Достоверный и правдоподобный вывод в интеллектуальных системах - Вагин В.Н., Головина Е.Ю., Загорянская А.А., Фомина М.В.

Автор: Вагин В.Н. Головина Е.Ю. Загорянская А.А. Фомина М.В.

Теги: исследование операций кибернетика прикладная математика и информатика

ISBN: 5-9221-0474-8

Год: 2004

Похожие

Многокритериальная оптимизация. Математические аспекты

Системы счисления

Методы оптимизации в примерах и задачах

Принятие решений на основе нечетких моделей. Примеры использования

Текст

УДК 519.816
ББК 32.81
В 12
Вагин В. Н., Головина Е. Ю., Загорянская А. А., Фомина М. В.
Достоверный и правдоподобный вывод в интеллектуальных систе-
системах / Под ред. В.Н. Вагина, Д.А. Поспелова. — М.: ФИЗМАТЛИТ, 2004. —
704 с. - ISBN 5-9221-0474-8.
Рассматриваются методы достоверного (дедуктивного) и правдоподоб-
правдоподобного (абдуктивного, индуктивного) выводов в интеллектуальных системах
различного назначения. Приводятся методы дедуктивного вывода на графо-
графовых структурах: вывод на графе связей, графе дизъюнктов, вывод на иерар-
иерархических структурах. Даются различные виды параллелизма при выводе на
графовых структурах. Описываются как классические, так и немонотонные
модальные логики: логики убеждения и знания, немонотонные логики Мак-
Дермотта и Дойла, автоэпистемические логики Мура, логики умолчания
Рейтера. Приводятся основы теории аргументации и методы абдуктивного
вывода. Рассматриваются базовые принципы построения систем обучения и
принятия решений и даются задачи обучения «без учителя» и «с учителем».
Излагаются индуктивные методы для случая с неполной информацией и
методы теории приближенных множеств.
Для студентов, аспирантов, обучающихся по направлениям «Приклад-
«Прикладная математика и информатика», «Информатика и вычислительная техни-
техника» и специальностям «Прикладная математика» (по областям), «Приклад-
«Прикладная математика и информатика», а также для специалистов в области ис-
искусственного интеллекта, интеллектуальных систем управления и принятия
решений.
ISBN 5-9221-0474-8 © физматлит, 2004

СОДЕРЖАНИЕ
Предисловие 10
Введение 12
I. ДОСТОВЕРНЫЙ ВЫВОД
Глава 1. Автоматическое доказательство теорем 24
1.1. Нормальные и стандартные формы 25
1.2. Логические следствия 35
1.3. Процедура вывода Эрбрана 38
1.4. Принцип резолюции 41
1.5. Линейная резолюция 48
1.6. Вывод в языке Пролог 54
1.6.1. SLD-резолюция E4). 1.6.2. Стратегии поиска в языке
Пролог E8). 1.6.3. Предположение о замкнутости мира F1).
1.6.4. Синтаксис и семантика языка Пролог F2). 1.6.5. Реали-
Реализация на языке Пролог моделей представления знаний и меха-
механизмов вывода на них F9).
Глава 2. Вывод на графе связей 81
2.1. Последовательная процедура доказательства методом гра-
графа связей 82
2.2. Стратегии поиска в графе связей 86
2.3. Достоинства процедуры дедуктивного вывода на графе
связей 87
2.4. Параллельный вывод на графе связей 88
2.4.1. Метод OR-параллельной резолюции (89). 2.4.2. DCDP-
параллельный вывод (91). 2.4.3. AND-параллельная резолю-
резолюция (94).
2.5. Модификация процедур параллельного вывода 97
2.5.1. Принципы создания эвристической функции (97).
2.5.2. Эвристическая функция HI (98). 2.5.3. Применение
эвристической функции HI при решении задачи «Стимрол-
лер» A00).
2.6. Сравнение эффективности 104
2.7. Система параллельного вывода PIS (Parallel Inference
System) на графе связей 107
2.7.1. Автоматический выбор параллельных методов вы-
вывода A08). 2.7.2. Математический препроцессор A09).
2.7.3. Методы ускорения и анализ результатов для задачи о
N ферзях A12). 2.7.4. Полученные результаты A15).

Содержание
Глава 3. Вывод на графе дизъюнктов 116
3.1. Типы параллелизма в дедуктивном выводе 116
3.2. Последовательный алгоритм вывода на раскрашенных гра-
графах дизъюнктов 119
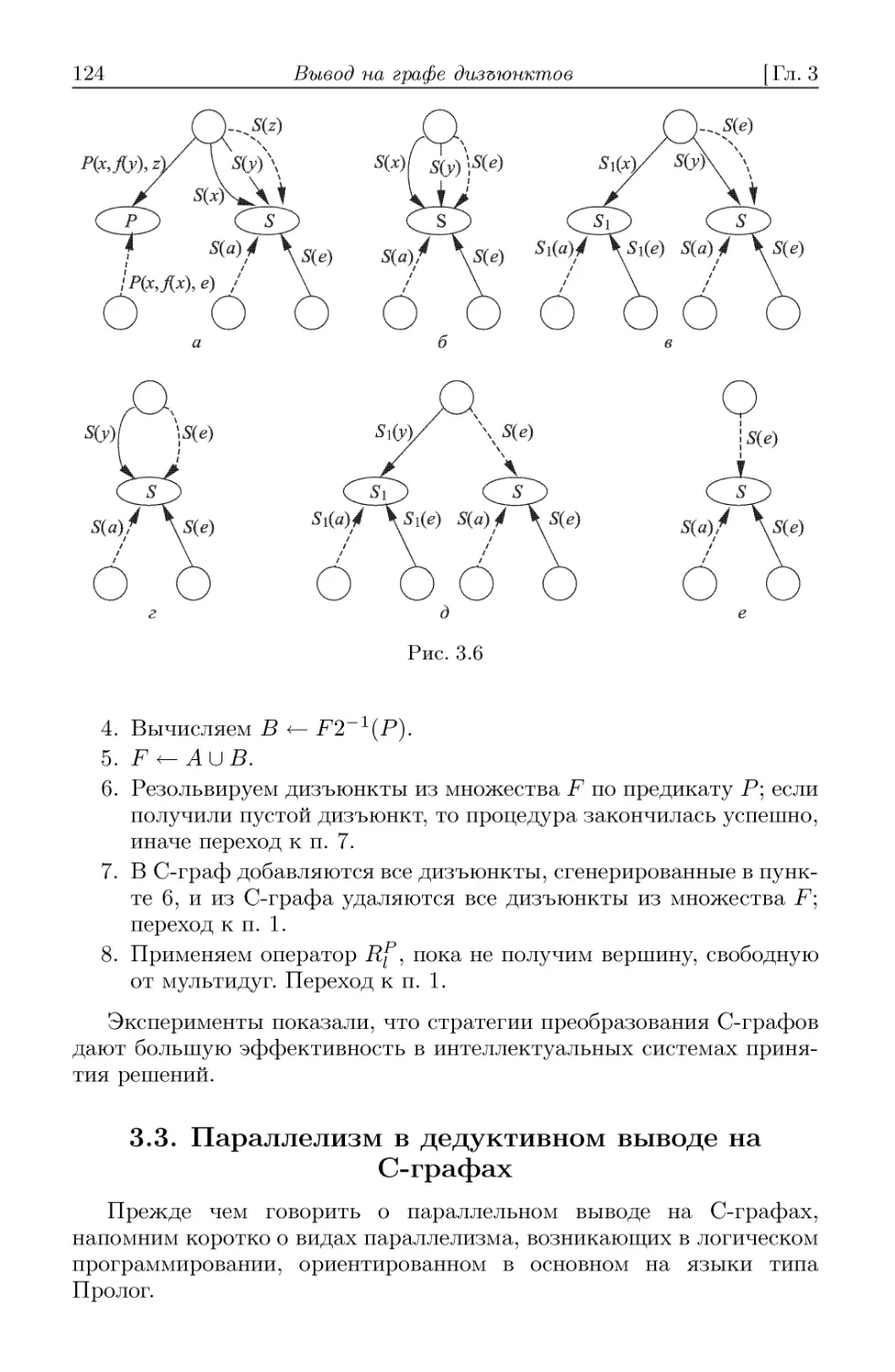
3.3. Параллелизм в дедуктивном выводе на С-графах 124
3.4. Сравнение эффективности процедур дедуктивного вывода 134
Глава 4. Вывод на аналитических таблицах 136
4.1. Метод аналитических таблиц для логики высказываний . . 136
4.2. Метод аналитических таблиц для логики предикатов пер-
первого порядка 143
4.3. Метод аналитических таблиц в логическом программиро-
программировании 153
4.3.1. Реализация метода аналитических таблиц для логики вы-
высказываний на языке Пролог A53). 4.3.2. Реализация мето-
метода аналитических таблиц для логики предикатов 1-го поряд-
порядка A59).
Глава 5. Вывод на иерархических структурах 186
5.1. Многоуровневая упорядоченно-сортная алгебра 186
5.1.1. Необходимость разработки механизмов вывода на иерар-
иерархических структурах A86). 5.1.2. Введение в многоуровневую
алгебру A88). 5.1.3. Моделирование подтипов и наследова-
наследования A89). 5.1.4. Описание параметрического полиморфизма
аппаратом двухуровневой алгебры A91).
5.2. Многоуровневая логика как язык представления знаний в
интеллектуальных системах 194
5.2.1. Способы задания иерархических структур в многоуров-
многоуровневой логике A94). 5.2.2. Синтаксис многоуровневой логи-
логики A98). 5.2.3. Описание двух видов иерархической абстракции
и иерархической структуры множеством правильно построен-
построенных формул многоуровневой логики A99). 5.2.4. Логический
вывод в многоуровневой логике B04).
5.3. Система моделирования проблемной области «Инфолог» . . 215
5.3.1. Назначение и структура системы «Инфолог» B15).
5.3.2. Концептуальный язык описания сложноструктуриро-
сложноструктурированной проблемной области B19). 5.3.3. Реализация системы
«Инфолог» B22).
II. АРГУМЕНТАЦИЯ И АБДУКЦИЯ
Глава 6. Данные и знания в интеллектуальных систе-
системах 224

Содержание
6.1. Характерные особенности знания 224
6.2. Знание как обоснованное истинное убеждение 234
6.3. He-факторы знания 240
6.4. Зачем нужны нетрадиционные логики? 248
Глава 7. Монотонные классические модальные логики 255
7.1. Исчисление предикатов первого порядка как основа постро-
построения модальной логики 255
7.2. Вспомогательная логика как основа перехода к модальному
исчислению высказываний 257
7.3. Постулаты, основные теоремы и правила модального исчис-
исчисления высказываний 259
7.4. Система S1 261
7.5. Система S4 271
7.6. Система S5 275
7.7. Семантика возможных миров Крипке 276
Глава 8. Немонотонные модальные логики 281
8.1. Логики убеждения и знания 281
8.2. Немонотонные логики Мак-Дермотта и Дойла 287
8.3. Автоэпистемические логики 292
8.4. Логики умолчаний 301
8.5. Системы поддержки истинности 312
8.5.1. Системы поддержки истинности, основанные на обоснова-
обоснованиях C15). 8.5.2. Системы поддержки истинности, основанные
на предположениях C17).
Глава 9. Немонотонные логики в логическом програм-
программировании 321
9.1. Семантика логических программ: краткий обзор 323
9.1.1. Нормальные логические программы C23). 9.1.2. Расши-
Расширенные логические программы C30). 9.1.3. Зачем нужна новая
семантика для расширенных программ? C36).
9.2. WFSX — фундированная семантика для расширенных ло-
логических программ 337
9.2.1. Интерпретации и модели C37). 9.2.2. Определение
WFSX C40). 9.2.3. Существование семантики C43).
9.2.4. Нисходящие процедуры вывода для WFSX C45).
9.3. Работа с противоречиями 356
9.3.1. Удаление противоречий C58). 9.3.2. Паранепротиво-
речивая WFSX C60). 9.3.3. Декларативные ревизии C63).
9.3.4. Поддержка и устранение противоречий C70).
9.4. WFSX, семантика логических программ с двумя отрицани-
отрицаниями и автоэпистемическая логика 375

6 Содержание
9.4.1. Общая семантика для программ с отрицаниями двух ви-
видов C76). 9.4.2. Автоэпистемические логики для WFSX C89).
9.5. WFSX и логика умолчаний 401
9.5.1. Язык умолчаний D02). 9.5.2. Некоторые необходимые
принципы для теорий умолчаний D05). 9.5.3. О-теория умол-
умолчаний D08). 9.5.4. Сравнение с семантикой Рейтера D13).
9.5.5. Сравнение со стационарной семантикой умолчаний D14).
9.5.6. Связь семантики теории умолчаний и логических про-
программ с явным отрицанием D15). 9.5.7. Определение WFSX
с помощью Г D16).
Глава 10. Системы аргументации и абдуктивный вывод 419
10.1. Системы пересматриваемой аргументации 420
10.1.1. Основы теории аргументации D20). 10.1.2. Обзор систем
аргументации D36).
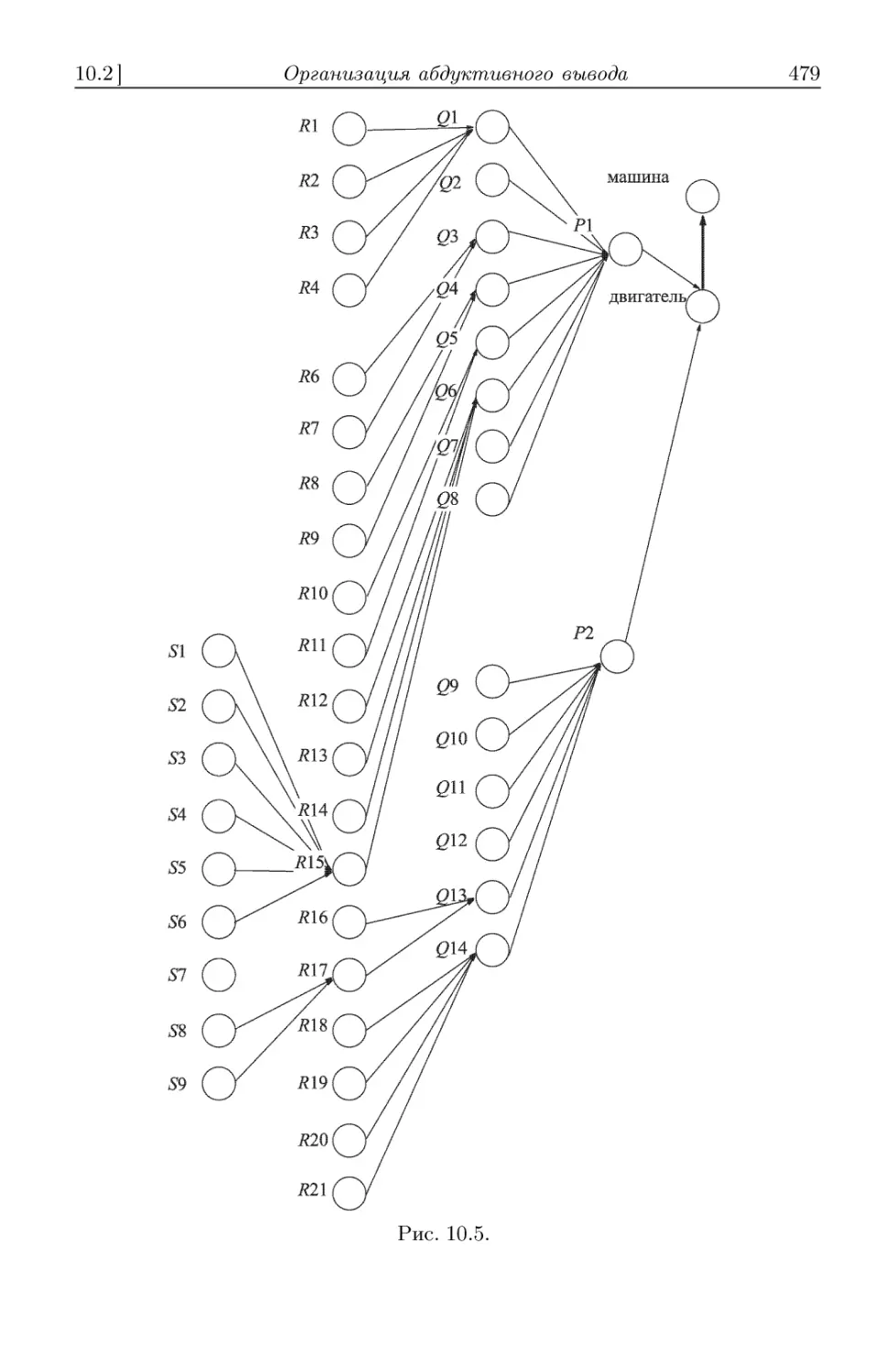
10.2. Организация абдуктивного вывода 444
10.2.1. Понятие абдуктивного вывода D44). 10.2.2. Подходы к
характеризации абдукции D48). 10.2.3. Подходы к вычислению
абдуктивных объяснений D56). 10.2.4. Метод вероятностных
абдуктивных рассуждений в сложноструктурированных про-
проблемных областях D66).
10.3. Абдукция и аргументация в логическом программировании 481
10.3.1. Аргументационная семантика логических программ и ее
вычисление D81). 10.3.2. Роль аргументации в организации
абдуктивного вывода D96).
III. ИНДУКЦИЯ И ОБОБЩЕНИЕ
Глава 11. Базовые принципы построения систем обуче-
обучения и принятия решений 503
11.1. Системы поддержки принятия решений 505
11.2. Задачи извлечения знаний из баз данных 510
11.3. Способы представления исходной информации в интеллек-
интеллектуальных системах 518
11.4. Структурно-логические методы обобщения 523
Глава 12. Задача обучения «без учителя» 534
12.1. Алгоритм, основанный на понятии порогового расстояния . 535
12.2. Алгоритм MAXMIN 538
12.3. Алгоритм «К средних» 541
12.4. Распознавание с использованием решающих функций .... 545
12.4.1. Построение решающих функций по критерию мини-
минимального расстояния E46). 12.4.2. Разделяющие решающие

Содержание
функции E47). 12.4.3. Линейные решающие функции E49).
12.4.4. Построение решающих функций методом потенциа-
потенциалов E52).
12.5. Распознавание на основе приближенных признаков 556
Глава 13. Обучение с учителем 558
13.1. Постановка задачи 558
13.2. Алгоритм ДРЕВ 563
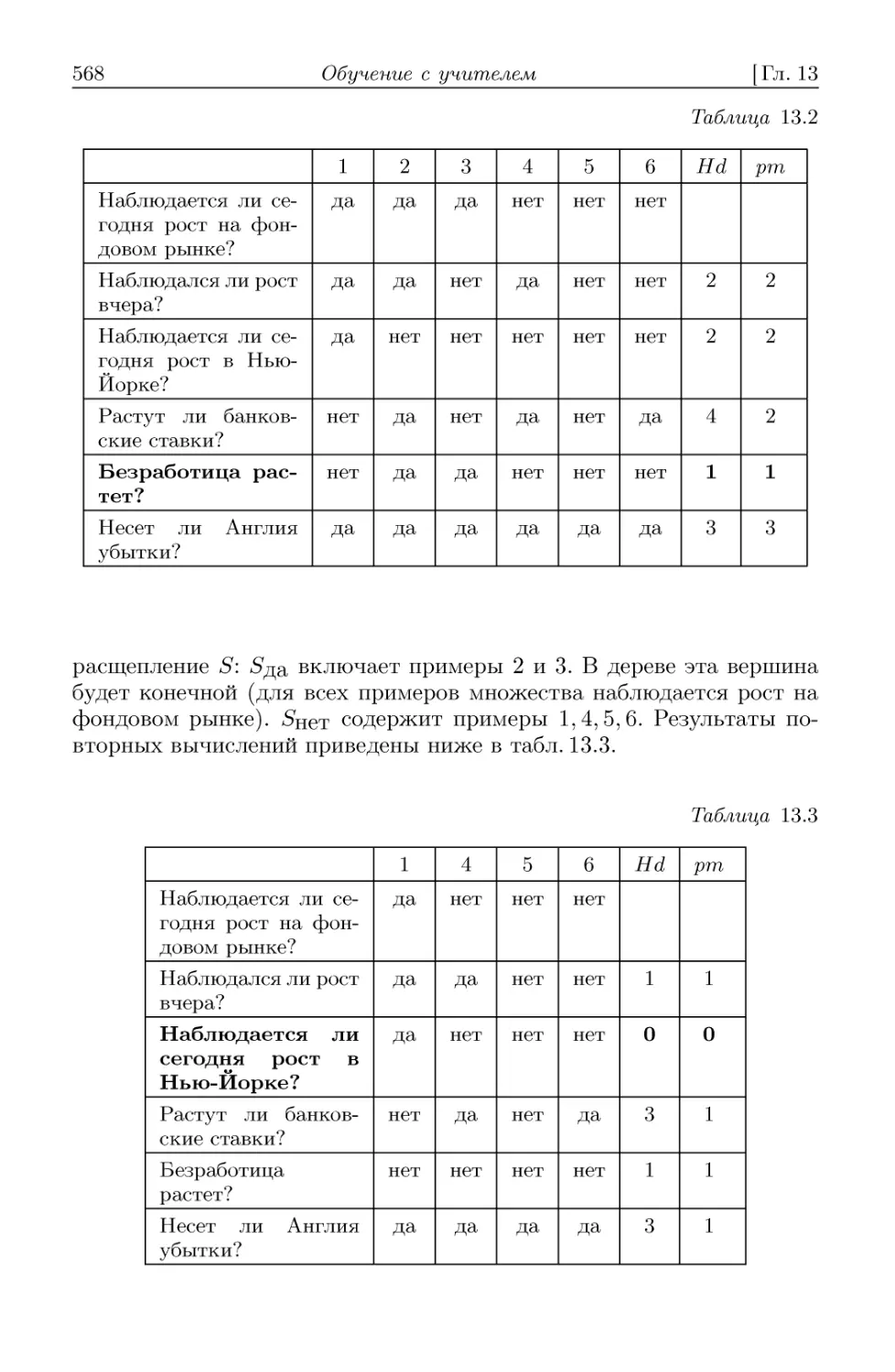
13.3. Построение решающего дерева с использованием метрики
Хемминга 566
13.4. Индукция решающих деревьев 569
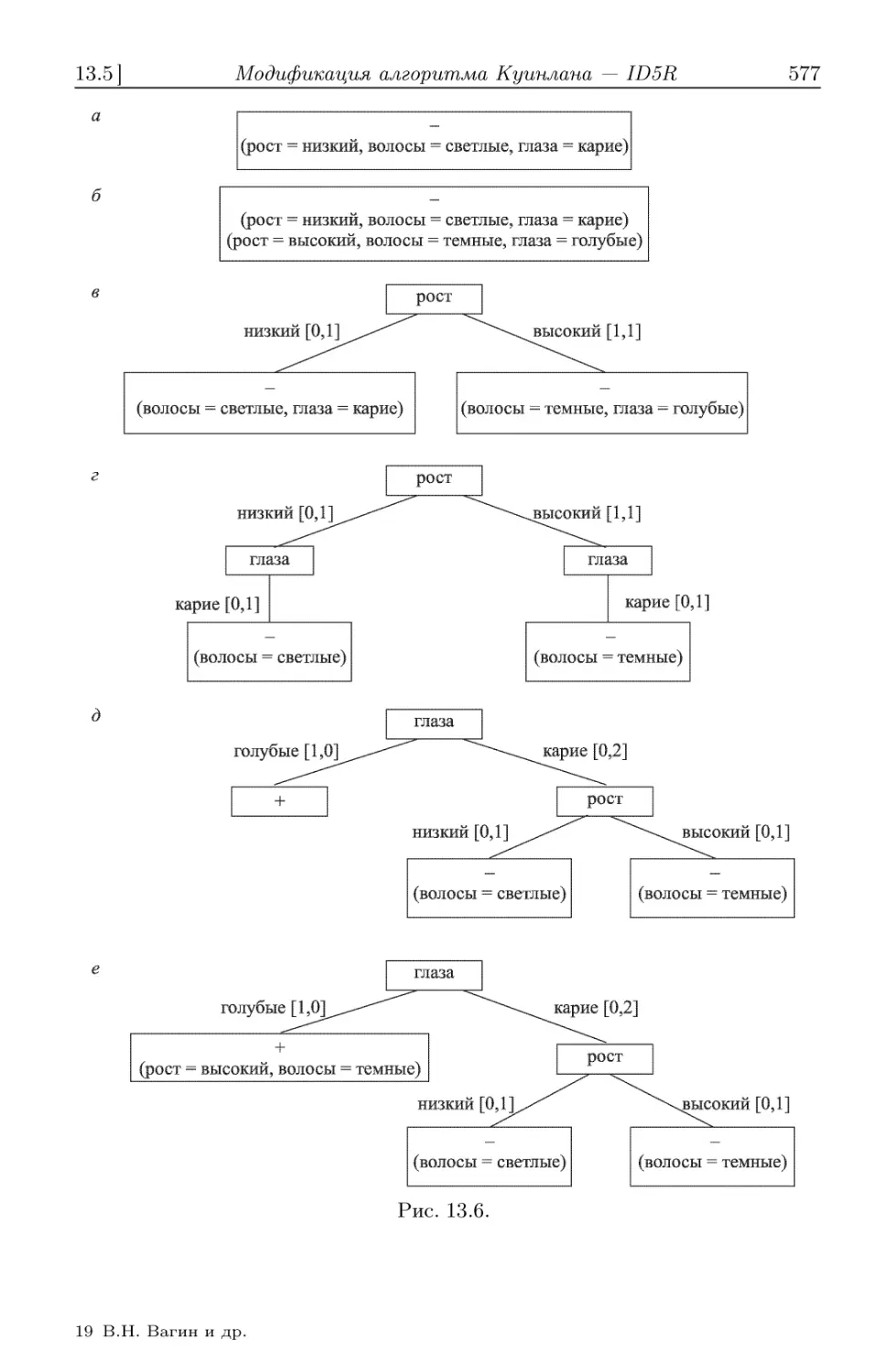
13.5. Модификация алгоритма Куинлана — ID5R 574
13.6. Алгоритм Reduce 579
13.7. Фокусирование 583
13.8. Алгоритм EG2 589
Глава 14. Индуктивные методы для случая неполной
информации 596
14.1. Проблемы извлечения знаний из баз данных 596
14.1.1. Ограниченная информация E97). 14.1.2. Искаженная
информация E98). 14.1.3. Большой размер баз данных E98).
14.1.4. Изменение баз данных со временем E99).
14.2. Алгоритм извлечения продукционных правил из большой
базы данных 600
14.3. Подход с использованием приближенных множеств 603
14.3.1. Основные понятия теории приближенных мно-
множеств F04). 14.3.2. Алгоритм RS1, использующий прибли-
приближенные множества F08). 14.3.3. Информационные системы с
неопределенностью F11).
14.4. Алгоритм распознавания объектов в условиях неполноты
информации 621
Литературный комментарий 633
К введению 633
К части I 634
К главе 1 634
К главе 2 636
К главе 3 638
К главе 4 639
К главе 5 640
К части II 642
К главе 6 642
К главе 7 644
К главе 8 645

Содержание
К главе 9 647
К главе 10 650
К части III 655
К главе 11 655
К главе 12 657
К главе 13 659
К главе Ц 661
Предметный указатель 663

Низкий поклон тебе, Учитель.

Предисловие
Идея написания книги возникла у авторов в ходе обсуждения
научных результатов на различных конференциях и семинарах по
проблемам искусственного интеллекта. Большое влияние на выбор
тематики оказала книга Д. А. Поспелова «Моделирование рассужде-
рассуждений. Опыт анализа мыслительных актов»*, в которой описываются
дедуктивные и правдоподобные модели, учитывающие особенности
человеческих рассуждений. Блестяще написанная, совмещающая до-
доступность чтения со строгим изложением сложных логических про-
проблем, эта книга явилась своеобразным стимулом для продолжения
исследований по достоверным и правдоподобным рассуждениям, итог
которых воплотился в данном издании.
Авторы, конечно, осознают, что дать полную картину исследова-
исследований по достоверным и правдоподобным рассуждениям в одной книге
невозможно, поэтому в ней отражены личные пристрастия авторов к
освещению тех или иных проблем. При этом авторы все-таки надеют-
надеются, что излагаемый материал привлечет внимание не только узкого
круга специалистов по математической логике, но и многочисленных
профессионалов, занимающихся разработкой интеллектуальных си-
систем принятия решений, в частности, экспертных систем и систем
управления сложными технологическими объектами.
Для того, чтобы читатель смог получить цельное представление
о рассматриваемых проблемах, в книге, наряду с оригинальными
работами авторов, составляющих единую научную группу, изложен
ряд результатов других российских и зарубежных ученых, тем более,
что некоторые проблемы и методы такие, как метод аналитических
таблиц или проблема аргументации и абдукции, почти не освещались
в отечественной литературе.
Чтобы не затруднять чтение книги, в тексте нет библиографиче-
библиографических ссылок. Вся использованная литература указана в конце книги,
где дан также краткий обзор работ, на которые ссылаются авторы
и которые помогут читателю углубить свои знания об обсуждаемых
проблемах.
Выбор материала книги определялся следующими соображения-
соображениями: во-первых, желанием охватить достаточно широкий круг про-
проблем, связанных с использованием математической логики в разного
рода интеллектуальных системах различного назначения, во-вторых,
М.: Радио и связь, 1989. 184 с.

Предисловие 11
стремлением сделать изложение весьма разнородного материала еди-
единым и связным, в-третьих, как уже говорилось, собственными на-
научными интересами авторов. Насколько удачно это удалось сделать,
судить читателям, и мы заранее благодарны тем, которые укажут на
замеченные недостатки и недоработки.
Для чтения книги требуются знания в объеме стандартных курсов
вузов по дискретной математике, математической логике, теории при-
принятия решений и языкам программирования. По мнению одного из ав-
авторов, а именно В. Н. Вагина, желательно, чтобы читатели ознакоми-
ознакомились с его монографией «Дедукция и обобщение в системах принятия
решений»*, в которой изложены основные понятия математической
логики и модели представления знаний, а также описаны алгоритмы
дедукции и обобщения понятий по признакам и структурам. Как бы
то ни было, все основные понятия вводятся в данную книгу. Каждый
читатель может избрать свой порядок чтения глав в зависимости
от своих интересов. Читателю, не знакомому или мало знакомому
с предметом, рекомендуется изучение материала в той последова-
последовательности, в какой он приведен в книге. Читатели, интересующиеся
выборочно какой-либо одной проблемой, например, только абдукци-
абдукцией, могут ограничиться чтением соответствующих глав, опустив или
бегло просмотрев остальные.
Материал книги распределен между авторами следующим об-
образом. В. Н. Вагин подготовил предисловие, введение, главу 1 (за
исключением § 1.6), главы 2,3,6,7,8; глава 4 написана совместно
В. Н. Вагиным и Е. Ю. Головиной, которая изложила также § 1.6 гла-
главы 1, главу 5, §10.2.4 главы 10. А. А. Загорянская написала главы 9, 10
(кроме §10.2.4), а М. В. Фомина — главы 11, 12, 13, 14. Естественно, за
все опечатки, описки и ошибки все авторы несут равную ответствен-
ответственность.
Авторы приносят свою искреннюю благодарность редактору этой
книги Д. А. Поспелову и рецензентам Э. В. Попову и Г. С. Плесневичу.
Редактор книги Д. А. Поспелов пытался сделать все возможное, чтобы
книга стала четко структурированной и единой по стилю и замыслу,
но, к сожалению, в силу ряда обстоятельств он так и не сумел добиться
конечного результата.
М.: Наука, 1988. 384 с.

Однажды Лебедь, Рак да Щука
Везти с поклажей воз взялись
И вместе трое все в него впряглись.
И. А. Крылов
Введение
С возникновением интеллектуальных систем различного назначе-
назначения и перенесением центра тяжести на модели и методы представле-
представления и обработки знаний существенно изменяется аппарат формаль-
формальных рассуждений, комбинирующий средства достоверного и правдо-
правдоподобного выводов. На наш взгляд, логика есть наука о рассуждениях,
и от разработки формальных моделей различных форм рассуждений
зависит успех создания действительно интеллектуальных систем.
Не вдаваясь в детали определения интеллектуальной системы
(ИнтС), отметим ее основные компоненты:
ИнтС = РИС + ПИС + ИнИн + АП,
где РИС — рассуждатель интеллектуальной системы, состоящий из
генератора гипотез, доказателя теорем и вычислителя; ПИС — по-
поисковая информационная система, которая доставляет информацию,
релевантную цели рассуждения; ИнИн — интеллектуальный интер-
интерфейс (диалог, графика, обучение пользователя работе с системой);
АП — подсистема автоматического пополнения базы данных (БД) и
базы знаний (БЗ) из текстов, образующих информационную среду для
интеллектуальных систем.
Под рассуждением понимается построение последовательности ар-
аргументов, вынуждающих принятие некоторого утверждения, которое
и является целью рассуждения. Особенностями рассуждения, отлича-
отличающими его от логического вывода, и в частности, от доказательства,
в стандартном понимании являются
• открытость множества возможных аргументов;
• использование метатеоретических, и в частности, металогиче-
металогических средств, с помощью которых осуществляется управление
логическими выводами, применяемыми в процессе рассуждения;
• использование правил не только достоверного вывода, но и прав-
правдоподобного вывода.
Очевидно, что логический вывод в стандартном понимании ма-
математической логики — частный случай рассуждений, когда множе-
множество аргументов фиксировано, нетривиальные металогические сред-
средства (например, проверка на непротиворечивость) не используются
и применяются только правила достоверного вывода, по которым

Введение 13
из истинных аргументов (посылок) можно получить лишь истинные
заключения.
В широком смысле к достоверному выводу и относится дедук-
дедуктивный вывод, который в настоящее время хорошо изучен и иссле-
исследован. В классической логике дедуктивный вывод рассматривается
как вывод от общего к частному. Дедукция — в высшей степени
идеализированная и ограниченная форма рассуждений, и если мы
хотим моделировать некоторые аспекты человеческих рассуждений
(здравый смысл, неопределенность, противоречивость информации и
т.п.), то дедукции будет совершенно недостаточно, и нужно привле-
привлекать не дедуктивные или правдоподобные формы рассуждений, такие
как абдукция и индукция.
Термин «правдоподобное рассуждение» принадлежит Д. Пойа;
примерами правдоподобных рассуждений в смысле Д. Пойа являются
индукция через простое перечисление, аналогия и различные схемы
недостоверных (в двузначной логике высказываний) выводов.
Д. Пойа сформулировал два возможных принципа вывода по
аналогии:
• «предположение становится более правдоподобным, когда ока-
оказывается истинным аналогичное предположение»;
• «предположение становится несколько более правдоподобным,
когда становится более правдоподобным аналогичное предполо-
предположение».
Пусть рФ- упомянутые выше предположения, тогда принци-
принципам Пойа отвечают, соответственно, следующие схемы правдоподоб-
правдоподобных выводов:
(р аналогично Ф,
Ф истинно,
(р более правдоподобно;
(р аналогично Ф,
Ф более правдоподобно,
(f несколько более правдоподобно.
Здесь «ср несколько более правдоподобно» понимается в том смыс-
смысле, что без информации о правдоподобности Ф ср было бы менее
правдоподобным.
Формальные уточнения схем таких правдоподобных выводов свя-
связаны, во-первых, с формализацией средства описания структуры дан-
данных предметной области, и, во-вторых, с формализацией «степени
правдоподобия ср». Существенность сходства структур в выводах по
аналогии была отмечена еще И. Г. Лейбницем.

14 Введение
Индукция обеспечивает возможность перехода от единичных фак-
фактов к общим положениям, законам. Говоря об истории исследования
индуктивных рассуждений, следует отметить Ф. Бэкона, который
впервые попытался формализовать индуктивные выводы посредством
таблиц причин. Ф. Бэкон явился родоначальником исследований «эм-
«эмпирической структурной индукции», целью которой является обнару-
обнаружение эмпирических зависимостей в виде индуктивных обобщений,
полученных на основе сравнения объектов, имеющих структуру и вхо-
входящих в явления, которые представляются примерами и контрприме-
контрпримерами. Учение Ф. Бэкона об индукции было развито Д. С. Миллем, ко-
который предложил свои известные методы сходства, различия, остат-
остатков и сопутствующих изменений.
Рассматривая индукцию как недедуктивное рассуждение, можно
выделить аргументы, обеспечивающие некоторую (частичную) под-
поддержку заключения, т. е. если посылки истинны, они дали бы неко-
некоторое основание, хотя и неполностью убедительное, принять данное
заключение истинным; при этом остается некоторая возможность по-
получить ложное заключение. Аргументы такого типа Салмон называл
«индуктивными аргументами». Далее он классифицирует их следу-
следующим образом:
• аргументы, основанные на выборках;
• аргументы, полученные по аналогии;
• статистические силлогизмы.
Аргументы, основанные на выборках, представляют индуктивные
обобщения. При обобщении также имеет место логический процесс
перехода от единичного к общему, от менее общего к более общему
знанию. Это понятие довольно близко смыкается с понятием ин-
индуктивного вывода, хотя в современной логике индуктивный вывод
трактуется более широко и рассматривает не только умозаключения
от частного к общему, но и вообще все те логические отношения, когда
истинность проверяемого знания нельзя достоверно установить на
основании тех знаний, истинность которых нам известна, а можно
лишь определить, подтверждается ли первое знание последними, а
если да, то с какой степенью.
Индуктивные обобщения имеют следующую форму:
Х% наблюдаемых явлений F есть G\
поэтому (приблизительно) Х% всех F есть G.
Аргументы, полученные по аналогии, выглядят следующим
образом:
объекты типа X имеют свойства F\, F^,..., Fk;
объекты типа Y имеют свойства F\, F2,..., Fk, а также свой-
свойство G;
поэтому объекты типа X имеют также свойство G.

Введение 15
Наконец, статистические силлогизмы имеют следующую форму:
Х% всех явлений F есть G;
а есть F]
поэтому а есть G.
Здесь процент всех явлений понимается как значительный («боль-
(«большой»), ибо в противном случае заключение будет: а не есть G.
Можно разделить индуктивные аргументы на статистические и
категорные, понимая последние как имеющие некоторую форму рас-
рассуждений. Так, например, категорное индуктивное обобщение имеет
следующий вид:
все наблюдаемые явления F есть G\
поэтому все F есть G.
Независимо от того, являются ли индуктивные аргументы ста-
статистическими или категорными, главная проблема заключается в
способе их оценивания. Чтобы узнать степень убеждения некоторой
гипотезы (гипотетического заключения) Н при некотором основании
(доводе) Е, можно прибегнуть к вероятностной формализации индук-
индуктивной поддержки этой гипотезы и вычислить условную вероятность
Р(Н\Е), что реализуется в теории подтверждения (confirmation
theory). Сторонник этой теории Карнап прямо указывал на возмож-
возможность рассмотрения степени подтверждения гипотезы Н путем осно-
основания Е как на степень общезначимости индуктивного аргумента
типа «Е, поэтому Н» и подчеркивал возможность обрабатывать эту
«индуктивную общезначимость» как аналог дедуктивной общезначи-
общезначимости. Он писал, что, называя теорию индуктивного вывода не де-
дедуктивной, термин «вывод» в индуктивной логике мы не понимаем
в том же самом смысле, как в дедуктивной. Обе логики, как дедук-
дедуктивная, так и индуктивная, едины в одном: они исследуют логические
отношения между утверждениями, но если первая изучает отношение
выводимости одних утверждений из других, то вторая — степень
подтверждения утверждений, которая рассматривается как некоторая
числовая мера. Другими словами, теория подтверждений сама по себе
не устанавливает отношение логического следствия, поскольку лю-
любое основание только подтверждает любую гипотезу в определенной
степени. Индуктивная логика, основанная на теории подтверждений,
является логикой оценки гипотезы, а не ее образования. Поскольку
меры убеждения выражают субъективные оценки агента об истинно-
истинности гипотез, то процедуры оценки истинности гипотез являются тем
средством, который отвечает на вопрос: «Насколько правдоподобна
эта гипотеза при данном основании?»
Возвращаясь к категорным индуктивным аргументам, можно про-
продолжить разделение недедуктивных рассуждений на индуктивные и
абдуктивные. Если в индуктивных выводах некоторые факты, уста-
устанавливаемые для отдельных явлений, переносятся на весь класс таких

16 Введение
явлений, то в абдуктивных выводах имеет место вывод от частного к
частному.
Абдуктивные выводы были предложены одним из создателей ма-
математической логики Ч. Пирсом. В своей попытке классифицировать
аргументы он следовал силлогистике Аристотеля. Гениальный мысли-
мыслитель древности выбрал для формализации именно дедуктивные рас-
рассуждения, в которых истинные посылки порождают только истинные
заключения. Пирс разработал свою теорию силлогистики. Рассмот-
Рассмотрим в качестве примера аристотелевский силлогизм «Barbara».
1. Все студенты из группы А-13-2000 юны.
2. Эти студенты являются студентами группы А-13-2000.
3. Следовательно, эти студенты юны.
Истинность заключения не вызывает сомнений, если истинны две
посылки. Считая первую посылку главной (Пирс называл ее правилом
(rule)), а вторую — меньшей (он назвал ее случаем (case)), Пирс из
этого силлогизма построил еще два других. Заключение он называл
результатом (result).
I. Случай: Эти студенты являются студентами группы А-13-2000.
Результат: Эти студенты юны.
Правило: Все студенты из группы А-13-2000 юны.
П. Правило: Все студенты из группы А-13-2000 юны.
Результат: Эти студенты юны.
Случай: Эти студенты являются студентами группы А-13-2000.
В первом силлогизме из случая и результата осуществляется вывод
правила, а во втором из правила и результата — случай.
Нетрудно заметить, что первый силлогизм относится к категорно-
му индуктивному обобщению. Второй силлогизм Пирс назвал приня-
принятием гипотезы (термин «абдукция» он ввел позже).
Таким образом, Пирс пришел к следующей классификации выво-
вывода: вывод делится на дедуктивный (или аналитический) и синтетиче-
синтетический, который, в свою очередь, подразделяется на индукцию и приня-
принятие гипотезы. Следовательно, индуктивное обобщение соответствует
в его классификации индукции.
В 1902 г. Пирс писал, что, уделяя слишком много внимания силло-
силлогистическим формам рассуждений, он недостаточно останавливался
на трех формах рассуждений — абдукции, дедукции и индукции,
которые идентифицировались, по его понятиям, с тремя стадиями
научного исследования — генерацией гипотез, предсказанием и оцен-
оценкой соответственно. Имея ряд наблюдаемых явлений и сопоставляя
их, исследователь приходит к какой-то начальной гипотезе, затем
получает из нее какие-то заключения (следствия), которые должны

Введение 17
быть истинными, если исходная гипотеза истинна, и затем сопостав-
сопоставляет с некоторой степенью достоверности предсказанные заключения
с реальностью. Первую стадию образования гипотез при объяснении
наблюдаемых явлений он назвал абдукцией, вторую стадию вывода
предсказанных заключений из гипотез — дедукцией и последнюю,
путем оценки этих заключений, — индукцией.
Абдукция по Пирсу определяется как процесс формирования объ-
объяснительной гипотезы из наблюдаемых явлений реальной действи-
действительности, и он считал этот процесс инсайтом (подобно «вспышке» в
голове) и не подлежащим алгоритмизации. Как и любой акт озарения,
инсайт не свободен от ошибок, и в основе абдукции, по мнению Пир-
Пирса, лежит «мистическая сила догадки». Вот его абдуктивная форма
вывода:
— наблюдается некоторый факт С;
— если утверждение А было бы истинным, факт С был бы чем-то
само собой разумеющимся;
— следовательно, имеется причина подозревать, что А истинно.
О наблюдаемом факте С можно сказать, что он истинен и не явля-
является логическим следствием, полученным из нашего знания реального
мира. Вторая посылка интерпретируется как «А логически влечет С».
Истинность этой посылки очевидна, если истинен С, и под «логически
влечет» следует понимать материальную импликацию. Пирс назвал
утверждение А объяснением С или объяснительной гипотезой факта
С. К гипотезе он предъявляет требование ее экспериментальной ве-
рифицируемости, ибо в противном случае она не может быть индук-
индуктивно оценена. Правда, сама верификация нужных гипотез требует
дополнительных затрат, и по этой причине абдукцию Пирс называл
как «вывод наилучших объяснений».
Индукция идентифицируется Пирсом как процесс тестирования
гипотезы посредством отобранных предсказаний. Идея об обеспече-
обеспечении верифицированного предсказания дальнейшей поддержки гипо-
гипотезы близка к понятию подтверждения, которое обсуждалось ранее.
Главное отличие от теории подтверждения состоит в том, что с точки
зрения Пирса в индукции с помощью предсказаний гипотеза тестиру-
тестируется только по отобранным порциям довода, и, следовательно, оценка
гипотезы носит в некотором смысле ограниченный характер.
Таким образом, Пирс отделяет процесс образования гипотез от
их тестирования, и, по его мнению, абдукция является процессом
генерации объяснительных гипотез, а индукция соответствует методу
тестирования гипотез и их оценки.
Рассмотрим более подробно логические аспекты абдукции и ин-
индукции в плане их применения в интеллектуальных системах, будь
это системы диагностики и планирования действий, или системы

18 Введение
обучения и понимания естественного языка. Так как абдукция и ин-
индукция являются не дедуктивными формами рассуждений, считаем,
что основная функция абдукции заключается в обеспечении объяс-
объяснений наблюдаемых явлений или событий, а функция индукции — в
обеспечении обобщений наблюдений.
Для представления знаний имеем язык предикатов первого поряд-
порядка, предикаты которого делятся на наблюдаемые и ненаблюдаемые
или фоновые, в зависимости от того, описывают ли они наблюдае-
наблюдаемые объекты и явления или нет. Имеют место знания трех типов:
знание предметной области или фоновое (background) знание пред-
представляет собой общую теорию, касающуюся только ненаблюдаемых
предикатов; знание переднего плана (foreground knowledge) является
общей теорией, связывающей наблюдаемые предикаты с фоновыми;
и, наконец, знание примеров (иногда называемое знанием сценария)
состоит из формул, содержащих только ненаблюдаемые предикаты,
возможно выведенные из некоторого подмножества таких предикатов.
Знание примеров может быть частью фонового знания. Наблюда-
Наблюдаемые предикаты являются выполнимыми наблюдениями в отличие
от предсказаний, истинностное значение которых неизвестно. Знание
примеров обычно содержит описания объектов или ситуаций пред-
предметной области рассуждений в терминах ненаблюдаемых предикатов.
Описание ненаблюдаемого объекта или индивидуума становится из-
известным только после формирования гипотезы, которая может быть
абдуктивной или индуктивной. Однако эта гипотеза способна обес-
обеспечить предсказание ненаблюдаемого объекта, получив доступ к его
описанию.
Отсюда можно определить цель индукции как вывод знания перед-
переднего плана из наблюдений и другой известной информации, состоящей
обычно из фонового знания и знания примеров. Эти наблюдения мы
и пытаемся обобщить в новое знание переднего плана.
Если в индукции идет процесс обобщения, то в абдукции из наблю-
наблюдений и другой известной информации мы выводим знание примеров.
Возможные абдуктивные гипотезы строятся из специфических нена-
ненаблюдаемых предикатов, называемых абдуцентами, и, таким образом,
абдуктивная гипотеза является гипотезой, которая пополняет знание
примеров о наблюдаемом объекте или явлении.
Отсюда абдуктивная гипотеза предназначена для объяснений на-
наблюдений, а индуктивная — для их обобщений. Если абдуктивное
объяснение состоит только из знания примеров, то, очевидно, для
абдукции нужна также и общая теория знания переднего плана, свя-
связывающая наблюдение с фоновыми предикатами с целью объяснения
этих наблюдаемых явлений. Абдуктивное объяснение, таким образом,
имеет смысл только относительно данной теории переднего плана.
Что касается индукции, то в ней объяснение играет иную роль, чем
в абдукции. Например, когда мы говорим, что все студенты группы

Введение 19
А-13-2000 юны, то этот тип объяснений носит универсальный харак-
характер, и он был получен не из теории, а путем обобщения конкретных
примеров: «Эти студенты являются студентами группы А-13-2000»
и «Эти студенты юны». Можно сказать, что индуктивные гипотезы
не объясняют конкретные объекты и явления, а скорее объясняют
частоты, с которыми эти наблюдения встречаются (в данном примере
неюных студентов из группы А-13-2000 не наблюдалось). Отсюда в ин-
индуктивной гипотезе на первое место выходит обеспечение обобщений
наблюдаемых объектов и явлений, и объяснительная гипотеза будет
индуктивной только в случае, если она обобщает. А это и является
категорным индуктивным обобщением, когда исходя из истинности
конкретных примеров (выборки) делаем вывод об истинности всей
популяции.
Следует также заметить, что в абдукции имеется обобщение, вы-
выраженное только в общей теории фонового знания, в то время как в
индукции мы получаем новые обобщения, не содержащиеся в общей
теории фонового знания.
Индуктивное обобщение наиболее часто исследуется в машинном
обучении, когда имеют место наблюдения неизвестного понятия, взя-
взятые в форме описания примеров (положительных примеров) и контр-
контрпримеров (отрицательных примеров). Цель состоит в определении
понятия, которое правильно отличает примеры от контрпримеров.
Пусть дана общая теория фонового знания Т, содержащая описа-
описание примеров и контрпримеров в виде множеств Р и N фундаменталь-
фундаментальных (означенных) литер. Требуется определить гипотезу Н в рамках
языка логики предикатов первого порядка, такую, что:
• для всех примеров р Е Р: Т U Н N р;
• для всех контрпримеров п Е N: T U Н ? п.
Одна из серьезных проблем в машинном обучении заключается
в обеспечении метода обучения «адекватным» множеством примеров
и контрпримеров. Термин «адекватный» неформально здесь понима-
понимается как достаточный для успешного обучения понятия, что в свою
очередь выдвигает тяжелое условие для понимания, какие примеры
достаточны (а какие нет) при решении этой задачи. Отметим также,
что в логическом программировании множества Р и N могут содер-
содержать более сложные выражения, нежели фундаментальные факты.
Индуктивные методы также применяются для проблемы обнару-
обнаружения знаний (knowledge discovery). Дан некоторый довод (основание)
Е и требуется определить гипотезу Н в рамках языка логики преди-
предикатов первого порядка, такую, что:
• Н истинна в модели то, сконструированной из Е;
• для всех формул g в рамках данного языка, если g истинна в
то, то Н N д.

20 Введение
Предполагая, что модель то является минимальной эрбрановской
моделью, гипотеза Н представляет аксиоматизацию всех утвержде-
утверждений, истинных в этой модели.
Существенной особенностью процесса индукции является роль
отобранной индуктивной гипотезы Н, состоящей в расширении су-
существующей теории Т (фонового знания) на новую теорию Т' =
= Т U Н. Таким образом, выбранная гипотеза Н обеспечивает связь
между наблюдаемыми и ненаблюдаемыми предикатами, которой не
доставало в исходной теории Т. Если абдукция с помощью абдуцентов
расширяет знание примеров, то подлинное обобщение теории Т про-
происходит только путем индукции. Можно сказать, что если в абдукции
теория Т фиксируется, и варьируется только знание примеров, то
в индукции, наоборот, фиксировано знание примеров, а подвержена
изменению (расширению) теория Т.
Как в индуктивных, так и в абдуктивных рассуждениях имеют-
имеются специфические факты (примеры), которые затем должны быть
объяснены. Но если индукция рассматривает примеры как примеры
понятия, а объяснения как общие объяснения понятия, то в абдукции
примеры рассматриваются как специфические наблюдения, а объяс-
объяснения — как некоторые другие специфические факты, истинность
которых подтверждает эти наблюдения.
Рассмотрим на примере взаимодействие между абдуктивными и
индуктивными рассуждениями. Пусть дана теория фонового знания
Т: «Все студенты МЭИ юны» и наблюдение О: «Все студенты группы
А-13-2000 юны». Тогда объяснение этого наблюдения будет выражено
гипотезой Н: «Все студенты группы А-13-2000 являются студентами
МЭИ». Взаимодействие между индукцией и абдукцией зависит от
выбора наблюдаемых предикатов и абдуцентов.
Предположим, что в качестве наблюдаемого предиката мы выбра-
выбрали Юн(ж), а абдуцентом является СтМЭИ(ж). Тогда гипотеза Н среди
всех возможных абдуцируемых расширений теории Т, соответствую-
соответствующих разным абдуцируемым утверждениям знания примеров, непро-
непротиворечивых с Т, выбирает данное конкретное. В этом выбранном
расширении наблюдение О выводится, и поэтому, согласно абдуктив-
ной теории Т, гипотеза Н объясняет это наблюдение. Заметим, что эта
гипотеза не обобщает данное наблюдение, т. е. наблюдаемый предикат
Юн (ж) действует только в рамках наблюдения О.
Теперь при анализе этого примера мы исходим из того, что на-
наблюдаемым предикатом является СтМЭИ(ж), предполагая, что любой
из наблюдаемых студентов является студентом МЭИ. Образуя ту же
самую гипотезу Н, что и раньше, и имея в виду уже индуктивную
проблему, эта гипотеза становится индуктивной и обладает обобщаю-
обобщающим действием на наблюдениях по предикату СтМЭИ(ж). Но откуда
появились наблюдения по предикату СтМЭИ(ж)? Они могут быть
получены из теории Т как выбранные абдуктивные объяснения при

Введение 21
наблюдениях по предикату Юн (ж). Здесь мы уже имеем гибридный
процесс, первая ступень которого использует абдукцию как наблюде-
наблюдение на абдуцируемых предикатах, а вторая ступень — индукцию для
обобщения этого множества наблюдений, получая общее утверждение
на абдуцируемых предикатах.
Таким образом, абдукция может быть использована для извлече-
извлечения из данной теории Т и наблюдений О абдуцированной информации
О', которая затем на уровне индукции дополняет эту теорию до новой
Тх, такой, что Т1 N О1'. Затем этот процесс может быть повторен.
В свете современных воззрений дедукция, абдукция и обобщение
взаимосвязаны, дополняют друг друга и присутствуют в той или иной
степени в интеллектуальных системах. В связи с большими объема-
объемами перерабатываемых данных и знаний, высокими требованиями к
точности и времени обработки, необходимостью работы с неполной,
противоречивой и неопределенной информацией проблема автомати-
автоматизации процессов дедукции, абдукции и обобщения становится одной
из наиболее важных проблем при создании интеллектуальных систем
различного назначения. Так, в частности, при разработке динами-
динамических экспертных систем, характеризующихся неполной, противо-
противоречивой и меняющейся во времени информацией, большое значение
приобретают исследования по немонотонным рассуждениям. В та-
таких рассуждениях при получении дополнительной информации мо-
может потребоваться пересмотр (ревизия) некоторых ранее сделанных
заключений, которые окажутся несовместимыми с новой информа-
информацией. Правила немонотонного вывода относятся к правдоподобным
выводам.
Таким образом, данная книга состоит из трех частей, каждая из
которых посвящена дедукции, абдукции и индукции соответственно.
В первой части, содержащей пять глав, рассмотрены проблемы до-
достоверного вывода. Глава 1 носит обзорный характер и посвящена
автоматическому доказательству теорем, в котором главный акцент
сделан на метод резолюции, его модификации и применение этого
метода в языке Пролог. В следующих двух главах рассмотрены ме-
методы вывода на графовых структурах. Авторы отдали предпочтение
этим методам ввиду их хорошего распараллеливания и возможности
сравнения эффективности работы на тестовой задаче «Стимроллер».
В главе 4 описан метод аналитических таблиц, который малоизве-
малоизвестен русскоязычному читателю вследствие малого количества лите-
литературы по этому методу на русском языке.
И, наконец, вывод на иерархических структурах приведен в гла-
главе 5. Здесь главное внимание было уделено описанию многоуровневой
алгебры и многоуровневой логики, а также механизму вывода в такой
логике.

22 Введение
Во второй части, также состоящей из пяти глав, дан аппарат клас-
классических модальных логик, немонотонных модальных логик, описаны
системы аргументации и абдуктивный вывод.
Глава б посвящена характерным особенностям знания; подчерки-
подчеркивается роль не-факторов знания в правдоподобных рассуждениях и
нетрадиционных логик в искусственном интеллекте.
Аппарат классических модальных логик изложен в главе 7. Здесь
рассматриваются не только формальные системы модальной логики,
но и семантическая сторона этой проблемы.
Предлагаемые в главе 8 немонотонные модальные логики опе-
оперируют с неполным, противоречивым, динамически изменяющимся
знанием. Сначала рассмотрены логики убеждения и знания, затем
описаны универсальные аксиоматические модальные системы Мак-
Дермотта и Дойла, которые были модифицированы с привлечением
моделирования идеально разумного агента, интроспективно рассуж-
рассуждающего об исходном множестве предположений (автоэпистемические
логики Мура). Далее описываются логики умолчаний Рейтера и си-
системы поддержания истинности БД.
Глава 9 посвящена исследованию фундированной семантики для
расширенных логических программ (WFSX). С помощью этой се-
семантики можно представлять вывод по неполной информации, аб-
абдуктивный вывод, вывод с умолчаниями, выполнять обработку про-
противоречий.
Системы аргументации и абдуктивный вывод представлены в гла-
главе 10. Дается обзор систем аргументации и показывается, что теория
аргументации может успешно применяться для организации абдук-
тивного вывода. Излагаются подходы к вычислению абдуктивных
объяснений, описывается метод вероятностных абдуктивных рассуж-
рассуждений и дается применение абдукции и аргументации в логическом
программировании.
Третья часть книги, состоящая из четырех глав, посвящена ин-
индуктивному обобщению в интеллектуальных системах. Другие виды
индукции в книге не рассматриваются.
Так, в главе 11 описываются системы поддержки принятия реше-
решений и роль извлечения данных и знаний из БД в таких системах.
В главе 12 рассматривается класс алгоритмов, решающих задачу
обучения без учителя. Затем приводятся алгоритмы распознавания с
использованием решающих функций.
Алгоритмы обучения с учителем описаны в главе 13. Дан широкий
спектр алгоритмов такого класса и показано, что эти алгоритмы
оперируют с объектами, содержащими качественные признаки. Поиск
наиболее существенных сочетаний признаков проводится с помощью
аппарата логических функций.
И, наконец, последняя 14-я глава посвящена индуктивному обоб-
обобщению для случая неполной информации. Системам извлечения зна-

Введение 23
ний часто приходится работать с уже готовыми БД, в которых инфор-
информация может быть искажена, и значения некоторых атрибутов могут
содержать ошибки в результате измерений или даже отсутствовать.
Приводится алгоритм извлечения продукционных правил из большой
БД, и описывается подход для извлечения знаний с использованием
приближенных множеств.
Басня И. А. Крылова, отрывок из которой предваряет введение,
как известно, заканчивается пессимистически. Мы же будем надеять-
надеяться, что после прочтения этой книги «воз» все же сдвинется с места,
и читатели будут иметь более оптимистический настрой при решении
проблем, связанных с достоверными и правдоподобными рассуждени-
рассуждениями. Дай же Бог!

Часть I
ДОСТОВЕРНЫЙ ВЫВОД
Также и много других собрать бы я мог доказательств,
Чтобы еще подтвердить несомненность моих рассуждений;
Но и следов, что я здесь лишь наметил, довольно,
Чтобы ты чутким умом доследовал все остальное.
Лукреций
Глава 1
АВТОМАТИЧЕСКОЕ ДОКАЗАТЕЛЬСТВО
ТЕОРЕМ
Автоматическое доказательство теорем ведет свое начало от осно-
основополагающих работ Эрбрана, который еще в 30-х годах XX в. пред-
предложил механическую процедуру дедуктивного вывода. В 60-е годы
усилиями Ньюэлла и Саймона был создан общий решатель проблем,
доказывающий теоремы формальной логики, разработанной Расселом
и Уайтхедом, которые считали, что для математики достаточно иметь
формальный вывод теорем из основных аксиом.
Однако результаты Чёрча и Тьюринга о неразрешимости логики
предикатов первого порядка в какой-то степени оттеснили работы
Эрбрана на задний план. Интерес к ним возрос лишь в 60-е годы, когда
Гилмор реализовал эрбрановскую процедуру вывода на компьютере.
Действительно, если нет процедуры для проверки противоречивости
(общезначимости) формул логики предикатов первого порядка, то
самое большее, что молено сделать — это проверить противоречивость
(общезначимость) формулы, если она на самом деле таковой и явля-
является. Гилмору удалось доказать с помощью процедуры Эрбрана ряд
простых теорем из логики высказываний и логики предикатов первого
порядка, но его программа столкнулась с неразрешимыми трудностя-
трудностями при доказательстве более сложных теорем логики предикатов.
Ненамного эффективнее был метод Девиса и Патнема, с помощью
которого были доказаны некоторые теоремы из логики предикатов
первого порядка, не доказанные Гилмором. В 1964-1965 гг. независи-
независимо друг от друга появились обратный метод установления выводимо-
выводимости Маслова и принцип резолюции Робинсона. В те же годы Шани-
Шаниным и его коллегами было разработано несколько версий алгоритма
машинного поиска естественного логического вывода в исчислении
высказываний (АЛПЕВ). Разработка версий системы АЛПЕВ и ма-
машинных алгоритмов вывода на основе обратного метода и принципа

1.1] Нормальные и стандартные формы 25
резолюции показала принципиальную возможность машинных дока-
доказательств теорем.
Сейчас принято считать, что автоматические рассуждения на
основе формальной логики относятся к слабым (weak) методам до-
доказательства теорем, и чисто синтаксические методы управления по-
поиском не способны обрабатывать огромное пространство поиска при
решении задач практической сложности. Поэтому альтернативой яв-
являются неформальные методы поиска, ad hoc стратегии, эвристики
и рассуждения здравого смысла, которые человек использует при
решении проблем.
Однако методы доказательства теорем, основанные на формаль-
формальной логике типа логики предикатов первого порядка, остаются все
еще сильным оружием при манипулировании знанием и их нельзя
игнорировать. Продолжающийся интерес к автоматическому дока-
доказательству теорем заключается в симбиозе человека и машины при
решении сложных проблем, когда на долю человека остаются задачи
декомпозиции сложной проблемы на ряд подпроблем, поиска нуж-
нужных эвристик для сокращения пространства поиска, а автоматиче-
автоматическому решателю доводится выполнять формальные манипуляции со
знанием на основе методов вывода. Ярким примером использования
этого симбиоза являются экспертные системы, основанные на прави-
правилах, нашедшие широкое применение в медицине, геологии, управле-
управлении производством, транспортом, тепловыми и атомными станциями
и т. п.
Конечно, доминирующий в автоматическом доказательстве теорем
метод резолюции не является панацеей от всех бед, сопровождаю-
сопровождающих процедуры доказательства теорем, и мы вправе надеяться на
появление более совершенных процедур дедуктивного вывода. Это
касается и языка Пролог, неплохо зарекомендовавшего себя при ре-
решении логических проблем. Здесь можно согласиться с точкой зре-
зрения Н. Н. Непейводы, утверждавшего, что «есть смысл использовать
Пролог для кусков программ, обладающих исключительно сложной
логикой при явном задании вариантов. Все вычислительные части
программ при этом стоит писать на других языках и иметь либо
Пролог-программу, вызывающую вычислительные модули, либо (ска-
(скажем) Паскаль-программу с внешней Пролог-подпрограммой».
1.1. Нормальные и стандартные формы
При разработке методов автоматического доказательства теорем
необходимо представить все формулы, как логики высказываний, так
и логики предикатов первого порядка, в некотором стандартном виде.
В дальнейшем слова «первого порядка» будут опускаться, а логика
предикатов будет считаться расширением логики высказываний за

26 Автоматическое доказательство теорем [Гл. 1
счет введения предикатов, квантора общности V и квантора суще-
существования 3. Простые высказывания в логике высказываний будем
называть атомами, принимающими два значения: истина (И) или
ложь (Л). Символы И и Л называются истинностными значениями.
Сложные высказывания (формулы) будут образовываться из про-
простых с помощью логических связок -н (не), & (конъюнкция), V (ди-
(дизъюнкция), —> (импликация), <-> (эквивалентность).
Для логики предикатов определим понятия терма, атома и фор-
формулы. Здесь мы имеем:
xi, #2,..., хп,... — предметные переменные;
ai, а2,... а/с,... — предметные константы;
Pj1, Рр,..., Р^,..., Qrk,... — предикатные буквы;
Д1, /р,..., /^,..., #?,...- функциональные буквы.
Верхний индекс предикатной или функциональной буквы указыва-
указывает число аргументов, а нижний служит для различения букв с одним
и тем же числом аргументов. В дальнейшем верхний индекс будем
опускать.
Правила конструирования термов:
1) всякая предметная переменная или предметная константа есть
терм;
2) если fi — функциональная буква и ti,t2,...,tn — термы, то
fi(ti,t2,...,tn) —терм;
3) других правил образования термов нет.
Например, ж, у и 1 — термы, mult и plus — двухместные функцио-
функциональные символы, тогда plus(?/, 1) и mult(x, plus(?/, 1)) — также термы.
Правила образования атомов (атомарных формул):
1) всякое переменное высказывание X есть атом;
2) если Pi — предикатная буква, а ti,t2,...,tn — термы, то
РД^Ъ ^2, • • • ,tn) есть атом;
3) других правил образования атомов нет.
Формулы логики предикатов конструируются по следующим пра-
правилам:
1) всякий атом есть формула;
2) если Аи В — формулы их — предметная переменная, то каждое
из выражений -.Д А & Б, А V Б, А -> Б, А <-> Б, Ух А и ЗхА
есть формула;
3) других правил образования формул нет.

1.1] Нормальные и стандартные формы 27
Для того чтобы сократить количество скобок в формуле, исполь-
используем правила силы операций:
1) связка -л сильнее связок & , V, —>, <->;
2) связка & сильнее связок V, —», <->;
3) связка V сильнее связок —», <->;
4) связка —> сильнее связки <-».
Внешние скобки всегда будем опускать, и вообще везде, где не
возникает двусмысленностей, будем пользоваться минимумом скобок.
Кроме того, всегда предполагаем, что свободные и связанные пере-
переменные обозначены разными буквами, и если один квантор находится
в области действия другого, то переменные, связанные этими кванто-
кванторами, также обозначены разными буквами.
Пример 1.1.
Пусть Р(х) и N(x) обозначают соответственно «х есть положи-
положительное целое число» и «ж есть натуральное число». Тогда утвержде-
утверждение «Всякое положительное целое число есть натуральное число. Чис-
Число 5 есть положительное целое число. Следовательно, 5 есть натураль-
натуральное число» будет записано на языке логики предикатов следующим
образом:
\/х(Р(х) -> N(x))
РE)
NE)
Отметим, что для перевода предложений с русского языка на
язык логики предикатов в общем случае не существует механических
правил. В каждом отдельном случае нужно сначала установить, каков
смысл переводимого предложения, а затем пытаться передать тот же
смысл с помощью предикатов, кванторов и термов. Для иллюстрации
того, что при переводе могут возникнуть трудности, приведем доволь-
довольно несложные высказывания.
Пример 1.2.
1. Все люди — животные: Vy(S(y) —> С (у)).
2. Следовательно, голова человека является головой животного:
VxCy(S(y) к V(x,y)) -> 3z(C(z) к V(x,z))). Здесь S(x) - «х -
человек»; С(х) — «х — животное»; V(x,y) — «х является голо-
головой у».
Если перевод первого высказывания довольно прост, то с пере-
переводом второго возникают сложности, связанные с определением его
семантики.
Формулы логики высказываний и логики предикатов имеют смысл
только тогда, когда имеется какая-нибудь интерпретация входящих в
нее символов.

28 Автоматическое доказательство теорем [Гл. 1
Пусть дана формула логики высказываний Б hIi, X2,..., Хп —
атомы, встречающиеся в этой формуле. Тогда под интерпретацией
формулы логики высказываний В будем понимать приписывание ис-
истинностных значений атомам Xi, Х2,... , Хп, т.е. интерпретация —
это отображение /, сопоставляющее каждому атому Xi (г = 1,п)
некоторое истинностное значение.
Под интерпретацией в исчислении предикатов будем понимать
систему, состоящую из непустого множества D, называемого обла-
областью интерпретации, и какого-либо соответствия, относящего каж-
каждой предикатной букве Р™ некоторое n-местное отношение в D (т. е.
Dn —> {И, Л}), каждой функциональное букве /гп — некоторую п-
местную функцию в D (т.е. Dn —> D) и каждой предметной кон-
константе di — некоторый элемент из D. При заданной интерпретации
предметные переменные мыслятся пробегающими область D этой
интерпретации, а логическим связкам —<, & , V, —>-, <->¦ и кванторам
придается их обычный смысл.
Для данной интерпретации любая формула без свободных пере-
переменных представляет собой высказывание, которое может быть ис-
истинным или ложным, а всякая формула со свободными переменными
выражает некоторое отношение на области интерпретации, причем
это отношение может быть истинным для одних значений переменных
из области интерпретации и ложным для других.
Пример 1.3.
Дана формула P(fi(xi,X2),a). В качестве области интерпретации
берем множество всех натуральных чисел N и интерпретируем Р(х,
у) как х ^ у, /i(xi, X2) — как х\ + Х2 и а = 5. Тогда -P(/i(xi,X2),a)
представляет отношение х\ + ^2 ^ а, которое верно для всех упорядо-
упорядоченных троек < ^1, &2? ^з > целых положительных чисел, таких, что
h + b2 > b3.
Пример 1.4.
Дана замкнутая формула (т. е. формула без свободных перемен-
переменных) V#i3x2-A(x2, ?i). Пусть область интерпретации — множество
натуральных чисел N и А (ж, г/) — интерпретируем как х ^ у. Тогда
записанное выражение оказывается истинным высказыванием, утвер-
утверждающим существование наименьшего целого положительного числа.
Для выяснения факта, истинна или ложна формула в данной
интерпретации /, необходимо, задав область интерпретации, интер-
интерпретировать прежде всего все термы, входящие в формулу, затем
атомы и, наконец, саму формулу.
Если область интерпретации D конечна, то в принципе можно
выяснить истинность или ложность любой формулы, перебрав все
различные элементы множества Dn, где п — число различных пере-
переменных, входящих в формулу. Однако на практике D часто настолько

1.1] Нормальные и стандартные формы 29
велика или бесконечна, что о переборе не может быть и речи. Поэтому
логический вывод оказывается просто необходим.
Формула логики высказываний (предикатов), которая истинна во
всех интерпретациях, называется общезначимой формулой. Анало-
Аналогично формула логики высказываний (предикатов), которая ложна
во всех интерпретациях, называется противоречием.
Кроме того, будем называть формулу выполнимой, если она ис-
истинна по крайней мере в одной интерпретации. Аналогично, формула
называется опровержимой, если она ложна по крайней мере в одной
интерпретации. Отсюда очевидно, что формула А общезначима тогда
и только тогда, когда ^А невыполнима, и А выполнима тогда и только
тогда, когда ^А опровержима.
Интерпретация, при которой истинностное значение формулы есть
И, называется моделью этой формулы. Любую формулу удобно пред-
представить в виде так называемой нормальной формы. Атом или его
отрицание будем называть литерой.
Говорят, что формула логики высказываний В представлена
в конъюнктивной нормальной форме (КНФ) тогда и только
тогда, когда она имеет форму В = В\ & В2 & ... & Бш, где
каждая из Bi (г = 1,га) есть дизъюнкция литер. Например, В =
= (Xi V ^Х2) & (->Xi VI2V ^Х3) & Х3 представлена в КНФ.
Аналогично говорят, что формула логики высказываний В пред-
представлена в дизъюнктивной нормальной форме (ДНФ) тогда и толь-
только тогда, когда она имеет форму В = В\ У В2 У ... V Бш, где
каждая из Bi (г = 1,га) есть конъюнкция литер. Например, В =
= (-.Xi & ^Х2 & Х3) V (Xi & Х2) V ^Х3 представлена в ДНФ.
Любая формула исчисления высказываний может быть преобра-
преобразована в нормальную форму с помощью следующего алгоритма.
Шаг L А <-> В = (А -> В) & (Б -> А).
А^ В = ^AV В.
^А = А.
-\а & В) = -А V -Б / 3аКОНЫ Де"М°Ргана-
ШагЗ.
АУ (В & С) = (АУ В) & (А V С) (для КНФ).
A&EVC)=ifeEVi&C (для ДНФ).
Пример 1.5.
Получим КНФ для формулы (А —> (Б V ->С)) —> Z).
-^ (В V -.С)) -^D = (-iVSV^)^D = ^(^A У ВУ^С)У D =
= (А & ^Б & С) V ?> = (А У D) & (-.Б V D) & (С V ?>).

30 Автоматическое доказательство теорем [Гл. 1
Пример 1.6.
Получим ДНФ для формулы -.(А & В) & (А V Б).
-.(А & Б) & (А V В) = (-.А V -.Б) & (А V Б) =
= ((-.А V -.Б) & А) V ((-.А V -.Б) & В) =
В логике предикатов также имеется нормальная форма, называе-
называемая пренексной нормальной формой (ПНФ). Необходимость введения
ПНФ будет обусловлена в дальнейшем упрощением процедуры дока-
доказательства теорем.
Сначала рассмотрим некоторые равносильные формулы в исчис-
исчислении предикатов. Напомним, что две формулы F и Ф равносильны,
т. е. F = Ф, тогда и только тогда, когда истинностные значения этих
формул совпадают при любой интерпретации F и Ф. Для подчерки-
подчеркивания факта, что переменная х входит в формулу F, будем писать
F[x], хотя F может содержать и другие переменные.
Имеем следующие пары равносильных формул:
\/xF[x] WO
\JxF[x) & Ф = \Jx(F[x) & Ф);
3xF[x] V Ф = 3x(F[x] V Ф);
3xF[x] & Ф = 3x(F[x] & Ф).
при условии, что переменная х не входит свободно в формулу Ф. Рав-
Равносильность этих формул очевидна, так как формула Ф не содержит
свободно ж, поэтому не входит в область действия кванторов.
Далее имеем
\/xF[x] & \/хФ[х] = \/x(F[x] & Ф[ж]),
3xF[x] V ЗхФ[х] = 3x(F[x] V Ф[х\).
Доказательство этих двух равносильностей оставляем читателю.
Однако
\/xF[x] V \/хФ[х] ф \/x(F[x] V Ф[ж]),
3xF[x] & ЗхФ[х] ф 3x(F[x] & Ф[ж]).
Действительно, взяв область интерпретации D = {1,2} и положив
при некоторой интерпретации F[l] = И и F[2] = Л, а Ф[1] = Л и
Ф[2] = И, получим в левой части первого неравенства значение Л,
а в правой — И. Аналогично доказывается и второе неравенство. В
последних двух случаях производим переименование связанных пере-
переменных, т. е.Ух F[x] V УжФ[ж] = Ух F[x] УУу Ф[у] = УхУу (F[x\ V Ф[г/]),
Зх F[x) & ЗхФ[х) = Зх F[x) & ЗуФ[у] = 3x3y(F[x] & Ф[у]) при усло-
условии, что переменная у не появляется в F[x].

1.1] Нормальные и стандартные формы 31
Теперь дадим определение ПНФ. Говорят, что формула F логики
предикатов находится в ПНФ тогда и только тогда, когда ее мож-
можно представить в форме 3iXi ^2^2 ••• Ягхг Му где 31^, * — 1?г>
есть либо Ухг, либо Зжг и М — бескванторная формула. Иногда
^1^1 ^2^2 ••• ^г^г называют префиксом, а М — матрицей форму-
формулы F.
Например, формула Fx = ЗхУу (Q(x,y) V P(f(x)) -> R(x,g(y)))
находится в ПНФ, а формула F2 = Ух(Р(х) —> 3yQ(x, у)) — не в ПНФ.
Существует алгоритм, преобразующий произвольную заданную
формулу в равносильную ей формулу, имеющую пренексный вид.
Алгоритм состоит из следующих шагов.
Шаг 1. Исключение логических связок <-> и —». Многократно (пока
это возможно) делаем замены: F <-> Ф = (-I.F V Ф) & (F V —"Ф),
F -^ Ф = ^F V Ф. Результатом этого шага будет формула, равно-
равносильная исходной и не содержащая связок ^ и —».
1/7аг 2. Продвижение знака отрицания -н до атома. Многократно
(пока это возмож:но) делаем замены:
^F = F,
n(FVO) = ^^&^Ф,
^(F& Ф) = ^FV^O,
Очевидно, что в результате выполнения этого шага получается
формула, у которой знаки отрицания -н могут стоять лишь перед
атомами.
Шаг 3. Переименование связанных переменных. Многократно (по-
(пока это возможно) применяется следующее правило: найти самое левое
вхождение переменной, такое, что это вхождение связано (некоторым
квантором), но существует еще одно вхождение этой же переменной;
затем сделать замену связанного вхождения на вхождение новой пе-
переменной.
Шаг 4. Вынесение кванторов. Для этого используем следующие
равносильности:
XxF[x] V Ф = Xx(F[x] V Ф),
XxF[x] & Ф = Hx(F[x] & Ф),
\/xF[x] & \/хФ[х] = \/x(F[x] & Ф[ж]),
3xF[x] V ЗхФ[х] = 3x(F[x] V Ф[ж]),
XlXF[x] V Х2хФ[х] = XlXX2y(F[x} V Ф^]),
XlXF[x] & Х2хФ[х] = X1xX2y(F[x] & Ф[у]),
где ^Л, ^Ii и ^2 — кванторы либо V, либо 3.

32 Автоматическое доказательство теорем [Гл. 1
После выполнения четвертого шага формула приобретает пренекс-
ный вид: >Ii?i ^2^2 • • • HrxrM, где >^, ? {V, 3} для г = 1,г.
Пример 1.7.
Пусть F = \/х{Р{х) <-> 3xR(x)) —> VyQ(y). Применяя алгоритм,
получаем следующую последовательность формул.
Шаг!.
Ух[(^Р(х) V 3xR(x)) & (Р(х) V ->3xR(x))] -+ VyQ(y),
-Nx[(--P(x) V 3xR(x)) & (P(x) V -.ЗжД(ж))] V Vt/Q(i/).
Шаг 2.
) V ЗжД(ж)) & (Р(ж) V ^Зж^(ж))]} V VyQ(y),
) V ЗжД(ж)) V -.(Р(ж) V ^Зж^(ж))} V Vt/Q(i/),
) & -.ЭжД(а;)) V (-.Р(ж) & ^3xR
Зх{(Р(х) & ^Зж^(ж)) V (-.Р(ж) & ЗжД(ж))} V
Зж{(Р(ж) & Уж--Д(ж)) V (--Р(ж) & 3xR(x))} V
Я/агЗ.
(г) & Уа;-ВД) V (-Р(г) & ЭжД(ж))} V
& Vw^R(w)) V (-Р(г) & Зж^(ж))} V VyQ(y).
Шаг А.
3z\/w3x\/y{(P(z) & ^R(w)) V (-Р(г) & Д(ж)) V Q(y)}.
Таким образом, мы ограничимся формулами, имеющими пренекс-
ный вид. Однако можно рассматривать еще более узкий класс фор-
формул, так называемых V-формул.
Формула F называется V-формулой, если она представлена в ПНФ,
причем кванторная часть состоит только из кванторов общности, т. е.
F = \/х\\/х2 ... VxrM, где М — бескванторная формула.
Отсюда возникает задача устранения кванторов существования в
формулах, представленных в ПНФ. Это можно сделать путем введе-
введения сколемовских функций.
Пусть формула F представлена в ПНФ. F = 3iXi ^2^2 • • • ^ЯгхгМ',
где X,-e{V,3}, j=T^F.
Пусть Xi A ^ г ^ г) — квантор существования в префиксе
З1Х1З2Х2... ^rxr- Если г = 1, т.е. ни один квантор общности не
стоит впереди квантора существования, то выбираем константу с
из области определения М, отличную от констант, встречающихся
в М, и заменяем х\ на с в М. Вычеркиваем из префикса квантор
существования ^А\Х\. Если перед квантором существования ^ сто-
стоит >1д, 3^2,..., 5ijm кванторов общности, то выбираем т-местный
функциональный символ /, отличный от функциональных символов
в М, и заменяем xi на f(xji,Xj2,... ,^jm)? называемую сколемовской

1.1] Нормальные и стандартные формы 33
функцией, в М. Квантор существования ^Хг вычеркиваем из пре-
префикса. Аналогично удаляются и другие кванторы существования в
ПНФ. В итоге получаем V-формулу. Опишем алгоритм последователь-
последовательного исключения кванторов существования.
Алгоритм Сколема
Шаг 1. Формулу представить в ПНФ.
Шаг 2. Найти наименьший индекс г такой, что 3Ii, ^2, • • •, ^г-i
все равны V, но ^ — 3. Если г = 1, т.е. квантор 3 стоит на первом
месте, то вместо х\ в формулу М подставить константу с, отличную
от констант, встречающихся в М, и квантор 3 удалить из префикса.
Если такого г нет, то СТОП: формула F является V-формулой.
Шаг 3. Взять новый (г — 1)-местный функциональный символ /^,
не встречающийся в F. Заменить F на формулу
( ) 1, . . . , Xr].
Шаг 4. Перейти к шагу 2.
Пример 1.8.
Пусть F = 3x\/y\/z3u\/v3w (P(x,y) V -^R(z,u,v) & Q(u,w)). При-
Применяя алгоритм Сколема, получаем следующую последовательность
формул:
\Jy\Jz3uVv3w (Р(с, у) V -.Д(г, щ v) & Q(u, w));
\Jy\Jz\Jv3w (Р(с, 2/) V ^R(z, /B/, z), v) & Q(/B/, z), ^));
Vi/VzV^ (P(c, y) V -i?(z, /B/, z), v) & Q(/B/, z),pB/, z, v))).
Переход от формулы в пренексной форме к V-формуле не за-
затрагивает свойство формулы быть невыполнимой (противоречивой).
Это доказывается следующей теоремой. Как правило, все теоремы
будут даваться без доказательств. Желающие доказать их могут по-
попробовать сделать это сами или обратиться к книгам, указанным в
литературном комментарии.
Теорема 1.1. Пусть формула F задана в ПНФ и преобразована в
V-формулу. В этом случае F в пренексной форме логически невыпол-
невыполнима тогда и только тогда, когда невыполнима V-формула F.
Аналогичная теорема имеет место и для общезначимых формул.
Однако следует заметить, что если имеется выполнимая формула
F, то может оказаться, что V-формула для F будет невыполнимой.
Действительно, пусть F = Зх Р{х) и соответствующая ей V-формула
есть Р(с). Тогда, задавая область интерпретации D = {1, 2} и интер-
интерпретируя РA) = Л и РB) = И и положив с = 1, получаем, что F
в пренексной форме выполнима, а V-формула в этой интерпретации
невыполнима.
2 В.Н. Вагин и др.

34 Автоматическое доказательство теорем [Гл. 1
Таким образом, алгоритм Сколема, сохраняя свойство невыполни-
невыполнимости (противоречивости), приводит произвольную формулу, имею-
имеющую пренексный вид, к V-формуле.
Рассмотрим теперь преобразование бескванторной части (матри-
(матрицы) к виду так называемых дизъюнктов (clauses). Дизъюнктом назы-
называется формула вида Li VL2 V.. .VL&, где Li (г = 1, к) — произвольная
литера.
Дизъюнкт, не имеющий литер, называется пустым дизъюнктом
(?). По определению он всегда ложен. Дизъюнкты, соединенные зна-
знаком & , образуют КНФ. Существует простой алгоритм равносильного
преобразования произвольной бескванторной формулы в КНФ (см.
также алгоритм получения КНФ и ДНФ для логики высказываний,
данный ранее). Здесь дадим его в развернутом виде.
Алгоритм, приведения к КНФ
Шаг 1. Дана формула F, составленная из литер с применением
связок & и V. Предполагается, что в формуле исключены скобки
между одинаковыми связками, т. е. нет выражений вида
Фх V (Ф2 V Ф3), (Фх V Ф2) V Ф3,
или
Фх & (Ф2 & Фз)> (Ф1 & Фг) & Фз-
Шаг 2. Найти первое слева вхождение двух символов "V(" или ")V"
(здесь предполагается, что скобка не является скобкой атома). Если
таких вхождений нет, то СТОП: формула F находится в КНФ.
Шаг 3. Пусть первым вхождением указанной пары символов явля-
является "V(". Тогда взять наибольшие формулы
Ф1,Ф2,...,Фг,Ф1,Ф2,...,Фв,
такие, что в F входит формула
F1 = Фх V Ф2 V Фг V (Фх & Ф2 & ... & ФД
которая связана с вхождением "V(". Заменить формулу F\ на формулу
(Фх V Ф2 V . .. V Фг V Фх) & (Фх V Ф2 V . .. V Фг V Ф2) & ... &
& (фх у ф2 V... V Фг УФз).
Шаг 4. Пусть первым вхождением является ")V". Тогда взять
наибольшие формулы
такие, что в F входит формула
Fi = (Фх & Ф2 & ... & Фз) V Фх V Ф2 V ... V Фг,

1.2] Логические следствия 35
связанная с вхождением ")V". Заменить F\ на формулу
(Фх V Фх V Ф2 V . .. V Фг) & (Ф2 V Фх V Ф2 V . .. V Фг) & ... &
& (Фз У ФХУ Ф2 V... УФГ).
1/7аг 5. Перейти к шагу 2.
Пример 1.9.
Преобразуем формулу F = Р{х) V P(a)V((R(x,y) V ->Q(y)) &
& Р(ж) & (Д(ж,а) V НЭЫ & Р(а)))) в КНФ. ~~
F = (Р(х) V Р(а) V Д(ж, 2/) V -,Q(y)) & (Р(ж) V Р(а) V Р{х)) &
& (Р(ж) V Р(а) V Д(ж, а) V(-.QB/) & Р(а))) =
= (Р(ж) V Р(а) V Д(ж, 2/) V -,Q(y)) & (Р(ж) V Р(а)) &
& (Р(ж) V Р(а) V Д(ж, а) V ->Q(y)) & (Р(ж) V Р(а) V Д(ж, а) V Р(а)) =
= (Р(ж) V Р(а) V Д(ж, 2/) V ^QB/)) & (Р(ж) V Р(а)) &
& (Р(х) V Р(а) V Д(ж, а) V --QB/)) & (Р(ж) V Р(а) V Д(ж, а)).
Здесь чертой подчеркнуты вхождения "V(". Кроме того, в ал-
алгоритме надо предусмотреть приведение подобных членов, а также
всевозможные склеивания и поглощения.
Итак, последовательным применением алгоритма приведения к
ПНФ, алгоритма Сколема и алгоритма приведения к КНФ с со-
сохранением свойства невыполнимости любая формула F может быть
представлена набором дизъюнктов, объединенных кванторами общ-
общности. Такую формулу будем называть формулой, представленной в
Сколемовской стандартной форме (ССФ).
В дальнейшем формулы вида Ух\Ух2 ... Vxr[Z)x & D2 & ... & Dk\,
где Di, Дг> • • • > Dk ~ дизъюнкты, а хх, Х2,..., хг — различные пере-
переменные, входящие в эти дизъюнкты, будет удобно представлять как
множество дизъюнктов S = {Di, D2,..., Dk}. Например, множеству
дизъюнктов S = {->Р(ж,/(ж)),Р(ж,2/) V ^R{x,g{y)),Q{x) V P(x,a)}
соответствует следующая формула, представленная в ССФ:
Vx4ybP(x,f(x)) & (P(x,y)V^R(x,g(y))) & (Q(x)VP(x,a))). И, нако-
нец, когда говорят, что множество дизъюнктов S = {D\, D^-,..., Dk}
невыполнимо (противоречиво), то всегда подразумевают невы-
невыполнимость формулы Ух\Ух2 ...yxr[Di & D2 & ... & Dk], где
хх, #2,..., хг ~~ различные переменные, входящие в дизъюнкты.
1.2. Логические следствия
Как мы уже упоминали, исчисление предикатов первого порядка
является примером неразрешимой формальной системы. В доказан-
доказанной А. Чёрчем теореме говорится об отсутствии эффективной про-
процедуры при решении вопроса относительно произвольной формулы
исчисления предикатов первого порядка, является ли эта формула

36 Автоматическое доказательство теорем [Гл. 1
теоремой. Однако при доказательстве заключительного утверждения
(цели) из начальной системы аксиом, посылок мы придерживаемся
правила, что если все аксиомы и посылки принимают истинност-
истинностное значение И, то и заключительное утверждение также принимает
значение И. Из-за этого ограничения иногда исчисление предикатов
первого порядка называют полуразрешимым. Рассмотрим пример.
Пример 1.10.
Горничная сказала, что она видела дворецкого в гостиной. Гости-
Гостиная находится рядом с кухней. Выстрел раздался на кухне, и мог быть
услышан во всех близлежащих комнатах. Дворецкий, обладающий хо-
хорошим слухом, сказал, что он не слышал выстрела. Детектив должен
доказать, что если горничная сказала правду, то дворецкий солгал.
1. Р —> Q: если горничная сказала правду, то дворецкий был в
гостиной.
2. Q —> R: если дворецкий был в гостиной, то он находился рядом
с кухней.
3. R —> L: если дворецкий был рядом с кухней, то он слышал
выстрел.
4. М —> ^L: если дворецкий сказал правду, то он не слышал
выстрела.
Требуется доказать, что если горничная сказала правду, то дво-
дворецкий солгал, т. е. Р —> ->М.
Представим посылки в КНФ: (-.Р V Q) & (-.Q V R) & (-.Д V L) &
& (-iM V -iL). Аналогично заключение: ^Р V ->М.
Задавая интерпретации, в которых истинны посылки, нетрудно
обнаружить, что будет истинно и заключение. Желающие могут вы-
выписать истинностную таблицу, чтобы в этом убедиться.
Таким образом, если даны формулы F\, F2,..., Fn и G, то говорят,
что формула G является логическим следствием F\, F2,..., Fn (или
G логически следует из Fi, F2,..., Fn) тогда и только тогда, когда
для любой интерпретации I, в которой F\ & F2 & ... & Fn истинна,
G также истинна.
Для обозначения логического следования формулы G из посылок
Fi, F2,..., Fn будем писать Fi, F2,..., Fn N G. Символ N есть
некоторое отношение между формулами, причем, если посылки
соединены знаком & , то имеет место двуместное отношение:
F\ & F2 & ... & Fn N G. Теперь приведем две простые, но важные
теоремы, связывающие понятия логического следования с понятиями
общезначимости и противоречивости.
Теорема 1.2. Даны формулы Fi, F2,..., Fn и G. Формула G яв-
является логическим следствием формул F\, F2,..., Fn тогда и только
тогда, когда формула F\ & F2 & ... & Fn —> G общезначима, т. е.

1.2] Логические следствия 37
N Fi & F2 & ... & Fn -> G. Формула Fx & F2 & ... & Fn -> G назы-
называется теоремой, a G называется заключением теоремы.
Теорема 1.3. Даны формулы Fi, F2,..., Fn и G. Формула G яв-
является логическим следствием формул F\, .F2, • • •, Fn тогда и только
тогда, когда формула F\ & F2 & ... & Fn & ^G противоречива.
Таким образом, факт, что данная формула является логическим
следствием конечной последовательности формул, сводится к доказа-
доказательству общезначимости или противоречивости некоторой формулы.
Следовательно, имеется полная аналогия при выводе заключения
теоремы из множества аксиом или посылок в формальной системе,
и многие проблемы в математике могут быть сформулированы как
проблемы доказательства теорем.
Обозначим общезначимую формулу через ¦, а противоречивую —
через П. Вернемся к примеру 1.10 и покажем, что формула
(-.Р V Q) & (-.Q V R) & (-.Д V L) & (-.М V -.L) -> (-.Р V -.М)
общезначима.
Действительно,
-.[(-.Р V Q) & (-.Q V Д) & (-.Д V L) & (-.М V -.L)] V ^Р V ^М =
= Р &^QVQ k^Ry R&^LV M &LV ^PV ^M =
Аналогично мож:но показать противоречивость формулы
(-.Р V Q) & (-.Q V Д) & (-.Д V L) & (-.М V -.!,) & ^(^Р V --М) =
= п.
Подобный подход мож:но использовать и для логики предикатов.
Вернемся к примеру 1.2 и покажем, что конъюнкция посылки и
отрицания заключения есть противоречивая формула, т. е. \/y(S(y) —>
-> C(y))Sz^xCy(S(y)SzV(x,y)) -+ 3z(C(z) & V(x,z))) = П. Для
этого приведем ее к ССФ. Посылка имеет вид —iS(y) V С (у).
Отрицание заключения
& V(x,y)) V 3z(C(z) & V(x,z))) =
V nV(i, у)) V 3z(C(z) & У(х, 2))) =
V nV(i, y) V (C(z) & У(ж, г))) =
= 3x3yWz(S(y) & У(х, у) & (-,С(г) V -,^(ж, г))),
и ССФ имеет вид S(b) & У (а, 6) & ЬС{г) V -.У(а, z)).
Таким образом,
V С(Ь)) & 5F) & V(a, 6) & (-.С(Ь) V -,F(o, 6)) =
& 5F) & V{a, Ъ) к ^С{Ъ) V С{Ь) &
&F(a,6)&^F(a,6) = П.

38 Автоматическое доказательство теорем [Гл. 1
Примененный здесь подход для получения общезначимой (проти-
(противоречивой) формулы, конечно, далек от практического применения. В
дальнейшем будут даны более эффективные процедуры доказатель-
доказательства общезначимости или противоречивости формул.
В заключение отметим, что из двух теорем A.2 и 1.3), как правило,
применяется теорема 1.3, т.е. если формула G является логическим
следствием формул Fi, F2,..., Fn, то надо доказать противоречивость
формулы F\ & F2 & ... & Fn & -iG. Так как в этой формуле заключе-
заключение теоремы G опровергается, то и процедуры поиска доказательства
называются процедурами поиска опровержения, т. е. вместо дока-
доказательства общезначимости формулы доказывается, что отрицание
формулы противоречиво, и потери общности нет.
1.3. Процедура вывода Эрбрана
Ранее мы установили, что множество дизъюнктов S невыполнимо
тогда и только тогда, когда оно принимает значение «ложь» при всех
интерпретациях на любых областях. Однако в силу невозможности
рассмотрения подобных интерпретаций хорошо было бы найти та-
такую специальную область интерпретации, установив на которой факт
невыполнимости множества дизъюнктов, можно было бы сделать вы-
вывод о невыполнимости этого множества на любых других областях
интерпретаций. Такая область, к счастью, имеется, и она называется
универсумом Эрбрана. Определим его.
Пусть Щ — множество констант, появляющихся во множестве
дизъюнктов S. Если в S нет констант, то в Hq включается неко-
некоторая константа, например, Но = {а}. Для г = 1,2,... iJ^+i =
= Hi U {/n(ti, ^2,..., tn)}, где fn — все n-местные функциональные
символы, встречающиеся в S, a ti,t2,...,tn — элементы множества
Hi. Тогда будем Н = Н^ называть универсумом Эрбрана для S, а
Hi — его уровнем г.
Пример 1.11.
Пусть 5 = {Р(х, a, g(y)) V -.Q(x), -Р(/(ж), а, у) V Q(a)}. Тогда
Но = {а};
Я1 = {а,/(а),?(а)};
Я2 = {aJ(a),g(a)J(f(a))J(g(a)),g(f(a)),g(g(a))y,
Пример 1.12.
Пусть S = {Q{x) V ^R(y),P(y) V -Q(x)}. Тогда Н = Щ = Щ =

1.3] Процедура вывода Эрбрана 39
Если под выражением понимать терм, множество термов, атом,
множество атомов, литеру, множество литер, дизъюнкт или множе-
множество дизъюнктов, то под фундаментальным выражением будем по-
понимать выражение, в котором все переменные заменены элементами
универсума Эрбрана. Так, фундаментальным примером дизъюнкта
будем называть дизъюнкт, полученный заменой всех переменных в
этом дизъюнкте элементами универсума Эрбрана таким образом, что
все вхождения одной и той же переменной в дизъюнкт заменяются
одним и тем же элементом универсума.
Множество фундаментальных атомов вида Pn(?i, ?2, • • • tn), где
Рп — все n-местные предикатные символы, встречающиеся во мно-
множестве дизъюнктов S и ?i, ^2,... tn — элементы универсума Эрбрана,
называется атомарным множеством или эрбрановской базой для S.
Обозначим эрбрановскую базу через А.
Пример 1.13.
Пусть 5 = {Q(x), -P(/(x)) V -Q(x)}. Тогда
А =
Фундаментальные примеры: Q(a), ^P{f{a)) V ^Q{a) и т. п.
Определим теперь интерпретацию на универсуме Эрбрана и назо-
назовем ее ^-интерпретацией. Говорят, что интерпретация /я является
^-интерпретацией для множества дизъюнктов S, если выполнены
следующие соответствия:
• каждому предикатному символу Рп соответствует некоторое п-
местное отношение в Н\
• каждому функциональному символу /J1 соответствует некоторая
n-местная функция в Н (т. е. функция, отображающая Нп в Н);
• каждой предметной константе а^ из S соответствует некоторая
константа из Н (т. е. все константы отображаются на самих себя).
Пусть А = {Ai, A2,..., Ak,... } является эрбрановской базой для
S. Тогда ^-интерпретация /я может быть представлена множеством
/я = {^l? f^2> • • • ? wtyfc? • • • }? в котором rrij есть Aj или ^Aj для
j = 1,2,.... При этом, если rrij есть Aj, то Aj имеет значение И, в
противном случае — Л.
Пример 1.14.
Пусть S = {-.Р(/(ж)) V Q(x),R(x)}. Тогда
А =

40 Автоматическое доказательство теорем [Гл. 1
Примеры ^-интерпретаций:
Ih = {P(a), Q(a), R(a), P(/(o)), Q(/(o)), R(f(a)),...},
I2H = {^P(a), -nQ(a), -пД(а),
При /^ оба дизъюнкта выполнимы; при 1\ первый дизъюнкт
выполним, второй нет; при /^ оба дизъюнкта невыполнимы, т. е.
принимают значение Л.
В случае, если интерпретация задана не на универсуме Эрбра-
на, а на произвольной области D, то можно установить следующее
соответствие между этими интерпретациями. Пусть дана интерпре-
интерпретация / на некоторой области D. Говорят, что i^-интерпретация /я
соответствует интерпретации /, если имеет место следующее: пусть
/ii, /12, • • •, hn, • • • — элементы Н, и пусть каждый hi отображается на
некоторый элемент di области D; тогда, если любой P(di,d2,...,dn)
принимает значение И (Л) при интерпретации /, то P(h\, /12, • • •, hn)
также принимает значение И (Л) при 1н- Существует следующая
теорема.
Теорема 1.4. Множество дизъюнктов S невыполнимо тогда и
только тогда, когда S ложно при всех ^-интерпретациях.
Доказательство «тогда» очевидно, а «только тогда» легко
доказывается от противного введением соответствия между Н-
интерпретацией и некоторой произвольной интерпретацией. В
дальнейшем будем рассматривать только Н-интерпретации, и
называть их просто интерпретациями /. Таким образом, для
установления невыполнимости множества дизъюнктов необходимо и
достаточно рассмотреть только ^-интерпретации. Процедура вывода
Эрбрана основывается на его теореме.
Теорема 1.5. (теорема Эрбрана). Множество дизъюнктов S
невыполнимо тогда и только тогда, когда существует конечное невы-
невыполнимое множество Sf фундаментальных примеров дизъюнктов S.
Таким образом, для установления невыполнимости множества
дизъюнктов необходимо образовать множества Si, S2,..., ?п фунда-
фундаментальных примеров дизъюнктов и последовательно проверять их на
ложность. Теорема Эрбрана гарантирует, что если множество дизъ-
дизъюнктов S невыполнимо, то данная процедура обнаружит такое п, что
Sn является ложным.
Процедура вывода Эрбрана состоит из двух этапов: сначала на-
находится множество всех фундаментальных примеров дизъюнктов, и
затем, применяя мультипликативный метод, из КНФ получают ДНФ.

1.4] Принцип резолюции 41
Пример 1.15.
Пусть S = {Р{х) V -<&х, g(x)), -P(/(ffl)), Q(y, z)}. Находим
Н = {а, /(о), д(а), /(/(a)), f(g(a)), g(f(a)), g(g(a)),...}
и фундаментальные примеры дизъюнктов:
Sw = {P(f(a)) V
Затем с помощью мультипликативного метода убеждаемся в невыпол-
невыполнимости S:
) V -Q(/(a), 5(/(а)))) & -Р(/(а)) & Q(/(a), g(f(a))) =
= P(f(a)) к -пР(/(а)) & Q(f(a),g(f(a))) V -Q(/(a),5(/(a))) &
& -пР(/(а)) & Q(f(a),g(f(a))) = П V П = П.
Недостаток процедуры вывода Эрбрана состоит в экспоненциаль-
экспоненциальном росте множества фундаментальных примеров Si при увеличе-
увеличении г. Мультипликативный метод, использованный Гилмором при
машинной реализации этой процедуры, также неэффективен. Как
легко видеть, даже для малого множества из десяти двухлитерных
фундаментальных примеров дизъюнктов существует 210 конъюнкций
в ДНФ. Вот почему Гилмор смог доказать только простые теоремы.
Иной поход предложил Дж. Робинсон, который ввел принцип резолю-
резолюции, являющийся теоретической базой для построения большинства
методов автоматического доказательства теорем.
1.4. Принцип резолюции
Основная идея принципа резолюции заключается в проверке, со-
содержит ли множество дизъюнктов S пустой (ложный) дизъюнкт П.
Если это так, то S невыполнимо. Если S не содержит П, то следующие
шаги заключаются в выводе новых дизъюнктов до тех пор, пока не
будет получен ? (что всегда будет иметь место для невыполнимого
S). Таким образом, принцип резолюции рассматривается как правило
вывода, с помощью которого из S порождаются новые дизъюнкты.
По существу принцип резолюции является расширением Modus
Ponens на случай произвольных дизъюнктов с любым числом литер.
Действительно, имея Р и Р —> Q, что равносильно ^Р V Q, можно
вывести Q путем удаления контрарной пары Р и пР. Расширение
состоит в том, что если любые два дизъюнкта С\ и С2, имеют кон-
контрарную пару литер (Р и ~>Р), то, вычеркивая ее, мы формируем
новый дизъюнкт из оставшихся частей двух дизъюнктов. Этот вновь
сформированный дизъюнкт будем называть резольвентой дизъюнк-
дизъюнктов С\ И С2-

42 Автоматическое доказательство теорем [Гл. 1
Пример 1.16.
Пусть d : PV^Q V Д, С2 : ^PV^Q. Тогда резольвента С: ^QVR.
Обоснованность получения таким образом резольвенты вытекает
из следующей теоремы.
Теорема 1.6. Резольвента С, полученная из двух дизъюнктов С\
и С^2, является логическим следствием этих дизъюнктов.
Если в процессе вывода новых дизъюнктов мы получим два одно-
литерных дизъюнкта, образующих контрарную пару, то резольвентой
этих двух дизъюнктов будет пустой дизъюнкт П.
Таким образом, выводом пустого дизъюнкта ? из невыполнимого
множества дизъюнктов S называется конечная последовательность
дизъюнктов Ci, Сг,..., С&, такая, что любой Ci (г = l,fc) является
или дизъюнктом из S, или резольвентой, полученной принципом ре-
резолюции, и Ck = ?•
Вывод пустого дизъюнкта может быть наглядно представлен с
помощью дерева вывода, вершинами которого являются или исходные
дизъюнкты, или резольвенты, а корнем — пустой дизъюнкт.
Пример 1.17.
Пусть S:
2.
3.
4.
Тогда резольвенты будут:
5.
6. -QC,4),
7. ПE,6).
Дерево вывода представлено на рис. 1.1.
PvQ
Приведем пример вывода формулы из множества посылок прин-
принципом резолюции. Напомним, что доказательство вывода формулы G

1.4] Принцип резолюции 43
из множества посылок F\, F2i • • •, Fn сводится к доказательству про-
противоречивости формулы Fi & F2 & ... & Fn & ^G (процедура опро-
опровержения).
Снова рассмотрим пример 1.10. Имеем следующее множество
дизъюнктов:
1.-PVQ,
2. ^QVR,
ЗТЭ \ / Т
. 1/Х V _L/,
4. ^М V -iL,
и отрицание заключения ^(^Р V —<Af)
5. Р,
6. М.
Дерево вывода представлено на рис. 1.2.
Р
Если в логике высказываний нахождение контрарных пар не вызы-
вызывает трудностей, то для логики предикатов это не так. Действительно,
если мы имеем дизъюнкты типа
d : Р{х) V -пД(х),
то резольвента может быть получена только после применения к С\
подстановки д(у) вместо х.
Имеем
С[ : Р(д(у)) V

44 Автоматическое доказательство теорем [Гл. 1
Однако для случая
очевидно, никакая подстановка в контрарную пару неприменима, и
никакая резольвента не образуется. Дадим определение того, что
является подстановкой.
Подстановкой будем называть конечное множество вида
{ti/xi, t2/x2, • • • > tn/xn}i где любой ti — терм, а любая xi — переменная
A ^ г ^ п), отличная от ti.
Подстановка называется фундаментальной, если все ti A ^ г ^ п)
являются фундаментальными термами. Подстановка, не имеющая
элементов, называется пустой подстановкой и обозначается через е.
Пусть в = {ti/xi, t2/x2,..., tn/xn} — подстановка и W — выраже-
выражение. Тогда W0 будем называть примером выражения W, полученного
заменой всех вхождений в W переменной Xi A ^ г ^ п), на вхождение
терма ti. WB будет называться фундаментальным примером выра-
выражения W, если в — фундаментальная подстановка.
Например, применив к W = {P(x,f(y)) V ^Q(z)} фундаменталь-
фундаментальную подстановку в = {a/x,g(b)/y, f(a)/z}, получим фундаменталь-
ный пример W6 = {Р{а, f(g(b))) V -Q(/(a))}.
Пусть е = {t1/x1,t2/x2,...,tn/xn} и Л = {щ/уииъ/уъ,...,
Um/Ут} — Две подстановки. Тогда композицией <д о Л двух
подстановок 6 и А называется подстановка, состоящая из множества
{t1\/x1,t2\/x2,..., tn\/xn, ui/yi, u2/y2, • • •, ит/ут}, в котором
вычеркиваются все tiX/xi в случае tiX = Xi и Uj/yj, если yj находится
среди Ж1,ж2,...,жта.
Пример 1.18.
е = {g(x,y)/x,z/y} и Л = {a/x,b/y,c/w,y/z}. в о Л =
= {#(а, Ь)/ж, г//г/, а/ж, Ь/г/, с/'Ш, i//z} = {g(a, b)/x, c/w, y/z}.
Можно показать, что композиция подстановок ассоциативна, т. е.
(9oA)o/i = 9o(Ao/i).
Подстановку в будем называть унификатором для множества
выражений {Wb W2,..., Wk}, если Wi9 = W29 = ... = WkS. Будем
говорить, что множество выражений {Wi, W2,..., W&} унифицируе-
унифицируемо, если для него имеется унификатор. Унификатор а для множества
выражений {Wi, W2,..., W&} называется наиболее общим унифика-
унификатором (НОУ) тогда и только тогда, когда для каждого унификатора
в из этого множества выражений найдется подстановка А такая, что
в = сто А.
Пример 1.19.
W = {P(x,a,f(g(w))),P(z,y,f(u))}. Тогда а = {z/x,a/y,g(w)/u}
есть НОУ, а в = {b/x,a/y,g(c)/u,b/z,c/w} есть унификатор, т.е.
{Ъ/х, а/у, g(c)/u, b/z, c/w} = {z/x, а/у, g(w)/u} о {b/z, c/w}.

1.4] Принцип резолюции 45
Опишем теперь алгоритм унификации, который находит НОУ,
если множество выражений W унифицируемо, и сообщает о неудаче,
если это не так.
Алгоритм унификации
1. Установить к = 0, Wk = W, сг/с = е. Перейти к шагу 2.
2. Если Wfc не является одноэлементным множеством, то перейти к
шагу 3. В противном случае положить а = ак и окончить работу.
3. Каждая из литер в Wk рассматривается как цепочка симво-
символов, и выделяются первые подвыражения литер, не являющиеся
одинаковыми у всех элементов Wk, т.е. образуется так назы-
называемое множество рассогласований типа {xkjtk}. Если в этом
множестве Xk — переменная, a tk — терм, отличный от хк, то
перейти к шагу 4. В противном случае окончить работу: Wk не
унифицируемо.
4. Пусть ак+\ = сгк о {tk/xk} и Wk+i = Wk{tk/xk}.
5. Установить к = к + 1 и перейти к шагу 2.
Пример 1.20.
Найти НОУ для W = {Р(у, g(z), /(ж)), Р(а, ж, /М))}.
1. fc = 0, сг0 =? и Wo = ИЛ
Так как Wo не является одноэлементным множеством, то перей-
перейти к шагу 3.
2. {г/, а}, т.е. {а/г/}.
3. а! = ст0 о {а/у} = е о {а/г/} = {а/г/}.
Wi = WoWl/} = {Р(а, g(z), /(х)), Р(а, х, f(g(a)))}.
4. Так как W\ опять неодноэлементно, то множество рассогласова-
рассогласований будет {g(z),x}, т.е. {g(z)/x}.
5. а2 = сух о {g(z)/x} = {a/y,g(z)/x}.
W2 = W1{g(z)/x} = {P(a,g(z)J(g(z))),P(a,g(z)J(g(a)))}.
6. Имеем {z,a}, т.е. {a/z}.
7. ct3 = cr2 о {a/z} = {a/y,g(a)/x,a/z}.
W3 = W2{a/z} = {P(a,g(a)J(g(a))),P(a,g(a)J(g(a)))} =
= {P(a,g(a)J(g(a)))}.
<7з = {a/y,g(a)/x,a/z} есть НОУ для W.
Можно показать, что алгоритм унификации всегда завершается на
шаге 2, если множество W унифицируемо, и на шаге 3 — в противном
случае.
Если две или более одинаковые литеры (одного и того же
знака) дизъюнкта С имеют НОУ <т, то С а называется фактором
дизъюнкта С.
Пример 1.21.
Пусть С = Р(х) V Р(д(у)) V -.Д(ж). Тогда НОУ а = {д(у)/х} и
фактор дизъюнкта С а = Р{д{у)) V

46 Автоматическое доказательство теорем [Гл. 1
Пусть С\ и Съ — два дизъюнкта, не имеющие общих переменных
(это всегда можно получить переименованием переменных). И пусть
Li и L2 = —iZ/i — литеры в дизъюнктах С\ и С2 соответственно,
имеющие НОУ а. Тогда бинарной резольвентой для С\ и С2 является
дизъюнкт вида С = (С\о — L\o~) U (С2& — L2CF). Бинарная резольвента
может быть получена одним из четырех способов:
1) резольвента для С\ и С2;
2) резольвента для С\ и фактора дизъюнкта С^\
3) резольвента для фактора дизъюнкта С\ и С2;
4) резольвента для фактора дизъюнкта С\ и фактора дизъюнкта
С2.
Пример 1.22.
Пусть d = P(f(g(a))) V ^Д(Ь), С2 = ^Р{х) V -Р(/Ы) V Q(?/).
Тогда С2<7 = Сз = -|Р(/(г/)) VQ(|/), и резольвентой для Ci и Сз будет
С = -iR(b) V Q(g(a)) (a = g(a)/y).
Принцип резолюции обладает важным свойством — полнотой,
которое устанавливается следующей теоремой.
Теорема 1.7. (Теорема о полноте Дж. Робинсона). Множе-
Множество дизъюнктов S невыполнимо тогда и только тогда, когда суще-
существует вывод принципом резолюции из S пустого дизъюнкта.
Так как исчисление предикатов первого порядка полу разрешимо,
то для выполнимого множества дизъюнктов S в общем случае проце-
процедура, основанная на принципе резолюции, будет работать бесконечно
долго.
Приведем два примера, иллю-
S(b) -uSOO v C(y) стрирующих принцип резолюции
для логики предикатов. Вернем-
Вернемся к примеру 1.2. В разд. 1.2 по-
^V{a,z) сылку и отрицание заключения
мы уже представили в виде на-
о V(a, b) бора дизъюнктов:
2.
3. V(a,b),
4.^C(z)V^V(a,z).
Дерево вывода изображено на
РисЛ-3 рис. 1.3.
Пример 1.23.
Существуют студенты, которые любят всех преподавателей. Ни
один из студентов не любит невежд. Следовательно, ни один из пре-
преподавателей не является невеждой.

1.4] Принцип резолюции 47
Запишем эти утверждения на языке логики предикатов и приведем
их к виду дизъюнктов:
Ух(С(х)
Здесь С(х) — х есть студент; Р(х) — х есть преподаватель; Н(х) — х
есть невежда; L(x,y) — х любит у.
ССФ первой посылки имеет вид: Чу (С (а) & (-*Р(у) V L(a,y))).
ССФ второй посылки имеет вид: ЧхЧу{-^С{х) V -^Н(у) V -iL(x, у)).
ССФ отрицания заключения имеет вид: ->Чу(->Р(у) V ->Н(у)) =
= ЭгН-Р(г/) v яы) = зу(Р(у) & я(у)) = р(ь) & н{ь).
Таким образом, имеем следующий набор дизъюнктов:
1. С(а),
2.
4. Р(Ь),
5. Н(Ъ).
Дерево вывода представлено на рис. 1.4.
С(а) ^C(x)v~
Рис. 1.4
Принцип резолюции является более эффективной процедурой,
нежели процедура вывода Эрбрана. Но и он страдает существен-
существенными недостатками, заключающимися в формировании всевозмож-
всевозможных резольвент, большинство из которых оказывается ненужными.
Многочисленные модификации принципа резолюции направлены на
нахождение более эффективных стратегий поиска нужных дизъюнк-
дизъюнктов. Желающие могут обратиться к комментарию в конце книги, где
перечислена литература, описывающая эти модификации.

48 Автоматическое доказательство теорем [Гл. 1
Отметим, что основными способами устранения причин «экспонен-
«экспоненциального взрыва», имеющего место при доказательстве теорем прак-
практической сложности, являются использование семантики, различных
эвристик и встраивание в правила вывода и алгоритмы унификации
специфики конкретной предметной области.
Как правило, будем удалять из рассмотрения порождаемые дизъ-
дизъюнкты типа тавтологий, так как невыполнимое множество дизъюнк-
дизъюнктов, содержащее дизъюнкт-тавтологию, остается снова невыполни-
невыполнимым после его удаления.
Аналогично будем вычеркивать поглощенные дизъюнкты, которые
также не меняют невыполнимость множества дизъюнктов. Дизъюнкт
С\ поглощает дизъюнкт С2 тогда и только тогда, когда имеется под-
подстановка S, такая, что С\5 С С^- Дизъюнкт С2 называется поглощен-
поглощенным дизъюнктом. Например, пусть С\ = Р{х) и С^ = P(a)\/R(y). Если
S = {а/х}, то Сг5 = Р(а). Тогда Р{а) С Р{а) V R{y), и d поглощает
С^2, т.е. С^ можно без ущерба для вывода вычеркнуть.
Также будем удалять так называемые чистые (pure) дизъюнкты.
Литера, чье отрицание отсутствует во множестве дизъюнктов, назы-
называется чистой. Дизъюнкт, содержащий чистую литеру, естественно,
не может участвовать в выводе пустого дизъюнкта и поэтому может
быть удален из множества дизъюнктов.
1.5. Линейная резолюция
Линейная резолюция довольно легко может быть реализована на
ЭВМ, обладает простой структурой и полнотой. Ее частный случай —
входная резолюция — является встроенным механизмом дедуктивного
вывода в языке логического программирования Пролог.
Линейным выводом из множества дизъюнктов S называется по-
последовательность дизъюнктов С\, С2,..., Ст, в которой С\ Е S, а
каждый член Q+i, (г = 1,2,...,га — 1), является резольвентой дизъ-
дизъюнкта Ci (называемого центральным дизъюнктом) и дизъюнкта Bi,
(называемого боковым дизъюнктом), который удовлетворяет одному
из двух условий: 1) Bi Е S (г = 1,2,...,т — 1); 2) Bi является
некоторым дизъюнктом Cj, предшествующим в выводе дизъюнкту
Ci, т.е. j < г (рис. 1.5).
Пример 1.24.
Пусть S = {PVQ, ^PVQ, Py^Q, ^Py^Q}. Тогда линейный вывод
пустого дизъюнкта из S представлен на рис. 1.6.
Отметим, что из четырех боковых дизъюнктов три принадле-
принадлежат S, и только один дизъюнкт Q является центральным дизъюнк-
дизъюнктом. Линейная резолюция полна, что устанавливается следующей
теоремой.

1.5]
Линейная резолюция
49
.О -^ v-.fi
.ОС
Рис. 1.5
Рис. 1.6
Теорема 1.8. Множество дизъюнктов невыполнимо тогда и толь-
только тогда, когда существует линейный вывод пустого дизъюнкта.
Линейная резолюция может быть существенно усилена введением
понятия упорядоченного дизъюнкта и использованием информации о
резольвированных литерах.
Идея упорядочения дизъюнктов заключается в рассмотрении
дизъюнкта как последовательности литер, а не как множества литер.
Отсюда упорядоченным дизъюнктом будем называть дизъюнкт с
определенной последовательностью литер.
Говорят, что литера L^ старше литеры L\ в упорядоченном дизъ-
дизъюнкте тогда и только тогда, когда L2 следует за L\ в последова-
последовательности, определенной упорядоченным дизъюнктом. Отметим, что
старшая (наибольшая) литера дизъюнкта является последней литерой
дизъюнкта, а младшая литера — первой. Например, в упорядоченном
дизъюнкте Р(а)\/ Р(Ь)\/ Р(с) Р(с) является старшей литерой, а Р(а) —
младшей.
Если две или больше литер (с одинаковыми знаками) упорядочен-
упорядоченного дизъюнкта С имеют НОУ <т, то упорядоченный дизъюнкт, по-
полученный из последовательности С а вычеркиванием любой литеры,
идентичной младшей литере, называется упорядоченным фактором
дизъюнкта С.
Пусть имеется упорядоченный дизъюнкт С = Р{х) V R(x) V Р(а),
тогда а = {а/х} и С а = P(a)\/R(a)\/P(a). Здесь имеются две идентич-
идентичные литеры Р(а). В соответствии с определением младшей литерой
считается литера, расположенная левее. Для получения упорядочен-
упорядоченного фактора надо из С а удалить литеру, идентичную младшей. В на-
нашем примере это последняя литера. Следовательно, упорядоченным
фактором будет последовательность литер Р(а) V R(a). Отметим, что
связывание понятия упорядоченных дизъюнктов с линейной резолю-
резолюцией не нарушает ее полноты, но существенно увеличивает эффек-

50 Автоматическое доказательство теорем [Гл. 1
тивность метода. Другим усилением линейной резолюции является
использование информации о резольвированных литерах. Обычно при
выполнении резолюции образование резольвенты происходит путем
удаления резольвированных литер. Однако оказывается, что эти ли-
литеры несут полезную информацию, которая может быть использована
для усиления линейной резолюции.
Вернемся к примеру 1.24. Мы видим, что один из боковых дизъ-
дизъюнктов (дизъюнкт Q) не является входным дизъюнктом. Было бы
полезно найти необходимое и достаточное условие, при котором цен-
центральный дизъюнкт, полученный ранее, становится боковым. Это
условие может быть определено, если используется понятие упоря-
упорядоченных дизъюнктов и информация о резольвированных литерах
записывается соответствующим образом. Вывод, использующий оба
эти понятия, называется линейным упорядоченным выводом (OL-
выводом).
Таким образом, сначала образуем резольвенты для упорядоченных
дизъюнктов. Пусть С\ и С2 — упорядоченные дизъюнкты. Упоря-
Упорядоченная бинарная резольвента дизъюнктов С\ и С^ (не имеющих
общих переменных) определяется следующим образом. Пусть L\ и
L2 = ~*Li — литеры в Ci и С*2 соответственно. Если Li и L2 имеют
НОУ сг, и С есть упорядоченный дизъюнкт, полученный из конка-
конкатенации последовательностей С\о и С^о путем удаления L\o и L^o
и вычеркивания из оставшейся последовательности любой литеры,
которая идентична младшей литере последовательности, то С назы-
называется упорядоченной бинарной резольвентой.
Например, если С\ = P(x)VQ(x)V^R(x) иС2 = ^P(a)VQ(a) —упо-
—упорядоченные дизъюнкты, то конкатенация С\о и С^о', где а = {а/ж},
дает последовательность Р(а) V Q(a) V ->R(a) V ->Р(а) V Q(a). Удалив
Р{а) и -нР(а), а также старшую литеру Q(a), получим упорядоченную
бинарную резольвенту С = Q(a) V -iR(a). Теперь вместо удаления
обеих резольвированных литер будем оставлять в резольвенте первую
из них, но помечать ее особым образом. Будем записывать резольвиро-
ванные литеры в рамке и называть их обрамленными литерами. Если
за обрамленной литерой не следует никакая другая литера, то будем ее
вычеркивать. Таким образом, продолжая вышеуказанный пример, по-
получим следующую упорядоченную резольвенту: Р(а) \/Q(a)\/^R(a).
Возвращаясь к примеру 1.24, получим упорядоченный линейный
вывод, представленный на рис. 1.7. Рассмотрим на этом рисунке под-
подчеркнутую резольвенту. Отличительной чертой данной резольвенты
является то, что в нее входит литера -нР, являющаяся дополнением к
обрамленной литере | Р |. Это обстоятельство и является указанием на
необходимость использования центрального дизъюнкта Р в качестве
бокового. Резольвируя | Р |v Q V^P с Р, мы получим | Р |v Q V

1.5] Линейная резолюция 51
Так как за этими обрамленными литерами не следует никакой другой
литеры, то, вычеркивая их, получим пустой дизъюнкт П.
Упорядоченный дизъюнкт С будем
Р v Q ^ yO P v -.g называть редуцируемым упорядоченным
дизъюнктом тогда и только тогда, когда
последняя литера в С унифицируется с
отрицанием некоторой обрамленной ли-
литеры в С.
Таким образом, при получении ре-
редуцируемого упорядоченного дизъюнкта
нет необходимости искать, с каким из
полученных ранее дизъюнктов он обра-
образует линейную резолюцию. Вместо это-
этого можно просто вычеркнуть последнюю
литеру в этом упорядоченном дизъюнкте. Будем называть это вы-
вычеркивание операцией редукции. Операция редукции позволяет не за-
запоминать в OL-выводе промежуточные дизъюнкты. Эта особенность
OL-вывода делает его очень удобным при машинной реализации. Опе-
Операцию вычеркивания обрамленных литер, за которыми не следуют
никакие другие литеры, будем называть операцией сокращения.
Редуцируемый упорядоченный дизъюнкт образуется применением
операций редукции и сокращения. Упорядоченная бинарная резоль-
резольвента упорядоченных дизъюнктов С\ и С^ получается конкатенацией
последовательностей С\о и С^о~, где а есть НОУ для литер L\ и
L2 = —iZ/i в С\ и Съ соответственно, путем:
1) заключения в рамку L\g\
2) вычеркивания Ь^о~\
3) вычеркивания любой необрамленной литеры, которая идентич-
идентична младшей необрамленной литере последовательности;
4) применения операции сокращения.
Теперь формально определим OL-вывод. Пусть дано множество
упорядоченных дизъюнктов S и упорядоченный дизъюнкт С\ из S.
Линейный вывод дизъюнкта Сп из S с начальным дизъюнктом С\
называется OL-выводом, если выполнены следующие условия:
1) для г = 1,2,..., п — 1, Ci+i является упорядоченной резольвентой
дизъюнкта Ci (называемого центральным упорядоченным дизъ-
дизъюнктом) и дизъюнкта Bi (называемого боковым упорядоченным
дизъюнктом), при этом резольвированная литера в Q (или в
упорядоченном факторе С г) является последней литерой Q;
2) Bi является или некоторым дизъюнктом Cj, j < i (если Cj есть
редуцируемый упорядоченный дизъюнкт), или дизъюнктом из S
(во всех остальных случаях). Если Bi есть некоторый дизъюнкт
Cj (j < г), то Ci+i — редукция дизъюнкта Q;
3) в выводе нет тавтологий.

52 Автоматическое доказательство теорем [Гл. 1
Определение упорядоченного дизъюнкта может быть использова-
использовано для доказательства следующего утверждения. В OL-выводе, если
Ci есть редуцируемый упорядоченный дизъюнкт, то существует цен-
центральный упорядоченный дизъюнкт Cj (j < г), такой, что редукция
Ci+i дизъюнкта Ci является упорядоченной резольвентой Ci с неко-
некоторым частным случаем дизъюнкта Cj.
Следующая теорема устанавливает полноту OL-резолюции (Лав-
ленд, Ковальский, Кюнер).
Теорема 1.9. (о полноте OL-резолюции). Если С является
упорядоченным дизъюнктом в невыполнимом множестве упорядо-
упорядоченных дизъюнктов S и если #-{С} выполнимо, то существует OL-
опровержение из S с начальным упорядоченным дизъюнктом С.
Рассмотрим пример реализации OL-резолюции.
Пример 1.25.
Преподаватели принимали зачеты у всех студентов, не являющих-
являющихся отличниками. Некоторые аспиранты и студенты сдавали зачеты
только аспирантам. Ни один из аспирантов не был отличником. Сле-
Следовательно, некоторые преподаватели были аспирантами.
Пусть С(х), О(х), Р(х), А{х) и S(x,y) означают «х есть студент»,
«х есть отличник», «х есть преподаватель», «х есть аспирант» и «ж
сдает зачеты у». Тогда на языке исчисления предикатов имеем
Ух(С(х) & -,О{х) -+ Зу(Р(у) & S(x, у)))
Зх(А(х) & С[х) &
Зх(Р(х) & А(х))
или в стандартной форме:
3. С(а);
4. А(а)-
6. -.О(ж) V -.А(ж);
7. -пР(ж) V--A(x).
Дерево OL-вывода пустого дизъюнкта изображено на рис. 1.8.
Отметим, что OL-вывод успешно конкурирует со многими резо-
люционными методами вывода за счет простоты организации поиска.
Эта простота объясняется тем, что не нужно запоминать промежу-
промежуточные дизъюнкты, а также тем, что здесь всегда определен один из
резольвируемых дизъюнктов.

1.5]
Линейная резолюция
53
OL-вывод — это по существу то же самое, что и метод элими-
элиминации моделей, как назвал его Лавленд, или специальный SL-вывод
по определению Ковальского и Кюнера, т. е. разновидность линейной
О(х) v
,О А(а)
/) -,C(jc) v O(x) v 5(jc, j
di v -iC(fl) v \S(a,fja)i v A(f(a))
v -,Qa) v fe Д «)) v U(f «)) v Ша) v O(«) СГ Л
Рис. 1.8
резолюции с функцией выбора (selection function). Возвращаясь к
примеру 1.24, мы обнаружили, что невозможно построить линейный
вывод пустого дизъюнкта, если в качестве боковых дизъюнктов брать
только дизъюнкты из исходного множества S (центральный дизъюнкт
Q стал боковым). Назовем дизъюнкты из исходного множества S
входными дизъюнктами. Тогда резолюция, у которой хотя бы один из
двух дизъюнктов при резольвировании является входным, называется
входной резолюцией. Входная резолюция проста, эффективна, но в
общем случае, к сожалению, как было видно из примера 1.24, неполна.
Однако она полна для множества так называемых хорновских дизъ-
дизъюнктов.
Дизъюнкт называется хорновским, если он содержит не больше
чем одну положительную литеру. Он имеет в общем случае
вид: -iPi V ^Р2 V ... V ^Рп V Q или в импликативной форме:
Pi & Р2 & ... & Рп -> Q.
Возвращаясь к примеру 1.10, в котором детектив должен доказать,
что, если горничная сказала правду, то дворецкий солгал, мы видели,
что дерево вывода (см. рис. 1.2) линейно, и вывод пустого дизъюнкта
был получен с помощью входной резолюции. В этом примере все
дизъюнкты из S были хорновскими в отличие от примера 1.24, где
дизъюнкт Р У Q — нехорновский.

54 Автоматическое доказательство теорем [Гл. 1
1.6. Вывод в языке Пролог
1.6.1. SLD-резолюция
В языке Пролог используется упорядоченная входная резолюция,
т. е. литеры резольвируются в фиксированном порядке строго слева
направо. Иногда систему вывода в языке Пролог называют SLD-
резолюцией, т. е. SL-резолюцией для дефинициальных (definite) дизъ-
дизъюнктов, где под дефинициальным дизъюнктом понимают хорновский
дизъюнкт.
Логической программой является множество универсально
квантифицированных выражений в логике предикатов вида
Q <— Pi & Р2 & ... & Рп. Здесь применяется обратная имплика-
тивная запись выражения. Q и Д (i = 1?^) являются позитивными
литерами, причем Q — заголовок (голова) дизъюнкта, а конъюнкция
Pi — тело.
Очевидно, что множество выражений является множеством хор-
новских дизъюнктов, которые могут быть трех видов:
1) <— Pi & Р2 & ... & Рп — множество целей, которые надо
доказать;
Qi <—
2) > — факты;
<2m <- J
3) Q <- Pi & Р2 & ... & Рп — правило.
Литералы в целевом утверждении <— Pi,...,Pn (n > 0) интер-
интерпретируются как задачи или цели, которые должны быть решены
или достигнуты. Если целевое утверждение содержит переменные
Xi,..., Х&, то можно считать, что оно задает следующую цель:
• найти такие Х\,..., Х\~, при которых достигаются цели
Pi,...,Pn (n > 0); или
• найти такие Xi,..., Х&, которые решают задачи Pi,..., Рп
(п > 0).
Процедура Q <— Pi,..., Рп интерпретируется как метод поиска
решения задачи или достижения цели:
• для того, чтобы решить задачу Q, надо решить подзадачи
Рь .. .,РП; или
• для того, чтобы достигнуть цель Q, надо достигнуть подцели
рь...,р„.
Если имеется множество целей вида <— Pi & Р2 & ... & Рп, то
на каждом шаге вычисления интерпретатор произвольно выбирает

1.6] Вывод в языке Пролог 55
некоторое Pi для 1 ^ г ^ п. Затем он недетерминированно выбирает
дизъюнкт Р1 <— Ri & R2 & ... & Rm, такой, что Р1 унифицируется
с Pi подстановкой в и таким образом сокращает множество целей.
Новый дизъюнкт имеет вид
(Pi &Р2& ... &Д-1 &
Процесс недетерминированного сокращения цели продолжается до
получения пустого множества целей.
Этот процесс можно представить с помощью ИЛИ-дерева (дерева
поиска), вершины которого составляют целевые утверждения. Потом-
Потомки вершины — альтернативные целевые утверждения, выводимые из
целевого утверждения данной вершины. Концевые вершины дерева
соответствуют неразрешимым либо пустым целевым утверждениям,
которые представляют решения. Композиция подстановок, использу-
используемых на пути от корневой вершины к пустой, примененная к перемен-
переменным исходного целевого утверждения, дает требуемый результат.
Рассмотрим пример. Для простоты и ясности изложения пример
рассматривается без учета подстановок. Пусть имеется набор проце-
процедур (или хорновских дизъюнктов):
• А\ <— -Oi, JD2 О. JD2 <—
. Л\ <— Oi, O2 D. Oi <—
3. А2 <- Вх 7. С2 <-
4. В\ <- 8. Di <-
и исходное целевое утверждение (Go) <— Ai,A2. Поддеревья дерева
поиска приведены на рис. 1.9, на котором введены следующие обозна-
обозначения:
G3:^Ai,Di Glb:^C2\D1
Ltq'. <— JD\ , _l>2
G7: ^— C2j A2
G8: <— Gi, A2
t9
Gq: ^C1,C2,D1 G2°-
/^i , a ^1' — ^2
Gn: ^ A2 G22-^C1
G\2'. <— B2,D\ G23: ? (пустой дизъюнкт)
На рис. 1.9 деревья Gi, G2 и G3 определяют поддеревья дерева
поиска, соответствующего исходному целевому утверждению Gq.

56
Автоматическое доказательство теорем
[Гл. 1
&и Gu Gu G13 Gu G13 G14
П8М18 419 418418 420
^23^23^23 ^23
Л Л Л
418 419 418 420 М19 Ч0
GriGi* Gy\ G
^23 ^23^23 ^23
I" fi I" fi fi fi fi
^lS^lS ftl^iefte fe^lS ?21 ^18 <?22^23 <^2
uia G"oa Cjo'iG'ia G"91 C-Foa G'o'i G"9'
^12 ^13 ^14 <|15 ^16 Oil Gu (fll
I I I I I I I I I I I I I I I I
"~~1 f^ f4* f*i ^°i f~4 z1*™^ f~^ Z1*™^ ^""^ f** f^ ?^ f^ ?^
19 418 420 419 420 418 421 418 422 ^23 ^23419 420^23 b7
G23 G23 G23 G23 G23 G23
Рис. 1.9
Процесс недетерминированного сокращения цели также молено
представить в виде И-дерева (дерева доказательства). Непосредствен-
Непосредственными потомками корня дерева являются литералы («вызовы») или
подцели Pi (г = 1,п) исходного целевого утверждения <— Pi,...,Pn
(п ^ 0). Подцель Pi (г = 1,п), к которой применяется процедура
Pi ^— В\,..., Вш, получает в качестве потомков подцели В\,..., Вш.
Унификатор U далее применяется к каждой из вершин дерева.
На рис. 1.10 представлена последовательность деревьев доказа-
доказательств (без учета подстановок), соответствующая ветви дерева по-
поиска на рис. 1.9, которая задана вершинами Go, Gi, Gq, G12, Gis, G23.
Недетерминизм может быть устранен за счет наложения порядка
выбора целей. В любом случае все результаты, найденные недетер-
недетерминированно, могут быть обнаружены с помощью исчерпывающего
упорядоченного поиска. Таким образом, основная цель практическо-

1.6]
Вывод в языке Пролог
57
А А
G0:<-AhA2
н
ъВъА2
А. А.
Г Т1
G.:<
г1
л г
Di
U U
Рис. 1.10
г1
В2 D-
U П П
го языка логического программирования заключается в обеспечении
программиста средствами управления и, если возможно, сокращения
ненужных ветвей в дереве пространства поиска.
Абстрактная спецификация логических программ имеет ясную
семантику, заключающуюся в резолюционной системе опровержения.
Ван Эмден и Ковальский показали, что наименьшей интерпретацией,
на которой логическая программа истинна, является интерпретация
самой программы. Цена, заплаченная практическими языками логи-
логического программирования (такими, как язык Пролог) за управление
в поисковом пространстве, заключается в том, что программы могут
вычислять только подмножество своих ассоциированных интерпрета-
интерпретаций.
Последовательный язык Пролог является аппроксимацией интер-
интерпретатора для модели логического программирования, предназначен-
предназначенной для эффективного выполнения на обычной ЭВМ. Язык Пролог
использует как упорядочение целей в дизъюнкте, так и упорядочение
дизъюнктов в программе при управлении поиском подцелей строго
слева направо в множестве целей.
Таким образом, если дано множество целей <— Pi & Р2 & ... & Рп
и программа 'Р, интерпретатор языка Пролог последовательно ищет
первый дизъюнкт в 'Р, чей заголовок унифицируется с Р\. Если
этот дизъюнкт имеет вид Р1 <— R\ & R2 & ... & Rm с унифи-

58 Автоматическое доказательство теорем [Гл. 1
катором в, целевой дизъюнкт теперь приобретет следующий вид:
(Дх & R2 & ... & Rm & Pi & Р2 & ... & Рп)в.
Затем интерпретатор пытается сократить самую левую цель Ri,
используя в программе V первый дизъюнкт, который унифицируется
с R]_. Пусть он имеет вид R1 <— L\ & L2 & ... felfc с унификатором
сг. Тогда цель становится
(Li & L2 & ... & Lfe & Д2 & ... kRmk
P2hPzh ... &PnNocr.
Заметим, что список целей обрабатывается как стек, осуществляя
поиск в глубину. Если интерпретатор при унификации терпит неудачу,
то происходит возврат (бектрекинг) в самую последнюю точку выбора
унификации, восстанавливаются все связи (bindings), сделанные в
этой точке выбора, и выбирается следующий дизъюнкт в 'Р, который
будет унифицироваться с самой левой целью. Таким образом, язык
Пролог осуществляет поиск в пространстве дизъюнктов слева направо
и в глубину.
Напомним, что если множество целей сводится к пустому дизъ-
дизъюнкту П, то композиция унификаций в о а о ... о г\ обеспечивает ин-
интерпретацию, при которой исходное множество целей было истинным.
1.6.2. Стратегии поиска в языке Пролог
Отметим, что для приведенного примера, состоящего из восьми
хорновских дизъюнктов, дерево поиска имеет достаточно большую
размерность. Отсюда возникает задача: как найти все альтернативные
решения, представляющие композиции подстановок, используемых на
пути от корневой вершины к пустой; или, иначе говоря, как найти все
пути, идущие от корневой вершины к пустым.
В качестве таких стратегий поиска выбраны поиск только «в глу-
глубину» (depth-first search), основополагающий в языке Пролог, поиск
только «в ширину» (breadth-first search) и поиск только «наилучшего»
(best-first search).
Рассмотрим метод поиска только «в глубину» на примере набора
процедур (или хорновских дизъюнктов), описанных в предыдущем
примере.
На рис. 1.11 и рис. 1.12 приведены поддеревья дерева доказатель-
доказательства, которые соответствуют представлению поиска методом «в глу-
глубину». Целевым утверждением является Go :<— А\, А2. Стратегия вы-
вычисления выбирает самую левую подцель А\ в Go. Стратегия поиска
выводит из Go целевое утверждение G\ :<— В\,В2,А2. Ищут первую
подстановку для В\, затем для В2. Выбирают подцель А2, которая
решается полностью: находятся все альтернативные подстановки при
первых подстановках для В\ и В2. Далее при первой подстановке
для В\ осуществляют поиск второй подстановки для В2 и повторяют

1.6]
Вывод в языке Пролог
59
G0:<-Al9A2
Gi:<-BhB2,A2
G4: <- Въ А2
в
Ал А
л
и и
1, А2
Ах А,
и и
и п п
G23: <- П
Рис. 1.11
аналогичные действия с ^2- После того, как найдены все подстановки
для ?>2, ищут вторую подстановку для В\ и т. д. Этот процесс поиска
решений представлен на рис. 1.11, на котором закрашенной областью
(см. рис. 1.11 в) отмечены вершины, раскрытые в этом процессе. Невы-
Невыделенные вершины раскрываются в дальнейшем (см. рис. 1.11 г, д, е).
Когда найдены все подстановки для В\, осуществляется возврат (бек-
(бектрекинг) для нахождения нового целевого утверждения для Ai, и
повторяются действия, аналогичные рассмотренным выше. Этот про-
процесс поиска решений представлен на рис. 1.12.
Допустим, поиск осуществляется методом «в ширину». Непосред-
Непосредственными потомками корня дерева являются подцели А\ и А^
(см. рис. 1.10а). К подцели А\ применяется процедура 1, которая
получает в качестве потомков подцели Bi и В2 (см. рис. 1.106). Ана-
Аналогичные действия применяют к подцели А^ (см. рис. 1.10в), а затем

60
Автоматическое доказательство теорем
[Гл. 1
А л2
л2
А л2
Q с2
G2<-Ci,C2,A2
G7 <r- Съ А2
б
А2
С, С2
и и
и п п
г д
Рис. 1.12
к подцелям В\ тлВ^. На рис. l.lOe закрашенной областью обозначены
вершины, которые были раскрыты в процессе поиска решений.
Предшествующие деревья непосредственно восстанавливаются из
последнего дерева, если известен порядок, в котором выбираются
подцели. Вообще деревья доказательств, соответствующие последо-
последовательным целевым утверждениям, расположенным на одной ветви
дерева поиска, образуют последовательность, каждый член которой
получается из предшествующего путем подвешивания поддерева к
вершине, помеченной выбранным вызовом.
Заметим, что для ускорения процесса нахождения решений в
настоящее время существуют различные параллельные реализации
языка Пролог, основанные на AND-параллелизме (параллельное ре-
решение подцелей целевого утверждения Д (г = 1, п), что соответствует
параллельному построению вершин И-дерева) и OR-параллелизме
(параллельное выполнение процедур, определяющих подцель
Р^ [% = 1,п), что соответствует параллельному построению вершин
И Л И-дерева).

1.6] Вывод в языке Пролог 61
Кроме бектрекинга на порядок выполнения дизъюнктов в логиче-
логической программе оказывает влияние специальное целевое утверждение
«!», называемое отсечением, которое используется для останова ме-
механизма бектрекинга. Доказательство цели-отсечения всегда закан-
заканчивается успешно, и после этого не могут быть пере доказаны цели,
стоящие в целевом утверждении до отсечения, включая головную
цель.
1.6.3. Предположение о замкнутости мира
Важным вопросом, касающимся интерпретатора языка Пролог,
является предположение о замкнутом мире. В этом предположении
считается, что имеет место полное знание о данной предметной об-
области, т. е. нет «брешей» в этом знании. В исчислении предикатов
доказательство —iP(x) предполагает, что Р(х) ложно при каждой
интерпретации. Интерпретатор языка Пролог на основе алгоритма
унификации предлагает более ограниченный вариант, чем нахожде-
нахождение опровержения методом резолюции. Вместо рассмотрения всех
интерпретаций, он исследует только те, которые явно присутствуют в
базе данных.
Пусть ai, a2,..., ап составляют область определения переменной ж,
являющейся термом предиката Р. Интерпретатор языка Пролог при
унификации использует:
1) аксиому об уникальности имен, т. е. для всех атомов а^ Ф dj^ если
только они не идентичны; это означает, что атомы с разными
именами различны;
2) аксиому замкнутого мира Р(х) —> Р(а\) V Р(аг) V ... V Р(ап)у
которая означает, что возможными примерами отношения явля-
являются только те факты, которые представлены в спецификации
проблемы (в базе данных (БД));
3) аксиому замыкания предметной области (х = а\)У(х = аг) V... V
V(x = an), которая гарантирует, что определены только те
атомы, которые встречаются в спецификации проблемы.
Эти три аксиомы в интерпретаторе языка Пролог выражены неяв-
неявно. Они могут рассматриваться как добавленные к множеству хорнов-
ских дизъюнктов, составляя описание проблемы и, таким образом,
ограничивая множество возможных интерпретаций на запрос.
Интуитивно это означает, что в языке Пролог предполагаются
ложными все цели, которые не могут быть доказанными как истин-
истинные. Это может привести к следующей ситуации: если истинностное
значение цели неизвестно в текущей БД, Пролог предполагает, что она
ложна. Это явление известно как отрицание при неудаче (negation as
failure).

62
Автоматическое доказательство теорем
[Гл. 1
1.6.4. Синтаксис и семантика языка Пролог
В настоящее время существуют многочисленные версии языка
Пролог, которые мало отличаются друг от друга. Для понимания
дальнейшего изложения материала приведем краткое описание одной
из версий языка Пролог, а именно языка C-Prolog, созданного Уоррен
и Перейра. Синтаксис языка C-Prolog близок к синтаксису исчисления
предикатов первого порядка. Однако существует ряд различий между
C-Prolog и исчислением предикатов. В C-Prolog, например, символ
«:-» заменяет символ импликации «<—» в исчислении предикатов.
Другие различия между этими языками приведены в табл. 1.1.
Таблица 1.1
Русский
и
или
только если
не
Исчисление
предикатов
&
V
Prolog
not
Предикатные имена, переменные и константы языка Пролог пред-
представляются последовательностью алфавитных символов, которые на-
начинаются с буквы. Переменная представляется строкой алфавитных
символов, начинающейся с заглавной буквы, а предикатные имена и
константы представляются строками, начинающимися со строчных
букв. Как видно из приведенной таблицы, логические связки исчис-
исчисления предикатов также присутствуют в синтаксисе языка Пролог.
Программа на языке Пролог представляет собой набор специфи-
спецификаций, заданных в исчислении предикатов и описывающих объекты и
отношения проблемной области. На набор спецификаций, описываю-
описывающих факты проблемной области (истинные утверждения), ссылаются
как на БД. Заметим, что выражения языка Пролог, используемые в
БД, являются примерами фактов. В Прологе определяются и прави-
правила, описывающие отношения между фактами, используя логическую
импликацию (:-), разделяющую правило на две части: левую и пра-
правую. Напомним, что правила в языке Пролог являются хорновскими
дизъюнктами. Таким образом, левая часть правила состоит из одного
предиката, который представляет одну положительную литеру в хор-
новском дизъюнкте. Правая часть правила состоит из любого числа
предикатов, разделенных «,» ( & ) и/или «;» (V). Далее в качестве
примера зададим следующее утверждение: «X и Y являются друзья-
друзьями, если X любит Z и Y любит Z» в виде правила языка Пролог:
friends(X,Y):-likes(X,Z),likes(Y,Z).

1.6] Вывод в языке Пролог 63
Пролог обычно реализован как интерпретатор, хотя существуют
версии языка Пролог, которые позволяют осуществлять компиляцию
части или всех спецификаций БД для более быстрого поиска.
Пользователь вводит запрос как ответ на подсказку языка Про-
Пролог: ?-. Далее активизируется, описанный в предыдущих пунктах,
механизм поиска в «глубину» с возвратом для получения ответа на
запрос.
Вышеописанных сведений о синтаксисе языка Пролог по нашему
мнению вполне достаточно для того, чтобы понять приведенные ниже
реализации методов поиска «в глубину», «в ширину» и «наилучшего»,
а также рассмотренные в следующих пунктах реализации на этом
языке моделей представления знаний и механизмов вывода в них,
выполненные Люгером и Стабблфилдом из монографии, опублико-
опубликованной в 1998 г. (см. литературный комментарий). Ознакомление с
этим материалом значительно углубит Ваши знания о языке Пролог
и его возможностях.
Опишем реализации методов поиска «в глубину», «в ширину»
и «наилучшего» на языке Пролог. Рассмотрим эти методы поиска
применительно к задаче поиска в пространстве состояний целевого со-
состояния — решения задачи. В реализациях этих методов используется
переменная Closed_set, которая содержит все состояния на текущем
пути плюс состояния, которые были отвергнуты при использовании
«бектрекинга» (возврата). Так, в переменной Closed_set содержится
путь от начального состояния к текущему. Для хранения информации
об этом пути создается упорядоченная пара [State,Parent], кото-
которая задает для каждого состояния его родителя. Для начального
состояния Start эта пара имеет вид: [Start,nil], которая определяет
отсутствие родителя у начального состояния. Таким образом, эти
пары используются для перегенерации решающего пути, хранимого в
переменной Closed_set .В реализациях методов поиска используется
предикат path, который имеет три аргумента (терма): Open_stack и
Closed_set, являющиеся списками, а также аргумент Goal, исполь-
используемый для задания целевого состояния.
Рассмотрим реализацию на языке Пролог метода поиска «в глуби-
глубину». В этой реализации текущее состояние State является следующим
состоянием для раскрытия и заносится в список, задаваемый перемен-
переменной Open_Stack. Поиск начинается посредством вызова предиката go,
который в свою очередь инициирует вызов предиката path. Заметим,
что при этом начальное состояние Start не имеет родителя и списки,
задаваемые переменными Open_stack и Closed_set являются пусты-
пустыми. Приведем описание дизъюнкта go, при задании которого исполь-
используются обычные предикаты для работы со стеком. Отметим, что во
всех нижепредставленных реализациях эти предикаты не приводятся
для того, чтобы не загромождать описание реализаций методов на
языке Пролог.

64 Автоматическое доказательство теорем [Гл. 1
go(Start, Goal) :-
empty_stack(Empty_open),
stack([Start,nil],Empty _open, Open_stack),
empty_set(Closed_set),
path(Open_stack, Closed_set, Goal).
Приведем описание дизъюнкта path.
path(Open_stack,_,_) :- empty_stack(Open_stack),
write('No solution found with these rules').
path(Open_stack, Closed_set, Goal) :-
stack([State, Parent], _, Open_stack), State = Goal,
write('A Solution is Found!'), nl,
printsolution([State, Parent], Closed_set).
path(Open_stack, Closed_set, Goal) :-
stack([State, Parent], Rest_open_stack, Open_stack),
get_children(State,Rest_open_stack,Closed_set,Children),
add_list_to_stack(Children, Rest_open_stack,
New_open_stack), union([[State, Parent]], Closed_set,
New_closed_set), path(New_open_stack, New_closed_set,
Goal),!.
get_children(State,Rest_open_stack,Closed_set,Children):-
bagof(Child, moves(State, Rest_open_stack, Closed_set,
Child), Children).
moves(State, Rest_open_stack, Closed_set, [Next, State]) :-
move(State, Next),
not(unsafe(Next)),
not(member_stack( [Next,_],Rest_open_stack)),
not(member_set( [Next,_], Closed_set)).
Дизъюнкт move (Present_state,Next_state) :-. . . описывает спе-
специфику задачи и для каждой задачи задает ее уникальное описание.
Одно из описаний дизъюнкта move приведено для решения задачи —
головоломки «Переправа через реку» в п. 1.6.5.1.2.
Предикат print solution используется для распечатки решения
от начального состояния к целевому. Ниже приведем его описание:
printsolution( [State, nil], _) :-
write(State), nl.

1.6] Вывод в языке Пролог 65
printsolution( [State, Parent], Closed_set) :-
member_set([Parent, Grandparent], Closed_set),
printsolution( [Parent,Grandparent],Closed_set),
write(State), nl.
Рассмотрим реализацию метода поиска «в ширину». В ней ис-
используются те же переменные и дизъюнкты, что и при реализа-
реализации метода поиска «в глубину». Существенные отличия заключаются
в дизъюнктах path, в которых первым аргументом является пере-
переменная Open_queue, начальным значением которой является пустой
список. Процесс поиска заканчивается, когда «голова» переменной
Open_queue идентична целевому состоянию Goal. В список, задавае-
задаваемый переменной Open_queue, последовательно заносятся все потомки
текущей вершины для раскрытия. Приведем реализацию дизъюнктов
go, path и moves для этого метода.
go(Start, Goal) :-
empty_queue(Empty_open_queue) ,
enqueue([Start, nil], Empty_open_queue,Open_queue),
empty_set(Closed_set),
path(Open_queue, Closed_set, Goal).
path(Open_queue, _,_):-
empty_queue(Open_queue),
write('Graph searched, no solution found.').
path(Open_queue, Closed_set, Goal) :-
dequeue([State, Parent], Open_queue,_), State = Goal,
write('Solution path is:'), nl,
printsolution([State, Parent], Closed_set).
path(Open_queue, Closed_set, Goal) :-
dequeue([State, Parent],Open_queue,Rest_open_queue),
get_children(State,Rest_open_queue,Closed_set,Children),
add_list_to_queue(Children,Rest_open_queue,
New_open_queue),
union([[State,Parent]],Closed_set,New_closed_set),
path(New_open_queue, New_closed_set, Goal),!.
get_children(State,Rest_open_queue,Closed_set,Children):-
bagof(Child, moves(State, Rest_open_queue,
Closed.set, Child), Children).
moves(State, Rest_open_queue, Closed_set, [Next,State]) :-
move(State,Next),
3 B.H. Вагин и др.

66
Автоматическое доказательство теорем
[Гл. 1
not(unsafe(Next)),
not (member_queue ( [Next, _] , Rest_open_queue) ) ,
not(member_set( [Next,_],Closed_set)).
Одним из наиболее эффективных методов поиска является метод
поиска «наилучшего», который позволяет значительно сократить пе-
перебор в пространстве состояний. Поэтому опишем реализацию этого
метода на языке Пролог и покажем, за счет чего сокращается перебор
при поиске целевого состояния в пространстве состояний. Этот метод
относится к эвристическим.
Реализация метода поиска «наилучшего» является модификацией
метода поиска «в ширину», в которой очередь вершин заменяется
на приоритетную очередь вершин для раскрытия, упорядоченных
на основе оценочной функции. Отметим, что оценочная функция
предложена Н. Нильсоном и имеет вид: f(n) = g(n) + h(n), где в
качестве д(п) можно выбрать стоимость пути на дереве поиска от
корневой (начальной) вершины к вершине п, которая получается в
результате суммирования стоимостей дуг, вычисленных на пути от
корневой вершины к вершине п. h(n) — эвристическая функция, опре-
определяемая спецификой проблемной области. Рассмотрим метод поиска
«наилучшего» на примере.
Пример 1.26.
Предположим, что литеры хорновских дизъюнктов, приведенных
в примере п. 1.6.1., соответствуют задачам, которые должны быть
решены для достижения исходно-
исходного целевого утверждения. Пусть
любой литере соответствует чис-
число, обозначающее стоимость реше-
решения данной задачи. Тогда задача
доказательства исходного целево-
целевого утверждения может быть пере-
переформулирована в задачу нахожде-
нахождения наилучшего по стоимости пу-
пути достижения исходного целево-
целевого утверждения. Для решения этой
задачи исходные хорновские дизъ-
дизъюнкты задаются при помощи графа «И/ИЛИ», вершинами которого
являются литеры хорновских дизъюнктов (рис. 1.13).
Далее зададим оценочную функцию /(п) = д{п) + /i(n), в которой
h(n) — эвристическая функция: v(n) —> min, где v(n) — стоимость
решения задачи щ д(п) задает «глубину» размещения вершины п в
графе, т. е. количество вершин, которые находятся на пути от корне-
корневой вершины до вершины п.
Рис. 1.13

1.6] Вывод в языке Пролог 67
Пусть v{Ax) = 5, v{A2) = 3, v(Bi) = 2, v(B2) = 1, v(d) = 3,
v(C2) = 4, «(Di) = 6.
Наилучший по стоимости путь достижения цели Go, представлен-
представленный на рис. 1.13, для /(п) —> ram, строится следующим образом:
1)
2)
3)
4)
5)
6)
Go
G3
G'6
G12
G20
Gig
<-Ai,?>i
^DuBhB2
<- B2
<--Bi
Заметим, что цель Gf6 отличается от цели Gq перестановкой литер.
Далее рассмотрим реализацию метода поиска «наилучшего» на
языке Пролог. В реализации метода д(п) задает глубину вершины при
раскрытии, т. е. определяется числом вершин, находящихся на пути от
корневой вершины к вершине п. Упорядочивание вершин производит-
производится каждый раз вновь после вызова предиката path. Таким образом,
вычисление оценочной функции осуществляется для каждой верши-
вершины, добавляемой в список, который задается переменной Open_pq, и
ее значение используется для упорядочивания этого списка. В реали-
реализации данного метода для задания каждого состояния используется
список из пяти элементов, который содержит описатель состояния;
родительское состояние; целое число, задающее глубину раскрытия
в дереве; целое число, задающее значение эвристической функции;
сумму третьего и четвертого элементов списка. Первые два элемента
списка, задающего состояние, являются обычными. Третий элемент
является результатом добавления 1 к значению глубины родительской
вершины. Четвертый элемент определяется значением эвристической
функции, вычисленной для этой вершины. Пятый элемент списка
используется для упорядочивания состояний в списке, задаваемого
переменной open_pq.
Приведем реализацию метода поиска «наилучшего» на языке Про-
Пролог. Алгоритм выполняется, как и в предыдущих реализациях, по-
посредством вызова предиката go, в котором nil является родителем
вершины Start и Н — эвристическим значением начальной (корневой)
вершины Start.
go(Start, Goal) :-
empty_set(Closed_set),
empty_pq@pen),
heuristic(Start, Goal, H) ,
insert_pq([Start, nil, 0, H, H], Open, Open_pq),
path(Open_pq, Closed_set, Goal).
3*

68 Автоматическое доказательство теорем [Гл. 1
Далее приведем дизъюнкты, задающие предикат path:
path(Open_pq,_,):-
empty_pq(Open_pq),
write('Graph searched, no solution found.').
path(Open_pq, Closed_set, Goal):-
dequeue_pq([State, Parent,_,_,_], Open_pq,_),
State = Goal,
write('The solution path is:'), nl,
printsolution([State, Parent,_,_,_], Closed_set).
path(Open_pq, Closed_set, Goal) :-
dequeue_pq([State, Parent, D, H, S], Open_pq,
Rest_open_pq), get_children( [State, Parent, D, H, S] ,
Rest_open_pq, Closed_set, Children, Goal),
insert_list_pq(Children, Rest_open_pq, New_open_pq),
union( [[State, Parent, D, H, S]], Closed_set,
New_closed_set),
path(New_open_pq, New_closed_set, Goal),!.
get .children является предикатом, который создает всех детей вер-
вершины State. Приведем дизъюнкты для задания этого предиката:
get_children([State,_,D,_,_], Rest_open_pq, Closed_set,
Children, Goal):-
bagof(Child, moves([State,_,D,_,_], Rest_open_pq,
Closed.set, Child, Goal), Children).
moves([State,_,Depth,_,_], Rest_open_pq, Closed_set,
[Next, State, New_D, H, S], Goal):-
move(State, Next),
not(unsafe(Next)),
not(member_pq([Next,_,_,_,_] , Rest_open_pq)),
not(member_set( [Next,_,_,_,_], Glosed_set)),
New_D is Depth + 1,
heuristic(Next, Goal, H),
S is New_D + H.
В заключение отметим, что предикат print solution используется
для распечатки пути решения. Дизъюнкт, задающий этот предикат,
имеет вид
printsolution ([State, nil,_,_,_],_) :-
write(State), nl.

1.6] Вывод в языке Пролог 69
printsolution( [State, Parent,_,_,_], Closed_set) :-
member_set([Parent, Grandparent,_,_,_], Closed_set),
printsolution([Parent, Grandparent,_,_,_], Closed_set),
write(State), nl.
1.6.5. Реализация на языке Пролог моделей представления
знаний и механизмов вывода на них
1.6.5.1. Реализация продукционного вывода
1.6.5.1.1. Реализация алгоритмов планирования. Одной из важ-
важных компонент в современных интеллектуальных системах, в частно-
частности в системах поддержки принятия решений, является подсистема
планирования. В настоящее время разработаны различные методы
планирования, основанные на исчислении предикатов и реализован-
реализованные с использованием языка Пролог. Рассмотрим реализацию алго-
алгоритмов планирования действий робота на языке Пролог, на которой
продемонстрируем основные моменты решения задач данного класса.
Для решения задачи планирования обычно выделяются два типа
состояний: начальное состояние и конечное состояние, описываемые
предикатами. Для нашего примера начальным состоянием является
следующее расположение кубиков и мапипулятора (hand): кубики
«В» и «С» находятся на столе, кубик «А» стоит на кубике «В»,
манипулятор расположен над кубиком «С». Конечным состоянием
является следующее расположение кубиков: кубики «А» и «В» на-
находятся на столе, а кубик «С» стоит на кубике «В». Начальное и
конечное состояния описываются следующими списками предикатов:
start = [hand_empty, on_table(b), on_table(c), on(a, b),
clear(c), clear(a)];
goal = [hand_empty, on_table(a), on_table(b), on(c, b),
clear(a), clear(c)].
Далее строится пространство состояний, начальные уровни кото-
которого представлены на рис. 1.14. Затем задается предикат, описываю-
описывающий перестановку кубиков. Этот предикат имеет имя «move», и он
задает четыре возможности для перестановки кубиков, описанные с
использованием предикатов «add» и «del», которые используются для
добавления и удаления из списка заданных элементов:
move(pickup(X), [hand_empty, clear(X), on(X,Y)],
[del(hand_empty), del(clear(X)), del(on(X,Y)),
add(clear(Y)), add(holding(X))]).
move(pickup(X), [hand_empty, clear(X), on_table(X)],
[del(hand_empty), del(clear(X)), del(on_table(X)),

70
Автоматическое доказательство теорем
[Гл. 1
М - манипулятор
Рис. 1.14
add(holding(X))]).
move(putdown(X), [holding(X)], [del(holding(X)),
add(on_table(X)),add(clear(X)), add(hand.empty)]).
move(stack(X,Y), [holding(X), clear(Y)], [del(holding(X)),
del(clear(Y)), add(hand.empty), add(on(X,Y)),
add(clear(X))]).
Предикат move имеет три аргумента. Первый из них обозначает
имя действия, которое выполняется со своими аргументами. Второй
аргумент представляет список предусловий: предикаты, которые дол-
должны быть истинны в описании состояния мира, к которому приме-
применяется правило перестановки кубиков, заданное предикатом move.
Третьим аргументом является список добавляемых и удаляемых пре-
предикатов, т. е. предикатов, которые добавляются к состоянию мира
или удаляются из него для того, чтобы создать новое состояние как
результат применения данного правила.
Опишем действия, выполняемые рекурсивным генератором плана
или планировщиком.
1. Поиск предиката move.
2. Проверка для предиката move предусловий.
3. Предикат change.state создает новое состояние (Child.state),
используя списки предикатов для добавления и удаления.
4. Предикат member.stack проверяет, не встречалось ли получен-
полученное состояние ранее.
5. Оператор stack заносит новое состояние (Child.state) в
New.moves.stack.

1.6] Вывод в языке Пролог 71
6. Оператор stack заносит новое имя состояния (name) в
New_been_stack.
7. Рекурсивно вызывается предикат plan для поиска следующего
состояния, при этом используется Child_state и обновленные
New_moves_stack и New_been_stack.
Процедурой поиска является метод поиска «в глубину» с возвра-
возвратом, реализованный в языке Пролог и заканчивающийся при нахо-
нахождении целевого состояния.
Приведем программу реализации планировщика.
plan(State, Goal, _, Move_stack) :- equal_set(State, Goal),
write("moves are"), nl,
reverse_print_stack(Move_stack).
plan(State, Goal, Been_stack, Move_stack) :- move(Name,
Preconditions, Actions), conditions_met(Preconditions,
State),
change_state(State, Actions, Child_state),
not(member_stack(Child_state, Been_stack)),
stack(Name, Been_stack, New_been_stack),
stack(Child_state, Move_stack, New_move_stack),
plan(Child_state, Goal, New_been_stack,
New_move_stack),!.
plan(_, _, _) :- write("No plan possible with
these moves!").
conditions_met(P, S) :- subset(P, S).
change_state(S, [] , S).
change_state(S, [add(P) I T], S_new) :-
change_state(S, T, S2),
add_if_not_in_set(P, S2, S_new),!.
change_state(S, [del(P) I T], S_new) :-
change_state(S, T, S2),
delete_if_in_set(P, S2, S_new),!.
reverse_print_stack(S) :- empty_stack(S).
reverse_print_stack(S) :- stack(E, Rest, S),
reverse_print_stack(Rest), write(E), nl.
Зададим предикат go для инициализации аргументов предиката
plan, также опишем предикат test для задания тестов, содержащих
начальное и целевое состояния.
go(Start, Goal) :- empty_stack(Move_stack),
empty_stack(Been_stack), stack(Start, Been_stack,
New_been_stack),
plan(Start, Goal, New_been_stack, Move_stack).

72 Автоматическое доказательство теорем [Гл. 1
test :- go([hand_empty, on_table(b), on_table(c), on(a, b),
clear(c), clear(a)],
[hand_empty, on_table(a), on_table(b), on(c, b), clear(a),
clear(c)]).
Результатом работы программы планировщика является список
действий на экране монитора, которые необходимо выполнить для
достижения заданного целевого состояния из заданного начального
состояния.
1.6.5.1.2. Применение языка Пролог для решения головоломок.
Рассмотрим еще одну реализацию продукционной модели в языке
Пролог на примере решения одной из наиболее популярных головоло-
головоломок — о волке, козе и капусте. Приведем описание старинной задачи:
«Найти последовательность, которую должен выполнить человек для
перевоза в лодке через реку волка, козы и капусты. При этом в лодке
может поместиться только один человек, а с ним или волк, или коза,
или капуста. Но если оставить волка с козой без человека, то волк
съест козу, если оставить козу с капустой, то коза съест капусту, а
в присутствии человека никто никого не съест». Решением задачи
является такая последовательность пересечений реки, при которой
указанные условия должны быть выполнены. Для решений задачи
строится граф возможных состояний, на котором ищут пути (после-
(последовательности состояний), удовлетворяющие условиям задачи. Граф
состояний строится на основе следующих рассуждений: лодка может
быть использована в четырех случаях, а именно, для перевоза чело-
человека и волка, человека и козы, человека и капусты и только человека.
Состоянием мира является некая комбинация характеристик на двух
берегах. Некоторые состояния представлены на рис. 1.15.
Состояние мира описывается предикатом state(F,W,G,C), термы
которого задают местоположение человека (F), волка (W), козы (Ои
капусты (С) .Предположим, что река протекает с севера на юг, и для
обозначения берегов используем е (восточный берег) и w (западный
берег). Начальное состояние задается предикатом state(w,w,w,w),
описывающим, что все (человек, волк, коза и капуста) находятся на
западном берегу.
Следует отметить, что выбор подходящего представления для ре-
решений задачи является одной из наиболее важных проблем, которая
должна быть разрешена. Для выбранного представления различные
состояния мира создаются за счет различных пересечений реки, ко-
которые задаются при помощи изменения значений термов предика-
предиката state. Другие представления данной задачи, конечно, тоже воз-
возможны.
Рассмотрим граф состояний для решения задачи переправы. В
начале мы игнорируем тот факт, что некоторые состояния являются
бесполезными. На рис. 1.16 представлена часть графа, на котором

1.6]
Вывод в языке Пролог
73
state(w,w,w,w) FWGC
state(e,w,efw) WC
state(w,w,e,w) FWC
state(e,w,e, e) W
state(w,w,w,e) FWG
state(e,e,wfe) G
state(w,e,w,e) FG
W
FG
FCG
С
FWC
WC
FWGC
Рис. 1.15
ищется путь решения задачи. Предикат path вызывается рекурсивно
для поиска решения задачи.
state(w, w, w,w)
state(e,e,w,w) state(e,w,e,w) state(e,w,w,e) state(e,w,w,w)
state(w,e#w,w) state(wfwrerw) state(w,w,w,e)
state(e,e,e,w) state(e,e,w,e) state(e,w,e,e)
Рис. 1.16
Продукционные правила или хорновские дизъюнкты использу-
используются для задания изменения состояний в процессе поиска решения

74 Автоматическое доказательство теорем [Гл. 1
задачи. Зададим эти правила в виде правил в языке Пролог, ле-
левая часть которых описывается предикатом move. Далее на них бу-
будем ссылаться как на правила «move». Первое правило определим
для человека, переправляющего волка. Это правило должно при-
применяться для переправы человека и волка как с восточного берега
на западный, так и с западного берега на восточный, и не должно
применяться, когда человек и волк находятся на различных бере-
берегах реки. Таким образом, данное правило должно преобразовывать
состояние state(e,e,G,C) в состояние state(w,w,G,C) и состояние
state(w,w,G,C) в состояние state(e,e,G,C),H не должно применять-
применяться к состояниям state(e,w,G,C) и state(w,e,G,C). Переменные G и
С представляют в действительности тот факт, что они могут быть
связаны с любой из констант w или е. Заметим, что производятся
некоторые состояния, которые на самом деле являются бесполезными.
Правило move срабатывает только тогда, когда человек и волк
находятся на одном из берегов реки. После срабатывания правила они
находятся на противоположном берегу реки. При этом коза и капуста
не изменяют своего местоположения:
move(state(X, X, G, С), state(Y, Y, G, С)):- орр(Х, Y) .
орр(е, w).
opp(w, e).
Таким образом, правило срабатывает, когда в состоянии, представ-
представленном первым параметром предиката move, человек и волк находятся
в одном месте. Когда правило сработало, возникает новое состояние,
задаваемое вторым параметром предиката move, и в нем человек и
волк находятся на противоположных берегах (значение X противо-
противоположно значению Y). Для возникновения нового состояния должны
быть выполнены два условия:
• значения первых двух параметров предиката state должны
быть одинаковые;
• в новом состоянии эти значения изменяются на противополож-
противоположные старому.
Первое условие в процессе унификации проверяется неявно. Если
необходимо, то проверка первого условия может быть сделана явно, с
использованием следующего правила:
move(state(F, W, G, С), state(Z, Z, G, С)):- F = W,
opp(F, Z) .
Данное правило является эквивалентным предыдущему. Заметим,
что Пролог может делать «назначения» посредством связывания зна-
значений переменных при унификации.

1.6] Вывод в языке Пролог 75
Первая версия правила move является более эффективным пред-
представлением с точки зрения времени вывода, поскольку при унифика-
унификации не рассматриваются хорновские дизъюнкты, если их первые два
параметра не являются одинаковыми.
Рассмотрим предикат, тестирующий каждое новое состояние на
полезность, т. е. на то, чтобы «никто никого не съел в процессе
переправы». Заметим, что унификация играет важную роль в этой
проверке. Любое состояние, в котором второй и третий параметр оди-
одинаковы и отличны от первого параметра, является бесполезным, по-
поскольку волк съедает козу. Соответственно, если третий и четвертый
параметры одинаковы и отличны от первого параметра, то состояние
также является бесполезным, поскольку коза съедает капусту. Таким
образом, бесполезные (unsafe) ситуации могут быть представлены
следующими правилами:
unsafe(state(X, Y, Y, С)):- opp(X, Y).
unsafe(state(X, W, Y, Y)):- opp(X, Y).
Отрицание может быть добавлено к предыдущему правилу:
move(state(X, X, G, С), state(Y, Y, G, С)) :- орр(Х, Y) ,
not(unsafe(state(Y, Y, G, C))).
Подобным образом создаются продукционные правила для чело-
человека, перевозящего козу и капусту на другой берег. Отметим, что
команда writelist в каждом продукционном правиле печатает трас-
трассу текущего правила. Команда reverse_print_stack применяется в
заключительном состоянии пути для того, чтобы распечатать путь
найденного решения.
Приведем текст программы на языке Пролог для решения по-
поставленной задачи. Описание в языке Пролог предикатов unsafe,
writelist, reverse_print_stack, member_stack, stack не дается,
чтобы не загромождать описание реализации продукционной модели.
move(state(X, X, G, С), state(Y, Y, G, С)) :- орр(Х, Y) ,
not(unsafe(state(Y,Y,G,C))), writelist(["try
farmer takes wolf", Y, Y, G, C]).
move(state(X, W, X, C), state(Y, W, Y, C)) :- opp(X, Y),
not(unsafe(state(Y, W, Y, C))),
writelist(["try farmer takes goat", Y, W, Y, C]).
move(state(X, W, G, X), state(Y, W, G, Y)) :- opp(X, Y),
not(unsafe(state(Y, W, G, Y))),
writelist["try farmer takes cabbage", Y,W,G,Y]).
move(state(X, W, G, C), state(Y, W, G, C)) :- opp(X,Y),

76 Автоматическое доказательство теорем [Гл. 1
not(unsafe(state(Y, W, G, C))), writelist(["try
farmer takes self", Y, W, G, C]).
move(state(F, W, G, C), state(F, W, G, C)) :-
writelist("Backtrack from:", F, W, G, C]), fail.
path(Goal, Goal, Been_stack) :-
write("Solution Path Is:"),
nl, reverse_print_stack(Been_stack).
path(State, Goal, Been_stack) :- move(State,Next_state),
not(member_stack(Next_state, Been_stack)),
stack(Next_state, Been_stack, New_been_stack),
path(Next_state, Goal, New_been_stack), !.
opp(e, w).
opp(w, e).
Приведенная программа на языке Пролог вызывается посредством
предиката go, который инициализирует рекурсивный вызов предиката
path. Для того, чтобы легче запустить программу на выполнение,
определяется предикат test, в котором задаются начальные и конеч-
конечные состояния:
go(Start, Goal) :- empty_stack(Empty_been_stack),
stack(Start, Empty_been_stack, Been_stack),
path(Start, Goal, Been_stack).
test:- go(state(w, w, w, w), state(e, e, e, e)).
Приведем трассировку выполнения программы.
?- test.
try farmer takes goat -e w e w
try farmer takes self -w w e w
try farmer takes wolf -e e e w
try farmer takes goat -w e w w
try farmer takes cabbage -e e w e
try farmer takes wolf -w w w e
try farmer takes goat -e w e e
BACKTRACK from e w e e
BACKTRACK from w w w e
try farmer takes self -w e w e
try farmer takes goat -e e e e
Solution Path Is:
state(w, w, w, w)
state(e, w, e, w)
state(w, w, e, w)
state(e, e, e, w)

1.6]
Вывод в языке Пролог
77
state(w, e, w, w)
state(e, e, w, e)
state(w, e, w, e)
state(e, e, e, e)
В заключение заметим, что порядок срабатывания правил для
генерации новых состояний из каждого состояния является детерми-
детерминированным и определяется порядком, в котором эти правила разме-
размещены в продукционной модели.
1.6.5.2. Реализация вывода па семантических сетях. Од-
Одним из достоинств сетевого представления знаний является исполь-
использование в нем механизма наследования свойств. Рассмотрим реали-
реализацию на языке Пролог этого механизма в простейшей семантиче-
семантической сети, описывающей фрагмент иерархии воздушных лайнеров.
В семантической сети, изображенной на рис. 1.17, вершинам соответ-
соответствуют такие объекты, как ТУ154, АН76, и такие классы объектов,
как воздушный лайнер, самолет, самолет с технологией «stealth»
(самолет-невидимка), самолет класса «ТУ», самолет класса «АН».
Напомним, что отношение «класс —подкласс» (ISA) является осново-
основополагающим отношением в семантической сети.
видимость для радаров
виден
ISA
перевозка
пассажиров и
грузов
исшльзование
m
ISA /
видимость для радаров/ ISA
не виден
самолет-
невидимк
использование
бревые
действия
Рис. 1.11/
Для описания семантической сети в языке Пролог используются
предикаты: isa(Type, Parent), обозначающий, что объект Туре яв-
является представителем класса Parent, и hasprop(Object, Property,

78 Автоматическое доказательство теорем [Гл. 1
Value) , задающий свойства объектов. Предикат hasprop обозначает,
что Object имеет свойство Property со значением Value. Object и
Value являются вершинами в семантической сети, и Property явля-
является именем ребра, соединяющего их.
Приведем список предикатов, описывающий фрагмент иерархии
воздушных лайнеров, заданный семантической сетью, представленной
на рис.1.17.
isa (airplane, liner).
isa (airsphere, liner).
isa (stealth, airplane).
isa (TU, airplane).
isa (AN, airplane).
isa (TU154, TU).
isa (AN76, AN).
hasprop (stealth, application, war_actions).
hasprop (stealth, see_for_radar, no).
hasprop (airplane, application, fly).
hasprop (airplane, see_for_radar, yes).
Опишем рекурсивный алгоритм поиска объектов в семантической
сети, обладающих заданным свойством. Заметим, что свойства опи-
описываются в семантической сети на самом верхнем уровне и имеют
значения «истина». Используя механизм наследования, можно по-
получить свойства, которыми обладают объекты или подклассы неко-
некоторого надкласса, если описаны свойства надкласса. Так, свойство
«видимость для радаров» задается для воздушных лайнеров и всех
его подклассов. Исключения описываются на том уровне, на котором
размещены объекты, не обладающие заданным свойством. Например,
в представленной на рис. 1.17 семантической сети описаны верши-
вершины, отражающие тот факт, что самолеты с технологией «stealth»
(самолеты-невидимки) являются невидимыми для радаров и не ис-
используются для перевозки пассажиров и грузов.
Предикат hasproperty начинает поиск свойств для объектов, рас-
расположенных на нижнем уровне. Если свойство для объекта в явном
виде не задано, то hasproperty ищет isa-связь для перехода к над-
классу, для которого далее определяется, обладает ли он заданным
свойством и т. д. Если надклассов больше нет, и hasproperty не нашел
объекта или класса, обладающего заданным свойством, то результа-
результатом алгоритма поиска является неудача (fail).
Представим на языке Пролог описанную выше процедуру поиска.
hasproperty(Object, Property, Value) :- hasprop(Object,
Property, Value).

1.6]
Вывод в языке Пролог
79
hasproperty(Object, Property, Value) :- isa(Object,Parent),
hasproperty(Parent, Property, Value).
Заметим, что указанная процедура осуществляет поиск «в глу-
глубину» с возвратом в семантической сети, которая задает иерархию
наследования. В следующем пункте опишем механизм наследования
в фреймовом представлении и реализацию множественного наследо-
наследования на языке Пролог.
1.6.5.3. Реализация, вывода на фреймовых структурах.
Семантическая сеть может быть представлена в виде структур фрей-
фреймов. Представим в виде фреймов фрагмент семантической сети, за-
заданный на рис. 1.17. Необходимо напомнить, что фрейм задается име-
именем фрейма и списком слотов, в которых определяются свойства и
их значения. Примеры фреймов, используемых для описания выше-
вышеописанного примера, приведены на рис. 1.18. Слот isa во фреймах
используется для задания иерархии на них. В нем находится список
исключений и значений, заданных по умолчанию.
Ими: воздушный лайнер
Isa:
Свойство: видимость для радаров
(да)
Default:
Ими: самолет
Isa: воздушный лайнер
Свойство: использование(перевозка
пассажиров и грузов)
Default:
Ими: самолет с технологией
«stealth»
Isa: самолет
Свойство: видимость для
радаров (нет); использование
(боевые действия)
Default:
Ими: АН
Isa: самолет
Свойство:
Default:
Имм: ТУ
Isa: самолет
Свойство:
Default:
Рис. 1.18
Опишем фреймы, заданные на рис. 1.18, в виде конструкций языка
Пролог.
frame(name(airliner),isa(" "), [see_for_radar(yes)],[ ]).
frame(name(airplane),isa(airliner),[application(fly)] ,[ ]) .
frame(name(stealth),isa(airplane),[see_for_radar(no),
application(war_action)],[ ]) .

80 Автоматическое доказательство теорем [Гл. 1
frame(name(AN),isa(airplane),[ ] ,[ ]).
frame(name(TU),isa(airplane),[],[]).
Приведем текст процедур, позволяющих обрабатывать заданные
конструкции.
get(Prop, Object) :- frame(name(Object),_,
List_of.properties,.), member(Prop, List_of.properties).
get(Prop, Object) :- frame(name(Object),_,_,
List_of.defaults), member(Prop, List_of.defaults).
get(Prop, Object):- frame(name(Object), isa(Parent), _, _),
get(Prop, Parent).
Если структура фреймов описывает сетевую, а не древовидную
иерархию, т. е. необходимо поддерживать множественное наследова-
наследование, то нужно внести изменения как в выбранное представление
фреймов на языке Пролог, так и в стратегию поиска. Сначала из-
изменим представление фрейма следующим образом: в предикате isa
зададим список надклассов объекта Object. Так, каждый надкласс в
списке является родителем объекта, имя которого задается в первом
аргументе фрейма. Далее необходимо внести изменения в процедуру
поиска, которая будет поддерживать множественное наследование.
Определим процедуру Get .multiple следующим образом:
net(Prop, Object) :- frame(name(Object), isa(List), _, _),
get_multiple(Prop, List).
get_multiple(Prop, [Parent I]) :- get(Prop, Parent).
get_multiple(Prop, [_I Rest]) :- get_multiple(Prop, Rest).
В заключение заметим, что список правил языка Пролог может
быть задан в слоте фрейма. Например, можно задать в слоте фрейма
список правил для получения различных вариантов ответа на вопро-
вопросы, касающиеся данного объекта. Такие списки правил можно рас-
рассматривать в какой-то степени как методы, которые играют важную
роль в объектно-ориентированном программировании.

В словах заключена великая сила,
если только Вы не сцепляете их одно с
другим в слишком длинную цепь.
Д. Биллингз
Глава 2
ВЫВОД НА ГРАФЕ СВЯЗЕЙ
При обработке большого объема данных, а также при решении
задач, характеризующихся экспоненциальным ростом пространства
поиска, особое значение приобретает проблема эффективности проце-
процедур дедуктивного вывода.
Для эффективной работы с множествами дизъюнктов большой
мощности процедура вывода должна отвечать следующим требова-
требованиям:
• по возможности сокращать пространство поиска контрарной па-
пары на каждом шаге резольвирования;
• исключать из дальнейшего рассмотрения дизъюнкты, которые
не могут быть использованы в процессе доказательства;
• в процедуре вывода должен быть реализован эффективный ал-
алгоритм выбора контрарных пар для резольвирования;
• поиск доказательства должен производиться сразу по несколь-
нескольким направлениям.
Этим условиям удовлетворяет процедура параллельного вывода
на графе связей Ковальского.
Проблема поиска контрарных пар решается путем сохранения ин-
информации о потенциально резольвируемых предикатах в графе свя-
связей. Таким образом, установление потенциальной резольвируемости
производится один раз при создании графа связей, и нет необхо-
необходимости в просмотре всего множества дизъюнктов на каждом шаге
резольвирования — достаточно лишь просмотреть дизъюнкты, полу-
полученные в результате резольвирования на последнем шаге. Исключение
дизъюнктов, которые не могут быть использованы в доказательстве,
достигается с помощью простой процедуры нахождения «чистых»
литер. Для эффективного выбора контрарной пары можно использо-
использовать эвристические оценки, а также любые существующие алгоритмы
вывода. Для организации поиска доказательства сразу по нескольким
направлениям процедура вывода на графе связей может быть распа-
распараллелена.

82 Вывод на графе связей [Гл. 2
2.1. Последовательная процедура доказательства
методом графа связей
Рассмотрим исходную последовательность дизъюнктов:
С\, Съ,..., Ck, состоящих из предикатов Р\, Р2,..., Pi. Поставим
в соответствие каждому предикату вершину в графе связей. Два
узла соединяются ненаправленным ребром, называемым связью, если
соответствующие предикаты потенциально образуют контрарную
пару (что означает возможность резольвирования данных преди-
предикатов после применения к ним унификатора и переименования
соответствующих переменных). Узлы, соответствующие предикатам,
принадлежащим одному дизъюнкту, группируются вместе в графе
связей. Во время построения графа при определении предикатов —
потенциальных кандидатов на резольвирование — следует (хотя
это потребует дополнительных вычислительных затрат) пометить
каждую связь соответствующим наиболее общим унификатором
(НОУ).
С каждой связью в графе связей ассоциируется единственная
резольвента, являющаяся результатом резольвирования предикатов,
соединенных данной связью. После генерации резольвенты не состав-
составляет особого труда добавить ее в граф. Новые связи дизъюнкта-
резольвенты могут быть вычислены с использованием имеющейся
информации о наследуемых связях дизъюнктов-потомков. НОУ для
новых связей будет представлять собой композицию унификатора
резольвированной связи и связи дизъюнкта-предка.
Таким образом, процесс резольвирования для данной связи пред-
представляет собой получение резольвенты, добавление резольвенты в
граф связей, добавление связей резольвенты в граф связей и удаление
«старых» связей и дизъюнктов из графа связей.
Удаление «старых» связей и дизъюнктов производится по следу-
следующей схеме:
1) когда резольвента сгенерирована и добавлена в граф, связь,
которая породила резольвенту, удаляется из графа связей;
2) если вершина не имеет связей, то дизъюнкт, которому эта вер-
вершина (предикат) принадлежит, удаляется из графа вместе со
всеми связями;
3) если дизъюнкт является тавтологией, то он удаляется со всеми
принадлежащими ему предикатами и связями.
В значительной мере гибкость и мощь процедуры вывода является
следствием ее недетерминизма, так как на каждом шаге алгоритма
может быть выбрана любая связь для резольвирования. Для точного
определения процедуры вывода необходимо обратить внимание на де-
детали, особенно на вопросы, связанные с факторизацией, поглощением

2.1] Последовательная процедура доказательства методом 83
дизъюнктов, удалением дизъюнктов-тавтологий и чистых дизъюнк-
дизъюнктов.
Таким образом, последовательный алгоритм вывода на графе свя-
связей имеет следующий вид.
Алгоритм 2.1.
1. Выбор связи из множества связей.
2. Резольвирование связи и получение резольвенты. Удаление свя-
связи, по которой производилось резольвирование.
3. Если получена пустая резольвента, то успешное завершение,
иначе помещение резольвенты в граф, добавление ее связей,
удаление дизъюнктов-тавтологий и чистых дизъюнктов, выпол-
выполнение операций факторизации и поглощения дизъюнктов.
4. Если граф не содержит ни одного дизъюнкта, то неуспешное
завершение алгоритма, иначе переход к шагу 1.
Рассмотрим работу алгоритма дедуктивного вывода на приме-
примере 1.23 (см. главу 1).
Пример 2.1.
Граф связей для данного множества дизъюнктов изображен на
рис. 2.1.
Рассмотрим основные шаги алгоритма. На первом шаге
производится выбор связи для резольвирования и резольвирование
выбранной связи. Прорезольвированная связь
С(а) Н(Ъ) удаляется. Выберем для резольвирования
связь 1.
На втором шаге происходит резольвирова-
iC(jc) v-!#(>) v-iLfo у) ние по этой связи, в результате которого мы
получаем дизъюнкт 6: -^Н(у) V -iL(a, г/). Уда-
Удаляем связь 1 и переходим к шагу 3 алгоритма.
Р(Ъ) 4 uP(v) v Па у) На третьем шаге проверяем, является ли
р полученный на предыдущем шаге дизъюнкт
пустым. Так как дизъюнкт б не является пу-
пустым дизъюнктом, добавляем его в граф связей. Также добавляем
связи дизъюнкта 6. Полученный граф связей изображен на рис. 2.2.
Дизъюнкты С (а) и ->С(х) V ->Н(у) V ^L(x,y) содержат чистые
литеры С (а) и -iC(x), то есть являются чистыми дизъюнктами и под-
подлежат удалению из графа связей. После удаления данных дизъюнктов
получаем граф связей, изображенный на рис. 2.3.
Данный граф связей не содержит дизъюнктов-тавтологий и чи-
чистых дизъюнктов, подлежащих удалению. Операции факторизации и
поглощения дизъюнктов также являются неприменимыми к данному
множеству дизъюнктов, поэтому переходим к шагу 4 алгоритма.
Граф связей, изображенный на рис. 2.3, не содержит пустого дизъ-
дизъюнкта, поэтому переходим к шагу 1.

Вывод на графе связей
[Гл.2
С(а) Нф)
|_
2
) v —H(y) v —1,(х, у) —Н(у) v —\L(a, у)
3 6
)vL(a,y)
Нф)
РФ)— >P(y)vL(a,y)
Рис. 2.2
Рис. 2.3
Выберем для резольвирования связь 5. После резольвирования
по этой связи получаем дизъюнкт 7: -iL(a, Ь). Удаляем связь 5 и
переходим к шагу 4 алгоритма.
Дизъюнкт 7 не является пустым дизъюнктом, поэтому добавляем
его в граф связей. Также добавляем связи дизъюнкта 7. Полученный
граф связей изображен на рис. 2.4.
Нф)
Рф)
-Н(у)\/-Ца9у)
6
4 v Ца, у)
-Ца9 Ь)
7
(a, b)
7
Рис. 2.4
Рис. 2.5
Дизъюнкты Н(Ъ) и —iH(y) V^L(a, г/) содержат чистые литеры Н(Ъ)
и ^Н(у), то есть являются чистыми дизъюнктами и подлежат удале-
удалению из графа связей. После удаления данных дизъюнктов получаем
граф связей, изображенный на рис. 2.5.
Данный граф связей не содержит дизъюнктов-тавтологий и чи-
чистых дизъюнктов, подлежащих удалению. Операции факторизации и
поглощения дизъюнктов также являются неприменимыми к данному
множеству дизъюнктов, поэтому переходим к шагу 4 алгоритма.
Граф связей, изображенный на рис. 2.5, содержит дизъюнкты, по-
поэтому переходим к шагу 1.
Выберем для резольвирования связь 7. После резольвирования по
этой связи получаем дизъюнкт 8: -пР(Ь). Удаляем связь 7 и переходим
к шагу 3 алгоритма.
Дизъюнкт 8 не является пустым дизъюнктом, поэтому добавляем
его в граф связей. Также добавляем связи дизъюнкта 8. Полученный
граф связей изображен на рис. 2.6.

2.1] Последовательная процедура доказательства методом 85
Дизъюнкты -iL(a, Ь) и ~^Р(у) V L(a,y) содержат чистые литеры
—iL(a, Ь) и L(a,?/), то есть являются чистыми дизъюнктами и подле-
подлежат удалению из графа связей. После удаления данных дизъюнктов
получаем граф связей, изображенный на рис. 2.7.
-~Ца, Ъ)
P(b)— J>(y)vL(a,y)
Рис. 2.6 Рис. 2.7
Данный граф связей не содержит дизъюнктов-тавтологий и чи-
чистых дизъюнктов, подлежащих удалению. Операции факторизации и
поглощения дизъюнктов также являются неприменимыми к данному
множеству дизъюнктов, поэтому переходим к шагу 4 алгоритма.
Граф связей, изображенный на рис. 2.7, содержит дизъюнкты, по-
поэтому переходим к шагу 1.
Выберем для резольвирования связь 8. После резольвирования по
этой связи получаем дизъюнкт 9: П. Удаляем связь 8 и переходим к
шагу 3 алгоритма.
Дизъюнкт 9 является пустым дизъюнктом, следовательно исход-
исходное множество дизъюнктов является невыполнимым. Завершение ра-
работы алгоритма.
Доказана полнота и состоятельность процедуры вывода на графе
связей. Вышеприведенный алгоритм является недетерминированным.
Для реализации его на детерминированной машине он нуждается в
детерминированной процедуре выбора резольвируемой связи. В дан-
данном вопросе возможно использование нескольких основных методик,
например, выбор связи, активация которой приведет к уменьшению
количества дизъюнктов в графе, количества связей или количества
вхождений предикатов в дизъюнкты. Идеальная ситуация возникает в
случае, когда связь соединяет пару предикатов, не имеющих никаких
других связей (так как в этом случае резольвирование приведет к
удалению родительских дизъюнктов и всех связей родительских дизъ-
дизъюнктов). Также к упрощению графа приводит слияние одинаковых
предикатов из дизъюнктов-родителей. Еще одним фактором, влияю-
влияющим на выбор связи, является единственность связи для предиката,
что приводит, как сказано ранее, к удалению дизъюнкта, содержащего
этот предикат после резольвирования. В случае, когда упрощения
графа добиться не удается, следует выбрать связь, резольвирование
которой приведет к минимальному усложнению графа связей. В этой

86 Вывод на графе связей [Гл. 2
ситуации следует отдавать предпочтение связям, резольвенты кото-
которых содержат наименьшее количество предикатов.
2.2. Стратегии поиска в графе связей
В графах связей стратегия поиска заключается в проблеме выбора
связи для резольвирования на каждом шаге резольвирования. Эта
проблема аналогична проблеме выбора последовательности резольви-
резольвирования предикатов во многих традиционных системах вывода. Боль-
Большинство методов, использованных в этих системах, без значительных
усложнений могут быть применены и к выводу на графе связей.
Основное отличие графа связей от других способов дедуктивного
вывода — облегчение получения информации о еще нерезольвиро-
ванных предикатах. Эта информация может быть использована раз-
различными способами, одним из наиболее интересных является вычис-
вычисление нижних границ сложности опровержения данной резольвенты.
Очень грубую оценку, равную количеству предикатов в резольвенте,
получить легко. Стратегии поиска повышают свою эффективность
при более точном определении нижней границы. Число предикатов
в дизъюнкте, как эквивалент нижней границы, аналогичен поиску
на один уровень в графе связей. Поиск на один уровень означает,
что все предикаты в дизъюнкте имеют связи с другими предикатами.
Оценка нижней границы может быть значительно уточнена при ис-
использовании поиска на п уровней в графе связей. В нижеприведенном
примере будет рассмотрен метод вычисления значений, оценивающих
с помощью поиска на п уровней в графе связей, минимальное чи-
число резольвируемых связей, необходимых для достижения цели G.
Вычислительные затраты, необходимые для расчета этих значений,
являются линейной функцией от п. Поиск на п уровней не учитыва-
учитывает возможность существования тавтологий, факторов дизъюнктов и
слияния предикатов в дизъюнктах.
Величина hn(G) оценивает минимальное число резольвируемых
связей, необходимых для достижения цели G. h\(G) вычисляется
путем утверждения, что каждый предикат в каждом дизъюнкте,
соединенном связью с G, может быть достигнут за один шаг, путем
активации единственной связи. Таким образом, h\{G) — минимальное
значение числа предикатов в дизъюнктах, соединенных связью с G.
В общем случае
т г=1,1т
где Ki~ предикатные литеры дизъюнктов, соединенных связью с G,
вида Сш = ^G V К\ V ... V Ktm.
Вообще говоря, hn — нижняя граница числа резольвент, которые
необходимо сгенерировать для опровержения G.

2.3] Достоинства процедуры дедуктивного вывода на графе связей 87
Поиск на несколько шагов вперед можно использовать для вычис-
вычисления значений /in, что позволит производить оптимальный выбор
генерируемой связи. Рассмотрим вычисление hn на примере.
Пример 2.2.
Исходное множество дизъюнктов
2. Д V^Q V^P
3. Р
4. -.Д.
Граф связей для множества дизъюнктов изображен на рис. 2.8.
Табл. 2.1 иллюстрирует процесс нахождения значения hn.
Таким образом, hn = /г2 = hi. Рассмотрим
более подробно процесс вычисления hn(Q).
hi(Q) = 3, так как минимальное число литер во
всех дизъюнктах, соединенных связью с литерой
Q, равно 3 (дизъюнкт 2: Д V ^Q V -.Р).
/i2(Q) = 3, так как минимум по всем дизъюнк-
дизъюнктам, соединенным связью с Q (в данном случае это
единственный дизъюнкт 2: Д V ^Q V ->Р), сумм J^ hn-i(Ki), равен
г=1,/т
/г1(Д)+/г1(->Р) = 1 + 1 = 2, и, таким образом,
Л2(<2) = 1 + minI Yl hn-AKi)] = 1 + 2 = 3. (Сго = R V -.Q V -.Р).
е
Рис. 2.S
Следовательно, hn(Q) = /12(Q) = hi(Q) = 3. Аналогично находит-
находится /i2 для остальных литер.
1аблица 2.1
-^р
р
^R
кг
3
1
1
1
3
3
h2
3
1
1
1
3
3
2.3. Достоинства процедуры дедуктивного вывода
на графе связей
Рассмотрим основные проблемы, характерные для процедур вы-
вывода, и покажем преимущество процедуры дедуктивного вывода на
графе связей над другими методами.

88 Вывод на графе связей [Гл. 2
1. Проблема нахождения контрарной пары. Проблема нахождения
контрарной пары — одна из основных проблем, существенно снижаю-
снижающих эффективность процедур дедуктивного вывода. Особенно замет-
заметно это проявляется при достаточно большом количестве дизъюнктов.
В наиболее неудачных случаях требуется просмотреть все множество
дизъюнктов, прежде чем будет найдена контрарная пара предикатов
для резольвирования. Много времени занимает проверка возможно-
возможности резольвирования предикатов, которые не резольвируемы.
Для графов связей проблема поиска контрарной пары решается
путем сохранения информации о потенциально резольвируемых пре-
предикатах в графе связей. Таким образом, установление потенциальной
резольвируемости производится один раз при создании графа свя-
связей, и нет необходимости в просмотре всего множества дизъюнктов
на каждом шаге резольвирования — достаточно лишь просмотреть
дизъюнкты, полученные в результате резольвирования на последнем
шаге.
2. Проблема препроцессорной обработки. Препроцессорная обра-
обработка переводит множество дизъюнктов во множество, содержащее
меньшее количество дизъюнктов, предикатов или связей. Препроцес-
Препроцессорная обработка множества дизъюнктов проводится не только на
шаге инициализации множества дизъюнктов, но и на каждом шаге
вывода. В процедуре дедуктивного вывода на графе связей препро-
препроцессорная обработка включена в саму процедуру, и на каждом шаге
алгоритма производится удаление «чистых» дизъюнктов, поглощен-
поглощенных дизъюнктов и дизъюнктов-тавтологий, что значительно ускоряет
и упрощает вывод.
3. Проблема модификации алгоритма вывода. Одно из основных
достоинств метода дедуктивного вывода на графе связей — это воз-
возможность «встраивать» процедуры из других методов в данный метод
вывода. Это достигается путем изменения процедуры выбора связи
для резольвирования. Так, например, метод гиперрезолюции может
быть встроен в процедуру вывода на графе связей. Таким образом,
алгоритм дедуктивного вывода на графе связей позволяет аккумули-
аккумулировать в себе достоинства других методов.
2.4. Параллельный вывод на графе связей
Рассмотрим три метода вывода: OR-параллельный вывод, AND-
параллельный вывод и DCDP-параллельный вывод на графе связей
в логике предикатов первого порядка.
Основной операцией в опровержении графа связей является резо-
резолюция связи, в которой выделяется связь, и соответствующие термы
пар литер-вершин унифицируются. После этого вычисляется резоль-
резольвента, и она входит в граф. Связь удаляется, и соответствующие связи
вычисленной вершины-резольвенты вставляются в граф. Резолюция

2.4] Параллельный вывод на графе связей 89
графа имеет полезное свойство: она не требует поиска для того, чтобы
определить связи вычисленной резольвенты и пары дизъюнктов для
дальнейшего резольвирования. Мы можем резольвировать любую па-
пару дизъюнктов, соединенных ребром, так как все ребра соединяют
контрарные пары. Резольвента всегда наследует связи, соединяющие
литеры-вершины дизъюнктов, инцидентных резольвированной связи.
Использованная единожды связь удаляется из графа, чем до-
достигается ограничение излишней резолюции между данной парой
дизъюнктов. Множество дизъюнктов, соответствующее графу связей,
невыполнимо, если мы можем вывести пустой дизъюнкт из графа
связей. Связи графа могут быть выделены сверху вниз, снизу вверх
или комбинацией обоих методов. Поскольку все пространство поиска
проблемы известно, то на каждом шаге мы можем использовать эври-
эвристическую информацию, чтобы выделить лучших кандидатов на ре-
зольвирование. Для повышения эффективности вывода используются
различные стратегии упрощения графа связей, такие как удаление
чистых дизъюнктов, тавтологий и поглощенных дизъюнктов.
2.4.1. Метод OR-параллельной резолюции
Граф связей Ковальского является основой для разработки алго-
алгоритмов параллельной резолюции. Наличие полного пространства по-
поиска предполагает возможность использования стратегий параллель-
параллельного вычисления для повышения эффективности процедуры вывода.
В случае OR-параллелизма система вывода параллельно сопо-
сопоставляет некоторое целевое утверждение с головами дизъюнктов-
кандидатов, подходящих для данного сопоставления. При этом осу-
осуществляется унификация литер и генерация новых дизъюнктов по
методу резолюции для предикатов первого порядка.
Алгоритм OR-параллельной резолюции включает следую-
следующие этапы.
1. Выбор множества связей для OR-параллельного резольвирова-
резольвирования.
2. Параллельное резольвирование всех связей из выбранного мно-
множества. Удаление выбранных связей.
3. Если получена пустая резольвента, то успешное завершение,
иначе помещение резольвент в граф, добавление их связей, уда-
удаление дизъюнктов-тавтологий и чистых дизъюнктов, выполне-
выполнение операций факторизации и поглощения дизъюнктов.
4. Если граф не содержит ни одного дизъюнкта, то неуспешное
завершение алгоритма, иначе переход к п. 1.
OR-параллельная резолюция позволяет одновременно резольвиро-
резольвировать более одной связи, и, следовательно, не нужно выбирать одну
наилучшую связь.

90
Вывод на графе связей
[Гл.2
Рассмотрим пример OR-параллельного дедуктивного вывода на
графе связей.
Пример 2.3.
Исходное множество дизъюнктов
1. Q(c)
2. Q(b)
3. R(x) V -,Q(y) V -
4. P(b)
5. -ni?(x) V S(x, y) V
6. T(j/) V
7. B(o)
8.
9. Б (ж) V -¦C(x) V
10. D(c)
11. F(b)
12. F(c)
13. CF)
Допустимыми мнолсествами OR-связей для графа связей, изобра-
изображенного на рис. 2.9, являются {Iх, 2х} и {10х, 11х} (в данном и после-
последующих примерах мы не рассматриваем множества связей для па-
параллельного резольвирования, состоящие из одной связи). Желающие
могут довести пример до конца.
R(pc)v
4'
Q(c) Q{b)
l'\ /2'
-.e(v)v^p(x)-
-i%)v5(ij)v-ir(x)
—\F(y) \
F(b)
7'
f —h^CFj z) v —B(z)
F(c)
J'
5r
-РФ)
-B(x)v
7
9'
К,) V —iLjyy)
12'
C(b)
В(а)
D(c)
Рис. 2.9
OR-параллелизм является наиболее простым в реализации видом
параллелизма в дедуктивном выводе на графе связей. Процедура
OR-параллельного вывода сводится к нахождению множества связей
предикатной литеры дизъюнкта и последующему резольвированию с
удалением дизъюнкта, содержащего предикатную литеру, по которой
производилось резольвирование. В данной ситуации особое значение
приобретает задача нахождения множества связей, резольвирование
по которым приведет к максимальному упрощению графа связей. Так
как предварительное резольвирование всех связей и нахождение среди
них оптимальной связи является вычислительно неэффективным, то

2.4] Параллельный вывод на графе связей 91
для выбора связи необходимо использовать эвристики. Выбор эври-
эвристических функций подробно рассмотрен ниже.
2.4.2. DCDP-параллельный вывод
Одной из разновидностей параллельного вывода на графе связей
Ковальского является DC- параллелизм. В случае DC-параллелизма
(distinct clause parallelism) мы резольвируем те связи, для кото-
которых дизъюнкты, соединенные этими связями, различны. Мы будем
рассматривать ограниченный DC-параллелизм, сохраняющий логи-
логическую непротиворечивость. Такой параллелизм называется DCDP-
параллелизмом (parallelism for distinct clauses, edge distinct pair).
Определение 2.1. Дизъюнкты называются смежными, если су-
существует одна или несколько связей, соединяющих литеры одного с
литерами другого.
Определение 2.2. Множеством D СВР-связей называется мно-
множество связей, которые соединяют пары различных дизъюнктов, если
дизъюнкты каждой пары не являются смежными со всеми дизъюнк-
дизъюнктами остальных пар.
В качестве иллюстрации данных определений рассмотрим вы-
выбор множества DCDP-связей для графа связей из примера 2.3 (см.
рис. 2.9).
Для рассматриваемого множества дизъюнктов можно записать
следующие пары смежных дизъюнктов: {A),C)},{B),C)},{C),D)} и
т. д. Таким образом, одним из множеств DCDP-связей будет {Iх, 6х, 9х}.
Проверим выполнение условия из определений: связь (Iх) соединяет
дизъюнкты A) и C), связь Fх) — дизъюнкты F) и G), связь (9х) —
дизъюнкты (9) и A0). Дизъюнкты A) и C) не смежны с F), G), (9)
и A0); F) и G) не смежны с A), C), (9) и A0); (9) и A0) не смежны
с A), C), F) и G).
В качестве других примеров множеств DCDP-связей можно приве-
привести {2х, 6х, 12х}, {4х, 12х}, {Iх, 6х, 10х}. Сложность оптимального выбора
DCDP-связей эквивалентна проблеме оптимальной раскраски графа.
Доказано, что DCDP-параллельная резолюция корректна. Счита-
Считаем, что исходное множество дизъюнктов не имеет чистых литер и
тавтологий. Предварительно построим исходный граф связей. Если
граф связей содержит пустой дизъюнкт, то он невыполним и, сле-
следовательно, алгоритм достиг конечного состояния. Алгоритм DCDP-
параллельной резолюции отличается от алгоритма OR-параллельной
резолюции 1-м шагом, на котором, в случае DCDP-параллельной
резолюции, происходит выбор множества DCDP-связей и проводится
параллельное резольвирование по всем связям из выбранного множе-
множества.
Рассмотрим проблему выбора DCDP-связей. Пусть все связи име-
имеют метки. Пусть L — некоторая связь графа связей.

92 Вывод на графе связей [Гл. 2
Определение 2.3. Множеством конфликтных с L связей на-
называется множество таких связей, которые не могут быть DCDP-
связаны с L.
Определение 2.4- Множество связей, DCDP-связанных с X, на-
называется множеством совместимых с L связей.
Данные множества можно формально определить следующим об-
образом:
Cnf (L) = AdjLink (L) (J j|J AdjLink (г)}, B.1)
^GAdjLink(L)
где Cnf (L) — множество конфликтных с L связей; AdjLink (L)- мно-
множество ребер (исключая X), соединенных с парой дизъюнктов, инци-
инцидентных L; Cmp (L) = Lset — Cnf (L) — множество совместимых с L
связей; Lset — все множество связей графа связей.
Рассмотрим в качестве примера построение множеств Cnf(Iх) и
Cmp(l/) = Lset — Cnf (Iх) для графа связей, изображенного на рис.2.9:
AdjLink A) = {2х, 3х, 4х}
AdjLink B) = {Iх, 3х, 4х}
AdjLink C) = {Iх, 2х, 4х}
AdjLink D) = {Iх, 2х, 3х, 5х, 7х}
Таким образом, Cnf (Iх) = {Iх, 2х, 3х, 4х, 5х, 7х}, а СтрAх) = Lset -
- Cnf(lx) = {6х, 8х, 9х, 10х, 11х, 12х}.
Используя формулу B.1), можно получить для каждой связи гра-
графа конфликтное множество. Затем надо создать раскрашенный граф,
в котором каждая вершина соответствует связи исходного графа, и
вершины, смежные с вершиной X, составляют множество конфликт-
конфликтных с L связей в исходном графе.
Вспомогательный граф для графа связей, изображенного на
рис. 2.9, показан на рис. 2.10. Каждая вершина имеет номер связи; в
скобках указан номер цвета. Таким образом, мы получаем следующие
множества одного цвета, что соответствует множествам DCDP-связей:
{Iх, 6х, 9х}, {2х, 8х}, {3х, 10х}, {5х, 12х}, {4х}, {7х}, {11х}. Заметим, что при
другой расстановке цветов можно получить иные множества DCDP-
связей, например: {Iх, 6х, 8х}, {2х, 9х}, {3х, 12х}, {5х}, {4х}, {7х}, {11х},
{10х}.
Рассмотрим модификацию алгоритма DCDP-параллельного вы-
вывода. Недетерминизм определения множества DCDP-связей, в прин-
принципе, может оказывать влияние на эффективность работы алгорит-
алгоритма. Необходимо напомнить, что при определении множества DCDP-
связей необходимо определить дизъюнкты, параллельное резольви-
рование которых позволяет максимально упростить граф связей. В

2.4]
Параллельный вывод на графе связей
93
этом случае первостепенное значение приобретает не задача нахожде-
нахождения оптимальной (или субоптимальной) раскраски графа, результа-
результатом которой является получение множества внутренне независимых
подмножеств графа максимальной мощности (в случае оптимальной
раскраски) или получение раскраски, при которой максимальная
12\5)
GI1
CI0'
B)8'
4\4)
FO'
5>E)
мощность множеств вершин одного цвета равна максимальной мощ-
мощности вершин одного цвета в случае оптимальной раскраски, а задача
нахождения множества DCDP-связей, резольвирование которых поз-
позволяет упростить граф связей. Так как нахождение всех возможных
множеств DCDP-связей, резольвирование по этим связям и определе-
определение наиболее подходящего варианта резольвирования является вычис-
вычислительно неэффективным, необходимо использование эвристик для
определения потенциально лучших кандидатов на резольвирование.
Для разных видов параллельного вывода можно предложить различ-
различные эвристики. Подробно вопрос выбора эвристик будет рассмотрен
ниже.
Рассмотрим модификацию процедуры нахождения множества
DCDP-связей. Обозначим множество DCDP-связей как DCDPset, a
множество связей, которые могут быть потенциально добавлены во
множество DCDPset как AVAILset.
Пусть AVAILset = {Множество связей графа связей}.
DCDPset = {}.

94 Вывод на графе связей [Гл. 2
На первом шаге работы алгоритма производится оценка связей
из множества связей AVAILset по выбранному эвристическому крите-
критерию.
После оценивания связей производится сортировка по степени
убывания значения оценки. Связь с наибольшим значением оцен-
оценки — обозначим ее L — удаляется из множества связей AVAILset
и добавляется во множество связей DCDPset. Из множества связей
AVAILset удаляются также и все связи, соединяющие дизъюнкты,
являющиеся смежными с дизъюнктами, которые соединяет связь L.
Если множество AVAILset не пусто, то происходит переход на шаг 1.
Таким образом, в результате работы алгоритма мы получаем суб-
субоптимальное множество DCDP-параллельно резольвируемых связей.
2.4.3. AND-параллельная резолюция
Определение 2.5. Дизъюнкт, все связи которого резольвируются
параллельно, называется SUN-дизъюнктом.
Определение 2.6. Дизъюнкты, соединенные с литерами SUN-
дизъюнкта, называются сателлитными.
При AND-параллелизме все связи, соединенные с литерами SUN-
дизъюнкта, резольвируются одновременно. Все резольвенты помеща-
помещаются в граф вместе со всеми наследуемыми связями сателлитных
дизъюнктов. SUN-дизъюнкт и все его связи удаляются из графа.
Доказана корректность AND-параллельной резолюции.
В резолюции связей унификация комбинируется с выводом. Для
ускорения вывода и бектрекинга сохраняются все НОУ. Также необхо-
необходимо обеспечить корректную унификацию разделенных переменных.
Переменная называется разделенной, если она имеет более чем одно
вхождение в дизъюнкт. Чтобы формально выразить это, введем нес-
несколько обозначений.
Определение 2.7.
1\ V 1ъ V ... V 1п : общий вид SUN-дизъюнкта, где U — г-я литера
дизъюнкта;
1ц V Cli : общий вид j-vo дизъюнкта, где 1ц — j-я литера дизъ-
дизъюнкта, соединенная с i-й литерой SUN-дизъюнкта, а Си — остальная
часть дизъюнкта;
ац : НОУ для термов пары контрарных литер : 1ц в сателлитном
дизъюнкте и li в SUN-дизъюнкте;
Sv (X) : функция, принимающая значение истина, если пере-
переменная X является разделенной переменной для рассматриваемых
предикатов, и ложь — в противном случае;
Const (у) : функция, принимающая значение истина, если аргу-
аргумент у — константа, и ложь — в противном случае;
Var (у) : функция, принимающая значение истина, если аргумент
у — переменная, и ложь — в противном случае.

2.4] Параллельный вывод на графе связей 95
Определение 2.8. Комбинация НОУ o~ij и &2к непротиворечива,
если истинно следующее выражение:
Wx(Sv(x) & Const(x • <Jij) & Const(x • <72/c) & (^ • Gij = X • <72/c))V
Mx{Sv{x) & Const(x • aij) & Var(x • cr2/c))V
Wx(Sv(x) & Const(x
Wx(Sv(x) & Var(x • a2k)
где ж • сг — результат применения подстановки сг к переменной х (здесь
мы не рассматриваем возможность связи переменной с функциональ-
функциональным термом).
Пример 2.4.
Пусть Р (ж, y,z) V Q (х) V D (ж, у) — SUN-дизъюнкт и
^Р (и, v, с) V K(w) и ^Q (v) — сателлитные дизъюнкты. Мы
рассматриваем контрарные пары: P(x,y,z) - ^P (u,v,c) с НОУ
а1 = {и/х,у/у,с/г} и Q(x) — ->Q(v) с НОУ а2 = {v/ж}. В этом
случае комбинация НОУ непротиворечива по определению 2.8, так
как разделенная переменная х связывается с переменными и и
v. Если сателлитные дизъюнкты имеют вид ^Р (a, v, с) V K(w) и
->Q(b), то комбинация НОУ cri = {a/x^v/y^c/z} и <Т2 = {6/ж} будет
противоречивой, так как переменная ж связывается с различными
константами. Если комбинация а^ и а2к непротиворечива, мы можем
получить согласованный унификатор.
Определение 2.9. Множество кортежей согласованного унифи-
унификатора получается следующим образом:
°SV= U {U/Xi},
ГЛР +. - / i * ^k' если 3<J* (Const (Xi * *<*)
1^ x^ если Vcr^ (Const {Xi • cr^j = jalse)
ство разделенных переменных, а = cr^y (J {кортежи для неразделен-
неразделенных переменных}. Резольвентой в этом случае является Cljj4j\/'C2k'•a\
Для каждого НОУ переменные SUN-дизъюнкта, которые связаны
с одной и той же переменной сателлитного дизъюнкта, сохраняются во
множестве, называемом «var-of-same-inst». НОУ может иметь более
одного такого множества.
Рассмотрим общий случай, когда множество var-of-same-inst не пу-
пусто. Будем использовать обозначение var-of-same-inst[I', а] для ссылки
на 1-е множество переменных унификатора а, таких, которые должны
быть связаны с одним и тем же значением. Пусть group 1 и group 2
содержат все множества var-of-same-inst унификаторов g\j и о^к со-
соответственно. Пусть х\ G group 1 и х^ G groupi. Для любых х\ и
Х2, если xi П Ж2 ^ 9, то должна быть по крайней мере одна пере-
переменная, общая для х\ и Х2- Следовательно, х\ и х^ комбинируются

96 Вывод на графе связей [Гл. 2
для формирования нового множества var-of-same-inst согласованного
унификатора для aij и (Т2к-
Пример 2.5.
Пусть имеются следующие множества var-of-same-inst:
var-of-same-inst[l,aij] = {2/1,2/2},
var-of-same-inst[2,aij\ = {2/3,2/4},
var-of-same-inst\5,aij] = {2/5,2/б},
var-of-same-inst[l,G2k] = {2/1,2/6 },
var-of-same-inst[l,G2k] = {2/2,2/7},
= {{2/1,2/2}, {2/3,2/4}, {2/5,2/e}},
i, 2/б}, {2/2,2/т}}-
Обе группы не пусты. Следовательно, мы начинаем с х\ = {2/1,2/2}
из group 1. Каждое множество из group 2 имеет общую перемен-
переменную с group 1 и, следовательно, помечается. Создается новое множе-
множество new-same-inst[l,a] = {2/1,2/2,2/6,2/7}- Помеченные множества из
group 1 и group 2 удаляются. Теперь множества выглядят следующим
образом: groupl = {{2/1,2/2}, {2/3, y^},group2 = { }.
Оставшиеся в group 1 множества проверяются на наличие общих с
множеством neu>-same-ms?[l, сг] переменных. Множество {2/5,2/6} име-
имеет такие переменные, и оно включается в new-same-inst[l,(r]. Затем
множество {2/5,2/6} удаляется из groupl. Так как group2 пуста, алго-
алгоритм заканчивается со следующим результатом: new-same-inst[l, а] =
= {2/1,2/2,2/5,2/6,2/7}, new-same-ms?[l,cr] = {2/3,2/4}.
Если все переменные во множестве new-same-inst связаны с терма-
термами —переменными унификаторов aij и <72&? то они непротиворечивы.
Если, по крайней мере, одна переменная во множестве new-same-inst
связана с константным термом, остальные переменные множества
должны быть связаны либо с тем же самым константным термом,
либо с термом-переменной пары унификаторов.
Этот алгоритм может быть распространен на любое число унифи-
унификаторов для любого числа дизъюнктов.
Алгоритм AND-параллельной резолюции отличается от алгорит-
алгоритма OR-параллельной резолюции 1-м шагом, на котором, в случае
AND-параллельной резолюции, происходит выбор SUN-дизъюнкта и
вычисление комбинации унификаторов всех связей SUN-дизъюнкта
как результат непротиворечивого связывания общих переменных. Со-
Согласование НОУ всех связей может быть сделано параллельно. Для
каждого согласованного НОУ вычисляются соответствующие резоль-
резольвенты. После этого SUN-дизъюнкт удаляется.
Рассмотрим выбор множества AND-связей для графа связей из
примера 2.3 (см. рис. 2.9). Допустимыми множествами AND-связей яв-

2.5] Модификация процедур параллельного вывода 97
ляются, например, {5х, 4х, 7х} (SUN-дизъюнкт - дизъюнкт 5) и {5х, &}
(SUN-дизъюнкт — дизъюнкт 6).
2.5. Модификация процедур параллельного вывода
2.5.1. Принципы создания эвристической функции
Как было указано выше, при выборе связи для резольвирования в
графе связей можно использовать различные эвристические функции
оценки. В случае параллельного резольвирования необходимо делать
выбор множества связей, отвечающих некоторым условиям. Стоит
отметить, что неудачный выбор связи может привести к экспоненци-
экспоненциальному росту количества дизъюнктов при решении сложных задач,
что сделает процедуру вывода практически непригодной. В то же
время удачный выбор связи может значительно увеличить эффектив-
эффективность процедуры вывода. Например, резольвирование единственной
связи предикатной литеры в дизъюнкте приведет к появлению так
называемого «чистого» дизъюнкта, который должен быть удален.
Удаление «чистого» дизъюнкта в свою очередь может привести к кас-
каскадному удалению других дизъюнктов и к эффекту «снежного кома».
В результате структура графа связей может значительно упроститься.
Рассмотрим основные принципы, которых необходимо придерживать-
придерживаться при создании эвристических функций оценки связи:
1) число литер в резольвируемых дизъюнктах должно быть по
возможности минимальным;
2) число связей у резольвируемых дизъюнктов должно быть мини-
минимальным;
3) число связей у литер, по которым резольвируются дизъюнкты,
должно быть минимальным;
4) НОУ резольвируемой связи должны иметь подстановки вида
с/ж, где с — константный или функциональный терм, х — пе-
переменная.
Поясним смысл каждого из принципов.
Принцип A) служит для упрощения результирующего графа
связей, так как дизъюнкты с малым числом литер, как правило,
имеют меньшее число связей. Также резольвирование по дизъюнк-
дизъюнктам, имеющим малое количество литер, позволяет получить одно-
двулитеральные дизъюнкты, которые могут быть эффективно ис-
использованы в дальнейшем процессе вывода.
Принцип B) также служит для упрощения результирующего гра-
графа связей, так как резольвирование дизъюнктов с малым числом
связей после резольвирования приводит к получению дизъюнктов
также с малым числом связей.
4 В.Н. Вагин и др.

98 Вывод на графе связей [Гл. 2
Принцип C) отдает предпочтение связям, резольвирование кото-
которых позволяет получить «чистые» дизъюнкты, а при их удалении
значительно упрощается структура графа связей.
То же самое молено сказать и о принципе D) — при резольвирова-
нии по связи, содержащей подстановку константы вместо переменной,
мы получаем в результате дизъюнкт, содержащий константные тер-
термы. Подобный дизъюнкт имеет, во-первых, малое число связей, а во-
вторых, может быть эффективно использован при резольвировании.
Отметим, что из всех типов параллельного вывода наиболее требо-
требовательным к выбору эвристики является DCDP-параллельный вывод.
Это объясняется наименьшими требованиями DCDP-параллельного
вывода к выбору резольвируемого дизъюнкта (дизъюнктов). При OR-
резольвировании мы резольвируем все связи одной из литер OR-
дизъюнкта. При AND-резольвировании мы резольвируем по всем
связям SUN-дизъюнкта. Таким образом, нельзя исключить из вы-
выбранного множества связей те связи, резольвирование по которым
на данном шаге может оказаться бесполезным или малоэффектив-
малоэффективным. Естественно, при выборе дизъюнкта в AND-параллельном ре-
резольвировании или предикатной литеры в OR-параллельном выводе,
используются различные функции эвристической оценки, но данные
оценки распространяются на все множество связей в целом, в то время
как при DCDP-параллельном выводе происходит последовательный
отбор связей, и на каждом шаге добавляется связь, удовлетворяющая
условиям и имеющая наилучшее значение оценки.
При разработке процедур вывода было проанализировано и ис-
испытано несколько возможных эвристических функций. Рассмотрим
некоторые из них и приведем полученные результаты. В описанной
ниже эвристической функции HI учитываются все принципы A)—D).
2.5.2. Эвристическая функция HI
При создании эвристической функции HI функция оценки связи
была представлена как линейная комбинация функций оценки объ-
объектов, входящих в связь (унификатор, дизъюнкты и предикатные
литеры, участвующие в связи).
Пусть Weight-Link — значение эвристической оценки для связи.
Тогда:
WeightLink = kc\ause • (Clausemeur + Clause2Heur) + UniHeur • КпЛ
eur + Pred2Heur),
где ClauseiHeur — значение эвристической оценки первого дизъюнк-
дизъюнкта; Clause2Heur — значение эвристической оценки второго дизъюнк-
дизъюнкта; UniHeur — значение эвристической оценки унификатора связи;
r — значение эвристической оценки предикатной литеры из

2.5] Модификация процедур параллельного вывода 99
первого дизъюнкта, участвующей в связи; Ргес^неиг — значение эври-
эвристической оценки предикатной литеры из второго дизъюнкта, участ-
участвующей В СВЯЗИ; fcuni? ^clause? &pred ? [lj ЮО] — ПрОИЗВОЛЬНЫе КОЭффи-
циенты.
Поясним введенные обозначения более подробно.
2.5.2.1. Вычисление эвристической оценки дизъюнкта.
Эвристическая функция оценки должна учитывать изменения ха-
характеристик графа связей в процессе вывода (например, изменение
количества связей и количества литер в дизъюнктах). Рассмотрим
следующую эвристическую функцию оценки дизъюнкта, учитываю-
учитывающую принципы A) и B):
ClauseHeur = &i • ClauseNumberOfLiterals + k^ • ClauseNumberOfLinks,
где ClauseNumberOfLinks — число связей дизъюнкта; ClauseNumber-
ClauseNumberOfLiterals — число предикатных литер дизъюнкта; к\, &2 — произволь-
произвольные коэффициенты, выбираемые перед началом работы алгоритма,
исходя из таких характеристик графа, как среднее число литер и
связей для дизъюнкта.
Пусть, например, среднее число литер для дизъюнкта равно 1,8, а
среднее число связей равно 3,6. Тогда в качестве значений коэффици-
коэффициентов к\ и &2 молено выбрать к\ = 3, 6/1, 8 = 2 и к^ = 1. В этом случае
оба принципа A) и B) учитываются в одинаковой степени. В процессе
вывода значения характеристик могут изменяться. В этом случае
первоначально выбранные значения коэффициентов «устаревают», и
один из принципов получает больший вес, чем другой. Для того,
чтобы избежать подобной ситуации, необходимо изменять значения
коэффициентов в процессе вывода.
Введем следующие обозначения:
AverageLinkCount — среднее число связей для дизъюнкта;
AverageClauseLength — среднее число предикатных литер в дизъ-
дизъюнкте.
Тогда можно предложить следующие значения коэффициентов к\
и fc2: к\ = AverageLinkCount/AverageClauseLength и кч = 1. В этом
случае оба принципа A) и B) учитываются одинаково на протяжении
всего процесса вывода. Окончательный вид эвристической функции
оценки дизъюнкта:
AverageLinkCount
ClauseNumberOiLiterals+
AverageClauseLength
+ ClauseNumberOfLinks.
2.5.2.2. Вычисление эвристической оценки унификатора.
Эвристическая оценка унификатора обязана учитывать принцип D)
4*

100 Вывод на графе связей [Гл. 2
(унификаторы резольвируемой связи должны иметь подстановки ви-
вида с/ж, где с — константный или функциональный терм, х — перемен-
переменная). Также эвристическая функция учитывает изменение значений
характеристик графа.
Пусть Unineur — значение эвристической оценки для унификатора.
Тогда вычисляем значение Unineur следующим образом:
AverageLinkCount
ШНеиг ~
NumberOfConstantSubst + NumberOfFuncSubst'
где NumberOfConstantSubst — число подстановок в унифика-
унификаторе вида {с/ж}, (с — константный терм, а х — переменная);
NumberOfFuncSubst — число подстановок в унификаторе вида {//ж},
(/ — функциональный терм, а х — переменная).
2.5.2.3. Вычисление эвристической оценки предикатной
литеры. Эвристическая оценка предикатной литеры обязана учи-
учитывать также принцип C) (число связей у литер, по которым резоль-
вируются дизъюнкты, должно быть минимальным), а сама эвристи-
эвристическая функция учитывает изменение значений характеристик графа.
Пусть PredHeur — значение эвристической оценки для предикатной
литеры. Тогда вычисляем значение PredHeur следующим образом:
PredHeur = PredNumberOfLinks • AverageClauseLength,
где PredNumberOfLinks — число связей предикатной литеры.
2.5.2.4- Выбор коэффициентов. Коэффициенты fcUnb ^clause?
/Cpred выбираются опытным путем. При моделировании были выбраны
следующие отношения коэффициентов: kun\ = /cpred = A/10) • kc\ause.
При данном соотношении коэффициентов больший вес придается
принципам A) и B).
Таким образом, в эвристической функции HI учитываются все
принципы A)—D), причем существует возможность изменения весов
каждого из этих принципов. Также учитываются возможные измене-
изменения характеристик графа.
Применение эвристической функции HI позволило улучшить эф-
эффективность работы алгоритмов параллельного вывода на задачах
практической сложности.
2.5.3. Применение эвристической функции HI при решении задачи
« Стимро ллер »
В данном разделе остановимся более подробно не на результатах, а
на процессе работы алгоритмов параллельного дедуктивного вывода
на задаче «Стимроллер».
Задача «Стимроллер» была сформулирована Шубертом в 1978 г. в
качестве тестовой для систем автоматического доказательства теорем

2.5] Модификация процедур параллельного вывода 101
и подробно рассмотрена Стикелем. Она заключается в нахождении
логической корректности следующего рассуждения.
A) Существуют волки, лисы, птицы, гусеницы и улитки. B) Волки,
лисы, птицы, гусеницы и улитки — животные. C) Существуют злаки.
D) Злаки — растения. E) Каждое животное либо ест все растения,
либо ест всех животных, которые меньше него и едят некоторые
растения. F) Гусеницы и улитки меньше птиц. G) Птицы меньше лис.
(8) Лисы меньше волков. (9) Волки не едят лис и злаки. A0) Птицы
едят гусениц. A1) Птицы не едят улиток. A2) Гусеницы и улитки
едят некоторые растения. Следовательно, A3) существует животное,
которое ест некоторых питающихся злаками животных.
Запишем условие задачи «Стимроллер» на языке исчисления пре-
предикатов первого порядка. Каждое из понятий можно представить
соответствующим предикатом. Введем предикаты, которые будем ис-
использовать при формальном доказательстве.
А(Х) : X — животное;
В(Х) : X — птица;
С(Х) : X — гусеница;
F(X) : X - лиса;
G{X) : X — злак;
Р(Х) : X — растение;
S(X) : X — улитка;
W(X) : X - волк;
E(X,Y) : ХестУ;
М(Х, Y) : X меньше, чем Y.
Множество посылок задачи может быть записано следующим об-
образом:
1) W(w) (Существуют волки)
2) F(f) (Существуют лисы)
3) В(Ъ) (Существуют птицы)
4) С {с) (Существуют гусеницы)
5) S(s) (Существуют улитки)
6) G(g) (Существуют злаки)
7) ^W(X) V A(X) (Волки — животные)
8) ^F(X) V A(X) (Лисы — животные)
9) ^В(Х) V А(Х) (Птицы — животные)
10) -'С(Х) V А(Х) (Гусеницы — животные)
11) ^S(X) V A(X) (Улитки — животные)
12) --G(X) V P(X) (Злаки — растения)

102 Вывод на графе связей [Гл. 2
13) ^А(Х)V^A(Z) V^P(F)V-.P(V)VE(X, Y)V^M(Z, X)V^E(Z, V)V
V.E7(X, Z) (Каждое животное либо ест все растения, либо ест всех
животных, которые меньше него и едят некоторые растения)
14) -.С(Х) V -пБ(У) V М(Х, У) (Гусеницы меньше птиц)
15) ^S(X) V --Б(У) V М(Х, У) (Улитки меньше птиц)
16) ^В(Х) V --F(y) V М(Х, У) (Птицы меньше лис)
17) -F(X) V --И^(У) V М(Х, У) (Лисы меньше волков)
18) ^W(X) V --F(y) V ^Е(Х, У) (Волки не едят лис)
19) ^W(X) V --С(У) V -.Я(Х, У) (Волки не едят злаки)
20) ^В(Х) V ^C(Y) V ^(X, У) (Птицы едят гусениц)
21) ^В(Х) V --5(У) V --^(Х, У) (Птицы не едят улиток)
23) ^с\х)УЕ{ХМХ)) )(Гусеницы едят некоторые растения)
24 ^(X)VP(i(X) 1.л. ,
25) ->5(Х) V Е(Х i(X)) )(Улитки едят некотоРые растения)
где X, У, Z, У — переменные, w, /, 6, с, 5, ^ — константы, /г и г — сколе-
мовские функции.
Заключение задачи можно записать следующим образом:
3X3Y(A(X) & А(У) & (?(Х, У) & 3Z(G(Z) & Я(У, Z)))) или его
отрицание в виде
26) ^А(Х) V -.А(У) V --G(Z) V --^(Х, У) V -.^(У, Z) (Не существует
животного, которое ест некоторых, питающихся злаками, жи-
животных)
Необходимо отметить, что существует несколько вариантов записи
дизъюнкта для заключения задачи «Стимроллер».
Задача «Стимроллер» характеризуется экспоненциальным ростом
пространства поиска, поэтому для эффективной работы при решении
данной задачи процедура вывода должна, во-первых, по возможности
сокращать множество дизъюнктов и, во-вторых, выбирать наилуч-
наилучшие, или близкие к наилучшим, связи для резольвирования. (Под наи-
наилучшими связями мы понимаем связи, резольвирование по которым
приближает нас к решению задачи).
Очевидно, что программы автоматического доказательства тео-
теорем не всегда принимают оптимальные решения на различных эта-
этапах процесса доказательства. Для эффективного решения задач во
многих случаях требуется дополнительная информация об исходном
множестве дизъюнктов. Нами была сделана попытка создания мощ-
мощной процедуры дедуктивного вывода, не требующей дополнительной
информации для решения поставленной задачи. Для этого процедура
дедуктивного вывода на графе связей была распараллелена. Кроме
того, были разработаны эвристические функции оценки связи.

2.5] Модификация процедур параллельного вывода 103
В результате сравнения выясняется, что «ход рассуждения» авто-
автоматической процедуры мало совпадает с человеческим. Человек при
решении старается разбивать задачу на подзадачи и делать общие, а
не частные выводы (например, «Волки не едят растения» или «Птицы
едят растения»). Автоматическая же процедура вывода пытается по-
получить множество частных фактов (например, «Лиса / ест птицу Ь»)
и пробует найти доказательство путем подстановки частных фактов
в исходные посылки. Данный факт говорит о том, что при создании
процедур не удалось произвести хотя бы приблизительное моделиро-
моделирование хода рассуждений человека.
Несмотря на это, на некоторых шагах резольвирования процедуры
вывода принимали верные решения. Например, в процессе решения
задачи методом OR-параллельного вывода было получено следующее
множество дизъюнктов:
S = (l)US',
где
A) = ^А(Х) V ^A(f) V ^P(g) V ВД g) V -М(/, X) V ВД /),
S1 = {М(/, w), A(w), A(/), P(g), ^E(w, /), ^E(w, g)}.
Очевидно, что данное множество дизъюнктов является невыпол-
невыполнимым, и доказательство этого сводится к поочередному резольви-
рованию дизъюнкта 1 и дизъюнктов из подмножества S'. Но данное
множество является подмножеством общего множества дизъюнктов,
в которое входит около 200 дизъюнктов. Таким образом, нахождение
именно этого невыполнимого подмножества и его последовательное
опровержение является сложной задачей для процедуры автомати-
автоматического доказательства теорем. Однако процедура OR-параллельного
опровержения смогла найти это подмножество и доказать его невы-
невыполнимость максимально коротким способом.
Процедура AND-параллельного вывода нашла доказательство при
обработке множества из 225 дизъюнктов, встретив дизъюнкты
1. ^W(X) V -.С(У) V ^B(Z) V ^F(V)
2. W(w)
3. F(f)
4. В(Ъ)
5. G(g)
Процедура DCDP-параллельного вывода показала наилучшие ре-
результаты и получила больше всего фактов, совпадающих с человече-
человеческим ходом рассуждений. Это объясняется наибольшей чувствитель-
чувствительностью процедуры DCDP-вывода к выбору эвристической функции.

104 Вывод на графе связей [Гл. 2
Несмотря на выбор неоптимальных связей для резольвирова-
ния, процедуры параллельного вывода показали неплохие результа-
результаты. Количество промежуточных дизъюнктов для процедуры DCDP-
параллельного резольвирования составило 200, а количество унифи-
унификаций — 2200. На некоторых шагах резольвирования, как было ука-
указано выше, процедуры вывода действовали весьма «разумно». Таким
образом, выбор эвристической функции HI повысил эффективность
процесса вывода.
2.6. Сравнение эффективности
Сравнение процедур вывода является сложной задачей. Матема-
Математический анализ эффективности редко применим, поэтому обычно
используется сравнительный анализ алгоритмов на основе результа-
результатов работы алгоритмов на наиболее известных задачах логического
программирования. К таким задачам относятся задачи «Задача о N
ферзях» (при N > 10), «Ханойские башни» (при количестве башен
п > 5), а также задача «Стимроллер».
В данной ситуации особое значение приобретает способность ал-
алгоритма проводить направленный вывод, не генерировать излишних
дизъюнктов, а также быстро определять кандидатов на резольвиро-
вание и получать соответствующую резольвенту. Подобным требо-
требованиям удовлетворяют алгоритмы дедуктивного вывода на графах
связей, так как пространство поиска на каждом шаге является легко
обозримым (в графе одновременно хранится информация обо всех
кандидатах на резольвирование), дизъюнкты, которые не могут ре-
результативно участвовать в процессе вывода (дизъюнкты с чистыми
литерами — литерами без связей), удаляются из графа связей вместе
со всеми связями, значительно упрощая его структуру. Быстрота
вывода обеспечивается однократным вычислением и постоянным хра-
хранением унификатора для каждой связи. Также достоинством про-
процедуры вывода на графе связей является возможность адаптации
существующих алгоритмов для вывода на графе связей, что позволяет
комбинировать достоинства существующих алгоритмов вывода и ал-
алгоритмов вывода на графах связей. Недостатками процедуры вывода
на графе связей являются необходимость пересчета графа связей на
каждом шаге резольвирования с вычислением новых связей и унифи-
унификаторов и необходимость хранения всего графа связей в оперативной
памяти. Параллельный вывод на графах связей позволяет частично
решить проблему необходимости пересчета графа на каждом шаге
резольвирования, так как одновременно резольвируются несколько
связей. Недостатком процедур параллельного вывода является гене-
генерация некоторого количества бесполезных, лишних дизъюнктов, что
вытекает из самого принципа организации параллельного вывода,
когда резольвируются все связи одновременно. В данной ситуации

2.6]
Сравнение эффективности
105
является целесообразным резольвировать те множества связей, удале-
удаление которых после резольвирования позволит максимально упростить
граф связей.
Подобная попытка, путем введения эвристической функции выбо-
выбора следующей связи, была реализована в алгоритме параллельного
резольвирования.
Ниже рассмотрены результаты работы нескольких алгоритмов де-
дедуктивного вывода на графе связей, разработанных другими автора-
авторами, на тестовой задаче «Стимроллер». Результаты вывода без исполь-
использования многосортных логик для задачи «Стимроллер» представлены
на рис. 2.11а, б.
12000
10500
9000
7500
6000
4500
3000
1500
а) Количество успешных унификаций б) Количество промежуточных дизъюнктов
Stfckei/CG-SOS-TR Щ McCune/UR
Stickel/CG
Stlckel/CG-TR
McCune/LUR
DP-параллельный
зод на графе связей
AND-параллельный
вывод на графе связей
OR-параллельный
вывод на графе связей
Последовательный
вывод на графе связей
Рис. 2.11. CG — стратегия вывода с использованием графа связей. SOS —
вывод на графе связей с использованием целевого утверждения, как мно-
множества поддержки. TR — вывод с использованием Theory Links, которые
являются расширением стандартного метода резолюции. UR — Вывод с
использованием Unit-резолюции — модификации метода резолюции. LUR —
Вывод с использованием Linked Unit-резолюции — модификации метода
UR-резолюции
Приведенные результаты нуждаются в пояснении. Как показано
Стикелем, к данным по сравнению эффективности алгоритмов стоит

106 Вывод на графе связей [Гл. 2
относиться весьма осторожно, так как в различных реализациях одни
и те же характеристики могут вычисляться по-разному. Особенно это
касается временных характеристик, так как они крайне зависят от
языка реализации и конфигурации машины, на которой проводился
вывод. Весьма сложно сравнивать производительность символьной
LISP-машины и компьютера с архитектурой PC. Поэтому в работу
не были включены результаты сравнения временных характеристик
программ вывода.
Такие характеристики, как число промежуточных дизъюнктов и
число унификаций, являются более общими, но и к их использованию
стоит относиться внимательно. Например, некоторые из использован-
использованных методов позволяют получать резольвенту путем одновременного
резольвирования по нескольким дизъюнктам, поэтому такая характе-
характеристика, как число промежуточных дизъюнктов меняет свой смысл. В
случае использования алгоритмов параллельного вывода может быть
более полезным использование характеристики «количество шагов
вывода», так как на каждом шаге резольвирования мы можем по-
получить больше чем один дизъюнкт.
Количество успешных унификаций также не является универсаль-
универсальной характеристикой для оценки эффективности, так как в этом слу-
случае не учитывается количество неудачных попыток унификации и не
рассматривается проблема нахождения произведения унификаторов.
В графе связей, как было сказано выше, нет необходимости в нахожде-
нахождении контрарных пар для полученных дизъюнктов резольвент, так как
они наследуют связи дизъюнктов-родителей, а унификаторы новых
связей вычисляются путем объединения унификатора связи, по кото-
которой проводилось резольвирование, и унификатора связи дизъюнкта-
родителя. Задача умножения унификаторов требует определенных
вычислительных затрат, но никак не учитывается при получении
характеристики «Количество успешных унификаций».
Таким образом, приведенная статистика является лишь приблизи-
приблизительным инструментом для сравнения алгоритмов вывода. Некоторое
отставание процедур вывода, реализованных в программе, от лучших
алгоритмов других авторов не позволяет говорить о неэффективности
разработанных алгоритмов. Наоборот, показанные результаты свиде-
свидетельствуют о достаточно высокой эффективности процедур парал-
параллельного вывода, так как они сопоставимы по производительности
с лучшими разработками в плане создания эффективных процедур
дедуктивного вывода. В качестве достоинств процедуры параллель-
параллельного вывода на графе связей стоит отметить простоту реализации,
возможность модификации с помощью применения эвристических
функций оценки, умение работать с исходным множеством дизъ-
дизъюнктов без выделения дизъюнктов-аксиом и дизъюнктов-целей, без
предварительного упорядочивания предикатных литер в дизъюнкте,

2.7] Система параллельного вывода PIS на графе связей 107
в то время как алгоритмы других авторов требуют выделения данных
параметров и более сложны в реализации.
Необходимо отметить зависимость работы алгоритмов от струк-
структуры графа связей. В графах связей с большой удельной связно-
связностью, для которых мощность множества DCDP-связей мала, наи-
наилучшие результаты показываются при использовании алгоритма OR-
параллельной резолюции. В случае низкой связности графа свя-
связей наилучшие результаты дает использование DCDP-параллельного
вывода. AND-параллельный вывод показывает наилучшие результа-
результаты, когда имеется множество однолитеральных дизъюнктов и SUN-
дизъюнкт с большим количеством литер. Таким образом, наиболее
мощной модификацией алгоритма параллельного дедуктивного вы-
вывода на графе связей было бы сочетание одновременно OR-, DCDP- и
AND-параллелизма, с выбором каждого из вариантов в зависимости
от значения эвристической оценки для множества выбранных связей.
Полученные результаты свидетельствуют о том, что процедура
параллельного вывода является одной из наиболее эффективных и
может применяться при решении задач практической сложности.
2.7. Система параллельного вывода PIS (Parallel
Inference System) на графе связей
Система PIS является законченным программным комплексом,
позволяющим вводить и обрабатывать множества дизъюнктов, а так-
также наблюдать за ходом доказательства в формульном или графиче-
графическом виде.
Процесс обработки исходного множества дизъюнктов начинается с
его ввода в систему в виде текстового файла определенного формата
или ввода в специализированном встроенном редакторе. После того,
как множество дизъюнктов введено, по желанию пользователя можно
выбрать метод доказательства теорем: последовательный, DCDP-,
OR- или AND-параллельный. Данная система разрабатывалась как
обучающая и демонстрационная, и настройка системы по автоматиче-
автоматическому выбору подходящего параллельного метода разработана в виде
дополнительной функции.
Процесс доказательства отображается на экране в виде трансфор-
трансформируемого на каждом шаге множества дизъюнктов или в виде графа
связей. По желанию пользователя возможно дублирование вывода
результатов работы системы в виде текстового файла. Также можно
выбрать шаг, с которым пользователь просматривает результаты.
В связи с ограниченным пространством и разрешающей способ-
способностью экрана, просмотр результатов в графическом виде возможен
лишь для небольших задач, что в точности соответствует обучающим
и демонстрационным целям данной разработки.

108 Вывод на графе связей [Гл. 2
Однако отсутствие визуального представления для сложных задач
не означает невозможности их решения. Расширение системы PIS за
счет надстройки автоматического выбора метода решения и матема-
математического препроцессора позволяет использовать ее для решения за-
задач практической сложности. Более подробно вопрос о необходимости
реализации такого препроцессора и результатах его использования
будет рассмотрен ниже.
Процесс доказательства теорем в системе PIS заканчивается в слу-
случае окончания выполнения алгоритма или при желании пользователя
прервать работу. При успешном завершении процесса пользователь
либо получает сообщение о выводе пустого дизъюнкта, либо видит
результат работы в виде полученного дизъюнкта ANS (список пара-
параметров) (от английского answer — ответ).
2.7.1. Автоматический выбор параллельных методов вывода
На каждом шаге необходимо принимать решение о том, какой
из параллельных методов следует применять. Сначала проверяется
возможность применения DCDP-параллельной резолюции. Для этого
строится вспомогательный граф (см. разд. 2.4.2) и находятся макси-
максимальные по мощности DCDP-множества. Если их мощность равна
1, то следует рассмотреть возможность применения OR- и AND-
параллельной резолюции. В случае, если при выборе дизъюнктов при
резольвировании удаляется только одна связь, возникает необходи-
необходимость сделать один шаг с использованием последовательного метода.
Рассмотрим работу надстройки автоматического выбора парал-
параллельного метода на примере решения тестовой задачи раскраски
карты.
Пример 2.6.
Исходное множество дизъюнктов задачи о раскраске карты:
0) {^N(x, у) V -.iVB/, z) V -,N(x, z) V С(ж, у, z)}
1) {N(r,b)}
2) {N(b,r)}
3) {N(g,r)}
4) {N(r,g)}
5) {N(b,g)}
6) {N(g,b)}
7) {^С(ж, г/, г)}, где x,y,z — переменные, г, 6, g — константы, обо-
обозначающие цвета красный, голубой и зеленый.

2.7] Система параллельного вывода PIS на графе связей 109
Строим вспомогательный граф. Все DCDP-множества имеют мощ-
мощность, равную единице. Следовательно, DCDP-параллельный алго-
алгоритм не дает преимуществ по сравнению с последовательным алго-
алгоритмом. Используем AND-параллельный алгоритм. В качестве SUN-
дизъюнкта берется 0-й дизъюнкт (как имеющий больше всего связей).
НОУ: r/x,b/y,g/z.
Таким образом, за один шаг получен пустой дизъюнкт.
2.7.2. Математический препроцессор
Необходимость математического препроцессора для обработки
множества дизъюнктов становится очевидной, если рассмотреть
задачи, классическим примером которых может служить «задача о
восьми ферзях». Более того, любая задача, требующая выполнения
некоторых математических действий для проверки истинности
условий, не может быть оптимально решена без такого препроцессора,
а в некоторых случаях решение вообще невозможно.
Математический препроцессор базируется на распознавании на
этапе предварительной обработки некоторого множества встроенных
или введенных функций. В качестве базисных используются эле-
элементарные арифметические функции: сложение (ADD), вычитание
(SUB), деление (DIV), умножение (MUL), взятие по модулю (ABS), а
также суперпозиции элементарных арифметических функций: функ-
функции модуля суммы (AADD), модуля разности (ASUB), модуля част-
частного (ADIV), модуля произведения (AMUL); операции сравнения на:
равенство (EQ), неравенство (NEQ), меньше (LT) и больше (GR), а
также логические функции NOT, AND и OR. Операндами в арифме-
арифметических функциях могут быть числовые константы и переменные,
принимающие числовые значения. Те из арифметических операций,
которые дают числовой результат, могут также использоваться в
качестве операндов. Операндами в логических функциях могут быть
те константы и переменные, которые принимают логические значе-
значения. Операции сравнения дают логический результат и могут быть
использованы в качестве операндов в логических функциях. Логи-
Логические функции тоже могут быть использованы в них в качестве
операндов. Логические функции могут также являться функциями-
ограничениями на резольвирование для того или иного дизъюнкта. В
этом случае функция присоединяется к дизъюнкту при помощи логи-
логической операции & . Тогда запись дизъюнкта выглядит следующим
образом: {(<исходный дизъюнкт>) & (<функция-ограничение>)}.
Определение 2.10. Функция называется означенной полностью,
если в ней нет операндов-переменных.
Нетрудно заметить, что для означенной полностью логической
функции всегда может быть вычислено ее значение.

110 Вывод на графе связей [Гл. 2
Резольвирование дизъюнктов с функциями-ограничениями произ-
производится только при условии, что функция означена не полностью или
означена полностью и имеет значение true. В первом случае резольви-
резольвирование производится по обычным правилам, так как в этом случае
функция-ограничение воспринимается только препроцессором, а для
остальных процедур «видим» только сам исходный дизъюнкт. Однако
процедура применения подстановки выполняется как для исходного
дизъюнкта, так и для функции-ограничения.
Если функция означена полностью и имеет значение true, то она
удаляется, и дизъюнкт приобретает стандартный вид. В том случае,
если функция означена полностью и имеет значение false, то дизъ-
дизъюнкт удаляется из множества дизъюнктов как не соответствующий
своим ограничениям.
Рассмотрим в качестве примера задачу о четырех ферзях. Условие
того, что ферзь X — Y не бьет ферзя XI — У1, можно записать в
следующем виде: Y не равен Y\ и Y\ —Y не равен модулю XI — X
(при условии, что мы задаем шаблон для расположения ферзей по оси
X и XI = 1, Х2 = 2, ХЗ = 3, Х4 = 4).
Запишем это условие для распознавания в препроцессоре. Оно
будет иметь следующий вид: AND(NEQ(F, П), NEQ(ASUB(F1, У),
SUB(X1,X))).
Тогда множество дизъюнктов для задачи о четырех ферзях можно
записать следующим образом:
Пример 2.7.
{queen(l, 1)}
{queen(l, 2)}
{queen(l, 3)}
{queen(l, 4)}
{queenB,1)}
{queenB,2)}
{queenB,3)}
{queenB, 4)}
{queenC,1)}
{queenC, 2)}
{queenCJ3)}
{queenCJ 4)}
{queenD:, 1)}
{queen(A,2)}
{queenD:, 3)}
{queenD:J 4)}
J ( —1/77/ ppfi [ 1 T^O I \/ —\Ctll PPH ( ^) "VГ~\ I \/ —\Ctll PPll ( *\ "V^^) I \/ —\Ctll PPH ( A. "V'*\ I \/
V ANS(rO,ri,F2,r3)) & (AND(NEQ(F0,ri), NEQ(ASUB(ri,F0),
1)) & AND(NEQ(rO,r2),NEQ(ASUB(F2,rO),2)) & AND(NEQ(F0,
УЗ), NEQ(ASUB(F3,rO), 3)) & AND(NEQ(ri,F2), NEQ(ASUB(F2,

2.7] Система параллельного вывода PIS на графе связей 111
У1), 1)) & AND(NEQ(ri,F3), NEQ(ASUB(F3,ri), 2)) &
AND(NEQ(F2,r3), NEQ(ASUB(F3,r2), 1)))},
где сначала задаются все возможные расположения ферзей на поле
4 х 4, а затем описывается правило их расстановки, причем функции
имеют в данной ситуации смысл ограничений.
На каждом шаге препроцессор просматривает множество дизъ-
дизъюнктов, чтобы выполнить все математические операции. Как только
найдена функция со всеми означенными операндами, препроцессор
выполняет действия над ними и меняет функцию на ее результат.
Это приводит к тому, что другие функции становятся означенными и
т. д. до тех пор, пока не останется больше неозначенных функций.
Например, если на N-м шаге после резольвирования последнего
дизъюнкта и дизъюнкта {queen(l, 3)} (НОУC/У0)) была получена
резольвента
{(-^queenB,Yl) V ^queenC,Y2) V ^queenD,Y3)V ANSC,ri,F2,
УЗ)) & (AND(NEQC,yi), NEQ(ASUB(yi,3), 1)) & AND(NEQC,
У2), NEQ(ASUB(y2,3), 2)) & AND(NEQC,y3), NEQ(ASUB(y3,3),
3)) & AND(NEQ(yi,y2),NEQ(ASUB(y2,yi), 1)) & AND(NEQ(yi,
УЗ), NEQ(ASUB(y3,yi),2)) & AND(NEQ(y2,y3), NEQ(ASUB(y3,
Y2), 1)))} (#),
то препроцессор не может ничего упростить. Однако, если на следу-
следующем шаге резольвировать полученный дизъюнкт [К) и дизъюнкт
{queenB,1)} (НОУ{1/У1}), то резольвента {К + 1), имеющая вид
{(-.дгхеегсC,У2) V -.дгхеегсD,УЗ)У ANSC,1, У2, УЗ)) &
& (AND(NEQC, 1), NEQ(ASUBA, 3), 1)) & AND(NEQC,y2),
NEQ(ASUB(y2,3),2)) & AND(NEQC,y3), NEQ(ASUB(y3,3), 3)) &
& AND(NEQ(l,y2), NEQ(ASUB(y2,1), 1)) & AND(NEQ(l,y3),
NEQ(ASUB(y3,l), 2)) & AND(NEQ(y2,y3), NEQ(ASUB(y3,y2),
может быть упрощена во время работы препроцессора, так
как AND(True,NEQ(ASUB(l,3),l)) = AND(True,NEQB,1)) =
= AND (True, True) = True и, следовательно, (К + 1) будет иметь
вид
{(-.дгхеепC,У2) V ^queenD,Y3)V ANSC,1, У2, УЗ)) &
& (AND(NEQC,y2), NEQ(ASUB(y2,3), 2)) & AND(NEQC,y3),
NEQ(ASUB(y3,3),3)) & AND(NEQ(l,y2), NEQ(ASUB(y2,1), 1)) &
& AND(NEQ(l,y3), NEQ(ASUB(y3,l), 2)) & AND(NEQ(y2,y3),
NEQ(ASUB(y3,y2), 1))) } (if + 1).
Для того, чтобы ускорить процесс вычисления, в системе преду-
предусмотрен ввод нестандартных функций. Для этого объявляется пере-
перечень имен и тел функций в определенном формате. Тело функции
пишется в нотации языка Си и затем компилируется в системе.
Рассмотрим в качестве примера описанную выше задачу о четырех
ферзях. Введем функцию-ограничение СОШ1ЕСТ(У0, У1, У2, УЗ). Ее
тело можно записать в нотации языка Си следующим образом:

112 Вывод на графе связей [Гл. 2
{return((TO != Yl) && (abs(Fl -ГО) != 1) & & (ГО != У2) &&
(abs(F2 - ГО) != 2) & & (ГО != УЗ) & & (аЬй(УЗ - УО) != 3) & &
(У1 != У2) && (аЬ8(У2 - У1) != 1) & & (У1 != УЗ) &&
(аЬй(УЗ - У1) != 2) & & (У2 != УЗ) && (аЬй(УЗ - У2) != 1))}.
Тогда правило расстановки ферзей будет иметь вид
{(-^queen(l, УО) V ^queenB, Yl) V -.gueenC, У2) V -.gueenD, Y3)W
V ANS(Vo,yi,y2,y3)) & СОККЕСТ(У0,У1,У2,УЗ)}.
После этого работа с введенной функцией не отличается от работы
со встроенными функциями. Ускорение происходит за счет того, что
запись математических операций и их выполнение в качестве функ-
функций языка Си может быть во много раз быстрее, чем выполнение этих
операций, записанных в виде встроенных функций. К тому же запись
получается более наглядной и компактной.
2.7.3. Методы ускорения и анализ результатов для задачи
о N ферзях
Результат программной реализации процесса опровержения с по-
помощью графа связи Ковальского можно рассматривать по-разному.
Во-первых, установлена принципиальная возможность реализации
данного метода на ЭВМ. Во-вторых, показаны способы эффективного
распараллеливания на базе графа связи Ковальского. Данная реали-
реализация позволяет также выявить некоторые возможности ускорения
процесса опровержения, которые оказываются весьма существенными
для ряда классов задач. Получены также количественные оценки
ускорения параллельного вывода относительно последовательного.
Один из основных методов ускорения — сокращение перебора
возможных кандидатов на резольвирование при AND-параллельной
резолюции графа связи за счет использования функций-ограничений.
Рассмотрим его более подробно. Допустим, что на некотором шаге
мы выбрали SUN-дизъюнкт S = si V S2 V ... V sn и определили
множество сателлитных дизъюнктов Si, S2,..., Sn. В самом простом
случае каждая литера SUN-дизъюнкта соединена только с одним из
сателлитных дизъюнктов. Этот случай не подлежит упрощению за
счет сокращения перебора связей. Однако для ряда задач, напри-
например, для раскрасок карт, для задачи о N ферзях и прочих, своди-
сводимых к ним, подграф в общем случае имеет вид, представленный на
рис. 2.12.
В таком подграфе при поиске согласованного НОУ необходим пол-
полный перебор всех комбинаций связей. Для уменьшения этого перебора
используются как условия согласованности унификатора (см. опреде-
определение 2.7), так и функции-ограничения. Идея состоит в следующем.
Пусть мы имеем комбинацию S^, Si2,..., S^, где ii,..., ц G {1,..., n}.
В том случае, если для первых к ^ п элементов Si*, Si*,..., Si* данной

2.7]
Система параллельного вывода PIS на графе связей
113
Рис. 2.12
комбинации установлен факт их несоответствия условию согласо-
согласованности или функции-ограничению, то не имеет смысла не только
проверять оставшиеся элемен-
элементы, но и все другие комбина-
комбинации, начинающиеся с элементов
Si*, Si*,..., Si*. Это очевидное
ограничение перебора приводит
к хорошим результатам на прак-
практике.
Рассмотрим снова при-
пример 2.7. Существует 256 вариантов подстановки значений в
функцию CORRECT(yO, У1, У2, УЗ). Ограничение резольвирования
по условию согласованности унификатора здесь не работает, так как
все предикаты содержат разные переменные. Поэтому используем
функцию-ограничение. Для упрощения индексации дизъюнктов,
являющихся сателлитными, будем записывать лишь значения Yi, т. е.
комбинация A, 2, 3, 4) определяет попытку резольвирования дизъ-
дизъюнкта (^queen(\, УО) V'^queenB, У1) V^^ixeenC, У2) V^^ixeenD, У3)\/
V АМ8(У0,У1,У2,УЗ)) & CORRECT(yO,yi,y2, УЗ) с дизъюнкта-
дизъюнктами queen(l,l), queenB,2), queen(b, 3) и g?xeenD,4).
Теперь рассмотрим, какие же из этих комбинаций действитель-
действительно необходимо проверять, учитывая функцию-ограничение из при-
примера 2.7:
У0 = 1, У1 = 1 (не выполняется условие У0!= У1);
УО = 1, У1 = 2 (не выполняется условие abs(yi — У0)!= 1);
УО = 1, У1 = 3,У2 = 1 (не выполняется условие У0!= У2);
УО = 1, У1 = 3,У2 = 2 (не выполняется условие аЬв(У2 - У1)!= 1);
УО = 1, У1 = 3,У2 = 3 (не выполняется условие У1!= У2);
УО = 1, У1 = 3,У2 = 4 (не выполняется условие abs(Y2 — У1)!= 1);
УО = 1, У1 = 4,У2 = 1 (не выполняется условие У0!= У2);
УО = 1, У1 = 4,У2 = 2 (не выполняется условие abs(Y2 - У0)!= 1);
УО = 1, У1 = 4,У2 = 3 (не выполняется условие abs(Y2 — У1)!= 1);
УО = 1, У1 = 4,У2 = 4 (не выполняется условие У1!= У2);
УО = 2, У1 = 1 (не выполняется условие abs(yi — У0)!= 1);
У0 = 2, У1 = 2 (не выполняется условие У0!= У1);
УО = 2, У1 = 3 (не выполняется условие abs(yi — У0)!= 1);
УО = 2, У1 = 4, У2 = 1, УЗ = 1 (не выполняется условие У2! = УЗ);
У0 = 2, У1 = 4, У2 = 1, УЗ = 2 (не выполняется условие
аЬй(УЗ-У2)!= 1);
У0 = 2, У1 = 4, У2 = 1, УЗ = 3 (получена необходимая комбинация).

114
Вывод на графе связей
[Гл.2
СМ
СМ
I
1 о
Й
Он
И1С
и
о
§
^ ^
О
СМ
о
т—1
_Г
^ N
СМ
^"
со"
со
X
о
т—1
т—|
со"
со"
оо"
о
т—1
ю"
см"
ь-"
со
о
X
о
т—1
о
со
со
ю
00
о"
т—1
т—1
СО
т—1
т—1
см
ь-"
со
см
X
см
т—1
о
см
см
^г
со"
ю"
см
т—1
о
т—1
со"
т—1
см"
оо"
т—1
со
X
о
т—1
=
см
т—1
со"
ю"
см"
со"
т—1
т—1
см
т—1
ю
т—1
СО"
т—1
ь-"
т—1
оо"
о"
со
СО
X
СО
т—1
о
о
со
и
S
ю
т—1
со"
ю"
см"
оо"
ю"
см"
т—1
СО"
со"
т—1
т—1
СО
оо"
т—1
ь-"
т—1
т—1
^"
т—1
о"
со
00
X
00
т—1
о
ю
=
т—1
со
^-^
т—1
со"
ю"
см"
^"
со"
ю"
т—1
см"
оо"
т—1
о"
ь-"
т—1
СО"
т—1
сТ
т—1
оо"
о
т—1
со"
т—1
со
о
X
о
см
о
00
см
и
S
т—1
т—1
со"
ю"
см"
^1
аГ
т—1
т—1
ю"
т—1
т—1
см
оо"
т—1
о"
см
ь-"
т—1
О5
т—1
ь-"
см"
т—1
о"
т—1
00
СО
¦^г
т—1
СО"
т—1
со"
со
т—1
см
X
т—1
см
о
со
т—1
и
S
ю
со"
ю
см"
^"
аГ
т—1
со"
т—1
оо"
т—1
о"
см
см"
см
аГ
т—1
см
о"
т—1
00
со"
со"
см
СО"
см"
т—1
ю"
т—1
ь-"
т—1
со
со
см
X
со
см
о
о
со
=
т—1
т—1
со"
ю"
см"
^"
^-Г
^^
со"
—н
ю"
т—1
аГ
т—1
т—1
см
^"
см
см
ю"
см
со"
см
СО"
оо"
о"
т—1
ь-"
т—1
СО"
оо"
т—1
см"
т—1
ь-"
т—1
см"
см
со
ю
см
X
ю
см
о
ю
со
и
S
см
т—1
со"
ю"
см"
аГ
т—Г
т—1
со"
т—1
ю"
^^
ь-"
—н
аГ
т—1
со"
см
ю"
см
ь-"
см
см
со"
см
со"
т—1
ь-"
со"
т—1
оо"
см"
т—1
см
оо"
т—1
о"
см
см"
см
со
t^
см
X
см

2.7] Система параллельного вывода PIS на графе связей 115
Заметим, что мы исследовали только 16 комбинаций, причем все,
кроме последней, — лишь частично. В том случае, если перебирать все
варианты без ограничения, то подходящий вариант был бы найден на
115-м шаге.
Если использовать классическое ограничение по условию согласо-
согласованности унификатора, то в данной задаче было бы проведено 114
резольвирований и 114 бектрекингов, прежде чем был бы получен
ответ. В нашем случае мы имеем лишь одно резольвирование.
Для задач типа раскраски карты условие согласованного уни-
унификатора работает подобно функции-ограничению и также дает
значительное сокращение перебора. При условии применения тако-
такого сокращения опровержение графа связи с использованием AND-
параллельной резолюции дает ускорение в 5-10 раз по сравнению с
AND-параллельной резолюцией с полным перебором и в 50-70 раз по
сравнению с последовательным опровержением.
2.7.4. Полученные результаты
Решение задачи о N ферзях с использованием AND-параллельной
резолюции и функций-ограничений в том виде, как это описано в
разд. 2.7.2, приводит к результатам, представленным в табл. 2.2.
Применение DCDP-параллельной резолюции для задач этого клас-
класса не дает ускорения относительно последовательной резолюции, так
как мощность всех возможных DCDP-множеств не превышает еди-
единицы.

Узкая полосынька
Клиношком сошлась, —
Не вовремя косынька
На две расплелась!
Н. Клюев
Глава 3
ВЫВОД НА ГРАФЕ ДИЗЪЮНКТОВ
В данной главе рассматриваются типы параллелизма в дедуктив-
дедуктивном выводе: параллелизм на уровне термов, на уровне дизъюнктов и
на уровне поиска. Описывается алгоритм дедукции на раскрашенных
графах дизъюнктов с использованием операторов удаления и расщеп-
расщепления вершин, и приводятся пять типов параллелизма, возникающих
в этом алгоритме. Дается сравнение процедур вывода на тестовой
задаче «Стимроллер».
3.1. Типы параллелизма в дедуктивном выводе
Так как система дедуктивного вывода в общем случае недетер-
минирована, проблема управления поиском вывода актуальна для
построения эффективных решателей проблем. Одним из путей реше-
решения этой проблемы является параллелизм, который может быть реа-
реализован как мулытипоиск и распределенный поиск. В мультипоиске
стратегии приписывают каждому параллельному процессу свой план
поиска, в то время как стратегии распределенного поиска выдают
каждому параллельному процессу свою порцию пространства поиска.
Эти два подхода не являются взаимоисключающими, между ними
имеется связь.
Говоря о стратегиях поиска, прежде всего следует упомянуть о
стратегиях, основанных на упорядочении (ordering-based strategies).
Необходимо отметить, что среди них имеются как стратегии, ориен-
ориентированные на расширение (expansion) множества дизъюнктов, по-
получаемого путем резолюции, так и на сокращение (contraction) это-
этого множества путем поглощения. Упорядочение здесь понимается
как наличие обоснованного порядка среди дизъюнктов, подлежащих
процедуре поиска вывода. Стратегии, основанные на упорядочении,
используют поиск только «наилучшего» (с применением эвристик)
и, как правило, не очень восприимчивы к разрешению целей. Од-
Однако использование в них семантических (например, семантической
резолюции) или поддерживающих (резолюция множества поддержки)
требований настраивает поиск на разрешение целей. Стратегии, осно-

3.1] Типы параллелизма в дедуктивном выводе 117
ванные на упорядочении, являются синтетическими, получаемыми
образованием одних цепочек вывода из других.
Другим типом стратегий является стратегия редукции подцелей
(subgoal-reduction strategy), реализованная в линейной резолюции или
в аналитических таблицах (см. главу 4). Название этой стратегии
подчеркивает тот факт, что вычисление цели состоит в редукции ее
подцелей и затем их разрешении, как это имеет место в линейной
резолюции. Если в подходе, основанном на упорядочении, стратегии
ограничивают поиск наложением некоторых локальных требований
на каждый шаг вывода, то стратегии редукции подцелей ограничива-
ограничивают поиск наложением требований на саму форму вывода, например,
в линейной резолюции имеем линейное дерево вывода. Эти стратегии
являются по сути аналитическими, так как при выводе происходит
разложение формулы на подформулы, и ищется их невыполнимость
(в случае методов опровержения). Стратегии редуцирования подцелей
обычно используют поиск только в глубину вместе с бектрекингом,
хотя в принципе линейное опровержение можно найти, используя
любой план поиска, включая поиск только в ширину или «наилуч-
«наилучшего». Однако поиск только в глубину предпочтителен вследствие
построения за один раз только одной ветви доказательства, и только
при неудаче происходит возврат и построение другой ветви.
При классификации параллелизма дедуктивного вывода будем
различать:
• параллелизм на уровне термов (parallelism at the term level);
• параллелизм на уровне дизъюнктов (parallelism at the clause
level);
• параллелизм на уровне поиска (parallelism at the search level).
Типы параллелизма в дедуктивном выводе представлены на
рис. 3.1.
В параллелизме на уровне термов данными, над которыми мо-
может быть произведена параллельная обработка, являются термы или
литеры. В методах доказательства теорем имеет место параллельное
сопоставление литер и параллельная унификация, когда термы под-
подставляются параллельно вместо переменных. В системах переписыва-
переписывания имеет место параллельное переписывание термов. Этот вид па-
параллелизма относится к параллелизму низшего уровня и отличается
довольно большой связностью между данными.
В параллелизме на уровне дизъюнктов данными, над которыми
производится параллельная обработка, являются формулы некоторо-
некоторого языка. В системах, основанных на языке Пролог, имеет место AND-
параллелизм и OR-параллелизм. Другие типы параллельных выводов
были рассмотрены в главе 2. В данной главе также будут описаны
некоторые формы параллелизма на графовых структурах.

118
Вывод на графе дизъюнктов
[Гл. 3
Параллелизм
на уровне термов
Параллелизм
на уровне дизъюнктов
Параллелизм
на уровне поиска
Параллельное
сопоставление
Параллельная
унификация
Параллельное
переписывание
термов
AND-параллелизм
OR-параллелизм
Другие формы
параллельных
выводов
Рис. 3.1
Гомогенные
системы
вывода
Распреде-
Распределенный
поиск
X
Гетерогенные
системы
вывода
Мульти-
поиск
Отметим, что проблема управления на этом уровне представляется
как проблема расписания задач. Управление параллельными вывода-
выводами с помощью расписания задач осуществляется применением как
стратегий, основанных на упорядочении, так и стратегий редукции
подцелей.
В параллелизме на уровне поиска различают распределенный по-
поиск и мультипоиск. Ключевой фактор в классификации методов с
параллельным поиском заключается в дифференциации и комбини-
комбинировании активности дедуктивных процессов. Принцип разделения
пространства поиска на ряд подпространств положен в основу распре-
распределенного поиска, в котором существенную роль играет организация
связи между порциями пространства.
Другая возможность организации параллельного поиска заклю-
заключается в обработке всего пространства поиска различными планами
поиска, что осуществляется мультипоиском. Чтобы каждый процесс
мог воспользоваться результатами других процессов, здесь также
необходима связь между ними.
Еще одна возможность параллелизма на уровне поиска представ-
представляется в допущении процессам иметь разные или одну и ту же систему
вывода. В первом случае такую систему вывода назовем гетероген-
гетерогенной, а в последнем — гомогенной. В гетерогенных системах вывода
параллелизм применяется для комбинирования стратегий редукции
подцелей и стратегий, основанных на упорядочении, причем для про-
процессов редукции подцелей имеется возможность использования дизъ-
дизъюнктов, образованных процессами, основанными на упорядочении.
Рассмотрим подробнее типы параллелизма в дедуктивном выводе
на графовых структурах, названных С-графами (Clause graphs).

3.2] Последовательный алгоритм вывода на раскрашенных графах 119
3.2. Последовательный алгоритм вывода
на раскрашенных графах дизъюнктов
Как и в выводе на графе связей данный вывод относится к резо-
люционному типу и является методом опровержения.
Исходное множество дизъюнктов будем представлять в имплика-
тивной форме. Граф дизъюнктов состоит из дизъюнктных вершин,
т. е. вершин, которым соответствуют исходные дизъюнкты, предикат-
предикатных вершин (на рисунках — овальные вершины) и дуг, взвешенных
предикатами и помеченных двумя цветами.
Рассмотрим правило раскраски графов дизъюнктов: если имеется
дизъюнкт вида А —> Б, то условие дизъюнкта А будет «раскрашено»
на графе цветом Ц1 (соответствующие дуги изображены непрерыв-
непрерывной линией), а заключение — цветом Ц2 (прерывистой линией). Это
правило распространяется также на случай множества условий и
заключений дизъюнкта и на его частные случаи. Поясним сказанное
примером.
Пример 3.1.
Пусть имеется следующий набор утверждений:
1) если куб 1 находится в месте а, то куб 2 также находится в том
же месте;
2) если куб 1 находится в месте а, то куб 3 находится в месте в;
3) куб 1 находится в месте а.
В дизъюнктной форме эти утверждения имеют следующий вид:
С\) Б(куб 1,а) -> Б(куб 2, а);
С2) Б(куб 1,а) -> Б(куб 3, в);
СЗ) -> Б(куб 1, а)(или И -> Б(куб 1, а)).
Граф дизъюнктов будет иметь вид, показанный на рис. 3.2. Здесь
Съ Сг? Сз ~ исходные дизъюнкты, а В — предикатный символ. Отме-
Отметим, что если имеется утверждение типа «Куб 3 не находится в месте
а», то оно будет записано в виде
Б(куб 3,а) —> Л или Б(куб 3,а) —>, что
позволяет выражать отрицание фактов.
Представление в раскрашенном виде
графов дизъюнктов дает эффективную
индексацию информации и уменьшает
перебор при поиске нужных утвержде-
утверждений, что позволяет обрабатывать графы
большой размерности.
Такие графы дизъюнктов будем называть С-графами. Формально
С-граф задается четверкой вида L =< С, Р, F\,F2 >, где С — мно-
множество дизъюнктных вершин, Р — множество предикатных вершин,

120
Вывод на графе дизъюнктов
[Гл. 3
F\ — отображение С в Р, причем это отображение осуществляется
на дугах, «раскрашенных» цветом Ц1, и ^ - отображение С в Р,
которое осуществляется на дугах, «раскрашенных» цветом Ц2.
Опишем алгоритм преобразования С-графов для невыполнимого
множества дизъюнктов, результатом которого является получение
пустой сети — противоречия, т. е. ситуации, в которой находится как
факт, так и его отрицание (аналог пустого дизъюнкта).
Сначала рассмотрим основные операторы преобразования С-
графов. Эти операторы следующие:
1) оператор удаления вершины;
2) оператор расщепления вершины.
Будем говорить, что предикатная вершина свободна от мультидуг,
если число дуг, выходящих из одной и той же какой-нибудь другой
вершины и входящих в данную вершину, не больше единицы.
1. Оператор удаления вершины. Если в С-графе имеется вершина,
которая свободна от мультидуг, тогда граф всегда может быть преоб-
преобразован так, чтобы он не содержал этой вершины. Если таких вершин
несколько, то все они могут быть удалены из графа. Например, на
рис. 3.3,а вершины Р и R свободны от мультидуг, а вершина Q имеет
мул ьти дуги.
Рис. 3.3
Правило удаления вершины следующее: если в С-графе имеется
вершина Р и этой вершиной связаны дизъюнкты с\, с^,..., сп, то после
всевозможных резольвирований дизъюнктов с\, с^,..., сп по преди-
предикату Р из графа удаляются дизъюнкты с\, с^,..., сп и добавляются
новые дизъюнкты, полученные резольвированием ci, C2,..., сп. На-
Например, после удаления вершины R на рис. 3.3.а получаем С-граф,
который показан на рис. 3.3,6 Вершина будет также удалена из графа
в случае «чистого» дизъюнкта.
Покажем, что такое преобразование является корректным. Обо-
Обозначим оператор удаления вершины Р через Up. Сначала докажем
эквивалентность такого преобразования для фундаментальных при-
примеров.

3.2] Последовательный алгоритм вывода на раскрашенных графах 121
Допустим, имеется множество фундаментальных примеров дизъ-
дизъюнктов
S = {Р V Гь Р V Г2,..., Р V Гп, ^Р V Пь ^Р V П2,...,
где Fi, Г2,..., Гп; Щ, П2,..., Пт; Ф1, Ф2,..., Ф/ являются дизъюнкта-
дизъюнктами, которые не содержат предиката Р. Это соответствует тому, что в
С-графе предикатная вершина Р свободна от мультидуг.
После применения оператора Up множество дизъюнктов S примет
вид
Si = {Г1 V Щ,..., Ti V Пт, Г2 V Щ,..., Гп V Пь ...,
ГПУПГО,ФЬФ2,...,Ф|}.
Чтобы показать корректность (эквивалентность) [/-преобразова-
[/-преобразования, рассмотрим два случая.
1. Множество дизъюнктов S выполнимо тогда и только тогда,
когда при каждой интерпретации или {Г]_, Г2,... ,ГП}, или
{IIi, П2,... ,Пт} принимают значение И. Это значит, что
множество дизъюнктов Si также выполнимо.
2. Множество S не выполнимо тогда и только тогда,
когда S' = {ni,n2,...,nro^i^2,...^j} и S" =
= {Fi, Г2,..., Гп, Ф1, Ф2,..., Ф/} являются также невыполни-
невыполнимыми множествами. Это значит, что множество дизъюнктов Si
также не выполнимо.
Этим доказывается корректность [/-преобразования. Для доказа-
доказательства корректности (эквивалентности) [/-преобразования в общем
случае логики предикатов первого порядка применим теорему Эрбра-
на и лемму подъема.
2. Оператор расщепления вершины. Оператор расщепления вер-
вершины применяется при наличии в предикатной вершине мультидуг.
Обозначим его через Rf, что означает расщепление вершины Р по
дуге /.
Например, для С-графа на рис. 3.4,а после применения оператора
Rf образуется С-граф, изображенный на рис. 3.4,6
Формально оператор расщепления определим следующим обра-
образом. Пусть имеется множество дизъюнктов S = {Р\/Г,Ф}, где Р\/Г —
дизъюнкт, в котором компонент дизъюнкта Г содержит также литеру
Р, а Ф — любое подмножество дизъюнктов. Тогда после применения
оператора R множество S примет вид Sf = {Pi V Г, [Ф] х' ,Ф}, где
[Ф] х' означает подстановку литеры Pi вместо Р в формуле Ф.

122
Вывод на графе дизъюнктов
[Гл. 3
Рис. 3.4
Доказано, что оператор расщепления, примененный к невыпол-
невыполнимому множеству дизъюнктов, снова приводит к невыполнимому
множеству. Имеется следующая теорема.
Теорема 3.1. Пусть S — невыполнимое множество дизъюнктов,
представленное С-графом. Тогда после применения оператора рас-
расщепления вершины Rf снова получаем невыполнимое множество
дизъюнктов Si.
Алгоритм вывода пустого С-графа с использованием опера-
операторов удаления и расщепления приведен ниже.
1. Если в С-графе присутствуют вершины, к которым применим
оператор Up, то после использования этого оператора данные
вершины удаляются.
2. Если имеются вершины с мультидугами, то применяем опера-
оператор расщепления Rf -, результатом которого являются вершины,
свободные от мультидуг. После этого снова применяем оператор
U и т. д., пока не получим противоречие в графе.
Рассмотрим примеры решения задач с применением операторов
Up и Rf.
Пример 3.2.
Пусть задано следующее множество дизъюнктов:
R{x)
S(a)
Q(x)
T(x)
S(x),
Т(Ъ),
Соответствующий С-граф показан на рис. 3.5,а. При последова-
последовательном применении оператора Up получаем С-графы, показанные на
рис. 3.5,6, в, г, причем на последнем рисунке получаем противоречие.
Это говорит о том, что исходное множество дизъюнктов противоре-
противоречиво.

3.2] Последовательный алгоритм вывода на раскрашенных графах 123
Щ/ \Щх)
Рис. 3.5
о
Т(х)
О
При доказательстве противоречивости множества S в примере 3.2
мы использовали только оператор Up, так как С-граф не содержал
мультидуг. Теперь рассмотрим пример, где используются как опера-
оператор Up, так и оператор Rf.
Пример 3.3.
Пусть задано множество дизъюнктов
S(e) - .
Соответствующий С-граф показан на рис. 3.6,а. После применения
оператора Up имеем граф, представленный на рис. 3.6,6 Далее после-
последовательное применение операторов RnU приводит к получению про-
противоречивого графа. Соответствующие шаги показаны на рис. 3.6,в,
г, д, е.
Алгоритм вывода на С-графе.
1. Если в С-графе имеется вершина, которая свободна от мульти-
мультидуг, то переход к п. 2, иначе к п. 8.
2. Выделяем предикатную вершину Р, которая свободна от муль-
мультидуг.
3. Вычисляем А <- F1~1(P).

124
Вывод на графе дизъюнктов
[Гл. 3
4. Вычисляем В <- F2~1(P).
5. F ^ Аи В.
6. Резольвируем дизъюнкты из множества F по предикату Р; если
получили пустой дизъюнкт, то процедура закончилась успешно,
иначе переход к п. 7.
7. В С-граф добавляются все дизъюнкты, сгенерированные в пунк-
пункте б, и из С-графа удаляются все дизъюнкты из множества F\
переход к п. 1.
8. Применяем оператор Rf, пока не получим вершину, свободную
от мультидуг. Переход к п. 1.
Эксперименты показали, что стратегии преобразования С-графов
дают большую эффективность в интеллектуальных системах приня-
принятия решений.
3.3. Параллелизм в дедуктивном выводе на
С-графах
Прежде чем говорить о параллельном выводе на С-графах,
напомним коротко о видах параллелизма, возникающих в логическом
программировании, ориентированном в основном на языки типа
Пролог.

3.3] Параллелизм в дедуктивном выводе на С-графах 125
Обычно интерпретатор логических программ начинает
свою работу с целевого утверждения, например, такого, как
<— Р(х) & Q(x) & R(y) ? состоящего из трех подцелей Р(х), Q(x)
и R(y) и пытается с помощью принципа резолюции вывести пустой
дизъюнкт. Для этого он ищет подходящий дизъюнкт, который
разрешает подцель, скажем, Р(х) и формирует новое целевое
утверждение. В образующемся дереве вывода возникают следующие
виды параллелизма.
1. OR-параллелизм. Система вывода параллельно сопоставляет
некоторое целевое утверждение с головами дизъюнктов-
кандидатов, подходящих для такого сопоставления. При этом
параллельно происходит унификация соответствующих литер и
генерация новых дизъюнктов.
2. AND-параллелизм. Система вывода параллельно решает две или
более подцелей, находящихся в целевом утверждении. Здесь
появляются довольно сложные проблемы. Так, в вышеприве-
вышеприведенном целевом утверждении две подцели Р(х) и Q(x) имеют
общую переменную ж, и система вывода должна гарантировать,
что при параллельном разрешении этих подцелей переменная
х будет связана с одним и тем же значением. В ином случае
возникает противоречие, которое необходимо разрешить.
Будем называть переменную х простой переменной, если она появ-
появляется в дизъюнкте только один раз (конечно, при последовательной
унификации переменная будет также простой и при более чем одном
ее вхождении в дизъюнкт).
Как мы уже знаем, переменная х называется разделенной, если
она имеет более чем одно вхождение в дизъюнкт при условии парал-
параллельной унификации (т. е. один и тот же терм должен быть связан с
каждым вхождением этой переменной).
При унификации простой переменной с некоторым термом не обра-
образуется, как говорят, никакой связи, а осуществляется простая подста-
подстановка этого терма вместо переменной. При унификации разделенной
переменной с некоторым термом формируется так называемая среда
связей, представляющая собой список разделенных переменных и их
подстановок (примеров) для проверки непротиворечивости этих свя-
связей при параллельной унификации. Естественно, что система вывода
может эффективно использовать AND-параллелизм лишь при усло-
условии простых переменных и требует довольно сложной организации в
случае разделенных переменных.
В процессе доказательства утверждений в логических моделях,
реализованных в виде соответствующих С-графов, можно выделить
Здесь используется нотация языка Пролог.

126
Вывод на графе дизъюнктов
[Гл. 3
несколько типов параллелизма (используем алгоритм вывода с опера-
операторами удаления и расщепления вершин).
а. Параллелизм в процессе унификации, осуществляемый внутри
одной вершины, свободной от мультидуг. Относящиеся к предикатной
вершине дизъюнкты резольвируются по литере, принадлежащей этой
вершине, т. е. осуществляется параллельная унификация аргументов
литеры цвета 1 B) с аргументами литер-кандидатов цвета 2 A) и
параллельная генерация новых дизъюнктов.
Пример 3.4.
Имеем невыполнимое множество дизъюнктов
Cl. QkM^,
С2. M&H^Q,
СЗ. F & М -> Я,
С4. -> М,
СЬ. -> F.
В представленном на рис. 3.7,а графе, описывающем данное мно-
множество дизъюнктов, вершине М соответствуют три дизъюнкта (С1,
G2, СЗ) с литерой М цвета 1 и один дизъюнкт (С4) с литерой М
цвета 2. Их параллельная унификация (для простоты аргументы ли-
литер опущены) сопровождается также параллельной генерацией новых
дизъюнктов б, 7, 8, изображенных на рис. 3.7,6^ (причем происходит
копирование дизъюнкта 4 столько раз, сколько имеется дизъюнктов-
кандидатов на параллельную унификацию, в нашем случае 3 раза).
©
Рис. 3.7
Заметим, что параллельную унификацию не надо путать с парал-
параллельной обработкой всех аргументов литеры одновременно. В нашем
случае аргументы литеры обрабатываются последовательно.
Этот вид параллелизма соответствует OR-параллелизму в логиче-
логических программах.

3.3] Параллелизм в дедуктивном выводе на С-графах 127
б. Параллельное удаление вершин, свободных от мультидуг, не
имеющих общих дизъюнктов, т. е. параллельное применение операто-
оператора удаления вершин. Для выбора вершин, не имеющих общих дизъ-
дизъюнктов, можно применить простое эвристическое правило: выбирают-
выбираются вершины с минимальным числом дуг, связывающих их с другими
вершинами.
Пример 3.5.
Имеем невыполнимое множество дизъюнктов
Cl.
C2.
СЗ.
C4.
C5.
N -> P,
M ^T,
-> MV Д,
Сб.
C7.
C8.
C9.
CIO.
Соответствующий им граф показан на рис. 3.8,а. Параллельно
удаляем вершины Р, Q, М (возможны другие варианты). В результате
получаем граф, представленный на рис. 3.8,6 Затем аналогично уда-
удаляем одновременно вершины S и R. Получаем граф, представленный
на рис. 3.8,в.
в. Параллельная стяжка мультидуг одного цвета (если это воз-
возможно) как внутри одной вершины, так и среди множества вершин,
что соответствует получению фактор-дизъюнктов в принципе резо-
резолюции.
Пример 3.6.
На рис. 3.9,а показан граф, соответствующий следующему множе-
множеству дизъюнктов:
С2. R(uJ(x))bR(v,w)
СЗ.
Здесь для дизъюнктов 2 и 3 имеем наиболее общие унификаторы
Gi = {u/v, f(x)/w} и <72 = {f(x)/w, y/z} соответственно, что приводит
их к виду
СИ. Д(«,/(*))->,
СЗ'.
и к графу, представленному на рис. 3.9,6
г. Параллельное расщепление внутри одной вершины, имеющей
несколько мультидуг. С помощью оператора расщепления производим
параллельное расщепление внутри одной вершины, имеющей несколь-
несколько мультидуг (неважно, одного или разных цветов).

128
Вывод на графе дизъюнктов
[Гл. 3
MX М „--' / R
Рис. 3.8
с?
\I\f(x),y)
R(a,x)y \P(x,y)
Рис. 3.9

3.3]
Параллелизм в дедуктивном выводе на С-графах
129
Пример 3.7.
Имеем
С\.
С2. P(
СЗ.
С4.
Р(х,у) -+ P(f(x),y),
P(g(x),y)VP(a,z),
что соответствует графу на рис. 3.10,а. Производим параллельное рас-
расщепление трех мультидуг (трех «лепестков») вершины Р с помощью
оператора расщепления, в результате чего получаем четыре вершины
Pi, P2, Рз? Р (их число на единицу больше числа «лепестков»),
четыре копии дизъюнкта 4, три копии «расщепленного» дизъюнкта
1, две копии «расщепленного» дизъюнкта 2 с его дублированием в
вершине Р и «расщепленный» дизъюнкт 3 с его дублированием в
вершинах РиР3 (см. рис. 3.10,б').
Для наглядности введем следующий фиктивный порядок расщеп-
расщепления (хотя никакого «порядка» нет, так как все делается параллель-
5 В.Н. Вагин и др.

130
Вывод на графе дизъюнктов
[Гл. 3
но): сначала расщепляется мультидуга A—Р), затем B—Р) и, наконец,
мультидуга C — Р).
д. Параллельное расщепление нескольких вершин, имеющих муль-
тидуги. Параллельно применяем оператор расщепления к вершинам,
имеющим мультидуги.
Пример 3.8.
На рис. 3.11,а представлен граф, соответствующий следующему
множеству дизъюнктов:
С2. Р(щу)
СЗ. -
С4. Q(u,v)^.
Имеем две вершины с мультидугами, расщепление которых можно
производить параллельно. В результате получим граф, показанный на
рис. 3.11,5.
v)
Рис. 3.11
Параллельное удаление вершин, свободных от мультидуг и не
имеющих общих дизъюнктов, можно производить одновременно с
параллельной унификацией внутри этих вершин (т. е. комбинация

3.3] Параллелизм в дедуктивном выводе на С-графах 131
параллелизмов типа аи б). Аналогично, если имеется несколько вер-
вершин с мультидугами, то молено произвести параллельное расщепление
этих вершин с параллельным расщеплением внутри каждой такой
вершины (т.е. комбинация параллелизмов типа гид).
Приведем теперь параллельный алгоритм вывода на С-графах.
Алгоритм PAL
1. Если в С-графе имеются вершины, свободные от мультидуг, то
переход к п. 2, иначе к п. 8.
2. Выделяем предикатные вершины Р, Q,..., R, не имеющие общих
дизъюнктов (эвристическое правило: выбираются вершины с ми-
минимальным числом дуг, связывающих их с другими вершинами).
3. Параллельно вычисляем
А2 <- F^(Q),
Ат <- Fr\R),
где F-f^P) — отображение предикатной вершины Р в множество
дизъюнктов, ей соответствующих, для цвета 1, и А\А2,..., Ат —
списки.
4. Параллельно вычисляем
где F^X(P) — отображение вершины Р в множество дизъюнктов,
ей соответствующих, для цвета 2, и В\, ?>2, • • •, Вь — списки.
5.
D1 <- A1 иБь
D2 <— A2 иБ2,
6. Параллельное резольвирование дизъюнктов из множеств
Di, D2,..., Di по предикатам Р, Q,..., R одновременно с па-
параллельной унификацией внутри каждой предикатной вершины
Р, Q,...,i?. Если получили пустой граф (противоречие), то
процедура закончилась успешно, иначе переход к п. 7.
7. В С-граф добавляются все дизъюнкты, сгенерированные в
пункте б, и из графа удаляются все дизъюнкты из списков
5*

132 Вывод на графе дизъюнктов [Гл. 3
D\, D2,..., Di, т. е. удаляются параллельно вершины Р, Q,..., R.
Переход к п. 1.
8. Произвести параллельную стяжку мультидуг одного цвета в
вершинах Р, Q,..., R, если это возможно (что соответствует на-
нахождению фактор-дизъюнктов) и переход к п. 1, иначе переход
к п. 9.
9. Используя оператор расщепления вершины, произвести парал-
параллельное расщепление вершин с мультидугами одновременно с
параллельным расщеплением внутри каждой вершины, имею-
имеющей несколько мультидуг, до тех пор, пока не получим вершины,
свободные от мультидуг. Переход к п. 1.
Для иллюстрации алгоритма приведем пример.
Пример 3.9.
Имеем невыполнимое множество дизъюнктов, С-граф для которо-
которого представлен на рис. 3.12,а.
С1. М(с, а) & R(a, и) -> Q(f(x), z),
С2. M(z,y)bF(x,y)^H(x,z),
СЗ. М(и, v) & H(v, w) -> Q(u, w),
C4. Г(г/, г;) -> Д(а, x) V М(щ v),
Cb. -+ S(w, c) V T(x, u) V R(b, v),
C6. F(c, y) & H(x, c) & S(u, d) ^,
C7. Q{x,y)
C8.
C9.
CIO. -^F(c,a),
«Зажигаем» граф с трех сторон, т.е. активизируем вершины Q,
F, Т (на рис. 3.12,а они заштрихованы). После параллельного уда-
удаления этих вершин получаем граф, изображенный на рис. 3.12,6.
Затем последовательно удаляем вершины Н и S, причем в вершине
S дизъюнкты не унифицируемы, поэтому они удаляются вместе со
своей вершиной (см. рис. 3.12,в, г). Производим параллельную стяжку
мультидуг в вершине М и удаляем вершину R вместе со своим дизъ-
дизъюнктом. Получаем граф, показанный на рис. 3.12,Л Затем вершину
М расщепляем и имеем противоречие (см. рис. 3.12,е, ж), что говорит
о невыполнимости исходного множества дизъюнктов.
Отметим, что в предложенной процедуре параллельной дедукции
поиск и вывод осуществляется не только «сверху вниз» или «снизу
вверх» или их комбинацией, но и по всем возможным «фронтам» С-
графа одновременно. Как говорят, метод «атакует» С-граф со всех
возможных сторон.

3.3]
Параллелизм в дедуктивном выводе на С-графах
133
R(b, vp^'Siw, c) S(u,
C)
, c)
M(u, c) M(w, a)
A
M(w, a)
M(b,a) M(d, c) M,(b, a) M,(d, c) M(b, a) M(d, c) M(b, a) M{d,c)
Рис. 3.12
Алгоритм параллельного вывода может быть использован при
реализации параллельной машины вывода. Предлагавшиеся до сих
пор архитектуры параллельных машин вывода ориентированы, глав-
главным образом, на языки логического программирования типа Пролога,

134 Вывод на графе дизъюнктов [Гл. 3
которые на наш взгляд страдают существенными недостатками. Эти
недостатки связаны не только с ограниченностью процедуры вывода
(хорновские дизъюнкты, неполная входная резолюция, поиск только
«в глубину», порядок разрешения литер), но также и с тем, что языки
логического программирования на сегодняшний день ориентированы,
главным образом, на фон-неймановскую архитектуру машин, что,
конечно, является недостаточным для создания принципиально новых
образцов вычислительной техники.
3.4. Сравнение эффективности процедур
дедуктивного вывода
В главе 2 уже говорилось об эффективности различных алго-
алгоритмов вывода и приводилось сравнение процедур вывода на тесто-
тестовой задаче «Стимроллер». Напомним, что в целях уменьшения про-
пространства поиска в процессе нахождения решения и, таким образом,
сокращения времени вывода в алгоритмах дедукции используются
следующие стандартные средства, уменьшающие число промежуточ-
промежуточных дизъюнктов в резолюционных доказательствах, и две полезные
стратегии, специфичные только для алгоритма вывода на С-графах:
• применение операции факторизации (при графической интер-
интерпретации вывода эта операция названа стяжкой одноцветных
мультидуг);
• удаление дизъюнктов, связанных с «чистыми» литерами;
• удаление дизъюнктов-тавтологий;
• удаление поглощенных (subsumed) дизъюнктов;
• применение стратегии «предпочтение единичным дизъюнктам»;
• удаление дизъюнктов-дублеров;
• первоочередное удаление предикатных вершин без мультидуг;
• первоочередное удаление предикатных вершин, в которые вхо-
входит наименьшее число дуг.
На рис. 3.13,а, б представлены результаты работы нескольких
алгоритмов дедуктивного вывода на тестовой задаче «Стимроллер».
Следует отметить, что здесь не рассматриваются случаи многосорт-
многосортных логик.
Алгоритм дедуктивного вывода на раскрашенных С-графах явля-
является наиболее эффективным для решения задачи «Стимроллер», что
определяется ее представлением в виде графа дизъюнктов, который
имеет множество независимых вершин. При работе алгоритма проис-
происходит стяжка сети, на каждом шаге резольвирование идет по несколь-
нескольким вершинам, что повышает эффективность алгоритма вывода.

Истинно знать что-либо —
значит, знать его причины.
Ф. Бэкон
Глава 4
ВЫВОД НА АНАЛИТИЧЕСКИХ ТАБЛИЦАХ
Метод аналитических таблиц (или метод семантических таблиц,
или метод Хинтикка) является эффективной процедурой доказатель-
доказательства теорем, как для логики высказываний, так и для логики предика-
предикатов первого порядка. Он, как и метод резолюции, относится к методам
опровержения, т. е. для доказательства общезначимости формулы А
доказывается ее противоречие (~*А). Но если метод резолюции рабо-
работает с формулами, представленными в КНФ, то метод аналитических
таблиц оперирует с формулами, представленными в ДНФ. Вывод
осуществляется на бинарных деревьях, вершины которых отмечены
формулами, причем вершина называется концевой, если она не имеет
потомков, простой, если она имеет только одного потомка и дизъ-
дизъюнктивной, если она имеет двух потомков. Каждая ветвь дерева
представлена конъюнкцией формул, а само дерево — дизъюнкцией
своих ветвей.
4.1. Метод аналитических таблиц для логики
высказываний
Все формулы логики высказываний разделим на два класса:
мулы конъюнктивного типа или формулы а, состоящие из двух
компонент cei и «2, и формулы дизъюнктивного типа или формулы
/3, также имеющие две компоненты C\ и /?2 (табл. 4.1).
Таблица 4.1
Формулы конъюнктивного типа
а
Х&У
-(XV У)
-(* - У)
^х
ai
X
X
-.х
X
а2
Y
-У
-У
-.х
X
Формулы дизъюнктивного типа
^(Х & Y)
XVY
X^Y
Pi
^Х
X
-^х
Р2
-У
У
У

4.1]
Метод аналитических таблиц для логики высказываний
137
Таким образом, для каждого булева означивания v (т. е. приписы-
приписывания пропозициональным переменным значений И и Л) формул а и
C имеем
Отсюда для каждых а и /3 формулы се <-> (ai & a^) и /3 ^ (/?i V/^)
являются тавтологиями.
При доказательстве методом аналитических таблиц иногда вводят-
вводятся символы «И» и «Л» и определяются так называемые означенные
формулы типа ИХ или ЛХ, где X — формула логики высказывания
(неозначенная).
При любой интерпретации означенная формула ИХ является ис-
истинной, если X есть И, и ложной, если X есть Л. Также ЛХ является
истинной, если X есть Л, и ложной, если X есть И. Таким образом,
истинностное значение ИХ совпадает с формулой X, а истинностное
значение ЛХ совпадает с —lX". Отсюда табл. 4.1 для означенных фор-
формул можно переписать в виде табл. 4.2.
1аблица 4.2
Формулы конъюнктивного типа
И(Х & У)
Л(ХУУ)
Л(Х -> У)
и^х
л^х
ai
ИХ
лх
их
лх
их
ИУ
ЛУ
ЛУ
лх
их
Формулы дизъюнктивного типа
Л(Х & У)
И(Х V У)
И(Х -> У)
лх
их
лх
ЛУ
ИУ
ИУ
Введем еще два определения.
Степенью означенной формулы ИХ или ЛХ является число ло-
логических связок в формуле X. Пропозициональная переменная имеет
степень 0, такую же степень имеют И и Л. Заметим, что cei, ot^ и /?i, /?2
имеют степень меньшую, чем се и /3, а именно, г (се) = r(cei) +r(c^2) +1;
r(/3) = r(/?i) + г(/?2) + 1? где г(Х) — степень формулы X.
Сопряжением означенной формулы является результат изменения
И на Л и наоборот. Так, сопряжение ИХ есть ЛХ, а сопряжение ЛХ
есть ИХ.
Возвращаясь к табл. 4.1 и 4.2 заметим, что они могут быть обоб-
обобщены в два правила:
правило а: _с^; правило C:
C
а2

138
Вывод на аналитических таблицах
[Гл.4
Первое правило говорит, что если формула X есть се, то к дереву
надо добавить вершину, отмеченную формулой а\ и затем на этой же
ветви другую вершину, отмеченную «2- Второе правило гласит, что
если X есть /3, надо расщепить идущую от вершины C ветвь на две
ветви и вершину на левой ветви отметить формулой C\, а на другой —
формулой /?2- Возвращаясь к проблеме логического следования фор-
формулы из посылок, заметим, что для любой интерпретации, в которой
формула а истинна, истинны будут как cei, так и а^. Аналогично для
любой интерпретации, в которой формула C истинна, будет истинна
/?1 ИЛИ /?2-
Определение 1^.1. Замкнутой ветвью называется ветвь, которая
содержит формулу ИХ и ее сопряжение ЛХ, т.е. контрарную пару
(X и ^Х), или истинностное значение Л.
Определение Ji.,2. Дерево (или таблица) называется замкнутой,
если все его ветви замкнуты.
Правила а и C назовем правилами расширения таблицы
(табл. 4.3).
Таблица 4.3
-.-.X
X
^и
л
^л
и
а
а2
C
Pi\P2
Если на дереве вершина отмечена формулой ^^Х, добавим
вершину-потомок, обозначенную X. Аналогично добавляются
вершины, отмеченные Л и И для формул ^И и -J1. Формулы
типа а и C были объяснены ранее.
Поскольку метод аналитических таблиц основан на процедуре
опровержения, то для доказательства общезначимости формулы X
надо построить дерево (таблицу) для ЛХ(^Х), которое будет замк-
замкнутым.
Аналитическая таблица для X есть упорядоченное бинарное де-
дерево, вершины которого являются формулами, строящимися следу-
следующим образом. Сначала помещаем ^Х в корень дерева и расширя-
расширяем аналитическую таблицу с помощью правил расширения таблицы
(аи/3).
Дадим индуктивное определение таблицы для X. Пусть даны два
упорядоченных бинарных дерева Т\ и Т^. Будем называть Т^ непо-
непосредственным расширением дерева 7\, если Т^ может быть получено
из Т\ путем применения правил а и C. Дерево Т является аналитиче-
аналитической таблицей для X, если существует конечная последовательность
деревьев G\, Тг,... ,ТП = Т) такая, что Т\ содержит единственную
вершину, соответствующую X, и для любого г < п T^+i является
непосредственным расширением Т^.

4.1]
Метод аналитических таблиц для логики высказываний
139
Теперь докажем с помощью метода аналитических таблиц обще-
общезначимость следующей формулы:
(Q -> г)) -> ((р -^ q)
г)).
Справа от формулы будем ставить в скобках номер формулы, из
которой будет получено то или иное следствие. Для простоты во
всех примерах будем использовать неозначенные формулы, для чего
символ И будем опускать, а вместо Л ставить -п. При построении
таблицы каждая замкнутая ветвь будет заканчиваться символом П.
4. -.p
6. р^>
7. ->{р
B)
Я C)
-г) C)
10. -.р F) 11. g F)
12. рG) 14. рG)
13.-г G) 15.- г G)
? ?
18.-
22.
23.-
пр(8)
р(9)
пг(9)
19.
24.
25.-
Q
Р
-\Г
(8)
(9)
(9)
20."
26.
27.-
ip
р
(8)
(9)
(9)
21.
28.
29.
9(8)
р(9)
-г (9)
П
П
?
?
Таблица строится следующим образом. На первом шаге к исходной
формуле применяем -п. Затем используется правило се, в результате
которого имеем две формулы с номерами 2 и 3. К формуле 2 применя-
применяем правило /3, в результате которого получаем разветвление дерева на
две ветви с формулами 4 и 5. В каждой ветви к формуле 3 применяем
правило се, в результате которого получаем формулы б, 7, 8, 9. Затем
идет дальнейшее ветвление дерева по правилам C до тех пор, пока не
получаем замкнутую ветвь.
Из таблицы видно, что все ветви дерева замкнуты; это говорит о
противоречивости формулы ^Х или об общезначимости X, где X —
формула (р —> (q —> г)) —> ((р —> q) —> (р —> г)). В дальнейшем
будем замыкать ветвь символом П, как только впервые будет найдена
контрарная пара или символ Л. В данном примере шаги 13, 15, 23,
24, 25, 27 лишние, и поэтому их можно было бы игнорировать. Таким
образом, общее число шагов — 23.
При анализе данного примера нетрудно видеть, что раннее при-
применение правила C приводит к неоправданному дублированию шагов
вывода. Это значительно удлиняет процедуру вывода. Более эффек-
эффективное решение по длине шагов вывода заключается в приоритете
правила а над правилом /3, что позволит сократить повторение одной

140 Вывод на аналитических таблицах [Гл. 4
и той же формулы на различных ветвях дерева. В качестве подтвер-
подтверждения этого высказывания решим тот же самый пример, применяя
сначала правило се, а потом C.
12. -.g (9) 13. г (9)
? ?
Очевидно, что второй вывод, включающий 13 шагов, короче, чем
первый. Таким образом, приоритет правила а над правилом C позво-
позволяет в какой-то степени уменьшать недетерминированность примене-
применения этих правил.
В общем, чтобы показать, что формула G логически следует из
формул F\, F2,..., Fn, мы должны сконструировать замкнутую ана-
аналитическую таблицу для формулы ->[Fi & F2 & ... & Fn —> G] или
Fi & F2 & ... & Fn & -.G.
Теперь нам осталось показать, что метод аналитических таблиц
обладает непротиворечивостью и полнотой.
Как обычно, под непротиворечивостью будем понимать невозмож-
невозможность доказать этим методом формулу и ее отрицание одновременно.
Множество S формул логики высказываний называется выполнимым,
если имеется хотя бы одна интерпретация v (булево означивание),
на которой каждая формула из S будет истинной. Назовем некото-
некоторую ветвь дерева в выполнимой, если множество пропозициональных
формул на этой ветви выполнимо, т. е. принимает значение И. Отсюда
дерево (или таблица) Т выполнимо, если, по крайней мере, одна ветвь
на этом дереве будет выполнимой.
Пусть таблица Т2 является непосредственным расширением таб-
таблицы Т\ с помощью правил расширения таблицы (се, C ). Нетрудно
показать, что если таблица Т\ выполнима, то выполнимой будет и
таблица Т2. В силу выполнимости Т\ на этом дереве имеется, по
крайней мере, одна ветвь в, которая истинна.
Если дерево Т2 получено из Т\ добавлением вершин-потомков с
помощью правил аи C к некоторой ветви 0i, то в случае несовпадения

4.1] Метод аналитических таблиц для логики высказываний 141
01 и 0 ветвь 0 останется выполнимой. Отсюда выполнимым будет и
дерево Т2. Если 0 совпадает с 0i, то в случае применения правила а
ветвь 0 расширится на две вершины а\ иа2. Так как правило а явля-
является правилом конъюнктивного типа, то в силу v{a) = И, истинными
будут также v(a\) и v(a2). Следовательно, дерево Т2 также будет
выполнимым. Если к 0 = 01 применяется правило дизъюнктивного
типа C, то из истинности v(/3) следует, что по крайней мере одна из
ветвей v(Pi) или v(/32) будет также истинной. Отсюда и дерево Т2
тоже будет выполнимым.
Таким образом, любое расширение выполнимой таблицы также
выполнимо. Применяя метод математической индукции, получаем,
что если корень любого дерева является истинным в заданной интер-
интерпретации v, дерево (таблица) тоже будет истинным в v. Но замкнутая
таблица не может быть истинной ни при какой интерпретации, т. е.
корень замкнутой таблицы должен быть невыполнимым. Отсюда сле-
следует, что метод аналитических таблиц является непротиворечивым,
из чего вытекает теорема о состоятельности этого метода.
Теорема 4.1. Если формула X выводима (доказуема) методом
аналитических таблиц, то она общезначима.
Утверждение, обратное теореме 4.1, представляет собой полноту
метода аналитических таблиц, т. е. если формула X общезначима,
то она доказуема методом аналитических таблиц. Однако сначала
покажем, что если имеется открытая (незамкнутая) ветвь на дереве,
то таблица будет выполнимой.
Определение 4-3- Назовем ветвь 0 таблицы полной, если для
любой се-формулы, входящей в 0, сх\ и а2 также входят в 0, и для
любой /3-формулы, входящей в 0, по крайне мере, одна из формул C\
или /32 входит в 0.
Определение 4-4- Таблица Т называется полной, если любая
ветвь этой таблицы является замкнутой или полной.
Покажем, что если таблица Т является полной открытой таблицей
(открытой в том смысле, что хотя бы одна ветвь является открытой),
то корень таблицы Т является выполнимым.
Пусть 0 — полная открытая ветвь таблицы Т и Я — множество
пропозициональных формул из 0, называемое пропозициональным
множеством Хинтикка, удовлетворяющее следующим условиям:
Но: для любой пропозициональной переменной А, ни А, ни ее сопря-
сопряжение ^А не принадлежат Я одновременно;
Нц Л ^Я,-И^Я;
Я2: если -.-.Z e Я, то Z е Я;
Я3: если a G Я, то а\ G Я и а2 G Я;
Я4: если C е Я, то /?i G Я или C2 е Я.

142 Вывод на аналитических таблицах [Гл. 4
Например, пустое множество является тривиальным множеством
Хинтикка или множество всех пропозициональных переменных так-
также является множеством Н. Множество {Р & (-iQ —> R),P,(^Q —>
—> R), ——Q, Q} является множеством Хинтикка.
Лемма Хинтикка. Любое пропозициональное множество Хин-
Хинтикка выполнимо.
Эта лемма доказывается индукцией по числу логических связок
в формуле, т. е. по степени элементов из Н. Из леммы Хинтикка
вытекает доказательство следующей теоремы.
Теорема 4.2. Любая полная открытая ветвь таблицы является
выполнимой.
Приведем теорему о полноте метода аналитических таблиц.
Теорема 4.3 (о полноте). Если формула X общезначима, то она
доказуема методом аналитических таблиц.
Отсюда становится понятным, что для любой общезначимой фор-
формулы X таблица, начинающаяся с —X, должна быть замкнутой, ибо
в противном случае открытая ветвь говорила бы, что —X выполнима,
а это противоречит условию.
Пример 4.1.
Докажем методом аналитических таблиц пример, который до это-
этого был доказан с помощью принципа резолюции (см. пример 1.10 и
рис. 1.2)
(Р
* (У?
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
П
13
(g-> r), i
-i[(p —> q)
(Р - <7)&i
р —> g
g —> г
г^ I
771 —> -i/
F
т
D) 12
•-9E)
П ^
15.-г
?
& (q -> г)&
(д -^ г)& (г -
п)
•9 D)
\^
14. г E)
F) 16. 1
17.-1 m G)
П
-> ^г) к jp —>
(г_> |)& (ш
-^ 1)& (m -^
F)
^\
18.-1 G)
П
—> -iQ —> (
A)
A)
B)
B)
B)
B)
C)
C)
(9)

4.2]
Метод аналитических таблиц для логики предикатов
143
В заключение заметим, что для конечного множества Хинтикка
Н лемма Хинтикка эффективно задает интерпретацию, на которой
Н выполнимо. Если формула X не является тавтологией, то в полной
таблице для ^Х найдется контрпример, т. е. интерпретация, в которой
формула X принимает значение Л.
Пример 4.2.
Дана формула (р V q) —> (р & q). Построим полную таблицу для
этой формулы.
1.
2.
3.
-•[(pv
pVq
^(pk
a)
p&?)]
(i)
(i)
Таблица имеет две полные открытые ветви. Рассмотрим полную
открытую ветвь с концевой вершиной 7. В соответствии с теоремой
4.2, которая гласит о выполнимости полной открытой ветви, имеем
интерпретацию р — И и q — Л, в которой исходная формула ложна (или
ее отрицание выполнимо). Аналогично на другой полной открытой
ветви имеем р — Л и q — И, что также говорит о ложности исходной
формулы.
4.2. Метод аналитических таблиц для логики
предикатов первого порядка
Так как логика предикатов первого порядка является расшире-
расширением логики высказываний, то естественно к существующим ранее
формулам добавить формулы с кванторами. Одну группу формул
универсального типа назовем 7-формулами, а другую группу формул
экзистенционалъного типа — E-формулами (табл. 4.4).
Таблица 4.4
Формулы универсального типа
7
УхФ
7(а)
Формулы экзистенционального типа
6
ЗжФ
-1\/хФ
<5(а)
Ф^
Здесь а — любой параметр, а запись Ф^ означает, что в формуле Ф
переменной х присвоен параметр а. В дальнейшем присвоение будем

144
Вывод на аналитических таблицах
[Гл.4
понимать как подстановку и Ф^ — как результат подстановки а вместо
всех вхождений х в Ф.
Определим подстановку для любой формулы Ф по следующей
индуктивной схеме:
1) если Ф — атомарная формула, то Ф^ — результат подстановки
а вместо любого вхождения х в Ф;
2) [Ф & F}% = Ф* & ?%;
[Ф Vi4S = <D*VF*;
[Ф ^ F]* = Ф* ^ F*;
3)
Ф}1 = УхФ;
[Эх Ф}* = ЗжФ.
Но для переменной у, отличной от х,
Определение ^.5. Замкнутой формулой будем называть формулу
Ф такую, что для любой переменной х и любого параметра а Ф^ = Ф.
Как и раньше, введем понятие степени г(Ф) формулы Ф. Степенью
г(Ф) формулы Ф является число вхождений логических связок и
кванторов.
1. Любая атомарная формула имеет степень 0.
2. г(--Ф) =г(Ф) + 1,
г(Ф & F) = г(Ф V F) = г(Ф -^ F) =
3.
=г(Ф) + 1,
=г(Ф) + 1.
Как и для логики высказываний, если речь идет об означенных
формулах, формула 7 является формулой И[УхФ] или Л[Зх]Ф] и j(a)
является соответственно ИФ^ или ЛФ^. Аналогично формула S будет
любой формулой типа И[ЗжФ] или Л[\/жФ], а 5(а) — соответственно
^, ЛФ^ (табл. 4.5).
Таблица 4.5
Формулы универсального типа
7
И[УжФ]
Л[ЗжФ]
7(а)
ИФ?
ЛФ^
Формулы экзистенционального типа
6
И[ЗжФ]
Л[УжФ]
6(а)
ЛФ?

4.2 ] Метод аналитических таблиц для логики предикатов 145
При любой интерпретации в универсуме U будут выполняться
следующие утверждения:
F\: а истинна тогда и только тогда, когда истинны а\ и«25
F2: C истинна тогда и только тогда, когда, по крайней мере, истинна
/?1 ИЛИ /?2 5
F%: 7 истинна тогда и только тогда, когда формула j(k) истинна для
любого k Е U;
F4: S истинна тогда и только тогда, когда формула S(к) истинна, по
крайней мере, для одного к Е U.
Как следствие вышеизложенных фактов, имеем следующие зако-
законы, касающиеся выполнимости формул.
Пусть S — любое множество замкнутых формул, подобных се, /3,
7, S.
Gi: Если S выполнимо и а Е S, то {S, ai, a^} также выполнимо.
G2: Если 5 выполнимо и /3 Е 5, то, хотя бы одно из двух множеств
{#, /?i}, {S, /З2} также выполнимо.
G3: Если /S выполнимо и 7 ^ *^, то для любого параметра а множе-
множество {S, 7(a)} также выполнимо.
G4: Если S выполнимо и E Е 5 и если с — любой новый параметр,
который не является элементом 5, то {S, 5(с)} также выполнимо.
Последний закон нуждается в пояснении. Пусть по гипотезе име-
имеется интерпретация / всех предикатов из S в некотором универсуме
U и отображение V всех параметров из S в элементы из U такое, что
для каждой замкнутой формулы Ф Е S [/-замкнутая формула Фу
истинна при этой интерпретации /. В частности, Sv истинна при /.
Замкнутая формула 5V является формулой, не имеющей параметров,
но с константами из С/, и эта формула является замкнутой формулой
экзистенционального типа (назовем ее Si). Поскольку Si истинна в /,
то, согласно утверждению F±, имеется, по крайней мере, один элемент
к из U такой, что формула Si(k) истинна в интерпретации /. Теперь
отображение V определяется по всем параметрам из {S,5(c)}, за
исключением параметра с. Расширим отображение V за счет опреде-
определения V(c) = к и назовем это расширение V*. Теперь V* определяется
по всем параметрам {S,5(c)}. Очевидно, для каждой формулы Ф Е S
Ф является тем же самым выражением, что и Ф^. Таким образом,
Фу истинна в интерпретации /и [?(с)]у есть та же самая замкнутая
формула, что и Si(k). Отсюда [?(с)]у истинна в /. Следовательно,
для каждой формулы Ф Е {S,5(c)} ФУ истинна в интерпретации /.
Таким образом, множество {$, S(c)} выполнимо.
Теперь мы можем сформулировать четыре правила вывода при
работе с аналитическими таблицами, два из которых были сформули-
сформулированы для логики высказываний, а два — для логики предикатов

146 Вывод на аналитических таблицах [Гл. 4
первого порядка (возвращаясь к табл. 4.3, не забудем о правилах
вывода для ^^Х, ^И и —Л).
а
Правило а: —;
OL2
правило C:
1
правило 7: / ч ? где а — любой параметр;
l{a)
правило 5: , где с — новый параметр, не принадлежащий S.
6 (с)
В случае означенных формул правила j и 5 будут выглядеть
следующим образом:
ИУж Ф ЛЗж Ф
правило
ИФГ ЛФ!
г ИЗж Ф ЛУж Ф
правило о: х , , где с — новый параметр.
Для неозначенных формул эти два правила будут выглядеть сле-
следующим образом:
Ух Ф ^Зх Ф
правило
ф
*
_ Зх Ф -Ых Ф
правило о: ——, —, где с — новый параметр.
^с "'^с
Правила j и S также называются правилами расширения таблицы.
Поясним правило S. Это правило является формализацией нефор-
неформального аргумента, довольно часто используемого в математике.
Пусть мы доказали, что существует предмет ж, обладающий некото-
некоторым свойством Ф, т.е. доказали утверждение ЗхФ(х). Мы могли бы
ввести имя для этого предмета, скажем с, и записать Ф(с). Конечно,
мы не утверждаем, что свойство Ф выполняется для каждого с, но, по
крайней мере, для одного оно выполняется. Если мы последовательно
покажем, что для другого свойства Q существует предмет х такой,
что Q(x), то неправомерно было бы дать то же самое имя с этому
предмету, потому что с уже обладает свойством Ф, и мы не уверены,
что он имеет оба свойства Ф и Q. Естественно, лучше взять новый
константный символ или параметр, скажем 6, и считать Q(b). Это и
является причиной для оговорки в правиле S.
Безусловно, мы можем либерализовать правило E, считая, что
параметр а — новый, раньше не вводился правилом S и не входил в 5-
формулы. Идея либерализации состоит в том, что при доказательстве
замкнутой формулы типа 7, скажем УхФ(х), мы выводим Ф(а).

4.2 ] Метод аналитических таблиц для логики предикатов 147
Мы не договаривались, что а является именем любого конкретного
предмета, просто Ф(а) выполняется для каждого значения а. Если мы
доказываем формулу типа ЗхФ(х), правомерно сказать, что имеется
х такое, что для того же самого а Ф(а) будет также выполняться. При
этой либерализации доказательства формул могут быть сокращены и
это будет продемонстрировано на примере.
Правила расширения таблицы (се, /3, 7? ^) не детерминированы,
т. е. они говорят, что можно сделать, а не то, что нужно сделать.
Но в отличие от пропозиционального случая в логике предикатов
возможно многократное (в худшем случае бесконечное) повторение
правил расширения таблиц без получения замкнутого дерева, хотя
оно может существовать. Источником такой трудности является j-
правило. В качестве тривиального примера рассмотрим ветвь, содер-
содержащую как Зж^Р(ж), так и \/уР(у). Применение 5-правила к первой
формуле добавит вершину ^Р(б), где Ъ — новый параметр. Но ис-
использование 7-правила для второй формулы приведет к добавлению
вершин P(ci), Р(с2),..., где Ci, С2,... — различные параметры, отлич-
отличные от Ъ. Хотя здесь замыкание очевидно, останова не будет в силу
бесконечного добавления соответствующих вершин. В более трудных
случаях дело еще усложняется. Если в логике высказываний можно
довольствоваться строгими таблицами, т. е. таблицами, при констру-
конструировании которых ни к одной формуле правила расширения таблиц
(се, C) дважды не применяются на одной и той же ветви, то в логике
предикатов дело обстоит не так. Более того, в логике высказываний
доказано, что, если X — общезначимая формула, процесс конструи-
конструирования строгой таблицы закончится на уровне атомарно замкнутой
таблицы, т. е. таблицы, все ветви которой замыкаются атомарными
контрарными парами Р и -нР.
В логике предикатов первого порядка при построении замкнутой
таблицы для общезначимой формулы допускается повторное исполь-
использование 7~Ф°РМУЛ на одной и той же ветви. Рассмотрим пример.
Пример 4.3.
Доказать общезначимость формулы Зу(ВхР(х) —> Р(у)).
2. -,[ЗхР(х) -+ Р(а)] A)
3. ЗхР(х) B)
4. ^Р(а) B)
5. Р(Ь) C)
6. -п[ЗхР(х) -+ Р(Ъ)] A)
7. ЗхР(х) F)
8. -пР(Ь) F)
?

148 Вывод на аналитических таблицах [Гл. 4
В этом доказательстве правило 7 было применено дважды. В
либеральной версии это правило применяется один раз, в результате
чего получаем более короткое доказательство.
1. -,[Зу(ЗхР(х) -+ Р(у))]
2. -,[ЗхР(х) -+ Р(а)] A)
3. ЗхР(х) B)
4. ^Р(а) B)
5. Р(а) C)
П
Теперь обратимся к состоятельности и полноте метода аналитиче-
аналитических таблиц для логики предикатов первого порядка. Прежде всего,
расширим определение множества Хинтикка для этой логики.
Пусть Е — множество формул логики предикатов первого порядка;
Еи — множество всех замкнутых U-формул, где U — множество
предметов или универсум предметов, а [/-формула — формула логики
предикатов первого порядка, определенная на этом универсуме, при-
причем сюда входит «чистая» (pure) формула, не содержащая констант
как специальный случай.
Определение 2^.6. Множеством Хинтикка 1-го порядка (для уни-
универсума U) называется множество Я ([/-формул) такое, что выпол-
выполняются следующие условия:
Hq: для любой атомарной формулы А из Еи ни А, ни ее сопряжение
^А не принадлежат Я одновременно;
Яц Л ^Я,-И^Я;
Я2: если ^^Z e Я, то Z G Я;
Я3: если а е Я, то а\ е Я и а2 G Я;
Я4: если C е Я, то fa G Я или C2 G Я;
Я5: если 7 G Я, то для каждого a G [/, 7(а) ^ ^5
Яб: если E G Я, то, по крайней мере, для одного элемента а Е U
6(a) G Я.
Так же как и для пропозиционального случая, пустое множество
является тривиальным множеством Хинтикка 1-го порядка. Если в
логике предикатов первого порядка имеется бесконечное число за-
замкнутых термов (т. е. термов, имеющих функциональные символы и
константы), тогда любое множество Хинтикка 1-го порядка, содержа-
содержащее 7-замкнутую формулу, должно быть бесконечным.
Лемма Хинтикка для логики предикатов первого поряд-
порядка. Любое множество Хинтикка Я 1-го порядка для универсума U
является выполнимым (в смысле логики 1-го порядка).

4.2 ] Метод аналитических таблиц для логики предикатов 149
Доказательство проходит методом индукции по числу логических
связок в формуле (по степени формулы). Мы должны найти атомар-
атомарное означивание для Еи, в котором все элементы из Н будут истинны.
Затем предполагаем, что формула X имеет степень большую, чем О,
и каждый элемент из Н меньшей степени истинен по индуктивному
предположению. Тогда мы должны доказать, что и сама формула X
будет истинной. Так как сама формула X является одной из се-, /3-, j-
или S-формул, то нетрудно видеть, что X будет истинна.
Теперь рассмотрим, каким образом лемма Хинтикка может быть
использована для доказательства состоятельности и полноты метода
аналитических таблиц для случая логики предикатов первого поряд-
порядка. Прежде всего, рассмотрим лемму Кёнига.
Лемма Кёнига. Бесконечное дерево, которое конечно древовид-
древовидно, должно иметь бесконечную ветвь.
Дерево называется конечно древовидным, если каждая его верши-
вершина имеет конечное число потомков (возможно 0).
Лемма Кёнига утверждает, что если мы не
допускаем бесконечного ветвления, то примером
бесконечного дерева может быть только дерево,
показанное на рис. 4.1.
В логике высказываний таблица всегда закан-
заканчивается после конечного числа шагов. Для ло-
логики предикатов первого порядка таблица, как
мы уже видели, может продолжаться бесконеч- ис' '
но долго без какого-либо замыкания. Если это так, и генерируется
бесконечное дерево, то по лемме Кёнига, оно содержит бесконечную
ветвь в. Эта ветвь открыта. Зададимся вопросом: «Составляют ли
элементы этой ветви в множество Хинтикка?» Отрицательный ответ
может быть получен при следующем рассуждении.
Для любой формулы X степени больше, чем 0, на ветви в эта
формула выполнима на В, если
1) X есть се, и сеi и се 2 находятся на ветви в; или
2) X есть /3, и, по крайней мере, одна из формул /3i или /32 нахо-
находится на ветви в; или
3) X есть 7? и Для каждого параметра a j(a) находится на ветви
в; или
4) X есть 5, и, по крайней мере, для одного а 5(а) находится на
ветви В.
Теперь предположим, что Т — конечная таблица, и ветвь в
содержит две 7~Ф°РМУЛЫ? скажем 71 и 72- При использовании
7i-формулы к ветви будут добавляться вершины с формулами
7i(ai)j 7i (а2), • • • ,7i(an), • • • Для всех ai, а2,..., ап,... Таким образом,
будет порождаться бесконечная ветвь, на которой 71 выполнима.

150 Вывод на аналитических таблицах [Гл. 4
В этом случае мы пренебрегли 72- В другом случае можно
сделать выполнимой 7~Ф°РМУЛУ на ветви, но пренебречь одной
или несколькими се-, C- или E-формулами. В любом случае имеется
много способов порождения бесконечного дерева (таблицы) без
привлечения множества Хинтикка. Ключевой проблемой является
нахождение систематической процедуры, гарантирующей получение
бесконечного дерева, каждая открытая ветвь которого является
множеством Хинтикка.
Одной из таких систематических процедур является процедура
порождения дерева, на каждом шаге которого определенные вершины
дерева объявляются «использованными» (например, путем отметки
таких вершин). Процедура начинается с помещения формулы (чья
выполнимость проверяется) в корень. Пусть был выполнен n-й шаг.
Если на этом шаге была получена замкнутая таблица, то останов.
Также будет останов, если на каждой открытой ветви были использо-
использованы все неатомарные вершины. В противном случае конструирова-
конструирование таблицы продолжается путем отбора неиспользованной вершины
X минимального уровня (т. е. как можно ближе к корню) и которая
находится на открытой ветви. Чтобы сделать процедуру полностью
детерминированной, можно, например, отобрать на дереве самую ле-
левую неиспользованную вершину минимального уровня. Расширение
таблицы происходит следующим образом. Отбирается любая откры-
открытая ветвь в, проходящая через вершину X и
1) если X есть се, происходит расширение ветви в на (в, cei, a^);
2) если X есть /3, расширение распространяется на две ветви:
(в, ft) и (в, /32);
3) если X есть 5, то берется новый параметр с, до сих пор не
появлявшийся на дереве, и расширение идет на ветвь (в, 5(с));
4) если X есть j (это довольно деликатный случай), берем первый
параметр а такой, что j(a) не встречалась на в и расширяем
ветвь на (В, 7(а)? 7)- Другими словами, добавляем 7(а) к В и
затем повторяем вхождение j\ раз.
Выполнив все эти действия, в зависимости от того, является ли
формула X се-, /3-, j- или E-формулой, объявляем вершину использо-
использованной и этим завершаем (п + 1)-й шаг нашей процедуры.
Говоря неформально, системность спуска по дереву заключается
в выполнении се-, 5- и /3-формул. Что касается 7-формул, то сначала
присоединяем первый пример j(a), затем — второй пример j(b) и т. д.
Иногда может оказаться, что при систематическом построении таб-
таблицы после конечного числа шагов таблица будет все еще незамкнута,
хотя все неатомарные вершины каждой открытой ветви были уже
использованы. Это говорит о том, что на любой открытой ветви ни
одна из 7"Ф°РМУЛ так и не появилась. Следовательно, в этом случае
элементы открытой ветви являются множеством Хинтикка.

4.2] Метод аналитических таблиц для логики предикатов 151
Таблицу будем называть систематической, если к ней применима
систематическая процедура. Заметим, что дерево, порожденное та-
такой процедурой, строго говоря, не является либеральной таблицей,
поскольку нет правил для таблицы, учитывающих произвольные по-
повторения 7-формул (или любых других формул).
Таким образом, порождение законченной систематической табли-
таблицы с открытыми ветвями приводит к получению множества Хин-
тикка, что выражается приведенной ниже теоремой.
Теорема 4.4. Для любой законченной систематической таблицы
элементы каждой открытой ветви являются множеством Хинтикка
(для счетного универсума U параметров).
Из теоремы 4.4 и леммы Хинтикка вытекает следующая теорема.
Теорема 4.5. В любой законченной систематической таблице Т
каждая открытая ветвь выполнима (в смысле логики 1-го порядка).
Отсюда очевидна теорема о состоятельности метода аналитиче-
аналитических таблиц для логики предикатов первого порядка.
Теорема 4.6. Если формула X логики предикатов первого поряд-
порядка доказуема методом аналитических таблиц, то она общезначима.
Также очевидна непротиворечивость этого метода для логики пре-
предикатов первого порядка. Из теоремы 4.5 легко доказывается пол-
полнота метода аналитических таблиц для логики предикатов первого
порядка.
Теорема 4.7 (о полноте). Если X является общезначимой
формулой логики предикатов первого порядка, то она доказуема
методом аналитических таблиц, т. е. существует замкнутая таблица
для -iX.
С помощью теоремы 4.5 можно доказать теорему Левенгейма —
Сколема.
Теорема 4.8 (Левенгейма — Сколема). Пусть L — язык пер-
первого порядка и пусть S — множество замкнутых формул этого языка.
Если S выполнимо, то S выполнимо в счетной модели.
Возвращаясь к систематическим таблицам, отметим, что в общем
случае систематическая таблица имеет длину большую, нежели таб-
таблица, сконструированная наудачу, случайно. Но зато в отличие от
случайной систематическая таблица всегда гарантирует решение, если
исходное множество формул общезначимо.
Для уменьшения недетерминированности выбора правил се, /3, j и S
сначала будем использовать все а- и E-правила (нет ветвления). Затем
применим все /3-правила и только после этого — 7-пРавило? причем
в вершине, располагающейся как можно дальше от корня (обратите
внимание: в предыдущем случае было как можно ближе к корню).
Как и в логике высказываний, назовем таблицу атомарно за-
замкнутой, если каждая ветвь дерева содержит некоторую атомарную
формулу и ее отрицание (т.е. контрарную пару Р и ->Р). Таким

152 Вывод на аналитических таблицах [Гл. 4
образом, систематическая процедура называется атомарно замкнутой
или атомарно открытой, если в систематической таблице каждая
ветвь атомарно замкнута или существует, по крайней мере, одна
ветвь, элементы которой являются множеством Хинтикка. Таким об-
образом, если формула X общезначима или ^Х невыполнима, то суще-
существует не просто замкнутая таблица, а атомарно замкнутая таблица
для X.
Докажем методом аналитических таблиц пример, который был до
этого доказан с помощью принципа резолюции.
Пример 4.4. (см. пример 1.23)
Зх(С(х) & V у(Р(у) -. L(x, у))), Ух(С(х) - Уу(Н(у) -
->¦ -|Дж, ф)) Уу(Р(у) ->• ->Н(у))
1. ^[Зх{С{х) & V у(Р{у) -» Цх, у))) & ЩС(х) -+ Уу(Н{у) ->
A)
3. \/х(С{х) -> Му{Н(у) -л -Дж, у))) A)
4. —i\/y(P(y) —> —iH(y)) A)
5. С(а) & Vj/(P(?/) —> i(a, у)) B)
6. -(РF) -> ->ЯF)) D)
7. С(а) E)
8. V2/(P(y) - L(o, t/)) E)
9. P(b) F)
10. — H(b) F)
11. ЯF) A0)
12. P(b) -» До, 6) (8)
13. -P(&) A2) 14. Да, 6) A2)
? 15. C(a) -> V^Я(у) -»• -Да, у)) C)
16.-аа) A5) 17. Vy(H(y)
? 18.
В заключение покажем, что в случае конечного универсума U
метод аналитических таблиц может быть использован для доказа-
доказательства выполнимости формулы. Известно, что для выполнимой
формулы имеется, по крайней мере, одна открытая ветвь В, чьи
элементы составляют множество Хинтикка для конечного универсума
U тех параметров, которые встречаются, хотя бы в одном элементе
этой ветви. Поэтому бессмысленно расширять таблицу дальше, и в
соответствии с леммой Хинтикка элементы ветви в составляют мно-

4.3] Метод аналитических таблиц в логическом 153
жество Хинтикка, которое будет выполнимо в конечном универсуме.
Рассмотрим пример.
Пример 4.5.
Докажем, что формула \/х(Р(х) V Q(x)) —> (\/хР(х) V \/xQ(x))
выполнима.
1. ^[Ух(Р(х) V Q(x)) -> (Ух Р(х) V Ух Q(x))]
2. Ух (Р(х) V Q(x)) A)
3. ^(Ух Р{х) V Ух Q{x)) A)
4. ^УжР(ж) C)
5. -.Уж <5(ж) C)
6. --Р(а) D)
7. -0F) E)
8. Р(а) V Q(a) B)
9. P(b)yj^b) B)
10. Р(а) (8) ll.Q(a) (8)
П ^^^"^\
12. Р(Ь) (9) 13.0E) (9)
П
Имеется одна открытая ветвь в с концевой вершиной 12. Для
U = {а, Ь} в этой ветви две се-вершины A, 3), две /3-вершины (8, 9),
две E-вершины D, 5) и одна 7-вершина B) выполнимы. По лемме Хин-
Хинтикка все формулы ветви в истинны при следующей интерпретации:
Р(а) = Л, Р(Ъ) = И, Q(a) = И, Q(b) = Л. Отсюда исходная формула
выполнима.
4.3. Метод аналитических таблиц в логическом
программировании
4.3.1. Реализация метода аналитических таблиц для логики
высказываний на языке Пролог
Опишем реализацию метода аналитических таблиц для логики
высказываний на языке Пролог, выполненную Фиттингом. В начале
приведем положения, которые легли в основу разработанной версии.
• Аналитические таблицы являются строгими.
• Правила аналитических таблиц позволяют проверять ветвь на
замыкание (на основе атомарного замыкания).
• Метод аналитических таблиц в общем случае не является де-
детерминированным, поэтому Фиттингом предложена очередность
применения правил.

154 Вывод на аналитических таблицах [Гл. 4
• Аналитические таблицы представляются в виде списка своих
ветвей, в котором каждая ветвь является списком своих формул.
Далее, если при применении правил получили, что ветвь является
замкнутой, то она удаляется из списка. Пустой список ветвей свиде-
свидетельствует о замкнутости таблицы.
Фиттинг отмечает, что если к формулам применяются правила
расширения таблиц и при этом исходные формулы, к которым прави-
правила применялись, удаляются, то имеет место расширение таблицы.
Таким образом, реализация метода аналитических таблиц состоит
из 2-х частей:
• 1-я часть — программа задания формулы в виде ДНФ;
• 2-я часть — проверка ветви на замыкание.
Определение ^.7. Если дизъюнкт (clause) есть дизъюнкция ли-
литер, то в двойственной КНФ ДНФ конъюнкция литер представляет
собой конъюнкт (Фиттинг назвал его Dual Clause Form — форма,
двойственная к дизъюнкту). Отсюда формула логики высказываний
представима в ДНФ, если она является дизъюнкцией конъюнктов.
Приведенная ниже программа возвращает значение Y, которым
является список конъюнктов, составляющих ДНФ.
/* Dual Clause Form Program. Программа задания формулы в виде
днф. */
?-орA40, fy, neg).
?-орA60, xfy, [and, or, imp, revimp, uparrow, downarrow,
notimp, notrevimp]).
/* member (Item, List) — проверка, что Item входит в List. */
member(X, [X I _]).
member(X, [_ I Tail]) :- member(X, Tail).
/* remove(Item, List, Newlist) — Newlist является результатом удале-
удаления всех вхождений Item из списка List. */
remove (X, [],[]).
remove(X, [X I Tail], Newtail) :- remove(X, Tail,
Newtail).
remove(X, [Head I Tail], [Head I Newtail]) :-
remove(X, Tail, Newtail).
/* conjunctive(X) — X является се-формулой. */
conjunctive(_ and _).
conjunctive(neg(_ or _)).

4.3] Метод аналитических таблиц в логическом 155
conjunctive(neg(_ imp _)).
conjunctive(neg(_ revimp _)).
conjunctive(neg(_ uparrow _)).
conjunctive(_ downarrow _).
conjunctive(_ notimp _).
conjunctive(_ notrevimp _).
/* disjunctive (X) — X является /3-формулой. */
disjunctive(neg(_ and _)).
disjunctive(_ or _) .
disjunctive(_ imp _).
disjunctive(_ revimp _).
disjunctive(_ uparrow _).
disjunctive(neg(_ downarrow _)).
disjunctive(neg(_ notimp _)).
disjunctive(neg(_ notrevimp _)).
/* unary(X) — X является двойным отрицанием или отрицанием
константы. */
unary (neg neg _).
unary(neg true).
unary(neg false).
/* components(X, Y, Z) — Y и Z являются компонентами формулы
X в соответствии с се- и /3-правилами. */
components(X and Y, X, Y).
components(neg(X and Y), neg X, neg Y).
components(X or Y, X, Y).
components(neg(X or Y), neg X, neg Y).
components(X imp Y, neg X, Y).
components(neg(X imp Y), X, neg Y).
components(X revimp Y, X, neg Y).
components(neg(X revimp Y), neg X, Y).
components(X uparrow Y, neg X, neg Y).
components(neg(X uparrow Y), X, Y).
components(X downarrow Y, neg X, neg Y).
components(neg(X downarrow Y), X, Y).
components(X notimp Y, X, neg Y).
components (neg (X notimp Y) , neg X, Y).
components(X notrevimp Y, neg X, Y).
components(neg(X notrevimp Y), X, neg Y).
/ component(X, Y) — Y является компонентой унарной формулы X.
I
/* ^
*

156 Вывод на аналитических таблицах [Гл. 4
component(neg neg X, X).
component(neg true, false),
component(neg false, true).
/* singlestep(Old, New) — New является результатом применения
шага процесса расширения таблицы к Old, являющейся дизъ-
дизъюнкцией конъюнкций. */
singlestep([Conjunction I Rest], New) :-
member(Formula, Conjunction),
unary(Formula), component (Formula, Newfomula),
remove(Formula, Conjunction, Temporary),
Newconjunction = [Newformula I Temporary],
New = [Newconjunction I Rest].
singlestep([Conjunction I Rest], New) :- member(Alpha,
Conjunction),
conjunctive (Alpha),
components(Alpha, Alphaone, Alphatwo),
remove(Alpha, Conjunction, Temporary),
Newcon = [Alphaone, Alphatwo I Temporary],
New = [Newcon I Rest].
singlestep([Conjunction I Rest], New) :- member(Beta,
Conjunction),
disjunctive(Beta),
components(Beta, Betaone, Betatwo),
remove(Beta, Conjunction, Temporary),
Newconone = [Betaone I Temporary],
Newcontwo = [Betatwo I Temporary],
New = [Newconone, Newcontwo I Rest].
singlestep([Conjunction I Rest], [Conjunction I Newrest]):-
singlestep(Rest, Newrest).
/* expand(Old, New) — New является результатом применения к
таблице Old шага расширения таблицы, сделанного много раз
(насколько это возможно). */
expand(Dis, Newdis) :- singlestep(Dis, Temp),
expand(Temp, Newdis).
expand(Dis, Dis).
/* dualclauseform(X, Y) — Y является двойственной формой для X
(днф). */
dualclauseform(X, Y) :-expand([[X]], Y).
В реализации метода аналитических таблиц дизъюнкт
dualclausef orm(X,Y), используемый для запуска приведенной выше

4.3] Метод аналитических таблиц в логическом 157
программы нахождения ДНФ Y для формулы X, должен быть
удален, поскольку в нем нет необходимости.
Далее для реализации данного метода необходимо добавить дизъ-
дизъюнкты, проверяющие таблицу на замыкание. Они имеют следующий
вид:
/* closed (Tableau) — проверка на то, что каждая ветвь таблицы
содержит контрарную пару. */
closed([Branch I Rest]) :- member(false, Branch),
closed(Rest).
closed([Branch I Rest]) :- member(X, Branch),
member(neg X, Branch),
closed(Rest).
closed([ ] ).
Затем необходимо задать вызов предиката expand, осуществляю-
осуществляющий расширение таблицы, и вызвать предикат closed, проверяющий
полученную таблицу на замыкание. Таким образом, предикат test,
выполняющий эти операции, имеет вид
/* test(X) — создание полного расширения таблицы для формулы
^Х и проверка ее на замкнутость. */
test(X) :- expand([[neg X] ] , Y), closed(Y).
Фиттинг отмечает, что существует некоторая трудность, связанная
с эффективностью использования предиката test. Если формула X,
задаваемая в предикате test, является доказуемой, то вызов преди-
предиката expand заканчивается успешно, и затем вызов предиката closed
также заканчивается успешно (как ожидалось). В то же время, если
формула X не является доказуемой, то вызов предиката expand будет
закончен успешно, но вызов предиката closed завершится неудачей,
что приведет к бектрекингу (поиску новых значений) для предиката
expand. Но если предикат expand может успешно завершиться для
нескольких значений (путей), то предикат closed никогда успешно не
завершится. Следовательно, перед окончанием программы с неудачей
будет выполнено много путей для нахождения расширения формулы,
заданной в ДНФ. Для того, чтобы предотвратить ненужный бек-
бектрекинг, используется оператор отсечения языка Пролог (!). Таким
образом, предикат test заменяется приведенным ниже предикатом,
который является более эффективным в случае, когда формула не
является теоремой.
test(X) :- expand([[neg X] ] , Y) , !, closed(Y) .

158 Вывод на аналитических таблицах [Гл. 4
Если пользователь программы желает, чтобы в качестве ее выпол-
выполнения выдавался ответ «формула является теоремой» или «формула
не является теоремой», то в предикат test нужно добавить предикаты
if _then_else и write. Таким образом, получается следующая версия
предиката test:
/* if_then_else(P, Q, R) — если Р — истинно, то Q; в противном
случае R. */
if_then_else(P, Q, R) :- Р, !, Q.
if_then_else(P, Q, R) :-R.
/* test(X) — создание полного расширения таблицы для формулы
^Х и проверка на замкнутость. Если таблица замкнутая, то X —
теорема, в противном случае X не является теоремой. */
test(X) :- expand([[neg X] ] , Y) , !,
if_then_else(closed (Y), yes, no).
yes :- write ("Propositional tableau theorem"), nl.
no :- write ("Not a propositional tableau theorem"),
nl.
Следует отметить, что существует еще одна проблема, связанная
с неэффективностью представления. Пусть мы хотим доказать тав-
тавтологию (Р & Q) V -i(P & Q). Таблица для нее будет начинаться с
формулы ->((Р & Q) V -i(P & Q)), затем используется се-правило, на
основе которого формула разбивается на две формулы: -i(P & Q)
и ^^(Р & Q). С теоретической точки зрения таблица является за-
замкнутой, поскольку одна из формул является отрицанием другой. Но
если для доказательства этой формулы использовать приведенную
выше программу, то она будет производить расширения в форме
конъюнктов перед проверкой ветви на замыкание. В этом случае
формула не будет доказана, поскольку контрарную пару образуют ее
подформулы, а не литеры. Для того, чтобы устранить этот недоста-
недостаток, Фиттинг разработал новую версию предиката expand, который
назвал expand_and_close. Ниже приведем программную реализацию
этого предиката.
expand_and_close(Tableau) :- closed(Tableau).
expand_and_close(Tableau) :-
singlestep(Tableau, Newtableau), !,
expand_and_close(Newtableau).
Заметим, что в приведенной реализации предиката
expand_and_close используется оператор отсечения языка Пролог,
который предотвращает генерацию ненужных расширений. Следует

4.3] Метод аналитических таблиц в логическом 159
сказать, что приведенная реализация является корректной и без
оператора отсечения, но менее эффективной.
Далее необходимо сделать последнее расширение в предикате test,
чтобы учесть новую версию предиката expand_and_close. Таким об-
образом, предикат test имеет следующий вид:
/* test(X) — создание полного расширения таблицы для формулы
^Х и проверка на замкнутость. Если таблица замкнутая, то X
— теорема, в противном случае X не является теоремой. */
test(X) :- if_then_else(expand_and_close([[neg X] ] ) ,
yes, no).
Поскольку вслед за Фиттингом нами приведено несколько реали-
реализаций метода аналитических таблиц, зададимся вопросом: какая из
реализаций является лучшей? Если мы попытаемся доказать фор-
формулу, подобную F V -iF, где F — формула, то последняя версия
предиката test является, очевидно, лучшей. Но для других типов
формул эта версия предиката test является неудачной, поскольку
увеличивается время на их доказуемость. Таким образом, ответ на
поставленный вопрос можно дать такой: выбор лучшей реализации
метода аналитических таблиц зависит от наших знаний о формуле,
т. е., другими словами, эвристики здесь играют не последнюю роль.
Следует отметить еще одну деталь, приводящую к неэффективно-
неэффективности заключительной версии метода аналитических таблиц. Предполо-
Предположим, что аналитическая таблица построена до момента, начиная с ко-
которого она разветвляется на 5 ветвей, 4 из которых являются замкну-
замкнутыми. Предикат, названный expand_and_close, будет тестировать на
замкнутость все ветви таблицы и найдет ветвь, которая не является
замкнутой. Затем применяется правило расширения таблицы, и снова
вся таблица тестируется на замкнутость ветвей. Но 4 ветви были
замкнутыми, и, естественно, замкнутыми и остались. Поэтому нет
необходимости проверять их вновь, и более удачной версией програм-
программы является та, в которой удаляется из таблицы ветвь с обнаруженой
замкнутостью. Читателю предлагается модифицировать последнюю
версию реализации метода аналитических таблиц так, чтобы только
что обнаруженная замкнутость ветви, удалялась из таблицы. Желаем
успеха в разработке лучшей версии реализации метода аналитических
таблиц для пропозициональной логики!
4.3.2. Реализация метода аналитических таблиц для логики
предикатов 1-го порядка
4» 3.2.1. Алгоритм унификации. Перед описанием реализа-
реализации метода аналитических таблиц для логики 1-го порядка приведем
основные теоретические положения, лежащие в его основе. Одним

160 Вывод на аналитических таблицах [Гл. 4
из фундаментальных алгоритмов в методах автоматического доказа-
доказательства теорем является алгоритм унификации. В настоящее время
известно огромное множество различных версий алгоритмов унифи-
унификации. Ниже мы рассмотрим алгоритм унификации, введенный Ро-
Робинсоном, для принципа резолюции, поскольку именно этот алгоритм
выбран Фиттингом для реализации метода автоматического доказа-
доказательства теорем на основе аналитических таблиц. Напомним основные
определения.
Определение 2^.8. Пусть имеются два терма t и и, каждый из
которых содержит переменные. Тогда подстановка а такая, что ta =
= иа¦, называется унификатором t и и.
Определение Ji.,9. Пусть о~\ и о~2 — две подстановки. Говорят, что
<72 — более общая подстановка, чем <7i, если для некоторой подста-
подстановки Т О\ = О~2Т.
Пример 4.6.
<П = {f(g(a,h(z)))/x,g(h(x),b)/y,h(x)/z}
сг2 = {f(g(x,y))/x,g(z,b)/y}
Здесь <72 — более общая подстановка, чем <7i, потому что а\ = <72Т,
где г = {а/ж, h(z)/y, h(x)/z}.
Заметим, что каждая подстановка является более общей к самой
себе, поскольку а = ае.
Утверждение 4.1. Если as более общая подстановка, чем <72, и
<72 более общая, чем <7i, то as более общая, чем cri.
Определение J^-IO. Пусть t\ и t^ — два терма (определение можно
расширить и более чем на два терма). Подстановка а — унификатор
для t\ и ^2, если ti<7 = t2<7. tiH^2 унифицируемы, если они имеют уни-
унификатор. Подстановка а называется наиболее общим унификатором
(НОУ), если она является более общим унификатором, чем другой
унификатор.
Пример 4.7.
Два терма f(y,h(a)) и f(h(x),h(z)) можно унифициро-
унифицировать, используя подстановку {h(x)/y,a/z}. Также подстановка
{k(w)/x,h(k(w))/y,a/z} — унификатор, но первая подстановка
является более общей.
Определение 2^.11. Область изменения переменной для подста-
подстановки а есть множество переменных, которые встречаются в термах
вида хсг, где х — переменная.
Утверждение 4.2. Предположим, что как <7i, так и а^ — НОУ
для t\ и ^2- Тогда имеется переименование переменных ? для области
изменения переменных для а\ такое, что <7i? = a^-
Подстановка ? есть переименование переменных для множества V
переменных, если

4.3] Метод аналитических таблиц в логическом 161
1) для каждой х G V xt; — переменная;
2) для ж, у G V (х ф у) х^ и у? — различные.
В приведенных выше примерах используется задание термов
в линейной форме. Существует и другая форма задания термов,
а именно, форма записи терма в виде дерева. Например, терм
f(g(x, у, /г(а, k(b)))) можно представить в виде упорядоченного дерева
(рис. 4.2), где аргументы терма — потомки этого дерева.
Далее приведем определение расширенного представления дерева,
которое является более удобным для реализации алгоритма унифика-
унификации.
х у h
а к
Ь
Рис. 4.2 Рис. 4.3
Определение 4.12. Расширенное представление дерева терма
есть дерево, в котором имя каждой вершины расширено целым чи-
числом, представляющим порядковый номер потомка для заданного
родителя.
В качестве примера приведем расширенную версию дерева для
предыдущего примера, изображенную на рис. 4.3.
Определение 4.13. Пусть t\ и t^ — два терма. Пара рассогла-
рассогласования для этих термов есть пара d\i& efe, где d\ — подтерм t\ и
^2 — подтерм ^2 такие, что расширенные деревья для d\ и d^ имеют
различные имена вершин, соответствующих корням деревьев d\ и^,
таких, что путь, ведущий от корня t\ вниз к корню d\ и путь, ведущий
от корня ^2 к корню 6^2, один и тот же.
Пример 4.8.
Рассмотрим термы: f(g(a,x),h(c,j(y,x))) и f(g(a,x),h(c,k(z))).
Расширенные деревья, соответствующие этим термам, представлены
на рис. 4.4, на котором также указана пара рассогласования для этих
термов.
Заметим, что на обоих деревьях путь от корневой вершины вниз
к подтермам, составляющим пару рассогласования, один и тот же
{< /, 0 >,< /г, 2 >}. В рассмотренном примере имеется только одна
6 В.Н. Вагин и др.

162 Вывод на аналитических таблицах [Гл. 4
Пара рассогласования: j(y, x), k(z)
Рис. 4.4
пара рассогласования, хотя их может быть и больше. Если два тер-
терма отличаются, то должна быть одна и более пар рассогласований.
Также, если а унифицирует различные термы t\ и ?2, он должен
унифицировать каждую пару рассогласований этих термов.
Теперь дадим алгоритм унификации по Робинсону (см. также
разд. 1.4).
Алгоритм унификации.
Пусть а := е\
while t\G ф t2<J do
begin
найти пару рассогласований d\ и с^ для tier, ^сг;
если ни di, ни efe не являются переменными, то FAIL (неудача);
пусть ж, содержащаяся как в di, так ив^, а также или в d\ или
^2, является переменной
и пусть ? является одним из d\ или efe;
если х входит в ?, то FAIL;
иначе а := a{x/t}
end.
Теорема 4.9 (унификации). Пусть t\ и ?2 — термы. Если ti и
^2 неунифицируемы, то алгоритм унификации заканчивается с FAIL
(неудача). Если t\ и t^ унифицируемы, то алгоритм унификации
заканчивается без FAIL, и конечное значение а будет НОУ для t\
и ?2.
Поскольку существует необходимость в унификации более чем
одной пары термов, разработан алгоритм многократной унификации,
в основе которого лежит процедура сведения к бинарной унификации.
Рассмотрим алгоритм многократной унификации.
Предположим, что {to, ?1, ?2? • • • ? tn} — множество термов. Унифи-
Унификатором для данного множества является подстановка а такая, что
to<j = t\G = ... = tna. Как обычно, НОУ есть унификатор, который
является более общим, чем любой другой унификатор. Многократная

4.3 ] Метод аналитических таблиц в логическом 163
унификация может быть довольно просто сведена к последователь-
последовательности выполнения задач бинарной унификации. Предположим, что
{to, ti, ?2, • • •, tn} имеет унификатор. Определим последовательность
подстановок, каждая из которых вычисляется алгоритмом бинарной
унификации следующим образом:
G1 — НОУ ДЛЯ to И t\.
G2 — НОУ ДЛЯ toCTi И t<2,(J\-
СГ3 — НОУ ДЛЯ ?оСГ1<72 И
Оп — НОУ ДЛЯ ?оСГ1<72 • • • ап-\
Далее объявляем, о~\о~2... о~п-\оп — НОУ для множества
{to, ti, ^2,..., tn}. Таким образом, мы выполнили многократную
унификацию.
Следует отметить, что существуют и другие подходы к созданию
алгоритмов унификации. Один из таких подходов основан на нахо-
нахождении согласующейся (concurrent) унификации. Вместо подстановки
а, унифицирующей термы t и и, удобно иногда говорить, что имеется
решение уравнения t = и. Предположим, что мы имеем уравнения
to = uo,ti = 1x1,...,tn = ип. Подстановка а является результатом
решения каждого уравнения.
Далее мы приведем теоретические положения, на которых бази-
базируется метод автоматического доказательства теорем на основе ана-
аналитических таблиц для логики предикатов 1-го порядка. Отметим,
что вышеописанный алгоритм унификации играет в этом методе клю-
ключевую роль. (Реализация алгоритма унификации на языке Пролог,
приведена в п. 4.3.2.3).
4-3.2.2. Аналитические таблицы со свободными перемен-
переменными. Главная практическая сложность в реализации метода ана-
аналитических таблиц для логики предикатов 1-го порядка заключается
в правиле 7? которое позволяет добавлять в ветвь, содержащую фор-
формулу 7? Ф°РМУЛУ т@> гДе ^ ~~ Фундаментальный пример. Следует
отметить, что существует бесконечное множество подстановок в фор-
формулу 7? и ранее созданные решатели теорем осуществляли перебор
примеров некоторым систематическим способом. Однако это не явля-
является эффективным. Для оперирования с формулами типа 7 Фиттинг
предложил следующую процедуру. Она заключается в добавлении в
ветвь, содержащую формулу 7, формулу 7(ж)? гДе х ~ 'новая свободная
переменная, которая принимает значение при использовании алгорит-
алгоритма унификации, замыкающего ветвь. Именно эта процедура и дала
название данному параграфу. Но эта процедура не является панацеей
от всех проблем, поскольку здесь возникает трудность при исполь-
использовании правила S. Теперь мы не можем быть уверены в том, что
параметр, используемый в правиле 5, является новым. Для решения
этой проблемы было использовано более сложное понятие параметра,
6*

164
Вывод на аналитических таблицах
[Гл.4
чем то, которое использовалось до сих пор. Таким образом, если фор-
формула S встречается на ветви, то в конец ветви добавляется формула
8(f(xi, • • • > хп)), где / — новый функциональный символ и х\,..., хп —
все свободные переменные, встречающиеся на этой ветви. В этом
случае неважно, какие значения принимают переменные х\,... ,хп,
поскольку f(x\,... ,хп) является отличной от любой из них. Здесь
необходимо использовать процедуру для проверки появления пере-
переменной (occurs_check). Введенные символы называются сколемовски-
ми функциональными символами. Следует отметить, что правило S
может использоваться после любого применения правила j, которое
вводит свободные переменные, используемые в качестве аргументов
в сколемовских функциях. Особо выделяется случай, когда ни одно
из правил 7 не применялось, т. е. никакая свободная переменная не
была введена. В этом случае сколемовский функциональный символ
должен быть 0-местным. Но 0-местный функциональный символ яв-
является просто константой, т. е. параметром в обычном смысле. Эти
рассуждения приводят к следующему определению.
Определение 4-14- Пусть L = L(R,F,C) — язык 1-го порядка.
Пусть par — счетное множество константных символов, не входящих
в С. Также пусть sko — счетное множество функциональных симво-
символов, не входящих в F (называемых сколемовскими функциональными
символами), включающее бесконечно много 1-местных, 2-местных и
т. д. функциональных символов. Тогда через Lsko обозначим язык
1-го порядка: Lsko = L(R, FUsko, CUpar), где R — счетное множество
предикатных символов.
Следует отметить, что доказательства строятся из замкнутых фор-
формул языка L, также при этом используются формулы языка Lsko.
Таким образом, механизм доказательства совпадает с описанным в
разд. 4.2, за исключением правил, оперирующих с кванторами. Так,
пропозициональные правила расширения таблиц и правила замыка-
замыкания ветви одинаковы, а правила оперирования с формулами, имею-
имеющими кванторы, различны и берутся из таб. 4.6.
Таблица 4.6
7
70)
(где х — свободная пере-
переменная)
S
5(f(xi,...,xn))
(где / — новый символ сколемовской
функции и х\,...,хп — все используе-
используемые в ветви свободные переменные)
Далее приведем определение и правило подстановки.
Определение 4-15- Пусть а — подстановка и Т — таблица. Рас-
Расширим действие а на Т путем получения подстановки Та, которая

4.3 ] Метод аналитических таблиц в логическом 165
является результатом замены каждой формулы X в Т на Ха. Гово-
Говорят, что а свободна для Т при условии, что а свободна для каждой
формулы в Т.
Правило подстановки для таблицы. Если Т — таблица для
множества замкнутых формул S из L и подстановка а свободна для
Т, тогда Та также является таблицей для S.
Как обычно, табличным доказательством со свободными пере-
переменными формулы X является замкнутая таблица для {^Х}, при
построении которой используются правила расширения для пропози-
пропозициональной логики (правила а и C), правила оперирования с кванто-
кванторами (правила j и 5), описанные выше, и правило подстановки для
таблицы.
Рассмотрим примеры, поясняющие метод аналитических таблиц
со свободными переменными.
Пример 4.9.
Доказать формулу: 3w\/xR(x,w, f(x,w)) —> 3w\/x3yR(x,w,y).
,w, f(x,w)) —> 3uNx3yR(x,w,y)]
2.3wVxR(x,wJ(x,w)) A)
3.^3wVx3yR(x,w,y) A)
4. \/xR(x,aJ(x,a)) B)
,y) C)
uy) E)
7.R(v2,aJ(v2,a)) D)
г;з) F)
Приведем поясняющий комментарий.
B) и C) получаются из A) путем применения правила а.
D) выводится из B) вследствие правила S. В нем а — 0-местный
сколемовский функциональный символ, т. е. параметр.
E) получается из C), если применить правило 7? которое вводит
новую свободную переменную v\.
F) следует из E) путем применения правила E, с учетом введения
одноместного сколемовского функционального символа Ъ.
G) получается из D), если примененить правило 7, которое вводит
новую свободную переменную v^-
Затем (8) выводится из F) с помощью правила 7, вводящего новую
свободную переменную v%.
Теперь применим правило подстановки для таблицы, используя
подстановку а = {a/^i, Ь(а)/г>2, /(Ь(а), a)/vs} и построим замкнутую
таблицу получением контрарной пары G) и (8). Подстановка триви-
тривиально свободна, поскольку все подставленные термы замкнуты.

166 Вывод на аналитических таблицах [Гл. 4
Рассмотрим следующий пример, в котором строится аналитиче-
аналитическая таблица со свободными переменными для доказательства заклю-
заключения известной тестовой задачи «Стимроллер» (см. разд. 2.5.3).
Пример 4.10.
Имеем:
3xW(x),
3xF(x),
ЗхВ(х),
ЗхС(х),
3xS(x),
Vx(W(x) -> А(х)),
Vx{F(x) -> А(х)),
Ух(В(х) -> А(х)),
\/х(С(х) -> А(х)),
Vx(S(x) -+ А(х)),
3xG(x),
Vx(G(x) -+ Р(х)),
\/xVyVz\/v[(A(x) & Р(у) -> Е(х,у)) V (A(z) & P(v) & M(z,x) &
bE(z,v)^E(x,z))],
УхЩС(х) & B(y) -+ М(х,у)} & \/x\/y[S(x) & В (у) -> М(х,у)],
WxVy[B(x)kF(y)^M(x,y)},
Vx\/y[F(x) kW(y) -> М(х,у)],
bF(y)^^E(x,y)\,
k G(y) ^ ^E(x,y)},
& S(y) -* ^E(x,y)}
Vx3y[C(x) ^ P(y) & E(x,y)},
h ЗхЗуЩх) & A(y) & [E(x,y) &
Построим аналитическую таблицу со свободными переменными
для доказательства заключения.

4.3 ] Метод аналитических таблиц в логическом 167
# т
^ ^iTH Н ^ ^ 5» 5* ^
f о jo п ^—' ^—' - ci - ^ ~
I ^^^bq bq ^l^^^^
н н н н н н н н н
ттттт>>>>>>>>

168
Вывод на аналитических таблицах
[Гл.4
1^ об
см см
1—1
г
см
CJ
СЗ
в
Г
ю
см
CJ
со
СО
со
CQ
Г
со
со
СО
см
CJ
со
в
СО
со
г
ю
со
00
см
CJ
об
со
ю
г
со
oi
со
см
CJ
ю
со
см
г
т-Ч
со
CJ
со
43. Р
г
см
44. Р
00
см
CJ
45. Е
оо
О:
47. Р
оо
г
со
оо
С*
48. Р
см
CJ
00
оо
оо
49. Я
о
г
ю
о
50. -.(
о
г
со
ю
г
см
ю
Г
ю
ю
см
CJ
о
см
CJ
СЗ

4.3]
Метод аналитических таблиц в логическом
169
со
ю
т—1
ю
ю
Г
об
ю
Г
1^
ю
oi
ю
Oi
со
а
см
со
СО
со
О
cj
Г
СО
г
со
СО
со
Г
см
СО
см
CJ
п"
СО
см
CJ
со
т—1
с^
CJ
со
СО
СО
со
ю
ю
СО
cJ
oi
СО
СО
Г
об
СО
ю
г
СО
00
см
CJ
со
т—1
п
СО
см
CJ
ю
т—1
CJ
оо
т-Ч
оо
О
74. М(с, Ъ)
оо
г
со
Г
см
ю
см
CJ
оо
п
СО
см
CJ
1—1
о
СО
о
Ю
о
00
о
Г
oi
г
об
см
CJ
о
СЗ
п
ю
см
CJ
п
Т
(М
т-Ч
00
т
5^
СМ
00
00
(М
со
00
г
СО
00
г
ю
00
г
00
СО
см
CJ
(М
?>
CJ
п
00
см
CJ
п
oi
00
(М
об
00
см
г
т—1
Oi
?>
г
о

170
Вывод на аналитических таблицах
[Гл.4
00
CM
CJ
CM
CJ
П
CM
CJ
П
со
CM
^r ?
^ со
<3 1
ю ^
CM ^
^ bq
T
CM
^ ^ ^
со со
CM CM
CO |
^ ч
Ю
CM
со
CM

о
О
1-4
со
см
с^
Ю
^—n СМ
со ?Ь
, ч со
ю ^
см ^
^ 1
oi ой
Qi
^^
см
со
см
СО
см
^—^
со
см
^—^
Ю
СО
CJ
Ю
см
со
см
*—у—'
?
см
-?'
г
об
со
см
г
1-4
CJ
см
п
СО
со
CJ
со
см
со
п
со
ю
см
г
104.
со
см
\^
ю
см
г
со
о
1—1
со
г
102.
^—V
ю
см
5^
г
о
CJ
со
см
ю
см
см
CJ
со
см
'25,
п
00
CJ
со
см
п
00
со
CJ
ю
см
п
оо
см
m
s ч
оо
S1
CM
oo
CM
^—^
CM
T'
Ю
о
oo
CM
m
oo
CM
CM
г
об
о
1—1
^—V
oo
CM
г
О
1—1
^-^
CM
г
CO
О
1-4
CO
CO
CJ
oo
CM
CO
CO
CJ
CM
CJ
П
oo
CM
CM
г
oi
о
1—1
oo
CM
&
m
г
о
1-4
1-4
CO
CJ
oo
CM
CO
CM
CJ
П
CM
oo
CM
CM
г
1—1
1—1
1—1
oo
CM
CM
г
CO
1—1
1—1
s—V
CM
г
CM
1—1
1—1
CO
CJ
CM
28,,
CO
П
Oi
CO
CJ
CM
П

4.3] Метод аналитических таблиц в логическом 171
Остановимся на проблеме реализации метода аналитических таб-
таблиц со свободными переменными. Напомним, что перед введением
свободных переменных в таблицу перед нами стояла проблема выбора:
«Какие термы нужно применять в правиле 7?»- Теперь эта проблема
видоизменилась: «Какие значения следует применять вместо свобод-
свободных переменных?». Но сейчас мы имеем очевидный ответ: «следует
применять подстановки, которые делают ветвь замкнутой, и эти под-
подстановки молено определить, используя алгоритм унификации».
Следует отметить, что процедура замыкания таблицы наклады-
накладывает ряд ограничений, одним из которых является то, что в ней
используется правило атомарного замыкания.
Определение 4.16. Правило атомарного замыкания с помощью
НОУ. Предположим, что Т-таблица для множества S замкнутых фор-
формул языка L и некоторая ветвь Т содержит А и -н.В, где А и В —
атомарные формулы. Тогда Та также является таблицей для S, где
а — НОУ для А и В.
Поскольку правило атомарного замыкания с помощью НОУ есть
как раз специальный случай правила подстановки таблицы, его до-
добавление в систему не будет влиять на свойство состоятельности
метода аналитических таблиц. И можно доказать, что система полна,
даже когда все применения правила подстановки таблицы ограничены
применениями правила атомарного замыкания с помощью НОУ.
4-3.2.3. Реализация алгоритма унификации на языке
Пролог. В настоящее время существует несколько алгоритмов
унификации, которые отличаются от алгоритма унификации,
предложенного Робинсоном. Фиттинг предложил реализацию
алгоритма унификации на языке Пролог, которая имеет следующие
особенности. Во-первых, в алгоритме унификации унифицирующая
подстановка (НОУ) а создается с помощью успешно составленных
простейших подстановок, которые часто называют связками
(bindings). Во-вторых, в предложенном алгоритме не выполняется
вычисление композиции подстановок, а происходит запоминание
каждой связки. Для запоминания подстановок (связок) используется
список окружения (environment list), состоящий из элементов [х,?],
означающих, что вхождения х заменяются на t. Специфичной чертой
данной замены является то, что связка ?, в свою очередь, может быть
заменена другими переменными, содержащимися в списке окружения.
Если при унификации термов встречаются функциональные символы
/(...) и #(...), то унификация невозможна и, таким образом, нет
необходимости проверять на унифицируемость аргументы функций
/ и р.
Для того, чтобы не было конфликтов с переменными языка
Пролог, разработчики данного алгоритма используют выражение

172 Вывод на аналитических таблицах [Гл. 4
variable(X) для обозначения того, что X является свободной перемен-
переменной языка L.
/* variable(X) — X является свободной переменной. */
variable(var(_)).
Кроме того, для оценивания терма Term в окружении Env был
введен предикат partialvalue(Term,Env,Result). Если терм не яв-
является свободной переменной, или является свободной переменной
без связывания в окружении Env, то Result совпадает с Term без
изменения. В то же время, если связка для терма Term в окружении
Env найдена, то процесс оценивания применяется к связке. Приведем
реализацию предиката part ialvalue.
/* partialvalue(X, Env, Y) — Y является частично вычисленным зна-
значением терма X в окружении Env, где окружение Env является
списком подстановок. */
partialvalue(X, Env, X).
partialvalue(X, Env, Y) :- member([X I Z], Env),
partialvalue(Z, Env, Y).
/* member(X, Y) — X является элементом списка Y. */
member (X, [X I_].
member(X, [_|Y]) :- member(X, Y).
Для реализации алгоритма введены также несколько предикатов,
описанных ниже. Они используются для выполнения проверки термов
на унифицируемость.
/* in(X, T, Env) — X является вхождением в терм Т в окружении
Env. */
in(X, T, Env) :- partialvalue(T, Env, U),
(X == U; not variable(U),
not atomic(U), infunctor(X, U, Env)).
infunctor(X, U, Env) :- U == [ _ I L], inlist(X, L, Env).
inlist(X, [T|_], Env) :- in(X, T, Env).
inlist(X, [_|L], Env) :- inlist(X, L, Env).
Приведем непосредственно предикат унификации: unify (Terml,
Term2, Env, Newenv). Предикат unify принимает значение истина, если
результат унификации термов Terml и Term2 в окружении Env влечет
создание нового окружения Newenv. Для более подробного объяснения
приведенной ниже реализации предиката unify заметим, что в языке

4.3] Метод аналитических таблиц в логическом 173
Пролог вместо логической связки «or» пишется «;». Для того, чтобы
унифицировать два предиката Terml и Term2, сначала оцениваются
их значения, т. е. осуществляется разбиение на термы (переменные,
константы, функции). Затем, если выделенным элементом является
переменная, то она связывается с другим выделенным элементом
после проверки их на унифицируемость. Таким образом, если выде-
выделенный элемент заменяется на более сложный, например, переменная
заменяется на функцию, то далее выделяются аргументы у функции,
и осуществляется их унификация.
/* unify (Terml, Term2, Env, Newenv) — унификация термов Terml
и Term2 в окружении Env, создавая новое окружение Newenv,
где Env - старый список подстановок, Newenv — новый список
подстановок. */
unify(Terml, Term2, Env, Newenv) :-
partialvalue(Terml, Env, Vail),
partialvalue(Term2, Env, Val2),
((Vail == Val2, Newenv = Env);
(variable(vail), not in(Vall, Val2, Env),
Newenv = [[Vail, Val2] I Env]);
(variable(Val2), not in(Val2, Vail, Env),
Newenv = [[Val2, Vail] I Env]);
(not variable(Vail), not variable(Val2),
not atomic(Vail), not atomic(Val2),
unifyfunctor (Vail, Val2, Env, Newenv))).
/* unifyfunctor(Fun 1, Fun2, Env, Newenv) — унификация функцио-
функциональных термов Funl и Fun2 в окружении Env, производя новое
окружение Newenv. */
unifyfunctor(Funl, Fun2, Env, Newenv) :-
Funl = [FunSymb I Argsl],
Fun2 = [FunSymb I Args2],
unifylist(Argsl, Args2, Env, Newenv).
/* unifylist(Listl, List2, Env, Newenv) — начиная с окружения Env и
унифицируя каждый терм в Listl с соответствующим термом в
List2, создаем окружение Newenv. */
unifylist([ ], [ ], Env, Env).
unifylist([Headl I Taill], [Head2 I Tail2], Env, Newenv) :-
unify(Headl, Head2, Env, Temp),
unifylist(Taill, Tail2, Temp, Newenv).
Следует заметить, что в приведенной выше реализации алгоритма
унификации опущены предикаты, необходимые для проверки термов

174 Вывод на аналитических таблицах [Гл. 4
на унифицируемость (связанность). Рассмотрим реализацию преди-
предиката unify, в которой учтена такая проверка термов.
/* unify(Terml, Term2) — проверка Terml и Term2, являются ли они
унифицируемыми. */
unify(X, Y) :- var(X), var(Y) , X = Y.
unify(X, Y) :- var(X), nonvar(Y), not_occurs_in(X, Y),
X = Y.
unify(X, Y) :- var(Y), nonvar(X), not_occurs_in(Y, X),
Y = X.
unify(X, Y) :- nonvar(X), nonvar(Y), atomic(X), atomic(Y),
X = Y.
unify(X, Y) :- nonvar(X), nonvar(Y), compound(X),
compound(Y), term_unify(X, Y).
not_occurs_in(X, Y) :- var(Y), X != Y.
not_occurs_in(X, Y) :- nonvar(Y), atomic(Y).
not_occurs_in(X, Y) :- nonvar(Y), compound(Y),
functor(Y, F, N),
not_occurs_in@, X, Y).
not_occurs_in(N, X, Y).
not_occurs_in(N, X, Y) :- N > 0, arg(N,Y,Arg),
not_occurs_in(X,Arg), N1 is N - 1,
not_occurs_in(Nl,X,Y).
term_unify(X, Y) :- functor(X, F, N), functor(Y, F, N),
unify_args(N, X, Y).
unify_args@, X, Y).
unify_args(N, X, Y) :- N > 0, unify.arg (N, X, Y),
N1 is N - 1, unify_args(Nl, X, Y).
unify_arg(N, X, Y) :- arg(N, X, ArgX), arg(N, Y, ArgY),
unify(ArgX, ArgY).
compound(X) :- functor(X, _, N), N > 0.
4-3.2.4- Реализация метода аналитических таблиц для
логики предикатов 1-го порядка па языке Пролог. Хотя боль-
большинство реализаций метода доказательства теорем выполнено на
основе принципа резолюций, здесь мы рассмотрим реализацию этого
метода с использованием аналитических таблиц, выполненную Фит-
тингом, поскольку в последние годы указанный метод выбран как
один из перспективных для доказательства теорем. Далее мы приве-
приведем реализацию метода, основанного на методе аналитических таблиц

4.3] Метод аналитических таблиц в логическом 175
в логике 1-го порядка со свободными переменными, на языке Пролог.
Отметим, что правила подстановки, используемые в методе аналити-
аналитических таблиц, основаны на нахождении НОУ, который строится для
замыкания ветви. В качестве пояснения к приведенной ниже реализа-
реализации метода заметим, что переменные языка Пролог используются как
свободные переменные в формулах прикладного языка, и формулы
удаляются из ветви, только если они могут быть унифицированы.
/* member (Item, List) — Item является элементом списка List. */
member[X, [X I _]).
member(X, [_ I Tail]) :- member(X, Tail).
/* remove (Item, List, Newlist) — Newlist является результатом удале-
удаления всех вхождений элемента Item из списка List. */
remove(X, [ ] , [ ]).
remove(X, [Y I Tail], Newtail) :-
X == Y, remove(X,Tail, Newtail).
remove(X, [Y I Tail], [Y I Newtail]) :-
X != Y, remove(X, Tail, Newtail).
/* append (List A, ListB, Newlist) — Newlist является результатом
соединения списков List А и ListB. */
append([ ], List, List).
append([Head I Tail], List, [Head I Newlist]) :-
append(Tail, List, Newlist).
/* Пропозициональные операторы: neg, and, or, imp, revimp, uparrov,
downarrow, notimp и notrevimp */
?-opA40, fy, neg).
?-opA60, xfy, [and, or, imp, revimp, uparrov, downarrow,
notimp, notrevimp]).
/* conjunctive(X) — X является се-формулой. */
conjunctive(_ and _).
conjunctive (neg (_ or _)).
conjunctive(neg(_ imp _)).
conjunctive(neg(_ revimp _)).
conjunctive(neg(_ uparrow _)).
conjunctive(_ downarrow _) .
conjunctive(_ notimp _).
conjunctive(_ notrevimp _).
/* disjunctive(X) — X является /3-формулой. */

176 Вывод на аналитических таблицах [Гл. 4
disjunctive(neg(_ and _)).
disjunctive(_ or _) .
disjunctive(_ imp _).
disjunctive (_ revimp _) .
disjunctive(_ uparrow _).
disjunctive(neg(_ downarrow _)).
disjunctive(neg(_ notimp _)).
disjunctive(neg(_ notrevimp _)).
/* unary (X) — X является двойным отрицанием или отрицанием
константы. */
unary(neg neg _).
unary(neg true).
unary(neg false).
/* binary_operator(X) — X является бинарным оператором. */
binary_operator(X) :- member(X, [and, or, imp, revimp,
uparrow, downarrow, notimp,
notrevimp]).
/* components(X, Y, Z) — Y и Z являются компонентами формулы
X, определенными в соответствии с правилами а и C. */
components(X and Y, X, Y).
components (neg (X and Y), neg X, neg Y) .
components(X or Y, X, Y).
components (neg(X or Y), neg X, neg Y).
components(X imp Y, neg X, Y).
components (neg (X imp Y), X, neg Y).
components (X revimp Y, X, neg Y).
components (neg(X revimp Y), neg X, Y).
components (X uparrow Y, neg X, neg Y).
components (neg (X uparrow Y), X, Y).
components (X downarrow Y, neg X, neg Y).
components(neg(X downarrow Y), X, Y).
components(X notimp Y, X, neg Y).
components (neg(X notimp Y), neg X, Y).
components(X notrevimp Y, neg X, Y).
components(neg(X notrevimp Y), X, neg Y).
/* component (X, Y) — Y является компонентой формулы X. */
component (neg neg X, X).
component (neg true, false.),
component (neg false, true).

4.3] Метод аналитических таблиц в логическом 177
Заметим, для задания кванторов используется функциональ-
функциональная нотация языка Пролог. Таким образом, формула УхР(х)
представляется 2-х местной функцией all(x,p(x)). Аналогично
формула ЗхР(х) представляется, как some(x,p(x)). Затем формула
Зх(Р(х) —> УхР(х)) записывается в следующем виде: some(x,p(x)
imp all(x,p(x))). Следует отметить, что реализация метода
аналитических таблиц наряду с обычными логическими связками
( & , V, -л, —> ) поддерживает нетрадиционные логические связки,
например, эквивалентность, стрелку Пирса и штрих Шеффера.
/* universal (X) — X является 7-формулой. */
universal(all(_, _)).
universal(neg some(_, _)).
/* existential(X) — X является E-формулой. */
existential(some(_, _)).
existential(neg all(_, _)).
/* literal(X) — X является литерой. */
literal(X) :- not conjunctive(X), not disjunctive(X),
not unary(X), not universal(X),
not existential(X).
/* atomicfmla(X) — X является атомарной формулой. */
atomicfmla(X) :- literal(X), X != _neg_.
Отметим, что формулы а и C имеют компоненты, а формулы 7 и
S имеют примеры. Запись примера предполагает, что известен способ
построения подстановки термов для свободных переменных в фор-
формуле. Для нахождения подстановки служит предикат sub, который
также разбивает формулу на подформулы, обеспечивая добавление
следующего уровня. В реализации метода формулы, термы и подста-
подстановки представляются списками.
/* sub(Term, Variable, Formula, NewFormula) — NewFormula являет-
является результатом подстановки Term во все вхождения свободной
переменной Variable в формулу Formula. */
sub(Term, Variable, Formula, NewFormula) :-
sub_(Term, Variable, Formula, NewFormula), !.
sub_(Term, Var, A, Term) :- Var == A.
sub_(Term, Var, A, A) :- atomic(A).
sub_(Term, Var, A, A) :- var(A).
sub_(Term, Var, neg X, neg Y) :- sub_(Term, Var, X, Y).
sub_(Term, Var, F(X,Y), F(U,V)) :- binary.operator(F),
sub_(Term, Var, X, U), sub_(Term, Var, Y, V).

178 Вывод на аналитических таблицах [Гл. 4
sub_(Term, Var, all(Var, Y), all(Var, Y)).
sub_(Term, Var, all(X,Y), all (X, Z)) :-
sub_(Term, Var, Y, Z).
sub_(Term, Var, some(Var, Y), some(Var, Y)).
sub_(Term, Var, some(X, Y), some(X, Z)) :-
sub_(Term, Var, Y, Z).
sub_(Term, Var, Functor, Newfunctor) :-
Functor = [F | Arglist],
sub_list(Term, Var, Arglist, Newarglist),
Newfunctor = [F I Newarglist].
sub_list(Term, Var, [Head I Tail], [Newhead I Newtail]) :-
sub_(Term, Var, Head, Newhead),
sub_list(Term, Var, Tail, Newtail).
sub_list(Term, Var, [ ], [ ]).
Понятия примеров j- или E-формул могут быть легко охарактери-
охарактеризованы.
/* instance(F, Term, Ins) — F является квантифицированной форму-
формулой, и Ins является результатом удаления квантора и замещения
всех свободных вхождений квантифицированной переменной на
вхождение терма Term.
7
instance(all (X,Y), Term, Z) :- sub_(Term, X, Y, Z).
instance(neg some(X,Y), Term, neg Z) :- sub_(Term, X, Y, Z).
instance(some(X,Y), Term, Z) :- sub_(Term, X, Y, Z).
instance(neg all(X,Y), Term, neg Z) :- sub_(Term, X, Y, Z).
Каждый раз, когда применяется правило 5, вводится новый функ-
функциональный символ. Далее используется символ сколемовской функ-
функции fun(n), где п является числом, которое увеличивается на 1 ка-
каждый раз при использовании правила 5. Для запоминания текущего
значения числа п применяют механизм, описанный далее. Для нача-
начала вводят предикат funcount, который запоминает текущий номер
сколемовской функции. Начальное значение номера равно 1, и оно
определяется записью funcount A). Затем каждый раз, когда исполь-
используется правило 5, вызывается предикат newfuncount. Далее приме-
применяют предикаты retracts и asserts для извлечения программного
предиката funcount (n) и замещения его на новый программный пре-
предикат funcount (n+1). Отметим, что этот механизм является не очень
логичным для языка Пролог, но Фиттинг не считает его неудобным.
Для того, чтобы пользователь этой программы имел возмож-
возможность доказывать несколько различных формул, был введен предикат
reset, который просто сбрасывает значение funcount к 1.

4.3] Метод аналитических таблиц в логическом 179
/* funcount(N) - N является текущим индексом сколемовской функ-
функции. */
funcountA).
/* newfuncount(N) - N является текущим индексом сколемовской
функции, увеличенным на 1. */
newfuncount(N) :- funcount(N), retract(funcount(N)),
M is N + 1, assert(funcount(M)).
/* reset - сбрасывание индекса сколемовской функции к 1. */
reset :- retract(funcount(_)), assert(funcountA)), !.
/* sko_fun(X, Y) - X является списком свободных переменных, Y яв-
является списком символов сколемовских функций, примененных
к этим переменным и неиспользуемым. */
sko_fun(Varlist, Skoterm) :- newfuncount (N),
Skoterm = [fun [N I Varlist]].
Итак, мы описали работу с правилом 5. Рассмотрим теперь
механизм работы с правилом 7- Для работы с этим правилом была
введена сложная структура, которая называется «записываемой
ветвью» (notated branch). Она представляет собой структуру
nb (Not at ion, Branch), где Branch является списком формул, а
Notation содержит информацию, которая связывается с ветвью.
Вводятся два вспомогательных предиката, которые работают с этой
структурой.
/* notation (Notated, Information) — Notated является записываемой
ветвью, Information содержит связанную с ней информацию. */
notation(nb(X, Y), X).
/* branch(Notated, Branch) — Notated является записываемой вет-
ветвью, Branch является частью этой ветви. */
branch(nb(X, Y), Y).
Затем вводится предикат single step, который используется для
расширения таблицы по соответствующим правилам и для проверки
ветви на замкнутость. Источником трудностей здесь является правило
7- Для работы с ним предлагается перейти от 7 к j(t) для любого кон-
константного терма t в формулах, не содержащих свободные переменные.
Такое правило можно применять несколько раз к одной и той же фор-
формуле, используя каждый раз различные константные термы. Следует
отметить, что существует бесконечное число константных термов,

180 Вывод на аналитических таблицах [Гл. 4
и, таким образом, процесс расширения таблицы может никогда не
завершиться, и, следовательно, никогда не будет достигнут шаг, при
котором ветвь станет замкнутой. Подобная проблема возникает также
при работе с таблицами, содержащими свободные переменные. Но
после всего сказанного выше, следует заметить, что если существовал
бы некоторый процесс, который всегда приводил бы к завершению
таблиц 1-го порядка за конечное число шагов, то существовала бы
разрешающая процедура для логики 1-го порядка. Однако знаме-
знаменитый результат, известный как теорема Чёрча, свидетельствует об
отсутствии подобной процедуры.
Путь, ведущий к преодолению этой трудности, основан на огра-
ограничении числа применений 7~пРавила ПРИ доказательстве методом
таблиц. Для этого используется метод Q-depth, заключающийся в
следующем. Когда 7~пРавило было применено максимальное число
раз, которое определяется заранее в виде значения Q-depth, оно может
больше никогда не применяться. Таким образом, используя метод
Q-depth, можно построить замыкание расширения таблицы (ни одно
из правил не может быть применено), за конечное число шагов, и
далее переходить к этапу тестирования замыкания. Таким образом,
доказательства являются конечными. Если выражение X является
доказуемым, то имеется доказательство, в котором сделано конечное
число применений 7"пРавила- Следовательно, если X является ис-
истинным, то оно будет доказуемо, если использовать метод Q-depth.
В принципе применяя каждый раз большее значение для метода
Q-depth, можно получить доказательство истинности любого выра-
выражения при условии игнорирования проблемы временной сложности и
ограниченного объема памяти. С другой стороны, ложность выраже-
выражения эквивалентна его недоказуемости на основе метода Q-depth любой
размерности, и это никогда не может быть выполнено, даже если будет
сделано бесконечное число шагов.
Отметим, что при создании автоматического метода аналитиче-
аналитических таблиц, реализованного на языке Пролог, была использована
идея Р. Смальяна, заключающаяся в том, что ветвь рассматривается
как нить, по которой осуществляется движение всегда сверху вниз, и
сначала применяются правила для отрицания и правила се, а затем
остальные правила. С учетом этой идеи был реализован метод, в
котором формула удаляется из ветви, если она не является формулой
7, и затем добавляются ее компоненты (для формул а и C) или
примеры (для формул 5). В качестве пояснения Фиттинг отмечает,
что он реализовал на языке Пролог метод, в котором добавление
компонент к началу ветви является удобным, хотя это теоретически
не обоснованно. В то же время, если выбрана формула 7? то она
удаляется из ветви, добавляется соответствующий пример, и затем
добавляется новое вхождение формулы j в конец ветви. Изложенные

4.3] Метод аналитических таблиц в логическом 181
выше положения гарантируют то, что каждый раз, когда рассматри-
рассматривается формула 7 на ветви, осуществляется повторение этой формулы
в ее исходном виде.
Еще одной проблемой, возникающей при реализации метода, явля-
является случай, когда каждая ветвь содержит формулу j. Для решения
данной проблемы была предложена обработка нитевидного представ-
представления таблицы, являющегося списком записываемых ветвей, подобно
приоритетной очереди. Далее работа начинается с 1-й ветви, затем
со второй и т. д. и продолжается до тех пор, пока не встретится
формула 7- Когда правило 7 применяется, то ветвь перемещается в
конец списка ветвей. Это гарантирует распространение применения
правила 7 на все ветви с помощью метода Q-depth.
Затем вводятся предикаты single step, которые имеют 4 аргумен-
аргумента. Первые два аргумента представляют аналитическую таблицу до
и после применения правила расширения таблицы как в пропозици-
пропозициональном случае. Два следующих аргумента представляют соответ-
соответствующее количество применения правила 7? используемое в Q-depth
до и после его применения. Последние два аргумента используются
только при работе с правилом j. Заметим, что переменные языка
Пролог взяты в качестве свободных переменных.
/* singlestep(OldTableau, OldQdepth, NewTableau, NewQdepth) -
применение одного правила расширения таблицы к таблице
OldTableau с заданным числом применений 7-правил OldQdepth.
При этом создается новая таблица NewTableau, и осуществля-
осуществляется изменение числа применений правила 7 OldQdepth на
NewQdepth. */
singlestep([01dNotated I Rest], Qdepth, [NewNotated I Rest],
Qdepth) :-
branch(OldNotated, Branch),
notation@1dNotated, Free),
member(Formula, Branch),
unary (Formula),
component(Formula, NewFormula),
remove(Formula, Branch, TempBranch),
NewBranch = [NewFormula I TempBranch],
branch(NewNotated, NewBranch),
notation(NewNotated, Free).
singlestep([OldNotated I Rest], Qdepth, [NewNotated I Rest],
Qdepth) :-
branch(OldNotated, Branch),
notation@1dNotated, Free),
member(Alpha, Branch),
conjunctive(Alpha),
components(Alpha, AlphaOne, AlphaTwo),

182 Вывод на аналитических таблицах [Гл. 4
remove (Alpha, Branch, TempBranch),
NewBranch = [AlphaOne, AlphaTwo I TempBranch],
branch(NewNotated, NewBranch),
notation(NewNotated, Free).
singlestep([OldNotated I Rest], Qdepth,
[NewOne, NewTwo I Rest], Qdepth):-
branch(OldNotated, Branch),
notation@1dNotated, Free),
member(Beta, Branch),
disjunctive(Beta),
components(Beta, BetaOne, BetaTwo),
remove (Beta, Branchy, TempBranch),
BranchOne = [BetaOne I TempBranch],
BranchTwo = [BetaTwo I TempBranch],
branch(NewOne, BranchOne),
notation(NewOne, Free),
branch(NewTwo, BranchTwo),
notation(NewTwo, Free).
singlestep([OldNotated I Rest], Qdepth, [NewNotated I Rest],
Qdepth) :-
branch(OldNotated, Branch),
notation@1dNotated, Free),
member(Delta, Branch),
existential(Delta),
sko_fun(Free, Term),
instance(Delta, Term, Deltalnstance),
remove(Delta, Branch, TempBranch),
NewBranch = [Deltalnstance I TempBranch],
branch(NewNotated, NewBranch),
notation(NewNotated, Free).
singlestep([OldNotated I Rest], OldQdepth, NewTree,
NewQdepth) :-
branch(OldNotated, Branch),
notation@1dNotated, Free),
member(Gamma, Branch),
universal(Gamma),
OldQdepth > 0,
remove(Gamma, Branch, TempBranch),
NewFree = [V I Free],
instance(Gamma, V, Gammalnstance),
append([Gammalnstance I TempBranch], [Gamma], NewBranch),
branch(NewNotated, NewBranch),
notation(NewNotated, NewTree),
append(Rest, [NewNotated], NewTree),
NewQdepth is OldQdepth - 1.

4.3 ] Метод аналитических таблиц в логическом 183
singlestep([Notated I OldRest], OldQdepth,
[Notated I NewRest], NewQdepth) :-
singlestep@1dRest, OldQdepth, NewRest, NewQdepth).
Заметим, что предикат expand имеет аргумент для задания значе-
значения в методе Q-depth.
/* expand(Tree, Qdepth, Newtree) — создание полного расширения
таблицы Newtree для таблицы Tree с заданным числом приме-
применений правила j. */
expand(Tree, Qdepth, Newtree) :- singlestep(Tree, Qdepth,
TempTree, TempQdepth),
expand(TempTree, TempQdepth,
Newtree).
expand(Tree, Qdepth, Tree).
Ветвь считается замкнутой, если она содержит литеры X и -Y,
где X и Y унифицируемы. Заметим, что для проверки унифицируе-
унифицируемости нельзя воспользоваться встроенной в язык Пролог процедурой
унификации. В реализации метода аналитичческих таблиц использу-
используется реализация алгоритма унификации, составленная Стирлингом и
Шапиро.
/* unify (Terml, Term2) — Terml и Term2 являются унифицируемы-
унифицируемыми. */
unify(X, Y) :- var(X), var(Y) , X = Y.
unify(X, Y) :- var(X), nonvar(Y), not_occurs_in(X, Y),
X = Y.
unify(X, Y) :- var(Y), nonvar(X), not_occurs_in(Y, X),
Y = X.
unify(X, Y) :- nonvar(X), nonvar(Y), atomic(X), atomic(Y),
X = Y.
unify(X, Y) :- nonvar(X), nonvar(Y), compound(X),
compound(Y), term_unify(X, Y).
not_occurs_in(X, Y) :- var(Y), X != Y.
not_occurs_in(X, Y) :- nonvar(Y), atomic(Y).
not_occurs_in(X, Y) :- nonvar(Y), compound(Y),
functor(Y, F, N),
not_occurs_in(N, X, Y) .
not_occurs_in(N, X, Y) :- N > 0, arg(N, Y, Arg),
not_occurs_in(X, Arg), N1 is N - 1,
not_occurs_in(Nl, X, Y).
not_occurs_in@, X, Y).

184 Вывод на аналитических таблицах [Гл. 4
term_unify(X, Y) :- functor(X, F, N),
functor(Y, F, N),
unify_args(N, X, Y).
unify_args(N, X, Y) :- N > 0, unify_arg(N, X, Y),
N1 is N - 1, unify_args(Nl, X, Y).
unify_args@, X, Y).
unify_arg(N, X, Y) :- arg(N, X, ArgX), arg(N, Y, ArgY),
unify(ArgX, ArgY).
compound(X) :- functor(X, _, N), N > 0.
В приведенной реализации алгоритма унификации тестируются
только атомарные замыкания на основе правила атомарного замыка-
замыкания. Приведем описания предиката closed, тестирующего замыкание
ветви.
/* closed (Tableau) — каждая ветвь таблицы содержит контрарную
пару после подстановки нужных значений вместо свободных
переменных. */
closed([Notated I Rest]) :- branch(Notated, Branch),
member(false, Branch),
closed(Rest).
closed([Notated I Rest]) :- branch(Notated, Branch),
member(X, Branch), atomicfmla(X),
member(neg Y, Branch),
unify(X, Y),
closed(Rest).
closed([ ] ).
Рассмотрим описания предикатов, составляющих заключительную
часть программы. Для того, чтобы запустить программу для форму-
формулы X, необходимо задать глубину метода поиска (Q-depth) и выпол-
выполнить запрос test(X,Y).
/* if_then_else(P, Q, R) — если Р — истинно, то Q; в противном
случае, если Р — ложно, то R. */
if_then_else(P, Q, R) :- Р, !, Q.
if_then_else(P, Q, R) :- R.
/* test(X, Qdepth) — создание полного расширения таблицы для
формулы ^Х с заданным числом применений 7~пРавил и те~
стирование на замыкание. */
test(X, Qdepth) :- reset, branch (Notated, [neg X]),

4.3]
Метод аналитических таблиц в логическом
185
notation(Notated, [ ]),
expand([Notated], Qdepth, Tree),
if_then_else(closed(Tree), yes(Qdepth)
no(Qdepth)), !, fail.
yes(Qdepth) :- write("First-order tableau theorem
at Q-depth"),
write(Qdepth), write(".") , nl.
no(Qdepth) :- write("Not first-order tableau theorem
at Q-depth"),
write(Qdepth), write(".") , nl.

Строй членов мира, как, всмотревшись ближе,
Увидел ты, уступами идет
И, сверху взяв, потом вручает ниже.
Данте Алигьери
Глава 5
ВЫВОД НА ИЕРАРХИЧЕСКИХ СТРУКТУРАХ
Одной из важных особенностей современных проблемных областей
является сложноструктурированность. Поэтому разработка методов
представления и обработки знаний в сложноструктурированных про-
проблемных областях весьма актуальна. В последние годы наблюдается
резкий рост количества работ, относящихся к обработке иерархиче-
иерархических структур. К настоящему времени в этой области сформировалось
несколько направлений исследований, наиболее перспективными из
которых являются алгебраический и логические подходы. Поэтому
ниже приведем описание наиболее практически значимых результатов
исследований, относящихся к этим подходам.
5.1. Многоуровневая упорядоченно-сортная
алгебра
5.1.1. Необходимость разработки механизмов вывода на
иерархических структурах
Перед тем, как покажем необходимость разработки механизмов
вывода на иерархических структурах, напомним, что одним из при-
признаков сложной системы по Г. Буч и Л. А. Растригину является иерар-
иерархичность. Этот признак особенно существенен для современных про-
проблемных областей, при описании которых часто используется термин
«сложноструктурированность». Поэтому далее мы и будем его исполь-
использовать для отражения сложной структуры проблемной области. Для
сложноструктурированных проблемных областей характерно наличие
огромного числа систем, связанных друг с другом информационными
связями и состоящих в свою очередь из подсистем, и т. д. до элемен-
элементарных подсистем.
Следует отметить, что использование механизмов вывода в слож-
сложноструктурированных проблемных областях является наиболее важ-
важным. Во-первых, эти механизмы позволяют «сжать» экстенсиональ-
экстенсиональную составляющую базы знаний, т. е. получить факты на основе ло-
логических выражений (аксиом), содержащихся в интенсиональной со-
составляющей базы знаний. Во-вторых, позволяют осуществить провер-
проверку информации, содержащейся в базе знаний, на непротиворечивость.

5.1] Многоуровневая упорядоченно-сортная алгебра 187
И в-третьих, пополнить интенсиональную составляющую базы знаний
новыми знаниями, отражающими специфику сложноструктурирован-
сложноструктурированной проблемной области. Перечисленные способы применения меха-
механизмов вывода делают его неотъемлемой частью интеллектуальных
систем, функционирующих в сложноструктурированных проблемных
областях.
Конечно, все описанные в предыдущих главах механизмы вывода,
в силу общности, применимы к сложноструктурированным проблем-
проблемным областям. Но следует заметить, что эффективность их использо-
использования в таких проблемных областях резко уменьшается за счет того,
что для описания сложноструктурированных проблемных областей
используется огромное количество структурных зависимостей, для
формализации которых в исчислении предикатов первого порядка
нет других средств, кроме предикатов. Использование предикатов
для задания структурных зависимостей загромождает описание про-
проблемной области, снижает его наглядность и резко уменьшает, что
существенно, эффективность процедур вывода. Поэтому в настоящее
время весьма актуально создание языков представления знаний и
механизмов вывода в них, позволяющих описывать структурные от-
отношения, не прибегая для этого к предикатам. Одним из таких языков
представления знаний является многоуровневая логика, созданная
японскими учеными С. Осуга и X. Ямаучи, которые также создали и
механизмы вывода в ней. Многоуровневой логике посвящена вторая
(большая) часть данной главы.
Вернемся теперь к алгебраическому подходу обработки иерархи-
иерархических структур. В последние годы наблюдается всплеск количества
работ, относящихся к этому подходу, о чем свидетельствует множество
статей, выставленных на обсуждение в Internet. Это связано прежде
всего с тем, что и по настоящее время не решена задача создания удоб-
удобного представления сложноструктурированной информации в базах
данных и не созданы эффективные средства манипулирования ею.
Одним из решений этой задачи является создание средств обработ-
обработки сложноструктурированной информации на основе многосортной
и многоуровневой алгебр. Они являются математическим аппаратом
для манипулирования сложными объектами, которые представляют
собой множества объектов, множества подмножеств объектов и т. д.
Краткому изложению этих алгебр посвящена первая часть данной
главы. Авторы приносят извинения за некоторую фрагментарность
в изложении материала, поскольку окончание разработки этих ал-
алгебр еще далеко впереди. Данный материал решили включить в на-
настоящую книгу, поскольку многосортную и многоуровневую алгебру
можно рассматривать как математический фундамент для создания
систем управления базами данных (СУБД) нового поколения, к кото-
которому по праву можно отнести объектно-ориентированные СУБД.

188 Вывод на иерархических структурах [Гл.5
Многоуровневая упорядоченно-сортная алгебра (multi-level order
sorted algebra или кратко MLOSA) была разработана М. Ируингом для
описания отношений между типами и является формальным базисом
для определения понятий на основе единого формализма. MLOSA
является интеграцией многосортной алгебры (many-sorted algebra или
кратко MSA) и упорядоченно-сортной алебры (order-sorted algebra
или кратко OS A). MS А была введена Р. Гутингом, Р. Цикари и
Д. Чоем как основа для создания языка запросов, и в дальнейшем
была использована для определения алгебры манипулирования
сложными объектами. MSA обеспечивает создание правильно-
структурированных типов системы. В отличие от MSA OSA позволяет
поддерживать иерархию типов и наследование. М. Ируинг и Р. Гутинг
ввели второй уровень в OS А для описания результатов применения
типовых конструкторов к видам, которыми являются множества
сортов одноуровневой алгебры. Также эти ученые описали трехуров-
трехуровневую алгебру для формального описания операций с переменным
числом аргументов. OSA используется для манипулирования типами
данных, а также иерархиями типов данных. Следует отметить,
что OS А используется в функциональных моделях, содержащих
функции, моделирующие атрибуты объектов и отношения между
ними.
5.1.2. Введение в многоуровневую алгебру
Многоуровневая алгебра (multi-level algebra или кратко MLA) при-
применяется для создания БД, имеющих специфичную структуру, и язы-
языков запросов. В основе модели таких БД лежит система множеств, ис-
используемая для представления типов данных и объектов, и функции,
задающие атрибуты и отношения, определенные на этих множествах,
которые и образуют алгебру. Развитием MLA является MLOSA, кото-
которая применяется для манипулирования объектами в описанной выше
модели данных, а также для обработки специфичных схем. Далее
кратко рассмотрим релевантные нотации и обоснуем использование
MLOSA.
Классическая реляционная алгебра является универсальной или
односортной алгеброй, т. е. она имеет простые домены, чьими эле-
элементами выступают отношения, заданные таблицами, и набор функ-
функций, определенных на этих доменах. Развитием реляционной алгебры
является MSA, которая имеет ряд преимуществ перед реляционной
алгеброй для создания языка запросов. Одно из таких преимуществ
состоит в возможности интеграции арифметических функций и функ-
функций агрегации в такой алгебре. Следует отметить, что понятия «под-
«подтип» и «наследование» также введены в MSA. Сложные типы объек-
объектов строятся из простейших типов с помощью применения конструк-
конструкторов типов. Функции, которые служат конструкторами типов, при-

5.1] Многоуровневая упорядоченно-сортная алгебра 189
меняются к разнообразным классам типов, т. е. их сигнатуры обыч-
обычно содержат типовые выражения с переменными, определенными на
множествах имен типов. Обычно говорят, что такие функции задают
свойство «полиморфизм». Полиморфизм в OSA является ограничен-
ограниченным. Так, следует отметить, что, в общем, модельный параметриче-
параметрический полиморфизм посредством одного уровня алгебры невозможен,
и поэтому была разработана двухуровневая алгебра, описывающая
типы и конструкторы типов. Значения на втором уровне в такой
алгебре рассматриваются как имена сортов на первом уровне. Идея
представления произвольного числа уровней формализуется в ML А.
Двухуровневая алгебра используется как аппарат, в котором может
быть определена экстенсиональная составляющая сложноструктури-
сложноструктурированной БЗ.
5.1.3. Моделирование подтипов и наследования
М. Ируинг и Р. Гутинг провели моделирование подтипов и насле-
наследования на основе OSA. Для этого была определена многосортная
сигнатура, упорядоченно-сортная сигнатура и сигнатура специфика-
спецификации. Приведем определения этих сигнатур, которые необходимы для
дальнейшего изложения материала.
Определение 5.1. Многосортная сигнатура есть пара (?, XI)? где
S — множество сортов и X] есть S* —>¦ S — семейство операций:
{J2Ws\w ^ #* и s e ?}, в котором S* — декартово произведение
элементов s Е S. Операция а Е J2W s имеет арность w и ранг ws.
Определение 5.2. Упорядоченно-сортная сигнатура есть тройка
(?, <, Х!)> в которой (?, J2) есть многосортная сигнатура, (?, <) есть
частично-упорядоченное множество, и операции в X! удовлетворяют
условию монотонности:
а е Y^ n Yl ^w ^ w'^w' ^ ?) ^ s ^ 5''
w,s w' ,s'
где е — пустая строка.
Пусть (#, ^, XI) есть алгебра А, содержащая для каждого сорта s E
Е S множество sA (носитель s) и для каждого символа операции aw^s
функцию o~As:: wA —> sA , где (ws)A = wA • sA и еА = {0}. Алгебра А
должна удовлетворять следующим условиям:
A) s < sf => sA С s/A;
w,s w' ,s'

190 Вывод на иерархических структурах [Гл.5
Пример 5.1.
В качестве примера приведем многосортную сигнатуру, состоя-
состоящую из множества сортов S = {Самолет, Радиолокационная станция
(РЛС), Взлетная полоса, Поток сообщений, ... } и множества опера-
операций: назначить взлетную полосу, назначить время взлета и посадки,
записать в график и т. д.
Иерархии типов данных и типов объектов определяются посред-
посредством частичного порядка на сортах. Рассмотрим на примере задание
иерархии типов данных и типов объектов.
Пример 5.2.
Иерархии типов данных и типов объектов приведены на рис. 5.1.
На них могут быть определены следующие операции:
обеспечить прием/передачу потока сообщений: Самолет —> РЛС;
назначить взлетную полосу: Самолет —> Взлетная полоса;
назначить время взлета: Самолет —> Число.
Объект управления
Поток РЛС Самолет Взлетная
сообщений полоса
Число
Целое Вещественное
Рис. 5.1
Следует отметить, что для операции «Обеспечить прием/передачу
потока сообщений» объекты сорта «Самолет» являются исходными
данными, объекты сорта «РЛС» — результирующими данными.
Заметим, что определение OSA не позволяет задать наследование.
Для того, чтобы задать наследование, М. Ируинг и Р. Гутинг ввели
сигнатуру спецификаций.
Определение 5.3. Любая упорядоченно-сортная сигнатура есть
в то же время сигнатура спецификации. Индуцированная сигнатура
(S, ^,IND(J^)) определяется следующим образом:
w")}

5.1] Многоуровневая упорядоченно-сортная алгебра 191
Это определение описывает наследование функций сверху вниз. К
J2 добавляются операции а, определенные на подтипах w" из w с тем
же результатом, как для типов s.
5.1.4. Описание параметрического полиморфизма аппаратом
двухуровневой алгебры
Функции, определенные на различных типах, описывающих подоб-
подобные структуры, поддерживают параметрический полиморфизм. Для
таких функций область определения и область значений определяется
посредством одной сущности, содержащей переменные, описываю-
описывающие параметры типов. В общем, переменные типов определяются на
подмножестве множества, элементами которого являются все имена
типов. Для того, чтобы определить множество имен типов и на-
назначить ему имя, введено понятие «множество видов». Фактически,
виды являются сортами, входящими в состав другой сигнатуры, за-
заданной на 2-м уровне, и ее носителями являются множество сортов
1-го уровня. Операции, определенные на 2-м уровне, называются
конструкторами типов. Функции, входящие в такие конструкторы,
устанавливают соответствие между видами, т. е. они устанавливают
соответствие одного или более сортов одного вида и сорта другого
вида. Поэтому 2-й уровень называется сигнатурой/алгеброй видов.
Далее определяются конструкторы типов и дается определение п-
уровневой сигнатуры.
Определение 5-4- Упорядоченно-сортной сигнатурой является
сигнатура 1-го уровня. Пусть задана n-уровневая сигнатура (#, ^, J2)
и n-уровневая алгебра В (носителем алгебры В является множе-
множество В). Тогда упорядоченно-сортная сигнатура (S", ^', Y^ ) есть
n + 1-уровневая сигнатура, заданная на (#, ^, J^) и Б, если выполнено
условие: S' = U SB.
ses
Тогда алгебра A (Sf, ^', J2 ) есть n + 1-уровневая алгебра, если для
каждой операции aWiS Е Y1 существует функция aws (конструктор
типов от crw,s), и если для каждого t E S': t = cr^)S(?i,..., tn) (где
w = 5Ь..., 5П и U е sf , г = 1,...,п) имеется tA = aws(tf,... ,t^).
Функцию g_w^s определяет семантический конструктор, входящий
в состав J^. Говорят, что А зависит от В и от семантического кон-
конструктора из J^.
Поясним определение 5.4, расширив предыдущий пример 5.2 за
счет добавления сортов объектов «Система поддержки управления
(СПУ)», «Принимаемый поток сообщений», «Передаваемый поток
сообщений», а также добавления на 2-м уровне к множеству видов
S = {Аэропорт, Объект управления, Диспетчер, Поток сообщений}
конструктора «диспетчер», используемого для построения сортов ви-

192
Вывод на иерархических структурах
[Гл.5
да «Диспетчер». На основе вышесказанного зададим сигнатуру 2-го
уровня.
Ord: Поток сообщений ^ Объект управления; СПУ, Объект управ-
управления < Аэропорт.
Тс: Принимаемый поток сообщений, Передаваемый поток сообще-
сообщений —> Поток сообщений.
Поток сообщений, РЛС, Самолет, Взлетная полоса —> Объект
управления.
СПУ, Объект управления —> Аэропорт.
Диспетчер: Объект управления —> Диспетчер, где
Ord задает спецификацию порядка, где s,t,v,w является короткой
записью того, что s ^ v; t ^ v; s ^ w; t ^ w.
Тс является конструктором типов на 1-м уровне, «диспетчер» яв-
является семантическим конструктором типов на 2-м уровне. Иерархия
подтипов приведена на рис. 5.2.
Аэропорт
СПУ
Диспетчер
Поток сообщений
Принимаемый поток
сообщений
Взлетная полоса
Передаваемый поток
сообщений
Рис. 5.2
Для обозначения сортов на 2-м уровне вводятся кавычки. Так,
«Поток сообщений»={Принимаемый поток сообщений, Передава-
Передаваемый поток сообщений};
«Объект управления»={Поток сообщений, РЛС, Самолет, Взлет-
Взлетная полоса};
«Диспетчер» является множеством сортов, которые могут быть
получены путем применения конструктора «диспетчер» к сорту «Объ-
«Объект управления». Так,
«Диспетчер» = {диспетчер (Поток сообщений), диспетчер (РЛС),
диспетчер (Самолет), диспетчер (Взлетная полоса)}.
Семантический конструктор «диспетчер» определяется так:

5.1] Многоуровневая упорядоченно-сортная алгебра 193
Для всех 5G «Объект управления» диспетчер(<5>) =<s> * (для
его обозначения вводится запись < диспетчер (s) >), где < s > * —
вид «Диспетчер».
Вид «Диспетчер» содержит только сорта, получаемые с помощью
применения конструктора «диспетчер» к сорту «Объект управления».
Таким образом определяется персонал по обслуживанию взлетной
полосы, обеспечению взлета — посадки самолетов и взаимодействию
с РЛС. Сорта, которые являются подмножествами вида «Диспетчер»,
могут быть определены путем применения конструктора «диспетчер»
к подмножествам вида «Объект управления». Так, имеем диспет-
чер(Самолет), диспетчер (РЛС) и т.д.
Следует отметить, что типы функций, поддерживающих полимор-
полиморфизм, обычно описываются при помощи схем типов, например, тип
операции «обслуживание» может быть определен так:
Для всех а Е «Объект управления»
обслуживает: диспетчер (се) —> строка символов, где «строка симво-
символов» определяет имя диспетчера, который обслуживает объект а.
Запись типа операции может быть представлена следующим
образом:
обслуживает: диспетчер (объект управления)^ строка символов, что
тоже самое, что Диспетчер —>¦ строка символов.
Если операция применяется более чем к одному сорту, то она
может быть представлена следующим образом:
прием/передача: Поток сообщений^Время.
Данная запись обозначает оператора «приема/передачи» для лю-
любых комбинаций принимаемых и передающих сообщений РЛС, явля-
являющихся подмножествами множества «Поток сообщений».
Для определения одних и тех же элементов в различных позициях
сигнатуры вводится индексирование видов. Например, оператор срав-
сравнения, который может быть применен к любым двум объектам одного
сорта вида «Число», имеет следующий вид:
<,<,>,>: Число; х Число; -> BOOL,
где тип данных BOOL содержит два значения {истина, ложь} .
Таким образом, MLA позволяет:
• представить спецификации всех типов полиморфизма (подти-
(подтипов, ad hoc и параметрического);
• в едином формализме представить новые структуры (примеры,
графы, гетерогенные последовательности объектов);
• выражать детали подтипов для конструирования типов;
• использовать стандартные методы для синтаксической проверки
статичных типов.
7 В.Н. Вагин и др.

194 Вывод на иерархических структурах [Гл.5
Теперь перейдем к рассмотрению логического подхода. Большой
вклад в область обработки иерархических структур внесли и вносят
японские логики С. Осуга и X. Ямаучи, которые создали многоуровне-
многоуровневую логику (Multi-layer logic или коротко MLL) и механизмы вывода
в ней. MLL является фундаментом логического подхода к обработке
иерархических структур. Более точно ее можно рассматривать как
интеграцию логического подхода и подхода, основанного на семан-
семантической сети, к построению языка представления знаний. Поэтому
ниже приведем ее описание и модификацию, позволяющую увеличить
эффективность процедуры дедуктивного вывода.
5.2. Многоуровневая логика как язык
представления знаний в интеллектуальных
системах
5.2.1. Способы задания иерархических структур в многоуровневой
логике
Отметим, что ISA- и Part-of-иерархии являются основополагающи-
основополагающими структурами для описания сложноструктурированной проблемной
области. Для представления ISA- и Part-of-иерархий в MLL исполь-
используется иерархическая абстракция и иерархическая структура. Иерар-
Иерархическая абстракция представляет граф, вершинам которого соответ-
соответствуют классы объектов или их представители, а ребрам — отношения
«класс-подкласс», либо «часть — целое». Иерархическая абстракция
является многоуровневой структурой. Уровни в иерархической аб-
абстракции, соответствующей отношению «класс — подкласс», выде-
выделяются в соответствии с принципом наследования свойств. Классы
и их представители располагаются на различных уровнях, поскольку
описания (атрибуты) класса наследуются его представителями. Меха-
Механизм наследования свойств позволяет «сжать» базу знаний, т. е. сде-
сделать ее более компактной. В иерархической абстракции, соответству-
соответствующей отношению «часть — целое», уровни выделяются в соответствии
с принципом декомпозиции, который является основополагающим
при моделировании сложноструктурированных проблемных областей.
Класс объектов и классы, из которых он состоит, располагаются на
различных уровнях.
Атрибуты классов объектов или их представителей (объектов) и
отношения между классами объектов, исключая структурные отно-
отношения, в иерархической абстракции могут быть описаны правильно
построенными формулами (ППФ). Когда некоторая ППФ описывает
класс объектов (или объекты) в иерархической абстракции, она соеди-
соединяется с соответствующей ему вершиной. Пример ППФ, описывающей
объекты в иерархической абстракции, приведен на рис. 5.3, где ф —

5.2] Многоуровневая логика как язык представления знаний 195
обозначение константы; —> — обозначение структурных отношений;
> — обозначение ссылки на ППФ.
Cx/#5)(Vj/x) Поступают (у, принтер)
' функциональная подсистема #S
объем памяти (N, 20 К)
программная / \ \^^ /время реакции Ш, 0,02 с)
компонента / f ^\_к If ..
/2О --ТУ
\\
тип (данное k, int)
данное 1 данное к «обработка»
Рис. 5.3
В то же время, любая ППФ, задающая некоторое описание про-
проблемной области, должна использовать в качестве термов классы
объектов (или объекты), с которыми она соединена в иерархической
абстракции. Иногда существует необходимость представлять в ППФ
не только объекты, с которыми описание связано непосредственно, но
и классы объектов (или объекты), с которыми описание связано кос-
косвенно. Эти классы объектов (или объекты) расположены в иерархиче-
иерархической абстракции на более низких уровнях от вершины, которой соот-
соответствует описание. Пример такой ППФ описывает вершину «функ-
«функциональная подсистема», представленную на рис. 5.3: «Существует
некоторая программная компонента в функциональной системе ^fS
такая, что все ее результирующие данные поступают на принтер».
Чтобы описать модель проблемной области и определить в ней
операции, необходим специальный язык. Этот язык определяется как
расширение логики предикатов первого порядка. Поскольку он имеет
дело с многоуровневыми (иерархическими) объектами, его назвали
языком многоуровневой логики.
MLL можно рассматривать как расширение многосортной логики
за счет введения метода структурирования типов в синтаксис и семан-
семантику логического языка. Структурирование типов (сортов) позволяет
сократить область определения терма и тем самым увеличить эффек-
эффективность дедуктивного вывода.
Рассмотрим базовые отношения, которые задаются в MLL. Фигур-
Фигурные скобки будем использовать как метасимвол для представления

196 Вывод на иерархических структурах [Гл.5
множества объектов. Так, d = {Ьь 62,... ,ЬП} является множеством
и bi = {ан, &2г, • • • ? атг}? * — 1, • • •, 71, является подмножеством из d.
Следующие отношения объявляются как базовые.
1. «Element of», которое обозначается х Е X (объект х является
элементом множества X) и является средством для задания
отношения «элемент—множество».
2. «Power set of», которое обозначается Y = *Х и исполь-
используется для отражения того, что Y является множеством,
состоящим из подмножеств множества X (не включая
пустого множества). Например, если d = {1,2,3}, то *d =
= {{1}, {2}, {3}, {1,2}, {1,3}, {2,3}, {1,2,3}}. Мощность |*d| =
= 2^ — 1, где \d\ = N. Поскольку *d является множеством,
можно определить множество подмножеств 2-го порядка на d,
как *(*d). Это обозначается как *2d. Таким образом, множество
подмножеств n-ого порядка, обозначаемое *nd, определяется
как *(*(n-1)d).
3. «Product set of», которое обозначается Y = Х\ х Х2 х ... х Хт или
т
Y = Л X^ и используется для задания того, что Y представляет
г=1
собой декартово произведение из Х\, Х2,..., Хт.
4. «Component of», которое обозначается YVX и задает, что X яв-
является компонентом Y. Если Y содержит несколько компонент,
т. е. YVXi, У VX2,..., YVXs, то специальный метасимвол О
используется для обозначения: < Y >= {Xi, X2,... ,Х#}. Со-
Содержательно, X^, г = 1,..., s представляет собой подмножество
элементов одного сорта, каждый из которых является частью Y.
Среди базисных отношений B) и C) являются специальными
операторами для генерации новых сортов из заданных. Рассмотрим
производные отношения в силу их важности для описания иерархи-
иерархических структур, которые определяются через композицию базисных
отношений.
(Iх) «Subset of», которое обозначается X С У и определяет, что
X является подмножеством Y. Это отношение является ком-
композицией двух отношений: Z = *У и X Е Z, т.е. С=е о*.
Множественное отношение «Subset-of» задает ISA-иерархию на
множестве классов объектов проблемной области.
Bх) «Part of», которое обозначается Y > х и определяет, что х
является частью Y. Это отношение является композицией двух
отношений: >=? oV. Отношение «Part of» используется для
задания Part-of-иерархии на множестве классов объектов про-
проблемной области.

5.2]
Многоуровневая логика как язык представления знаний
197
Поскольку отношение «Part
of» является композицией отноше-
отношений «Component of» и «Element
of», иерархическая абстракция, со-
соответствующая отношению «Part
of», представляется так, как по-
показано на рис. 5.4. Такое изобра-
изображение иерархической абстракции
называется иерархической струк-
структурой, которая используется для
задания Part-of-иерархии предста-
представителей классов в экстенсиональ-
экстенсиональной составляющей базы знаний
(БЗ) (базы данных (БД)) интел-
интеллектуальной системы.
Представление иерархической
структуры на рис. 5.4 являет-
является стандартной формой в MLL.
Иерархическая структура, изобра-
изображенная на этом рисунке, являет-
является многоуровневой. Уровни в ней,
как и в иерархической абстрак-
абстракции, выделяются в соответствии
уровень i+l
функциональная подсистема /
#S I
программная
"^компонента
(пку
Рис. 5.4
а) Форма представления иерархии
наследования (ISA-иерархия)
интенсио-
интенсиональная
состав-
составляющая БЗ
экстенсио-
экстенсиональная
составляю-
составляющая БЗ (БД)
б) Форма представления иерархии
подчинения (Part-of-иерархия)
Ш|
а') интенсиональная б') экстенсиональная
составляющая БЗ составляющая БЗ (БД)
(иерархия представи-
представителей классов)
Рис. 5.5

198
Вывод на иерархических структурах
[Гл.5
\ /
с наследованием свойств. Так, классы объектов и их представители,
которые находятся в отношении «Element of», располагаются на раз-
различных уровнях, а классы объектов, которые находятся в отношении
«Component of» — на одном уровне, поскольку нет наследования
свойств между ними.
Графические формы представления иерархической абстракции и
иерархической структуры представлены на рис. 5.5. На рис.5.5,а изоб-
изображена иерархическая абстракция, соответствующая ISA-иерархии
классов объектов, которая задается в интенсиональной составляющей
БЗ интеллектуальной системы; ниж-
нижний уровень этой иерархии соответству-
соответствует представителям классов, содержа-
содержащихся в экстенсиональной составляю-
составляющей БЗ (БД). На рис. 5.5,б'дана форма
представления иерархии подчиненности
(Part-of-иерархия).
Одним из недостатков иерархи-
иерархических абстракций, соответствующих
ISA- и Part-of-иерархиям классов объ-
объектов, является то, что класс объек-
объектов может принадлежать к обоим ви-
видам абстракций, что приводит к дуб-
дублированию описания класса объектов,
и, как следствие этого, к неэффектив-
неэффективному использованию памяти ЭВМ. По-
Поэтому дальнейшим направлением иссле-
исследований может быть объединение двух
видов абстракций в одну обобщенную
иерархическую абстракцию и изучение наследования в ней. Пример
обобщенной абстракции представлен на рис. 5.6.
5.2.2. Синтаксис многоуровневой логики
Для дальнейшего изложения материала представим синтаксис
MLL и ее основные определения.
Алфавит:
A) константы: а, 6, с,...; X, Y, Z (константные множества), ...;
B) переменные: ж, г/, г,...;
C) функциональные символы: /, д, /г,...;
D) предикатные символы: Р, Q, i?,...;
E) кванторы: V, 3;
F) отрицание: "";
G) логические связки: &, V, —>;
(8) вспомогательные символы: ф,*,/,/',/У,{,},(,).

5.2] Многоуровневая логика как язык представления знаний 199
Термы:
A) любая константа и переменная являются термом;
B) если / есть n-местный функциональный символ и ?i,?2,...,?n
являются термами, то /(?]_, ?2, • • • •> tn) есть терм;
C) все термы получаются применением A) и B).
Правила образования ППФ:
F1) если Р является n-местным предикатным символом и
ti, ?2, • • •, tn есть термы, то P(?i, ?2, • • •, tn) является ППФ
(атомарной формулой);
F2) если FuG — ППФ, то ^F, F&G, F V G, F -> G являются ППФ;
F3) если F — ППФ и х — предметная переменная, то
1) (\/x/y)F и Cx/y)F являются ППФ, где у есть константа или
переменная;
2) (\/x/y)F и Cx/y)F являются ППФ, где у есть константа
или переменная;
3) (Ух//y)F и (Зх//y)F являются ППФ, где у есть константа
или переменная;
F4) других правил образования ППФ нет.
5.2.3. Описание двух видов иерархической абстракции и
иерархической структуры множеством правильно построенных
формул многоуровневой логики
Принципиальной разницей между MLL и многосортной логикой
(MSL) является форма представления иерархической абстракции и
иерархической структуры с помощью множества ППФ. MSL опи-
описывает явно отношение «элемент-множество» между объектами в
префиксе ППФ в форме x/d, где х является элементом множества
(сорта) d.
Для задания иерархической абстракции, соответствующей ISA-
иерархии, MLL использует расширение этого формализма. Так, MLL
позволяет работать с сортами, представляющими собой структури-
структурированные единицы, элементами доменов которых могут быть множе-
множества, множества подмножеств и т. д.
Для описания иерархической абстракции и иерархической струк-
структуры, соответствующих Part-of-иерархии классов объектов и Part-of-
иерархии представителей классов, аппарат MSL использовать неудоб-
неудобно, поскольку в основе этих иерархий лежат отношения, в схемы кото-
которых входят различные сорта, a MSL рассматривает сорта как отдель-
отдельные, независимые единицы, и в ней нет средств, кроме предикатов,
позволяющих описывать эти отношения. Использование предикатов

200 Вывод на иерархических структурах [ Гл. 5
для описания этих отношений усложняет и загромождает описание
проблемной области и снижает эффективность дедуктивного вывода.
Для задания Part-of-иерархии в MLL введено три вида специальных
знаков слэшей.
Слэшем называется некоторый разделитель, который использует-
используется в префиксе формулы. Так, простой слэш (Qx/X) используется для
обозначения, что х является элементом множества X (х Е X), простой
«жирный» слэш (Qx/X) обозначает, что х определен на множестве,
элементами которого являются компоненты объекта Х(Х>х), двойной
слэш (Qx/ /X) обозначает, что х определен на множестве, элементами
которого являются части объекта Х(Х > ж), где Q Е {V, 3}.
Если объект Y имеет в качестве компоненты объект X, то для
того, чтобы определить свойства объекта х Е X, который является
частью объекта У, мы можем написать формулу
(Qx//#Y)G(x), E.1)
где ф — обозначение константного множества; Q : V или 3; G{x) —
предикат, описывающий свойства объекта х (атрибут).
Формула E.1) записана в стандартной форме для MLL. Если объ-
объект Y имеет в качестве компонент несколько объектов, как показано
на рис. 5.4, то для того, чтобы задать нужную нам компоненту X объ-
объекта У, необходимо использовать селектор, который представляется
предикатом F(X,Y). Для этого случая, чтобы определить свойства
xGl, являющегося частью объекта У, мы можем написать формулу
(ЗХ/W) (Qx/X) [F(X, Y)kG(x)},
которая может быть преобразована к стандартной форме:
(Qx//#Y)[F(x,Y)&zG(x)].
Используя формализм задания структурных отношений в префик-
префиксе формулы, мы предлагаем замену селектора, который представляет-
представляется предикатом и используется для нахождения нужной компоненты
некоторого объекта, на композицию префикса. Рассмотрим предло-
предложенное нами расширение синтаксиса MLL.
Пусть объект #У имеет в качестве компонент несколько объектов,
т.е. < jfY >= {Xi} , г = 1... TV, тогда префикс может содержать
запись вида
(Q(x/Xi)//#Y),
Xi задает сортность ж, которой в прикладном исчислении соот-
соответствует класс объектов предметной области. Щ^-Y будем называть
>-предком для х по иерархии Part of. Запись E.2) содержательно
означает, что х определена на множестве частей #У, которые имеют
сортность Х^

5.2] Многоуровневая логика как язык представления знаний 201
Таким образом, мы развили правила образования ППФ, которые
теперь имеют следующий вид:
F1. Если Р является n-местным предикатным символом и
ti, ?2, • • •, tn есть термы, то P(?i, ?2, • • •, tn) является ППФ
(атомарной формулой).
F2. Если FnG- ППФ, то ^(F), (F&G), (FVG)y(F -> G) являются
ППФ.
F3. Если F — ППФ и х — предметная переменная, то
1) (\/x/y)F и Cx/y)F являются ППФ, где у есть константа или
переменная;
2) (Vx/y)F и Cx/y)F являются ППФ, где у есть константа
или переменная;
3) (\/х//y)F и (Эх//y)F являются ППФ, где у есть константа
или переменная;
4) (V(x/Z)//y)F и C(x/Z)//y)F являются ППФ, где у есть
константа или переменная, Z есть константное множество.
F4. Других правил образования ППФ нет.
Преимущества модифицированных правил построения ППФ:
• во-первых, не затрачивается время на унификацию предиката-
селектора, а расширенный нами синтаксис префикса логической
формулы позволяет сделать означивание термов по структурам
проблемной области и далее осуществить проверку значений
переменных на удовлетворение условию, задаваемому матрицей
логической формулы;
• во-вторых, не затрачивается память на хранение многочислен-
многочисленных фактов проблемной области для означивания переменных
в предикате-селекторе.
Из рассмотренного выше следует, что это расширение синтаксиса
MLL повышает эффективность дедуктивного вывода по памяти и
быстродействию.
Приведем пример логического выражения, содержащегося в ин-
интенсиональной составляющей БЗ, и на нем покажем преимущества
использования аппарата MLL для формализации сложноструктури-
сложноструктурированной предметной области по сравнению с аппаратом многосорт-
многосортной логики (MSL).
Пример 5.3.
Программная компонента ж, входящая в состав системы поддерж-
поддержки управления фР, обеспечивает посадку самолета г/, приписанного к
аэропорту фА, если имеется
• ЭВМ ?, на которой функционирует х;

202 Вывод на иерархических структурах [ Гл. 5
• радиолокационная станция (РЛС) s, соединенная с ЭВМ t\
• поток информации ^/1, содержащий поток сообщений ti, при-
принимаемый РЛС 5, и содержащий класс сообщений ri, описыва-
описывающий самолет у и обрабатываемый х;
• поток информации #/2, содержащий поток сообщений ?2, пере-
передающийся РЛС s, в который входит класс сообщений Г2, имею-
имеющий сведения, необходимые для посадки самолета у, вырабаты-
вырабатываемый х и принимаемый у.
Структуры проблемной области представлены на рис. 5.7.
Запись в MSL:
{фА/ Аэропорт) (#Р/СПУ) (Зж/программная_подсистема)
(У|//самолет)C5/РЛС)C^/ЭВМ)(#/1/поток_информации)
(#/2/поток_информации)C^1/поток_сообщений)
Cri /класс_сообщений) C^/поток_сообщений)
(Зг2/класс_сообщений)
Содержит(#Р, х) & Содержит(#А, у) & Содержит(#А, s) &
& Содержит(#Д?)&
& Функционирует (ж, t) & Соединена(з, t) & Содержит (#/1, ti) &
& Принимает_РЛСE, ti) & Содержит(^1, ri) & Описывает(г1, у) &
& Обрабатывает(ж,Г1) & Содержит(#/2, ?2) & Передает_РЛСE, t2)&
& Содержит(^2, г2) & Вырабатывает(ж, Г2) &
& Принимает_самолет(|/, Г2) -^ Обеспечивает_посадку(ж, г/)
Запись в MLL:
C(ж/программная_система)//#Р)(\/(|//самолет)//#О)
(Э(в/РЛС)//#А)(Э(*/ЭВМ)//#А) C(?1/поток_сообщений)//#/1)
C(г1/класс_сообщений)//^1)C(^2/поток_сообщений)//#12)
C (г2 /класс_сообщений) //?2)
Функционирует (ж, t) & СоединенаE, t) & Принимает_РЛСE, t\) &
& Описывает (ri, г/) & Обрабатывает(ж, ri)& Передает_РЛСE, ^)&
& Вырабатывает(ж, гг) & Принимает_самолет(|/, гг) -^
-^ Обеспечивает_посадку(ж, г/)
Из рассмотренного выше примера следует, что аппарат MLL уве-
увеличивает эффективность дедуктивного вывода по сравнению с MSL
за счет сокращения пространства поиска. Это сокращение достигается
структуризацией проблемной области и представления структурных
отношений в префиксе логической формулы, что влечет удаление
большого числа предикатов, которые загромождают описание про-
проблемной области и снижают эффективность дедуктивного вывода.
Таким образом, MLL позволяет сделать описание сложнострук-
сложноструктурированной проблемной области более наглядным за счет задания
структурных отношений в префиксе логической формулы, без ис-
использования предикатов, и, как следствие этого, позволяет увеличить

5.2] Многоуровневая логика как язык представления знаний 203
#Р
Программная
система
PI P2 РЗ
Q#O
Самолет
TU154
AN74 IL86
ЭВМ
РЛС
SUN 1000 SUN 10000 Pentium
133
РЛС1 РЛС2 РЛСЗ
MF11
Поток_сообщений
(MF)
MF13
MF21
Поток_сообщений
(MF)
МСШ MC112 MC113
6 Ь О
MC211
MC212 MC213
————— — Отношение «Component-of» (V)
— Отношение «Element-of» (E)
— Отношение «Part-of» (>)
Рис. 5.7
эффективность работы механизма дедуктивного вывода. Структу-
Структурирование проблемной области также позволяет увеличить эффек-
эффективность дедуктивного вывода за счет существенного сокращения
пространства поиска. Следовательно, MLL является гибким форма-
формализмом для представления знаний о реальной сложноструктуриро-

204 Вывод на иерархических структурах [ Гл. 5
ванной проблемной области и может быть выбрана в качестве языка
представления знаний для ее описания.
5.2.4. Логический вывод в многоуровневой логике
Неотъемлемой частью любой БЗ являются механизмы обработки
знаний, одним из которых является дедуктивный вывод.
Дедуктивный вывод позволяет
• получать новые знания из знаний, представленных в БЗ;
• осуществлять контроль информации, представленной в БЗ, на
непротиворечивость;
«сжать» экстенсиональную составляющую БЗ (за счет получе-
получения экстенсионалов атрибутов и отношений при помощи дедук-
дедуктивного вывода);
• получать ответы на запросы пользователей.
Необходимо предусмотреть работу дедуктивного вывода в откры-
открытой проблемной области. Рассмотрим процесс дедуктивного вывода
более подробно. В процесс дедуктивного вывода вовлекаются два
важных алгоритма: алгоритм сколемизации и алгоритм унификации.
Эти алгоритмы в MLL являются дальнейшим развитием соответству-
соответствующих алгоритмов исчисления предикатов первого порядка. Исходная
формула для алгоритма сколемизации должна быть представлена в
пренексной нормальной форме.
5.2.^.1. Алгоритм сколемизации. Рассмотрим особенности
алгоритма сколемизации в MLL. Алгоритм сколемизации основыва-
основывается на следующих положениях:
А) сколемовская функция включает в качестве аргументов все пе-
переменные, которые связаны квантором V и которые расположе-
расположены слева от квантора 3, за исключением переменной, которая
является >-предком переменной, связанной квантором 3;
Б) >-предок и домен должны быть включены в сколемовскую
функцию и в матрицу для процедуры унификации. Они сохра-
сохраняются в форме (x/X)//Y.
Объясним положение (А) на примере. Поскольку построение ско-
лемовской функции не зависит от числа компонентов объектов, при-
приведем случай, когда объекты состоят из одной компоненты. При этом
области определения термов однозначно определяются их >-предками
по иерархической структуре. Пусть иерархическая структура задана
и имеет форму, представленную на рис. 5.8. Рассмотрим формулу:
(Ух1//Х)(Зх0//х1)Р(х1,х0). E.3)
Формула E.3) читается следующим образом: для любого объекта
xi, который является частью объекта X, (на рис. 5.8 это ai, <22, аз)? су-
существует объект хо, который является частью объекта xi, (на рис. 5.8

5.2]
Многоуровневая логика как язык представления знаний
205
это Ъц или bi2 или ... или bik, если х\ есть ai, и 621 или 622 или ...
или &2п? если xi есть <22, и 631 или 632 или ... или бзт? если xi есть
аз), такой, что P(xi,xq).
V 1 °\2 D\k
Рис. 5.8
В классическом алгоритме сколемизации хо заменяется на функ-
функцию /c(xi), т.е. получим формулу с учетом положения (Б):
Поскольку иерархическая структура является фиксированной, то
фиксированными являются и все структурные отношения в ней
и, следовательно, области определения термов. Поскольку функция
f с{х\//X)//(х\//X) определена на множестве частей объекта, задан-
заданного переменной xi, то она не зависит непосредственно от перемен-
переменной х\//X. Следовательно, функция /с заменяется на «обобщенную»
константу В с, которой может быть любая константа Ъц или Ъ\ъ или
... или bik, если х\ есть ai, и 621 или 622 или ... или &2п? если х\
есть а2, и Ь^\ или 632 или ... или бзт? если х\ есть аз, и на которую
заменяется переменная xq в классическом алгоритме сколемизации,
если она связана квантором 3 и стоит на первом месте в префиксе. В
результате получим формулу
Отсюда следует, что при построении сколемовской функции для
переменной хо переменная х\ «мысленно» вычеркивается из пре-
префикса. Это положение может быть распространено на произвольную

206 Вывод на иерархических структурах [ Гл. 5
формулу MLL. Пусть задана формула
b .., хп). E.4)
Применим классический алгоритм сколемизации к формуле E.4).
Получим выражение
Р(Х!//Хи ..., Xn-i//Xn-U f(xi//Xu ..., »n_i//Xn_i)//(»i//Xi)).
Поскольку / определена на множестве частей объекта, за-
заданного переменной х\/ /Х\, значение функции / не зависит
непосредственно от переменной х\//Х\, и, следовательно, пере-
переменная хп в алгоритме сколемизации заменяется на функцию
f(x2//X2,..., xn_i//Xn_i)//(xi//A:i).
Рассмотрим алгоритм сколемизации в MLL с учетом введенного
расширения синтаксиса.
Алгоритм сколемизации в MLL.
Пусть формула представлена в виде
(Qi(xi/X1)//Y1)(Q2(x2/X2)//Y2)...(Qr(xr/Xr)//Yr)P(x1,x2,..,xr),
где Q G {V, 3}, Xi — сортность переменной л^, Уг ~ >-предок пере-
переменной Xi, г = 1 -т- г, Р — бескванторная формула (или матрица). (В
качестве У^, г = 1 -i- r может быть константа или переменная).
Шаг 1. Найти наименьший индекс г такой, что Qi, Q2? • • • ? Qi-i все
равны V, a Qi = 3. Если такого г нет, то перейти к шагу 4. Если г =
= 1, то Xi заменяется на константу (@a/Xi)//Yi во всех вхождениях
в матрицу и на @а во всех вхождениях Xi в префикс в виде >-предка
другой переменной.
Замечание. Специальный символ @ означает, что @а может быть
любой константой сорта Х^, обозначающей часть объекта У^.
Если г ^ 1, то перейти к шагу 3.
Шаг 2. Квантор Qi = 3 вычеркивается. Перейти к шагу 1.
Шаг 3. Все переменные с индексом до г сравнить с >-предком
г-й переменной. Если совпадения нет, то взять новый (г — 1)-местный
функциональный символ /^. Переменная Xi заменяется на сколе-
мовскую функцию (fi(xi,X2, • • • ,Xi-i)/Xi)//Yi во всех вхождениях в
матрицу и на функцию /г(хь Х2, • • • ,Xi-i) во всех вхождениях Xi в
префикс. Перейти к шагу 2.
Если имеются совпадения (т. е. имеется переменная Xj (j < г) под
квантором V, которая является и >-предком заменяемой переменной)
и если г — 2 равняется нулю, то Xi заменяется на (@a/Xi)//xj во всех
вхождениях в матрицу и на @а во всех вхождениях в префикс как
>-предок другой переменной, и перейти к шагу 2.
Если г — 2 не равняется нулю, то взять (г — 2)-местный функ-
функциональный символ, не встречавшийся в формуле. Переменная Xi
заменяется на сколемовскую функцию (/г(жь #2, • • • ? xi-2)/Xi)//xj во

5.2] Многоуровневая логика как язык представления знаний 207
всех вхождениях в матрицу и на функцию /г(хь #2? • • • ixi-2), где
Xk ф Xj , k = 1 -г i - 2 во всех вхождениях в префикс как предок
другой переменной. Перейти к шагу 2.
Шаг 4- Если кванторов V нет, то Стоп. Если в префиксе формулы в
качестве >-предков выступают сколемовские функции, то аргументам
функции приписываются их домены и >-предки.
Всем переменным, стоящим под квантором V, в матрице формулы
приписываются их домены и >-предки, за исключением случая, когда
переменная является >-предком другой переменной.
Кванторы V опускаются, предполагая, что они существуют.
Стоп
Пример 5.4.
Рассмотрим использование алгоритма. Предположим, что объекты
X, У, Z имеют в качестве компонент несколько объектов.
(V(x1/D1)//X)C(y1/D2)//Y)(V(y0/D3)//y1)C(x0/D4)//x1)
(\/(z1/D5)//Z)P(xuxo,yi,yo,z1).
Шаг l.i = 2
Шаг 3.
(V(xl/D1)//X)C(yl/D2)//Y)(V(y0/D3)//fl(xl))C(x0/D4)//xl)
(y(zi/D5)//Z)P(xi,x0, (fi(Xl)/D2)//Y, j/o,*i)
Шаг 2.
(V(xl/Dl)//X)(V(yo/D3)//fl(xl))C(xo/D4)//xl)(V(zl/D5)//Z)
P(x1,x0,(f1(x1)/D2)//Y,y0,z1)
Шаг 1Л = Ъ
Шаг 3.
(W(x1/D1)//X)(W(yo/D3)//f1(x1))C(xo/D4)//x1)(W(z1/D5)//Z)
Шаг 2.
(W(x1/D1)//X)(W(y0/D3)//f1(x1))(W(z1/D5)//Z)
P(xi,(f2(yo)/D4)//x1,(f1(x1)/D2)//Y,yo,z1)
Шаг 1. г нет
Шаг I
(yo/D3)//Mx1/D1)//X),(z1/Db)//Z)
Стоп.

208 Вывод на иерархических структурах [ Гл. 5
5.2.4-2. Алгоритм, унификации. Рассмотрим особенности ал-
алгоритма унификации в MLL.
1. Термы в MLL унифицируются при выполнении условий унифи-
унификации, которые являются одинаковыми для >-предков и доме-
доменов: ХСУиХПУ^О.
2. Пусть х является термом уровня i и, в то же время, он является
>-предком терма следующего нижележащего уровня. Терм х
унифицируется и автоматически унифицируется >-предок тер-
терма следующего нижележащего уровня.
Алгоритм унификации для MLL.
1. Установить к = 0, И4 = W, Sk = ?, где W — унифицируемые
выражения, Sk — наибольший общий унификатор и е — пустая
подстановка.
2. Если Wk является одноэлементным множеством, то S = Sk и
стоп. В противном случае переход к п. 3.
3. Каждая из литер в Wk рассматривается, как цепочка символов,
и выделяются первые подвыражения литер, не являющихся оди-
одинаковыми у всех элементов Wk , т. е. образуется так называемое
множество рассогласований типа {(vk/Vk)//V, (tk/Tk)//T}.
Если или Vk — переменная, a tk — терм, или Vk — функция, а
tk — переменная или функция, то перейти к п. 4.
В противном случае стоп: W не унифицируемо.
4. Проверка условий унификации >-предков. Если V С Т или
VГ)Т = Z^-ф 0) (условия унификации выполняются), то перейти
к п. 5. В противном случае стоп: W не унифицируемо. Если >-
предками являются термы и они совпадают, то перейти к п. 5. В
противном случае стоп: W не унифицируемо.
5. Проверка условий унификации доменов:
а) если Vk — переменная, определенная на домене 14, a tk кон-
константа, определенная на домене Т, и Т С У, то перейти к п. 6. В
противном случае стоп: W не унифицируемо.
б) если Vk — переменная, определенная на домене 14, a tk —
переменная, определенная на домене Tk, и Tk П Vk = Zk(^ 0), то
перейти к п. 6. В противном случае стоп: W не унифицируемо.
в) если Vk — переменная, определенная на домене 14, a tk —
функция, определенная на домене Т&, и Tk П 14 = Zk(^ 0), то
перейти к п. 6. В противном случае стоп: W не унифицируемо.
г) если Vk — функция, определенная на домене 14, a tk функция,
определенная на домене Т^, и Т^ С 14 или 14 ^ Tk ,то перейти
к п. 6. В противном случае стоп: W не унифицируемо.
6. Если Vk — переменная, a tk — константа или функция, то
Sfc+i = Sk о {tk/vk} и И4+1 = Wk{tk/vk}, где о — композиция

5.2] Многоуровневая логика как язык представления знаний 209
подстановок, а запись Wk{tk/vk} обозначает замену Vk на tk в
Wk (см. примечание).
Если Vk — переменная, tk — переменная, то Sk+i =
= Sk о {zk/tkjZk/vk} и Wfc+i = Wk{zk/tk,Zk/vk}, где zk —
переменная, отличная от Vk и^.
Если Vk и tk — функции, то в унифицируемое выражение
подставляется функция, область значений которой является
подмножеством области значений другой функции.
Примечание. Запись {tk/vk} означает замену (vk/Vk)//V на
(tk/Tk)//T во всех вхождениях Vk как терма и замену Vk на tk
во всех вхождениях Vk как >-предка. Это положение верно и в
случае, когда Vk и tk определены на термах.
7. к = к + 1, перейти к п. 2.
В случае, когда объекты состоят из одной компоненты, сорт-
сортность термов не указывается в префиксе и шаг проверки унифи-
унификации доменов термов в формулах пропускается, поскольку об-
области определения термов однозначно задаются их >-предками.
Рассмотрим пример использования алгоритма унификации. При-
Пример приведен для случая, когда объекты в качестве компонент имеют
несколько объектов. Иерархические структуры проблемной области
приведены на рис. 5.9.
Пример 5.5.
W = {P((ai/Ai)//X, (хо/Хо)//аи (
(f((xo/Xo)//a1)/Wo)//y1),
P((vi/Vi)//V, (gdw^Wj.y/wyXo)/^!, (wi/Wi)//W, (wo/Wo)//wi)}
1. W0 = W; S0=e
2. {(ai/Ai)//X, (vi/Vi)//V} — множество рассогласований
3. Полагаем, что X С V и А\ С V\,
4. 5i = 50
(f((xo/Xo)//a1)/Wo)//y1),
P((a1/A1)//X,(g((w1/W1)//W)/X0)//a1,
(wi/Wi)//W, (wo/Wo)//wi)}
5. {(xo/Xo)//ai, (g((wi/Wi)//W)/Xo)//ai} — множество рассогла-
рассогласований.

210
Вывод на иерархических структурах
[Гл.5
Рис. 5.9
). *Ь2 = Oi О
(wo/Wo)//Wl)}
7. {(г/1/У1)//У, (wl/Wl)//W} — множество рассогласований
8. Полагаем, что W П Y = Z(^ 0) и Wx П Y1 = Zx(? 0).

5.2] Многоуровневая логика как язык представления знаний 211
9. S3 = S2o{z/y1,z/w1}
(wo/Wo)//z)}
10. {(f((g((z/Z1)//Z)/X0)//a1)/W0)//z, (wo/Wo)//z} - множество
рассогласований
11. 54 = S3 о {f((g((z/Z1)//Z)/X0)//a1)/w0}
(g((z/Z1)//Z)/X0)//a1, (z/Z^f/Z,
1)//Z)/Xo)//a1)/Wo)//z)} =
(g((z/Z1)//Z)/X0)//a1, (z/Z^f/Z,
12. W4- одноэлементное множество; S = S&.
Стоп.
В качестве процедуры вывода используется линейная входная ре-
резолюция, которая является полной для хорновских дизъюнктов и
обладает большой эффективностью.
5.2.^.3. Особенности использования линейной входной
резолюции в многоуровневой логике. Рассмотрим особенности
использования линейной входной резолюции в MLL с упорядоченны-
упорядоченными дизъюнктами. Связывание понятия упорядоченных дизъюнктов
с линейной входной резолюцией не нарушает ее полноты, но
существенно увеличивает эффективность метода.
Пусть S — конечное множество упорядоченных дизъюнктов Хор-
на, полученное после удаления кванторов V и 3.
S содержит следующие дизъюнкты:

212 Вывод на иерархических структурах [Гл.5
где т — количество всех положительных упорядоченных дизъюнктов
Хорна из S (фактов); р — количество всех смешанных упорядоченных
дизъюнктов Хорна из S (фактов); к — количество всех отрицательных
упорядоченных дизъюнктов Хорна из S (фактов).
Рассмотрим одно из применений дедуктивного вывода, а именно,
получение экстенсионалов отношений, которое позволяет значительно
сократить экстенсиональную составляющую БЗ. Для этого случая в
качестве верхнего центрального дизъюнкта возьмем отрицание пре-
предикатной литеры, имя которой соответствует имени отношения, экс-
тенсионалы которого нужно определить: ->Cj, j = 1 -г- m -\-p.
Для центрального дизъюнкта возможны два случая:
1) Cj(j = 1 -т- m + р) является А^ г = 1тт.
2) Cj(j = 1 -т- m + р) является Am+i, г = 1 -!-р.
Из всех известных модификаций линейной входной резолюции
возьмем наиболее эффективную — метод поиска в глубину. Для
первого случая, используя метод поиска в глубину, получаем набор
экстенсионалов отношения, имя которого соответствует центральному
дизъюнкту. Во втором случае метод поиска в глубину повторяем для
каждой посылки В^к, к = 1-^-щ, входящей в логическое предложение,
заключением которого является Am+i, г = 1 -i-p.
Особенности линейной входной резолюции в MLL следующие:
• возможные значения термов (их домены) при резольвировании
определяются по иерархической структуре;
• существенное сокращение пространства поиска, которое влечет
увеличение эффективности дедуктивного вывода, достигаемое
за счет особенности /.
Приведем в качестве примера использование дедуктивного вывода
для получения экстенсионалов отношения
Поступают(у, принтер),
где у есть результирующие данные программных компонент х неко-
некоторой функциональной системы #5, т. е.
(Зх/ /#S) C (^/Результат) / /х) Поступают(у, принтер).
Поскольку принцип резолюции основан на процедуре опроверже-
опровержения, отрицание приведенной выше формулы используется в качестве
верхнего центрального дизъюнкта
->[Cх / /'#S)C(y /Результат) / /'х) Поступают(у, принтер)] =
= (Ух//#S) (У (у/Результ&т)//х)^ Посту пают(у, принтер). E.5)
Применяя алгоритм сколемизации к формуле E.5), получим
^ Посту пают( (^/Результат) //ж, принтер). E.6)

5.2] Многоуровневая логика как язык представления знаний 213
Если запрос касается описания некоторой вершины и описания
ее нижележащих вершин по иерархической структуре, как в рас-
рассматриваемом примере, мы выводим не пустой дизъюнкт, а предикат
ответа. И формула E.6), которая выступает в качестве центрального
дизъюнкта, имеет вид
-л Поступают((у / Результат) //ж, принтер )V
V ANSWER(a;//#S, (у/Результат)//х).
Рассматриваемый пример представляет запрос 1-го вида. В случае,
если запрос касается описания только самих вершин и не касается
описаний их нижележащих вершин по иерархической структуре, то
при получении ответа на запрос выводится пустой дизъюнкт и выда-
выдается список значений переменных, означивание которых произошло в
процессе вывода. Такие запросы являются запросами 2-го вида.
В качестве примера запроса 2-го вида рассмотрим запрос: «Найти
все программные компоненты функциональной системы #S такие,
что объем оперативной памяти, занимаемый ими, не превосходит
200 кб», который представляется формулой
(Vz//#S)(Vi//REAL) Объем_памяти(>, y)kLE(y, 200).
Запрос 2-го вида, являясь частным случаем запроса 1-го вида,
выделяется в силу того, что большинство запросов имеют сходную
с ним форму.
Пусть в интенсиональной составляющей БЗ хранится множество
аксиом, одной из которых является аксиома
(Зх/ /^S)(\/y/Результат) / /х) Соединена_ ЭВМ(х, принтер)&
& Время _ получения(у, 0.01с) —> Поступают(у, принтер) E.7)
и в экстенсиональной составляющей БЗ хранится множество фактов,
среди которых находятся
Соединена _ ЭВМ (ПК^, принтер), ? = 1тпи
Время _получения(Р^ 0.01с), j = 1 -i- r.
Применяя алгоритм сколемизации к формуле E.7), получим
Соединена_ 9BM(ua//#S, принтер)&
&:Время_ получения{{у/Результат)//@а, 0.01с) —>
—> Поступают^ (^/Результат) //@а, принтер),
где @а — обобщенная константа.
Цепочка вывода в виде дерева вывода представлена на рис. 5.10.

214
Вывод на иерархических структурах
[Гл.5
-пПоступают((у/Результяп:у/х, принтер) v
vANSWER(x//#S,(y/Pe3yflbTax)//x) /^\
принтер)у
у-тВремя_получения((у'/Результат)
//@a,0.01c)vANSWER(@a //#S,
(у/Результат)// @а)
—1Время_получения((у/Результг^)
//ПК^О.01 c)vANSWER(nKi //#S,
(у/Результату/ПК,.),
i = 1 + и
iCoeduHeHa_3BM(@a//#S,
принтер)у
//@a,0.01c)v
тат)//@а,
принтер)
Соединена_Э2?М(ПК1.,1финтер), / =1 + я
х = ПК,., у = Р/ (i = 1 + п; ] = 1 + г)
Рис. 5.10
Множество ПКг, г = 1 -i-n, которые входят в состав функцио-
функциональной системы фБ, определяем по иерархической структуре, пред-
представленной на рис. 5.4, и для каждого ПК^ находим факт Соедине-
Соединена _ ЭВМ (ПК^, принтер). Затем определяем множество Pj, j' = 1 -Z-K,
которые являются результатами ПК^. Для каждой пары {IIK^Pj}
находим факт Время_ получения (Pj,0.01c). Ответом на запрос будет
множество пар {ПК^, Pj}, являющихся значениями переменных х и у
соответственно.
Разработанные алгоритмы дедуктивного вывода для предложен-
предложенного расширения синтаксиса MLL положены в основу интеллектуаль-
интеллектуальной системы моделирования сложноструктурированной проблемной
области «Инфолог».
5.2.4-4- Иерархическая абстракция и продукционная мо-
модель. Из рассмотренного следует, что MLL является удобным сред-
средством для формализации структурного аспекта проблемной области.
Иерархическую абстрактную структуру удобно использовать и при

5.3] Система моделирования проблемной области «Инфолог» 215
описании проблемной области продукционной моделью представления
знаний, которая применяется для отражения динамики изменения
проблемной области, когда для ее задания требуется несколько де-
десятков тысяч продукционных правил.
Иерархическая абстрактная структура позволяет разбить продук-
продукционные правила на блоки в соответствии с принадлежностью к
элементам структуры, принятие решений в которых они задают, и
использовать механизм наследования продукционных правил. Меха-
Механизм наследования продукционных правил позволяет «сжать» базу
знаний, сделать ее более компактной. Рассмотрим механизм наследо-
наследования продукционных правил на примере.
Пусть задана иерархическая структура, которая описывает неко-
некоторую абстрактную проблемную область «Аэропорт». Иерархическая
структура состоит из трех уровней детализации:
1-й уровень — Аэропорт;
2-й уровень — РЛС, классы самолетов (ТУ, ИЛ, АН, ...);
3-й уровень — представители классов РЛС, самолетов (конкретные
объекты).
Управление работой аэропорта задается множеством продукцион-
продукционных правил, которые разбиваются на блоки в соответствии с уровнями
в иерархической структуре следующим образом:
• в блок 1-го уровня входят продукционные правила, которые
описывают принципы управления аэропортом в целом;
• в блоки 2-го уровня входят продукционные правила, которые
описывают управление классами РЛС и самолетов;
• число блоков 3-го уровня определяется количеством представи-
представителей классов РЛС и самолетов.
В каждый блок 3-го уровня входят продукционные правила, ко-
которые задают специфические законы управления конкретным само-
самолетом или РЛС. Остальные продукционные правила, которые задают
общие законы управления классами РЛС и самолетов, могут быть
получены благодаря механизму наследования.
Таким образом, иерархическая структура позволяет создать
иерархию продукционных правил и использовать принцип насле-
наследования продукционных правил, подобно механизму наследования
свойств в ISA-иерархии.
5.3. Система моделирования проблемной области
«Инфолог»
5.3.1. Назначение и структура системы «Инфолог»
В основе любой интеллектуальной системы лежат формализмы
представления знаний и манипулирования ими с целью имитации

216
Вывод на иерархических структурах
[Гл.5
рассуждений человека для решения поставленных задач. Одной из
важных проблем, которая встает перед разработчиками интеллекту-
интеллектуальной системы, является проблема моделирования проблемной обла-
области, т. е. создание модели проблемной области в компьютере и опреде-
определение соответствия между смоделированными объектами и объектами
реального мира, а также представление знаний экспертов о ней. «Ин-
фолог» — информационно-логическая система, предназначенная для
представления сложноструктурированной информации и дедуктивно-
дедуктивного вывода на ее основе. Программное средство «Инфолог» создано
для поддержки задач, решаемых разработчиками интеллектуальных
систем на этапе моделирования проблемной области. Она позволяет
пользователю описать требуемую проблемную область: задать объ-
объекты, атрибуты объектов, определить различные отношения между
объектами, описать закономерности проблемной области в виде ло-
логических выражений, а также реализовать запросы, требуемые для
получения тех или иных фактов.
«Инфолог» может быть использована в качестве компоненты ин-
интеллектуального репозитория (информационной базы проекта) С ASE-
системы. В этом качестве «Инфолог» служит для:
• пополнения модели знаний CASE-системы о самой себе (пред-
(представление этих знаний в репозитории облегчает разработчикам со-
создание программного обеспечения (ПО) в CASE-системе);
• пополнения репозитория на
основе моделирования предмет-
предметной области разрабатываемой си-
системы и самой системы, кото-
которое осуществляется при проведе-
проведении начальных этапов в жизнен-
жизненном цикле ПО различными груп-
группами разработчиков. Отметим,
что моделирование программных
систем (выделение классов объ-
объектов, отношений и атрибутов)
является основой для формали-
формализации начальных требований к
программной системе на этапе
анализа и базой для выделения
классов объектов программной
системы и требований к ним, ко-
которые необходимо реализовать,
на этапе проектирования;
• проверки информации,
представленной в репозитории CASE-системы, на непротиворечи-
непротиворечивость;
подсистема управления
моделями предметных
областей
подсистема
моделирования
БЗ
модель предметной
области
подсистема
просмотра
компонента
перевода запроса
компонента
логического вывода
Рис. 5.11

5.3]
Система моделирования проблемной области «Инфолог» 217
• получения значений атрибутов и экстенсионалов отношений с
помощью логического вывода, что позволяет «сжать» экстенсиональ-
экстенсиональную составляющую репозитория;
• получения ответов на запросы пользователя.
Основные компоненты системы «Инфолог» представлены на
рис. 5.11. Функциональная структура системы «Инфолог» изображе-
изображена на рис. 5.12.
Система «Инфолог»
подсистема
управления
моделями
предметной
области
-начать раз-
разработку
новой
модели
-продолжить
разработку
модели
-удалить
модель
-выход
подсистема
модели-
моделирования
подсистема
просмотра
- выделение
классов
объектов
предметной
области,
определение
их атрибу-
атрибутов и отноше-
отношений между
ними
- определение
- просмотр
ISA-
иерархии
классов
объектов
- просмотр
Part-of-
иерархии
классов
объектов
структуры L просмотр
выделенных классов
компо-
компонента
перевода
запроса
-ввод
текста
запроса
- форми-
формирование
запроса
классов отношений
(построение
ISA- и Part-of-
иерархии на
классах объектов,
определение их
атрибутов и
отношений)
- определение
представителей
классов
-построение
Part-of-иерархии
на представителях
- определение
значений атрибутов
Рис
5.12
компо-
компонента
логичес-
логического
вывода
-ввод
логи-
логического
предло-
предложения
-форми-
-формирование
ответа
Рассмотрим основные компоненты системы «Инфолог». Централь-
Центральной компонентой системы «Инфолог» является БЗ, которая служит

218 Вывод на иерархических структурах [Гл.5
для представления модели проблемной области. Процедурная состав-
составляющая БЗ содержит процедуры для вычисления экстенсионалов
(фактов) отношений и атрибутов и процедуры, которые могут вызы-
вызываться в процессе дедуктивного вывода для изменения информации,
в ней хранящейся.
Для пополнения БЗ служит подсистема моделирования. Она поз-
позволяет выполнить следующие операции:
• выделить классы объектов выбранной для разработки предмет-
предметной области, определить их атрибуты и отношения между клас-
классами объектов, составить описание классов объектов, атрибутов
и отношений;
• определить структуры выделенных классов объектов, т. е. по-
построить ISA- и Part-of-иерархии на классах объектов проблемной
области; определить атрибуты классов объектов и отношения
между ними; задать их описание. Существует возможность поис-
поиска классов объектов и выхода на самый верхний уровень иерар-
иерархии. Реализован контроль уникальности имени класса объектов
и схемы отношения.
Эти функции реализуют моделирование (пополнение) интенсио-
интенсиональной составляющей выбранной проблемной области.
Функциями, реализующими моделирование (пополнение) экстен-
экстенсиональной составляющей выбранной проблемной области, являются
следующие:
• определение представителей классов объектов, задание Part-of-
иерархии на представителях классов, описание представителей
классов;
• задание значений атрибутов или способов их определения.
Подсистема управления моделями проблемных областей предна-
предназначена для загрузки описания выбранной проблемной области. Под-
Подсистема просмотра служит для просмотра структур (ISA- и Part-
of-иерархий) классов объектов выбранной проблемной области и от-
отношений, сгруппированных по следующим классам: семантические,
структурные, каузальные и функциональные. При просмотре иерар-
иерархий классов объектов реализованы следующие возможности: доба-
добавить, удалить, изменить класс объектов и осуществить поиск класса
объектов.
Компонента логического вывода служит для получения экстен-
экстенсионалов отношений и атрибутов (фактов) выбранной проблемной
области и для проверки информации, представленной в модели про-
проблемной области, на непротиворечивость. Она состоит из следующих
подсистем:

5.3]
Система моделирования проблемной области «Инфолог»
219
• подсистема ввода логических выражений;
• подсистема просмотра логических выражений;
• подсистема ввода запросов;
• подсистема формирования ответа на основе логического вывода.
Структура компоненты логического вывода представлена на
рис. 5.13. В основе компоненты логического вывода лежат механизмы
обработки знаний, описанные в разд. 5.2.4 (алгоритмы сколемизации,
унификации и входной линейной резолюции для MLL).
подсистема
ввода
логических
предложений
подсистема
ввода
запроса
разработчика
подсистема
просмотра
логических
предложений
подсистема формирот ания ответа
отрицание запроса
сколемизация запроса
линейная входная резолюция
-ответ на запрос
база знаний
база данных
СУБД
Рис. 5.13
5.3.2. Концептуальный язык описания сложноструктурированной
проблемной области
Для разработки системы моделирования проблемной области
очень важным фактором является выбор языка представления
знаний, т. к. от этого будет зависеть и мощность самой системы.
Однако чем мощнее будет язык представления знаний, тем более
высокой квалификацией должен обладать пользователь, который
будет в дальнейшем работать с данной системой. Ему необходимо
будет знать данный язык для построения запросов и ввода аксиом.

220 Вывод на иерархических структурах [ Гл. 5
В нашем случае в качестве языка представления знаний исполь-
используется язык MLL. И хотя пользователь, не зная его, может описать
классы объектов и отношения между ними, используя функциональ-
функциональные возможности программного средства «Инфолог», тем не менее,
для создания запросов необходимо знание синтаксиса MLL. Это, ра-
разумеется, предъявляет ряд определенных требований к пользователю.
Для того, чтобы облегчить работу с программным средством «Ин-
«Инфолог», нами разработан концептуальный язык запросов. Во второй
версии программного средства «Инфолог» поддерживается концеп-
концептуальный язык запросов. Он реализован в модуле q_analis.c. Исполь-
Использование данного модуля в системе позволяет пользователю вводить
запрос не на языке MLL, а на ограниченном естественном языке,
который неподготовленному пользователю несомненно ближе и не
требует знания языка MLL.
Далее кратко опишем созданный концептуальный язык. В хо-
ходе исследований были разработаны 9 шаблонов, которые позволяют
представить основное количество запросов. Таким образом, следуя
какому-либо из данных шаблонов, пользователь может построить
запрос. При этом сам текст запроса он вводит на естественном языке.
Пользователь не заботится о том, какой язык представления знаний
используется в данной системе; это позволяет ему «подняться» на
один уровень выше. После непосредственного описания самой про-
проблемной области, практически неподготовленный пользователь может
создавать запросы и получать результаты.
Например, так выглядит запрос, записанный на естественном язы-
языке: «Определить программные компоненты (ПК) проектируемой си-
системы Р, обеспечивающие взлет-посадку самолетов» и на языке MLL:
C(ж/ПК_обработки)//#Р)C(?//самолет)//#О)
обесп_взлет_посадку(ж, у) —> .
На концептуальном языке этот запрос имеет следующий вид:
«Определить ПК_обработки, являющиеся частью проектируе-
мая_система Р, и самолеты, являющиеся частью объект_управления
О, находящиеся в отношении обесп_взлет_посадку».
Как видно из примера, для того, чтобы задавать запросы, запи-
записанные на концептуальном языке, знание языка MLL не требуется.
Ниже представим разработанные шаблоны.
1. Определить, имеет ли <#объект1>, который является частью
<#объект2>, атрибут <G> со значением <#R>.
2. Определить, находится ли <#объектц>, который является ча-
частью <#объект1>, в отношении <G> с <#объект22>, который
является частью <^объект2>.
3. Определить значение атрибута <G> <#объект1>, который яв-
является частью <#объект2>.

5.3] Система моделирования проблемной области «Инфолог» 221
4. Определить <объекты>, являющиеся частью <#объект!>, с
которыми <# объект2>, являющийся частью <#объектз>, на-
находится в отношении <G>.
5. Определить <объекты>, являющиеся частью <#объект!>, име-
имеющие атрибут <G> и значение атрибута.
6. Определить <объекты>, являющиеся частью <#объект1>, и
<объекты>, являющиеся частью <#объект2>, находящиеся в
отношении <G>.
7. Определить <объекты>, которые имеют атрибут <Р> со зна-
значением <R>, являющиеся частью <#объект1>, содержащегося
в <#объект2>.
8. Определить <объекты>, имеющие атрибут <Р>, и его значе-
значения, которые являются частью <#объект1>, содержащегося в
9. Определить <объекты>, имеющие атрибут <Р>, и значения
которого { >,<,=,^,^, ^ } константы <#i?>, являющиеся
частью <# объект! >, содержащегося в <#объект2>.
Рассмотрим внутреннюю структуру программного модуля, реа-
реализующего концептуальный язык. Его основу составляет процедура
lexanal. Для передачи запроса из головного модуля используется бу-
буфер ipText. Запрос помещается в него при считывании содержания
текущего окна. При этом текст запроса может быть введен из файла
или с клавиатуры. Информация из IpText обрабатывается функцией
syntanal, которая выбирает лексемы и передает их вызывающей про-
процедуре. Получая лексемы, lexanal сравнивает их с эталонными и про-
проверяет соответствие тому или иному шаблону. Для того, чтобы текст
запроса был более приближен к естественному языку, пользователю
позволяется вводить слова в любом падеже или числе.
Например, следующий запрос:
«Определить ПК обработки, являющиеся частью проектируемой
системы Р, и самолеты, являющиеся частью объекта управления О,
находящиеся в отношении обесп_взлет_посадку»
будет более понятен, чем:
«Определить ПК_обработки, являющиеся частью проектируе-
мая_система Р, и самолеты, являющиеся частью объект_управления
О, находящиеся в отношении обесп_взлет_посадку».
Для осуществления такой возможности была реализована попол-
пополняемая библиотека data.lib. Данная библиотека содержит основу сло-
слова и его представление в БЗ. Таким образом, например, при вводе
пользователем слова «самолета», оно интерпретируется при постро-
построении запроса на языке MLL в «самолет». Это является необходимым

222
Вывод на иерархических структурах
[Гл.5
условием для создания правильного запроса. В процессе работы со-
собирается массив слов, используемых в запросе. При окончании об-
обработки текста запроса по полученным данным создается запрос на
языке MLL.
Описанный выше модуль позволяет переводить основное количе-
количество запросов на ограниченном естественном языке на язык MLL. При
этом от пользователя требуется приложение минимальных усилий,
ему не надо изучать язык MLL; основная задача ложится на систему.
Также плюсом данного модуля является высокая скорость работы.
После преобразования запрос вновь появляется в окне экрана, и
пользователь может видеть результат. После этого ему требуется за-
запустить преобразованный запрос, который попадает в модуль вывода.
5.3.3. Реализация системы «Инфолог»
Разработанная версия системы «Инфолог» работает под управле-
управлением MS Windows 3.1 и выше, Windows NT.
Система «Инфолог» поставляется в виде загрузочного модуля
КМ.ЕХЕ и файлов *.dat, которые содержат описание (заголовки)
таблиц, представленных в БЗ. ПО системы «Инфолог» включает 11
модулей, написанных на языке Си++ с использованием библиотеки
Engine, объем которых составляет около 4000 операторов. Объем за-
Класс объектов
Уровень
Подкласс
«Целое»
Уровень
«Часть»
Тип
отношения
Имя
отношения
Имя класса
объектов 1
Имя класса
объектов 4
Арность
Метод
определе-
определения экстен-
сионала
Объект»
Описание
Класс объектов
Атрибут
Имя
предло-
предложения
1
Имя
терма
1
Имя
домена
1
Имя
>-
пред-
предка 1
Имя
терма
4
Имя
домена
4
Имя
> -
пред-
предка 4
Имя
предло-
предложения
4
Рис. 5.14

5.3]
Система моделирования проблемной области «Инфолог» 223
грузочного модуля системы «Инфолог» составляет 382 Кб. Структура
некоторых таблиц, содержащихся в БЗ, представлена на рис. 5.14.
Таблицы экстенсиональной составляющей БЗ (БД) создаются си-
системой «Инфолог» в процессе моделирования предметной области.
Структура некоторых из них представлена на рис. 5.15.
Класс объектов
Представитель
Представитель
«целого»
Уровень
Представитель
«части»
Класс
«целого»
Класс
«части»
Атрибутi
Имя класса
объектов
Значение
Тип
атрибута
Способ
определения
значения
Отношение i
Имя класса
объектов 1
Имя класса
объектов 4
Рис
5.15
Система «Инфолог» поддерживает «свободное соединение» БЗ
и БД под управлением СУБД Paradox. Такая реализация системы
«Инфолог» обеспечивает использование всех возможностей СУБД
Paradox, таких, как распределенная обработка, высокая производи-
производительность, сложный контроль, обеспечение целостности и безопасно-
безопасности данных, восстановление БД, поддержка больших БД.

Часть II
АРГУМЕНТАЦИЯ И АБДУКЦИЯ
Мы живем, точно в сне неразгаданном,
На одной из учебных планет...
Много есть, чего вовсе не надо нам,
А того, что нам хочется, нет...
И. Северянин
Глава 6
ДАННЫЕ И ЗНАНИЯ В
ИНТЕЛЛЕКТУАЛЬНЫХ СИСТЕМАХ
Рассмотренные методы дедуктивного вывода относятся к досто-
достоверным, т. е. из множества посылок, имеющих выделенные истинност-
истинностные значения, выводимы заключения, также имеющие лишь выде-
выделенные истинностные значения. Так как в двузначной логике выде-
выделенным истинностным значением является «истина», то из истинных
посылок не выводимы ложные заключения.
Дедуктивные выводы в настоящее время хорошо изучены, и авто-
автоматическое доказательство теорем является старейшей ветвью искус-
искусственного интеллекта. Конечно, формальные, синтаксические методы
дедуктивного вывода не способны обрабатывать сложные прикладные
области с большим пространством поиска нужной информации. Необ-
Необходимо разрабатывать эвристические методы управления таким по-
поиском, применять ad hoc стратегии, которые использует человек при
решении различных проблем. Таким образом, на первый план выдви-
выдвигаются рассуждения «здравого смысла», рассуждения, оперирующие
с неполной, противоречивой, неточной, неопределенной информацией,
где главную роль играет правдоподобный вывод. Но прежде чем
переходить к основным методам правдоподобного вывода — абдукции
и индукции, — необходимо остановиться на основных особенностях
данных и знаний, применяемых в интеллектуальных системах раз-
различного назначения.
6.1. Характерные особенности знания
Данные и знания есть основные понятия системы представления
знаний, являющейся одной из главных компонент интеллектуальной
системы принятия решений. Исторически в теории и практике про-
программирования понятие «данные» видоизменялось и усложнялось.

6.1] Характерные особенности знания 225
Сначала под данными понимались двоичные слова фиксированной
длины. С развитием структуры вычислительных машин происходило
развитие информационных структур для представления данных. По-
Появились способы описания данных в виде векторов и матриц, возник-
возникли списочные и иерархические структуры. В настоящее время в язы-
языках программирования высокого уровня используются абстрактные
типы данных, структура которых задается программистом. Появле-
Появление БД знаменовало собой еще один шаг на пути организации работы
с данными. Специальные средства, образующие систему управления
БД (СУБД), позволяют эффективно манипулировать с данными, при
необходимости извлекать их из БД и записывать в нужном порядке в
БД.
Таким образом, данные — это факты, характеризующие объекты,
процессы и явления предметной области, а также их свойства.
По мере развития исследования в области интеллектуальных си-
систем возникла концепция знаний, которая стала доминирующей в
исследованиях по искусственному интеллекту.
Как считает Д. А. Поспелов, можно выделить шесть этапов для
усложнения данных и превращения их в знания. Охарактеризуем суть
каждого этапа.
1. Внутренняя интерпретируемость.
На заре программирования каждой информационной единице —
данному — программист отводил определенную ячейку памяти, кото-
которой соответствовал ее адрес в памяти, т. е. приписанное ей уникальное
имя. Такое приписывание имени информационной единице приводило
к тому, что только сам программист знал содержимое, скрывающееся
под тем или иным именем. При необходимости он использовал это
содержимое в программе, вызывал его по имени, причем машине не
было известно, что скрывается за тем или иным именем.
Переход от физических адресов к относительным, а позднее и к
символьным создал большие удобства для программиста. Он освобо-
освобождался от забот по распределению реальной памяти в машине. Ав-
Автоматически распределяя физическую память, машина формировала
таблицу соответствий, в которой относительным или символьным ад-
адресам соответствовали физические адреса, назначаемые машиной. Но
и в этом случае машина не получала информации о том, что именно
скрывается за введенными программистом именами, соответствующи-
соответствующими относительным или символьным адресам. Имена информационных
единиц не подвергались ее анализу, и машина не могла ответить ни
на один запрос, который касался бы содержимого ее памяти, если
программист не составил для ответа специальной программы.
Если, например, в память машины нужно было записать сведения
о студентах университета, представленные в табл. 6.1, то без внутрен-
внутренней интерпретации в память машины была бы занесена совокупность
из четырех машинных слов, соответствующих строкам этой таблицы.
8 В.Н. Вагин и др.

226
Данные и знания в интеллектуальных системах
[Гл.6
Таблица 6.1
Ф.И.О.
Железнов В.П.
Попов П.С.
Иванов А.П.
Петухова С.С.
Год рож-
рождения
1979
1981
1978
1983
Факуль-
Факультет
АВТ
ГТ
ЭТ
ПТ
Курс
4
3
5
2
№ зачетной
книжки
М1273
Г523
Э1451
Т485
Специализация
Прикладная
математика
Гадиотехника
Электротехника
Теплоэнергетика
Информационная единица, которой, например, приписано имя
«Железнов В. П.», выглядит так: (<Год рождения, 1979> <Факуль-
тет, АВТ> <Курс, 4> <№ зачетной книжки, М1273> <Специализа-
ция, прикладная математика>). Круглые скобки здесь служат для
выделения содержания информационной единицы, а угловые скобки
выделяют в ней самостоятельные части, называемые обычно слота-
слотами. Полная запись информационной единицы, таким образом, имеет
вид: (Имя информационной единицы <Имя 1-го слота, Значение 1-го
слота> <Имя 2-го слота, Значение 2-го слота> ... <Имя n-го слота,
Значение n-го слота>).
При этом информация о том, какими группами двоичных раз-
разрядов в этих машинных словах закодированы сведения о студентах,
у системы отсутствуют. Они известны лишь программисту, который
использует данные табл. 6.1 для решения возникающих у него задач.
При переходе к знаниям в память машины вводится информа-
информация о некоторой протоструктуре информационных единиц («шапка»
таблицы в нашем примере). Она представляет собой специальное ма-
машинное слово, в котором указано, в каких разрядах хранятся данные
о Ф.И.О., годах рождения, факультетах, курсах, номерах зачетных
книжек и специализациях. При этом должны быть заданы специаль-
специальные словари, в которых перечислены имеющиеся в памяти системы
Ф.И.О., года рождения, факультеты и т.п. Все эти атрибуты могут
играть роль имен для тех машинных слов, которые соответствуют
строкам таблицы. По ним можно осуществлять поиск нужной инфор-
информации. Каждая строка таблицы будет экземпляром протострукту-
ры. В настоящее время СУБД обеспечивает реализацию внутренней
интерпретируемости всех информационных единиц, хранимых в ре-
реляционной БД.
2. Структурированность.
Сначала данные обладали очень простой внутренней структурой
типа «машинное слово — совокупность разрядов». Затем, когда от-
отдельные машинные слова стали объединяться в более сложные струк-
структуры (например, в списки), появилась возможность работать с инфор-
информационными единицами с более богатой внутренней структурой. Для

6.1]
Характерные особенности знания
227
таких информационных единиц должен выполняться «принцип мат-
матрешки», т. е. рекурсивная вложимость одних информационных единиц
в другие. Каждая информационная единица может быть включена в
состав любой другой, и из каждой информационной единицы можно
выделить некоторые ее составляющие. Другими словами, должна
существовать возможность произвольного установления между от-
отдельными информационными единицами отношений типа «часть —
целое», «род — вид» или «элемент — класс».
Таким образом, информационная единица может задаваться в ви-
виде структуры, показанной на рис. 6.1, где Р? означает имя слота j-ro
уровня вложенности с порядковым номером г, Р — имя всей инфор-
информационной единицы, т\ — значение слота с порядковым номером г в
j-м уровне.
р
р\
р\
л
р\
d
р\
4
Pi
Рис. 6.1
I
шерет
&
к
*§
ПЫ
I
ватели
Препода
Железное
В.П.
Попов
П.С.
Жуков
В.А.
Крюков
А.Т.
Год
рожд.
1979
Фак-т
АВТ
Курс
4
№кн.
М1273
Спец.
ПМ
Год
рожд.
1981
Фак-т
РТ
Курс
3
№кн.
Р523
Спец.
Радио-
Радиотехника
Год
рожд.
1955
Фак-т
АВТ
Каф.
пм
Долж.
доц.
Какой
курс
читает
Дискрет-
Дискретная мате-
математика
Год
рожд.
1953
Фак-т
РТ
Каф.
РПУ
Долж.
проф.
Какой
курс
читает
Радио-
прием-
приемники
Рис. 6.2
Видно, что информационная единица задается так, что ее первый
слот в качестве своего значения содержит к слотов второго уровня, а

228 Данные и знания в интеллектуальных системах [ Гл. 6
все остальные слоты первого уровня не разбиваются на более мелкие
единицы. Иногда в представлении знаний вместо термина «слот j-ro
уровня» используют специальные названия для частей информацион-
информационной единицы. Например, части слота 1-го уровня называют ячейками,
а их части — фасетами.
Между слотами разных уровней (точнее, между их именами) мо-
могут устанавливаться отношения различного типа. На рис. 6.2 (см.
также рис. 6.1) показан пример многоуровневой информационной еди-
единицы. Она имеет глубину вложения слотов, равную четырем. Именем
слота первого уровня служит слот «работники университета». На
втором уровне два слота: «студенты» и «преподаватели». На третьем
уровне имена слотов — это «Железнов В. П.», «Попов П. С.» и т.д.
Остальные слоты вместе с их значениями являются слотами четвер-
четвертого уровня.
Информационные единицы, структурированные таким образом,
обычно называются фреймами. Они также обладают внутренней ин-
интерпретируемостью и наличием внутренней структуры связей.
3. Связность.
Между информационными единицами может быть также пре-
предусмотрена возможность установления внешней структуры связей
различного типа. Например, информационные единицы могут быть
связаны каузальным отношением, задающим причинно-следственные
связи, или отношением «аргумент — функция», связанным с вычис-
вычислением определенных функций. Можно также говорить об отношении
структуризации, задающем иерархию информационных единиц.
Между информационными единицами могут устанавливаться так-
также пространственные и временные отношения, а также отношения,
определяющие порядок выбора информационных единиц из памяти
машины или указывающие на то, что две информационные единицы
несовместимы друг с другом в одном описании.
Наиболее полно различные типы связей воплощены в общей моде-
модели представления знаний, называемой семантической сетью, пред-
представляющей собой иерархическую сеть, в вершинах которой находят-
находятся информационные единицы. Эти единицы снабжены индивидуаль-
индивидуальными именами. Дуги такой сети соответствуют различным связям
между информационными единицами. При этом иерархические связи
определяются отношениями структуризации, а неиерархические свя-
связи — отношениями иных типов. Так, в качестве иерархических связей
выступают отношения ISA (is an instance of) и АКО (a kind of). ISA-
отношение связывает элементы (примеры) класса с самим классом,
включающим группу объектов (явлений, процессов), обладающих об-
общими свойствами. АКО-отношение используется для связи одного
класса с другим. Например, индивидуальный объект «Попов П. С.»
связывается ISA-отношением с классом «группа А-13-99», который, в

6.1] Характерные особенности знания 229
свою очередь, связывается АКО-отношением с более общим классом
«факультет АВТ».
4. Шкалирование.
Отдельные информационные единицы могут соотноситься между
собой с помощью различных шкал. Простейшие из них — метрические
шкалы. С их помощью можно устанавливать количественные соот-
соотношения и порядок тех или иных совокупностей информационных
единиц.
Метрические шкалы, у которых начало отсчета абсолютно, т. е. не
зависит ни от событий, ни от момента или места нахождения, называ-
называются абсолютными. Примером такой абсолютной метрической шкалы
является начальное событие «Рождество Христово», от которого мы
отсчитываем историческое время. С помощью этой шкалы можно
упорядочить по возрасту всех людей, известных интеллектуальной
системе, и ответить на любой вопрос, связанный с их возрастом.
Другой тип метрических шкал — относительные метрические
шкалы. Начало отсчета на них меняется и каждый раз служит пред-
предметом специального договора. Очень часто это начало определяется
текущим моментом высказывания или местом нахождения. Такое
высказывание как «Через полчаса я буду на кафедре прикладной
математики» проецируется именно на относительную шкалу. Для от-
относительных шкал используют те же единицы измерений, что и для
абсолютных.
Наконец, еще один вид шкал — порядковые шкалы. На них фик-
фиксируется лишь порядок информационных единиц. Примером такой
шкалы может служить шкала тяжести преступлений, имеющая место
в юриспруденции. В этой шкале кража — преступление менее зна-
значительное, чем убийство, а мелкое хулиганство менее значительно,
нежели кража. Другим примером порядковой шкалы является шкала
оценок обучающихся в университете: неудовлетворительно, удовле-
удовлетворительно, хорошо, отлично. На этой шкале нет никакой метрики,
и мы не можем количественно оценить, насколько оценка «хорошо»
превосходит оценку «удовлетворительно».
Среди порядковых шкал выделяют нечеткие порядковые шка-
шкалы. Их иногда называют лингвистическим шкалами. Пример такой
шкалы «никогда — всегда». Метки на ней характеризуют частоту
появления событий или процессов. Шкала ограничена с двух сторон
маркерами «никогда» и «всегда». В первом случае частота появления
события равна нулю, во втором — единице. Остальным маркерам,
которым соответствует упорядоченный список нечетких квантифика-
квантификаторов типа «очень редко», «редко», «не часто — не редко», «часто»,
«очень часто», соответствуют не точечные деления, а некоторые ин-
интервалы, величина и расположение которых зависят от интерпретации
словесных оценок, относящихся к шкале. Например, можно считать,

230 Данные и знания в интеллектуальных системах [ Гл. 6
что маркеру «редко» соответствует случай, когда частота появления
события лежит в интервале от 0,2 до 0,3.
Для нечетких квантификаторов при построении такой шкалы
молено равномерно разделить отрезок между концевыми маркерами
на столько отрезков, сколько промежуточных маркеров в ней нахо-
находится или опросить экспертов с целью определения границ отрезков,
соответствующих каждому из промежуточных маркеров.
В теории нечетких множеств, как известно, используются функции
принадлежности, интерпретируемые как характеристические функ-
функции для нечетких множеств. Функция принадлежности для множе-
множества А обозначается символом /хд(х). Ее значение, равное 0, соответ-
соответствует утверждению, что данный элемент х не принадлежит А, а ее
значение, равное 1, свидетельствует о его безусловной принадлежно-
принадлежности данному множеству. Промежуточные значения /хд(ж) не следует
трактовать в вероятностном смысле, так как степень принадлежности
элемента к нечеткому множеству не обязана иметь статистическую
природу.
Следует отметить, что нечеткие квантификаторы фиксируют
лишь порядок, образующийся на нечетких шкалах. Например, что
значит «редко»? Во фразах типа «Я редко бываю в кинотеатре»
и «Редко удается поехать в зарубежную командировку» вряд ли
говорится об одинаковой частоте случающихся событий. Трудность
сравнения между собой информационных единиц, расположенных на
различных нечетких шкалах, решается путем введения универсаль-
универсальных нечетких шкал, на которые с помощью специальных процедур
проецируются различные нечеткие шкалы, соответствующие одним и
тем же спискам нечетких квантификаторов.
Кроме абсолютных и относительных метрических шкал,
порядковых шкал и их смешанных типов, следует отметить
оппозиционные шкалы. Как считает Д. А. Поспелов, именно оппо-
оппозиционные шкалы заложили основу восприятия мира человека не
как хаотического набора ситуаций и фактов, а как определенным
образом упорядоченного их единства. Бинарная оппозиция типа
противопоставления двух фактов, явлений или свойств — левое
и правое, мужское и женское, — лежит в основе мировосприятия
у всех народов мира. Такая шкала образуется с помощью пар
слов-антонимов. Примерами могут быть пары: красивый —
безобразный, хороший — плохой, сильный — слабый и т. п. В
середине оппозиционной шкалы находится нейтральное значение
типа: не красивый — не безобразный, не хороший — не плохой
и т. п.
Постигая закономерности физического мира, с помощью оппози-
оппозиционных шкал можно любое понятие естественного языка как бы
спроецировать на второй план. Отсюда и употребляются эпитеты
«острый» ум, «недалекий человек» и т. п.

6.1] Характерные особенности знания 231
5. Семантическая метрика.
На множестве информационных единиц упорядочение сведений в
когнитивных структурах человека происходит благодаря не только
оппозиционным шкалам, но также и ассоциативным связям, харак-
характеризующим ситуационную близость этих единиц. Эту связь можно
было бы назвать отношением релевантности для информационных
единиц. Такое отношение дает возможность выделять в информацион-
информационной базе некоторые типовые ситуации (например, «покупка», «учеба»,
«отдых»). Отношения релевантности при работе со знанием позволяет
сузить пространство поиска нужной информации и обнаруживать
знания, близкие к уже найденным.
Другая оценка близости информационных единиц опирается на
частоту появления тех или иных ситуаций или конкретных представи-
представителей в типовых ситуациях. Выбор того или иного конкретного пред-
представителя из возможных подчиняется закону частоты его появления.
Если, например, провести с представителями социума, в котором мы
живем, эксперимент, в ходе которого испытуемый должен не заду-
задумываясь давать ответы на вопросы экспериментатора о названиях
конкретных представителей типовых ситуаций или слов-понятий, то
результат в подавляющем числе случаев будет демонстрировать дей-
действие закона частоты появления. Если мы просим назвать поэта, то,
как правило, русский человек даст ответ «Пушкин», а не «Байрон».
На требование назвать инструмент, мы, как правило, получим ответ
«молоток».
Такие эксперименты показывают, что у нас «на языке» готовые
ответы на возможные запросы к нашей памяти всегда те, которые
соответствуют наиболее часто встречавшемуся верному ответу. По-
Подобный механизм позволяет при дефиците времени на обдумывание и
поиск нужной информации в памяти всегда иметь нужные «клише»,
наиболее часто встречавшиеся в нашей жизни.
6. Наличие активности.
В связи с непрерывным развитием теории и практики программи-
программирования программы и данные, с которыми эти программы работали,
были отделены друг от друга. В программе было сосредоточено про-
процедурное знание. Оно хранило в себе информацию о том, как надо
действовать, чтобы получить нужный результат. Машина выступала
в роли мощного калькулятора, в котором программа играла роль
активатора данных.
Знания другого типа, которые обычно называют декларативными,
хранили в себе информацию о том, над чем надо выполнять эти
действия. Процедурное знание формировало обращение к деклара-
декларативному знанию, воплощенному на первом этапе развития програм-
программирования в пассивно лежащие в памяти машины данные.
Для интеллектуальных систем складывается противоположная си-
ситуация. Не процедурные знания активизируют декларативные, а на-

232 Данные и знания в интеллектуальных системах [ Гл. 6
оборот, та или иная структура декларативных знаний оказывается
активатором для процедурных знаний. Появление в базе фактов
или описаний событий, установление связей может стать источником
активности системы. Совокупность средств, обеспечивающих работу
со знанием, образует систему управления базой знаний (СУБЗ), раз-
разработка которой сейчас выполняется.
В развитых моделях представления данных можно выделить два
компонента: интенсиональные представления и экстенсиональные
представления. Оба компонента хранятся в БД. При этом в ее экс-
экстенсиональную часть входят конкретные факты, касающиеся пред-
предметной области (например, строки табл. 6.1), а в интенсиональную
часть — схемы связей между атрибутами, выраженные в виде общих
законов (постулатов). Будем рассматривать БД, в которых хранятся
конкретные факты о предметной области как экстенсиональные БД
(ЭБД), а БД для хранения общих законов — как интенсиональные
(ИБД). Если экстенсиональные представления относятся к данным,
то относительно интенсиональных представлений единого мнения нет.
Разработчики БД говорят в этом случае о схемах БД, а представи-
представители искусственного интеллекта — о знаниях в проблемной области.
Естественно, мы будем придерживаться второй точки зрения.
Поясним на примере понятия экстенсионального и интенсиональ-
интенсионального представления знаний. Возьмем понятие ПРЕДШЕСТВУЕТ (со-
(сокращенно ПРЕД). Интенсиональный смысл этого понятия состоит в
том, что ПРЕД есть бинарное отношение, определенное на множестве
предметов и удовлетворяющее следующим условиям:
1) если х ПРЕД уиу ПРЕД z, то х ПРЕД z\
2) не существует xi, Х2, ..., хш таких, что х\ ПРЕД Х2,
х2 ПРЕД жз, • • •, хт ПРЕД хх.
Экстенсиональное представление понятия ПРЕД получается то-
тогда, когда это понятие интерпретируется как множество всех пар
предметов, для которых это отношение истинно.
Пусть, например, предметная область состоит из всех двоичных
слов длины п. Предположим, что отношение ПРЕД определено сле-
следующим образом: о\о~2 ... оп ПРЕД /?i/?2 • • • Рп тогда и только тогда,
когда Gi ^ /?i, <72 ^ /?2> • • • > 0п ^ /Зп. Тогда экстенсиональным пред-
представлением понятия ПРЕД будет множество пар: @0... 00, 00... 01),
@0... 00, 00... 10), ..., @0... 0, 10... 0), @0... 01, 00... 11), @0... 001,
00... 101), ..., @0... 01, 10... 01), ..., @1... 11, 11... 11). Легко пока-
показать, что число этих пар равно в данном примере Зп — 2П.
При таком экстенсиональном представлении имеется простой ал-
алгоритм, выясняющий для любой пары ж, у Е {0,1}п, верно ли, что
х ПРЕД у. Этот алгоритм заключается просто в поиске данной пары
(ж, у) среди пар экстенсионального представления. Если такая пара

6.1] Характерные особенности знания 233
найдена, то ответом будет: «верно, что х ПРЕД г/»; если же такой
пары нет, то ответом будет: «неверно, что х ПРЕД г/».
Конечно, опираясь только на интенсиональные представления 1)
и 2) нельзя выяснить верно ли для конкретной пары (ж, г/), что
х ПРЕД у. Нужна дополнительная информация об интерпретации.
Можно, однако, рассматривать «комбинированные» экстенсиональное
и интенсиональное представления, которые позволяют отвечать более
эффективно на такие вопросы.
Эффективность алгоритмов вывода очень сильно зависит от вы-
выбранных экстенсиональных и интенсиональных представлений. Чисто
экстенсиональное представление приводит к неэффективным алго-
алгоритмам (в том случае, если экстенсиональное представление понятий
велико) или же вообще не позволяет дать алгоритм (в том случае,
когда экстенсиональное представление бесконечно). С другой сторо-
стороны, чисто интенсиональное представление не позволяет фиксировать
интерпретацию, в частности, ее область: необходимо также и экс-
экстенсиональное представление. Логика предикатов первого порядка
показывает, что в определенном смысле произвольное знание можно
выразить почти чисто интенсионально: единственным экстенсиональ-
экстенсиональным представлением является экстенсиональное представление поня-
понятия ИСТИНА. Однако проблемы распознавания в языке логики пре-
предикатов первого порядка либо вообще алгоритмически неразрешимы,
либо имеют трудоемкие алгоритмы (алгоритмы с весьма высокими
нижними оценками по времени и памяти).
Таким образом, в ЭБД конкретные факты находятся в экстенси-
экстенсиональной форме посредством соответствующих кортежей (n-ок) от-
отношений. ИБД служит для хранения общих законов (постулатов),
представленных в виде правильно построенных выражений логики
предикатов первого порядка. Введение интенсиональной части БД
очень важно с точки зрения дедуктивного вывода и позволяет перей-
перейти к рассмотрению дедуктивных БД, являющихся составной частью
дедуктивных систем принятия решений. Отсюда понятно различие
между обычными БД и дедуктивными: в дедуктивных БД для вывода
новых фактов из общих законов используются методы автоматическо-
автоматического доказательства теорем, в то время как в обычных БД пользователь
должен писать более сложные предложения для запроса, в том числе
необходимые ему общие законы. Кроме того, дедуктивные механизмы
вывода должны являться, на наш взгляд, интегральной частью любой
технологии БД и, как следствие, любой интеллектуальной системы.
Возвращаясь к табличному представлению данных, отметим, что
экстенсиональное отношение — это определенным образом выделен-
выделенное подмножество декартова произведения доменов, относящихся
к некоторому набору атрибутов. Например, содержимое табл. 6.1
есть подмножество декартова произведения доменов, соответствую-
соответствующих атрибутам: «Ф.И.О.», «Год рождения», «Факультет», «Курс»,

234 Данные и знания в интеллектуальных системах [ Гл. 6
«№ зачетной книжки», «Специализация». В схеме баз данных такому
экстенсиональному отношению будет соответствовать интенсиональ-
интенсиональное отношение R(Ai,A2,...,Am). Имя этого отношения совпадает
с именем экстенсионального отношения (например, для табл. 6.1 R
представляет собой «список студентов данного университета»), а в
качестве его аргументов выступают атрибуты, домены которых ис-
использовались для образования соответствующего экстенсионального
отношения.
Табличное представление данных, протоструктура которых опре-
определяется экстенсиональными отношениями, а схема БД — интен-
интенсиональными отношениями, является характерным для реляцион-
реляционных БД.
6.2. Знание как обоснованное истинное убеждение
По мере развития исследований в области интеллектуальных си-
систем возникла концепция знания, которая объединила в себе многие
черты процедурной и декларативной информации.
Хотя строгого понятия знания и не существует, само это понятие
волновало лучшие умы человечества, начиная с древних греков. Так,
по Платону знание делится на чувственное и интеллектуальное.
Чувственное знание — низший вид, интеллектуальное — высший.
Каждая из этих сфер в свою очередь делится на «мышление» (noesis)
и «рассудок» (dianoia). Под «мышлением» Платон понимает дея-
деятельность одного лишь ума, свободную от примеси чувственности,
непосредственно созерцающую интеллектуальные предметы.
Второй вид интеллектуального знания — «рассудок». Под «рассуд-
«рассудком» Платон понимает такой вид интеллектуального знания, при ко-
котором познающий также пользуется умом, но уже не ради самого ума,
а для того, чтобы понимать чувственные вещи. «Рассудок» Платона
уже не непосредственный, не интуитивный, а опосредствованный,
«дискурсивный» вид знания. Рассудок, согласно Платону, ниже ума
и выше ощущений.
Чувственное знание Платон также делит на две области: «веру»
(pistis) и «подобие» (eicasia). С помощью «веры» мы воспринимаем
вещи в качестве существующих и утверждаем их в этом качестве.
«Подобие» — вид уже не восприятия, а представления вещей, или ин-
интеллектуальное действование с чувственными образами вещей. «По-
«Подобие», по Платону, — мыслительное построение, основывающееся на
«вере».
Платон различает знание и мнение. Одно истинное мнение еще не
дает знания, и для возникновения знания к истинному мнению долж-
должно присоединится еще нечто — «смысл». Но Платон идет еще дальше.
Как бы ни понимать «смысл», то ли как выражение в слове, то ли
как перечисление элементов, то ли как указание на отличительный

6.2] Знание как обоснованное истинное убеждение 235
признак, прибавка «смысла» к «правильному мнению» не создает и
не может создать того, что зовут знанием.
Таким образом, знание не есть ни ощущения, ни правильное мне-
мнение, ни соединение правильного мнения со смыслом. Мнение не есть
незнание, но оно не есть и знание: оно темнее знания и яснее незнания.
В отличие от мнения знание есть потенция, особый род существую-
существующего. Род этот характеризует направленность: знание направляется
к своему предмету, и всякая потенция, направляющаяся к одному и
тому же и делающая одно и то лее, называется той же самой в отличие
от всякой, направленной на иное и делающей иное.
Математические предметы и математические отношения Пла-
Платон выделяет в особый предмет знания. В системе видов знания
математическим предметам также принадлежит некое «серединное»
место. Это место между областью «идей» и областью чувственно
воспринимаемых вещей, а также областью их отображений. «Идеи»
постигаются только посредством знания, и знание возможно только
относительно «идей». В отличие от «идей» математические предметы
и математические отношения постигаются посредством рассуждения,
или размышления рассудка. Это и есть второй вид знания.
Чувственные вещи постигаются посредством мнения (doxa). О них
невозможно достоверное знание, их нельзя постигнуть с помощью
рассуждения; если их можно постигнуть, то лишь недостоверно, ги-
гипотетически.
Почему же математические предметы занимают середину между
подлинным знанием и мнением? Дело в том, что математические
предметы родственны и вещам, и «идеям». Предметы эти как «идеи»
неизменны; природа их не зависит от отдельных экземпляров, пред-
представляющих их в чувственном мире. Математики вынуждены, считает
Платон, прибегать для достижения своих предметов к помощи отдель-
отдельных фигур, как в геометрии. Фигуры эти рисуются или представляют-
представляются посредством воображения. Именно поэтому математическое знание
не есть знание, совпадающее с тем, при помощи которого постигаются
«идеи». Оно совмещает в себе черты истинного знания с некоторыми
чертами мнения.
Русскому слову «наука» соответствует древнегреческое «епист-
эмэь, которое в языке эллинов первоначально понималось как «уме-
«умение», «искусство», «опытность», затем — как «знание» и, наконец, как
«научное знание». Для Платона «епистэмэ» — достоверное знание, а
не субъективное мнение. Так же понимал этот термин и Аристотель —
ученик, последователь и критик Платона.
Научное, или достоверное, знание для Аристотеля — не резуль-
результат веры, некритически воспринятой традиции, субъективного опыта.
Оно — результат логического рассуждения, направленного на откры-
открытие начал, причин и элементов того, что дано нам в непосредственном

236 Данные и знания в интеллектуальных системах [ Гл. 6
чувственном опыте: «... всякое знание, основанное на рассуждени-
рассуждениях ... имеет своим предметом, — говорится в «Метафизике», — более
или менее точно определенные причины и начала».
«Знать лее, почему нечто есть, — значит знать через причину» —
пишет Аристотель во «Второй аналитике». Научное знание должно
быть также логически доказательным: нужно не просто выявить
причину данного предмета, но и доказать, что для этого предмета
именно она, а не нечто иное, является причиной. Поэтому Аристотель
подчеркивает: «... наука связана с доказательством... ».
Аристотель абсолютизировал научное знание и считал, что не
может быть науки ни о привходящем (случайном), ни о преходя-
преходящем (изменчивом). Случайное как таковое не может быть предметом
никакого вида знания. Нельзя сказать, чтобы Аристотель игнори-
игнорировал правдоподобное знание, принцип правдоподобия, который в
латиноязычной философии получил название пробабилизма (от лат.
«пробабилис» — вероятный, правдоподобный, возможный). Он опре-
определяет правдоподобное как «то, что кажется правильным всем или
большинству людей... ». Здесь он говорит об особом типе умозаклю-
умозаключения, которое строится из правдоподобных положений. Гениальный
Стагирит называл его «диалектическим». Но такое умозаключение он
вовсе не считал научным, доказательным, ведь доказательство имеет
место только там и тогда, где и когда мы исходим непосредственно
или опосредствованно из безусловно истинных положений. Следова-
Следовательно, в отличие от скептиков, Аристотель допускал возможность
абсолютно достоверного знания и именно его считал научным.
Как правило, определение знания носит метафорический харак-
характер, начиная от знаменитого высказвания «знание — сила» и кончая
определениями, данными в различных энциклопедических справоч-
справочниках.
В области искусственного интеллекта этот ключевой термин мы
будем употреблять как следующую метафору: знание — это обосно-
обоснованное истинное убеждение (вера). Здесь каждое слово нуждается
в объяснении: что такое убеждение (belief), истина и обоснование
(подтверждение) ?
Интересно отметить, что до появления вычислительных машин,
задолго до эры искусственного интеллекта в Большой энциклопедии
(под ред. С. Н. Южакова, СПб, т. 9, 1902 г.) было дано следующее
определение этого термина: «Знание в объективном смысле то же,
что истинное знание (познание), в субъективном — убеждение в его
истине по реальным причинам. В первом отношении оно противопо-
противополагается заблуждению, как неистинному знанию, во втором — вере,
мнению».
В этой цитате те же самые «три кита», на которых зиждется это
метафорическое понятие. Начнем с «убеждения» (веры). Пусть име-
имеется база знаний для описания реального мира (предметной области),

6.2] Знание как обоснованное истинное убеждение 237
состоящая из пары <БЗо, Кс>, где БЗо — совокупность утверждений
на языке некоторой логики ?, например, логики предикатов первого
порядка, и \-?, — отношение выводимости (доказуемости) в этом языке
С. В этом случае утверждение Р Е БЗо тогда и только тогда, когда
БЗо ^с Р.
Пусть дана некоторая интеллектуальная система А, основанная на
знании, со своей БЗ. Предполагается, что в этой системе утверждение
Р имеет место только тогда, когда Р находится в БЗ этой системы,
т. е. убеждение есть нечто, литералъно представленное в БЗ.
Конечно, в такой БЗ могут находиться какие угодно утвержде-
утверждения. Однако потребуем, чтобы такие утверждения были истинными,
непротиворечивыми друг другу, хотя это может потребовать обосно-
обоснования.
Фундаментальным понятием семантики является понятие истины
реального мира. Мы будем рассматривать истину в модели, где под
моделью и понимается реальный мир. Состояние реального мира поз-
позволяет приписать семантические значения «истинно» или «ложно»
(истинностные значения) к утверждениям интеллектуальной систе-
системы А. Так, для логики предикатов первого порядка имеет место
семантика А. Тарского, состоящая из тройки < D,R,F >, где D —
непустое множество предметов (индивидуумов), называемое областью
интерпретации (универсумом), a R и F являются множествами отно-
отношений и функций соответственно между предметами, содержащимися
в описываемом реальном мире.
Интерпретация представляет собой распространение исходных
положений какой-либо формальной системы на реальный мир. Она
придает смысл каждому символу формальной системы и устанавлива-
устанавливает взаимно однозначное соответствие между символами формальной
системы и реальными предметами. Если в логике высказываний ин-
интерпретация формулы понимается как приписывание истинностных
значений пропозициональным символам этой формулы, то в логике
предикатов первого порядка, как известно, каждому n-местному пре-
предикатному символу формулы соответствует n-местное отношение (т. е.
Dn —> {И,Л}); каждому n-местному функциональному символу — п-
местная функция (т. е. Dn —> D) и каждой константе — некоторый
предмет из D. Говорят, что интерпретация является моделью БЗ тогда
и только тогда, когда все утверждения в БЗ становятся истинными
в этой интерпретации.
Как правило, системы, основанные на знании, имеют дело с одним
знанием или с одним убеждением (верой). Для таких систем логи-
логика предикатов первого порядка пополняется оператором К, где КР
читается как «Известно (верно), что утверждение Р истинно». Имеем
ли мы дело со знанием или убеждением относительно утверждения Р,
зависит только от того, представлена ли в БЗ или нет аксиома вида
КР —> Р, которая читается как «Если известно, что Р истинно, тогда

238 Данные и знания в интеллектуальных системах [ Гл. 6
утверждение Р действительно истинно». Если эта аксиома представ-
представлена, то имеет место знание, если нет — убеждение.
Конечно, в динамически изменяющемся мире истинность некото-
некоторых утверждений может меняться. Тут мы подходим к пояснению
слова «обоснованное» в метафорическом определении понятия «зна-
«знание».
Действительно, чтобы убедиться в истинности или ложности неко-
некоторого утверждения, надо обосновать его статус новыми объяснения-
объяснениями, фактами или наблюдениями, и в зависимости от подтверждения
или опровержения его истинности, перевести это утверждение в статус
или знания, или ошибочного убеждения. Будем называть убеждение
гипотезой, которая по мере ее обоснования превращается или в зна-
знание (в случае, если все объяснения, факты или наблюдения говорят
о ее истинности), или в ошибочное убеждение, которое надо удалить
изБЗ.
В качестве примера рассмотрим три утверждения.
1. Все студены юны или \/х (Студент(ж) —> Юн(х)).
2. Петров — студент или Студент (Петров).
3. Петров юн или Юн(Петров).
Если мы убеждены, что первые два утверждения истинны, то ис-
истинность третьего утверждения достоверно подтверждена вследствие
правила дедуктивного вывода Modus Ponens. Обоснование третьего
утверждения здесь не требуется, если нам удалось обосновать ис-
истинность первых двух (такое обоснование легко сделать для второго
утверждения, но что касается первого утверждения, возникают труд-
трудности с квантором «все»).
Теперь считаем, что истинны первое и третье утверждения. Вы-
Выдвигаем гипотезу: «Студент ли Петров?» Эта гипотеза перейдет в
статус знания, если мы усилим нашу веру в эту гипотезу путем до-
дополнительных объяснений, фактов или наблюдений, одно из которых,
например, может быть следующим: «Петров учится на факультете
вычислительной техники». Этот тип рассуждений носит название
абдуктивного вывода, к рассмотрению которого мы перейдем ниже.
Наконец, имеется третья возможность, когда истинны второе и
третье утверждения. Выдвигается гипотеза в виде общего закона:
«Все ли студенты юны?» Этот пример является примером индуктив-
индуктивного умозаключения, обоснование которого является трудной задачей.
Говорят, что классификация утверждений о реальном мире на
убеждения, гипотезы и знание выражает эпистемический статус
утверждений. Большинство теорий о реальном мире на данном пе-
периоде исследований являются знанием, так как они подтверждаются
многочисленными объяснениями, фактами и наблюдениями.
Кроме эпистемического статуса утверждений имеется еще и ассер-
ассерторический статус. Рассмотрим следующее утверждение: «Студенты
юны». Его можно трактовать по-разному.

6.2] Знание как обоснованное истинное убеждение 239
1. «Все студенты юны». Как уже говорилось, это слишком сильное
утверждение из-за квантора «все». По-видимому, исключения в
реальной жизни все-таки бывают.
2. «Обычно (в большинстве случаев, как правило) студенты юны».
Это утверждение предполагает некоторую возможность (веро-
(вероятность) того, что студенты юны.
3. «Студенты юны». В этом случае исключения, конечно, пред-
предполагаются, но и признается неявно некоторая связь (какая?)
между студенчеством как некоторым социумом и его возрастом.
Отсюда вытекают три различных подхода при определении смыс-
смысла (семантики) утверждений.
В первом случае имеет место так называемый аналитический
(дефинициальный) тип утверждений, т.е. тот тип, когда истинность
утверждений не подвергается сомнению, как не подвергаются сомне-
сомнению утверждения типа «квадрат — равносторонний прямоугольник»
или «Земля вращается вокруг Солнца». Конечно, к этому типу неже-
нежелательно относить утверждения вроде нашего примера, так как име-
имеются не юные студенты, если считать юность до 23 лет.
Во втором случае подчеркивается стереотипный взгляд на утвер-
утверждения, в котором имеет место типичный случай. Известно, что в
искусственном интеллекте теория прототипов широко используется
в системах представления знаний, основанных на фреймах, в кото-
которых выводится стереотипная ситуация. Но если в классической ло-
логике предикатов первого порядка, как правило, используется вывод
с аналитическими утверждениями (достоверный вывод), то в выводе
с прототипами находят применение вероятностные, нечеткие и т. п.
схемы (правдоподобный вывод).
Третий случай страдает отсутствием строгого формализма при
описании смысла того или иного утверждения. Здесь можно говорить
лишь о выдвижении некоторой гипотезы, которая будет подтвер-
подтверждаться или опровергаться при наличии дополнительных фактов,
объяснений или наблюдений.
Таким образом, в семантической теории знания основная труд-
трудность заключается в том, что истинностное значение утверждения
может быть как известно, так и неизвестно, независимо от того, какое
оно в действительности. Если мы охарактеризуем БЗ как один из
возможных миров, то некоторое утверждение будет истинным тогда
и только тогда в этом мире, когда оно истинно во всех возможных
мирах, совместимых с нашей БЗ.
Пусть, например, мы имеем в БЗ следующие три утверждения.
1. Профессор(Бурлаков).
2. Профессор(Фролов) V Профессор(Коптев).
3. \/ж(Профессор(ж) —> Работник_Университета(ж)).

240 Данные и знания в интеллектуальных системах [ Гл. 6
Здесь утверждается, что Бурлаков и Фролов или Коптев являются
профессорами как в этой БЗ, так и во всех возможных мирах, совме-
совместимых с ней, чего нельзя сказать о других индивидуумах, не перечис-
перечисленных в нашей БЗ. Аналогично, в мире нашей БЗ легко вывести, что
Бурлаков также является работником университета. Таким образом,
наша БЗ может быть охарактеризована как один из возможных ми-
миров, в котором некоторое утверждение будет истинным тогда и только
тогда, когда оно истинно во всех возможных мирах, совместимых с
БЗ. Недостаток этого подхода заключается в том, что моделирование
знаний влечет логическое всеведение, т. е. все логические следствия
убеждений должны быть обоснованы.
Альтернативным к подходу возможных миров является так на-
называемый синтаксический подход, который изоморфен только явно
заданному множеству утверждений БЗ. Так, возвращаясь к примеру
нашей БЗ, мы имеем только три заданных утверждения, считающихся
истинными. Однако никакие выводимые утверждения типа «Бурла-
«Бурлаков является работником университета» не должны быть в БЗ, что
позволяет избежать логического всеведения. Все, что обосновано, яв-
явно присутствует в БЗ. Правда, при таком подходе не обосновывается
утверждение Профессор(Коптев) V Профессор(Фролов) в силу его
явного отсутствия в БЗ, с чем трудно согласиться.
Упомянем еще об одном подходе, связывающем понятие возмож-
возможного мира с миром ситуаций. Из утверждений, в том числе и выво-
выводимых, будут поддерживаться только те, которые релевантны данной
ситуации. Так, для нашего примера истинны будут утверждения о
том, что Бурлаков является профессором, а также что Фролов или
Коптев — тоже профессора, причем, если обосновано утверждение
Профессор(Фролов) V Профессор (Коптев), то обосновано и Профес-
сор(Коптев) V Профессор(Фролов). Выводимое утверждение о Бурла-
кове как работнике университета также обосновано, если обосновано
утверждение, что все профессора являются работниками университе-
университета.
Таким образом, ситуационный подход расширяет стандартную
структуру возможных миров, и если в «возможных мирах» опреде-
определяется истинностное значение всех утверждений, то в ситуационном
подходе истинностное значение может быть как определено, так и не
определено.
6.3. He-факторы знания
В идеале было бы замечательно, если БЗ интеллектуальной систе-
системы содержала бы только аналитические утверждения, обоснование
которых не требуется. К сожалению, данные и знание, описываю-
описывающие сущности и связи какой-либо проблемной области, как правило,

6.3] Не-факторы знания 241
неполны, противоречивы, немонотонны, неточны, неопределенны и
нечетки. Остановимся на этих особенностях знания.
В классических логических системах свойство полноты обычно
формулируется следующим образом: для множества формул с задан-
заданными свойствами исходная система аксиом и правил вывода должна
обеспечить вывод всех формул, входящих в это множество.
Важно также свойство непротиворечивости, суть которого сво-
сводится к тому, что исходная система аксиом и правил вывода не должна
давать возможность выводить формулы, не принадлежащие заданно-
заданному множеству формул с выбранными свойствами. Например, полные
системы аксиом и правил вывода в классическом исчислении пре-
предикатов первого порядка позволяют получить любую общезначимую
формулу из множества общезначимых формул и не дают возможности
получить какие-либо формулы, не обладающие этим свойством.
Однако на практике трудность получения полной и непротиворе-
непротиворечивой БЗ состоит в том, что знания о некой конкретной проблемной
области, как правило, плохо формализованы или не формализованы
совсем, а значит, трудно или даже невозможно сформулировать и
те априорные свойства, которым должны удовлетворять формулы,
выводимые в данной системе.
От полноты содержащейся в БЗ информации зависит и полнота
ответов на запросы, предъявляемые к БЗ. Если в БЗ, содержащую
сведения о студентах и преподавателях данного университета, посту-
поступил запрос «Бурлаков — профессор?», то ответ будет положительным,
если это на самом деле так. В случае неудачи с этим запросом могут
быть два варианта: а) Бурлаков — не профессор и б) статус Бурлакова
неизвестен. Первый вариант имеет место, если мы придерживаемся
предположения о замкнутости мира (Рейтер), рассматривающего
факты, которые не могут быть найдены (выведены) в БЗ, как их
отрицания. О втором варианте трудно что-либо сказать. Таким об-
образом, если в БЗ содержатся сведения только о нескольких препо-
преподавателях университета, хотя их на самом деле намного больше, то,
естественно, такая неполная БЗ и будет давать ответы только об этих
преподавателях. Возможен случай, когда система «знает» о других,
неизвестных ей преподавателях. Можно отметить, что проблеме об-
обработки запросов при неполноте знаний посвящена логика вопросов
и ответов {эротетическая логика), в которой наряду с обычными
истинностными значениями {И, Л} добавлены еще два: «неизвестно»
и «противоречиво».
Что касается противоречивости знания, то ее последствия в силу
потери разницы между истиной и ложью (вспомним, что из противо-
противоречия выводима любая формула (ex falso quodlibet), т.е. А,^А \- В)
поистине катастрофически. При представлении и обработке противо-
противоречивых знаний возникают две проблемы. Первая касается ассимиля-
ассимиляции (усвоения) противоречивой информации, т. е. способности вклю-

242 Данные и знания в интеллектуальных системах [ Гл. 6
чать в БЗ противоречия и возможности работать с противоречивой
БЗ. Вторая проблема заключается в аккомодации (приспособлении)
противоречивого знания, т.е. такой модификации БЗ, при которой
она становится непротиворечивой. Эти две проблемы тесно связаны
между собой, и от их совместного решения зависит общая проблема
вывода утверждений в противоречивой БЗ.
На первый взгляд, исходя из здравого смысла, проблема ассими-
ассимиляции противоречий может быть разрешена путем введения порядка
реализации вывода, т. е. сначала пытаются вывести рассуждения, свя-
связанные с частными фактами, нежели с общими законами. Рассмотрим
следующую БЗ.
1. Студенты изучают биологию или Ух (Ст(х) —»Биол(х)), предпо-
предполагая, что все студенты изучают биологию.
2. Рыбин — студент или Ст(Рыбин). Отсюда следует, что студент
Рыбин изучает биологию.
Однако, введение в эту БЗ дополнительной информации,которая
носит более частный и уточняющий характер, блокирует предыдущий
вывод, отдавая предпочтение этим частным утверждениям.
1. Студенты радиотехнического факультета не изучают биологию
или Ух (СтРад(ж) —> ^Биол(ж));
2. Рыбин — студент радиотехнического факультета или
СтРад(Рыбин).
Отсюда выводимо, что студент Рыбин не изучает биологию.
Трудность нахождения порядка реализации вывода заключается,
конечно, в семантике утверждений, которая в общем случае неоче-
неочевидна. Можно говорить, что утверждение В выводимо из гипотез
Ai,^,..., Ап (или Ai,^,..., Ап Ь Б), если каждая гипотеза реле-
релевантна этому утверждению. Но построение такой релевантной ло-
логики связано с большими трудностями. Здесь можно найти связь с
ситуационной семантикой, где выводы делаются только в пределах
ситуации, которая имеет место в данный момент. Естественно, при
переходе к другой ситуации имеет место ревизия БЗ, и выведенные
ранее утверждения не должны использоваться для вывода новых.
Проблема ассимиляции противоречия имеет место и в уже упо-
упоминавшейся эротетической логике. Если, например, из одного ис-
источника получено, что Студент (Петров) истинно, а из другого —
^Студент(Петров) истинно, то в этой логике данному утверждению
будет приписано истинностное значение «противоречиво», что дает
возможность работать с противоречивой информацией.
Что касается аккомодации противоречия, то проблема заключа-
заключается в обработке так называемых «подозрительных» формул (т. е.
формул, которые могли бы быть противоречивыми) в качестве гипо-
гипотез. Так как эти формулы находятся среди формул, общезначимость

6.3] Не-факторы знания 243
которых не вызывает сомнений, то возникают вопросы установления
непротиворечивости «подозрительных» формул, нахождения и опи-
описания множества формул, выдвигаемых в качестве гипотез, и нако-
наконец, каким образом эти гипотезы могут взаимодействовать с другими
утверждениями для дедуктивного вывода новых утверждений. Конеч-
Конечно, поддержка истинности таких утверждений должна проверяться
исключениями, которые имеют место в реальной БЗ, что приводит к
ее ревизии и усложняет саму процедуру вывода.
В классической логике предикатов первого порядка отношение
выводимости удовлетворяет следующим свойствам:
1) рефлексивности: Ai,A2,... ,Ап Ь А^ г = 1,п, т.е. вывод за-
заключения, идентичного одной из посылок, есть общезначимая
операция;
2) транзитивности: если А\, А^ ..., Ап Ь В\ и
Ai,^,..., Ап, B\ \- Е>2, то А\, A2,..., Ап h B2, т. е. промежуточ-
промежуточные результаты можно использовать для вывода заключения В^;
3) монотонности: если А\, А?,,..., Ап \- ?>i, то
А\, A2,..., Ап, {F} \- Bi, где {F} — множество добавочных
утверждений, т. е. добавочно введенные утверждения не отме-
отменяют ранее выведенное утверждение В\.
К сожалению, свойство монотонности не выполняется для ди-
динамических проблемных областей, БЗ которых содержит неполную,
неточную и динамически изменяющуюся информацию. Рассуждения
в таких БЗ часто предположительны, правдоподобны и должны под-
подвергаться пересмотру. Довольно очевидно, что для таких пересмат-
пересматриваемых рассуждений логическая система должна быть немонотон-
немонотонной. Это значит, что пересматриваемые рассуждения не являются в
классическом смысле общезначимыми, и если заключение В выводимо
из посылок Ai,^,..., Ап, существует модель для {Ai, A2,..., Ап} U
U {F}, не подтверждающая В.
Например, «Петров юн» не является общезначимым следствием из
двух посылок: «Большинство студентов юны» и «Петров — студент».
Оно просто выполнимо с этими посылками. И, следовательно, это
заключение принадлежит к возможно выполнимому на основе этих
двух посылок образу мира.
Конечно, если у нас нет дополнительной информации, то мы по
умолчанию полагаем: «Если Вы не знаете ничего другого, то пред-
предположите, что все студенты действительно юны». Тогда унаследовав
это свойство, можно вывести, что и Петров, будучи студентом, также
юн. При поступлении новой информации предположения могут стать
невыполнимыми с новым множеством посылок и будут отвергнуты.
Узнав, например, что Петров не юн, и получив, таким образом, про-
противоречивую БЗ, мы или отвергнем ранее выведенное заключение,
или потребуем дополнительной информации.

244 Данные и знания в интеллектуальных системах [ Гл. 6
Такой тип немонотонных рассуждений был реализован в логике
умолчаний и будет рассмотрен наряду с другими типами немонотон-
немонотонных логик позднее. Отметим только, что проблема немонотонности
тесно связана с проблемами неполноты и противоречивости знаний.
При описании динамически изменяющегося реального мира мы
часто имеем дело с неточной информацией, которая будучи поме-
помещенной в БЗ обрабатывается как истинная информация, хотя это
не соответствует действительности. Например, пусть в БЗ хранятся
следующие сведения:
Студент(Петров),
Читать_курс(Фролов, Математическая логика).
Однако эти сведения могут не соответствовать действительности,
если студент Петров месяц назад был отчислен из университета, а
Фролов уже читает другой курс.
Неточность относится к содержанию информации (или значению
сущности) и наряду с неполнотой и противоречивостью должна обя-
обязательно учитываться при представлении знаний в БЗ. Неточная ин-
информация может быть как непротиворечивой, так и противоречивой.
Так, например, возраст студента Петрова, записанный в БЗ, равен
32 годам, хотя ему на самом деле 23. Это пример непротиворечивой,
хотя и неточной информации. Может быть и другая ситуация, когда
по ошибке в БЗ ему записали 123 года, что противоречит действи-
действительности, так как возраст людей, как правило, колеблется от 0 до
100 лет.
Для того, чтобы неточные данные стали точными, можно восполь-
воспользоваться ранее упоминавшимся модальным оператором К, который
подчеркивает, что если известно, что некоторое утверждение истинно,
то оно на самом деле истинно. Например, если известно, что все
находящиеся в БЗ личности являются студентами, то это на самом
деле так, или Ух (К Студент (ж) —> Студент (ж)).
К неточности будем относить также величины, значения которых
могут быть получены с ограниченной точностью, не превышающей
некоторый порог, определенный природой соответствующих парамет-
параметров. Очевидно, что практически все реальные оценки являются неточ-
неточными, и сама оценка неточности также является неточной. Примеры
неточности данных встречаются при измерении физических величин.
В зависимости от степени точности измерительного прибора, от пси-
психического состояния и здоровья человека, производящего измерения,
получаемое значение величины колеблется в некотором интервале.
Поэтому для представления неточности данных мы можем исполь-
использовать интервал значений вместе с оценкой точности в качестве меры
доверия к каждому значению.
Если неточность относится к содержанию информации, то неопре-
неопределенность — к ее истинности, понимаемой в смысле соответствия
реальной действительности (степени уверенности знания). Каждый

6.3] Не-факторы знания 245
факт реального мира связан с определенностью информации, которая
указывает на степень этой уверенности. Понятия «определенности»
и «уверенности» довольно трудно формализуемы, и для их опре-
определения чаще всего используются количественные меры. Основная
идея такой меры заключается во введении функции неопределенности
unc(p), понимаемой как определенность того, что высказывание р,
содержащееся в БЗ, истинно, т. е. говорят, что утверждение р более
определенно, чем q, если unc(p) ^ unc(q).
Традиционным подходом для представления неопределенности яв-
является теория вероятностей — хорошо разработанная на сегодняш-
сегодняшний день математическая теория с ясными и общепринятыми аксио-
аксиомами.
Пусть Q — конечное множество утверждений, замкнутое относи-
относительно отрицания и конъюнкции (т. е. любая суперпозиция функций
из множества Q снова принадлежит О), а 0 и / обозначают проти-
противоречивое и общезначимое утверждения соответственно в множестве
Q. Тогда вероятностная мера V, определенная на Q, представляет
собой определенность (вероятность, правдоподобность, уверенность)
утверждения такую, что
2. РA) = 1;
3. V(p Vq)= V(p) + V(q), если р & q = 0.
Однако классическая теория вероятностей страдает рядом недо-
недостатков, и до сих пор не утихают споры насчет того, какого рода
действительность хотят выразить с помощью этой теории. Напри-
Например, как найти вероятностную меру V для конкретного множества
утверждений или на основании чего должно выполняться равенство
V(q) + V(^q) = 1. Действительно, если БЗ конкретно неизвестно, яв-
является ли Петров студентом или нет, то почему Р(Студент(Петров)) +
+ Р(^Студент(Петров)) = 1?
Основной вопрос, возникающий при выборе функции неопреде-
неопределенности для множества утверждений, заключается в нахождении
ограничений этой функции теми утверждениями, которые логически
или вероятностно связаны между собой. Решение этого вопроса обес-
обеспечивается правилом Байеса:
V{H\EuE2,...,En)
где V(H | Ei, Еъ, • • •, Еп) — условная вероятность утверждения Н при
условии Ei, E2j..., Еп, т.е. это вероятность того, что утверждение Н
истинно, если истинны утверждения (события) Ei, E2,..., Еп.
Однако на практике определить вероятность того, что
утверждения Ei, E2,..., Еп истинны, и условную вероятность

246 Данные и знания в интеллектуальных системах [ Гл. 6
V (Ei, E2, • • •, Еп | Н) довольно трудно. Конечно, можно упростить
проблему и считать, что утверждения Ei статистически независимы,
т.е. V (ЕъЕ2,...,Еп) = V(Ei) • V(E2) • ... • V(En). Однако
насколько достоверно и обоснованно предположение о статистической
независимости Ei — это вопрос, требующий дополнительного анализа
для каждого конкретного случая. Другое упрощение касается
статистической независимости утверждения Ei при условии Н,
т.е. V(EUE2, ...,Еп\Н)= Г(Ег \ Н) ¦ V(E2 | Я) ¦... ¦ V(En \ H).
В теории Демпстера — Шейфера требование к условию V(q) +
+ V(~^q) = 1 ослаблено, и вместо него имеет место V(q) + V(^q) ^ 1.
Здесь основным средством для распределения и манипулирования
степенями уверенности утверждений является функция вероятност-
вероятностной меры Mr, представляющая собой распределение базовых вероят-
вероятностей на все возможные утверждения. Исходя из этого распределе-
распределения, поддержка утверждению р определяется как sup(p) = У^ Mr(g),
если {q —> р}, т.е. вероятностная мера любого утверждения q, из
которого следует р, кладется в общую копилку для р.
Правдоподобность утверждения р определяется следующим обра-
образом: pls(p) = 1 — sup(^p). Легко показать, что sup(p) ^ pls(p). Отсюда
степень уверенности утверждения р определяется доверительным
интервалом: conf(p) = [sup(p), pis(p)].
Возвращаясь к примеру, является Петров студентом или нет, мы
получим доверительный интервал [0, 0], если в БЗ нет никаких сведе-
сведений о студенте Петрове, и conf(^p) = [1,1], если Петров не является
студентом.
Однако и в подходе Демпстера — Шейфера имеются свои трудно-
трудности. Так, неясно, что делать при выборе утверждений, доверительные
интервалы которых перекрываются или значительно отличаются раз-
размерами.
Таким образом, и классическая теория вероятностей, и теория
Демпстера — Шейфера нуждаются в обосновании в каждом конкрет-
конкретном случае, когда мы имеем дело с неопределенностью. И только
тщательный анализ видов неопределенности может дать ответ, какой
из подходов более предпочтителен.
Наконец, остановимся на проблеме представления нечетких зна-
знаний, являющейся ключевой при разработке интеллектуальных си-
систем различного назначения. Нечеткие знания по своей природе раз-
разнообразны и могут быть условно разделены на следующие катего-
категории: неточность, недоопределенность, неоднозначность, словом, лю-
любые нечеткости, между которыми нельзя провести четкой границы.
Один из способов описания нечеткости основывается на понятии
нечеткого множества, введенного Л. Заде. Пусть X — произвольное
непустое множество. Нечетким множеством А множества X назы-
называется множество пар: А = { < /ла(х)/х > }, где xGl

6.3] Не-факторы знания 247
Функция /1д : X —> [0,1] называется функцией принадлежности
нечеткого множества А, а X — базовым множеством. Для каждого
конкретного значения xGl величина 1Лд(х) принимает значения из
замкнутого интервала [0, 1], которые называются степенью принад-
принадлежности элемента х нечеткому множеству А. Носителем нечеткого
множества А называется подмножество А множества X, содержащее
те из X, для которых значения функции принадлежности Ца{х) > 0.
Например, пусть X — множество натуральных чисел. Тогда его
нечеткое множество А «очень малых» чисел может быть таким:
А = {< 1/1 >, < 0, 8/2 >, < 0, 7/3 >, < 0, 6/4 >, < 0, 5/5 >, < 0, 3/6 >,
< 0,1/7 >}.
Носителем нечеткого множества А является множество А =
= {1,2,3,4,5,6,7}. Отметим, что носитель нечеткого множества —
это обычное, «четкое» подмножество множества X.
В настоящее время существует целый ряд моделей представления
нечеткости в интеллектуальных системах, среди которых модель ко-
коэффициентов уверенности в MYCIN, вероятностная логика Ниль-
сона, теория свидетельств Шейфера, теория возможностей Заде,
модель голосования Бэлдвина, лингвистическая модель в MILORD и
др. Несмотря на различную природу нечеткости, формализованную в
моделях, мы можем условно разбить эти модели на три группы по ти-
типу нечетких множеств, используемых для оценок объектов (значений,
функций принадлежности) в моделях. К первой группе относятся мо-
модели с числовым значением функции принадлежности: модель коэф-
коэффициентов уверенности, вероятностная логика. Вторая группа вклю-
включает в себя интервально-значные модели: теория свидетельств, теория
возможностей, модель голосования и т. д. Третья группа — нечетко-
значные модели, в частности, лингвистическая модель в MILORD.
Если не учитывать внешние проявления знаний в разных моделях,
которые могут изменяться с одной модели на другую, то можно пред-
представить любое нечеткое знание в формальном виде М : Z, где М —
некоторое нечеткое выражение, отражающее понятия, утверждения,
отношения, правила и т. п., a Z — мера доверия к тому, что М истинно.
В моделях с числовым значением Z обычно представляет собой
действительное число (в большинстве случаев число из интервала
[0, 1]) и интерпретируется как степень уверенности в истинности
выражения М. Формальным аппаратом для выражения меры доверия
Z в интервально-значных моделях является интервал. В различ-
различных моделях нижняя и верхняя границы интервала объясняются по
разному. Они могут быть нижней и верхней вероятностями, как в
теории свидетельств, степенями необходимости и возможности в тео-
теории возможностей, необходимой и возможной поддержками в модели
голосования и пр.

248 Данные и знания в интеллектуальных системах [ Гл. 6
Нечетко-значные модели обычно применяются в случаях, в кото-
которых лингвистические переменные используются для описания объ-
объектов предметной области. Лингвистические переменные могут быть
языковой единицей (словом, словосочетанием и др.), отражающей
свойства объектов, лингвистическим квантором, определенным на
множестве объектов и т. п. При этом Z интерпретируется лингви-
лингвистическим значением и представляется некоторым нечетким множе-
множеством.
6.4. Зачем нужны нетрадиционные логики?
Как известно, классическая логика типа логики предикатов перво-
первого порядка есть формальная система, состоящая из множества термов
и операций, множества правил конструирования правильно постро-
построенных выражений (синтаксиса), системы аксиом и множества пра-
правил вывода. Она дает различные средства формализации и анализа
правильности дедуктивных рассуждений. Язык классической логики
является основой для выражения декларативных знаний, где рас-
рассуждение определяется как операция доказательства общезначимости
(противоречивости) логического утверждения.
Так, логика предикатов первого порядка с равенством дает воз-
возможность
• выразить, что нечто обладает определенным свойством, не ука-
указывая, что именно (роль 3-квантификации);
• выразить, что каждый элемент некоего класса обладает опре-
определенным свойством, без указания, что представляет из себя
каждый такой элемент (роль V-квантификации);
• выразить, что хотя бы одно из двух утверждений истинно, не
говоря, какое именно (роль дизъюнкции);
• явно сказать, что нечто ложно (роль отрицания);
• утверждать или оставлять неустановленным тот факт, что два
различных выражения означают один и тот же объект (роль
равенства).
Эти парадигмы полезны и подчас необходимы при решении многих
проблем искусственного интеллекта.
Велика роль формальной логики также в семантическом анализе
знаний и обосновании выводов. Представить знание — это значит
выразить в некотором формализме имеющийся у нас образ мира.
Соответствие между миром и его представлением устанавливается
семантическим анализом. Такой анализ имеет целью определить объ-
объекты представления и уточнить образ мира, определяемый представ-
представлением. Следовательно, оно должно позволить осуществлять анализ

6.4] Зачем нуоюны нетрадиционные логики? 249
истинности высказываний о мире. Иначе говоря, для плодотворно-
плодотворности представления нужно, чтобы оно могло быть предметом анализа,
использующего информацию из этого представления для выявления
того, что свойственно миру, а что нет. С этой точки зрения обоснован-
обоснованный вывод или дедукция «подтверждаются» видением мира, который
определяется семантическим анализом представления.
Семантический анализ представленного в некотором формализме
знания должен позволять определить, что в этом воображаемом мире
влечет истину, а что — ложь. Даже если анализ облечен другими ас-
аспектами, подобная операция относится по определению к компетенции
формальной логики, и делает особенно полезным обращение к теории
моделей.
Классическая логика формализует строго корректные рассужде-
рассуждения и, к сожалению, не принимает во внимание некоторые аспекты че-
человеческих рассуждений (здравый смысл, неопределенность, противо-
противоречивость, нечеткость информации). Имея дело с неполной, неточной,
противоречивой или нечеткой информацией, человеческие рассужде-
рассуждения всего лишь правдоподобны и должны подвергаться пересмотру
(ревизии). Для представления такой информации, ее семантическо-
семантического анализа и обоснования выводов и разработаны нетрадиционные,
«нестандартные» логики, являющиеся расширением классических ло-
логик. Эти расширения касаются языка логики и понятия вывода.
Вернемся к примеру о том, что большинство студентов юны.
Мы видели, что связывание этого утверждения квантором общности
приводило к его состоятельности, если не было исключений. Любое
исключение типа «Петров — студент, но он не юн» приводило к проти-
противоречию БЗ. Перечисление всех исключений становится нереальным
при работе с прикладными системами. Таким образом, роль квантора
общности при анализе рассуждений здравого смысла может быть
подвергнута сомнению.
Однако не перечисляя все исключения, мы можем выразить ис-
исключение неявным образом, например, Зх Студент (х) & пЮн(х) —
существуют неюные студенты без указания их имен. Такого типа
формулы сложны при обработке вследствие нечеткости термина «су-
«существуют». Можно ли ограничиться одним неюным студентом или
их большинство? Отсюда и роль квантора существования также ста-
становится недостаточной при анализе и выводе рассуждений здравого
смысла.
Далее, если в БЗ имеется факт «Иванов — студент», то вывод
«Иванов юн» может быть осуществлен только введением предполо-
предположения об уникальности имен, т.е. ^(Иванов = Петров). Тогда для
вывода желаемых заключений в логике предикатов с равенством
необходимо сначала доказать, что эти заключения не попадают под
случай исключений.

250 Данные и знания в интеллектуальных системах [ Гл. 6
Если закон исключенного третьего (terbium поп datur) выпол-
выполняется в классической формальной логике, то он может не вы-
выполняться в нетрадиционных логиках. Действительно, почему Сту-
дент(Петров) \/^Студент(Петров) = И, когда мы можем считать, что
статус Петрова не известен.
Роль отрицания также может быть неоднозначной в подобных
логиках. Будем называть факты, принимающие значение «ложь»,
негативными фактами. Они явно присутствуют в БЗ. Кроме явного
отрицания в БЗ могут находиться факты, которые не доказуемы
в данной системе, как их отрицания (negation as failure), если мы
придерживаемся предположения (гипотезы) о замкнутом мире. Со-
Соде ржательно это значит, что факт —\q считается доказуемым, если
любое доказательство q терпит неудачу. Придерживаясь этого пред-
предположения, считаем, что в знании предметной области нет «брешей»
и это знание полно.
К сожалению, при анализе случаев пересматриваемых рас-
рассуждений предположение о замкнутом мире не всегда бы-
бывает продуктивным. Пусть Т — множество формул, и име-
имеет место предположение о замкнутом мире, т.е. ASS(T) =
— {"¦(/ I Q ~ атомарная формула и notT Ь q}. Тогда для случая
Т = {а V Ь} в ASS(T) находятся как ^а, так и -ib, которые вместе с
{а V Ь} дают противоречие.
Что касается вывода и его свойств, прежде всего, остановимся
на правилах вывода Modus Ponens и Modus Tollens. Как мы уже
видели на примере о том, что большинство студентов юны и Петров —
студент, вывод о юности Петрова получается применением правила
Modus Ponens. Считая эти утверждения выполнимыми, мы оставляем
возможность для пересмотра (ревизии) заключения при поступлении
новой информации. Сложнее обстоит дело с правилом Modus Tollens,
которое получается применением теоремы дедукции и аксиомы кон-
трапозиции к утверждению р —> q, т. е. если р —> q Ь -iq —> ~^р и
выводимо -|#, то будет выводимо ^р или h p ^ g и h ^, тоЬ^р.
Возвращаясь к нашему примеру, имеем
1) большинство студентов юны;
2) Петров не юн.
Следовательно, применяя правило Modus Tollens, получим: «Пет-
«Петров не является студентом». Интуитивно чувствуется, что для таких
выполнимых утверждений, если двигаться от следствия к причине,
степень уверенности конкретного факта, связанного с причиной, ста-
становится недостаточной для подобного вывода.
Из всех свойств вывода остановимся на свойстве немонотонности.
Как мы уже видели, свойство монотонности препятствует прямой
формализации пересматриваемых рассуждений. Следовательно, с чи-
чисто синтаксической точки зрения построение немонотонной системы
вывода делает необходимым ослабление свойств дедуктивных систем

6.4] Зачем нуоюны нетрадиционные логики? 251
классической логики. Логика умолчаний Рейтера является одной из
версий немонотонных рассуждений. В ней немонотонность обуслов-
обусловлена необщезначимостью правил вывода, присущих той или иной
прикладной области.
Тесно связан с рассуждениями по умолчанию абдуктивный вы-
вывод, теория которого была заложена Пирсом. Формально абдукция
устанавливает, что из Р —> Q и Q возможно вывести Р. Однако
абдукция является несостоятельным правилом вывода, означающим,
что заключение необязательно истинно для каждой интерпретации, в
которой истинны посылки.
Пусть Т/г, / и /г — три множества замкнутых формул языка логики
предикатов первого порядка, представляющие знание о рассматри-
рассматриваемой предметной области, наблюдаемое событие этой области и
объяснение этого события соответственно. Предположим, что / сов-
совместимо с Т/г (т.е. Т/г & / выполнимо), но / не является логическим
следствием Т/г, т. е. Т/г не объясняет /. Следовательно, необходимо
вывести дополнительные факты /г, объясняющие / в предполагаемой
интерпретации, описанной Т/г.
С формальной точки зрения экзистенционально квантифициро-
ванная конъюнкция /г литер есть абдуктивное объяснение наблюда-
наблюдаемого события относительно знания Т/г, если Т/г, /г N /, где, как и
раньше, N — знак логического следования.
Пример 6.1.
Т/г: Ух (Студент)» -> Юн(ж))
/: Юн(Петров)
/г: Студент (Петров), Студент (Иванов) & ^Юн(Иванов), Сту-
Студент (Петров) & Смертен (Петров) — три абдуктивных
объяснения наблюдаемого события / относительно Т/г.
Заметим, что представление абдуктивного объяснения в виде
конъюнкции фактов является синтаксическим ограничением, отлича-
отличающим абдукцию от других моделей объяснений, например, от индук-
индуктивного обобщения.
Ключевой вопрос в абдуктивных рассуждениях заключается в на-
нахождении так называемых «интересных» объяснений. Эти объясне-
объяснения могут быть формально охарактеризованы двумя семантическими
свойствами: непротиворечивостью и минимальностью. Интуитивно
минимальные и непротиворечивые абдуктивные объяснения интерес-
интересны в том смысле, что они являются довольно общими фактами от-
относительно Т/г и не вступают в противоречие со знанием предметной
области.
Считаем, что абдуктивное объяснение /г для наблюдаемого
события / относительно Т/г непротиворечиво (с Т/г), если Т/г & /г —

252 Данные и знания в интеллектуальных системах [ Гл. 6
выполнимая формула. Продолжая пример 6.1, видим, что Сту-
Студент (Петров) — непротиворечивое абдуктивное объяснение события
Юн(Петров) относительно Ух (Студент(ж) —> Юн(х)). Однако,
другое объяснение Студент (Иванов) & ^Юн(Иванов) является
противоречивым абдуктивным объяснением наблюдаемого события
Юн(Петров) относительно Ух (Студент(ж) —> Юн(х)), так как
одновременно были бы выводимы Юн(Иванов) и ^Юн(Иванов).
Аналогичным образом абдуктивное объяснение h для события /
относительно Т/г минимально, если каждое абдуктивное объяснение
для наблюдаемого события / относительно Т/г, являющееся логиче-
логическим следствием /г, эквивалентно /г.
Из примера 6.1 видно, что Студент (Петров) — минимальное аб-
абдуктивное объяснение события Юн (Петров) относительно Ух (Сту-
(Студентах) —> Юн(х)), а Студент(Петров) & Смертен(Петров) тако-
таковым не является. Очевидно, что свойство минимальности устраняет
объяснения, которые не являются общими. Так, из двух объяснений
Студент(Петров) и Студент (Петров) & Смертен(Петров) общим объ-
объяснением является Студент (Петров).
Подробнее проблему абдукции и процедуры абдуктивного вывода
мы рассмотрим ниже. Здесь же отметим, что процесс абдукции может
быть выполнен с помощью процедуры дедуктивного вывода следую-
следующим образом: Т/г, /г N / тогда и только тогда, когда Т/г, -i/ N -п/г.
Этот результат получается благодаря применению теоремы дедукции
и аксиомы контрапозиции.
В другой немонотонной логике, предложенной Мак-Дермоттом и
Дойлом, вводится оператор М, интерпретируемый в качестве «непро-
«непротиворечивого» (как, впрочем, и в логике умолчания). Тогда утвержде-
утверждение типа «Как правило (обычно, в большинстве случаев), студенты
юны» будет записано в следующем виде: \/ж(Студент(ж) & МЮн(х) —>
—> Юн(х)), т. е. если кто-то является студентом и это не противоречит
тому, что он юн, то этот кто-то действительно юн. Если в БЗ вво-
вводится информация типа «Петров — студент» и невозможно вывести
^Юн(Петров), т.е. М Юн(Петров) истинно, то можно сделать вывод
о том, что Петров юн.
Однако система вывода здесь немонотонна, поскольку введение
добавочной информации может блокировать предыдущий вывод. На-
Например, после добавления нового факта, что Петров не юн, перво-
первоначальное заключение будет отвергнуто, так как в данном случае
М Юн (Петров) не будет истинным.
Трудность вывода в немонотонной системе Мак-Дермотта заклю-
заключается в том, что понятие «непротиворечивости» здесь довольно «сла-
«слабое» в том смысле, что истинностные значения утверждений Р и М Р
не связаны между собой никаким отношением, т. е. пара {М Р, ^Р}
необязательно может быть противоречивой.

6.4] Зачем нуоюны нетрадиционные логики? 253
Мур развивает идею немонотонного вывода дальше, вводя два
типа рассуждений по умолчанию. Первый тип рассуждений характе-
характеризуется тем, что имеет дело с фактами, касающимися внешнего мира:
вообще объекты типа X имеют свойство Р. Если А — объект типа X,
то можно сделать вывод, что А (по-видимому) обладает свойством Р.
Например, если Петров — студент, то можно сделать вывод, что (по-
видимому) Петров юн.
Второй тип рассуждений, названный автоэпистемическим, каса-
касается рассуждений, связанных с чьими-то убеждениями (верами). Этот
тип пересматривается, исходя из текущего состояния знаний агента,
из его интроспективной природы. Например, если мне ничего не из-
известно о том, что Петров не юн, то я делаю вывод, что Петров, будучи
студентом, юн. Механизм рассуждений интроспективен и основан на
предположении, что все знания, касающиеся этого вопроса, таковы:
«Если бы Петров был не юн, то я бы об этом знал». Иначе говоря,
можно потребовать от рассуждений «общезначимости» относительно
этого состояния знаний. Пересматриваемый характер рассуждений
проистекает из зависимости от состояния знаний. Оно присуще рас-
рассуждающему агенту и может изменяться.
Появление нетрадиционных логик связано также с прикладны-
прикладными аспектами создания различного рада интеллектуальных систем,
в частности, экспертных систем. Эти системы служат для решения
диагностических и классификационных проблем, проблем управле-
управления и принятия решений. Знания в таких системах представляются
продукциями, имеющими вид: «Если А\ и А2 и ...и Ап, то Б»,
где Ai (г = 1,п) — условия, а В — выполняемое действие. Чтобы
подчеркнуть «экспертный» характер таких продукций, в них добавлен
так называемый «фактор определенности», подчеркивающий степень
неопределенности данного условия и заключения. Неопределенность
знания, таким образом, обрабатывается с помощью распространения
факторов определенности от условий продукций к их заключениям.
Хотя здесь в явной форме исключения не обрабатываются, неопре-
неопределенность в продукциях предполагает существование исключений.
Факторы определенности выражаются численно с привлечением тео-
теории вероятностей или аппарата нечеткой логики. Однако такой подход
сталкивается с большими трудностями в силу отсутствия строгой
семантики при взвешивании продукций факторами определенности.
Здесь проявляется проблема обоснования (подтверждения) числен-
численного значения фактора определенности, которая усугубляется кон-
конфликтными ситуациями в продукциях, приводящих к конфликтным
заключениям. Наглядным примером является хорошо известная си-
система MYCIN, в которой факторы определенности, распространяемые
дедуктивно по цепочке вывода, определяются в терминах относитель-
относительной разницы между апостериорной и априорной вероятностями.

254 Данные и знания в интеллектуальных системах [ Гл. 6
Хотя экспертные системы с факторами определенности продолжа-
продолжают развиваться и проявляют завидное упорство к дальнейшему рас-
распространению, нетрадиционные логики для обработки неопределен-
неопределенной, противоречивой, неточной и нечеткой информации продолжают
вносить свой вклад в модели и методы представления и обработки
знаний.
Резюмируя сказанное, отметим, что при представлении и обработ-
обработке неполных, противоречивых и немонотонных знаний в интеллекту-
интеллектуальных системах необходим аппарат таких нетрадиционных логик,
как логика умолчания, немонотонная модальная логика, автоэпи-
стемическая логика и ряд других. Для представления и обработки
нечетких знаний, отражающих неточность, неопределенность, неод-
неоднозначность знаний, используются такие нестандартные логики, как
вероятностная логика, логика возможности, нечеткая логика и дру-
другие.
Естественно, охватить спектр всех нетрадиционных логик в одной
книге невозможно. Поэтому мы остановимся лишь на немонотонных
нетрадиционных логиках, да и то в неполном объеме, как будет пока-
показано ниже.

Следи за тем, как здесь мой шаг ведет
К Познанью истин, для тебя бесценных,
Чтоб знать потом, где пролегает брод.
Данте Алигьери
Глава 7
МОНОТОННЫЕ КЛАССИЧЕСКИЕ
МОДАЛЬНЫЕ ЛОГИКИ
Идея применения аппарата модальных логик в задачах представ-
представления знаний для интеллектуальных систем различного назначения
начинает завоевывать все более прочные позиции наряду с такими
общепризнанными моделями, как семантические сети и их разно-
разновидности — фреймы. Для инженерии знаний важны не только фор-
формальные системы модальной логики (так называемые синтаксические
системы), но и возможные интерпретации или модели таких систем,
т. е. семантика. Мы остановимся как на синтаксической, так и на
семантической стороне этой проблемы. Для лучшего понимания немо-
немонотонных рассуждений сначала изложим основные понятия классиче-
классических модальных логик, которые положены в основу построения логик
немонотонного типа. Изложение начнем с исчисления предикатов пер-
первого порядка, являющегося базой для построения модальных логик.
7.1. Исчисление предикатов первого порядка как
основа построения модальной логики
1. Аксиомы классического исчисления высказываний (Рас-
(Рассела — Бернайса).
1.1. Ь (рУр) ->р,
1.2. hp^(pV^),
1.3. h(pVq)^(qVp),
1.4. b(p->g)->((rVp)->(rVg)),
где р, q, r — пропозициональные переменные.
Понятие правильно построенной формулы (в дальнейшем прос-
просто формулы) определяется обычно и здесь не приводится.
2. Аксиомы исчисления предикатов, выраженные в виде
схем.
2.1. Ь Ух(Р -> Q) -> (УхР -> VxQ).
2.2. Пусть у/х есть результат подстановки у вместо каждого
свободного вхождения переменной х в Р. Тогда, если у не
окажется связанной в Р на тех местах, где переменная х
была свободной, то Ь УхР —> (у/х)Р.

256 Монотонные классические модальные логики [ Гл. 7
2.3.
Здесь Р и Q — предикаты исчисления предикатов, а х и у —
предметные переменные.
3. Правила вывода. Правило подстановки в нашей системе со
схемами аксиом не требуется.
3.1. Modus ponens (правило отделения): если h P и h P ^ Q, то
I-Q.
3.2. Правило обобщения: если Ь Р, то Ь УхР при условии, что
х не свободна в Р.
4. Определения.
4.1. ЗжР означает -Ых^Р.
4.2. Р ^Q означает \/ж(Р -> Q).
4.3. Р <^—> Q означает Ух(Р <-> Q).
X
Приведем (без вывода) основные теоремы (написанные в виде
схем) и правила предложенного исчисления.
5. Отрицание.
5.1. h^\/xP^3x^P.
5.2. h\/xP^^3x^P.
5.3. Ь ^ЗхР <г+ Ух^Р.
5.4. Ь ЗжР ^ -Nx^P.
6. Подчинение (переменная г/ не связана в Р на тех местах,
где х свободна).
6.1. ЬУжР^ (у/х)Р(= 2.2).
6.2. Ь (г//ж)Р -> ЗжР.
6.3. h VxP -^ ЗжР.
7. Дистрибутивность кванторов по отношению к & и V.
7.1. Ь \/х(Р & Q) ^ (VxP & VxQ).
7.2. h (VxP V VxQ) -> Vx(P V Q).
7.3. h Зж(Р V Q) ^ (ЗжР V 3xQ).
7.4. h Зж(Р & Q) -+ CxP & 3xQ).
7.5. h Зж(Р & Q) -> ЗжР.
8. Дистрибутивность кванторов по отношению к -^ и <-».
8.1. h Vx(P -^ Q) -^ (VxP -^ VxQ)(= 2.1).
8.2. Ь (Vx(P -^ Q) & VxP)
8.3. Ь Vx(P -^ Q) -^ (ЗжР
8.4. Ь (Vx(P -^ Q) & ЗжР)
8.5. h \/x(P <r+ Q) -^ (\/xP <r+ \JxQ).
8.6. h Vx(P ^ Q) -^ (ЗжР ^ 3xQ).
9. Правила дедукции.
9.1. Если h Vx(P -^ Q), то Ь VxP -
9.2. Если h Vx(P -^ Q), то h ЗжР -^ 3xQ.

7.2 ] Вспомогательная логика как основа перехода 257
9.3. Если Ь Ух(Р ^ Q), то Ь МхР <-> MxQ.
9.4. Если Ь Vx(P <-> Q), то h ЗжР <-> 3xQ.
Здесь логические связки —> и <-> представляют собой обыч-
обычные импликацию и эквивалентность соответственно (иногда их
называют материальными связками), а —> и <—> называются
X X
формальными связками.
7.2. Вспомогательная логика как основа перехода к
модальному исчислению высказываний
В логике предикатов первого порядка всякое предложение (фор-
(формула свободных переменных) — это утверждение о некотором опреде-
определенном факте. Но в естественном языке часто говорят о допустимости
чего-либо, о гипотетических событиях, целях, которые можно пытать-
пытаться достигнуть. Большая часть фраз языка может быть то истинной,
то ложной в зависимости от обстоятельств, текущего момента, точки
зрения каждого из нас. В естественных языках модальности «воз-
«возможный», «необходимый» выражаются вспомогательными глаголами,
такими как «могу» и «должен».
Модальные характеристики высказываний изучались на всем про-
протяжении развития логики. Еще Аристотель наряду с ассерторической
силлогистикой, т.е. теорией умозаключений из утверждений вида «Р
присуще всякому SV, «Р не присуще ни одному 5», «Р присуще неко-
некоторому /S» и «Р не присуще некоторому SV, рассматривал и модаль-
модальную силлогистику. В посылки и заключение модального силлогизма
могут входить утверждения вида «Р необходимо присуще всем $», «Р
возможно присуще всем S» и т. д. (такое использование модальных
выражений получило впоследствии название модальностей de re). Хо-
Хотя общепринятого построения модальной силлогистики Аристотеля
мы не имеем, своеобразие его силлогистики состоит в том, что он
допускал переход от необходимой большей посылки и ассерторической
меньшей к необходимому заключению: от «Р необходимо присуще М»
и «М присуще S» к «Р необходимо присуще S».
Возможность и необходимость называются алетическими модаль-
модальностями или модальностями возможности. Так же, как кванторы V
и 3 вводились в синтаксисе логики первого порядка, можно построить
формальный язык, используя пару понятий возможно/необходимо
как кванторы, действующие на формулы. Логическая система, ба-
базирующаяся на операторах «возможно, что» и «необходимо, чтобы»,
называется логикой возможного или алетической логикой.
Для обозначения модальности «необходимо» используется символ
П. Формула DF читается «необходимо, чтобы F» или «F необходимо».
Формула DF истинна тогда и только тогда, когда F необходимо истин-
истинна. Двойственный ? оператор обозначается (}. Формула (}F читается
9 В.Н. Вагин и др.

258 Монотонные классические модальные логики [ Гл. 7
«возможно, что F» или «F возможно». (}F истинна, если F может ока-
оказаться истинной. Один из этих операторов принимается за основной, а
другой определяется через него и отрицание (эквивалентность DF =
= ^(}^F можно установить, применяя доводы, подобные тем, которые
используются при доказательстве соотношения \/xF = -*3x^F).
В естественном языке употребляются и другие модальные формы,
которые можно перенести в логику. Деонтическая логика вводит
модальности «разрешено» и «обязательно», реализующие модальные
языковые конструкции «разрешается» и «надо, чтобы». Эпистеми-
ческая логика или логика знания исследует модальности «знания»
и «веры», тогда как временная логика вводит модальности «иногда»
и «всегда» («в будущем» и «в прошлом») вместе с их отрицаниями
«часто» и «никогда». Иногда для обозначения совокупности всех этих
логик используют термин модальная логика. Но старейшая среди
них — алетическая логика. Поэтому чаще всего именно ее называют
модальной.
Модальная логика в отличие от логики предикатов первого по-
порядка рассматривает утверждения при некоторых обстоятельствах,
случаях. Мы не придаем термину «случай» точного значения, напри-
например, не отождествляем случай с моментом времени или с возможными
мирами, по крайней мере, в принципе. Точные значения этого термина
могут быть введены в приложениях модальной логики. Заметим толь-
только, что различие случаев не должно отождествляться с различием
индивидов или предикатов. Для обозначения «случая» или «обсто-
«обстоятельства» введем соответствующую переменную t. Это переменная
особого рода, отличная от предметных переменных. Фразу «событие
р происходит в случае t» запишем как pt. Утверждение «событие р
происходит с необходимостью» выразимо на нашем вспомогательном
языке с помощью \ftpt (для любого t событие р происходит в случае
?), а «событие р возможно» — через 3tpt (для некоторого t событие р
произойдет в случае t).
В логике высказываний р является произвольным предложением
в том смысле, что оно обозначает утверждение о произвольных мыс-
мыслимых фактах. В модальной логике в разных случаях факты могут
иметь различное содержание. Поэтому символ р в излагаемой ниже
модальной логике будет обозначать утверждение о произвольном со-
содержании факта в любом из случаев.
Перед тем, как перейти собственно к модальному исчислению вы-
высказываний, рассмотрим некоторое промежуточное (вспомогательное)
исчисление, в котором в каждый предикат введена дополнительная
переменная ?, а модальности выражены посредством кванторов.
Задан бесконечный список переменных р, q, г, s,..., которые в на-
нашем вспомогательном исчислении будем обозначать Р, Q, i?, S,..., а
переменную t — через Т. Предложения этого исчисления определя-
определяются рекурсивно следующим образом:

7.3 ] Постулаты, основные теоремы и правила 259
1) выражения вида РТ — предложения. Однако ни Р, ни Т в
отдельности предложениями не являются;
2) если М и N — предложения, то -.М, M&N,M\/N,M^N,
М ^ N — тоже предложения;
3) если М — предложение, то УТМ и ЗТМ — тоже предложения.
Постулаты вспомогательного исчисления формулируются «парал-
«параллельно» постулатам исчисления предикатов 1-го порядка. При этом
необходимо учесть следующее:
1) правило образования должно быть таким, чтобы выражение
К'ТКТРТ (где К и КУ обозначают V или 3) было правильно
построенным. В К'ТКТРТ самое правое Т связано внутренним
квантором КТ;
2) правило обобщения, параллельное правилу C.2), существенно;
3) можно доказать, что К'ТКТРТ строго эквивалентно сводится
к КТРТ;
4) не существует аналога аксиомы B.3), т.е. вспомогательное ис-
исчисление является аналогом исчисления одноместных предика-
предикатов.
Очевидно, что если некоторое выражение исчисления предикатов
1-го порядка доказуемо, то соответствующее ему выражение вспомо-
вспомогательного исчисления тоже доказуемо.
Теперь перейдем к модальному исчислению высказываний посред-
посредством следующей замены:
pt, qt, rt, ..., Vt, 3t, —», <—>
на p, q, r, ..., П, 0, =>, «=> .
Эта замена ввиду взаимно однозначного соответствия сохраняет до-
доказуемость.
7.3. Постулаты, основные теоремы и правила
модального исчисления высказываний
Постулаты
1. Все аксиомы исчисления высказываний A.1-1.4).
2. Правило подстановки: всякая доказуемая формула остается до-
доказуемой, если вместо пропозициональной переменной подста-
подставить некоторую формулу.
3. Modus ponens C.1).
4. Определения символов &, —>, <-», т.е. P&Q означает
^(^Р V -iQ), Р —> Q означает ^Р V Q, Р <-> Q означает
9*

260 Монотонные классические модальные логики [ Гл. 7
5. Правило: если Ь Р, то Ь ПР.
6. Аксиомы для модальности.
6.1. Ь П(р -> д) -> (Пр -> О?).
6.2. Если Р — собственная модальность, т.е. предложение, со-
содержащее непустой набор ? и 0> то Ь Р —> ПР.
6.3. hDp^p.
6.4. Если Р — формула исчисления предикатов 1-го порядка, то
Р — формула в модальном исчислении высказываний. Если
Р и Q — формулы, то -нР, Р V Q, ПР — тоже формулы.
7. Определения.
7.1. ОР означает ^П^Р.
7.2. Р => Q означает П(Р -> Q).
7.3. Р ^ Q означает П(Р ^ Q).
Основные теоремы и правила
Приведем выводимые формулы (теоремы) и правила, соответству-
соответствующие теоремам и правилам исчисления предикатов первого порядка.
8. Отрицание.
8.1. Ь ^Пр^ 0^
8.2. Ь Пр ^ -.<>^
8.3. Ь ^0р <г+ П^
8.4. Ь Op — —¦?—i^
9. Субординация.
9.1. Ь Пр —>¦ р.
9.2. Ьр^ Op-
9.3. h Пр ^ Op-
0. Дистрибутивность
и V.
10.1. ЬП(р&<?) ^
10.2. h (ПрУП^) ¦
ю.з. hO(pv^) ^
10.4. h 0(p & q) —
10.5. h 0(p & q) —
> (Пр<5
-^П(р
¦(Opv
» Op-
1. Дистрибутивность
условных связок.
11.1. h (p=>^) ->
11.2. h ((p=>^) &
11.3. h (p=>^) -^
11.4. h ((p=>^) &
11.5. h (p&q) -+
11.6. h Ид -^
(Пр^
Пр)^
(Op-
OpH
(Op-
(Пр^
модальностей относительно &
lUq).
У q).
г 0<?)«
модальностей относительно
Uq).
> Uq.
0<?)«
Og).
Uq).

7.4] Система SI 261
12. Правила дедукции.
12.1. Если Ь Р => Q, то Ь DP -> DQ.
12.2. Если Ь Р => Q, то Ь OP -> 0Q.
12.3. Если Ь P ^ Q, то Ь DP <-> DQ.
12.4. Если h P ^ Q, то Ь OP *¦
В дальнейшем символы =4> и -Ф=> будем называть строгими услов-
условными связками, а символы —> и <-> — по-прежнему материальными
связками.
Рассмотренное нами модальное исчисление высказываний удобно
в эвристическом смысле благодаря наличию простого соответствия
между ним и одноместным исчислением предикатов первого поряд-
порядка. Однако, «ввиду своей силы», оно является в некотором смысле
«тривиальной системой». Поэтому интересно было бы рассмотреть
более «слабые» системы, в которых модальность и строгие связки
характеризовались бы менее узкими условиями.
Очевидный путь для получения таких систем состоит в замене
некоторых аксиом на более слабые при условии (которое мы счита-
считаем здесь выполненным), что преобразуемые или опускаемые аксио-
аксиомы независимы от остальных аксиом. В результате получим такие
важные в классической модальной логике системы, как SI, S4 и S5,
которые понадобятся нам для дальнейшего, преимущественно семан-
семантического, изложения.
7.4. Система S1
Назовем системой 1 (или S1) систему со следующими постулатами.
1. Аксиомы (исходные предложения).
1.1. \- р & q => р.
1.2. bp&g=>g&p.
1.3. h((pkq)kr)^(pk(qkr)).
1.4. h p => р & р.
1.5. Ь ((р => q) & (g => г)) => (р => г).
1.6. Ьр^ Op-
Последняя аксиома A.6) независима от предыдущих пяти аксиом,
в чем можно убедиться посредством следующей матрицы (группа IV
Льюиса — Лэнгфорда). Напомним, что аксиома называется независи-
независимой от остальных аксиом, если она не выводима (не доказуема) из них.
a. Значения: 1, 2, 3, 4.
b. Выделенные значения (т. е. значения, которые должны будут
принимать истинные предложения): 1,2.

262
Монотонные классические модальные логики
[Гл.7
р
1
2
3
4
^Р
4
3
2
1
Ор
2
2
2
4
Согласно определениям имеем:
&
1
2
3
4
1
1
2
3
4
2
2
2
4
4
3
3
4
3
4
4
4
4
4
4
Р
1
2
3
4
-<>Р
3
3
3
1
?р
1
3
3
3
V
1
2
3
4
1
1
1
1
1
2
1
2
1
2
3
1
1
3
3
4
1
2
3
4
1
2
3
4
1
1
1
1
1
2
3
1
3
1
3
3
3
1
1
4
3
3
3
1
1
2
3
4
1
1
3
3
3
2
3
1
3
3
3
3
3
1
3
4
3
3
3
1
Аксиомы A.1-1.5) принимают выделенные значения 1 и 2, т.е.
будут истинными. Однако аксиома 1.6 имеет значение 3 для р = 1
или для р = 3.
2. Исходные правила.
2.1. Правила образования формул.
Пропозициональная переменная — формула. Если Р и Q —
формулы, то -нР, фР, Р & Q — тоже формулы.
2.2. Правило подстановки.
Доказуемое предложение остается доказуемым, если вмес-
вместо входящей в него пропозициональной переменной всюду
подставлена некоторая формула.
2.3. Правило соединения.
Если h P и h Q, то h P & Q.
2.4. Правило отделения (modus ponens) для =>.
Если Ь Р и Ь Р => Q, то Ь Q.
2.5. Правило замены строго эквивалентных. Если h P <^> Q,
то доказуемая формула останется доказуемой, если в ней
некоторые вхождения Q заменить на Р.
3. Определения.
& -.Q).
& -.Q).
> Q) & (Q -> Р).
& -.Q).
Q) k (Q ^ Р).
3.1. Р V Q означает ^(^Р
3.2. Р ^ Q означает -.(Р
Р <-> Q означает (Р
Р ^ Q означает
Р ^ Q означает (Р
ПР означает ^О^Р
3.3.
3.4.
3.5.
3.6.
Отметим, что в аксиому 1.5 входит & , следовательно, необходимо
иметь аксиомы, определяющие & . Отсюда правило соединения 2.3
становится необходимым.
Правило отделения 2.4 является само по себе более строгим, чем
обычное правило modus ponens. Однако его высокая степень строгости

7.4]
Система SI
263
является таковой лишь по видимости, т. к. обычный modus ponens
может быть тоже выведен в этой системе.
Покажем, что если h P ^ Q и h Р, то \- Q.
1. Ь Р —> Q гипотеза.
2. ЬР гипотеза.
3. Ь Р & (Р —> Q) по правилу соединения 2.3
4. Ь (Р & (Р —> Q)) => Q доказательство в 5.31 ниже.
5. \~ Q по правилу 2.4.
Можно показать, что система аксиом S1 непротиворечива. Для
этого достаточно построить матрицу, в которой каждое Р, доказуе-
доказуемое в системе, принимало бы только выделенные значения, а ^Р не
принимало бы выделенных значений. Это имеет место для следующей
матрицы (группа V Льюиса — Лэнгфорда).
a. Значения: 1, 2, 3, 4.
b. Выделенные значения: 1,2.
р
1
2
3
4
^Р
4
3
2
1
Р
1
2
3
4
¦р
1
2
1
3
&
1
2
3
4
1
1
2
3
4
2
2
2
4
4
3
3
4
3
4
4
4
4
4
4
Согласно определениям получим следующие матрицы:
р
1
2
3
4
-<>Р
4
3
4
2
?р
2
4
3
4
V
1
2
3
4
1
1
1
1
1
2
1
2
1
2
3
1
1
3
3
4
1
2
3
4
1
2
3
4
1
2
2
2
2
2
4
2
4
2
3
3
3
2
2
4
4
3
4
2
1
2
3
4
1
2
4
4
4
2
4
2
4
4
3
4
4
2
4
4
4
4
4
2
Любая доказуемая формула Р имеет выделенное значение, поэто-
поэтому ^Р имеет значения 4 или 3, которые не являются выделенны-
выделенными. Таким образом, система S1 непротиворечива (непротиворечивость
можно также доказать, используя обычную @, 1)-матрицу для & , -н,
дополненную соотношением (}р = р (т. е. (}0 = 0 и ^1 = 1)).
В классической модальной логике модальность — это последова-
последовательность символов -л, & и (} или любое выражение, которое может
заменять (согласно определению) такую последовательность. Сте-
Степень модальности равна числу символов (} (или ?), содержащихся в
модальности.
4. Теоремы и выводимые правила.
4.1. Если h(P&Q)^i?,hPn
1. Ь (Р & Q) => R гипотеза.
2. Ь Р гипотеза.
), то Ь Д.

264 Монотонные классические модальные логики [ Гл. 7
3. Ь Q гипотеза.
4. Ь Р & Q по правилу соединения B.3).
5. Ь i? из 1 и 4 по правилу B.4).
4.2. Принцип тождества.
4.2.1. Ьр^р.
1. \- р => р & р аксиома 1.4.
2. Ь р & р => р из аксиомы 1.1 подстановкой р вместо q.
3. Ь р => р из A) и B) по аксиоме 1.5.
4.2.2. Ь р ¦<=> р из 4.2.1 и определения 3.5.
4.2.3. Если Р означает Q, то Ь Р <Ф4> Q.
1. ЬР^ Риз 4.2.2.
2. Ь Р ¦<=> Q подстановка по определению «Р означает Q».
4.2.4. Если Ь P ^ Q, то h P =ф Q.
1. h P 44> Q гипотеза.
2. ЬР^ Риз 4.2.1.
3. h P ^> Q согласно правилу 2.5 замены строго эквива-
эквивалентных.
4.2.5. Если Ь Р ^ Q, то h Q => Р.
4.2.6. Если Ь Р ^ Q, то h Q ^ Р.
4.2.7. Если Ь Р ^ Q, то h ^P ^ -.Q.
4.2.8. Если Ь Р ^ Q, то h (Д & Р) ^ (Д & Q).
4.2.9. Если Ь Р ^ Q, то h (Д V Р) ^ (Д V Q).
4.2.10. Если Ь Р ^ Q, то h DP ^ DQ.
4.2.11. Если h Р & Q, то h OP & OQ.
4.2.12. Если h Р ^ Q, то h ^<>Р ^ ^OQ.
4.3. Конъюнкция.
4.3.1. ^pkq^qkp.
1. bp&g=>g&p аксиома 1.2.
2. \-q&zp^p&zq подстановка.
3. Ь р & g' 44> q & р из A) и B) по определению 3.5.
4.3.2. Ьр^р&р.
1. \- р ^> р & р аксиома 1.4.
2. Ь р & р => р подстановка в аксиому 1.1.
3. Ь р 4=> р & р из A) и B) по определению 3.5.
4.3.3. Ь р & (<? & г) ^ (р & q) & г.
1. Ь (р & ^) & г => р & (^ & г) аксиома 1.3.
2. Ь р & (</ & г) 44> р & (г & q) из 4.2.2 замена по 4.3.1.
3. Ь р & (^ & г) 44> (г & q) & р замена по 4.3.1.
4. Ь (г & q) & р => г & (^ & р) подстановка из аксиомы 1.3.

7.4] Система SI 265
5. h (г & q) & p => r & (p & g) замена по 4.3.1.
6. h (r & g) & p =4> (p & g) & г замена по 4.3.1.
7. h p & (g & r) => (p & g) & г замена по C).
8. h p & (g & r) <Ф4> (p & g) & г из A) и G) по определению
3.5.
4.4. Отрицание.
4.4.1. Ь (-ip => q) <Ф4> (-i^ => р).
1. \~ (->р & -i^) -Ф=> (-i^ & -ip) подстановка в 4.3.1.
2. Ь -0(-р & ^q) & "-<>(-¦« & -Р) из 4.2.12.
3. h (-ip =4> ^) 44> (-i^ ^> р) по определению 3.4.
4.4.2. Ь ^^р <^р.
1. |—ip ^> ^р подстановка в 4.2.1.
2. I—i^p => р замена по 4.4.1.
3. I—i^^^p => ^^p подстановка в B).
4. I—i^^^p =4> р из C) и B) по аксиоме 1.5.
5. I—ip => ^^^p замена по АЛЛ.
6. I—i^^p => ^p подстановка в B).
7. I—i^^p 4=> ^р из E) и F) по определению 3.5.
8. I—i^(p <^ ~^р) из 4.2.1 по определению 3.4.
9. I—>()(р & ^^^р) замена по G).
10. Ь р ^> ^^р по определению 3.4.
11.1—'^р 44> р из B) и A0) по определению 3.5.
4.4.3. Ь (р => ^) <^ (-i^ => -пр).
1. h (^^p ^ q) ^ (~^q ^ ~>р) подстановка в 4.4.1.
2- Ь (р => q) ^ (~"^ ^ ~"р) замена по 4.4.2.
4.4.4. h (pVg') 44> ^(^р & ->q) из определения 3.1 по правилу 4.2.3.
4.4.5. I—i(p&g)<^> (—i_pV—i^) доказывается из 4.4.4 подстановкой
^р вместо р и —1(/ вместо ^, затем 4.4.2.
4.5. Дизъюнкция.
4.5.1. hp^ (p Vp).
1. Ь р ^> р & р аксиома 1.4.
2. I—ip ^> ^р & ^р подстановка.
3. h ^р =Ф ^(^р & -пр) по 4.2.7.
4. Ь р => р V р по 4.4.2 и определению 3.1.
Аналогично доказывается Ь (р\/р) =>¦ р, отсюда Ь (jpVp) -^ р.
4.5.2. hp ^ pV q.
1. h (-ip & -i^) ^> ^p подстановка в аксиому 1.1.
2. h ^^p =ф ^(^р & -.g) no 4.4.3.
3. h p ^> p V ^ по определению 3.1 и замене по 4.4.2.

266 Монотонные классические модальные логики [ Гл. 7
4.6. Материальная импликация.
4.6.1. Ь -.(р -> q) & (р & -.д).
1. Ь (р —> q) ¦<=> ->(р & ->(/) из определения 3.2 по правилу
4.2.3.
2. I—i(p —> </) ¦<=> ^^(р & ->(/) по правилу 4.2.7.
3. I—i(p —> д) -Ф=> (р & -i^) замена по 4.4.2.
4.6.2. ^ (p^q) ^ bpVq).
1. Ь (р —> (?) ¦<=> ->(р & ->(/) из определения 3.2. по правилу
4.2.3.
2- Ь (р —> О) О (^Р V ^q) по 4.4.5.
3. Ь (р -^ ^f) ^ (^p V gf) по 4.4.2.
4.6.3. Ьр^ (^р^р).
1. hp^ (pVр) по 4.5.1.
2. h р & (^р V р) по 4.4.2.
3. Ьр^ (^р^р). по 4.6.2.
5. Выводы в системе S1.
5.1. Строгая импликация.
5.1.1. Ь (р =ф ^) ^ П^(р & ^).
1. \~ (р => q) ^ ^()(р & ~"^) из определения 3.4 по правилу
4.2.3.
2- Ь (р ^ q) <=> ^()^^(р & ~1^) замена по 4.4.2.
3. \~ (р ^ q) <^ П~>(р & ~>^) по определению 3.6.
5.1.2. \- (р ^ q) <^ П(р -^ ^) из 5.1.1 по определению 3.2.
5.1.3. \~ (р ^ q) <^ П(^р V ^) доказывается из 5.1.2 и 4.6.2 с
применением правила 4.2.10.
5.2. Антилогизм. Импортация-экспортация.
5.2.1. Ь ((р & q) =Ф г) ^ ((р & -.г) =Ф -.^).
1. Ь (</ & -пг) 44> (->г & q) подстановка в 4.3.1.
2. Ь (р & (^ & -.г)) ^ (р & (-.г & ^)) по правилу 4.2.8.
3. Ь ((р & ^) & -.г) ^ ((р & -г) & q) no 4.3.3.
4. Ь ((р & q) & -.г) ^ ((р & -.г) & -.-.^) по 4.4.2.
5. h -0((р & <?) & -г) ^ --0((р & --г) & -.-.^) по 4.2.12.
6. Ь ((р & ^) ^> г) 44> ((р & -ir) ^> -п^) по определению 3.4.
5.2.2. h ((р & q) => г) ^ ((q & -.г) => -р).
1. \- ((р & ^) & -пг) -Ф4> (р & (q & -ir)) подстановка из 4.3.3.
2. Ь ((р & q) & -.г) ^ ((^ & -т) & р) по 4.3.1.
3. h ((р & <?) & -г) ^ ((^ & -.г) & -.-.р) по 4.4.2.
4. Ь -0((р & q) & -г) ^ -.<>((? & -г) & ^^р) по 4.2.12.
5. \- ((р & q) => г) 44> ((# & -ir) ^> -пр) по определению 3.4.

7.4] Система SI 267
5.2.3. Ь ((р & q) => r) <& (р => (q -> г)).
1. \- ((р & q) & -ir) -Ф=> (р & (д & -ir)) подстановка в 4.3.3.
2. Ь ((р & д) & -.г) ^ (р & -.(gf -> г)) замена по 4.6.1.
3. Ь ->ф((р & <?) & ~>г) -Ф=> ^О(р & ^(<2 —> О) по правилу
4.2.12.
4. Ь ((р & </) =4> г) -Ф=> (р =4> (д —> г)) по определению 3.4.
5.2.4. Ь ((р & -<г) => -tq) <^ (р => (^ -^ г)) из 5.2.3 замена по
5.2.1.
5.3. Modus ponens с материальной импликацией.
5.3.1. ^(pk{p^q))^q.
1. \- (р & -п^) =4> (р & -i^) подстановка в 4.2.1.
2. Ь (р & -.(р & -.^)) =Ф ^g no 5.2.I.
3. h (р & (р —> #)) ^ ^^^ по определению 3.2.
4. Ь (р & (р -^ ^)) =ф q по 4.4.2.
5.3.2. Если h P ^ Q и h P, TohQ Доказано раньше.
5.4. Сложные силлогистические выводы.
5.4.1. Ь ((р =Ф ^) & ((^ & 5) => г)) =ф ((р & 5) =ф г).
1. Ь (((* & -г) => ^) & (^ => -пр)) => ((s & -г) => -пр)
подстановка в аксиому 1.5.
2. Ь (((^ & 5) => г) & (-.^ => -пр)) =ф ((р & 5) =ф г) по 5.2.2,
используемому дважды, и правилу 4.2.6.
3. Ь ((^ & 5 ^> г) & (р ^> </)) ^> ((р & s) => г) по контрапози-
ции 4.4.3.
4. Ь ((р =Ф q) & ((^ & 5) => г)) =Ф ((р & 5) => г) по 4.3.1.
5.4.2. Если Ь Р =Ф Q и h (Q & 5) => R, то h (P & 5) => Д из
5.4.1 по правилу 4.1.
5.4.3. Ь ((р =Ф ^) & (^ =Ф г) & (г => s)) => (р => s).
1. h ((^ => г) & (г ^> s)) => (q => s) подстановка в аксиому
1.5.
2. Ь ((^ =4> s) & (р ^> #)) =4> (р ^> s) из аксиомы 1.5 по 4.3.1.
3. Ь ((^ =Ф г) & (г => s) & (р ^> ^)) =Ф (р => s) по правилу
5.4.2, принимая A) за Р =Ф Q, а B) — за (Q & 5) =Ф Д.
4. h ((р =Ф ^) & (q => г) & (г => s)) => (р => 5) по 4.3.1.
6. Явные модальности в S1.
6.1. Строгие импликации, эквивалентные модальностям.
6.1.1. Ь Пр^ (-^р^>р).
1. Ьр^ (pVp) no 4.5.I.
2. Ь р ^ (^^р V р) по 4.4.2.
3. Ь Dp ^ П(^^р V р) по 4.2.10.
4. Ь Пр 44> (-<р => р) замена по 5.1.3.

268 Монотонные классические модальные логики [ Гл. 7
6.1.2. Ь П^р ¦<=> (р =4> -ip) доказывается из 4.5.1, 4.2.10 и 5.1.3.
6.2. Отрицания модальностей.
6.2.1. I—'О^Р ^ Пр из определения 3.6 по 4.2.3.
6.2.2. Ь <Ьр ^ ^Пр.
1. Ь -.-.<Ьр ^ ^Пр из 6.2.1 по 4.2.7.
2. Ь 0^.Р ^ ~>Пр замена по 4.4.2.
6.2.3. Ь ^П^р ^ Ор.
1. I—O-ip -Ф=> 0^^.Р подстановка в 6.2.2.
2. I—О^р <Ф4> Ор замена по 4.4.2.
6.3. Modus ponens с модальными утверждениями.
6.3.1. Ь ((р=>д)&Пр) =фП^.
1. h ((^ => -пр) & (-р => р) & (р => д)) => (^ => q)
подстановка в 5.4.3.
2. Ь ((р =Ф ^) & (-.^ =Ф -пр) & (^р =Ф р)) =Ф (-.^ => q) no 4.3.I.
3. Ь ((р =4> ^) & (-<р ^> р)) ^> (-i^ => q) замена по 4.4.3 и
4.3.2.
4. Ь ((р => ^) & Пр) => ?# замена по 6.1.1.
6.3.2. h (р =ф ^) =ф (Пр -> П^) из 6.3.1 по 5.2.3.
6.3.3. h ((р => q) & Op) => Og.
1. h ((-i^ ^> -ip) & П~>^) ^ ?-'Р подстановка в 6.3.1.
6.3.4
6.3.5
2
3
4
1
2
3
•М(р
•М(р
.h((p
.h((p
• l-((p
.h((p
=>¦ (/)
=>¦ ^)
> q) —,
z г) =
=>(r
& г =
&r)
&
&
&
п^^
^п-
Op)
>@р-
)&[
g') &
') ^П
пр) =Ф"
^0^
¦^ 0<?)]
Dp) =
-^p замена по 4.4.3.
nD^g no
замена i
зз 6.3.3 i
(r => q).
^П(г-
П(г^(
> (r => q]
5.2.1.
io 6.2.3.
io 5.2.3.
¦* q) подстановка в 6.3.1.
\) замена по 5.2.3.
) замена по 5.1.2.
7. Общие метатеоремы для S1.
7.1. Если Р доказуема в немодальном исчислении высказываний
(Ь Р), то Ь ПР (т.е. ПР доказуема в S1). Доказательство
проводится следующим образом.
7.1.1. Если Р — одна из четырех аксиом Рассела —Бернайса
A.1-1.4), то Ь ПР (см. эти аксиомы в разд. 7.1).
7.1.1.1. Ь n((pVp) ->p).
1. hp^ (pVp) no 4.5.1.
2. h (p Vp) ^> p по правилу 4.2.5.
3. Ь П((р V р) -^ р) замена по 5.1.2.

7.4] Система SI 269
7.1.1.2. h П(р^ (pVq)).
1. Ьр=> (pVg) по 4.5.2.
2. h D(p -^(pV q)) замена по 5.1.2.
7.1.1.3. hQ((PV^(gVp)).
1. \~ (pVq) ¦<=> (qVp) из 4.3.1, правила 4.2.7 и определения
3.1.
2. h (р V g) =4> (q Vp) по правилу 4.2.4.
3. Ь n((pVg) -> (qVp)) замена по 5.1.2.
7.1.1.4. h 0((р ^q)^ ((r Vp) -+ (г V <?))).
1. Ь (р& (p->g)) =Ф<?по 5.3.1.
2. Ь ((р -> д) & -.^) => ^р по 5.2.2.
3. Ь (-.^ & (р -^ ^)) =ф ^р по 4.3.1.
4. Ь (-<р & -ir) ^> (-ir & -пр) подстановка в аксиому 1.2.
5. Ь (-i^ & (р -^ ^) & -пг) ^> (->г & ->р) по правилу 5.4.2,
принимая C) заР^> Q, а D) — за (Q & 5) ^> i?.
6. h ((p -> ^) & -г & -.gf) =Ф (-.г & -р) по 4.3.1 и 4.3.3.
7. Ь ((р -^ ^) & -i(r V ^)) ^> ^(г V р) замена по 4.4.4.
8. Ь (р -^ ^) =ф ((г V р) -^ (г V д)) по 5.2.4.
9. h П((р -^ ^) -> ((г Vp)^(rV ^))) замена по 5.1.2.
7.1.2. Если h Q выведена из h P по правилу подстановки для
немодального исчисления высказываний, то Ь \Z\Q получа-
получается из h DP по правилу подстановки 2.2 для S1.
7.1.3. Если Ь Q выведена изЬР^^иЬРпо правилу Modus
Ponens, то h \DQ доказывается из Ь П(Р -^ Q) и h DP .
1. h П(Р -^ Q) гипотеза.
2. hP^Q no 5.I.2.
3. \~ ПР гипотеза.
4. h (Р => Q) & ПР по правилу соединения 2.3.
5. Ь BQ по 6.3.1.
7.1.4. Если Ь Q выведена из h P посредством подстановки со-
согласно следующим определениям: р & g означает ^(^pV^g);
р —> ^ означает ^р\/ q и р ^ q означает (р -^ q) & (^ -^ р),
то Ь DQ выводится из \- ПР.
1. h П(р & q) гипотеза.
2. h(p&^)^-(-pV^).
3. Ь П(р & ^) ^ П(^(^р V -.^)) по 4.2.10.
4. h D(^(^pV^^)) по правилу замены строго эквивалентных
2.5.
Аналогично доказываются с помощью 4.6.2, определения
3.3 и правила 4.2.3 остальные две формулы.
Таким образом, если формула Р доказуема в немодальном ис-
исчислении высказываний, то ПР доказуема в S1.

270 Монотонные классические модальные логики [ Гл. 7
7.2. Если Ь ПР, то Ь Р (Р доказуема в S1).
1. Ь ПР гипотеза.
2. Ь ^Р => Р замена по 6.1.1.
3. Ь (q & р) =4> g подстановка в аксиому 1.1.
4. Ь (р & </) =4> q замена по 4.3.1.
5. Ь (ПР & -.Р) => ^Р подстановка в D).
6. Ь (DP k^P)^ P из E) и B) по аксиоме 1.5.
7. Ь ПР => (-.Р -> Р) по 5.2.3.
8. Ь ПР => Р замена по 4.6.3.
9. \~ Р из A) и (8) по правилу Modus Ponens 2.4.
7.3. Если Ь Р -^ Q, то Ь Р =Ф Q.
1. hn(P^Q) по 7.1.
2. hP^Q no 5.I.2.
8. Теоремы, специфические для S1.
8.1. I—'0.Р =>¦ ^Р из аксиомы 1.6. по 4.4.3.
8.2. Ь Пр^р.
1. I—^О^Р ^ ^^Р подстановка в 8.1.
2. Ь Пр => р замена по 4.4.2. и по определению 3.6.
8.3. Ь ППр =4> р из 8.2 подстановкой и 8.2 по аксиоме 1.5.
8.4. Ь Пр => (}р из 8.2 и аксиомы 1.6 по аксиоме 1.5.
8.5. Ь(р^)^(р^з).
1. \~ П(р —> q) ^> (p -^ q) подстановка в 8.2.
2. Ь (р ^> ^) ^> (р —> ^) замена по 5.1.2.
8.6. h (р & (р => д)) => д.
1. h ((р =Ф ^) & р) => ^ из 8.5 по 5.2.3.
2. h (р & (р ^> q)) => q замена по 4.3.1.
Заметим, что аксиома 1.6 может быть получена из 8.6 следую-
следующим образом.
1. \- ((р => ~>р) & р) ^ ^р подстановка в 8.6.
2. Ь (р => ^р) =4> (р —> -пр) замена по 5.2.3.
3. \- П^р ^> ^р замена по 6.1.2 и подстановка в 4.6.3.
4. Ь ^^р =Ф ^П^р по 4.4.3.
5. Ьр^ Орпо 4.4.2 и 6.2.3.
Т.к. аксиомы 1.6 и 8.6 дедуктивно эквивалентны (т.е. могут
быть выведены друг из друга), то 8.6 можно принять в качестве
аксиомы вместо 1.6.

7.5] Система S4 271
8.7. Правило 7.2 (если Ь ПР , то Ь Р) можно применить к 8.2-8.6.
Например:
а) Ь Dp —> р из 8.2 или
б) если Ь DP , то Ь ОР.
1. Ь DP гипотеза.
2. Ь DP => OP no 8.4.
3. Ь фР по правилу 2.4.
Это позволяет выводить из каждой теоремы Ь ПР теорему
До сих пор матрицы использовались для доказательства независи-
независимости аксиом. Можно ли построить характеристическую матрицу для
S1 (т. е. матрицу, на которой формула принимает выделенное значение
тогда и только тогда, когда эта формула доказуема в системе)?
Дугунджи показал A940 г.), что не существует конечной характе-
характеристической матрицы для S1. Это доказательство справедливо и для
S2, S3, S4 и S5.
7.5. Система S4
Так как системы S2 и S3 целиком находятся в S4, мы их опустим
и остановимся на весьма важной системе S4. Почти все теоремы,
доказуемые в следующей системе S5, доказуемы также и в S4. Тем
не менее, S4 не имеет тривиальной простоты системы S5, так как
сохраняет 12 различных собственных модальностей.
9. Постулаты S4.
Система S4 определяется как система, получаемая добавлением к
постулатам S1 аксиомы
9.1.
Ясно, что вместо 9.1 можно взять в качестве аксиомы двойствен-
двойственную формулу
9.2. Ь Dp => ППр.
Аксиома 9.1 ведет к строгим эквивалентностям.
9.3. ь ООр <& Ор.
1. \~ (}р => (}(}р подстановка в аксиому 1.6.
2. Ь ООр => Ор аксиома 9.1.
3. Ь ООр ^ Ор из A) и B) по определению 3.5.
9.4. Ь ППр 4=> Пр из 9.3 по двойственности.

272 Монотонные классические модальные логики [ Гл. 7
Таким образом, «возможно» в этой системе отождествляется с
«возможно, что возможно» и вообще с неограниченным повторени-
повторением символа «возможно». Аналогичное положение имеет место и для
символа необходимости.
Аксиома 9.1 независима от аксиом S1, так как на матрицах группы
V Льюиса — Лэнгфорда (см. эту группу при доказательстве непроти-
непротиворечивости S1), которым удовлетворяет S1, она принимает значение
3 при р = 4.
Постулаты S4 непротиворечивы, так как все они удовлетворяют
матрицам группы III Льюиса — Лэнгфорда, отличающейся от группы
V только одной матрицей:
V
1
2
3
4
Ор
1
1
1
4
Покажем, что S4 включает в себя системы S2 и S3. Это видно из
следующих теорем.
9.5. Ь
1. \~ ПП(р —> q) -Ф=> П(р —> q) подстановка в 9.4.
2. Ь П(р => q) <Ф4> (р => q) замена по 5.1.2.
9.6. Ь 0(р & q) => Op аксиома S2.
1. \- ((р & q) =4> р) -Ф=> П((р &z q) ^ р) подстановка в 9.5.
2. Ь ((р & q) => р) & ^)(р & </)) ^> ^)р подстановка в 6.3.3.
3. h П((р &</)=> р) из аксиомы 1.1 по A).
4. Ь 0(р & q) =Ф Ор из C) и B) по 6.3.5.
9.7. Ь (р => ^) => (Ор => 0^) аксиома S3.
1. h D(p ^ g) => П(Ор —> 0^) подстановка в 6.3.2, применением
Modus Ponens 2.4 для 6.3.2 и 6.3.4, затем по 7.1 и 5.1.2.
2. Ь (р => ^) =Ф (Op => 0q) по 9.5 и 5.1.2.
Таким образом, S2 и S3 выводимы из постулатов системы S1 при
добавлении соответственно 9.6 и 9.7 и поэтому содержатся в S4.
Показано, что в системе S3, содержащейся в S4, имеется не более
40 несводимых собственных модальностей (т. е. модальностей степени
высшей, чем нуль), а если добавить к ним две несобственные модаль-
модальности р и -нр, то будет не более 42 несводимых модальностей.

7.5] Система S4 273
В S4 имеется ровно 14 несводимых модальностей, из них 12 соб-
собственных модальностей и 2 несобственных (р и -~>р). Парри показал,
что если с помощью 9.3 свести (}(}р к фр, а с помощью 9.4 свести ППр
к Пр, то 40 собственных модальностей сведутся к 12.
10. Теоремы и правила, доказуемые в S4.
10.1. hDg^(|)^ Dq).
1. Ь (}(р & д) =4> Ор аксиома S2 9.6.
2. Ь Пр =4> П(р V q) из A) по двойственности.
3. Ь Пд => П(д V -нр) подстановка.
4. Ь \3q => П(^р V g) замена по Ь (д V -нр) <Ф4> (-<р V #).
5. Ь П<? => (р => д) по 4.6.2 и.5.1.2.
6. Ь ППд =4> (р =4> \3q) подстановка в E).
7. Ь Пд =4> (р ^> П^) замена по 9.4.
10.2. Теоремы импортации и экспортации становятся строгими экви-
валентностями.
10.2.1. Ь ((Пр & П^) =ф Пг) ^ (Пр =ф (П^ => Пг)).
1. h ((р & д') ^> г) ^> (р ^> (^ ^ г)) из 5.2.3 по правилу 4.2.4.
2. Ь (-i(/ ^> ^p) ^> ((}^q ^> О^р) подстановка в аксиому 9.7.
3. Ь (р =Ф ^) =Ф (-<>-р => --О-1^) по 4.4.3.
4. h (р ^> ^) ^> (Пр => П^) по определению 3.6.
5. Ь (р ^> (q -^ г)) ^> (Пр => (qf ^> г)) подстановка в D) и
5.1.2.
6. Ь (^ ^> г) ^> (П^ ^> Пг) подстановка в D).
7. Ь (Пр => (q => г)) => (Пр => (П^ => Пг)) по правилу S2:
если h Q => Д, то h (Р =Ф Q) =Ф (Р =Ф Д).
8. h ((р & q) => г) => (Пр => (П^ =ф Пг)) из A), E) и G) по
5.4.3.
9. Ь ((Пр & П^) =ф Пг) =Ф (ППр => (ПП^ =ф ППг)) подста-
подстановка в (8).
10. h ((Пр& П^) => Пг) =Ф (Пр => (П^ =ф Пг)) замена по
9.4.
11. h (q ^> г) ^> (^ —> г) подстановка в 8.5.
12. h (р ^> (^ => г)) =4> (р ^> (q —> г)) по правилу S2: если
h Q =ф Д, то Ь (Р =Ф Q) =Ф (Р =Ф Д).
13. Ь (р => (^ => г)) => ((р & q) => г) замена по 5.2.3.
14. h (Пр ^> (Q/ ^> Пг)) ^> ((Пр & П^) => Пг) подстановка
в A3).
15. Ь ((Пр & П^) =ф Пг) ^ (Пр => (П^ =ф Пг)) из A0) и A4)
по определению 3.5.

274 Монотонные классические модальные логики [ Гл. 7
10.2.2. Ь (Пр => (Bq => Пг)) <& (Bq => (Пр => Пг)).
1. \- (q =4> r) => (q —> г) подстановка в 8.5.
2. Ь (р => (д => г)) =^ (р => (<? ^ г)) из A) по правилу S2:
если Ь Q => R, то Ь (Р => Q) => (Р =ф Д).
3- Ь (р => (Л "^ г)) ^ ((р & ^r) =^ -¦(/) из 5.2.4 по правилу
4.2.6.
4. h (p =>
5. h (p =>
6. h (p =>
7. h (-.g =
8. h (p =>
9. h (p =>
10. ^ (q =
5.1.2.
(q -> г)) <=
(<? - О) 4
(<7 -^ г)) =
> -Р) ^ (<
«) ^ (ПР
> (р -^ г))
11. h (p => (q => r))
5.4.3.
12. h (Пр
ка в A1).
13. Ь (Пр
9.4.
14. Ь (Dg
в A1) и 9
15. Ь (Пр
^> (Bq =>
=> (Bq =4
=> (Пр^
.4.
^(?^
по определению 3.5
^ (я. =^
4> (^ =4
> (^ ^
>^ =^
=Ф Пд'^
=> (С
> -.(р & -.г)) по 4.4.3.
> (р -^ г)) по определению 3.2.
> (р -^ г)) по правилу 4.2.4.
- О^р) подстановка в 9.7.
^0^<?) по 4.4.3.
1 по определению 3.6.
~\q ^ (р => г)) подстановка в (9) и
=> (П^ =Ф (р =ф г)) из B), F) и A0) по
?г)) =
>Пг))
ПГ)) :
Пг)L
=4> (??# =Ф (Пр ^> Пг)) подстанов-
^> (П^ => (Пр ^> Пг)) замена по
=^> (Пр ^> (П^ => Пг)) подстановка
* (Bq => (Пр =Ф Пг)) из A3) и A4)
10.3. Если Ь Р, то Ь ПР . Чтобы доказать это правило, достаточно
показать, что если Р — аксиома S4, либо формула, выводимая в
ней, то \- ПР .
1. Все аксиомы S4 имеют форму Р => Q. По 9.5, если Ь Р => Q,
то h П(Р ^> Q)] таким образом, если R — аксиома системы S4,
то Ь BR.
2. Если Q выведена из Р по правилу подстановки 2.2, то очевид-
очевидно, что Ь BQ может быть выведена из Ь ПР.
3. Если Р & Q выведена из Р и Q по правилу соединения 2.3, то
согласно Ь (Пр & П^) =ф П(р & ^), h П(Р & Q) следует из h ПР
и Ь DQ. Ь (Пр & Bq) =4> П(р & q) доказывается в системе S2.
4. Если Q выведена из Р и Р => Q по правилу отделения 2.4,
то по 6.3.1 Ь DQ следует из h DP и h P ^> Q (которая строго
эквивалентна Ь П(Р ^> Q) согласно 9.5).
5. Если Q выведена из Р по правилу замены строго эквивалент-
эквивалентных 2.5 или по определениям, то очевидно, что Ь BQ следует из
ЬПР.

7.6] Система S5 275
10.4. Следствиями 10.3 являются, например, такие правила вывода:
10.4.1. Если Ь Р -> Q, то Ь DP -> UQ.
1. Ь Р —> Q гипотеза.
2. bP^Qno 10.3 и 5.1.2.
3. Ь ПР -> BQ по 6.3.2.
10.4.2. Если Ь Р <-> Q, то Ь P ^ Q по 10.3 и
h D(p f^ g) <^ (p <^ g) (доказано в S2).
10.4.3. Правило замены материально эквивалентных.
Если Ь Р <-> Q, то доказуемая формула остается доказуе-
доказуемой, если все вхождения Р заменить в ней на Q (из 2.5 по
10.4.2).
10.5. Некоторые другие теоремы.
10.5.1. Ь П(р V -пр) ^ (р V -пр).
1. \~ П(р V -ip) =4> (р V -пр) подстановка в 8.2.
2. hpV^p.
3. hD(pV^p) из B) по 7.1.
4. Ь П(р V -пр) ^> ((р V ^р) ^> П(р V ^р)) подстановка в 10.1.
5. Ь (рУ^р) => D(pV^p) из C) и D) по 2.4 (Modus Ponens).
6. h П(р V -^р) 44> (р V ^р) из A) и E) по правилу 2.3 и
определению 3.5.
10.5.2. Ь 0(р & ^р) 44> (р & -лр) из 10.5.1 по двойственности.
7.6. Система S5
11. Постулаты S5.
Постулаты S5 определяются как постулаты S1, к которым добав-
добавляется аксиома
ил. Ь0р
Эта аксиома независима от постулатов S1, так как согласно мат-
матрице группы V Льюиса — Лэнгфорда она имеет значение 4 при
р = 3. Она также не противоречит постулатам S1, ибо матрица
группы III Льюиса — Лэнгфорда удовлетворяет как самим этим
постулатам, так и 11.1.
11.2. Докажем следующие строгие эквивалентности.
11.2.1. Ь
1. \- П^)р => фр подстановка в 8.2.
2. Ь \3{)р 4=> (}р из A) и аксиомы 11.1 по определению 3.5.
11.2.2. Ь (}\3р 4=> Пр из 11.2.1 по двойственности.

276 Монотонные классические модальные логики [ Гл. 7
11.3. Можно вывести в S5 аксиому 9.1 системы S4, поэтому S5 содер-
содержит систему S4.
1. \~ П(}р =>¦ ^}р подстановка в 8.2.
2. Ь ОПОр => Ор замена по 11.2.2.
3. Ь ООр =>¦ Ор замена по 11.2.1.
Так как в S4 имеются 14 несводимых модальностей, то и в S5 они
имеют место. Однако их число можно уменьшить в S5 до 6: четыре
из них являются собственными модальностями, имеющими первую
степень, а именно: «возможно» (фр) и «невозможно» (^(}р или П^р);
«необходимо» (Пр) и «не необходимо» или «случайно» (~Ор или ф->р),
а также две несобственные модальности (р и —>р).
Таким образом, мы рассмотрели различные системы модального
исчисления высказываний, не касаясь модального исчисления преди-
предикатов первого порядка, которое может быть получено путем введения
соответствующих постулатов для формул, содержащих кванторы по
предметным переменным.
7.7. Семантика возможных миров Крипке
Рассмотрим теперь один из способов интерпретации модальных
систем при помощи структур, предложенных С. Крипке. Здесь будет
четко прослеживаться связь между синтаксисом и семантикой, т. е.
между системами аксиом и интерпретирующими отношениями.
Модальное исчисление высказываний по-прежнему задается бес-
бесконечным списком пропозициональных переменных (атомарных фор-
формул), комбинируя которые при помощи связок & , -л и П, можно полу-
получить правильно построенные формулы, обозначаемые как А, В, С ...
Модальное исчисление высказываний будет называться нормаль-
нормальным, если оно содержит следующие схемы аксиом и правила вывода:
А1. ПА^А.
A3. П(А -> В) -> (ПА -> ПБ).
R1. Если \- А и \- А ^ В, то \- В (правило Modus Ponens).
R2. Если h А, то h \DA (в ненормальных системах правило R2 не
выполняется).
Система, содержащая только вышеприведенные схемы аксиом
и правила вывода, называется системой М (системой Фейса —
фон Вригта, иногда системой Т). Система S4 получается из М
добавлением схемы аксиом А4: ПА —> ППА Брауэрова система
получается из М добавлением брауэровой схемы аксиом А —> П()А.

7.7] Семантика возможных миров Крипке 277
Наконец, система, эквивалентная S5, может быть определена как
система М с добавленной схемой аксиом А2: ^\ЗА —> П-ОА Известно
также, что S4 плюс брауэрова схема аксиом эквивалентна S5.
Нормальной модельной структурой называется упорядоченная
тройка < G, W, R >, где W — некоторое непустое множество (уни-
(универсум), элементы которого могут рассматриваться как «точки соот-
соотнесения» или «возможные миры», в которых высказывание истинно
или ложно; G Е W — некоторый выделенный элемент этого множе-
множества, иначе «действительный мир»; R — отношение доступности,
определенное на множестве W, на которое наложено единственное
требование рефлексивности.
Модальная формула будет оцениваться в лоне некоего «универсу-
«универсума» различных «возможных миров». Точнее, анализ истинности некой
модальной формулы зависит от рассматриваемого возможного мира.
Если два мира Hi и Щ принадлежат универсуму W, то доступность
мира Нъ из мира Hi обозначается как Hi R Н^- Нормальную модель-
модельную структуру будем также называть М-модельной структурой.
М- (S4-, S5-, брауэровой) моделью формулы А из М- (S4-, S5-,
брауэровой) системы называется двуместная функция Ф(Р, Я), соот-
соответствующая данной М- (S4-, S5-, брауэровой) модельной структуре
< G, W, R >. Первая переменная Р пробегает множество атомарных
подформул А, а вторая переменная Н пробегает элементы W. Эта
функция принимает значения на множестве {И, Л}.
Для данной модели Ф, соответствующей модельной структуре
< G, W, R >, определим для каждой подформулы В формулы А
и всякого Н Е W оценку — значение Ф(В, Н) (которое может быть И
или Л), т.е. определим однозначное расширение Ф, первый аргумент
которого пробегает все подформулы А, а не только атомарные под-
подформулы. Для атомарных В (т. е. для пропозициональных перемен-
переменных) соответствующие значения Ф(В,Н) уже определены выше. Для
сложных формул оценка определяется индукцией по числу связок в
формуле.
Пусть Ф{В,Н) и Ф{С,Н) уже определены для каждого Н Е W.
Если Ф(В,Н) = Ф(С,Я) = И, то Ф(Б & С, Я) = И; в противном
случае Ф(Б к С, Н) = Л. Если Ф(Б,Я) = И, то Ф(-Б, Я) = Л; в
противном случае, т. е. если Ф(?>, Я) = Л, то Ф(->В, Я) = И. Наконец,
определим Ф(ПЯ,Я): если Ф(В,Н') = И для всех Н' из W, таких
что Я R Ях, то положим Ф(ПЯ,Я) = И; в противном случае, т.е.
когда существует такое Ях, что Я R Н' и Ф(В,Н') = Л, положим
Ф(ПБ,Я) = Л.
Формулу А назовем истинной в модели Ф, связанной с модельной
структурой < G, И7, R >, если Ф(А, G) = И и ложной, если
Ф(А, G) = Л. Формулу А назовем общезначимой, если она истинна во
всех своих моделях, и выполнимой, если она истинна хотя бы в одной
из моделей.

278 Монотонные классические модальные логики [ Гл. 7
Из множества «возможных миров» выделяем «действительный
мир» — элемент G. Каждая атомарная формула (т. е. пропозицио-
пропозициональная переменная) Р получает некоторое истинностное значение в
каждом мире Н\ в действительности это значение есть Ф(Р,Н).
Интуитивно отношение R может пониматься следующим образом:
для данных двух миров Hi,H^ G W, «Hi R Н^» читается как «Н^
возможен относительно Hi», «возможен в Hi» или «зависит от Hi»;
это значит, что каждое высказывание, истинное в Н^^ возможно в Н\.
Один мир является теперь возможным относительно некоторого дру-
другого. Очевидно, что каждый мир возможен относительно себя самого
(рефлексивность отношения R), т.е. всякое высказывание, истинное
в Н, является также возможным в Н. Мы оцениваем формулу А
как необходимую в мире Hi, если она является истинной в каждом
мире, возможном относительно Н\\ иными словами, Ф(ОА, Н\) =
= И тогда и только тогда, когда Ф(А, Н2) = И для каждого Щ
такого, что Hi R Н^- Двойственным образом, формула А возможна в
мире Hi тогда и только тогда, когда существует мир Н^ возможный
относительно Hi, в котором А истинна.
Выясним, при каком условии отношение R будет обладать свойст-
свойством транзитивности, т. е. следует ли из того, что Hi R Н2 и Н2 R Н%
утверждение Hi R Н%! Сказать, что Н2 R Н%, — значит, сказать,
что каждая формула А, истинная в Н%, является возможной в Н^
(т.е. формула §А истинна в Н^)\ но тогда, поскольку Н\ R Н^ то
отсюда в свою очередь следует, что формула (}А является возможной
(«возможно, что возможно» А и (}(}А истинна) в Hi. Но Hi R H3,
значит, если А истинна в Н%, то А возможна в Н\\ однако выше
мы установили, что по меньшей мере, возможно, что А возможна
в Hi. Это приводит к требованию дополнительной аксиомы: (}(}А —>
—> (}А «возможно, что возможна А, означает, что А возможна», а
это аксиома редукции S4. В соответствии с этим будем называть
модельную структуру с транзитивным отношением R (не забывая о
рефлексивности) 84-модельной структурой.
Аналогично можно показать, что брауэрова аксиома приводит к
симметричности R. Действительно, предположим, что имеет место
А —> \3{)А и Hi R i?2- Тогда Н^ R Hi будет установлено, если мы
сможем доказать, что всякое утверждение, истинное в Н\, возможно
в i?2- Но если А истинна в Н\, то согласно брауэровой аксиоме (О(}А
истинна в Hi)()A необходимо в Hi, т.е. (}А истинна во всех мирах,
возможных относительно Hi. В частности, (}А истинна в Н^^ что и
требовалось доказать.
Аксиомы редукции классической модальной логики позволяют
установить простые свойства (помимо рефлексивности) отношения R.
Если мы считаем, что отношение R имеет место для каждой пары
элементов из W, то тем самым утверждается, что каждое возможное
высказывание является необходимо возможным, т. е. это приводит к

7.7] Семантика возможных миров Крипке 279
характеристической аксиоме S5. К той же аксиоме мы придем, считая
R отношением эквивалентности.
Пусть отношение R* является «транзитивным замыканием» от-
отношения R, т. е. Hq R* Я означает существование таких Hi,..., Нп =
= Я, что для любого г < п имеет место Щ R Щ+i. Модель-
Модельная структура < G, W, R > называется связной, если для всех
Я g W G R*H.
Модель называется связной, если она определена на связной мо-
модельной структуре. Модель Ф является моделью формулы А тогда и
только тогда, когда А истинна в Ф, в противном случае Ф является
контрмоделью для А.
Покажем, что каждая выполнимая формула имеет связную модель
или, что то же, что каждая необщезначимая формула имеет связную
контрмодель.
Пусть А выполняется в модели Ф(Р, Я), определенной на модель-
модельной структуре < G, W, R >. Пусть W есть множество всех Н Е W
таких, что G R* Я, a Rr является ограничением R на W', и пусть
ФХ(Р, Я) есть Ф, ограниченная условием, что Н пробегает W. Тогда
< G, W', Rr > есть модельная структура, и Фх является моделью в
< G, W', Rf >. Очевидно, что Фх связана. Мы докажем по индукции,
что Ф'(В, Н) = Ф(В, Н) для каждой подформулы В формулы А и для
каждого Н Е W (следовательно, окажется, что Фх является искомой
моделью А, т.к. Ф(Д G) = И, Ф'(A, G) = И).
Если В атомарна, то этот результат получается немедленно. Если
утверждение уже доказано для С и D, и В есть С & D или -iC,
то проверка утверждения для В тривиальна. Если В есть ПС, то
проделываем шаг индукции следующим образом: заметим, что если
Я е W, то Я R! Hf влечет Hf e Wf, & следовательно, Н R Hf. По
индуктивному предположению, для Н' Е И^ Ф(С, Ях) = ФХ(С, Н').
Тогда
1) Ф(ПС, Я) = И тогда и только тогда, когда для всякого Н' Е W
такого, что Я Д Ях, Ф(С, Ях) = И;
2) ФХ(ПС, Я) = И тогда и только тогда, когда для всякого Н' Е И^
такого, что Я Д Н', Ф\С, Н') = И.
Предыдущее обсуждение показывает, что если Я Е И^, то правые
части A) и B) эквивалентны; так, Ф(П\С, Я) = И тогда и только тог-
тогда, когда Ф'(ПС, Я) = И, а следовательно, Ф(ПС, Я) = Ф'(ПС, Я),
что и требовалось доказать.
Доказанное предложение приводит к тому, что можно было бы
ограничиться рассмотрением только связных моделей. Очевидно, что
если в связной модели Д есть отношение эквивалентности, то лю-
любые два мира связаны с данным отношением; этим объясняется то,

280 Монотонные классические модальные логики [ Гл. 7
что модельная структура с подобным отношением есть 85-модельная
структура.
Дадим еще несколько определений, относящихся к связным мо-
моделям.
Тройка < G, И7, S >, где W — множество, G Е W, а 5 — отноше-
отношение, определенное на W (не обязательно рефлексивное), называется
деревом, a G — его корнем или началом, если
1) не существует Н Е W такого, что Н S G;
2) для каждого Н ? W, кроме G, существует единственное Н7
такое, что Н' S Н\
3) для каждого Н eW G S*H.
Если Н S Л', то Н мы назовем предшественником .Н7; в терминах,
связанных с S, W можно охарактеризовать как область определения
S, a G — как единственный элемент W, не имеющий предшественника.
Можно сказать, что S является древовидным отношением, если суще-
существуют G и W, удовлетворяющие сформулированным выше условиям.
М-модельная структура < G, W, R > называется древовидной,
если существует такое отношение S, что < G, W, S > является
деревом, a R — наименьшее рефлексивное отношение, содержащее S
(рефлексивное отношение, «порожденное» S). Очевидно, что в этом
случае Hi R Н^ тогда и только тогда, когда Hi S Н^ или Hi = Н^.
Аналогично определяются брауэрова, S4-, 85-модельные структу-
структуры как древовидные структуры с условием, что R — наименьшее
рефлексивное и симметричное отношение для брауэровой структуры;
рефлексивное и транзитивное отношение для S4 и отношение эквива-
эквивалентности для S5 соответственно.
Очевидно, что каждая древовидная модельная структура связна.
Согласно условию C) для каждого Н Е W G S*H; а поскольку
S С. R, то получаем, что S* С R*. В S5 каждая конечная или счетная
связная модельная структура является древовидной 85-модельной
структурой. Это может не выполняться для S4. Действительно, су-
существуют связные 85-модельные структуры (например, W = {G, Н}
и отношение R связывает все пары), являющиеся древовидными
85-модельными структурами, но не являющиеся древовидными S4-
модельными структурами.
Модель, ассоциированная с древовидной модельной структурой,
называется древовидной моделью.
Можно показать, что семантическая теория не потеряет общности,
если рассматривать только древовидные модели. Кроме того, эти
модели допускают наглядное диаграммное представление.

Я сейчас курю восхитительную мысль с
обаятельным запахом. Ее смолистая нега
окутала мой разум точно простыней.
В. Хлебников
Убеждение — это не начало, а венец
всякого познания.
И. Гёте
Глава 8
НЕМОНОТОННЫЕ МОДАЛЬНЫЕ ЛОГИКИ
Рассматриваемые в данной главе немонотонные модальные ло-
логики оперируют с неполным, неточным, зачастую противоречивым,
динамически изменяющимся знанием. Рассуждения здравого смысла
часто не монотонны, т. е. оказываются предположительными, прав-
правдоподобными и должны подвергаться пересмотру (ревизии). Такие
рассуждения неточны и пересматриваемы по самой своей природе или
из-за той информации, на основании которой они построены. Бывают
случаи, когда корректные по сути рассуждения могут пересматри-
пересматриваться, когда они основаны на таких договоренностях (соглашениях),
которые выходят за рамки информации (знания), на основе которой
они приняты.
Сначала будут рассмотрены логики убеждения и знания, затем
описаны универсальные аксиоматические модальные системы Мак-
Дермотта и Дойла, которые будут модифицированы, с привлечением
моделирования идеально разумного агента, интроспективно рассуж-
рассуждающего об исходном множестве предположений (автоэпистемические
логики Мура). Далее будет дан подход, основанный на немонотонных
правилах вывода, в котором используются умолчания, индуцирующие
так называемые расширения классических логических теорий (логики
умолчаний Рейтера).
В заключение рассмотрены две системы поддержания истинности
БД: система TMS (Truth-Maintenance System) и ATMS (Assumption-
Based Truth-Maintenance System).
8.1. Логики убеждения и знания
Главной функцией модальной логики является формализация мо-
модальностей «необходимости» и «возможности». Другим ее примене-
применением является моделирование и анализ парадигм «убеждения» и
«знания». Для этого различные логические системы используют фор-
формальные языки с модальными операторами «убеждения» и «знания».

282 Немонотонные модальные логики [ Гл. 8
В рамках логик убеждения и знания оператор ? принимает соответ-
соответственно значения «предполагается» и «известно». Двойственный ему
оператор (} принимает соответственно значения «противоположное не
предполагается» и «противоположное неизвестно».
Пусть С — модальный язык высказываний, р и q — метаперемен-
ные, представляющие формулы в языке С. Модальные операторы в
С обозначим символами L и М, где Пр есть Lp и (}р — Мр, причем,
как и раньше Lp = ^М^р.
Напомним, что нормальная модальная система (см. разд. 7.7) —
это четверка, состоящая из
• множества всех теорем логики высказываний, область действия
которых распространена на формулы модального языка выска-
высказываний L;
• схемы аксиомы дистрибутивности L(p —> q) —> (Lp —> Lq)
(в классике As), обозначаемой буквой К. Схема К утверждает,
что «Если необходимо, что р влечет q, то из необходимости р
вытекает необходимость q»;
• правила Modus Ponens: если Ь р и Ь р —> q, то Ь #;
• модального правила вывода необходимости: если Ь р, то Ь Lp.
Формула р необходимо истинна при условии, что р истинна (см.
также разд. 7.7).
Обогатим нормальную модальную систему следующими схемами
аксиом.
Схема аксиомы знания: Lp —>¦ р (в классике А\).
В немонотонных модальных системах эту схему обозначают бук-
буквой Т. Она утверждает: «то, что известно — верно». Эту схему до-
добавляют к нормальной модальной системе, чтобы оператор L означал
«известно». Напротив, схемы Т не будет в системе аксиом, форма-
формализующих «предположение», ибо оно может быть ошибочным. Нор-
Нормальная модальная система, пополненная схемой Т, перенимает имя
от двух входящих в нее схем модальных аксиом: она обозначается
через КТ.
Схема аксиомы позитивной интроспекции: Lp —> LLp.
Эта схема обозначается цифрой 4. Когда модальный оператор L
означает «известно», схема 4 утверждает: «Если мне известно р, то
я знаю, что известно р». Если же модальный оператор L означает
«предполагается», то схема 4 гласит: «Если я предполагаю, что р
подтверждается, то я предполагаю, что я предполагаю, что р под-
подтверждается».
Описанная схемой 4 возможность интроспекции (от лат.
introspecto — смотрю внутрь, то же, что самонаблюдение) нужна
для формализации совершенного интроспективного интеллекта.
Нормальная модальная система, пополненная схемами аксиом Т и 4,
обозначается КТ4 (или в классической модальной системе S4).

8.1] Логики убеждения и знания 283
Схема аксиомы негативной интроспекции: Мр —> LMp.
Эта схема обозначается цифрой бив логиках знания и убежде-
убеждения формализует совершенную негативную интроспекцию. Схема 5
эквивалентна следующей схеме: ^Lp —> L^Lp. Когда оператор L
означает «известно», то схема 5 утверждает: «Если я не знаю, что р
подтверждается, то я знаю, что я не знаю, что р подтверждается».
Если же оператор L означает «предполагается», то она гласит: «Если
я не предполагаю, что р подтверждается, то я предполагаю, что я не
предполагаю, что р подтверждается».
Это свойство, конечно, чрезвычайно обременительно. Оно выража-
выражает совершенное понимание пределов нашего знания или убеждения.
Нормальная модальная система, пополненная схемами аксиом Т, 4 и
5, обозначается КТ45 (или в классической модальной системе S5).
Выбор модальной системы зависит от моделируемого понятия.
Подробнее об этом выборе будет написано ниже.
Вернемся к семантике возможных миров Крипке. Структурой
будем называть пару ^5 = (И7, R), где W — непустое множество (уни-
(универсум) возможных миров, а Д — бинарное отношение доступности
на множестве W, т. е. некоторое подмножество из W x W.
Пусть Р — множество атомов (или высказываний) модального
языка С. Тогда Р-моделью на структуре (И7, R) называется тройка
АЛ = (И7, R, V), где оценка V — отображение из Р в 2W (т.е. мно-
множество всех подмножеств множества W), сопоставляющая каждому
высказыванию р Е Р подмножество V(p) из W.
Неформально это значит, что V(p) интерпретируется как множе-
множество возможных миров из If, в которых высказывание р истинно.
Если нет никакой двусмысленности в контексте, то префикс Р в
определении модели будем опускать и говорить просто о модели.
Пусть w E W и А — модальная формула в языке С. Для семан-
семантической оценки формул из С желательно иметь в виду конкретный
мир w из универсума W вместе с рассматриваемой оценкой V. Ре-
Рекурсивно определяют отношение семантического следования N между
моделями и формулами языка. Запись А4 \=w А отражает семантику
формулы А и означает, что А истинна в мире w для модели Ad.
Эта семантика определяется следующим образом:
• М Nw И,
• Ai \=w р, если w E V(p),
• АЛ \=w А\ —> А2, если из АЛ \=w A\ следует АЛ \=w A2,
• А4 \=w LA, если из w R t вытекает, что А4 \=t А для всех t E W.
Последнее правило выражает тот факт, что формула LA истин-
истинна в мире w модели АЛ, если формула А истинна во всех мирах

284 Немонотонные модальные логики [ Гл. 8
t, находящихся в отношении R с миром w. Это правило учитыва-
учитывает желательные значения модального оператора L. Действительно,
в логике необходимости формула LA представляет необходимость
формулы А: «А необходимо в данном мире» интуитивно означает
подтверждаемость А во всех мирах, доступных из данного. В то
же время, в логике знания формула LA означает «А известно» и,
следовательно (интуитивно), А подтверждается во всех возможных
мирах, какие только можно вообразить на основе некоего множества
знаний и предположений.
Семантическая оценка (означивание) формул И, -iA, MA, A\ V А^,
А\ & Аъ и А\ <-> Аъ получается из базовых семантических отношений
с помощью эквивалентных преобразований, позволяющих записать
константу И, оператор М и связки V, & , <-> в виде формул, по-
построенных из константы Л, оператора L и связок —< и —>-. Например,
из соотношения ^А = А —> Л и правила двойственности выводятся
следующие семантические правила:
• ЛЛ \=w -*А, если ЛЛ ?w A;
• ЛЛ \=w MA, если ЛЛ \=t А хотя бы для одного t Е W такого, что
w Rt.
Введем ряд понятий.
Формула А из С общезначима в модели ЛЛ = (И7, R, V) тогда и
только тогда, когда она истинна во всех мирах этой модели, т. е. если
А4 \=w А для всех w E W. Это обозначается так: А4 N А.
Формула А из С общезначима в структуре ^s = (И7, R) тогда
и только тогда, когда А общезначима в любой модели (И7, R, V),
т.е. если ЛЛ N А для всех моделей ЛЛ. Это обозначается следующим
образом: SNA.
Формула А из С общезначима тогда и только тогда, когда А
общезначима в любой структуре S. Символьная запись: N А.
Необходимой истиной в мире w называется формула, которая
подтверждается во всех мирах ?, достижимых из w. Отсюда формула
LA читается так: «А необходимо истинна».
Возможной истиной в мире w называется формула, которая под-
подтверждается хотя бы в одном из миров, достижимых из w. Отсюда
формула МА читается так: «возможно, что А истинна».
Введем реальный мир G. Формула А, которая необходимо истинна
в реальном мире G, будет истинна и во всех мирах, достижимых из
реального мира, в частности, и в самом реальном мире G. Таким
образом, формула LA —> А истинна в рассматриваемой структуре.
Если формула А истинна в реальном мире G, то она будет ис-
истинной хотя бы в одном из миров, доступных из реального мира G.
Значит, формула А —> МА истинна в рассматриваемой структуре.
Рассмотрим список свойств, которым может обладать отношение
доступности R.

8.1] Логики убеждения и знания 285
1. Рефлексивность: \/w(wRw).
2. Симметричность: 4uNt(wRt —> tRw).
3. Репродуктивность: Vw3t(wRt).
4. Транзитивность: WuNtWu(wRt & tRu —> wRu).
5. Евклидовость: WuNtWu(wRt & W-Ru —> tRu).
6. Частичная функциональность: \/w\/t\/u(wRt & wi^ix -^ t = u).
7. Функциональность: Vw3H(wRt) (обозначение 3!t означает: суще-
существует одно и только одно ?).
8. Слабая плотность: \/w\/t(wRt —> 3u(wRu & uRt)).
9. Слабая связность: \/uNt\/u{wRt & W-Ru -^ ti?u V' t = и У uRt).
10. Слабая направленность: VwVtVu(wRt & wifoz -^ 3v(tRv & uRv)).
Этому списку свойств отношения R соответствует список схем
формул.
l.LA^A (T) б.МА^ЬА.
2.А^ LMA (В) 7. МА <-> LA
3. LA -^ MA (D) 8. LLA -^ LA.
A.LA^LLA D) 9. L(A & LA -^ В) V Ь(Б & ?Б -^ A) (L).
5. МА -> LMA E) 10.
В скобках справа около некоторых схем формул указаны истори-
исторические названия соответствующих схем аксиом.
Следующая теорема дает точное описание вышеупомянутого соот-
соответствия.
Теорема 8.1. (Р. Голдблатт). Если задана структура ^5 = (И7, R),
то отношение R тогда и только тогда обладает конкретным из свойств
1-10, когда соответствующая схема формул истинна в Э.
Эта теорема имеет фундаментальное значение. Именно ею объяс-
объясняется тот успех, который имела реляционная семантика с тех пор,
как ее ввел Крипке. Такие структуры хорошо приспособлены для
применения.
Однако отметим, что есть и такие достаточно привычные свойства
отношения R, которые не соответствуют общезначимости никакой
модальной схемы. Таковы, например, следующие три свойства:
• иррефлексивность: Ww->(wRw)]
• антисимметричность: \/uNt(wRt & tRw —> w = t)\
• асимметричность: 4uNt(wRt —> -*(tRw)).

286 Немонотонные модальные логики [ Гл. 8
Возвращаясь к нормальным модальным системам, следует
заметить, что если {Л^ | г Е /} — какое-либо множество нормальных
логик, то их пересечение П{Лг | г Е /} является нормальной
логикой. В частности, логика К, определенная соотношением
К = П {Л^ | Л^ есть нормальная логика}, т.е. пересечение всех
нормальных логик есть наименьшая нормальная логика. Следующая
теорема показывает важность этой «минимальной» логики.
Теорема 8.2. (Р. Голдблатт). Формула А является теоремой ло-
логики К тогда и только тогда, когда А общезначима (т. е. истинна во
всех структурах).
Следующие отношения выполняются в любой нормальной логике:
Ьл
Ьл
Ьл
Ьл
Ьл
А^
А < >
М(А
LAW
М(А
В =^Ь
Б^Ь
V В)
LB-
&Б)
ALA
a LA
+ L(A
-> LBn
^ LB и
iV MB,
У В),
А к MB.
ЬЛМА
ЬЛМА
-^ MB,
^ MB,
Существует соответствие между выбором схем основных аксиом
данной формальной системы и свойствами отношения доступности
между возможными мирами семантической характеристики этой си-
системы. Проиллюстрируем это соответствие следующими теоремами.
Теорема 8.3. Формула А является теоремой логики КТ тогда
и только тогда, когда А истинна во всех структурах, в которых R
рефлексивно.
Теорема 8.4. Формула А является теоремой логики S4 тогда
и только тогда, когда А истинна во всех структурах, в которых R
рефлексивно и транзитивно.
Теорема 8.5. Формула А является теоремой логики S5 тогда
и только тогда, когда А истинна во всех структурах, в которых R
рефлексивно, транзитивно и евклидово (т. е. R — отношение эквива-
эквивалентности) .
Теоремы 8.3-8.5 можно обосновать с использованием следующей
леммы.
Лемма 8.6. (Р. Голдблатт). Если нормальная логика Л содержит
какую-либо из схем 1—10 (см. список свойств отношения доступности
R), то существует отношение RA (названное каноническим для Л),
обладающее соответствующим свойством.
Структура возможных миров семантически характеризует различ-
различные модальные системы в зависимости от свойств отношения доступ-
доступности.

8.2] Немонотонные логики Мак-Дермотта и Доила 287
Схема КТ может быть выбрана в нормальной модальной систе-
системе, если соответствующая семантическая характеризация свойств мо-
модального оператора L будет состоять из множества возможных миров,
связанных рефлексивным отношением доступности R. Аналогично,
если выбрать систему КТ45 (она же S5) для аксиоматизации свойств
оператора L, то соответствующая семантическая характеризация бу-
будет состоять из множества возможных миров, связанных между собой
отношением R, являющимся отношением эквивалентности.
8.2. Немонотонные логики Мак-Дермотта и Дойла
Немонотонные логики Мак-Дермотта и Дойла являются универ-
универсальными аксиоматическими системами, рамки которых аналогичны
модальным системам необходимости и возможности, пополненные
правилом вывода выполнимых утверждений. В этих логиках имеем
формулы вида р, ^р и Мр («р возможна»), истинность которых соот-
соответствует факту, что р доказуема, опровергаема и возможна. Интуи-
Интуитивно ясно, что р возможна всякий раз, когда она не опровергаема,
т. е. ^р недоказуема.
Понятия «возможно» и «необходимо» могут интерпретироваться
как «непротиворечиво» и «доказуемо» («известно»). Тогда в рам-
рамках немонотонной логики Мак-Дермотта и Дойла утверждение ти-
типа «обычно (как правило, типично) студенты юны» будет записано
следующим образом: Ух (Ст(х) & М Юн(х) —> Юн(х)), т.е. если
кто-то — студент и он возможно (или это не противоречит) юн, то он
действительно юн. Если в БЗ поступил факт, что Петров — студент
(Ст(Петров)) и ^Юн(Петров) невозможно вывести (доказать), т.е.
факт М Юн(Петров) истинен, то мы действительно делаем вывод,
что Петров юн.
Построим модальный язык первого порядка ?, предложенный
Мак-Дермоттом.
1. Пусть С, X, F и Р — множества символов индивидных констант,
переменных, функций и предикатов соответственно.
2. Множество термов из С определяется по индукции следующим
образом. Терм из С — либо константа из С, либо переменная
из X, либо выражение /f(?i, ?2, • • • ? tn), где /гп — п-местная
функция из F, a ti, ^2,..., tn — термы из С.
3. Атомарная формула из С— это выражение вида -Р/Х^ъ ^2? • • • ? ^п)?
где PJ1 — n-местный предикат из Р, a ti,t2,...,tn — термы
из С. Символ п в дальнейшем у предикатов и функций будем
опускать.
4. Множество формул из С определяется по индукции: формула
из С — либо атомарная формула, либо -нр, либо р —> q, либо

288 Немонотонные модальные логики [ Гл. 8
Мр, либо \/х р. Здесь р и q — формулы из ?, М — модальный
оператор (О), х — переменная из X.
Теперь зададим немонотонную аксиоматическую систему. Она со-
содержит следующие элементы:
1) «нелогические сведения», являющиеся формулами из С со ста-
статусом дополнительных аксиом (посылок);
2) схемы логических аксиом;
3) логические правила вывода.
Схемы классических аксиом (Клини).
а) Р^ (q^p).
б)
в)
г)
д)
(Р
(-"
Ух
\/х
—>
?-
р-
(р
(Я
¦» -
—>•
пр) -^ ((-
Pt/x, гДе
^) "^ (Р
\\Р ~^
терм t
-^Ух ,
^) -^ (Р —
) -^«),
'свободен
д), если ж
для х в р,
не фигурирует в
Говорят, что терм t свободен для переменной х в формуле р, если
ни х, ни произвольная переменная из t не квантифицированы в р. Как
и раньше, через Pt/X обозначается формула, полученная из р путем
одновременной замены всех вхождений х на t.
Схемы модальных аксиом.
а) Схема аксиомы знания Т: Lp —> р. Она соответствует аксиоме
А\ в нормальном модальном исчислении высказываний.
б) Схема аксиомы дистрибутивности К: L(p —>¦ q) -^ (Lp —>¦ Lg'),
что соответствует Аз в нормальном модальном исчислении вы-
высказываний.
в) Схема Баркан: (Ух)Ьр —> L(\/x)p.
г) Схема аксиомы позитивной интроспекции 4: Lp —>¦ LLp, или А^
в нормальном модальном исчислении высказываний. Напомним,
что нормальная модальная система, пополненная схемами акси-
аксиом К, Т и 4, обозначается КТ4 (или, в классической манере, S4).
д) Схема аксиомы негативной интроспекции 5: Мр —> LMp, что
эквивалентно ^Lp —> L^Lp. Аналогично, нормальная модальная
система, пополненная схемами аксиом К, Т, 4 и 5, обозначается
КТ45 (или, в классической манере, S5).
Правила вывода:
а) Modus ponens: p,p ^ q\- q.
б) Правило универсального обобщения: р\- Ух р.
в) Правило необходимости: р\- Lp (формула р необходимо истинна
при условии, что р истинна).

8.2] Немонотонные логики Мак-Дермотта и Доила 289
г) Правило немонотонного вывода: «Нельзя вывести ^р» Ь Мр.
Это правило так называется потому, что система должна сама
обеспечивать отказ от своих выводов. Применение данного пра-
правила может динамически блокироваться.
Правило немонотонного вывода хорошо высвечивает тройствен-
тройственную роль, предположительно им выполняемую.
1. Оно позволяет выводить, что некоторое утверждение возмож-
возможно, т. е. выполнимо с точки зрения логики. Применяя прави-
правило, можно вывести формулы вида Мр. Искомое значение для
формулы Мр есть «р возможно» или же «р выполнимо». Для
осуществимости этого надо, чтобы ~^р не было выводимо, что
обеспечивается проверкой условия правила немонотонного вы-
вывода.
Между тем для эффективной реализации этого приписанного
модальному оператору М значения надо, чтобы оно обладало
свойствами модальных операторов, выраженных схемами мо-
модальных аксиом этой системы.
2. Правило косвенно позволяет принять как «истинные» всего
лишь выполнимые формулы. (Например, если Мр выведено по
правилу немонотонного вывода и если в данной системе со-
содержится дополнительная аксиома Мр —>¦ р, то по Мр можно
вывести р). Применение этого способа означает также переход
от констатации выполнимости некоего выражения к его утвер-
утверждению. Данной системе присуща, в некотором смысле, спо-
способность воспринимать как истинные формулы с установленной
выполнимостью.
3. Правило придает данной системе немонотонный характер.
Например, если эта система позволяла вывести формулу Мр
(или вообще формулу q, вытекающую из Мр) и если добавлена
новая аксиома, позволяющая в этой системе вывести -нр, то
формулу q надо отвергнуть.
Однако правило немонотонного вывода приемлемым, вообще гово-
говоря, не является. Оно зацикливает определение отношения выводимо-
выводимости. Его условия (называемые предусловиями) позволяют проверять
(до вывода) выполнимость некоего утверждения вместе с уже выве-
выведенными утверждениями в этой системе из существующего множества
посылок, т. е. правило определяет выводимость в терминах выво-
выводимости. Чтобы убедиться в получении противоречия, рассмотрим
следующую формулу: Mq —> -^q. Если мы используем эту формулу
как одну посылку, то благодаря правилу немонотонного вывода ->q
выводима тогда и только тогда, когда -iq не выводима (понятно, что
10 В.Н. Вагин и др.

290 Немонотонные модальные логики [ Гл. 8
-н(/ выводима по правилу Modus Ponens, когда Mq выводима, a Mq, в
свою очередь, выводима по правилу немонотонного вывода, когда не
выводима -|#).
Для решения проблемы зацикливания в определении правила
немонотонного вывода, а также проблемы характеризации множеств
выводимых формул, опишем неподвижные (фиксированные) точки
отображения системы вывода во множество посылок А. Интуитивно
неподвижные точки соответствуют множествам убеждений (предпо-
(предположений), которые могут быть получены применением стандартных
правил вывода классической логики и добавлением формул вида Мр,
т. е. это такое устойчивое множество формул, что никакую новую (не
входящую в рассматриваемое множество) формулу нельзя вывести с
соблюдением свойства выполнимости.
Рассмотрим сначала одну из монотонных классических модальных
систем КТ, или S4, или S5 и назовем ее S. Определим Ths(A) как
множество формул языка ?, выводимых в системе S из множества
посылок (дополнительных аксиом) A: Ths(A) = {р Е С \ A \-s p}, т.е.
Ths{A) — множество классических теорем из А.
Возьмем одну из немонотонных модальных систем и определим
множество предположений В из С относительно А как Assа{В) =
= {Mq \q E С (q не имеет свободных переменных) и -i</ ф. B}\Ths(A),
т. е. это множество формул, предположительных относительно мно-
множества В или множество формул, выполнимых вместе с формулами
из множества В, но недоказуемых в модальной системе S с использо-
использованием множества посылок А.
Нас интересуют такие множества В формул из ?, которые являют-
являются неподвижными точками оператора NMa(B) = Th(A U Ass a(B)).
Предположим, что В — неподвижная точка оператора NMa, т.е.
= В. В этом случае В содержит
1) все посылки А;
2) все монотонные теоремы для А;
3) множество формул Mq, которые можно непротиворечиво доба-
добавить к В;
4) все теоремы из 1), 2) и 3).
Таким образом, неподвижные точки NMa соответствуют множе-
множествам формул, интуитивно «санкционированных» посылками из А
при предполагаемой интерпретации М, и надо найти решения рекур-
рекуррентного уравнения В = Th(A U Assa(B)).
Правая часть этого уравнения есть множество всех модальных
следствий, выводимых из объединения множества посылок А и фор-
формул, предположительных относительно искомого множества В. Мно-
Множество В является неподвижной точкой этого уравнения и называется
Немонот.^. Оно устойчиво и состоит из всех модальных следствий,

8.2] Немонотонные логики Мак-Дермотта и Доила 291
выводимых из объединения множества А и множества формул, пред-
предположительных относительно этого Немонот.^4 множества.
Таким образом, решения приведенного выше рекуррентного урав-
уравнения дают (неконструктивно определяемые) максимальные мно-
множества формул, выводимых с использованием множества посылок
А и с сохранением свойства выполнимости. Эти множества содержат
все логические следствия из множества посылок А, а также все пред-
предположительные относительно них формулы.
Обозначим через ТН(А) множество теорем, получаемых в резуль-
результате применения к множеству посылок А системы немонотонного
вывода, причем применение это осуществляется в соответствии со
следующим соотношением:
ТН(А) =?U (пНемонот.Л),
т. е. берется пересечение всех неподвижных точек (говорят, что непо-
неподвижные точки минимальны). Таким образом, статус теорем при-
придается формулам, принадлежащим всем неподвижным точками из
немонотонной модальной системы. Это соответствует взгляду, что в
случае конфликтной информации логика не должна отдавать пред-
предпочтение ни одному из конфликтных заключений. При отсутствии
неподвижных точек ТН(А) определяется как множество всех формул
из С.
Отношение немонотонной выводимости, соответствующее системе
немонотонного вывода, обозначается через |~ и определяется следу-
следующим образом. Пусть Qi и Q2 — подмножества из L. Имеем Qi \~Q2
тогда и только тогда, когда Q2 С TH(Qi). Множество Q2 формул
становится с данного момента множеством теорем для множества
посылок Qi тогда и только тогда, когда любая формула из Q2 при-
принадлежит всем неподвижным точкам множества Q\.
Проблема в подходе с неподвижной точкой заключается в том, что
в общем случае неподвижные точки трудно описать и найти, посколь-
поскольку их определение неконструктивно. Варьируя порядок применения
выводов, имеем ноль, одну или больше неподвижных точек. Приведем
несколько примеров, предложенных Мак-Дермоттом и Дойлом.
Пример 8.1.
А\ = { }. Если множество посылок пусто, то имеется одна непо-
неподвижная точка. Она содержит все общезначимые формулы и форму-
формулы вида {Mq \ q не является противоречием}.
Пример 8.2.
А2 = {Мр —> р}. Имеется одна неподвижная точка, содержащая
как Мр, так и р.
Пример 8.3.
As = {Мр —> р, ^р}. Имеется одна неподвижная точка. Она не со-
содержит ни Мр, ни р. Так как А2 С Аз, имеем пример немонотонности.
ю*

292 Немонотонные модальные логики [ Гл. 8
Пример 8.4.
А^ = {Мр —>¦ —i^, М q —>¦ ^р}. У этого множества посылок имеются
две неподвижные точки F\ и F2. Неподвижная точка F\ содержит Mq
и -пр, но не содержит Мр и -i#, a F2 содержит Мр и -ig, но не Мд и -пр.
Действительно, если Fi не содержит -iq, то она содержит Мд, откуда
по правилу Modus Ponens вытекает, что она содержит ->р. То же самое
верно и для i^.
Пример 8.5.
А5 = {Мр —> ^р}. Неподвижных точек здесь нет. Действительно,
если бы неподвижная точка не содержала —<р, то она содержала бы
Мр. Следовательно, она содержала бы ^р в противоречии с предпо-
предположением. Если бы она содержала -нр, то содержала бы и Мр. Поэтому
формула Мр —>¦ ^р была бы выполнимой. Приходим к противоречию,
ибо ^р и Мр не могут одновременно фигурировать в одном выполни-
выполнимом множестве.
Основное достоинство немонотонной логики Мак-Дермотта состо-
состоит в методе неподвижной точки, используемом для характеризации
устойчивых множеств заключений немонотонной системы, а также в
применении модальной логики для формализации пересматриваемых
рассуждений.
Впрочем, выбор подходящей для рассмотрения модальной системы
остается проблематичным. Желая сопоставить модальному оператору
М значение «быть выполнимым», Мак-Дермотт заметил, что наи-
наиболее приемлемой модальной логикой является та, которая соответ-
соответствует немонотонной S5-системе. Однако эта логическая система
обнаруживает неожиданное свойство: если A |^S5P? то А Ь$5 Р-
Иначе говоря, в немонотонной 85-системе нет теоремы, которая
не была бы теоремой в соответствующей монотонной классической
системе S5. Мак-Дермотт подверг сомнению полезность немонотонной
85-системы и посоветовал (не приводя абсолютно убедительных аргу-
аргументов) выбрать для формализации немонотонности немонотонную
84-систему.
В следующем разделе мы покажем, как можно перестроить ло-
логику Мак-Дермотта, привлекая моделирование идеально разумного
субъекта, интроспективно рассуждающего об исходном множестве
предположений. Тогда проблема выбора модальной системы решится
удовлетворительно.
8.3. Автоэпистемические логики
Автоэпистемические логики (АЭЛ) имеют своим предметом фор-
формализацию интроспективных (т. е. зависящих от текущего состояния
знаний агента) и идеально разумных рассуждений об исходном мно-
множестве предположений. Вместо формализации понятия непротиво-
непротиворечивости в АЭЛ рассматривается идеальный агент, рассуждающий

8.3] Автоэпистемические логики 293
о своих собственных убеждения (верах). Предполагается, что такой
агент имеет полные интроспективные способности в том смысле, что
он знает, что он знает утверждение р всякий раз, когда он знает р, и
он знает, что он не знает р всякий раз, когда он не знает р.
Под идеально разумными понимаются утверждения, идеализи-
идеализированные в двух аспектах: из исходного множества предположений
можно выводить только ожидаемые логические следствия, и все эти
логические следствия надо принять во внимание. Таким образом, для
рассуждений нужны неограниченные ресурсы.
Подобные рассуждения немонотонны, ибо множество основных
предположений агента может со временем меняться, что чревато
противоречиями для некоторых выводов. Такими интроспективны-
интроспективными рассуждениями можно моделировать многочисленные виды пере-
пересматриваемых рассуждений (в частности, для формализации таких
рассуждений применяются модальные логики знания и убеждения,
см. разд. 8.1).
Столнекер и особенно Мур развили основанный на модальной
логике метод для формализации немонотонных, интроспективных и
идеально разумных рассуждений.
Разработанную ими АЭЛ можно рассматривать как результат ре-
реконструкции немонотонной логики Мак-Дермотта, состоящий в за-
замене парадигм выводимости и выполнимости на формализацию ин-
интроспективных способностей рассуждений.
В этом контексте модальный оператор М и двойственный ему опе-
оператор L формализуют соответственно «обратное не предполагается»
и «предполагается» (вместо выполнимого и выводимого). Модальные
операторы в АЭЛ позволяют выразить соотношение между тем, что
предполагается и тем, что истинно в мире. Например, мы можем выра-
выразить, что если Петров — студент, и мы не предполагаем, что он не юн,
тогда он действительно юн, т. е. Ст(Петров) & ^Ь^Юн(Петров) —>
—> Юн(Петров). Синтаксически это представление эквивалентно пред-
представлению в немонотонной модальной логике Мак-Дермотта.
Рассмотрим язык и семантику АЭЛ. Язык Ср получается ограни-
ограничением модального языка Мак-Дермотта С на свою пропозициональ-
пропозициональную компоненту и использованием модального оператора L (двой-
(двойственного М) для построения модальных формул. Формула вида Lq
интерпретируется следующим образом: «Предполагается, что q под-
подтверждается».
Назовем теорией множество формул языка ?р, автоэпистеми-
ческой теорией — подмножество Т из Ср, представляющее какое-то
полное и состоятельное множество предположений, которое идеаль-
идеально разумный агент может построить на основе множества А исходных
предположений. Сначала уточним, каковы семантические свойства,
которыми должно обладать подобное множество формул Т.
Введем некоторые определения (Мур).

294 Немонотонные модальные логики [ Гл. 8
• Интерпретация высказываний автоэпистемической теории Т
приписывает значения истинности формулам множества Т. При-
Приписывание подчиняется классическим правилам оценки слож-
сложных формул логики высказываний. Оно придает произвольное
значение истинности пропозициональным константам и форму-
формулам вида Lp («предполагается р»).
• Модель высказываний автоэпистемической теории Т — это ин-
интерпретация высказываний из Т, в которой подтверждаются все
формулы теории Т.
• Автоэпистемическая интерпретация автоэпистемической тео-
теории Т — это интерпретация высказываний из Т, для которой
всякая формула вида Lp подтверждается тогда и только тогда,
когда р G Т. Таким образом, при автоэпистемической интерпре-
интерпретации формула Lp подтверждается в том и только в том случае,
если р принадлежит множеству Т предположений данного аген-
агента.
• Автоэпистемическая модель автоэпистемической теории Т —
это автоэпистемическая интерпретация, в которой подтвержда-
подтверждается всякая формула из Т.
На эти семантические рассмотрения дадим понятие полноты и
состоятельности (вместо выполнимости), приспособленные к авто-
эпистемичности.
1. Автоэпистемическая теория Т семантически полна тогда и
только тогда, когда она содержит все формулы, подтвержда-
подтверждающиеся во всех автоэпистемических моделях Т. (Интуитивно:
Т полна тогда и только тогда, когда Т содержит все форму-
формулы, которые данному агенту семантически позволено вывести в
предположении истинности всех его гипотез.)
2. Автоэпистемическая теория Т состоятельна относительно мно-
множества А основных предположений тогда и только тогда, когда
любая автоэпистемическая интерпретация Т, являющаяся мо-
моделью А, является также и моделью теории Т. (Интуитивно:
это позволяет гарантировать, что предположения некоего аген-
агента, составляющие автоэпистемическую теорию, истинны тогда и
только тогда, когда истинны основные предположения из мно-
множества А.)
Зададим синтаксическую характеризацию автоэпистемическим
теориям Т, обладающим семантическими свойствами полноты и
состоятельности относительно множества А исходных предположе-
предположений. Ввиду трудности конструктивной характеризации множеств
выводимых формул немонотонной системы дадим неконструктивное
определение автоэпистемических теорий Т, таких, что их полные

8.3] Автоэпистемические логики 295
и состоятельные множества предположений идеально разумный
агент в состоянии построить на основе множества А исходных
предположений.
Будем говорить, что автоэпистемическая теория Т устойчива,
если Т есть множество замкнутых формул из Ср, удовлетворяющее
следующим условиям:
1) если {pi...jPn} CI Т и {pi...jPn} 1~ <L гДе 1~ ~~ отношение
выводимости в логике высказываний, то q G Т;
2) если р G Т, то Lp G Т;
3) если р ф Т, то ^Lp G Т.
Первое правило утверждает, что агент предполагает все логиче-
логические следствия (логическое всеведение). Второе правило гарантирует,
что формула «предполагается р» принадлежит множеству Т предпо-
предположений этого агента, если р — предположение этого агента. Третье
правило утверждает, что формула «р не предполагается» фигурирует
во множестве предположений того же агента, если формулы р там нет.
Автоэпистемическая теория Т называется теорией, основанной на
множестве посылок А (предположений, дополнительных аксиом), ес-
если все формулы из Т находятся среди общезначимых следствий из
множества A U {Lp | p e T} U {^Lp | p ф Г}.
Справедливы следующие утверждения (Мур).
• Автоэпистемическая теория Т семантически полна тогда и
только тогда, когда она устойчива.
• Автоэпистемическая теория Т состоятельна относительно мно-
множества А основных посылок (предположений) тогда и только
тогда, когда она основана на А.
• Наконец, назовем устойчивым расширением множества исход-
исходных предположений А множество предположений Т, которое
устойчиво и основано на А. Устойчивые расширения являются
максимальными состоятельными множествами предположе-
предположений, которые идеально разумный агент в состоянии вообразить
на основе исходного множества предположений.
При анализе немонотонной АЭЛ напомним, что Мак-Дермотт
обнаружил одну особенность, связанную с тем, что каждая теоре-
теорема из немонотонной 85-системы является теоремой из монотонной
системы S5. Этот факт можно объяснить, привлекая АЭЛ. Мак-
Дермотт рассматривает неподвижные точки Т системы вывода своей
немонотонной логики, приложенной к множеству А предположений
(дополнительных аксиом). Эти точки можно сравнить с максималь-
максимальными состоятельными множествами предположений идеально разум-
разумного агента. Определение Мак-Дермотта, ограниченное на пропози-
пропозициональную компоненту, в сущности, эквивалентно следующему: Т

296 Немонотонные модальные логики [ Гл. 8
является неподвижной точкой относительно А тогда и только тогда,
когда Т есть множество модальных следствий (в системе М (КТ), S4
или S5) из A U {^Lp \p^T}.
Правило немонотонного вывода позволяет вывести формулу вида
Мр, если формула ^р не принадлежит рассматриваемой неподвижной
точке Т. Иначе говоря, опираясь на отношение двойственности между
модальными операторами М и L, можно с помощью этого правила
осуществить вывод формулы вида ^Lp, если формула р не принад-
принадлежит рассматриваемой неподвижной точке. Но тогда в логике Мак-
Дермотта неподвижная точка состоит из всех модальных следствий
из объединения множества формул ^Lp с указанной характеризацией
и множества А дополнительных аксиом (предположений).
Напротив, устойчивое расширение Т в АЭЛ определяется сле-
следующим образом: Т является устойчивым расширением А тогда и
только тогда, когда Т есть множество общезначимых следствий из
A U {Lp |р е Т} U {-.Lp \р?Т}.
Легко заметить, что в определении неподвижной точки, данном
Мак-Дермоттом, в совокупности аксиом нет (!) множества {Lp\p Е
Е Т}. Мур описывает природу этой неполноты следующим образом:
«При автоэпистемическом видении модального оператора L мысля-
мыслящий субъект, использующий немонотонную логику Мак-Дермотта,
всеведущ относительно всего им не предполагаемого, но может полно-
полностью игнорировать им предполагаемое». В самом деле, он не включает
в число аксиом формулы вида «Я предполагаю, что р подтверждает-
подтверждается», которые квалифицируют положительные предположения агента.
Рассмотрим положение о том, что любая теорема немонотонной
85-системы является теоремой в монотонной системе S5. Это можно
объяснить следующим образом. Немонотонная 85-система содержит
схему аксиомы знания, т. е. Lp —> р. Для автоэпистемического анализа
немонотонности эта схема кажется слишком обременительной, так как
она утверждает: «Все, что предполагается, истинно» (а не «То, что
известно — верно», как раньше). Это было бы приемлемо в логике
знания, но не в логике убеждения (веры).
Если мы хотим построить немонотонную систему, то использова-
использование логики знания представляется неподходящим. Все выведенное не
имеет больше статуса общезначимого в классическом смысле, ибо
есть возможность ревизии (пересмотра). Это кажется трудно совме-
совместимым со схемой аксиомы, требующей истинности всего предпола-
предполагаемого. Поскольку ничто не позволяет выделить в системе Мак-
Дермотта общезначимые утверждения и утверждения со статусом
всего лишь выполнимых формул, эту схему аксиом, видимо, надо
исключить.
В то же время, как считает Мур, немонотонная 85-система содер-
содержит также схему аксиомы Мр —> LMp, применяя которую совместно

8.3] Автоэпистемические логики 297
со схемой аксиомы знания, можно обосновать предположение в любой
формуле.
Следовательно, нет такой формулы, которая отсутствовала бы во
всех неподвижных точках множества вспомогательных аксиом, полу-
получаемого с помощью немонотонной 85-системы. В частности, не суще-
существует теоремы вида ^Lp (эквивалентной М^р) ни в какой теории,
базирующейся на немонотонной 85-системе, ибо такая теорема име-
имела бы обоснование, построенное с помощью правила немонотонного
вывода из логики Мак-Дермотта. Мур толкует этот факт следующим
образом: «Идеально разумный субъект, который предполагается не
совершающим ошибок, склонен предполагать все таким образом, что
внешний наблюдатель не может сделать никаких выводов относитель-
относительно того, что этот субъект не предполагает».
Предлагается и еще один путь: не отвергать схему аксиомы
Мр —> LMp, чтобы тем самым получить немонотонную 84-систему,
а отбросить схему аксиомы знания Lp —>¦ р, что приведет к
немонотонной системе, основанной на модальной слабой 85-системе
(иногда обозначаемой как К45).
Впрочем, Мур показал, что система вывода, содержащая произ-
произвольное подмножество схем модальных аксиом, присущих слабой S5-
системе, дает всегда одни и те же устойчивые расширения (независимо
от выбора указанного подмножества). Таким образом, АЭЛ может
обойтись без явного упоминания схем модальных аксиом.
Как и в немонотонной логике Мак-Дермотта, в АЭЛ имеются
множества посылок (предположений), дающих 0; 1 или много рас-
расширений. Например, если А = {Lp}, то нет способа получения р из
А всякий раз, когда добавляются модальные формулы. Поэтому ^Lp
должно содержаться в каждом расширении. Но так как это противо-
противоречит А, то отсюда вытекает, что в этом случае нет расширения.
Возвращаясь к нашему примеру (с. 293), имеем
1) Ст(Петров) & ^Ь^Юн(Петров) —> Юн(Петров),
2) Ст(Петров).
Так как нет способа вывести ^Юн(Петров) из посылок, то
^Ь^Юн(Петров) содержится в расширении. Отсюда имеем одно
расширение, содержащее Юн(Петров).
Если мы добавим еще две посылки:
3) Иметь_детей(Петров) & ^Ь^Юн(Петров) —> ^Юн(Петров),
4) Иметь_детей(Петров),
то получим два расширения одно из которых содержит формулу
Юн(Петров), а другое — ее отрицание (^Юн(Петров)).

298 Немонотонные модальные логики [ Гл. 8
Описанная нами семантика АЭЛ имеет то достоинство, что, ис-
используя ее, молено характеризовать предположения агента, незави-
независимо от того, разумен он или нет. Между тем данная семантика ока-
оказалась неудобной для использования, будучи неконструктивной в том
смысле, что в ней нет правил, позволяющих оценивать предположения
агента о сложных формулах, исходя из его предположений и/или
непредположений о составных частях формул. Это положение вещей
вполне приемлемо для случая неразумного агента, ибо нельзя априори
установить никакой связи между его предположениями. Напротив,
предположения разумного агента подчиняются неким отношениям, из
которых можно попытаться извлечь пользу.
С этой целью Мур предложил альтернативную семантическую
характеризацию своей АЭЛ. Эта новая семантика, основанная на по-
понятии возможных миров, позволяет построить конечные модели для
автоэпистемических теорий и дает возможность доказать существова-
существование полных и состоятельных относительно некоторого множества по-
посылок автоэпистемических теорий, что было бы трудно осуществить
с помощью первоначально указанной семантической характеризации.
Основным результатом, на котором базируется эта новая характе-
ризация, является следующее утверждение: Т есть множество фор-
формул, подтверждающихся во всех мирах 85-полной структуры (т. е.
структуры относительно системы S5, для которой любой возможный
мир доступен из другого, неважно какого, возможного мира) тогда
и только тогда, когда Т является устойчивой автоэпистемической
теорией.
Таким образом, любая автоэпистемическая интерпретация / устой-
устойчивой автоэпистемической теории Т может характеризоваться струк-
структурой St типа S5 и некой оценкой V. Структура возможных миров
специфицирует предположения идеально разумного агента, тогда как
оценка определяет то, что действительно подтверждается в реальном
мире.
Точнее, автоэпистемическая интерпретация I автоэпистемиче-
автоэпистемической теории Т есть пара I =< St, V >, где
• St — 85-полная структура (представленная множеством своих
возможных миров, каждый из которых символизирован множе-
множеством подтверждающихся позитивных и негативных пропозици-
пропозициональных констант);
• V — оценка истинности в реальном мире для пропозициональ-
пропозициональных констант из Ср.
Автоэпистемическая теория Т является множеством всех формул,
истинных во всех мирах из St.
Рассмотрим пример автоэпистемической интерпретации:
/ = <St,V> с St = {{q,p},{q, ^р}} и V = {p,q}. 85-полная
структура St составлена из двух возможных миров. В первом

8.3] Автоэпистемические логики 299
формулы q и р истинны. Во втором истинны формулы q и -пр.
Оценка V указывает, что р и q истинны в реальном мире. / —
автоэпистемическая интерпретация автоэпистемической теории Т,
содержащей все формулы, истинные во всех мирах структуры St из
/. В данном случае Т сводится к единственной формуле q.
I называется автоэпистемической моделью теории Т, составлен-
составленной из множества формул, истинных во всех мирах из St, когда любая
формула из Т подтверждается в /.
Второй результат дает средство проверки, является ли авто-
автоэпистемическая интерпретация / для Т автоэпистемической моделью
для Т.
Если / =< St, V > — автоэпистемическая интерпретация для Т,
то / является автоэпистемической моделью для Т тогда и только
тогда, когда V — элемент из St, что означает выполнимость оценки
V вместе с данной оценкой, задаваемой в одном из возможных миров
структуры St (т.е., реальный мир — один из миров, совместимых с
предположениями данного субъекта).
В нашем примере / — автоэпистемическая модель для Т, ибо
оценка V реального мира выполнима вместе с оценкой, заданной в
первом возможном мире структуры St.
Эти два результата интересны тем, что они индуцируют метод
проверки принадлежности формулы к устойчивому расширению ис-
исходного множества посылок.
Напомним, что устойчивое расширение Т множества А основных
предположений (посылок) есть устойчивое множество предположе-
предположений, основанное на А.
В силу первого результата автоэпистемическая теория Т устой-
устойчива, если ее можно представить 85-полной структурой возможных
миров. Чтобы автоэпистемическая теория Т была устойчивым рас-
расширением, нужно, чтобы Т была основана на множестве А исходных
предположений (следовательно, чтобы Т была состоятельна относи-
относительно А). Иначе говоря, любая автоэпистемическая модель посылок
А должна также быть и моделью для Т. В силу второго результата
оценка реального мира каждой из этих автоэпистемических моделей
посылок должна быть выполнимой вместе с оценкой в одном из воз-
возможных миров структуры St для автоэпистемической интерпретации.
Мур предложил разрешающую процедуру для автоэпистемиче-
автоэпистемической логики. Приведем один простой ее вариант.
Пусть А — множество посылок.
1. Строим все оценки, возможные для пропозициональных кон-
констант, появляющихся в А. Они будут характеризовать 85-полные
структуры возможных миров языка для А.
2. Выбираем структуры возможных миров, для которых любая
формула из А подтверждается во всех мирах.

300 Немонотонные модальные логики [ Гл. 8
3. Для каждой из этих структур St строим все автоэпистемические
интерпретации < St, V >, соответствующие всем оценкам V
пропозициональных констант, которые появляются в А.
4. Проверяем для каждой автоэпистемической интерпретации
< St, V > выполнение или невыполнение утверждения: «любая
формула из А истинна в < St, V > тогда и только тогда, когда
V принадлежит St». В случае выполнения St характеризует
некое устойчивое расширение для А.
5. Чтобы проверить принадлежность данной формулы устойчиво-
устойчивому расширению, представленному посредством St, выясняем,
подтверждается ли эта формула в St.
Пример 8.6.
Пусть множество исходных предположений А = {~^Lp —>¦ q\. Оно
содержит только одну формулу, означающую «Если я не предполагаю
р, то q подтверждается». Докажем, что
• идеально разумный агент, имеющий множество исходных пред-
предположений А, состоящее из одного элемента, получит устойчивое
расширение Т, содержащее высказывание q, но не р;
• не может существовать ни устойчивого расширения, содержаще-
содержащего р, но не q, ни устойчивого расширения, содержащего одновре-
одновременно р и q.
1. Предположим, что какое-то устойчивое расширение Т для А
содержит q, но не р. В этом случае 85-полной структурой,
связанной с множеством предположений Т, будет St =
Эта структура отражает два возможных мира: в первом под-
подтверждаются q и р, во втором — q и -пр. Истинные формулы
во всех мирах этой структуры соответствуют формулам, пред-
предполагаемым данным агентом. Таким образом, Т — устойчивая
автоэпистемическая теория.
Рассмотрим все автоэпистемические интерпретации для Т. Они
составлены из структуры возможных миров, отражающей пред-
предположения данного агента, и из произвольной оценки истинно-
истинности V в реальном мире. В рассматриваемом языке имеются лишь
две пропозициональные константы; значит, оценок — четыре:
{Pj о]-, {Pj ^ч}-) {^Pj q}-, {^P-, ^O.}- Из четырех автоэпистемических
интерпретаций / =< St, V > только первая и третья превраща-
превращают в истинное основное предположение ^Lp —> q. Так как оценка
V для каждой из этих интерпретаций A и 3) совпадает с оценкой
возможного мира данной структуры, то теория Т основана на
множестве посылок А, и, следовательно, является устойчивым
расширением А.

8.4] Логики умолчаний 301
2. Предположим, что Т содержит р, но не q. Структура возможных
миров будет тогда St = {{р, q}, {р, ^<?}}. Рассмотрим оценку V =
— {^Р? о}- Она, служит основой автоэпистемической интерпрета-
интерпретации / =< St, V > теории Т, подтверждающей А. Так как V не
соответствует оценке какого бы то ни было мира этой структуры,
то Т не может быть устойчивым расширением А.
3. Предположим, что Т содержит р и q. Единственно возможным
является мир {р, q}. Так как существует автоэпистемическая ин-
интерпретация, подтверждающая А и заданная этим возможным
миром и оценкой V = {^р, ->(/}, для которой У не соответствует
единственному возможному миру данной структуры, то Т не
может быть устойчивым расширением А.
Области применения семантики АЭЛ весьма разнообразны. Она
позволяет характеризовать заключения, ожидаемые от системы, спо-
способной к совершенной интроспекции. Это особенно полезно, когда
запрашивают БД или БЗ об их собственных пределах знаний.
Между тем эффективное применение АЭЛ ограничено возмож-
возможностями языка высказываний и громоздкостью разрешающей про-
процедуры.
8.4. Логики умолчаний
Логики умолчаний, введенные и развитые Рейтером для фор-
формализации рассуждений, являющихся всего лишь выполнимыми, во
многих отношениях аналогичны логикам, описанным в предыдущих
главах. В частности, Рейтер интерпретирует умолчания точно так же,
как Мак-Дермотт и Дойл, т. е. утверждение «А есть обычно (как пра-
правило, типично) В» интерпретируется как «Если х есть А и непротиво-
непротиворечиво предположить, что х есть В, тогда х есть В». Однако логики
Рейтера отличаются от модальных подходов одним важным аспектом:
вместо расширения логического языка и представления умолчаний в
языке, умолчания используются как дополнительные правила выво-
вывода, индуцируя так называемые расширения классических логических
теорий. Умолчания определяют, каким образом логическая БЗ может
быть расширена на множество предположений (убеждений), содержа-
содержащее формулы, логически невыводимые в классическом смысле из БЗ.
При неполной информации мы вынуждены получать всего лишь
правдоподобные предположительные заключения. Часто имеются
утверждения, которые в большинстве случаев истинны, но допускают
исключения. Логика первого порядка не является подходящей для
выражения исключений, так как она требует явного упоминания всех
исключений, что на практике невозможно выполнить

302 Немонотонные модальные логики [ Гл. 8
Если известно, например, что обычно студенты юны и Петров —
студент, то выводимо, что Петров юн. Но не все студенты юны, имеют-
имеются студенты, которым около или за 30 лет (предполагая, что юность
длится лет до 23). Естественно сделать общее заключение, что Петров
юн, если нет никакой другой дополнительной информации. Это и есть
рассуждение с умолчанием.
Логики умолчаний позволяют формализовать такие рассуждения
а:М/3 ЛЛ
в виде правил вывода, называемых умолчаниями: . Интуи-
7
тивный смысл этого правила: если мы убеждены в се и если /3 не
противоречит тому, в чем мы убеждены (не противоречит тому, что
известно), то мы убеждаемся и в 7-
И таким образом, правило «студенты обычно юны» выразимо в
Ст(ж) : МЮп(х)
виде: ^ , т.е. если х — студент и если это не про-
Юн(х)
тиворечит тому, что х юн, то выводимо «х юн». Общее правило с
исключениями гласит, что обычно (как правило, типично) студенты
юны. Это правило умолчания позволяет обрабатывать исключения
без их предварительной идентификации.
Система логики умолчаний представляется теорией с умолчания-
умолчаниями, состоящей из некоторого множества особо выделенных формул
и правил вывода. В ней содержатся формулы логики предикатов,
представляющие основную информацию о прикладной системе, об-
обрабатываемую в соответствии с имеющимися аксиомами, а также
имеются правила умолчаний, отражающие исключения.
Для такой системы существует несколько (ноль или больше) мно-
множеств выводимых предположений. Эти множества представляют раз-
различные картины мира, которые можно вообразить, исходя из теории
с умолчаниями.
Опять обозначим через С язык предикатов первого порядка. Пра-
Правило умолчания (сокращенно: умолчание) D — это выражение вида
g(x):M/3i(x),...,M/3m(x) f , о f , о < ^ < ^ л.
— , где се(х), /?i(x),... ,/?ш(х) и 7(х) — фор-
7vx/
мулы языка ?, свободные переменные у которых выбраны среди х =
= (xi ... ,хп); а(х) называется предпосылкой умолчания D; /ЗДх) —
обоснованием умолчания D {г = 1,га); 7(х) ~~ следствием умолчания
D\ M — некий символ метаязыка (например, «непротиворечиво»).
Умолчание D называется замкнутым тогда и только тогда, когда
а(х), /?i(x),..., /3m(x) и 7(х) не содержат свободных переменных. При
этом можно использовать более простые обозначения се, /?i,...,/3m и
7 соответственно.
Свободные переменные умолчания считаются V-квантифицирован-
ными. Область действия этих кванторов простирается на все чле-
члены умолчания. Незамкнутое умолчание называется открытым. Оно

8.4] Логики умолчаний 303
представляет общую схему вывода. Его конкретизацией является за-
замкнутое умолчание, полученное заменой всех свободных переменных
открытого умолчания на константы языка С (с соблюдением неявного
закона об области действия свободных переменных умолчания).
Теория с умолчаниями А — это пара (Z},F), где D — множество
умолчаний, F — множество замкнутых формул из С. Она называется
замкнутой тогда и только тогда, когда все умолчания из D замкнуты.
Теория с умолчаниями А = (D,F) подразумевает некоторое (нуле-
(нулевое или большее) число множеств предположений, которые выводимы
с использованием множества формул F, и удовлетворяют свойству
выполнимости. Эти множества предположений называются расшире-
расширениями данной теории с умолчаниями. Расширения теории с умолчани-
умолчаниями явно определены здесь лишь для замкнутых теорий. Открытую
теорию можно преобразовать эффективным образом в замкнутую,
заменяя каждое открытое умолчание множеством всех его конкре-
конкретизации, получаемых посредством применения открытых умолчаний
к универсуму Эрбрана данной теории. Используя это преобразование,
полученные для замкнутых теорий с умолчаниями результаты можно
распространить на открытые теории (когда они конечны). Заметим,
что теории, содержащие функциональные символы ненулевой арно-
арности, имеют бесконечную эрбранову область.
Прежде чем приступить к формализации, охарактеризуем инту-
интуитивно свойства, которыми должно обладать расширение замкнутой
теории с умолчаниями. Расширение — это подмножество основных
сведений системы, включающее все выводимое (по правилам класси-
классической логики и/или логики умолчаний).
Пусть X — подмножество формул из ?, Thc(X) — множество
замкнутых формул, общезначимо выводимых из X по классическим
правилам вывода из С: Thc{X) = {w\w G C,w замкнута и X \- w}.
Пусть А = (D,F) — замкнутая теория с умолчаниями, S — под-
подмножество замкнутых формул в С. Обозначим через Г(?) наименьшее
подмножество в ?, удовлетворяющее следующим трем условиям:
1) F С ГE),
2) Thc(T(S)) = ГE),
3) если a:M/3l''"'M/3m e D, а е ГE) и ^,..., -/Зт ф S, то
7 € ГE).
Множество формул Е С С является расширением для А тогда и толь-
только тогда, когда Т(Е) = Е (т. е. Е — неподвижная точка оператора Г).
Первое условие гарантирует то, что известно о мире, содержится в
каждом расширении. Второе условие говорит, что убеждения должны
быть дедуктивно замкнуты, и третье подразумевает тот эффект, что
имеет место столько умолчаний, сколько их возможно относитель-
относительно самого расширения. Кроме того, условие минимальности делает

304 Немонотонные модальные логики [ Гл. 8
невозможным «нефундаментальные» убеждения, т. е. неозначенные
убеждения.
Расширение Е можно охарактеризовать так. Строим последо-
последовательность формул Ei, полагая Е$ = F и i^+i = Thc(Ei) U
U {7 | — —— G D и a G Я* и -./?b..., -./?ш ? Я} для г =
= 0,1, 2,... Множество Я есть расширение для А тогда и только тогда,
ОО
когда Е = (J i^.
г=0
Теория с умолчаниями иногда позволяет вывести несколько рас-
расширений из одного множества посылок. Если предпосылка а всегда
истинна, то ее можно опустить.
Пример 8.7. (Мак-Дермотт, Дойл).
Эта теория обладает расширением Е = Thc({-*P, ~~i*S'}).
Пример 8.8.
Пусть А = (D, F), где D = < -—— > и F = 0. Эта теория не имеет
расширений.
Пример 8.9. (Мак-Дермотт, Дойл).
Пусть А = (?>,F), где D = \ '-——, '-—— i и F = 0. У этой
теории два расширения: Е\ = Ткс({^А}) и Е^ =
Пример 8.10. (Рейтер).
/тл г,ч ^ (А:МЗхР(х) :МА
Пусть А = (D,F), где D = { ^
F = 0. Расширений два: Ях =
Например, первым умолчанием из D можно формализовать
«Большинство профессоров университета имеет степень доктора»:
Проф_унив(ж) : МCу Конкр(у, доктор) & Имеет (х,г/))
Зу Конкр(у, доктор) & Имеет(ж, у)
Как показывает пример 8.8, некоторые теории с умолчаниями не
обладают расширениями. Существование расширений гарантировано,
если следствие и обоснование одного и того же умолчания совпадают.
Такие теории называются нормальными. Они состоят из нормальных
„ а(х) : М/3(х)
умолчании —^-L.
Кроме интересного свойства допускать хотя бы одно расширение,
нормальная теория с умолчаниями обладает свойством полумонотон-
полумонотонности: если увеличить множество умолчаний, то полученная теория
допускает расширение, включающее какое-то расширение исходной

8.4] Логики умолчаний 305
теории. Практически важное следствие этого свойства состоит в воз-
возможности построения такой теории доказательств, в которой исполь-
использованные умолчания проявляются локальным образом.
Пусть D' и D — два множества замкнутых и нормальных умол-
умолчаний, таких, что D' С D. Пусть Е' — расширение для замкнутой
и нормальной теории А' = (D',F) и пусть также А = (D,F). Тогда
А имеет расширение Е такое, что Е' С Е. При добавлении нового
умолчания к теории, если имеет место полу монотонность, все, что
было выведено в старой теории, останется выводимым в теории с но-
новым умолчанием. Отсюда нет необходимости проверять предыдущие
выводы при применении нового умолчания.
Можно ли построить теорию доказательств для логик умолча-
умолчаний, в частности, для замкнутых нормальных теорий? Сформулируем
вопрос точнее. Даны замкнутая нормальная теория А и замкнутая
формула / из С. Существует ли метод проверки наличия для А
расширения Е, содержащего /?
Для получения ответа Рейтер определил доказательство в теории
с умолчаниями следующим образом. Пусть А = (D,F) — замкну-
замкнутая нормальная теория и / — замкнутая формула из С. Конечная
последовательность D$, D\,..., Dk конечных подмножеств из D есть
доказательство для / в А тогда и только тогда, когда
1) FU{KC(D0)}hf,
2) F U {KC(Di)} Ь ATT(A-i) Для г = ТД,
3) Dk = 0,
4) FU{KC(Di) | 0 ^ г ^ к} выполнимо, где KC(Di) — конъюнкция
следствий и KT(Di) — конъюнкция предпосылок умолчаний
из А-
Итак, доказательство есть последовательность подмножеств умол-
умолчаний. Его можно интерпретировать следующим образом. Первое
подмножество (Dk) выбирается пустым. Последовательно строятся
Dk-i-, • • •, D\, Dq. Множество основных аксиом с добавленной к нему
конъюнкцией следствий из всех умолчаний Do должно обеспечивать
доказательство / классическим образом. Из построения подмноже-
подмножества Di-i вытекает, что множество F (с добавленной к нему конъ-
конъюнкцией следствий из Di) должно позволять доказывать классиче-
классическим образом предпосылки из 1Л-1 и? следовательно, гарантировать
применимость умолчаний из Di-\. Глобальная применимость всех
умолчаний устанавливается проверкой выполнимости объединения F
и конъюнкций следствий всех использованных умолчаний.
Заметим, что в определении не говорится, как строить подмноже-
подмножества Di и не приводится разрешающей процедуры для используемого
отношения доказательства (из классической теории предикатов пер-
первого порядка). Более того, оно предполагает проверку выполнимости

306 Немонотонные модальные логики [ Гл. 8
некой формулы из ?, тогда как множество замкнутых выполнимых
формул из С не является рекурсивно перечислимым.
Метод Рейтера сочетается со свойством полноты. Пусть / —
замкнутая формула из С. Нормальная теория А (замкнутая и вы-
выполнимая) обладает расширением Е (содержащим /) тогда и только
тогда, когда / обладает доказательством в А.
К сожалению, во всей общности проблема проверки существования
расширения с данной замкнутой формулой не полуразрешима (т. е.
неразрешима). Это не столь неожиданно. Тем не менее, в некоторых
случаях она поддается практическому решению (особенно когда огра-
ограничиваются рамками высказываний).
Нормальные умолчания выглядят достаточно привлекательными
при представлении многих форм рассуждений. Свойства формальных
систем, составляющих нормальные теории, особенно выигрышны в
силу следующих обстоятельств. Следствие и обоснование нормаль-
нормального умолчания совпадают. Следовательно, нормальные умолчания
неприменимы, когда ложность их следствий доказана. Эти умолчания
не могут вводить невыполнимости, опровергать обоснования из дру-
других ранее примененных нормальных и своих собственных умолчаний.
Итак, нормальные теории полумонотонны, всегда обладают хотя бы
одним расширением и представляют довольно простую теорию дока-
доказательств.
Между тем в ходе применения нормальных умолчаний могут
возникнуть неприятные осложнения. В частности, взаимодействие
различных нормальных правил может приводить к нежелательным
заключениям. Поэтому иногда необходимо блокировать транзитив-
транзитивность между умолчаниями. Например, рассмотрим нормальную тео-
теорию А = (D,F), где D содержит два нормальных умолчания:
1) «обычно студенты университета являются взрослыми», или в
Ст(ж) : МВз(ж)
символьном ^ . . ;
Вз(х)
2) «обычно на работу берут взрослых», или в символьном ви-
Вз(ж) : МР(х)
де: — и где г — множество из одного элемента
Р{х)
{Ст(Петров)}.
Правила из D позволяют по умолчанию вывести, что сту-
студента университета взяли на работу. Это нежелательный вывод.
Осложнение предотвращается с помощью третьего нормального
умолчания: «обычно студентов не берут на работу». Таким образом,
получается нормальная теория А' = (D',F), где D' — множество
Г Ст(ж) : МВз(х) Вз(ж) : МР(х) Ст(ж) : М^Р(х)
умолчаний: < ————-^ , — , ч—-^, — ——-^
У \ Вз(ж) ' Р(х) ' -.Р(ж)
Для данного студента множество D' может дать два расширения
}¦

8.4] Логики умолчаний 307
теории Ах (соответствующих различной занятости студента):
Т/1?({Ст(Петров), Вз(Петров), ^Р(Петров)}) и Г/1/:({Ст(Петров),
Вз(Петров), Р(Петров)}).
Тем не менее, разумно потребовать блокирования транзитивности
между двумя первыми правилами из D. Следовало бы также
выделить априори расширение, соответствующее ситуации, когда
студента не принимают на работу. Это можно осуществить
модификацией второго правила, чтобы оно не могло быть применено
в исключительном случае — «взрослый является студентом».
Итак, для теории А" = (D",F), где D" есть | Ст(ж)
\ Вз(ж)
Ст(ж) : М^Р(х) Вз(ж) : М(Р(х) & -.Ст(ж)) '
v получаем желаемое
-пР(х) ' Р{х)
расширение Т/г^({Ст(Петров), Вз(Петров), ^Р(Петров)}).
Третье умолчание D" полунормальное ^ т. е. имеет вид
а(х) : М(/?(х) fe 7(х))
/3(х)
Таким образом, полунормальное умолчание явно управляется до-
дополнительным условием в обосновании. Теория с полунормальными
умолчаниями не обязательно обладает расширением. Она теряет неко-
некоторые достоинства нормальных теорий, в частности, полумонотон-
полумонотонность.
Системы сетевого и объектного представлений часто позволяют
выразить наследование свойств с исключениями и встроить механиз-
механизмы вывода, связанные с этими методами. Поведение таких систем
редко бывает корректным и полностью охарактеризованным. Соот-
Соответствующие методы довольно плохо освоены. Если наследственные
свойства между классами и подклассами можно относительно легко
охарактеризовать в классической логике, то исследование исключе-
исключений требует определенных ухищрений. Логика умолчаний очерчивает
естественные рамки для формализации систем представления знаний
и рассуждений с исключениями.
Между тем прямое обращение к теории с умолчаниями (в част-
частности, к нормальной) простым не является. Наследственная система
обеспечивает передачу свойств по транзитивности. Когда к системе
добавляются исключения, транзитивность свойств должна допускать
возможность блокирования.
В литературе предложены различные формализмы систем пред-
представления с механизмами наследования свойств.
1. Можно использовать полунормальные умолчания, как это сде-
сделали Этерингтон и Рейтер. Исключения для наследования свойств
явно перечислены в умолчаниях. Этерингтон определил подкласс по-
полунормальных умолчаний (связанных отношением зависимости), для
которых соответствующие полунормальные теории всегда обладают

308 Немонотонные модальные логики [ Гл. 8
хотя бы одним расширением. Он предложил процедуру эффективного
построения полунормальных теорий.
2. Можно использовать нормальные умолчания с неявным поряд-
порядком, подчиненным иерархии моделируемой структуры, как было пред-
предложено в работах Турецкого. Можно не упоминать явно исключения
в умолчаниях.
3. Можно использовать таксономические теории с умолчаниями
(не являющиеся ни нормальными, ни полунормальными). Они обла-
обладают единственными расширениями. Подробнее об этом можно узнать
из работ Фройдевакса.
В заключение приведем пример.
Пример 8.11.
Нормальные умолчания:
, Ст(х) : Юн(х)
d\ = ' . .——?- — обычно студенты юны;
Юн(х)
(ж)
как правила, юные люди одиноки:
Од(ж)
ж) : Юн(ж)
одинокие люди юны:
аз = т\
Юн(х)
Ст(ж) & Род(х) : Жен(ж) V Сож(ж)
d4 = — ( , -г-, обычно студенты, име-
Жен (х) V Сож(ж)
ющие детей, женаты или являются сожителями;
Сож(х): Юн(х)
а$ = ' . ч—-^ — сожители юны.
Юн(х)
Формулы:
Fi = \/х(^Од(х) V
F2 = \/х(^Од(х) V
F3 = Уж(^Сож(ж) V -Жен(ж)).
Дадим несколько примеров запросов. Формула / является ответом
на запрос к БЗ, представленной с помощью D = {di,... ,^5} и F =
= {Fi, F2, F3}, если существует, по крайней мере, одно расширение Е
для (.D, F) такое, что f E Е.
1. Если Мария — студентка, то каков ее семейный статус? Добавим
к F формулу F^ = Ст(Мария). Тогда Ai = (D,F U F4) имеет
расширение Е\. Е\ содержит: Ст(Мария), Юн(Мария), Од(Мария),
^Жен(Мария), ^Сож(Мария), т.е. Мария — студентка, юна и
одинока.
2. Если Мария — студентка и замужем, то каков ее статус?
К F добавляем F^ = Ст(Мария) и F$ = Жен(Мария). А2 =
= (D,F U {^4,^5}) имеет расширение Е^, содержащее: Ст(Мария),
Юн(Мария), Жен(Мария), ^Сож(Мария), ^Од(Мария). Здесь имеет
место немонотонность: добавление F^ приводит к расширению Е^,
в котором блокируется Од(Мария). Точнее имеем свойство полумо-

8.4] Логики умолчаний 309
нотонности нормальных умолчаний, которое ограничивает необходи-
необходимость ревизии старых доказательств.
3. Если Мария юна, каков ее статус? Добавляем Fq = Юн(Мария).
Для A3 = (D,FUFq) имеем расширение Е%, содержащее: Юн(Мария),
Од(Мария), ^Жен(Мария), ^Сож(Мария), но неизвестно, студентка
она или нет.
4. Мария — студентка и, может быть, имеет детей. Каков ее статус?
_. / ч : Род(Мария)
Добавляем F^ = Ст(Мария) и два умолчания: а« = -г -1 и
Род(Мария)
: ^Род(Мария)
tt = «Может быть» говорит о существовании двух
tt7 = .:
^Род(Мария)
типов расширений: она может иметь и может не иметь детей. А4 =
= {D U {^б, d>?}, F U {i7^}} дает три расширения: Е±, Е'4 и Ef(. Каждое
из них содержит: Ст(Мария), Юн(Мария). Кроме этого, Е^ содер-
содержит: Род(Мария), Жен(Мария) V Сож(Мария), ^Од(Мария); Е'А со-
содержит: Род(Мария), Од(Мария), ^Жен(Мария), ^Сож(Мария); Е'{
содержит: ^Род(Мария), Од(Мария), ^Жен(Мария), ^Сож(Мария).
Мы не знаем точно, одинока ли Мария или нет, лишь знаем как о
возможности ее быть одинокой (F'/± и Е%), так и не быть (Ед). Заметим,
что эта ситуация отличается от предыдущей, в которой наше знание о
студентке или не студентке Марии не было представлено. Здесь факты
Ст(Мария) и Юн(Мария) необходимы, так как они присутствуют во
всех трех расширениях, в то время как факт Од(Мария) возможен,
т.е. он содержится не во всех расширениях.
5. Теперь модифицируем умолчания d\ -т- d$ путем использования
так называемых «свободных» умолчаний или нормальных умолчаний
без предпосылок.
, _ : Ст(ж) -> Юн(ж) #
1 ~ Ст(ж) -^ Юн(ж) '
: Юн(ж) ^ Од(х)
U2 Юн (х) -+ Од(ж) '
= : Од(х) -+ Юн(ж)
3 Од(ж) -^ Юн(ж) '
, _ : (Ст(ж) & Род(ж)) -^ (Жен(ж) V Сож(ж)) #
4 ~ (Ст(ж) & Род(ж)) -^ (Жен(ж) V Сож(ж)) '
_ : Сож (ж) -> Юн(ж)
5 ~ Сож (х) -+ Юн(ж) '
Тогда 1У = {d^ -^ 6^5}. Умолчания d\ и d^ имеют разный смысл:
d\ выражает знание по обстоятельствам, a d[ — постоянное знание.
Умолчание d\ говорит о том, что когда речь идет о студенте, то пред-
предполагаем, что он априори юн. В случае d[ с самого начала известно,

310 Немонотонные модальные логики [Гл. 8
что любой человек, если он — студент, априорно юн.
Имеем запрос: Мария не юна. Каков ее статус? К F добавляем F? =
= -л Юн (Мария). В случае с (D,FUF?) ничто не может быть выведено,
кроме теорем, полученных из F. Единственное, что известно, это то,
что Мария не юна. Во втором случае для А5 = {D'', FUF?) расширение
Е$ содержит: ^Юн(Мария), Ст(Мария) —> Юн(Мария) и по кон-
трапозиции ^Ст(Мария). Аналогично, ^Од(Мария), ^Сож(Мария).
Таким образом, Мария — не студентка, не одинока и не сожительница.
Насколько правомерно применять контрапозицию?
6. Запрос: я не могу точно вспомнить, говорила ли Мария
мне о том, что она — студентка или одинока? Добавляем Fg =
= Ст(Мария) \/Од(Мария). В случае с (D, FUFg) мы не имеем ничего
касающегося Марии, в то время как при (D', F U Fg) расширение Eq
содержит: Ст(Мария) —> Юн(Мария), Од(Мария) —> Юн(Мария) и
Ст(Мария) V Од(Мария), и следовательно, Юн(Мария).
7. Если Мария — студентка и имеет детей, то каков ее статус?
Добавляем F4 = Ст(Мария) и F9 = Род(Мария). А7 = (D,FU {F4 U
U Fg}) допускает два расширения: Е? и Е'7. Каждое из них содержит:
Ст(Мария), Юн(Мария), Род(Мария) (используем d\). Кроме того, Е7
содержит: Жен(Мария) V Сож(Мария), ^Од(Мария) (полученное из
оЦ). Е'7 содержит: Од(Мария), ^Жен(Мария), ^Сож(Мария). В дан-
данном случае такая двойственность статуса Марии здесь нежелательна.
Поэтому предпочтительнее выбрать Е7, поскольку информация, со-
содержащаяся в сЦ, более специфична, чем та, которая получена из d\
и 6^2- Таким образом, в рассуждениях здравого смысла сЦ? касающееся
более конкретного случая, ведет себя как исключение по отношению
к общим правилам d\ и d^. Отсюда ему можно дать приоритет. Но
кто будет устанавливать эти предпочтения?
Выходом из создавшегося положения может быть введение по-
,„ Юн(ж) : -Род(ж) & Од(ж)
лунормальных умолчании типа а2 = -^ ^ —?-, что
Од(ж)
означает: «Быть родителем есть исключение из факта, что юная
персона должна быть априори одинокой». Пусть D" = (D\{d2}) U
U{d'{}. Тогда Ах7 = {D"\ FU{F4, ^9})} имеет единственное расширение
Е7, соответствующее здравому смыслу. Заметим, что (D", F U F±)
допускает то же самое расширение Ei, что и Ai.
Главный недостаток такого представления умолчаний заключает-
заключается в немодульности написания правил умолчания, т. е. добавление
новых исключений может потребовать добавления новых формул для
обоснования полунормальных умолчаний и, следовательно, модифи-
модификации уже существующих правил.
Для сохранения модульности с каждым умолчанием di будем свя-
связывать предикат утверждения ^г(х), означающий, что умолчание di

8.4] Логики умолчаний 311
может быть применено к х. Этих предикатов столько, сколько умол-
умолчаний. Для нашего примера имеем
_ CT(aQ:K)H(a:)fefli(aO
1 " Юн(ж)
,„ _ Юн(ж) : Од (ж) & R2(x)
d ;
,,„ _ Од(д) : Юн(х) & Д3(д)
3 " Юн(х)
,„ _ (Ст(ж) & Род(ж)) : ((Жен(ж) V Сож(х)) & Д4(ж)) _
4 ~ Жен(ж) V Сож(ж)
,„ _ Сож(ж) : Юн(х) & Д5(ж)
5 "
Для того, чтобы дать предпочтение d'l' над d'^, введем умолчание
dgX, которое блокирует d!^. Умолчание d!§ выражает тот факт, что
быть студентом и родителем не допускает вывода быть одиноким, если
он был юным, т. е.
,„, _ Ст(ж)&Род(ж):-.Д2(ж)&Д6(а:)
Имеем D1" = {d'l' -i- d'^'}. Умолчание d!§ играет здесь управля-
управляющую роль, указывая, что d'l' является исключением для d!^. В
этом случае А!" = {D'",F U {F4,Fg} имеет единственное расши-
расширение Е'7", которое содержит Ст(Мария), Юн(Мария), Род(Мария),
Жен(Мария) V Сож(Мария), ^Од(Мария), ^R2 (Мария) с сохранени-
сохранением модульности.
Установим соотношение между логикой умолчаний и АЭЛ. На
первый взгляд может показаться, что логика умолчаний менее выра-
выразительна, нежели АЭЛ, поскольку в ней нет возможности выводить
умолчания из других формул, так как они не являются частью языка.
Тем не менее, как это ни удивительно, Конолиге показал, что АЭЛ и
логика умолчаний эквивалентны. Эквивалентность здесь понимается
в том смысле, что расширения теории с умолчаниями являются точно
частью теории первого порядка, т. е. не содержащими оператор L фор-
формулами некоторого класса расширений АЭЛ, так называемых строго
основанных расширений. Понятие строгой основанности гарантирует,
что каждая замкнутая формула / имеет вывод, который не зависит
от Lf.
Конолиге показал, что каждая автоэпистемическая теория может
быть эквивалентно представлена в так называемой нормальной фор-
форме, в которой формулы имеют вид: ^La V LE\ V ... V LCn V 7? где
се, /?i,..., /Зп, 7 не содержат оператора L (^La и/или L/Зг могут быть
опущены).

312 Немонотонные модальные логики [Гл. 8
Такой вид формулы представляется как умолчание
а : -¦/?!,..., ~-/?п
7
и обратно (оператор L может быть опущен). Если предпосылка ^La
опущена, то предполагается, что она всегда истинна.
Например, если в АЭЛ мы имели
Ст(Петров) & ^Ь^Юн(Петров) —> Юн(Петров),
Ст(Петров):Юн(Петров)
то в нормальном умолчании -—^А /тт ^—— •
Пусть А — множество замкнутых формул АЭЛ в нормальной
форме и пусть Е — расширение для А. Пусть А' — множество за-
замкнутых формул ^La V LCi V ... V LCn V 7 для А такое, что ни одно
из /?i,... ,/Зп не содержится в Е. Расширение Е строго основано на
А тогда и только тогда, когда Е = {р \ A! U LAf U ^LE N$s p}, где
LA! — множество формул \Lp\p Е Ах}, ^LE — {^Lp\p ф Е}, a Nss
обозначает логическое следствие с ограничением модальных индексов
для устойчивых множеств (SS — stable sets).
Конолиге доказал следующую теорему.
Теорема 8.7. Для любого множества замкнутых формул А авто-
эпистемической логики имеется эффективно конструктивная теория
с умолчаниями (D, F) и обратно, для каждой теории с умолчаниями
(D,F) имеется эффективно конструктивное множество замкнутых
формул А автоэпистемической логики такое, что Е является рас-
расширением теории с умолчаниями тогда и только тогда, когда оно
является подмножеством теории первого порядка для расширений,
строго основанных на А.
Результат этой теоремы, доказанной Конолиге, удивителен. Мур
понимал свою логику как формализацию автоэпистемических рас-
рассуждений, но не как формализацию рассуждений по умолчанию.
Эквивалентность этих логик предполагает, что формы немонотонных
рассуждений хотя и различны, но как автоэпистемические рассуж-
рассуждения, так и рассуждения по умолчанию не обязательно требуют
различных формализации.
8.5. Системы поддержки истинности
К сожалению, немонотонные логики в их общей форме не явля-
являются даже полу разрешимыми, как это имеет место в классической
логике предикатов первого порядка. Но это ни в коей мере не означает,
что мы должны отказаться от создания автоматических решателей
проблем для немонотонного случая. Тот же Рейтер в своей логике
умолчаний предложил процедуру доказательства для нормальных

8.5] Системы поддержки истинности 313
умолчаний (см. разд. 8.4). Этерингтон дал недетерминированную про-
процедуру конструирования расширений произвольных конечных теорий
с умолчаниями. Конечность здесь означает то, что число переменных,
констант, предикатных символов и умолчаний конечно, к тому же в
его процедуре отсутствуют и функции. Г. Бревка в своей книге (см.
Литературный комментарий к главе 8) описал модальный решатель
для умолчаний, который может быть интерпретирован и для авто-
эпистемической логики. Здесь также на язык первого порядка был
наложен ряд ограничений, связанных с замкнутыми формулами, с
конечным числом констант и отсутствием функций.
В данном разделе мы остановимся на системах поддержки истин-
истинности (Truth Maintenance Systems — TMS) и на их двух разновидно-
разновидностях — системах поддержки истинности, основанных на обоснованиях,
и системах поддержки истинности, основанных на предположениях.
TMS используются для сохранения логической целостности за-
заключений системы вывода. Положенный в основу таких систем ме-
метод поддержки истинности реализован в рамках автономной системы
(как это сделали Дойл и ДеКлир), которая работает совместно с
решателем проблем и поддерживает вывод в единственном актив-
активном пространстве. Принцип функционирования системы состоит в
следующем. С каждым выведенным заключением связывается неко-
некоторая качественная характеристика, представляющая собой список
обоснований этого заключения. Каждое обоснование является спис-
списком тех заключений, исходя из наличия и/или отсутствия которых в
соответствии с некоторым правилом было непосредственно выведено
данное заключение. Возможность учета в правилах и обоснованиях
отсутствия заключений позволяет осуществить построение немоно-
немонотонных рассуждений. Все заключения, выведенные решателем, либо
принадлежат активному пространству (миру), либо находятся вне
его. Активному пространству принадлежат все исходные данные, а
также все заключения, имеющие хотя бы одно обоснование в активном
пространстве. Будем называть такое обоснование действительным.
В ходе вывода решатель может делать предположения, т. е. вводить
в активное пространство заключения, не имеющие действительных
обоснований.
При выводе некоторого заключения его характеристика расширя-
расширяется за счет обоснования, представляемого правилом вывода. Здесь
возможен следующий случай. Пусть правило подтвердило некоторое
заключение, находящееся в настоящий момент вне активного про-
пространства. В результате заключение получило действительную под-
поддержку и вышло в активное пространство, что может привести к тому,
что некоторые обоснования для следствий из этого заключения станут
действительными, т. е. тоже перейдут в активное пространство. Если
в активном пространстве вывелось противоречие, то это означает, что

314 Немонотонные модальные логики [Гл. 8
лежащее в его основе множество предположений является противо-
противоречивым, несовместным. Чтобы выявить это множество, выполняется
процедура возврата по зависимостям. В результате одно из предполо-
предположений удаляется из активного пространства. Несовместимое множе-
множество предположений запоминается, чтобы в будущем не повторилась
данная ситуация, и все следствия из удаленного предположения также
удаляются из активного пространства.
Интеллектуальные системы, поддерживающие пересматриваемые
рассуждения, должны строго обосновывать каждый вывод заклю-
заключения и затем в свете появившихся новых убеждений пересматри-
пересматривать поддержку такого заключения. Один из способов решения этой
проблемы заключается в пересмотре алгоритма бектрекинга. Исто-
Исторически бектрекинг был катализатором создания систем поддержки
истинности. Бектрекинг является систематическим методом исследо-
исследования всех альтернатив точек решения в проблемах, основу которых
составляет поиск. Однако существенным недостатком классического
алгоритма бектрекинга является то, что он систематически (и всле-
вслепую) возвращается назад по дереву решений из тупиковых состоя-
состояний и ищет следующую альтернативу для выбора. Такой бектрекинг
иногда называют хронологическим бектрекингом. Естественно, такая
систематическая проверка всех альтернатив поиска решений неэф-
неэффективна, требует много времени и для больших пространств поиска
часто бесполезна.
Для избежания избыточных вычислений было бы желательно в
процессе поиска возвратиться сразу в ту точку поиска, где име-
имеется конфликтная ситуация, пропуская промежуточные точки, ко-
которые вели бы к ней в процессе систематического осмотра. Такой
бектрекинг называется зависимо-направленным (dependency-directed
backtracking).
Рассмотрим пример для немонотонных рассуждений. Нам требу-
требуется обнаружить некое утверждение р, которое непосредственно не
выводимо. Однако имеется правдоподобное предположение q, которое,
если оно истинно, будет поддерживать р. Итак, если q предполагается
истинным, то р выводимо. Продолжая наше рассуждение и основыва-
основываясь на р, мы делаем заключения о г и s. Но мы в процессе рассуждений
нашли заключение о t и и, не прибегая к поддержке р, г и s. Наконец,
приходим к выводу, что наше раннее предположение q ложно. Что
делать в данном случае? Хронологический бектрекинг будет пере-
перепроверять наши шаги рассуждений, идя в обратном порядке отно-
относительно того, в котором они были сделаны. Зависимо-направленный
бектрекинг сразу будет идти обратно к источнику противоречия, а
именно к первому предположению q. После этого отменяются р, г и s.
Конечно, мы можем проверить, можно ли вывести г и s независимо
от р и q, так как их поддержка может быть осуществлена из других

8.5] Системы поддержки истинности 315
источников. Наконец, так как t и и были выведены независимо от р,
г и 5, нам не нужно их пересматривать.
Таким образом, для применения зависимо-направленного бектре-
бектрекинга в системе рассуждений мы должны
• связать каждое произведенное заключение с его обоснованием.
Обоснование должно содержать все факты, правила и предпо-
предположения, использованные для вывода этого заключения;
• обеспечить механизм нахождения ложного предположения с об-
обоснованием, ведущим к противоречию;
• отменить ложное предположение;
• создать механизм для отслеживания отменяемого предположе-
предположения и отменить любое заключение, использующее в рамках сво-
своих обоснований отменяемое предположение.
Конечно, отменяемые заключения необязательно должны быть
ложными, они могут быть перепроверены, если появятся какие-либо
обоснования.
Мы представим два типа систем поддержки истинности с
зависимо-направленным бектрекингом. Первой подобной системой
является система поддержки истинности, основанная на обосновании.
8.5.1. Системы поддержки истинности, основанные на обоснованиях
Одна из самых ранних систем поддержки истинности была раз-
разработана Дойлом и называлась системой поддержки истинности,
основанной на обосновании (Justification-Based Truth Maintenance
System — JTMS). JTMS была автономной системой, связанной с реша-
решателем проблем, и снабжающей решатель информацией о том, каким
утверждениям следует верить, основываясь на текущих обоснованиях.
JTMS имеет три главных операции: inspection (инспектирование),
modification (модификация) и updating (обновление). С помощью пер-
первой операции система инспектирует сеть обоснований, получая от ре-
решателя проблем запросы типа: «Следует ли верить утверждению р?»,
«Почему следует верить утверждению р?», «Какие предположения
лежат в основе утверждения р?».
Назначение второй операции заключается в модификации сети за-
зависимостей информацией от решателя проблем. Модификации вклю-
включают добавление новых утверждений, добавление или удаление по-
посылок, добавление противоречий и обоснование убеждения (веры) в
данное утверждение.
С помощью третьей операции происходит обновление сети зависи-
зависимостей. Операция обновления перевычисляет метки всех утверждений
методом, не противоречащим текущим обоснованиям.
Приведем пример построения сети зависимостей для следующих
утверждений.

316
Немонотонные модальные логики
[Гл.,
Рис. 8.1
1. Если кто-то — прилежный студент и это не противоречит тому,
что он хорошо учится, то он действительно хорошо учится:
\/ж(Ст_прил(ж) & МУч_хор(ж) —> Уч_хор(ж)).
2. Лентяи учатся плохо: Уг/(Лен(г/) —>¦ —1"Уч_хор(г/)).
3. Петров — прилежный студент: Ст_прил(Петров).
4. Петров — лентяй: Лен(Петров).
Введем графическую нотацию для обоснований.
Обоснование посылки (факта) показано на рис. 8.1.
Обоснование вида < iVi,..., N3; | JV^+i,..., iVm —>
—> iV >, где iVb ...,Nj — IN-вершины, iVj+i,...,
Nm — OUT-вершины, a N — следствие (консеквент) обоснования,
представлено на рис. 8.2. Вершины могут рассматриваться как уни-
уникальные имена для формул, ассоциированных с ними. Интуитивно
обоснования могут читаться так:
«Если мы убеждены (IN) в вер-
вершинах N\,..., Nj;, а в вершины
iVj+i,..., Nm не верим (OUT), то в
вершину N следует верить (IN)».
Обоснования без OUT-вершин
называются монотонными обосно-
обоснованиями. Если как OUT-, так и IN-
вершины отсутствуют, обоснование
называется обоснованием посылок.
Разметка сети зависимостей
должна обладать следующими
свойствами:
• вершина размечена IN тогда и
только тогда, когда имеется, по крайней мере, одно истинное обоснова-
обоснование для нее. Отсюда обоснование общезначимо тогда и только тогда,
когда, находясь в состоянии убеждения (веры), все ее IN-вершины
размечены IN, а все ее OUT-вершины — OUT;
• для каждой вершины, отмеченной IN, существует нециклический
аргумент, т. е. вершина не может обосновывать саму себя.
Сеть обоснования убеждения, что Петров хорошо учится, показана
на рис. 8.3. Из рисунка видно, что для поддержки этого заключения на
вентиль нужно подать убеждение, что Петров — прилежный студент,
и взять отрицание от убеждения ^Уч_хор(Петров).
Рис. 8.2
Уч_хор(ПетровI
Рис. 8.3

8.5] Системы поддержки истинности 317
Имея такую информацию от данной сети обоснований, решатель
проблем убежден, что посылка Уч_хор(Петров) истинна, и так как
нет других доводов, то нет и никакого противоречия в том, что
прилежные студенты хорошо учатся.
Теперь предположим, что добавлена посылка обоснования
Лен(Петров), т.е. соответствующая ей вершина будет размечена
как IN. Это добавление приводит к заключению, что Петров учится
плохо (^Уч_хор(Петров)), и убеждение Уч_хор(Петров) больше
не поддерживается. Обоснование этой новой ситуации отражено на
рис. 8.4.
ГЛ Г
V*4 Ст_прил(Петров)
IN1— ^
Рис. 8.4
Как видно из рис. 8.3 и 8.4, JTMS представлена сетью зависимо-
зависимостей, которая рассматривает только отношения между атомарными
утверждениями и их отрицаниями, а затем организует их в отношение
поддержки того или иного убеждения.
Следует заметить, что JTMS имеет дело только с зависимостями
между убеждениями и не касается содержимого самих убеждений, т. е.
убеждения можно просто заменить идентификаторами типа ni, П2,...,
которым соответствуют вершины в сети.
Применяя операции модификации и обновления, сеть обоснований
может перестраиваться, меняются также обоснования путем возврата
по самой сети с помощью зависимо-направленного бектрекинга. Име-
Имеются также более современные системы, в которых JTMS и решатель
проблем объединены в единое представление (см. литературный ком-
комментарий к главе 8).
8.5.2. Системы поддержки истинности, основанные на
предположениях
Вторым типом систем являются системы поддержки истинности,
основанные на предположениях (Assumption-Based Truth Maintenance
Systems — ATMS). Термин «основанный на предположениях» был
введен ДеКлиром, хотя идеи, связанные с предположениями, выдви-
выдвигались также Мартинсом и Шапиро.
Как и в случае с TMS, ATMS реализована в виде автономной
подсистемы, которая может работать совместно с различными типами
решателей, ориентированных на логику предикатов первого порядка.
Допускается расширение метода на случай решателя проблем, исполь-
использующего немонотонные правила вывода.

318 Немонотонные модальные логики [Гл. 8
Рассмотрим суть метода поддержки истинности, основанного на
предположениях. С выводимыми заключениями, как и в TMS, сопо-
сопоставляются качественные характеристики, образованные из списков
обоснований, но в ATMS каждое обоснование содержит не только
список посылок правила, исходя из которого было получено заклю-
заключение, но и список предположений, принятие которых позволило его
вывести, т. е. контекст пространства, в котором выведено заключение.
Основные операции ATMS заключаются в построении обоснований
заключений, исходя из обоснований посылок применяемых правил,
а также в анализе обоснований противоречий. Вывод противоречия
говорит о несовместности предположений, в рамках которых сде-
сделан вывод. При появлении противоречивых множеств предположе-
предположений происходит просмотр обоснований всех имеющихся к данному
моменту заключений и удаление тех контекстов, в которые входят
противоречивые множества.
ATMS позволяет строить интерпретации для выводимых решате-
решателем вариантов решений. Возможны различные способы связи реша-
решателя с ATMS для реализации различных стратегий вывода решений.
К достоинствам данного метода относится то, что он сохраняет все
выведенные промежуточные результаты, что значительно повышает
эффективность поиска решений с возвратами. Метод предоставляет
возможность одновременной работы с различными альтернативными
решениями, например с помощью метаправил. Принципы работы с
обоснованиями являются наиболее простыми среди методов данной
группы: обработка обоснований сводится к операциям над множе-
множествами. Метод допускает наиболее эффективную реализацию, обеспе-
обеспечивает простую настройку на различные стратегии решения задач и
типы решателей, предоставляет большие возможности по управлению
функционированием ATMS.
Контекст ATMS — это множество предположений, сформирован-
сформированное в соответствии с предположениями о непротиворечивости окруже-
окружения, которое состоит из всех вершин, выведенных из этих предполо-
предположений.
Характеристическое окружение для контекста — множество
предположений, из которых может быть получена каждая вершина
контекста. Каждый контекст имеет, по крайней мере, одно характе-
характеристическое окружение, и когда предположения не имеют никаких
обоснований, обычно контекст имеет только одно характеристическое
окружение.
В данной системе, в отличие от JTMS, метки являются множе-
множествами посылок (предположений) и строятся самой ATMS. ДеКлир
различает вершины-посылки, которые выполняются как универсаль-
универсально квалифицированные формулы, и вершины, которые могут быть
предположениями, сделанными решателем проблем, и которые позже
могут быть отменены.

8.5]
Системы поддержки истинности
319
Преимущество ATMS по сранению с JTMS заключается в доба-
добавочной гибкости, которую ATMS обеспечивает при рассмотрении мно-
многих возможных состояний убеждения (веры). Посредством разметки
убеждений множеством посылок, при котором они выполняются, име-
имеем не одно состояние убеждения (в JTMS все вершины, отмеченные
IN), а ряд возможных состояний, т.е. множество всех подмножеств
поддерживающих посылок. Создание различных множеств убежде-
убеждений или возможных миров допускает сравнение результатов, полу-
полученных от различных выборов посылок, существование различных
решений, обнаружение противоречий и их разрешение.
Целью вычислений ATMS является нахождение минимального
множества посылок, достаточных для поддержки каждой вершины
сети. Метка минимальна, если никакое окружение метки не является
надмножеством других окружений, т. е. для любой метки с окружени-
окружением Е не должно существовать другой метки с окружением Е' такой,
что Е1 С Е. На примере, взятом у Мартинса, покажем распростране-
распространение и комбинирование меток.
Пример 8.12.
Пусть мы имеем ATMS-сеть, представленную на рис. 8.5. В этой
сети ni, П2, пз и П4 являются посылками (предположениями), и пред-
предполагается, что они истинны. Сеть зависимостей отражает различные
связи. Так, посылки п\ и П2 служат для поддержки п^, которая в
свою очередь поддерживает щ, поддерживаемую также пз- Посылки
пз и П4 поддерживают tiq, поддерживающую щ (заметим, что пз
поглощает пз & п±, т. е. пз V пз & п^ = пз).
D—©«¦>»
((nh п2), щ)
К(щ))
Рис. 8.5
Так как каждое непротиворечивое окружение характеризует кон-
контекст, то если имеется п предположений, то контекстов будет 2П.
Рис. 8.6 демонстрирует решетку окружений для предположений (ni,
П2, пз, П4). Вершины на решетке представляют собой окружения.
Просматривая решетку снизу вверх, можно найти все надмножества
окружений, а идя сверху вниз — все подмножества окружений.

320
Немонотонные модальные логики
[Гл.,
Решетка подмножеств посылок дает способ визуализации про-
пространства комбинаций посылок, и если некоторая посылка «подозри-
«подозрительна» (т.е. убеждение в ее истинности ставится под сомнение), с
помощью решетки можно определить ее связь с другими подмноже-
подмножествами поддержки посылок. Так, например, вершина п$ на рис. 8.5
будет поддержана всеми множествами посылок, которые находятся
наверху (щ, п2) в решетке рис. 8.6.
(щ, щ)
ATMS удаляет противоречия путем вычеркивания из вершин тех
множеств посылок, которые оказались противоречивыми. Например,
надо пересмотреть поддержку рассуждений для случая, когда верши-
вершина П5 (рис. 8.5) оказалась противоречивой. Поскольку метка для n$
есть (ni, П2), то, естественно, это множество посылок определяется
как противоречивое. При обнаружении этого противоречия все мно-
множества посылок, находящиеся в отношении надмножества к (ni, П2)
на рис. 8.6, размечаются как противоречивые (на рис. 8.6 они обведены
овалами) и удаляются из сети зависимостей. В этой ситуации одна из
возможных разметок, поддерживающая вершину щ рис. 8.5, должна
быть удалена.
Кроме рассмотренных систем поддержки истинности имеется еще
ряд других. Так, в TMS, основанной на логике (Logic-Based TMS —
LTMS), утверждения представлены клозами, которые могут быть ис-
использованы для вывода истинностных значений других утверждений.
Система LTMS очень похожа на JTMS. Кроме того, имеется также
система рассуждений, работающая с многократными убеждениями
(Multiple Belief Reasoner — MBR), аналогичная ATMS, за исключе-
исключением того, что решатель проблем и TMS объединены в одну систему.
Подробнее о различных видах систем поддержки истинности можно
прочитать в Литературном комментарии к главе 8.

Существует достаточно
света для тех, кто хочет ви-
видеть, и достаточно мрака для
тех, кто не хочет.
Б. Паскаль
Глава 9
НЕМОНОТОННЫЕ ЛОГИКИ В ЛОГИЧЕСКОМ
ПРОГРАММИРОВАНИИ
Формализмы немонотонного вывода обеспечивают изящную се-
семантику для логического программирования (в частности, объяс-
объясняя отрицание как неудачу). Они позволяют понять, как логическое
программирование может быть использовано для формализации и
решения некоторых задач в области искусственного интеллекта. В
то же время теория немонотонного вывода получает практическое
применение благодаря существованию процедур логического програм-
программирования.
В логическом программировании истина понимается в автоэпи-
стемическом смысле: истина — это доказуемость на основании зна-
знаний агента. Возможна ситуация, когда не удается доказать ни само
утверждение, ни его отрицание, находясь на данном уровне знаний,
тогда истинностное значение этого утверждения не определено. Сле-
Следовательно, не выполняется закон исключенного третьего: q\/->q (это
правило при необходимости требуется явно указывать в программах).
Процедурная природа логического программирования требует,
чтобы каждое заключение имело поддержку в виде некоторого опре-
определенного правила, тело которого используется для вычисления зна-
значения истины, а его головой является данное заключение. Этим
логическое программирование отличается от анализа ситуаций, где
применимы альтернативные правила. То есть заключения должны
быть процедурно обоснованы известными фактами, и запрещается
переходить к заключениям, к которым не было явного обращения.
Пролог широко известен как язык логического программирования.
Он успешно применяется для решения некоторых задач искусствен-
искусственного интеллекта, но, к сожалению, страдает рядом недостатков:
11 В.Н. Вагин и др.

322 Немонотонные логики в логическом программировании [ Гл. 9
1) допустимы отрицательные заключения, но они выводятся толь-
только по умолчанию (или неявно), то есть в случае, когда по-
позитивное заключение не достигается за конечное число шагов
(основная форма Предположения о замкнутости мира);
2) используемый вид отрицания может работать с неполной инфор-
информацией, предполагая ложным все, что не оказывается истинным
за конечное число шагов. Но остаются бесконечные вычисления
даже для конечных программ.
Рассмотрим простой пример, иллюстрирующий п.1. Предполо-
Предположим, что необходимо запрограммировать следующее утверждение:
«Школьный автобус может пересекать железную дорогу при усло-
условии, что нет приближающегося поезда». Как известно, в Прологе
для выражения отрицания используется оператор not, реализованный
правилами
not(P) :- Р, l.fail.
not(P).
Тогда приведенное предложение будет представляться правилом:
пересекать :- по1:(поезд).
Но в этом случае разрешается пересекать дорогу, когда нет информа-
информации ни о присутствии, ни об отсутствии поезда. Здесь лучше было бы
использовать явное отрицание (->)
пересекать :- ^поезд.
Это правило утверждает: «Автобус может пересекать железную
дорогу, если водитель уверен, что нет приближающегося поезда».
Перед нами стоит следующая задача: «Найти такую семантику,
которая подходящим образом определяла бы смысл программ». В
качестве такой семантики мы рассмотрим фундированную семантику
для расширенных логических программ (Well Founded Semantics for
eXtended logic programs — WFSX). Эта семантика использует два вида
отрицания: явное и неявное. В результате возникают противоречия,
для которых требуется специальная обработка. Например, разреша-
разрешается принимать не все предположения по умолчанию, а только те,
которые не приводят к противоречию.
Преимуществами фундированной семантики для расширенных ло-
логических программ являются: выразительность, возможность обра-
обработки циклов, характеризация и объединение различных форм выво-
вывода. WFSX обладает следующими структурными свойствами:
• простота: используется всего два итеративных оператора фик-
фиксированной точки без привлечения трехзначной логики;
• кумулятивность: добавление лемм не изменяет семантики про-
программы;
• рациональность: семантика не изменяется при применении от-
отрицания к недоказуемому утверждению;

9.1] Семантика логических программ 323
• релевантность: нисходящее вычисление истинностного значе-
значения литеры использует только граф вызовов, расположенный
ниже этой литеры.
С помощью фундированной семантики WFSX можно представ-
представлять вывод по неполной информации, абдуктивный вывод, вывод с
умолчаниями; выполнять обработку противоречий. Этой семантике
соответствуют такие формы представления знаний, как правила, пра-
правила с умолчаниями, исключения и др.
9.1. Семантика логических программ:
краткий обзор
9.1.1. Нормальные логические программы
В этом разделе мы рассмотрим
• язык нормальных логических программ, определения;
• ранние подходы к семантике нормальных программ и их свойс-
свойства;
• устойчивые модели и фундированную семантику как новые и
важные семантические базисы.
9.1.1.1. Язык нормальных логических программ. Введем ряд
обозначений и определений:
• А — алфавит языка Lang — это конечное или бесконечное мно-
множество констант, предикатных и функциональных символов и
счетное множество различных символов переменных;
• Терм над А определяется рекурсивно: переменная; константа;
выражение вида /(ti,..., tn), где / — функциональный символ
A, ti — термы;
• Атом над А — это выражение вида p(?i, ...,?n), где р — преди-
предикатный символ A, ti — термы;
• Литера — это атом А или его отрицание not А. Литеры по
умолчанию (defaults) имеют вид not A.
• Терм называется фундаментальным, если он не содержит пе-
переменных. Множество всех фундаментальных термов (атомов)
над А называется универсумом (базой) Эрбрана Н.
• Нормальная логическая программа — это множество правил
вида: Н <— Li,..., Ln (n ^ 0), где Н — атом и Li — литеры,
символ «,» обозначает конъюнкцию. Правила вида «Н <—» за-
записываются как Н.
• Нормальная логическая программа определена тогда и только
тогда, когда ее правила не содержат литер по умолчанию.
11*

324 Немонотонные логики в логическом программировании [ Гл. 9
• Фундаментальная версия нормальной логической программы
Р — это (может быть, бесконечное) множество фундаменталь-
фундаментальных правил, полученных из Р заменой всеми возможными спо-
способами каждой переменной элементом из универсума Эрбрана.
В дальнейшем будем считать, что алфавит А содержит все символы
рассматриваемой программы Р и ничего больше. Определим теперь
двузначные и трехзначные эрбрановские модели и интерпретации
нормальных логических программ.
Определение 9.1. (Двузначная интерпретация). Двузнач-
Двузначная интерпретация I нормальной логической программы Р — это
любое подмножество базы Эрбрана Н программы Р.
Любая двузначная интерпретация может рассматриваться как
множество Т U notF (здесь notjai,..., ап} = {not ai,.. .,not an}), где
T — множество атомов, истинных в /, и F = Н \Т — множество
атомов, ложных в /. Любой атом либо истинен, либо ложен, т. е.
Н= Т U F. Интерпретации программы Р могут рассматриваться как
«возможные миры», представляющие возможные состояния наших
знаний о смысле Р. Так как эти знания могут быть неполными,
возникает необходимость описывать неопределенные атомы.
Определение 9.2. (Трехзначная интерпретация). Под
трехзначной интерпретацией I программы Р понимается множество
TU not F, где Т и F — непересекающиеся подмножества эрбрановской
базы Н программы Р.Т — часть /, содержащая все фундаментальные
атомы, истинные в /, а F — все фундаментальные атомы, ложные в /;
истинностное значение оставшихся атомов не определено. Очевидно,
двузначные интерпретации — частный случай трехзначных.
Утверждение 9.1. Любая интерпретация / = Т U not F может
быть эквивалентно представлена функцией /: Н —> У, где V =
= {0,1/2,1}, определяемой следующим образом:
{О, если not A G /
1, еслиАе/
1/2 — в противном случае
Для определения модели нам потребуется функция оценки истин-
истинности.
Определение 9.3. (Оценка истинности). Если / — интерпре-
интерпретация, то оценка истинности /, соответствующая /, это функция,
которая определяется рекурсивно:
/ : С —>¦ V, где С — множество всех формул языка.
• Если А — фундаментальный атом, то 1(А) = 1(А).
• Если S — формула, то I(notS) = 1—I(S).

9.1] Семантика логических программ 325
• Если S и V — формулы, то
?, V)) = min(/Ef), /(V)) (здесь запись (S,V) представляет
конъюнкцию S&V);
— /(У <— S) = 1, если 7E) < I(V); в противном случае I(V <— 5) =
= 0.
Определение 9.4- (Трехзначная модель). Трехзначная ин-
интерпретация 7 называется трехзначной моделью программы Р тогда
и только тогда, когда для каждого фундаментального примера пра-
правила программы Н <— В выполняется: 7(i7 <— В) = 1.
Двузначная модель определяется аналогично трехзначной. В даль-
дальнейшем нам потребуются определения упорядочений интерпретаций
и моделей.
Определение 9.5. (Классическое упорядочение). Если 7 и J —
две интерпретации, то мы говорим, что 7 ^ J , если 7(А) ^ J(A)
для любого фундаментального атома А. Если / — набор интерпрета-
интерпретаций, то интерпретация I E I называется минимальной в /, если не
существует интерпретации JeI: J^InJ^I. Интерпретация
7 называется наименьшей в /, если I ^ J для любой интерпретации
J Е I. Модель М программы Р минимальная (наименьшая), если она
минимальная (наименьшая) среди всех моделей Р.
Определение 9.6. (Упорядочение по Фиттингу). Если 7 и J —
две интерпретации, то мы говорим, что Ip ^ J, тогда и только тогда,
когда 7 С J. Если / — набор интерпретаций, то интерпретация I E I
называется F-минимальной в /, если не существует интерпретации
Jg/:Jf^7hJ^7. Интерпретация 7 называется F-наименьшей в
/, если Ip ^ J для любой интерпретации J Е I. Модель М программы
Р F-минимальная G^-наименыпая), если она 7^-минимальная (F-
наименыпая) среди всех моделей Р.
Заметим, что классическое упорядочение соответствует количе-
количеству истинных атомов, а упорядочение по Фиттингу — количеству
информации (определенности).
9.1.1.2. Семантика. Прежде всего попытаемся ответить на во-
вопрос: «Зачем необходимо определять точный смысл или семантику ло-
логических программ?» Декларативная семантика, которую мы и бу-
будем изучать, обеспечивает математически точное определение смысла
программы, не зависящее от процесса ее выполнения. Процедурная
семантика — это процедурный механизм, способный давать ответы
на запросы. Корректность такого механизма определяется сравнением
его работы со спецификацией, полученной по декларативной семан-
семантике. Без декларативной семантики пользователю потребовалось бы
знание всех процедурных аспектов, чтобы писать корректные про-
программы. Приведем примеры определения декларативной семантики.

326 Немонотонные логики в логическом программировании [ Гл. 9
Семантика наименьшей модели определяется с помощью мини-
минимизации позитивной информации, т. е. она ограничивается факта-
фактами, явно вытекающими из программы. Все остальное предполагается
ложным (Предположение о замкнутости мира).
Пример 9.1.
Предположим, программа имеет вид
способный_математик(Х) <— физик(Х)
физик(Эйнштейн)
президент(Сорес)
Для этой программы существует несколько двузначных моделей.
Наибольшая из них предполагает, что Эйнштейн и Сорес одновремен-
одновременно президенты, физики и способные математики. Вряд ли такое описа-
описание можно считать корректным. Естественнее считать, что отсутствие
дополнительной информации говорит о том, что можно допустить
противное. В этом случае мы получим наименьшую двузначную мо-
модель:
{ физик (Эйнштейн), способный _ математик (Эйнштейн),
президент (Сорес)}.
Так как единственная наименьшая модель существует для любой
определенной программы, то можно определить семантику наимень-
наименьшей модели для таких программ: атом А истинен в программе Р
тогда и только тогда, когда он принадлежит наименьшей модели Р (в
противном случае значение А ложно). Недостатком такой семантики
является то, что она не может применяться к программам с отрица-
отрицанием по умолчанию. Действительно, пусть Р = {р <— not q} , тогда
существуют две минимальные модели: {р} и {д}, и, следовательно, не
существует наименьшей модели.
Пополнение (completion) предикатов Кларка было предложено для
определения семантики нормальных логических программ с отрица-
отрицанием по умолчанию. В основе определения семантики лежала сле-
следующая идея: «Мы часто используем слово «если», когда имеем в
виду «тогда и только тогда»». Например, программа, описывающая
натуральные числа, имеет вид
нат(О)
нат(след(Х)) <— нат(Х)
Отсюда не следует, что только 0, 1,... — натуральные числа.
Вероятно, имелось в виду следующее:
нат(Х) & X = 0V (ЗУ : X = след (Y) & нат(У)).
Семантика пополнения программы Р определяется двузначной мо-
моделью пополнения для Р. Эта семантика также имеет некоторые недо-
недостатки. Так, пополнение непротиворечивых программ может быть
противоречиво. Например, для программы {р <— not p} пополнением
будет программа {р -Ф=> not p}.

9.1] Семантика логических программ 327
Семантика Фиттинга для нормальных логических программ
представляет собой трехзначное обобщение моделей Кларка. Эта се-
семантика не является рекурсивно перечислимой. К сожалению, се-
семантика Фиттинга унаследовала некоторые проблемы, связанные с
семантикой пополнений Кларка. Рассмотрим пример.
Пример 9. 2.
Пусть программа определяется правилами
ребро (а, Ъ)
ребро (с, d)
ребро (d, с)
достижимо (а)
достижимо (X) <— достижимо (Т), ребро (Y,X)
Эта программа определяет, какие вершины достижимы из верши-
вершины а орграфа. С помощью семантики Фиттинга нельзя заключить,
что вершины cud недостижимы из а. Эта трудность связана с тем,
что существуют симметричные правила: ребро (с, d) и ребро (d, с).
Обнаружен и еще один недостаток семантики пополнений (как
двух-, так и трехзначной): она плохо представляет транзитивное за-
замыкание. После первых не совсем удачных попыток исследователи
предложили определять семантику для программ из некоторого уз-
узкого класса.
9.1.1.2.1. Семантика устойчивых моделей. Идея, лежащая в
основе этой семантики, пришла из формализмов немонотонного
вывода: литеры-умолчания not А, которые могут приниматься
или отвергаться, понимаются в эпистемическом смысле, т. е.
считается, что А не предполагается. Если истина присваивается
некоторому множеству литер по умолчанию (гипотез), а ложь —
остальным, то получаются некоторые следствия в соответствии с
семантикой определенных программ. Если эти следствия полностью
подтверждают исходные гипотезы, то они и образуют устойчивую
модель.
Определение 9.7. (Оператор Гельфонда —Лифшица). Пусть Р —
нормальная логическая программа и / — двузначная интерпретация.
Р
GL-трансформация Р по модулю / — это программа —, полученная
из Р с помощью выполнения следующих операций:
• удалить из Р все правила, содержащие литеры по умолчанию
not А такие, что А Е /;
• удалить из оставшихся правил все литеры по умолчанию.
Р
Так как — — определенная программа, то существует единствен-
единственная наименьшая модель J. Мы определяем Г(/) = J. Из приведенного

328 Немонотонные логики в логическом программировании [ Гл. 9
определения следует, что фиксированные точки оператора Г для про-
программы Р всегда являются моделями Р.
Определение 9.8. (Семантика устойчивых моделей). Двузнач-
Двузначная интерпретация / логической программы Р есть устойчивая мо-
модель Р тогда и только тогда, когда Г(/) = /. Атом А программы Р
истинен по отношению к семантике устойчивой модели тогда и толь-
только тогда, когда А принадлежит всем устойчивым моделям программы
Р.
Пример 9.3.
Пусть программа Р задается правилами
а <— not b
b <— not a
с <— not d
d <— not e
p^b
Устойчивыми моделями Р являются I\ = {p, a,d} и /2 = {p, 6, d},
поэтому pud истинны в семантике устойчивых моделей. Трансфор-
Р
мация это программа
h
а <—
р ^ а
р <— 6
Тогда F(/i) = {р, a,d} = /1, т.е. 1\ — действительно устойчивая
модель. Аналогично можно проверить, что и 1^ является устойчивой
моделью.
Семантика устойчивых моделей не всегда может успешно приме-
применяться. Для некоторых программ не существует устойчивых моделей.
Например, пусть Р = {a <— not а}. Тогда либо а Е /, либо а ф I. В
первом случае правило удаляется из Р, и а ^ Г(/), тогда / ф Г(/) и
Р
в результате / не является устойчивой моделью. Во втором случае —
не содержит not a, поэтому а Е Г(/) и снова / ф Г(/).
Даже для программ, имеющих устойчивые модели, их семантика
не всегда приводит к желаемым результатам. Так у программы Р
а <— not b
b <— not a
с <— not a
с <— not с
существует единственная устойчивая модель / = {с, Ь}. Трансформа-
Р
ция это программа

9.1] Семантика логических программ 329
поэтому {с, Ь} — наименьшая модель, а Ъ и с — следствия семантики
устойчивых моделей для Р. Если добавить с к Р, то Ъ не будет след-
следствием программы в этой семантике, так как устойчивыми моделями
в этом случае будут 1\ = {с, Ь} и 1^ = {с, а}. Другими словами, в се-
семантике устойчивых моделей нарушается свойство кумулятивности.
Более того, по программе Р нельзя вывести следствие 6, используя
нисходящие методы. Действительно, начав с цели <— 6, процедура
достигнет только первых двух правил, откуда Ъ вывести не удается,
т. е. нарушается свойство релевантности.
Вычисление устойчивых моделей является NP-полной задачей
даже для простых классов программ (например, логических
программ исчисления высказываний). Кроме того, из-за исполь-
использования двузначной интерпретации теряется выразительность
семантики.
9.1.1.2.2. Фундированная семантика. Эта семантика свободна от
недостатков семантики устойчивых моделей и представляет собой
естественное обобщение для случая трехзначных интерпретаций.
Для формализации понятия частичных устойчивых моделей язык
программ расширяется добавлением пропозициональной константы
и, которая не определена в любой интерпретации, т. е. для любой
интерпретации /: /(u) = /(not и) = 1/2. В неотрицательной про-
программе посылки являются либо атомами, либо и. Для любой неот-
неотрицательной программы существует трехзначная наименьшая мо-
модель.
Определение 9.9. (Г*-оператор). Пусть Р — нормальная ло-
логическая программа и пусть / — трехзначная интерпретация. Рас-
Р
ширенная GL-трансформация Р по модулю / — это программа —,
полученная из Р выполнением следующих операций:
• удалить из Р все правила, содержащие литеры по умолчанию
not А такие, что 1(А) = 1;
• заменить в оставшихся правилах Р такие литеры not А, для
которых 1(А) = 1/2, на и;
• удалить из оставшихся правил все литеры по умолчанию.
Существует единственная трехзначная модель J. Мы определяем
г* (/) = J.
Определение 9.10. (Фундированная семантика). Трехзначная
интерпретация / логической программы Р — это частичная устойчи-
устойчивая модель Р тогда и только тогда, когда Г*(/) = /. Фундированная
семантика Р определяется единственной F-наименыпей частичной
устойчивой моделью Р и может быть получена с помощью (восходя-
(восходящей) итерации Г*, начиная от пустой интерпретации.

330 Немонотонные логики в логическом программировании [ Гл. 9
Пример 9. 4.
Для программы Р из примера 9.3 фундированная модель находит-
находится с помощью итераций оператора Г*, начиная с пустой интерпрета-
интерпретации:
1) Г*({}) — наименьшая трехзначная модель для программы:
а <— и
Ь<- и
с <— и
d <— и
р <— а
Г*({}) = {not e}
2) Г*({not e}) — наименьшая трехзначная модель для программы:
а <— и
6^ и
с ^— и
р ^— а
р ^— 6
Г*({not e}) = {d, not e}
3) F*({d, not e}) — наименьшая трехзначная модель для программы:
а <— и
6^ и
р ^— а
р <— 6
F*({d, not e}) = {d, not e, not с}
4) F*({d, not e, not с}) — наименьшая трехзначная модель для про-
программы:
а <— и
6^ и
d^
р <— а
р ^— Ъ
F*({d, not e, not с}) = {d, not e, not с} — это и есть фундированная
модель. Очевидно, по этой модели выходит, что d — истина, е и с —
ложь, а, Ъ и р не определены.
9.1.2. Расширенные логические программы
В логических программах для дедуктивных баз знаний, пред-
представления знаний и немонотонного вывода полезно применять явное
отрицание —<. В этом разделе мы рассмотрим
• обоснование введения двух отрицаний;

9.1] Семантика логических программ 331
• расширение языка программирования для учета явного отрица-
отрицания;
• обзор различных видов семантики.
В нормальных логических программах негативная информация
представляется неявно, т. е. невозможно явно утверждать ложность,
и высказывания считаются ложными, если нет причин верить в их
истинность. В некоторых случаях это действительно необходимо. На-
Например, база данных явно утверждает, что существует связь между
пунктами, и отсутствие связи говорит о том, что соединения не су-
существует. Но в других случаях приходится сталкиваться с серьезным
ограничением. Явная негативная информация играет важную роль в
естественных рассуждениях и выводе здравого смысла.
Рассмотрим пример: пусть имеется утверждение о студентах-
заочниках: «Заочники не юны». На языке логического программиро-
программирования это утверждение может быть представлено следующим обра-
образом:
не_юн(Х) <— заочник(Х), где не_юн — предикат.
Заметим, что при этом не охватывается связь между предикатом
не_юн(Х) и предикатом юн(Х). Действительно, предположим, что
еще требуется представить утверждение «студенты юны». Очевидно,
его можно представить правилом
юн(Х) <— студент(X).
Теперь нетрудно заметить, что если некто является студентом-
заочником, то он оказывается юн и не юн одновременно, и противоре-
противоречие не будет обнаружено, так как предикаты юн и не_юн различны.
Значение связи предиката и его отрицания возрастает, если требуется
представлять исключения из правил.
Итак, необходимо иметь явное отрицание в голове правил. Но
существуют причины и для применения явного отрицания в теле
правил. Вернемся к примеру, приведенному в начале этой главы.
Высказывание: «Школьный автобус может пересекать железную
дорогу при условии, что нет приближающегося поезда» нельзя вы-
выражать правилом вида
пересекать <— not поезд,
так как это правило позволяет автобусу пересекать железную дорогу,
когда нет информации как о присутствии, так и об отсутствии поезда.
В случае, когда определено явное отрицание, ситуация изменяется:
пересекать <— -н поезд.
Следовательно, автобус может пересекать железную дорогу, если
шофер уверен, что нет приближающегося поезда.
Различие между not р и ~^р в логической программе существенно
всякий раз, когда мы не можем допустить, что доступная позитивная
информация о р полна, т. е. не можем допустить, что отсутствие
информации о р явно описывает его ложность.

332 Немонотонные логики в логическом программировании [ Гл. 9
Существование двух отрицаний повышает выразительность языка,
например, высказывание: «Если водитель не уверен, что поезд не
приближается, то он должен снедать» представляется правилом
снедать <— not поезд.
Другая причина введения отрицания — симметрия между позитив-
позитивной и негативной информацией. Особенно важно то, что негативную
информацию часто оказывается проще представить, чем позитивную.
Пример 9. 5.
Пусть предикат дуга(Х, Y) выражает, что в графе существует дуга
от вершины X к вершине Y. Для определения терминальной вершины
проще определить те вершины, которые не являются терминальными:
^терминальная (X) <— дуга(Х, Y)
терминальная(X) <— not ^терминальная(X)
Введение двух видов отрицаний позволяет обобщить связи между
логическим программированием и формализмами немонотонного вы-
вывода. Так, с помощью нормальных логических программ не удается
^а : ~^Ъ
представить даже простые правила логики умолчаний вида ,
с
а : Ъ
, а с помощью двух отрицаний удается расширить класс связан-
ных немонотонных формализмов.
9.1.2.1. Описание языка. Язык расширенных логических про-
программ представляет собой расширение языка нормальных логических
программ. В определения вносятся перечисленные ниже изменения.
• Объективная литера над алфавитом А — это атом А или -А.
• Символ «-I» обозначает дополнительные литеры в смысле явно-
явного отрицания:
-.-.А = А.
• Литера — это объективная литера L или not L (т. е. литера по
умолчанию).
• Расширенная Эрбрановская база — это множество всех фунда-
фундаментальных объективных литер А.
• Расширенная логическая программа — это конечное множество
правил вида Н <— Li,...,Ln (n ^ 0), где Н — объективная
литера и Li — литеры. При п = 0 символ «<—» может опускаться.
• Расширенная база Эрбрана Н программы Р — расширенная
Эрбрановская база алфавита, состоящего из всех констант, пре-
предикатных и функциональных символов, явно присутствующих
в Р.
• Интерпретация определяется по расширенной базе Эрбрана
так же, как и для нормальных логических программ.

9.1] Семантика логических программ 333
Определение 9.11. (Каноническая программа). Расширенная ло-
логическая программа Р является канонической тогда и только тогда,
когда для любого правила в Р: Н <— Body, если L Е Body, то
not^L E Body, где L — произвольная объективная литера.
Определение 9.12. (Семантическое ядро). Расширенная логиче-
логическая программа Р — семантическое ядро тогда и только тогда, когда
любое правило в Р имеет вид Н <— not Li,..., not Ln (n ^ 0).
9.1.2.2. Семантика.
9.1.2.2.1. Семантика, основанная на устойчивых моделях. Се-
Семантика ответных множеств — обобщение семантики устойчивых
моделей для языка расширенных программ. Ответное множество
расширенной программы Р — это устойчивая модель нормальной
программы, полученной из Р заменой объективных литер вида ^L
на новые атомы, скажем, -i L.
Определение 9.13. (Г*-оператор). Пусть Р — расширенная ло-
логическая программа и / — двузначная интерпретация (по отношению
Р
к not). GL-трансформация Р по модулю / — это программа —,
полученная из Р с помощью следующих правил:
1) обозначить все объективные литеры в Н вида ^А атомом
2) заменить в Р и / эти объективные литеры новыми обозначени-
обозначениями;
3) выполнить следующие операции:
а) удалить из Р все правила, содержащие литеры not А, где
АеЦ
б) удалить из оставшихся правил все литеры по умолчанию.
Р
Так как — — определенная программа, то существует единствен-
единственная наименьшая модель J. Если J содержит пару А и ->_А, то Г(/) =
= Н, иначе, пусть J' — интерпретация, полученная из J заменой ^ _А
на ->А, тогда Г(/) = J''.
Определение 9.Ц. (Семантика ответных множеств). Дву-
Двузначная интерпретация / расширенной логической программы Р —
это ответное множество Р тогда и только тогда, когда Г(/) =
= /. Объективная литера L программы Р истинна при семантике
ответных множеств тогда и только тогда, когда L принадлежит
всем ответным множествам Р; L — ложна тогда и только тогда, когда
^L истинна; в противном случае L не определена.

334 Немонотонные логики в логическом программировании [ Гл. 9
Пример 9. 6.
Пусть дана программа
юн(Х) <— студент(Х), not ^юн(Х)
->юн(Х) <— заочник(Х), not юн(Х)
студент (X) <— заочник(X)
заочник (Джон)
Ответными множествами будут:
h = {юн (Джон), студент (Джон), заочник (Джон)}
/2 = {^юн(Джон), студент (Джон), заочник (Джон)}.
Действительно, 1\ — ответное множество, так как — удаляет
h
второе правило для Х = Джон (так как not юн(Джон) находится в
теле этого правила, и юн(Джон) Е /i), и удаляет по^юн(Джон) из
тела первого правила (так как ^юн(Джон) ^ /]_). Легко проверить,
что наименьшая модель результирующей определенной программы
совпадает с 1\. Аналогично, для /2, когда удаляется первое правило,
(по^юн(Джон) находится в его теле, и ^юн(Джон) ^ /2), и
not юн (Джон) удаляется из тела второго правила (так как
юн (Джон) ф /]_).
По определению нетрудно проверить, что для программ без явного
отрицания ответные множества совпадают с устойчивыми моделями.
Расширенная программа противоречива по отношению к семан-
семантике ответных множеств (AS-противоречивая программа), если у нее
нет непротиворечивых ответных множеств. Например, для програм-
программы Р = {а; ^а} единственное ответное множество {а, ^а} противоре-
противоречиво.
Пример 9. 7.
Пусть Р имеет вид (здесь аЪ — предикат, определяющий аномаль-
аномальность X по отношению к первому правилу)
юн(Х) <— студент(Х), not ab(X)
студент (Джон) <—
^юн(Джон) <—.
У Р не существует непротиворечивых ответных множеств.
Действительно, так как не существует правил, определенных
Р
для аЬ(Джон), и, по определению, — не добавляет правил к Р,
независимо от /, то наименьшая модель — никогда не может
содержать аЬ(Джон). Следовательно, любой кандидат (S) на
Р
ответное множество не должен содержать аЬ(Джон), и тогда —
всегда содержит правило:
юн (Джон) <— студент (Джон).
Так как студент (Джон) и ^юн(Джон) — истинны, то достигнуто
противоречие.

9.1] Семантика логических программ 335
Утверждение 9.2. Для любой ^^-противоречивой программы
существует единственное противоречивое ответное множество, совпа-
совпадающее с ее Эрбрановской базой Н.
Оказывается, что других ответных множеств для противоречивых
программ не существует, так как справедлива представленная ниже
лемма.
Лемма 9.1. Расширенная программа не может иметь два от-
ответных множества, одно из которых — собственное подмножество
другого.
Отсутствие ^^-противоречивости не гарантирует существования
ответных множеств. Заметим, что нормальные программы не могут
быть ^^-противоречивыми, но у них может не быть ответных мно-
множеств, что является существенным недостатком.
Отрицание в ответных множествах не выражает некоторые свой-
свойства классического отрицания. Например, не выполняется свойство
«исключенного третьего», так как А V ^А может и не быть истиной
для каждого атома А в ответном множестве.
Существует семантика е-ответных множеств, обобщающая
устойчивые модели на класс расширенных логических программ.
Явно отрицательные атомы в расширенных программах играют роль
исключений, поэтому предпочтение отдается негативным литерам.
Пример 9.8.
Пусть задана программа Р:
юн(Х) <— студент(X)
^юн(Х) <— заочник(X)
студент (X) <— заочник(X)
заочник (Джон)
Возможны следующие заключения: юн (Джон) и ^юн(Джон). По-
Поэтому единственное ответное множество — это вся база Эрбрана.
В семантике е-ответных множеств утверждение ^юн(Джон) пред-
предпочтительнее, чем юн(Джон), поэтому е-ответное множество имеет
вид
{заочник(Джон), студент(Дснсон), ^юн(Джон)}.
9.1.2.2.2. Фундированная семантика.
Определение 9.15. (Фундированная семантика с псевдоотрица-
псевдоотрицанием). Трехзначная интерпретация / — частичная устойчивая модель
расширенной логической программы Р тогда и только тогда, когда
Г — частичная устойчивая модель нормальной программы Рх, где Г
и Р1 получены соответственно из / и Р заменой каждой объективной
литеры вида ^А новым атомом, скажем, ^_А.
Фундированная семантика с псевдоотрицанием Р определяется
единственной F-наименыпей частичной устойчивой моделью Р.

336 Немонотонные логики в логическом программировании [ Гл. 9
Смысл символа «-i» не соответствует смыслу классического отри-
отрицания. Рассмотрим программу Р:
Ъ <— а
Ъ <— -па.
Для классического отрицания Ъ — следствие Р, так как аУ ^а —
тавтология. Но фундированной моделью программы Р является мно-
множество {not a, not ^а, not 6, not ^6}, и, таким образом, b не есть
следствие программы Р.
9.1.2.2.3. Другие подходы. В отличие от случая нормальных ло-
логических программ семантика расширенных программ определена не
для всех программ, т. е. некоторые программы остаются противоре-
противоречивыми. Иногда это свойство является серьезным недостатком.
Пример 9. 9.
Программа Р:
^р <— not q
р^-
противоречива в семантике всех видов, так как для q нет правила, и
not q должно быть истинным.
Существует семантика, не принимающая гипотез, приводящих к
противоречию, т. е. для приведенного примера она принимает р, а
not q не допускается. Может быть и другой подход — паранепроти-
воречивая семантика, в которой принимается противоречивая инфор-
информация.
9.1.3. Зачем нужна новая семантика для расширенных программ?
Ни один из описанных вариантов семантики не охватывает смысла
расширенных программ. Можно выделить ряд недостатков:
• некоторые непротиворечивые программы не имеют ответных
множеств, например, программа Р = {а <— not а};
• даже для программ с ответными множествами их семантика
не всегда дает ожидаемые результаты; добавление к программе
лемм (доказанных фактов) изменяет семантику (нарушается
кумулятивность);
• процесс вывода для ответных множеств не может основываться
на нисходящих методах даже для непротиворечивых программ
(нарушено свойство релевантности);
• вычисление ответных множеств iVP-полно даже для логических
программ исчисления высказываний. Для логических программ
с предикатами в общем случае невозможно вычислить ответные
множества с помощью конечных аппроксимаций;
• из-за двузначности интерпретации теряется выразительность;
• семантика е-ответных множеств несимметрично обрабатывает
позитивную и явно негативную информацию;

9.2] WFSX — фундированная семантика 337
• фундированная семантика с псевдоотрицанием свободна от этих
недостатков и не отдает предпочтения негативным атомам, но
при этом теряются важные свойства, связывающие отрицания в
ответных множествах.
Пример 9.10.
Рассмотрим программу Р:
а <— not Ъ
Ъ <— not a
Если ^а — новый атомарный символ (->_а), то фундированная
семантика дает: {^а, not^fr}, так что ^а — истина, и а не определен.
В результате разрывается связь между отрицаниями (-ia — явное
утверждение ложности а, тогда и not а должно быть истинно).
Пример 9.11.
Пусть дана программа (она представляет следующее утверждение:
«Если ничего не известно о забастовке водителей автобусов, то
можно ехать на автобусе»)
автобус <— not забастовка
^забастовка
Интуитивно, ^забастовка влечет not забастовка. Чтобы связать
оба отрицания в расширенных логических программах, вводится
принцип когерентности: «Пусть L — объективная литера расширен-
расширенной логической программы Р. Если ^L принадлежит семантике Р, то
литера not L должна принадлежать этой семантике». Заметим, что
ответные множества согласуются с когерентностью.
Кроме того, классическое отрицание в логических программах не
отвечает свойству поддерживаемости (supportedness), которое тре-
требует, чтобы для каждой программы Р объективная литера L была
истинной только в том случае, когда существует правило для L,
чье тело истинно. Это свойство вызвано природой эпистемического
знания. Следует отметить, что различают эпистемическую истину,
которая основывается на истинности других объективных литер или
литер по умолчанию, и онтологическую истину, которая не зависит
от поддержки (например, L V ->L).
9.2. WFSX — фундированная семантика для
расширенных логических программ
9.2.1. Интерпретации и модели
Определение 9.16. Интерпретация I языка Lang — это любое
множество Т U not F, где Т и F — непересекающиеся подмножества
объективных литер над базой Эрбрана, при этом
если ^L G Т, то L E F (принцип когерентности).

338 Немонотонные логики в логическом программировании [ Гл. 9
Множество Т содержит все фундаментальные объективные лите-
литеры, истинные в /, множество F — ложные в /. Истинностное значение
оставшихся объективных литер не определено.
Два типа отрицания связаны по когерентности: если ^L Е /, то
not L Е /. Из приведенного определения следует, что выполняется
условие непротиворечивости.
Утверждение 9.3. (Условие непротиворечивости). Если / = Т U
U not F — интерпретация программы Р, то не существует такой пары
объективных литер А и ^А программы Р, что А Е Т и ^А Е Т.
Пример 9.12.
/ = {а, -па, ^Ь} не является интерпретацией, так как
1) а и ^а принадлежат / (противоречие);
2) not Ъ не принадлежит /, хотя ~^Ъ Е / (не выполняется принцип
когерентности).
Интуитивно объяснить смысл интерпретации можно следующим
образом:
• атом А — истинен (явно ложен) в интерпретации / тогда и
только тогда, когда А Е / (~^А Е /);
• позитивная (негативная) объективная литера А (~>А) ложна в /
тогда и только тогда, когда not А Е / (not ^A E /);
• атом А не определен в / в противном случае.
Как и в разделе 9.1, интерпретацию можно представить в ви-
виде функции. Точнее, любая интерпретация / = Т U not F может
быть эквивалентно представлена как функция / : Н —> V, где
V = {0,1/2,1}:
1(А) = 0, еслипо1А е /;
/(А) = 1, если А е /;
1(А) = 1/2, в противном случае.
Определение 9.17. (Оценка истинности). Если / — интерпре-
интерпретация, то оценка истинности /, соответствующая /, — это функция
/: С —> V (здесь С — множество всех формул языка), рекурсивно
определяемая следующим образом:
• если L — объективная литера, то I(L) = I{L)\
• если S = not L — умолчание, то /(not L) = 1 — I(L);
• если 5 и V - формулы, то /(E, V)) = min(/Ef), I(V));
• если L — объективная литера и S — формула, то

9.2] WFSX — фундированная семантика 339
S) = { lj если^(^) ^ /(?) или
( 0, в противном случае
Ясно, что дополнительное (по отношению к фундированной семан-
семантике) второе условие для случая I(L <— S) = 1 (I(->L) = 1 и /E) т^ 1)
не влияет на вычисление формул без «-i». Оно позволяет заключе-
заключению с (при условии, что выполняется ->с) быть независимо ложным,
когда для некоторого правила посылки имеют неопределенное зна-
значение. В частности, явное отрицание «—<» может замещать ложным
значением неопределенность заключений правил с неопределенным
телом.
Определение 9.18. (Модель). Интерпретация / является моделью
программы Р тогда и только тогда, когда для каждого фундаменталь-
фундаментального примера правила программы, Н <— />, выполняется: 1{Н <— В) =
= 1.
Пример 9.13.
Пусть дана программа
Ъ <— а
а <— not a, not с
с <— not ^с
^с ^— not с
Моделями этой программы являются
Ml = {^6, not 6}
М2 = {^6, not 6, с, not ^c}
МЗ = {^6, not 6, с, not -ic, not a}
М4 = {^6, not 6, not с, ^с}
М5 = {^6, not 6, -па, not а}
Мб = {^6, not 6, ^а, not а, с, not ^c}
М7 = {^6, not 6, not ^а}
М8 = {^6, not 6, с, not -ис, not ^а}
М9 = {^6, not 6, с, not -ic, not а, not ^а}
М10 = {^6, not 6, not с, -ic, not ^а}
Заметим, что среди этих моделей
1) МЗ, Мб и М9 — классические модели (в соответствии с определе-
определением 9.4);
2) Ml, М2, М4, М7, М8 и М10 — неклассические модели, так как тело
правила Ъ <— а не определено и голова ложна, т. е. /(голова) < /(тело);
3) М5 — неклассическая модель, так как /(голова) < /(тело) (ложь <
< не определено) для правила а <— not a, not с.

340 Немонотонные логики в логическом программировании [ Гл. 9
9.2.2. Определение WFSX
Введем понятие устойчивости моделей и, используя его, определим
семантику WFSX. Напомним, что в языке логических программ вы-
высказывание и определяется следующим образом: /(и) = 1/2 для любой
интерпретации. Тогда назовем неотрицательной такую программу,
посылки в которой — объективные литеры или и.
/Р
Определение 9.19. ( — — трансформация). Пусть Р — расши-
расширенная логическая программа и / — интерпретация. Трансформация
р
— (Р по модулю /) — это программа, получаемая из Р выполнением
следующих операций:
• удалить из Р все правила, содержащие умолчание L = not A,
где А е /;
• удалить из Р все правила, содержащие в теле такую объектив-
объективную литеру L, что ^L Е /;
• удалить из всех оставшихся правил программы Р такие умолча-
умолчания L = not А, что not A E /;
• заменить все оставшиеся умолчания высказыванием и.
Заметим, что вторая операция применяется только к расширен-
расширенным программам и требуется для выполнения свойства когерентно-
когерентности. По определению, результирующая программа неотрицательная.
Определение 9.20. (Оператор least), least (P), где Р — неотри-
неотрицательная программа, — это множество литер Т U not F, полученное
следующим образом:
• пусть Р1 — неотрицательная программа, полученная заменой в
Р каждой негативной объективной литеры ^L на атом «^_L».
• пусть Т' U not F' — наименьшая трехзначная модель Р'.
• TUnot F получается из T'Unot F' с помощью обратной замены.
Определение 9.21. (Оператор Ф*^. Пусть Р — неотрицательная
программа, / — интерпретация Р; А и Ai — все фундаментальные
атомы. Тогда Ф* (I) — это множество атомов, определенное правилами
= 1 тогда и только тогда, когда существует такое
правило А <— Ai,..., Ап в программе Р, что I{Ai) = 1, г ^ п.
Ф*(/)(А) = 0 тогда и только тогда, когда либо для каждого
правила А <— А\,..., Ап существует такое г ^ п, что I(Ai) = 0,
либо не существует правил с головой А и 1(А) = 0.
= 1/2 в противном случае.

9.2] WFSX — фундированная семантика 341
Теорема 9.1 (Трехзначная наименьшая модель). Трехзначная
наименьшая модель для неотрицательной программы — это наимень-
наименьшая фиксированная точка оператора \I/*(not Н), где Н — эрбранов-
ская база программы.
Теорема 9.2. Для каждой неотрицательной программы множе-
множество литер least (P) существует и является единственным.
Пример 9.14.
Оператор least не всегда дает интерпретацию. Пусть задана про-
программа Р:
а <—
Тогда least (P) = {а, -па, ~^Ъ} не является интерпретацией, так как не
выполняются свойства когерентности и непротиворечивости.
Чтобы выполнялось свойство когерентности, если нет противоре-
противоречия, определим частичный оператор, переводящий любое непротиво-
непротиворечивое множество литер в интерпретацию.
Определение 9.22. (Оператор Coh). Пусть QI = QTUnot QF —
такое множество литер, что QT не содержит пары объективных литер
Аи пА Тогда Coh(QI) — интерпретация Т U not F такая, что Т =
= QT и F = QF U {—iZ/|Z/ G Т}. Оператор Coh не определен для
противоречивого множества литер.
/р\
Очевидно, результат Coh (least I — I) всегда будет интерпретацией,
J,
если он определен. Но применение оператора Coh к WFM не дает
семантики и приводит к странным результатам.
Пример 9.15.
Дана программа Р:
а <— not b
b <— not a
Для программы Р фундированная модель, WFM, есть М = {^а,
not^fr}. Тогда Coh(M) = {^a, not а, not^fr} является интерпретацией,
но в ней не учитываются следствия: присутствует not а, в то время
как b — прямое следствие — отсутствует. Поэтому Coh(M) не является
моделью, так как для правила b <— not а тело истинно, а голова не
определена.
Обобщим оператор Г* для того, чтобы учитывать следствия Coh.
Определение 9.23. (Оператор Ф). Пусть Р — логическая про-
грамма, / — интерпретация и J = least ( — I. Тогда если существует
Coh(J), то ФрA) = Coh(J), иначе ФрA) не определен.

342 Немонотонные логики в логическом программировании [ Гл. 9
Определение 9.24- (WFSX, PSM, WFM). Интерпретация / рас-
расширенной логической программы Р называется частичной устой-
устойчивой моделью (Partial Stable Model — PSM) программы Р тогда и
только тогда, когда ФрA) = /. F-наименыпая PSM называется фунди-
фундированной моделью (Well Founded Model — WFM). Семантика WFSX
программы Р определяется множеством всех PSM программы Р.
Пример 9.16.
У программы Р = {а, ^а} нет семантики.
Определение 9.25. (Противоречивая программа). Расширенная
логическая программа противоречива тогда и только тогда, когда у
нее нет семантики, т.е. не существует интерпретации /: Фр(/) = /.
Пример 9.17.
Рассмотрим программу Р:
с <— not Ъ
Ъ <— not a
а <— not a
Определяя семантику Р, находим модель PSM= {^6, с, not 6, not -ic,
* 1 ТТ - Р ) b^U {
not ^а}. Действительно, = < > и ее наименьшая модель
{ \ J* J
есть {с, -ib, not 6, not -ic, not ^a}. Следовательно, <I>p(PSM) = PSM.
Если же ~^Ъ считать просто новым атомом, то эта нерасширенная
программа будет иметь единственную PSM = {^fr}, которая не яв-
является когерентной интерпретацией. Интересно отметить, что PSM
не является моделью в классическом смысле, так как для второго
правила: PSMF) = 0 < PSM(not a) = 1/2. Интуитивное объяснение
может быть таким: истинность ~^Ъ (или независимая ложность Ъ)
заменяет любое правило для Ъ с неопределенным телом, так что not Ъ
становится скорее истинным (и Ъ ложным), чем неопределенным. Это
необходимо предполагать, если мы считаем, что факт ~^Ъ в программе
предназначен для определения ложности Ъ.
Теорема 9.3 (PSM являются моделями). Каждая PSM программы
Р — это модель Р.
Вернемся к вопросу о необходимости дополнительной операции,
введенной в трансформации по модулю.
Пример 9.18.
Пусть программа Р имеет вид
с <— а
^а
а <— Ъ
Ъ <— not Ъ

9.2] WFSX — фундированная семантика 343
Единственная PSM — это / = {^а, not a, not с, not -ib, not ^c}.
Фактически,
least I — ) = {^а, not с, not -но, not ^c} и
ь I V/
Ф(/) = /. V
Если бы не было второй операции в определении трансформации, то
Р
— содержала бы правило с <— а, и с было бы скорее не определено,
чем ложно. Это противоречило бы принципу когерентности, так как
^а влечет not а, и поскольку единственное правило для с имеет в
теле а, то должно выполняться еще и not с. Роль новой операции —
обеспечить распространение лжи как следствия всякой литеры not L,
полученной из ^L по когерентности. Рассмотрим теперь программу
Р' в каноническом виде:
с <— a, not^a
6 <— not 6
Единственная PSM: / = {^a, not a, not с, not -ib, not ^c}. — =
(^ 1
= < b ^ и >. Из-за того, что программа имеет канонический вид,
(a^b J
вторая операция не используется (первое правило удаляется первой
операцией).
Р\
Теорема 9.4 (Компактная версия — 1. Пусть Р — каноническая
Р
расширенная логическая программа, / — интерпретация. Тогда —
может быть эквивалентно определена как программа, получаемая из
Р выполнением следующих операций:
• удалить из Р все правила, содержащие умолчание
L = not А : А е I.
• удалить из всех оставшихся правил Р их умолчания
L = not A : not Ael.
• заменить все оставшиеся умолчания на высказывание и.
9.2.3. Существование семантики
Мы определили WFM как F-наименыпую PSM, так как выполня-
выполняется следующая теорема.
Теорема 9.5 (Существование семантики). Для непротиворечи-
непротиворечивой программы всегда существует единственная F-наименыпая PSM.

344 Немонотонные логики в логическом программировании [ Гл. 9
Более того, литера L принадлежит каждой PSM непротиворечивой
программы тогда и только тогда, когда L принадлежит .Р-наименьшей
PSM программы Р.
Определение 9.26. (Итеративное построение WFM). Чтобы по-
получить конструктивное восходящее определение WFM для заданной
непротиворечивой программы Р, мы определяем следующую беско-
бесконечную последовательность {1а} интерпретаций Р:
= ФРAа)
Is = U{/a|ce < 5} для конечного натурального 5.
Утверждение 9.4. Существует наименьшее натуральное число
Л: 1\ — фиксированная точка оператора Фр, и WFM= I\.
Конструктивное восходящее определение требует знания a priori,
является ли программа непротиворечивой.
Теорема 9.6. Программа Р противоречива тогда и только тогда,
когда для последовательности 1а существует такое натуральное число
/ р\
А, что ФрA\) не определен, т.е. least — содержит пару объектив-
ных литер А и -нА
При восходящем вычислении WFM программы Р необходимо на-
начать строить описанную последовательность. Если на некотором шаге
оператор Фр нельзя применить, то следует закончить итерации, так
как Р — противоречивая программа. В ином случае продолжать до
тех пор, пока не будет получена наименьшая фиксированная точка
оператора Фр, т.е. WFM.
Пример 9.19.
Дана программа Р:
а <— not a
^а
Строим последовательность:
^о = {}
h = Coh Meast ( тт ) ) = Coh(least({a <- u, ^a <- })) = Coh({^a}) =
= {^a,not a}
h = Coh (least ( 7 ) ) = Coh (least({a <-, ^a <- })) =
V \{-a> not a}77 V V1 S))
= Coh ({a, ->a}),
т. е. результат не определен и, следовательно, программа Р противо-
противоречива.

9.2] WFSX — фундированная семантика 345
Пример 9.20.
Дана программа Р:
а <— not Ъ
Ъ <— not a
Строим последовательность:
/i = Coh ( least ( — I I = Coh(least({a <- u, b <- u, ^a <- })) =
= Coh({^a, not ^b}) = {^a, not a, not
h = Coh least
= Coh(least({a ^— u, 6 <—, ^a ^— })) =
= Coh({6, -ia, not ^^}) = {b, ->a, not a, not ^b} = /3.
Следовательно,WFM = {6, -ia, not a, not ^6}.
Теорема 9.7 (Обобщение фундированной семантики). Для про-
программ без явного отрицания WFSX совпадает с фундированной се-
семантикой.
9.2.4. Нисходящие процедуры вывода для WFSX
Подобные процедуры необходимы на практике для целевых запро-
запросов к программе об истинности литер, когда не обязательно вычис-
вычислять заранее всю WFM. Трудно переоценить важность для этой цели
структурных свойств, которыми обладает WFSX и которые делают
возможным существование подобных процедур (этого нет в других
видах семантики).
Определим сначала полную и состоятельную нисходящую харак-
теризацию WFSX с помощью семантических деревьев, а затем, осно-
основываясь на этой характеризации, построим процедуру вывода. Чтобы
гарантировать завершение, по крайней мере для конечных фундамен-
фундаментальных программ, введем правила, ограничивающие пространство
поиска и исключающие как циклическую положительную рекурсию,
так и циклическую рекурсию через отрицание по умолчанию.
9.2.4»I» Характеризация WFSX с помощью семантиче-
семантических деревьев. Нисходящая характеризация опирается на постро-
построение И-деревьев (Т-деревьев), узлам которых присваивается статус
успешных или неуспешных. Успешное (неуспешное) дерево имеет
успешный (неуспешный) корень. Если литере L соответствует успеш-
успешное дерево с корнем в L, то L E WFM; в противном случае,
т. е. когда все деревья для L неуспешные, L ф WFM. Узлам не

346 Немонотонные логики в логическом программировании [ Гл. 9
присваивается статус неизвестности, т. е. неуспех не означает лож-
ложность, а свидетельствует о том, что нам не удалось доказать истин-
истинность.
Рассмотрим сначала программы без явного отрицания. Мы пред-
предполагаем, что атомы, не имеющие правил, терпят неуспех, а истин-
истинность означает успех. Атомы разрешаются (определяется их истин-
истинностное значение) по правилам программы, и выполняется правило
отрицания как неудачи, т. е. not L успешно, если L терпит неуспех, и
неуспешно, если L успешно.
Пример 9.21.
Пусть программа Р имеет вид: Р = {р <— р}. Тогда существует
единственное дерево для р:
р
I
р
Это дерево является бесконечным, поэтому р терпит неуспех и
not p успешно. Таким образом для решения проблемы положитель-
положительной рекурсии правило неуспеха может применяться и к бесконечным
ветвям.
Для рекурсии через отрицание по умолчанию решение не является
столь простым, поскольку нам необходимо доказать неуспех как для
L, так и для not L. Поэтому правило отрицания как неудачи в данном
случае не работает. Чтобы справиться с этой проблемой, вводится
новый вид деревьев — TU-деревья, — которые скорее доказывают
неложность, чем истинность. TU устанавливается для истинности
и неопределенности. В этом случае для любого L доказательство
истинности not L неуспешно тогда и только тогда, когда существует
доказательство неложности L.
TU-деревья строятся аналогично Т-деревьям: атомы, для кото-
которых нет правил в программе, — это неуспешные листья (т. е. они
не истинны и не являются неопределенными). Истина успешна, ато-
атомы разрешаются по правилам программы (литера L истинна или
не определена, если существует правило для L, тело которого ис-
истинно или не определено), и not L терпит неуспех, если L успеш-
успешно при доказательстве истинности, а в противном случае not L
успешно.
С деревьями этих двух типов легко определить статус литеры L,
участвующей в рекурсии через отрицание по умолчанию. Действи-
Действительно, литера L не определена в WFS тогда и только тогда, когда
L имеет статус неуспеха, если находится в Т-дереве, и успеха — если
находится в TU-дереве.

9.2]
WFSX — фундированная семантика
347
Пример 9.22.
Пусть Р = {р <— not p}. Чтобы доказать истинность р, мы строим
Т-деревья для этой литеры. Существует единственное дерево:
not р
Узел not p неуспешен, если существует успешное TU-дерево для р, и
успешен в противном случае. Для р существует всего одно TU-дерево
(далее такие деревья будем заключать в рамку):
1
по
э
tp
Следовательно, существует рекурсия для р через отрицание по
умолчанию. В TU-дереве литере р назначается статус успеха и, сле-
следовательно, not р в Т-дереве терпит неуспех. Поэтому доказательство
истинности р терпит неуспех.
Рассмотрим, как обобщить характеризацию для работы с явным
отрицанием в WFSX. Обработка расширенных программ во многом
похожа на обработку нормальных программ, где вместо атомов ис-
используются объективные литеры. Основное отличие обобщения для
расширенных программ состоит в обработке отрицания как неудачи.
Чтобы выполнялся принцип когерентности, должен быть дополни-
дополнительный способ доказательства not L, т. е. литера not L должна быть
успешной, если успешна литера -iL.
Пример 9.23.
Дана программа Р:
а <— not Ъ
Ъ <— not a
Для этой программы WFSX есть
дерево имеет вид
Ъ
а, 6, not а, not ^b}. Для Ъ Т-
not a
В соответствии с методами, используемыми для нормальных про-
программ, чтобы доказать not а, необходимо рассмотреть все TU-деревья
для а. Существует единственное TU-дерево:
с
по
1
t Ъ

348
Немонотонные логики в логическом программировании
[Гл.9
Так как это случай рекурсии через отрицание по умолчанию, то
not Ъ успешно и, следовательно, not а терпит неуспех. Однако, так
как ^а истинно, то по когерентности not а (а, значит, и Ь) должно
быть успешно. Поэтому для расширенных программ в Т-дереве not L
успешно тогда и только тогда, когда все TU-деревья для L неуспеш-
неуспешны или существует успешное Т-дерево для -iL, и терпит неуспех в
противном случае. Что касается TU-деревьев, not L успешно в тех
же случаях, что и для нормальных программ, и еще в том случае,
когда ^L истинно (т.е. существует успешное Т-дерево для -iL). ^L в
случае неопределенности не связан с неложностью not L (в примере
9.23 неопределенность с не запрещает принять истинность not —<с).
Необходимо соблюдать осторожность при доказательстве неложно-
неложности, так как требование когерентности сильнее неопределенности.
Пример 9. 24.
Дана программа Р:
с <— а
а <— b
b <— not b
WFSX имеет вид: {^a, not a, not c, not -ib, not ^c}. Можно показать,
что если а в первом правиле заменить на 6, то истинностное значение
с не сохраняется.
Проблема развертывания объективных литер без изменения се-
семантики решается следующим образом: в семантическом дереве при
развертывании узлов должны быть дополнительные потомки, соот-
соответствующие отрицанию по умолчанию для дополнений объективных
литер в выбранном правиле, т. е. необходимо выполнять неявное при-
присоединение not ^L для объективных литер L.
В примере 9.24 существует единственное дерево для not с без
дополнительных потомков: оно содержит единственный узел not с.
Так как не существует правил для -не, то все Т-деревья для ^с
неуспешны. Поэтому, чтобы доказать not с, мы должны рассмотреть
все TU-деревья для с. Единственное такое дерево имеет вид
а
I
ъ
I
not b
Это дерево успешно, так как not b в TU-дереве участвует в рекурсии
через отрицание. Поэтому Т-дерево для not с неуспешно, что является
некорректным результатом, так как not с Е WFM. Заметим, что

9.2]
WFSX — фундированная семантика
349
проблема возникает из-за того, что а в TU-дереве развертывается до
Ъ. Следовательно, результат для а становится тем же, что и для Ъ.
Однако Ъ и а имеют различные истинностные значения в WFM (Ъ не
определено, а — ложно).
Если добавляются дополнительные потомки, то TU-дерево для с
имеет вид
Это дерево неуспешно, так как not ^a терпит неуспех, следовательно,
not с в Т-дереве успешно, как и требовалось.
Перейдем к обобщению полученных результатов.
Определение 9.27. (Т-дерево, TU-дерево). Т-дерево Т(А) (со-
(соответственно, ТЬт-дерево TU(A)) для произвольной фиксированной
фундаментальной расширенной логической программы Р есть И-
дерево с корнем, помеченным А, и узлами, помеченными литерами.
Т-деревья (соответственно, TU-деревья) строятся от корня к листьям
последовательным развертыванием новых узлов по следующим пра-
правилам:
1) для узла п, помеченного объективной литерой А: если не
существует правил для А в Р, то п — лист; в противном случае,
выбрать (недетерминированно) одно правило: А <— B\,...,Bj,
not ?>j+i, • • •, not Bk из Р, где Bi — объективные литеры. В
Т-дереве потомками п будут: В\,..., Bj^ not ?>j+i,..., not B^\
в TU-дереве существуют еще и дополнительные потомки:
not -1.В1,..., not ^Bj.
2) узлы, помеченные умолчаниями, являются листьями.
Определение 9.28. (Успех и неуспех для WFSX). Каждый узел
в Т-дереве (соответственно, в TU-дереве) имеет связанный с ним
статус успеха или неуспеха. Все бесконечные деревья неуспешны.
Конечное Т-дерево (соответственно, TU-дерево) успешно, если его
корень успешен, и неуспешно в противном случае. Статус узла в ко-
конечном дереве определяется в соответствии с правилами, указанными
в табл. 9.1.

350
Немонотонные логики в логическом программировании
[Гл.9
Таблица 9.1
N
1
2
3
4
5
Положение
узла в дереве
Лист
Лист
Лист
Лист
Внутренний
(не лист)
Пометка узла
Истина (true)
Объективные
литеры, не
являющиеся
истинными
not A
not A
Тип
дерева
т, ти
т, ти
Т
ти
Т
ти
т, ти
Дополнительные
условия
1) Все вспомогатель-
вспомогательные TU-деревья с
корнем в А
неуспешны или
2) существует успеш-
успешное Т-дерево с корнем
^А
1) Все Т-деревья с
корнем в А неуспеш-
неуспешны или
2) существует успеш-
успешное Т-дерево с корнем
^А
Существует успешное
вспомогательное TU-
дерево с корнем А
Существует успешное
Т-дерево с корнем А
Все потомки успешны
Существует неуспеш-
неуспешный потомок
Статус
узла
Успех
Неуспех
Успех
Успех
Неуспех
Неуспех
Успех
Неуспех
После применения этих правил статус некоторых узлов может
остаться неопределенным из-за бесконечной рекурсии через отрица-
отрицание по умолчанию. Неопределенным узлам в Т-деревьях присваива-
присваивается статус неуспеха, а в TU-деревьях — статус успеха.
Теорема 9.8 (Корректность по отношению к WFSX). Пусть Р —
фундаментальная (быть может, бесконечная) расширенная логиче-
логическая программа, М — ее фундированная модель, соответствующая
WFSX, и пусть L — произвольная фиксированная литера. Тогда
1) если 3 успешное Т-дерево с корнем L, то L Е М (состоятель-
(состоятельность);
2) если L Е М, то 3 успешное Т-дерево с корнем в L (полнота).

9.2] WFSX — фундированная семантика 351
Эта теорема гарантирует корректность только для непротиворечи-
непротиворечивых программ. Однако с помощью введенной хар акте риз ации можно
определить, является ли программа противоречивой.
Теорема 9.9 (Противоречивые программы). Расширенная про-
программа Р противоречива тогда и только тогда, когда существует
некоторая объективная литера L программы Р такая, что существует
успешное Т-дерево для L и существует успешное Т-дерево для -iL.
Данное определение позволяет характеризовать WFM для нор-
нормальных программ. Но можно сделать некоторые упрощения: так
как доказательство для литеры ^L в нормальных программах тер-
терпит неуспех, то п. 3 таблицы 9.1 может быть определен следующим
образом: «Лист п в Т-дереве (TU-дереве), помеченный литерой not A
успешен, если все TU-деревья (Т-деревья) с корнем А неуспешны
(при построении TU-дерева не требуется включать дополнительные
потомки)».
Альфереш и Перейра доказали, что описанный метод (даже с
упрощениями) корректен по отношению к фундированной семантике
нормальных программ.
9.2.4-2. SLX — Процедура вывода для WFSX. Основыва-
Основываясь на характеризации с помощью семантического дерева, несложно
определить нисходящий вывод для WFSX, — SLX (extended Selected
Linear).
Определение 9.29. (SLX-T-вывод). Пусть Р — расширенная про-
программа, R — произвольное фиксированное правило вычисления. SLX-
Т-вывод GOj Gi,... для G в программе Р через R определяется как
Go = G. Пусть Gi есть <— Li,..., Ln, и предположим, что R выбирает
литеру Lfc(l ^ k ^ п). Тогда
• если Lk — объективная литера и входное правило:
Lk <— i?i,..., Bm, то выводимая цель — это:
• если Lk = not А, то если существует SLX-T-опровержение для
^А в Р или не существует SLX-TU-опровержения для А в Р, то
выводимая цель есть
• в противном случае Gi — последняя цель в выводе.
Определение 9.30. (SLX-TU-вывод). Пусть Р — расширенная
программа и R — произвольное фиксированное правило вычисления.
SLX-TU-вывод Go, Gi,... для G в программе Р через R определяется
как Go = G. Пусть Gi есть <— Li,...,Ln и предположим, что R
выбирает литеру Lk(l ^ к ^ п). Тогда

352 Немонотонные логики в логическом программировании [ Гл. 9
• если Lk — объективная литера, то
- если существует SLX-T-опровержение для -iL^, то Gi —
последняя цель в выводе;
- в противном случае, если входное правило есть:
Lk <— Бь ... ,Вт,
то выводимая цель есть:
<— Li,..., Lk-i, В\,..., Вт, Lfc+i,..., Ln\
- если не существует правила для Lk, то Gi — последняя цель
в выводе;
• если Lk — умолчание вида not А, то
- если существует SLX-T-опровержение для <— А в програм-
программе Р, то Gi - последняя цель в выводе;
- если все SLX-T-выводы для <— А являются SLX-T- неуспеш-
неуспешными, то выводимая цель есть:
<— Li,..., Lk-i, bfc+i,..., Ln\
- из-за бесконечной рекурсии через отрицание по умолча-
умолчанию может случиться, что описанных случаев окажется
недостаточно для определения выводимой цели. Тогда, по
определению, выводимой целью будет также
Определение 9.SI. (SLX-опровержение и неуспех). SLX-T-
опровержение (соответственно, SLX-TU-опровержение) для литеры
G в программе Р — это конечный SLX-T-вывод (соответственно,
SLX-TU-вывод), завершающийся пустой целью (<— ?). SLX-T-вывод
(SLX-TU-вывод) для литеры G в программе Р есть SLX-T-неуспех
(SLX-TU-неуспех) тогда и только тогда, когда этот вывод не является
опровержением, т. е. бесконечен или заканчивается целью, отличной
от пустой.
Теорема 9.10 (Состоятельность SLX). Пусть Р — непротиворе-
непротиворечивая расширенная логическая программа, L — произвольная ли-
литера из Р. Если существует SLX-T-опровержение для <— L в Р, то
L е WFM(P).
Теорема 9.11 (Теоретическая полнота SLX). Пусть Р — непроти-
непротиворечивая расширенная программа, и L — произвольная литера из Р.
Если L G WFM(P)y то существует SLX-T-опровержение для <— L в Р.
Теорема 9.12 (Противоречивые программы). Если Р — проти-
противоречивая программа, то существует литера L Е Н, для которой
существует SLX-T-опровержение как для <— L, так и для <— —<L.

9.2] WFSX — фундированная семантика 353
9.2.4-3. О достиснсении останова SLX-процедуры. Хотя
SLX состоятельна и полна для WFSX, она не является эффективной
даже для конечных фундаментальных программ. SLX не содержит
механизма для обнаружения циклов, поэтому полнота является лишь
идеальной. Как и WFS для нормальных программ, WFSX, вообще
говоря, не вычислима, поэтому в общем случае нельзя гарантировать
завершение.
Чтобы обеспечить останов, по крайней мере, для конечных фун-
фундаментальных программ, введем правила, отсекающие SLX-выводы и
исключающие как циклическую положительную рекурсию, так и цик-
циклическую рекурсию через отрицание по умолчанию (отрицательную
рекурсию). Будем использовать два вида предшественников вывода:
• локальные предшественники назначаются литерам в выводи-
выводимых целях и используются для выявления циклической поло-
положительной рекурсии. Чтобы включать локальных предшествен-
предшественников, заменим литеры в целях парами Li : Si, где Li — литера
и Si — множество ее локальных предшественников.
• глобальные предшественники назначаются выводам и использу-
используются для выявления циклической отрицательной рекурсии.
В И-дереве локальные предшественники литеры — это литеры,
появляющиеся на пути от корня дерева к данной литере. Глобальные
предшественники вспомогательного вывода — это локальные предше-
предшественники породившей его литеры L и цель предшествующего вывода,
в котором появилась литера L. Для вывода верхней цели не существу-
существует глобальных предшественников. Глобальные предшественники мо-
могут быть поделены на два множества: глобальные Т-предшественники
и глобальные TU-предшественники (в зависимости от того, в каком
выводе они были получены).
Чтобы справиться с проблемой останова для циклической положи-
положительной рекурсии, достаточно гарантировать, что не будут строиться
бесконечные выводы. Этого можно достичь, если ни одна из выбран-
выбранных литер, принадлежащих своему множеству локальных предше-
предшественников, не развертывается.
Первое правило обрезки. Пусть Gi — цель в SLX-выводе (Т или
TU) и пусть Lk — литера, выбранная правилом R. Если L& принад-
принадлежит своим локальным предшественникам, то Gi — последняя цель
в выводе.
Лемма 9.2 (Редукция отрицательных циклов). В SLX-T-выводах
все циклические отрицательные рекурсии могут быть выявлены, если
рассматривать только их глобальных предшественников.
Пример 9. 25.
Отрицательный цикл в программе Р = {а <— not 6, Ъ <— not а} не
выявляется ни с помощью единственной проверки того, принадлежат
12 В.Н. Вагин и др.

354 Немонотонные логики в логическом программировании [ Гл. 9
ли цели в SLX-T-выводе своим глобальным TU-предшественникам, ни
с помощью единственной проверки принадлежности литер в SLX-TU-
выводе своим глобальным Т-предшественникам. Строятся следующие
выводы:
Таблица 9.2
SLX-T-вывод
<— а
^not Ъ
SLX-TU-вывод
^not a
SLX-T-вывод
<— а
^not Ъ
SLX-TU-вывод
^not a
Объективная литера а из SLX-T-вывода не появляется в SLX-TU-
вывод ах. То же касается и Ъ. Все SLX-T-выводы для ^а неуспешны.
Единственная проверка принадлежности литеры в SLX-TU-
выводах своим глобальным TU-предшественникам не выявляет
рекурсии, например, в следующей программе:
^а <— not a
Лемма 9.2 дает второе правило обрезки.
Второе правило обрезки. Пусть Gi — цель в SLX-T-выводе и
пусть Lk — литера, выбранная правилом R. Если Lk принадлежит
множеству глобальных Т-предшественников, то Gi — последняя цель
в выводе.
Теорема 9.13 (Исключение циклической рекурсии для WFSX).
Первое и второе правила обрезки необходимы и достаточны для того,
чтобы гарантировать исключение всех положительных и отрицатель-
отрицательных рекурсий.
Заметим, что в правилах обрезки не используются TU-пред-
шественники.
Определение 9.32. (SLX-T-вывод с предшественниками). Пусть
Р — расширенная программа и R — произвольное фиксированное
правило вычисления. SLX-T-вывод Go, Gi,... для G в программе Р по
правилу R с Т-предшественниками ST определяется как Go = G : {}.
Пусть Gi есть <— L\ : Si,..., Ln : Sn и предположим, что R выбирает
литеру Lk : S&A ^ к ^ п). Тогда
• если Lk — объективная литера, Lk ф S& U ST, и входное правило
есть Lk <- Бь...,Бт,
то выводимая цель есть
<— L\ : Si,..., Lk-i : S&_i, B\ : S ,..., Bm : S , Lk+i : S^+i,...,
Ln : »bn,
где Sf = Sk U {Lk};
• если Lk — это not А, то если существует SLX-T-опровержение
для <— ^А : {} в программе Р с Т-предшественниками ST U Sk

9.2] WFSX — фундированная семантика 355
или если не существует SLX-TU-опровержения для <— А : {} в
программе Р с теми же предшественниками, выводимой целью
будет:
<— Li : Si,..., Lk-i : S&_i, Ь/c+i : S&+i,..., Ln : Sn;
• в противном случае Gi — последняя цель в выводе.
Определение 9.33. (SLX-TU-вывод с предшественниками).
Пусть Р — расширенная программа и R — произвольное фикси-
фиксированное правило вычисления. SLX-TU-вывод Go,Gi,... для G в
программе Р по правилу R с Т-предшественниками ST определяется
как Go = G : {}. Пусть Gi есть <— Li : Si,..., Ln : Sn и предположим,
что i? выбирает литеру L& : S&A ^ /с ^ п). Тогда
• если L/c — объективная литера,
- если L/c G Sfc или не существует правила для L&, то G^ —
последняя цель в выводе;
- иначе, если существует SLX-T-опровержение для
<— ^Lk '. {} с Т-предшественниками ST', то G^ — последняя
цель в выводе;
- в противном случае, если входное правило есть
Lfc <— i?i,..., Вт, то выводимой целью будет:
<— Li : Si,..., L/c-i : Sfc_i, 5i : S ,..., Бт : S , L^+i : S&+i,
..., Ln : on,
где 5' = 5fc U {Lk};
• если Lfc — это not A, to
- если существует SLX-T-опровержение для <— A : {} в про-
программе Р с Т-предшественниками ST, то G^ — последняя
цель в выводе;
- в противном случае выводимой целью будет:
<— L\ : Si,..., L/c-i : Sfc_i, L/c+i : Sfc+i,..., Ln : Sn.
Теорема 9.14 (Корректность процедуры SLX с предшественника-
предшественниками). Пусть Р — непротиворечивая расширенная программа. Тогда
• если L G WFM(P), то существует SLX-T-опровержение для
<— L : {} с пустыми Т-предшественниками. Более того, все вспо-
вспомогательные выводы, используемые в опровержении, конечны,
и их число также конечно;
• если L ф WFM(P), то все SLX-T-выводы для <— L : {} с пу-
пустыми Т-предшественниками конечны и заканчиваются целью,
отличной от <— ? Более того, все необходимые вспомогательные
выводы конечны, и число их конечно.
12*

356 Немонотонные логики в логическом программировании [ Гл. 9
9.3. Работа с противоречиями
Как отмечалось, WFSX определена не для каждой программы,
т. е. некоторые программы противоречивы и не имеют смысла. Однако
для некоторых программ это может быть слишком сильным ограниче-
ограничением.
Пример 9. 26.
Рассмотрим утверждения
• обычно студенты юны (если не доказана аномальность студента
по отношению к свойству «быть юным»);
• Джон — студент и не юн;
• Сократ — человек.
Они естественным образом выражаются программой (ab — предикат
аномальности)
юн(Х) <— студент(Х), not ab(X)
студент(Джон)
^ юн (Джон)
человек(Сократ)
Для этой программы не существует WFSX. Хотя, интуитивно, мы
можем сказать, что Сократ — человек и Джон — студент. Разумно
также заключить, что Джон не юн, так как правило, говорящее, что он
не юн, будучи фактом, сильнее того, которое заключает, что Джон юн.
В самом деле, всякий раз, когда предположение вызывает противоре-
противоречие, кажется логичным иметь возможность отменить предположение,
чтобы избежать противоречия, т. е. вывод по противоречию — это
вывод «от противного».
Оказывается, приемлемость одной гипотезы может находиться в
условной зависимости от приемлемости другой. Это типично при
предположении повреждений в устройстве, где всякий раз предпо-
предположению более серьезных повреждений отдается предпочтение по
сравнению с менее серьезными, являющимися следствиями. Более
того, может вводиться критерий предпочтения, определяемый поль-
пользователем или ориентированный на прикладную область.
Пример 9.27.
Следующая программа описывает состояния велосипеда:
-л неустой ч и вое _ колесо <— not сдутая_шина, not сломанные_спицы
сдутая_шина <— пропускает_ниппель
сдутая_шина <— дырявая_камера
^нет_света <— not неисправен_генератор
Дополнительно известно наблюдение: неустойчивое колесо.
Можно определить смысл программы следующим образом:
{неустойчивое _ колесо, not неисправен _ генератор, ^нет_ света,
not нет_света, not nponyекает_ниппель, not дырявая_камера}, не

9.3] Работа с противоречиями 357
принимая ни гипотезы not сдутая_шина, ни not сломанные_спицы,
так как если принять любую из них, то при допущении остальных
возникает противоречие. Но, возможно, желательно, чтобы в этом
случае семантика глубже учитывала модель велосипеда и снова,
будучи скептической, не принимала бы ни not пропу екает _ ниппель,
ни not дырявая_ камера.
Чтобы выполнить подобные эпистемиологические требования,
можно ввести понятие оптативного принятия гипотез. Оптативные
гипотезы — это гипотезы, которые в случае приемлемости могут
приниматься, а могут и нет. В то же время в случае приемлемости
могут быть приняты и гипотезы, не являющиеся оптативными.
Оптативные гипотезы могут задаваться пользователем или выво-
выводиться из программы при заданном критерии (например, гипотеза не
должна зависеть от остальных). Такая очень скептическая семантика
моделирует разумного агента, считающего программу абсолютно
правильной, и всякий раз, когда он сталкивается с приемлемой
гипотезой, приводящей к противоречию, он не принимает ее.
Разумный агент предпочитает скорее считать программу корректной,
чем допустить, что приемлемая гипотеза обязательно должна быть
принята.
WFSX моделирует менее скептических агентов, которые сталки-
сталкиваясь с противоречивым сценарием, предпочитают скорее считать
программу неправильной, чем допустить, что приемлемые гипотезы
не будут приняты. Такой агент более уверен в своем критерии прием-
приемлемости: приемлемая гипотеза принимается раз и навсегда; если же
возникает противоречие, то наверняка проблема в программе, а не в
индивидуальной приемлемости каждой приемлемой гипотезы. Если
же проблема в программе, то требуется ее пересмотр.
Эта точка зрения оправдана, если мы думаем, что программа —
это нечто динамическое, т. е. каждая программа получается в ре-
результате ассимиляции (усвоения) знаний предыдущей программой.
Если при ассимиляции знаний возникает противоречие, то необходимо
выполнить процесс пересмотра для восстановления непротиворечиво-
непротиворечивости.
Ковальский утверждает, что понятие ограничений целостности
(integrity constraints) необходимо в логическом программировании как
для обработки и представления знаний, так и для их ассимиляции.
Проблема противоречивости возникает в случае, когда не удовле-
удовлетворяются ограничения целостности. Если некоторое новое знание
не совместимо с ограничениями целостности, то процесс пересмот-
пересмотра должен восстановить соблюдение ограничений. В расширенном
логическом программировании мы можем рассматривать требование
непротиворечивости как удовлетворение ограничениям целостности
вида <— L, -iL. Мы будем использовать ограничения целостности в
форме отрицаний (denials).

358 Немонотонные логики в логическом программировании [ Гл. 9
Пример 9.28.
Пусть программа должна утверждать, что: «Не известно никого,
кто являлся бы и республиканцем, и демократом». Это знание может
быть легко представлено с помощью ограничения целостности:
<— демократ(X), республиканец(Х).
Вернемся к примеру о Джоне (9.26). Можно считать, что эта
программа — результат усвоения знаний предыдущей БЗ. Например,
мог быть добавлен факт о том, что Джон не юн. В WFSX результи-
результирующая программа противоречива. Один из способов восстановления
непротиворечивости программы состоит в том, чтобы добавить пра-
правило, утверждающее, что аЬ(Джон) не может быть ложно, т.е. это
утверждение может привести к противоречию:
аЬ(Джон) <— not аЬ(Джон).
В результате программа становится непротиворечивой, и ее
WFSX — это {человек (Сократ), ^юн(Джон), студент (Джон),
not юн(Джон)}, что согласуется с интуицией.
Как утверждает Рейтер, главная идея ограничений целостности
состоит в том, что только определенные состояния программы явля-
являются приемлемыми, и эти ограничения предназначены для указания
этих приемлемых состояний. Ограничения целостности могут быть
двух типов:
1) Статические ограничения зависят только от текущего состоя-
состояния программы и не зависят от предыдущих состояний. (При-
(Пример — задача о демократах и республиканцах).
2) Динамические ограничения зависят от двух и более состояний
программы. Например, приобретаемые работником знания не
могут исчезать (они накапливаются).
Мы будем рассматривать только статические ограничения целост-
целостности в форме отрицаний. Программа с правилами целостности (или
ограничениями) — это множество правил плюс множество отрицаний
или правил целостности вида
_L <- Ab...,An,not ?b...,not Бш,
где Ai,..., Ап, ?>i,..., Вш — объективные литеры, и п + т > 0. Сим-
Символ _1_ обозначает ложь. Программа Р с семантикой S удовлетворяет
ограничениям целостности тогда и только тогда, когда Р ? s_l_.
9.3.1. Удаление противоречий
Итак, чтобы справиться с противоречиями, возникающими из-
за предположения о замкнутости мира, вместо определения более
скептической семантики можно использовать менее скептическую
семантику, дополненную процессом пересмотра, восстанавливающим

9.3] Работа с противоречиями 359
непротиворечивость всякий раз, когда нарушаются ограничения це-
целостности.
Определим процесс пересмотра, восстанавливающий непротиворе-
непротиворечивость по отношению к WFSX. Этот процесс связан с разрешением
отменять предположения об истинности негативных литер. Множе-
Множество литер, для которых может быть пересмотрено допущение об
их истинности, называется множеством пересматриваемых литер и
может быть любым подмножеством not H.
Мы будем считать, что любые литеры по умолчанию могут быть
пересмотрены. Предполагается, что пересматриваемые литеры ука-
указываются пользователем. Мы определим скептический процесс пере-
пересмотра, который включает все варианты пересмотра и ни одному из
них не отдает предпочтения. Рассмотрим непротиворечивую програм-
программу Р:
р <— not q
^р <— г, not t
Допустим, что дана дополнительная информация г. Предлагаются
следующие модели для Р U {г}:
{г} — минимальная модель
{г, р, not -ip, not q}
{r, -ip, not p, not t}.
Последние две модели пытаются минимально изменить WFM про-
программы Р, чтобы принять новую информацию. Например, вторая
модель предпочитает считать t неопределенным в отличие от случая
предположения замкнутости мира, а третья делает неопределенным
значение q. {r} предполагает неопределенными и t, и q. При этом
выполняются необходимые и достаточные изменения в соответствии
с новой информацией, т. е. не отдается предпочтения ни одной из
пересматриваемых литер.
Ревизии — это программы, получаемые единственным образом из
исходной, для которых каждая из непротиворечивых моделей являет-
является WFSX. Для приведенного примера ревизиями являются следующие
программы:
PU{r}U{t ^ not t}
PU{r}U{q^ not q}
PU{r}U{tf- not t] q <- not q}
Заметим, что правило вида L <— not L делает неопределенной гипоте-
гипотезу not L.

360 Немонотонные логики в логическом программировании [ Гл. 9
9.3.2. Паранепротиворечивая WFSX
Для того, чтобы выполнить пересмотр, необходимо сначала опре-
определить противоречивые множества, порождаемые программой в пара-
непротиворечивой семантике. Основная идея — вычислить все след-
следствия программы, включая те, которые приводят к противоречиям, и
те, которые следуют из противоречий.
Пример 9.29.
Пусть задана программа Р:
а <— not Ъ (I)
^а <— not с (II)
d<- not a (III)
е <— not ^a (IV)
Для программы Р справедливы следующие утверждения:
1) not Ь и not с выполняются, так как не существует правил для Ъ
и с;
2) ^а и а следуют из п. 1 и правил I и II;
3) not а и not ^a следуют из п. 2 и принципа когерентности;
4) d и е выполняются по п. 3 и правилам III и IV;
5) not d и not е выполняются по п. 2 и правилам III и IV, единствен-
единственным для due;
6) not ^d и not ^е следуют из п. 4 и принципа когерентности.
В результате все множество следствий есть
{not 6, not с, -на, а, not а, not ^а, d, e, not d, not e, not -id, not ^e}.
Будем считать, не теряя общности, что программы всегда нахо-
находятся в каноническом виде. Определим сначала интерпретацию для
паранепротиворечивого случая.
Определение 9.34- (р-интерпретация). р-интерпретация / —
это любое множество Т U not F такое, что если ^L Е Т, то L E F
(когерентность).
Определение 9.35. (Оператор CohP). Пусть QI = QTU
not QF — множество литер. Мы определяем оператор Cohp(QI)
как р-интерпретацию Т U not F такую, что Т = QT и
Заметим, что в этих определениях не требуется, чтобы множества
Т и F не пересекались.
Р
В компактной версии —трансформации (см. теорему 9.4) мож-
можно применять первые две операции в произвольном порядке, так
как условия их применения независимы при любой интерпретации.
Возможность потенциального конфликта остается при применении

9.3] Работа с противоречиями 361
и первой, и второй операций, но этого не происходит, так как если
некоторое А Е /, то not A ^ /, и наоборот. Но это не выполняется в
случае р-интерпретаций р/, где множеству pi могут принадлежать А
и not А. Следовательно, результат будет зависеть от порядка приме-
применения операций.
Рассмотрим, например, программу из примера 9.29 и найдем
Р
трансформацию -. Если приме-
{а, -па, not ^а, not а, not о, not с)
нять сначала операцию 1, а затем 2, то получается:
• правила III и IV удаляются, так как и а, и ^а принадлежат р-
интерпретации;
• not Ъ и not с удаляются из правил, так как они принадлежат
р-интерпретации.
В результате программа имеет вид
а <—
Но если изменить порядок применения операций, то:
• not Ъ, not с, not a, not ^a удаляются из правил, так как они
принадлежат р-интерпретации;
• так как больше нет литер в теле правил, то другие операции не
применяются.
Результирующая программа:
е <—
Чтобы трансформация не зависела от порядка применения опера-
операций, определим соответствующую трансформацию для паранепроти-
воречивого случая как недетерминированную по порядку применения
этих операций.
( Р
Определение 9.36. ( — р — трансформация). Пусть Р — кано-
каноническая расширенная логическая программа и пусть / — р-ин-
терпретация. Под — р-программой мы понимаем любую программу,
полученную из Р сначала путем недетерминированного применения
следующих операций (до тех пор, пока они не будут неприменимы):
• удалить все правила, содержащие умолчания L = not А, такие
что А Е /;
• удалить из правил их умолчания L = not А такие, что not A E /.

362 Немонотонные логики в логическом программировании [ Гл. 9
Затем все оставшиеся умолчания необходимо заменить на выска-
высказывание и. Чтобы получить все следствия программы, далее приводя-
приводящие к противоречиям и следующие из противоречий, мы рассмотрим
Р
следствия всех таких —р-программ.
Определение 9.37. (Фр-оператор). Пусть Р — каноническая
расширенная логическая программа; / — р-интерпретация; Р&, где
Р
k G К, — все возможные результаты применения — р. Тогда
фР(Л = U CohP{least{Pk)).
кек
Теорема 1.15 (Монотонность для Фр). Оператор Фр монотонный
по отношению к включению множеств р-интерпретаций.
Следовательно, для каждой программы существует наименьшая
фиксированная точка, и она может быть получена с помощью итера-
итераций оператора Фр, начинающихся с пустого множества.
Определение 9.38. (Паранепротиворечивая WFSX). Паранепро-
тиворечивая WFSX канонической расширенной логической програм-
программы Р, обозначаемая через WFSXP(P), — это наименьшая фиксирован-
фиксированная точка оператора Фр, примененного к Р. Если некоторая литера
принадлежит паранепротиворечивой WFSX программы Р, то будем
записывать Р \=р L.
Утверждение 9.5. WFSXP(P) определена для любой программы
с ограничениями целостности 1С.
Пример 9.30.
Вычислим паранепротиворечивую WFSX для программы из при-
примера 9.29. Р уже находится в каноническом виде. Начнем с пустого
Р
множества. Единственная программа, получаемая из — р — это Род
(здесь и далее используется нумерация Д,ь гДе * ~~ номер интерпре-
интерпретации, а к — номер программы, полученной в результате применения
Р
трансформации —р):
J-i
а <— и
^а <— и
d <— и
е <— и
и /i = Cohp(least(P0,i)) = {not b, not с}.
Р
По — р получаем единственную программу Pi,i:
h
а <—
и
и

9.3] Работа с противоречиями 363
и /2 = Cohp(least(Pi i)) = {a, not ^а, ^а, not а, not 6, not с}.
Р
Результатом — р являются четыре программы:
±2
Р2,1 • О* <— Р2,2 • О* <— Р2,3 : О* <— Р2,4 • 0> <~
Например, Ргд получается с помощью применения второй операции
к правилам III и IV, так как not а и not ^a принадлежат 1^. ^2,4
получается применением первой операции к правилам III и IV, что
возможно, так как аи^а принадлежат /2.
Легко видеть, что /з = Фр(/2) = {not 6, not с, ^а, а, not а,
р
not ^а, d, e, not d, not e, not -id, not ^e}. Применяя — р получаем
/ 3
ту же программу, следовательно, Фр(/з) = h, т- е. /з — наименьшая
фиксированная точка оператора Фр, и поэтому она является WFSX^
программы Р.
Определение 9.39. (Противоречивая программа). Программа Р
с языком Lang, в котором А — атом, и множеством ограничений
целостности 1С противоречива тогда и только тогда, когда Р U 1С U
U {!_ <- А, ^А\А е Lang} |=p _L.
Утверждение 9.6. Для непротиворечивой программы Р паране-
противоречивая WFSX совпадает с WFSX.
9.3.3. Декларативные ревизии
Перед тем, как рассмотреть вопрос о том, какие предположения
необходимо пересмотреть, чтобы устранить противоречие, начнем с
определения того, как включить в программу ревизию, устраняющую
некоторое пересматриваемое предположение, т. е. правила специаль-
специального вида, препятствующие ложности объективных литер в моделях
программы.
Определение 9.40. (Подавляющее правило). Подавляющее пра-
правило (inhibition rule) для умолчания not L есть L <— not L. Через
IR(S), где S — множество умолчаний, будем обозначать множество
IR(S) = {L^- not L\ not L e S}.
Эти правила устанавливают, что если not A — истина, то А —
также истина, и в результате возникает противоречие. Интуитивно
это то же самое, что и ограничение целостности вида _1_ <— not A.
Технически разница в том, что удаление такого противоречия в случае

364 Немонотонные логики в логическом программировании [ Гл. 9
подавляющих правил выполняется самой WFSX, а в случае ограни-
ограничений целостности — нет.
Утверждение 9.7. Пусть Р — любая программа такая, что для
объективной литеры L, P^ -iL. Тогда: Р U {L <— not L} Kp not L.
Более того, если не существует других правил для L, то истинностное
значение L не определено в WFSXP(P).
Такие правила при добавлении в программу позволяют сделать
умолчания неопределенными в паранепротиворечивой WFSX.
Чтобы декларативно определить ревизии противоречивой про-
программы, начнем с рассмотрения результирующих WFSX для всех
возможных ревизий программы Р с подавляющими правилами. Они
получаются удалением пересматриваемых предположений, даже если
некоторые ревизии остаются все еще противоречивыми программами.
Заметим, что, возможно, несколько различных ревизий фактиче-
фактически соответствуют одной и той же в том смысле, что они приводят к
одинаковым следствиям.
Пример 9. 31.
Рассмотрим программу Р:
JL <— not a
а <— b
Ъ <— а
а <— с
с пересматриваемыми литерами Rev = {not a, not 6, not с}.
Заметим, что добавление правил а <— not а или Ъ <— not Ъ (можно
одновременно) приводит к одним и тем же следствиям. Интуитивно
они являются одной и той же ревизией, так как неопределенность а
приводит к неопределенности 6, и наоборот.
Пересматриваемые литеры not а и not Ъ неразделимы, и поэтому
не имеет значения, какие подавляющие правила будут добавлены в
программу (для а, 6, или и то, и другое). В дальнейшем мы объединим
эти ревизии в одну стандартную, которая добавляет оба правила.
Определение 9.41- (Неразделимые литеры). Пусть Р — расши-
расширенная логическая программа с пересматриваемыми литерами Rev.
Множество Ind(S') D S неразделимых литер (indissociable literals)
множества умолчаний S — это наибольшее подмножество множества
Rev такое, что
• Ind(S) С WFSXP(P) и
• WFSXP(P U IR(S)) П Ind(S') = {} (если последнее условие не
выполняется, положить Ind(S') = {}).
Таким образом Ind(S') — множество всех пересматриваемых литер,
истинностные значения которых изменяются с истины на неопреде-
неопределенность, как только добавляются подавляющие правила для каждого
умолчания из S.

9.3] Работа с противоречиями 365
Нетрудно видеть, что такое наибольшее множество всегда суще-
существует (так как Ind монотонный оператор), и что Ind — оператор за-
замыкания. Более того, справедливо и приведенное ниже утверждение.
Утверждение 9.8. Пусть М = WFSXp(PUlR(S)) для некоторого
подмножества S множества Rev, тогда WFSXp(PUlR(lnd(S)T))=M.
В примере 9.31 Ind({not a}) = Ind({not b}) = {not а, not b} и
Ind({not с}) = {not a, not 6, not с}.
Определение 9.2^2. (Подмодель). Подмодель (противоречивой)
программы Р с ограничениями целостности 1С и пересматриваемы-
пересматриваемыми литерами Rev есть любая пара <М, Д>, где R — подмножество
множества Rev, замкнутое относительно неразделимых литер, т. е.
\/S С Д, Ind(S) Сйи
М = WFSXP(P U {L <- not L\ not L e Д}).
В подмодели <M, R> назовем R ревизией подмодели, М — след-
следствиями ревизии подмодели. Подмодель противоречива тогда и толь-
только тогда, когда М противоречиво (т.е. либо М содержит _1_, либо
не является интерпретацией). Заметим, что подмодели в точности
соответствуют ревизиям программы.
Существование WFSXP(P) для любой программы Р (утв. 9.5) га-
гарантирует, что М существует для каждого подмножества множества
Rev. Более того, так как Ind — оператор замыкания, то выполняется
приведенное ниже утверждение.
Утверждение 9.9. Множество всех подмоделей <М, R> любой
программы Р с пересматриваемыми литерами Rev образует полную
решетку (по включению множеств) на ревизиях подмоделей.
Решетка подмоделей для примера 9.31 представлена на рис. 9.1
(для каждой подмодели, изображенной в эллипсе, вверху записано
множество М, а под ним — R).
{not a, not b, not с}
{not с}
{not a, not b}
{_L, not a, not b, not c]
Рис. 9.1.

366
Немонотонные логики в логическом программировании
[Гл.9
Пример 9.32.
Рассмотрим программу Р с пересматриваемыми литерами
Rev = {not q, not r, not b}:
p <— not q
^p <— not r
a <— not 6
Ее решетка подмоделей представлена на рис. 9.2, где отмеченные
жирной линией подмодели противоречивы. Противоречивые модели
представлены не полностью.
Рис. 9.2.
Так как мы будем выполнять пересмотр противоречия с минималь-
минимальными изменениями, то нас будут интересовать те подмодели, которые
непротиворечивы и являются минимальными в решетке подмоделей.
Определение 9.43. (Минимальная непротиворечивая под-
подмодель). Подмодель <М, R> — минимальная непротиворечивая
подмодель (MNS — minimal noncontradictory submodel) программы
Р тогда и только тогда, когда она непротиворечива и не существует
другой непротиворечивой подмодели <МХ, В!> такой, что В! С R.
По определению, каждая MNS программы Р соответствует ре-
ревизии программы Р вида Р U RevRules (RevRules — множество
подавляющих правил для некоторой ревизии подмодели), которая
гарантирует непротиворечивость, и для любого множества правил

9.3] Работа с противоречиями 367
Rev Rules7 С Rev Rules, замкнутого относительно неразделимых ли-
литер, Р U RevRules' противоречиво. Другими словами, каждая MNS
соответствует такой ревизии программы Р, которая восстанавлива-
восстанавливает непротиворечивость и добавляет минимальное множество правил
подавления для пересматриваемых литер, замкнутое относительно
неразделимых литер.
Пример 9.33.
Пусть дана программа Р где s(X) обозначает число, на 1 боль-
большее X:
p(X)^p(s(X))
а <— not p(s(X))
Пусть Rev = {not p(i)\i > 0}. Единственными множествами подавля-
подавляющих правил, которые удаляют противоречие, являются такие мно-
множества IR(Sk), что Sk = {not p(i)\ i > к}. Ни одно из них не является
минимальным. Тем не менее, замыкание относительно неразделимых
литер есть S = {not p(i)\ i > 0}. Таким образом, единственная непро-
непротиворечивая модель — это <М, S>, где М = {^а, not а}, которая и
является единственной MNS. Заметим, что в действительности М —
модель для каждой из перечисленных ревизий.
Очевидно, что литеры в ревизии подмодели на самом деле изменя-
изменяют свое истинностное значение при добавлении подавляющих правил.
Утверждение 9.10. Если <М, R> — это MNS программы Р, то
R С WFSXP(P).
Определение 9-44- (Минимально пересмотренная программа).
Пусть Р — программа с пересматриваемыми литерами Rev, и
<М, R> — некоторая MNS программы Р. Минимально пересмот-
пересмотренная программа (MRP — minimally revised program) для Р есть
PUIR(R), т. е. программа Р, к которой добавлено одно подавляющее
правило для каждого элемента R.
Утверждение 9.11. Если Р непротиворечива, то ее единственная
MNS — это <WFSX(P),{}> и сама Р является минимально пересмот-
пересмотренной.
Пример 9.34.
Минимально пересмотренные программы для программы Р из
примера 9.32 — это
MRPi
MRP2
= {P
= {p
<— not
<— not
q\ ^i
q- -njr
? ^— not
) ^— not
r;
r;
a
a
<— not
^— not
b;
b]
q
r
<— not
^— not
^} и
r}.
Каждая из этих двух программ есть трансформация исходной, ко-
которая минимальным образом устраняет противоречие, отменяя пред-
предположение об истинности для некоторых пересматриваемых литер
с помощью правил подавления. В этом примере можно избежать

368
Немонотонные логики в логическом программировании
[Гл.9
противоречия для р либо вернувшись к предположению замкнутости
мира о ложности q (истинности not q), либо о ложности г (соответ-
(соответственно, программы MRP\ и MRP^). Так как нет причин присваивать
неопределенное значение только q или только г, то естественно, что
результатом скептической ревизии должно быть присвоение неопре-
неопределенного значения обеим литерам.
Определение 9.45. (Скептическая ревизия). Скептическая под-
подмодель программы Р — это объединение <Mj,Rj> всех MNS про-
программы Р. Скептически пересмотренная программа Р — это про-
программа, полученная из Р путем добавления к ней правил подавления
для каждого элемента множества Rj.
Необходимо гарантировать, что скептическая ревизия действи-
действительно устраняет противоречие в программе.
Утверждение 9.12. Пусть <Mi,i?i> и <M2,i?2> — две любые
непротиворечивые подмодели. Тогда подмодель <M,R\ U i?2> также
непротиворечива.
Пример 9. 35.
Рассмотрим противоречивую программу Р с пересматриваемыми
литерами Rev = {not g, not a, not b}:
p <— not q
q <— not r
r <— not s
^p <— not a
^a <— not b
На рис. 9.3 показана решетка подмоделей для программы Р, где
MNS отмечены штриховой линией, а скептические подмодели выде-
выделены жирной линией.
{г, not s, p, not q}
{not a, not Щ
{r, not s, -i p, -i a, not a, no
^ - ^ {no
Рис. 9.3.

9.3] Работа с противоречиями 369
Пример 9. 36.
Рассмотрим программу, представляющую так называемый ромб
Никсона:
J_ <— пацифист (X), милитарист (X)
пацифист(Х) <— квакер(Х), not аЬ_квакер(Х)
милитарист(X) <— республиканец(Х), not ab_республиканец(Х)
квакер (Никсон)
республиканец(Никсон)
Эта противоречивая программа Р имеет две MRP:
• к Р добавляется правило аЬ_ квакер <— not ab_ квакер]
• к Р добавляется правило
аЬ_ республиканец <— not ab_ республиканец.
Обе эти программы имеют непротиворечивые WFSX:
{милитарист (Никсон), квакер (Никсон), республиканец(Никсон),
not ab_республиканецНиксон)}
и
{пацифист (Никсон), квакер (Никсон), республиканец(Никсон),
not ab_ квакер (Никсон)}
(соответственно, для первой и второй ревизий).
Скептическая подмодель программы получается с помощью добав-
добавления двух правил подавления. Ее WFSX — это {квакер(Никсон), рес-
республиканец (Никсон)}. Здесь видна необходимость требования един-
единственности скептической ревизии, так как нет смысла отдавать пред-
предпочтение ни одному из утверждений «Никсон — пацифист» или «Ник-
«Никсон — милитарист».
У некоторых программ может и не существовать пересмотренной
версии. Это происходит в том случае, когда противоречие основыва-
основывается на непересматриваемых литерах.
Пример 9. 37.
Рассмотрим программу Р с пересматриваемыми литерами
Rev = {not с}:
а <— not Ъ
^а
Ъ <— not с
с
Подмодели Р - это <WFSXP(P),{}> и <WFSXP(P U {с <- not с}),
{not c}>. Так как обе эти подмодели противоречивы, то у Р не
существует MNS и, следовательно, не существует ревизий. Заметим,
что если бы not Ъ было пересматриваемым, то у программы была бы
ревизия Р U {Ъ <— not Ъ}. Если бы not Ъ не было в первом правиле,
то Р не имела бы ревизий, независимо от выбора пересматриваемых
литер.

370 Немонотонные логики в логическом программировании [ Гл. 9
Определение 9.46. (Непересматриваемая программа). Противо-
Противоречивая программа Р с пересматриваемыми литерами Rev не пере-
пересматриваема тогда и только тогда, когда у нее не существует непро-
непротиворечивой подмодели.
9.3.4. Поддержка и устранение противоречий
Подмодели характеризуют возможные ревизии и критерий ми-
минимальности. Конечно, вряд ли процедура поиска минимальной и
скептической подмоделей может быть основана на их определении:
потребовалось бы сгенерировать все возможные ревизии и затем вы-
выбрать те, которые необходимо. Определим процедуру пересмотра и
покажем, что она согласуется с определенными ранее ревизиями.
Процедура основывается на понятиях поддержки противоречия
и множествах удаления противоречий. Информативно, поддержка
противоречия — это множества пересматриваемых литер из WFSXp,
которые достаточны для поддержки _1_. Из их истинности неизбежно
следует истинность _1_.
Множества удаления противоречия строятся по множествам под-
поддержки противоречия. Они представляют собой минимальные мно-
множества таких литер, выбранных из множеств поддержки, что любое
множество поддержки _1_ содержит, по крайней мере, одину литеру из
множества удаления противоречия. Следовательно, если все литеры в
некотором множестве удаления противоречия имеют неопределенные
значения, то не существует поддержки для _1_.
Пример 9. 38.
Рассмотрим программу из примера 9.32. Ее единственным множе-
множеством поддержки противоречия является {not q, not r} и ее множества
удаления противоречия — это {not q} и {not r}. Допустим, что q было
бы не определено как результат правил для q. В этом случае _1_ также
было бы не определено, и программа становится непротиворечивой.
То же случилось бы, если бы г было не определено. Ни одно другое
множество, не содержащее ни одну из этих двух альтернатив, не
обладает этим свойством.
Определение 9.47. (Поддержка литеры). Множества поддерж-
поддержки (support set) литеры L, принадлежащей WFSXP программы Р с
пересматриваемыми литерами Rev (каждое из них представляется как
SS(L)), получаются следующим образом.
• если L — объективная литера:
- если существует факт для L, то поддержка L — это
SS(L) = {};
- для каждого правила: L <— В\,... ,?>n, n ) 1 вР такого,
что {?>i,..., Бп} С WFSXp(P), существует поддержка L

9.3] Работа с противоречиями 371
вида SS(L) = [jSSj^(Bi) для каждой комбинации одного
г
j(i) с каждым г;
• если L = not А (А — объективная литера):
- если L Е Rev, то поддержка L — это SS(L) = {L};
— если L ^ Rev и не существует правил для А, то поддержка
L - это SS(L) = {};
- если L ^ Rev и существуют правила для А, выбрать из каж-
каждого правила для А такую литеру Z/, что ее дополнение по
умолчанию not V Е WFSXP(P). Для каждой такой литеры
существует несколько SS(L'), и каждое из них состоит из
поддержки для каждого дополнения по умолчанию, not Z/,
выбранных литер;
— если ^А Е WFSXp(P), то существуют еще множества под-
поддержки SS(L) = SSk(^A) для каждого к.
Пример 9.39.
Рассмотрим программу Р из примера 9.35. Ее паранепротиворе-
чивые фундированные следствия — это WFSXp(P) = {not 5, г, not q,
р, not -ip, not 6, -на, not a, -ip, not p}. Множества поддержки для р
вычисляются следующим образом:
• из единственного правила для р заключаем, что множества под-
поддержки для р — это множества поддержки для not q;
• так как not q — пересматриваемая литера, то одно из множеств
поддержки — это {not q};
• так как ->q ^ WFSXp(P), то не существует других множеств
поддержки для q.
Поэтому единственная поддержка для р — это {not q}. Теперь
можно определить множества поддержки для ^р:
• из единственного правила для ~^р можно заключить, что множе-
множества поддержки ^р совпадают со множествами поддержки для
not a;
• так как not a — пересматриваемая литера, то {not a} — под-
поддержка;
• так как ^а Е WFSXP(P), то множества поддержки для ^а также
поддерживают not a;
• из единственного правила для ^а заключаем, что множества
поддержки ^а также являются множествами поддержки для
not b;
• аналогично, как и для not q, можно заключить, что единствен-
единственной поддержкой not Ъ является {not Ъ}.

372 Немонотонные логики в логическом программировании [ Гл. 9
В результате у литеры ^р есть две поддержки: {not а} и
{not Ъ}.
Пример 9.40.
Множествами поддержки а в примере 9.33 являются
SSi(a) = {notp(l)}
SSi(a) = {not p(i)}
Утверждение 9.13 (Существование поддержки). Литера
L G WFSXp программы Р тогда и только тогда, когда у литеры
L существует, по крайней мере, одна поддержка SS(L).
Определение 9.1^8. (Поддержка противоречия). Поддержка про-
противоречия для программы Р — это поддержка _1_ в программе, полу-
получаемая из Р путем добавления к ней ограничений вида _1_ <— L, ^L
для каждой объективной литеры L языка программы Р.
Далее рассматриваются программы, к которым уже добавлены все
такие ограничения.
Пример 9. 41.
Множества поддержки противоречия программы Р из примера
9.35 — это объединение пар из множеств поддержки для р и —<р. Со-
Согласно результатам примера 9.39, Р имеет два множества поддержки
противоречия: {not q, not a} и {not q, not b}.
Поддержка противоречия — это множества пересматриваемых ли-
литер, истинных в WFSXp программы и принадлежащих одному из
множеств поддержки противоречия (т.е. _1_). Определив множества
пересматриваемых литер, которые вместе поддерживают некоторую
литеру, нетрудно построить такие множества пересматриваемых ли-
литер, что при полной их неопределенности истинность этой литеры
обязательно становится необоснованной. Чтобы избежать построения
лишних множеств, определим эти множества как замкнутые по отно-
отношению к неразделимым литерам.
Определение 9.49. (Множество удаления). Предварительное
множество удаления (pre-removal set) литеры L, принадлежащей
WFSXp программы Р, — это множество литер, образованное объеди-
объединением некоторых непустых подмножеств из каждого SS(L). Мно-
Множество удаления (RS) литеры L — это замыкание относительно
неразделимых литер предварительного множества удаления для L.
Если SS(L) — пустое множество, то, по определению, единственное
RS(L) пусто. Заметим, что для литер, не принадлежащих WFSXP(P),
RS не определяется.
Определение 9.50. (Минимальное множество удаления). В про-
программе Р RSm(L) — минимальное множество удаления тогда и

9.3] Работа с противоречиями 373
только тогда, когда не существует множества RSi(L) в Р такого, что
RSm(L) D RSi(L). Мы будем обозначать минимальное RS для L через
MRSP{L).
Определение 9.51. (Множество удаления противоречия). Мно-
Множество удаления противоречия (CRS — contradiction removal set)
программы Р — это минимальное множество удаления литеры _1_, т. е.
CRS для Р - это MRSP(±).
Пример 9.42.
Рассмотрим программу Р из примера 9.31. Единственная поддерж-
поддержка для _1_ — это SS(-L) = {not а}. Поэтому единственное предвари-
предварительное множество удаления для _1_ — это также {not а}. Так как
Ind({not a}) = {not а, not 6}, то единственным множеством удаления
противоречия является {not a, not b}.
Пример 9.43.
Множества удаления _1_ в программе из примера 9.35 — это
RSi = {not q}; RS2 = {not q, not a, not b};
RSs = {not q, not b}; RS4 = {not a, not b};
RS$ = {not q, not a}.
Множества RSi и RS^ — множества удаления противоречия. Они
в точности соответствуют ревизиям минимальных непротиворечивых
подмоделей (см. рис. 9.3).
Пример 9.44.
Единственное CRS для программы из примера 9.33 есть CRS =
= {not p(i)\ i > 0}.
Очень важно гарантировать, что множества удаления противоре-
противоречия действительно удаляют противоречие.
Лемма 9.3. Пусть Р — противоречивая программа со множеством
удаления противоречия CRS. Тогда Р U IR(CRS) непротиворечива.
Следующие теоремы доказывают, что этот процесс согласуется с
ревизиями, рассмотренными выше.
Теорема 9.16 (Состоятельность множеств CRS). Пусть R — непу-
непустое множество CRS противоречивой программы Р. Тогда <М, R> —
это MNS программы Р, где М = WFSX(P U IR(R)).
Теорема 9.17 (Полнота множеств CRS). Пусть <М, R> — это
MNS с R ф {} для противоречивой программы Р. Тогда R — это
CRS программы Р.
Теорема 9.18 (Непересматриваемые программы). Если {} — CRS
программы Р, то Р — непересматриваемая.
Теорема 9.19 (Скептически пересмотренная программа). Пусть
Р — противоречивая программа со множествами CRS вида Rk,

374 Немонотонные логики в логическом программировании [ Гл. 9
где k G К. Скептически пересмотренная программа для Р есть
Р U {L <- not L| not L e U #fc}-
кек
Пример 9.45. Рассмотрим программу Р:
JL <— not a
а <— Ъ
со множеством Rev = {not а, not b}. Подмодели Р есть:
< {not а, not 6, _L}, {} >
< {not 6}, {not а} >
< {}, {not a, not b} > .
В результате ее единственная MNS (и скептическая подмодель) —
это вторая из приведенных подмоделей. Заметим, что не существует
подмодели с ревизией {not 6}, так как
Ind({not b}) = {not a}.
Если бы мы учитывали такую ревизию, то скептической подмоделью
была бы третья подмодель. Единственной поддержкой для _1_ является
{not а}, и она совпадает с единственным CRS.
Пример 9. 46.
Вспомним пример о студентах (9.26), где Rev = {not ab(X)}. Един-
Единственная поддержка для _1_ — это {not аЬ(Джон)} и в результате она
совпадает с единственным множеством CRS. Поэтому единственной
MRP и скептически пересмотренной программой является исходная
программа, дополненная правилом аЬ(Джон) <— not аЬ(Джон), а ее
WFSX есть:
{студент(Джон), ^юн(Джон), not юн(Джон), человек(Сократ)},
как и ожидалось.
Пример 9.47.
Рассмотрим программу
поход <— not дождь
плавание <— not дождь
плавание <— not холодная_ вода
J_ <— поход, плавание
и пусть Rev = {not дождь, not холодная_ вода}. Множества поддерж-
поддержки для _1_ — это {not дождь} и {not дождь, not холодная_ вода}. В
результате для программы существует два множества удаления:
{not дождь} U {not дождь} = {not дождь}
{not дождь} U {not дождь,
not холодная_ вода} = {not дождь, not холодная_ вода}.
Единственное CRS и, следовательно, MRP, — это {not дождь}. Тогда
скептически пересмотренная программа имеет вид

9.4] WFSX, семантика логических программ 375
J_ <— поход, плавание
поход <— not дождь
дождь <— по? дождь
плавание <— not дождь
плавание <— по? холодная_ вода
и WFSX = {по? холодная _вода, плавание}.
Пример 9. 48.
Вспомним программу Р из примера 9.37. Ее паранепротиворечивая
WFSX есть {с, -на, not а, not 6, а, not ^а}. Поддержка для _1_ полу-
получается путем объединения множеств поддержки для а и множеств
поддержки для -^а. Так как единственным правилом для ^а является
факт, то единственная поддержка — это {}. Множества поддержки
для а — это множества поддержки для not 6, а для not Ъ — множества
поддержки для с. Снова, так как единственное правило для с — это
факт, то его единственной поддержкой является {}. Следовательно,
единственная поддержка _1_ — это {}, и в итоге Р нельзя пересмотреть.
9.4. WFSX, семантика логических программ с
двумя отрицаниями и автоэпистемическая логика
В последние годы были предприняты попытки изучения взаи-
взаимосвязей между логическим программированием и формализмами
немонотонного вывода. Такие связи оказались взаимовыгодными. С
одной стороны, немонотонные формализмы обеспечивают изящную
семантику для логических программ, особенно в том, что касается
смысла отрицания по умолчанию, и помогают понять, как логическое
программирование используется для формализации различных типов
задач в искусственном интеллекте. С другой стороны, эти формализ-
формализмы выигрывают благодаря существующим процедурам логического
программирования. Более того, с помощью логического программи-
программирования были установлены связи между немонотонными формализ-
формализмами.
Идея рассматривать логические программы как автоэпистемиче-
ские теории впервые возникла у М. Гельфонда, который предложил
обозначать каждую негативную литеру not L логической программы
как r^BL (трансформация Гельфонда), т.е. not L получает эписте-
мическое прочтение: «Нет повода иметь убеждение в истинности L».
П. Бонатти изучал различные трансформации между литерами с от-
отрицанием по умолчанию и литерами со степенью убеждения «belief
literals», чтобы показать, как различные виды семантики логических
программ могут быть получены из автоэпистемических логик.
В случае расширенного логического программирования взаимо-
взаимосвязи с формализмами немонотонного вывода позволяют уточнить
смысл явного отрицания (-i) и его связь с отрицанием по умолчанию.

376 Немонотонные логики в логическом программировании [ Гл. 9
9.4.1. Общая семантика для программ с отрицаниями двух видов
Логическую программу Р молено представить в виде множества
общих дизъюнктов ^_Р, которое будет называться дизъюнктивной
логической программой. Множество общих дизъюнктов — это, как
обычно, множество дизъюнктов вида L\ V ... V Ln, где Li — либо
атом А, либо его классическое отрицание ~ А (отрицание в классиче-
классической логике). Мы будем различать явное отрицание «-i» и настоящее
классическое отрицание «~», так как необходимо наиболее полно
охарактеризовать отрицание «-i».
Модели и интерпретации дизъюнктивных логических программ —
это просто классические модели и интерпретации множеств общих
дизъюнктов. Высказывания вида not_A (перевод умолчаний not A
из программы Р для дизъюнктивной логической программы ^_Р)
будем называть умолчаниями, а все остальные высказывания — объ-
объективными высказываниями.
Опишем стационарную и устойчивую семантику для программ с
двумя видами отрицания. Рассмотрим параметризуемую схему. Для
этого необходимо определить сначала два вида общей семантики для
нормальных логических программ, расширенных дополнительным
отрицанием: первая семантика расширяет стационарную семантику
для нормальных логических программ (она эквивалентна фундиро-
фундированной семантике), а вторая — семантику устойчивых моделей. Это
примеры общей семантики, так как здесь делаются минимальные
предположения о дополнительном виде отрицания. Напротив, смысл
отрицания по умолчанию оказывается полностью определенным в
этих общих видах семантики. В дальнейшем схема будет обобщена,
чтобы параметризовать ее и по отношению к отрицанию по умолча-
умолчанию.
Определим стационарное расширение нормальных программ.
Определение 9.52. (Минимальные модели). Минимальная мо-
модель теории (или множество общих дизъюнктов) Т — это модель М
теории Т, обладающая следующим свойством: не существует мень-
меньшей модели N теории Т, совпадающей с М на высказываниях-
умолчаниях.
Если формула F истинна во всех минимальных моделях теории
Т, то мы пишем: Т |=circ F и говорим, что F минимально следу-
следует из Т. Это равносильно параллельному очерчиванию Мак-Карти
(McCarthy's Parallel Circumscription): CIRC(T;O;D) теории Т, в ко-
которой объективные высказывания О минимизируются при фиксиро-
фиксированных высказываниях-умолчаниях D.
Определение 9.53. (Стационарное расширение нормальных про-
программ). Стационарное расширение нормальной программы Р — это
любая непротиворечивая теория Р*, удовлетворяющая следующему

9.4] WFSX, семантика логических программ 377
уравнению фиксированной точки:
Р* = -_PU {not_A|P* |=circ~A} U {~not_A|P* |=circ А},
где А — произвольный атом, ^_Р — программа, полученная из Р
путем замены каждой литеры вида not L на not_L. (Заметим, что
п_Р и Р* - это всегда множества хорновских дизъюнктов.)
Пример 9.49.
Рассмотрим программу Р:
а <— not a
Ъ <— not а, с
d <— not b,
для которой дизъюнктивной программой является ^_Р:
а V ^not_a
Ъ V ~not_a V ~c
d V ~not_b
Единственным расширением Р является Р* = ^_Р U {not_6,
not_c, ^not_d}. Действительно, минимальными моделями Р* будут
следующие (для ясности в примерах будут показаны все литеры, и
позитивные, и негативные):
{not_a, not_6, not_c, ^not_d, a, ~Ь, ^с, d}
{^not_a, not_6, not_c, ^not_d, ^a, ^b, ^c, d}
Так как из Р* следуют ^ 6, ^ с и d, то программа должна содер-
содержать {not_6, not_c, ^not_d} и лишь эти литеры по умолчанию.
Оказывается, наименьшее стационарное расширение нормальной
логической программы дает ее фундированную семантику, поэтому
мы займемся расширением WFS с помощью явного отрицания, чтобы
получить WFSX.
Чтобы расширить это определение для логических программ со
вторым отрицанием «—<» общего вида, мы дополнительно преобразуем
все такие литеры с отрицаниями в новые атомы.
Определение 9.54- (Дизъюнктивная программа ^_Р для Р).
Дизъюнктивная программа ^_Р для расширенной логической про-
программы Р — это множество хорновских дизъюнктов, полученное с
помощью обозначения каждой литеры в Я по следующим правилам:
^А обозначается новым атомом ^_А,
not А обозначается атомом not_A,
not ^A обозначается атомом not_^_A,

378 Немонотонные логики в логическом программировании [ Гл. 9
последующей заменой в Р таких литер их новыми обозначениями,
и, наконец, интерпретацией связки правил «<—» как материальной
импликации, обозначаемой символом «=>».
Пример 9. 50.
Пусть Р = {а <— ^Ь}. Дизъюнктивная программа ^_Р — это:
—1 _Р = {^_Ь => а} или, что эквивалентно, ^_Р = {а V ^^Ь}.
Модели расширенной программы определяются моделями ее дизъ-
дизъюнктивных расширений с помощью обратного преобразования.
Определение 9.55. (Смысл дизъюнктивной программы Р*).
Смысл дизъюнктивной программы Р* определяется объединением
множеств всех атомов:
А таких, что Р* |= А
^А таких, что Р* |= ^_А
not А таких, что Р* |= not_A
not ^А таких, что Р* |= not_^_A, где
Р* |= L означает, что литера L принадлежит всем (классическим)
моделям (множества общих дизъюнктов) Р*.
Для определения второго вида отрицания необходимо ввести в
^_Р аксиомы АХ^, определяющие его свойства. Например, если
мы хотим, чтобы второе отрицание было классическим отрицанием,
мы должны добавить к ^_Р множество дизъюнктов: {^_А -Ф=>^ А\
A G Я}, где символ «<^>» обозначает материальную эквивалентность
и используется для сокращения записи: -н А =>^А и ~А => ^_А. В
этом случае семантика Р не зависит от того, выполнялась ли первая
часть преобразования к ^_Р или нет.
Мы хотим, чтобы эта общая семантика была расширением стаци-
стационарной семантики. Тогда мы должны гарантировать, что семантика
программы, в которой отсутствует ^-отрицание, такая же, как и для
стационарной семантики, независимо от вида используемых в общей
схеме аксиом ^-отрицания. Для этого необходимо сначала миними-
минимизировать с помощью очерчивания атомы языка Р, и только потом
можно минимизировать атомы с символами подчеркивания.
Пусть М и N — две модели программы ^_Р и Mpos (соответ-
(соответственно, iVpos) — подмножество М (соответственно TV), получающееся
с помощью удаления из него всех литер вида ^_L. Мы говорим, что
М~ ^ N тогда и только тогда, когда
Mpos С iVpos V (Mpos = iVpos Л М С N).
Это определение эквивалентно классическому, к которому добавляет-
добавляется условие, чтобы выполнялось, например, следующее соотношение:
модель Mi = {^_а} меньше модели М^ = {а}.
Теперь минимальные модели определяются аналогично определе-
определению 9.52, но уже с этим новым отношением ~ ^. Эквивалентность

9.4] WFSX, семантика логических программ 379
между минимальностью и очерчиванием достигается с помощью упо-
упорядоченного предикатного очерчивания CIRC(T;O;D) теории Т, в
котором минимизируются объективные высказывания О. Сначала
минимизируются высказывания, имеющие вид, отличный от ^ _А^ а
затем — высказывания вида ~^_А, причем высказывания-умолчания
D — фиксированные параметры.
Определение стационарного расширения программ оказывается
обобщением определения 9.53, которое параметризуется множеством
аксиом АХ^ , определяющих ^_А, и использует новое понятие упо-
упорядоченной минимальности.
Определение 9.56. {Стационарные АХ ^-расширения.) Стацио-
Стационарное расширение программы Р, расширенной по АХ^, — это любая
непротиворечивая теория Р*, удовлетворяющая следующему уравне-
уравнению фиксированной точки:
Р* = -_Р U AX^ U {not_L|P* |=circ~?}U -not_L|P* |=Circ L},
где L — любое произвольное объективное высказывание, а АХ^ —
множество аксиом для ^-отрицания в программе Р.
Стационарное расширение Р* программы Р получается с помощью
добавления к соответствующей дизъюнктивной программе ^_Р ак-
аксиом, определяющих ^-отрицание, и отрицаний по умолчанию not_L
только лишь для тех литер L, которые ложны во всех минимальных
моделях Р*. Смысл отрицания по умолчанию состоит в том, что в
любом стационарном расширении Р* not_L оказывается истинным
лишь в том случае, если Р* минимально влечет ^L. Заметим, что
определение АХ^ влияет на то, будет ли ~ L принадлежать всем
минимальным моделям Р*, сокращая количество моделей.
Известно, что для любого позитивного высказывания А любой
теории Т приведенное определение |=circ дает следующий результат:
Т |=circ А = Т |= А. В этом случае непосредственно по определению
9.56 оказывается справедливым следующее утверждение.
Утверждение 9.14. Непротиворечивая теория Р* — это стаци-
стационарное расширение программы Р, расширенной по АХ^, тогда и
только тогда, когда
• Р* получается путем добавления к п_Р и АХ^ некоторых
высказываний-умолчаний not_A и ^not_A, где А — объектив-
объективное высказывание;
• Р* удовлетворяет свойствам:
Р* |= not_A = P*
Р* |=-not_A = P* \=A
для любого объективного высказывания А.

380 Немонотонные логики в логическом программировании [ Гл. 9
Пример 9. 51.
Рассмотрим программу Р:
р <— а
р <— ^а
q <— not р,
где символ «-I» обозначает классическое отрицание в программе Р,
т. е.
Дизъюнктивная программа для Р — это следующая программа:
р V ~а
р v ^j^a
q V ~not_p
Единственным стационарным расширением Р является следую-
следующее:
Р* = ^_Р U AX^ U {-not_p, not_^_p,
not_q, ~not_^_q, not_a, ~not_^_a}.
Фактически, единственной минимальной моделью для Р? является
{^not_p, not_^_p, not_^, ^not_^_^, not_a,
и условия утверлсдения 9.14 выполнены.
Обратим внимание на то, что отношение ~^ отдает предпочтение
именно этой модели по сравнению с другими, которые могли бы
быть минимальными, если бы использовалось обычное отношение ^.
Например, классическая минимальная модель — это модель
{^not_p, not_^_p, not_g, ^not_^_g, not_a,
которая не будет минимальной по отношению к ~^.
Если отрицание «-<» в программе Р определить с помощью АХ^ =
= {^_а =>^a, ^_p ^^p, ^_q ^^q}, т. е. использовать сильное отри-
отрицание в том смысле, что отрицание «-i» влечет классическое отрица-
отрицание в ^_Р, то единственным стационарным расширением программы
Р будет Р2* = ^_Р U AX^ U {not_p, not_^_p, ^ not_q, not_^_qy
not_a, not_^_a}.

9.4] WFSX, семантика логических программ 381
Фактически, единственной минимальной моделью для Р^ являет-
является:
{not_p, not_^_p, ^not_g, not_^_g, not_a,
и снова условия утверждения 9.14 выполнены.
Определим теперь семантику программы, основанную на ее стаци-
стационарных расширениях по отношению к некоторому АХ^.
Определение 9.57. {Стационарная АХ ^-семантика). Стацио-
Стационарная АХ^-модель программы Р определяется смыслом программы
Р*, где Р* — стационарное АХ^-расширение программы Р. Стаци-
Стационарная АХ ^-семантика расширенной программы Р — это множе-
множество всех стационарных АХ^-моделей программы Р. Если S = {М&
k G К} — семантика Р, то предполагается, что смысл Р определяется
как М = р| Мк.
кек
Пример 9. 52.
Смысл программы из примера 9.51 определяется множеством
{Pi ^<L ^ai n°t <L n°t ai n°t ^P}> если используется классическое
отрицание, и множеством {g, not p, not -np, not -na, not a, not ^a},
если используется сильное отрицание.
Пример 9. 53.
Рассмотрим программу Р:
а <— not b
-¦a,
где «-i» — слабая форма отрицания, определяемая с помощью
АХ^ = {~А => ^_А\А е Н}.
Единственным стационарным расширением Р будет
которое определяет смысл программы Р как М = {a, -ia, not 6, ^6}.
Тот факт, что а и ^а одновременно принадлежат М, не составляет
проблемы, так как слабая форма отрицания это допускает. Заметим,
что утверждение ^А => ^_А эквивалентно утверждению А V ^_А,
т.е. разрешаются модели, содержащие как А, так и ^_А. Литера ~^Ъ
также появляется в М благодаря использованию слабого отрицания.
Утверждение 9.15 (Обобщение стационарной семантики).
Пусть Р — (нерасширенная) нормальная логическая программа,
и пусть АХ^ таково, что ни один дизъюнкт вида А\ V ... V Ап,
где {Ai,... ,Ап} С Я не является ее логическим следствием. М —

382 Немонотонные логики в логическом программировании [ Гл. 9
стационарная АХ^-модель программы Р тогда и только тогда, когда
М (по модулю ^-литер) — стационарная модель Р.
Все множества аксиом АХ^, используемые в дальнейшем, удо-
удовлетворяют ограничению, накладываемому в утверждении 9.15. Это
ограничение на вид АХ^ предназначено для исключения необычных
определений ^-отрицания, в которых позитивные литеры могут быть
следствиями лишь аксиом, независимо от программы.
Пример 9.54.
Пусть Р = {а <— Ь} и АХ^ = {а V ^^_6, ^_Ь}. У программы Р
существует АХ^-модель: {a, not —<а, not 6, ^fr}, которая не является
стационарной моделью Р. Заметим, что а находится в модели будучи
логическим следствием АХ^ вне зависимости от программы.
Параметризуемая схема. Устойчивые модели имеют 1:1 соот-
соответствие с устойчивыми расширениями , а последние могут быть
получены просто заменой |=circ на |=cwa в определении стацио-
стационарного расширения нормальных программ, где CWA (Closed World
Assumption) обозначает предположение о замкнутости мира.
Подобно стационарной семантике расширенных программ может
быть получено общее определение устойчивой семантики расширен-
расширенных программ, если использовать следующее условие для добавления
отрицания по умолчанию: Р* |=cwa^-^- Таким образом в общем слу-
случае в схему желательно привнести новый параметр, чтобы определить
способ добавления в расширение отрицания по умолчанию.
Определение 9.58. (<АХ^, notcond>-расширение).
<АХ^, notcond>-расширение расширенной программы Р — это
любая непротиворечивая теория Р*, удовлетворяющая следующему
уравнению фиксированной точки:
Р* = ^_Р U AX^ U {not_L| notCond(b)} U {~not_L| P* |= L},
где L — любое произвольное объективное высказывание.
Определение общей семантики подобно определению стационарной
семантики.
Определение 9.59. (<АХ^, notcon(\>-семантика).
<АХ^, пот,СОпс1>-модель программы Р определяется смыслом
программы Р*, где Р* — это <АХ^, notcond>-pacniHpeHHe программы
Р. Семантика программы Р — это множество всех <АХ^, notcond>-
моделей Р. Смысл программы Р определяется пересечением всех
моделей.
Устойчивая АХ^-семантика определяется как общая семантика,
для которой notCond(^) = P* Hcwa^^- При таком определении ут-
утверждения 9.14 и 9.15 остаются в силе и для устойчивых моделей.
9.Ji..l.l. Свойства отрицания «^». Рассмотрим некоторые
свойства расширенных логических программ и покажем для неко-
некоторых АХ^, подчиняется или нет результирующая семантика таким

9.4] WFSX, семантика логических программ 383
свойствам. Точнее, Альфереш и Перейра проанализировали следую-
следующие случаи для общих схем стационарной и устойчивой семантики:
• классическое отрицание, т.е. АХ^ = {^_А <f=^~A\A Е Н};
• сильное отрицание, т.е. АХ^ = {^_А =4>^А\А Е Н};
• слабое отрицание, т.е. АХ^ = {^А => ^_А|А Е Д"};
• псевдоотрицание, т.е. АХ^ = {}.
В следующем разделе будет приведено новое определение для
WFSX с использованием явного отрицания, которое задается с по-
помощью АХ^ = {}, и notCond(b) = Р* |=circ ~ L V Р* |= ^_L.
Альтернативно можно определить WFSX через стационарную АХ^-
семантику, если ввести явное отрицание с помощью аксиомы АХ^ =
= {~^_А => not_A| А Е Н}. Остановимся на свойствах лишь
^-отрицания.
Свойство 9.1 (Внутренняя непротиворечивость). Семантика
внутренне непротиворечива тогда и только тогда, когда для
любой программы Р, если М — стационарная (соответственно,
устойчивая) модель Р, то ни для какого атома А Е Н не
выполняется {А, ^А} С М. Другими словами, семантика внутренне
непротиворечива, если нет необходимости проверять непротиворе-
непротиворечивость результирующих (стационарных или устойчивых) моделей
программы.
Пример 9. 55.
Пусть программа Р — это
а <— not Ъ
^а <— not 6,
где -л — слабое отрицание. Единственным стационарным расширением
Р будет
Р* = ^_Р U {~А => ^
Единственной минимальной моделью Р* будет
{a1~not_a1 ^_a, ^not_^_a, ~Ь, ^^_6, not_b, not_^_b},
которая непротиворечива. Однако Р* получает противоречивый
смысл: {a, -ia, not_b, not_^_b}.
Как показано в предыдущем примере, семантика со слабым от-
отрицанием не обязательно является внутренне непротиворечивой. То
же относится и к семантике с псевдоотрицанием. Семантика с клас-
классическим или строгим отрицанием внутренне непротиворечива, так
как по самому определению АХ^, для каждого атома А Е Н
~А\/ ~^_А Е Р* для каждого расширения Р* любой программы Р, и
в результате никакая модель Р* не может содержать одновременно А

384 Немонотонные логики в логическом программировании [ Гл. 9
и ^_А. Таким образом, смысл Р* никогда не содержит одновременно
Свойство 9.2 (Когерентность). Семантика когерентна тогда и
только тогда, когда для любой программы Р и объективной литеры
L если М — стационарная (соответственно, устойчивая) модель Р, то
из ^L Е М следует, что и not L Е М.
Как отмечалось выше, это свойство играет важную роль, если
мы рассматриваем второе отрицание как средство для определения
ложности литер. В этом случае когерентность может пониматься сле-
следующим образом: «Если А объявлено ложным, то необходимо пред-
предполагать его ложность по умолчанию». Оказывается, что и для ста-
стационарной, и для устойчивой семантики когерентность эквивалентна
непротиворечивости.
Теорема 9.20. Стационарная (устойчивая) семантика когерентна
тогда и только тогда, когда она непротиворечива.
Свойство 9.3 (Обоснованность). Семантика необходимо обосно-
обосновывающая тогда и только тогда, когда для любой программы Р
всякий раз, когда М — стационарная (соответственно, устойчивая)
модель Р, для каждой объективной литеры L, если L Е М, то в Р
существует по крайней мере одно правило вида
L <— В\,..., Bnj not C\,..., not Cm такое, что:
{?i,...,?n,notCb...,notCm} С М.
Так как для любой программы Р: ^_PU {not_L| P* ^ciRC-^} —
программа из хорновских дизъюнктов, то стационарная (или устой-
устойчивая) семантика такая, что АХ^ не содержит ни одного дизъюнкта
с позитивными высказываниями, необходимо является обосновываю-
обосновывающей. Таким образом, семантика с псевдо- или сильным отрицанием
будет необходимо обосновывающей.
Семантика, которая использует в АХ^ дизъюнкты с позитивными
высказываниями не обязательно будет обосновывающей. Например,
если -л — классическое отрицание необходимая обоснованность не
выполняется.
Пример 9.56.
Рассмотрим программу Р:
Единственная стационарная {~^_А 43- ~ А} модель — это
М = {not а, -па, not 6, ^b}. Так как -^Ъ Е М и не существует правила
для -иЬ, то семантика не является необходимо обосновывающей.

9.4] WFSX, семантика логических программ 385
Это свойство тесно связано с использованием логики как языка
программирования. Истинность объективных литер не предполагает-
предполагается до тех пор, пока не будут представлены правила, устанавливаю-
устанавливающие их истинность, другими словами, за исключением высказываний-
умолчаний, не предполагается никакой неявной (скрытой) информа-
информации. Если необходимо получить результат по предыдущей программе,
то требуется записать:
или, если вводится дизъюнкция:
а <— Ъ
Ъ У^Ъ.
9.4 АЛЛ. Фиксация множества АХ^ и условия notcond(L). Пред-
Представим еще раз некоторые виды семантики для расширенных про-
программ, просто определяя конкретное множество АХ^ и условие
notcond(iv) по отношению к введенной общей семантике. В результате
молено лучше понять, какой тип второго отрицания используется в
каждой семантике, каковы основные различия между ними, и как
они соотносятся с WFSX. Начнем с семантики ответных множеств
для программ с непротиворечивыми ответными множествами.
Теорема 9.21 (Семантика ответных множеств). Интерпретация
М — это ответное множество программы Р тогда и только тогда,
когда М — устойчивая АХ^ = {^_А =>^А| А Е ifj-модель Р (по
отношению к синтаксическому представлению моделей).
В определении ответных множеств литеры по умолчанию не вклю-
включаются в модели, поэтому последнее замечание предполагает удале-
удаление всех литер по умолчанию в моделях в соответствии с исходным
определением.
Теорема 9.21 приводит к заключению, что семантика ответных
множеств расширяет семантику устойчивых моделей с помощью силь-
сильного отрицания. Поэтому семантика ответных множеств непротиворе-
непротиворечива, когерентна и является обосновывающей. Заметим, что если вме-
вместо сильного отрицания использовать псевдоотрицание, то непротиво-
непротиворечивость результирующей модели все равно сохраняется, но свойства
когерентности и внутренней непротиворечивости будут нарушены.
Теорема 9.22 (Стационарная семантика с классическим отри-
отрицанием). Интерпретация М — стационарная модель программы Р
тогда и только тогда, когда М — стационарная АХ^ = {^_А <f=^~A\
А е Н}-модель Р.
13 В.Н. Вагин и др.

386 Немонотонные логики в логическом программировании [ Гл. 9
Эта семантика не удовлетворяет свойству обоснованности. Тем
не менее, эта семантика — единственная из рассматриваемых здесь,
которая вводит «настоящее» классическое отрицание в нормальных
логических программах. Альфереш и Перейра утверждают, что если
ее сравнивать с другими видами семантики с сильным отрицанием,
то преимущество данной семантики невелико, так как если разрешить
добавление дизъюнкции к логическим программам с сильным отри-
отрицанием, то программист сможет устанавливать отрицание, похожее
скорее на классическое, нежели на сильное. Это может быть сделано
просто с помощью добавления правил в форме А V ^А для каждого
атома. Более того, программист имеет возможность устанавливать,
какое отрицание — сильное или классическое — желательно исполь-
использовать для каждого атома языка, путем выбора — добавлять или нет
для этого атома дизъюнктивное правило.
ДУГ8Хисильное отрицание
Теорема 9.23 (WFSX и сильное отрицание). Если интерпретация
М является стационарной АХ^ = {^_А =4>^ А\ А Е ifj-моделью
программы Р, то М — WFSX-частичная устойчивая модель програм-
программы Р.
Таким образом, WFSX дает семантику для большего количества
программ, и всегда, когда обе семантики определяют смысл програм-
программы, WF-модель WFSX является (возможно, собственным) подмноже-
подмножеством модели стационарной семантики с сильным отрицанием.
Пр имер 9. 57.
Рассмотрим программу Р:
бреет(джон,Х) <— not бреет (Х,Х)
идти_ обедать(X) <— бреет(У,Х)
^идти_ обедать (джон),
которая утверждает: «Джон бреет каждого, кто не бреется сам»,
«Если X был кем-то побрит, то X идет обедать в ресторан»,
и «Джон не идет обедать». Согласно WFSX, фундированная
модель программы (и единственная частичная устойчивая модель)
- это М: {^идти_ обедать (джон), not идти _ обедать (джон),
not сбреет (джон, джон)}. Заметим, что М не является моделью в
обычном смысле, так как для второго правила значение истинности
головы (ложь) меньше, чем истинностное значение тела (неопреде-
(неопределенность).
Вспомним, что ^-отрицание в WFSX «сильнее» неопределенности
(в данном случае идти_ обедать (джон)). Истинность ^L — это явное
объявление того, что L ложно.
Любая семантика, согласующаяся с утверждением 9.14, и, в част-
частности, стационарная семантика с сильным отрицанием, не может
иметь М как модель программы: not _идти_ обедать (джон) находит-
находится в расширении тогда и только тогда, когда ^ идти_ обедать (джон)

9.4] WFSX, семантика логических программ 387
принадлежит всем минимальным моделям этого расширения, но если
бы это выполнялось, то (по второму правилу) rsjбреет(джон, джон)
должно быть также во всех минимальных моделях, откуда необхо-
необходимо следует, что not бреет (джон, джон) принадлежит расшире-
расширению.
Для того, чтобы восстановить WFSX по общей схеме, необходимо
ввести новое условие для добавления отрицания по умолчанию, по
которому литера по умолчанию not L обязательно должна принадле-
принадлежать расширению в случае, когда явное отрицание ^_L находится во
всех моделях.
Теорема 9.24 (Семантика WFSX). Интерпретация М — частич-
частичная устойчивая модель канонической программы Р тогда и только
тогда, когда М — стационарная АХ^ = {^_А => not_A| А Е Н} —
модель Р.
Альтернативно, М — частичная устойчивая модель Р тогда и
только тогда, когда М представляет смысл такой программы, что
Р* = ^_Р U {not_L\ Р* \=cmc~L или
Р* |= ^_L} U {~not L|P* |= L}.
Пример 9. 58.
У программы Р из примера 9.57 есть единственное расшире-
расширение (использованы сокращенные названия предикатов и констант:
идти_ обедать — о, бреет — б, джон — д):
Р* = ^_Р U {not_o(d), ~not_^_o(d), not_^_6(d,d)}.
Минимальными моделями являются следующие:
{not_6(d,d), not_^_6(d,d), not_o(d),~not_-^_o(d),
б(д,д),~^_б(д,д), о(д), ^_
Во всех моделях имеем
), следовательно, необходимо добавить not_^_6(d,d);
• ~^_о(д), следовательно, необходимо добавить ~ not_^_o(d), и,
по второму дизъюнкту, not_o(d).
Заметим, что согласно первому варианту теоремы 9.24, нет необхо-
необходимости добавлять not_o(d), так как это заключение является след-
следствием при заданных в АХ^ аксиомах. Семантика Р определяется
смыслом программы Р*, т.е. {->о(д), not о(д), not ^б(д,д)}, который и
определяет единственную частичную WFSX-модель.
13*

388 Немонотонные логики в логическом программировании [ Гл. 9
9.^.1.1.2. Логические программы с ^-отрицанием и дизъюнкцией.
Основываясь на сходстве между общим определением стационарной
семантики для расширенных программ и стационарной семантики для
нормальных логических программ, нетрудно обобщить стационарную
семантику расширенных логических программ на расширенные дизъ-
дизъюнктивные логические программы.
Сначала необходимо расширить определение для ^_Р на случай
дизъюнктивных программ. Это определение получается добавлением
к определению 9.54 следующего предложения: «Проинтерпретируем
связку V в логических программах как классическую дизъюнкцию».
Определение 9.60. Стационарное АХ ^-расширение для расши-
расширенной дизъюнктивной программы Р — это любая непротиворечи-
непротиворечивая теория Р*, удовлетворяющая следующему уравнению фикси-
фиксированной точки (предполагается, что есть дистрибутивная аксиома:
not (А & В) = not A V not В):
Р* = ^_Р U AX^ U {not F\ P* |=circ~^},
где F — произвольная конъюнкция позитивных (соответственно, нега-
негативных) объективных литер.
Имея это определение, можно задать семантику подобно тому, как
это было сделано в начале настоящего раздела (9.4.1) для стацио-
стационарной и устойчивой семантики программ с двумя видами отрица-
отрицаний.
Пример 9.59.
Рассмотрим программу Р:
р <— not a
р <— not ~^Ъ
а V ^Ъ
и пусть АХ^ — это аксиомы сильного отрицания. Единственным
стационарным АХ^-расширением программы Р является
Р* = ^_Р U AX^ U {not_^_a, not_b,~not_p,
not_^_p, not_a V not_^_b,~not_aV ~not_-i_b}.
В результате единственной стационарной АХ^-моделью будет
{р, not -ip, not ^a,not b}.
Теперь открывается широкое поле для исследования взаимодей-
взаимодействия между отрицанием «—<» и дизъюнкцией в семантике расширен-
расширенных программ и сравнительного анализа различных видов семантики
по отношению к дизъюнкции.

9.4] WFSX, семантика логических программ 389
Пример 9. 60.
В примере 9.56 показано, что программа Р
а <— Ъ
-¦а,
рассматривающая «—<» как классическое отрицание, имеет единствен-
единственную стационарную модель: М = {not а, —<а, not 6, ^fr}, что нарушает
свойство обоснованности. Для
восстановления этого свойства программу необходимо переписать
в виде
Нетрудно показать, что единственной стационарной моделью Р2 при
-л — сильном отрицании будет М.
Известно, что определение, подобное 9.60, делает дизъюнкцию
в программах исключающей (см. пример 9.59). Чтобы дизъюнкция
была «включающей» для нерасширенных дизъюнктивных программ,
необходимо использовать «слабое расширенное предположение о за-
замкнутости мира».
9.4.2. Автоэпистемические логики для WFSX
Выше были определены некоторые свойства каждого из
^-отрицаний, но не было дано эпистемического смысла этих отрица-
отрицаний. Альфереш и Перейра построили немонотонную эпистемическую
логику с двумя модальностями — доказуемостью и убеждением, с
помощью которой можно выразить различия между определенными
ранее ^-отрицаниями.
В этом подходе для второго вида отрицания предлагается ис-
использовать дополнительную модальность. Поэтому, чтобы определить
общий перевод между расширенными программами и некоторой эпи-
стемической логикой, последняя должна включать две модальности.
При этом объективная литера ^А (соответственно, А) должна чи-
читаться как «доказана ложность А» (соответственно, «доказана истин-
истинность А»), что обозначается как Е~А(ЕА). Запись not L читается
как «имеется убеждение в том, что L не доказано» и обозначается с
помощью Br^EL. E соответствует эпистемическому знанию, которое
определяется пропозициональной доказуемостью, и связано с модаль-
модальностью М следующим образом: Е =r^M^j.
9.4.2.I. Автоэпистемические логики Мура и Пшимусин-
ского. Пропозициональный автоэпистемический язык — это любой

390 Немонотонные логики в логическом программировании [ Гл. 9
пропозициональный язык Lang, обладающий свойством: для любо-
любого высказывания А в Lang, далее называемого объективным, алфа-
алфавит этого языка содержит соответствующее высказывание убеждения
(belief proposition) XA, т. е. высказывание, имя которого состоит из
символа X, за которым следует А. При этом смысл LA выражается
предложением: «А принимается как убеждение».
Автоэпистемическая теория — это любая теория Т над автоэписте-
мическим языком (причем символ «~» будет обозначать классическое
отрицание в теории). Следующее определение устойчивого автоэпи-
стемического расширения эквивалентно определению Мура.
Определение 9.61. (Устойчивое автоэпистемическое расшире-
расширение). Непротиворечивая теория Т* — это устойчивое автоэпистеми-
автоэпистемическое расширение теории Т тогда и только тогда, когда
• Т* = Т U .?>, где В (возможно пустое) множество литер убежде-
убеждения, т. е. литер в форме LA или ^ХА, {А — объективное выска-
высказывание) и
• Т* удовлетворяет следующим условиям:
Т* |= LA = Т* \=А
Т* \=~LA = Т* К А
Это определение выражает позитивную и негативную интроспек-
интроспекцию разумного агента: агент убежден в истинности некоторого выска-
высказывания А тогда и только тогда, когда А принадлежит всем моделям
его знания; и у агента нет повода быть убежденным в истинности
А(~ LA) тогда и только тогда, когда А не принадлежит всем моделям
его знания.
Заметим, что в автоэпистемическом определении Мура оператор
убеждения L мог применяться к любой формуле, и поэтому соответ-
соответствующим образом модифицируется определение расширения.
Пример 9. 61.
Рассмотрим следующую автоэпистемическую теорию Т:
студент(Х) & ~L ah (X) => юн(Х)
студент (а)
студент (Ь)
аЬ(Ь)
Единственным устойчивым расширением Т является следующее (ис-
(используются сокращенные названия предикатов):
Т U {Lc{a), Lc(b), Lab(b), Ью{а), ~Lab(a), ~Ью{Ъ)}.
Здесь утверждается, что агент со знаниями Т убежден, что а и Ъ —
студенты, Ъ — аномальный студент и а юн, и у агента нет повода быть
убежденным в том, что а — аномальный и Ъ юн.

9.4] WFSX, семантика логических программ 391
Конечно, некоторые автоэпистемические теории могут иметь нес-
несколько устойчивых расширений.
Пример 9. 62.
У теории Т
а V Lb
Ъ V La
два расширения, а именно, Т U {Ха, ^Lb} и Т U {Z6, ^La}. Каждое из
данных расширений может рассматриваться как состояние убежде-
убеждений, т. е. агент со знаниями Т имеет два возможных состояния убежде-
убеждений: либо он убежден в истинности айв этом случае у него нет повода
быть убежденным в истинности 6, либо наоборот. Скептический агент
с этими состояниями убеждений не будет убежден или не убежден ни
в истинности а, ни в истинности Ъ.
Пшимусинский выделяет четыре недостатка автоэпистемической
логики Мура.
1. У вполне разумных теорий может не быть устойчивых расшире-
расширений. Например, для теории
разбитая _ машина
можно_ починить V L можно_ починить
нет устойчивого расширения, так как ни одно непроти-
непротиворечивое добавление убеждений к теории не позволяет
вывести L можно_ починить. Если нет убеждения в том,
что можно_ починить, то возникает противоречие, и агент
должен остаться агностиком, так как нельзя иметь или не иметь
убеждения в истинности высказывания можно_ починить. Тем
не менее агент должен быть убежден, по крайней мере, в том,
что машина разбита.
2. Даже те теории, у которых существуют устойчивые расширения,
в автоэпистемической логике Мура не всегда получают есте-
естественно ожидаемую семантику.
Пример 9. 63.
Робот запрограммирован так, что он может переносить деньги из
банка 1 в банк 2. Существует два возможных пути, обозначаемых а и Ъ.
Робот выбирает один из них, если у него нет повода быть убежденным
в том, что на этом пути могут возникнуть препятствия. Если он не
может выбрать ни одного пути, то он должен отдать предпочтение
пути а. После выбора пути робот сигнализирует: «я выхожу» и пыта-
пытается попасть в банк 2. Эта задача может быть естественным образом
формализована с помощью автоэпистемической теории
L препятствие (а) & ^L препятствие (Ъ) => выбрать (Ъ)

392 Немонотонные логики в логическом программировании [ Гл. 9
L препятствие (Ь) & ^Х препятствие (а) => выбрать (а)
~L препятствие (а) & ~L препятствие (Ъ) => выбрать (а)
выбрать (а) => сигнал
выбрать (Ь) => сигнал
Единственное устойчивое расширение охватывает предполагаемый
смысл, т. е. у робота нет повода быть убежденным в том, что есть
препятствия на каком-либо из путей, и поэтому он выбирает путь а и
сигнализирует.
Допустим теперь, что к теории добавлено знание, что есть некото-
некоторое препятствие на одном из путей, но не известно на каком, т. е.
препятствие (а) V препятствие (Ь)
Результирующая теория имеет два устойчивых расширения, каждое
из которых содержит L сигнал, и одно содержит L выбрать(а), а
другое — L выбрать(Ь). Согласно устойчивым расширениям, у скеп-
скептического агента нет убеждения ни в истинности утверждения вы-
выбрать (а), ни в истинности утверждения выбрать(Ъ), т.е. робот не
выберет ни один из путей, что вполне разумно. Но тем не менее,
такой агент будет убежден в истинности высказывания сигнал, т. е.
робот сообщит: «Я выхожу», что не соответствует нашим ожида-
ожиданиям.
3. Устойчивые расширения не могут быть эффективно вычислены
даже для простых классов теорий, например, для пропозицио-
пропозициональных программ. Это существенный недостаток, если требу-
требуется выполнять представление знаний или рассуждений.
4. Так как всегда требуется явно указывать все убеждения агента,
то при устойчивых расширениях теряется выразительность.
Для того, чтобы преодолеть перечисленные недостатки, Пшиму-
синский ввел общее понятие автоэпистемических логик замкнутых
убеждений, и представил автоэпистемические логики очерчивания
как важный частный случай. Понятие автоэпистемической логики
замкнутых убеждений естественным образом возникает как обобще-
обобщение автоэпистемической логики Мура. Сначала Пшимусинский от-
отметил, что в определении устойчивого расширения запись Т* К А
может быть заменена на Т* |=cwa~A и поэтому устойчивые рас-
расширения могут рассматриваться как частный случай расширений,
основанных на общих понятиях позитивной и негативной интроспек-
интроспекции.
Определение 9.62. (Автоэпистемическое расширение). Непро-
Непротиворечивая теория Т* — автоэпистемическое расширение теории Т
тогда и только тогда, когда
• Т* = Т U В, где В — (возможно пустое) множество литер
убеждения, т. е. литер вида LA или ~LA, где А — объективное
высказывание и

9.4] WFSX, семантика логических программ 393
• Т* удовлетворяет следующим условиям:
Т* |= LA = Т* |=ор А
Т* \=~LA = T* |=ci~A
где |=ор — общий оператор следования открытых убеждений (пози-
(позитивная интроспекция) и |=ci — общий оператор следования замкнутых
убеждений (негативная интроспекция).
Различные автоэпистемические логики получаются в зависимо-
зависимости от выбора позитивной и негативной интроспекции. Основываясь
на этом общем определении, Пшимусинский определяет расширения
очерчивания, просто выбирая |= как позитивный и |=circ как нега-
негативный оператор интроспекции (|=circ определяется, как и ранее,
но фиксируются высказывания в форме LA вместо not_A). Пшиму-
Пшимусинский показал также, что при таком определении расширения все
перечисленные недостатки устраняются, и что с помощью трансфор-
трансформации Гельфонда между нормальными логическими программами
и автоэпистемическими теориями (где not L понимается как ~?L),
приведенное расширение эквивалентно фундированной семантике.
9.4-2.2. Логика убеснсдений и доказуемости. Альфереш и
Перейра определили эпистемическую логику ЕВ с модальностями
убеждения и доказуемости, и показали, что она охватывает семан-
семантику WFSX. Остановимся подробнее на этих результатах. Рассмот-
Рассмотрим сначала определенные расширенные логические программы (т. е.
логические программы без отрицания по умолчанию) и определения
модальной логики для интерпретации таких программ. Затем эта
логика будет расширена с тем, чтобы можно было работать с вы-
высказываниями, принимаемыми как убеждения (belief propositions). И
наконец, рассмотрим, как связана ЕВ-лоткдь и WFSX.
Доказуемость в определенных расширенных ло-
логических программах. Чтобы объяснить и сделать доступным
смысл модальности доказуемости, начнем с более простой задачи,
заключающейся в том, чтобы определить смысл расширенных
логических программ без отрицания по умолчанию, т. е. множеств
правил вида
где каждое Li — это атом А или его явное отрицание ->А.
Не теряя общности, будем считать, что все правила фундаменталь-
фундаментальные, т. е. не содержат переменных.
Желательно, чтобы семантика этих программ была монотонной и
не поддерживала бы контрапозицию, т. е. должны различаться прави-
правила вида а ^ b a ^b ^ ^а. Правила рассматриваются как (однонаправ-
(однонаправленные) «правила вывода». Заметим, что в трансформации Гельфонда
это не выполняется: оба правила переводятся в правило Ъ => а.

394 Немонотонные логики в логическом программировании [ Гл. 9
Пример 9. 64.
По трансформации Гельфонда программа Р
а <— Ъ
переводится в теорию Т (здесь знак ~ соответствует явному отрица-
отрицанию -н):
Отсюда следует {^ а, ~ Ъ\ и семантика Р (как для WFSX, так и для
ответных множеств) есть {^а}. Заметим, что ~ 5 выводится в Т с
помощью применения контрапозиции к первому правилу.
Причина возникновения этой проблемы в том, что ^А переводится
в «А есть ложь», и связка правила «<—» понимается как матери-
материальная импликация. Напротив, семантика расширенных логических
программ склонна интерпретировать ^А как «А доказуемо ложно» в
смысле обоснованности (grounded sense) и «<—» — как отношение вы-
выводимости. Для того, чтобы охватить этот смысл, вводится оператор
модальности Е, соответствующий (пропозициональной) «доказуемо-
«доказуемости» или «эпистемическому знанию», и правило (9.1) переводится в
правило вида
h ... hELn => EL0, (9.2)
где всякая литера с явным отрицанием ^А переводится в Е~А и чи-
читается как «А доказуемо ложно», и всякий атом А переводится в ЕА
и читается как «А доказуемо истинно».
Эта трансляция непосредственно охватывает интуитивное понима-
понимание смысла правила: «если все Li,..., Ln доказуемы, то и Lq доказу-
доказуемо» и не объединяет контрапозиции: а <— Ъ становится ЕЪ => Еа,
тогда как -^Ъ <— ^а дает Е^а => Е^Ъ.
Для обеспечения гибкости подхода делается ряд предположений
относительно Е, который определяется как оператор необходимо-
необходимости в наименьшей нормальной модальной системе — модальной ло-
логике К. Эта логика включает лишь Modus Ponens, необходимость
(necessitation), дистрибутивность относительно конъюнкции и акси-
аксиому
К : E(F ^G)^ (EF => EG).
В логике К Е двойственно по отношению к оператору модаль-
модальной непротиворечивости (consistency) М, т.е. Е =r^M^j. Этой слабой
модальной логики уже достаточно для определения WFSX, если до-
добавить к ней модальность убеждения и немонотонность, а также эта
логика может отражать и другой смысл Е при введении большего
количества аксиом.

9.4] WFSX, семантика логических программ 395
Так как в настоящее время нас интересует лишь семантика моно-
монотонных (определенных) расширенных логических программ, то немо-
немонотонный вариант этой логики не требуется.
Выше уже отмечалось, что трансляция (9.2) может охватывать
и семантику расширенных логических программ. Следующая теоре-
теорема уточняет это утверждение для семантики ответных множеств и
WFSX.
Теорема 9.25. Пусть Р — расширенная логическая программа и
Т — теория, получаемая из Р с помощью трансляции (9.2). Если ни
для какого атома А не выполняется Т \~к ЕА и Е ~ А, то справедливо
следующее:
Т Ьк ЕА = Р \=AS A = P |=wfsx A
Т Ьк Е~А = Р \=as ^A = P |=wfsx --A,
где \~s обозначает, как обычно, отношение следования в модальной
логике S, и Р \=as L, соответственно, Р |=wfsx L, означает, что L
принадлежит всем ответным множествам, соответственно, всем ча-
частичным устойчивым WFSX-моделям, программы Р.
Убеждениеидоказуемость. Помимо явного отрицания рас-
расширенные логические программы также позволяют использовать от-
отрицание по умолчанию, которое является немонотонным и обычно
понимается как высказывание, принимаемое в качестве убеждения
(belief proposition). Таким образом, требуется добавить к модальной
логике К немонотонный оператор убеждения.
Рассмотрим сначала, какие убеждения следуют из определенных
расширенных логических программ. Такие программы без труда мо-
могут быть переведены во множества хорновских дизъюнктов, что обес-
обеспечивает существование единственной минимальной модели. Поэтому
будем сначала считать, что «Агент убежден в истинности каждой
формулы, принадлежащей минимальной модели теории», т. е. если
Т |=min F, то BF (интроспекция).
Пример 9. 65.
Программа из примера 9.64 переводится в теорию Т:
ЕЪ^ Еа
для которой наименьшей моделью будет {Е~а} (сюда не вошли нере-
нерелевантные литеры). Поэтому у агента со знаниями Т есть следующие
убеждения: ВЕ^а, В^Еа, В^ЕЪ, В~Е~Ъ.
Более того, потребуем, чтобы для разумных агентов из Т |= EL
следовало бы, что В^Е^Ь (когерентность). В этом контексте коге-
когерентность утверждает, что всякий раз, когда L доказуемо истинно,
обязательно должно быть убеждение в том, что нельзя доказать
ложность L (заметим, что B^E^L = BML). В приведенном примере

396 Немонотонные логики в логическом программировании [ Гл. 9
результат не согласуется с этим правилом. Но в общем случае это
не так.
Пример 9. 66.
Рассмотрим теорию Т = {Еа; Е^а}, для которой наименьшей мо-
моделью будет {Еа, Е~ а}, и ВЕа и BE ^ а выполняются по интро-
интроспекции. Более того, по когерентности, агент должен поддерживать
как В~Е~а, так и В^Еа.
Этот тип вывода (рассуждений) может показаться странным,
так как агент убежден в истинности взаимодополнительных
(complementary) формул (например, убеждения в истинности Еа
и Е~а). Но, как будет показано ниже, при введении аксиом для В
можно определять противоречия в интуитивно противоречивой
теории Т, т. е. нельзя будет одновременно иметь убеждения в
истинности доказанных взаимодополнительных высказываний.
Как и для Е, относительно В делаются незначительные предпо-
предположения для достижения гибкости, и, кроме того, этого оказывается
достаточно для характеризации семантики WFSX.
Более точно, для оператора убеждения В предполагаются следу-
следующие аксиомы:
• для любой тождественно ложной формулы F выполняется ~BF;
• для любых формул F и G выполняется B(F&G) = BFhBG.
Можно доказать, что из этих аксиом следует, что для любой фор-
формулы F выполняется
BF ^~B~F.
Следовательно, если иметь убеждения в истинности двух взаимнодо-
полнительных формул BY и B^F, то возникнет противоречие, так
как B~F ^~BF.
В итоге для теории Т, получающейся из определенной расширен-
расширенной логической программы, множество убеждений агента представ-
представляет собой замыкание относительно приведенных выше аксиом для
множества
{BF\ T hmin F} U {B~E~F\ T |= EF},
как требуется по интроспекции и когерентности соответственно.
Для того, чтобы добавить к логике К немонотонный оператор
убеждения, рассмотрим, в каких случаях добавляются к теории фор-
формулы вида BF или ~BF (далее называемые формулами убеждений).
В этих случаях уже нельзя использовать операцию замыкания. Для
того, чтобы в теориях можно было работать с формулами убеждений,
необходимо рассмотреть, как и в случае АЭЛ, расширения теорий.
Расширение теории Т — это фиксированная точка уравнения Т* =
= Т U Bel, где Bel — множество формул убеждений, зависящих от

9.4] WFSX, семантика логических программ 397
Т*. Интуитивно, каждое расширение устанавливается для определен-
определенного состояния убеждений разумного агента. Если поступить таким
образом, то возникнет новая проблема: «Какой вид немонотонности
можно ввести для таких теорий?», или другими словами, «При каких
условиях агент может наращивать собственное множество убежде-
убеждений?».
Для решения этой проблемы существует два подхода:
• первый подход представляет автоэпистемическую логику (АЭЛ)
Мура и рефлексивную АЭЛ. Он основывается на предположе-
предположении о замкнутости мира и охватывает двузначную (тотальную)
семантику логических программ;
• второй подход основывается на GCWA и охватывает трехзнач-
трехзначную (или частичную) семантику логических программ.
Альфереш и Перейра следуют второму подходу. Приведем фор-
формальное определение эпистемической логики. Для этого сначала будет
расширен язык пропозициональной логики с помощью модальных
операторов Е и В для «доказуемости» и «убеждения» соответствен-
соответственно. Теории, как и раньше, определяются рекурсивно. Более того,
предполагается, что любая теория содержит все аксиомы логики К
для Е и две описанные ранее аксиомы для В.
Определение 9.63. (Минимальные модели). Минимальная мо-
модель теории Т — это модель М для Т такая, что не существует мень-
меньшей модели N для Т, совпадающей с М на высказываниях убеждений.
Если F истинно во всех минимальных моделях теории Т, то мы
пишем Т |=min F.
Расширение Т* соответствует состоянию убеждений, при котором
агент убежден в истинности F, если Т* |=min F, и не убежден в
истинности F, если Т* |=т1п^ F. Отметим, что если принять акси-
аксиомы, введенные для В, то второе утверждение включается в пер-
первое. Фактически, по первому утверждению, если Т* |=т1п^ F, то
B~F и из аксиом для В следует, что ~BF. Как было показано для
определенных расширенных логических программ, при рассмотрении
теории с доказуемостью и убеждением возникает новая возможность
получения убеждений (когерентность), а именно, если Т* |= EF', то
В~ E^F. В результате расширения формализуют следующее понятие
убеждения В:
BF = F минимально выводимо, или F =^E^G и EG выводимо.
Определение 9.64- (Расширение). Расширение теории Т — это
непротиворечивая теория Т*, удовлетворяющая следующему уравне-
уравнению фиксированной точки:
Т* = TU{BF\ T* \=m[nF}U{B~E~G\ T* \= EG}.

398 Немонотонные логики в логическом программировании [ Гл. 9
Пример 9. 67.
Рассмотрим следующую автоэпистемическую теорию Т (модифи-
(модификация примера 9.65):
~ВЕ~юн(Х) & Естудент(X) => Еюн(Х)
Е студент (а)
Е студент (Ь)
Е^юн(Ъ),
где последний дизъюнкт выражает, что доказано, что Ъ не юн.
Единственным расширением будет: TU {ВЕс(а)у ВЕс(Ь)у ВЕю(а)у
ВЕ~ю(Ъ), В~Е~ с{а), В~Е~ ф), В~Е~ю(а), В~Ею(Ъ)}, кото-
которое утверждает, что агент со знаниями Т убежден в том, что а и
Ъ —студенты, Ъ не юн, а юн, и у него нет убеждения в истинности
того, что а и Ъ не являются студентами, что а не юн и Ъ юн.
Пример 9. 68.
В общем случае не обязательно иметь или не иметь убеждения
в истинности высказывания А. Например, рассмотрим следующие
утверждения:
• если имеется убеждение в том, что машина не может быть
отремонтирована, то тогда доказуемо, что она не может быть
отремонтирована;
• если нет убеждения в том, что кто-то сможет отремонтировать
машину, то доказуемо, что будет вызван эксперт;
• доказано, что эксперт не будет вызван.
Эти утверждения представляются следующей автоэпистемической
теорией Т:
В~Еможно_ починить_ машину => Еможно_ починить_ машину
В~Еможно_ починить_ машину => Евызвать_ эксперта
Е^ вызвать _ эксперта
Единственным расширением будет:
Т U {BEг^вызвать_ эксперта, В~Евызвать_ эксперта},
которое утверждает, что агент убежден в том, что эксперт не будет
вызван, и у него нет убеждения в том, что эксперт будет вызван.
Подобно автоэпистемическим теориям Мура, ^^-теории могут
иметь несколько расширений.
Пример 9.69.
Рассмотрим теорию Т, описывающую ромб Никсона:
Е республиканец (никсон)
Е квакер (никсон)
Ереспубликанец(Х), Вг^Епацифист(X) => E^jпацифист(X)
Еквакер(X), В~Е~пацифист(X) => Епацифист(Х)
У теории Т существует три расширения, получающиеся путем объ-
объединения Т и множеств (использованы сокращенные названия преди-
предикатов и констант):

9.4] WFSX, семантика логических программ 399
1) {ВЕр(н), ВЕк(н), ВЕп(н), В~Е~р(н), В~Е~к(н),
2) {ВЕр(н), ВЕк(н),
В~Еп(н)};
3) {ВЕр(н), ВЕк(н), В^Е^р(н), В~Е~к(н)}.
Они утверждают следующее: в первом случае принимается как
убеждение, что Никсон — пацифист, во втором — что Никсон не паци-
пацифист, и в третьем случае остается неопределенным, считать Никсона
пацифистом или не считать его таковым.
Если скептический агент сталкивается с несколькими расширени-
расширениями (т. е. с несколькими возможными состояниями убеждений), то он
должен принимать лишь те высказывания, которые являются общими
для всех расширений. В приведенном примере это третье расширение.
Связь с расширенными логическими программами.
Вспомним, что расширенная логическая программа — это множество
правил вида
Lo <— Li,..., Lm, not Lm+i,..., not Ln, (9.3)
где Li — объективная литера, т. е. либо атом А, либо его отрицание —^А.
Как показано выше, атом А переводится в ЕА и явно отрицатель-
отрицательный атом ^А — в Е~А. В рефлексивной автоэпистемической логике
литеры вида not L переводятся в X^XL, что читается как «известно,
что L не известно». В нашем подходе мы переводим not L в В~ EL,
т. е. «принимается как убеждение (или может быть допущено), что L
не доказуемо». В результате каждое правило вида (9.3) переводится
следующим образом:
ELU ..., ELm, Б- ELm+u ..., Б- ELn => EL0. (9.4)
Определение 9.65. (Модели и расширение). Модель М расши-
расширенной логической программы Р соответствует расширению Т* тогда
и только тогда, когда
• для объективной литеры L выполняется: L Е М 43- Т* |= BEL;
• для литеры not L выполняется: not L Е М 4=> Т* |= B^EL.
Теорема 9.26 (WFSX, доказуемость и убеждение). Пусть Т —
теория, получающаяся по канонической расширенной логической про-
программе Р с помощью перевода (9.4). Тогда существует 1:1 соответ-
соответствие между частичными устойчивыми WFSX-моделями программы
Р и расширениями Т.
Эта связь полезна как для WFSX, так и для .ЕБ-логики . С одной
стороны, логика представляет интуитивно более верный взгляд на
WFSX, особенно в том, что касается понимания WFSX как средства
для моделирования способности агента доказывать что-либо и для

400 Немонотонные логики в логическом программировании [ Гл. 9
моделирования убеждений разумного агента. В результате становится
более понятным, как в рамках WFSX решать задачи представления
знаний и рассуждений, и как оценивать результаты WFSX. В част-
частности, логика показывает, что явное отрицание соответствует дока-
доказательству ложности, отрицание по умолчанию — убеждению, что
литера не доказана, а неопределенность — отсутствию убежденности
как в ложности, так и в истинности литеры.
В то же время для класса теорий, получающихся из некоторых рас-
расширенных логических программ, «логика может быть реализована»
с использованием процедур, определенных для WFSX. Более того,
для этого класса логика удовлетворяет свойствам кумулятивности,
рациональности, релевантности и ряду других свойств, которым удо-
удовлетворяет WFSX. Установленные взаимосвязи позволяют получить
новые результаты в эпистемической логике и приводят к алгоритмам,
используемым в расширенном логическом программировании.
9.4-2.3. Дальнейшие разработки. Так как язык ЕВ является
более общим, чем язык расширенных логических программ, то логика
ЕВ может служить инструментом для дальнейших обобщений расши-
расширенного логического программирования, например, дизъюнкции. Все,
что для этого требуется, — определить трансляцию дизъюнктивных
расширенных программ в логику.
Другим возможным обобщением расширенного логического про-
программирования может быть использование модальных операторов
логики, допускающих конъюнкцию и дизъюнкцию.
Благодаря связи ЕВ-логики и расширенного логического програм-
программирования удается решить ряд задач. Например, рассмотрим более
подробно задачу устранения противоречий или пересмотр убеждений.
В расширенном логическом программировании предложено несколько
подходов для решения этой задачи, в основе которых лежит следую-
следующая идея: литеры not L рассматриваются как предположения, так
что если предположение приводит к противоречию, то необходим его
пересмотр. В эпистемической логике это переформулируется следу-
следующим образом: «Если в результате интроспекции оказывается, что
не существует ни одного расширения, то необходимо пересмотреть
убеждения».
Пример 9. 70.
Пусть имеется теория Т:
В^Е аЪ => Елетает
Е^летает
Она непротиворечива, но не имеет расширений. Это происходит из-за
того, что г^ЕаЪ истинно во всех минимальных моделях и поэтому, по
интроспекции, в них должно быть добавлено В^ ЕаЪ, что приводит к
противоречию. Причем это типичный пример того, когда в результате

9.5] WFSX и логика умолчаний 401
интроспекции возникает противоречие (подобное явление характерно
и для логик Мура).
Для того, чтобы определить смысл непротиворечивых теорий, не
имеющих расширений, можно использовать два подхода:
1) определить более скептическое понятие расширения, использу-
использующее в интроспекции меньше высказываний, принимаемых как
убеждения;
2) минимально пересматривать теорию, чтобы получить расшире-
расширения.
Исключение возникновения противоречий в логике ЕВ равно-
равносильно ослаблению условий для интроспекции. Дополнительно мож-
можно вводить высказывания-убеждения исключительно для выбранного
подмножества формул, минимально следующих из теории. При этом,
конечно, разрешаются не все подмножества. В частности, можно рас-
рассматривать лишь максимальные подмножества. Изучение дополни-
дополнительных условий предпочтения на этих подмножествах равносильно
соответствующим исследованиям для расширенного логического про-
программирования.
Благодаря эквивалентности автоэпистемической логики и WFSX,
устранение противоречий в этой логике эквивалентно устранению
противоречий для логического программирования.
9.5. WFSX и логика умолчаний
Идея установления связи между логическим программированием и
теориями умолчаний состоит в следующем: перевести каждое правило
программы в правило-умолчание и затем сравнить расширения тео-
теории умолчаний с семантикой соответствующей программы. Поводом
для проведения таких исследований послужило то, что с одной сто-
стороны, появляется возможность использования логического програм-
программирования как структуры для немонотонного вывода, и, с другой
стороны, — вычислять расширения логики умолчаний с помощью ал-
алгоритмов, разработанных для логических программ. Для того, чтобы
установить связь фундированной семантики с расширениями теории
умолчаний, Альфереш и Перейра сначала определяют основные прин-
принципы, которым должна удовлетворять семантика теории умолчаний,
а затем определяют специальную теорию умолчаний, согласующуюся
с этими принципами.
В настоящее время наблюдается все более активное использование
логического программирования с явным отрицанием как инструмента
для выполнения немонотонного вывода, поэтому благодаря резуль-
результатам, полученным этими исследователями, появляется возможность
применять логическое программирование как средство для представ-
представления теорий умолчаний. Наличие установленной связи позволяет

402 Немонотонные логики в логическом программировании [ Гл. 9
лучше прояснить смысл логических программ, сочетающих явное от-
отрицание и отрицание по умолчанию. В частности, удается установить,
как явное отрицание соотносится с классическим отрицанием в теории
умолчаний, и глубже понять особенности использования правил в рас-
расширенных логических программах. Подобно умолчаниям, правила в
программах являются однонаправленными, так что их контрапозиции
задаются явно: связка «<—» — не материальная импликация, а скорее
похожа на отношение выводимости.
Так как WFSX определяется с помощью монотонного операто-
оператора фиксированной точки, то эта семантика обладает желательными
вычислительными свойствами, включающими наличие нисходящих
и восходящих вычислительных процедур. Так как фундированная
семантика состоятельна по отношению к семантике умолчаний Рей-
Рейтера, то всякий раз, когда существует расширение, мы обеспечиваем
наличие состоятельных методов для вычисления пересечения всех
расширений для важного подмножества теорий умолчаний Рейтера.
Представляемая семантика теорий умолчаний определена для
ограниченного языка, в котором предпосылки (prerequisites) и обосно-
обоснования (justifications) — конечные множества фундаментальных литер,
заключением также является литера, и все формулы, не входящие в
правила-умолчания, представлены лишь литерами. Отметим, что, как
обычно, при установлении соответствия теорий умолчаний и логиче-
логических программ, язык теорий уже ограничен подобным образом. Более
того, далее будет показано, что теории умолчаний с ограниченным
языком представления тем не менее обладают такой же выразитель-
выразительной силой, как и логические программы с явным отрицанием.
В данном разделе приводится описание семантики для теории
умолчаний и показывается ее связь с семантикой WFSX. Основываясь
на этой связи, можно дать альтернативное определение WFSX, опира-
опирающееся не на трехзначную, а лишь на двузначную логику. Это дости-
достигается с помощью введения такого определения Г-оператора Гельфон-
да — Лифшицца, для которого уже установлена связь с умолчаниями
Рейтера. В результате WFSX можно рассматривать как частичную
двузначную семантику, в которой неопределенными являются те ли-
литеры, относительно которых не может быть доказана ни ложность, ни
истинность, т. е. литеры, истинность которых в трехзначной логике не
известна.
9.5.1. Язык умолчаний
Рассмотрим сначала пропозициональные языки умолчаний и неко-
некоторые известные логики умолчаний.
Определение 9.66. (Правило умолчания). Пропозициональное
умолчание d — это тройка d =< p(d), j(d), c{d) >, где p{d) и c(d) —

9.5] WFSX и логика умолчаний 403
пропозициональные формулы и j(d) — конечное подмножество пропо-
пропозициональных формул. p(d) (Соответственно, j(d) и c(d)) называется
предпосылкой (соответственно, обоснованием и следствием) умолча-
умолчания d. Умолчание d также обозначается следующим образом:
P(d) :
c(d) ¦
Определение 9.67. (Теория умолчаний). Теория умолчаний А —
это пара (Z), W), где W — множество пропозициональных формул и
D — множество правил-умолчаний.
Как отмечалось выше, определение семантики теорий умолчаний
дается здесь для ограниченного языка, достаточного, тем не менее,
для установления связей с расширенными логическими программами.
Определение 9.68. (Ограниченная теория умолчаний). Ограни-
p(d) : j(d)
ченное правило-умолчание — это правило вида — , где р(а),
c(d)
j(d) и c(d) — литеры. Ограниченная теория умолчаний А — это пара
(D,W), где W — множество литер и D — множество ограниченных
правил-умолчаний.
Рассмотрим кратко ряд известных видов семантики теорий умол-
умолчаний для пропозиционального случая. Затем рассмотрим фундиро-
фундированную и стационарную логики умолчаний, соответствующие фун-
фундированной и стационарной семантике нерасширенных логических
программ.
9.5.1.1. Семантика умолчаний Рейтера. Каждой теории
умолчаний А Рейтер ставит в соответствие оператор Гд, действую-
действующий на множествах объективных литер, которые называются контек-
контекстами.
Определение 9.69. (Оператор Гд,). Пусть А = (Д W) — пропо-
пропозициональная теория умолчаний и пусть Е — произвольное множество
объективных литер, называемое контекстом. Тогда Та(Е) — наимень-
наименьший контекст, для которого справедливо следующее:
1) он содержит W;
2) он замкнут по отношению ко всем правилам вывода вида ,
где — е D и -¦/ ф Е для каждого / е j(d).
суй)
Интуитивно, Та(Е) представляет множество всех объективных
литер, выводимых из W и Е, замкнутое относительно всех правил-
умолчаний, обоснования которых не противоречат Е.
Определение 9.70. (Расширения умолчаний Рейтера). Контекст
Е — это расширение теории умолчаний А тогда и только тогда, когда
Е = ГА(Е).

404 Немонотонные логики в логическом программировании [ Гл. 9
Осторожная (cautious) семантика умолчаний для А — это кон-
контекст, содержащий все объективные литеры, принадлежащие всем
расширениям А. Оказывается, расширения умолчаний могут рассмат-
рассматриваться как рациональные (rational) множества заключений, дедук-
дедуктивно выводимых из А.
Одной из проблем, связанных с логикой умолчаний Рейтера, яв-
является то, что она может иметь множественные расширения, и в этом
случае осторожная семантика умолчаний уже может и не быть рас-
расширением. Если рассматривать расширения лишь как рациональные
множества заключений, то, к удивлению, можно обнаружить, что ни
одно из этих множеств не совпадает с осторожной семантикой.
Пример 9.71.
«с . ^а с . ^1 \
—' ? —' г > Iе} ) > У к°-
Ъ а ) J
торой существует два расширения: Е\ = {а,^Ь,с} и Е2 = {6, ^а,с}.
Осторожная семантика умолчаний дает {с}, причем это множество
само не является расширением, а значит, согласно семантике Рейтера,
не будет и рациональным множеством заключений.
Другая проблема заключается в том, что в тех случаях, когда
ожидается существование вполне определенного смысла, расширение
может и не существовать (т.е. смысл не будет определен).
Пример 9.72.
Для теории умолчаний ( < > , {р} ) не существует расширений.
Хотя р — это факт и естественно считать р истинным.
9.5.1.2. Фундированная и стационарная семантика
умолчаний для нормальных логических программ. Рас-
Рассмотрим два подхода, которые связывают нормальные логические
программы с теориями умолчаний и решают отмеченные проблемы
логики умолчаний Рейтера.
Берел и Субрахманиан предложили фундированную семанти-
семантику для пропозициональных теорий умолчаний, которая определяет
смысл теорий умолчаний с множественными расширениями. Более
того, семантика определяется для всех теорий, назначая каждой из
них единственное расширение.
Пусть А = (D,W) — теория умолчаний, и пусть оператор Гд(.Б)
определен так же, как и раньше. Так как оператор Гд(.Е) антимоно-
антимонотонный, то Гд(.Е) — монотонный оператор, и поэтому имеет наимень-
наименьшую фиксированную точку.
Определение 9.71. (Фундированная семантика).
• Формула F истинна в теории умолчаний А по отношению
к фундированной семантике тогда и только тогда, когда
F G lfp(Y2) (здесь Ifp — наименьшая фиксированная точка);

9.5] WFSX и логика умолчаний 405
• формула F ложна в теории умолчаний А по отношению к фун-
фундированной семантике тогда и только тогда, когда F ф #/р(Г2)
(здесь gfp — наибольшая фиксированная точка);
• в противном случае говорят, что истинностное значение F не
известно (или не определено).
Эта семантика определена для всех теорий и эквивалентна семан-
семантике фундированных моделей для нормальных логических программ.
Позже Пшимусинская и Пшимусинский обобщили эту работу, введя
понятие стационарных расширений умолчаний.
Определение 9.72. (Стационарное расширение). Для данной
теории умолчаний А Е — стационарное расширение умолчаний тогда
и только тогда, когда
. Е = Г\(Е) и
• ЕС Гд(Я).
Определение 9.73. (Стационарная семантика умолчаний).
Пусть Е — стационарное расширение для теории умолчаний А. Тогда
• формула L истинна в Е тогда и только тогда, когда L Е Е\
• формула L ложна в Е тогда и только тогда, когда L ^ Гд(.Б);
• в противном случае истинностное значение L считается неопре-
неопределенным.
Было показано, что эта семантика эквивалентна стационарной
семантике нормальных логических программ.
Заметим, что каждая теория умолчаний имеет по крайней мере
одно стационарное расширение. Наименьшее стационарное расшире-
расширение умолчаний всегда существует и соответствует фундированной
семантике теории умолчаний. Более того, наименьшее стационарное
расширение умолчаний может быть вычислено с помощью итераций
монотонного оператора Гд.
Пример 9. 73.
Рассмотрим теорию умолчаний из примера 9.72. Имеем: Гд({р}) =
= {р, q} и Гд({р}) = {р}. Следовательно, р истинно в теории А.
9.5.2. Некоторые необходимые принципы для теорий умолчаний
Обоснуем ряд принципов, которым должна удовлетворять семан-
семантика теории умолчаний, и свяжем ее с логическими программами,
расширенными явным отрицанием, для которых выполнение этих
принципов весьма желательно.
Свойство 9.4 (Единственность минимального расширения). Мы
говорим, что теория умолчаний удовлетворяет свойству единствен-
единственности минимального расширения, если всякий раз, когда она имеет
расширение, у нее существует и минимальное расширение.

406 Немонотонные логики в логическом программировании [ Гл. 9
Как известно, теории умолчаний Рейтера не согласуются с этим
принципом, что становится очень важным особенно в том случае,
когда мы рассматриваем осторожную версию семантики умолчаний.
Пример 9.74.
Рассмотрим следующую теорию умолчаний:
Г республиканец(Х) : ^пацифист(Х) квакер(Х) : пацифист(Х
\ -л пацифист (X) ' пацифист (X)
{республиканец(никсон), квакер (никсон)}
С помощью семантики Рейтера находим два расширения:
Ei = {пацифист (никсон), республиканец(никсон), квакер (никсон)} и
Еъ = {-^пацифист (никсон), республиканец(никсон), квакер (никсон)}.
В результате осторожная семантика Рейтера дает:
{республиканец(никсон), квакер (никсон)}.
Как отмечалось выше, если рассматривать расширение как раци-
рациональное множество заключений, то кажется странным, что осторож-
осторожная семантика сама не образует такого множества. Если же обеспе-
обеспечить выполнение свойства единственности минимального расшире-
расширения, то с этой проблемой удается справиться. Более того, наличие
свойства единственности облегчает поиск итерационных алгоритмов
для вычисления осторожной версии семантики умолчаний.
Определение 9.Ц. (Объединение теорий). Объединение двух
теорий умолчаний Ai = (Di,Wi) и А2 = (Дг?^) c языками L(Ai)
и ^(Аг) — это теория А = Ai U A2 = (Di U D2, Wi U W2) с языком
Пример 9. 75.
Рассмотрим две теории умолчаний:
Классическая теория умолчаний, фундированная семантика и стаци-
стационарная семантика определяют {Ь} как единственное расширение для
Аг. Так как языки данных теорий умолчаний не связаны, то можно
ожидать, что Ъ будет включаться во все расширения объединения
этих теорий. Но оказывается, что и фундированная, и наименьшая
стационарная семантика делают значение Ъ неопределенным в объеди-
объединенной теории. Это происходит потому, что данные виды семантики не
являются модулярными. В данном случае существует нежелательное
взаимодействие между правилами-умолчаниями обеих теорий при их
объединении. Классическая теория умолчаний, будучи модулярной,
дает два расширения: {^а, Ъ} и {а, 6}, но в результате не удается

9.5] WFSX и логика умолчаний 407
определить единственное минимальное расширение для объединения
теорий.
Свойство 9.5 (Модулярность). Пусть даны Ai и А2 — две
теории умолчаний с непротиворечивыми расширениями такие, что
L(Ai) П ^(Аг) = {}, и пусть объединение теорий есть А = Ai U
U A2, причем для этих теорий известны расширения ЕА1, ^Д2 и -^д-
Семантика для теории умолчаний модулярна тогда и только тогда,
когда:
УА(Уг АеЕгА1^Ук Ае ЕкА)
\/A(\/j AeEJA2^\/k Ae ЕкА).
Неформально, семантика теории умолчаний модулярна, если лю-
любая теория, получающаяся объединением двух непротиворечивых тео-
теорий с несвязанными языками, содержит следствия каждой из теорий
в отдельности.
Утверждение 9.16. Логика умолчаний Рейтера модулярна.
Пример 9.76.
Теория умолчаний ( < d\ = , 6^2 = —7— р {} ) имеет два клас-
сических расширения {а} и {Ь}. Стационарная семантика умолчаний
дает еще одно расширение — {}.
Пример 9. 77.
Пусть (.D, W) — это ( < d\ = , 6^2 = —7— \ , {^«} ) • Единствен-
ным классическим расширением будет {^а,6}. В наименьшем стаци-
стационарном расширении Е = Т2А(Е) = {-^a},j{d2) G Е, но с(^) ф Е.
Определение 9.75. (Применимость умолчаний). Пусть дано рас-
расширение Е, тогда
• умолчание d применимо в Е 44> p{d) С Е и ~^j{d) П Е = {};
• применимое умолчание d применяется в Е <=> c(d) E Е.
В классической семантике умолчаний каждое применимое умолча-
умолчание применяется. Это препятствует наличию свойства единственности
минимального расширения. Так, в примере 9.76 из-за того, что одно
умолчание всегда применяется, нельзя получить единственное мини-
минимальное расширение.
Для того, чтобы гарантировать единственность минимального рас-
расширения, можно так определить семантику, чтобы применимое умол-
умолчание могло применяться, или не применяться в зависимости от
каких-либо условий. В результате утрачивается понятие максималь-
максимального применения умолчаний, которое используется в классической
теории. В примере 9.77 необходимо, чтобы по крайней мере правило
^2 было применено.

408 Немонотонные логики в логическом программировании [ Гл. 9
Альфереш и Перейра предлагают сохранить принцип единствен-
единственности минимального расширения наряду с понятием максимального
применения умолчаний, что нашло отражение в принципе «принуди-
«принудительности» (enforcedness).
Свойство 9.6 (Принудительность). Пусть дана теория А с расши-
расширением Е, тогда умолчание d принуждаемо в Е тогда и только тогда,
когда p(d) G Е и j(d) С Е. Расширение является принудительным,
если все принуждаемые умолчания в D применены.
Всякий раз, когда Е является расширением, если умолчание при-
принуждаемо, то оно должно быть применено. Заметим, что принуж-
принуждаемое умолчание всегда является применимым. Другими словами,
если d — принуждаемое умолчание и Е — расширение, то правило-
умолчание d должно пониматься как правило вывода: p(d)Jj(d) —> c(d)
и в результате должно выполняться: c(d) G Е.
И фундированная, и стационарная семантика поддерживают ми-
минимальные расширения, для которых принуждаемые умолчания не
применяются (см. пример 9.77). Но в этом примере они все же допус-
допускают принудительное расширение: {6, ^а}, хотя в общем случае это
не выполняется.
Пример 9.78.
Пусть (Z), W) = ( < , , > , {^b\ I. Единственным стаци-
\{ с Ъ а ) )
онарным расширением будет {^fr}, и оно не является принудитель-
принудительным.
Основываясь на описанном понятии принудительности, Пшиму-
синская и Пшимусинский определяют насыщенные теории умолча-
умолчаний.
Определение 9.76. (Насыщенная теория умолчаний). Теория
умолчаний А = (D, W) является насыщенной тогда и только тогда,
когда для каждого правила-умолчания * g D если p(d) G W
c(d)
и j(d) e W, то c(d) e W.
Для данного класса теорий умолчаний эти исследователи дока-
доказали, что и стационарная, и фундированная семантика умолчаний
согласуются с принципом принудительности. Но требование насыщен-
насыщенности является очень сильным ограничением, так как оно требует
выполнения некоторого замыкания теории W.
9.5.3. П-теория умолчаний
Альфереш и Перейра вводят семантику теории умолчаний, кото-
которая является модулярной и удовлетворяет принципу принудительно-
принудительности для каждой ограниченной теории умолчаний. Более того, если
эта семантика определена, то она дает единственное минимальное

9.5] WFSX и логика умолчаний 409
расширение. В дальнейшем, если не возникает недоразумений, мы
ссылаемся на ограниченные правила-умолчания и теории просто как
на правила-умолчания и теории.
Для того, чтобы установить связь между теориями умолчаний
и расширенными логическими программами, необходимо обеспечить
выполнение принципа модулярности для семантики теории умолча-
умолчаний во всех случаях, кроме противоречивых ситуаций. Рассмотрим
следующий пример, в котором возникает противоречие.
Пример 9. 79.
Для теории умолчаний ( < —, — > , {}) два правила-умолчания с
пустыми предпосылками и обоснованиями должны всегда применять-
применяться, что, очевидно, приводит к противоречию. Отметим, что это же
происходит и в том случае, если теорию умолчаний переписать как
Вернемся к примеру 9.75, с помощью которого была по-
показана немодулярность стационарной семантики умолчаний
(D = < , —, — > и {} — наименьшее стационарное расширение).
I ^а а о )
В самом деле, Гд({}), имея и а, и -*а, по дедуктивному замыканию
определяет -пЬ. В результате на второй итерации уже нельзя
применить третье умолчание. Чтобы этого не произошло, необходимо
подавить добавление ~^Ъ к Гд({}), что можно сделать, если запретить
при дедуктивном замыкании в Г использование заключений,
вызывающих противоречие.
В описанном ограниченном языке проблема решается просто, так
как все формулы — это лишь литеры, и подавление может быть
выполнено с помощью переименования негативных литер.
Определение 9.77. (Т'А). Пусть А = (D, W) — пропозициональ-
пропозициональная теория умолчаний и Е — контекст. Пусть Е' — наименьшее
множество атомов, для которого выполняется следующее:
1) оно содержит W'\
p(d)f
2) оно замкнуто относительно всех правил вывода вида таких,
Суп)
что — gDh -if ^ Е для каждого / Е j(d)\ и / ^ Е для
с(а)
каждого -i_/ E j(d)f'.
Здесь W (соответственно p(d)', j(d)' и c(d)/) получаются из W
(соответственно p(d), j(d) и c(d)) заменой в нем каждой негативной
литеры ^А новым атомом ^_А. Г'А(Е) получается из Е' заменой
каждого атома вида ^_А на —iA.

410 Немонотонные логики в логическом программировании [ Гл. 9
Рассмотрим снова пример 9.77, который показывает, что стацио-
стационарные расширения умолчаний не всегда являются принудительны-
принудительными. Непринудительным (наименьшим) расширением является Е =
= Г2(Е) = {^а}, где Т(Е) = {^а,а,6}. В полученной семантике
^а истинно и а имеет неопределенное истинностное значение. Этот
результат не согласуется с нашей интуицией. Чтобы справиться с
этой проблемой, мы должны гарантировать, что для расширения Е
выполняется следующее:
Vd g D ^c(d) eE^ c(d)
т. е. если —ic(d) — истина, то c(d) — ложь (здесь прослеживается
сходство с принципом когерентности).
Нетрудно видеть, что это условие удовлетворяется полу нормаль-
нормальными теориями умолчаний: если —<c(rf) принадлежит расширению, то
не должно применяться никакое полунормальное правило с заключе-
заключением c(d). Этот принцип используется в семантике умолчаний.
Определение 9.78. (Полунормальная версия теории умолчаний).
Для заданной теории умолчаний А ее полунормальная версия As
получается путем замены в А каждого правила-умолчания вида
p(d):j(d),c(d)
, P(d):j(d) iS
d = . 7N на правило-умолчание вида а = ;Чг•
с[а) с[а)
Определение 9.79. (Оператор Q&). Для теории А определяется
следующий оператор:
ПА(Е)=Г'А(Г'АЗ(Е)).
Определение 9.80. (ft-расширение). Пусть А — теория умолча-
умолчаний, Е является ^-расширением тогда и только тогда, когда
• Е =
. ЕСГ'АЗ(Е).
Основываясь на ^-расширениях, Альфереш и Перейра определяют
семантику теории умолчаний.
Определение 9.81. (ft-семантика умолчаний). Пусть А — теория
умолчаний, Е — расширение А и L — литера, тогда
• L истинна по отношению к расширению Е <^=> L Е Е\
• L ложна по отношению к расширению Е 4=> L ф TfAS(E);
• в противном случае L не определена.
Q-Семантика умолчаний для А определяется множеством всех
^-расширений для А. Осторожная Q-семантика умолчаний для А
определяется наименьшими ^-расширениями для А.

9.5] WFSX и логика умолчаний 411
Здесь предполагается, что выполняются следующие требования:
каждое расширение Е должно быть подмножеством для TfAS(E).
Если этого не делать (т. е. рассматривать в качестве расширений все
фиксированные точки О), то семантика допускала бы в некоторых
расширениях одновременную ложность и истинность литер.
Пример 9. 80.
/f:na :п5 a:na &:nM \
Для теории умолчаний А = < , —-—, , >, су-
\[ а о с с ) '
ществуют четыре фиксированные точки О
а ' b '
)чки Од:
"р/ / 771 >
р' (т? \
1 as -С/4
С
1 = iC
1 = {^
| = {]
С
i,c}
^
Е4 = {a, b, с}
Расширением является лишь Е\, и поэтому Е\ определяет Q-
семантику умолчаний для А. Отметим, что, например, а Е Е2 и
а ^ Где.(^г)- Поэтому если Е2 рассматривалось бы как расширение,
то а было бы одновременно и истинно, и ложно в Е2. Более того,
согласно интуиции, ни одно расширение не должно содержать с,
так как для каждого правила с заключением с предпосылки не
совместимы с обоснованием. В Е2 с истинно, так как а, будучи
истинным, удовлетворяет предпосылкам и одновременно, будучи
ложным, удовлетворяет обоснованиям. Приведенное определение
расширения гарантирует, что никакая пара противоречивых литер не
принадлежит Е.
Утверждение 9.17. Если Е — ^-расширение теории умолчаний
А, то не существует такой литеры L, что {L, ^L} С Е.
Пример 9.81.
Рассмотрим те
Единственным ее расширением является {^а,6}. Действительно,
/ Г : ic : >Ь : >a : 1
Рассмотрим теорию умолчаний А = < , , ——, — > , \ \
\[ с а о ^а)
В результате ^а и b истинны, с не определено иоип& ложны.
Нетрудно видеть, что для некоторых теорий может и не быть Q-
расширений. Рассмотрим следующий пример.
Пример 9.82.
У теории А = ( < -, — >, {} j не существует ^-расширений.

412 Немонотонные логики в логическом программировании [Гл. 9
Определение 9.82. (Противоречивая теория). Теория умолча-
умолчаний А противоречива тогда и только тогда, когда у нее не существует
^-расширений.
Чтобы гарантировать существование наименьшего расширения,
была доказана следующая теорема.
Теорема 9.27 (ft — монотонный оператор). Если А — непротиво-
непротиворечивая теория, то Qa — монотонный оператор.
Определение 9.83. (Итеративное построение). Для того, чтобы
получить конструктивное определение для наименьшего (по отноше-
отношению включения множеств) ^-расширения теории, определяется сле-
следующая бесконечная последовательность {Еа}:
Ео = {}
Ea+i = &(Еа)
Е$ = U {Еа\а < 5} для конечного натурального 5.
По теореме 9.27 и теореме Кнастера — Тарского для описанной
последовательности должно существовать наименьшее натуральное
Л такое, что Е\ — наименьшая фиксированная точка оператора Q.
Если Е\ — ^-расширение, то оно является наименьшим. В противном
случае, согласно приведенному ниже утверждению, для теории не
существует ^-расширений.
Утверждение 9.18. Если наименьшая фиксированная точка Е
оператора Од не является ^-расширением для А, то у теории А не
существует ^-расширений.
Пример 9.83.
Рассмотрим теорию умолчаний А из примера 9.81. Чтобы полу-
получить наименьшее расширение для А, построим следующую последо-
последовательность:
Ег = Гд (Гдя ({})) = Г'А({с, а, Ъ, -о}) = {-а}
?2 = 1д(Г'дя(М)) = ГА({с,Ъ,^а}) = Ьа,Ъ}
Ез = Гд(Г'дя({-а,Ь})) = Т'А({с,Ь,^а}) = {^а,Ъ} = Е2
Так как Е^ С Гд^-Ег)? то Е^ — наименьшее ^-расширение для А.
Пример 9. 84.
Пусть А = ( \ -, — \ , {} ). Построим последовательность:
Via ^a J /
Ео = {]
Ei =Г'Д(ГДЗ({})) =Г'д({а,-а}) = {а^а}
Ei = ГА(ГАЗ({а,^а}) = Г'д({}) = {а,^а} = Ех

9.5] WFSX и логика умолчаний 413
Так как не выполняется условие Е\ С T'^S{E\), то у теории А не
существует ^-расширений.
Установлено, что описанная семантика умолчаний удовлетворяет
всем принципам, представленным в разд. 9.5.2. Точнее, доказаны при-
приведенные ниже теоремы.
1. Если для теории А существует расширение, то существует един-
единственное наименьшее расширение Е (единственность минималь-
минимального расширения).
2. Если Е — ^-расширение для теории А, то Е — принудительное
расширение (принудительность).
3. Пусть Lai и La2 — языки двух теорий умолчаний. Если
Lai П La2 = {}, то для любых соответствующих расширений
Ei и Е/2 всегда существует расширение Е для теории А = Ai U
U A2 такое, что Е = Ei U Е^.
9.5.4. Сравнение с семантикой Рейтера
Сравнивая О-семантику для теорий умолчаний с семантикой Рей-
Рейтера, Альфереш и Перейра доказали, что для ограниченных теорий
умолчаний первая семантика является обобщением последней в том
смысле, что всякий раз, когда семантика Рейтера (Г-расширение)
может определить смысл теории (т. е. у теории существует по крайней
мере одно Г-расширение), то О-семантика тоже определяет смысл
этой теории.
Более того, всякий раз, когда обе семантики могут определить
смысл теории, О-семантика состоятельна по отношению к пересече-
пересечению всех Г-расширений. Поэтому оказывается возможным исполь-
использовать монотонный оператор фиксированной точки для вычисления
подмножества пересечения всех Г-расширений.
Теорема 9.28. Рассмотрим теорию А такую, что определена
О-семантика. Тогда каждое Г-расширение будет и ^-расширением.
Теорема 9.29 (Обобщение семантики Рейтера). Если теория А
имеет по крайней мере одно Г-расширение, то у нее существует одно
^-расширение.
Теорема 9.30 (Состоятельность по отношению к семантике Рейте-
Рейтера). Если теория А имеет Г-расширение, то всякий раз, когда литера L
принадлежит наименьшему ^-расширению, она также принадлежит
пересечению всех Г-расширений.
Интересно отметить, что если для определения Q использовать
любое другое сочетание операторов, подобных Г (операторы
Гд5,Гд,Гд5 и Гд), то получается семантика, состоятельная по
отношению к семантике Рейтера, но новая семантика уже не будет
так «похожа» на семантику Рейтера, как О-семантика. Под словами
«не будет так похожа» мы понимаем, что наименьшие фиксированные

414 Немонотонные логики в логическом программировании [ Гл. 9
точки новой семантики — подмножества пересечения всех расширений
семантики Рейтера, которые меньше (по отношению к включению
множеств), чем наименьшая фиксированная точка для Q. Поэтому Q-
семантика является наилучшим приближением семантики умолчаний
Рейтера по сравнению с остальными.
Утверждение 9.19. Пусть А — непротиворечивая теория умол-
умолчаний, тогда:
1) lfp(T'ASr'A) с lfp(T2s);
2) lfP(T'ASr'A) с lfp(T'l);
3) lfp(r'AS 2) С lfp(U);
4) lfp(T'A2)Clfp(n).
9.5.5. Сравнение со стационарной семантикой умолчаний
Приведем кратко результаты сравнения О-семантики со ста-
стационарными расширениями. Не всегда стационарное расширение
является ^-расширением, поскольку, как уже отмечалось, немоду-
немодулярные и непринудительные стационарные расширения не могут
быть ^-расширениями. Следующий пример показывает, что не всегда
^-расширение является стационарным расширением.
Пример 9. 85.
f ( : ->Ь : ->а : ->а : 1 г.
Пусть дана следующая теория А : < , ——, , —- > , \\
VI с Ъ а ^Ъ)
Единственным ^-расширением для А будет {с, ^6}, но оно не является
стационарным расширением.
Как уже отмечалось, для насыщенных теорий умолчаний стаци-
стационарная семантика удовлетворяет принципу принудительности. Од-
Однако даже для этого класса теорий стационарная семантика может
не совпадать с О-семантикой. Причина состоит в том, что в общем
случае стационарные расширения не являются модулярными.
Пример 9. 86.
Теория умолчаний в примере 9.75 является насыщенной и имеет
немодулярное стационарное расширение.
Тем не менее, для большого класса случаев эти виды семантики
совпадают. В частности, справедливо следующее утверждение.
Утверждение 9.20. Если для каждого умолчания
d = * eld) — позитивная литера, то Q совпадает с Г\.
c(d)

9.5] WFSX и логика умолчаний 415
9.5.6. Связь семантики теории умолчаний и логических программ с
явным отрицанием
Как оказалось, ^-расширения эквивалентны частичным устойчи-
устойчивым моделям расширенных логических программ.
Определение 9.84- (Программа, соответствующая теории
умолчаний). Пусть А = (?),{}) — теория умолчаний. Мы говорим,
что расширенная логическая программа Р соответствует А тогда и
только тогда, когда
{аь ... ,ап} : {Ьь ... ,ЬШ}
• для каждого умолчания вида Е А
с
существует правило с <— ai,..., an, not —i&i,..., not ^6m E P;
• программа P не содержит никаких других правил.
Определение 9.85. (Интерпретация, соответствующая кон-
контексту.) Интерпретация / программы Р соответствует контексту Е
теории умолчаний Т тогда и только тогда, когда для каждой объек-
объективной литеры L программы Р (и литеры L теории Т) выполняется
0^L(?EkL(? T'AS(E).
Следующая теорема связывает два вида семантики.
Теорема 9.31. Пусть А = (?),{}) — теория умолчаний, соответ-
соответствующая программе Р. Е — ^-расширение для А тогда и только
тогда, когда интерпретация /, соответствующая Е, является частич-
частичной устойчивой моделью программы Р.
Следуя этой теореме, можно сказать, что явное отрицание — это
не более чем классическое отрицание в (ограниченных) теориях умол-
умолчаний и наоборот. Так как ?1-семантика умолчаний — это обобщение
Г-семантики умолчаний (см. теоремы 9.29 и 9.30), и так как семантика
ответных множеств соответствует Г-семантике умолчаний, то оказы-
оказывается, что семантика ответных множеств — частный случай WFSX.
Кроме того, и другие свойства ^-расширений также могут быть «пе-
«переведены» в свойства моделей расширенных логических программ,
например, модулярность, единственность минимального расширения
и т. п.
В то же время, используя приведенную теорему, можно применять
нисходящие процедуры логического программирования для вычисле-
вычисления расширений по умолчанию. В частности, в соответствии с теоре-
теоремой 9.30, нисходящие процедуры для WFSX могут быть использованы
как состоятельные нисходящие процедуры для логики умолчаний
Рейтера.

416 Немонотонные логики в логическом программировании [ Гл. 9
Пример 9. 87.
Рассмотрим программу Р:
с <— not с
а <— not b
b <— not a
Этой программе соответствует теория умолчаний
([ Л \
Л ([ \^с \ Ь \^а \ Л \ TZ
А = < , , ——, — > , \ \ . Как уже вычислено в примере
\[ с а о ^а) )
9.81, единственным ^-расширением для А является Е = {^а, Ь} и
Tf^s(E) = {^a, 6, с}. PSM, соответствующая этому расширению, есть
М = {^а, not а, 6, not -ib, not ^с}. Нетрудно проверить, что М —
единственная PSM для программы Р.
9.5.7. Определение WFSX с помощью Г
Используя взаимосвязь логических программ и теорий умолчаний,
Альфереш и Перейра определили WFSX, опираясь не на трехзначную,
а на частичную двузначную логику. Рассмотрим, как определяется
для логических программ понятие, соответствующее полунормально-
полунормальности для теорий умолчаний.
Определение 9.86. (Полунормальная версия программы). Полу-
Полунормальная версия программы Р — это программа Ps, получающаяся
из Р добавлением к (возможно пустому) телу Body каждого правила
вида L <— Body литеры по умолчанию not -iL, где ^L — дополнение
L по отношению к явному отрицанию.
Для краткости, когда Р ясно из контекста, будем использовать
T(S) для обозначения Tp(S), и Ts(S) для обозначения Tps(S).
Теорема 9.32 (Частичные устойчивые модели). Пусть Р — рас-
расширенная логическая программа, тогда М = Т U not F — частичная
устойчивая модель программы Р тогда и только тогда, когда
1) Т = ГГ5Т;
2) Т С Г3Т.
Более того, F = {L\ L ^ Г^Т}, и те элементы Г^Т, которые не
принадлежат Т, оказываются неопределенными в М. В дальнейшем
Т будут называться генераторами для М.
Заметим, что в этих альтернативных определениях каждая модель
PSM полностью определяется истинными в ней объективными лите-
литерами.
Теорема 9.33 (Фундированная модель). Пусть Р — непротиворе-
непротиворечивая программа. М = Т U not F — фундированная модель програм-
программы Р тогда и только тогда, когда Т — наименьшая фиксированная
точка для ITs и Т генерирует М.

9.5] WFSX и логика умолчаний 417
В результате оказывается, что WFM может быть получена с по-
помощью итераций ГГ^ из пустого множества (заметим, что роль Г^
состоит в том, чтобы обеспечить выполнение принципа когерентно-
когерентности). Если в результате будет найдена фиксированная точка S, то
она содержит объективные литеры, истинные в WFM. Ложные лите-
литеры находятся при сравнении с Г^, т.е. это те литеры, которые не
принадлежат TsS. Можно также определить итеративное построение
ложных в WFM литер, а истинные литеры находить с помощью
ложных. Следующее утверждение помогает нам определить подобное
итеративное построение.
Утверждение 9.21. Пусть Р — непротиворечивая программа.
Тогда: rs(lfp(Trs)) = gfp(TsT).
Определим теперь два монотонных оператора: один из них позво-
позволяет по заданному множеству истинных объективных литер находить
дополнительные истинные объективные литеры, а другой — по задан-
заданному множеству ложных объективных литер находить дополнитель-
дополнительные ложные объективные литеры.
Определение 9.81. Для программы Р определим T(S) = ГГs(S),
F(R) = H — ГГs(H — R), где Н обозначает эрбрановскую базу
программы Р.
Теорема 9.34. Для любой непротиворечивой программы опера-
операторы Т и F являются монотонными.
Теорема 9.35. Пусть Р — непротиворечивая программа. Тогда
WFM(P) = lfp(T) U not lfp(F).
Пример 9.88.
Пусть дана программа Р:
с <— 6, not с
а <— not Ъ
Ъ <— not a
Покажем два альтернативных способа вычисления WFM.
1. Начнем с пустого множества истинных объективных литер и
будем выполнять последовательно итерации, чтобы найти все
истинные объективные литеры, до тех пор, пока не будет полу-
получена фиксированная точка:
Т2 = rrs{-a} = Г{с, Ь, ^а} = {Ь, ^а
Т3 = rrs{b, -a} = Г{с, b, ^a} = {Ъ,
14 В.Н. Вагин и др.

418 Немонотонные логики в логическом программировании [ Гл. 9
В результате WFM= T3 U not (Л" - TST3) = {Ъ, ^а} U not (Л" -
— {с, Ъ, ^а}) = {b, ^a} U {not a, not -ib, not ^c}.
2. Начнем с пустого множества ложных объективных литер и
будем выполнять последовательно итерации, чтобы найти все
ложные объективные литеры, до тех пор, пока не будет получена
фиксированная точка:
F1 = H- YSV(H - {}) = Н - Ysba} = H - {с, Ъ, -а} = {а, -6, -с};
F2 = Н - Г5Г(с, Ъ, ^а) = Н - Ts{b, -а} = Н - {с, Ъ, ^а} = {а, -.Ь, ^с}.
В результате WFM = Г(Л - F2) U not F2 = Г{с, 6, ^а} U
U {not a, not -ib, not ^c} = {6, ^а} U {not а, not -ib, not ^c}.

... исчерпать сей предмет невоз-
невозможно: уж кажется, насказано
много, ан нет — недосказано еще
больше...
Д. Боккаччо
Глава 10
СИСТЕМЫ АРГУМЕНТАЦИИ И
АБДУКТИВНЫЙ ВЫВОД
Абдукция — это процесс формирования объясняющей гипотезы.
Точнее, при заданной теории и наблюдении, предложенном для объ-
объяснения, абдуктивный вывод должен определить одно или более наи-
наилучших объяснений наблюдения на основе заданной теории. Термин
«абдукция» впервые ввел американский философ Пирс.
Приведем простейший пример абдуктивного вывода. Пусть извест-
известно правило «Все шары в этой коробке белые» и результат наблюдения
«Эти шары белые», тогда по абдукции можно заключить, что «Дан-
«Данные шары взяты из этой коробки» (причина-объяснение).
В искусственном интеллекте приложением-прототипом абдукции
является задача диагностики. В этом случае абдукция использует-
используется для обнаружения в соответствии с некоторой известной теорией
системы причины наблюдаемого неправильного поведения системы.
Из других возможных приложений абдукции наиболее важными яв-
являются следующие: задача наблюдения, основанного на моделях; за-
задача распознавания плана, в которой с помощью абдукции по на-
наблюдаемым действиям агента делается попытка обнаружить цели его
деятельности; задача понимания естественного языка, в которой по
сравнению с задачей диагностики требуется рассматривать наиболее
полное множество абдуктивных объяснений; временной вывод и пла-
планирование; задача накопления и усвоения знаний, в которой в базу
знаний добавляются абдуктивные объяснения, описывающие новые
для нее явления; задачи вывода по умолчанию.
На сегодняшний день теория аргументации проявила себя как
мощное средство моделирования различных форм правдоподобного
вывода. Основная идея аргументационного вывода состоит в том, что
14*

420 Системы аргументации и абдуктивный вывод [ Гл. 10
утверждению можно доверять, если оно может быть аргументиро-
аргументированно защищено от атак аргументов. Как оказалось, теория аргумен-
аргументации может успешно применяться и для организации абдуктивного
вывода.
10.1. Системы пересматриваемой аргументации
10.1.1. Основы теории аргументации
Системы для пересматриваемой аргументации содержат (иногда
неявно) следующие пять элементов:
1) лежащий в основе логический язык;
2) определение аргумента;
3) определение конфликта между аргументами;
4) определение поражения аргумента;
5) определение оценки аргументов, которая может использоваться
для определения понятия пересматриваемого логического след-
следствия.
Аргументационные системы строятся над логическим языком и
связанным с ним понятием отношения следования с помощью опре-
определения понятия аргумента. Это отношение следования предпола-
предполагается монотонным: новые посылки не могут отменить (сделать не
действительным) аргумент, а могут лишь вызвать новые контраргу-
контраргументы. Некоторые аргументационные системы предполагают наличие
конкретной логики, другие же оставляют лежащую в основе логику
неопределенной частично или полностью, поэтому последние системы
могут работать с различными логиками, что делает их скорее карка-
каркасами (структурами), нежели системами. Понятие аргумента соответ-
соответствует доказательству (или существованию доказательства) в базовой
логике.
В литературе по аргументационным системам можно найти три
базовые формы аргументов:
1) иногда аргументы определяются как дерево выводов, основанное
на посылках;
2) иногда — как последовательность таких выводов, то есть как
дедукция;
3) некоторые системы определяют аргумент как пару: посылки —
заключения, оставляя неявным то, как лежащая в основе логика
осуществляет доказательство заключения по посылкам.
Данг предложил аргументационную систему, оставляющую
внутреннюю структуру аргумента полностью неопределенной.

10.1] Системы пересматриваемой аргументации 421
Аргумент — примитивное понятие, и Данг занимается лишь
способами взаимодействия аргументов. Это наиболее абстрактный
подход.
Понятия логики и аргумента соотносятся со стандартными пред-
представлениями о логической системе. Оставшиеся три элемента — это
то, что делает аргументационную систему структурой для пересмат-
пересматриваемой аргументации. Первое — это понятие конфликта между
аргументами (или атаки, или контраргумента). Существует два типа
конфликтов:
1) опровержение (rebutting) аргумента (у аргументов противоре-
противоречивые заключения) — это симметричная форма атаки;
2) подрыв (undercutting) аргумента — несимметричная форма ата-
атаки:
а) один аргумент делает предположение о недоказуемости (по-
(подобно тому, как это делается в логике умолчаний) и другой
аргумент доказывает то, что предполагалось недоказанным
первым аргументом;
б) один аргумент отрицает связь между посылками и заключе-
заключением другого аргумента. Эта связь может быть нарушена
только у не дедуктивных аргументов, т. е. у индуктивных,
абдуктивных или аргументов-аналогий.
Определение того, является ли атака успешной, — еще один эле-
элемент аргументационных систем. Оно имеет вид бинарного отношения
между аргументами, устанавливая отношение «атакует и не слабее»
(слабая форма) или «атакует и сильнее» (сильная форма). Могут ис-
использоваться различные названия: «поражение» (Праккен, Сартор),
«атака» (Данг, Бондаренко), «интерференция» (Луи). Далее будем
слабую форму называть поражением, а сильную — строгим пораже-
поражением.
В различных работах отличаются также понятия оценки резуль-
результата вычислений. В искусственном интеллекте многие считают очень
важным принцип специфичности. Но Поллок, Праккен и Сартор
утверждают, что специфичность не является основным принципом
практического вывода, а представляет собой лишь один из образцов,
которые могут использоваться, а могут и нет. Для этого некоторые
аргументационные системы параметризуются по критерию, опреде-
определяемому пользователем. Праккен и Сартор даже утверждают, что
критерии оценки являются частью теории прикладной области и
могут оспариваться, как и все в этой теории, т. е. аргументационные
системы должны работать с пересматриваемыми по этим критериям
аргументами.
Понятие поражения определяется бинарным отношением на мно-
множестве аргументов. Оно не говорит нам о том, с какими аргументами

422 Системы аргументации и абдуктивный вывод [ Гл. 10
можно выиграть спор, а лишь говорит об относительной силе двух
индивидуальных конфликтующих аргументов. Конечный статус аргу-
аргумента зависит от взаимодействия между всеми доступными аргумен-
аргументами: возможна ситуация, когда аргумент А поражает аргумент Б, но
сам аргумент А поражается аргументом С, т. е. С «восстанавливает»
В. Следовательно, требуется определить статус аргументов на базе
всех возможных способов их взаимодействия. Праккен и Вресвейк
считают, что это определение должно охватывать, во-первых, восста-
восстановление аргументов, и, во-вторых, следующий принцип: «Аргумент
не может быть подтвержден до тех пор, пока не подтверждены все
его подаргументы» (принцип композиционности Вресвейка).
Заметим, что часто восстановление происходит с помощью атаки
на подаргумент атакующего аргумента. Именно определение статуса
аргументов дает конечный
результат работы аргументационной системы. По статусу аргумен-
аргументы разбиваются обычно, по крайней мере, на два класса:
• аргументы, с которыми можно выиграть спор (подтверждаю-
(подтверждающие);
• аргументы, с которыми можно проиграть спор (отвергающие).
Иногда выделяют класс аргументов, с которыми спор остается
нерешенным, т. е. защищающие аргументы. Статус аргументов опре-
определяет статус заключений. Эти понятия могут быть определены как
в декларативной, так и в процедурной форме. При декларативном
определении используются определения с фиксированной точкой, за-
задающие приемлемость некоторых множеств аргументов (при задан-
заданных множествах посылок и критериях оценок). При этом не опреде-
определяется процедура проверки на принадлежность аргумента этому мно-
множеству. При процедурном определении задается процедура проверки
на принадлежность аргумента множеству приемлемых аргументов. В
результате декларативная форма определения аргументационной си-
системы может считаться ее теоретико-аргументационной семантикой, а
процедурная — ее теорией доказательства. Возможно, что в то время,
когда аргументационная система имеет теоретико-аргументационную
семантику, для лежащей в ее основе логики построения аргументов
определена теоретико-модельная семантика в обычном смысле, на-
например, семантика логики предикатов первого порядка или семантика
возможных миров в модальной логике.
Возникает вопрос: должна ли логика немонотонного вывода иметь
теоретико-модельную семантику? Некоторые исследователи утвер-
утверждают, что для немонотонного вывода требуется не модельная тео-
теория, а теоретико-аргументационная семантика.
Традиционно модельная теория использовалась в логике для опре-
определения смысла логических констант формальных языков. Формулы

10.1] Системы пересматриваемой аргументации 423
таких языков говорят о свойствах действительного мира. Теоретико-
модельная семантика определяет смысл логических констант, опи-
описывая то, каким будет мир, если выражение с этими константами
истинно; и задает логическое следование с помощью выяснения того,
что еще должно быть истинным, если посылки являются истинными.
Для умолчаний это означает, что их семантика должна определяться в
терминах того, как обычно или типично выглядит мир, когда умолча-
умолчания истинны, а логическое следование задается с помощью выделения
наиболее нормальных миров, моделей и ситуаций, удовлетворяющих
посылкам.
Но существует и другой подход (Поллок, Вресвейк, Луи): смысл
умолчаний нужно искать не по связи с действительностью, а по их
роли в диалектическом исследовании. Связь посылок и заключения
пересматриваема, т. е. существует некоторое дополнительное свойство
доказательства. Центральные понятия пересматриваемого вывода —
это понятия атаки, опровержения и поражения аргументов, которые
не являются «пропозициональными», т. е. их смысл не охватывается
естественным образом связью между высказыванием и миром. Этот
подход определяет «теоретико-аргументационную» семантику для по-
подобных понятий. Главная идея — охватить множества аргументов,
которые велики настолько, насколько это возможно, и адекватно
защитить их от атак. При таком подходе отмечается, что модельная
теория также важна, и ей отводится особое место. Модельная теория
должна применяться к базовым составляющим аргументационной
системы (логический язык и отношение следования, определяющие
аргумент).
Некоторые исследователи (Гефнер и Перл) интерпретируют аргу-
ментационные системы как теории доказательства для семантики вы-
выводимости по предпочтению. Но успех предпочтительной семантики
аргументационных систем определяется естественностью критериев
для предпочтения моделей. Естественные критерии в свою очередь
могут быть определены лишь для некоторых частных случаев, но еще
необходимо показать, что они могут быть найдены для более общих
аргументационных систем, например для тех, в которых допускаются
индуктивные или абдуктивные аргументы.
10ЛЛЛ. Основные свойства семантики, основанной на
аргументах. Рассмотрим семантику аргументационных систем,
т. е. условия, которым должны удовлетворять множества подтвер-
подтвержденных аргументов. Аргументационные системы связаны не с истин-
истинностью высказываний, а с подтверждением принятия высказывания
как истинного. Остановимся на понятии подтвержденного аргумента.
Пусть на множестве аргументов определено отношение поражения,
тогда может быть дано определение статуса аргумента.

424 Системы аргументации и абдуктивный вывод [ Гл. 10
Определение 10.1. Аргументы либо подтверждаются, либо не
подтверждаются. Аргумент подтверждается, если все аргументы,
поражающие его не подтверждаются. Аргумент не подтверждается,
если он поражается подтвержденным аргументом.
Пример 10.1.
Пусть аргумент В поражает аргумент А, а аргумент С поража-
поражает аргумент В. Например, А = «Твити не летает будучи птицей»,
В = «Твити не летает, так как он — пингвин», С = «Наблюдение,
говорящее о том, что Твити — пингвин, не является надежным». Ана-
Анализируя взаимоотношения аргументов, находим: С подтверждается,
так как он не поражается никаким аргументом. Аргумент В не под-
подтверждается, так как В поражается аргументом С. Следовательно,
А подтверждается, так как хотя А поражается аргументом В, но
его статус восстанавливается аргументом С, поскольку С делает В
неподтвержденным.
Если аргументы равной силы интерферируют, то неясно, какой из
аргументов останется непораженным.
Пример 10.2.
Пусть аргумент А поражает В, и аргумент В поражает А. С
процедурной точки зрения здесь возникает цикл, а с декларативной —
существуют два возможных способа назначения статуса по определе-
определению 10.1: аргумент А подтверждается, а В — нет, и наоборот.
Было предложено два подхода к решению проблемы:
1) изменить определение 10.1 так, чтобы статус присваивался
единственным образом, и если возникает «неразрешимый
конфликт», то конфликтующие аргументы получают статус
«не подтверждается»;
2) можно допустить несколько вариантов назначения статуса. Ар-
Аргумент истинно подтверждается, если он получает этот статус
при всех возможных назначениях.
Существует и другая проблема — самопоражающие (self-defeating)
аргументы.
Пример 10. 3.
Пусть аргумент А поражает аргумент А. Предположим что, А
не подтверждается. Тогда все аргументы, поражающие А, не под-
подтверждаются. Следовательно, аргумент А должен подтверждаться.
Возникает противоречие. Если же аргумент А подтверждается, то
снова приходим к противоречию.
Таким образом, принимая определение 10.1, необходимо предпола-
предполагать, что самопоражающие аргументы отсутствуют.
10.1.1.2. Назначение уникального статуса аргументам,.
Назначение аргументу уникального статуса можно выполнить дву-
двумя способами: определить назначение статуса в терминах оператора

10.1] Системы пересматриваемой аргументации 425
фиксированной точки или ввести рекурсивное определение для поня-
понятия подтвержденного аргумента, определяя дополнительно понятие
подаргумента.
Определения фиксированной точки. Поллок, Симари,
Луи, Праккен и Сартор используют подход, связанный с понятием
восстановления. Здесь учитывается следующее наблюдение: аргумент,
пораженный другим аргументом, может быть подтвержден, если он
восстанавливается третьим аргументом. В результате Данг дает опре-
определение понятию приемлемости (определение 10.2).
Определение 10.2. Аргумент А приемлем по отношению к мно-
множеству аргументов S тогда и только тогда, когда каждый аргумент,
поражающий А, поражается аргументом из множества S.
Аргументы множества S могут рассматриваться как аргументы,
способные к восстановлению статуса аргумента А, если А поражается.
Но одного понятия приемлемости оказывается недостаточно. Пусть в
примере 10.2 S = {А}. Нетрудно видеть, что А приемлем по отно-
отношению к S, так как все аргументы, поражающие А (т. е. аргумент
В), поражаются самим аргументом А из S. Очевидно, мы не хотим,
чтобы аргумент восстанавливал сам себя. Вот почему необходимо
использовать оператор фиксированной точки.
Определение 10.3. Пусть Args — множество аргументов, упоря-
упорядоченное бинарным отношением поражения. Тогда оператор F опре-
определяется так:
• F: Pow(Args)^ Pow(Args) (Pow — степень множества);
• F(S) = {ie Args| А приемлем по отношению к S}.
У оператора F существует наименьшая фиксированная точка. Ес-
Если аргумент приемлем по отношению к S, то он приемлем по отноше-
отношению к любому надмножеству S, т. е. F — монотонный. Чтобы не было
самовосстановления, будем считать, что подтвержденные аргументы
принадлежат наименьшей фиксированной точке. Для примера 10.2
множества {А} и {В} являются фиксированными точками, но не наи-
наименьшими, поэтому ни один из аргументов не защищен от поражения:
F@) = 0.
Определение 10.4- Аргумент подтверждается тогда и только
тогда, когда он является элементом наименьшей фиксированной точ-
точки оператора F.
Утверждение 10.1. Рассмотрим следующую последовательность
аргументов:
. F0 = 0;
• i^+! — {^4 G Args| А приемлем по отношению к F}.
Выполняются следующие свойства:

426 Системы аргументации и абдуктивный вывод [ Гл. 10
оо
1) Все аргументы в (J F1 подтверждаются.
г=0
2) Если каждый аргумент поражается, самое большее, конечным
числом аргументов, то аргумент подтверждается тогда и только
ОО
тогда, когда он принадлежит (J F1.
г=0
При итеративном построении сначала добавляются все аргументы,
которые не поражаются никаким из аргументов, и каждое новое при-
применение F добавляет все аргументы, восстановленные аргументами,
уже находящимися в построенном множестве. Это достигается бла-
благодаря использованию понятия приемлемости. Пусть мы применяем
F для i-ro шага: тогда для любого аргумента А, если все аргументы,
поражающие А, сами поражаются аргументом из Fl~1, то А Е F1.
Например, для примера 10.1 получаем
F1 = F@) = {С};
F3 = F(F2) = F2.
Доказано, что применение оператора F эквивалентно двукратному
применению оператора G, т.е. F = G°G.
Определение 10.5. Пусть Args — множество аргументов, упоря-
упорядоченное бинарным отношением поражения. Тогда оператор G опре-
определяется как
• G: Pow(Args)^ Pow(Args);
• G(S) = {А Е Args| А не поражается никаким аргументом в S}.
Рассмотрим последовательность, получаемую с помощью итера-
итеративного применения оператора G к пустому множеству, и определим,
что аргумент А подтверждается тогда и только тогда, когда, начиная
с некоторого шага (уровня) п в последовательности, А остается в Gm
При ВСеХ 771 ^ П.
Определение 10.6. Определим уровни при доказательстве:
• все аргументы принадлежат множеству на уровне 0;
• аргумент принадлежит множеству на уровне п+1 тогда и только
тогда, когда он не поражается никаким аргументом на уровне щ
• аргумент подтвержден тогда и только тогда, когда существует
такое значение т, что для любого п ^ т аргумент принадлежит
множеству уровня п.
Это определение связано с определением 10.5, подобно тому, как
утверждение 10.1 соответствует определению 10.3. Например, для
примера 10.1 находим, что подтвержденными аргументами являются

10.11
Системы пересматриваемой аргументации
427
А и С. Действительно, С принадлежит множеству на всех уровнях, а
А появляется на втором уровне и остается далее на всех последующих
уровнях.
Уровень
Множество аргументов
0
А, В,С
1
С
2
А, С
3
А, С
Для примера 10.2 подтвержденными оказываются и аргумент А, и
аргумент В.
Уровень
Множество аргументов
0
А, В
1
А, В
2
А, В
3
А, В
Рассмотрим бесконечную цепь аргументов: Ai, А^ ..., Ап,..., по-
поражающих друг друга: А\ поражается аргументом А^ ... поражается
аргументом Ап ... Наименьшая фиксированная точка цепи пуста, так
как ни один из аргументов не восстанавливается, т. е. F@) = 0.
Заметим, что существуют две другие фиксированные точки, которые
удовлетворяют определению 10.1, т.е. множество всех А^ где г —
нечетное, и множество всех А^ где г — четное.
Оправдываемые аргументы. Главная особенность приве-
приведенных определений в том, что они позволяют различать два типа
подтвержденных аргументов. Например, в примере 10.1 хотя аргу-
аргумент В и поражает аргумент А, аргумент А все же подтверждается,
так как его восстанавливает аргумент С. Рассмотрим еще один при-
пример.
Пример 10. 4.
Пусть имеется три аргумента А, В иС: А поражает Б, В поражает
А и А поражает С. Интерпретация может быть следующей:
А = «Диксон — пацифист, так как он квакер, и у него нет писто-
пистолета, так как он пацифист»;
В = «Диксон не пацифист, так как он республиканец»;
С = «У Диксона есть пистолет, так как он живет в Чикаго».
По определениям 10.4и10.бни один аргумент не подтверждается.
Для А и В это верно, поскольку они связаны, как и в примере 10.2,
а для С — поскольку этот аргумент поражается аргументом В. Здесь
становится явным главное отличие между двумя примерами. В отли-
отличие от примера 10.1, аргумент А хотя и не подтверждается, но и не по-
поражается ни одним подтвержденным аргументом. Следовательно, А
сохраняет потенциальную возможность не допустить подтверждения
С: не существует подтвержденных аргументов, восстанавливающих
аргумент С путем поражения аргумента А. В результате аргумент

428 Системы аргументации и абдуктивный вывод [ Гл. 10
А оказывается так называемым зомби-аргументом, т. е. он не под-
подтверждается, и в то же время, не полностью опровергнут. Поэтому у
аргумента А некоторый средний статус, при котором он все еще может
влиять на статус других аргументов. Этот статус в дальнейшем будем
обозначать как «оправдываемый» (defensible).
Определение 10.7. Будем называть аргумент аннулированным
тогда и только тогда, когда он не подтверждается, и либо самопо-
самопоражается, либо поражается подтвержденным аргументом. Аргумент
оправдываемый тогда и только тогда, когда он не подтверждается и
не аннулируется.
Пример 10. 5.
Рассмотрим два аргумента А и В: аргумент А поражает сам себя
и поражает аргумент В. Интуитивно желательно, чтобы В подтвер-
подтверждался, так как единственный поражающий его аргумент является
самопоражающим. Однако F@) = 0, поэтому ни А, ни В не под-
подтверждаются. Более того, оба этих аргумента являются оправдыва-
оправдываемыми, так как они не поражаются подтвержденными аргументами.
Следовательно, требуется модифицировать определения 10.3 и 10.6,
чтобы аргумент А в этом примере аннулировался, а аргумент В —
подтверждался.
Определение 10.8. Поллок определяет подтверждение аргумен-
аргумента следующим образом:
• аргумент находится на уровне 0 тогда и только тогда, когда он
не поражает сам себя;
• аргумент находится на уровне п + 1 тогда и только тогда, когда
он принадлежит уровню 0 и не поражается никаким аргументом
на уровне щ
• аргумент подтверждается тогда и только тогда, когда суще-
существует такое значение т, что для каждого п ^ т аргумент
принадлежит уровню п.
Дополнительные условия, говорящие о том, что аргумент не пора-
поражает сам себя, и что он принадлежит уровню 0, позволяют исключить
все самопоражающие аргументы для каждого уровня, и делают невоз-
невозможным для них исключение других аргументов.
Возможен и другой подход (Праккен, Сартор), когда вводится
специальный «пустой» аргумент, который не поражается никаким
другим аргументом и, по определению, поражает любой самопора-
самопоражающий аргумент.
Рекурсивные определения. Существует еще один подход
к назначению уникального статуса аргументам. Он состоит из двух
частей: во-первых, сделать явной идею о том, что аргументы обычно
строятся по шагам, начиная от промежуточных, и заканчивая фи-
финальными заключениями (например, в примере 10.4 промежуточное

10.1] Системы пересматриваемой аргументации 429
заключение — «Диксон — пацифист» и финальное — «У Диксона нет
пистолета»). Заметим, что главное интуитивное замечание об оценке
аргументов состоит в том, что аргумент не может быть подтвержден,
если не подтверждены все его подаргументы. Во-вторых, ограничить
восстановление случаями, когда оно достигается атакой на подаргу-
мент. Для введения формализованных определений будем считать,
что у аргументов существуют подаргументы.
Определение 10.9. Аргумент А подтверждается тогда и только
тогда, когда
• А не является самопоражающим аргументом и
• все подаргументы аргумента А подтверждаются и
• все аргументы, поражающие аргумент А, самопоражаются или
имеют по крайней мере один подаргумент, который не подтвер-
подтверждается.
Возникает вопрос: как удается избежать множественного присва-
присваивания статуса? Это определение по-разному обрабатывает два вида
восстановления. Интуитивно, аргументы могут быть восстановлены
двумя способами. В примере 10.1 способ, с помощью которого аргу-
аргумент С восстанавливает аргумент А, состоит в атаке на подаргумент
В, т.е. аргумент для заключения, что Твити — пингвин. Сделаем эту
связь подаргументов явной, изменив пример (обозначим через Х~
подаргумент аргумента X).
Пример 10. 6.
Рассмотрим четыре аргумента: А, .?>, В~ и С такие, что аргу-
аргумент В поражает аргумент А и аргумент С поражает аргумент В~.
Согласно определению 10.9, А и С подтверждаются, В и В~ — не
подтверждаются (В не подтверждается по второму условию). Итак,
аргумент С восстанавливает аргумент А, не поражая аргумент В
непосредственно, а поражая его подаргумент В~.
Другой вид восстановления можно проиллюстрировать на примере
10.1.
Пример 10. 7.
Рассмотрим три аргумента Ау В и С: А поражается Ву В поража-
поражается С. Возможна следующая интерпретация:
А = «Твити летает, так как он — птица»;
В = «Твити не летает, так как он — пингвин»;
С = «Твити летает, так как он необычный пингвин».
По определениям 10.3 и 10.6 и аргумент А, и аргумент С подтвержда-
подтверждаются. В частности, А подтверждается, так как он восстанавливается с
помощью аргумента С. Однако по определению 10.9 только аргумент
С подтверждается. Это происходит из-за того, что третье условие
определения 10.9 требует, чтобы аргумент А не мог поражаться ни
одним аргументом: оно не оставляет возможности восстановления

430 Системы аргументации и абдуктивный вывод [ Гл. 10
с помощью прямого поражения аргументов, поражающих аргумент
А. Следовательно, аргумент С не восстанавливает А. Это кажется
интуитивно верным: можно заключить, что Твити летает не из-за
того, что он — птица, а из-за того, что он — необычный пингвин.
Интуитивное различие между двумя типами восстановления в том,
что в примере 10.6 аргументы поражают друг друга по отношению к
различным заключениям, тогда как в примере 10.7 все конфликты
происходят по отношению к одному и тому же заключению. В то
время, как неявная форма восстановления (с помощью поражения по-
даргумента) соответствует базовому принципу аргументации, пример
10.7 показывает, что с прямым восстановлением все не так очевидно.
Возникает вопрос: удастся ли с помощью этого подхода исключить
множественное присвоение статуса в примере 10.2? Заметим, что опре-
определение 10.9 не допускает восстановления аргументов по отношению
к их конечным заключениям. И А, и В не подтверждаются, так как
оба эти аргумента поражаются по отношению к их конечным за-
заключениям («Никсон — пацифист или не пацифист»). Единственный
способ восстановить аргумент А = «Никсон — пацифист» состоит в
поражении подаргумента В = «Никсон — республиканец».
В определениях фиксированной точки мы неявно предполагали,
что один из способов поражения аргумента — это поражение одно-
одного из его подаргу ментов. И в подходе, использующем рекурсивные
определения, мы допускаем, что, напротив, поражение аргумента не
зависит от поражения подаргумента. Отсюда вытекают практически
важные следствия. Если подход фиксированной точки применяется
для системы, различающей аргументы и подаргу менты по другим со-
соображениям, то необходимо доказать, что второе условие определения
10.9 выполняется. Так как приведенные определения аргументов и
поражения довольно абстрактны, приведем еще несколько примеров.
Оказывается, определение 10.9 не совсем корректно. Рассмотрим
следующий пример (это версия примера 10.4, в котором подаргументы
определены явно).
Пример 10. 8.
Пусть даны аргументы А~, А, В и С: А~ и В поражают друг
друга, аргумент А поражает аргумент С. Можно ввести следующую
интерпретацию:
А~ = «Диксон — пацифист, так как он — квакер»;
В = «Диксон — не пацифист, так как он — республиканец»;
А = «У Диксона нет пистолета, так как он — пацифист»;
С = «У Диксона есть пистолет, так как он живет в Чикаго».
Согласно определению 10.9, С подтверждается, так как единственный
аргумент, поражающий аргумент С, — это аргумент А, который содер-
содержит неподтвержденный подаргумент, т.е. аргумент А~. Интуитивно,
аргумент А должен сохранять свою способность к предотвращению

10.1] Системы пересматриваемой аргументации 431
аргумента С, так как подаргумент аргумента А не поражается под-
подтвержденным аргументом.
Существует способ изменения определения 10.9: его нужно сделать
явно «трехзначным», изменив фразу «не подтверждается» в третьем
условии на «аннулируется».
Определение 10.10. Будем считать, что аргумент аннулируется
тогда и только тогда, когда он не подтверждается и либо поражает
сам себя, либо он сам или один из его подаргументов поражается под-
подтвержденным аргументом. Аргумент оправдывается тогда и только
тогда, когда он не подтверждается и не аннулируется.
Определение 10.11. Аргумент А подтверждается тогда и толь-
только тогда, когда выполняется
• А не поражает сам себя и
• все подаргументы аргумента А подтверждаются и
• все аргументы, поражающие аргумент А, поражают сами себя,
или имеют по крайней мере один подаргумент, который аннули-
аннулируется.
Для примера 10.8 получается следующий результат: ни один из
аргументов не поражает сам себя. Чтобы определить, подтверждается
ли аргумент С, мы должны определить статус аргумента А. Аргумент
А поражает аргумент С, следовательно, аргумент С подтверждается,
если аргумент А аннулируется. Так как аргумент А не поражается,
то он может аннулироваться лишь тогда, когда его подаргумент А~
аннулируется. Ни один подаргумент аргумента А~ не поражается, но
сам аргумент А~ поражается аргументом В. Тогда если аргумент
В подтверждается, то аргумент А~ аннулируется. Аргумент В не
подтверждается, так как он поражается аргументом А~, и аргумент
А~ не поражает сам себя и у него нет аннулированных подаргу ментов.
Но тогда аргумент А не аннулируется, т. е. аргумент С не подтвержда-
подтверждается. Таким образом все аргументы оправдываемы, что может быть
легко доказано.
Сравнение рекурсивных определений и опреде-
определений с фиксированной точкой. Сравнивая рекурсивные
определения и определения с фиксированной точкой, можно заметить,
что для примера 10.7 результаты применения этих определений
различны: интуитивно, лучшим кажется определение с рекурсией.
Рекурсивное определение (модифицированное, трехзначное) может
работать с зомби-аргументами так же, как и определения с
фиксированной точкой. Определения 10.9 и 10.11 не всегда дают
однозначное установление статуса аргумента.

432 Системы аргументации и абдуктивный вывод [ Гл. 10
Пример 10. 9.
Пусть имеется четыре аргумента А~, А, В~, В: аргумент А пора-
поражает аргумент В~, аргумент В поражает аргумент А~. Определение
10.9 дает два назначения статуса:
1) А~, А подтверждаются;
2) В~, В подтверждаются.
Кроме того, определение 10.11 еще дает такой вариант назначения
статуса, когда все аргументы оправдываемы. Очевидно, последний
вариант наиболее желателен, но, не прибегая к помощи определений
с фиксированной точкой, по-видимому, нельзя получить один лишь
этот результат.
Оценивая подход «назначения уникального статуса», мы видим,
что он может быть аккуратно формализован, если используются
определения с фиксированной точкой, тогда как, возможно, более
понятный способ введения рекурсивных определений сталкивается
с некоторыми проблемами. Но и применяя подход с определениями
с фиксированной точкой, можно столкнуться с рядом проблем: с
существованием плавающих аргументов и плавающих заключений.
Пример 10.10.
Рассмотрим аргументы А, В, С и D: А поражает Б, В поражает
А, А поражает С, С поражает D. Так как ни один из аргументов
не защищен от поражения, по определению 10.4 находим, что все
они оправдываемы. Но для аргументов С и D можно получить и
другое решение: так как аргумент С поражается и аргументом А, и
аргументом В, то аргумент С должен быть аннулирован: постольку,
поскольку статус аргумента С принят, отпадает необходимость раз-
разрешать конфликт между аргументами А и В. В результате статус
аргумента С «плавает» в зависимости от статуса аргументов А и В:
и если аргумент С должен быть аннулирован, то аргумент D должен
быть подтвержден, так как аргумент С — единственный аргумент,
поражающий аргумент D.
Пример 10.11.
Предположим, что у аргументов существуют заключения. Рас-
Рассмотрим аргументы А~, А, В~, В: А~ и В~ поражают друг друга, А и
В имеют одно и то же заключение. Возможна, например, следующая
интерпретация:
А~ = «Брайт — голландец, так как он родился в Голландии»;
В~ = «Брайт — норвежец, так как его родители — норвежцы»;
А = «Брайт любит кататься на коньках, так как он — голландец»;
В = «Брайт любит кататься на коньках, так как он — норвежец».
Как бы ни был разрешен конфликт между аргументами А~ и В~,
всегда спор завершается с аргументом, заключающим, что Брайт

10.1] Системы пересматриваемой аргументации 433
любит кататься на коньках, т. е. нам необходимо принять это заклю-
заключение как истинное, хотя оно и не поддерживается подтвержденным
аргументом. Другими словами, статус этого заключения «плавает» в
зависимости от статуса А~ и В~.
Решить подобные проблемы позволяет подход с назначением мно-
множественного статуса для аргументов.
10.1.1.3. Назначение множественного статуса аргумен-
аргументам,. При таком подходе разрешается назначать соревнующимся
аргументам А и В равной силы два варианта статуса: 1) аргумент А
подтверждается за счет аргумента В; 2) аргумент В подтверждается
за счет аргумента А. Обе эти ситуации удовлетворяют определению
10.1. Будем говорить, что аргумент А истинно подтверждается, если
он получает этот статус при любых назначениях.
Определение 10.12. Назначение статуса множеству аргументов
X, упорядоченному бинарным отношением поражения, состоит в на-
назначении каждому аргументу либо статуса «принадлежит», либо «не
принадлежит» (но не одновременно), удовлетворяющего следующим
условиям:
• аргумент принадлежит, если все аргументы, поражающие его,
имеют статус «не принадлежит»;
• аргумент не принадлежит, если он поражается аргументом,
имеющим статус «принадлежит».
Заметим, что условия те же, что и в определении 10.1. Для примера
10.2 существует два возможных варианта назначения статуса:
• аргумент А имеет статус принадлежит, а аргумент В — не
принадлежит;
• аргумент А имеет статус не принадлежит, а аргумент В —
принадлежит.
Аргументационная система должна определять, когда можно оправ-
оправданно принимать аргумент. Так как и аргумент А, и аргумент В могут
иметь статус «принадлежит» и «не принадлежит», то ни аргумент
А, ни аргумент В не подтверждаются.
Определение 10.13. При данном множестве аргументов X и от-
отношении поражения на X, аргумент подтверждается тогда и только
тогда, когда он имеет статус принадлежит при любых назначениях
статуса множеству X.
Существует два вида неподтвержденных аргументов:
1) аргументы отсутствуют во всех расширениях;
2) аргументы принадлежат некоторым расширениям.

434 Системы аргументации и абдуктивный вывод [ Гл. 10
Определение 10.14- Дано множество аргументов X и отношение
поражения на X:
• аргумент аннулируется тогда и только тогда, когда он имеет
статус «не принадлежит» при любых назначениях статуса мно-
множеству X]
• аргумент называется оправдываемым тогда и только тогда, ког-
когда он имеет статус «принадлежит» при некоторых назначениях,
и статус «не принадлежит» — при остальных.
Нетрудно доказать эквивалентность определений 10.7 и 10.14. Под-
Подходы уникального и множественного назначения статуса не эквива-
эквивалентны. Рассмотрим пример 10.10. Аргументы Аи В образуют четный
цикл, так что при подходе множественного назначения статуса, либо
аргумент А, либо аргумент В, могут иметь статус «принадлежит», но
не одновременно. В результате мы получаем два варианта назначения
статуса:
1) аргументы А и D получают статус «принадлежит», аргументы
В и С — «не принадлежит»;
2) аргументы В и D получают статус «принадлежит», аргументы
А и С — «не принадлежит».
При уникальном назначении статуса все аргументы оправдывае-
оправдываемы, аргумент С подтверждается, аргумент D — аннулируется. Подход
множественного назначения статуса позволяет работать с плавающи-
плавающими заключениями.
Определение 10.15. Статус заключений определяется следую-
следующим образом:
• заключение ср подтверждается тогда и только тогда, когда
каждое назначение статуса дает статус «принадлежит» аргу-
аргументу с заключением ср;
• заключение (р оправдывается тогда и только тогда, когда (р не
подтверждается и является заключением оправдываемого аргу-
аргумента;
• заключение ср является аннулируемым заключением тогда и
только тогда, когда (р не оправдывается и не подтверждает-
подтверждается, и кроме того является заключением аннулируемого аргу-
аргумента.
Если первое условие заменить на «ср — подтверждаемое заключе-
заключение тогда и только тогда, когда (р — заключение подтвержденного
аргумента», то будет выражено более сильное понятие, при котором
плавающие заключения не подтверждаются.

10.1] Системы пересматриваемой аргументации 435
Пример 10.12.
Пусть А, В и С — три аргумента, представляющие треугольник: А
поражает С, В поражает А, С поражает В. При применении определе-
определения 10.13 возникают некоторые проблемы, так как для этого примера
не удается определить статус аргументов:
1) пусть аргумент А имеет статус «принадлежит». Тогда, так как
А поражает С, то С получает статус «не принадлежит». Так
как С «не принадлежит», то В получает статус «принадле-
«принадлежит», тогда А должен получить статус «не принадлежит»,
и мы приходим к противоречию;
2) пусть аргумент А имеет статус «не принадлежит». Тогда, так
как А поражает С, то С получает статус «принадлежит». Так
как С «принадлежит», то В получает статус «не принадле-
принадлежит», тогда А должен получить статус «принадлежит», и мы
снова приходим к противоречию.
Заметим, что аргументы, поражающие сами себя — особый случай
примера 10.12, т. е. здесь аргументы В и С идентичны А. Это означает,
что множества аргументов, содержащие аргумент, который поражает
сам себя, не получают статуса.
10.1.1.4- Сравнение подходов уникального и мноснсе-
ственного назначения статуса аргументам. Возникает
вопрос: как связаны между собой подходы уникального и множе-
множественного назначения статуса? Иногда говорят, что они соответствуют
скептическому и доверчивому подходам к выводу пересматриваемых
заключений: если скептически настроенный агент сталкивается с
неразрешимым конфликтом двух аргументов, он не выводит никакого
заключения, а доверчивый агент выбирает любое заключение,
или несколько заключений одновременно, и будет использовать
их следствия.
С точки зрения Праккена и Вресвейка, это некорректная интер-
интерпретация. При решении, что принять как подтвержденное убеждение,
важно не то, сколько назначений статуса выполняется, а как аргу-
аргументы оцениваются при этих назначениях. И это оценивание охва-
охватывается понятиями «подтвержденный» и «оправдываемый», что в
результате отражает различие между скептическими и доверчивыми
выводами. И так как было показано, что различие между подтвер-
подтвержденными и оправдываемыми аргументами может быть сделано в
обоих подходах, то они, следовательно, не зависят от типа вывода —
скептического или доверчивого.
Подход множественного назначения статуса больше подходит для
определения множеств аргументов «идущих вместе». Действительно,

436 Системы аргументации и абдуктивный вывод [ Гл. 10
подход уникального назначения статуса делает оправдываемыми ар-
аргументы на индивидуальной основе, а при множественном назначе-
назначении они оправдываемы, если принадлежат множеству аргументов со
статусом «принадлежит», и, следовательно, могут быть защищены
одновременно. Даже если два оправдываемых аргумента не поражают
друг друга, они могут быть несравнимы в том смысле, что ни одно
назначение статуса не делает их одновременно принадлежащими мно-
множеству аргументов со статусом «принадлежит».
Пример 10.13.
Пусть аргументы Аи В поражают друг друга, аргумент В поража-
поражает аргумент С, аргумент С поражает аргумент D. Хотя аргументы А и
D не поражают друг друга, аргумент А имеет статус «принадлежит»
тогда и только тогда, когда аргумент D имеет статус «не принадле-
принадлежит». При подходе уникального назначения статуса это выразить
сложнее.
Подход уникального назначения статуса успешно справляется с
проблемой «зомби-аргументов». Эта проблема возникает лишь в слу-
случае рекурсивных двузначных определений.
Подходы различаются, главным образом, обработкой плавающих
заключений и аргументов. Например, смысл, который вкладывается
в подтверждение заключения «Брайт любит кататься на коньках» из
примера 10.11, отличается от смысла, вкладываемого в подтвержде-
подтверждение заключения «Твити летает» из примера 10.1. Лишь в примере
10.1 заключение поддерживается подтвержденным аргументом. Ана-
Аналогично, статус аргумента D из примера 10.10 отличается от статуса
аргумента А из примера 10.1. Хотя оба аргумента нуждаются в по-
помощи других аргументов чтобы стать подтвержденными, аргумент,
поддерживающий аргумент А, сам подтверждается, а аргументы, под-
поддерживающие аргумент Z), лишь оправдываемы.
10.1.2. Обзор систем аргументации
На сегодняшний день разработан широкий спектр аргументаци-
онных систем, отличающихся определениями базовых элементов и
уровнями абстракции. Приведем краткое описание ряда аргумента-
ционных систем, которое дает представление о современном уровне
развития теории аргументации.
Абстрактная аргументационная система, которую
разработали Дан г, Ковальский, Бондаренко и Тони,
определена как в декларативной, так и в процедурной формах. Эту
систему можно использовать для исследования различных аргумента-
ционных систем, с ее помощью можно представить ряд немонотонных
логик. В данной системе авторы полностью абстрагируются от
внутренней структуры аргументов и природы множества аргументов.
Предполагается лишь, что существует некоторое множество

10.1] Системы пересматриваемой аргументации 437
аргументов, упорядоченное бинарным отношением «поражения»
(или «атаки» — у авторов подхода). Для множеств аргументов
определяются так называемые аргументационные расширения,
которые должны охватывать различные типы пересматриваемых
следствий. Определения расширений даются в декларативной форме,
т. е. они объявляют некоторые множества аргументов как имеющие
определенный статус.
Аргументационной структурой (AF) является пара (Args,
defeat), где Args — множество аргументов и defeat — бинарное
отношение на множестве Args. Структура AF называется конечной
в том случае, когда каждый аргумент в Args поражается, самое
большее, конечным числом аргументов из Args. Множество
аргументов является бесконфликтным, если ни один аргумент
множества не поражается аргументами этого множества. Множество
Args может пониматься как множество всех аргументов, которые
могут быть построены в данной логике из данного множества
посылок.
В этой системе поражение интерпретируется в слабом смысле,
т. е. как «атакует и не слабее». Таким образом два аргумента мо-
могут поражать друг друга. Центральным понятием аргументационной
структуры является приемлемость: «Аргумент А приемлем по отно-
отношению к множеству аргументов S тогда и только тогда, когда каждый
аргумент, поражающий А, поражается аргументом в S». Аргументы
в S могут рассматриваться как
аргументы, способные восстанавливать А, если А поражается.
Например, для задачи 10.1 А.Р-структура содержит множество Args
= {А, Б, С} и defeat = {(Б, А), (С,В)}, т.е. В строго поражает А
и С строго поражает В. Аргумент А приемлем по отношению к
{С}, {А, С}, {Б,С} и {А, Б,С}, но он не является приемлемым по
отношению к 0 и {В}.
Еще одним важным понятием является допустимость множества
аргументов: «Бесконфликтное множество аргументов S допустимо
тогда и только тогда, когда каждый аргумент в S приемлем по от-
отношению к S». Для нашего примера множества 0, {С} и {А, С} —
допустимые, а все остальные подмножества для {А, Б,С} не будут
допустимыми.
Используя понятия приемлемости и допустимости, авторы это-
этого подхода определили различные «аргументационные расширения»,
которые соответствуют назначению аргументам некоторого статуса.
Приведем для примера определение устойчивого расширения (приме-
(примеры определения других расширений можно найти в разд. 10.3.1 приме-
применительно к логическим программам). Бесконфликтное множество ар-
аргументов S является устойчивым расширением тогда и только тогда,
когда каждый аргумент, не принадлежащий S, поражается некоторым
аргументом множества S. Для примера 10.1 устойчивым расширением

438 Системы аргументации и абдуктивный вывод [ Гл. 10
будет лишь множество {А, С}. Если для примера с ромбом Никсона
A0.2) определить аргументационную структуру с Args = {А, В} и
defeat = {(А, В), (Б, А)}, то окажется, что существует два устойчивых
расширения {А} и {В}.
Для абстрактной аргументационной системы был получен ряд
результатов, касающихся существования аргументационных расши-
расширений и связей между различными видами семантики. Разработчики
этого подхода также изучали и процедурные формы для различных
видов аргументационной семантики.
Преимуществом данного подхода является то, что он обеспечивает
изящную общую структуру для исследования различных аргумента-
аргументационных систем. Авторы подхода показали, что некоторые немонотон-
немонотонные логики могут быть переведены в аргументационные системы. В
результате появляется возможность для определения альтернативной
семантики немонотонных логик. Например, Данг показал, что семан-
семантика логики умолчаний соответствует устойчивой семантике аргумен-
аргументационной системы, и для этой логики можно определить другую
аргументационную семантику, гарантирующую наличие расширений.
В то же время, из-за абстрактности подхода, разработчикам конкрет-
конкретных систем придется определять внутреннюю структуру аргументов,
способы их взаимодействия и смысл отношения поражения для аргу-
аргументов.
Аргументационная система, разработанная Пол-
локом, была им же реализована в виде программного комплекса
OSCAR. В этой системе логический язык — логика предикатов
первого порядка; аргументы представляются последовательностью
высказываний, связанных схемами вывода, определяющими как
достоверный, так и правдоподобный вывод; отношение поражения
аргументов определяется в зависимости от используемых схем
вывода (допускаются и опровержение, и подрыв). Определение
конфликтующих аргументов остается неявным. Статус аргументов
определяется с помощью множественного подхода, причем использу-
используется предпочтительная семантика (см. разд. 10.3.1). При реализации
системы Поллок использует частичные вычисления, что особенно
важно при ограниченных ресурсах.
Обычно в аргументационных системах определение аргумента
основывается на понятии выводимости в базовом логическом языке.
Но иногда оказывается полезным определять специальные правила
построения новых аргументов. Это важно, например, в случае фор-
формализации предположительного вывода. При предположительном вы-
выводе мы «предполагаем» нечто, что не может быть выведено из ис-
исходных данных (ВХОДа), выводим заключения из предположений,
и затем «исключаем» предположения, чтобы получить связанное за-
заключение, которое больше не зависит от исходного предположения. У

10.1] Системы пересматриваемой аргументации 439
Поллока аргумент, основанный на ВХОДе, представляет собой конеч-
конечную последовательность строк аргумента o~i =< Xi,pi,Vi >, где Xi —
множество высказываний, являющееся множеством предположений
строки г, Pi — высказывание и. щ — степень подтверждения. Строка
аргумента получается из предыдущих строк по одному из правил
образования аргумента. Приведем примеры таких правил:
• Вход: если р Е ВХОДу и а — аргумент, то для любого X : а,
< X, р, оо > — тоже аргумент;
• Предположение: если а — аргумент, X — множество высказы-
высказываний и р Е X, то сг, < Х,р, оо > — тоже аргумент;
• Дилемма: если а — аргумент и некоторая строка а есть
< Х,р V q, v >, а также в а есть строки: < X U {p},r,[i > и
< X U {q}, r, <f >, то сг, < X, г, min {z/, /i, ?} > — тоже аргумент.
Рассмотрим пример предположительного вывода. «Предположи-
«Предположительно, студенты, сдавшие сессию без троек, получают стипендию;
предположительно, студенты, относящиеся к льготной категории,
получают стипендию. Иван сдал сессию без троек или относится
к льготной категории. Следовательно, предположительно, Иван
получает стипендию». Такой вывод может быть формализован
следующим образом. По условию, у нас есть правдоподобные
доводы (ПД): (ПД-1) без_троек(Х) — ПД силы v для получа-
получает _стипендию(X); (ПД-2) льготная _категория{Х) — ПД силы
/i для полу чает _ стипендию {X). ВХОД = {без _ троек (Иван)
V льготная_ категория (Иван)}. Тогда аргумент, утверждающий,
что Иван получает стипендию, имеет вид
1) <0, без _ троек (Иван) V льготная _штего1рия(]Авал), сю > (это
описание ВХОДа);
2) <{без_троек(Ив&н_)}, без _ троек (Иван), оо > (Предположе-
(Предположение);
3) <{без_троек(Ив&п)}у полу]чает _ стипендию (Иван), v > B и
ПД-1);
4) <{льготная_категория(И.вал)}, льготная_категория(Ивал),
сю > (Предположение);
5) <{льготная_категория(И.вал)}, полу'чает _ стипендию (Иван),
v > D и ПД-2)>;
6) <0, полу'чает_ стипендию (Иван), min{z/, /i} > C, 5 и Дилемма).
Заметим, что строка 1 утверждается как абсолютный факт, в
строках 2 и 4 временно предполагается истинность высказываний
без _ троек (Иван) и льготная_категория(И.вал) соответственно.
Строки 3 и 5 получаются на основе сделанных предположений, а
строка б утверждает, что Иван получает стипендию, не используя

440 Системы аргументации и абдуктивный вывод [ Гл. 10
никаких предположений, благодаря существованию правила
Дилеммы.
Если говорить об аргументационной системе Поллока в целом, то
следует отметить, что она опирается на глубокую философскую (эпи-
(эпистемологическую) теорию пересматриваемого вывода. Эта аргумента-
ционная система логически очень богата: в ней определены линейные
и предположительные, дедуктивные и не дедуктивные (статистиче-
(статистические и индуктивные) аргументы, для которых определены конфликты
двух типов. Из-за того, что Поллок при разработке аргументацион-
аргументационной системы использовал понятия эпистемологии, его систему нельзя
непосредственно применить для специфического практического вы-
вывода. Например, понятия, связанные с вероятностями, сложно учесть
при выводе для аргументов с приоритетами.
Абстрактная аргументационная структура Лина и
Шоэма. Лин и Шоэм разработали абстрактную аргументационную
структуру и ряд методов для того, чтобы сформулировать некоторые
системы вывода по умолчанию в рамках аргументационной теории.
В этой работе логический язык явно не определяется; используются
монотонные и немонотонные правила вывода для построения аргу-
аргументов, которые представляют собой деревья с пометками на дугах.
Понятия конфликтующих аргументов и их сравнение не определяют-
определяются. Вместо этого вводится понятие структуры аргументов, которая
содержит множество посылок аргументов, все подаргументы для ка-
каждого аргумента, и множество заключений аргументов в структуре
дедуктивно замкнуто и непротиворечиво. Как оказалось, структуры
аргументов с дополнительными свойствами полноты очень похожи на
семантику устойчивых расширений для аргументационных систем.
Аргументационная система Вресвейка опирается на ар-
аргументационную систему Лина и Шоэма, дополняя ее определени-
определениями конфликта аргументов и статуса конфликтующих аргументов.
Логический язык не определяется явно, но предполагается, что он
содержит символ _1_, обозначающий противоречие, а также множество
монотонных и немонотонных правил вывода. Аргументы представ-
представляются деревьями, и на множестве аргументов вводится отношение
упорядочения по силе. Выделяется два типа конфликтов: подрыв и
опровержение, причем конфликтовать аргумент может не только с
единичным аргументом, но и с множеством аргументов. При опре-
определении семантики используются аргументационные последователь-
последовательности, которые формируются из структур аргументов. С помощью
таких последовательностей определяются частичные вычисления.
Для практических приложений абстрактной системы Вресвейк
предполагает, что объектный язык позволяет представлять пересмат-
пересматриваемую условную зависимость ср > ф и пересматриваемое правило
ср,ср>ф
вывода вида ¦ . В системе Вресвейка в качестве контраргу-
Ф

10.1] Системы пересматриваемой аргументации 441
мента выступает множество аргументов: «Множество аргументов Е
не сравнимо с аргументом т тогда и только тогда, когда заключения
Е U {г} вызывают _1_». Необходимость использования множеств аргу-
аргументов объясняется тем, что в данной аргументационной структуре
язык явно не определяется и, следовательно, теряется выразительная
сила при распознавании противоречий. Следствием недостатка вы-
выразительности является то, что множество аргументов <ji, ..., сгп, не
сравнимых с г, не может быть добавлено к какому-либо аргументу
а', который противоречит т. Поэтому и приходится рассматривать
множества аргументов.
Вресвейк не вводит явно понятие конфликтов подрыва, он утвер-
утверждает, что может формализовать их как аргументы для пересматри-
пересматриваемой условной зависимости. Для этого Вресвейк предполагает, что
язык абстрактной аргументационной системы замкнут относительно
отрицания (-i), конъюнкции (&), материальной импликации (D) и пе-
пересматриваемой импликации (>). В результате оказывается возмож-
возможным выразить правила вывода (являющиеся метаязыковыми поняти-
понятиями) в объектном языке. Правила метауровня, в которых используют-
используются символы «—>¦» (строгое правило вывода) и «=>» (пересматриваемое
правило вывода), представляются с помощью соответствующих сим-
символов импликации объектного языка: <О» и «>». При данных пред-
предположениях Вресвейк формально определяет опровергающие и под-
подрывающие аргументы. Например, пусть сгиг — аргументы в рассмат-
рассматриваемой аргументационной системе с заключениями (риф соответ-
соответственно, причем г сильнее, чем а. Пусть также (/?i,..., срп => ср — верх-
верхнее правило аргумента а. Тогда вводятся следующие определения:
• поражение-опровержение. Если ф = -к/?, то т — аргумент,
опровергающий а. Таким образом заключение опровергающего
аргумента противоречит заключению аргумента, который он
поражает;
• поражение-подрыв. Если ф = ->(^i,...,^n > Ф), т-е- если ф —
это отрицание последнего правила аргумента а^ установленное
в объектном языке, то г — аргумент, подрывающий а. Таким
образом заключение подрывающего аргумента противоречит по-
последнему правилу вывода того аргумента, который он поражает.
Для оценки статуса аргументов Вресвейк использует следующее
определение: аргумент «в силе» (in force) на основе множества посы-
посылок тогда и только тогда, когда
1) аргумент эквивалентен посылке или
2) все подаргументы «в силе» и последнее правило вывода является
дедуктивным или
3) все подаргументы «в силе», последнее правило вывода являет-
является пересматриваемым, и для каждого множества несравнимых

442 Системы аргументации и абдуктивный вывод [ Гл. 10
аргументов по крайней мере один элемент слабее данного аргу-
аргумента или не «в силе».
Для примера с ромбом Никсона можно определить, что аргумент
«квакер» «в силе» тогда и только тогда, когда аргумент «республи-
«республиканец» не «в силе». Если конфликтующие аргументы имеют равную
силу, как в случае с ромбом Никсона, то необходимо использовать
множественные устойчивые расширения.
Оценивая подход Вресвейка, Праккен утверждает, что в нем уде-
уделяется меньше внимания деталям сравнения аргументов, чем в под-
подходе Поллока, и в противоположность подходу Данга, формализуется
лишь один тип пересматриваемого следования. Тем не менее, подход
достаточно глубоко проработан в том, что касается структуры аргу-
аргументов и процесса аргументации.
Аргументационная система, разработанная Прак-
кеном и Сартором, обобщает фундаментальную семантику
абстрактной аргументационной структуры Данга и др. для случая,
когда используются приоритеты аргументов. Предполагается, что
объектный язык содержит связку «=>», используемую в логическом
программировании для формирования правил на литерах, а также
существует два вида отрицания — явное и неявное, и предикатный
символ <<^<», устанавливающий приоритеты в языке. Аргумент
представляется конечной последовательностью фундаментальных
примеров правил. В структуре аргумента выделяется подаргумент,
заключение и гипотеза. При конфликте аргументов возможен
как подрыв, так и опровержение. Причем при определении вида
поражения аргумента учитываются и приоритеты, определенные для
правил. С помощью скептической семантики определяется статус
аргумента: подтверждаемый, аннулируемый или оправдываемый.
При формулировке этой аргументационной системы может исполь-
использоваться и язык логики умолчаний. Система сформулирована как в
процедурной, так и в декларативной форме.
Симари и Луи разработали аргументационную
систему, предназначенную для характеризации условий, при
которых аргументационная структура является предпочтитель-
предпочтительной. При этом рассматривается лишь синтаксический подход.
Знания агента представляются парой (.К*, А). Множество К
представляет непересматриваемые знания, которые должны быть
непротиворечивы. А — конечное множество пересматриваемых
правил, которые выражаются средствами метаязыка. Дополнительно
определяется мета-мета взаимосвязь, которая соотносит формулы
из множества К и фундаментальные примеры из множества
А с формулой h. Эта взаимосвязь «|^» — пересматриваемое
следование — представляет вывод из К к h с использованием
фундаментальных примеров из множества А (приложение правила

10.1] Системы пересматриваемой аргументации 443
Modus Ponens). Аргумент определяется следующим образом:
«Подмножество Т фундаментальных примеров элементов множества
А является аргументом для предложения h тогда и только тогда,
когда
1) К U T |~ h (T влечет ft);
2) К U T |^_1_ (T не противоречиво с X);
3) ^ЗТ' С Т такого, что К U Г' |~ h (T — минимально)».
Аргументационная структура образуется аргументом Т и форму-
формулой ft, и записывается как <Т, ft>. Аргумент <Т, h\> — подаргумент
для аргумента <S, /i2> тогда и только тогда, когда Т С S. Заметим,
что здесь аргумент определяется не как дерево или цепочка выводов,
а как неупорядоченный набор правил, которые вместе приводят к
некоторому заключению.
Конфликт аргументов определяется следующим образом: «Аргу-
«Аргумент <Т, h\> — это контраргумент для аргумента <S, /i2> тогда и
только тогда, когда у аргумента <$, /i2> существует подаргумент
<S", h> такой, что <Т, h\> не согласуется с <Sf,h>, т.е. К U
U {h\,h} \- _L». Для сравнения аргументов используется специфич-
специфичность: «Аргумент А поражает аргумент В тогда и только тогда, когда
А не согласуется с подаргументом В~ для В и А более специфичный,
чем В~».
Симари и Луи предложили специальное исчисление аргументов,
обладающее интересными математическими свойствами. К ограниче-
ограничениям подхода можно отнести то, что используются лишь двуместные
умолчания, поэтому не различаются поражение как подрыв и как
опровержение (этот недостаток преодолевается в системе Праккена
и Сартора).
В заключение приведем кратко основные результаты сравнитель-
сравнительного анализа аргументационных систем, выполненного Праккеном и
Вресвейком.
1. Большинство систем аргументации могут быть переведены из
одной системы в другую. Например, понятие аргумента как
множества (Симари, Луи) может быть переведено в понятие
аргумента как дерева (Лин, Шоэм).
2. Аргументационные системы различаются, главным образом, из-
за различного уровня абстракции по отношению к лежащему
в основе логическому языку, структуре аргументов и природе
отношений поражения.
3. Некоторые аргументационные системы расширяют уже извест-
известные ранее системы. Например, подход Данга и др. обобщается
для случая, когда у аргументов имеются приоритеты, в подходе
Праккена и Сартора.

444 Системы аргументации и абдуктивный вывод [ Гл. 10
4. Основное различие систем состоит в различном понимании пере-
пересматриваемого следования. Вообще говоря, существование раз-
различных определений не представляет собой проблемы, а яв-
является свойством области пересматриваемой аргументации. В
конечном счете, выбор понятий определяется практическими
соображениями.
5. Подход Данга и др. может рассматриваться как универсальный,
если это вообще возможно в области аргументации.
6. Некоторые аргументационные системы формализуют «логиче-
«логически идеального» агента, а другие реализуют идею частичных
вычислений, т. е. вычисления аргументов не по отношению ко
всем возможным аргументам, а лишь по отношению к аргу-
аргументам, которые в действительности были построены агентом.
Снова различные системы оказываются полезными для разных
контекстов практических приложений.
10.2. Организация абдуктивного вывода
10.2.1. Понятие абдуктивного вывода
Абдукция предназначена для поиска объяснений или причин на-
наблюдаемых явлений и фактов. Соответствующий вывод имеет форму
(в теории вывода Пирса):
• наблюдается удивительный факт С (то есть этот факт не следует
из наших знаний о мире);
• если бы А было бы истинным, то С могло бы произойти {А —
объясняющая гипотеза);
• следовательно, можно предположить, что А истинно.
В силлогистической теории Пирса под абдукцией понимается вы-
вывод по схеме: даны правило и результат, требуется вывести частный
случай — причину.
В искусственном интеллекте под абдуктивным выводом понима-
понимается вывод наилучшего абдуктивного объяснения. Причем «наилуч-
«наилучшим» считается такое объяснение, которое удовлетворяет специаль-
специальным критериям, определяемым в зависимости от решаемой задачи и
используемой формализации.
В настоящее время наблюдаются разногласия, как в определении
термина «абдукция», так и свойств абдуктивного вывода. Например,
Флеч отмечает: «Характеристической чертой абдукции является объ-
объяснение». При абдуктивном выводе теория Т, описывающая домен,
предполагается неполной. Наблюдение дает новую информацию, ко-
которая должна дополнить имеющееся описание. Поэтому абдуктивное
описание имеет смысл только относительно этой теории Т, из которой

10.2] Организация абдуктивного вывода 445
оно построено. Теорию Т можно расширить как представление всех
ее возможных абдуктивных расширений Т U А, где А — гипотеза —
результат абдуктивного вывода, объясняющая имеющееся наблюде-
наблюдение. При этом абдуктивное следование в теории Т определяется как
дедуктивное следование в каждом из ее абдуктивных расширений.
В то же время под процессом абдукции можно понимать выбор
одного из абдуктивных расширений теории Т, в котором выполня-
выполняется данное наблюдение. Обычно множество гипотез, которое может
выступать в качестве объяснений, ограничивается специальным мно-
множеством так называемых абдуцентов. Вид множества абдуцентов, по
мнению Флеча и Какаса, отражает уровень наших знаний о домене.
Например, если абдуцентами могут быть лишь фундаментальные
факты, то это возможно только тогда, когда теория Т достаточно
полно описывает домен. Как отмечают Флеч и Какас, «Цель абдук-
абдукции — отобрать расширение и выполнить с ним вывод, раскрывая
таким образом потенциал к обобщению, заложенный в теории Т».
Пол указывает на то, что правило в абдуктивном силлогизме
Пирса не обязательно должно выражать связь-импликацию, то есть
Л > С С
в правиле вывода для абдукции: —-—, А может быть причиной
С пли доводом в пользу того, чтобы С было истинным.
Габбай утверждает, что при абдукции, то есть объяснении наблю-
наблюдения, не выводимого в заданной теории Т логики L1, необходимо
модифицировать теорию Т, либо добавляя к ней объяснение-гипотезу
А, либо удаляя А из Т. Габбай также отмечает следующие свойства
механизма абдукции:
1) абдукция — это понятие метауровня;
2) абдукция зависит от теории доказательства логики L1;
3) абдукция может изменять логику, то есть новые правила, по-
получаемые по абдукции, могут изменять теорию доказательства
логики L1;
4) для выполнения абдукции требуется еще одна логика L2, то
есть определение абдуктивного механизма включает процедуру
для абдукции (компонента объяснения) и логику L2 (компонента
правдоподобия);
5) абдуктивный вывод может быть неуспешным.
Таким образом, согласно исходному определению абдукции как
наилучшего объяснения, требуется решать две задачи: найти объяс-
объяснение и определить наилучшее объяснение, то есть специальный кри-
критерий. Дюбуа и Прад считают, что ключевой проблемой для абдукции
является назначение некоторого статуса абдуктивному заключению,
например, степени правдоподобия или, по крайней мере, упорядочить
возможные причины наблюдаемого явления по их относительному
правдоподобию.

446 Системы аргументации и абдуктивный вывод [ Гл. 10
Боргельт и Крузе, напротив, утверждают, что абдуктивный вы-
вывод следует рассматривать отдельно от оценки гипотез. Как опре-
определил Лукасевич, все логические выводы могут быть поделены на
. „ А^В, А,
два класса: дедукцию (со схемой — ) и редукцию (со схе-
„ А^В,В,
мои ). Дедукция позволяет сделать явными все истинные
утверждения, определяемые заданным множеством утверждений, а
редукция позволяет обнаруживать объяснения для утверждений, опи-
описывающих, например, новые факты. Редуктивный вывод не сохраняет
истину, но с его помощью можно получать новую информацию. К
редукции можно отнести как индуктивный, так и абдуктивный вывод.
Тогда определение абдукции может быть дано следующим образом:
«Абдукция — это редуктивный вывод, в котором заключение является
частным утверждением».
Если использовать понятия формальной логики, то под частным
утверждением понимается фундаментальная формула, не содержа-
содержащая ни свободных, ни связанных переменных. Абдуценты также пред-
представляются лишь фундаментальными формулами. Если же заключе-
заключение не является фундаментальной формулой, то такой вывод назы-
называется индуктивным. Абдуктивный вывод может привести к ложным
заключениям даже при истинных посылках, поэтому его заключение и
называется гипотезой. Проблема заключается в том, что обычно не все
объясняющие выводы с фундаментальными заключениями считаются
абдуктивными, так как для этого они должны предлагать объяснение,
лучшее, чем все другие объясняющие выводы. Как уже отмечалось,
смысл термина «наилучшее объяснение» определяется критериями,
зависящими от домена приложения. Поэтому не удивительно, что
существует так же много различных интерпретаций термина «абдук-
«абдукция», как и критериев оценки гипотез.
Например, Боргельт и Крузе приводят следующие примеры кри-
критериев:
1) связь между посылками и следствием (требуется, чтобы объяс-
объясняющая гипотеза представляла собой довод в пользу наблюде-
наблюдения или причину наблюдения, а это понятия семантики, которые
сложно определить);
2) связь с другими утверждениями (другие утверждения могут
опровергать или поддерживать гипотезу, что влияет на ее прав-
правдоподобие);
3) экономия (требуется, чтобы объяснения были максимально про-
простыми) ;
4) вероятность (учитывается вероятность данного объяснения для
имеющегося наблюдения).

10.2] Организация абдуктивного вывода 447
Дополнительно Пол предлагает разделять критерии на глобаль-
глобальные, которые проверяются на множестве всех возможных гипотез-
объяснений, и локальные, которые применяются при генерации ги-
гипотез, чтобы избежать построения «лишних» объяснений.
В искусственном интеллекте работы по абдукции ведутся пример-
примерно с 70-х гг. XX века. Можно выделить следующие этапы разработок
(по МакИлрайт):
• механизация абдуктивного вывода G0-е — начало 80-х гг.);
• определение и формализация понятия абдуктивного вывода,
предлагаются структуры и формальные характеризации (80-е —
начало 90-х гг.);
• результаты по вычислительной сложности задачи абдукции (на-
(начало 90-х гг.);
• применение абдуктивного вывода к различным задачам гипо-
гипотетического вывода, выполняется более формальная характе-
ризация прикладных задач и предлагаются новые определения
наилучшего объяснения (90-е гг.);
• установление связей абдукции с другими видами немонотонного
вывода (90-е гг.).
Анализируя работы по абдукции, Пол подчеркивает ключевую
роль представления причинно-следственных связей в базовой теории
для решения задачи абдукции. Он выделяет следующие подходы к
реализации абдуктивного вывода:
1) подход, основанный на покрытии множеств (базовая теория
имеет очень простую структуру: причинно-следственные связи
представляются просто импликацией);
2) подход на основе логики (более общий подход, реализующий
методы генерации и отбора гипотез, но должно быть использова-
использовано специальное представление знаний, определяющее, возмож-
возможно, неявно причинно-следственные связи (например, логические
программы));
3) подход на уровне знаний (модель определяется в зависимости
от типа доверия; вводится семантическое определение оператора
объяснения, то есть достигается независимость от соответству-
соответствующего представления знаний);
4) вероятностные методы (задача абдуктивного вывода понимается
как поиск наиболее вероятного объяснения наблюдения; приме-
применяются каузальные сети, для которых определяется некоторое
понятие правдоподобия).
Заметим, что в искусственном интеллекте до последнего времени
работы по абдукции и индукции велись независимо. Но, по-видимому,

448 Системы аргументации и абдуктивный вывод [ Гл. 10
перспективным является рассмотрение абдукции, индукции и дедук-
дедукции в рамках одной системы. При этом абдукция используется для
получения гипотез, объясняющих наблюдения. Дедукция позволяет
выполнять вывод с использованием этих гипотез и получать некото-
некоторые предсказания. С помощью индукции на основе этих предсказаний
можно определить общие правила и оценить, насколько они согласу-
согласуются с реальностью.
Остановимся подробнее на подходах 1-3; четвертому подходу по-
посвящен разд. 10.2.4.
10.2.2. Подходы к характеризации абдукции
10.2.2.1. Подходы, основанные на покрытии множеств.
Предполагается, что заранее задано множество возможных гипотез,
и множество объяснений отбирается из числа этих гипотез. Выби-
Выбираемое подмножество должно представлять наилучшее объяснение
для наблюдения; оно определяется с использованием покрытий, мер
правдоподобия и т. п. Так как гипотезы строятся с использованием
множества ранее известных кандидатов, то такой подход иначе назы-
называется «сборкой» (assembly) гипотез.
Например, Аллемань дает следующее определение: «Домен для
сборки гипотез определяется тройкой (Ф,0,е), где Ф — конечное
множество гипотез, Q — множество наблюдений, е — отношение,
связывающее Ф и Q. е(Ф) Называется мощностью объяснения мно-
множества гипотез Ф и определяет множество наблюдений, учитываемых
Ф. Задача сборки дается множеством наблюдений ff С Ц, которые
должны быть объяснены».
Для того, чтобы можно было использовать эту формальную мо-
модель на практике, требуются дополнительные предположения о до-
домене Ф:
1) предположение вычислимости (оно важно для всех моделей,
основанных на покрытии множеств): для любого множества
Фх С Ф может быть вычислено е(Фх), т.е. всегда известно, какие
наблюдения объясняются какими множествами гипотез;
2) предположение независимости. Пусть Ф1 С Ф и Ф2 С Ф, тогда
е(Ф1иФ2) =е(Ф1)ие(Ф2). Выполнение этого свойства важно при
пошаговом вычислении соответствия е, т. е. если известно е(Ф].),
то е(Ф2) = е(Ф1 U {(/?}) может быть легко найдено присоединени-
присоединением е({(р}) к известному множеству е(Ф].);
3) предположение монотонности. Пусть Ф1 С Ф, Ф2 С Ф, тогда
должно выполняться: е(Ф].) С е(Ф2);
4) предположение о разрешимости (accountability assumption).
Функция а : Ф —> ГГ, где а{ф) = {со е Щ ЗФ1 С Ф с (р е Фг :
ио G е{Ф\) пои ф (ФД{(/?})} вычислима. Функция а(ф) определяет

10.2] Организация абдуктивного вывода 449
те наблюдения, которые не могут быть объяснены без ср. Если
выполняется монотонность, то се((р) С е((р).
Подходы, основанные на покрытии множеств, сильно зависят от
заранее определенного соответствия е, которое сразу задает надмно-
надмножество искомых объяснений. Таким образом здесь в действительности
не существует механизма генерации гипотез, а, скорее, определяется
процедура накопления, отбирающая релевантные гипотезы из этого
надмножества. Отметим ряд недостатков, присущих данному под-
подходу:
• вычислимость соответствия не критична для выбора возможных
объяснений. Все причинно-следственные связи, релевантные за-
задаче, должны быть представлены до выполнения абдуктивной
процедуры;
• требуется выполнение ряда предположений (независимости, мо-
монотонности и т.п.), поэтому приложения ограничиваются доме-
доменами, с которыми «легко» работать;
• небольшие изменения в лежащей в основе теории могут приве-
привести к значительным трудностям, так как может потребоваться
переопределение функции е.
В результате можно сделать вывод о том, что данный подход
удобен для решения задач диагностики (когда известны все причинно-
следственные связи, и они могут быть представлены с помощью
функции), причем лежащая в основе теория не должна подвергаться
изменениям.
10.2.2.2. Подходы, основанные на логике. Наибольший объ-
объем исследований по абдукции основывается на логических моделях.
Знания, представленные в некотором логическом языке для дедук-
дедуктивного вывода, могут быть также использованы и для абдукции.
Абдуктивная система состоит из логической теории Т над языком
Lang и множества предложений А языка Lang, которые называются
абдуцентами (иногда выделяется множество предикатов, которые мо-
могут использоваться в предложениях-абду центах).
Если предложение (р — результат абдуктивного процесса поиска
объяснения для ш, то оно должно удовлетворять условиям
• TUip hcj;
• Т U (р непротиворечиво;
• ср е А.
Таким образом, абдукция здесь определяется над глобальными
логическими свойствами: непротиворечивостью и выводимостью, что
является некоторым ограничением этого подхода. Кроме того, неявно
предполагается, что знания о причинно-следственных связях, которые
15 В.Н. Вагин и др.

450 Системы аргументации и абдуктивный вывод [ Гл. 10
используются для поиска абдуктивных объяснений, должны быть
представлены в теории Т. Например, импликация в теории Т мо-
может интерпретироваться двояко: как причинно-следственная связь (в
предложениях с абдуцируемыми предикатами) и как материальная
импликация (в остальных случаях).
Рассмотрим примеры реализации логического подхода к абдук-
абдукции.
Простые каузальные теории. Конолиге дает следующее
определение: «Пусть (С\Е,Т) — простая каузальная теория, опреде-
определяемая над языком Lang, т.е. С — множество причин, Е — множество
следствий и Т — логическая теория над Lang. Тогда объяснение
множества наблюдений Q Е Е — это конечное множество предло-
предложений Ф: Ф непротиворечиво с Т; Т U Ф Ь О, где ?1 — конъюнкция
всех w G О, Ф — минимальное по включению множеств подмноже-
подмножество».
Здесь прослеживается сходство с подходом, основанным на по-
покрытии множеств: абдуктивный процесс связывает множество наблю-
наблюдений — элементов предопределенного множества Е с множеством
причин, ограниченным множеством С. Но отсутствует соответствие
е, определяющее для каждой гипотезы данные, с ней связанные. Со-
Соответствующие связи выражаются в логической теории материальной
импликацией «от причин к следствиям».
Абдукция в логическом программировании. Эшги и
Ковальский рассматривают абдукцию в контексте логического про-
программирования с ограничениями целостности. Они показали, что «от-
«отрицание как неуспех» может быть смоделировано, если негативные
условия сделать абдуцируемыми и в качестве ограничений целостно-
целостности использовать подходящие отрицания и дизъюнкции. В результате
определяется семантика отрицания как неуспеха (NAF), обобщающая
семантику устойчивых моделей.
При таком подходе логические программы с NAF преобразуются в
абдуктивную структуру, в которой могут быть определены ограниче-
ограничения целостности более общего вида, чем просто отрицания. Для этого
абдукция определяется следующим образом:
«Структура (Т,1,А) является абдуктивной тогда и только тогда,
когда
• Т — теория хорновских дизъюнктов без отрицаний;
• I — множество ограничений целостности;
• А — множество предикатных символов-абдуцентов».
Для заданной абдуктивной структуры (Т,1,А) множество гипотез
Ф — абдуктивное решение по запросу q тогда и только тогда, когда
• Ф состоит из множества атомов-абду центов, не содержащих пе-
переменных;

10.2] Организация абдуктивного вывода 451
• ТиФЬд;
• Т U Ф U / непротиворечиво.
Отметим, что ограничения целостности используются как кри-
критерий отбора для объяснений. Гипотезы, не удовлетворяющие им,
исключаются третьим условием. Ограничение на то, что Ф не должно
содержать переменных, не является существенным, так как можно
дополнительно применить процедуру сколемизации и обратной ско-
лемизации (Кокс и Петржиковский).
Рассмотрим, как программы с NAF преобразуются в абдуктивную
структуру:
1) отрицания g заменить на новые символы g*;
2) добавить ограничения целостности вида: \/x(-~*(g*(x) &g(x))) и
Vx(g(x)Vg*(x));
3) определить множество абдуцентов как множество д*.
В результате выполнения такого преобразования пространство по-
поиска оказывается практически эквивалентным исходному, но вместо
проверки доказуемости условий с отрицаниями с помощью NAF, про-
проверяется непротиворечивость для абдуцируемых предикатов.
Абдуктивное доказательство содержит две фазы:
1) абдуктивная фаза — это стандартная SLD-резолюция, которая
позволяет найти абдуцируемые предикаты из А;
2) фаза непротиворечивости, состоящая в проверке ограничений
целостности с помощью прямого вывода из соответствующих
ограничений целостности отрицания абдуцируемого предиката,
причем этот вывод должен закончиться неуспехом за конечное
число шагов (обратная резолюция).
Разработчики данного подхода показали, что абдукция может рас-
рассматриваться как расширение логического программирования с помо-
помощью преобразования программ, работающих с NAF, в абдуктивную
структуру, которая по крайней мере так же мощна, как и исходный
формализм. Дедукция используется, чтобы направить генерацию аб-
дуктивных объяснений, и обеспечивает состоятельность процесса, т. е.
ТиФ Ь ?1, где Q описывает факты, которые должны быть объяснены.
Так как описанная процедура доказательства состоятельна только
по отношению к определенному классу логических программ, то бы-
были предложены различные расширения. Например, Данг разработал
альтернативную состоятельную семантику без дизъюнктивных огра-
ограничений целостности, используя предпочтительные расширения.
Абдуктивное логическое программирование. Какас и
Манкарелла определили семантику обобщенных устойчивых моделей
для абдуктивных структур. Она охватывает более общий случай, так
15*

452 Системы аргументации и абдуктивный вывод [ Гл. 10
как абдуцентами могут быть и позитивные литеры. В этом случае
абдуктивная структура задается тройкой (Тх, A U Ar, IU Г) с позитив-
позитивными абдуцентами в А и негативными абдуцентами в преобразован-
преобразованном виде в i'. В результате различается вывод по умолчанию (по-
(посредством NAF) и гипотетический вывод (не по умолчанию). Тони и
Ковальский определили преобразование таких логических программ
к нормальным логическим программам с NAF.
Позднее была предложена аргументационная структура как семан-
семантика для немонотонного вывода, обобщающая описанные идеи (Тони,
Ковальский). Точнее, аргументационная структура — это четверка
• Т — теория в некотором формальном языке;
• Ь — монотонное отношение выводимости в этом языке;
• А — множество предположений — предложений языка;
• I — множество ограничений целостности — отрицаний, таких,
что по крайней мере одна литера в ограничении целостности
помечается как удаляемая в случае нарушения целостности.
Предложение называется немонотонным следствием, если оно мо-
монотонно следует из теории, расширенной приемлемым множеством
предположений. Тони и Ковальский предложили различные варианты
приемлемых множеств в зависимости от понятия атаки между мно-
множествами предположений. В простых терминах, множество атакует
предположение, если существует ограничение целостности, которое
выполняется для теории, дополненной предположением, но которое
нарушается, если добавить другие предположения из атакующего
множества. Таким образом, могут быть определены различные мно-
множества предположений: устойчивые множества, частично-устойчивые
множества, предпочтительные множества, соответствующие устойчи-
устойчивым моделям, частично-устойчивым моделям и т. п. для нормальных
логических программ.
Бревка и Конолиге предложили альтернативную семантику, охва-
охватывающую логические программы, логику умолчаний и автоэписте-
мическую логику. Абдуктивное логическое программирование уже
успешно применяется во многих областях, в которых требуется вы-
выполнять вывод по абдукции.
Абдукция и изменение немонотонной теории. Иноуи
и Сакама распространили понятие абдукции на автоэпистемические
теории. Их целью было охарактеризовать немонотонное изменение
или пересмотр автоэпистемической теории с формулой ии по отноше-
отношению к минимальному объяснению ии.
Авторы используют автоэпистемическую фоновую теорию Т и
множество А автоэпистемических абдуцируемых формул. Помимо
«классического» определения объяснения формулы ии (позитивного

10.2] Организация абдуктивного вывода 453
объяснения) с помощью Т U ср \= ио для (р Е А, также учитыва-
учитывается то, что удаление формулы тоже может объяснять наблюдение.
Эти негативные объяснения формулы ио характеризуются с помощью
Т\ср |= ио. Кроме того, определяются позитивные или негативные
антиобъяснения с помощью правил: TUcp ?- ио и Т\р ?- ио соответствен-
соответственно. Объяснение может характеризоваться как множеством, которое
должно быть добавлено к теории, так и множеством, которое должно
быть удалено.
В результате под абдуктивной структурой понимается пара (Т,А),
в которой Т и А — автоэпистемические теории. Для формулы ио пара
(Ф+,Ф_), где Ф+ и Ф_ содержат примеры элементов из А, является
объяснением ио по отношению к абдуктивной структуре, если:
• (ТиФ+)\Ф_|=ы;
• (Т U Ф+)\Ф_ непротиворечиво.
Антиобъяснение определяется аналогично с первым условием вида
Заметим, что если Ф_ = 0 для любого объяснения, то приведенное
определение описывает «классическую» абдукцию для логики первого
порядка. Минимальность объяснения определяется по отношению к
минимальности подмножеств Ф_ и Ф+. Изменение автоэпистемиче-
ской теории Т рассматривается как построение ((Т U Ф+)\Ф_) для
минимального объяснения (Ф+, Ф-) формулы ш, если ио должно быть
помещено в Т, и для минимального анти-объяснения (Ф+,Ф_), если
ио должно быть удалено.
Авторы утверждают, что этот подход определяет более общую
структуру, чем предыдущие, и лучше охватывает понятие абдукции
Пирса. Помимо генерации гипотетических объяснений для некоторого
наблюдения, формализуется также и их ревизия. Если эксперимен-
экспериментальная проверка дает новую информацию, т. е. могут быть получе-
получены новые наблюдения, то проверка предыдущих объяснений может
привести к ревизии гипотез.
10.2.2.3. Подход на уровне знаний. Подход на уровне зна-
знаний (knowledge-level approach) предложен Левеком и основывается на
модели убеждения. Абдукция определяется по отношению к эписте-
мическим состояниям и не зависит от символьного представления.
Абдукция в логике неявного и явного убеждения.
Подход на уровне знаний рассматривает абдукцию в контексте неяв-
неявных и явных убеждений. Для неявных убеждений это подход согласу-
согласуется с общими идеями, лежащими в основе логических моделей, опи-
описанных выше. Но дополнительно он позволяет изменять модель убеж-
убеждения, таким образом, получается очень общее определение абдукции,
которое не зависит от соответствующего представления знаний.

454 Системы аргументации и абдуктивный вывод [ Гл. 10
Пусть задан пропозициональный язык Lang. Убеждения форму-
формулируются в языке Lang*, атомарные предложения которого имеют
форму В а с а Е Lang. Индексы используются для обозначения типа
убеждения. Эпистемическое состояние е определяет, какие предло-
предложения языка Lang являются убеждениями, т. е. е |= В\а для убеж-
убеждений типа Л. Будем говорить, что (р объясняет ои по отношению к
е(ср ехр1Л си) тогда и только тогда, когда е |= (В\(ср D oj)$z^B\^cp).
Таким образом ср является объяснением для со, если мы убеждены,
что (р влечет со (подразумевается материальная импликация), и если
нет убеждения в том, что -к/? истинно. Последнее условие определя-
определяет проверку непротиворечивости по отношению к рассматриваемому
множеству убеждений.
Это определение допускает множественные объяснения. Поэтому
и определяется синтаксический критерий отбора, ограничивающий
возможные объяснения. Объяснения с меньшим количеством пропо-
пропозициональных букв являются предпочтительными (причем р и ^р
считаются различными). Множество литер LITS(ce) формулы а опре-
определяется следующим образом:
• LITS (false) = 0;
• LITS(p) = {р} для атома р\
• LITS(--a) = {т\ т е LITS(ce)};
• LITS(a&/3) = LlTS(a V /3) = LITS(ce) U LITS(/3).
Согласно Левеку, формула а проще, чем формула C (а -< C) тогда и
только тогда, когда LITS(ce) С LITS(/3). Теперь мож:но определить ми-
минимальное объяснение: «ср минимально объясняет ии по отношению к
эпистемическому состоянию е и типу убеждения Л, т. е. (р min _explA ои
по отношению к е, тогда и только тогда, когда (р ехр1Л ии по отношению
к е и не существует такого (р* -< ср, что (р* ехр1л ии по отношению к е».
Абдуктивный процесс долж:ен возвращать дизъюнкцию всех мини-
минимальных объяснений, т. е. в качестве семантической характеризации
можно определить оператор объяснения:
EXPLAINA[e,cj] = \\{(р | (р min _explA ии по отношению к е}||, где
\\ср\\ — множество всех моделей, в которых ср — истина.
Алгоритм, выполняющий вывод по абдукции, называется кор-
корректным, если он возвращает в точности все минимальные объяс-
объяснения по отношению к эпистемическому состоянию. Пусть резуль-
результаты абдуктивной процедуры описываются функцией explain(T,cj),
т. е. explain(T, ои) дает объяснения ои по отношению к теории Т. Тогда
корректность может быть охарактризована равенством:
EXPLAIN\[R\(T),и] = ||explain(T,cj)||, где функция R\ переводит
множества предложений в эпистемические состояния по отношению к
выбранному типу убеждения Л.
Абдукциякакпересмотр убеждений. Бутилье и Бечер да-
дали логическую спецификацию объяснения, основанную на пересмотре

10.2] Организация абдуктивного вывода 455
эпистемического состояния агента. Они используют качественное по-
понятие правдоподобия, так как определению абдуктивного объяснения
в терминах дедуктивного вывода присущ ряд недостатков:
1) пересматриваемость абдуктивных объяснений не может быть
выражена монотонной выводимостью;
2) предпочтение некоторых объяснений по отношению к другим
может быть выражено лишь на металогическом уровне;
3) противоречивые объяснения не могут быть объяснены.
Вероятностные подходы или выбор подходящего представления
знаний в терминах аномальных исключений позволяют справиться
с проблемами 1 и 2. Рассматривая накопление знаний в более широ-
широком контексте (Какас) или модели пересмотра (Иноуи, Сакама), про-
противоречивые наблюдения могут быть объяснены, если предыдущие
допущения вызвали противоречие. В этом случае противоречивые
гипотезы можно исключить. Бутилье и Вечер предложили семейство
бимодальных логик, которое позволяет справиться со всеми тремя
проблемами. Упорядочение по правдоподобию на возможных мирах,
качественно охватывающее предпочтение, семантически описывает
процесс пересмотра и позволяет определить различные понятия объ-
объяснения.
Пусть язык Lang состоит из счетного множества пропозициональ-
пропозициональных переменных, классических связок и модальных операторов ? и
?х. Семантика дается в терминах возможных миров. Согласно Бути-
Бутилье и Вечеру, СТ40-модель — это М = (И7, ^, /i), где W — множество
возможных миров, ^ — рефлексивное транзитивное бинарное отноше-
отношение на W, /i переводит пропозициональные переменные языка Lang в
2W, т.е. /i(-P) — это множество миров, где Р истинно.
Предложения в Lang интерпретируются как обычно. Истинность
модальной формулы F в мире w Е W(M \=w F) задается правилами:
• М \=w BF & для Vv : v < w, M \=v F\
• M \=w \3fF -Ф=> для \/v : не выполняется v ^ w,M \=v F.
Таким образом, \3F выполняется в w, если F выполняется во всех
эквивалентно правдоподобных или более правдоподобных мирах, и
\3fF — истина, если F — истина во всех менее правдоподобных мирах.
Если К — множество убеждений, то в К-модели пересмотра мак-
максимально правдоподобные миры — это в точности те, в которых К
выполняется. Пересмотр К с помощью F, обозначаемых Кр, опреде-
определяется с помощью правила: |\Kp\\ = {w : w |= F nv < w влечет v ? F}
для w E W из фиксированной СТ40-модели. \\S\\ обозначает миры,
удовлетворяющие каждому предложению F E S. Поэтому, если К
пересматривается с помощью F, то F выполняется в максимально
правдоподобных мирах.

456 Системы аргументации и абдуктивный вывод [ Гл. 10
Интуитивное соображение, лежащее в основе объяснения ср для
cj, состоит в следующем: убеждение в истинности ср должно быть
достаточно для убеждения в истинности ии. В логическом языке это
может быть выражено с помощью следующего определения условной
зависимости ср => ии:
ср => и = defD"(cp D О(ср&П(ср D о;))), где П" и О — модальные
операторы, обозначающие истину во всех мирах и истину в некото-
некотором эквивалентно или более правдоподобном мире соответственно.
Упорядочение по правдоподобию должно определяться приложени-
приложением (агентом или программой) для отображения его эпистемического
состояния.
Пусть М — К-модель пересмотра, отражающая эпистемическое со-
состояние агента со множеством убеждений К. Предсказывающее объ-
объяснение для наблюдения ии (относительно М) — это любое ср Е Langp^
(LangPL — пропозициональный язык — подмножество Lang) такое,
что (Все означает, что а — убеждение)
1) М |= (Вер = Вои)&(В^(р = В^ио) (ср принимается тогда же, когда
и ии);
2) М |= ср => ии (убеждение в истинности ср влечет убеждение в
истинности а;);
3) М |= ^ои => -ар (ср достаточно для и).
Заметим, что в данном подходе в качестве предпочтительных
выбираются наиболее правдоподобные объяснения. Объяснения, не
являющиеся предсказывающими, которые не приводят к убеждению
в истинности наблюдения, но делают предположение о его истинности
«разумным», также могут быть учтены, если ввести более слабое
понятие ревизии. В рассматриваемом подходе к абдукции определе-
определена очень общая структура, зависящая от эпистемического состояния
агента.
10.2.3. Подходы к вычислению абдуктивных объяснений
10.2.3.1. Подходы к генерации гипотез. Наиболее важная
часть абдуктивной процедуры — это образование новой теории, объ-
объясняющей данные наблюдений. Можно выделить две группы методов
для генерации гипотез, которые существенно зависят от соответству-
соответствующей формальной модели:
• генерация с помощью какой-либо формы линейной резолюции и
• генерация с использованием ATMS (система поддержки истин-
истинности, основанная на предположениях).
В ряде работ показано, что формы линейной резолюции могут ис-
использоваться для генерации гипотез в моделях, основанных на логике
(Поупл, Эшги, Ковальский, Какас, Консоул, Кокс, Петржиковский).

10.2] Организация абдуктивного вывода 457
Линейная резолюция и сколемизация. Процедуры
(Кокс, Петржиковский) основываются на линейной резолюции и
обратной сколемизации (могут объясняться факты, описываемые
произвольной формулой, содержащей переменные).
Пусть Т — логическая теория и ии — формула (факт, который
требуется объяснить). Т также обозначает конъюнкцию всех формул
в Т. Т Y- ии (исключается тривиальный случай). Причина ср для ии в
Т — это формула, определяемая следующими условиями:
\~ UJ И
• ср непротиворечиво с Т.
Для вычисления причины ср выполняется следующее:
1) преобразовать Т в дизъюнктивную форму;
2) выполнить отрицание ии и затем линейную резолюцию со входом:
множество дизъюнктов из Т и некоторый элемент из ^ио как
входной (top) дизъюнкт.
3) Так как ТУ- ои, то можно выделить два случая:
- дедукция не завершается;
- дедукция завершается с некоторой «мертвой точкой» —
дизъюнктом d.
4) Пусть D — множество всех «мертвых точек». Тогда для каждого
d G D необходимо выполнить следующие шаги:
- выполнить отрицание d, получив конъюнкцию литер
- применить алгоритм обратной сколемизации, т. е. заменить
все сколемовские термы в р^ на универсально квалифици-
квалифицированные переменные (в результате будет получена форму-
формула ср = Q\X\ ... QkXk(qi& • • • &(Zn)? гДе Qi — универсальные
квантификаторы).
В результате будет найдена (р — причина-объяснение для ои в Т.
Этот алгоритм использует критерий отбора. Все вычисляемые объяс-
объяснения (р являются базовыми, т. е. любое объяснение ср' для ср является
тривиальным ((// влечет ср непосредственно). В большинстве случаев
критерий минимальности также удовлетворяется. Если ср — вычислен-
вычисленное объяснение, то не существует более специфического объяснения
х такого, что х D (р. Это является следствием алгоритма резолюции,
который работает до тех пор, пока нельзя будет выполнить очередной
шаг резолюции. Единственное исключение — случай, когда одна мерт-
мертвая точка включается в другую. Приведенный алгоритм не является

458 Системы аргументации и абдуктивный вывод [ Гл. 10
полным, т. е. существуют случаи, когда не все базовые и минимальные
объяснения могут быть найдены.
Упрощение задачи с помощью линейной резолюции.
Вместо того, чтобы добавлять отрицание наблюдения ио к логической
теории, Поупл пытается напрямую показать, что Т D ои. Наблюде-
Наблюдение преобразуется в дизъюнктивную форму. Рассматривая каждый
дизъюнкт в отдельности, можно разбить задачу доказательства ои на
эквивалентное множество подзадач. Дизъюнкт в логической теории
интерпретируется как вид правила, и с помощью обратного ветвления
можно прийти к узлам, которые не дадут узлов-потомков, т. е. кото-
которые не могут быть доказаны по множеству аксиом. Это и будут кан-
кандидаты для объясняющих гипотез. Когда все различные подзадачи
рассмотрены, оказывается сгенерированным все множество гипотез.
Поупл предлагает следующую процедуру:
1) преобразовать теорию Т в КНФ без квантификаторов;
2) использовать сколемизацию универсально квантифицирован-
ных переменных для преобразования ои в ДНФ:
— устранить импликацию;
— сократить количество отрицаний;
— заменить каждую универсально квантифицированную пе-
переменную на сколемовскую функцию, которая в качестве
аргументов имеет переменные всех кванторов существова-
существования, находящихся перед квантором всеобщности;
— удалить кванторы существования;
— преобразовать результирующее выражение в ДНФ;
3) рассматривая все возможные сочетания для удовлетворения
дизъюнкции cj, можно разбить задачу на п различных, но экви-
эквивалентных формулировок, где п — количество дизъюнктов. На-
Например, пусть си = (di V... V'dn-\\/'dn) = (^di& ... &^dn_i) D dn.
Если к Т добавить конъюнкцию ^di& ... &^dn_i, то задача сво-
сводится к доказательству dn. Этот процесс может быть повторен
с каждым di, так что в результате получается п различных
формулировок задачи;
4) дизъюнкты в Т интерпретируются как продукции с одной ли-
литерой слева, поэтому к дизъюнктов позволяют образовать к
различных правил, в которых каждый дизъюнкт образует левую
часть;
5) попытаться решить любую подзадачу с помощью обратного
ветвления. В результате может быть получено п различных
множеств мертвых точек;

10.2] Организация абдуктивного вывода 459
6) заметим, что для любой подзадачи предположение di состоит из
(возможно, унарной) конъюнкции. Теперь предпочтение отда-
отдается тем мертвым точкам, которые учитывают наибольшее ко-
количество конъюнктов, подлежащих объяснению. Эти эвристики
учитываются механизмом вывода с помощью процесса отбора,
который называется синтезом с использованием частичных дере-
деревьев. Он устанавливает, что всякий раз, когда это возможно, ли-
литеры, появляющиеся в различных деревьях доказательства, по-
построенных для каждого конъюнкта наблюдения, должны быть
унифицированы. Результирующий унификатор учитывает обе
верхние литеры соответствующих деревьев доказательства, т. е.
оба наблюдения объясняются. Из нескольких подходящих ги-
гипотез предпочтение отдается тем, которые учитывают больше
наблюдений.
Следует отметить, что в процессе синтеза Поупл реализует про-
процедуру отбора, которая выбирает лишь те гипотезы, которые под-
подтверждаются несколькими наблюдениями. Для задач диагностики
предлагается выбирать лишь один абдуцируемый предикат, который
объясняет наблюдение. В этом случае синтез выполняется лишь по
отношению к вхождениям этого предиката.
Процедура доказательства для абдуктивного
логического программирования. Фунг и Ковальский
разработали IFF-процедуру доказательства для абдуктивного
логического программирования, которая является состоятельной
и полной по отношению к трехзначной семантике пополнения для
абдуктивных логических программ.
Пусть задана абдуктивная логическая структура (Т,/,А),
где Т содержит пополнение логической программы в iff-форме:
P(xi,..., хп) <-> D\ V ... V Dm, где Р — это либо «=», true, false, либо
абдуцент в А, а каждое Di — конъюнкция литер и переменные х
неявно универсально квантифицированы. Ограничения целостности
задаются множеством импликаций:
а\ V ... V ап <— Ь]_& ... &6т, га, п ^ 0.
А содержит абдуцируемые предикатные символы. Абдуктивное
решение для запроса q — это пара (Ах, а) с фундаментальными абду-
цируемыми атомами в А' и подстановкой фундаментальных термов
для переменных в запросе так, что
• Т U Comp(A') U СЕТ |= qa и
• Т U Comp(A/) U СЕТ |= /, где Сотр(А/) — пополнение А! в
терминах iff-onpeделений, как показано выше, а СЕТ — теория
равенств Кларка. Все другие абдуценты в А эквивалентны false.

460 Системы аргументации и абдуктивный вывод [ Гл. 10
Приведем процедуру доказательства IFF. Пусть q — исходный
запрос, тогда необходимо построить узел, соединяя q со множеством
ограничений целостности, и затем применять следующие правила
вывода, пока это возможно:
• развертывание: заменить атом, который появляется как конъ-
конъюнкт в узле или условии импликации, на тело его определения;
• распространение: резольвировать атом с импликацией в том же
узле;
• расщепление: использовать законы дистрибутивности для обра-
образования двух узлов-потомков;
• разбор вариантов: если х = t появляется в условии импликации,
создать один узел-потомок для х = t и один для x^t;
• факторизация: если два абдуцента Р(х) и Р(у) появляются в уз-
узле, то создать два узла-потомка, в одном из которых аргументы
идентичны, а в другом — различны;
• правила перезаписи для эквивалентности применяются для
имитации унификации;
• логические преобразования применяются для того, чтобы пере-
переформулировать импликации и упростить выражения, содержа-
содержащие true и false.
Нисходящая IFF-процедура состоит из двух фаз: развертывание,
расщепление и преобразования с правилами перезаписи и анализом
вариантов, когда это возможно, составляют первую фазу, а вторая
фаза включает распространение и факторизацию, вероятно, с ис-
использованием преобразований и анализом вариантов. Авторы не дают
стратегии для применения правил вывода, но утверждают, что пол-
полнота достигается для любой произвольной стратегии. Построенное в
результате решение является минимальным.
ATMS как абдуктивная процедура. Семантическая
характеризация дается оператором объяснения: ЕХРЬАШд[е,а;] =
= ||{(/?|(/?min _explAcj по отношению к е}||. Для разработки абдуктив-
ного алгоритма требуется синтаксическая теория, которая позволяет
выполнять реальное вычисление простейших объяснений. Дадим
такое синтаксическое определение объяснения, и покажем, как может
быть разработана абдуктивная процедура в зависимости от типа
убеждения Л.
В случае неявного убеждения абдуктивный вывод может модели-
моделироваться с помощью ATMS. Левек определяет функцию V для двух
множеств дизъюнктов ЕиГ. Если Г — множество дизъюнктов, кото-
которые должны быть объяснены, и Е содержит дизъюнкты-убеждения по
отношению к А, то V(X, Г) определяет соответствующие минимальные

10.2] Организация абдуктивного вывода 461
объяснения. Точнее, V(E,F) = /х(Ф), где Ф — множество, определяе-
определяемое следующим образом:
ф = {-iz\\/y е Е, г/ <? z и для Ух е Г, Зу е Е, ж П г/ ф 0 и (г/ - х) С г},
a /i определяет минимальное множество по отношению к включению
множеств.
Функция V может интерпретироваться, например, таким образом.
Во-первых, дизъюнкты г, которые мы ищем, не должны быть рас-
расширением некоторых у Е Е, т.е. множества дизъюнктов-убеждений.
Это необходимо для того, чтобы избежать противоречий в случае,
когда ^z позже будет добавлено ко множеству убеждений в качестве
объяснения.
Во-вторых, z должно удовлетворять другому условию. Если в
действительности возможно объяснить все наблюдения в Г, то для
каждого наблюдения х Е Г должно существовать убеждение у Е Е,
которое хотя бы частично объясняет его, т. е. х и у имеют общие
литеры: х П у ф 0. Дизъюнкты z выбираются таким образом, что
они содержат каждую литеру г/, которая не является частью соот-
соответствующего наблюдения х. Если в последующем z с отрицанием
добавляется ко множеству убеждений Е, то в результате множество
наблюдений Г должно быть истинно. Формула ^z отрицает в точности
те дизъюнкты из г/, которые не связаны с наблюдениями.
Таким образом, оставшиеся дизъюнкты каждого у, которые яв-
являются частью наблюдений, должны быть истинными. Если могут
быть найдены различные множества дизъюнктов z, то они образуют
альтернативные объяснения. Наконец, функция /i, применяемая ко
множеству дизъюнктов -iz, определяет минимальное множество по
отношению к включению множеств (объяснение не должно содержать
больше литер, чем это необходимо).
В целом, ATMS — одно из возможных средств для генерации
абдуктивных объяснений. Если учесть результаты Селмана и Левека,
то оказывается, что ATMS, с вычислительной точки зрения, — наи-
наилучшая процедура. Она находит некоторое объяснение вместо всех
возможных. Если рассматривать явные убеждения, то можно найти
и более простую вычислительную процедуру, которая позволяет ре-
рекурсивно вычислять неявные убеждения. Это очень общий подход,
дающий возможность исследовать и другие типы убеждений.
10.2.3.2. Подходы к отбору гипотез. Результатом работы
абдуктивной процедуры является множество возможных объяснений.
Так как это множество может быть очень большим, то кажется ра-
разумным исключить «менее интересные» гипотезы, чтобы выиграть в
эффективности последующего вычислительного процесса. Большин-
Большинство описанных абдуктивных процедур уже включает подобный кри-

462 Системы аргументации и абдуктивный вывод [ Гл. 10
терий отбора для того, чтобы исключить, например, генерацию самих
наблюдений как тривиальных объяснений.
Принципы отбора основываются на эвристиках, которые пытаются
определить хорошие объяснения. Эти эвристики зависят частично от
области приложения. Но могут применяться также и синтаксические
критерии, например, чтобы исключить тривиальные объяснения.
Пирс утверждает, что должны отбираться самые простые с психо-
психологической точки зрения гипотезы, т. е. наиболее интуитивные объяс-
объяснения. Это сложно реализовать, поэтому такое требование обычно ин-
интерпретируется как логическая и синтаксическая простота. Гипотезы,
содержащие лишние литеры, или те гипотезы, которые включаются
в другие, нежелательны. Однако существует и негативный результат:
Левек утверждает, что невозможно сформулировать критерий отбора
только лишь на семантической основе.
Рассмотрим различные подходы к обнаружению наиболее подхо-
подходящих объяснений. Большинство из них — это методы, реализующие
некоторым образом принцип «лезвия Оккама». Тем не менее предла-
предлагается и альтернативный подход, основанный на метрике когерентно-
когерентности. Этот подход также дает метод определения подходящего уровня
специфичности.
Критерии простоты. Независимо от соответствующих крите-
критериев, определяющих уровень специфичности, т. е. уровень абстракции
объяснения, в общем случае все принятые гипотезы должны удовле-
удовлетворять некоторым основным условиям, формализующим синтакси-
синтаксическую простоту. Хороший пример — критерии, которым должны
удовлетворять гипотезы, сгенерированные по алгоритму Кокса.
Пусть Т — база знаний логики первого порядка и Ф — множество
гипотез для наблюдения и. Если ср Е Ф — гипотеза-кандидат, то она
должна удовлетворять следующим условиям:
• непротиворечивость: Т & ср непротиворечиво (это требование
предъявляется ко всем моделям, основанным на логике);
• нетривиальность: -up D со, т. е. наблюдение не является прямым
следствием гипотез (в частности, исключается тот случай, когда
ии само синтезируется как подходящее объяснение);
• фундаментальность: любое непротиворечивое объяснение для
ср является тривиальным, т. е. предпочтение отдается наиболее
специфичному объяснению в том смысле, что для самого объяс-
объяснения не существует нетривиального объяснения;
• минимальность: для всех гипотез (pf для ии : ср D (pf влечет cpf =
= (/?, т.е. не существует более общей гипотезы для а;, чем ср (в
том смысле, что все лишние литеры или кванторы всеобщности,
не являющиеся необходимыми, исключены из объяснений).
Заметим, что если ср D ф — часть теории, что ф не будет сгенериро-
сгенерировано. Это является следствием применяемого алгоритма резолюции,

10.2] Организация абдуктивного вывода 463
который выполняется до тех пор, пока это возможно, и ср является
единственно возможной мертвой точкой. Таким образом метод, осно-
основанный на резолюции, всегда гарантирует выполнение свойства фун-
фундаментальности. Фундаментальность уже реализует стратегию для
определения подходящего уровня специфичности множества объясне-
объяснения, которая называется «наиболее специфичной абдукцией». Объяс-
Объяснения, удовлетворяющие свойствам непротиворечивости, минималь-
минимальности и нетривиальности, реализуют принцип «лезвия Оккама», если
он интерпретируется синтаксически. Однако множество интересую-
интересующих гипотез, отобранных таким образом, может быть снова слишком
велико, и обычно требуется дополнительный отбор для того, чтобы
получать гипотезы определенного уровня специфичности. Аппельт и
Поллок рассматривают два вида критериев: глобальные критерии и
локальные критерии.
Глобальные критерии. Методы отбора, основанные на гло-
глобальных критериях, рассматривают множество предложений как це-
целое. Среди таких критериев различают: сравнение мощностей, наиме-
наименее предположительная или наименее специфичная абдукция, наибо-
наиболее специфичная абдукция и минимальная аномальность.
Сравнение мощностей используется только в диагностических си-
системах и гарантирует принятие лишь тех гипотез, которые приводят к
неправильной работе наименьшего количества компонентов. Поэтому
система приложения должна определяться в терминах различных
компонентов, для которых поведение входов и выходов полностью
определено (это не выполняется для задач понимания естественного
языка или планирования).
Наименее предположительные или наиболее специфичные объяс-
объяснения определяются следующим образом: пусть h\ и h^ — гипотезы
и Т — логическая теория, тогда h\ — менее предположительная или
специфичная гипотеза, чем h^ тогда и только тогда, когда TU/12 |= h\.
Поэтому наименее предположительные или специфичные объясне-
объяснения — это те, которые обеспечивают наиболее общее объяснение.
Абдуктивный процесс, реализующий этот вид отбора, был предложен
Стикелем. Могут отбираться и наиболее специфичные объяснения,
которые сами не имеют нетривиальных объяснений. Эта стратегия
кажется полезной для диагностики неполадок, когда требуются очень
подробные знания о природе неполадки.
Аппельт предлагает для распознавания плана использовать соче-
сочетание наиболее и наименее специфичной абдукции. Тем не менее все
равно остается проблема решения, какая стратегия должна приме-
применяться в каждом конкретном случае. Более того, возможны ситуации,
когда не существует единственного наименее или наиболее специфич-
специфичного объяснения, и требуется дальнейший отбор. Дюпрэ и Розотто по-
показали, как аксиомы абстракции вместе с абдуктивной теорией могут
использоваться для вычисления наиболее абстрактных объяснений,

464 Системы аргументации и абдуктивный вывод [ Гл. 10
т. е. объяснений, допускающих минимум предположений. Использо-
Использование иерархии абстракций увеличивает эффективность вычисления
объяснений путем исключения построения непредпочтительных ги-
гипотез вместо того, чтобы впоследствии применять критерий отбора.
Абстракции также могут использоваться для того, чтобы сосредото-
сосредоточить поиск на более детальных объяснениях.
Минимальная аномальность. Пул определяет абдуктивную струк-
структуру, которая основывается на спецификации предположений ано-
аномальности и нормальности. Как утверждает Аппельт, внутренняя
проблема этого подхода — это тот факт, что минимально аномальные
предположения могут противоречить «наилучшему» объяснению.
Локальные критерии. Чтобы избежать недостатков преды-
предыдущих подходов, были введены локальные критерии, позволяющие
отбирать наилучшие гипотезы еще до завершения вычисления всех
возможных объяснений. Здесь выделяют статистические методы Бай-
еса, взвешенную абдукцию и абдукцию, основанную на стоимостях.
Статистические методы Байеса. Для отбора «наиболее вероят-
вероятных» гипотез может использоваться стандартная теория вероятно-
вероятностей. Пул описывает прагматически оправданную структуру вероят-
вероятностей для хорновской абдукции. Она определяется над теориями,
состоящими из множества определенных клозов, представляющих об-
общие знания, и ряда «несвязанных объявлений», определяющих мно-
множество несвязанных и покрывающих гипотез с ассоциированными с
ними вероятностями. Каждое несвязанное множество устанавлива-
устанавливается для множества примеров независимых и взаимноисключающих
гипотез, сумма вероятностей которых дает 1. Пул показывает, что
любое вероятностное знание, представимое в дискретной сети убеж-
убеждений Байеса, может быть представлено в этой структуре. Подход
в результате дает простую логическую формулировку, которая се-
семантически прозрачна и, кроме того, допускает простую реализацию.
Но при этом требуется, помимо прочих предположений, разбиение
пространства гипотез на независимые альтернативы, что часто бы-
бывает сложно выполнить. О'Рурк описывает обобщение, позволяющее
генерировать не только наиболее вероятные объяснения, но также и
наиболее важные. Причем последнее определяется с помощью теории
принятия решений.
Взвешенная абдукция. Аппельт и Поллак для того, чтобы на-
направить процесс применения правил, назначают весовые множители
для всех литер в посылке. В результате правила приобретают вид:
cpi & ... &^n D (р. Веса \±i используются для вычисления стоимости
предположения литер. Это делается с помощью умножения стоимости
предположения следствия на весовой множитель рассматриваемой
литеры в посылке. Например, если ф имеет стоимость с, то ф\ мо-
может рассматриваться со стоимостью с*ц\. В абдуктивной процедуре

10.2] Организация абдуктивного вывода 465
предпочтение отдается множеству предположений с наименьшей сто-
стоимостью.
Теоретико-модельная семантика подхода основывается на предпо-
предпочтении моделей. С помощью взвешенной абдукции модели теории
Т ограничиваются так, что отбрасываются модели, которые явля-
являются подчиненными согласно ограничениям предпочтения моделей.
Предполагается, что на моделях Т установлен частичный порядок
предпочтений. Веса в правилах интерпретируются как дополнитель-
дополнительные ограничения на этот порядок. Если дано правило сра D ф с весом
а < 1, то это означает, что каждая модель, удовлетворяющая (р&ф,
предпочитается некоторой модели, удовлетворяющей ^ср&ф.
Чарняк и Шимони отмечают, что для случая се > 1 не определена
семантика, поэтому может моделироваться лишь наиболее специфич-
специфичная абдукция. Более того, взвешивание правил должно привести к
непротиворечивому упорядочению без циклов, что делает еще более
сложным определение весов вновь добавляемых правил.
Абдукция, основанная на стоимости. Чарняк и Шимони пытают-
пытаются найти наилучшее объяснение наблюдения с помощью поиска до-
доказательства минимальной стоимости. Подходящая семантика дается
булевской сетью доверия. Более точно авторы представляют правила
взвешенной абдукции в виде направленного ациклического графа
(DAG — Directed Acyclic Graph) и показывают, что поиск модели
этого графа с минимальными стоимостями соответствует поиску мно-
множества абдуктивных гипотез наименьшей стоимости. Предложенный
алгоритм опирается на эвристики поиска в графе DAG для обнару-
обнаружения частичных объяснений, которые затем расширяются. Чтобы
определить семантику, строится булева сеть доверия, основанная на
взвешенном И/ИЛИ направленном ациклическом графе (WAODAG —
Weighted AND/OR DAG). Показано, что поиск модели минимальной
стоимости, т. е. предположений минимальной стоимости, соответству-
соответствует поиску назначения максимальной апостериорной вероятности дан-
данным фактам для сети доверия. Эти идеи кажутся перспективной стра-
стратегией для широкой области приложений. Но для применения этого
подхода должны быть известны вероятности. Кроме того, знания
домена и, в частности, связи между объяснениями и наблюдениями,
должны быть представимы в терминах правил, которые могут быть
преобразованы в DAG.
Когерентность объяснений как критерий отбора. Вместо пред-
представления принципа «лезвия Оккама» как синтаксической простоты,
Энг и Муни определили метрику когерентности, которая помогает
найти наиболее интуитивные объяснения. Поиск объяснений направ-
направляется эвристиками (лучевой поиск), чтобы увеличить эффектив-
эффективность. Метрика также определяет уровень специфичности.
Как утверждают авторы подхода, принцип «лезвия Оккама» недо-
недостаточен для приложений понимания текста и распознавания плана.

466 Системы аргументации и абдуктивный вывод [ Гл. 10
Они предлагают отбирать те объяснения, которые лучше всего свя-
связывают между собой все наблюдения. Это означает, что они пред-
предпочитают объяснения, у которых больше связей между любой парой
наблюдений, где связи интерпретируются как направленные пути в
графе доказательства. Более точно метрика определяется следующим
образом:
где I — количество наблюдений, N — количество узлов в графе доказа-
доказательства, Nij — количество различных узлов в графе доказательства
таких, что существует последовательность направленных ребер от п&
к щ и от щ к rij, где щ и rij — наблюдения (последовательности могут
быть пустыми), iVB) — масштабирующий множитель, обеспечиваю-
обеспечивающий выполнение условия С Е [0,1]. Числитель — это сумма количества
узлов в графе, которые одновременно поддерживают интерпретацию,
представленную этим графом.
Для определения «хорошего» объяснения рассматриваются все
возможные связи узлов, т.е. несколько различных графов доказатель-
доказательства. Выбирается интерпретация, представляемая графом с самой
высокой когерентностью. Метрика может быть вычислена за время
О (IN + e), используя поиск в глубину.
К преимуществам подхода можно отнести следующее: когерентные
объяснения обычно также и синтаксически просты (так как унифи-
унификация сопутствует предпочтению тесных связей), метод не допускает
«слишком много степеней свободы», как, например, в случае взве-
взвешенной абдукции, где веса правил могут быть выбраны произвольно.
Кроме того, метрика помогает определить уровень специфичности,
так как доказательство подцели выполняется при обратном ветвлении
лишь в том случае, когда оно может увеличить общую когерентность.
Когерентность объяснений кажется многообещающим подходом
для систем, поведение которых не может быть заранее определено
для всех случаев (например, для моделирования человеческого мыш-
мышления).
10.2.4. Метод вероятностных абдуктивных рассуждений в
сложноструктурированных проблемных областях
В настоящее время абдуктивный вывод признан одним из наиболее
эффективных механизмов диагностики, так как довольно адекватно
моделирует рассуждения человека в процессе нахождения объясне-
объяснений. Абдуктивный вывод — это вывод, при котором формируются и
оцениваются гипотезы объяснений наблюдаемых явлений. В послед-
последние годы резко возрастает количество применений диагностических

10.2] Организация абдуктивного вывода 467
программных средств, основанных на механизмах абдуктивного выво-
вывода, в различных сферах деятельности человека, а также увеличивает-
увеличивается сложность задач, решаемых такими средствами. Поскольку одним
из признаков сложной системы, для диагностики которой исполь-
используются программные средства, является, по Г. Буч, иерархичность,
возникает необходимость разрабатывать новые методы диагностики,
позволяющие не только обнаруживать неисправности, но и объяснять
причины их возникновения в сложноструктурированных проблемных
областях.
В настоящее время разработано несколько методов абдуктивных
рассуждений в сложноструктурированных проблемных областях. Од-
Одним из таких методов, предложенным Консоулом и Дюпрэ, являет-
является иерархическая абдуктивная схема рассуждений для нахождения
объяснений в сложноструктурированных проблемных областях. На
определениях этого метода базируется разработанный авторами ме-
метод вероятностных абдуктивных рассуждений, позволяющий обнару-
обнаруживать аномалии в поведении сложноструктурированных объектов.
Введение в предложенный метод вероятностей позволяет упорядочить
огромное количество найденных объяснений по наиболее подходящим
для данной ситуации.
10.2.4-1- Основные определения. Нахождение объяснений
причин возникновения аномальных ситуаций в сложнострукту-
сложноструктурированных объектах имеет ряд особенностей, среди которых
существенными являются следующие:
1) объяснения не должны быть слишком детализированными, ког-
когда более общих подробностей достаточно для объяснения причин
возникновения явлений;
2) слишком абстрактные объяснения могут быть излишними, когда
должны быть приведены более детальные объяснения.
Приведем определения понятий метода абдуктивных рассуждений
(Консоул и Дюпрэ), используемых авторами в разработанном ме-
методе вероятностных абдуктивных рассуждений, который позволяет
учесть приведенные выше особенности использования абдуктивного
вывода в сложноструктурированных проблемных областях. Отметим,
что данные определения являются распространением определений,
представленных в разд. 10.2.1 и 10.2.2, на сложноструктурированную
проблемную область.
Определение 10.16. Иерархия объяснений есть пара <TEjTa>,
где Те есть множество аксиом объяснений, в котором каждая аксиома
есть хорновский дизъюнкт:

468
Системы аргументации и абдуктивный вывод
[Гл. 10
Г\
РЗ
Рис. 10.1.
здесь Р1&Р2& ... &P/v есть непосредственное объяснение Q; Та есть
множество аксиом абстракций, в котором каждая аксиома имеет вид
Р —> Q, где Р есть объект, более специфичный, чем Q (Q есть абстрак-
абстракция Р).
Примечание. Аксиомы абстракций задают ISA- и Part-of-
иерархии на объектах проблемной области.
Для каждой формулы Р —> Q
в множестве аксиом абстракций уро-
уровень Р меньше, чем уровень Q
(level(P) < level(Q)) и ЗР : level (P) =
= 0.
На рис. 10.1 приведен пример гра-
графической формы задания иерархии
объяснений. Графической интерпре-
интерпретацией иерархии объяснений является
семантическая сеть, вершинам кото-
которой соответствуют литеры, представ-
представляющие элементарные высказывания,
принимающие значения «истина» или
«ложь». В семантической сети выде-
выделяются два типа ребер для задания
аксиом из множеств Те и Та соответственно. Для задания акси-
аксиом из множества Та используются ребра, выделенные жирной ли-
линией.
На рис. 10.1 множества Те и Та имеют вид
ТЕ = {Р1&Р2 -> Ql, Д1&Д2 -> Q1, РЗ -> Q2};
ТА = {РЗ -> Р2}.
Определение 10.17. Множество наблюдаемых литер назовем на-
наблюдением (OBS).
Определение 10.18. Абдуктивная теория (AT) задана, если
определены множество Т = Те U Та и наблюдение (OBS).
Определение 10.19. Абдуцентной литерой назовем литеру, ко-
которая не является литерой заключения в Хорновском дизъюнкте
D,\/D E Те-
Определение 10.20. Конъюнкцию абдуцентных литер назовем
абду центом.
Определение 10.21. Объяснение наблюдений из Т есть множе-
множество Е = {^1,..., Еп}, где Ei (г = 1, п) — есть множество абдуцентов
для наблюдения Oi E OBS, n — число наблюдаемых литер, такое, что
Т U E \- Oi для каждой наблюдаемой литеры Oi E OBS и из Т U Е
невыводимо ^Oi] T U Е совместно; только из Т невыводимо СИ.

10.2] Организация абдуктивного вывода 469
Выделяют два типа объяснений в сложноструктурированных про-
проблемных областях:
• поддерживающие объяснения, которые отражают особенность
1, а именно: объяснения не должны быть слишком детализи-
детализированными (например, нахождение объяснений наблюдений с
использованием только множества Те)',
• предпочтительные объяснения, которые отражают особенность
абдукции в сложноструктурированных проблемных областях, а
именно: слишком абстрактные объяснения могут быть излиш-
излишними.
Перед описанием метода приведем ряд положений, на которых он
базируется:
• литера, соответствующая вершине в иерархии объяснений, в том
числе и наблюдаемая литера, не являющаяся абдуцентной лите-
литерой, должна быть объяснена с использованием Та только тогда,
когда часть построенного объяснения не может быть расширена
добавлением новых литер для объяснения наблюдаемой литеры
из множества OBS при помощи Те',
• для того, чтобы устранить генерацию высокоуровневых объяс-
объяснений, алгоритм начинается с объяснения наблюдаемых литер
самого нижнего уровня, таким образом, предотвращается поиск
литер для объяснения О Е OBS при помощи множества аксиом
Те, когда О уже подкреплено поддерживающими объяснениями,
сделанными на нижележащем уровне.
Положим, что аксиомы в Та используются для задания Part-of-
иерархии на объектах проблемной области.
Примечание. Аксиомы в Та, задающие Part-of-иерархию на объ-
объектах проблемной области, можно рассматривать как множество огра-
ограничений целостности, поскольку если компонента объекта неисправ-
неисправна, то и сам объект является неисправным.
10.2.4-2. Описание метода вероятностных абдуктивных
рассуждений в сложноструктурированных проблемных об-
областях. Далее приведем описание метода абдуктивных рассужде-
рассуждений в сложноструктурированной проблемной области. Как видно из
представленных выше определений, формулировка задачи абдуктив-
абдуктивного вывода в сложноструктурированных проблемных областях явля-
является обычной для абдуктивных рассуждений, а именно: нахождение
объяснений наблюдений с использованием абдуктивной теории. Од-
Однако существует следующее уточнение формулировки задачи: объяс-
объяснение наблюдений осуществляется не только на основе множества ак-
аксиом объяснений Т#, но и множества аксиом абстракции Та, которое

470 Системы аргументации и абдуктивный вывод [ Гл. 10
используется обычно для задания структуры объектов проблемной
области. Следует отметить, что аксиомы из множества Та определяют
уровни в иерархии объяснений.
Множество аксиом абстракции Т_д, как было сказано выше, можно
рассматривать как ограничения целостности в задаче абдуктивных
рассуждений. Метод абдуктивных рассуждений в сложнострукту-
сложноструктурированной проблемной области начинается с нахождения множе-
множества абдуцентов для наблюдений наименьшего уровня, что можно
интерпретировать, как, например, нахождение объяснений причин
возникновения явлений в элементарных объектах, если аксиомы из
множества Та используются для задания структурного отношения
«часть — целое» (Part-of). После того, как найдено множество абду-
абдуцентов для наблюдений наименьшего уровня происходит поднятие на
один уровень вверх по иерархии объяснений и, если на нем отмечены
наблюдения, которые необходимо объяснить, то начинается процесс
нахождения их объяснений.
Этот процесс имеет особенность, которая заключается в том, что
если литера А используется для объяснения некоторого наблюдения,
т.е. является посылкой аксиомы из Те, выбранной для объяснения
наблюдения, и эта литера А уже объяснена на нижележащем уровне,
т. е. литера А является заключением аксиомы из Та, посылка которой
объяснена на нижележащим уровне, то, с учетом аксиомы из Та,
объяснение найденное на нижележащем уровне является объяснени-
объяснением литеры А. Таким образом, описанный выше процесс позволяет
«связывать» объяснения наблюдений, расположенных на различных
уровнях в иерархии объяснений. Далее поднимаемся на следующий
уровень по иерархии объяснений. Если на нем отмечены наблюдения,
которые необходимо объяснить, то повторяем вышеописанный про-
процесс и т. д., пока не будут объяснены все наблюдения на всех уровнях
иерархии объяснений.
Следует отметить, что в результате данного процесса нахождения
объяснений наблюдений обнаруживается большое количество различ-
различных объяснений. Поэтому возникает задача их упорядочивания по
наиболее подходящим для данной ситуации. Для этого в описанный
метод абдуктивных рассуждений введен подсчет вероятности абду-
цента.
Для пояснения процесса нахождения объяснений в сложнострук-
сложноструктурированной проблемной области, приведем пример и после него
опишем алгоритмы, лежащие в основе описанного метода вероятност-
вероятностных абдуктивных рассуждений.
Рассмотрим пример получения множества абдуцентов с исполь-
использованием аксиом из Та для иерархии объяснений, представленной на
рис. 10.2. В данном примере предполагается, что наблюдаемые литеры
присутствуют на двух уровнях.

10.2]
Организация абдуктивного вывода
471
Of
Рис. 10.2.
На рис. 10.2 заданы следующие аксиомы:
ТЕ = {R№R2 -> Oj, Q -> Д1, Р1&Р2 -> Р, Z1&Z2 -> Р};
Тл = {Р ^ Q}.
Получим множество абдуцентов Ej для наблюдаемой литеры Oj:
1) {Д1&Д2};
2) {Q&#2};
3) {{Р1&Р2, Zl&Z2}&i?2} = {Р1&Р2&Д2, Z\hZ2hRl).
Покажем, что Т U Ej Ь Oj, где Т = Те U Тд на основе принципа
резолюции:
1. ^Oj (в основе принципа резолюции лежит процедура опровер-
опровержения)
2. Р\
3. Р2
4. Д2
5. Z\
6. Z2
7. -лвхч
8. ^Q Vffl
9. ^P1V
10. -.Zl
11. ^PV
12. -.mv-u
13. -.m
14. -.Q
15. -.P2VP
16. P
17. Q
18. П
R2 A,7)
D,12)
(8,13)
B,9)
C,15)
A1,16)
A4,17)

472 Системы аргументации и абдуктивный вывод [ Гл. 10
Далее приведем описание алгоритмов, лежащих в основе метода
вероятностных абдуктивных рассуждений в сложноструктурирован-
сложноструктурированной проблемной области. Эти алгоритмы базируются на модифици-
модифицированном методе поиска в ширину.
10.2.4-3. Алгоритмы вероятностных абдуктивных рас-
рассуждений в сложноструктурированной проблемной обла-
области.
Алгоритм получения объяснений (мноснсества Е) для на-
наблюдаемых литер О G OBS. Алгоритм вероятностных абдуктив-
абдуктивных рассуждений в сложноструктурированной проблемной области
состоит из двух алгоритмов:
• алгоритма для нахождения всех возможных абдуцентов для на-
наблюдаемой литеры Oj GOBS наименьшего уровня;
• алгоритма для нахождения всех возможных абду центов для на-
наблюдаемой литеры Oj GOBS, где Oj GOBS не является литерой
наименьшего уровня.
Приведем описание алгоритма вероятностных абдуктивных рас-
рассуждений в сложноструктурированной проблемной области. Предпо-
Предположим, что абдуктивная теория задана, т.е. заданы множества Те,
Та и OBS.
Шаг 1. На иерархии объяснений отмечаются вершины, которые
соответствуют наблюдаемым литерам.
Шаг 2. Нахождение номера наименьшего уровня, в котором отме-
отмечены вершины, как наблюдаемые. Результат: номер уровня (г).
Шаг 3. Нахождение всех возможных абдуцентов для наблюдаемой
литеры Oj GOBS уровня г. Результатом является Ег- = {-К-]_,..., Щп},
где п — число абдуцентов для Oj\ Ег^A = 1..п) — абдуцент для Oj.
Шаг 3 повторить для всех наблюдаемых литер уровня г. Результа-
Результатом шага 3 является: Ег = {Е\,..., Е^} где m — число наблюдаемых
литер на уровне г; Е* (j=l..m) — множество абдуцентов для Oj.
Шаг 4- Нахождение всех возможных абдуцентов для наблюдаемой
литеры Oj GOBS уровня /с, где к > г. Шаг 4 повторить для всех
наблюдаемых литер уровня к.
Шаг 5. Если существуют Oj GOBS, которые еще не объяснены, то
перейти к шагу 4. В противном случае СТОП.
Результатом алгоритма нахождения объяснений для наблюдаемых
литер OgOBS есть множество объяснений Е: Е = иЕгу где Ег =
= {Е\,...,-Ё^}, где EjQ=l..m) — множество абдуцентов для наблю-
наблюдаемой литеры Oj GOBS уровня г; m — число наблюдаемых литер на
уровне г.
Далее последовательно приведем описания всех алгоритмов, на-
начиная с алгоритма для нахождения всех возможных абдуцентов для

10.2] Организация абдуктивного вывода 473
наблюдаемой литеры Oj Е OBS наименьшего уровня г, на котором
отмечены вершины, соответствующие наблюдаемым литерам.
Алгоритм, для нахоснсдения всех возмоснсных абдуцентов
для наблюдаемой литеры Oj e OBS наименьшего уровня
Пусть Щ = {Oj}.
Шаг 1. Если Oj — абдуцентная литера, то вернуть Ej = {Oj}.
Шаг 2. Нахождение непосредственных объяснений для элементов
множества Ej , т. е. аксиом из Т, заключениями которых являются
элементы множества Ej, с учетом метода поиска в ширину. Если суще-
существуют хорновские дизъюнкты Dl, D2 Е Те Dl: Р1&Р2& .. .&Рп —>
—> Oj и D2: Ш&Д2&.. .&Rm —> Oj, то нахождение непосредствен-
непосредственных объяснений для Е) = {Р1&Р2& ... &Рщ Д1&Д2& ... &Rm}, т. е.
заменить Oj на посылки аксиом из множества Те, и отметить вер-
вершины, соответствующие литерам PI, P2,..., Рп, Ш, i?2,..., Rm, на
иерархии объяснений. В противном случае использовать аксиому из
множества Та вида Р\ —> Oj, найти непосредственные объяснения
для Ej = {PI} и отметить вершину Р1 на иерархии объяснений.
Шаг 3. Вычисление вероятностей полученных элемен-
элементов из множества Ej. Пусть конъюнкция литер А Е Ej.
к
Р{А) = П P(Ai\Hi,..., Hq), где к — число литер в конъюнкции
г=1
A, P(Ai\Hi,..., Hq) — условная вероятность литеры Ai в конъюнкции
A; ill, • • •, Hq — литеры, соответствующие вершинам в иерархии
объяснений, используемые при выводе литеры А^. Если Р(А) < а
(а — пороговое значение), то А — абдуцент для Oj .
Для того, чтобы вычислить значение условной вероятности ли-
литеры, соответствующей вершине, необходимо выполнить следующие
действия.
А) Задание значений вероятностей вершинам иерархии объяс-
объяснений P(Q), Р(Р1),..., Р(Рп); на ребрах иерархии объяснений —
P(Q|P1),..., P(Q\Pn), где Р1& ... кРп -^QeTE.
Б) Вычисление условных вероятностей по теореме Байеса, т. е.
Отметим, что гипотезы объяснений, заданные литерами и вероят-
вероятностями, являются независимыми.
В) Замена P(Pi) на P(Pi\Q) при отметке вершины Pi.
Шаг 4- Переход к шагу 2 до тех пор, пока конъюнкции литер
из множества Ег- будут содержать только абдуцентные литеры, т.е.
станут абдуцентами для Oj (иначе — нахождение аксиом для литер
PI, P2,..., Рщ Ш, Д2,..., Rm).
Шаг 5. Упорядочивание элементов (абдуцентов) множества Ej по
убыванию значений условных вероятностей. СТОП.

474 Системы аргументации и абдуктивный вывод [ Гл. 10
Ниже приведем алгоритм для нахождения всех возможных абду-
центов для наблюдаемой литеры Oj Е OBS уровня /с, где к не яв-
является наименьшим уровнем, на котором присутствуют наблюдаемые
литеры.
Алгоритм для нахоснсдения всех возмоснсных абдуцентов
для наблюдаемой литеры Oj E OBS
0. Е) = {Oj}
1. Если Oj — абдуцентная литера, то возврат Ej = {Oj}.
2. Нахождение непосредственных объяснений для элементов мно-
множества Ej, т.е. аксиом из Т, заключениями которых являют-
являются элементы множества Ej с учетом метода поиска в ширину.
Пусть существует аксиома Р —> Q Е Т_д, где Q — литера,
непосредственное объяснение которой находим, Р — отмеченная
литера уровня к — 1. Пусть Е\~х — множество абдуцентов для
наблюдаемой литеры Ог уровня к — 1. Положим, что Е^~г явля-
является также множеством абдуцентов для литеры Р уровня к — 1,
допуская при этом избыточность, поскольку множество Е^~г
кроме абдуцентов литеры Р содержит и другие элементы. Тогда
необходима замена литеры Q на множество абдуцентов Е^~г во
всех вхождениях Р в множество Ej и приведение множества Ej
к множеству, элементами которого являются конъюнкции литер.
В случае отсутствия такой аксиомы, действия, выполняемые на
этом шаге, аналогичны действиям шага 2 алгоритма для нахо-
нахождения всех возможных абдуцентов для наблюдаемой литеры
наименьшего уровня.
Остальные шаги алгоритма аналогичны шагам алгоритма для
нахождения всех возможных абдуцентов для наблюдаемой литеры
наименьшего уровня.
Таким образом, используя описанный шаг алгоритма, мы мо-
можем «связывать» наблюдаемые литеры, т. е. находить объяснения
нескольким наблюдаемым явлениям. Приведенный алгоритм, позво-
позволяющий «связывать» объяснения наблюдений, можно рассматривать,
как некоторое приближение к нахождению минимальных объясне-
объяснений.
Поскольку одной из важных проблем в методах абдуктивных рас-
рассуждений является проверка найденных объяснений на непротиворе-
непротиворечивость, далее приведем описание этой процедуры.
10.2.4-4- Процедура проверки найденных объяснений на
непротиворечивость. В качестве процедуры проверки найденных
объяснений на непротиворечивость предлагается использовать метод
автоматического доказательства теорем, предложенный М. Фитингом
и описанный в главе 4. Имеем Т U Е Ь Oj. На основании теоремы о

10.2] Организация абдуктивного вывода 475
логическом следствии (см. раздел 1.2.) доказано, что T&E&z^Oj явля-
является противоречивой формулой. Для того, чтобы выяснить, что най-
найденное множество объяснений Е является непротиворечивым, необхо-
необходимо показать, что Т U E Y- Oj (очевидно, что непротиворечивость Е
вытекает из невозможности одновременного доказательства Е и —\Е).
Отсюда, если дерево аналитической таблицы с корнем T&E&^Oj
замкнуто, а дерево с корнем T&E&^^Oj содержит открытую ветвь
(она отмечена символом «*» в таблице), то тем самым будет доказана
непротиворечивость множества объяснений Е. Процедура построения
аналитической таблицы повторяется для всех наблюдаемых литер.
Напомним, что для исчисления высказываний открытая ветвь (что
говорит о выполнимости формулы) всегда конечна, но для исчисления
предикатов 1-го порядка конечность имеет место только для конечно-
конечного универсума (см. гл.4).
В качестве примера построим аналитическую таблицу для теории
Т, представленной на рис. 10.2, и найденного множества объяснений
Е (рис. 10.3). Из построенной таблицы видно, что таблица с корнем
T&zE&z^Oj замкнута, а таблица с корнем T&zE&z^^Oj содержит от-
открытую ветвь (помечено символом «*»), что говорит о непротиворе-
непротиворечивости множества объяснений.
10.2.^.5. Примеры применения разработанных алгорит-
алгоритмов абдуктивного вывода в сложноструктурированных
проблемных областях. Приведем два примера получения
множества абдуцентов для наблюдений.
Пример 10.14.
Дано: OBS = Q,TE = {Р1&Р2 -> Q,P11 -> Р1,А1&А2 -> Q},
заданные на иерархии объяснений, (рис. 10.4).
Используя вышеописанные алгоритмы, найдем множество объяс-
объяснений Е = {Р11&Р2, А1&А2}.
Далее, используя принцип резолюции, покажем, что Т U Е Ь Q,
где Т = Те, поскольку Тд = 0.
2. -.P11VP1
4. Pll
5. P2
6. Al
7. A2
8. ^P1V^P2
9. PI
10. -.P2
11. П
Из примера
: A,3)
B,4)
(8,9)
E,10)
видно, что только из Т не выводимо

476
Системы аргументации и абдуктивный вывод
[Гл. 10
Условные обозначения
1.-.-.0-
2.О/
3.Rl&R2^Oj
4. Q->R1
5.Р1&Р2^Р
6. Z1&Z2^P
7.P->6
8.Р1&Р2&Д2
9. Z1&Z2&JG
10. PI
11.P2
12. Л2
13. Zl
14. Z2
15.Л2
16. -.(Д1&Д2)
17. O/
18.-Л1
19. ^J?2 (П12)
20.^6
21.Л1
22.^6
23.Ш(П18)
24. ^(P1&P2)
25. P
26. ^(P1&P2)
27. P
28. ^(P1&P2)
29. P
30. -тР1 (П10)
31. —lP2(D11)
32. ^(Z1&Z2)
33. P
34. -тР1 (П10)
35.-^2 (П11)
36. ^(Z1&Z2)
37. P
38. -J>1 (П10)
39.^P2(D11)
40. ^(Z1&Z2)
41. P
42. -tZI (П13)
43. ^Z2 (П14)
44. ^P (ПЗЗ)
45. Q (П20)
46. -tZI (DO)
47. ^Z2 (П14)
48. ^P (П37)
49. 0(*)
50. -tZI (П13)
51.^Z2(D14)
52.^P(D41)
53.0(D22)
Рис. 10.3.
Пример 10.15.
Пример вероятностных абдуктивных рассуждений для обнаруже-
обнаружения неисправностей двигателя автомобиля. Двигатель работает, если
выполнены следующие условия:
• легко запускается, т.е. заводится не позднее, чем через 10-15
оборотов коленвала или 6-8 сек. Норма — 1-5 сек. Предел —
8 сек. 1 < Pl.tz < 5 (Мах = 8);

10.2] Организация абдуктивного вывода 477
• работает устойчиво на холостом ходу, обеспечивая постоянное
число оборотов в минуту. 950 ^ Р2.от ^ 1000(= const) .
Р11
Q
Рис. 10.4.
Опишем неисправности двигателя автомобиля и возможные при-
причины их возникновения. Обозначим Pl.tz>8 через Р1. Возможные
причины данной неисправности: (Q1) нет топлива в карбюраторе;
(Q2) неисправность электрооборудования; (Q3) система пуска карбю-
карбюратора не отрегулирована; (Q4) система пуска карбюратора неисправ-
неисправна; (Q5) не открывается клапан ЭПХХ; (Q6) неисправность системы
зажигания; (Q7) не отрегулирована система зажигания; (Q8) наличие
воды в топливе.
Обозначим Р2.от < const через Р2. Возможные причины: (Q9)
не отрегулирована система холостого хода; (Q10) не отрегулирована
система зажигания; (Q11) засорен карбюратор; (Q12) низкое качество
бензина; (Q13) подсос воздуха через прокладки, шланги; (Q14) неис-
неисправна система газораспределения (износ или регулировка).
Возможные причины неисправности (Pl.tz > 8)&Q1: (Rl) нет топ-
топлива в баке; (R2) засорен топливопровод; (R3) неисправен топливный
насос; (i?4) установлен неправильный зазор (больше 1 мм).
Возможные причины неисправности (Pl.tz > 8)&Q3: (RQ) воз-
воздушная заслонка не приоткрывается при запуске на нужный зазор
B,8 мм); (R7) дроссельная заслонка не приоткрывается на зазор
1,5 мм.
Возможные причины неисправности (Pl.tz > 8)&Q4: (R8) не ра-
работают приводы заслонок (воздушной или дроссельной); (R9) неис-
неисправна мембрана.
Возможные причины неисправности (Pl.tz > 8)&Q5: (Ш0) обрыв
или короткое замыкание провода, ведущего к клапану; (Ш1) неиспра-
неисправен клапан.
Возможные причины неисправности (Pl.tz > 8)&Q6: (R12) неис-
неисправна катушка; (ШЗ) обрыв или короткое замыкание центрального

478 Системы аргументации и абдуктивный вывод [ Гл. 10
провода; (RU) грязные или неисправные свечи; (Rib) неисправность
прерывателя-распределителя зажигания.
Возможные причины неисправности (Р.от < const2)&Q13: (Ш6)
засорен карбюратор; (R17) подсос воздуха через прокладки.
Возможные причины неисправности (Р2.от < const)&Q14: (Ш8)
прогар клапанов; (R19) износ распределительного вала; (.R20) полом-
поломка пружин клапанов; (R21) износ втулок клапанов.
Возможные причины неисправности (Pl.tz > 8)tkQ6tkRlb: (SI)
пробой бегунка; (S2) трещина на крышке; (S3) пробой конденсатора;
(SA) износ контактов; (Sb) загрязнение; (S6) обрыв или короткое за-
замыкание внутреннего провода; E7) механическое повреждение вала.
Возможные причины неисправности (Р2.от < const)&C13&i?17:
(S8) ослаблен крепеж; (S9) износ прокладок.
Формализуем перечисленные утверждения в виде аксиом. Таким
образом, имеем следующее множество аксиом:
ТЕ={ Ql-> PI, Q2^ PI, Q3^ PI, Q4^ PI, Qb^ PI, Q6^ PI,
Q7^ PI, Q8^ PI, Д1-> Ql, R2^ Ql, R3^ Ql, RA^ Ql, R6^ Q3,
R7^ Q3, R8^ Q4, R9^ Q4, R10^ Qb, Rll^ Qb, R12^ Q6, R13^
-^ Q6, RU-^ Q6, Rlb^ Q6, 51^ Д15, S2^ Rib, S3^ Rib, S4^ Rib,
Sb^ Rib, S6^ Rib, S7^ Rib, Q9^ P2, Q10^ P2, Qll^ P2,
-^ P2, Q13^ P2, QU^ P2, R16^ Q13, R17^ Q13, R18^ QU,
-^ QU, R20^ QU, R21^ QU, S8^ R17, S9^ R17}.
Та = {двигатель—^автомобиль}
Графическое представление иерархии объяснений неисправностей
двигателя автомобиля приведено на рис. 10.5.
Пусть имеем наблюдение Р1, обозначающее Pl.tz>8. Тогда мно-
множество абдуцентов Е на основе разработанного алгоритма строится
следующим образом.
1. Множество абдуцентов для наблюдаемой литеры Р1 уровня 0:
El = {Ql, Q2, Q3, QA, Qb, Q6, Q7, Q8}
2. El ={R1, R2, R3, R4, Q2, R6, R7, R8, R9, RIO, Rll, R12, R13,
RU, Rib, Q7, Q8}
3. El ={R1, R2, R3, RA, Q2, R6, R7, R8, R9, RIO, Rll, R12, R13,
RU, SI, S2, S3, SA, Sb, S6, S7, Q7, Q8}
Построенные объяснения удовлетворяют ограничению целостно-
целостности, которое задано аксиомой из Та, поскольку двигатель, являющий-
являющийся неотъемлемой частью автомобиля, неисправен, следовательно, и
автомобиль является неисправным.
Очевидно, что из ТЕ U El Ь Р1.
Для того, чтобы показать, что найденное множество объяснений
является непротиворечивым (из Те иЕ± не выводимо ->Р1) построена
аналитическая таблица с корнем T^&i^&^^Pl, которая не являет-
является замкнутой, что свидетельствует о том, что найденное множество

10.2]
Организация абдуктивного вывода
479
о
Рис. 10.5.

480
Системы аргументации и абдуктивный вывод
[Гл. 10
объяснений является непротиворечивым. Описание аналитической
таблицы, содержащей 114 шагов, приведено в табл. 10.1. В таблице
использованы следующие обозначения: р — номер формулы (шага),
А — номер предыдущей формулы, Б — номер формулы, породившей
Данную. Таблица 10.1
р
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
Формула
-.-.Р1
Р1
Q1->P1
Q2^Pl
Q3^Pl
Q4^P1
Qb^Pl
Q6^P1
Q7^P1
Q8^P1
Rl^Ql
R2^Ql
R3^Ql
RA^Ql
R6^Q3
R7->Q3
RZ^QA
RV^QA
RIO^ Q5
mi^ Q5
Д12-> Q6
Д13-> Q6
Д14-> Q6
Д15-> Q6
Sl-> Rib
S2^ Rib
S3^ Rib
S4^ Rib
S5^ Rib
S6^ Rib
S7^ Rib
А(Б)
1A)
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
P
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
Формула
Д13
RU
SI
S2
S3
S4
S5
S6
S7
Q7
QS
-Ql
PI
-.Д1 (П32)
Ql (П55)
-.Д1 (П32)
Ql
~^Q7 (П53)
PI
^Q8 (П54)
PI
^R2 (ПЗЗ)
Ql
-^R3 (П34)
Ql
-^R4 (П35)
Ql
-^R6 (П37)
Q3
^R7 (П38)
Q3
A
43
44
45
46
47
48
49
50
51
52
53
54
54
55
55
56
56
60
60
62
62
64
64
66
66
68
68
70
70
72
72
Б
3
3
11
11
11
11
9
9
10
10
12
12
13
13
14
14
15
15
16
16
P
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
Формула
^Ш4 (П45)
Q6
-.?1 (П46)
Rib
-^S2 (П47)
Rib
^S3 (П48)
Rib
-^S4 (П49)
Rib
^55 (П50)
Rib
^S6 (П51)
Rib
-^S7 (П52)
Rib
пД15 (П102)
Q6
^Q6 (П104)
PI
^Q5 (П80)
PI
^Q4 (П76)
PI
^Q3 (П74)
PI
^Q2 @36H
A
86
86
88
88
90
90
92
92
94
94
96
96
98
98
100
100
102
102
104
104
106
106
108
108
110
110
112
112
Б
23
23
25
25
26
26
27
27
28
28
29
29
30
30
31
31
24
24
8
8
7
7
6
6
5
5
4
4

10.3
| Абдукция и аргументация в логическом программировании
481
Таблица 10.1 (продолжение)
Р
32
33
34
35
36
37
38
39
40
41
42
43
Формула
Ш
R1
R3
R4
Q2
R6
R7
R8
R9
то
R11
R12
А(Б)
31
32
33
34
35
36
37
38
39
40
41
42
Р
75
76
77
78
79
80
81
82
83
84
85
86
Формула
-^R8 (D39)
Q4
-^R9 (D40)
Q4
-.Д10 (D41)
Q5
-.Д11 (П42)
Q5
-.Д12 (D43)
Q6
-.Д13 (П44)
Q6
A
74
74
76
76
78
78
80
80
82
82
84
84
Б
17
17
18
18
19
19
20
20
21
21
22
22
P
Формула
A
Б
Поскольку аналитическая таблица с корнем Te&zE®&z—i—iP1 не яв-
является замкнутой (содержит две открытые ветви), из Те U Е® не
выводимо —iPl. Из построенной аналитической таблицы видно, что
таблица с корнем Te&cE®&l-iP1 является замкнутой, следовательно,
из Те U Е® выводимо Р\. Из этого
следует, что построенное объяснение Е® является непротиворечи-
непротиворечивым.
Описанный пример нахождения объяснений неисправности ав-
автомобиля свидетельствует о том, что существует достаточно много
объяснений некоторого явления, которые желательно упорядочивать.
Для этого в разработанный алгоритм абдуктивного вывода и введен
расчет вероятностей найденных объяснений.
10.3. Абдукция и аргументация в логическом
программировании
10.3.1. Аргументационная семантика логических программ и ее
вычисление
Рассмотрим различные способы определения аргументационной
семантики логических программ в соответствии с подходом Данга,
Тони и Какаса. В общем случае аргументационная структура
состоит из теории Р в некоторой базовой монотонной логике,
множества гипотез-кандидатов Hyp и бинарного отношения
атаки между множествами гипотез (по терминологии авторов,
16 В.Н. Вагин и др.

482 Системы аргументации и абдуктивный вывод [ Гл. 10
вместо термина «поражение» будем использовать термин «ата-
«атака»), удовлетворяющего следующим фундаментальным свойст-
свойствам:
• ни одно множество гипотез не может атаковать пустое множе-
множество гипотез;
• атаки монотонны, т.е. для всех A, АХ,А,АХ С Hyp, если А
атакует А, то если А С Af, то Af атакует А, и если А С А',
то А атакует А';
• атаки компактны, т. е. для всех А, А С Hyp, если А атакует А,
то существует конечное Af С А такое, что А атакует А.
Будем считать, что отношение атаки определяется только на ко-
конечных подмножествах множества Hyp. Различные примеры этой
абстрактной аргументационной структуры соответствуют различным
немонотонным формализмам. Для специального случая логическо-
логического программирования Р — логическая программа, множество гипо-
гипотез — это Hyp = {not р | р — атом, не содержащий переменных, в
эрбрановской базе программы Р}, и лежащая в основе логика —
это классическая логика определенных хорновских программ. Дан-
Данные программы получаются с помощью замены каждой негативной
литеры в программе Р и во множестве гипотез Hyp новым пози-
позитивным атомом. Мы будем обозначать эти программы тем же сим-
символом Р и отношение следования в этой логике — через |= (если
не определяется иначе, мы будем предполагать, что программы, со-
содержащие переменные, представляют множество примеров этих про-
программ, не содержащих переменных, над заданным универсумом Эр-
брана).
Для данной программы Р конъюнкция литер G (не содержащих
переменных) — это немонотонное следствие Р по отношению к неко-
некоторой семантике тогда и только тогда, когда существует множество
гипотез А, разрешенное в этой семантике такое, что Р U A |= G.
Различные виды семантики логических программ разрешают раз-
различные множества гипотез. Все виды семантики, которые будут рас-
рассмотрены, могут быть сформулированы в терминах следующего отно-
отношения атаки между множествами негативных литер, не содержащих
переменных.
Определение 10.22. Множество гипотез А атакует другое мно-
множество гипотез А (по гипотезе not p) тогда и только тогда, когда
Р U А \= р для некоторого not p в А.
Заметим, что это определение удовлетворяет всем указанным
выше свойствам. Так как отношение |= компактно, то и атака
компактна. Может быть бесконечно много атак на некоторое
множество гипотез.

10.3] Абдукция и аргументация в логическом программировании 483
Пример 10.16.
Рассмотрим фундаментальную версию программы:
р <— q(x), not r{x)
r(x)
и множество До = {not p}. Существует бесконечно много конечных
атак на До, т.е. {not r@)}, {not r(succ@))}, {not r(succ(succ(O)))}
и т. п.
10.3.1.1. Предпочтительные расширения и семантика
допустимости. Предпочтительные расширения и частично
устойчивые модели определяются по максимальным допустимым
множествам гипотез. В рамках абстрактной аргументационной
структуры допустимые множества определяются указанным образом.
Определение 10.23. Множество гипотез Д допустимо тогда и
только тогда, когда для всех множеств гипотез А, если А атакует Д,
то Д атакует А-Д.
Интуитивно, Д допустимо тогда и только тогда, когда Д может
быть защищено от любой атаки А. Множество гипотез, атакующее
само себя, не может быть допустимым, так как не существует атаки
на пустое множество. В дальнейшем мы будем работать с допусти-
допустимыми множествами гипотез, а не с предпочтительными расширени-
расширениями. Любое допустимое множество гипотез «содержится» в некото-
некотором предпочтительном расширении, и поэтому для определения того,
выполняется ли запрос в предпочтительном расширении и семантике
частичных устойчивых моделей, достаточно определить, выполняется
ли запрос в семантике допустимых множеств.
Пример 10.17.
Пусть имеется программа
s <— not г
г <— not s
Множество Д1 = {not s} допустимо, так как любая атака на Ai -
это надмножество множества Д2 = {not r}, которое атакуется мно-
множеством Д]_. Аналогично, Д2 является допустимым. Но множество
Д]. U Д2 не допускается, так как атакует само себя. Следовательно,
множества Д1 и Д2 максимально допустимы и соответствуют предпо-
предпочтительным расширениям Р.
Пример 10.18.
Рассмотрим программу из примера 10.17, дополненную правилом
q <— not s. До = {not q} не допускается, так как оно не атакует атаку
16*

484 Системы аргументации и абдуктивный вывод [ Гл. 10
{not s}. Но множество До U D, где D = {not r} допустимо, так как
оно атакует атаку {not s} (и, следовательно, все атаки на До U D,
так как любая из них содержит not s). Если множество До дополнить
множеством D, то можно получить допустимое (и предпочтительное)
множество {not q, not r}.
Множество D играет роль защиты для До. Вообще, построение
допустимого множества Д может быть выполнено по шагам, начи-
начиная от заданного множества гипотез До, с помощью добавления к
До подходящих защит. Существование нескольких допустимых (и
предпочтительных) множеств гипотез обусловливает существование
нескольких подходящих защит для заданного множества До, и в
результате необходим недетерминированный выбор защит в теории
доказательства.
Пример 10.19.
Добавим к программе из примера 10.17 правила
t <— not q
q <— not s
q <— not r
Тогда оказывается, что множество До = {not t} не допускается, но
До U Di, где D\ = {not r} и До U D2, где D2 = {not s} допускаются (и
являются предпочтительными).
На самом деле не каждая потенциальная защита может быть
применена к До-
Пример 10.20.
Рассмотрим программу
s <— not г
г <— not г
Множество До = {not 5} не является допустимым, так как атака А =
= {not г} на До не атакуется множеством До. Множество D = {not r}
может быть возможной защитой для До, так как атакует А. Более
того, D содержится в каждой возможной атаке на А. Однако До U D
не допускается, так как D и, следовательно, До U D атакует само себя
(не существует допустимого надмножества для До).
10.3Л.2. Устойчивые теории и семантика слабой устой-
устойчивости. Устойчивые теории получаются из максимальных слабо
устойчивых множеств гипотез. Они определяются в абстрактной ар-
гументационной структуре приведенным ниже способом.
Определение 10.24- Множество гипотез Д слабо устойчиво тог-
тогда и только тогда, когда для всех множеств гипотез А, если А атакует
Д, то A U Д атакует А-А.

10.3] Абдукция и аргументация в логическом программировании 485
Интуитивно, атака А на А может быть использована в конъюнк-
конъюнкции с А, чтобы защитить А от А. Заметим, что аналогично случаю
допустимых множеств, множество гипотез, которое атакует само себя,
не может быть слабо устойчивым.
Тривиально, любое допустимое множество гипотез слабо устойчи-
устойчиво, но не наоборот (см. пример 10.20). Мы уже видели, что А = {not s}
не является допустимым для программы из этого примера. Однако А
слабо устойчиво, так как любая атака А на А — это надмножество
{not г}, которое атакуется самим {not г} и поэтому — A U А. А —
также максимальное слабо устойчивое множество, соответствующее
устойчивой теории Р.
Можно доказать, что любое слабо устойчивое множество гипотез
«содержится» в некоторой устойчивой теории. В дальнейшем мы
будем заниматься вычислением лишь слабо устойчивых множеств
гипотез.
10.3.1.3. Семантика приемлемости. Семантика допустимо-
допустимости и слабой устойчивости — частные случаи более общей аргумента-
ционной семантики приемлемости. Формально, приемлемость опреде-
определяется как наименьшая фиксированная точка оператора F на множе-
множестве всех бинарных отношений, определенных на множестве гипотез
Hyp. Этот оператор можно охарактеризовать с помощью следующе-
следующего неформального рекурсивного определения приемлемости: «Мно-
«Множество гипотез А приемлемо по отношению к другому множеству
гипотез Ао тогда и только тогда, когда для всех множеств гипотез А,
если А атакует А—Ао, то А не является приемлемым по отношению
к A U Ао». Можно привести и еще одно определение.
Определение 10.25. Множество гипотез А приемлемо по от-
отношению к другому множеству гипотез Ао тогда и только тогда,
когда для всех множеств гипотез А, если А атакует А—Ао, существует
множество гипотез D такое, что D атакует А-(Аи Ао) и D приемлемо
по отношению к A U A U Ао. Множество гипотез приемлемо тогда и
только тогда, когда оно приемлемо по отношению к пустому множе-
множеству гипотез.
Следовательно, приемлемость — это бинарное отношение на мно-
множестве гипотез Hyp с центральным понятием «А приемлемо по отно-
отношению к Ао», где Ао может рассматриваться как множество специаль-
специально выбранных гипотез (контекст), относительно которых исследуется
приемлемость А.
Базовый случай для приведенного рекурсивного определения
определяется следующим образом:
• (ВС1) множество гипотез А приемлемо по отношению к другому
множеству гипотез Ао, если не существует множества гипотез А,
атакующего (А—Ао). (В частности, так как не может быть атак

486 Системы аргументации и абдуктивный вывод [ Гл. 10
против пустого множества гипотез, то условие ВС1 выполняется,
когда А - До = 0);
• (ВС2) А приемлемо по отношению к Ао, если А С Ао.
Отметим, что множество гипотез А, атакующее само себя, не
может быть приемлемым, так как не существует атаки на пустое
множество.
Формулировка приемлемости в определении 10.25 сразу же приво-
приводит к следующему утверждению: «Слабо устойчивые и допустимые
множества гипотез приемлемы».
Подобно случаю допустимых и слабо устойчивых множеств, мно-
множество D в определении семантики приемлемости играет роль за-
защиты против атаки А. Теория доказательства для данной семанти-
семантики строит приемлемые множества А с помощью постепенного нара-
наращивания подходящим образом исходных подмножеств множеств А
гипотезами-защитами для того, чтобы гарантировать приемлемость
А. Более того, снова выбор подходящих защит является недетермини-
недетерминированным, и некоторые возможные защиты могут оказаться неподхо-
неподходящими. Однако в случае приемлемых множеств существует допол-
дополнительный вид недетерминизма, состоящий в отделении тех частей
выбранных защит, которые могут быть помещены в заключительные
множества А. Это иллюстрируется следующим примером.
Пример 10.21.
Пусть дана программа
р <— not q
q <— not t,
причем и Ai = {not p, not t} и А2 = {not p} приемлемы. В самом
деле, нетрудно видеть, что Ai допустимо, и, следовательно приемле-
приемлемо. Более того, все атаки на А2 содержат not g, и можно показать,
что они неприемлемы по отношению к А2, используя тот факт, что
атака {not q} неприемлема по отношению к А2, что доказывается
следующим образом:
• {not q\ приемлемо по отношению к А2, только если существует
защита D, атакующая A-({not g}UA2), где А = {not t} атакует
{not g}-A2={not q}, и такая, что D приемлемо по отношению к
{not <?}UA2 U А;
• но A-({not g}UA2)={not t} и не существует атаки против {not t}.
В этом примере при заданном исходном множестве А2 = {not p}
потенциальная защита {not ?}, выбираемая для доказательства того,
что атака {not q\ против А2 не приемлема по отношению к А2, может
добавляться, а может и нет, ко множеству А2 для того, чтобы постро-
построить приемлемое множество, так как в обоих случаях результирующее
множество приемлемо.

10.3] Абдукция и аргументация в логическом программировании 487
Пример 10.22.
Дана программа
р <— not q
q <— not r
г <— not 5
5 <— not g.
Для этой программы множество А = {not q} приемлемо. Действи-
Действительно, все атаки против А содержат not q, и может быть показано,
что они неприемлемы по отношению к А, с учетом того факта, что
атака Ai={not q} неприемлема по отношению к А, который доказы-
доказывается следующим образом:
• Ai приемлемо по отношению к А, только если существует защи-
защита D, атакующая A-(Ai U А) = {not г}, где А = {not r} атакует
Ai — А, и такая, что D приемлемо по отношению к AuAiUA =
= {not r, not q, not p};
• любое такое множество D должно содержать not s и является
приемлемым по отношению к A U Ai U А, только если суще-
существует защита D'', атакующая Af-(A U Ai U А) с Af = {not q},
атакующим D-(A U Ai U А), и такое, что Dr приемлемо по
отношению KiUAiUAUi'UD.
• но A'-{A U Ai U А) = 0 и следовательно, такого множества D' не
существует. (Аналогично, множества А2 = {not r}, A3 = {not 5}
не являются приемлемыми).
В этом примере при заданном приемлемом множестве А = {not p}
защита {not r}, выбираемая для доказательства того, что атака
{not q} против А неприемлема по отношению к А, не должна добав-
добавляться к А. Это необходимо на промежуточном уровне для защиты от
атаки {not q} и, хотя она приемлема по отношению к {not р, not q}, она
неприемлема по отношению к пустому множеству и, следовательно,
не может добавляться к А.
10.3.1.4- Семантика фундированных моделей. До сих пор
мы рассматривали семантику логических программ, которая является
доверчивой по природе и разрешает в общем случае более одного мно-
множества гипотез, а значит требует выбора при определении немонотон-
немонотонных следствий Р. Важной скептической семантикой для логического
программирования, разрешающей лишь одно множество гипотез, яв-
является семантика ^/-моделей. В рамках абстрактной аргументаци-
онной структуры, ^/-модель может быть формально выражена как
наименьшая фиксированная точка оператора F на множестве всех
унарных отношений, определенных на множестве гипотез Hyp, анало-
аналогично случаю приемлемости. Неформально рекурсивное определение
дается следующим образом.

488 Системы аргументации и абдуктивный вывод [ Гл. 10
Определение 10.26. Множество гипотез А — w f -приемлемо тог-
тогда и только тогда, когда для всех множеств гипотез А, если А атакует
А, то существует множество гипотез D такое, что D атакует AnD —
^/-приемлемо.
Как и для случая приемлемости, множество D играет роль защиты
для А. Базовый случай для ^/-приемлемости определяется следую-
следующим образом:
(ВС) множество А — ^/-приемлемо, если ни одно множество
гипотез А не атакует А.
Рассмотрим программу из примера 10.21. И пустое множество, и
множество Ао = {not t} являются ^/-приемлемыми, так как никакое
множество гипотез их не атакует. Заметим, что пустое множество все-
всегда ^/-приемлемо, так как на него не существует атак. Следователь-
Следовательно, множество Ai = {not р\ — ^/-приемлемо, так как оно может быть
защищено ^/-приемлемым множеством Ао. Действительно, каждая
атака против Ai должна содержать гипотезу not q, которая атакуется
множеством Ао. Наконец, множество Ао U Ai — u>/-приемлемо.
Рассмотрим программу из примера 10.17. Ai = {not s} не явля-
является ^/-приемлемым. Каждая атака против Ai содержит гипотезу
not r, которая может быть защищена лишь множеством гипотез,
содержащим Д]_. Это означает, что для того, чтобы Ai было wf-
приемлемым, нам требуется ^/-приемлемость множества Д]_. В ре-
результате оказывается, что Ai не может принадлежать наименьшей
фиксированной точке соответствующего оператора F. Другими сло-
словами, ^/-приемлемость Ai не может быть сведена к базовому случаю
ВС определения, т. е. ко множеству гипотез, которое не атакуется ни
каким другим множеством. Аналогично, А2 = {not r} не является wf-
приемлемым. Единственным ^/-приемлемым множеством является
пустое множество.
Аналогичная ситуация возникает и для программы в примере
10.20. Множество {not r} не является ^/-приемлемым, так как оно
атакует само себя, и любая возможная защита должна содержать саму
гипотезу not r. Снова не может быть достигнут базовый случай ВС.
Более того, множество {not s} не является ^/-приемлемым, так как
любое множество, защищающее его, должно содержать not r, которое
не может быть ^/-приемлемым. Следующее утверждение показывает
связь ^/-приемлемости и ^/-модели.
Утверждение 10.2. Для данной логической программы Р:
• Если М = (/+, /~) — ^/-модель Р, то Ам = {not р \р е 1~} —
максимальное ^/-приемлемое множество.
• Если А — ^/-приемлемо и (/+, /~) — ^/-модель Р, то /д = {р \ р
принадлежит эрбрановской базе программы Р и PU А |= р} С /+
и /~ = {р | not р е А} С /~.

10.3] Абдукция и аргументация в логическом программировании 489
Непосредственное следствие второго утверждения: «Если А —
максимальное ^/-приемлемое множество гипотез, то (/д, /д) — wf-
модель Р». Так как каждое ^/-приемлемое множество гипотез «со-
«содержится» в ^/-модели, мы можем ограничиться вычислением -не-
-неприемлемых множеств гипотез.
Следующее утверждение обеспечивает свойство ^/-семантики, по-
полезное для определения теории и процедуры доказательства.
Утверждение 10.3. Множество гипотез А — ^/-приемлемо то-
тогда и только тогда, когда каждое множество гипотез Ах С A wf-
приемлемо.
Два рекурсивных определения скептической семантики wf-
моделей и доверчивой семантики приемлемости очень похожи.
Существенная разница между этими двумя видами семантики
состоит в следующем: в то время, как в случае приемлемости защиты
подтверждаются в контексте множеств гипотез (самого А, других
защит и даже атак), в случае ^/-приемлемости все защиты должны
быть универсально подтверждены, независимо от того, защищают
они гипотезы или атаки, в конце концов сводя их к защитам, которые
не могут быть атакованы.
Таким образом, в то время, как теория доказательства для при-
приемлемости может расширять исходное множество гипотез Ао с по-
помощью некоторой защиты D (как показано в примере 10.18), теория
доказательства для ^/-приемлемости не расширяет Ао, а продолжает
строить (вложенные) защиты до тех пор, пока для некоторой защиты
не будет существовать ни одной атаки. Отметим, что в этом случае,
как заключительная защита, так и каждая из «ранних» защит, яв-
являются ^/-приемлемыми и, следовательно, объединение всех таких
защит также ^/-приемлемо.
10.3.1.5. Процедура доказательства для аргументацион-
ной семантики. Процедура доказательства основывается на се-
семантике аргументации, сформулированной в терминах И-деревьев.
Будем считать, что в дереве есть подветвь (от одного узла — вниз
по направлению к другому), поддерево (с корнем в фиксированном
узле). Узлы в дереве — это множества целей, и каждый узел помечен
как «атака» или «защита». Термин «узел» обозначает или вершину
дерева, или множество гипотез, связанное с этой вершиной.
Определение этих деревьев параметризовано по отношению к
функции goal-branch, возвращающей для каждого дерева и узла в
дереве множество гипотез. Деревья для допустимых, слабо устойчи-
устойчивых, ^/-приемлемых и приемлемых множеств гипотез получаются с
помощью различного выбора функции goal-branch. Для всех подоб-
подобных вариантов выбора множество гипотез, возвращаемое функцией
goal-branch для заданного дерева и заданного узла в дереве, — это
подмножество объединения всех множеств гипотез по ветви дерева от
корня к самому узлу, исключая этот узел.

490 Системы аргументации и абдуктивный вывод [ Гл. 10
Будем считать, что заданы программа Р и соответствующее мно-
множество гипотез Hyp. Процедура доказательства работает непосред-
непосредственно с программой Р, которая может содержать переменные. Но
цель G и сгенерированное множество А не должны содержать пере-
переменных. Вообще говоря, процедуру доказательства несложно моди-
модифицировать, чтобы она, дополнительно к возвращаемым множествам
гипотез, в качестве решения возвращала бы подстановки для перемен-
переменных, так что ограничение для G не является существенным. Узлы в
промежуточных деревьях для процедуры доказательства — это цели,
которые могут содержать переменные и атомы. Используемые при
этом деревья называются целевыми.
Определение 10.21. Пусть целевая ветвь (goal-branch) — это
любая функция, такая, что для заданного дерева с целями в узлах
и фиксированного узла в дереве она возвращает множество гипотез.
Тогда целевое дерево (goal-tree) — это помеченное дерево Т, для кото-
которого справедливо:
• (GT1) каждый узел — это цель, помеченная либо как цель-атака,
либо как цель-защита;
• (GT2) корень, помечен как цель-защита;
• (GT3) каждый узел, помеченный как цель-атака, имеет един-
единственного потомка, помеченного как цель-защита;
• (GT4) каждый узел, помеченный как цель-защита, может иметь
произвольное количество потомков, помеченных как цели-атаки;
• (GT3-4) для каждого узла G — потомка узла G' существует
гипотеза not р Е G' — goal-branch(T,Gf) такая, что Р U G |= р
(здесь Р и G обозначают множество всех примеров, не содержа-
содержащих переменных, а негативные литеры в G обрабатываются как
атомы);
• {GTb) каждая ветвь Т конечна.
Цели-атаки и цели-защиты в целевых деревьях лишь потенциально
атакуют гипотезы своих родительских узлов. Действительные атаки
получаются при редукции (с помощью резолюции) всех атомов в
целевых узлах до гипотез. Если некоторые из атомов в целевом узле
не могут быть редуцированы, то целевой узел не представляет ника-
никакой атаки на свой родительский узел. Более того, редукция может
порождать некоторые неминимальные атаки.
Пусть дана программа
р <— not q
q <— not q, not r
и гипотеза not p. При редукции атома р вычисляется как минимальная
атака {not д}, так и неминимальная атака {not q, not r}.

10.3] Абдукция и аргументация в логическом программировании 491
Процедура доказательства для различных видов семантики полу-
получается из общего определения вывода целей с помощью подстановки
параметров goal-branch и extend-goal-root, а также с помощью исполь-
использования и построения подходящей функции goal-culprits.
Определение 10.28. Пусть дано целевое дерево Т и узел N в Т
такой, что ветвь из корня к N в Т — это Щ, iVi,..., Ni = N для г ^ 0,
тогда функция goal-branch определяется следующим образом:
• ^/-семантика: goal-branch(T,iV) = 0;
• семантика допустимости: goal-branch(T, N) = {h\ h G Nj П
П Hyp, j = 0,..., г — 1 и Nj; — цель-защита в Т};
• семантика слабой устойчивости и приемлемости:
goal-branch(T, N) = {h\ h e Nj П Hyp, j = 0,..., г - 1}.
Если N — корень, то goal-branch(T, N) = 0 для всех видов
семантики.
Определение 10.29. Для любого узла — цели N в данном целе-
целевом дереве Т, (N П Hyp) — goal-branch(T,iV) — есть слабая часть
узла N.
Если N — узел-атака, то любая гипотеза в слабой части TV, атаку-
атакуемая единственным потомком N в Т, — это виновник в N. Функция
виновников (culprit) — это любая функция goal-culprits, действующая
из множества целевых деревьев в степень множества Hyp, такая, что
для любого данного целевого дерева Т и любого целевого узла-атаки
Gа-) не являющегося листом Т, goal-culprits(T) содержит в точности
одного виновника для Ga- Заметим, что goal-culprits не возвращает
виновников для целей-атак, у которых нет потомков.
Определение 10.30. Для h G Hyp отношение extend-goal-root
определяется следующим образом:
• для u>/-семантики extend-goal-root (/г, по);
• для семантики допустимости и слабой устойчивости extend-goal-
root (/г,yes);
• для семантики приемлемости extend-goal-root (/г, yes), extend-
goal-root (/г, по).
Гипотезы в целях-защитах отбираются одна за одной в целевых
выводах и никогда не добавляются к корню в ^/-семантике, всегда
добавляются к корню в семантике допустимости и слабой устойчиво-
устойчивости и могут добавляться, а могут и не добавляться к корню в случае
семантики приемлемости. Для того, чтобы получить целевые деревья,
ветви которых содержат перемежающиеся атакующие и защищающие
целевые узлы, при выводе цели узлы могут не только добавляться в

492 Системы аргументации и абдуктивный вывод [ Гл. 10
целевые деревья, но и замещаться новыми узлами после выполнения
резолюции.
В определении вывода цели, приводимом ниже, мы обозначим
правило отбора литер в целевых узлах символом «5R». Мы будем
предполагать, что правило Э? безопасно, т. е. негативные литеры отби-
отбираются правилом Э? лишь тогда, когда они не содержат переменных.
Более того, будем предполагать, что каждый целевой узел G в целевом
дереве разделен на две части: первая часть называется Gaheady — это
множество гипотез, которое прозрачно для правила Э?. Отсюда, 5ft(G)
будет устанавливаться для 3?(G—Galready). Более того, 5ft(G) = J_ тогда
и только тогда, когда (G - Galready) = 0.
Определение 10.31. При заданных goal-branch и extend-root вы-
вывод цели для не содержащей переменных цели G — это последова-
последовательность целевых деревьев Т\,... ,Тп такая, что Т\ содержит лишь
(непомеченный) корень G, являющийся целью-защитой, и при задан-
заданном Ti (г = 1,..., п — 1) дерево T^+i строится по алгоритму построения
целевых деревьев, приведенному ниже.
Алгоритм построения целевых деревьев
Пусть имеется дерево Ti (см. определение 10.31) и N — отобранный
в нем узел (непомеченный), тогда дерево T^+i находится следующим
образом.
(а) Если N — цель-атака и 5ft(iV) ф J_, то
•(«atom) Если 3ft(iV) = q, где q — атом, и Gi,...,Gm(m > 0) — все
резольвенты N по q (в программе Р), то T^+i — это Ti, где TV
заменяется на Gi,..., Gm как узлы целей-атак, являющиеся по-
потомками родителя узла N и Galready = ... = Ga^eady = Naheady.
Отметим, что если m = 0, то N удаляется из Ti и не появляется в
Ti+i. Это эквивалентно удалению потенциальной атаки (iV), которой
не соответствует действительная атака.
Если 5R(iV) = not ^, где д — атом, то
- если not q e goal-branch(T^,iV), то Ti+1 — это Ti с узлом iValready,
замененным на iValreadyU{not q}.
- если not q ф. goal-branch(T^,iV), то T^+i — это Ti, где
1) N помечен;
2) not ^ записан как виновник TV;
3) {^} добавлен как (непомеченный) узел цели-защиты узла N, и
4) (только для семантики приемлемости) для каждого узла цели-
защиты D, отличного от родителя узла N в ветви, ведущей к N в

10.3] Абдукция и аргументация в логическом программировании 493
дереве Т^ и такого, что А — потомок узла D в ветви, содержащей
iV, а А\,..., Ап — все потомки Z), являющиеся надмножествами
А в Ti, расширенные узлы целей-атак А' = Аи {not q}, A[ = А\ U
U {not q},..., А^ = Ат U {not g} добавляются как дополнитель-
дополнительные (непомеченные) потомки узла D в T^+i.
^/already _ ^already ^/already _ ^already ^/already _ ^already
Отметим, что первая гипотеза, отбираемая в узле цели-атаки, выби-
выбирается как виновник, и узел цели-атаки сразу же помечается. Следо-
Следовательно, помеченные узлы атак-целей не могут быть множествами
гипотез. Если N — цель-атака и 5ft(iV) = 1, то не существует дерева
Tj+i, и узел N не может быть помечен (это соответствует неуспеху).
Альтернативно, мы можем получить случай а± для 5ft(iV) = J_, просто
пометив N (это также приведет к неуспеху в соответствии с опреде-
определением 10.32).
(б) Если N — узел цели-защиты, то
• (S±) Если 5ft(iV) = J_, то Т^+1 — это Т^, в котором N помечен.
Отметим, что узел цели-защиты помечается лишь тогда, когда все
гипотезы в нем были сгенерированы (с помощью развертывания ато-
атомов) и переведены в часть already. Следовательно, помеченные узлы
целей-защит — это множества гипотез.
(^atom) Если 5ft(iV) = (/, где q — атом, то необходимо выбрать резоль-
резольвенту G' узла N по q (в программе Р), и T^+i — это Т^, где iV
заменяется на узел цель-защиту G' и G"already = ^already
•Enaf) Если 5ftGV) = not ^, где ^ — атом, то
- если not q e goal-branch(T^,iV), то Ti+1 — это Г*, где iValready
заменяется на iValreadyu{not q};
- если not q ф goal-branch(T^,iV), то
- если extend-goal-root (not q, yes) и not q ^ culprits(T^), то T^+i —
это T^, где
1) iValready заменяется на iValready U {not q};
2) корень 7V|_i — это Rf = R U {not ^}, где R — корень
11 ^d
3) {g'} добавляется как дополнительный узел цели-атаки, яв-
являющийся потомком R/;
если extend-goal-root (not q, no) и (только для случая семантики
приемлемости) not q ^ culprits(T^at), где Тщ — поддерево Т^ с
корнем в iV, то Т^+1 — это Т^, где

494 Системы аргументации и абдуктивный вывод [ Гл. 10
1) iValready заменяется на JValready U {not q} и
2) {q} добавляется как дополнительный узел цели-атаки, яв-
являющийся потомком N.
Заметим, во-первых, что extend-goal-root (not g, yes) применяется
как в случае допустимости и слабой устойчивости, так и в случае
семантики приемлемости. Во-вторых, extend-goal-root (not q, no) при-
применяется как в случае ^/-семантики, так и в случае семантики прием-
приемлемости. Проверка в случае extend-goal-root (not q, no) для приемлемо-
приемлемости заключается в том, что отобранные гипотезы не появляются как
виновники в поддереве ниже цели-защиты, и является необходимой,
так как защиты строятся постепенно, и новое появление not q в узле
цели-защиты может «вывести из строя» ранее выбранного виновника
not q в ветви, расположенной ниже узла цели-защиты. Эта проверка
отсутствовала в теории доказательства, но она аналогична проверке,
необходимой при развертывании корня.
Нетрудно видеть, что выполняется следующее утверждение.
Утверждение 10.4. Каждое дерево в выводе целей является
целевым деревом.
Определение 10.32. Пусть заданы goal-branch и extend-root, тог-
тогда успешный вывод цели для цели G (без переменных) — это конечный
вывод цели Ti,..., Тп для G, где все узлы в Тп помечены и все листья
в Тп — это цели-защиты. Если А — корень Тп, то мы будем говорить,
что вывод цели вычисляет Апо С.
Отметим, что так как каждый помеченный узел цели-защиты в
выводе цели необходимо является множеством гипотез, то и А, вы-
вычисляемое в успешном выводе цели, — это множество гипотез.
Пример 10.23.
Рассмотрим программу
w(X) <^n
vC)
8C)
На рис. 10.6 показан успешный вывод для G = {u>C)}, вычисляющий
А = {not pC), not tC)} по отношению к выбору параметров для
семантики допустимости, слабой устойчивости и приемлемости. Т^ и
Тз получены по EatOm-niary (литера, отобранная правилом Э?, подчерк-
подчеркнута). Т^ получается по ?naf-inary. T5 — это Т^ с помеченным корнем,
которое получается по шагу 5±. Tq получается по шагу ceatom при

10.3] Абдукция и аргументация в логическом программировании 495
резольвировании рC) со вторым правилом программы. Т? получается
по шагу cenaf. Tg находится по шагу Satom. Tg — по шагу 5naf, направляя
not tC) в корень. Тю — это Tg с удаленным правым узлом цели-
атаки {?C)}, выполненным по шагу ceatom (нет резольвент для ?C)).
Тц — это Ti2 с непомеченным узлом цели-защиты на втором уровне
и получается это дерево по шагу 5atom при отобранном иC, У). Ti2
получается из Тц по шагу 5±.
*{notpC)}
*{sC%notqC)}
{notpC),v(M
*{notpC)}
*{sC),notqC)}
{not tC\ uC,Y)}
{notpC)}
{nopC)}
*{not/iC), not tC)}
{not tC), uC.Y)\
*{notpC)}
{sC% not gC)}
*{notpC% not tC)}
*{sC),notqC)}
Рис. 10.6.
Утверждение 10.5. Дана цель G (без переменных), тогда, если
существует успешный вывод цели, вычисляющий А из G по отноше-
отношению к разрешенным вариантам параметров goal-branch и extend-goal-
root, то А — решение для G по отношению к семантике, соответству-
соответствующей выбору параметров (свойство состоятельности).
Процедура доказательства не является полной. Одна из причин
неполноты — обычное возможное возникновение зацикливания. Дру-
Другая причина, которая сохраняется далее в случае пропозициональных
программ, следует из того факта, что успешные выводы должны быть
конечными.
Пример 10.24.
Рассмотрим программу: р^ри множество {not p}. Оно являет-
является допустимым, слабо устойчивым, приемлемым и ^/-разрешенным.
Однако процедура доказательства не может это определить, так как
резолюция на шаге ceatom зацикливается.
Кроме того, рассмотрим программу из примера 10.16 и множе-
множество гипотез {not p}. Оно является допустимым, слабо устойчивым,
приемлемым и ^/-разрешенным. Но процедура доказательства не
может это определить, так как она не может определить, что каждая
из бесконечного множества атак на {not p} контратакуется пустым
множеством.
Чтобы справиться с неполнотой процедуры доказательства, необ-
необходимо интегрировать ее с конструктивными методами проверки от-
отрицания и зацикливания. В случае, например, пропозициональных

496 Системы аргументации и абдуктивный вывод [ Гл. 10
программ следующий метод обнаружения циклов может быть легко
включен в процедуру доказательства: если атака требует доказатель-
доказательства атома р, то {not р} добавляется как защита против атаки. Следо-
Следовательно, на шаге ceatom с отобранным атомом р мы можем добавить
в дерево {not p} как специальную цель-защиту. Тогда, если в защите
этой гипотезы мы снова потребуем, чтобы р терпел неудачу в цели-
атаке последующего шага ceatom? мы можем использовать предыду-
предыдущую защиту {not p}, и таким образом, прекратить цикл.
10.3.2. Роль аргументации в организации абдуктивного вывода
Теория аргументации может успешно применяться для органи-
организации абдуктивного вывода. Например, процедура доказательства,
описанная в разд. 10.3.1.4, позволяет находить абдуктивное объясне-
объяснение для целевого запроса G, который можно считать наблюдением,
по теории Т — логической программе. Этим объяснением является
множество гипотез-умолчаний А, которое необходимо добавить к ис-
исходной программе, чтобы в заданной аргументационной семантике
можно было заключить G по теории Т. Рассмотрим пример.
Пример 10.25.
Пусть теория описывает работу встроенного аккумулятора ком-
компьютера. Аккумулятор работает (w), если он не находится в режиме
подзарядки (not с). Аккумулятор заряжается, если не разомкнута
основная цепь питания (not и). Цепь питания считается разомкнутой,
если напряжение в сети ниже заданного уровня (not п). Эта теория
может быть представлена с помощью следующей логической програм-
программы Р: {w <— not с; с <— not щ и <— not n}.
Пусть абдуцентами являются {not с, not и, not n}. Найдем решение
задачи абдукции для запроса Q = {w} и семантики допустимости. Де-
Дерево Т\ содержит единственный узел-защиту — корень {w}. Применяя
правило для узла-защиты, когда L есть атом, получаем дерево Тг,
содержащее лишь корень {not с}. Теперь можно применить правило
для узла-защиты, когда L содержит отрицание по умолчанию. В
результате дерево Тз — это дерево Тг, к корню которого добавлен
узел-потомок атака {с}. Выбрав {с} текущим узлом в Тз, переходим
к дереву Т4, в котором узел {с} заменен на узел-атаку {not и} как
резольвенту узла {с} по программе Р. Применяя правило для узла
атаки при L = not и, получаем из дерева Т^ дерево Т$: узел атаки
{not и} помечается, потомком этого узла становится защита {и}.
Дерево Tq находим, заменив по правилу для узлов-защит узел {и}
на его резольвенту {not n} по программе Р. Для семантики допусти-
допустимости разрешается добавлять гипотезы к корню, поэтому узел {not n}
отмечается, и гипотеза not n добавляется к корню (корень дерева Т?
содержит гипотезы {not с, not n}), дополнительным потомком которо-
которого становится атака {п}. Переходя к дереву Tg, обнаруживаем, что для

10.3] Абдукция и аргументация в логическом программировании 497
узла атаки {п} не существует резольвент по программе Р, то есть этой
потенциальной атаке не соответствует действительная атака, поэтому
в дереве Tg атака {п} удаляется. Помечая корень в дереве Tg, так как
он не содержит не обработанных ранее литер, получаем дерево Тд. На
этом процедура успешно завершается, и абдуктивным объяснением
запроса Q = {w} является множество гипотез {not с, not n}. Мы
нашли, что аккумулятор работает, если он не находится в режиме
подзарядки и напряжение в сети ниже заданного уровня.
Пример 10. 26.
Предположим, что теория описывает работу робота в некоторой
сложной системе. Мы будем использовать следующие предикаты:
w(x,y,z) — робот может перейти из точки х в точку у, выполняя
действие z\
р(х) — запрещено покидать точку х;
v(x) — работа в точке х завершена;
s(х) — произошла авария в точке х\
a(z,y) — переход в точку у с выполнением действия z невозмо-
невозможен;
Ь(у) — точка у недоступна;
c(z,y) — в точке у необходим результат действия z\
d(z) — действие z должно быть выполнено как можно скорее;
к (у) — нахождение в точке у опасно;
q(x) — получен управляющий сигнал, требующий покинуть точ-
точку х\
t(x) — в точке х робот работает автономно;
и(х,у) — в точке х получено информационное сообщение под
номером у.
Применяя описанные предикаты можно предложить, например,
такую программу
w(x, у, z) <— not p(x), v(x), not a(z, у)
(робот может перейти из точки х в точку г/, выполняя действие г, если
нет запрета покидать точку ж, работа в точке х завершена, и переход
в точку у при выполнении действия z возможен)
a(z,y) <- Ъ(у), not c(z,y)
(переход в точку у при выполнении действия z невозможен, если точка
у недоступна и нет необходимости в выполнении действия z в точке у)
c(z,y) <- d(z),not k(y)

498 Системы аргументации и абдуктивный вывод [ Гл. 10
(действие z необходимо в точке у, если действие z должно быть
выполено как молено скорее и нахождение в точке у не связано с
опасностью)
р(х) <— s(x),not q(x)
(запрещено покидать точку ж, если в точке х произошла авария и нет
управляющего сигнала, требующего срочно покинуть точку х)
q(x) <— not t(x), и(х, 2)
(получен управляющий сигнал, требующий срочно покинуть точку ж,
если в точке х робот не работает автономно (без внешнего управления)
и полученное в точке х информационное сообщение имеет код 2.)
vC)
(работа в точке р 3 завершена)
8C)
(в точке р 3 произошла авария)
гхC,2)
(в точке р 3 получено информационное сообщение с кодом 2)
6E)
(точка р 5 недоступна)
dG)
(действие р 7 должно быть выполнено как можно скорее.)
Пусть абдуцентами являются все умолчания для используемых
предикатов. Найдем решение задачи абдукции для запроса G =
= {u>C,2,2)} и семантики допустимости. Другими словами, известно,
что робот перешел из точки р 3 в точку р 2, выполнив действие
р 2. Необходимо выяснить, почему он смог это сделать. Дерево Т\
содержит единственный узел-защиту — корень {^C,2,2)} (рис. 10.7).
Деревья Т^ и Тз получены по ?atOm-Hiary (литера, отобранная пра-
правилом 5R, подчеркнута). Т^ получается по ?naf-inary. T5 — это Т±, в
котором узел-атака заменен на два атакующих узла по правилу ceatom-
Tq получается по шагу ceatom, так как в программе есть факт 5C).
Tj получается по шагу cenaf- Tg находится по шагу SatOm- Tq — по
шагу ?atomj так как в программе есть факт иC,2). Тю — это Тд с
добавленным к корню умолчанием not tC) (использовано правило
^naf)- Дерево Тц — получено из Тю при применении правила 5naf.
Для того, чтобы получить дерево Ti2, было использовано правило
c^atom- В результате построения деревьев Т13 и Т14 выясняется, что для
каждой атаки существует защита, и получается полностью помечен-
помеченное дерево Ti5. Процедура завершается успешно, корень последнего
дерева содержит абдуктивное объяснение для исходного запроса G:
{not pC), not aB,2), not ?C)}. Полученный результат говорит о том,
что робот перешел из точки р 3 в точку р 2, выполнив действие р 2,
потому что не было запрещено покидать точку р 3, переход в точку

10.3] Абдукция и аргументация в логическом программировании 499
G={wC,2,2)}
{not/?C), notaB,2)}
fcffi}
{not/?C), not аB,2)}
*{notgC)}
{not/7C), not gB.2). not <3)}
*{notgC)}
*{notb)}
¦{not/<3), not aB,2), not *C)}
*{notgC)} {notcfi,!)}
*{tioUC)}
{not/7C).vC).notflB.2)}
{noti?C),notaB,2)}
{sC}} {notgC)}
{по^C),шЛаB,2)}
•{not^C)}
{not tC% nC.2)>
Гц
¦{notpC), not aB,2), not <3)}
*{no'tgC)} {oG.2)}
*{not<3)}
*{notpC), not flB,2), not <3)}
*{notfC)} {dm} {notiB)}
*{not<3)}
{not/>C). not лB,2)}
{not/?C), not aB,2)}
{not gC)>
{not/7C),notaB,2)}
*{notgC)}
{not tf3)}
¦{not/7C), not aB,2), not <3)}
*{not^C)} {Щ}} {notcB,2)}
*{not<3)}
*{not/?C), not аB,2), not tC)}
*{notqC)}
*{nottC)}
Рис. 10.7.
p 2 с выполнением действия р 2 был возможен, и в точке р 3 робот не
работал в автономном режиме.
Приведем результаты работы процедуры для других запросов в
случае использования семантики допустимости:
• наблюдение wC,2,1) объясняется гипотезами not p C), not aA,2),
not tC);
• гипотезы not pC), not аG,5), not fcE), not tC) объясняют на-
наблюдение гу C,5,7);
• если в исходную программу вместо факта vC) добавить факт
v(X), то объяснением для наблюдения гуA,5,7) будут гипотезы
not p(l), not aG,5), not fcE).
Какас, Ковальский и Тони предложили использовать аргумен-
аргументацию для выполнения абдуктивного вывода, когда множество аб-
дуцентов содержит не только умолчания, но и позитивные преди-
предикаты (абдуктивное логическое программирование). В соответствую-
соответствующей абдуктивной структуре применяются ограничения целостности.
В искусственном интеллекте при представлении знаний ограничения
целостности позволяют задавать допустимые состояния базы знаний.
Если же рассматриваются логические программы, то применение

500 Системы аргументации и абдуктивный вывод [Гл. 10
ограничений целостности дает возможность задавать, например, же-
желательные свойства программ. В этом случае задача абдукции опреде-
определяется следующим образом: «Для заданного множества предложений
Т (представления теории) и предложения G (наблюдения), задача
абдукции может быть охарактеризована как задача поиска множества
предложений А (абдуктивного объяснения для G) такого, что
1) TUA \=G,
2) Т U Д удовлетворяет ограничениям целостности /».
Пусть <Р, А, /> — абдуктивная структура, где Р — программа,
А — множество абдуцентов, / — множество ограничений целостности.
В этом случае М(А) (Д С А) называется обобщенной устойчивой
моделью структуры <Р, А, /> тогда и только тогда, когда М(А) —
устойчивая модель для Р U А и М(А) |= / (здесь определяется
смысл ограничений целостности). Напомним, что устойчивая модель
М программы Р, не содержащей переменных, определяется как такое
множество атомов, не содержащих переменных, которое совпадает с
минимальной моделью программы Рм, получающейся из Р по прави-
правилам
1) удалить из Р все правила, содержащие литеру not А, где А Е М;
2) удалить все литеры вида not А из оставшихся правил.
После того, как определена обобщенная устойчивая модель, абдук-
тивное объяснение наблюдения Q в структуре <Р, А, /> определяет-
определяется как любое подмножество Д множества А такое, что М(Д) — обоб-
обобщенная устойчивая модель структуры <Р, А, /> и М(А) |= Q. Проце-
Процедура доказательства в этом случае содержит две фазы: абдуктивную
фазу, в ходе которой выполняется стандартная SLD-резолюция, гене-
генерирующая гипотезы; и фазу непротиворечивости, состоящую в про-
проверке того, удовлетворяют ли гипотезы ограничениям целостности.
Эта процедура оказывается несостоятельной. Для достижения состо-
состоятельности было предложено использовать аргументационную семан-
семантику, единым образом работающую как с ограничениями целостности,
так и с NAF (отрицанием как неуспехом) с помощью специально
определенного понятия атаки. Если в программе Р заменить все нега-
негативные литеры not p(t) на p*(t) (в результате получится программа
Р*) и положить А* = {р* | для V предиката р программы Р}, то можно
определить новую абдуктивную структуру < Р*, A U А*, / U /* >, где
/* — множество ограничений целостности вида: VX^[p(X)&p*(X)]
и У Х\р(Х) Vp*(X)]. Тогда отношение атаки для аргументов Е и Д
можно определить следующим образом:
1) аргумент Е атакует аргумент Д (Е attacks Д) через NAF тогда
и только тогда, когда Р* U Е Ь р для некоторого р* G Д или
а* Е Е для некоторого абдуцента а в Д;

10.3] Абдукция и аргументация в логическом программировании 501
2) аргумент Е атакует аргумент А (Е attacks А) через ограниче-
ограничение целостности —<(Li& ... &ЬП) в / тогда и только тогда, когда
Р* U Е \~ Li,..., Li-i, Li+i,..., Ln для некоторого Li в А.
В качестве иллюстрации применения теории аргументации для
интерпретации абдуктивной процедуры доказательства рассмотрим
пример из области диагностики. Предположим, что анализируется
поведение некоторой системы. В ее работе обнаружено отклонение
от нормального поведения, которое может вызывать некоторая неис-
неисправность А. Кроме того, известно, что текущие значения парамет-
параметров системы можно установить с помощью двух контрольных те-
тестов, причем тесты связаны соотношением: проверка первого теста
считается успешной, если ничего не известно об успехе выполнения
проверки второго теста. Второй тест успешен, если в системе имеется
неисправность В. Невозможными являются ситуации, когда имеется
неисправность А и успешна проверка первого или второго теста. Со-
Соответствующая логическая программа Р имеет вид
обнаружено_ отклонение <— неисправность_ А]
успешен_тест_1 <— not успешен_тест_2\
успешен_ тест_ 2 <— неисправность_ В.
Ограничения целостности / задаются условиями
-^[неисправность _ А & у спешен _ тест _1];
-^[неисправность_А & успешен_тест_2].
Множество абдуцентов А содержит: {неисправность_А, неисправ-
неисправность В}.
Пусть требуется найти объяснение для наблюдения обна-
обнаружено _ отклонение. По программе находим, что возможной
причиной наблюдаемого явления может быть неисправность_ А
(то есть А={неисправность_А}). Теперь необходимо проверить, не
вызовет ли предположение о неисправности А противоречия. Для
этого найдем контраргументы для аргумента {неисправность_А}.
Существует два таких аргумента:
1) {успешен_тест_2*}. Этот контраргумент атакует аргу-
аргумент {неисправность _ А} через ограничение целостности
^[неисправность_А & успешен_тест_1] в /, так как по
программе из у спешен _тест _2? следует успешен_тест_1.
2) {неисправность_В}. Этот контраргумент атакует аргу-
аргумент {неисправность _ А} через ограничение целостности
^[неисправность_А & успешен_тест_2] в /, так как по
программе из неисправность_ В следует успешен_ тест_ 2.
Атака аргумента {успешен_тест_2*} контратакуется аргумен-
аргументом {неисправность_ В} через NAF, так как предположение об истин-
истинности гипотезы неисправность_ В влечет истинность утверждения
успешен_тест_2. Гипотезу неисправность_В можно добавить ко

502 Системы аргументации и абдуктивный вывод [ Гл. 10
множеству А, так как единственная атака {неисправность_В*} про-
против этого аргумента тривиально контратакуется аргументом {неис-
{неисправность _В}. Но аргумент {неисправность_В} атакует аргумент
{неисправность_ А} (см. п. 2). Следовательно, множество А атакует
само себя, что вызывает неуспех процедуры доказательства. Заме-
Заметим, что если убрать второе ограничение целостности, то решением
задачи абдукции будет множество А = {неисправность_ А, неисправ-
неисправность В}.
Если вместо семантики обобщенных устойчивых моделей для
абдуктивной структуры использовать аргументационную семантику
К М-допустимости, то абдуктивная процедура доказательства стано-
становится состоятельной. Здесь множество гипотез А К М-допустимо тогда
и только тогда, когда для любого множества гипотез Е, такого, что
справедливо отношение Е attacks А выполняется: аргумент А атакует
аргумент (Е-А) лишь через NAF.
Заметим, что мы рассмотрели особенности решения с помощью
аргументации задачи абдукции для случая, когда базовая теория
представлена логическими программами. Если в качестве гипотез мо-
могут выступать лишь умолчания, для поиска абдуктивных объяснений
можно использовать различные виды аргументационной семантики,
для вычисления которых существует единая модель. В случае аб-
дуктивного логического программирования применение аргумента-
аргументации позволяет справиться с проблемой несостоятельности обычной
абдуктивной процедуры. Таким образом, теорию аргументации можно
рассматривать как средство реализации абдуктивного вывода, поз-
позволяющее определять наилучшее абдуктивное объяснение как «вы-
«выигравшее» в ходе определения статуса множеств гипотез-аргументов
по правилам конкретной семантики при заданном отношении атаки.
В настоящее время остается открытым вопрос о том, в каких слу-
случаях следует отдать предпочтение той или иной аргументационной
семантике, какими свойствами обладают полученные абдуктивные
объяснения.

Часть III
ИНДУКЦИЯ И ОБОБЩЕНИЕ
Как будто был к дверям подобран ключ.
Как будто был в тумане яркий луч.
Про «Я» и «Ты» звучало откровенье...
Мгновенье — мрак! И в бездну канул луч.
Омар Хайям
Глава 11
БАЗОВЫЕ ПРИНЦИПЫ ПОСТРОЕНИЯ
СИСТЕМ ОБУЧЕНИЯ И ПРИНЯТИЯ
РЕШЕНИЙ
Индукция и формирование индуктивных понятий играют боль-
большую роль в жизни людей. В отличие от дедуктивных выводов, хо-
хорошо изученных в настоящее время, индуктивные выводы гораздо
хуже поддаются формализации. Индуктивный вывод, или обобщение,
основан на построении некоторого общего правила (закона) на осно-
основании конечного числа наблюдаемых фактов. Индуктивные выводы,
которые делает человек, достаточно тесно связаны со статистически-
статистическими моделями; достоверность таких выводов в значительной степени
зависит от полноты того набора фактов, которым он пользуется при
формировании гипотез. Может ли компьютер выполнять аналогич-
аналогичную функцию — строить новые гипотезы на основе наблюдаемых
фактов? Ответ на этот вопрос дает раздел искусственного интеллекта,
исследующий проблемы индукции и обобщения. Поскольку нельзя
ввести универсальные формальные правила, по которым делаются
индуктивные выводы в науке и в повседневной жизни, определим круг
проблем, рассматривающихся в этой части.
Прежде всего, из всех возможных задач, связанных с построением
индуктивных зависимостей, выделим круг задач, называемых задача-
задачами индуктивного формирования понятий. К ним относятся задачи,
которые моделируют возможность человека формировать описания,
охватывающие множество примеров некоторого понятия. В основе
процесса индуктивного формирования понятий лежит умение челове-
человека выделять некоторые наиболее общие или характерные фрагменты
среди описаний отдельных примеров понятия, избавляясь от мелких,

504 Базовые принципы построения систем обучения [Гл. 11
незначительных характеристик, присущих конкретным примерам по-
понятия.
Обычно люди пытаются понимать свое окружение, упрощая его.
Создание подобной упрощенной модели называется индуктивным обу-
обучением. В процессе обучения человек наблюдает свое окружение и
определяет взаимосвязи между объектами и событиями в этом окру-
окружении. Он группирует сходные объекты в классы и конструирует
правила, предсказывающие поведение объектов такого класса.
Подобным образом может обучаться и компьютер. Изучение и
компьютерное моделирование процесса обучения является одним из
предметов исследования в области искусственного интеллекта, назы-
называемой машинным обучением (Machine Learning). Как правило, систе-
система машинного обучения пользуется не единичными наблюдениями, а
целыми (конечными) множествами наблюдений сразу. Такое множе-
множество называется обучающим множеством или обучающей выборкой.
Одной из практически ценных при поиске индуктивных законо-
закономерностей является добыча (анализ) данных из баз данных (Data
Mining). Хотя извлечение знаний из баз данных является одной из раз-
разновидностей машинного обучения, существуют аспекты, существенно
отличающие его от других приложений машинного обучения. Первое
и главное состоит в том, что базы данных, как правило, проекти-
проектируются без учета потребностей специалистов в области обобщения.
Системам извлечения знаний приходится работать с уже готовыми
базами данных, рассчитанными на нужды других приложений. В
них вовсе не обязательно присутствуют атрибуты, которые могли бы
облегчить процесс обучения.
Второе важное отличие состоит в том, что реальные базы данных
достаточно часто содержат ошибки. В то время как для машинного
обучения используются тщательно подобранные данные, алгоритмы
извлечения знаний из баз данных вынуждены иметь дело с зашум-
ленными и подчас противоречивыми данными.
Дальнейшим развитием этого направления стала разработка
средств обнаружения знаний, представленных в базах данных в
неявной форме (Knowledge Discovery in Databases). Такие средства и
системы могут быть применены в машинном обучении, распознавании
образов, при извлечении знаний для экспертных систем, и многих
других задачах искусственого интеллекта.
В работах, посвященных созданию интеллектуальных систем,
основанных на индуктивных методах, используются термины
классификация и распознавание. Эти понятия, семантически близкие,
на самом деле не однозначны. Под задачей распознавания будем
понимать в первую очередь задачу формирования решающего
правила, на основании которого объекты, принадлежащие классу,
могут быть отделены от остальных. По сути, когда мы говорим о
получении решающего правила, речь идет о создании алгоритма,

11.1] Системы поддержки принятия решений 505
способного эффективно отличить объекты, принадлежащие классу,
от прочих.
Решающее правило может быть задано по-разному. Прежде все-
всего, любое решающее правило — это набор условий, которым долж-
должны удовлетворять примеры формируемого понятия. Способ задания
решающего правила может быть различным (например, логическое
выражение, дерево решений, набор продукционных правил), однако,
как будет показано далее, достаточно легко можно перейти от одного
представления к другому. Разрабатывая алгоритм формирования ре-
решающего правила, исследователь заинтересован в получении правила,
наиболее достоверного или наиболее точно отражающего особенности
примеров класса. Решающее правило также должно быть максималь-
максимально компактным: правило, просто перечисляющее все свойства всех
объектов обучающей выборки, не имеет ценности.
Задача классификации в рамках этой части будет пониматься
нами как задача отнесения вновь предъявленных объектов, отличных
от объектов обучающей выборки, к тому или иному классу на основе
построенного решающего правила. Речь идет о проверке полезности
полученного решающего правила на множестве контрольных приме-
примеров: правило, способное верно расклассифицировать только объекты
исходной выборки, нельзя признать удачным.
Предлагается рассмотреть два метода обучения. В обучении с учи-
учителем учитель определяет классы и предлагает примеры объектов
каждого класса. Система должна найти общие свойства объектов
каждого класса, сформировав тем самым описание класса. Описание
класса вместе с самим классом дает нам классифицирующее правило
«Если <описание> то <класс> », которое может быть использовано
для предсказания класса объектов, неизвестных системе ранее. Дру-
Другой метод обучения — обучение без учителя — предполагает, что
системе предъявляется совокупность объектов, не разделенных на
классы. Количество классов также может быть неизвестным. Система
должна сама определить классы объектов, основываясь на общих
свойствах объектов из данного множества примеров.
В данной главе обсуждается применение методов индукции и об-
обобщения в интеллектуальных системах различного назначения. Рас-
Рассматривается структура таких систем. Обсуждаются реальные про-
проблемы, стоящие перед разработчиками. Дается понятие объекта ис-
исследования, рассматриваются способы его описания.
11.1. Системы поддержки принятия решений
Системы поддержки принятия решений (английский эквивалент —
DSS: Decision Support System) — это компьютерные системы, предна-
предназначенные для усовершенствования процесса управления предприя-
предприятием или иным сложным объектом. Цель таких систем — обеспечение

506 Базовые принципы построения систем обучения [Гл. 11
быстрого и надежного анализа и визуализации деловой информации,
синтез информации с целью получения новых знаний об объекте
управления и выработки управляющих решений. Примером такой
системы может быть система оперативно-диспетчерского управления
в энергетике. Системы поддержки принятия решений для энергообъ-
энергообъединения работают в режиме реального времени и являются основным
звеном в комплексной системе защиты энергоблоков от ошибочных
действий оперативно-диспетчерского персонала. В настоящее время
для решения задач принятия решений при оперативном управлении
энергообъектами (типа энергоблоков) атомных и тепловых электро-
электростанций и обучения лиц оперативно-диспетчерского персонала требу-
требуется более 100 интеллектуальных диалоговых систем поддержки при-
принятия решений семиотического типа, внедрение которых, учитывая
опыт западных стран, даст многомиллионный экономический эффект.
Системы поддержки принятия решений состоят из следующих
основных структурных элементов:
- хранилище информации (массив данных и знаний);
- средства управления данными (накопление, хранение, манипу-
манипулирование, защита и т.д.);
- средства аналитической обработки данных (Data Mining);
- средства синтеза управляющих решений (моделирование, про-
прогнозирование, оптимизация, анализ альтернатив).
Большинство систем поддержки принятия решений относятся
к системам оперативной (динамической) аналитической обработки
(Online Analytical Processing или OLAP). Цель таких систем — обес-
обеспечить интерактивную обработку сложных запросов, а также после-
последующий многопроходный анализ, чтобы предоставить пользователю
возможность анализировать в оперативном режиме большие массивы
разнообразных данных, выявлять взаимосвязи, определять тенденции
развития событий и прогнозировать состояние объекта управления.
Инструментарий систем поддержки принятия решений обычно вклю-
включает в себя широкий набор средств статистического анализа данных,
средства выявления тенденций и прогнозирования, а также функции
моделирования, агрегирования и объединения данных, средства оп-
оптимизации.
Многочисленные попытки использовать традиционные системы
оперативной обработки транзакций, так называемые OLTP-системы
(Online Transaction Processing) для поддержки принятия решений, как
правило, заканчивались неудачей по следующим причинам.
1. Данные, накапливаемые в недрах OLTP-систем, труднодоступ-
труднодоступны, обладают излишней подробностью, могут охватывать или
слишком короткие временные интервалы, или, наоборот, форми-
формироваться в неподходящие моменты времени. Кроме того, между

11.1] Системы поддержки принятия решений 507
различными транзакционными системами, как правило, не со-
соблюдаются одинаковые правила именования, кодировки и из-
измерения переменных. Для принятия решений такие «сырые»
данные не годятся и требуют предварительной обработки.
2. Информация, необходимая для принятия решений, часто рас-
располагается на разных платформах (разные ОС, СУБД), отчего
задача ее извлечения требует квалификации и опыта работы с
разными СУБД, а также хорошего знания структур баз данных
отдельных OLTP-приложений.
3. Уровень компьютерных знаний управленцев обычно относитель-
относительно невысок, поэтому даже после того, как данные собраны и
приведены к приемлемому для анализа виду, работать с ними
напрямую конечный пользователь вряд ли сможет, так как для
этого потребуется хорошее владение запросами на языке SQL —
базовом средстве доступа к данным, используемым в OLTP-
системах.
По этим причинам обеспечение менеджеров необходимой для при-
принятия решений информацией обычно возлагалось на специальные
информационные службы. Однако вскоре стало очевидным, что тра-
традиционная информационная технология, основанная на встраивании
аналитических средств в транзакционные системы, «неповоротлива»,
ограничена и не может служить основой при построении систем под-
поддержки принятия решений, обладающих таким важным свойством,
как быстрота извлечения важной деловой информации.
Признанием этого факта стало рождение новой информаци-
информационной технологии, технологии информационных хранилищ (Data
Warehouse). В отличие от баз данных традиционных OLTP-систем,
где данные подобраны в соответствии с конкретными приложениями,
информация в информационных хранилищах ориентирована на
задачи поддержки принятия решений. Это автономная, специальным
образом организованная база данных, которая ориентирована на
хранение информации, необходимой для принятия решений и
оснащена OLAP-инструментарием.
Архитектура OLAP-системы определяется типом хранилища дан-
данных, на котором она основывается. Различают три вида информаци-
информационных хранилищ.
1. Виртуальное (логическое) хранилище. В его основе лежит ре-
позитарий метаданных, которые описывают источники данных
(БД, внешние файлы и т.д.), SQL-запросы, процедуры обработ-
обработки и представления информации. Доступ к ним обеспечивает
программное обеспечение промежуточного слоя (middleware).
Избыточность данных минимальная, пользователь-аналитик ра-
работает фактически с «живыми» данными OLTP-систем, что

508 Базовые принципы построения систем обучения [Гл. 11
сопровождается снижением их производительности и реальной
угрозой нарушения их работоспособности.
2. Централизованное хранилище. Это самый распространенный
способ организации OLTP-систем. В качестве СУБД обычно
используются либо профессиональные реляционные, либо мно-
многомерные СУБД, специально приспособленные для построения
OLTP-систем. Наполнение централизованного хранилища про-
производится из баз данных транзакционных систем и внешних ис-
источников путем обработки (компиляции) первичных, «сырых»,
детальных данных.
3. Распределенное информационное хранилище. Такая форма
свойственна крупным организациям с большим числом
удаленных филиалов, являющихся автономными центрами
принятия решений. В этом случае для каждого управленче-
управленческого уровня открывается свой фрагмент информационного
хранилища, называемый информационной витриной (data mart)
и реализуемый в виде отдельной локальной базы данных, куда
копируется из центрального хранилища только та информация,
которая необходима для данного подразделения.
В настоящее время распространены в основном два принципа
организации архитектуры OLTP-систем: на основе многомерных баз
данных (MDDB или Multidimensional Database) и на основе исполь-
использования реляционных баз данных (ROLAP или Relational OLAP).
Многомерные базы данных преобразуют содержимое хранилищ дан-
данных таким образом, чтобы информация была представлена в виде
многомерного «куба» (гиперкуб или поликуб), для чего предваритель-
предварительно производится множество вычислений (консолидация, фильтрация,
форматирование и т. д.) над данными, содержащимися в разных тран-
транзакционных OLTP-систем ах, в итоге образующих многомерные пред-
представления данных, которые хранятся как части указанного куба. В
ROLAP-системах функции поддержки принятия решений реализу-
реализуются в виде надстройки над реляционной СУБД. Благодаря гибким
и мощным инструментам оптимизации запроса, присущих реляцион-
реляционным СУБД, сервер ROLAP создает многоуровневую архитектуру, в
рамках которой клиент ROLAP имеет дело с многомерными представ-
представлениями данных (типа «звезды», метаданные). Каждая из этих двух
архитектур имеет свои преимущества и недостатки.
Компания Red Brick Systems, известная своими продуктами по
организации и эксплуатации хранилищ данных, опубликовала доку-
документ, в котором сформулировала 10 требований, которым должна
удовлетворять реляционная СУБД, чтобы ее можно было назвать
сервером информационного хранилища.
1. Скорость загрузки (Load Performance). Необходимость периоди-
периодической загрузки новых данных в хранилище в узких временных

11.1] Системы поддержки принятия решений 509
рамках требует, чтобы производительность процесса загрузки
составляла сотни миллионов записей (несколько Гбайт в час), и
она не должна становиться причиной искусственного ограниче-
ограничения размера хранилища.
2. Технология загрузки (Load Processing). Чтобы загрузить или
откорректировать данные в хранилище, требуется произвести
целый ряд действий: преобразование данных, фильтрацию, пе-
переформатирование, проверку целостности, организацию физи-
физического хранения, индексирование и обновление метаданных.
Все эти действия должны выполняться как единая и неделимая
операция.
3. Управление качеством данных (Data Quality Management). Ана-
Анализ реальных явлений предъявляет высокие требования к каче-
качеству данных. В хранилище должна быть обеспечена локальная
и глобальная согласованность, а также ссылочная целостность,
даже при наличии огрехов в исходных базах данных.
4. Скорость обработки запросов (Query Performance). Интерпре-
Интерпретация реальных явлений и анализ текущей ситуации не должны
замедляться или становиться практически невозможными из-за
низкой производительности реляционной СУБД. Сложные за-
запросы, важные для принятия решений, должны обрабатываться
за секунды или минуты, но ни в коем случае за дни.
5. Масштабируемость в широких пределах (Terabyte Scalability).
Применяемая РСУБД не должна иметь никаких архитектурных
ограничений на размер хранилища данных. От нее требуется
поддерживать модульную и параллельную обработку, сохранять
устойчивость к локальным авариям, при этом скорость обработ-
обработки запроса должна зависеть от его сложности, а не от размеров
хранилища.
6. Обслуживание большого числа пользователей (Mass User
Scalability). Сервер БД должен поддерживать сотни и даже
тысячи конкурирующих пользователей без снижения скорости
обработки запросов.
7. Сети хранилищ данных (Networked Data Warehouse). Часто
несколько локальных хранилищ (Data mart) взаимодействуют
в более крупной сети хранилищ данных. Сервер должен обеспе-
обеспечивать координацию перемещения данных между такими храни-
хранилищами, а пользователь должен иметь возможность обращаться
к нескольким хранилищам с одной клиентской станции.
8. Администрирование (Warehouse Administration). Администра-
Администраторы должны быть способны выполнять свои функции в сети
хранилищ из одного физического центра. Очень большие мас-
масштабы хранилищ и временная цикличность требуют наличия
гибких и удобных средств администрирования РСУБД.

510 Базовые принципы построения систем обучения [Гл. 11
9. Интегрированные средства многомерного анализа (Integrated
Dimensional Analysis). Для обеспечения высокопроизводитель-
высокопроизводительной аналитической обработки в базовой РСУБД необходимо
иметь средства, поддерживающие работу с многомерными дан-
данными: удобные функции вычисления агрегированных показате-
показателей и инструменты, автоматизирующие генерацию таких пред-
предварительно вычисленных агрегированных величин.
10. Развитые функции формулирования запросов (Advanced Query
Functionality). Конечным пользователям необходимы мощные и
в то же время простые в использовании средства для выполне-
выполнения аналитических расчетов, последовательного и сравнитель-
сравнительного анализа, а также для согласованного доступа к детальной
и агрегированной информации. Желательно, чтобы эти средства
были встроены в РСУБД и не требовали использования языка
запросов SQL.
OLAP-технология тесно связана с методами математической ста-
статистики и полезна для проверки заранее сформулированных гипотез
и предварительного анализа данных. Следующим этапом развития
процесса анализа данных стала разработка систем, предназначенных
для трансформации данных, накопленных в информационных храни-
хранилищах или витринах (Data Mart), в информацию, способную помочь
в принятии правильных решений.
11.2. Задачи извлечения знаний из баз данных
В разные годы понятию поиска полезных закономерностей сре-
среди необработанных («сырых» данных) было дано множество назва-
названий, включая обнаружение знаний в области баз данных (Knowledge
Discovery in Databases, сокращенно KDD), анализ данных (Data
mining), извлечение знаний (Knowledge Extraction), обнаружение ин-
информации (Iinformation Discovery), сбор информации (Information
Harvesting), археология данных (Data Archaeology), обработка моде-
моделей данных (Data Pattern Processing). Термин обнаружение знаний в
области баз данных (или KDD) был введен в 1989 г. и описывает
широкий процесс поиска данных, в особенности, высокий уровень
применения основных методов поиска данных. Термин Data mining
используется главным образом статистиками, аналитиками данных
и в системах управления информацией, в то время как KDD по
большей части используется в области искусственного интеллекта и в
исследованиях по машинному обучению.
Системы обнаружения знаний в базах данных (KDD) являются
объектом интереса для специалистов в области машинного обучения,

11.2]
Задачи извлечения знаний из баз данных
511
распознавания образов, баз данных, статистики, искусственного ин-
интеллекта, сбора данных для экспертных систем и наглядного пред-
представления данных. Системы KDD разработаны на основании методов,
алгоритмов и технологий, взятых из различных областей. Общей
целью является извлечение знаний из данных, хранящихся в больших
базах данных.
В областях машинного обучения и распознания образов KDD ча-
частично совпадает с системами Data mining. Системы обнаружения
знаний нацелены на разработку теорий и алгоритмов для выявления
образов или классов, которые можно интерпретировать как полезные
и интересные знания. У таких систем также много общего со статисти-
статистикой, со специальным исследовательским анализом данных. Системы
KDD всегда располагают встроенными конкретными статистически-
статистическими процедурами для моделирования данных и подавления шума в
данных.
Целевые j данные
данные |
Рис. 11.1.
Процесс обнаружения знаний в базах данных является интерак-
интерактивным и итеративным, состоит из нескольких этапов, каждое после-
последующее решение принимается пользователем самостоятельно. Авторы
Брахман и Ананд излагают практический взгляд на процесс KDD,
подчеркивая взаимодействующую природу данного процесса. Процесс
обнаружения знаний может включать в себя повторения и допускает
возврат с одного этапа к другому по нескольку раз. Основные эта-
этапы процесса KDD (без учета возможных повторений) представлены
на рис. 11.1. Большая часть предварительной работы над процессом
KDD сосредоточена на этапе Data Mining или извлечения данных.
Однако остальные этапы также крайне важны для успешного функ-
функционирования процесса KDD. Рассмотрим более детально шаги этого
процесса.

512 Базовые принципы построения систем обучения [Гл. 11
1. Исследование и осмысление прикладной области, или первич-
первичных знаний, из которых надо извлечь информацию, а также
формулирование целей пользователя.
2. Формирование планового набора данных, как множества (под-
(подмножества) объектов, на которых возможно использование про-
процедур обнаружения знаний.
3. Предварительная подготовка и обработка данных: общие опе-
операции, такие, как устранение шумов (помех), сбор необходимой
информации для моделирования и оценивания шумов (помех),
выбор стратегий обработки областей с неполными данными.
4. Планирование и предварительная обработка данных: выявление
полезных особенностей для представления данных в зависимо-
зависимости от поставленной цели. Используется снижение размерности
информации и методы преобразования для снижения рассмат-
рассматриваемого числа переменных или поиск инвариантов для пред-
представления данных.
5. Определение задачи Data Mining: в зависимости от конечной
цели это может быть классификация, регрессия, кластеризация
и т. п.
6. Выбор алгоритма, решающего задачу Data Mining: задачу поис-
поиска классов, образов в предъявленных данных. При этом необ-
необходимо учитывать как особенности данных, так и пожелания
пользователя.
7. Собственно Data Mining: поиск интересных для пользователя
зависимостей в одной (или нескольких) из возможных форм — в
виде классификационных правил, деревьев решений, регресси-
регрессионных схем, кластеризации и т. п.
8. Интерпретация выявленных классов, образов. Возможно, при
желании, возвратиться к любому из семи предыдущих этапов
для выполнения новой итерации.
9. Консолидация выявленных знаний: добавление новых знаний в
базу знаний какой-либо функционирующей системы, либо до-
документирование результатов и предоставление их пользователю
в виде отчета. При этом необходимо проверить полученные ре-
результаты на предмет конфликта с уже существующими (добы-
(добытыми ранее) знаниями.
Одной из наиболее важных задач, решаемых в рамках систем
KDD, является задача Data Mining. Data Mining включает в себя под-
подборку моделей, а также выявление классов из предъявленных данных.
Выбор модели существенно влияет на полученные в итоге знания,
поскольку одной из составляющих общего процесса KDD является
проверка того, сколь полно отражают принятые модели интересные и
полезные знания. Отметим, что здесь часто приходится полагаться на

11.2] Задачи извлечения знаний из баз данных 513
субъективное суждение человека относительно данного процесса. Су-
Существует два основных математических формализма, использующих-
использующихся при подборке моделей: статистический подход, принимающий во
внимание недетерминированные эффекты модели (например, f(x) =
= аж+е, где е может являться Гауссовской произвольной переменной),
тогда как логическая модель является чисто детерминированной и не
допускает двусмысленностей в процессе моделирования. Статистиче-
Статистический подход в реальных системах Data Mining используется практи-
практически повсеместно, при этом всегда остается неуверенность в том,
насколько соответствуют построенные объекты (классы) объектам,
существующим в реальном мире.
Многие методы Data Mining базируются на концепциях машинного
обучения, распознавания образов и статистике, а именно на класси-
классификации, кластеризации, построении графовых моделей и т. д. Класс
алгоритмов для решения данных проблем очень широк, и проблема
выбора конкретного метода может представлять сложность как для
опытных аналитиков, так и для новичков. Кроме того, многие (если
не все) методы, которые используются в Data Mining, могут быть рас-
рассмотрены как расширения или гибриды небольшого числа основных
методов и принципов.
Две главные цели Data Mining можно сформулировать как про-
прогноз (предсказание) и получение описаний классов объектов. При
прогнозировании используются некоторые переменные или области
баз данных, чтобы предсказать неизвестные или будущие значения
других переменных, интересующих пользователя. Описание базиру-
базируется на обнаружении классов данных, которые затем могут быть
интерпретированы человеком. Построение описания класса включа-
включает нахождение зависимостей между данными, включенными в этот
класс. В контексте KDD описание считается более важным, чем про-
прогноз. Это контрастирует с распознаванием образов и применением
машинного обучения (такого, как распознавание речи), где прогноз
обычно является непосредственной целью.
Перечислим основные принципы решения задач Data Mining.
1. Классификация изучает способы построения функции, способ-
способной отнести элемент данных к одному или нескольким извест-
известным классам (классифицировать элемент). Классификационные
методы могут использоваться в областях исследования поведе-
поведения финансового рынка, автоматизированного выявления объ-
объектов в больших базах данных и многих других.
2. Регрессия изучает построение функций, способных связать
предъявленный элемент данных с важной предсказывающей
переменной. Существует множество примеров применения
регрессии: прогнозирование прироста биомассы в лесу на
основе микроизмерений, оценка вероятности смертельного
17 В.Н. Вагин и др.

514 Базовые принципы построения систем обучения [Гл. 11
исхода для пациента по результатам диагностических тестов,
прогнозирование спроса на новый товар как функция рекламной
компании.
3. Кластеризация (группирование) обычно относится к задачам
определения — то есть получения конечного множества классов,
групп, категорий описаний данных. Полученные классы могут
быть взаимоисключающими (непересекающимися) или допус-
допускать более широкое представление в виде иерархии классов. В
качестве примеров применения кластеризации можно назвать
такие задачи, как обнаружение однородных подгрупп для поль-
пользователей маркетинговых баз данных, определение подкатего-
подкатегорий спектров инфракрасных измерений небесных тел. С кла-
кластеризацией тесно связана задача оценки плотности вероятно-
вероятности, которая формулируется как получение оценки возможной
многомерной функции плотности вероятности всех переменных
(полей) для базы данных.
Следующим этапом Data Mining является разработка алгоритмов
для решения ранее сформулированных задач. Три главных компонен-
компонента любого алгоритма Data Mining включают представление модели,
оценку модели и метод поиска решения.
1. Представление модели — это язык для описания выявленных
классов. Если представление слишком ограничено, тогда ника-
никакое количество подготовительного времени и никакое количе-
количество примеров не смогут обеспечить точную модель данных. Та-
Таким образом, важно, чтобы аналитик полностью осознавал пред-
представительное допущение, которое может быть присуще конкрет-
конкретному методу. Также очень важно, чтобы автор (разработчик) ал-
алгоритма точно указал, какое представительное допущение было
принято конкретным алгоритмом. Заметим, что более мощные
представительные средства для моделей повышают опасность
чрезмерного соответствия полученного описания класса обуча-
обучающему множеству, которое может закончиться снижением точ-
точности обнаруживаемых данных.
2. Оценка модели позволяет установить, насколько те или иные
классы (сама модель и ее параметры) соответствуют критериям
процесса KDD. Оценка предполагаемой точности основана на
пересечении утверждений. Оценка описательного качества мо-
модели включает точность предсказания, новизну, практическую
полезность и понятность подходящих моделей. Для такой оценки
используются как логический, так и статистический критерии.
Например, принцип максимальной вероятности выбирает пара-
параметры для модели, которая наилучшим образом подходит для
тренажерных данных.

11.2] Задачи извлечения знаний из баз данных 515
3. Метод поиска объединяет поиск параметров и поиск модели.
- Здесь предусматривается поиск для параметров, которые
надо оптимизировать, критериев оценки модели на основе
исследуемых данных и фиксированного способа представ-
представления модели.
- Поиск модели заключается в исследовании семейства моде-
моделей, для каждой из которых дается оценка с использовани-
использованием метода поиска параметров. При реализации метода по-
поиска модели обычно используются приемы эвристического
поиска, т. к. размер пространства возможных моделей часто
не позволяет (даже запрещает) применить полный перебор.
Рассмотрим наиболее популярные методы решения задач Data
Mining в зависимости от того, какая модель представления знаний
может быть выбрана.
Деревья решений и решающие правила имеют простую форму
представления, что делает такие модели относительно несложными
для пользователя. Однако ограничения для представления знаний в
виде дерева или решающего правила способны существенно понизить
функциональную форму (а значит и силу) самой модели. Усложнение
модели делает ее более эффективной для предсказания, но одновре-
одновременно может быть и более сложной для понимания пользователем.
Существует множество вариантов нахождения решающих деревьев
и решающих правил (алгоритмы для их построения будут подробно
описаны в главе 13). Деревья и решающие правила используются для
предсказательного моделирования, для классификации (этот подход
используется в работах авторов Апта и Хонга, а также Файяда, Дьер-
говского и Вэйра) и регрессии, хотя они в равной степени могут при-
применяться для описательного моделирования, как показано в работе
Агравала.
Методы нелинейной регрессии включают множество разнообраз-
разнообразных приемов, ставящих целью прогнозирование соответствия тех или
иных линейных и нелинейных комбинаций основных функций (сигмо-
идов, сплайнов, многочленов) с комбинациями вводимых переменных.
Примерами являются нейронные сети, адаптивные сплайн методы,
прогнозы последующих регрессий и т. д.
Методы, основанные на примерах, базируются на простых идеях.
Для описания приближенной модели используется множество извест-
известных объектов из базы данных, удовлетворяющих некоторым требо-
требованиям. Далее новые объекты оцениваются по их сходству с этими
«простыми» примерами. Сходство или различие выражается через
расстояние в многомерном пространстве признаков. Такие методы
сочетают в себе классификацию по методу «ближайших соседей»,
регрессионные алгоритмы, подобные алгоритмам, предложенным в
17*

516 Базовые принципы построения систем обучения [Гл. 11
1991 г. Дасарати, и системы вывода, базирующиеся на примерах, как
описано в работе Колоднера, опубликованной в 1993 г. Для методов,
основанных на примерах, важным является наличие метрики, хорошо
разделяющей примеры в пространстве признаков.
Методы, основанные на примерах (так же, как и нелинейная ре-
регрессия), зачастую являются ассимптотически мощными по прибли-
приблизительным характеристикам, но в то же время, бывает трудно интер-
интерпретировать результаты, поскольку сама модель «скрыта» в наборах
данных.
Графовые модели определяют вероятностные зависимости, кото-
которые лежат в основе конкретной модели, использующей графовую
структуру. Принципы работы с такими моделями изложены в ста-
статье Перла за 1988 г. и в более поздней работе Уиттекера. В своей
простейшей форме модель определяет напрямую, какие переменные
непосредственно зависят от других. Естественно, эти модели примени-
применимы для переменных с дискретными и категориальными значениями,
но возможно и расширение для вещественных значений переменных
в некоторых частных случаях. В задачах искусственного интеллекта
данные модели были первоначально внедрены в рамках вероятност-
вероятностных экспертных систем, где структура модели и параметры (условные
вероятности, связанные с дугами графа) задавались экспертами. За
последнее время была проведена работа по созданию методов извлече-
извлечения структуры и параметров графовой модели прямо из базы данных
(авторами таких методов являются Бантайн и Хекерман). Критерии
оценки модели базируются на байесовой форме. Первичные знания,
такие как, например, частичное упорядочение переменных, базиру-
базирующееся на причинных отношениях, могут быть очень полезными в
сокращении пространства поиска для строящейся модели.
В то время, как деревья решений и решающие правила имеют
ограниченное представление, в пропозициональной логике, реляцион-
реляционное обучение (известное также под названием индуктивное логическое
программирование) использует более гибкие средства языка логики
первого порядка. В подобных системах можно легко обнаружить
такие формулы, как X = Y. Многие научные исследования, на-
направленные на поиск методов оценки модели реляционного обучения,
являются логическими по происхождению.
Перечислим основные проблемы, возникающие перед разработчи-
разработчиками при исследованиях в области KDD.
Большие базы данных. Базы данных с сотнями полей и таблиц,
миллионами записей и мультигигабайтными размерами в настоящее
время являются обычными, и уже начинают появляться терабайтные
A012 байт) базы данных. Для работы с такими базами даных тре-
требуются специальные приемы, включая аппроксимационные методы и
развитие мощных средств параллельной обработки.

11.2] Задачи извлечения знаний из баз данных 517
Большая размерность. Часто встречается не только большое чи-
число записей в БД, но и очень большое число полей (атрибутов, пе-
переменных), поэтому важна проблема размерности. В случаях повы-
повышения размера поискового пространства возникают проблемы для
представления модели (комбинаторный взрыв). Также повышается
вероятность, что алгоритм Data Mining найдет фиктивные, ложные
классы. Способ решения таких проблем — разработка методов для
уменьшения размерности задач, а также использование информации,
полученной ранее, чтобы выявлять «лишние» переменные.
Переполнение. Результат работы алгоритма может сильно зави-
зависеть от представительности входного набора данных. Если объем
данных невелик, алгоритм может исчерпать данные, получив при
этом плохую модель. Возможные решения включают в себя прежде
всего статистические методы и стратегии.
Изменения данных и знаний. Быстрая смена (нестационарных)
данных может сделать прежде сформированные классы неверными. К
тому же переменные, определенные в данном приложении БД, могут
быть со временем модифицированы, удалены или расширены новыми
определениями. Возможные решения включают инкрементные мето-
методы для обновления классов и обработку изменений в данных, как
средство для поиска изменений в классах.
Отсутствующие и зашумленные данные. Эта проблема особенно
остра в деловых БД. В США данные переписи, по сообщению, содер-
содержат ошибки в 20% случаев. Важные данные могут быть потеряны,
если БД не была разработана с расчетом на применение систем KDD.
Возможные решения включают более сложные статистические стра-
стратегии для идентификации скрытых переменных и зависимостей.
Комплексные отношения между полями. Иерархически структу-
структурированные атрибуты или переменные, отношения между атрибутами
и более сложные средства для представления понятия о содержи-
содержимом БД нуждаются в алгоритмах, которые способны эффективно
использовать подобную информацию. Исторически сложилось, что
алгоритмы поиска в данных были разработаны для простых записей
«атрибут-значение», хотя уже разрабатываются новые методы для
анализа дифференцированных отношений между переменными.
Понятность классов. Во многих приложениях важно предста-
представить «открытые» знания наиболее понятным для человека образом.
Возможные решения включают графические представления, правила
структурирования с ориентированными ацикличными диаграммами,
естественно-языковое представление и методы для визуализации дан-
данных и знаний.
Взаимодействие с пользователем и знаниями, полученными ра-
ранее. Многие реальные системы KDD не являются интерактивными и
не могут использовать предшествующие знания о проблеме, кроме са-

518 Базовые принципы построения систем обучения [Гл. 11
мых простых случаев. Использование базовых знаний было бы крайне
валено на всех шагах процесса извлечения знаний из данных.
Интеграция с другими системами. Одиночная система поиска
знаний из данных не может быть очень полезной. Возникает проблема
интеграции с системами визуализации, средствами чтения данных с
сенсоров в реальном времени, средствами взаимодействия с СУБД.
11.3. Способы представления исходной
информации в интеллектуальных системах
Человек, решающий задачу выбора целесообразного поведения в
той или иной ситуации, прежде всего анализирует существенные и
несущественные обстоятельства, влияющие на принимаемое решение.
Процесс выделения существенных для данной задачи обстоятельств
можно представить как разбиение входных ситуаций на классы, об-
обладающие тем свойством, что все ситуации из одного класса требуют
одних и тех же действий. Оценка входной ситуации человеком проис-
происходит на основе совокупности сигналов, поступающих от его органов
чувств. На основании этих сигналов мозг вырабатывает команды,
которые обеспечивают реакцию человека на ситуацию. Сигналы по-
поступают от рецепторов (зрительных, тактильных и др.). Совокупность
таких сигналов формирует представление человека о ситуации.
Вычислительная машина, на которой моделируется аналогичный
процесс, должна обладать возможностью получать описание входной
ситуации от внешних «рецепторов» в виде различных наборов дан-
данных. Очевидно, объем информации, который получает компьютер,
несоизмеримо меньше объемов информации, с которыми имеет дело
человек; кроме того, такая информация будет представлена исклю-
исключительно в численной форме. Для того, чтобы эффективно оценить,
относятся ли различные ситуации к одному классу, или, по-другому,
к понятию, интеллектуальная система должна иметь возможность
рассмотреть и оценить ряд конкретных примеров таких ситуаций,
включенных в обучающее множество.
Обучение на основе примеров является типичным случаем индук-
индуктивного обучения и широко используется в интеллектуальных систе-
системах. На основе предъявленных примеров (и, возможно, контрприме-
контрпримеров) интеллектуальная система должна сформировать общее понятие,
охватывающее примеры и исключающее контрпримеры. Источником
примеров, на которых осуществляется обучение, может быть учи-
учитель — то есть лицо, которое заранее знает концепцию формируе-
формируемого понятия и подбирает наиболее удачные обучающие выборки.
Источником примеров для обучения может быть внешняя среда, с
которой взаимодействует интеллектуальная система. В этом случае
обучающие выборки формируются случайным образом в зависимо-
зависимости от внешних факторов. Обучение на таких выборках существенно

11.3] Способы представления исходной информации 519
сложнее. Наконец, источником примеров для обучения может стать
сама интеллектуальная система. Например, в случае взаимодействия
интеллектуального робота с внешней средой действия самого робота
могут привести к созданию обучающей выборки, то есть образуется
множество сходных ситуаций с известными результатами, которые
можно затем обобщить.
Если обучающие выборки содержат только положительные приме-
примеры формируемого понятия, обучение на таких примерах может приве-
привести к построению чрезмерно общих индуктивных понятий. Такие по-
понятия смогут охватить все предъявленные примеры, но с их помощью
бесполезно пытаться различить два близких объекта, принадлежащих
на самом деле к разным классам. Гораздо эффективнее использовать
для обучения множество, содержащее как положительные, так и от-
отрицательные примеры некоторого понятия. При этом снижается риск
получения чрезмерно общих индуктивных описаний.
Для системы машинного обучения принципиально важным явля-
является вопрос, что поступает на вход системы, в каком виде предъяв-
предъявляются примеры понятия, включенные в состав обучающего множе-
множества. Все рассмотренные ниже методы решения задач индуктивного
построения понятий базируются на концепции признакового описа-
описания примера понятия, а именно: любой элемент обучающей выбор-
выборки, который может быть представлен в системе, полностью опре-
определяется набором свойств, или признаков. Такое задание объекта
исследования называется признаковым описанием объекта. Нами не
рассматривается случай, когда необходимо сгруппировать по классам
объекты, характерной чертой которых является наличие структуры:
примером таких объектов могут быть химические соединения, кри-
кристаллические решетки, графы и др. Также мы не будем рассматри-
рассматривать случай, когда описание объектов классификации задано в виде
формул исчисления предикатов первого порядка (описание ситуаций,
семантических сетей и т.п.). Подобные модели описания объектов
крайне интересны, но их рассмотрение выходит за рамки данной
книги.
Традиционно объекты, рассматриваемые в рамках интеллектуаль-
интеллектуальной системы, задаются в виде набора признаков. Описания различных
объектов отличаются значениями признаков. Под обобщением обыч-
обычно понимается переход от рассмотрения единичного объекта о или
некоторой совокупности объектов О к рассмотрению обобщенного
понятия Z), которое
а) отображает характерные для этого множества логические отно-
отношения между значениями признаков;
б) является достаточным для разделения объектов, принадлежа-
принадлежащих множеству, и объектов, ему не принадлежащих с помощью
некоторого правила распознавания.

520 Базовые принципы построения систем обучения [Гл. 11
Для описания объекта будем использовать признаки
А\, ^2,..., Ап. Каждый объект о Е О характеризуется набором
конкретных значений этих признаков (атрибутов) о = {ai, a2,..., an},
где ai — значение i-ro признака. Такое описание объекта называют
признаковым описанием; признаками могут служить цвет, размер,
форма, скорость, вес, цена и т.п. Обозначим через
множество допустимых значений i-ro признака: a^ E
Формирование понятий по сути является процессом выделения
закономерностей, свойственных множествам объектов.
Рассмотрим отдельные виды признаков. Основой для работы лю-
любой системы индуктивного формирования понятий является множе-
множество векторов признаков, описывающих объекты. Входной вектор X
содержит компоненты х^ называемые далее признаками, или атрибу-
атрибутами объекта. Значения, которые могут принимать признаки объекта,
относятся к трем основным типам: количественные, или числовые,
качественные и шкалированные. То, какие значения принимают при-
признаки, может оказать большое влияние на процесс обобщения.
В случае числовых признаков на множестве значений призна-
признаков может быть введена метрика, позволяющая дать количествен-
количественную оценку значения признака. Это значит, что различные значения
признаков можно сравнивать между собой в количественном плане.
Часто такие значения являются результатом измерений физических
величин, таких, как длина, вес, температура и др.
В случае, если признаки могут иметь качественный характер, но
при этом их значения можно упорядочить друг относительно друга,
говорят, что такие значения образуют ранговую или порядковую шка-
шкалу. Примерами таких шкал порядка могут быть ряды типа {большой,
средний, маленький} или {горячий, теплый, холодный}. С помощью
таких шкал порядка можно судить, какой из двух объектов является
наилучшим, но нельзя оценить, сколь близки или далеки эти объекты
по некоторому критерию.
Третий случай заключается в том, что значения признаков имеют
чисто качественный характер, связать эти значения между собой не
удается. Примерами таких значений могут быть цвет = {красный,
желтый, зеленый} или материал = {стекло, дерево, пластмасса, же-
железо}.
Рассмотрим пример задания обучающей выборки с разными ти-
типами признаков. Ниже представлена выборка описаний состояний
нескольких больных, страдающих некоторым заболеванием, а также
состояний людей, не страдающих этим заболеванием.
Пример обучающей выборки для К^~ и К~ приведен в табл. 11.1.
Каждая строка в таблице соответствует одному объекту класси-
классификации. Любой объект характеризуется семью признаками, среди
которых есть количественные (температура), качественные (пол, что
болит) и шкалированные (например, возраст). Выборки такого типа

11.3]
Способы представления исходной информации
521
Таблица 11.1
Выборка
1
2
3
4
5
6
7
8
Возраст
Пожилой
Пожилой
Пожилой
Средний
Пожилой
Пожилой
Пожилой
Пожилой
ТТотт
11UJ1
Жен.
Муж.
Муж.
Жен.
Жен.
Муж.
Муж.
Муж:.
Стадия
болезни
Средняя
Средняя
Поздняя
Начальная
Начальная
Начальная
Начальная
Начальная
Что
болит
Голова
Голова
Голова
Голова
Нет
Спина
Нет
Голова
Темпера-
Температура, °С
36,6
36,4
36,7
37,8
38,0
36,3
36,6
38,2
Прочие
ощущения
Озноб
Озноб
Озноб
Никаких
Нет аппетита
Нет аппетита
Нет аппетита
Озноб
Выборка К
1
2
3
4
Возраст
Молодой
Средний
Пожилой
Пожилой
Пол
Муж:.
Жен.
Жен.
Муж.
Стадия
болезни
Средняя
Начальная
Поздняя
Что
болит
Нет
Живот
Руки
Ноги
Темпера-
Температура, °С
36,6
37,7
36,7
36,4
Прочие
ощущения
Никаких
Тошнота
Никаких
Нет аппетита
являются исходными данными для алгоритмов распознавания и клас-
классификации.
Поскольку задача распознавания состоит в отнесении объекта к
одному из классов признаков, одним из способов сравнения объектов
является их сравнение на основе мер близости (сходства). Если из-
известны объекты некоторого класса, то можно оценить меру близости
объекта классу на основании значений меры близости (или сходства)
данного объекта и объектов, принадлежащих классу. Объект следует
отнести к тому классу, для которого мера близости максимальна.
Для числовых объектов мерой близости является расстояние. Рас-
Расстояние D(X, Y) между двумя объектами X и У может быть опреде-
определено по одной из формул:
Z •
k=l
\(xk-ykn
к=1
,Y) = max \xk - Ук\ ,
к

522 Базовые принципы построения систем обучения [Гл. 11
где X, Y — векторы (наборы) значений признаков двух объектов,
хк-> У к — соответствующие значения k-го признака объектов, п — об-
общее число признаков. В дальнейшем будем использовать обозначение
D(X,Y), когда расстояние можно ввести любым из перечисленных
способов. Отметим, что если речь идет о расстоянии по Евклиду (фор-
(формула Di(X,Y)), будем применять также общепринятое обозначение
\X-Y\.
Признаки, характеризующие объект, можно рассматривать как
детерминированные и вероятностные. Детерминированными призна-
признаками будем называть признаки, принимающие конкретные числовые
значения. Достаточно часто для определения близости двух объектов
используют значения признаков, не совпадающие с действительными,
а предварительно подвергают эти значения масштабированию.
Приближенные, (размытые) признаки характерны тем, что при
измерении значения такого признака возможны погрешности, то есть
нельзя с уверенностью сказать, каково значение признака. Для при-
приближенных признаков в качестве меры близости может быть исполь-
использован риск, связанный с решением о принадлежности объекта классу.
Рассмотрим подробнее различные подходы к решению задачи об
отнесении объекта к некоторому классу. Самым простым вариантом
системы, решающей задачу распознавания, являются системы без
обучения. В таких системах заранее известны классы, к которым
могут относиться предъявляемые объекты, а также критерии отне-
отнесения объекта к классу. Примером такой системы может служить
система автоматического контроля качества деталей. Предположим,
что деталь характеризуется двумя признаками: это длина и диаметр.
Существует два класса деталей — годные и бракованные. Деталь
считается годной, если ее параметры удовлетворяют условиям: дли-
длина = 100 =Ь 5 мм, диаметр = 8 ± 0, 5 мм. Таким образом, нам известны
как сами классы, так и критерии отнесения предъявленной детали к
каждому из классов.
Более сложными являются системы с обучением. В системах с
обучением не задан алгоритм разделения предъявляемых объектов
на классы. Процесс создания и оптимизации такого алгоритма и на-
называется обучением. Для обучения используется определенный набор
объектов, называемый далее обучающим множеством или обучающей
выборкой. Далее мы остановимся на рассмотрении систем с обучением
более подробно.
В системах с обучением структура алгоритмов, классифицирую-
классифицирующих объекты, тесно связана с видом информации, представленной
в обучающей выборке. Будут рассмотрены два варианта обучающих
выборок. В первом случае исходная информация, на основании ко-
которой создается искомый алгоритм, представлена в виде обучающего
множества, не разделенного на классы. Это значит, что для объектов
обучающего множества не задано, к каким классам они принадле-

11.4] Структурно-логические методы обобщения 523
жат. Таким образом, заранее неизвестны не только характеристики
классов, но и их количество. Задача обучения сводится к разделению
объектов выборки на группы объектов, «сходных» друг с другом
(классы). Процесс построения алгоритма, разделяющего затем объ-
объекты по степени их сходства, называется обучением «без учителя».
Примером задач такого типа могут быть задачи классификации расте-
растений, химических соединений, обработка статистических исследований
и т. п.
В другом случае исходная информация представлена в виде мно-
множества объектов, для каждого из которых известно, к какому из
классов он отнесен. При этом нам неизвестны критерии отнесения
объектов к какому-либо классу. В случае, если в выборку вошли
не все примеры классов, можно считать, что число классов также
неизвестно. Здесь задача обучения состоит в построении алгоритма,
позволяющего отнести предъявленный объект к одному из известных
классов. Процесс построения такого алгоритма назовем управляемым
обучением или обучением «с учителем». Будем считать, что алго-
алгоритм распознавания построен правильно, если для любого объекта из
обучающей выборки он дает правильный результат.
Частным случаем алгоритмов обучения с учителем является за-
задача формирования единственного обобщенного понятия на основе
предъявленного множества примеров и контрпримеров данного поня-
понятия. Действительно, если объекты обучающей выборки относятся к
классам К\, К^-,... Кп, мы можем рассмотреть
отдельно задачу построения алгоритма распознавания для
класса К.^ считая при этом объекты, принадлежащие классам
К\,... Ki-i, Ki+i,..., Кп, — контрпримерами.
11.4. Структурно-логические методы обобщения
В системах, моделирующих мышление, обобщение понимают как
процесс получения знаний, объясняющих имеющиеся факты, и спо-
способных объяснять, классифицировать или предсказывать новые. В
общем виде задача обобщения была сформулирована Михальским сле-
следующим образом: по совокупности наблюдений (фактов) F, совокуп-
совокупности требований и допущений к виду результирующей гипотезы Н, и
совокупности базовых знаний и предположений, включающих знания
об особенностях предметной области, выбранном способе представле-
представления знаний, допустимых операторов, эвристик и др., сформировать
гипотезу Н : Н => F (Н «объясняет» F).
Форма представления и общий вид гипотезы Н, а также выбран-
выбранные модели обобщения зависят от цели обобщения и выбранного спо-
способа представления знаний. Согласно Михальскому, можно выделить
модели обобщения по выборкам и модели обобщения по данным. В
первом случае совокупность фактов F имеет вид обучающей вы-

524 Базовые принципы построения систем обучения [Гл. 11
борки — множества объектов, каждый из которых сопоставляется с
именем некоторого класса. Целью обобщения в этом случае может
быть
- формирование понятий, то есть построение по данным обучаю-
обучающей выборки для каждого класса максимальной совокупности
его общих характеристик;
- классификация, или построение по данным обучающей выборки
минимальной совокупности характеристик, которая отличала
бы элементы одного класса от элементов других классов;
- определение закономерности последовательного появления со-
событий.
К моделям обобщения по выборкам относятся лингвистические
модели, методы автоматического синтеза алгоритмов и программ по
примерам. В моделях обобщения по данным априорное разделение
фактов по классам отсутствует. Здесь могут ставиться такие цели:
• получение гипотезы, обобщающей данные факты;
• выделение образов на множестве наблюдаемых данных, группи-
группировка данных по признакам;
• установление закономерностей, характеризующих совокупность
наблюдаемых данных.
По способу представления знаний и допущений на общий вид объ-
объектов, вошедших в обучающую выборку, методы обобщения делятся
на методы обобщения по признакам и структурно-логические (кон-
(концептуальные) методы. В первом случае объект обучающей выборки
представляются в виде совокупности значений косвенных признаков.
Методы обобщения и распознавания различаются для качественных
и количественных признаков. В формально-логических системах, ис-
использующих структурно-логические методы обобщения, вывод общих
следствий из данных фактов называется индуктивным выводом. Пра-
Правило вывода гипотезы Н из фактов F называют индуктивным, если
из истинности Н следует истинность F, а обратное неверно.
Гипотезы, полученные в результате индуктивного вывода, нуж-
нуждаются в оценке разумности, достоверности. В ряде исследований
для подтверждения или отрицания выдвигаемой гипотезы использу-
используются методы автоматического порождения новых элементов обучаю-
обучающей выборки, которые выдаются затем для классификации человеку-
эксперту. Решающее правило переопределяется, пока не будет достиг-
достигнута равновесная ситуация.
Рассмотрим кратко связь между задачей обобщения и классифи-
классификации и задачами, решаемыми в рамках теории вероятностей и ма-
математической статистики. Фактически, в математической статистике
также ставятся и решаются задачи вывода новых знаний на основании

11.4] Структурно-логические методы обобщения 525
анализа совокупности наблюдений. В статистике устанавливаются
частотные закономерности появления событий, то есть определяются
общий вид и параметры функций распределения вероятностей собы-
событий по данным наблюдений, делаются выводы о степени статисти-
статистической зависимости наблюдаемых случайных величин, принимаются
решения о выборе гипотезы, о характеристиках случайного события
на основании применения байесовской процедуры последовательного
анализа наблюдений. Общая задача формирования гипотез по дан-
данным наблюдений, рассматриваемая как одно из направлений развития
интеллектуальных систем, не ограничивается установлением стати-
статистических закономерностей. Известны формально-логические модели
выдвижения статистических гипотез, рассмотренные в работах Гаека
и Гавранека.
Главной особенностью структурно-логических методов, в отличие
от признаковых методов, является использование в обучающих вы-
выборках объектов, имеющих внутреннюю логическую структуру. Та-
Такими объектами могут быть последовательности событий, иерархи-
иерархически организованные сети, алгоритмические и программные схемы.
Примеры таких объектов молено встретить в работах Р. Михальского,
В. К. Финна, Д.А.Поспелова. Поскольку в следующих главах будут
детально рассмотрены именно методы обобщения по признакам, в
этом разделе мы остановимся подробнее на структурно-логических
методах. Сначала обсудим методы индуктивного вывода в формаль-
формальных исчислениях, а затем — методы обобщения на семантических
сетях.
Основой каждой модели индуктивного вывода является набор пра-
правил (схем) индуктивного вывода. В работах Плоткина за основную
схему вывода была выбрана схема индуктивной резолюции. Приведем
эту схему в обозначениях, данных Михальским:
Р & Fi => К
& |= Fi V F2 => К
^Р & F2 ^ К
или в другой форме
Р & Fi => К
V |= Fi & F2 => К
(знак |= обозначает отношение индуктивного следования).
Эта схема применяется в классическом исчислении предикатов
первого порядка вместе с алгоритмом антиунификации. Результатом
применения правила индуктивной резолюции к двум предложениям
является их «наименее общее обобщение».

526 Базовые принципы построения систем обучения [Гл. 11
Михальский строил схему индуктивного вывода в рамках модифи-
модификации языка исчисления предикатов первого порядка, включающей
обобщенные кванторы и префиксную запись отношений равенства и
неравенства. Помимо принципа индуктивной резолюции используют-
используются следующие схемы вывода:
СТХ & S =>К\= СТХ => К (селекция)
СТХ k[L = Ri)^K |= СТХ & [L = R2] => К,
где Ri С R2 С DOM(L) (расширение)
СТХХ =Ф К |= СТХХ V СТХ2 => К (добавление)
СТХ k[L = a)^K
\=СТХ &[L = [a,...,z]]=>K
СТХ k[L = z}^ К
(переход к интервалу)
F[a]
|= 4vF(y) (классическая индукция).
F[i\
В данных схемах СТХ обозначает контекстное описание свойств
(атрибутов) некоторого индуктивного понятия, полученное ранее.
Схемы вывода позволяют получить «более общие» описания инте-
интересующего нас понятия. Рассмотрим простой пример. Пусть СТХ
соответствует описанию «объекты — круглые», S — «объекты —
коричневые», а К обозначает понятие «мяч» (СТХ & S => К).
Тогда на основании правила селекции можно получить более общее
утверждение: «Круглые объекты являются мячами» (СТХ => К).
Схема формирования гипотез по обучающей выборке (метод «звез-
«звезды») заключается в применении к множеству фактов и полученных
утверждений всех возможных правил вывода (как индуктивных, так и
дедуктивных). На каждом этапе поиска выбирается определенное ко-
количество наиболее «перспективных» согласно выбранным эвристикам
гипотез. Процесс заканчивается, когда достигается цель обобщения.
Правила индуктивного вывода, используемые в ДСМ-методе, осно-
основываются на схемах, предложенных в работах Милля. Принципы
установления причинно-следственных отношений, которые предло-
предложил Милль, основываются на идеях выделения сходства и различия в
наблюдаемых ситуациях внешнего мира. Так, принцип единственного
различия гласит: «Если после введения какого-либо фактора появ-
появляется, или после удаления его исчезает, известное явление, причем
мы не вводим и не удаляем никакое другогое обстоятельство, которое
могло бы иметь в данном случае влияние, и не производим никако-
никакого изменения среди первоначальных условий явления, то указанный
фактор и составляет причину явления».

11.4] Структурно-логические методы обобщения 527
Схематически этот принцип можно описать так: пусть в ситуации,
при наличии факторов а, 6, с наблюдалось появление d] при наличии
факторов 6, с явление d не наблюдалось. Ситуации, относящиеся к
первой группе, назовем положительными примерами, а ситуации из
второй группы — контрпримерами. Для исключения случая, когда d
появляется случайным образом, требуется повторение событий первой
и второй групп не менее п раз. Если п с точки зрения эксперимента-
экспериментатора достаточно для уверенного вывода, то, используя принцип един-
единственного различия, можно утверждать, что а является причиной,
ad — следствием (между and имеет место причинно-следственное
отношение).
Второй основополагающий принцип рассуждения Милля носит
название принципа единственного сходства. Его можно сформулиро-
сформулировать следующим образом: «Если все обстоятельства явления, кроме
одного, могут отсутствовать, не уничтожая этого явления, то это одно
обстоятельство находится в отношении причинной связи с явлением,
при условии, что приняты были все меры к тому, чтобы никаких
других обстоятельств, кроме принятых во внимание, налицо не ока-
оказалось».
Схематическое представление этого принципа Милля выглядит
следующим образом. Пусть многократно (не менее п раз) при нали-
наличии факторов а,Ъ,с наблюдалось появление d. Также наблюдалось
не менее п событий, когда при наличии факторов а, Ъ наблюдалось
появление d. Также имела место группа событий (не менее п), когда
наличие одного лишь фактора а приводило к появлению d. Здесь
все примеры являются положительными. По принципу единственного
сходства отсюда вытекает, что and связаны причинно-следственным
отношением.
Еще один принцип, введенный Миллем, носит название принципа
единственного остатка. Он гласит: «Если вычесть из какого-либо
явления ту часть его, которая, согласно прежним исследованиям, ока-
оказывается следствием известных причин, присутствующих в явлении,
то остаток явления есть следствие остальных причин».
Введем схему для пояснения принципа остатка. Пусть многократ-
многократно (не менее п раз) при наличии факторов а,Ъ,с наблюдалось появ-
появление due. Также многократно наличие факторов Ъ и с приводило к
появлению е. Следовательно, and связаны причинно-следственным
отношением, а факторы 6, с являются возможными причинами е.
При использовании методов индуктивных рассуждений, которые
предложил Милль, важную роль играет способ выделения признаков,
или фактов, посредством которых описывается ситуация. ДСМ-метод
(или метод Джона Стюарта Милля) был реализован научной группой
под руководством В. К. Финна. На основе этого метода можно строить
различные интеллектуальные системы, способные к поиску скрытых
закономерностей в процессе обучения.

528 Базовые принципы построения систем обучения [Гл. 11
Введем три множества: причины А = (ai, a2,..., ар), следствия
В = (Ь]_, &2? • • • ^ Ьт) и множество оценок Q = (<?ь <?2, • • •, Qi)- Выражение
вида
di => bj\ qk
будем называть положительной гипотезой. Такая гипотеза может
быть выражена утверждением: «а^ является причиной bj с оценкой
достоверности (/&» . Выражение вида
ai ^> bj; qk
будем называть отрицательной гипотезой и свяжем его с утвержде-
утверждением «ai не является причиной bj с оценкой достоверности qk». Далее
будем положительные гипотезы обозначать кратко как п+ г j /с, а
отрицательные — как п~ i j к. Среди значений qk выделим два специ-
специальных, которые можно обозначить как 0 и 1. Значение 0, приписанное
положительной или отрицательной гипотезе, означает, что соответ-
соответствующее утверждение является ложным. Приписывание гипотезам
значения оценки, равного 1, означает, что данная гипотеза является
тождественно истинной. Все остальные оценки, отличные от 0 и 1,
будут представляться рациональными числами вида s/n, где величина
п характеризует «дробность» используемых оценок достоверности.
Отметим, что чем больше п, тем с большей точностью оценивается
степень достоверности гипотез.
Суть ДСМ-метода в следующем. Рассматривается группа положи-
положительных примеров, в которых ищем некоторую часть описания объек-
объектов, общую для определенной совокупности примеров из группы. Если
такие фрагменты описаний удалось выделить, они могут считаться
кандидатами в причины. Таких кандидатов может быть несколько.
Образуем матрицу М+, в которой строки соответствуют выделенным
кандидатам а^, а столбцы — следствиям bj. На пересечении строк и
столбцов будут записываться оценки достоверности qk для гипотез
n+ i j к. Для множества отрицательных примеров аналогично стро-
строится матрица М~, содержащая оценки достоверности отрицательных
гипотез п~ г j к. Отметим, что кандидаты в причины в матрицах М+
и М~ могут частично совпадать.
Для оценки обоснованности гипотезы в ДСМ-методе используется
квантор /ш, т Е {0,1/(п — 1), 2/(п — 1),..., 1}. Значение т = 1/(п — 1)
соответствует гипотезам, достоверность которых неизвестна, значение
т = 1 — истинным гипотезам. Если применяемое правило вывода под-
подтверждает гипотезу, то значение т возрастает, если не подтверждает,
то значение т уменьшается.

11.4] Структурно-логические методы обобщения 529
На каждом шаге работы ДСМ-метода множества положительных
и отрицательных примеров могут пополняться. Новые наблюдения
будут либо подтверждать, либо опровергать сформированные гипоте-
гипотезы. В этом случае оценки достоверности построенных гипотез надо
либо увеличивать, либо, соответственно, уменьшать. Таким образом,
в процессе накопления новой информации оценки гипотез или при-
приближаются к 0 или 1, или ведут себя «неустойчиво». Гипотезы, досто-
достоверность которых стала меньше некоторого нижнего порога, могут
исчезать из матриц М+ и М~. При достижении некоторого верхнего
порога достоверности гипотеза может быть признана в системе как
установленный факт.
Новые гипотезы формируются не только на основании выделения
в примерах определенного сходства. Они могут использовать также
метод различия. Различие в описаниях групп примеров может порож-
порождать гипотезы, включаемые в М+ и М~. Кроме того, в ДСМ-методе,
помимо прямой реализации идей Милля, используются некоторые
выводы по аналогии. Для этого на множестве описаний объектов
вводится тем или иным способом понятие сходства. Если, например,
речь идет о структурных формулах химических соединений, то мерой
сходства для них может быть совпадение самих структур при различ-
различных химических элементах в их позициях, либо, наоборот, наличие в
некоторых фиксированных позициях структуры одинаковых элемен-
элементов. Существует в этом методе и правило отрицательной аналогии,
а также градация тех и других правил по существенности сходства.
Таким образом, ДСМ-метод демонстрирует возможность проведения
правдоподобных рассуждений весьма широкого спектра.
Получивший широкую известность GUHA-метод позволяет фор-
формировать множество «всех интересных гипотез» о наблюдаемых дан-
данных. Гипотезы, порождаемые GUHA-методом, имеют вид ф ^ (р, где
ф и ср — утверждения, имеющие единственную свободную перемен-
переменную ж, а знак «^» означает связывающий х ассоциативный или
индуктивный квантор: (~х)(ф,(р). Выражение ф ^ (р в зависимости
от выбранного квантора может служить для представления широкого
диапазона зависимостей между ф и ср (от логического следования, до
статистической корреляции). Для утверждений специального класса
метод позволяет сформировать такое подмножество гипотез, что все
остальные следуют из них в соответствии с принятым набором правил
вывода. Для оценки рациональности ответа на вопрос / индуктивного
вывода вводится вероятностная мера наблюдения.
В качестве языка представления знаний (отдельно рассматривают-
рассматриваются языки представления эмпирических и теоретических утверждений)
используется модификация языка исчисления предикатов первого по-
порядка с обобщенными кванторами. Каждому квантору q ставится в
соответствие функция Asfq, вычисляющая значение его истинности
на каждой модели < М, /i, /2, • • •, /п > •> где М — непустое множество

530 Базовые принципы построения систем обучения [Гл. 11
из некоторого семейства М, а Д, Д,..., fn — набор логических функ-
функций, определенных на этом множестве.
Квантор q, определенный на моделях < М,ф,ср >, называют
ассоциативным в следующем случае. Пусть ам — количество элемен-
элементов М, на которых ф и ср одновременно истинны, Ъм — количество
элементов, на которых ф истинно, а (р — ложно; см : ф ложно, (р
истинно; Aм'- как ф, так и (р ложно.
Тогда если umi ^ «М2,^М1 < Ъм2,см\ ^ см2, и dMi ^ ^М2,
то для ассоциативного квантора условие Asfq < М.2-)ф-)^р >= 1,
влечет Asfq < Mi, ф,<р >= 1. Определение импликативного квантора
аналогично для условий ам1 ^ ^М2 и 6мi ^ ^М2-
Для задания GUHA-метода требуется определить ассоциативный
или импликативный квантор ^, квантор эквивалентности 4=> и еще
ряд характеристик (например, запрет или разрешение использовать
дедуктивные правила вывода). Особое внимание уделяется методам
формирования гипотез ф ~ (/?, таких, что ф представляет собой
элементарную конъюнкцию, а (р — элементарную дизъюнкцию од-
одноместных предикатов. С помощью языка, использующего понятие
случайной модели < Ма, Д, /2,..., /п >, где а Е ? — случайный
параметр, вводится вероятностная мера достоверности гипотез и рас-
рассматриваются статистические гипотезы. Важный класс ассоциатив-
ассоциативных (и импликативных) кванторов образуют кванторы, функции Asf
которых являются тестами для проверки статистических гипотез.
GUHA-метод нашел применение в медицине, социологии, лингвисти-
лингвистике, строительстве.
Применение аппарата семантических сетей для решения задач
классификации и формирования понятий позволяет получать обоб-
обобщенные представления множеств объектов, имеющие наглядную се-
семантическую трактовку, и использовать в процессе обобщения семан-
семантику таких понятий, как «признак», «имя», «класс», «отношение».
Роль языка представления наблюдений и классов (понятий) играет
выбираемый формализм семантической сети.
Рассмотрим методы обобщения на сетях. Пусть Z — множество
объектов. Каждый объект z E Z представляется сетью, называемой
семантическим графом, который включает вершины двух типов:
объектные и предикатные. Объектной вершине приписывается имя
объекта, имя базового класса объекта и вектор его признаков.
Предикатной вершине приписывается имя отношения (возможно,
с отрицанием). Семантический граф, предназначенный для
представления объекта z E Z, распадается на иерархически
упорядоченное множество р-подграфов, служащих для представления
объекта г, его частей (р-потомков), частей его частей и т.п.

11.4] Структурно-логические методы обобщения 531
Обобщенный семантический граф также представляется в виде
набора обобщенных р-подграфов (ор-подграфов). Каждый ор-подграф
предназначен для представления множества М = т(д) объектов.
Объектной вершине первого уровня op-подграфа приписывается имя
множества М, имя базового класса Т: М С Т и совокупность /i огра-
ограничений на изменения значений признаков объектов из М. Объектная
вершина v второго уровня взвешена именем множества Mv, которое
может быть получено из множеств, представимых на ор-подграфах
применением к ним конечного числа операций объединения и пере-
пересечения. Предикатным вершинам op-подграфов приписаны выраже-
выражения логики исчисления высказываний, в которых роль высказываний
играют имена отношений между объектами. На тг-предикатных вер-
вершинах обобщенного семантического графа отображаются отношения,
выполняющиеся на множестве значений признаков различных объек-
объектов.
Обобщения д на семантической сети получаются применением
к элементам д Е v+ операторов обобщения, таких, например, как
удаление вершины из графа, замена значения признака множеством
значений, замена имени отношения Q на предикатной вершине вы-
выражением L = Q V R. Часто обобщение формируется «от против-
противного». За исходный элемент принимается «наиболее общий» граф д,
покрывающий все элементы базового класса Т. Все остальные обоб-
обобщенные семантические графы получаются в результате применения
к д конечного числа ограничивающих операторов, таких, например,
как ввод предикатной вершины, ввод конъюнктивного члена в пре-
предикатную вершину, удаление дизъюнктивного члена из предикатной
вершины, сужение допустимого множества изменения значений при-
признака. Процесс формирования обобщенных представлений классов
ведется по уровням обобщенного семантического графа (согласно
иерархии р-подграфов), начиная с нижних, методом ветвей и гра-
границ.
Рассмотрим несложный пример обобщения на семантической сети.
Пусть имеются два утверждения:
1. «Если кусок железа 1 нагреть до температуры 1500 °С, то он
расплавится».
2. «Если кусок железа 2 нагреть до температуры 2000 °С, то он
расплавится».
Пусть BI — предикат «быть куском железа», HEAT — «нагреть»,
MELTS — «расплавиться». Тогда можно записать:
1) В1(Ъй1)ШЕАТ(Ъй1,1Б00°С) -> MELTS'(bit 1);
2) BI(bit2)kHEAT(bit2, 2000°С) -> MELTS(bit2).

532 Базовые принципы построения систем обучения [Гл. 11
Посылкам вывода в данных выражениях соответствуют семанти-
семантические графы G\ и G2, представленные на рис. 11.2 а, б. Обобщен-
1/
HEAT
2
ob
Т°
I
1500 °С
G1
MELTS
G2
1Х
HEAT
2
ob
Т°
I
2000 °С
MELTS
Рис. 11.2.
ный семантический граф, соответствующий наименее общему обоб-
обобщению графов G\ и G2, обозначим G0. Этот граф представлен на
рис. 11.3. Обобщенному семантическому графу G0 соответствует пре-
предикат Ig°(Xj t), эквивалентный выражению
BI(x)&HEAT(x,t)&A500°C
2000°С) и
Vx, t(IGo(x, t) => MELTS(x)),
или «Если любой кусок железа нагреть до температуры от 1500 °С до
2000 °С, то он расплавится». Чтобы проверить, относится ли новый
граф G к классу таких ситуаций, необходимо убедиться в изоморфной
наложимости G0 на некоторый подграф семантического графа G.
Если такое наложение возможно, то семантический граф G относится
к тому же классу ситуаций, что и графы G\ и G2.

11.4]
Структурно-логические методы обобщения
533
ob
/
BI
/ 1 ob
HEAT
2
Т°
1500°-
2000° С
MELTS
Рис. 11.3.
Все перечисленные выше методы предоставляют возможность ра-
работы с объектами, обладающими внутренней структурой. Такой вид
обобщения, безусловно, один из наиболее сложных. В следующей
главе мы рассмотрим методы обобщения объектов по признакам.

Раньше, чем разрывать навозную кучу,
надо оценить, сколько на это уйдет
времени и какова вероятность того,
что там есть жемчужина.
А. Б. Мигдал
Глава 12
ЗАДАЧА ОБУЧЕНИЯ «БЕЗ УЧИТЕЛЯ»
В этой главе будет рассмотрен класс алгоритмов, решающих за-
задачу обучения «без учителя». Важность данного класса алгоритмов
в том, что реальные признаки, описывающие объекты распознава-
распознавания, очень часто бывают именно количественными, или числовыми.
Известно, что человек плохо воспринимает информацию, представ-
представленную в виде больших наборов чисел. Первым и крайне важным
этапом решения задачи обобщения в таком случае будет переход от
количественных признаков к признакам качественным или хотя бы
к шкалируемым. Здесь большую помощь могут оказать алгоритмы
рассматриваемого типа. Дадим более строгую формулировку задачи
обучения «без учителя».
Пусть обучающая выборка содержит М объектов:
X = {Xi, X2,... Хм}- Каждый из этих объектов представляет
собой n-мерный вектор Xi значений признаков:
Xi =< Хц,Хг2,...,ХгП >,
где Xij — значение j-ro признака для г-го объекта, п — количество
признаков, характеризующих объект.
Напомним, что признаки, используемые для описания объекта,
чисто количественные, к ним применимы введенные в предыдущей
главе меры близости.
Требуется в соответствии с заданным критерием разделить набор
X на классы, количество которых заранее неизвестно. Под критерием
подразумевается мера близости всех объектов одного класса между
собой. Будем считать, что работа алгоритма завершена успешно, если
классы, сформированные в результате работы алгоритма, достаточно

12.1] Алгоритм, основанный на понятии порогового расстояния 535
компактны и, возможно, выполнены некоторые дополнительные кри-
критерии.
При решении задачи обучения «без учителя» самыми несложными
являются алгоритмы, основанные на мерах близости. Для достижения
цели — компактного формирования классов — введем понятие точки-
прототипа, или точки в n-мерном пространстве признаков, являющей-
являющейся наиболее «типичной» представительницей построенного класса. В
дальнейшем расстояние от объекта до класса будет заменяться рас-
расстоянием от объекта до точки-прототипа. Точка-прототип может быть
сопоставлена каждому сформированному классу, и при этом вовсе
не обязательно существование реального объекта, соответствующего
точке-прототипу. Представим алгоритмы этого типа на нескольких
примерах.
12.1. Алгоритм, основанный на понятии порогового
расстояния
Пороговый алгоритм — один из самых несложных алгоритмов,
базирующихся на понятии меры близости. Критерием отнесения объ-
объекта к классу здесь является пороговое расстояние Т. Если объ-
объект находится в пределах порогового расстояния от точки-прототипа
некоторого класса, то такой объект будет отнесен к данному классу.
Если исследуемый объект находится на расстоянии, превышающем
Т, он становится прототипом нового класса. Самая первая точка-
прототип может выбираться произвольно. Результатом работы такого
алгоритма будет разбиение объектов выборки X на классы, где в ка-
каждом классе расстояние между точкой-прототипом и любым другим
элементом класса не превышает Т. Пороговое расстояние Т определим
как половину расстояния между двумя наиболее удаленными друг от
друга точками обучающей выборки.
Алгоритм, 12.1.
1. Выбрать точку-прототип первого класса (например, объект Х\
из обучающей выборки). Количество классов К положить рав-
равным 1. Обозначить точку-прототип Z\.
2. Определить наиболее удаленный от Z\ объект Xf по условию
D(Z1,Xf) = maxD(Z1,Xi),
где D(Zi,Xi) — расстояние между Z\ и Х^ вычисленное одним
из возможных способов. Объявить Xf прототипом второго клас-
класса. Обозначить Xf как Z^- Число классов К = К -\- 1.
3. Определить пороговое расстояние Т = D(Zi, Xf)/2.
Построить Xf = Х\{ХЪ Xf}.

536
Задача обучения «без учителя»
[Гл. 12
4. Выбрать Xj e X1.
5. Вычислить расстояние от
до всех точек-прототипов:
= 1, 2,
6. Определить ближайшую к рассматриваемому объекту точку-
прототип Zp по условию
7. Если D(Zp,Xj) < Т, отнести объект Xj к классу р [Zv является
прототипом этого класса) и удалить его из X'. Иначе объявить
Xj прототипом нового класса. Обозначить Xj как Zk+i- Число
классов К увеличить на 1: К = К + 1. Удалить Xj из X'.
8. Если Xх = 0 (то есть обучающее множество исчерпано), то
КОНЕЦ. В противном случае перейти к шагу 4.
Пример 12.1.
Рассмотрим пример работы алгоритма, основанного на вычис-
вычислении порогового расстояния. Пусть каждый объект из множества
объектов, представленных в табл. 12.1, задан двумя признаками (мо-
(модель — точка на плоскости) (рис. 12.1).
Таблица 12.1
Координаты
объектов
Точки-прототи-
Точки-прототипы классов
Расстояние от Z\
до объектов
Расстояние от Z2
до объектов
Расстояние от Zo>
до объектов
Xi
B; 2)
х2
C;3)
1,4
6,7
Хз
B; 4)
2
7,3
х4
G;1)
5,1
5,4
х5
(8; 5)
6,7
1,4
4Д
х6
(9;1)
7,05
5
2
х7
(9; 2)
7,0
4
2,2
х8
(9; 6)
Z2
8,05
Выберем в качестве точки-прототипа первого класса точку Х\
из обучающей выборки (обозначается далее Z\). В таблице пред-
представлены расстояния от этой точки до объектов Х2 — Xg. Наибо-
Наиболее удаленным объектом для Z\ будет Х%. Пороговое расстояние
Т = - D(Zi, Xg) = 4,02. Точка Xg становится точкой-прототипом вто-
второго класса и обозначается далее Z^. Рассматриваем точки множества

12.1] Алгоритм, основанный на понятии порогового расстояния 537
123 456 789
Рис. 12.1.
Xr = X\{Xi, Ху}. Это точки Х^ — Xj. Анализируем их последователь-
последовательно. Точки Х2 и Хз будут отнесены к классу 1 (прототип — Z\).
Точка Х4 имеет ближайшим прототипом Z\, однако, поскольку
расстояние D(Zi,X±) > Т, точка Х4 становится прототипом нового
(третьего) класса (обозначаем ее далее Zs).
Для Х5, Xq и Х7 ближайшими прототипами станут, соответствен-
соответственно, Z2, ^з, Zs- Поскольку условие D(Zp,Xj) < Т не нарушается
(наименьшие расстояния — 1,4; 2; 2,2), новых классов не возникнет.
Окончательное распределение представлено в табл. 12.2.
Таблица 12.2
Класс 1
Класс 2
Класс 3
Прототип
X!
B; 2)
х8
(9; 6)
х4
G;1)
Элементы класса
Х2 Хз
C;3) B; 4)
х5
(8; 5)
Хб Х7
(9;1) (9; 2)
К достоинствам рассмотренного алгоритма следует отнести про-
простоту реализации и небольшой объем вычислений. Очевидны также
его недостатки, а именно, не предусмотрено уточнение разбиения.
В результате расстояние от объекта до точки-прототипа класса мо-
может оказаться больше, чем расстояние от этого объекта до точки-
прототипа другого класса. Результат, кроме того, сильно зависит

538 Задача обучения «без учителя» [Гл. 12
от порядка рассмотрения объектов X, а также от способа вычисле-
вычисления порогового расстояния (молено использовать и другие формулы
для подсчета Т). Из этого обсуждения следует, что полезно было
бы использовать алгоритмы, допускающие многократную коррекцию
формируемых классов, например, можно было бы менять пороговое
расстояние Т и проводить многократное уточнение разбиения.
12.2. Алгоритм MAXMIN
Рассмотрим алгоритм, более эффективный по сравнению с преды-
предыдущим и являющийся улучшением порогового алгоритма. Исходным
данным для работы алгоритма будет, как и раньше, выборка X.
Объекты этой выборки следует разделить на классы, число и харак-
характеристики которых заранее неизвестны.
На первом этапе алгоритма все объекты разделяются по классам
на основе критерия минимального расстояния от точек-прототипов
этих классов (первая точка-прототип может выбираться произволь-
произвольно). Затем в каждом классе выбирается объект, наиболее удаленный
от своего прототипа. Если он удален от своего прототипа на рассто-
расстояние, превышающее пороговое, такой объект становится прототипом
нового класса. Отметим, что в этом алгоритме пороговое расстояние
не является фиксированным, а определяется на основе среднего рас-
расстояния между всеми точками-прототипами, то есть корректируется
в процессе работы алгоритма. Если в ходе распределения объектов
выборки X по классам были созданы новые прототипы, процесс
распределения повторяется. Таким образом, в алгоритме MAXMIN
окончательным считается разбиение, для которого в каждом классе
расстояние от точки-прототипа до всех объектов этого класса не
превышает финального значения порога Т.
Для вычисления порогового расстояния Т между К точками-
прототипами воспользуемся следующей формулой. Для произвольно-
произвольного числа классов К пороговое расстояние вычисляется как половина
среднего расстояния между точками-прототипами, то есть
г=1 j=i+l
Алгоритм, 12.2.
1. Выбирается первоначальная точка-прототип (например, Х\).
Она становится точкой-прототипом первого класса и обознача-
обозначается далее Z\. Число классов полагаем равным 1 : К = 1.
2. Определяется Xf — наиболее удаленный от Z\ объект. Xf ста-
становится точкой-прототипом нового класса и обозначается далее

12.2]
Алгоритм MAXMIN
539
3. Находим пороговое расстояние Т.
4. Для всех объектов обучающего множества строится мат-
матрица расстояний до каждого из имеющихся прототипов:
D(XuZk), i = l,...M, k = l,...,K.
5. Каждый объект относится к классу по критерию наиболь-
наибольшей близости к точке-прототипу: Xi отнесен к классу р, если
D(XuZp)=mmD(XuZk).
к
6. В каждом классе к определяется объект Х/&, наиболее удален-
удаленный от точки-прототип a: D(Xik,Zk) = max D(X, Z&), где Rk —
X?Rk
множество объектов класса к.
7. Для всех найденных объектов проверяется условие:
D(Xlk,Zk)<T,k=l,...,K.
Если для некоторого Х\ь это условие не выполнено, он становит-
становится точкой-прототипом нового класса, число классов К = К -\- 1.
8. Если новых классов не создано, то КОНЕЦ. Иначе — перейти к
шагу 9.
9. Вычисляется новое значение Т как среднее расстояние между
прототипами.
10. Перейти к шагу 4.
Пример 12. 2
Рассмотрим работу алгоритма MAXMIN на примере. Как и в
предыдущем случае выберем объекты, которые заданы двумя при-
признаками. Обучающая выборка представлена на рис. 12.2. Координаты
точек обучающей выборки даны в табл. 12.3.
123456789
Рис. 12.2.

540
Задача обучения «без учителя»
[Гл. 12
Таблица 12.3
Координаты
точек
Первая точ-
точка-прототип
Расстояние
Хг
B; 2)
Zt
х2
C;2)
1
Хз
D; 2)
2
E; 4)
3,6
F; 5)
5
х6
G; 2)
5
G; 5)
5,8
Xs
(8;1)
6,1
(9; 2)
7
В качестве первой точки произвольно выбирается Х\. В таблице
даны расстояния от этой точки до остальных. Наиболее удаленной от
Z\ будет Х9. Пороговое расстояние Т = -L>(Xi,X9) = 3,5. Точка Х9
объявляется прототипом второго класса и обозначается Z^.
Матрица расстояний для двух классов представлена в табл. 12.4.
Таблица 12 А
Координаты
Расстояние
Z?(Zi,Xf)
Zi = B,2)
Расстояние
D(Z2,Xj)
Z2 = (9,2)
Х2
C;2)
1
6
D; 2)
2
5
Х4
E; 4)
3,6
4,5
х5
F; 5)
5
4,3
х6
G; 2)
5
2
Х7
G; 5)
5,8
3,6
Х8
(8;1)
6,1
1,4
Разделение на классы по критерию минимального расстояния до
точки-прототипа дает следующий результат:
класс 1 = {Xi, Х2, Хз, Х4}, класс 2 = {Х5, Хб, Х7, Xg, Xg}.
Найдем в каждом классе точку, максимально удаленную от про-
прототипа. В классе 1 — это Х4, поскольку D(Z\,X±) = 3,6 > Т
(Т = 3,5), Х4 становится прототипом нового — третьего класса и
обозначается далее также Z$. Новая итерация начинается с вычисле-
вычисления порогового расстояния и построения новой матрицы расстояний.
т _ Р(ХиХ9) + Р(ХиХ4) + Р(Х4,Х9) _ 7 + 3,6 + 5 _ 2 б
Матрица расстояний для трех классов представлена в табл. 12.5.
Разделение точек на классы даст следующий результат:
класс 1 — {Xi, X2, Х3}, класс 2 — {Хб, Xg, Xg}, класс 3 — {Х4, X5, X7}.

12.3J
Алгоритм
«if средних»
541
Таблица 12.5
Координаты
Расстояние
Z?(Zi,X,-)
Zx =B,2)
Расстояние
D(Z2,X3)
Z2 = (9,2)
Расстояние
D(Z3,X3)
Z3 = E,4)
x2
C;2)
l
6
о о
D; 2)
2
5
2,3
х5
F; 5)
5
4,3
1,4
Х6
G; 2)
5
2
2,8
Х7
G; 5)
5,8
3,6
2,3
Х8
(8;1)
6,1
1,4
4Д
Найдем в каждом классе точку, максимально удаленную от про-
прототипа. В классе 1 — это Хз. Расстояние D(Zi^Xs) = 2 < Т = 2,6.
В классе 2 искомая точка — Xq. Так как 1}(^2,Хб) = 2, для второго
класса условие выполнено. В классе 3 наиболее удаленной является
точка Ху. D(Zs, Х7) = 2,3 < Т. В соответствии с пунктом 8 алгоритма
новый класс не создается, и алгоритм завершает работу.
Алгоритм позволяет получить лучшее разбиение точек на классы,
поскольку разбиение многократно уточняется. Это снижает чувстви-
чувствительность алгоритма к ошибкам в обучающем множестве, а также к
выбору порядка рассмотрения объектов. Недостатком является необ-
необходимость многократно вычислять расстояние между объектами.
12.3. Алгоритм «К средних»
Рассмотрим алгоритм, решающий задачу обучения «без учителя»
при одном дополнительном условии: количество классов, к которым
могут принадлежать элементы обучающей выборки, заранее извест-
известно (классов — К). В такой ситуации первоначально выбираются К
точек-прототипов (например, первые К объектов обучающей выборки
X). Затем все объекты обучающей выборки X распределяются по
классам по критерию наименьшего расстояния от точек-прототипов
этих классов. В каждом из сформированных классов определяется
новая точка-прототип как «средняя» точка данного класса. Если
точки-прототипы при этом изменяются, то распределение объектов
по классам выполняется заново. Признаком окончания работы алго-
алгоритма здесь будет совпадение разбиений на классы на двух последо-
последовательных итерациях. В окончательном разбиении каждый объект из
X должен оказаться ближе к «центру» то есть к прототипу своего
класса, чем к прототипу любого другого класса. Заметим также, что

542
Задача обучения «без учителя»
[Гл. 12
в алгоритме «К средних» точки-прототипы могут не совпадать ни
с одним реальным объектом из X, поскольку они определяются как
«средние» точки своих классов.
Алгоритм 12.3.
1. Обозначим номер итерации 5 = 0. Выбираются К начальных
точек-прототипов:
Z = {Zf,Zs2,...,ZsK}n3X.
2. Выполняется итерация 5 = 5 + 1.
3. Строится матрица расстояний. Каждый объект Х\ Е X отно-
относится к одному из классов l,2,...i^ по признаку ближайшего
расстояния до точки-прототипа.
4. Для каждого из сформированных классов вычисляется новая
точка-прототип. Для этого значение каждого признака для
точки-прототипа класса к определяется как среднее арифмети-
арифметическое значений этого признака по всем объектам к-ro класса,
сформированного на текущей итерации 5:
хещ
где xskj — значение j-ro признака для определяемой точки-
прототипа класса /с, (к = 1, 2,..., К), Rsk — множество объектов,
отнесенных к классу к на s-й итерации, \Щ,\ — мощность этого
множества, j = 1, 2,..., п, поскольку каждый объект обучающей
выборки содержит п признаков.
5. Если для всех (к = 1,2,..., К) верно, Zsk = Z?~\ то КОНЕЦ,
иначе — переход к шагу 2.
Пример 12. 3.
Рассмотрим пример работы данного алгоритма. Обучающая вы-
выборка представлена в табл. 12.6. Требуется разбить эту выборку на
три класса (К = 3).
Коорди-
Координаты
X
B;
i
2)
х2
B; 4)
X
C;
"з
4)
х4
C;8)
X
D;
5
7)
х6
E; 9)
х7
F;D
Ха
F; 8)
Таблица
х9
G;D
X!
(8;
12.6
0

12.3]
Алгоритм «К средних»
543
Прежде всего, выберем начальные точки-прототипы. Пусть
Z\ = Xi, Z^ = Х3, Z% = Х4. Выполняем итерацию 1. Матрица
расстояний от точек-прототипов до остальных объектов представлена
в табл. 12.7.
Таблица 12.7
Коорди-
Координаты
Zi
z2
z3
Хх
B; 2)
0
-
-
х2
B; 4)
2
1
4Д
Хз
C;4)
-
0
-
х4
C;8)
-
-
0
х5
D; 7)
5,4
3,2
1,4
х6
E; 9)
7,6
5,4
2,3
х7
(б;1)
4Д
4,2
7,6
х8
F; 8)
7,2
5
3
х9
G;1)
5,1
5
8,05
Хю
(8;i)
6,05
5,8
8,6
Проведем разбиение на классы по критерию минимального рас-
расстояния: класс 1 — Х\,Хч; класс 2 — Хз,Х2,Хд,Хю; класс 3 —
X4,X5,X6,Xg. Расчет точек-прототипов для каждого класса даст
значения Z\ = D; 1,5), Z\ = E; 2,5), Z\ = D,5; 8).
Построим новую матрицу расстояний от точек-прототипов до
остальных объектов (табл. 12.8).
Таблица 12.8
Коорди-
Координаты
z\ =
= D; 1,5)
z\ =
= E; 2,5)
z3 —
= D,5; 8)
Хх
B; 2)
2
3
6,5
х2
B; 4)
3,2
3,35
4,7
Хз
C;4)
2,7
2,5
4,3
х4
C;8)
6,6
5,85
1,5
х5
D; 7)
5,5
4,6
1,1
х6
E; 9)
7,6
6,5
1Д
х7
(б;1)
2
1,8
7,2
х8
F; 8)
6,8
5,6
1,5
х9
G;1)
3
2,5
7,4
Хю
(8;1)
4
3,4
7,8
Новое разбиение на классы по критерию минимального расстояния
до прототипа: класс 1 — Xi, X2; класс 2 — Хз, Х7, Xg, Хю; класс 3 —
Х4,Х5,Хб,Х8 . Рассчитаем координаты точек-прототипов на итера-
ции 2: Z\ = B;3), ^22 = F; 1,75), Z32 = D,5; 8).
Итерация 3. Снова построим матрицу расстояний (табл. 12.9). Лег-
Легко заметить, что класс 3 уже стабилен.

544
Задача обучения
«без учителя»
[Гл. 12
Таблица 12.9
Коорди-
Координаты
zl =
= B;3)
= F;1,75)
z3 =
= D,5; 8)
B; 2)
1
4
6,5
х2
B; 4)
1
4,6
4,7
х3
C;4)
1,4
3,75
4,3
Х4
C;8)
5,1
6,9
1,5
х5
D; 7)
4,47
5,6
1Д
Х6
E; 9)
6,7
7,3
1Д
х7
F;1)
4,47
0,75
7,2
х8
F; 8)
6,4
6,25
1,5
х9
G;1)
5,4
1,25
7,4
Х10
(8;1)
6,3
2,1
7,8
¦ ¦ ¦
123456789
Рис. 12.3.
На основании матрицы расстояний разбиваем выборку на
классы: класс 1 — Х15Х2,Хз; класс 2 — Х7,Хд,Хю; класс 3 —
X4,X5,X6,Xg. Точки-прототипы для классов имеют координаты
Z\ = B,33; 3,33), Z% = G,0; 1,0), Z\ = D,5; 8,0).
Из рис. 12.3 видно, что классы окончательно сформированы. Вы-
Выполнение четвертой итерации по тем же правилам даст разбиение,
равное предыдущему, и алгоритм заканчивает работу. Заметим, что
в качестве точек-прототипов полезно брать не первые К объектов из
X, а максимально различные между собой объекты.
Алгоритмы, рассмотренные в этой главе, обладают одним общим
свойством: с их помощью для обучающей выборки X решается зада-
задача классификации, то есть строится разбиение примеров обучающей
выборки на классы. Вспомним, что алгоритмы обобщения должны
успешно решать и задачу распознавания, то есть задачу распреде-

12.4] Распознавание с использованием решающих функций 545
ления вновь предъявляемых примеров по классам. Последнее требует
наличия четко сформулированного решающего правила, или алгорит-
алгоритма, позволяющего отнести новый объект X к одному из классов.
12.4. Распознавание с использованием решающих
функций
Прежде всего необходимо дать понятие решающей функции. В си-
системах распознавания по признакам, где любой объект распознавания
представим как вектор X = (xi,X2,... ,хп), образованный значени-
значениями признаков Xj, j = 1,2,..., п, введем функцию /(xi,..., хп) от
значений признаков. Пусть по значениям этой функции принимается
решение об отнесении объекта к одному из известных классов (или
о том, что объект не может быть отнесен ни к одному из классов).
Назовем такую функцию решающей функцией.
Существуют различные способы построения решающих функций.
Прежде всего решающая функция может строиться как выражение,
значение которого отражает расстояние между классифицируемым
объектом и классом (прототипом класса). Решающая функция может
представлять собой также уравнения границ между классами. В этом
случае вектор X = (xi, Х2, • • • , хп) представим точкой в п-мерном
пространстве признаков. При удачном выборе признаков для распо-
распознавания объекты, принадлежащие одному классу, группируются в
некоторую область — кластер. Если эти области достаточно четко
очерчены (классы четко разделимы), то можно построить гиперпо-
гиперповерхности, разделяющие классы. В частном случае, когда, например,
объект характеризуется только двумя признаками, моделью будет
плоскость, на которой расположены точки, отображающие объекты
распознавания. Разделяющие поверхности будут представлять собой
кривые на плоскости. Для трехмерного случая (объект задается тремя
признаками) границами между классами будут разделяющие поверх-
поверхности. Задача поиска решающей функции есть задача отыскания
уравнений таких поверхностей.
Чтобы распознать объект X относительно классов 1, 2,..., К на
основе решающих функций, необходимо или сравнивать расстояния
между X и прототипами заданных классов, или оценить положение
X относительно разделяющих классы гиперповерхностей. Поскольку
распознавание возможно только относительно известных классов,
для решения такой задачи необходимо разбить на классы элемен-
элементы обучающей выборки X, например, с помощью одного из выше-
вышеизложенных алгоритмов, затем построить решающие функции для
отнесения объекта к одному из классов. Следующий шаг — отнесение
объекта X к одному из классов на основе построенных решающих
функций (непосредственно задача распознавания).
18 В.Н. Вагин и др.

546 Задача обучения «без учителя» [Гл. 12
12.4.1. Построение решающих функций по критерию минимального
расстояния
Простейшим способом распознавания некоторого объекта X яв-
является сравнение расстояний между данным объектом и объектами-
прототипами всех известных классов. Предъявляемый объект X счи-
считается принадлежащим классу /с, если выполняется условие \Х — Z^\ =
= min(|X—Zi\), где i = 1, 2,..., К — классы, Zi = (zi, z^-,..., zn) — век-
г
тор, характеризующий объект-прототип класса г. В качестве объекта-
прототипа класса можно использовать его «геометрический центр»
(как в алгоритме К средних). Расстояние между предъявленным объ-
объектом X и прототипом г-то класса Zi может быть найдено, например,
как обычное евклидово расстояние:
\
3 = 1
Для упрощения вычислений вместо непосредственного расчета
величины \Х — Zi\ можно построить другие решающие функции,
значения которых связаны определенным образом с расстоянием. Рас-
Рассмотрим один из методов получения решающей функции.
Найдем квадрат расстояния между X и прототипом Z^:
\Х -Zz\2 = f>, - zl3f = (Х- Zi) • (X - Z%f =
3 = 1
= X • Хт - X • Zj - Z% • XT + Z% • Zj.
j
В данном выражении X — вектор-переменная, Zi — вектор-
константа, Хт — транспонированный вектор. Заметим, что произве-
произведение X • Хт не связано с конкретным классом, и, следовательно,
не внесет вклад в оценку близости двух объектов. Отбросим его,
а оставшуюся часть формулы умножим на (-1). Результатом будет
следующая решающая функция:
х-г1 + гг-хт-гг- zj.
После умножения на (-1) была получена функция, принимающая
максимальное значение при минимальном расстоянии от объекта X
до прототипа. Получен критерий распознавания: объект X относим к
классу /с, если выполняется условие
Очевидно, потребуется построить К решающих функций, по одной
для каждого класса. Заметим, что для К классов можно строить

12.4]
Распознавание с использованием решающих функций
547
решающих функций в случае, когда для каждой пары
классов строится своя решающая функция. К достоинствам метода
можно отнести также отсутствие областей неопределенности, то есть
областей значений признаков, для которых объект не может быть
отнесен ни к одному классу. Однако метод хорош только в случае,
если точки, соответствующие объектам класса, образуют выпуклые
области.
12.4.2. Разделяющие решающие функции
Рассмотрим метод построения решающих функций как получение
уравнений границ, разделяющих классы. Первоначально рассмотрим
самый простой случай — случай двух классов. Тогда задача сводится
к построению только одной решающей функции. Такая функция дол-
должна принимать положительные значения для объектов одного класса
и отрицательные — для другого класса. В случае, когда классов
несколько, можно использовать различные стратегии.
Метод 1. Сначала какой-либо класс (обозначим его класс 1) счи-
считаем первым, а все остальные классы в совокупности — вторым.
Найдем решающую функцию, отделяющую класс 1 от остальных.
Аналогично построим функцию, отделяющую класс 2 от остальных
и т.д. (рис. 12.4). Всего построим К решающих функций. Решение о
принадлежности объекта X классу к принимается, если выполняется
условие Dk(X) > 0, Di(X) < 0 для всех г ф к.
Рис. 12.4.
В таком методе распознавания имеются неопределенные области,
в которых объект не может быть отнесен ни к одному классу.
18*

548
Задача обучения «без учителя»
[Гл. 12
Метод 2. Находится решающая функция для разделения каждой
пары классов. Количество решающих функций здесь будет равно
К{К-\)
количеству пар классов: — -.
. X
XXX
X
X
Рис. 12.5.
Решение о принадлежности X классу к принимается, если вы-
выполнено условие: Dki(X) > О, г = 1,2,..., К, г ф к. При таком
подходе возможно наличие единственной области неопределенности
(на рис. 12.5 — в центре). Объекты, попадающие в эту зону, не могут
быть отнесены ни к одному классу.
Метод 3. Следующий подход основан на устранении областей
неопределенности и является комбинацией методов 1 и 2 (рис. 12.6).
X X
X
Рис. 12.6.

12.4] Распознавание с использованием решающих функций 549
Если можно построить линейные решающие функции, будем гово-
говорить, что классы линейно разделимы.
12.4.3. Линейные решающие функции
Рассмотрим алгоритм построения линейных решающих функций.
п
Линейная функция имеет следующий вид: D(X) = wo + J2 wj ' хз-
Цель алгоритма — найти коэффициенты Wj решающей функции D(X)
методом последовательного уточнения. Рассмотрим случай двух клас-
классов (выше было показано, какими приемами можно свести к этому
случаю вариант нескольких классов). Основой для вычисления коэф-
коэффициентов Wj является анализ обучающей выборки X, где известна
заранее принадлежность объектов X классу 1 или классу 2. Далее эти
два класса обозначим С\ и С2.
Решающая функция считается построенной, если все объекты
обучающей выборки X распознаются этой функцией правильно, то
есть D(X) > 0, если X Е Ci, и, соответственно, D(X) < 0, если
I G С*2. Коррекция коэффициентов решающей функции выполня-
выполняется по следующему правилу: коэффициенты решающей функции
увеличиваются при неправильном распознавании объекта из класса
С\, уменьшаются при неправильном распознавании объекта из класса
С2 и остаются без изменения, если распознавание идет правильно.
Если на некотором шаге произойдет корректировка коэффициентов
решающей функции, счетчик правильно распознанных объектов, обо-
обозначаемый далее как сч, сбрасывается на ноль, поскольку мы перешли
к новой функции, и теперь ее надо проверить заново на всех элементах
обучающей выборки.
Алгоритм завершается, когда окажется, что построенная решаю-
решающая функция D(X) правильно распознает все объекты обучающего
множества.
Алгоритм 12.4-
1. Получить обучающую выборку X = (Xi, X2,..., Хм), элементы
которой принадлежат непересекающимся классам С\ или С^-
2. Установить в ноль счетчик правильно распознанных объектов:
сч = 0.
3. Установить номер итерации равным нулю: к = 0.
4. Задать начальные значения коэффициентов Wj в решающей
функции (например, Wj = 0 для j = l,2,...,n). Получим ре-
решающую функцию Dq(X).
5. Выбираем класс С\ в качестве текущего класса.
6. Переход к новой итерации: к = к + 1.

550
Задача обучения «без учителя»
[Гл. 12
7. Выбрать очередной объект Хь текущего класса (класса С\).
Если класс С\ исчерпан, объявить текущим классом класс Сг,
выбрать первый объект этого класса.
8. Вычислить новые значения коэффициентов решающей функции
на итерации к: w^ = w^1 + с • Xkj, где с — множитель, опреде-
определяемый из условия
С = <i 1 V^ k-1 ^ n
¦1, 2^ wj ' xkj > 0, и лк t o2;
0 прг^ правильном распознавании.
9. Если с = 0, сч = сч + 1 (увеличиваем на 1 число правильно
распознанных объектов), иначе сч = 0.
10. Если сч = М — общему числу объектов обучающей выборки X,
то КОНЕЦ, иначе перейти к шагу 6.
Приведенный алгоритм обеспечивает построение решающей функ-
функции во всех случаях, когда классы являются линейно разделимыми.
Пример 12. 4.
Рассмотрим пример работы алгоритма построения линейной раз-
разделяющей функции. В табл. 12.10 дана обучающая выборка — объек-
объекты, принадлежащие двум классам.
Таблица 12.10
Класс С\
Класс Сг
Точки X
1
2
3
4
5
6
Координаты точек
<1; 2>
<1; 3>
<3; 3>
<4;1>
<5; 2>
<6; 2>
Каждый объект задается двумя числовыми значениями и может
интерпретироваться как точка на плоскости (рис. 12.7). Цель — полу-
получить линейную разделяющую функцию, которая дает положительные
значения для точек 1, 2 и 3 и принимает отрицательные значения для
точек 4, 5, 6. Функция должна иметь вид F(X) = г^о +wi -x\ -\-W2 -Х2-
Выполняем итерацию 0. Коэффициенты г^о = ^1 = ^2 = 0-

12.4] Распознавание с использованием решающих функций 551
1 - 2щ + Зх2 = О
X,
Рис. 12.7.
Выполняем итерацию 1. Выбираем первый объект класса С\ —
вектор Х\ =< 1, 2 >. Значение функции F{X\) =0 + 0-1 + 0-2 = 0,
по правилу П8 необходима коррекция коэффициентов при значении
множителя с = 1. Вычисляем новые коэффициенты функции:
^о = ^о + с = 0 + 1 = 1; w\ = W! + с • хх = 0 + 1 • 1 = 1;
w\ = w2 + с • х2 = 0 + 1 • 2 = 2. Получаем F1(X) = 1 + х\ + 2 • ж2-
Выполняем итерацию 2. Вычислим последовательно значения
F:(X) для элементов выборки: F:(< 1,2 >) = 1 + 1-1 + 2-2 =
= б > 0; Fx(< 1,3 >) = 1 + 1 • 1 + 2 • 3 = 7 > 0; Fx(< 3,3 >) =
= 13 > 0. Все элементы класса С\ распознаны правильно. Выбираем
текущим класс С2. Fx(< 4,1 >) = 1 + 1-4 + 2-1 = 7> 0 —
объект распознан неправильно. Необходима коррекция коэффициен-
коэффициентов при значении множителя с = — 1. Wq = Wq + с = 1 — 1 = 0;
w{ = w\-\-c- x\ = 1 — 1-4 = —3;
= 2 — 1-1 = 1. Новая
функция F2(X) = х2 — 3 • х\.
Выполняем итерацию 3. Вычисляем значения функции для эле-
элементов выборки F2(< 1,2 >) = 2 — 3-1 = —1 < 0. Необходима
коррекция коэффициентов с поправкой с = 1: Wq = Wq -\- с = 0 -\- 1 =
= 1; w\ =w\ + с-Ж1 = -3 + 1-1 = -2; w% = w\ + c-x2 = 1 + 1 -2 = 3.
Новая функция F3(X) = 1 — 2xi + Зж2.
Начинаем новую итерацию с проверки значений F3(X) на эле-
элементах выборки: F3(< 1,2 >) = 5 > 0; F3(< 1,3 >) = 8 > 0;
F3(< 3,3 >) = 4 > 0. Переходим к проверке объектов класса С2:
F3(< 4,1 >) = -4 < 0; F3(< 5, 2 >) = -3 < 0; F3(< б, 2 >) = -5 < 0.
Все объекты выборки разделены правильно, таким образом получена
искомая решающая функция F(X) = 1 — 2xi + Зж2. На рис. 12.7 дана
геометрическая интерпретация решения.

552
Задача обучения «без учителя»
[Гл. 12
12.4.4. Построение решающих функций методом потенциалов
Иногда точки обучающей выборки невозможно разделить, исполь-
используя линейные функции. На рис. 12.8 приведен пример такой обучаю-
обучающей выборки. В случае, если классы невозможно разделить линейно,
используется метод потенциалов, предназначенный для построения
нелинейных решающих функций.
XXX
XX А А
X — элементы первого класса
4i — элементы второго класса
XXX
III 1111
Рис. 12.8.
Само название «метод потенциалов» связано со следующей интер-
интерпретацией. Предположим, что любой точке из обучающего множе-
множества соответствует некоторый объект, обладающий зарядом (наподо-
(наподобие электрического). Объекты разных классов имеют заряды разных
знаков: положительные и отрицательные. В любой точке п-мерного
пространства признаков такие заряды создадут некоторый потенци-
потенциал, являющийся суммой потенциалов отдельных зарядов. Величина
потенциала прямо пропорциональна величине заряда и обратно про-
пропорциональна расстоянию до него.
Известно, что линии, соединяющие точки с одинаковыми потен-
потенциалами, называются эквипотенциалями. В таких условиях каждый
класс отделен от другого «потенциальной долиной», имеющей нулевой
потенциал. Такая нулевая эквипотенциаль представляет собой грани-
границу между классами; ее уравнение и будет решающей функцией.
Функция, описывающая закон изменения потенциала, создаваемо-
создаваемого зарядом, помещенным в точку Хс, может быть задана по-разному.
Рассмотрим два варианта:
2) F(X,XC) = — тг~5"? гДе « > 0 — константа (можно
1 -\- а • X — Хс
принять а = 1).

12.4] Распознавание с использованием решающих функций 553
Если рассматривать расстояние по Евклиду, вторая функция при-
примет вид
F(X, Хс) = , где коэффициент а = 1.
Рассмотрим алгоритм построения решающей функции как раз-
разделяющей границы D(X), отделяющей области положительного и
отрицательного потенциалов. При описании алгоритма используем
обозначения, принятые в описании алгоритма построения линейной
разделяющей функции. Легко заметить, что оба алгоритма имеют
много общего.
Алгоритм 12.5.
1. Получить обучающую выборку X = (Xi, Х2,..., Хм), элементы
которой принадлежат классам С\ или С2.
2. Установить в ноль счетчик правильно распознанных объектов:
сч = 0.
3. Установить номер итерации равным нулю: к = 0.
4. Начальное значение решающей функции D°(X) = 0.
5. Выбрать в качестве текущего класса класс С\.
6. Выполнение новой итерации: к = к + 1. Если к > М, примем
к = 1.
7. Выбрать очередной объект Хк из текущего класса. Если теку-
текущий класс исчерпан, то объявить текущим класс С2 и выбрать
из него первый объект.
8. Построить новую решающую функцию:
Dk(X) = Dk~\X) + с • F(X, Xk),
где множитель с выбирается из условий
( 1, если Вк~х (Хк) < 0 и Xfc e Ci;
с = < -1, если Вк~х (Хк) > 0 и Хк е С2]
У 0 при правильном распознавании.
9. Если с = 0, то сч = сч + 1, иначе сч = 0.
10. Если сч = М, то КОНЕЦ, иначе перейти к шагу 6.
Заметим, что при выполнении пункта 8 на первой итерации всегда
получим значение множителя с = 1, так как D°(Xi) = 0, Х\ Е С\.

554
Задача обучения «без учителя»
[Гл. 12
Пример 12. 5
Пример работы алгоритма рассмотрим для обучающей выборки,
представленной в табл. 12.11.
Таблица 12.11
Класс С\
Класс Сг
Точки X
1
2
3
4
5
6
Координаты точек
<2;4>
<4;1>
<4; 6>
<4; 2>
<6; 2>
<6; 5>
Как следует из рис. 12.9, между точками классов нельзя провести
линейную границу.
123 456789 Xt
Рис. 12.9.
Воспользуемся методом потенциалов, причем для вычисления
нелинейной границы предлагается использовать функцию второго
типа. Поскольку каждая точка задана двумя координатами, функция
примет вид
F{X,XC) =
- х1сJ + (х2 - х2сJ '
Рассмотрим выполнение алгоритма по шагам.
Итерация 0. Искомая функция D°(X) = 0. Проверяем элементы
обучающей выборки. D°(< 2,4 >) = 0, необходима коррекция при
с=1.

12.4] Распознавание с использованием решающих функций 555
Итерация 1. Строим решающую функцию D1(X) = 1/A +(xi — 2J +
+ (х2 — 4J). Проверим элементы обучающей выборки для класса С\\
2?«2,4» 1>0; ^«4,1» ттт^ >0;
D1(<4,6>) = ->0.
Для элементов класса С\\ Dx{< 4,2 >) = - > 0. Распознавание
ошибочно, поэтому выбираем множитель с = —1, и начинаем коррек-
коррекцию функции.
Итерация 2.
On - 2J + {х2 - 4J l + (xi-4J + (x2-2J*
Проверяем элементы обучающей выборки:
D\< 2, 4 >) = 1 - 1 > 0; D2(< 4,1 >) = ^ - 1 < 0.
Необходима коррекция при с = 1.
Итерация 3. Новая функция примет вид
- 2J + (х2 - 4J 1 + On - 4J + (х2 - 2J
1
Выполним проверку для элементов класса С\\
D\< 2,4 >) = 1 - 1 + ^ > 0; D\< 4) 1 >) = 1 - i + 1 > 0;
^«4,6»Л_1 + 1>
Проверяем элементы класса С^'-
D\< 4,2 >) = 1 - 1 + \ < 0; Д3(< 6,2 >) = 1 - I + I > 0.
Необходима коррекция функции при значении с = — 1.
Итерация 4 • Новая функция содержит четыре компонента:
_ 2J + (Ж2 _ 4J
1
1 + (Ж1 - 4J + (х2 - IJ 1 + (Ж1 - бJ + (х2 ~ 2J '

556
Задача обучения «без учителя»
[Гл. 12
123456789 Xj
Рис. 12.10.
Выполним проверку для элементов класса С\\
4 111 4
^ ' ^~ "9 + 141> ' ^ ' >
Переходим к проверке элементов класса С2'-
D4(< 4,2>) = |-1 + |-|<0; D4(< 6, 2 >) = А- - i + 1 - К 0;
Все объекты обучающей выборки функция D4(X) разделила пра-
правильно, следовательно, она является искомой решающей функцией.
Работа алгоритма завершена. На рис. 12.10 представлена графическая
интерпретация решения.
12.5. Распознавание на основе приближенных
признаков
Значения, которые принимают признаки в обучающих выборках,
часто являются результатами измерений различных параметров. Лю-
Любые измерения связаны с возможностью возникновения ошибок, та-
таким образом числовые значения признаков мы получаем с некоторой
достоверностью, или уверенностью в их истинности. В ситуациях,
когда вероятность получения неверных значений достаточно велика,
введем в рассмотрение риск, связанный с решением об отнесении
объекта к некоторому классу. Под риском будем понимать «цену»,
связанную с правильным или неправильным распознаванием объек-
объекта. Например, риском может служить величина потерь, связанная с

12.5] Распознавание на основе приближенных признаков 557
тем, что робот неправильно обработает деталь, ошибочно отнеся ее к
другому классу.
Введем матрицу рисков, связанных с правильными и ошибочными
решениями:
R =
Rn R12 ••• Rim
R21 R22 - - - R2M
R
m2
где Rij — риск, связанный с отнесением к классу j объекта, в дей-
действительности принадлежащего классу г, М — общее число классов.
В матрице имеются диагональные элементы — Rn. Они отображают
риск, связанный с правильным решением (обычно Rn ^ 0, и эту
величину можно рассматривать как выигрыш, достигнутый за счет
правильного распознавания).
Пусть для распознавания предъявлен объект, у которого известны
значения признаков X = (#i, #2, • • • ,хп). Назовем это событием А.
Значение риска, связанное с решением о принадлежности объекта
X классу Cj при условии, что имеет место событие А, выражается
формулой
м
R(X e Cj\A) = R(Cj\A) =
Здесь P(Ci\A) — условная вероятность принадлежности объекта X
классу Ci при наблюдаемых значениях признаков, R^ — риск того,
что объект в действительности принадлежал классу г, а его ошибочно
отнесли к классу j. Условные вероятности P(Ci\A) находим по фор-
формуле Байеса:
Р{СЛА) . /№)-^1й) ,
Е P(Ci) -P(A\C,)
г=1
где P(Ci) — априорная вероятность появления объекта, принад-
принадлежащего классу г, она может быть известна, например, из ста-
статистических данных; P(A\Ci) — вероятность появления признаков
X = (xi, X2, • • •, хп) у объекта, принадлежащего классу г.
Решение о том, что объект X принадлежит классу Cz, принима-
принимается в случае, если риск, связанный с данным решением, минимален:
R(CZ\A) =minR(d\A).
i
Введенное правило распознавания называется критерием Байеса.
Применение этого правила обеспечивает минимальный средний риск,
то есть риск, усредненный по всем возможным решениям задачи
распознавания.

Я уже не знаю того, чему научился,
а немногое, что еще знаю, просто угадал.
Н. Шамфер
Глава 13
ОБУЧЕНИЕ С УЧИТЕЛЕМ
Алгоритмы, исследованные в предыдущей главе, решали задачи
классификации и распознавания для числовых признаков. Качествен-
Качественные, а также шкалированные признаки не использовались, потому
что для подобных признаков сложно ввести меру, задающую бли-
близость объектов. При исследовании объектов, содержащих качествен-
качественные признаки, необходимо определять близость или сходство объектов
прежде всего на основании совпадения качественных значений. Важ-
Важным моментом является определение правильных сочетаний значений
некоторых качественных признаков. Поиск наиболее существенных
сочетаний признаков удобно проводить с помощью аппарата логиче-
логических функций. Алгоритмы, использующие такой подход, относятся к
алгоритмам обучения с учителем и будут рассмотрены в настоящей
главе.
13.1. Постановка задачи
Поставим задачу обобщения понятий по признакам. Пусть имеется
множество объектов, состоящее из положительных и отрицательных
примеров формируемых понятий. Назовем такое множество обучаю-
обучающей выборкой. На основании обучающей выборки необходимо постро-
построить понятие, разделяющее положительные и отрицательные объекты.
Под обобщением, как правило, понимается переход от рассмотре-
рассмотрения единичного объекта о или некоторой совокупности объектов Т к
рассмотрению множества объектов V такого, что о Е V или Т С V.
Здесь в качестве объекта может рассматриваться как реальный объ-
объект, так и модель некоторого процесса или явления.
Пусть О = {oi, 02,..., оп} — множество объектов, кото-
которые могут быть представлены в интеллектуальной системе
S. Каждый объект характеризуется г признаками. Обозна-
Обозначим через Zi,Z2,...,Zr множество допустимых признаков, где
Zk = {zki,Zk2,--">Zkm} (I < к < г) и Zki являются значениями

13.1] Постановка задачи 559
признаков. Каждый объект о^ G О, 1 ^ i ^ п, представляется
как множество значений признаков, т.е. Oi = {%kj}, гДе zkj €= %k^
l^/c^r,l^j^m. Такое описание объекта называется
признаковым описанием. В качестве признаков объектов могут
использоваться количественные, качественные, либо шкалированные
признаки.
В основе процесса обобщения лежит сравнение описаний исходных
объектов, заданных совокупностью значений признаков, и выделение
наиболее характерных фрагментов этих описаний. В зависимости от
того, входит или не входит объект в объем некоторого понятия, на-
назовем его положительным или отрицательным объектом для этого
понятия.
Пусть О — множество всех объектов, представленных в некоторой
системе знаний, V — множество положительных объектов и W —
множество отрицательных объектов. Будем рассматривать случай,
когда О = V U W, V П W = 0, W = Q ^ и W% П W5 = 0 (г + j).
г
Пусть К — непустое множество объектов такое, что К = К+ U К~,
где К+ С V и К~ С W. Будем называть К обучающей выборкой. На
основании обучающей выборки надо построить правило, разделяющее
положительные и отрицательные объекты обучающей выборки.
Понятие, таким образом, сформировано, если удалось построить
решающее правило, которое для любого примера из обучающей вы-
выборки указывает, принадлежит ли этот пример понятию или нет. Ал-
Алгоритмы, которые мы исследуем, формируют решение в виде правил
типа «ЕСЛИ условие, ТО искомое понятие». Условие представляет-
представляется в виде логической функции, в которой булевы переменные, от-
отражающие значения признаков, соединены логическими операциями
конъюнкции, дизъюнкции и отрицания. Решающее правило является
корректным, если оно в дальнейшем успешно распознает объекты, не
вошедшие первоначально в обучающую выборку.
Проблема формирования понятий по признаковым описаниям бы-
была сформулирована М. М. Бонгардом. Процедура обучения по Бон-
гарду является более сложным вариантом обучения «с учителем»
и основывается на двух этапах: обучении и экзамене. В процедуре
обучения используются две выборки примеров. Одна группа содер-
содержит примеры, относящиеся к понятию, а вторая выборка содержит
контрпримеры.
Результатом обучения будет некоторое решающее правило. Оно
должно позволять принять решение об отнесении конкретных при-
примеров к понятию. Правило считается корректным, если оно успешно
разделяет все примеры и контрпримеры обучающей выборки.
После того, как распознающее правило на обучающей выборке
построено, проводится экзамен — с помощью распознающего правила
надо разделить объекты новой, экзаменационной выборки на приме-

560
Обучение с учителем
[Гл. 13
ры и контрпримеры. Если решающее правило правильно проводит
такое разделение, обучение заканчивается. Если результат экзамена
неудовлетворителен, то можно проводить дополнительное обучение на
новой обучающей выборке (например, к исходной обучающей выборке
можно добавить примеры, на которых при распознавании возникали
ошибки).
В отличие от алгоритмов обучения без учителя основное внимание
будем уделять качественным признакам. Главная задача алгоритмов
обобщения заключается в построении решающего правила, которое в
дальнейшем используется для распознавания новых объектов. Кри-
Критерии качества построенных правил — это компактность и высокое
качество распознавания вновь предъявленных объектов.
Прежде чем перейти к рассмотрению реальных алгоритмов обуче-
обучения с учителем, исследуем способы задания решающего правила на
примере.
Пример 13.1.
В табл. 13.1 приведен пример обучающего множества. Здесь каж-
каждый объект имеет четыре атрибута: класс, рост, цвет волос и цвет
глаз.
Таблица 13.1
Класс
-
-
+
-
-
-
+
Рост
Низкий
Высокий
Высокий
Высокий
Низкий
Высокий
Низкий
Волосы
Светлые
Темные
Светлые
Темные
Темные
Светлые
Светлые
Глаза
Карие
Карие
Голубые
Голубые
Голубые
Карие
Голубые
Наблюдая примеры, приведенные в таблице, сформулируем зако-
закономерность их разделения на классы: все голубоглазые объекты со
светлыми волосами относятся к классу +; все темноволосые объекты,
либо светловолосые, но с карими глазами, относятся к классу —. Заме-
Заметим также, что признак рост не влияет на выбор класса. Рассмотрим
способы описания полученных решений в автоматизированной сис-
системе.
Первый способ задания решающего правила — использование ло-
логических функций. Две функции, задающие классы + и —, могут

13.1] Постановка задачи 561
иметь вид:
Р+(Х) = (глаза = голубые) & (волосы = светлые)
Р~ (X) = (волосы = темные)\/
V (волосы = светлые) & (глаза = карие).
Такой способ представления знаний о построенных классах исполь-
используется в алгоритме ДРЕВ, рассмотренном ниже.
Представление знаний с помощью деревьев решений с успехом
было использовано в ряде систем обучения с учителем, например, в
алгоритме ID3 Куинлана.
Дерево решений — это дерево, внутренние узлы которого представ-
представляют собой проверки для входных примеров из обучающего множе-
множества, а вершины-листы являются категориями, классами (примеров).
Пример дерева решений приведен на рис. 13.1. Дерево решений ка-
каждому входному примеру ставит в соответствие номер класса (или
выходное значение) путем фильтрации этого примера через узлы
проверки дерева сверху вниз. Результаты каждой проверки являются
взаимоисключающими и исчерпывающими. Например, проверка Т^
в дереве, изображенном на рис. 13.1, имеет три возможных исхода:
самый левый относит входной пример к классу 3, средний перена-
перенаправляет входной пример вниз к проверке Т4, а самый правый относит
пример к классу 1. Мы будем следовать обычной договоренности об
изображении узлов-листьев номерами классов.
Существует несколько характеристик, по которым деревья реше-
решений могли бы различаться:
1. Проверки могут быть многопризнаковыми (выполняется про-
проверка нескольких признаков входного примера за один раз) или

562
Обучение с учителем
[Гл. 13
однопризнаковыми (выполняется проверка только одного при-
признака) .
2. Проверки могут приводить к двум результатам или более чем к
двум. (Если все проверки приводят к двум результатам, то мы
получаем двоичное дерево решений).
3. Признаки (или атрибуты), которые используются в узлах
дерева, могут быть качественными или количественными.
Бинарные признаки могут рассматриваться как любые из
них.
4. Классов может быть два или более. Если мы имеем два класса, и
объекты классификации представляют собой двоичные входные
векторы, то дерево реализует булеву функцию и называется
булевым деревом решений.
Удобно использовать дерево реше-
решений с пометками на ребрах. В нем вер-
вершины, не являющиеся концевыми, по-
помечены именами атрибутов, ребра —
допустимыми значениями соответству-
соответствующего атрибута, и концевые верши-
вершины — именами классов. Процесс клас-
классификации заключается в прохожде-
прохождении пути из корня к листьям, сле-
следуя ребрам, соответствующим значени-
значениям атрибутов объекта.
На рис. 13.2 приведен пример дере-
дерева решений для обучающей выборки из
табл. 13.1.
Еще один способ представления решающего правила — продукции.
Продукционные правила представляются в виде
если <посылка>, то <заключение>
В системах извлечения знаний в качестве посылки выступает
описание объекта через его свойства, а заключением будет вывод о
принадлежности объекта к определенному классу. Примером такого
продукционного правила является
если рН < б, то жидкость — кислота.
В экспертных системах часто используются правила, в которых
посылкой является описание ситуации, а заключением — действия,
которые необходимо предпринять в данной ситуации. Основные до-
достоинства, благодаря которым продукционные правила получили ши-
широкое распространение, заключаются в следующем:
1) продукционные правила легки для восприятия человеком;
2) отдельные продукционные правила могут быть независимо до-
добавлены в базу знаний, исключены или изменены, при этом не
светлые/7
глаза
голубые/ V1
+
волосы
темныеЧ
карие
\
-
-
Рис. 13.2

13.2] Алгоритм ДРЕВ 563
требуется перепрограммирование всей системы. Как следствие
этого, представление больших объемов знаний не вызывает за-
затруднений;
3) с помощью продукционных правил выражаются как деклара-
декларативные, так и процедурные знания.
Решающие деревья более сложны для понимания, чем продук-
продукционные правила, что является их недостатком. С другой стороны,
любое решающее дерево может быть преобразовано в набор про-
продукционных правил: каждому пути от корня дерева до концевой
вершины соответствует одно продукционное правило. Его посылкой
является конъюнкция условий «атрибут — значение», соответствую-
соответствующих пройденным вершинам и ребрам дерева, а заключением - имя
класса, соответствующего концевой вершине. Так, приведенное выше
решающее дерево может быть записано в виде следующего набора
продукционных правил:
если волосы = светлые & глаза = голубые то класс = «+»
если волосы = светлые & глаза = карие то класс = « —»
если волосы = темные то класс = « —».
Эти наиболее популярные модели описания класса объектов равно-
равносильны. Перейдем к рассмотрению конкретных алгоритмов, исполь-
использующих такие модели.
13.2. Алгоритм ДРЕВ
Данный алгоритм является методом качественного обобщения по
признакам. Он был предложен как развитие алгоритма обобщения
Э. Ханта CLS. Ставится цель построения обобщенного понятия на
основе анализа обучающей выборки S, содержащей примеры К+ и
контрпримеры К~. При этом формируется логическая функция при-
принадлежности к обобщенному понятию, которая служит классифици-
классифицирующим правилом. В этой логической функции булевы переменные,
отражающие значения признаков, соединены операциями конъюнк-
конъюнкции, дизъюнкции и отрицания.
На первом этапе работы алгоритма делается попытка сформиро-
сформировать обобщенное конъюнктивное понятие на основе поиска призна-
признаков, значения которых являются общими для всех объектов выборки
К+ и не встречаются среди контрпримеров К~. Результатом дол-
должна стать логическая функция П^, значение которой равно 1 на
всех примерах из выборки К+ и равно нулю на всех контрпримерах
из К~.
Затем формируется обобщенное дизъюнктивное понятие Пд, по-
построение которого начинается с выбора среди элементов К+ такого
признака Ai, который является наиболее существенным для обобщен-
обобщенного понятия. Для выбранного признака ищется значение с', которое

564 Обучение с учителем [Гл. 13
называют разделяющим значением, так как на его основе происхо-
происходит разбиение выборок К^~ и К~ на две пары подвыборок: К^ и
lfj~, К^г и KZi (здесь К^ и К± содержат примеры со значения-
значениями с', а К^г и KZi соответственно содержат примеры со значения-
значениями ^сх).
В алгоритме ДРЕВ наиболее важное значение признака определя-
определяется с помощью одного из критериев существенности Ф1, Ф2,..., Ф9.
Критерии Ф1, Ф2,..., Ф9 составляют набор эвристических правил,
встраиваемых в алгоритм; эти правила могут взаимозаменяться в
диалоге с пользователем и тем самым оказывать влияние на вид
получаемой функции принадлежности или решающего дерева. По-
Поскольку множества значений признаков не наделены никакой струк-
структурой, позволяющей извлекать дополнительную информацию, основ-
основным параметром, влияющим на существенность значений признаков
в формулах, соответствующих Ф-7', служит частота появления их в К+
и К~. В качестве примера критерия существенности может быть взят
следующий:
Ф = max ( XZij ) ,
где Xzi:j — частота появления j-ro значения i-ro признака в примерах
и контрпримерах, а щ — число различных значений i-ro признака в
примерах и контрпримерах. Здесь разделяющее значение с1 = Cij, для
которого этот критерий выполняется.
После разбиения выборок на подвыборки на основе найденного
значения с' к каждой паре подвыборок применяется аналогичная
процедура. В результате работы алгоритма формируется дерево ре-
решений, конечным вершинам которого либо сопоставлены подвыборки,
для которых существует обобщенное конъюнктивное понятие, либо
подвыборка обратилась в пустое множество.
Алгоритм ДРЕВ.
1. Формирование П^ на множестве S = К+ U К~. В случае успеха
переход к п. 2, иначе — к п. 3.
2. Печать П^ и исключение признаков, вошедших в Ик-
3. Выбор признака Ai и нахождение разделяющего значения с'.
4. Разбиение выборок на две пары подвыборок.
5. Формирование П^ на подвыборках. В случае неудачи — возврат
к шагу 3, иначе — переход к шагу 6.
6. Формирование и печать Пд. Конец.

13.2]
Алгоритм ДРЕВ
565
Алгоритм основан на разбиении выборок частных примеров на
подвыборки в соответствии с наличием в них разделяющих значе-
значений признаков (см. ниже) и позволяет получать логическую функ-
функцию принадлежности ценой небольшого числа просмотров этих выбо-
выборок.
На первом этапе работы алгоритм пытается построить конъюнк-
конъюнктивное обобщенное понятие П^:
По = h
r\
& hr2
h
rm jm.
Для этого берется теоретико-множественное пересечение
где каждое К^ понимается как упорядоченное по признакам множе-
множество значений.
Построение П^ (дизъюнктивной формы обобщенного понятия)
начинается с поиска среди элементов К+ такого значения с' признака
г, которое является наиболее существенным для формирования поня-
понятия. Наиболее важное значение признака определяется с помощью
одного из критериев существенности Ф1, Ф2,..., Ф9, введенных выше.
Пример 13.2.
Рассмотрим пример из области медицинской диагностики. В
табл. 11.1 была представлена выборка описаний состояний нескольких
больных, страдающих определенным заболеванием, а также
состояний нескольких людей, не страдающих этим заболеванием.
На рис. 13.3 представлено дерево решений, построенное алгоритмом
ДРЕВ для диагностики заболевания на основе анализа обучающей
выборки из табл. 11.1.
пожилой возраст
"| пожилой возраст
Щ kz1}
] головные средний возраст &
" женский пол &
нач. стадия &
головные боли &
t = 37,8 & никаких
прочих ощущений

566 Обучение с учителем [Гл. 13
В результате функция принадлежности, построенная алгоритмом
ДРЕВ, будет иметь вид:
Болезнь Z = Пожилой возраст & ( Головные боли & Озноб V Нет
головной боли & Нач. стадия & Нет аппетита) V Средний возраст &
& Жен. пол & Нач. стадия & Головные боли & t = 37,8 & Никаких
прочих ощущений.
К основным достоинствам алгоритма ДРЕВ можно отнести его
компактность, быстроту сходимости, простой вид формируемых им
понятий. Достоинством алгоритма также является то, что в алгорит-
алгоритме ДРЕВ на каждом шаге из дальнейшего рассмотрения удаляются
признаки, имеющие для всех примеров и контрпримеров одинаковые
значения и, следовательно, не несущие существенной информации.
Это может быть особенно важно, если мы имеем дело с большим
количеством признаков, и многие из них несущественны.
13.3. Построение решающего дерева с
использованием метрики Хемминга
Дерево решений — это по сути алгоритм, представленный в спе-
специальной форме. Рассмотрим алгоритм, который строит бинарное
дерево на основании поиска существенного (разделяющего) значения
некоторого признака. Каждой вершине дерева приписывается вопрос
«Обладает ли пример данным значением признака?», а дуги взве-
взвешиваются ответами (Да, Нет). Конечные (висячие) вершины дерева
будут помечены утверждениями, соответствующими решениям.
Распознавание начинается с корневой вершины, откуда строится
путь до конечной (висячей) вершины. В каждом внутреннем узле
необходимо отвечать на вопрос и выбирать соответствующую дугу,
ведущую к следующему вопросу. Заметим, что вершины с одинако-
одинаковыми вопросами могут встречаться несколько раз в разных местах
дерева, но в каждом конкретном пути от «корня» к «листу» каждый
вопрос встретится только один раз.
Рассмотрим рекурсивный алгоритм построения бинарного дерева
на основе обучающей выборки S (далее будем называть этот алгоритм
АМХ — «Алгоритм, основанный на метрике Хемминга»).
Для предъявленной обучающей выборки S ищется наиболее важ-
важный вопрос, который помещается в корневую вершину дерева. На-
Например, при решении задачи выбора меню для обеда, в корневую
вершину разумно поместить вопрос, является ли клиент вегетариан-
вегетарианцем. Обучающее множество S в соответствии с ответами ДА, НЕТ
разделяется на две подвыборки. Далее для каждой подвыборки снова
ищется наиболее важный вопрос и порождаются две новые ветви.
Процесс завершается, когда использованы все вопросы.
Для нахождения наиболее важного вопроса используется следу-
следующий подход. Предположим, обучающее множество S содержит К

13.3] Построение решающего дерева 567
примеров. Построим метрику на множестве вопросов и упорядочим S
по следующему правилу. Для каждого вопроса Q строится i^-арный
кортеж, где j-й элемент в кортеже имеет значение
. _ Г 1, если j-й пример из S дает ответ ДА на вопрос Q,
1 0 в противном случае.
Расстояние между двумя вопросами определяется как расстояние
между двумя двоичными векторами по Хеммингу. Обозначим такое
расстояние между векторами X и Y как Hd(XJY). При этом из
рассмотрения исключаются вопросы, на которые все примеры из S
дают одинаковый ответ (все 0 или все 1).
Для искомого свойства Р и множества объектов S строится кортеж:
длины К по правилу: j-e значение в кортеже Р равно 1, если j-u
пример из S обладает искомым свойством Р\ j-e значение в кортеже
Р равно 0, если j-й пример из S этим свойством не обладает. Чтобы
выбрать наиболее важный вопрос, ищем среди всех подходящих во-
вопросов Q такой, чья связь с Р наиболее тесная. Для этого восполь-
воспользуемся правилом: ищем рт = min{Hd(P, Q), К — Hd(P,Q)}, то есть
берем наименьшее расстояние по Хеммингу от Q до Р и от Q до ^Р
(рт далее называем псевдометрикой).
Когда наиболее важный вопрос выбран, выполняется расщепление
обучающего множества на 5да и бнет, затем для каждого подмноже-
подмножества выполняются аналогичные вычисления.
Пример 13.3.
Рассмотрим пример построения дерева решений для анализа пове-
поведения Лондонского фондового рынка. Пусть главные факторы, влия-
влияющие на фондовый рынок, это
- состояние на вчерашний день;
- состояние фондового рынка в Нью-Йорке;
- банковские тарифы (ставки);
- процент безработицы;
- перспективы для Англии.
В табл. 13.2 приведено обучающее множество из шести примеров.
Пусть наша цель — построить дерево, определяющее, наблюдается
ли рост на Лондонском фондовом рынке. Искомое свойство «Сегодня
наблюдается рост». Ищем расстояние по Хеммингу (Hd) между этим
свойством и каждым атрибутом. Так, для атрибута «Банковские став-
ставки растут» расстояние по Хеммингу Hd(l 11000, 010101) =4
(значения различны в 4-х позициях). Тогда Hd = 4, К — Hd = б — 4 =
= 2, minD,2) = 2. Следовательно, рт («Сегодня наблюдается рост»,
«Банковские ставки растут») = 2.
Поскольку критерием выбора является минимальное значение рт,
выбираем наиболее важный вопрос «Безработица растет?». Проведем

568
Обучение с учителем
[Гл. 13
Таблица 13.2
Наблюдается ли се-
сегодня рост на фон-
фондовом рынке?
Наблюдался ли рост
вчера?
Наблюдается ли се-
сегодня рост в Нью-
Йорке?
Растут ли банков-
банковские ставки?
Безработица рас-
растет?
Несет ли Англия
убытки?
1
да
да
да
нет
нет
да
2
да
да
нет
да
да
да
3
да
нет
нет
нет
да
да
4
нет
да
нет
да
нет
да
5
нет
нет
нет
нет
нет
да
6
нет
нет
нет
да
нет
да
Hd
2
2
4
1
3
рт
2
2
2
1
3
расщепление S: 5да включает примеры 2 и 3. В дереве эта вершина
будет конечной (для всех примеров множества наблюдается рост на
фондовом рынке), бнет содержит примеры 1,4,5,6. Результаты по-
повторных вычислений приведены ниже в табл. 13.3.
Таблица 13.3
Наблюдается ли се-
сегодня рост на фон-
фондовом рынке?
Наблюдался ли рост
вчера?
Наблюдается ли
сегодня рост в
Нью-Йорке?
Растут ли банков-
банковские ставки?
Безработица
растет?
Несет ли Англия
убытки?
1
да
да
да
нет
нет
да
4
нет
да
нет
да
нет
да
5
нет
нет
нет
нет
нет
да
6
нет
нет
нет
да
нет
да
Hd
1
0
3
1
3
рт
1
0
1
1
1

13.4]
Индукция решающих деревьев
569
Из результата видно, что когда безработица не растет, Лондонский
фондовый рынок в точности следует за Нью-Йоркским. Приведем
ниже окончательное дерево решений (рис. 13.4).
Рост на Лондонском
фондовом рынке
Есть рост на фондовом
рынке Нью-Йорка?
Рост на Лондонском
фондовом рынке
Падение на Лондонском
фондовом рынке
Рис. 13.4.
Заметим, что в алгоритме АМХ, так же, как и в представленном
выше алгоритме ДРЕВ, выбор наиболее существенного признака мо-
может определяться на основании эвристических критериев, задаваемых
пользователем.
13.4. Индукция решающих деревьев
Алгоритм ID3 (Induction of Decision trees, разработан
P. Куинланом) формирует решающие деревья на основе примеров.
Каждый пример имеет одинаковый набор атрибутов (признаков),
которые можно рассматривать как качественные признаки. Этот
алгоритм относится к алгоритмам обучения с учителем, таким
образом, обучающая выборка, необходимая для его работы, содержит
положительные и отрицательные примеры формируемого понятия.
В соответствии с терминологией автора назовем признаки, или
атрибуты, которые задают свойства каждого примера обучающей
выборки, предсказывающими атрибутами. Такие признаки могут
быть бинарными, количественными либо качественными. Единствен-
Единственный признак, который для каждого примера задает, принадлежит
ли он формируемому понятию или нет, назовем целевым, или
предсказываемым атрибутом. Этот атрибут является бинарным
и также входит в обучающую выборку.

570
Обучение с учителем
[Гл. 13
Пример 13. 4.
Пусть есть набор примеров, в каких погодных условиях молено и в
каких нельзя играть в гольф. Предсказывающими атрибутами здесь
являются
- прогноз погоды G {солнечно, пасмурно, дождливо},
- температура Е [10, 33] (в градусах Цельсия),
- влажность Е [0, 100] (в процентах),
- ветер Е {true, false} (либо есть ветер, либо ветра нет).
Целевой или предсказываемый атрибут в этом примере — Играть
ли в гольф — принимает два значения: {Да — играть, Нет — не
играть}. Обучающее множество приведено в табл. 13.4.
Таблица 13.4
Прогноз
погоды
Солнечно
Солнечно
Пасмурно
Дождливо
Дождливо
Дождливо
Пасмурно
Солнечно
Солнечно
Дождливо
Солнечно
Пасмурно
Пасмурно
Дождливо
Темпе-
Температура
29
27
28
21
20
18
18
22
21
24
24
22
27
22
Влажность
85
90
78
96
80
70
65
95
70
80
70
90
75
80
Ветер
false
true
false
false
false
true
true
false
false
false
true
true
false
true
Играть ли
в гольф?
Не играть
Не играть
Играть
Играть
Играть
Не играть
Играть
Не играть
Играть
Играть
Играть
Играть
Играть
Не играть
Заметим, что в этом примере два атрибута имеют непрерывные
значения. Алгоритм ID3 не может непосредственно работать с атри-
атрибутами, имеющими непрерывные области определения, хотя ниже мы
рассмотрим способ расширения алгоритма на случай непрерывных
атрибутов.
Алгоритм строит такое решающее дерево, в котором с каждым
узлом ассоциирован атрибут, являющийся наиболее информативным
среди всех атрибутов, еще не рассмотренных на пути от корня дерева.
В качестве меры информативности обычно используется теоретико-
информационное понятие энтропии, хотя возможны и другие под-
подходы.

13.4] Индукция решающих деревьев 571
Если имеется п равновероятных значений атрибута, то вероят-
вероятность р каждого из них равна 1/п и информация, сообщаемая нам
значением атрибута, равна -logp = logn (здесь и далее log обозначает
логарифм по основанию 2). В общем случае, если мы имеем дискрет-
дискретное распределение Р = (pi,P2> • • • >Рп)? то передаваемая информация
или энтропия Р вычисляется по формуле
Чем более равномерным является распределение, тем больше его
энтропия.
Если множество S примеров разбито на попарно непересекаю-
непересекающиеся классы Ci, C2,..., С&, то информация, необходимая для то-
того, чтобы идентифицировать класс примера, равна Info(S) = 7(Р),
где Р — дискретное распределение вероятностей появления соответ-
соответствующего примера, сопоставленное набору классов Ci, С2,..., С&:
Р = ( -г^р, -г§г, • • •, -г^г ), где \dl \S\ — мощности как отдельных
V /
классов, так и всей выборки соответственно.
В нашем примере с игрой в гольф Info(S) = /(9/14,5/14) =
= 0, 94. Здесь 14 — количество примеров в обучающей выборке, 9
и 5 — количество примеров для выборок К^~ и К~ соответственно.
Разбив множество примеров на основе значений некоторого атри-
атрибута А на подмножества Si, S2,..., Sn, мы можем вычислить Info(S)
как взвешенное среднее информации, необходимой для идентифика-
идентификации класса примера в каждом подмножестве:
Так, для атрибута Прогноз погоды в примере с игрой в гольф мы
получим 1п/о(Прогноз погоды, S) = 5/14*7B/5, 3/5)+4/14*7D/4, 0) +
+ 5/14*7C/5, 2/5) = 0, 694.
Величина Gain^A, S) = Info{S) — Info{A,S) показывает количество
информации, которое мы получаем благодаря атрибуту А. Алгоритм
ID3 использует эту величину для оценки информативности атрибута
при построении решающих деревьев, что позволяет получать деревья
минимальной высоты.
Алгоритм 7723 основан на следующей процедуре рекурсивного
характера.
1. Выбирается атрибут для корневого узла дерева, и формируются
ветви для каждого из возможных значений этого атрибута.

572
Обучение с учителем
[Гл. 13
2. Дерево используется для классификации обучающего множе-
множества. Если все примеры на некотором листе принадлежат одному
классу, то этот лист помечается именем этого класса.
3. Если все листья помечены именами классов, алгоритм заканчи-
заканчивает работу. В противном случае узел помечается именем оче-
очередного атрибута, и создаются ветви для каждого из возможных
значений этого атрибута, после чего алгоритм снова выполняет
шаг 2.
В примере с игрой в гольф получим следующее решающее дерево
(рис. 13.5).
дождливо
< 75 75 True \ False
Ы И
Рис. 13.5.
Ниже приведен псевдокод алгоритма ID3.
Алгоритм, ID3
Алгоритм ID3 (А: множество предсказывающих атрибутов,
С: целевой атрибут,
S: обучающее множество)
результат решающее дерево
начало
если S = 0, то вернуть одну вершину со значением «ошибка»
если S состоит из примеров с одинаковым значением атрибута С,
то вернуть одну вершину со значением атрибута С
если А = 0, то вернуть одну вершину со значением атрибута С,
наиболее частым среди примеров из S
Пусть D — атрибут с наибольшим значением Gain(D, S) среди всех
атрибутов из А.
Пусть dj, j = 1, 2,..., т — значения атрибута D, a Sj,
j = 1,2,...,тп — подмножества обучающих примеров, состоящие из
примеров со значением dj для атрибута D
Вернуть дерево с корнем, помеченным D и дугами, помеченными
d\, 6^2,..., dm, соединяющими корень с деревьями
ID3(A\{D}, С, Si), ID3(A\{D}, С, S2),... ,ID3(A\{D}, С, Sm);
конец

13.4] Индукция решающих деревьев 573
Рассмотрим оценку вычислительной сложности алгоритма ID3.
Положим для простоты, что размер областей определения всех атри-
атрибутов одинаков и равен Ъ. Количество рекурсивных вызовов в худшем
случае составит 1 + Ъ + Ъ2 + ... + Ьк~г, где к — количество атрибутов,
а общая сложность составит
к-1
г=0
где С (г) — сложность одного шага алгоритма (как мы увидим в
дальнейшем, она зависит от глубины рекурсивной вложенности).
Единственная трудоемкая операция, выполняемая на одном ша-
шаге алгоритма, это выбор атрибута D с максимальным значением
Gain(D, S). При этом количество альтернатив и размеры подмноже-
подмножества обучающих примеров сужаются с увеличением глубины рекур-
рекурсивной вложенности. На уровне г они составляют соответственно к — г
и п/Ъг, где п — количество примеров. Для того, чтобы вычислить
Gain(D, S), достаточно одного просмотра множества примеров, по-
поэтому общее число операций составит
Подставив это выражение в сумму, определяющую общую слож-
сложность, и выполнив очевидные преобразования, получим
к-1
С (IDS) = п ^(к -г)= О(к2п).
г=0
Аналогичный результат получен в работе Утгоффа с использова-
использованием несколько иной методики доказательства.
Рассмотрим, как обрабатываются атрибуты, имеющие непрерыв-
непрерывные значения. Даже если некоторый атрибут А имеет непрерывную
область определения, в обучающем множестве имеется лишь конечное
множество значений с\ < с^ < ... < сп. Для каждого значения q
мы разбиваем примеры на те, у которых значение А ^ q, и те, у
которых А > Сг. Для каждого из возможных разбиений мы вычисля-
вычисляем Gain(A, S) и выбираем наиболее информативное разбиение. Так
было получено разбиение по значению 75 для атрибута Влажность
в примере с игрой в гольф.
Сравним алгоритм ID3 с ДРЕВ и АМХ. Первые два из рассмот-
рассмотренных выше алгоритмов строят только бинарные деревья решений,
тогда как каждый узел в дереве, построенном алгоритмом /D3, может
иметь более двух потомков. Это обусловлено тем, что в алгоритме
ID3 на каждом шаге определяется важнейший признак, а в алгорит-
алгоритмах ДРЕВ и АМХ — важнейшее (разделяющее) значение признака.

574 Обучение с учителем [Гл. 13
Признак может иметь несколько значений, а на вопрос «Обладает
ли пример каким-либо значением признака?» молено дать только два
ответа: Да или Нет. Поэтому в тех случаях, когда признаки имеют
больше двух значений, наиболее подходящим является алгоритм ID3.
Алгоритмы ДРЕВ и АМХ также можно использовать и в этих слу-
случаях, потому что любое дерево решений можно представить в виде
бинарного. Но такое дерево будет более громоздким и не очень удоб-
удобным для использования, поскольку придется иметь дело с длинными
путями.
Алгоритм ID3 хорошо зарекомендовал себя в широком спектре
приложений. Он обеспечивает высокое качество классификации, а
учет статистических закономерностей позволяет ему работать с за-
шумленными данными. После того, как алгоритм был впервые опуб-
опубликован, ряд исследователей предложили различные усовершенство-
усовершенствования алгоритма. Так, в статье Утгоффа предложена инкрементная
версия алгоритма, которая позволяет не создавать дерево заново при
добавлении одного примера, а перестроить его. Это свойство важно
для того, чтобы учесть изменения в базах данных. В работе Нуньеса
предложена версия алгоритма, позволяющего использовать допол-
дополнительную информацию о предметной области. Наконец, в статье
Мингера рассмотрены различные методики упрощения решающих
деревьев и проведено их экспериментальное сравнение.
13.5. Модификация алгоритма Куинлана — ID5R
В своей работе Утгофф предложил инкрементную версию алго-
алгоритма ID3 под названием ID5R. Решающее дерево, простроенное
этим алгоритмом, совпадает с решающим деревом, которое было бы
построено с помощью алгоритма /D3, что позволяет использовать ал-
алгоритм IDbR как прямую замену ID3 в тех случаях, когда требуется
инкрементное обучение. Инкрементная версия сохраняет предыдущий
вариант дерева решений, а при добавлении новых примеров лишь
перестраивает его. Алгоритм хранит достаточно информации, чтобы
при появлении нового примера заново вычислить информативность
каждого атрибута и перестроить дерево таким образом, чтобы наибо-
наиболее информативный атрибут оказался в вершине дерева.
Формально решающее дерево алгоритма IDbR имеет вид
1. Лист, с которым связаны:
a) имя класса,
b) множество описаний примеров, принадлежащих классу.
2. Корневая вершина, с которой связаны:
c) проверка атрибута с ответвлением к другим решающим де-
деревьям (свое поддерево для каждого возможного значения

13.5] Модификация алгоритма Куинлана — ID5R 575
атрибута), а также счетчики положительных и отрицатель-
отрицательных примеров для каждого значения,
d) неиспользованные атрибуты, каждый с набором счетчиков
(для всех возможных значений) положительных и отрица-
отрицательных примеров.
Как видно, разметка решающего дерева отличается от разметки,
используемой в алгоритме ID3, поэтому его интерпретация также
несколько отличается. Когда дерево используется для классификации
обучающего примера, от корня дерева проходится путь в соответствии
со значениями атрибутов в узлах проверки до тех пор, пока не будет
достигнут лист, в котором все примеры принадлежат одному классу.
Если достигнутый лист содержит примеры разных классов, то алго-
алгоритм развертывает его в поддерево и продолжает работу.
Алгоритм ID5R выглядит следующим образом. Он получает на
входе решающее дерево и очередной обучающий пример и выдает
обновленное решающее дерево.
Алгоритм, IDR5
Алгоритм ID5R (Т: решающее дерево,
s: обучающий пример)
результат решающее дерево
начало
если Т = 0, то вернуть лист с именем класса из обучающего
примера и множеством примеров, содержащим один обучающий
пример s
если Т — лист и пример принадлежит тому же классу, что и Т,
то добавить пример к списку примеров листа и вернуть Т
иначе
если Т — лист, то преобразовать его в дерево высоты 1, выбрав
решающий атрибут произвольным образом, обновить счетчики по-
положительных и отрицательных примеров для каждого значения
решающего атрибута
если текущий решающий атрибут не является наиболее информа-
информативным, то перестроить дерево таким образом, чтобы наиболее ин-
информативный атрибут оказался в корне дерева, рекурсивно устано-
установить наилучший атрибут для всех поддеревьев, обновить поддерево,
находящееся под значением решающего атрибута, присутствующем
в s.
Вернуть Т
конец если
конец
Пример 13. 5.
Рассмотрим работу алгоритма на примере табл. 13.5. Каждый при-
пример описывается тремя атрибутами: рост, цвет волос и цвет глаз.

576
Обучение с учителем
[Гл. 13
Класс
-
-
+
-
-
+
-
+
Рост
Низкий
Высокий
Высокий
Высокий
Низкий
Высокий
Высокий
Низкий
Волосы
Светлые
Темные
Светлые
Темные
Темные
Рыжие
Светлые
Светлые
Глаза
Карие
Карие
Голубые
Голубые
Голубые
Голубые
Карие
Голубые
Таблица 13.5
Изначально решающее дерево является пустым. После первого
примера (—, рост = низкий, волосы = светлые, глаза = карие),
дерево превращается в лист (рис. 13.6 а). Следующий пример также
является отрицательным, поэтому он просто добавляется к списку
примеров, давая дерево, изображенное на рис. 13.6 б. Третий пример
(+, рост = высокий, волосы = светлые, глаза = голубые) — положи-
положительный, поэтому лист преобразуется в дерево высоты 1. Решающий
атрибут выбирается произвольным образом, в данном случае им яв-
является атрибут рост. Сразу после преобразования дерево имеет вид,
изображенный на рис. 13.6 в (в квадратных скобках показано количе-
количество положительных и отрицательных примеров соответственно), но
наиболее информативным является атрибут глаза. Поэтому первым
шагом будет преобразование непосредственных поддеревьев таким
образом, чтобы атрибут глаза являлся их решающим атрибутом. В
данном случае оба поддерева являются листьями, поэтому они раз-
разворачиваются в деревья с использованием атрибута глаза в качестве
решающего атрибута (рис. 13.6 г), после чего атрибуты рост и цвет
глаз меняются местами (рис. 13.6 д).
Заметим, что поддерево под вершиной, помеченной значением гла-
глаза = голубые, пока пусто, так как процесс построения дерева еще не
закончен. Следующим шагом является проверка решающих атрибу-
атрибутов на нижних уровнях дерева. Так, атрибут рост сейчас является
решающим не потому, что он наиболее информативный, а в резуль-
результате преобразования дерева на предыдущем шаге. После проверки
оказывается, что рост является более информативным, чем волосы,
поэтому перестройки этого поддерева не требуется.
Наконец, последний шаг алгоритма — это обновление поддерева
под признак глаза = голубые. В результате получается структура,
изображенная на рис. 13.6 е.

13.5]
Модификация алгоритма Куинлана — ID5R
577
(рост = низкий, волосы = светлые, глаза = карие)
(рост = низкий, волосы = светлые, глаза = карие)
(рост = высокий, волосы = темные, глаза = голубые)
(волосы = светлые, глаза = карие) (волосы = темные, глаза = голубые)
низкий [ОД]
высокий [1,1]
(рост = высокий, волосы = темные)
Рис. 13.6.
19 В.Н. Вагин и др.

578
Обучение с учителем
[Гл. 13
Очевидно, что правое поддерево с корнем рост может быть свер-
свернуто в лист, поскольку все его примеры принадлежат одному классу.
Однако алгоритм IDbR не выполняет это действие, так как неизвест-
неизвестно, окажется ли подобное свертывание полезным. С одной стороны, в
свернутом виде поддерево будет занимать меньше места и его легче
обновлять, но, с другой стороны, разворачивание вновь листа в дере-
дерево — достаточно трудоемкая операция. Эксперименты, проведенные
автором алгоритма, показывают, что в общем случае сворачивание
поддерева не дает положительного эффекта.
Оставшиеся примеры обрабатываются аналогичным образом. В
результате получается следующее решающее дерево (рис. 13.7).
светлые [2,2]/темные [ОД
!ыжые [1,0]
голубые [2,0] карие [0,2] голубые [0,2] карие [ОД]
рост рост
низкий [1,0] выский [1,0]
(рост = высокий
рост = низкий)
\ низкий [ОД] высокий [ОД]
Рис. 13.7.
(рост = высокий
глаза = голубые)
высокий [ОД]
После сжатия этого дерева, сворачивая, где возможно, поддеревья
в один лист, мы получим дерево, изображенное на рис. 13.8. Такое же
дерево будет построено алгоритмом ID3 на этих восьми обучающих
примерах.
светлые [2,2]
голубые [2,0]
рыжие [1,0]
(рост = высокий, глаза = голубые)
(рост = высокий, глаза = карие)
(рост = низкий, глаза = карие)
(рост = высокий,
глаза = голубые)
+
(рост = высокий)
(рост = низкий)
(рост = высокий)
(рост = низкий)
Рис. 13.8.

13.6] Алгоритм Reduce 579
Утгофф провел теоретическую оценку вычислительной сложности
алгоритма ID5R и осуществил ряд экспериментов. В худшем случае
количество операций составляет
C(IDbR) = О(п-к-Ък),
где п — размер обучающего множества (количество примеров), к —
количество атрибутов, Ъ — максимальное количество различных зна-
значений одного атрибута. Сравним этот алгоритм с методом «гру-
«грубой силы», когда после добавления каждого обучающего примера
заново строится решающее дерево с помощью алгоритма ID3. Такой
алгоритм получил название ID3f. Легко показать, что C(ID3f) =
= Oik2 • n2).
Поскольку обычно к • Ък > /с2, то на малом количестве примеров
метод «грубой силы» работает быстрее. Однако по мере увеличения
количества примеров вклад множителя п2 становится все более зна-
значительным, в то время как к • Ък остается постоянным. Поэтому на
большом обучающем множестве (а именно этот случай нам наиболее
интересен) алгоритм ID5R работает быстрее.
Алгоритм IDbR строит решающее дерево инкрементно, модифи-
модифицируя решающее дерево таким образом, чтобы наиболее информа-
информативный атрибут всегда проверялся первым. Хотя алгоритм сохраняет
обучающие примеры в решающем дереве, они используются только в
процессе изменения структуры дерева, а не обрабатываются каждый
раз при добавлении нового примера. Алгоритм строит такое же реша-
решающее дерево, что и оригинальный алгоритм ID3.
Вычислительная сложность алгоритма IDbR на больших обучаю-
обучающих множествах ниже, чем у метода «грубой силы», что подтвержде-
подтверждено эмпирическим сравнением на одних и тех же обучающих выборках.
Результаты сравнения даны в работе Утгоффа.
13.6. Алгоритм Reduce
Характерной чертой алгоритма ID3 является то, что для де-
детерминированных (без шума) входных данных примеры обучающего
множества всегда классифицируются правильно. Когда алгоритм ID3
применяется к данным, которые могут содержать значения в некото-
некоторой степени случайным образом искаженные, например, в результате
ошибок, измерения, результирующее решающее дерево становится
слишком большим и сильно ветвящимся. В этом случае предлагается
построение решающего дерева разбить на три части. Сначала с по-
помощью алгоритма ID3 или ID5R строится первоначальное большое
дерево, затем это дерево подвергается упрощению с целью удаления
ветвей с низкой статистической достоверностью. Последним этапом
является обработка дерева для повышения его понятности.
19*

580 Обучение с учителем [Гл. 13
В работе Мингера проведено сравнение нескольких методов упро-
упрощения деревьев. Основываясь на результатах этой работы, мы рас-
рассмотрим алгоритм Reduce, предложенный Куинланом в 1987 г. Ал-
Алгоритм Reduce формирует последовательность упрощенных деревьев,
и для его работы необходимо наличие тестового множества приме-
примеров. Алгоритм работает следующим образом: сначала полное дерево
используется для классификации примеров тестового множества, и
для каждого узла дерева запоминается количество примеров каждого
класса. Затем для каждого узла вычисляется количество ошибок,
допущенных в процессе классификации и количество ошибок, которое
было бы допущено, если бы соответствующее поддерево было редуци-
редуцировано в лист. Из всех узлов дерева выбирается тот, который дает
наибольший выигрыш в количестве ошибок, и преобразуется в лист.
Процесс повторяется до тех пор, пока не останется узлов, редукция
которых уменьшает общее количество ошибок.
Алгоритм Reduce
алгоритм Reduce (T: решающее дерево,
S: множество тестовых примеров)
результат упрощенное решающее дерево
начало
для всех s G S
классифицировать пример s по дереву Т, увеличивая счетчик, со-
соответствующий классу примера, в каждом узле дерева
конец для
повторять
для всех t — узлов дерева Т
вычислить количество ошибок Eo(t) в поддереве с корнем в t\
вычислить количество ошибок Ei(t), которое будет допущено, если
поддерево будет преобразовано в лист
вычислить выигрыш G(t) = Eo(t) — E\(t)
конец для
найти to : maxG(t) = G(to)
если G(to) > 0 то преобразовать поддерево to в лист
пока G(t0) > 0
вернуть Т
конец
Пример 13. 6.
Рассмотрим работу алгоритма на примере из предыдущего разде-
раздела. Пусть имеется решающее дерево (рис. 13.9) и множество тестовых
примеров, представленных в табл. 13.6.
Классифицируя первый пример ( —, низкий, светлые, голубые), мы
проходим по пути дерева волосы —> светлые —> глаза —> голубые —>
—> +, т.е. этот пример классифицирован ошибочно. Так как этот

13.6]
Алгоритм Reduce
581
светлые/ темные
глаза
голубые / \ карие
]
Рис. 13.9.
Таблица 13.6
Класс
-
-
+
+
-
+
-
Рост
Низкий
Высокий
Высокий
Высокий
Низкий
Низкий
Высокий
Волосы
Светлые
Темные
Светлые
Темные
Темные
Рыжие
Светлые
Глаза
Голубые
Карие
Голубые
Карие
Голубые
Голубые
Голубые
пример отрицательный, мы увеличиваем счетчик отрицательных при-
примеров в каждом узле дерева. Дерево принимает вид, приведенный на
рис. 13.10
(в квадратных скобках, как и ранее, показывается количество
положительных и отрицательных примеров соответственно).
+
[ОД]
[0,0]
Рис. 13.10.
Аналогичным образом классифицируются остальные тестовые
примеры, после чего дерево выглядит следующим образом
(рис. 13.11).

582
Обучение с учителем
[Гл. 13
волосы
[3,4]
светлые/темные\
глаза
[1,2]
[1,2]
голубые/ Хкарие
+
[1,2]
[0,0]
Рис. 13
.11.
\рыжые
[1,0]
После того, как все примеры тестового множества классифици-
классифицированы, алгоритм вычисляет количество ошибок в каждом подде-
поддереве. Для поддерева с корнем глаза количество ошибок составляет
Ео(глаза) = 2, а для всего дерева Ео(волосы) = 3. Если теперь
все поддерево с корнем глаза заменить на один лист со
значением « —», то количество ошибок составит Е\(глаза) = 1, т.е.
количество ошибок уменьшится на G{глаза) = Eq(глаза)—Е\(глаза) =
= 1. Проведя аналогичные подсчеты для всего дерева, получаем
Ei(волосы) = 3, G(волосы) = 0.
Таким образом, поддерево с корнем глаза обеспечивает наиболь-
наибольший выигрыш в количестве ошибок и редуцируется в лист (рис. 13.12).
волосы
[3,4]
ветлыб// темные\
[1,2]
Рис.
[1,2]
13.12
Х^рыжые
+
[1,0]
На следующей итерации алгоритма остается только одна возмож-
возможность для редукции — узел волосы, но, как нетрудно проверить, такая
редукция приведет к увеличению общего количества ошибок, поэтому
на этом работа алгоритма заканчивается.
Дадим оценку вычислительной сложности алгоритма Reduce. Обо-
Обозначим размер тестового множества через п и количество узлов ис-
исходного дерева как р. Классификация выполняется п раз и в худшем
случае приведет к перебору всех р вершин дерева. Поэтому на клас-
классификацию примеров тестового множества требуется пр операций.
Вычисление Eo(t) и E\(t) для всех узлов можно произвести за один
просмотр дерева снизу вверх. Поскольку каждая редукция поддерева
приводит к уменьшению узлов дерева как минимум на один, а общее
количество редукций не может быть больше р, то на цикл редукции

13.7] Фокусирование 583
будет затрачено не более р2 операций. Таким образом, вычислитель-
вычислительная сложность алгоритма Reduce С (Reduce) = О(пр + р2).
Эксперименты, проведенные Мингером, показывают, что исполь-
использование алгоритма Reduce приводит к значительному уменьшению
количества узлов в решающем дереве. В зависимости от количества
шума в обучающем множестве, количество узлов уменьшалось от 2
до 10 раз. При этом точность классификации, выраженная как отно-
отношение количества ошибок к общему числу примеров, увеличивалась
на 25%.
Таким образом, применение алгоритма Reduce способно суще-
существенно упростить дерево решений и повысить точность классифи-
классификации, но требует наличия отдельного множества тестовых примеров.
13.7. Фокусирование
Важным шагом вперед при решении задачи обобщения понятий
является получение решающих правил (продукций, деревьев), кото-
которые содержат не только логические функции от конкретных значе-
значений признаков, но включают более общие закономерности, напри-
например, обобщенные значения тех же атрибутов. Рассмотрим метод фо-
фокусирования, где предполагается, что над значениями каждого из
атрибутов Ai построена иерархия типа «класс — подкласс», называе-
называемая ISA-иерархией. Элементы нижнего уровня являются значениями
атрибутов сц, Q2, • • •, с%п и встречаются в обучающем множестве S.
Элементы верхних уровней соответствуют более общим понятиям, т. е.
подмножествам Sij С Dom(Ai).
Важным требованием к подобной иерархии является то, что каж-
каждые два элемента должны иметь наименьшую верхнюю грань, т. е. это
должно быть не просто частично упорядоченное множество, а верх-
верхняя полу решетка. На практике это требование легко удовлетворить,
добавив Dom(Ai) на вершину иерархии.
Каждому элементу иерархии соответствует конъюнкт вида
Ai Е Sij в формируемых правилах, причем правило содержит в
точности по одному конъюнкту для каждого предсказывающего
атрибута:
Аг е Slh & А2 е S2J2 & ... & Ат е Smjm - С.
Естественно, конъюнкт вида Ai Е Dom(Ai) тождественно истинен
и может быть опущен.
Для работы алгоритма фокусирования необходимо также наличие
отрицательных примеров в обучающем множестве. С помощью отри-
отрицательных примеров учитель ограничивает набор допустимых обоб-
обобщений и может определить, когда обучение должно быть завершено.
Алгоритм формирует результат в виде обобщенного продукционного
правила, выраженного через известные предикаты.

584 Обучение с учителем [Гл. 13
Целью алгоритма фокусирования является нахождение конъюнк-
конъюнктов в условии правила. В иерархии каждого атрибута алгоритм от-
отслеживает два указателя, называемые нижним L и верхним U. L
указывает на наиболее ограничивающее условие, которое может быть
конъюнктом правила. Правильный конъюнкт является обобщением
любого из конъюнктов, расположенных ниже L. Указатель U отмеча-
отмечает наименее ограничивающее условие, которое может быть конъюнк-
конъюнктом. Все условия, не являющиеся специализацией U, не могут быть
конъюнктами, так как противоречат контрпримерам.
Алгоритм фокусирования.
1. Найти первый положительный пример и установить в каждой
иерархии указатель L на значение, соответствующее значению
атрибута в этом примере, а указатель U — на вершину иерархии.
2. Пусть / — очередной пример. Если это положительный пример,
то в каждой иерархии установить L, как наименьшую верхнюю
грань предыдущего положения L и вершины, соответствующей
текущему значению атрибута.
3. Если / является отрицательным примером и существует в точно-
точности одна иерархия, в которой вершина, соответствующая теку-
текущему значению атрибута, лежит ниже U и не ниже L, мы имеем
дело с ближним промахом. В этой иерархии следует установить
U как наименьшую верхнюю грань:
а) вершины, на которую указывает U и всех нижележащих
вершин;
б) вершины, на которую указывает L и всех вышележащих
вершин;
в) вершин, не лежащих выше текущего значения атрибута.
4. В противном случае (/ является отрицательным примером и су-
существует более одной иерархии, в которой вершина, соответству-
соответствующая текущему значению атрибута, лежит ниже U и не ниже
L), мы имеем дело с дальним промахом. Возможные действия в
данном случае будут рассмотрены отдельно.
5. Если существует иерархия, в которой L ф U", выбрать следую-
следующий пример и перейти к шагу 2. В противном случае СТОП.
Когда алгоритм останавливается, L и U указывают на одну и ту
же вершину в каждой иерархии. Эти вершины и являются искомыми
конъюнктами.
Рассмотрим подробнее пункт 4 алгоритма. Когда существует бо-
более одной иерархии, в которой вершина, соответствующая текущему
значению атрибута, лежит ниже U и не ниже L, мы не знаем, в какой
из них следует опустить [/, чтобы учесть контрпример. Существует
несколько стратегий для обработки дальних промахов:

13.7] Фокусирование 585
1) игнорировать их и не изменять положения указателей;
2) запросить пользователя, какую иерархию выбрать;
3) упорядочить обучающее множество таким образом, чтобы поло-
положительные примеры предшествовали отрицательным;
4) рассмотреть все возможные случаи. Это потребует введения
новых пар указателей для каждого случая. В конце обучения
будет ясно, какой выбор был правильным.
Пример 13. 7.
Целью исследования являются фразы естественного языка (ан-
(английского). Надо вывести правило, позволяющее выяснить, надо ли
ставить неопределенный артикль «а» перед словом или нет. Понятия,
или предикаты, которые образуют базу знаний, делятся на четыре
независимые группы.
Группа 1. Def(x), Indef(x).
Группа 2. Singular (ж), Plural(x).
Группа 3. agent(х, г/), object(х, г/),
Группа 4. Past(x), Present(x), Future(x).
В первой группе предикатов задается, является ли х {х — любое
слово) определенным или неопределенным объектом. Вторая груп-
группа определяет единственное или множественное число объекта х.
Группа 3 определяет, является х агентом или объектом действия в
ситуации у. В группе 4 задается время действия — прошедшее, насто-
настоящее или будущее. Для каждой группы задаем иерархию понятий в
виде диаграммы частичного порядка, или полурешетки. На высших
уровнях таких структур располагаются дизъюнктивные отношения.
Дизъюнкции более высокого уровня будут более общими, чем дизъ-
дизъюнкции низших уровней. Таким образом, каждая структура будет
аналогом ISA-иерархии (иерархии класс — подкласс). На рис. 13.13
приведены иерархические структуры для рассматриваемого примера.
true true
Definite Indefinite Singular Plural
true true
not_speculative
agent object
Past Present Future
Рис. 13.13.

586
Обучение с учителем
[Гл. 13
Цель алгоритма — построить продукционное правило в виде:
IF условия THEN АРТИКЛЬ (ж, «а»).
Построенное алгоритмом правило должно содержать конъюнкцию
предикатов из каждой группы.
В табл. 13.7 приведена обучающая выборка из пяти примеров —
предложений на английском языке. В каждом предложении выделе-
выделено исследуемое слово. Правая часть таблицы содержит предикаты,
приписанные этому слову.
Таблица 13.7
р
1
2
3
4
5
Фразы
A dog chases balls.
Dogs chase balls.
John chased a dog.
Dogs will chase
a ball.
John will chase dogs.
Предикаты
базы знаний
Indef(x), Singular(x),
Present(x), agent (ж, у)
IndefO), PluraK»,
Present(x), agent (ж, у)
Indef(x), Singular(x),
Past (ж), object (ж, у)
Indef(x), Singular(x),
Future(x), object (ж, у)
Def(x), Singular(x),
Future(x), agent (ж, у)
Ставить ли
артикль «а»
Да
Нет
Да
Да
Нет
Пусть примеры рассматриваются алгоритмами в этом порядке.
Первым анализируется положительный пример. Положение указате-
указателей U, L, соответствующих ему, показано на рис. 13.14: L указывает на
вершины Indef, Singular, Present, agent; верхний указатель U в каждой
структуре установлен на корневую вершину, помеченную true.
Untrue
true
Definite L -» Indefinite L -»> Singular Plural
Untrue
not_speculative
Past X -> Present Future
Рис. 13.14.
true
L -> agent object

13.7]
Фокусирование
587
Второй экземпляр обучающей выборки — контрпример. Имеет-
Имеется единственная структура, для которой текущее значение атрибута
(Plural) не ниже L. На этой структуре понижаем указатель U так,
чтобы он находился не ниже L (рис. 13.15).
U-> true
true
Definite L -» Indefinite U -* L-* Singular Plural
17 ^ true
Untrue
not^speculative
L -» agent object
Past L ™> Present Future
Рис. 13.15.
Третий пример выборки также положительный. Соответствующие
ему предикаты приведены в табл. 13.7. Здесь мы повышаем указатель
L до корневой вершины true в структуре agent — object. Мы также по-
повышаем указатель L до вершины non-speculative в структуре времен;
эта вершина будет обобщением случаев Past и Present (рис. 13.16).
true
true
Definite L -» Indefinite 17 -> L ™> Singular Plural
U-* true
true
L -> not^speculative
L -> agent object
Past Present Future
Рис. 13.16.
Четвертый положительный пример обладает свойством Future, это
показывает, что все варианты задания параметра «время» покрыва-
покрываются положительными примерами, указатель L для дерева времен
устанавливается на корневую вершину true. Последний элемент обу-
обучающей выборки — также контрпример. На рис. 13.17 показано окон-

588 Обучение с учителем [Гл. 13
чательное распределение указателей после обучения. Теперь сформу-
сформулируем результат:
Indef(X) & Singular(X) & true & true => АРТИКЛЬ(Х, «а»).
Можно отбросить части true в конъюнкции. Окончательный резуль-
результат: ЕСЛИ X неопределенное и в единственном числе ТО ставим
перед ним артикль «а».
true true
Definite U^L^> Indefinite U^L^ Singular Plural
^U^ true L^U^ true
not_speculative
agent object
Past Present Future
Рис. 13.17.
Метод фокусирования не приспособлен для работы с зашумленны-
ми данными. Если исходные данные содержат шум или противоречи-
противоречивы, произойдет одно из двух:
1) либо для некоторого положительного примера значение атрибу-
атрибута не окажется ниже вершины, указываемой U\
2) либо для отрицательного примера новое положение U окажется
ниже L.
Таким образом, сильными сторонами метода фокусирования явля-
являются
• обучение является инкрементным, если только не надо переупо-
переупорядочивать обучающее множество;
• не требуется запоминать обучающие примеры;
• автоматически распознается момент, когда обучение должно
быть завершено;
• результат обучения является оптимальным в том смысле, что
находится наиболее общее правило, не противоречащее контр-
контрпримерам.
С другой стороны метод фокусирования имеет и недостатки:
• довольно много предположений об исходных данных;

13.8] Алгоритм EG2 589
• в случае дальних промахов часть информации может быть уте-
утеряна или метод становится ненадежным;
• метод не может работать с противоречивыми данными и данны-
данными, содержащими шум.
В этом плане метод фокусирования является методом классическо-
классического машинного обучения и не может быть непосредственно применен,
например, для работы с базами данных.
13.8. Алгоритм EG2
Рассмотренные ранее алгоритмы семейства ID3 никак не исполь-
используют информацию о предметной области. В работе Нуньеса пред-
предложен алгоритм EG2, который позволяет пользователю задать ISA-
иерархию над значениями каждого атрибута. Кроме того, алгоритм
вводит экономический критерий в процесс классификации. Например,
врач, принимая человека с головной болью, не назначает ему сразу
томографию головного мозга, хотя этот тест является наиболее ин-
информативным. Вместо этого он задает простые вопросы и назначает
более экономичные проверки, чтобы исключить простые случаи.
В то время как алгоритм ID3 использует чисто информационную
метрику (количество информации) для выбора решающего атрибута,
алгоритм EG2 использует несколько иной подход. Критерием для вы-
выбора атрибута является функция стоимости информации (Information
Cost Function, ICF). Эта функция определяется как отношение меж-
между стоимостью атрибута и его различающей способностью:
где cos t(Ai) — функция стоимости атрибута, Gain(Ai) — информатив-
информативность атрибута (введена в разд. 13.4), ио — переменная для управления
критерием экономичности. Алгоритм выбирает атрибут с наимень-
наименьшим значением ICF'.
Алгоритм EG2 осуществляет две формы обобщения: подъем по
дереву обобщения и объединение значений операцией или. Первая из
них — подъем по дереву обобщения — это обобщение, использован-
использованное в алгоритме фокусирования. Для выполнения такого обобщения
алгоритм учитывает ISA-иерархии, ассоциированные с атрибутами.
Пусть, например, с атрибутом форма ассоциирована иерархия, пред-
представленная на рис. 13.18.
Тогда на следующих обучающих примерах может быть
построено обобщенное решающее дерево, представленное на
рис. 13.19.

590
Обучение с учителем
[Гл. 13
Кривая
Треугольник Квадрат Пятиугольник
Эллипс
Рис. 13.18.
Многоугольник
Класс
+
+
+
Форма
Квадрат
Треугольник
Пятиугольник
Круг
Эллипс
Рис. 13.19.
Если же ISA-иерархия отсутствует, используется вторая форма
обобщения — объединение отдельных значений атрибутов операцией
или (рис. 13.20).
\ Треугольник V
\ Пятиугольник
Класс
Форма
Квадрат
Треугольник
Пятиугольник
Круг
Эллипс
Рис. 13.20.

13.8] Алгоритм EG2 591
Будем называть структурированными атрибутами те из них, ко-
которые имеют ассоциированную ISA-иерархию. В обучающих при-
примерах могут встречаться только значения, расположенные на ниж-
нижнем уровне иерархии, будем называть эти значения наблюдаемыми.
Остальные значения в ISA-иерархии будем называть абстрактными.
Заметим, что наблюдаемое значение может принадлежать нескольким
абстрактным значениям.
Алгоритм работает следующим образом. Сначала выбира-
выбирается атрибут с наименьшей функцией стоимости информации.
Затем формируется список L, состоящий из самых общих
абстрактных значений и наблюдаемых значений, для которых
нет абстрактных значений. Затем алгоритм пытается постро-
построить поддерево, соответствующее первому значению в списке.
Если полученное поддерево является полным и непротиворе-
непротиворечивым, поддерево запоминается для дальнейшего обобщения
(понятия полноты и непротиворечивости будут рассмотрены
ниже), в противном случае абстрактное значение разбивается
на значения следующего уровня, и они добавляются в спи-
список.
Для усиления обобщения алгоритм пытается объединять очеред-
очередные элементы списка с помощью операции или. Если поддерево, соот-
соответствующее новому условию, остается полным и непротиворечивым,
оно сохраняется, в противном случае используется дерево, полученное
на предыдущем шаге.
Дерево решений называется противоречивым, когда суще-
существуют два примера, которые принадлежат разным классам,
но классифицируются одинаково. В этом случае алгоритм
сначала пытается построить менее сильное обобщение, и, если
ни одно из обобщений не является приемлемым, используются
только наблюдаемые значения, точно так же, как в алгорит-
алгоритме ID3.
Полнота дерева решений определяется измерением пропорции на-
наблюдаемых значений в листьях поддерева:
т п
Е EMU)
полнота = , где
т • п
{1, если лист j содержит наблюдаемое значение г,
О, если лист j не содержит наблюдаемого значения г.
Если каждый лист содержит каждое наблюдаемое значение, то полно-
полнота равна 1. Обобщение считается приемлемым, если величина полноты
превосходит некоторый порог с?, определенный пользователем.

592 Обучение с учителем [Гл. 13
Алгоритм, EG2
Алгоритм EG2(A: множество предсказывающих атрибутов,
С: предсказываемый атрибут,
S: обучающее множество)
результат решающее дерево
начало
если все примеры в S имеют одинаковое значение атрибута С, то
вернуть одну вершину, помеченную этим значением
если А = 0, то вернуть одну вершину со значением атрибута С,
наиболее частым среди примеров из S
выбрать атрибут D с наименьшим значением ICF(D)
L := {абстрактные значения верхнего уровня} U {наблюдаемые
значения атрибутов, не принадлежащих никакому абстрактному
значению}
G := 0 (текущее обобщение)
Т := 0 (текущее поддерево)
То := 0 (формируемое поддерево)
пока L ф 0 выполнить
упорядочить L от более общих значений к менее общим
с := первый элемент списка L
построить выборку <jd(S) = {$ ? S\s удовлетворяет G V (D = с)}
t:=EG2(A\{D},C,aD(S))
если t — непротиворечиво и полно, то
G:=GV(D = c)
T:=t
L := L\{c}
иначе
если G ф 0 то То := То U Т
иначе если с — абстрактное значение, то
L := L\{c} U { список значений, подчиненных с}
конец если
G:=0
Т:=0
конец если
конец пока
То :=T0UT
вернуть То
конец
Пример 13. 8.
Рассмотрим работу алгоритма на следующем примере. Заданы
четыре атрибута: форма, цвет, размер и материал. Стоимость их

13.S
Алгоритм EG2
593
измерения 10, 30, 50 и 100 единиц соответственно. На значениях
первых трех атрибутов построены следующие иерархии (рис. 13.21).
Форма
Треугольник Квадрат Пятиугольник
/
Круг
Кривая
/
isa
\isa
Эллипс
Цвет
Розовый
Размер
Рис. 13.21.
Обучающее множество составляют примеры, приведенные в
табл. 13.8.
Чтобы выбрать первый атрибут, алгоритм вычисляет информа-
информативность каждого атрибута и его функцию стоимости информации:
Gain (форма) = 0, 061
Gain (цвет) = 0,119
Gain (раз мер) = 0,167
Gain (материал) = 0,186
ICF'(форма) = 252,27
1С?(цвет) = 360, 54
ICF(pa,3Mep) = Ш,Ъ7
ICF(материал) = 733, 98
Как видно, хотя атрибут материал является наиболее информа-
информативным, более выгодным отношением стоимость/информативность
обладает атрибут форма, поэтому он выбирается в качестве решаю-
решающего в корне дерева.

594
Обучение с учителем
[Гл. 13
Таблица 13.8
Класс
+
+
+
-
-
-
-
-
+
+
+
+
Форма
Квадрат
Квадрат
Треугольник
Треугольник
Квадрат
Круг
Круг
Эллипс
Эллипс
Эллипс
Круг
Треугольник
Цвет
Красный
Синий
^Желтый
Розовый
Розовый
Красный
Синий
Желтый
Синий
Розовый
Синий
Синий
Размер
Большой
Маленький
Средний
Большой
Средний
Маленький
Маленький
Маленький
Большой
Средний
Большой
Средний
Материал
Металл
Пластик
Металл
Кожа
Кожа
Пластик
Металл
Пластик
Кожа
Дерево
Дерево
Пластик
Теперь список L заполняется наиболее общими значениями
атрибута форма: L = {многоугольник, кривая} и алгоритм
пытается построить поддерево, соответствующее обобщению
форма = многоугольник. Построенное поддерево оказыва-
оказывается полным и непротиворечивым, так
что обобщение принимается (рис. 13.22).
На следующем шаге алгоритм пытает-
пытается построить еще более сильное обобще-
обобщение форма = многоугольник V форма =
= кривая, но такое обобщение не является
непротиворечивым, поэтому оно отверга-
отвергается, и алгоритм приступает к построе-
построению отдельного поддерева для значения
форма = кривая. Окончательное решаю-
решающее дерево приведено на рис. 13.23.
Средняя стоимость классификации по
этому дереву составляет 50 единиц. Дере-
Дерево, построенное алгоритмом ID3 для того же обучающего множества,
содержит 15 вершин, и его стоимость классификации равна 108 еди-
единицам.
Дадим оценку вычислительной сложности алгоритма EG2. Клю-
Ключом к оценке вычислительной сложности этого алгоритма является
определение количества повторений внутреннего цикла и, следова-
следовательно, количества рекурсивных вызовов.
Основной
Рис. 13.22

13.8] Алгоритм EG2 595
Форма
i
Многоугольник у
Основной / \ маленький / \Маленышй
Рис. 13.23.
Пусть Ъ — количество наблюдаемых значений, ad — количество
абстрактных значений. Количество неудачных попыток обобщения
путем подъема по дереву обобщения не может быть больше d. Худший
случай наблюдается в том случае, если ISA-иерархия представляет
собой цепь вида А\ isa ^2,^2 isa A3,... ,Ad-i isa Ad, и ни одна из
попыток обобщения не приводит к успеху. В то же время, поскольку
алгоритм удаляет все уже задействованные значения из списка L,
общее количество итераций не будет больше, чем Ъ + d.
Заметим, что вычисление функции ICF не сложнее, чем инфор-
информативности Gain, поэтому, повторяя рассуждения, проведенные при
оценке сложности алгоритма ID3, получим
к-1 к-1
г=0 г=0
Алгоритм EG2 позволяет использовать дополнительные знания о
предметной области, представленные в виде ISA-иерархии на значени-
значениях атрибутов обучающих примеров. Методы обобщения, заложенные
в алгоритме, — подъем по дереву обобщения и объединение значений
операцией или — позволяют получать более компактные решающие
деревья, с большей вероятностью отражающие реальные взаимосвязи
в представленных данных.
Учет оценок стоимости, осуществляемый алгоритмом EG2, явля-
является весьма важным для реальных систем, так как позволяет избе-
избежать неоправданно дорогих, хотя и информативных решений.

И вот почему — в ожидании
Не верим мы темным часам:
Мы бродим в неконченом здании,
Мы бродим по шатким лесам!
В. Брюсов
Глава 14
ИНДУКТИВНЫЕ МЕТОДЫ ДЛЯ СЛУЧАЯ
НЕПОЛНОЙ ИНФОРМАЦИИ
Необходимость применения методов обобщения информации в
сложных системах обусловлена как построением обобщенных моде-
моделей данных (знаний), так и обработкой больших массивов данных,
хранящихся в базах данных. Современные информационные техно-
технологии предоставляют возможность собирать и хранить информацию
из большого числа источников в количестве, которое еще недавно
рассматривалось бы как невозможное. Такое явление наблюдается во
многих областях: финансы, банковское дело, статистика, розничная
торговля, управление и диагностика и т. п. Например, система наблю-
наблюдения за Землей, которую использует НАСА, способна выдавать дан-
данные в объеме несколько гигабайт в час. Хотя современные технологии
баз данных допускают экономное хранение таких больших потоков
данных, основной проблемой является использование этих потоков
данных для анализа. Анализ подразумевает прежде всего осмысление
данных в зависимости от контекста, от поставленной цели. Это поиск
скрытых закономерностей, которые невозможно выявить с помощью
простых запросов к базе данных. Как мы уже выяснили, научное
направление, которое занимается решением подобных проблем, по-
получило название Data Mining (анализ данных) и Knowledge Discovery
in Databases (обнаружение знаний в базах данных). В главе 11 упоми-
упоминались основные проблемы, связанные с извлечением знаний из баз
данных. Рассмотрим этот аспект подробнее.
14.1. Проблемы извлечения знаний из баз данных
Обсуждая вопросы поиска классифицирующих правил, мы неявно
предполагали, что такие правила существуют. В частности, мы пред-
предполагали, что существуют детерминированные классифицирующие
правила. Хотя такое предположение может быть верным для искус-

14.1] Проблемы извлечения знаний из баз данных 597
ственно созданных обучающих множеств, используемых в машинном
обучении, оно наверняка не выполняется применительно к реальным
базам данных.
Использование базы данных в качестве обучающего множества
вызывает следующие трудности. Во-первых, информация в базе дан-
данных ограничена, так что не вся информация, необходимая для опре-
определения класса объекта, доступна. Во-вторых, доступная информа-
информация может быть повреждена или частично отсутствовать. Наконец,
большой размер баз данных и их изменение со временем рождает
дополнительные проблемы.
14.1.1. Ограниченная информация
Как было сформулировано выше, задача системы извлечения зна-
знаний состоит в построении правил, определяющих класс объекта на
основе значений предсказывающих атрибутов. Проблема состоит в
том, что не все атрибуты, реально определяющие класс объекта,
присутствуют в базе данных. Поэтому не всегда возможно построение
правил, корректно классифицирующих объекты в терминах извест-
известных атрибутов.
Один из подходов к решению этой проблемы состоит в ограниче-
ограничении множества правил детерминированными правилами, не содержа-
содержащими вероятностных оценок. Отрицательной стороной этого подхода
является то, что большая часть ценной информации, скрытой в базе
данных, так и останется не открытой.
С другой стороны, мы можем искать правила, которые не обяза-
обязательно классифицируют все объекты корректно, а показывают веро-
вероятность того, что объект, удовлетворяющий описанию, принадлежит
классу. Такие вероятностные правила предоставляют очень важную
информацию об отношениях в базе данных. Например, отношение
между курением и раком легких не является корректным, т. е. курение
не является ни необходимым, ни достаточным условием для заболе-
заболевания раком, тем не менее такое отношение представляется весьма
важным.
Если ни один из предсказывающих атрибутов не имеет отношения
к классификации, получается, что атрибуты и класс объектов никак
не связаны. В этом случае нельзя найти даже вероятностных правил.
Например, бесполезно искать связь между фамилией и фактом забо-
заболевания раком.
Корректность найденных описаний может быть проверена раз-
разделением базы данных на две части. Первая часть используется в
качестве обучающего множества, а вторая — в качестве проверочно-
проверочного. Правило будет корректным, если вероятность каждого правила,
вычисленная для проверочных примеров, не слишком отличается от
вероятности, предсказанной в процессе обучения.

598 Индуктивные методы для случая неполной информации [ Гл. 14
14.1.2. Искаженная информация
Далее если база данных содержит всю информацию, необходимую
для корректной классификации объектов, некоторые данные могут не
соответствовать действительности. Например, значения каких-либо
атрибутов могут содержать ошибки в результате измерений или субъ-
субъективных суждений. Ошибка в значениях предсказываемых атрибу-
атрибутов приводит к тому, что некоторые объекты в обучающем множестве
классифицированы неправильно. Несистематические ошибки такого
рода обычно называются шумом.
Шум вызывает две проблемы: сначала при построении правил,
а затем при классификации объектов с использованием этих пра-
правил. Когда система извлечения данных строит описания на основе
зашумленных данных, она должна учитывать сам факт искажения
данных. Как правило, эта проблема решается с использованием ста-
статистических методов для определения того, какие значения следует
считать истинными. Основная идея заключается в том, что небольшое
количество исключительных данных рассматривается как шум и не
участвует в построении правил.
При классификации зашумленных данных точность классифи-
классификации, естественно, уменьшается. Интересное свойство, отмеченное
Куинланом, заключается в том, что правила, построенные на данных,
содержащих некоторое количество шума, классифицируют новые дан-
данные с шумом даже лучше, чем правила, построенные на чистых
примерах. Так что при построении правил для реальных приложений,
которые практически всегда содержат то или иное количество шума,
следует использовать реальные примеры, также содержащие ошибки.
Другим примером искажения информации является отсутствие
отдельных значений атрибутов. Такие примеры могут быть просто
исключены из рассмотрения, или вместо отсутствующих значений
можно подставить наиболее вероятные. Другой способ состоит в ис-
использовании отдельного значения < пусто > для отсутствующих зна-
значений.
14.1.3. Большой размер баз данных
Как мы установили в начале этой главы, основным отличием из-
извлечения знаний из баз данных от традиционных методов машинного
обучения является использование базы данных в качестве обучающего
множества. Системы машинного обучения используют небольшие обу-
обучающие множества, состоящие из тщательно подобранных примеров.
Базы данных, наоборот, обычно очень велики как в смысле количества
атрибутов, так и в смысле количества объектов, представленных в
базе данных.
С одной стороны, большое количество атрибутов дает нам боль-
больше шансов на то, что мы сможем найти подходящие описания
классов. С другой стороны, увеличение числа атрибутов приводит к

14.1] Проблемы извлечения знаний из баз данных 599
увеличению размеров пространства поиска. Очевидно, для любой ре-
реальной базы данных размер пространства поиска будет очень боль-
большим, так что ни один из методов полного перебора не может быть
применен. Необходимо использовать знания о предметной области и
эвристики для сокращения перебора.
В процессе поиска мы должны проверять качество созданных опи-
описаний. Как было показано ранее, расчет критерия качества требует
некоторой статистики по всем объектам обучающего множества. При-
Применительно к базам данных это выливается в запросы. Выполнение
запроса по целой базе данных со многим количеством объектов может
занять очень много времени. Чтобы обойти эту проблему, можно
использовать методы, предложенные Холшеймером и Керстеном. Во-
первых, можно конструировать сразу несколько описаний за один
проход по базе данных. Во-вторых, можно использовать для вычис-
вычисления качества правил относительно небольшую представительную
выборку. После того, как найдены лучшие правила, они проверяются
с использованием всей базы данных. Если существует значительное
количество неправильно классифицированных объектов, они добав-
добавляются в выборку и процесс повторяется еще раз.
14.1.4. Изменение баз данных со временем
Базы данных постоянно обновляются. Информация добавляется,
изменяется или удаляется. Следовательно, знания, извлеченные из ба-
базы данных ранее, уже не соответствуют содержащимся в ней данным.
Очевидно, что обучающаяся система должна адаптироваться к подоб-
подобным изменениям. Необходимо также учесть, что свежая информация
более ценна, чем старая.
Каждый раз при изменении базы данных мы можем либо кон-
конструировать систему правил с нуля, либо использовать инкрементное
обучение (incremental learning), когда знания, полученные на преды-
предыдущих этапах, используются для построения новых знаний. В этом
разделе мы рассмотрим задачу извлечения знаний из баз данных и
ряд общих методов ее решения. Хотя извлечение знаний из баз данных
является одним из видов машинного обучения, ему присущи свои
особенные черты.
1) Базы данных создаются из расчета требований конкретных при-
приложений, а не специально для машинного обучения.
2) Информация, содержащаяся в базах данных, как правило,
неполна. Свойства объектов, необходимые для корректной
классификации, не обязательно представлены в базе данных.
3) Отдельные значения могут содержать ошибки или вовсе отсут-
отсутствовать.
4) Базы данных очень велики.
5) Базы данных изменяются со временем.

600 Индуктивные методы для случая неполной информации [ Гл. 14
От того, насколько система извлечения знаний сможет справиться
с этими проблемами, зависит успех ее практического применения.
Рассмотрим один из алгоритмов, который используется в реальной
системе Data Mining.
14.2. Алгоритм извлечения продукционных правил
из большой базы данных
Система извлечения продукционных правил из баз данных, опи-
описанная в работах Холшеймера и Керстена, поддерживает связь с
СУБД Monet и работает с исходными данными, представленными в
форме реляционной таблицы. Эта таблица велика: она может содер-
содержать несколько сотен тысяч объектов со многими атрибутами. Ал-
Алгоритм должен найти правила, которые определяют принадлежность
объекта к некоторому множеству — классу. Класс задается пользо-
пользователем. Это означает, что пользователь должен провести разделение
базы данных на две части: первая содержит объекты, принадлежащие
классу, и составляющие тем самым множество положительных при-
примеров Р, в то время как вторая содержит все остальные, образующие
множество отрицательных примеров N. Наиболее простым способом
задания класса для пользователя может быть возможность явно ука-
указать в реляционной таблице один из атрибутов в качестве целевого
(что возможно не всегда).
Правила формируются в виде <D> —> <С>, где С — это класс, а
D — условие, составленное как конъюнкция простых условий вида
<атрибут> — <значение>. Условия могут быть равенствами для
символьных атрибутов, либо неравенствами для числовых атрибутов.
Условие D определяет выборку из базы данных тех объектов, для
которых оно верно. Рассмотрим выборки из множеств положительных
и отрицательных примеров, обозначаемые в дальнейшем (Jd{P) и
(T]j{N) соответственно.
Правило считается корректным, если оно покрывает все положи-
положительные примеры и не покрывает ни одного отрицательного, то есть
&d(P) = Р и cd(N) = 0. На практике можно найти крайне мало кор-
корректных правил, чаще правило выполняется с той или иной степенью
достоверности. Поэтому с каждым правилом R мы свяжем следую-
следующую вероятностную оценку качества: Q(R) = : . ——, где
\aD(P)\ + \aD(N)\
\а\ обозначает мощность множества.
Очевидно, для корректного правила Q(R) = 1. Целью алгорит-
алгоритма является извлечение правил с наибольшим показателем качества
Q(R).
Работа алгоритма поиска начинается с «тривиального» правила с
пустой посылкой Rq : true —>< С >, приписывающего все объекты
базы данных классу С. Оценка качества этого правила есть просто

14.2] Алгоритм извлечения продукционных правил 601
вероятность того, что произвольно выбранный объект базы данных
принадлежит этому классу. Следующим шагом является расширение
(уточнение) правила за счет добавления в его левую часть условия
< атрибут> = <значение>, что приводит к новому правилу R\ : А =
= а —к С >.
Чтобы получить результат за приемлемое время, алгоритм следует
эвристическому правилу: выбираются расширения с наиболее высокой
оценкой качества. Такая стратегия используется во многих системах
обучения.
Поиск расширения правила с наилучшей оценкой качества требу-
требует полного перебора, поэтому во избежание комбинаторного взрыва
количество промежуточных правил ограничивается использованием
стратегии «поиска по лучу»: для дальнейшего расширения предлага-
предлагается использовать не более чем w лучших правил предыдущего шага.
Выделенные правила используются для порождения новых расши-
расширений до тех пор, пока длина правила не превысит заданной поль-
пользователем величины d, либо не удастся получить улучшение оценки
качества. Число w называется шириной луча, ad — глубиной поиска.
Алгоритм ЦЛ.
Алгоритм (Т: таблица базы данных, d: глубина поиска, w: коли-
количество лучей, С: целевой атрибут)
результат R — множество продукционных правил
начало
So :={начальное правило Ro}
R:=S0
Построение на основе Т по атрибуту С таблиц примеров Лз и ^о
для начального правила Rq
к := 0 (индекс глубины поиска)
пока к < d и имеет место улучшение выполнить
Sk+i ¦= 0
для всех правил Щ Е Sk выполнить
для всех столбцов Fj ф Щ выполнить
Вычислить оценку качества для всех правил вида
R% & (Fj = vn) -^< С >.
Добавить лучшие w правил к S&+1.
конец для
конец для
Sfc+i := лучшие w правил Sk+i.
Построить таблицы примеров для Pi и Ni для всех правил
Ri E Sfc+i
R:=RUSk+1
к:=к + 1
конец пока
конец

602 Индуктивные методы для случая неполной информации [ Гл. 14
С каждым правилом Ri : D —>< С > связана своя таблица поло-
положительных Pi и отрицательных Ni примеров. Таблица Pi содержит
все объекты, принадлежащие классу С, для которых выполняется
посылка D, в то время, как таблица Ni содержит все объекты, не
принадлежащие классу С, для которых тем не менее выполняется
посылка D.
Для уточненного правила R'fai^Fj = ип) —>< С > создаются
новые таблицы примеров. При этом не возникает необходимости осу-
осуществлять выборку над всей базой данных, достаточно использовать
уже имеющиеся таблицы примеров, поскольку, очевидно, Р[ С Д и
Щ С N,.
Пример 14.1.
Рассмотрим пример вывода продукционных правил с помощью
данного алгоритма для базы данных страховой компании. В базе
данных компании хранятся сведения о клиентах, застраховавших свои
автомобили, такие, как имя, пол, возраст, место рождения, марка
автомашины, ее цена и т. п. На основании этих сведений предлагается
построить продукционные правила, пригодные для выявления кате-
категории водителей, склонных попадать в аварию. Страховая компания
заинтересована в выявлении таких клиентов, чтобы потребовать с них
более высокие страховые взносы.
В качестве обучающей выборки был использован фрагмент базы
данных, содержащий 25 000 записей. К атрибутам каждой записи
добавлен бинарный атрибут «аварийность»; его значения «да» —
субъект попадал в аварию, либо «нет» — водитель в аварию не по-
попадал. Среди элементов обучающей выборки ровно половина записей
относится к владельцам машин, попавших в аварию, другая половина
записей — контрпримеры. Предлагается построить дерево поиска при
условиях: использовать 5 лучей, глубина поиска 3.
Правило Rq : true —>¦ «аварийность» = да приписывает все объ-
объекты таблицы к искомому классу с оценкой (вероятностью) 0,5 или
50%. На первом шаге алгоритма это правило дополняется условием
«возраст» G [19; 21]. Этому условию удовлетворяют 1743 записи из
таблицы; вероятность того, что водители этой группы попадали в
аварию, составила 55,2%. Новое правило R\ : {«возраст» ^ 21) —>
«аварийность» = да называется расширением начального правила.
На рис. 14.1 представлен фрагмент дерева поиска по 5 лучам с глуби-
глубиной 3.
В каждом узле дерева представлены собственно условие, размер
покрытия и оценка качества. Например, правило {«пол» = муж) &
^{«возраст» ^ 22) покрывает 1349 примеров и 60,8% из них относятся
к классу «аварийный водитель».
Правила, которые порождает алгоритм, классифицируют коррект-
корректно не все объекты; скорее они показывают вероятность того, что объ-

14.3]
Подход с использованием приближенных множеств
603
нет условии1
[25000/0,5]
возраст <21
/[1743/0,552]
пол = жен
[11620/0,463]
пол = муж
[13380/0,532]
пол = муж —
[1001/0,607]
город = Детройт -
[171/0,591]
™цена авто < 19999
[322 / 0,655]
¦ цена авто < 29999
[84/0,679]
город =Вашингтон цена авто > 79995
[192/0,583] [12/0,667]
возраст^ 22
[1349/0,608]
город = Нью-Йорк
[2432 / 0,479]
категория = прокат
[33 / 0,242]
возраст > 62 -
[1617/0,478]
город = Майами
[160/0,406]
Рис. 14.1.
ект принадлежит классу. Корректность построенных правил можно
проверить, например, разделив базу данных на две части: первая
используется в качестве обучающего множества, а вторая — в качестве
проверяющего (экзамен).
14.3. Подход с использованием приближенных
множеств
Неполнота информации, которую иногда приходится использовать
в системах машинного обучения, требует специальных подходов, от-
отличных от методов классической логики. Это могут быть методы
статистики, методы нечеткой логики, основанные на теории нечетких
множеств Заде. Основной проблемой нечеткой логики, затрудняющей
использование таких методов в экспертных системах и системах ма-
машинного обучения, является определение значений вероятности или
степени принадлежности.
Теория приближенных множеств (rough sets theory) была предло-
предложена в начале 80-х годов математиком Павлаком как новое средство
для работы с нечеткостями. В дальнейшем эта теория развивалась
многими исследователями и применялась для решения разнообразных
задач. Главное преимущество теории приближенных множеств в том,
что она не требует никакой предварительной или дополнительной
информации о данных (информации о вероятностях или о степени
принадлежности элемента множеству). Мы рассмотрим, как теория
приближенных множеств может быть использована для решения за-
задачи извлечения знаний из баз данных.

604 Индуктивные методы для случая неполной информации [ Гл. 14
14.3.1. Основные понятия теории приближенных множеств
Основной подход, связанный с теорией приближенных множеств,
основан на идее классификации. Эта теория помогает решить про-
проблему неточных знаний. Неточные знания или понятия могут быть
определены приближенно в рамках заданного обучающего множества,
если использовать понятия верхнего и нижнего приближений. Ниж-
Нижнее приближение включает те объекты обучающей выборки, которые
наверняка принадлежат понятию, верхнее приближение включает все
объекты, которые возможно принадлежат понятию. Разница между
этими двумя приближениями образует граничную область и содержит
объекты, которые не могут быть классифицированы наверняка на
основе имеющейся информации.
В соответствии с основной постановкой задачи обучения «с учи-
учителем», данной в главе 13, исходными данными для задачи обобще-
обобщения является обучающее множество. Обучающие множества, которые
рассматриваются в книге, состоят из объектов, представленных на-
наборами атрибутов. При обучении «с учителем» один из атрибутов,
называемый далее решающим атрибутом, служит для разделения
обучающего множества на примеры и контрпримеры формируемого
понятия.
Пусть на обучающем множестве О введено R С О х О — отно-
отношение неразличимости или эквивалентности на О. Допустим, что
R — отношение эквивалентности. Упорядоченную пару Р = (О, R)
будем называть пространством аппроксимации или пространством
приближений. Скажем, что если (ж, у) Е R, то х и у неразличимы в Р
по значениям атрибутов из D. Классы эквивалентности по отношению
к R называются элементарными множествами или атомами в Р.
Обозначим все множество классов эквивалентности как R*(D) =
— {еъ е2> • • • ? ?п}. Пустое множество является также элементарным
для любого пространства приближений. Любое конечное объединение
элементарных множеств в Р назовем составным множеством в Р.
Семейство составных множеств в Р будем обозначать Def(P).
Пусть X С О. Под нижним приближением множества X в Р будем
понимать наибольшее составное множество в Р, содержащееся в X, а
под верхним приближением X в Р — наименьшее составное множе-
множество в Р, содержащее X. Обозначим нижнее и верхнее приближения
множества X в пространстве Р через РХ и РХ соответственно.
Множество Впр(Х) = РX — Р_Х будем называть границей X в Р.
Обозначим далее нижнее приближение РХ = Lowerр(Х) = (J е^.
_ eiCX
Верхним приближением называется РХ = Upperр(Х) = (J е^.
Пара <Lower(X), Upper(X)> составляет приближенное множество.
Для множества X в пространстве приближений Р = (O,R) опреде-
определяется мера точности аппроксимации. Она определяется только для

14.3]
Подход с использованием приближенных множеств
605
конечных множеств и вычисляется следующим образом:
цр(Х) = —= , где |Х| — мощность множества X.
Вместо цр(Х) мы также будем писать /i^(X). Заметим, что
0 < /^р(Х) < 1, и jJLp(X) = 1, если X определяемо в Р; если X
неопределяемо в Р, то fip(X) < 1.
Пример 14. 2.
В процессе изложения основных понятий теории приближенных
множеств будем использовать следующий пример, приведенный в
табл. 14.1.
Таблица 14.1
Имя
Джо
Мэри
Питер
Пол
Кэти
Образование
Среднее
Среднее
Неполное среднее
Высшее
Аспирантура
Высокий доход
Нет
Да
Нет
Да
Да
Положим D= {Образование}, тогда обучающая выборка разбива-
разбивается на четыре класса эквивалентности:
R*(D) = {{Джо, Мэри}, {Питер }, {Пол }, {Кэти }}.
Здесь в1={Джо, Мэри}, е2 ={Питер}, е3 = {Пол}, в4={Кэти}.
Любое объединение элементарных множеств называется состав-
составным множеством. Так, множество {в2, ез}={Питер, Пол} — составное
множество.
Пусть в нашем примере X — класс людей с высоким доходом.
Тогда
РХ ={Пол, Кэти}
РХ ={ Пол, Кэти, Джо, Мэри}
Впр(Х) = РХ -РХ ={Джо, Мэри}.
Приближенные множества могут быть использованы для класси-
классификации объектов следующим образом.
Назовем Pos(X) = Р_{Х) положительной областью, Neg(X) =
= S\P(X) — отрицательной областью, и Bnd(X) = Р(Х)/Р(Х) —
граничной областью. Мы можем сформировать следующие правила:
Описание Pos(X) —> X,
Описание Neg(X) —> -iX,
Описание Bnd(X) —> возможно X,

606
Индуктивные методы для случая неполной информации [ Гл. 14
где описание множества включает набор характерных атрибутов. На-
Например, в нашем случае мы получим правила:
(Образование = Высшее) V (Образование = Аспирантура) —> Вы-
Высокий доход
(Образование = Неполное среднее) —> Низкий доход
(Образование = Среднее) —> Возможно высокий доход.
На рис. 14.2 представлена диаграмма приближенного множества.
Рассмотрим следующие важные свойства приближенных множеств.
Как было определено выше, на множестве X введем ЙСХхХ — от-
отношение неразличимости или эквивалентности на X. Упорядоченная
пара Р = (X, R) образует пространство приближений. Рассмотрим
множества У С X, Z С X.
Ш Множество
13 Верхнее приближение
¦ Нижнее приближение
П Граница
П Отрицательные объекты
Рис. 14.2.
Два произвольных множества Y и Z приближенно равны снизу в
Р, если равны их нижние приближения в пространстве Р: PY = PZ.
Обозначим приближенное равенство снизу Y tz, Z.
Множества Y и Z приближенно равны сверху, если совпадают их
верхние приближения: PY = PZ. Обозначим приближенное равен-
равенство сверху Y ~ Z.
Если два множества приближенно равны сверху и снизу одновре-
одновременно, они называются приближенно равными и обозначаются как
Y &Z.
Справедливы также следующие соотношения:
1. PY С Г С TY
2. PI = PI = 1
3. Р0 = Р0 = 0
4. P(YHZ) =PYnPZ
5. P(FUZ) = PFUPZ
6. РУ = -Р(-У)
7. PY = -Р(-У)

14.3] Подход с использованием приближенных множеств 607
Здесь 0 обозначает пустое множество, 1 обозначает все множе-
множество X.
Рассмотрим далее специальный вид пространств приближений,
используемых при классификации объектов на основе значений их
атрибутов. С каждым атрибутом ассоциировано множество значений.
Описание объекта задано, если выбрано одно значение для каждого
атрибута. Для более точного выражения этой идеи введем понятие
информационной системы.
Под информационной системой IS понимается четверка
IS=(O,Q,V,p),
где О — множество, называемое обучающим множеством в IS; эле-
элементы О называются объектами, Q — множество атрибутов (при-
(признаков), q Е Q будет обозначать далее один атрибут из множества.
Q разделяется на два непересекающихся подмножества: условные
атрибуты С и решающие атрибуты D, т. е. Q = С U D, V = (J Vq —
множество значений атрибутов; Vq называется доменом q, или мно-
множеством значений атрибута q. р : О х Q —> V — описательная
функция, такая что р(х, q) Е Vq для каждого q E Q и х Е О. Описа-
Описательная функция, таким образом, определяет значение атрибута для
заданного объекта.
Определим функцию рх : Q —> V, такую что рх(я) = р(х, q) для
каждого q E Q и х Е О; рх назовем описанием х в IS. Скажем, что
объекты ж, у Е О неразличимы по отношению к q <E Q в пространстве
приближений, если px(q) = py(q), и будем записывать xqy\ очевидно,
что q есть отношение эквивалентности. Объекты х,у Е О неразличи-
неразличимы по отношению kPcQb IS, (записывается хРу), если Р = р| р.
Если Р = Q, скажем, что х и у неразличимы в IS л будем записывать
х IS у вместо xQ у.
Очевидно, что Р — отношение эквивалентности, таким образом,
информационная система IS = (O,Q,V, p) определяет единственным
образом пространство приближений As = {О,IS), где IS есть отно-
отношение неразличимости, образованное информационной системой IS.
Если х Е О и рх есть описание х в IS, то мы допускаем, что рх
есть также описание класса эквивалентности для IS, содержащего
х. Скажем, что подмножество X С О описываемо в IS, если X
определяемо в Ajs'-, если X неопределяемо в Ajs, X будем называть
неописываемым в IS. Описание определяемого множества IS состоит
из QO описаний его элементарных множеств. Описание пустого мно-
множества обозначим через Л.
Рассмотрим алгоритм построения продукционных правил, осно-
основанный на теории приближенных множеств, и называемый далее RS1.

608 Индуктивные методы для случая неполной информации [ Гл. 14
14.3.2. Алгоритм RS1, использующий приближенные множества
Обучающее множество S содержит объекты о Е S. Каждый объект
представлен вектором признаков, или атрибутов. Все атрибуты услов-
условно разделяются на два подмножества: описательные xi,X2,... ,хп и
целевой (решающий) атрибут d. Сначала в обучающем множестве на-
находятся элементарные множества. Затем строятся объединения этих
множеств и находятся верхнее и нижнее приближения. Далее прибли-
приближения редуцируются, чтобы устранить избыточность информации. В
итоге получаются две системы продукционных правил, для верхнего
и нижнего приближений соответственно.
Введем меру точности аппроксимации для множества С в про-
пространстве приближений Р =< S,R(D) >:
\lower(C)\
\upper(C)\'
где |Х| — мощность множества; такая оценка будет существовать
только для конечных множеств.
Ядро и сокращение (редукция) — две фундаментальные концеп-
концепции приближенных множеств. Дадим определение сокращения. Пусть
В С А — некоторое подмножество информационных атрибутов. Атри-
Атрибут q E В назовем излишним в множестве атрибутов В С А, если
POSb(D) = POSb-{q}{D). В противном случае атрибут q назовем
необходимым атрибутом. Напомним, что область POSb(D) включает
все объекты обучающей выборки, которые могут быть отнесены к
классу D без классификационной ошибки. Излишний атрибут может
быть удален без изменения отношения эквивалентности между объ-
объектами. Если каждый атрибут из В С D является необходимым по
отношению к D, то В называется ортогональным по отношению в
D. Подмножество атрибутов В С А определяется как сокращение в
информационной системе, если В ортогонально по отношению kDh
POSa(D) =POSb(D).
Сокращение — существенная часть информационной системы, ко-
которая может различать все объекты, различимые исходной информа-
информационной системой. Ядро — общая часть всех сокращений.
Пусть S — обучающая выборка, D — целевой атрибут,
Р =< S, R(D) > — пространство приближений и X С S — множество,
для которого мы хотим найти описание. Необходимо
1) найти атомы для S]
2) найти верхнее и нижнее приближения для X в Р;
3) вычислить точность аппроксимации;
4) найти сокращения для Lowerр(Х)и Upperp(X).

14.3]
Подход с использованием приближенных множеств
609
Пример 14. 3.
Рассмотрим работу алгоритма на примере. Обучающее множество
О, приведенное в табл. 14.2, содержит набор записей, описывающих
допустимые погодные условия для игры в гольф. Требуется получить
описание множества X, которое состоит из записей, в которых содер-
содержатся допустимые условия для игры (для подобных записей атрибут
«Играть ли в гольф» принимает значение «играть»).
Таблица 14.2
О
XI
Х2
Хз
Х4
Х5
х6
Х7
х8
х9
Хю
Прогноз
погоды
Пасмурно
Солнечно
Солнечно
Пасмурно
Пасмурно
Дождливо
Солнечно
Дождливо
Дождливо
Пасмурно
Влаж-
Влажность, %
87
80
80
75
75
80
80
80
85
87
Ветер
Ложь
Истина
Истина
Истина
Истина
Ложь
Истина
Ложь
Ложь
Ложь
Играть ли
в гольф?
Играть
Играть
Играть
Играть
Играть
Не играть
Не играть
Не играть
Не играть
Играть
1) Атомами для О являются Е\ = {xi,xio}, ^2 = {^2,^3,^7}?
Е3 = {ж4,ж5}, Е4 = {х6,х8}у Еъ = {х9}.
2) Нижнее и верхнее приближения соответственно Lower О(Х) =
= {ж1,жю,Ж4,ж5} и Uppero(X) = {хъ х10, х2, ж3, Ж7, я4, хъ}-
3) Точность аппроксимации равна 4/7 ~ 0,57.
4) Заметим, что в Lowerо(Х) и Upperо(Х) содержатся повторяю-
повторяющиеся записи — их нужно отбросить.
В результате мы получим систему продукционных правил для
классификации погодных условий с целью принятия решения о том,
играть или не играть в гольф. Точнее, это будут две системы правил,
для нижнего и верхнего приближений соответственно. Их смысл в
следующем. Нижнее приближение дает нам уверенную классифика-
классификацию ситуаций, в то время как верхнее — лишь возможную.
Нижнее приближение:
если (Прогноз погоды = Пасмурно) & (Влажность = 87) &
& (Ветер = Ложь), то Играть ли = играть
20 В.Н. Вагин и др.

610 Индуктивные методы для случая неполной информации [Гл. 14
если (Прогноз погоды = Пасмурно)& (Влажность = 75)&
& (Ветер = Истина), то Играть ли = играть
Верхнее приближение:
если (Прогноз погоды = Пасмурно) & (Влажность = 87)&
& (Ветер = Ложь), то Играть ли = играть
если (Прогноз погоды = Солнечно) & (Влажность = 80)&
& (Ветер = Истина), то Играть ли = играть
если (Прогноз погоды = Пасмурно) & (Влажность = 75)&
& (Ветер = Истина), то Играть ли = играть
Обратим внимание на невысокую точность аппроксимации, что
может показаться плохим признаком. На самом деле это связано с
противоречивостью данных. Если подробнее рассмотреть обучающее
множество (табл. 14.2.), то можно заметить, что 2-я, 3-я и 7-я записи
совпадают, но принадлежат к разным классам ситуаций.
Ниже приводится псевдокод алгоритма RS1.
Алгоритм RS1.
Функция RS1 (А: множество информационных атрибутов,
D: решающий атрибут,
S: обучающее множество )
возвращает две системы продукционных правил.
Начало:
1. Нахождение элементарных множеств или атомов ei, в2,..., еп.
На первом этапе просмотр S, поиск неразличимых объектов
среди полностью определенных и построение элементарных мно-
множеств. Для этого 1-й объект сравнивается с N — 1 оставшимся,
2-й — с N — 2, и т. д (|?| = N). На втором этапе просмотр
S и сравнение каждого неполностью определенного объекта с
каждым имеющимся атомом. Сравнение производится только
для информационных атрибутов из А.
2. Нахождение нижнего и верхнего приближений. Пусть {е^}
(j = 1,...,/с) — множество атомов, X С S — множество,
приближения к которому ищем. Множество X вычисляется на
основе значений решающего атрибута D.
2.1. Нахождение нижнего приближения.
Lower(X) := 0;
для j от 1 до к
нц
если ej С X, то Lower(X) := Lower(X) U ej
кц

14.3] Подход с использованием приближенных множеств 611
2.2. Нахождение верхнего приближения.
Upper(X) := 0;
для j от 1 до к
нц
если X С Ef\eJ), то ej пометить, как лишний иначе
Upper {X) := Upper (X) U ej
кц.
3. Точность аппроксимации вычисляется как
/i(X) : = Lower(X)/Upper(X).
4. Найти сокращения для приближений. От каждого элементарно-
элементарного множества оставить по одному его представителю.
5. По вычисленным верхнему и нижнему приближениям построить
систему продукционных правил
Pos(X) -> X,
Neg(X) -+ -X,
Bnd(X) —> возможно X.
Конец RSI.
Для примера «Игра в гольф», приведенного выше, результатом
работы алгоритма RS1 будет следующая система продукций:
1) если (Прогноз погоды = Пасмурно) & (Влажность =
= 87%V75%) & (Ветер = Безразлично), то Играть ли = играть
2) если (Прогноз погоды = Дождливо) & (Влажность = 80%)&
& (Ветер = Ложь), то Играть ли = не играть
3) если (Прогноз погоды = Солнечно) & (Влажность = 80%)&
& (Ветер = Истина), то Играть ли = возможно играть.
Отличительной особенностью алгоритма RS1 является возмож-
возможность обработки обучающего множества, в котором есть объекты с
отсутствующими значениями атрибутов. Помещая неполностью за-
заданные объекты во все возможные элементарные множества, алго-
алгоритм устраняет неполноту информации. В данном случае очевидно
преимущество RS1.
14.3.3. Информационные системы с неопределенностью
В общем, информационная система четко представляет объекты.
Это значит, что для данного объекта в базе данных и для заданного
свойства (пара атрибут — значение) не существует неопределенности
независимо от того, имеет объект это свойство или нет. Это есть
ограничение целостности. Оно ограничивает нашу представительную
20*

612 Индуктивные методы для случая неполной информации [Гл. 14
силу в двух направлениях. Во-первых, все объекты в рассматривае-
рассматриваемом множестве должны быть представлены единообразно. Во-вторых,
представительная сила также ограничивается из-за четкого описания
объектов, т. е. нет способа выразить степень представленности объек-
объекта. Таким образом, у объекта либо имеется, либо не имеется некоторое
свойство.
Для обработки объектов с неопределенностью и различными
степенями важности будет рассмотрена информационная система с
неопределенностью. В информационной системе с неопределенностью
с каждым объектом связан коэффициент неопределенности и
и степень важности d. Коэффициент неопределенности — это
вещественное число из диапазона [0, 1]. Если и = 1, то мы имеем
полностью положительный объект. Если и = 0, то мы имеем
полностью отрицательный объект. Степень важности d выражает
важность объекта в информационной системе. Как будет показано
ниже, произведение d x и позволяет вычислить класс положительных
объектов, а произведение d х A — и) — класс отрицательных объектов.
Информационной системой с неопределенностью (ИСН) называ-
называется шестерка UIS = (О, Q, V, р, и, d), где О — непустое множество
объектов, Q — множество атрибутов (признаков), Q = С U D, С —
непустое множество условных атрибутов, D — решающий атрибут с
коэффициентом неопределенности и, V = |J Vc — множество значе-
сес
ний условных атрибутов; Vc называется доменом с, р : О х С ^ V —
описательная функция, такая что р(ж,с) Е Vc для каждого с Е С и
х Е О, d(x) — функция, связывающая с каждым объектом х Е О,
степень важности этого объекта.
Пример 14. 4.
В табл. 14.3 представлена информационная система с неопределен-
неопределенностью (ИСН). В ней условными атрибутами являются С = {cl,c2}
со значениями Vc\ = {0,1}, VC2 = {0,1,2}, решающий атрибут есть
D = {dec}. С каждым объектом связана степень его важности d.
Таблица 14.3
О
1
2
3
4
5
6
с\
0
0
0
1
1
1
с2
0
1
2
0
1
2
dec
0,75
0,67
0,35
0,75
0,67
0,35
d
4
3
4
4
3
4

14.3] Подход с использованием приближенных множеств 613
Для обработки зашумленных данных в ИСН мы будем исполь-
использовать концепцию относительных ошибок классификации. Основная
идея заключается в том, чтобы выявить граничную область между
положительной и отрицательной областями в соответствии с неко-
некоторыми классифицирующими факторами. Целью является создание
нескольких строгих правил, которые всегда были бы правильными.
В реальности каждый класс (положительный или отрицательный) в
информационной системе может содержать шум. Введем два класси-
классификационных фактора Рр и Np, такие что 0 ^ Рр, Np ^ 1. Рр и Np
могут быть одинаковой величины и могут одновременно существо-
существовать. Они определяются путем оценки степени шума соответственно
в положительной и отрицательной областях. Пусть имеется непустое
множество I, I С О. Мера относительной ошибки классификации
множества X по отношению к положительному классу Pciass и отри-
отрицательному классу Nciass определяется следующим образом:
сР{х) = ЕКЧ1»»)) для всех хеХ, хсо,
/ j di
CN(X) = ?(Д*'Ц*) для всех xgI, ХСО,
ld
где Yl di — сумма степеней важности объектов, принадлежащих к
множеству X, XX^г • щ) — сумма степеней важности выведенного
положительного класса, ^2(di • A — щ)) — сумма степеней важности
выведенного отрицательного класса.
Если мы при классификации относим объекты из множества X
к положительному классу, мы можем получить ошибку Ср(Х). Если
мы относим объекты из множества X к отрицательному классу, мы
можем получить ошибку Сдг(Х). Основываясь на мере относитель-
относительной ошибки классификации, можно определить множество объектов,
которые принадлежат к положительному классу, если и только если
ошибка Ср(Х) не превышает заданного уровня точности Рр, или мно-
множество объектов, принадлежащих к отрицательному классу, если и
только если ошибка Сдг(Х) не превышает заданного уровня точности
Np. Таким образом,
Pciass 2 X если и только если Ср(Х) ^ Рр,
Ndass 2 X если и только если Сдг(Х) ^ Np,
в противном случае множество объектов X принадлежит граничной
области.
Пример 14. 5.
Допустим, что имеется информационная система, представленная
в табл. 14.3 и заданы Рр = 0,3 и Np = 0,6. В этой системе существуют
следующие элементарные множества: Ei = {xi}, i = 1... 6. Нетрудно

614 Индуктивные методы для случая неполной информации [Гл. 14
вычислить степени относительной ошибки классификации:
з.
4 -
4 -
3-
4-
(i,
(i,
(i,
(i,
4
3
/^_
/^_
0-
3
0-
¦о,
¦о,
¦о,
¦о,
67)
35)
75)
67)
35)
Ср(з) = 4>A-Q4-Q?35) = о, 65 Слг(з) = i^ = о, 35
3A,00,67) 3-0,67
C7pE) = = 0, 33 CN(b) = = 0, 67
4(l,00,35) 4-0,35
CpF) = = 0, 65 CNF) = —-— = 0, 35
Теперь можно сказать, что Pciass = {-^ъ ^4} и Nciass = {^3, Eq}.
В оригинальной модели приближенных множеств пространство
приближений определяется как пара А = (O,R), которая состоит
из непустого конечного множества объектов и отношения эквива-
эквивалентности Д на О. Отношение эквивалентности называется также
отношением неразличимости.
В обобщенной модели приближенных множеств объекты, принад-
принадлежащие к одному элементарному множеству, воспринимаются как
идентичные, и может оказаться невозможным различать их.
Используя классификационные факторы Рр и Np, получим сле-
следующее обобщение концепции приближенной аппроксимации. Пусть
пара А = (O^Rp^n) будет пространством приближений. Для произ-
произвольного X С О его положительное нижнее приближение POSp(X)
определяется как объединение тех элементарных множеств, чьи клас-
классификационные критерии гарантируют, что относительная ошибка
Ср(Е) множества X не будет превосходить Рр
POSp(X) = U{E e Rp,n : СР(Е) < Рр}.
Отрицательное нижнее приближение NEGn(X) определяется как
объединение тех элементарных множеств, чьи классификационные
критерии гарантируют, что относительная ошибка Cn(E) множества
X не превосходит Np
NEGN{X) = U{E e Rp,n : CN{E) < Np}.
Верхнее приближение положительной области UPPp(X) опреде-
определяется как объединение тех элементарных множеств, чьи классифи-
классификационные факторы гарантируют, что относительная ошибка Cn{E)

14.3] Подход с использованием приближенных множеств 615
множества X превосходит Np
UPPp(X) = U{E e Rp,n : CN(E) > Np}.
Верхнее приближение отрицательной области UPPn(X) опреде-
определяется как объединение тех элементарных множеств, чьи классифи-
классификационные критерии гарантируют, что относительная ошибка Ср(Е)
множества X превосходит Рр
UPPN(X) = U{E е RP,N : CN(E) > Рр}.
Граничная область BNDpjy(X) множества X есть объединение
элементарных множеств, не принадлежащих ни к положительной, ни
к отрицательной области множества X:
BNDP,N(X) = U{E e Rp,n : Е ф POSP, NEGN}.
Для ИСН из табл. 14.3 будем иметь
POSP(D) = {E1,Ei}
NEGN(D)={ES,E6}
= {E1,E2,E4,E5}
= {E2,E3,E5,E6}
Чтобы формально определить меру зависимости атрибутов между
множеством условных атрибутов С С Q и множеством решающих
атрибутов D С Q, Q = С U D, определим С как множество классов
эквивалентности отношения Rp,n(C) и, аналогично, определим D
как множество классов эквивалентности Rpyjy(D) = {Pciass, Nciass}.
Для заданных классификационных факторов Рр и Np скажем, что
множество решающих атрибутов D неточно зависит от множества
условных атрибутов С со степенью ^(C^D, Pp, iV/з), если
где INT(C, D, Pp, Np) есть объединение положительных и отрица-
отрицательных нижних приближений всех элементарных множеств разби-
разбиения D = {Pciass, Nciass} в пространстве приближений (O,Rp,n(C))]
IMP(X) — функция важности, связывающая сумму степеней важно-
п
сти всех объектов в X, такая что IMP(O) = J2 di для всех объектов
г=1
Xi Е О И
IMP(INT(C,D,PI3,NI3))=
pos=l neg=l
xpos e POSP(X), xneg e NEGN{X).

616 Индуктивные методы для случая неполной информации [Гл. 14
Предыдущую формулу можно записать в виде
а Ъ
г=1
Неформально говоря, степень зависимости j(C, D, Рр, Np) атрибу-
атрибутов D от атрибутов С с уровнями точности Рр и Np есть пропорция
этих объектов x^gO, которые могут быть классифицированы в соот-
соответствующие классы разбиения D (положительный и отрицательный
классы) с уровнем ошибки меньшим, чем желаемая величина (Рр, Np),
на основе информации,
представленной классификацией С.
Пример 14. 6.
Для ИСН, приведенной в табл. 14.3, мы можем вычислить степень
зависимости между условными атрибутами С и решающим атрибутом
D. Для классификационных факторов Рр = 0,3 и Np = 0,6 получим
POSP(D) = {ЕЪЕ4}, NEGN(D) = {Е3, Е6}.
Степень зависимости между С и D есть
4+4+4+4
7(С; D; 0,30; 0,60) = = 0,73.
Пусть имеется ИСН UIS = (O,Q,V, p,u,d), P С С, заданы клас-
классификационные факторы Pp,Np. Дадим несколько определений.
Атрибут р G Р называется излишним в Р, если
7(Р — {a}, D, Рр, Np) = j(P, D, Рр, Np), иначе атрибут а называется
необходимым.
Если все атрибуты а^ G Р являются необходимыми в Р, то Р
называется ортогональным.
Подмножество Р С С называется сокращением С в ИСН, если Р
ортогонально и j(P, D, Рр, Np) = j(C, D, Рр, Np).
Относительное сокращение множества условных атрибутов будет
определяться как неизбыточное независимое подмножество условных
атрибутов, с помощью которого можно различить все объекты, раз-
различимые с помощью полного множества атрибутов.
В обобщенной модели сокращение множества условных атрибутов
С по отношению к множеству решающих атрибутов D является под-
подмножеством RED(C,D,Pp,Np), которое удовлетворяет следующим
двум критериям:
1) <у(С, D, Рр, Np) = <y(RED(C, D, Рр, Np), D, Pp, Np);

14.3] Подход с использованием приближенных множеств 617
2) нет атрибута, который мог бы быть исключен из RED(C, D, Рр,
iV/з), без воздействия на первый критерий.
Пример 14.7.
Рассмотрим удаление условного атрибута с\ из табл. 14.3. Пусть
заданы Рр = 0,3 и Np = 0,6. Тогда получим следующие классы
эквивалентности: Е\ = {ж1,ж4}, Е^ = {ж2,ж5}, Е<$ = {жЗ,жб}. Таким
образом,
2-4-A,0-0,35) 2-4-0,35
СрC) = = 0,65 CWC) = = 0,35
о о
и мы получим POSpiC') = {Ei}, NEGN(C') = {ЕА} (С = {х2}).
7(С"; Г>; 0,30; 0,60) = ^ = 0,73.
Из предыдущего примера мы знаем, что
7(С; ?>; 0,30; 0,60) = 7(С"; D; 0,30; 0,60),
поэтому Gх = {х2} является сокращением для С.
Идея сокращения наиболее полезна в тех приложениях, где необ-
необходимо найти самое важное семейство условных атрибутов, ответ-
ответственных за причинно-следственное отношение, а также полезна для
исключения несущественных атрибутов из информационной систе-
системы. Заметим, что для информационной системы может существо-
существовать более одного сокращения. Каждое сокращение в множестве
из RED(C,D,Pf3,Nf3) может быть использовано как альтернативная
группа атрибутов, которые могут представлять исходную информа-
информационную систему с классификационными факторами Рр, Np. Важной
проблемой является выбор оптимального сокращения из множества
RED(C,D,Pfi,Np).
Алгоритм RS2 является модификацией алгоритма RS1. В нем реа-
реализованы обобщения, описанные выше. По сравнению с RS1, разница
состоит в формате представления объектов и способе вычисления
приближений. Алгоритм RS2 позволяет обрабатывать информацию с
неопределенностью двух видов: когда отсутствуют значения некото-
некоторых атрибутов у объектов и когда объекты представлены с некоторой
степенью уверенности. Также модифицирован способ вычисления со-
сокращений множества. Перечислим основные шаги алгоритма.
Пусть U IS = (O,Q,V,p,u,d) — информационная система, Аи is ~
пространство приближений и X С О — множество, для которого мы
хотим найти описание. Необходимо:

618 Индуктивные методы для случая неполной информации [Гл. 14
1) найти атомы для О;
2) найти AUISX и AUISX\
3) вычислить точность аппроксимации;
4) найти сокращения для AUISX и
Пример 14. 8.
Рассмотрим пример. Обучающее множество — О — (табл. 14.4)
снова содержит набор записей, описывающих допустимые погодные
условия для игры в гольф. Мы хотим получить описание множества
X, которое состоит из записей, содержащих допустимые условия для
игры. Зададим классификационные факторы Рр = 0,2 и Np = 0,6.
Таблица 14.4
О
XI
х2
хз
Х4
хъ
Хб
Х7
х8
х9
хю
Прогноз
погоды
Пасмурно
Солнечно
Солнечно
Пасмурно
Пасмурно
Дождливо
Солнечно
Дождливо
Дождливо
Пасмурно
Влажность
87
80
80
75
75
80
80
*
85
87
Ветер
Ложь
Истина
Истина
*
Истина
Ложь
Истина
Ложь
Ложь
Ложь
Играть
ли?
1
0,87
1
0,93
1
0
0,21
0,01
0
0,73
Важность
3
2
4
2
3
6
2
2
4
3
1) Атомами для О являются Е\ = {xi, хю}, Е2 = {^2, #з> х7}-> Ез =
= {ж4,ж5}, ЕА = {жб,ж8}, Еъ = {х9,х8}.
2) Степени возможных ошибок классификации равны Ср{Е\) =
= 0,135, СР(Е2) = 0,028, Ср(Е3) = 0,28, СР(Е4) =
= 0,9975, СР{Еъ) = 0,9967, CN(E1) = 0,865, CN(E2) = 0,77,
CN(E3) = 0,972, CN(E4) = 0,0025, CN(E6) = 0,0034. С
учетом Рр и Np получим нижнее и верхнее приближения
соответственно: POSp(X) = {х1,хю,Х4,Хб} и UPPp(X) =
3) Точность аппроксимации равна 4/7 ~ 0,57.
4) Заметим, что в ASX и AsX содержатся повторяющиеся запи-
записи — их нужно отбросить. Также отбросим излишние атрибуты.

14.3] Подход с использованием приближенных множеств 619
В результате, как и ранее, получим две системы продукционных
правил.
Нижнее приближение:
если Прогноз погоды = Пасмурно & Влажность = 87, то
Играть ли = +
если Прогноз погоды = Пасмурно & Влажность = 75, то
Играть ли = +
Верхнее приближение:
если Прогноз погоды = Пасмурно & Влажность = 87, то
Играть ли = +
если Прогноз погоды = Солнечно & Влажность = 80, то
Играть ли = +
если Прогноз погоды = Пасмурно & Влажность = 75, то
Играть ли = +
Этот метод имеет расширенные возможности по обработке про-
противоречивой и неполной информации. Он формирует продукционные
правила с минимальными условными частями.
Алгоритм RS2
Функция RS2 (С: множество условных атрибутов,
D: решающий атрибут,
О: обучающее множество,
Рр, Np: классификационные факторы) возвраща-
возвращает две системы продукционных правил.
Начало:
1. Нахождение атомов. На первом этапе просмотр О, поиск нераз-
неразличимых объектов среди полностью определенных и построение
атомов. Для этого 1-й объект сравнивается с N — 1 оставшимся,
2-й — с N — 2 и т.д. (\О\ = N). На втором этапе просмотр
О и сравнение каждого неполностью определенного объекта с
каждым имеющимся атомом. Сравнение производится только
для условных атрибутов из С.
2. Нахождение нижнего и верхнего приближений. Пусть {Ej}
(j = 1,..., к) — множество атомов, X С О — множество, прибли-
приближения к которому ищем. Множество X вычисляется на основе
значений решающего атрибута D.
2.1. Нахождение нижнего приближения. POSp(X) := 0; в цик-
цикле для j = 1 до к для каждого атома Ej проверить
Cp(Ej) ^Рр? если да, то POSP{X) := POSP{X) U Ej.

620 Индуктивные методы для случая неполной информации [ Гл. 14
2.2. Нахождение верхнего приближения. UPPp(X) := 0; в цик-
цикле для j = 1 до к для каждого атома Ej проверить
Cn(Ej) ^ Np? если да, то Ej пометить, как лишний, иначе
Ej пометить, как необходимый. АХ есть объединение необ-
необходимых атомов.
3. Точность аппроксимации вычисляется как
ц(Х) = \Posp(X)\/\UppP(X)\.
4. Найти сокращения для приближений. От каждого атома в мно-
множестве оставить по одному его представителю. Для каждого
приближения найти зависимые атрибуты и удалить их из при-
приближения.
Конец RS2.
Для оценки возможностей алгоритма RS1 проведем его сравнение
с алгоритмом IDS. Алгоритм IDS строит дерево решения, a RS1 —
систему продукционных правил. Продукционные правила являются
более удобными и гибкими. Однако дерево решения может быть легко
сведено к системе продукционных правил. В этом вопросе можно
считать алгоритмы схожими.
Существенным моментом является длина полученных описаний.
Дело в том, что алгоритм RS1 включает в полученное описание
все доступные атрибуты. Алгоритм IDS — напротив, строит дерево
минимальной длины (для этого на каждом шаге он выбирает наибо-
наиболее информативный атрибут). Выбор оптимальной длины описания
представляет проблему. С одной стороны, небольшие описания легче
воспринимаются человеком, в них быстрее осуществляется поиск. С
другой стороны, минимизируя описание, мы можем отбросить атри-
атрибуты, в общем случае влияющие на классификацию.
Алгоритм IDS имеет возможность обработки атрибутов, имеющих
непрерывные области определения. Все значения таких атрибутов
разбиваются на два диапазона, при этом выбирается порог, дающий
наибольший прирост информации. Это позволяет построить всего две
ветви для поддерева на данном этапе. Таким образом, мы получаем
слабо ветвистое дерево, упрощая полученный результат. В отличие от
IDS, RSI не имеет механизмов обработки непрерывных атрибутов.
Он, например, будет рассматривать записи
<красный, 81, светло, 125>,
<красный, 81.2, светло, 125>,
<красный, 81.3, светло, 125>
как различные, помещать их в различные классы эквивалентности.
Будет получена система продукционных правил, в которой три прави-
правила, возможно, будут описывать один и тот же объект. В этой области
преимущество IDS очевидно.

14.4] Алгоритм распознавания объектов 621
Рассмотрим отдельно непрерывные и дискретные атрибуты. Алго-
Алгоритм ID3 хорошо справляется с непрерывными атрибутами, и шум в
таких данных почти не окажет влияния на результат. Все равно все
значения будут разбиты на два диапазона, а наличие отклонений от
действительности может только сместить границы диапазонов. Для
алгоритма RS1 разброс значений еще более увеличит количество эле-
элементарных множеств и, следовательно, размер полученного описания.
Что касается атрибутов с дискретными значениями, то здесь дело
обстоит по-другому. Алгоритм /D3, используя статистику, выбирает
наиболее часто встречаемые значения. Это позволяет «не замечать»
случайных искажений. В этом случае RS1 тоже показывает хоро-
хорошие результаты. Так как заранее неизвестно, какие значения считать
истинными, а какие — искаженными, алгоритм строит две системы
продукционных правил. Одна дает уверенную классификацию, но
при этом возможно, что не все объекты, принадлежащие к понятию,
попадут под эту классификацию, т. е. эта система неполная. Вторая
система будет описывать все положительные объекты, но под это
описание могут попасть и некоторые отрицательные. Для разной
степени точности классификации мы будем иметь различные системы
правил. Как видно из сказанного, в зависимости от ситуации лучше
подойдет тот или иной метод. Отметим способ, который расширит об-
область применения алгоритма RS1. Предварительно можно заменить
непрерывный атрибут дискретным, разбив весь диапазон непрерыв-
непрерывных значений на 2—5 отрезков.
Были получены оценки для вычислительной сложности каждого
алгоритма: Сщз = О(к2 • TV), Crsi = О (к • N2). Таким образом,
на больших обучающих множествах (\U\ = N ^> 100) ID3 будет
выдавать результаты существенно быстрее, чем RS1.
Основным достоинством подхода с использованием приближенных
множеств является его способность работать с неточными и даже про-
противоречивыми исходными данными. Главный недостаток заключается
в высокой вычислительной сложности алгоритма генерации правил.
14.4. Алгоритм распознавания объектов в условиях
неполноты информации
Как было упомянуто выше, реальные базы данных часто могут
содержать неполную, либо некорректную информацию. Исследуется
случай, когда обучающая выборка содержит примеры такого типа.
Здесь каждый объект можно интерпретировать как вектор, получен-
полученный путем измерений ряда параметров. Некоторые из параметров
при этом могут получать ошибочные значения, либо просто быть
неизвестными в результате помех и сбоев в контурах измерений.
Сама обучающая выборка представляет множество положительных
примеров.

622 Индуктивные методы для случая неполной информации [ Гл. 14
Изложенный в работе авторов алгоритм решает задачу отнесения
объектов такого типа к одному из известных классов К\, К^ ..., Кш.
Вследствие неполноты информации классификация каждого объек-
объекта может быть неоднозначной. В таком случае предлагается искать от-
ответ с некоторой оценкой достоверности, то есть в виде множества пар:
< K\,[i\ >, < К2,112 >,...,< Кт, iim >, где iii представляет досто-
достоверность того, что предъявленный объект принадлежит г-му классу.
Ставится задача построить решающее правило R, которое поз-
позволит сопоставить произвольному объекту пару < К.^ jii >, либо
несколько таких пар. Исходным данным для построения решающего
правила является обучающая выборка /, содержащая примеры, для
которых известна их принадлежность к определенному классу (обуче-
(обучение с учителем). Само решающее правило организуется в виде дерева,
называемого деревом разбора, которое формируется на основе зонного
представления признаков. Признаки, характеризующие объект, явля-
являются либо количественными, либо качественными, и могут содержать
неизвестные или неверные значения.
Сформулируем задачу более строго. Пусть имеется множество
объектов, таких, что для описания каждого объекта используется
набор атрибутов < т\\, 7Г2,..., тгп >, причем значение каждого из
признаков может быть неизвестно. Каждый объект х принадлежит
одному из классов Kj, j = l,m. Для каждого класса Kj, j = 1,га
задана информация Ij в виде множества положительных примеров.
Множества таких выборок по всем классам составляют общую обуча-
обучающую выборку /:/ = /]_ U /2 U ... U /ш.
Требуется на основе обучающей выборки / построить решающее
правило (алгоритм), позволяющее сопоставить произвольному объек-
объекту х пару < Kj,/ij >, где Kj — класс, /ij понимается как достовер-
достоверность принадлежности этого объекта классу. Далее надо применить
построенное решающее правило для классификации других предъяв-
предъявленных объектов. Будем строить последовательный алгоритм, базиру-
базируясь на идее последовательного анализа значений признаков входного
объекта х.
Сам алгоритм и схема последовательной классификации основаны
на зонном представлении признаков объектов. Для каждого числово-
числового признака тг^ определяется диапазон изменений его значений: d7Ti.
Для этого в пределах обучающей выборки / находятся наибольшее и
наименьшее значения признака среди всех представленных в выборке
значений, и берется их разность.
Для исследования корреляции значений признака тг^ соответствен-
соответственно классам К\, К^,..., Кш, диапазон изменения значений разбиваем
на равные участки, называемые далее зонами. Число зон определяет-
определяется формулой Ad^i = d^i/lll, где Ad^i ~ ширина зоны, |/| — мощность
обучающей выборки /.

14.4] Алгоритм распознавания объектов 623
Разбив диапазоны значений обучающих признаков на зоны и про-
произведя для каждого признака тг^, г = 1, п, разметку соответствия его
значений, представленных в общей обучающей выборке /, зонам, мож-
можно определить, представители каких классов из / попали в каждую
зону. Класс Kj будем называть сопоставляемым для определенной
зоны рассматриваемого признака тг^, если в обучающей выборке /j,
соответствующей классу Kj найдется пример, значение которого по-
попадает в эту зону.
Введем функцию F, называемую далее функцией существенности
признака. Функция существенности F принимает значения в интер-
интервале @, 1); в соответствии с ней наиболее существенным следует
признать признак, для которого по всем классам К число классов,
одновременно сопоставленных каждой зоне, минимально.
Значения функции F могут быть получены в процессе диалога
с экспертом на этапе генерации системы; если эксперт затрудняется
упорядочить признаки по существенности, предлагается использовать
следующую эмпирическую формулу, в соответствии с которой наи-
наиболее существенным является тот признак, для которого по всем
классам Kj,j = l,ra, число классов, одновременно сопоставляемых
каждой зоне, минимально:
\
где т — число классов, nz — число зон по рассматриваемому призна-
признаку;
, ( 1 — если класс Ki является сопоставляемым для j-й зоны;
г°' ~ | 0 — в противном случае,
тг — число классов, для которых в общей обучающей выборке / по
рассматриваемому признаку имеется информация (т. е. не все значе-
значения неизвестны).
Вычисленные по этой формуле значения функции существенности
позволяют упорядочить признаки объекта по убыванию существен-
существенности, что определяет порядок выбора признаков последовательным
правилом классификации.
В связи с возможным разбросом значений, представленных в обу-
обучающей выборке /, введем понятие гипотетических классов. Разброс
оценивается экспертом на этапе построения решающего правила пу-
путем задания одной из следующих оценок: 3 — существенный разброс,
2 — несущественный, 1 — разброс практически отсутствует. Для учета

624 Индуктивные методы для случая неполной информации [ Гл. 14
возможного попадания значений числовых признаков тг^, г = 1,п,
распознаваемых объектов за пределы диапазона d^i, вводим две вспо-
вспомогательные зоны: для значений признака тг^, меньших тт(тгг); и для
/
значений признака тг^, больших тах(тгг).
Ширина этих зон вычисляется исходя из введенной экспертом
оценки разброса с учетом семантических ограничений, накладывае-
накладываемых на значения данного признака. Разброс значений числовых при-
признаков имеет место не только для крайних зон, но и для промежуточ-
промежуточных. Если зона помечена именем класса, то можно предположить, что
при классификации встречаются примеры объектов этого же класса
со значением рассматриваемого признака, попадающим в соседние
зоны. Класс, сопоставляемый зоне вследствие возможного разброса
значений признаков из других зон, будем называть гипотетическим
для данной зоны.
При построении решающего правила R введем оценку /i, называе-
называемую далее достоверностью принадлежности объекта классу. Введе-
Введение этой оценки связано с тем, что по каждому признаку тг^, г = 1, п,
каждой зоне могут быть сопоставлены несколько классов. Достовер-
Достоверность fi будет использована при оценке гипотез о принадлежности
объекта х каждому из сопоставленных зоне классов. Оценки /i будут
вычисляться для каждой зоны каждого признака по всем классам
(как сопоставляемым, так и гипотетическим) по правилам, рассмот-
рассмотренным ниже. Вычисление достоверности для сопоставляемых зоне
классов можно разбить на следующие этапы.
Шаг 1. Для каждого сопоставляемого зоне класса Kj подсчи-
тывается отношение числа примеров, представленных в обучающей
выборке Ij, значение рассматриваемого признака которых попадает в
эту зону, к числу примеров этой же выборки /j, для которых значе-
значение рассматриваемого признака определено. Полученное отношение
умножается на 100%.
Шаг 2. Для всех сопоставляемых данной зоне классов суммиру-
суммируются полученные значения (в процентах), и полученный результат
принимается за 100%.
Шаг 3. Для каждого сопоставляемого зоне класса Kj значение, по-
полученное на первом шаге, делится на суммарное значение, полученное
на втором шаге, что дает искомое значение достоверности.
Так как гипотетические классы введены на случай возможного
попадания значений признаков в определенные зоны, то достовер-
достоверность для гипотетических классов не может быть вычислена на основе
анализа значений, представленных в обучающей выборке. Эта досто-
достоверность может быть оценена интуитивно с учетом оценки разброса
значений числовых признаков, введенной экспертом.
Пусть для некоторой зоны класс Kj является сопоставляемым с
достоверностью jij. Чем больше оценка разброса, тем в большее число

14.4] Алгоритм распознавания объектов 625
близлежащих зон возможно попадание значений анализируемого при-
признака при распознавании, т. е. для большего числа зон класс является
гипотетическим.
Примем, что если для некоторой зоны класс Kj является сопо-
сопоставляемым, а соседние зоны не помечены именем этого класса, то
попадание значений анализируемого признака в эти зоны наблюдается
хотя бы в два раза реже, нежели в основную зону. Следовательно,
и достоверности для гипотетических классов этих зон должны быть
хотя бы в два раза меньше достоверности для сопоставляемого клас-
класса Kj.
При вычислении достоверностей для гипотетических классов мы
ориентируемся на «наихудший случай», т. е. лучше завысить досто-
достоверность, чем недооценить ее. Это объясняется тем, что если факт
принадлежности объекта гипотетическому классу будет опровергать-
опровергаться в ходе распознавания, то и достоверность для этого класса будет
уменьшаться в процессе вывода решения.
В соответствии с этими соображениями, если для некоторой зоны
класс Kj уже является гипотетическим с достоверностью //, и на эту
зону накладывается достоверность //', учитывающая разброс какой-
нибудь другой близлежащей зоны, то окончательная достоверность
/i для гипотетического класса Kj вычисляется следующим образом:
/i = max(//, ц").
Рассмотрим далее структуру решающего правила R. Результатом
работы первого этапа алгоритма является решающее правило i?, пред-
представленное в базе знаний. Решающее правило R содержит зонное
представление признаков tti ,..., тгп. Для каждого признака указано
его имя, тип (количественный или качественный) и информация по
всем зонам. Первая и последняя зоны каждого числового признака —
вспомогательные, они используются для учета разброса значений,
выходящего за пределы диапазона значений, представленных в обуча-
обучающей выборке /. Для каждой зоны указаны: интервал охватываемых
ею значений, число примеров обучающей выборки, попавших в дан-
данную зону по каждому из классов Kj, j = 1, т (значение —1 означает,
что данный класс является гипотетическим для рассматриваемой
зоны), а также достоверности принадлежности объекта каждому из
классов.
Поясним механизм применения построенного решающего правила
для распознавания конкретного объекта х. При распознавании про-
происходит наложение значений признаков классифицируемого объекта
на зонное представление признаков, содержащееся в базе знаний.
Анализ начинается с наиболее существенных признаков, (в смысле
определения принадлежности объекта классу).
По первому признаку, который подлежит анализу, ищется зона,
в которую попадает значение признака. Из этой зоны считывается
информация о достоверностях для сопоставляемых и гипотетических

626 Индуктивные методы для случая неполной информации [ Гл. 14
классов, которая заносится в список L\. Это первоначальный список
классов, к которым может принадлежать распознаваемый объект,
и их достоверностей. Информация по следующему анализируемому
признаку заносится в список L^. Из списков L\ и L^ формируется
результирующий список Lr по правилам, изложенным ниже. Далее
результирующий список выступает в роли списка L\ и т. д. Процесс
продолжается, пока не будут проанализированы все признаки распо-
распознаваемого объекта х или пока в результирующем списке не останется
один класс.
Итак, в ходе последовательного анализа признаков происходит
отсечение ненужных классов и осуществляется корректировка зна-
значений достоверности для оставшихся в списке классов. Если значе-
значение очередного подлежащего анализу признака неизвестно, то про-
происходит переход к анализу следующего по существенности признака.
Процедура поэтапного анализа значений признаков с использованием
построенной базы знаний может быть представлена в виде так назы-
называемого «дерева разбора». Вершине дерева соответствует множество
всех возможных классов, ярусу — очередной анализируемый признак.
При движении по «дереву разбора» сверху вниз происходит вывод
решения.
Рассмотрим подробно алгоритм последовательной классификации
объектов при неполной исходной информации.
Алгоритм, последовательной классификации
Шаг 1. Вычислить значение функции существенности F для
каждого признака тг^, г = 1, п.
Шаг 2. Выстроить признаки в последовательность в порядке
убывания их существенности.
Шаг 3. in = 0.
Шаг 4 • Если значения всех признаков распознаваемого объекта
неизвестны, то переход к шагу 19.
Шаг 5. Перейти к анализу наиболее существенного признака
распознаваемого объекта.
Шаг 6. Если значение подлежащего анализу признака неизвест-
неизвестно, то переход к шагу 18.
Шаг 7. гп = гп + 1.
Шаг 8. В базе знаний, содержащей решающее правило, найти
зону, в которую попадает значение анализируемого признака.
Шаг 9. Если гп = 1, то переход к шагу 13.
Шаг 10. Сформировать список Li, выписав из найденной зоны
классы с соответствующими им значениями достоверности (до-
(достоверности для гипотетических классов выписывать со знаком
минус).

14.4] Алгоритм распознавания объектов 627
Шаг 11. Переписать в результирующий список Lr информацию
из списка L\.
Шаг 12. Переход к шагу 17.
Шаг 13. Сформировать список L^ аналогично списку L\.
Шаг 14- Из списков L\ и L2 сформировать результирующий
список Lr по правилам, изложенным ниже.
Шаг 15. in = in- 1.
Шаг 16. Переписать в список L\ информацию из результирую-
результирующего списка Lr.
Шаг 17. Если в результирующем списке Lr содержится один
класс с ненулевым значением достоверности, то переход к ша-
шагу 20.
Шаг 18. Если не все признаки распознаваемого объекта проана-
проанализированы, то переход к шагу 5, иначе переход к шагу 20.
Шаг 19. Сформировать результирующий список Lr, присвоив
всем классам одинаковую достоверность, равную 1/т, где т —
число классов.
Шаг 20. Конец.
Рассмотрим подробнее правила формирования результирующего
списка Lr из списков Li и L2 (шаг 14 алгоритма).
1. Если в список L2 вошли сопоставляемые классы, номера кото-
которых не совпадают с номерами ни сопоставляемых, ни гипотети-
гипотетических классов списка Li, то
1.1) в результирующий список их не вносить;
1.2) просуммировать их достоверности;
1.3) полученное значение распределить между сопоставляемы-
сопоставляемыми классами списка L^ пропорционально их достоверно-
стям.
2. Если в список L^ не вошли какие-нибудь из сопоставляемых
классов списка L\ (ни в качестве сопоставляемых, ни в качестве
гипотетических) то
2.1) в список Lr эти классы не вносить;
2.2) их достоверности распределить между оставшимися сопо-
сопоставляемыми классами списка L\ пропорционально их до-
стоверностям;
2.3) сопоставляемые классы списка Li, вошедшие в качестве
сопоставляемых в список L2, внести в список Lr с усред-
усредненными (по спискам L\ и L2) значениями достоверности.

628 Индуктивные методы для случая неполной информации [ Гл. 14
3. Если в список L2 вошли сопоставляемые классы списка L\ в
качестве сопоставляемых, то занести их в список L^ в качестве
сопоставляемых классов с усредненными (по спискам L\ и L^)
значениями достоверности.
4. Если в список L^ вошли сопоставляемые классы списка L\ в
качестве гипотетических классов, то занести их в список Lr в
качестве гипотетических классов с усредненными (по спискам
L\ и L12) значениями достоверности и со знаком минус.
5. Если в список L^ не вошли гипотетические классы из списка L\
(ни в качестве сопоставляемых, ни в качестве гипотетических)
то их следует пропустить при составлении списка Lr.
6. Если в список L2 вошли гипотетические классы из списка L\ в
качестве гипотетических, то занести их в список Lr в качестве
гипотетических классов с усредненными (по спискам L\ и L^)
значениями достоверности со знаком минус.
7. Если в список L2 вошли гипотетические классы, номера которых
не совпадают с номерами ни сопоставляемых, ни гипотетических
классов из списка Li, то их следует вычеркнуть из списка L2-
8. Если в список L^ вошли гипотетические классы списка L\ в
качестве сопоставляемых классов, то занести их в список Lr
в качестве гипотетических классов с усредненными (по спискам
L\ и L<2) значениями достоверности и со знаком минус.
Пример 14. 9.
Рассмотрим пример работы алгоритма последовательной класси-
классификации. Обучающая выборка / представлена в табл. 14.5.
Проведем расчет функции существенности F по каждому из при-
признаков Pi, г = 1,4. Определим ширину зоны dP\ для признака Р\.
dPx = 80 - 3 = 77. |/| = 11. Тогда МРг = 77/11 = 7, 00. Разбив далее
диапазон изменения значений признака Р\ на зоны и определив для
каждой зоны сопоставляемые ей классы, вычислим значение функции
F для признака Р\ с использованием введенной выше формулы.
FPl=l-
Промежуточные результаты расчета значений Fpx приведены в
табл. 14.6.

14.4]
Алгоритм распознавания объектов
629
Таблица 14.5
Имя признака
Тип признака
1\ —примеры
объектов
класса К\
/2 —примеры
объектов
класса Къ
/з —примеры
объектов
класса Кз
Pi
количествен-
количественный
10
15
20
3
70
80
22
44
35
Р2
качествен-
качественный
20
10
18
20
10
20
18
18
10
Рз
качествен-
качественный
1
1
2
to I I to
1 to to 1
p4
количествен-
количественный
15
19
14
13
21
25
24
3
33
44
Таблица 14.6
p зоны, j
1
2
3
4
5
6
7
8
9
10
11
DP!
(ЗД0)
(ЮД7)
A7,24)
B4,31)
C1,38)
C8,45)
D5,52)
E2,59)
E9,66)
F6,73)
G3,80)
С опоставимые
классы
1,2
1
2,3
-
3
3
-
-
-
2
3
Uo\ г =1,3
1, 1, 0
1, 0, 0
0, 1, 1
0, 0, 0
0, 0, 1
0, 0, 1
0, 0, 0
0, 0, 0
0, 0, 0
0, 1,0
0,0,1
2, 3, 4
1, 1, 0
0, 0, 0
0, 1, 1
0, 0, 0
0, 0, 0
0, 0, 0
0, 0, 0
0, 0, 0
0, 0, 0
0, 0, 0
0, 0, 0
1, 2, 1
Для признака Р2 роль зоны играет дискретное значение
(табл. 14.7).
Fp2 = 1 - (J + \ + ^ /6 « 1 - 0, 778 = 0, 222.

630 Индуктивные методы для случая неполной информации [ Гл. 14
Таблица 14.7
р зоны, j
1
2
3
DP2
20
10
18
С опоставимые
классы
1, 2, 3
2,3
2,3
hj; г= 1,3
1,1, 1
0, 1, 1
0, 1, 1
1,3,3
^ ^; г = 1, 3
2,2,2
0,1,1
0,1,1
2,4,4
Аналогично получим Fp3 « 0,167, Fp4 « 0, 681.
Таблица Ы.<
Имя
признака
Pi
Р2
Рз
Р4
Р
зоны
1
2
3
dPx
0,000 + 3,000
3,000 + 10,000
10,000 + 17,000
Кг
-0,20
0,60
1,00
к2
1,00
0,40
-0,30
к3
0,00
-0,10
-0,20
12
13
1
2
3
1
2
1
2
73,000 + 80,000
80,000 + 94,000
20
10
18
1
2
0,00 + 3,00
3,00 + 6,727
0,00
0,00
0,63
0,00
0,00
1,00
0,14
-0,06
-0,12
-0,20
-0,10
0,21
0,57
0,40
0,00
0,43
-0,06
-0,12
1,00
1,00
0,16
0,43
0,60
0,00
0,43
1,00
1,00
6
7
17,909 + 21,636
21,636 + 25,364
0,5
-0,25
0,50
1,00
-0,21
-0,11
12
13
40,273 + 44,00
44,00 + 55,182
0,00
0,00
0,00
0,00
1,00
1,00

14.4]
Алгоритм распознавания объектов
631
Упорядочивая признаки по существенности, получим: Pi1P2iP^>.
Именно в таком порядке далее будет проводиться анализ признаков
предъявленных объектов.
В табл. 14.8 приведена база знаний решающего правила, на осно-
основе которой будет проводиться распознавание конкретных объектов.
В этой таблице для каждой зоны каждого признака даны значе-
значения достоверностей принадлежности объектов каждому из классов
Kj, j = 1,3. Со знаком минус указаны значения достоверностей для
гипотетических классов.
Таблица 14.9
Имя признака
Значение признака
Pi
78
Р2
-
Рз
-
Р4
20
Пусть для распознавания системе предъявлен объект, представ-
представленный в табл. 14.9. Определим на основе построенного решающе-
решающего правила, к какому классу принадлежит данный объект. Пер-
Первый анализируемый признак — Р\. Его значение, равное 78, по-
попадает в зону р 12 (см. табл. 14.8). Будет сформирован список
Li : 2(-0,20), 3A,00).
Поскольку значения признаков Р2, Рз отсутствуют, следующим
анализируем признак Р^. Его значение, равное 20, попадает в зону 6.
Будет сформирован список L2 : 1@,50), 2@,50), 3(-0,21).
Построим результирующий список Lr по правилам, изложенным
ранее. Так, в списке L2 появился новый сопоставляемый класс —
класс 1. Модифицируем список L2 (п. 1 правил построения резуль-
результирующего списка): 2A,00), 3(—0,21).
Сопоставляемый класс 3 списка L\ вошел в список L2 как
гипотетический. Согласно п. 4 правил, заносим класс 3 в список
Lr как гипотетический со значением достоверности, равным
Класс 2 согласно п. 8 правил заносим в результирующий
список как гипотетический со значением достоверности, равным
@,20 + 1,00)
= = 0,60. Поскольку значения признаков
Р2,Рз неизвестны, мы закончили анализ всех признаков объек-
объекта. Результат распознавания: объект принадлежит классу 2 с
достоверностью 0,60; объект принадлежит классу 3 с достовер-
достоверностью 0,65.
Алгоритмы, рассмотренные выше, использовали для анализа пре-
прежде всего качественные признаки. Вспомним, что алгоритм ID3

632 Индуктивные методы для случая неполной информации [ Гл. 14
позволяет в случае количественных признаков разбить область зна-
значений только на две зоны. Обучающие выборки для алгоритмов
ID3, ДРЕВ не должны содержать объектов с неизвестными значе-
значениями, хотя после того, как решающие правила сформированы, их
можно использовать для классификации объектов с неизвестными
значениями некоторых атрибутов. Еще одной характерной особен-
особенностью алгоритма последовательной классификации является пред-
представление решающего правила в виде информационной базы, бо-
более сложной, чем рассмотренные выше представления. Предложен-
Предложенный алгоритм имеет невысокую вычислительную сложность, опре-
определяет принадлежность предъявленного объекта одному из множе-
множества классов, но не подходит для случая чисто качественных приз-
признаков.

К введению 633
Литературный комментарий
К введению
Понятие интеллектуальной системы было взято из [0.1]. Желаю-
Желающие подробно ознакомиться с классификацией типов выводов, тео-
теорией правдоподобных выводов и ДСМ-методом автоматического по-
порождения гипотез могут обратиться к работам [0.2, 0.3]. Философские
понятия основных типов рассуждения — дедукции и индукции —
освещены в [0.4].
Вопросы силлогистики Аристотеля и проблемы автоматизации до-
достоверных и правдоподобных рассуждений даны в прекрасной книге
[0.5]. В работах [0.6, 0.7, 0.8] подробно излагается роль абдукции и
индукции в философии и логике, приводится теория силлогистики и
инференциальная теория Пирса, показывается взаимодействие между
абдукцией и индукцией, описывается индукция и абдукция в ма-
машинном обучении. Статья [0.6] оказала сильное влияние на создание
введения, особенно той части, которая касается силлогистики Пирса
и его инференциальной теории.
0.1. Финн В. К. Правдоподобные рассуждения в интеллектуальных си-
системах типа ДСМ // Итоги науки и техники. Сер. «Информатика».
Т. 15. Интеллектуальные информационные системы. — М.: ВИНИ-
ВИНИТИ, 1991. С. 54-101.
0.2. Финн В. К. Правдоподобные выводы и правдоподобные рассужде-
рассуждения // Итоги науки и техники. Сер. «Теория вероятностей. Мате-
Математическая статистика. Теоретическая кибернетика». Т. 28. — М.:
ВИНИТИ, 1988. С. 3-84.
0.3. Финн В. К. Интеллектуальные системы: проблемы их развития и
социальные последствия // Будущее искусственного интеллекта /
Под ред. К. Е. Левитина, Д. А. Поспелова. — М.: Наука, 1991. С. 157-
177.
0.4. Философский словарь / Под ред. И.Т.Фролова. — М.: Политиздат,
1980. 444 с.
0.5. Поспелов Д. А. Моделирование рассуждений. Опыт анализа мысли-
мыслительных актов. — М.: Радио и связь, 1989. 184 с.
0.6. Flach P. A., Kakas А. С. On the Relation between Abduction
and Inductive Learning // Handbook of Defeasible Reasoning and
Uncertainty Management Systems. V. 4: Abductive Reasoning and
Learning / Ed. by Dov. Gabbay and Ph. Smets. — Kluwer Academic
Publishers, 1998-2001-32. P. 1-39.

634 К части I
0.7. Flach P. A. Logical Characterisations of Inductive Learning // Ibid.
P. 155-196.
0.8. Bergadano F., Cutello V., Gunetti D. Abduction in Machine Learning //
Ibid. P. 197-229.
К части I
К главе 1
В этой главе даны основные положения автоматического доказа-
доказательства теорем, наиболее развитой области искусственного интеллек-
интеллекта. Прежде всего следует отметить разработку Ньюэллом и Саймоном
общего решателя проблем (GPS), с помощью которого были доказаны
многие теоремы формальной логики [1.1, 1.2].
Вопросам автоматического доказательства теорем посвящены
работы [1.3-1.19]. Здесь стоит отметить оригинальный подход
С. Ю. Маслова, базирующийся на методе обратного вывода [1.8], на
основе которого было создано несколько систем поиска вывода [1.9].
Описание алгоритма машинного поиска естественного логического
вывода в исчислении высказываний (АЛПЕВ), предложенного
Н.А.Шаниным и его коллегами, можно найти в [1.10]. Изложение
классического метода дедукции Эрбрана было взято из [1.3, 1.13].
Описание принципа резолюции для логики высказываний и логики
предикатов основывалось на работах [1.3, 1.5—1.7, 1.11]. Линейная
резолюция и ее частный случай — входная резолюция — подробно
даны в [1.12-1.15].
Общие соображения о дедуктивных моделях и взаимосвязях меж-
между формальной логикой и логическим программированием описаны
в [1.4, 1.16-1.20]. В работе [1.21] рассмотрены вопросы, связанные с
предположением о замкнутом мире.
Изложение теоретических основ языка Пролог приведено в книгах
[1.4, 1.22-1.27]. Описанию языка Пролог как языка логического про-
программирования посвящены книги [1.28-1.31]. Описания реализаций
методов поиска «в глубину», «в ширину» и «наилучшего» на языке
Пролог приведены в [1.15]. Вопросы реализации моделей представле-
представления знаний на языке Пролог, примеры планирования действий робота
и решения головоломок освещены в [1.15]. Желающие ознакомиться
с основами прикладной логики могут обратиться к [1.32].
1.1. Newell A., Simon H. GPS: A Program that Simulates Human Thought /
Ed. by Feigenbaum E. A. and Feldman J. // Computers and Thought. —
N.Y.: McGraw-Hill, 1963.
1.2. Computers and Thought / Ed. by Feigenbaum E. A., Feldman J. — N.Y.:
McGraw-Hill, 1963.

К главе 1 635
1.3. Chang С. L., Lee R. С. Т. Symbolic, Logic and Mechanical Theorem
Proving. — N.Y., London: Acad. Press, 1973. (Русский перевод: Ма-
Математическая логика и автоматическое доказательство теорем. —
М.: Наука, 1983. 358 с).
1.4. Kowalski R. Logic for Problem Solving. — N.Y.: Elsevier North-Holland,
1979. (Русский перевод: Логика в решении проблем. — М.: Наука,
1990. 280 с).
1.5. Loveland D. W. Automated Theorem Proving: a Logical Basis. — N.Y.:
North-Holland, 1978.
1.6. Wos L., Overbeek R., Lusk E., Boyle J. Automated Reasoning:
Introduction and Applications. Englewood Cliffs. — N.Y.: Prentice-Hall,
1984.
1.7. Wos L. Automated Reasoning, 33 Basic Research Problems. — N.Y.:
Prentice-Hall, 1988.
1.8. Маслов С Ю. Обратный метод установления выводимости в класси-
классическом исчислении предикатов // ДАН СССР. Т. 159. р 1. 1964. С. 17-
20.
1.9. Давыдов Г. В., Маслов С. Ю., Минц Г. Е. и др. Машинный алгорифм
установления выводимости на основе обратного метода // Исследо-
Исследования по конструктивной математике и математической логике. Зап.
науч. сем. ЛОМИ АН СССР. - Л.: Наука, 1969. Т. 16. С. 8-19.
1.10. Шанин Н. А., Давыдов Г. В. и др. Алгорифм машинного поиска есте-
естественного логического вывода в исчислении высказываний. — М.: Л.:
Наука, 1965.
1.11. Robinson J.A. A Machine Oriented Logic Based on the Resolution
Principle // Journal of the ACM. 1965. V. 12. P. 25-41. (Русский
перевод: Машинно-ориентированная логика, основанная на принципе
резолюции // Кибернетический сб. Нов. сер. р 7. — М.: Мир, 1970.).
1.12. Kowalski R., Kuehner D. Linear Resolution with Selection Function //
Artificial Intelligence. 1971. V. 2. P. 227-260.
1.13. Вагин В. Н. Дедукция и обобщение в системах принятия решений. —
М.: Наука, 1988. 384 с.
1.14. Вагин В. Н. Дедуктивный вывод на знаниях // Справ. Искусствен-
Искусственный интеллект. Кн. 2. Модели и методы / Под ред. Д. А. Поспелова. —
М.: Радио и связь, 1990. С. 89-105.
1.15. Luger G. F., Stubblefield W. A. Artificial Intelligence. Structures and
Strategies for Complex Problem Solving. — Addison Wesley Longman,
Inc., 1998. 824 p.
1.16. Carlo Zaniolo et al. Advanced Database Systems. — San Francisco:
Morgan Kaufmann Publishers, Inc. 1997. 572 p.
1.17. Вагин В. Н. Дедуктивные модели // Представление знаний в
человеко-машинных и робототехнических системах. Т.А.: Фундамен-
Фундаментальные исследования в области представления знаний. — М.: ВИ-
ВИНИТИ, 1984. С. 36-47.

636 К главе 2
1.18. Вагин В.Н., Головко А. В. Дедуктивные базы данных в системах
управления // Изв. АН СССР. Техническая кибернетика. №2. 1987.
С. 60-73.
1.19. Stickel M. E. An Introduction to Automated Deduction // Lecture Notes
in Computer Science. N. 232. Fundamentals of Artificial Intelligence / Ed.
by W. Bibel and Ph. Jorrand. — Spriger-Verlag, 1986. P. 75-131.
1.20. Van Emden M., Kowalski R. The Semantics of Predicate Logic and a
Programming Language // Journal of the ACM. 1976. V. 23. P. 733-742.
1.21. Reiter R. Deductive Question-Answering on Relational Data Bases //
Logic and Data Bases. — N.Y.: Plenum Press, 1978. P. 149-177.
1.22. Barr A., Feigenbaum E. A. The Handbook of Artificial Intelligence. —
Pitman, 1981. V. 1-3.
1.23. Campbell J. A. Implementation of Prolog. — Ellis Horwood, 1984.
1.24. Horovitz E., Sahni S. Fundamentals of Data Structures. — Pitman, 1976.
1.25. Тейз А., Грибомон ТТ., Луи Ж. и др. Логический подход к искус-
искусственному интеллекту: от классической логики к логическому про-
программированию / Пер. с франц. — М.: Мир, 1990. 432 с.
1.26. Лорьер Ж.-Л. Системы искусственного интеллекта / Пер. с франц. —
М.: Мир, 1991. 568 с.
1.27. Логическое программирование. Сб. статей / Под ред. В.Н.Ага-
В.Н.Агафонова. — М.: Мир, 1988.
1.28. Брагпко И. Программирование на языке ПРОЛОГ для искусствен-
искусственного интеллекта. — М.: Мир, 1990. 560 с.
1.29. Clocksin W. F., Mellish С S. Programming in Prolog. — Spinger-Verlag,
1981. (Русский перевод: Клоксин У., Меллиш К. Программирование
на языке ПРОЛОГ. — М.: Мир, 1987).
1.30. Sterling L., Shapiro E. The Art of Prolog. — Cambridge: MIT Press,
MA, 1986. (Русский перевод: Стерлинг Л. Шапиро Э. Искусство
программирования на языке ПРОЛОГ. — М.: Мир, 1989).
1.31. Доорс Дснс., Рейблейн А. Р., Вадера С ПРОЛОГ — язык программи-
программирования будущего / Пер. с англ. — М.: Финансы и статистика, 1990.
144 с.
1.32. Непейвода Н.Н. Прикладная логика. — Новосибирск: Изд-во НГУ,
2000. 490 с.
К главе 2
Метод вывода на графе связей был разработан Р. Ковальским,
и его описание взято из [2.1]. Проблема полноты и состоятельности
метода вывода на графе связей рассмотрена в [2.2, 2.3]. Параллель-
Параллельным методам вывода на графе связей, особенно DCDP- и AND-
параллелизму, было посвящено много работ. Мы придерживались
изложения параллелизма в выводе на графе связей по работам [2.4-
2.9]. В качестве основных тестовых задач были рассмотрены задачи
о N ферзях и «Стимроллер» [2.10, 2.11]. Программирование зада-

К главе 2 637
чи о N ферзях с применением DCDP- и AND-параллелизма было
осуществлено Н. О. Салапиной [2.12-2.16]. Изложение OR-, DCDP- и
AND-параллелизма на графе связей для задачи «Стимроллер» да-
дано по работам [2.17-2.20]. Разработка эвристической функции HI и
программного обеспечения при решении задачи «Стимроллер» при-
принадлежит А. И. Аверину.
2.1. Kowalski R. A Proof Procedure Using Connection Graphs // J. of the
ACM. 1975. V.22D). P. 572-599.
2.2. Bibel W. On the Completeness of Connection Graph Resolution //
Proceedings GWAI-81, Informatik-Fachberichte 47 / Ed. by
J.H.Siekmann. — Berlin: Springer-Verlag, 1981. P. 246-247.
2.3. Siekmann J., Stephan W. Completeness and Soundness of the Connection
Graph Procedure // Interner Bericht 7/76. — Inst. fur Informatik I,
Universitat Karlsruhe, FRG, 1976.
2.4. Loganantharaj R. Theoretical and Implementation Aspects of Parallel
Link Resolution in Connection Graphs. PhD thesis // Dep. of Сотр.
Sci., Colorado State University, 1985.
2.5. Loganantharaj R., Mueller R. A. Parallel Theorem Proving with
Connection Graph // 8th Int. Conf. on Autom. Deduc, LNCS 230, 1986.
P. 337-352.
2.6. Loganantharaj R., Mueller R. A., Oldehoeft R.R. Connection Graph
Refutation: Aspects of AND-parallelism // Tech. Report CS-85-10,
Department of Computer Science, Colorado State University, 1985.
2.7. Cheng P.D., Juang J. Y. A Parallel Resolution Procedure Based on
Connection Graph // Proc. of 6th Nat. Conf. on Art. Intell. (AAAI 87),
Seattle, Washington, 13-17 July 1987. P. 13-17.
2.8. Hornung G., Knapp A., Knapp U. A Parallel Connection Graph Proof
Procedure // German Workshop on Artificial Intelligence, LNCS. —
Berlin: Springer-Verlag, 1981. P. 160-167.
2.9. Munch К. Н. A New Reduction Rule for the Connection Graph Proof
Procedure // J. of Automated Reasoning. 1988. V. 4. P. 425-444.
2.10. Stickel M. F. Schubert's Steamroller Problem: Formulations and
Solutions // Ibid. 1986. V. 2. P. 89-100.
2.11. Братко И. Программирование на языке Пролог для искусственного
интеллекта / Пер. с англ. — М.: Мир, 1990. 560 с.
2.12. Вагин В. Н., Еремеев А. П., Салапина Н. О. Организация параллель-
параллельного вывода в системах поддержки принятия решений // Сб. изб.
работ по грантам в обл. информатики, радиоэлектроники и систем
управления. — СПб, 1994. С. 58-63.
2.13. Vagin V. N., Salapina N. О. Parallel Inference on Connection Graphs //
Proceedings of the 1998 IEEE ISIC/CIRA/ISAS Joint Conference,
Gaithersburg, MD, September 14-17, 1998. P. 204-209.

638 К главе 3
2.14. Вагин В.Н., Салапина И.О. Система параллельного вывода с ис-
использованием графа связи // Изв. РАН. Теория и системы управле-
управления. 1998. №5. С. 39-47.
2.15. Вагин В.Н., Салапина Н. О. Программная реализация системы па-
параллельного вывода PIS с использованием графа связей // КИИ'98.
Шестая национальная конференция с между народным участием.
Труды конференции. Пущино, 1998. Т. 1. С. 250-256.
2.16. Vagin V. М., Salapina N. О. A System of Parallel Inference with the Use
of a Connection Graph // J. of Сотр. and Syst. Sci. Int. 1998. V. 37.
№5. P. 699-707.
2.17. Аверин A.M., Вагин В.Н., Хамидулов М.К. Исследование алгорит-
алгоритмов параллельного вывода на задаче «Стимроллер» // Изв. РАН.
Теория и системы управления. 2000. №5. С. 92-100.
2.18. Аверин А. И., Вагин В. Н., Хамидулов М. К. Методы параллельного
вывода на графовых структурах // Седьмая нац. конф. по иск. инт. с
межд. участием (КИИ-2000). — М.: Физматлит, 2000. Т. 1. С. 181-189.
2.19. Averin A.I., Vagin V. N., Khamidulov M.K. The Investigation of
Algorithms of Parallel Inference by the Steamroller Problem // J. of
Сотр. and Syst. Sci. Int. 2000. V.39. №5. P. 758-765.
2.20. Аверин А. И., Вагин В.Н. Параллелизм в дедуктивном выводе на
графовых структурах // Автоматика и телемеханика. 2001. №10.
С.54-64.
К главе 3
Описание типов параллелизма на уровне термов, на уровне дизъ-
дизъюнктов и на уровне поиска в дедуктивном выводе взято из [3.1].
Последовательный алгоритм дедукции на С-графах был разрабо-
разработан В. Г. Кикнадзе и В.Н.Вагиным и дан в [3.2, 3.3]. Пять типов
параллелизма в выводе на раскрашенных С-графах предложены
В.Н.Вагиным и рассмотрены в [3.2, 3.4-3.9]. Сравнение эффектив-
эффективности различных процедур дедуктивного вывода было проведено на
тестовой задаче «Стимроллер» и описано в [3.10, 3.11]. Программная
реализация параллельного алгоритма вывода на С-графе принадле-
принадлежит М. К. Хамидулову.
3.1. Bonacina M. P. A Taxonomy of Parallel Strategies for Deduction // Ann.
of Math, and Artificial Intell. 2000. 29 A, 2, 3, 4). P. 223-257.
3.2. Вагин В. Н. Дедукция и обобщение в системах принятия решений. —
М.: Наука, 1988. 384 с.
3.3. Вагин В.Н., Кикнадзе В. Г. Дедуктивный вывод на семантических
сетях в системах принятия решений // Изв. АН СССР. Техническая
кибернетика. 1984. №5. С. 106-120.
3.4. Вагин В. Н. Параллельная дедукция на семантических сетях // Там
же. 1986. №5. С. 51-61.

К главе 4 639
3.5. Vagin V. N. Parallel Deduction in Inference Machines // Artificial
Intell. and Information-Control Systems of Robots-87. Elsevier Science
Publishers B. V. (North-Holland). 1987. P. 479-482.
3.6. Вагин В. H., Васильев М. Ю. Абстрактная схема параллельной маши-
машины логического вывода // Изв. АН СССР. Техническая кибернетика.
1988. №5. С. 195-207.
3.7. Вагин В.Н., Васильев М.Ю. Программное моделирование парал-
параллельной системы логического вывода // Новые инф. технол. в пла-
планировании, управлении и в производстве. Матер, сем. МДНТП им.
Ф.Э.Дзержинского. — М.: 1991. С. 105-112.
3.8. Vagin V. N. Parallel Inference on Logical Networks // Automated
Reasoning. Proc. of the IFIP/WG 12.3 Int. Workshop on Autom. Reas.
Beijing, P. R. China, 13-16 July 1992. North-Holland, 1992. P. 305-310.
3.9. Vagin V. N. Parallel Inference in Situation Control Systems //
Architectures for Semiotic Modelling and Situation Analysis in Large
Complex Systems. Proc. of the 1995 ISIC Workshop. 10th IEEE Int.
Symp. on Intell. Cont. 1995. Monterey, California. P. 109-116.
3.10. Аверин А. И., Вагин В. Н., Хамидулов М. К. Методы параллельного
вывода на графовых структурах // Тр. VII нац. конф. по иск. инт. с
межд. участием. Т. 1. — М.: Физматлит, 2000. С. 181-189.
3.11. Averin A.I., Vagin V. N., Khamidulov M.K. The Investigation of
Algorithms of Parallel Inference by the Steamroller Problem // J. of
Сотр. and Syst. Sci. Int. 2000. V.39. №5. P. 758-765.
К главе 4
Полное описание метода аналитических таблиц дано в книге [4.1],
из которой был почерпнут основной материал для написания этой
главы. М. Фиттинг продолжил дело своего учителя Р. Смальяна и
изложил этот метод с точки зрения применения теории автоматиче-
автоматического доказательства теорем в логическом программировании [4.2].
Этот же автор дал реализацию метода аналитических таблиц для
пропозициональной логики и логики предикатов первого порядка на
языке Пролог. Е. Ю. Головина применила этот метод для решения
тестовой задачи «Стимроллер», описанной в [4.3]. Желающие могут
также ознакомиться с этим методом по книге [4.4].
4.1. Smullyan R. M. First-Order Logic. — Berlin, Heidelberg, N.Y.: Springer-
Verlag, 1968. 158 p.
4.2. Fitting M. First-Order Logic and Automated Theorem Proving. — N.Y.:
Springer-Verlag, 1990. 511 p.
4.3. Stickel M. F. Schubert's. Steamroller problem: formulation and
solution // Journal of Automated Reasoning. 1986. V. 2. P. 89-100.
4.4. Хвостова К. В., Финн В. К. Проблемы исторического познания в
свете современных междисциплинарных исследований. — М.: РГГУ,
1997. 256 с.

640 К главе 5
К главе 5
В работах [5.1, 5.2] описана многоуровневая упорядоченно-сортная
алгебра для описания взаимодействия типов. В [5.3] дана многосорт-
многосортная алгебра, как основа для создания языка запросов, и показано ее
использование для определения манипулирования сложными объек-
объектами. В [5.4] была разработана упорядоченно-сортная алгебра, позво-
позволяющая описывать иерархию типов и наследование. Также использо-
использованию двухуровневой OSA посвящена работа [5.5]. В [5.6] изложены
преимущества интеграции различных типов функций (арифметиче-
(арифметических, функций агрегации и ADT-функций) в многосортной алгебре.
В [5.7] отмечено, что невозможен, в общем, модельный параметриче-
параметрический полиморфизм посредством одного уровня алгебры и разработана
двухуровневая алгебра, описывающая типы и конструкторы типов.
М. Ируинг и Р. Гутинг в [5.2] определили многосортную сигнатуру,
упорядоченно-сортную сигнатуру и сигнатуру спецификации. В [5.8]
введено понятие «множество видов». Многоуровневая логика разра-
разработана С. Осугой, X. Ямаучи в [5.9, 5.10].
Описанию использования многоуровневой логики в качестве язы-
языка представления знаний в экспертных системах, CASE-системах,
системах поддержки принятия решений и семиотических системах
посвящены работы [5.11-5.27]. В этих работах Е. Ю. Головиной развит
синтаксис многоуровневой логики, разработаны механизмы вывода
для модифицированного синтаксиса, позволяющие увеличить эффек-
эффективность процедуры дедуктивного вывода. Приведены также резуль-
результаты моделирования сложноструктурированной проблемной области
«Аэропорт» и дано описание разработанного программного средства
моделирования сложноструктурированной проблемной области «ИН-
ФОЛОГ», в основе которого лежит аппарат многоуровневой логики и
механизмы вывода в ней. Первая версия этого программного средства
«ИНФОЛОГ» была разработана Е. Ю. Головиной. В разработке вто-
второй версии, функционирующей под Windows 3.1 и выше, Windows NT,
принимали участие Е. Ю. Головина и Ф. Ф. Оськин.
5.1. Erwing M. Specifying Type Systems with Multi-Level Order-Sorted
Algebra // 3rd Int. Conf. On Algebraic Method, and Software Technol.
1993. P. 179-188.
5.2. Erwing M., Guting R.H. Explicit Graphs in a Functional Model for
Spatial databases // Report 110, FernUniversity Hagen. 1991. Revised
Version. 1993.
5.3. Guting R.H., Zicari R., Choy D.M. An Algebra for Structured Office
Documents // ACM Transactions on Office Information Systems. 1989.
V.7. №4. P. 123-157.

К главе 5 641
5.4. Goguen J.A., Meseguer J. Order-Sorted algebra I: Partial and
Overloaded Operations, Errors and Inheritance // Report. SRI
International. 1989.
5.5. Guting R.H.. Second-Order Signature: A Tool for Specifying Data
Models, Query Processing and Optimization // ACM SIGMOD Conf.
On Management of Data. 1993. P. 277-286.
5.6. Guting R. H. Geo-Relational Algebra. A Model and Query Language
for Geometric Database Systems // Int. Conf. On Extending Database
Technol. 1988. P. 506-527.
5.7. Leszczylowski J., Witsing M. Polymorphism, Parameterization and
Typing. An Algebraic Specification Perspective // Symp. on Theor. Asp.
of Computer Sci. 1991. P. 1-15.
5.8. Cardelli L. Types for Data Oriented Languages // Int. Conf. On
Extending Database Technol. 1988. P. 1-15.
5.9. Ohsuga S., Yamauchi H. Multi-layer Logic — a Predicate Logic
Including Data Structure as Knowledge Representation Language // New
generation computing. 1985. V. 3. №4. P. 451-485.
5.10. Ohsuga S. Toward Inlelligent CAD Systems // Computer Aided Desing.
1989. V.21. №5. P. 315-337.
5.11. Вагин В. H., Головина Е. Ю. Многоуровневая логика — модель пред-
представления знаний в экспертных системах // III конф. по ИИ. КИИ-92.
Сб. науч. тр. Т. 1. — Тверь: Центрпрограммсистем, 1992. С. 16-18.
5.12. Вагин В.Н., Викторова Н.П., Головина Е.Ю. Многоуровневая ло-
логика как модель представления знаний в CASE-системе // Изв. РАН.
Техническая кибернетика. 1993. №5. С. 172-185.
5.13. Вагин В. Н., Головина Е. Ю. Моделирование сложноструктурирован-
сложноструктурированной предметной области в системах принятия решений // II межд.
научн.-техн. сем. «Теор. и прикл. проб л. моделирования предметных
областей в системах баз данных и знаний». Тез. докл. / Под ред.
Б.В.Игнатенко. — Киев: Concept Ltd, 1993. С. 73-75.
5.14. Головина Е. Ю. Объектно-ориентированный подход к моделирова-
моделированию предметной области // Изв. РАН. Техническая кибернетика.
1994. №2. С. 43-47.
5.15. Vagin V. N., Golovina E. Yu. Creating a Knowledge-based Repository
of CASE Environment for Intelligent Tutoring Systems // Proc. of
JCKBSE/94. JapanCIS Symp. on Knowledge Based Software Eng/94.
Pereslavl-Zalesski, 1994. P. 42-46.
5.16. Vagin V. N., Viktorova N.P., Golovina E. Yu. Multilayer Logic as a
Knowledge Representation Model in the CASE System // J. of Сотр.
and Syst. Sci. Int. 1995. V.33. №3. P. 72-83.
5.17. Вагин B.H., Головина Е.Ю. Построение репозитория, основанного
на знаниях, в CASE-технологии // Вест. МГТУ. Сер. «Приборостро-
«Приборостроение». Изд. МГТУ им. Н.Э.Баумана. 1995. №2. С. 17-26.
5.18. Vagin V.N., Golovina E. Yu., Salapina N. О. Intelligent CASE for
Decision Making Systems // Proc. of JCKBSE'96. Sec. Joint Conf.
21 B.H. Вагин и др.

642 К части II
on KnowledgeBased Software Eng. Sozopol, Bulgaria. September 21-22.
1996. P. 122-127.
5.19. Вагин В. Н., Головина Е. Ю. Формальная модель предметной области
CASE-системы // Сб. науч. тр. V-й нац. конф. с межд. участием
«Искусственный интеллект-96». — Казань: ЗАО ПО «Спецтехника»,
1996. Т.З. С. 433-437.
5.20. Вагин В. Н., Головина Е. Ю., Салапина Н. О. Искусственный интел-
интеллект в CASE-технологии // Программные системы и продукты. —
Тверь: НИИ «Центрпрограммсистем», 1996. №3. С. 13-21.
5.21. Vagin V.N., Golovina E.Yu. Artificial Intelligence in CASE-
technology // Тез. докл. межд. конф. «New Inf. Technol. in Sci. Educ.
and Business» (IT+SE/97). Украина, Крым, Ялта, 15-24 мая 1997.
P. 59-63.
5.22. Vagin V. N., Golovina E. Yu. Knowledge Representation Language in
Semiotic Systems // Proc. of the 1997 Int. Conf. on Intell. Syst.
and Semiotics: A Learning Perspective / Ed. by A. M. Meystel. —
Washington: U.S. Government Printing Office, 1997. P. 50-53.
5.23. Вагин B.H., Головина Е.Ю., Оськин Ф. Ф. Модели и методы пред-
представления знаний в CASE-технологии // Интеллектуальные системы.
Т. 2. Вып. 1-4. — М.: Изд. ц. РГГУ, 1997. С. 115-134.
5.24. Vagin V. N., Golovina E. Yu. Knowledge Model in Semiotic Systems //
Seventh Intern. Conf. Artificial Intelligence and Information-Control
Syst. of Robots. AIICSR/97. Second Workshop on Applied Semiotics.
Sept. 15, 1997. Smolenice Castle, Slovakia. P. 61-66.
5.25. Головина Е. Ю. Применение методов искусственного интеллекта в
CASE-технологиях // Третья межд. летняя школа-семинар по иск.
интелл. для студ. и аспир. (Браславская школа — 1999): Сб. науч.
тр. — Мн.: БГУИР, 1999. С. 66-74.
5.26. Головина Е. Ю. Метод построения семиотических CASE-систем //
Компьютерная хроника. 2000. №4. С. 3-23.
5.27. Головина Е. Ю. Модель представления знаний в семиотической си-
системе // Сб. докл. межд. конф. по мягким вычислениям и измерени-
измерениям (SCM'2000). СПб., май, 2000. Т2. С. 109-113.
К части II
К главе 6
Основные характерные особенности данных и знаний были рас-
рассмотрены Д.А.Поспеловым и его учениками в [6.1, 6.2]. Вопросам
применения данных и знаний в интеллектуальных системах посвя-
посвящены работы [6.3, 6.4]. Философско-логический подход к метафори-
метафорическому определению понятия знаний дан в [6.5-6.9]. В [6.9] так-
также подробно изложены три основных механизма мышления: дедук-
дедукция, абдукция и индукция, освещены вопросы семантической теории

К главе 6 643
знания, а также if е-факторы знания: неполнота, немонотонность,
противоречивость, неточность, относительность, неопределенность и
нечеткость, if е-факторы знания рассмотрены также в [6.10, 6.11].
Вопросам представления и обработки неопределенности и нечеткости
знания на основе теории вероятностей, теории Демпстера-Шейфера,
теории возможностей и нечеткой логики посвящены работы [6.12,
6.13, 6.14]. Подробное изложение логики вопросов и ответов дано в
[6.15]. Различным видам немонотонных логик типа абдукции, логики
умолчания, модальной логики, автоэпистемической логики и других
посвящены работы [6.16-6.24].
6.1. Кондрашина Е. Ю., Литвинцева Л. В., Поспелов Д. А. Представление
знаний о времени и пространстве в интеллектуальных системах. /
Под ред. Д.А.Поспелова. — М.: Наука, 1989. 328 с.
6.2. Искусственный интеллект. Кн. 2. Модели и методы: Справ. / Под
ред. Д.А.Поспелова. — М.: Радио и связь, 1990. 304 с.
6.3. Гаврилова Т. А., Хорошевский В. Ф. Базы знаний интеллектуальных
систем. — СПб.: Питер, 2000. 384 с.
6.4. Вагин В. П. Дедукция и обобщение в системах принятия решений. —
М.: Наука, 1988. 384 с.
6.5. Асмус В. Ф. Платон. — М.: Мысль, 1975. 220 с.
6.6. Платон. Соч. в 3-х тт. / Под ред. В. Ф. Асмуса и А. Ф. Лосева. Т. 1. —
М., 1968.
6.7. Чанышев А. П. Аристотель. — М.: Мысль, 1987. 221 с.
6.8. Аристотель. Соч. в 4-х тт. — М., 1975-1983.
6.9. Delgrande J. P., Mylopoulos J. Knowledge Representation: Features of
Knowledge // Fundamentals of Artificial Intelligence. An Advanced
Course. Lect. Notes in Computer Science / Ed. by W. Bibel and
Ph. Jorrand. — Springer-Verlag, 1986. V. 232. P. 3-36.
6.10. Нариньяни А. С He-факторы: неточность и недоопределенность —
различие и взаимосвязь // Изв. РАН. Теория и системы управления.
2000. №5. С. 44-56.
6.11. Вагин В. П. if е-факторы знания и нетрадиционные логики // Третья
межд. школа-семинар по иск. интелл. для студ. и аспир. (Браслав-
ская школа-1999). Сб. науч. тр. Беларусь, 1999. С. 10-14.
6.12. Dempster A. P. A Generalization of Bayesian Inference // J. of the Royal
Stat. Soc. 1968. V.30. P. 205-247.
6.13. Дюбуа Д., Прад А. Теория возможностей. Приложения к представ-
представлению знаний в информатике. — М.: Радио и связь, 1990. 287 с.
6.14. Zadeh L. A. Fuzzy Logic and Approximate Reasoning // Synthese 30.
1975. P. 407-428.
6.15. Белнап if., Стил Т. Логика вопросов и ответов. — М.: Прогресс,
1981. 288 с.
21*

644 К главе 7
6.16. J. of App. Non-Classical Logics. Sp. Iss. Uncertainty, Conditionals and
Non-Monotonicity. 1991. V. 1. №2. 310 p.
6.17. Int. J. of Intell. Syst. Sp. Iss. Reasoning under Incomplete Information
in Artificial Intelligence. 1990. V. 5. №4. 472 p.
6.18. Тейз А., Грибомон 77., Луи Ж. и др. Логический подход к искус-
искусственному интеллекту. От классической логики к логическому про-
программированию. — М.: Мир, 1990. 429 с.
6.19. Reiter R. A Logic for Default Reasoning // Artif. intell. 1980. V. 13.
P. 81-132.
6.20. Marquis P. Extending Abduction from Propositional to First-Order
Logic. P. 141-155 // Lecture Notes in Artificial Intelligence. V. 535. /
Ed. by Ph. Jorrand, J. Kelemen. — Fundamentals of Artificial Intelligence
Research. Springer-Verlag, 1991. 255 p.
6.21. McDermott D., Doyle J. Non-Monotonic Logic I // Artif. Intell. 1980.
V.13. P. 41-72.
6.22. Moore R. С Semantical Considerations on Non-Monotonic Logic //
Proc. IJCAI-83, Karlsruhe, 1983. P. 272-279.
6.23. Vagin V. N. Non-Classical Logics in Semiotic Systems // CAI'98. Sixth
Nat. Conf. with Int. Participants. Proc. Workshop App. Semiotics and
Abstracts of CAI'98. V. III. 1998. P. 34-39.
6.24. Вагин В. Н. Зачем нужны нетрадиционные логики? // Межд. форум
информатизации-98: Докл. межд. конф. «Информационные средства
и технологии», 20-22 октября 1998. — М.: Станкин, Т. 1. С. 6-14.
К главе 7
Большая часть этой главы основывается на самом полном изло-
изложении формальных систем модальной логики в замечательной книге
Р. Фейса [7.1], в которой систематически изложены основные положе-
положения модальной логики, но которую автор так до конца своей жизни
и не успел переработать. В этой же книге в разделе «Дополнения»
С.А. Крипке дан семантический анализ модальной логики как для
нормальных, так и ненормальных модальных исчислений высказыва-
высказываний [7.2, 7.3]. Читатели, более подробно интересующиеся семантиче-
семантическими исследованиями модальных и интенсиональных логик, могут
обратиться к [7.4, 7.5]. Некоторые сведения о модальных логиках
можно найти в [7.6].
7.1. Фейс Р. Модальная логика. — М.: Наука, 1974. 520 с.
7.2. Крипке С. А. Семантический анализ модальной логики. I. Нормаль-
Нормальные модальные исчисления высказываний // Модальная логика. —
М.: Наука, 1974. С. 254-303.
7.3. Крипке С. А. // Там же. С. 304-323.
7.4. Семантика модальных и интенсиональных логик / Под общ. ред.
В.А.Смирнова. — М.: Прогресс, 1981. 424 с.

К главе 8 645
7.5. Модальные и интенсиональные логики и их применение к проблемам
методологии науки / Под. ред. В.А.Смирнова. — М.: Наука, 1984.
368 с.
7.6. Кузин Л. Т. Основы кибернетики. Т. 1. Математические основы ки-
кибернетики. — М.: Энергоатомиздат, 1994. 576 с.
К главе 8
Нетрадиционным логикам, в частности, немонотонным, посвящено
в последние двадцать лет так много литературы, что перечислить все
книги и статьи по этим логикам не представляется возможным. Из
книг укажем только те, которые оказали наибольшее влияние на на-
написание этой главы — [8.1, 8.2, 8.18, 8.23]. Описание модальных логик
знания и убеждения было взято в основном из [8.1, 8.2], некоторые
теоремы для этих логик были заимствованы из [8.3]. Семантика воз-
возможных миров для модальных логик дана в соответствии со статьей
[8.4].
Немонотонные модальные логики Мак-Дермотта и Дойла пред-
представлены в [8.5, 8.6], и их описание базируется на этих работах.
Столнекер [8.7] и особенно Мур [8.8, 8.9, 8.10] развили основанный
на модальной логике метод для формализации немонотонных, интро-
интроспективных и идеально разумных рассуждений и создали автоэпи-
стемическую логику. Мур в [8.8] предложил также альтернативную
семантическую характеризацию своей автоэпистемической логики.
Логики умолчаний разработаны Рейтером для формализации рас-
рассуждений, являющихся всего лишь выполнимыми [8.11]. Теория с по-
полунормальными умолчаниями, позволяющая блокировать ненужную
транзитивность между умолчаниями, рассмотрена в [8.12, 8.13, 8.14].
В [8.14] была также предложена процедура эффективного построения
полунормальных теорий.
Использованию нормальных умолчаний с неявным порядком,
подчиненным иерархии моделируемой структуры, посвящена статья
[8.15]. В [8.16, 8.17] показано, что таксономические теории с
умолчаниями обладают единственными расширениями.
В книге [8.18] представлены логические основы немонотонных
рассуждений и описаны как основные немонотонные логики, так и
немонотонные формальные системы.
В последние годы резко возрос интерес к системам поддержки
истинности, служащим для сохранения логической целостности за-
заключений системы вывода. Подробное описание систем поддержки
истинности и их разновидностей можно найти в [8.19—8.24]. Нотация
для рис. 8.1-8.4 была взята в адаптированном виде из [8.25]. Жела-
Желающие ознакомиться с более поздними версиями систем поддержки
истинности, включая LTMS и MBR, могут обратиться к [8.26-8.29].

646К главе 8
8.1. Тейз А., Грибомон 77., Луи Ж. и др. Логический подход к искусствен-
искусственному интеллекту: от классической логики к логическому программи-
программирования / Пер. с франц. — М.: Мир, 1990. 432 с.
8.2. Тейз А., Грибомон 77., Юлен Г. и др. Логический подход к искус-
искусственному интеллекту: от модальной логики к логике баз данных /
Пер. с франц. — М.: Мир, 1998. 494 с.
8.3. Goldhlatt R. Logics of Time and Computation. Lecture Notes. №7. —
Centre for the Study of Lang, and Inf., 1987.
8.4. Kripke S. A. Semantical Considerations on Modal Logic // Reference and
Modality. — London: Oxford Univ. Press, 1971. P. 63-72.
8.5. McDermott D., Doyle J. Non-Monotonic Logic I // Artif. Intell. 1980.
V. 13. №1-2. P. 41-72.
8.6. McDermott D. Non-Monotonic Logic II: Non-Monotonical Modal
Theories // J. ACM. 1982. V. 29. №1. P. 34-57.
8.7. Stalnaker R. A Note on Non-Monotonic Modal Logic // Note non publee,
Dept. of Philosophy. Cornell Univ., Ithaca, N.Y., 1980.
8.8. Moore R. C. Possible-World Semantics for Auto-Epistemic Logic //
Proc. AAAI-Workshop on Non-Monotonic Reasoning, New Paltz, N.Y.,
October 1984. P. 344-354.
8.9. Moore R. C. Semantical Considerations on Non-Monotonic Logic //
Artif. Intell. 1985. V. 25. №1. P. 75-94.
8.10. Moore R. C. Autoepistemic Logic // Non-Standard Logics for
Automated Reasoning. — London: Acad. Press, 1988. P. 105-136.
8.11. Reiter R. A Logic for Default Reasoning // Artif. Intell. 1980. V. 13.
№1-2. P. 81-131.
8.12. Reiter R., Criscuolo G. On Iteracting Defaults // Proc. IJCAI-81, 1981.
P. 270-276.
8.13. Etherington D. W., Reiter R. On Inheritance Hierarchies with
Exceptions // Proc. AAAI-83, 1983. P. 104-108.
8.14. Etherington D. W. Formalizing Nonmonotonic Systems // Artif. Intell.
1987. V.31. №1. P. 41-85.
8.15. Touretzky D. S. The Mathematics of Inheritance Systems // Res. Notes
in Artif. Intell. London: Pitman, 1986.
8.16. Froidevaux С Taxonomic Default Theory // Proc. ECAI-86, Brighton,
1986. P. 123-129.
8.17. Froidevaux C, Kayser D. Inheritance in Semantic Networks and in
Default Logic // Non-Standard Logics for Automated Reasoning. —
London: Acad. Press, 1988.
8.18. Brewka G. Non-monotonic Reasoning: Logical Foundations of
Commonsense. — Cambridge: Cambridge University Press, 1991.
165 p.
8.19. Forbus K. D., DeKleer J. Building Problem Solvers. — Cambridge, MA:
MIT Press, 1993.

К главе 9 647
8.20. DeKleer J. An Assumption-Based Truth Maintenance System // Artif.
Intell. 1986. V. 28. P. 127-162.
8.21. DeKleer J. Extending the ATMS // Ibid. 1986. V. 28. P. 163-196.
8.22. DeKleer J. Problem Solving with the ATMS // Ibid. P. 197-224.
8.23. Luger G. F., Stubblefield W.A. Artificial Intelligence: Structures and
Strategies for Complex Problem Solving. — Addison Wesley Longman,
Inc. 1988. 824 p.
8.24. Doyle J. A Truth Maintenance System // Artif. Intell. 1979. V. 12.
8.25. Goodwin J. An Improved Algorithm for Non-Monotonic Dependency Net
Update // Technical Report LITH-MAT-R-82-23. Dep. of Сотр. Sci. and
Inf. Sci., Linkoping University, Linkoping, Sweden, 1982.
8.26. McAllester D.A. A Three-Valued Truth Maintenance System // MITAI
Lab., Memo 473, 1978.
8.27. Martins J., Shapiro S. C. A Model for Belief Revision // Artif. Intell.
1988. V.35(l). P. 25-79.
8.28. Martins J., Shapiro S. C. Reasoning in Multiple Belief Spaces // Proc.
of the Eighth IJCAI, San Mateo, CA: Morgan Kaufmann, 1983.
8.29. Martins J. A Structure for Epistemic States // New Directions for
Intelligent Tutoring Systems. Costa, ed. NATO ASI Series, F. Heidelberg:
Springer-Ver lag, 1991.
К главе 9
В этой главе рассмотрены различные способы применения логи-
логического программирования как средства для представления знаний и
для выполнения ряда форм вывода: вывода по противоречивой базе
знаний, вывода для автоэпистемических логик, вывода по умолча-
умолчанию. Основой для написания главы послужила книга [9.1], в которой
Альфереш и Перейра представили результаты своих исследований за
четырехлетний период работы.
Краткий обзор видов семантики логических программ выполнен
по работе [9.1], с. 5-35. Существование единственной наименьшей мо-
модели для каждой определенной программы доказано в [9.2]. Описание
пополнения предикатов Кларка можно найти в [9.3]. Определение се-
семантики Фиттинга для нормальных логических программ приводится
в [9.4]. Семантика устойчивых моделей была впервые определена
в работе [9.5] Гельфондом и Лифшицем. Фундированная семантика
нормальных логических программ была введена в [9.6], а ее альтерна-
альтернативные определения можно найти, например, в [9.7] или [9.8]. В работе
[9.9] обосновывается необходимость введения второго отрицания для
выполнения вывода здравого смысла. Семантика ответных множеств,
исторически первая семантика, определенная для расширенных логи-
логических программ, была описана в [9.10]. Семантика для расширенных
логических программ, опирающаяся на фундированную семантику
для нормальных логических программ, предложена в работе [9.11].

648 К главе 9
Фундированная семантика для расширенных логических
программ была предложена Альферешем и Перейрой, и ее
описание приведено по книге [9.1], с. 37-48. В частности, здесь
можно найти доказательства теорем существования семантики
WFSX, монотонности оператора Ф и эквивалентности WFSX и
фундированной семантики для случая нормальных логических
программ. Более подробно ознакомиться с процедурой вычисления
WFSX и доказательством ее корректности можно по работе [9.1],
с. 187—206. В момент написания книги [9.1], существовала лишь одна
процедура доказательства для расширенных логических программ,
которая не определена для программ с функциональными символами
[9.12].
В разд. 9.3 рассмотрен подход Альфереша и Перейры к устранению
противоречий в расширенных логических программах для семантики
WFSX. Более подробное изложение этого подхода можно найти в
[9.1], с. 129-166. Здесь дополнительно приводится описание подхода,
заключающегося в том, чтобы не устранять возникшие противоречия,
а избегать их, используя сценарии. Авторы доказали эквивалентность
этих двух подходов. Заметим, что существуют и другие подходы к
работе с противоречивыми программами ([9.13, 9.14]), определяющие
паранепротиворечивую семантику, а не устраняющие противоречия с
помощью пересмотра программы.
Идея рассмотрения логических программ как автоэпистемических
теорий возникла впервые у М. Гельфонда [9.15]. В [9.16] предприня-
предпринята попытка изучить различные преобразования между литерами по
умолчанию и литерами убеждений, чтобы показать, как семантика
логических программ может быть получена по семантике автоэписте-
мической логики. Определение стационарной семантики для нормаль-
нормальных логических программ можно найти, например, в [9.17]. Транс-
Трансляция из расширенных логических программ с семантикой ответных
множеств в рефлексивные автоэпистемические теории и обратно впер-
впервые была представлена в [9.18] и [9.19]. Описание автоэпистемической
логики Мура можно найти в [9.20], а автоэпистемической логики
замкнутых убеждений — в [9.8]. Связь автоэпистемической логики
знаний и мнений с логическими программами отражена в работе
[9.21].
Впервые взаимосвязи логических программ и теории умолчаний
были рассмотрены в работах [9.22] и [9.23]. Описание классической
логики умолчаний Рейтера можно найти в [9.24]. Фундированная и
стационарная семантика логики умолчаний определены в [9.25] и [9.26]
соответственно.
9.1. Alferes J. J., Pereira L. M. Reasoning with Logic Programming. — Berlin:
Springer-Verlag, 1996.

К главе 9 649
9.2. Van Emden M., Kowalski R. The semantics of predicate logic as
programming language // J. of ACM. 1976. V.4B3). P. 733-742.
9.3. Clark K. Negation as failure // Logic and Data Bases / Ed. by H. Gallaire,
J. Minker - N.Y.: Plenum Press, 1978. P. 293-322.
9.4. Fitting M., Kripke-Klene A. Semantics for logic programs // J. of LP.
1985. V.2D). P. 295-312.
9.5. Gelfond M., Lifschitz V. The stable model semantics for logic
programming // 5th Int. Conf. on LP / Ed. by R. Kowalski,
K. A.Bowen. — MIT Press, 1988. P. 1070-1080.
9.6. Van Gelder A., Ross K. A., Schlipf J. S. The well-founded semantics for
general logic programs // J. of the ACM. 1991. V.38C). P. 620-650.
9.7. Przymusinska H., Przymusinski T. Semantic issues in deductive
databases and logic programs // Formal Techniques in AI / Ed. by
R. Banerji. — North Holland: a Source-book, 1990. P. 321-367.
9.8. Przymusinski T. Autoepistemic logic of closed beliefs and logic
programming // LP&NMR / Ed. by A. Nerode, W. Marek,
V.S.Subrahmanian. — MIT Press, 1991. P. 3-20.
9.9. Wagner G. A database needs two kinds of negation // Mathematical
Foundations of Database Systems / Ed. by B. Thalheim, J. Demetrovics,
H.D.Gerhardt. - LNCS 495, Springer-Verlag, 1991. P. 357-371.
9.10. Gelfond M., Lifschitz V. Logic programs with classical negation // 7th
Int. Conf. on LP / Ed. by Warren and Szeredi. — MIT Press, 1990.
P. 579-597.
9.11. Przymusinski T. Extended stable semantics for normal and disjunctive
programs // 7th Int. Conf. on LP / Ed. by Warren and Szeredi. — MIT
Press, 1990. P. 459-477.
9.12. Teusnik F. A proof procedure for extended logic programs // Proc.
ILPS'93. - MIT Press, 1993.
9.13. Sakama S. Extended well-founded semantics for paraconsistent logic
programs // Fifth Generation Сотр. Syst., ICOT, 1992. P. 592-599.
9.14. Wagner G. Reasoning with inconsistency in extended deductive
databases // 2nd Int. Ws. on LP&NMR / Ed. by L.M.Pereira and
A. Nerode. — MIT Press, 1993. P. 300-315.
9.15. Gelfond M. On Stratified autoepistemic theories // AAAI'87. — Morgan
Kaufmann, 1987. P. 207-211.
9.16. Bonatti P. Autoepistemic logics as a unifying framework for the
semantics of logic programs // Int. Joint Conf. and Symp. on LP / Ed.
by K. Apt. — MIT Press, 1992. P. 417-430.
9.17. Przymusinski T. Stationary semantics for disjunctive logic programs and
deductive databases // North American Conf. on LP / Ed. by Debray
and Hermenegildo. — MIT Press, 1990. P. 40-57.
9.18. Lifschitz V., Schwartz G. Extended logic programs as autoepistemic
theories // 2nd Int. Ws. on LP&NMR / Ed. by L. M. Pereira, A. Nerode. —
MIT Press, 1993. P. 101-114.

650 К главе 10
9.19. Marek V., Truszczynski M. Reflexive autoepistemic logic and logic
programming // Ibid. P. 115-131.
9.20. Moore R. Semantics considerations on nonmonotonic logic // Artif.
Intell. 1985. V. 25. P. 75-94.
9.21. Пшимусинский Т. Рассуждения на основе знаний и мнений // Про-
Программирование. 1998. №1. С. 18-50.
9.22. Bidoit N., Froidevaux С. General logic databases and programs: default
semantics and stratification // J. of Inform, and Comput. 1988.
9.23. Bidoit N., Froidevaux C. Minimalism subsumes default logic and
circumscription is stratified logic programming // Int. Symp. on
Principles of Database Syst. ACM Sigact-Sigmod, 1987.
9.24. Reiter R. A logic for default reasoning // Artif. Intell. 1980. V. 13. P. 68-
93.
9.25. Baral C, Subrahmaniac V. S. Dualities between alternative semantics
for logic programming and nonmonotonic reasoning // LP&NMR /
Ed. by A.Nerode, W. Marek, V. S. Subrahmanian. — MIT Press, 1991.
P. 69-86.
9.26. Przymusinska H., Przymusinski T. Stationary default extensions //
Tech. Report, Dep. Of Computer Science, California State Polytechnic
and Dep. Of Computer Science, Univ. Of California at Riverside,
1993.
К главе 10
В этой главе представлены основные подходы к организации аб-
дуктивного вывода и к построению систем пересматриваемой аргу-
аргументации. На сегодняшний день не существует формальной теории
аргументации. Праккен и Вресвейк предприняли попытку описать
основные свойства семантики, базирующейся на аргументации [10.1].
Изложение основ теории аргументации приводится по этой работе.
Обзор систем аргументации также выполнен по работе [10.1], и до-
дополнительно использована работа [10.2], где описан ряд разработок по
теории аргументации в искусственном интеллекте и примеры их прак-
практических приложений. Более подробное изложение аргументационной
семантики Данга можно найти в [10.3], где, в частности, утверждает-
утверждается, что логическое программирование и другие формализмы немо-
немонотонного и пересматриваемого вывода в искусственном интеллекте
основываются на принципах теории аргументации. В работе [10.4]
описано, как различные системы для вывода по умолчанию могут
быть представлены с помощью теории аргументации. В частности,
здесь в качестве систем для вывода по умолчанию приводятся сле-
следующие: логика умолчаний, логическое программирование, автоэпи-
стемические логики, немонотонные модальные логики, логика очер-
очерчивания. Система для пересматриваемой аргументации с приоритета-
приоритетами, являющаяся обобщением теоретико-аргументационного подхода

К главе 10 651
к семантике логического программирования Данга, также описана в
[10.4]. Более подробно ознакомиться с другими аргументационными
системами можно по работам [10.5-10.9].
Для интересующихся вычислительными аспектами построения ар-
гументационных систем могут оказаться полезными статьи [10.10]
и [10.11]. Например, в [10.11] определяются абстрактные процедуры
доказательства для выполнения «доверчивого» и «скептического»
немонотонного вывода по отношению к теоретико-аргументационной
формализации немонотоннного вывода, предложенной в [10.4]. Эти
процедуры определяются на основе процедуры доказательства для
вычисления «доверчивых» следствий в семантике допустимых рас-
расширений, примером которой может служить процедура, описанная в
[10.10].
Следует отметить также работы В. К. Финна, в которых предла-
предлагается четырехзначная логика аргументации А^ с дополнительными
истинностными значениями противоречия и неопределенности. Пред-
Представленная теория аргументации может рассматриваться как сред-
средство автоматизированного рассуждения, полезное для формализации
рассуждений в гуманитарных науках [10.12, 10.13]. В работе [10.14]
для логики аргументации А^ вводится понятие логического следова-
следования и исследуются его свойства. С вероятностным подходом к по-
построению аргументационных систем можно познакомиться, например,
по работам [10.15, 10.16]. Подобные теории аргументации соединяют
классическую логику с теорией вероятностей и представляют собой
альтернативный подход к немонотонному выводу в условиях неопре-
неопределенности. Примеры применения теории аргументации для модели-
моделирования различных форм правдоподобного вывода можно найти в
[10.17].
Описание понятия абдуктивного вывода проведено, главным об-
образом, по книге [10.18]. В частности, использована работа [10.19], в
которой приводятся описания абдуктивного и индуктивного вывода
и их особенностей в сравнении. Различные подходы к определению
абдуктивного вывода и абдукции описаны по работам [10.20-10.23].
Этапы разработок по абдукции даны по МакИлрайт [10.24]. Описание
подходов к хар акте риз ации абдукции выполнено в соответствии с
работой [10.20].
Заинтересованному читателю можно порекомендовать дополни-
дополнительно следующие работы: [10.25], в которой представлен подход,
основанный на покрытии множеств; [10.26], в которой описываются
простые каузальные теории; [10.27], представляющую собой обзор раз-
различных способов организации абдуктивного вывода для случая, когда
базовая теория представляется логическими программами; [10.28], в
которой понятие абдукции определяется применительно к автоэпи-
стемическим теориям; [10.29], в которой описан подход к абдукции на
уровне знаний, предложенный Левеком; [10.30], где Бутилье и Вечер

652 К главе 10
рассматривают абдукцию как пересмотр убеждений. Дополнительно в
работе [10.18] молено найти ряд статей, посвященных вероятностному
подходу к организации вывода по абдукции, а в [9.1] (С. 107-128)
приводится описание подхода к выполнению абдуктивного вывода для
расширенных логических программ (см. гл. 9).
Подходы к вычислению абдуктивных объяснений освещаются в ра-
работах [10.24] и [10.20], на основе которых выполнен обзор в разд. 10.2.3.
Дополнительно, по подходу к генерации гипотез с помощью резолю-
резолюции можно рекомендовать работы [10.27], [10.31], [10.32]. ATMS как
одно из возможных средств для генерации абдуктивных объяснений
рассматривается в [10.29] и [10.27]. Глобальные и локальные критерии
к отбору гипотез можно найти в работе [10.33].
При описании метода вероятностных абдуктивных рассуждений в
сложноструктурированных проблемных областях были использованы
работы [10.34-10.37]. В работе [10.34] приведены признаки сложной
системы, одним из которых является иерархичность. Поэтому в [10.37]
предложен метод вероятностных абдуктивных рассуждений в слож-
сложноструктурированной проблемной области, который является инте-
интеграцией и развитием методов абдуктивных рассуждений, описанных
в работах [10.35] и [10.36]. В работе [10.37] разработаны алгоритмы
абдуктивных рассуждений, процедура проверки найденных объясне-
объяснений на непротиворечивость и представлены примеры использования
разработанных алгоритмов абдуктивного вывода в сложноструктури-
сложноструктурированной проблемной области.
Описание аргументационной семантики логических программ вы-
выполнено в соответствии с работой [10.10]. Более подробно с абстракт-
абстрактным подходом к определению аргументационной семантики можно по-
познакомиться, например, по работе [10.4]. Приведенная в разд. 10.3.1.5
процедура доказательства для аргументационной семантики более
подробно описана в [10.10], где также можно найти и описание теории
доказательства. Роль аргументации в организации абдуктивного вы-
вывода освещена в работе [10.38]. Некоторые вопросы применения аргу-
аргументации для абдуктивного вывода в логическом программировании
рассматриваются в работе [10.27].
10.1. Prakken H., Vreeswijk G. Logics for defeasible argumentation //
Handbook of Philosophical Logic. V. 4. — Kluwer Academic Publishers,
Dordrecht etc., 2001.
10.2. Chesnevar C. /., Maguitman A. G., Loui R.P. Logical models of
argument // ACM Computing Surveys. 2000. V.31. №4. P. 337-383.
10.3. Dung P. M. On the acceptability of arguments and its fundamental role
in nonmonotonic reasoning, logic programming and n-person games //
Artif. Intell. 1995. V. 77. P. 321-357.

К главе 10 653
10.4. Bondarenko A., Dung P.M., Kowalski R. A., Toni F. An abstract,
argumentation-theoretic framework for default reasoning // Ibid. 1997.
V. 93A-2). P. 63-101.
10.5. Prakken H., Sartor G. A system for defeasible argumentation with
defeasible priorities // Proc. of the Int. Conf. on Formal Aspects of
Practical Reasoning, Bonn, Germany: Springer Verlag, 1996.
10.6. Pollock J. L. Cognitive carpentry. A blueprint for how to build a
person. — Cambridge, MA: MIT Press, 1995.
10.7. Lin F., Shoham Y. Argument systems. A uniform basis for nonmonotonic
reasoning // Proc. of the First Int. Conf. on Principles of Knowledge
Representation and Resoning. San Mateo, CA: Morgan Kaufmann
Publishers Inc, 1989. P. 245-255.
10.8. Vreeswijk G. A. W. Abstract argumentation systems // Artif. Intell.
1997. V.90. P. 225-279.
10.9. Simari G. R., Loui R.P. A mathematical treatment of defeasible
argumentation and its implementation // Ibid. 1992. V. 53. P. 125-157.
10.10. Kakas A. C, Toni F. Computing argumentation in logic
programming // J. of Logic and Comput. 1999. V.9. P. 515-562.
10.11. Kakas A. C, Mancarella P., Toni F. Argumentation-based proof
procedures for credulous and sceptical non-monotonic reasoning // Tech.
report. 2001. 26 p.
10.12. Финн В. К. Об одном варианте логики аргументации // Интеллек-
Интеллектуальные системы и общество: Сб. статей. — М.: РГГУ, 2001. С. 206-
251.
10.13. Финн В. К. Логика исторических рассуждений // Проблемы исто-
исторического познания в свете современных междисциплинарных иссле-
исследований. — М.: РГГУ, 1997. 256 с.
10.14. Таран ТА. Иследование тавтологий логики аргументации А± //
Информационные процессы и системы. 2001. №5. С. 28-35.
10.15. Haenni R., Kohlas J., Lehmann N. Probabilistic argumentation
systems // Series: Linkoping Electronic Art. in Сотр. and Inf. Sci. 2000.
V.5.
10.16. Krause P., Ambler S., Elvang-Gorans son M., Fox J. A logic of
argumentation for reasoning under uncertainty // Comput. Intell. 1995.
V. 11. P. 113-131.
10.17. Вагин В.Н., Загорянская А. А. Аргументация в правдоподобном
выводе // Труды конф. КИИ'2000. Т. 1. М.: Изд. физ.-мат. лит. 2000.
С. 165-173.
10.18. Abductive reasoning and learning // Handbook of defeasible reasoning
and uncertainty management systems / Ed. by Dov M. Gabbay, P. Smets.
V. 4. — Kluwer Acad. Publishers, Dordrecht Hardbound, 2000. 448 p.
10.19. Flach P. A., Kakas A.C. On the Relation between Abduction and
Inductive Learning // Ibid. P. 1-33.
10.20. Paul G. AI Approaches to Abduction // Ibid. P. 35-99.

654 К главе 10
10.21. Gabbay M. Abduction in Labelled Deductive Systems // Ibid. P. 99-
155.
10.22. Dubois D., Prade H. An Overview of Ordinal and Numerical Approaches
to Causal Diagnostic Problem Solving // Ibid. P. 231-281.
10.23. Borgelt C, Kruse R. Abductive Inference with Probabilistic
Networks // Ibid. P. 281-315.
10.24. Mcllraith S. A. Logic-Based Abductive Inference // Knowledge Systems
Laboratory, Stanford Univ., Stanford, С А 94305-9020, July 6, 1998. 29 p.
10.25. Allemang D., Tanner M., Bylander Т., Josephson J. Computational
complexity of hypothesis assembly // Proc. of the 10th Int. Joint Conf.
on Artif. Intell., 1987. P. 1112-1117.
10.26. Konolige K. Closure + minimization implies abduction // PRICAI-90,
Nagoya, Japan, 1990.
10.27. Kakas A. C, Kowalski R. A., Toni F. The role of abduction in logic
programming // Handbook of Logic in Artificial Intelligence and Logic
Programming / Ed. by D. M. Gabbay, C.J. Hogger and J.A. Robinson. —
Oxford University Press, 1998. P. 235-324.
10.28. Inoue K., Sakama С Abductive framework for nonmonotonic theory
change // Proc. of the 14th Int. Joint Conf. on Artif. Intell., 1995. P. 204-
210.
10.29. Levesque H. A knowledge-level account of abduction // Proc. of the
11th Int. Joint Conf. on Artif. Intell., 1989. P. 1061-1067.
10.30. Boutilier C, Becher V. Abduction as belief revision // Artif. Intell.,
1995. V. 77. P. 43-94.
10.31. Cox P., Pietrzykowski T. Causes for events: Their computation and
application // Proc. CADE 86. 1986. P. 608-621.
10.32. Pople H. E. On the mechanization of abductive logic // Proc. of the 3rd
Int. Joint Conf. on Artif. Intell. 1973. P. 147-151.
10.33. Appelt D.E., Pollack M. Weighted abduction for plan ascription //
Techn. report, Artif. Intell. Center and Center for the Study of Language
and Information, SRI International, Menlo Park, California, 1990.
10.34. Буч Г. Объектно-ориентированное проектирование с примерами
применения // Пер. с англ. — М., 1992.
10.35. Console L., Dupre D. Т. Choices in abductive reasoning with
abstraction axioms // J. of Logic and Comput. 1999. Vol. 1E).
10.36. Poole D. Probabilistic Horn abduction and Bayesian networks // Artif.
Intell. 1993. Vol.64.
10.37. Головина Е. Ю. Абдуктивный вывод в инструментальных средствах
для создания динамических систем поддержки принятия решений //
Труды конгресса «Искусственный интеллект в XXI веке». — М.: Изд.
физ.-мат. лит., 2001. С. 50-60.
10.38. Вагин В.Н., Загорянская А. А. Организация абдуктивного вывода
средствами теории аргументации // Там же. С. 13-20.

К главе 11 655
К части III
К главе 11
Проблемам индукции и индуктивного вывода в интеллектуальных
системах уделяется большое внимание. В основу многих алгоритмов
обобщения положены идеи, выдвинутые М. М. Бонгардом [11.1]. Обзор
основных понятий и методов, связанных с проблемами индуктивного
обобщения, дан в [11.2].
В настоящее время алгоритмы индуктивного обобщения широко
используются для проектирования экспертных систем, систем машин-
машинного обучения, систем поддержки принятия решений, Data Mining и
других. Разработчикам таких систем часто приходится решать про-
проблемы, связанные с тем, что необходимо обеспечить взаимодействие
алгоритмов индукции с реальными базами данных.
Роль индукции и обобщения в системах поддержки принятия ре-
решений (DSS), использующих OLAP-технологию, обсуждается в [11.3,
11.4]. При этом основные требования к OLAP-продуктам сформулиро-
сформулированы в [11.5, 11.6]. В работе [11.7] излагается история развития систем
Data Mining и KDD, обсуждается их взаимосвязь и перспективы
развития. Прикладные системы, использующие идеи KDD, описаны в
[ 11.8, 11.9, 11.10].
Для получения индуктивных понятий обычно приходится исполь-
использовать обучение на основе примеров. Принципы обобщения на основе
примеров рассмотрены в книге [11.11]. В работах [11.12, 11.13] при-
приводятся алгоритмы обучения на основе примеров. Модели, которые
строят обобщенное понятие в виде графа, рассмотрены в [11.14, 11.15].
Алгоритмы, использующие в качестве обучающего множества базу
данных, приведены в [11.16, 11.17].
Индуктивное формирование понятий находит применение в экс-
экспертных системах. Идеи применения алгоритмов обобщения для по-
пополнения базы знаний экспертной системы обсуждаются в [11.18,
11.3]. Задача автоматического образования гипотез в интеллектуаль-
интеллектуальной системе рассмотрена в работе авторов Гаека и Гавранека [11.19].
Среди различных стратегий построения индуктивных понятий
важное место занимает обобщение на основе признаков. Индуктивное
обобщение понятий по признакам — одна из широко известных задач
искусственного интеллекта. В работе [11.11] рассматривается задача
индуктивного обучения на примерах, представленных прежде всего в
виде признаков. Метрики в пространствах признаков даны в [11.20],
там же обсуждается стратегия выбора метрики в зависимости от
предметной области.
Особенности построения обобщенных понятий на основе анализа
объектов, обладающих структурой, обсуждаются в ряде работ. Ме-
Методы индуктивного вывода в формальных исчислениях приводятся

656 К главе 11
в [11.21, 11.11]. Принципы индуктивных рассуждений, предложен-
предложенные Миллем, высказаны и обоснованы в [11.22]. Обзорное изложение
ДСМ-метода можно найти в [11.23], а более подробно ознакомиться
с этим методом можно в [11.24]. GUHA-метод, используемый для
порождения индуктивных гипотез на основе наблюдаемых данных,
излагается в [11.19]. Решение задачи обобщения на основе использо-
использования аппарата семантических сетей обсуждается в [11.2]; пример,
приведенный в качестве иллюстрации, взят из [11.21].
11.1. Бонгард М. М. Проблема узнавания. — М.: Наука, 1967. 320 с.
11.2. Вагин В. Н., Викторова Н. П. Обобщение и классификация знаний //
Искусственный интеллект. Кн. 2. Модели и методы: Справочник /
Под ред. Д. А. Поспелова — М.: Радио и Связь, 1992. С. 82-89.
11.3. Попов Э. В., Фоминых И. Б., Кисель Е. Б., Шапот М. Д. Статические
и динамические экспертные системы. — М.: Финансы и статистика,
1996. 319 с.
11.4. Вагин В.Н., Загорянская А. А. Извлечение данных как наиболее
важное приложение технологии информационных хранилищ // Про-
Программные продукты и системы. 2000. №1. С. 2-11.
11.5. Codd E.F. Providing OLAP (On-line Analytical Processing) to User-
Analysts: An IT Mandate. — Codd and Associates, 1993.
11.6. Свинарев С. Десять требований Red Brick System // Комьютеруик-
Москва. 1996. Т. 2. С. 45.
11.7. Fayyad U., Piatetsky-Shapiro G., Smith P. From Data mining to
Knowledge Discovery: an Overview // Advances in Knowledge Discovery
and Data Mining. — Cambridge: AAAI Press / The MIT Press, 1996.
P. 1-36.
11.8. Apte C, Hong S. J. Predicting Equity Returns from Securities Data with
Minimal Rule Generation // Ibid. P. 541-560.
11.9. Fayyad U., Djorgovski G., Weir N. Automating the Analysis and
Cataloging of Sky Surveys // Ibid. P. 471-493.
11.10. Agrawal R., Mannila H., Srikant R. et al. Fast Discovery of Association
Rules // Ibid. P. 307-328.
11.11. Michalski R.S., Carhonell J. G., Mitchell T.M. Machine Learning. An
Artincal Intelligence Approach. — Springer-Verlag, 1984. 567 p.
11.12. Dasarathy B. Nearest Neighbor (NN) Norms: NN Pattern Classification
Techniques. Los Alamitos, Calif.: The AIII Press., 1991.
11.13. Kolodner J. Case-Based Reasoning. — San-Francisco: Morgan
Caufmann, 1993.
11.14. Pearl J. Probabilistic Reasoning in Intelligent Systems. — San-
Francisco: Morgan Caufmann, 1988.
11.15. Whittaker J. Graphical Models in Applied Multivariate Statistics. —
N.-Y.: Wiley, 1990.

К главе 12 657
11.16. Buntine W. Graphical Models for Discovered Knowledge // Advances in
Knowledge Discovery and Data Mining. — Cambridge: AAAI Press/The
MIT Press., 1996. P. 59-82.
11.17. Heckerman D. Bayesian Networks for Knowledge Discovery // Ibid.
P. 273-306.
11.18. Гаврилова Т. А., Червинская К. Р. Извлечение и структурирование
знаний для экспертных систем. — М.: Радио и связь, 1992. 200 с.
11.19. Гаек Т., Гавранек П. Автоматическое образование гипотез: матема-
математические основы общей теории. — М.: Наука, 1984. 280 с.
11.20. Фор А. Восприятие и распознавание образов. — М.: Машинострое-
Машиностроение, 1989. 272 с.
11.21. Plotkin G. D. A further note on inductive generalization // Machine
Intellect. 1971. V.6. P. 101-124.
11.22. Милль Д. С. Система логики силлогистической и индуктивной /
Пер. с англ. — М.: Книжное дело, 1900.
11.23. Поспелов Д. А. Моделирование человеческих рассуждений в интел-
интеллектуальных системах // Лекции Всесоюзной школы по основным
проблемам искусственного интеллекта и интеллектуальным систе-
системам. — Минск: 1990. С. 29-47.
11.24. Финн В. К. О машинно-ориентированной формализации правдо-
правдоподобных рассуждений в стиле Бэкона — Милля // Семиотика и
информатика. 1983. Вып. 20. С. 35-101.
К главе 12
Задача классификации и распознавания образов является одной из
признанно важных задач искусственного интеллекта [12.1]. Одним из
известных направлений в этой области является задача обучения без
учителя. Рассматривается проблема разбиения множества объектов
на заданное либо неизвестное число классов. Критерием группиро-
группирования объектов обычно является близость между собой объектов
одного класса и удаленность объектов разных классов. Такое требо-
требование подразумевает введение метрики на множестве предъявленных
объектов, поэтому объекты распознавания представляются наборами
признаков, имеющих количественные значения.
Широко известен статистический подход к решению таких задач;
он основан на байесовской теории принятия решений. Классическими
работами в этой области являются [12.2, 12.4]. Ряд алгоритмов ав-
автоматической классификации и группирования рассмотрены в [12.3,
12.5]. Ясный и наиболее современный обзор методов, основанных на
статистическом подходе, дан в [12.6].
Разделение классов в пространстве признаков, имеющих коли-
количественные значения, выполняется методами построения решающих
функций. Эти методы хорошо изучены и дают наглядную геометриче-
геометрическую интерпретацию, многие из них детально изложены в [12.2, 12.8,

658 К главе 12
12.9]. Построение линейных и квадратичных разделяющих функций
приводится в [12.7]; там же рассматривается практическое приме-
применение предложенных алгоритмов в такой интересной области, как
сейсмология. Использование методов распознавания при построении
систем машинного зрения обсуждается в [12.10]. Следует назвать
также посвященные проблеме решающих функций очень полезные
работы [12.11, 12.12, 12.13]. Связь проблем распознавания образов и
машинного обучения рассматривается в [12.14, 12.15].
12.1. Журавлев Ю. И., Гуревич И. Б. Распознавание образов и анализ
изображений // Искусственный интеллект. Кн. 2. Модели и методы.
Справ. / Под ред. Д. А. Поспелова. — М.: Радио и Связь, 1990. С. 149-
191.
12.2. Дуда Р., Харт П. Распознавание образов и анализ сцен. — М.: Мир,
1976. 511 с.
12.3. Смородинский С. С, Батин Н.В. Алгоритмы и программные сред-
средства интеллектуальных систем принятия решений. Ч. 2. — Мн.: БГУ-
ИР, 1994. 68 с.
12.4. Ту Дснс., Гонсалес Р. Принципы распознавания образов. — М.: Мир,
1978. 411 с.
12.5. Айвазян С. А., Бухштабер В.М., Енюков И. С, Мешалкин Л. Д.
Прикладная статистика. Классификация и снижение размерности. —
М.: Финансы и статистика, 1989. 128 с.
12.6. Дюк В. А., Самойленко A. Data Mining: учебный курс. — СПб: Питер,
2001. 366 с.
12.7. Грешилов А. А., Мальцев В. 77., Пархоменко В. П. Принятие решений
с помощью обобщенных линейных разделяющих функций. — М.:
Радио и связь, 2000. 480 с.
12.8. Горелик А. Л., Скрипкин В. А. Методы распознавания. — М.: Высш.
шк, 1989. 232 с.
12.9. Аркадьев А. Г., Браверман Э.М. Обучение машины классификации
объектов. — М.: Наука, 1971. 192 с.
12.10. Козлов Ю. М. Адаптация и обучение в робототехнике. — М.: Наука,
1990. 248 с.
12.11. Себестиан Г. Процессы принятия решений при распознавании об-
образов. — Киев: Техника, 1965. 151 с.
12.12. Классификация и кластер / Под ред. Р. Райзина. — М.: Мир, 1980.
389 с.
12.13. Айзерман М. А., Браверман Э.М., Розоноер Л. И. Метод потенци-
потенциальных функций в теории обучения машин. — М.: Наука, 1970. 384 с.
12.14. Sklansky «/., Wassel G. N. Pattern Classifiers and Trainable Mashines. —
Springer Verlag, New York, Heidelberg, Berlin. 1981.
12.15. Фор А. Восприятие и распознавание образов. — М.: Машинострое-
Машиностроение, 1989. 272 с.

К главе 13 659
К главе 13
Процедура обучения с учителем, предложенная Бонгардом [13.1],
широко используется в системах машинного обучения и индуктивного
формирования понятий. Объекты, на которых проводится обучение
(обучающая выборка), представлены наборами признаков [13.2]. В
[13.2] дается строгая постановка задачи индуктивного обобщения.
Важным фактором индуктивного обобщения является выбор мо-
модели для представления результатов обобщения. В [13.2, 13.3, 13.4,
13.5] обсуждаются наиболее популярные модели для представления
результатов распознавания. Работа [13.6] показывает связь продукци-
продукционных моделей и моделей решающих деревьев.
Алгоритмы количественного и качественного распознавания по
признакам, в основе которых лежит формирование конъюнктивно-
дизъюнктивного понятия, приведены в работах [13.7, 13.2]. Одной из
широко распространенных моделей для представления результатов
распознавания является модель решающего дерева. Известен целый
ряд модификаций для таких моделей. Так, в [13.8] рассмотрен алго-
алгоритм построения дерева решений на основе меры близости распознаю-
распознающих признаков и целевого признака. Работа [13.9] приводит алгорит-
алгоритмы построения дерева решений по примерам на основе идеи метода
«ближайшего соседа». В [13.10, 13.4] дается сравнение различных спо-
способов построения решающих деревьев и обсуждается эффективность
этих методов.
Классический метод распознавания — индукция решающих дере-
деревьев, основанный на введении оценки информативности признаков —
дан в работах Куинлана и его последователей [13.6, 13.11, 13.12,
13.13, 13.14]. Обобщение с учетом таксономических отношений на ка-
качественных признаках (фокусирование, алгоритм EG2) рассмотрено
в работах [13.8, 13.14]. Пример работы алгоритма фокусирования взят
из [13.8]. Обсуждение особенностей таксономических отношений в
моделях искусственного интеллекта дано в [13.15]. Следует отметить,
что в [13.14] вводится «экономический» фактор для выбора порядка
рассмотрения признаков при построении дерева решений. Эффектив-
Эффективные методы упрощения дерева решений предлагаются в [13.16].
Важность использования подсистем обобщения для получения ин-
индуктивных знаний (метазнаний) в экспертных системах обсуждает-
обсуждается в [13.17, 13.18]. Большой интерес представляют методы построе-
построения обобщенных понятий на основе структурных объектов обучения;
такие методы называют методами структурного обобщения знаний.
Этот класс алгоритмов подробно исследован в [13.19, 13.20].
13.1. Бонгард М. М. Проблема узнавания. — М.: Наука, 1967. 320 с.
13.2. Вагин В. Н. Дедукция и обобщение в системах принятия решений. —
М.: Наука, 1988. 384 с.

660 К главе 13
13.3. Мешалкин В. П. Экспертные системы в химической технологии.
Основы теории, опыт разработки и применения. — М.: Химия, 1995.
154 с.
13.4. Вагин В. Н., Федотов А. А., Фомина М. В. Методы извлечения и об-
обобщения информации в больших базах данных // Изв. РАН. Теория
и системы управления. 1999. №5. С. 45-59.
13.5. Вагин В. Н., Викторова Н. П. Обобщение и классификация знаний //
Искусственный интеллект. Кн. 2. Модели и методы. Справ. / Под ред.
Д. А. Поспелова — М.: Радио и связь, 1990. С. 82-89.
13.6. Quinlan J. R. Generating production rules from Decision Trees // Proc.
of IJCAI 87. Milan. 1987. P. 304-307.
13.7. Хант Э., Мартин Д., Стоун Ф. Моделирование процесса формиро-
формирования понятий на вычислительной машине. — М.: Мир, 1970. 302 с.
13.8. Hutchinson A. Algoritmic Learning. — Oxford: Claredon Press, 1994.
434 p.
13.9. Aha D. W., Kibler D., Albert M. K. Instance-based Learning Algoritms //
Machine Learning. 1991. V.6. P. 37-66.
13.10. Куликов А. В., Фомина М. В. Исследование алгоритмов извлечения
и обобщения знаний // В сб. МФИ_2000. Докл. «Информационные
средства и технологии». Т. 2. — М: МЭИ, 2000. С. 76-79.
13.11. Quinlan J. R. Induction on Decision Trees // Machine Learning. 1986.
V.I. P. 81-106.
13.12. Quinlan J. R. Improved Use of Continuous Attributes in С 4.5 // J. of
Artif. Intell. Res. 1996. V. 4. P. 77-90.
13.13. Utgoff P. E. Incremental induction of Decision Trees // Machine
Learning. 1989. V. 4. P. 161-186.
13.14. Nunez M. The Use of Background Knowledge in Decision Tree
Induction // Machine Learning. 1991. V. 6. P. 231-250.
13.15. Brachman R. What IS-A is and isn't - an Analysis of Taxonomic Links
in Semantic Networks // Computer. 1983. V. 16. № 10. P. 30-36.
13.16. Minger J. An Empirical Comparison of Pruning Methods for Decision
Tree Induction // Machine Learning. 1989. V. 4. P. 227-243.
13.17. Попов Э. В. Экспертные системы. Решение неформализованных за-
задач в диалоге с ЭВМ. — М.: Наука, 1987. 288 с.
13.18. Лоръер Ж. Л. Системы искусственного интеллекта. — М.: Мир,
1991. 586 с.
13.19. Вагин В. Н., Викторова Н. П. Вопросы структурного обобщения и
классификации в системах принятия решений // Изв. АН СССР.
Техническая кибернетика. 1982. №5. С. 64-73.
13.20. Вагин В. Н., Викторова Н. П. Задачи обобщения в системах приня-
принятия решений. Формирование классов объектов и отношений выбора
на семантических сетях // Изв. АН СССР. Техническая кибернетика.
1985. №5. С. 3-17.

К главе Ц 661
К главе 14
Одной из наиболее интересных задач, которые решаются в рамках
современных экспертных систем и систем обобщения, является задача
извлечения обобщенных понятий из обучающих выборок, содержащих
неполную или неточную информацию. Такими выборками могут быть
реальные базы данных, хранящие огромные объемы различных сведе-
сведений. Проблемы, возникающие при попытке получить обобщение для
таких исходных данных, обсуждаются в [14.1, 14.2].
Многие из рассмотренных в предыдущей главе алгоритмов могут
быть успешно модифицированы для случая обучения по неполным
и нечетким данным. Известны такие модификации для алгоритма
Куинлана [14.3] и его последователей. Варианты таких алгоритмов
приведены в работах [14.2, 14.4, 14.5].
Применение идей индуктивного формирования понятий в реаль-
реальных системах Data Mining рассматривается в [14.6, 14.7] на примере
системы Monet. В [14.8] приводится оригинальный алгоритм, который
был использован в реальной системе обобщения при неполной входной
информации.
Интересным подходом к решению задач индуктивного формирова-
формирования понятий при неполной информации стала теория приближенных
множеств, разработанная Павлаком, и изложенная в [14.9, 14.10].
Многие авторы успешно развивают это направление. Алгоритм RS1,
изложенный в данной главе, описан в [14.11], там же приведены
оценки сложности алгоритма. В [14.12] обсуждается использование
приближенных множеств в системе, основанной на логике предикатов
первого порядка. В работах [14.13, 14.14] рассматривается модифика-
модификация алгоритма RS2.
14.1. Vagin V. N., Fedotov A. A., Fomina М. V. Methods of Data Mining and
Knowledge Generalization in Large Databases // J. of Сотр. and Syst.
Sci. Int. 1999. V.38. №5. P. 714-727.
14.2. Федотов А. А., Фомина М.В. Система формирования обобщенных
продукционных правил на основе анализа больших баз данных //
Сб. науч. трудов Шестой нац. конф. по иск. интел. КИИ-98. Т. 1.
Пущино, Россия. 1998. С. 287-292.
14.3. Quinlan J. R. Induction of Decision Trees // Machine Learning. 1986.
V.I. P. 81-106.
14.4. Куликов А. В., Фомина M. В. Разработка алгоритма обобщения зна-
знаний // КИИ'2000. Седьмая нац. конф. по иск. интел. Т. 1. — М.:
Физматгиз, 2000. С. 135-142.
14.5. Пицишин Ю. Б., Фомина М.В. Разработка алгоритма обобщения
для поиска скрытых закономерностей в больших базах данных //
1С AI'2001 Международный конгресс «Искусственный интеллект в
XXI веке». Т. 1. — М.: Физматгиз, 2001. С. 221-227.

662 К главе Ц
14.6. Holsheimer M., Kersten M. L. Architectural Support for Data Mining //
AAAI-94 Workshop Knowledge discovery in Databases / Ed. by
U.M.Fayyad and R. Uthurusamy. — Seattle, Washington, 1994. P. 217-
228.
14.7. Holsheimer M., Siebes A. Data mining: the search for knowledge in
databases // Technical Report CS-R9406, CWI, 1994. 78 p.
14.8. Вагин В. Н., Гулидова В. Г., Фомина М. В. Распознавание состояний
сложного объекта при неполной входной информации // Изв. АН
СССР. Техн. кибернетика. 1992. №5. С. 120-132.
14.9. Pawlak Z. Rough classification // Int. J. of Man-Machine Studies. 1984.
V.20. P. 469-483.
14.10. Pawlak Z. Rough Sets // Int. J. of Inf. and Сотр. Sci. 1982. V. 11.
P. 341-356.
14.11. Aasheim О. Т., Solheim H. G. Rough Sets as a Framework for Data
Mining // Project Report. Faculty of Computer Systems and Telematics,
The Norwegian University of Science and Technology, Trondheim, 1996.
150 p.
14.12. Parsons S., Kubat M., Dohnal M. A rough Set Approach to Reasoning
under unsertainty // Technical Report. J. of Experim. and Theor. Artif.
Intell.
14.13. Zirako W. Variable Precision Rough Sets Model // J. Сотр. and
System Sci. 1993. V.46. №1. P. 39-59.
14.14. Zirako W. Analysis of Uncertain Information in the Framework of
Variable Precision Rough Sets // Found, of Сотр. and Decision Sci.
1993. V. 18. №3,4. P. 381-396.

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Абдуктивная
гипотеза 465
логическая программа 459
логическая структура 459
процедура 449, 454, 456, 461,
464
процедура доказательства
501, 502
система 449
структура 450, 451, 453, 464,
499, 500
теория 463, 468, 469
Абдуктивное
доказательство 451
логическое программирова-
программирование 451, 452, 459, 499,
502
объяснение 419, 444, 450, 455,
461, 496-498, 500, 502,
652, 682
описание 444
расширение 445
решение 450, 459
следование 445
Абдуктивный
аргумент 421, 423
вывод 16, 238, 251, 252, 323,
419, 420, 444-447, 466,
467, 496, 499, 650-652,
680-682
механизм 445
процесс 450, 454, 463
силлогизм 445
Абдукция 13, 251, 252, 419, 444-
450, 453, 456, 465, 633,
642, 651, 663, 672, 681
Абдукция, основанная на стоимо-
стоимости 464, 465
Абдуцент 18, 446, 449-451, 468,
470, 472, 473, 478, 496,
498-500
Абдуцентная литера 468, 469, 473
Абдуцируемый предикат 451, 459
Абсолютная
метрическая шкала 229
Абстрактная
аргументационная
система 438, 441
структура 440, 484
Абстрактное
значение 591
объяснение 467
Абстракция 468
Автоматизированное
рассуждение 651, 681
Автоматическое
доказательство теорем 634,
639, 664, 669
Автоэпистемическая
абдуцируемая формула 452
интерпретация 294, 298
логика 254, 375, 393, 401, 452,
643, 645, 647, 648, 650,
673, 675, 677, 678, 680
Мура 391, 392, 397, 648,
678
Мура и Пшимусинского
389
замкнутых убеждений
392, 648, 678
знаний и мнений 648, 678
очерчивания 392
модель 299
теория 293, 375, 390, 393, 452,
453, 648, 651, 678, 681
Мура 398
теория Т 398
фоновая теория 452

664
Предметный указатель
Автоэпистемические
логики (АЭЛ) 292, 295, 297,
298, 301, 311, 312
Автоэпистемический
тип рассуждений 253
Агностик 391
Адаптивный сплайн метод 515
Администрирование 509
Аккомодации 242
Аксиома 237, 238, 245, 261, 289
АХ^ 378, 379
абстракции 469
контрапозиции 252
объяснений 467, 469
Аксиомы Рассела — Бернайса 255
Активатор 231, 232
Активность 231
Алгоритм 632
EG2 589, 594, 595, 659, 689
ID3 561, 569-575, 578, 579,
589, 591, 594, 595, 620,
621, 631
ID5R 574, 575, 578, 579
RS1 608, 610, 611, 617, 620,
621, 661, 691
RS2 617, 619, 661, 691
«К средних» 541, 542
AND-параллельной резолю-
резолюции 96
Data Mining 514, 517
DCDP-параллельного выво-
вывода 92, 135
DCDP-параллельной резо-
резолюции 91
MAXMIN 538, 539
OR-параллельная резолю-
резолюция 96
OR-параллельной резолю-
резолюции 91
PAL 131
Reduce 580, 582, 583
АМХ 566, 569
ДРЕВ 561, 563-566, 569, 573,
574
Кокса 462
Куинлана 661, 691
Алгоритм
Сколема 33-35, 204-206, 212,
213, 219
абдуктивного вывода 481
автоматической классифи-
классификации 657, 687
антиунификации 525
вероятностных абдуктивных
рассуждений 472
входной линейной резолю-
резолюции 219
вывода на С-графе 123
вывода на графе связей 83
вывода пустого С-графа 122
генерации правил 621
группирования 657, 687
извлечения знаний 504
индукции 655, 685
количественного и каче-
качественного распознава-
распознавания по признакам 659
многократной унификации
162
обобщения 544, 560, 563, 655,
685
обратной сколемизации
457
обучения
без учителя 560
на основе примеров 655,
685
с учителем 558, 560, 569
параллельного дедуктивного
вывода 135
получения объяснений для
наблюдаемых литер 472
последовательной классифи-
классификации 626, 628
построения целевых дере-
деревьев 492
преобразования С-графов
120
приведения к КНФ 34, 35
распознавания 521, 523
резолюции 457, 462
семейства IDS 589

Предметный указатель
665
Алгоритм
сколемизации 204-206, 212,
213, 219
сколемизации в MLL 206
унификации 45, 61, 159-163,
171, 173, 184, 204, 208,
209, 219
фокусирования 583, 584, 589,
659, 689
Алгоритмы количественного и
качественного распо-
распознавания по признакам
689
Алетическая
логика 257, 258
модальность 257
АЛПЕВ 24, 634, 664
Алфавит 323, 324, 390
АМХ 574
Анализ
вариантов 460
данных 510, 596
признаков 631
Аналитическая
таблица 117, 136, 138, 145,
153, 154, 159, 160, 163,
181, 478
со свободными перемен-
переменными 166
Аннулированный
аргумент 428
подаргумент 431
Аннулируемое
заключение 434
Аннулируемый
аргумент 434
статус аргумента 442
Аномальная ситуация 467
Антилогизм 266
Антиобъяснение 453
Апостериорная вероятность 253
Априорная вероятность 253, 557
Аргумент 420, 421, 424-444, 460,
500, 501
-аналог 421
«в силе» 441
Аргументационная
последовательность 440
семантика 438, 481, 496, 500,
502, 652, 682
семантика Данга 650, 680
система 420-423, 433, 436,
438, 440, 442-444, 651,
681
структура 437, 443, 452, 481,
483, 487
теория 440
Аргументационное
расширение 437, 438
Аргументационный
вывод 419
Аргументация 499, 650, 652, 680,
682
Аргументы 422
Археология данных 510
Ассерторическая силлогистика
257
Ассерторический статус утвер-
утверждений 238
Ассимиляция
(усвоение) противоречивой
информации 241
знаний 357
Ассоциативный квантор 529, 530
Атака 421, 423, 429, 437, 452, 481-
483, 485, 486, 488, 489,
496, 498, 500, 501
аргументов 420, 423
Атом 323, 332, 333, 338, 340, 346,
377, 383, 386, 393, 394,
399, 409, 490, 493, 500,
604, 609, 610, 618, 620
Атомарная формула 199
Атомарное множество 39
Атрибут 200, 217, 226, 233, 504,
517, 520, 560, 562, 569-
573, 575, 579, 583, 584,
588-590, 592, 593, 595,
597, 598, 600, 602, 604,
606-608, 611, 616-618,
620-622, 632
Ациклический граф DAG 465

666
Предметный указатель
База
Эрбрана 324, 335, 337
данных 331, 504, 507, 509,
510, 513-516, 589, 596,
599, 601-603, 621, 655,
661, 685, 691
знаний 236, 330, 499, 562, 625,
626, 631, 647, 677
Базовый класс 531
Бектрекинг 58, 59, 61, 63, 94, 115,
117, 157, 314
Бимодальная логика 455
Бинарная
резольвента 46
унификация 163
Бинарное
дерево 566
дерево решений 573
Бинарный
атрибут 602
признак 562, 569
Ближний промах 584
Блокирование транзитивности
306, 307
Боковой упорядоченный дизъ-
дизъюнкт 51
Брауэрова система 276
Булева
переменная 559
сеть доверия 465
функция 562
Булево
дерево решений 562
означивание 137, 140
Вектор признака 520
Вера 234
Вероятностная
зависимость 516
логика 247, 254
мера 245, 246, 530
наблюдения 529
экспертная система 516
Вероятностное
абдуктивное рассуждение
476
Вероятностное
правило 597
Вероятностный метод 447
Вероятность 446
абдуцента 470
Верхнее приближение 604, 606,
608-611, 618-620
отрицательной области 615
положительной области 614
Верхняя полурешетка 583
Вершина
дизъюнктивная 136
концевая 136
простая 136
Ветвь
выполнимая 140
полная 141
Взвешенная абдукция 464-466
Виновник 491-494
Виртуальное (логическое) храни-
хранилище 507
Витрина 510
Внешняя среда 518
Внутренняя
интерпретируемость 225
непротиворечивость 383
Возможная истина в мире 284
Возможные миры 277, 298, 324,
455
Восстановление 425, 429, 430
аргументов 422
статуса 425
Временная логика 258
Временной вывод 419
Вспомогательный вывод 353
Второе правило обрезки 354
Вход 439
Входная резолюция 53, 134, 634,
664
Входной дизъюнкт 53, 457
Выборка 523, 535, 538, 544, 551,
563, 565, 600, 602, 661,
691
Вывод 313
на графе связей 119
по абдукции 452, 454

Предметный указатель
667
Вывод
по аналогии 13, 529
по умолчанию 323, 419, 452,
647, 650, 677, 680
пустого дизъюнкта 42, 53
решения 626
целей 491
цели 492, 494, 495
Выводимость 438, 449
Выполнимая формула 33, 277
Высказывание
убеждения 390
умолчание 376, 385
Генератор 416
Генерация 453
абдуктивных объяснений 451
гипотез 447, 456, 652, 682
с использованием ATMS 456
Гетерогенная система вывода
118
Гипотеза 238, 327, 357, 442, 445,
446, 448, 451, 462-464,
482-484, 488, 490, 491,
493, 496, 503, 523, 524,
526, 528
-аргумент 502
-умолчание 496
релевантна 242
Гипотетический
вывод 447, 452
класс 623-628, 631
Глобальные
Т-предшественники 353, 354
TU-предшественники 353
предшественники 353
Глобальный критерий 447, 463
Глубина поиска 601
Головоломки 72
Гомогенная система вывода 118
Граница 604
Граничная область 604, 605, 615
Граф
«И/ИЛИ» 66
дизъюнктов 119
доказательства 466
Граф
связей 81-87, 98, 636, 666
связей Ковальского 81, 89,
91, 112
Графическая интерпретация
468
Графовая модель 516
Группа
III Льюиса — Лэнгфорда 272
IV Льюиса — Лэнгфорда 261
V Льюиса — Лэнгфорда 263
Группирование 514
ДНФ 136, 154, 157, 458
ДРЕВ 632
ДСМ-метод 526-529, 656, 686
ДСМ-метод автоматического по-
порождения гипотез 633,
663
Дальний промах 584, 589
Данные 225, 240
Двоичное дерево решений 562
Двоичный вектор 567
Двойственная форма 156
Двузначная
интерпретация 324, 327-329,
333
логика 402
модель 325
семантика логических
программ 397
Двуместное умолчание 443
Двухуровневая
OSA 640, 670
алгебра 189, 191
Дедуктивная модель 634, 664
Дедуктивное
замыкание 409
правило вывода 530
Дедуктивные
БД 233
рассуждения 248
системы принятия решений
233
Дедуктивный
аргумент 440

668
Предметный указатель
Дедуктивный
вывод 13, 81, 87, 88, 100, 102,
104, 106, 107, 116, 117,
124, 134, 449, 455, 503,
638, 640, 668, 670
на графовых структурах
118
Дедукция 13, 420, 446, 448, 451,
633, 642, 663, 672
Действительная атака 492, 497
Действительный мир 278
Декартово произведения доменов
233
Декларативная
ревизия 363
семантика 325
Декларативное знание 231, 248,
563
Деонтическая логика 258
Дерево 280
вывода 42, 53
выполнимо 140
доказательства 459
замкнутое 138
конечно древовидное 149
обобщения 595
поиска 602
разбора 622, 626
решений 505, 516, 561, 562,
564, 566, 567, 569, 574,
583, 591, 620, 659, 689
Деревья
доказательств 60
решений 512, 515
Детерминированное классифици-
классифицирующее правило 596
Детерминированный признак
522
Дефинициальный дизъюнкт 54
Диагностическая система 463
Диаграмма частичного порядка
585
Диалектическое исследование
423
Диапазон
значений 625
Диапазон
изменения значений призна-
признака 628
Дизъюнкт 34, 35, 39, 40, 42, 47, 55,
58, 81, 97, 125, 154
боковой 48, 50
пустой 46
сателлитный 94, 95, 112
упорядоченный 49, 50
центральный 48, 50
Дизъюнктивная
нормальная форма 29
программа 377, 379, 380
форма 457
обобщенного понятия 565
Дизъюнктивное
ограничение целостности 451
правило 386
Дизъюнктные вершины 119
Дизъюнкты
поглощенные 48
смежные 91
тавтологий 48, 83-85, 88, 89,
134
чистые 48
Дилемма 439
Динамическое ограничение 358
Дискретное
значение 516
распределение 571
распределение вероятности
571
Дискретный атрибут 621
Доверительный интервал 246
Доверчивая семантика 489
Доверчивый вывод 435
Довод 445, 446
Доказательство 420
Доказуемость 389
Домен 234, 445, 607, 612
Допустимое множество 484, 485
гипотез 483, 486, 489
Допустимость 494
множества аргументов 437
Достоверное рассуждение 633,
663

Предметный указатель
669
Достоверность 556, 625-627
выводов 503
принадлежности 624, 625
Древовидная
модель 280
структура 280
Древовидное отношение 280
Евклидово расстояние 546
Единственность минимального
расширения 413, 415
Зависимо-направленный бектре-
бектрекинг 314
Зависимый атрибут 620
Задача
«Стимроллер» 100-102, 104,
134, 166, 637-639, 667-
669
Data Mining 512, 513, 515
абдуктивного вывода 469
абдукции 447, 496, 500, 502
диагностики 419, 449, 459
извлечения
знаний из баз данных 599,
603
обобщенных понятий из
обучающих выборок
661, 691
индуктивного
обобщения 659, 689
обучения на примерах 655,
685
построения понятий 519
искусственного интеллекта
516
классификации 505, 523, 558,
657, 687
наблюдения 419
накопления и усвоения зна-
знаний 419
о N ферзях 104, 112, 115
о восьми ферзях 109
о четырех ферзях 110, 111
обобщения 523, 534, 604, 656,
Задача
обобщения
и классификации 524
понятий 583
понятий по признакам 558
обучения 523
«без учителя» 534, 535,
541, 657, 687
«с учителем» 604
оценки плотности вероятно-
вероятности 514
планирования 69
поддержки принятия реше-
решений 507
поиска классов 512
понимания естественного
языка 419, 463
представления знаний и рас-
рассуждений 400
принятия решений 506
раскраски карты 108, 115
распознавания 504, 521, 522,
544, 557
образов 657, 687
плана 419
сборки 448
устранения противоречий
400
формирования гипотез 525
Заключение 442, 443
аргументов 440
теоремы 37
Закон
дистрибутивности 460
исключенного третьего 250
Замкнутая
аналитическая таблица 140
ветвь 138
таблица 150
формула 28, 145
Замкнутое умолчание 302
Замкнутые формулы 164, 165, 171
Запрос 450
Зашумленные данные 517, 588,
598, 613

670
Предметный указатель
Защита 484, 486, 487, 489, 494,
496, 498
Защищающий аргумент 422
Знание 225, 232-238, 240, 241, 390
Значение
достоверностей принадлеж-
принадлежности объектов 631
достоверности 626-628, 631
признака 520
Зомби-аргумент 428, 431, 436
Зона 623-625, 628, 631
Зонное представление признаков
622, 625
И-дерево 56, 60, 345, 349, 353, 489
ИЛ И-дерево 55, 60
ИСН 612, 615, 616
Идеально разумные рассуждения
292
Идеально разумный агент 298
Идентификация класса примера
571
Иерархическая
абдуктивная схема рассуж-
рассуждений 467
абстрактная структура 214,
215
абстракция 194, 195, 197-
199, 214
связь 228
структура 186, 194, 196-199,
204, 205, 209, 212-215,
585
Иерархичность 186, 467, 652, 682
Иерархия 584, 591, 593
классов 514
объяснений 467, 469, 470,
472, 473
понятий 585
типов 640, 670
Извлечение знаний 504, 510, 511
из баз данных 598
Излишний атрибут 608, 616
Импликативный квантор 530
Импортация-экспортация 266
Индексирование метаданных 509
Индуктивная
гипотеза 656, 686
зависимость 503
закономерность 504
резолюция 525
Индуктивное
знание 659, 689
логическое программирова-
программирование 516
обобщение 14, 16, 655, 685
обучение 504, 518
описание 519
понятие 503, 519, 526, 655,
685
правило вывода 524
следование 525
умозаключение 238
формирование понятий 503,
655, 659, 685, 689
Индуктивный
аргумент 421, 423, 440
вывод 14, 446, 503, 524, 525,
529, 651, 655, 681, 685
квантор 529
Индукция 13, 14, 17, 447, 503, 633,
642, 655, 663, 672, 685
решающих деревьев 569, 659,
689
Индуцированная сигнатура 190
Инкрементное обучение 599
Инспектирование 315
Интеллектуальная система 12,
233, 234, 237, 240, 246,
247, 253-255, 314, 505,
518, 519, 525, 527, 558,
633, 642, 655, 663, 672,
685
Интеллектуальное знание 234
Интеллектуальный репозиторий
216
Интенсиональная
логика 644, 674
составляющая базы знаний
186, 187, 198, 201, 213
составляющая проблемной
области 218

Предметный указатель
671
Интенсиональные
(ИБД) 232
представления 232, 233
Интервал 247
Интерпретатор 58
Интерпретация 28, 30, 36, 40, 57,
138, 140, 141, 143, 145,
233, 237, 251, 255, 290,
294, 318, 332, 336-343,
378, 385, 393, 415, 432,
435, 466, 501, 575
/342
высказываний 294
дизъюнктивных логических
программ 376
Интерференция 421
Интроспективная природа 253
Интроспективные рассуждения
292
Интроспекция 395, 396, 400, 401
Инференциальная теория Пирса
633, 663
Информативность атрибута 589,
593
Информативный атрибут 620
Информационная
база 632
витрина 508
единица 226, 228, 230, 231
метрика 589
система 607, 608, 611-613,
617
с неопределенностью 612
технология 507
Информационное хранилище 507,
510
Информационный
атрибут 608, 610
Информация 571
Искажение информации 598
Искусственный интеллект 239,
248, 321, 375, 419, 444,
447, 499, 503, 504, 510,
634, 650, 657, 659, 664,
680, 687, 689
Истинная формула 277
Истинностные значения 26
Исчисление
аргументов 443
высказываний 336
предикатов 46, 52
первого порядка 255, 259-
261, 276, 519, 525
Итеративное построение 412, 417,
426
КМ-допустимость 502
КНФ 136, 154, 458
К аноническая
программа 333, 387
расширенная логическая
программа 343, 361,
362, 399
Категориальное значение 516
Категория 561
Каузальная сеть 447
Каузальное отношение 228
Качественный признак 520, 524,
534, 559, 560, 562, 569,
622, 631, 632
Квантифицированная формула
178
Квантор 27, 28, 143, 177, 178, 257,
276, 302
общности 26, 249, 458
существования 26, 249, 458
эквивалентности 530
Класс 504, 505, 511, 514, 517-519,
522-524, 529, 534-549,
551-557, 560-563, 574,
578, 580, 598, 601-603,
622-624, 626, 628, 631,
632, 657, 687
данных 513
объекта 597
отрицательных объектов
612
положительных объектов
612
примера 571
разбиения 616
ситуаций 532, 610

672
Предметный указатель
Класс
эквивалентности 604, 605,
617, 620
Классификационное правило 512
Классификационный
критерий 614
метод 513
фактор 613, 614, 615-619
Классификация 504, 512, 513, 515,
521, 524, 582, 583, 594,
597-599, 604, 609, 616,
620-622, 632
и формирование понятий 530
объектов 607
Классифицируемый объект 625
Классифицирующее правило 505,
563, 596
Классифицирующий фактор 613
Классическая
логика определенных хор-
новских программ 482
теория умолчаний 406
Классическое
отрицание 376, 380, 381, 383,
384, 386, 389, 390, 402,
415
упорядочение 325
Кластер 545
Кластеризация 512-514
Клоз 464
Когерентное объяснение 466
Когерентность 384, 395-397, 466
объяснений 465
Количественный признак 520,
524, 534, 559, 562, 569,
622, 632
Количество
информации 571, 589
лучей 601
Комбинаторный взрыв 517, 601
Компактная версия 343
Компактность 560
Композиция подстановок 44, 55,
171
Компонент
объяснения 445
Компонент
правдоподобия 445
Конечный статус аргумента 422
Консеквент 316
Конструктивное восходящее
определение 344
Конструкторы типов 189, 191, 192
Контекст 403, 404, 409, 415, 485,
489
ATMS 318
Контекстное описание
атрибутов 526
свойств 526
Контрапозиция 393, 394
Контраргумент 420, 421, 441, 443,
501
Контрарная пара 42-44, 81, 82,
88, 95, 106, 138, 139, 147,
151, 157, 158, 165, 184
Контрарные литеры 94
Контрмодель 279
Контрольный пример 505
Контрпример 518, 523, 527, 559,
563, 564, 566, 584, 587,
588, 602
Конфликт 421, 430, 432, 435, 440,
442
аргументов 440, 443
между аргументами 420
Конфликтное множество 92
Конфликтующий аргумент 424,
438
Концептуальный язык 221
запросов 220
Концепция
относительных ошибок клас-
классификации 613
приближенной аппроксима-
аппроксимации 614
Конъюнкт 154, 158, 583, 584
наблюдения 459
Конъюнктивная нормальная
форма 29
Конъюнктивное обобщенное по-
понятие 565
Конъюнкция 245, 251, 264, 305

Предметный указатель
673
Корень 280
Кортеж: 567
Косвенный признак 524
Коэффициент неопределенности
612
Критерий
Байеса 557
выбора 567
для предпочтения моделей
423
минимального расстояния
538, 546
минимальности 457
отбора 451, 457, 462, 464, 465
оценки 421
предпочтения 356
приемлемости 357
простоты 462
распознавания 546
существенности 564, 565
экономичности 589
Кумулятивность 322, 329, 336
Левенгейма — Сколема 151
Лексемы 221
Лемма
Кёнига 149
Хинтикка 142, 143, 148, 149,
152, 153
подъема 121
Либерализация 146, 147
Либеральная таблица 151
Лингвистическая
модель 247
шкала 229
Лингвистические переменные 248
Линейная
входная резолюция 211, 212
разделяющая функция 550,
553
резолюция 48, 49, 117, 456-
458, 634, 664
решающая функция 549
функция 552
Линейный
аргумент 440
Линейный
вывод 48
пустого дизъюнкта 49
упорядоченный вывод (OL-
вывод) 50
Литера 29, 39, 41, 45, 49, 50, 53,
54, 97, 323, 332
обрамленная 50
по умолчанию 323, 327, 329,
332, 359, 377, 385, 387,
648, 678
убеждения 390, 392, 648, 678
Логика
К 396
возможного 257
возможности 254
вопросов 643, 673
высказываний 237, 258, 295,
531
знания 258, 296
немонотонного вывода 422
необходимости 284
очерчивания 650, 680
предикатов первого порядка
233, 237, 239, 243, 248,
257, 258, 312, 317
предикатов первого порядка
с равенством 248, 249
убеждений и доказуемости
393
убеждения 296
умолчаний 244, 251, 252, 254,
281, 301-303, 305, 307,
311, 332, 401, 421, 442,
452, 643, 645, 650,673,
675, 680
Рейтера 404, 407, 648, 678
Логическая
модель 449, 453, 513
программа 54, 328, 329, 341,
376, 386, 402, 416, 437,
452, 481, 482, 487, 488,
496, 499, 501, 502, 648,
651, 652, 678, 681, 682
с явным отрицанием 415
простота 462
22 В.Н. Вагин и др.

674
Предметный указатель
Логическая
система немонотонная 243
теория 449
функция 558, 560, 563, 583
принадлежности 565
целостность 313
Логические связки 26, 28
Логический язык 420
Логическое
всеведение 240, 295
выражение 505
преобразование 460
программирование 153, 321,
332, 357, 375, 401, 442,
450, 451, 482, 634, 639,
647, 650, 652, 664, 669,
677, 680, 682
следование 251, 423, 529
следствие 36-38, 42, 252, 293,
295, 381, 382
Локальные предшественники 353
литеры 353
Локальный критерий 447, 464
Лучевой поиск 465
М-модельная структура 277
Максимально правдоподобные
миры 455
Максимальное
применение умолчаний 407,
408
слабо устойчивое множество
485
Масштабирование 522
Масштабируемость 509
Математическая статистика 524
Математический препроцессор
109
Математическое знание 235
Материальная
импликация 17, 266, 378, 394,
402, 450, 454
эквивалентность 378
Материальные связки 257, 261
Матрица 31
расстояний 542-544
Матрица
рисков 557
Машинное обучение 504, 510, 511,
513, 589, 597, 599, 603,
633, 658, 663, 688
Мера
близости 521, 534, 535
зависимости атрибутов 615
информативности 570
относительной ошибки клас-
классификации 613
сходства 529
точности аппроксимации
604, 608
Метазнание 659, 689
Металогический уровень 455
Метауровень 445
Метафорическое определение по-
понятия знаний 642, 672
Метаязык 442
Метод
Data Mining 513
OR-параллельного вывода
103
Q-depth 180, 181, 183
Рейтера 306
Хинтикка 136
абдуктивных рассуждений
467, 470, 474, 652, 682
абдукции 224
автоматического доказа-
доказательства теорем 474
аналитических
таблиц 136-143, 148, 149,
151-154, 156, 159, 171,
174, 177, 180, 183, 639,
669
вероятностных
абдуктивных рассужде-
рассуждений 466, 467, 469, 472,
652, 682
ветвей и границ 531
вывода на графе связей 636,
666
генерации 447
дедукции Эрбрана 634, 664

Предметный указатель
675
Метод
диагностики 467
индуктивного вывода 655,
685
индуктивных рассуждений
527
индукции 149, 224, 505
качественного обобщения по
признакам 563
машинного обучения 598
нелинейной регрессии 515
неподвижной точки 292
обобщения 505, 595
информации 596
на сетях 530
объектов по признакам
533
по признакам 524, 525
обратного вывода 634, 664
опровержения 119, 136
основанный на примерах 515
поддержки истинности,
основанного на пред-
пол ожениях 318
поиска 515
«в глубину» 63, 71
«в ширину» 65, 472-474
«наилучшего» 66, 67
параметров 515
последовательного уточне-
уточнения 549
потенциалов 552, 554
правдоподобного вывода 224
распознавания 547
резолюции 21, 89, 105, 135,
136
семантических таблиц 136
структурного обобщения
знаний 659, 689
установления выводимости
24
фокусирования 583, 588
элиминации моделей 53
Метрика 516, 520, 567
Хемминга 566
когерентности 462, 465
22*
Метрические шкалы 229
Механизм
генерации гипотез 449
наследования 215
наследования продукцион-
продукционных правил 215
наследования свойств 77
Минимальная
аномальность 463, 464
модель 325, 376, 379-381,
397, 500
непротиворечивая подмо-
подмодель 366
Минимально пересмотренная
программа 367
Минимальное
абдуктивное объяснение 252
множество удаления 372
объяснение 474
Минимальность 462
объяснения 453
Минимальный средний риск 557
Мир ситуаций 240
Мнения 235
Многократная унификация 163
Многомерная база данных 508
Многопризнаковая проверка 561
Многосортная
алгебра (MSA) 187, 188, 640,
670
логика (MSL) 134, 195, 199,
201, 202
сигнатура 189, 190, 640, 670
Многоуровневая
алгебра (MLA) 187-189, 193
логика (MLL) 187, 194-204,
206, 211, 212, 214, 219-
222, 640, 670
у поря доченно- сортная
алгебра (MLOSA) 188,
640, 670
Множественное
наследование 80
присвоение статуса 430
Множество
AND-связей 96

676
Предметный указатель
Множество
DCDP-связей 91, 93, 107
Хинтикка 142, 143, 148-150,
152
аксиом 37
аргументов бесконфликтное
437
видов 640, 670
внутренне независимых под-
подмножеств графа 93
гипотез 485, 487-489, 492-
494, 502
дизъюнктов 35, 38, 39, 41, 46,
81, 119
значений атрибутов 607
классов эквивалентности 615
конфликтных связей 92
литер 454
общих дизъюнктов 376
оценок 528
поддержки 371, 375
литеры 370
противоречия 372
посылок 37
правил вывода 248
предположений 452
предсказывающих атрибу-
атрибутов 592
примеров 523
рассогласований 45, 208-211
решающих атрибутов 616
совместимых связей 92
тестовых примеров 583
удаления
RS 372
противоречий 370
противоречия 373
целей 489
Модальная
логика 255, 258, 261, 278, 281,
292, 293, 393, 422, 643,
644, 673, 674
К 394
знания 645, 675
убеждения 645, 675
силлогистика 257
Модальное
исчисление 259, 261, 276
исчисление высказываний
276
нормальное 276
правило вывода необходимо-
необходимости 282
Модальность 257, 263, 389
возможности 257
доказуемости 393
убеждения 393, 394
Модальный
оператор 456
оператор К 244
решатель 313
Модель 325, 328, 339, 342, 359,
367, 377, 378, 385, 390,
399
БЗ 237
высказываний 294
голосования 247
дизъюнктивных логических
программ 376
знаний 216
индуктивного вывода 525
коэффициентов уверенности
247
обобщения 523
по выборкам 523, 524
по данным 523, 524
представления знаний 515,
634, 664
программы 363
реляционного обучения
516
решающих деревьев 659, 689
убеждения 453
формулы 29, 277, 279
Модельная теория 423
Модельный параметрический по-
полиморфизм 640, 670
Модификация 315
Модульность 311
Модулярная семантика 408
Модулярность 407, 415
Монотонная выводимость 455

Предметный указатель
677
Монотонное
отношение выводимости 452
правило вывода 440
Монотонность 449
Монотонные обоснования 316
Монотонный оператор 365, 412,
417
Мощность обучающей выборки
622
Мультидуги 120-124, 126, 127,
129-132
Мультипликативный метод 41
Мультипоиск 116, 118
Мышление 234
Наблюдаемая литера 472, 474
Наблюдаемое значение 591
Наблюдаемые данные 656, 686
Наблюдение 419, 448, 450, 456,
458, 459, 461, 465, 466,
468, 469, 496, 499-501,
504, 525, 529
Набор
признаков 519
продукционных правил 505
Надмножество 483
объяснений 449
Назначение
множественного статуса ар-
аргументам 433
статуса 432-434, 436, 437
Наиболее
информативное разбиение
573
информативный атрибут
574-576, 579
общий унификатор (НОУ)
44, 46, 49, 50, 82, 94-97,
109, 111, 112, 127, 160,
162, 163, 171, 175, 208
правдоподобное объяснение
456
специфичная абдукция 463
Наибольшая фиксированная точ-
точка 405
Наилучшее объяснение 446, 447
Наименее
общее обобщение 525
предположительная абдук-
абдукция 463
предположительные или
наиболее специфичные
объяснения 463
специфичная абдукция 463
Наименьшая
верхняя грань 584
модель 326, 327, 329, 333,
334, 342
трехзначная модель 330, 340
фиксированная точка 341,
362, 404, 412, 414, 427,
485, 487
Наименьшее стационар-
Наименьшее стационарное расширение 407
Наследование 640, 670
свойств 307
Насыщенная теория умолчаний
408, 414
Наука 235
Нахождение атомов 619
Невыполнимая формула 33
Негативная
интроспекция 390, 392, 393
литера 359, 375, 409, 482, 490,
492, 500
объективная литера 388
Негативное
антиобъяснение 453
Негативные факты 250
Негативный
абдуцент 452
атом 337
оператор интроспекции 393
Недедуктивные аргументы 440
Недетерминизм 56, 82
Недетерминированный выбор 484
Нейронная сеть 515
Нелинейная
регрессия 516
решающая функция 552
Немодульность 310
Немодулярность 409

678
Предметный указатель
Немонотонная
логика 436, 438, 643, 645, 673,
675
Дойла 287
Мак-Дермотта 287
модальная
логика 254, 281, 650, 680
система 282
модальная логика Мак-
Дермотта и Дойла 645,
675
формальная система 645, 675
эпистемическая логика 389
Немонотонное
правило вывода 440, 317
рассуждение 21, 645, 675
следствие 452, 482, 487
Немонотонность 308, 643, 673
Немонотонный
вывод 321, 330, 401, 422, 447,
452, 650, 651, 680, 681
формализм 482
Ненормальное модальное исчис-
исчисление высказываний
644, 674
Необходимая
истина в мире 284
формула 278
Необходимый атрибут 616
Неозначенные формулы 137, 139,
146
Неопределенность 244, 400, 611,
617, 643, 651, 673, 681
Неотрицательная программа 329,
340
Непересматриваемая
литера 369
программа 370, 373
Неподвижная точка оператора
303
Неподвижные (фиксированные)
точки 290
Неполнота 643, 673
информации 611
Непосредственное
объяснение 468, 473
расширение таблицы 140
Непрерывный атрибут 570, 621
Непротиворечивая
модель 359, 367
подмодель 368
Непротиворечивое
абдуктивное объяснение 252
Непротиворечивость 140, 449, 462
Неразделимая литера 364, 367,
372
Неразличимый объект 610, 619
Неразрешимый конфликт 424
Нерасширенная дизъюнктивная
программа 389
Несимметричная форма атаки
421
Неточное знание 604
Неточность 244, 643, 673
Нетрадиционные логики 248-250,
253, 254
Нетривиальность 462
Неуспешное дерево 345
Нечеткая
логика 254, 603
порядковая шкала 229
Нечеткие
знания 246, 254
квантификаторы 229, 230
Нечетко-значные модели 248
Нечеткое множество 246, 248
Нечеткость 603, 643, 673
Неявная форма восстановления
430
Неявное убеждение 453
Нижнее приближение 604, 606,
608-611, 618, 619
Нисходящая
процедура логического про-
программирования 415
характеризация 345
Нормальная
логическая программа 326,
329, 331, 332, 336, 376,
386, 393, 404, 405, 452,
647, 677
с NAF 452

Предметный указатель
679
Нормальная
модальная система 282, 286,
394
модельная структура 277
программа 335, 347, 351, 382
теория 304, 306
теория с умолчаниями 304
форма 29, 311
Нормальное
модальное исчисление
высказываний 644, 674
умолчание 304, 306, 312, 645,
675
Нормальные миры 423
Носитель нечеткого множества
247
Область
изменения переменной 160
интерпретации 28, 237
неопределенности 548
Обнаружение
знаний 504, 510, 511
в базах данных 596
информации 510
Обновление 315
Обобщение 464, 503, 519, 523, 524,
526, 531, 533, 558, 589,
591, 592, 594, 595, 655,
685
на основе
признаков 655, 685
примеров 655, 685
Обобщенная
модель
данных 596
приближенных множеств
614
устойчивая модель 500
Обобщенное
дизъюнктивное понятие 563
конъюнктивное понятие 563,
564
понятие 519, 523, 563, 659,
689
представление классов 531
Обобщенное
продукционное правило 583
Обобщенный
квантор 526, 529
семантический граф 531
Обоснование 313, 316, 402, 403,
409, 411
посылок 316
умолчания 302, 304
Обоснованность 384
Обработка моделей данных 510
Образование новой теории 456
Обрамленные литеры 50
Обратная
резолюция 451
сколемизация 451
Обратное ветвление 458
Обучающая
выборка 504, 505, 518-520,
522-526, 534-536, 539,
541, 542, 545, 549, 550,
552-556, 558-560, 562,
563, 565, 566, 569, 571,
586, 587, 602, 604, 605,
608, 621-625, 628, 632,
659, 689
Обучающаяся система 599
Обучающее
множество 504, 514, 518, 519,
522, 541, 549, 552, 560,
566, 567, 570, 573, 579,
583, 585, 588, 592-594,
597-599, 603, 604, 607,
609-611, 618, 619, 655,
685
Обучающий
признак 623
пример 572, 573, 575, 579,
588, 589, 595
Обучение 518, 522, 559, 560, 588
без учителя 505, 523, 534
на основе примеров 655, 685
по неполным и нечетким
данным 661, 691
с учителем 505, 523, 559, 604,
622

680
Предметный указатель
Общая семантика 385
Общезначимая формула 29, 38,
147, 241, 277, 291
Общезначимость 36, 37
Объединение теорий 406
Объект
-прототип 546
исследования 505
классификации 519, 520, 562
распознавания 534, 545, 657,
687
управления 506
Объективная литера 332, 333,
335, 337, 338, 340, 341,
344, 347-349, 351, 354,
358, 364, 370, 372, 384,
385, 389, 399, 403, 404,
415-418
Объективное высказывание 376,
379, 382, 390, 392
Объектная вершина 530
Объектно-ориентированные
СУБД 188
Объектный язык 441
Объяснение 444-446, 448, 452-
455, 461, 463-467, 469,
474, 478, 481, 499, 501
-гипотеза 445
базовое 457
наблюдений 450, 468
Объяснительная гипотеза 17
Объясняющая гипотеза 444, 446,
458
Объясняющий вывод 446
Ограничение целостности 357,
358, 362, 363, 365, 450-
452, 459, 469, 478, 499-
501, 611
Ограниченная теория умолчаний
403, 408, 413
Ограниченное правило-
умолчание 403, 409
Ограниченный язык 409
Однопризнаковая проверка 562
Односортная алгебра 188
Означенные формулы 137, 144
Онтологическая истина 337
Оператор
F 425
G 426
К 237
Rf 123
Rf 124
Up 122, 123
Г* 341
ГА 403
Од 410
Ф 341
ФР 344
Ф* 340
Coh 341
Cohp 360
least 340, 341
Гельфонда — Лифшица 327,
402
антимонотонный 404
замыкания 365
модальной непротиворечи-
непротиворечивости 394
модальности Е 394
монотонный 404
обобщения 531
объяснения 447, 454
отсечения 157-159
расщепления 122
расщепления вершины 121
следования
замкнутых убеждений 393
открытых убеждений 393
убеждения 390, 395, 396
удаления вершины 120
фиксированной точки 402,
413, 425
Операция
замыкания 396
редукции 51
сокращения 51
факторизации 134
факторизации дизъюнктов
89
Описание 607
класса 505

Предметный указатель
681
Описательная функция 607, 612
Описательное моделирование 515
Описательный атрибут 608
Оппозиционная шкала 230
Оправдываемый
аргумент 427, 428, 434, 435
статус аргумента 442
Определение
с фиксированной точкой 431,
432
фиксированной точки 425
Определенная
логическая программа 395
программа 327, 333, 334, 647,
677
расширенная логическая
программа 393, 396, 397
Опровергающий аргумент 441
Опровержение 38, 438, 440, 442,
443
аргумента 421
аргументов 423
Оптативная гипотеза 357
Орграф 327
Осторожная
О-семантика умолчаний 410
семантика умолчаний 404,
406
Отбор гипотез 447, 461
Отвергающий аргумент 422
Ответное множество 334-336, 385,
394, 395
расширенной программы 333
Открытая ветвь 481
Открытое умолчание 302
Относительная
метрическая шкала 229
ошибка 614
Относительное
правдоподобие 445
сокращение множества
условных атрибутов
616
Относительность 643, 673
Отношение
«класс-подкласс» 77
Отношение
extend-goal-root 491
выводимости 237, 243, 289,
295, 394, 402
доступности 277
немонотонной выводимости
291
неразличимости 604, 606,
607, 614
поражения 423, 425, 426, 433,
437, 438, 443
релевантности 231
следования 420
эквивалентности 604, 606—
608, 614
Отрицание 245, 389
как неуспех 450, 500
по умолчанию 326, 347, 348,
379, 382, 387, 393, 395,
400, 402, 496
при неудаче 61
Отрицательная
аналогия 529
гипотеза 528
область 605
множества 615
рекурсия 353
Отрицательное нижнее прибл
жение 614, 615
Отрицательный
класс 613, 616
объект 558, 559, 621
пример 519, 528, 569, 576,
581, 583, 584, 588, 600,
602
Отсечение 61
Оценка 277
аргументов 420
гипотез 446, 529, 624
достоверности 524, 622
информативности 571
истинности 324, 338
качества 600-602
модели 514
обоснованности гипотезы
528
бли-

682
Предметный указатель
Оценка
разброса 624
степени шума 613
Оценочная функция 66, 67
Очерчивание 378
Пара рассогласования 161, 162
Параллелизм
в процессе унификации 126
на графовых структурах 117
на уровне дизъюнктов 117
на уровне поиска 118
на уровне термов 117
Параллельная
машина вывода 133
стяжка мультидуг одного
цвета 127
унификация 125, 126, 130,
131
Параллельное
очерчивание 376
расщепление внутри одной
вершины 127
расщепление нескольких
вершин 130
резольвирование 90-92, 97,
131
удаление вершин, свободных
от мультидуг 127
Параллельный
алгоритм вывода на С-
графах 131
вывод 124
Параметрический полиморфизм
189, 191
Паранепротиворечивая
WFSX 360, 362, 375
семантика 336, 360, 648
Паранепротиворечивая семанти-
семантика 678
Паранепротиворечивое фундиро-
фундированное следствие 371
Первое правило обрезки 353
Пересматриваемая
аргументация 421
с приоритетами 650, 680
Пересматриваемая
литера 359, 364, 365, 367-372
условная зависимость 441
Пересматриваемое
логическое следствие 420
правило вывода 440, 441
предположение 364
следование 442
следствие 437
Пересматриваемые рассуждения
293
Пересматриваемый вывод 423,
650, 680
Пересмотр
автоэпистемической теории
452
убеждений 400, 454, 652, 682
эпистемического состояния
агента 455
Пересмотренная версия 369
Плавающее заключение 432, 434
Плавающие заключения и аргу-
аргументы 436
Плавающий аргумент 432
Планирование 463
Планировщик 70—72
Плотность вероятности 514
Поглощение дизъюнктов 83—85,
89
Поглощенные дизъюнкты 134
Подавляющее правило 363, 364,
366, 367
Подаргумент 422, 425, 429-431,
440-443
Подветвь 489
Подвыборка 564, 566
Поддерево 489
Поддерживающее объяснение 469
Поддержка 372
литеры 370
принятия решений 506
противоречия 370, 372
Подмодель 365, 369
Подобие 234
Подрыв 438, 440-443
аргумента 421

Предметный указатель
683
Подрывающий аргумент 441
Подстановка 44, 55, 97, 144, 160,
490
Подтверждаемый статус аргу-
аргумента 442
Подтверждающий аргумент 422
Подтверждение аргумента 428
П одтвержденное убеждение 435
Подтвержденный аргумент 423,
425, 426, 428, 431, 435,
436
Подход
к абдукции на уровне знаний
651, 681
множественного назначения
статуса 434, 435
на уровне знаний 453
назначения уникального ста-
статуса 432
уникального назначения 436
уникального назначения ста-
статуса 434, 435
Подцели 54
Подъем по дереву обобщения 589
Позитивная
интроспекция 390, 392, 393
литера 382, 414, 452
объективная литера 388
Позитивное
антиобъяснение 453
высказывание 379, 384
объяснение 453
Позитивный
абдуцент 452
атом 482
предикат 499
Поиск
методом
«в глубину» 58, 79
«в ширину» 59
модели 515
скрытых закономерностей
596
Поисковое пространство 517
Покрытие множеств 447, 448, 450,
651, 681
Полиморфизм 189, 193
Полностью
отрицательный объект 612
положительный объект 612
помеченное дерево 498
Полнота 140, 294, 350
Положительная
гипотеза 528
область 605
множества 615
рекурсия 346
Положительное
нижнее приближение 614,
615
Положительный
и отрицательный пример 575
класс 613, 616
объект 558, 559, 621
пример 519, 527, 528, 569,
576, 581, 584, 586-588,
600, 602, 621, 622
Полумонотонность 307, 309
Полунормальная
версия
программы 416
теории умолчаний 410
теория умолчаний 410
Полунормальное
правило 410
умолчание 307, 310
Полу нормальность 416
Полуразрешимая логика 312
Полурешетка 585
Помеха 512
Помеченное дерево 490
Понятие 518
ревизии 456
сходства 529
Пополнение 459
предикатов Кларка 326, 647,
677
Поражение 421, 432, 437, 442, 443,
482
-опровержение 441
-подрыв 441
аргумента 420, 423, 430

684
Предметный указатель
Пороговое расстояние 535, 536,
538-540
Пороговый алгоритм 535, 538
Порядковая шкала 229, 230, 520
Построение графовых моделей
513
Потенциальная атака 492, 497
Потенциальная защита 484
Потомок узла D 493
Правдоподобие 446-448, 455
Правдоподобное
знание 236
рассуждение 13, 529, 633
Правдоподобное рассуждение 663
Правдоподобность утверждения
246
Правдоподобный
вывод 239, 419, 438, 651, 681
довод 439
мир 456
Правила 54
конструирования правильно
построенных выраже-
выражений 248
расширения таблиц 138, 146,
147, 154
Правило
а 137, 139-141, 146, 165, 176,
180
C 137, 139, 140, 146, 165, 176
6 146, 163, 165, 178, 179
7 146, 148, 163-165, 171, 179,
181, 183
-умолчание 401-403, 406,
408-410
Байеса 245
атомарного замыкания 171
вывода 393, 441, 460, 529
вывода для абдукции 445
индуктивного вывода 526
классификации 623
метауровня 441
немонотонного вывода 289
обобщения 256
перезаписи для эквивалент-
эквивалентности 460
Правило
подстановки 165
распознавания 519, 557
селекции 526
умолчания 302, 402
фундаментальное 393
Правильно построенные форму-
формулы (ППФ) 194, 195, 199,
201
Правильный конъюнкт 584
Предварительное множество уда-
удаления 372, 373
Предикат 27, 101, 258
аномальности 356
полуразрешимый 36
селектор 201
утверждения 310
Предикатная вершина 119, 121,
123, 530, 531
Предикатный символ 237, 313,
323
Предметная
константа 26, 28
переменная 26, 28
Предположение 439
вычислимости 448
монотонности 448
независимости 448
о замкнутости мира 61, 241,
250, 322, 326, 358, 359,
368, 382, 397, 634, 664
о разрешимости 448
Предположительный
аргумент 440
вывод 438, 439
Предпосылка 402, 409, 411
умолчания 302
Предпочтение моделей 465
Предпочтительная семантика
423, 438
Предпочтительное
множество 452, 484
объяснение 469
расширение 451, 483
Предсказательное
моделирование 515

Предметный указатель
685
Предсказываемый
атрибут 569, 570, 592, 598
Предсказывающая переменная
513
Предсказывающее объяснение
456
Предсказывающий атрибут 569,
570, 597
Представительное допущение 514
Представление
знаний 561, 647, 677
модели 514
теории 500
Пренексная нормальная форма
30, 33, 204
Препроцессор 111
Препроцессорная обработка 88
Префикс 31, 201, 202, 205, 207, 209
формулы 200
Приближенно равное множество
606
Приближенное множество 604,
605, 608, 614, 621, 661,
691
Приближенный признак 522, 556
Приемлемая
гипотеза 357
Приемлемое
множество 486, 487
гипотез 489
предположений 452
Приемлемость 357, 425, 426, 437,
485, 487
Признак 515, 519, 520, 556, 557,
559, 561, 563, 569
Признаковое
описание 520, 559
объекта 519
Признаковый
метод 525
Применимое умолчание 407
Применимость умолчаний 407
Пример 516, 518
класса 505
понятия 503, 519
Принудительное расширение 408,
413
Принудительность 408
Принуждаемое умолчание
408
Принцип
«лезвия Оккама» 462, 463,
465
декомпозиции 194
единственного
остатка 527
различия 526
сходства 527
единственного различия 527
единственности минималь-
минимального расширения 408
индуктивной резолюции 526
когерентности 337, 338, 343,
347, 360, 410, 417
композиционности Вресвей-
ка422
максимальной вероятности
514
модулярности 409
наследования свойств 194
принудительности 408, 414
резолюции 24, 41, 42, 46, 47,
125, 127, 142, 152, 160,
471, 475, 634, 664
специфичности 421
Принятие гипотезы 16
Приоритет 443
аргументов 442
Причина 445, 528
-объяснение 457
наблюдения 446
Причинно-следственная связь
447, 449
Причинно-следственное отноше-
отношение 527, 617
Пробабилизм 236
Проблема
обнаружения знаний 19
обоснования 253
противоречивости 357
расписания задач 118

686
Предметный указатель
Проблема
распознавания образов 658,
688
Проблемы извлечения знаний
596
Проверка 561
целостности 509
Проверочный пример 597
Прогнозирование 513, 515
Программа 332
с правилами целостности 358
Продукционная модель 75, 77,
214, 659, 689
Продукционное правило 73, 75,
215, 562, 563, 586, 600-
602, 607, 619, 620
Продукция 253, 562, 583
Пролог 57, 61, 63, 67, 69, 72, 74-
76, 78-80, 117, 124, 125,
133, 153, 157, 158, 163,
171, 173, 174, 177, 178,
180, 181, 183, 321, 322,
634, 639, 664, 669
Пропозициональная
буква 454
логика 397, 516
переменная 455
программа 392, 495
теория умолчаний 409
формула 403
Пропозициональное
множество Хинтикка 141
умолчание 402
Пропозициональный
автоэпистемический язык
389
язык 454
Простая
каузальная теория 450, 651,
681
переменная 125
Пространство
аппроксимации 604
поиска 451, 516, 599
приближений 604, 606, 607,
614, 615, 617
Пространство
признаков 516, 545, 655, 657,
685, 687
Противоречивая
гипотеза 455
программа 351, 363, 373
теория 412
формула 38
Противоречивость 36-38, 43
Противоречивый
сценарий 357
Противоречие 29, 409, 651, 681
Протоструктура 234
информационных единиц
226
Прототип 535-541, 543, 545
Процедура
AND-параллельного вывода
103
DCDP-параллельного выво-
вывода 103
DCDP-параллельного
резольвирования 104
OR-параллельного вывода
90
OR-параллельного опровер-
опровержения 103
вывода
для WFSX 351
вывода Эрбрана 40, 41, 47
вычисления WFSX 648, 678
доказательства 312, 489-491,
495, 500, 502, 651, 652,
681, 682
IFF 460
для абдуктивного логиче-
логического программирова-
программирования 459
накопления 449
обнаружения знаний 512
обучения 559
с учителем 659, 689
опровержения 43, 138, 212,
471
отбора 459
пересмотра 370

Предметный указатель
687
Процедура
сколемизации 451
унификации 183
Процедурная семантика 325
Процедурное знание 231, 563
Процесс
KDD 511, 514
абдукции 445
аргументации 442
извлечения знаний 518
классификации 562, 580, 589
обнаружения знаний 511
обобщения 520, 559
обучения 504, 527, 597
опровержения 112
отбора 459
пересмотра 357, 359, 455
синтеза 459
Прямое восстановление 430
Псевдометрика 567
Псевдоотрицание 383-385
Пустая подстановка 44, 208
Пустое множество гипотез 486
Пустой
аргумент 428
граф 131
дизъюнкт 34, 41, 42, 51, 58,
85, 89, 91, 109, 120, 124,
125
Равносильная формула 30
Разбор вариантов 460
Разброс 623
значений 625
Развертывание 460
атомов 493
Разделенная переменная 94, 95,
125
Разделяющая функция 658, 688
Разделяющее
значение 564
признака 573
Разумный агент 357, 397
Ранговая шкала 520
Раскрашенный граф 92, 119
Распознаваемый объект 626
Распознавание 504, 524, 545, 546,
550, 553, 556-558, 560,
566, 625, 631, 659, 689
образов 504, 511, 513
Распознающее правило 559
Распознающий признак 659, 689
Распределенное информационное
хранилище 508
Распределенный поиск 116, 118
Распространение 460
Расстояние 522
по Евклиду 522, 553
по Хеммингу 567
Рассудок 234
Рассуждения 12, 235
здравого смысла 281
Расчет вероятностей 481
Расширение 303, 304, 386, 387,
390, 397-399, 401, 406,
408, 410, 411, 413-415,
438, 445
логики умолчаний 401
очерчивания 393
семантики Рейтера 414
теории 303, 396
теории умолчаний 403
умолчаний 404
Расширенная
GL-трансформация 329
дизъюнктивная логическая
программа 388
логическая программа 322,
332, 333, 335, 340, 342,
352, 364, 377, 382, 395,
399, 400, 402, 403, 409,
415, 647, 652, 677, 682
программа 336, 347, 351, 355,
385
эрбрановская база 332
Расширенное
логическое программирова-
программирование 357, 400, 401
представление дерева терма
161
Расщепление 460
Рациональность 322

Предметный указатель
Ревизия 249, 359, 363, 364, 367,
369, 370, 453
БЗ 242
гипотез 453
минимальных непротиворе-
непротиворечивых подмоделей 373
подмодели 365-367
программы 365, 366
Регрессионная схема 512
Регрессионный алгоритм 515
Регрессия 512, 513, 515
Редуктивный вывод 446
Редукция 52, 446, 490, 582, 608
атома 490
отрицательных циклов 353
Редуцируемый упорядоченный
дизъюнкт 51, 52
Резольвента 41, 42, 48, 50, 86, 88,
89, 94, 95, 104, 106, 111,
492, 493, 495, 496
Резольвирование 81, 85, 88, 89, 91,
93, 98, 102-104, 109, 110,
113, 115, 134
Резолюция 490, 492, 495, 652, 682
входная 48
линейная 48
Рекурсивное определение 428, 431
Рекурсивный
алгоритм 566
генератор плана 70
Рекурсия 347
через отрицание по умолча-
умолчанию 346, 350, 352
Релевантная гипотеза 449
Релевантность 323, 329, 336
Реляционная
СУБД 508
база данных 508
таблица 600
Реляционное обучение 516
Репозитарий метаданных 507
Рефлексивная
АЭЛ 397
автоэпистемическая
логика 399
теория 648, 678
Решатель проблем 315, 317, 634,
664
Решающая функция 545-553, 555,
556, 658, 688
Решающее
дерево 563, 564, 569-572,
574-576, 578-580, 583,
589, 592, 594, 659, 689
правило 504, 505, 515, 516,
524, 545, 559, 560, 562,
583, 622-626, 631, 632
Решающий атрибут 575, 576, 589,
604, 607, 608, 610, 612,
615, 619
Решение задачи классификации
544
Решетка подмоделей 365, 368
Риск 556, 557
Родительский узел 490
Ромб Никсона 369, 398, 438, 442
СТ40-модель 455
СУБД 508
Monet 600
Самовосстановление 425
Самопоражающий аргумент 424,
428, 429
Сбор информации 510
Сборка гипотез 448
Свободная
переменная 27, 163-165, 171,
177, 179, 181, 184, 446
переменная х 529
Свободные переменные 179
Свободные умолчания 309
Свойство
внутренней непротиворечи-
непротиворечивости 385
выполнимости 291
единственности минималь-
минимального расширения 405-
407
когерентности 340, 341, 385
кумулятивности, рациональ-
рациональности, релевантности
400

Предметный указатель
689
Свойство
минимальности 251
монотонности 250
немонотонности 250
непротиворечивости 241, 251
обоснованности 386, 389
поддерживаемости 337
полноты 241
полумонотонности 304
состоятельности 495
Связанная переменная 27, 446
Связки 171
Связная
модель 279
модельная структура 279
Связность 228
Селектор 200
Семантика 237, 239, 242, 255, 283,
285, 293, 298, 321, 322,
336, 342, 348, 357, 358,
375, 378, 382, 385-388,
391, 393, 394, 402, 406,
408, 414, 438, 446, 452,
465, 482, 483, 487, 489,
491, 494, 495, 502, 647,
650, 677, 680
е-ответных множеств 335,
336
WFSX 340, 342, 393, 396, 648,
678
Рейтера 404, 413
Фиттинга 327, 647, 677
аргументации 489
аргументационных систем
423
возможных миров Крипке
283, 422, 645, 675
допустимости 485, 491, 494,
496, 498, 499
допустимых
множеств 483
расширений 651, 681
логики умолчаний 438
логических программ 325
наименьшей модели 326
необходимо обосновываю-
обосновывающая 384
обобщенных устойчивых мо-
моделей 451, 502
определенных программ 327
ответных множеств 333, 385,
395, 415, 647, 677
отрицания как неуспеха 450
приемлемости 485, 491-494
программы 322
расширенных
логических программ 394
программ 388
с классическим отрицанием
383
с псевдоотрицанием 383
слабой устойчивости 484,
485, 491, 494
и приемлемости 491
со слабым отрицанием 383
со строгим отрицанием 383
теории умолчаний 405, 407,
409, 415
теорий умолчаний 403
умолчаний 407, 413
умолчаний Рейтера 402, 414
устойчивых
моделей 327-329, 385
расширений 440
устойчивых моделей 450,
647, 677
фундированных моделей
405, 487
Семантика, основанная на устой-
устойчивых моделях 333
Семантическая
метрика 231
оценка (означивание) 284
сеть 77, 78, 194, 228, 255, 468,
519, 525, 530, 531, 656,
686
теория знания 643, 673
характеризация 454
Семантический
анализ 248
граф 530, 532

690
Предметный указатель
Семантический
конструктор 191, 192
конструктор типов 192
Семантическое
дерево 345, 348
ядро 333
Семиотическая система 640, 670
Сервер информационного храни-
хранилища 508
Сетевое представление знаний 77
Сети хранилищ данных 509
Сеть
зависимостей 315, 316, 319
обоснования 317
обоснования убеждения 316
Сигнатура 189
спецификации 189, 190, 640,
670
Силлогистика
Аристотеля 633, 663
Пирса 633, 663
Силлогистическая теория Пирса
444
Сильное отрицание 380, 381, 383-
386, 388
Симметричная форма атаки 421
Синтаксическая простота 462
Синтаксическая теория 460
Синтаксический
критерий 462
подход 240, 442
Синтаксическое представление
моделей 385
Синтез с использованием частич-
частичных деревьев 459
Система
Data Mining 513
KDD 511, 512, 517
Monet 661, 691
PIS 107, 108
51 261
52 271
53 271
54 271, 282
55 271, 275
M 276
Система
T 276
Фейса — фон Вригта 276
аксиом 36, 248
аргументации 419, 436, 650,
680
без обучения 522
вывода 516, 645, 675
извлечения
данных 598
знаний 504, 562, 597, 600
индуктивного формирова-
формирования понятий 520
машинного обучения 504,
519, 598, 603, 655, 659,
685, 689
обнаружения знаний 511
обобщения 661, 691
обучения 601
с учителем 561
оперативной
аналитической обработки
506
обработки транзакций 506
пересматриваемой аргумен-
аргументации 420, 650, 680
поддержки
истинности 645, 675
принятия решений 505-
507, 640, 655, 670, 685
поддержки истинности
(TMS) 313, 314
поддержки истинности,
основанная на обос-
обосновании (JTMS) 315
поддержки истинности,
основанные на пред-
предположениях (ATMS)
317
представления знаний 224,
239, 307
продукционных правил 609-
611, 619-621
распознавания по признакам
545
с обучением 522

Предметный указатель
691
Система
управления
информацией 510
управления базами данных
(СУБД) 187, 223
управления базой знаний
(СУБЗ) 232
Систематическая
процедура 150, 152
таблица 152
Ситуационная близость 231
Ситуационная семантика 242
Скептическая
подмодель 368, 369, 374
ревизия 368, 369
семантика 357, 358, 442, 487,
489
Скептически пересмотренная
программа 368, 373
Скептический
агент 391, 399
вывод 435
процесс пересмотра 359
Сколемизация 457, 458
С ко л емовская
стандартная форма (ССФ)
35, 37, 47
функция 32, 102, 164, 165,
178, 204-206, 458
Скорость
загрузки 509
обработки запросов 509
Слабая
устойчивость 494
форма отрицания 381
часть узла 491
Слабо
устойчивое множество гипо-
гипотез 486, 489
Слабое
отрицание 381, 383
расширенное предположение
о замкнутости мира 389
Следствие 403, 528
умолчания 302, 304
ревизии подмодели 365
Сложноструктурированная
информация 187, 216
предметная область 201
проблемная область 186, 187,
194, 202, 204, 214, 219,
467, 469, 470, 472, 475,
640, 652, 670, 682
Сложноструктурированность 186
Сложноструктурированный объ-
объект 467
Слот 79, 80, 226, 228
Слэш 200
Смысл 234
дизъюнктивной программы
378
программы 382, 387
Событие 557
Совершенная интроспекция 301
Согласующаяся унификация 163
Сокращение 608, 616-618, 620
для приближений 611
Сопоставляемый класс 624, 625,
627, 628, 631
Сопряжение означенной форму-
формулы 137
Составное множество 604, 605
Состояние убеждения 391, 397,
399
Состоятельность 294, 350
Специальный SL-вывод 53
Специфичность 443
Список окружения 171
Сравнение мощностей 463
Среда связей 125
Статистика 511
С татистическая
гипотеза 530
корреляция 529
Статистический
аргумент 440
метод 517
Байеса 464
подход 513
Статическое ограничение 358
Статус 424, 428, 429, 431, 433-435,
437, 441, 502

692
Предметный указатель
Статус
аргумента 423, 432, 438, 442
заключений 422
конфликтующих аргументов
440
литеры 346
неуспеха 349
успеха 349
Стационарная
АХ^-модель 381, 382, 388
АХ^-семантика 381, 383
логика умолчаний 403
модель 382-385, 389
семантика 376, 378, 381, 383,
384, 406, 408, 409, 648,
678
нормальных логических
программ 388, 405
расширенных программ
388, 382
с классическим отрицани-
отрицанием 385
с сильным отрицанием 386
умолчаний 405, 407, 414
Стационарное
АХ^-расширение 388
расширение 379-382, 408,
409, 414
нормальной логической
программы 376, 377
умолчаний 405, 410
Стек 58
Степень
г(Ф) формулы Ф 144
важности 612, 613, 615
возможных ошибок класси-
классификации 618
достоверности 600
гипотез 528
зависимости 616
множества 425, 491
модальности 263
означенной формулы 137
подтверждения 439
правдоподобия 445
принадлежности 247, 603
Степень
точности классификации 621
уверенности 617
утверждения 246
Стоимость
классификации 594
предположения литер 464
Стратегии аналитические 117
Стратегия
«поиска по лучу» 601
вычисления 58
поиска 58, 80
редукции подцелей 117, 118
Стрелка Пирса 177
Строгая
импликация 266
основанность 311
таблица 147
Строгие условные связки 261
Строгое
поражение 421
правило вывода 441
Структура аргументов 438, 440,
442
Структурированность 226
Структурированный атрибут 591
Структурно-логический метод
524, 525
Структурный объект обучения
659, 689
Существенность 623, 626, 631
Схема
аксиомы знания 282, 296
аксиомы негативной интро-
интроспекции 283
аксиомы позитивной интро-
интроспекции 282
вывода 438
Схемы БД 232
Сходство 521
Сценарий 648, 678
Счетчик правильно распознан-
распознанных объектов 549
Таблица
атомарно замкнутая 151

Предметный указатель
693
Таблица
выполнима 140
замкнутая 138
полная 141
систематическая 151
Тавтология 51, 82, 86, 89, 91, 137,
143, 158, 336
Таксономическая теория с умол-
умолчаниями 645, 675
Таксономические теории 308
Теорема
Байеса 473
Кнастера — Тарского 412
Чёрча 180
Эрбрана 40, 121
дедукции 252
Теоретико- аргу ментационная
семантика 422
Теоретико-модельная семантика
422, 423, 465
Теория 397, 409, 489
Демпстера — Шейфера 246,
643, 673
аргументации 419, 420, 436,
496, 501, 502, 650, 651,
681
вероятностей 245, 464, 524,
643, 651, 673, 681
возможностей 247, 643, 673
доказательства 422, 445, 486,
489, 494, 652, 682
нечеткой логики 643, 673
пересматриваемого вывода
440
правдоподобных выводов
633, 663
приближенных множеств
603, 605, 607, 661, 691
принятия решений 464, 657,
687
равенств Кларка 459
с полунормальными умолча-
умолчаниями 307, 645, 675
свидетельств 247
умолчаний 302, 303, 401, 403,
404, 407-413, 415, 416,
648, 678
Рейтера 402, 406
хорновских дизъюнктов 450
Терм 26-28, 39, 44, 45, 61, 63, 100,
125, 323
Тестовое множество 582
Точка-прототип 535-544
Точность аппроксимации 608—
611, 618, 620
Транзитивное замыкание 279, 327
Транзитивность 307
Трансформация 328, 340, 342,
343, 361, 367
Гельфонда 375, 393, 394
Трехзначная
интерпретация 324, 329, 335
логика 322
модель 325, 329
наименьшая модель 329, 341
семантика
логических программ 397
пополнения 459
Тривиальное объяснение 462
Убеждение 236, 389, 454, 456
Удивительный факт 444
Узел 489
N 492
-атака 491, 498
-защита 496
-потомок 496
Умолчание 302, 338, 340, 349, 352,
376, 402, 403, 408, 409,
423, 498, 499, 502
Универсальная нечеткая шкала
230
Универсальный квантификатор
457
Универсум 145, 148, 151-153, 237,
277, 283
Эрбрана 38-40, 303, 323, 324,
482
Уникальный статус 424

694
Предметный указатель
Унификатор 44, 56, 58, 82, 95,
96, 98, 100, 104, 106, 112,
113, 115, 160, 162, 163,
459
Унификация 58, 74, 75, 89, 94,
104, 106, 125, 162, 171-
173, 201, 209, 460, 466
Упорядочение
по Фиттингу 325
по правдоподобию 455, 456
Упорядоченная
бинарная резольвента 50, 51
входная резолюция 54
резольвента 52
У поря доченно- сортная
алебра (OSA) 188-190
сигнатура 189-191, 640, 670
Упорядоченный
дизъюнкт 49, 50
фактор дизъюнкта 49
Управление качеством данных
509
Управляемое обучение 523
Управляющее решение 506
Уравнение фиксированной точки
377, 379, 382, 388, 397
Уровень
абстракции 436
абстракции объяснения 462
ошибки 616
при доказательстве 426
специфичности 462, 465, 466
точности 616
Условие непротиворечивости
338
Условная
вероятность 473, 516, 557
зависимость 456
Условный атрибут 607, 612, 615—
617, 619
Успешное дерево 345
Успешный вывод цели 494
Устойчивая
АХ^-семантика 382
автоэпистемическая теория
298
Устойчивая
модель 323, 328, 333-335,
382-384, 452, 500
семантика 376, 383, 384
аргументационной систе-
системы 438
расширенных программ
382
теория 484, 485
Устойчивое
автоэпистемическое расши-
расширение 390
множество 452
расширение 295-297, 299,
300, 382, 390-392, 437
Устойчивость моделей 340
Утверждения 240
Учитель 518, 583
Фаза непротиворечивости 451,
500
Факт 54, 503
Фактор
дизъюнкта 45, 46, 86, 127,
132
определенности 253
Факторизация 460
Факторизация дизъюнктов 82-85,
89
Фасеты 228
Фиксированная
точка 363, 411, 416-418, 422,
425, 430
оператора 328, 344
уравнения 396
Фильтрация 509, 561
Фокусирование 583, 659, 689
Формализм немонотонного выво-
вывода 332, 375
Формальная система 248
Формальные связки 257
Формирование понятий 524
Формируемое понятие 519
Формула
а 136, 177, 180
р 136, 177, 180

Предметный указатель
695
Формула
6 144, 164, 177, 180
7 144, 177, 180
Байеса 557
выполнимая 29
общезначима в модели 284
общезначима в структуре
284
опровержимая 29
убеждения 396
Фрейм 79, 228, 239, 255
Фундаментальная
версия нормальной логиче-
логической программы 324
литера 402
объективная литера 338
подстановка 44
программа 345, 353
расширенная логическая
программа 349
семантика 442
формула 446
Фундаментальное выражение 39
Фундаментальность 462
Фундаментальные примеры
дизъюнктов 39, 40,
41, 121
Фундаментальный
абдуцируемый атом 459
атом 325, 340
пример 44, 163, 325, 442
правил 442
правила программы 339
терм 323
факт 445
Фундированная
и стационарная семантика
403
логика умолчаний 403
модель 330, 336, 341, 342,
350, 416
программы 386
семантика 322, 323, 329, 337,
339, 345, 376, 377, 393,
401, 404, 406, 408
WFSX 323
Фундированная
семантика
для расширенных логиче-
логических программ 337, 648,
678, 677
с псевдоотрицанием 335,
337
Функции
неопределенности 245
принадлежности 230
Функциональный символ 178,
237, 303, 323
Функция
V 461
goal-branch 489, 491
goal-culprits 491
важности 615
виновников 491
ограничение 112, 113, 115
означенная полностью 109
принадлежности 247, 564,
566
распределения вероятностей
525
стоимости информации 589,
591, 593
существенности 626, 628
признака 623
Ханойские башни 104
Характеристическое окружение
318
Хорновская абдукция 464
Хорновский дизъюнкт 53, 54, 58,
62, 66, 73, 75, 134, 211,
377, 384, 395, 467, 468,
473
Хранилище данных 509
Хронологический бектрекинг 314
Целевая ветвь 490
Целевое
дерево 490-492, 494
утверждение 54, 55
Целевой
атрибут 569, 570, 601, 608

696
Предметный указатель
Целевой
вывод 491
запрос 496
признак 659
узел 490, 491
Целевой признак 689
Цель 54
-атака 490, 493, 496
-защита 490-496
Централизованное хранилище
508
Центральный упорядоченный
дизъюнкт 51, 52
Циклическая
отрицательная рекурсия 353
положительная рекурсия
345, 353
рекурсия через отрицание по
умолчанию 345
Частичная
двузначная логика 416
устойчивая модель 329, 342,
386, 387, 415, 416
расширенной логической
программы 335, 415
Частично
упорядоченное множество
583
устойчивая модель 452, 483
устойчивое множество 452
Четырехзначная логика аргумен-
аргументации 651, 681
Числовой признак 520, 558
Чистая формула 148
Чистые
дизъюнкты 83-85, 88, 89, 97,
98, 120
литеры 83-85, 91, 104, 134
Чувственное знание 234
Ширина
зоны 622, 624, 628
луча 601
Шкала порядка 520
Шкалирование 229
Шкалированный признак 520,
558, 559
Штрих Шеффера 177
Шум 511, 512, 598, 621
Эвристика 459, 462, 465, 599
Эвристическая
оценка 107
дизъюнкта 99
предикатной литеры 100
унификатора 99
функция 105, 106
функция HI 98, 100, 637, 667
Эвристический
критерий 569
поиск 515
Эвристическое правило 564, 601
Экзамен 559, 560, 603
Экзаменационная выборка 559
Экземпляр протоструктуры
226
Экономия 446
Экспертная система 21, 253, 254,
504, 511, 562, 603, 640,
655, 659, 661, 670, 685,
689, 691
Экспоненциальный взрыв 48
Экстенсионал 217, 218
Экстенсионалы отношений 212
Экстенсиональная
составляющая базы знаний
186, 197, 198, 204, 212,
213, 218, 223
Экстенсиональные
БД (ЭБД) 232
представления 232, 233
Элементарная
дизъюнкция 530
конъюнкция 530
Элементарное
высказывание 468
множество 604, 605, 608, 610,
611, 613-615, 621
Энтропия 570
Эпистемическая
истина 337

Предметный указатель
697
Эпистемическая
логика 258, 397, 400
ЕВ 393
Эпистемический
смысл 389
статус утверждений 238
Эпистемическое
знание 394
состояние 453, 454, 456
агента 456
Эпистемология 440
Эрбрановская
база 335, 417, 482, 488
программы 341
модель 324
Эрбрановская база 39
Эротетическая логика 241, 242
Эффективность алгоритмов 233
Явное
отрицание 330, 332, 334, 346,
375, 383, 393-395, 400-
402, 405, 415, 416
убеждение 453
Ядро 608
Язык
запросов 640, 670
запросов SQL 510
логики первого порядка 516,
529
логических программ 340
логического программирова-
программирования 331
многоуровневой логики 195
нормальных логических про-
программ 323, 332
представления знаний 187,
194, 204, 220, 529
расширенных логических
программ 332
умолчаний 402
Ячейки 228
AF-структура 437
A S- противоречивая
334
программа
AS-противоречивость 335
С-граф 638, 668
ЕВ-логика 393, 399-401
ЕВ-теорпя 398
F-минимальная 325
//-интерпретация 39
Не-факторы знания 643, 673
К-модель пересмотра 456
MRSp 373
TVP-полно 336
Р-моделью 283
U- преобразования 121
U- формула 148
Г-расширение 413
Г-семантика умолчаний 415
Г*-оператор 329
О-расширение 410-415, 416
О-семантика 413, 414
О-семантика умолчаний 410, 411
Фр-оператор 362
а-правило 151, 155, 158
а-формула 141, 149, 150, 154, 175
р- правило 151, 155
/3-формула 141, 149, 150, 155, 175
E-правило 147
E-формула 143, 146, 149, 150, 177,
178
E-правило 151
V-формула 32-34
7-правило 147, 151, 180, 184
7-формула 143, 147, 149-151, 177,
178
ор-подграф 531
р-интерпретация 360, 361
р-подграф 531
и>/-модель 487-489
и>/-приемлемое множество гипо-
гипотез 489
и>/-приемлемость 488
w/-семантика 489, 491, 494
АКО (a kind of) 228
AND-параллелизм 60, 117, 125,
636, 666
AND-параллельная резолюция
94, 108, 112, 115

698
Предметный указатель
AND-параллельный алгоритм
109
AND-параллельный вывод 88, 107
AND-резольвирование 98
ATMS 460, 461, 652, 682
Автоэпистемическое расширение
392
C-Prolog 62
С-граф 118-125, 131, 132, 134
CASE-система 216, 640, 670
СЕТ 459
CLS 563
CRS 373, 374
Семантика 386
Data Mining 514, 596, 655, 661,
685, 691
DC-параллелизм 91
DCDP-множества 108, 109
DCDP-параллелизм 91, 636, 666
DCDP-параллельная резолюция
108, 115
DCDP-параллельный алгоритм
109
DCDP-параллельный вывод 88,
91, 98, 107
GL-трансформация 333
GUHA-метод 529, 530, 656, 686
ICF 589, 595
iff-определение 459
IFF-процедура 459
ISA (is an instance of) 228
ISA-иерархия 194, 196, 198, 199,
215, 218, 468, 583, 585,
589, 590, 595
K45 297
KDD 510, 513, 516, 655, 685
Knowledge Discovery in Databases
596
KT282
KT4 288
KT45 283, 288
LTMS 320
MBR 320
MDDB 508
MNS 366, 367, 369, 374
Modus Ponens 238, 250, 256, 290,
394, 443
Modus Tollens 250
MRP 367, 369, 374
NAF 501
NP-полная задача 329
OL-вывод 51, 52
OL-опровержение 52
OL-резолюция 52
OLAP 506
OLAP-технология 510, 655, 685
OLTP-приложение 507
OLTP-система 506-508
OLAP-система 507
OR-дизъюнкт 98
OR-параллелизм 60, 89, 90, 117,
125, 126, 637, 667
OR-параллельная резолюция 89,
107, 108
OR-параллельный вывод 88, 90,
98
OR-резольвирование 98
OR-связи 90
OSCAR 438
Part-of-иерархия 194, 196-199,
218, 468, 469
PSM 342, 343, 416
ROLAP 508
SLD-резолюция 54, 500
SLX 351, 353
SLX-T-вывод 351, 352, 354, 355
с предшественниками 354
SLX-T-неуспех 352
SLX-T-опровержение 351, 352,
354, 355
SLX-TU-вывод 351, 352, 354
с предшественниками 355

Предметный указатель 699
SLX-TU-неуспех 352
SLX-TU-опровержение 351, 352,
355
SLХ-вывод 353
SLX-опровержение 352
SQL-запросы 507
SUN-дизъюнкт 94-98, 107, 109,
112
Т-дерево 345-350
Т-предшественники 355
TU-дерево 346-350
TU-предшественники 354
WAODAG 465
WFM 341-345, 348, 351, 352, 355,
359, 417, 418
WFS 346, 353, 377
WFSX 345, 347, 348, 351, 353,
354, 356-359, 362-364,
369, 372, 374, 375, 377,
383, 385-387, 394, 395,
399-402, 415, 416
WFSXP 363, 371, 372
WFSX-модель 387

Vagin V. N., Golovina E. Yu., Zagoryanskaya A. A., Fomina M.V.
Exact and Plausible Reasoning in Intelligent Systems / Ed. by V. N. Vagin,
D. A. Pospelov — M.: Fizmatlit, 2004 — 704 с
The methods of exact (deductive) and plausible (abductive, inductive)
reasoning in intelligent systems are considered. The deductive methods
on graph structures are given: the inference on connection graphs, clause
graphs and hierarchical structures. The distinct types of parallelism of
inference on graph structures are reviewed. The classical modal logics
SI, S4, S5 are described. The following types of nonmonotonical modal
logics as logics of belief and knowledge, nonmonotonical McDermott's and
Doyle's logics, autoepistemic Moore's logics and default Reiter's logics are
proposed. The foundations of the argumentation theory and methods of
abductive inference are given. The basic principles of building machine
learning systems and decision making ones are considered. The problems
of learning «without teacher» and «with teacher» are described. The
inductive methods for the case with incomplete information and methods
of the rough sets theory are presented.
The monograph is intended for students and postgraduates teaching
on «Applied Mathematics and Informatics», «Informatics and Computer
Science» and for specialists in areas of Artificial Intelligence, Intelligent
Control and Decision Making Systems.

CONTENTS
Preface 10
Introduction 12
I. EXACT REASONING
Chapter 1. Automatic Theorem Proving 24
1.1. Normal and Standard Forms 25
1.2. Logical Consequences 35
1.3. Herbrand's Inference Procedure 38
1.4. Resolution Principle 41
1.5. Linear Resolution 48
1.6. Inference in the Prolog Language 54
Chapter 2. Inference on Connection Graphs 81
2.1. The Sequential Proof Procedure by the Connection Graph
Method 82
2.2. Search Strategies in a Connection Graph 86
2.3. Advantages of the Inference Procedure on a Connection
Graph 87
2.4. Parallel Inference on Connection Graphs 88
2.5. Modification of Parallel Inference Procedures 97
2.6. Comparison of the Efficiency 104
2.7. The Parallel Inference System (PIS) for a Connection Graph 107
Chapter 3. Inference on Clause Graphs 116
3.1 Types of Parallelism in Deductive Inference 116
3.2. The Sequential Inference Algorithm in Color Clause Graphs 119
3.3. Parallelism in Deductive Inference on C-Graphs 124
3.4. The Efficiency Comparison of Deductive Inference Procedures 134
Chapter 4. Inference on Analytic Tableaux 136
4.1. The Method of Analytic Tableaux for Propositional Logic . . 136
4.2. The Method of Analytic Tableaux for First-Order Predicate
Logic 143
4.3. The Method of Analytic Tableaux in Logic Programming . . 153
Chapter 5. Inference in Hierarchical Structures 186

702 Contents
5.1. Multi-level Order-Sorted Algebra 186
5.2. Multi-layer Logic as a Knowledge Representation Language
in Intelligent Systems 194
5.3. The System of Simulating a Problem Domain «INFOLOG» . 215
II. ARGUMENTATION AND ABDUCTION
Chapter 6. Data and Knowledge in Intelligent Systems 224
6.1. Peculiarities of Knowledge 224
6.2. Knowledge as a Justified True Belief 234
6.3. Non-Factors of Knowledge 240
6.4. Why the Nontraditional Logics Need? 248
Chapter 7. Monotonic Classic Modal Logics 255
7.1. First-order Predicate Calculus as a Base of Building Modal
Logic 255
7.2. Auxiliary Logic as a Base of Transferring to Modal
Propositional Calculus 257
7.3. Postulates, Main Theorems and Rules of Modal Propositional
Calculus 259
7.4. SI System 261
7.5. S4 System 271
7.6. S5 System 275
7.7. Semantics of Cripke's Possible Worlds 276
Chapter 8. Non-Monotonic Modal Logics 281
8.1. Belief and Knowledge Logics 281
8.2. McDermott's Non-Monotonic Logics 287
8.3. Autoepistemic Logics 292
8.4. Default Logics 301
8.5. Truth Maintenance Systems 312
Chapter 9. Non-Monotonic Logics in Logic Programming 321
9.1. Semantics of Logic Programs: overview 323
9.2. WFSX — a Well-Founded Semantics for Extended Logic
programs 337
9.3. Operation with Inconsistency 356
9.34. WFSX, Semantics of Logic Programs with Two Negations
and Autoepistemic Logic 375
9.5. WFSX and Default Logic 401
Chapter 10. Argumentation Systems and Abductive Reasoning . 419
10.1. Defeasible Argumentation Systems 420

Contents 703
10.2. Organization of Abductive Inference 444
10.3. Abduction and Argumentation in Logic Programming .... 481
III. INDUCTION AND GENERALIZATION
Chapter 11. Basic Principles of Building Learning and Decision-
Making Systems 503
11.1. Decision Support Systems 505
11.2. Problems of Knowledge Extraction from Databases 510
11.3. The Ways of Original Information Representation in
Intelligent Systems 518
11.4. Structure-Logic Generalization Methods 523
Chapter 12. The Problem of Learning a Teacher Free 534
12.1. The Algorithm Based on the Notion of a Threshold Distance 534
12.2. MAXMIN Algorithm 538
12.3. The «K middle» Algorithm 541
12.4. Recognition with Using the Decision Functions 545
12.5. Recognition Based on Rough Features 556
Chapter 13. Learning with a Teacher 558
13.1. Setting up the Problem 558
13.2. The DREV Algorithm 563
13.3. Building a Decision Tree with Using Hamming's Metrics . . 566
13.4. Induction of Decision Trees 569
13.5. Modification of the Quinlan's Algorithm — ID5R 574
13.6. The Reduce Algorithm 579
13.7. Focusing 583
13.8. The EG2 Algorithm 589
Chapter 14. Inductive Methods for the Case of Incomplete
Information 596
14.1. Problems of Knowledge Extraction from Databases 596
14.2. The Algorithm of Extracting Production Rules from a Large
Database 600
14.3. Approach with Using Rough Sets 603
14.4. The Algorithm of Object Recognition in Conditions of
Incomplete Information 621
Bibliography 633

Научное издание
ВАГИН Вадим Николаевич
ГОЛОВИНА Елена Юрьевна
ЗАГОРЯНСКАЯ Анастасия Анатольевна
ФОМИНА Марина Владимировна
ДОСТОВЕРНЫЙ И ПРАВДОПОДОБНЫЙ ВЫВОД
В ИНТЕЛЛЕКТУАЛЬНЫХ СИСТЕМАХ
Редактор Е.Ю. Архарова
Оригинал-макет: Е.М. Граменицкая
ЛР №071930 от 06.07.99. Подписано в печать 09.04.04.
Формат 60x90/16. Бумага офсетная. Печать офсетная.
Усл. печ. л. 44. Уч.-изд. л. 46. Заказ №
Издательская фирма «Физико-математическая литература»
МАИК «Наука/Интерпериодика»
117997, Москва, ул. Профсоюзная, 90
E-mail: fizmat@maik.ru, fmlsale@maik.ru
http://www.fml.ru
Отпечатано с диапозитивов
в ОАО «Чебоксарская типография № 1»
428019, г. Чебоксары, пр. И. Яковлева, 15
ISBN 5-9221-0474-8
9 78592204746