Текст
Г Г Малинецкий
А. Б. Потапов
СОВРЕМЕННЫЕ
ПРОБЛЕМЫ
НЕЛИНЕЙНОЙ
ДИНАМИКИ
Эдиториал УРСС • Москва • 2000
Настоящее издание осуществлено при финансовой
поддержке Российского фонда фундаментальных
исследований (проект № 98-01-14092)
Малинецкий Георгий Геннадьевич, Потапов Алексей Борисович
Современные проблемы нелинейной динамики. — М.: Эдиториал УРСС,
2000. - 336 с.
ISBN 5-8360-0110-3
В книге рассматриваются некоторые ключевые проблемы современной нелиней-
нелинейной динамики. Концепция авторов сводится к тому, что принципиальные трудности,
с которыми столкнулся этот междисциплинарный подход, требуют новой парадигмы.
В книге сделана попытка наметить ее возможные контуры. На смену эре диссииативны.х
структур и эре динамического хаоса должна прийти новая эпоха. Если многие кон-
концепции и базовые математические модели ранее приходили в синергетику из физики,
химии, гидродинамики, то теперь их основными поставщиками становятся нейронаука,
теория риска, биология, теоретическая история, психология и другие области, свя^иные
с анализом сложных необратимо развивающихся спаем.
Обсуждается ряд оригинальных результатов, касающихся математического моде-
моделирования нелинейных явлении и анализа временных рядов. Большое внимание уделено
таким бурно развивающимся и синергетике подходам как теория инершгальных много-
многообразий, реконструкции аттракторов, теория русел и джокеров, теория нейронных сетей.
Это делает книгу интересной для специалистов в нелинейной динамике и смежных
областях.
Более чем двадцатилетнее развитие синергетики заставляет подвести предвари-
предварительные итоги и заново оценить основные идеи, модели, концепции, отредактированные
в ходе большого пройденного пути, осмыслить «язык» нелинейной науки. Этому по-
посвящена значительная часть книги, что делает ее полезной широкому кругу студентов,
аспирантов и всем, кто хочет ознакомиться с конкретным математическим содержанием
нелинейной динамики.
Группа подготовки и мания:
Директор — Доминго Марин Рикой
Заместители директора — Наталья Финогеиова, Ирина Макеева
Компьютерный дизайн — Виктор Романов
Верстка — Наталия Бекетова
Редакционно-корректурные работы — Елена Кудряшова, Анлрей Стулов
Обработка графики — Елена Ефремова
Обработка текста — Евгений Макаров
Техническая поддержка — Наталья Аринчева
Издательство «Эдиториал УРСС". 113208, г. Москиа. ул. Чертановская, д. 2/11, к.м.
Лицензия ЛР №064418 от 24.01.96 г. Гигиенический сертификат ма выпуск книжной
продукции №77.ФЦ.Х.953.И.270.3.99 oi 30.03.99 г. Подписано к печаш 10.05.2000 г.
Формат 60x88/16. Тираж 1000 Ж1. Печ. л. 21. Зак. № 2 .
Oi печатано в АООТ «Политсх-4». 129110, [. Москва, ул. Б. Переяславская, 46.
785836 001100 >
ISBN 5-8360-0110-3
© Г. Г. Малинецкнй,
А. Б. Потапов, 2000
© Эдиториал УРСС. 2000
Содержание
Глава 1. Предисловие, или игры со сложностью б
1.1. Время оправдывать надежды 7
1.2. Новая парадигма. Внешнее оправдание 15
1.3. Логика нелинейной динамики 25
ЧАСТЫ
Нелинейная динамика и хаос: основные понятия
Глава 2. Язык нелинейной динамики 37
2.1. От истории к современности. Взгляд с птичьего полета ... 37
2.2. Простое и сложное поведение 42
2.3. Порядок в хаосе 45
2.4. Прообразы динамического хаоса — 1. Сдвиг Бернулли ... 49
2.5. Прообразы динамического хаоса — 2.
Проблема турбулентности. Лоренц, Рюэль и Такенс 50
2.6. Прообразы динамического хаоса — 3.
Небесная механика, Пуанкаре и «подкова Смейла» 56
Глава 3. Динамические системы и нх устойчивости 60
3.1. Что такое динамическая система? 60
3.2. Уравнения движения и отображение ?>'(") 62
3.3. Инвариантные множества 64
3.4. Простейшие инвариантные множества и их устойчивость . 65
3.5. Асимптотическое поведение, физический смысл
и разнообразные устойчивости 72
Глава 4. Бифуркации неподвижных точек динамических систем 86
4.1. Что такое бифуркация? 86
4.2. Теорема о центральном многообразии: выделение
существенных размерностей для анализа бифуркации .... 89
Глава 5. Инвариантная мера динамических систем 102
5.1. Откуда приходит случайность? 102
5.2. Инвариантная мера и уравнение Перрона—Фробениуса . . 104
5.3. Неразложимые, или эргодические, меры 109
5.4. Устойчивость и сходимость мер 111
5.5. Несколько важных теорем 112
5.6. Примеры непрерывных инвариантных мер 114
5.7. Численное исследование мер. Гистограммы 115
5.8. Динамические системы с шумом 117
5.9. Шум и «физическая мера» 118
5.10. Заключение. Зачем нужна инвариантная мера 119
Содержание
ЧАСТЬ II
Нелинейная динамика: подходы, результаты, надежды
Глава 6. Параметры порядка и ииерциальные многообразия *22
6.1. Самоорганизация '^2
6.2. Инерциальные многообразия,
оценка размерности аттрактора 127
Глава 7. Жесткая турбулентность ее упрощенные модели 148
7.1. Кратко об истории 148
7.2. Как выглядят пики жесткой турбулентности в QTDGL ... 150
7.3. Нелинейное уравнение Шредингера
и его автомодельные решения 152
7.4. Автомодельная обработка
и приближение «замороженной формы»:
упрощенная модель ограничения пика по высоте 154
7.5. Макроскопическое описание жесткой турбулентности . . . 157
7.6. О возможном статистическом описании жесткой
турбулентности 159
7.7. Жесткая турбулентность и переключающая
перемежаемость 161
7.8. Чем интересна жесткая турбулентность? 169
Глава 8. Нейронные сети 171
8.1. Нейронаука 171
8.2. Элементарные представления о работе мозга 173
8.3. Модель Хопфилда 176
8.4. Смысл хаоса 184
8.5. Многослойные нейронные сети 191
Глава 9. Энтропии и размерности аттракторов 204
9.1. Энтропия динамической системы 204
9.2. Размерности аттракторов динамических систем 207
Глава 10. Ляпуновские показатели 218
10.1. Устойчивость и показатели Ляпунова 218
10.2. Мультипликативная эргодическая теорема 224
10.3. Некоторые свойства ляпуновских показателей 228
10.4. Связь ляпуновских показателей
с другими характеристиками 230
10.5. Как вычисляют ляпуновские показатели? 232
Глава 11. Реконструкция аттракторов по временным рядам 239
11.1. Временные ряды и их обработка 239
11.2. Статистические методы обработки 240
11.3. Идея реконструкции аттрактора. Теорема Такенса 244
11.4. Выбор параметров реконструкции 249
Глава 12. Обработка временных рядов —
важнейшие алгоритмы нелинейной динамики 258
12.1. Расчет фрактальной размерности аттрактора 259
12.2. Свойства корреляционного интеграла.
Оценка энтропии и другие полезные применения 262
Содержание 5
12.3. Предсказание временных рядов 270
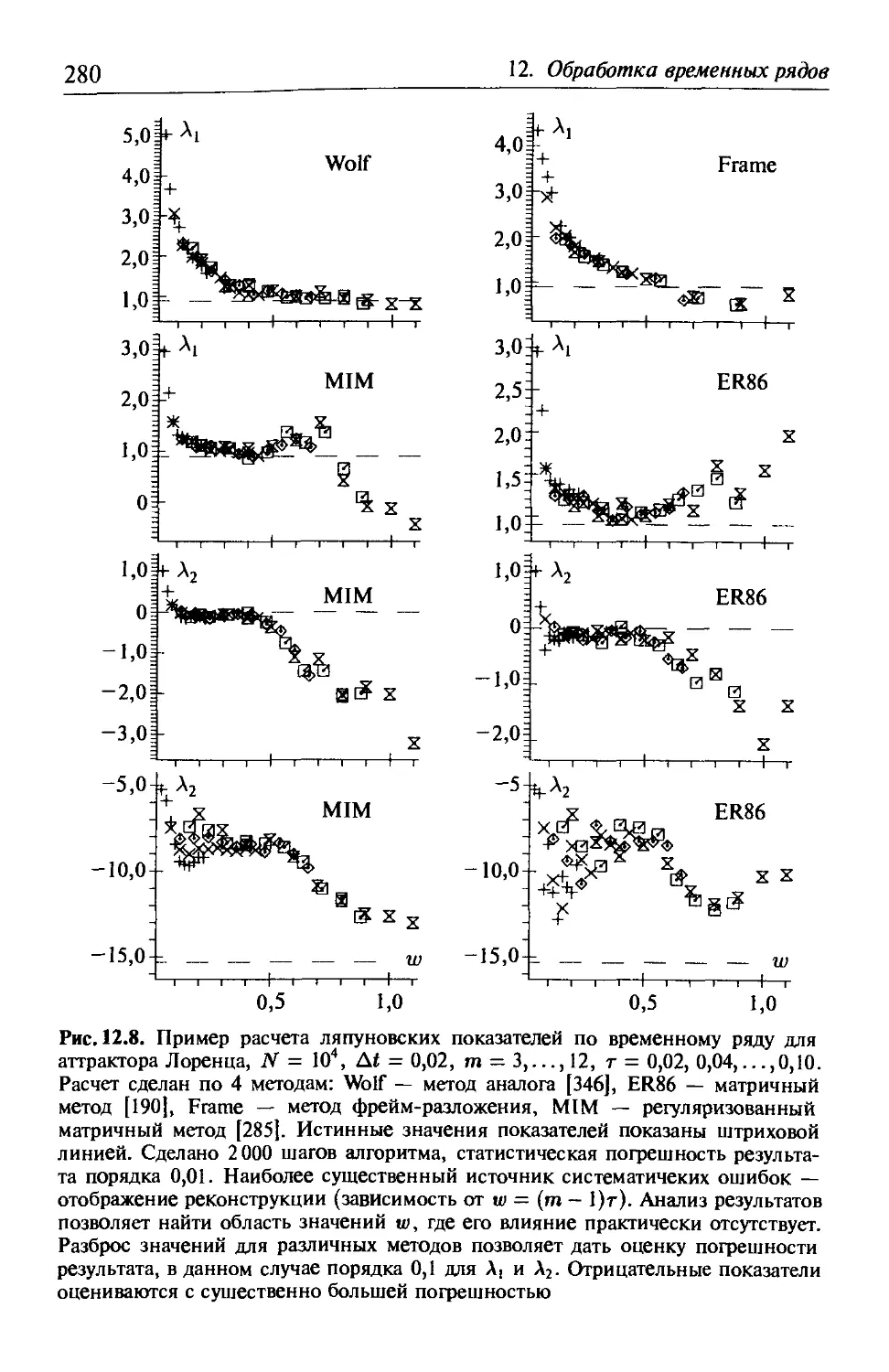
12.4. Оценка ляпуновских показателей по временному ряду . . . 275
12.5. Заключение. Что дали алгоритмы нелинейной динамики? . 281
Глава 13. Когда применимы алгоритмы нелинейной динамики? 283
13.1. Проклятие размерности 283
13.2. Порог фрактальности и трудности реконструкции 285
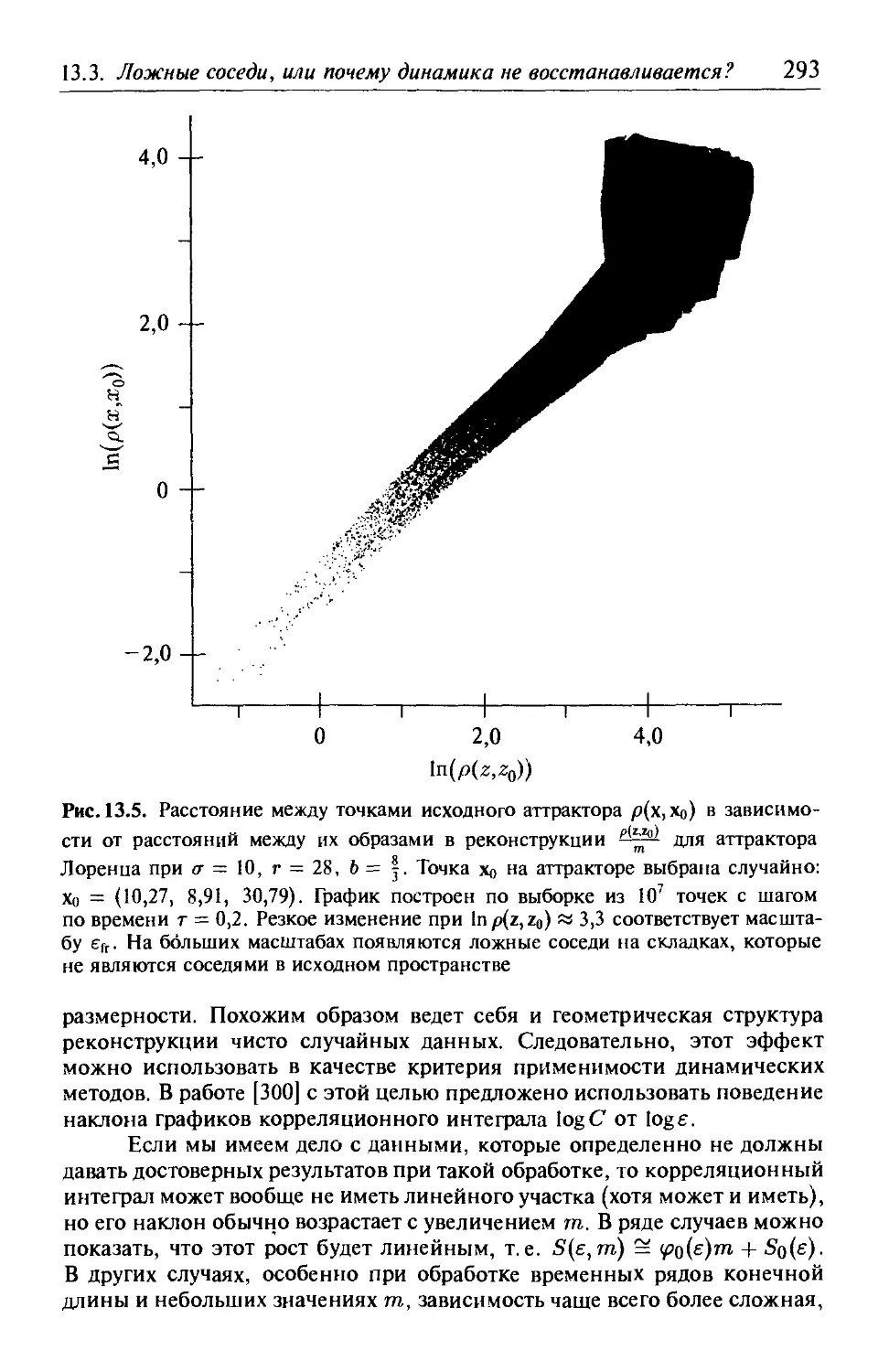
13.3. Ложные соседи, или почему динамика
не восстанавливается на больших масштабах? 289
13.4. Алгоритмы нелинейной динамики для временных рядов
как способы решения некорректной задачи 294
Глава 14. Русла и джокеры, или как сопрячь динамику со статистикой? . . . 298
14.1. Прогнозирование сложной динамики:
почему мозг может, а реконструкции — нет? 299
14.2. Предикторы и трехслойные нейронные сети 300
14.3. Когда сложная динамика может быть предсказуема?
Русла и джокеры 301
14.4. Как искать русла? 304
14.5. Что находится в конце русла? 305
14.6. Модельный пример 305
14.7. Выводы и гипотезы 309
Задачи 312
Список литературы 317
Предисловие,
или игры со сложностью
Игру нельзя отрицать. Можно отрицать почти
все абстрактные понятия: право, красоту, истину,
добро, дух, Бога. Можно отрицать серьезность.
Игру — нельзя.
Й. Хейзинга. Homo Ludens
Эта книга посвящена ключевым концепциям и нескольким новым
идеям нелинейной динамики — широко обсуждаемого и используемо-
используемого междисциплинарного подхода. Естественно было бы в начале книги
упомянуть предшествующие работы и перейти к анализу конкретных
проблем и теорий. Однако состояние области исследований, все чаще на-
называемой нелинейной наукой, и ее перспективы, на наш взгляд, требуют
вначале обратить внимание на некоторые общие вопросы. Это позволит
увидеть за отдельными деревьями лес, оценить место обсуждаемых задач
в общем контексте, развеять иллюзию ясности, простоты и оптимизма
там, где для этого нет оснований.
Легко и приятно писать про новую, молодую научную дисциплину,
которая может с легкостью раздавать обещания, делиться надеждами,
не задумываться о своих пределах, внутренней логике, принципиальных
ограничениях. Именно в таком стиле обычно писали о синергетике —
теории самоорганизации — и нелинейной динамике в последние двадцать
лет [7], [10], [11], [18], [28], [40], [41], [42], [68], [77], [76], [92], [93[, [94],
[95], [104], [108], [119], [125], [133]. Однако положение дел меняется.
Нелинейная наука выглядит сейчас как общепризнанная, перспек-
перспективная, респектабельная область. Регулярно проводятся десятки научных
конференций, шпрингеровская серия по синергетике подошла к сто-
стотомному рубежу. Портфели журналов «Physica D. Nonlinear Phenomena»,
«Nonlinearity», «Chaos», «Прикладная нелинейная динамика», «Physical Re-
Review ?» и других изданий, целиком посвященных нелинейной науке,
заполнены научными материалами. «Успехи физических наук», «Журнал
экспериментальной и теоретической физики», «Успехи математических
наук» и «Журнал вычислительной математики и математической физи-
физики», не говоря уже о «Physical Review Letters», «Physics Letters», «Journal of
Statistical Physics», охотно публикуют «нелинейные» статьи.
Специалисты по синергетике входят в моду и становятся популяр-
популярны. Их приглашают журналисты и банкиры, политики и администраторы.
Даже в «Парке юрского периода» глубокая мысль о том, что прежде чем
1.1. Время оправдывать надежды
что-то сделать, надо хорошенько подумать, вложена в уста специалиста
по нелинейной динамике. Главные синергетики регулярно собираются
на «рабочие группы» и обсуждают, как выращивать юных синергетиков.
Несмотря на все это, идеи, методы и алгоритмы нелинейной ди-
динамики иногда успешно применяются в радиоэлектронике, медицине,
биофизике, химических технологиях, психологии и еще в десятках других
областей. Можно надеяться, что этот очень полезный для любого междис-
междисциплинарного подхода рост «вширь» будет продолжаться еще много лет.
Однако рост «вглубь» столкнулся с серьезными трудностями, которые сей-
сейчас представляются принципиальными, а не техническими. Посмотрим
на них «с птичьего полета», отвлекаясь от множества конкретных деталей.
1.1. Время оправдывать надежды
Анри Пуанкаре в начале века обратил внимание на то, что в разви-
развитии большинства наук наблюдается два противоположных процесса. То
вдруг исследования позволяют увидеть за сложностью, многообразием,
обилием фактов и гипотез внутреннюю логику, ясность и простоту (ти-
(типичный пример из истории науки — возникновение химии из алхимии).
То вдруг за простейшими, очевидными, твердо установленными вещами
обнаруживается глубина и сложность. Наверно, возраст любого научного
подхода можно оценивать по числу таких поворотов. Два таких поворота
можно увидеть и в нелинейной динамике.
Грубо в предшествующем развитии синергетики можно выделить
два периода, две парадигмы. Первый период условно можно назвать
«эпохой диссипативных структур». В эту эпоху удивлялись, начиная
с А.Тьюринга [341], тому, что сложные системы могут вести себя просто.
В пространственно-распределенных системах, потенциально обладающих
бесконечным числом степеней свободы, происходит самоорганизация —
выделение небольшого числа переменных, параметров порядка, опреде-
определяющих динамику всей системы.
Основное понятие синергетики — самоорганизацию — можно
пояснить с помощью следующей простой картинки (рис. 1.1). Пусть
в начальный момент времени пространственное распределение какой-
нибудь интересующей нас величины определяется сложной «изрезанной»
функцией и(х), например, такой, как показано на рис. 1.1а (слева).
«Сложность» и «изрезанность» может быть выражена на языке предста-
вления Фурье: и(х) = Y2 а* cos ( пг ) • Они связаны с тем, что значения
*=о v '
многих коэффициентов Фурье а* (амплитуды гармоник, как их называют
физики) близки по величине.
В процессе эволюции, благодаря вязкости, теплопроводности или
каким-то другим процессам, неоднородности и резкие перепады сглажи-
сглаживаются и может возникнуть намного более простой профиль, например,
показанный на рис. 1.15 (справа). Его «простота» выражается в том, что
он достаточно точно определяется совсем небольшим числом Фурье-
1. Предисловие, или игры со сложностью
20 fc
Рис. 1.1. Иллюстрация понятия «самоорганизация»
коэффициентов а*. Именно их в этом случае и называют параметрами
порядка. Во-первых, потому, что они достаточно точно характеризу-
характеризуют возникшую упорядоченность, а во-вторых, потому что их немного.
Уменьшение числа существенных переменных, спонтанно происходящее
в процессе эволюции, вначале и стали называть самоорганизацией.
Любимые символы эпохи — система «реакция—диффузия», не-
неустойчивость Тьюринга, ячейки Бенара, проблема морфогенеза, модель
брюсселятора, спиральные волны. (Читателя, который впервые читает
книгу по синергетике, не должны смущать эти названия. С заоблачных
высот мы скоро спустимся на землю и обсудим основные понятия после-
последовательно и подробно.) В этот период за такими явлениями, как возник-
возникновение колебательных химических реакций или спонтанное появление
упорядоченности в открытых гидродинамических системах, в задачах
физики плазмы, в нелинейной оптике и динамике популяций, удалось
увидеть общие механизмы. Их описание было дано с помощью близких
моделей и одних и тех же математических структур. За внешним мно-
многообразием и сложностью открылась общность и внутренняя простота.
Оказалось, что о многих открытых, далеких от равновесия системах следу-
следует спрашивать, «что произойдет в конце концов на больших характерных
1.1. Время оправдывать надежды
временах?» Математическими образами таких устойчивых, предельных
режимов явились притягивающие множества в фазовом пространстве
или аттракторы. При этом простейшим аттракторам — неподвижным
точкам — соответствуют стационарные, не меняющиеся со временем
структуры, более сложным — предельным циклам — различные периоди-
периодические, волновые режимы.
Принципиальным оказалось наличие диссипативных процессов
(вязкости, диффузии, теплопроводности). Они позволяли исследуемым
системам «забыть» начальные данные и независимо от их «деталей» сфор-
сформировать с течением времени одни и те же или похожие стационарные
распределения изучаемых переменных. Иными словами, немного (а ино-
иногда и сильно) изменив начальный профиль, в конце мы обычно получаем
то же самое стационарное распределение переменных. Чтобы подчеркнуть
это обстоятельство, данные структуры, с легкой руки И. Р. Пригожина,
стали называть диссипативными структурами.
Типичная постановка задачи в этот период — выяснить, как ме-
меняется число и конфигурация возникающих структур при изменении
какого-нибудь внешнего параметра и начальных данных. Эту задачу ста-
стали называть построением бифуркационной диаграммы. При этом под самим
термином бифуркация подразумевали изменение числа или устойчивости
решений определенного типа. Простота заключалась в том, что
— упрощенными математическими моделями различных процессов
оказались одни и те же уравнения;
— хотя процессы в исследуемых системах разворачивались во времени
и в пространстве и описывались уравнениями в частных производ-
производных, качественное поведение удавалось понять с помощью про-
простейших динамических систем (обычно с помощью одного-двух
обыкновенных дифференциальных уравнений);
— множество различных нелинейных процессов и неустойчивостей
оказались воплощением одних и тех же простейших бифуркаций.
Математическим аппаратом нелинейной динамики на этом этапе
были качественная теория и теория бифуркаций динамических систем
на плоскости. Эти разделы математики интенсивно разрабатывались с на-
начала века и к 70-м годам были хорошо поняты научным сообществом.
Они долго и успешно применялись в теории колебаний [2, 3]. Это, не в
последнюю очередь, обеспечило первые успехи синергетики и быстро
пришедшую к ней популярность.
Синергетика развивалась настолько быстро и успешно, что за ка-
какие-то 5-7 лет превратилась из занятия физиков-теоретиков в объект
интереса ученых из разных областей естественных наук, инициирова-
инициировала постановку ряда оригинальных экспериментов. Однако со временем
выяснилось, что число систем, где можно наблюдать «в сравнительно
чистом виде» предсказываемые диссипативные структуры, весьма неве-
невелико. Более того, поиск диссипативных структур во многих интересных
физических системах, не говоря уже о прикладных задачах, зачастую тре-
требовал учета многих других усложняющих картину явлений, нелинейных
1. Предисловие, или игры со сложностью
эффектов. Явления, аналогичные в главном, на качественном уровне,
оказывались различными в деталях, что обнаруживалось при более глу-
глубоком и точном исследовании.
Прежде чем взглянуть на вопросы, которые оставил в наследство
этот этап развития, и пойти дальше, мы хотим предостеречь читателя.
Как-то один студент объяснил авторам этой книги, что «синергетики
уже прошли диссипативные структуры и сейчас надо заниматься другими
задачами». Пришлось напомнить ему про известный разговор Эйнштей-
Эйнштейна со школьницей. Девочка выразила искреннее удивление, что такой
взрослый дядя может заниматься физикой, которую они уже прошли год
назад. Вопрос, что «прошла» данная область науки, а что — нет, совсем
не так очевиден, как казалось нашему собеседнику.
Например, сейчас многие области физики «открывают для се-
себя» явление самоорганизации и процессы формирования диссипативных
структур. В частности, многие эксперты полагают, что создание приборов
с использованием нанопроводов, оптико-электронных систем на кван-
квантовых точках, одноэлектронных приборов потребует нового поколения
технологий, использующих пространственную самоорганизацию, само-
самоформирование и другие нелинейные эффекты [1, 27, 52, 74]. Открытое
и объясненное в последние годы в лазерной термохимии явление возник-
возникновения стержневых структур при движении по поверхности окисляюще-
окисляющегося материала лазерного луча постоянной интенсивности также находит-
находится в рамках обрисованной парадигмы нелинейной динамики [60]. Сюда
можно отнести и недавно появившиеся задачи — проекты ускорения эле-
элементарных частиц в кильватере мощной электромагнитной волны [22].
Или теорию мощных атмосферных вихрей, объясняющую нелинейные
эффекты, наблюдавшиеся при столкновении кометы Шумейкера—Леви
с Юпитером в 1994 г. [58]. Прекрасно, что об этих явлениях можно
говорить на языке, десяток лет назад выработанном нелинейной ди-
динамикой, опираться на сформулированные ранее понятия и базовые
математические модели. Более того, успешная реализация какого-либо
из упомянутых проектов может изменить и само направление нелиней-
нелинейной динамики, поставить новые фундаментальные задачи. И с этой точки
зрения, самоорганизацию, диссипативные структуры, параметры порядка
никак нельзя назвать «пройденным материалом».
Однако специалистов по синергетике, как, вероятно, и теоретиков
в других областях, интересует прежде всего, до каких пределов можно
продвинуться в ранее выбранном направлении и где нужны новые идеи
и теории.
Эра диссипативных структур оставила в наследство нелинейной
науке несколько сложных вопросов.
Каковы условия самоорганизации? При каких условиях процессы
в нелинейных средах, описываемые уравнениями в частных производных,
в строгом смысле, а не на физическом уровне строгости, определяются
конечномерной динамической системой (скажем, системой конечного
числа обыкновенных дифференциальных уравнений)? Какие переменные
в конкретных случаях оказываются параметрами порядка?
1.1. Время оправдывать надежды 11
Ответ на сформулированные вопросы и строгое обоснование кон-
концепции параметров порядка стали одним из главных успехов последнего
десятилетия. Этот ответ, который дает теория инерциальных многообра-
многообразий, мы обсудим в настоящей книге.
Можно ли построить содержательную качественную теорию систем
параболических уравнений, например, типа реакция—диффузия
щ -D\uxx + f(u,v),
vt = D2vxx+g(u,v),
O^x^l, u(x,0) = ио(х), v(x,0) = vq(x), [)
Мг,"х|х=<У = 0
по аналогии с качественной теорией систем обыкновенных дифферен-
дифференциальных уравнений
x = f(x,A), x = (xl,...,xN),
х@) = хо, A2)
которая (например, при N — 2) определяет типы аттракторов, типичные
бифуркации и т.д.?
На важность этой задачи, позволяющей представлять свойства ре-
решений дифференциальных уравнений в частных производных, не решая
их, указывал Р. Фейнман. Он связывал ее с будущей эрой пробуждения
человеческого разума [122]. Поскольку почти все фундаментальные физи-
физические теории, начиная с электродинамики, теории упругости, квантовой
механики, гидродинамики сформулированы на языке этих уравнений,
проблему их качественного исследования трудно переоценить.
Большие усилия, вложенные в построение качественной теории
нелинейного уравнения теплопроводности
21 = div (fc(T)gradT) + Q(T), A.3)
показали, что и здесь продвижение является очень трудным [311, 129].
Качественная теория, отражающая в основном эффекты, давно понятые
с помощью компьютерного моделирования, потребовала новых матема-
математических идей, существенно опирающихся на то, что мы имеем дело
с одной переменной Г, а не с их набором.
Одной из надежд, возлагавшихся на нелинейную науку, был вывод
и анализ фундаментальных уравнений. Например, В. Гейзенберг полагал,
что такое уравнение может дать спектр масс элементарных частиц. Ряд
принципиальных нелинейных уравнений, среди которых, в частности,
уравнение A.3), выдвигался и в других областях [72, 112, 142, 311]. Тео-
Теоретическое исследование развитой турбулентности также часто сводится
к анализу уравнения Навье—Стокса при больших числах Рейнольдса. Эти
задачи часто оказывались связаны с построением сложных стационарных
или автомодельных решений, анализом решений, время существова-
существования которых ограничено, либо с изучением задач с малым параметром
при старшей производной. При этом аналитические методы, как пра-
правило, не позволяют строить такие решения и приходится прибегать
12 1. Предисловие, или игры со сложностью
к компьютерному моделированию. Однако «перевод» дифференциальных
уравнений и гладких функций на дискретный язык оказался также доста-
достаточно сложной процедурой. Сложность зависит от того, какие свойства
дифференциальных уравнений мы хотим передать в дискретной модели.
И стандартные приемы — разностные схемы, например, консерватив-
консервативные (в которых выполняются аналоги законов сохранения [110]), или
спектральные методы — часто оказываются неэффективными. В качестве
типичного примера можно привести классические нелинейные уравне-
уравнения — уравнение Кортевега—де Фриза щ + иих + иххх = 0 и кубическое
уравнение Шредингера iipt = ipxx — \ip\2ip, возникшие соответственно в
теории волн на поверхности воды и в нелинейной оптике. Показано, что
каждое из этих уравнений имеет бесконечное число законов сохранения.
Последнее объясняет замечательные качественные явления, описываемые
этими уравнениями. Однако до сих пор не предложен алгоритм построе-
построения разностных схем, имеющих заданное число законов сохранения для
данных уравнений. Более сложные методики, например, использующие
адаптивные сетки [38] или схемы, наследующие алгебраическую структу-
структуру исходных уравнений [188], также требуют ясных представлений о том,
что мы хотим увидеть. Но именно это, как правило, и хочется узнать.
Один из подходов, на наш взгляд, связан с уточнением постановок
ряда задач, с расширением класса используемых моделей. К примеру,
с описанием ряда явлений на языке клеточных автоматов, дифференциа-
дифференциально-разностных уравнений и т.д. Некоторые из открывающихся здесь
возможностей мы обсудим в этой книге.
Построение бифуркационной диаграммы и нахождение зависимо-
зависимости решений от параметров потребовало разработки достаточно сложного
аппарата [57] и создания целого арсенала различных численных методов.
Однако есть и принципиальные трудности. Если в случае простейших
стационарных или периодических решений можно четко и ясно опреде-
определить, что такое бифуркация и чем одно решение отличается от другого, то
для многих более сложных аттракторов это представляет собой открытую
проблему.
Следующий период в развитии нелинейной динамики условно можно
назвать периодом динамического хаоса. В эту эпоху удивлялись тому,
что простые динамические системы могут вести себя сложно. Исходя
из анализа простейших динамических систем с несколькими степенями
свободы, были поняты принципиальные ограничения на получение ди-
динамического прогноза [116]. Это позволило поставить задачу определения
пределов предсказуемости для различных нелинейных процессов [103].
На рубеже XIX века великий французский математик и астроном
П.Лаплас утверждал, говоря современным языком, что располагая до-
достаточно мощной вычислительной техникой, можно заглянуть вперед
и назад как угодно далеко. Нелинейная динамика показала, что это
не так, и помогла оценить горизонт прогноза для конкретных систем.
Другими словами, одним из ключевых понятий на этом этапе стала
чувствительность к начальным данным — экспоненциальное (в среднем)
разбегание двух бесконечно близких траекторий для класса хаотических
1.1. Время оправдывать надежды 13
аттракторов (см. рис. 1.2). Скорость
этого разбегания определяется стар-
старшим ляпуновским показателем, а ско-
скорость «расползания» большого количе-
количества бесконечно близких траекторий —
колмогоровской, или метрической эн-
энтропией динамической системы. В силу у - ^—хц+\
чувствительности к начальным данным "-"""^
нельзя сравнивать траекторию объекта
и модели (пусть даже идеальной) «по-
«поточечно», на одни и те же моменты „ , , „
' , Рис. 1.2. Одно из ключевых поня-
времени - сколь угодно малая ошиб- тии _ чувствительность к началь.
ка в начальных данных будет экспо- ным данным — экспоненциальное
ненциально нарастать и спустя некото- (в среднем) разбегание двух беско-
рое время мы обнаружим, что модель нечно близких траекторий для клас-
в сравнении с объектом «пошла другим са готических аттракторов
путем». Поэтому либо приходится ограничиваться кратковременными
прогнозами, либо изыскивать адекватные способы сравнения поведения
модели и объекта. Одним из них может быть использование некоторых
функционалов от траектории, так называемых количественных характе-
характеристик хаоса. И. Пригожий и И.Стенгерс [105], например, полагают, что
для хаотических систем «траектория» есть величина невоспроизводимая,
а потому несущественная, а важной и измеримой характеристикой ста-
становится вероятность обнаружения траектории в той или иной области,
т. е. инвариантная мера динамической системы.
В центре внимания исследователей оказались методы анализа вре-
временных рядов, проблема сравнения теории и эксперимента, задачи по-
построения прогнозирующих систем, определение законов движения объ-
объекта по ряду наблюдений.
И здесь вновь возникло несколько глубоких принципиальных во-
вопросов. Из них наиболее важными представляются следующие (к ним мы
будем не раз возвращаться в этой книге).
Алгоритмы определения количественных характеристик хаоса, по-
построения предсказывающих систем, извлечения динамики из ряда на-
наблюдений достаточно «капризны». Они требуют большой выборки весьма
точных измерений предшествующих состояний объекта. Живые существа
такими данными для обучения не располагают, поэтому неясно, как им
удается эффективно ориентироваться в быстро меняющейся обстановке.
Это особенно удивительно, когда предшествующий опыт невелик и ранее
не было возможности действовать методом проб и ошибок. Другими сло-
словами, у нас возник класс задач, очень сложный для компьютеров (или,
по крайней мере, для разработчиков алгоритмов) и сравнительно легко
решаемый биологическими объектами.
С другой стороны, большинство алгоритмов анализа данных, ис-
использующих представления нелинейной динамики, эффективны, когда
размерность фазового пространства системы невелика. Как заметил один
14 1- Предисловие, или игры со сложностью
известный специалист, «все алгоритмы хорошо работают только для си-
системы Лоренца». Как следует действовать в случае систем большой раз-
размерности? Как продвинуться от простейших модельных задач теории
динамического хаоса к реальности?
Символами этой эпохи стали логистическое отображение, система
Лоренца, канторово множество, теория универсальности.
Возникло странное противоречие между красивыми и ясными об-
общими представлениями нелинейной динамики и трудностью приложе-
приложения развитых алгоритмов и теорий к исследованию многих открытых
нелинейных систем. Противоречие гораздо более острое, чем в физике
или химии. За простоту и общность идей синергетики сейчас прихо-
приходится платить высокую цену. От «теории всего» — каковой некоторые
гуманитарии представляют себе синергетику — не приходится ждать
конкретных результатов и методов. Сложившуюся ситуацию можно по-
пояснить, исходя из тринитарного подхода, развиваемого в нашей стране
Р. Г. Баранцевым [12]. В соответствии с ним достаточно сложные объекты
не укладываются в черно-белую схему дуальных категорий (горячо-
холодно, плохо—хорошо), а требуют привлечения триад (например,
рацио—эмоцио—интуицио, простота—точность—область приложимости
и т.д.). При этом одна категория выступает в качестве своеобразно-
своеобразного оппонента двух других. Например, чем больше простота и шире
область приложений, тем меньше точность и конкретность. Это имен-
именно та ситуация, с которой столкнулась синергетика. Ряд исследователей
экстраполирует такую тенденцию и всерьез полагает, что синергетика
должна получить статус философской теории, а может быть даже заме-
заменить диалектику. Однако те, кто хочет по-прежнему видеть синергетику
на твердом естественнонаучном основании и полагают, что философия
науки не должна становиться главной частью последней, все чаще скло-
склоняются к мыслям о новой парадигме синергетики, пусть не столь общей
и простой, но зато более конкретной и глубокой.
Одним из главных результатов предшествующего развития нели-
нелинейной динамики, по-видимому, является создание «языка», на котором
можно описывать многие нелинейные явления. К нему следует отнести
новые понятия, вобравшие в себя опыт исследования многих конкретных
систем — «аттракторы», «диссипативные структуры», «области притя-
притяжения», «кризисы», «режимы с обострением», «параметры порядка»,
«инерциальные формы» и другие. Его частью являются базовые мате-
математические модели — подкова Смейла, отображение Хенона, система
Лоренца, логистическое отображение, уравнение Макей—Гласса и другие
замечательные объекты. Зная, как они устроены, можно предполагать,
как ведет себя исследуемая система. Особенно важен возникший набор
вопросов, которые нелинейная наука советует задавать, исходя из накоп-
накопленного опыта относительно новых явлений. Постановка компьютерных
или натурных экспериментов, исходя из общих представлений, почему
это интересно, очень часто оправдывала себя в последние десятилетия.
Иногда у студентов и аспирантов возникает ощущение, что «ма-
«математики все это давно знали». И действительно, взяв книгу П.Халмо-
1.2. Новая парадигму. Внешнее оправдание 15
ша [126] по эргодической теории или работу Э. Хопфа [23] о рассеивающих
биллиардах, выполненные задолго до эры динамического хаоса, неволь-
невольно удивляешься, как много было известно и впоследствии переоткрыто.
И тем не менее мир прорлем, который открылся с возникновением нели-
нелинейной науки, оказался\гораздо шире тех задач, которые ставили перед
собой предшествующие Математические теории. Нелинейная наука, разу-
разумеется, вбирает их представления и методы, но совсем не сводится к ним.
Во многом это обусловлено широким использованием компьютерного
моделирования. Результаты многих численных расчетов нередко оказы-
оказывались парадоксальны и требовали новых идей и подходов. На их основе
впоследствии удалось получить строгие математические результаты.
Этот язык настолько важен, что в этой книге его «буквам», «сло-
«словам» и «фразам» уделено несколько глав. Рассказывая о сегодняшнем
состоянии нелинейной науки, приходится опираться на эти понятия, а,
заглядывая в будущее, нужно видеть, каких конструкций в нем не хватает.
Хотя «мода» на диссипативные структуры и динамический хаос спадает,
как ни странно, многие вопросы, относящиеся к ним, так и не были
изложены, если не полно, то хотя бы ясно, системно и в одном ме-
месте. Поэтому тех, кто знакомится с синергетикой, часто удивляет, зачем
нужно вводить многие понятия. С другой стороны, часть из того, что
применяется, обычно не поясняют, считая, что читатель или слушатель
все и так прочтет между строк. Некоторые книги, по выражению нашего
коллеги, «вываливают большой объем информации, с которым непонят-
непонятно что делать дальше: то ли стараться немедленно использовать, то ли
поскорее забыть». Поэтому мы постарались в нескольких главах изложить
минимальный скелет основной части нелинейной динамики, выбросив
все, что можно, а также обратить внимание на литературу, в которой
можно уточнить детали.
Специалистов по нелинейной динамике на конференциях послед-
последних лет можно сравнить с театральными режиссерами. Одни спектакли
у них удались и отошли в прошлое, другие играются сейчас, но главные
мысли — о будущем, о следующей парадигме.
Альберт Эйнштейн полагал, что для развития теории нужно «внеш-
«внешнее оправдание» — наличие вопросов о мире, задаваемых «извне», на ко-
которые она должна ответить, и «внутреннее совершенство» — следование
внутренней логике той области, в которой строится теория. По-видимому,
это можно отнести к научным парадигмам.
1.2. Новая парадигма. Внешнее оправдание
Прежде чем определить контуры новой парадигмы нелинейной
динамики, ее возможные сверхзадачи, место в общенаучном контексте,
взглянем на развитие науки в целом.
Прогноз Станислава Лема о замедлении темпов развития науки,
об уменьшении ее социальной роли и об оценке ее обществом, сделан-
сделанный в книге «Сумма технологии» [75], оправдывается. Знание все реже
16 1. Предисловие, или игры со сложностью
связывают с силой, а науку — с производительной силой, как было еще
лет 20 назад. И дело не только в том, что экспоненциальный рост числа
ученых и затрат на науку, имевший место в 60-е годы, стабилизировался
и вести исследования по всему фронту интересных проблем оказалось
невозможно, как и предсказывал Лем. На передний план вышли другие
задачи, иной социальный заказ.
Наука стала важной областью технологии после того, как с конца
прошлого века на ее основе началось стремительное совершенствование
средств защиты и нападения. Радио и компьютеры, самолеты и космиче-
космические корабли развивались и применялись прежде всего в военном секторе
экономики. Однако в большой степени эта задача исчерпала себя, многие
высокоэффективные виды оружия снимаются с вооружения и уничтожа-
уничтожаются, началась «гонка разоружения». Разумеется, противоборство про-
продолжается, но его научная компонента стала гораздо меньше, чем раньше.
С другой стороны, производство товаров и технологий — другой
заказчик науки — тоже изменилось. Ограниченность многих важнейших
ресурсов сейчас диктует отказ от многих товаров, услуг, проектов. По-
видимому, эта тенденция будет нарастать.
При этом возникли новые сферы научной активности. Это широ-
широкий круг проблем, связанный с устойчивостью и безопасностью развития.
Глобальные изменения климата, экологической ситуации, техносферы,
экономики и других ключевых систем показали неготовность современ-
современной науки отвечать на многие кардинальные вопросы. Большинство
из них связаны с коллективным поведением и с прогнозом поведения
сложных систем в различных условиях. Поэтому нелинейная динамика
здесь может сыграть важную роль.
Специализация науки, ее прикладные успехи в XX веке имели
ряд побочных последствий. Возникла своеобразная цеховая раздроблен-
раздробленность — непонимание и незнание специалистами происходящего даже
в смежных областях, отсутствие научной картины мира. Это оказывает
сдерживающее влияние на развитие самой науки — многое переоткры-
переоткрывается в соседних областях, а многие проекты выполняются в контексте,
смысл которого к моменту окончания работы оказывается утраченным.
Отношение к ученым в обществе напоминает взгляд на средневековых
ремесленников, нужных для того, чтобы производить разные товары.
Научные школы все чаще перенимают дух цеховой замкнутости.
Один из создателей квантовой механики Е. Вигнер [30] полагал,
что есть два подхода к научному осмыслению мира, которые предлагают-
предлагаются, соответственно, физикой и психологией, между которыми не может
быть переброшен мост. В такой утрате надежды на построение единой
самосогласованной научной картины реальности он видел одно из прин-
принципиальных ограничений для развития самого научного знания.
Исходя из этого, особенно необходимой становится разработка
междисциплинарных подходов. Поэтому нелинейная динамика, связан-
связанная с поиском единых механизмов в нелинейных явлениях различной
природы, в физических, химических, биологических, социальных си-
системах, выходит на первый план. Единство мира, с точки зрения этого
1.2. Новая парадигма. Внешнее оправдание 17
подхода, проявляете»», в универсальности математических моделей, опи-
описывающих реальность» в возможности построить математическое описа-
описание данного явления с\ различной точностью с помощью одного набора
«кубиков» — базовых Моделей. Поэтому роль нелинейной науки в об-
общенаучном контексте как «языка междисциплинарного общения» может
оказаться очень большой.
В настоящее время цивилизация проходит очень крутой поворот.
Меняются не только политические, экономические, социальные траек-
траектории отдельных стран, этносов, регионов, но и их исторические пути.
Решения, которые принимаются сейчас, могут изменить сценарий раз-
развития, жизнь людей на много поколений вперед. Поэтому ключевой
становится проблема выбора норм, целей, приоритетов, экономических,
социальных, политических и иных технологий.
Цена принимаемых решений здесь очень велика. Например, по
оценкам экспертов, последний кризис обойдется мировой экономике
более чем в триллион долларов. Экономические реформы последних лет
в России привели к тому, что страна, занимавшая второе место в мире
по валовому внутреннему продукту, оказалась на пятнадцатой позиции.
Диапозон управляющих воздействий здесь также очень широк. Ре-
Реализуя идею устойчивого и безопасного развития, Швеция отказывается
от атомной энергетики. Во Франции, где более 70% электроэнергии
вырабатывается на АЭС, форсированное развитие этого сектора эконо-
экономики, напротив, рассматривается как эффективный способ сохранения
окружающей среды.
Возникает принципиальная общая задача построения альтернатив-
альтернативных сценариев развития сложных, необратимо развивающихся систем.
Эти проблемы тем более актуальны, поскольку приходится выбирать
не между хорошим и лучшим, а между плохим и очень плохим вариантом.
Проблема «проектирования будущего», поиска устойчивых и безо-
безопасных траекторий развития имеет непосредственное отношение к не-
нелинейной динамике. В самом деле, социально-технологические объекты
представляют собой сложные иерархические системы, различные процес-
процессы в которых разворачиваются на разных характерных временах. Степень
их неустойчивости, их пределы предсказуемости также различны. В эко-
экономической системе горизонт прогноза резко уменьшился: если еще 15 лет
назад нормой в мире было 5-летнее директивное или индикативное пла-
планирование, то сейчас об этом говорить не приходится. В мире становится
все больше предложение «быстрых денег» и все меньше предложение
«медленных». Но, с другой стороны, устойчивое развитие общества тре-
требует медленно меняющихся стратегических целей, шкалы общественных
ценностей и норм, культуры и идеологии. Нужна техника, теории, фор-
формализм, который позволял бы анализировать возможную динамику таких
«разновременных систем» и на этой основе направлять развитие.
Такие исследовательские программы, получившие название тео-
теоретической истории или исторической механики, активно обсуждаются
в последние годы [59, 88]. История выступает идеальным пилишном
для тестирования, совершенствования и верифскации таких методик.
18 1. Предисловие, илц игры со сложностью
При этом следует отдавать себе отчет, что многие ситуации, альтернати-
альтернативы, возможные решения, возникающие сейчас, являются стандартными,
каноническими, не раз разыгрывавшимися на исторических подмост-
подмостках. В то время как другие оказываются принципиально новыми, где
опираться на исторические аналоги не приходится. Этот круг междисци-
междисциплинарных, «плохо поставленных проблем», связанных с организацией
общества и его перспективами является важнейшим «социальным зака-
заказом» и для нелинейной динамики, и для всей современной науки.
Другая сверхзадача связана с проблемой человека или, как сейчас
часто говорят, с парадигмой нейронауки. XX век показал, что концеп-
концепции просветителей, полагавших, что знание, технологии, информация,
избавят людей от войн, эксплуатации, многих бед и несчастий, были
слишком грубым приближением. Оказалось, что многие «модели челове-
человека», предлагавшиеся гуманитарными науками, неприменимы к нынешней
реальности. Поэтому здесь также возникла потребность использовать ар-
арсенал и методику естественных наук для анализа массового сознания,
задач социальной психологии, социологии, анализа и прогнозирования
индивидуального и коллективного поведения.
Однако человек оказался загадкой не только с социальной, но и
с «технической» точки зрения. В частности, время срабатывания нервной
клетки — нейрона — в миллион раз превышает время такта персонального
компьютера. Скорость передачи информации в нервной системе также
в миллион раз меньше, чем в электронной вычислительной машине.
Кроме того, в отличие от элементов компьютера, нейроны нередко
«выходят из строя за время службы», поэтому возникает сложная задача
перезаписи информации с одних «носителей» на другие. Вместе с тем
такая столь «несовершенная» и «ненадежная» система, как наш мозг,
с легкостью справляется со многими задачами управления движением,
поиска закономерностей, распознавания образов, принятия решений,
которые ставят в тупик суперкомпьютеры. Например, ребенок нескольких
лет от роду свободно отличает кошку от собаки в жизни, на картинке,
по телевизору, хотя конкретного животного, которого ему показывают
сейчас, он раньше никогда не видел. Кроме того, он, не затрудняясь,
заявляет, если необходимо, что показанное ему ни кошкой, ни собакой
не является. Вычислительным машинам это пока недоступно.
Все это говорит о том, что мы в мозге и компьютере, по-видимому,
имеем дело с другими принципами восприятия, передачи, обработки,
анализа информации. При этом важно подчеркнуть, что речь идет не об
уточнении отдельных деталей или интересных подробностях. Пока мы
не располагаем ответами на многие «наивные» вопросы. Каково нейрофи-
нейрофизиологическое значение сна в целом и его отдельных стадий в частности?
Как кодируется информация в нервной системе? Существует ли здесь еди-
единый универсальный «психологический код», по аналогии с «химическим
кодом» (одним набором химических элементов, входящим во все веще-
вещества) или генетическим кодом (одним набором оснований и аминокислот,
используемым всеми живыми организмами)? Какие изменения на ней-
робиологическом уровне происходят при обучении сложным навыкам?
1.2. Новая парадигма. Внешнее оправдание 19
Работа последних десятилетий по математическому и компьютер-
компьютерному моделированию элементов психики, по анализу механизмов са-
самоорганизации в мозге и в нервной системе показали эффективность
междисциплинарного подхода и в этой области. По существу, речь идет
о развивавшейся еше в 30-х годах идее гештальта — целостного обра-
образа, который возникает на основе небольшого набора данных об объекте
(своеобразных параметров порядка) и позволяет домысливать его дру-
другие свойства. В основе парадигмы нейронауки лежит предположение,
что сложное целесообразное функционирование биологических объектов
обусловлено коллективным поведением, взаимодействием простейших
функциональных единиц, например, нейронов. Разным типам решаемых
задач соответствуют различные алгоритмы самоорганизации (способы
установления взаимосвязей между элементами ансамбля, обычно назы-
называемого нейронной сетью или нейрокомпьютером). Анализ этих алгоритмов,
которые использует природа или которые разумно применять в компью-
компьютерных системах (так называемая искусственная психика), представляется
одной из наиболее важных и перспективных задач современной нау-
науки [29, 64, 120].
Следует обратить внимание еще на несколько принципиальных
трудностей, связанных с анализом организма человека и других биоло-
биологических систем, где идеи нелинейной динамики также могут сыграть
большую роль. На возникшую проблему все чаще стали обращать вни-
внимание биофизики и специалисты по математическому моделированию
в биологии. Парадоксальные физические идеи и размерностные оценки,
сделанные Э. Шредингером в книге «Что такое жизнь с точки зрения
физики?» [132], дали мощный начальный толчок биофизическому под-
подходу. Становление «автоколебательной идеологии», в большей степени
связанное с Пущинской научной школой, также помогло многое понять
в поведении биологических систем. При этом замечательные явления
удалось описать и смоделировать, опираясь на поразительно простые,
по нынешним меркам, системы двух или трех обыкновенных дифферен-
дифференциальных уравнений.
Многократное усложнение моделей, ставшее возможным благо-
благодаря быстрому прогрессу вычислительной техники, дало гораздо бо-
более скромные, чем ожидалось, результаты. Зачастую оно не приводило
ни к «пониманию явления», ни к «новым качественным результатам»,
ни к «надежным количественным показателям», близким к тем, которые
можно ожидать на основе натурных экспериментов. Да и сам тезис о том,
что «современная теоретическая биология — это раздел вычислительной
математики», тоже незаметно начал сходить с арены. Обратим внима-
внимание на то, что эта ситуация является общей и для детальных моделей
колебательных химических реакций, и для «продвинутых» моделей фо-
фотосинтеза, и для программ, анализирующих конформацию достаточно
сложных молекул, и для многих других объектов. Все чаще вычислитель-
вычислительный эксперимент занимает в сотни и в тысячи раз больше времени, чем
тот же процесс в реальности.
20 1. Предисловие, или игры со сложностью
На наш взгляд, ситуация очень похожа на то положение, в котором
находилась метеорология до работы Э. Лоренца, когда неувязки со сред-
среднесрочным прогнозом погоды относили к тому, что в лаборатории стоит
не последняя, а только предпоследняя модель компьютера, и к тому,
что сотрудники недостаточно изобретательны, а аспиранты не слишком
трудолюбивы.
Все упомянутые системы обладают отличительной общей чертой,
не позволяющей их упрощать, пользуясь стандартными приемами. Они
в определенных случаях могут функционировать в режиме гигантских
усилителей. Например, при повреждении стенки кровеносного сосуда
включается цепь химических реакций, скорости которых на пять порядков
превышают характерные скорости для реакций, текущих в норме.
Наличие таких усилителей приводит к ряду очевидных особенно-
особенностей таких систем.
— Весьма высокая избирательность и чувствительность к воздействиям
определенного типа. Иначе система просто не могла бы работать,
если бы усиливалось слишком много сигналов. Может быть, с этим
связаны эффекты сверхмалых концентраций и доз, аномальная
чувствительность к изменениям солнечной активности, слабым
электромагнитным и звуковым полям в определенных диапазонах.
— Принципиальная роль нелинейных эффектов. Любой сигнал, после
того как он усилен до значительной величины, должен быть стаби-
стабилизирован, ограничен, скомпенсирован.
— Коллективные эффекты при наличии мощных механизмов поло-
положительной обратной связи приводят к тому, что явления, харак-
характерные для одного уровня организации материи, могут проявляться
на другом. Типичный пример такого поведения — лазер, в котором
законы квантовой механики, описывающие «в нормальных услови-
условиях» только динамику микрочастиц, определяют макроскопическое
поведение.
С точки зрения поиска новых явлений на границе между раз-
различными уровнями организации, особый интерес представляет теория
сознания, выдвинутая известным математиком и физиком-теоретиком
Р. Пенроузом в его последней книге «Тени сознания» [291]. В соответ-
соответствии с этой теорией, в основе сознания лежит невычислимый процесс.
Другими словами, не существует алгоритма, логического, детерминиро-
детерминированного или вероятностного, с помощью которого можно было бы решать
те же задачи, которые приходится иногда решать нашему сознанию.
Несуществование таких алгоритмов для ряда математических задач
ранее было доказано. Например, такой задачей является проблема замо-
замощения плоскости без пробелов и наложений набором плиток заданной
формы. В принципе не может быть построен алгоритм, на вход кото-
которого можно было бы подать набор плиток, а на выходе получить ответ,
разрешима ли задача замощения для этого набора.
Если бы гигантский компьютер был приемлемой моделью для на-
нашего мира или сознания, то тогда места для невычислимости бы не было.
1.2. Новая парадигма. Внешнее оправдание 21
Квантовомеханическое рассмотрение (компьютеры, в которых детерми-
детерминированным образом меняются не сами состояния, а вероятности найти
систему в разных состояниях) не меняет этого вывода.
Чтобы гипотеза невычислимости работала, должны быть парадок-
парадоксальные, неисследованные явления на границе между разными уровнями
организации. Р. Пенроуз видит их на границе, где квантовые свойства
объектов меняют классическое макроскопическое поведение. Хрестома-
Хрестоматийный пример — классический опыт по дифракции электрона на двух
щелях, в результате которого на экране за щелями возникает характерная
дифракционная картина. При движении к экрану электрон обладает вол-
волновыми свойствами и описывается ^-функцией; сталкиваясь с экраном,
он «становится» классической частицей. Происходит редукция, приво-
приводящая к «уничтожению» квантовых свойств микрообъекта и появлению
классических. Эту редукцию естественно назвать «субъективной», по-
поскольку она связана с процедурой наблюдения, со взаимодействием
микрообъекта с макроскопическим прибором.
Р. Пенроуз предположил, что существует и другое явление, которое
играет принципиальную роль в феномене сознания и придает невычи-
невычислимость ряду мыслительных процессов, которое он назвал «объектив-
«объективной редукцией». Такая редукция, по его гипотезе, прерывает «квантовую
жизнь» любой системы, даже если никаких измерений не проводится.
Она происходит, когда в системе слишком много частиц, либо когда
в ней накопилось очень много энергии, либо когда она слишком долго
изолирована от среды и живет в так называемом сцепленном состоянии
(вновь коллективные эффекты).
Определенное обоснование такого взгляда дают результаты актив-
активно развиваемой сейчас нанобиологии. Один из основателей этой области
исследований С. Хамерофф обратил внимание на своеобразные вычисле-
вычисления, проводимые в микротрубочках цитоскедета клетки. Эти структуры
представляют собой цилиндрические трубочки диаметром 25 нм, состо-
состоящие из молекул-димеров, так называемых тубулинов. Тубулины могут
существовать по крайней мере в двух пространственных конфигурациях
(конформациях). Для изменения конформации достаточно перемещения
одного электрона. Исходя из физических соображений и косвенных экс-
экспериментальных данных, Р. Пенроуз и С. Хамерофф заключили, что боль-
большая совокупность тубулинов и демонстрирует объективную редукцию,
ответственную за ряд принципиально важных механизмов сознания [73].
Другими словами, в решении этой сверхзадачи современной нау-
науки представления о коллективном поведении, о выделении параметров
порядка, самоорганизации, другие подходы нелинейной динамики, по-
видимому, окажутся очень важными.
Третья сверхзадача пока не имеет короткого красивого названия.
Условно ее можно назвать теорией риска и безопасности. На наш взгляд,
само выделение ее в качестве сверхзадачи существенно запоздало. До сих
пор на защиту людей от природных и техногенных катастроф, на обеспече-
обеспечение устойчивости развития социально-технических систем часто смотрят
22 1. Предисловие, или игры со сложностью
как на инженерную, техническую проблему, решение которой в основ-
основном сдерживается несовершенством управляющих структур. Приведем
несколько аргументов, показывающих, что такой взгляд не адекватен
нынешней реальности.
В Московском физико-техническом институте разницу между науч-
научными и техническими задачами поясняли на первых курсах следующим
образом. Технические задачи, безусловно, имеют решение, и вопрос
лишь в том, сколько оно будет стоить, кто, как и за какой срок его
получит. В отличие от них научные задачи могут как иметь, так и не
иметь решения. Анализ глобальных изменений ряда тенденций мировой
динамики показывает, что построение и реализация самосогласованно-
самосогласованного социально-технологического сценария развития мирового сообщества
сейчас выступает не как политическая или техническая, а как научная
проблема. Достаточно напомнить, что многие оптимистичные надежды,
высказывавшиеся 40-50 лет назад, не оправдались. Форсированное раз-
развитие технологий не привело к сокращению разрыва между развитыми
и развивающимися странами, как мечтал Чарльз Сноу, а, напротив,
увеличило этот разрыв. Надежда на термоядерную энергетику, альтерна-
альтернативные источники, которые позволили бы отказаться от ряда опасных
технологий, связанных с эксплуатацией АЭС, от потребления части не-
невосполнимых ресурсов, пока пришлось отнести в отдаленное будущее.
Междисциплинарный характер проблемы и ее новизна связаны
с тем, что наша технологическая цивилизация оказалась в области па-
параметров, где не бывала раньше. Это касается и объемов используемых
ресурсов, и масштабов взаимодействия с окружающей средой. Приме-
Применяемые атомные технологии приводят к возникновению радиоактивных
отходов, которые будут представлять опасность на геологических време-
временах, превышающих 100 тысяч лет. Биотехнологии существенно меняют
мир обитающих на Земле микроорганизмов, заставляя принимать в рас-
расчет масштабы, которыми человек раньше не оперировал. Здесь в гораз-
гораздо более жесткой постановке, чем в других областях, встает проблема
выделения параметров порядка и управления сложной системой. В иде-
идеале следовало бы видеть упорядоченный и систематизированный набор
наиболее серьезных угроз для человечества и возможных воздействий,
позволяющих их парировать.
Попытка осмыслить этот круг задач показала существенный про-
пробел в методах анализа сложных нелинейных систем и в соответствующих
теоретических представлениях. В настоящее время для характеристики
многих сложных социально-технологических объектов часто употребляет-
употребляется термин «системный кризис». Обычно в него вкладывается два смысла.
Первый — наличие сложной структуры причинно-следственных связей,
которые не позволяют решить одну возникшую проблему, вырвав ее
из этой структуры. Сама структура определяет коридор возможностей
и цели, которые разумно ставить. Понятно, к примеру, что попытка по-
построить процветающий технополис, ориентированный на компьютерные
технологии, в средневековом окружении, вероятно, не удастся. С другой
стороны, опыт показал, что цели всей системы и следующие из них
1.2. Новая парадигма. Внешнее оправдание 23
правила взаимодействия частей не могут быть подменены целями и инте-
интересами какой-либо подсистемы. Там, где это происходит, весьма велика
опасность распада, деградации, катастрофы.
Многие задачи, связанные с обеспечением безопасности, с упра-
управлением риском, являются проблемами системного уровня. Поэтому,
казалось бы, для их решения, как и для исследования многих про-
проблем, возникающих в связи с системным кризисом ряда принципиально
важных общественных структур, естественно воспользоваться системным
анализом.
К сожалению, этот подход, разрабатывавшийся с начала века и бур-
бурно обсуждавшийся с 60-х годов, так и не был создан. Точнее говоря, он
не был доведен до того уровня, когда вполне определенные достаточно
общие методики стало возможным применять к конкретным задачам.
Известные авторам примеры удачного анализа систем обычно демон-
демонстрируют изобретательность и фантазию их создателей, а также глубокое
понимание ими существа дела и принципиальные трудности, связанные
с обобщением предложенных методов.
Тем не менее можно предположить, что и в этой области привлече-
привлечение идей и аппарата нелинейной динамики может оказаться полезным.
Приведем один пример. Традиционные общества обычно имели веками
складывавшуюся систему социальных, экономических, технологических
и иных взаимосвязей, которая тщательно оберегалась. Это давало воз-
возможность опираться на накопленный опыт, легко искать исторические
прецеденты, медленно эволюционно совершенствовать систему. В эпоху
быстрых социально-технологических перемен число взаимосвязей мно-
многократно возрастает. При этом опыта, на основе которого можно было
бы судить, насколько дорого и опасно то или иное принимаемое реше-
решение, естественно, нет. Поэтому возникает задача анализа и редактирова-
редактирования появляющихся причинно-следственных связей. Последнюю технологию
приходится применять все чаще. Это, например, отказ от производства
хлорфторуглеродов (фреонов), по мнению экспертов, представляющих
основную опасность для озонового слоя, отказ от ряда видов гербицидов,
от некоторых созданных высокоэффективных видов оружия и т. д.
При этом понятно, что многие взаимосвязи нельзя рассматривать
по отдельности, «вырвав из контекста». Какие же системы взаимосвя-
взаимосвязей заслуживают первоочередного внимания и потенциально могут быть
наиболее опасны?
Для большого класса систем ответ на этот вопрос уже получен
в нелинейной динамике при анализе совершенно другого класса задач.
Исследование добиологической эволюции показало, что следует рассма-
рассматривать не отдельные процессы, ферменты, механизмы, а циклические
последовательности химических реакций, в которых продукт последней
реакции является исходным веществом для первой. Именно между таки-
такими циклическими структурами причинно-следственных связей, которые
М.Эйген назвал гиперциклами, и происходит конкуренция. Эта конку-
конкуренция в свою очередь многократно увеличивает скорость эволюционных
процессов. При этом автокаталитические последовательности реакций,
24 1. Предисловие, или игры со сложностью
где один из промежуточных продуктов может выступать в качестве ката-
катализатора какой-либо реакции, входящей в цикл, получают преимущество
в конкурентной борьбе.
В мире аналогичных циклов живем и мы. Это биогеохимические
циклы, системообразующие циклы в экономике, циклы воспроизводства
общественных структур. Поэтому новые возникающие циклы, принципи-
принципиально влияющие на ранее существовавшие, или связи, обеспечивающие
взаимодействие циклов разной природы, заслуживают особого внимания
как потенциально опасные.
Еще одна причина, по которой теория риска и безопасности ока-
оказывается выделенной из общего круга научных задач, состоит в том,
что здесь мы сталкиваемся с проблемой, масштабы которой растут.
Например, за последние тридцать лет число природных бедствий и тех-
техногенных катастроф с большим экономическим ущербом увеличилось,
по сравнению с предшествующим уровнем, вчетверо. Число жертв и мас-
масштаб потерь от них сейчас сравнимы с соответствующими показателями
для региональных конфликтов. Если за последние двадцать лет число
беженцев, покинувших дома из-за таких конфликтов, составило пример-
примерно 13 миллионов человек, то резкое ухудшение состояния окружающей
среды, прежде всего из-за аварий и катастроф привело к переселению
10 миллионов.
Если в ходе американской ядерной бомбардировки Нагасаки поги-
погибло и было ранено более 140 тысяч человек, то для аварии на химическом
комбинате в Бхопале этот показатель составил 220 тысяч. Масштабы тех-
техногенных аварий и природных катастроф приближаются по числу жертв
и материальному ущербу к потерям в результате военных конфликтов.
Сейчас в этой области делается стратегический выбор, от кото-
которого зависит, насколько безопасным будет наш мир в следующем веке.
Какова же роль нелинейной динамики в этом выборе? Каковы ее ны-
неншние возможности и перспективы? Какие цели следует иметь в виду
при обсуждении новой парадигмы? К этим проблемам мы будем не раз
возвращаться в книге. Тем не менее, общий подход к ним, на наш
взгляд, может быть следующим. Пройденный нелинейной наукой путь
(созданные теории, модели, формализованный аппарат, накопленный
опыт) уже сейчас позволяет более просто и эффективно анализировать
и решать многие крупные научно-технические задачи. Уже сейчас нели-
нелинейная динамика имеет огромный опыт компьютерного моделирования,
«понимания» результатов компьютерного моделирования сложных си-
систем. Этот опыт уже сейчас может и должен быть перенесен во многие
области научных исследований и технологических разработок. Уже сей-
сейчас нелинейная динамика предлагает новый междисциплинарный подход
к образованию, позволяющий «увидеть лес за деревьями», рассмотреть
«единое во многом». Уже сейчас язык, предлагаемый нелинейной наукой,
позволяет эффективно взаимодействовать представителям различных на-
научных дисциплин, активно проникает в культуру всего общества.
XX век стал веком специализации науки, системного анализа, рас-
расчленения общей картины на множество отдельных фрагментов. За сто-
1.3. Логика нелинейной динамики 25
летие был выполнен гигантский объем исследований. XXI век, на наш
взгляд, станет веком возврата к целостности, к всестороннему осмысле-
осмыслению общих проблем. При этом ключевыми становятся технологии свое-
своеобразной системной интеграции, системного синтеза. Последние, с одной
стороны, должны позволять принимать решения, создавать технологии
на основе нескольких дисциплин и имеющегося опыта, выделять главное
в изучаемой ситуации. С другой стороны, они должны выявлять те фраг-
фрагменты нашего незнания, которые необходимо заполнить при решении
данной конкретной задачи. Это дело будущего. Многие научные подходы
сталкиваются в различном контексте с теми же проблемами и ищут свои
ответы на поставленные вопросы. Однако нелинейная наука имеет здесь
несколько важных преимуществ. В ходе ее развития для ряда систем уже
научились выделять ключевые переменные, ведущие процессы, пара-
параметры порядка, уже удалось эффективно исследовать ряд проблем на
стыке естественных и гуманитарных дисциплин, уже удалось выявить ряд
общих свойств сложных нелинейных систем. Иными словами, для новой
парадигмы синергетики есть серьезное «внешнее оправдание» и большие
основания надеяться на успех.
1.3. Логика нелинейной динамики
По-моему, такие полеты были возможны всегда,
просто кто-нибудь должен был об этом догадать-
догадаться и попробовать научиться так летать, а время
здесь ни при чем. Может быть, мы опередили
моду.
Р. Бах. Чайка Джонатан Ливингстон
Поворот, к которому подошла нелинейная динамика, можно срав-
сравнить по направленности и относительному масштабу с несколькими
крупными событиями в истории культуры и науки.
Самая близкая аналогия — это Реформация. Мартин Лютер осо-
осознавал отрыв прекрасно развитой утонченной теологии от острых задач,
которые прихожанам и служителям церкви приходилось решать здесь
и сейчас. С падением морального авторитета и уменьшением реаль-
реальной пользы, которую институт Церкви приносил простым смертным,
возникла потребность добиться понимания учения гораздо большим ко-
количеством людей. Для того, чтобы сохранить главное, Лютеру пришлось
отказаться от множества деталей, возможностей, тонкостей, сосредо-
сосредоточиться на основном и, естественно, упростить учение. Кроме того,
протестантство смогло очертить свою сферу компетенции и конкретно
выделить те области, которые в эту сферу не входят. Внешне это выглядит
как шаг назад, отказ от решения поставленных вначале задач и подмена
одних проблем другими. Но, как считают многие историки, именно этот
ход и оказался чрезвычайно важным и плодотворным.
Многократно похожий процесс имел место и в математике. Лю-
Любимые школьные забавы — теоремы синусов, косинусов и операции
26 1. Предисловие, или игры со сложностью
с тригонометрическими функциями приобрели популярность и вошли
в фундамент естествознания только в Новое время. Древние математи-
математики и астрономы, начиная с Птолемея, и средневековые исследователи
имели дело с гораздо более сложной и специфической областью —
сферической тригонометрией. Однако самыми важными и полезными,
на наш сегодняшний взгляд, оказались тривиальные, с точки зрения
предшественников, случаи, относящиеся к плоскости.
Еще более поучительно развитие нелинейного анализа, связанного
с изучением квазилинейных уравнений в частных производных, с иссле-
исследованием ударных волн в различных системах. Классический путь, пред-
предполагающий доказательства гладкости решений, их единственности и су-
существования в свое время стал настолько сложен, что пришлось изменить
само понятие решения. Возникла концепция обобщенных решений, были
развиты представления о некорректных задачах и методах регуляризации,
предложена техника анализа разрывов и разработаны соответствующие
разделы вычислительной математики. Заметим, что компьютерное моде-
моделирование, расчет решений на ЭВМ сами по себе являются громадным
упрощением. Дифференциальные и разностные операторы могут обла-
обладать совершенно различными свойствами и для большинства интересных
нелинейных задач установить строго их взаимосвязь пока не удается.
Кроме того, нельзя забывать, что конечная точность представления дан-
данных вносит совершенно новый элемент. Исследователи не взяли барьер.
Они обошли его.
На наш взгляд, в похожем положении сейчас находится наука в це-
целом и нелинейная динамика в частности. Кризисные явления послед-
последнего времени и глобальные неблагоприятные изменения, происходящие
в мире, показали, что у нас нет ясных и жизненно важных представле-
представлений о пределах возможностей науки. Ученые поразительно редко говорят
о том, чего они не могут. Обычно они «просят гранты» под будущие успехи
или рапортуют о достижениях. Поэтому у непосвященных создается вна-
вначале иллюзия всемогущества, а потом глубокое разочарование человека,
обманутого в лучших чувствах. Уже несколько десятков лет и журналисты,
и исследователи говорят о том, что многие проблемы являются междис-
междисциплинарными. Но именно с этой позиции нужно подойти и к нашему
незнанию. Ведь не так важно, что конкретно не знают физики, химики
или социологи. Важно, что научное сообщество не знает как целое, за ка-
какие задачи оно не берется. Кроме того, есть разные уровни незнания.
И наша беда состоит в том, что мы зачастую не представляем, насколько
глубоко мы не знаем тех или иных вещей. Поэтому анализ структуры на-
нашего незнания, определение пределов компетенции сейчас представляются
исключительно важными. (Классический пример Сократа, занимавше-
занимавшегося поддержкой принятия решений в Афинах, показывает, что анализ
этих вопросов может быть занятием неблагодарным и опасным.)
По-видимому, следует разделить «знание» различных явлений и их
«понимание». В первом случае речь может идти о научной техноло-
технологии, оправдывающей сложный формализованный аппарат, дорогостоя-
дорогостоящие эксперименты и многочисленные наблюдения. Во втором — нам
1.3. Логика нелинейной динамики 27
нужна простая, ясная картина, идеи и понятия, которые могут не позво-
позволять рассчитать, вычислить, получить конкретную прибыль, но укажут
направление, в котором следует двигаться, а также место того или иного
события или явления в нашей картине мира.
Спросим себя, когда сложные вещи оказываются важны и полезны
в науке? Во-первых, когда на основе этих вещей удается предложить
технологию, приводящую к созданию какого-либо продукта. Например,
у нас есть работающий персональный компьютер. Методы проектирова-
проектирования, расчета и оптимизации микросхем могут быть весьма сложными,
«неизящными», громоздкими и дорогими. Однако само наличие тако-
такого продукта, с одной стороны, «сворачивает» многочисленные знания
и данные из разных областей, начиная с квантовой механики и кончая
микроэкономикой, а с другой — оправдывает развитие ряда разделов
прикладной науки.
Во-вторых, может оказаться, что определенная научная теория
играет важную роль в существующей научной картине мира. При этом
одни части этой теории могут быть ясными, простыми и красивыми, а то,
что придает ей стройность и законченность — сложным, изощренным
и трудоемким. Напомним знаменитый афоризм о тем, что физик-теоре-
физик-теоретик, когда его просят рассчитать устойчивость стола с четырьмя ножками,
быстро приносит решение задачи об устойчивости стола с одной ножкой
и с бесконечным числом ножек, а затем всю жизнь пытается рассчитать
устойчивость стола с произвольным числом ножек. Тем не менее и по-
последняя задача может иметь большой смысл, несмотря на ее небольшое
прикладное значение. Она может замкнуть научную картину в некоторой
области, превратив ее в систему знаний. Последняя же система в кон-
контексте других теорий может оказаться небольшим, простым, полезным
элементом.
В-третьих, проводя такие исследования, мы можем наткнуться как
на новую простоту, так и на существенные пробелы в наших знани-
знаниях, которые изначально не были видны. Однако большинство усилий
современной науки тратится не на проведение таких работ, а на то,
чтобы получить понимание каких-то явлений. И с этой точки зрения
естественно взглянуть и на нелинейную динамику.
В течение всего времени ее развития от этой области исследова-
исследования в основном просили не деталей, тонкостей, работающих изделий
или высокоточных измерений, а принципов, идей, запретов, качествен-
качественной картины различных явлений. Пожалуй, она в наибольшей степени
оправдывает слова А. Эйнштейна о том, что современный ученый ничего
не хочет знать, но все хочет понимать. Другими словами, синергети-
синергетика и нелинейная динамика задумывались и развивались как подходы,
направленные на понимание.
С этой точки зрения, наиболее важными в нелинейной динамике
являются методы упрощения нашей реальности. Каждая наука имеет свои
алгоритмы упрощения. Химики в качестве упрощающего предположения
считают, что основой являются химические свойства объектов, в механике
упрощение связано с тем, что влиянием огромного количества взаимодей-
28 1. Предисловие, или игры со сложностью
ствий можно пренебречь. Поэтому можно рассматривать падение камня
в поле тяжести Земли, не заботясь об ее вращении, электромагнитных
полях, а иногда даже и о сопротивлении воздуха. Отсюда и маятни-
маятники, наклонные плоскости, сообщающиеся сосуды, которые объясняют
поразительно много. Математики, занимающиеся асимптотическим ана-
анализом, полагают, что в каждой интересной системе найдется малый или
большой параметр, который позволит написать простые соотношения
или сведет задачу к известной.
Нелинейная динамика предложила свои алгоритмы упрощения.
С их развитием и совершенствованием, с их осмыслением мы и связываем
будущее этой области. Можно сказать, что эти алгоритмы являются
достаточно общими, выходящими за рамки отдельных задач, областей,
объектов исследования. Наверное, лет двадцать назад такие алгоритмы
назвали бы системными.
Один из самых главных алгоритмов связан с предположением
о масштабной инвариантности процессов, протекающих на разных уров-
уровнях. Простейший пример масштабной инвариантности дают фрактальные
множества. Несмотря на наличие сложной структуры, они могут выгля-
выглядеть одинаково или почти одинаково в разных масштабах.
Это предположение для каких-то явлений может не выполняться.
Студентам-физикам и инженерам обычно объясняют, что уменьшение
пространственных, временных или иных масштабов в 10-100 раз может
привести к возникновению других явлений, к изменению относительной
важности различных факторов и механизмов. Например, закономерно-
закономерности, характерные для атомной физики (масштаб 10~8 см), для ядерной
A0~14 см), физики элементарных частиц A0~20 см) существенно отлича-
отличаются. Про объекты этих наук следует задавать разные вопросы и рассчи-
рассчитывать на разные ответы.
С другой стороны, психологи, занимающиеся исследованием взаи-
взаимодействия в группе людей, видят одни и те же закономерности, имеем
ли мы дело с Советом министров, районной администрацией или ро-
родительским комитетом. Однако если объект обладает масштабной инва-
инвариантностью, то возникает множество различных интересных эффектов,
неожиданных возможностей, совершенно новых задач. Например, обыч-
обычные методы измерения для таких объектов могут не работать, в то время
как необычные парадоксальные представления о площади, объеме и дли-
длине могут быть адекватными этой реальности.
Этот способ упрощения имеет и еще один глубокий смысл. Если
раньше ученые часто спрашивали, как устроена природа, то теперь
не менее важным становится вопрос о том, как мы могли бы устроить,
сконструировать, представить или изобразить ту или иную вещь. Отчасти
наука при этом берет на себя некоторые функции техники, которую рань-
раньше связывали с конструированием и придумыванием различных систем.
Современное программирование, развитие вычислительной техники, ор-
органической химии, микробиологии позволяют предугадать один из путей
эволюции науки XXI века — увеличение «конструкторского», «инженер-
1.3. Логика нелинейной динамики 29
ного» компонента деятельности в сравнении с поиском новых эффектов,
теоретическим анализом.
Например, простейшие самоподобные фрактальные структуры мо-
могут приводить к поразительно красивым и сложным картинкам. Про-
Простое в одном представлении оказывается сложным в другом. Поэтому
на основе такого фрактального упрощения реальности возникли алгорит-
алгоритмы обработки изображений, сжатия информации, создания различных
материалов, обладающих необычными свойствами. Если мы не можем
найти такую вещь в природе, то можем попытаться создать ее.
Главная идея и надежда нелинейной динамики состоит в том,
что многие сложные системы могут быть просто описаны с помощью
нескольких переменных — параметров порядка. Именно это в перспек-
перспективе позволяет надеяться на понимание. Психологи утверждают, что
человек в состоянии управлять системами, в которых нужно контроли-
контролировать не более 5-7 параметров, активно взаимодействовать не более чем
с 7-9 людьми. Поэтому если выясняется, что управляющих параметров
более десятка или людей больше 20, то нужно думать о способах дальней-
дальнейшего упрощения ситуации. Известная шутка о том, что задача, в которой
менее 2 переменных — не задача, а более 8 — неразрешима, с точки
зрения понимания шуткой не является.
Поэтому ответ на вопрос, откуда берутся параметры порядка и по-
почему сложная система может вести себя просто, является для всей не-
нелинейной науки ключевым. Этот вопрос во многом удалось прояснить
благодаря теории бифуркаций и теории инерциальных многообразий.
Оказалось, что в наиболее важных областях пространства пара-
параметров, где меняется число или устойчивость решений, систему можно
описывать с помощью одних и тех же соотношений. Однако за эту
простоту мы платим тем, что делаем свой анализ локальным. Он отно-
относится только к окрестности точки бифуркации в пространстве параметров
и обычно к решениям малой амплитуды.
Но, к глубокому удовлетворению приверженцев нелинейной дина-
динамики, оказалось, что в природе существует и другой механизм упрощения.
Для многих сложных систем, потенциально обладающих бесконечным
числом степеней свободы, с течением времени происходит самооргани-
самоорганизация — выделение параметров порядка, принадлежащих инерциальному
многообразию, которые являются главными, и остальных переменных,
которые целиком подчинены параметрам порядка. Пожалуй, здесь мы
имеем дело со сложным исследованием, требующим развитой техники,
которое вносит ясность и системность в существующие представления.
Для разнообразия обратим внимание на несколько возражений,
которые высказываются при обсуждении этой теории. Во-первых, за общ-
общность теории мы платим отсутствием конкретных уравнений, которые бы
описывали динамику параметров порядка на инерциальном многообра-
многообразии. Во-вторых, эти уравнения, существование которых доказывается,
не являются универсальными для разных нелинейных систем. В-третьих,
о том, что происходит самоорганизация и выделение параметров поряд-
порядка, в синергетике говорят уже более 20 лет, поэтому на первый взгляд
30 1. Предисловие, или игры со сложностью
достаточно изощренная математическая теория не привносит здесь ни-
ничего нового. Понятно, что самоорганизация связана с диссипативными
процессами — вязкостью, теплопроводностью, трением и прочими.
Теория инерциальных многообразий позволила решить ключевую
задачу — она показала, где находится область того, что мы знаем, где мы
можем надеяться на получение простого конечномерного описания, а где
можно ожидать сюрпризов. Пожалуй, теория инерциальных многообра-
многообразий [333] по значению и смыслу ближе всего к работе Дж. фон Неймана
«Математический аппарат квантовой механики» [91]. Обе работы многим
известным процедурам, приемам, подходам, которые на интуитивном
уровне применялись и раньше, придали ясность и строгий математичес-
математический смысл.
Знание пределов, очерченных теорией инерциальных многообра-
многообразий, в которых можно рассчитывать на конечномерное описание, помогло
поставить вопрос о том, что же находится за этими пределами. Чтобы
нарушать каноны, надо их ясно представлять. За этими пределами лежит
важный и интересный класс явлений, связанных с редкими катастрофи-
катастрофическими событиями. Как уже отмечалось, именно такие события играют
особую роль в теории риска и безопасности. В этой книге мы обратим вни-
внимание только на один класс таких явлений. Они связаны с так называемой
жесткой турбулентностью — возникновением редких пространственно
локализованных пиков гигантской амплитуды на турбулентном фоне.
В течение основного времени система ведет себя так, как будто в ней есть
небольшой набор параметров порядка, эффективно описывающих всю
эволюцию. Но иногда система как будто становится «очень многомер-
многомерной». Однако самое главное состоит не в сложности, а в том, что меняется
сам набор параметров порядка. Для турбулентного фона это одни параме-
параметры, для стадии роста пика — другие, для процесса его распада — третьи.
Исследование жесткой турбулентности также позволило придать некото-
некоторую законченность большому циклу работ, связанных с возникновением
нестационарных диссипативных структур в нелинейных средах с сильной
положительной обратной связью [56,109]. В таких средах также возникают
пространственно локализованные гигантские пики с сокращающейся по-
полушириной. Описывать их можно в рамках одного параболического урав-
уравнения с нелинейным источником. И действительно оказалось, что стадию
роста пика модели такого рода передают вполне удовлетворительно.
У А. Эйнштейна глубокую неудовлетворенность вызывал стати-
статистический характер квантовой механики. Он считал, что Бог в кости
не играет. В теории нестационарных структур [56] можно наблюдать мно-
множество сложных красивых эффектов, однако Бог должен распоряжаться
начальными данными. Встает вопрос, может ли это все наблюдаться
в природе и кто же на самом деле распоряжается начальными данными?
Исследование жесткой турбулентности позволило указать конкретные
механизмы, решающие эти задачи. Одна математическая и физическая
теория, развивавшаяся более двух десятков лет, стала восприниматься
не как вещь в себе, а как способ описания целого, которое в других
случаях может вести себя хаотическим или иным образом.
1.3. Логика нелинейной динамики 31
Исследование жесткой турбулентности позволило и далее про-
продвинуться по пути упрощения. Оказалось, что жесткая турбулентность,
характерная для сред с кубической нелинейностью в многомерном случае,
может существовать и в одномерных задачах с более сильной нелиней-
нелинейностью. Для того, чтобы упростить и понять это, можно «обменять»
размерность пространства на степень нелинейности среды.
Однако расчеты и их анализ не означают полного понимания моде-
моделируемого явления. В некоторых науках «понимаю» значит «могу исполь-
использовать». В нелинейной динамике «понимаю» значит «могу предложить
простую конечномерную модель». Этот принципиально важный уровень
понимания жесткой турбулентности удалось достичь благодаря усилиям
С. В. Ершова, модель которого мы также кратко обсудим. Замечательной
чертой этой модели, представляющей собой трехмерное отображение,
является возможность его детального аналитического исследования.
Для многих актуальных задач современной нелинейной динамики
характерно наличие принципиально важных малых параметров. Напри-
Например, это может быть единица деленная на число Рейнольдса в теории
турбулентности. Эти параметры могут быть настолько малы, что возмож-
возможность прямого численного моделирования таких явлений не представится
в ближайшее десятилетие. Нужен другой уровень понимания и дру-
другие подходы к упрощению. Жесткая турбулентность тоже наблюдается
в системах с малыми параметрами, характеризующими диссипативные
свойства системы. Поэтому «просто посчитать» многие статистические
характеристики оказывается невозможно даже для трехмерного отображе-
отображения. Модель С. В. Ершова показывает тот желаемый уровень понимания,
к которому хотелось бы стремиться во многих других сложных задачах,
относящихся к области нелинейной динамики. Результат исследования
жесткой турбулентности важен и с точки зрения прогнозов. Оказалось,
что явление, выглядевшее неожиданностью и катастрофой для исходных
переменных модели, вполне объяснимо и предсказуемо, если анализи-
анализировать определенный набор усредненных характеристик. Иначе говоря,
выход за пределы, очерченные строгой математической теорией, очень
быстро дал блестящие результаты.
В средние века многие философы считали, что основной задачей
ученых и мудрецов должно быть не наблюдение, описание и моделиро-
моделирование существующего, а прогноз и конструирование будущего. В рам-
рамках этой парадигмы работы Нострадамуса были вполне ортодоксальны.
И сейчас прогноз находится в центре внимания нелинейной динамики.
В нелинейной динамике появляется замечательная возможность
в полной мере реализовать установку И. Ньютона, полагавшего, что он
гипотез не измышляет. Поэтому на всю нашу науку и методы прогноза
можно взглянуть как на прием анализа временных рядов. Наши наблю-
наблюдения — временные ряды. Наша цель — на основе предыстории предска-
предсказать, что будет дальше. Поэтому после рождения теории динамического
хаоса стало ясно, что радужные надежды относительно глобальной пред-
предсказуемости, возможности заглянуть как угодно далеко вперед и назад,
о которых уверенно писал Лаплас, несбыточны. Поэтому приходится
32 1. Предисловие, или игры со сложностью
ставить более скромные цели и разрабатывать наилучшие пути их до-
достижения. Этому аспекту мы уделяем большое внимание, анализируя
количественные характеристики хаоса, методы обработки эксперимен-
экспериментальных данных, типичные проблемы, которые возникают при изучении
нелинейных систем.
Можно сказать, что в некотором смысле родоначальником анализа
временных рядов является Платон. Он сформулировал притчу о пеще-
пещере, в которой находятся прикованные к стене узники. Узники могут
наблюдать только тени проходящих людей и проносимых предметов. Пе-
Перед ними возникает задача реконструкции реальности, находящейся вне
пещеры. Платон смотрел на проблему достаточно оптимистично, пола-
полагая, что узникам доступно почти все. Развитие астрономии во многом
подтверждает этот вывод. Несмотря на причудливые траектории, описы-
описываемые планетами по небосводу, Кеплеру удалось предложить простую
и красивую модель, связанную с движениями по эллипсу. К сожалению,
анализ даже весьма простых систем показывает, что процедура рекон-
реконструкции аттракторов, своеобразного восстановления многомерной ди-
динамики по временному ряду, далеко не всегда применима и эффективна.
Чтобы не измышлять гипотезы, надо иметь весьма обширную априорную
информацию и относительно простую динамику. В еще большей мере
это относится к пониманию изучаемых процессов.
По-видимому, долгий путь, пройденный специалистами по времен-
временным рядам, многочисленные работы по обработке данных в нелинейной
динамике показывают, что мы столкнулись не с технической, не с матема-
математической, а с принципиальной проблемой. Нам нужно менять основную
идею и используемые представления.
Заметим, что почти все, что мы понимаем, нам удается предста-
представить в виде наглядных образов. Это означает, что мы обречены иметь
дело, по крайней мере на уровне понимания, с двух-трехмерным про-
пространством. Именно с ними и должны быть связаны наши алгоритмы
упрощения. Можно предположить, что в той реальности, с которой мы
имеем дело и которую в большой степени конструируем, удается находить
двух- и трехмерные проекции, в которых и находятся все ключевые пара-
параметры важной для нас ситуации. Наше искусство, как индивидуальное,
так и видовое, и состоит в том, чтобы эффективно выделять эти проекции
и менять их по мере того, как изменилась ситуация или мы начинаем
заниматься проблемами другого уровня.
В книге предлагается некоторый способ формализации этого есте-
естественного взгляда. Мы стараемся жить в мире с весьма высокой степенью
предсказуемости. Однако это удается не всегда. Есть области параметров,
где реальность становится слишком сложной и нам не удается просчитать
причинно-следственную связь между нашими поступками и конечным
результатом. В этих областях параметров более естественным представля-
представляется не динамическое описание, не построение логических конструкций,
а вероятностные или игровые модели. Эмоции, мораль, культура могли
возникнуть как реакция на эти ситуации выбора. К сожалению, во многих
важных случаях не удается опираться на предшествующий опыт. Поэтому
1.3. Логика нелинейной динамики 33
алгоритмы прогноза и способа действий в этих ситуациях должны быть
также необычными. Грубо говоря, нам надо учиться на очень малом
числе не очень значительных чужих ошибок. К примеру, почти все круп-
крупные аварии XX века имели предшественников — аварии того же типа,
но меньшего масштаба. В тех странах, где из этого были извлечены уроки,
сделаны выводы и изменены нормы безопасности, техническая политика
или организационные структуры, реагирующие на такие угрозы, многих
бед удалось избежать. Грубо говоря, мы здесь не можем действовать
интуитивно, закрывать глаза или надеяться на лучшее. Формализация
этих представлений ведет к другим вопросам относительно изучаемых
процессов, к другим моделям, другим методам управления. Первые шаги
на этом пути описаны в настоящей книге.
Один из принципиальных уроков развития компьютерного моде-
моделирования и нелинейной динамики состоит в том, что весьма небольшая
часть наших знаний навыков и представлений может быть эффективно
формализована. Как ни странно, мы гораздо чаще, чем хотелось бы, «все
понимаем, но сказать не можем». Поэтому особую роль приобретают
методы, техники, формализм, которые позволяют извлекать эти знания
и переводить их в форму, допускающую передачу и многократное исполь-
использование. Одной из наиболее популярных и перспективных техник такого
рода являются нейронные сети. В идеале они способны создать наше
«второе я», обучаясь на наборе примеров, которые мы им предоставляем.
В рамках предшествующего подхода, связанного с выделением
маломерных проекций, мы выдвигаем гипотезу о природе «непостижимой
эффективности» нейронных сетей при решении многих задач анализа
и прогноза. Непостижимой эффективности математики в естественных
науках удивлялся Е. Вигнер. Однако гораздо более естественно удивиться
тому, насколько эффективно может быть смоделировано то, для чего
у нас нет удовлетворительного математического описания.
В самом деле, отталкиваясь от нейронных сетей, можно пред-
представить себе совершенно другой способ моделирования и осмысления
реальности. Можно представить себе компьютерные модели, которые
непосредственно обучаются на наборе экспериментов, не используя ка-
каких-либо уравнений, а затем предсказывают, что будет в этой системе.
Моделью становится не уравнение и алгоритм его численного решения,
а нейронная сеть, обученная решать эту задачу. «Понимание» в этом кон-
контексте будет означать, что сеть очень простая и человеку удается легко
проследить, как устроен этот черный ящик, дающий правильные ответы.
Нейронные сети, как мы показываем, потенциально обладают
прекрасными возможностями находить маломерные проекции. Поэтому,
возможно, они и оказываются очень полезными при решении многих
задач, для которых нет удовлетворительной формализации. Идеалом бы-
было бы предложить набор алгоритмов выделения маломерных проекций
и областей, где простые и ясные представления уже не работают. В од-
одних случаях это могло бы дать новые алгоритмы прогноза временных
рядов. В других — системы предупреждения о тех ситуациях, с которыми
мы ранее не сталкивались и которые требуют предельной осторожно-
2 Зак.2
34 1. Предисловие, или игры со сложностью
ста. В третьих — информацию о том, что изучаемый объект на самом
деле описывается с помощью нескольких параметров порядка. Наряду
с индикаторами температуры, давления, влажности нам были бы очень
нужны индикаторы «простоты» и «сложности». Работы по компьютерно-
компьютерному прогнозу землетрясений показывают, что эти надежды гораздо ближе
к реальности, чем кажется на первый взгляд.
Другая гипотеза, заслуживающая внимания, связана с ролью хаоти-
хаотической динамики в анализе и распознавании образов. Одними из главных
вопросов при анализе психики являются алгоритмы забывания и пере-
переключения внимания на другие объекты. Мозг тоже определенным образом
занимается самоорганизацией и выделением параметров порядка, кон-
концентрируя внимание на главных образах, устраняя ложные, отправляя
второстепенные на периферию сознания. На наш взгляд, роль дисси-
пативных процессов, обеспечивающих такую самоорганизацию, могут
играть элементы, обладающие хаотической динамикой. Один модельный
пример, подтверждающий этот взгляд, мы также разбираем в книге.
Междисциплинарность позволяет не только упрощать, но и вы-
выделять новые явления, на которые раньше внимание не обращалось.
Обычно эти явления находятся на границе различных уровней органи-
организации. Во многих интересных случаях научные дисциплины занимаются
детальным анализом явлений, происходящих на одном уровне, а междис-
междисциплинарные подходы обращают внимание на то, что происходит между
ними. Типичный пример — самоорганизованная критичность. Обычный
подход фиксирует внимание на детерминированном поведении, будь то
одномерное отображение или уравнение в частных производных, либо
на чисто статистическом описании. На границе между этими уровнями
существует большая область нелинейных процессов, которые также могут
приводить к редким катастрофическим событиям. В этой области есть
своя внутренняя простота и свои механизмы упрощения. Они связаны
с непосредственным влиянием локальных правил, обеспечивающих взаи-
взаимодействие элементов системы или их выбор из имеющегося множества,
на глобальную статистику. Эта статистика во многих случаях оказывается
степенной в большом интервале масштабов. Последнее означает, что
редкие катастрофические события происходят не настолько редко, чтобы
ими можно было пренебречь. Эта область очень быстро развивается и в
теоретическом, и в прикладном плане.
Разнообразие и сложность исследования нелинейных систем, в ко-
которых процессы разворачиваются во времени и пространстве, ставят но-
новые проблемы перед нелинейной динамикой. Традиционный путь связан
с уравнениями в частных производных, с выводом аппроксимирующих
их разностных схем, со сложной техникой построения сеток в приклад-
прикладных задачах, с многочисленными компьютерными расчетами. Трудности
традиционного подхода хорошо известны, методы преодоления возника-
возникающих препятствий за последние полвека также были детально изучены.
Поэтому естественно возникает мысль пойти радикальным, альтернатив-
альтернативным путем — описывать различные нелинейные процессы сразу на дис-
дискретном языке, считая, что сама измеряемая величина может принимать
1.3. Логика нелинейной динамики 35
конечный набор значений. Этот подход, развиваемый в теории клеточ-
клеточных автоматов, имеет очевидные достоинства. Среди них возможность
высокоскоростных параллельных вычислений на так называемых маши-
машинах клеточных автоматов; очевидность алгоритмов, позволяющих строить
неплохие автоматы для задач переноса, газовой динамики, химической
кинетики и многих других; отсутствие проблем с аппроксимацией, схо-
сходимостью и сложными разностными сетками; наличие экологической
ниши, в которой трудно или даже невозможно писать уравнения в част-
частных производных, но довольно легко придумывать клеточные автоматы.
Однако главная проблема теории клеточных автоматов, на наш
взгляд, также является не технической (сколько клеток, какая точность,
какое быстродействие), а принципиальной. И связана она не с рас-
расчетами конкретных объектов, а с пониманием. С начала нашего века,
когда на уравнения в частных производных смотрели как на сложный
экзотический объект, прошло много времени. В той или иной степени
благодаря усилиям поколений ученых удалось построить качественную
теорию для многих таких объектов. Для разных областей и разных урав-
уравнений ее объем достижений различен. Проблема клеточных автоматов
состоит в том, что на сегодняшний день такой качественной теории нет.
Более того, неизвестно, может ли быть построена эта теория. Если бы
это удалось сделать, методы компьютерного моделирования могли бы
радикально измениться.
В этом разделе и во всей книге мы попытались выделить параметры
порядка в развитии нелинейной динамики. Однако сама эта область
представляет собой нелинейную, открытую, необратимо развивающуюся
систему, для которой процедура выделения параметров порядка может
оказаться некорректной. Что от нее можно ожидать?
Прояснения и упрощения основных представлений. Новых методов
упрощения реальности. Растущего влияния на области исследований,
связанные с системным анализом.
И, конечно, неожиданностей и новых парадоксов.
ЧАСТЬ I
Нелинейная динамика и хаос:
основные понятия
Язык нелинейной динамики
При чередующемся главенстве то одной, то дру-
другой науки или искусства игра игр превратилась
в некий универсальный язык, дававший возмож-
возможность игрокам выражать и соотносить разные
значения в осмысленных знаках.
Г. Гессе. Игра в бисер
2.1. От истории к современности. Взгляд с птичьего полета
Принципиальный шаг в математическом моделировании явлений
природы был сделан 300 лет назад И. Ньютоном. Его с полным правом
можно считать родоначальником нелинейной динамики. С точки зрения
этого подхода главное из того, что предложил Ньютон — способ описы-
описывать различные явления с помощью дифференциальных уравнений или
динамических систем. Это совершенно неочевидный шаг. Во-первых,
он предполагает, что изучаемый объект описывается конечным набором
чисел. Во-вторых, скорость изменения этих чисел зависит от состояния
объекта в тот же самый момент, а не раньше или не позже. И, наконец,
реальные зависимости могут описываться гладкими дифференцируемыми
функциями. Оказалось, что эти представления позволяют не только ясно
и просто выразить фундаментальные законы, но и являются тем языком,
Иа котором удобно говорить о явлениях природы. Свое развитие он по-
получил в математической физике, начавшейся с Лапласа, Эйлера, Коши.
За небольшим исключением, все современные физические теории —
электродинамика, квантовая механика, теория упругости, гидромеханика
и многие другие — опираются именно на этот язык.
В основе современного математического моделирования лежат
обыкновенные дифференциальные уравнения. (Уравнения в частных
производных, с которыми имеет дело математическая физика, можно
рассматривать как их обобщение на бесконечномерные фазовые про-
пространства. Это требует перехода от математического анализа, с которым
имели дело Ньютон и Лейбниц, к функциональному, ставшему важным
инструментом математики XX века.) Согласно традициям, сложившимся
в XVIII-XIX веках, основным типом математической модели в физике
являлись дифференциальные уравнения, описывающие некую реально
Существующую систему. Эти уравнения необходимо составить, исходя
из законов физики, а затем найти их решение.
Под решением понималась некоторая вполне конкретная функция,
зависящая от времени и начальных данных. Если же аналитически ре-
33 2. Язык нелинейной динамики
шение построить не удавалось (т. е. нельзя было предъявить его в виде
формулы, написанной на бумаге), то использовались численные или
приближенные методы. Последние рассматривались, однако, как методы
«второго сорта». Действительно, эти методы позволяют исследовать по-
поведение решения только на конечном временном интервале, а численные
методы, к тому же, только для некоторых фиксированных начальных
данных. Знание же решения в аналитическом виде избавляет от этих
проблем. Лучше всего подобную точку зрения выражает афоризм, при-
приписываемый Н.Е.Жуковскому: «Механиком является не тот, кто пишет
уравнения, а тот, кто пишет их так, что они интегрируются».
Тем не менее оказалось, что существует много задач, в том числе
и практически важных, где интегрирующееся уравнение написать невоз-
невозможно. Однако проблема построения решения на сколь угодно больших
временах остается. Такова, например, задача трех тел в небесной механи-
механике. В самом деле, естественно узнать, удалится ли одно из тел сколь угодно
далеко от двух других или, напротив, никогда не покинет некую область
пространства. А может быть они будут беспрестанно сталкиваться друг
с другом? При этом оказываются важны не координаты и скорости, а сам
тип поведения, ответ на вопрос, чего можно ждать от такой системы.
Следовательно, возникает необходимость создания качественной тео-
теории дифференциальных уравнений. Ее основы были заложены А. Пуанкаре
в конце XIX - начале XX века. В этой теории ставится задача выяснить
свойства решений дифференциального уравнения, не решая его. Для это-
этого необходимо исследовать решения, отвечающие либо всем возможным
начальным данным, либо достаточно широкому их классу и в идеале
выяснить, с каких начальных данных куда попадет траектория на боль-
больших характерных временах. Основным понятием качественной теории
становится не решение (как функция), а пространство, называемое фазо-
фазовым, точки которого представляют различные состояния системы, и его
преобразования, которые определяют уравнения динамики. Тогда можно
спросить, что в конце концов произойдет с траекториями системы, если
начинались они, скажем, в некотором кубике фазового пространства.
Если Декарт перевел геометрию на алгебраический язык, то здесь про-
происходит обратный процесс — представления теории дифференциальных
уравнений переводятся на язык геометрии. Вместо того, чтобы писать
формулы, математики начали рисовать картинки.
Другими словами, качественная теория дифференциальных урав-
уравнений приводит к геометрической трактовке уравнений движения как
однопараметрического (зависимость от времени) семейства преобразова-
преобразований фазового пространства. При этом особенно интересными оказыва-
оказываются автономные системы дифференциальных уравнений, для которых
эти преобразования образуют группу (композиция двух преобразований
дает третье преобразование из того же семейства). Таким образом мы
приходим к более общему понятию — динамической системе, т. е. группе
преобразований фазового пространства. Группы могут быть непрерывные
и дискретные (т.е. время может меняться непрерывно, i ? R1, или
2.1. От истории к современности. Взгляд с птичьего полета 39
принимать только целые значения, ? G Z1). В пер- у^ X.
вом случае они часто называются потоками, во X ^ V
втором — отображениями или каскадами. Диффе- \ V Ч
ренциальные уравнения определяют потоки, зада- i . 1
вая в каждой точке пространства вектор скорости, * г *
или, как говорят, при помощи векторного поля * /* jf
(см. рис. 2.1). Переход к геометрической трактовке "* у, ^
приводит к тому, что многие основные термины
носят геометрический смысл — траектория, мно- Рис>2-1- Пример век-
v _ п торного поля
жество, многообразие, размерность и т.д. Одним
из основных понятий в настоящее время является понятие притягиваю-
притягивающего множества в фазовом пространстве, или аттрактора.
Несмотря на то, что геометрический подход успешно применяется
достаточно длительное время, составляет основу нелинейной динамики,
дает возможность предсказывать новые эффекты в ряде областей, отече-
отечественные программы и курсы дифференциальных уравнений во многом
отвечают традициям XIX века. Исключений здесь немного [8, 94].
Таким образом, нелинейная динамика вначале возникла не как
отдельная наука, а, скорее, как одна из «дополнительных глав» совре-
современного курса дифференциальных уравнений или динамических систем.
Однако пока мы пояснили лишь вторую половину термина — динами-
динамика. Остановимся на нелинейности. Одним из главных и парадоксальных
Проявлений нелинейности является хаотичность или динамический хаос.
Именно исследование динамического хаоса привело к пересмотру наших
взглядов на моделирование явлений природы и на наши возможности
давать прогноз. Поэтому пора остановиться на хаотичности.
Одна из любимых тем философов — соотношение случайности
и детерминизма. В физике для них применялись разные типы моделей —
для случайных процессов использовались методы теории вероятностей,
для детерминированных — писались дифференциальные уравнения. Де-
Детерминизм понимался как возможность (при желании) вычислить, исходя
из настоящего состояния системы, ее будущее. Классическая теорема
о непрерывности и дифференцируемости решений дифференциальных
уравнений по начальным данным вселяла оптимизм и уверенность в спра-
справедливости такого подхода. В самом деле, если мы немного ошибемся
в описании прошлого состояния, то и в будущем ошибка также будет
небольшой. Более того, почти во всех практически важных ситуаци-
ситуациях временное поведение системы (или ее желательное поведение) было
Довольно простым — стационарным или колебательным.
Метод Фурье, широко применяемый в линейной математической
физике, наглядно демонстрировал, что сложные колебания можно пред-
представить как композицию нескольких простых (заметим, что спектраль-
спектральный анализ данных до сих пор остается одним из основных инструментов
анализа результатов эксперимента). Математически это означало переход
от окружности (образ периодического процесса в фазовом простран-
пространстве) к произведению нескольких окружностей, т. е. многомерному тору.
40 2. Язык нелинейной динамики
Предполагалось, что и для нелинейных систем сложные колебания то-
тоже отвечают движению по поверхности тора в фазовом пространстве.
Естественно, что в подобной картине нет места неупорядоченному, хао-
хаотическому поведению, потому и открыли явление динамического хаоса
на 30 или на 70 лет позднее, чем могли бы.
Главный «концептуальный» толчок этому открытию дала работа
американского математика С. Смейла, предложившего в 1965 отображе-
отображение, известное под названием «подкова Смейла», о котором речь пойдет
дальше. Было показано, что временному поведению динамической систе-
системы может отвечать движение точки не по тору и вообще не по гладкому
множеству, а по «бесконечно разорванному» (впоследствии такие объекты
получили название фрактальных множеств или фракталей, фракталов),
и такая ситуация может быть типичной — так называемой «грубой»
или «структурно устойчивой», т. е. от нее нельзя избавиться маленьким
исправлением системы.
При этом непрерывная зависимость и даже дифференцируемость
по начальным данным сохраняется на любом конечном временнбм ин-
интервале, т.е. противоречия с классической теоремой нет. Однако эта
зависимость становится все более и более «рваной», подобно функции
/(ж) = sin(ix) — формально она непрерывна по х при любом t, но на
практике при достаточно большом t ни один физик таковой ее не сочтет.
Естественно, что и прогноз при помощи подобных функций возможен
только на небольших временах, пока производная -^^ не слишком
велика.
Поведение хаотической динамической системы во времени ока-
оказывается довольно сложным. В некоторых аспектах оно может быть
неотличимо от чисто случайного процесса, например, такого как под-
подбрасывание монеты (для подковы Смейла это несложно доказывается).
Получается, что динамическая система объединяет в себе глобальную
устойчивость (траектория не уходит из некоторой области фазового про-
пространства) с локальной неустойчивостью — малые погрешности начальных
данных нарастают, близкие траектории расходятся.
Обратим внимание на важное изменение точки зрения. Класси-
Классическая теория обыкновенных дифференциальных уравнений, которую
обычно преподают студентам, имеет дело с поведением на конечном вре-
временном интервале. Именно конечность временного интервала позволяет
доказывать многие теоремы и строить вычислительные алгоритмы. Не-
Нелинейная динамика интересуется асимптотическим поведением системы,
когда время стремится к бесконечности.
После того, как возможность подобной ситуации была осознана,
началась тихая революция во взглядах на случайное и детерминированное,
возникли термины «динамический хаос», «странный аттрактор». Оказа-
Оказалось, что хаотическое поведение может наблюдаться в весьма простых
системах, таких как система трех обыкновенных дифференциальных урав-
уравнений. Более того, оказалось, что пример такой системы был опубликован
за несколько лет до появления самого термина «странный аттрактор» (зна-
2.1. От истории к современности. Взгляд с птичьего полета 41
менитая статья американского метеоролога-теоретика Э. Лоренца в Jour-
Journal of Atmospheric Science, 1963), но прошел незамеченным из-за непод-
неподготовленности научной аудитории к восприятию новых взглядов.
В начале 70-х годов концепция динамического хаоса позволила
предложить новый подход к некоторым классическим задачам, напри-
например, к проблеме гидродинамической турбулентности — анализу сложной
картины течения жидкости при больших скоростях. Предшествующие
теории предполагали, что для описания турбулентности нужны модели
с очень большим числом степеней свободы (примерно по два диффе-
дифференциальных уравнения на одну возникающую частоту в спектре наблю-
наблюдаемого сигнала). Концепция динамического хаоса позволяет надеяться,
что хотя бы в некоторых случаях за сложным временным поведением
может скрываться сравнительно простая математическая модель. Подоб-
Подобные представления возникли и в связи с рядом задач в области химии.
Концепция сочетания локальной неустойчивости с глобальной устойчи-
устойчивостью породила надежды у некоторых биологов и социологов (которые,
прайда, пока так и остаются надеждами). Итак, с середины 70-х годов
началось триумфальное шествие динамического хаоса. Странные аттрак-
аттракторы стали находить всюду, и возникла настоятельная необходимость
разработки методов исследования хаотического поведения и его количе-
количественной характеризации. Встал вопрос, как отличить странный аттрактор
от нестранного, какой из двух аттракторов более странный и т. п.
Интереснее всего, что почти вся необходимая для анализа хаоти-
хаотических динамических систем математическая техника к 70-м годам была
уже разработана. А именно:
— в 60-х годах была практически завершена теория ляпуновских ха-
характеристических показателей, разработанных для исследования
устойчивости решений [55, 53];
— существовало понятие инвариантной меры, позволяющее приме-
применять к динамическим системам некоторые методы теории вероят-
вероятностей (фактически это понятие было использовано еще Пуанкаре
для доказательства его известной теоремы о возвращении решения
в окрестность большинства точек) [94];
— была тщательно исследована структура траекторий динамических
систем со сложным временным поведением и понята важность так
называемых гомоклинических траекторий, в окрестности которых
имеет место сложное временное поведение;
— существовали понятия аттрактора, инвариантного множества и т. п.,
ставшие центральными в хаотической динамике, многие из которых
были предложены в том или ином виде Пуанкаре и Биркгофом
в первой трети XX века.
Таким образом, в 70-е и 80-е годы во многом происходило оформле-
оформление концепции с использованием ранее разработанной техники. Новые
результаты главным образом были связаны с разработкой эффектив-
эффективных численных методов, с расчетом характеристик динамических систем
42
2. Язык нелинейной динамики
по временным рядам. Много внимания было уделено фракталам и кон-
концепциям типа параметров порядка. В последней исследуется вопрос о том,
системе скольких дифференциальных уравнений отвечает поведение ис-
исследуемой динамической системе на аттракторе.
2.2. Простое и сложное поведение
Прежде чем рассказывать об ос-
основных понятиях и идеях нелинейной
динамики, приведем примеры того, что
считается простым и сложным времен-
временным поведением. Пояснять удобнее все-
всего, показывая траекторию динамичес-
динамической системы на рис. 2.2. Если фазовое
пространство двумерно (плоскость или
ее часть), то можно показать саму тра-
траекторию, если нет — то ее двумерную
проекцию. В последнем случае возмож-
возможны самопересечения проекции траекто-
траектории, хотя в самом фазовом пространстве
траектории пересекаться не могут. Это
Рис. 2.2. Схема областей притяже-
притяжения. При различных начальных
данных решение выходит на ат-
аттракторы различных типов. На ри-
рисунке 1 — область притяжения
неподвижной точки; 2 — цикла;
3 — более сложного аттрактора
следует из теоремы единственности для
систем обыкновенных дифференциаль-
дифференциальных уравнений. Если из одной точки
фазового пространства «выходили» бы
две различные траектории, то это означало бы неединственность реше-
решения. Система в окрестности такой точки не знала бы, куда ей двигаться.
Если же условия теоремы единственности нарушаются, то такая ситуация
может возникнуть. Пример: уравнение х = /(ж) = ж1/3, ж@) = 0, имеет
два решения, x(t) = 0 и x(t) = (у) , однако /(ж) в точке х = 0 не
дифференцируема и условия теоремы единственности нарушены.
Особые или неподвижные точки х* системы уравнений х = f(x)
(т.е. такие точки, в которых f(x*) = 0) не являются исключением.
Функция x(t) = х* является решением, а другие траектории обычно
бесконечно долго стремятся к этой точке. Например, в уравнении х — —х,
ж@) = хо, неподвижная точка х* = 0, решение x(t) = х^е~*, lim x(t) = 0,
<->00
однако ни в какой конечный момент времени Т функция х(Т) Ф 0.
В уравнении х = х, х@) = хо, напротив, траектории могут покидать
окрестность особой точки за сколь угодно большое время.
Заметим, что нас будет интересовать асимптотическое поведение
динамической системы. Как правило, оно оказывается проще, чем на-
наблюдаемое при произвольно взятых начальных данных. На рисунке это
выглядит таким образом, что с течением времени траектории, выходя-
выходящие из различных начальных точек, стремятся собраться в некоторых
выделенных, сравнительно небольших областях фазового пространства
2.2. Простое и сложное поведение
43
(«аттракторах»), которые затем уже не покидают (рис. 2.2). Картина на-
напоминает ситуацию в бассейне реки или моря — маленькие ручейки текут
вниз с гор, сливаются в реки и в конце концов попадают в море. Поэтому
иногда область, откуда траектории стремятся к аттрактору, т. е. его область
притяжения, иногда называют бассейном притяжения (basin of attraction).
Таким образом, поведение динамической системы можно разделить на два
этапа: переходное поведение, пока траектория стремится к аттрактору,
и асимптотическое, когда траектория находится на самом аттракторе или
настолько близко к нему, что расстоянием можно пренебречь. Поскольку
переходное поведение преходяще, а асимптотическое вечно, внимание
исследователей обычно сосредоточено именно на последнем. Заметим
также, что динамические системы, к которым относится данная карти-
картина, называют диссипативными (определение будет дано позднее). Кроме
них существуют так называемые консервативные системы, у которых нет
деления на переходное и асимптотическое поведение. Судьба системы
при этом определяется начальными данными. Консервативные системы
часто встречаются в физике, когда при построении модели можно прене-
пренебречь диссипативными процессами — теплопроводностью, диффузией,
трением и т. п. Характерный пример — маятник без трения.
Как уже отмечалось, динамические системы могут описывать либо
непрерывное изменение состояния при непрерывном течении времени,
либо дискретные изменения в дискретные моменты времени. В первом
случае она является системой обыкновенных дифференциальных уравне-
уравнений или потоком, во втором — отображением или каскадом. Простота
и сложность временного поведения у них оказывается похожей, однако
отображения, порождающие качественно похожее поведение, оказыва-
оказываются проще потоков, поэтому некоторые эффекты предпочтительнее
исследовать именно для отображений.
Для потоков простейшим видом асимптотического поведения явля-
является отсутствие всяких временных изменений. В фазовом пространстве
при этом существует точка, называемая неподвижной точкой, которой
и отвечает данный тип поведения (рис. 2.3). Чтобы быть аттрактором,
она должна быть устойчивой, что показано при помощи траектории,
стремящейся к ней. Более сложным является периодическое поведе-
поведение, которому отвечает предельный цикл (рис. 2.4). Простому поведению
У It
у,
Рис. 2.3. Неподвижная точка
Рис. 2.4. Периодический режим
44
2. Язык нелинейной динамики
Рис. 2.5. Двухчастотный ре-
режим (тор)
отвечают простые модели — устойчивая неподвижная точка может опи-
описываться всего одним уравнением, скажем, х = —ж, предельный цикл
требует уже двух уравнений (сложные циклы могут требовать и больше),
например z = (iw + a - \z\2)z, z = x + iy (здесь при а < 0 реализуется
устойчивая неподвижная точка, при а > 0 — предельный цикл).
Следующий шаг усложнения — это
квазипериодические колебания, когда в сис-
системе наблюдаются две частоты ш\ и иг,
причем их отношение ^ — иррациональ-
иррациональное число. Эта ситуация реализуется толь-
только если размерность фазового пространства
не меньше трех (модель должна включать
не менее трех уравнений). Асимптотиче-
Асимптотическое поведение соответствует заполнению
траекторией поверхности двумерного тора,
поэтому данный режим иногда для крат-
краткости называют просто 2-тор (рис. 2.5). Да-
Далее степень сложности может нарастать
в двух направлениях. Во-первых,
может увеличиваться число неза-
независимых частот, и траектория мо-
может регулярно заполнять 3-тор, 4-
тор и т.д. Во-вторых, может воз-
возникнуть режим, получивший назва-
название динамического хаоса (рис. 2.6).
На вид он не является строго детер-
детерминированным, хотя и совсем слу-
случайным его не назовешь. Траекто-
Траектория в этом случае никакой гладкой
гиперповерхности в фазовом про-
пространстве не заполняет, аттрактор
оказывается «всюду дырявым». Как
и тор, возникать хаос может толь-
только тогда, когда размерность фазо-
фазового пространства не меньше трех,
потоки на плоскости хаоса лишены. Слож-
Сложность хаотических режимов тоже может быть
различной, этому собственно и были уделе-
уделены большие усилия специалистов по нели-
нелинейной динамике.
Похожим образом анализируется и
сложность асимптотических режимов для ди-
динамических систем с дискретным временем
отображений. Обычно их записывают в виде итерационного процесса —
в виде формулы, определяющей, как следующее состояние определяется
по предыдущему, xn+i = f(xn). Здесь также существуют неподвижные
Рис. 2.6. Хаос
Рис. 2.7. Неподвижная точка,
цикл и аналог тора в отобра-
отображениях
2.3. Порядок в хаосе
45
ТОЧКИ X* = f(x*) И ЦИКЛЫ Х2 =
f(xi), ..., xm = f(xm_i), xi =
f(Xm). Тору отвечает непериодиче-
непериодическое поведение, при котором точ-
точки регулярно заполняют одномер-
одномерную кривую (например, отображе-
отображение окружности в себя <р„+\ =
ipn + а, где =— иррационально
(рис. 2.7)). Существуют и хаотиче-
хаотические режимы: если от f требо-
требовать обратимости, то они возни-
возникают в пространстве размерности
больше единицы. Пример этого да-
дает аттрактор Хенона
У
0,4
0,2
-0,20
-0,40
-1,0-0,5 0 0,5 1,0
х
— 1 — ахп
Уп+1 — Ь
а =1,4,
B.1)
Рис. 2.8. Хаос (аттрактор Хенона). Кре-
Крестиком показана одна из двух неустой-
неустойчивых неподвижных точек
= 0,3,
показанный на рис.2.8. Если от f не требовать обратимости, т.е. до-
допускать отображение нескольких точек в одну, то хаос возможен даже
в одномерном случае. Пример этого дает логистическое отображение.
2.3. Порядок в хаосе
Каковы же основные черты и закономерности хаотических режи-
режимов?
Во-первых, очень часто на асимптотической стадии траектория
притягивается к притягивающему множеству, обладающему фрактальной
структурой, или фракталу. Простейший и широко известный пример
фрактала — это канторово множество, схема построения которого приве-
приведена на рис. 2.9. Отличительной чертой, присущей многим (но не всем!)
фракталам, является то, что увеличенная часть такого множества ока-
оказывается подобна всему множеству (определение фрактала будет дано
позднее, оно связано с понятиями топологической и хаусдорфовой раз-
размерностей). На рис. 2.10 показаны увеличенные детали аттрактора Хе-
Хенона B.1): видно, что подобие действительно имеет место. Аттракторы,
имеющие фрактальную структуру, называют странными.
Рис. 2.9. Первые пять ша-
шагов построения канторова
множества
46
2. Язык нелинейной динамики
0,5 +
-0,5+. . , . х 0,1601-
I ifmп i ч 111 и i м и 111111111 п 11111
-1,0 0 1,0 2,0
0,25; -
0,20 j -
0,55 0,60 0,65 0,70
У
0,190-
0,185--
0,40 0,60 0,80 1,00
T I I П
0,620 0,630 0,640
Рис. 2.10. Иллюстрация фрактальной структуры аттрактора Хенона. Квадратик
выбирается в окрестности неподвижной точки, обозначенной крестиком
Во-вторых, движение обычно оказывается локально неустойчивым,
т.е. почти любые близкие траектории расходятся, не покидая при этом
аттрактора. Движение оказывается неустойчивым по Ляпунову, в отличие
от циклов и торов, где оно устойчиво (напомним, что решение x(t) назы-
называется устойчивым по Ляпунову, если для любого г найдется 6, такое что
для любого решения x(t), такого что |х@) — ж@)| < 6, \x(t) — x(t)\ < e,
t > 0; если к тому же \x(t) - x(t)\ ^5 0, то решение называют асим-
асимптотически устойчивым). Расстояние I между траекториями при малых I
в среднем обычно экспоненциально увеличивается, i~ exp (Xt), где А > 0
называется старшим ляпуновским показателем (на самом деле показа-
показателей несколько, но самый важный среди них — наибольший). Чем
больше А, тем более хаотичным выглядит движение. На рис. 2.11 при-
приведена зависимость расстояния между двумя траекториями отображения
Хенона, первоначально очень близкими. Аттракторы, динамика которых
характеризуется положительным ляпуновским показателем, называют ха-
хаотическими.
В-третьих, если в качестве начальных данных взять не точку, а неко-
некоторый, пусть очень малый, объем в фазовом пространстве, то с течением
2.3. Порядок в хаосе
47
Рис. 2.11. Расходимость близких траекторий для аттрактора Хенона. Точками
показано изменение расстояния г между двумя первоначально очень близкими
траекториями в начальный момент г = 10~5. Сплошная линия показывает
эволюцию бесконечно близкой траектории (нормировка выбрана так, чтобы
на первых итерациях она совпадала с предыдущим случаем). Штриховая линия
показывает среднюю скорость расходимости бесконечно близких траекторий
г = гоехр(А<), где А = 0,418... — старший ляпуновский показатель, время
изменяется дискретно, t = п
времени система начнет этот маленький объем, «каплю», размазывать
по всему аттрактору, и возникает эффект перемешивания (рис. 2.12). Та-
Таким образом, если в начальный момент времени мы знали состояние
системы достаточно точно, с малой ошибкой, то со временем ошибка
начнет нарастать, и спустя некоторое время, зависящее от скорости пе-
перемешивания (заметим, что скорость перемешивания обычно не связана
каким-либо простым образом с величинами ляпуновских показателей),
окажется, что о состоянии системы можно сказать лишь, что оно «где-то
на аттракторе». На больших временах характеризовать систему можно,
только указав вероятность появления траектории в окрестности некото-
некоторой точки. Таким образом, мы приходим к вероятностному описанию
динамического хаоса, к понятиям инвариантной меры и энтропии —
степени хаотичности системы. Аттракторы, обладающие свойством пе-
перемешивания, часто называют перемешивающими, или стохастическими
аттракторами. Однако доказать или проверить свойство перемешивания
обычно очень трудно. Тем не менее, в большинстве случаев хаотичность
скорее всего влечет за собой и стохастичность аттрактора.
Аттрактор Хенона оказывается одновременно странным, хаотиче-
хаотическим и, по-видимому, стохастическим. Однако это не всегда так. Су-
Существуют странные нехаотические аттракторы, простейшим примером
которых служит инвариантное множество в логистическом отображении
х„+1 = ахп(\ - хп), х € [0,1]; при некотором а = аж (см. [10]) оно
имеет фрактальную структуру, но ляпуновский показатель А = 0. Бывает
и наоборот, при а = 4 А = 1п2 = 0,693..., в то время как инвариантное
множество — это весь отрезок [0,1] и у него нет фрактальной структуры.
Получаем, что хаотичность не влечет странности. Заметим, однако, что
обе эти ситуации «негрубые», т. е. в некотором смысле нетипичные.
48
2. Язык нелинейной динамики
0,4
0,2-
о-
-0,2-
-0,4-
У
I , I I I I I Hill hiItT1
-0,1 0 1,0
0,4-
0,2-
о-
-0,2-
-0,4-
У
1 1 I I П 1 1 II 1 1 ! 1 1 1 I 1 МI
10
))
1 х
0,4-
0,2-
o--
-0,2-
-0,4--
У
0,4-
0,2-
o-
-0,2-
-0,4-
У
-0,1 0
1,0
ъ
-0,1 0
-0,1 0 1,0
Рис. 2.12. Растекание малого фазового объема по аттрактору Хенона
2.4. Прообразы динамического хаоса — 1
49
Как уже было сказано, хаотические режимы могут иметь различную
степень не только хаотичности, но и сложности. Однако характеризовать
сложность числом независимых (некратных) частот в спектре невозмож-
невозможно, поскольку спектр оказывается сплошным, и в этом динамический
хаос также похож на истинный. Но можно измерять сложность как размер
минимальной математической модели, способной воспроизвести наблю-
наблюдаемый процесс, или, что то же самое, измерять ее геометрическими
характеристиками аттрактора. В результате мы приходим к фракталь-
фрактальным размерностям и размерностям, связанным с понятием инерциального
многообразия.
Еще один подход к анализу хаотических динамических систем
состоит в детальном исследовании структуры траекторий, приводящей
к хаотическому поведению. Это, вероятно, один из наиболее глубоких
и сложных подходов к проблеме, но изложение этих вопросов требует
достаточно серьезной подготовки читателя. Изложение многих вопросов
и обширный список литературы можно найти, например, в [9], [48], [92].
2.4. Прообразы динамического хаоса — 1.
Сдвиг Бернулли
Рассмотрим одну из классических хк+1
задач теории вероятностей — последо-
последовательность случайных подбрасываний
монеты, которая может с равной ве-
вероятностью выпадать каждой из сто-
сторон — «орлом» или «решкой». Будем
первому исходу ставить в соответствие О,
второму — 1. Тогда результату бес-
бесконечной серии подбрасываний мож-
можно сопоставить строку из нулей и еди-
единиц или действительное число 0 ^
ж ^ 1, двоичное представление которого
имеет вид 0,ою2о3...о*... , например, р„с.2.13. Отображение хш =
0,0110100011... . Если 0 ^ ж < 0,5, то 2itmodl
результат первого броска — 0, если
0,5 ^ ж < 1 — то 1. Чтобы получить результат второго подбрасыва-
подбрасывания, надо сдвинуть строку на 1 символ влево, т.е. умножить ж на 2,
и оставить только дробную часть. Таким образом, необходимо выпол-
выполнить преобразование ж„+1 = /(ж„), где /(ж) — 2ж при 0 ^ ж ^ 0,5
и /(ж) — 2ж — 1 при 0,5 ^ ж ^ 1, т. е. /(ж) = 2ж mod 1. Мы получили ото-
отображение отрезка в себя — динамическую систему. Таким образом, если
мы выберем некоторую точку ж и рассмотрим ее итерации, сопоставляя
каждому хк целую часть от 2хк, то результат будет неотличим от по-
последовательности подбрасываний монеты. Мы получили «случайную»
последовательность, сгенерированную детерминированным алгоритмом,
причем в зависимости от начальной точки может быть воспроизведена
любая последовательность (рис. 2.13).
50 2. Язык нелинейной динамики
Аттрактора (области притяжения) в данном случае нет, поскольку
фазовое пространство — отрезок [0,1] — заполняется траекториями пол-
полностью. Локальная неустойчивость очевидна — если в качестве начальных
данных выбрать две близкие точки, то расстояние между их образами
на каждой итерации будет удваиваться, Л = In 2. Таким образом мы
получили одну из простейших динамических систем с хаотическим пове-
поведением. Заметим, что она необратима, поскольку две точки отображаются
в одну.
2.5. Прообразы динамического хаоса — 2.
Проблема турбулентности. Лоренц, Рюэль и Такенс
— А вы видели, как течет река?
А. Моруа
С одним из самых загадочных объектов современной науки мы
сталкиваемся ежедневно. Речь идет об известном всем турбулентном,
сильно завихренном течении жидкости. Исследования этого явления
были начаты еще в прошлом веке. Были созданы и успешно применялись
инженерные и математические модели для расчета характеристик труб
или кораблей, однако понимания причин и «корней» этого явления нет
во многом и по сию пору.
Математическое описание течений жидкости было предложено еще
в начале прошлого века — это так называемые уравнения Навье—Стокса.
Они представляют собой не что иное как запись второго закона Ньютона,
дополняемого законом сохранения вещества (так называемое уравнение
неразрывности). Наиболее просто уравнения выглядят в случае несжи-
несжимаемой жидкости, когда уравнение неразрывности сводится к условию
divV = 0:
V« + (VV)V = i/ДУ - Vp + F,
где р — давление, F — объемная сила, V — вектор скорости из трех
компонент V\, Vi и V-$. Уравнения оказываются нелинейными, поэтому
аналитически удается исследовать только простейшие течения, когда за-
завихренности либо нет совсем, либо она регулярная. В основном изучены
были двумерные течения жидкости, для которых возможно применение
методов теории функций комплексного переменного. Объяснить же удо-
удовлетворительно структуру сложных трехмерных течений, опираясь на эти
уравнения, не удавалось.
Было выдвинуто несколько гипотез (см., например, [117]). Во-
первых, это гипотеза Лере. Она опирается на удивительный факт —
несмотря на большие усилия, до сих пор не удалось доказать глобаль-
глобальное (для неограниченного промежутка времени) существование решений
уравнений Навье—Стокса. Лере предположил, что турбулентность —
это процесс постоянного разрушения старых решений и возникновения
новых. Во-вторых, гипотеза Ландау. В соответствии с ней турбулент-
турбулентное течение — это просто тор очень большой или даже бесконечной
2.5. Прообразы динамического хаоса — 2 51
размерности. Ничего нереального в этой гипотезе нет, но изучение ста-
статистических свойств турбулентности показало, что она не согласуется
с экспериментальными данными. В-третьих, существовали гипотезы и о
том, что турбулентные режимы могут вообще не описываться урав-
уравнениями Навье—Стокса или для них может не выполняться условие
несжимаемости divV = 0. Наконец, в 1971 г. Рюэлем и Такенсом была
высказана еще одна гипотеза, связанная с идеей динамического хаоса
и представляющаяся сейчас наиболее предпочтительной.
Прежде чем рассказать о ней, вернемся к концу 50-х - началу
60-х годов, когда в Америке уже получили распространение компьютеры
и началось широкое применение численных методов решения обыкно-
обыкновенных дифференциальных уравнений. Именно благодаря компьютер-
компьютерному моделированию и появилась первая работа, в которой не только
было обнаружено явление динамического хаоса, но также и достигнуто
понимание проблемы.
Е. Н. Лоренц был метеорологом-теоретиком, и как-то раз его знако-
знакомый, Б. Сольцмен, рассказал ему о сложном поведении решений некото-
некоторой системы обыкновенных дифференциальных уравнений, полученной
из уравнений конвекции жидкости. Надо заметить, что задача о конвек-
конвекции в слое жидкости — одна из классических, на которой «точило и точит
зубы» не одно поколение гидродинамиков любого профиля — и теоре-
теоретиков, и вычислителей, и экспериментаторов. Она состоит в следующем.
Рассмотрим слой жидкости между двумя горизонтальными пластина-
пластинами, температура которых поддерживается постоянной, причем нижняя
горячее верхней на ДГ. Движение жидкости и перенос тепла описы-
описывается системой уравнений Навье—Стокса и теплопроводности. Экспе-
Экспериментальное исследование ситуации при различных ДГ показало, что
при малых перепадах температур не происходит вообще ничего — жид-
жидкость находится в покое, работает только теплопроводность, температура
линейно убывает от дна к поверхности. Затем при достижении некото-
некоторого критического перепада температур ДГС такое однородное состояние
становится неустойчивым. Далее могут возникать шестигранные ячейки
на поверхности жидкости, или конвективные валы (рис. 2.14). При воз-
возникновении валов распределения скорости и температуры не зависят
от одной из координат, и задачу можно считать двумерной. При даль-
дальнейшем увеличении ДТ валы начинают колебаться, затем колебания
становятся все более сложными и развивается турбулентное движение.
Рис. 2.14. Конвективные валы
52 2. Язык нелинейной динамики
Аналитически можно получить лишь решение в виде стационарных кон-
конвективных валов, все прочие режимы можно исследовать только прибли-
приближенно или численно. Обычно при этом ищут решения, периодические
по горизонтальным координатам х\ и Х2. Специальным образом поста-
поставленные гидродинамические эксперименты подтверждают правомерность
такого подхода (в общем же случае ситуация оказывается гораздо слож-
сложнее). Функции, входящие в уравнение (поле скорости и температуры),
можно искать в виде ряда Фурье по пространственным координатам вида
Если разлагаемые функции достаточно гладкие по г, то фактически вид
решения будет определяться коэффициентами при нескольких первых
гармониках, остальными же можно пренебречь.
Далее можно подставить такие конечные разложения для V и Т
в уравнения. Затем отбросим возникающие благодаря нелинейности про-
пространственные гармоники, которыми ранее пренебрегли (например, если
п + тп достаточно велико, то из произведения cos mx cos nx оставляем
только 0,5cos(n — m)x). После этого получим систему обыкновенных
дифференциальных уравнений для коэффициентов Qjkn- Такая процеду-
процедура широко применяется в физике и вычислительной математике и на-
называется методом Галеркина. Этот же метод можно применять и для
получения упрощенных моделей явлений, поскольку иногда количество
существенных мод оказывается поразительно малым. Тогда оказывает-
оказывается, что суть процессов, которые формально описываются уравнениями
в частных производных, бесконечномерными динамическими системами,
можно передать при помощи всего нескольких ОДУ.
С системой такого типа для уравнений Навье—Стокса и теплопро-
теплопроводности и имел дело Лоренц. Для простоты рассматривался двумерный
случай, когда от переменной xi ничего не зависит. Тогда от двумерного
вектора скорости можно перейти к скалярной величине — потенциалу
скорости ip, V\ = Ц, К3 = -|?. При этом условие divV = g? + ?g = О
выполняется автоматически, а для функции ip получается одно уравнение
четвертого порядка. Вместо температуры использовалось ее отклонение
от линейного равновесного профиля &. Полная система уравнений име-
имела вид
dip дА'ф dip dAip _ 2 *?
дх 1 дхз dxj дх\ dxi
dip dti дф dti , , dip
tf + -L -I. = кд20 + ДТЯГ1 —,
' дхх дх3 9«з dxi ' 9xi'
где g, a, v и к — некоторые коэффициенты. Линейный анализ по-
показывает, что при ДТС однородное состояние становится неустойчивым
2.5. Прообразы динамического хаоса — 2
53
по отношению к возмущениям вида
~У
Логично было предположить, что эти моды будут играть наиболее важную
роль и в дальнейшем, так что использовались следующие разложения:
. firax\\ .
cm i I cir
¦X(t)V2sm[ -
У
Подстановка этих разложений в уравнения после перехода к новому
безразмерному времени приводит к следующей системе:
X = a(Y - X), Y = rX -Y- XZ, Z = XY- bZ.
Здесь а = ? — так называемое число Прандтля, г = ^, Ь = -ц^,
где а — отношение расстояния между плоскостями к горизонтальному
периоду, так называемое «аспектное отношение» (aspect ratio). Именно эта
система уравнений в настоящее время известна как «система Лоренца».
Некоторые результаты не требуют применения численных методов.
Легко получить, что при г < 1 существует только одно устойчивое
состояние X = Y = Z = 0. При г > 1 оно становится неустойчивым
и возникают два новых, ненулевых: Z = г — 1, X = Y, X1 = Ь(г — 1).
Затем, при г = 24,74 они также становятся неустойчивыми, и возникают
нерегулярные колебания, которые наблюдались в численном счете.
Далее Лоренц показал, что траекто-
траектории этой системы при всех положитель-
положительных значениях параметров должны вхо-
входить в некоторую сферу в фазовом про-
пространстве X, Y, Z. Можно показать, что
2 22
р
y2 I y2
< 0 вне этой сферы (подробнее
)
мы рассмотрим этот вопрос в гл. 3). Следо-
Следовательно, используя современную термино-
терминологию, можно сказать, что у системы суще-
существует аттрактор, который находится внутри
этой сферы (рис. 2.15). Далее, в той же ра-
работе были приведены численные расчеты
для значений параметров а — 10, b = j,
г = 28, когда наблюдались нерегулярные конеч„ое BpeMa входят внутрь
колебания. Их характерный вид предста- некоторого множества (погло-
влен на рис. 2.16 рядом с аттрактором Ло- щающее множество, на рис.—
ренца, одним из самых популярных объ- круг) и впоследствии не поки-
ектов нелинейной науки. Оказалось, что дзкхг его, значит внутри него
с хорошей точностью можно считать, что есть аттРакт°Р
траектории двигаются по «раздваивающейся» поверхности. Но самое,
Рис. 2.15. Схема доказатель-
доказательства существования аттракто-
аттрактора. Если все траектории за
2. Язык нелинейной динамики
10 15 20 25 30
-10 0 10 x(t)
11,1 .Ill, I, I,,
-10
10
Рис. 2.16. Аттрактор Лоренца. Временое поведение: a) X(t), б) Z(t); проекции
траектории на плоскость: в) X, Y, г) X,Z.
пожалуй, важное наблюдение было следующим. Лоренц построил график
локальных максимумов Z(t), причем по оси абсцисс откладывал преды-
предыдущее значение Zn, а по оси ординат — следующее, Zn+\. Оказалось, что
точки (Zn+\,Zn) с хорошей точностью ложатся на одномерную кривую
вида Zn+\ = f(Zn), причем производная -*Цр везде больше 1 (рис. 2.17).
Отсюда Лоренц сделал вывод о неустойчивости траекторий и в качестве
2.5. Прообразы динамического хаоса — 2
55
34,90 - -
34,85--
34,80 - -
30
45 Zk
~i—I—i—i—i—i—I—i—i—i—i—I—i—i
34,00 34,05 34,10 Zk
Рис.2.17. Аттрактор Лоренца: а) точки (Zt+\,Zt) с хорошей точностью ложатся
на одномерную кривую вида Z/,+l = /(#*), 10 000 точек; б) увеличенный фрагмент
графика
поясняющего примера привел отображение ж„+1 = 1 — |1 — 2ж„|, обла-
обладающее теми же свойствами, что и рассмотренное выше отображение
х„+1 = 2ж„ mod 1. Таким образом, перед нами пример вполне «реальной»
системы, демонстрирующей хаотическое поведение.
Более поздние исследования показали, что на самом деле ре-
результаты Лоренца не имеют отношения к наблюдаемой в большинстве
гидродинамических экспериментов конвекции. В более точных двумер-
двумерных галеркинских аппроксимациях вообще нет никакого хаоса, а только
квазипериодические колебания. По-видимому, турбулентность и хаос воз-
возникают только в трехмерных течениях жидкости. Тем не менее, в иссле-
исследованиях по динамическому хаосу система Лоренца — одна из основных
моделей и объект испытаний множества методик.
Интересно, что в течение долгого времени результаты Лоренца
не были восприняты. Интерес к ним возник только после того, как
в 1971 г. математики Д. Рюэль и Ф.Такенс предложили новую концеп-
концепцию турбулентности. Основываясь на представлениях С. Смейла, они
показали, что системы, где есть аттрактор в виде 3-тора, можно малым
изменением превратить в системы с аттрактором, имеющим весьма слож-
сложную структуру, который они назвали «странным аттрактором». Однако
работы Смейла были основаны не на исследованиях турбулентности,
а на теории динамических систем, которая выросла из исследований
по небесной механике и гамильтоновым системам.
56 2. Язык нелинейной динамики
2.6. Прообразы динамического хаоса — 3.
Небесная механика, Пуанкаре и «подкова Смейла»
Одним из основных объектов исследований математиков прошлого
века были уравнения движения планет — небесная механика. Уравне-
Уравнения эти принадлежат к классу так называемых гамильтоновых систем.
Переменные, входящие в уравнения, называются обобщенными коорди-
координатами q{ и обобщенными импульсами р{, а сами уравнения движения
выражаются через так называемую функцию Гамильтона H(p,q):
дН дН ¦ i лг
Для гамильтоновых систем выполняется закон сохранения энергии
Е = Н, поскольку легко получить, что Ё = 0. В самом деле,
днан
Однако часто в системах такого типа существуют и другие законы сохра-
сохранения, и если их всего N штук, то система называется вполне интегриру-
интегрируемой. В этом случае от переменных р и q можно перейти к другим парам
переменных, также имеющим смысл обобщенных координат и импуль-
импульсов, но таким образом, чтобы новыми обобщенными импульсами стали
сохраняющиеся величины Jj, называемые «действие», а обобщенными
координатами ipi — так называемые «углы», поскольку они циклически
изменяются от 0 до 2я\ При этом функция Гамильтона зависит только
от J, так что система уравнений в переменных действие-угол имеет вид
дН
Ji = 0, ф(--—-=ш{= const.
OJi
Таким образом, самое сложное поведение, которое может наблюдаться
во вполне интегрируемой системе — это колебания с N независимыми
частотами, т. е. ЛГ-тор. Возможно, этот результат также сыграл не послед-
последнюю роль в том, что динамический хаос был открыт только в 70-е годы
нашего века. Однако еще в 1880-х годах Пуанкаре проводил исследование
уравнений небесной механики, поскольку уже для задачи трех тел доказать
полную интегрируемость не удавалось. Пуанкаре это также не удалось,
однако он показал, что если аппроксимировать потенциал полиномом ко-
конечной степени, то система будет вполне интегрируемой. Кроме того, им
был получен ряд важных результатов, развитых впоследствии Биркгофом
и составивших основу современной теории динамических систем. В част-
частности, им была отмечена сложность поведения системы в окрестности так
называемой гомоклинической траектории (траектория стремится к неко-
некоторой неподвижной точке или периодической траектории как при t -* со,
так и при t —» -оо).
2.6. Прообразы динамического хаоса — 3
57
Ранее мы упоминали только устойчивые неподвижные точки ди-
динамических систем. Однако гамильтоновы системы относятся к консер-
консервативным системам, в которых не бывает аттракторов, и типичными
неподвижными точками для них являются центры, окруженные контину-
континуумом периодических траекторий (устойчивые точки), и седла, в которые
траектории по одним направлениям входят, по другим — выходят (не-
(неустойчивые точки) (см. рис. 2.18). Совокупность всех траекторий, входя-
входящих в такую точку, образует ее устойчивое многообразие, всех выходящих
из нее — неустойчивое многообразие. Точно также устойчивое и неустой-
неустойчивое многообразия существуют и у циклов, и у торов. Так вот, оказалось,
что существуют траектории, называемые гомоклиническими, которые стре-
стремятся к одному и тому же тору (циклу или неподвижной точке) как при
t —> со, так и при t —> —со (рис. 2.19). Они должны проходить через точки
пересечения устойчивого и неустойчивого многообразия, называемые го-
гомоклиническими точками, причем в случае N > 1 такие пересечения могут
быть типичными, т. е. неустранимыми при малых изменениях системы.
Пуанкаре отметил, что в окрестности гомоклинических траекторий воз-
возможно очень сложное временное поведение, однако насколько сложное,
до 60-х годов было неясно.
Ситуацию помогла прояснить конструкция, предложенная амери-
американским математиком С. Смейлом; впоследствии она получила название
«подкова Смейла». Преобразование подковы отображает внутренность
единичного квадрата в изогнутую полосу, дважды пересекающую его
У,
а б
Рис. 2.18. а) Центр, б) Седло и его устойчивое и неустойчивое многообразие, по
которым траектория, соответственно, приходит в неподвижную точку и уходит
из нее ,
а б
Рис. 2.19. Гомоклиническая и гетероклиническая точки на плоскости
58
2. Язык нелинейной динамики
(см. рис. 2.20). Это преобразование
обратимо, что характерно для га-
мильтоновых систем, и обратное
преобразование имеет тот же вид,
но полосы располагаются не верти-
вертикально, а горизонтально. Смейл по-
показал, что: 1) инвариантное множе-
множество отображения (которое перехо-
переходит в себя) является, как мы сейчас
говорим, фрактальным; 2) ему отве-
отвечает временное поведение, неотли-
неотличимое от последовательности бро-
D С
D
С
В
А В С D
А В
Рис. 2.20. Отображение, получившее
саний монеты (как и в случае ото- название «подкова Смейла»
бражения ж„+1 = 2xnmodl); 3) эта
ситуация может быть типична и неустранима при помощи малых из-
изменений системы. Последний результат оказался особенно важным, так
как означал, что подобные конструкции могут существовать и в природе,
когда реализуется сложное временное поведение. Оказалось, что в случае
гомоклинических структур реализуется качественно похожее отображе-
отображение. Таким образом было найдено, что вполне интегрируемые системы
не охватывают класс всех важных систем, и могут существовать другие,
в которых реализуется явление динамического хаоса. Переход к хаосу
в гамильтоновых системах, получивший название «разрушение инва-
инвариантных торов» или теории Колмогорова—Арнольда—Мозера (КАМ),
разобран в ряде книг, например, [21], и далее мы этой темы касаться
не будем. Основные идеи теории диссипативных и гамильтоновых систем
оказываются существенно различны, и далее мы сосредоточим внимание
на диссипативных системах.
Однако отображение типа подковы оказалось очень важным и для
теории диссипативных систем. В частности, оно служит качественным
объяснением формирования сложной фрактальной структуры странных
аттракторов. После того, как это объяснение было предложено, француз-
французский специалист по небесной механике М. Хенон (М. Нёпоп) предложил
великолепную иллюстрацию, построив отображение плоскости в себя, ре-
реализующее те же стадии, что и отображение Смейла, в виде композиции
трех отображений:
• образование складки: щ = х, v\ — у + 1 — ах2;
• сжатие: «2 = Ь, ^2 = v\;
• поворот, возвращающий прежнюю ориентацию: «з = vi, Щ = «2 •
В результате получается двумерное отображение, получившее название
«отображение Хенона», и имеющее вид
я„+1 = 1 - axl + уп, уп+1 = Ьхп.
Оно уже упоминалось раньше в этой главе. Для случая а = 1,4, Ь = 0,3
траектория этого отображения показана на рис. 2.8, а на рис. 2.10 показана
и возникающая у него фрактальная структура.
2.6. Прообразы динамического хаоса — 3 59
Вместо заключения
Разумеется, история динамического хаоса гораздо богаче, чем наш
небольшой схематический набросок. Например, свои прообразы есть
и в физике лазеров, где, как утверждается, система Лоренца была получена
совсем в другом контексте и на год раньше. Однако тогда задача состояла
не в изучении сложного поведения, а наоборот, в стабилизации режимов
генерации. Поэтому странный аттрактор в этой системе тогда открыт не
был. Однако система была выписана, и если бы Лоренц не опубликовал
своих работ, его аттрактор нашел бы кто-нибудь другой.
Своя предыстория была и в радиофизике, где развивалась теория
нелинейных колебаний. Там была своя, не менее драматическая история
создания генераторов хаоса (см., например, [41, 108]).
Этот перечень можно продолжать. Видимо, когда-нибудь история
динамического хаоса будет написана достаточно полно. Однако нам хоте-
хотелось бы отметить, что открытие в 70-х годах нашего века динамического
хаоса сыграло ключевую роль в создании нелинейной динамики. Оно
показало, что даже в простейших детерминированных системах суще-
существуют принципиальные ограничения на получение динамического про-
прогноза, т. е. предсказания, в какой точке фазового пространства окажется
система через заданный интервал времени. Важную роль в открытии
динамического хаоса сыграло компьютерное исследование системы Ло-
Лоренца. Понимание этого явления, введение новых понятий и концепций
оказалось связано с изучением простейших одномерных и двумерных
отображений — подковы Смейла, логистического отображения, кусочно-
линейного одномерного отображения х^.+\ = 1 — 2|жц|, отображения
Хенона. Эти исследования привели к новому взгляду на динамические
системы, на математическое моделирование многих явлений, на проце-
процедуру сопоставления теории и эксперимента, позволили переосмыслить
ряд предшествующих математических результатов.
Динамические системы
и их устойчивости
3.1. Что такое динамическая система?
Ранее приводились многочисленные примеры динамических си-
систем (ДС). Поясним теперь, что именно мы будем понимать под этим
термином.
Вообще говоря, в разных книгах можно найти различные толкова-
толкования этого термина, например, такие:
— это синоним термина «система обыкновенных дифференциальных
уравнений» (ОДУ)
x = f(x,«);
— это синоним термина «автономная система обыкновенных диффе-
дифференциальных уравнений»
х = g(x);
— это математическая модель некоторой механической системы.
Мы будем придерживаться точки зрения, принятой, например,
в работах [55, 111]. Согласно ей, понятие ДС является обобщением
понятия автономной системы дифференциальных уравнений и включает
в себя два основных компонента: фазовое пространство Р (метрическое
пространство или многообразие) и однопараметрическую непрерывную
или дискретную группу (полугруппу) <р*(х) или <p(x,t) его преобразований.
Параметр группы, обозначаемый t — это время. В случае полугруппы
рассматриваются только значения времени t ^ 0. Проще говоря, ip*1 (x) —
это вектор, представляющий решение изучаемого уравнения в момент t\
с начальным условием х.
Однако столь общее определение обычно не требуется, поэтому мы
поясним, что будет пониматься под ДС чаще всего.
В качестве фазового пространства Р практически во всех важных
и нужных случаях выступают:
— га-мерное евклидово пространство или некоторая его область (на-
(например, отрезок [0,1]);
— га-мерный тор (например, окружность);
— произведение raj -тора и гаг-мерного евклидова пространства, нечто
вроде «обобщенной бесконечной трубки» или ее части;
3.1. Что такое динамическая система? 61
— в некоторых приложениях теории динамических систем удобно
распространять данный подход и на системы, описываемые урав-
уравнениями в частных производных, в этом случае в качестве Р
обычно используются гильбертовы функциональные пространства,
например, Li.
Других примеров фазовых пространств мы рассматривать не будем.
Отображение <р в этом случае, по крайней мере локально, является
обычной вектор-функцией векторного аргумента. То есть для любого
вектора (точки) хЕРи (^0 (целого или действительного) существует
единственный вектор (точка) ^'(х) ? Р-
Для отображения <р должны выполняться свойства полугруппы или
группы (ниже они перечислены). В последнем случае оно должно быть
определено и для t < 0, иначе говоря, функция (р*(х) должна быть
определена и обратима при любом -оо < t < оо: если у = ^'(х)> то
х = *>~Чу)-
1. ^°(х) — х (начальное условие).
2. Для любых t\,t2 (в случае полугруппы ^ 0) и х € Р у>'2(у>''(х)) =
р(|+B(х).
3. В дальнейшем мы ограничимся только кусочно-дифференцируе-
кусочно-дифференцируемыми функциями <р. Для систем с непрерывным временем мы
будем предполагать, что <р дифференцируема по t и дважды кусочно
дифференцируема по совокупности аргументов.
Из свойства 3 следует, в частности, непрерывность по начальным
данным на любом конечном интервале времени.
Гладкость правых частей нужна, в частности, для того, чтобы
исключить неединственность. Заметим, что в примере из предыдущей
главы х = ж1/3 = F(x), х@) — 0, производная F(x) в нуле не существует,
поэтому эта система не принадлежит классу функций, о которых идет
речь (или надо в качестве фазового пространства использовать область
ж>0).
Траекторией, проходящей через точку х, будем называть множе-
множество {(р((х)}, где t принимает все допустимые значения @ ^ t < оо
для необратимых <р и —сю < t < оо для обратимых).
Траекторией, начинающейся в точке х, или положительной полу-
полутраекторией точки х называется множество {<р*(х): t ^ 0}. Очевидно, что
такая полутраектория единственна.
Неподвижной точкой (fixed point) xo называется траектория, такая
что ^'(хо) = хо при всех /.
Периодической траекторией называется траектория, не являющаяся
неподвижной точкой и такая, что для некоторого Т и произвольного t
выполнено равенство (pt+T(\) = ^'(х)- Минимальное Т, для которого
справедливо это соотношение, называется периодом.
Для точки х € Р ее образом для отображения (р( при некотором
фиксированном t называется у = ^'(х)- в свою очередь, х называется
прообразом у. Для обратимого отображения <р прообраз каждой точки
62 3. Динамические системы и их устойчивости
существует и единственен. Для необратимого отображения прообразов
может быть несколько.
Напомним, что траектории динамической системы не могут пере-
пересекаться (иначе будет нарушена единственность отображения <р, тогда
из точки пересечения начинались бы сразу две траектории).
3.2. Уравнения движения и отображение <р\х)
Сразу заметим, что чаще всего отображение <р'(х) неизвестно.
В большинстве практически важных случаев его можно построить только
численно. Зачем в таком случае вообще вести о нем речь? Во введе-
введении уже говорилось, что часто представляет интерес асимптотическое
поведение решения при t -+ oo. Таким образом, чаще всего интересны
свойства именно отображения у'(х) при больших t, а не локальные свой-
свойства при малых временах t, которые можно почерпнуть непосредственно
из дифференциальных уравнений. И сама хаотическая динамика обязана
своим появлением весьма неожиданным свойствам некоторых подобных
отображений ip. Если бы они всегда были известны, то большинство ма-
математических моделей были бы так же просты, как задачи из школьного
учебника физики, и наши возможности анализа явлений природы были
бы неизмеримо больше. Но мир, в котором мы живем, оказался иным.
Динамические системы обычно задают в виде уравнений движения.
Последние позволяют по точке х в момент времени t найти точку,
отвечающую следующему моменту времени: t + dt для непрерывного
времени и * + 1 для дискретного. То есть вместо того, чтобы определять
всю траекторию сразу, задают правило, по которому она находится
шаг за шагом. Такой способ оказывается гораздо более универсальным,
чем задание отображения в явном виде: например, для большинства
хаотических систем в математике пока просто не существует конструкций,
позволяющих записать такие функции ^'(х) Для данного t, минуя все
промежуточные моменты времени.
Таким образом, одна из основных задач хаотической динамики
состоит в том, чтобы по уравнениям движения исследовать свойства
отображения <р'(х).
Если время меняется дискретно, то задается правило, по которому,
зная х в момент t, находят точку, отвечающую моменту времени t+ 1. Это
дает отображение x(+i = f(x<) (функция f явно от времени не зависит).
Таким образом, f(x) = ^'(х) = v(x)- Очевидно, что (р2(\) = f(f(x)),
<р3(х) = f (f (f(x))) и т.д. Подобным способом можно в принципе найти <р
для любого t.
Если время меняется непрерывно, то динамическую систему задают
в виде автономной системы ОДУ вида х = F(x). Покажем, как связаны
функции F и <р. Пусть в некоторый момент t состояние динамической
системы описывается точкой х = x(t). Тогда x(t + dt) — x + dx = x + ?dt.
С другой стороны,
3.2. Уравнения движения и отображение <р*(х) 63
UE UE /=0
Функцию F(x) часто называют векторным полем. Оно задает касательную
к траектории в каждой точке фазового пространства — подробно это об-
обсуждается во многих учебниках по теории дифференциальных уравнений.
Как по заданному векторному полю построить отображение <р'(х)?
Надо просто найти решение x(t) дифференциального уравнения х = F(x)
при начальных данных х@) = хо, тогда (р*(хо) = х@- Таким образом,
аргумент х функции ^'(х) ~~ это начальные данные для системы ОДУ.
Следовательно, производная ff' — это производная решения по на-
начальным данным. Она используется, например, при расчете ляпуновских
показателей.
Рассмотрим несколько примеров.
Пример, х = ах. Решением уравнения с начальными данными х@) = х0
будет x(t) = е"'хо. Поэтому <р'(х) = е"'х. Легко проверить, что все груп-
групповые свойства выполняются.
Пример, х = — у, у = х. Аналогично находим решение для начальных
данных х = хо, у = уо'- x(t) = accost - j/osin', J/@ = zosint + y0cost.
Функцию <f>'(x) удобно записать в матричном виде:
_ /zcost-j/sintN _ /cost -sint\ /x\ =д(х\
~ \a;sint + j/cost/ ~ \sint cost/ \y) ~ \y) '
Матрица А осуществляет поворот на угол t на плоскости (х, у). Компози-
Композиция двух поворотов снова будет поворотом.
Пример, х = Ах, А — постоянная матрица. Решение часто записывают
в символическом виде, таком как x(t) = exp (tA)xo, ехр(А) = 1 + А +
Т + • • • + 1Г + • • • • Тогда
р'(х) = ехр(М)х. C.1)
Получаем обобщение первого примера, но если раскрыть эту запись, по-
получится комбинация экспонент, тригонометрических функций, а в случае
кратных собственных значений — эти функции, возможно, будут домно-
жены на полиномы от t.
Следует заметить, что, согласно нашему определению, не любая авто-
автономная система уравнений определяет динамическую систему. Например,
для уравнения х = 1 + ж2 траектория за конечное время уходит в беско-
бесконечность. При любых i > 0 найдется х, для которого ipf(x) не определено.
В заключение приведем два примера, когда отображение (р*(х)
обладает свойствами полугруппы.
Пример. Логистическое отображение xk+l = axk(l - xk), 0 < о ^ 4, не-
необратимо — каждому хк+] соответствуют два прообраза. В самом деле,
квадратное уравнение, определяющее значение хк, — это
2 л
ахк — ахк + хк+\ = U.
64 3. Динамические системы и их устойчивости
При Жц., < f оно имеет два корня. Или то же самое на геометрическом
языке: прямая, параллельная оси абсцисс, пересекает параболу аж*A —ж*)
в двух точках с абсциссами р\ и рг- Следовательно, р\ и рг являются про-
прообразами ж*+1- Поэтому отображение <рк(х) определено только при fc ^ 0.
Пример. Для уравнения х = х — хъ , х 6 R', решения обращаются за ко-
конечное время в бесконечность для отрицательных значений t. Причем
для любого t < 0 существуют начальные данные, такие что решение «не
доживет» до этого момента. Поэтому отображение <р'(х) также определено
только при t ^ 0.
3.3. Инвариантные множества
Пусть задано некоторое множество Л&Р. Функцией от множества Л
(р*(Л) будем называть множество образов всех точек из Л.
Если для всех t > 0 <р*(А) С Л, то множество Л будем называть по-
положительно инвариантным. Если для всех допустимых t <р*(А) = Л, то Л
называется инвариантным множеством динамической системы. Поэтому
образом инвариантного множества является само это множество (полно-
(полностью), а образом положительно инвариантного множества является или
само множество, или только его часть.
Примерами инвариантных множеств являются: все фазовое про-
пространство; траектория, определенная для —оо < t < оо; неподвижная
точка; цикл. Положительно инвариантным множеством, в частности,
является положительная полутраектория.
Пример, х = -2х, у = -у. Очевидные инвариантные множества: точка
{х = 0, у = 0}, ось х, ось у. Примерами положительно инвариантных
множеств будут отрезки на осях х или у, содержащие точку @,0), скажем,
{х = 0, -1 < у < 1}, или круг {х,у: х2 +у2 < 1}.
Проще всего вопрос об инвариантных множествах решается для ли-
линейных динамических систем — их можно указать явно и в общем виде.
Линейные дифференциальные уравнения с постоянной матрицей
обсуждались выше, а линейные отображения с постоянными коэффици-
коэффициентами имеют вид
xn+i - Вх„.
Здесь просматривается очевидная аналогия с дифференциальными урав-
уравнениями. Каждому ОДУ можно сопоставить отображение с шагом т
по времени, тогда В = ехр(тЛ.) C.1), однако далеко не для всякого
отображения можно найти дифференциальное уравнение.
Собственные значения матрицы А будем обозначать Aj, В — /Xj.
Очевидно, что если В = ехр(тЛ.), то /ij = ехр(тА,).
Для линейных отображений отображение <р также легко выписы-
выписывается в явном виде:
<рп(х) = Впх.
Вопрос об инвариантных множествах в данном случае решается просто —
это будут линейные оболочки (подпространства) собственных векторов
матрицы А (или В). Среди них выделяют три:
3.4. Простейшие инвариантные множества и их устойчивость
65
1. Es (устойчивое, stable) — подпростран-
подпространство собственных векторов, для которых
Re А, <0 (или \щ\ < 1).
2. Еа (неустойчивое, unstable) — подпро-
подпространство собственных векторов, для ко-
которых ReAj > 0 (или |/Xj| > 1).
3. Ес (центральное, center) — подпростран-
подпространство собственных векторов, для которых
ReA; = 0 (или \т\ = 1).
Эти подпространства используются при
линеаризации динамических систем в ок- Рис. 3.1. Подпространства
рестности неподвижных точек (рис. 3.1). Е", Е? и EF
3.4. Простейшие инвариантные множества и их устойчивость
Мы рассмотрим основные свойства простейших инвариантных
множеств динамических систем — неподвижных точек и циклов (рис. 3.2).
Хаотического поведения для них, естественно, наблюдаться не может,
однако они существенны по следующим причинам:
— для них получено наибольшее число строгих результатов, поэтому,
в некотором смысле, они являются гордостью теории динамических
систем и одним из основных источников примеров и задач;
У
д ¦ е
Рис. 3.2. Типы неподвижных точек
3 3.1К. 2
66 3. Динамические системы и их устойчивости
— они иллюстрируют некоторые важные подходы и понятия, которые
обобщаются на более сложные режимы: гиперболичность, сечение
Пуанкаре, устойчивость, бифуркации.
Видимо, поэтому исследование динамических систем обычно на-
начинают с анализа возможных неподвижных точек и циклов и во всех
курсах нелинейной динамики им уделяется особое внимание. Мы также
пойдем привычным путем, но постараемся пройти его быстро, обращая
внимание только на ключевые вехи.
Заметим одно важное отличие данного раздела: мы будем обсуждать
инвариантные множества, которые состоят из одной единственной траек-
траектории. Поэтому в данном случае никаких других определений устойчи-
устойчивости, кроме обычной устойчивости по Ляпунову, обсуждаемой во всех
курсах дифференциальных уравнений, нам не потребуется.
3.4.1. Неподвижные точки обыкновенных дифференциальных уравнений
Рассмотрим систему ОДУ
х = F(x). C.2)
Неподвижные точки хо должны быть решениями системы алгебраических
уравнений F(x) = 0. Чаще всего поиск их не слишком сложен, сложнее
определить их устойчивость. Иногда для этого можно использовать метод
функции Ляпунова, если таковую удается построить, но стандартным
подходом является линеаризация системы в окрестности неподвижной
точки. Возьмем х = xo+fu, где е мало, и, подставив в уравнение, получим
)(U'l')+... = Аи + О(е),
где Aij = ЦМх=х<> ~~ это матрица Якоби. Далее возникает стандартная
задача исследования свойств системы линейных ОДУ с постоянными ко-
коэффициентами и = Аи, о чем упоминалось в предыдущем разделе. Связь
решений линеаризованной и исходной систем устанавливает следующая
теорема.
Теорема Гробмана—Хартмана. Если у матрицы А нет собственных значений
с нулевой действительной частью, то существует гомеоморфизм (взаимно
однозначное непрерывное, но, возможно, не дифференцируемое отображе-
отображение) h, определенный в некоторой окрестности U точки \q, который
локально отображает траектории нелинейной системы в траектории лине-
линеаризованной системы. Отображение h сохраняет тип траекторий и может
быть выбрано таким образом, чтобы сохранить параметризацию по времени.
Доказательство теоремы см., например, в [8, 128].
Неподвижные точки, в которых у матрицы А нет собственных зна-
значений с нулевой действительной частью, называются гиперболическими,
или невырожденными. Таким образом, согласно теореме, линеаризован-
линеаризованная система дает исчерпывающую информацию относительно устойчи-
устойчивости гиперболической неподвижной точки, причем не только по отно-
3.4. Простейшие инвариантные множества и их устойчивость 67
шению к бесконечно малым, но и к конечным возмущениям (их макси-
максимально допустимая амплитуда зависит от размера окрестности U).
Для негиперболических неподвижных точек (когда Ес ф 0) суще-
существуют примеры, когда поведение траекторий линеаризованной и исход-
исходной системы принципиально различно. Например, для
У = -х - ех2у,
в линеаризованной системе точка @,0) всегда является центром и устой-
устойчива, в то время как в нелинейной системе она является негиперболиче-
негиперболическим фокусом, асимптотически устойчивым при е > 0 и неустойчивым
при е < 0. Это становится очевидно, если записать уравнения движения
в полярных координатах
г = -?T3cos20sin20,
в = -1 -?T2cos30sin0.
При малых е поведение этой системы должно быть близко к поведе-
поведению системы г = -^-, в = -1, для которой решение можно найти
аналитически.
3.4.2. Периодические решения (циклы) автономных систем ОДУ
Рассмотрим периодическое решение системы вида C.2) x(t + Т) —
x(t). Аналитически подобные решения построить обычно не удается,
поэтому применяются численные методы. Аналитическое исследование
периодических решений, как правило, проводят в достаточно общем
виде, и наиболее часто используется для этой цели построение так на-
называемого сечения Пуанкаре, при помощи которого исследование свойств
периодической траектории сводится к анализу свойств неподвижной точ-
точки некоторого отображения — отображения Пуанкаре. Во-первых, это
удобно, а во-вторых, позволяет избавиться от неприятной ситуации —
нулевого собственного значения у матрицы в системе ОДУ.
Сначала напомним некоторые сведения из теории линейных ОДУ
с периодическими коэффициентами. Пусть
u = A{t)u, A(t + T) = A(t). C.3)
Можно показать, что в этом случае существует замена переменных,
превращающая систему с периодическими коэффициентами в систему
с постоянными коэффициентами.
В дальнейших рассуждениях используется понятие фундаменталь-
фундаментальной матрицы Ф. Рассмотрим систему линейных дифференциальных урав-
уравнений общего вида
u = A(t)u, u@) = uo,
где u(t) — га-мерный вектор. Если матрица А невырождена, то среди
всевозможных решений, отвечающих различным начальным данным uo,
3*
68 3. Динамические системы и их устойчивости
можно выделить ровно п линейно независимых u^(t), ..., u^(t) (разу-
(разумеется, такой выбор неединствен). Рассматривая их как столбцы некото-
некоторой матрицы Ф(?)> мы получим, что:
1) эта матрица удовлетворяет уравнению Ф = А(Ь)Ф;
2) поскольку любые п линейно независимых решений образуют
базис, то любое решение можно представить в виде комбинации базисных
решений, откуда
u(t) = ^2 CiU^'\t) = &(t)c, с - const.
Вектор с можно найти из начальных условий
Тогда
n(t) = Ф(*)Фо V
То есть фундаментальная матрица позволяет выразить решение уравне-
уравнения u(t) через начальные данные щ. Заметим, что ФD) = Ф(Офо' "" тоже
будет фундаментальной матрицей. Она отвечает выделенным начальным
данным Ф@) = I, где I — единичная матрица, и носит название норми-
нормированной фундаментальной матрицы. Фундаментальных матриц много, но
нормированная единственна. Очевидно, что u(t) = Ф(?)ио, поэтому Ф(?)
дает отображение <р*(и) = Ф(?)и для рассматриваемой линейной системы.
Для систем с постоянной матрицей А Ф(?) = exp (tA).
Определитель фундаментальной матрицы
называется определителем Вронского. Поскольку фундаментальная ма-
матрица невырождена, W Ф 0. Для него можно получить уравнение
п
W = (trA)W, где trA = ^2Ац — след матрицы А. Он понадобит-
1
ся нам в главе, посвященной ляпуновским показателям динамических
систем.
Для линейных отображений также можно ввести понятия фунда-
фундаментальной матрицы и определителя Вронского, хотя они редко встреча-
встречаются на практике.
Вернемся теперь к системам с периодическими коэффициентами.
Поскольку фундаментальная матрица Ф(?) удовлетворяет уравнению Ф =
4(*)Ф, то
Ф(* + Т) = A(t + Т)Ф(* + Г) = А(*)Ф(* + Т),
т.е. Ф(< + Т) будет другой фундаментальной матрицей. Так как любое
решение можно выразить как комбинацию фундаментальных решений, то
ф(* + Т) = Ф(*)Б,
где В — постоянная матрица. Она называется матрицей монодромии,
а ее собственные значения /х,- — множителями, или мультипликатора-
мультипликаторами Флоке. Преобразованием подобия (две матрицы А и В называются
3.4. Простейшие инвариантные множества и их устойчивость 69
подобными, если существует матрица С, такая что А = СВС~1) можно
привести В к диагональному виду Зв = diag(/xi,... ,Цп)- Далее, пред-
представим ^ как ехр(!ГА/ь), т.е. А* = У^Чп/х*. Величины А* называются
характеристическими показателями, и с их помощью можно «прологариф-
«прологарифмировать» Зв, т.е. Зв = exp(TJ«), где 3r = diag(Ai,..., А„). Используя
обратное преобразование подобия, получим В = exp{TR). Характери-
Характеристические показатели являются собственными значениями матрицы R.
Обозначим теперь Z{t) = Ф(?)ехр(-Ш). Тогда
Z{t + Т) = Ф(* + Г) exp (-TR) exp (-tR) =
То есть Ф(?) = Z{t)exp{tR). Таким образом, фундаментальную матрицу
можно выразить как произведение периодической матрицы на экспо-
экспоненту постоянной. Очевидно, что если сделать замену v{t) = Z{t)~lu{t),
то система с периодическими коэффициентами u = A(t)u превратится
в систему с постоянными коэффициентами v = jRv. Однако на практике
найти эту замену почти никогда не удается, и анализ (например, нахожде-
нахождение множителей Флоке или характеристических показателей) приходится
проводить численно.
Пусть теперь дана система ОДУ х = F(x) .имеющая периодическое
решение xo(t) ¦ Для исследования ее устойчивости можно воспользоваться
линеаризацией. Положим x(t) = xo(t) +eu(t), тогда
u = с (F(xo + ей) -х0) = е~](F(x0 + ей) - F(xo)) = DF(xo(t))u + ... .
Таким образом, поведение близких траекторий должно описываться ли-
линейной системой вида C.3). Однако вопрос об устойчивости периодиче-
периодического решения x(t) оказывается нетривиальным, поскольку матрица R
всегда имеет хотя бы одно нулевое собственное значение, что не позволяет
сделать вывод об устойчивости. Покажем это.
Поскольку исходная система для х автономная, то если \(t) —
решение, то x(t + т) тоже будет решением для любого г (это просто сдвиг
вдоль траектории), т. е. x(t + т) = F(x(t + г)). Продифференцируем это
соотношение по г, положим г = 0 и обозначим v(t) — xo(t). Получим
у = A(t)v, но xo(t+T) = X(,(t), поэтому и v(t + T) = v(t). Иными словами,
уравнение u = A(t)u имеет хотя бы одно периодическое решение v(t).
Выразим его через фундаментальную матрицу:
y(t) = Ф(*)с = Z(t) exp (tR)c = v(t + T) =
= Z(t + T) exp {tR) exp {TR)c = Ф(*) exp {TR)c,
т.е.
exp {TR)c = с
Таким образом, с — это собственный вектор матрицы монодромии
с собственным значением ft — 1 и матрицы Д с А = 0.
Несмотря на то, что формально вопрос об устойчивости решить
в такой ситуации нельзя (не выполнено условие известной теоремы
70 3. Динамические системы и их устойчивости
Ляпунова), казалось бы, этот нулевой характеристический показатель А
связан только с движением по циклу и не должен влиять на устойчивость.
Оказывается, это действительно так, и можно строго обосновать это
утверждение, что достигается при помощи построения сечения Пуанкаре.
Построение сечения Пуанкаре. Попытаемся избавиться от показа-
показателя, связанного с движением вдоль цикла. Ранее уже упоминалось,
что каждая динамическая система с непрерывным временем порождает
отображение вида
Однако оно не избавляет от упомянутого выше нулевого показателя А,
поскольку инвариантность относительно сдвига вдоль цикла остается.
Избавиться от нее можно, только избавившись от самого движения по ци-
циклу. Для этого в га-мерном пространстве выбирается некоторая гладкая
(га — 1)-мерная гиперповерхность S, к которой предъявляются два требо-
требования: циклическая траектория не должна ее касаться (по возможности ее
выбирают так, чтобы траектории пересекали ее почти перпендикулярно)
и должна пересекать ее только один раз в некоторой точке so, двигаясь
в данном направлении — с одной стороны S на другую (для удобства
обозначений точки, принадлежащие поверхности S, будем обозначать
не х, a s). Возможно еще одно пересечение при движении в обратном
направлении, если поверхность S определена глобально, но иногда S
определяют только в окрестности so, и тогда цикл пересекает S один раз.
Благодаря непрерывности ip близкие к циклу траектории также не будут
касаться S, и по крайней мере в окрестности цикла можно построить
так называемое отображение первого возвращения, или отображение
Пуанкаре (рис. 3.3).
Очевидно, что ^г(во) = so. Возь-
Возьмем некоторую точку s ?S при t = 0
и рассмотрим траекторию ^Ч8)- Обо-
Обозначим через r(s) момент времени, ко-
когда траектория впервые снова пересе-
пересечет S в некоторой точке si = (pT^(a),
«двигаясь» в том же направлении, т.е.
при 0 < t < r(s) либо (pf(s) <? S, либо
V>'(s) G S, но F(s) и F(v>'(s)) — вектора,
определяющие направление движения - ^^ Схема п ния сече.
лежат по разные стороны от S. Заметим, ния Пуанкаре
что точка S] существует, если s лежит
достаточно близко к циклу. Определим теперь новую динамическую си-
систему с дискретным временем к, фазовым пространством которой будет
поверхность 5, а сама система будет порождаться отображением
g:S-+S, si+1 = g(Sjfc) = И*>Ы, SGSCP.
Теперь к нумерует моменты пересечения траекторией поверхности Пу-
Пуанкаре, а цикл превращается в неподвижную точку xq. Заметим, что
3.4. Простейшие инвариантные множества и их устойчивость 71
размерность нового фазового пространства будет на единицу меньше.
Обозначим через В\ матрицу производных jDg(so). Существует теоре-
теорема [86], которая утверждает, что собственные значения щ матрицы В\,
i = 1,...,п — 1, совпадают с собственными значениями матрицы мо-
нодромии В, за исключением значения ft = 1, отвечающего движению
вдоль цикла.
Таким образом, сечение Пуанкаре позволяет свести задачу об устой-
устойчивости периодического решения к задаче об устойчивости неподвижной
точки отображения g, поэтому оно может быть весьма полезно при иссле-
исследованиях бифуркаций периодических режимов. Однако гораздо чаще оно
используется для сложных временных режимов с тем, чтобы упростить
наблюдаемую картину и перейти от потока к отображению меньшей раз-
размерности. Доказать существование сечения, обладающего такими же по-
полезными свойствами, в общем случае, т. е. для непериодических режимов,
нельзя, пересечения поверхности S могут быть нерегулярными и тогда
отображение g будет слишком сложным или утратит важную информацию
об исследуемой системе. Однако численное построение отображения мо-
может дать понимание качественной картины явления и помочь подобрать
упрощенную модель, объясняющую ее. Особенно полезно отображение
Пуанкаре для исследования некоторых потоков в R3, сильно сжимающих
фазовый объем, когда двумерное отображение Пуанкаре оказывается по-
почти одномерным и может быть таковым весьма точно аппроксимировано,
что позволяет провести очень детальное исследование. В частности, для
системы Лоренца реализуется именно эта ситуация [7, 10, 326].
3.4.3. Неподвижные точки и циклы отображений
Для отображений xn+i = f(xn) неподвижная точка должна удовле-
удовлетворять соотношению хо = f(xo). Устойчивость ее исследуется точно так
же, как и в случае ОДУ. Возьмем х = хо + ?и, тогда
"п+1 = ?~l (f(x0 + eun) - х0) = е (f(x0 + eun) - f(xo)) =
Таким образом, задача сводится к исследованию рассмотренного выше
линейного отображения с постоянной матрицей:
un+1 = Вип.
Неподвижная точка хо отображения называется гиперболической, если
у матрицы В нет собственных значений /х,-, таких что |/ii| = 1.
Для гиперболических точек отображений также существует теорема
Гробмана—Хартмана.
Теорема Гробмаиа—Хартмана. Пусть f: R" -+ W имеет непрерывную первую
производную. Тогда в некоторой окрестности U гиперболической точки хо
существует гомеоморфизм h, взаимно однозначно отображающий траек-
траектории исходной системы на траектории линеаризованной системы, т. е.
такой, что /i(f(x)) = Df(xo)h(x) для любого х € ЕЛ
72 3. Динамические системы и их устойчивости
Таким образом, и для гиперболических точек отображений устой-
устойчивость по отношению к бесконечно малым и малым конечным возму-
возмущениям определяется свойствами матрицы В.
Исследование периодических траекторий отображений легко
сводится к случаю неподвижной точки. Достаточно просто перейти
от xn+i = f(xn) к Т-Й итерации функции f:
х„+, = g(xn) = fr(xn) = f (f(.. .f(xn)...)).
г
Тогда периодической траектории, состоящей из последовательности точек
хо, х 1,..., хг = хо, будут соответствовать Т неподвижных точек отображе-
отображения g. Аналогом матрицы В для неподвижной точки будет произведение
матриц
B = ?>f(x,)?>f(x2)...?>f(xr).
Понятие гиперболичности и теорема Гробмана—Хартмана естественным
образом обобщается на цикл любого конечного периода Г, и иссле-
исследование устойчивости таких гиперболических циклов не представляет
принципиальных трудностей.
Все сказанное можно проиллюстрировать на примере простейшего
одномерного отображения х^+х = /(я*). Неподвижная точка х* = f(x*)
устойчива, когда а = | j* | < 1. В этом случае в некоторой окрест-
окрестности этой точки по теореме Гробмана—Хартмана траектория эквива-
эквивалентна сходящейся геометрической профессии (а:*+1 — х*) = а(ж* — х*)
или Xk+\ = axk + A — а)х*. Неподвижная точка неустойчива при
а = | ? ' | > 1, тогда геометрическая прогрессия оказывается расходя-
расходящейся. Точка теряет устойчивость, когда j* ' = ± 1.
Цикл отображения периода р (иногда его обозначают Sp), соответ-
соответственно, устойчив, когда
jxi) df(xp)
< 1.
dx dx
Этому циклу отвечает р устойчивых точек х\,..., хр отображения
v
3.5. Асимптотическое поведение, физический смысл
и разнообразные устойчивости
3.5.1. О понятии устойчивости
Для неподвижных точек и циклов важной характеристикой ока-
оказывается устойчивость (траектории) по Ляпунову. Но во введении был
показан пример хаотического режима, для которого близкие траектории
3.5. Разнообразные устойчивости 73
расходятся, т. е. устойчивости по Ляпунову нет. Однако общая картина
траекторий хорошо воспроизводится в различных расчетах для разных на-
начальных данных, так что в каком-то смысле нечто должно быть устойчиво.
Следовательно, хаотическая динамика — это хороший повод поговорить
на тему устойчивости.
Как известно, все, что может испортиться — портится. Обычно
считается, что на все в мире действует некий случайный шум — малое
нерегулярное внешнее воздействие неопределенной природы. Интуитив-
Интуитивно это понятно: мы описываем явление на одном уровне организации,
а влияние других уровней, которое, разумеется, имеет место, естественно
учесть, вводя в уравнение параметры или малый шум. Если проявле-
проявление какого-нибудь эффекта коренным образом зависит от этого шума,
то он, скорее всего, каждый раз будет происходить по-разному. Иначе
говоря, не будет повторяемости и воспроизводимости результата. Объек-
Объектами научного исследования обычно являются воспроизводимые явления,
а потому они должны на малое внешнее воздействие отвечать малым же
' изменением результата. Это свойство называется устойчивостью, и им
должны обладать и математические модели, описывающие изучаемые
явления, в том числе и динамические системы. Отсутствие устойчиво-
устойчивости обычно воспринимают как отсутствие физического (химического,
биологического, социологического или иного) смысла у модели.
Как уже говорилось, у динамической системы два основных «ком-
«компонента» — фазовое пространство Р и его преобразование <р, и оба
они, в принципе, могут быть объектом воздействия шума. Во-первых,
Чпум может слегка изменять начальные данные или в процессе эволюции
.«сталкивать» точку, определяющую текущее состояние системы, с одной
траектории на другую, близкую. Образно этот процесс можно представить
себе так, как будто мы имеем дело не с траекторией (например, кривой),
а с пучком траекторий (трубкой, окружающей кривую) некоторого ко-
конечного диаметра. Для описания движения важно знать не только то, как
будет вести себя данная траектория, но также представлять и поведение
близких к ней траекторий, т. е. всего упомянутого пучка. Во-вторых, само
(отображение может зависеть от каких-либо внешних параметров, о су-
существовании которых мы можем и не догадываться. Шум может на эти
параметры влиять, меняя тем самым отображение. Иногда это несуще-
несущественно, иногда — фатально. Например, для отображения хп+\ = цх„
Малое изменение /х несущественно при \ц\ Ф 1. В противном случае оно
Может качественно изменить поведение последовательности {жп}> и х„,
Вместо того чтобы оставаться постоянным, может устремиться к нулю
Рис. 3.4. Шум и «трубка траекторий»
74 3. Динамические системы и их устойчивости
или бесконечности. Топологические свойства траекторий при этом могут
измениться. На основе таких представлений и возникли определения
обычной и структурной устойчивости.
Заметим, что устойчивость обычно тесно связана с асимптотичес-
асимптотическим поведением системы, с понятиями предельного множества, притя-
притягивающего множества, аттрактора, неблуждающего множества, поэтому
естественно рассматривать их совместно.
Вкратце устойчивостью можно назвать воспроизводимость при на-
наличии шума некоторого свойства системы. Однако необходимо понимать,
воспроизводимость каких деталей существенна, а каких нет. Скажем, если
какое-то свойство системы ненаблюдаемо в принципе или наблюдаемо,
но с большим трудом, то модели, в которых отсутствует устойчивость
по данному признаку, могут быть вполне осмысленными. При этом
выбор нужного определения устойчивости во многом определяется ин-
интуицией исследователя. Перечислим некоторые традиционные признаки
и соответствующие им понятия устойчивости.
1. Воспроизводимость отдельной траектории системы. Ей соответ-
соответствует обычная устойчивость по Ляпунову — малые отклонения начальных
данных ведут к малым искажениям траектории. Это одно из наиболее
популярных определений устойчивости, однако оно не выполнено для си-
систем с хаотическим поведением. Как правило, с понятием устойчивости
по Ляпунову тесно связано понятие w-предельного множества.
2. Воспроизводимость асимптотического поведения ансамбля траек-
траекторий, т. е. все траектории, начинающиеся в некоторой области фазового
пространства, будут притягиваться к одному и тому же инвариантно-
инвариантному множеству, при этом устойчивость каждой отдельной траектории
не предполагается. Таким образом определяется устойчивость инвари-
инвариантного множества по Ляпунову, которая тесно связана с понятием ат-
аттрактора. Некоторое отношение к этому имеет определение устойчивости
по Лагранжу — компактность траектории, т.е. принадлежность ее неко-
некоторому ограниченному множеству для евклидовых пространств. Однако
это понятие не получило достаточного распространения, и мы не будем
в дальнейшем его касаться.
3. Воспроизводимость повторного появления траектории в сколь угод-
угодно малой окрестности некоторой ее точки, т. е. своеобразное обобщение
свойства периодичности. Этому признаку отвечает так называемая устой-
устойчивость по Пуассону. С ней оказывается тесно связано понятие неблужда-
неблуждающего множества динамической системы, а также свойство эргодичности
и понятие инвариантной меры.
4. Воспроизводимость при возмущениях tp топологической структуры
траекторий динамической системы (количество и взаимное расположение
инвариантных и предельных множеств, направление движения по траек-
траектории и т. п.), которой соответствует понятие структурной устойчивости
или «грубости». Понятие структурной устойчивости привело к выделению
класса так называемых гиперболических динамических систем (гипербо-
(гиперболическая теория), для которых структурная устойчивость может быть
3.5. Разнообразные устойчивости 75
доказана (в рассмотренном выше примере хп+\ = цхп гиперболичность
сводится к требованию \ц\ ф 1).
Как связаны эти четыре понятия? Структурная устойчивость стоит
особняком, из устойчивости траекторий по Ляпунову обычно следует
устойчивость инвариантного множества, откуда в свою очередь следует
устойчивость по Пуассону. Впрочем, не исключено, что существуют
патологические примеры, нарушающие эту цепочку.
Рассмотрим теперь упомянутые понятия более подробно.
3.5.2. Предельные множества и устойчивость траекторий по Ляпунову
Оба этих понятия относятся к одной траектории, начинающейся
в точке х, т. е. к множеству ^'(х)-
Точка р называется w-предельной точкой для х, если существу-
существует последовательность U —<• оо, такая что ^('(х) ~* Р- Множество всех
ш -предельных точек для данной траектории называется ш-предельным
множеством и обозначается w(x). Аналогично, если у'(х) определено
для отрицательных t, можно определить а-предельные точки, для кото-
которых U —* —оо, и множество а(х).
Множество ш(х) состоит из полных траекторий, т. е. если р ? ш(х),
то ^'(р) е w(x)- Следовательно, Цх) является инвариантным множе-
множеством.
Перейдем теперь к устойчивости. Траектория ^'(хо) называется
устойчивой по Ляпунову, если для любого е > 0 найдется 6 > 0, та-
такое что при ||х - хо|| < 6 для всех t > 0, ||v'(x) ~ V((xo)|| < ?¦ Если
||v'(x) - V*(xo)|| -+ О ПРИ t —> °°> то траектория называется асимптотиче-
асимптотически устойчивой.
Существует два способа исследования устойчивости — по отноше-
отношению к бесконечно малым возмущениям и по отношению к конечным.
Исследование устойчивости по отношению к бесконечно малым
возмущениям проводится путем линеаризации отображения. Предпола-
Предполагается, что <р дважды дифференцируемо по х. Возьмем х = хо + ещ
и рассмотрим отношение *° vx°+g'/~»> W _ Устремив е —* 0, получим ли-
линейное отображение u(t) = Xty'(xo)u<). Если существует число М, такое
что ||u(t)|| < М при всех t, то движение устойчиво, в противном случае —
нет. Для неподвижных точек устойчивость определяется собственными
значениями \i матрицы В = jDy>'(xo) = exp(tA) или собственными зна-
значениями А матрицы А. Для периодических траекторий ту же роль играют
мультипликаторы Флоке и характеристические показатели. Для про-
произвольного временного поведения их обобщением служат ляпуновские
показатели, которые мы рассмотрим позднее.
Доказательство устойчивости по отношению к конечным возмуще-
возмущениям обычно гораздо труднее. Правда, при выполнении ряда ограничений
на <р оно следует из устойчивости к бесконечно малым возмущениям,
при этом определяется и масштаб возмущений, для которых устойчи-
устойчивость выполняется. Для неподвижных точек дифференциальных уравне-
76 3. Динамические системы и их устойчивости
ний иногда применяется метод функции Ляпунова (см., например, [99]).
Здесь мы не будем на нем останавливаться. Как уже указывалось во
введении, в системах, где наблюдается динамический хаос, траектории
оказываются неустойчивыми по Ляпунову, а w-предельные множества
могут быть очень сложными. Поэтому для описания подобных режимов
широко используют понятия притягивающего множества и аттрактора.
3.5.3. Притягивающие множества, аттракторы.
Устойчивость множества по Ляпунову. Поглощающее множество
В случае, когда траектория неустойчива, но не уходит из неко-
некоторой ограниченной области фазового пространства, естественно пред-
предположить, что какая-то устойчивость движению присуща. Определим
необходимые понятия.
Напомним, что множество А называется положительно инвари-
инвариантным, если при t > 0 (р'(Л) С Л, и просто инвариантным, если
<р((А) = А. Окрестностью множества А называется открытое множе-
множество U, включающее замыкание множества Л, т.е. А вместе со всеми
предельными точками, в том числе граничными. Расстоянием между
точкой х и множеством А называется Z=dist(x, A) = infye^ ||x — у||. е-ок-
рестностью U множества А называется окрестность, все точки которой
удалены от А не более чем на е.
Замкнутое инвариантное множество А С Р называется притягива-
притягивающим множеством, если для него существует окрестность U, такая что
для всех х € U, <р*(х) —> А при t —> оо. Наибольшее U, удовлетворяющее
этому определению, называется областью притяжения А.
Реже используют термин «множество, устойчивое по Ляпунову».
Множество А называется устойчивым по Ляпунову, если для любого
? > 0 найдется 6 > 0, такое что для любого х, такого что dist(x, A) < 6,
и любого t > 0 dist(p'(x)>-4) < ?• Если к тому же dist(p'(x), A) -+ О
при t —> оо, то А называют асимптотически устойчивым. Таким образом,
притягивающее множество — это множество, асимптотически устойчивое
по Ляпунову.
Казалось бы, этого определения достаточно для описания асимпто-
асимптотического поведения любой системы, однако существует ряд примеров,
показывающих, что притягивающее множество может, несмотря на инва-
инвариантность, содержать внутри себя «много лишнего». Очень популярным
примером является система
ж = ж-ж3, у = ~у.
Легко проверить, что отрезок —1<х<1,у = 0 является притягиваю-
притягивающим множеством, однако практически все траектории при t —> оо будут
стремиться к одной из двух устойчивых неподвижных точек х = ±1,
у = 0. В некоторых случаях ситуация оказывается аналогичной, но более
сложной для анализа. Поэтому используется также понятие «аттрактор» —
меньшее множество, к которому стремятся «почти все траектории» дина-
динамической системы. Наиболее популярное определение аттрактора на се-
3.5. Разнообразные устойчивости 77
годняшний день таково: аттрактором Л называется притягивающее мно-
множество, содержащее всюду плотную траекторию, или, что то же самое,
содержащее точку х, для которой ш(х) = Л. Иногда это свойство назы-
называют неразложимостью. Согласно этому определению, в рассмотренном
выше примере отрезок [—1,1] аттрактором не является, а аттракторов
два — неподвижные точки ±1. Областью притяжения каждого из них
является соответствующая полуплоскость, не включающая ось у. Если
аттрактор единственный и его областью притяжения является все фазовое
пространство, его называют универсальным, или глобальным.
Вообще говоря, общепринятого определения аттрактора в настоя-
настоящее время нет, и, скорее всего, это связано с тем, что в практических
задачах подчас встречаются ситуации, для которых такое понятие трудно
определить. Например, для системы в полярных координатах
г = г-г3, i? = l-costf
притягивающим множеством служит окружность г — 1, и меньшего «ат-
«аттрактора» выделить нельзя; с другой стороны, все траектории рано или
поздно будут притягиваться к точке г = 1, i? = 0. Поэтому удовле-
удовлетворительно определить понятие аттрактора в этом примере невозможно.
В некоторых случаях предпочитают не делать различия между аттрактором
и притягивающим множеством, как, например, в книге Р. Темама [333].
Определение аттрактора полезно для того, чтобы знать, что именно
искать. Однако в большинстве практических случаев аттрактор найти
не удается, в лучшем случае можно численно получить траекторию, ле-
лежащую «практически на аттракторе». Тем не менее очень важно знать,
существует аттрактор, или нет. Для этого используют так называемые
поглощающие множества, которые построить гораздо легче. Допустим,
что удалось найти некоторое множество В в фазовом пространстве, куда
траектории входят, а обратно уже не выходят — остаются в нем навсегда.
Если В компактно (или в случае конечномерного фазового простран-
пространства просто ограничено), то в нем все траектории должны стремиться
к некоторому предельному множеству, которое можно обозначить ш(В).
Существует теорема, утверждающая, что ш(В) — Л — притягивающее
множество [333].
Итак, пусть задано множество U С Р (возможно, что U = Р).
Положительно инвариантное множество В С U (т. е. <р*(В) С В при t > 0)
называется поглощающим в U, если любая траектория, начинающаяся
в точке х?М,в течение конечного времени входит в В. Если В компактно,
то существует Л = ш(В), которое будет притягивающим множеством, т. е.
для х G U dist (у'(х), А) -> 0 при t -» оо.
В отличие от аттрактора и притягивающего множества, поглощаю-
поглощающее множество неединственно, можно построить семейство вложенных
друг в друга поглощающих множеств. Более того, поглощающее множе-
множество можно построить наиболее удобным для доказательства его свойств
способом. Чаще всего его строят как сферу или эллипсоид в фазовом
пространстве и доказывают, что расстояние от точки траектории ^'(х)
78 3. Динамические системы и их устойчивости
до центра сферы с течением времени должно уменьшаться. Например,
это нетрудно показать для системы Лоренца.
X = -о-Х + o-Y,
Y = rX -Y - XZ,
Z = -bZ + XY.
Представим Z как Z — z + г + а, X и Y заменим на х и у, тогда
уравнения перепишутся как
х = —ах + <гу | х,
у - -ах -y-xz \y,
z — -bz + ху - Ь(г + а) \ z.
Домножим уравнения, соответственно, на х, у, z и сложим. Тогда
получим
d(x2 + у2+ z2)
2dt
= -ах - у - bz - Ь(г + a)z.
Обычно предполагается, что 6 > 1, поэтому член — bz1 представим как
-г2 — F — l)z2; первое слагаемое сохраним, а второе «аннигилируем»
с членом -b(r + a)z:
Обозначим Я2 = х2 + у2 + z2, I - min(<r, 1), -у2 = 2{Ь - 1) (^rf)) . тогда
или
-±—- + 21R2 = exp (-2lt) — (exp {2lt)R2)
at at
Интегрируя это неравенство от 0 до t, получим
3.5. Разнообразные устойчивости 79
R2(t) < R2@)exp(-2lt) +72(l - exp
To есть, если в качестве поглощающего множества выбрать шар радиуса
До > 7> то траектория войдет в него за время, не превышающее
после чего R(t) < До- Следовательно, данный шар действительно явля-
является поглощающим множеством для системы Лоренца, которая обязана
иметь внутри него притягивающее множество.
Таким образом, доказательство существования аттрактора сводится
к доказательству существования поглощающего множества. Эта техника
может быть применена не только к обыкновенным дифференциальным
уравнениям, но также и к уравнениям в частных производных [333].
Она кажется простой, однако построение нужной цепочки неравенств
в каждом конкретном случае может быть далеко не тривиальной задачей.
3.5.4. Неблуждающее множество и устойчивость по Пуассону
В случае сложных временных режимов, таких как автоколебания
с несколькими независимыми частотами и хаос, поведение траектории
не является периодическим, однако немного напоминает таковое: траек-
траектория, побывав в какой-нибудь точке, с течением времени возвращается
в ее окрестность и проходит достаточно близко от нее. Чем дольше по-
подождать, тем ближе к точке траектория пройдет. Это свойство близости
движения к периодическому и положено в основу понятия неблуждаю-
неблуждающего множества и устойчивости по Пуассону.
Точка р называется неблуждающей для динамической системы, если
для любой окрестности U точки р и для любого сколь угодно большого
Т > 0 найдется t > Т, такое что <р*(К) П U ф 0. В противном слу-
случае точка называется блуждающей. Множество всех неблуждающих точек
динамической системы называется неблуждающим множеством и обо-
обозначается ?1. Множество всех блуждающих точек открыто (если точка
блуждающая, то существует ее окрестность, целиком состоящая из таких
точек, в противном случае точка будет неблуждающей), а неблуждающее
множество замкнуто.
Очевидно, что неподвижные точки, а также все точки периодиче-
периодических траекторий являются неблуждающими. Для более сложных аттрак-
аттракторов, при условии, что они являются компактными, удается установить
даже более сильное свойство — устойчивость по Пуассону. Это результат
известной теоремы Пуанкаре о возвращении. Однако теорема использует
понятие инвариантной меры, и мы остановимся на ней в следующей
главе. Приведем только определение.
Точка р называется (положительно) устойчивой по Пуассону, если
для любой ее окрестности U и для любого Г > 0 найдется t > Т, такое
что <р*(р) G U. Очевидно, что точка, устойчивая по Пуассону, является
неблуждающей; обратное, вообще говоря, неверно [94].
80 3. Динамические системы и их устойчивости
Понятие неблуждающего множества используется главным образом
в теоретических построениях. В практических приложениях эти понятия
встречаются довольно редко, поскольку обычно свойство неблуждания
для какой-либо точки либо очевидно, либо очень трудно доказуемо. То же
справедливо и для устойчивости по Пуассону.
3.5.5. Структурная устойчивость и гиперболичность
Рассмотренные ранее типы устойчивости были связаны с поведе-
поведением траекторий в фазовом пространстве, при этом отображение <р было
фиксировано и мы просто интересовались его свойствами. Перейдем
теперь к устойчивости по отношению к возмущениям самого отображе-
отображения <р, которую будем условно называть <р-устойчивостью (это не обще-
общепринятый термин, он используется здесь просто как сокращение длинной
фразы «устойчивость по отношению к возмущениям отображения <р»).
Суть проблемы можно пояснить при помощи простого примера.
Пусть Р = W (прямая) и рассмотрим обыкновенное дифференциальное
уравнение
х = ах — х .
Если а < 0, то в нуле есть единственная устойчивая неподвижная точка,
если а > 0, то неподвижных точек три: х = 0 и х2 = а. Теперь получим
возмущенное уравнение, добавив в правую часть некоторую функцию 6F;
для простоты возьмем 6F = бах. Тогда новая динамическая система будет
иметь вид
х = (а + 6а)х — х ,
где 6а может быть сколь угодно малым, но неопределенного знака. Тогда,
если а ф 0, то в случае \6а\ < \а\ поведение динамической системы
качественно не изменится. Если же а = 0, то добавка может качественно
изменить поведение решения, превратив устойчивую неподвижную точку
в неустойчивую и породив две новых устойчивых. Можно рассматривать
влияние и других возмущений: в этом случае от 6F обычно требуют,
чтобы она была ограничена в какой-либо норме (скажем, С1) и отлична
от нуля только в ограниченной области.
Итак, для исследования у»-устойчивости необходимо рассматри-
рассматривать не фазовое пространство Р, а пространство динамических систем,
определенных на Р. Для краткости будем обозначать его D(P) (на-
(например, это может быть подмножество пространства всех непрерывно
дифференцируемых функций на Р). Для нас существенно только, чтобы
в этом пространстве было определено понятие расстояния между ди-
динамическими системами или малой окрестности данной динамической
системы. Временной эволюции в пространстве D нет, а действие шума
(возмущения 6<р) сводится к тому, что точка, отвечающая динамической
системе <р, сдвигается на небольшое расстояние е = \\б<р\\. Как опреде-
определять устойчивость в таком случае? Необходимо, чтобы все достаточно
близкие динамические системы были в некотором смысле эквивалентны
данной, т.е. все системы должны быть разделены на классы эквива-
эквивалентности, и устойчивость будет достигаться, если такому классу будет
3.5. Разнообразные устойчивости 81
соответствовать «толстое множество» или «случай общего положения»
(в обычном трехмерном пространстве «толстыми» будут множества с не-
ненулевым объемом — шар, куб и т.д., а «тощими» — множества нулевого
объема — точка, отрезок, плоская фигура и т.д.). Таким образом, проблема
у>-устойчивости требует построения удачной и «дискретной» классифика-
классификации (т. е. когда классифицирующий признак меняется дискретно — либо
постоянен, либо меняется скачком) динамических систем, при которой
все пространство динамических систем D(P) было бы разбито на толстые
множества-классы, а все тощие были бы только их границами раздела,
на которых бы наблюдались бифуркации, связанные с переходами дина-
динамической системы из одного класса в другой при изменении управляющих
параметров. Иными словами, при удачной классификации должна быть
возможность «подойти» к любой динамической системе сколь угодно
близко по цепочке у-устойчивых систем (или, что то же самое, должна
существовать возможность сколь угодно малым возмущением любую ди-
динамическую систему превратить в у>-устойчивую). Иначе говоря, у»-устой-
чивые динамические системы должны быть плотны в пространстве D(P).
В противном случае возможны были бы типичные пути изменения дина-
динамических систем, состоящие из одних бифуркаций, что кажется бессмы-
бессмысленным (как развитие без эволюции, состоящее из одних качественных
скачков). Такая ситуация возникает, когда классифицирующий признак
может изменяться непрерывно. Непрерывно изменяющиеся инварианты
называются модулями, примером модуля может служить период цикла
для потоков. При построении классификации модулей следует избегать.
Необходимо, однако, помнить, что «качественное отличие» зави-
зависит от того, какой признак положен в основу классификации; от этого
же зависит и определение понятия «бифуркация». В настоящее время
общепринятым считается использование в качестве классифицирующего
признака понятия топологической эквивалентности, а соответствующая <р-
устойчивость носит название «структурной устойчивости», с ним же свя-
связано и общепринятое понятие бифуркации. Понятие структурной устой-
устойчивости идеально подходит для исследования простейших временных
режимов — неподвижных точек, циклов и 2-торов (автоколебаний с дву-
двумя независимыми частотами). Для систем с более сложным поведением
оно оказалось недостаточным — среди них структурно устойчивые систе-
системы не всюду плотны [8, 113, 224]. Поэтому уже более 20 лет идет поиск
более удачного классифицирующего признака для таких систем, но удо-
удовлетворяющего всех результата пока не получено. Тем не менее, на поня-
понятии структурной устойчивости основана значительная часть современной
теории динамических систем, поэтому перейдем к ее рассмотрению.
Само это понятие было предложено в 1937 г. в статье А. А. Андроно-
Андронова и Л. Р. Понтрягина. Оно, в свою очередь, требует определения двух
других понятий — «возмущения» и «топологической эквивалентности».
Пусть дана некоторая функция F(x) ? С1. Возмущенной функцией,
или возмущением ?\ G С1 амплитуды е будем называть любую функцию,
для которой существует компактное множество К., вне которого Fi = F,
82 3. Динамические системы и их устойчивости
а на К. для 6F = F-Fj норма функции и ее производных не превосходит е,
т.е. ||№||<еи ||И| <е [224].
Возмущение динамической системы определяется либо как возму-
возмущение векторного поля F(x) для потоков C.2), либо как возмущение
отображения f(x) = ?>'(х)-
Две динамических системы <р\ и <р2 называются топологически
эквивалентными, если существует непрерывная, но не обязательно диф-
дифференцируемая функция h (гомеоморфизм), отображающая траектории
одной динамической системы в траектории другой. Направление време-
времени должно сохраняться, но в случае потоков масштаб времени может
изменяться. То есть для любой точки х и любого t\ существует такое <2.
(^J()
Речь идет о замене временной переменной t и фазовой пере-
переменной х. Рассмотрим, например, замену переменной х = h(y) для
одномерного отображения
**+! = /(**), Л(Яь+О = /(%*)), Ин-1 = Л"'(/(М»)))=вЫ-
Если функция h(y) — непрерывная и взаимно однозначная (чтобы по
данному х можно было найти у и наоборот, а также чтобы близким
значениям х\, xi соответствовали близкие у\, yi), то отображения
ж*+1 = /(ж*) и 2йь+] — д(ук) топологически эквивалентны.
Динамическая система <р*(х) называется структурно устойчивой,
если существует е > 0, такое что все возмущения tp амплитуды, мень-
меньшей е, топологически эквивалентны ip.
Почему от h требуется только непрерывность, а масштаб времени
может меняться? Это сделано, чтобы избежать упомянутых выше модулей.
Если от h потребовать дифференцируемости, то окажутся неэквивалент-
неэквивалентными динамические системы
х — -х, у = —у
и
х=-х, у=-A+е)у,
независимо от величины е, хотя очевидно, что в обоих случаях поведе-
поведение будет качественно одним и тем же. Изменение масштаба времени
необходимо, чтобы были эквивалентными две динамические системы
с одинаковыми периодическими траекториями, но разными периодами
обращения (иначе говоря, классифицирующим признаком будет служить
замкнутость траектории, а не ее период).
Топологическая эквивалентность (как почти все в нелинейной ма-
математике) бывает локальной и глобальной, т. е. справедливой в некоторой
окрестности некоторой точки или множества (локально), или же во всем
фазовом пространстве (глобально).
Для доказательства эквивалентности иногда используют так назы-
называемое гомологическое уравнение (подробнее см. в [8]). Проиллюстриру-
Проиллюстрируем его на примере динамической системы, порожденной отображением
хв+] = f(xn). Допустим, мы добавили к f(x) малое возмущение eg(x),
3.5. Разнообразные устойчивости 83
и получили новую систему yn+i = f(yn) + eg(yn). Для выполнения свой-
свойства структурной устойчивости необходимо, чтобы существовала функция
Н(х) = х + eh(x), такая что у„ = Н(х„) для всех и. Иными словами,
у„+1 = Н(х„+1) = H(f(xn)) = f(H(xn)) +eg(H(xn)),
или
f(x) + eh(f(x)) = f(x + eh(x)) + eg(x + eh(x)).
Это уравнение необходимо решить относительно функции h. Если е
мало, можно разложить f в точке х в ряд и отбросить члены О(е2), тогда
получится
h(f(x)) - Df(x)h(x) = g(x).
Для того чтобы система была структурно устойчивой, это уравнение,
называемое гомологическим, должно быть разрешимо для любой функции
g G С1. Как оказалось, для его разрешимости существенны спектральные
свойства матрицы Df.
Для неподвижной точки соответствующий результат носит название
«теоремы о структурной устойчивости седла» или теоремы Гробмана—
Хартмана (см. выше).
Для потоков х = F(x) теорема формулируется аналогично, за ис-
исключением того, что требуется отсутствие у матрицы А — DF(\q) соб-
собственных значений с нулевой действительной частью, т. е. Re Л Ф 0. Если
вспомнить аналогию В — ехр(тА), то очевидно, что оба требования
эквивалентны.
Как уже говорилось, неподвижные точки, для которых выполнено
условие \fi\ ф 1 или Л Ф 0, получили название гиперболических. Для пе-
периодических траекторий можно аналогичным образом определить свой-
свойство гиперболичности, сводя задачу к исследованию неподвижной точки
отображения Пуанкаре (для потоков) или нужной степени отображения
(для каскадов). В случае более сложного временного поведения также
можно определить понятие гиперболичности, требующее непрерывного
расщепления касательного пространства на растягивающее и сжимающее
подпространства [55, 191].
Из гиперболичности следует структурная устойчивость динамиче-
динамической системы. Однако исследовать на гиперболичность любую конкрет-
конкретную систему, встречающуюся на практике, обычно невероятно трудно.
На сегодняшний день имеется считанное число хаотических аттракто-
аттракторов, для которых свойство гиперболичности доказано. Тем не менее,
в теоретических построениях предположение о гиперболичности оказы-
оказывается полезным и часто используется. Существует даже раздел теории
динамических систем, называемый гиперболической теорией [55, 191].
Что на сегодняшний день известно о структурной устойчивости ди-
динамических систем? Полностью исследованы свойства потоков на плос-
плоскости. К нарушениям структурной устойчивости в этом случае приводит,
во-первых, наличие негиперболических неподвижных точек (нарушение
локальной структурной устойчивости), а во-вторых, наличие так назы-
называемых седловых связок (saddle connections), когда неустойчивое мно-
многообразие одного седла является устойчивым многообразием (подробнее
84 3. Динамические системы и их устойчивости
об этих многообразиях будет говориться в главе о бифуркациях) другого
или даже того же седла, гетеро- и гомоклинические траектории. При ма-
малом возмущении такой динамической системы связка может нарушиться.
Структурная устойчивость двумерных потоков — это утверждение тео-
теоремы Лейксото: динамическая система, порожденная векторным полем
гладкости С на компактном двумерном многообразии М, структурно
устойчива, если и только если: 1) число неподвижных точек и замкнутых
траекторий конечно и каждая из них является гиперболической, 2) от-
отсутствуют седловые связки и 3) неблуждающее множество состоит только
из неподвижных точек и периодических траекторий. Если М — ориенти-
ориентированное многообразие, то множество структурно устойчивых векторных
полей открыто и плотно в пространстве всех полей той же гладкости. До-
Доказательство подобных утверждений достаточно сложно, поэтому касаться
его в этой книге мы больше не будем. Вместе с тем сам факт, что кажуще-
кажущееся очевидным на первый взгляд утверждение удалось строго обосновать,
представляется весьма важным. Обратим внимание на то, что в истории
нелинейной динамики принципиальные трудности на пути доказатель-
доказательства различных утверждений оказывались признаком нового нелинейного
явления или необходимости кардинально изменить постановку задачи.
Достаточно напомнить проблемы, с которыми столкнулся А. Пуанкаре
при анализе задачи трех тел, предвосхитившие проблематику теории ди-
динамического хаоса в гамильтоновых системах, работу Смейла, открывшую
поток статей по рождению хаотических аттракторов, и многие другие.
Если векторное поле задано на плоскости, то утверждение тео-
теоремы может относиться к любой положительно инвариантной области,
например, к поглощающему множеству.
Итак, для двумерных потоков топологическая эквивалентность по-
порождает хорошую их классификацию. Для потоков более высокой раз-
размерности и отображений такого результата нет. Более того, построены
примеры динамических систем, в окрестности которых нет ни одной
структурно устойчивой (см., например, [8]); т.е. в пространстве ди-
динамических систем есть области, где структурно устойчивые системы
не плотны, а потому структурная неустойчивость может быть типичным
признаком. В этом не было бы ничего страшного, если бы привычное
понятие бифуркации в значительной степени не утрачивало смысл для по-
подобных систем. Однако сейчас вопрос о том, что такое «качественное
отличие» для структурно неустойчивых систем, остается открытым.
3.5.6. Еще раз о проблеме устойчивости
Менее всего нам хотелось бы, чтобы после прочтения этой главы
у читателей сложилось впечатление, что проблемы, связанные с устой-
устойчивостью динамических систем, носят абстрактный характер и речь идет
лишь о наведении «математического лоска» на результаты уже во многом
завершенных исследований.
Говоря об устойчивости, нужно решить, сохранение каких свойств
системы для нас наиболее важно и возмущения каких классов мы считаем
допустимыми. Например, при анализе генераторов шума, используемых
3.5. Разнообразные устойчивости 85
для скрытой передачи информации — одной из наиболее быстро развива-
развивающихся областей нелинейной динамики [40, 42] — и генераторов случай-
случайных чисел, в основе которых лежат динамические системы, желательные
свойства и возмущения будут совершенно различными. Пока математи-
математически формализовать интуитивные представления специалистов, работа-
работающих в разных областях нелинейной науки и отражающих накопленный
в них опыт, удалось лишь в небольшой степени. Это, безусловно, одна из
задач, которая возникает при создании новой парадигмы синергетики.
Кроме того, в настоящее время приобрела популярность идея устой-
устойчивого развития мирового сообщества, отдельных государств и регионов.
Об этом часто говорят политики, этим кругом междисциплинарных
проблем начали активно заниматься исследователи. Сложилась ситуация,
когда разные политические силы, различные научные школы и отдельные
исследователи вкладывают в эти слова совершенно разный смысл. При
этом по-разному понимается, какие свойства существующей сложной
системы надо сохранить и развить, а какими пожертвовать. По-разному
понимаются возможные допустимые возмущения и управляющие воздей-
воздействия, не говоря уже о целевых функциях.
По-видимому, первая математическая модель, представляющая со-
собой динамическую систему и описывающая такие переменные, как про-
промышленное производство, загрязнение, население и другие глобальные
факторы в пределах всей Земли, была предложена в начале 70-х годов
Дж. Форрестером. Далее такие модели, описывающие мировую динамику,
получили широкую известность. В Советском Союзе и затем в России
исследования такого плана на высоком уровне проводились в Вычисли-
Вычислительном центре Академии наук в научной школе Н. Н. Моисеева.
Дж. Форрестер пришел в свое время к неутешительным выво-
выводам о неустойчивости «траектории», выбранной нашей цивилизацией.
Н. Н. Моисеев и его коллеги показали неприемлемость крупномасштаб-
крупномасштабной ядерной войны с эколого-климатической точки зрения.
Казалось бы, большинство моделей этого класса представляет собой
системы обыкновенных дифференциальных уравнений, и представления
об устойчивости по Ляпунову, структурной устойчивости, аттракторах
здесь должны быть непосредственно применимы. Оказалось, что это не
так, что ситуация значительно сложнее. Даже если не считать, что мы
имеем дело с быстро и необратимо развивающейся системой (например,
предположить, что технологический прогресс замедлился), то непосред-
непосредственно использовать результаты математической теории устойчивости не
удается. Дело в том, что мы имеем дело со сложной иерархической си-
системой, в которой происходят взаимосвязанные процессы с различными
характерными временами. И хаос на одних временах и уровнях организа-
организации обеспечивает упорядоченность на других. Научиться анализировать
устойчивость таких систем и осмыслить само понятие устойчивости —
дело будущего.
Бифуркации неподвижных точек
динамических систем
В настоящее время теория бифуркаций динамических систем, каза-
казалось бы, разработана весьма детально [9, 57, 86]. Тем не менее, результаты,
которые были бы одновременно и достаточно общими, и строгими, по-
получены лишь для неподвижных точек, либо для случаев, которые можно
свести к анализу неподвижных точек (например, для циклов). Результаты
для более сложных режимов и инвариантных множеств получены только
в случае, если на систему наложены очень сильные ограничения.
Тем не менее, несмотря на то, что неподвижные точки — про-
простейший тип инвариантных множеств, исследование их бифуркаций
оказывается полезным по следующим причинам.
— Этот тип бифуркаций охватывает много практически важных слу-
случаев.
— Они позволяют получить довольно много простых, красивых и в то
же время строгих аналитических результатов.
— Они дают некоторую строгую основу для исследования качествен-
качественных трансформаций динамических систем и позволяют выработать
систему взглядов на эту проблему.
— Они дают возможность строго обосновать существование простых
и в то же время типичных математических моделей, исследование
которых дает информацию о широком классе явлений (теория
нормальных форм и теорема о центральном многообразии).
В теории бифуркаций, которую считают обычно неотъемлемой
частью нелинейной динамики, удалось выделить некоторые типичные
бифуркации и указать характерные свойства систем в их окрестности. Этот
результат оказался столь удачным и интересным, что в настоящее время
понятия, связанные с бифуркациями, проникают в самые различные
отрасли знания.
Мы рассмотрим несколько центральных идей теории бифуркаций,
а в заключение остановимся на нерешенных проблемах. В изложении
некоторых результатов мы будем следовать книге [224], большая часть
примеров заимствована оттуда же.
4.1. Что такое бифуркация?
В некоторых статьях «синергетиков» появляются фразы типа «точка
бифуркации в фазовом пространстве». Сразу заметим, что в фазовом про-
4.1. Что такое бифуркация? 87
странстве точек бифуркации не бывает. Они связаны не с исследованием
одной конкретной системы с фиксированными параметрами, а с исследо-
исследованием семейства динамических систем, зависящего от к параметров ^:
1р*(х,A\,. ..,/**). При изменении параметров /t,- поведение траекторий
в фазовом пространстве может качественно изменяться. Значения {fii},
при которых происходят эти качественные изменения, и называются
точками бифуркации.
Это, однако, «гуманитарное» определение, поскольку понятие «ка-
«качественное изменение» можно трактовать весьма вольно. Однако в слу-
случае неподвижных точек, циклов и ряде других случаев можно опираться
на понятие топологической эквивалентности и структурной устойчивости:
будем считать качественно различными системы, не являющиеся тополо-
топологически эквивалентными. Поскольку для гиперболических неподвижных
точек (циклов) доказана структурная устойчивость, кандидатами на точ-
точки бифуркации автоматически становятся те значения параметров //;,
при которых точка (цикл) оказываются негиперболическими. Это дает
простой и мощный инструмент поиска точек бифуркации.
Итак, бифуркационным значением ц
или точкой бифуркации называется зна-
значение ц, при котором динамическая си-
система является структурно неустойчи-
неустойчивой. Поскольку структурная устойчи-
устойчивость бывает локальной и глобальной,
то выделяют, соответственно, локальные
и глобальные бифуркации [9]. Мы будем
говорить о локальных бифуркациях.
Рассмотрим пример: уравнение
х-^х-х =F(x,fi). D.1) Рис. 4.1. Пример бифуркацион-
Негиперболическую особую точку нахо- нои Диаграммы. Как это принято,
дим из условий F(x,») = 0, Fi(a:^) = 0. Устойчивые решения обозначены
Это * = 0, „ = (Легко проверить! что Г™ГГ НеУСТ°ЙЧЙ-
при ft < О особая точка одна, х = О,
а при ц > 0 — три, х = 0 и х = ±s/Ji. Это изображено на бифурка-
бифуркационной диаграмме 4.1. В данном случае диаграмма имеет вид вилки,
от этого и произошло слово «бифуркация» (от французского bifurcation —
раздвоение, ветвление. Термин был введен А. Пуанкаре в 1885 г. в рабо-
работе, посвященной фигурам равновесия самогравитирующих вращающихся
жидких тел).
Аналогичная бифуркация возникает и в отображениях, например,
Х„+1 = A + Ц)Х„ ~х\ = f(x,fl).
Бифуркационная диаграмма выглядит так же.
Таким образом, в различных системах могуг возникать однотипные
бифуркации. Поэтому естественно поставить вопрос об их классифи-
классификации. Одной из характеристик, используемых с этой целью, является
коразмерность.
88 4. Бифуркации неподвижных точек динамических систем
Бифуркации можно классифицировать по тому, для скольких соб-
собственных значений матрицы J9F нарушается условие гиперболичности
ReAj Ф 0 (или |А<| ^ 1 для Di). Исходя из этого, можно говорить о том,
сколько параметров ^ должно быть в модели для того, чтобы данная
бифуркация была типичной. Собственные значения также можно рас-
рассматривать как функции от параметров fi: Aj(/*i,... ,//*). Тогда условие
нарушения гиперболичности ReAj = 0 можно рассматривать как систему
уравнений относительно fi. Например, для того, чтобы два действитель-
действительных собственных значения одновременно обратить в 0, необходимо найти
решение системы двух уравнений
¦¦¦,&) = о-
Это система двух уравнений относительно к неизвестных. Разумеется,
не зная конкретного вида функций А;(/*],...,/**)> невозможно сделать
выводов, справедливых для каждой системы, но существуют утвержде-
утверждения, относящиеся к типичным ситуациям. В данном конкретном случае
типичными будут следующие ситуации:
— если к = 1, то решения обычно нет, т.е. бифуркация такого типа
скорее всего в данном семействе наблюдаться не будет;
— если к = 2, то бифуркация может наблюдаться в одной или не-
нескольких точках пространства параметров;
— если к > 2, то в типичном случае негиперболические точки будут
располагаться на поверхности размерности к - 2 в пространстве па-
параметров. То есть могут наблюдаться даже не точки, а поверхности
бифуркации.
В общем случае, если необходимо одновременно удовлетворить то
условиям, то потенциальные точки бифуркации будут располагаться
на (к — т)-мерной поверхности. Величину то называют коразмерностью
бифуркации, показывая тем самым, что существенно не количество пара-
параметров, а количество условий. (Вообще, коразмерность поверхности —
это разность между размерностью пространства и размерностью поверх-
поверхности.) Строгое определение коразмерности можно найти в работах,
посвященных теории бифуркаций [9, 57] или теории катастроф [100].
Таким образом, коразмерность бифуркации показывает, от сколь-
скольких параметров должна зависеть динамическая система, чтобы бифур-
бифуркация для нее была типичной. Чем выше коразмерность, тем более
экзотической будет бифуркация.
Мы будем рассматривать только самые типичные бифуркации —
коразмерности 1, которые наблюдаются в однопараметрических семей-
семействах. Оказывается (это будет показано ниже), все важные особенно-
особенности таких систем можно продемонстрировать, ограничиваясь системами
с размерностью фазового пространства 1 или 2.
Заметим, однако, что коразмерность бифуркации, связанная со
свойствами матрицы ?>F, характеризует ее не полностью, и «внутри»
4.2. Теорема о центральном многообразии 89
одной коразмерности возможны различные типы бифуркационных диа-
диаграмм. Например, если в примере D.1) несколько изменить функцию
F(x, ft) = v + fix — ж3 (например, нарушается симметрия, функция пере-
перестает быть нечетной), бифуркационная диаграмма изменится. Подобные
вопросы исследует так называемая теория несовершенств [57].
4.2. Теорема о центральном многообразии:
выделение существенных размерностей
для анализа бифуркации
В этом разделе мы приведем некоторые пояснения, почему имеет
смысл рассматривать и анализировать бифуркации малой коразмерности
в моделях, включающих 1-2 уравнения, в то время как почти все реальные
системы имеют размерность существенно больше 1.
Рассмотрим в окрестности значения параметра fi — 0 систему
х = fix - ж3,
Очевидно, что для исследования бифуркции второе уравнение несу-
несущественно и его можно безболезненно выбросить, понизив порядок
системы. Оказывается, в окрестности точки бифуркации эта ситуация
типична, причем не только для подобных модельных примеров, но и
в общем случае. Дело в том, что для негиперболических неподвижных
точек оказываются несущественными все те размерности, которые отве-
отвечают за «гиперболическую часть» спектра. Проблема только в том, как
найти эти существенные размерности. Это позволяет сделать теорема
о центральном многообразии. Сформулируем ее для потоков, для ото-
отображений она формулируется аналогично.
Теорема о центральном многообразии. Пусть F — векторное поле на W
гладкости С, имеющее в нуле неподвижную точку (F@) = 0). Выделим
три подпространства собственных векторов матрицы DF@) в зависимости
от знака действительной части собственных значений Re Л:
— Е* (устойчивое подпространство, stable) — подпространство соб-
собственных векторов, у которых Re Л < 0;
— Еи (неустойчивое подпространство, unstable) — подпространство
собственных векторов, у которых Re Л > 0;
— Е° (центральное подпространство, center) — подпространство соб-
собственных векторов, у которых Re A = 0.
Тогда существуют устойчивое Ws, неустойчивое Wu и центральное Wc,
инвариантные относительно F многообразия, которые касаются в нуле со-
соответственно Es, Еи и Ес. Ws и Wu единственны и имеют гладкость С,
в то время как Wc имеет гладкость С1""' и не обязательно единственно.
Заметим, что в почти всех практически важных случаях неустойчи-
неустойчивое подпространство и многообразие отсутствуют, поскольку наибольший
90 4. Бифуркации неподвижных точек динамических систем
интерес представляют бифуркации, в которых устойчивые неподвижные
точки теряют устойчивость. Поэтому мы ограничимся лишь случаями,
когда присутствуют только Ws и Wc.
Однако сначала поясним, какая польза может быть от знания этих
многообразий. Дело в том, что траектории системы экспоненциально
сходятся к центральному многообразию, и реально свойства системы
в окрестности особой (или неподвижной) точки зависят только от того,
что происходит на Wc. А так как это многообразие инвариантно, то его
можно принять за новое фазовое пространство некоторой динамической
системы меньшей размерности и анализировать только проекцию исходной
системы на центральное многообразие.
Поиск центрального многообразия облегчается тем, что оно каса-
касается Е? в самой особой точке. Если выделить в явном виде координаты,
отвечающие направлениям Ес (х) и направлениям ЕР (у), то, согласно
теореме, Wc можно искать как некоторую поверхность, описывающуюся
соотношением у = h(x), причем h@) = 0, Dh(O) = 0. После этого можно
было бы строить проекцию на поверхность. Однако реально поступают
еще проще и рассматривают «проекцию проекции» на центральное под-
подпространство Ес. Существует теорема о том, что поведение такой двойной
проекции качественно совпадает с поведением исходной динамической
системы в окрестности неподвижной точки.
Поясним основные моменты более подробно. Запишем исходную
систему в виде двух частей, отвечающих введенным выше координа-
координатам х и у.
x = Bx + f(x,y)>
y = Cy + g(x,y). v " ;
Подставив в первое уравнение вместо у функцию h(x), получим проекцию
векторного поля на центральном многообразии (некоторой неизвестной
системы вида X = f(x)) на центральное подпространство Е°:
x = Bx + f(x,h(x)). D.3)
Существует теорема, утверждающая, что если неподвижная точка (х,у) = 0
системы D.2) локально асимптотически устойчива (неустойчива), то же
справедливо и для неподвижной точки х = 0 системы D.3).
Остается найти функцию h(x). Уравнение для нее можно получить
из второго соотношения D.2), подставляя h(x) вместо у:
у = Dh(x)x =Dh(x){Bx + f(x,h(x))) - Ch(x) + g(x,h(x)).
To есть для h(x) получаем систему уравнений в частных производных
Dh(x) (Bx + f (x,h(x))) - Ch(x) - g(x,h(x)) = 0 D.4)
с граничными условиями
h@) = 0, Dh@) = 0.
Естественно, что найти его точное решение не удается почти никогда.
Однако можно сравнительно несложно найти его сколь угодно точную
4.2. Теорема о центральном многообразии 91
аппроксимацию в виде ряда Тейлора. Для этого в уравнение D.4) подста-
подставляют разложение h(x) в ряд с произвольными коэффициентами, после
чего получают соотношения для искомых коэффициентов.
Пример. Рассмотрим систему
у=-у-а(х + уI + /3(ху + уг),
которая выбрана так, что Е? и Е° совпадают с осями у и х (для произ-
произвольно заданной системы сначала необходимо выполнить преобразование
переменных, чтобы привести ее к подобному виду). Поскольку оба подпро-
подпространства одномерны, то уравнение для Wc ищем в виде у = h(x). Тогда
/»'(*) (а(х + hI - /3(xh + Л2)) + h + a(x + ЛJ - p(xh + h1) = 0.
Подставляя разложение для h вида Л = ахг + Ьхъ +... и приравнивая к ну-
нулю выражения при хг, х3 и т.д., после довольно громоздких вычислений
находим выражения для коэффициентов и получаем
h(x) = -ах1 + аDо - р)хъ + О(хА).
Теперь можно записать приближенное уравнение для х
х = а(х + ЛJ - p(xh + Л2) = ах2 + а(р - 2о)х3 + О(г4),
(если о = 0, необходимо использовать больше членов разложения).
Заметим, что в исключительных случаях разложение в ряд не рабо-
работает. Один из таких примеров приведен в [224]: х = —ж3, у — -у + х2.
Проекции на центральное многообразие можно строить и для
отображений. Однако мы не будем останавливаться на этом моменте,
который подробно обсуждается в той же книге.
4.2.1. Центральное многообразие и анализ бифуркаций
Теорема о центральном многообразии в том виде, как она приве-
приведена выше, мало пригодна для анализа бифуркаций. Действительно, она
относится к одной фиксированной динамической системе, в то время как
для бифуркационного анализа необходимо исследовать семейство дина-
динамических систем, зависящее от одного или нескольких параметров. Про-
Проблема решается при помощи весьма элегантного приема: динамическая
система дополняется фиктивными уравнениями для параметров fi: fi = 0.
Тогда параметры попадают в «расширенное центральное многообразие»
и можно рассматривать уже параметрические семейства динамических
систем.
В общем виде методика выглядит следующим образом. Рассмотрим
расширенную систему:
92 4. Бифуркации неподвижных точек динамических систем
Уравнение для центрального многообразия ищем в виде у = h(x, fi),
подставляем у в третье уравнение и находим нужное количество членов
в разложении h(\,fi). Затем, подставив результат в первое уравнение,
находим укороченную систему:
Рассмотрим пример, квадратичное уравнение Дюффинга, преобра-
преобразованное в систему:
й = v,
v - ри - и2 - v, (^ '
где /3 — параметр, близкий к 0. Особыми точками являются v — 0, и — 0
и и — р. Обе они становятся негиперболическими при /3 = 0, когда они
совпадают. Собственными значениями линеаризованной системы в точке
(it,v) = 0, /3=0
(J)-O-O (:)-*(:)
являются 0 и —1. Соответствующие собственные векторы удобно пред-
представить как столбцы матрицы
-а -о
Тогда преобразование подобия, приводящее матрицу А = TJT'1 к диа-
диагональному виду, имеет вид J = Т~1АТ. Обозначим новые перемен-
переменные (ж, у). Переход к ним осуществляется преобразованием
(:)¦'(:)• О-'О-О-:)(:)•
Тогда систему D.5) можно записать в виде
(*)-[(:-?)¦'(-:-:)](:)¦(-!:#)•
Расширенная система будет иметь вид
х = Р(х + у)-(х + уJ,
/3 = 0,
у - -у - (х + у) + (х + уJ-
Будем искать центральное многообразие в виде
у = h(x,p) = ах2 + Ьхр + ср2 + О((\х\ + |/3|K).
Уравнение для центрального многообразия будет иметь вид
У=7Гх+мР = 1Г№Х + h)~(x + hJ) =-h~(x + h) + (x + hJ.
ax dp ox
4.2. Теорема о центральном многообразии 93
Подставляя разложение для h, получаем с точностью до квадратичных
членов
Bах + ЬР + .. .)(р(х + ...) + ...)+ {ах2 + foc/3 + с/32) +
+ р(х + ах2 + Ьхр + ср2) - (х + ... J = O((|as| + |/3|K).
Раскрывая скобки и приравнивая нулю коэффициенты при ж2, х/Э и /Э2,
находим а— 1, Ь— — 1, с = 0. Следовательно,
j, = х2 - рх + 0@x1 + |/3|K).
Поэтому искомая укороченная система, определяющая устойчивость осо-
особой точки, имеет вид
х = /3A - р)х - A - /3)я2 + О{(\х\ + |/3|K).
Таким образом, анализ простых моделей может давать весьма по-
подробную информацию о бифуркациях в достаточно сложных системах.
Более того, иногда метод построения проекции на центральное мно-
многообразие позволяет даже строить упрощенные модели для некоторых
бифуркаций уравнений в частных производных.
4.2.2. Типичные нелинейности и идея метода нормальных форм
Даже после того, как размерность исследуемой модели уменьше-
уменьшена, все равно количество возможных правых частей остается слишком
большим. Было бы важно выделять среди них типичные модели, исследо-
исследование которых давало бы информацию не об одной из них, а о широком
классе объектов. Именно эту проблему призваны решить методы теории
нормальных форм.
Заметим, что для гиперболических особых и неподвижных точек
такой результат уже упоминался выше. Согласно теореме Гробмана—
Хартмана, в некоторой окрестности динамическая система топологически
эквивалентна некоторой линейной системе. Поэтому последние можно
рассматривать в качестве типичных. Заметим, однако, что теорема не га-
гарантирует, что замена, осуществляющая переход к линейной системе,
будет дифференцируемой.
Рассмотрим систему ОДУ вида х = F(x), у которой в нуле име-
имеется особая точка. Предположим, что все собственные значения матри-
матрицы Z)F(O) различны и равны Ai,...,An, а переменные выбраны таким
образом, что матрица ?>F@) диагональна. Таким образом, система урав-
уравнений имеет вид
ii = XiXi +9i(xi,...,xn), t= l,...,n,
или х = Лх + g(x), где д исчезает в нуле вместе с производными. Будем
искать нелинейную замену х = h(y) — у + Р(у), тогда
#h(y)y = F(h(y)), y=(ZJh(y))-'F(h(y)), D.6)
или
( )~1( ) D.7)
94 4. Бифуркации неподвижных точек динамических систем
Естественно, что найти такую замену, чтобы обратить исследуемую си-
систему в линейную, в общем случае невозможно, поэтому используют
последовательное исключение членов разложения gi(x\,...,xn) в ряд
Тейлора: квадратичных, кубических и т.д. Предположим, что наимень-
наименьшая степень нелинейных членов <& равна к, выберем тогда в качестве
Р(у) полином степени к. Предполагая, что |у| мало, и оставляя только
члены порядка к, из D.7) получим
" дР
5*(у) - J21
,-=1 oyi
(здесь учтено, что с точностью до членов порядка к, A+?>Р)~' =/—?>Р).
Поскольку мы хотим исключить члены порядка к, следует выбрать Р так,
чтобы
Ег Л D8)
з=\ Оу>
Заметим, что соотношение D.8) можно рассматривать отдельно для ка-
каждого из мономов вида Р = у\'... j/**. Но для таких мономов
dyj
поэтому левая часть системы D.8) принимает вид (Л; — 52 fy Aj) Pi. Следо-
вательно, условие разрешимости D.8) будет следующим. Члены порядка к
можно исключить, если не обращается в ноль ни одно из выражений
j j
Если это справедливо для любого к ^ 2, то уравнения можно линеаризо-
линеаризовать вплоть до любого порядка.
Пример. Рассмотрим систему
У = -У
Здесь А| = 1, А2 = — 1 и условие D.9) имеет вид
fci-fc^l, *,-*2^-1,
поэтому, например, члены вида х2у и ху2 при помощи описанной проце-
процедуры невозможно исключить из системы. Заметим, что рассматриваемая
система является гиперболической, однако дифференцируемой замены пе-
переменных, при помощи которой можно было бы линеаризовать систему,
построить не удается.
Выше была изложена лишь основная идея метода нормальных
форм. Многие существенные детали не были упомянуты, их можно най-
найти в книгах, таких как [21, 224, 8]. Мы также не будем рассматривать
4.2. Теорема о центральном многообразии
95
применение метода нормальных форм для отображений. Для нас важ-
важно было проиллюстрировать следующую мысль: спектр линеаризованной
системы позволяет выделить некоторые «существенные» нелинейные чле-
члены. Поэтому можно ожидать, что для некоторых явлений можно построить
наиболее «типичные» модели, которые и естественно исследовать в первую
очередь. В том числе и для бифуркаций неподвижных точек.
4.2.3. Простейшие бифуркации и их нормальные формы
Наиболее распространенные бифуркации имеют коразмерность 1
и происходят, когда в линеаризованной системе дифференциальных урав-
уравнений возникает одно нулевое или два мнимых комплексно сопряжен-
сопряженных собственных значения. (В отображениях, соответственно, одно дей-
действительное или пара комплексно сопряженных собственных значений,
по модулю равных 1.) Рассмотрим их.
Пусть задано одно дифференциальное уравнение, зависящее от
единственного параметра:
x = F(x,fi), F@,0) = 0,
= 0.
При помощи идей метода нормальных форм можно попытаться ис-
исключить старшие степени в разложении F(x,fi) в ряд. Результат, есте-
естественно, зависит от конкретной функции, например, от того, обращается
или нет в ноль F,, @,0) и другие производные — это определяет, какие
именно члены останутся в максимально упрощенной функции. Заметим,
что подобным анализом занимается и теория катастроф [100].
Наиболее типичной и чаще всего встречающейся является бифурка-
бифуркация типа «седло-узел» (saddle-node) (рис. 4.2). Она возникает при условии
-f/j@,0) Ф 0, Fxx@,0) Ф 0, а в окрестности точки бифуркации система
приводится к виду
х = ц-х2. D.10)
Рис. 4.2. Примеры бифуркаций типа седло-узел: а) одновременное возникно-
возникновение устойчивого и неустойчивого решений; б) одновременное исчезновение
решений, которое может приводить к «катастрофе»
96
4. Бифуркации неподвижных точек динамических систем
Несколько более экзотическими, но довольно часто встречающимися
являются бифуркации типа «обмен устойчивости» (transcritical) (рис. 4.3 а)
х = цх-х2 D.11)
(она встречалась в примере построения проекции квадратичного урав-
уравнения Дюффинга на центральное многообразие), и бифуркация типа
«вилки» (pitchfork) (рис. 4.1, 4.36)
х = цх-х3. D.12)
Заметим, что эта бифуркация весьма популярна среди физиков-теорети-
физиков-теоретиков, поскольку на ней основаны некоторые теории, объясняющие спон-
спонтанное нарушение симметрии (устойчивая неподвижная точка х — О
при у. < 0 отвечает симметричному состоянию, например, отсутствию
намагниченности, а рождающиеся неподвижные точки х = ±y/Ji — со-
состоянию с нарушенной симметрией). В частности, на этой бифуркации
основана теория фазовых переходов II рода, предложенная Ландау. В ней
чаще всего роль ц играет отклонение температуры от критического зна-
значения, а величина х носит название «параметр порядка». Впоследствии
этот термин был заимствован Г. Хакеном и использован в синергетике.
\
Рис. 4.3. Примеры бифуркаций типа: а) обмен устойчивости; б) типа вилки, под-
критическая: устойчивое решение исчезает, а нового решения в его окрестности
не возникает. Такая ситуация ведет к возникновению скачков, анализом которых
занимается теория катастроф. См. также рис. 4.1, где показана надкритическая
бифуркация типа вилки, когда новые решения плавно отходят от старого при
увеличении параметра ft, и скачки не возникают
Для того, чтобы в системе возникали бифуркации, отличные
от D.10), функция F должна удовлетворять некоторым дополнительным
условиям, которые, однако, нередко реализуются в конкретных задачах,
например, благодаря наличию какой-либо симметрии. В принципе, ни-
ничто не мешает рассматривать и более сложные функции, скажем, такие
как fix3 - ж5, но в нашей практике они никогда не встречались. Заметим,
что при нарушении симметрии все «высшие» бифуркации распадают-
распадаются на некоторое количество бифуркаций типа седло-узел (подробнее
см. [57], замечания об упоминавшейся теории несовершенств).
4.2. Теорема о центральном многообразии 97
Другой типичной бифуркацией коразмерности 1 является бифур-
бифуркация рождения предельного цикла из неподвижной точки (бифуркация
Хопфа или Андронова—Хопфа). При этом в линеаризованной системе
возникает пара чисто мнимых собственных значений Л = ±ш. Поэтому
минимальная модель, в которой возможна бифуркация Хопфа, должна
содержать два уравнения. Методами теории нормальных форм в типичном
случае уравнения приводятся к виду
х = dfix - (w + сц)у + (ах - Ьу)(х2 + у2),
2 2 И-»3)
у = (ш + cfi)x + dfiy + (bx + ау)(х +у ).
Более обозримое выражение получится, если перейти к комплексной
записи. Обозначим
W = х + гу, с\ = d + ic, сг = а + ib,
тогда D.13) принимает вид
W = {ш + (ic\)W + c2W \W\2.
Заметим, что многие физические модели, в которых исследуется возник-
возникновение колебательных режимов, имеют похожий вид. Что, как видим, не
удивительно, поскольку это действительно минимальная модель, «ухва-
«ухватывающая суть дела».
Другой достаточно информативный вид выражение D.13) прини-
принимает при переходе к полярным координатам х = rcos0, у = г sin в:
г = dfir + ar ,
в = и> + cfi + br2.
В такой записи неподвижной точке отвечает г = 0, а периодическому ре-
решению — г = const > 0. Из первого уравнения видно, что по радиальной
компоненте рождение (или исчезновение) цикла происходит по схеме
бифуркации типа вилки.
Исследование устойчивости возникающего цикла требует получе-
получения коэффициентов а и d. Это довольно громоздкая процедура, на кото-
которой мы не будем останавливаться; соответствующие формулы приводятся,
например, в [224, 86].
У отображений
хп+\ =/(хп,ц)
Возникают почти те же бифуркации, что и у дифференциальных урав-
уравнений. Бифуркациям коразмерности 1 отвечает негиперболическая не-
неподвижная точка (х — 0), в которой матрица Df @,0) имеет одно соб-
собственное значение |А| = 1 (минимальная модель одномерна) или два
Комплексно сопряженных собственных значения Л, А, |А| = |а| = 1
(минимальная модель двумерна).
Последний случай — бифуркацию Хопфа в отображениях — мы
рассматривать не будем, поскольку вопрос слишком сложен, требует
4 Зак. 2
98
4. Бифуркации неподвижных точек динамических систем
громоздких формул и учета большого количества деталей [224, 9j. Рас-
Рассмотрим только случай бифуркации в одном отображении, когда А = ±1.
В случае А = 1 наиболее типичной является бифуркация седло-
узел, уравнения для которой приводятся к виду
хп+\ =xn+fi-x2n.
Несколько менее типичными, но достаточно распространенными явля-
являются бифуркации типа вилки и обмена устойчивости,
хп+х = A + ц)х„ - xl,
х„+\ =A+ц)хп-х1.
3,0
X
1,0;
0,5;
0;
-0,5;
-1,0;
-^—-~_
1 1 1 I i 1 1 1 1 I 1
3,5
a
гптттЬттпттт
4,0 a
111111 1 1 1 1 1 1 1 1 1 1 II 1 1 1 1 1 1 1 1 1
0,90
1,00
1,10 1,20
б
1,30
1,40
Рис.4.4. Переход к хаосу в а) логистическом отображении: xk+l = axk(\ — xt);
б) отображении Хенона: г*+| = 1 — ах\+у, yk+\ = bxk, b — 0,3. Бифуркационным
параметром является а
4.2. Теорема о центральном многообразии 99
А вот аналога для случая Л = -1 нет среди бифуркаций непо-
неподвижных точек дифференциальных уравнений. Рассмотрим в качестве
примера отображение
хп+х = -xn+n-x2n=f{x,ii), D.14)
где fi предполагается малым. У этого отображения есть неподвижная
точка вблизи нуля, xq = §, |/'(«о,^)| = И + 2жо| = l+fi. При переходе ц
через ноль эта точка теряет устойчивость, однако новых неподвижных
точек не возникает.
Рассмотрим, однако, вторую итерацию этого отображения
= х„ + xl - (х„ + х\ - ц) .
Его неподвижные точки удовлетворяют соотношению х = f2(x,fi),
-(х + х2- цJ ={ц- х2)Bх
х2-(х + х2- ц) ={ц- х2)Bх
Вторая скобка дает уже известную неподвижную точку отображения /,
а первая — две дополнительные точки при fi > 0, которые не являются
неподвижными точками D.14). Следовательно, из неподвижной точки
рождается периодическая траектория с периодом 2. Поэтому бифурка-
бифуркация и получила название «бифуркация удвоения периода». Подробно
о бифуркации удвоения один из авторов уже писал в [10].
4.2.4. Цепочки бифуркаций, сценарии перехода к хаосу
и некоторые нерешенные вопросы
Мы рассмотрели бифуркации неподвижных точек. Для периодиче-
периодических траекторий ОДУ можно построить сечение Пуанкаре и рассматри-
рассматривать бифуркации отображения, порождаемого этим сечением. Поэтому,
в частности, для циклов ОДУ бифуркации удвоения периода встречаются.
Иногда удается проанализировать бифуркации и более сложных режимов,
например, ге-торов.
Бифуркации можно условно разделить на те, которые приводят
к усложнению временного поведения (например, бифуркация Хопфа,
бифуркации рождения странного аттрактора в маломодовых моделях),
и те, которые временную сложность не меняют. Последовательность
усложняющих бифуркаций может приводить к возникновению сложных,
хаотических режимов. Причем были найдены некоторые достаточно ти-
типичные цепочки бифуркаций, встречающиеся в целом ряде динамических
систем. Они получили название сценариев перехода к хаосу. Некоторые
из них таковы:
Сценарий Ландау: бесконечная последовательность бифуркаций
Хопфа, хаос как бесконечномерный тор.
100 4. Бифуркации неподвижных точек динамических систем
Сценарий Рюэля—Такенса: точка—цикл—2-тор—странный аттрак-
аттрактор—?
Сценарий Фейгенбаума: бесконечная последовательность бифурка-
бифуркаций удвоения—странный нехаотический аттрактор (цикл бесконечного
периода)—хаос.
Сценарий Помо—Манневиля: переход к хаосу через «перемежае-
«перемежаемость»—промежуточный режим, когда интервалы хаотического поведе-
поведения сменяются практически регулярными участками, связанными с про-
прохождением траектории вблизи неподвижной точки. Строгой теории здесь
нет, есть только несколько моделей, качественно, а иногда и количе-
количественно объясняющих эффект. Возникает перемежаемость при значениях
параметров недалеко от точки бифуркации [18].
Есть и другие, менее известные сценарии. Некоторые из них свя-
связаны не с локальными, а с глобальными бифуркациями, например, когда
при изменении параметра происходит столкновение двух инвариантных
множеств (кризисы аттракторов, гомоклинический взрыв в системе Ло-
Лоренца [326]), возникновение петли седлоузла [7, 9].
Таким образом, переход к хаосу удалось неплохо описать и проана-
проанализировать. Остались, однако, две проблемы.
Во-первых, так и не удалось найти какого-то одного или небольшо-
небольшого числа универсальных сценариев. Чем больше примеров динамических
систем исследуется, тем больше разновидностей такого перехода обнару-
обнаруживается. Поэтому первые результаты, о которых речь шла выше, посте-
постепенно теряют ореол общепризнанности. Например, каскад бифуркаций
удвоения должен встречаться во всех системах, описываемых одномер-
одномерными отображениями с квадратичной вершиной, однако реально такие
системы встречаются довольно редко.
Во-вторых, усложнение самого хаоса в терминах бифуркаций до на-
настоящего времени практически никак не описано. Одной из причин
этого является большая сложность структуры траекторий на странном
аттракторе, проследить за изменениями которой, а тем более доказать то-
топологическую эквивалентность, по-видимому, практически невозможно.
Другой является то, что само понятие топологической эквивалентности
может оказаться неадекватным в таких ситуациях.
По-видимому, для описания усложнения хаоса необходима какая-
то другая характеристика, более устойчивая по отношению к практичес-
практически ненаблюдаемым деталям тонкой структуры траекторий. Одна из идей,
предлагавшаяся Зиманом [352], состоит в том, чтобы рассматривать изме-
изменения инвариантной меры при бесконечно малом шуме (см. следующую
главу). Другая возможная идея заключается в том, чтобы использовать
совсем грубую характеристику динамической системы — минимальное
количество динамических переменных, необходимое для описания на-
наблюдаемого процесса (так называемая размерность минимального инер-
циального многообразия — см. далее в этой книге). Однако обе они пока
не получили сколько-нибудь глубокого развития и остаются на уровне
«перспективных подходов к проблеме». Возможно, их развитие также
связано с новой парадигмой нелинейной динамики.
4.2. Теорема о центральном многообразии 101
Небольшое заключение
Отметим, что применение теоремы о центральном многообразии
и теории нормальных форм приводит к системам обыкновенных диффе-
дифференциальных уравнений. В то же время многие «классические» уравнения
нелинейной динамики являются уравнениями в частных производных.
Можно ли их получить с помощью аналогичных подходов? Начиная
с Г. Хакена, этому вопросу уделяли большое внимание [125]. При этом
обычно рассматривали уравнение с малым параметром при старшей
пространственной производной вблизи точки какой-нибудь бифуркации.
Считали, что решение зависит от «быстрых» и «медленных» координат,
а затем, усредняя уравнения по «быстрым» переменным, получали урав-
уравнение, зависящее от медленных [10, 255]. Некоторые свойства одного
из таких уравнений: обобщенного, зависящего от времени уравнения
Гинзбурга—Ландау (оно же уравнение Курамото—Цузуки, в англоязыч-
англоязычной литературе TDGL, Complex Time-Dependent Ginzburg— Landau Equa-
Equation), связанные с явлением жесткой турбулентности, а также с оценкой
размерности его аттрактора, мы обсудим в этой книге. Такой вывод
«на физическом уровне строгости» был типичен для задач нелинейной
динамики в первые два десятилетия ее развития. Однако в последние
годы, благодаря работам С. А. Кащенко и его научной школы в Ярослав-
Ярославском университете, был предложен формализм, позволяющий получать
модельные уравнения как аналоги нормальных форм, так называемые
квазинормальные формы [63].
В заключение сделаем замечание, которое можно рассматривать
и как вывод к данной главе. Замечательной чертой современной физики
является поразительная эффективность простых нелинейных моделей.
Более того, список базовых нелинейных моделей составлен в основ-
основном физиками. Достаточно напомнить фигурировавшее в этой главе
уравнение Wt = W — A + iq) \W\ W, введенное в теории турбулент-
турбулентности Л.Д.Ландау и оказавшееся нормальной формой для бифуркации
Андронова—Хопфа, уравнение Кортевега—де Фриза, с 1895 года дожи-
дожидавшееся возможностей компьютерной имитации, уравнение Бюргерса
щ + иих — ихх и многие другие. Можно сказать, что на таких моделях
стоит почти вся физика. Методы теории бифуркаций (теорема о цен-
центральном многообразии и теория нормальных форм) показывают, что
построение таких простых моделей, по крайней мере в некоторых случа-
случаях, может быть не только искусством, но и строго обоснованным научным
подходом.
Инвариантная мера
динамических систем
5.1. Откуда приходит случайность?
Как уже говорилось во введении, неустойчивость траекторий ха-
хаотических динамических систем приводит к тому, что сколь бы малой
ни была погрешность в определении исходного состояния, при пред-
предсказании будущего поведения системы эта погрешность будет нарастать,
пока наконец не достигнет размера аттрактора. После этого попытки
динамического предсказания становятся лишенными всякого смысла.
В то же время можно разбить область фазового пространства, в ко-
которой содержится аттрактор, на ячейки и для каждой ячейки построить
отношение
время, проводимое траекторией в /-Й ячейке
Ui(t) = .
полное время движения t
Оказывается, что при t —* со это отношение стремится к некоторой фик-
фиксированной для данной ячейки величине, причем отклонения от среднего
значения уменьшаются с ростом t. Это напоминает стремление частоты
случайного события к его вероятности при увеличении числа испытаний,
которое и лежит в основе теории вероятностей.
Возникает аналогия между теорией вероятностей и теорией динами-
динамических систем: множеству в фазовом пространстве мы можем приписать
некоторое число, имеющее смысл, аналогичный понятию вероятности.
Подобно тому, как в теории вероятностей вводят меру на пространстве
случайных событий (в случае дискретного пространства — это вероят-
вероятность элементарного события, а в случае непрерывного — плотность
вероятности), можно определить некоторую меру в фазовом простран-
пространстве, связанную с динамической системой. Эта мера получила название
инвариантной меры. В данном случае она инвариантна (т. е. не меняется)
при временном сдвиге траектории — переходе от x(t) к x(t + r). Мера по-
позволяет множеству в фазовом пространстве сопоставить некоторое число,
которое можно интерпретировать как вероятность того, что траектория
посетит данное множество.
Определив таким образом понятие вероятности, можно применять
к динамическим системам статистические методы, например, ввести
понятия средней величины, дисперсии, различных моментов распреде-
распределений, корреляций, энтропии и т.п., а также получать для них оценки.
Для динамических систем с регулярным поведением, как правило, это
5.1. Откуда приходит случайность? 103
не имеет большого смысла, но в случае динамического хаоса статистика
оказывается весьма подходящим языком для его описания. Кроме того,
при этом естественно получается и способ описания поведения дина-
динамических систем, на которые действует случайный шум. Заметим, что
инвариантная мера динамической системы неединственна, она может
быть связана как с устойчивым по Ляпунову множеством (аттрактором),
так и с неустойчивым. Добавление малого шума позволяет избавиться
от «лишних», неустойчивых мер.
К понятию инвариантной меры можно прийти и иным путем, ле-
лежащим, кстати, в основе ее строгого определения. Рассмотрим не одну
траекторию, а целый ансамбль, начальные данные для которого распреде-
распределены в фазовом пространстве с некоторой плотностью вероятностей Р(х)
(т.е. изначально вводится некоторая вероятностная мера). «Включим» те-
теперь временную эволюцию, динамику — отображение х —>у>'(х). При этом
вероятность оказаться в бесконечно малой окрестности точки х для
какой-нибудь траектории из рассматриваемого ансамбля и в окрестности
ее образа <р((х) должны совпадать, т. е. Р(х) dx = P(<p\x),t) dtp*{x). Одна-
Однако из-за преобразования пространства <р размер этой бесконечно малой
окрестности, вообще говоря, изменится, а потому изменится и плот-
плотность вероятности. Преобразование пространства х —><р*(х) порождает
преобразование плотности вероятности Р(х) —> Р(х, t) — ?(P(x),t). Если
же при таком преобразовании плотность остается неизменной, ее назы-
называют инвариантной. Оператор С. получил название оператора Перрона—
Фробениуса. Можно поставить задачу исследования асимптотического
поведения P(x,t). Если оказывается, что, независимо от начального
распределения, Р(х, t) стремится к инвариантной мере, то говорят, что
динамическая система обладает свойством перемешивания (начальное
распределение «перемешивается» и «растекается» по всему аттрактору,
подобно тому, как капля чернил в стакане воды при перемешивании
распространяется по всему стакану).
Вообще, связь теории динамических систем и теории вероятностей
оказывается довольно глубокой. Дело в том, что задолго до современной
нелинейной динамики в теории вероятностей рассматривалась модель
стационарных последовательностей случайных величин или стационар-
стационарных случайных процессов, основанная на использовании динамических
систем [131, 54]. В основе теории вероятностей лежит понятие про-
пространства событий, на котором вводится вероятностная мера. Оказалось,
что стационарные случайные последовательности можно представить как
результат действия некоторого отображения на пространстве случайных
событий при условии, что это отображение сохраняет меру или мера
для него является инвариантной. Поэтому понятие инвариантной ме-
меры позволяет использовать результаты теории вероятностей для анализа
динамических систем.
Выше говорилось о двух различных подходах к введению понятия
инвариантной вероятностной меры для динамической системы. И соот-
соответствующие меры могли бы также оказаться различными. Тем не менее,
104 5. Инвариантная мера динамических систем
они совпадают, и этот факт носит название эргодического свойства —
среднее по времени равно среднему по мере (или по ансамблю).
Перейдем теперь к более подробному рассмотрению указанных
вопросов.
5.2. Инвариантная мера и уравнение Перрона—Фробениуса
5.2.1. Ъшы вероятностных мер
Прежде всего напомним, что мера (любая) — это обобщение
понятий длины, площади, объема на случай множеств А достаточно
общей природы. Иными словами, мера — это отображение или функция:
(множество А) —> (действительное неотрицательное число ц(А)). Функция
эта удовлетворяет следующим условиям:
— для любого измеримого множества А, т. е. для которого ц(А)
определено, ц(Л) > 0;
— если АП В = 0, то ц(Аи В) = ц(А) + ц(В);
— мера пустого множества равна нулю, /i@) = 0.
Само число (i(A) называют мерой множества А.
Если мера пространства, которому принадлежат измеримые мно-
множества А (в дальнейшем это будет фазовое пространство Р), равна 1
(ц(Р) = 1), то мера ц называется вероятностной.
Для множеств в Евклидовом пространстве наиболее известной
является мера Лебега ць (см., например, [66]). С ее помощью определяют
интеграл Лебега, так что Hl(A) = / dx, например, длина отрезка [а,Ь]
А
Ъ
представима в виде / dx. Однако мера Лебега не единственно возможная.
а
Если взять какую-либо интегрируемую функцию f(x) > 0, то можно
ввести другую меру, Hf(A) = J f(x)dx. Эта мера, естественно, будет
А
отличаться от меры Лебега; функция / как бы учитывает неравноценность
различных частей пространства. Например, если в некоторой области В
f(x) = 0, то, даже если fib(B) = со, Ц/(В) = 0. Если мы найдем такую
+оо
функцию р(х), что / р(х) dx = 1, то на прямой будет определена
— 00
некоторая вероятностная мера цр.
Носителем меры (обозначается supp, от английского слова support —
поддерживать) иногда называется множество <S, на котором она «сосре-
«сосредоточена», т.е. минимальное множество, дополнение которого имеет
нулевую меру ц.
В дальнейшем мы будем предполагать, что Р — это евклидово
пространство. На нем принято выделять три типа вероятностных мер.
1. Абсолютно непрерывная мера. Она определяется путем задания
некоторой непрерывной функции р(х) ^ 0, называемой плотностью
вероятности. Как говорилось выше, в этом случае мера множества А
5.2. Инвариантная мера и уравнение Перрона—Фробениуса 105
определяется как Jp(\)d\. Носителем непрерывной меры должно быть
А
множество с ненулевой мерой Лебега.
2. Дискретная мера. Она сосредоточена на конечном или счетном
множестве точек х,, каждой из которых приписано некоторое значе-
значение вероятности — число Р,-. Мера любого множества в этом случае
определяется просто как сумма вероятностей точек, принадлежащих ему.
Дискретную меру также можно представить в виде плотности вероятно-
вероятности, если воспользоваться 5-функцией:
Интегральное представление меры множества остается таким же, как
и для непрерывной меры.
Заметим, что возможны комбинированные случаи, когда мера
является непрерывной на некотором многообразии, например, на окруж-
окружности, которая, в свою очередь, является частью плоскости. Такие меры
могут быть представлены в виде произведения непрерывной функции
на 5-функцию. Такие меры мы будем относить к дискретным, посколь-
поскольку мера Лебега их носителя равна нулю, но меру множества можно
представить как интеграл от некоторой обобщенной функции.
3. Сингулярная мера. Если мера не является ни дискретной, ни не-
непрерывной, ни их комбинацией, то она называется сингулярной. Как
и дискретная, она сосредоточена на множестве, у которого мера Лебега
равна нулю, но само это множество не является ни многообразием (т. е.
локально не эквивалентно евклидову пространству меньшей размерно-
размерности), ни счетным множеством точек. Основной трудностью описания
таких мер является отсутствие интегрального представления — ни обыч-
обычные, ни обобщенные функции для этого непригодны. Меру любого
множества определить можно, а разумную плотность вероятности — нет.
В качестве примера построим сингулярную меру на обычном кан-
торовом множестве (см. введение). Для этого дополним процесс «из-
«измельчения отрезков» определением меры каждого из них. Изначально
припишем отрезку [0, 1] меру Ро = 1> на первом шаге каждому из двух
отрезков длины /1 = 5 меРУ Pi = j. на втором шаге каждому из четырех
отрезков длины h = ц меру Р^ — \, и т.д., на fc-м шаге каждому из 2*
отрезков длины h = 3~* меру Р* = 2~*. То, что получится при к —> со,
и будет сингулярной мерой. Вероятность каждой точки канторова мно-
множества определить нельзя, Pi —> 0, плотность на нем — тоже, поскольку
¦f- —> со. В то же время любому отрезку конечной длины можно приписать
вполне определенное значение меры.
Таким образом, в случае сингулярных мер плотность вероятности
не вводят, а пишут просто (i(A), например, fi(dx).
Несмотря на неудобство описания, сингулярные меры очень ши-
широко встречаются в хаотической динамике, поскольку носителями меры
зачастую являются фрактальные множества. Чтобы избежать сингулярных
106 5. Инвариантная мера динамических систем
мер и получить вместо них абсолютно непрерывные, на динамическую
систему иногда накладывают малый шум амплитуды е.
5.2.2. Средние значения и корреляции
Напомним, что в теории вероятностей средним значением функции
случайной величины f(x) называется (/) = f f(x)p(x)dx. Используя
более общее понятие меры, можно определить среднее по мере ц как
(/) = f f(x)n(dx). Это выражение будет справедливо и в случае сингу-
сингулярной меры, когда /i(dx) не представимо в виде р(х) dx.
Ковариацией двух функций /и</ называется величина
Cov (/,</) = <(/-(/»(</ -(</»).
Дисперсией функции / называется D(f) = (r(fJ = Cov(/,/), где a(f) —
среднеквадратичное отклонение, а коэффициентом корреляции, характе-
характеризующим независимость двух случайных функций / и g —
Cov (/,</)
В теории вероятностей рассматривают также случайные величины, зави-
зависящие от времени — случайные процессы f (<). При каждом значении t
функция ?(<) — это случайная величина с некоторым законом распре-
распределения p((x,t), и для нее стандартным образом определяются среднее
(?(<)) и дисперсия #(?(<)) ¦ Однако такие одномоментные распределения
характеризуют случайный процесс неполно, более детальной характери-
характеристикой являются двухмоментные распределения p^(x\,X2,t\,t2). Можно
вводить и трех, четырех и более моментные распределения, но на практи-
практике ограничиваются двухмоментными. Точнее, на практике интересуются,
насколько независимы случайные величины ?(t\) и ?(<г)> т.е. откло-
отклонением двухмоментного распределения P((x\,X2,t\,t2) от произведения
одномоментных P((x\,t\)p({x2,t2). Для этого вводится характеристика,
называемая автокорреляционной функцией
K{tUt2) = <(?(<,) - <?(<!)» (?(<2) - (№)»)•
Наиболее часто встречаются так называемые стационарные случайные
процессы, когда K(t\,t2) = K(t\ - <г).
Рассмотренные выше характеристики связаны с усреднением по
вероятности или, как говорят, по мере. Но эти характеристики чаще
всего невозможно измерить в эксперименте, когда сведения о случайной
величине ограничиваются измеренным временным рядом или, как гово-
говорят, реализацией случайного процесса x(t). Тогда используют временное
среднее
1
{х)Т= Шп| Jx(t)dt.
5.2. Инвариантная мера и уравнение Перрона—Фробениуса 107
Аналогично вводится временная автокорреляционная функция
г
КТ(т) = lim i f(x(t) - (я!)т) (x(t + т)~ (х)т) dt.
0
В случае, когда средние по времени {-)т и по мере (-^ совпадают,
говорят, что случайный процесс обладает эргодическим свойством или
является эргодическим.
Для динамических систем также можно говорить о среднем по вре-
времени и по инвариантной мере. Свойство эргодичности для них также
является весьма важным и в простейших случаях может быть строго
доказано. Автокорреляционная функция также является одной из важ-
важных характеристик. В частности, если наблюдается экспоненциальное
затухание корреляций, это может свидетельствовать о том, что динамиче-
динамическая система обладает свойством перемешивания и в некотором смысле
на больших временах ведет себя аналогично случайному процессу.
5.2.3. Преобразование плотности вероятности при замене переменных
Рассмотрим сначала простейший случай, когда фазовое простран-
пространство одномерно, например, представляет собой прямую или отрезок.
Пусть х — случайная величина с плотностью распределения р(х). По-
Построим новую случайную величину у = f(x) и найдем ее плотность
вероятности q(y). Выберем некоторое значение у и маленький отрезо-
чек [у —/,j/ + -/], тогда его мера (вероятность) будет равна q(y)Ay.
Далее, найдем все точки Xi, такие что f(x{) = у, их может быть несколь-
несколько, поскольку монотонность функции / не предполагается. Напомним,
что у называется образом точки ж,-, одна (любая) точка ж* — прообразом
точки у, а совокупность всех точек ж,- — полным прообразом точки у.
В отрезочек Ау под действием отображения / попадут точки отрезочков
длиной Axi около точек Xi, мера каждого из которых равна p(xi)Ax{.
Очевидно, что мера Ау должна быть равна сумме мер всех Axi, т. е.
Далее, ^ = трпл[ > откуда окончательно получаем соотношение
В случае пространств более высокой размерности и замены переменных
у = f(x) соотношение остается похожим, но вместо формулы преобра-
преобразования длин используется формула преобразования бесконечно малых
объемов, т.е. вместо /' — якобиан преобразования J = det (щ)'-
108 5. Инвариантная мера динамических систем
Ту же самую формулу можно записать и иначе, используя свойства
^-функции, в виде свертки
г
- у)р(х) dx. E.2)
Соотношение E.2) получается при замене переменной хна f в кратном
интеграле, тогда dx = df/|J|, возникает сумма по всем корням уравнения
f(x) = у, а согласно свойствам 5-функции,
6(f-y)g(f)df =
5.2.4. Уравнение Перрона—Фробениуса. Инвариантная мера
Рассмотрим теперь динамическую систему — отображение xn+i =
f(xn). Пусть на n-м шаге в фазовом пространстве определена плотность
вероятности рп(х). Как она изменится на п+ 1-м шаге после действия
преобразования f? Будем рассматривать отображение как замену пе-
переменных, переход от переменной х к f(x), тогда для преобазования
плотности вероятности, согласно E.2), получим
P»+i(y) = /«('(х) - y)pn(x)dx = AW,
?f называется оператором Перрона—Фробениуса для отображения f (х). Это
линейный несамосопряженный оператор со сложной структурой спектра.
Подобно тому, как для некоторой начальной точки динамическая
система порождает последовательность точек, траекторию, для началь-
начальной плотности вероятности, меры, она порождает последовательность
вероятностных мер. Эту аналогию между мерами и траекториями можно
было бы развивать и дальше, вводить для мер аналоги инвариантных
множеств и т. п. Однако наиболее важными оказались два понятия. Это
аналоги неподвижной точки и сходимости к асимптотически устойчивой
неподвижной точке — инвариантная мера и сходимость мер.
Если плотность вероятности не меняется под действием операто-
оператора С{, то ее называют инвариантной. Она должна удовлетворять уравнению
Перрона—Фробениуса (УПФ)
Однако, как сказано выше, в случае сингулярной меры плотность ве-
вероятности не существует, поэтому чаще используют несколько иное
определение инвариантной меры, основанное на том же принципе, что
и УПФ: мера множества должна быть равна мере его полного прообраза
f-'И-
5.3. Неразложимые, или эргодические, меры 109
Итак, мера ц называется инвариантной мерой динамической
системы х„+1 = f(xn), если для любого измеримого множества А
р(А) = /i(f~'(^)). Если же отображение f обратимо, то каждая точка
имеет только по одному образу и прообразу, и их можно менять местами.
В этом случае для инвариантной меры fi(A) = n(f(A)) = /i(f~'(«4)).
5.2.5. Инвариантная мера для потоков. Уравнение непрерывности
Пусть задана динамическая система <р*(х), порожденная дифферен-
дифференциальным уравнением х = F(x). Такая динамическая система для каждо-
каждого т порождает отображение xn+i = f(xn) = <рт(х„), поэтому определение
инвариантной меры для отображений переносится на потоки без измене-
изменений. В случае, если рассматривать непрерывную плотность вероятности,
можно получить аналог уравнения Перрона—Фробениуса для потоков.
Запишем УПФ для некоторого отображения <рт(х):
Продифференцируем это соотношение по г и положим г = 0. Учитывая,
что <р°(х) = х, <^|т=0 = F(X) и M^±ll = М^±1); получим
^g^ = Jp(x, t) (V«(x - y) • F(x)) dx
(далее, интегрируя по частям, «перебросим» дифференцированнее 5-фун-
кции на pF и получим)
- Jdiv (p(x, t)F(x))«(x - у) dx = -div (p(y, t)F(y)).
+ div(p(x,t)F(x))=0.
Или, окончательно
dp(x,t)
m
To есть мы получили просто уравнение непрерывности. Такое же уравнение
описывает поток некоторой сжимаемой жидкости, движущейся со ско-
скоростью F(x), который «увлекает распределение вероятностей за собой»,
причем р(х, t) играет роль плотности этой жидкости.
Инвариантная плотность вероятности не зависит от времени, т. е.
должна удовлетворять уравнению div (p(x)F(x)) = 0.
5.3. Неразложимые, или эргодические, меры
Инвариантная мера не меняется под действием отображения, по-
порождающего динамическую систему, поэтому ее носителем должно быть
некоторое множество, во-первых, инвариантное, а во-вторых, неблу-
неблуждающее (одной инвариантности может не хватить, поскольку среди
точек инвариантного множества могут быть блуждающие). Простейшим
примером являются особые и неподвижные точки. Очевидно, что мера,
110 5. Инвариантная мера динамических систем
сосредоточенная на них, является дискретной и имеет вид 6(х — xq).
Это справедливо как для каскадов, так и для потоков. Если имеется
несколько неподвижных точек, устойчивых или неустойчивых, то каждая
из них служит носителем своей собственной меры. Более того, можно по-
построить сколько угодно комбинированных мер, выбирая несколько точек
с различными вероятностями, но такие меры обычно не представляют
интереса, поскольку для них не выполняются эргодические теоремы.
Дадим определение эргодической меры. Инвариантная мера у,
называется неразложимой или эргодической, если ее нельзя представить
в виде комбинации нескольких различных инвариантных мер. Или иначе,
если некоторое инвариантное множество А имеет положительную меру
ц(А) > 0, то мера его дополнения должна быть равна нулю: д(Р\Л) = 0.
Пример. Рассмотрим уравнение х = х — ж3. У него есть три неподвижных
точки «i = 0, а;2,з = ±1. Соответственно, у него три эргодических меры:
p,(i) = 6(х), р2,ъ(х) = 6(х ± 1). Кроме того, можно построить сколько
угодно неэргодических инвариантных мер вида
p(x) = api(x) + pp2(x)+'yp}(x), а+ /3 + 7 = 1, а,/3, 7 > 0.
Мера р не будет эргодической, так как мера инвариантного множества х,
/*(а:,) = а > 0, а мера его дополнения равна /3 + 7 # 0.
Более сложным примером неблуждающего множества является пе-
периодическая траектория — цикл. Для случая циклов отображений мера
также будет дискретной; если цикл образуют точки xi,X2,... ,х„, то
инвариантная мера будет иметь вид
1=1
В случае потоков ситуация несколько более сложная. Рассмотрим
динамическую систему на окружности # = a+cos#, a > 1. Инвариантная
мера (плотность вероятности) должна удовлетворять уравнению
fl))
М
или
(a + cos0) = a,
(а + cos ¦&)
2х
Значение а определяется из условия нормировки J pd/d = 1. Таким обра-
0
зом, мы получили на окружности непрерывную меру. Она неоднородна,
так как скорость движения по окружности в разных точках неодинакова,
поэтому в разных частях окружности движущаяся точка проводит различ-
различное время. Отсюда вероятность найти точку в разных частях окружности
неодинакова. Это и отражает зависимость р(#).
Если теперь рассмотрим ту же окружность, но уже на плоскости,
с уравнениями в полярных координатах г = r — r3, # = a + cosi?, то та же
5.4. Устойчивость и сходимость мер 111
инвариантная мера на окружности станет дискретной и будет иметь вид
a+costf • Очевидно, она будет эргодической. Кроме того, появится еще одна
эргодическая мера, носителем которой будет неподвижная точка г = 0.
Точно так же существуют инвариантные меры, носителями которых
являются торы и более сложные инвариантные множества, такие как
странные аттракторы. В последнем случае мера оказывается сингулярной.
5.4. Устойчивость и сходимость мер
Когда динамическая система обладает хаотическим поведением,
в ряде случаев (это доказано), если не всегда (в это верят), у нее наряду
с аттрактором существует бесконечное число неустойчивых периодичес-
периодических орбит (если эти орбиты к тому же всюду плотны на неблуждающем
множестве, то говорят, что динамическая система удовлетворяет «аксио-
«аксиоме А»). Каждый из этих неустойчивых циклов является носителем своей
эргодической меры, так что эргодических мер оказывается бесконечно
много. С другой стороны, очевидно, что не все меры существенны,
и наблюдаемому в эксперименте (численном или натурном) поведению
отвечает только одна из них. Такие меры получили название «физи-
«физических», они связаны с определенными свойствами устойчивости. Как
устойчивое инвариантное множество обладает окрестностью, все точки
которой стремятся к нему при t —> со, так и малые возмущения устойчи-
устойчивой меры должны «затухать» с ростом t. Очевидно, что носителем такой
устойчивой меры должно быть притягивающее множество, аттрактор.
Существует два способа введения понятия устойчивости меры.
Первый связан с добавлением бесконечно малого случайного шума, ам-
амплитуда которого стремится к нулю (это определение мы рассмотрим
позже при обсуждении физических мер). Другой связан с исследова-
исследованием сходимости последовательности мер р„ под действием оператора
Перрона—Фробениуса С. При этом одна трудность связана с необходимо-
необходимостью исследования спектра оператора С, а другая — с тем, что пределом
последовательности непрерывных мер часто бывает мера сингулярная,
т.е. само уравнение следует понимать в обобщенном смысле и использо-
использовать интегрирование по мере, а не по плотности вероятностей. Эти во-
вопросы весьма сложны и мы их затрагивать не будем. Заметим только, что
скорость сходимости мер зависит от их гладкости. Например, непрерыв-
непрерывные распределения «хорошо» сходятся к инвариантным, распределение
же в виде 5-функции сходиться вообще не будет, оставаясь таким всегда.
Со сходимостью мер оказывается связанным и другое важное свой-
свойство динамических систем, тесно связанное с хаотическим поведением —
перемешивание. Для него существует несколько эквивалентных опреде-
определений, на первый взгляд, весьма различных. Одно из них в нестрогой
форме упоминалось выше (просто сходимость мер). Другое таково.
Пусть Л — аттрактор динамической системы, и на нем существует
инвариантная мера ц. Если в начальный момент на множестве В, принад-
принадлежащем аттрактору Л, задано некоторое распределение вероятностей,
112
5. Инвариантная мера динамических систем
то с течением времени, благодаря неустойчивости траекторий, это рас-
распределение «расплывается» по всему аттрактору и стремится с точностью
до множителя к распределению, соответствующему инвариантной мере.
В результате мера части образа множества В, попадающей в некоторое
другое множество С, стремится с точностью до множителя к мере ц(С).
То есть
lira
[—¦00
Перемешивание — более силь-
сильное свойство, чем эргодич-
эргодичность. Из него, например, сра-
сразу вытекает, что автокорреля-
автокорреляционная функция динамиче-
динамической системы должна экспо-
экспоненциально убывать, а ско-
скорость убывания связана со
скоростью сходимости меры
к инвариантной. Однако, если
для эргодичности существуют
теоремы, показывающие, что
этим свойством обладает боль-
большинство реальных систем, то
перемешивание требует дока-
доказательства в каждом отдель-
отдельном случае. Многие верят, что
наличие положительного ля-
пуновского показателя (т. е.
экспоненциальное разбегание
близких траекторий, подроб-
подробно о которых рассказано ни-
ниже) свидетельствует о пере-
перемешивании: это утверждение,
насколько известно авторам,
/*(»)•
4,0
6,0 t
-0,5;
О
4,0
6,0 t
Рис. 5.1. Автокорреляционные функции для
переменных жиг системы Лоренца
не доказано, хотя и не опровергнуто. Математики предпочитают об этом
не говорить. Большинству физиков это довольно очевидно, даже несмо-
несмотря на существование примеров, показывающих, что скорость сходимо-
сходимости меры и скорость убывания автокорреляционной функции напрямую
с ляпуновскими показателями никак не связаны. Простейший из таких
примеров — это система Лоренца. Если рассчитать автокорреляционную
функцию для компонент х и z (см. рис. 5.1), они будут разительно отли-
отличаться, хотя ляпуновский показатель и скорость сходимости меры в обоих
случаях одни и те же.
5.5. Несколько важных теорем
Существует несколько важных теорем, использующих понятие ме-
меры. Утверждения, содержащиеся в них, очень часто бывают нужны
5.5. Несколько важных теорем 113
при исследовании конкретных задач, хотя детали доказательства необхо-
необходимы далеко не всегда. Пусть заданы фазовое пространство Р и динами-
динамическая система ?>'(х), х €Р.
Теорема Крылова—Боголюбова (существование инвариантной меры). Если
компактное множество Л С Р инвариантно относительно динамической
системы <р*(х), то существует хотя бы одна вероятностная мера ц (т. е.
ц(Р) =1), инвариантная относительно <р. ц может быть выбрана таким
образом, что она будет неразложимой или эргодической.
Эргодическая теорема. Если ц — эргодическая инвариантная мера, то по-
почти для всех х по мере ц и для любой непрерывной измеримой функции
g(x): P —>R' существует среднее по времени, которое равно среднему по ин-
инвариантной мере:
t+T
'm ™ / 5Mx,r))dr= g(\)n(dx).
^оо 1 J J
t P
Иногда этот результат записывают в виде
t+T
h ^ )dT> E3)
(имеется в виду слабая сходимость, т. е. сходимость интегралов). Данное
утверждение служит обоснованием методов расчета инвариантных мер
путем построения гистограмм.
При пользовании этой теоремой следует только помнить, что «по-
«почти все по мере fi» может существенно отличаться от «почти все по мере
Лебега». Например, если ц сосредоточена в одной точке, то «почти
для всех х» на самом деле будет относиться только к этой точке, т.е.
«почти нигде» по мере Лебега.
Терема о возвращении (Пуанкаре). Эта теорема включает два утвержде-
утверждения:
а) Возвращение множеств. Пусть ft — инвариантная мера динамической
системы <р*(х), Л — измеримое множество и ц(Л) > 0. Тогда существует
такое t, \t\ > 1, что fi(A П <р(А,<)) > 0. (То есть доказывается, что
носителем инвариантной меры является неблуждающее множество.)
б) Возвращение траекторий. Если Р — фазовое пространство со счетной
базой (например, евклидово пространство или область в нем — см. [66]),
а инвариантная мера ц — вероятностная, т. е. ц(Р) = 1, то почти все
точки х в смысле меры ц устойчивы по Пуассону. Иными словами, для любой
окрестности U точки х и любого Т найдется такое t > Т, что у'(х) € U.
Мера ц множества точек х, для которых это свойство не выполняется,
равна нулю.
114 5. Инвариантная мера динамических систем
Резюме. Таким образом, из приведенных теорем следует, что если
у динамической системы существует (компактный) аттрактор, то на нем
существует инвариантная мера, для движений на аттракторе существуют
средние по времени (например, автокорреляционная функция), а траек-
траектории, даже если и не являются периодическими или квазипериодичес-
квазипериодическими, возвращаются в сколь угодно малую окрестность почти всех точек
аттрактора.
5.6. Примеры непрерывных инвариантных мер
Выше уже приводились примеры сингулярных мер, локализован-
локализованных на неподвижных точках и циклах. Рассмотрим теперь пару приме-
примеров для хаотических одномерных отображений — одних из немногих,
для которых инвариантная мера непрерывна и выражение плотности
вероятности для нее можно получить аналитически.
Первый пример — это отображение
хп+\ = 2a;nmod 1 = f(xn). E.4)
Для него |/'(а;)| = 2, поэтому уравнение Перрона—Фробениуса имеет
вид (считая, что существует непрерывная плотность вероятности р(х))
E.5)
Подставляя это выражение в его же правую часть, находим
рС) = ЯРШ +р(^) + р(^) +р(^)]-
Применяя подстановку п раз, получим
РХ ~2\=сЛ 2" )-+Jpixdx-L
Можно проверить (совершенно аналогично), что эта мера устойчива, т. е.
произвольная непрерывная мера будет сходиться к ней (это означает, что
система E.4) перемешивающая).
Точно так же можно доказать существование устойчивой непре-
непрерывной инвариантной меры с р(х) =const для отображения «тент» или
tent map, которое записывают в двух вариантах (один сводится к другому
заменой переменных):
хп+1 = 1-2|*„|, яв G [-1,1] E.6)
или
xn+l = l-\2xn-l\, *е[0,1]. E.7)
Другой широко известный пример — логистическое отображение
для одного из значений параметра при квадратичной нелинейности:
хя+1 = 1-2x1, яв € [-1,1]- E.8)
5.7. Численное исследование мер. Гистограммы 115
Сделав замену х — - cosirO, 0 ? [0,1], находим
- cosirOn+] = 1 — 2 (cos7r#n) = — cos27r6n,
т.е.
9"+l = \2-20n, Hi
что можно преобразовать к виду E.7). Для 0, следовательно, будет су-
существовать непрерывная постоянная плотность р(в) = 1. Отсюда можно
найти плотность распределения для х с помощью обычных приемов
теории вероятностей:
р(х) = ' -. E.9)
Таким образом, явно получить выражение для плотности вероят-
вероятности удается в основном для простейших одномерных отображений.
5.7. Численное исследование мер. Гистограммы
Инвариантная мера может представлять интерес либо как само-
самостоятельная характеристика динамической системы, либо, например, как
средство посчитать какие-нибудь средние значения, которые не удается
получить как временные средние. Если просто хочется кинуть взгляд
на примерное распределение вероятностей, то носитель меры или какую-
то область фазового пространства, содержащую его, просто разбивают
на достаточно малые подмножества А{ и рассчитывают достаточно длин-
длинную траекторию, содержащую N точек х*. Затем (см. начало главы) меру
каждого множества приближенно оценивают как fi(Ai) = ^, где ЛГ; —
число точек, попавших в А{, т.е. фактически при помощи гистограммы.
Этот метод, однако, хорош только когда N{ достаточно велики. Если же
интерес представляют области, где траектория появляется очень редко,
то для них такие оценки будут давать неприемлемо большую ошибку
(поскольку относительная погрешность ''л') = ^ ~ -^ ). В этом слу-
случае необходимо либо аппроксимировать меру гладким распределением,
либо решать уравнение Перрона—Фробениуса, либо вообще отказаться
от исследований такого рода.
Встречаются задачи иного типа, связанные, например, с при-
приложениями теории информации к динамическим системам. Для них
необходимо строить разбиения фазового пространства, оценивать меру
каждого из них, а затем рассчитывать энтропию, взаимную информацию
и тому подобные характеристики. При таком подходе трудностей можно
частично избежать, если разбивать носитель меры на части, примерно
равные не по мере Лебега (объему), а по инвариантной мере ц, т. е. такие,
для которых все ЛГ; будут примерно одинаковы и ни одно из них не будет
слишком мало. Тогда оценки нужных величин будут наиболее надежными.
116
5. Инвариантная мера динамических систем
Рис. 5.2. Пример двумерной гистограммы для
отображения Хенона, составленной по 2 • 107
точкам
-2 Ее
-31-
A z _
С I _
В качестве примера на
рис. 5.2 приведена двумерная
гистограмма для отображе-
отображения Хенона. Она получена
по 20 миллионам точек на
сетке 200 х 60. Она дает неко-
некоторое представление о неод-
нородностях меры. Несмо-
Несмотря на то, что число ячеек А{
гистограммы невелико, а за-
заполненных (n(Ai) Ф 0) все-
всего 850, сходимость значений
n(Ai) оказывается довольно
медленной. Чтобы охаракте-
охарактеризовать ее, рассчитывались
-61-
¦ ¦ I ¦ I I I I ¦ I I I I ¦ I I И I I ¦ II I I ¦ М , I ¦ Г¦
4,0 4,5 5,0 5,5 6,0 6,5 7,0 Igt
Рис. 5.3. Представление о скорости сходимости гистограммы дает график изме-
изменений lg(max|6/*(|) за каждые 10000 итераций
0,5860
0,5840
0,5820
0
100000
Рис. 5.4. Сходимости среднего по времени (х2} для атрактора Хенона на первых
105 итерациях
5.8. Динамические системы с шумом 117
изменения оценок ц(А{) после каждых 10000 итераций, тах|<5^|. График
на рис. 5.3 показывает, что эта величина убывает примерно как {. Анало-
Аналогичная закономерность наблюдается и для сходимости средних значений;
грубую оценку с точностью до 2-3 знаков получить нетрудно, а серьезное
ее улучшение требует очень больших объемов вычислений. На рис. 5.4
показано, как изменяется вычисленное по траектории аттрактора Хенона
t
длиной t значение x2(t) — ?"' ^,х2. Введенная величина х2 определяет
зависимость среднего по времени от времени усреднения t. Видно, что
вариации оценки среднего значения уменьшаются довольно медленно.
5.8. Динамические системы с шумом
Рассмотрим отображение xn+| = f(xn) и будем считать, что на ка-
каждом шаге к х добавляется малый шум амплитуды е, так что результиру-
результирующее отображение имеет вид
х„+, = f(xn) + е?п.
Пусть случайная величина ? распределена с плотностью вероятно-
вероятности Нс(\). Для простоты будем считать, что Н не зависит от п. Тогда
изменение плотности вероятности при переходе от п-го шага к (п + 1)-му
будет определяться, во-первых, оператором Перрона—Фробениуса, опи-
описывающим действие f, и, во-вторых, сверткой результата с функцией Н —
распределением суммы двух случайных величин f(xn) и е?„. Таким обра-
образом, окончательно получаем
= J dzHc(y-z) J dxpn(xN(z-f(x)) =
= JdxH?(y - f(x))Pn(x) = Сс,,(р„).
Инвариантная плотность вероятности должна удовлетворять уравнению,
называемому иногда уравнением Хакена:
). E.10)
В отличие от УПФ, это обычное интегральное уравнение с непрерывным
интегрируемым ядром, и все его решения — также функции непрерывные.
Таким образом, введение сколь угодно малого шума позволяет избавиться
от сингулярных мер.
В случае потоков обычно к F(x) добавляют винеровский случай-
случайный процесс малой амплитуды. (Это однородный гауссовский процесс
?(<) с независимыми приращениями. Он широко используется в физике,
например, как одна из моделей броуновского движения.) В результате
из исходной динамической системы получается стохастическое диффе-
дифференциальное уравнение
X=F(X)+ ?««),
118 5. Инвариантная мера динамических систем
а для эволюции плотности вероятности получается так называемое урав-
уравнение Фоккера—Планка (см., например, [125])
^^ + div (p(x, i)F(x)) = ?V2p(x, t),
где диффузионный член описывает расплывание распределения из-за
шума (заметим, что таким простым видом уравнение обязано именно
винеровскому процессу, а если к динамической системе добавить другой
случайный процесс, уравнение будет гораздо сложнее; видимо, именно
по этой причине винеровский процесс столь популярен). Как и в случае
уравнения Хакена, его решения являются непрерывными функциями,
и сингулярности инвариантной меры исчезают.
Инвариантная мера должна удовлетворять уравнению
div (p(x)F(x) - eVp(x)) = 0.
Особенно простым является случай, когда динамическая система является
градиентной, т. е. F(x) = -VU(\). Тогда одним из стационарных решений
уравнения Фоккера—Планка будет функция
а простейшим его случаем при U(\) = х2 будет распределение Гаусса.
5.9. Шум и «физическая мера»
Понятие «физической меры» возникло из следующего простого
соображения. Инвариантных мер у динамической системы много, может
быть даже бесконечно много. Но если взять, к примеру, ту же систему
Лоренца или Хенона, получить численно достаточно длинную траекто-
траекторию на аттракторе и постараться вычислить сумму E.3), то результат
будет отвечать не бесконечному числу мер, а некоторой одной, вполне
конкретной, выделенной, которая и отвечает реальному, «физическому»
поведению системы, и которую чаще всего и надо иметь в виду, ко-
когда упоминается свойство эргодичности. Такую меру принято называть
физической, или колмогоровской.
Удовлетворительного определения физической меры, годящегося
на все случаи жизни, по-видимому, пока не существует. Одна из доволь-
довольно общих идей в этом плане приписывается Колмогорову. Она связана
с тем, что в реальных системах всегда присутствует малый шум. Как уже
говорилось выше, шум значительно упрощает все вопросы, связанные
с мерами, поскольку беспощаден к неустойчивым мерам. Если дина-
динамическая система обладает единственным (глобальным) аттрактором, то
введение малого шума действительно решает все проблемы. Остается
единственная мера (решение уравнения Хакена или Фоккера—Планка),
которая при е —* 0 стремится к нужной физической мере.
5.10. Заключение. Зачем нужна инвариантная мера 119
Проблемы возникают, когда у динамической системы аттракторов
несколько. В этом случае добавление гауссового шума или винеровско-
го случайного процесса приводит к тому, что траектория может иногда
перескакивать с одного аттрактора на другой (очень редко могут возни-
возникать очень большие всплески), а потому мера системы с таким шумом
растечется по всем аттракторам сразу. В таких случаях общепринятого
определения физической меры нет. Можно лишь указать возможные пути
преодоления возникающих трудностей.
Первый из путей связан с понятием так называемых мер Синая—
Рюэля—Боуэна (SRB) [191]. Это меры, которые непрерывны вдоль не-
неустойчивых направлений (неустойчивого многообразия). В ряде случаев
доказано, что сумма E.3) сходится к SRB-мере, причем не только для
точек аттрактора, а для некоторого множества положительной меры Лебе-
Лебега. Для систем, удовлетворяющих аксиоме А (периодические траектории
всюду плотны на неблуждающем множестве), доказана единственность
SRB-меры. Таким образом, возможно, что SRB-меры являются строгим
определением для физических мер. Кроме того, для SRB-мер доказан
ряд других важных результатов, например, для них справедливо тожде-
тождество Песина (связь ляпуновских показателей и метрической энтропии
динамической системы) в теории ляпуновских показателей.
Другим путем к введению физических мер могло бы быть введение
«специальных шумов», не перебрасывающих траектории с одного аттрак-
аттрактора на другой. Например, если к отображению добавить шум с малой
максимальной амплитудой, а не дисперсией, скажем, равномерно распре-
распределенный на отрезке [-е,е], то можно избежать ухода с экспоненциаль-
экспоненциально притягивающего аттрактора (воздействие шума может накапливаться
только как арифметическая прогрессия, а убывание отклонения идет
в геометрической). Видимо, можно предложить аналогичные построения
и для потоков, т.е. добавлять не винеровский процесс, а дифференциру-
дифференцируемую, но в каком-либо смысле случайную функцию, однако какие-либо
теоретические построения на этот счет широко, по крайней мере, неиз-
неизвестны. Либо применимость таких результатов очень ограничена, либо
хорошего теоретического аппарата нет (уравнение Фоккера—Планка уже
не годится).
5.10. Заключение. Зачем нужна инвариантная мера
Чаще всего поисками самой инвариантной меры при решении
практических задач не занимаются, а ограничиваются оценками меры
каких-либо множеств в фазовом пространстве. Важен сам факт суще-
существования меры. А этот факт используется, когда для исследования
динамической системы применяются статистические методы. Наиболее
распространенными являются следующие:
— использование методов усреднения для получения усредненных
уравнений движения;
— теория показателей Ляпунова (например, тот факт, что показатели
совпадают почти для всех х по инвариантной мере);
120 5. Инвариантная мера динамических систем
— понятия метрической энтропии и вероятностных фрактальных раз-
размерностей, одно из наиболее часто встречающихся применений
которых — обработка временных рядов методами теории динами-
динамических систем — будет рассмотрено далее в этой книге.
Без рассказа об инвариантной мере эти темы будут трудны для
понимания. Именно для этого и написана данная глава.
ЧАСТЬ II
Нелинейная динамика:
подходы, результаты, надежды
Параметры порядка
и инерциальные многообразия
6.1. Самоорганизация
В части книги, посвященной языку нелинейной науки, основны-
основными моделями были простейшие отображения и системы обыкновенных
дифференциальных уравнений. Однако одним из основных объектов ма-
математического моделирования и анализа большинства физических теорий
являются нелинейные среды. Основным аппаратом, который использу-
используется при исследовании нелинейных сред, являются уравнения в частных
производных. Формально они описывают системы с бесконечным числом
степеней свободы. Однако не все степени свободы играют одинаковую
роль. В нелинейной диссипативной системе обычно удается выделить
конечное, а иногда и небольшое число переменных, к которым «подстра-
«подстраиваются» все остальные. Эти переменные обычно называют параметрами
порядка.
Их введение можно пояснить на следующем простом примере,
о котором речь шла уже во введении. Возьмем функцию и(х), заданную
на интервале от 0 до I. Ее можно разложить в ряд Фурье и найти ампли-
амплитуду каждой гармоники. Пусть функция и(х) имеет сложный изрезанный
вид (см. рис. 1.1а). В ее поведении не видно какой-либо закономер-
закономерности или упорядоченности. При этом амплитуды многих гармоник а^
сравнимы между собой. Напротив, гладкая функция на рис. 1.15 ведет
себя очень просто, в ней легко заметить закономерности: она близка
к периодической. Для того чтобы передать ее профиль, достаточно задать
амплитуды всего нескольких гармоник. Если процесс идет так, что ко-
количество гармоник большой амплитуды уменьшается, то в системе будет
возникать упорядоченность, будет происходить самоорганизация.
Посмотрим, как меняются со временем амплитуды коэффициен-
коэффициентов Фурье решений в простейших линейных и нелинейных уравнениях.
Задачу для линейного уравнения теплопроводности
Т, = аТхх,
(Кх<г, Т(х,0) = Щх), Tx@,t) = Tx(l,t) = Q F.1)
можно свести к бесконечной системе обыкновенных дифференциальных
00
уравнений, разложив функцию Т в ряд Фурье T(x,t) — ?) C'm(<)cosBji)
m=0
6.1. Самоорганизация
123
и подставив ее в уравнение F.1):
00 .
m=0 m=0
Будем домножать эти уравнения последовательно на cosEj?) и интегри-
i
ровать от 0 до I. Напомним, что при тфп J«^(^у5) cos(Ij?)dx = 0.
о
Это дает нам бесконечную систему уравнений
п = 0,1,2,....
F.2)
В силу линейности задачи все уравнения в получаемой системе будут
независимы.
Пусть нас интересует ре-
решение задачи F.1) на моменты * Т ^о
времени t > t\, и ответ мы хо-
хотим получить с достаточно вы-
высокой точностью е. Посмотрим
на рис. 6.1, на котором пока-
показано, как меняются амплитуды
нескольких первых гармоник со
временем. Чем больше номер
гармоники, тем быстрее умень-
уменьшается ее амплитуда. В результа-
результате, чтобы получить ответ с точ-
точностью е = 0,001 при t > t\
(см. рис. 6.1), нам нужно решить
только первые пять уравнений
в F.2), на моменты с t > ti до-
достаточно трех уравнений, а на
моменты t > t-\ хватит двух. Это
Рис. 6.1. Уравнение теплопроводности: из-
изменение амплитуды нескольких первых
гармоник со временем
замечательный факт — вместо решения всей бесконечной системы F.2),
начиная с некоторого момента времени, достаточно решить всего не-
несколько уравнений. Указание точности и времени, начиная с которого
нам нужен ответ, очень упростило задачу.
Такой подход был развит Г. Хакеном и для анализа нелинейных
диссипативных систем. Пусть мы знаем уравнения в частных произ-
производных, описывающие такую систему. Поступая с ними так же, как
при выводе F.2) из уравнения теплопроводности, получим бесконечную
систему уравнений
F.3)
В этих уравнениях Ст — коэффициенты Фурье. Члены ^тСт обу-
обусловлены диффузионными (или другими диссипативными) процессами,
124
6. Параметры порядка и инерциальные многообразия
О < 71 < 72 < • • • < 7m < • • •, а /о, /i,..., /m, ¦ ¦ ¦ — нелинейные функ-
функции, которые могут зависеть от амплитуд всех гармоник. Система F.3)
гораздо сложнее, чем F.2) — в ней все уравнения связаны. Однако
посмотрим вновь на зависимости Cm(t) для какого-нибудь нелинейного
уравнения, полученные с помощью ЭВМ. В качестве примера возьмем
уравнение
Щ = ruxx + Q(u), F.4)
где Q(u) = и - 2и3. Уравнения такого типа используются в некоторых
математических моделях биологии в связи с анализом эпидемий, рас-
расселением особей с определенным набором признаков. Одно из первых
уравнений такого рода было исследовано в 1937 году А. Н. Колмогоровым,
И. Г. Петровским и Н. С. Пискуновым [65].
Здесь видна та же закономерность (см. рис. 6.2), что и для линейного
уравнения (см. рис. 6.1): амплитуды гармоник с высшими номерами
убывают быстрее, и с опре-
определенного момента ими мож-
можно пренебречь. Учитывая это,
можно построить приближен-
приближенный
метод анализа системы F.4). Бу-
Будем считать, что характерное
0,6
0,4
0,2
0
-0,2
-0,4
Рис. 6.2. Уравнение F.4): амплитуды гармо-
гармоник с высшими номерами убывают быстрее,
и с определенного момента ими можно пре-
пренебречь
время изменения переменных
Cq,C\, ... ,Cm_i равно 6. На-
Например, это может быть наи-
наименьшее время, за которое од-
одна из этих переменных может
измениться в е раз. Предпо-
Предположим теперь, что переменная
Ст меняется гораздо быстрее.
Это вполне разумное предполо-
предположение, поскольку чем выше номер гармоники, тем быстрее она может
измениться, подстроившись под предыдущие. Это обусловлено членом
—7mCm. Как мы видели в рассмотренном примере с линейным и нели-
нелинейным уравнением теплопроводности, коэффициенты 7т пропорцио-
пропорциональны т2, т.е. быстро растут с ростом т.
Аналогичное предположение используется уже более полувека в хи-
химической кинетике под названием метода квазистационарных концентра-
концентраций. Быстро протекающие реакции при этом считаются протекающими
мгновенно. Это позволяет во многих случаях переходить от большой
системы обыкновенных дифференциальных уравнений к системе малого
числа дифференциальных и набору алгебраических уравнений. Из по-
последних иногда удается выразить медленно меняющиеся «квазистацио-
«квазистационарные» концентрации быстрых переменных. Их «быстрота» и состоит
в том, чтобы за малое время выйти на этот медленный квазистационар-
квазистационарный режим. Строгое математическое обоснование этого приема было дано
6.1. Самоорганизация
125
А. Н. Тихоновым и дало начало новому направлению в асимптотическом
анализе.
Фундаментальное допущение о том, что 6 > j-, получило название
адиабатического приближения.
Предположим также, что выполнены неравенства 7т <С 7m+t <¦
7т+2 < ¦.. . Они говорят о том, что процессы, описываемые первыми
т + 1 уравнениями, идут гораздо медленнее остальных. Если, кроме того,
функции /т таковы, что применимо адиабатическое приближение, то
мы придем к системе т. + 1 дифференциальных и последовательности
алгебраических уравнений
/„(C0)Ci,... ,
n = 0,l,...,m- 1,
о = -
_i, cm
F.5)
которые описывают процессы с характерными временами т > ~.
Допустим, что нам удалось выразить амплитуды Ст, Ст+\, Ст+2,...
через Со, С\,..., Cm_ i из последовательности алгебраических уравнений
(или мы знаем, что Ст, Ст+\ и остальные моды гораздо меньше, чем пер-
первые т). Тогда цель достигнута: указав точность и характерные времена,
мы приходим к системе т дифференциальных уравнений
F.6)
с
которая значительно проще, чем исходная система. Этот подход оказал-
оказался плодотворным при исследовании ряда задач физики лазеров и при
решении многих других задач.
Мы уже обращали внимание на то,
что в системах двух автономных обык-
обыкновенных дифференциальных уравнений
единственными аттракторами могут быть
устойчивые особые точки и устойчивые
предельные циклы. Такие же аттракторы
могут существовать и в более сложных си-
системах с N > 2. Но тогда и в них бу-
будет происходить эффективное уменьше-
уменьшение степеней свободы при t —* оо. До-
Допустим, в системе есть предельный цикл.
Чтобы характеризовать координату точки
на этом цикле, достаточно одной величи-
ны в (например, это может быть угол ,,
как в случае, показанном на рис. 6.3). Из- тя цикла
менение величины в может быть задано
одним уравнением: в — д(в), где функция в характеризует неравномер-
неравномерность изменения угла. Остальные переменные можно выразить через эту
координату: X) = /ц@), ..., xN = hN(9). To есть в этом случае уста-
установившийся режим можно описать с помощью гораздо более простой
математической модели, чем исходная система уравнений.
126 6. Параметры порядка и инерциальные многообразия
По аналогии с этой ситуацией, попробуем сформулировать близкое
утверждение для моделей, которые описывают процессы в нелинейных
средах. Эти модели можно представить в виде
u, - Lu + f(u),
u(x, 0) = uo(x), 5(u) |хеГ= q(<). F.7)
х€Г, п = (и, (х,«),..., м,(М)).
Здесь состояние системы в данный момент характеризуется не N
числами, как в системе N автономных обыкновенных дифференциальных
уравнений, а р функциями И|,... ,ир, зависящими от пространственных
координат. Вектор х = (х\,... ,xN) принадлежит области G с грани-
границей Г; L — оператор, в который входят пространственные производные.
Формально эта система с бесконечным числом свободы. Чтобы опре-
определить ее эволюцию, надо вначале задать ее состояние ио(х) в каждой
точке области G. К примеру, такой вид имеет уравнение теплопровод-
теплопроводности F.1), которое мы обсудили в начале этой главы. Это одномерная
задача, поэтому N — 1 и х не вектор, а скаляр, и в этом случае скаляр,
р — \. Область G — отрезок 0 < х < /. Член Lu = Duxx описывает
процесс теплопроводности.
Вернемся к системе F.7). Пусть она также является диссипатив-
ной. Тогда ее поведение при t —> оо может быть охарактеризовано п
функциями времени а\(t),...,an(t), которые связаны уравнениями вида
J = g(a), я@) = яо, а(<)= (а, («),..., МО)- F-8)
Функции а„(<) в этом случае естественно назвать параметрами порядка.
При этом функции и при t —» оо могут быть выражены через а:
u(x,t) = h(ei(t),...,or@,x).
Это фундаментальное утверждение представляет ту основу, на ко-
которой строится анализ большинства процессов в нелинейных средах.
Чтобы подчеркнуть его принципиальное значение, назовем это утвержде-
утверждение основной догмой.
Ранее мы обсуждали уравнение Колмогорова—Петровского—Пис-
кунова, возникающее в теории горения, экологии, биофизике, рассма-
рассматривая решение в ограниченной области. С течением времени решение
стремилось к стационарному. Но возможна и другая постановка задачи,
когда область бесконечна. Тогда при t —» оо его решения и(х, t) выходят
на автомодельное решение типа бегущей волны: и = f(x — ct). При t —» оо
его можно характеризовать одним параметром, например, координатой
точки ?, где «(?,?) = 0,5тах(м(х,t)). При <—>оо ? = х — ct, где х
определяется начальными данными.
Функцию / и скорость волны с можно определить, решая неко-
некоторое дифференциальное уравнение. Это довольно просто сделать с по-
помощью ЭВМ, а в отдельных случаях и аналитически. Такая процедура
позволяет получить и = ft(?) = f(x — ct). В любом случае это уравнение
для / и с оказывается несравненно проще исходной задачи. Еще раз
6.2. Инерциалъные многообразия, оценка размерности аттрактора 127
подчеркнем — все бесконечное число степеней свободы определяется
одним параметром порядка, который линейно зависит от времени.
Далее мы обсудим методы, позволяющие оценить число параметров
порядка по данной модели или по экспериментальным данным. Сейчас
практически нет методов, которые позволяли бы эффективно восстано-
восстановить зависимость h(a, x). Однако, как мы убедимся далее, использование
основной догмы, самым тесным образом связанной с подходом синер-
синергетики, с концепцией параметров порядка, подчас приводит к хорошим
результатам даже в тех случаях, когда ее применение не удается строго
обосновать. Особое значение это утверждение приобрело в связи с ис-
исследованием хаоса в нелинейных средах.
Ранее это утверждение использовалось как эвристическое сообра-
соображение при построении различных упрощенных моделей. Именно из этих
соображений из уравнений гидродинамики выводилась система Лоренца
и ее обобщения.
В последние годы для ряда нелинейных систем основную догму
удалось строго обосновать в теории инерциальных многообразий. Одну
из базовых моделей, где удается получить строгие результаты, далее мы
рассмотрим более подробно. В последнее время концепция параметров
порядка начинает использоваться при построении численных алгоритмов
решения нелинейных задач.
6.2. Инерциальные многообразия,
оценка размерности аттрактора
Обсуждая концепцию параметров порядка, мы говорили об основ-
основной догме, о возможности описывать решения уравнения в частных
производных при t —» оо с помощью некоторой конечномерной дина-
динамической системы. Интуитивно это кажется вполне вероятным для рас-
распределенных диссипативных систем. Для определенности можно считать,
что в таких системах происходят процессы диффузии, теплопроводности
или есть вязкость. В математических моделях такие процессы описыва-
описываются оператором Лапласа с некоторым коэффициентом. Чем выше номер
гармоники (номер собственной функции), тем меньше собственные зна-
значения этого оператора. Поэтому высшие гармоники должны сильно
убывать, быть малыми по величине и не оказывать существенного влия-
влияния на динамику системы. Отправляясь от этих интуитивных физических
соображений, в последние годы удалось сделать важный шаг и получить
строгие результаты.
6.2.1. Уравнение Курамото—Цузуки (или Гинзбурга—Ландау)
Обсудим подробнее применение этих идей и соответствующего
формализма для одной из базовых математических моделей, занимающей
особое место в нелинейной динамике. Этой моделью является уравнение
WT = (±1 + ico)W + A + ici)WRR - A + ic2) \W\2 W. F.9)
128 6. Параметры порядка и инерциальные многообразия
Оно естественно возникало при моделировании множества различных
процессов, протекающих в нелинейных средах. Оно использовалось при
описании ветровых волн на воде и морфогенеза, возникновения турбу-
турбулентных режимов в гидродинамике и ряда неустойчивостей в плазме,
самоорганизации, возможной в ходе колебательных химических реакций,
и ряда явлений в твердом теле.
Однако еще более важным является следующее обстоятельство.
Огромный класс нелинейных сред, широко изучавшихся в нелиней-
нелинейной динамике и синергетике, описывается системой уравнений типа
реакция—диффузия, зависящей от параметра А:
+ Fl(X,Y,X). v""v/
Как было понято в эру диссипативных структур, типичным являет-
является следующее поведение. Обычно эти уравнения имеют стационарное
пространственно-однородное решение (Xq,Yq), которое И.Пригожиным
было названо термодинамической ветвью. Это решение устойчиво, если
А < Aq. Поведение решений после потери устойчивости термодинамиче-
термодинамической ветви определяется спектром линеаризованной задачи для уравне-
уравнения F.10) в окрестности решения (Xq,Yq) и точки бифуркации Ао.
Если при А = Ао одно простое собствен-
собственное значение проходит через нуль, возникают
пространственно-неоднородные стационарные ре-
решения. Такое поведение в системе F.10) впервые
было обнаружено А.Тьюрингом при исследова-
исследовании математической модели морфогенеза [341].
Его часто называют неустойчивостью Тьюринга или
диффузионной неустойчивостью. Типичная зависи-
о Л мость амплитуды стационарного решения А от
Рис. 6.4. Схема бифур- параметра А будет такой, как показано на рис. 6.4.
кации Тьюринга в урав- Здесь легко узнать типичную бифуркационную
нении F.10) — это диаграмму — «вилку», с которой мы сталкива-
обычная бифуркация лись, обсуждая язык нелинейной динамики. Од-
типа «вилки», но в бес- нако следует подчеркнуть, что здесь речь идет
конечномерной дина- о явлениИ; возникающем именно в распределен-
мическои системе ной системе решение (Хо, у0) в пространственно-
однородной системе (в которую переходит F.10) при D\ = Dj = 0)
устойчиво. Неустойчивость обеспечивается сильно различающимися ко-
коэффициентами диффузии («короткодействующий активатор» и «дально-
действующий ингибитор», как говорят химики и биологи). Диффузия
здесь выступает в нетрадиционной дестабилизирующей роли.
Если при А = Ао у линеаризованной задачи два чисто мнимых зна-
значения (два комплексно сопряженных собственных значения проходят че-
через мнимую ось), то происходит упоминавшаяся в предыдущей части кни-
книги бифуркация Андронова—Хопфа, и в системе начинаются колебания.
Уравнение F.9) описывает поведение двухкомпонентных сред в ок-
окрестности точки бифуркации в обоих случаях. В нем W{R,T) — ком-
6.2. Инерциальные многообразия, оценка размерности аттрактора 129
плексная функция, величины со, с\, ci — действительные постоянные,
значения которых определяются по коэффициентам D\, Z>2, функциям
Fi(X, Y, А) и их производным. Знак плюс в правой части этого уравнения
соответствует области параметров А > Ао, минус — А < Ао. Именно это
и было показано в 1975 г. И. Курамото и Т. Цузуки [255], [256].
Очевидно, уравнение F.9), зависящее от трех действительных по-
постоянных, гораздо проще, чем исходная математическая модель, завися-
зависящая от двух нелинейных функций F\ (X, Y, А) и ^(-Х", Y, А).
Поясним смысл переменных W, R, Т. Возможность перейти от
систем вида F.10) к уравнению F.9) связана с наличием малого параметра
е = |А — Aol'/2. Решение уравнения F.10) в этом случае можно записать
в виде
еЬе2 = Const,
где Xq, Yq — термодинамическая ветвь. Функция W зависит от медлен-
медленных переменных R — ех, Т = e2t; f = e'k'x в случае неустойчивости
Тьюринга, / = е1Ш»', если происходит бифуркация Хопфа. Значения fcc
и и>о, естественно, определяются величинами собственных значений
линеаризованной задачи при А = Ао. Параметр fcc определяет «простран-
«пространственный период» возникающих стационарных диссипативных структур,
параметр и>о — частоту, с которой происходят колебания вблизи точки би-
бифуркации. Иначе говоря, переменные R и Т в уравнении F.9) — это мед-
медленные переменные, определяющие модуляцию по времени и простран-
пространству простейших решений /, вид которых следует из линейного анализа.
Вывод уравнения F.9), предложенный И. Курамото и Т. Цузуки,
опирался на традиционные приемы асимптотического анализа и был
сделан на физическом уровне строгости. Однако позже было показано,
как оно возникает для систем в конечной области с малой диффузией
D\ ~ ed\, Z>2 ~ e^2 [63]. По-видимому, оно было первой квазинор-
квазинормальной формой, полученной для систем реакция—диффузия. Позже
аналогично были получены и другие уравнения такого типа [10].
Без ограничения общности в уравнении F.9) можно положить
со = 0 (это обеспечивается заменой Whob = We>Cot) и выбрать знак плюс.
Когда выбран знак минус, можно показать, что lim ||W||2 = 0. Такой
(->оо
результат представляется естественным, поскольку в этой области пара-
параметров устойчива термодинамическая ветвь Xq, Yq.
Исследованию краевой задачи
Wt = W + (l + ic\)Wxx - A + ia) \W\2 W,
Q^x^l, 0<t<oo, W(x,Q) = W0(x), F.11)
было посвящено огромное количество работ. Их обширная библиография
приведена в книгах [10], [56], [256]. Задача F.11) имеет множество раз-
5 Зак.2
130 6. Параметры порядка и шерциальные многообразия
ных решений от пространственно-однородных W(x,t) ~ ехр(—гс2< + ш),
а = const, автомодельных W(x, t) = Д(х)ехр (—iwt + ia(x)) до двухча-
стотных (аналогов инвариантных торов) и хаотических.
Хаотические режимы описывают так называемый диффузионный
хаос — возникновение непериодических, турбулентных режимов в среде,
каждый элемент которой в отсутствие остальных (Wxx = 0) стремится
к периодическому решению. Чем больше длина области /, тем более
сложные хаотические режимы возможны в такой системе.
Подобно тому как с помощью метода Галеркина для уравнений
гидродинамики, описывающих конвекцию, была получена система Ло-
Лоренца, здесь также можно получить конечномерную модель. Простейшая
модель такого типа имеет вид
17)- ^/(cos в + a sin в),
+ з|) -2?j/(cos0-c2sin0)-2fc27/,
в = с2B? - |) +sin0B? + т/) + c2cos0B? - i/) + 2c,fe2,
где используется Галеркинская аппроксимация
k = у, 9(t) = 92(t) - 0,@-
Три уравнения для ?, 7/, в вместо четырех для ?, »/, 9\, 02 получаются
благодаря тому, что исходное уравнение обладает симметрией — оно
инвариантно относительно преобразования W —> We'", a — const.
Так же как модель Лоренца, динамическая система F.12) при
определенных значениях параметров описывает динамический хаос, т. е.
имеет странные аттракторы, некоторые из которых были детально иссле-
исследованы [10].
Вместе с тем в одном важном отношении система F.12) отличается
от системы Лоренца. Множество работ, выполненных в 80-е годы, пока-
показали, что хаос, наблюдающийся в экспериментах с подогреваемым снизу
слоем жидкости, принципиально отличается от хаотических аттракторов
в системе Лоренца. В том двумерном течении, описать которое была
призвана система Лоренца, имеют место только периодические решения.
Чтобы получить их в конечномерной галеркинской модели, нужно брать
не три, а около сотни гармоник. Этот эффект получил название явления
ложного хаоса. Другими словами, анализируя исключительно интересную
саму по себе модель Лоренца, мы ничего не узнаем об исходном течении.
Двухмодовая система F.12) находится в совершенно другом от-
отношении к исходному уравнению Курамото— Цузуки. Было показано,
что когда длина области невелика (/ < 1,5тг + 2тг), то между решениями
исходного уравнения и двухмодовой системы есть не только качествен-
качественное, но и количественное соответствие. Причем оно относится не только
к простейшим периодическим, но и к хаотическим аттракторам, и к
сценариям их возникновения при изменении параметров. Это позволяет
6.2. Инерциальные многообразия, оценка размерности аттрактора 131
найти какой-либо интересный эффект в упрощенной системе F.12) и
затем достаточно легко обнаружить его в исходном уравнении, описыва-
описывающем диффузионный хаос.
Другими словами, комплексные амплитуды двух первых гармоник
являются параметрами порядка, к которым подстраиваются остальные
степени свободы, когда длина области невелика. Но если это так, то
аттрактор уравнения Курамото— Цузуки должен в точности описываться
некоторой конечномерной динамической системой. В последнее десяти-
десятилетие в теории инерциальных многообразий появились методы, позволя-
позволяющие доказывать это. Отметим, что этот круг работ обладает не только
«академической ценностью», но и «эвристическим потенциалом». Ста-
Становится понятно, где нас могут ожидать неожиданности, где параметров
порядка оказывается гораздо больше, чем можно было бы предположить.
Следующая глава наглядно подтверждает эту мысль.
Встает вопрос, почему в случае системы Лоренца это не так,
почему подход, обсуждаемый ниже, применим к очень немногим ги-
гидродинамическим задачам. Некоторые «формальные» причины этого мы
обсудим в конце главы. Однако здесь можно привести простое физи-
физическое соображение. Уравнение Курамото—Цузуки описывает ситуацию
«взаимодействующих осцилляторов», каждый из которых сам по себе
обладает автоколебательной динамикой. Благодаря диффузионному чле-
члену A + ic\)Wxx амплитуды высших пространственных гармоник быстро
убывают. В гидродинамической системе каждый «элемент системы» не
обладает какой-то собственной динамикой, которую он может демон-
демонстрировать в отсутствие остальных. Турбулентность здесь в большей
степени свойство «целого», а не «взаимодействующих частей». Кроме
того, член (v, V)v обеспечивает перекачку энергии от низших гармоник
к высшим. Поэтому и параметров порядка, даже если они существуют,
обычно гораздо больше, чем в системах реакция—диффузия.
Заглядывая вперед, можно сказать, что теория инерциальных мно-
многообразий позволяет объяснить поразительную эффективность галеркин-
ских уравнений для уравнения Курамото—Цузуки в одномерном случае.
Оказалось, что аттракторы этого уравнения действительно определяются
системой конечного числа обыкновенных дифференциальных уравне-
уравнений. Другими словами, это уравнение является мостом между уравне-
уравнениями в частных производных и обыкновенными дифференциальными
уравнениями.
6.2.2. О некоторых идеях теории ннерциальных многообразий
Идеи теории, обосновывающей конечномерность аттракторов для
распределенных систем и называемой теорией инерциальных многообра-
многообразий, мы и обсудим в этом пункте. После этого будет рассмотрено их
приложение к уравнению Курамото—Цузуки.
Обсуждая основную догму, мы отмечали, что важно иметь в виду,
какой именно аттрактор уравнения мы рассматриваем (их может быть
очень много) и что является параметрами порядка. Для получения оценок
132
6. Параметры порядка и инерциалъные многообразия
сверху естественно предположить, что мы можем столкнуться с худшей
ситуацией, и получать результаты для всех возможных аттракторов ис-
исследуемой задачи
u = u(r,t), M(r,0)
ащ (г, t) + bu(r, t) = g(r)
rGG + Г,
при г ? Г.
F.13)
Представление о всех возможных установившихся режимах формализует-
формализуется в понятии глобального, или максимального, аттрактора (в зарубежной ли-
литературе его иногда называют универсальным аттрактором). Введем опре-
определение. Полугруппой {(p',t > 0}, отвечающей уравнению F.13), назовем
семейство операторов <р', действующих в банаховом пространстве Е,
которому принадлежит решение ipf: Е -* Е. Причем (р (щ) - u(t), где
u{t) — решение задачи F.13). (Предполагается, что решение задачи F.13)
существует и единственно.) Максимальным аттрактором полугруппы {<р1}
или уравнения F.13) называется также замкнутое ограниченное множе-
множество U С Е, которое обладает:
1) свойством инвариантности >р*(и) = U для t > 0;
2) свойством притяжения: для любого ограниченного множества
ВСЕ расстояние distE(yj'(B),Z7) -+ 0 при t -* оо, где dist(X, Y) =
mpinfyeY\\x-y\\E.
Существование максимального аттрактора
доказано для большого класса дифференциаль-
дифференциальных уравнений и отображений. Максимальный
аттрактор определяет асимптотическое поведе-
поведение решений изучаемых уравнений при всех воз-
возможных начальных данных. Поэтому он может
описывать множество предельных режимов, бо-
более широкое, чем множество режимов, наблю-
наблюдаемое в реальном или вычислительном экс-
эксперименте. Например, в уравнении Курамото—
Цузуки при любых значениях параметров су-
существует бесконечное количество неустойчивых
симметричных решений. Они также должны вхо-
входить в максимальный аттрактор, как и те множе-
множества, которые характеризуют поведение решений
при t —* оо в случае типичных начальных данных.
В качестве параметров порядка будем вы-
выбирать коэффициенты Фурье по системе соб-
собственных функций {ф„} линейной задачи. В этом
представлении решение уравнения в частных про- п='
изводных представляет собой точку в пространстве ф\,ф2,--- u(x,t) =
оо
X) Сп(()фп(т) (см. рис. 6.5), в котором по координатным осям отклады-
ваются соответствующие коэффициенты Фурье.
Рис. 6.5. Решение урав-
уравнения в частных про-
производных представляет
собой точку в простран-
ф\,ф-1,... u(x,t) =
6.2. Инерциальные многообразия, оценка размерности аттрактора 133
Число «существенных» переменных N — С\,..., Сц, необходи-
необходимых для однозначного восстановления решения и(Х, t) при t —> оо
(и, соответственно, Сц+\,Сц+2,...) будем называть Фурье-размерностью
максимального аттрактора (исходный английский термин Fourier span-
spanning dimension). Это число дает оценку сверху фрактальной размерности
любого аттрактора, возможного в этой системе. (В частности потому, что
Cn(t) могут быть далеки от параметров порядка, которых может быть
в идеальном случае намного меньше, чем N.)
Поскольку система диссипативна, решение ее естественно счи-
считать гладким. Так как решение рассматривается в ограниченной области
пространства, можно предположить, что оно будет принадлежать функ-
функциональному пространству ?2[G] с нормой \\u\\i =
|
Коэф-
\\QNa(t)\\2 < \\PNa(t)\\2-
фициенты Фурье, естественно, возникают в пространствах со скалярным
произведением (p,q) = / p(r)q(r) dr, т. е. в гильбертовом пространстве Н.
в
Основная идея теории инерциальных многообразий сводится к сле-
следующему. Пусть Ррг — оператор проектирования на первые N фурье-
мод: @|,..., фп), Qn = 1 —Pn — оператор проектирования на оставшиеся
моды (<Pn+i,<Pn+2,---)- Рассмотрим два решения задачи — u(t) и u'(t).
Для краткости зависимость от пространственной координаты г будем
опускать. Пусть разность двух решений a(t) = u'(t) - u(t) удовлетворяет
так называемому неравенству конуса
F.14)
Из последнего равенства следует, что высшие фурье-гармоники решений
u(t) и u'(t) (с номерами большими N) могут отличаться, только когда
отличаются низшие. В самом деле, если п низших гармоник совпадают
у двух решений, то ||Pjvtt(<)||2 = 0, но тогда по этому неравенству и
||Qjva(?)|| = 0. Таким образом, высшие моды (CN+\,CN+2, ¦ ¦.) определя-
определяются низшими, что позволяет для функции u(t) на аттракторе X ввести
отображение Ф:
Ф(Рлгм) = QNu.
Неравенство конуса гарантирует, что отображе-
отображение Ф определено корректно. В самом деле, если
выполнено равенство
PNu = PNu,
то в силу неравенства F.14) QtfU = QffU1.
Геометрическую интерпретацию неравен-
неравенству конуса дает рис. 6.6. Для простоты про-
пространство Н здесь изображено трехмерным,
РцН представляет собой горизонтальную плос-
плоскость.
Возьмем какую-нибудь точку на какой-
либо траектории u(t), принадлежащей макси-
F.15)
QNH
Рис. 6.6. Геометрическая
интерпретация неравен-
неравенства конуса
134 6. Параметры порядка и инерциальные многообразия
мальному аттрактору. Из неравенства конуса следует, что ни одна из тра-
траекторий максимального аттрактора не лежит внутри конуса, показанного
на рис. 6.6. Отсюда ясно, что любая траектория изучаемой системы од-
однозначно проектируется на плоскость РцН: каждой точке в плоскости
РцН отвечает не более одной точки на аттракторе в пространстве Н.
Используем эти соображения для исследования максимально-
максимального аттрактора уравнения Курамото—Цузуки. Пусть начальные данные
Wq(x) принадлежат аттрактору PjyWo € Pn (проекция аттрактора). Это
предположение позволяет не рассматривать переходный процесс, а со-
сосредоточить внимание на асимптотическом поведении решения. Тогда
QnWq = <&{PNWt)), где W(t) — решение уравнения
W(t) = W + (\+ic])Wxx-(l+ic2)\W\2W, W@) = W0 F.16)
с периодическими граничными условиями
W(l,t) = W@,t).
Решение W(t) может быть представлено в виде
где г&(<) = PtfW(t) — конечномерный вектор, лежащий в простран-
пространстве PffH, эволюция которого определяется уравнением
щ = w + A + icx)wxx-PN{(\ + tc2)|t& + Ф[г»]|2(г& + Ф[ад])},
г&@) = PNWQ.
Уравнение F.17) получено проектированием уравнения F.16) на конеч-
конечномерное пространство Р^Н. Оно представляет собой конечномерную
систему обыкновенных дифференциальных уравнений для компонент
вектора w — (С\,..., CV).
Дифференциальное уравнение для Cj (I ^ j < N) можно полу-
получить также в методе Галеркина, домножив на <pj (I ^ j ^ N) и взяв
скалярное произведение, то есть проинтегрировав по области G (в случае
уравнения F.16) — по отрезку 0 < х < /).
Обратим внимание на отличие уравнения F.17), называемого инер-
циалънои формой, от системы уравнений, полученных в случае метода
лг
Галеркина, в котором решение ищется в виде W = ?) С;(<H„(х). В ме-
тоде Галеркина следует положить QnW — Ф(Р^\?) = 0. Уравнение F.17)
дает не приближенное, а точное описание эволюции первых N фурье-
мод решения W(x,t) при t -* оо. В отличие от метода Галеркина функ-
функция Ф неизвестна, известно только, что она существует. Равенство F.15)
означает, что при t —» оо удовлетворяется бесконечное число равенств
Cj = hj(C{,..., CN), N + 1 ^ j < оо, т. е. именно то равенство, которое
фигурирует в основной догме.
Пусть {С\(t),...,CN(t)} — решение уравнения F.17). Пусть все
функции
6.2. Инерциальные многообразия, оценка размерности аттрактора 135
„
Ф
принадлежащие максимальному аттрактору
(соответствующие различным начальным дан-
ным), лежат в некоторой области простран-
пространства Н, называемой инерциальным многообра-
многообразием (см. рис. 6.7). Функции {С| (t),..., CN(t)}
принадлежат проекции инерциального много-
многообразия на пространство Р^Н.
При анализе конкретного уравнения
в частных производных ключевым моментом
является проверка неравенства конуса. Обыч-
но эта проверка проводится в два этапа.
1. Получение априорных оценок изуча- Рис-6.7. Иллюстрация по-
емого уравнения при t - оо при всех воз- ня™я инерциального мно-
lv v r, - гообразия
можных начальных данных. При этом обычно
недостаточно иметь оценки в норме L2, нужны оценки и в норме С —
!M)|
2. Доказательство неравенства конуса для аттрактора изучаемых
уравнений
Hm (||QW0||2 " 11^а@||2) < 0. F.18)
Рассмотрим оба этих этапа более подробно, следуя работе [187].
6.2.3. Априорные оценки решений уравнения Курамото—Цузуки
Перейдем к первому шагу для уравнения Курамото—Цузуки. Вве-
Введем два интеграла
M(t)=J\W(x,t)\2dx= \\W(t)\\22, E(t)=J\W,(x,t)\2dx=\\Wt(t)\\l.
о о
Домножим уравнение F.16) на W*(x,t) и проинтегрируем от 0 до /
W*Wt = W*W + A + ic\)W*Wxx - A + ic2)\W\2WW\
J W"Wt dx = M(t) + A + ici) \W*WX - J W*XWX dx\ - F {g)
0 I ° 0
-(l+iC2)J\Wfdx.
0
В случае второй краевой задачи 1^@,<) = Wx(l,t) и задачи с пери-
периодическими краевыми условиями, которые мы и будем иметь в виду,
VF*Wj:|0= 0. Заметим, что JW?Wxdx = E(t). Возьмем комплексно
о
136 6. Параметры порядка и инерциальные многообразия
сопряженное равенство к F.19)
1 i
Г WW* dx = M(t) + A - ic\)E{t) - A - ic2) f \W\4 dx.
0
Сложим два последние равенства
i
f(W*Wt + Wt*W) dx = 2M(t) - 2E(t) - 2 f \Wf dx.
о
Поскольку члены слева равны jMt, получим
1
о
Напомним неравенство Коши—Шварца, справедливое для функций
из?2:
¦у
\(f,h)\ = I fhdr ¦¦
G G G
I/I2*
I f
Следовательно, / <te / |W|4 <te ^ M2, (/ = |W|2, ft = 1). Таким образом,
о о
1 dlijt) .. _ Af2 ^ ., M1
2 "л ^M-?- — ^M--r.
Поэтому М^)'-1^»!. Решим уравнение jM(=M-jH применим
теорему сравнения для одного автономного обыкновенного дифференци-
дифференциального уравнения. В силу этой теоремы M(t) < М(<), если М@) ^ М@),
так как правая часть уравнения для M(t) меньше правой части уравнения
для M(t). Тогда найдем
( 00
Отметим, что J \W\2 dx — ?) С2 (мы считаем, что система {фп} ор-
о *=1
тонормирована). Следовательно, ||W||2 равна расстоянию г от точки,
соответствующей решению, до начала координат в фазовом простран-
пространстве {ф\,ф2,---} (см. рис.6.3). Следовательно, независимо от начальных
данных
r2(t) = M^l[l-exp(-2t)]~l. F.21)
Получим оценку для величины E(t). Продифференцируем исходное урав-
уравнение по х, домножим его на W% и проинтегрируем по х от 0 до /:
6.2. Инерциальные многообразия, оценка размерности аттрактора 137
W*xWxt = W'W, + A + ic{)W*xWxxx - A
i /
Jw*xWxt = E-{\ + ic\) J \WXX\2 dx -
0 °,
f \W\2\WX\2 dx + J W2W*2 dx J.
0 0
Комплексно сопряженное равенство
i i
J WxW*t = Я - A - ici) У \WXX\2 dx -
0 0
I
Учитывая, что ^ = J{WxtWx + WxWxt)dx, и сложив последние равен-
о
ства, получим
\™=E-J\Wxx\2dx-2j\W\2\Wx\2dx-
,
о F.22)
Выписывая последний член в правой части, мы учли очевидные
равенства a*b* — (ab)* и a*b + ab* = 2Re(a*b), где а и b — произвольные
комплексные числа. Второй член справа можно оценить следующим
образом
' ' ' ,,Л I ,,,
W*WXX dx < (J \W\2 dx) (j \WXX\2 dx) .
0 0 0 0
( J
Следовательно, J \WXX\2 dx ^ jj. Далее рассмотрим отдельно два случая.
0
Если коэффициент ci мал: \ст\ < Vb, то |1 + 1С2\ = A + <^I/'2 < 2. В этом
случае
/ i
-2 J \W\2\WX\2dx - Re[(l + ic2)J W2w;2dx\ <
138 6. Параметры порядка и инерциальные многообразия
i
< (-2+|l+tc2|) I \WX\2\W\2dx ^ 0.
О
Поскольку эти члены всегда неположительны, то отбросив их в форму-
формуле F.22), получим неравенство
\дЕ Е2
Учтем, что M(t) < i[l - ехр(-2<)] = M(t), при t > I, M(t) < M(i)
и применим теорему сравнения. Рассмотрим уравнение
1 &*¦
-!,=!-=—. F.23)
2 М{1) V ;
Проведя те же выкладки, что и при выводе неравенства F.21), получим
®('>=1-схр(-2*)-
Таким образом, при t > I E(t) < E(t), где E(t) определяется формулой,
полученной из F.23). Эта формула дает априорную оценку производ-
производной Wx.
Получим теперь оценку функции W(x,t) в норме с ||W||C =
max |W(x,<)|. В данном случае эта оценка совпадает с оценкой в норме
пространства L00. Заметим, что
— \W\2 = WW* + WXW* = 2Re(WW*).
ox
Интегрируя последнее равенство от хо до х, получим
х
|W(x,<)|2 = \W(xo,t)\2 + f 2Re(WW*)dx.
В силу неравенства Коши—Шварца получим
|W(x,<)|2 ^ \W(xo,t)\2 + 2M(t)l/2E(t)l/2. F.24)
Это неравенство справедливо и для точки х, где функция W(x,<)
достигает максимума W(x,t) = max W(x, t).
Проинтефируем уравнение по хо, считая, что в неравенстве F.24)
слева стоит W(x,i)
/_ i
\W(x,tf\dx = l\W(x,t)\2^J
О О
/
[\
6.2. Инерциальные многообразия, оценка размерности аттрактора 139
= М + 21МтЕт => \\W(t)\\2 < — + 2М|/2Я|/2. F.25)
Напомним, что последнее неравенство справедливо при |с2| < л/3.
В случае |с2| > л/3 оценка будет несколько сложнее. Пусть S =
max{0,— 2 + |1 + *с2|}.
При |с2| > л/3 <5 > 0, и
i i
-2 / |W|2|Wx|2da:-Re|(l + »C2) f W2W*2 dx] <
•/ L J J
^sJ\W\2\W,\2dx^S\\W(t)\\2eEl.
Отметим, что оценка F.25) справедлива при всех значениях пара-
параметров С[, С2 и 1. Следовательно,
Поэтому при |с2| > л/3 получаем из F.22)
Членом, ограничивающим решение, является член —jg-, кото-
который с ростом Е растет быстрее всех остальных. Отметим, что оцен-
оценка F.25) верна во всем пространстве параметров. Введем обозначение
lim M(t) = Moo, lim E(t) = Д».
f^oo ' t^oo '
Имея в виду теорему сравнения для одного обыкновенного диффе-
дифференциального уравнения и проводя такие же рассуждения, как при выводе
оценки F.23), убедимся, что Еж будет определяться особой точкой урав-
уравнения
—2
~Ef = E — h oMqqE + 216Mqq E =$-
2 Moo
Е
=>¦ 1 — + бМда + 216мЦ еЦ — 0.
Последнее равенство представляет собой квадратное уравнение
1/2
относительно Е^ .
- iW00( I -|- бМпо), (г ^г\
(Ь.2Ь)
140 6. Параметры порядка и инерциальные многообразия
Подставляя формулу F.26) в неравенство F.25), получим
. F.27)
Отметим еще один частный случай Ci = 0. При этом уравнение
Курамото—Цузуки переходит в систему типа реакция—диффузия. До-
множим исходное уравнение на W*, комплексно сопряженное к нему
уравнение на^и сложим
W*Wt + Wt*W = 2W*W + W*WXX + WWXX - 2|W|4 =4>
=> jt\W\2 = 2\W\2 + \W\]X - 2\WX\2 - 2\W\4.
Используем принцип максимума. Пусть в момент t в точке жд
|W(a;o,f)| достигает локального максимума. В этой точке \WX\2 = 0,
l^lL ^ 0. Следовательно,
^|^(Ж0,0|2 < \W(xo,t)\2 - 2|^(Ж0,0|4.
Вновь пользуясь теоремой сравнения для одного обыкновенного
дифференциального уравнения, получим
hm\W(x,t)\] ^ 1. F.28)
Подытожим полученные оценки для максимального аттрактора:
lcil^v/3, C2 — произвольное,
\с\ | > л/3, с2 — произвольное,
C2 — произвольное, ||W||e < 1 +2/;
^ ' '
где 5 = { ^}
С] — произвольное, с2 = 0, \\W\tf: < 1.
6.2.4. Доказательство неравенства конуса
Перейдем ко второму шагу — доказательству неравенства кону-
конуса. Вновь будем рассматривать два решения уравнения F.16): W(x,t)
и W^a;, t) и их разность а = W'(x, t) — W(x, t). Записав уравнение для W
и для W, и вычитая из первого второе, получим
о, = о + A + tci)oM + A + ic2)(W'\W'\2 - W\W\2).
Спроектируем функцию a(x,t) на пространство, натянутое на пер-
первые N фурье-гармоник: р = PNa. Проекция p(x,t) удовлетворяет урав-
уравнению
pt = р + A + iCl)pM - A + ic2)PN(\W'\2W' - \W\2W). F.30)
6.2. Инерциальные многообразия, оценка размерности аттрактора 141
Проекция на ортогональное дополнение Qt/H, q — Q^a, удовле-
удовлетворяет уравнению
qt = q + A + ic2)qxx - A + ic2)QN(\W'\ V - \W\2W). F.31)
Принципиальным моментом является следующий: оператор Лапласа, взя-
взятый с отрицательным знаком, ограничен сверху некоторым числом к^
в пространстве Рц?1 и ограничен снизу числом k^+i в простран-
пространстве Qr/H.
Важное значение для проверки условия конуса имеет разность меж-
между &ДГ+1 и ktf (в англоязычной литературе для этой разности используется
специальный термин «spectral gap» (спектральная щель)).
Домножим равенство F.30) на р*, равенство, сопряженное к F.30),
на р и сложим. Разделив полученное соотношение пополам, придем
к неравенству
-Re[(l+iC2) fp'(\W'\2W'~\W\2Wdx)],
L 0 J
о
При получении равенства мы учли самосопряженность оператора
Лапласа
i i i
I P(-P*xs)dx= I 'P'xPx dx = I p*(-pxx) dx
0 0 0
(последняя цепочка равенств получается в результате интегрирования
по частям). Кроме того, в неравенстве F.32) использовано тождество
i
A + *с2) У (\W'\ V - \W\2W)p'(x) dx +
о ;
+ A - ic2) J(\W*'\W*' - \\У*\2иг')р(х) dx =
0
= 2ReT(l +«C2) jp"(x){\W'\2W' - \W\2W) dx].
о
Домножая равенство F.31) на q*, равенство, сопряженное уравне-
уравнению F.31) на q(x), складывая и деля пополам, получим
142 6. Параметры порядка и инерциапьные многообразия
i
- Re[(l+ic2) f q*(x)(\W'\2W' -\W\2W)dx\. F.33)
о
Как в задаче с периодическими краевыми условиями, так и в задаче
с условием отсутствия потоков на границе, имеет место равенство
kN+\ =kN + k\. F.34)
В случае второй краевой задачи, в частности, fco = 0>
Используя соотношение F.34), перепишем неравенство F.33) в виде
F.35)
2 ~ k2N\\q\\\ - fc,Bfeff + *,) IMli -
- Re[A + гс2) J q*(x)(\W'\2W' - \W\2W) dx\.
о
Разность между величинами fc#+i и к^ обеспечивает существование тре-
третьего члена в правой части неравенства F.33), который играет ключевую
роль в проверке неравенства конуса.
Разность двух решений равна
Проверим тождество
\W'\2W' - \W\2W = a(\wf + \W\2) + a*WW'. F.36)
Левая часть тождества равна
(W + a) (W* + a*) (W + а) - WW*W =
= (WW* + aW* + Wa* + aa*) x (W + a) - WW*W =
= WW*W + aW*W + W2a* + aa*W +
+ aWW* + a2W* + Wa*a + a2a* - WW*W.
(Первый и последний члены в последнем равенстве справа сокращаются.)
Правая часть тождества F.36) равна
a((W + a)(W* + a*) + WW*) + a*W(W + а) =
= a(WW* + aW* + Wa' + aa* + WW*) + a*W2 + a*aW =
= aWW* + oV + Waa* +a2a* + aWW* + a*W2 + aa'W.
Сравнивая почленно, убедимся, что обе части равенства F.36) совпадают.
6.2. Инерциальные многообразия, оценка размерности аттрактора 143
Введем функцию
Щ = \\QNa\\22 - \\PNa\\l = \\q\\l - \\p\\l
Точка, соответствующая функции W'(t), находится внутри конуса,
построенного из точки W(t) (см. рис. 6.6), если L(t) > 0, на конусе, если
L(t) = О, внутри конуса L(t) < 0.
Вычитая неравенство F.32) из неравенства F.35), получим нера-
неравенство для L(t)
r I 1 F.37)
- Re|0 +ic2)j (q* -V')(\W'\2W - \W\2W) fej .
о
Преобразуем последний член этого неравенства, имея в виду тождество
F.36) и соотношения
= Я*Р ~ V\ + 94* - VV = 2» lm(q*p) + \q\2 - |р|2,
5 = -Re J(l +ic2) j{q* -p*)(\W'\2W' - \W\2W) dx\ =
о
о
i
i
= - Re [A + ic2) I(\q\2 - \p\2) (\W'\2 + \W\2)
0
;
- Re[(l + ic2)f 2Ит(Ч'р)(\иг'\2 + \W\2) dx\ -
о
;
- Re[(l + ic2) f(qt2 -p*2)WW'dx\.
0
(
Отметим, что / = /(|g|2 - \p\2) (\W'\2 + \W\2) dx — действительное
0
число. Следовательно, Re((l +ic2)l) — —I.
144
6. Параметры порядка и инерциальные многообразия
Кроме того, из тех же соображений получим
;
-Re[(I + ic2)J2i\m{qtp){\Wl\2 + \W\2) dx\ =
О
/
= 2c2Jlm(q'p)(\W'\2 + \W\2)dx.
Следовательно,
/
+ \W\2) dx + 2c2j
0
- Re ГA + ic2) J {q2 - p2) WW' dx\.
\W\2) dx -
Напомним неравенство Гельдера
ь
-1 \
dx I
/
(р-О/р
, 1 < p < +oo.
При р-2
ь
S < (\\W'\\2c + \\W\\2) j \p\2 dx + 2(\\W'\\2C + \\W\\2) \c2\ I \q\\p\ dx
В последнем неравенстве ||W||c — наибольшая из оценок
ll^'ll2-
Таким образом, неравенство F.37) можно переписать в виде
< A 4)? feBfc k)\\\\2 +
fcW + kl)\\q\\22
2(HPll2 + H?ll2)]-
F.38)
6.2. Инерциальные многообразия, оценка размерности аттрактора 145
На этом этапе можно выбрать число гармоник JV, гарантирующее
существование инерциального многообразия.
^|)} F.39)
Обсудим подробнее этот выбор. Мы хотим, чтобы вне конуса L —
\\ч\\г ~ \\р\\\ > 0 =*¦ ||д||2 > \\p\\\ величина L(t) убывала. Поэтому заменим
||р||2 на большую величину ||д||2 (вне конуса) в неравенстве F.38).
Тогда условие F.39) гарантирует выполнение двух неравенств: при
L > 0, A - fc^)L < О
Следовательно, вне конуса
поэтому величина L(t) экспоненциально убывает. Когда L = О, то
и в этом случае -щ ^ 0. Следовательно, если, начиная с какого-то
момента времени ?, условие конуса, характеризующее разность двух ре-
решений, начинает выполняться, то оно будет выполняться и в дальнейшем
при i < t < 00.
Поскольку для второй краевой задачи при условии отсутствия
потоков k] = j, kfi = ?p, из неравенств F.39) следует
(,40)
Проекция на первых N гармоник однозначно определяет движе-
движение на аттракторе исследуемой задачи. Однако эта проекция может иметь
особенности, некоторые из которых мы будем обсуждать, рассматри-
рассматривая проблемы реконструкции аттракторов. Для того чтобы особенностей
не было и отображение обладало многими другими полезными свой-
свойствами, исходя из ряда топологических соображений, часто используют
следующую оценку
где D — Фурье-размерность универсального аттрактора, d — фрактальная
размерность любого конкретного аттрактора исследуемой системы.
Исходя из неравенств F.29) и F.40), имеем: |с]| < л/3, с2 —
произвольное
146 6. Параметры порядка и инерциальные многообразия
\с\ | > л/3, С2 — произвольное,
0
С] — произвольное, ci = О,
Таким образом, имеет место замечательный факт: динамика об-
обсуждаемого уравнения в частных производных на больших временах
определяется системой конечного числа обыкновенных дифференциаль-
дифференциальных уравнений. Это делает понятным успех упрощенных конечномерных
моделей, построенных на основе метода Галеркина, для небольших про-
пространственных областей. Причина успеха — малое отличие этих уравне-
уравнений от соответствующих инерциальных форм.
Существование инерциальных форм указывает на принципиаль-
принципиальную возможность создания нового поколения алгоритмов для численного
исследования нелинейных дифференциальных уравнений. В самом деле,
допустим, что мы умеем эффективно аппроксимировать инерциальную
форму. Если Фурье-размерность невелика, это должно давать хорошее
описание временной динамики решения. Приближенно решая определен-
определенное число алгебраических уравнений, можно получить достаточно точное
описание пространственной структуры решения. Методы, использую-
использующие эту идею, были построены для уравнения Курамото—Сивашинского
щ + и«х + «и + ихххх =0 и ряда других нелинейных уравнений. Как
правило, они не только намного экономичнее простейших разностных
схем, но и лучше передают бифуркации исследуемых аттракторов.
Обратим внимание на то, что в соответствии с полученными оцен-
оценками Фурье-размерность очень быстро растет с ростом длины области.
Фрактальная размерность реальных хаотических аттракторов (в частно-
частности, ляпуновская размерность), как показали расчеты, растет существенно
медленнее. Эти величины даже для небольших областей (I ^ 10) могут
отличаться на несколько порядков. Вероятно, для анализа реальных хао-
хаотических аттракторов могут быть построены более тонкие оценки.
Отметим, что приведенное рассуждение не проходит для много-
многомерного случая. Формально это происходит потому, что спектральный
интервал kN+\ — kff для многомерного оператора Лапласа недостаточно
велик и неравенство конуса проверить не удается. Высказываются гипо-
гипотезы о том, что эти математические трудности связаны не с недостатками
используемого математического аппарата, а со свойствами модели. Была
выдвинута гипотеза, получившая название гипотезы о жесткой турбу-
турбулентности. В соответствии с ней, свойства уравнения Курамото—Цузуки
в двумерном и трехмерном случае могут кардинально отличаться от изу-
6.2. Инерциальные многообразия, оценка размерности аттрактора 147
ценных ранее свойств одномерных решений. В двумерном случае возмож-
возможны хаотические режимы, в ходе которых могут возникать существующие
конечное время и локализованные в пространстве структуры, амплитуда
которых может намного превышать амплитуду основного хаотического
фона. В трехмерном случае наряду с такими режимами, получившими на-
название «жесткой турбулентности», возможны режимы с обострением, когда
решение при определенных начальных данных существует только конеч-
конечное время. К обсуждению этой гипотезы мы вернемся в следующей главе.
Существование инерциальных многообразий в последние годы бы-
было доказано для ряда математических моделей, возникающих в нелиней-
нелинейной оптике, гидродинамике, физике атмосферы. Концепция параметров
порядка, служившая отправной точкой при анализе ряда физических
явлений, сейчас становится источником новых математических идей,
новых вычислительных алгоритмов.
Мы не случайно уделили много внимания применению теории
инерциальных многообразий к конкретному уравнению. Именно этот
подход может стать прообразом того, какими могут быть «понимание»
и численный анализ уравнений, описывающих процессы в нелинейных
средах. В самом деле, говоря о языке нелинейной науки, мы затра-
затрагивали теорему о центральном многообразии, показывающую, почему
и в каких случаях анализ бесконечномерных систем может быть сведен
к исследованию обыкновенных дифференциальных уравнений. При этом
предполагается существование какого-нибудь простого решения, около
которого можно было бы линеаризовать исследуемую модель.
Здесь мы имеем дело с принципиально иным механизмом упроще-
упрощения, когда такого решения не требуется. Более того, можно представить
себе, что появится возможность численно строить инерциальные формы
для уравнений в частных производных или даже делать это, непосред-
непосредственно исходя из экспериментальных данных. В настоящее время в этом
направлении уже сделано несколько удачных шагов.
Важно это и еще по одной причине. Упоминавшиеся сценарии воз-
возникновения динамического хаоса и понимание того, как возникает турбу-
турбулентность в разных ситуациях, пока очень далеки от расчета тех конкрет-
конкретных величин, которые интересуют инженеров, технологов, метеорологов.
Возможно, при разработке обсуждаемой парадигмы эту пропасть удастся
в ряде задач преодолеть. Для этого надо научиться строить инерциальные
формы. Эта задача некорректна, поскольку решение неединственно — из
бесконечномерного пространства можно успешно проектировать на са-
самые разные конечномерные подпространства. Иногда неясно, какой здесь
должна быть разумная регуляризация. Пока здесь используется очевид-
очевидный прием — поиск правых частей в виде полиномов небольшой степени,
включающих малое число членов. Еще более важная задача — научить-
научиться численно восстанавливать необходимое число остальных переменных,
подстраивающихся к параметрам порядка. Возможно, здесь наиболее
подходящим инструментом окажутся нейронные сети, о которых в этой
книге тоже пойдет речь. С этим кругом задач, несомненно, придется
иметь дело при разработке новых подходов в нелинейной динамике.
Жесткая турбулентность
и ее упрощенные модели*
7.1. Кратко об истории
Уравнение Курамото—Цузуки (или Гинзбурга—Ландау), о котором
шла речь в предыдущей главе, имеет очевидное двумерное обобщение
Wt = (l + ic\)AW + A + ico)W - A + ic2) \W\2 W. G.1)
Именно оно в случае двумерного лапласиана и представляет основной
интерес при моделировании ветровых волн на поверхности океана, опи-
описании морфогенеза, анализе колебательных химических реакций, про-
протекающих на поверхности. Для этого уравнения было выполнено много
работ, в которых были найдены те же решения, что и в одномерной зада-
задаче: периодические и двухчастотные режимы, диффузионный хаос. Были
исследованы бифуркации, связанные с симметрией, которая возникает,
если это уравнение решать в квадратной области [10], а также найдены
решения, описывающие спиральные волны в полярных координатах:
W(r,0,t) = S(r)exp(iu)t + ia(r) +гтв), x-rcos9, y = rsin6.
Естественно, возник вопрос, есть ли в многомерном аналоге уравнения
Курамото—Цузуки принципиальные качественные отличия от поведения
решений одномерной задачи.
Надежду на это давали априорные оценки решений и попытки
применить к его анализу теорию инерциальных многообразий. Оценки
показывали аномально большие значения ряда величин, характеризую-
характеризующих решения. Доказательство существования инерциальной формы и,
соответственно, эквивалентности этого уравнения на аттракторе неко-
некоторой конечномерной системы также не удалось получить. Величина
^лг+1 ~ ^лг в двумерном случае оказывается меньше, чем в одномерном,
что не позволяет использовать технику, описанную в предыдущей главе.
В 1990 г. было опубликовано сообщение о том, что при больших с\
и С2 в двумерном и трехмерном уравнениях G.1) наблюдается так называ-
называемая «жесткая турбулентность» (hard или strong turbulence) — хаотический
режим с редкими, но исключительно высокими выбросами [149, 321, 177].
В 1992 г. была опубликована работа [240], где специально исследовались
подобные выбросы, но уравнение было слегка модифицировано:
* Эта глава написана С. В. Ершовым, Г. Г. Малинецким, А. Б. Потаповым.
7.1. Кратко об истории 149
1) предполагалось, что с\ = С2 = v = -;
2) уравнение поделили на v и изменили масштаб времени vt —> t;
3) для случая одной пространственной переменной использовали бо-
более сильную нелинейность (о причинах будет сказано ниже), т.е.
\W\2 -» |W|4.
Таким образом, реально исследовалось уравнение
Wt = (г + e)Wxx +(i-e)\W\AW + eW. G.2)
(Для краткости, следуя англоязычной традиции, будем обозначать это
уравнение QTDGL (от quintic time-dependent Ginzburg—Landau equation).)
Кроме того, в тех же работах приводилось качественное объяснение
причин возникновения жесткой турбулентности в G.2). При е —> 0 оно
превращается в нелинейное уравнение Шредингера (НУШ)
Wt=iWa,+i\W\*W, G.3)
которое детально исследовалось в 70-80-е годы как модель, каче-
качественно объясняющая некоторые закономерности задач физики плаз-
плазмы [351, 310, 260, 259]. Известно, что при достаточно сильной нелиней-
нелинейности, т.е. когда показатель степени в нелинейном члене \W\ превышает
критическое значение д (d — размерность пространства), типичные его
решения развиваются в режиме с обострением. Таким образом, в од-
одномерном пространстве обостряющиеся решения наблюдаются при 4,
в двумерном — при 2 (классическая нелинейность TDGL), в трехмер-
трехмерном — при j. Видимо, именно поэтому жесткую турбулентность сначала
обнаружили в двумерной задаче, а уже потом был найден аналог, допус-
допускающий ее исследование в одномерном случае. Важным отличием НУШ
является наличие трех законов сохранения:
1) «массы» М — J \W\2 dx;
2) «импульса» Р = % f (W*W - WW*) dx;
3) «энергии» Е = j{\Wx\2 - \ \W\6) dx.
Эти величины впоследствии окажутся существенными и для опи-
описания жесткой турбулентности.
Среди результатов, описанных в [240], отметим следующие.
1) Было подтверждено предположение о том, что при малых пиках
профиль W^a;,*) в области растущих больших пиков хорошо описыва-
описывается решением уравнения Шредингера, причем форма пика при этом
сохраняется, т. е. соответствующее решение является автомодельным.
2) Было исследовано статистическое распределение пиков по наи-
наибольшей высоте Л, до которой они дорастали, и оказалось, что в до-
достаточно широком интервале масштабов оно описывается степенной
промежуточной асимптотикой p(h) ~ h~~a, где а = 7 -г- 8. Для малых h
распределение оказывается иным, а наличие в уравнении членов, пропор-
пропорциональных е, по-видимому, ограничивает максимальную высоту пиков
сверху (хотя доказательства этого факта представлено не было).
150 7. Жесткая турбулентность и ее упрощенные модели
Трудно сказать, является ли такое значение а большим или ма-
малым. Это зависит от интерпретации величины W. Если смысл имеют
величины |W| или \W\2, то распределение можно считать эффективно
ограниченным, т.е. очень большие пики не будут существенно влиять
на среднее и дисперсию осмысленных величин (едва ли существенно
отсутствие восьмых или даже четвертых моментов). Но если смысл имеет
величина \W\4, то дисперсия может быть бесконечной, и мы получаем
модель ситуации, типичной для некоторых катастрофических событий:
редкие большие выбросы вносят существенный вклад в среднее и опре-
определяющий — в дисперсию [81].
Неясно, насколько типичной моделью подобных событий являет-
является G.2). Но поскольку подобных моделей единицы, каждая из них может
заслуживать исследования, хотя бы в некоторых аспектах. В частности,
для G.2) представляется интересным ответить на следующие вопросы:
— Каким образом начинается рост пика и каким образом он прекра-
прекращается?
— Каково происхождение степенного распределения наибольшей вы-
высоты пиков?
— Можно ли воспроизвести основные элементы жесткой турбулент-
турбулентности на более простых моделях?
7.2. Как выглядят пики жесткой турбулентности в QTDGL
Прежде всего, обсудим, как выглядит явление жесткой турбулент-
турбулентности (ЖТ) в численных экспериментах. Значения е выбирались в интер-
интервале 0,014-0,0001. Задача решалась в области длины L с периодическими
граничными условиями.
В коротких областях при L < 5 никакого сложного временного
поведения не наблюдалось. В областях «среднего размера» (L = 10 -=- 80)
наблюдалась «однопиковая» ЖТ, т. е. в каждый момент времени суще-
существовало не более одного пика. Типичное поведение решения показано
на рис. 7.1, где приведены мгновенные профили для нескольких харак-
характерных стадий.
1. Первоначально существует пространственно однородная «турбу-
«турбулентность», т.е. нерегулярные медленные пространственно-вре-
пространственно-временные колебания, когда профиль гладкий, a \W\ < 1.
2. Затем внезапно начинает расти пик. Рост его оказывается столь
быстрым, что окружающий фон выглядит «замороженным». Эф-
Эффективная ширина пика сокращается, хотя в некоторых перенор-
перенормированных переменных его форма остается почти постоянной.
3. После достижения максимальной амплитуды (тем большей, чем
меньше е), начинается распад пика. Его высота быстро убывает,
а эффективная ширина растет. Этот процесс оказывается даже
более быстрым, чем рост пика (см. рис. 7.2). Но теперь форма
пика меняется даже в перенормированных переменных, и когда
высота доходит до значений порядка 2-3, «колокольчик» пика
7.2. Как выглядят пики жесткой турбулентности в QTDGL
151
4
О
2
1
О
-1
О
10 15 20 х
10 15 20 х
10 15 20 х
-0,6
10 15 20 х
О 5 10 15 20 х 0 5
г з
Рис. 7.1. Пример развития и распада гигантского пика жесткой турбулентности
превращается в быстро осциллирующий «изрезанный» волновой
пакет с огибающей в виде колокола.
4. Затем остатки пика — «пятно» длины порядка 1 и амплитуды
\W\ < 1, заполненное «пространственными колебаниями», начи-
начинает расползаться по всей области. При этом высшие гармоники
затухают из-за действия диссипативного члена —eWxx, в то время
как собственно диффузия происходит независимо от е и наблюда-
наблюдается даже в невозмущенном уравнении G.3).
5. Наконец, вся область оказывается заполнена такими простран-
пространственными колебаниями, и характерное время сглаживания про-
профиля составляет j. И только после сглаживания может вырасти
новый пик.
В областях большой длины могут вырастать одновременно несколь-
несколько пиков, но в дальнейшем мы ограничимся лишь случаем одного пика.
152
7. Жесткая турбулентность и ее упрощенные модели
500
700 900
1100
<-2оооо
1300 1500 1700 1900
545,1 545,15 545,20 545,25
J-20000
Рис. 7.2. Временная эволюция высоты пика
545,30
7.3. Нелинейное уравнение Шредингера
и его автомодельные решения
Мы уже говорили, что динамика пиков в уравнении G.2) тесно
связана с автомодельными решениями G.3). Чтобы показать это, удобно
записать G.2) в переменных амплитуда-фаза, W(x,t) = p(x,t)e%ip^x^:
pt = ~2(рхрх - pipxx + е(-р(<рхJ + рхх -р5 +р),
Pft = Рхх ~ Р5 ~ р(<рхJ + еB<РхРх + Р<Рхх)-
Полагая е = 0, получим соответствующее представление для G.3).
Для анализа пика с центром в точке жо удобнее перейти к автомо-
дельным переменным p(x,t) - -Щ, (p(x,t) = Ф(?,<), ? = ^, где
L(t) — ширина пика, а также к медленному времени т, dr — -jjr\-
7.3. Нелинейное уравнение Шредингера и его автомодельные решения 153
Получим
Rr = (?LL - 1Щ)Щ +{jy~ Ф«)л + е(-ЩФ(J + % - R5 + L2R),
RФT = % + R5 + RQ^LL - Ф() + г(Д«% + 2R(Ф()
(здесь L — ^). При е = 0 эта система допускает точное автомодель-
автомодельное решение, для которого R(?,t) = Rq(?), где До(?) удовлетворяет
следующему уравнению
а для фазы получаем соотношение
Для 6, с, а и L нетрудно получить следующие уравнения
2 2
6Т = с + а, Сг = -ас + 7, ат = —о — 4/3, LT = —aL,
где а, р и 7 ~ константы. Из последнего уравнения следует, что
^L2 = -2а, а так как высота пика и L~42, то именно параметр а
управляет ростом пика.
Из двух последних уравнений следует, что
откуда
Таким образом, получаем, что в уравнении G.3) возможны два закона
роста пика при приближении момента обострения if. а) при /3 < О
|W(seo,t)| ~ (tf -t)/4; б) при /3 = 0, |W(aso,*)| ~ (tf - t)~]>2. В случае
-у = /3 = 0 уравнение для Щ(?) можно решить аналитически:
обычно решение нормируют так, чтобы Ло@) = 1, что соответствует
Как указывалось в [240], решения с /3 = 0 неустойчивы и в числен-
численном счете не реализуются, решения же, отвечающие /3 < 0, устойчивы
и в численном счете действительно был получен похожий закон роста.
Заметим, что нелинейное уравнение Шредингера G.3) допускает обра-
обращение времени t —» -t, W —> W, и наряду с растущими пиками долж-
должны существовать и затухающие. При обращении времени неустойчивые
154 7. Жесткая турбулентность и ее упрощенные модели
решения могут стать устойчивыми, поэтому можно ожидать, что решения
для /9 = 0 будут описывать стадию распада пика. Численный счет показы-
показывает, что данное решение действительно является хорошей асимптотикой
для стадии начала распада пика (рис. 7.2).
7.4. Автомодельная обработка
и приближение «замороженной формы»:
упрощенная модель ограничения пика по высоте
Автомодельные решения, однако, неспособны объяснить, почему
прекращается рост пика. Общие слова о том, что «рост прекращает дис-
диссипация», неудовлетворительны. Как уже говорилось, решение остается
почти автомодельным и в начале фазы распада, а следовательно, дисси-
диссипация, которая должна была бы ограничивать «остроту» пика и делать
решение неавтомодельным, существенной роли не играет. Поэтому ну-
нужен какой-либо иной механизм, зависящий от диссипативных членов.
Качественно описать нужный эффект помогла приближенная модель,
которую можно назвать «приближение замороженной формы пика».
Для численно построенных профилей W(x,t) можно произвести
автомодельную обработку. Пусть максимум ^(ж,*)! расположен в неко-
некоторой точке xq. Введем L(t) — . ' , f = ^jjQ и рассмотрим профиль
Щ?,1) — \w(xt)\ • Оказалось> чт0 во время роста и начала распада пика
профили R(?, t) вблизи его центра и вплоть до f я 3 -е- 5 практически
не меняют своей формы и близки к автомодельному виду. В то же время
аналог величины a, <pg{O,t), где <р(?, t) — фаза W(x,t), в момент на-
начала распада пика резко изменяет знак. Поэтому можно предположить,
что эволюция пика связана не с изменением формы, а с изменениями
амплитуды, полуширины и фазы. Попытаемся построить приближенную
модель, основанную на следующих предположениях.
Будем считать, что форма профиля остается практически постоян-
постоянной в перенормированных координатах, т.е. |W(x,t)| = g(t)Ro(?) (для
строго автомодельных профилей g(t) = Д—, но мы оставим профилю
возможность отклоняться от автомодельного решения по высоте при со-
сохранении формы), а фаза имеет тот же вид, что и для автомодельного
случая: у>(?, i) = b(t) + c(t)? - 2i^i-. Анализ реальных профилей для вы-
высоких пиков показал, что эти предположения вполне оправданы. Более
того, чтобы упростить выкладки, положим c(t) = 0; это означает, что
максимум пика не движется.
Подставим теперь в уравнения W(x,t) = G(<)До(?)е*"^'(). Тогда мы
получим
gR - gLL'^R' = -gL'2B<p'R' + <p"R) +
+ egL~2(RL2 + R" - V'2R - gAL2R5),
7.4. Автомодельная обработка 155
- Г»" п2Т'2
-L R --aL
или
' + Д) + e(RL2 + R" -
R + a4tLR = R" -
2 4
По очереди умножим эти уравнения сначала на R, затем на -2?R'
и проинтегрируем по ? от -оо до оо. Для удобства введем обозначения
In = jRndt, S2 = Н2&<%' J = S(R'f «, G = f?2(R'J d?. Будем
полагать, что при |^| —> оо Д убывает по крайней мере экспоненциаль-
экспоненциально, поэтому подстановки вида ^-R"!^ обращаются в 0. Кроме того,
профиль мы считаем с хорошей точностью симметричным, а потому ин-
интегралы с нечетным подынтегральным выражением будем отбрасывать.
Интегрированием по частям несложно получить, что
- 2 J R"(R' df = J, -if R5(R' d{ = ^/6.
Удобно также сделать замену времени t —> т, т.е. L2f = fT. Тогда
из первого уравнения получим
- J - ~S2
- g*L2lA,
(l2L2 + J- 3a2S2 - \g*L2I(, J .
| I2) + e (l2L2 + J- 3a2S2 - \
а из второго
hbr - jS2 + ^L~lLrS2 = -J- jS2 +g*L2I6,
3aT 3a i 3a2 1
S + L~XLS J S +
о,
(
3aT 3a i 3a 1 л э о,
hbT - ~S2 + - L~XLTS2 = J- —S2 + -g*L2h + e-(AG - I2).
Заметим, что g входит в правые части полученных уравнений только
в комбинации ц—д^-Ь.Ъ случае автомодельного решения эта комбинация
представляет собой сохраняющуюся величину и пропорциональна «массе»
пика. Теперь она может изменяться и можно получить уравнение для ее
изменения, используя уравнения для д к L.
156 7. Жесткая турбулентность и ее упрощенные модели
После несложных преобразований получается следующая система
для основных параметров
J
LT = -aL + O{e).
Оказалось, что члены, обозначенные как О(е), для качественного анализа
несущественны и их можно не учитывать. Таким образом, получается сле-
следующая качественная картина эволюции пика. В результате процессов,
не описываемых данным приближением, формируются начальные усло-
условия, когда а > О, а масса пика ц > цц. Тогда для а получаем фактически
автомодельное уравнение, в котором
,3 = ^(/4) V) < О,
352
но медленно нарастает со временем; согласно второму уравнению, масса
медленно убывает. Начинается рост пика практически по автомодельному
закону, L быстро уменьшается, а а медленно убывает до тех пор пока fi
не перейдет через критическое значение цо. После этого а меняет знак
и начинает быстро убывать. Столь же быстро начинает расплываться и сам
пик, и вскоре начинает меняться его форма, после чего приведенный
анализ становится неприменим — пик «размораживается».
Заметим, что можно несколько усложнить исследование, добавив
в соотношение для фазы линейный член (который считался нулевым),
и разрешить вершине пика перемещаться. Для этого необходимо полу-
получить дополнительную пару приближенных уравнений, умножая исходные
уравнения на -2?Й и интегрируя их как обычно. Однако никаких прин-
принципиально новых качественных выводов это не дает, за исключением
того, что при малых а2 коэффициент при линейном члене должен убы-
убывать, а пик, следовательно, симметризоваться.
Результаты данного раздела позволяют сделать ряд выводов и пред-
предположений.
1. Уравнение G.2) обладает очень интересным механизмом остановки
роста пика. Члены порядка е обеспечивают не столько диссипацию
энергии пика, сколько нечто вроде «обращения времени», развора-
разворачивающего рост пика вспять. Образно говоря, система оказывается
снабжена не «тормозами», а «рулем». Непонятно, насколько общим
мог бы быть подобный механизм управления крупномасштабными
событиями и в какие системы он мог бы быть «встроен». В этой
связи интересно также вспомнить, что в 70-е годы директор ИФА
АН СССР академик А. М. Обухов говорил про управление погодой,
что человечество едва ли может остановить или ликвидировать,
скажем, циклон. Но можно пытаться малыми воздействиями пере-
перевести его на другую, безвредную для нас траекторию.
7.5. Макроскопическое описание 157
2. На этапе развития пика, когда фон можно считать замороженным,
а рост пика описать довольно простой моделью, в системе на ко-
короткое время появляется небольшое число «параметров порядка»:
о, L и ft. Два из них — характеристики пика, а третий может
быть определен и для иных образований, в том числе и для всей
области. Поскольку в нелинейном уравнении Шредингера пол-
полная масса сохраняется, в G.2) ей отвечает медленно меняющаяся
величина. Возникает вопрос, нельзя ли хотя бы в каких-нибудь
аспектах характеризовать всю систему, а не только отдельный пик,
при помощи нескольких параметров порядка.
3. Основными кандидатами на эту роль будут масса, энергия и им-
импульс — то, что сохраняется в G.3).
Для энергии пика тоже можно попытаться выписать приближенное
соотношение, но оно оказывается не слишком информативно. Можно
только утверждать, что когда полуширина сокращается настолько, что
L « у*?, начинается быстрый рост энергии. На основании численных ре-
результатов и некоторых приближенных рассуждений можно получить, что
максимальная энергия пика будет составлять примерно max E ~ econst/e.
При малых L изменение оказывается очень большим, поэтому в течение
некоторого небольшого интервала времени в районе достижения пиком
максимума энергия не будет меняться медленно.
7.5. Макроскопическое описание жесткой турбулентности
Итак, рассмотрим, как будут вести себя масса, энергия и импульс
для уравнения G.2). Из уравнения можно получить закон их изменения:
G.4)
lPpx - (p<pxf - p6 - (^J) v, dx.
Интересно, что импульс почти не играет роли в исследуемых процессах.
Во всех расчетах, где его начальное значение было близко к нулю, оно
таковым и оставалось с некоторыми незначительными флуктуациями.
Напротив, энергия и импульс оказались весьма информативны. Харак-
Характерный пример их эволюции приведен на рис. 7.3. Отметим следующее.
1. Возникновение пика откликается мощным и очень быстрым вспле-
всплеском энергии.
2. На этапах распада пика, когда профиль становится весьма изрезан-
изрезанным, энергия монотонно уменьшается. Фактически, она позволяет
характеризовать изрезанность, поскольку включает Wx.
158
7. Жесткая турбулентность и ее упрощенные модели
3. После того как пик исчезает и начинается переходный процесс,
энергия равномерно убывает. Пока она не достигнет значений ~ 1,
новые пики не возникают (для области длиной 20). Чаще всего
пики возникали при Е = 0,8 -=- 1,3.
4. Масса меняется гораздо слабее. После возникновения пика она
начинает убывать до тех пор пока Е > М, затем она начинает
опять нарастать.
300 500 700 900 1100 1 300 1500 1700 1900
?-20000
545,2 545,22 545,24 545,26 545,28 545,30
?-20000
Рис. 7.3.
В случаях, когда в системе существует хорошее разделение вре-
временных масштабов, т. е. любой процесс можно отнести либо к быстрым,
либо к медленным, эффективным способом исследования модели явля-
является усреднение по быстрым переменным. При этом можно было бы
использовать тот факт, что статистические характеристики малых фоно-
фоновых флуктуации должны быть практически теми же, что и у нелинейного
уравнения Шредингера. А для эволюции медленных переменных должна
получиться система вида
АЕ
= 2eE-2eFE(E,M,P),
dt
dM
~dT
= 2e(M-E)--eFM(E,M,P),
7.6. О возможном статистическом описании турбулентности 159
На ранних стадиях распада пика, когда \W\ < 1, а пространствен-
пространственные градиенты велики, \WX\ ¦< \W\, многие члены в G.4) становятся
несущественны, поэтому
— и 2еЕ - 2е( [ \wxx\2 dx
dt \J
dt
Входящее в эту систему среднее удалось получить численно, и результи-
результирующее уравнение для данной стадии оказалось на удивление простым:
dE 1
— я-ес(М,Е)Е2,
dt
где с (М, Е) — практически константа.
Заметим, что на самой ранней стадии распада пика значение энер-
энергии может быть очень велико (~ econstl?), а потому изменение энергии
не является медленным. Поэтому разделения временных масштабов нет
и техника усреднения вполне могла бы не работать. Но особенностью
данной задачи является то, что техника оказывается применима. Одна
из причин этого в том, что для нелинейного уравнения Шредингера
интеграл J \WXX\ dx почти совсем не флуктуирует. Поэтому простран-
пространственное усреднение как бы частично заменяет временное.
Однако на турбулентном фоне, когда распад предыдущего пика
закончился, а следующий еще не возник, мгновенные значения массы
и энергии медленно и не слишком регулярно дрейфуют в небольшой
области, где энергия мала, а масса сравнительно велика. Это поведение
больше всего напоминает траектории вблизи устойчивой неподвижной
точки с шумом. Рост нового пика оказывается внезапным и может
начаться в любой части указанной области.
Поэтому детерминированное маломодовое описание в терминах
энергии и массы хорошо описывает релаксационные процессы перехода
пик—фон, но практически совсем не описывает процессы, происходящие
на фоне, а потому не может предсказать момент начала нового пика и его
характеристики. В связи с этим была предпринята попытка дополнить
динамическое описание статистическим.
7.6. О возможном статистическом описании
жесткой турбулентности
Минимальные требования к статистической модели сводятся к то-
тому, что она должна предсказывать распределение межпиковых интервалов
и распределение пиков по высоте (или, что почти то же самое, по энер-
энергии) . Для этого надо определить вероятность i(M, E, Р) того, что при дан-
данных значениях массы, энергии и импульса начнется рост пика, а также
160
7. Жесткая турбулентность и ее упрощенные модели
вероятность того, что он дорастет до заданных значений энергии. Вообще
говоря, существует возможность развить подобный подход детально и вы-
выписать соответствующее кинетическое уравнение. Но оно оказывается
столь сложным, что его невозможно решить ни аналитически, ни числен-
численно. Поэтому мы даже не будем его здесь приводить. Отметим, что един-
единственным простым и красивым результатом этого подхода является опре-
определение формы границы области
на плоскости М,Е, внутри ко-
которой возможно возникновение
пиков, т.е. у(М,Е,Р) > 0 (см.
рис. 7.4). В термодинамическом
пределе, когда систему можно ха-
характеризовать плотностями энер-
энергии, массы, импульса, практичес-
практически не зависящими от длины обда-
обдари _ . сти, для этого оказывается доста-
достаточно соображений симметрии.
Известно, что нелинейное уравнение Шредингера инвариантно
относительно преобразования
7 = 0
Предсказываемая
граница
которому соответствует преобразование плотностей средних величин
(т.— -р- и т. д., где D — длина области)
т =
т
А'
= "Г*> Р ~
A2'
Поскольку t' —
' — р-
пространственная плотность вероятности возник-
возникр
новения пика на интервале [t, t + dt] (т. е. число событий в единицу
времени на единицу длины) меняется как 7' = $• С другой сторо-
стороны, i(M,E,P) — это та же функция, но от других аргументов, по-
поэтому 7(т>р!лт) = д?'р'. Если пренебречь импульсом, то получим,
что 7(>™,е,0) = m37(l,^r,0). Зафиксировав длину области и перехо-
переходя от плотностей снова к массе, энергии и импульсу, получим, что
7(Af, J5,0) = M37(jfr), и, следовательно, уравнение границы должно
иметь вид Е = const • М3.
Таким образом, уравнение G.2) оказалось слишком сложной моде-
моделью, не допускающей сколько-нибудь полного исследования статистиче-
статистических свойств жесткой турбулентности. Поэтому встал вопрос о создании
более простой модели, допускающей детальное исследование.
Хорошим объектом могли бы стать системы, демонстрирующие так
называемую on-off перемежаемость [210, 211, 212, 228, 294, 343, 348].
Но необходимо учесть и качественные особенности G.2), что не слишком
просто. О разработке подобной модели речь пойдет в следующем разделе.
7.7. Жесткая турбулентность и переключающая перемежаемость 161
7.7. Жесткая турбулентность
и переключающая перемежаемость
Сам термин «on-ofF intermittency» — переключающая перемежае-
перемежаемость — появился в 1993 г. [294]. Как утверждали авторы этой работы, ими
был описан новый тип перемежаемости, связанный с возникновением
гигантских выбросов. Классическая перемежаемость Помо и Манневи-
ля [270] была связана с близостью системы к точке тангенциальной бифур-
бифуркации. В результате этой бифуркации теряет устойчивость неподвижная
точка соответствующего отображения. Когда траектория проходила вбли-
вблизи этой точки, являющейся слабо неустойчивой, в течение некоторого
времени в системе наблюдалась «ламинарная фаза», сменявшаяся затем
интервалом хаотического поведения. В соответствии с тремя типичными
бифуркациями различали и три типа перемежаемости: I (седло-узел),
II (Хопфа) и III (удвоения периода).
В работе [284] был предложен более общий тип бифуркации,
«blow-out», когда при А < 0 в системе существует устойчивое инвариант-
инвариантное многообразие, на котором система ведет себя хаотически, а при А > 0
оно становится неустойчивым и начинает резко выбрасывать траекто-
траектории в перпендикулярном направлении (скорость отбрасывания зависит
от фантазии авторов). Если такую систему дополнить механизмом возвра-
возвращения выброшенной траектории обратно к многообразию, то будет реали-
реализован хаотический режим, перемежающийся редкими выбросами. Кстати,
авторы [343] специально отмечали, что их работа была навеяна аналогия-
аналогиями с солнечными циклами, рыночными ценами акций и развитием био-
биологических видов, а также тем, что для таких режимов скорее всего будет
неприменима теорема Такенса (о ней речь будет идти в главе, посвящен-
посвященной реконструкциям аттракторов), поскольку траектория много времени
проводит на инвариантном многообразии, а поэтому она не способна
характеризовать направления, в которых ее выбрасывает неустойчивость.
Таким образом, переключающую перемежаемость можно рассма-
рассматривать как обобщение классической перемежаемости. Однако это ско-
скорее руководство к действию, способ построения моделей, чем конкретная
схема. Поэтому едва ли имеет смысл говорить относительно общих и фун-
фундаментальных свойств такой перемежаемости (статистика, спектр и т. п.).
Меняя тип и размерность инвариантного многообразия, динамику на нем
и механизмы ухода и возвращения, скорее всего, можно получать очень
сильно отличающиеся характеристики. Поэтому в этой главе сделана по-
попытка воспроизвести некоторые характерные черты жесткой турбулент-
турбулентности в QTDGL при помощи принципов реализации переключающей
перемежаемости на простых моделях, предложенных в работах [294, 343].
Заметим, что само QTDGL можно отнести к классу подобных моделей, хо-
хотя и не простых. Однако для него инвариантное многообразие неизвестно,
а его ортогональное дополнение имеет слишком большую размерность.
Основными чертами мы будем считать следующие: наличие инва-
инвариантного многообразия или множества, способного терять устойчивость;
наличие медленно меняющейся величины, характеризующей текущее со-
6 i.iK 2
162 7. Жесткая турбулентность и ее упрощенные модели
стояние системы; и взаимодействие между быстрыми и медленными
переменными, регулирующее поведение системы.
Описанное выше грубое качественное понимание столь непростого
и богатого феномена, как жесткая турбулентность, никоим образом
не является достаточным. Однако его вполне хватит для построения
упрощенной модели.
Коль скоро мы знаем так мало, нет особого смысла оснащать
ее тонкими деталями; напротив, она должна быть максимально грубой,
чтобы передавать лишь наиболее общие свойства жесткой турбулентности.
Будем пытаться воспроизвести поведение в уравнении QTDGL на другой
«элементной базе», используя отображения:
Во-первых, пусть будет лишь одна медленная переменная; она
заменит один из параметров в отображении для быстрых переменных.
Назовем ее для преемственности «энергией» Е, так как, по-видимому,
именно энергия играет наибольшую роль среди интегралов движения
в QTDGL.
Во-вторых, пусть регулярная (межпиковая) фаза соответствует дви-
движению быстрых переменных по хаотическому аттрактору, свойства кото-
которого медленно меняются с изменением той медленной переменной. Когда
же она переходит через некоторое критическое значение, пусть происходит
кризис этого аттрактора, так что в нем появляется «дырка», через которую
траектория покидает его и начинается «рост пика».
Однако когда-то этот рост должен смениться распадом, при ко-
котором траектория быстрой системы возвращается в ограниченный ат-
аттрактор. Иными словами, этот аттрактор вновь становится глобально
притягивающим (даже для бесконечно удаленных точек).
Подобная перестройка может быть достигнута либо за счет энергии
(«параметрически»), либо за счет быстрых переменных («динамически»).
Первый способ проще; однако он мало соответствует происходящему
в QTDGL.
В-третьих, исходя из сказанного, мы потребуем, чтобы рост пика
прерывался при достижении какими-то из быстрых переменных порого-
пороговых значений.
Конечно, после этого они не могут устремиться к аттрактору все
сразу, поскольку как только они чуть отступят за этот порог, тут же притя-
притяжение вновь смениться отталкиванием, и т.д.; и подобные колебания за-
закончатся падением на неподвижную точку рядом с пороговым значением.
Поэтому, в то время как одна группа быстрых переменных начала
возвращение на аттрактор, другая группа должна продолжать удаляться
от него. Так должно продолжаться до тех пор пока все переменные
первой группы не попадут на аттрактор; и лишь после этого начнется
возвращение по оставшимся переменным.
Поэтому быстрая система должна содержать как минимум две пере-
переменных, и притом не слишком сильно связанных.
В-четвертых, пусть быстрое отображение при фиксированной энер-
энергии будет кусочно-линейным. Это снимет массу проблем с бифуркациями
и тонкостями поведения при различных значениях параметров.
7.7. Жесткая турбулентность и переключающая перемежаемость 163
Сформулируем (пока словесно) вид динамической системы.
Есть два связанных одномерных отображения с переменными х
и у и параметром Е. При малом Е имеется регулярный аттрактор,
который траектория никогда не покидает. Когда же энергия превышает
пороговое значение Есг, происходит кризис аттрактора, и начинается уход
траектории (х, у) на бесконечность. Когда у переходит через (достаточно
большое) пороговое значение, динамика х обращается, и эта переменная
устремляется назад в аттрактор. Когда она попадает туда (и пока там
остается), переменная у также устремляется в аттрактор.
Теперь пусть Е уже не постоянный параметр, но медленная пе-
переменная. Пусть в течение регулярной фазы она медленно убывает, так
что если бы не обострение, она сошлась бы к неподвижной точке Е„,
лежащей ниже критического значения: Е, < Есг. В действительности она
до нее не дойдет, так как случится кризис аттрактора, траектория покинет
его и закон изменения медленной переменной (усредненное уравнение)
изменится. Значения быстрых переменных станут расти, а вместе с ними
начнет расти и энергия. Как только она превысит критическое значе-
значение Ес[, «дырка» в аттракторе закроется, т.е. он вновь станет глобально
притягивающим.
Быстрые же переменные будут продолжать расти независимо от ве-
величины энергии. Когда переменная у переходит через пороговое зна-
значение, динамика х обращается, и эта переменная устремляется на-
назад в аттрактор. Энергия начинает убывать, но медленнее, чем росла.
Наконец х возвращается в аттрактор, после чего у также устремляется
туда. Из-за медленности убывания энергии, в этот момент она все еще
много больше критической. Так что х остается в аттракторе надолго, и у
успевает вернуться туда. Итак, теперь обе быстрые переменные загнаны
в аттрактор, где и меняются хаотическим образом. Энергия медленно
убывает, до тех пор пока не достигнет своего критического значения. Тут
возникнет новый пик, и т.д.
Теперь небольшая деталь. Пусть у нас есть параметр, который
и определяет скорость эволюции энергии, т.е. отношение быстрого
и медленного масштаба времени. Оказывается, что при е —» 0 обострение
начинается при значении энергии, практически совпадающим с крити-
критическим: Е —> ЕС[ - 0. А это значит, что «дырка» в аттракторе очень мала.
Она находится там, где коснулись границы аттрактора и его области при-
притяжения, т. е. две линии, и потому в общем случае является окрестностью
точки. Иными словами, пики начинаются при практически одинаковом
значении не только энергии, но и быстрых переменных. Следовательно,
они и завершатся практически одинаковыми — без того их разброса,
который характерен для жесткой турбулентности в уравнении QTDGL.
Преодолеть это несоответствие довольно просто. Именно, пусть
при переходе энергии через критическое значение вначале открывается
дырка только для х, а у остается в аттракторе до тех пор, пока х не станет
достаточно большим. И пусть лишь тогда переменная у сможет покинуть
аттрактор.
6*
164
7. Жесткая турбулентность и ее упрощенные модели
к<
В результате обострение будет
начинаться с разных (в пределах раз-
размера дырки, который, как мы уви-
увидим ниже, есть ~ е1//3) значений х
и у. Пока х не достигнет того значе-
значения X, при котором откроется дыр-
дырка для у, эта переменная движется
по хаотическому аттрактору, и перво-
первоначальный разброс значений растет:
Ау„ ~ е'/3е"*». Одновременно (ото-
(отображение по а; вне аттрактора линей-
линейно (см. рис. 7.5)) хп ~ (if)". Так что
к моменту, когда х = X, разброс значений у составит
Рис. 7.5. Отображение /(х,к,а)
и если потребовать, чтобы
то разброс значений у будет порядка единицы. Тут откроется дырка для у-
траектории, и если она мала, то пройдет достаточно много времени, пока
траектория туда попадет. Поскольку стартовые условия очень разные:
Ау ~ 1, то и время достижения дырки Т\ (считая за 0 момент, когда
х = X) также будет сильно различаться. Наконец, начнется рост у —
с практически одинаковых начальных условий (в окрестности дырки).
Поэтому интервал времени Тг от выхода ^-траектории из аттрактора
до достижения порогового значения (когда х начнет убывать), будет
практически постоянным.
Таким образом, после перехода через критическое значение х будет
расти в течение времени Т\ + Ti, и потому максимальное значение будет
Ятах = -У х {Kt) ' 2- Благодаря разбросу Ti максимальное значение
жтах будет меняться от пика к пику случайным образом.
Итак, мы пришли к трехмерному отображению:
Уп
«i > 1, У > Усг,
«i < 1, У < Усг,
Уп+1
1+е
\-\У«\' *~
> -1,
G.5)
En+i =Еп~ е(Еп + х„),
Е
а(Е) = аа
с быстрыми переменными х и у и медленной «энергией» Е. Вид функ-
функции / показан на рис. 7.5. Связь быстрых переменных с медленной
осуществляется через член, содержащий хп в третьем уравнении.
7.7. Жесткая турбулентность и переключающая перемежаемость
165
Параметр е — произвольное малое число; 70 = 0,5, uq — 0,5,
7 = 0,122. Критическое значение осг зависит от ао и у; при указан-
указанных выше величинах асг = -0,2668.... Соответствующее значение Есг
произвольно; мы положили Ес[ = 0,3. Значение а^, соответствующее
большой энергии, также произвольно и только должно быть меньше асг;
мы положим о,» = -0,8.
Наклон внешних ветвей есть к? — 4, «г = 0,1, к? — 2, к~ = 0,1,
а критические значения, при которых происходит переключение наклона
*сг = -3,й:г = - Ю000.
На рис. 7.6 показаны временные ряды в окрестности пика для спе-
специально выбранных параметров е — 0,02, 70 = 0,5, усг = -100, при кото-
которых пики достаточно низкие и широкие, чтобы их можно было показать
на рисунке:
100 150 200
Рис. 7.6. Эволюция переменных системы в окрестности пика. Тонкая сплошная
линия — log |х|, жирная сплошная линия — log|t/|, пунктир — log |??|. Чтобы
обеспечить приемлемые масштабы, расчет произведен при нетипичных значениях
параметров: ?=0,02, 7о = 0,5, усг = -100 (при параметрах, использованных
в расчетах статистических характеристик, пик был бы слишком узкий и высокий)
Рассмотрим теперь качественное описание динамики пика.
Межпиковая фаза. После распада очередного пика траектория бы-
быстрой системы возвращается на аттрактор и спустя несколько итераций
на нем устанавливается инвариантное распределение. Энергия медленно
убывает.
Выброс по х. Когда энергия падает ниже критического значе-
значения .Есг, те- оказывается, что а > асг, в аттракторе двумерного отобра-
отображения (первые два отображения G.5)) происходит кризис и открывается
«дырка», через которую а;-траектория начинает уходить на бесконеч-
бесконечность по закону х„ ~ (at) ¦ Пока |ж| много меньше, чем |, динами-
динамика у -траектории приближенно описывается уравнением
Уп+\ = f(yn,Ky,a0).
166 7. Жесткая турбулентность и ее упрощенные модели
Хотя это отображение и имеет отталкивающую ветвь, попасть на нее из ат-
аттрактора невозможно, поэтому движение у остается пока ограниченным
и хаотическим.
Выброс по у. На самом деле, динамика у -траектории описывается
отображением
\ех I
? „, г» = 7о , "
Поскольку отображение
+ \ ТО
Уп + \ = 1(Уп,Ку ,Оо) + —
уже не имеет аттрактора (траектории покидают его и уходят на бесконеч-
бесконечность), то когда \х\ достигает величины -, в аттракторе появляется дырка,
и траектория может покинуть его. Кризис аттрактора происходит при
г-г - 1/2
1 _ 1 сг _ -—•
Заметим однако, что дырка эта не слишком большая, так что выход из ат-
аттрактора может произойти далеко не сразу. В течение этого времени \х\
продолжает расти, так что добавочный член Г„ меняется. Следователь-
Следовательно, разные траектории покидают аттрактор при разных значениях Г,
и получается «растянутый» кризис.
Прекращение роста по х. Когда у превышает (по модулю) ве-
величину усг, внешняя ветвь для ж-отображения становится сжимающей
и рост х сменяется еще более быстрым убыванием: хп ~ («j)"- До тех пор
пока переменная х не уменьшится настолько, что пересечет критическое
значение хс[, координата у продолжает расти, уп ~ (*?)"¦
Распад пика. Когда х уменьшится настолько, что пересечет крити-
критическое значение ха, внешняя ветвь для у -отображения становится сжи-
сжимающей и рост у сменяется еще более быстрым убыванием: уп ~ (к^) .
Пока \у\ не станет меньше \усг\, внешняя ветвь для а;-отображения оста-
остается сжимающей, так что траектория, уже лежавшая правее жсг, попадает
в область притяжения аттрактора, из которой она уже не может выскочить
на внешнюю ветвь отображения.
Поэтому даже после того, как \у\ окажется меньше \усг\ и внешняя
ветвь для ж-отображения станет растягивающей, это уже не может вы-
выбросить ж-траекторию, так как к этому времени она находится в области
притяжения ограниченного аттрактора.
Координата у продолжает убывать, и в конце концов попадает
на аттрактор. Внешняя ветвь соответствующего отображения так и оста-
остается сжимающей.
Начинается новая межпиковая фаза, и т.д.
Система оказывается замечательна тем, что при малом е в ней
можно аналитически рассчитать:
7.7. Жесткая турбулентность и переключающая перемежаемость 167
— параметры «дырки», из которой убегает траектория;
— плотность вероятности для х и у к моменту образования дырки;
— вероятность выхода траектории через дырку, т. е. начала роста пика;
— распределение значений параметра а на момент роста пика;
— распределение х и у после выхода из аттрактора.
Это дает возможность получить распределения максимальных ве-
величин и в пике (рис. 7.7 и 7.8). Видно, что на рисунках теоретическая
прямая практически не отличается от результатов вычислительного экс-
эксперимента.
-6
а,
-7
О 200 400 600
Рис. 7.7. Логарифм гистограммы распре-
распределения lg|xmax|. Левее левого конца
кривой распределение обращается в нуль
и потому не построено. Расчет прове-
проведен при ? = 10 , 7о = 0,27. Тонкая
прямая имеет наклон 3,34-10~3, в то
время как аналитическое соотношение
при использованных параметрах дает
Pig|*maxl (С) = const * е'00346^, так что пред-
предсказанный наклон составляет 3,46-10
а.
-4
С
-6
«г
0
100 200
ig(-y)
Рис. 7.8. Логарифм гистограммы распре-
распределения lg |t/max |. Левее левого конца кри-
кривой распределение обращается в нуль
и потому не построено. Расчет прове-
проведен при ? = 10" , 7о = 0,27. Тонкая
прямая имеет наклон 1,109-10, в то
время как теоретическое приближение
при использованных параметрах дает
PblvmuKO = const * e~Ofiuii, так что пред-
предсказанный наклон составляет 1,15-10~2
Распределение для |жтах|
= (ТО - Гсг)
G.6)
168 7. Жесткая турбулентность и ее упрощенные модели
Распределение для максимумов у:
Pv^max) = const* l^
{О, \уп
1, Itt,
где значение нормировочного множителя:
const = -?* С, (то - Гсг) С2 Ш
lg< V е6а;сг G0 - ГсгJ
Максимальное значение энергии пика также можно оценить через
максимум х, откуда получается, что распределение пиков как по мак-
максимальной, так и по конечной энергии, когда х вернется на аттрактор,
ведет себя как ~ Етах |Gо~ "'.
Ниже построена экспериментальная гистограмма распределения
log E в момент завершения пика. Для сравнения проведена прямая линия,
показывающая наклон графика в логарифмических координатах (рис. 7.9).
Рис.7.9. Логарифм гистограммы распре-
распределения lj>E в момент окончания пика.
Левее левого конца кривой распределение
обращается в нуль и потому не построено.
Р 6
.ар _-,
у у р
Расчет проведен при е — 10~6, 7о = °>27.
Тонкая прямая имеет наклон 3,34-10 3,
в то время как теоретическое приближе-
приближение при использованных параметрах дает
200 400 600 PlgE(C) = const xe^'«, так что пред-
сказанный наклон составляет 3,46
После распада пика энергия спадает по закону Еп+\ = A -е)Еп,
пока не снизится до величины порядка единицы. После этого потребует-
оA) „ , ,
ся -^ итерации чтобы было достигнуто критическое значение энергии
и возник новый пик. Таким образом, межпиковый интервал имеет дли-
длительность
е е
где J5end — энергия в конце пика.
Пренебрегая величиной 0A) и используя полученные ранее соот-
соотношения, получаем распределение длительности межпиковой фазы:
рт(Т) RJ С\е(то - Гсг) е~с>€ 70"г" (Г-Гт™> х i j' mm'
I м ¦*• >^ *mini
7.8. Чем интересна жесткая турбулентность? 169
где Tmin — минимальная и средняя длительность межпиковой фазы,
которые равны
1 С? 1
Tmin = - log(Т> « T +
? (то-ГсгJ
7.8. Чем интересна жесткая турбулентность?
Явление жесткой турбулентности и подходы, которые мы обсудили
в этой главе, могут оказаться очень важными с точки зрения развития
новой парадигмы синергетики. Эти подходы демонстрируют возможные
способы упрощения, «понимания» сложных явлений и их математичес-
математического моделирования. Поэтому еще раз обратим на них внимание.
1) Разделение сложного явления на несколько стадий, анализ и от-
отдельное описание каждой из них, выделение ведущих процессов.
Затем согласование, «сшивание» разных описаний, своеобразный
системный синтез. Заметим, что в отличие от традиционных прие-
приемов асимптотического анализа мы не можем «заморозить» на этом
этапе быстрые или медленные процессы, а должны рассматривать
их взаимодействие. Вероятно, вопросы взаимодействия явлений,
происходящих на разных уровнях организации, будут находиться
в центре внимания при создании новых подходов в нелинейной
науке. По-видимому, такая «межуровневая динамика» является ти-
типичной для многих сложных систем. В 70-е годы в физике атмосфе-
атмосферы, в метеорологии была популярна идея о разделении масштабов,
выделении «погоды» и «климата» и раздельном описании обоих.
Большие усилия в этом направлении не привели к положительным
результатам, поскольку связь между быстрыми и медленными про-
процессами оказалась гораздо более важной и сложной, чем казалось
ранее. Такая же проблема — построение согласованного описания
макро- и микроэкономики — является открытой в современном
экономическом анализе.
2) Наличие стадий, на которых в сложной системе коренным образом
меняется набор параметров порядка и проблема предсказания таких
стадий. Эта проблема является важнейшей при прогнозе редких
катастрофических событий.
3) Возврат к построению аналитических моделей для сложных систем
с малыми параметрами. Широкое использование компьютерного
эксперимента еще недавно порождало эйфорию и иллюзию не-
неограниченных возможностей исследований. Однако ряд задач не-
неизбежно были и будут тяжелы для существующих и перспективных
компьютеров. Поэтому на новом уровне приходится возвращаться
к аналитическим моделям, делая при этом упрощающие предполо-
предположения, совершенно нетрадиционные для «докомпьютерной эры».
170 7. Жесткая турбулентность и ее упрощенные модели
4) Редкие катастрофические события, которые в истории нашей циви-
цивилизации играли и играют важнейшую роль, требуют иного подхода
к математическому моделированию. Например, уравнение, рассма-
рассматривавшееся в этой главе, описывает в упрощенном виде процессы
на поверхности атмосфера—океан. Ряд исследователей высказывал
гипотезу, что именно нелинейные процессы на этой границе от-
ответственны за аварии на буровых платформах — одних из самых
дорогих и грандиозных инженерных сооружений в истории. Однако
аварии эти исчисляются десятками, поэтому говорить о статистике
не приходится. Исходя из основных принципов, это явление также
не удается описать. Таких явлений очень и очень много. Поэтому
остается строить феноменологические модели и корректировать их
после каждой из происшедших катастроф либо по мере накопления
новых знаний. Техника такой коррекции только начинает созда-
создаваться. Сейчас по этому пути идут многие разработчики атомных
электростанций. Однако сами «алгоритмы корректировки» могут
обосновываться на известных моделях нелинейной динамики, опи-
описывающих редкие катастрофические события. Разработка таких ал-
алгоритмов может стать важным направлением в нелинейной науке.
8
Нейронные сети
8.1. Нейронаука
Сегодня мы не можем сказать с уверенностью,
содержит ли уравнение Шредингера и лягушек,
и композиторов, и даже мораль, или там ничего
похожего и быть не может. Мы не можем сказать,
требуется ли что-либо сверх уравнения, вроде
каких-то богов, или нет. Поэтому каждый из нас
может иметь на этот счет свое особое мнение.
Р. Фейнман
Вычислительные машины дали очень много нелинейной динами-
динамике. Они позволили исследовать математические модели, возникающие
в разных областях, и обнаружить множество интересных нелинейных эф-
эффектов. Сейчас нелинейная динамика «возвращает долги» компьютерным
наукам и вычислительной технике.
Компьютерное моделирование играет важную роль в междисципли-
междисциплинарном подходе, называемом нейронаукой. Этот подход призван ответить
на вопрос, как работает мозг, какие психические события определяются
паттернами нервных импульсов в мозге. Нейронаука возникла на стыке
многих научных дисциплин. Среди них нейрофизиология, биохимия,
когнитивная психология, математика, вычислительная техника.
Развитие нейронауки показало, что основным способом понимания
протекающих в мозге процессов, осмысления имеющихся эксперимен-
экспериментальных данных, постановки новых проблем является построение и ис-
исследование математических моделей. Естественно, следует отдавать себе
отчет, что путь от нынешнего состояния работ в этой области к глубо-
глубокому пониманию принципов работы мозга, по-видимому, очень длинен.
Модели скорее отвечают на вопрос, как могли бы работать те или иные
системы, в каких-то чертах согласующиеся с данными об архитектуре,
функциях, особенностях мозга. Тем не менее исследования в нейронауке
уже открыли пути для создания новых компьютерных архитектур и наде-
наделению вычислительных систем своеобразной интуицией, ассоциативной
памятью, способностью к обучению и обобщению поступающей инфор-
информации, т.е. возможностями, которые раньше считались прерогативами
живых систем.
Огромный интерес, проявляемый к этим работам в последние
пятнадцать лет, обусловлен несколькими причинами. В 60-е и 70-е
годы большие надежды возлагались на научное направление, называемое
искусственным интеллектом. Предполагалось, что, опираясь на логику,
172 8. Нейронные сети
дискретную математику, можно будет создать программное обеспечение,
решающее широкий круг задач: от доказательства теорем и сочинения
стихов до шахматной игры, медицинской диагностики, государственного
планирования. Несмотря на отдельные успехи в решении конкретных
задач, на этом пути возникли принципиальные трудности.
Во многих случаях формализация процедур оценки ситуации и вы-
выработки решения оказалась очень сложной. Их программная реализация,
создание детальных инструкций для гигантского числа возможных ситуа-
ситуаций, с которыми может встретиться компьютерная система, также требует
очень больших затрат. В частности, одним из принципиальных моментов,
заставивших США в свое время отказаться от системы полномасштаб-
полномасштабной противоракетной обороны с элементами космического базирования
(программа «звездных войн»), стали трудности создания программного
обеспечения. Ряд экспертов оценивали объем работы по созданию такой
системы в сотни тысяч человеко-лет работы высококвалифицированных
разработчиков.
Это заставило искать новые принципы и по-новому взглянуть
на поразительную способность человеческого мозга ориентироваться
в незнакомой, не встречавшейся ранее ситуации, управлять движением,
принимать быстрые и достаточно точные решения, распознавать образы.
В самом деле, трехлетний ребенок с легкостью отличает кошку от со-
собаки в жизни, на картинке, при разном освещении. Для компьютерных
программ это нерешенная проблема.
Второе обстоятельство, способствовавшее бурному развитию ней-
ронауки и большому интересу к ней, — успехи биологии. В последние
сорок лет стало ясно, как в ряде важных случаев проходится путь от взаи-
взаимодействия отдельных молекул до реакции организма как целого. На но-
новом уровне, связанном с развитием молекулярной биологии, стала ясна
универсальность многих биологических механизмов. Появилась надежда,
что благодаря новым методам, инструментам, идеям этот путь может
быть пройден и для процессов, связанных с восприятием, сознанием,
психикой.
Наконец, развитие точных наук, успехи в исследовании нели-
нелинейных математических моделей помогли сформулировать новые идеи
в этой области. Основная идея состоит в том, что восприятие, обу-
обучение, мышление, другие функции мозга обусловлены коллективным
процессом, приводящим к согласованной работе ансамблей достаточно
просто устроенных нервных клеток — нейронов. Самоорганизация («само-
(«самопрограммирование») таких ансамблей и является ключом к объяснению
функций мозга. Работы по исследованию памяти человека и животных
показали, что нельзя выделить в мозге одной четко локализованной струк-
структуры, отвечающей за запоминание. Это заставляет предположить, что мы
имеем дело с распределенной системой. Простым физическим прообра-
прообразом ситуации, которая, вероятно, имеет место, является голограмма.
Голограмма дает возможность записывать и хранить информацию
с помощью когерентных пучков света. Принцип ее получения — запись
на фотопластинке интерференционной картины, возникающей при на-
8.2. Элементарные представления о работе мозга
173
ложении падающего и рассеянного фиксируемым объектом монохрома-
монохроматического излучения. Если осветить зафиксированную на фотопластинке
интерференционную картину лучом того же лазера, то он при рассея-
рассеянии даст изображение первоначального объекта. При этом информация
о данной точке на поверхности объекта оказывается «рассредоточенной»
по всей поверхности фотопластинки-голограммы.
Испортив часть голограммы, мы не утратим изображение объекта,
а лишь сделаем его менее четким. Это кардинально отличается от ор-
организации стандартной «фотографической» памяти. Отрезав и выбросив
кусок фотографии, мы утратим возможность узнать, что на нем было
запечатлено.
Другую «математическую метафору»
распределенной памяти дает преобразова-
преобразование Фурье. В самом деле, пусть нам дан
некоторый силуэт. Его контур можно хра-
хранить в виде графика некоторой функции x(t)
(ом. рис. 8.1 в), заданной в дискретном на-
наборе точек (*i,*2> - - -1 *jv)- Однако его можно
хранить и в виде набора Фурье-гармоник,
например,
Ск = ±
cos (,?
«Забыв» значения х в отдельных точ-
точках, мы довольно быстро теряем предста-
представление о картинке в целом (см. рис. 8.16).
«Забыв» старшие коэффициенты Фурье, мы
всего лишь делаем контур более размытым
(см. рис. 8.1 в). Поэтому, работая с ненадеж-
ненадежными элементами, лучше иметь дело с коэф-
коэффициентами Фурье, чем с исходным конту-
контуром — «класть все яйца в одну корзину».
В этой главе мы вначале рассмотрим
элементарные представления о работе голов-
головного мозга, которые в том или ином виде
отображают различные модели, а также об-
Рис. 8.1. Искажения, вноси-
вносимые при различных способах
записи информации, меняют
картину по-разному: а) ис-
исходный силуэт; 6) картина,
которая возникает, если «ис-
«испорчена» часть функции x(t);
в) картина, возникающая,
если высшие коэффициенты
Фурье Ск утрачены
судим несколько базовых математических моделей в этой области.
8.2. Элементарные представления о работе мозга
Более сотни лет назад Сантьяго Рамон-и-Кахаль использовал
для исследования нервных клеток новый метод их окраски солями
серебра, предложенный К. Гольджи. Это стало началом научного ис-
исследования мозга. Оказалось, что мозг содержит около 1012 нейронов,
и состоит из некоторого набора дискретных функциональных единиц.
174
8. Нейронные сети
Рис. 8.2. Схематиче-
Схематическое изображение
типичного нейрона:
1 — тело клетки, 2 —
дендриты, 3 — ак-
аксон, 4 — один из
синапсов
V, MB,
80
40
0
-40
-80
Рис. 8.3. Типичный вид потенциала
действия в точке нейрона, располо-
расположенной на аксоне
Типичный нейрон представлен на рис. 8.2. Он со-
состоит из тела клетки и сильно разветвленных дре-
древовидных отростков, получивших название дендри-
тов. Дендриты получают информацию от других
нейронов. За передачу информации отвечает длин-
длинный неразветвленный отросток, называемый аксо-
аксоном. Участки контакта между нейронами получили
название синапсов. Они обеспечивают превращение
электрических импульсных сигналов, распространя-
распространяющихся как волна по аксону, в химические. Эти
импульсы получили название потенциалов действия.
Потенциалы действия, приходя в синапсы, вызывают
в них выделение веществ, называемых нейромедиато-
рами. Нейромедиаторы диффундируют через узкую
щель между синапсом данного и дендритом связан-
связанного с ним нейрона. Рецепторы дендритов таковы,
что с их помощью нейрону удается осуществлять
обратное преобразование — превращать химические
сигналы в потенциалы действия.
Число синапсов у разных клеток различно.
У так называемых пирамидных клеток около 104
синапсов, у клеток Пуркинье их более 15 • 104. Ти-
Типичный закон изменения потенциала действия, из-
измеренного в одной из точек аксона, представлен
на рис. 8.3. Характерный временной
масштаб здесь имеет порядок милли-
миллисекунд. Амплитуда и форма импуль-
импульсов обычно считаются постоянными.
Изменение состояния клетки про-
проявляется в изменении частоты генера-
генерации потенциалов действия. Это наво-
наводит на мысль, что, вероятно, для си-
систем мозга характерно частотное ко-
кодирование информации, а сам нейрон
напоминает электронную схему, ко-
которую в импульсной технике называ-
называют блокинг-генератором. При подаче
t
на вход такой схемы сигнала он генерирует «стандартный импульс» за-
заданной формы и амплитуды. Этот автоколебательный процесс таков, что
после каждого такого «взрыва» система оказывается невосприимчивой
к внешним воздействиям. Последнее состояние называют рефрактерным.
Можно сказать, что мы имеем дело с возбудимой системой, которая
может находиться в фазе покоя (до того, как пришел потенциал дей-
действия), возбуждения (в то время, как импульс пришел) и рефрактерности
(в течение определенного временного интервала сразу после прохожде-
прохождения импульса). Наличие рефрактерного периода определяет предельную
8.2. Элементарные представления о работе мозга 175
возможную частоту генерации потенциалов действия. Она не превыша-
превышает 200 Гц.
Нейрон является типичным нелинейным элементом, действующим
по принципу «все или ничего». Когда суммарный сигнал, приходящий
от других нейронов, превышает некоторое критическое значение, гене-
генерируется «стандартный» импульс. В противном случае нейрон «молчит».
Потенциалы действия служат не только для передачи и обработ-
обработки информации. Они могут изменять те нервные сети, по которым
передаются. Эта пластичность синапсов и нейронных сетей является,
в соответствии с нынешними воззрениями, основой для обучения.
Даже поверхностное сопоставление мозга и электронно-вычисли-
электронно-вычислительной машины показывает, как сильно отличаются эти объекты.
Ключевое отличие состоит в том, что мозг является «самопрограм-
«самопрограммируемой машиной», способной создавать, модифицировать, совершен-
совершенствовать программы своей деятельности.
Хотя и мозг, и компьютер состоят из большого количества эле-
элементарных структур (в одном случае нейронов, в другом — триггеров,
соединенных определенным образом), между ними есть принципиальная
разница. Элементы компьютера являются весьма ненадежными структу-
структурами. Выход из строя любого из них может означать выход из строя всей
системы. По мере взросления человека число нейронов снижается. Этот
процесс происходит неравномерно. Однако к старости, как утвержда-
утверждают специалисты, ряд структур мозга может терять 30-40 % клеток. Тем
не менее это не обязательно приводит к нарушениям умственной деятель-
деятельности. Пока неясно, какова возможная архитектура такого «компьютера
с исчезающими элементами».
Разительно отличаются количественные характеристики обеих си-
систем. Максимальная скорость нервного импульса сейчас оценивается
в 100 м/сек. Это примерно в миллион раз меньше, чем скорость распро-
распространения электрического сигнала по хорошему проводнику. Тактовая
частота современных персональных компьютеров около сотен мегагерц.
Предельная тактовая частота нейронных систем примерно в миллион раз
меньше.
Чем же обеспечивается исключительная эффективность работы
мозга при решении огромного количества задач в сравнении с ком-
компьютерами? В настоящее время общепринятая точка зрения объясня-
объясняет это параллельной работой множества «элементарных процессоров»,
а также совершенной архитектурой системы, позволяющих эффективно
«распараллеливать задачу». Попытки создания вычислительных машин
с высокой степенью параллельности — многопроцессорных комплексов,
транспьютеров, машин клеточных автоматов, — показали, что создание
параллельных алгоритмов, при которых части вычислительной системы
не мешают друг другу и не слишком долго ждут результатов от других ча-
частей, представляет весьма сложную задачу. По-видимому, природе в ходе
эволюции удалось найти очень удачное ее решение.
Кроме того можно ожидать, что в мозге реализованы исключитель-
исключительно эффективные алгоритмы обучения нейронных ансамблей, обеспечи-
обеспечивающие эффективную коррекцию и самонастройку программ.
176 8. Нейронные сети
Следует отметить, что при анализе такой системы, как мозг, трудно
отделить ключевые факторы от второстепенных, принципы действия
от деталей «технической реализации». Мнения специалистов на этот счет
часто расходятся.
Для нейронов характерно довольно большое структурное разно-
разнообразие. Внешне клетки Пуркинье и клетки структуры мозга, называе-
называемой бледным шаром, выглядят совершенно по-разному. Возможно, эти
существенные различия следует учитывать в моделях. Число известных
нейромедиаторов приблизилось к пятидесяти. Вероятно, это также важ-
важный фактор, обеспечивающий «развязку» различных информационных
каналов или повышающий надежность и живучесть всей системы. Нако-
Наконец, исследования Д. Хьюбела и Т. Визела по анализу зрительной коры
привели к обнаружению важной структурной особенности в организа-
организации мозга. Было обнаружено, что нейроны с одинаковыми функциями
сгруппированы в виде колонок, своеобразных модулей, пронизывающих
кору. Модуль может включать более 100 тысяч клеток, большинство ко-
которых образует локальные нейронные сети. Может быть, ключ к разгадке
психических процессов связан с алгоритмами и механизмами взаимодей-
взаимодействия таких модулей? В отличие от компьютера, принципы организации
памяти мозга неизвестны. И это приводит к кардинально отличающимся
взглядам на то, что же мозг может запомнить.
Несмотря на большое количество нерешенных проблем в этой
области, в нейронауке были достигнуты крупные успехи. К ним можно
отнести новое поколение препаратов для лечения психических забо-
заболеваний, названных нейролептиками, и создание нейрокомпьютерных
вычислительных систем.
8.3. Модель Хопфилда
Нейронная сеть Хопфилда, по-видимому, является сейчас наиболее
популярной математической моделью в нейронауке. Это обусловлено ее
простотой и наглядностью. Кроме того, она оказалась близка по сво-
своему математическому описанию к объекту, детально исследовавшемуся
в статистической физике — модели спиновых стекол.
Сеть Хопфилда показывает, каким образом в принципе может быть
организована память в сети из элементов, которые не являются очень
надежными.
Обратим внимание на несколько важных особенностей памяти жи-
животных и человека, которые интересно было бы воспроизвести в модели.
Ассоциативность, устойчивость по отношению к шуму. Представим
себе память как некоторый «черный ящик». Для того чтобы система
могла впоследствии вспоминать информацию, ее следует вначале обучить.
Другими словами, элементарная формализация работы запоминающего
устройства приводит к следующей картине. Пусть на вход «черного
ящика» подается некоторый входной образ ?*,", содержащий N бит
информации. Допустим, нам нужно обучить устройство распознавать М
8.3. Модель Хопфилда 177
различных образов, которые мы назовем ключевыми. На выходе «черного
ящика» по предъявлении данного ключевого образа должен появляться
выходной образ, который мы будем обозначать ?°ut. Пространства входных
и выходных образов могут быть как одинаковыми, так и различными.
Пример. Множество {?",/* = 1,...,М] может представлять фотографии
коллег, {?)?",/1 = \,...,М} — их имена; {?™} — имена друзей, {??"'} —
номера их телефонов.
В процессе обучения определенным образом устанавливаются связи
между данным ключевым образом ?™(ц = 1,..., М) и желаемым выходом
if/?"}- Естественно предположить, что в процессе работы устройства оно
должно по предъявлении ?™ на входе выдавать ??"' на выходе. Кроме того
будем требовать, чтобы при предъявлении «близких», «похожих» на данный
ключевой образ ?'" образах ?'" «черный ящик» вспоминал «настоящий»
ключевой образ {J? и, соответственно, на выходе давал неискаженный
образ ?°ш.
Пример. ?'" — запомненная устройством памяти картинка, ?'" — какой-
нибудь фрагмент этой картинки или она сама с наложенным на нее шумом,
?out — неискаженная картина, хранящаяся в памяти; ?" — запомненный
фрагмент текста, ?" — фраза или несколько слов из этого текста, ?"" — би-
библиографические данные о тексте, содержащем предъявленный фрагмент;
?'" — «идеальная» кардиограмма, соответствующая данному заболеванию,
?1" — кардиограмма данного больного, ?"" — диагноз, указывающий
с каким заболеванием столкнулись врачи.
Иначе говоря, у создаваемого «черного ящика» должны возни-
возникать верные ассоциации. Понятно, что такое распознавание предъявлен-
предъявленных образов может быть полезно для справочных и поисковых систем,
для оценки ситуации.
Ясно также, что важная проблема состоит в определении «похоже-
«похожести», другими словами, нормы в пространстве образов ||{J" — {J"||. Разные
нейронные сети, вообще говоря, имеют разные нормы. Тот образ, который
одна сеть считает похожим на данный, другая может таковым не считать.
И выбирать между ними приходится, исходя из своих представлений о ре-
решаемой задаче. Это компетенция не нейронной сети, а того, кто обратился
к ее помощи.
Распределенный характер хранения р
информации, высокая надежность. Будем ,
исходить из обсуждавшихся представле-
представлений о работе мозга. Поскольку в мозге
не удается указать конкретного элемента, 0,5
отвечающего за хранение данного образа,
будем считать, что информацию об объек-
объекте хранит не один элементарный «нейрон» q 77j jqq aV%
в «черном ящике», а целая группа. Кро- '
ме того желательно, чтобы создаваемое Рис-8.4. Желаемая зависимость
устройство, как и в случае мозга, было бы вероятности правильного распо-
способно действовать и при потере или знаванияр от доли вышедших из
г строя нейронов а
выходе из строя части элементов. Было
j 78 8. Нейронные сети
бы хорошо, чтобы вероятность правильного распознавания для создава-
создаваемой нейронной сети в зависимости от доли уничтоженных элементов
вела себя так, как показано на рис. 8.4.
Быстрый доступ к информации. Несмотря на крайне медленную,
в сравнении с компьютерами, скорость передачи сигналов и инерцион-
инерционность элементов мозга, наша память работает весьма быстро. Вероятно,
мозг не просматривает всю информацию, которой он располагает, а дей-
действует гораздо рациональнее. Желательно, чтобы создаваемый «черный
ящик» также позволял бы определять выходной образ по входному до-
достаточно быстро.
Универсальность и адаптивность. Важно было бы обеспечить струк-
структуру «черного ящика», позволяющую иметь дело с различными входными
образами ?j,n (изображения, звук, запахи и т.д.). Должна быть обес-
обеспечена возможность перенастроить нейронную сеть, меняя рецепторы,
периферию, число образов и т.д.
Сопоставим эти требования с организацией памяти традиционных,
«фон-неймановских» компьютеров. В рамках этой архитектуры весьма
трудно обеспечить устойчивость по отношению к шуму. Достаточно
сложно иметь дело со входным образом ?^п, если число бит N, необ-
необходимое для его кодировки, велико, даже в том случае, если мы умеем
вычислять норму ||?jln — ?Jn||- Кроме того, мы сталкиваемся с необходи-
необходимостью перебирать различные ключевые образы, сравнивая их с данным.
Естественно, это может потребовать много времени.
Основная идея построения сети Хопфилда непосредственно свя-
связана с качественной теорией дифференциального уравнения х = v(x),
где х — скаляр. Напомним, что аттракторами этого уравнения могут
быть только особые точки х*, v(x*) = 0. На прямой, являющейся фазо-
фазовым пространством этой системы, устойчивые особые точки чередуются
с неустойчивыми. Последние определяют границы области притяжения
устойчивых точек. Точка устойчива, если дх ' < 0, и неустойчива, если
Сопоставим аттракторам этого уравнения ^абор ключевых обра-
образов ?Jf (fi = 1,...,М). Предъявляемым образам ? будет соответствовать
начальное значение х@). Распознавание образа будет соответствовать
выходу на аттрактор.
Предъявленный образ будет близок к данному ключевому, если он
попадает в его область притяжения (см. рис. 8.5). Для этого уравнения
существует функция Ляпунова или потенциал
X
U(x) = - J v(y)dy, v(x) = ~, C(x) = U(x).
Следовательно, решение уравнения
* = »(*), as(O) = f, (8.1)
8.3. Модель Хопфилда
179
при ? —> оо стремится к одному из клю-
ключевых образов ?^n, v{^) = 0. Други-
Другими словами, если бы и входные обра-
образы, и ключевые образы были бы дей-
действительными числами, то вычисли-
вычислительная система, решающая уравнение
(8.1), могла бы играть роль запоминаю-
запоминающего «черного ящика». Обучению такой
«сети» соответствовало бы построение
функции v(x) с устойчивыми особы-
особыми точками в точках числовой оси ?^п
U
Рис. 8.5. Уравнение (8.1) позволяет
(и = 1,... , М); им соответствуют мини- Реализовать простейший вариант
мумы потенциальной функции. Функ- ассоциативной памяти
цию v(x) можно построить так, чтобы неустойчивые особые точки ж*
(v(X).) = 0) принимали заданные значения (см. рис. 8.5). Они определяют
области притяжения ключевых образов и говорят о том, какие числа ?
«похожи друг на друга» и на известный ключевой образ. Обратим внима-
внимание на важную деталь — здесь мы можем задавать по своему усмотрению
не только ключевые образы, но и их области притяжения.
Реальные ситуации, с которыми приходится сталкиваться и в кото-
которых применяются нейронные сети,_разумеется, гораздо сложнее. Прежде
всего потому, что предъявляемые ? и запомненные образы ?Jf предста-
представляют собой векторы большой размерности. Например, это могут быть
изображения и в ? «записана» информация о цвете каждого пиксела
на экране.
Тем не менее общая идея и постановка задачи остается такой же.
Если считать, что исследование аттракторов заданной динамической си-
системы — прямая задача качественной теории, то здесь мы имеем дело
с обратной задачей. При ее решении следует построить динамическую
систему, обладающую заданным набором аттракторов (а в идеале и за-
заданными областями притяжения этих аттракторов). Эта задача является
некорректной. Самые разные динамические системы могут иметь одни
и те же аттракторы. (В самом деле, самые разные функции U(x) могут
иметь экстремумы в одних и тех же точках.) Поэтому можно упростить
ситуацию, считая, например, что мы имеем дело с динамическими систе-
системами специального вида, у которых есть к тому же функция Ляпунова.
Этот подход используется в модели Хопфилда и во множестве других
нейронных сетей. Нейронные сети, имеющие функцию Ляпунова или
ее аналог, в этой области исследований часто называют конвергентными
(от английского to converge — сходиться).
Чтобы описать нейронную сеть, надо:
— определить динамику ее отдельных элементов — нейронов;
— задать архитектуру сети;
— определить правила, по которым нейроны будут взаимодействовать
друг с другом;
180 8. Нейронные сети
— описать алгоритм обучения, т. е. формирования связей для решения
поставленной задачи.
Последний пункт является особенно важным. Чтобы подчеркнуть
его значение, в зарубежной литературе алгоритмы обучения нейронных
сетей иногда называют «искусственной психикой», а само направление
работ — коннекционизмом (от английского to connect — связывать).
Мы рассмотрим классическую, дискретную версию модели Хоп-
филда, хотя основные идеи ее построения непосредственно связаны
с непрерывной моделью (8.1). Кроме того, в литературе можно найти
непрерывные сети такого же типа.
Будем обозначать через S(t) активность нейрона в момент вре-
времени t. Эта величина дискретна и может принимать значение +1, что
соответствует состоянию «возбуждения», и —1, что отвечает «тормо-
«торможению». Эта дискретность отражает нелинейный, пороговый характер
функционирования нейрона и известный из нейробиологии принцип
«все или ничего».
Пусть h(t) внешнее воздействие, оказываемое на нейрон, на-
например, со стороны других нейронов. Традиционной моделью теории
нейронных сетей является нейрон Мак-Каллока—Питтса. Его динамика
определяется соотношением
{! $}Jjj; (8.2)
(случай h(t) = 0 не рассматриваем). Очевидно, sign (ft) — это просто
знак функции h. Время считаем дискретным: t = 1,2,... . Будем иметь
в виду, что мембранный потенциал нейрона i в момент времени t
зависит от состояния других нейронов. Чтобы описать это обстоятельство
в модели, будем считать, что воздействие на данный нейрон со стороны
других определяется взвешенной суммой
M'+1) = X>jSj@- (8-3)
j
Веса связей J^ являются идеализированным описанием взаимодей-
взаимодействия между дендритами данного нейрона и синапсами других. Иногда
для каждого нейрона вводят локальный порог Gj, по превышении кото-
которого нейрон переходит в активное состояние:
Будем считать, что архитектура сети такова, что каждый нейрон
связан с каждым. Величины J^ удобно представлять в виде квадратной
матрицы размером N х N, называемой матрицей связей J = {Jij}.
Итак, эволюция состояния сети {S;(?)} определяется дискретной
динамической системой
N 1
\ K*"<iV, * = 1,2 (8.4)
8.3. Модель Хопфилда 181
Входной образ, который предъявляется для распознавания ?, соот-
соответствует начальным данным для системы (8.4)
f={S,-@),i=l,...,JV}. (8.5)
Эти представления нейронауки, отраженные в модели, имеют пря-
прямой аналог в теории спиновых стекол. Клетке-нейрону соответствует
спин; состоянию покоя (возбуждения) — ориентация спина —1 (+1);
синаптическим весам — связи ,7^; возбуждающим связям — J;j > 0;
тормозным — J^ < 0; порогам в,- — локальные поля.
Модель (8.4) значительно упрощает предположение о том, что связи
симметричны
Jij = Jji, Л* = 0, l^i,j,k^N. (8.6)
Вообще говоря, это предположение гораздо более оправдано в те-
теории спиновых стекол, чем в моделях нейронауки, где связи между
синапсами одного нейрона и дендритами другого являются однонапра-
однонаправленными.
Назовем величину
N N
Е = -ч ? ? j<js'sj+? G«? (8-7)
г i=i j=\
энергией. Можно сказать, что для рассматриваемой модели эта величина
играет роль функции Ляпунова. В самом деле, представим себе, что
в момент времени t + At мы изменили значение переменной S только
для одного нейрона с номером k: Sk(t + At) = Sk(t) + AS. Очевидно,
сумма (8.7) при этом изменится на величину
АЕ = ~2 ? JkJSJAS" - 2 ? JJkSJASk ~
- ^JuSjiASkJ + QkASk = ASk [- ?) JkjSj +
L j=l
Принципиальной здесь является возможность «свернуть» обе сум-
суммы в одну и избавиться от квадратичного по AS члена, что обеспечивается
выполнением равенств (8.6). Но выражение в квадратных скобках в фор-
формуле (8.8) будет противоположно по знаку величине ASk, если состояние
нейрона будет меняться по правилу (8.4). Именно поэтому величина АЕ
будет неположительна. Более строгие рассуждения, учитывающие, что
состояние может менять не один, а несколько нейронов, приводят к тому
же выводу.
Обратимся теперь к алгоритму обучения нейронной сети. Этот ал-
алгоритм позволяет по заданному набору ключевых образов ?j,n, 1 ^ fi ^ М,
найти матрицу связей J.
132 8. Нейронные сети
Обозначим через ^ значение переменной Si (т.е. состояние *-го
нейрона), в случае входного образа с номером ц. В модели Хопфилда
значения пороговых параметров Gj выбраны равными нулю, а матрица
связей определяется правилом обучения Хебба
1 и
Jij = uYlbxti» при **'> Jii=z0-
Правило Хебба было предложено, исходя из следующих нейро-
нейрофизиологических представлений. Обучение нейронных ансамблей, по-
видимому, связано с возникновением положительных обратных связей.
Очевидно, эти связи должны, в первую очередь, устанавливаться между
теми нейронами, которые при выполнении одной задачи оказываются
в одинаковом (например, возбужденном) состоянии. При этом эффек-
эффективность взаимодействия соответствующих синапсов и дендритов должна
возрастать. В модели это должно соответствовать увеличению веса связи,
например, между i-м и j-м нейроном Зц. Другими словами, в форму-
формуле (8.9) подсчитывается общее число раз, которое нейроны оказывались
в одинаковом состоянии при предъявлении всем М ключевых образов,
и далее нормируется на число нейронов. Аналогичные рассуждения про-
проводятся, если нейроны, как правило, оказываются в противофазе и между
ними возникает отрицательная обратная связь.
Характерная метафора, которую здесь иногда используют — со-
соскальзывание камня по глинистому склону: чем больше раз камень
скользил по одному пути, тем глубже становится возникшая колея и тем
с большей вероятностью он будет двигаться по ней же.
Убедимся, что в ключевых образах ?J,n, /х = 1,... ,М в нейронной
сети, обученной по правилу Хебба, действительно достигается минимум
функционала энергии. Подставим соотношение (8.9) в формулу (8.7)
при G,- = О
, N N . N N , М
EE
M f/ JV 42 JV , M
M f/ JV 42 JV , M
где гпц = jf J2 S&ii- Очевидно, Sjtj — 1. Условие i ф j в (8.10) следует
»=i
из формулы (8.6).
Величина m^, очевидно, соответствует корреляции, или скалярному
произведению, данной нейронной конфигурации и ключевого образа ft.
8.3. Модель Хопфилда 183
Формула (8.10) определяет квадратичную формулу относительно компо-
компонент вектора {Si}. Если ключевые образы ортогональны друг к другу
с _ Г 1, если ц =
то mi = 1, т,2 = 0, тз = 0, ..., если Si = ?,i. Значение энергии в этом
случае равно Е({\) = - у + у. В точности таким же оно будет и для других
ключевых образов. Если бы тп^ были непрерывными величинами, то
можно было бы проверить, что -к— = 0, а матрица ,«-af ч отрицательно
определена. То есть энергия Е, как функция го^, имеет локальный
минимум. Если образы выбраны наугад, то можно ожидать, что
1
ТПц ~
Значение энергии в этом случае близко к нулю (~ Ц- — 4f), что суще-
существенно выше.
Итак, соотношения (8.4), (8.5), (8.9) полностью определяют дина-
динамику сети Хопфилда, в которой при определенных условиях ключевым
образам соответствуют аттракторы.
Излюбленным тестом для модели Хопфилда является распозна-
распознавание картинок, изображающих различные буквы алфавита. На рис. 8.6
показаны три входных образа — изображения букв А, У, К, которым
в соответствии с правилом Хебба обучена сеть. Затем показано, како-
какова эволюция нейронной конфигурации в случае искаженной буквы А.
При этом достаточно быстро происходит выход на аттрактор, соответ-
соответствующий ключевому образу. В силу того, что все элементы действуют па-
параллельно, распознавание обычно происходит всего за несколько шагов.
Важной характеристикой нейронной сети является отношение чи-
числа ключевых образов М, которые могут быть запомнены, к числу
нейронов сети N
_ М
Для модели Хопфилда в литературе часто указывается а = 0,14. Однако
такая оценка может иметь место только в случае, если образы близки
к некоторому набору взятых наугад векторов. Обычно коэффициент а
существенно меньше.
Для многих нелинейных систем, в которых возможны коллек-
коллективные процессы, можно выделить ведущие переменные, параметры
порядка, к которым подстраиваются все остальные степени свободы
исследуемой системы. Для модели Хопфилда такие параметры также су-
существуют. Их роль играют величины, называемые корреляциями между
образами [67]:
1 N
i=\
184
8. Нейронные сети
1 I
¦¦ II
¦¦ •¦
¦J. я
У
\»
:: .:¦
:: -••
step : 1
•• ¦•
¦¦ ¦•
•SSS •• ¦"•
/ "
a1"-!;:::-!:
:: ::
:::: ::!:
e: .1Z11E+06
step : 3
••
J 4
i-\
n ::
Haazau»»!.'
II !i
a* .::
e: .1740E*06
step : 7
••
¦• ¦•
/ \
t %
••«¦•¦•¦•¦¦¦¦•¦¦¦I
..............и
II ••
:: ::
a :;
e: .1861E*O6
Рис. 8.6. Пример распознавания образа сетью Хопфилда. В верхнем ряду —
ключевые образы. В нижнем — распознавание буквы «А», на которую наложен
шум. Параметр step соответствует номеру шага Т, е — энергии представленной
конфигурации S(t). За несколько шагов сеть верно распознает образ
Традиционный вопрос, который возникает при анализе сети: мож-
можно ли записать в дополнение к имеющимся М образам еще один ?м+\
так, чтобы он также стал аттрактором исследуемой системы, а остальные
продолжали оставаться аттракторами. В последние годы было показано,
что ответ на этот вопрос однозначно определяется корреляциями между
образами [67]. Интуитивно понятно, что чем больше корреляция ново-
нового образа с одним из уже записанных, тем «труднее» нейронной сети
запомнить и распознать его.
8.4. Смысл хаоса
Для модели Хопфилда характерны два существенных недостатка.
Первый в литературе называется «ложной памятью», существованием
«призраков», «фантомов», «ложных образов». Суть этого явления пока-
показывает рис. 8.7. Здесь также сеть обучена распознавать изображения трех
букв. Каждое из них является аттрактором соответствующей динамичес-
динамической системы. Снизу показан процесс распознавания, когда на изображе-
изображение буквы А наложен довольно большой шум. Здесь также происходит
выход на аттрактор, но на такой, который не совпадает ни с одним
из ключевых образов. Другими словами, обучая нейронную сеть по пра-
8.4. Смысл хаоса
185
: :
¦ ¦
¦ i
¦ •
Y
Г ¦¦"
i '¦-.,
step : 0
"If» "IB.", m SI
e: -.3692ЕЧН
steD : 1
¦::! "v;.y *
e: -.?544E*05
StCD : 6
¦
¦ ¦ ¦
e: -.1530E*06
Рис. 8.7. Эффект «ложной памяти». Верхний ряд — набор ключевых образов,
которым обучена сеть. Нижний ряд иллюстрирует выход сети на стационарную,
не зависящую от времени конфигурацию. Эта конфигурация не соответствует ни
одному ключевому образу.
вилу Хебба, мы получили наряду с «настоящими», желаемыми, еще
и набор паразитных аттракторов.
Другой недостаток связан с достаточно простым мысленным экспе-
экспериментом. Предположим, что сеть «научена» распознавать изображение
кошки и собаки. Допустим, что мы предъявили изображение птицы.
Пусть траектория сети благополучно миновала все ложные образы. Про-
Произошло распознавание, функционал энергии уменьшился и достиг ло-
локального минимума, и сеть распознала в предъявленном изображении
собаку. Будем ли мы удовлетворены результатом? Очевидно, нет. Отсюда
ясен еще один существенный недостаток: сеть не умеет говорить «не
знаю», она распознает, даже если для этого нет никаких оснований.
Ниже мы обсудим модифицированную модель Хопфилда. В этой
модели предпринята попытка устранить оба недостатка, усложнив модель
нейрона. Идеализированный нейрон Мак-Каллока—Питтса мгновенно
реагирует на состояния соседей, причем независимо от того состояния,
в котором в данный момент находится он сам. Это противоречит ряду
нейрофизиологических данных, утверждающих, что реальный нейрон
является чрезвычайно сложной инерционной системой.
Исследование электрической активности при распознавании за-
запахов млекопитающими показало, что принципиальную роль в этом
процессе играют регулярные и хаотические колебания. Распознавание
186 8. Нейронные сети
запахов начинается с обонятельных рецепторов, которые выстилают но-
носовые ходы. Они вступают в контакт с молекулами пахучего вещества
и посылают сигнал клеткам обонятельной луковицы. Каждому запаху со-
соответствует определенный паттерн активности рецепторов, который часто
бывает искаженным, так как в результате турбулентных завихрений вды-
вдыхаемого воздуха не все рецепторы взаимодействуют с пахучим веществом.
Из результатов, полученных профессором У. Фрименом и его кол-
коллегами, следует, что когда активность рецепторов отсутствует, активность
обонятельной луковицы носит низкоамплитудный, нерегулярный и, по
всей видимости, хаотический характер.
Когда животное вдыхает знакомый запах, активность становится
периодической. В каждой точке обонятельной луковицы колебания по-
потенциала электроэнцефалограммы синфазны, но отличаются по амплиту-
амплитуде. При этом каждому знакомому запаху отвечает свой пространственный
паттерн амплитуд, своеобразная стоячая волна, которая не изменяется
в течение всего времени постановки опыта.
Было установлено, что если вдыхаемый запах незнаком, то ак-
активность обонятельной луковицы остается хаотической. Однако, если
в процессе обучения на данный запах будет выработан условный ре-
рефлекс, то и ответ становится периодическим.
Итак, можно сказать, что в состоянии покоя и при вдыхании
незнакомого запаха активность обонятельной системы хаотична, что ха-
характеризуется как состояние «не знаю». При распознавании выученного
образа активность системы периодична и, вероятно, определяется не-
некоторым предельным циклом. На основе проведенных экспериментов
У. Фримен пришел к выводу о том, что «без хаотического поведения
нейронная система не может добавить новый запах к своему репертуару
уже выученных запахов».
Чтобы отобразить эти наблюдения в модели, предположим, что рас-
распознавание запахов обеспечивается некоторой нейронной сетью хопфил-
довского типа. Однако пусть нейроны в этой сети обладают более сложной
динамикой, чем элементы, введенные Мак-Каллоком и Питтсом. Отме-
Отметим, что в последних не используется абсолютная величина входа h.
Существенным является только ее знак. Логично было бы предположить,
что при больших h переход в состояние возбуждения действительно про-
происходит быстро, а при уменьшении |А| его скорость уменьшается. Кроме
того, нейробиологические данные говорят о том, что состояние нейрона
в последующий момент зависит не только от внешних воздействий, но и
от состояния самого нейрона в предыдущий момент времени.
Чтобы учесть эти два обстоятельства, будем считать, что динамика
одиночного нейрона определяется некоторым одномерным отображением
S(t+l)=F(S(t),V(t)), (8.11)
зависящим от величины входа V, как от параметра. Величину входа в этой
модели обозначим V, поскольку она будет вычисляться несколько иначе,
чем входная функция h в модели Хопфилда. Величину S(t) также будем
считать не дискретной, а непрерывной величиной. Пусть при V > О
8.4. Смысл хаоса
187
это отображение представляется горизон-
горизонтальным отрезком, что соответствует ней-
нейрону Мак-Каллока—Питтса (см. рис. 8.8а).
Допустим теперь, что правый конец отрез-
отрезка закреплен, а левый может вращаться во-
вокруг этой точки как вокруг оси. Очевидно,
что если угол между отрезком и горизон-
горизонталью не равен нулю, то переход в состоя-
состояние возбуждения уже не будет мгновенным
(см. рис. 8.8 б). В этом случае величина S(t)
будет приближаться к + \ экспоненциаль-
экспоненциально, причем чем больше угол, тем медленнее
приближение.
Если обозначить зависимость угла
наклона от внешнего воздействия V через
функцию K(V), то отображение F(S, V)
в формуле (8.11) для V > 0 запишется
в виде
F(S, V) = 1 + E
Соответственно, при V < О
-1
/
/
S(H
-1 ^
р
/
-I1
/
/
+1
-1
-1);
+1
-f
-1
.,).
+1
i
\
/
V»
k(h,
У/
/
f
v>
//
0< V
f
+1
1
+1
1
у
+1
'< 1
S(t)
S(t)
S(t)
Оба эти соотношения можно запи-
записать в виде одной формулы
F{S, V) = sign V + E - sign V)K(V),
где функция К(V) симметрична, поло-
положительна и монотонно стремится к нулю
при V —> оо. При K(V) < 1 отображение
является сжимающим. Его аттрактор — не- в
подвижная точка. Рис. 8.8. Каждый нейрон моде-
С уменьшением величины внешнего лируется одномерным отобра-
воздействия V угол наклона K(V) увели- жением S(t+\) = F[S(t),V(t)),
чивается. Ряд данных нейробиологии сви- зависящим от внешнего воз-
детельствует в пользу того, что при сильном Дейс™ия v(l) как от параме-
гиперполяризующем или деполяризующем ^ а> *»» больших V данный
„ „ нейрон эквивалентен нейрону
воздействии поведение нейрона регулярно Мак-Каллока-Питтса; б) для
(в нашей модели это соответствует значе- не очень больших значений
Ниям параметров F < -1 и К » +1), V > 1 состояние возбуждения
а при некотором промежуточном воздей- «+1» все еще является устой-
ствии поведение нейрона хаотично. Пусть ч.ивой неподвижной точкой;
этому диапазону воздействий отвечает ин- в> при V < l отображение ста-
1 у 1 новится растягивающим, а ди-
тервал -1 < V < +1. намика нейрона — хаотической
Потребуем, чтобы при малом вход-
Ном воздействии |V| < 1 модель нейрона также обладала бы хаотиче-
хаотическим поведением. Для этого достаточно, чтобы в этом случае отобра-
188
8. Нейронные сети
жение (8.11) было растягивающим. Этого можно добиться, положив
K(V)> 1 при всех |7| < 1, и
F(S,V)=
(8.12)
Функция К(V) — 1+|у. и отображения F(S, V) для различных значений V
представлены на рис. 8.9.
/
7,
II
'1
/
Л
-1
о
1
V
Рис. 8.9. Вид функции K(V), задающей угол наклона кусочно-линейного,
кусочно-непрерывного одномерного отображения, определяющего динамику
одиночного нейрона. В квадратиках сверху показана функция F(S, V) при зна-
значениях V, отложенных по оси абсцисс. При |VJ > 1 одномерное отображение
сжимающее, при |V| < 1 — растягивающее
Итак, построенное одномерное отображение, описывающее дина-
динамику нейрона, выбрано так, что при сильном положительном (V > 1)
или отрицательном (V < —1) воздействии нейрон переходит в состояние
возбуждения или торможения соответственно, а при слабом внешнем воз-
воздействии активность нейрона хаотична. Различные типы динамики оди-
одиночного нейрона при фиксированном входе V представлены на рис. 8.10.
V=0,7
V=-0,7 \Z\ \ЛЛЛЛЛЛЛЛЛА/
V=-\,\ 0 ^^
Рис. 8.10. Активность одиночного ней-
нейрона в зависимости от внешнего воздей-
воздействия V. Для наглядности S(t) и S(t+ 1)
соединены отрезком. При V = 0,7
(V = -0,7) динамика нейрона явяется
хаотической, но нейрон проводит боль-
большую часть времени в состоянии возбу-
возбуждения (торможения). При 5 = 0 оба
состояния (возбуждения и торможения)
являются равноправными
Обучение, как и в классической модели Хопфилда, будем проводить
в соответствии с правилом Хебба
м
J" =
Для описания взаимодействия нейронов введем параметр А, имеющий
смысл «силы» взаимодействия между нейронами
8.4. Смысл хаоса 189
Из формул (8.11) и (8.12) следует, каково будет поведение такой сети
в двух предельных случаях. При А = 0 она распадается на N несвязанных
одномерных отображений с хаотическим поведением. При А —> оо она
эквивалентна стандартной модели Хопфидда со всеми присущими ей
недостатками.
В частности, даже не при очень больших соотношениях ^ суще-
существует огромное количество «ложных образов», т. е. аттракторов, не со-
совпадающих ни с одним из ключевых образов fp, 1 < /х ^ М.
При анализе обобщенной сети Хопфидда, построенной по описан-
описанному выше рецепту, был обнаружен чрезвычайно интересный эффект [51].
Оказалось, что эта нейронная сеть умеет «бороться» с ложными обра-
образами, делая неустойчивыми соответствующие им неподвижные точки
отображения.
Будем рассматривать входной образ {S,, 1 ^ i ^ N} как вектор S@).
Пусть А < оо. Стартуя с некоторого начального состояния S@), век-
fpp S(t) попадает в область притяжения какого-либо аттрактора не сразу,
i после некоторого переходного процесса, который можно назвать «раз-
Яышлением». Чем больше похож входной образ S@) на какой-либо ключе-
I 5Й образ, тем меньшее время необходимо нейронной сети для размыш-
j ения. Соответственно, чем меньше похож предъявленный образ S@)
It ранее запомненные, тем большее время требуется нейронной сети
дая принятия решения.
,,; По прошествии достаточно большого времени Г вектор S(t) может
водиться к устойчивой неподвижной точке. |Vi| > I, Si находится
¦Окрестности +1 или -1 и ViSi > 0 для всех г. Если же для какого-либо
Жйрона \Vi\ < 1, то активность нейронной сети хаотична.
1 При проведении численных экспериментов перед нейронной сетью
врвилась задача распознать предъявленный случайный образ S@) за ко-
Щчное число шагов Г = 250. По истечении этого времени сеть может
ркодиться в одном из трех состояний:
— состояние правильного распознавания, когда S(<) сходится к од-
одному из запомненных образов;
— состояние ошибочного распознавания, когда S(t) сходится к лож-
ложному образу;
— состояние «не знаю», когда нейронная сеть находится все еще
в стадии размышления, либо вышла на хаотический аттрактор.
Если обозначить через р\, р2, рз, соответственно, вероятность
ввильного распознавания, ошибочного распознавания и состояния
знаю» (pi + Р2 + рз = 1), то зависимость этих величин от «силы
аптических связей А», как показывают расчеты, выглядит следующим
эм (см. рис. 8.11).
190
8. Нейронные сети
о
Рис. 8.11. Типичная зависимость от параметра А вероятностей правильного рас-
распознавания (pi), ошибочного распознавания (р2) и состояния «не знаю» (р3).
При А"' = 0 хаос отсутствует и данная модель эквивалентна модели Хопфил-
да. При увеличении А вероятность правильного распознавания не только не
уменьшается, но, наоборот, увеличивается. При 0,3 < А~' < 0,5 все ложные
образы потеряли устойчивость и нейронная сеть либо дает правильный ответ,
либо переходит в состояние «не знаю»
Обратимся к результатам типичного расчета. В этой сети N = 128,
М = 8, образы ?,,, 1 ^ ц ^ M выбраны наугад.
При А = оо, как и в классической модели Хопфидда, вероятность
попасть в ложный образ значительно превышает вероятность правильного
распознавания. Но уже при А = 5 нейронная сеть намного реже попадает
в ложные образы, а при еще меньшем значении А практически все
ложные образы потеряли устойчивость.
Однако за эту удивительную способность бороться с ложными
образами приходится платить тем, что с уменьшением А увеличивается
время, необходимое нейронной сети для размышления, и увеличивается
вероятность того, что нейронная сеть не успеет принять решение за от-
отведенное время Г (кривая рз на рис. 8.11). В стандартной сети выход
на аттрактор происходил бы за 5-6 итераций. Тем не менее, существует
большой участок значений параметра А, при которых нейронная сеть
хорошо справляется с распознаванием за приемлемое время.
Заметим, что параметр А не влияет на количество и положение
в фазовом пространстве неподвижных точек. Он влияет лишь на их
устойчивость.
При большом А, как и в модели Хопфилда, рядом с запомненны-
запомненными образами могут находиться ложные образы. При уменьшении этого
параметра, как показывает анализ областей притяжения, первыми «поги-
«погибают» неподвижные точки, соответствующие ложным образам. В то же
время область притяжения неподвижных точек, которые соответствуют
запомненным образам, не только не уменьшается, но даже увеличивается.
В настоящее время общепризнанным в нейронауке является пред-
представление о важной роли хаоса в работе мозга. Большие периодические
участки энцефалограммы обычно свидетельствуют о приступах эпилеп-
8.5. Многослойные нейронные сети
191
сии. Излишняя упорядоченность во многих случаях свидетельствует о се-
серьезных заболеваниях. В литературе описано более десятка гипотез от-
относительно механизмов мозга, «использующих» динамический хаос. По-
Построенное обобщение модели Хопфилда позволяет выдвинуть еще одно
предположение. Хаос может быть одним из средств борьбы с «ложной»
памятью. Он может соответствовать состояниям «не знаю», в которых
информации для принятия решения, либо времени недостаточно.
8.5. Многослойные нейронные сети
8.5.1. Нейросети и задача интерполяции
Для модели Хопфилда прообразом служили динамические систе-
системы вида х = v(x), а основной задачей было конструирование систем,
обладающих ассоциативной памятью.
Однако не менее важным представляется другой круг проблем,
при решении которых желательно, чтобы вычислительные системы обла-
обладали аналогами интуиции и «умели учиться на собственных ошибках».
Приведем две типичные задачи.
Допустим, мы располагаем
прекрасной диагностической ап-
аппаратурой, которая дает обшир-
обширную информацию о состоянии
больных. Пусть кроме этого мы
имеем большой набор историй
болезней, показывающий, с ка-
какими заболеваниями обращались
пациенты. Было бы желательно
Иметь своеобразного компьютер-
компьютерного эксперта, который, исхо-
исходя из результатов обследований,
а также предыдущего опыта, вы-
высказывал бы мнение относитель-
относительно диагноза.
Эту задачу можно фор-
формализовать следующим образом.
Пусть результаты обследования
больного определяются набором
Переменных (а\,..., а^). Состо-
Состояние больного характеризуется
Точкой в этом N -мерном фазо-
фазовом пространстве (см. рис. 8.12). Разным заболеваниям в этом про-
пространстве, по-видимому, соответствуют различные группы близких точек.
Например, множество точек {Sm} характеризует пациентов с m-ным за-
заболеванием. Если точки множества Sm не близки, а случайным образом
разбросаны по пространству, то это факт в пользу того, что наша диа-
диагностика для этого заболевания неэффективна. (Нет одного или группы
Рис. 8.12. Типичная картина, возникаю-
возникающая в задачах диагностики
192
8. Нейронные сети
признаков, определяемых переменными а„, по которым можно было
бы отличать больных от здоровых.) Именно на этом этапе нужен опыт
и истории болезней. Допустим, нам удалось построить в этом многомер-
многомерном пространстве области G\,..., Gm,..., в каждую из которых входят
только точки соответственно из множеств Si,...,Sm,... и не входят
другие (см. рис. 8.12).
Тогда можно было бы создать компьютерную систему, которая
по результатам обследования, т.е. конкретному набору переменных
(S1,..., ujv) для данного больного определяла бы принадлежность соот-
соответствующей точки множеству Gm, 1 ^m^M. Это дало бы возможность
предположить, что мы имеем дело с заболеванием т. Если точка не по-
попала ни в одну из построенных областей, то это позволяло бы утверждать,
что пациент не болеет теми болезнями, выявлять которые должна была
бы предполагаемая диагностика.
Другими словами, нам надо решить задачу, которая сводится к про-
проблеме интерполяции в ЛГ-мерном пространстве, т.е. к определению зна-
значения функции в заданной точке в некоторой области по известному
набору значений в точках bi,...,b?. В задачах диагностики, например,
эта функция может равняться единице в области G\, двойке вС2,пвС„
и нулю вне всех этих областей. Несмотря на простоту постановки задачи,
при создании компьютерных систем обычно возникает множество труд-
трудностей. Во-первых, пространство может иметь очень высокую размер-
размерность, что, естественно, затрудняет интерполяцию. Во-вторых, мы обыч-
обычно не знаем, как уменьшить число переменных и воспользоваться каким-
нибудь простым логическим алгоритмом. В-третьих, области Gm могут
иметь достаточно сложную геометрию, к примеру, не быть выпуклыми.
Другая задача связана с прогно-
прогнозом. Пусть нам дан ряд измерений ве-
величины о — О],..., ojv . Исходя из этих
данных, надо предсказать значение
ajvfi. Допустим, что нам очень по-
повезло, и значение «m+i (то = 1,2,...)
зависит только от числа ат, т. е. суще-
существует зависимость
= f(am)-
(8.13)
В этом случае стратегия решения
задачи такова. Для простоты предполо-
предположим, что все элементы последователь-
последовательности {ат} принадлежат интервалу j,
т.е. функция / отображает этот ин-
интервал в себя. Рассмотрим плоскость
{ат,о,т+\}- Имеющаяся выборка из N элементов позволяет определить
N — 1 точку на этой плоскости: (ai,a2),(a2,a3),(*3>a4)j--. . Очевидно,
эти точки должны лежать на непрерывной однозначной кривой, урав-
уравнение которой задается формулой (8.13) (см. рис. 8.13). Следовательно,
Рис. 8.13. Задача прогноза поведе-
поведения динамической системы по вре-
временному ряду сводится к проблеме
интерполяции
8.5. Многослойные нейронные сети
193
нужно произвести интерполяцию по iV - 1 точке и приближенно най-
найти зависимость у — f(x). Обозначим эту функцию, приближающую /,
через /. В известных точках кривой эти функции должны совпадать:
am+i=f(am), m=l,...,N-\. (8.14)
Пользуясь построенной функцией /, можно подставить в нее
значение пц и найти приближенное значение ац+\: aN+\ и /(а^).
Существует множество методов построения функции / или алго-
алгоритмов интерполяции. Два самых простых иллюстрирует рис. 8.14. В пер-
первом случае значение / в точке х считается таким же, как у известного
ближайшего соседа из множества {хт}, 1 ^ т < N - 1. Естественно,
такая интерполяция кусочно-постоянными функциями имеет большой
недостаток. Во-первых, ее точность невелика, во-вторых, она «склеива-
«склеивает» образы различных точек х, принадлежащих одному интервалу.
¦*т+1.,
¦т+\
f
Рис. 8.14. Простейшие типы интерполяции: а) интерполяция кусочно-постоян-
кусочно-постоянными функциями; б) интерполяция кусочно-линейными функциями
Во-втором случае интерполяция производится с помощью кусоч-
кусочно-линейных функций. Здесь точность выше. Кроме того, интерполяция
локальна, — чтобы определить приближенное значение функции в про-
промежуточных точках интервала, достаточно знать ее только в краевых
точках интервала (см. рис. 8.14).
Наконец, можно действовать в соответствии с методом Лагранжа.
Пусть значение функции в точке ж, равно yi. Приближенное значение /
вычисляется как сумма N - 1 слагаемого
(x-x2)(x-x3)...(x-xN^)
J/JV-1;
(х - х2)(х -х3)...(х- xN-2)
(8.15)
(xN-\ - Ж|)(ЖЛГ_) - Х2) . . - (Ждг.! - Ждг-2)
Очевидно, множитель при у\ таков, что в точке х\ равен единице,
а в точках х2,... ,х^-\ равен нулю. Точно так же множитель при у2
равен единице в х2 и нулю в остальных точках множества {хт}.
7 1ак.:
194 8. Нейронные сети
Поэтому график многочлена (8.15) проходит через все точки (ж,-,2/;)>
1 ^ i ^ N — 1. Поскольку, чтобы задать многочлен степени к, достаточ-
достаточно задать его значения в (к + 1)-й точке, то формула (8.15) позволяет
находить не приближенные, а точные значения, если функция у — f(x)
является многочленом степени ниже iV — 1.
Несмотря на высокую точность, этот способ интерполяции также
обладает существенными недостатками. Здесь велик объем вычислений,
интерполяция нелокальна — изменение значения уь в точке х/. скажется
на всех точках функции /.
Наконец, следует иметь в виду, что при интерполяции, по-види-
по-видимому, придется использовать ЭВМ, которая хранит числа с конечной
точностью и, соответственно, вносит ошибку округления. Это может
привести к тому, что в ходе вычислений придется делить одно малое
число, заданное с большой погрешностью, на другое. Естественно, это
понизит точность, с которой приближается функция /.
Теория интерполяции является одной из наиболее развитых обла-
областей вычислительной математики. Однако попытка использовать боль-
большинство алгоритмов в случае пространства высокой размерности или
в ситуациях, когда элементы множества {zj} и {?/,¦} заданы с некоторой
погрешностью, наталкивается на большие трудности. Даже задача поиска
соседей (возникающая, если мы хотим воспользоваться локальными ал-
алгоритмами интерполяции) в многомерном пространстве может оказаться
совсем не простой и потребовать использования специальных численных
методов.
Нейронные сети определенным образом решают интерполяцион-
интерполяционные задачи. В ряде случаев эти решения оказываются вполне удовлетвори-
удовлетворительными. На их основе удается создавать замечательные распознающие,
диагностирующие, предсказывающие системы. Однако теория таких си-
систем, позволяющая априорно оценивать, в каких задачах на что можно
рассчитывать, сегодня находится в начале своего развития.
8.5.2. Обучение персептрона
Основные идеи и проблемы, возникающие при создании интер-
интерполирующих сетей, можно проиллюстрировать на примере простейших
однослойных сетей, предназначенных для распознавания изображений.
Такие сети были предложены Мак-Каллоком и Питтсом в пятидесятые
годы и названы персептронами (от английского perception — восприятие).
Схема такой системы показана на рис. 8.15.
Допустим, что система обучена, т.е. веса о>; подобраны таким
образом, чтобы распознавать предъявляемые образы х. Будем считать,
что х — n-мерный вектор х = (х\,...,хп). Персептрон действует сле-
следующим образом. Вначале суммирующий элемент вычисляет величину
п
S = ~Y^Xi<i>i. Затем этот сигнал подается на некоторый нелинейный
пороговый элемент. Если величина S превышает порог, то элемент сра-
срабатывает (система говорит, к примеру, «да»). В противном случае система
не срабатывает и персептрон отвечает «нет».
8.5. Многослойные нейронные сети
195
S
в S
Рис. 8.15. Схема простейшего персептрона, который должен отличать согласные
буквы от гласных
Как же обучить такую систему? Для этого, так же как в модели
Хопфилда, надо предъявить множество ключевых образов {?к} и тех
ответов, которые, по нашему мнению, нейронная сеть должна давать
по предъявлении этих ключевых образов. Обозначим множество этих от-
ответов П(?к). Множество упорядоченных пар {?ц,П(?к)} будем называть
обучающей выборкой.
Для примера представим себе простейший персептрон, которому
предъявляются черно-белые изображения различных букв и который
должен определять, является ли показанная ему буква гласной. Если эта
буква гласная, то на выходе должно возникнуть число 1 («да»), если
согласная, то 0 («нет»).
Чувствительное устройство (например, сканер), которому предъ-
предъявляется изображение, разобьем на элементарные квадратики (см.
рис. 8.15). Пусть, если тп-й квадратик «темный» (черных пикселов в нем
больше, чем белых), то величина хт равна единице, в противном слу-
случае — нулю. То есть ?i = (х\,... ,х]„), где 1 в индексе вектора ?
соответствует первой предъявленной букве, ?2 = (жр ¦ • • >zm) и т-Д-
Идею обучения (т. е. настройки весов шт) можно пояснить с помо-
помощью следующей притчи. Допустим, что в некотором королевстве королю
приходится довольно часто принимать ответственные решения. Для этого
ему надо советоваться со своими министрами или экспертами. Других
экспертов взять ему неоткуда и нужно опираться на имеющихся. Как
повысить эффективность принимаемых решений? Надо смотреть, ка-
какие советы давали эксперты и были ли правильны принятые решения.
На основе этого опыта король может выяснить, как следует относиться
к экспертам. Естественно, решать проблемы голосованием неразумно.
Одних экспертов следует слушать и поступать так. как они советуют, дру-
других следует слушать и поступать наоборот. Различное отношение короля
к разным экспертам и определяют величины {шт}.
Алгоритм обучения можно описать следующим образом: если
на (i + 1)-м шаге обучения персептрон выдал правильный ответ, то
веса связей не меняются
ч4+1=. (8.16)
г
196 8. Нейронные сети
Здесь нижний индекс соответствует номеру связи, верхний — шагу
по времени. Пусть хт — значение на входе т-го нейрона.
Допустим, ответ неправильный. Пусть он равен нулю, в то время
как при правильном ответе персептрон должен выдавать единицу. Тогда
a4+1=a4 + zm. (8.17)
Иными словами, мы увеличиваем вес, значение элементов, голосую-
голосующих «за» в этом случае.
Если выдан неправильный ответ «единица», то
a4+1=fc4-zm. (8.18)
После этого на вход подается тот же образ и вновь корректируются
связи, если ответ неправильный.
Формулы (8.16), (8.17), (8.18) могут быть записаны в более простой
и компактной форме, если ввести величину рассогласования между реаль-
реальным ответом на г-м шаге R' и желаемым ответом Л—6 = (Д'(?,) — П(?,)).
(Аргумент ?s показывает, что нейронной сети был предъявлен s-й ключе-
ключевой образ.)
Тогда формулы (8.16), (8.17), (8.18) можно записать в виде
<"m+1=<4. + Ai, ^i = 6flXi. (8.19)
В последнем равенстве 6 — уже введенная величина рассогласования.
Нетрудно проверить, что домножение на величину ж*, которое принято
в литературе, не меняет формул с (8.16) по (8.18). Числовой коэффициент
г) < 1 носит название «скорости обучения». Этот коэффициент вводят,
чтобы изменение весов связей при обучении не было слишком быстрым.
Этот алгоритм обучения получил название «дельта-правила».
Встает вопрос, каким входным образам ?s можно обучить пер-
персептрон. В начале развития этого направления исследований казалось,
что принципиальных ограничений здесь не существует: взяв достаточно
большой входной вектор х и обучая нейронную сеть достаточно долго,
можно аппроксимировать любую область G в пространстве входных обра-
образов (если точка оказалась внутри области G, персептрон говорит «да»,
если вне ее — «нет»).
Исследование простейших персептронов позволило разделить два
важные понятия, связанные с этими системами. Первое понятие —
персептронная представляемость. Определенная логическая функция или
множество в пространстве входных образов обладает этим свойством, если
существует набор весов {шт}, с помощью которых в ответ на заданные
ключевые образы {?„} персептрон будет давать желаемые ответы {fi(?s)}.
Однако для того, чтобы настроить веса таким образом, должна существо-
существовать некоторая систематическая обучающая процедура, позволяющая
по обучающей выборке найти желаемое множество весов {шт}. (Такой
процедурой может быть, например, обсуждавшееся дельта-правило.) На-
Наличие такой процедуры для конкретных задач означает, что персептрон
обладает свойством обучаемости.
8.5. Многослойные нейронные сети
197
Исследования Ф. Розенблатта, проведенные в 60-е годы, показали,
что простейшие персептроны при весьма общих условиях обладают свой-
свойством обучаемости, если функция, которую они должны реализовать,
относится к персептронно представляемым. Но как велико последнее
множество? И вообще, существуют ли функции, которые в него не входят?
Работы М. Минского, также выполненные в 60-е годы, показали,
что этих функций очень много, что персептронной представляемостыо
не обладают даже очень простые функции. Этот вывод заставил боль-
большинство исследователей прекратить работы в области нейронных сетей.
Возрождение интереса к интерполирующим сетям в 80-е годы было связа-
связано с переходом к многослойным нейронным сетям и к новым алгоритмам
обучения.
Классический пример М. Минского связан с функцией «исключа-
«исключающее ИЛИ». Это простейшая функция двух аргументов, каждый из ко-
которых может быть нулем или единицей. Она должна принимать значение
единица, только когда один из аргументов равен единице. Обозначим
один вход через х, другой через у. Соответственно входные векторы ?
будут иметь две компоненты (?х,?у)- Обучающие пары для этой функции
представлены в таблице.
0
1
0
1
0
0
1
1
п
0
1
1
0
точки
Ао
Во
В\
А\
В\ в плоскости
Этим образам соответствуют точки Aq, Bq, A\
UxAy} (см. рис. 8.16).
Обратимся теперь к простейшему пер-
септрону. Суммирующий элемент на выходе
дает функцию S = и)\?х + шг^у. Переключе-
Переключение нелинейного элемента будет происхо-
происходить при выполнении условия
ш\(х + u>2iy = G, (8.20)
где в — порог. Мы считаем, что у нас
есть нейрон Мак-Каллока—Питтса — П =
2 —• В таком представлении он на
выходе дает +1 или 0, а не +1 и — 1,
как раньше. Уравнение (8.20) определяет Рис. 8.16. Пространство вход-
некоторую прямую на плоскости {?z,?j,}.
Над прямой он будет давать одно значение
выхода (например, +1), под прямой — другое (например, 0). Точки, соот-
соответствующие функции «исключающее ИЛИ», должны лежать в вершинах
198
8. Нейронные сети
квадрата AqB\A\Bq (см. рис. 8.16). Причем точки Aq и А\ должны лежать
по одну сторону от прямой, а точки Во и В\ по другую. Но из рис. 8.16
ясно, что такой прямой не существует. Точки Aq,A\ и Bq,B\ нельзя
разделить прямой. Функции, обладающие этим свойством, называются
линейно неразделимыми.
Если рассмотреть ситуацию, когда персептрон имеет п двоичных
входов, то число возможных входных образов будет равно 2". Соответ-
Соответственно, число логических функций от этих аргументов будет 22 . Если
в случае двух аргументов из 16 различных возможных функций линейно
разделимы 14, то при п — 6 из примерно 1,8 х 1019 разделимы только
1,5 х 107. Функции, которые сможет распознать рассмотренный персеп-
персептрон, являются не правилом, а редким исключением даже при небольших
значениях п.
Возвращаясь к притче с королем и министрами, можно сказать, что
при такой системе управления могут быть приняты только достаточно
простые решения. Поэтому нужна более сложная структура.
8.5.3. Многослойные сети
Вспомним задачу о диагностике. Пусть у нас, как на рис. 8.16,
на вход сети подается два диагностических параметра ?х и ?у. Для просто-
простоты будем считать, что это непрерывные величины. Пусть областью G, ко-
которая соответствует болезни, является треугольник (см. рис. 8.17). Можно
ли, исходя из рассмотренной нейронной сети, построить систему для диа-
диагностики в этом случае? Рассмотренная ранее однослойная сеть позволяла
в одной полуплоскости говорить «да», в другой полуплоскости — «нет».
Треугольник можно рассматривать как фигуру, вырезанную из плоскости
тремя прямыми А\А2, В\В2, С\С2 (пусть у нас есть три нейрона в пер-
первом слое, на каждый из которых подается вектор (?х,?у) (см. рис. 8.18)).
Подберем веса {ш} так, чтобы первый нейрон говорил «да» (т. е. на вы-
выходе вырабатывал 1), когда точка в плоскости (?х,?у) лежит выше A\Aj,
о
Рис. 8.17. Простейшая задача диа-
диагностики, в которой надо опреде-
определить, попадет ли точка внутрь за-
заштрихованного треугольника
Рис. 8.18. Простейший двухслойный
персептрон, который может решить
задачу, представленную на рис. 8.17
8.5. Многослойные нейронные сети
199
что, очевидно, можно сделать. Второй нейрон будет говорить «да», когда
точка лежит ниже B\Bj, третий — когда ниже С\С2- Выходы всех этих
нейронов подадим на один нейрон второго слоя, который говорит «да»,
когда все три нейрона предыдущего слоя говорят «да». Это можно сделать,
установив веса связей между элементами первого слоя равными единице,
а порог элемента второго слоя установив чуть меньше трех.
Итак, переход от однослойной к двухслойной нейронной сети по-
позволяет построить диагностирующую систему в этом случае. В притче
о короле это означает, что каждому министру (нейрону первого слоя)
нужен штат экспертов. Они определяются весами {ш„} нейронов первого
слоя. Но построенная система имеет очень серьезный недостаток. Фи-
Фигуры, которые можно реализовать в плоскости {?х,€у}> должны лежать
по одну сторону от прямой, т. е. фигура должна быть выпуклой. Фигуры,
представленные на рис. 8.12, которые вполне могут возникнуть в задачах
компьютерной диагностики, двухслойной сети недоступны (см. также
рис. 8.19).
Однако с этой задачей вполне может справиться трехслойная сеть
(см. рис. 8.20). Представим себе, что во втором слое имеется два нейрона.
Один говорит «да», когда точка попадает в треугольник А\ AjA^. Другой
говорит «да», когда точка не попадает в треугольник В\В2Вз. И нейрон
в выходном третьем слое говорит «да», когда «да» сказали оба нейрона
второго слоя. Как видим, чтобы принимать решение в таких случаях,
королю надо иметь министров, к мнению которых следует, вообще
говоря, относиться по-разному. Тем надо иметь помощников, которым,
в свою очередь, надо иметь экспертов.
Рис. 8.19. В задачах компью-
компьютерной диагностики могут воз-
возникать невыпуклые области
Рис. 8.20. Трехслойная нейронная сеть мо-
может решить задачу, которую иллюстрирует
рис. 8.19
Если {?,} не двумерные векторы, а векторы более высокой размер-
размерности, то придется иметь дело не с плоскостью, а с пространством, и не
с прямыми, а с гиперплоскостями. Однако принципиально это картины
не меняет.
200
8. Нейронные сети
Из сказанного ясно, что возможности трехслойных сетей велики.
Но встает вопрос, как же учить такие сети. Как подстраивать веса в каждом
из трех слоев, исходя из имеющейся обучающей выборки? По существу,
в королевстве надо принять общие законы, определяющие, как следует
менять отношение к министрам, помощникам, экспертам в зависимости
от результатов их работы. Поэтому большой интерес к таким сетям
оказался связан с созданием эффективных алгоритмов обучения.
8.5.4. Алгоритм обратного распространения ошибки
Идея этого алгоритма проста. Королю, министрам, помощникам
на своем уровне следует оценивать, чей вклад в принятие неверного
решения был наибольшим. Отношение к ним следует менять в первую
очередь. С другой стороны его можно рассматривать как некоторое
обобщение дельта-правила.
В качестве нелинейного элемента в трехслойных сетях часто ис-
используют не нейрон Мак-Каллока—Питтса, а нейрон, реализующий
функцию, называемую сигмоидом (см. рис. 8.21)
Эта функция удобна, поскольку она имеет простую производную
dy
dx
= »(!-»)¦
(8.21)
Рассмотрим нейронную сеть, представленную на рис. 8.22.
У,,
1
0 х
Рис. 8.21. Функция «сигмоид»,
обычно используемая при постро-
построении нейронных сетей
Рис. 8.22. При обучении трехслойных
нейронных сетей часто используется
алгоритм обратного распространения
ошибки
Прямой проход
Пусть j — типичный элемент выходного слоя, * — типичный эле-
элемент слоя, предшествующего выходному. Активность элемента выходно-
выходного слоя определяется по следующей схеме. На первом шаге вычисляется
взвешенная сумма
Y^ (8-22)
8.5. Многослойные нейронные сети 201
где у,- — уровень активности г-го элемента в предшествующем слое,
u>ij — все связи между i-м и j-м элементом.
Затем нелинейный элемент вычисляет активность выходного эле-
элемента
Пусть мы имеем уже обученную трехслойную сеть, на вход которой
подается некоторый вектор. Тогда по этому алгоритму осуществляется
сначала переход от нейронов первого слоя к элементам второго, а затем
от элементов второго к нейронам третьего, которые и дадут «ответ сети»
на «заданный вопрос». На этом работа сети кончается.
Если сеть еще не обучена, то результат, полученный после прямого
прохода, может нас не устроить. При предъявлении входного вектора ?s
нз обучающей пары на выходе может быть получен после прямого прохода
ответ у(?5), не совпадающий с желаемым П(?я). Тогда нужен обратный
проход, позволяющий корректировать веса ш^.
Обратный проход
Шаг 1. После определения активности выходных элементов у,-
в результате прямого прохода вычисляется ошибка
3
где j/j и ?lj — j-t компоненты соответствующих векторов; аргумент
цля краткости будем опускать. Если е = 0, то веса не меняются. В про-
противном случае надо перейти к следующему шагу.
Шаг 2. Оценка того, насколько быстро меняется ошибка при из-
изменении активности выходного элемента
EAj = -^=yj-nj. (8.24)
Шаг 3. Оценка того, насколько быстро меняется ошибка при из-
изменении суммарного входа выходного нейрона — Xj
Именно здесь и используется «удобное» выражение для производ-
производной сигмоида (8.21).
Шаг 4. Оценка того, как быстро меняется ошибка при изменении
Весов связей ц/у
де де дх<
= -— = —-. —^ = Eli'¦ Уг- (8-26)
du)ij dxj oujij
202 8. Нейронные сети
Значение последней производной получается при дифференциро-
дифференцировании формулы (8.22).
Шаг 5. Оценка того, насколько велик вклад в ошибку i-ro элемента
слоя, предшествующего выходному
где мы вновь воспользуемся формулой (8.21).
Шаг 6. Подстройка весов ш^ с помощью некоторого варианта
дельта-правила
ыу(п + 1) = wy(n) + vEWij(n), n = 0,1,2,..., (8.28)
где п — номер прохода (подразумевается, что все величины в фор-
формулах (8.23)—(8.27) относились к проходу п), rj — скорость обучения,
коэффициент, лежащий в интервале от 1 до 0,01.
Шаг 7. Получив на шаге 5 величину ЕА{ для нейронов слоя, пред-
предшествующего выходному (например, второго слоя, если выходной —
третий), мы оказались в точности в том же состоянии, как после ша-
шага 2 для нейронов выходного слоя. Другими словами, заменив EAj
на EAi, мы можем, пользуясь формулами (8.23)—(8.28), подстроить ве-
веса, связывающие элементы слоя, предшествующего выходному, с его
предшественником (например, первого со вторым).
После того, как все веса в нейронной сети подстроены, опять
осуществляется прямой проход. Величина п увеличивается на единицу.
Вычисляется величина ошибки е (шаг 1). И если она неприемлема
(превышает точность, с которой мы хотим обучить сеть), то следует
перейти к шагу 2 и т. д.
Метод обратного распространения ошибки по своей идее близок
к методу градиентного спуска. В этом методе при поиске максимума
функции и(х\,..., хр) выбирается начальная точка а а (а\,..., ар) и на-
находится направление, при движении в котором функция убывает быстрее
„ аи(») euU)
всего. Для этого вычисляются частные производные -gyp, • • •, -j^ и де-
делается шаг по градиенту. Это дает новую точку В. И так далее. Грубо
говоря, в методе градиентного спуска мы с помощью метода Эйлера
решаем уравнение х = — -^, аттрактор которого соответствует минимуму
функции U.
Во многих случаях при минимизации функционалов применение
метода градиентного спуска и его модификаций дает отличные резуль-
результаты. Именно поэтому под разными названиями в различных областях
исследований он неоднократно переоткрывался. То же самое относится
и к алгоритму обратного распространения ошибки. Он тоже является
одним из самых известных, простых и надежных методов обучения ней-
росетей. После того, как его предложил П. Вербос в 1974 г., он также
несколько раз переоткрывался.
8.5. Многослойные нейронные сети 203
Оба метода имеют ряд важных ограничений. С помощью обоих
этих методов ищется локальный, а не глобальный минимум некоторой
потенциальной функции. Сменив начальную точку а, мы можем по-
попасть в другой локальный экстремум. Кроме того, если потенциал имеет
«овражную» структуру, т.е. путь к минимуму идет по дну глубокого
извилистого «ущелья» функции U(x\,...,х„), то эти методы могут по-
потребовать много времени. Анализ ряда типичных задач показывает, что
структура потенциала, возникающего при обучении нейросетей, часто
оказывается именно такой.
Кроме того, при обучении многослойной сети может возникнуть
явление, называемое «параличом сети». Оно проявляется в том, что,
несмотря на длительное время обучения, ошибка может практически
не убывать, оставаясь достаточно большой. Такая ситуация может воз-
возникнуть, если веса связей и значения активностей велики по модулю.
При этом вход ряда нейронов оказывается на «крыльях» сигмоида, где
производная мала. Поэтому сеть может слабо реагировать на коррекцию
весов, Это одна из причин, по которой часто используют не сам алгоритм
обратного распространения ошибки, а его модификации. Другая причи-
причина — необходимость обойтись меньшим числом нейронов и повысить
надежность работы сети. (В самом деле, если два нейрона первого или
второго слоя говорят «да» или выдают близкие значения на всей обуча-
обучающей выборке, то, очевидно, можно обойтись одним.) Разработка таких
подходов, которая сейчас интенсивно ведется, важна и в связи с пробле-
проблемой «прозрачности сети». Допустим, что обученная сеть оказалась очень
эффективной при решении некоторой задачи. Тогда желательно не только
считать и диагностировать, но и понимать. Хорошо было бы несколько
упростить сеть, чтобы понять, какие признаки являются решающими
для сети. Другими словами, сделать ее работу «прозрачной».
При изучении нелинейных явлений нейронные сети могут высту-
выступать в двух различных качествах. Они могут использоваться для анализа,
диагностики, прогноза, поиска закономерностей, которые в дальней-
дальнейшем могут быть использованы при построении традиционных моделей.
В самом деле, прогнозирующая сеть сама по себе тоже представляет
своеобразную имитационную модель изучаемого процесса.
Нейронные сети также могут быть использованы как инструмент
для моделирования различных нелинейных систем. На сегодняшний день
они представляют собой один из немногих прообразов организованной
сложности, характерной для ряда физических, многих биологических,
технических и социальных систем.
Энтропии и размерности аттракторов
9.1. Энтропия динамической системы
9.1.1. Энтропия как мера неопределенности. Информация
В теории информации энтропию вводят для систем, которые могут
находиться в некоторых состояниях, которые мы будем обозначать х;,
с некоторыми вероятностями р; = p{x.i) [134]. Допустим, мы узнали,
что система достоверно находится в состоянии х*. Насколько ценно,
информативно такое сообщение? Очевидно, что это зависит от «неопре-
«неопределенности» системы. Скажем, если все р< кроме рн равны нулю, то
почти ничего нового мы не узнаем. Если же различных состояний мно-
много и они почти равновероятны, то сообщение очень сильно уменьшает
неопределенность, а потому содержит значительную информацию.
Проблема количественного измерения неопределенности и ин-
информации в данном контексте рассматривалась Шенноном. Им было
показано, что при весьма разумных предположениях очень полезной
характеристикой состояния неопределенности (и, соответственно, полу-
получаемой информации) оказывается энтропия, определяемая как
Я = -"^2 Pi 1°8 Pi-
i
В свою очередь мерой информации, содержащейся в сообщении, является
изменение энтропии. В частности, если сообщение полностью определяет
текущее состояние системы, то после его получения Н = 0. Тогда
информация, содержащаяся в сообщении, / = АН = Щ.
Логарифмы используют либо натуральные, либо по основанию 2.
В последнем случае единица информации называется бит (сокращение
от binary digit). Например, если некоторая система может с равной
вероятностью находиться в одном из двух состояний, то сообщение о ее
текущем состоянии несет информацию в 1 бит.
9.1.2. Энтропия динамической системы
Пусть задана некоторая динамическая система и ее инвариантная
мера, которую будем считать физической. Разбив фазовое пространство
на непересекающиеся множества Ai с диаметром не больше е и вычислив
меру каждого р, = fi(Ai), можно определить информацию, которую дает
знание текущего состояния системы с точностью е. А что будет происхо-
происходить с нашими знаниями с течением времени? Если система хаотическая,
9.1. Энтропия динамической системы 205
т.е. перемешивающая, то с течением времени образ почти всех А^ будет
иметь непустое пересечение со всеми остальными А,-. Это означает, что,
хотя при t — 0 неопределенность с точностью е отсутствовала, в даль-
дальнейшем она будет увеличиваться. Перемешивающая система с течением
времени увеличивает неопределенность своего состояния. В таком случае
иногда говорят, что система производит информацию. Скорость про-
производства информации или неопределенности при е —> 0 называется
(метрической) энтропией динамической системы (это пока не строгое
определение, а пояснение сути дела).
В качестве примера рассмотрим динамическую систему
хп+] = 2xnmod 1, 0 ^ х < 1. (9.1)
Ее физическая мера непрерывна, однородна, постоянна; плотность р = 1.
Если мы разобьем отрезок [0,1) на N частей длиной е — jy, то мера
каждого из них р,- = е, а энтропия системы Н = —iVeloge = logiV.
Для простоты будем считать, что N — 2*. Тогда определение текущего
состояния системы с точностью е даст информацию к бит.
Допустим, теперь известно, что исходное состояние принадлежит
некоторому элементу. Тогда нам известно, что одно из р,- = 1, остальные
Pi = 0, j ф i (внутри же г-го интервала распределение вероятности
будем считать равномерным). Поэтому после измерения с точностью е
в начальный момент неопределенность отсутствует, а энтропия системы
Но = 0. На следующем шаге образом е-отрезка будут два аналогичных
отрезка, плотность распределения станет вдвое шире и вдвое ниже. Обо-
Обозначим их номера г\, %2, р., = Pi2 =; \, тогда Н\ = log2. Аналогично
можно показать, что Hi = 21og2, ..., Ht = Hog2, t ^ к. На к-и шаге
образ исходного отрезка покроет весь отрезок [0, 1) и далее энтропия уве-
увеличиваться не будет. Таким образом, за одну итерацию неопределенность
возрастает на log2 или на 1 бит, т.е. система производит информацию
со скоростью 1 бит за итерацию. Забегая немного вперед, отметим, что
метрическая энтропия в данном случае и будет равна К = log 2.
Если вспомнить, что данная система описывает сдвиг Бернулли
(см. введение), то интерпретация становится очевидной. Конечная точ-
точность е означает, что мы знаем конечное число к = Iog2(j) двоичных
разрядов в представлении числа. Каждая итерация означает сдвиг числа
влево и потерю одного известного знака. За к итераций будут потеряны
все известные знаки, и мы ничего не сможем сказать о состоянии системы
в тот момент.
Заметим, что энтропия динамической системы К определяет время
предсказуемости для динамической системы: если относительная погреш-
погрешность данных о ее состоянии равна е, то
T^'l
Заметим, однако, что предсказуемость можно понимать в двух смыслах:
1) «объемном», как нарастает количество фазовых объемчиков Ai, по ко-
206 9. Энтропии и размерности аттракторов
торым расползается пятно первоначальной погрешности, и 2) «линей-
«линейном», как нарастает разница между истинной и возмущенной траекторией
||у>((х) - <р((х + ебх) ||. Энтропия К связана с первой трактовкой предска-
предсказуемости, вторая трактовка связана с понятием показателей Ляпунова А;,
о которых речь пойдет в следующей главе. Во втором случае также можно
ввести несколько иное время предсказуемости
Amaxlog-,
О
однако по порядку величины обе оценки обычно совпадают, поэтому
пользоваться можно любой из них. Таким образом, энтропия К является
весьма существенной характеристикой динамической системы.
Дадим теперь определение метрической энтропии динамической
системы, или энтропии Колмогорова—Синая. Пусть дана динамическая
система, например, отображение xn+i = f(xn) и ее инвариантная мера ц
на компактном носителе А (см. гл. 5). В большинстве практически важ-
важных случаев это физическая мера и аттрактор, но, вообще говоря, можно
определить энтропию и для других компактных инвариантных множеств.
Пусть также задано разбиение А на конечное число измеримых мно-
множеств А{. Далее будем обозначать множество точек, отображаемых в А{
отображением f*, как f~k(Ai). Рассмотрим теперь разбиения, порождае-
порождаемые таким «обратным» отображением:
• на первом шаге разбиение на множества А) := А;;
• на втором шаге разбиение на A\J^. = А^ П f~' (Ai2), т. е. это те точки
из множества -4^, которые на следующем шаге попадут в Ai2;
• на третьем шаге разбиение на A\Jii:>:= А^ П f~'(.4,-2) П Г~2(^,),
т. е. это те точки из множества А^, которые на следующих двух
шагах попадут сначала в А^, а затем в А^;
• и т. д.
Затем вычислим энтропию каждого разбиения
•|>2-¦¦•*
Если обозначить е = max diam Aj, то энтропией динамической системы
i
называется
К (и) = lim Urn f#(*+I) - Я<*Л = lim Urn k
?_0fc->oo\ / <r->0fc—oo
т.е. асимптотический прирост неопределенности для разбиения беско-
бесконечно малого диаметра. Иногда предел к —» оо сам по себе влечет
измельчение разбиений, тогда первый предел не нужен.
Определенная таким образом энтропия зависит от использованной
меры. Если о мере ничего не говорится, то подразумевается «физическая
9.2. Размерности аттракторов динамических систем 207
мера». Кроме метрической существует еще и так называемая тополо-
топологическая энтропия [20], определение которой не использует понятия
меры. Мы не будем на этом останавливаться, упомянем лишь только,
что топологическая энтропия равна sup К{ц), где sup берется по всем
ц
эргодическим инвариантным мерам.
Отметим одно интересное свойство энтропии. Если отображение ip
динамической системы обратимо, то энтропия для прямого и обратного
отображений (но одной и той же меры ц!) совпадает. Но важно, что
чаще всего физические меры для прямого и обратного отображения
не совпадают, поэтому противоречия со здравым смыслом здесь нет.
Заметим также, что на практике определение энтропии для ее рас-
расчета практически никогда не используется. Либо оценивается энтропия jfiT
при помощи ляпуновских показателей, либо обобщенная энтропия Ki
при помощи корреляционного интеграла.
9.1.3. Обобщенные энтропии (энтропии Реньи)
Обычная, или шенноновская, энтропия обладает одним замеча-
замечательным свойством: если необходимо рассчитать суммарную энтропию
двух независимых подсистем, то она будет равна сумме энтропии каж-
каждой из них. То же свойство, соответственно, будет справедливо и для
информации.
Однако, если отказаться от этого свойства, то можно ввести и другие
меры неопределенности состояния — энтропии Реньи Hq:
Покажем, что при q —> 1 Ня стремится к обычной шенноновской энтро-
энтропии. Положим q = 1+7, 7 < 1 • Тогда р\ = р{-р[ = р^1"* = PiA+7 lnp»).
Я, =li
7-
1+7
Если подставить в определение энтропии К Hq вместо Н, то получим
обобщенные энтропии динамической системы Кя. Наибольший интерес
среди них представляет Кг, для которой существуют удачные алгоритмы
расчета, но об этом речь пойдет ниже в разделе про обработку временных
рядов.
9.2. Размерности аттракторов динамических систем
Поскольку в теории динамических систем используют геометриче-
геометрические характеристики множеств в фазовом пространстве, не удивительно,
что речь заходит и о размерностях. Кроме того, размерность — одна
208 9. Энтропии и размерности аттракторов
из характеристик, которую можно применять как к обычным евклидовым
пространствам и их областям, к торам, сферам и т.д., короче, к мно-
многообразиям, так и к фрактальным множествам типа канторова. Более
того, определение фрактального множества основано как раз на понятии
размерности.
Важны размерности еще и потому, что это одни из немногих харак-
характеристик, которые в некоторых случаях можно оценить по временному
ряду, получая таким образом существенную характеристику динамичес-
динамической системы непосредственно по экспериментальным данным.
Размерностей, однако, существует много. Не все они одинаково
важны, поэтому мы остановимся только на наиболее часто встреча-
встречающихся.
Для чего может пригодиться знание размерности? Размерность ха-
характеризует сложность аттрактора динамической системы, т. е. позволяет
дать ответ на вопрос, какое минимальное количество переменных долж-
должна включать соответствующая математическая модель, или хотя бы дать
оценку этой величины (чаще всего снизу).
9.2.1. Геометрические размерности
Наиболее важной характеристикой множеств является топологи-
топологическая размерность dr. Это наиболее привычная всем величина, кото-
которая равна п для n-мерного евклидова пространства Шп или п-мерного
многообразия (которое локально эквивалентно R"). Однако ее можно
определить и для более сложных множеств, например, канторова [87].
Первое общее определение размерности было дано Л. Брауэром
для компактов и метрических пространств и строится по индукции.
Пустому множеству приписывается размерность d = — 1. Далее, перего-
перегородкой между множествами А и В называется замкнутое множество Ф,
такое что его дополнение — это сумма двух множеств С и D, С П D = 0,
из которых одно содержит А, а другое — В. Предположим, что дано
определение множества и пространства размерности ^ п. Тогда говорят,
что пространство X имеет размерность ^ п+ 1, если между любыми дву-
двумя замкнутыми множествами А и В, А П В = 0, имеется перегородка
размерности ^ п.
Например, точка имеет размерность 0, поскольку две не совпада-
совпадающие точки можно считать разделенными пустым множеством. Счетное
множество точек также имеет размерность 0. Прямая имеет размерность 1,
так как любые два не пересекающихся отрезка с не совпадающими кон-
концами можно разделить точкой, плоскость можно разделить линией, и т. д.
Канторово множество имеет размерность d? = 0 (оно не содержит ни
одного отрезка и любые его части можно считать разделенными пустым
множеством).
Другой подход к понятию размерности был предложен А. Лебегом
(хотя строгое доказательство утверждений принадлежит также Л. Брауэру)
и определяется посредством покрытий. Пусть дан компакт X и его
покрытие открытыми множествами диаметра не более е. Размерностью
9.2. Размерности аттракторов динамических систем 209
называется наименьшее число п такое, что для любого е > 0 существует
такое покрытие, что каждая точка X принадлежит не более чем п + 1
покрывающему множеству. Тот факт, что топологическая размерность
канторова множества равна 0, также очевиден — его можно покрыть
непересекающимися отрезками, так что каждая точка будет принадлежать
только одному из них.
Другой важной размерностью является хаусдорфова размерность,
которая и позволяет дать определение фрактального множества. Она
также связана с покрытием исследуемого множества или метрического
пространства множествами А* такими, что diam.4j < е. Далее, пусть
т(е,р) — inf X)(diam Ai)p, где нижняя грань берется по всем возможным
{ЛЛ i
покрытиям с diartiA,- < e. Тогда хаусдорфова размерность определяется
как dB = sup [р: supm(s,p) > О}.
?>0
Смысл этого определения можно пояснить на следующем примере.
Возьмем квадрат со стороной А на плоскости в трехмерном простран-
пространстве и покроем его кубиками со стороной е. Количество таких кубиков
N(e) = G) . а диаметр кубика d — л/Зе. Здесь множитель л/3 возникает,
поскольку мы покрываем плоскость трехмерными кубиками. Далее со-
составим сумму s(e,p) = ^2,dp = N(e)dp = Аер~2. Зависимость этой суммы
i
от е существенно зависит от р. Если р < 2, то s при уменьшении е не-
неограниченно растет, поэтому sups(e,p) дает бесконечное значение. Если
?>0
же р > 2, то с уменьшением е s(s,p) —> 0, поэтому inf по всем покрытиям
с диаметром < е даст 0. Существует выделенное значение р — 2, которое
равно топологической размерности квадрата и является точной верхней
гранью значений р, для которых s > 0. (Это, разумеется, не доказатель-
доказательство, а просто пояснение к определению хаусдорфовой размерности: что
дают входящие в него inf и sup.) Тем не менее, существует доказатель-
доказательство того факта, что хаусдорфова размерность n-мерного многообразия
йц = п, т. е. совпадает с топологической размерностью.
Для канторова множества доказано, что dH = log3 2 = {^|. Воспро-
Воспроизводить здесь доказательство этого факта мы не будем, но пояснения,
аналогичные случаю квадрата, можно дать.
Покроем канторово множество отрезками длины е (для простоты
пусть е = 3~*, т. е. совпадает с длиной отрезков, возникающих на fc-м ша-
шаге построения канторова множества). Количество таких отрезков N = 2*,
тогда s(e,p) — 2*3~р* = B- 3~р)к. Измельчение покрытия (е -» 0) экви-
эквивалентно к —> оо, поэтому поведение s зависит от того, больше или
меньше 1 выражение в скобках 2 • 3"^. Выделенному значению р будет
отвечать случай 2 • Ъ~р = 1, т. е. 2 = У или р = Iog3 2.
Следует, однако, заметить, что такие «пояснения» иногда могут
дать неверный результат. То есть они дают значение не хаусдорфовой
размерности, а другой величины, емкости dc > dH. Один из примеров,
когда dc> dH, будет приведен ниже.
210 9. Энтропии и размерности аттракторов
Таким образом, для канторова множества dr = 0, a dg = Iog3 2 =
0,6309.... Множества, для которых хаусдорфова размерность строго боль-
больше топологической размерности, называются фрактальными множествами,
или фракталами. При этом предполагается, что множество принадле-
принадлежит n-мерному евклидову пространству или многообразию, и диаметр
покрывающего множества вычисляется в метрике этого пространства
или многообразия. (Дело в том, что значение йц может зависеть от то-
того, каким образом вычисляется диаметр множества, т. е. от используемой
метрики. А метрику можно определять по-разному и, соответственно, по-
получать разные значения ё,ц, причем оказывается [87], что точная нижняя
грань du по всем возможным метрикам равна df. Поэтому определение
фрактала требует фиксации метрики.)
Странные аттракторы чаще всего являются фрактальными множе-
множествами, поэтому естественно использовать как одну из их характеристик
хаусдорфову размерность. Однако вычислить ее в большинстве случаев
невозможно — определение не позволяет предложить никакого числен-
численного алгоритма, например, из-за невозможности найти численно точную
нижнюю грань по всем покрытиям. Поэтому численно делаются оценки
другой величины — (предельной) емкости dc-
Пусть дано множество А (предполагается, что задана также метри-
метрика — способ вычисления расстояний). Обозначим через N(e) минимальное
число шаров радиуса е, необходимое для того, чтобы покрыть А. Емко-
Емкостью множества А называется предел
если он существует. Если предел не существует (такие примеры есть,
но на практике они обычно не встречаются; о проблемах численного
определения размерностей будем говорить дальше), то вводят верхнюю
и нижнюю емкости — как верхний и нижний пределы.
Заметим, что в определении шары можно заменить, например,
кубиками (кстати, в некоторых метриках «шарами» и будут кубики).
В [87] приводится по сути то же самое определение, но соответствующая
размерность носит название «метрическая размерность», шары названы
«эталонами меры», а покрытие производится эталонами не радиуса е, а ра-
радиуса ^ е (но так как число их должно быть минимальным, это неважно).
Определение емкости фигурирует в основе большинства числен-
численных методов оценки размерности. Используется, однако, не минимальное
количество шаров (кубиков), а какое получится, но различные математи-
математические патологии редко проявляются в численном счете, так что разница
оказывается несущественной.
Для канторова множества оценку dc дать очень легко. Количество
покрывающих отрезков N = 2к, а их размер е = 3~к, откуда немедленно
получаем dc — i^fl = '°8з 2- В данном случае dc = du, но, вообще говоря,
для произвольного множества можно лишь утверждать, что dc > du.
9.2. Размерности аттракторов динамических систем 211
Очень поучительный пример дает множество точек последовательности
Хп = ^. Для него dH = 0, в то время как dc = \ ¦
9.2.2. Вероятностные размерности
Вероятностные размерности используют понятие меры и энтропии
(просто энтропии, а не метрической энтропии динамической системы).
Предполагается, что на исследуемом множестве А определена мера и что
все упоминаемые в этом разделе множества измеримы. Разобьем это
множество на минимально возможное количество непересекающихся
подмножеств А; таких, что diamAj < е, и вычислим энтропию этого
разбиения
Я(е) = - Y^ Pi In ft, p,-
Если бы мы рассматривали случай абсолютно непрерывной меры на мно-
множестве в К", для которой существует плотность вероятности р(х), то
могли бы записать, что при е —> 0 pi = p(xi)Vi, где Х{ ? Ai, a Vi RJ e" —
объем (мера Лебега) Ai. Тогда
Pilne" = "ОМ - nine.
При e —» 0 первый член ограничен, а второй неограниченно растет, так
Н(е)
что отношение --^г стремится к п, т.е. к размерности множества —
носителя меры. Как оказалось, это справедливо и для фрактальных
множеств. Таким образом, скорость расходимости энтропии при измель-
измельчении разбиения можно использовать для оценки размерности странных
аттракторов, существование меры для которых доказано.
Информационной размерностью D\ множества А будем называть
предел
()
1 с ln(e)'
Кроме обычной шенноновской энтропии можно использовать для этой
цели и обобщенные энтропии Реньи Нч. Соответствующие размерно-
размерности обычно называют обобщенными размерностями Dq. В этом случае
для покрытия рассчитывается величина
Я„(е) = П-</)"'In V»?,
*-о 1п(е)
Очевидно, что в случае q = 0 мы получаем емкость, при q -» 1 — инфор-
информационную размерность, а при q = 2 соответствующая размерность носит
212 9. Энтропии и размерности аттракторов
название корреляционной размерности или корреляционного показателя.
О выделенное™ случая q = 2 мы будем говорить в разделе про обработку
числовых данных.
Пример. Пусть на канторовом множестве задана однородная мера, которую
будем строить так: на fc-м шаге построения каждому из 2* отрезков
длины 3** припишем значение меры 2~*, т.е. е = 3~*, pi = 2~k. Тогда
Н = -^p.lnp, = Jfeln2, lne = -JHn3,
1
In 2
Можно в этом примере рассчитать и обобщенные размерности. ^2,р] =
2*2''* = 21'"'**, Hq = fcln2, откуда находим, что для всех q Dq = D, =
dH — dc- Таким образом, для однородной меры на канторовом множестве
все размерности совпадают.
Рассмотрим теперь более сложный случай. На каждом шаге постро-
построения будем приписывать меру по-другому: когда из отрезка с мерой р
удаляется средняя часть, то левой половине приписываем меру ар,
а правой A — а)р, 0 < а < 1. Таким образом, возникает «пирамида»
вероятностей:
1
а A-а)
а2 аA-а) аA - а) A-аJ
и т.д. Воспользуемся тем, что для каждого р = а'A - а)*~' количество
таких членов определяется биномиальным распределением. Поэтому
Я, = (I - »)-' lo^0»»**1 " «)'(*"°) = *A - «)'''"(«' + С "
Подставив сюда 9 = 0, можно убедиться, что получается правильное
значение dc- Чтобы получить значение D\, можно воспользоваться
определением, но проще сделать переход q —» 1. Положим q = 1 +7,
7< 1. Тогда
а» = аа1 = ае7'па S аA + jlna),
o)),
alna + (l-a)ln(l-a)
Di=lim—7 In
T-0 1пЗ 1пЗ
9.2. Размерности аттракторов динамических систем 213
Положим для определенности а = j, тогда получим
D°= пТз ~ °'6309'
21п2
1I = !- зьз -0'5794'
Л, = -1„!=Ша 0,5350.
1пЗ
Это иллюстрация общей закономерности: если р > ^, то Dp < D,.
Заметим, что размерности Dq можно определить и для отрицательных
значений q. В частности, можно найти D±oo как предел соответствующих
значений Dq. В нашем примере, если считать, что а < 0,5, то
п - 1п^ ~а) п - 1па
In 3 In 3
Спектр обобщенных размерностей характеризует неоднородность сингу-
лярностей меры. Для того, чтобы охарактеризовать сингулярность меры
в окрестности некоторой фиксированной точки х, вводят поточечную
размерность dp. Ее определяют следующим образом. Обозначим через
В(е,х) шар радиуса е с центром в точке х. Поточечной размерностью
называется предел (если он существует)
?->о In e
То есть если размерность сушествует, в окрестности точки х мера шара
радиуса е ведет себя как edp. Очевидно, что для меры Лебега в R" пото-
поточечная размерность каждой точки равна п. На однородном канторовом
множестве поточечная размерность каждой точки одинакова и совпадает
со всеми прочими размерностями. А вот для построенной неоднородной
меры на канторовом множестве поточечные размерности большинства
точек оказываются разными. Наиболее «разреженной» оказывается мера
в окрестности самой левой точки (при а < 0,5), наиболее «густой» —
в окрестности самой правой. Для них поточечную размерность нетрудно
оценить, и она оказывается равна, соответственно, D-,» и D^. Прочие
значения Dq могут быть равны поточечным размерностям для точек с ее
промежуточными значениями. Таким образом, спектр обобщенных раз-
размерностей показывает, в каких пределах могут находиться значения dp.
Во избежание путаницы следует, однако, заметить, что поточеч-
поточечная размерность, вообще говоря, может не иметь абсолютно никакого
отношения к топологической размерности ни исследуемого множества,
ни пространства или многообразия, к которым оно принадлежит. Это
просто локальная характеристика меры и не более того. Наиболее впе-
впечатляющим и предостерегающим примером может служить то же самое
неоднородное канторово множество на отрезке. Топологическая размер-
размерность множества d? = 0, самого отрезка 1, хаусдорфова размерность
214 9. Энтропии и размерности аттракторов
и емкость дают промежуточное значение. Если же мы выберем, скажем,
а = 5> т° получим, что поточечная размерность самой левой точки,
совпадающая с D-,», равна 2. Уменьшая а, т.е. делая эту точку «все
менее вероятной», можно получить сколь угодно большое значение dp.
Однако такие точки практически не дают вклада в значения Dq при q > 1,
и дают довольно слабый вклад при 0 ^ q ^ 1. Поэтому, если нас инте-
интересуют не захватывающие подробности и детали фрактальной структуры
аттрактора динамической системы, а лишь оценка числа существенных
переменных динамической системы, то отрицательные значения q следует
исключить, и, вообще говоря, достаточно ограничиться расчетом какой-
нибудь одной размерности. Чаще всего используют корреляционную
размерность Х?2- Вообще говоря, на практике для странных аттракторов
детали фрактальной структуры оказываются несущественны: для систем
размерности больше 2-3 их не удается исследовать ни численно, ни ана-
аналитически, а на малых масштабах их истребляет шум.
Можно показать, что для произведения двух одномерных канто-
ровых множеств в двумерном пространстве его размерность равна сумме
размерностей одномерных множеств.
Если же Вас интересует именно фрактальная структура или какая-
нибудь диффузия на фракталах, то, скорее всего, упомянутые размер-
размерности — это совсем не то, чем следует пользоваться. Тем более, что
и подходящей вероятностной меры может не оказаться...
9.2.3. «Динамические размерности»
и минимальные инерциальиые многообразия
Термин «динамическая размерность» не является устоявшимся, он
был использован в [137] и последующих работах, хотя величина, о которой
пойдет речь дальше, для аттракторов динамических систем упоминается
примерно с 1987 года, но под разными именами, а то и вовсе без
специального имени. Она также тесно связана с принципом подчинения
мод, который был положен в основу синергетики Г. Хакеном в 1975 г.,
и с понятием инерциального многообразия, предложенного в 1985 г.
(см. главу про инерциальные многообразия). Корни же его, скорее всего,
кроются в веках.
Суть подхода заключается в том, что движение динамической си-
системы на аттракторе обычно проще, чем в общем случае, поэтому, если
опустить переходный процесс, то переменные, входящие в динамическую
систему, должны разделиться на две группы: «существенные», которые
определяют динамику, и «несущественные», которые к первым под-
подстраиваются и следуют за ними. В синергетике первые были названы
«параметрами порядка», а вторые — подчиненными модами. Однако там
этот подход был «физическим», т.е. нестрогим, хотя и плодотворным.
Похожие подходы возникли и в математической физике, но они
были связаны главным образом с проблемой турбулентности, о кото-
которой говорилось во введении. Дело в том, что уравнения Навье—Стокса
9.2. Размерности аттракторов динамических систем 215
формально бесконечномерны, а в то же время некоторые режимы тре-
требуют для своего описания всего несколько переменных. После того, как
в 70-е годы родилась концепция странных аттракторов, и идея о том, что
сложная временная динамика может наблюдаться в простых моделях, за-
завоевала достаточную популярность, возникла мысль: а нельзя ли в задачах
гидродинамики как-то выделить эти существенные переменные. Если бы
это удалось сделать, то проблема турбулентности была бы почти решена,
во всяком случае удалось бы исключить многие концепции, например,
сценарий Ландау (бесконечномерный тор), а возможно, и гипотезу Лере
(несуществование дифференцируемых решений неограниченно долго).
В этом направлении работали несколько групп выдающихся математиков
(Ладыженская, Бабин, Вишик, Темам, Фояш, Селл и многие другие).
В ряде случаев подобную концепцию удалось реализовать, кроме, разу-
разумеется, самого интересного случая, ради которого все и затевалось —
трехмерной задачи для уравнений Навье—Стокса. Но сейчас нам, однако,
важнее то, что в ходе этих исследований была изобретена весьма удачная
терминология — группой Фояша и Темама была предложена концепция
инерциального многообразия [333].
Возможно, что на русский язык его правильнее было бы переводить
не «инерциальное», как сейчас принято, а «инерционное». Название, ви-
видимо, происходит из гидродинамики — иногда течения с большой длиной
волны, для которых вязкость почти несущественна, называют инерци-
инерционными. Амплитуды длинноволновых гармоник и оказываются теми
самыми «существенными переменными», для которых можно получить
упрощенную модель и, в частности, иногда свести бесконечномерную
задачу к конечномерной. Слово «многообразие» возникает потому, что,
с геометрической точки зрения, траектории вместо того, чтобы осваи-
осваивать все доступное фазовое пространство, притягиваются к некоторой
поверхности конечной (а иногда и малой) размерности — многообразию.
Обычно подход иллюстрируется следующим образом. Рассмотрим
некоторое дифференциальное уравнение х = F(x); вектор х может быть
как конечномерным, так и бесконечномерным. Допустим, что компонен-
компоненты х можно разделить на две части: и конечной размерности т и v — то,
что останется, так что система запишется в виде u = Fi(u,v), v = F2(u,v).
Пусть также существует положительно инвариантное множество (поверх-
(поверхность) В, задаваемое соотношениями
* = Ф(и), (9.2)
такое что на нем второе уравнение автоматически выполняется, т.е.
3j<&(u) — F2(u, Ф(и)) = 0. При этих условиях исходная n-мерная система
дифференциальных уравнений будет эквивалентна системе т дифферен-
дифференциальных уравнений
й = Р,(и,Ф(и)) (9.3)
и п-т алгебраических уравнений (9.2). Для того, чтобы подобная си-
ситуация на асимптотической стадии была типичной, множество В должно
216 9. Энтропии и размерности аттракторов
быть притягивающим, т. е. асимптотически устойчивым. Такое асимпто-
асимптотически устойчивое (т.е. экспоненциально притягивающее траектории)
положительно инвариантное дифференцируемое многообразие В, со-
содержащее аттрактор системы, называется инерциальным многообрази-
многообразием (ИМ). Многообразие В задается уравнениями (9.2), а динамическую
систему меньшей размерности (9.3) для и, фазовым пространством ко-
которой служит В, называют инерциальной формой. Детали и пример
построения инерциального многообразия см. в соответствующей главе
этой книги.
Наличие у системы инерциального многообразия позволяет иссле-
исследовать асимптотическое поведение не самой системы, а ее инерциальной
формы. Это напоминает проекцию уравнений на центральное многообра-
многообразие, упрощающую исследование свойств системы в окрестности точки
бифуркации.
Приведем простой пример.
Пример. Рассмотрим систему в цилиндрических координатах
г = г - г3, I? = I, z = -z. (9.4)
С течением времени траектории сходятся к предельному циклу, лежащему
в плоскости г = 0, который и будет инерциальным многообразием раз-
размерности 1. Другим инерциальным многообразием будет вся плоскость
z = 0 или круг достаточно большого радиуса с центром в точке @, 0, 0).
В первом случае инерциальной формой будет одно уравнение 0 = 1, во
втором — первые два уравнения системы (9.4).
Этот пример иллюстрирует следующие важные моменты.
— Инерциальное многообразие неединственно. Существует последо-
последовательность вложенных друг в друга инерциальных многообразий
и соответствующих им инерциальных форм.
— Существует одно выделенное ИМ минимальной размерности, ко-
которое мы будем называть минимальное ИМ — МИМ. Его, как
правило, нельзя однозначно отобразить на евклидово пространство
той же размерности. В случае, если сам аттрактор асимптотичес-
асимптотически устойчив и является многообразием (цикл, тор), он совпадает
с МИМ.
— Если необходимо, чтобы ИМ являлось евклидовым пространством
или было эквивалентно ему, его размерность должна быть доста-
достаточно большой.
Таким образом, если динамическая система обладает минимальным
инерциальным многообразием размерности d^, то на асимптотической
стадии ее поведение описывается при помощи dN существенных перемен-
переменных. Эта величина является одной из наиболее существенных характери-
характеристик динамической системы и «сложности» ее поведения. Вообще говоря,
все измерения фрактальных размерностей для аттракторов динамических
систем обычно оправдывают тем, что они дают оценку dN снизу.
Устоявшегося названия для djv в настоящее время нет. В статьях
использовались различные термины: геометрическая размерность [159],
9.2. Размерности аттракторов динамических систем 217
динамическая размерность [137], число параметров порядка [125], ло-
локальная внутренняя размерность [231] или число независимых степеней
свободы [151] (в последнем случае это должно быть if- так как это термин
из механики, где на одну степень свободы приходится две переменных).
Пользоваться можно любым названием, а можно продолжить этот ряд
и изобретать новые.
Величина djv могла бы представлять интерес как параметр для
классификации динамических систем. Если усложнение, скажем, ги-
гидродинамических течений идет путем увеличения числа существенных
степеней свободы, то при помощи djv можно было бы разбить все режи-
режимы на классы эквивалентности с одинаковыми значениями dN и изучать
«бифуркации инерциальных многообразий» [45]. Однако реальных дости-
достижений на этом пути пока нет. Во-первых, нет подходящей техники для
подобного анализа, во-вторых, классификация может оказаться слишком
грубой для практических целей. Наконец существует возможность, что
аттракторы наиболее интересных гидродинамических течений, по край-
крайней мере формально, всегда бесконечномерны, просто «толщина» по
большинству направлений у них очень мала, а усложнение идет не путем
увеличения количества размерностей, а путем изменения «толщин».
На этом мы завершим данный раздел. Заметим, что в теории конеч-
конечномерных динамических систем понятие инерциального многообразия
практически не используется, обычно достаточно термина «аттрактор».
Насущная потребность в нем возникает только при рассмотрении вопро-
вопросов обработки временных рядов и методов реконструкции аттракторов,
но об этом позднее.
10
Ляпуновские показатели
В начале книги уже говорилось, что одной из особенностей хаоти-
хаотических режимов является неустойчивость каждой траектории, принадле-
принадлежащей хаотическому аттрактору. Очень удачной количественной мерой
этой неустойчивости оказались так называемые характеристические по-
показатели Ляпунова (ляпуновские показатели, ЛП). Они оказались одной
из важнейших характеристик аттрактора, поскольку позволяют оценить
— фрактальную размерность аттрактора;
— энтропию динамической системы;
— характерное время предсказуемости поведения системы.
Эти величины были предложены А. М. Ляпуновым в ходе его исследо-
исследований по теории устойчивости для описания свойств линейных систем
обыкновенных дифференциальных уравнений (ОДУ). Однако в теории
Ляпунова они характеризовали только устойчивость положения равно-
равновесия, т. е. одну траекторию. Следующим важным шагом, показавшим
большую важность и более широкую применимость ЛП, стало доказа-
доказательство В. И. Оселедцем в 60-е годы мультипликативной эргодической
теоремы, согласно которой для хаотических систем набор ЛП характери-
характеризует не отдельную траекторию, а весь аттрактор, т.е. ЛП одни и те же
для почти всех (по инвариантной мере) траекторий на аттракторе. (Заме-
(Заметим, что в теореме Оселедца рассматривается более общая ситуация, но в
рамках данной книги мы не будем углубляться в детали.) В 70-80-е годы
был доказан ряд теорем, связывающих ЛП с энтропией и размерностями
аттракторов динамических систем. Наконец, в 1979 г. был предложен
простой и эффективный численный алгоритм расчета ЛП по известным
уравнениям движения.
10.1. Устойчивость и показатели Ляпунова
В главе, посвященной динамическим системам и простейшим инва-
инвариантным множествам, говорилось об исследовании устойчивости непо-
неподвижных точек при помощи линеаризации уравнений движения и анализа
собственных значений матрицы линеаризованной системы. Для перио-
периодических траекторий аналогичный подход связан с построением сечения
Пуанкаре, т.е. со сведением ситуации к случаю неподвижной точки.
Ляпуновские показатели предлагались как обобщение этого подхода на
случай траектории более общего вида. Тогда линеаризация приводит к
неавтономной линейной системе, для которой нет матрицы, собственные
10.1. Устойчивость и показатели Ляпунова 219
значения которой можно было бы исследовать. Однако можно предло-
жить некоторые усредненные аналоги собственных значений. При их
исследовании ряд существенных результатов удалось получить при помо-
помощи эргодической теоремы. Соответствующий результат получил название
«мультипликативной эргодической теоремы».
Как и в случае неподвижной точки, набор ляпуновских показа-
показателей не всегда полностью характеризует устойчивость соответствующей
траектории. Тем не менее, он несет весьма существенную информацию
о системе.
Пусть задана динамическая система с непрерывным временем
x = F(x), х@) = Х A0.1)
или с дискретным
хш = f(xfc), xo = X, A0.2)
где X — начальные данные. Нас интересует, как изменится x(t) (соот-
(соответственно, Хц), если начальным данным дать бесконечно малое прира-
приращение 6Х, т.е. рассмотреть бесконечно близкую траекторию x(t) + 6x(t)
или разность 6x(t) (соответственно, дхь). Для весьма широкого класса
систем решение дифференцируемо по начальным данным для конечных
значений t, поэтому
6x(t) = ФЦNХ,
где ФB) — матрица производных решения по начальным данным
Для линейных систем Ф(?) совпадает с нормированной фундаментальной
матрицей (см. ниже).
По заданному начальному возмущению 6Х можно найти 6x(t),
решая соответствующую линейную систему 6х = DF(x(t)Nx, 6х@) = 6Х
(или tfx/t+i = Df(xkNxk, бхо = 6Х). В силу линейности амплитуда ре-
решения несущественна, важен только «коэффициент прироста» решения
за время t, поэтому от бесконечно малых величин 6х можно перейти к
конечным и (можно, например, считать, что 6х = ей, а бесконечно малая
амплитуда е, входящая множителем как в правую, так и в левую части
уравнений, сокращается). Таким образом, исследование устойчивости
приводит нас к линейным системам
u = A(t)u, A(t)=D?(x(t)), u@) = U A0.3)
и
11*+, =Внщ, Bk = Df(xk), uo = U. (Ш.4)
Начальное возмущение U FX — eU) определяет направление, в котором
мы выбираем бесконечно близкую траекторию в точке X.
Заметим, что, строго говоря, векторы х и и принадлежат к разным
пространствам: х принадлежит фазовому пространству динамической
системы, аи — так называемому касательному пространству в точке х.
220
10. Ляпуновские показатели
Рис. 10.1. Иллюстрация понятия каса-
касательного пространства к многообразию
в различных точках
Разницу проще всего проиллюстри-
проиллюстрировать для динамической системы,
заданной на некоторой поверхно-
поверхности, скажем, когда фазовым про-
пространством отображения является
сфера. Тогда касательное простран-
пространство можно представить себе как
касательную плоскость в некоторой
точке Xjt, рис. 10.1. Оператор Df(xt)
отображает касательное простран-
пространство в точке х* в касательное про-
пространство в точке хц+1. Этот при-
пример показывает, что, вообще гово-
говоря, касательные пространства в разных точках — это разные пространства.
Однако их несложно отождествить. Если же фазовое пространство евк-
евклидово, то такое отождествление получается естественно. Более того,
в последнем случае их можно отождествить и с исходным пространством.
Тогда, напротив, трудно объяснить, что все эти пространства различны.
В дальнейшем мы ограничимся только случаем, когда фазовое простран-
пространство — это n-мерное евклидово пространство W.
Для систем A0.3), A0.4) решение бывает удобно выразить через
нормированную фундаментальную матрицу Ф, которая удовлетворяет тем
же самым уравнениям
Ф =
Ф@) = I
A0.5)
Фо = -?- A0.6)
Тогда u(t) = Ф(*)и (щ = Ф*и).
В общем случае для одних направлений U близкие траектории
будут экспоненциально удаляться, для других — экспоненциально сбли-
сближаться, для третьих расстояние остается примерно тем же или меня-
меняется медленнее, чем экспоненциально. Для неподвижной точки, когда
A(t) = А = const (В). ;В = const), эти случаи соответствуют собствен-
собственным значениям с Rev > 0, Rev < 0, Rev = 0 (\ц\ > \, \ц\ < \, \р\= \).
Здесь и далее v, \i — собственные значения соответственно А и В. Для
того, чтобы охарактеризовать ситуацию в общем случае, А.М.Ляпунов
ввел так называемый характеристический показатель решения u(t):
A(u)= limrhnlu^)!-
A0.7)
Сначала в качестве примера подробнее рассмотрим, чему будут
равны значения А(и) в случае неподвижной точки для системы A0.1),
\(t) = X = const. Для простоты предположим, что все собственные зна-
значения Vi матрицы А вещественны, различны и пронумерованы в порядке
убывания: v\ > V2 > ... > vn. Обозначим соответствующие им собствен-
собственные вектора через r('), Ar^ = v^1', |№')|| = 1. Тогда г(') образуют базис
10.1. Устойчивость и показатели Ляпунова
221
в касательном пространстве в точке X, в общем случае неортогональный.
Любое решение A0.3) u(t) можно представить как комбинацию базисных
решений Uj(<) = e"'V'), отвечающих начальным данным Uj(O) = гМ. Если
= Yl c'e
'e"lfr@-
A0-8)
Пусть j — номер, такой что с\ = ci = ... = Cj_i =0, Cj ф 0. Тогда
очевидно, что
i=j
1=7+1
А(и) = lim -t
lim - In
,-=j+l
Таким образом, характеристический показатель может принимать толь-
только п различных значений {v\,V2,- ¦ ¦ ,vn} в зависимости от начальных
данных.
В общем случае у матрицы А могут быть кратные и комплексные
собственные значения. В этом случае соответствующих вещественных
собственных векторов может не быть, а будут минимальные инвариантные
подпространства Щ (для любого u G R, Аи G Щ) размерности dj —
dimRj, i = l,...,m, d\ + d2 + ¦¦¦ + dm = n.
Хорошо известно, что действительную матрицу А можно при
помощи преобразований подобия А' = САС~^ привести к блочно-
диагональному виду, когда на диагонали стоят блоки следующего вида.
— обычные диагональные элементы (блок 1 х 1), которым отвеча-
отвечают обычные собственные векторы, соответствующее инвариантное
пространство одномерно;
блоки 2x2 вида
(а -Ь\
\Ь а)'
отвечающие паре комплексно сопря-
сопряженных собственных значений. Такому блоку соответствует двумер-
двумерное инвариантное подпространство, в котором действие матрицы
сводится к комбинации вращения и растяжения. Действительных
собственных векторов нет;
— жордановы блоки к х к, например, при
к = 2 I „ I.
При а ф 0
у такой матрицы А;-мерное инвариантное пространство, но всего
один собственный вектор.
Каждому подпространству Rj будут отвечать собственные зна-
значения v с одинаковыми действительными частями Rei/, и для всех
222 10. Ляпуновские показатели
u ? Rj характеристический показатель будет равен именно этому зна-
значению А = Rei/. Размерность dj = dimRj называют кратностью соот-
соответствующего показателя А. В дальнейшем мы будем предполагать, что
в ряду показателей каждый из них встречается столько раз, какова его
кратность, так что всего показателей ровно п штук, а упорядочены они
по убыванию: А) ^ Аг ^ ... ^ А„. Если и имеет ненулевые проекции
на несколько Rj, то А(и) будет равен наибольшему среди показателей
для этих подпространств, т.е. показателю А; с наименьшим номером г.
Заметим, что кратность показателей может быть больше кратности соб-
собственных значений матрицы А, поскольку показатели действительные,
а собственные значения, вообще говоря, комплексные.
В данном случае также можно выбрать базис линейно независимых
векторов rW, так чтобы каждый вектор принадлежал одному из Rj
(но не все из них могут быть собственными векторами .4), а для решений
с начальными данными u;@) = rW A(u,) = Aj.
А.М.Ляпунов [80] рассматривал случай линейных систем общего
вида с переменными коэффициентами
t
i = A(t)u, net", птГ1 [\\А{т)\\с1т < оо. A0.9)
о
Вместо выделения инвариантных подпространств Ляпунов ввел понятие
нормальной системы линейно независимых решений: система решений
{u\(t),U2(t),... ,un(t)} называется нормальной, если для любой другой
линейно независимой системы {fi;(?)} A(flj(t)) ^ \(ui{t)). Сам набор
показателей А), А2,..., Ап (среди них могут быть совпадающие, т. е. крат-
кратные показатели), как показал Ляпунов, не зависит от выбора нормальной
системы решений и является характеристикой данной линейной систе-
системы A0.9). Для любого решения u(t) ф 0 показатель А(и) может принимать
только одно из этих значений. В рассмотренном выше примере с непо-
неподвижной точкой нетрудно проверить, что система решений, для которой
U;@) = И'), является нормальной.
Все сказанное справедливо и для отображений A0.4), с той разни-
разницей, что вместо Rez/ будет использоваться |/i| для собственных значений
матрицы В. Аналогично для циклов систем ОДУ ляпуновские показатели
равны логарифмам модулей множителей Флоке (см. гл. 3).
Характеристические показатели Ляпунова часто называют про-
просто ляпуновскими показателями (ЛП). Среди всего набора ляпунов-
ских показателей наиболее важен наибольший (старший) А]. Поскольку
для почти всех начальных данных U будет иметь ненулевую проек-
проекцию на направление гО, то случаем общего положения (т.е. в не-
некотором смысле типичной ситуацией) будет A(u) = Aj. Чтобы полу-
получить меньшее значение показателя А(и) = А,-, необходим специаль-
специальный выбор начальных данных; в простейшем случае одномерных Rj
U G span {r«,r(i+1),... ,r(")}\span {#+*),... ,r(")}.
10.1. Устойчивость и показатели Ляпунова 223
Кроме обычных показателей А(и), характеризующих одно решение,
т.е. растяжение или сжатие в одном направлении, используют показатели
порядка т > 1, характеризующие изменение m-мерных фазовых объемов
(тп ^ га). Пусть u\(t), U2(t), ..., um(() — линейно независимые реше-
решения, a Vol (u\(t),U2(t),... ,um(t)) — объем образуемого ими т-мерного
параллелепипеда,
Vol(ubu2,...,um)=
det
(ui.ui) ... (ubum)
(um,U|) ... (um,Um)
A0.10)
Ляпуновским показателем порядка т называется
«m(ui,U2,...,um) = lim -lnVol(ui,U2,...,um).
Подобно тому, как типичным значением А(и) является А], типичным
значением кт является А)+Аг + ... +Ат. Чтобы добиться иных значений,
необходим специальный выбор начальных данных.
Среди всех кт выделяется показатель re-го порядка, для которого
можно получить дополнительные результаты. Дело в том, что любой
набор п линейно независимых решений образует фундаментальную ма-
матрицу Ф@> определитель которой называют определителем Вронского
W(t) = det<?(t). Объем Vol (ubu2,... ,un) = \W(t)\. В главе 3 при-
приводились соотношения для случая ОДУ A0.3): W — (lTA(t))W или
t
= trA(t). Отсюда сразу получаем, что к„ = lim - / (itA(t)) dr.
0
В прикладных задачах чаще всего существует точный предел (знак верх-
верхнего предела можно убрать, система является правильной по Ляпунову
— см. ниже), поэтому
к„ = <tr4),
т.е. среднему по времени от следа матрицы А.
Аналогично, в случае отображения A0.4) фундаментальная матрица
удовлетворяет уравнению Ф*+1 = -В*Фь откуда Wk+\ = Wf. x detSj.
, t
Поэтому кп = lim - )> In |det Bf. \, т. е. чаще всего
^°°1 tt
tt
«n = (ln|detB|).
Как видим, в соотношения для к„ и вообще не входит, поэтому
этот показатель можно рассматривать как характеристику всей линейной
динамической системы в целом. Согласно его значению динамические
системы подразделяют на консервативные, сохраняющие re-мерные фа-
фазовые объемы (к„ = 0) и диссипативные (к„ < 0), подробнее об этом
будет сказано ниже.
224 10. Ляпуновские показатели
Если теперь вернуться к исходной системе A0.1) или A0.2) и
ее траектории x(t), то набор ЛП для систем A0.3) или A0.4) будет
характеризовать устойчивость этой траектории. В этой связи выделяют
класс так называемых правильных по Ляпунову систем. Система A0.3)
называется правильной, если существует предел
t
1
lim -
<->оо t
0
с
f 1гА(т)ёт = к„ = М+Х2 + ¦¦¦ +А„. A0.11)
Аналогично, система A0.4) называется правильной, если существует
предел
\im -S^\n\detBk\ = кп = Х{ +A2 + ... +А„. A0.12)
k=\
Для неправильных систем предел может не существовать или может
нарушаться равенство. Однако на практике неправильные по Ляпунову
системы обычно не встречаются и соотношения A0.11) и A0.12) всегда
полагаются справедливыми. Для правильных систем доказано, что если
А] < 0, то траектория x(t) асимптотически устойчива, если Aj > 0 —
неустойчива.
Более детальное изложение теории ляпуновских показателей можно
найти, например, в книгах [55, 25] и обзоре [53].
Заметим, что набор ляпуновских показателей иногда называют
ляпуновским спектром соответствующей динамической системы.
10.2. Мультипликативная эргодическая теорема
Если теперь вместо произвольной линейной системы с матри-
матрицей A(t) рассмотреть линеаризованную систему A0.3) или A0.5), то,
вообще говоря, набор показателей будет зависеть от базовой траекто-
траектории х((), т.е. будет характеризовать траекторию, а не аттрактор. Фунда-
Фундаментальное значение ляпуновским показателям придала мультипликатив-
мультипликативная эргодическая теорема, доказанная в 1968г. В. И. Оселедцем. Согласно
ей, ляпуновские показатели совпадают почти для всех траекторий по
инвариантной мере ц.
В настоящее время существует несколько различных доказательств
этой теоремы, а сама она представляет собой довольно большой ком-
комплекс утверждений. Мы рассмотрим лишь некоторые из них, с нашей
точки зрения, наиболее интересные. Кроме того, мы ограничимся ее
формулировкой только для случая отображений хк+] = /(х*) (напомним,
что каждой системе ОДУ можно сопоставить подобное отображение
x(t) -> x(t + т) = <pT(x(t)), т. е. /(х) = ipT(x)).
Обозначим хо = х, и пусть Фк — фундаментальная матрица для ли-
линеаризованной системы A0.4). Мультипликативная эргодическая теорема
предполагает, что траектория х* может быть продолжена до бесконеч-
бесконечности в обе стороны, т.е. при к —» ±оо, и при каждом хк существует
10.2. Мультипликативная эргодическая теорема 225
фк = Dipk(x). Это, вообще говоря, справедливо не для всех точек х. На-
Например, для уравнения х = х - г3 и соответствующего ему отображения
при \х@)\ > 1 обратная траектория при t < 0 уходит в бесконечность
за конечный промежуток времени. Поэтому будем предполагать, что х
принадлежит инвариантному множеству, которое является носителем не-
некоторой инвариантной меры р. (или, как говорят, преобразование /
сохраняет меру р.). Матрицы Ф* предполагаются невырожденными, а ма-
матрицы Вк ¦= Df(xk) будем полагать ограниченными.
Тогда
1) для почти всех х по мере р. существуют точные значения ляпу-
новских показателей всех порядков при t -+ ±оо, т.е. линеаризованная
система является правильной по Ляпунову;
2) значения показателей Aj совпадают для почти всех х по мере р\
3) касательное пространство TMfa) в каждой точке х* распадается
на прямую сумму подпространств Rj(xt), так что если и@) € R;(xo), то
ton —, 'nllu@ll = i'V Подпространства инвариантны в том смысле,
t->±oo Щ
что если х*+1 = Цхк), то Щхк+\) = ВкЩхк).
Таким образом, почти для всех точек х по мере р. линеаризованная
система оказывается правильной по Ляпунову. Такие точки также называ-
называют правильными. Согласно теореме, это свойство оказывается типичным
но инвариантной мере.
Используя факт существования инвариантных подпространств Rj,
Нетрудно показать, что ляпуновские показатели являются средними по
мере от некоторого функционала, зависящего от х. Для простоты снова
Предположим, что все показатели различны, т.е. все подпространства
Rj(xjt) одномерны. Тогда в касательных пространствах можно выбрать
базисы {rW(Xfc)}, причем так, что они тоже будут инвариантными:
Г')(хк+]) = цд*^,)/* )ц [55]. Иногда такой базис называют базисом Оселедца.
Заметим, что вектора г('Цхк) определены с точностью до знака.
Рассмотрим теперь решение линеаризованной системы u*+i =
В*и*, начальные данные для которой Uo = rM(xo). Тогда, последовательно
Подставляя r(')(Xjt+i) • ||в4г(')(х*)|| вместо ВкА'Цхк), получим
||Вог(О(хо)|| = ... =
= B*V°(x*-l)- K-2r(i)(x*-2)|| •... • \\Bi^(xi)\\ ¦ ||BorW(xo)||,
откуда
^
8 За к 2
226 10. Ляпуновские показатели
Поскольку линеаризованная система является правильной почти для
всех хо по мере ц,
. *-1
Аналогично, для систем с непрерывным временем можно получить соот-
соотношение
t
(Здесь использовано соотношение (г, At) = (Л*г,г) = (г, А*т), справедли-
справедливое для действительных А и г.) Однако применить эти соотношения на
практике не удается, поскольку векторы г(')(х) почти никогда неизвест-
неизвестны. Более того, даже численно в большинстве случаев можно получить
только гО(х) (наиболее растягивающее направление) и г(")(х) (направле-
(направление, становящееся наиболее растягивающим при обращении времени).
На рис. 10.2 приведен пример направлений, отвечающих инвариантным
подпространствам для аттрактора Хенона (п = 2): Rj (длинный штрих)
и R2 (короткий штрих). Видно, что угол между ними, как правило, не
прямой, а в некоторых точках он даже может приближаться к нулю.
Однако инвариантные подпространства Wi = span{r(')(x),rB)(x),
...,r(')(x)} численно найти удается при помощи алгоритма Бенетти-
на и др. [155], который мы рассмотрим в конце главы. В нем по-
получаются другие вектора е(')(х), такие что образуемые ими подпро-
подпространства оказываются теми же самыми, span{eO(x),... ,е(')(х)} =
span {rO(x),... ,г(')(х)}. Они оказываются тесно связаны с другим вари-
вариантом мультипликативной эргодической теоремы, предложенном в 1979 г.
Д. Рюэллем [191].
Как указывалось выше, и* можно выразить через фундаментальную
матрицу Ф* = Df*(x) и начальные данные U: щ — Ф*и. Выражение,
входящее в определение ляпуновского показателя, можно переписать
следующим образом:
* 1П I|U*" = 2Jfc 1 ()
Как показал Рюэлль, если преобразование f(x) сохраняет меру /i, а на
Df(x) наложены те же условия, что и в теореме Оселедца, то для почти
10.2. Мультипликативная эргодическая теорема
227
-1,0
У-
0:
-
-
-0,0020:
-0,0040-
_
-0,0060;
-
Xх"
X
*\* х
S
// 1
у
X
X
1 1 | , т
у
Ж
0,7000
0,7020
0,7040
0,7060 х
Рис. 10.2. Пример направлений, отвечающих инвариантным подпространствам
для аттрактора Хенона: R| (длинный штрих) и R2 (короткий штрих). Увеличена
область, в которой угол между направлениями очень мал
всех х по мере ft существует предельная матрица
G00(x)= 1ип(Ф1Ф4)|/2*.
Jfc-fOO
Логарифмы собственных значений этой матрицы А,- = lnij — это набор
ляпуновских показателей, отвечающих точке х, (т.е. для почти всех х
собственные значения /,- совпадают; заметим, что /,- = ех' иногда назы-
называют ляпуновскими числами). Собственные вектора g^(x) этой матрицы
228
10. Ляпуновские показатели
образуют ортонормированный базис в касательном пространстве к точ-
точке х. Их связь с векторами г(')(х) довольно очевидна: они получаются,
если векторы {И')(х)} ортонормировать, начиная с последнего:
A0.15)
где коэффициенты Cij определяются из условия ортонормированности
базиса {g}. (Если ортонормировать начиная с первого, то начальным
данным U = gW в общем случае будет отвечать показатель не А;, а А),
поскольку будет ненулевая проекция на направление гО(х).)
Если отображение f обратимо, то для обратного отображения f~'
и траектории, продолженной в обратную сторону до бесконечно-
бесконечности (Xfc_i = f~'(xfc), и*-] = Df"'(xt)u/i), можно построить аналогич-
аналогичную матрицу G_oo(x) = lim (Ф^Ф*I' . Ее собственные значения
Г; = jr1 = е~Л', а собственные вектора е(')(х) получаются ортогона-
лизацией Грама—Шмидта системы {г(')(х)}, но начиная с первого, т.е.
A0.16)
Именно этот набор векторов и получается в упомянутом алгоритме
Бенеттина.
Различные формулировки и варианты доказательства мультипли-
мультипликативной эргодической теоремы приводятся в работах [96, 242, 36, 191].
10.3. Некоторые свойства ляпуновских показателей
Отметим важное свойство ЛП. Если уравнения движения динами-
динамической системы инвариантны относительно некоторого преобразования,
характеризующегося непрерывно изменяющимся инвариантом, то у си-
системы обычно есть нулевой ЛП, связанный с этим преобразованием.
10.3. Некоторые свойства ляпуновских показателей 229
В самом деле, пусть x(a,t) — однопараметрическое семейство траекто-
траекторий, причем tp'(-) явно от а не зависит. Тогда x(a,t) = <р*(х(а, 0)), а
т.е. u(t) = fa'' — решение линеаризованной системы A0.3) или A0.4)
для начальных данных U = ¦ д„ ¦ Если справедливо соотношение
где с\ и С2 не зависят от времени, то характеристический показатель
для этого решения будет равен нулю. Следовательно, в ляпуновском
спектре динамической системы должен быть нулевой показатель.
Частным случаем этой ситуации является сдвиг по времени для ав-
автономных систем ОДУ х = F(x). Если x(t) решение, то x(t + а) — тоже
решение. Так как ^ = х = F(x), то условие A0.17) сводится просто
к требованиям, чтобы на траектории не было неподвижных точек. Таким
образом, для аттракторов ОДУ, отличных от неподвижных точек, должен
быть по крайней мере один нулевой ляпуновский показатель.
С точки зрения не линеаризованной, а исходной динамической
системы ляпуновские показатели характеризуют скорость разбегания бес-
бесконечно близких траекторий, а показатели высших порядков — скорость
изменения бесконечно малых фазовых объемов.
Динамические системы, для которых n-мерный фазовый объем
уменьшается, называются диссипативными. Если фазовый объем сохраня-
сохраняется, то такие системы носят название консервативных. У консервативных
систем всегда существует хотя бы один закон сохранения. Как говорилось
выше, наличие закона сохранения часто влечет существование соответ-
соответствующего ему нулевого ляпуновского показателя.
Для диссипативных динамических систем сумма ляпуновских по-
показателей всегда отрицательна, к„ < 0.
Если от системы дифференциальных уравнений A0.1) х = F(x) с на-
набором ляпуновских показателей А) ...А„ перейти к отображению A0.2):
xk+\ = f(x*), xk = x(t), xk+\ = x(t + r) = ipT(x(t)), то ляпуновскими
показателями для этого отображения будут А'; = \т. Аналогично, если от
отображения перейти к некоторой его степени F"(x) = /(/(... /(х)...)),
m ,
то для нового отображения показатели будут в m раз больше, А; = тп\{.
Если от системы дифференциальных уравнений перейти к сече-
сечению Пуанкаре и соответствующему отображению на единицу меньшей
размерности, то в спектре показателей для отображения не будет нуле-
нулевого показателя, «отвечающего» за сдвиг вдоль траектории, остальными
показателями будут Xt — \ (т), где (т) — среднее время возвращения на
плоскость Пуанкаре.
230 10. Ляпуновские показатели
При обращении времени (но для той же самой инвариантной
меры /i!) «типичными» ляпуновскими показателями будут —Л„, —Ап_),
..., -А). Однако при этом вместо аттрактора, к которому притягиваются
траектории при t —* оо, нужно рассматривать неустойчивое множество —
репеллер, к которому траектории притягиваются при t —* -оо.
Упомянутые свойства позволяют делать некоторые априорные вы-
выводы о ляпуновских показателях динамических систем, исходя лишь из
анализа уравнений движения. Рассмотрим два примера.
Пример. Для системы Лоренца
—а
т — z
У
а
-1
а;
0
—а;
-Ь
(у)
F(x) = (r-z)x-y , D?(x) =
xy-bz J
поэтому tr(UF(x)) = -(a + 1+Ь). Так как след от х не зависит, он
и будет средним значением. Таким образом, для аттракторов системы
Лоренца всегда А, + А2 + А3 = -(it + 1 + Ь). Кроме того, если аттрактор —
не неподвижная точка, то один из показателей равен нулю. В случае
предельного цикла А| = 0, А2з < 0> для хаотического аттрактора А| > 0,
А2=0, А3<0.
Пример. Для отображения Хенона
откуда detDf(x) = —Ь, поэтому Ai + А2 = In \Ь\.
Такие соотношения бывают полезны для контроля численных рас-
расчетов ляпуновских показателей.
10.4. Связь ляпуновских показателей
с другими характеристиками
Ляпуновские показатели — это одни из немногих характеристик,
которые с довольно высокой точностью могут быть рассчитаны по из-
известным уравнениям движения (как именно — рассказано чуть дальше).
Оказывается, что по ним можно многое сказать о динамической системе,
о наблюдаемом режиме, о размерности аттрактора, если таковой имеется,
и об энтропии динамической системы.
Хаотические и нехаотические режимы. Динамическому хаосу отве-
отвечает неустойчивость каждой отдельной траектории, т. е. наличие хотя бы
одного положительного ляпуновского показателя. В этом случае соответ-
соответствующий аттрактор называют «хаотическим». Как правило, хаотические
аттракторы имеют сложную фрактальную структуру. Растяжение по од-
одним направлениям компенсируется сжатием и формированием складок
по другим. В настоящее время основной иллюстрацией этого процесса
является подкова Смейла.
Следует, однако, заметить, что фрактальная структура у аттрактора
или иного инвариантного множества может возникать и при отсутствии
10.4. Связь ляпуновских показателей с другими характеристиками 231
хаотичности — как периодическая структура с бесконечным периодом
или при наличии разбегания траекторий, но слабее экспоненциального.
Такой аттрактор называют «странный нехаотический»; примером может
служить аттрактор Фейгенбаума для логистического отображения. В этом
случае А) = 0.
Регулярные периодические или квазипериодические режимы не
имеют в ляпуновском спектре положительных показателей, а для к не-
независимых частот имеют к (для ОДУ) или к — 1 (для отображений)
нулевых показателей. Поэтому для случая дифференциальных уравнений
у цикла один нулевой показатель, у тора — два, у 3-тора — три и т.д.
Для отображений у цикла нулевых показателей обычно нет, у тора — 1,
у 3-тора — 2 и т. д. Эта закономерность легко объяснима: когда аттракто-
аттрактором является «хорошее множество», m-мерное многообразие, т-мерный
фазовый объем должен сохраняться. Притяжение к аттрактору требует,
чтобы фазовые объемы больших размерностей сжимались. Это и отражено
в ляпуновском спектре.
Тем не менее, количество независимых частот можно выяснить
не всегда, так как нулевые показатели могут быть связаны и с наличием
сохраняющихся величин. Для диссипативных систем наличие законов со-
сохранения, вообще говоря, нетипично, однако соответствующие примеры
существуют.
Ляпуновская размерность. Знание ляпуновских показателей позво-
позволяет оценить и фрактальную размерность аттрактора. Эта оценка выгля-
выглядит, на первый взгляд, странной, но может быть получена достаточно
к
естественным путем. Напомним, что кк = X)^i> и ПУСТЬ к — такое
•=1
число, что к),«2,- •• >Кк ^ 0, а кк+\ < 0, т.е. fc-мерный фазовый объем
не уменьшается, а к+ 1-мерный — сокращается. Выше говорилось, что
для аттракторов-многообразий фазовый объем, отвечающий размерности
аттрактора, сохраняется. Для хаотических аттракторов обычно получается
так, что Kk > 0, а кк+\ < 0, и целой размерности, обладающей таким
свойством, не существует. Однако можно попытаться найти подходящую
дробную размерность. Для этого аппроксимируем зависимость kj — n(j)
кусочно линейной функцией n(j) — aj + b. Эта функция обязательно
обратится в ноль в некоторой промежуточной точке j — di, к < dL <
к + 1. Это значение и принимается за оценку размерности аттрактора,
которая получила название ляпуновская размерность. Получим для нее
выражение. Как говорилось выше ak + b = кк, а(к+ 1) + Ь = кк — |А*+1|,
т.е. а = -|Ajt+i|, b = к,;. + к\Хк+\\, а для ляпуновской размерности
получаем соотношение - \Хк+\\ dL + nk+k \\k+\\ = 0 или
^ A0.18)
Соотношение A0.18) очень часто используется на практике. Доказано не-
несколько теорем, согласно которым dL дает оценку сверху для хаусдорфо-
вой размерности аттрактора, правда иногда вместо обычных ляпуновских
232 10. Ляпуновские показатели
показателей используют так называемые «глобальные ляпуновские по-
показатели», которые больше или равны обычным [333]. Соответствующая
оценка размерности также будет больше.
Энтропия динамической системы. Пусть у динамической системы j
строго положительных показателей Aj > 0. Для энтропии К\ существует
i
строгая оценка К\ ^ J2 Л;. Однако на практике обычно считают, что
выполняется точное равенство
Для SRB-мер, упоминавшихся в гл. 5, оно доказано строго. Для про-
прочих энтропии Kq аналогичных оценок нет, но поскольку чаще всего
все Kq при не слишком больших q близки, то приближенно можно
пользоваться A0.19).
10.5. Как вычисляют ляпуновские показатели?
Аналитически ляпуновские показатели можно найти либо для про-
простых аттракторов (неподвижная точка), либо для одномерных отображе-
отображений, например, типа «тент». Для прочих случаев их рассчитывают чи-
численно. Однако, как правило, в численном счете можно находить только
«типичные» значения величин. В частности, если численно решать A0.3)
или A0.4), то из-за ошибок округления практически всегда будет полу-
получаться значение показателя А(и) = А). Однако, как говорилось выше, ти-
типичным значением для Kj будет сумма j наибольших показателей. Поэто-
Поэтому для численного расчета нескольких показателей используют эволюцию
фазовых объемов, как это было предложено в работе Бенеттина и др. [ 155].
При таком подходе можно рассчитывать любое число показателей —
от 1 до ге. Для простоты будем считать, что определяются все показатели.
Чтобы задать n-мерный фазовый объем, необходимо п линейно не-
независимых решений линеаризованной системы ц(')(?). Обычно начальные
данные ц(')@) выбирают ортонормированными, что гарантирует линей-
линейную независимость. Далее, казалось бы, необходимо одновременно про-
проводить численный расчет и систем A0.3) или (Ю.4), находить j-мерный
фазовый объем Vj(t) = Vol (u(')(t),... ,u^(t)) no формуле A0.10) и вы-
вычислять величину kj(t) = ?"' \nVj(t). Если значение этой величины уста-
устанавливается с ростом t, его можно было бы принять в качестве оценки
обобщенного ляпуновского показателя к,- = Ai + A2 + ... + Xj, и тогда
Aj — Kj — Kj_\.
Однако такой простой подход оказывается неработоспособным по
двум причинам.
1. Произвольно выбранные начальные данные ц(')@) обычно со-
содержат ненулевую компоненту в направлении наибольшего растяжения
10.5. Как вычисляют ляпуновские показатели? 233
гО(х@)), а если нет, то она обычно
возникает в ходе расчетов из-за оши-
ошибок округления. Поскольку эта ком-
компонента растет как ~ eA'f, спустя не-
некоторое время она станет доминирую-
доминирующей, все п векторов v[l\t) развернут-
развернутся в направлении г(')(х(?)) и станут
практически коллинеарны (рис. 10.3). p,,c.10.3. в ходе эволюции вектора
После этого расчет образуемого ими uw(t) стремятся развернуться в на-
объема станет невозможен из-за ко- правлении наибольшего растяжения,
нечной точности представления дан- поэтому спустя некоторое время они
ных в ЭВМ. Хорошая иллюстрация могут стать почти коллинеарными
этого эффекта приведена в [346].
2. Сама величина eA|f может за сравнительно небольшое время
выйти за пределы машинной точности. Обычно это время существенно
меньше, чем требуемое для расчета ляпуновского показателя.
Таким образом, необходима борьба с коллинеарностью векторов и
выходом за пределы машинной точности.
Первая проблема решается при помощи процедуры ортогонализа-
ции векторов и(')(?), т.е. переходу к новой системе решений п0)(?) =
¦(|)@, u(i)@ = u(')(?)+ ?cyii(.?)(t). Поскольку уравнения для uW(t)
линейны, u('\t) также будет решением, а так как ортогонализация не
меняет значения объема, Vol (uOty),.. ¦ ,uW@) = Vol(u(')(<),... ,fiW(t)),
то u('>(t) будет системой решений, отвечающей тем же самым значениям
показателей Kj. Затем проводится дальнейший расчет решений п(')(?). Во-
Вообще говоря, они сразу же перестанут быть ортогональными, поэтому спу-
спустя некоторое время ортогонализацию необходимо будет повторить. Если
Йроводить ее достаточно часто, то проблема коллинеарности отпадает.
Для ортогонализованной системы решений
voi (пО)(о,...,й^(О) = ||аA)(
поэтому каждое из решений Ф\г) будет «отвечать» за свой показатель Aj,
'* ||u(')(t)|| ~ eA(f. Остается решить проблему переполнения. Она реша-
решается при помощи запоминания текущего значения <rW(<) = 1п||п(')(?)|| и
[Нормализации v(')(t) = Z^fL ¦ Далее полагаем u^(t) = \('\t) и повторяем
§сю процедуру. Нормализация делает объем единичным, как в начальный
ромент, но не меняет направлений, а потому не меняет и приращения
|вбъема на следующем этапе расчета. Поэтому после следующей ортогона-
ации надо просто добавить к <T^'\t) следующее значение
234 10. Ляпу'новские показатели
Мы описали основные этапы. Сформулируем теперь полный алго-
алгоритм расчета ляпуновских показателей. Сначала рассмотрим случай ото-
отображений A0.2), A0.4).
1. Задаем п ортонормированных векторов Vq , t = 1,...,и, присваи-
присваиваем <Tq =0, to = 0, Uq = Vq , а также определяем шаг перенор-
перенормировки At. Проще всего положить At — 1. (Предполагается, что
точка хо принадлежит аттрактору.)
2. Делаем итерацию отображений, т.е. находим х*+1 = f(x*)> о>ь+] ~
L>f(xt)u<°.
3. Ортогонализуем систему векторов и?+] и получаем й^р
п
¦Й-, = -Й-, + ХЗ
4. Увеличиваем <т(') на логарифм нормы соответствующего вектора:
й°к+\ — ln||"!fc+i||> "k+i ~ "к + ^<7*+]> увеличиваем t: tk+] =
tk + At. В качестве текущей оценки ляпуновского показателя можно
использовать А*(?) = у11.
5. Нормируем систему векторов й{.+р получаем ортонормированный
базис на следующем шаге vi'i, = «t1 и заносим его снова в
Нй II
вектора u: Щ^ = vJV j.
6. Повторяем пункты 2-5 нужное число N раз.
7. Получаем окончательную оценку ляпуновского показателя. В про-
стейших случаях выбирают А;(<) S -f-, или А<(<) = j^ X) 6<тк —
" к=\
2jF<r^''), несколько лучшая оценка получается, если использовать
линейную аппроксимацию (г? — \$к + const.
Для дифференциальных уравнений A0.1), (Ю.З) алгоритм остается
тем же самым за исключением следующих моментов.
— Шаг перенормировки At можно выбирать достаточно произ-
произвольно, но он не должен быть слишком велик; очень малым
его выбирать тоже обычно бессмысленно — это ведет к лиш-
лишним затратам машинного времени.
10.5. Как вычисляют ляпуновские показатели? 235
— Вместо итерации отображений необходимо решить диффе-
дифференциальные уравнения х = F(x), u^ = D?(x)u^ на отрезке
[*ti*t+i] Длины At с начальными данными х = х(?*), и = и(?*).
Далее в алгоритме вместо u^i используется u^(i*+i). Векто-
(•) *
pa vk будут определяться только в точках г*.
— При численной реализации алгоритма уравнения для х и и
следует решать не раздельно, а совместно. То есть необходимо
эти две системы объединить в одну, объединив вектор х и
п векторов ц(') в один (п + п2)-мерный вектор w, а затем
численно решать эту объединенную систему вида w = H(y/).
Это связано с особенностями численных методов решения
дифференциальных уравнений, реализованных в стандартных
пакетах программ.
— При аппроксимации уравнений движения х = F(x) разност-
разностной схемой дифференциальные уравнения заменяются ото-
отображением х*+1 = g(xit,ft), где h — шаг разностной схемы.
В простейшем случае схемы Эйлера используется отображение
Xj+i = х* + rF(xjb). Результат расчета ляпуновских показате-
показателей, естественно, будет зависеть от выбранного значения т,
но при т —» 0 эта зависимость обычно исчезает. Поэтому
желательно убедиться, что результат не зависит от выбранной
разностной схемы, т. е. вида функции g и шага по времени h
(например, что результаты для двух методов и значений h и ^
практически совпадают).
Можно показать [197], что с ростом tj. ортонормированные векто-
|iavj. стремятся ке(')(х*) (см. A0.16)). Эта сходимость экспоненциальная,
||vi° - е<°(х*)|| ~ ехр(-7Л), Ъ = тт{|А<_, - А,|,|А,- - А,+ 1|}.
Вдесь надо заметить, что вектора eW, как собственные вектора ма-
матрицы Goo, определены с точностью до знака, поэтому можно всегда
Читать, что знак выбран так, что v^ —» еМ, а не vj. —» — е^.) Более
(ого, в [197] показано, что погрешность, вносимая в 6а}!', пропорцио-
пропорциональна ||vj. — е(')(х*)||. Поэтому при расчете можно улучшить точность,
|сли в течение нескольких первых итераций не регистрировать значе-
Вм да). , а сначала дать векторам Vj. сойтись с достаточной точностью
Описанный алгоритм был предложен в 1979 г. [155] и с тех пор
Ьвсеместно применяется, зачастую с небольшими добавлениями и улуч-
юниями. Вектора v^ иногда называютляпуновскими векторами, a e(')(xt)
ыли названы стационарными ляпуновскими векторами [197].
236
10. Ляпуновские показатели
Существует несколько эквивалентных формулировок данного ал-
алгоритма. Во-первых, его можно представить как эволюцию ортонорми-
рованного базиса векторов {vj, } —> {vj^.,}:
v@ _
v
VB)
v
? V
A0.21)
где отображения J^ включают уравнения движения вместе с процедурой
ортонормализации Грама—Шмидта. Ляпуновские показатели при этом
получаются как усредненный функционал на векторах v:
В работе [213] были получены аналогичные соотношения для случая диф-
дифференциальных уравнений. Сама процедура Грама—Шмидта в матричном
виде называется фД-разложением на ортогональную матрицу Q, столбцы
которой образуют ортонормированный базис {v[. }, и верхнюю треуголь-
треугольную матрицу R, тогда 6а\ — \nRiik. Соответствующая формулировка
алгоритма приводится, например, в [191].
-1,620
-1,625
-1,630 HI , , iMMiMnlrnnnMl
0 10000 20000 30000 40000
Рис. 10.4. Сходимость оценок ляпуновских показателей Ai, Аг для аттрактора
Хенона
10.5. Как вычисляют ляпуновские показатели?
237
2000
2500
Рис. 10.5. Сходимость оценок ляпуновских показателей для аттрактора Лоренца
Наконец, поскольку vj. —* е(')(х*), то с использованием векто-
векторов e(')(Xjt) можно написать выражение для ляпуновских показателей,
аналогичное A0.13):
A0.22)
= <ln|(e«(f(x)),Df(x)eW(x))|),
238 10. Ляпуновские показатели
или для случая дифференциальных уравнений аналог A0.14)
A0.23)
В заключение сделаем несколько замечаний. В описанном алгорит-
алгоритме не обязательно вычислять все показатели. Если использовать т < п
векторов ц(') (или v(')), то будут получены т наибольших показателей.
Это существенно для систем большой размерности или дифференциаль-
дифференциальных уравнений в частных производных.
«Побочным» результатом алгоритма является поле направлений
eW(x). Кроме того, можно получить и вектора gW(x) A0.15), если
рассчитать траекторию х*, к — 1,...,ЛГ, а затем запустить алгоритм
расчета показателей в обратном направлении от х# к Х|, т.е. с обра-
обращением времени. Тогда чк —* g'"'(x^) (наибольшим показателем при
обращении времени станет — А„), \к —* g("~t)(xfc) и т.д. А вот из ин-
инвариантных направлений г(")(х*) можно найти только гО(х*) = е(')(х*),
г^"Нх*) = g^(x*) (см- Рис- Ю-2), и для отображений в случае п — 3
направление гB)(х*) как пересечение плоскостей {е(')(х*),еB)(х*)} и
{g^(x*)j8^(x*)}- Л1" дифференциальных уравнений всегда известно
одно из инвариантных направлений — это касательная к траектории.
Небольшое резюме
Если известны уравнения движения динамической системы, а под
рукой имеется компьютер, то расчет ляпуновских показателей — это срав-
сравнительно простой способ получить весьма существенную информацию
об аттракторе динамической системы. В настоящее время такой расчет
для хаотических систем стал общепринятым. В отдельных случаях его
проводят даже для довольно сложных уравнений в частных производных,
таких как уравнения Навье—Стокса (см., например, [249]).
Есть большой класс задач, где расчет ляпуновских показателей
имеет не только академический, но и прикладной интерес. Это задачи,
связанные с определением горизонта предсказуемости Т для данной си-
системы. Обычно считают, что Т ~ т-. От этой величины зависит, на какое
Л]
«в среднем» время можно предсказывать поведение системы (посколь-
(поскольку Aj характеризуют весь аттрактор), насколько часто надо измерять ее
состояние при мониторинге и т. д. В ряде случаев удается определить
ляпуновские показатели по временному ряду — множеству измерений
состояния системы с заданным интервалом по времени (об этом речь
будет идти дальше). При сравнении теории таких явлений с экспери-
экспериментом сопоставление ляпуновских показателей является очень важным
элементом.
11
Реконструкция аттракторов
по временным рядам
11.1. Временные ряды и их обработка
Временные ряды — один из давних объектов статистического ана-
анализа. Скалярным временным рядом мы будем называть массив из N
чисел, представляющих собой значения некоторой динамической пе-
переменной x(t) с постоянным шагом At по времени, т.е. в моменты
tt — to + (i — l)At: Xi = x(ti), i = 1,... ,N. Подобные временные ря-
ряды являются основным результатом экспериментов, как натурных, так
и вычислительных. Потому и методы их обработки развивались давно.
В качестве основных побудительных мотивов обычно указывают задачи
метеорологии или, более широко, геофизики (записи давления, темпера-
температуры, солнечной активности и т. п.), и финансового анализа (цены акций,
товаров, курсы валют).
В последнее время к ним присоединились физиология и медицина.
Кроме того, большое количество временных рядов дают астрономические
наблюдения. Однако последний случай не слишком интересен, поскольку
математические модели, описывающие системы небесных тел, известны
достаточно давно, а потому обработка наблюдений не представляет каких-
либо принципиальных или концептуальных трудностей — уравнения знаем,
осталось найти входящие в них параметры (однако алгоритмических
и вычислительных проблем может быть сколько угодно).
В случае же, например, метеорологических данных трудности воз-
возникают именно принципиальные: неизвестно, какой именно математи-
математический объект следует поставить в соответствие полученным данным.
В силу такой неопределенности в течение длительного времени к ана-
анализу временных рядов подходили с позиций математической статистики.
Использовался соответствующий математический аппарат, включающий
понятия последовательностей случайных величин, случайных процессов,
статистических моделей, стохастических дифференциальных уравнений.
Были также выделены две основные задачи анализа временных рядов.
1. Задача идентификации. При ее решении делается попытка отве-
ответить на вопрос, каковы параметры системы, породившей данный вре-
временной ряд. Параметры могут быть самыми различными — статистиче-
статистические распределения, параметры статистических моделей, спектральные
свойства и т. п. Важно, что эти параметры могут помочь идентифициро-
идентифицировать (распознать) систему, т. е. отличить ее от других. Проблемы такого
типа возникают, например, в задачах медицинской или технической
240 11. Реконструкция аттракторов по временным рядам
диагностики — необходимо отличить норму от различных патологий,
не разрушая систему, а используя доступные измерению характеристики.
2. Задача прогноза. Она состоит в том, чтобы по данным наблюде-
наблюдений предсказать будущие значения измеряемых характеристик или, более
широко, будущее состояние анализируемого объекта.
Статистика предложила первые подходы к решению этих задач.
Нелинейная динамика внесла свой весьма существенный вклад, однако
не столько в сами практические методики, сколько в их концептуальное
обоснование. До нее методы, дававшие зачастую неплохие результаты,
выглядели несколько мистически. Поэтому сначала мы несколько слов
скажем об основных чертах статистических подходов, а потом обратимся
к методам нелинейной динамики.
11.2. Статистические методы обработки
В основе многих статистических методов обработки лежит понятие
статистической модели. По сути, это те же самые динамические систе-
системы с шумом, которые рассматривались в гл. 5, однако теперь акцент
делается не столько на динамике, сколько на шуме. Предполагается, что
на такую систему действует некоторый «стандартный» некоррелирован-
некоррелированный гауссовый шум, а для выходного сигнала появляется некоторое свое
характерное распределение и свои характерные временные корреляции,
обязанные своим появлением динамике. Задача обработки заключается
в том, чтобы построить динамическую часть таким образом, чтобы она
преобразовывала шум во временной ряд, в некотором смысле аналогич-
аналогичный обрабатываемому. В каком именно смысле — зависит от контекста.
Можно требовать только совпадения нескольких моментов распределе-
распределения, можно требовать совпадения и более тонких характеристик, на-
например, плотности распределения, особенностей спектра или деталей
динамики, скажем, наличия редких больших выбросов.
Каким образом строились статистические модели? Поскольку пред-
предполагается, что известен лишь сам временной ряд х*, а также всегда мож-
можно создать «шум» — последовательность некоррелированных и одинаково
распределенных случайных величин & с нулевым средним (Е& = 0), то
возможностей немного. Остается только предположить, что г'-й элемент
ряда Xj можно представить как некоторую функцию т предшествующих
элементов x,_i,... ,Xj_m и А; + 1 случайных величин &,... ,&_*
х,- = F(xi-h..., x,_m,&,..., &-*)• A1.1)
(«Тебе придется сделать добро из зла, поскольку его больше не из чего
сделать».) Раньше, примерно до 1980 г. чаще всего ограничивались
линейными функциями F, т.е. моделями вида
т k
Xi = а0 + J2 ciiXi-j + J2 Ь&ч. A1.2)
j=\ j=0
Для них было изобретено даже специальное название: ARMA, от слов Аи-
toRegression — авторегрессия, первая сумма в A1.2), и Moving Average —
J1.2. Статистические методы обработки 241
скользящее среднее, вторая сумма. Коэффициенты a,j и bj определяют,
например, методом наименьших квадратов. Подробно об этой и других
подобных задачах можно прочитать в книгах, посвященных построению
статистических моделей и оцениванию их параметров, там же приводятся
и статистические классификации моделей (см., например, [62, 79, 19]).
Получение искомых коэффициентов можно рассматривать как возмож-
возможное решение задачи идентификации, а соотношение A1.2) можно ис-
использовать и для прогноза следующего значения по т предыдущим.
В качестве прогнозируемой величины обычно используется среднее зна-
т
чение &i = Ext = <щ + YL <4xi-j (предполагается, что предшествующие
j=l
значения известны точно). Заметим в этой связи, что шум является со-
совершенно необходимой и неотъемлемой частью таких линейных моделей.
В отсутствие шума поведение модели чаще всего абсолютно не похоже
на исследуемый ряд. Поэтому подобные «линейные прогнозы» можно
делать лишь на сравнительно небольшое число шагов вперед.
Иногда модели типа A1.2) называют также линейными цифровы-
цифровыми фильтрами, поскольку процесс порождения временного ряда такой
системой по сути представляет собой фильтрацию некоррелированного
Шума. (Поэтому и шум совершенно необходим — нет шума, значит нечего
фильтровать, не из чего «приготовить» сигнал.) Однако при построении
Цифровых фильтров задачи ставятся иначе; необходимо так подобрать
коэффициенты at, b{, чтобы добиться нужных спектральных свойств вы-
выходного сигнала. Решается задача не идентификации, а преобразования
временных рядов.
Почему в данном случае вообще можно вести речь о фильтрации?
Соотношение A1.2) — это дискретный аналог свертки двух сигналов
ш(<) и ?(t) с финитными (не равными нулю только на конечном отрезке
времени [0,Т]) функциями a(t) и b(t):
Т Т
x(t) = I a{r)x{t -r)dr+ I b(r)Z(t - т) dr.
Вспомним, что преобразование Фурье Х(и>) = / x(t)e ш* dt свертки
—оо
оо
*(*) = / a(T)v(t - r)dt равно произведению преобразований Фурье,
—оо
X(u) = A(u)Y(u). Тогда
Х(ы) = А(ы)Х(ш) + В(ШK(ы), Х(ш) = { *^ Щш). A1.3)
Подбор функций а и b позволяет так преобразовать спектр шума Щш),
чтобы он стал аналогичен спектру анализируемого сигнала.
Аналог соотношения A1.3) существует и для дискретных сигна-
сигналов. Предположим, что х< и & — периодические последовательности
242 11. Реконструкция аттракторов по временным рядам
с периодом N, г = 0,... ,N - 1. Тогда в суммах, входящих в A1.2), мож-
можно использовать циклическое изменение индексов — вместо -1 писать
N - 1, вместо — 2 — N — 2ит. д. Аналогично вместо N можно писать О,
вместо N + 1 писать 1. Такое суммирование с циклически меняющимися
индексами носит название циклической дискретной свертки.
Далее, комплексным дискретным преобразованием Фурье (ДПФ или
DFT) последовательности х* называется
Хк = В?Т({х{})к = J2Xiexp (-J^)
А; = 0,..., N - 1, j — мнимая единица, р- = — 1. Интересно, что
обратное преобразование имеет тот же вид, но под экспонентой стоит
знак «+» и добавляется множитель JV~'. Для быстрого вычисления таких
сумм существует алгоритм быстрого преобразования Фурье (БПФ). Он
работает не для любых N, наиболее распространены версии, требующие,
чтобы N = 2т.
Если последовательность х, удовлетворяет A1.2), нетрудно пока-
показать, что ДПФ Х{ и & (Xk и Н*, соответственно) связаны соотношением
Хк = CfcHjfc. Здесь С/с — характеристика цифрового фильтра. Суще-
Существенно, что она не зависит от &. Таким образом, при помощи ДПФ
и БПФ можно выполнять бытрую свертку. Вообще говоря, цифровая
обработка сигналов — это отдельная интересная область, на которой мы
сейчас не можем останавливаться. Можно порекомендовать в этой связи,
например, книгу [107].
Главных причин популярности (П.2) было две: это единственная
модель, для которой можно получить какие-либо аналитические резуль-
результаты, а ее построение и использование требует сравнительно небольших
затрат машинного времени.
Можно строить и более сложные нелинейные статистические мо-
модели вида A1.1) (для них иногда используют термин NARMA), но в этом
случае построение модели требует более существенных затрат и сильно
затрудняет получение каких-либо аналитических оценок. В частности,
довольно сложно получить аналитическое выражение для среднего зна-
значения правой части. Чтобы преодолеть эту трудность, иногда сразу строят
детерминированную модель для прогноза среднего значения [106]. Кроме
того, нелинейные модели уже сами по себе могут порождать нетриви-
нетривиальное временное поведение, так что простая картина фильтрации шума
может оказаться неприменимой.
Нелинейные модели делят на два типа: параметрические и непара-
непараметрические. Параметрическими называют модели, для которых функция
F(x, ?,a) одна и та же для всех х и ? и зависит от нескольких параме-
параметров а, которые и необходимо как можно точнее найти по временному
ряду. Непараметрические методы используют локальные аппроксима-
аппроксимации в окрестности некоторого набора точек {х/ь,?*}, так что функция
получается как набор кусочных аппроксимаций в окрестностях задан-
заданных узлов (чаще всего кусочно-линейных). Каждая из таких локальных
JJ.2. Статистические методы обработки 243
функций, разумеется, тоже зависит от параметров, но набор параметров
свой в каждой окрестности, так что термин «непараметрическая регрес-
регрессия» несколько странен, хотя широко используется в статистике (см.,
например, [127] и приведенный там обширный список литературы).
Статистические модели такого типа широко применяются, одна-
однако У них есть один существенный дефект. Непонятно, имеют ли они
какое-либо отношение к действительным уравнениям динамики системы
иди нет. Некоторые аргументы в пользу того, что такая связь может
иметь место, дают модели, описываемые уравнениями m-й степени ви-
вида х(т) = /(x(m~'v ..,x',x) + ?(<). Разностные схемы для них будут
иметь вид A1.1). Далее, некоторые модели, описываемые системами т
ОДУ первого порядка, можно свести к одному уравнению m-го порядка.
Но с другой стороны, существует огромное количество неустойчивых
разностных схем, поведение которых имеет мало общего с аппрокси-
аппроксимируемыми уравнениями. Поэтому подход следует признать разумным,
хотя и недостаточно обоснованным. Его обоснование и было весьма су-
существенным вкладом нелинейной динамики в анализ временных рядов.
Бывают и другие ситуации, когда вид уравнений модели известен
и измерению доступны все основные переменные, входящие в них. Такие
Ситуации, видимо, встречаются не только в небесной механике и физике.
Иногда считается, что существуют эксперты в экономических вопросах,
|оторые знают, какими уравнениями следует описывать те или иные
йпуации, но не знают, какие параметры туда подставить. Тогда задача
|5удет состоять в том, чтобы аккуратно определить значения параме-
|ров и выписать, например, детерминированные уравнения для средних
величин и моментов. Построение таких уравнений — одна из приклад-
|шх задач теории случайных процессов. Полученные уравнения можно
использовать как для анализа текущей ситуации, так и для прогнозирова-
прогнозирования (в качестве прогноза и в этом случае разумно давать математическое
ржидание следующего члена ряда).
Мы сознательно не остановились на многих серьезных проблемах
анализа временных рядов, таких как удаление тренда, получение стати-
яических или спектральных оценок, стационарности, фильтрации шума
1 т. п. [19]. Они не столь важны для пояснения общей идеи, хотя без них
гевозможно полноценное практическое воплощение описываемых идей.
В заключение приведем один пример нелинейной стохастической
модели для ряда измерений солнечной активности [325]. В качестве
Предсказанных величин солнечной активности Yn используются
ip\ = 1,90693, ?>2 = -0,98751,
01 = 0,78512, -д2 = -0,40662, а = 0,03,
Где ап — независимые случайные величины, имеющие гауссово распре-
распределение с нулевым средним и дисперсией а = 0,4.
244 11. Реконструкция аттракторов по временным рядам
11.3. Идея реконструкции аттрактора. Теорема Такенса
Итак, идеи авторегрессионного анализа использовались довольно
давно, но, по-видимому, связь авторегрессионных моделей с динамичес-
динамическими системами, описывающими исследуемые процессы, всерьез не ана-
анализировалась. Однако такой вопрос возник, когда в конце 70-х годов
проводились экспериментальные исследования для подтверждения идей
маломодовой нелинейной динамики. Группа американцев, изучавших
гидродинамические течения, опубликовала в 1980 г. работу «Геометрия
по временному ряду» [285], в которой показала, что можно получить
удовлетворительную геометрическую картину странного аттрактора не-
небольшой размерности, если вместо переменных х, входящих в уравнения
динамической системы, использовать тп-мерные вектора, получаемые
из элементов временного ряда по тому же принципу, что и в задачах
авторегрессии
Zt = {x,-,Xi+i,...,Xi+m-l}- A1.4)
В том же году голландский математик Ф. Такенс доложил о своей
знаменитой теореме, опубликованной годом позже [329]. Именно она
лежит в основе всех алгоритмов анализа временных рядов методами
нелинейной динамики. Поэтому остановимся на ней подробнее.
Теорема Такенса основана на тех же идеях, что и известная теорема
Уитни из курсов дифференциальной геометрии [115]. Строгих форму-
формулировок мы давать не будем, это уведет нас в сторону, а дадим лишь
несколько пояснений.
fc-мерное многообразие — это обобщение понятия «гладкая fc-мер-
ная поверхность в n-мерном пространстве, которую локально в окрестно-
окрестности каждой точки можно параметризовать А; евклидовыми координатами».
Глобально же она может быть устроена по-разному, как сфера, тор, не-
нечто бутылковидное, сфера с ручками и т. п. Теперь остается представить
себе то же самое, но уже без n-мерного пространства. Это и будет
многообразие как абстрактный математический объект, который можно
обозначить Мк. Когда такое многообразие реализуется в виде поверхно-
поверхности Sk в п-мерном пространстве, которая не пересекается сама с собой,
то говорят, что оно вложено в R". Само вложение можно представить себе
как дифференцируемую векторную функцию F, определенную на Мк,
щш которой отображение М* —> Sk является взаимно однозначным и су-
существует обратная дифференцируемая функция F~', отображающая Sk
обратно в Мк. То есть Sk = F(Mk) и Мк - F~x(Sk). Заметим, что F~l
определена только на Sk, в противном случае она не могла бы быть одно-
однозначной. Выбирая разные F и п, можно получить различные представле-
представления одного и того же многообразия. Если все F и F~l дифференцируемы,
то про эти представления говорят, что они диффеоморфны друг другу.
Теперь пусть на многообразии Мк (или на какой-либо поверхно-
поверхности Sk, диффеоморфной ему) определена векторная функция, нужное
количество раз дифференцируемая и отображающая Мк в тя-мерное евк-
евклидово пространство К™. То, что получится в К™, т. е. будет образом Мк,
будет являться вложением или нет?
11.3. Идея реконструкции аттрактора. Теорема Такенса 245
Пусть Мк — как минимум дважды дифференцируемое много-
многообразие [115], a g(x) — некоторая дважды дифференцируемая функция,
отображающая Мк —> Rm, для которой матрица производных ^- имеет
ранг А;. Последнее условие необходимо, чтобы при отображении не полу-
получился объект меньшей размерности; скажем, плоскость не отображалась
в одномерную кривую (или, как говорят, ранг отображения должен
быть равен А;). Такое отображение будет давать погружение многообра-
многообразия Мк в Rm при условии, что m > 2k 4- 1 (теоремы Уитни [115]).
Погружение локально аналогично вложению, но может содержать са-
самопересечения, а потому глобально невозможно определить обратное
отображение. Например, если в качестве многообразия рассматривать
окружность, то на плоскости эллипс будет вложением, а восьмерка —
только погружением. Точке пересечения восьмерки будут соответствовать
две различные точки окружности. Поэтому теоремы Уитни оказалось
недостаточно для обоснования методов обработки временных рядов.
Осталось пояснить, что за многообразие М и функция М -> Rm
имеются в виду и какое отношение все сказанное имеет ко временным
рядам. Пусть задана динамическая система <р'(х) с фазовым простран-
пространством Р. Будем считать, что числа, образующие временной ряд, являются
значениями некоторой «наблюдаемой» — скалярной функции состояния
динамической системы х(<):
В качестве многообразия М, фигурирующего в теореме Уитни, может
использоваться либо само фазовое пространство Р, либо какое-либо ин-
инвариантное многообразие Md из Р. Во многих случаях, когда переходные
процессы закончились и можно считать, что траектория находится прак-
практически на аттракторе, удобно в качестве Мd рассматривать минимальное
инерциальное многообразие (МИМ), о котором ранее говорилось в раз-
разделе «Динамические размерности».
Теперь рассмотрим подробнее построение z-векторов A1.4). Пусть
временной шаг между элементами временного ряда равен г, а векто-
вектора х(?;) будем для краткости обозначать х,-. Тогда очевидно, что
Поэтому
Xi = h(\i) = Фо(х;),
xi+2 = h(xi+2) =
xi+w_, = Ь(*+т_
xi+m = h(xi+m) =
246 11. Реконструкция аттракторов по временным рядам
Мы связали все компоненты вектора Zj с одним и тем же состоянием
динамической системы х,-. Следовательно, существует векторная функ-
функция, которую мы, следуя Такенсу, обозначим Л, отображающая вектора
х,- € Md в точки яг-мерного евклидова пространства Rm,
Zi = Л(х,), х; е Md, zi e Em.
То есть мы пришли к ситуации, описанной в условиях теоремы Уитни,
где роль отображения g играет Л, а роль многообразия — Md. В теореме
предполагается, что Md, ft и ^ по крайней мере дважды дифференци-
дифференцируемы, а для всех неподвижных точек и циклов с периодами кт, к < d,
предполагается, что у них все собственные значения простые и не рав-
равны 1, a h(x) для них различны. Тогда теорема Такенса утверждает, что
случаем общего положения, т. е. типичным свойством отображения Л будет
то, что при т ^ Id + 1 оно будет давать вложение Мd в Rm. Образ Md
в Rm будем обозначать Sd: Sd = A(Md), и, согласно теореме, в типичном
случае у него не должно быть самопересечений.
«Вложение» в данном случае будет означать, что:
1. Функция Л будет дифференцируема и будет иметь обратную диф-
дифференцируемую Л~', определенную на Sd: Md = A~'(Sd).
2. Каждой траектории динамической системы будет соответствовать
ее образ в z-пространстве. Причем для образов будут иметь место
те же свойства, что и для исходных траекторий, в частности, через
каждую точку Sd будет проходить одна и только одна z-траектория.
3. На Sd можно определить динамическую систему. Действительно,
х,- =A(zi), Xj+i -(pT(xi),
ZieS". A1.6)
Ф отображает Sd в Sd, а вне поверхности Sd отображение Ф
не определено. Если оставить только последнюю компоненту этого
соотношения, получим другой вариант, который можно записать
в виде «отображения с запаздыванием» или «нелинейной авторе-
авторегрессии»
Xi = F(xi-\,... ,Xj_m).
Данное соотношение может быть использовано для решения задачи
прогнозирования временного ряда.
4. Таким образом, мы имеем два отображения:
xi+i = ipT(xi) = Ф(х<), х е Md, Ф: Md - Md
Их можно рассматривать как отображения, связанные невырожден-
невырожденной и обратимой заменой переменных z = Л(х) или как различные
представления одного и того же отображения. Следовательно, ха-
характеристики, инвариантные относительно невырожденной заме-
замены, у обеих систем должны совпадать. К ним относятся фракталь-
фрактальные размерности аттрактора, набор обобщенных энтропии и все d
|j,3. Идея реконструкции аттрактора. Теорема Такенса 247
ляпуновских показателей. Поэтому указанные свойства можно пы-
пытаться определять по экспериментальным данным, не зная всех
переменных динамической системы. Можно пытаться восстано-
восстановить (аппроксимировать) и саму функцию Ф(г).
Как следует понимать слова о «типичном свойстве» отображе-
отображения Л? Строгие формулировки сложны и говорить мы о них не будем.
Типичность понимается примерно таким же образом, как в случае утвер-
утверждений «в типичном случае две прямые на плоскости пересекаются»
или «в типичной ситуации три прямых на плоскости не пересекаются
в одной точке». Подобное пояснение можно дать и к теореме Такенса.
В ней, фактически, используется предположение, что в случае общего
положения ранг Л равен d.
Допустим, что нам захотелось найти точку самопересечения по-
поверхности Sd, т.е. две различные точки Х],Х2 € Md, %\ ф *г, такие что
Л(х,) = Л(х2). A1.7)
Это соотношение можно рассматривать как систему m нелинейных ал-
алгебраических уравнений для определения 2d неизвестных — компо-
компонент X), Х2. При тп > Id число уравнений будет больше числа неиз-
вестных, поэтому в типичном случае решений, а, следовательно, и точек
Самопересечения быть не должно. Но в каждом конкретном случае до-
доказать их отсутствие — задача нетривиальная. Чаще всего при анализе
экспериментальных данных отсутствие самопересечений принимается
на веру или специально проверяется. Более того, если самопересече-
самопересечений немного по сравнению с общим числом точек, то, как правило,
щ наличие не влияет на результаты большинства алгоритмов. Скажем,
И для окружности, и для восьмерки оценка размерности будет одной
и той же. Однако большое количество самопересечений или даже про-
просто наличие близких к самопересечениям складок способно радикально
Повлиять на результаты. Об этом мы расскажем позднее.
Таким образом, с практической точки зрения, хорошее погружение
Может быть почти так же хорошо, как и вложение. Кроме того, окрест-
окрестности точек самопересечения могут никогда не посещаться траекторией,
в таких ситуациях их можно просто игнорировать или рассматривать
не все Md, а только его часть, содержащую аттрактор.
Однако могут существовать такие сочетания задержки т, наблю-
наблюдаемой h(x) и динамической системы у'(х), при которых вложения
не получится. Однако, хотя такая ситуация и «нетипична», с ней впол-
вполне можно столкнуться на практике. Приведем несколько простейших
Примеров.
1. Неудачным примером наблюдаемой будет сохраняющаяся ве-
величина. В этом случае все фазовое пространство отображается в точку,
При этом ранг отображения Л оказывается меньше d. Ситуация не явля-
является случаем общего положения.
2. Неудачным примером сочетания задержки и исследуемого ат-
аттрактора динамической системы будет т, равное или кратное периоду
248^^х^Реконструктя^^
или одному из периодов для n-тора. В не-
STSSSJS А бу/ех меньше *. но такой выбор г
™удет случаем обшего положения.
3 Интересно, что простейшие примеры можно найти и во всем
известной системе Лоренца х = а(у - х), у = (г - z)x - у, z = ху - bz.
Исходное фазовое пространство Р = R?. Если в качестве наблюдаемой
рассматривать переменные х или у, то окажется, что все R3 не вклады-
вкладывается в Rm отображением Л: вся ось z, которая является инвариантным
подпространством, отображается в одну точку z = 0. Однако хаотический
аттрактор Лоренца не содержит оси z, а потому реконструкция оказыва-
оказывается корректной. Если же в качестве наблюдаемой выбрать z, то ситуация
оказывается хуже: из-за того, что уравнения инвариантны относительно
замены (x,ytz) —> (—х,— у, z), на аттракторе для любой траектории х(<)
всегда найдется симметричная ей х(<), такая что Л(х(?)) = Л(х(?)). По-
Поэтому реконструкция по переменной z, вообще говоря, может содержать
сколь угодно много самопересечений. Тем не менее, обычно оценки
фрактальной размерности для таких реконструкций оказываются теми
же, что и для реконструкций по переменной х.
4. В качестве последнего примера проблем с реконструкцией рас-
рассмотрим систему
* = F(x,y), y = G(y). A1.8)
Измеряя какие-либо компоненты у, невозможно судить о полном со-
состоянии системы, включающем х (ранг отображения Л, построенного
по у, не может быть больше размерности вектора у). Однако то, что G
не зависит от х, также не является случаем общего положения, если
рассматривать G как элемент множества функций {G(x,y)}. Но если ко
второму уравнению сделать малую добавку, т. е. рассмотреть уравнение
у = G(y) 4- ef(x, у), то ситуация общего положения восстанавливается.
Если решения системы A1.8) стремятся к таким, для которых
х = g(y), то возникает описанный ранее случай системы с инерциальным
многообразием (пространство векторов у) и инерциальной формой (урав-
(уравнение у = G(y)). В этом случае, даже если мы анализируем полное состоя-
состояние системы и измеряем некоторую функцию /i(x, у), то на самом деле мы
получаем информацию лишь относительно минимальной инерциальной
формы у = G(y), поскольку /i(x,y) = /i(g(y),y) = h(y). Следовательно,
основным объектом исследований при анализе временных рядов для траекто-
траекторий на аттракторе являются не сами динамические системы, а ихминималь-
ные инерциальные формы на минимальном инерциальном многообразии (МИФ
на МИМ). Для полной динамической системы с фазовым пространством
{х, у} функция Л окажется «нетипичной» и не будет давать вложения.
Таким образом, из теоремы Такенса не следует, что вектора A1.4)
всегда позволяют исследовать свойства динамической системы по времен-
временному ряду. Такое исследование возможно лишь как правило, из которого
всегда есть исключения.
Если теперь кратко суммировать содержание данного раздела, мож-
можно сказать, что теорема Такенса подводит строгую математическую основу
11.4. Выбор параметров реконструкции 249
под идеи нелинейной авторегрессии. После работ Такенса и др. почти
те же самые идеи, использовавшиеся в статистике, иногда фигурируют
часто под другими названиями — реконструкция аттрактора, фазового
пространства, динамической системы, прогнозирование методами нели-
нелинейной динамики и т. п. Тем не менее, кроме собственно обоснования
некоторых старых идей, нелинейная динамика позволила предложить не-
несколько действительно новых подходов к исследованию временных рядов,
а также новые характеристики систем, которые могут быть использованы
для их идентификации.
11.4. Выбор параметров реконструкции
11.4.1. Задача выбора оптимальных параметров
При всей своей простоте практическая реализация идей рекон-
реконструкции часто сталкивается с проблемами. Возникают они из-за того, что
длина обрабатываемого ряда всегда ограничена, во-первых, возможностя-
возможностями хранения информации, во-вторых, скоростью обработки, и в третьих,
стационарностью исследуемого объекта — важно знать, в течение какого
времени мы можем полагать, что исследуем одну и ту же динамическую
систему (как только изменится у'(х), вектора z начнут строиться по-
другому). Проблема стационарности вообще является бичом большинства
методов анализа временных рядов и о ней разговор особый. Для простоты
пока будем полагать, что имеется временной ряд из N чисел, которые
являются значениями некоторой наблюдаемой, характеризующей одну
и ту же динамическую систему. Тогда реконструированные z-вектора
A1.4) дадут N — т точек на поверхности Sd G Rm, по которым надо будет
судить о динамической системе Ф и ее аттракторе. Объем информации,
который можно извлечь из этого множества точек, вообще говоря, зави-
зависит от свойств поверхности (насколько она искривлена, закручена и т. п.)
и от свойств функции Ф(г) (насколько велики ее производные). Так как
точек конечное число, то существует некоторое характерное расстояние I
между точкой и ее ближайшим соседом. Меньшие масштабы будут не-
неразрешимы для данного временного ряда. Если на масштабах порядка I
поверхность Sd сильно искривлена, а функция Ф(г) сильно изменяется,
то методы нелинейной динамики будут, скорее всего, бесполезны. Эта
же проблема в несколько ином виде встречается, например, в задачах
цифровой обработки сигналов (так называемая теорема Котельникова).
Считается, что если временной интервал между отсчетами равен At,
то частоты больше чем 1/2Д< разрешить невозможно. Однако в зада-
задачах реконструкции свойства Sd и Ф(г) априорно неизвестны, поэтому
аналогичных оценок (скажем, кривизна или производная, не превыша-
превышающие ~ i~') сделать невозможно. Можно только разумно распорядиться
несколькими свободными параметрами. Чаще всего это тит.
В предыдущем разделе уже говорилось, что свойства Sd и *(z)
зависят от динамической системы <р, наблюдаемой h, задержки т и раз-
размерности векторов т (иногда ее называют «размерность вложения»).
250
11. Реконструкция аттракторов по временным рядам
Обычно первые два фактора менять невозможно. Для отображений фик-
фиксирован и временной шаг. Для непрерывных систем, вообще говоря, т
можно менять. Относительно размерности вложения m теорема Такенса
требует только, чтобы она не была слишком мала; верхней границы,
с точки зрения теоремы, нет. Поэтому можно сформулировать задачу
оптимального выбора параметров реконструкции, так чтобы получаемый
набор реконструированных векторов был наиболее информативен.
Пример различных реконструкций для аттрактора Лоренца показан
на рис. 11.1. Свойства реконструкции характеризуют графики корреля-
корреляционного интеграла, приведенные справа. Наклон этого графика должен
давать оценку размерности аттрактора Лоренца Di = 2,06. Отклонения
наклона на линейном участке от штриховой линии можно рассматривать
как характеристику качества реконструкции. Видно, что при слишком
малых и слишком больших задержках т реконструкция оказывается ис-
испорченной искажениями.
log2C -,
-20;-
1 ) П I I (I I М I I ГII III 1II IIJ '1II ! М JI II ! Г J
-10 0 10
'l I I I I I
I I I I I I I I I I I I I I I
log,e
log2C -,
-10-
-20
iiiiiiiiliiii in iiIiiiiiiiiiIhuiiiii
I |4тТ1 I ITF'D I I I ) I I I I I t i
-10
0
10
-5
11.4. Выбор параметров реконструкции
251
Рис. 11.1. Зависимость свойств реконструкции аттрактора Лоренца от т, m = 5.
а) т = 0,015; ?) т = 0,15; в) т = 1,5; г) т = 7,5. Справа приведены графики
корреляционного интеграла, наклон которых должен давать оценку размерности
Х>2 — 2,06 (истинному значению отвечает штриховая линия)
Таким образом, для оценки информативности реконструкции не-
необходимы критерии ее качества. Следует сразу заметить, что исчерпыва-
исчерпывающих критериев качества на сегодня не существует. Любой из описанных
ныне в литературе критериев выбора т и m — это не догма, а лишь
руководство к действию. В том смысле, что для каждого критерия суще-
существуют ситуации, в которых он вообще не будет работать или будет давать
далеко не оптимальные значения. А потому при практическом использо-
использовании реконструкции не самым худшим оказывается простой подбор т
и тп: произвести расчет некоторой величины (скажем, размерности 1?г)
для нескольких т и для последовательности тп = тщ, тпц + 1, то + 2
252 11. Реконструкция аттракторов по временным рядам
и т.д., пока результат не перестанет зависеть от m. r можно подбирать,
например, исходя из минимизации некоторой ошибки метода.
Тем не менее мы приведем несколько популярных рекомендаций
по выбору параметров реконструкции. Но сначала сделаем несколько
предварительных замечаний.
1. Вообще говоря, следует различать два временных интервала —
интервал между элементами временного ряда At = U+\ — U и интер-
интервал (временной сдвиг, запаздывание, задержка) т между компонентами
вектора г. Они не обязаны совпадать. Можно выполнить процедуру
реконструкции даже для непрерывной скалярной функции x(t):
z(i) = {x(t), x(t + t), x(t + 2т),...,x(t + (m- 1)т)}. A1.9)
Более того, доказательство теоремы Такенса не требует даже, что-
чтобы временные сдвиги между компонентами были одинаковы. То есть
в принципе можно даже строить реконструированные вектора как
z(t) = {x(t), x(t + Т]), x(t +тг),... ,x(t + Tm_i)} [191], важно только,
чтобы способ был один и тот же для всех z(i), т. е. набор задержек т* дол-
должен быть всегда один и тот же. В принципе, можно даже поставить задачу
оптимизации набора задержек, однако неясно, насколько существенный
выигрыш можно получить.
На практике, разумеется, цифровые системы непрерывных функ-
функций не измеряют, поэтому т всегда кратно At. В теоретических же
рассуждениях, напротив, часто удобнее считать наблюдаемую непрерыв-
непрерывной функцией и анализировать вектора вида A1.9).
Для непрерывных реконструкций можно поставить задачу восста-
восстановления дифференциальных уравнений ^ = f2(z) no экспериментальным
данным [219]. Практически же для этого достаточно, чтобы At было
мало, тогда % 3 *%&.
2. Не обязательно соотносить момент t именно с первым элемен-
элементом z-вектора. Иногда удобнее считать, что он относится к некоторой
промежуточной точке, например, к середине временного интервала, за-
захватываемого вектором. Один из таких примеров мы рассмотрим ниже.
3. Вообще говоря, реконструкции можно строить не только по ска-
скалярным временным рядам. Можно строить вектора и из нескольких
наблюдаемых. При этом, однако, возникнет небольшая проблема, свя-
связанная с тем, как вычислять расстояние между такими векторами (т.е.
как, например, из метров, литров и килограмм получать одно число —
расстояние). Однако она обычно вполне разрешима.
В литературе можно найти много рекомендаций и способов выбора
задержки т и размерности вложения т, например, [262, 207, 216]. Как
уже говорилось выше, ни на одно из них нельзя полностью полагаться.
В простейших модельных случаях они все обычно работают, а для неко-
некоторого произвольного, а особенно экспериментального, временного ряда
результаты очень часто бывают невразумительны. Поэтому несколько
общих принципов мы сформулируем, но важно не терять чувство меры
и здравый смысл.
11.4. Выбор параметров реконструкции ~.„
11.4.2. Выбор размерности реконструкции т
Одна из основополагающих идей при анализе получившейся ре-
реконструкции состоит в следующем. Если реконструируется траектория
динамической системы, то через каждую точку должна проходить только
одна траектория, т. е. удовлетворительная реконструкция не должна со-
содержать самопересечений траектории. Разумеется, что самопересечений
в массиве дискретных точек Z; скорее всего никогда не будет, поэтому
ищут так называемых «ложных близких соседей» — пары векторов, кото-
которые оказались близкими в реконструкции, но их прообразы находились
далеко. Для поиска таких пар предлагались две идеи, которые на самом
деле сводятся к одному и тому же.
Пусть J- и Zj — два близких соседа в реконструкции размерно-
(m+l) (m+1)
сти т, а ъ\ и zj соответствуют им в реконструкции размерности
т + 1. Если мы имеем дело с истинно близкими соседями, то они чаще
всего будут близки в обеих реконструкциях (редкие исключения возмож-
возможны из-за особенностей исследуемой динамической системы). В то же
время ложные близкие соседи в реконструкции т, как правило, превра-
превращаются в отдаленных с ростом т. Пары, для которых ||z,- — г™ [| мало,
a ||zj — zjm+ 'I — нет, и получили название «ложных ближайших
соседей» или false nearest neighbours — FNN. Если теперь увеличивать т
и оценивать количество FNN, то при достижении нужной размерно-
размерности, при которой достигается правильная реконструкция, это количество
резко уменьшается. По уменьшению можно найти минимальное т.
Практически тот же метод можно получить путем иных рассужде-
рассуждений. Если реконструкция при данном т корректна, то отображение Ф(г),
z,+i = Ф(г,), должно быть непрерывным и дифференцируемым. Тогда
для близких векторов Zj и Zj должны быть близки и их образы Zj+i
и Zj+1. Таким образом, получается несколько иное определение ложных
близких соседей, но суть остается той же самой, тем более что в обо-
обоих случаях речь идет об одних и тех же элементах временного ряда.
Из второй формулировки становится понятно, откуда возникает неболь-
небольшое количество FNN в корректных реконструкциях — это просто места,
где производная Ф(г) велика или, что то же самое, траектории быстро
расходятся в стороны друг от друга.
При всей своей интуитивной очевидности данная методика не до-
допускает практически полезной строгой формулировки, поскольку ис-
использует нестрогие понятия «близкие» и «не близкие» пары. Строго их
определить невозможно, потому что свойства функции Ф(г) априорно
неизвестны. Поэтому при численной реализации метода и приходится
опираться на интуицию и здравый смысл.
Иногда отсутствие ложных соседей в реконструкции можно об-
обнаруживать и по косвенным признакам, измеряя некоторую величину
для различных т и определяя значение, при котором результат почти
перестает зависеть от т.
11- Реконструкция аттракторов по временным рядам
11.4.3. Выбор временного интервала г
Первоначально для выбора задержки использовали качественную
идею о том, что если компоненты, образующие вектор, будут «неза-
«независимы» друг от друга, то реконструированные вектора будут нести
в себе «наибольшее количество информации о системе». Простейший
способом добиться такой «линейной» независимости — это выбрать т
близким к первому нулю автокорреляционной функции для ряда Xj.
Более сложным вариантом была методика, основанная на теории ин-
информации и использовавшая первый минимум взаимной информации
для x(t) и x(t +t) [207, 208, 209]. Для этого по временному ряду изго-
изготовляются гистограммы, аппроксимирующие распределение x(t) (оно же
будет и для x(t + т)) и совместное распределение x(t) и x(t + т). Да-
Далее по построенным гистограммам рассчитываются энтропии и взаимная
информация. Результат, однако, оказался интересным. Для простых мо-
модельных систем вроде системы Лоренца почти любой разумный выбор т
был если и не хорош, то и не плох. Для более сложных систем, в которых
нет одного ярко выраженного «псевдопериодического» поведения ока-
оказалось, что данные методики иногда просто невозможно использовать,
поскольку автокорреляционная функция может вовсе не иметь первого
нуля, а функция взаимной информации — первого минимума. Обе про-
просто монотонно убывают с ростом т. Иногда ноль или минимум есть,
но в качестве т оказывается далеко не оптимальным. Поэтому делались
попытки разработать более сложные методы, напоминающие технику
выбора размерности вложения т. Детали здесь опять таки излагать мы
не будем, опишем только важнейшие из них. Самым интересным, пожа-
пожалуй, оказалось то, что на качество реконструкции влияет не сама по себе
величина т, а временной интервал, захватываемый вектором z — между
последним и первым его элементами. Мы будем называть его окном ре-
реконструкции и обозначать w = (m — 1)т. Ниже мы будем предполагать,
что т достаточно велико, чтобы удовлетворять условию теоремы Такенса.
Влияние w на реконструкцию отличается от влияния т, хотя
и может быть иногда интерпретировано также в терминах «ложных сосе-
соседей». Удобнее его характеризовать термином «искажения реконструкции».
Можно выделить два типа искажений. Один возникает, когда w слишком
мало, проявляется, как правило, только для систем с непрерывным вре-
временем, и о нем можно получить представление на простейшем примере
реконструкции сигнала cos< (см. задачи в конце книги). Он заключается
в том, что образ реконструируемого множества оказывается «спрессован»
вдоль некоторых направлений (рис. 11.1 в). Из-за этого, во-первых, воз-
возникают ложные соседи, а во-вторых, для изучения деталей аттрактора
необходимо различать очень мелкие масштабы, для чего в свою очередь
нужны очень большие выборки; время измерения должно быть порядка
времени возвращения в очень малую окрестность точки.
Второй тип искажений возникает, когда w слишком велико,
но только для хаотических систем.(рис. 11.1 в,г). Дискретность или не-
непрерывность времени не важна. Характерным временным масштабом
в этом случае выступает К~{ — величина, обратная энтропии дина-
11.4. Выбор параметров реконструкции _,
мической системы. Этот тип искажений немного похож на резул
действия «подковы Смейла»: множество как бы подвергается растяжению
и складыванию, и вплоть до некоторых масштабов будет исследовать-
исследоваться не структура самого множества, а структура получившихся складок
При этом на соседних складках тоже возникают ложные соседи и на боль-
больших масштабах реконструкция может выглядеть как объект существенно
большей размерности, чем на самом деле.
Рассмотрим теперь действие искажений при малых длинах окна.
В данном случае удобно соотнести момент t с серединой вектора z,
а размерность т считать нечетным числом, хотя это и не принципиально.
Итак, пусть
Будем считать, что функция x(t) m раз дифференцируема, а аргумент х
представим в долях половины длины окна, x(t — a j), где а принимает т
дискретных значений as: от а\ = — 1 до ат = +1. Тогда
w\ , „ aw ., , 1 / aw
)x(t) + — Х(*)+{
Обозначим через е^+ь А; = 0,...,то— 1, вектор, компоненты которого
представляют собой просто значения (а„)к. Тогда
Далее ортонормируем систему векторов е*. Это даст не что иное как
систему векторов v*, компонентами которых будут значения дискретных
полиномов Л ежандра, подобно тому как ортогонализация полиномов вида
Qk(ce) = а* Дает непрерывные полиномы Лежандра. Для разложения z
по у* получится соотношение, аналогичное A1.10)
m-l
k=0
где Ак = O(wk). Значения А^ можно приближенно получить как Ак —
(z,Vjt), если заменить дискретные полиномы непрерывными, а сумму
в скалярном произведении — интегралом:
1
* J'x(t + ~
11. Реконструкция аттракторов по временным рядам
Если воспользоваться соотношением
то, интегрируя по частям, получим
1
Г(*+1 + 1/2)
(Здесь <* — некоторая точка отрезка [t - |,< - f ], но с нужной нам
точностью х<*)(<*) S ж(*)(<).)
С помощью значений Л* можно примерно оценить «размеры» ре-
реконструированного множества в направлении v* как среднеквадратичное
отклонение
<»¦»>
Таким образом, область значений w, где проявляется «эффект слишком
малых задержек», можно определить, как область справедливости соотно-
соотношения A1.11). Проверить справедливость этих закономерностей, скажем,
для системы Лоренца, можно просто выполнив анализ главных ком-
компонент (построение ковариационного базиса, базиса Карунена—Лоэва)
для массива векторов Zj.
Идея его построения очень проста. Пусть имеется N векторов
Zj G Rm; для простоты будем считать, что (z) = iV~'^Zi = 0. Су-
Существует ли какое-либо выделенное направление, на которое вектора
имеют наиболее существенные проекции? Проще всего такое утверж-
утверждение формализовать так: найти максимум по координатам вектора а
для выражения N~l ХН2"8) ПРИ условии а2 = 1. Это обычная задача
на условный экстремум и легко показать, что минимизируя функцио-
функционал -N^'^te.a) - 5(а2 - 1), мы приходим к задаче на собственные
t
значения Ся = 5а, где Ctj = JV Х^г1*г0' ~ ковариационная матри-
i
ца, Zik — fc-я компонента вектора z,-. Собственные вектора а* мат-
матрицы С, образующие ортонормированный базис, обычно располагают
в порядке убывания собственных значений 5*. Легко получить, что
11.4. Выбор параметров реконструкции 257
Sk — (як,СЯк) = iV~' 53 (ziiat) ¦ Таким образом, я\ дает решение задачи
t
максимизации ЛГ~' ^(zj,a) , am — минимизации, аг — максимизации
при дополнительном условии а ± aj и т.д. Описанная техника носит
много названий — анализ главных компонент, построение ковариаци-
ковариационного базиса или базиса Карукена—Лоэва. Она широко используется
в статистике, при обработке данных и т.д.
Оказалось, что при малых w направления главных компонент
для векторов реконструкции практически совпадают с v*, а средние
проекции на них действительно пропорциональны 5* ~ wk [216]. С ро-
ростом w они постепенно выравниваются и момент «выравнивания» можно
принять за точку wt исчезновения эффекта малых w. Для нее можно
получить приближенное выражение, если приравнять а(Ао) = о{А\), т. е.
V2a(x) = —^ или
Как указывалось в [216], оптимальное значение длины окна рекон-
реконструкции часто несколько меньше; скажем, для системы Лоренца оно
составляет примерно %?¦. Следует заметить, что соотношение A1.12) опре-
определяет только порядок величины, вблизи которого скорее всего лежит
оптимум. Как и все приводимые в данном разделе результаты, его следует
воспринимать в качестве руководства к действию, а не строгого рецепта,
даже несмотря на несколько мистический множитель VT2. Например,
для сигнала x(t) = cos(^) легко получить, что wt — V3j = 0,55T.
Оптимальное w (см. задачи по реконструкции гармоничекого сигнала)
близко к 0,25 Т — также примерно вдвое меньше.
Ограничения для w сверху также можно получить, но это сделать
сложнее. Мы вернемся к этой теме при обсуждении корреляционно-
корреляционного интеграла и оценке энтропии Kq по экспериментальным данным.
Соответствующая оценка имеет вид
Kw<0(l)lnN.
То есть для нехаотических систем серьезных ограничений сверху нет,
а для хаотических можно сделать некоторые оценки по эксперименталь-
экспериментальным данным.
Задача выбора оптимальной наблюдаемой для построения рекон-
реконструкции в литературе не рассматривалась. Видимо такая постановка
нетипична для натурных экспериментов, а потому и интереса большого
не представляет. Возможно, к подобному классу задач можно отнести
проблему формирования сводных экономических индексов (биржевых,
ценовых, потребительских и т. п.), однако, насколько нам известно, в кон-
контексте теории динамических систем данный вопрос не рассматривался.
12
Обработка временных рядов —
важнейшие алгоритмы
нелинейной динамики
При обработке временных рядов обычно решают несколько типов
задач. Во-первых, задачи измерения некоторых характеристик динами-
динамических систем, инвариантных относительно замены переменных. К ним
относятся размерности аттрактора, ляпуновские показатели, энтропии.
Иногда удается исследовать какие-нибудь топологические свойства ат-
аттрактора. Иногда ставится задача аппроксимации уравнений движения
по экспериментальным данным, например, чтобы попытаться понять
механизмы простейших бифуркаций и выяснить, моделями какого ти-
типа такие данные лучше всего описывать. Подобные задачи относятся
к проблеме идентификации.
Ко второму типу можно отнести задачи динамического прогноза
временных рядов. В этом случае, фактически, тоже приходится решать за-
задачу восстановления динамической системы по временному ряду, но соб-
собственно уравнения движения интереса не представляют, к ним относятся
как к «черному ящику» — важно, чтобы по входному сигналу правильно
вырабатывался выходной. Такой подход характерен, например, для ап-
аппроксимирующих нейронных сетей типа персептронов — после того, как
сеть обучена, почти никто никогда не интересуется, какова структура
сформировавшихся связей и какой же функциональной зависимости она
соответствует.
К третьему типу можно отнести другую часть задач идентифика-
идентификации, когда нужно каким-либо образом классифицировать исследуемые
системы, скажем, для диагностических целей. Но при этом абсолютно
несущественно, измеряем ли мы инвариантные характеристики динами-
динамической системы или же нечто совершенно экзотическое, пригодное толь-
только для данного узкого круга задач. Важно только, чтобы классификация
работала эффективно и по возможности быстро. Многие успешные реше-
решения задач такого типа вообще не используют представления нелинейной
динамики, хотя иногда они оказываются полезны или даже незаменимы.
При решении таких задач «третьего типа» возможны курьезы, ко-
когда какой-либо алгоритм (скажем, расчет корреляционной размерности)
применяют в ситуации, где он не может и не должен работать, но по-
получают число или кривую, которая служит хорошим классификатором.
Затем этот результат снабжают интерпретацией в терминах свойств ди-
динамических систем и получают совершенно неверные суждения (авторам
12.1. Расчет фрактальной размерности аттрактора 259
немножко стыдно, у них за плечами тоже есть одна похожая работа,
но мы не скажем, какая).
Почему возможны такие ситуации? Дело в том, что каждый из опи-
описанных ниже алгоритмов — это только преобразователь чисел. Он может
работать с простыми детерминированными данными и служить для оцен-
оценки параметров динамических систем. Он может обработать и чисто
случайные данные, и результаты будут также случайными числами (воз-
(возможно, усредненными). Различить подобные ситуации и правильно их
интерпретировать можно далеко не всегда и именно для этого требуется
опыт; чем больше, тем лучше.
Поэтому существует и четвертый тип задач — определить, с данны-
данными какого типа имеет дело обработчик. Следует ли данные рассматривать
как детерминированные и применять «детерминированные» интерпрета-
интерпретации. Или следует относиться к данным как к случайным? Получается
задача «идентификации временного ряда».
Мы рассмотрим некоторые алгоритмы для задач первого, второго
и четвертого (в следующей главе) типов. На полноту данное изложение
не претендует, мы постараемся изложить несколько важнейших идей.
12.1. Расчет фрактальной размерности аттрактора
Расчет любой из фрактальных размерностей аттрактора по вре-
временному ряду представляет значительный интерес, поскольку позволяет
оценить (обычно снизу) минимальное число существенных динамичес-
динамических переменных <2дг, необходимых для описания наблюдаемых процессов.
Как уже говорилось выше, существует много названий этой величины —
число параметров порядка, динамическая размерность или размерность
минимального инерциального многообразия.
Исторически первыми были попытки определения емкости dc
(см. раздел про размерности аттракторов). Численные методы следовали
сформулированному определению, за исключением того, что опускался
этап минимизации количества накрывающих множеств. Алгоритм, таким
образом, получался примерно следующий. Предполагается, что по вре-
временному ряду построена тя-мерная реконструкция и в распоряжении
исследователя находится набор векторов щ (хотя, вообще говоря, это
могут быть и точки исходного фазового пространства х<).
1. Задаем некоторое е, разбиваем область фазового пространства,
в которой лежат анализируемые вектора, на кубики со стороной е и под-
подсчитываем, сколько кубиков накрывают все известные нам точки. Полу-
Получаем одно значение М(е).
Здесь необходимо обратить внимание читателя, что полное количе-
количество кубиков в большом m-мерном кубе, содержащем аттрактор, для т
порядка 10 может быть огромным (скажем, порядка 1020). Но подавля-
подавляющее большинство из них нам не нужно, потому что туда не попадет
ни одной точки Zj. В любом случае М(е) не может быть больше числа
векторов, т.е. всегда М(е) < N. На самом деле число нужных нам куби-
кубиков еще меньше и можно построить быстрые и эффективные алгоритмы
9*
260
12. Обработка временных рядов
для расчета М(е). Одна из идей может быть следующей. Поделим все
координаты векторов на е и оставим только целую часть, преобразовав
вектора z* в новые вектора щ. Тогда для всех векторов г, попадающих
в одну ячейку, полученные вектора п будут совпадать. То есть М(е) просто
будет равно количеству различных векторов щ. В такой постановке задача
выглядит уже как задача для начинающих программистов и с использова-
использованием быстрой сортировки можно создать алгоритм, требующий порядка
NlogN операций. Так что первый шаг больших проблем не представляет
и переходим ко второму.
2. Допустим, что мы вычислили М(е) для различных е. Теперь
по полученным данным необходимо оценить размерность. Как следует
из определения емкости, при малых е М(е) должно вести себя как
~ e~dc, а в таком случае logAf(e) = — dcloge. Поэтому оценивание
емкости по полученным данным сводится к
а) поиску «наиболее линейного» участка зависимости logM(e)
от log e;
б) построению на этом участке линейной аппроксимации вида
logM(e) = bloge + с, например, по методу наименьших квадратов; в ка-
качестве оценки емкости берется dc = —b.
Наиболее трудно формализовать
в этом алгоритме выбор линейного
участка, по которому следует оцени-
оценивать емкость. Пример расчета для ат-
аттрактора Хенона приведен на рис. 12.1.
Алгоритмы такого типа получили
название подсчет ячеек или box counting.
Первые численные оценки размерно-
размерностей странных аттракторов были сде-
сделаны именно с их помощью. Одна-
Однако довольно быстро выяснилось, что
алгоритм обладает некоторыми серьез-
серьезными недостатками. Во-первых, ока-
оказалось, что даже в случае простейших
аттракторов, вроде аттрактора Хенона,
получение хорошего результата требует Рис. 12.1. Пример оценки емкости
очень длинных выборок — миллионы
16
12
16
20
log2en
24
28
р
для аттрактора Хенона. Длина ряда
5
точек и даже более. Для более коротких N = 20 ¦ Более короткие выборки
не позволяют получить хорошей ли-
линейной зависимости для log2 M(e)
выборок часто не получается хорошего
линейного участка. Во-вторых, вели-
величину М(е) не всегда удается хорошо оценить, поскольку в ряде случаев
весьма заметный вклад вносят редко посещаемые области аттрактора.
В некоторые из них точки Zj не попадут и оценка для М окажется
заниженной. Более того, в [223] было показано, что для аттрактора Ло-
Лоренца при малых е не наблюдается сходимости М(е) даже при N ~ 107.
Исходя из этого был сделан вывод о «непрактичности» алгоритмов типа
box counting.
12.1. Расчет фрактальной размерности аттрактора 261
Поэтому внимание было обращено к вероятностным размерно-
размерностям Dq. Напомним, что в их основе лежит вычисление обобщенных
энтропии Нч = A — q)~x log (Y^pI) > гДе Pi — мера i-ro кубика, покры-
покрывающего аттрактор. При q > 1 основной вклад в сумму, стоящую под
знаком логарифма, будут давать наиболее посещаемые кубики, а влияние
редко посещаемых будет незначительным. Таким образом, одну проблему
удается решить. Используя те же разбиения на кубики, можно для каждо-
каждого разбиения вычислить Hq(e), а затем, аналогично емкости, оценить Dq
путем линейной аппроксимации Hq(e) ? —Dqloge + c. Однако такая
методика также требует больших выборок.
Революционной оказалась следующая идея.
Сумму Cq(e) = (Y^pJ) > называемую иногда обобщенным корреляци-
корреляционным интегралом, можно представить в виде
т. е. как среднее (в общем случае среднее геометрическое) значение меры
кубика размера е. Идея заключалась в том, чтобы оценить это среднее
как можно точнее, а для этого рассчитать меру кубика или шара радиуса е
с центром в каждой точке z,-, а затем усреднить полученные значения
по всем таким шарам. Будем обозначать через fc,(e) число точек Zj внутри
е-шара с центром в точке z,-. Тогда его меру можно приближенно оценить
В случае q = 2 это соотношение существенно упрощается,
a Cj часто называют просто корреляционным интегралом. Последняя
сумма — это просто удвоенное число пар точек, расстояние между
которыми не превосходит е. Таким образом, мы приходим к широко
известному определению корреляционного интеграла
числопарсЦцд||<?
полное число пар Zj, Zj
Оказалось, что для того, чтобы оценить размерность ?>2 по корреляци-
корреляционному интегралу, необходимы выборки существенно меньшей длины,
чем в предыдущих случаях. Методика оценки та же самая — линей-
линейная аппроксимация зависимости logC(e) = -?>2юёе + с по «наиболее
линейному» участку. Саму размерность ?>2 называют корреляционной
размерностью или корреляционным показателем.
Алгоритм расчета ?>2 был предложен в 1983 г. П. Грассбергером
и И. Прокаччиа [222] и с тех пор, видимо, является самым популярным
262 12. Обработка временных рядов
алгоритмом нелинейной динамики для временных рядов (для уравнений
движения таковым является расчет ляпуновских показателей). Но платой
за достоинства является большой объем вычислений — расчет требует
O(N2) операций. Поэтому довольно большие усилия были направлены
на создание эффективных алгоритмов его реализации, и на этом пути
был достигнут ряд серьезных успехов [221, 337, 83].
Однако оказалось, что корреляционный интеграл обладает большим
количеством дополнительных достоинств и позволяет оценить уровень
шума в системе, отличать хаотические системы от нехаотических, оценить
энтропию Кг- Короче, он оказался неисчерпаем почти как электрон
и атом, и потому заслуживает подробного рассказа.
12.2. Свойства корреляционного интеграла.
Оценка энтропии и другие полезные применения
Корреляционный интеграл можно рассчитывать как для точек
в исходном фазовом пространстве %i, так и для реконструированных
векторов Zj. В первом случае при благоприятных обстоятельствах мож-
можно оценить только размерность исследуемой системы. Во втором случае
корреляционный интеграл становится функцией не только е, но и па-
параметров реконструкции т и т (или т и w). Зависимость от двух по-
последних параметров и позволяет (естественно, тоже при благоприятных
обстоятельствах) диагностировать хаотичность, уровень шума, оценивать
энтропию, время предсказуемости, верхний предел допустимой длины
окна реконструкции wmax.
12.2.1. Сравнение результатов для разных т
н коррекция метрики (нормы г -векторов)
В ходе анализа нам будет необходимо сравнивать значения кор-
корреляционного интеграла, вычисленные при различных значениях т;
задержку т мы считаем при этом фиксированной. Однако, если мы
будем использовать обычное евклидово расстояние
\
- zjkJ, A2.3)
то с увеличением т все расстояния будут монотонно увеличиваться,
а среднее квадратичное расстояние (||г< — Zj||2) ~ т. Это в свою очередь
приводит к тому, что одни и те же характерные участки на графике
С(е) будут относиться к разным значениям е (можно привести и не-
несколько более строгую аргументацию, основанную на статистической
интерпретации корреляционного интеграла [300], но сейчас мы этого
делать не будем). В некоторых случаях подобный сдвиг масштабов может
препятствовать использованию описанных ниже алгоритмов. Поэтому,
если предполагается совместная обработка корреляционного интеграла
12.2. Свойства корреляционного интеграла 263
для нескольких значений т, то необходимо использовать коррекцию ме-
метрики — нормировать расстояние на размерность т [206]. Вместо A2.3)
следует вычислять расстояния как
A2.4)
*=l
Метрику A2.3) иногда обозначают как ||-||2 или L2. Скорректированную
метрику A2.4) мы будем обозначать ||-||2с или Ljc-
При расчете корреляционного интеграла часто используют и две
другие метрики:
*=1
и
Вообще говоря, каждая из метрик имеет свои достоинства и недостатки.
Например, ||||2 и ||||2С изотропны. При использовании \\-\\1 или ||||1С
(если необходимо сравнивать различные т),
т ¦ i
„_ -м V^ \Zik-Zjk\
можно получить наиболее быстрые алгоритмы расчета (экономия на воз-
возведении в квадрат) [101]. Для нормы A2.5), которую иногда называют L^
или sup-норма, также можно построить быстрый алгоритм, и кроме то-
того, данная норма не нуждается в коррекции. Для нее, однако, интервал
значений е, на котором изменяется корреляционный интеграл, обычно
несколько короче, что не всегда удобно.
Итак, далее будем предполагать, что расстояния между векторами
вычисляются в скорректированных нормах \\-\\\с, 1ИЬс или в норме ||-||,Х1.
Но еще раз напомним, что необходимо это не для оценки размерности,
а для иных применений корреляционного интеграла.
12.2.2. Оценки энтропии
Напомним, что обобщенный корреляционный интеграл был пред-
предложен как способ расчета энтропии Реньи для некоторого разбиения ат-
аттрактора на кубики, но затем разбиение подменялось усредненной мерой
одного кубика. Забудем теперь об этой подмене, зафиксируем масштаб
разбиения и посмотрим, что получится, если увеличивать размерность
реконструкции т.
Пусть наблюдаемая х изменяется в пределах от xmin до хтах.
Разбиение этого отрезка на участки [a:,-,Xj+i] длиной е (не путайте точ-
точки разбиения ж; с элементами временного ряда а;,-) порождает некоторое
разбиение аттрактора в исходном фазовом пространстве на множества А{,
264
12. Обработка временных рядов
(это будет множество всех векторов хк, для которых h(xk) принадлежит i-
му отрезку). В простейшем случае, когда х — просто одна из компонент
вектора х, получится нарезка аттрактора гиперплоскостями на «ломтики».
Теперь представим себе двумерную реконструкцию с разбиением на отрез-
отрезки [5j,5j+i] по обеим координатам вектора г. Пусть некоторая точка гк
попала в кубик {г, j }: это будет означать, что х* € Л,-, а х^+1 ? Aj. To есть
кубики будут отвечать разбиению «2-го порядка» на множества A\j ,
а «минус логарифм» корреляционного интеграла для него — log Cq —
энтропии этого разбиения Щ (е). Рассуждая таким же образом, мы по-
получим, что m-мерная реконструкция будет соответствовать некоторому
разбиению m-го порядка, а корреляционный интеграл — давать Hq(e).
Тогда можно ожидать, что при малых е Я, '(е) - щт'(е) —> KqT или
'^ ' —* Кчт, когда m —> оо (напомним, что энтропия динамической
системы Kq отвечает свойствам отображения <pl(x), а для отображе-
О -10
-20
От
О
-4
2,5;
2,0;
1,5;
1,0;
0,5;
0
-2 0 2
log2e
^~ ^
i i
4
\
—4 —
2 0
log2e
-10-
-10
-10
б
5
log2e
Рис. 12.2. Пример расчета корреляционного интеграла (верхний) в норме Ьгс
и соответствующая оценка энтропии (нижний): а) Аттрактор Лоренца, г =
At = 0,02, m = 40,60,80,...,200, истинное значение Кг я 0,9; б) Аттрактор
Хенона, г = At = 1, m = 3,4,5,..., 10, истинное значение Кг а 0,36
12.2. Свойства корреляционного интеграла
265
ния ут(х)> которое отвечает временному шагу реконструкции аттракто-
аттрактора т, соответствующее значение энтропии будет равно Кчт).
В приведенных рассуждениях есть, правда, один изъян. Опре-
Определение энтропии динамической системы включает еще один шаг —
измельчение исходного разбиения, т.е. diam.4j —¦ 0. Однако в нашем
случае для типичной наблюдаемой h диаметр разбиения не будет умень-
уменьшаться даже при е —> 0 (при уменьшении толщины ломтиков их ширина
остается той же). Поэтому остается надеяться, что с ростом тп будет
уменьшаться диаметр множества Л|, ,- , тогда измельчение исходного
разбиения можно опустить.
Таким образом, строгого доказательства того, что корреляционный
интеграл имеет отношение к энтропии, нет, но можно ожидать, что
при малых е и достаточно больших тп
log С, = Dq loge - Kqw + const. A2.6)
Здесь использована длина окна реконструкции w = (тп— 1)т вместо тпт,
что иногда удобнее. Заметим, что величина const может зависеть от m
и т, однако эта зависимость менее выражена.
Следовательно, фиксируя в A2.6) масштаб е и исследуя зависимость
от w, можно оценить энтропию динамической системы Kq.
Пример расчета корреляционного интеграла в норме Lie приведен
на рис. 12.2.
Однако соотношение A2.6) позволяет делать не только количе-
количественные, но и качественные выводы. Согласно ему, если система ха-
хаотическая, то при увеличении т график корреляционного интеграла
должен проходить все ниже и ниже. По этому признаку можно иногда
Рис. 12.3. Пример графиков корреляционного интеграла: а) для нехаотическои
системы C-тор); б) для чисто случайных данных, равномерно распределенных
на отрезке [0,1]
266
12. Обработка временных рядов
просто сделать вывод о хаотичности системы. Для сравнения на рис. 12.3
приведены графики для нехаотической системы — 3-тора — и для чисто
случайных данных. Видно качественное отличие от рис. 12.2.
12.2.3. Альтернативный алгоритм и оценки Кг
Ограничимся далее только случаем q — 2, когда все алгоритмы рас-
расчета существенно упрощаются. Перепишем соотношение A2.6) несколько
иначе,
C(e,w) ~ e°2 exp(-K2w). A2.7)
Далее вспомним соотношение A2.2), согласно которому C(e,w) можно
интерпретировать как вероятность того, что во множестве реконструи-
реконструированных векторов Zi для случайно выбранной пары расстояние между
ними будет не больше е. Параметры реконструкции тиг при этом пред-
предполагаются фиксированными. Соотношение A2.7) означает, что в рекон-
реконструкциях с большим w должно быть очень мало близких пар. Действи-
Действительно, для хаотической системы очень трудно найти два длинных куска
временного ряда, которые повторяли бы друг друга с хорошей точностью.
Откажемся теперь от последнего предположения и построим из од-
одного и того же временного ряда много реконструкций для различных
значений размерности т: т^ < т < m\j. Это будет отвечать значениям
окна реконструкции wl < w < w\j. Будет ли A2.7) справедливо для тако-
такого «сводного» ансамбля векторов? При малых е и не слишком малых w
логично предположить, что будет. В таком случае ^ можно уже при-
0
log2e
Рис. 12.4. Пример расчета wR для системы Лоренца. На масштабах Iog2? от —3
до 1 график стремится к значению wR и 1,1, что хорошо согласуется со значением
К2 а 0,9
12.2. Свойства корреляционного интеграла 267
ближенно рассматривать как совместную плотность вероятности, т. е. как
вероятность того, что для данной пары векторов расстояние = е, а длина
окна реконструкции равна w.
Зафиксируем теперь масштаб е, тогда распределение пар векторов
по длине окна при фиксированном расстоянии будет близко к экспонен-
экспоненциальному, p(w) = Ae~K2W. Среднее для такого распределения
Г wp(w)dw
w« = ^7 = -, ; 1 "u^J0 w _j A2.8)
J p(w)dw
To есть, вычислив среднюю длину реконструкции для данного е, мы
получим величину, обратную энтропии. Достоинством метода будет то,
что искомая величина вычисляется сразу, без дополнительных преобра-
преобразований. Напомним, что ожидать подобную зависимость имеет смысл
только на малых масштабах. Пример расчета wr для системы Лоренца
приведен на рис. 12.4.
12.2.4. Оценка уровня шума и статистические тесты
Корреляционный интеграл не обязательно рассчитывать только
для наблюдаемых траекторий динамических систем, можно обрабатывать
данные любого типа. Однако интерпретация результатов должна быть
различной, т.е. желательно знать, что мы обрабатываем, или уметь
сделать соответствующий вывод по полученным результатам.
Предположим, что мы обрабатываем временной ряд чисто случай-
случайных величин Х{. У специалистов-статистиков есть специальный термин
для «эталона» таких величин — HD-данные, от английского independent
and identically distributed, т. е. независимые и одинаково распределенные.
Однако нам понадобятся свойства не самой величины х, а случайной
величины yij = \x{- Xj \, которая служит основным «материалом» для рас-
расчета расстояний ||z; — Zj\\. Пусть случайные величины у распределены
у
с плотностью р(у), а их функция распределения F(y) = f p(x)dx.
—00
Очевидно, что р(у) — F(y) = 0 при у < 0. Для вычисления расстояний
воспользуемся нормой Ц-Ц^ A2.5). Тогда тот факт, что Цг^-гуЦоо < е, озна-
означает, что одновременно должны выполняться неравенства y;+*J+* < e,
к = 0,..., т— 1. Поскольку входящие в эти неравенства у — независимые
величины, то вероятность такого события, т. е. значение корреляционного
интеграла
C{e) = F{e)m. A2.9)
Если плотность вероятности не имеет особенностей в нуле, т. е. р(у) =
Ро + Р\У + ¦ ¦ ¦ при малых у, то F(e) = рое + Щ- + ..., а
logC(e) = mloge + log (po + О(е)), A2.10)
268
12. Обработка временных рядов
т.е. для таких плотностей р(у) размерность получающегося множества
всегда равна размерности пространства реконструкции то. Для других
плотностей результат может оказаться иным, но нетрудно получить общее
правило, если при j -> 0 р(у) ~ у0 (еще раз напомним, что р —
распределение не ж, а разностей \х{ - Xj\\), то значение размерности
получится равным A+/8)то. Не столь важно велика эта оценка или мала,
важно, что она монотонно возрастает с увеличением т.
Этот результат и используется в качестве детектора некоррелирован-
некоррелированного или слабо коррелированного шума. Подчеркнем, что некоррелирован-
некоррелированность может быть существенна. Построены примеры случайных сигналов
со спектром вида f~a, когда в шуме доминируют низкочастотные ком-
компоненты, а корреляции убывают очень медленно [338], для которых су-
существуют такие длины выборок N и такие интервалы масштабов [е\, ?2].
на которых рассчитанный по такой выборке корреляционный интеграл
ведет себя как logC(e) = Dlogs. Оценка «размерности» D зависит от а,
но при достаточно большом т не зависит от т. Такой сигнал легко при-
принять за детерминированный для системы с аттрактором размерности D.
Мы будем считать, что не имеем дела с подобной ситуацией.
Предположим, что мы ис-
исследуем временной ряд маломодо-
вой динамической системы, к ко-
которому в процессе измерения доба-
добавился малый шум /z?;, т. е. данные
имеют вид Xi = h(xi) + /z&, /z ма-
мало. Что получится при расчете кор-
корреляционного интеграла? На мас-
масштабах е > ii влияние шума бу-
будет несущественно, и корреляци-
корреляционный интеграл получится почти
таким же, как и в отсутствие шума.
На малых масштабах е < ц дан-
данные будут выглядеть как случай-
случайные, и можно ожидать, что корре-
корреляционный интеграл будет похож
на случай A2.10). Таким образом,
-2
Рис. 12.5. Пример корреляционного ин-
интеграла для системы Лоренца с шумом
на графике log С от loge должны быть две области: на больших масштабах
при достаточно больших то наклон стабилизируется, а на малых посто-
постоянно увеличивается с ростом то. По такому поведению корреляционного
интеграла можно установить наличие шума и примерно определить его
амплитуду. Пример такой зависимости для системы Лоренца, на которую
наложен шум, приведен на рис. 12.5.
Иногда можно сделать и более точные оценки. Рассмотрим поведе-
поведение наклона корреляционного интеграла, S(e, то) = d %f?y ¦ Для данных
с шумом на больших масштабах S(e, то) = ?>2 > а на малых, где сказывается
влияние шума, S(e,m) = фа(е)тп + const. Функцию </>о(е) можно полу-
получить из рассчитанных значений корреляционного интеграла. Заметим,
12.2. Свойства корреляционного интеграла
269
что для чисто случайных данных A2.10) </>о(е) = ~&. Если предполо-
предположить, что наложен гауссовый шум с нулевым средним и неизвестной
дисперсией, то значение дисперсии можно установить по полученной
функции фо(е). Такое определение уровня шума будет точнее, если,
разумеется, сделанные предположения верны [318].
Здесь следует сделать одно важное замечание. Выше говорилось,
что случайные, но коррелированные данные можно принять за детерми-
детерминированные. Возможен и противоположный случай — данные для хао-
хаотической системы в случае короткой выборки можно принять за случай-
случайные. Поясним почему. На графике корреляционного интеграла можно
выделить два характерных масштаба: максимальное расстояние между
точками етах и масштаб, начиная с которого график корреляционного
интеграла становится почти линейным и ниже которого можно иссле-
исследовать фрактальные свойства, ?fr. Очевидно, что С(етах) = 1, а на
масштабах меньше ?fr должно быть справедливо соотношение A2.6), т. е.
logC(?fr) = I>2 logefr - Kirm + c — c\- KjTm. Поэтому средний наклон
на участке [efr, emax] будет равен
S =
A log С Кит — с\
=
Aloge log(emax/efr)
-ат + Ь,
т.е. будет линейно расти с увеличением т. Если выборка недостаточно
длинная, то масштабы меньшие ?fr могут оказаться неразрешенными
о
Рис. 12.6. Пример корреляционного интеграла для системы Лоренца, усложнен-
усложненной добавкой периодического сигнала (размерность D2 = 3,06). а) В случае
короткой выборки N = 103 данные воспринимаются как случайные, наклон на
наиболее линейном участке монотонно возрастает с увеличением размерности
вложения т, размерность аттрактора определить невозможно, скорее всего, такой
ряд можно обрабатывать только статистическими методами; б) при увеличении
размера выборки до N = 104 удается разрешить меньшие масштабы, на которых
появляется линейный участок, отвечающий размерности 3,06
270 12. Обработка временных рядов
и данные скорее всего будут интерпретироваться как случайные. На са-
самом же деле это проявление искажений, характерных для реконструкций
хаотических систем при слишком больших длинах окна w. Искажения
связаны с искривлением и образованием складок, из-за которых рекон-
реконструированный аттрактор на больших масштабах выглядит как объект
большей размерности, чем на самом деле, подобно скомканному листу
бумаги. Пример такой ситуации приведен на рис. 12.6.
Отметим еще одно использование корреляционного интеграла, свя-
связанное со случайными данными и статистикой. Вспомним, что для неза-
независимых случайных данных справедливо соотношение A2.9). По откло-
отклонению от этого соотношения можно судить о зависимости или независи-
независимости данных друг от друга. В частности, довольно широкую известность
приобрел так называемый BDS-тест (по инициалам авторов), но это уже
относится скорее к статистике, чем к нелинейной динамике [317, 316, 347].
12.3. Предсказание временных радов
Задача прогноза — видимо, одна из старейших задач анализа вре-
временных рядов [50, 19]. О статистическом подходе к ее решению немного
было сказано в главе про реконструкцию. Теперь мы расскажем о под-
подходах, основанных на представлениях нелинейной динамики. Предпола-
Предполагается, что мы имеем дело с реконструкцией некоторой динамической
системы по скалярному временному ряду, т. е. с набором z-векторов. В той
же главе говорилось, что согласно теореме Такенса должно существовать
некоторое отображение Ф(я), такое что
«.-+1=Ф(*) A2.11)
или
xi+k = F(n), A2.12)
где к соответствует искомой координате вектора Z;+i. Все динамические
методы прогноза основаны на различных методах аппроксимации одной
из форм этого отображения.
Следует сразу сделать важное замечание. Задача прогнозирования
возникла задолго до появления синергетики и нелинейной динамики
и называлась она «предсказанием случайных процессов» [50, 19]. Какое
бы обоснование не изобреталось авторами концепций прогноза, на этапе
практической реализации все сводилось к построению тех же самых
функций A2.11) или A2.12), наилучшим образом аппроксимирующих
доступную предысторию временного ряда. Все равно больше прогноз
делать не из чего, а если какая-то проблема может быть решена без
теории одними лишь не слишком сложными инженерными приемами,
она обычно довольно быстро решается. Поэтому основное, что внесла
в дело прогнозирования нелинейная динамика, сводится к следующему.
1. Был найден удачный объект для тестирования и приложения таких
методов. Им оказались отнюдь не случайные процессы, а мало-
модовые динамические системы с хаотическим поведением, вроде
системы Лоренца.
12.3. Предсказание временных рядов 271
2. Было предложено строгое математическое обоснование всей концеп-
концепции прогноза временных рядов с точки зрения динамики (теорема
Такенса).
3. Исходя из этой теоремы и концепции минимального инерциально-
го многообразия, можно указать на некоторые ограничения, которые
должны быть наложены на функции Ф или F. Напомним, что со-
согласно теореме Такенса, отображение будет существовать только на
некоторой поверхности, а не во всем Rm.
Последнее обстоятельство, способствовавшее развитию идей про-
прогноза именно в наши дни, связано не с нелинейной динамикой, а с рас-
распространением и большой доступностью компьютеров и нейросетевых
программных продуктов. Оказывается, что аппроксимирующие много-
многослойные нейронные сети (персептроны) действительно способны учи-
учитывать требования, накладываемые на функциональные аппроксимации,
а потому не случайно они оказались одним из основных практических
инструментов прогноза.
Методы прогнозирования обычно делят на локальные, глобальные
и третий тип, «глобальные с локальными свойствами» (лучшего назва-
названия пока не придумали). Ниже мы будем обсуждать аппроксимацию
только скалярной функции A2.12); если необходимо построить вектор-
векторную аппроксимацию, то все сказанное ниже будет относиться к каждой
из компонент аппроксимируемой функции.
Решаемую задачу можно сформулировать следующим образом.
Имеется временной ряд, заданы параметры реконструкции и для N век-
векторов Zj известны значения искомой функции, т. е. Fj = F(z{) (потому что
известны следующие за Ъ{ члены временного ряда). Требуется найти зна-
значение искомой функции в новой точке г, х = F(z). Априорные сведения
о функции F весьма скудны. Во-первых, если параметры реконструкции
выбраны правильно, можно ожидать, что F, скорее всего, будет непре-
непрерывна и дифференцируема. Во-вторых, чаще всего она определена не во
всем пространстве векторов z, а только на поверхности некоторой раз-
размерности dN <т, хотя конкретное значение dfj обычно неизвестно. Не-
Неизвестно также, можно ли корректно доопределить F во всем z-простран-
стве. Таким образом, математически задача поставлена весьма скверно,
поэтому решается она не столько на математическом, сколько на физи-
физическом или техническом уровне строгости. Тем не менее, эксперименты
показывают, что для модельных задач можно получить неплохой прогноз.
Неплохой обзор методик прогнозирования приведен в статье [136].
12.3.1. Локальные методы
Локальные методы названы так потому, что функция F или Ф стро-
строится как множество локальных аппроксимаций в окрестностях отдельных
точек, причем сшивать друг с другом эти отдельные аппроксимации
не требуется. В статистике для подобного подхода используется термин
«непараметрическая регрессия».
272 12. Обработка временных рядов
Для поиска F(z) найдем к ближайших соседей точки г, будем
обозначать их zo,-, i = I,...,к. Предположим, что в окрестности точ-
точки г функцию F можно аппроксимировать полиномом степени га, т.е.
будем искать ее в виде F(z) = Рп(%). Полином Pn(z) зависит от ~ тп
параметров, коэффициентов. Их значения можно определить методом
наименьших квадратов, минимизируя функционал
Разумеется, к должно быть больше числа коэффициентов полинома.
По этой причине очень редко используются полиномы степени выше 2,
обычно только при т < 3. Поэтому реальная классификация локальных
методов выглядит следующим образом.
Методы нулевого порядка. В этом случае от полинома остается толь-
только константа. Для ее выбора либо находят одного ближайшего соседа zo
и полагают F(z) — F(zq), либо делают взвешенную сумму по нескольким
ближайшим соседям
F(z) =
Выбор весов д,- — самостоятельная задача; возможный выбор, например,
5i = exp(-c||z-zoi||) или gt = ||ж — zo,-||" и т.д. В случае удачного
выбора весов метод работает не намного хуже методов первого порядка,
но существенно устойчивее.
Методы первого порядка. Полином 1-го порядка содержит т + 1
неизвестную константу, которые можно представить как скаляр и вектор;
тогда
F(z) = ao + (a,z).
Их значения несложно определить методом наименьших квадратов и по-
построить прогноз. Единственным недостатком метода можно считать тот
факт, что если с его помощью необходимо делать прогноз поведения
на много шагов вперед, то изредка он оказывается неустойчив и приводит
к неограниченному росту решения. На простейших модельных задачах
было показано, что точность такой аппроксимации составляет О(е), где
e = max||z-zoi||.
Нелинейные локальные аппроксимации. Для них, вообще говоря,
порядок точности может быть О(е2) и выше, однако их использование
связано с дополнительными проблемами. Во-первых, из-за большого ко-
количества коэффициентов количество соседей должно быть велико, что за-
заставляет увеличивать окрестность, а потому снижает точность. Во-вторых,
при использовании нелинейных аппроксимаций очень актуальной стано-
становится проблема, связанная с выбором существенных переменных, число
12.3. Предсказание временных рядов 273
которых обычно меньше т. В противном случае, если точки z, лежат
на поверхности размерности dfj < m, то среди одночленов, входящих
в -P(z), появятся линейно зависимые, что несколько затрудняет исполь-
использование метода наименьших квадратов. Правда, если произвести отбор
линейно независимых одночленов, то это может в ряде случаев быть
эквивалентно переходу к поверхности меньшей размерности. В-третьих,
иногда возможны проблемы и с устойчивостью таких аппроксимаций.
Следует, правда, оговориться, что авторам неизвестны случаи
успешного применения локальных нелинейных предикторов для про-
прогнозирования не модельных, а каких-либо реальных экспериментальных
данных. Поэтому данный пункт представляет, скорее всего, лишь мето-
методический интерес.
12.3.2. Глобальные и глобально-локальные методы
К глобальным методам обычно относят те, в которых делается ап-
аппроксимация уравнений динамики единой функцией во всей используе-
используемой области z-пространства, т. е. сразу по всему множеству N известных
пар {Fi,Zi}. К этому методу прибегают обычно в тех случаях, когда
необходимо не столько прогнозирование, сколько последующее анали-
аналитическое исследование полученных уравнений движения, либо нужны
глобальные идентификационные характеристики всей системы в целом.
В качестве аппроксимирующей функции используются обычно многочле-
многочлены -Pn(z). Для определения коэффициентов многочлена решают задачу
минимизации полной ошибки
= mm.
Методу присущи все те же недостатки, что и локальным нелинейным
аппроксимациям, но устранить их труднее. Иногда метод следует рассма-
рассматривать скорее как статистическую модель, поскольку тот факт, что F(z)
определена лишь на некоторой dN-мерной поверхности, в данном случае
учесть почти невозможно. Однако авторам известны примеры, когда гло-
глобальные аппроксимации вполне успешно использовались для получения
детерминированных моделей, в том числе и дифференциальных уравне-
уравнений, причем поведение модели хорошо соответствовало особенностям
исследуемого объекта. Поэтому априорно ругать или хвалить данный
метод крайне трудно.
При обработке экспериментальных данных чаще используют два
других метода, которые можно назвать глобальные аппроксимации с локаль-
локальными свойствами. К ним относятся метод радиальных базовых функций
и нейронные сети — персептроны. О персептронах мы рассказали в гла-
главе, посвященной нейронным сетям. Здесь мы остановимся только на
радиальных базовых функциях.
Радиальные базовые функции. Радиальные базовые функции пред-
предлагались для аппроксимации неизвестных функций многих переменных
274 12. Обработка временных рядов
по набору известных точек [136, 167]. С их помощью также можно постро-
построить аппроксимацию уравнений динамической системы. Для этого выби-
выбирается М точек-центров Zck (которые, вообще говоря, могут не совпадать
с каким-либо реконструированным вектором Z;) и базовая или базисная
функция одной переменной ф(г). Отображение F строится в виде
м
1
а коэффициенты а* определяются из условия минимизации функционала
ошибки
?(/,^)) ?(/<-!>*«*) =min>
• i V 1 '
где
Ф« = *(||ж,--гс*||).
В матричной форме это соотношение записывается в виде
(Фа-fJ =min.
Откуда следует, что вектор коэффициентов а является решением системы
линейных уравнений
Ф*Фа = Ф*Г
В ряде работ было показано, что для широкого класса функций гр(г)
матрица Ф*Ф будет невырожденной, и, следовательно, методика будет
осуществима.
Основным недостатком данной методики, как и для глобальных ап-
аппроксимаций, является то, что она не учитывает тот факт, что функция F
определена только на МИМ динамической системы. Вообще говоря,
построенная аппроксимация может иметь весьма отдаленное отноше-
отношение к уравнениям исходной динамической системы, даже если она дает
хороший прогноз. В литературе были описаны ситуации, когда для пре-
предикторов, дававших наилучший краткосрочный прогноз, все ляпуновские
показатели были отрицательны, в то время как исходная динамическая
система была хаотической [324, 325]. В связи с этим подобные аппрок-
аппроксимации точнее было бы называть статистическими моделями, а не
аппроксимациями уравнений движения.
Модификацией метода радиальных базисных функций является
метод ядер плотности — также статистическая модель [127]. При этом
функция гр(г) используется для аппроксимации плотности вероятно-
вероятности p(z) и условной вероятности
pc(z|u) = J2 Ai*(W* ~ *+lllMll" - ««И)-
В качестве предсказания для следующего значения используется среднее
значение по условной вероятности
= J
12.4. Оценка ляпуновских показателей по временному ряду 275
12.4. Оценка ляпуновских показателей по временному ряду
12.4.1. Сколько показателей измеримо?
Ляпуновские показатели — тоже очень важные характеристики
динамической системы, и для их оценки также было предложено не-
несколько алгоритмов. Сразу заметим, что чаще всего удается с разумной
точностью измерить только старший, наибольший показатель Х\. Очень
редко — два старших. Большее количество удается измерить только
для модельных экспериментов, когда обрабатываемый ряд порождается
динамической системой малой размерности.
Начнем с того, что собственно измеряется или может быть в прин-
принципе измерено. В главе, посвященной реконструкции аттракторов, мы
отмечали, что реконструированные вектора связаны отображением Ф(г),
таким что zi+i = Ф(г,). Если исследуется траектория на аттракторе,
а именно такое предположение делается в большинстве случаев, то ее
размерность будет совпадать с размерностью минимальной инерциаль-
ной формы dfi, и ровно столько ляпуновских показателей (а не т),
совпадающих с показателями исходной динамической системы в х-про-
странстве, оно будет иметь. Остальные п - йц показателей исходной
системы связаны с процессами притяжения к аттрактору и не могут быть
исследованы по реконструкции траектории на аттракторе. Итак, по вре-
временному ряду может быть определено < йц ляпуновских показателей. Сама
величина d^, к сожалению, неизвестна, но для построения некоторых
алгоритмов важен сам отмеченный факт.
Далее, определение ляпуновских показателей требует исследования
бесконечно близких траекторий. Однако в распоряжении исследовате-
исследователя имеется только одна траектория. Но, как мы отмечали ранее, она
возвращается спустя некоторое время в достаточно малую окрестность
почти всех своих точек. Поэтому в окрестности почти каждой точки мож-
можно найти другие участки той же траектории, которые и можно считать
другими траекториями. С их помощью и делаются оценки ляпуновских
показателей.
Существующие в настоящее время алгоритмы оценки ляпуновских
показателей можно разделить на два больших класса.
12.4.2. Матричные методы
Алгоритмы, связанные с восстановлением в каком-либо виде урав-
уравнений движения, аппроксимацией матрицы ?>f и расчетом показателей,
называют матричными методами. Получение уравнений движения по ре-
реконструированным векторам мы обсудили в предыдущем разделе, где
речь шла о прогнозе. Техника расчета здесь та же, что и для анали-
аналитически заданных уравнений движения — метод Бенеттина и др. [155].
Суть методики достаточно проста, но практическое воплощение сильно
затруднено по той причине, что аппроксимация уравнений движения
включает определение большого количества параметров, а вычисленные
значения показателей чаще всего весьма чувствительны к большинству
из них. Немного поменяв параметр метода, например, размер окрестно-
276 12. Обработка временных рядов
сти в которой ведется поиск соседей или количество ближайших соседей,
по которым ведется аппроксимация, или что-то еще, можно получить
заметно отличающиеся результаты. Для каждого конкретного тестового
примера, скажем, системы Лоренца, всегда можно подогнать параме-
параметры метода так, чтобы он давал хорошие результаты. Примеры нетрудно
найти в журнальных публикациях и книгах. Вообще, хорошо работать
над решением задачи, зная ответ заранее. Но когда ответ неизвестен,
использовать метод становится затруднительно.
Существует, правда, одна интересная идея, касающаяся уточнения
истинных значений показателей при варьировании параметров метода.
Она предложена У. Парлитцем [287] и основана на том, что при обраще-
обращении времени в динамической системе ляпуновские показатели меняют
знак, оставаясь теми же самыми по абсолютной величине. Поэтому,
если мы обработаем временной ряд сначала от начала к концу, а потом
от конца к началу, то есть шанс, что при сопоставлении результатов
можно отличить истинные показатели от ложных. Метод не застрахован
от ошибок, но дает хоть какую-то уверенность. Другие детали реализации
метода мы обсуждать не будем по причине слишком большого числа
возможных вариантов.
12.4.3. Методы аналога
Это методы, связанные с непосредственным измерением скорости
расходимости близких траекторий, или методы аналога. Существует две
реализации метода, одна из которых предложена в 1985 г. Вольфом
и др. [346]. Подробно останавливаться на ней мы не будем, а опишем
основную идею.
Чтобы оценить старший ляпуновский показатель, необходимо в те-
течение длительного времени знать поведение достаточно близкой тра-
траектории. В данном методе предполагается построить «синтетическую»
траекторию u(t) из отдельных кусочков, имеющихся в наличии. Будем
по-прежнему обозначать «основную» траекторию z(i), а «соседние» тра-
траектории через zoi(t); соответственно, iij(<) = zo*(t) — Zi(t). Обозначим че-
через L(t) длину ||iij(<)||. В момент to выбирается одна из соседних траекто-
траекторий, zoi (to), и полагаем u(f) = "'Ал... Когда в некоторый момент t\ норма
llui(OII становится слишком велика и выбранную соседнюю траекторию
больше нельзя считать близкой, производится смена соседа (см. рис. 12.7).
При этом для «старой» длины будем писать L'(t\), а для «новой» L(t\),
как показано на этом рисунке. Выбирается zo2(t\) так, чтобы направления
u I (t \) и иг (t 1) были как можно ближе друг к другу. Далее до некоторого tj
полагаем u(t) = .у 1"\.у . Затем снова производим смену и т. д. Спустя
п шагов в качестве оценки старшего ляпуновского показателя получаем
А M_!_/rtal!LMl + taJ!5M+ , 1п I
1 - tt riM')ii iMtoii+ ""+ iK
Метод можно обобщить на fc-мерные фазовые объемы и вычислять сум-
сумму к показателей, но уже при к = 2 практическая реализация метода
12.4. Оценка ляпуновских показателей по временному ряду 277
Рис. 12.7. Схема метода [346] для оценки старшего ляпуновского показателя
по временному ряду
сталкивается с большими трудностями. Поэтому в подавляющем боль-
большинстве случаев метод используется для оценки только старшего пока-
показателя. Двумя очень важными достоинствами метода являются: 1) очень
малое количество подбираемых параметров метода — размер окрест-
окрестности, максимальное удаление от траектории и допуск на угол между
векторами при смене близкой траектории; 2) независимость реализации
метода от размерности пространства реконструкции т.
В 1993-1994 г. в двух независимых друг от друга работах была пред-
предложена еще одна методика оценки старшего ляпуновского показателя,
обладающая теми же достоинствами, но вдобавок не требующая смены
траекторий [307, 246], Методика использует двойное усреднение. Сначала
определяется средний локальный коэффициент разбегания близких тра-
/*\ /Н»('+«)||\
ектории в данной точке r(t) = ( ,| ,.ц" >, где усреднение проводится по
всем ближайшим траекториям или, что то же самое, по всем ближайшим
соседям ZQi(t). Затем получают оценку старшего ляпуновского показателя
Ai = (r(t)), где усреднение проводится по всем точкам z(i). Обоснование
этой методики предложено в работе [197].
12.4.4. Комбинированная методика: фрейм-разложение
Можно предложить комбинированную методику. Алгоритм Бенет-
тина и др. используют эволюционирующие векторы uj. , и?|, = Dmj. ,
а затем используют их для оценки ляпуновского показателя А,-. В матрич-
матричных методах получают аппроксимацию матрицы Ш, а затем с помощью
этой аппроксимации рассчитывают следующее значение u^p Однако,
если не ставить целью расчет всех показателей, а ограничиться только А],
то можно было бы попытаться построить иЦ,, не восстанавливая всю
матрицу Df.
Рассмотрим идею метода подробнее. Допустим, мы «привели» век-
вектор и'1' вдоль траектории в точку z*. Далее мы анализируем следующий
шаг, отображение г* —> Zk+\- Рассмотрим ближайших соседей точки г*,
278 12. Обработка временных рядов
z* , j = l,...,e. Образы ближайших соседей на следующем шаге zki+\
нам также известны. Поэтому на самом деле мы знаем набор векторов
yj = zkj — г*, которые на следующем шаге отображаются в fj = z^.+i ~zk+\ ¦
Именно по набору пар (yj,9j) в матричных методах строится аппрокси-
аппроксимация оператора Df.
Однако если бы мы могли просто получить разложение вектора ик '
по этим векторам, ик — Ylcjyj> то на следующем шаге мы могли бы
«собрать» вектор иЦ,: ujj.^, = ^ с,уу. То есть вместо матрицы Df можно
j
попытаться получить набор коэффициентов с,-. Разложение необходимо
выполнять по системе линейно-зависимых векторов уу. В теории вейвлет-
преобразований системы линейно зависимых векторов называют фрейм-
фреймами [182], поэтому данный метод мы назвали методом фрейм-разложения.
Мы использовали следующий подход.
Пусть задано несколько векторов yj, i = 1,... ,s, и ляпуновский
вектор ик . Будем полагать, что ||и^ '|| = 1, и искать разложение в виде
ч = ? ^у; тогда u = ^°^^ где ук =
Заметим, что, вообще говоря, в реальных расчетах вектор щ
может немного отклоняться от линейной оболочки span{yi}. Поэтому
разложение будем обозначать
S
8 = Х^У'- A2ЛЗ)
i=l
Подобное разложение, как правило, неединственно, поэтому необходимы
дополнительные условия. Строго говоря, необходимо решать следующую
задачу: найти max(uj.',g) при условии g2 = 1 и, например, ?)с? = min.
Однако это приводит к обобщенной задаче на собственные значения, что
делает методику слишком сложной. Поэтому будем решать более простую
задачу. Будем искать g, такое что (ик , g) = 1 и g2 = min. Очевидно, что
если ик € span{yi}, то ее решение совпадает с предыдущим случаем,
если же нет, то решение будет пропорционально проекции щ.' на это
подпространство и далее его надо будет лишь перенормировать таким
образом, чтобы g2 = 1. Однако второй подход оказывается существенно
проще, поскольку, как будет показано ниже, благодаря линейности усло-
условия (<4 ,g) = 1 по коэффициентам задача сводится к решению обычной
системы линейных уравнений, а не к задаче на собственные значения.
На коэффициенты разложения A2.13) наложим следующие требо-
требования.
1. Угол между ик и с;у* не должен быть больше |. Этого можно
добиться, например, выбирая с< ~ щ(щ ,у»)|(uj. ,yt)f, P > 0.
12.4. Оценка ляпуновских показателей по временному ряду 279
2. 2 а? = min — все «лишние» коэффициенты, для которых со-
соответствующие вектора почти ортогональны ujj. , должны быть
близки к 0.
3. Чем дальше находится соседняя точка (т. е. чем больше длина век-
вектора у<), тем меньший вклад должен вносить он в окончательный
результат, поэтому выберем с, ~ {го + |Ух I) ^ -
Таким образом, наибольший вклад должны давать ближайшие век-
вектора, имеющие то же направление, что и щ. .
Запишем
Задачу на условный экстремум можно записать следующим образом
^
где параметр 6q > 0 обеспечивает равенство нулю тех коэффициентов
для которых Ki = 0. Далее получаем систему уравнений для а,-:
Решая эту систему, находим значения ~, после чего значение \i опреде-
определяется из условия нормировки (и];' ,g) = 1.
Метод оказался не намного сложнее обычных методов аналога
и показал неплохую работоспособность.
12.4.5. Зависимость результатов от свойств реконструкции
и коррекция ошибок
Мы рассказали о нескольких методах, которые призваны расчиты-
расчитывать одни и те же величины. Возникает естественный вопрос: а зачем
нужно много методов, неужели недостаточно одного? Оказывается, что
наличие нескольких методов может быть принципиально важно. Связано
это с тем, что в реконструкциях по временному ряду могут возникать
искажения. Подробно мы расскажем о них в следующей главе, а частич-
частично они иллюстрировались в предыдущей главе (рис. 11.1). Искажения,
в свою очередь, приводят к систематическим ошибкам в результатах, и
наличие нескольких различных методов расчета ляпуновских показателей
иногда помогает установить истинное значение и оценить погрешность.
Пример расчета для аттрактора Лоренца по нескольким методикам
показан на рис. 12.8. Результаты приведены в зависимости от длины
окна реконструкции w = (m — 1)т. Длина выборки составляла N = 104.
280
12. Обработка временных рядов
Frame
-15,0-,
1,0
0,5
1,0
Рис. 12.8. Пример расчета ляпуновских показателей по временному ряду для
аттрактора Лоренца, JV = 104, At = 0,02, т = 3,...,12, г = 0,02, 0,04,.. .,0,10.
Расчет сделан по 4 методам: Wolf — метод аналога [346], ER86 — матричный
метод [190], Frame — метод фрейм-разложения, MIM — регуляризованный
матричный метод [285]. Истинные значения показателей показаны штриховой
линией. Сделано 2000 шагов алгоритма, статистическая погрешность результа-
результата порядка 0,01. Наиболее существенный источник систематичеких ошибок —
отображение реконструкции (зависимость от и = (га - 1O"). Анализ результатов
позволяет найти область значений w, где его влияние практически отсутствует.
Разброс значений для различных методов позволяет дать оценку погрешности
результата, в данном случае порядка 0,1 для А, и А2. Отрицательные показатели
оцениваются с существенно большей погрешностью
12.5. Заключение. Что дали алгоритмы нелинейной динамики? 281
При расчете сделано 2000 шагов алгоритма, что дает статистическую
погрешность ~ 0,01. Однако реальная точность оказывается существенно
хуже. При некоторых значениях w рассчитанные значения Х\ и Аг
получаются близкими к истинным, хотя погрешность обычно больше,
чем среднеквадратичное отклонение, полученное в ходе расчета.
Следовательно, требуется исключить влияние систематических оши-
ошибок. Расчет для многих w позволяет найти область значений w, где зави-
зависимость от этого параметра практически отсутствует. Однако на результат
могут оказывать влияние и другие факторы (неоднородность инвариант-
инвариантной меры, особенности геометрии и т. п.), причем воздействие их на
разные методики оказывается, вообще говоря, различным. Анализ ре-
результатов показывает, что разброс в оценках для разных алгоритмов при
обработке одной и той же выборки позволяет оценить реальную погрешность
расчета, связанную с систематическими ошибками. В нашей практике
встречались примеры, когда использование только какого-либо одно-
одного алгоритма не позволяло получить оценки ляпуновского показателя.
Только совместное использование 4 методов с контролем, путем расче-
расчета энтропии Kiy позволило получить оценку нескольких показателей.
Кроме того, расчет по матричным методам при различных значениях djv
(предполагаемое количество параметров порядка и размерность восста-
восстанавливаемой матрицы Df) и сравнение результатов с методами аналога
(которые не зависят от djv) позволяют в ряде случаев установить и
значение djy.
В заключение сформулируем еще раз основные рекомендации.
— Необходимо проводить расчет ляпуновских показателей несколь-
несколькими методами. Желательно одновременно провести расчет раз-
размерности и энтропии при помощи корреляционного интеграла
и сравнить со значениями, получающимися согласно значениям
ляпуновских показателей.
— Полезную информацию может давать расчет показателей для обра-
обращенного во времени временного ряда.
— Желательно исследовать зависимость результатов от длины окна ре-
реконструкции w. Это позволяет идентифицировать систематические
ошибки, вносимые реконструкцией.
Таким образом, достаточно надежный результат расчета ляпунов-
ляпуновских показателей по временному ряду можно получить только как итог
большой серии расчетов при помощи нескольких алгоритмов.
12.5. Заключение. Что дали алгоритмы нелинейной динамики?
Если задаться целью кратко сформулировать, что дали миру алго-
алгоритмы нелинейной динамики, то можно, видимо, сказать следующее.
— Алгоритмы позволили изучить переход к хаосу в целом ряде мало-
модовых хаотических систем. Это нелинейные радиофизические,
химические системы, NMR-лазер, сигналы изолированного серд-
сердца, текущий водопроводный кран, простейшие гидродинамические
282 12. Обработка временных рядов
течения, сложные маятники с магнитами и катушкой с током и
еще несколько подобных систем (см., например, [136]).
— Алгоритмы позволили предложить новые методы диагностики.
В частности, расчет корреляционного интеграла для электроэн-
электроэнцефалограмм позволил классифицировать мозговые травмы, что не
удавалось сделать никакими другими способами [47].
— Алгоритмы нелинейной динамики позволили предложить новые
концепции в теории связи [40] и в криптографии.
В следующей главе мы остановимся на некоторых трудностях,
возникших на этом пути.
13
Когда применимы алгоритмы
нелинейной динамики?
Алгоритмы нелинейной динамики для обработки временных рядов
выглядят весьма привлекательно. Действительно, кому же не понравится
идея получить уравнения движения неизвестной системы непосредствен-
непосредственно из эксперимента. Однако оказалось, что экспериментальных времен-
временных рядов, для которых аппарат нелинейной динамики действительно мог
бы быть эффективно использован, очень немного. В литературе можно
найти сигналы от сравнительно простых электронных схем, хаотичес-
хаотические колебания в некоторых лазерах, отдельные, специальным образом
организованные эксперименты в гидродинамике, несколько сравнитель-
сравнительно простых сигналов в физиологии. И все. Для произвольно взятого
временного ряда, например, метеорологических наблюдений или сей-
сейсмограмм, результаты редко оказываются вразумительными. Почему так
происходит? Когда можно использовать динамические подходы, а когда
лучше пользоваться статистическими? В данной главе речь пойдет именно
об этом.
13.1. Проклятие размерности
Пусть перед нами стоит задача оценить размерность некоторого
множества по конечному множеству точек, принадлежащих ему. Будем
считать, что ситуация идеальная: множество обладает масштабной инва-
инвариантностью, так что правильная оценка размерности может быть сделана
без предельных переходов е —> 0, изменение масштаба, на котором за-
заметна инвариантность, не слишком велико (для канторова множества —
в 3 раза), а точки по множеству распределены достаточно однородно.
Пусть размерность множества равна d. Сколько точек необходимо, чтобы
ее оценить?
Естественно предположить, что для того, чтобы обнаружить мас-
масштабную инвариантность множества, необходимо изменить масштаб хотя
бы в 10 раз. Если бы рассматриваемое множество было бы d-мерным
кубом со стороной а, то необходимо, чтобы расстояние до ближайшего
соседа точки составляло ~ 0,1а. То есть на одну точку должен прихо-
приходиться объем ~ @,1а) , тогда необходимое для заполнения куба число
точек N ~ " А = \0d. Обычно исследуемое множество кубом не явля-
@,1 о)
ется, однако общая асимптотика должна сохраниться. В экспериментах
редко доступны пригодные для обработки выборки длиннее, чем 105.
284 13. Когда применимы алгоритмы нелинейной динамики ?
Немедленно получаем, что множество размерности d > 5 едва ли удастся
успешно обработать. В общем случае трудностей следует ожидать, если
нарушается неравенство
rf < lg2V.
Более оптимистическую оценку можно получить из свойств кор-
корреляционного интеграла. Пусть точки на множестве распределены с не-
некоторой специальной неоднородностью, так что график корреляцион-
корреляционного интеграла представляет собой идеальный отрезок прямой с накло-
наклоном d. Очевидно, что максимальное значение корреляционного интеграла
составляет Стах = 1, а минимальное Cm;n = JV . Тогда логарифм изме-
изменения масштаба, соответствующего этому линейному участку, составит
^ J
— I
Поскольку минимально допустимое значение р мы положили равным 10,
то получаем, что по выборке длины N невозможно правильно оценить
размерность большую, чем 21gJV, т.е.
d< 2lgN.
Для выборки длиной N = 105 получаем ограничение d < 10.
В задачах прогноза временных рядов, когда аппроксимируется
функция
х„ = Ф(х„_1,... ,ж„_т) = Ф(г„_т), A3.1)
получить подобные оценки несколько сложнее. Дело в том, что какой-
нибудь прогноз можно дать всегда при помощи метода «нулевого по-
порядка»: Ф(г) = Ф(го), где zo — ближайшая точка, в которой известно
значение, или взвешенная сумма, полученная по нескольким ближайшим
соседям точки zo, Ф(г) = ^* wk$(zok)- To есть для прогноза используется
одна или несколько наиболее близких ситуаций в прошлом. Заметим, что
метод радиальных базовых функций можно рассматривать как обобщение
этого подхода.
Наибольший же интерес при прогнозировании представляет ошиб-
ошибка прогноза. «Типичную» ошибку можно оценить как \6х\ » ||-ОФ(го)|| •
||z — zoll (здесь ||ЛФ(го)|| — норма матрицы производных для ото-
отображения Ф(г)). Чтобы приблизительно оценить ||z — zo||, можно вос-
воспользоваться приведенными выше рассуждениями о заполнении точ-
точками d-мерного куба: на одну точку приходится объем ~ ~, который
можно оценить приближенно и как ~ ("z~?°") , тогда ||z - zo|| = 2aN~^d.
Поэтому для приближенной оценки ожидаемой относительной ошибки
прогноза получаем ео ~ ||х>Ф(жо)|[ • N~^d. Оценить ||1)Ф(го)|| весьма
сложно: в грубых оценках считается, что она порядка 1. Таким же образом
можно оценить ошибку прогноза для локального линейного предиктора
(метод «первого порядка»), ?] и ||1JФ(го)|| • N~2ld [136].
Успех методов нелинейной динамики, описанных в предыдущей
главе, можно объяснить использованием небольшого d A-ЬЗ), а также тем
13.2. Порог фрактальности и трудности реконструкции 285
фактом, что при малых г как правило ||.ОФ(го)|| и 1, a ||х>2Ф(го)|| также
ОA) или даже близко к 0. Если положить ||.ОФ(го)|| и ||1?2Ф(го)|| и 1,
7V « 103, d = 2, мы легко получим, что ео ~ 0,03, ?] и 0,001. Близкие
значения и получаются в численных экспериментах для модельных систем
(см. [136] и ссылки в этой работе).
Для экспериментальных данных, таких как временные ряды в фи-
физиологии, медицине или экономике, размерность d обычно неизвестна,
но едва ли она меньше 5. Оценки производных также не могут быть
получены. Но даже если положить ||.ОФBо)|| f» ||ХJФBо)|| и 1, N и 103,
d = 5, то получим ео и 0,3, е\ и 0,1. В отношении медицины сказать
трудно, но в экономических и финансовых прогнозах такая точность,
как правило, никого не устраивает. Таким образом, и в задачах прогно-
прогноза применимость методов обусловлена пределом по размерности. То же
справедливо и для задач оценки ляпуновских показателей.
Тем не менее, существуют ситуации, когда для реальных сложных
систем делались хорошие прогнозы, обычно с помощью нейронных
сетей (в печати надежной информации на этот счет нет, поскольку все
успешные финансовые прогнозы сразу становятся коммерческой тайной,
однако краткие заметки в газетах и многочисленные слухи утверждают,
что такое в самом деле случается). Позднее мы попытаемся объяснить
этот феномен.
13.2. Порог фрактальности и трудности реконструкции
Приведенные оценки сделаны для идеального случая. Они дают
правильную асимптотику N > \0d. Реальные аттракторы отличаются
тем, что к асимптотике добавляется некоторый множитель. И он может
оказаться отнюдь не малым. Поэтому более реальная оценка имеет вид
N > iVoIOd. В данном разделе речь пойдет именно о множителе Щ.
Самая главная причина его возникновения — нелинейность ис-
исследуемой системы, кривизна аттрактора и иные причины, вызывающие
неоднородность свойств аттрактора на масштабах больше некоторого по-
порога ?fr. Выражается это в том, что график корреляционного интеграла
при е > ?fr утрачивает линейность, а вектор у = z — zo при ||z - zo|| > ?fr
уже нельзя считать касательным и использовать для оценки ляпуновских
показателей и построения линейных предикторов. Чем меньше мас-
масштаб ?fr, тем больше множитель Nq. Зависимость JVo(efr), скорее всего,
имеет степенной характер, Щ ~ ?fTd.
Строгих выражений масштаба ?fr нет, но можно сделать некото-
некоторые предположения и с их помощью получить приближенные оценки.
Рассмотрим две достаточно близкие точки аттрактора \\ и Х2- Времен-
Временная эволюция отображает их в некоторые другие точки k\ = <p(xi,t)
и Х2 = <p{x2,t). Соответственно, вектор у = хг — Х] отображается
в у = <р(х{ +y,t) - (p(\ut)=g(xi,y,t).
Пусть ||у|| настолько мала, что для этого вектора отображение
g(x\,y,t) можно считать линейным при t = O(\). А пока оно оста-
2gg 13. Когда применимы алгоритмы нелинейной динамики?
ется линейным, то те элементы аттрактора, которые оно отображает
друг в друга, можно рассматривать как аффинно-подобные (когда ко-
коэффициент растяжения по различным направлениям может отличаться).
Но именно при помощи таких отображений создают самоподобные фрак-
фракталы, для которых оценки размерности можно получать без предельного
перехода е —* О, например, при помощи корреляционного интеграла.
Поэтому можно предположить, что масштабу, на котором заканчивает-
заканчивается линейная зависимость на графике корреляционного интеграла, будет
соответствовать «утрата линейности» отображения д.
Если система хаотическая, то отображение д(х\,у,t) должно быть
в среднем растягивающим, а длина у должна расти как ~ ext. Но при
достижении некоторого масштаба нелинейные члены станут существен-
существенными и отображение больше нельзя будет считать линейным. Попробуем
получить оценку для этого масштаба. Очевидно, что
у = д(х,у, t) = tp(x + у, t) - <р(х, t) = Dy{x, t)y+-D2<p(x, t)(y, у) + ....
В качестве верхнего «предела линейности» выберем масштаб, при котором
величина линейного и квадратичного членов будут совпадать
\\D<p(x,t)y\\?i\\D2<p(x,t)(y,y)\\=?{r-
Тогда, используя оценки
получаем, что
\\DM*,t)\\'
Однако, полученная величина будет характеризовать только одно какое-
либо t и только одну точку х. Чтобы получить характеристику аттрак-
аттрактора в целом, необходимо исследовать поведение усредненной величины
при достаточно больших t. Поэтому, вообще говоря, нас интересует
величина
<)||2
Усреднение логарифма выбрано с тем, чтобы влияние малых членов
не было пренебрежимо малым, поскольку они в данном случае суще-
существенны. Сушествует ли предел A3.2) — неизвестно, однако численные
расчеты для модельных систем показывают, что усредняемая величина
довольно быстро устанавливается и далее с ростом t практически не ме-
меняется. Пример показан на рис. 13.1. Заметим, что рассчитанная величина
действительно хорошо согласуется с верхней границей линейного участка
на графике корреляционного интеграла.
13.2. Порог фрактальности и трудности реконструкции
287
0,8:-
0,6 Е
0,4 Ё-
Ц Т7ТГГГ7Т77ТТТ777Г7ГТТТ777ГГГГТТ77Т777ГГП—
0 10 20 30 40 50 t
а
-4,0
-6,0 :^
100<
0 500 1000 1500 2000
I I I I I
150 200t
Рис. 13.1. Численный расчет масштаба фрактальности (eft(x,t)}x для аттракторов:
а) Хенона (усреднение по 20000 точек); б) Лоренца (усреднение по 2000 точек).
Роль усреднения видна из графиков sfr(\,t); в) аттрактор Хенона; г) аттрактор
Лоренца. На двух последних графиках масштаб по оси г логарифмический. Тот
факт, что для аттрактора Хенона наблюдаются столь сильные скачки, порядка 106,
может означать, что какие-либо проблемы с оценкой размерности возможны. То,
что усреднение скачки устраняет, означает, что проблемы не слишком серьезны.
Как показало специальное исследование, причина эффекта в «остриях» или «за-
«заостренных складках» на аттракторе, где действительно нарушается самоподобие,
но на оценках размерности это практически не сказывается
Однако для некоторых систем величина ?fr может оказаться весьма
малой. Тогда применение методов нелинейной динамики окажется под
вопросом. Простейшим примером могут служить генераторы случайных
чисел вида хп+\ = (ax+b) mod 1, а, 6 > 1. Линейность этого отображения
будет заметна только на масштабах меньше е = а'', а для практически
используемых версий эта величина оказывается близкой к машинной
точности.
288 13. Когда применимы алгоритмы нелинейной динамики ?
Перейдем теперь к проблемам реконструкции. Отображение
z = A(x), подробно обсуждаемое в главе, посвященной реконструкции,
может быть дополнительным фактором, сильно увеличивающим величи-
величину Щ. Его свойства зависят в первую очередь от длины окна реконструк-
реконструкции w = (т - 1)г (см. там же). При малых го (по сравнению с некоторым
характерным временным масштабом wq) реконструированный аттрактор
как бы оказывается подвергнут аффинному преобразованию — сжатию
пропорционально (^) , Л = 0,1,..., d— 1, для разных направлений. По-
Поэтому реально ?fr при реконструкции домножается на (~) (на боль-
больших масштабах реконструкция будет выглядеть как объект размерности
меньше, чем d), a Nq, соответственно, на
При больших же го из свойств корреляционного интеграла можно по-
получить, что Nq будет домножаться на величину порядка ехр(^и'),
где Ki — энтропия динамической системы (см. главу про обработку вре-
временных рядов, свойства корреляционного интеграла). То есть получаем,
что связь между величинами Nq для исходного аттрактора (Nqx) и его
реконструкции (JVbz) следующая:
) \ A3.3)
Эта функция должна иметь минимум вблизи wq и -%-, который и со-
соб
ответствует наилучшему выбору го. Если Kjwq ^ 1, то правильным
выбором го можно добиться хорошего качества реконструкции. Это спра-
справедливо, например, для аттрактора Лоренца (K^wq = 0,3) и некоторых
других хаотических динамических систем малой размерности.
Однако ситуация существенно меняется, если в системе существует
несколько сильно различающихся временных масштабов: например, ко-
когда существенный вклад в размерность дают медленные процессы с харак-
характерными временами w\ > too (например, если x(t) = жо(^-) — х\ (^)),
зависимость Nqz от w может быть более сложной. При w\ > w > too
компоненты, связанные с xq, будут реконструироваться удовлетвори-
удовлетворительно, а компоненты, связанные с х\, будут давать существенный вклад
только в одну-две проекции г. Следовательно, пока w < w\, рекон-
реконструкция будет порождать серьезные искажения и Nfc > N^. Если
при этом K2it>\ > 1, то для w ^ -щ будут сильны искажения за счет
малости ад, а когда они станут малы и w будет близко к W|, хаотичность
будет вызывать искажения другого рода, проявляющиеся при больших го.
Следовательно, N^ должно всегда существенно превышать Nqx, даже
в случае оптимального го (рис. 13.2). Таким образом, возможны ситуации,
когда реконструкция по скалярному временному ряду может оказаться
вообще плохо применимой. Одним из таких случаев вполне могут ока-
оказаться турбулентные течения жидкостей. Тогда необходимо применять
13.3. Ложные соседи, или почему динамика не восстанавливается? 289
C)
A)
Рис. 13.2. Схема зависимости -^: A) нехаотическая система, нет принципиаль-
принципиальных ограничений сверху на и;; B) маломодовая хаотическая система, существует
интервал значений w, для которого обработка по реконструкции почти так же
эффективна, как в исходном пространстве; C) сложная система с широким спек-
спектром, Nz всегда должно быть много больше, чем Nx, предпочтительна обработка
векторного ряда, позволяющего избежать процедуры реконструкции
другие подходы, например, использовать векторный временной ряд, из-
измеряя достаточное число различных характеристик объекта и используя
их для построения фазовых векторов.
Пример такой ситуации приведен на рис. 13.3 о, где показаны
результаты оценивания размерности по реконструкциям скалярного вре-
временного ряда для 23-модовой галеркинской системы, описывающей трех-
трехмерную конвекцию в слое жидкости [266]. В то же время оценить раз-
размерность по массиву векторов х оказывается возможно (рис. 13.36).
13.3. Ложные соседи, или почему динамика
не восстанавливается на больших масштабах?
Мы обсудили вопрос о том, почему могут возникнуть проблемы
с оценкой размерности: необходимо разрешать очень малые масштабы,
что для систем большой размерности требует гигантских выборок. Та-
Такие выборки обычно невозможно получить, а если даже иногда удается,
то возникает проблема стационарности данных. Грубо говоря, надо быть
уверенным в том, что за длительное время наблюдений объект не изме-
изменился и в конце наблюдений мы имеем дело с той же самой динамической
системой, что и в начале. Без этого сама идея реконструкции повисает
в воздухе. Проверка же стационарности представляет собой самостоя-
самостоятельную проблему. Более того, в случае энцефалограмм, кардиограмм,
временных рядов, порождаемых сложными биологическими объектами,
именно нестационарность хаотического сигнала является функционально
обусловленной и принципиально важной.
290
13. Когда применимы алгоритмы нелинейной динамики?
Рис. 13.3. а) Зависимость от w наклона графика корреляционного интеграла на
наиболее линейном участке для 23-модовой галеркинской системы, описывающей
конвекцию [266, 265]. Значения т = 0,125, 0,625, 1,25, 3,75, при каждом т т
принимает 35 значений от 6 до 40. Наклон монотонно растет, что обычно
интерпретируется как случайный характер данных. В данном случае этот эффект
связан со свойствами реконструкции. См. также рис. 12.6; б) расчет размерности
для той же задачи, но с использованием 11, 17 и 23 компонент исходных фазовых
векторов х. Оценка размерности D2 и 5 (наклон штриховой линии)
Более того, если на данные наложен шум амплитуды 6, то полу-
получение очень длинных выборок вообще может не иметь смысла, посколь-
поскольку разрешить структуру аттрактора на масштабах меньше S все равно
не удастся.
13.3. Ложные соседи, или почему динамика не восстанавливается? 291
Чаще всего приходится иметь дело с относительно короткими
выборками, длина которых может даже не превышать Щ. Допустим,
размерность по ним определить нельзя, нет масштабной инвариантности.
Но, казалось бы, можно обойтись и без этого. Если бы удалось решить
проблему прогноза или оценить ляпуновский показатель, этого могло бы
оказаться достаточно для многих практических задач. Более того, если
заданы точки в исходном фазовом пространстве (или хороший вектор-
векторный временной ряд), то при условии достаточной гладкости (в смысле
ограничения на производные, а не в смысле существования последних)
исследуемой динамической системы задача, по-видимому, решается. Од-
Однако искажения реконструкции, обсуждаемые в предыдущем разделе,
приводят к возникновению эффекта, препятствующего решению этой
задачи. Возникают ложные соседи в реконструкции.
Напомним, что при аппроксимации отображения A3.1) в некоторой
точке zo, используются значения в ближайших соседних точках z*, Ф^).
При этом предполагается, что для близких пар точек {zo,z^} в реконстру-
реконструированном пространстве их прообразы в исходном пространстве {хо,х*}
также близки. Однако свойства отображения реконструкции z = Л(х) ока-
оказываются таковы, что данное предположение иногда нарушается. В ре-
реконструкции возникают ложные соседи. Их условно можно разделить
на два типа, которые иногда называют ложными ближайшими соседями
(False Nearest Neighbours — FNN) и ложными соседями на складках (False
Neighbours on Folds — FNF). Они соответствуют двум типам искажений,
упомянутых в предыдущем разделе: FNN возникают при слишком ма-
малых длинах окна реконструкции w, a FNF — при слишком больших.
Схематически возникновение ложных соседей показано на рис. 13.4.
Для аттракторов малой размерности обычно существует интервал
значений параметров т и т, при которых соседи FNN уже исчезли,
а соседи FNF еще не возникли. Для аттракторов большой размерности
оба типа ложных соседей могут даже сосуществовать. Именно из-за этого
эффекта реконструкция может стать вообще неприменима для динами-
динамических методов обработки временных рядов.
Смешение истинных и ложных соседей ведет к двум следствиям.
1) На следующем временном шаге ложные соседи ведут себя не так,
как истинные. Поскольку мы не можем их различить, вся динамика
на масштабах больших ?fT начинает выглядеть случайной. (При
«одинаковых» начальных условиях получается разный результат.)
2) Ложные соседи обычно занимают все доступные размерности. По-
Поэтому множество точек z* на масштабах, больших чем ?fr, будет вы-
выглядеть как объект размерности большей, чем исходный аттрактор.
Этот рост «эффективной размерности» с увеличением т напоми-
напоминает увеличение размерности в случае случайных данных (см. главу,
посвященную описанию алгоритмов нелинейной динамики).
Проиллюстрируем эффект возникновения ложных соседей на склад-
складках простым примером. На рис. 13.5 показано соотношение между раз-
размерами окрестности точки в реконструированном (z) и исходном (х)
292 13. Когда применимы алгоритмы нелинейной динамики?
\Щ\ Ш
t • • •
\ *. *._¦. *
Рис. 13.4. Схема возникновения различных типов ложных соседей: а) хорошая
реконструкция, данных достаточно, чтобы разрешить истинную окрестность точ-
точки (масштабы меньше, чем efr), т.е. методами нелинейной динамики можно
пользоваться; б) та же реконструкция, но данных слишком мало, как обычно
и бывает в случае аттракторов большой размерности, и из-за кривизны аттрактора
возникают ложные соседи на складках (FNF). Этот эффект часто не позволяет
различить хаотические и стохастические данные; в) другой эффект — ложные
ближайшие соседи (FNN) из-за неверного выбора параметров реконструкции:
точки, удаленные на аттракторе, оказываются рядом в одномерной проекции.
В отличие от предыдущего случая FNN исчезают, когда размерность вложе-
вложения т и запаздывание т выбраны верно. Однако для реконструкций аттракторов
большой размерности оба типа ложных соседей могут даже сосуществовать.
Корреляционный интеграл обнаруживает наличие ложных соседей
пространствах для системы Лоренца, -ыло взято 107 точек на ат-
аттракторе с шагом т = 0,2, равным запаздыванию в реконструкции,
и рассчитаны расстояния от случайно выбранной точки на аттракторе
Хо = A0,27, 8,91, 30,79) и ее образа zo = Л(хо) в 12-мерной реконструкции
до всех точек траектории. При т = 12, с одной стороны, выполнены усло-
условия теоремы Такенса и FNN отсутствуют, а с другой стороны, интервал
между началом и концом z-вектора w = (т - \)т достаточно велик, что-
чтобы начали образовываться складки. Заметим, что для аттрактора Лоренца
необходимы специальные усилия, чтобы эффекты, типичные для систем
большой размерности, стали заметны. На рисунке /з(х,хо) — расстояние
между точками в исходном пространстве, а р(г, zo) — расстояние между
их реконструкциями. При lnp(z,zo) = lnefr = 3,3 появляются ложные
соседи на складках, которые отвечают резкому обрыву на облаке точек.
Такое возникновение ложных соседей будет препятствовать работе
любых алгоритмов, использующих окрестности точек: методов оценки
ляпуновских показателей и большинство алгоритмов прогноза. Методика
нелинейной авторегрессии, тем не менее, может работать даже в такой си-
ситуации, но ее при этом следует рассматривать скорее как статистический,
а не как динамический метод.
Разрешение достаточно малых масштабов, вообще говоря, возмож-
возможно только для динамических систем малой размерности. Для систем
большей размерности, как и для маломодовых систем с очень сложной
динамикой, малые масштабы остаются неразрешенными, а потому про-
процедура реконструкции дает с ростом m структуру все большей и большей
13.3. Ложные соседи, или почему динамика не восстанавливается? 293
4,0 --
2,0
0 --
-2,0--
о
4,0
2,0
ln(p(z,zQ))
Рис. 13.5. Расстояние между точками исходного аттрактора р(х, Хо) в зависимо-
зависимости от расстояний между их образами в реконструкции ^г~ для аттрактора
Лоренца при а = 10, г — 28, Ь = |. Точка хо на аттракторе выбрана случайно:
х0 = A0,27, 8,91, 30,79). График построен по выборке из 107 точек с шагом
по времени т = 0,2. Резкое изменение при lnp(z, z0) ~ 3,3 соответствует масшта-
масштабу еГг. На больших масштабах появляются ложные соседи на складках, которые
не являются соседями в исходном пространстве
размерности. Похожим образом ведет себя и геометрическая структура
реконструкции чисто случайных данных. Следовательно, этот эффект
можно использовать в качестве критерия применимости динамических
методов. В работе [300] с этой целью предложено использовать поведение
наклона графиков корреляционного интеграла log С от loge.
Если мы имеем дело с данными, которые определенно не должны
давать достоверных результатов при такой обработке, то корреляционный
интеграл может вообще не иметь линейного участка (хотя может и иметь),
но его наклон обычно возрастает с увеличением т. В ряде случаев можно
показать, что этот рост будет линейным, т.е. S(e,m) = <ро{е)т + Sq(e).
В других случаях, особенно при обработке временных рядов конечной
длины и небольших значениях га, зависимость чаше всего более сложная,
294 13. Когда применимы алгоритмы нелинейной динамики?
однако в большинстве ситуаций она удовлетворительно аппроксимиру-
аппроксимируется линейной зависимостью. Исследование зависимости наклона от т
может помочь разрешению вопроса о том, позволяет ли реконструкция
судить о свойствах аттрактора или нет (по самым разным причинам —
недостаточно данных, слишком сложная динамика, данные не детерми-
детерминированные, а случайные и т. п.).
Если в некотором интервале масштабов реконструкция не содер-
содержит ложных соседей, то применение методов нелинейной динамики
будет оправдано. Однако это еще не гарантирует хорошего качества ре-
результатов. Кроме того, они могут быть хорошими для одних методов
и плохими для других. Так, например, для некоторых типов аттракто-
аттракторов существует проблема определения размерности из-за так называемых
лакун или иных геометрических неоднородностей. В этом случае кор-
корреляционный интеграл может вообще не содержать линейных участков,
а размерность определяют лишь по усредненному поведению в доста-
достаточно широком интервале масштабов. Если данных недостаточно, то
размерность определить не удастся, хотя ряд может быть предсказуем,
ляпуновские показатели измеримы и т.д. [300]. Для предлагаемой мето-
методики, несмотря на то, что она использует корреляционный интеграл, это
не будет препятствием — поскольку отклонения от линейной зависимо-
зависимости связаны со структурой исходного аттрактора, они будут повторяться
для различных т, а потому практически не повлияют на вид <ро(е).
Таким образом, корреляционный интеграл (точнее, скорость роста
локального наклона >ро(е)) может служить детектором случайных сосе-
соседей [300], а значит с его помошью можно пытаться решать вопрос о том,
применимы ли динамические методы для обработки данного временно-
временного ряда, или же необходимо использовать статистические подходы, или
как-либо комбинировать динамические и статистические методики. Спе-
Специальное исследование, проведенное в [300], показало, что пороговым
значением служит <ро(е) = 0,05 -г 0,1. При меньших значениях <ро(е) алго-
алгоритмы нелинейной динамики обычно применимы, при больших — нет.
13.4. Алгоритмы нелинейной динамики для временных рядов
как способы решения некорректной задачи
Рассмотрим теперь проблематику корректности задач оценки па-
параметров динамических систем по временному ряду: размерностей, эн-
энтропии, ляпуновских показателей, а также параметров аппроксимации
уравнений движения. Сделаем несколько обобщающих замечаний.
Задача оценки параметров динамической системы по временному
ряду является некорректной. Добавление сколь угодно малого шума
радикально меняет динамику на бесконечно малых масштабах, в то время
как в определение размерностей, энтропии и ляпуновских показателей
входит предельный переход е —> 0. Поэтому добавление шума может
сколь угодно сильно изменить данные характеристики.
13.4. Алгоритмы нелинейной динамики для временных рядов 295
Таким образом, данная задача напоминает проблему численного
дифференцирования, и способы преодоления трудностей в обоих случа-
случаях похожи. Вместо характеристики, которая фигурирует в определении,
например, фрактальной размерности d{T, вычисляются некоторые другие
величины G(e, N), которые зависят от масштаба е и должны стремиться к
искомым, если 1) амплитуда шума 6 стремится к нулю и 2) длина обраба-
обрабатываемого ряда N стремится к бесконечности, так что точки траектории
заполняют весь аттрактор. Поэтому можно утверждать только, что
der = lim lim limG(e, N).
Реально же всегда обрабатывается временной ряд конечной длины, на
который может быть наложен шум. Поэтому расчет производится на
некотором интервале масштабов [с^ег]. и без достаточно сильных огра-
ограничений на исследуемую функцию G(e,N) априорно установить связь
между G(e,N) и G@, оо) невозможно.
Однако можно выделить класс систем, для которых эта задача будет
корректной при условии выполнения ряда ограничений на уровень шума
(он должен быть достаточно малым, но может быть ненулевым) и длину
временного ряда (он должен быть достаточно длинным, но не бесконеч-
бесконечным). Для того чтобы система принадлежала к этому классу, она должна
удовлетворять некоторым требованиям, обсуждаемым ниже, которые мы
для краткости будем называть «регуляризующими предположениями».
То, что такие системы существуют, показывают примеры маломодовых
динамических систем с хаотическим поведением, для которых харак-
характеристики измеримы с хорошей точностью по конечному временному
ряду [136], при условии, что используется «подходящий» функционал
G(e,N). Обычно при обработке данных предполагается, что регуляризу-
ющие предположения справедливы и исследуемая система принадлежит
этому классу, поэтому предельные переходы можно опустить, а просто
рассматривать G(e,N) на «достаточно малых масштабах» е < ?fr.
Таким образом, регуляризация задачи оценки параметров динамичес-
динамической системы прежде всего требует разработки подходящего функционала
G(e, N) для оцениваемой величины d{r. Однако при выполнении расчета,
вообще говоря, в рамках одного алгоритма, как правило, невозможно дать
строгую оценку погрешности \G(e, N) — d{T , поскольку, во-первых, мас-
масштаб ?fr обычно априорно неизвестен и его приходится оценивать по ре-
результатам тех же самых алгоритмов. Во-вторых, сам функционал G(e, N)
зависит не только от свойств аттрактора исследуемой системы, но также
и от отображения реконструкции, от способов аппроксимации производ-
производных отображения по ближайшим соседям и т. п., влияние которых очень
сложно учесть. В результате на конечных масштабах возможно возникно-
возникновение систематических ошибок, которые не устраняются статистическим
усреднением результата по всем точкам аттрактора. Это накладывает
отпечаток на всю стратегию разработки алгоритмов и их применение.
Помимо систематических ошибок, следует упомянуть также и о дру-
других проблемах, таких как необходимость по набору отдельных точек
296 13. Когда применимы алгоритмы нелинейной динамики?
в евклидовом пространстве оценивать размерность проходящей через
них поверхности, на которой определено отображение динамической
системы, несуществование решения задачи реконструкции отображения
динамической системы вне искомой поверхности и т. п.
Для каждой конечной длины временного ряда N можно предло-
предложить пример, когда влияние какого-нибудь фактора вносит погрешность
результата ОA) при сколь угодно малом возмущении динамической
системы. Например, система может включать несколько мод с очень
малой амплитудой, которые практически незаметны для наблюдателя,
но меняют «истинную размерность» аттрактора: возмущение системы
на величину О(е) при обработке дает погрешность оценки размерности
6d = 1, не определяются и соответствующие ляпуновские показатели.
Однако предсказание с точностью е оказывается возможным.
Другой пример приведен на рис. 13.4: по конечному набору то-
точек одномерная кривая интерпретируется как двумерный объект, или
наоборот — двумерный объект как одномерный.
Отметим наиболее важные требования к динамической системе,
при выполнении которых задача обработки становится корректной. Как
уже говорилось, они позволяют отказаться от перехода к пределу е —> О
и работать на конечных, иногда не очень малых масштабах. В свою оче-
очередь, их нарушение может служить источником систематических ошибок.
1. Свойства отображения Ф. Теорема Такенса требует, чтобы ото-
отображение динамической системы было по крайней мере дважды
непрерывно дифференцируемо. Кроме того, поскольку вместо про-
производных зачастую используют конечные разности, предполагает-
предполагается, что производные не просто непрерывны, но и «не слишком
велики».
2. Особенности геометрической структуры аттрактора динамической
системы и неоднородности инвариантной меры. Вообще говоря, срав-
сравнительно редко посещаемые участки аттрактора могут вносить до-
достаточно существенный вклад в измеряемые характеристики, чтобы
сделать погрешность неприемлемо большой. При использовании
алгоритмов нелинейной динамики, особенно оценок размерности,
предполагается «однородность» свойств аттрактора начиная с не-
некоторого масштаба efr.
3. Длина выборки и точность измерений предполагается достаточной
для применимости методов нелинейной динамики, в частности,
реконструкции по Такенсу. Если характеристики при помощи не-
некоторого функционала G(e,N) необходимо расчитывать на мас-
масштабах е < ?fr, то необходимо, чтобы уровень шума был хотя бы
в несколько раз меньше ?fr, а аттрактор должен быть заполнен точ-
точками с достаточной плотностью, чтобы растояние до ближайшего
соседа также было в несколько раз меньше ?fr. Это предположение
может быть подвергнуто проверке, для чего предлагался ряд оце-
оценок [323, 192, 266] и методик выбора параметров реконструкции.
Один из тестов был описан в предыдущем пункте [300].
13.4. Алгоритмы нелинейной динамики для временных рядов 297
Все упомянутое накладывает отпечаток на формулировки и осо-
особенности применения алгоритмов нелинейной динамики для обработки
временных рядов, а также позволяет сделать ряд выводов.
— Как правило, не следует ограничиваться использованием какого-
либо одного алгоритма; необходимо согласованное использование
нескольких алгоритмов. Это может позволить проверить выпол-
выполнение используемых предположений и оценить достоверность ре-
результатов.
— Не следует требовать от методов больше, чем они способны да-
давать. В связи с этим важно применять «предостерегающие» тесты,
оценки и алгоритмы, упоминавшиеся выше. Часто помогает также
исследование зависимости результата от параметров метода. Иногда
следует ограничиться качественной информацией.
— Весьма важным оказывается поиск наиболее информативных ха-
характеристик и создание алгоритмов с «наименьшим искажением
информации» — требующих минимума гипотез и переносящих
некоторые проблемы с этапа обработки данных на этап интерпре-
интерпретации.
— Следует различать задачу диагностики и задачу оценки параметров
динамической системы. Рассчитываемые величины могут быть хо-
хорошими диагностирующими признаками даже тогда, когда они не
имеют непосредственного отношения к параметрам динамической
системы.
Удовлетворить таким требованиям довольно сложно, и видимо по-
поэтому среди десятков предложенных в 80-90-х годах алгоритмов «выжили»
очень немногие.
14
Русла и джокеры, или как сопрячь
динамику со статистикой?
Мы не станем пытаться проанализировать все
взаимоотношения, а ограничимся лишь теми,
которые необходимы для построения простых
моделей. Иными словами, мы не ставим своей
задачей построение общей теории, а хотим со-
сосредоточиться лишь на частичном объяснении
динамики...
Дж. Сорос. Алхимия финансов
В предыдущей главе мы обсудили ограничения возможностей ди-
динамических методов. Высказывалось также предположение, что будущее
связано с сочетанием динамических и статистических методов. Один
из подходов такого типа предлагается в данной главе. Он основан на пред-
предположении о неоднородности фазового пространства сложной динами-
динамической системы. Предполагается, что в некоторых областях, называемых
руслами, существенные аспекты динамики могут быть описаны маломо-
довыми динамическими системами, отвечающими некоторым проекциям
малой размерности. Если траектория многократно возвращается в область
русла, точек может оказаться достаточно для построения аппроксимации
соответствующей маломодовой модели. В других областях, названных
областями джокеров, данных недостаточно для восстановления сложной
многомерной динамики, и более адекватным может стать статистичес-
статистическое описание (попав в эту область, траектория может иметь различное
будущее; джокер как бы заменяет несколько разных функций).
Такой взгляд на проблему описания сложной динамики приводит,
во-первых, к отказу от некоторых ключевых понятий нелинейной динами-
динамики (например, для кусочного описания становятся неприменимы понятия
аттрактора, его размерности, ляпуновских показателей и т. п.); во-вторых,
к изменению взгляда на модели сложных систем вообще. Становится оче-
очевидно, что для объекта может не быть «правильной единой модели», а опи-
описание может строиться как комплекс маломодовых русел, среди которых
бессмысленно искать «правильное», но следует отслеживать «текущее».
Проблема идентификации тоже меняет свое содержание: сложные систе-
системы можно классифицировать, например, по количеству и типу русел.
Поэтому, в связи с особенностями подхода, мы остановимся глав-
главным образом на проблеме прогнозирования, роли нейронных сетей и их
возможной связи с поиском русел.
14.1. Прогнозирование сложной динамики 299
14.1. Прогнозирование сложной динамики:
почему мозг может, а реконструкции — нет?
Одной из основных проблем в нейронауке является обработка
больших объемов информации. Мозг человека и животных научился
находить хорошие решения подобных задач в ходе эволюции. Именно
быстрая обработка информации о постоянно изменяющейся ситуации
вокруг нас и помогла выжить в борьбе за существование.
Эта быстрая обработка информации необходима для того, чтобы
— быстро изменять стратегии поведения, принимая во внимание раз-
различные факторы, чтобы принять правильное решение в различных
ситуациях (то есть, чтобы находить «параметры порядка» сложных
ситуаций);
— обучаться не только путем проб и ошибок (в большом числе
ситуаций второй попытки просто не будет), а путем тренировки
здравого смысла, интуиции, т. е. «внутренней предсказывающей
системы» (психологи называют это опережающим отражением);
— реагировать быстро (для этого необходимо быстро «забывать» не-
несущественные детали или отправлять их в долговременную память,
оставляя быструю кратковременную память только для самой важ-
важной информации).
Таким образом, мозг обладает очень эффективными способами
самоорганизации в обработке информации, и разумно взглянуть на про-
проблемы современной нелинейной динамики с точки зрения нейронауки.
А главная проблема состоит в том, что все предлагавшиеся методы эффек-
эффективны только для маломодовых систем, т. е. с числом наиболее существен-
существенных переменных 5-10. Но это неравенство оставляет за пределами приме-
применимости нелинейной динамики почти все практически важные ситуации.
Тем не менее, при помощи нейронных сетей иногда оказывается
возможно делать предсказания в ситуациях, которые должны быть безна-
безнадежны, с точки зрения упоминавшихся оценок эффективности методов
нелинейной динамики, например, для финансовых временных рядов.
Отсюда можно сделать два вывода:
1) должно существовать разумное объяснение подобных фактов, а воз-
возможно, и способы преодоления упомянутых ограничений;
2) нейронные сети обладают какими-то важными особенностями,
существенно повышающими эффективность такой обработки дан-
данных.
Ниже предлагается одно из возможных объяснений.
Основная идея состоит в том, что фазовое пространство динами-
динамической системы неоднородно. Поэтому в нем могут существовать места,
где для описания динамики может требоваться меньшее количество пере-
переменных, чем в общем случае или чем для полного, глобального описания.
Тогда систему можно характеризовать при помощи ее проекции небольшой
размерности. Такие проекции мы назвали руслами.
300 14. Русла и джокеры, или как сопрячь динамику со статистикой?
Но многослойные нейронные сети выполняют операции, которые
сильно напоминают проецирование: в них вычисляется взвешенная сумма
входных сигналов. Следовательно, если требуемая проекция малой раз-
размерности существует, нейронная сеть могла бы ее найти. Более того, как
говорилось ранее, проецирование должно быть необходимым элементом
большинства предикторов. Возможно, что именно способность строить
различные проекции объясняет успехи искусственных нейронных сетей
(а может быть, и настоящего мозга тоже).
Следовательно, идеи нейронауки позволяют прийти к заключе-
заключению, что возможным путем исследования сложных динамических систем
является поиск таких локальных маломодовых русел. Но если с такой
точки зрения «маломодовых» русел взглянуть на всю сложную динамику
в целом, то мы увидим, что в каких-то местах русла теряют способ-
способность прогнозирования. Ситуация может выглядеть так, словно чисто
(или почти чисто) детерминированное поведение быстро сменяется по-
почти непредсказуемым, кажущимся совершенно случайным. Такие области
вероятностного описания мы будем называть областями джокеров, а пра-
правила (обычно вероятностные), по которым начинает функционировать
система, когда попадает в область джокера — джокерами. Название связа-
связано с тем, что карта джокер во многих карточных играх может исполнять
роль любой выбранной карты, что резко повышает неопределенность.
Следовательно, другой идеей является исследование свойств маломодо-
маломодовых систем с джокерами.
Используя эти термины, можно сказать, что мозг обладает ис-
исключительными способностями находить русла, а джокеры соответствуют
очень сложным ситуациям, с трудом поддающимся анализу. В подобных
ситуациях мозг может активизировать механизмы эмоций, которые в не-
некоторых аспектах могут выглядеть как случайные, вероятностные.
Возможно, что рассмотрение сложных систем с точки зрения джо-
джокеров и русел может дать новые практически полезные идеи. В этой
главе мы покажем, как данный подход вытекает из проблемы прогноза
временных рядов. Развитый подход позволяет объяснить ряд известных
фактов и предложить новые идеи для разработки численных методов.
14.2. Предикторы и трехслойные нейронные сети
Рассмотрим основные компоненты трехслойной нейронной сети:
R линейные _^ Сигмоидная _+ линейные _^ Сигмоидная _^ R
ход ~* комбинации ~* функция (<г) комбинации ~* функция (<г) ~* '
где (т(ж) — так называемая «сигмоидная» функция (например, а(х) =
A + е~х)" ). Поскольку нас интересует прогноз следующего члена вре-
временного ряда по т предшествующим, будем предполагать следующую
архитектуру сети. В ней т входных нейронов, некоторое количество
нейронов в скрытом слое и единственный выходной нейрон. На вход
подаются т предыдущих значений x,-_i,x,-_2,...,Xi_m или г^т.
14.3. Когда сложная динамика может быть предсказуема? 301
Линейные комбинации вида
к=\
можно рассматривать как одновременное вычисление компонент для не-
нескольких проекций, т. е. компонент Рпг. Затем вычисляется сигмоидная
функция u{yj). Как правило, для подобных целей используют функцию
с насыщением, которую приближенно можно рассматривать как кусоч-
кусочно линейную: на «рабочем» участке <т(ж) = сх, а вне его а{х) = ±1.
При помощи членов dj рабочий интервал можно сдвигать, добиваясь
того, чтобы для данного набора входных параметров значение j/, либо
попадало внутрь него («компонента активна»), либо вне его («компонента
неактивна»). В принципе это позволяет активизировать только я необ-
необходимых компонент yj, а значит получить на нейронах скрытого слоя
необходимую проекцию Р„г.
На следующих двух этапах вычисляется функция X = <т(^ BjHj).
Это не что иное как локальная линейная аппроксимация неизвестной
функции. Причем все эти локальные аппроксимации оказываются со-
согласованы между собой, подобно сплайнам (получающаяся функция
непрерывна и, в зависимости от выбора и(х), сколько-то раз дифферен-
дифференцируема).
Следовательно, трехслойные сети фактически воплощают основ-
основное требование теоремы Такенса: проецирование + аппроксимация. Это
позволяет объяснить и еще один факт, известный из литературы: увели-
увеличение числа слоев, как правило, не улучшает ситуацию (см., например,
[167, 261]). Комбинация двух проекторов эквивалентна некоторому тре-
третьему проектору, а комбинация двух линейных аппроксимаций снова
дает линейную аппроксимацию. Поэтому можно ожидать, что основные
свойства многослойных нейронных сетей можно получить и на трехслой-
трехслойных при соответствующем выборе числа скрытых нейронов и сигмоидной
передаточной функции.
14.3. Когда сложная динамика может быть предсказуема?
Русла и джокеры
Основная идея
Рассмотрим теперь вопрос о предсказании сложной динамики.
Выше мы отмечали ограничения, с которыми сталкиваются методы
прогноза. Но они были связаны только с «глобальной» предсказуемо-
предсказуемостью, т. е. с возможностью восстановить полную динамическую систему
в z-представлении
гп+] = Ф(г„). A4.1)
Для сложной системы эта задача неразрешима. Но может быть, можно
делать локальные прогнозы?
302 И. Русла и^жокерь^лик^^Е^ь динамикУ со статистикой?
В пользу этой идеи говорит и упоминавшаяся способность нейрон-
нейронных сетей к построению таких прогнозов. Но, как указывалось в пре-
предыдущем разделе, нейронные сети обладают высокими «проецирующими
способностями». Поэтому было бы разумно рассмотреть вопрос о «пред-
«предсказуемости в проекции малой размерности».
Предположим, что локально, в некоторой области G я-мерно-
го фазового пространства поведение сложной системы приближенно,
но с хорошей точностью может быть описано маломодовой моделью
с размерностью фазового пространства щ < я. Тогда, если данная траек-
траектория в течение времени наблюдений достаточное число раз проходила
через область G, то этого может быть не достаточно для того, что-
чтобы восстановить полную исходную я-мерную систему, но достаточно,
чтобы восстановить я i -мерную функцию, дающую возможность делать
локальный прогноз. При таких обстоятельствах не возникает никаких
противоречий с ограничениями методик прогноза.
Более того, эта гипотеза позволяет объяснить, почему именно ней-
нейронные сети могут случайно находить такие области G и строить локаль-
локальные предикторы. Как уже говорилось, они формируют большое число
проекций исходного фазового пространства, и если для предсказаний
достаточно Я] < я параметров, то сеть в принципе может обнаружить су-
существование области G и сформировать соответствующий маломодовый
предиктор. Иными словами, подход русел и джокеров — это попыт-
попытка использовать идеи маломодовой нелинейной динамики для анализа
сложных систем большой размерности.
14.3.1. Как могут возникать русла?
Рассмотрим теперь высказанную идею более подробно. Предполо-
Предположим, что для динамической системы xn+i = /(х„) существует область G,
где функция /(х) имеет вид
/(х) = /, (Р„,х) + 7/2(х), х € G С R".
Здесь 7 < 1, а РП] — проектор на подпространство размерности п\ < я.
Эту проекцию можно рассматривать как плоскость (в общем случае
поверхность) Р, проходящую через некоторую точку хо € G, а оператор
Р„, — как проектор на нее. Обозначим ,акже п\ координат на Р как
и = Рщх, а прочие я - п\ — через v = (/ - Р„,)х. Тогда /(х) = /|(и) +
7/2A1, v), и на поверхности Р мы получаем отображение
ni+i=Pni/i(ni)+7i>nl/2(n,-,Vi), uijUi+, GP. A4.2)
Если точность необходимого прогноза позволяет отбросить второй член,
например, если 7 очень мало, то динамику можно приближенно свести
к Я| -мерной:
U.-+1 =Рп,Мт). A4.3)
Таким образом, если необходимо предсказывать компоненту и, это можно
сделать при помощи A4.3). Предсказание компоненты v также иногда
возможно, если их зависимость от самих себя несущественна или имеет
14.3. Когда сложная динамика может быть предсказуема?
303
очень простой вид. Некоторые же компоненты вектора х могут остаться
непредсказуемыми.
Отметим, что A4.3) фактически является уравнением русла, свя-
связанного с областью G.
14.3.2. Русла и прогноз временных рядов
Рассмотрим теперь, как идею русел можно применить для про-
прогнозирования временных рядов. В этом случае мы будем иметь дело
с динамической системой A4.1) и ее компонентой
хп = Ф(жп_1,...,жп_т)ЕЕФ(гп_т). A4.4)
Будем предполагать, что полная система имеет большую размерность,
но где-то в реконструированном пространстве К существуют обла-
области Gk, где можно использовать подход маломодовых русел. Размерность
русла можно приближенно оценить при помощи методики, использован-
использованной в п. 2. Примем за необходимую точность 1 %, т. е. ~ 0,01, и положим
||?)Ф(го)|| « ||Х>2Ф(а5о)|| « 1 и N и 103. Тогда для метода 1-го порядка
е\ и N~2ld или
d^2 = 3. A4.5)
Следовательно, необходимо искать область, где динамику можно
предсказать по 3-6 наиболее важным компонентам вектора г или, иными
словами, определить проектор Рщ (заметим, что вектор z может или даже
должен иметь большую размерность). Если такая проекция найдена,
построение предиктора можно проводить при помощи обычных методов.
Следовательно, использование русел может позволить упростить
структуру предикторов, а потому дает возможность делать прогнозы
для систем большой размерности, которые в общем случае оказыва-
оказываются вне пределов применимости методов маломодовой нелинейной
динамики.
Отметим однако, что точность прогноза в этом случае ограничена
не только 1) ошибками исходных данных и 2) хаотичностью динамической
Точность
прогноза
Рис. 14.1. Схема возникновения русла. В неко-
некоторой области G различные траектории могут
оказаться близкими в проекции. Тогда в этой
проекции динамика становится частично пред-
предсказуемой. Однако такая «модель в проекции»
будет иметь принципиально ограниченную точ-
точность. Ситуация похожа на использование мето-
методов усреднения, когда усредненная модель полу-
получается как «проекция» на подпространство мед-
медленно меняющихся мод. Однако, в отличие от
них, здесь модель справедлива только при попа-
попадании траектории в область G. Как только тра-
траектория исходной системы покинет эту область,
предсказуемость в проекции будет утрачена
304 14. Русла и джокеры, или как сопрячь динамику со статистикой?
системы. Серьезным источником ошибок может быть 3) отброшенный
член в A4.2), который накладывает свои ограничения на ошибку прогно-
прогноза и в рамках маломодового подхода не может быть уменьшен (рис. 14.1).
Поэтому более адекватной моделью для русла могла бы быть динамиче-
динамическая система с наложенным шумом, но, возможно, этот «шум» должен
обладать некоторыми динамическими чертами, чтобы воспроизводить
свойства проекции траектории в пространстве большой размерности.
14.4. Как искать русла?
Поиск русел представляется сложной задачей. Здесь мы хотели бы
ограничиться несколькими краткими замечаниями.
Задача эта тесно связана с другими методами, ранее предлагав-
предлагавшимися в нелинейной динамике и статистике. Можно в этой связи
упомянуть методику ложных ближайших соседей [136], поиск зависимых
переменных [317, 316] или попытки использовать идеи анализа главных
компонент [160]. Однако все эти методы носят глобальный характер,
в то время как русла требуют локальных подходов. Поэтому необходимо
развивать новые способы анализа.
По-видимому, наиболее многообещающим представляется стан-
стандартный подход поиска функциональной зависимости между последова-
последовательными реконструированными векторами, который обычно использу-
используется для определения правильной размерности вложения [178, 136, 172].
Идея метода довольно проста: если существует функциональная зависи-
зависимость между Z; и Zj+i, то, если ||zi+i — zJ+i|| мало, то же самое должно
быть справедливо и для их образов под действием A4.1), т.е. ||z;+] -Zj+|||
также должно быть мало. (Другой путь использования той же идеи состоит
в сравнении расстояний в реконструкциях для размерностей вложения т
и т + 1.) Вероятно, для поиска русел можно было бы использовать по-
похожую технику, но только в некоторой проекции, которая в свою очередь
должна быть найдена.
Таким образом, мы приходим к следующей задаче: для реконструк-
реконструкции большой размерности (т может быть велико) найти а) проекцию
малой размерности, т.е. п\ = 3-6 ортонормальных векторов а*, опре-
определяющих проектор РП[х — $^(х,а*)аь и б) область G, где естественно
ожидать функциональную зависимость между Pn,Zi и Pniz,-+i. Одним
из возможных подходов может быть исследование соотношения между
||-Pn,(zi - Zj)|| и ||Pn,(Zi+i-Zj+i)||, изучение распределения потенци-
потенциально зависимых пар в проекции и подбор векторов а*. Эта задача
требует огромных вычислительных затрат и, возможно, необходимо пре-
прежде построить эффективные численные алгоритмы для этой цели, чтобы
добиться производительности, сравнимой с нейронными сетями.
14.5. Что находится в конце русла ?
305
14.5. Что находится в конце русла?
Внутри русла может быть получено простое описание сложной
системы. А что произойдет, когда русло закончится (т.е. траектория
уйдет из области G), в то время как нам хотелось бы оставаться в рамках
маломодового описания реальности? Простые модели более не способны
давать детерминированный прогноз, и единственным способом в какой-
то степени оставаться в рамках парадигмы маломодовой нелинейной
динамики — это допустить случайное, вероятностное поведение модели
системы. То есть, мы полагаем, что существуют области «7* (джокеры),
где поведение траектории становится случайным. Например, джокер
может отправить траекторию назад в некоторую (или в любую) точку
того же русла G или другого, или траектория может некоторое время
перемещаться между несколькими джокерами и т. п. Схематически это
показано на рис. 14.2.
Рис. 14.2. Схема представления сложной
динамики как комбинации русел и джо-
джокеров. На рисунке приведены 2 русла (G,
и G2) и 3 джокера (J,, J2, J}). Чер-
Черные стрелки показывают детерминирован-
детерминированное описание динамики (траектории модели
для проекции), «пустые» стрелки показы-
показывают действие джокеров: когда траектория
попадает в область джокера (заштрихован-
(заштрихованную), она может с некоторой вероятностью
направиться в некоторую точку русла или
к другому джокеру
Свойства одномерных отображений с джокерами различных типов
изучались в [152, 153]. Было показано, что присутствие джокера может
резко изменить бифуркационную диаграмму и даже подавить возникно-
возникновение хаоса.
14.6. Модельный пример
Приведем теперь простой модельный пример, позволяющий про-
продемонстрировать понятия русел и джокеров. Рассмотрим хаотическую
систему, состоящую из двух связанных частей, каждая из которых в свою
очередь является хаотической системой:
xn+i = /, (xn) + /i(xn)pi (у„), х G ДП|,
Уп+i = /г(Уп) + /*<№(хп), У G Я.
Предполагается, что размерность х мала. Изменяющуюся связь мы выбе-
выберем таким образом, чтобы внутри некоторой области ц(х„) = 0, а вне ее —
ц(хп) Ф 0. То есть, когда х попадает в G, у нас получается для х почти
независимая подсистема xn+i = /i(xn). Таким образом, получается русло.
1 1 Чак. :
306 14. Русла и джокеры, или как сопрячь динамику со статистикой?
Получим затем временной ряд для некоторой наблюдаемой х„ = Л(хп)
и посмотрим, удастся ли данное русло найти по временному ряду. За-
Заметим, что именно хороший выбор наблюдаемой делает данный пример
простым и избавляет нас от тяжелой процедуры поиска нужной проекции.
В приведенном ниже примере в качестве отображения /i(xn) мы
использовали модифицированное отображение Хенона
A4.6)
Ж2,п+1 = 2sin — = V(*i,n), xn
Модификация необходима для того, чтобы траектория не уходила на бес-
бесконечность, как это случается в исходном отображении Хенона. В ка-
качестве отображения /г(Уп) мы использовали три идентичных отображе-
отображения A4.6) с постоянной связью. Результирующая система имеет следую-
следующий вид
Ж1,п+1 =<p(xitn,X2,n)+H(X]in)ylfl, Х2.П+1 =
2/1,п+1 = <Р(У\,п,У2,п) + №> —^ -, 2/2,п+1 =
, v 2/1,п +2/5,п \ ¦ I
2/3,п+1 = (Р(УЗ,я,У4,п) +№ 2 ' J/4'n+1 =
2/5,я+1 = <Р(У5,п,Уб,п) + Р0УЗ,п, 2/6,п+1 =
1 - thEx)
Ч(х) = № ^ . a:n = ft(xn) = a:iini
о=1,4, 6 = 0,3, W = 0,3.
Из вида функции ц{х) следует, что область G соответствует х\п > 0.
Такой выбор не случаен, поскольку в этой полуплоскости у отображения
/i(xn) имеется неподвижная точка, и траектория иногда проводит не-
несколько последовательных итераций в ее окрестности. Иными словами,
благодаря такому выбору, в области траектория проводит несколько по-
последовательных итераций, что может быть важно для обнаружения русла
по временному ряду.
На первый взгляд, временной ряд для A4.7) почти не отличается
от ряда для невозмущенной системы A4.6), но при помощи корреляци-
корреляционного интеграла (а еще лучше — его наклона) эффект переменной связи
легко наблюдаем (см. рис. 14.3). Из этого графика можно сделать вывод,
что скорее всего обрабатываемый ряд порожден маломодовой динамиче-
динамической системой, но постоянный рост наклона с увеличением размерности
вложения делает его несколько «случайным». Следовательно, в проекции
на плоскость х мы получаем описанную выше ситуацию: маломодовая
динамика внутри G и более сложное поведение вне ее. В данном слу-
случае «джокер» оказывается слабым и просто добавляет небольшой «шум»
к маломодовому «сигналу».
14.6. Модельный пример
307
0 'I I
-10
Рис. 14.3. График корреляционного интеграла log2 C(e) от log2 e и его наклона
для временного ряда наблюдаемой xtj модельной системы A4.7). Длина ряда
N = 104, размерность вложения т = 4, 6, 8, 10, 12, 14, 16. Видно, что набор г-
векторов не выглядит случайным, скорее они образуют «нечто небольшой
размерности», но структура этого множества меняется с ростом т, а наклон
постепенно растет. Обычно такое поведение интерпретируют как присутствие
шума. В нашем случае с точки зрения маломодового русла это влияние джокера,
а с точки зрения всей системы A4.7) это следствие проблем с применимостью
теоремы Такенса: из-за переменной связи fj(x) наблюдаемая X\ti не позволяет
реконструировать всю систему целиком
Чтобы применить наш подход к анализу полученного временного
ряда, необходимо в реконструированном пространстве найти область
русла G. (Еще раз заметим, что здесь нам не нужно искать нужную
проекцию малой размерности, достаточно просто взять небольшое ц).
Чтобы найти русло, мы использовали сравнительно простую методику,
которую можно назвать тест на линейное предсказание (ТЛП).
Его идею можно пояснить следующим образом. Как уже указы-
указывалось ранее, прогноз временного ряда означает интерполяцию функ-
308 14. Русла и джокеры, или как сопрячь динамику со статистикой?
ции Ф(г) A4.4) в нужной точке г по известным значениям в соседних
точках <&(zofc). Для простоты рассмотрим одномерный случай: пусть да-
дана некоторая функция /(ж), значения которой известны в дискретных
точках ж,-, /,¦ = f{xi), и необходимо интерполировать значение функции
в некоторой точке х Е [zj,Zj+i]. Также для простоты будем считать, что
точки ж,- образуют равномерную сетку, т.е. x,+ i — Xi = Л для всех i.
Тогда линейная аппроксимация, использующая соседние точки /;+j и /*,
имеет вид
Да) S Un(fit Л+,,х) = ах + Ь= fi+1+ fi + ~^(х - хе),
2 2га
Погрешность данной аппроксимации можно приближенно оценить как
е ~ f"(x)h2, га = Х{+\ - ж,, а вторую производную можно аппроксими-
аппроксимировать второй разностью, тогда
.н,2 ~ /• + ! - 2/« + /i-1 ,2 /i+l ~ 2/t + /i-1
/Л =—__—h = _ =
j Л = ^-''Л+ьж>') ~ f{-
Следовательно, пофешность аппроксимации можно по порядку вели-
величины оценить как разницу между значением / в некоторой точке и ее
линейной аппроксимацией по ближайшим соседям. (Отсюда и обозначе-
обозначение Lin.) Такую форму оценки погрешности легко обобщить на многомер-
многомерный случай. Так мы приходим к идее ТЛП. Будем оценивать «качество»
точки Z* следующим образом:
1. Выберем некоторое количество к — ко > т + 2 ближайших сосе-
соседей точки z,, Zjt, s = 1,..., к, где известны значения Ф(г^), и построим
линейную аппроксимацию Lfc(z) по этим к соседям (но не используя
для построения аппроксимации саму точку z,), где Ф(г<) также извест-
известно. Таким образом, мы получим две величины, е| = |x,fc(z,) — Ф(г,)|
и е2 = max \Lk(zjt) - Ф(г,-,)|.
2. Затем будем уменьшать к: будем по одной отбрасывать те точ-
точки Zj#, для которых операция отбрасывания дает наибольшее уменьшение
погрешности е — |Lj._|(z,) — Ф(г,) . Повторяем эту процедуру до тех пор
пока (а) к > т + 2 и (б) уменьшение е составляет по крайней мере 2%.
3. В результате получаем некоторое новое к < ко и значения
е3 = jis(zi) - Ф(гО|, ?4 = max \b-k(zjt) - Ф(г,-,)|.
Как оказалось, во многих случаях при помощи ?],...,?4 можно
произвести довольно удачную классификацию точек i\. Один из ре-
результатов приведен на рис. 14.6. Точками показаны «хорошие» точки,
а крестиками — «плохие». Область русла выделяется довольно просто.
Таким образом, мы получаем область хорошей предсказуемости для на-
нашего ряда и простое правило для проверки принадлежности ему вектора.
14.7. Выводы и гипотезы
309
Можно сделать вывод, что по крайней мере в некоторых ситуациях подход
русел и джокеров может оказаться полезным.
1.0:
0,5;
о;
0.5:
1,0:
1 1 1 1 |l|+i \-
-1,0-0,5 0 0,5 1,0
а) т = 2
-1,0-0,5 0 0,5 1,0 х,
б)т-6
Рис. 14.4. Результаты применения теста на линейное предсказание (ТЛП) для ко-
короткого (JV = 103) временного ряда наблюдаемой xti, порожденного модельной
системой A4.7). Крестиками показаны «плохие» точки, точками — «хорошие»,
в которых хороший прогноз возможен. При применении ТЛП к проекции малой
размерности (т = 2, график а) область русла, отвечающая полуплоскости я, > 0,
ясно выделяется по отсутствию плохих точек. Для проекции большей размерности
(т = 6, график 6, координатами на графике служат последние две компоненты
6-мерного z-вектора) ТЛП почти неспособен обнаружить русло. Следовательно,
методика поиска русел требует поиска подходящей проекции
14.7. Выводы и гипотезы
Таким образом, наша гипотеза состоит в том, что для сложных си-
систем большой размерности может оказаться полезным подобное описание
в терминах джокеров и русел. В определенном смысле его можно рассма-
рассматривать как обобщение символической динамики, в других аспектах —
как систему сопряженных простых моделей.
Можно предположить, что большинство успешных научных тео-
теорий приводят к успеху, когда проекция реальности, с которой они имеют
дело, оказывается связана с каким-либо руслом (или, если хотите, со-
создание такой успешно предсказывающей теории и показывает, что русло
существует и найдено). В идеальном случае очень устойчивых причинно-
следственных связей можно оставаться в рамках логики, конструкций
типа «Если ... то»; тут раздолье для идеализации, для людей, которые
умеют доказывать теоремы.
На следующем уровне находится физика. Ей посчастливилось —
она в большинстве ситуаций имеет дело с глобальными руслами, когда
можно выделить и описывать почти изолированную подсистему (об окру-
окружении можно забыть), когда существенными оказываются одни и те же
310 14. Русла и джокеры, или как сопрячь динамику со статистикой?
переменные и можно всегда пользоваться одними и теми же уравнениями
(дополнительность является скорее исключением, а не правилом). Прав-
Правда, до теорем обычно дело не доходит, да и на бумажке можно посчитать
немного, приходится часто обращаться к помощи компьютера.
В экономике, социологии, психологии, истории ситуация сложнее.
Успехи выдающихся экономических теорий, различных психологичес-
психологических школ показывают, что русла есть и здесь. Однако, во-первых, они
локальны, т. е. обладают предсказывающей силой только в какой-то впол-
вполне определенной ситуации, при выполнении определенных требований.
А, во-вторых, от них нельзя требовать очень точных и очень длительных
прогнозов (хотя от создателей можно потребовать эту точность оценить).
Поэтому нужно очень точно оговаривать допущения, исходные посылки.
На первый план выходит определение истока (когда посылки начинают
быть справедливы) и устья русла (когда они больше не выполняются),
а точнее, определение джокеров — если нельзя указать следующего русла.
Почему русла важны? Потому что понимание, на основе которого
можно принимать решения, дают только простые модели, а втиснуть в них
действительность можно только отбрасывая «лишнее». По-видимому,
на подсознательном уровне мозг решает подобные задачи очень быстро,
однако сознательный выбор нужных переменных и его обоснование тре-
требует времени, иногда очень большого. Ведь умели же люди очень точно
кидать камни и пускать стрелы задолго до Галилея и Ньютона. Мозг бы-
с фо прикидывает нужные траекторию и усилия, но никто точно не знает
каким образом. Надо только немного потренироваться. Преуспевающие
бизнесмены хорошо ориентируются на биржах и рынках, но обычно
не создают экономических теорий и, видимо, почти не пользуются ими.
То же самое наблюдается в управлении коллективами людей, сложными
объектами, нетрадиционной медицине и т. п. Однако такое эмпиричес-
эмпирическое знание, хотя и приводит к успеху, обычно не может быть передано
другим людям, не становится достоянием общества. Его можно переда-
передавать только небольшой группе близких соратников личным примером, да
и то не всегда. Наука, обеспечивающая передачу информации, обучение,
формализованное описание, обслуживает и отражает весьма небольшую
часть наших знаний, навыков и представлений. Заметим, например, что
социальные теории обычно успешнее всего объясняют прошлое. Пока
теория создается, ситуация успевает измениться и старая проекция уже
может не отражать сути дела. Найденное русло оказалось пройдено, и те-
текущая ситуация соответствует джокеру или пока не найденному руслу
в неизвестной проекции.
Что же делать в такой ситуации? Принципиальным становится
определение структуры нашего незнания, осмысление ситуаций, где еще
могут существовать русла, а также техники, позволяющей переходить
от одних русел к другим, от одних теорий к их альтернативам. Может,
к примеру, оказаться, что неокейнсианство и монетаризм — это не альтер-
альтернативное описание одной реальности, а теории, относящиеся к разным
руслам. Поэтому может оказаться, что вопросы «Вы за или против?», «Кто
прав?» лишены смысла. Следует просто осознать, к объекту какой теории
14.7. Выводы и гипотезы 311
ближе реальность, которую предполагают моделировать или тем более ме-
менять. Это необходимо, чтобы не пришлось «импровизировать» или, хуже
того, «подгонять» существующую реальность под неадекватную теорию.
Вероятно, именно здесь и может быть развита новая парадигма
нелинейной динамики и математического моделирования. Возможно,
следует отказаться (хотя бы частично) от построения общих теорий,
а «сосредоточиться лишь на частичном объяснении динамики», на со-
создании «частных теорий», для построения которых было бы достаточно
сравнительно небольшого объема информации. Такого, который может
быть собран, переработан и осмыслен за разумный промежуток времени.
И для этого концепция русел и джокеров представляется многообеща-
многообещающей. Определение русел и джокеров в социальных науках, экологии,
теории риска представляется захватывающей задачей.
Но помимо таких «философских» выводов мы ожидаем, что подход
русел и джокеров может быть полезен и в ряде более прозаических задач,
таких как прогноз временных рядов. Одно из возможных применений
описано в данной главе.
Задачи
1. Для системы дифференциальных уравнений в полярных координа-
координатах г — г(\ — г2), Ь = 1 построить отображение <р'(х).
2. Показать, что круг {х, у: х2 + у2 < 1} является положительно
инвариантным множеством для системы х = —2х, у = -у.
3. Для каких матриц В существует матрица А, такая что В = ехр (тАI
4. Для матриц 2x2 найти условия, при которых матрица имеет: а) одно
нулевое собственное значение; б) два чисто мнимых собственных
ч + ( 0 1 \ ч
значения; в) жорданову форму I „ „ 1; г) жорданову форму
О 0
5. Иногда логистическое уравнение записывают в виде хп+\ = \хпх
A - хп), х € [0,1]. Как будет выглядеть выражение для инвари-
инвариантной меры при А = 4 (указание: преобразуйте логистическое
отображение к треугольному отображению, для которого инвари-
инвариантная мера постоянна)?
6. Дано отображение с шумом хп+\ = ах„ + ?„, \а\ < 1, где ?„ — слу-
случайная величина, такая что —е < ?„ < е, а исходное распределение
х локализовано на отрезке [-е,е]. Покажите, что распределение х
всегда останется локализованным на отрезке [тгш> "Ro[] •
7. Покажите, что энтропия максимальна, если все состояния х,- си-
системы равновероятны.
8. Пользуясь определением энтропии, покажите, что для отображе-
отображения хп+] = 2ж„тосН, 0 ^ х < 1, и физической инвариантной
меры (р = 1) она равна In 2. В качестве начального разбиения
используйте А\ = [0, j) и Аг — [j, l).
9. У этого отображения есть бесконечно много других мер, сосре-
сосредоточенных на неустойчивых циклах, отвечающих рациональным
точкам отрезка [0,1). Покажите, что энтропия для таких мер рав-
равна 0. (Результат разумный, так как когда точка движется по циклу,
неопределенность не увеличивается.)
10. Пользуясь определением емкости, показать, что емкость множества
хп = - равна 2, т. е. что количество покрывающих отрезков растет
как е"'/2.
11. Покажите, что для произведения двух одномерных канторовых
множеств в двумерном пространстве его размерность равна сумме
размерностей одномерных множеств.
12. Как надо поделить отрезок при построении канторова множества,
чтобы емкость была равна j ?
Задачи 313
13. Постройте фрактальное множество, емкость которого равна це-
целому числу. (Этот пример показывает, что иногда встречающееся
определение фрактального множества как множества с дробным
значением размерности не вполне корректно, хотя в большинстве
практически важных случаев оно вполне пригодно; вообще говоря,
целое значение фрактальной размерности — ситуация нетипичная,
«не грубая».)
14. Что представляет собой минимальное инерциальное многообразие
для динамической системы в полярных координатах: г = гA — г2),
в = а + cos в при различных а?
15. Предположим, что Х{ и ?,- — периодические последовательности
с периодом N, t = 0,..., JV — 1. Тогда в суммах, входящих в модели
авторегрессионного типа, можно использовать циклическое изме-
изменение индексов — вместо —1 писать N — 1, вместо —2 — iV - 2
и т.д. Аналогично вместо N можно писать 0, вместо N + 1 — 1.
Такое суммирование с циклически меняющимися индексами носит
название циклической дискретной свертки. Далее, комплексным
дискретным преобразованием Фурье (ДПФ или DFT) последова-
последовательности Х{ называется
Хк = DFT({Xi})k = ]Г>,ехр (-
?<
t=0
к = 0,... ,N — 1, j — мнимая единица, j2 = — 1. Покажите,
что а) обратное преобразование имеет тот же вид, но добавляется
множитель Г и под экспонентой стоит знак +; б) пусть по-
m к
следовательность х, удовлетворяет ж; — ац + ^ а;Ж;_у + ^ bj^j\
j=] j=0
покажите, что ДПФ ж, и f,- (X^ и Ец, соответственно) связаны
соотношением X). = AkELk и получите выражение для А)..
16. Пусть наблюдаемая имеет вид x(t) = cos(<). Покажите, что при
т — 2 реконструкция при всех т кроме некоторых выделенных
будет эллипсом.
17. Покажите, что в условиях предыдущей задачи реконструкция
при любом т почти всегда будет эллипсом, лежащим в не-
некоторой плоскости. Указание: сначала покажите, что z(t) —
е\ (г) • cos(i) + е2(т) • sin(i).
18. Сколько существует инвариантных мер у динамической системы?
а) ж„+1 = 2ж„ при ж„ < 0,5 и жп+] = 2 - 2ж„ при ж„ > 0,5;
в)г = г(г-1)(г-2)(г-3), в=\.
19. Даны два отображения: жп+1 = 2жптос) 3, 0 < ж < 3 и хп+\ =
3xnmod 2, 0 < ж < 2. Чему равны их ляпуновские показатели?
Энтропия какого из них больше?
314 ^ Задачи
20. Дано отображение Хенона х„+\ = 1 - аж„ + у„, у„+\ = Ьх„. У него
есть неподвижные точки и циклы периода 2. Найти их ляпуновские
показатели.
21. Дано преобразование пекаря жп+1 = ^ при уп < 0,5 и хп+х = 24р*
при у„ > 0,5, j/n+i = 2Уп mod 1. Найти его ляпуновские показатели,
энтропию и размерность аттрактора.
22. При построении обычного канторова множества (удаление средней
трети отрезка) одновременно определяется заданная на нем сингу-
сингулярная мера: если некоторому отрезку на n-м шаге была приписана
вероятность р, то его левой трети приписывается вероятность jj,
а.правой -Ц- (т.е. получаем последовательность 5, 5 ~~* ЗП"> 8Т>
gy, gj —»...). Найти для этой меры обобщенные размерности Dq
для q — 0, ±2, ±оо.
23. На отрезке [0,1] равномерно распределены N точек х\ — 0,...,
хц — 1. Считая их «траекторией» некоторой динамической систе-
системы, найти корреляционный интеграл С(е). Можно ли по нему
найти размерность отрезка (d =1)?
24. Что может означать наличие одного или нескольких нулевых ля-
пуновских показателей? Может ли ляпуновская размерность от-
отличаться от корреляционной на несколько единиц? (Например,
dL = 5,4, а ?>2 = 3,35.)
25. Расскажите, что Вы думаете о динамической системе, если изме-
измеренный набор ляпуновских показателей выглядит как
а) -1, -1, -2, -3, ...;
б) 0, -1, -1, -2, -3, ...;
в) 0, 0, 0, -1, -1, -2, -3, ...;
г) 0,1, 0, 0,-1, -1, -2, -3, ...;
д) 0,5, 0,1, 0,-1, -1, -2, -3, ....
26. При построении канторова множества оставляют каждый раз не |,
а I отрезка. Какова емкость полученного множества?
27. Покажите, что динамические системы х = -х и х = -ж3 тополо-
топологически эквивалентны. Какая из них структурно устойчива?
28. Постройте отображение Пуанкаре для системы х + х + х = cos 2?r?
в сечении t = 0. (Указание: замените явно входящее время на новую
динамическую переменную и, й — 1, которая будет меняться
циклически от 0 до 2я\ То есть фазовым пространством новой
трехмерной автономной системы будет произведение плоскости Д2
и окружности 51.)
29. Рассмотрим систему
х + (ц + х2)х + х + х3 - 0.
Найти точки бифуркации и определить их тип.
Задачи
315
х2),
30. Дана динамическая система (и > 0)
х = jx + y(z -
у = 72/ + х(Ъг + 1 -ж2),
z - -2z(u + xy).
При каких значениях 7 У системы могут быть аттракторы, отличные
от неподвижной точки?
31. Рассмотрим систему
х-цх- х(х2 + у1) - ху2,
у = у-у(х2 + у2)-ух2.
Показать, что у данной системы существует аттрактор и найти
точки бифуркации.
32. Для системы Лоренца
х = а(у - х),
y = (r-z)x- у,
z = xy- bz,
показать, что г — 1 — точка бифуркации. Построить систему
на центральном многообразии с точностью до кубических членов
и показать, что происходит бифуркация типа вилки.
33. Как нужно изменить систему Лоренца, чтобы вместо бифуркации
типа вилки происходила бифуркация типа седло-узел? Приведите
пример.
34. Найти ляпуновские показатели для системы х + х + х = cos 2тг/.
35. Рассмотрим модель Хопфидда, в которой jy > 0, 1 < г < N,
1 ^ j ^ N. Какова типичная конфигурация в этом случае? Каким
материалам соответствует такое поведение? Каковы будут ответы
на те же вопросы, если j < 0?
36. В спиновых стеклах известны эффекты, называемые фрастрация-
ми, — изменение ориентации отдельного спина не меняет энергию
системы. Рассмотрите три спина и выясните, при каком соотно-
соотношении знаков j\2, J23. J\3 этот эффект возможен?
37. Нейронная сеть Хопфидда, состоящая из 9 элементов, обучена двум
ключевым образам
1
1
1
1
0
0
0
0
0
0
0
0
0
0
1
1
1
1
Какова будет финальная конфигурация, если на вход сети подан
образ
0 1 0
,is Задачи
38. При численном исследовании описанного дискретного варианта
сети Хопфилда, в котором состояния всех элементов обновля-
обновлялись синхронно, было обнаружено, что при некоторых начальных
конфигурациях происходит выход на циклы S2. Объяснить это
явление. Как оно согласуется с наличием функционала Ляпунова?
39. В конце прошлого века Эббингаузом были поставлены класси-
классические эксперименты, которые легли в основу теории обучения.
Испытуемым предъявлялось на определенное время множество
бессмысленных слов из трех букв. Затем выяснялось, насколько
точно запомнено это множество. Оказалось, что в подавляющем
большинстве случаев вероятность ошибки зависела от числа предъ-
предъявлений множества N как Р т Ce~XN, С = const. Постройте
математическую модель, объясняющую эту зависимость.
40. Оказалось, что закон Эббингауза не верен для ситуаций, в ко-
которых происходит длительное обучение сложным навыкам (под-
(подготовка операторов атомных электростанций, пилотов самолетов-
истребителей и т.д.). Вначале время принятия решения меняется
в зависимости от времени обучения Г как т = то+Се~хт, где посто-
постоянные то, С, А, естественно, зависят от способностей обучаемого.
Затем происходит «качественный скачок» и время т существенно
уменьшается. Объясните это явление, имея в виду подход теории
бифуркаций либо концепцию параметров порядка.
41. Построить простейшую нейронную сеть, которая по предъявленно-
предъявленному вектору (fx>Cy>?z) определяет, попала ли соответствующая точка
в кубик с ребром а заданной ориентации с центром в заданной
точке пространства.
42. Предложите простейшую нейронную сеть, предсказывающую дви-
движение исследуемого объекта на основе его предыстории.
Список литературы
1. Алферов Ж. И. История и будущее полупроводниковых гетерострук-
тур // Физика и техника полупроводников. 1998. № 32. С. 3-18.
2. Андронов А. А. Динамические системы на плоскости. М.: Наука, 1961.
3. Андронов А. А. Бифуркации динамических систем. М.: Наука, 1962.
4. Анищенко B.C., Павлов А.Н., Янсон КБ. Седло-фокус в модели
электрической активности сердца человека // Письма в ЖТФ. 1996.
Т. 22. №4. С. 78.
5. Анищенко В. С, Сапарин П. И. Нормированная энтропия как диагно-
диагностический признак реакции сердечно-сосудистой системы человека
на внешнее воздействие // Изв. вузов. Прикладная нелинейная ди-
динамика. 1993. Т. 1. № 3, 4. С. 54.
6. Анищенко В. С, Сапарин П. И., Курте Ю., Витт А., Фосс А. Анализ
динамики сердечного ритма человека на основе критерия пере-
перенормированной энтропии // Изв. вузов. Прикладная нелинейная
динамика. 1994. Т. 2. №3, 4. С. 55.
7. Анищенко В. С. Сложные колебания в простых системах. М: Наука,
1990. 312 с.
8. Арнольд В. И. Дополнительные главы теории обыкновенных диффе-
дифференциальных уравнений. М.: Наука, 1978. 304 с.
9. Арнольд В. И., Афраймович В. С., Ильяшенко Ю. С., Шильников Л. П. Те-
Теория бифуркаций // Итоги науки и техники. Современные проблемы
математики. Фундаментальные направления. 1985. Т. 5. С. 5-220.
10. Ахромеева Т. С, Курдюмов СП., Малинецкий Г. Г., Самарский А. А.
Нестационарные структуры и диффузионный хаос. М.: Наука, 1992.
544 с.
11. Бабин А. В., Вишик М. И. Аттракторы эволюционных уравнений. М.:
Наука, 1989. 296 с.
12. Баранцев Р. Г. О тринитарной методологии // Между физикой и ме-
метафизикой: наука и философия. СПб.: Наука, 1998. С. 51-61.
13. Белолипецкий А. А., Тер-Крикоров А. М. О фундаментальных решениях
нелинейного уравнения теплопроводности // Журн. вычисл. матем.
и матем. физ. 1984. Т. 24. № 6. С. 850-863.
14. Белоцерковский О. Численный эксперимент в турбулентности: от по-
порядка к хаосу. М.: Наука, 1997. 206 с.
15. Вельский Ю. Л., Веденяпин А. Б., Дмитриев А. С, Зенков Л. Р., Стар-
Старков CO., Васильев П.П. Диагностика патологических состояний
мозга на основе анализа электроэнцефалограмм методами нели-
нелинейной динамики // Радиотехника и электроника. 1993. Вып. 9.
С. 1625-1635.
31 g Список литературы
16. Беляев Ю.Н., Монахов А. А., Яворская И.М. Устойчивость сфериче-
сферического течения Куэтта в толстых слоях при вращении внутренней
сферы // Изв. АН СССР. Механика жидкости и газа. 1978. №2.
С. 9-15.
17. Беляев Ю.Н., Яворская И.М. Сферическое течение Куэтта — пере-
переходы и возникновение хаоса // Изв. АН СССР. Механика жидкости
и газа. 1991. N° 1. С. 10-18.
18. Берже П., Помо И., Видаль С. Порядок в хаосе. М.: Мир, 1991.
19. Бокс Док., Дженкинс Г. Анализ временных рядов. Прогноз и упра-
управление. М.: Мир, 1974.
20. Боуэн Р. Методы символической динамики. М.: Наука, 1979. 245 с.
21. Брюно А. Д. Локальный метод нелинейного анализа дифференциаль-
дифференциальных уравнений. М.: Наука, 1979. 255 с.
22. Буланов С. В., Есиркепов Т.Ж., Каменец Ф. Ф., Наумова Н. М., Пегора-
ро Ф., Пухов А. М. Лазерные методы ускорения заряженных частиц //
Радиотехника (Электромагнитные волны). 1995. № 12. С. 49-55.
23. Бунимович Л. А. Системы гиперболического типа с особенностями //
Итоги науки и техники. Современные проблемы математики. Фун-
Фундаментальные направления. М.: ВИНИТИ, 1988. Т. 2. С. 173-204.
24. Буссе Ф. Вихри и волны. М.: Мир, 1984. 199 с
25. Былое Б.Ф., Виноград Р.Э., Гробман Д.М., Немыцкий В. В. Теория
показателей Ляпунова и ее приложения к теории устойчивости. М.,
1966.
26. Вайнштейн СИ., Зельдович Я.Б., Рузмайкин А.А. Турбулентное ди-
динамо в астрофизике, Новосибирск: Наука, 1980. 352 с.
27. Валиев К.А., Кудрявцев С.Е., Левин В.Л., Мордвинцев В.М., Сава-
син В. Л. Память на основе нано-мим-диода с углеродистой активной
средой // Микроэлектроника. 1997. №26. С. 3-11.
28. Васильев В. А., Романовский Ю. М., Яхно В. Г. Автоволновые процессы.
М.: Наука, 1987. 240 с.
29. ВеденовА.А. Математическое моделирование элементов мышления.
М.: Наука, 1988.
30. Вигнер Е. Этюды о симметрии. М.: Мир, 1971. 318 с.
31. Гантмахер Р. Теория матриц. М., 1953.
32. Герценштейн С. Я., Родичев Е. Б., Шмидт В. М. Взаимодействие трех-
трехмерных волн во вращающемся горизонтальном слое, подогреваемом
снизу // Докл. АН СССР. 1978. Т. 238. № 3.
33. Гидродинамические неустойчивости и переход к турбулентности.
М.: Мир, 1984. 344 с.
34. Гиззатулина СМ., Малинецкий Г.Г., Потапов А.Б., Рузмай-
Рузмайкин А. А., Рукавишников В. Д. Размерность геодинамического аттрак-
аттрактора по данным о вариации длины суток. ИПМ им. М. В. Келдыша
АН СССР (препринт), 1988. № 95. 25 с.
35. Гилмор Р. Прикладная теория катастроф. М.: Мир, 1984. Т. 1, 2.
Список литературы 319
36. Гольдштейд И. Я., Маргулис Г. А. Показатели Ляпунова произведения
случайных матриц // Успехи мат. наук. 1989. Т. 44. Вып. 5. С. 13-60.
37. Грибков Д.А., Грибкова В. В., Кравцов Ю.А., Кузнецов Ю.И., Ржа-
нов А. Г. Восстановление структуры динамической системы по вре-
временным рядам // Радиотехника и электроника. 1994. Вып. 2.
С. 269-277.
38. Дегтярев Л. М., Дроздов В. В., Медведев С. Ю. Численное моделиро-
моделирование равновесия и устойчивости тороидальной плазмы. М.: ИПМ
АН СССР, 1989.
39. Деруссо П., Рой Р., Клоуз Ч. Пространство состояний в теории
управления. М.: Наука, 1970.
40. Дмитриев А. С, Панас А. И., Старков С. О. Динамический хаос как
парадигма современных систем связи // Зарубежная радиоэлектро-
радиоэлектроника. Успехи современной радиоэлектроники. 1997. N° 10. С. 4-26.
41. Дмитриев А. С, Кислое В.Я. Стохастические колебания в радиофи-
радиофишке и электронике. М.: Наука, 1989.
42. Дмитриев А. С, Старков С. О. Передача сообщений с использовани-
использованием хаоса и классическая теория информации // Зарубежная радио-
радиоэлектроника. Успехи современной радиоэлектроники. 1998. №11.
С. 4-32.
43. Дубровин В. Н., Новиков С. П., Фоменко А. П. Современная геометрия.
М.: Наука, 1979. 760 с.
44. Дымников В. П., Филатов А. Н. Основы математической теории кли-
климата. М.: ВИНИТИ, 1994. 254 с.
45. Ершов С. В., Потапов А. Б. Бифуркации инерциальных многообразий
в модельной задаче. ИПМ им. М. В. Келдыша АН СССР (препринт),
1991. №8.
46. Ершов С. В., Потапов А. Б. Размерность реконструкции аттракторов
и упорядочение ближайших соседей. ИПМ им. М. В. Келдыша РАН
(препринт), 1995. №8. 12 с.
47. Ефремова Т.М., Куликов М.А., Резвова И. Р. Участие нелинейных
динамических процессов в формировании высокочастотной ЭЭГ
кролика // Журн. высшей нервной деятельности. 1991. Т. 41. С. 998-
1006; Куликов М.А. Частное сообщение.
48. Заславский Г. М., Сагдеев Р. 3. Введение в нелинейную физику. От ма-
маятника до турбулентности и хаоса. М.: Наука, 1988. 368 с.
49. Зельдович Я. Б., Соколов Д. Д. Фракталы, подобие, промежуточная
асимптотика // Успехи физ. наук. 1985. Т. 146. Вып. 3. С. 493-506.
50. Ивахненко А. Г., Лапа В. Г. Предсказание случайных процессов. Киев:
Наукова думка, 1971.
51. Ижикевич Е. М., Малинецкий Г. Г. О возможной роли хаоса в нейро-
системах // Докл. РАН. 1992. Т. 326. С. 626-632.
52. Илькаев Д. Р., Кривоспицкш А.Д., Окшин А.А., Орликовский А.А.,
Семин Ю. Ф. Нестандартные методы формирования субмикронных
320 Список литературы
структур в микроэлектронике // Микроэлектроника. 1996. №25.
С. 339-345.
53. Итоги науки и техники. Математический анализ. М., 1974. Т. 12.
С.71-146.
54. Итоги науки и техники. Современные проблемы математики. Фун-
Фундаментальные направления. М.: ВИНИТИ, 1985. Т. 1. 243 с.
55. Итоги науки и техники. Современные проблемы математики. Фун-
Фундаментальные направления. 1985. Т. 2. 312 с.
56. Итоги науки и техники. Современные проблемы математики. Но-
Новейшие достижения. М.: ВИНИТИ, 1986. Т. 28. 316 с.
57. Йосс Ж., Джозеф Д. Элементарная теория устойчивости и бифурка-
бифуркаций. М.: Мир, 1983. 304 с.
58. Каменец Ф. Ф., Пухов А. М., Иванов М. Ф., Фортов В. Е. Образование
вихревых структур в атмосфере Юпитера в результате падения фраг-
фрагментов кометы Шумейкера—Леви-9 // Письма в ЖЭТФ. 1994. Т. 60.
Вып. 6. С. 383-387.
59. Капица С. П., Курдюмов С. П., Малинецкий Г. Г, Синергетика и про-
прогнозы будущего. М.: Наука, 1997. 285 с.
60. Карлов Н. В., Кириченко Н.А., Лукьянчук Б. С. Лазерная термохимия.
М.: Центрком, 1995.
61. Като Т. Теория возмущений линейных операторов. М.: Мир, 1972.
62. Кашьяп Р.Л., Рао А. Р. Построение динамических стохастических
моделей по экспериментальным данным. М.: Наука, 1983.
63. Кащенко С. А. О квазинормальных формах для параболических урав-
уравнений с малой диффузией // Докл. АН СССР. 1988. Т. 299. № 5.
С. 1049-1052.
64. Кащенко С. А., Майоров В. В., Мышкин И. Ю. Исследование колебаний
в кольцевых нейронных системах // Докл. РАН. 1993. Т. 333. №5.
С. 594-597.
65. Колмогоров А.Н., Петровский И. Г., Пискунов И. С. Исследование
уравнения диффузии, соединенной с возрастанием количества ве-
вещества, и его применение к одной биологической проблеме //
Бюллетень МГУ. 1937. Т. 1. № 6. С. 1-26.
66. Колмогоров А. Н., Фомин С. В. Элементы теории функций и функци-
функционального анализа. М.: Наука, 1977.
67. Костылев И. А., Малинецкий Г. Г., Потапов А. Б. Параметры порядка
в нейронной сети Хопфилда // Журн. вычисл. матем. и матем. физ.
1994. Т. 34. С. 1733-1740.
68. Ланда П. С. Нелинейные колебания и волны. М.: Наука, Физматлит,
1997. 495 с.
69. Ланда П. С, Четвериков В. И. К вопросу о вычислении максимально-
максимального ляпуновского характеристического показателя по одной экспери-
экспериментальной реализации // Журн. Техн. Физ. 1988. Т. 58. С. 433-441.
70. Ландау Л. Д., Лившиц Е. М. Квантовая механика. Нерелятивистская
теория. М.: Наука, 1974. 752 с.
Список литературы 321
71. Ландау Л. Д., Лифшиц Е. М. Гидродинамика. М.: Наука, 1986. 736 с.
72. Лахно В. Д., Чуев Г. Н. Связанные состояния фононов в адиабатичес-
адиабатической теории полярона и F-центра. Пущино: препринт НИВЦ НЦБИ,
1987.
73. Левкович-Маслюк Л. И. Физическая личность // Компьютерра. 13 ок-
октября 1997. № 40. С. 27-30.
74. Леденцов Н.Н., Устинов В.М., Щукин В.А., Копъев П. С, Алфе-
Алферов Ж. И., Бимберг Д. Гетероструктуры с квантовыми точками: полу-
получение, свойства, лазеры: Обзор // Физика и техника полупроводни-
полупроводников. 1998. №32. С. 385-410.
75. Лем С. Сумма технологии. М.: Текст, 1996.
76. Лоскутов А. Ю. Хаотичность динамических систем и подавление
хаоса: основные понятия // Физическая мысль России. 1997. № 2-3.
С. 6-35.
77. Лоскутов А. Ю., Михайлов А. С. Введение в синергетику. М.: Наука,
1990.
78. Лукащук С.Н., Фалькович Г. Е., Черных А. И. О вычислении размер-
размерностей аттракторов по экспериментальным данным // Журн. прикл.
мех. и техн. физ. 1989. № 1. С. 99-104.
79. Льюнг Л. Идентификация систем. Теория для пользователя. М.:
Физматлит, 1991.
80. Ляпунов А. М. Собр. соч. М.—Л., 1956. Т. 2. С. 7-263.
81. Малинецкий Г. Г., Подлазов А. В. Парадигма самоорганизованной кри-
критичности. Иерархия моделей и пределы предсказуемости // Изв.
вузов. Прикладная нелинейная динамика. 1997. Т. 5. № 5. С. 89-106.
82. Малинецкий Г. Г., Потапов А. Б. О вычислении размерностей стран-
странных аттракторов. ИПМ им. М. В. Келдыша АН СССР (препринт),
1987. №101.
83. Малинецкий Г. Г., Потапов А. Б. О вычислении размерностей стран-
странных аттракторов // Журн. вычисл. матем. и матем. физ. 1988. Т. 28.
№7. С. 1021-1037.
84. Малинецкий Г. Г., Потапов А. Б. Геометрия странных аттракторов
и вычисление ляпуновских показателей по временным рядам. ИПМ
им. М. В. Келдыша АН СССР (препринт), 1991. № 13. С. 28.
85. Малинецкий Г. Г., Потапов А. Б. Русла и джокеры: о новых методах
прогноза поведения сложных систем. ИПМ им. М. В. Келдыша РАН
(препринт), 1998. № 32. 20 с.
86. Марсден Дж., Мак-Кракен М. Бифуркация рождения цикла и ее
приложения. М.: Мир, 1980. 368 с.
87. Математическая энциклопедия. М.: Советская энциклопедия, 1985.
Т. 1-5.
88. Математическое моделирование исторических процессов. М.: МГУ,
1998.
89. Мозер Ю. Лекции о гамильтоновых системах. М.: Мир, 1973. 167 с.
,22 Список литературы
90 Монин А. С. О природе турбулентности // Усп. физ. наук. 1978. Т. 125.
Вып. 1. С. 97-122.
91. Нейман Док. Теория самовоспроизводящихся автоматов. М.: Мир,
1971.
92. Неймарк Ю. И.,Ланда П. С. Стохастические и хаотические колебания.
М.: Наука, 1987. 424 с.
93. Нелинейные волны: самоорганизация: Сб. статей / Ред. А. В. Гапо-
нов-Грехов, М. И. Рабинович. М.: Наука, 1983.
94. Немыцкий В. В., Степанов В. В. Качественная теория дифференци-
дифференциальных уравнений. М.—Л.: ОГИЗ, 1947.
95. Николис Г., Пригожий И. Самоорганизация в неравновесных систе-
системах. М.: Мир, 1979. 512 с.
96. Оселедец В. И. Мультипликативная эргодическая теорема. Характе-
Характеристические показатели Ляпунова динамических систем // Труды
Моск. мат. общества. 1968. Т. 19. С. 179-210.
97. Павлов А. Н., Янсон Н.Б. Применение методики реконструкции ма-
математической модели к электрокардиограмме // Изв. вузов. При-
Прикладная нелинейная динамика. 1997. Т. 5. № 1. С. 93.
98. Павлов А.Н., Янсон Н.Б., Анищенко B.C., Гриднев В. И., Довгалев-
ский П. Я. Диагностика сердечно-сосудистой патологии методом вы-
вычисления старшего показателя Ляпунова по последовательности RR-
интервалов // Изв. вузов. Прикладная нелинейная динамика. 1998.
Т. 6. №2. С. 3-14.
99. Понтрягин Л. С. Обыкновенные дифференциальные уравнения. М.:
Наука, 1982. 331 с.
100. Постон Т., Стюарт И. Теория катастроф и ее приложения. М.: Мир,
1980. 607 с.
101. Потапов А. Б. Программы вычисления корреляционного показате-
показателя и оценки обобщенной энтропии по временному ряду. ИПМ
им. М. В. Келдыша АН СССР (препринт), 1991. № 27. С. 31.
102. Потапов А. Б. Качество реконструкций хаотических аттракторов
и выбор параметров реконструкции. ИПМ им. М. В. Келдыша РАН
(препринт), 1995. № 13. 28 с.
103. Пределы предсказуемости: Сб. статей / Ред. Ю.А.Кравцов. М.:
Центрком, 1997.
104. Пригожий И., Стенгерс И. Порядок из хаоса. Новый диалог человека
с природой. М.: Прогресс, 1986. 432 с.
105. Пригожий И., Стенгерс И. Время, хаос, квант. М.: Прогресс, 1994.
106. Пугачев B.C., Синицын И.Н. Стохастические дифференциальные
системы. М.: Наука, 1985.
107. Рабинер Л. Р., Гоулд Б. Теория и применение цифровой обработки
сигналов. М.: Мир, 1978. 495 с.
108. Рабинович М.И., Трубецков Д. И. Введение в теорию колебаний
и волн. М.: Наука, 1984. 432 с.
Список литературы 323
109. Самарский А.А., Галактионов В. А., Курдюмов СП., Михайлов А. П.
Режимы с обострением в задачах для квазилинейных параболических
уравнений. М.: Наука, 1986. 480 с.
НО. Самарский А.А., Попов Ю.П. Разностные методы решения задач
газовой динамики. М.: Наука, 1980. 352 с.
111. Синай Я. Т. Современные проблемы эргодической теории. М.: Физ-
матлит, 1995.
112. Скотт Э. Волны в активных и нелинейных средах в приложении
к электронике. М.: Советское Радио, 1987. 368 с.
113. Смейл С. Дифференцируемые динамические системы // Успехи мат.
наук. 1970. Т. 25. № 1. С. 113-185.
114. Соколов И. М. Размерности и другие геометрические критические
показатели в теории протекания // Успехи физ. наук. 1986. Т. 150.
Вып. 2. С. 221-255.
115. Стернберг С. Лекции по дифференциальной геометрии. М.: Мир,
1970.
116. Странные аттракторы. М.: Мир, 1981.
117. Струминский В. В., Скобелев Б. Ю. Странные аттракторы и турбулент-
турбулентность // Механика неоднородных и турбулентных потоков / Отв.
ред. акад. В. В. Струминский. М.: Наука, 1989.
118. Тер-Крикоров А. М. Вихри и внутренние волны в стратифицирован-
стратифицированной жидкости // Прикл. матем. и мех. 1995. Т. 59. № 3. С. 443-450.
119. Трубецков Д. И. Колебания и волны для гуманитариев. Саратов: Изд.
УНЦ «Колледж», 1997. 394 с.
120. Уоссермен Ф. Нейрокомпьютерная техника. М.: Мир, 1992. 237 с.
121. Федер Е. Фракталы. М.: Мир, 1991.
122. Фейнмановские лекции по физике. М.: Мир, 1977.
123. Фракталы в физике. М.: Мир, 1988. 672 с.
124. Хайтун В. Механика и необратимость. М.: Янус, 1996. 445 с.
125. Хакен Г. Синергетика. М.: Мир, 1980. 404 с.
126. Халмош П. Р. Лекции по эргодической теории. М.: ИЛ, 1959. 147 с.
127. Хардле В. Прикладная непараметрическая регрессия. М.: Мир, 1993.
349 с.
128. Хартман Ф. Обыкновенные дифференциальные уравнения. М.: Мир,
1970. 720 с.
129. ХейлДж. Теория функционально-дифференциальных уравнений. М.:
Мир, 1984. 421 с.
130. Шарковский А.Н., Майстренко Ю.А., Романенко Е.Ю. Разностные
уравнения и их приложения. Киев: Наукова думка, 1986. 280 с.
131. Ширяев А. Н. Вероятность. М.: Наука, 1980. 574 с.
132. Шредингер Э. Что такое жизнь с точки зрения физики? М.: Мир,
1962.
133. Шустер Г. Детерминированный хаос. Введение. М.: Мир, 1988. 240 с.
. Список литературы
134 Яглом A.M., Яглом И. М. Вероятность и информация. М.: Наука,
1973. 511 с.
135. Янсон Н. Б., Павлов А. Н., Бала нов А. Г., Анищенко В. С. Задача рекон-
реконструкции математической модели применительно к электрокардио-
электрокардиограмме // Письма в ЖТФ. 1996. Т. 22. № 16. С. 57.
136. Abarbanel H.D.I., Brown R., Sidorowich J.J., Tsimring L.S. The analysis
of observed chaotic data in physical systems// Rev. Mod. Phys. 65 A993).
P. 1331-1391.
137. Abarbanel H. D.I., Kennel M. B. Local false nearest neighbors and dynam-
dynamical dimensions from observed chaotic data // Phys. Rev. E. 47 A993).
P. 3057.
138. Abraham N. B.,AlbanoA. M., Das В., DeGuzman G., Young S., Gioggia R. S.,
Puccioni G. P., Tredicce J. R. Calculating the dimension of attractors from
small data sets // Phys. Lett. A. 114 A986). P. 217.
139. Aguirre L.A., Billings S.A. Retrieving dynamical invariants from chaotic
data using NARMAX models// Int. J. Bifurc. Chaos. 5 A995). P. 449-474.
140. Albano A.M., Abounadi J., Chyba Т.Н., Searle C.E., Yong S. Low-
dimensional chaotic attractors for an unstable inhomogeneously broad-
broadened, single-mode laser// J. Optical Soc. of Amer. B. 2 A985). P.47-55.
141. Albano A. M., Muench J., Schwartz C, MeesA. I., Rapp P. E. Singular-value
decomposition and the Grassberger—Procaccia algorithm // Phys. Rev.
A. 38A988). P. 3017-3026.
142. Alflmov G.L., Eleonsky KM., Kulagin N.E., Lerman L.M., Silin V.P.
On existence of nontrivial solution for the equation Дм - и + и3 = 0 //
Physica D. 44 A990). № 1-3. P. 168-177.
143. Anishchenko V. S., Postnov D. E., Saparin P. I., Safonova M.A. Diagnostics
of self-oscillating systems by methods of nonlinear dynamics // Applied
Nonlinear Dynamics. 1 A992). P. 10.
144. Babloyantz A., Destexhe A. Low-dimensional chaos in an instance of
epilepsy// Proc. Natl. Acad. Sci. USA. 83 A986). P. 3513-3517.
145. Babloyantz A., Destexhe A. Is the normal heart a periodic oscillator? //
Biol. Cybernetics. 58 A988). P. 203.
146. Badii R., Broggi G., Derighetti В., Ravani M. Dimension increase in filtered
chaotic signals // Phys. Rev. Lett. 60 A988). № 11. P. 979-982.
147. Badii R., PolitiA. Statistical description of chaotic attractors: the dimension
function // J. Stat. Phys. 40 A985). P. 725-750.
148. Bakker R., Schouten J. C, Tokens F., van den Bleek С. М. Neural network
model to control an experimental chaotic pendulum // Phys. Rev. E. 54,
pt.A A996). P. 3545-3552.
149. Bartucelli M., Constantin P., DoeringC. R., Gibbon J. D., GisselfaltM. On the
possibility of soft and hard turbulence in the complex Ginzburg—Landau
equation // Physica D. 44 A990). P. 421-444.
150. Bauer M., Heng H., Martienssen W. Characterization of spatiotemporal
chaos from time series // Phys. Rev. Lett. 71 A993). P. 521.
Список литературы 325
151. Bayly B.J., Goldhirch J., Orszag S.A. Independent degrees of freedom of
dynamical systems // J. Sci. Computing. 2 A987). P. 111-121.
152. Bellachook L. V., Malinetskii G.G. Tricks of jokers on one-dimensional
maps. Proc. 5 Int. Spec. Workshop Nonlinear Dynamics of Electronic
Systems. Moscow, 1997.
153. Bellachook L.V., Malinetskii G.G. Tricks of jokers on one-dimensional
maps // M. V. Keldysh Inst. Appl. Math, (preprint), 1997. № 24.
154. Belyaev Y. M., Yavorskaya I. M. Nonuniqueness and multiparametric study
of transition to chaos in the spherical Couette flow // European Journal
of Mechanics B. 10 A991). P. 267.
155. Benettin G., Galgani L., Giorgilli A., Strelcin J. M. Lyapunov characteristic
exponents for smooth dynamical systems and for hamiltonian systems; a
method for computing all of them: Pt. 1, 2 // Mechanica. 15 A980). № 1.
P. 9-20, 21-30.
156. Blank M. Pathologies generated by round-off in dynamical systems //
Physica D. 78 A994). P. 93-114.
157. Bonetti M., Meinart R., Boon J.B., Olivary D. Chaotic dynamics in a
periodically excited air jet // Phys. Rev. Lett. 55 A985). P. 492-495.
158. Brandstater A., Swinney ILL. Strange attractors in weakly turbulent
Couette-Taylor flow // Phys. Rev. A. 35 A987). P. 2207-2220.
159. Broomhead D. S., Jones R. Time-series analysis // Proc. R. Soc. Lond. A.
423 A989). P. 103.
160. Broomhead D. S., King G. P. Extracting qualitative dynamics from experi-
experimental data // Physica D. 20 A986). P. 217-236.
161. Broomhead D. S., Huke J. P., Jones R. Signals in chaos: a method for the
cancellation of deterministic noise from discrete signals // Physica D. 80
A995). P. 413-432.
162. Broomhead D.S., Jones R., King G.P. Topological dimension and local
coordinates from time series data // J. Phys. A. 20 A987). P. L563-L569.
163. Brown R. Calculating Lyapunov exponents for short and/or noisy data
sets // Phys. Rev. E. 47 A993). P. 3962-3969.
164. Bunimovich L.A., Sinai Ya. G. Spacetime chaos in coupled map lattices //
Nonlinearity. 1 A988). №4. P. 491-516.
165. Cao L., Hong Y., Fang H., He G. Predicting chaotic time series with
wavelet networks // Physica D. 85 A995). P. 225-238.
166. Casaleggio A., Corana A., Ridella S. Correlation dimension from electro-
electrocardiograms // Chaos, Solitons & Fractals. 5 A995). P. 713-726.
167. Casdagli M. Nonlinear prediction of chaotic time series // Physica D. 35
A989). P. 335-356.
168. Casdagli M. Chaos and deterministic versus stochastic non-linear mod-
modelling// Statist J. R. Soc. B. 54 A991). P. 303-328.
169. Casdagli M., Eubank S., Farmer J. D., Gibson J. State space reconstruction
in presence of noise // Physica D. 51 A991). P. 52.
170. Castro R., Sauer T. Correlation dimension of attractors through interspike
intervals // Phys. Rev. E. 55, pt. A A997).
326 Список литературы
171. Cawley R., Hsu G.-H. Local-geometric-projection method for noise reduc-
reduction in chaotic maps and flows // Phys. Rev. A. 46 A992). P. 3057-3082.
172. Cenys A., Pyragas K. Estimation of the number of degrees of freedom from
chaotic time series// Phys. Lett. A. 129 A988). P.227-230.
173. Chaos. 5 A995). P. 1-215. (Результаты по обработке физиологических
данных).
174. Chaos. 7 A997). №4. P. 509-687. (Спец. выпуск по управлению
хаосом).
175. Cohen A., Procaccia I, Computing the Kolmogorov entropy from time
signals of dissipative and conservative dynamical systems // Phys. Rev. A.
31 A985). P. 1872.
176. Collet P., Eckmann J. P. Iterated maps on the interval as dynamical systems.
Basel—Stuttgart: Birkhauser, 1980. 248 p.
177. Collet P. Thermodynamic limit of the Ginzburg-Landau equation //
Nonlinearity. 7 A994). P. 1175-1190.
178. Cremers J., Hubler A. Construction of differential equation from experi-
experimental data // Z. Naturforsch. 41 a A987). P. 797-802.
179. Crisanti A., Paladin G., Vulpiani A. Products of random matrices in
statistical physics. Springer, 1993.
180. Crutchfleld J. P., Farmer J. D., Packard N. H, Shaw R. Chaos // Sci. Am.
255A986). P. 46.
181. Cutler С D. A review of the theory and estimation of fractal dimension //
Dimension Estimations and Models / Tong H., ed. Singapore: WS, 1993.
P. 1-107.
182. Daubechies I. The wavelet transform, time-frequency localization and
signal analysis // IEEE Trans. Inf. Theory. 36 A990). P. 961-1005.
183. Davies M. E. Reconstructing attractors from filtered time series // Physi-
caD. 101 A997). P. 195-206.
184. Deppish J., Bauer H.-U., Geisel T. Hierarchical training of neural networks
and prediction of chaotic time series// Phys. Lett. A. 158 A991). P. 57-62.
185. Dimensions and Entropies in Chaotic Systems. Berlin: Springer, 1986.
257 p.
186. Ding M., Grebogi C, Ott E., Sauer Т., Yorke J.A. Estimating correlation
dimension from a chaotic time series: when does plateau occure? //
Physica D. 69 A993). P. 404-424.
187. Doering С A., Gibbon J.D., Holm D.D., Nikolaenko B. Low-dimensional
behaviour in the complex Ginzburg-Landau equation // Nonlinearity. 1
A988). P. 279-309.
188. Dorodnitsyn V.A. Finite difference models entirely inheriting continuous
symmetry of original differential equations // International Journal of
Modern Physics С 1994. №5. P. 723-734.
189. Dressier U., Farmer J. D. Generalized Lyapunov exponents corresponding
to higher derivatives // Physica D. 59 A992). P. 365.
190. Eckmann J.-P, Kamphorst S. O., Ruelle D., Ciliberto S. Liapunov exponents
from time series// Phys. Rev. A. 34 A986). P.4971-4779.
Список литературы 327
191. Eckmann J. P., Ruelle D. Ergodic theory of chaos and strange attractors //
Rev. Mod. Phys. 57 A985). №3. P. 617-656.
192. Eckmann J.-P., Ruelle D. Fundamental limitations for estimating dimen-
dimensions and Liapunov exponents in dynamical systems // Physica D. 56
A992). P. 185-187.
193. EllnerS. Estimating attractor dimensions from limited data: a new method,
with error estimates // Phys. Lett. A. 133 A988). P. 128-133.
194. Ellner S., Gallant A. R., McCaffrey D., Nychka D. Convergence rates and
data requirements for Jacobian-based estimates of Lyapunov exponents
from data // Phys. Lett. A. 153 A991). P. 357-363.
195. Ershov S. V. On slow motions in chaotic systems // Phys. Lett. A. 176
A993). P. 186-194.
196. Ershov S. V. Lyapunov exponents as measure averages // Phys. Lett. A.
176A993). P. 89-95.
197. Ershov S. V., PotapovA. B. On the concept of stationary Lyapunov basis //
Physica D. 118 A998). P. 167-198.
198. Ershov S.V., Potapov A. B. Macrodynamics: Large-scale structures in
turbulent media // J. Stat. Phys. 69 A992). P. 763-811.
199. Farmer J. D., Ott E., Yorke J.A. The dimension of chaotic attractors //
Physica D. 7 A983). № 1-3. P. 153-180.
200. Farmer J. D., Sidorowich J. J. Predicting chaotic time series // Phys. Rev.
Lett. 59A987). P. 845-848.
201. Farmer J.D., Sidorowich J.J. Exploiting chaos to predict the future and
reduce noise // Evolution, Learning and Cognition / Lee Y. C, ed. World
Scientific. Singapore, 1988. P. 227.
202. Feigenbaum M. J. Universal behaviour in nonlinear systems // Los Alamos
Sci. 1 A980). №1. P. 4-27.
203. Foias С, Sell G. R., Temam R. Inertial manifolds for nonlinear evolutionary
equations // J. Differential Equations. 73 A988). № 2. P. 309-353.
204. Fraedrich K. Estimating the dimension of weather and climate attractors //
J. Atmospheric Science. 43 A986). P. 419-432.
205. Franaszek M. Optimized algorithm for the calculation of correlation
integrals // Phys. Rev. A. 39 A989). P. 5440-5443.
206. Frank M., Blank H.-R., Heindl J., Kaltenhauser M., Kochner //., Kreis-
che W., Mailer N., Poscher S., Sporer R., Wagner T. Improvement of Kj-
entropy calculations by means of dimension scaled distances // Physica D.
65A993). P. 359-364.
207. Eraser A. M. Reconstructing attractors from scalar time series: a comparison
of singular systems and redundancy criteria // Physica D. 34 A989). P. 391.
208. Fraser A. M. Information and entropy in strange attractors // IEEE Trans.
Inf. Theory. 35 A989). P. 245-262.
209. Fraser A. M., Swinney H. L. Independent coordinates for strange attractors
from mutual information // Phys. Rev. A. 33 A986). P. 1131-1140.
210. Fujisaka #., Ishi #., Inoue M., Yamada T. Intermittency caused by chaotic
modulation. II // Progr. Theor. Phys. 76 A986). P. 1198-1209.
328 Список литературы
211. Fujisaka Н., Yamada Т. A new intermittency in coupled dynamical
systems// Progr. Theor. Phys. 74 A985). P.918-921.
212. Fujisaka H., Yamada T. Intermittency caused by chaotic modulation. Ill //
Progr. Theor. Phys. 77 A987). P. 1045-1055.
213. Geist K., Parlitz. U., Lauterborn W. Comparison of different methods for
computing Lyapunov exponents // Progr. Theor. Phys. 83 A990). 875 p.
214. Gencay R., Dechert W. An algorithm for the n Lyapunov exponents of
an n-dimensional unknown dynamical system // Physica D. 59 A992).
P. 142-157.
215. Gershenfeld N. A. Dimension measurement on high-dimensional systems //
Physica D. 55 A992). P. 135-154.
216. Gibson J. F., Farmer J. D., Casdagli M., Eubank S. An analytic approach
to practical state space reconstruction // Physica D. 57 A992). P. 1.
217. Gizzatulina S. M., Malinetskii G. G., Potapov А. В., Ruzmaikin A. A., Rukav-
ishnikov V. D. Dimension of geomagnetic attractor from the data on length
of day variations // Physics of the Earth and Planetary Interiors. 59 A990).
P. 170-181.
218. Goldhirsch /., Sulem P.-L., Orszag S.A, Stability and Lyapunov stability
of dynamical systems: a differential dynamics approach and a numerical
method // Physica D. 27 A987). P. 311.
219. Gouesbet G. Reconstruction of vector fields of continuous dynamical
systems from numerical scalar time series // Phys. Rev. A. 43 A991).
P. 5321-5331.
220. Govindan R.B., Narayanan K., Gopinathan M.S. On the evidence of
deterministic chaos in ECG: Surrogate and predictability analysis //
Chaos. 8A998). P. 495-502.
221. Grassberger P. An optimized box-assisted algorithm for fractal dimen-
dimensions // Phys. Lett. A. 148 A990). P. 63.
222. Grassberger P., Procaccia I. Estimation of the Kolmogorov entropy from
a chaotic signal // Phys. Rev. A. 28 A983). №4. P. 2591-2593; Grass-
Grassberger P., Procaccia I. Measuring the strangeness of strange attractors //
Physica D. 9 A983). № 1, 2. P. 189-208.
223. Greenside H.S., Wolf A., Swift J., Pignataro T. Impracticality of a box
counting algorithm for calculating the dimensionality of strange attrac
tors // Phys. Rev. A. 25 A982). №6. P. 3453-3456.
224. Guckenheimer J., Holmes P. Nonlinear oscillations, dynamical systems and
bifurcations of vector fields. N.Y.: Springer, 1983. 453 p.
225. Hall G. M., Bahar S., Gauthier D. J. Experimental control of chaotic point
process using interspike intervals // Phys. Rev. E. 58 A998). P. 1685-1689.
226. Halsey C, Jensen M. N, Kadanqff L., Procaccia /., Shraiman B. I. Fractal
measures and their singularities. The characterization of strange sets //
Phys. Rev. A. 33 A986). P. 1141-1151.
227. Hammel S. M., Yorke J. A., Grebogi C. Numerical orbits of chaotic processes
represent true orbits // Bull. Amer. Math. Soc. 19 A988). P. 465-469.
Список литературы 329
228. Hammer P. W., PlattN., Hammel S. M., HeagyJ. F., Lee B. D. Experimental
observation of on-off intermittecy // Phys. Rev. Lett. 73 A994). P. 1095-
1098.
229. Hata M. Fractals in mathematics // Patterns and waves. Qualitative analys
of nonlinear differential equations. Tokyo: Kinokuniya, 1988. P. 259-278.
230. HavstadJ. W., Ehlers C. L. Attractor dimension of nonstationary dynamical
systems from small data sets. Phys. Rev. A. 39 A989). P. 845-851.
231. Hediger Т., Passamante A., Farell M.E. Characterizing attractors using
local intrinsic dimensions calculated by singular-value decomposition and
information-theoretic criteria // Phys. Rev. A. 41 A990). P. 5325.
232. Hegger R., Kantz H, Olbrich E. Problems in the reconstruction of highdi-
mensional deterministic dynamics from time-series. Nonlinear analysis of
physiological data / H. Kantz, J. Kurths, G. Mayer-Kress, eds. Springer,
1998.
233. Hegger R., Kantz H, Schmuser, Diestelhorst M., Kapsch R.-R, Beige H.
Dynamical properties of ferroelectric capacitor observed through nonlinear
time series analysis // Chaos. 8 A998). P. 727-736.
234. Holzfuss J., Lauterborn W. Liapunov exponents from a time series of
acoustic chaos// Phys. Rev. A. 39 A989). P.2146-2152.
235. Holzfuss J., Mayer-Kress G. An approach to error-estimation in the
application of dimension algorithms // Dimensions and Entropies in
Chaotic Systems. Berlin etc.: Springer, 1986. P. 114-122.
236. Hunt F. Error analysis and convergence of capacity dimension algorithms //
SIAM J. Appl. Math. 50 A990). P. 307-321.
237. Isliker H., Kurths J. A test for stationarity: finding parts in time series
apt for correlation dimension estimates // Int. J. Bifurc. Chaos. 3 A993).
P. 1573.
238. Ivanov D.K, Posch H.A., Stumpf Ch. Statistical measures derived from
the correlation integrals of physiological time series // Chaos. 6 A996).
P. 243-253.
239. Ivanov P.Ch., Rosenblum M.G., Peng C.-K, Mietus J., Havlin S., Stan-
Stanley H. E., Goldberger A. L. Scaling behaviour of heartbeat intervals obtained
by wavelet-based time series analysis // Nature. 383 A996). P. 323.
240. Iwasaki H., Toh S. Statistics and structures of strong turbulence in a
complex Ginzburg-Landau equation // Progr. Theor. Physics. 87 A992).
P. 1127.
241. Janson N. В., Pavlov A. N., Neiman А. В., Anischenko V. S. Reconstruction
of dynamical and geometric properties of chaotic attractors from interspike
intervals // Phys. Rev. E. 58 A998). P. R4-R7.
242. Johnson R. A., Palmer К J., Sell G. R. Ergodic properties of linear dynamical
systems // SIAM J. Math. Anal. 18 A987). P. 1.
243. Judd К An improved estimator of dimension and some comments on
providing confidence intervals // Physica D. 56 A992). P. 216-228.
244. Judd K, Mees A. On selecting models for nonlinear time series //
Physica D. 82 A995). P. 426-444.
330 Список литературы
245. Kadtke J. Classification of highly noisy signals using global dynamical
models// Phys. Lett. A. 203 A995). P. 196-202.
246. Kantz H. A robust method to estimate the maximal Lyapunov exponent of
a time series // Phys. Lett. A. 185 A994). P.77.
247. Kaplan D. T. Exceptional events as evidence for determinism // Physica D.
73A994). P. 38-48.
248. Kaplan D. Т., Glass L. Direct test for determinism in a time series // Phys.
Rev. Lett. 68 A992). P. 427-430.
249. Keefe L., Moin P., Ют J. The dimension of attractors underlying periodic
turbulent Poiseuille flow // J. Fluid Mech. 242 A992). P. 1-29.
250. Kennel M. В., Isabelle S. Method to distinguish possible chaos from colored
noise and to determine embedding parameters // Phys. Rev. A. 46 A992).
P. 3111—3118.
251. Kirby M., Miranda R. Nonlinear reduction of high-dimensional dynamical
systems via neural networks // Phys. Rev. Lett. 72 A994). P. 1822-1825.
252. Kostelich E.J., Schreiber T. Noise reduction in chaotic time-series data: a
survey of common methods// Phys. Rev. E. 48 A993). P. 1752-1763.
253. Kostelich E.J., Yorke J.A. Noise reduction in dynamical systems// Phys.
Rev. A. 38 A988). P. 1649-1652.
254. Kruel Th.-M., Eiswirth M., Schneider F. W. Computation of Lyapunov
spectra: effect of interactive noise and application to a chemical oscillator//
Physica D. 63 A993). P. 117-137.
255. Kuramoto Y, Tsuzuki T. Reductive perturbation approach to chemical
instabilities // Progr. Theor. Phys. 52 A974). P. 1399-1401; Kuramoto Y,
Tsuzuki T. On the formation of dissipative structures in reaction-diffusion
systems// Progr. Theor. Phys. 54 A975). P.687-699.
256. Kuramoto Y. Chemical oscillations, waves and turbulence. Berlin: Springer,
1984. 156 p.
257. Kurths J., Herzel H. An attractor in a solar time series // Physica D. 25
A983). P. 165.
258. Kurths J., VossA., Saparin P., Witt A., Kleiner H.J., Wessel N. Quantitative
analysis of heart rate variability // Chaos. 5 A995). С 88.
259. Landman M.J., Papanicolau G.C., Sulem C, Sulem P.L. Rate of blowup
for solutions of the nonlinear Shrdinger equation at critical dimension //
Phys. Rev. A. 38a A988). P.3837-3843.
260. LeMesurier J., Papanicolau G.C., Sulem С Local structure of the self-
focusing singularity of the nonlinear Shrdinger equation // Physica D. 32
A988). P. 210-226.
261. Lefebvre J.H., Goodings D.A., Kamath M. V., Fallen E. L. Predictability
of normal heart rhythms and deterministic chaos // Chaos. 3 A993).
P. 267-276.
262. Liebert W., Pawelzik K, Schuster H.G. Optimal embedding of chaotic
attractors from topological considerations // Europhys. Lett. 14 A991).
P. 521; Buzug Th., PflsterG. Optimal delay time and embedding dimension
Список литературы 3 31
for delay-time coordinates by analysis of the global static and local
dynamical behaviour of strange attractors // Phys. Rev. A. 45 A992).
P. 7073; Rosenstein M.T., Collins J.J., De Luca C.J. Reconstruction
expansion as a geometry-based framework for choosing proper delay
times Physica D. 73 A994); Kennel M.B., habelle S. Method to
distinguish possible chaos from colored noise and to determine embedding
parameters // Phys. Rev. A. 46 A992). P. 3111.
263. Liebert W., Schuster H. G. Proper choice of the time delay for the analysis
of chaotic time series// Phys. Lett. A. 142 A989). P. 107-111.
264. Mane R. On the dimension of the compact invariant sets of certain
non-linear maps // Lect. Notes in Math. Berlin: Springer. 898 A981).
P. 230-242.
265. Malinetskii G. G., Potapov А. В., Rakhmanov A. I., Rodichev E, B. Limita-
Limitations of delay reconstruction for chaotic systems with broad spectrum //
Phys. Lett. A. A993) 179. P. 15.
266. Malinetskii G.G., Potapov А. В., Rakhmanov A.I. Limitations of delay
reconstruction for chaotic dynamical systems // Phys. Rev. E. 48 A993).
P. 904-912.
267. Malraison В., Atten P., Berge P., Dubois M. Dimension of strange attractors:
an experimental determination for the chaotic regime of two convective
systems // J. Physique. 44 A983). P. L897-L902.
268. Mandelbrot В. В. Fractals: form, chance and dimension. San Francisco:
Freeman Comp, 1977. 365 p.
269. Manneville P., Pomeau Y. Different ways to turbulence in dissipative
dynamical systems // Physica D. 1 A980). №2. P. 219-226.
270. Manneville P., Pomeau Y. Different ways to turbulence in dissipative
dynamical systems// Physica D. 1 A980). P.219-226.
271. Manuca R., Savit R. Model misspecification tests, model building and
predictability in complex systems// Physica D. 93 A996). P.78-100.
272. Martinerie J. M., Albano A. M., Mees A. /., Rapp P. E. Mutual information,
strange attractors and the optimal estimation of dimension // Phys. Rev.
A. 45A992). P. 7058.
273. Mayer-Kress G. Localized measures for non-stationary time-series of
physiological data // Integrative Psychological and Behavioral Science. 29
A994). P. 203.
274. Mayer-Kress G., Haken H. The influence of noise on the logistic model //
J.Stat. Phys. 26 A981). № 1. P. 149-171.
275. McCarthy D. D., Babcock А. К The length of day since 1656 // Physics of
Earth and Planetary Interior. 44 A986). P. 281-292.
276. MilnorJ. On the concept of attractor // Commun. Math. Phys. 99 A985).
№2. P. 177-198.
277. Muldoon M. R., MacKay R. S., Huke J. P., Broomhead D. S. Topology from
time series // Physica D. 65 A993). P. 1-16.
278. Murray D. B. Forecasting a chaotic time series using an improved metric
for embedding space // Physica D. 68 A993). P. 318-325.
332 Список литературы
279. Nerenberg M.A.H., Essex С. Correlation dimension and systematic geo-
geometric effects // Phys. Rev. A. 42 A990). P. 7065-7074.
280. Nese J. M. Quantifying local predictability in phase space // Physica D.
35A989). P. 237-250.
281. Nicolis C, Nicolis G. Is there climatic attractor? // Nature. 31 A984).
P. 529-532; Grassberger P. Do climatic attracror exist? // Nature. 326
A986). P. 609-602; Grassberger P. Letter to Editor // Nature. 326 A987).
№6112. 523 p.
282. Nonlinear analysis of physiological data / H. Kantz, J. Kurths, G. Mayer-
Kress, eds. Springer, 1998.
283. Olbrich E., Kantz H. Inferring chaotic dynamics from time-series: on which
length scale determinizm becomes visible // Phys. Lett. A. 232 A997).
P. 63.
284. Ott E., Sommerer J.C. Blowout bifurcations: the occurence of riddled
basins and on-off intermittency // Phys. Lett. A. 188 A994). P. 39.
285. Packard N. H., Crutchfleld J. P., Farmer J. D., Shaw R. S. Geometry from
a time series // Phys. Rev. Lett. 45 A980). P. 712.
286. Palus M. Coarse-grained entropy rates for characterization of complex
time series // Physica D. 93 A996). P. 64-77.
287. Parlitz U. Identification of true and spurious Lyapunov exponents from
time series // Int. J. Bifurc. Chaos. 2 A992). P. 155.
288. Pavlos G. P., Karakatsanis L., Latoussakis J. В., Dialetis D., Papaioannou G.
Chaotic analysis of a time series composed of seismic events recorded in
Japan // Int. J. Bifurc. Chaos. 4 A994). P. 87-98.
289. Pawelzik K., Schuster H. G. Generalized dimensions and entropies from a
measured time series // Phys. Rev. A. 35 A987). № 1. P. 481-484.
290. Pawelzik K., Schuster H. G. Generalized dimensions and entropies from a
measured time series // Phys. Rev. A. 35 A987). P. 481-484.
291. Penrose R. Shadows of the Mind. Vintage, 1995.
292. Physica D. 58 A992).
293. Pikovsky A. S. On the interaction of strange attractors // Z. Phys. B. 55
A984). P. 149-154.
294. Platt N., Spiegel E.A., Tresser С On-off intermittency: a mechanism for
bursting// Phys. Rev. Lett. 70 A993). P.279-282.
295. Pompe B. Measuring statistical dependencies in a time series // J. Stat.
Phys. 73 A993). P. 587.
296. Potapov A. B. Distortions of reconstruction for chaotic attractors // Physi-
Physica D. 101A997). P. 207-226.
297. Potapov A. B. Time-series analysis: when dynamical algorithms can be
used // Proc. 5 Int. Specialist Workshop Nonlinear Dynamics of Electronic
Systems. Moscow. June 26-27, 1997. P. 388-393.
298. Potapov A. B. Are R-R-interval data appropriate to study the dynamics
of heart? Nonlinear analysis of physiological data / H. Kantz, J. Kurths,
G. Mayer-Kress, eds. Springer, 1998. P. 117-127.
Список литературы 333
299. Potapov А. В. Characteristic scales of reconstruction distortions // Int. J.
Bifurc. Chaos. 8 A998). P. 835-841.
300. Potapov A., Kurths J. Correlation integral as a tool for distinguishing
between dynamics and statistics in time series data // Physica D. 120
A998). P. 369-385.
301. Provenzale A., Smith L.A., Vio R., Murante G. Distinguishing between
low-dimensional dynamics and randomness in measured time series //
Physica D. 58 A992). P. 31-49.
302. Ramsey J.B., Yuan H.-J. Bias and error bars in dimension calculations
and their evaluation in some simple models // Phys. Lett. A. 134 A989).
P. 287.
303. Ramsey J.B., Yuan H.-J. The statistical properties of dimension calcula-
calculations using small data sets // Nonlinearity. 3 A990). P. 155.
304. Rapp P. E. Chaos in the neurosciences: cautionary tales from the frontier //
Biologist. 40 A993). P. 89-94.
305. Rombouts S. A. R. В., Keunen R. W. M., Stam C. J. Investigation of nonlinear
structure in multichannel EEG // Phys. Lett. A. 202 A995). P. 352-358.
306. Rosenblum M., Kurths J. A model of neural control of the heart rate //
Physica A. 215 A995). P. 439-450.
307. Rosenstein M.T., Collins J.J., De Luca C.J. A practical method for
calculating largest Lyapunov exponents from small data sets // Physica D.
65A993). P. 117.
308. Roux J. C, Simoyi R. //., Swiney H. L. Observation of a strange attract or //
Physica D. 8 A983). P. 257-266.
309. Ruelle D. Deterministic chaos: the science and the fiction. Proc. Roy. Soc.
London A. 427 A990). P. 241.
310. Rypdal K., Rasmussen J.J., Thomsen K. Similarity structure of wave-
collapse // Physica D. 16 A985). P. 339-357.
311. Samarskii A.A., Galaktionov V.A., Kurdjumov S. P., Mikhailov A. P. Blow-
Blowup in Quasilinear Parabolic Equations. Berlin—New York: Walter de
Gruyter, 1995.
312. Sano M., Sawada Y. Measurment of the Lyapunov spectrum from a chaotic
time series// Phys. Rev. Lett. 55 A985). P. 1082-1085.
313. Sato S., Sano M., Sawada Y. Practical methods of measuring the gener-
generalized dimension and the largest Lyapunov exponent in high dimensional
chaotic systems// Progr. Theor. Phys. 77 A987). P. 1-5.
314. Sauer T. Interspace interval embedding of chaotic signals // Chaos. 5
A995). P. 127-132.
315. Sauer Т., Yorke J.A., Casdagli M. Embedology // J. Stat. Phys. 65 A991).
P. 579.
316. Savit R., Green M. Dependent variables in broad band continuous time
series// Physica D. 50 A991). P.521-544.
317. Savit R., Green M. Time series and dependent variables // Physica D. 50
A991). P. 95-116.
Список литературы
318 Schreiber T Determination of the noise level of chaotic time series //
' Phys. Rev. E. 48 A993). P.R13-R16.
319. Schreiber Т., Kaplan D.T. Nonlinear noise reduction for electrocardio-
electrocardiograms // Chaos. 6 A996). P. 87-92.
320. Schuster H. G. Information content of chaotic signals // Physica Scripta.
40A989). №3. P. 367-372.
321. Shraiman B.I., Pumir A., van Saarloos W., Holienberg P.C., Cate H.,
Holen M. Spatiotemporal chaos in the one-dimensional complex
Ginzburg—Landau equation // Physica D. 57 A992). P.241.
322. Sieber M. Experiments on the attractor dimension for turbulent pipe
flow // Phys. Lett. A. 122 A987). P. 467-470.
323. Smith L.A. Intrinsic limits on dimension calculations // Phys. Lett. A.
133A988). №6. P. 283-288.
324. Smith L. A. Identification and prediction of low-dimensional dynamics //
Physica D. 58 A992). P. 50-76.
325. Smith L.A. Local optimal prediction: exploiting strangeness and the
variation of sensitivity to initial conditions // Phil. Trans. R. Soc. Lond.
A. 348A994). P. 371-381.
326. Sparrow С The Lorenz equations: bifurcation, chaos and strange attractors.
Berlin: Springer, 1982. 269 p.
327. Stoop R., Meier P. F. Evaluation of Lyapunov exponents and scaling
functions from time series // J. Opt. Soc. Am. B. 5 A988). P. 1037-1045.
328. Stoop R., Parisi J. Calculation of Lyapunov exponents avoiding spurious
elements// Physica D. 50 A991). P.89-94.
329. Tokens F. Detecting strange attractors in turbulence // Lect. Notes in
Math. Berlin: Springer. 898 A981). P. 336-381.
330. Tokens F. Estimation of dimension and order of time series // Nonlinear
Dynamicsl Systems and Chaos / Broer H. W., van Gills S. A., I. Hoveijn,
F. Takens, eds. Progress in Nonlinear Differential Equations and Their
Applications. Birkhauser, Basel etc. 19 A996).
331. Takens F. On the numerical determination of the dimension of an
attractor // Lecture Notes in Math. Springer. 1125 A985). P. 99-106.
332. Tang X. Z, Tracy E. R., Boozer A. D., de Brauw A., Brown R. Reconstruc-
Reconstruction of chaotic signals using symbolic data. Phys. Lett. A. 190 A994).
P. 393-398.
333. Temam R. Infinite-dimensional dynamical systems in mechanics and
physics. Springer, 1988.
334. Theiler J. Spurious dimension from correlation algorithms applied to
limited time-series data // Phys. Rev. A. 34 A986). № 3. P. 2427-2432.
335. Theiler J. Efficient algorithm for estimating the correlation dimension
from a set of discrete points // Phys. Rev. A. 36 A987). P. 4456.
336. Theiler J. Lacunarity in a best estimator of fractal dimension // Phys. Lett.
A. 133 A988). P. 195.
337. Theiler J. Estimating fractal dimension // J. Opt. Soc. Am. A. 7 A990).
P. 1055.
Список литературы 335
338. TheilerJ. Some comments on the correlation dimension of 1//° noise //
Phys. Lett. A. 155 A991). P. 480-493.
339. Theiler J. On the evidence for low-dimensional chaos in an epileptic
electroencefalogram // Phys. Lett. A. 196 A995). P. 335-341.
340. TheilerJ., Eubank S., Longtin A., Galdrikan В., Farmer J.D. Testing for
nonlinearity in time series: the method of siurogate data // Physica D. 58
A992). P. 77-94.
341. Turing A. On the chemical basis of morphogenesis // Phil. Trans. Roy.
Soc. London. 1952. Ser. A. 237. P. 37-52.
342. Vastano J.A., Kostelich E.J. Comparison of algorithms for determining
Lyapunov exponents from experimental data // Dimensions and entropies
in chaotic systems. Berlin: Springer, 1986. P. 100-107.
343. Venkataramani S.C., Antonsen T.M.Jr., Ott E., Sommerer J.C. On-off
intermittency: power spectrum and fractal properties of time series //
Physica D. 96 A996). P. 66-99.
344. Voss H., Kurths J. Reconstruction of non-linear time delay models from
data by the use of optimal transformations // Phys. Lett. A. 234 A997).
P. 336-344.
345. Wilson T. D., Keefe D. H. Characterizing the clarinet tone: measurement of
Lyapunov exponents, correlation dimension and unsteadiness // J. Acoust.
Soc. Am. 164 A998). P. 550-561.
346. Wolf A., Swift J. В., Swinney H.L., Vastano J.A. Determining Lyapunov
exponents from a time series // Physica D. 16 A985). № 3. P. 285-317.
347. Wu K., Savit R., Brock W. Statistical tests for deterministic effects in broad
band time series // Physica D. 69 A993). P. 172-188.
348. Yamada T, Fujisaka H. Intermittency caused by chaotic modulation. I //
Progr. Theor. Phys. 76 A986). P. 582-591.
349. Ying-Cheng L., Lerner D. Effective scaling regime for computing correlation
dimension from chaotic time series // Physica D. 115 A998). P. 1-18.
350. Yip K.-R, Marsh D.J., Holstein-Rathlou N.-H. Evidence of low-
dimensional chaos in renal blood flow control in genetic and experimental
hypertension // Physica D. 80 A995). P. 95-104.
351. Zakharov V. E. Collapse and self-focusing of Langmuir waves // Handbook
of Plasma Physics 11 / A. A, Galeev, R.N. Sudan, eds. P. 81-121.
Amsterdam: North Holland. 1981. XIV+850 p.
352. Zeeman E. Stability of dynamical systems // Nonlinearity. 1 A988).
P. 115-155.
!
I
i
I в/.
Уважаемые читатели!
Уважаемые авторы!
Издательство УРСС специ&тизируется на
выпуске учебной и научной литературы, в том
чисте монографий, журналов, трудов ученыч
Российской Академии Наук, научно-исслсдова-
тетьских институтов и учебных заведений.
Основываясь на широком и плодотворном
сотрудничестве с Российским фондом фундачен-
и шных исследований и Российским гуманитарным научным фондом, мы
предлагаем авторам свои услуги на выгодных экономических условиях.
При этом мы берем на себя всю работу по подготовке издания — от набора,
редактирования и верстки до тиражирования и распространения.
Среди недавно вышедших книг мы предлагаем Вам следующие.
Ма.шнсикип Г.Г. Хаос. С1р\ктуры. Вычислительный эксперимент.
Введение в нелинейную динамику.
Пригожим И.. Стенгсрс И. Время, хаос, квант.
Пригожий И., Спн'нгерс И. Порядок из хаоса.
Боирчук А.К.. Гай Я Г.. Головач Г.П.. Ляшко И.И. Справочное пособие
но высшем ма!ематике (Антидемидович). Т. 1-5.
Боровков А.А. Теория вероятности.
Боровков А. А. Эргодичность и устойчивость случайных процессов.
Пытн'в Ю.П. Возможность. Элементы теории и применения.
Дубровин Б. А.. Новиков СП.. Фоменко А. Т. Современная геометрия.
Методы и приложения. Т. 1.2.
Морозов А.Д. и др. Инвариантные множества динамических систем в Windows.
ГиеЛенки Б.В. О математике.
Корстстян А. В. Устойчивость стационарных движений.
Рубикон В.А. Классические калибровочные поля.
Петрашень М.И., Трифонов Е.Д. Применение теории групп
в кванювой механике.
ЭльсгопцЛ.Э. Дифференциальные уравнения н вариационное исчисление.
Арнольб В.И. Математические методы классической механики.
Магари.1-И)ьяев Г.Г.. Тихомиров В. М. Выпуклый анализ и его приложении.
Самарский А.А. и др. Задачи и упражнения по численным метолач.
Эоелинг В. и др. Физика процессов эволюции.
Табор .\/. Хаос и интегрируемость в нелинейной динамике.
Наши книги можно приобрести в магазинах:
«Библио-Глобус» (м. Лубянка, ул. Мясницкая, 6. Тел. 928-87-44)
«Московский дом книги- (ул. Новый Арбат, 8. Тел. 290-45-07)
«Дом технической книги» (Ленинский пр., 40. Тел. 137-06-3
«С.-Пб. дом книги' (Невский пр., 28)
а также в книжных киосках МГУ (Воробьевы горы)
По всем вопросам Вы можете обратиться к нам:.
тел./факс 135-44-23, тел. 135-42-46
или электронной почтой urss@urss.ru
Потным каталог издании представлен
в Internet: http-//urss.ru