АРИвМЕТНКА,
57/ ('%)
й-яп
СОСТАВЛЕННАЯ
УЧИТЕЛЕМЪ МАТЕМАТИКИ,
ВЪ МОСКОВСКОМЪ ДВОРЯНСКОМЪ ИНСТИТУТА
В. Аглоблиныжъ.
. }
I
МОСКВА.
ВЪ ТИПОГРАФШ НИКОЛАЯ СТЕПАНОВА.
1846

ч'к. МАУ ЧНАА
пЕ« А.*ОГИ1:»“скА£2
БийЛИОГг.\
*М. К. Д. У ш и и с ц с гф
N9
ПЕЧАТАТЬ ПОЗВОЛЯЕТСЯ
ст> ттмъ, чтобы по отпечатанш представлено было въ Ценсурныи
Комитета узаконенное число экземпляровъ. Москва, 1844 года,
Декабря 1 дня.
Ценсорь И. Снегиревъ.

APII0METHKA.
ПРЕДВАРИТЕЛЬНЫЯ П0НЯТ1Я.
А. Величиною или колигсство.иь называется
все то, что имЬетъ свойство увеличиваться и
уменьшаться; напр. вЬсь, время, разстоящя, ка¬
питалы и проч. Чтобы иметь ясное понятие о ве¬
личине, должно выл 1гъ]штпъ ciio величину; а для
сего должно сравнить ее съ величиною однород¬
ною, известною намъ, и смотреть какимъ образомъ
первая составлена изъ последней. Сля известная
величина, условно взятая и служащая мЪрою
всЬмъ однороднымъ съ нею величинамъ, называет¬
ся единицею. Выводъ сравнения величины съ ея
единицею называется гыслолгь.
2. Сравнивая величины съ единицами ихъ,ветре-
чаемъ два случая: или иъмгъряелтя величина
больше единицы и для составлешя ея нужно по¬
вторить единицу некоторое определенное число
разъ; или излньрнелшя величина меньше еди¬
ницы, и для составлешя ея нужно повторить
определенное число разъ не всю единицу, а только
некоторую ея часть: въ первомъ случае выводъ
сравнешя величины съ единицею, показывающш
сколько разъ целая единица должна повториться

%
для составлешя измеряемой величины, называется
цгълымъ числомц а во второмъ случае выводъ
.сравнения величины, съ единицею, показывающш
сколько разъ некоторая часть единицы должна
повториться для составлешя измеряемой вели¬
чины, называется дрибыо- Следовательно ц/ьдое
число есть собрате пгьсколькихъ однпродпыхь
едшшиц а дробь есть собрате нгъсколькихъ
одинакихъ долей едипгл^ы. Какъ цЬлыя числа,
такъ й дроби делятся еще на два рода, или при
составленш ихъ означается родъ единицы, или
не означается. Въ нервомъ случае они называют¬
ся юиеновапиылш числалш; во второмъ — от¬
влеченными.
5.	Наука, излагающая способы подвергать веемъ
возможнымъ измЬнсшямъ числа и уметь прикла¬
дывать cin изченешя къ решение вопросовъ. встре-
чаемыхъ въ общежитш, называется Afiuejuemu-
кою.
Аривметику естественно разделить на три глав-
ныя отделешя:
1-е огпдгьлеий: числа отвлеченныя.
Н-е отд/ьлен1е: числа именованные.
Ш-е отдтълсше: приложете споеобовъ вычи-
« cлeнiя къ рещешю вопросовъ, встречаемых ъ въ
общежи»*и.

5
ОТДЕЛЕН Е 1-е.
ОБЪ ОТВЛЕЧЕГШЫХЪ ЧИСЛАХЪ.
Прежде нежели пристуиимъ къ изложение спо-
собовъ ВСГ.ХЪ возможныхъ ЙЗМЪНеИШ, производи-
мычъ въ общежитш надъ числами или къ изло¬
жение) способовъ вычнолетя, должно научиться
называть числа и изо бражать ихъ сокращенными
знаками, что сосгавдяетъ предметь счислен’ ко¬
торое слЪдов. бываеть двоякое: словесное и пись¬
менное.
С Ч И С Л Е НI Е.
а) словесное.
Л. Всякая величина можетъ быть увеличена и
уменьшена, а потому и всякое число можетъ быть
увеличено и уменьшено; слЪдов. числа могутъ
быть разнообразны до безконечности, и какъ вся¬
кое число имЬетъ свое название, то и названия
чиселъ могутъ быть разнообразны до безконеч¬
ности, и если бы не существовало между сими
назвашями нЪкотораго рода зависимости, то удер¬
жать ихъ въ памяти не было бы никакой возмож¬
ности. Чтобы подчинить cm назван!я зависимо¬
сти, должно было придумать нисколько родовыхъ
названш чиселъ, которыми бы можно было об¬
нять назвашя всЬхъ возможныхъ чиселъ. Для сего
придуманы различной величины единицы, кото¬
рый отличены между собою назван ями порядковъ
так. обр.: единицы перваго порядка, единицы вто-
раго порядка, третьяго, четвертаго и т. д. поряд¬
ковъ; въ единицу втора го порядка включено нЬ-

которое определенное, совершенно условное число
единицъ перваго порядка; въ обыкновенномъ об-
щепринятомъ счнслеми въ единице втораго по¬
рядка заключается десять едииицъ перваго по¬
рядка — отъ того и самое счислете называется
деслтишое — и ыя единица втораго порядка
называется деслткомъ; единица третьяго порядка
заключаетъвъсебе столько-жедесятковъ, т. е. десять
единицъ втораго Порядка и называется согпнею; еди¬
ница четвертаго порядка заключав тъ съ себе де¬
сять единицъ третьяго порядка и называется
гпысягрю; единица пятаго порядка заключаетъ
въ себе десять единицъ четвертаго порядка и на¬
зывается деслткомъ тысягь; единица шестаго
порядка заключаетъ въ себе десять единицъ пя¬
таго порядка и называется сотнею тысягъ; ,еди-
ница седьмаго порядка заключаетъ въ себе де¬
сять единицъ шестаго порядка и называется мил-
люномЬу далее следуютъ вътакомъ же порядке
десятки, сотни, тысячи, десятки тысячь, сотни
тысячь миллюновъ; потомъ биллюны съ теми же
порядками единицъ, какъ и мцллюны; потомъ
триллионы, квадриллюны и т. д. — Для выраже¬
ния числа единицъ перваго порядка придуман**
сдедующш назвашя: одинъ, два, три, четыре, пять,
шесть, семь, восемь и девять; присовокупляя къ
девяти единицамъ перваго порядка еще единицу
того же порядка, получимь единицу втораго по¬
рядка или десятокъ; десятки считаются такъ-же,
какъ и единицы перваго порядка, присовокупляя
только къ вышеуломянутымъ девяти назвашямъ
простыхъ единицъ назвате родовой единицы так.

7
обр. два десятка, три десятка, четыре десятка,
пять десятковъ и т. д., или сокращено: двадцать,
тридцать, сорокъ, пятьдесятъ, шестьдесятъ, семь-
десятъ, восемьдесятъ и девяносто; прибавляя къ
девяти десяткамъ еще одинъ десятокъ, получимъ
десять десятковъ или единицу третьяго порядка т.
е. сотню; сотни считаются также, какъ и десятки, т.
е. одна сотня, дв4 сотни, три сотии и т. д., или
сокращенно: сто, двести, триста, четыреста, пять-
сотъ, шестьсотъ, семьеотъ, восемьсотъ, девятьсотъ;
прибавляя къ девяти сотнямъ еще одну сотню,
иолучимъ десять сотень или -тысячу и счетъ ты-
сячамъ производимъ так.: обр. одна тысяча, двЪ
тысячи, три тысячи и т. д. до десяти тысячь,
причемъ составляется десятокъ тысячь, и потомъ
опять счнтаемъ: одинъ десятокъ тысячь, два де¬
сятка тысячь, три десятка тысячь, или сокращен¬
но: десять тысячь, двадцать тысячь, тридцать
тысячь, и т. д.; такимъ же образомъ доходимъ
до сотенъ тысячь, миллюновъ, десятковъ миллю¬
новъ и т. д., употребляя названия первыхъ девяти
чиселъ съ присовокуплен емъ къ ни.мъ названш
единицъ различныхъ порядковъ. Назвашя для
среднихъ чиселъ, заключающихся между различ¬
ными числами единицъ одного и разныхъ поряд¬
ковъ составляются также изъ вышеуномянутыхъ
названiii первыхъ девяти чиселъ и родовой еди¬
ницы так. обр.: между однимъ и двумя десятками
находятся девять чиселъ, которыя составляются
изъ одного десятка съ присовокуплен «емъ къ нему
единицъ перваго порядка', именно: десять и одинъ
десять и два, десять и три, десять и четыре, или

8
сокращенно: одинаддать, двенадцать, тринадцать,
четырнадцать и т. д.;_ между двумя и тремя де
сятками опять находятся девять чиселъ: двадцать
одинъ, двадцать два, двадцать три и т. д. произ¬
водится счетъ до девяносто девяти; придавая къ
сему числу единицу, получимъ сто; между одною
сотнею и двумя сотнями опять помещаются де¬
вять чиселъ, выраженный единицами третьяго и
втораго порядковъ такъ: сто десять, сто двадцать,
сто тридцать и т. д.; между каждыми двумя изъ
сихъ чнселъ помещаются еще девять чиселъ, вы-
раженныя единицами третьяго, втораго и перваго
порядковъ такъ: сто одинъ, сто два, сто три и
т. д. до сто десяти, потомъ сто одинадцать, сто
двенадцать, сто сорокъ одинъ, сто пять-
десятъ два,  до ста девяносто девяти; потомъ
двести и опять такой же счетъ до триста и т.
д.	до девятьсогь девяносто девяти; прибавляя къ
сему числу единицу, получимъ единицу четвер¬
таго порядка или тысячу; назватя для среднихъ
чигелъ между различными числами простыхъ
тысячь будутъ составлены изъ названш четвер¬
таго и третьяго порядковъ единицъ; потомъ ~ зъ
четвертаго, третьяго и втораго порядковъ еди¬
ницъ; наконецъ изъ четвертаго, третьяго втораго
и перваго порядковъ единицъ. СлЪдое. назватя
для среднихъ чиселъ между различнымъ числомъ
единицъ одного и того же порядка будутъ соста¬
вляться изъ названш родовой единицы разематри-
ваемаго порядка и постепенно изъ единицъ всЪхъ
предыдущнхъ порядковъ до перваго включитель¬
но; такъ средтя числа въ шестомъ порядкЬ бу-

9
дутъ составлены изъ единицъ шестаго и пятаго
порядковъ; шестаго пятаго и четвертаго; шестаго
пятаго, четвертаго и третьяго; шестаго, пятаго,
четвертаго, третьяго и втораго; шестаго, пятаго,
четвертаго, третьяго, втораго и перваго; напр.
Сто двадцать три тысячи пятьсотъ — это число
составлено изъ единицъ шестаго, пятаго, четвер¬
таго и третьяго порядковъ.
в) ПИСЬМЕННОЕ.
Б.* Изъ предыдущаго слЪдуетъ, что для выра-
жешя всякаго возможнаго числа приняты за ос¬
нование назватя первыхъ девяти чиселъ и назва¬
тя родовыхъ единицъ разнЫхъ порядковъ; со¬
единяя ciii назватя по известному закону', выра¬
женному въ предыдущемъ член-fe, можно выразить
на обыкновенномъ язык* всякое данное число.
Основываясь на семъ и самое изображение чиселъ
посредствомъ сокращенныхъ знаковъ надобно было
подчинить также какому' нибу дь закону, помопцю
коего съ наивозможно-меньшимъ числомъ знаковъ
можно было бы изобразить всЬ возможный чи¬
сла. Для сего принято изображать первыя девять
чиселъ посредствомъ слЪдующихъ Арабскихъ зна¬
ковъ, называемы къ цыФрами:	2,	3,	W-,	5,	6,	7,
8 и 9. Помощгю сихъ знаковъ можно было бы
изображать и число единицъ разныхъ порядковъ,
но для еего надобно было бы изобрЪсть также
знаки и для изображешя родовыхъ единицъ раз¬
ныхъ порядковъ; такъ напр, чтобы изобразить
5 десятковъ, надобно было бы къ циФр-fe 5 при¬
совокупить знакъ, выражающ н десятки; тоже са¬

40
мое должно сказать и объ единицахх другихъ
порядковъ. Но вмёсто того, чтобы придумывать
разные знаки для изображения единицъ разныхъ
порядковъ, согласились» въ слЬдующемъ весьма
важномъ условш: изображать вышеупомянуты¬
ми девятые ирфралш есть порядки единице во
всякол1Ъ прсдложснномъ гислгь, поставляя пныя
цифры одну подлпг другой нагиная съ правой
руки, каждую на лиъстгь, соотпвшпствеиномъ
тол1у порядку единицъ, гасло которыхъ выра¬
жается сею цифрою; такъ напр, на первомъ
мёстё съ правой руки ставить цифру, означаю¬
щую простыя единицы, на второмъ — единицы
втораго порядка (десятки), на третьемъ — еди¬
ницы третьяго порядка (сотни), и такъ далЁе.
Пусть напр., требуется выразить цифрами число
двести тридцать пять. Cie число заключает ь въ
сеоЁ 5 единицъ перваго порядка, 5 единицы вто¬
рого порядка и 2 единицы третьяго порядка, или
cie число состоитъ изъ 5 единицъ, 3 десятковъ и
2 сотней; слёдов. на первомъ мёстё съ правой
руки должно поставить цифру 5, на второмъ —
3, на третьемъ — 2, т. е. число двёсти трид "ать
нягь изобразится такъ: 235. Также число двад¬
цать пять тысячь четыреста семдесптъ пять изо¬
бразится такъ: 25475. — Но еслн-бы мы хотёли
изобразить ровное число единицъ какого нибудь
порядка, кром-ь перваго, то легко замЁтилн-бы,
что вышеупомянутый девять циФръ для сего не¬
достаточны; напр, чтобы изобразить число двад¬
цать, для сего должно цифру 2 поставить на
второмъ мёстё, а первое мЬсто простыхъ единицъ,

11
которыхъ въ предложенномъ чпслъ не находится,
должно замъстнть какныъ ннбудь знакомъ, который
бы саыъ по себъ не лмълъ никакого значешя:
такой знакъ есть нуль 0. Слъдователыю знакъ
ссй въ изображение числа долженъ поставляться
на ыъстахъ тъхъ порядковъ едпннцъ, которыхъ
не находится въ предложенномъ чнслъ; напр, три¬
ста изобразятся чрезъ 500; ибо предложенное чи¬
сло состоять изъ трехъ сотеиъ, десятковъ же и
единицъ не шгветъ; посему, - дабы дать циФр-в
5 значеше сотсиъ, т. е. дабы поставить ее въ изо¬
бражали числа на третьемъ мЪсть, должно пер-
выя два мЪста, на которыхъ должны были бы
стоять десятки и единицы и которыхъ въ пред¬
ложенномъ чнслв не находится, замЪстить двумя
пулями. — Помощпо сихъ десяти знаковъ, т. е.
девяти ццфръ п десятаго нуля, можно выразить
всякое возможное число, наблюдая при семъ выше-
показанныя правила. Пусть требуется изобразить
число: два миллюна сорокъ пять тысячь двадцать
три едшшцы. Число cie, какъ видимъ, состонтъ
пзъ сднпнцъ 7-го, 5-го, 4-го, 2-го п 1-го по-
рядковъ; слъдсв. единицы 6-го и 5-го порядковъ
должно замъстить нулями н будетъ: 2045023.
Также число семь тысячь пять миллгоновъ двъ-
стп тысячь четыре едшшцы изобразится такъ:
7005200004.
6.	При пзображенш чиселъ цифрами можно об¬
легчить себя слъдующпмъ весьма важнымъ замъ-
чантемъ: числа состоять изъ простыхъ единицъ,
десятковъ и сотенъ: потомъ изъ едшшцъ, десят-
. ковъ п сотеиъ тысячь; пзъ единицъ, десятковъ и

12
сотенъ миллюновъ; изъ единицъ, десятковъ п сотенъ
тысячь миллюновъ; и т. д.; следовательно единицы
разныхъ порядковъ можно разделить на клас¬
сы: простыхъ единицъ, тысячь, миллюновъ, ты¬
сячь миллюновъ, биллюиовъ, тысячь биллюновъ
ит. д.; въ каждомъ классе должно быть по три
цифры, изключая последняго класса къ левой
руке, въ которомъ можетъ быть две и одна цифра;
изобразивши сей последшй классъ цифрами, сле¬
дующее после него классы изображаются, идя
постепенно къ правой руке и изображая каждый
классъ тремя цифрами; есля въ какомъ нибудь
классе не будете доставать циФръ, то оныя за¬
мещаются нулями. Напр, пятьдесятъ три тысячи
миллюновъ четыреста семь миллюновъ двадцать
пять единицъ; изобразивши первый классъ отъ
левой руки 53 тысячи миллюновъ, за ннмъ не¬
посредственно поставимъ классъ миллюиовъ, т. е.
четыреста семь миллюновъ; но какъ въ семъ клас¬
се находятся только две цифры, именно цифра
сотенъ миллюновъ (четыреста) и цифра единицъ
миллюновъ (семь), то десятки миллюновъ долж¬
но заместить нулемъ и будете: 53407 мслл’юиовъ;
далее следуете классъ тысячь, котораго совсемъ
не находится въ предложенномъ числе; посе¬
му означимъ его тремя нулями, непосредственно
следующими за классомъ миллюновъ и будете
53407000 тысячь; наконецъ следуете классъ про-
стыхъедннпцъ, именно двадцать пять; въ семъ клас¬
се две только цифры: десяткп н единицы, следов,
место сотенъ должно заместить нулемъ, н будете
все число выражено такъ: 53407000025.

13
*
Если бы наоборотъ нужно было число, изо¬
браженное цифрами, выговорить на обыкновенномъ
языкё, то раздЁлнвши cie число отъ правой рукЁ
къ лёвои на классы такъ, чтобы въ каждомъ клас-
сё было по 3 цифры, изключая послёдняго къ
лёвой рукЁ, будемъ произносить отдёлыю каждый
классъ, начиная съ послёдняго къ лёвои рукЁ, и
присовокупляя къ каждому классу г!!»звате ему
принадлежащее. Напр. 5700432305413; раздЬлиг,-
ши cie число на классы, будетъ: 5,700,432,305,
413, пять биллюновъ семьсотъ тысячь четыреста
-тридцать два миллюна триста пять тысячь четы¬
реста тринадцать единицъ.
7.	Наконецъ остается еще сказать о счислеши
дробей, т. е. о выговариванш и изображенш ихъ.
Изъ чл. 2-го знаемъ, что дробъ вообще есть одна
или нёсколько долей единицы и что для с оста*
влешя дроби нужно повторить опредЁленное чи¬
сло разъ не всю единицу, а только нЁкоторуго
ея часть. Всякая величина меньшая единицы есть
часть или доля сей единицы; посему доли еди¬
ницы могутъ быть различныя; такъ величина,
которую нужно взять четыре раза, чтобы соста¬
вить цЁлуго единицу, есть четвертая ея доля;
величина, которую нужно взять 12-ть разъ для
составлешя цёлои единицы, есть двЬнадцатая ея
доля. И такъ при изображенш дроби нужно по-
*
казать, какая доля единицы повторялась для с<>
ставлетя данной дроби, и потомъ. сколько разъ
она повторялась. Слёдов. для изображения дроби
нужно два числа: одно, которое показывало бы,
какая доля единицы повторялась для составления

14-
дроби, а другое, показывающее, сколько разъ С:я
доля единицы повторялась въ данной дроби. Пер¬
вое называется знамепателсмъ, а второе — ги-
сли/пелс.иъ; условно согласились ихъ писать одно
подъ другимъ, отд Ьляя чертою и ставя всегда подъ
сею чертою знаменателя. Такъ напр, f значить,
что для с оста слегая данной дроби, нужно было
пятую долю единицы повторить три раза; выго¬
вариваются сш числа одно послЪ другаго, начи¬
ная съ числителя и прибавляя къ знаменателю
слоги ыхьу ыя или ап' напр, вышеозначенная
дробь выговорится: три пятыхъ доли или три
пятыя доли. Также ~ двё седьмыхъ или двЪ сед-
мыл; ~ три четвертыхъ или три четвертый (под¬
разумевается доли) или еще три четверти.
ПослЬ сего приступнмъ къ подробному нзло-
женно основныхъ дЪиствхй вычисления, произво-
димыхъ надъ числами, и начнемъ съ цЬлыхъ чн-
селъ.
Дёйсгв1я сш суть: сложеше, вычиташе, умно¬
жение и дЬлеше.
О СЛО/KEHI И.
8.	Слолесше есть дЬйствге, посредствомъ ко-
тораго несколько данныхъ чнселъ совокупляются
аь одно гнело. СлЪдов. посредствомъ сложешя
узнается число единицъ разныхъ порядковъ, на¬
ходящееся въ нескольких ъ данныхъ числахъ. Дан¬
ный для сложешя числа называются елагае.ны-
.мк, а число, произшедшее отъ сложешя и заме¬
няющее сооою всь данныя числа вместе, назы-

>15
ваегся суммою. Вмёсто того, чтобы говорить и
писать: такое-то число сложить съ такичъ-то, упо¬
требляете ясокрагцеиный знакъ кото; ый выго¬
варивается п.гюсъ или съ. Напр, пусть требуется
сложить числа:
3456 -f- 7840 -Ь 371 -4- 7819.
Поелику посредствомъ сложенгя должно найти
такое число, которое бы собою замЁняло вс-t дан-
ныл для сложешя числа, или такое число, кото¬
рое бы заключало въ сеоЬ столько единицъ раз¬
ныхъ порядковь, сколько находится ИХЪ ВО ВСЁХЪ
данныхъ числахъ, то для опредЬлешя, сколько на¬
ходится въ немъ единицъ разныхъ порядковъ,
должно узнать, сколько каждаго порядка единицъ
находится во всЬхъ данныхъ числахъ. Для опре-
дЬлешя простыхъ единицъ видимъ, что въ 1-мь
чнслё находится ихъ 6, во 2-мъ совсёмъ не на¬
ходится единицъ, въ 3-мъ находится 1, которая
слёдов. съ вышеупомянутыми 6 единицами соста¬
вить 7 единицъ, да въ Ч-мъ числё находится ихъ
9, который съ вышеупомянутыми 7 единицами
составятъ 16 единицъ. Итакъвъ сумчЁ будет-ь 1G
простыхъ единицъ. Поступая такнмъ же образомъ съ
единицами прочнхъ порядковъ найдемъ, что въ
суммЁ . будетъ 17 десятковъ, 23 сотни и 17 ты¬
сячь. Теперь надобно всё сш порядки единицъ 1
•
выразить по 5 ча. однимъ числомъ, которое и
будетъ искомая сумма: 16 простыхъ единицъ,
составляютъ 1 десятокъ и 6 единицъ, и такъ
цифра 1 будетъ принадлежать къ единпцамъ 2-го
порядка и потому иа первомъ мёстё отъ правой
руки въ суммЁ будетъ стоять цив>ра 6, далЁе 1

46
десятокъ да 47 десятковъ, входящихъ въ сумму
составятъ 48 десятковъ; но 48 десятковъ с оста-
вляютъ 4 сотню и 8 десятковъ; слЬдов. въ 4 8
десяткахъ цифра 4 отойдетъ къ единицамъ 2-го
порядка и на второмъ м*ст* въ сумм* будетъ
стоять только цифра 8; дал*е 4 сотня, да 23 сотни
составятъ 24 сотни, которыя въ свою очередь
составляютъ 2 тысячи н 4 сотни; сл'Ьдов. на тре-
сьемъ мЬстё въ сумм* будетъ стоять цифра 4,
а цифра 2 отойдетъ къ тысячамъ, которыя вмЬ-
ст* съ 47 тысячами составятъ 19 тысячь, заклю-
чающихъ въ себъ 4 десятокъ тысячь и 9 про¬
стыхъ тысячь; и потому на четвертомъ м*ст* въ
сумм* будетъ стоять 9, а на пятомъ цифра 4 и
вся сумма выразится таким ъ образомъ: 4 9486.
Для облегчешя мо-	3456
жно производить ело-	78401
g	orrj	I	слагаемый,
жеше ^ак. обр.: дол-	371 1
жно подписать ела-	7849
еаемылгислаодно подъ 49486 сумма.
другилсь такъ, ггпобы единицы одного порядка
во вспхъ гислахъ находились въ одномъ верти-
кальномъ столбца» и потомъ каждый порядокъ
единицъ складывать отдтъльно’ если гисло еди¬
ницъ какого нибудь порядка выражается»одною
цифрою, то ее и въ сумлт» ставить подъ гер-
тою въ столбцть того же порядка единицъ; если
же гисло единицъ какого нибудь порядка выра¬
жается болтъе, нежели одною цифрою, то въ
столбцгъ складываемого порядка сдишщз ста¬
вится только первая цифра отъ правой ру-
кы, а всю осталькыя цифры придаются къ еди-
ницалсь слюдующаго къ лтъвой рушь стполбир.

слагаемый;.
сумма.
О В Ы Ч И Т А НI И.
* ы	*
9.	Выгиташе есть действ? е, посредствомъ кото-
раго определяется, чемъодно число больше другаго;
следов. посредствомъ сего действгя узнается, сколь¬
ко лишиихъ единицъ разныхъ порядковъ нахо¬
дится въ одномъ числе противъ другаго. Число,
изъ котораго вычитается другое, называется ум?нь-
шаемымъ\ то, которое вычитается называется
выштагмымъ; а число, произшедшее отъ дей-
ств1я вычитатя, называется осташкомъ или раз-
ностпо. Вместо того, чтобы говорить и писать
такое-то число вычитается изъ такого-то, упо¬
требляется сокращенный знакъ —, который вы¬
говаривается мапусъ или безъ. Пусть требуется
изъ 8976 вычесть 5343; 8976 — 5343.
Такъ какъ действие мъ вычнташя определяется
сколько лишннхъ единицъ разныхъ порядковъ
находится въ одномъ числе противъ другаго, то
въ разности должно найдти отдельно число про¬
стыхъ единицъ, десятковъ, сотенъ ri проч. лиш¬
ннхъ въ уменьшаемомъ числе противъ вычитаемаго.
Следов, въ разности число простыхъ едниицъ, де¬
сятковъ, сотенъ н проч. будетъ таково, что сло-
*
Воть еще примеры:
1) 85463 \	2)	"*3416	/
7 \ 3005 > слагаемый.	52817 1
2407 S	*	349)
800875 «умма.	40853	I
680304 ]
787739

18
живши cie число единицъ, десятковъ, сотенъ и проч.
съ единицами, десятками, сотнями и проч. вычи-
таемаго, получимъ соответстуюпце порядки единицъ
умсныпаемаго. После сего очевидно, что въ 3 едини*
цахъвычитаемаго недостаетъЗ единицъ до 6 единицъ
уменыпаемаго; следов. число единицъ въ разности
будетъ 3; также найдется, что число десятковъ въ
разности будетъ 3, число сотеиъ G и число тысячь 3.
Для облегчения вы-	897 6	уменьшаемое
читаше можно про-	5343	вычитаемое
изводить также, какъ	3633	разность,
и сложете т. е. подписавши одно число подъ
другимъ такъ, чтобы одинакге порядки единицъ
Находились въ одномъ вертикальномъ столбце, вы¬
читать каждый порядокъ единицъ отдельно и ци¬
фру соответствующей разности ставить подъ чер¬
тою въ томъ же столбце.
10.	Но присемъ действия встречается следующее
затруднете: можетъ случиться, что число еди¬
ницъ какого иибудь порядка въ уменьшаемомъ
числе будетъ меньше числа соответствуюпщхъ
единицъ того же порядка въ вычитаемомъ, тогда
действ1е вычитаю я производится следующимъ об-
разомъ: пусть требуется изъ 85413 вычесть 37242.
Отнимая 2 единицы вычи- 85413
таемаго отъ 3-хъ единицъ у- 37242
меньшаемаго, получимъ 1 еди- 481 7 1
ницу въ разности; потомъ следуетъ 4 десятка вы¬
честь изъ 1-го десятка; 4 десятка очевидно боль¬
ше 1-го десятка; но повышесказаниому, число де-
сятковъ въ вычитаемомъ должно быть таково, что
сложивши cie число съ десятками разности дол-

-19
жНЫ будемъ получить десятки уменьшаема го; изъ
сего заключаема, что число десятковъ разности
должно быть таково, что сложивши его съ чи-
сломъ десятковъ въ вычитаемомъ, получимъ не
одинъ десятокъ, но А А десятковъ, изъ коихъ *10
десятковъ, какъ составл я ющге въ совокупности
А сотню, отошли къ сотнямъ уменьшаема го; посему
надобно 5-знать еколькихъ десятковъ недостаетъ
въ 4-хъ десяткахъ вычитаемаго до А4 десятк овъ 5гмень-
гааемаго; очевидно 1-ми десятковъ; следов- цифра де¬
сятковъ въраэностибудетъ 7;потомъ З'же должно вы¬
читать 2 сотни вычитаемаго не изъ 4-хъ сотенъ умень
шаемаго, а изъ 3-хх: ибо одна -сотня отделена была
къ десяткамъ—так. обр. въ разности б5тдетъ А сотня;
потомъ 7 тысячь нельзя вычесть изъ 5 тысячь,
посему отъ десятковъ тысячь отдЬляемъ А деся¬
токъ тысячь и соединяемъ его съ простыми тыся¬
чами, тогда въ з’менынаемомъ число простыхъ
тысячь будетъ уже не 5, а А 5; слЬдов.	въ	7	ты-
сячахъ вычитаемаго недостаетъ 8 тысячь	до	А 5
тысячь }тиеньшаемаго, и потому въ разности ци¬
фра тысячь будетъ 8; накоиецъ вычитая 3 де¬
сятка тысячь изъ 7 десятковъ тысячь, получимъ
въ разности 4 десятка тысячь.
А А. Точно также должно поступать и въ томъ
случаЬ, когда въ уменьшаемомъ совсЬмъ не бу-
детъ находиться какого нибудь порядка единицъ.
Напр, требуется нзъ 5804 вычесть 4362.
Въ настоящемъ случаЬ де- 58*04
сятковъ въ з'меньшаемомъ не 4362
находится; слЬдов. число де- А 442
сдтковъ разности должно быть таково, что ело-

20
жипгаи его съ числомъ десятковъ вычитаемаго
получимъ ровно-10 десятковъ, составлягощихъ цЪ-
лу о сотню; посему въ 8 сотняхъ уменьшае.маго
заключается 4 лишняя сотня, произшедшая отъ
сложенл десятковъ вычитаемаго и разности; и такъ
беремъ отъ 8 сотенъ уменьшаемаго 4 сотню и
говоримт», что въ уменыпаемомъ находится не о
десятковъ, по 40 десятковъ; следов, въ 6 десяткахъ
вычитаемаго недостаетъ )[-хъ десятковъ до 40 де¬
сятковъ уменьшаемаго и потому циФра десятковъ
разности будетъ Н~; поступил по вышесказанному,
нолучимъ и остальныя цифры въ разности.
Пусть еще требуется изъ 0070 выче.ть 25793.
Вычитая 3 единицы изъ 40	Л0070
единицъ, получимъ въ разно- 25797
сти 7 единицъ; потомъ 9 де- 4 -4 % i i
сятковъ изъ 6 десятковъ вычитать нельзя и по¬
тому надобно отъ сотенъ отделить 4 сотню, ко¬
торая произошла отъ сложешя десятковъ вычи¬
таемаго и разности; но сотенъ совсЬмъ на нахо¬
дится въ уменыпаемомъ; изъ сего заключаема»,
что число сотенъ вычитаемаго съ числомъ сотенъ'
разности составило 9 сотенъ, къ которымъ при¬
дана была еще 1 сотня отъ десятковъ, что въ
совокупности составило 40 сотенъ или \ тысячу;
посему отъ тысячь уменьшаемаго надобно отде¬
лить 4 тысячу, произшедшую отъ сотенъ; но ты¬
сячь также не находится въ уменыпаемомъ; след,
число тысячь вычитаемаго таково, что 63'дз'чи
сложено съ числомъ тысячь разности, состзрляетъ
9 ты ячь, къ которымъ придана еще 4 тысяча,
произшедшая отъ сотенъ, что въ совокз'пносгн

и
составило 4 десятокь тысячь; посему въ десят
кахъ тысячь уменьшаемаго находится 4 лишшй
десятокь тысячь, произшеднни отъ простыхъ ты¬
сячь; отдЪляя сен десятокъ тысячь отъ Ч-хъ де¬
сятковъ тысячь уменьшаемаго, ■ говоримъ, что въ
уменьшаемомъ находится не нуль простыхъ ты¬
сячь, но 40; въ сихъ 40 тысячахъ находится 4
лишняя тысяча, произшедшая отъ сотенъ; от-
дЬляемъ ее отъ 40 тысячь, остается въ уменьшае¬
момъ 9 тысячь и 40 сотенъ; въ40 сотняхъ опять
находится одна лишняя сотня, произшедшая отъ
десятковъ; отдЬляемъ cito сотто, въ уменьшае¬
момъ будетъ уже 9 сотенъ, и 40 десятковъ вмЬ-
стЬ съ данными 6 десятками составятъ 46 десят¬
ковъ; слЬдов. 9 десятковъ вычитаемаго должно
будетъ вычесть изъ 46 десятковъ, въ разности
будетъ 7 десятковъ; 7 сотенъ отнимая отъ 9 со¬
тенъ, получимъ въ разности 2 сотни, и т. д. про¬
должая, получимъ всю искомую разность.
4 2. И такъ при вычитанш одного числа изъ
другаго должно наблюдать слЬдующее общее пра¬
вило:	должно	выгитаелюе гасло подписать
подъ )\исиышгелшлп так. обр. гтобы цифры
соогпегьгпствующнхъ порядковъ единицъ нахо¬
дились въ одполеь вертикальпол1Ъ столбшь, по-
толсь должно калсдую цифру выгитаелшго
выгитатъ отд/ьльно изъ соответствующей
цифры улкпыпаелтго; если цифра выгитаелш-
го будешь больше цифры улееньишелшго, или
на лаьстгь цифры у'мепъшаемаео будетъ на¬
ходиться нуль, то доллсно взять единицу отъ
тфры c.ubdj юищго порядка въ улгеньишелюмъ

22
и увеличить предыдущую ей къ правой рушь
цш/jpy или пуль (если от» находится на мть-
стшь ея) -10-ю единииряш; если въ у.иеньшае-
люлсь сряду находится нгьсколько нулей, то
первый только нуль отъ. правой руки уве.игш-
вается 40-ю едитщалсщ а есть остальные нули
только 9-ю единицами и потомъ производит¬
ся выштате какъ обыкновенно.
Прилишаше 4. Если какое нибудь число вы¬
чихается изъ единицы, имЪющей при себь столько
нулей, сколько находится циФръ въ данномъ тш-
слЪ, то разность въ семъ случаЪ называется Арио-
метихескилеь дополнсшелсь того числа- Следов.
Ариольетигеское дополнеше гисла есть раз¬
ность лес жду силсь гислолеъ и единицею непо¬
средственно высшаго порядка. Напр. 400 безъ
37 даетъ 63; также 40000 безъ 7538 даетъ 2462;
следов. 63 есть Аривметическое дополнение 37;
2462 есть Аривметическое дополнеше 7538 разу¬
меется до единицы слЪдующаго высшаго поряд¬
ка, т. е. въ первомъ случае до сотии, а во вто¬
ромъ, до десятка тысячь. Посредствомъ Ариеме-
тическаго дополнешя можно вычиташе обращать
въ сложеше. Напр, пусть требуется изъ 244 5 вы¬
честь 573; въ разности должно быть число 573-мя
единицами меньше противъ 2445; посему если
вместо того, чтобы отнять 573 отъ 2445 при-
дадимъ къ нему Аривметическое дополнеше 57 3-хъ,
то получимъ число целою тысячею больше про-
тивъ искомой разности: ибо въ самомъ числе 244 5
находятся 573 лишнгя единицы противъ разно¬
сти, да еще къ нему придали 427 (Ариеметич.

23
дополн. 573-хъ), что вмЪстЬ составятъ цЪлую ты¬
сячу; посему придавши Лриеметическое дополне¬
ние вычитаемаго къ 24:45, для получешя искомой
разности должны изъ найденной суммы вычесть
тысячу. И такъ вообще; чтобы обратить еыги-
matiic въ сложеше должно къ уменьшае.',ю.иу
числу придать Ариометихеское дополнеше вы-
читаелгиго и изъ найденной так. обр. еулг.чы
вычесть единицу высшаго порядка противъ въъ-
гитаелигго. Для отыскатя же Ариеметическаго
дополнения числа должно только единицы дан*
наго числа вычесть изъ 40, и всЪ nponia его. ци¬
фры изъ 9. Когда хотдтъ вычиташе обратить въ
сложение посредствомъ Ариеметическаго дополнения,
то cie дЬйспйе нзображаютъ такъ: подъ умень-
шаемымъпишутъ Ариемитнческое дополнеше вычи¬
таемаго, къ нему съ л'Ьвой руки приписываютъ
единицу и ставать надъ нею горизонтальную чер¬
ту, чтобы показать, что единица сего порядка
должна быть отнята отъ суммы. Напр, требует¬
ся изъ 8743 вычесть 783.
Прикладывая Ари- 8743
еметич. ' дополнеше 4247
къ 8743 получимъ 7930 искомая разность.
Въ сумм* 8930; отнимая отсюда тысячу, будетъ
7930 искомая разность. СлЪдов. подписавши чи¬
сла одно подъ другимъ, должно собственно про¬
изводить сложеше и въ томъ порядкЬ единицъ,
въ которомъ стоить 4 съ горизонтальною чертою
при сложенш отнять единицу изъ суммы. Еще
примъръ: изъ ЗЛ86 вычесть 257; будетъ:
к

ЗИ-86
m3
3229 искомая разность.
Нримгьгаше 2. Свойства чиселъ, входящих* в*>
дЬйствгя сложешя и вычиташя, суть сл*дуклщя:
ч*мъ (т. е. сколькими единицами) больше или
меньше слагаемый, т*мъ (т. е. столькими же еди¬
ницами) будетъ больше или меньше и сумма: ибо
въ сумм*, как* въ числ*, составленномъ изъ н*-
сколькихъ данныхъ чиселъ, находится столько
единицъ, сколько во всЪхъ данныхъ числах*.
СлЪдов. ч*м* больше или меньше будутъ данный
числа, тЬм* будетъ больше или меньше и число,
составленное изъ оныхъ. — Въ выгиташи: ч*мъ
больше или меньше будетъ уменьшаемое при од¬
ном* и том* же вычитаемом*, тЬм* больше или
меньше будетъ и разность: ибо разностпо опре¬
деляется число лишиихъ единиц* въ уменьшае¬
мом* против* вычитаемаго; следов. ч*мъ больше
или меньше будетъ уменьшаемое, т*мъ больше
или меньше будетъ въ нем* и число лишних*
единиц* против* одного и того лее вычитаемаго.
Напротив* чём* больше будетъ вычитаемое при
одном* и том* же уменьшаемом*, т*мъ будетъ
меньше разность, и ч*мъ меньше вычитаемое, т*мъ
больше разность: ибо съ увеличивашемъ выч. таема-
го число лишних* единиц* въ уменьшаемом* ста¬
новится меньше, и съ уменьшешем* вычитаемаго
число лишпицъ единиц* въ уменьшаемомъ ста¬
новится больше. Посему-то иногда при вычита-
нш вмЬсто того, чтобы уменьшать единицею ту
ЦИФру, от* которой было занято, можно оста-

гь
вить ее въ прежнемъ вид* и увеличить соотвАг-
ствующую цифру’ "вычитаемаго единицею:	ибо
при отнятш единицы отъ циФры уменьшаемаго,
соотв*тствую!цая цифра въ разности должна умень¬
шиться единицею, но то же самое уменынеше
произойдстъ съ цифрою разности и въ томъ слу-
ча*, когда будетъ увеличена цифра вычитаемаго
единицею. Напр, изъ 7565 вычесть 37ff9.
Вычитая 9 изъ 15 получимъ 7*565
въ разности 6; потомъ вм*сто 37^9
того, чтобы вычитать Ь изъ 3816
5, оставляемъ циФру уменьшаемаго въ прежнемъ
вид*, а цифру вычитаемаго Ч увеличиваемъ еди-
иицею и вычитаемъ 5 изъ 6; также вм*сто того,
чтобы вычитать 3 изъ 6, вычитаемъ Ч изъ 7.
ПОВЬРКИ СЛОЖЕН1Я И ВЫЧИТАШЯ.
13. Повгьркою Ариеметическаго дАнствгя на¬
зывается другое дьйствю, производимое для того,
чтобы увЬритьсл въ справедливости перваго д*й-
СТВ1Я.
Ловгьрка сложешя д/ълается ,слгъдующпмъ об-
разолсь: складываютъ первыя цифры слагаемыхъ
съ л*вой руки и найденную так. обр. сумму вы-
читаютъ изъ соотв*тствующей части въ ц*лой
сумм*, остатокъ приводятъ въ единицы сл*дую-
щаго низшаго порядка и соединяютъ его съ со-
отв±тствующею цифрою въ цЬлой сумм*, изъ сей
суммы вычитаютъ сумму вторыхъ цнФръ съ л*-
вой руки въ слагаемыхъ и продолжаютъ cie д*и-
CTBie до простыхъ едииицъ, которыя бывъ вы-

23
чтеиы изъ соотв±тствующихъ единицъ въ сумм*,
соединенныхъ съ остаткомъ (если олъ есть) отъ
десятковъ, дадутъ въ посл*днемъ оетатк* нуль,
если сложеше сдЪлано в*рно.
854-47
Нашедши сумму 4 507 QJ4, для	3692
пов'Ьрки д*йствш складыва-	53478
емъ сначала первыя цифры въ	84^19
слагаемыхъ съ лЪвой руки т.	^50794.
е. десятки тысячь, будетъ 43	24220
десятковъ тысачь; вычитаемъ ихъ изъ соотвЬтст-
вующаго порядка единицъ въ ц*лой сумм*, т. е.
изъ 45 десятковъ тысячь, получимъ въ остатка 2
десятка тысячь и пишемъ 2 внизу подъ чертою
подъ десятками тысячь; потомъ cin 2 десятка ты¬
сячь приводпмъ въ единицы сл±дующаго низшаго
порядка, т. е. въ тысячи, будетъ 20 тысячь, въ
сумм* тысячь не находится, посему сложивши
тысячи въ слагаемыхъ, т. е, 49 тысячь, вычтемъ
ихъ изъ упомянутыхъ 20 тысячь, получимъ въ
остатка одну тысячу; сш> тысячу приводпмъвъ
сотни н соединяемъ 40 сотенъ съ 7-ю сотнями,
находящимися въ сумм*, будетъ 47 сотенъ; изъ
снхъ 47 сотенъ вычитаемъ число сотенъ въ сла¬
гаемыхъ, т. е. 45 сотенъ, въ оетатк* получимъ 2
сотии и пишемъ ихъ подъ сотнями; 2 сш естни
приводпмъ въ десятки, будетъ 20 десятковъ, и по¬
елику десятковъ въ сумм* не находится, то изъ
20 десятковъ вычитаемъ число десятковъ въ сла¬
гаемыхъ, т. е. 48 десятковъ, въ остатк* получимъ
2 десятка н пишемъ ихъ подъ десятками; сш 2
десятка приводпмъ въ единицы, будетъ 20 единицъ,

27
соединяем* ихъ съ 4-мя единицами въ сумм*, бу¬
дет ъ 24 единицы; изъ сихъ 24 единицъ вычита¬
емъ единицы въ слагаемыхъ, т. е. 24 единицы и
получаемъ въ оетатк* нуль — слЬдов. * сложеше
сдЬлано в*рно.
Можно еще пов±рять еложеше н так. обр.: от¬
делить одно какое нибудь слагаемое, остальныя
вс* сложить вм*ст* и найденную так. обр. сум¬
му вычесть изъ общей суммы, и если въ разно¬
сти получится отд*ленцае слагаемое, то елзже-
Hie было сдЬлано в*рно.
Вычиташе пов*рвется сложешемъ: именно, ск¬
ладывая вычитаемое съ разностпо, получимъ въ
сумме уменьшаемое, если вычиташе было сдЬлано
В*рно.
Напр. Получивши разность	24343
5374, для поверки д*йств1я	4-8972
вычиташя сложнмъ ciio раз-	537 4
кость съ вычитаемым* 4 8972,	24343
получимъ въ сумме уменьшаемое 24343; слЬдов.
вычиташе было сдЬлано в*рно.
ф
ОБЪ УМНОЖЕНИЯ.
4 4. Умножить одно число на другое значитъ
наидти такое трепе число, которое бы составле¬
но было изъ перваго такъ, какъ второе составле¬
но изъ единицы. Посему если данный числа бу¬
дутъ цЬлыя, то для умножешя одного числа на
другое надобно первое число повторить столько
разъ, сколько разъ во второмъ повторяется еди¬
ница. Число, которое происходит* отъ д*йств1Я
умножешя, называется произведешемъ; число, изъ

28
котораго составляется произведете, называете я-
мнижил1Ы.иъ; а'число, которое показываетъ, сколь¬
ко разъ множимое должно быть повторено для
составленш произведенья, называется ятооките-
лежь. Оба числа вм-Ьст-ъ и множимое и множи¬
тель называются производителялш. Для того, что¬
бы. показать, что такое-то число умножается на
такое-то, употребляется знакъ X или (.)• СлЬдов.
8.	3 и 8 X 3 значить 8 должно умножить на 3.
И такъ, чтобы произвести умножеше одного чи¬
сла на другое, надобно первое число взять слагае-
* мычъ столько разъ, сколько находится единицъ
во второмъ. Ни пр. чтобы умножить 35 на 8 на¬
добно 35 взять слагаемымъ 8 разъ. Изъ сего ви¬
дно, что умножеше есть не что иное, какъ сложе¬
нье особеннаго рода, въ которомъ net слагаемый
равны между собою. СлЬдов. произведете всегда
должно быть однородно сь мноэкпмымъ: ибо
произведете составляется всегда изъ множимаго-
i 5. И такъ если множимое и множитель будутъ
числа, состоящая каждое изъ одной циФры, то
весьма легко найдти ихъ произведете. Напр, тре¬
буется 6 умножить на 7; для сего должно 6 еди¬
ницъ взять слагаемымъ 7 разъ, т. е. 6 -р- 8 -Р- б
6 -т- 6 -р- 6 -J- 6 и сумма 4-2 будетъ искомое про¬
изведенье. Для того, чтобы не складывать каждый
разъ множимое само съ собою нисколько разъ,
Паоагоръ, одинъ изъ Греческихъ мудрецовъ, со-
ставилъ такъ называемую таблицу умножешя,
въ которой заключаются Bet возможный произ¬
веденья первыхъ девяти чиселъ.

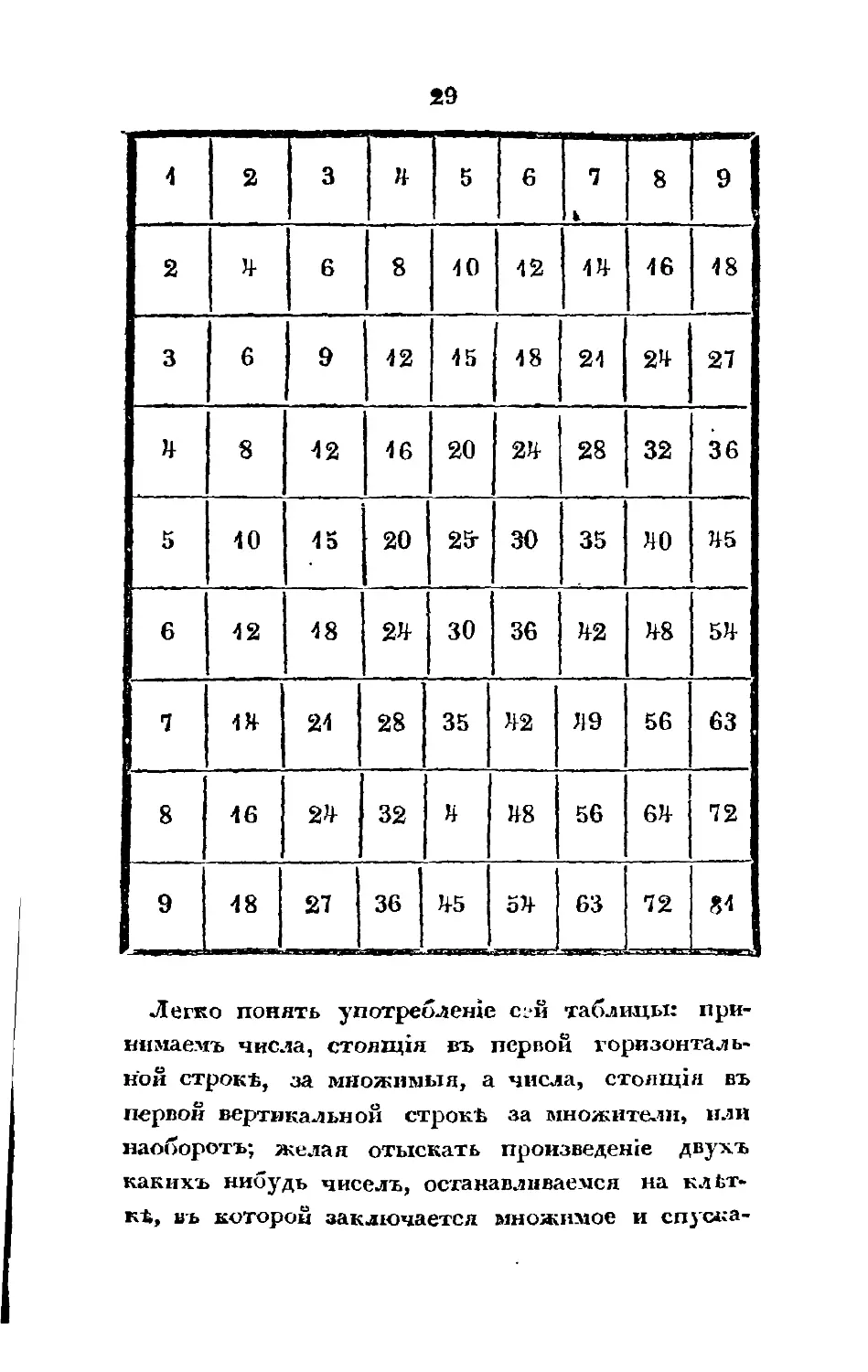
29
1
2
3
4
5
6
7
V
8
9
2
4
6
8
10
12
14
16
18
3
6
9
12
15
18
21
24
27
4
8
12
16
20
24
28
32
36
I 5
10
15
20
25-
30
35
40
45
6
12
18
24
30
36
42
48
54
7
14
21
28
35
42
49
56
63
8
16
24
32
Ч
48
56
64
72
9
18
27
36
45
54
63
72
81
Легко понять употреблеше с:й таблицы: при¬
нимаем* числа, столхщя въ первой горизонталь¬
ной строк*, за множимы я, а числа, стояния въ
первой вертикальной строк* за множители, или
наоборот*; желая отыскать произведение двухъ
какихъ нибудь чиселъ, останавливаемся на кл*т-
к*, въ которой заключается множимое и спуска-

30
ел1ся внизъ по вертикальной его строк* до тЬхъ
норъ, пока придемъ къ той горизонтальной стро-
к*, въ которой находится множитель; число, сто¬
ящее въ кл*тк*, на которой мы остановились, бу-
детъ искомое произведете. Напр. Желая умно¬
жить 8 на 7, въ первой горизонтальной строк*
останавливаемся на кл*тк* 8 и спускаемся внизъ
по вертикальной строк* до 7-й горизонтальной
строки, число 56, так. обр. найденное, будетъ ис¬
комое произведете.
При еемъ зам*тимъ предварительно: на какое
бы число мы не помножали нуль, всегда въ про-
изведенш получимъ нуль: ибо чрезъ повторете
нуля не можетъ составиться никакая величина.
"16. Теперь предложимъ себ* умножить число,
состоящее изъ н*сколькихъ циФръ на число, со¬
стоящее изъ одной цифры. Пусть напр, требует¬
ся 51И8 умножить на 8. Для отыскашя искомаго
произведения должно было бы, въел*дстте опре¬
деления умножешя, число 5JH8 взять слагаемымъ
8 разъ; но можно достигнуть до искомаго про¬
изведетя гораздо легчанпшмъ путемъ, руковод¬
ствуясь сл*дующими зам*ча«1лми: когда мы воз-
мемъ число 5JH 8 слагаемымъ 8 разъ для оты¬
скашя искомаго произведетя, то очевидно, что
каждый иорядокъ единицъ его повторится 8 разъ,
дабы опред*лнть число едшшцъ соотв*тетв.ующа-
го порядка въ произведении; посему произведе-
и е будетъ состоять изъ 8 единицъ, повтореняыхъ
8 разъ, изъ 1 десятка, повтореннаго также 8 разъ,
изъ Я сотенъ и нзъ 5 тысяч*, повторенных* то¬
же 8 разъ; но повторивши 8 разъ 8 единицъ, по-

34
лучкмъ по таблица умножешя въ произведен»!
64- единицы; 4 десятокъ будучи повторенъ В разъ
даетъ 8 десятковъ; 4 сотни, повторенный 8 разъ
дадутъ въ произведения 32 сотни и 5 тысячь, по¬
вторенный 8 разъ дадутъ НО тысячь; следов,
искомое произведен!с будетъ состоять изъ НО ты¬
сячь, 32 сотенъ, 8 десятковъ и 64 едкглцъ; ко •
671 единицы составляютъ 4 единицы и 6 десят¬
ковъ, которые бывъ соединены съ 8 десятками
произведетя составятъ \ 4 десятковъ, которые
опять составляютъ 4 сотню и У- десятка; но 4
сотня будучи соединена съ 32 сотнями произве¬
дения даетъ 33 сотни; 33 сотни составляютъ 3 ты¬
сячи и 3 сотни; придавши 3 тысячи къ 4Э ты-
слчаг.гъ произведения, получимъ 43 тысячи) сдЪд.
произведение будетъ состоять изъ 43 тысячь, 3
сотенъ, 4 десятковъ и 4 единицъ и потому выра¬
зится сл'Ьдующимъ числомъ: 43344.
Для облегчешя можно про- 5448
изводить умножеше сл-Ьдую- х8
щимъ образомъ: подписавши 43344
множителя подъ множимымъ должно повторять
каждый порядокъ единицъ множимаго отдельно;
если какой нибудь порядокъ единицъ при повто-
реши выражается одною цифрою, то ее ставятъ
подъ чертою подъ соотвЬтствующимъ порядкомъ
единицъ во множимомъ; если же какой нибудь
порядокъ единицъ при повторении выражается
двумя цифрами, то подъ соотвЪтствующимъ по¬
рядкомъ единицъ во множимомъ ставится только
первая цифра съ правой руки, а другая придается
къ числу повторенныхъ единицъ слЪдуюхцаго

32
высшаго порядка. Такъ напр, умножая 8 едя*
ннцъ на 8, получичъ 64- единицы, Л единицы ста-
вимъ подъ чертою подъ единицами, а 6 десятковъ
придаемъ къ числу повторенныхъ единицъ слё-
дующаго высшаго порядка, т. е. къ 1-му десятку,
повторенному 8 разъ или къ 8 десяткамъ, что
составитъ 4 7 десятковъ; опять Ч- десятка ставимъ
подъ десятками, а 4 сотню придаемъ къ числу
повторенныхъ сотеиъ и продолжаемъ так. обр.
далЁе, пока повторимъ всё порядки единицъ мно-
жнмаго столько разъ, сколько единицъ заключает¬
ся во множитель. Никогда не должно цифру, про-
изшедшую отъ повтореихя низшаго порядка еди¬
ницъ множимаго, придавать къ высшему порядку
единицъ его прежде повторения сего высшаго по¬
рядка; ибо придавши въ предыдущемъ примЁрЁ 6
десятковъ къ 4-му десятку, мы повторили бы 8
разъ не 4 десятокъ, какъ требовалось вонросомъ,
а 7 десятковъ, что и въ произведены дало бы не
8 десятковъ, а 56 десятковъ.
4 7. Прежде нежели нриступимъ къ умножению
чиселъ въ томъ случаЬ, когда оба производителя
состоятъ изъ нёсколькнхъ цнФръ, посмотримъ, ка-
кимъ образомъ умножается число на 40, 400,
и вообще на единицу съ нисколькими нулями.
Предложимъ сеоЁ воперпыхъ умножить 235 на 40.
Для умножешя 235 на 40 очевидно мы должны
будемъ число 235 повторить 40 разъ, т. е. взять
его слагаемымъ 40 разъ; но при семъ сложеши,
какъ видно, каждая единица числа повторится 40
разъ, т. е. каждая единица сдЪлается дееяткомъ и
5 единицъ даннаго числа сдЁлаютса 5 десятками;

33
также каждый десятокъ повторится 40 разъ и
следов. сдЬлается сотнею, так. обр. 3 десятка дан-
наго числа сдЬлаются 3 сотнями и так. дал.; каж¬
дая цнв>ра даннаго числа получить значеше въ 40
разъ большее; посему, чтобы получить произве¬
дете 235 на 40, надобно только каждой циФрЬ
даннаго числа дать значение въ 40 разъ большее
противъ настоящаго, т. е. единицы сделать де¬
сятками, десятки — сотнями и так. далЬс, а для
сего нужно только (чл. 5) прибавить къ данному
числу съ правой руки нуль, и будетъ искомое
произведете 2350. — Теперь умножпмъ 235 на
400; въ семь случаь надобно будетъ число 235
повторить 400 разъ; слЬдов. въ семъ случаЬ каж¬
дая единица сдЬлается сотнею, каждый десятокъ—
тысячею и так. дал.; слЬдов. и въ семъ случай
для отыскашя нскомаго произведет*! нужно толь¬
ко къ данному числу съ правой руки прибавить
два нуля. СлЬдов. вообще для умножешя какого
нибудь числа на единицу съ нисколькими нуля¬
ми, нужно къ данному числу прибавить столько
излей, сколько находится ихъ во множитель, и
чрезъ это получится искомое произведете.
Но если бы нужно было какое нибудь число
умножить не на единицу съ нЬсколькими нулями,
но на какую нибудь другую цифру, имЬющую
при себь также нЬсколько нулей, тогда дЬиств1е
производится слЬдующимъ ооразомъ: njcTb напр,
требуется число 384- умножить на 60; для сего
нужно бздетъ число 384- повторить 60 разъ; но
повторивши число 384 десять разъ, получимъ 3840,
число, въ которомъ заключается 40 чиселъ, рав-
3

34
иыхъ данному 384; вопросомъ же требовалось со¬
ставить такое число, въ которомъ бы заключалось
60 чиселъ, равныхъ данному, слЬд. въ 3840 недо¬
стаетъ еще 50 чиселъ, равныхъ данному; посему
взявши 3840 слагаемымъ 6 разъ, полу чимъ 6 чи-
селъ такихъ. изъ коихъ каждое заключаеть въ се¬
бе по \ 0 данныхъ чиселъ, и след. въ общей сум¬
ме ихъ будетъ данное число заключаться 60 разъ.
И такъ, чтобы умножить 384 на 60, должно къ дан¬
ному числу' приписать ну ль и повторить его 6 разъ.
Также для у'множешя числа на какое нибудь чи¬
сло сотенъ, или на какую иибудь цифру, имею¬
щую при себе два нуля, должно къ данному' мно¬
жимому приписать два нумя и повторить так. обр.
полученное число столько разъ, сколько сотенъ
находится во множителе. Но какъ мы заметили
въ чл. \ 5, что всякое число, помноженное на пуль,
даетъ въ произведен»! нуль, то при умноженш ка¬
кого нибудь числа на ци<ъру, имеющую при себе
нисколько нулей, можно прежде данное число по¬
множить на циФру множителя и потомъ къ полу¬
ченному так. обр. произведенйо приписать столь¬
ко нулей, сколько находилось ихъ во множитель;
так. обр. помножается всякое число на какую ни-
будь циФру съ нисколькими нулями. Теперь мож¬
но приступить къ тому случаю умножешя двухъ
чиселъ, когда оба производителя состоять изъ не-
СКОЛЬКНХЪ ЦИФръ.
48.	Пу сть теперь требуется 5893 уможить на 453.
По определении умножешя въ настоящемъ случае
число 5893 должно повторить 453 раза т. с. повто¬

35
рить его Зраза, да еще 50 разъ, да еще W00 разъ;
повторивши данное множимое 3 раза, получимъ
47679; повторивши его 50 разъ будетъ 29)1650: и на-
конецъ повторивши его W00 разъ, нмЬемъ 2357200;
слЬд. искомое произведете будетъ состоять изъ
трехъ частныхъ произведении 47679; 29W650 и
2357200. Соединивши сш три частныя произве-
детя вмЬстЬ , получимъ общее произведете
2669529.
Обыкновенно cie д/Ьистяге совер-
шаютъ так. обр-: подписываготъ	5893
множителя подъ множимымъ и ум-	XW 53
ножаштъ множимое отд-Ьльно на 4 7679
каждую цифру множителя, начн-	29W650
нал съ цифры единицъ; помно-	2357200
жая множимое на цифру десятковъ,	2669529
къ найденному произведенно приписываютъ съ пра¬
вой руки нуль; помножая на цифру сотенъ, при¬
писываютъ съ правой руки два нуля и вообще
столько нулей, сколько находится во множитель
цифръ, начиная отъ правой руки до той цифры,
на которую помножаютъ; наконецъ всЬ так. обр.
составленныя частныя произведешя складываютъ
вмЬстЬ и въ суммЬ получаютъ искомое произве¬
дете. Для облегчешя обыкновенно опускаютъ въ
частныхъ произведешяхъ нули; но при семъ должно
соблюдать, чтобы первая цифра съ правой руки
каждаго частнаго произведешя стояла подъ тою
цифрою множителя, на которую помножаютъ мно¬
жимое. Так. обр.:

36
5893
X>*53
Л679
294 65
23572
2669529
Нрн.итьг. \. Не должно думать, чтобы необхо¬
димо было всегда начинать умножете съ единицъ
множителя; можно начинать его съ какого угодно
порядка единицъ множителя и производить д*й-
CTBie въ какомъ угодно порядк-fe, строго только на¬
блюдая правило, чтобы первая ци®ра съ правой
руки въ ртыекиваемомъ частномъ произведении на¬
ходилась подъ тою цифрою множителя, на кото¬
рую помножаемъ множимое; такъ въ предыд} щемъ
пример!; можемъ начать дъйств5е умножешя съ со-
тенъ, потомъ умножать на единицы и наконецъ
ш десятки и тогда дЬнспйе расположится так.
обр.:
5893
Х'453
23572
>17679
29W65
2669529
Примтъг. 2. Если во множите.** на м1;ст! иЬ-
которыхъ порядковъ единицъ-стоять нули, то на
сш порядки единицъ не должно помножать мно¬
жимое: ибо всякое число, помноженное на нуль,
есть нуль, а посему надобно перейти къ тому по¬
рядку единицъ множителя, который имЪетъ зна¬
чительную цифру и на нее должно помножать

37
итожимое, наблюдая притомъ, чтобы первая циф¬
ра отъ правой руки сего частнаго произведения
стояла подъ тою цифрою множителя, на которую
помножаемъ множимое. Напр.
Можно объяснить себь cie д!,истые	3517
и так. обр.: умножить 3517 на 602	Х602
значить 3517 повторить два раза, да	70;№
еще 600 разъ; но повторивши его два 21102
раза, получимъ 70W, а повторивши 211 "J 21Н
его 600 разъ, будетъ 2110200; соединивши сш ча¬
стный произведения, будетъ:
703Л
2110200
211723^
Прн.шы. 3. Мы вндЪли (чл. 17), что если во мно¬
житель на концЬ находится нисколько нулей, то
при производств!; дЬЙствгя умножешя можно ихъ
опускать и прибавлять поел!, съ правой руки къ
найденному пронзведенно. Такимъ же- образомъ,
если бы и во множимомъ на концЬ находились ну¬
ли, то можно ихъ опустить при производств!. дЬЙ-
ствгя умножешя и послЬ прибавить съ правой ру¬
ки къ найденному пронзведенно. Иапр. пусть тре¬
буется Н500 умножить на 39. Отбросивши два ну¬
ля съ правой руки во множимомъ, помножаемъ
W-5 на 39, получимъ произведете 1755; но какъ
данное множимое было не >15, a )i500 или Л-5 со¬
тенъ и какъ произведете "(чл. 1Ч-) должно быть
однородно со множнмымъ, то и произведете долж¬
но содержать въ себъ не 1755 единицъ, а 1755 со¬
тенъ или 175500. Въ практик!, cie дьйствхе произ¬
водясь так. обр..-

435
475500
Также если бы и въ обоихъ производителяхъ бы¬
ли На КОТЩЬ НуЛИ, ТО ПрИ ПрОИЗВОДСТвЪ ДЬИСТВ1Я
можно ихъ опустить и послЬ въ произведенш съ
правой руки приписать столько нулей, сколько
находилось ихъ во множимомъ и во множителЪ.
Напр, пусть требуется 57000 умножить на 3500.
Опуская во множимомъ нули, будемъ 57 умножать
на 3500; по чл. 47 можемъ и во множитель опу¬
стить нули, и тогда придется 57 умножить на 35;
получивши произведете 4995, припншемъ къ нему
съ правой руки два нуля, прежде дЬиствхя опу¬
щенные въ множитель, будетъ, 499500—произведе¬
те 57 на 3500; но должно было не 57 единицъ
умножить на 3500, а 57 тысячь; посему вышенай-
де-нное произведете должно представлять собою
тысячи и слЬд. къ нему надобно приписать еще
три нуля и будетъ искомое произведете: 4 99500000.
Въ практикЬ cie дъйетые производить так. обр.:
57000
3500
285
474 '
499500000.
49.	Если бы нужно было какое нибудь число
умножить на другое число, которое само есть произ¬
ведете двухъ другихъ чиселъ, то вмьсто умноже-
Н1Я даннаго числа на другое данное, можно первое

39
число помножить на производители второго числа.
Напр, пусть требуется 35 умножить на 56; по тре¬
бование вопроса должно 35 повторить 56 разъ, т. е.
составить такое число, въ которомъ заключалось
бы 56 чиселъ, равныхъ 35; ко 56 салю есть произ¬
ведете 7 на 8; посему если мы умножимъ 35 на
7, то составили, число 255, въ которолп, заключает¬
ся 7 чиселъ, равныхъ 35; теперь, если мы число
255 возмемъ слагаемьшъ 8 разъ, то составимъ
8 такнхъ чиселъ, изъ коихъ въ каждомъ заклю¬
чается по 7 чиеелъ, равныхъ 35; слЪд. во вс*хъ
сихъ числахъ т. е. въ общей ихъ сумм* будетъ
заключаться 56 чиселъ, равныхъ 35—что и тре¬
бовалось вопросолгь; сл*д. 35. 56=35. 7. 8=255.
8=1960. Отсюда можно вывесть заключение та¬
кое: когда требуется перемножить между собою
три данныя числа, то должно сперва помножить
первое число на второе и найденное произведете
помножить на третье данное число. Если бы дано
было перелшожить между собою 5 данныя числа,
то по вышесказанному можемъ три посл Ьдтя чис¬
ла принять за производители одного множителя,
на котораго должно полпюжить первое данное чис¬
ло: ибо изъ предыдущаго видимъ, что одно какое
нибудь число можетъ происходить отъ умножешя
трехъ другихъ чиселъ; такъ \ 960 есть произведете
35. 7. 8. Принимая же при улшоженш 5-хъ чиселъ
три послВдшя числа за производители одного мно¬
жителя, умножимъ первое число на второе, най¬
денное произведете умножимъ на треие число и
наконецъ вновь так. обр. найденное произведете
3-хъ чиселъ умножимъ на четвертое данное число.

wo
Напр, требуется перемножить между собою числа
5. Т. 6. 3; умножая 5 на 1 будетъ 35, умножая
cie произведете на 6, получгохъ 210 и наконецъ
умножая 210 на 3, имЪечъ искомое произведете
630; слЬд. 5. 7. 6. 3=630. Точно такимъже обра-
зомъ должно поету'пать и при умножеиш между
собою нЬсколькнхъ данныхъ чиселъ.
20.	Наконецъ сдЬлаемъ последнее замЬчате ка¬
сательно умножетя цЪлыхъ чиселъ, состоящее въ
томъ, что произведете двухъ чиселъ не перемЬ-
няется въ какомъ бы иорядкЬ ни производили ум-
ножете сихъ чиселъ, т. е. подшожаемъ ли первое чи¬
сло на второе или второе на первое. Напр, пусть тре¬
буется 7 умножить на 9. Произведеше будетъ одно
и тоже: помножимъ ли 7 на 9 или 9 на 7 т. е. 7.
9=9. 7. Справедливость этого можно доказать слЪ-
дуюгцичъ образомъ: поелику у множить 7 на 9 зна¬
чить 7 повторить 9 разъ, слЬд. каждая единица 7-ми
должна повториться 9 разъ для составления искома-
го произведешя; и какъ 7 = 1 -|-1 -f-1 -f-1 -f-1 -f-1 -f-1,
то7. 9=1. 9-|-1. 9-f-1.9-J-1. 9-М- 9-f-1. 9-f-1. 9,
но 1. 9=9, и потому 7. 9=9—9—у—9—I—9—j—9—9—у—9;
а 9—Э—9—Р—9—у—Э—9—I—9 составляетъ 9, повторен¬
ное 7 разъ и равняется 9. 7; слЪд. 7. 9=9. 7.
Справедливость сего предложетя можно дока¬
зать и для всякаго числа производителей, т. е.
произведете нЬсколькихъ множителей не перемЬ-
няется въ какомъ бы норядкЬмы ни брали сихъ мно¬
жителей. Напр. перемножимъ между собою три чис¬
ла 3. 5. 7; по предыдущему члену надобно сперва
найти произведете двухъ первыхъ производителей 3.

Hi
. s
5; но no вышесказанному 3. 5=5. 3; слЬд.^3. 5. 7
= 5. 3. 7; далгъе по предыдущему же члену мож¬
но все производители, кроме перваго съ левой ру¬
ки, разсматривать за производители одного мно¬
жителя, на котораго надлежало бы умножнть'пер-
выи производитель 3; след. этотъ множитель мож¬
но разсматривать какъ произведете двухъ послЬд-
нихъ производителей 5. 7; но произведете двухъ
чиселъ не переменится отъ перемены порядка
производителей; посему множитель, на который
надлежало бы помножить первый производитель
3, останется одинъ и тотъ же, составимъ ли мы его
изъ 5. 7 или изъ 7. 5, а потому 3. 5. 7=3. 7. 5;
точно также можно доказать, что 3. 5. 7 =3. 7.
5=7. 3. 5 = 5. 7. 3 и проч. Такимъ же образомъ
можно доказать справедливость разбнраемаго на¬
ми предложешя при Ч-хъ, 5-ти и вообще при не-
сколькихъ множителяхъ. Польза сего замЪчашя
открывается при умноженш такихъ чиселъ, изъ
которыхъ множимое содержитъ въ себе менее
циФръ, нежели множитель; тогда можно наоборотъ
множителя принять за множимое, а множимое дан¬
ное за множителя. Напр, пусть требуется 53 умно¬
жить на 37И25. Принимая 53 за множимое, а
37Н-25 за множителя, должны будсмъ для опреде-
лешя искомаго произведешя составить пять част-
ныхъ произведении; но принимая 37)125 за мно.
жимое, а 53 за множителя, получимъ тоже самое
произведете, которое требуется вопросомъ; но для
отыскашя его должны будемъ составить только
два частныя произведешя.

52
О Д Ъ Л Е Н I И.
21. Разделить одно число на другое, значить
найти такое третье число, которое будучи умно¬
жено на второе, дало бы первое число. Первое чи¬
сло или то, которое требуется разделить на вто¬
рое, называется дгъламьииъ; второе число или то,
которое делить первое, называется д/ълитслемъ;
а третье число или то, которое определяется д*й-
стввемъ деления, называется гастнылъ. Для того,
чтобы показать, что одно число делится на дру¬
гое, употребляется знакъ (:), и вместо того, чтобы
говорить и писать: такое-то число делится на та¬
кое-то, ставятъ между ними знакъ две точки (:).
Напр, чтобы показать, что 8 делится на 2, изо-
бражаютъ cie дейспйе так. обр. 8 : 2.
22. Изъ предыдущаго видно, что делимое есть
произведете делителя на частное, изъ коихъ каж¬
дое можетъ быть принято за множимое и след,
за число, изъ котораго составляется делимое, какъ
произведете; и потому принимая частное за мно¬
жимое, можеяъ сказать, что разделить одно чи¬
сло на другое, значить найти такое третье число,
изъ котораго бы делимое было составлено такъ,
какъ делитель составленъ изъ единицы; или найти
такую часть делимаго, какую часть единица со-
ставляетъ относительно делителя. Напр. 56 разде¬
лить на 7; въ семъ примере 1 есть седьмая доля
делителя, следов, дЬнствтемъ делешя надобно оты¬
скать седьмую долю делимаго, т. е. такую вели¬
чину, чрезъ повторение которой 7 разъ получимъ
56; легко по таблице умножешя отыскать, что
искомое число будетъ 8. Принимая делителя за

^3
множимое, можемъ сказать, что раздоить од¬
но число на другое значить найти такое тре¬
тье число , которое бы такъ составлено бы¬
ло изъ единицы, какъ дЬлимое составлено изъ
дЬлителя; или найти такое число, которое содер¬
жало бы въ себь единицу столько разъ, сколько
разъ дЬлимое содержитъ въ себь дЬлителя. Напр.
36 разделить на Ч; следов, надобно узнать, сколько
разъ дЬлимое 36 содержитъ въ себь делителя Н-;
чтобъ узнать это, отнимечъ Ч отъ 36, останется
32, отнимемъ отъ 32 еще Ч, останется 23 и такъ
дадЬо продолжишь послЬдовательныя вычиташя
дЬлителя изъ уменьщающагося постепенно дЬ-
лимаго до тЬхъ поръ, пока получимъ въ остат-
кЬ нуль; тогда число послЬдовательныхъ вычита-
нш дЬлителя изъ дЬлнмаго и покажетъ, сколько
разъ cie послЬднее число содержитъ въ себь пер¬
вое — это и будетъ искомое частное; такъ въ
настоящемъ примЬрЬ можно отнимать Ч отъ 36
послЬдовательно 9 разъ, и потому 9 въ настоя¬
щемъ случаЬ будетъ искомое частное. Легко по¬
нять, что послЬдшя два опредЬлешя дьйств'по дЬ-
лсшя сами собою входятъ въ первое, выражен¬
ное въ предыдущемъ членЬ, т. е. раздЬлить одно
число на другое значить найти такое третье чи¬
сло, которое, будучи умножено на второе, дало
бы первое число.
23.	Понявши хорошо сш опредЬлешя дьйств1я
дЬлешя, легко приступить къ самому дЬиствйо.
Если дЬлимое будетъ состоять только изъ 2-хъ
цифръ, а дЬлитель изъ одной, то легко будетъ
опредЬлпть частное или числомъ послЬдователь-

чч
ныхъ вычитанш делителя изъ делима го, или отыс¬
кивая въ таблице умножения приличное число,
которое бы, будучи умножено на даннаго дели-
теля, дало въ произведепш данное делимое. Ио
при семъ можетъ встретиться следующее затру-
днеше: пусть напр, требуется 30 разделить на Ч;
производя последовательный вычитанхя дЬлителя
изъ дЬлимаго, увидимъ, что делитель можетъ быть
вычтеиъ изъ дЬлимаго Ч разъ и останутся еще
2 единицы, изъ которыхъ уже нельзя отнять де¬
лителя Ч; или отыскивая по таблице умножения
приличное число для частнаго, увидимъ, что Ч
будетъ мало, а 8 много; и такъ въ этомъ. случае
ловидимому нельзя определить настоящаго ча¬
стнаго. Постараемся же преодолеть это затрудне-
Hie: общее олределете делешя есть: разделить,
одно число на другое, значить найти такое третье
число, которое, бу дучи у множено на второе, дало
бы первое; въ настоящемъ случае требуется раз¬
делить 30 на Ч, сдЬдов. требугется найти такое
число, которое буду'чи умножено на Ч, дало бы
30; но мы видели, что Ч для сего мало, а 8 много:
ибо Н. 7=28, а W-. 8=32; и потому частное дол¬
жно быть более Ч и мен (.с 8; но между 7 и 8
разность есть только единица, следов, искомое
частное есть Ч съ несколькими долями единицы;
теперь все затруднение состоитъ въ томъ, чтобы
определить сколько должно быть долей въ част-
номъ и кактя доли единицы (чл. Ч); но разделяя
30 на Н-, мы нашли, что въ частномъ будетъ 7; 7
же будучи умножены на Ч, даютъ 28; так. обр.
въ делимомъ остаются еще 2 единицы, для ко-

45
торыхъ надобно пршскать въ частномъ такую
величину, которая, будучи умножена на 4, дала
бы 2 единицы; изъ сего заключаемъ, что въ
частномъ должно быть число таково, что оно
составляетъ 4-ю долю 2-хъ единицъ; следов, иско¬
мый доли единицы въ частномъ должны быть
выражены четвертыми долями; но какъ каждая
4-я доля единицы чрезъ повтореше 4-хъ разъ
даетъ только одну единицу, то для двухъ еди¬
ницъ должны быть двЬ четвертый доли, чрезъ
повтореше коихъ 4 раза составятся 2 единицы, и
потому въ частномъ будетъ дробъ и все част¬
ное отъ разд*лешя 30 на 4 выразится чрезъ 7, да
еще I или 7+“ или cie сокращенно пишутъ 7*, т.
е.	ставятъ дробъ частнаго подл* ц*лон его вели¬
чины безъ всякаго знака, и говорятъ частное есть:
семь единицъ и дв* четвертыхъ доли единицы.
Возмемъ еще подобный прин*ръ: пусть тре¬
буется разделить 47 на 8; отыскивая частное,
увндимъ, что оно будетъ бол*е 5 и менЬе 6: нбо
5. 8 = 40, a G. 8 = 48; посему искомое частное
будетъ 5 съ нисколькими долями единицы; для
онредЬлсшя сихъ долей разсуждаемъ такъ: по¬
елику 5 умноженное на 8 даетъ 40, то до даннаго
д Ьлимаго недостаетъ въ семъ чпсл* еще 7 единицъ и
потому въ частномъ къ 5 должна быть прибавлена
еще такая величина, которая будучи повторена
8 разъ, дала бы 7 единиц ь; слЬдов. cin величина
должна быть 8-я доля 7 еднннцъ, и какъ 8-я доля
о%пои единицы есть *, то 8-я доля 7 единиць бу¬
детъ ~ и потому искомое частное будетъ 5-4—~ или

Й6
Такимъ же образомъ найдется частное во вся-
комъ подобномъ случаЬ.
24.	Изъ предыд^щаго видно, что для опредЬ-
лешя частнаго надобно или отыскать его въ таб-
лицЬ умножешя, или вычитать дЬлителя изъ дЬ-
лимаго столько разъ, сколько это возможно; но
какъ, при дЬлеши чиселъ болЬе сложныхъ, неже¬
ли Kanin были предложены въ предыдущихъ чле-
нахъ отыскаше частнаго въ таблиц! умножешя
не возможно, а вычиташе дЬлителя изъ дЬлнмаго
продолжительно, то старались отыскать способы
болЬе общте, приличные всЬмъ возможнымъ чи-
сламъ и значительно облегчающее самое дЬиствтс.
Разсмотримъ же теперь, въ чемъ состоять сш спосо¬
бы. Чтобы удобнЬе изложить ихъ, раздЬлнмъ д ьйст-
Bie дЬлешя на два случая: \ ) когда дЬлимое состоитъ
изъ нЬсколькихъ цнфръ, адЬлитель изъ одной; 2)
когда дЬлимое и дЬлитель состоять изъ нЬсколь¬
кихъ циФръ.
\ -и слугссй: Пусть предложено 8316 раздЬлнть
на 6. Такъ какъ дЬистгйечъ дЬлешя спхъ дв>хъ
чиселъ должно отыскать такое третье число, ко¬
торое будучи помножено на 6, давало бы данное
дЬлимое 8316, то единицы, десятки и т. д. сего
искомаго числа должны быть таковы, что умно¬
живши ихъ на 6, должны бздемъ получить еди¬
ницы, десятки и т. д. даннаго дЬлпмаго. II такъ
вопервыхъ въ частномъ циа>ра единицъ должна
быть такова, что } множивши ее на 6, должны
будемъ въ пронзвсденш получить 6 единицъ и
можетъ быть нЬсколько десятковъ; одинъ взглядъ
на таблицу умножешя удостовЬряетъ, что сему

Wl
у СЛОВНО удОВЛСТВОрЯЮТъ цифры I и 6: въ первомъ
слу чаЬ получимъ 6 единицъ, а во второмъ 36 еди¬
ницъ, т. е. 6 единицъ и 3 десятка. II такъ какъ
ничто еще не определяете намъ взять ли ту или
другую цифру за циФру единицъ въ частномъ,то
беремъ но произволу I. Далее цифра десятковъ
въ частномъ должна быть такова, что умноживши
ее на делителя 6, должны б у демъ получить по
крайней Mt.pt II десятковъ, или вообще несколько
сотенъ и одинъ десятокъ; опять таблица умноже¬
ния удостоверить насъ, что нЬтъ ни одной такой
циФры, которая бы будучи умножена на 6, дава¬
ла несколько десятковъ и одну единицу; изъ сею
заключаемъ, что одинъ десятокъ въ делимомъ
произошелъ не отъ одного умножешя десятковъ
частнаго на делителя 6, но отъ десятковъ част-
наго, умноженныхъ на делителя и еложенныхъ съ
десятками, произшедшимн отъ умножешя еди¬
ницъ частнаго на делителя; и потому цифра I,
принятая нами за цифру сдшшцъ въ частномъ не
можетъ въ настоящемъ случае удовлетворять
вышесказанному условии: ибо произведете I на
6 не можетъ составить ни одного десятка. II такъ
приничаемъ за цифру единицъ въ частномъ чи¬
сле цпФру 6; произведшие 6 на дЪлителя 6
даете 36 или 6 единицъ и 3 десятка; и потому
для цифры десятковъ частнаго числа надобно npi-
искать та куч о цифру, которая бы будучи умно,
жена на 6 вместе.съ 3 десятками, произшедшимн
оть единиц ь, составила несколько сотснъ и одннь
я
десятокъ; следов, произведете десятковъ частнаго
на делителя должно быть пли 8 или 18 или 28,

или вообще произведение cie должно быть выра¬
жено двумя цифрами, изъ конхъ первая съ правой
руки должна быть 8, и потому за цифру десятковъ
въ частномъ можно взять или 3 или 8. Прини¬
мая 3, получимъ 3. 6 = 48 десятковъ, да еще 3
десятка будетъ всего 24 десятокъ, т. е. 2 сотни
и 1 десятокъ. Дал*е цифра сотенъ въ частномъ
должна быть такова, что умноживши ее на 6 и
сложивши съ произведешемъ 2 сотни, пронзшед-
Ш1Я отъ десятковъ, должны получить н-Ъсколько
тысячь и 3 сотни; слЬдов. произведете сотенъ
частнаго на делителя 6 должно быть или 4 4 или
21 или 34, или вообще выражено двумя цифрами,
изъ коихъ первая съ правой руки должна быть
4; но какъ по таблиц* умножешя ни одна изъ
девяти циФръ не удовлетворяетъ сему условно, то
заключаемъ, что не то число сотенъ, пропзшед-
шихъ отъ десятковъ, должно быть придано къ про-
изведенно сотенъ частнаго на дЬлнтеля 6. И по¬
тому за цифру десятковъ частнаго должно при¬
нять не 3, а 8. Умноживши 8 на 6 и придавши 3
десятка, произшедшге отъ единицъ, получимъ 54
десятокъ, т. е. 5 сотенъ и 4 десятокъ. II такъ ци¬
фра сотенъ въ частномь должна быть такова, что
умноживши ее на 6 и придавши 5 сотенъ, про-
изшедппя отъ десятковъ, получимъ нисколько
тысячь и 3 сотни; слЪдов. произведете цифры
сотенъ частнаго на дЬлителя 6 должно быть или
8 или 48 или 28, или вообще число, выраженное
двумя цифрами, изъ коихъ первая съ правой ру¬
ки есть 8; сему условно удовлетворяютъ цифры
3 и 8. Принимая 3 за цифру сотенъ въ частномъ,

>IG
будетъ 5-6 =18, да еще 5 сотенъ отъ десяЬковъ,
всего 23 сотни, т. е. 2 тысячи и 5 сотни. Нако¬
нец ь цифра тысячь въ частномъ должна быть
такова, что умноживши ее на делителя 6 и при¬
давши къ сему пронзведенно 2 тысячи отъ сотенъ,
получимъ 8 тысячь делима го; очевидно, цифра
тысячь въ частномь будетъ \. И такъ искомое ча¬
стное будетъ: 1386.
Всякой легко заметить можетъ, какая труд¬
ность представляется при определенен циФръ ча-
стиаго по предыдущему способу — надобно
брать ciii цифры по произволу и почти при каж¬
дой циФръ частнаго переделать два или несколько
одинакихъ действШ вычнслешя, и если бы дели¬
тель состоялъ более, нежели изъ одной циФры,
то почти не было бы никакой возможности опре¬
делить по сему способу цифры частнаго: и какъ
вся трудность состоитъ въ томъ, что не умеемъ
въ делимомъ, какъ въ сумме чаетныхъ произве¬
дений делителя на единицы, десятки, сотни и т.
д. частнаго, отделить енхъ чаетныхъ произведе¬
ний одного отъ другаго, то и старались открыть
для определенен частнаго другой спогобъ, въ ко-
торомъ бы въ продолжений самаго деисыця сш
чпетныя произведешя отделялись сами собою. Сего
условёя достигли на основаши следующихъ раз-
суждгнш: пусть предложено разделить 57348 на
Н. Поелику делимое есть произведете дЬлителя
на частное, то заключаю, что частное не можетъ
иметь более 5 циФръ, т. е. самый выешш поря¬
докъ единицъ въ частномъ есть десятокъ тысячь:
ибо если бы въ частномъ была хотя одна сотня
Jf

йт
Тысячь, то произведете 100000 на й дало бы ЙООООО,
число большее дел имаго; и такъ остается опреде¬
лить, сколько же находится десяткоЕь тысячь еъ
частномъ; опять очевидно, что болЬе одного де¬
сятка тысл 1ь въ частном ь быть не можетъ: ибо
произведшие 2 чъ десятковъ тысачь па Й даетъ
80000, число большее дЬлимаго; убедившись, что
Вь частномъ можетъ быть только одпнъ десятокъ
тысячь, возмемъ произп -деже сего десятка тысячь
частнаго на делителя Й н вычгемь cie произведе-
Jiie изъ десятковъ тысачь дЬлнмаго, т е. гыч-
темъ Й изъ 5, въ остатке получимъ I десятокъ
тысячь, произшсдннй отъ просгыхъ тысячь. При¬
ведя сей десятокъ тысячь г.ъ просты я тысячи и
соединяя съ ними 7 тысачь дел имаго, получимъ
всехъ простыхъ тысячь въ делнмомъ 17; опять
очевидно, что ъъ частномъ более Й-хъ тысячь
Сыть не можетъ: ибо 5 тысячь, будучи умноже¬
ны на делителя Й, даютъ 20 тысячь, число боль¬
шее 17 тысячь делимаго; и такь въ ча тномъ чи¬
сло тысячь будетъ выражено Й-мл; взявши про¬
изведете й-хъ тысячь частнаго на делителя й,
получимъ 18 тысячь; вычитая cie число тысячь
изъ 17 тыслчь дЬлимаго, будетъ въ остатке I ты¬
сяча, произшедшан отъ сотенъ. Приведя ciio ты¬
сячу еъ сотни и присоединяя къ числу сотенъ,
содержащихся вь сен тысяч Ь, число сотенъ, дан¬
ное въ делимом!, получимъ всего \ » сотенъ въ
делнмомъ п опять, ни ссяовашн подобныхъ выше¬
изложенному разсужден;й, заключаемь, что въ ча¬
стном ь более • -хъ сотенъ быть не можетъ; взявши
произведете сихъ з-хъ сотенъ частнаго на дели-

88
I
телп 8 п вычтя cie произведете изъ 43 сотен»
дЫюшгО) получимъ въ остатка 4 сотню, пронз-
шедшую отъ десятковъ. Приведя сно сотню въ
десятки и присоединяя къ нимъ данные въ дЬли-
ыомъ 8 десятка, получимъ всего въ дЬлпмомъ 48
десятковъ и въ частномъ число десятковъ будетъ
выражено цифрою 3; произведете 3-хъ десятковъ
на делителя 8, будучи вычтено изъ 48 десятковъ
дЬлимаго, даетъ въ остатке 2 десятка, пропзшед-
uiie оть единицъ- Приведя cin два десетка въ еди¬
ницы и присоединяя къ нимъ 8 единицъ дели¬
ма го, получимъ всего въ дЬлцмомъ 28 едннпцъ н
въ частномъ циФра еднницъ бу детъ 7; произве¬
дете ецхъ 7 едппицъ на делителя 8, будучи вы¬
чтено пзъ 28 единицъ дЬлимаго даетъ въ остат¬
ка нуль. Такимъ образо.мъ частное отъ дЪлешя
57388 на 8 будетъ выражено числомъ: 4 8337.
Въ практик-fe cie дЪнствте ра-
57388
8
сполагаютъ такнмъ образомъ:
8
48337
Определивши въ частномъ чи¬
4 7
сло единицъ самаго высшаго
4 G
порядка, какъ въ настоящемъ
43
случае 4 десятокъ тысячь, ио-
42
множаютъ cie число на дели¬
48
теля и произведете 8 десятка
42
тысячь вычитаютъ изъ соот»
28
ветствующаго порядка едн-
28
ницъ въ дЪлнмомъ, именно пзъ	О
5 десятковъ тысячь, въ остатка нолучаютъ 4 де¬
сятокъ тысячь, произшедийн отъ тысячь; сен де¬
сятокъ тысячь прнводятъ въ тысячи, будетъ 40
тысячь, да 7 тысячь въ дЬлпмомъ, что составить

49
вмЬстЬ 4 7 тысячь; въ частномъ должно быть
столько тысячь, что помноживши cie число ты¬
сячь на дЬлителя, получимъ или ровно 4 7 ты¬
сячь, или число меньшее 4 7: сему условно }до-
вдетворяють 4 тысячи; помноживши ихъ на дЬ¬
лителя, б}гдетъ 4 6 тысячь; вычитая 4 6 тысячь
изъ 4 7, въ оетаткЬ будетъ 4 тысяча; приведя cifo
тысяч}' въ сотни, будет/, 40 сотенъ и присоеди¬
нивши къ нимъ 3 сотни дЬлнмаго, пол} чимъ всего
43 сотенъ и найдемъ въ частномъ 3 сотни, ко¬
торыхъ произведете на дЬлителя дг стъ 4 2 сотенъ;
по вычнтан'и сихъ 4 2 сотенъ изъ 43, въ остаткЬ
• 7
б}’детъ 4 сотня или 40 десятковъ, да 4 десятка
въ дЬлнмомъ, составятъ 4 4 десятковъ; продолжая
так. обр. разеуждешя, подобныя вышензложен-
нымъ, опредЬлнмъ десятки и наконецъ единицы
въ частномъ и тогда или въ послЬдиемъ остаткЬ
будетъ Н}гль и частное число выразится ровно
какнмъ ннбздь цЬлымъ числомъ; или въ послЬ-
днемъ остаткЬ получи с,н какая ннбудь значитель¬
ная цифра и тогда частное выразится по чл 23-му
цЬлымъ съ дробъю.
Вотъ еще примЬры;
270579’'
7
52894653
8'
24
386542
48
CG4 4 834 —^
«0 29
~48
66
Ь6 28
48
64
45 44
If
5
42
4 4
8
24
"37
0
44
4 >
35
8
8
5

50
II-й Слугай: Пусть предложено 1216315 раз¬
делить на 37.
Самый высшш порядокъ
единицъ въ частномъ будетъ
десятки тысячь: ибо если бы
въ частномъ была одна сот¬
ня тысячь, то умноживши
ее на делителя, получили бы
въ пронзведешн 37 сотень
тысячь, между темъ, какъ
вь делнмомъ только 12 со¬
тенъ тысячь. Остается те¬
перь определить число десятковъ тысячь въ ча¬
стномъ; это число должно быть таково, что умно¬
живши его на делителя, должны получить или
ровно 121 десятокъ тысячь, какъ въ деликомъ,
или число меньшее этого; след, въ частномъ бу¬
детъ 3 десятка тысячь: ибо Й десятка тысячь, бу¬
дучи помножены на делителя даютъ 138 десятковъ
тысячь — число, большее делнчаго; вычитая про-
изведен'е 3-хъ десятковъ тысячь на делителя изъ
121 десятка тьюпчь въ делимомъ, получимъ вь
остатке 10 десятковъ тысячь; теперь, желая оты¬
скать тысячи въ частномъ, опредЬлимъ число ты¬
сячь въ делнмомъ; оставшееся 10 десятковъ ты¬
сячь составляюгь 100 тысячь да еще въ делн-
момъ 6 тысячь, всего будетъ 106 тысячь въ де¬
лимомъ; разсуждая подобно вышесказанному, най-
демъ въ частномъ 2 тысячи; вычитая произведе¬
те ихъ на делителя изъ 106 тысячь, получимъ
въ остатке 32 тысячи или 320 сотенъ, да 3 даи-
1216375^
111	I32875
"106
5Й
З'З
296
277
259
185
185
~тг

54
нып сохни въ дЪлимомъ, составяхъ всего 323 сот-»
нп, которымъ въ частномъ соотвЬтствуютъ 8 со*
тенъ; и такъ далЬе разсуясдая нодобнымъ оораэомъ,
доидемъ до опредЬлешя въ частномъ ннзшато по¬
рядка единицъ, х. е. простыхь единицъ.
Возмемъ еще болЪе сложный примЬръ: ntjсть
требуется *7ЧНЗ£7625 разделить на 875.
Самый высппй порядокъ
единицъ въ частномъ будетъ
сотни тысячь: ибо еслнбы
въ частномъ былъ одпнъ мил-
люнъ, то умножая его на
дТлителя, получили бы 875
миллюноиъ, а въ дЪлимомъ
только ЧЧЧ миллиона: раз-
суждзя такъ-же, какъ въ предыдз'гцемъ лрнмЬрЬ,
иаиде.мъ въ частномъ 5 сотенъ тысячь; вычитая
произведсше снхъ 5 сотенъ тысячь на дЪлнтеля
изъ	сотенъ	тысячь дЪличаго, ползгчимъ въ
остатка 68 сотенъ тысячь, или 680 десятковъ ты¬
сячь да 2 десятка тысячь въ дЬлпмомъ, всего бу¬
детъ 682 десятка тысячь; если бы въ частномъ
Сылъ одпнъ десятокъ тысячь, то умножая его на
дЪлителя полз чили бы 875 десятковъ тысячь —
число, большее десятковъ тысячь дЬлнмаго; изъ
сего заключаемы что въ частномъ не находится
ни одного десяа ка тысячь и посемзг па lubcTt лхъ
ставимъ нуль; теперь, желая спредЬлить число
тысячь въ частномъ, опредЬлнмъ сначала число
сныхъ въ дЬлпмомъ; 682 десятка тысячь состав-
ляютъ 682 J тысячь, да данныя 7 тысячъ въ д£-
Ь-1! .4-327625
4375
6827
64 25
7026
7000
2625
2625
0
875
507803

.тпмомъ составятъ пмЬстЬ 6827 тысячь, въ паст-
номъ соотвЬтствуютъ имъ 7 тысячь; разсуждая
подобнычъ образомъ, найдемъ всЬ цифры частна*
, го числа въ такомъ внд Ь, какъ out означены въ
прнмЬрЪ.
25.	Изъ всего вышесказаннаго можно выгееть
слЬдуюгце ■ общее правило для дЬлешя одного
цЬлаго числа на другое: доллсио написать дю-
ли/пеля съ правой спарены дгь нечто; отдп.-
лпть п.гъ верпчика.п.ною чертою и т дчерк-
путь дгьлитсля; поталь должно огпд/ьлить
вЪ дгЪЛП.нОЛП. СЪ Л/ЬСОП рЖ'Л СП10Л1К) ипф; ъ,
сколько находится < пыль въ д/ь.т/пел/ь, гели
д/ь.штель ланье сихъ птд/ьленпыхъ циф/ъ съ
д/ъ.шлюль-; въ п’ютивио.иъ слуга/ь должно съ
д/ь.н/люлгъ огпд/ьлить одною цофрою бол г ье про¬
тивъ д'ьлителя; поступивши так обр., полу-
гилсъ первое огпдгьльпое д/ьлн.иос; /поеда остает¬
ся ушат/, сколько ртъ д/ь.штель заключает¬
ся въ сел1ъ отд/ъльнольъ д/ьлилю.чъ — ото уз¬
нается слюгпря по толсу, сколько разъ пе/:сая
цифра съ л/ьвой pi ки въ д/ьлите.т. c/.dej/oicum-
ся въ одной или въ двухъ первыхь цифрагъ съ
лгьвой j/уки вь 01пд/ьлыюл1ъ д/олилсолчь, найден¬
ная цифра въ гас/пиомъ б) деть означать /пить
очес порядокъ единицъ, какой означаешь первая
цифра съ правой руки въ отс/ьл/ио.иъ дгъли-
молсъ; взявши прляыседчйе найден ион цифры
въ гаепшо.иъ на дчьлителя, вычтелп, ег<> изъ
отдгьльпаго д/ь.и:ло/г(>} къ остатку npunt-
шелчъ елгьдуюшую цифру пзъ д/ьли.паго, так.
сбр. полуги.иъ второе отдельное дчьлилюе; по-

53
добпо предыд)щелу найдется, cko.ii ко ра^ъыс
ernojh.e отдельное делилюе адеряснтъ съ се-
б/ь делителя; цифра еъ частнолп, отвечаю¬
щая ссл1Г, пишется съ правой руки первой
найденной еъ частномъ цифры и означаешь
тотъ oice порядокъ ■единицъ, капой озпа/аетъ
первая цифра съ правой руки во второмъ от-
дельио.иъ дгь.шлю.иъ; продолжая так. обр. да¬
лее, пол | силе все щ/фры съ искомо.нъ хаст-
по.иъ zttc.ie.
При семь должно обратить внпматс на следу¬
ющая два обстоятельства: 1 j Hauiediuu циф)ру въ
част иоле, отпил тощую како.иу пибудь от-
д/ьлънсму дгьлилю.иу, улшожимъ ciio цифру
на делителя, произведение вычте.нъ изъ от-
дгьльиаго дели.ипго и къ остатку прштшелрь
следующую ирфру изъ делилтго, полуночь
так. обр. новое отдельное деление; лю.псетъ
случиться, что cie повое отдельное дгьлилюе
будетъ меньше делителя, тогда въ частполп
па лиьсте цифры, отвплшощей сему и/пдгьль-
по.иу делилюлу, ставить пуль, къ и/адель-
нолеу de.ui.uo.uy, пршшсываютъ елтьдующую
гщфру изъ общаги делилшго и отыскиваюшъ съ
частполеь цифру, отвечающую сел1у пос.ted-
не. и у omde.thfio.ur делилю.иу. 2; Нашедши
цифру еъ час/пнолеъ, отв/ыаюиую кркслу ни¬
будь отдельполу делилюлу, уленоэнаютпъ ее
па делителя, .произведен1е вышгпаютъ изъ
о/пд/ьльпазо де.ш.иаго, полугаютъ въ остатке
число большее делителя—тогда это означаешь,
что взятая въ частпол1ъ цифра меньше нао~

5И-
t
лежащей и потому должно увеличить ее, что¬
бы получить ту цифру, которая въ салюмь
дгьлгь отвпчаетъ е ышесп az ап и с. ay оп.д/ьльнг^иу
дгьлиллслчу,
Прилиъч. Свойства чнсе гь, входящихъ въ д1ж-
ств1Я умножешя и делешя, суть следующая: А~)
Во сколько разъ увеличится пли уменьшится мно¬
жимое или иножптоль, во столько же разъ уве¬
личится или уменьшится и произведете: ибо чЬмь
большее или чемъ .меньшее число будемъ мно¬
жить на одного и того же множителя, темъ боль¬
шее или темь меньшее выйдетъ и произведете;
и наоборотъ, чЪмъ на большее или чемъ на мень¬
шее число полножимъ одно н тоже число, тЬмъ
большее или тёмъ меньшее выйдетъ и произведете;
если множимое и множитель увеличатся или
уменьшатся вместе, то и произведете увеличится
или уменьшится во столько разъ, во сколько
увеличились или уменьшились оба производителя
вместе; папр. если множимое увеличится въ 5 разъ,
а множитель въ 3 раза, то произведете увеличит¬
ся въ 4 5 разъ; ежели множимое увеличится —
во столько разъ, во сколько разъ множитель
уменьшится, или наоборотъ, то произведете ос¬
танется безъ перемены—это свойство можетъ слу¬
жить для поверки дЬиств1Я умножешя- 2) Во-
сколько разъ увеличится или уменьшится дели¬
мое, во столько же разъ увеличится или умень¬
шится и частное: ибо делимое есть произведете,
а делитель и частное—его производители: посему
если мы оставляемъ одного производителя (дели¬
теля) безъ перемены, а самое произведете увели-

55
чиваемъ или уменьшаемъ, то въ следствие преды—
дущаго замечания другой производитель (частное)
должень увеличиться или уменьшиться. Во сколь*
ко же разъ увеличится или уменьшится дели¬
тель, во столько разъ уменьшится или увеличится
частное: ибо при одномъ и томъ же произведет»!,
увеличивая одного производителя (делителя), дру¬
гой необходимо уменьшится; или уменьшая одно¬
го производителя (делителя), другой увеличится.
Если делимое и дЬлитель въ одно и тоже число
разъ увеличатся или уменьшатся, то частное оста¬
нется безъ перемены: ибо увеличивая или умень¬
шая одно делимое, увеличили» пли уменьшили» и
частное, а какъ въ тоже время увеличиваемъ или
умсньшаемъ и делитель, то частное въ следствие
сего, возвращается къ прежней своей величине..
ПОВЪРКИ УМНОЖЕШЯ и ДЪЛЕНЬЯ.
25. Умпожсше можно поверять по сделанному
нами злмечаьпо въ примЪчанш предыдущаго чле*
на, т. е. нашедшн искомое произведете, надобно
увеличить въ несколько разъ данное множимое
н во столько же разъ уменьшить данный множи¬
тель, или наоборотъ, ц потомъ вновь так. обр. най¬
денные множимое и множитель перемножить меж*
ду собою, и если выйдегъ прежнее произведете,
то умножеше сделано верно —Можно еще пове¬
рять умножеше н делешемъ так. обр.: разделить
произведете на множитель, и если верно было
сделано умножеше, то въ частномъ выйдетъ мно¬
жимое; либо р .зделнть произведете на множи-

56
мое, и въ частномъ выйдетъ множитель. Делен/е
можно поверять умножешемъ так. обр.: найден¬
ное частное помножить на делителя, произведете
должно быть равно делимому, если при делети
последнш остатокъ былъ нуль; если же при де¬
лении последнш остатокъ былъ какое нпбудь чис¬
ло, то л множивши при поверке частное на дели¬
теля, къ произведение, так. обр. полученному, дол¬
жно придать последнш остатокъ въ делетн, и сум¬
ма должна Сыть равна данному делимому.
О ДЪЛНТЕЛЯХЪ, ,
27. Числа по происхождению своему разделя¬
ются на два рода: на псрвопашльпыя и крат-
ныя. Первоначальными числами называются те,
которыя делятся безъ остатка на самнхъ себя и
единицу, пипр. 3,5,7,4 4,*43,97,203 и проч. Крат¬
ными называются те, которыя делятся безъ
остатка на кашя нибудь д pyrin числа, напр. 2'4 де¬
лится безъ остатка на 3 и на 8, отъ того н на¬
зывается числомъ кратнымъ 3-хъ и 8-мн. Всякое
число, которое делить другое число безъ остатка,
называется его дгълшпелемъ; такъ 3 и 8 суть де¬
лители 24-.
28. Чтобы разложить данное число на перво¬
начальные его производители, или другими ел ва¬
ми, чтобы отыскать все первоначальный числа,
- которыя будутъ делителями даннаго числа, долж¬
но делить его постепенно до техъ поръ, пока воз¬
можно, на все по порядку первоначальный числа.

57
Напр, требуется отыскать вс-fe первоначальные де¬
лители числа 480. Для сего разделимъ его снача¬
ла на 2, получимъ въ частнсмъ 240; и такъ какъ-
делимое равняется делителю, помноженному на
частное (чл. 24), то будетъ.	.
480=2.240
Поелику 240 есть само число кратное, то раз¬
деливши его на 2, получимъ въ частномъ 420;
посему
480=2. 240=2. 2. 420
Поступивши такимъ же образомъ со 4 20, полу¬
чимъ:
4 20=2. 60 и 480=2.2.2.60
Продолжая так. обр. дал he обнаруживать посте¬
пенно первоначальные делители, получимъ:
480=2.2.2 2.2.3.5
Обыкновенно зто дейетше располагаютъ так. обр.г
пишуть данное число, отделяютъ его вертикаль-
нош чертою и но правую руку сен черты mi¬
ni} ть первоначальные делители по порядку, какъ
находатъ оные, а по лев} ю руку черты подъ дан-
нымъ чнеломъ постеиепно гыходяшдя частниц.
Напр.
480|2
240,2
420 2
60 2
30 2
45 3
5 5

58
i
Возмемъ еще прнмЁръ. Требуется отыскать
яервоначальныхъ делителей числа 360.
360
2
А 80
2
90
2
И-5
3
А 5
3
5
5
СлЬд 360=2-2.2.3 3.5.
29. Нашедши всё первоначальные дЁлители дан¬
наго числа, для отыекашя всЬхъ прочнхъ цЬль-
ныхъ дЬлителей сего числа, докажемъ предвари¬
тельно следующее свойство чиселъ: всякое числоt
к тгорое дюлитъ безъ остатка одного изъ лшо-
окитслей даннаго произвсдсн1яу дгь.шг/го так-
оке безъ остатка и самое произведете. Напр.
56=7.8; 8 разделится на 2 безъ остатка н даетъ
частное JI; надобно теперь доказать, что частное
56 на 2 будетъ также цёлос число. Известно,
что во сколько разъ увеличится делимое при
одномъ и томъ же дЬлителЬ, во столько разъ уве¬
личится и частное; делимое 56 въ 7 разъ больше
дЪ.шмаго 8, слЬд. частное 56 на 2 будетъ въ 7
разъ больше частнаго 8 на 2; но частное 8 на 2
есть цёлос число, посему и частное 56 на 2 бу¬
детъ также цЁлое число въ 7 разъ большее Л-хъ.
Сл1>д. если какое ни будь число дЬлнтся на дру¬
гое число, то и всякое кратное нерваго числа
также разделится на второе число безъ остатка.
30. Поел* сего легко найти всВ цЬльные дЬ-
лителн даннаго числа, когда известны первона¬
чальные его делители: для сего стоить только
перемножать первоначальные дЬлнтелн между со¬

59
бою по 2, по 3, по ^ и такъ далке, совершенно
въ пронзвольномъ порядкЪ Напр, докажемъ, что
произведете 2.3.3 или число 48 будетъ цЪль-
нымь дЪлителемъ 360; поелику 360=2 2.2.3.3.5, то
взявши делители 2.3.3, остаются еще делители
2 2.5, которыхъ произведете будетъ 20; посему
360=4 8 20; послЬ сего очевидно, что одинъ про¬
изводитель 360, именно 48 дЬлитсл на 48 безъ
остатка, то по предыдущему члену и, 360 разд±-
лится на 4 8; такимъ же ' образомъ можно дока¬
зать, что и всякое произведете, составленное изъ
первоначальныхъ дЪлителей даннаго числа, бу¬
дет ь цЪльнымь дЪлителемъ сего числа.
Обыкновенно для отыскашя всЬхъ возмож-
ныхъ цЬльныхъ дЬлителей даннаго числа, соста¬
вляютъ сперва сложные дЪлители нзъ каждаго
огд Ьдешя первоначальныхъ и потомъ уже cm
сложные дЬлчтелн перемножаютъ между собою.
Так. обр. сложные дЬлители числа 360 бу¬
дутъ:
4.2Д,8,
4,3,9,
4,5,
Перемножая первый порядокъ на второ»*, бу¬
дет ъ:
4,2,4^,8,3,6,4 2,2^,9,4 8,36,72.
Перемножнвъ era поел Ьдще дЪлителц на 4 и 5,
получимъ:
4,2Л,8,3,6,4 2.2'к9,4 8,36,7 2,5,4 0,20,Л0,4 5,30,60,4 20,
Л5,90,4 80,360.
Вотъ вс* цельные д*лители числа 360.

60
i
31.	Для того, чтобы облегчить' разложеше дан*
наго числа на первоначальные делители, нужно
показать признаки делимости чиселъ на пергыя
10 чиселъ. Для лснентаго. же уразумЬшя сихъ
прнзнаковъ нужно предварительно доказать сле¬
дующее свойство чиселъ: веяния сумма делит¬
ся безъ остатка на то число, па которое де¬
лятся безъ остатка все ея слагаелчыл числа
по/юзпь. Напр. 63-27-J-36
Если 27 и 36 разделятся безъ остатка на 9,
то на cie число разделится и 63 безъ остатка:
ибо 27, разделенныя на 9, даютъ въ частномъ 3;
36 разделенныя на 9, даютъ въ частномъ Й; след,
число 9 въ 27 повторяется 3 раза а въ 36 по¬
вторяется Й раза; а какъ въ сумму входятъ все
слагаемый вместе, то въ сумме число 9 повто¬
рится 3 раза, да Й раза или 7 разъ, или вообще
какое нибудь целое число разъ; и след, сумма
будетъ также кратное число 9, а посему разде¬
лится на него (по чл. 29) безъ остатка.
32 На 2 делится всякое число, у котораго на
местЬ единицъ находится нуль или какое иибудь
четное число (2,й,6,8): ибо 10,100,1000 и т. д.
делятся на 2- безъ остатка, а потому (по чл. 29)
и всякое число десятковъ, сотенъ, тысячь и т. д.
разделится на 2 безъ остатка; след, для того,
чтобы все число разделилось на 2 безъ остатка,
нужно только, чтобы единицы его разделились
на 2 безъ остатка, что можетъ быть только въ
томъ случае, когда число единицъ будетъ «чет¬
ное.
На 3 и на 9 число делится тогда, когда сумма.

61
цифрт, которыми оно изображено, дЬлптся на 3
и на 9 безъ остатка: ибо всякое число десятковъ,
сотенъ, тысячь и т. д. можно принять за сумму,
т
состоящую изъ какого иибудь числа, кратна го
3-хъ или 9-ти, и нзъ такого числа единицъ, сколь¬
ко было десятковъ, сотенъ, тысячь п т. д. въ
ра осматриваемом* чнслЬ; напр.
А 0=3.3-М И 00=33.3_Н И 000=333.34-1;
40000=3333.3-5—1, и проч.
20=3.6-5~2;200=66.3-5-2;2000=666.?-1-2;
20000=6666.3-5—2, и проч.
30=9.3-5-3;300=99.3-j-3;3000=999.3-5-3;
30000=9999 3-J—3, и проч.
40= 12 3-{-Ч,Ч00='132.3-5—4;4000=1332.3-5-4;
40000=3 3332.3-5-4, и проч.
и т. д., т. е. надобно какое ннбудь число десят¬
ковъ, сотенъ, тысячь и т. д. разделить на 3,
тогда въ частномъ выйдеть какое нибудь число и
въ остаткЪ столько единицъ, сколько было десят¬
ковъ, согенъ, тысячь и т д. въ дЪлимомъ; напр,
разделивши 4000 на 3, получимъ въ частномъ
'1332 и въ остатка 4 и проч.
ПослЬ сего oeiieiib папр. число 4431 и посмо-
трпмъ, разделится ли оно на 3 безъ остатка: по¬
елику
4431 =4000-5-400-5-30-Н,
или въ с.гЬдстрле предыдущаго свойства чиселъ:
4433 = 1332.3-5-4-J-132.3-5-4-5-3.9-5-3-5-1,
всЬ слагаемый, нзъ кото5>ыхъ, какъ сумма, дан¬
ное число состонтъ, можно разделить на два раз-
ряда: одн 1, слагаемый—кратныя З-хъ^ дрдчтя—ис¬
кра тныя 3-хъ оудуть состоять нзъ такого числа

05
единицъ, сколько тысячь, сотенъ, десятковъ и еди-
шщъ въ данномъ числе; так. обр. соединивши от¬
дельно слагаемый кратныя 3-хъ и слагаемый не¬
кратный 5-хъ, изъ первыхъ составится число крат¬
ное 3-хъ (по чл. 31), а изъ вторыхъ составится чи¬
сло, которое будетъ заключать въ себь сумму циФръ
даннаго числа; и потому будетъ: 4431 =числ. кратн.
З-хъ+12; по чл. 31 чпсло 4431 тогда разделится
на 3 безъ остатка, когда разделятся на 3 безъ ос¬
татка его слагаемый; но первое слагаемое, какъ чис¬
ло кратное 3-хъ разумеется разделится на 3 безъ
остатка; след, для разделения на 3 числа 4431 не¬
обходимо, чтобы втород его слагаемое 12 делилось
па 3, т. е. чтобы делилась па 3 безь остатка сум¬
ма циФръ, которыми изображено данное число.
Тоже самое доказательство можно употребить и
для делимости числа на 9.
Всякое число делится на 4, когда две последняя
его цифры съ правой руки делятся на 4: нбо сотня
делится на 4, а потому и всякое число сотенъ, ты¬
сячь, десятковъ тысячь и т. д. какъ кратное сотни
также разделится на 4; след, для разделения дан¬
наго числа на 4, нужно только, чтобъ его десятки
въ совокупности съ единицами разделились на 4 безъ
остатка.
Всякое число делится безъ остатка на 5, когда
на месте единице его стоить о или 5: нбо десятокъ
делится на 5, а потому и всякое число десятковъ,
сотенъ, тысячь и т. д., какъ кратное десятка раз¬
делится на 5; след, для разделешя даннаго числа
на 5 нужно только, чтобы единицы его раздели¬
лись на 5.
5

66
Всякое число делится на 6 безъ остатка тогда,
когда оно делятся вдругъ и на 2 и па 5 резъ ос¬
татка — это слЕдуетъ пзъ чл. 30.
Чтобы узнать, делится ли число па 7 безъ остат¬
ка, должно раздвлнть его отъ правой руки къ ле¬
вой на грани, такъ, чтобы въ каждой грани заклю¬
чалось по три цифры, нзключая последней грани
къ л к вон руки, въ которой можетъ быть двЕ п од¬
на цифра, нотомъ с.южить нечетиыя грани отдель¬
но, а четны я грани отдельно, меньшую сумму вы¬
честь изъ большей суммы и если разность при семъ
полученная делится на 7 безъ остатка, то и все чи¬
сло раздЕлнтся на 7 безъ остатка; напр, число
17218070492 раздвлится на 7 безъ остатка: ибо
-s
раздЕлнвшн его на грани, будетъ: 17, 218,070,492;
возмемъ сумму нечетпыхъ граней, т. е. 1-й п 3-й
будетъ: 492+218—710, потомъ возмемъ сумму чет-
иыхъ граней, т. е. 2-й и 4-й будетъ: 070+17=87,
вычтемъ cfto сумму пзъ суммы нечетныхъ гранен,
т. е. пзъ 710, получимъ разность 623, которая раз¬
делится безъ остатка на 7, посему н все число даиное
раздвлится на 7 безъ остатка; и въ самомъ деле
разделивши 17218070492 на 7, получимъ въ част-
помъ 2459724356 и въ остаткъ нуль.
^ Всякое число делится безъ остатка на 8, когда
три последи!я его цифры съ правой руки делятся
безъ остатка па 8: ибо тысяча раздЕлнтся на 8 безъ
остатка, а потому п всякое число тысячь, десятковъ
тысячь н т. д., какъ кратное тысячи, раздЕлнтся по
ч.1. 29 на 8 безъ остатка; след, для того, чтобы
раздълнлось данное число на 8, нужно только, что¬

t
07
бы сотни его въ совокупности съ десятками и еди¬
ницами разделились на 8 безъ остатка.
На 10 делится всякое число, у котораго на мес¬
те еднннцъ находится нуль, или такое число, кото¬
рое состоите ровно изъ какого ыибудь числа десят¬
ковъ.
35. Общпмъ наибольшнмъ делителемъ двухъ пли
несколькихъ чиселъ называется самое большое чис¬
ло, на которое данпыя числа делятся безъ остатка.
Для того, чтобы отыскать общаго наибольшаго де¬
лителя двухъ или несколькихъ чиселъ, должно раз¬
ложить ciii числа на первоначальные делители по
чл. 28, потомъ взять тъхъ делителей, которые при¬
надлежать всъмъ даннымъ числаме, перемножить ихъ
между собою п так. обр. найденное произведете
будетъ общпмъ наибольшнмъ делителемъ данныхъ
чиселъ. Напр, требуется отыскать общаго наиболь-
шаго делителя между 560 и 480. Разлагая сш чи¬
сла на первоначальные делители, получимъ: 560 —
2.	2. 2. 3. 3. 5 и 480 = 2. 2. 2. 2. 2. 3. 5, обице
делители обонмъ чпсламъ будутъ: 2. 2. 2. 5. 5, про¬
изведете ихъ 120 будете общим ь панболышшъ де-
лителсмъ 360 и 480.	«
Пусть требуется еще найти общаго наибольшаго
делителя чиселъ 480, 540, 990 и 372. Разложивши
данныя числа на первоначальные делители, нолу-
чимъ:
480 = 2. 2. 2. 2. 2. 3. 5; 540 = 2. 2. 5. 3. 3. 5;
990 = 2. 3. 3. 5. И п 372=2. 2. 3. 51.
Обиде делители всехъ данныхъ чиселъ будутъ
2.	3, произведете ихъ 6 будетъ общнмъ наиболь-
шцмъ делителемъ всехъ 4-хъ данныхъ чиселъ.

f
68
34.	Есть еще другой способъ находить общш на-
ибольшш дьлнтель двухъ плн нъсколькнхъ чиселъ.
Разсмотрпчъ сей способъ:	пусть требуется напти
■общш наибольший дьлнтель чиселъ 480 и о72. Оче¬
видно, что общи! наибольший дълитель сихъ чиселъ
не можетъ быть больше меныиаго нзъ снхъ чиселъ,
т. е. не можетъ быть больше 372; посему онъ бу¬
детъ или равенъ сему числу или меньше его; для
того, чтобы общш наибольший дьлнтель данныхъ
чпеелъ былъ равепъ 572, надобно, чтобы 4S0 раз-
дълилосъ безъ остатка на 372; совершивши cie дъ-
лсше, полу'ншъ въ остаткъ 108; нзъ сего заключа-
емъ, что общш наибольшш дьлнтель двухъ данныхъ
чиселъ будетъ меньше 572; но пзвъетно, что дълн-
мос равняется пропзведешю дълителя на частное съ
остаткомъ, то
480 = 1. 372+108.
Если бы мы нашли самое большое число, на ко¬
торое раздвлились бы безъ остатка 372 н 108, то
(по чл. 31) и 480 раздълнлось бы на него безъ
остатка; сльд. вмъсто того, чтобы искать общш на¬
ибольший дьлнтель между числами 480 и 572, мы
должны искать его между числами 372 и 108; по¬
добно предыдущему заключаемъ, что сей общш на¬
ибольший дълптель не можетъ быть больше мень-
шаго изъ данныхъ чиселъ, т. е. 108; раздьлнвшн
572 на 108, получимъ: 372=3. 108+48; изъ сего
равенства и предыдущаго заключаемъ, что общш
наибольшш дьлнтель 480 и 572 будетъ тотъ же
самый, какой будетъ и чиселъ 108 и 48; разеуж-
дая подобно предыдущему, получимъ: 108=2. 48+
12; примьнивши къ сему равенству замъчашя, по-

ОУ '
добныя предыдущими, пайдемь, что 48=4. 12; слъд,
12 будетъ обидимъ наибольшнмъ дълителемъ 48 и
12, по о-му изъ предыдущичъ равеиствъ будетъ ва-
нбольшнмъ дълителемъ и 108; будучи же общпмъ
наибольшнмъ дълителемъ 48 к 108 будетъ нанболь-
шимъ дълителемъ по 2-му равенству и 572; буду¬
чи же общпмъ наибольшим'!» дълителемъ 372 и 108
по 1-му равенству будетъ н наибольшнмъ делителемъ
числа 480 и слЪд. будетъ искомое число--
Птакъ Эля отыскашя общаго наибольшаго дп>-
литвлп Эвухъ чиселъ надобно болыкее изъ данныхъ.
чиселъ раздгьлить иа метшее, на вышедийй прнсемъ.
дгьйствш остатокъ раздгьлить прежниь д/ълитель,
па второй остапюкъ раздгьлить первый остатокъ
и т. Э. продолжать дгъйспше до тгьхъ парь, пока
получится остатокъ, равный нулю, тогда поелгъд-
liiii дп,литель и будетъ общш иапбольийй дгълшиел&,
данныхъ чиселъ. Если бы при семъ дгьйствш вышелъ
озтатокъ равный едишщгь, то это значило быТ
что данпыя числа не имтотъ между собою ни¬
какого общаго дгьлителя и в» таномъ случагь на¬
зываются первыми между собою.
Все вышесказаниое дънств!е располагается так. обр.:.
1081372 3
л24
или лучше эго
нзобра
лучше эго 48 I0S ~
14148 4
О

70
35.	Если бы нужно было найти общаго наиболь¬
шая делителя между нисколькими данными числа¬
ми, то находятъ сперва по вышесказанному способу
общаго наибольшая делителя между двумя изъ дан-
ныхъ чиселъ; потомъ нщутъ второй общш напболь-
шш делитель между первымъ общнмъ наибольшимъ
делителемъ и третьнмъ изъ данныхъ чиселъ; далее
находятъ третий общш наибольший делитель между
вторымъ общнмъ наибольшимъ делителемъ и четвер-
тымъ изъ данныхъ чнселъ и т. д. до последняя
даннаго числа, тогда последит так. обр. найденный
общш наибольшш делитель будетъ общнмъ напболь-
шимъ делителемъ всехъ данныхъ чиселъ.
Пусть напр. требуется отыскать общш наиболь¬
ший делитель чиселъ 180, 210, 490 и 49‘5. Сперва
найдемъ общаго наибольшая делителя (по прсдыд.
чл.) между 180 и 210, это будетъ 30, потомъ меж¬
ду симъ числомъ и данньшъ третышъ числомъ 490
потому же,, способу найдемъ общий наибольший де¬
литель, это будетъ 10, это число будетъ общимъ
наибольшимъ делителемъ уже трехъ данныхъ чи¬
селъ, т. е. 180, 210 и 490; наконецъ потому же
способу найдемъ общш нанб. делитель между 10 и
посльднимъ даннымъ числомъ, т. е. 495, это будетъ
5, вотъ это-то число и будетъ общимъ наибольшимъ
делителемъ всехъ четырехъ дапныхъ чиселъ.
О ДРОБЯХ Ъ.
ПРОИСХОЖДЕШЕ И СВОЙСТВА ДРОБЕЙ.
56. Мы видели (чл. 2), что дробью называется
вообще величина, меньшая единицы или такая вели¬

I
71
чина, которая продета вл яетъ собою одну иди ни¬
сколько долей единицы н что (чл. 7) для полнаго
уразумыня п нзображешя дроби ^ нужно два числа;
одно, которое показываетъ сколько доле»! единицы
нужно для составлешя дроби, а другое, которое но-
казывастъ изъ какихъ долей единицы составлена
дробь; первое называется чнелнтелемъ, а второе —
знаменателем'»., оба вмБсть — членами дроби. Сльд.
чтобы составить какую шюудь дробь изъ единицы,
нужно сперва единицу раздьлить на столько рав-
пыхъ частей, какъ великъ долженъ быть знамена¬
тель искомой дроби (этимъ дъйс'гаемъ узнаемъ, изъ
какихъ частей единицы составляется дробь)—н по¬
томъ взять столько частей, какъ великъ долженъ
быть числитель—(этимъ дыкгтемъ узнаемъ, сколько
разъ прежде найденная часть единицы повторилась
для составлешя дроби). Напр, чтобы составить ^
единицы, нужно единицу раздьлить на 11 равныхъ
частей и взять такцхъ частей 5 — это будетъ зна¬
чить, что 11-я доля единицы повторилась 5 разъ
для составлешя дроби Поелику всякая величина
можетъ быть принята за единицу и всякая величи¬
на, какъ бы она мала не была, можетъ нмьть свои
доли, то н изъ всякой величины можно составить
желаемую дробь, раздьлнвши спо величину на столь¬
ко частей, какъ великъ знаменатель желаемой дро¬
би и взявши так. обр. одну найденную часть столь¬
ко разъ, какъ великъ числитель искомой дроби.
Напр, требуется взять f- доли капитала, состонщаго
изъ 4000 рублен; раздь.пишш 4000 на 5, получимь
800 рублей—это будеть пятая доля даннаго капи¬
тала; повторивши спо пятую долю 2 раза, получимь

72
искомую дробь f- равную 1600 рубл. Требуется най¬
ти ~ пуда; поелику въ цъломъ пудъ 40 Фунтовъ, то
разделивши 40 на 8, получимъ 5 Фунтовъ—это бу¬
детъ осьмая доля пуда; повторивши ейо долю 5 ра¬
за, найдемъ 15 фунтовъ—это и будетъ Д доли пуда.
37. Но нзъ какой бы единицы мы не составляли
дробь, всегда она должна быть меньше единицы, т.
е. въ дробь долей должно входить всегда меньше,
нежели въ единицу; а какъ число долей дроби озна¬
чается числителемъ, а число долей единицы — зна-
менателемъ, то во всякой дроби числитель должеиъ
быть меньше своего знаменателя. Напр. Д, ^т, т и т-
д.	Если мы возмемъ въ дробь столько долей, сколь¬
ко находится ихъ въ единицъ, то выйдетъ дробь,
равная единицъ — такая дробь слъд. есть та, у ко¬
торой числитель равенъ знаменателю; напр. |,	£,
и т- Д- Если же мы возмемъ въ дробь частей
болъе, нежели сколько находится ихъ въ едппицъ,
то выйдетъ дробь, большая единицы—такая дробь
слъд. есть та, у которой числитель больше своего
знаменателя; напр, Д, А и т. д.; таыя дроби на¬
зываются неправильными для отличхя отъ тъ\ъ дро¬
бен, у которыхъ числитель меньше своего знамена¬
теля и который называются правильными дробями.
58.	Изъ предыдущаго члена видно, что для со-
ставлешя всякой неправильной дроби потребна ве¬
личина, большая единицы:	ибо когда мы возмемъ
для составления Д всъ доли, заключаюнцяся въ еди¬
ницъ, то увидимъ, что должно кромъ сихъ Д долей
единицы взять еще f- доли нзъ другой единицы; по¬
сему и представляется вопросъ:	как. обр. опредЪ-
лить сколько нужно было единицъ для составления

1
73
какой нибудь неправильной дроби — это дъйете
обыкновенно выражается такъ:	пзключить	цтьлое
число изъ неправильной дроби: до ръшен'гя сего во¬
проса можйо достигнуть так. обр.: поелику въ не¬
правильной дроби числитель больше своего знамена¬
теля и какъ сей послъднш означаетъ число частей
единицы, , то очевидно, что сколько разъ это число
повторится въ числъ частей дроби, т. е. въ числите¬
ли, столько нужно единицъ для составлошя непра¬
вильной дроби; слъд. чтобы исключить цълое число
изъ неправильной дроби, должно числителя ея раз-
дълить на знаменателя. Напр. раздъливши чи¬
слителя на знаменателя, получимъ въ частномъ 2;
но 2 единицы заключають въ себъ только -f-fj сл%к
еще нужно было взять нзъ третьей единицы;
посему 2-f-T3- или 2Т\> Слъд. всякая непра¬
вильная дробь есть собственно или цъдое число или
цЪлое съ дробью.
59.	II наоборотъ можно всякое цълое число съ
дробью прнвесть въ неправильную дробь, т. е. вы¬
разить цЪлое число въ такихъ же доляхъ, въ ка-
кихъ выражена дробь, при немъ стоящая; напр.
требуется оД прнвесть въ неправильную дробь; для
сего разеуждаемъ такъ: поелику единица, нзъ ко¬
торой составлена дробь •§• выражена въ седьмых ъ
доляхъ и такихъ седьмыхъ долей въ ней находит¬
ся 7, то въ 5 едннпцахъ седьмыхъ долей будетъ
21 доля седьмая, да въ дроби еще 5 долей седь¬
мыхъ; слЪд. во вссмъ данномъ числв будетъ 26 до¬
лей седьмыхъ, т. е. 5^—^. Слъд. для приведешя
цгълага числа съ дробью въ неправильную дрооь
должно цгьлос число помножить на знаменателя

74
дроби, къ произведтио сему придать числителя
данной дроби и подъ сею суммою подписать дан¬
наго знаменателя.
40.	Замьтимъ, что кроив того происхождешя дро¬
би, какое мы объяснили въ чл. 36, можно еще про¬
исхождение оной объяснить и так. обр.:	всякую
дробь можно принять за частное, происшедшее отъ
двлешя меньшаго числа на большее, напр, требует¬
ся раздьлить 3 на 5; изъ чл. 22 явствуеть, что
раздьлить одно число на другое значить найти та¬
кую часть дьлимаго, какая означается дьлителемъ,
такъ въ настоящемъ случав раздьлить 3 на 5 зна¬
чить требуется найти пятую долю трехъ единнцъ;
но три единицы заключаютъ въ себь одну единицу
три раза, посему въ пятой доль трехъ единицъ пя¬
тая доля одной единицы будетъ заключаться три
раза или пятая доля трехъ единицъ будетъ заклю¬
чать въ себь три пяты я доли одной единицы, т. е.
искомое частное отъ раздьлешя 5-хъ на 5 будетъ
равно -f- или такой дроби, у которой числителемъ
будетъ двлимое, а знаменателемъ двлитель. Точно
также можно доказать, что -f- означаетъ или двъ
седьмыя доли одной единицы, или седьмую долю
двухъ единицъ; также означаетъ ил i семь три-
надцатыхъ одной единицы, или тринадцатую долю
семи единицъ и т. д.
Примтьч. Послъ сего легко доказать правило двле-
шя, изложенное въ чл. 25, т. е. въ томъ случаь,
когда дтлимое не дЬлнтся на двлнтеля безъ остатка,
для дополненш цЪлаго частнаго надобно подъ пос-
льднимъ остаткомъ подписать дълнтеля и придать
так. обр. найденную величину къ цьлому частному:

75
\
ибо пусть требуется \ 7 разделить на 5—это значить
иантн пятую долю семнадцати: нашедши частное 3,
помножимъ его на делителя и произведете 15 вы-
.чтемъ нзъ дел имаго 17, въ остатке получимъ 2; це¬
лое частное 5, которое мы нашли, не есть пятая
доля семнадцати, какъ требовалось вопросомъ, а
только пятая доля пятнадцати; след, прнсемъ деле-
нш остались еще 2 единицы ие разделенными, и
чтобы получить пятую долю семьнадцатн, надобно
къ 3, т. е. къ пятой доли пятнадцати единице при¬
дать еще пятую долю двухъ единицъ; а пятая доля
диухе единице, по изложенному въ семъ члене, бу¬
детъ ~ п след, полное частное отъ разделешя 17
на 5 будетъ З-pf или 5^.
41.	Перемены, которыя пронзводнмъ мы въ вы-
численш иадъ числами, нмеютъ целно или увеличить
или уменьшить числа; посему прежде всего раземо-
тримъ, как. обр. можемъ мы увеличивать и умень¬
шать дроби.
1)	Дробь увеличится, если увеличится ея числи¬
тель, а знаменатель останется безъ перемены: ибо
отъ увелнчешя числителя число однехъ п техъ
же частей, входящнхъ въ дробь, становится больше;
напр, въ дроби f- увеличивши числителя въ 2 раза,
самая дробь £ станете въ 2 раза больше прежней
дроби ибо и та и другая дробь составлена изъ
осьмыхъ долей единицы; но число сихъ долей во
второй дроби вдвое больше, нежели въ первой; а
потому н самая дробь будетъ вдвое более #; след,
дробь увеличивается во столько разъ, во сколько
разъ увеличивается ея числитель, оставляя безъ пе¬
ремены знаменателя.

2) Дробь еще увеличится, если уменьшится е.ч
знаменатель, а числитель останется безъ перемены:
пбо отъ уменьшенш зиаменателя части, изъ кото-
рыхъ составлена дробь, становятся крупнее, а число
ихъ остается одно и тоже; напр, въ дроби т%, у-
мсиьшивши знаменателя въ 2 раза, самая дробь
будетъ въ 2 раза больше предыдущей:	ибо	пер¬
вая дробь была составлена изъ пяти двеиадцатыхь
долей единицы, а вторая составлена также пзъ пяти
долей, но не двеиадцатыхъ, а шесты\ъ; каждая же
шестая доля вдвое больше двенадцатой доли одной,
и той же единицы; а потому ~ вдвое болте —г-.
Слтд. во сколько разъ уменьшится знаменатель
дроби, во столько же разъ увеличится дробь. Осно¬
вываясь на семъ, если въ какой нибудь дроби отбро¬
сить ея знаменателя, тогда дробь увеличится во
столько разъ, сколько было единицъ въ знаменателе:
ибо въ семъ случат мы ничто иное дтласмъ, какъ
дТлнмъ (т. е. умеиьшаемъ) знаменателя самаго на
себя. Напр, отбрасывая въ дроби 4 знаменателя 5,
получимъ целое число 3 въ 5 разъ большее •§-.
3) Дробь уменьшится если уменьшится ея числитель,
а знаменатель останется безъ перемены: ибо отъ умень-
шешя числителя число однихъ и техъ же частей, вхо-
дящнхъ въ дробь, становится меньше; напр, въ дроби
т£ уменьшивши числителя въ 3 раза, самая дробь т4-
будеть въ 3 раза меньше прежней: ибо во вторую
дробь трпдцатыхъ долей входить втрое меньше, не¬
жели въ первую. След, дробь уменьшается во столь¬
ко разе, во сколько разъ уменьшается ея числитель.
4)	Др°бь еще уменьшится, если увеличится ея
знаменатель, а числитель останется безъ перемены:

77
ибо отъ увеличешя знаменателя части, нзъ которыхъ
составлена дробь, становятся мелче, а число ихъ ос¬
тается одно н тоже; нппр. въ дроби f увеличивши
знаменателя вь i раза, самая дробь	будеть въ 4
'раза меньше прежн и дроби: ибо первая дробь со¬
ставлена нзъ четырехъ нятыхъ единицы, а вторая
составлена также нзъ четырехъ долей, но не пятыхъ,
а дпадцатыхъ; каждая же двадцатая доля въ 4 раза
меньше пятой доли; а потому и самая дробь въ
4 раза меньше Слвд. дробь уменьшается во столь¬
ко разъ, во сколько разъ увеличивается ся знаме¬
натель.
Итакъ дроби можно увеличивать и уменьшать
двоякимъ образомъ: увеличивая числителя дроби, а
знаменателя оставляя безъ перемъпы; или уменьшая
знаменателя дроби, а числителя оставляя безъ пе-
рсмъны — въ обонхъ сихъ случаяхъ дробь увелн-
чимъ. Уменьшая же числителя дроби, а знаменате¬
ля оставляя безъ перемъиы; пли увеличивая зна¬
менателя дроби, а числителя оставляя безъ пере-
мъны — въ обонхъ сихъ случаяхъ дробь умень-
шимъ.
Примтьч. Основываясь на семь, легко сравнивать
дроби, нмъюиця одншкнхъ числителей или однна-
кихъ знаменателен: ибо при одннакихъ числителяхъ
та дробь будетъ больше, у которой знаменатель
меньше, а при одннакихъ знаменателяхъ та дробь
будетъ больше, у которой числитель больше.
5)	Если къ числителю и знаменателю дроби при-
даднмъ одно н тоже число, то дробь увеличится:
ибо разность между знаменатслемъ и числителеиъ
означаетъ число долей, которыхъ недостастъ въ

78	'
дроби до единицы; придавши одно и то же число
къ знаменателю и числителю, cin разность (чл. 12
прнмьч. 2) не перемъпится; слъд. число долей, не-
достающихъ въ дроби до единицы, останется одно
и тоже; но въ первомъ случаъ величина сихъ долей
будетъ означена зиаменателемъ данной дроби, а во
второмъ тъмъ же знаменателемъ вмъстъ съ придан-
нымъ къ нему числомъ, такъ что знаменатель недо-
стающихъ долей во второмъ случат, будетъ болье,
нежели въ первомъ и потому во второмъ случаъ въ
дроби будетъ величина меньшая, нежели въ первомъ,
недоставать до единицы и слъд самая дробь будетъ
больше прежней; напр, въ дроби а недостаетъ А до
единицы; прндаднмъ къ числителю п знаменателю
дроби а по числу 5, получимъ Т*А; въ сен дроби до
единицы недостаетъ также 4-хъ долей, но не де-
вятыхъ, а двЪнадцатыхъ, т. е. -А^; но «я дробь мень¬
ше А; слъд. въ т%. меньшей величины недостаетъ
до единицы, нежели въ а и потому т\ больше А.
6) Если отъ числителя и знаменателя дроби от-
ннмемъ одно и тоже число, то дробь уменьшится:
причина сего таже, какъ и въ предыдущемъ примъ-
чанш; напр, въ дроби а недостаетъ А до единицы,
отнимемъ отъ числителя н знаменателя дроби А по
числу 2, получимъ дробь А, въ сей дроби до еди¬
ницы недостаетъ А; но А. болъе А; слъд. въ а недо¬
стаетъ до единицы большей величины, нежели въ
А а посему -f- меньше а.
7) Дробь не перемъннтъ своей величины, если
числителя и знаменателя ея умножимъ на одно н
тоже число: ибо умножая числителя дроби, увели¬
чить и самую дробь, во столько разъ, во сколько

79
увеличили ея числителя, а умножая знаменателя дроби,
уменьшимъ ее востолько же разъ, восколько прежде
увеличили, след, возвратнмъ ее къ прежней величи¬
не. Напр. |=tV Равенство сихъ дробей можно до¬
казать и так. обр.:	въ дроби частей берется
вдвое более, нежели въ -J, но за то части въ ^'а
вдвое менее частей въ |: ибо каждая десятая доля
вдвое менее каждой пятой доли единицы; а посему ~
все равно, что Также л =	и	т. д.
8)	Дробь не переменить своей величины, если чи¬
слителя н знаменателя оной раздел имъ на одно и
тоже число: ибо разделяя числителя дроби, умень¬
шимъ самую дробь, во столько разъ, во сколько у-
меньшили ея числителя, а разделяя знаменателя оной,
увеличит» ее во столько же разъ, во сколько прежде
уменьшили, след, возвратнмъ ее къ прежней вели¬
чине. Напр. —-=4- Равенство енхъ дробей можно
доказать п такъ:	частей во второй дроби вдвое
менее, нежели въ первой, но за то каждая часть,
входящая въ вторую дробь, вдвое более каждой
части, входящей въ первую дробь; а посему ~ все
равно, что Также|-4=44=т^=4=|.
Въ СЛЪДСТВ1С сихъ двухъ последнихъ свопствъ
дробей можно одну и ту же дробь представлять въ
различныхъ впдахъ не переменяя величины оной—и
на этомъ-то основываются новый свойства дробей,
такъ называемый сокращение дробей и приведете
дробей к» одному знаменателю.
СОКРАЩЕН1Е ДРОБЕЙ.
42.	Сократить дробъ значить представить ее вь
менъшемъ видтъ не перемпняя величины оной. Оче¬

80
видно сего достигаютъ, деля числителя и знамена¬
теля дроби на одно и тоже число. Напр. требуется
сократить дробь ffj; тотчасъ видно, что эта дробь
сократится на 5: ибо и числитель и знаменатель ея
можетъ разделиться безъ остатка на 5 (чл. 32 );
совершивши cie делете, получимъ:	I7777 = tW
5
Обыкновенно cie действие изображаютъ такъ: ~~ | tVtt
(По чл. 41. 8) дробь будетъ равна	Дробь
еще можно сократить на 9 (чл. 32) будетъ
О
5~	225	45	5
14 ‘ СлЬд' 630 — 126	14'
45
126
Такнмъ образомъ легко сократить всякую дробь,
руководствуясь признаками делимости чиселъ, изло¬
женными въ чл. 32.
Безъ сомнешя гораздо полезнее вместо повторе-
шя несколькнхъ сокращений, какъ въ предыдущемъ
примере, сделать одно сокращеше и представить
дробь въ самомъ меньшемъ виде, не перемьняя ве¬
личины оной — что бываете нужно для облегчены
вычисленш. Сего требовашя достигаютъ, отыскивая
(по чл. 33 или 54) общаго наибольшаго делителя
между числителемъ и знаменатслемъ и потомъ деля
на сен общЫ иаиболышй делитель и числителя и
знаменателя данной дроби. Напр, требуется сокра¬
тить дробь	Нашедши общЫ наибольшш дели¬
тель между 560 и 135, который есть 45, сократишь
на него дробь ц будетъ:
ь6	5	4	S
3 . m 175ГГ" 172|Т
- , также 	 __	;	—-	.
8	275 11	301 7
155
560
Дроби же	|4,	44|,	i»|.	будутъ	несократи-

81
'S
мыя: ибо числители и знаменатели ихъ суть числа
между собою первый (чл. 54).
ПРИВЕДЕИ1Е ДРОБЕЙ КЪ ОДНОМУ ЗНАМЕНА¬
ТЕЛЮ.
45. Мы сказали въ примеч. члена 41 какммъ об¬
разомъ можно сравнивать дроби, имеющая одина-
кихъ знаменателей пли одинакнхъ числителей и у-
знавать которая изъ нихъ больше или которая мень¬
ше; но если бы дроби имели разныхъ числителей
и знаменателей, то для сравнешя пхъ нужно было
бы привести оныя или къ одинакому числителю или
къ одинакому знаменателю; обыкновенно принято за
правило приводить дроби къ одинакому знаменателю:
ибо снмъ средствонъ можемъ не только определить
которая дробь больше, но и какою именно величи¬
ною одна дробь больше другой. Птакъ прнвесть
дроби къ одному знаменателю значить найти вме¬
сто данныхъ дробей друпя имъ равный, но выра-
женныя въ одинакнхъ доляхъ единицы, т. е. имею¬
щая одина каго знаменателя.
Пусть требуется прнвесть къ одному знаменате¬
лю дроби:
5	7	4	6	5
5’ 11’ 9’ 10’ 4'
Очевидно мы удовлетворнмъ требовании, если чи¬
слителя и знаменателя каждой дроби помножимъ на
знаменателей прочихъ дробей, кроме своего: ибо
при семъ дънствш числитель и знаменатель каждой
дроби будетъ помножаться на одно п тоже число
6

82
(произведете знаменателен прочихъ дробей), а пото¬
му получимъ шювь дроби, равныя даннымъ (чл. 41.
7)	н знаменатель каждой новой дроби будетъ соста-
вленъ пзъ произведешя всьхъ знаменателей данныхъ
дробен, а это лронзведеше будетъ одннакое въ ка-
комъ бы порядкъ пе брали мы спхъ производителен
(чл. 20) п слъд. знаменатель у всъхъ вновь полу-
чевныхъ дробей будетъ одппъ п тотъ же.
3.11	35.9	297.10	2970.4	11880
Итакъ:	5^9	= 493-i0 = 4950^ — 19в0о
7.5	55.9	515.10	5150.4	12600
ТГ5 “ 55^9 = 495.10 “ 4950.4 ~ 19800
4 5	20.11	220.10	2200.4	8800
05 “ 45.11	495.10 “ 4950.4 = T9S00
6.5	30.11	530.9	2970.4	11880
10.5	“50.11	550.9	4950.4	19S00
3 5	15.11	165.9	1485.10	14850
4.5	“2011	220.9“ 1980.10“ 19800
Слъд. вмъсто данныхъ дробей §•,	f по-
IV4IIM1 *	1 1 П IS6QO 8 800	II 8 8 о 14-8 Ь О TV1—
* J	19800’	19800 1 19ЯОО’ I 8 8 О О5 I9BOO*
перь очевидно, что самая большая пзъ данныхъ
Дробей есть:	= д, потомъ слъдуетъ	=
it. лалъе	^ п иаконецъ
Примгьч. Вышепоказанный способъ есть общш для
приведения всякнхъ дробей къ одинакому знаменате¬
лю; но опъ обыкновенно при вычпелешяхъ упот¬
ребляется только въ томъ случаъ, когда знаменате¬
ли данныхъ дробей будутъ числа первоначальный
или первыя между собою.
44.	Если знаменатели данныхъ дробей будутъ чи¬
сла кратныя, то можно легче, нежели по нредыду-

83
щему способу, привести таюя дроби къ одному зна¬
менателю: въ сс.чъ случаъ дъйстше пропзводятъ сле-
дующнмъ образомъ: разлагаютъ знаменатели дан¬
ныхъ дробей на первоначальные дтьлители, сравни-
ваютъ дгълители каждого знаменателя съ дгьлите-
лями прочпхъ знаменателей и вводятъ тть дгъли¬
тели въ каждый знаменатель, которыхъ въ немъ
не доспгаепгъ противъ прочихъ знаменателей, по¬
томъ перемножаютъ между собою одна введенные
дгълители и на произведете ихъ помнажаютъ чи¬
слителя и знаменателя каждой соответствующей
дроби. Очевидно, что снмъ средствомъ мы удовле¬
творюсь определенно данному въ чл. 43 приведение
дробей къ одному знаменателю: ибо чрезъ помноже-
ше числителя и знаменателя дроби на одно и тоже
число, получимъ дроби равныл даииымъ; а такъ какъ
число, на которое помножаемъ числителя и знамена¬
теля каждой дроби, есть произведете техъ перво-
начальныхъ делителей, которькъ недоставало пъ
знаменателе ея противъ знаменателей прочпхъ дан¬
ныхъ дробей, то и знаменатели вновь полученныхъ
дробен будутъ одинаковы: ибо въ каждый пзъ ипхъ
введутся те первоначальные делители, которыхъ въ
немъ недоставало противъ прочихъ знаменателен, и
след, каждый знаменатель будетъ произведете оди-
накихъ первоначальпыхъ делителей. Все cie легче
объяснится па примере. Пусть требуется привесть
къ одному знаменателю следуюиия дроби:	jj,
IS S
S6>	60 ■
Разлагая знаменатели данныхъ дробен на перво¬
начальные делители, получимъ:

84
24 = 3.	2.	2.	2	Сравнивая дълнтели перваго
36 = 2.	2.	3.	3	знаменателя съ дълителями про-
56 = 7.	2.	2.	2	чнхъ знаменателей, увидимъ,
60 = 2.	2.	3.	5	что въ первомъ знаменатели
противъ втораго недостаетъ дЪлителя 3, протнвъ
третьего дълителя 7 н противъ четвертаго дълнте-
ля 5; слъд. въ первый знаменатель должно ввести
дълнтели 3, 7 и 5; посту пивши такнмъ же образомъ
съ прочими знаменателями, иайдемъ каше дълнтели
должны быть введены въ каждый изъ данныхъ зна¬
менателей; отдълнвъ вводные дълнтели въ каждомъ
знаменателъ отъ собственныхъ его дълителей и пе-
ремножнвъ ciii вводные дЪлнте.ш между собою, по¬
лучимъ:
24 =	3.	2.	2.	2.
36 =	2.	2.	3.	3.
56 =	7.	2.	2.	2.
60 =	2.	2.	3.	5.
3.	5. 7 = 105
2. 5. 7 = 70
3. 3. 5= 45
2. 3. 7= 42
Итакъ числителя и знаменателя первой дроби
должно помножить на 105; второй дроби на 70;
третьей на 45, н четвертой на 42; совершивши все
cie, получимъ:
3.105	315	11.70	770	13.45	5S5
24.105 = 252U ’ 36.70 = 2520 ’ 56.45 — 2520 5
8.42	536
60 42	2520
Слъд. вмъсто данныхъ дробей f|, ff и -3-,
имъемъ:	лдо а*а п
о’ 2 5»	V 5 2 о 2 5 20
45.	Наконецъ есть случай, въ которомъ еще лег¬
че, нежели въ предыдущем ь члеяъ, приводятся дро¬
би къ одному знаменателю: ото именно тотъ случай,
когда одинъ нзъ знаменателей данныхъ дробен бу-

85
детъ число кратное вевхъ прочихъ знаменателей;
въ семъ случав этотъ кратный знаменатель п будетъ
общимъ знаменателемъ, къ которому должны быть
приведены всВ остальным дроби. Сего достпгаютъ,
двля сей кратный знаменатель на каждаго изъ про-
чичъ знаменателей н на соотввтствующее частное
умножая числителя п знаменателя каждой соотввт-
ствующей дроби. Напр, пусть требуется привесть
къ одному знаменателю елвдуюгщя дроби:
_5_ и -5.JL.
12	“	It. 6
ЗдВсь общимъ знаменателемъ будетъ 96. Раздв-
лпвши сей знаменатель отдВльио на 24, 12 и 48,
увндимъ, что числителя н знаменателя второй дро¬
би должно будетъ умножить на 4; третьей на 8; п
четвертой на 2; совершивши все cie, получимъ:
68. s~ a 	 4-0	»»■»
—	н г9--э = т”г. СлВд. вмвето
24*4.	9Ь}	13*8	48*2	06
данныхъ дробен |f, ff- и ff, получпмъ:	ff,
До. I, 5_я
3 6	96 *
46.	Иногда случается, что большей знаменатель не
будетъ число кратное вевхъ прочпхъ знаменателей,
а только ивкоторыхъ, но чрезъ помпожеше его на
какое нйбудь число сдв лается таковымъ; въ такомъ
случав всего выгоднве предварительно умножить его
на cie число и произведете так. обр. полученное
сдвлать по изложенному въ предыдущемъ членъ
способу общимъ знаменателемъ. Напр.	ff	и
—. Въ настоящемъ случав 56 будетъ число крат¬
ное вевхъ знаменателей, кромВ 24; но умноживши
56 на 2, получимъ 72, число кратное вевхъ знаме¬
нателей; так. обр. и сдвлаемъ 72 общимъ зиамена-
телемъ; для сего числителя п знаменателя первой
дроби должно будетъ умножить на 6 (ибо частное

86
72 на 12 есть 6); «торой на 4; третьей на 3; и чет¬
вертой на 2. Посему ■ -5'	= J4; * *—* =
1	•'13-6	7 * ’ I S - 4.	’О	H i
и	”	= 44*	И	слъд.	вмъсто	данныхъ дробей
”	нч	’•
8	S	II	„	и	„„	.	я_о	Ц	А Я	АЛ
Г7’	зТ	Ц	ПОЛУЧИМЪ.	-J,	—,	—	II	утг-
Наконецъ остается объяснить на какое число дол¬
жно помножать всякой разъ большш знаменатель,
чтобы сдълать его чнсломъ кратнымъ вс'Ъхъ дан¬
ныхъ знаменателен: чтобы найти tie число должно
большш знаменатель и тъ знаменатели, которыхъ
онъ не кратный, .разложить на первоначальные дъ-
лнтели и ввести въ большш знаменатель тъ дълн¬
тели, которыхъ въ немъ не достаетъ противъ дру-
гнхъ разложснныхъ знаменателей, перемножить cin
дЪлнтелн между собою н на произведете нхъ по¬
множить большей знаменатель, так. обр. полученное
число п будетъ общнмъ знаменателемъ, къ которому
прнведутся всъ дроби по способу показанному выше
въ семъ членъ. Такъ въ вышепрнведенномъ примъ-
ръ 36 болышй знаменатель п 24 другой знамена¬
тель, съ которымъ 56 не кратный; разложивши ciii
знаменатели на первоначальные дълнтели, будетъ:
36 = 2. 2. 3. 3
24 = 5. 2. 2. 2
Теперь очевидно, что въ 56 недостастъ дълнтели
2-хъ противъ 21 Прнведемъ еще къ одному знаме¬
нателю дроби:
7	15	5	8	13	_29
30’	40’ 27’ 60’	36 "	120'
Здъсь	болышй знаменатель	есть	120, число крат¬
ное	прочнхъ	знаменателен, кромъ	27 н 36.	Посему
разлагаемъ 120, 27 п 56 на первоначальные дъли-

S7
телн, будетъ:	120	=	2.	2.	2.	3.	5
27	=	3.	3.	3
36	=	2.	2.	3.	3
. Сравнивая дълнте.ш 120 съ дълнтелнми 27 и 56,
увпдимъ, что должно въ 120 ввести дълптелн 3 н
5, т. е. умножить 120 на 9 н сдълать число 1080
общпмъ знаменателемъ.
Поступая по вышесказанному, найдемъ:
7.56	252	13.27	551	5.40	200
30.36	1080’	40.27	108и	’	27.40	1680’
8.18	144	13.50	390	29.9	261
и
60.18	1080 36.30	1080’	120.9	10S0
Слъд- вмъсто данныхъ дробей	£-*,	f§
II	ПП JVIIIIUT' 2 5 2	S	Б	I	.8	00	144
iso *	Ш>1Ь.	jos	о9	хоао9	ю	so9 ю»о’ юно
II	.
1030
СЛОЖЕШЕ ДРОБЕЙ.
47.	При сложенш дробей можетъ быть два му¬
чая: пли данныя для сложешя дроби имъютъ одн-
накнхъ знаменателен, или разпыхъ.
1) Если слагаемыя дроби имъютъ одинакнхъ зна¬
менателен, т. е. выражены въ одинакнхъ доляхъ
единицы, то должно сложить однихъ числителей
пхъ и подъ суммою подписать общш ихъ знамена¬
тель. Напр. -L--+- ji 4- тт= Ту «ли по нзк.ио-
чеиш цълаго числа изъ неправильной дроби сумма
всъхъ данныхъ дробей выразится чрезъ 1Д.
2) Если слагаемый дроби имъютъ разныхъ знаме¬
нателен, т. е. составлены изъ долей различной ве¬

личины, то должно сперва привесть ciii дроби къ
одному знаменателю и потомъ поступить, какъ въ
предыдущемъ случав, т. е. сложить одннхъ числи¬
телей ихъ и подъ суммою подписать общш ихъ зна¬
менатель. Напр.
приведя ciii дроби по чл. 44 къ одному знаменате¬
лю, получимъ:
63	140	84	154	141
5U4	504	504	504	504*
Возмемъ еще примъръ. Пусть требуется сложить
дроби:
8	3	9	4	11
18"*" 28	36	+ 48 + 49 + 98*
ЗдЪсь можно 1-ю, 3-ю и 4-ю дроби привесть къ
одному знаменателю по чл. 46; также 2-ю, 5-ю и
6-ю привесть къ одному знаменателю по тому же
члену; тогда получимъ:
64	21	36	12	44	42
Ш + Т9б"НТ44+ 144+ 196"*" 196*
Теперь можно 1-ю, 5-ю и 4-ю дроби соединить
въ одну дробь; а 2-ю, 5-то и 6-ю также въ одну
Дробь, тогда вместо шести данныхъ дробей, полу¬
чимъ только две, именно: * Ц -J-
приведя ciii дроби по чл. 44 къ одному знаменате¬
лю, получимъ:
5488	3852	9340

89
или по сокращена! дроби на 4 сумма данныхъ дро¬
бен выразится чрезъ 1+7+ ■
48. Ежели при дробяХъ будутъданы для сложе-
шя и цълыя числа, то должно цълыя числа сло¬
жить отдельно, а дроби отдельно п сумму дробей
придать къ сумм® цълыхъ чиселъ; или целы я съ
дробями прнвесть въ неправильным дроби п потомъ
сложить ихъ по 1-му или 2-му случаю предыду-
гцаго члена. Папр.
34 -+-	-f- 2^.
Сложивши ц®лыя числа между собою, получимъ
въ сумм® 16. Сложивши между собою дроби от¬
дельно отъ цьлыхъ чнселъ, будетъ:	или	по
изключенш цълаго числа нзъ неправильной дроби
будетъ 1/Д; а потому вся сумыа=16+1^=17^.
Сл®д.
Пли приведя цьлыя числа съ дробями въ не¬
правильный дроби, будетъ:
32 ,99 ,137	101
9 * 24	18	Ж
Сложивши ciH дроби по чл. 47, получимъ:
64	198	137	101 _ 201	299	_	1608 897
18	~48 + Ж+ -48~Ж~* 48 ~ 144+144
 2505  	57
144 ~	144
Слъд. 5j + 4^ + 7fi + 2* = 17^
таже самая сумма, какая была найдена и прежде.
ВЫЧИТАШЕ ДРОБЕЙ.
49. При вычиташн дробен, также какъ и при сло-
женш оныхъ, можетъ встретиться два случая: или

90
данныя для вычиташя дроби будутъ нмЪть одина-
кнхъ знаменателен или разныхъ.
1)	Если данныя для вычиташя дроби нмыотъ о-
дннакнхь знаменателей, т. е. составлены изъ долей
одпнакой величины, то должно вычесть однихъ ихъ
числителей н подъ разностно подписать общш ихъ
знаменатель. Напр, изъ ■— вычесть будетъ:
I	I 3	13'
2)	Если данныя для вычиташя дроби пмЬютъ раз¬
ныхъ знаменателей, т. е. составлены изъ долей раз¬
ной величины, то предварительно надобно данныя
дроби привесть къ одному знаменателю н потомъ
уже вычесть одннхъ числителей н подъ разностно
подписать общш пхъ знаменатель. Напр, изъ ~
вычесть -5-. Приведя cm дроби къ одному знаме¬
нателю, получимъ:
33 __ 10 _ 23
72	72 “ 72'
18
Также —
35
14 _
126
. 70
_ 56
7
И 8
49 “
245
245
245
35
*
Примтьч. Сей разности можно достигнуть и дру-
гимъ образомъ: сокративши вычитаемую дробь на 7,
получимъ !■; а вмъсто уменьшаемой дроби можно
взять двЪ дроби, равныя ей, именно:	=	vf	~Ь v-
пли сокративши первую дробь на 5, будетъ:
18  8,2	18	14	8,22
35 ~ 35	7	“ ПОТОМу 35	49	35	7	7‘
Вычитая нзъ получимъ въ разности нуль, или
18_1J_ 8 о—1
55	49	55	35'
50.	Ежели въ вычитанш при дробяхъ будутъ да¬

91
ны целыя числа, то вычитаютъ целыя числа от¬
дельно, а дроби отдельно н разность дробен прнда-
ютъ къ разности целыхъ чиселъ; или целыя числа
съ дробями приводятъ въ неправнльиыя дроби и по¬
томъ вычитаютъ ихъ такъ, какъ показано въ преды-
дущемъ члене. Напр. пзъ 5| вычесть 4f; будетъ:
Ч —
Вычитая целыя, получимъ разность 1; для вычн-
ташя дробен а— ~ приведемъ ихъ къ одному зна¬
менателю, будетъ: ад— -я- = ейо разность прн-
дадимъ къ прежней целой разности, получимъ:	—
s	и о
Или приведя въ данномъ примере целыя съ дро¬
бями въ неправильным дроби, получимъ: ~ — ~,
вычитая ciii дроби, будетъ:
таже самая разность, какая и прежде была найдена.
Примтьч. Вычитая целыя числа отдельно, а дро¬
би отдельно, можетъ встретиться следующте затруд-
неше, именно вычитаемая дробь будетъ больше умень¬
шаемой дроби, такъ что отдельнаго вычнташя дро¬
бей сделать нельзя, тогда отъ целаго уменьшаемаго
отнпмаготъ единицу, обращаютъ ее въ те доли, въ
какнхъ выражена уменьшаемая дробь н складыва-
ютъ ее съ уменьшаемаго дробью и наконецъ дела-
ютъ вычитание, какъ показано въ семъ члене. Напр.
изъ 4-f вычесть 2А, будетъ:
Л* 	 0	4
Здесь вычитаемая дробь А больше уменьшаемой а,
посему отъ цвлаго уменьшаемаго 4 беремъ I, обра-
щаемъ ее въ седьмыя доли А а соединяемъ ciu дола
съ будетъ -1-, тогда вместо 4а — 2А, получимъ:
3— — 2А.
7	«

92
Поступая по вышесказанному въ семъ член®, бу¬
детъ:
3^ — 2A=lff-
7	а	3 5
51. Если требуется соединить въ одну дробь ни¬
сколько дробен, изъ которыхъ одн® требуется ело -
жить, а друг!я вычесть изъ нихъ, то по приведенш
сихъ дробен къ одному знаменателю складываютъ
отдельно дроби слагаемый и вычнтаемыя и сумму
вторыхъ дробей вычитаютъ изъ суммы первыхъ.
Напр.
-L - _ - _L?_U 1?	^4-i —-
24	36	48	9	56	12 49	25
приведя сш дроби къ одному знаменателю, получимъ:
80850 , 14700	18375	, 39200 ( 40950
176400 ^ 176400 ~ 176400	176400 ^ 176400
73500	14400	35280
176400 + 176400 _ 176400
соединивши въ одну дробь вс® слагаемыя дроби и
въ другую вс® вычитаемый, получпмъ:	—
I 2 7 15 5 — - ■ в 2 9 &. 5
I 7 6 4 О О I 7 6 40 о*
Еслибы въ вышеозначенномъ пртгьр-® при дробяхъ
находились и цьлыя числа, то должно бы слагае¬
мыя ц'Блыя числа соединить въ одно число, а вы¬
читаемый въ другое, сумму вторыхъ цБлыхъ чиселъ
вычесть изъ суммы первыхъ и найденную так. обр.
разность придать къ вышенайденной разности дробен.
УМНОЖЕШЕ ДРОБЕН.
52. При умножеши дробей можетъ быть четыре
случая: 1) или умножается дробь на цБлое число;
2)	или умножается цълое число на дробь; 3) или

' 93
умножается дрВбь на дробь; 4) или умножается це¬
лое число съ дробью на целое число съ дробью.
1)	Пусть требуется умножить дробь -f. на цЬлое
число 4, по чл. 14, умножить £ на 4 значить со¬
ставить третье число нзъ £ такъ, какъ 4 составле¬
но изъ единицы; но поелику 4 вчетверо больше
1, то для искомаго пронзведешя будетъ число
вчетверо большее f; но чтобъ найти число вчетве¬
ро большее £ надобно ciio дробь увеличить по чл.
41 т. е. или умножить числителя ея на 4 или раз-
дблнть на 4 ея знаменателя н такъ какъ не всегда
можно раздьлить знаменателя дроби на какое нибудь
число, то за общее правило для умножешя дроби па
цТ>лое число можно принять следующее: чтобы у-
множнтъ дробь на цгьлое число, то должно у мно¬
жить только на cie число одного ел числителя и
подписать подъ епмъ произведетемъ ея знаменате¬
ля; с.гвд. •§-. 4 = — = 2|-.
2)	Пусть требуется умножить цБлое число 5 на
дробь £. По смыслу умножешя въ настоящемъ слу¬
чав требуется взять три седьмыя доли пяти едн-
ницъ; но седьмая доля пяти единицъ по чл. 40 есть
£, а три такнхъ доли будутъ втрое больше сей
дроби, т. е. будутъ Слъд. чтобы умнозкить цп-
лое па дробь должно умножить цгьлое на числи¬
теля дашюй дроби и подписать подъ симъ произве-
дешемъ даннаго знаменателя. Птакъ 5.
. Примпч. Такъ какъ 5.|-=-75 п £. 5=*,-, то 5.£—
|-.5; с л ьд. правило, доказанное въ чл. 20, распростра¬
няется и на тб случал, въ копхъ производителями
будутъ числа дробны я.

94
Вышеозначенное правило умножешя целаго числа
на дробь можно доказать н так. об: пусть требует¬
ся 5 умножить на А; положили», что въ сен дроби
знаменателя 7 совсемъ не находится и вмъсто дан¬
наго множителя А возмемъ множителемъ целое число
3, которое въ 7 разъ (по чл.'41. 2) больше а. То¬
гда 5.3=13 это произведете въ 7 разъ больше ис-
комаго: ибо множитель 3 въ 7 разъ больше данна¬
го а, а потому для получешя нскомаго произведешя
должно 15 уменьшить въ 7 разъ, т. е. взять седь¬
мую долю 15, что и будетъ —След. 5. а=т~-
3)	Пусть требуется дробь а умножить на А. По
смыслу умножешя, въ настоящемъ случае требуется
найги такое трет! с число, которое бы пзъ а было
составлено такъ, какъ А составлено изъ единицы, т.
е. найти такое третье число, которое бы составляло
пять девятыхъ долей отъ трехъ четвертей единицы;
определпмъ сперва одну девятую долю f; такъ какъ
девятая доля какой ннбудь величины въ 9 разъ мень¬
ше сей величины, то для опредЬлешя девятой доли
а надобно сно величину уменьшить (по чл. 41) въ
9 разъ, т. е. или разделить ея числителя или умно¬
жить знаменателя ея на 9, и поелику первый спо¬
собе не всегда возможенъ, какъ п въ настоящел!ъ
случае, то для получешя девятой доли а умножпмъ
ся знаменателя на 9 н будетъ а_; но пять девятыхъ
долей а должны быть въ 5 разъ более одной ея
девятой долп, то для получешя пяти девятыхъ до¬
лей а должно девятую еядолю, т. е. аа увеличить
(по чл. 41) въ 5 разъ и будетъ След. а. А=аа.
П такъ для умножешя дроби на дробь должно
помножить числителя на числителя, а знаменате¬

95
ля iia знаменателя. Иногда можно cie умножеше
произвести н так. обр.: числителя множимой дроби
раздьлить на знаменателя множителя (если cie воз¬
можно) и частное поставить числителемъ въ произ¬
ведены, а знаменателя множимой дроби раздвлнть
на числителя множителя и частное поставить знаме-
иателемь въ произведены.
Вышеозначенное правило умножешя дроби на дробь
можно доказать и так. обр: пусть требуется ~ ум¬
ножить на положимъ, что во множители знамена¬
теля не находится п вместо даинаго множителя
возмемъ ыножнтелемъ цвлое число 5, тогда придется
л умножить на 5 ii будетъ — но cie произведете
въ 9	разъ больше	пскомаго:	ибо	множитель	5 про-
тпвъ	даннаго f	въ	9	разъ	(чл.	41,	2)	больше; по¬
сему для получешя искомаго произведенья должно
уменьшить въ 9 разъ (чл. 41, 3 и 4) и будетъ
rwi a	S S ■ ■ X 5
А*	4."	"9	5 6*
4)	Пусть требуется 5|- умножить на 4|-. Для сего
цълыя числа съ дробями припедемъ въ неправиль-
ныя дроби и потомъ будемъ поступать, какъ въ пре-
дыдущемъ случав, т$к. об.: 5-f. 4f=—^
24|А.
Лрпмтъч. 1. Изъ предыдущаго видно, что всякой
разъ, какъ миожнтелсмъ будетъ какая нибудь дробь,
произведете выходить меньше множимаго: ибо въ
такомъ случав всегда въ произведены получается
величина, представляющая собою одну или несколь¬
ко долей множимаго, какъ это можно видеть во 2 и
3 случав предыдущаго члена.

9G
Щ имтъч. 2. Очевидно также пзъ предыдущего,
что къ правилу умножешя дроби на дробь относит¬
ся и такъ называемое правило дроби дробей: нбо
взять ^ доли отъ единицы значнтъ по 3-му слу¬
чаю предыдущаго члена умножить |- на Также
взять отъ -§. отъ -| отъ значить отъ пяти ось-
мыхъ единицы взять три девятыя доли, отъ вели¬
чины так. обр. найденной взять двЪ седьмыя доли
п отъ величины так. обр. полученной взять нако-
нецъ три четверти. Взявши три девятыя доли отъ
пяти осьмыхъ единицы, получимъ: \взявши отъ
сен величины двъ седьмыя доли, будетъ:	и на-
конецъ взявши отъ сей величины три четверти, най-
дсмъ:	Итакъ,	чтобъ ръшнть сей вопросъ дол¬
жно было всЪ данныя дроби, начиная съ последней
перемпожить между собою; а для сего должно бы¬
ло перемножить всъхъ числителей ихъ между собою
и всъхъ знаменателей между собою; т. е.	=
Я О
2 0 16*
Также найдутся -§■ отъ £ отъ |- отъ отъ ~ че¬
тырехъ единицъ; будетъ: 4. Д-. Л. A. f =
53.	Пусть теперь требуется f-|-2-§— i i — Д | х.
умножить на Это обыкновенно пзображаютъ такъ:
Для сего всЪ дроби, зак.иочснныя въ скобкахъ,
соединяютъ по чл. 51 въ одну дробь, будетъ: —
потомъ ciio дробь умиожають на х по предыдущему
члену н‘будетъ: ffff. Слъд.
Cx + 2f— Н — rV + D- 1- = -Hff
Также ръшится и (^-bf- Д). (ЙД.-ДД + Д-).
Д.1я сего до.1жно все множимое прнвесть въ одну

97
дробь, а всего миожптеля въ другую и потомъ ciu
дроби перемножить между собою, п будетъ:
/ S 1 s 	 _4_л	 xs	I s\ 	 _I	loss 	 | S
\ I 8 "1” ТГ	3	6/	\лга	7	5	*Т" 35/	2"	525	IOSO	“
•Такпмъ же образол1Ъ решаются и все подобные
примеры.
ДЪЛЕШЕ ДРОБЕЙ.
54.	При двленш дробей, также какъ п при умно-
жеиш ихъ, можетъ быть четыре случая: 1) или де¬
лится дробь на целое число; 2) и.т делится целое
число па дробь; 5) или делится дробь на дробь; 4)
или делится целое число съ дробью па целое число
съ дробью.
1) Пусть требуется разделить на 5. Пзъ чл.
21 явствуетъ, что разделить одно число на другое
значить найти такое трет1е, которое будучи умноже¬
но на делителя даетъ въ произведеши делимое п по¬
тому въ настоящемъ случае искомое частное должно
быть таково, что увеличивши его въ 5 разъ, полу¬
чимъ делимое след, само по себе частное дол¬
жно быть въ 5 разъ меньше А н потому для отыска-
1пя его должно ~ уменьшить въ 5 разъ; поступая
по чл. 41, получимъ -fe. Слъд. ф: 5 = ^.
Нтакъ чтобы раздтълитъ дробь на цгьлое число,
должно знаменателя оной дроби помножить на
цгьлое число и поставить знаменателемъ въ част¬
номъ, а числителсмъ въ частномъ поставить чи¬
слителя дгълимой дроби.
2) Пусть требуется 7 разделить на Въ насто¬
ящемъ случае требуется найдти такое число, кото¬
рое будучи умножено на -§-, дало бы въ произведе-
7

98
ш’м 7; или другими словами: требуется найдтп такое
число, котораго три пятыя доли составляютъ 7; для
отыскашя сего числа разсуждаемъ так. обр.: поели¬
ку три пятыя его доли составляютъ 7, то одна пя¬
тая его доля будетъ въ о раза меньше 7, т. е. бу¬
детъ равна ~ п поелику во всемъ искомомъ чнслт.
плтыхъ его долей будетъ пять, то все искомое чи¬
сло будетъ состоять изъ пяти такихъ велнчинъ, какъ
i, т. е. оно будетъ въ 5 разъ больше поступая
по чл. 41, напдемъ для искомого числа величину
Ипгакъ чтобы раздтълить цтълое число на дробь,
должно цтълое число умножить на знаменателя
дроби и произведете написать въ частномъ числи¬
телемъ, а числителя дгьлящей дроби (дтълителя)
поставить въ частномъ знаменателемъ.
Cie правило можно доказать п другимъ образомъ:
пусть требуется 7 разделить на 4; положпмь, что
въ дълнтелъ совсъмъ не находится знаменателя 5 и
вместо даннаго дълителя -f- возмемъ дълптелемъ цъ¬
лое число о; тогда придется 7 раздълнть па 5, ча¬
стное число по чл. 40 выразится чрезъ Z- но cie
частное въ 5 разъ меньше нскомаго: ибо дълитель
3 противъ даннаго дълителя { въ 5 разъ больше,
а потому для полу чешя нскомаго частнаго должно ^
увеличить въ 5 разъ, поступая по чл. 41, полу-
3)	Пусть требуется £ раздълнть на -f. Въ насто-
ящемъ случав требуется найти такое число, которое
будучи умножено на J. даетъ А или такое число,
котораго пять девятыхъ долей составляютъ £ еди¬
ницы; для отыскашя сего числа разсуждаемъ так.
У- Слъд. 7: f.
а &
s
чимъ Слъд. 7: л.
3

99
обр.: поелику пять девятыхъ долей искомаго числа
составляютъ едшшцы, то одна девятая его доля
должна быть въ 5 разъ меньше ф; слъд. для опре-
дълешя сей девятой доли должно ф уменьшить въ
5 разъ; поступая по чл. 41, получимъ -4-, cin вели¬
чина будетъ девятая доля искомаго числа; н потому
цълое искомое число будетъ въ 9 разъ больше
и для получения его должно увеличить въ 9 разъ;
Лтакъ -чтобы раздгълитъ дробь на дробь, должно
■числителя дгьлимой дроби помножить на знамена¬
теля дгьллщей дроби (дгьлителп) и произведете по¬
ставить въ частномъ числителемъ, а знаменателя
дплимой дроби помиоз/сить tut числителя дплящей
дроби и произведшие поставить въ частномъ зна-
менателемъ.
Иногда можно cie дълеше произвести п так. обр.:
числителя дълимой дроби раздълить на числителя
дЪллщей и поставить въ частномъ числителемъ, а
знаменателя дълимой дроби раздълить на знаменате¬
ля дълящей п поставить знаменателемъ въ частномъ.
Вышеозначенное правило дълешя дроби па дробь
можно доказать п другнмъ образомъ: пусть требует¬
ся ф раздълить на -§.. Положимъ, что въ дЪлнтелЪ
совсЪмъ не находится знаменателя 9 и вмъсто дан¬
наго дЪлителя *. возмемъ дълителемъ цълое число
5, тогда придется ~ раздълить на 5; поступая по
чл. 41, получимъ но cie частное въ 9 разъ мень¬
ше искомаго: ибо дълптель 5 противъ даннаго дъли-
теля |- въ 9 разъ больше, а потому для получешя
искомаго частнаго должно увеличить въ 9 разъ
по чл. 41 нандемъ:	Слъд.
А* А
Ч " 9
S6
3 &
«в
a a

ICO
л
4)	Пусть требуется 5|- раздВлпть на Ъ\.' Приве¬
дя цт.лыя числа съ дробями въ неправильный дро¬
би, раздълпмъ потомъ cin дроби такъ, какъ въ пре-
дыдущемъ случае и будетъ:
2	•	JJL	     j	99
1Г*	°	о	8*	6	146	136 ’
Примтьч. Изъ предыдущаго видно, что всякой разъ,
какъ дълнтелемъ будетъ какая инбудь дробь, част¬
ное гыходитъ больше дълнмаго: причина сего заклю¬
чается въ томъ, что всякой разъ, какъ дълнтелемъ
будетъ дробь, частное число должно быть таково,
что одна или несколько какихъ ннбудь его долей
(сколько и какнхъ именно долей, это означается дъ-
лителемъ) равняются делимому, а потому все иско¬
мое частное будетъ больше даннаго дълнмаго.
55.	Пусть теперь требуется 5± — 2-^- -f-	—
разделить на Это обыкновенно пзображаютъ
такъ:
(К*   	I-5_> *
WT	Jh	>21	X
Для сего вес дроби заключенныя въ скобкахь со-
еднняютъ въ одну дробь и будете: -Ш, потомъ ciio
дробь д-влютъ по предыдущему члену на совер¬
шивши cie, получимъ
& = 6Н- Слъд. (5f-2^ + 3^ - 1JL):
Г6Х. _з —
SO* /j.
д = 6^
4 	 45
Такнмъ же образомъ решаются вес подобные при¬
меры.
Примтьч. Гакъ какъ четыре основныя дъйств1я
вычнелешя надъ дробями въ конечныхъ свонхъ вы-
водахъ приводятся КЪ ОСНОВНЫМЪ ДЪЙСТВ1ЯМЪ ВЫЧИ-
слешя надъ цълымн числами, такъ напр, въ сложе¬
ны п вычитанхн дробен по приведены П\ъ къ одно¬
му знаменателю, склэдываютъ н вычитаютъ одннхъ

101
числителей (разсматривая нхъ, какъ цълыя числа),
также въ умножешн и дълснш дробей множугъ «ли
дЬлштъ числителя на числителя, а знаменателя на
знаменателя (разсматривая нхъ также, какъ цълыя
- числа), то свойства «ълыхъ чиселъ, входящихъ въ
четыре основныя дъйств1я вычисленья, изложенный
въ чл. 11 примъч. 2 и въ чл. 25 прнмъч. прикла-
дываются безъ всякой переиъны и къ дробнымъ чн-
сламъ, входящпмъ въ четыре основныя дъйствш вы¬
числено] надъ дробями; повЪркп осиовныхъ дъйствш
вычисленья надъ дробями производятся такнмъ же
образомъ, какъ н надъ цьлыин числами (чл. 13 и 26).
О ДЕСЯТНЧНЫХЪ ДРОБЯХЪ.
*
ПРЕДВАРИТЕЛЬНЫ)! ПОНЯТ1Я О ДЕСЯТНЧНЫХЪ ДРОИЯХЪ И
ОСНОВНЫЯ ИХЪ СВОЙСТВА.
56.	Частный родъ дробей, пронсходящш отъ дЪ-
лсшя на 10 ит. л он единицы и постепенно уменьша¬
ющихся въ десятерномъ порядив частей ея заслу-
живаетъ особенное вппмашс по легкости своего нзо-
бражешя п удобности, съ каковою вводятся онъ въ
вычнслешя. II такъ если раздълнмъ единицу на 10
ровныхъ частей, то каждая часть будетъ десятая
доля единицы; если каждую десятую долю раздь-
лнмъ еще на 10 ровныхъ частей, то новая часть бу¬
детъ сотая доля единицы; раздъливиш каждую со¬
тую часть еще на 10 ровныхъ частей, получимъ
тысячную долю единицы и т. д  ташя дроби на¬
зываются десятичными. Слъд. въ каждой едншщь
заключается 10 десятыхъ долей, въ каждой деся¬

102
той долъ 10 сотых* долой, въ каждой сотой дол*
10 тысячныхъ долей н т. д И такъ десятичными
дробями называются тъ дроби, у которыхъ знаме¬
нателем* всегда бывает* единица съ несколькими
нулями. Посему f-, у^0, Го%6^ и т. д. будутъ дро¬
би десятнчныя.
57.	Въ слъдсттае основяаго услов1я десятерной ну¬
мерации по которому во всяком* изображенном* циф-ш
рамп цЪломъ 4iic.il; значеше каждой цифры зави¬
сит* отъ ывета ею занимаемаго и постепенно идя
отъ л т. вон руки къ правой въ 10 разъ уменьшается
(чл. 5), можно десятичпыя дроби изображать безъ
знаменателя так. обр.: написавши какое нибудь цЪ-
лое число, напр. 55 единиц*, если бы мы хотъли
еще написать какую ннбудь циФру съ правой руки
цифры единиц*, то написанная так. обр. цифра въ
слъдств1е помянутаго услов1я нумерацш означала бы
величину, въ 10 разъ меньшую единицы, слъд. эта
цифра означала бы десятый доли едшшцы; если бы
за цифрою так. обр. написанною захотъли бы еще
написать вправо цифру, то с1я послъдняя означала
бы величину, въ 10 разъ меньшую десятой доли;
слъд. эта ццФра означала бы сотыя доли единицы;
таким* же образомъ изобразили бы тысячныя, де-
сятитысячныя, стотысячный, мнлюнныя II т. д, до¬
ли; но для того, чтобы въ самом* изображенш от¬
личить доли отъ цълыхъ чиселъ согласились отдъ-
лять цълыя числа отъ долей запятото так. обр.
55,845 значит* 35 цълыхъ единицъ, 8 десятых*,
4 сотых* п 3 тысячных* доли. Послъ сего легко
изобразить безъ знаменателя слъдуюиця дроби: 3-^,
4^, 5^ и будетъ: 5,5 также 4.7 и 5,5; если бы на¬

103
добно было одну десятичную дробь, неимыощую
при себв ц-в л а го числа, изобразить безъ знаменате¬
ля, то на мБстБ цвлаго числа, для отли'ня его оть
долей, должно поставить нуль н отделить его запи¬
тою; посему изображенныя безъ знаменателя бу-
дутъ 0,5 это значить нуль цвлыхъ и пять деся-
тыхъ или просто пять десятыхъ.
Пусть требуется ~£~ изобразить безъ знаменате¬
ля: поелику при сей дроби не находится цвлаго чи¬
сла, то на мБстБ его поста вимъ нуль и отдвлнмъ
его запятою, да.гве вправо послв запятой въ слвд-
CTBie вышесказаннаго должны с.гвдовать на первомъ
мвств доли десятый, на второмъ—соты я; на треть-
емъ—тысячныл; на четвертомъ—десятитысячный и
т. д; обнаружимъ же въ данной дроби всБ посте¬
пенно так. обр. слвдующш доли, для сего числите¬
ля данной дроби, принимая его за цвлое число, раз-
ложимъ на разные порядки единицъ, изъ которыхъ
онъ состоитъ, и подъ каждымъ порядкомъ подпи-
шемъ знаменателя данной дроби (чл. 47. 1), будетъ:
543	500	40	3	500
Iow=Iooo+iooo+u»o- С°к!’а™!ШН Тбоо
40
на 100 и 	 на	10,	получимъ:
1000 J
543 __ 5	4	3
1000“ 10 + 100 + 1000'
И такъ данная дробь состоитъ изъ 5 десятыхъ
долей, 4 сотыхъ и 3 тысячныхъ и потому изобра¬
зится такъ: 0,543 ciio дробь можно читать так. обр.:
5 десятыхъ, 4 сотыхъ н 3 тысячныхъ; или прочи¬
тать вдругъ, какъ цвлое число, всБ ци<х>ры, означа-

104
Ю1ЩЯ десятичный доли и потомъ выговорить ПОСЛ'ЬД-
ыяго подразумт.иаемаго знаменателя, т. е. пятьсотъ
сорокъ три тысячныхъ.
Пусть еще требуется	изобразить	безъ	зпа-
мснателя; поступивши по вышесказанному получпмъ:
6466 	 8QOO I  Доо_ I» & о I  	6 ПЛИ ~8 *
Хоооо	IOOOO	I о о о о .* юооо ’ х о о о о * хоооо
  8	,	4	■ а . 	6	 Гил		О S456
 а о * IО О ' IО О О I хоооо' *	X О О О О	5	7
т. е. восемь тысячь четыреста пятьдссятъ шесть
десятнчныхъ.
Возмемъ еще прнмвръ: требуется	изобра¬
зить безъ знаменателя: поступивши по предыдуще¬
му, ПОЛуЧИМЪ:	7о30^ = Гоо^ + ЦГоом + Too^Z
И ЦТ  5.5 6    S  |	5	L	 в
* IOOOOО	Iо о о I хоооо I хо оооо *
Слъд. въ данной дроби десятыхъ и сотыхъ долей
не находится и потому замветпвшп ихъ пулями, по-
лучимъ:	= 0,00356.
Лослъ сего легко вывесть следующее правило:
чтобы изобразить десятичную дробь безъ знамена¬
теля, когда она находится въ видп? обыкновенной
дроби, должно поставить на мпсттъ цгълыхъ чи¬
селъ пуль, если цгълыхъ не находится при данной
дроби, отделить его занятою, и поелп запятой
поставить по порядку есть цифры числителя, если,
ихъ столько, сколько нулей въ знаменателть- если
же въ числшпел/ь цифръ мепгъс, нежели нулей въ
зиамснатсло, то сей недостатокъ должно замо¬
стить нулями, поставляя ихъ тотчасъ поелтъ за¬
пятой и потомъ уже поставить есть гуифры дан¬
ного чисмииеля.
Посему 1-Щ = 3^=3,517; г^^=0,000846
въ посльдней дроби нулей въ знаменатели 6, а
цифр ь вь числитель только 5; сльд. не достаетъ еще

105
3-хъ ццфръ, посему тотчасъ послъ запятой ставнмъ
три пуля п потомъ уже ставнмъ всъ цифры даннаго
числителя по порядку ихъ послЪдоватя въ ономъ.
Наоборот ь, если бы нужно было изобразить въ
видь обыкновенной дроби десятичную дробь, изоб¬
раженную безъ знаменателя, то должно бы было
все цифры, стояния после запятой поставить чпелк-
телемъ, а зпаменатслемъ единицу со столькими ну¬
лями, сколько было десятичныхъ знаковъ въ данной
дроби, считая въ число п\ъ н нули.
Прпмтьч. Зам'Бтимъ, что величина десятичной дро¬
би не зависитъ отъ числа десятичныхъ знаковъ, а
отъ величины цифры, означающей доли высшаго
разряда; напр. 0,35 больше, нежели 0,3486: ибо
изобразивши сш дроби въ вид е обыкновенныхъ, по-
лучнмъ:	и	и приведя ихъ къ одному зна¬
менателю	и —увндимъ справедливость
вышесказаннаго. Эго же самое можно объяснить и
так. обр.: въ дроби 0,35 находится о десятыхъ и
5 сотыхъ, въ дроби 0,34S6 находится также 3 де¬
сятыхъ, но уже не 5, а 4 сотыхъ, посему одной со¬
той не достаетъ до первой дроби; но какъ во второй
дроби находятся еще 8 тысячныхъ, то до одной со¬
той не достаетъ еще 2-\ъ тысячныхъ; но кромв 8
тысячныхъ находятся еще въ дроби 6 десятнтысяч-
ныхъ, то до 2-хъ тысячныхъ не достаетъ еще 14
десятитысячныхъ (считая въ каждой тысячной по 10
десятнтысячныхъ); слъд. во второй дроби ие доста¬
етъ до первой 14 десятнтысячныхъ; так. обр. мы
не только узнали, что 0,35 больше 0,5486, но и
опредълилн еще педостатокъ одной дроби противъ
другой.

106
58.	На осиоваши изображена десятичныхъ дро¬
бей безъ знаменателя легко объяснить слъдуюиця
свойства десятичныхъ дробей:
1) Чтобы увеличить десятичную дробь въ 10, 100,
1000,.... и вообще въ какое нибудь число разъ, оз¬
наченное единицею съ нисколькими нулями, должно
перенести запятую вправо черезъ столько десятич¬
ныхъ знаковъ, сколько находится нулей во множи¬
тели: ибо перенеся запятую въ дроби 0,83475 че¬
резъ одниъ зиакъ, получимъ дробь 8,3475 въ 10
разъ большую данной; потому что 8 десятыхъ въ
данной дроби сдьла.шсь въ новой дроби 8-ю еди¬
ницами; также 3 сотыхъ обратились въ 3 десятыхъ;
4 тысячныхъ въ 4 сотыхъ; 7 десятитысячныхъ въ
7 тысячныхъ п т. д. значеше каждой цифры, вхо¬
дящей въ данную дробь, увеличилось въ новой дро¬
би въ 10 разъ, а посему и самая дробь увеличилась
въ 10 разъ; перенеся въ предыдущей дроби 0,S3475
запятую черезъ два знака къ правой рукв, полу-
чимъ дробь 83,475 во 100 разъ большую дайной
потой же причпнв п т. д.
2) Чтобы уменьшить десятичную дробь въ 10,100
н т. д. и вообще въ какое ннбудь число разъ, озна¬
ченное единицею съ нисколькими нулями, должно
перенести запятую влъво черезъ столько знаковъ,
сколько находится нулей въ дълптелъ: ибо перене¬
ся запятую въ дроби 0,34 черезъ одннъ знакъ влъ¬
во, получимъ дробь 0,034 въ 10 разъ меньшую пре¬
дыдущей; потому что 3 десятыя ея доли сдълались
въ новой дроби 3-мя сотыми; также 4 сотыя обра¬
тились въ 4 тыся'шыя; слъд. значеше каждой циф¬

107
ры входящей въ дробь уменьшилось въ 10 разъ,
а потому п самая дробь уменьшилась въ 10 разъ;
перенеся занятую въ дроби 0,54 черезъ два знака,
получимъ 0,0034 дробь въ 100 разъ меньшую дан¬
ной: нбо въ новой дроби значсше каждой цифры во
100 разъ меньше, нежели въ предыдущей дроби
и т. д.
3)	Величина десятичной дроби не переменится,
если па конце оной съ правой руки прнпишемъ не¬
сколько нулей; пстр. 0,018 все равно, что 0,0180 и
0,01800 и 0,018000000: ибо ^=т^ _ _ж.-а_о_=
_ I 8 О О О Of>P
Хооооооооо *
Примтъч. На этомъ последнемъ свойстве основы¬
вается легкое средство приводить десятичныя дроби
къ одному знаменателю, т. е. выражать ихъ въ од-
ннхъ и техъ же доляхъ едшшцы; для сего должно
только въ техъ дробяхъ, въ которыхъ не достаетъ
несколькихъ десятичныхъ знаковъ противъ какой
нпбудь дроби, съ которою оне должны быть при¬
ведены къ одному знаменателю, заместить число не-
достающнхъ десятичныхъ знаковъ нулями, приписан¬
ными къ десятичнымъ дробямъ съ правой руки; напр.
требуется 0,05; 0,8463 и 0,013 прнвесть къ одному
знаменателю; здесь самый большш знаменатель есть
10000, прннадлежащш второй дроби, къ этому зна¬
менателю должны быть приведены и проч1я дроби;
для сего къ первой дроби должно приписать два
нуля съ правой рукн, а къ третьей дроби одннъ
нуль, тогда вместо данныхъ дробей получимъ рав-
ныя имъ: 0,0500; 0,8465 и 0,0150.

108
СЛОЖЕШЕ II ВЫЧИТАШЕ ДЕСЯТИЧНЫХЪ
ДРОБЕЙ.
59.	Такъ какъ взашшыя отпошенш между деся¬
тичными знаками тъже самыя, какъ и между знака¬
ми разныхъ порядковъ единицъ, то сложеше и вы¬
читание десятичныхъ дробен п повЬркн снчъ дЪнст-*
Bin производятся точно также, какъ ц въ цълыхъ
числахъ. Нлпр. требуется сложить между собою слъ-
дуюнйя десятнчиыя дроби: 0,017; 3,05; 21,00041
и 36,008; приведя сш дроби къ одному знаменате¬
лю, подпншемъ нхъ одну подъ другою такъ, чтобы
цифры, означающая десятнчиыя знаки одного раз¬
ряда стояли въ одномъ столбцъ, будетъ:
потомъ производнмъ сложеше де-	0,01700
сятнчныхъ знаковъ каждаго раз-	3,05000
ряда отдъльно п иаблюдаемъ	21,00041
здъсь тъже правила, какъ н въ	36,OOSOO
сложыпи цълыхъ чиселъ.	60,01541
Пусть требуется изъ 1S,004 вычесть 13,273536.
Приведя ciu дроби къ одному	18,004000
знаменателю , подпншемъ пхъ	13,273536
одну подъ другою н дълаемъ вы-	4,750464
читаше точно также, какъ н въ цвлыхъ чнслахъ.
УМНОЖЕШЕ II ДЪЛЕНТЕ ДЕСЯТИЧНЫХЪ
ДРОБЕЙ.
60.	Пусть требуется одну десятичную дробь 3,015
умножить на другую 0,23. Для сего во множимомъ

109
отброспмъ запятую, т. с. перенесемъ ее вправо че¬
резъ все десятнчиыя знаки и тоже самое сдълаемъ
во множптелъ, тогда вместо данныхъ десятичныхъ
дробен придется умножать цьлыя числа.
Умноживши cin цълыя числа, по-	5015
лучнмъ произведете 69345 едп-	X 25
ницъ; но cie произведение больше	9и45
нскомаго, потому что вместо данна- 6030
го множимаго мы взяли число въ	§9345
4000 разъ (чл. 5S. 4,) большее, отъ того произве¬
дете 69345 также въ 1000 разъ больше искомаго
(чл. 25, прим.) н потому должно уменьшить его въ
4000 разъ, т. е. перенести запятую, которая теперь
собственно находится после 5 едшшцъ, влево че¬
резъ три знака (чл. 58, 2) и будетъ 69,345; но cie
послвдпее произведете тогда было бы искомммъ,
когда бы при данномъ множимомъ 3,015 множителемъ
было цълое число 23, но cie число во 400 разъ
больше даинаго .множителя и потому произведете
69,345 еще во 100 разъ больше искомаго; умень¬
шивши его во 100 разъ, будетъ искомое произведе¬
те: 0,69345.
След, для умножешя одной десятичной дроби
на другую должно отбросить вь ппхъ зппятыя и
принять ихъ за цтълыя числа, пошомъ умножить
ciu числа между собою и въ произведеши так. обр.
получечпомъ отмгыттгь для десятичныхъ знаковъ
столько хщфръ, сколько было десятичныхъ знаковъ
во множимомъ и во мпожителтъ.
Пусть еще требуется 35,08 умножить на 27. От¬

110
бросивши во миожнмомъ запятую, умножнмъ 3508
на 27, будетъ:
найденное произведение 94716	3508
уменьшнмъ во 100 разъ и бу-	X 27
деть искомое произведете рав-	24556
но 947,16.	7016
94716
61.	Пусть теперь требуется десятичную дробь
34,025 раздълить на 0,18. ИзвЪстно (изъ примъч.
члена 25), что если дьлимое и дълнтель увеличатся
въ одно и тоже число разъ, то частное останется
безъ перемъны; принявши это во внимаше, отбро-
сшгь въ дълнмомъ и дълителт. заплтыя, тогда дъли-
мое увеличится въ 1000 разъ, а дълнтель во 100
разъ, и чтобы сравнять нхъ уееличешя, надобно дъ-
лнтеля, увеличенного уже противъ даннаго во 100
разъ, именно 18, увеличить еще въ 10 разъ, и тог¬
да вмъсто данныхъ дълпмаго и дълнтеля получимъ:
34025:180; раздЪливши ихъ какъ цълыя числа, по¬
лучимъ частное 1S9-1-, искомое, въ слт.дспйе выше*
замъчеииаго свойства чиселъ, входящихъ въ дъйсте
дъленпц слъд, 34,025: 0,18=189^.
Птакъ чтобы раздгълитъ одну десятичную дробь
на другую, должно привести ихъ сначала къ одно¬
му знаменателю, потомъ отбросить запятыя,
чрезъ что дгьлимая и дтьлящая дробь увеличатся
въ одно и тоже число разъ, и наконецъ раздтьлпть
ихъ какъ цгьлыя числа, частное число так. обр.
найденное п будетъ искомое.
Возмемъ еще примъръ. Пусть требуется 275,05
разд влить на 0,027л. Поступивши по вышссказан-

ж
ному правилу, получимъ: 275,05: 0,0275=275,0500:
0,0275=2750500: 275=10001^-.
Примгьч. I. ЗамЪчашя, сдьлаипыя нами въ утю-
жешн и дълеши дробей обыкновенныхъ (чл. 52
прим. 1. и чл. 54 прим.) прикладываются также и
къ дробямъ десятичнымъ.
Прпмтъч. 2. Дьлеше десятнчныхъ дробей можно
производить п так. обр.: отбросивши въ данныхъ
дълимомъ и двлителъ запятыя, раздьлить ихъ какъ
цьлыя числа и потомъ увеличить илп уменьшить най¬
денное частное сообразно съ правилами, изложен¬
ными въ прпмьч. чл. 25. Напр, возмемъ предыдущш
примьръ 54,025: 0,18; отбросивши запятыя, полу¬
чимъ 34025: 18 = 1890/j, но cie частное не будетъ
искомое: ибо увеличивши дълнмое въ 1000 разъ, ча¬
стное также увеличится въ 1000 разъ, ио какъ вмъ-
стъ съ дълнмымъ и дьлнтель былъ увеличенъ во
100 разъ, то частное увеличенное въ 1000 разъ
должно отъ увеличения дълителя уменьшиться во
100 разъ; слъд. оно будетъ больше искомаго част-
иаго только въ 10 разъ и потому должно уменьшить
его въ 10 разъ; для сего или прнведемъ 1890^ въ
одну дробь и раздълимъ потомъ на 10; или раздь-
лпмъ на 10 цвлое отдьльно, а дробь отдьльно и бу¬
детъ: 1890: 10 = 189;	10 = ^ = ^. Слъд.
искомое частное будетъ 189-^- тоже, какое п преж¬
де было найдено. Такнмъ же образомъ можно рь-
шать и всъ подобные примЪры.
Прпмтъч. 5. Въ сложсчнн, вычпташн н умноженш,
какъ видно изъ предыдущаго, нскомып числа, т. е.
сумма, разность п произведете выражаются также
десятичными дробями, какъ и данныя числа, между

112
тЬмъ какъ въ двлснш двлнмое и двлптель выража-
ются десятичными дробями, а частное обыкновенны¬
ми; посему и представляется вопросъ, как. обр. вы¬
ражать и въ двленш искомое частное также деся¬
тичными дробями, какъ выражены дълимое и дели¬
тель; а для сего надобно всякую обыкновенную дробь
уметь приводить въ десятичную, т. е. выражать ее
десятичными долями; рвшешемъ сего вопроса теперь
и займемся.
ОБРАЩЕШЕ ОБЫКНОВЕННЫХЪ ДРОБЕЙ ВЪ
ДЕСЯТНЧИЫЯ.
62.	Пусть требуется обыкновенную дробь при¬
вести въ десятичную. Мы вмдъди въ чл. 40, что
всякую дробь .можно принимать за частное, проис¬
ходящее отъ двлешя числителя на знаменателя и
что •§. напр, означаетъ пятую долю трехъ единицъ;
возмемъ же въ самомъ двлв ciio пятую долю трехъ
единицъ, т. е. совершимъ на самомъ деле то двле-
шс, которое требуется въ отон дроби; нзъ сего вид¬
но, что частное, которое мы найдемъ, должно быть
однородно съ двлимымъ: ибо оно должно собою
выражать никоторую долю, въ настоящемъ случаъ
пятую долю дв.шиаго.
РаздВляя 5 на 5, внднмъ, что	30	5
въ частномъ не будетъ пн од-	30	q q"
ной цвлон единицы, посему на	е *
мЬств еднннцъ ставимъ пуль н отдвлимъ его запя—
тою; потомъ поелнку въ каждой едпннцв содержит¬
ся 10 десятыхъ до.1ей, то въ 3-хъ единпцахъ бу-

113
детъ 30 десятычъ д вместо 3-хъ еддиицъ возмсмъ
величину ииъ равную именно 30 десятычъ долей и
какъ мы заметили, что частное должно быть одно¬
родно съ дълнмымъ, то раздъляя 30 десятыхъ на
5 единицъ нандемъ въ частномъ для пятой доли
величины 50 десятыхъ, 6 десятыхъ и въ остаткь
получимъ нуль- СлЕд. —■ =. 0,6.
Можно до этого же самаго равенства достигнуть
и другимъ образомъ: умножпмъ на 10, получимъ
~ или 6, величину въ 10 разъ большую •§; посему,
чтобы сравнять G съ надобно 6 уменьшить въ 10
разъ и будетъ ,в0- пли по чл. 57 имъемъ	0,6 и |-=0,6.
Возмеыъ еще примБръ: требуется ~ обратить въ
десятичную дробь.
Разделяя 7 на 25 увнднмъ, что въ	70	25
частномъ не будетъ ни одной целой	50 y gg
единицы и потому на мЕсхБ единицъ	200
ставнмъ нуль; потомъ вместо 7 еди-	^0
шщъ беремъ 70 десятыхъ долей и	"""
для двадцать пятой доли ихъ находимъ въ част¬
номъ 2 десятыхъ; повторивши ихъ 25 разъ, про¬
изведете 50 десятыхъ долей вычтемъ изъ 70 деся¬
тыхъ, получимъ въ остаткъ еще 20 десятыхъ до¬
лей; изъ сего заключаемъ, что 2 десятыхъ доли не
будетъ двадцать пятая доля 70 десятыхъ или 7
единицъ, а только 50 десятыхъ или 5 единицъ; ме¬
жду тЕмъ какъ 3 десятыхъ будетъ двадцать пятая
доля 75 десятычъ или величины большей 7 еди¬
ницъ; след- двадцать пятая доля 7 единицъ будетъ
больше 2-хъ десятыхъ и меньше 3-хъ десятыхъ, т.
е.	она будетъ равна 2 десятымъ единицы съ неко¬
торыми долями десятой доли единицы; десятичныя
8

114
50
49
0,571428571428571428.
доли по порядку менышя десятыхъ долей суть доли
сотыя; слъд. надобно въ частномъ еще отыскать
сотыя доли, а для сего надобно остатокъ отъ дъ.щ-
маго пли 20 десятыхъ долей привесть въ сотыя доли,
т. е. вместо 20 десятыхъ долей взять величину нмъ
равную (чл. 56) 200 сотыхъ, тогда для двадцать пятой
доли сей,величины будетъ 8 сотыхъ. Слъд. = 0,28.
Еще прнмъръ: требуется ~ обратить въ десятич¬
ную дробь.
Разделяя 4 на 40
7 увидимъ, что въ
частномъ вместо
едшнщъ должно
поставить нуль, по-
томъ 4 единицы
приводпмъ въ де-
сятыя доли п на-
ходпмъ для седь¬
мой доли 40 а де¬
сятыхъ, 5 деся¬
тыхъ, остатокъ 5
десятыхъ показы¬
ваете, что седьмая
доля 40 десятыхъ
будетъ больше 5
десятыхъ и мень¬
ше 6 десятыхъ н
потому въ частномъ
кромъ 5 десятыхъ
должно быть еще
пъеколько сотыхъ
долей; для оты¬
скашя сотыхъ до¬
10
7
~50
28
20
14
60
56
40
35
”50
49
10
7
"50
28
,20
14
-60
56

115
лей въ частномъ нрпводнмъ остатокъ въ дълимомъ
5 десятыхъ въ сотыя доли и находнмъ въ частномъ
для седьмой доли 50 сотыхъ, 7 сотыхъ; остатокъ
отъ дълнмаго 1 сотая показываетъ, что седьмая доля
4-хъ едниидъ будетъ болъе 57 сотыхъ п мснъе 58
сотыхъ, слъд. въ частномъ кромъ 57 сотыхъ будетъ
еще находиться нисколько тысячныхъ долей, для
отыскашя сихъ тысячныхъ долей остатокъ отъ дъ¬
лнмаго одну сотую приводнмъ въ тысячныя доли й
для седьмой доли 10 тысячныхъ находнмъ въ част¬
номъ одну тысячную и т. д. продолжая увиднмъ,
что послъ шести дъленш, именно когда мы найдемъ
въ частномъ 8 мнллюнныхъ долей, получатся въ
остаткъ отъ дълнмаго 4 мнллюнныя доли, которыя
приведя въ десятимпллюниыя доли, получимъ въ
дълнмомъ 40 десяттшллгонпыхъ долей н въ част¬
номъ для седьмой ихъ доли найдемъ 5 десятнмил-
люнныхъ долей, т. е. ту же самую цифру, какая
была въ частномъ для десятыхъ долей н потомъ
опять начнутъ въ частномъ повторяться тъ же циф¬
ры, какъ и прежде и въ томъ же самомъ порядкъ,
такъ что дълеше не можетъ никогда окончиться и
въ остаткъ никогда невындетъ нуль.
Еще прпмъръ:	пусть	требуется	обратить	въ
десятичную дробь.

116
Здвсь также 50 1 14
двдешс никогда | 0,55Т14285Т14285Т1428,
не окончится, но
С1Я дробь разли¬
чается отъ пре¬
дыдущей толь¬
ко гВмъ, что вь
ней первая ци¬
фра послв за¬
пятой именно 5
иеповторяехся, а
noBTopenie од-
нихъ и твхъ же
ццфръначинаст-
ся со второй ци¬
фры послв за¬
пятой.
Изъ всего пре¬
дыдущего можно вывесть следующее правило для
обращенгя простои дроби въ десятичную: должно
числителя раздплшпь на знаменателя а кань это
дгълыие въ правильной и сокращенной дроби нельзя
произвесть tin гръло, то на мпстгь цгьлыхъ поста¬
вишь въ частномъ нуль и потомъ числителя дан¬
ной дроби (принимая его за ц/ьлос число) прнвесть
въ дссятыя доли и въ частномъ отыскать соот¬
ветствующее число десятыхъ Золей, помножить
cie число на д/ълитсля и произведете вычесть пзъ
дп>лимаго, остатокъ отъ Ътлимаго, если онъ есть,
прнвесть въ сошыя доли и отыскать въ частномъ
соотвтыпствующее число сотыхъ долей, новый ос¬
татокъ отъ дп>ли.маго прнвесть въ тысячныя доли
100
98
20
14
60
56
40
28
120
112
80
ТО
100
98
2

пт
и отыскать вь частномъ соотвптствующее число
тысячныхъ долей и т. д. продолжать до ттъхъ
порь, пока или вь оспгапгкть выйдетъ нуль, или пач~
нуть въ частномъ повторяться, предыдущая его
цифры. — Или другимъ образомъ: должно числи¬
теля данной дроби умножить на 10, 100,	1000 и
вообще на единицу съ несколькими нулями, потомъ
произведете разделить на знаменателя и найденное
частное уменьшить во столько разъ, во сколько уве¬
личили прежде числителя данной дроби.
03.	Нзъ предыдущаго видно, что некоторый обык¬
новенный дроби приводятся въ десятнчиыя, имею¬
щая определенное число цифръ, а другхя приводятся
въ десятичныя, имеюпця неопределенное число циФръ.
Первыя называются точными десятичными, а вто-
рыя — безкопечными или псрюдическимщ въ енхъ
последнихъ собрате разныхъ цнфръ, повторяющихся
въ однояъ и томъ же порядке въ безконсчность на¬
зывается гщяодомъ. Перюдичесыя дроби еще раз¬
деляются на два вида:	на	простыя	перюдичесыя,
въ которыхъ перюдъ начинается тотчасъ после за¬
пятой и на емгыиенныя перюдичесыя, у которыхъ
перюдъ начинается спустя несколько знаковъ после
запятой. Въ перюде можетъ быть различное число
цнфръ — одна, две, три и т. д. но никогда не мо¬
жетъ быть въ перюде цнФръ более, нежели сколь¬
ко единице безъ одной въ знаменателе обыкновен¬
ной дроби, которую приводимъ въ десятичную: ибо
перюдъ, т. е. повтореше одннхъ н техъ же цифръ
въ частномъ происходить отъ одннакихъ остатковъ;
но предполагая, что при делении числителя на зна¬
менателя дроби каждый разъ выходятъ разные ос--

118
татки, и какъ каждый остатокъ долженъ быть
меньше делителя, т. е. знаменателя; то такнхъ чи¬
селъ можетъ быть только считая отъ 1 до чпсла,
которымъ выраженъ знаменатель; напр, если знаме¬
натель дроби будетъ число 57, то наибольшее чи¬
сло разныхъ остатковъ можетъ быть только 56.
64.	Теперь объяснимъ причину, по которой пеко-
торыя изъ обыкновенныхъ дробен приводятся въ
точныя десятнчиыя, а друг in въ псрюдичесыя и
прнтомъ простыя нлн сыешенпмл; нзъ чл. 62 вид¬
но, что для приведены обыкновенной дроби въ де¬
сятичную надобно умножить числителя обыкновен¬
ной дроби на 10, 100, 1 ООО н т. д. н потомъ раз-
дълнть cie произведете на знаменателя оно»; въ
правильной п прнтомъ несократимой дроби разу¬
меется числитель не только не делится на знаме¬
нателя, но даже и не имеете нн одного общаго съ
нимъ производителя, а по чл. 29 произведете тогда
делится на какое ннбудь число, когда одннъ про¬
изводитель его делится па cie число; въ настоящемъ
случае произведете состоите изъ числителя (кото¬
рый не делится на знаменателя) н единицы съ не¬
сколькими нулями; посему, для того, чтобы cie про¬
изведете разделилось на знаменателя, нужно, чтобы
на знаменателя делилась единица съ несколькими
нулями; а единица съ несколькими нулями делится
безъ остатка только на 2 и на 5 или на различ¬
ный произведены сихъ двухъ чиселъ, т. с. на чпсла
кратиыя только 2-хъ или 5-тн или обоихъ вместе.
Посему если знаменатель дроби будучи разложенъ
на первоначальные производители, имеете оными
только числа 2 н 5 или разлнчныя ихъ произве-

119
дешя, то дробь выразится точною десятичного. Чи¬
сло диФръ въ такой точной десятичной дроби зави-
сптъ также отъ производителей 2-хъ и 5-ти знаме¬
нателя; именно разложивши знаменателя данной
дроби на первоначальные производители, надобно
посмотръть, какое пзъ чиселъ 2 или 5 входнтъ боль¬
шее число разъ пропзводнтелемъ въ знаменатель н
сколько разъ cie число входнтъ пропзводнтелемъ въ
знаменатель, столько будетъ и цнфръ въ точной де¬
сятичной дроби, въ которую приводится данная
обыкновенная дробь; jump.	разложивши знаме¬
нателя сей дроби на первоначальные производители,
получимъ: 500—=2. 2. 5. 5. 5 здъсь число 5 входлтъ
пропзводнтелемъ большее число разъ, нежели %
прнтомъ 5 входить три раза пропзводнтелемъ, по¬
сему въ десятичной дроби, въ которую приводится
данная	будетъ	три дссятнчныхъ знака; н въ
самомъ дълъ = 0,680. Легко понять причину
этого, раземотръвши со вшшашемъ способъ приве¬
дения обыкновенных^» дробей въ десятичныя, изло¬
женный въ чл. 62; пзъ разематривашя сего способа
видно, что всякой разъ, какъ прнбавлясмъ мы къ
чиелптелю нуль пли другими словами умиожаемъ
его на 10, находнмъ въ частномъ одну циФру пли
одпнъ десятичный знакъ; а для того, чтобы совер¬
шилось дълеше числителя на знаменателя безъ ос¬
татка, надобно въ числителя ввести такой произво¬
дитель, который бы былъ число кратное знамена¬
теля; но 10 есть число кратное 2-хъ или 5-ти или
2. 5; слъд. каждый десятокъ, введенный множпте-
лемъ въ числитель соотвьтствуетъ въ знаменатели
множнтелямъ 2 или 5 или 2. 5; посему въ преды-

120
дущемъ примере прибавивши къ числителю нуль,
мы сделали его числомъ кратнымъ только 2. 5
след, надобно было еще ввести въ числителя мно¬
житель, который бы былъ число кратное 2. 5. 5;
прибавивши къ числителю еще нуль, т. е. умножив¬
ши его еще на 10, мы сдълаемъ его числомь крат¬
нымъ 2. 5. 2.	5 и потому надобно еще ввести въ
числителя множителемъ число кратное 5, т. е. къ
числителю прибавить еще нуль: так. обр. число ну¬
лей, прпбавляемыхъ къ числителю данной дроби
(или по чл. 62 число десятичныхъ знаковъ отыски-
ваемыхъ въ частномъ) равно наибольшему числу
разъ вхождения какого пнбудь нзъ чиселъ 2 или 5
пропзводителемъ въ знаменателя данной дроби.
Если въ знаменателя обыкновенной дроби не вхо-
дятъ производителями 2 или 5, а входятъ друпя
как1я нибудь числа, то дробь приведется въ nepi-
одическую и прптомъ простую: ибо въ настоящемъ
случаъ произведете числителя (какъ числа* не дъ-
лящагося на знаменателя) на единицу съ нъеколь-
KiiMii нулями (также какъ числа не дълящагося на
знаменателя) не раздълнтся безъ остатка на знаме¬
нателя; а какъ къ остатку для продолжения дъле-
шя должно будетъ также прибавить нуль (т. е.
умножить его на 10) и раздълнть на знаменатель,
то дълсше по вышесказанной же причннъ не совер¬
шится безъ остатка; н къ остатку опять надобно
будетъ прибавить нуль н т. д. до безконечностп; но
остатковъ разныхъ, какъ замътили мы въ чл. 65,
не можетъ быть много п потому поел Б нъеколькнхъ
дъленш необходимо станутъ повторяться прежше

ш
остатки, а потому станутъ повторяться л въ част¬
номъ прежшя цифры н дробь выйдетъ перюднческая.
Если въ знаменателя обыкновенной дроби вхо¬
дя тъ производителями % 5 и каыя ннбудь еще дру¬
гая числа, то дробь приведется въ перюдическую
смешенную, у которой перюдъ начнется послв за¬
пятой черезъ столько знаковъ, сколько разъ вхо¬
дить производителемъ въ знаменателя число 2 или
5; въ случаъ же обонхъ вмВетъ, надобно смотрвть
какое изъ нпхъ входнтъ большее число разъ про-
пзводнтелемъ въ знаменателя п сколько разъ это
число входнтъ производителемъ въ знаменателя, че¬
резъ столько циФръ послв запятой начнется перюдъ;
напр, въ дроби yV j разложивши знаменателя 12 на
первоначальные производители, нандемъ 12=2.2.5;
такъ какъ въ 12 входнтъ 2 пронзводимтелеъ два
раза, то черезъ дпв цпФры послв запятой начнется
перюдъ. II въ самомъ дЪлв ~ =0,41 666666
Въ дроби yytj знаменатель 12 50 = 2. 5. 5. 5. 7;
слъд. большее число разъ производителемъ вхо¬
дить число 5 и потому перюдъ начнется черезъ
три пнфры послв запятой. II въ самомъ двлв
0,0245714285714285
65.	Еслп при ръшенш какого ннбудь вопроса вхо¬
дить въ вычислеше перюднческая дробь, то само
собою разумеется, что нельзя вводить въ cie вычи¬
слеше всъхъ ея десятичныхъ знаковъ (ибо ихъ без-
численное множество), а только надобно ограничиться
нисколькими пзъ ннхъ, обыкновенно ограничиваются
одинмъ, двумя или тремя перюдами, а иногда и не
берутъ ни одного полиаго лерюда, смотря по уело-

122
вьамъ ръшасмаго вопроса; п даже въ конечныхъ
(точныхъ) десятнчныхъ дробяхъ, введен ныхъ въ вы-
чнслеше при рыиенш вопросовъ не трсбующнхъ
большой точности, пренсбрегаютъ нъсколькнмн де¬
сятичными знаками; но въ такомъ случаъ обыкно¬
венно дълаютъ погръшность, которую всегда легко
опредълнть п если она очень мала, то въ вопросахъ,
не требующихъ большой точности, оиа не едълаетъ
значительной ошибки; напр, ръшая какой нпбудь во-
просъ, положнмъ для ръшешя его получили выводъ,
выраженный такою дробью 0,2567 и положнмъ, что
въ семъ вонросъ за единицу принять былъ вер-
шокъ, то вмъсто вышеозначенной дроби для ръше¬
шя вопроса люжемъ взять ту же самую дробь толь¬
ко съ двумя первыми десятичными знаками, т. е.
0,25 вершка, тогда ошибка въ вопроси будетъ очень
незначительна: ибо прямое ръшеше вопроса есть
0,2567; но С1Я дробь больше взятой нами 0,25 и
меньше 0,26; слъд. принимая за ръшеше вопроса
0,25 вершка, мы дълаемъ въ вонросъ ошпбку, мень¬
шую одной сотой доли вершка; если бы мы взяли
для ръшешя вопроса дробь 0,256; то ошибка была
бы меньше тысячной доли вершка; такого рода вы-
чнелешя, т. е. ръшающш вопросъ съ нъкоторою по-
гръщностно, хотя незначительною, называются оы-
числстямп приближенными; п при такнхъ вычи-
слешяхъ чъмъ больше возмется десятпчныхъ зна-
ковъ въ точной десятичной дроби пли першдпческой,
тъмъ вычнелеше болъе будетъ подходить къ истин¬
ному.
Послъ сего очевидно, что всъ вопросы, въ вычн¬
елеше которыхъ входятъ перюднчесшя дроби, ръша-

123
ются только приближенно; если бы надобно было
такой вопросъ рЪшить точнычъ образомъ, то един¬
ственное для сего средство состояло бы въ томъ,
чтобы перюдпческую дробь, въ него входящую, за-
мъиить тою обыкновенною дробью, отъ которой она
произошла; а для сего нужно умъть всякую ncpio-
днческую дробь обращать въ обыкновенную—чъмъ
теперь мы и займемся.
ОБРАЩЕШЕ ПЕР ЮДИЧЕСКПХЪ ДРОБЕЙ ВЪ
ОБЫКНОВЕННЫЙ.
66.	Обращсше перюдическихъ дробей въ обык-
повенныя можно раздълнть на два случая: 1) обра¬
тить периодическую простую дробь въ обыкновен¬
ную н 2) обратить перюдпческую смъшеиную въ
обы кнове иную.
1)	Пусть требуется простую перюдпческую дробь
0,364564564	 обратить	въ	обыкновенную.	Поло-
жнмъ, что искомая обыкновенная дробь есть х, такъ
что х = 0,564564564
Умножимъ здЪсь х и дробь перюдпческую ему
равную на 1000, а вообще на единицу съ столькими
нулями, сколько цнФръ въ перюдъ, тогда (по чл.
58. 1.) получимъ; 1000 х = 564, 564364364	;
изъ сего равенства вычтемъ предыдущее равенство,
получимъ:
1000 х = 564,564364364
' х =: —0,564364364
999 а: = 564
поелику 999 х равняются 364, то одннъ х т. е.

124
искомая обыкновенная дробь будетъ въ 999 разъ мень¬
ше 564 или .т= ggf; слъд. 0,364564564	=
II такъ для обращетя простой псрюдической
дроби §ъ обыкновенную должно перюдъ поставить
числите.гемъ въ искомой обыкновенной дроби, а
зиамешапелемъ въ ней взять цифру 9, написан¬
ную столько разъ, сколько цифръ въ ncpiodn? дан¬
ной псрюдической дроби. Слъд. 0,555535	 = ff;
0,5608560S560S	=
Если бы въ данной периодической дроби бы¬
ли цълыя числа, то ихъ должно поставить при
дроби обыкновенной на мъстъ цълыхъ чиселъ, такъ:
3,575757	 =	3ff.
2)	Пусть теперь требуется смъшенную перюдп-
ческуго дробь 0,25747474	 обратить въ обыкно¬
венную. Положимъ, что искомая обыкновенная дробь
есть х, такъ что х = 0,23747474
Умножнмъ здъеь х п дробь перюдическую ему
равную па 100; а вообще па единицу съ столькими
нулями, сколько цифръ въ дроби до перюда; тогда
получимъ: 100 х = 23,747474
Получивши так. обр. нзъ псрюдической смъшен-
ной дроби перюдическую простую, умножнмъ 100 а?
и дробь равную пмъ на 100; а вообще на единицу
съ столышми пулями, сколько цифръ въ перюдъ,
тогда получимъ: 10000ж=2574,747474  ...; изъ сего
равенства вычтемъ предыдущее равенство, будетъ:
10000 х = 2574,747474
—100 х — —23,747474.:
9900 х = 2351
ц отсюда искомая обыкновенная дробь будетъ: т—~~

125
Можно и такимъ образомъ приводить въ обыкно¬
венную дробь перюдпческую смъшеиную: переие-
сслгь въ данной перюднческой дроби 0,23747474
запятую къ тон ццфръ, съ которой начинается пе¬
рюдъ, получимъ дробь во 100 разъ въ настоящемъ
случаъ большую данной, именно 23,747474	 ciio
дробь, какъ перюдпческую простую приведсиъ въ
обыкновенную но правилу предыдущаго случая и
будетъ:	25.747474	 =г:25^, но cie цълое съ
дробью во 100 разъ больше данной перюднческой
дроби; посему чтобы сравнять его съ оною, надобно
23j|- уменьшить во 100 разъ н будетъ (чл. 54. 4.)
Woo-; слъд. 0,23747474	=
II такъ чтобы обратить перюдпческую смгыаеп-
ную дробь въ обыкновенную, должно перенести въ
ней запятую къ той цпфртъ, съ которой начинает¬
ся перюдъ и вновь так. обр. полученную nepiodu-
ческую простую дробь обратить въ обыкновенную
и наконецъ найденное так. обр. цтълое съ дробью
уменьшить во столько разъ, во сколько прежде бы¬
ла увеличена данная перюдическая дробь при пере-
песенш запятой къ той цшфрть, съ которой начи¬
нался въ ней перюдъ.
О СОВОКУНЛЕНШ ДЕСЯТНЧНЫХЪ ДРОБЕЙ
СЪ ОБЫКНОВЕННЫМИ.
67.	Если въ сложешн, вычптанш, умножеиш и
дълепш вмъстъ съ десятичными дробями входятъ
дроби обыкновенный, то или обыкновенный дробя
ирпводятъ въ десятнчиыя и потомъ складываютъ,
«ычнхаютъ, умножаютъ н дълютъ нхъ, какъ деся-

. 126
тичныя дроби; или десятпчныя дроби приводить въ
обыкновенный II потом ь подвергаютъ ихъ дънств1ямъ
вычнслешя, какъ дроби обыкновенны». Если въ умно¬
жены или дъленш вмьсть съ обыкновенными дро¬
бями вчодять перюдичесыя, то всегда приводить
ихъ въ обыкновенный: ибо приведя въ семъ случаь
обыкновениыя дроби въ десятпчныя, мы при умно¬
жении или дъленш перюдцческнхъ дробен не знали
бы, черезъ сколько зиаковъ перенести запятую для
обращешя нхъ въ цьлыя числа, какъ ото требуется
правилами чл. 60 и чл. 61.
Пусть требуется изъ А вычесть 0,035; обративши ^въ
десятнчнуюдробь, получимъ: л =0,71428571428571....
Слад. — 0,055=0,7142S57142S57I....—0,035=
0,67928571428571
Обративши спо дробь въ обыкновенную получимъ:
0,67928571428571	= «ля-ддоад.
1	9VD99DOOO
Общи! иаиболыиш дьлнтель сен дроби (чл. 54)
есть 714285; сокративши оную дробь, будетъ:
6  о 055 — эг,т
7 	 *	  иоо-
Этоть же самый прпмъръ можно ръшнть и так.
обр.: обратнмъ десятичную дробь 0,055 въ обык¬
новенную; по чл. 57 имьемъ 0,055 = уууу тогда
7 — 0,055 -■§- — y^hj = f— или по сокращен»!
на 5 искомая разность будетъ у*^1- та же самая,
какъ н прежде. -
Пусть еще требуется (1 + 0,27-1-0,111111	)
умножить на (f-b 0,212121 -р Д).
Обративши во множнмомъ f въ десятичную дробь,
иолучнмъ: 0,4+0,27+0,11 ill 1.... — 0,78III 1111

ш
Обративши во множители u л въ дссатпчпыя
дроби, ниъсмъ:	0,75	4-	0,212121	 -р- 0,2 =
1,16212121
Слъд. (^4-0,274-0,111 111....)x(f+0,212121....-рл)
r= 0,7S111111 X 1,16212121
Пли приведя cin перюдичесшя дроби еъ простыл,
получимъ: 0,7Sill 111	 X	1,16212121
IIS Q_5_   Я О Я 8 О X 5
9900	U91QOOO*
Требуется сделать дълеше (§■ 4- 0,15 — 0,0128)
на (•§- — 0,002 4- i) приближенно до тысячныхъ до¬
лей — это значптъ, что въ конечномъ выводъ дол¬
жна быть такая десятичная дробь, у которой были
бы определены десятый, сотыя п тысячный доли.
Поелику л + 0,15 — 0,0128 = 0,4 + 0,15 —
0,0128 = 0,5572 и i — 0,002 + л =г 0,6 — 0,002+
0,25 = 0,848 то придется разделить 0,5572 на
0,848; поступая по чл. 61, найдемъ въ частномъ
дробь	обращая	се	въ	десятичную	(чл.	62)	и
останавливаясь при семъ обращеши па тысячныхъ
доляхъ, найдемъ искомое частное: 0,635.
О НЕПРЕРЫВПЫХЪ ДРОБЯХЪ.
«
6S.	Непрерывною дробью называется такая дробь,
у которой числителемъ бывает ь единица, а зиамспа-
телемъ цълое число съ дробью, которая сама чис.ш-
тслемъ пчъетъ единицу, а знамеиателемъ также цъ¬
лое число съ дробью и т. д.
При нзслъдованш о непрерывиыхъ дробяхъ на¬
добно разрешить слъдуюпце вопросы:	1)	какимъ

128
образомъ обыкновенную дробь обратить въ непре¬
рывную; 2) на оборотъ непрерывную дробь обра¬
тить въ обыкновенную; и 5) показать употреблеше
непрерывных'/, дробен.
69.	Пусть требуется дробь	обратить	въ	не¬
прерывную. Для сего числителя н знаменателя дан¬
ной дроби раздълнмъ на числителя, получимъ:
261 1
5571	13-f 178
261
такимъ же точно образомъ поступнмъ п съ дробью
т. е. числителя и знаменателя ея раздълпмъ на
числителя, будетъ: 178	 1	;	поставнмъ	ciio
261	1 4- 83 величину вмъ-
178 сто -'Ц въ вы¬
ражение данной дроби, получимъ: 261	1
3571“15+1
1+83
П8
поступивши съ дробью	также, какъ п съ пре¬
дыдущими дробями, иандемъ:	83	1
178 = “й+ 12	“
83
261 _ 1
35тТ 13 + 1
1 + i
2 + _12
83
потомъ продолжая такимъ же образомъ далве чи¬
слителя и знаменателя каждой вновь выходящей

129
дроби дилнть на числителя ея, найдемъ; 12	1
83	6-}-1 {
72
41	I
И 12	i + i_
11
и данная дробъ выразится наконецъ такою непре¬
рывною дробью:
261 __ 1
5571 ~15 +~ 1
1 + 1
2 + 1
6+1
1 + 1
11
СлЪд. для обращешя обыкновенной дроби въ не¬
прерывную должно чисУптсля и знаменателя ея раз-
дълнть нд числителя, съ полученною отъ сего дъй-
ств1Я въ знаменатель дробью поступить такимъ же
образомъ, т. е. числителя и знаменателя ея разде¬
лить на своего числителя п продолжать cie дъй-
ctbic до тг.хъ поръ, пока получится въ знаменатель
непрерывной дроби такая дробъ, у которой числи-
телемъ будетъ единица, какъ въ выше нзложенномъ
нрнмьрЪ дробъ Yf. Еслнбы для обращешя въ не-
прерывную дробъ дана была дробь неправильная,
то прежде сего обращешя должно бы было нзклю-
чнть цьлое число изъ неправильной дроби и уже
вышедшую послъ сего изключсшя дробь обратить
въ непрерывную.
9

»
130
JTfHMnv. Изъ предыдущаго способа видно, что не
всякая обыкновенная дробь можетъ быть обращена
въ непрерывную; именно тъ обыкновенный дроби, у
которыхъ числитель единица н тъ, у которыхъ зна¬
менатель — число кратное числителя не могутъ
быть обращаемы въ непрерывный дроби.
70.	Чтобы обратить данную непрерывную дробь
1
15+1
1 +1
¥+7
6 +~ Г
11
обратится въ следующую:
1
13+1
ттт
2+1
6 ч- 1
~~ГГ
1
15 + 1
1 +
поступая такнмъ же обра;
найдемъ слъдуюпця дроби:
въ обыкновенную; для се¬
го въ пое.тьднемъ знаме¬
натель непрерывной дро¬
би соедшшмъ цълое съ
дробью 1 -J- въ одну
дробь, будетъ i|, тогда
данная ненрерывнаядробъ
въ поелт.днемъ знамена¬
тели сен непрерывной
дроби раздълнмъ 1 на
будетъ:	11	данная
дробь будетъ:
I
+ i
О + 11
иъ далъе, постепенно

131
‘1 1 1 261
15+1	’13+1	513+178и3571
1+1	1+ S3	261
2+12	ТГ8	•
~83~
Слъд. 1
15 + Г
1 + 1
2+1.
6 + 1
1 + 1_
11
71.	Теперь остается показать употреблеше непре-
рывиыхъ дробей. Непрерывныя дроби употребля¬
ются въ вычнслешлхъ приблпженныхъ п именно на
слвдующемъ условие. часто случается, что при рв-
niciiin какого нибудь вопроса получается дробь обык¬
новенная несократимая и прнтомъ выраженная до¬
вольно въ большихъ числахъ, трудныхъ для удер¬
жания въ памяти, если это нужно, тогда можно по-
мощпо непрерывныхъ дробей найти дроби весьма
прпб.шженныя къ точной дроби и выраженныя го¬
раздо меньшпмп числами. Положнмъ, что при ръше-
iiiu какого нпбудь вопроса получили дробь ~£ аР-
шина. 15м вето сего точиаго рвшешя, которое нъко-
торымъ образомъ пе даетъ яснаго поняздя о найден¬
ной велнчпнв, возмемъ приближенное рвшеше так.
обр.:	обратнмъ спо дробь	въ	непрерывную,
получимъ:
261
551 Г

132
257 i
843 — 3+1
3+_l
1 + 1
1 + 1
3 + 1
10
Въ сей непрерывной дроби остановимся на пср-
вомъ ея знаменателя 3 и отброснмъ всю за нимъ
следующую величину, тогда вмъсто непрерывной
дроби, получимъ дробь i большую fff: ибо знаме¬
натель непрерывной дроби, равной уменьшился;
слЪд. принимая £, вмъсто	мы возмемъ больше,
нежели сколько нужно было; а если вмъсто Ц-§
возмемъ i, то cifl дробь будетъ меньше точнаго рЪ-
шеннг. ибо знаменатель непрерывной дроби былъ
5 -J- нъкоторая дробная величина, которую мы от¬
бросили и вмъсто оной къ 3 придали цълую еди¬
ницу; слъд. увеличили знаменателя дроби, отъ того
самая дробъ уменьшилась. II такъ	заключается
между J и { т. е. она меньше f- и больше i; раз¬
ность же между енмн дробями будетъ больше раз¬
ности между каждою изъ нихъ и дробью *	; раз¬
ность же между f 11 f есть TSi посему принимая f-
нлп ^ вмъсто	мы	едълаемъ	ошибку	менъе	~
аршина.
Если бы мы захотъли еще болъе приблизиться
къ точному ръшенйо и едълать чрезъ то меньшую
ошпоку, то надооно бы было остановиться въ выше¬
означенной непрерывной дроби на второмъ ея зна¬
менателя и отбросить всю внизъ за нимъ слЪдую-

133
щую величину; тогда бы вместо точнаго рыпешя
пришлось взять дробь 1 или по обраще-
3 + £
3
ши ея въ простую — и cin дробь была бы меньше
ибо - больше 1
843*
3 + 1
1 + 1
3 + 1
То"
слвд. 1 меньше 1
1
3	3+1
1 + 1
1 + 1
5 + 1
10
И такъ |ff будетъ заключаться между | и ^т.
е. она меньше f и больше — и потому принимая
ту или другую дробь вмъсто fff, мы сдълаемъ
ошибку ыенъе разности между | и — т. е. меяъе
7о аршина.
Если бы мы остановились на третьемъ знаменатель,
то получили бы дробь 1	большую дан-
3+1
3+JL
1
ной fff, къ которой требуется найти прибли-

134
женную величину: ибо £ болие 1^
1+1
1 + 1
3 + 1
10
посему 1	менъе	1	сльд.
3+1	3+1
1 1 + 1
1+1
3+1
10
болие 1
3+1	3+1
3 + 1
1 1 + 1
1 +т
5+ 1
ИГ
останавливаясь на четвертомъ знаменатель, получили
бы дробь меньшую данной, къ которой приближа¬
емся и т. д. вообще останавливаясь на знаменателяхъ
нечетныхъ мЬстъ, будемъ получать дроби, больпия
данной; а останавливаясь на знаменателяхъ четныхъ
мвстъ, будемъ получать дроби, менышя данной, къ
которой приближаемся; дроби так. обр. получаемыя,
между которыми заключается данная дробь и по¬
переменно то больная, то менышя оной называются
сближающимися дробями; принимая какую нибудь

цзъ сближающихся дробен вместо данной, мы сде-
лаемъ ошибку, меньшую разности между двумя по¬
следовательными сближающимися дробями Так. обр.
въ вышеозиаченпомъ примере останавливаясь на
третьемь и четвертомъ знаменателе, по.1учимъ для
сближающихся дробен следукящя дроби: ~4^ и
принимая ту или другую дробь вместо данной, мы
сделаемъ ошибку менее разности между сими сбли¬
жающимися дробями, т. е. менее аршина. Чтобы
еще яснее судить о прпблнжешн каждой нзъ спхъ
дробей Къ данной, обратные какъ сш сблнжаюнця-
ся дроби, такъ п данную въ дссятпчиыя, получимъ:
Iff = 0,3048635
-f-s = 0,307692307692
-ч- == 0,304547826.
Сравнивая ciu дроби между собою, увидимъ, чта
разность между данною и ~ заключается въ ты¬
сячныхъ доляхъ, нмешхо въ у4- заключается слиш-
комъ 3 тысячныя доли противъ данной; а разность
между данною и ~ заключается уже въ десяти-
тысячиыхъ доляхъ, именно въ ~ не достаетъ слиш-
комъ 5 десятитысячныхъ долей противъ данной;
след, если бы мы взяли ~ вместо данной дроби,
то сделали бы ошпбку менее тысячной до.ш аршина,
въ настоящемъ случае.
i Примтьч. 1. Непрерывный дроби нмеютъ множе¬
ство весьма любопытныхъ н съ пользою прлклады-
ваемыхъ къ разпымъ вычислешямъ свойстве, но пз-
следоваше оныхъ требуетъ некоторыхъ Алгебрап-
ческихъ сведений и потому более относится къ Ал¬
гебре, нежели къ Ариеметнке.

136
Примтъч. 2. Если непрерывный дроби входятъ вме¬
сте съ другими обыкновенными или десятичными
дробями въ некоторый дьйств1я вычпслешя, то для
производства надъ ними снчъ двнствш вычпслешя
предварительно приводить ихъ въ дроби обыкно¬
венный по чл. ТО и потомъ уже подвергают'!, ихъ
требуемымъ дънствхямъ вычпслешя.
О Т Д Ь Л Е II I Е II.
ОБЪ ИМЕНОВАПНЫХЪ ЧИСЛАХЪ.
72.	Мы сказали (чл. 1.), что имеиованпымъ чн-
сломъ называется такое число, при составлены ко-
тораго родъ единицы означается. Напр. 5 пудовъ, 7
рублей и т. д.; здесь видно, что первое число 5
составлено не пзъ какой ннбудь единицы, а именно
изъ единицы особаго рода, называемой пудомъ; так¬
же второе число 7 составлено нзъ определенной
единицы называемой рублемъ.
При измеренш какого нибудь рода величине у
каждаго народа употребляется некоторая единица,
имеющая свою определенную и постоянную вели¬
чину; с!я единица для измерешя ыеньшцхъ величшгъ
того же рода делится на некоторое определенное и
постоянное чпело частей, называемыхъ подъразде-
дешямп главной единицы; так. обр. для измерешя
веса тълъ принята за главную единицу особая ве¬
личина, называемая пудомъ; ая единица разделена
да 40 частей и каждая такая часть пуда названа
фуитомц след. Фунтъ есть подъразделенхе пуда, со¬
ставляющее сороковую pro часть; фунтъ, какъсоро-

137
косая часть пуда, снова раздвленъ на 32 части и
каждая так. обр. найденная часть Фунта названа
лотомъ; сл'Вд. лотъ есть нодъразд'Влеше Фунта, со¬
ставляющее тридцать вторую его часть, и т. д. Та-
ковыя подъраздьленхя главной единицы называются
еще низшими наименовашямщ а главная единица—
высшимъ паименоватемщ и такъ числа съ низшими
наимсновашямхх суть дроби, изображенный безъ зна¬
менателя (такъ какъ десятпчныя дроби): ибо этотъ
знаменатель однажды навсегда принять постоян-
нымъ; слъд. 5 Фунтовъ есть ничто иное, какъ пу¬
да, также 8 лотовъ есть ничто иное, какъ ~ Фунта:
ибо ^ пуда значить, что единица, которая въ на-
стоящемъ случав есть пудъ, раздВлена на 40 частей
и такихъ частей взято 5, что и составляетъ 5 Фун¬
товъ; также Фунта значить, что единица т. е.
Фунть раздВлена на 32 части и взято такихъ ча¬
стей 8, что и составить 8 лотовъ. Число, показы¬
вающее сколько единицъ низшаго наименованы со¬
держится въ единицъ высшаго, называется знамена-
телънымъ числомъ. Посему въ вышесказанныхъ при-
ыЪрахъ 40 и 32 суть числа знаменательный.
Именоваиныя чпсла, входянця въ вычпслехпе, бы-
ваютъ двухъ родовъ: простыл и сложныя. Про-
стымъ именованнымъ числомъ называется такое, ко¬
торое закдючаетъ въ себь одпнъ родъ единицы;
напр. 4 пуда; 5 стопъ; 7 Фунтовъ; 15 копВекъ и т.
д. Сложнымъ именованнымъ числомъ называется та¬
кое число, которое заключаеть въ себь единицы из-
въстнаго рода вмистъ съ подъраздвленхями сихъ еди¬
ницъ. Напр. 15 пУд- + 4 Ф?н- +18 лот-, 13 руб- +
23 ком- и т. д.

138
О РАЗЛИЧИЫХЪ МЪРАХЪ, УПОТРЕБЛЯЕМЫХЪ
БЪ POCC1IL
73.	Множество меръ, находящихся въ употрсбле-
ши у разлнчныхъ народовъ, можно разделить на 8
классовъ: 1) меры длины; 2) меры поверхностей; й)
меры объсмовъ телъ; 4) весы телъ; 5) монеты; 6)
мера времени; 7) мера бумаги н S) .мера окружности
Бъ Poccin для измерешя сихъ восьми родовъ вели¬
чине употребляются следуюхщя меры:
1.	меры длины.	2. мъры поверхностей.
Миля содержите въ себе Десятина содержите въ
7 верстъ; себе 2400 квадр. сажеиъ;
Верста. . . 500 сажеиъ; Квадратный сажень. 9
Сажень 3 аршина или 7 квадр. арш. или 49 квадр.
Русск. Футовъ;	русск. Футовъ;
Аршинъ. . 16 вершковъ; Квадратный Футъ. . 144
Футъ 12 Русск. дюймовъ;	квадр. дюйма;
Дюйме	10	лиши;	Квадратный дюйме. 100
Лишя . 10 скрупуловъ;	квадр. линш;
Квадратная лишя. . 100
квадр. скрупуловъ;
Примтъч. Въ межеванш сажень разделяется на 10
футовъ; Футъ на 10 дюймовъ; дюнмъ на 10 линши
лишя на 10 скрупуловъ.
5. МЪРЫ ОБЪЕМОВЪ.
Кубпческая сажень содержите въ себе 343 русск.
кубнч. Футовъ;
Кубчческш Футъ. . . 1728 кубнческнхъ дюймовъ;
Кубпческш дюймъ. . 1000 кубнческнхъ лннш;
Кубическая лннш.. . 1000 кубнческнхъ скрупуловъ;

139
Къ мерамъ объемовъ относятся также меры для
хлъбныхъ зеренъ и меры для жидкостей.
ЫЪРЫ ДЛЯ ХЛЪБНЫХЪ ЗВ- МБРЫ ДЛЯ ЖИДКОСТЕЙ.
РЕИЪ.
Четверть содержите въ Бочка содержите въ себе
себе 2 осмнны или 8	40	ведре;
четвернковъ;	Ведро. . .	10	штофов ь
Осмина. . .	4 четверика;	Штофъ. .	2	полуштоФа
Четверике. 4 четвертки;	пли	кружки;
Четвертка. 2 гарнца;
Гарнецъ. . 50 долей;
4.	мьры въеовыя.
Берковецъ содержитъ въ себе 10	пудовъ;
Пудъ	  40	Фуптовъ;
Фунте.	52	лота или 96 золоти.
Лотъ	 5	золотника;
АПТЕКАРСК1Й ВБСЪ.
Фунтъ содержитъ въ себе 12 укцпт пли около 84 золот.
Унцхя	8 драхме;
Драхма	5 скрупула
Скрупуле	  ...	20 грановъ;
5.	МОНЕТЫ.
а) Золотыя.	Ь)	Серебрения.
Пмпер1алъ= 10 рубл. зо- Рубль серебра содержитъ
лотыхъ содержите въ се- въ себе 3 руб. 50 к. мЪдп;
бъ 56 руб. 5 коп. м. Полтина серебра. 1 руб.
Полуимпериале = 5 рубл.	75	коп.	меди
золотыхъ содержитъ въ Четвертаке пли 25 коп.
себе 18 рубл. 2-~ коп. м.	серебра 87а коп. м.

140
Двугрнвенникъ пли 20
коп. серебра. 70 коп. м.
Пятиалтынникъ или 15 к.
серебра тоже что Поль¬
ской злотый. 52|- к. м.
Гривенникъ или 10 коп.
серебра. 35 коп. м.
Пять копеекъ серебра.
17f коп. м.
с) МтьЪныя.
Рубль меди содержать въ себь 10 гривенъ или 100 к.
Гривна	10	копеекъ.
Копейка.	 2	деньги.
Деньга	 2	полушки.
6.	М'ЪРА ВРЕМЕНИ.
Годъ содержитъ въ себь 12	ыесяцовъ;
Месяцъ	50	дней, т. е. 30 сутокъ;
Сутки	24	часа;
Часъ		60	минуть;
Минута	60	секуцдъ;
Примгьч. Годъ измеряется еще числомъ дней, въ
немъ содержащихся. Простой годъ содержитъ въ
себъ 565 дней. Високосный имъстъ 566. дней; ви¬
сокосный годъ следуетъ после каждыхъ трехъ про-
стыхъ годовъ. Чтобы узнать какой годъ высокосный,
ТО нужно ПОСЛЪДШЯ ДВЪ цифры числа, которымъ
выражается годъ, разделить на 4; если число cie
разделится на 4 безъ остатка, то годъ будетъ вы¬
сокосный; въ противномъ случае простой н нритомъ

141
число единицъ въ остатке покажете порядокъ года
п'ростаго отъ перваго прошедшаго высокоснаго. Напр.
1936 будетъ высокосиый: ибо 36: 4 = 9: но 1945
есть простой годе и притомъ первый следующей за
прошедшпмъ высокоснымъ: ибо 45 будучи разделе¬
ны на 4 дадутъ въ остатке 1.
7. МИРА БУМАГИ.	8.	МЬРА	ОКРУЖНОСТИ.
Стопа содержите въ себе Окружность круга содер-
20 дестей; жптъ въ себе 360 градус.
Десть	24	листа;	Градусе. . . 60 мннутъ;
Минута. . . 60 секунде;
Для означешя градусовъ употребляютъ знаке: (°);
для означешя минуть ('); для означешя секунде (*).
Посему 53 °	18' ■+■ 43" или какъ обыкновенно изо-
бражаютъ это 53° 18' 43" значите 53 градуса 18
минуть и 43 секунды.
Прежде нежели приступишь къ нзложенно основ-
иыхъ четырехъ денствш вычислены надъ именован¬
ными числами, научимся раздроблять числа боль-
шаго наименованы въ числа наименованы меньшаго
н превращать числа меньшаго наименования въ чи¬
сла наименовашя большаго.
РАЗДРОБЛЕШЕ ИМЕНОВАНПЫХЪ ЧИСЕЛЪ.
74.	Раздробление есть приведете чиселъ большаго
наименовашя въ числа меньшаго наименовашя. Напр.
требуется определить, сколько золотниковъ содер¬
жится въ 37 пудахъ; для сего определимъ сперва
сколько фунтовъ находится въ 37 нудахъ; поелику

' ш
въ каждомъ пудъ находится по 40 Фунтовъ, то въ
57 пудахъ будетъ Фунтовъ въ 57 разъ болъе, не¬
жели въ одномъ пудъ, т. е. въ 57 пудахъ будетъ
57. 40 = 1480 Фунтовъ; далъе поелику въ каждомъ
фунтЬ содержится 52 лота, то въ 1480 Фуптахъ
будетъ содержаться 1480. 52	47560	лотовъ;
наконсцъ въ 47560 лотовъ будетъ содержаться
47560. 5= 142080 золотнпковъ. II такъ 57 пУ^- =
14S0 Фи>1т- = 47560 ■*»"*• = 142080 30-1*
Пусть еще требуется -§- версты привести въ дюй¬
мы, т. е. узнать сколько будетъ дюймовъ въ ~ вер¬
сты. Поелику въ цълой верстЪ содержится 500 са¬
женъ, то въ пятой ея доли будетъ содержаться 100
саженъ, а въ трехъ пятыхъ ея доляхъ будетъ 500
саженъ т. е. чтобы узнать сколько въ дроби выс¬
шаго наименовашя содержится едшпщъ низшаго на-
имеиовашя, должно знаменательное число раздълить
па знаменателя данной дроби и частное умножить
на числителя оной, или другими словами должно
данную дробь высшаго наименовашя умножить на
знаменательное число и будетъ: Д веР- = Д. 500 =
500 салк- ; ПОТОМЪ ПО Предыдущему прнмвру 500 салк.
= 500.7=2100 Фзт- = 2100. 12 г 25200 дюймовъ.
Слъд. Д «гр- = 25200 Эю»-*..
Также обращая А фунта въ граны, получимъ:
А Фип‘ -А. 12 = ~7- у ищи = -А*. 8 = драхмъ =
- 5 = —скрупуловъ = ДА|Д.20=	—	гра-
новъ илн по исклгочеиш цълаго числа изъ непра¬
вильной дроби, будетъ: А Фи* — 5291д грана.
II такъ чтобы обратить простое именованное
число хрьлое или дробное большого наименовашя въ

143
наимсновате мепыиее, надобно постепенно приводить
его во всгь мсиъипп иаименовашя до экелаемаго,
умножая каждый разг. непосредственно большее на-
имеповатйе па знамена тельное его число.
I
Прп.ипч. 1. Можно раздробить данное простое
именованное, число въ желаемое меньшее нанмснова-
шс, не переводя его постепенно черезъ все менышя
иаименоваптл, заключающаяся между даппымт. на-
именовашеиъ н требуемымъ; для сего должно только
определить oTHomenie единицы даннаго нанменова-
IIIл къ единице желаемаго или другими словами
определить по таблице чл. 73 сколько едпнпцъ
требуемаго иаименовашя содержится въ единице дан¬
наго нанмсповашя, потомъ на найденное так. сбр.
число умножить данное для раздроблешя именован¬
ное число и получимъ желаемое. Папр. требуется
определить число вершкопъ въ 25 сажепяхъ; пое¬
лику въ сажени 3 аринша, а въ аршине 16 верш-
ковъ, то въ саженн 48 вершковъ; след. 25 сазк- —
25.48 = 1200 воршк.
Примтьч. 2. Если бы при дробномъ нмснопанномъ
чпеле высшаго панменовашя находилось п целое чи¬
сло того же папменовашя, то для раздроблешя его
въ низшее наименование должно бы было целое съ
дробью привести въ одну дробъ и поступить по
вышесказанному или целое привести отдельно въ
требуемое меньшее напменоваше, а дробъ отдельно
и после два так. обр. нанденныя чпсла сложить
вместе. Либо можно пзъ простого нменованнаго чп¬
сла сделать сложное, обративши дробъ его въ не¬
посредственно менышя наименования. Ilanp. 5,13 года

144
раздробить въ дни, для сего доли года 0,13 прпвс-
демъ сначала въ мвсяцы, будетъ 1,50 мвсяца; по-
томъ доли 0,56 мвсяца приведемъ въ дни, получимъ
16,8 дня; так. обр. 0,13 года = 1	16,8 Эн- .
Слъд. вмъсто даннаго простаго именованнаго числа
5,13 года, ыожемъ взять ложное именованное, ему
равное: 5 гоЭ- -Ь 1 М1ЬС• -+- 16,8 э,‘*;“ потомъ уже раз¬
дроблять cie сложное именованное число такъ, какъ
будетъ показано въ слъдующемъ члень.
75.	Пусть теперь требуется сложное именованное
число 27 Фу1- -Ь 4	+	о	драх.^_	{скр. _(_ 13 грая, раз¬
дробить въ меньшее напменоваше, т. е. узнать сколь¬
ко въ семъ сложномъ нменованномъ числъ находится
грановъ. Для сего 27 Фунтовъ по предыдущему
члену, обратнмъ въ унцш, будетъ 27 '/'■/“■=27.12=
324 унщямъ, къ сему числу унцш придадпмъ дан¬
ный 4 унцш, будетъ въ 27 Фуп- 4 !/«н- содержаться
328 унцш; cie число упцш обратнмъ въ драхмы,
будетъ 328 унцш = 528.8 = 2624 драхмамъ, прн-
даднмъ сюда даипыя 5 драхмъ, будетъ въ 27 Фун•-)-
4 янч- -Ь 5 содержаться 2629 драхмъ; cie число
драхмъ обратнмъ въ скрупулы и прпдадимъ данный
1 скрупулъ, получимъ: 27 Фу11- -+- 4 2/“ч + 5	+
1 ск1>-=. 7888 скруп. наконецъ обративши cie число
скрупуловъ въ граны и придавши данные 13 гра¬
новъ, получимъ: 27 Фун- 4	5	дР-	1	СКР’
13 гр- = 157773 гранамъ. Все cie дъйетше распола¬
гается так. обр.

145
Сллд. чтобы
раздробить сло¬
жное именован¬
ное ЧПСЛ о въ
меньшее наиме-
новаше, надобно
высшее наиме-
новашс его при¬
вести въ непо¬
средственно за
нимъ следую¬
щее, къ найден¬
ному так. обр.
числу придать
числоединицъсе¬
го непосредст¬
венно низшаго
наименовашя, со-
держащагося въ
фуч. ущ. дрпх. сир. гр.
37-i-4+5+l-i-13=157773 гр.
X 12
54
27
32 4 унцш
+ 4
328 уццш
X 8
2624 драхмы
+ 5
2629 драхмъ
X 3
7887 скрупуловъ
■+■ 1
7888 скрупудовъ
X 20
157760 грановъ
+ 13
157773 грановъ.
данномъ для раздроблстя именованномъ числе, по¬
лученную лит. обр. сумму обратить въ следующее
низшее наименовате и опять къ полученному чис¬
лу единицъ иоваго низшаго наименовашя придать
число единицъ того же наимсноватя, содержащееся
въ данном# числе, и так. обр. продолжать далее
до желаемого меныиаго наименовашя.
Вотъ еще прнмъръ: требуется 17 верст- + 345 саж-
_j_ 8 дюйм, привести въ .1Ш1П1.
10

146
Поступая по
вышесказанно¬
му, получимъ
8S45 сажеиъ;
cie' число са-
женъ прпво-
воднмъ въ не¬
посредствен! ю
низшее напме-
TioBanic — въ
футы (хотя
оныхъ п не
находится въ
данномъ пме-
повапномъ 4U-
агрст. гаж.
17-4- 345
Х.500 '
S3J0(T
4-345
8845 еаженъ
х7
дюп.к.
8 = 7429880 лннш.
(31915 футовъ
Х12
125850
61915
742980
4-8
742988 дюймовъ
Х10
742 У880 лшнй
слъ), получимъ 61915 Футовъ и такъ какъ въ дан-
помъ чнелт. Футовъ не находится, то безъ всякаго
лрпбавлешн Футовъ къ сему числу 61915 Футовъ,
прпводимъ нхъ въ дюймы, получивши 742988 дюн-
мовъ, прпводимъ пхъ вт. лшпн по требованно во¬
проса п нмьсмъ вмъсто даппаго сложиаго нменовапна-
го числа 7429880 лиши.
Если въ данномъ сложномъ пмеиоваппомъ чпелъ
находятся при цълыхъ н дроби, то можно въ каж-
домъ нанмснованш привести цълое съ дробью въ
одну дробь п потомъ при раздроблеши поступить
по вышесказанному; нлп .можно прежде раздробле-
П1Я освободиться въ сложномъ нмсноваппомъ чпелъ
отъ дробен во всъхъ напменовашяхт», кромь пос.гьд-
няго ппзшаго, а иногда и въ оиомъ, п потомъ по¬
ступить по предыдущему правилу. thmp. 25^- ".'/э-

147
-h 18f фу“- + 7-1 -h Ц Л0 ‘- ilpIIilL'CT:! ВЪ ЗОЛОТНИКИ.
Привода вь каждом;. папменованш цълос съ дробью
ВЪ ОДНу дробь, ПОЛучимЬГ	-1-	^5	Фи11-	ii b)»n._j_
-1 301-: обратшшш ~ нудл въ Фунты, пандсмъ ~ 40—
гДАД»/)!/»s придавши къ сему числу Фунтовъ ^Фун¬
та, пмг.смь -1 Н-/-Д -4- а-3 = «.унта; cie число Фун-
товъ приведешь въ лоты . 52 —	лота,
прндадпмъ сюда -г' лота, будетъ 5“а?52- -f- -’у- =
-?'®— лота; cie число лотовъ приведемъ въ золот¬
ники	3	=золоти., придадим ь сюда
4 золоти, будсгъ:	-+*	золоти,	или
но исключенш цълаго числа 92049, G золотника;
слъд Qol n'Jd- -h I Sf- Фуп- -+- 7уи",1--ь1^39-'-=920,Ю,С
золотника.
;j Можно это раздроблеше едълать и так. обр.:
освободнмсн въ даниомъ пмепопанпомъ чнелъ 25y,^.,/',•
18| Фип- -4- 7i лот. _[_ {*. зол. 0хъ дробей; приведя у
пугда въ Фунты, получимъ у. 40 = 20 фунт, придав¬
ши ciii 20 Фунтовъ къ даииымъ 18у Фунт, будетъ
5S-5- Фупт.; так. обр вмъсто 2лу “.Vй- -f- lSy Ф.Уа- шгъ-
елъ 25 пУд- -4- 58-f ФУ"-. потом ь обращая £ Фунта въ
лоты, получимъ: Д. 32	—	= 19у лот., придавая
сюда данные Ту лотовъ, будетъ 26лота и потому
25у пУь- + 18-| Фип- + 7у Аот- = 23 ":/й- + 3S Ф.г<1-
-4- 2С)~а м,:!-; приведя ~ .юта въ золотшш, будетъ:
5 = 9у =; золоти., придавая сюда 1узолот.,
получимъ: Ъ~- золоти, или i лотъ и ~ золоти.
Слъд. 25ун»й-с- lSf ФУ”-+ 7у-,0"*Ч- ly JfM- = 25"Уй- -+-
58 фуп- + 27 Avm- -j- ~ 30.tom. - поступивши СЪ СИЫЪ
именованнымъ числомъ по общему правилу, пап с мъ:
25 «уЭ.^_58 ф>уч- -4_ 27.*«»»•_}_ ^ зе-*.~92049,6 золоти.,
тоже число, какое и прежде было пандепо.

\
148
ПРЕВРАЩЕ111Е ИМЫЮВАППЫХЪ ЧИСЕЛЪ.
76.	Превращение есть приведете чиселъ ысньшаго
iiamieiioBania въ числа Сольшаго наименовашя. Напр.
требуется 864 гарнца привести въ четверти, т. е.
узнать сколько четвертей содержится въ 864 гарн-
цахъ; сначала узнаемъ сколько четвертокъ содер¬
жится въ 864 гарнца хъ; п поелику каждые два
гарнца составляютъ только одну четвертку, то чи¬
сло четвертокъ въ двое должно быть меньше числа
гарицевъ; слъд. чтобы узнать сколько четвертокъ
составляютъ 864 гарнца, должно cie число раздъ-
лнть на 2 и будетъ 864 гарнца = 864 : 2 = 432
четверткаыъ; потомъ поелику 4 четвертки составля¬
ютъ 1 четвернкъ, то число четвериковъ, содержа¬
щихся въ 432 четверткахъ, должно быть въ четве¬
ро меньше противъ числа четвертокъ и потому 432
четвертки = 432 : 4 г= 108 четвсрнкамъ; разсуждая
такнмъ же образомъ далъе найдемъ, что 108 четве¬
риковъ = 108 : 4 = 27 осминамъ и 27 осминъ =
27: 2 = 15^ четвертямъ. Слъд. 864 гарнца = 13i
четвертямъ.
Возмемъ еще примЪръ: 13 штофовъ привести въ
бочки, т. е. узнать какую долю бочки составляютъ
13 штофовъ. Такъ какъ 10 штофовъ составляютъ
только одно ведро, то число ведръ, содержащихся
въ 13 штофэхъ будетъ въ 10 разъ менъе числа што¬
фовъ, т. с. 13 штофовъ = 13: 10 rrr 1— или т-
Ю	ю
ведра п поелику 40 ведръ составляютъ одну бочку,
то число бочекъ, содержащихся въ ведра, будетъ
въ 40 разъ менъе числа ведръ, т. о. ведра =

149
if : 40 = ^ бочки. Слъд. 13 штофовъ=^ бочки.
Требуется узнать, какую доло пуда составить f
золотника. Поелику золотпикъ въ трое меньше лота;
то всякая доля золотника въ трое меньше такой же
доли лота; слъд. чтобы узнать какую долю лота
составить •§- золотника, должно ciio дробь раздълнть
на 3 и будетъ: f золоти. = ~ : 3 = ~ = i лота;
разсуждая такимъ же образомъ далъе, получимъ: f
золоти. = f лога — г*о Фунта = —пуда.
II так к, чтобы привести простое именованное
число цтьлос или дробное мсныиаго наименовашя вь
наименоваше большее надобно постепенно приводить
его во вегь слтьдующ1я больийя наименовашя So же-
ласмаго, дгьля каждый разъ мепыиее наименоваше
па знаменательное число непосредственно большего
шимеповашя. II здъеь, также какъ въ раздроблеши,
можно прямо привести данное меньшее наименоваше
въ желаемое большее; для сего надобно только узнать
по таблицъ чл. 73 сколько единицъ даннаго мень-
шаго наименовашя содержится въ единицъ желае-
ыаго большаго наименовашя и потомъ на найденное
так. обр. число раздълнть данное число меньшаго
наименовашя. Напр, требуется узнать, сколько пудовъ
содержится въ 19200 золотникахъ; нашедши, что въ
пудъ содержится 3840 золотнпковъ, получимъ: 19200
золоти. = 19200 : 3840 — 5 пудамъ.
77.	Иногда требуется меньшее наименоваше при¬
вести во всъ за ннмъ слъдующхя болышя нанмено-
вашя, тогда можно поступить так. обр.: привести
сначала данное меньшее наименование въ самое боль¬
шее однородное н потомъ доли сего большаго на-
нменовашя выразить въ иизшнхъ наименовашях.ъ.

150
какъ въ чл. 74 прим. 2. Напр. требуется 5684572
минуты привести въ часы, дни, мъсяцм и годы.
Поступал по предыдущему члену, наидемъ: 56845/2
мпиуты=5084572:51S40U = 10^ годамь. Здесь
518400 выражаете число минуть въ году'. Теперь
приведем ь дробь yviuHHr года въ непосредственно
нпзмпя наименовании	года =	12	=
месяца; потомъ ^Д50 месяца=	50	=
Далъс т дип=ЩЛА= П^часа; и па-
конецъ	час а=—• 60=52 ыииутамъ. Слъд. 56S4372
минуты = 10 '»*>• +11 мпс- н- 17 да ч-11 4ftC- -j- 52 «""■
Этотъ самый вопроса» можно решить п так. обр.;
прпведемъ меньшее папмсноиаше постепенно во всъ
за пимъ следующая болышя наименовашя, дъля его
по общему правилу на знаменательное число п за¬
мечая каждый разъ последше остатки въ делент,
какъ выражаюнце число едпшщъ мепьшаго наиме-
повашя, за нск.ночешемъ изъ делнмаго числа еди-
нпцъ большаго наименовашя. Напр, привести 5684572
минуты «ъ часы, дни, месяцы и годы. Разделивши
5684572 на 60, нолучнчъ въ частномъ 94759 часовъ
и въ остатке 52 минуты; сл г.д. 5684572 мин. =
94759 ч"с- + 52 разделивши 94759 час. на 24,
получимъ въ частномъ 3947 дней п въ остатке 11
часовъ, а потому 94739 чпс- = 5947И’»"*:-, раз¬
деливши 3947 дней на 30, найдемъ въ частномъ
131 лт,с. п 1(Ъ остатке 17 дней; наконецъ разделив¬
ши 151 месяцъ па 12, будете въ частномъ 10 го-
довъ н въ остатке 11 месяцовъ. След. 5684372 ми¬
нуты—94759	-ь 52 •»«*- =5947 *“• -|- И ,шс-
32 1,пп‘	151	л,аСш	—J—	17	—)—	11 час. _|_ 32 мин.

151
10 *o3..-{_ 11 мпс. 17 Э«.+ 11 час. _j_ gg М1Ш. gce
tie дьйстше располагается так. обр.	*
5684572
540
"284
240
’ 445
420
" 257
ISO
572
540
60
94759 часовъ
ЧЛС.
94739
72
227
216
ИЗ
96
179
168
24
5947 дней
11 часовь
52 минуты
50
диск.
3947
50
94
90
47
30
ЛffbC.
151
131 мьс. 12
12
10 годов?..
11 M1SC.
17 дней.
II такъ: 5684572 мин. = 10 «* + 11 •МПС.
11 час. 52 *«“•
17
78.	Если данное для прсвращешя число будетъ
сложное именованное, то надобно каждую его часть
отдьльно привести въ желаемое большее наииенова-
Hic и потомъ найденный так. обр. числа сложить
между собою. Папр. требуется 37 есрст. _j_	саж.
+ 3 фут. _j_ 9 дюйм, привести въ сажени.
37 вЧ,с,п. — 37.500 = 18500 спж-; 3 Фит- =
*т Q дюи.и. 	 -2- ~—г Л фита —- -JL Caatc.
II И		 12	4 J 	 28
СЛЪД. 37 еерст. -f 112 саж. _р 3 фут. _J_ 9 —

152
■— 18500 сляе- + 112 саж. _» спок. —|—	саж.
— 18612 ff саж-
Еще примтъръ: 26 пУд- +13 Фу». + 18 *от-
+ 2 30Л- привесть въ пуды.
I13* </5«,им-  -15. пш)л; {ft лот•  ■—г -3-	г—:	— 9—
до э 	 j ? m.\s		 S2 i,j	64.0
пуда* 9 золоти,	  » лота	 _^L.	_1_	фунта		—5-— пцЪа.
Э	^		 Ъ		 9 С	4-8 Л	1920
Слъд. 26	"2/э-	+13	'/’»“■ +	18 •*от*	+	2 эо-‘- =
26 »2/3- +	«уэ- + vb	,,уЭ' + чг^ n,J?- = 2С fff «г/Эд-
Еще примтъръ: 13° 17' 25" превратить въ десятич¬
ное число градусов ь, т. е. все это именованное число
превратить сначала въ градусы и потомъ дробь гра¬
дуса выразить въ десятнчныхъ доляхъ:
17' = ff°; 23" =	=	слъд.	13°	17'	25"	—
15° + ff“ +	15“	ffff;^ обративши	ffff въ
десятичную дробь,	получимъ: 15°	17'	25"	■= 15°,
28972222.. ....
Еще примтъръ: 53f «««* снж- -f- 15f «в. Фут--p. i 15*
Кв. дюйм- привести въ десятппы.
53i квадр. саж. = 53f: 2400 = десятины; 15f
квадр. Футовъ = 13i: 49 = -0/- квадр. саж. =
десятин. 11квадр. дюнмовъ = fff квад. Фут. —
Tf xh квадр- саж. =	десятины.
Слъд. 53i кв. саж.	кв-	Фут.	-(-	{	}5i	кв.	дюйм.
*97.. dec. _L_ A? *	dec.	_j_ *JLi	 Dec.	—	733059
i-sua	4-70400	~T~	saacesoo		 зкквваоо
десятины.
Примтьп. Два ciii дъйствп! — раздроблеше и превра-
щеню пмеиованныхъ чиселъ попираются одно другпиъ,
т. е. раздроблеше повъряется превращешеиъ, а пре-
вращешс раздроблешемъ.

'СЛОЖЕШЕ ПМЕПОВАННЫХЪ ЧПСЕЛЪ.
79.	Сложеше простыхъ именованпыхъ чиселъ де-
лается также, какъ и сложеше чиселъ отвлеченныхъ.
Напр, куплено 25-| иуда некотораго товара, потомъ
еще 27f пуд., еще 45^ пуд. п i 18-?- иуда того же
товара; сколько куплено всехъ пудовъ этого товара?
25-f- + 27х -+- 45|- + ii8i = 216 Ц пуда.
81). Чтобы сделать сложеше сложиыхъ пменован-
ныхъ чиселъ, должно подписать оныя числа одно
подъ другияъ такъ, чтобы единицы одного нанме-
повашя стояли въ одномъ вертикальиомъ столбце,
потоиъ сделать сложеше каждаго наименовашя от¬
дельно, начиная съ меньшаго; если сумма чиселъ
какого нибудь наименован! я составить одну или не¬
сколько еднницъ блпжайшаго большаго наименовашя,
то надобно ихъ отделить и приложить къ еднппцамъ
того большаго наименовашя Напр.
всуст. саж. фут. дюйм. лик.
132 + 248 + 4 + 11+5
485 + 349 + 3+ 8 +6
222 + 456 + 2 + 10 + 3
45 + 387 + 4+ 9 +4
186 + 492 + 3+ 11+8
1073 + 434 + 6+ 3 +6
Сложивши чпела, столица въ вертикальномъ столб¬
це линш, нандемъ 26 лиши; превративши cin 26
лпнш въ ближайшее большее наименоваше—въ дюй¬
мы (ЧЛ. 76), ПОЛуЧИМЪ 26 .IIIH. = 2 дюйм. _|_ 6
схн 6 лиши пншемъ въ сумме подъ лншямн, а 2
дюйма придаемъ къ числу дюймовъ ‘и находнмъ 51
дюнмъ = 4 Фит- + 3 дюйм,- опять сщ 3 дюйма типемъ
въ сумме подъ дюймами, а 4 Фута придаемъ къ чи-

слу ф) товъ ц находшгь 20 Футовъ = 2 саж- -|- G Фу,п'
и т. д.
ст. дсс. лис.
Еще прилиьръ:	24Si	4- 18-|- 4- 15*-
164- +15i+22i
215 -j- 19i 4- l8f
US* -ь 17i + 23i
774f- -f 12 + 7^
или освободясь отъ дробей, какъ едъдалц мы въ чл.
75, сумма выразится такъ: 774 *'“• -J- 15 ‘>сс- 4- 23^- l,tc*
Еще п[шмщ)ъ:	8°	15' 23//, 8
13 25 1G, 02
28 52 49, 4
13 48 55, 2
64" 22' 24//, 42
ВЫЧИТАШЕ ИМЕПОВАННЫХЪ ЧИСЕЛЪ.
81. Вычиханы простыхъ илииованиыхъ чиселъ
делается также, какъ н вычиташе отвлечеппыхъ.
llanp. требуется изъ 745|- год. вычесть 59G£ года.
745^ — 596| = 146 -З- года.
82. Чтобы сд елать вычиташе сложныхъ пменован-
ныхъ чиселъ, должно оиыя числа подписать од,по
подъ другимъ такъ, чтобъ сдинпцы одного нацме-
новаша стояли въ одиомъ вертпка.и>иоиъ столбце н
потомъ сделать вычиташе каждаго паименованы1 от¬
дельно, начиная съ меныиаго; если при вычптанщ
чпеелъ какого ннбудь наименовашя*число вычитаемое
будетъ больше своего уменьшаемаго, то должно взять,
къ нему единицу отъ блнжаншаго большаго наиме¬
нованы, раздробить ее въ это меньшее ианменоваша
и потомъ уже вычитать. Напр, требу ется изъ 155 боч«
4-	17 есд- -j- 5 вычесть 85 ^оч- -}- 29 6С^ -}- 4 Ш"1ш

155
По отняли отъ 5	155	(!о4-	-[- 17всЭ- + 5шт-
штоф. 4-хъ штоф.	85	-j- 29	+4
останется въ разно-	49	-+- 28	+ I
пости 1 штофъ; далъе 29 всдръ пзъ 17 ведръ нель¬
зя вычесть, посеву къ 17 кедрамъ прибавляешь одну
бочку, взятию отъ 155 бочекъ; въ бочкъ 40 ведръ,
слъд. вмъсто 17 ведръ тгвсмъ уже 57 ведръ, по
отняли отъ ннхъ 29 ведръ, останется въ разности
28 ведръ; н наконецъ 85 бочекъ должно угже отни¬
мать отъ 154 бочекъ, въ разности будетъ 49 бо¬
чекъ.
Еще примтърь:	ПуЪ.	фуи.	лот.	зол.
Въ ссмъ прпмъръ	28^ +	56-*- -Н	22л. -4-	1
1^ золоти, нельзя вы-	25у -+-	55у +	50f -4-	\ у
'I	. 3	*	г
честь нзъ одного	4|-	5У|- -+.	‘Ео—
золоти., посему беремъ отъ 22 лотовъ одппъ лотъ н
раздробляемъ его въ золотники, тогда li золотн.
должно будетъ вычитать пзъ 4-хъ золотннковъ, въ
разности останется 2л золотника; далъе 50^ лотовъ
нзъ 21i лота нельзя вычесть, посему къ 21-| лота
придаемъ 1 Фунтъ, взятьш отъ 36-*- Фунтовъ и по¬
томъ уже 50^ лотовъ вычитает, пзъ 55|- лота, въ
разности получимъ 25^- лога; опять 554- фунтовъ
вычптаемъ не нзъ 55-J Фунт., но нзъ 75f, въ разпо-
стп на\одго1ъ 39|- Фунта; н наконецъ по отнятие отъ
27*- пудовъ 23-f-, получимъ 4i пуда.
Еще примгъръ: требу етс я нзъ 28 верст. _j_ 112 саэ1С- -f-
1 арш- _у_ IQ efpni. вычс.сть 25|. версты. Для сего сна¬
чала ■§■ версты прнведемъ въ менышя ианл1сдювашя,
получпмъ:	версты :=	500 — 214-f- сажепн; f-
сяж. = f-. 5 = £ аршина; f- арш = f. 16 = 15л
вершка; слъд. 25|- версты = 25 вс1'ст' -у- 214 саж.

156
0 «;<!«• ■+- lof ое1>ш- Послъ сего дълаемъ вычиташе,
какъ въ предыдущнхъ прнмЪраХъ:
верст, сиза. прш. еерш.
2S -f-	И2	4- 1	-+-	№
25 +	214	+ 0	+	13#-
2 4-	598	4- 0	-+-	LQ
Пусть еще требуется	пзъ	5	4-	3-1	Э|1-	вычесть
8|. да- Въ умеш.шаемомъ чнелъ i дня приведя въ ча¬
сы, получимъ 8 часовъ; также въ вычитаемомъ чи¬
сли дня = £ . 24 = Of часа; f часа = |. 60 = 36
мииутамъ; притомъ 8 дней = 1 ксЭ- 4- 1 Эе“- Слъд.
5 вед. 4_ 5д.=5 «ей. _|- 3 да- 4- 8 i«c- и д,‘- = 1 псд• 4-
1 Эе«- 4_ 9час- 4- 56 мти н потому для вычнташя
имъемъ:
кед.	ди.	час.	мни.
5 +	3 4-	8	4-0
1 +	1 4-	9	+	56
4 4-	1 4- 22	4-	24
83.	Сложеше именованныхъ чиселъ можно новъ-
рять слъдующ. обр.: отдълшъ одно какое ннбудь
слагаемое, остальныя всъ сложить между собою п
найденную так. обр. сумму вычесть изъ общей сум¬
мы, прежде найденной при сложены всъхъ слагае¬
мыхъ п если въ разности выйдеть отдъленное слага¬
емое, то сложеше было сдЪлано върно.— Вычиташе
нмеиованпыхъ чиселъ повЪряется, складывая вычита¬
емое съ разностйо, въ сумиъ должно выдтн умень¬
шаемое, ес.ш вычиташе бьыо сдЬлано върно.
УМНОЖЕН IE IIMEIIOBA ННЫХЪ ЧИСЕЛЪ.
84.	Дънстйсмъ умножешя рыпаются такте вопро¬
сы, въ которыхъ по данному ко.ычеству, соотвътст—

157
пенному какой пнбудь едшпщт,, ищется такого же
рода количество, соответственное мношмъ едннн-
цамъ.
При умноженш простыхъ пменованныхъ чпсслъ
ыожегъ быть два случая: 1) п.ш одно множимое чи¬
сло именованное, а множитель — отвлеченное; 2) плн
н множимое н множитель — числа именованным Въ
обопхъ сихъ случаяхъ умножеше пменованныхъ чп¬
сслъ производится также, какъ н умножеше чиселъ
отвлеченныхъ н прнтомъ произведете всегда должно
быть однородно съ множнмымъ, а множитель принять
за число отвлеченное: ибо произведете всегда соста¬
вляется нзъ множнмаго такъ, какъ множитель со¬
ставляется изъ с,щшщы. JInnp. требуется 545^ пРш'
умножить на 55. Совершивши умножеше обыкповен-
нымъ образомъ, какъ въ чнелахъ отвлеченныхъ, но-
лучнмъ въ произведший 19092^ аршина.
Пусть еще требуется определить, сколько рублей
должно заплатить за 7 аршипъ, если за 1 аршнпъ
заплачено 55^ рублей? Очевидно въ 7 раза» болъе,
т. е. должно 55|- рубл. умножить на 7 аршнпъ,
принимая множителя 7 арш. за число отвлеченное;
получимъ: 55± P'J"- . 7 =	7 =	=	246f
рубля.
Никто прошелъ вх день 55? версты, спрашивает¬
ся сколько всрстъ пройдетъ онъ въ 18|. дня? Умно¬
жая ooi версты на l8i дня н принимая множителя
iSi дня за число отвлеченное, получимъ: 53i МРС-
18i = С J 4i версты.
S5. При умноженш сложныхъ пменованныхъ чп¬
сслъ можетъ Сыть три случая: 1) Множимое—число
сложное именованное, а множнте.и»—число отвлечен-

158
«ос; 2) множимое — число сложное именованное, а
множитель—число именованное простое: 5) множи¬
мое и множитель — числа сложный именованный. —
И здъеь ВО всъхъ трехъ сл>чаяхъ произведете дол¬
жно быть однородно съ множимым ь, а множитель при¬
нять за число отвлеченное.
1-й Случай. Въ семь случать, подписавши множи¬
теля подъ множимыми, должно умножать каждое
наимсиоваше отдельно, начиная съ мсныиаго, если
при у множен in какого нибудь паимспованЫ соста¬
вится. въ пропзеедешп нтьсколько единицъ ближай¬
шего большого наименовашя, то ихъ отдпляютъ и
придтотъ къ произведенйо числа сего ближайшего
большего шшменовапЫ на множителя. Напр.
пуд. фуп лот. зол.
Умножая 1 золоти, на 452,	58 -+- 25 -+- 50 -+- 1
полушчт. 452 золош. =	X 452
150 лот. Ф 3o.t.; о золоти. 17446 -+■ 24 -f 14 + 2
пишемъ въ произведен!!! подъ золотниками, a 15U
лотовъ прпдаднмъ послъ къ пронзведенно 50 лотовъ
на 452; [умноживши 50 лотовъ на 452, получимъ
13560 лотовъ, да еще 150 лотовъ будетъ 15710 =
42S ФУп- ■+■ 14 лот. [j. лотовъ пишемъ въ произве¬
дены подъ лотами; умножая 23 Фунта на 452, по¬
лучимъ 1059G Фунтовъ, да еще 428 фунтовъ, будетъ
10S24 Фунта = 270 пуд. _]_ 24 Фун~, 24 Фупта пн-
шемъ въ пропзведенш подъ Фонтами п далве шцемъ
произведете 58 на 452, находнмъ 17176 пу-
довъ.. да еще 210 иудовъ, будетъ всего 17446 нудовъ.
Еще нрнмъръ:	требуется S2+* го<>- -]_ мпс. _j_
14+ Эн- -j- 18+ vnc- ^ множить па 23+.

159
7.0
5
7.0	   5	I	I	О	   /	.)ZL 5
= 425a часа:	1936	-|-5A-j- 2 -(- 17a
обратпвши 425 часовъ въ ,щ, получпмъ 17 —
дня пли 17	-|-	17;	,шс-	слъд.	425а	часа	=
17 э“- -J- 17а ппс-■ 17|- часа ппшечъ въ произведе-
niii подъ часами, а 17 дней придаднмъ къ произве¬
дению 13а диен на 23|, которое есть: 13а . 25а =
r=r -bRA'i == 5|5 днямь, да еще 17 дней, всего
будет ь 552 дня г= 11 мпс. -{- 2 0,1; 2 дня пишемъ
въ произведены подъ днямп, а 11 мьсяцовъ прп-
дадпмъ къ произведенно 5а мъс. на 23а, которое
да еще 11 мьсяцовъ, всего будетъ 155а мьсяца =
11 год. _|_ 54 .wn.e.- 54. мьсяца ппшемъ въ пропзведе-
nin подъ мьсяцамн, а 11 годовъ придаднмъ къ про-
пзведепно 82а год. па 25а, которое есть: * *л . а*—
ixsao _ 1925 годаиъ, да еще 11 годовт», всего бу-
дстъ 195G годовъ. Въ семъ произведешн 19 36
^4 мп-с. _|_ О да. _[_ 17 в. час. можНО ОСВобоШТЬСЯ ОТЪ
дробей так. обр.: А мьс. = —|А дня гг 13а дня;
chi 13i дня должно придать къ 2 дпяиь въ пронз-
ведопш, будетъ 15* дня; потомъ А дня z=r часа=
8 часамъ п въ произведен!и вмг.сто 17а часа будетъ
25- часа = I 5,1 ■ + If; ,lnf-; 1 день придавая къ
прежпимъ 15 дпяиъ, полушчъ 16 дней; А часа =
ар° мни. = 59 лншутамъ; ель г- 193G го3 япс• -J-
Q да. _|_ 17а чпс-1936 г°3- -|_ 3 11 ">0. _j_ 10 Эя. -_J_
1 ЧЯС. _J_ 50 -«ИИ.
2-й Случай. Въ семъ случаь умножеше дьлается
также, какъ и въ первомъ случаь, только должно
= 124А мьсяца,

160
принять множителя за число отвлеченное. Напр.
сколько можно купить пудовъ, фуптовъ, лотовъ и
золотииковъ нъкотораго товара за 243 сереор. руб¬
ля, когда за 1 серебр. рубль покупается 5i "У5, -|-
2Si Фиа- + 15 -,om- -f- i~ 30Л- того же самаго това¬
ра? Для ръшешя сего вопроса надобно 5j пУдш -f-
28i Фун- + 15 яот- -j- li 30л- умножить на 243 се¬
ребр. рубля; принимая множитель 243 серебр. рубля
за число отвлеченное н производя умножеше какъ въ
прсдыдущемъ случаи, получимъ:
Фун’	лот,	зол,
5*	+	28*	+	15	+	Ц
х 243
1510i	+	21а	+	22	+	li
3-н лучай. Въ семъ случать должно мпоэтсите-
ля, какъ сложное именованное число, привесть въ
простое именованное и потомъ	поступить какъ
во 2-д1й случать, т. е. принять множителя, какъ
простое именованное число, за число отвлеченное;
а чтобы привесть множителя, какъ сложное име¬
нованное число въ простое именованное, то дол¬
о/сно есть его наимеиовашя привесть въ то наименова-
nie, единицть котораго соотвтьтспгвуетъ множимое
число. Напр.
Одннъ человъкъ въ часъ ндетъ по 5 etJ,c- -J-
118 сао,с- -J- 4 Фут- сколько верстъ прондетъ онъ въ
3 мгьс- —f- 15	-J-	4 чпс- -f- 25 ,шн? Здьсь множи¬
мое 5 ееРс- -j- 118 саж- -f- 4 Фут- соотвътствуетъ од¬
ному часу, посему множитель долженъ быть приве¬
ден ъ въ часы.
3 мпс- = 90 да. =2160 часамъ; 15 дней = 560
часамъ; и 25 минуть =	часа;	слъд. 3 мпс‘ +

161
15 Эп- + 4 ,inc- 25 лиги. — 21 GO чпг- -f- 360 чя« -j--
4 ««с. _j_ час. = 2524 ^ часа.
Принявши cie число за отвлеченное, поступаешь
какъ въ предыдущемъ случаь:
вере. слою,
5 -f- 118 + 4
X 2524 yz
13220^ + 325 * + о-f.
Еще прнмъръ:	Нъкоторая	артель работниковъ
съъдаетъ въ мъсяцъ 45i пуд- -f- IS4 Фуп, -[_ 29i -,0,n-
хлъба, сколько хлъба она съъстъ въ 5 г,,э- -|- 5
-j- 15i Эи- ? Здъсь множимое соотвътствуетъ одному ыъ-
сяцу; посему множитель долженъ быть приведет»
въ ыъсяцы. 3 года = 36 мъс ; 15| дней = ^ мъс.;
слъд. 3 го? -J- 5 мл,с• —|— 15-S.Эи- == 39 ^ мъсяца; прини¬
мая cie число за отвлеченное, получимъ:
пуд.	Фу	и-	лот,
454 + Щ +
	х	ЪЩ
1736Ц+37^ + 7Й
Еще прнмъръ: Иъсколько работниковъ въ одинъ
мъсяцъ ВЫМОСТИЛИ 22 ке- с"3'с’ -J- 13 ке- ФУт-^ СКОЛЬКО
квадратныхъ саженей вымостятъ они въ 4 МП>с- -|-
5Эи._р {2 ««с-? Здъсь множимое относится къ месяцу,
посему множителя должно привесть въ мъсяцы.
5 Эн. =: ~ мъс. = 4 мъс ; 12 час. = ft Дня — ^ ме¬
сяца; слъд. 4 -,,п’с- -[- 5 ди- -f- 12 чяс- = 4~ мъсяца;
посему нмъемъ:
ке. самс. ке. фут,
22 + 15
X 4Ц
93^ + 5^	11

162
ДЪЛЕШЕ И.МЕНОВЛННЫХЪ ЧИСЕЛЪ.
86.	Дт.пстпк'мь делешп рыпаются таше вопросы,
въ которыхъ по данному количеству, соотвътствен-
ному многимъ сдшшцамъ, ищется количество того
же рода, соответственное только одной единицъ; и
еще Tabic вопросы, въ которыхъ определяется, во
сколько разъ нькоторое количество больше или
меньше другаго количества съ инмъ однороднаго.
При деленш простыхъ нменованныхъ чиселъ мо¬
жетъ быть три случая: 1) Делимое — число име¬
нованное, а делитель — число отвлеченное; частное
въ семъ случае будетъ число именованное и при-
томъ однородное съ делимымъ:	ибо делимое есть
произведете делителя на частное; след- оно должно
быть однородно пли съ дЪлителемъ пли съ част-
нымъ; 2) делимое п делитель — числа именованный
и притомт> однородный; частное въ семъ случае бу-
дстъ отвлеченное или именованное, разнородное съ
делимымъ п делнтелемъ, смотря по вопросу; 3) де¬
лимое и делитель — числа именованныя разнород¬
ный; частное въ семъ случае будетъ число имено¬
ванное однородное съ делпыымъ. Во всехъ сихъ
трехъ случаяхъ дьлеше нменованныхъ чиселъ со¬
вершается какъ деленте чиселъ отвлеченныхъ.
1-й Случай. Пусть требуется 864 арш. разде¬
лить на 8. Совершивши делеше обыкновеннымъ
образомъ, получпмъ: 864 аРт-: 8 = 108 аршннамъ.
2-й Случай. Требуется определить, во сколько
разъ 495 верстъ больше 45 верстъ. Разделивши
495 на 45, какъ числа отвлеченный, получпмъ:

495 ве^с-:45веРс-=11. Слъд. 495 верстъ въ 11 разъ
больше 45 версть; так обр. въ семъ прпмъръ част¬
ное вышло число отвлеченное.
За стопу бълон бумаги заплачено 48 рублен, а за
стопу сърон бумаги заплачено 12 рублен, во сколь¬
ко разъ бълая бумага дороже сърон? Во сто.п ко,
во сколько цвна бълон бумаги больше цъпы сърой
бумаги; слъд. для ръшешя сего вопроса должно 48
раздвлить на 12 п будетъ: 48 РУб-: 12руб- =: 4 чи¬
сло отвлеченное.
Идя каждый день по 25 верстъ, во сколько дней
можно прондтн рззстояше 245 верстъ? II здесь для
ръшешя вопроса должно 245 верстъ разд влить на
25 верстъ и будетъ: 245 ееРс- ■ 25 ееРс- = 9+ дня.
Платя за каждый пудъ нъкотораго товара по 17
рубл., сколько пудовъ того же товара можно ку¬
пить на 85 рубл. 7 Раздъливши 85 рублей на 17
рубл., получимъ: 85 рубл. : 17рубл. = 5 пудовъ.
5-й Случай. За 15 пудовъ нъкотораго товара за¬
плачено 245 рублей, по какой цънъ обошелся пудъ?
Дъля 245 рублен на 15 пудовъ, найдемъ. 245 РУ6- :
15 пУд- = 16+ рубля.
Нъкто въ 18 дней прошелъ 169 верстъ, по сколь¬
ко верстъ шел ь онъ въ день? 169 ееРс- : 18дп- =
9^ версты.
87.	При дъленш сложныхъ именованныхъ чиселъ
можетъ быть также три случая: 1) Дълпмое — чи¬
сло сложное именованное, а дълнгель—число от вле¬
ченное или простое именованное, которое принимает¬
ся также за число отвлеченное; частное въ семъ

164
случаь будетъ число именованное, однородное съ
дълнмымъ; 2) дЪлимое и дълитель -— числа слож¬
ный нменованныя и притомъ однородный; частное
йъ семъ случай будетъ число отвлеченное или име¬
нованное, разнородное съ дълнмымъ и дълителемъ,
смотря по вопросу; 5) дъ.шмое и дълитель — числа
сложный именованный разнородныя; частное въ семъ
сл) чат. будетъ число именованное, однородное съ
дълнмымъ.
1-й Случай. Въ семъ случать написавши дтьли-
теля по правую сторону дгьлимаго и отдтъливши
его вертикальною чертою, пачинаютъ дгьлеше съ
лтьвой руки съ самого большого наименовашя; раз-
дтъливши cie самое большее наименоваше, остатокъ
отъ него при дгьленш произгиедшш раздробляютъ
въ елтьдующее меньшее наименоваше и складываютъ
его съ симъ наименовашемъ, даннымъ въ дгьлимомъ,
число так. обр, полученное дгьлютъ на данный дть-
литель и продолжаютъ так. обр, далтье до ттьхъ
поръ, пока не раздтълютъ самого меньшаго наиме-
новатя. Напр, требуется 490 верст. _|_ 84 саж. _j_.
5 Фит- + 6 Эю«м. раздълнть на 18
верст, саж. фут. дюйм.
56
дълимое И *^и
дълителя, 150
какъ слъ- 126
Написавши 490—|- 84—[— 5 —4—G
18
верст. саж. фут. Эюилс*
27+115+5+9
дуетъ, на- 4
чинаемъ дЪ- х
лить 490	2000
+ 84
верстъ на ~

165
1 У, въ ча¬
стномъ на-
ходнмъ чи¬
сло одно¬
родное съ
дълнмьшъ,
т. е. 27
верстъ; въ
остаткъ же
подучаемъ
4 версты;
сш 4 вер¬
сты раздро-
бляемъ въ ■
сажен н и
находимъ
2000 саж.
прикдады-
ваемъ къ
нимъ дан¬
ное число саженъ въ дълимомъ 84, имъемь 2084
сажени; рвздъливши cie число на 18, опять нахо-
дпмъ въ частномъ число однородное съ дълнмьшъ,
т. е. 115 саж. и въ остаткъ 14 саж., раздробляя
ихъ въ футы, получимъ 98 Фут. и приложивши къ
нимъ 5 фут., данные въ дъ.шмомъ, цмьемъ всего въ
дълимомъ 105 Фута; разделивши cie число Футовъ
на 18, найдемъ въ частномъ 5 Футовъ и въ остаткъ
15 Футовъ, раздробивши ихъ въ дюймы, получимъ
156 дюймов!» и придавши сюда 6 дюймовъ дъ.ш-
маго, найдемъ 162 дюйма, раздъ.швшп cie число
2084
18
“28
18
104
90
14
х 7
98
+5
103
90
13
X 12
26
13
156
+6
162
162

166
дюнмовъ на 18, будемъ иметь въ частномъ 9 дюн-
мовъ. След, частное будетъ равно:	27	верст. _j_
113 спж. 3 фут. _J_ 9 дюйм ъ
Пусть еще требуется 512|-cm- -J- 19|-®С|:' -|- 18-Ь лис.
раздълить на 13. Освободившись въ дЬлпмомъ отъ
дробей, получимъ:	512f	c,m-	-j-	19^	-j-	1Ь§	лпс- =:
515 cm. _j_ io дее- -f 2i лис.
Cm. dec. .тс. ■
И такъ: совершив- ti 13 —|— i0—1—
ши дълеше, какъ въ
предыдущемъ примъ- 1^5
ръ, дойдемъ наконецъ
13
ст. дсе. лпс.
39+10+^
до опредълешя ли- 6
4-20
стовъ въ частномъ; >
для сего должно б у- 120
детъ 2i листа раздъ- ~^9
лить на 15, имЪемъ:' 150
Од лис. ; 15 == ii лис. ; 1^9
тт	* * * <4 \
15 = Н	~т
Q &
Еще прнмъръ:	требуется	118	ФУ11- -j- 7 y,iai-
4 ai'- + 1 вир. _j_ 15 гр. раздъ лить на |..
Это обыкоовенно изображаюсь такъ: (118 Фун- -{-
7 Уп">- + 4	4-	1	в«р.	_р 15 гр.у. д.
По смыслу дълешя частное должно быть одно¬
родно съ дълимымъ: нбо дълпмое пзъ него состав¬
ляется и прнтомъ такъ составляется, что три ссдь-
мыя доли частнаго равны дълнмому; посему одна
седьмая доля частнаго будетъ въ три раза меньше
дълнмаго или седьмая доля частнаго найдется, когда
раздълнмъ дълпмое на 5, зная же седьмую долю
частнаго для опредълешя цълаго частнаго, должно

167
будетъ седьмую его долю умножить на 7; слъд.
чтобы определить въ семъ случаъ частное, должно
будетъ делимое раздълить на 5 и полученное так.
бр. частное умножить на 7 или что все равно,
умножить сначала данное дълимое на 7 и потомъ
найденное так. обр. число раздълить на 3. Умножая
118 Ф>Уп- + 7 »“'*•	4 ЪР- + 1 СКР■ + 13 гР- па 7, полу¬
чимъ: 830 Фу11- -J- 4 Упч- -]- 7 дР■ + 2 &¥■ + 11 гР- и
разделивши cie число, какъ въ нредыдущемъ при¬
мерь на 3, найдем ь искомое частное: 276 Ф‘Уп- -}-
9 упц. _|_ 5 Эр. _j_ 17 гр..
Щ
Пусть еще требуется 28-| "У3 -f- 34i Фип- -f- 22-^
лот. -|_ 1*. 30л. раздълить НЯ 5^, Т. С. (^8-i пуЪ-
54i Фу- + 22 f- """• + Ц зол-): ят-
Разсуждая п здъсь такь, какъ въ нредыдущемъ
примерь, увндимъ, что для получешя искомаго ча¬
стнаго должно данное дълимое умножить на 4 и
найденное произведете раздълить на 21.
Умножая дълимое на 4, получимъ: 115-^	-|-
19i ФУп- -+- 28 -,от-; освобождаясь въ сем ь числъ отъ
дробей, найдемъ, что 115 А»рЭ._]_ 19i«etf"--f- 28 •om.==
116 пУд- + 12 ФУ'1- + 6 Л0т- -f- 2 30л■; раздъливши cie
число на 21, будетъ искомое частное равно: 5
21 фуа. _j_ 17 лога- — зол..
2-и Случай. Въ семъ случаъ и дълимое и дъ.ш-
тель приводятся въ одннакое меньшее HaiiMCHoiianie
п потомъ дълются какъ числа отвлеченный; частное
въ семь случаъ будетъ смотря по вопросу или от¬
влеченное число, показывающее во сколько разъ дъ¬
лимое больше или меньше дълптеля; или число име¬
нованное, определяемое воиросомъ; если въ семъ

168
именоваиномъ числь при цъломъ числь будетъ на¬
ходиться дробь, то она раздробляется въ менышя
наименовашя. Напр■ требуется узнать во сколько
разъ 15 г,,э- +- 8 мпс- -+- 12 а“* больше 5 гоЬ- -+- 2 •ИП’С-;
раздробляя и то п другое число въ дни, получимъ:
{5 год. _j_ 8 мпс. 12 Эя. = 5652 ДНЯМЪ II 3 гид- -+ 2
,ип,с. = Ц40 днямъ; пос.гв сего 565 i : 1140—
во столько разъ первое именованное число больше
втораго.
Еще прими ръ: каждый день курьеръ проьзжаетъ
по 215 ecjicm. 113 сазк■ -+ 5 ФУт- во сколько дней
провдитъ ОИЪ раЗСТОЯШС ВЪ 8453 верст. _J_ 242 сазк. ]
Во столько дней, во сколько 8453 верст. 242 спЖш
больше 215 «ч»™»* +113 саок._1_5 фут., Посему обра¬
тивши и то и другое число въ Футы, получимъ:
8453 верст. 242 соме. — 29587194 Футамъ и 215
верст. —}— 113 еаж. _|_ 5 Ф>Ут- ГГГ 753296 ФутамЪ.
Итакъ: 29587194 Фут- : 755296 Фит- = 39тп^—7-а-
37660.8
ДНЯМЪ = 1 мпс. _|_ 9 дк._|_@ч«с._|_38дтн.—J_ 59”сек-
3-й Случай. Въ семь случаи дьлнтель—сложное
именованное число приводится въ простое именован¬
ное число и именно въ то наименоваше, къ единици
котораго относится искомое частное и потомъ со¬
вершается дилете какъ въ 1-мъ случаи. Напр, за
3 пуд. -Ь 18 Фу1- -J- 15 -*от- нъкотораго товара запла¬
чено 152. Руб- 92 «»»■, сколько стоить Фунтъ того
же товара? Здьсь искомое частное относится къ.фун-
ту, посему дьлнтель 3 "г/3- -[- 18 Фу11- -[-15 лот- дол-
женъ быть прнведенъ въ Фунты, т. е. 3 пуд- -|-
18 Фун. -4- 15 лот. — 158ff фунтамъ; сльд. 152 руб.-[-
92 коп. должно раздълнть на 138?|; поступивши

какъ въ 1-мь случав, найдемъ, что Фунтъ товара
стоить. 1 Ю'6- -j- 1O^-ff коп'-
Еще прнмъръ:	Нъкто въ 15 Эн- -J- час. _j_
13i яш i. проъхалъ 1680 веРст- + 245д с «ж. -f-5i Фу»1-,
по сколько верстъ ъхалъ онь въ день? Здъсь иско¬
мое частное относится къ дню; посему обративши
15Эн.	15-|Ш1Л- въ дни, получимъ:	дня.
Теперь задача обращается въ такую: нъкто въ
ISf-fff дня проъхалъ 1680 «J»cm -(-245icf,1,c ~\-Ь^Фут-,
по сколько верстъ ъхалъ опъ въ день? Очевидно,
что для ръшешя вопроса должно 1680 верст. _j_
24э^ С1,ж- -(- 5i &Ут- раздълить на 15|™§ или на
умноживши дълпмое на 5760, найдемъ:
9679656 верст. _j_ 408 спз,с- -{- 4 Ф;/т-, раздъ ливши cie
число на 88493, получимъ для искомаго частнаго:
“109 верст. _J_ 191 саж. _|_	Ф!/'“■.
Еще примъръ: на 3 ®сс- -J- 1500 кв• саж- -j- 4 кв- “Р-
употреблено ДЛЯ ПОСЪва li четверти _|_ { ОС.К. 1 гари.
зеренъ хлъба, по сколько четвернковъ зереиъ хлъ¬
ба пошло на каждую десятину? Приведя всего дъ-
лителя въ десятины, получимъ: 3* * | десятины;
СЛЪД. ДОЛЖНО раздълить 1 ~ четверти -]_ f осм. _j_ ] гари.
на 3ff§ нлн на	умножая дълпмое на 675,
имъемъ: 1360 чегав--j-1 осл‘--}-3 “'f'1-; раздълнвши cie
число на 2447, получимъ для искомаго частнаго:
j осм. _[_ j четвертка _j_	гари.. По ТЭКЪ КакЪ ВО-
просомъ требуется онредълить по сколько четвери-
ковъ зеренъ хлъба пошло на десятину, то найден¬
ное частное приведешь въ четверики п получимь:
loc.«._j-l четвертка _|_	ЧСТВСрнкамЪ.
88.	Умножеше и дълеше пменованныхъ чиселъ
I
ыовъраются точно также, какъ умножеше и дълеше

170
*отвлеченпыхъ чиселъ, т. е. для иовЪркн умножешя
должно произведете раздълить на множимое или па
/
множителя, въ частномъ получится множитель или
множимое, если умножеше было сдъ iano върно; для
новъркп же дълcnia должно частное умножить на
дълптеля, въ пронзведенш вындетъ дълимое, если
дълеше было сдълано върно. Но можно еще повър-
Kii умножешя н дълешя производить и так. обр.:
удвоить множимое н взять половину множителя и
так. обр. найденные вновь множимое н множитель
перемножить между собою, и если въ пронзведыпн
получится число равное прежнему произведение, то
умножеше было сдълано върно; для повърки же
дълешя должно удвоить дъ шмое и дълитель н по¬
томъ раздълить ихъ одно на другое, н если въ ча¬
стномъ вындетъ число равное прежнему частному, ”
то дЪлеше было сдълано върно. (чл. 25. прнмъч.).
Наконецъ въ заключение Teopin нменованныхъ чн-
селъ изложпмъ метрнчесшя мъры, принятый нынъ
во Францш н покажемъ cpaBiicuie • оныхъ ыъръ съ
Российскими мърами.
МЕТРИЧЕСК1Я МЪРЫ II СРАВ11ЕШЕ ОНЫХЪ
СЪ РОССШСКПМН МЕРАМИ.
89.	За единицу длины, въ новыхъ «ъранцузскнхъ
мърахъ принята десяти-мнлл1онная часть меридшна,
проходящаго черезъ Парижъ ц названа метромь.
Сен-то метръ служитъ основашемъ всей системы
метрическнхъ мъръ. Дабы составить мъры болышя
или меиышя метра, согласились употреблять слъ
двойня Гречесшя и Латннсшя слова:

myna, hilo, heclo, deca, deci, centi, milli,
который значутъ:
десять тысячь, тысяча, сто, десять, десятая, сотая,
тысячная доля н прибавлять вь концъ слово метръ
или другую главную единицу, какъ увидим ь въ ни¬
жеследующей таблнцъ.
,	1. мъры длины.
Одинъ метръ равняется 22,5 вершка Русскаго.
Декаметръ := J 0 метрамъ = 225 — —
Гектометръ= 100 — —=2250— — — — —
Километръ = 1000	22500
Миршметръ= 10000 —=225000 —	—
Децим етръ =  	= 2,25	 —
Центиметръ= -	— — = 0,225	—	— —
Мил л нмстръ=  	= 0,0225 	—
2.	МЬРЫ ПОВЕРХНОСТЕЙ.
За единицу поверхностей принять аръ, т. е. квад¬
ратный декаметръ.
Одинъ аръ равняется 22,09 квадр. сажени;
Декааръ—= 10 арамь = 220,9	 —
Гектоаръ =	100	=	2209 	—	—
Кнлоаръ— =	1000	—	=	221)90	—	—	—	—
Mupiapb— =	10000	—	=	22(J900	—	—	—	—
Децюръ — =	y- —	—	~	2,209 	—
Цеипаръ—=	— — = 0,2209 —
Мил.парь =	^ 0,02209
3.	МЬРЫ ОБЪЕМОВЪ.
За единицу объемовъ принять кубпчеепш метръ,
равный 0,102964 кубич. сажени.

172
Кратны я мъры сей единицы не подучили особен-
нычъ названш, только тысячная часть кубическаго
метра, называемая дециметра кубичесши=: 11,545 i 76
Кубнч. верни,овъ; а миллионная часть кубическаго
метра, называемая кубическш центи.иешра =
0,0115906^5 кубическ. всршковь.
Въ измъренш дровъ кубнческш метръ называет¬
ся стеромъ.
4.	МЪРЫ ВМЪСТИМОСТЕН ДЛЯ ЖИДКОСТЕЙ II ЗЕРЕН Ь.
За единицу вмъстпмостей прннятъ литра или ку¬
бическш дециметра.
Одинъ литръ равняется 11,545176	кубич. вершку
Дека.штръ = 10лптрамъ= 115,43176	—	—	-—	—
Гектолнтръ=100 = 1154,3176	—	—	—	—
Килолнтръ= 1000 — = 11543,176	—
А1иршлитръ=10000— = 115431,76
Децилитра, — -f-— — = 1,1545176 	—	—
Центнлнтръ=-^ = 0,11545176—- —
Мнллилитръ	—	=	0,011543176	—	'— —
*	5.	МЪРЫ	ВЪСА.
За единицу въсовъ прннятъ грамма, который рав¬
няется к/’.пптметру кубическому, наполненному де-
стиллпровапной водой при наибольшей густотъ, т. е.
при -j- 4° стог р. терм.
Одинъ граммъ равняется	0,25443 золоти.
Декаграммъ =10 граи.— — = 2,3443 золоти.
Г сктограмлъ = 100 —	=	23,445 -
Кнлограммъ = 1000	=	234,45
Мнр1аграммъ= 10000	 —	2344,5
Дсцнграммъ = ~	— — — = 0,023443—.
Центш раммъ= ^	—	0,0023443
_Миллнграммъ= —1	—	=	0,00023443

m
6 МОНЕТЫ.
За единицу монетъ принять франки
Одннъ Франкт. равняется 25,0244	коп.	сер.
Децимъ = ~ Франка — .-= 2,50244	коп.	сер.
Цснтнчъ =	— — — = 0,250244	коп.	сер.
Свсрьхъ сего находятся монеты въ 5 и въ2 франка
7.	РЛЗДЬЛЕШЕ ОКРУЖНОСТИ.
Французы рзздължоть окружность круга па 400
рагны.хъ частей или градусовъ, каждый градусь со¬
держать 400 минуть; и каждая минута 400 се-
кундъ; так. обр.
100° новыхъ — — — = 90° нрежняго дълешя.
4"	:	=	0",524
Нримтьц. Теперь легко числа, выраженным въ
метрическнхъ ыърахъ, перевести на числа, выражен¬
ный въ мЪрахъ Россшскнхъ и наоборотъ. Напр.
требуется 52килол‘- -J- 5 гектом. -[-48 метр. выразить
въ Россшскнхъ мърахъ; для сего прнведемъ это име¬
нованное число въ метры; 52 километра 52000
метр.; 5 гектом. = 300 метр. Слъд. 52 «моль _[_
5 гектом. _|_ | g метр. — 52548 метрамъ и поелику ка-
ждый метръ гг: 22,5 вершка, то 52548 метровъ =:
52348 . 22,5 = 4477455 вершк. = 49-—; версты.
Наоборотъ требуется 5 ИУЭ- -j- 8 'S'W1- -f- 5 лот- вы¬
разить въ метрическнхъ мърахъ. Для сего данное
именованное число раздробимъ въ золотники, полу¬
чимъ: 5	-f- 8 Фун- -f- 3 лот- = 49977 золотннкамъ;
далъе поелику 0,23445 золотника составляютъ одинъ
граммъ, то 23443 золоти, составятъ 400000 грам-

174
ыовъ; слъд. одпнъ золотннкъ будетъ въ 25443 раза
меньше 100000 граммовъ, т. е. 1 золоти. =
грамма; н 19977 золоти. — 80522—грамма; по
80000 грам. = 8 мнр1аграммамъ; 500 граымовъ = 5
гектограммамъ; 20 грамновъ := 2 декаграм.; и дробь
7зл4з грамма будучи обращена въ десятичную при¬
ближенно до тысячныхъ долей равна 0,970; слъд.
7*44^ гРам- == 0,970 грам. = 0,9 -(- 0,07; но 0,9=9
деннгр.; 0,07 =7 центигр.; посему 0,970 грам. ==: 9
децнгр. -(- 7 центигр
И слъд 5 пУд- -(- 8 Фу,1к -[- 5 лora• = 8 MiipiarpaM.
-(- 5 гектограм.-(-2 декаграм. 2 грам. 9 дециграм.
-(- 7 центнграм- —
ОТДЪЛЕШЕ III.
ПРПЛОЖЕШЕ ПРЕДЫДУЩИХЪ СПОСОБОВЪ
ВЫЧИСЛЕНЫ КЪ РБШЕППО ВОПРОСОВЪ,
- ВСТРЪЧАЕМЫХЪ ВЪ ОБЩЕЖИТИЕ
Теперь слъдуетъ изложить приложение предыду-
щихъ способовъ вычислешя къ рЪшенно практнче-
екпхъ вопросовъ, встръчаемыхъ въ общежитие Ръ-
шеше сихъ вопросовъ завнеитъ, крочъ вышеизло-
женныхъ способовъ вычислешя, отъ теорш отноше-
нш и пропорцш, которою теперь мы н займемся.
ОТПОШЕШЯ и ПРОПОРЦШ.
ОТНОШЕН1Я.
90. Ошпошешемъ вообще называется выводъ, по¬
лучаемый изъ сравнешя двухъ какихъ иибудь одно-
родныхъ велцчинъ Числа, какъ н всякг.т величины,

175
могутъ быть сравниваемы двоякнмъ образомъ: либо
при сравнено! двухъ чн елъ стараются определить
чемъ одно число больше или меньше другаго: либо
во сколько разъ одно число бо гьше или меньше
другаго; первый вопросе решается действ1емъ вы-
чнгашя п выводъ, получаемый отъ сего сравненш
называется оптошещемъ Лрпеметнчсскимъ или раз-
носпйю; второй вопросъ решается денствымъ делс-
шя н выводъ, получаемый отъ сего сравнешя на¬
зывается отпошетемъ Геометричеспимъ пли зиаме-
нателемъ отношешя. Числа, иходящ'ш въ то п дру¬
гое сравнешя называются предыдущими и поелтьду-
ющимъ членами. Такъ 8 — 6=2 и 12: 4 = 5; 8
въ первомъ сравнеп'и (Арпомстнческомъ) и 12 во
второмъ сравненш (Г еометрнчсскомъ) называются
предыдущими членами; а 6 въ первомъ сравненш и
4 во второмъ—последующими членами; 2 въ первомъ
сравненш называется разности о; п 5 во второмъ
сравненш — знамснсипелемъ отношешя.
След, въ Арпометичсскомъ сравненш: предыдущим
членъ равенъ своему последующему, сложенному съ
разностйо, а последующий чдепъ равенъ предыду¬
щему безъ разности, т. е. 8 = G—f—2 и 6=8 — 2.
Въ Геометрическомъ сравпенпм: предыдущим членъ
равенъ своему последующему, умноженному на зна¬
менателя отношешя, а последующий равенъ преды¬
дущему, разделенному на знаменателя отношешя, т.
е. 12 =4.5 и 4 = ^.
После сего пусть требуется определить какого
числа вдвое более число 15. Для решено! сего
вопроса сравннмъ 15 съ неизвестным ь числомъ, ко¬

торое для краткости назовемъ х (вообще въ послед-
ств1ч всегда будемъ неизвестный числа, входящая
въ вопросе, означать последними буквами Француз-
скаго алфавита какъ х, у. z,...); получпмъ: 15:а;=(2,
СЛ£Д X = J2- =
Какая дробь втрое менее •£■? Для решешя сего
вопроса сравиимъ л съ пснз вести ымъ х, будете:
л : х = 5, отсюда х = ± : 5 := и въ самомъ деле
t • _?L   Ю5 ■ 3
Т * 2 1	3	S
Также какое число 7-ю единицами менее 18?
Имеемъ: 18 — а; = 7 и а: = 18 — 7 = 11.
ПРОПОРЦШ.
91 Равенство двухъ отношенш называется пропор¬
цию. Если сравниваемый отношешя — Арнеыетиче-
ск'ш, то и пропорцш называется Ариомепгипескою;
если же сравниваемый отношешя — Геометрпчесшя,
то и пропорцш называется Геометрическою. Напр.
8 — 5=5 н 11 — 6 = 5
изъ равенства сихъ отношено! составляется Ариеме-
тнческая пропорщя: 8— 5 = 11 — 6, которая чи¬
тается так. обр.: 8 темъ более 5, чемъ 11 более
6; или 5 темъ менее 8, чемъ 6 менее 11; 8 — 5
называется первое отношеше, а 11 — 6 второе отно¬
шеше; 8 и 11 называются предыдущими членами
пропорцш. а 5 и 6 последующими ея членами; так¬
же 8 н 6 называются крайними членами пропорцш,
а 5 и 11 средними ел членами. Во всякой Арифме¬
тической пропорцш сумма крайпихъ члеповъ равна
всегда суммгь среднихъ члеповъ. Для доказательства
сего предложешя вообще заменить, что крайними
членами во всякой пропорцш называются предыду-

177
щ!й перваго отношешя и последующи! втораго, а
средними ея членами называются последующ»! пер¬
ваго отношешя и предыдущш втораго; потому сум¬
ма крайнихъ членовъ и сумма срединvi> членовъ бу-
, дутъ состоять изъ одного предыдущаго и одного
последующаго, т. е.
Предыдущш 1-го отнош. -ь последующи! 2-го
отнош.— сумма крайнихъ. Предыдущей 2-го отнош.
последующий 1-го отнош. сумма среднихъ.
Поставивши вместо предыдущихъ членовъ то, чему
они равны (чл. 90), получимъ:
Последуюпцй 1-го отнош. -4- разность ■+• после¬
дующи! 2-го отнош. — сумма крайнихъ. Последую¬
щий 2-го отнош. -f- разность ■+- последующи 1-го
отнош. сумма средихъ.
Изъ сего внднмъ , что та и другая сумма состоять
изъ двухъ последующихъ (которыхъ только и есть
въ пропорцш два) и разности (которая въ обоихъ
отиошешяхъ одинакова), т. е. обе суммы состоять
изъ одинакихъ слагаемыхъ и потому будутъ равны.
Применяя cm разсуждешя къ предыдущему приме¬
ру, пмееыъ:
8—5 =11—6
1
8 —(— G сумма крайнихъ
11 +5 сумма среднихъ
или
5 -J- 5 -j- 6 сумма крайнихъ
6 —5 —J— 3 сумма среднихъ.
След. 3-J-5-j-6=6-J-5-f-3 а потому и 8-j-6= ll-f-5.
II такъ пзъ двухъ равныхъ суммъ всегда можно со¬
ставить ариометическую пропоршю, принявши два
12

178
слагаемыя одной суммы за крайше члены пропорцш
а два слагаемый другой суммы за средше ея члены.
Напр. Т —1о = 9 —(- И; ИЗЪ сихъ суммь составится
такая пропорция 15 — 9—11 — i-
Доказанное выше свойство ариометической пропор¬
цш служить къ тому, чтобы по даннымъ трсмъ ея
членамъ находить четвертый пеи.шъстный. Папр. въ
npoiiopniii 12 —;г=19— 15 требу( тса определять
среднш членъ х\ поелику х -1- 19 = 12+ 15, или
Ж+19=27, то одинъ х будетъ девятнадцатью еди¬
ницами менъе 27, т. е. а; = 27— 19 = 8.
Также пзъ пропорнш 12 — 8= 19 — х; выходить
12 + х = 8 + 19 = 27 п х = 27 — 12 = 15.
Слъд. чтобы найти одинъ изъ среднихъ членовъ
ариометической пропорцш, должно изъ суммы
крайнихъ членовъ вычесть извпстпый средней; а
чтобы найти одинъ изъ крайнихъ членовъ арао-
метической пропорщи, должно изъ суммы среднихъ
членовъ вычесть извпстный крайнш.
Примтьч. Ариометическая пропорцш, въ которой
средше члены одинаковы, называется непрерывною
ариомспгическою пропорщсю; напр. 8 — 6 = 6-—-4
есть непрерывная ариометическая пропорцхя; сред¬
ни! членъ такой пропорцш называется среднимъ
Арно мет пч секи мъ пропорщоп альны мъ числомъ меж¬
ду. крайними ея членами; такъ 6 есть среднее Арие-
метпческое пропорцхональное число между 8 и 4.
Для опредълешя сего средняго члена, если онъ не-
извъетенъ, надобно сумму крайнихъ членовъ раздъ¬
лить на 2:	нбо желая опредЪлить въ пропорцш
8 — х = х — 4 среднш членъ, пмъемъ х +а?=8+4
или 2 х= 12; отсюда х = ^ = 6. Слъд. среднее

179
арпеметическое пропорщоиальнос число между дву¬
мя другими числами равняется всегда полъ-сумме •
сихъ др) гихъ чиселъ. Напр, среднее арнометиче-
ское проиорщональное число между 15 и 25 будетъ
20; ибо 25 -Ь 15 = 20.
2
92. Гели сравниваются два Геометричсскin отно-
шеыя, то изъ сравнен1я ихъ выходить пропорщя
Геометрнческая; папр.
8:4 = 2 и 18: 9 = 2;
пзъ равенства сихъ отношенш составляется Геоме¬
трическая пропорщя 8: 4.= 18: 9, которая чи¬
тается так,: обр.: во сколько разъ 8 больше 4, во
столько 18 больше 9; или во сколько разъ 4 мень¬
ше 8, во столько 9 меньше 18; или какъ обыкно¬
венно: 8 относится къ 4, такъ какъ 18 къ 9; 8:4 *
называется первое отношеше, 18 : 9 второе; 8 и 18
называются предыдущими членами пропорщи, а 4
и 9 последующими ея членами; также 8 и 9 назы¬
ваются крайними членами. пропорщи, а 4 и 18
средними ея членами. — Надобно заметить, что два
числа, входящая въ одно отношеше, должны быть,
разумеется, однородны, безъ чего нельзя сделать и
сравнены между ними; но числа одного отношешя
могутъ быть п разнородны съ числами другаго отно¬
шешя. Напр. 8 и 4 въ первомъ отношенш могутъ быть
пуды, а 18 и9 версты, т.е. 8пдд-: 4,,гя)-= 18веР-. 9	,
это значить 8 пудовъ во столько же больше 4 пу-
довъ, во сколько 18 верстъ больше 9 верстъ: при¬
чина этого заключается, очевидно, въ томъ, что зна¬
менатель отношешя въ Геометрическомъ сравнен in
есть всегда число отвлеченное, между темъ, какъ

180
в1ь Ариеметическомъ разность всегда однородна съ
- сравниваемыми числами и потому въ Ариеметнческой
пропорцш числа одного отношешя всегда должны
быть однородны съ числами другаго отношешя.
Во всякой Геометрической пропорцш произведете
крайнихъ членовъ равно произведеийо ея среднихъ
членовъ. Для доказательства сего предложешя во¬
обще замт.тпмъ, что каждое произведете состоитъ
изъ одного предыдущаго и одного послъдующаго, т. е.
Предыдущей 1-го отн. X послъдующш 2-го
отнош — произведете крайнихъ. Предыдущей 2-го
отнош. х послъдующш 1-го отнош. — произведете
среднихъ.
Поставивши вмъсто предыдущихъ членовъ то, чему
они равны (чл. 90), получимъ:
Послъдующш 1-го отнош. X знаменат. отнош. X
послъдующш 2-го отнош.— произведете крайнихъ.
Послъдующш 2-го отнош. X знаменат. отнош. X
послъдующш 1-го отнош.—произведете среднихъ.
Пзъ сего видимъ, что то и другое произведете со¬
стоитъ изъ двухъ послъдующпхъ (которыхъ только
и есть въ пропорцш два) и знаменателя отношешя
(который въ обонхъ отношешяхъ одннаковъ), т. е.
оба произведешя состоятъ изъ одииакихъ произво¬
дителен и потому будутъ равны.
Примъняя сш разеуждешя къ предыдущему при-
мъру, имъемъ:
8:4 = 18:9
8 . 9 произв. крайнихъ
18 . 4 произв. среднихъ
ИЛИ
4.2.9 и 9.2.4

181
Слад 4. 2.9=9. 2.4, а потому и8.9 = 18. 4.
И такъ изъ двуъъ равныхъ произведены всегда
можно составить Геометрическую пропорцпо, при¬
нявши два производителя одного произведет» за
крайше члены пропорцш, а два производителя
другаго произведения за средше ея члены. Нппр.
3 . 24 = 4 . 18; изъ сихъ произведены составится та¬
кая пропорщя: 24: 4 = 18: 3 или такая: 3:4=18:24
и та и другая пропорцш справедливы; въ первой
знаменатель отношешя есть б, т. е. 24:4 = 6 и
18:3 = 6; во второй знаменатель отношешя есть
дробь т. е. 3 : 4 = f и 18 : 24 = ff = f.
Мы могли бы въ предыдущемъ равенств!, двухъ
произведены 3. 24 = 4. 18 принять производители
втораго произведшая за крайще члены пропорпш, и
производители перваго произведет» за средше ея
члены и тогда составили бы еще новыя двт, про¬
порцш: 4 : 24=3 : 18 и 18 : 3 = 24 : 4, въ первой
пропорщи знаменатель отношешя есть дробь а во
второй число 6
Слъд. изъ равенства 3. 24=4. 18 двухъ произ¬
ведены составляются слъдуюнця пропорцш:
24: 4 = 18:3
3 : 4 = 18 : 24
4:24= 3: 18
18: 3=24:4
Всъ cm пропорцш будутъ справедливы, потому
что въ обоихъ отношешяхъ каждой изъ нихъ знаме¬
натель отношешя одинаковъ. Всъ cin пропорцш мо¬
гутъ быть выведены непосредственно пзъ одной
первой, именпо: для получения второй пропорщи на¬
добно было въ первой перемънпть мъста крайнихъ

182
ея членовъ; для получешя третьей надобно было въ
первой пропорцш крайнее члены сд ьлать средними,
а средше крайними; для получешя четвертой про¬
порцш надобно было въ первой пропорцш первое
ея отношеше сделать вторымъ, а второе—первымъ.
Изъ сего заключаемъ, что въ nponopuiii Геоме¬
трической можно переставлять члены разднчнымъ
образомъ, наблюдая только услов1е, чтобы произве¬
дете крайнихъ ея членовъ было равно произведе¬
нию среднихъ членовъ. Именно: можно переМЪнить
мъста крайнихъ н среднихъ членовъ вмъстъ и от-
дъльно; можно кранше члены сделать средними, а
средше— крайними, и можно еще переменить поря-
докъ отношений, т. е. первое отношеше сделать вто¬
рымъ, а второе — первымъ; вновь так. обр. состав-
ляемыя пропорцш будутъ справедливы, потому что
каждая будетъ заключать въ себе два равныя
отношешя.
Также можно въ пропорцш Геометрической, не
нарушая пропорцюнальности ея членовъ, умножить
или разделить из одно какое нибудь число:	1)	два
члена одного какого нибудь ея отношешя; 2) обо-
ихъ ея прсдыд^ щихъ: или о) обонхъ ея последуш-
щихъ: ибо въ первомъ случать, умножая или деля
два члена одного отношешя на одно какое ппбудь
число, мы знаменателя сего отношешя не цзмЬнимъ;
след, равенство двухъ отношений сохранится; во
второмъ случать, умножая или деля обонхъ прсды-
дущихъ на одно какое ппбудь число, мы ничто иное
сдвлаемъ, какъ увеличишь или уменышнгь въ одно
и тоже число разъ знаменателя отношешя въ обо-
ихъ отношениях ь пропорцш; и въ тпретьемъ случать,

183
умножая или дъля обоихъ послъдуюндихъ на одно
какое нибудь число, мы ничто иное сдЪлаемъ, какъ
уменьшимъ или увеличимъ въ одно и тоже число
разъ знаменателя отношения въ обопхъ отношешяхъ
пропорщи (чл. 25 примъч. 2).
95. Доказанное въ предыдущемъ членъ свойство
Геометрической пропорщи о равенствъ произведены
крайнихъ и среднихъ ея членовъ, служитъ къ тому,
чтобы по даннымъ тремъ членамъ ея находить че¬
твертый неизвъстный. Напр, въ пропорцш 12 : 6 —
16 : х требуется опредълнть крапнш членъ ж; по¬
елику 12.ж = б . 16 или 12 ж = 96, то одинъ ж
будетъ въ 12 разъ менъе 96, т. о. х = ~ = 8.
Также пзъ пропорцш 12:ж = 16:8 выходить '
16 . ж = 8 . 12 или 16 х — 96 и х —	= 6.
1 Ъ
Слъд. Чтобы найти одинъ из» крайнихъ чле¬
новъ Геометрической пропорцш, должно произведе¬
те среднихъ ея членовй разд/ълить па данный
крайниг, н чтобы найти одинъ изъ среднихъ ея
членовъ, должно произведете крашшхъ ея членов»
раздп>литъ на данный среднш.
Примгьч. 1. Геометрическая пропорщя, въ кото¬
рой срсдше члены одинаковы называется непрерыв¬
ною Геометрическою пропорщею. Напр. 32 : 16 =
16:8 есть непрерывная Геометрическая пропорщя;
среднш членъ такой пропорщи называется средним»
пропорцюнальнымъ членомъ между крайними ея
членами; такъ 16 есть среднее пропорциональное
число между 52 и 8. Опредълеше средняго члена
въ непрерывной Геометрической пропорщи, если онъ
нензиъстенъ, завнситъ отъ извлечения квздратныхъ
корней изъ чиселъ; а потому мы и упомянемъ объ

184
этомъ предмета, когда научимся извлекать квадрат¬
ные корни изъ чиселъ.
Примгьч. 2. Теперь покажемъ, какимъ образомъ
изъ всякой Геометрнческой пропорцш можно. соста¬
вить такъ называемыя сложный пропорцш, часто
встречаю шд ас я въ Г еомстрш; именно изъ всякой Ге¬
ометрической пропорцш можно составить слъдуюнця
сложныя:	1) Сумма или разность прсдыдущаго и
послтьдующаго въ одномъ отношенш относится къ
своему последующему такъ, какъ сумма или раз¬
ность прёдыдущаго и послтьдующаго въ другомъ
отношенш относится къ своему последующему.
Справедливость этой составной про пор иди можно до¬
казать так. обр.:	взявши	сумму	или разносib пре-
дыдущаго и послъдуюидаго въ одномъ отношенш
данной пропорцш и сравнивши ciio сумму или раз¬
ность съ послъдующимъ этого же отношешя, мы
получимъ новое Геометрическое отношенie, въ кото-
ромъ знаменатель отношешя будетъ различаться отъ
знаменателя отношешя въ данной пропорцш только
единицею; едълавши тоже самое въ другомъ отно¬
шенш данной пропорщи, получимъ новаго знамена¬
теля отношенш, различающегося отъ прежняго зна¬
менателя отношешя также единицею; слъд. новые
знаменатели отношенш будутъ равны, а потому и
самыя отношешя составятъ пропорщю. Напр, изъ
пропорцш 8:2 = 16: 4 получимъ пропорщю 8-(- 2 :
2 = 16 -|- 4 : 4; ибо 8 -(- 2 : 2 есть ничто иное, какъ
8-(-2 или	также	16-J- 4 : 4 есть ничто иное
2 какъ	А;	но	^ въ слъдств1е данной про¬
порщи равняется i” п |=: А; слъд. |	~	-f-	А
или —f- 2 = 1G 4 или 8 -J- 2 : 2 = 16-(-4: 4.
2	4

185
Также изъ 8 : 2	16 : 4, получимъ: 8 — 2 :	—
16 — 4:4; ибо § — % равняется ^ — |; потому
что § = ^ (по данной пропорцш) и | = | а посе¬
му и 8 — 2:2=16 — 4:4.
2) Сумма и ли разность предыдущаго и послть-
дующаго въ одиомъ опшошсиш относится къ сво¬
ему предыдущему такъ, какъ сумма или разность
прсдыдунхаго и послтъдующаго въ друге мъ отноше-
uiu относится къ своему предыдущему. Напр, пзъ
8 : 2 = 16:4, получимъ пропорцно. 8 ± 2: 8 =
16 + 4: 16; ибо выше было доказано, что изъ дан¬
ной пропорцш 8 : 2= 16 : 4 можно вывесть 8 ± 2:
2=16 + 4:4; переставивши въ данной пропорцш
и въ сей последней средше члены, получпмъ двь
слъдуюпця пропорщи: 8: 16=2:4 п 8 ± 2 : 16чь
4 = 2:4; въ сей последней пропорщи вмъсто отно¬
шешя 2: 4 можно взять ему равное (по первой про¬
порции) отношеше 8:16, тогда будетъ:	8+2:
16 + 4= 8:16, а переставивши въ сей пропорщи
средше члены, получимъ искомую пропорцно:
8 ±2: 8 = 16+ 4: 16.
3) Судиия или разность прсдыдущигсъ относится
къ суммть или разности послтьдующизсъ такъ, какъ
какой нибудь предыдущие относится къ своему по¬
следующему. Напр, пзъ пропорщи 8:2 = 16:4
можно вывесть, что 8 + 16:2+ 4 = 8 : 2 или
16:4; ибо переставивши въ данной пропорщи
средше члены, получимъ: 8 : 16 =2 : 4 , а по пре¬
дыдущему случаю сего прпмЪчашя изъ этон пропор¬
щи можно вывесть, что 8+16:8=2±4:2,
переставивши въ сей пропорщи средше члены, по¬
лучимъ искомую пропорция: 8±16:2±4 = 8: 2
или 16:4.

186
Также легко доказать, что изъ нъсколькихъ рав¬
ныхъ отношенш всегда можно составить пронорцно,
въ которой сумма или разность предыдущихъ встьхъ
данныхъ отношенш будетъ относиться къ суммгь
или разности послгьЪующихъ эпшхъ отношенш такъ,
какъ одинъ какой ннбудь предыдущие относится къ
своему поелпдующему. Напр, пусть даны отношешя:
8:2=16:4 = 12 : 5 = 20 : 5 = 56 : 9 = 24 : 6;
изъ енхъ отношений можно составить пропорции:
(8 dr 16 ± 12 ± 20 ± 36 ± 24): (2±4±3±5±
9±6) = 8: 2;
ибо взявши два первыя отношешя, по предыдуще¬
му имъемъ:
(8 ± 16) : (2 + 4) = 16 : 4. а поелику 16 : 4= 12:3,
то имъемъ: (8 ± 16) : (2 ± 4) := 12:3, изъ сей про¬
порщи, въ которой предыдупце члены 8 ± 16 и 12,
а послъ дую 1ще 2 ± 4 и 3 , получимъ новую про-
порщю : (8 ± 16 rt 12) : (2 ± 4 ± 5) = 12 : 3 ; а
поелику 12:5=20 : 5 , то (8 ± 16 ztz 12) : (2 i 4± 5)
=20 : 5 , отсюда (8± 16 ± 12±20) : (2 ± 4±5±5)
= 20 : 5 и т. д.
4.) Если нъеколько пропорцш перемножутся по¬
членно между собою, то вышедппя так. обр. про¬
изведешя будутъ также составлять пропорцию. Наир.
6: 5=10: 5*
8: 12 = 4 : 6
11:22= 7:14
б7« . 11 : 3 . 12 . 22= 10 . 4 . 7 : 5 . 6 . 14.“
Справедливость сего можно доказать тъмъ, что
всякая Геометрическая пропорщя есть ничто иное,
какъ двъ равныя дроби, слъд. при перемноженш
между собою пропорщи мы ничто иное дълаемъ,

187
какъ псремножаемъ нъсколько равныхъ дробей, а
потому н полученныя дроби въ произведенш будутъ
также равны и слъд. будутъ составлять пропорщю;
прнтомъ изображая пропорщю въ видъ дробей, пре¬
дыдущие ея члены будутъ числителями сихъ дро¬
бей, а послъдуюпйе — знаменателями; а какъ при
перемноженш дробей числители ихъ множутся от-
дъльно, а знаменатели отдъльно, то перемножеше
между собою нъсколькихъ равныхъ дробей есть
ничто иное, какъ почленное перемножеше пропорцш.
О ТРОЙНЫХЪ ПРАВИЛАХЪ.
94.	Тройными правиломъ въ Ариометикъ назы-
вается способъ по даннымъ тремъ числамъ задачи
опред-ьлять четвертое неизвъстное число, имъ про¬
порциональное, т. е. составляющее вмъстъ съ тремя
данными числами Геометрическую пропорщю. Изъ
сего видно, что для ръшешя Арнеметической задачи
троннымъ правиломъ, надобно, чтобы числа, въ нее
вход.ищя, составляли между собою два равныя от¬
ношешя, т. е. чтобы первое число было во столько
разъ больше или меньше втораго, во сколько разъ
трейе число больше или меньше четвертаго; если
между числами задачи находится такая зависимость,
то изъ нихъ можно составить Геометрическую про¬
порщю, въ которой по извъстнымъ тремъ членамъопре-
дълится легко четвертый неизвъстный членъ (чл. 93).
Гели изъ задачи составляется только одна Геоме¬
трическая пропорщя, то способъ опредълешя неиз-
въетиаго въ такой задачи называется тройнымъ
простымъ правиломщ если же изъ задачи состав¬

188
ляется нвсколько Геометрическихъ пропорщи, то
способъ опредълешя неизвъстнаго въ такой задачи
называется тройнымъ сложнымъ правилома.
ТРОЙНОЕ ПРОСТОЕ ПРАВИЛО.
95.	Мы сказали въ предыдущемъ членъ, что изъ
задачъ, относящихся къ тройному простому правилу,
всегда составляется одна Геометрическая пропорцгя;
слъд. во всякую задачу тройнаго простаго правила
входятъ только четыре числа, включительно съ не-
извЪстнымъ, изъ которыхъ надобно составить два
равныя отношешя или Геометрическую пропорцно;
посему числа, входящая въ задачу тройнаго простаго
правила, должны быть попарно однородны, дабы
можно было первое число сравнивать со вторымъ, а
Tperie съ четвертымъ. II такъ въ каждую задачу
тройнаго простаго правила входятъ два рода чиселъ,
изъ которыхъ надобно составить два равныя отно¬
шешя. Связь между сими двумя родами чиселъ въ
задачахъ тройнаго правила можетъ быть двоякая:
либо cin роды чиселъ находятся между собою въ
прямо мъ онгношенш, либо въ обратному. Объяс-
ннмъ этн выражешя примерами.
За 50 пудовъ нтькотораго товара заплачено 180
рублей; с пр. сколько надобно заплатить за 46 пу¬
довъ того же товара.
Чтобы составить изъ сей задачи Геометрическую
пропорцно (въ чемъ собственно и заключается вся
трудность рыисшя задачь тройнаго правила), выпц-
шемъ числа оной так. обр., чтобы однородныя чи¬
сла стояли одни подъ другими и противъ числа од¬

189
ного рода стояло соотвътствугощес число другаго
рода, такъ:
пуд.	руб.
30	180
46	х
потомъ разсуждаемъ так. обр.: если за 30 пуд. за¬
плачено 180 рубл., то за 46 пуд. надобно запла¬
тить больше, т. е. -чъмъ больше купимъ товара,
тъмъ больше и денегъ истратимъ.
И такъ если числа, входяхщя въ задачу, находят¬
ся между собою въ такой связи, что чъмъ болъе
или менъе возмется число одного рода, тъмъ будетъ
болъе или менъе и соотвътстг:} гощее ему число дру-
гаго рода, то числа задачи находятся между собою
въ прямомъ отношенш, т. е. въ какомъ отношенш
находится верхнее число къ нижнему въ одномъ
родъ чиселъ, въ такоыъ же отношенш находится
верхнее число къ нижнему и въ другомъ родъ чи¬
селъ; мл» во сколько разъ верхнее число больше
или меньше нижняго (или на оборотъ) въ одномъ
родъ чиселъ, во столько же разъ верхнее число
больше или меньше нижняго (или на оборотъ) и въ
другомъ родъ чиселъ. Посему, чтобы составить про¬
порцию изъ задачи тройнаго правила съ прямымъ
отношешемъ чиселъ, надобно какъ въ псрвомъ, такъ
и во второмъ отношенш составляемой пропорцш
верхшя числа сдълать предыдущими, а нижшя по-
слъдующпми, или на оборотъ, т. е.
30 : 46 = 180 : ж
или 46 : 30 = х : 180
какъ изъ той, такъ ц изъ другой пропорщи получимъ:
ас = 4AJS4S — 276 рубл.

190
Здъсь для окончательнаго опредълсшя величины
х надобно было помножить 46 на 180 и произве¬
дете раздълить на 50; но того же самаго резуль¬
тата можно‘достигнуть короче, сокращая знамена¬
теля н какой нибудь производитель (который воз¬
можно) числителя дроби на приличное число; такъ
въ дроби	числа	180	н	50	сократятся на 10
и будетъ	~э~» потомъ 18 и 5 сократятся
на 5 и будетъ:	= 46. 6=276.
Возмемъ еще прнмъръ:
15 человгькъ едтьлеиш юькопгорое дтъло въ 12 дней,
во сколько дней то же самое дтъло едтьлаютъ 45
человгькъ?
Выписавши числа задачи, какъ слъдуетъ:
чел.	дп.
15	12
45	х
разеуждаеиъ: если 15 человъкъ едълали никоторое
дъло въ 12 дней, то большее число люден то же
самое дъло едълаютъ скоръе, т. е. въ меньшее чи¬
сло дней; а изъ сего заключаемъ, что числа предло¬
женной задачи находятся между собою въ такой
связи, что чъмъ больше возмется число одного рода,
тъмъ меньше будетъ соотвътствующее ему число
другаго рода и слъд. числа задачи находятся между
собою въ обратномъ отношенш, т. е. во сколько
разъ въ первомъ родъ чиселъ верхнее число больше
или меньше ннжняго, во столько разъ въ другомъ
родъ чиселъ ннжнее число больше или меньше
верхняго; такъ что для составлешя пропорщи изъ
предложенной задачи надобно въ первомъ отношенш

19 f
сделать прсдыдущимъ верхнее число перпаго рода,.
а во втором ь — нижнее втораго рода; а послъду-
ющимъ въ п рвомъ отношенш сделать нижнее чи¬
сло перваго рода, а во второмъ — верхнее втораго
рода; либо предыдущнмъ въ первомъ отношенш
сд г.лать ннжнее число nejmaro - рода, а во второмъ—■
«верхнее втораго рода; а послъдующимъ въ первомъ
отношенш сделать верхнее число перваго родя, а
во второмъ нижнее втораго рода; н такъ получимъ:
15 : 45 = х: 12
или 45 : 15 = 12 : х
какъ изъ той, такъ и изъ другой пропорцш получимъ:
-у»	 is.ia
Л 	 4.5
н производя приличныя сокращсн1а въ сей величинъ
х, будетъ: х = 1-~- = —*2 = — = 4.
Изъ всего предыдущаго слт.дустъ, что задачи
тройнаго правила разделяются на два рода: на за¬
дачи тройнаго правила съ прямымъ отношешемъ чи¬
селъ и на задачи съ обратнымъ отношешемъ чи¬
селъ; и потому для ръшешя задачи тройнаго пра¬
вила выписавши числа приличнымъ образомъ, надоб¬
но прежде всего сообразить, въ какомъ между собою
отношенш находятся сш числа (в» прямомь: если
чъмъ болъе возмется число одного рода, тт.мъ болъе
будетъ и соотвЪтствующее ему число другаго рода;
п вь обратномъ: если чъмъ болъе возмется число
одного рода, тъмъ меиъе будетъ соотвътствующее
ему число другаго рода), потомъ по показаннымъ
выше правиламъ составить изъ сихъ чиселъ пропор -
щк> п опредЪлить въ ней неизвъстный членъ по
правиламъ чл. 93.

192
96.	Если чпсла задачи будутъ состоять изъ цЪ-
лыхъ чиселъ съ дробями, то для составлешя изъ
сихъ чиселъ пропорщи ciii цълыя числа съ дробями
приводятся въ неправильный дроби; также если чи¬
сла задачи будутъ сложный именованный числа, то
для составлешя изъ нихъ пропорщи, приводить ихъ
въ одпнашя менышя наименование Напр.
Корабль въ 5i сутокъ проплылъ 563-1 версты;
сколько верстъ проплывешь она въ 7 сутокъ?
сут.	верст.	\
5i	563i	>	прямое отношеше
7	х	)
Приведя ai сутокъ и 563-1 версты въ неправиль-
ныя дроби, получимъ пропорцио: ~ : 7 =г —s— : ас,
отсюда х =:	.	7: ^ = —гг,— — 7 i 6 ff версты.
На пару платья пошло аршхта сукна шири¬
ною въ 1 аРш- -f- 3 веРш ; сколько пойдешь на ту же
пару платья аршинъ сукна шириною въ i «/»»■-{- 9 верш.?
арт. вер.	арш.	1
1 -(- 3	3i	}	обратное отношеше
i -f- 9	х	)
Приведя i аРш- -f- 3 верш. и { арш. _|_ Q еерш-ш въ
вершки, получимъ пропорцию:
19 : 25 = х : I-, отсюда
х =	W	= 2 ТЪ аршина.
Примгьч. Если въ задачу входятъ простыя име¬
нованный числа одинакаго рода, но разныхъ наиме¬
нования, то для составлешя пропорцш изъ задачи
ciii простыя именованный числа разныхъ наимено¬
вали! приводятся къ одному наименовании. Напр.

19о
За вырьнте канавы глубиною въ 2 аршина за-
плачено и/ьсколькимъ работташмъ 28 рублей;
сколько рублей надобно заплатить тому оке са¬
мому числу работнпковъ за вырьнте канавы такой
же длины и ширины, какъ первая, а глубины въ 5
саженъ?
нрш,	рублЛ
2	28 /
} прямое отношеШе.
саж.	I	L
5	х	)
Для составлешя пропорцш изъ сей задачи на¬
добно 5 саженъ прнвесть въ аршины или 2 аршина
привесть въ сажени; въ первомъ случаъ будетъ про-
норщя: 2 : 15 = 28 : х ; во второмъ: £ : 5 = 28 : X)
изъ первой пропорщи выходитъ:	х г= —^ === 14 .
15 = 210 рублей; пзъ второй: х = 28 . 5 : ■§• =
*вддл-_ — 14, 5. 3 = 210 рублей.
ТРОЙНОЕ СЛОЖНОЕ ПРАВИЛО.
97.	Мы сказали (чл. 94), что изъ задачи трой-
наго сложнаго правила составляется Есегда пЪсколь-'
ко Геометр и ческихъ пропорцш; слъд. въ задачу
тройиаго сложнаго правила входнтъ нЪсколько ро-
довь чиселъ, н вся трудность ръшешя задачи трой-
наго сложнаго правила состонтъ въ томъ, чтобы
раздробить ее на нъсколько задачъ тройнаго про-
стаго правила, которыя ръшаются по правпламъ,
даннымъ въ чл. 95. Объяснимъ это прпмъромъ:
25 человтъкъ, работая ежедневно по 5 часовъ, въ
48 дней выткали 65 аршииъ сукна шириною въ
43

194
1 прш. _|_ 7 вер.. в0 сколько дней 30 человтькь, рабо¬
тая ежедневно по 4 часа, выткутъ 72 арщ. сукна
шириною вь 1	-J-	10	в17'"* ?
Здъсь данныхъ чиселъ въ задачъ уже не 5, какъ
въ задачахъ тройнаго простаго правила, но болъе
и именно 9; помощно сихъ данныхъ 9 чиселъ тре¬
буется опредълить 10-е неизвъстное число; напи¬
савши cin числа, какъ въ чл. 95 и приведя слож¬
ны» именоваиныя числа, входлщш въ задачу къ
одпнакому меньшему наименование, получимъ:
чел.	чпс.	дн.	врт.	верш.
25	5	18	65	23
50	4	а:	72	26
Въ сей задачъ искомое число дней заоиситъ отъ чи¬
сла людей, часовъ ежедневной ихъ работы, числа
аршинъ сукна и ширины его:	ибо съ измънешемъ
числа каждаго изъ сихъ родовъ и число дней, бу¬
детъ измЪняться; теперь вся трудность состоитъ въ
томъ, чтобы едълать cie искомое число дней запп-
симымъ отъ каждаго изъ упомлнутыхъ родовъ чи¬
селъ отдъльно, т. е. задачу тройнаго сложнаго пра¬
вила обратить въ нъеколько задачъ тройнаго про¬
стаго правила; для сего разсуждаемъ так. обр.: если
бы 50 человъкъ работали ежедневно 5 часовъ и
должны бы были выткать не 72 аршнна сукна ши¬
риною въ 26 вершковъ, по 65 аршинъ сукна ши¬
риною въ 25 вершка, т. е. при одинаковомъ числи
рабочихъ часовъ въ день должны были бы едълать
одпнакос дъло съ первыми 25 работниками, тогда
число дней, въ которое они едълали бы это дъло,
зависило бы только отъ числа работниковъ и въ

195
задачъ не надобно бы было обращать никакого внн-
машя на число рабочичъ часоиъ въ день, на число
аршинъ сукна и ширину его, и просто вмъсто
предложенной задачи получили бы следующую;
25 челостькъ, работал ежедневно по нисколько ча¬
совъ, едгьлали нгькопюрое дгьло съ 18 дней; во
сколько дней тоже самое дгьло едгьлаютъ 30 ра¬
ботников^ работал ежедневно по столько же ча-
совъ, какъ и первые 25 работниковъ ? Эту задачу
тройнаго простаго правила ръшимъ, какъ въ чл.
95, т. е.
чел.	Эн.	1
25	18	I	обратное отношеше.
30	х	\
■■ ■ ■ ■	^ ■ ■ I I—N
25 : 30 = х : 18 , отсюда х = ——
5.3=15 днямъ.
И такъ 30 человъкъ, работая ежедневно по столь¬
ко же часовъ, какъ и 25 человъкъ, т. е. по 5 ча-
совъ, едълаютъ тоже самое дъло въ 15 дней; но въ
предложенной *эадачъ тройнаго сложнаго правила
30 человъкъ работаютъ ежедневно не 5 часовъ,
какъ мы предположили, а 4 часа, и потому первую
ошибку въ нашемъ ръшеиш, произшедшую отъ чи¬
сла рабочихъ часовъ, нсправляемъ слъдующею зада¬
чею: нтьсколько человтькъ, работая ежедневно по 5
часовъ, едгьлали нгькопюрое дгьло въ 15 дней; во
сколько дней тоже самое число людей едгьлаютъ
пюже самое дгьло, работая ежедневно по 4 часа?
чае	Эн.	\
5	15	>	обратное отношеше.
4	х	)
5 ; 4 = х	15,	отсюда х =	—^	~	=	18|	дня.

196
II такъ они (т. с. 50 чсловъкъ), работая еже¬
дневно по 4 часа, едклзштъ это дт..ю въ lSf дня.
Обращая задачу тройнаго сложнаго правила пъ
первую задачу тройнаго простаго правила, вы ска¬
зали, что 50 чсловъкъ двлають тоже самое дъло,
какъ п 25 челошял., т. е. хкутъ 65 арш. сукна,
шприною въ 23 вершка: но по предложение задачи
тройнаго сложнаго правила они ткутъ 72 арш.
сукна, шириною въ 20 вершковъ и потому въ пай-
денномъ ръшенш 18^ дня заключаются еще дпъ
ошибки, зависящая отъ числа аршинъ с)кна н ши¬
рины его; первую ошибку исправляешь следующею
новою задачею тройнаго простаго правила: нисколь¬
ко человтъкъ 65 аршинъ сукна выткали съ 18| diuij
во сколько дней выткутъ они 72 аршина того же
сукна?
прш.	!>».	|
05	ISf	[ прямое отношеше.
72	гс	)
.	«
65 . <2 =	: х ; отсюда х = — — ; здЪсь можно
75 и 65 сократить на 5, а 72 и 4 на 4 н будетъ:
х — хд х* = SO If дня.
II такъ оО человъкъ выткутъ 72 аршпыа сукна,
шириною въ 25 вершка въ 20|| дня; по они дол¬
жны ткать такое сукно, котораго ширина не 23
вершка, а 26 вершковъ, н потому въ новомъ p i шешн
Дня находится еще ошибка, происходящая отъ
ширины сукна: ее исправляешь слъдующпо повою
задачею:	нисколько человгькъ выткали нисколько
аритпъ сукна, шириною въ 23 вершка въ 20|f йня;

197
во сколько дней выткутъ они столько же иришнъ
с) кик, шириною въ 26 верши. ?
Слъд. 50 че.ювтжь, работал ежедневно по 4 часа
пъ -Sii дня выткугь 72 арш. сукна шириною въ
26 всршковъ
11 такъ Эля ртыисшн задачи тройного сложного
правила должно написать числа о ной въ двп гори—
зонашльны я строки такъ, чтобы однородныя числа
заключались въ одномъ вершикальномъ столбцп, по¬
томъ взять изъ нихъ два какихъ ннбудь однород¬
ны хъ числа и dpyzia два числа, также однородным,
но изъ которыхъ бы одно было искомое или иеизвть-
сшиое х, выь оке друг1я однородные числа принять
одопаками въ об/ьихъ горизонтальныхъ сшрокахъ,
тогда задача тройнпго сложнаго правила обратится
въ задачу тройнпго проста го правила j ргъшивши ее,
найдемъ нензвтьашюе; потомъ должно взять опять
дца ктйя ннбудь однородный числа изъ оставлеп-
пыхъ прежде, изъ енхъ двухъ вновь езнтыхъ одно-
родпыхъ чисе.1ъ, изъ числа опредплепнаго въ пре¬
дыдущей задачи и нового нензвгьетпаго составить
опять новую задачу тройнпго простого правила н
опредтлшпь новое неизвпетное; потомъ опять взять
другая* два однородный числа, оставленная въ зада¬
чи нцюйпаго сложнаго правила; изъ сихъ двухъ
чиселъ, опредплепнаго въ предыдущей задачтъ не-
tepui. да.
25	20^§	прямое	отиошеше.
26	а?
26
а 7 0
I 5
х , отсюда х = 2 7 0
7	15	2	3	25

198
извтъсптаго и нового неизвестного опять составить
задачу тройного простого провала it т. д. про¬
должать до тпхъ поръ, пока не переберемъ по¬
степенно всгь прежде оставленные роды чиселъ въ
задачи* тройного слозкънаго правила — опредпленпое
так. обр. пеизвтъетное число изъ последней задачи
тройнаго простого правим и будетъ искомое чи¬
сло, удовлетворяющее ртиепйо задачи тройнаго
Сложного правила.
Пр импч. Можно ускорить ръшешс задачи трой¬
ного сложнаго л рапида тъмъ, что не опредълять
окончательно каждый разъ величину неизвъетнаго
выводимого пзъ каждой задачи тройнаго простаго
правила, входящей вЪ задачу тройного сложнаго
правила, а оставлять ее въ вндъ дроби, полученной
прямо изъ пропорщи до последней задачи, гдъ уже
произвесть всъ требуемый дъйств!я надъ числами
дроби, полученной при ръшеши сей послъдней за¬
дачи. Такъ напр, въ предыдущей задачъ, ръшан
первую задачу тройнаго простаго правила, входя¬
щую въ задачу тройнаго сложнаго правила, мы на-
ШЛИ, что
/г»	 a	s . х а
so
при составлснш второй задачи тройнаго простаго
правила расположись числа оной такъ:
час»	дн.
К	25*19
» О
4	ар
и составимъ пропорщю: 5 : 4 х : ?я•TR	дз-ь до-
торой х =:	;	при	составлены	третьей	задачи
тройнаго простаго правила расположпмъ числа оной
такъ;

/
199
арии
Ьп.
65
&*2 5-18
50.4
72
X
и состаиимъ пропорции:	65 : 72 = Тб* 1: xt ,,зъ
которой
Л, — ? 2 » 5 ■ 8 6 • I 8
~ 3 О * & • 6 G
и наконецъ при составлены! четвертой задачи трой¬
наго простаго правила расположимъ числа оной
такъ:
ёСрш.	cht.
QX	7 2 . & . 2 s . ia
з о • 4.' 6 &
26	х
и составить пропорцно: 25 г 26 = — ~: х ,
изъ которой
„ - . _ 72. S-25.I8.2S,
**'	3	О	.	4.	•	6 S • 2 3
Теперь для окончательная определения величи¬
ны х надобно перемножить между собою всъ про¬
изводители числителя и знаменателя отдъльно и
произведете первыхъ раздълнть на произведете
вторыхъ; но здъеь можно съ большою пользою упо¬
требить тъ еокращешя, о которыхъ упомянули мы
въ чл. 95; такъ 72 н 4 сократятся на 4 ; 5 и 30
на 5 ; 25 и 65 на 5 и будетъ: х —
г= *a~|-;-g-fv?g въ сея дроби 18 п 6 сократятся на
6; 26 и 13 на 13 н получпмъ наконецъ гс=—
= -Ч° = 23 тт А«я-
Ръшимъ еще какой ппбудь примъръ тройнаго
сложнаго правила: На 27 печей отпускается вь мть-
сяць 21 сажень дровъ 18 дюймовой мтъры. Сколько
потребно дровъ 7 футовой мгьры на 56 печей въгодъ?
»

200
Въ сен задачъ прежде всего миру дровъ надобно
выразить въ одинаконъ нлнмгнованш и тоже самое
едълать со временеяъ, въ продолженш котораго они
отпускаются на печи, т. е. 7 Футовъ привести въ
дюймы и годъ въ мЪсяпь?, тогда числа задачи изо¬
бразятся такъ:
nev.	Airoc.	саж.	др.	дюйм.
27	1	21	1S
36	12	х	84
Сначала опредълимъ, сколько нужно саиШнъ дровъ
48 дюймовой мъры на об печен въ одпнъ мъсяцъ;
для сего имъемъ;
псч.	спэ!с.	др.	\
27	21	>	прямое	отношеше.
56	х	)
27 : 36 — 21: х отсюда х = — j?5--
Потомъ онредълнмъ: сколько нужно саженъ дровъ
18 дюймовой мъры на 56 печей не въ мвсяцъ, а въ
уодъ; для сего имъемъ:
мп,г.	саж.	др.	^
1	(	прямое	OTHouieiiie.
12
х
1 : 12 =г	:	х	;	отсюда	х	=
II паконспъ онрсдЪлнмъ: сколько нужно саженъ.
дровъ не 18 дюймовой мъры, а 84 дюймовой мъры
на 56 нечем въ годъ; для чего имъемъ:
(hon.lt.	САЖ*	др. г
IS	|	обратное	отношение.
84	х	|

произведя въ сей дроби приличный сокращены,
получимъ:
х =	=	—	4. 18 = Т2 са,
а 7 • s 4	з	■	1 а
Женямъ.
Ръшеше задачъ, относящихся къ сльдующпмъ зц
спмъ правиламъ процснтовъ, учета векселей н това¬
рищества основывается на ръшепш задачъ тройнщо
правила, какъ увнднмъ мзъ нпжсслъдующаго.
ПРАВИЛО ПРОЦЕНТОВ^.
98.	Процентами называется условная плата за
деньги, занимасмыя или удерживаемый на извЪстное
время.
Сумма, отдаваемая въ проценты, называется капц-
цгаломъ. Проценты зависятъ отъ величины капита¬
ла, отъ времени его обращения н отъ таксы про¬
цент овъ. Таксою въ семъ случаъ называются про¬
центы или плата со 100 рублер въ годъ или въ
мъсяцъ. Наир, отдаютъ капиталь по 5 процентовъ,
здъеь 5 будетъ такса процентов'!» и это значить, что
каждые 100 рублен капитала черезъ годъ обратят¬
ся въ 105 рублен, г. с. вмъсто 100 рубл. взятыхъ
у заимодавца должнике мъ, сен нослъднш черезъ
годъ долженъ отдать ему 105 рублен.
Правило процснтовъ есть способъ, которымъ
опредт.ляготся проценты, получаемые съ нъкотораго
капитала въ извъстнос опредъленное время. Ciu
проценты бываютъ простые или сложные. Если
проценты, получаемые съ нъкотораго капитала но
истечении каждаго года не присоединяются для обо¬

202
рота къ сему капиталу а возвращаются заимодавцу,
то они называются простыми; если же проценты,
слъдуемые съ нъкотораго капитала по истеченш
каждаго года присоединяются къ самому капиталу
для новаго оборота на слт.дующш годъ, то они на¬
зываются сложными. Опредълсше сложныхъ про-
’ центовъ требуетъ знашя логарнемовъ и потому от¬
носится къ АлгебрЪ; въ Арнемстикъ же прсдла-
гаемъ опредълеше только простыхъ процснтовъ.
99.	Всъ задачи, относянцяся къ вычислении про¬
стыхъ процентовъ, могу тъ быть раздълсны на два
случая: или по извъстному капиталу ищутся про¬
центы, слъдуеыые съ этого капитала въ нъкоторое
время; пли по извъстньшъ процентамъ, полученнымъ
въ нъкоторое время съ непзвъстнаго капитала ищется
самый капиталъ. Задачи того и другаго случая ръ-
шаются по тройному правилу, какъ увидимъ изъ
ннжеслъдующихъ примъровъ.
i-й Случай.
Требуется опредтълитъ проценты въ годъ съ капи~
тали 4000рублей, отданного по 6 процентовъ со 100.
Для ръшешя сен задачи разеуждаемъ такъ: если
100 рубл. черезъ годъ приносятъ прибыли 6 р\б.,
то 4000 рубл. принесутъ прибыли больше 6 рубл.
и прнтомъ во столько разъ больше, во сколько 4000
руо.1. больше 100 рубл.; слъд. проценты съ дан-
иаго капитала къ процентамъ со 100 рубл. нахо¬
дятся въ такомъ же отношенш, въ какомъ данный
капиталъ ко 100 рублямъ, т. е. капиталы и про¬
центы ихъ находятся между собою въ прлмомъ от-

205
ношегня; и потому расположивши чпсла, какъ въ
тройномъ правили
руб. кап.	Руб.	прощ.
100	6
4000	х
составляемо пропорщю: 4000 : 100 = х : 6; отсюда
ос z= ~“-6 — 240 руб. Слъд. съ 4000 рубл. по- *
лучится въ годъ процентовъ 240 рублей.
Капиталь	25000 рубл.	отдапь	па	2	года	и	5
мпсяцовъ по	5 щюцентовь	со 100	въ годъ;	пайдтп
проценты со всего капитала за cie время.
Сначала опредълнмъ проценты со 100 руб. въ 2
года и 5 мъсяцовъ; для сего 2 года и 5 мъсяц. при-
ведемъ въ годы, будетъ: 2-^ и потомъ 5 процентовъ
умножимъ на 2-^ года, получимъ 12— рубля; и
текъ если со 100 рубл. въ 2 года и 5 мъсяц. по¬
лучается 12^- рубля, то сколько процентовъ полу¬
чится въ cie время съ 25000 рублен? Имъемъ;
руб. кап.	руб.	проц.
100 12^
25000	гс
100 : 25000 —	:	х; отсюда х =	—
3020^ рубля.
Найти проценты съ S000 рублей, отдаппыхъ на
218 дней по -f- рубля въ мтъсяцъ.
II здъсь сначала найдемъ проценты со 100 руб.
въ 218 дней; для сего привсдсмъ 218 дней въ мъ-
сяцы, будетъ ,| ,,а с;е ЧцСЛ0 умножимъ i рубля,
получимъ: ?8*0® рубля; потомъ

204
ptjo. кап.
100
sooo
рун. проц,
9.1 8
9 О
X
100 : B00U = 2,“ : X-, отсюда x
iM80_0_Q
90 100
X 'I fcft-
9
195’ j>yo.i
///о чно даль купцу 5I2SU рублей для торгосыхъ
рборотовъ, которые столь были удачны, что че-
]>сзъ гидь, с.шьсто у потребленного капитала, было
выручено ТВ:'00 рубл. Спрти. сколько проириповъ
составляешь прибыль?
Вь сей задачъ требуется определить таксу про-
цситовъ, т с. проценты со 100 рубл. въ тодъ; для
сесо вычитая лзъ 78200 рубл. собственный капи¬
таль 31280 руб., получимъ вь разности 46920 руб.
чистую прибыль купца; потомъ разсуждаемъ: . ес.ш
на 51280 рубл. получено прибыли 4G920 рубл., то
сколько получилось прибыли па каждые 100 руб.?
Имеем ь:
150 процентов'!».
1'лт>д. купецъ на каждые 100 рубл. получастъ
чистом прибыли 150 рублен.
Домъ, оцгьпспный вь 128и00 рубл, припесъ дохо¬
ду вь годь 16960 рублей. Сколько процептосъ со¬
ставляешь доходь, получаемый съ дома?
И здъеь, какъ въ предыдущем задачъ, требуется
определить таксу процентовъ ц потому нмъемь:
51'’S0: 500= 46920: .с; отсюда х =
 ft.в эв_о - юо,
"	3X980

руб. кап.
148000
руб. п;>оц.
109(>0
100
12S000 ; 100 = 16960 : гг; отсюда ,т =	=5
13£ процептовъ.
Слад, со 100 рубл. получаете» прибыли 13’ рублей.-
2-й Случаи.
Отдань нсизвпепишй Knnunut.tr, по 71 процентов®
п получено через?, годъ прибыли 474 рубля '44 коп.
Кинь велит, капитал?Л
ЗдЬсь по шпъстнои прибыли тр'буехсл отыскать
капиталь, г/ь котораго она получена; для сего раз-
су ждаемь так i; если 7| процстстоиь получаются иъ
годъ со 100 рубл., то 474 рубл. 24 коп. получатся
еъ капитала большаго 100 рубл. и притомь но
столько разъ большаго, со ckohi.ko разъ 474 рубл.
24 коп, больше 7i рубл. или 7.40 коп.: и шпону
нньемъ;
/>уб ка rib	коп.	npottf.
100	730
х	47424
100 : х = 750 : 47424; отсюда
х = —-4Д/‘о'1-00 = 6525-J рубл. = 6523 руб 20 коп.-
Отдан?, иеизвпептып капиталь по 5 процентов?*
в?, годъ и чрез?, 17 мгьелцовъ получено 840 руб. 15
коп. прибыли. Какъ ссликь капитальТ
Сначала нрпведемь прибыль съ нсизвъетнаго ка¬
питала къ одному году, т. с. узнаемь сколько полу-

206
чается прибыли съ неизвъетнаго капитала въ годъ,
если въ 17 мъсяцовъ получено 840 рубл. 15 коп ;
разделивши 840 рубл. 15 коп. на 17 мъсяцовъ, по¬
лучимъ прибыль съ неизвъетнаго капитала въ одпнъ
мЪсяцъ, умноживши ciio прибыль на 12, найдемъ
годовую прибыль съ неизвъетнаго капитала равною
59504— коп.; после сего имъемъ:
приведя 5 рубл. процентовъ въ копейки для срав¬
нения ихъ съ копъйками, составляемъ пропорцию:
100.	Векселемт, называется актъ и ли бнлетъ, да¬
ваемый должнпкомъ заимодавцу въ обезпечеше за¬
платы своего долга. Въ этомъ актъ обыкновенно
означается сумма, запятая должнпкомъ вместе съ
процентами, которые оиъ долженъ отдать заимодавцу
по истеченш изиъстнаго срока; такъ если вексель
дастся въ 3000 рубл. на два года, то въ сихъ 3000
рубляхъ заключается сумма, взятая въ заеыъ и про¬
центы въ два года приходяпреся на сно сумму.
Если вексель уплачивается за нисколько времени
до срока, то само собою разумеется, что должннкь
не обязанъ платить заимодавцу ту сумму, которая
означена въ вексель: ибо оиъ не пользуется день¬
руб. проц»
5
59304if коп.
ПРАВИЛО УЧЕТА ВЕКСЕЛЕЙ,

207
гами некоторое время (со дня уплаты долга до срока),
которое нмелъ бы полное право ими пользоваться,
чтобы после заплатить въ срокъ сумму, означенную
въ векселе; посему онъ вычитаете некоторое число
рублей изъ суммы, платимой въ срокъ—этотъ-то
вычетъ называется учетомъ векселя.
Способъ, которымъ определяется этотъ учстъ, на¬
зывается правиломъ учета векселещ онъ основы¬
вается на тройномъ правиле, какъ увиднмъ изъ ни—
жсгледующнхъ примеровъ.
Требуется учесть вексель в» 5000 рубл. по 5
процентовъ со ста, уплачиваемый за годъ до срока.
Учесть вексель, какъ мы сказали, значить найти
приличную сумму, платимую въ настоящее время
вместо означенной въ векселе платимой въ срокъ.
Для сего разсуждаемъ такъ: 100 рубл., которые
теперь должнике отдаете заимодавцу по прошсствш
года обратятся въ 105 рубл. т. е. если бы ciu 100
рубл. оставались у должника еще годъ, то по про-
шествш сего года онъ долженъ бы былъ отдать
заимодавцу ciu 100 рубл. и проценты на оные 5
рубл.; след, вопросе объ учете векселя обращается
въ такой: каждые 105 рубл., платимые въ срокъ,
соответствуютъ 100 рублямъ, платпмымъ въ насто¬
ящее время, то 5000 рубл., платимые въ срокъ, ка¬
кой соответствуютъ сумме, платимой въ настоящее
время? Очевидно большей, нежели 100 рубл. и во
столько разъ большей, во сколько разъ 5000 рубл.
Солее 105 рубл. и потому имсемъ:

208
рубл.
рубл.
105
100
5000
X
105: 5000= 100: ачотсю да х=	°	=47Clff	руб,
Слъд. вместо 5000 рубл. за годъ до срока дол¬
жно отдать 47(51— рубл а.
Пр имгъч. Само собою разумеется, что сумма, соб¬
ственно занятая должнпкомъ, возвращается вся спол¬
на заимодавцу во всякое время въ срокъ или до
срока, а учетъ конечно производится пзъ нроцен-
Товъ, которые наростаютъ па ciio сумму во время,
означенное въ векселе; посему можно прямо нахо¬
дить самые выключаемые проценты изъ суммы, оз¬
наченной въ векселе, так. обр.:	въ предыдущемъ
примере каждые 105 рубл., платимые въ срокъ, со¬
ответствуютъ 100 рублямъ, платпмымъ за годъ до
срока j след- нзъ каждыхъ 105 рубл., означенныхъ
въ векселе, выключается за годъ до срока 5 рубл.,
какая же сумма должна быть выключена изъ 5000
рубл., очначеннмхъ въ векселе:
руб.	руб.
105	5
5000	х
105 : 5000 = 5 : х ; отсюда х ■=. —°°°'* = 238-^
рублен.
След, изъ 5000 рубл., означенныхъ въ векселе,
должно вычесть за годъ до срока 23S-*T рубл. н
след, заплатить заимодавцу 5000—258^®т = 4761^4
рубл.; та же самая сумма, какая была найдена п въ
предыдущемъ члене. Впрочемъ сей последнш учетъ

209
и предыдущш служатъ одинъ другому повъркого,
именно: если предыдущш учетъ, сложенный съ симъ
послъднимъ учетомъ, даетъ сумму, означенную въ
вексель, то учетъ векселя сдъланъ върно.	1
101.	Въ торговлъ и у банкнровъ учетъ обыкно¬
венно дЪлается иначе: чтобы сдълать учетъ векселя,
торгующте н банкиры находятъ проценты, слъдуе-
мые съ суммы, означенной въ вексель въ продолже-
ше времени отъ дня платежа до срока и потомъ
вычитаютъ ciu проценты изъ вексельной суммы; такъ
въ примъръ прсдыдущаго члена учетъ сдълается
слъдующимъ образомъ:
руб.	руб.
100	5
5000	а:
100 : 5000 = 5 : х ; отсюда х	=	250руб.
т. е. за годъ до срока вмъсто 5000 рубл. должникъ
отдаетъ заимодавцу 5000—250=4750 рубл., менъе
Ujf рублями, нежели по способу предыдущаго
члена.
Впрочемъ очевидно, что способъ предыдущаго
члена върнъе сего послъдняго: ибо въ семъ послъд-
немъ способъ учетъ производится съ вексельной сум¬
мы, принимаемой за наличный капиталь заимодавца,
между тъмъ какъ эта сумма есть каппталъ его вмъ-
стъ съ процентами, съ которыхъ собственно и дол-
женъ производиться учетъ; посему принимая век¬
сельную сумму за наличный каппталъ заимодавца
(который всегда меньше сей суммы), должникъ со-
размърно съ симъ капиталомъ учнтаетъ изъ векселя
больше надлежащаго.
14

210
102.	Если учетъ векселя производится во время
большее или меньшее года до срока , то прежде
определения учета векселя надобно найти проценты,
слъдуемые со 100 рубл. за время, въ которое про¬
изводится учетъ векселя, сложить cin проценты со
100 рублями и потомъ поступить, какъ въ чл 100.
Напр. Цгъкто имгьетъ вексель въ 3646 рубл. сро-
комъ на 9 мтьепцовъ. Онъ нуждается въ деньгахъ,
и согласепъ, чтобы учетъ быль едгъланъ по 6 про-
центовъ въ годъ. Сколько елтьдуетъ ему получить?
Прежде всего опредълнмъ проценты со 100 рубл.
въ 9 мьсяцовъ; поелику въ годъ 6 процеитовъ. то въ
одинъ ыъсяцъ ~ или i процента, а въ 9 мьсяцовъ
рубля; слъд. 100 рубл, платимые теперь,
черезъ 9 мъсяцовъ обратятся въ 104i рубля, какая
же сумма должна быть отдана теперь, чтобы черезъ
9 мъсяцовъ обратилась она въ 3646 рубл., т. е.
руб.	руб.
100	104i
а;	3646
100 : х =	: 5646 ; отсюда х = —s&g.-ioo^a —
*	а	о	э
3488|.Я|. рубля; т. е. теперь долженъ владълецъ
векселя получить 3488 рубл. 99^~я коп.
Требуется учесть вексель въ 4000 рубл. по 7
процентовъ въ годъ за 15i мпещовъ до срока.
Проценты со 100 рубл. въ 13f мъсяцовъ составля¬
ютъ 7^. рубля; посему
рубл.	руь.
107’	100
4000	х
4000=100: ж; отсюда х=	^?iJ=37074||.py6.

211
С.il.д. вмъсто 4000 рубл. за 13а мъсяцовъ до срока
должно отдать 3707 рубл 99£~§. коп.
ПРАВИЛО ТОВАРИЩЕСТВА.
103.	Правило Товарищества есть способъ дълить
между нвеколькпмн товарищами общую ихъ при¬
быль пли убыль. При семъ дълежъ надобно обра¬
тить внимаше па елвдуюийя два обстоятельства:
1) Если капиталы, съ которыхъ получена общая
прибыль въ каком ь нибудь торгов щъ предпрппш,
были всъ вь обороте одинакое время, тогда, разу¬
меется, получитъ большую часть изъ общей при¬
были тотъ товарпщъ, которого каппталъ былъ боль¬
ше, т. е. въ семъ случаъ частный прибыли товари¬
щей будуть пропорцюнальны капиталамъ. 2) Если
капиталы были въ торговомъ предпр1атш разное
время, тогда нельзя сказать, что тотъ товарпщъ по-
лучнтъ большую часть общей прибыли, котораго
каппталъ былъ больше:	ибо п съ меньшим ь капп-
таломъ, но лежащимъ большее время въ торговомъ
прсдпрпи’ш, МОЖНО ПО 1учить большую прибыль—
въ семъ случаъ слЪд. частныя прибыли товарищей
будутъ пропорцюнальны капиталамъ и временамъ.
И такъ правило товарищества разделяется на два
случая:	дълнть общую прибыль или убыль нъ-
сколькихь точарищей 1) при капиталахъ, лежащнхъ
одниакое время; 2) при капиталахъ, лежащихъ раз¬
ное время въ торговомъ предпргятш.
1-й Случай.
Три купца согласились торговать вмтьстгъ: 1-к
употребилъ на общую торговлю 8000 рубл.; 2-й

212
употребилъ 5000 рубл. и 5-и употребиль Т000
рубл.-, по npoiuecmeiu нп>котораго времени они по¬
лучили 3000 рубл. прибыли-, требуется раздгьлшпъ
яту прибыль пропорционально (соразмтърно) ихъ
капиталамъ.
Для ръшешя сей задачи опредълимъ сперва об¬
щую сумму, на которую получена прибыль 3000
рубл.; сложивши капиталы трехъ товарищей, нмъ-
емъ 20000 рубл.; потомъ разсуждаемъ так. обр.:
если на 20000 рубл. пришлось прибыли 3000 руб.,
то сколько придется прибыли на 8000 рубл. т. е.
иа капиталъ перваго товарища; слъд. остается ръ-
шить задачу тройнаго простаго правила, т. е.
руб. кап.	Pi/б.	пр.
20000	3000
8000	а;
20000 : 8000 = 3000 : ж; отсюда х = ——
1200 рубл.
И такъ первый товарпщъ получить 1200 рубл.
прибыли.
Для опредълешя прибыли втораго товарища при¬
дется ръшпть подобную задачу, въ которой вмъсто
капитала перваго товарища надобно поставить капи¬
талъ втораго товарища, т. е.
руб. к пп.	Руб.	пр.
20000	3000
5000	ж
20000 : 5000 = 3000 : х\ отсюда х ■=.	—
80000
750 рубл.

215
Для опредълешя прибыли третьяго товарища
ръшаемъ слъдующую задачу.
Обыкновенно это ръшешс располагаютъ так. обр:
пишутъ капиталы одинъ подъ другнмъ, по правую
сторону снхъ капнталовъ пншутъ общую прибыль,
отдълившн ее отъ капнталовъ вертикальною чертою,
складываютъ частные капиталы въ общую сумму и
потомъ составляютъ вышеозначенный пропорцш, т.
е. какъ общш капитал ь относится къ частному ка¬
питалу какого нибудь товарища, такъ общая при¬
быль относится къ частной прибыла какого нибудь
товарища: Такъ
20000 : 8000 = 5000: зс ; х = 1200 р. при б. 1 товар.
20000 : 5000 — 3000 : х ; х = 750 р. . . . 2-го . .
20000 : 7000 = 5000 : х ; х = 1050 р. . . . 5-го . .
Сложивши частныя прибыли 1200 -|-750-f-1050=
3000 рубл. получимъ въ суммъ общую прибыль,
если ръшеше было сдълано върно.
РУ&- проц.
5U00
20000 : 7000 = 5000 : ж; отсюда х= ^
1050 рубл.
7 ООО Я ООО . .
3 0600
руб.
1-й товарищъ S000	ру<>- пР-
2- й	 5000	3000
5-й	 7000
20000 общш каппталъ.

214
2-й СЛУЧАЙ.
Три купца торговали смпашь и получили при¬
были 5000 рубл. ifepcbiii впгсъ 9000 рубл. па о
года; в торы й 7000 рубл. на 4 года и mpemiii 5000
рудл. па 6 лтыпъ. Сколько каждому слгьдуетъ по¬
лучить изъ общей прибыли?
Здъсь прибыль каждаго товарища завнситъ отъ
капитала его н отъ времени, въ продолжение кото¬
раго этотъ капиталъ былъ въ общемъ торговомъ
предпрйти. Чтобы опред елить въ семъ случав при¬
быль каждаго товарища, иадобно капиталы привесть
къ одпнакому времени, т. е. предложенную задачу
обратить въ задачу предыдущаго случая, въ кото-
ромъ прибыль каждаго товарища завиентъ оть од¬
ного только капитала. Сего достнгпемъ на основаны
слъдуюгцихъ разеуждеиш: первый говарнщъ внесъ
9000 рубл. на 3 года; но въ 3 года онь получить
съ 9000 рубл. туже самую прибыль, какую полу¬
чить онъ въ одинъ годъ съ капитала въ трое боль-
шаго 9000 рубл. т. е. съ капитала въ 27000 руб.;
также второй товарпщъ съ 7000 рубл. въ 4 года
получитъ такую же прибыль, какую съ 28000 руб.
въ годъ; и наконецъ третш товарищъ съ 5000 руб.
въ 6 лътъ получитъ туже самую прибыль, какую
получитъ оиъ съ 30000 рубл. въ одинъ годъ. II
такъ чтобы привесть капиталы къ одпнакому вре¬
мени, надобно данные капиталы помножить на со-
отвътствуюгщя имъ времена.
Потомъ вмъсто предыдущей задача придется ръ-
шнть слъдующую: три купца согласились торга-

215
вать вмтьстгь. Первый внес» 27000 рубл., второй
28000 рубл. и mpemiii 50000 рубл. По иетеченш
года они получили прибыли 5000 рубл. Требуется
опредтьлипгъ частную прибыль каждаго купца.
Поступая, какъ въ предыдущемъ случав, найдемъ:
руб.
1-й товарищъ 27000
•2_й	 28000
З-й	 50000
руб. приб.
5000
оощш капиталь.
85000
85000 : 27000 = 5000 : ж ; .г = 1588^ рубля
85000 : 28000 = 5000 : гс ; я; = 1647^ рубля
85000: 50000 = 5000 : х ; х = 17 рубля
И такъ 1-й товарищъ съ 9000 рубл. въ 3 года
получить прибыли 1588|^ рубля; 2-й товарищъ съ
7Q00 рубл. въ 4 года получить прибыли 1647—
рубля; З-й товарищъ съ 5000 рубл. въ 6 л-втъ по¬
лучить прибыли 1764ff рубля.
104.	Разсматривая предыдущая задачи, видимъ
что в!> правплъ товарищества никоторое данное чи¬
сло (общая прибыль) двлнхся на части (частныя при¬
были), пропорцгоиальныя другнмъ даннымъ числамь
(капиталамъ); посему правилу Товарищества можно
дать опредвлеше болъе общее, нежели какое мы
дали въ предыдущемъ членъ, а именно:	правило
товарищества есть способъ делить данное число на
части, нропорцюнальиыя другими даннымъ числахъ.
Напр, требуется раздгьлить число 45 па деть ча¬
сти, нропорцюнальиыя числамь 4 и 5.
Въ сен задачъ требуется найти двъ части, кото-
ры\ь сумма составляешь число 45 и прнтомъ ciu

216
частя должны быть между собою въ такомъ же от¬
ношенш, въ какомъ числа 4 и 5; посему 4 есть чи¬
сло, соответствующее одной части, а 5 число, со¬
ответствующее другой	части; сумма 4 -f- 5 будетъ
след, соответствовать сумме частей, т. е. 45 и по¬
тому приходится решить следующую задачу: если
девяти соответствуете 45, то четырсмъ какое чи¬
сло соответствуете? Имеемъ:
9	45
4	х
9 : 4 = 45 : х ; отсюда х = '--э^в- = 20.
Также для определения другой части 45 разсуж-
даемъ подобно предыдущему, т. е. если девяти со¬
ответствуете 45, то пяти какое число соответ¬
ствуете? Имеемъ:
9	45
5	х
9 : 5 = 45 : х ; отсюда х =	=	25.
И такъ одна часть 45 есть 20, другая 25; отно-
шеше снхъ частей есть 20 : 25 = ff- = £ = 4:5.
След, cifl задача решается, какъ задача правила
товарищества, принимая данное для разделешя чи¬
сла за общую прибыль, а числа, пропорцюнально
которымъ cie данное число должно быть разделено,
за капиталы товарищей. II потому имеемъ:
9
9 : 4 = 45 : а?; х = 20 первая часть 45.
9 : 5 = 45 : х; х ==: 25 вторая часть 45.

2iT
Требуется раздгълить число 70 па три части
татя, чтобы первая относилась ко второй и к»
третьей такъ, какъ число 7 относится къ 5 и къ 2.
Принимая здъсь 70 за общую прибыль, а числа
*7, 5 и 2, пропорцгоналыго которымъ число 70 дол¬
жно быть раздълеио за капиталы товарищей и по¬
ступая по предыдущему, найдемъ:
7
5	70
2
14
14 : 7 = 70 : х ; х = 35 первая часть 70
14 : 5 = 70 : х ; х =: 25 вторая часть 70
14 : 2 = 70 : х ; х — 10 третья часть 70	*
Отношеше первой части ко второй должно быть по
требованпо задачи таково же, какъ отношеше 7 къ 5,
и въ самомъ дълъ: 35 : 25 =	= £ = 7 : 5 ; отно¬
шение первой части къ третьей должно быть тако¬
во же, какъ отношеше 7 къ 2 и въ самомъ дълъ:
55 : 10 —П — 1 = 7: 2-
Ръшпыъ еще нисколько примЪровъ, относящихся
также къ правилу товарищества.
22 работникамъ поручено было выкопать каналъ.
По npouiecmein 12 дней они увтърплисъ, что не
могутъ кончить работу къ назначенному сроку, и
посему приняли въ товарищи еще 15 человт'ъ и
съ ними вмтъспгтъ работали еще 28 дней. Спрайте-
сколько слтъдуетъ выдать псрвымъ и послтьднимъ
работникамъ, если за всю работу заплачено 15S0
рублей?

218
Здъсь должно общую плату раздълнть пропор-
цюпально числу работнпковъ и времени, въ которое
они работали; упичтожнмъ прежде всего зависимость
платы отъ времени, т. е. прнведемъ число работпи-
ковъ къ одному дню; 22 работника работали преж¬
де один 12 диен и потомъ вмъстъ съ другими ра¬
ботниками работали еще 28 дней, слъд всего рабо¬
тали они 40 диен; само собою разумьетс.т, что 22
работникамъ за 40 дней падобпо заплатить такую
же сумму, какую приходится заплатить за одинъ
день числу работнпковъ вь 40 разъ большему 22
работнпковъ, т. е. 880 чсловъкамь; потомъ 15 ра¬
ботникамъ за 28 дней приходится такая же плата,
какая приходится за одинъ день числу работнпковъ
въ 28 разъ большему 15 работниковь, т. е. 420
человъкамъ; и потому имъемъ:
раб.	да.	раб.
22	40	г-	-880
15 	 28	=	420
1300
1580
1500:880 = 1580: х; отсюда х = 1069 руб. 55— коп.
1500: 420= 15S0: .т; отсюда х = 510 руб. 46^ кон.
Птакь 22 работникамъ приходится за 40 диен
1069 рубл. 55^ коп, а 15 работникамъ за 28 дней
510 рубл. 46^- кон.
Отецъ оставилъ четыремь своимъ сыповьямъ вь
наследство 15420 рубл. с» ттьмъ. чтобы они раз-
дгьлили ciio сумму соразмерно числу ихъ летъ.
Старшему было 2S л ыпъ, второму 24, третьему
20, а младшему 16. Спраш. сколько каждый пплу-
чилъ изъ наследстваI

219
28
24	15420
20
16
8S~
88 : 28 = 13420 : х ; х =4270 руб. получиль старш.
S8 : 24= 15420 : х ; х =5060 руб. нолучнлъ второй.
88 : 20 = 15420 : х ; х =5050 руб. получи ль третш.
88: 16 = 15420: ж; ж=24Юруб.получ. четвертый.
Четыре деревни должны внести 2564 рубля 80
копгьекъ соразмерно числу обывателей, въ нихъ на¬
ходящихся: въ первой 280 душъ, во второй 160,
въ третьей 450 , а въ четвертой 710. Спрашив.
сколько каждая деревня должна внести?
280
160
450
710
1600
256480 коп.
1000:280=250480:.х; д?=448р. 84 к. ст. внес. 1 деревн.
1600:160=256480:^; =256 р. 48 к.	2
1600:450=256480:х; =721 р. 55 к.	5
1600:710=256480:а;; ж=1138р. 15к.	4
ПРАВИЛО СМЪШЕШЯ.
105.	Задачи, относяппяся къ правилу смъшешя,
бываготъ двухъ родовъ: 1) ILiu по данным ь цьмамъ
и добротамъ смъшнваемыхъ веществъ ищется цъна
или доброта смъси; 2) 11ли по даниымъ цънамъ и
добротамъ разныхъ сортовъ веществъ ищется сколь-

220
ко отъ котораго сорта для смъшсшя взять должно.
Способъ определять отдьльно ту пли другую вели¬
чину, т. е. цьну смЬси пли величины частей, входя-
щнхъ въ смесь, называется праеиломъ смтыие/йя.
1-й Случаи.
106.	Смгыиивается трехъ сортовъ мука, именно:
23 фунта по 15 коп. за фунтъ; 32 фунта по 12
ко п. за фуптъ и 18 фунтовъ по 10 ко п. за фуптъ.
Спр. чего будешь стоить фунтъ смп>си?
Такъ какъ Фунтъ 1-го сорта муки стоить 15
коп, то 23 Фунта оной, положенные въ смыпеше
будутъ стоить 23 . 15 = 345 коп.; также 32 Фунта
2-го сорта, положенные въ смьсь, будутъ стоить
32.12 = 584 коп. п 18 фунтовъ 5-го сорта будутъ
стоить 18 . 10= 180 коп.; слъд. вся смесь, въ ко¬
торую входить 25	52 -f- 18 = 75 Фунта стоить
345	384—f-180=909 коп; теперь если 75 Фунта
смыленной муки стоять 909 коп., то одниъ Фуптъ
оной стоить въ 73 раза дешевле, т. е. онъ стоить
= 12 f-f коп. Слъд. сделавши вышеизложенное
смъшеше муки, каждый Фунтъ смъшенной муки бу¬
детъ стоить 12ff к. или почти 12 к. съ денежкою.
Все вышеизложенное дъйстте располагаютъ обык¬
новенно такшхъ образомъ:
Цепа за 23 Фунта 1-го сорта муки = 23 .15=545 к.
	-52	Фунта	2-го	сорта	—— = 52.12=584 к.
	18Фунт. 5-госорта —— = 18. 10=180 к.
всъ 75 Фунта муки стоять—	=909'	к.
одинъ Фунтъ смъсц стоить = 12— к.

221
Птакъ чтобы по даннымъ цтънамъ» итьсколькихъ
смтьшиваемыхъ веществъ опредтьлиигь цгьиу смгьсн,
долоюно данныя количества веществъ умножить
каоюдое на свою цтьну или доброту, потомъ какъ
данныя количества веществъ, такъ п цтъиы ихъ
сложить и сумму цтънъ раздтьлитъ на сумму ве¬
ществъ, частное покажетъ цтьну смтъси.
На основании сего правила можно рЪшить слъду-
юице прнмъры: 24 фунта серебра 85i пробы сплав¬
лены съ 36 фунтами серебра 70-й пробы. Спр. ка¬
кой пробы будетъ сплавленное серебро?
Прежде ръшешя сей задачи замътнмъ, что сере¬
бро, употребляемое для вещей разнаго рода, всегда
соединяютъ съ ыъдыо; таковая примъсь мъдп къ се¬
ребру называется лигатурою. Проба же серебра
есть число золотннковъ чнетаго серебра въ Фунтъ
серебра лнгатурнаго; с л li д. въ предложенной задачъ
фунтъ 1-го сорта серебра содержитъ въ 96 своихъ
золотннкахъ 83i золотника чистаго серебра; 2-го
сорта серебро въ каждомъ Фунтъ содержитъ 70 зо-
* лотнпковъ чистаго серебра и требуется опредълпть
сколько золотннковъ чиста го серебра будетъ въ
фунтъ смъсн. Поступая по предыдущему правилу,
найдемъ:
въ 24 Фунт. 1-го сорта чист, сереб. будетъ 2000 зол.
въ 36 Фунт. 2-го сорта — — — — — 2520 —
во всъхъ 60 Фунт, будетъ чист, серебра 4520 зол.
а въ одномъ Фунтъ будетъ чистаго серебра ==
75i золотника, т. е. смъшенное серебро будетъ
75§ пробы.

222
Сдгьлапо смгыиешс изъ двухъ сортовъ чая: пер¬
ваго сорта взято 45 фунтовъ, а втораго 24 фун¬
та. Спр. по какой цтънтъ слгьдуетъ продевать слиь-
шанный чай, если перваго сорта фунтъ стоить 8
рубл. 50 коп., а втораго 12 рубл и если притомъ
па все cMnuienie должно н.чшпь прибыли 100 руб.?
Цт.на за 45 Фунтовъ 1-го сорта чая = 382 руб. 50 коп.
		24 Фунта 2-го сорта чая =288 руб.
Всъ 6:) Фунтовъ стоятъ	670	руб. 50 коп.
Поелику купецъ долженъ получить ЮО рубл.
прибыли па всъ (>9 Фунтовъ смъшаниаго чая, то онъ
долженъ продать пхь за 770 рубл. 50 коп.; слъд.
Фунтъ смъшаниаго чая долженъ продаваться по
= 11 рубл. 10-| коп.
2-й Случай.
107.	Требуется едтълать смтыистс изъ двухъ сор¬
товъ кофе такъ, чтобы фунтъ емтъшанпаго кофе
спгоилъ 1 руб. 20 коп. Спраш., сколько надлежипгъ
взять фунтовъ кофе каждаго сорта, если перваго
сорта фунтъ стоить 1 руб. 50 коп, а втораго
1 руб. 5 коп.?
Для ръшешя сей задачи разсуждасмъ так. обр:
положимъ, что 1-го сорта коФе возьмемъ х Фунтовъ,
а втораго у Фунтовъ ; поелику каждый Фунтъ
1-го сорта кофс 10-ю копъйками дороже смъшаи-
наго коФе, то х Фунтовъ 1-го сорта коФе бу¬
дутъ 10. х копъйками дороже х Фунтовъ смъсп;
каждый же Фунтъ 2-го сорта коФе дешевле 15-ю
копъпками противъ фунта см г.шашшго кофс, у фун-

225
товъ 2-го сорта кофе будутъ 15. у копейками де¬
шевле у Фунтовъ смъсн; но какъ по требование за¬
дачи каждый Фуптъ смЪшанн >го кофс долженъ быть
ни дороже, нн дешевле 12U копеекъ, то х Фун-
топъ 1-го сорта и у Фунтов ь 2-го сорта должны
быть таковы, что излишекъ цены 10 х отъ пер¬
ваго сорта коФе противъ смеси долженъ быть уни-
чтоженъ недостаткомъ 15. у отъ втораго сорта кофс
противъ смЪси, т. с. надобно, чтобы число копеекъ,
содержащихся въ произведены 10 . х было равно
числу копеекъ, содержащихся въ произведен!» 15 . у-
Игакъ	10 . х =г 15 . у
Но изъ двухъ равныхъ пронзведенш всегда можно
составить пропорщю (чл. 92) и потому имъемъ:
х : у = 15 : Н)
Изъ сего заключаемъ, что части, входящш въ
смъшеше, пропорциональны разпостямъ цънъ между
ценами смъшиваемыхъ веществъ и ценою смъси;
прнтомъ количество вещества 1-го сорта, входящаго
въ смъшеше, относится къ количеству вещества
2-го сорта, такъ какъ разность между ценою ве¬
щества сего 2-го сорта и цъною смъсп относится
къ разности между ценою вещества 1-го сорта и
цъного смеси, т. е. количеству вещества 1-го сорта
соответствуете разность между цъною вещества
2-го сорта и цъною смеси, а количеству вещества
2-го сорта соответствуете разность между цъною
вещества 1-го сорта и цъною смеси След чтобы
найти части, входяиця въ смесь, то надобно коли¬
чество смъси раздълить на части пропорцюнальныя
разностямъ между ценами смъшиваемыхъ веществъ

224
и цъною смвси (чл. 104), помня присемъ, что cin
смъшпваемыя количества обратно пропорцюнальны
вышеупомянутымъ разиостямъ цъиъ, т. е. что раз¬
ности между цъиою вещества 2-го сорта п цъною
смъсн будетъ соотвьтствовать количество вещества
1-го сорта, а разности между цъною вещества
1-го сорта н цъною смЪсп будетъ соотвьтствовать
количество вешества 2-го сорта. Такъ какъ выше¬
упомянутая пропорциональность частей смъси рас¬
пространяется на всю вообще смъсь, то для опре-
двлетйя количества смъшиваемыхъ веществъ можно
1 Фунтъ смвси дълить на части обратно пропорцю-
нальныя разностямъ цънъ. Птакъ вопросъ обра¬
щается въ такой:	раздълнть	1 на части пропорщо-
нальныя числомъ 15 и 10; поступая по чл. 104,
имъемъ:
25
25 : 15 = 1 : х ; отсюда х	л
25 : 10 =: 1 : х ; отсюда х = |.§. = |.
и поелику соотвътствующее число 15-ти есть въ на¬
шей задачи количество вещества 1-го сорта, а со-
отвътствующее число 10-ти есть количество веще¬
ства 2-го сорта, то въ каждый Фунтъ смвси долж¬
но взять Фунта 1-го сорта ко®е и фунта
2-го сорта коФе.
Это д'Виств1е можно повврить слъдующнмъ обра¬
зомъ; л. фунта 1-го сорта съ -§- Фу нта 2-го сорта
составляютъ цвлын Фунтъ смЪсн, который стонтъ
120 коп.; но £ Фунта 1-го сорта стоять £ . 150

225
— * 5° = 78 коп. п j. <рунта 2-го сорта стоятъ
f . 105 =	г=:	42	коп.;	посему	78-J-42	=	120 коп.
II такъ: если смтыииваемыхъ веществъ будетъ
два рода, то для опредгълетя количества вещества
каждаго рода, входящаго въ смгъсь, долэ/сно взять
разности между цгытмн сихъ веществъ и цгьною
емтъеи; потомъ раздгьлпть по правилу товарище¬
ства фунтъ смгьси па части пропорцюнальныя
симъ разностям», тогда число найденное изъ той
пропорщи, въ которую входила разность между
цгьною смгьси и цгьною вещества 9.-го сорта, будет»
количество вегцества l-го сорта, входящаго въ
фунтъ смтьсщ а число найденное изъ той пропор¬
цш, въ которую входила разность между цгьною
смтьси и цгьною вещества 1-го сорта, будетъ коли- -
чество вещества 2-го сорта, входящаго въ фунтъ
смгьси.
Требуется едгълатъ сплавку тъ серебра 83J- про¬
бы и серебра 70-й пробы такъ, чпюбы сплавленное
серебро было 80-й пробы. Cnpaui. сколько фунпювъ
серебра каждой пробы падлезгеитъ взять дня со¬
ставлешя 25 фунтовъ сплавленнаго серебра требуе¬
мой пробы? '
Разность между добротою серебра 1-го сорта п
сплавленнаго серебра есть 85i — 80 = 5-|; разность
между добротою серебра 2-го сорта п сплавленнаго
серебра есть 80 — 70 =г 10. II такъ одннъ Фунтъ
сплавленнаго серебра должно раздълпть на части
обратно пропорцюнальныя чпеламъ я 10. По¬
ступая по предыдущему, получимъ:
15

226
13*
13i:3|-=l: ж; отсюда£C=f^fr=^0=iф.сер. 2сорт.
15i: 10= i: аг; отсюда #=■“*= |§ =f Ф.сер. 1 сорт.
Если въ одпнъ Фунтъ сплавлепнаго серебра вхо-
днтъ | Фунта серебра 1-го сорта и ~ Фунта серебра
2-го сорта, то въ 23 Фунтовъ сплавленнаго серебра
войдетъ . 25 = ^ = 18-|- Фунта серебра 1-го сор¬
та, и л. 25=^ = 6л Фунта серебра 2-го сорта.—
И въ самомъ дълъ въ 18л Фунта серебра 1-го сор -
та чнстаго серебра находится 1562л золотника; въ
6л Фунтахъ серебра 2-го сорта чистаго серебра на¬
ходится 437л золотннковъ; посему въ 23 Фунтахъ
сплавленнаго серебра находится чистаго серебра
1562л -f- 437л = 2000 золотннковъ, & въ одномъ
Фунтъ будетъ a°f-° = 80 золотннковъ, т. е. сдав¬
ленное серебро будетъ 80-й пробы.
108.	Если въ смъсь входятъ болъе двухъ сортовъ
веществъ, то для опредълешя количества вещества
каждаго рода, входящаго въ смъсь, нельзя поступать
по правилу предыдущего члена, какъ увидимъ пзъ
нпжеслъдующаго прнмъра:
Дмгьется три сорта муки: фунтъ l-го сорта
стоить 17 коп., 2-го сорта 12 коп. и 3-го сорта
9 коп., и требуется изъ встъхъ трехъ сортовъ едть-
латъ такую смпсь, которой фунтъ стоилъ бы 14 к.
Поступая по предыдущему члену, найдемъ, что
фупть муки 1-го сорта 3-мя копъйкамн дороже фун¬
та смъси, Фунтъ муки 2-го сорта 2-мя копъйкамн
дешевле фунта смъси и фунтъ муки 3-го сорта 5-ю

227
копейками дешевле Фунта смъси; называя чрезъ х,
у и z количества муки сихъ трехъ сортовъ, входя¬
щая въ смъсь, должны будеыъ сообразно разсужде-
нгямъ, сдъланнымъ нами въ предыдущемъ членъ за¬
ключить, что 3 . х = 2. у + 5. г; но такъ какъ
cie равенство не представляетъ собою равенства
двухъ произведенш, то изъ онаго нельзя составить
пропорщи и слъд, нельзя узнать какимъ чнсламъ
пропорцюнальны количества веществъ, входящихъ
въ смъсь.
II потому чтобы разръшить задачу подобную пред¬
ложенной, поступаютъ слъдующнмъ образомъ: сна¬
чала смъшиваютъ два вещества въ такую смъсь, ко¬
торой бы цъна была произвольна и потомъ уже схю
новую смъсь смъшиваютъ съ третышъ прежде остав-
лениымъ веществомъ въ требуемую задачею смъсь,
так. обр. предложенная задача приводится къ ръ-
шенпо задачъ предыдущего члена. Такъ въ выше-
предложенной задачъ смъшаемъ сначала муку 2-го
и 3-го сорта въ произвольную смъсь, которой цъна
была бы напр. 10 коп. за фунтъ. Поступая, какъ
въ предыдущемъ членъ, увидимъ, что надобно бу¬
детъ Фунтъ новой смЪси раздълнть на части про-
порцюнальныя разностямъ цънъ 2 и I.
2
1 *
~
3 : 2 = I : х ; отсюда х — ~ фунта муки 3-го сорт.
3 : 1 = 1 : х ; отсюда х = £ фунта муки 2-го сорт.
Потомъ смъшаемъ вновь так. обр. составленную
муку, которой цъна 10 коп. за Фунтъ съ мукою

228
1-го сорта, которой цъна за Фунтъ 17 коп., въ
смъсь, требуемую задачею, т. е. въ такую смъсь,
которой цъна 14 коп. Здъсь надобно будетъ 1 Фунтъ
смьси раздълить на части, пропорцюнальныя разно-
стямъ цънъ 3 и 4.
3
4	*
7
7 : 3~ 1 : х ; отсюда х= А ф. муки, котор. цЪн. 10 к.
7 : 4— I : х; отсюда #= А ф. муки, котор. цЪн. 17 к.
И такъ въ составъ каждаго Фунта требуемой смЪ-
си должно будетъ взять А Фунта муки 1-го сорта
и а. фунта муки, смъшенной изъ муки 2-го п 3-го
сорта; но поелику въ каждый фунть сей послЪдней
муки входнтъ А Фунта муки 3-го сорта и А Фунта
муки 2-го сорта, то въ а Фунта смъси ихъ будетъ
входить количество муки того и другаго сорта въ 7
разъ меньшее, т. е. а Фунта муки, которой цъна 10
коп. состоитъ пзъ ~ Фунта муки 2-го сорта п изъ
■— Фунта муки 3-го сорта; въ А Фунта муки, кото¬
рой цъна 10 коп. будетъ количество муки обоихъ
сортовъ, изъ которыхъ она состоитъ, въ 3 раза боль¬
шее, нежели въ А фунта ея, т. е. А Фунта муки, ко¬
торой цъна 10 коп. заключаютъ въ себъ или а
фунта муки 2-го сорта и ~ или f. Фунта муки
3-го сорта.
СлЪд. Фунтъ муки, которой цъна 14 коп., со¬
стоитъ изъ А Фунта муки 1-го сорта, фунта муки
2-го сорта и а Фунта муки 3-го сорта.

229
II въ самомъ	дълЪ	цъна	ф	ф.	муки	I	сор.	~	9|	к.
цъна	v	ф-	муки	2	сор.	=	1л	к.
цъна	-§■	ф.	муки	3	сор.	—	2£	к.
Слъд. цъна	смъшеннон	муки=9|--[- 1-§--{-Щ=	14	к.
Лримтъч. Поелику цъна 10 коп. за Фунтъ первой
смъси въ предложенной задачъ берется произволь¬
ною, то вопросъ нами разрЪшенный допускаетъ не-
опредъленное число ръшенш и вообще задачи, от-
носягщяся къ правилу смЪшешя, п въ которыхъ
смъсь составляется болъе, нежели изъ 2-хъ сор-
товъ веществъ, допускаютъ неопредълениое число
ръшенш; однакожъ и въ этомъ случав можно огра¬
ничить число ръшенш, такъ въ Предыдущемъ при-
мъръ составляя первую смъсь можно было цъну .ея
назначить или въ 10 коп. или въ 11 коп, т. с.
можно взять цъну произвольной смъси только между
цънамн смъшпваемыхъ веществъ:	ибо	нелъио	было
бы требовать изъ двухъ веществъ составить третье
такое, которое было бы дороже или дешевле ихъ
обоихъ. II такъ вышепредложенная задача допускаетъ
два ръшешя: одно вышенайденное нами, и другое
получаемое при положены произвольной 1 смЪси цъ-
ного въ 11 коп.
II такъ смъши'вая муки 2-го и 3-го сорта въ
вышспредложенной задачъ въ произвольную смъсь,
которой цъна 11 коп., получимъ:
1
2 1
3 .
3:1 = 1 : ос ; отсюда х = i Фунта муки 5-го сорта.
3 : 2 = 1 : х ; отсюда х = £ Фунта муки 2-го сорта.

230
Потомъ смъшивая ciio смъсь съ мукою 1-го сорта,
найдемъ:
3
3	*
6
6:3 = 1 :ж;отсгодаа:=£=£ф. мук. котор. цЪн. 11 к.
6:3= 1:а:; отсюда#=|^=£ф. мук.котор. цъи. 1Т к.
.1 Фунта муки, которой цъна 1 i коп. = Фунта
муки 2-го сорта § Фунта муки 3-го сорта.
Слъд. въ одинъ Фунтъ муки, которой цъна 14
коп., входить ■§- Фунта муки 1-го сорта; i Фунта
муки 2-го сорта и ^ Фунта муки 5-го сорта.
И въ самомъ дълъ цъна \ Фунта муки 1-го сор¬
та = ~ = 8§ коп.; цЪиа -i Фунта муки 2-го сорта
= 4 коп. и цъна Фунта муки 3-го сорта =
§ = 1|. коп.
Слъд. цъна муки сыъшанной = 8J —[— 4 -\- li=14 к.
109.	Послъ сего легко понять, какимъ образомъ
опредъляется количество каждаго вещества, входя-
щаго въ смъсь въ томъ случаъ, когда cia смъсь со-
стоить изъ 4-хъ, 5-тн, 6-ти и т. д. веществъ; имен¬
но когда смъсь состоитъ напр, изъ 4-хъ сортовъ ве¬
щества, то должно сперва два каме нибудь сорта,
напр. 1-й и 2-й смъшать въ какую нибудь произ¬
вольную смъсь, потомъ ciio смъсь смъшать съ 3-мъ
сортомъ въ новую произвольную смьсь; С1Ю новую
смъсь смъшать съ 4-ыъ сортомъ въ требуемую за¬
дачею смЪсь и накоиецъ вводный смъси замъннть
данными въ задачъ сортами вещества, изъ которыхъ
ciu смъси состоятъ.

231
При семъ надобно обратить внимаше на слъдую-
щее обстоятельство: если цъна смЪси, требуемой за¬
дачею, заключается между цъпамн двухъ как ихъ
нибудь сортовъ вещества, которые мы хотшгь сна¬
чала смъшать въ произвольную смъсь, то за цъну
сен произвольной смъси можемъ назначить какое
нибудь число, заключающееся между цънамп смЪ-
шпваемыхъ веществъ, кромъ цъны смъси, требуемой
задачею, притомъ если цъны остальиыхъ смъшивае-
мыхъ веществъ дешевле цъны смьси требуемой за¬
дачею, то нельзя принимать за цъну произвольной
смьси и среднее число, заключающееся между цЪ-
нами см вшиваемы хъ веществъ, но меньшее цъны
смъсн, требуемой задачею. Напр, смынивается че¬
тыре сорта вещества: цъна 1-го сорта 18 коп.;
цьна 2-го сорта 14 коп.; цъна 3-го сорта 11 коп.
и цъна 4-го сорта 8 коп.; цъна смъси назначается
въ 16 коп. Смешивая вещества 1-го и 2-го сорта
въ произвольную смъсь, не можемъ принять за цъну
сей смьси 16 коп.: ибо тогда требуемая емвеь состо¬
яла бы только изъ двухъ сортовъ, а не изъ четы¬
рехъ; также не можемъ принять за цъну произволь¬
ной смьси и 15 коп., ибо принимая за цвну сей
произвольной смъсн 15 коп., должны будемъ потомъ
смешивать вещества 3-хъ сортовъ, изъ коихъ цъна
i-го сорта 15 коп.; цъиа 2-го сорта 11 коп. и цъна
3-го сорта 8 коп. въ такую смъсь, которой цъна
16 коп.;—но эта задача будетъ нелъпа, потому что
требуется составить такую смъсь, которой цъиа до¬
роже каждаго изъ веществъ, въ нее входяпшхъ.
Итакъ остается за цъну произвольной смъсн при-
.нятъ 17 коп.; составивши эту смъсь, должны б у-

252
демъ потомъ смъшивать 3 сорта вещества, изъ ко-
ихъ цъна 1-го сорта 1Т коп.; цъна 2-го сорта 11
коп. и цъна 3-го сорта 8 коп. въ такую смъсь, ко¬
торой цъна 16 коп, какъ требуется задачею; опять
должны будемъ два кате нпбудь сорта смъшать въ
новую произвольную смъсь, наир. 1-й и 2-й сорты;
но смъшивая ciii сорты, увидимъ, что требуемое за¬
дачею смъшенге невозможно: ибо за цъпу новой про¬
извольной смъси не можемъ принять ни 16 коп.,
ни число меньшее 16 коп. по причинамъ, изложен-
нымъ выше; а пзъ сего и заключаемъ, что не вся-
йе два сорта, входящие въ задачу смъшешя для раз-
ръшев1я сей задачи, можно смыливать въ произволь¬
ную смъсь, н чтобы нзбъжать сего затруднешя, дол¬
жно всегда смъшивать въ произвольную смъсь два
таше сорта, между цънами которыхъ не заключает¬
ся цъна требуемой смЪси; при семъ можетъ встръ-
титься три случая: 1) когда въ задачу входитъ нъ-
сколько веществъ меньшей цъны противъ смъси п
одно только вещество большей цъны прогнвъ смъси;
2) когда въ задачу входитъ нъеколько веществъ
большей цъны противъ смъси и одно только веще¬
ство меньшей цъны противъ смъси; и 3) когда въ
задачу входитъ нъеколько веществъ большей цъны
противъ смЪсн и нъеколько веществъ меньшей цъны
противъ смЪси.
Въ первомъ случать емтыииваютъ въ произволь¬
ную емтъеь вещества метшей цтъны противъ требуе¬
мой емтъеи до ттьхп поръ, пока соедпнятъ ихъ вь
одну смтьсь, которую уже емтыииваютъ съ веще-
ствомъ большей цгьны противъ требуемой смтьсп;
такъ напр, въ вышенредложенной задачъ, которая

235
относится къ сему случаю, должно смъшать сперва
вещества меньшей цъны противъ смъси, напр, смъ-
шаемъ вещества 3-го н 4-го сорта въ смъсь, кото*
рой цъна пусть будетъ 9 коп; составленную так.
обр. смъсь смъшаемъ со 2-мъ сортомъ въ новую
произвольную смЪсь, которой цъна пусть будетъ 12
коп. и ciio послъднюю смъсь смъшаемъ съ 1-мъ
сортомъ въ требуемую задачею смъсь, которой цъна
16 коп.
Во второмъ случать емтъшиеаютъ въ произволь¬
ную смпсь вещества большей цгъны противъ тре¬
буемой емтъеи до пгтьхъ пора, пока соединять ихъ
въ одну смтьсь, которую уже емтъшиеаютъ съ ве-
щестеомъ меньшей цгъны противъ требуемой емгьси;
напр, требуется смъшать 4 сорта вещества: цъна
1-го сорта 27 коп.; цъна 2-го сорта 22 коп.; цъна
3-го сорта 19 коп. и цъна 4-го сорта 15 коп.; цъна
требуемой смъси 17 коп. Сначала смъшаемъ 1-й и
2-й сорты въ смъсь, которой цъна напр.. 25 коп.,
потомъ cito смъсь сосдшшмъ съ 3-мъ сортомъ въ
новую произвольную смъсь, которой цъна напр. 20
коп. и ciio новую смъсь соедншшъ уже съ 4-мъ
сортомъ въ требуемую смъсь, которой цъна 17 коп.
Въ шрапьсмъ случать емтъшиеаютъ есть вещества
большей цтьны противъ требуемой смтьсп въ одну
произвольную смтьсь и отдельно отъ нихъ емтъши-
ваюпгъ сеть вещества меныией цгъны противъ тре¬
буемой емтъеи въ другую произвольную смтьсь и на-
конец» ciu деть произвольный смтьсп сосдиняютъ
въ одтту требуемую задачею смтьсь. Напр.
Четыре сорта в инь, изъ коихъ ведро 1 -го сорта
стоить 30 рубл.; ведро 2-го сорта стоить 27

рубл.; ведро 5-го сорта стоить 20 рубл.; it ведро
4-го сорта стоить 16 рубл. надобно смтыиать
такъ, чтобы ведро смтыиеннаго вина стоило 24
рубл. Спр. сколько частей каждаго вина взять
должно для составлешя ведра вина емтъшеннаго1
Сначала смъшаемъ 1-й сортъ со 2-мъ въ произ¬
вольную смъсь, которой цъна пусть будетъ 28 руб.
тогда на основанш чл. 107 должны будемъ ведро
смъшсннаго вина дълить на части обратно пропор-
цюпальныя разностямъ цънъ 2 и 1 рубль, т. е.
3 : 2 = 1 : ос ; отсюда sc — ^ ведра вина 2-го сорта.
3 : 1 = 1 : ж ; отсюда х = i ведра вина 1-го сорта.
Итакъ ведро вина, котораго цъна 28 рубл. со¬
стоитъ изъ i ведра вина 1-го сорта и ~ ведра вина
Теперь отдельно отъ сего смЪшеНя соединимъ
5-й сортъ съ 4-ыъ въ новую произвольную смъсь,
которой цъна пусть будетъ 17 рубл., тогда ведро
внна въ 17 рубл. цЪною должны будемъ дЪлить на
части обратно пропорцюнальныя разностямъ цъпъ
5 н 1 рубль, т. е.
2
1
1
3
2-го сорта.
4
4 : 3 = 1 : х ; отсюда х
4 : 1 = 1 : х ; отсюда х ■=
~ f ведра впиа 4-го сорта.
= | ведра вина 5-го сорта.

235
Птакъ ведро вина, котораго цъна 17 рубл., со¬
стоитъ изъ £ ведра вина 3-го сорта и f ведра вина
4-го сорта.
Наконецъ нзъ енхъ двухъ смъсей, пзъ которыхъ
цъна одной 28 рубл., а другой 17 рубл., составимъ
требуемую смъсь, которой цъна 24 рубля. На осно-
ваиш чл. 107 должны будемъ ведро сей требуемой
смъсп дълпть на части обратно пропорцюнальныя
раэиостямъ цънъ 28 — 24 — 4 и 24 — 17 — 7, т. е.
11
11: 4= i: х\отсюдах =" ведр. вина, котор. цън. 17 р.
11: 7= 1: х;отсюалх=~ ведр. вина, котор. цън. 28 р.
Птакъ ведро вина цъною въ 24 рубля состоитъ
изъ ~ ведра вина цъною въ 28 рубл. и ведра
вина цъною въ 17 рубл.
Теперь замънимъ cin смъси данными въ задачъ
сортами вина, нзъ которыхъ состоять сш смъси.
Поелику ведро вина цъною въ 28 рубл. состоитъ
изъ i ведра вина 1-го сорта п \ ведра внна 2-го
сорта, то — ведра вина цъною въ 28 рубл. состоитъ
изъ ~~ ведра вина 1-го сорта и ~ ведра вина 2-го
сорта, a yj ведра вина цЪною въ 28 рубл. состоять
изъ yj- ведра вниа 1*го сорта и ~ ведра вина 2-го
сорта.
Также ведро внна цъною въ 17 рубл. состоитъ
изъ i ведра вина 3-го сорта и |- ведра вина 4-го
сорта; ~ ведра вина цъною въ 17 рубл. состоитъ
изъ -у ведра внна 3-го сорта н ~ ведра внна 4-го
сорта; ~ ведра вина цъною въ 17 рубл. состоятъ
изъ или Д ведра вина 3-го сорта и ~ или ~
ведра вина 4-го сорта.

236
Слад, ведро вина цъною въ 24 рубля состоптъ
изъ ~ ведра вина 1-го сорта, ~ ведра вина 2-го
сорта, — ведра вина 5-го сорта ц ■— ведра вина
4-го сорта.
II въ самомъ дълъ
цъна ведра вина 1-го сорта = ■— . 50 — 6^ р.
 	2-го	сорта	=	. 27 =: 11— р.
  	5-го сорта	. 20 = 1-^ р.
 77	4-го	сорта	=	. 16 = 4^*7 р.
Слад, цъна ведра вина смъшсинаго равна 6^--|-
1177 +	=	24	рублямъ.

I
I
I
I
i I
I

И ОБЪ ИЗВЛЕЧЕНЫ! КВАДРАТНЫХЪ И КУБИЧНЫХЪ
КОРНЕЙ ИЗЪ ЧИСЕЛЪ. (*)
I.	О КВАДРАТАХЪ И ОБЪ ИЗВЛЕЧЕН!И КВАДРАТНЫХЪ
КОРНЕЙ ПЗЪ ЧИСЕЛЪ.
110.	Квадратомъ или второю степенью какого
нибудь числа называется произведете, произшедшее
отъ умножения этого числа самаго на себя; или квад¬
ратом^ называется произведете, состоящее изъ
двухъ равныхъ производителей. Каждый изъ сихъ
производителей называется корнемъ квадратными
этого произведен!я пли этого квадрата. Если подан¬
ному числу ищется квадратъ его, то это дъйствге
называется возведеюемъ данного числа ей квадратъ
или во вторую степень. Если на оборотъ по дан¬
ному квадрату ищется корень его, то это дъйтйе
называется извлечешемъ корня квадратного изъ дан¬
наго квадрата.
Чтобы показать, что такое-то число возводится въ
квадратъ, для сего число cie заключаютъ въ скобки
и внъ этихъ скобокъ вверху съ правой ихъ сторо¬
ны ставятъ число 2, означая этимъ числомъ то, что
требуется сыскать произведете, состоящее изъ двухъ
равныхъ производителей. Напр, желая возвести въ
(') Некоторые Гг. Преподаватели послъ Ариеметшш пе-
реходатъ съ воспитанниками своими тотчасъ къ Гео-
метрш; посему я почедъ необходимостда присовоку¬
пить ciio статью къ моей Ариеметикъ.

240
квадратъ 7, изображаютъ это такъ: (7)2 =7.7 =
49; число 49 будетъ квадратъ числа 7; а на обо¬
ротъ число 7 будетъ квадратный корень числа 49.
Чтобы показать, что изъ такого-то квадрата извле-
каютъ квадратный его корень, то этотъ квадратъ
ставятъ подъ знакъ V"; напр, желая извлечь квад¬
ратный корень изъ 49, изображаютъ это дъшяые
такъ: |/49 = 7.
II такъ возвести данное число въ квадратъ зна-
читъ умножить это число само на себя. Извлечь
квадратный корень нзъ даннаго квадрата значить
найти такое число, которое, будучи умножено само
на себя, даетъ въ произведенш данный квадратъ.
111.	Изъ предыдущаго чл. видно, что возведете
чиселъ въ квадраты не представляетъ ннкакихъ
трудностей и требуетъ только одного дънштая умно¬
жешя, такъ напр, желая возвести число 576 въ
квадратъ, получимъ: (576)2 = 576 .576 = 531776.
Также желая	возвести	въ квадратъ какую нибудь
дробь, напр. А,	имъемъ: (д)2 = Д . Д =
Ио чтобы умЪть извлекать квадратные корни изъ
всякнхъ возможныхъ чиселъ, для этого надобно пред¬
варительно едълать слъдуюиця замЪчашя, отиосянй-
яся къ возведенно чиселъ въ квадраты:
1)	Взявши иервыя десять чиселъ:
1, 2,	5, 4, 5,	6, 7, 8, 9, 10,
и квадраты ихъ,	1, 4, 9, 16, 25, 56, 49, 64,	81,	100,
увидимъ, что если корень выражается одною циф¬
рою, то въ квадратъ его больше двухъ цпФръ быть
не можетъ ц что между числами, выраженными од¬
ною или двумя цифрами, находится только девять

241
такичъ чиселъ, которыя нмъютъ своими квадратны¬
ми корнами цълыя числа; всъ же друпя числа, яы-
раженныя одного или двумя цифрами, будуть имъть
своими корнями ц влыя числа съ дробями; напр, чи¬
сло 47 заключается между числами 56 п 49, т. е.
оно больше 56 н меньше 49, а потому и квадрат¬
ный корень его будетъ больше 6 н меньше 7; но
между 7 и 6 разность есть только единица, слъд.
квадратный корень 47 будетъ 6 съ какой нпбудь
дробью. Но замвтнмь здъсь, что если квадратный
корень какого нпб)дь цтьлаго пчела не выражается
цплымъ числомъ, то онъ не можетъ быть выра-
жепъ точнымъ образомъ и никакою дробью: ибо
положи «ъ, что извлекая квадратный корень изъ ка¬
кого нпбудь цълаго числа, нашли въ корнъ его цъ¬
лое число съ дробью (разумеется правильного п не¬
сократимою); приведя это цълое число съ дробью
въ одну дробь, получимъ дробь неправильную так¬
же несократимую (чл. 51), возведя эту неправиль¬
ную несократимую дробь въ квадратъ, получимъ въ
квадратъ новую неправильную и несократимую дробь
(чл. 29), изъ которой по изключепш цълаго числа,
получимъ цълое число съ дробью; но цълое число
съ дробью не можетъ быть равно никакому цълоыу
числу, слъд. корень, найденный нами, не будетъ кор-
немъ даннаго квадрата; напр, положнмъ, что извле¬
кая квадратный корень нзъ 47, получимъ въ корнъ
64; если это число есть корень 47, то квадратъ его
должеиъ быть раг.еиъ 47; но приведя 64 въ дробь,
получимъ	дробь неправильную несократимую;
возведя ciio дробь въ квадратъ, иаидемъ: (—)- =
яд. ДД|Д — 46--“- . Слъд б£ не можетъ быть
10

242
квадратным!, корнемъ 47; до такого же точно вы¬
года дойдемъ, если возмемъ вмъсто А другую дробь.
Слъд. точнаго корня нельзя определить для такого
цълаго квадрата, котораго квадратный корень не
можетъ выразиться цълымъ числомъ; въ семъ слу¬
чаъ можно только приблизиться (какъ увидимъ въ
послъдствш) къ корню его по желанно, т. е. мож¬
но найти вместо точнаго корня такую величину,
которая отличается отъ него такою малою величи¬
ною, какою мы захотимъ. Посему тъ числа, кото¬
рыхъ корни не выражаются цълымп числами, назы-
ваютъ неполными квадратами, а корни ихъ если-
чтама иррациональными пли несопзмгьрамыми съ
единицею: нбо ciu корни не могутъ быть точнымъ
образомъ выражены никакими долями единицы и
слъд. не могутъ быть измерены единицею; на обо-
ротъ те числа, которыхъ корни выражаются цъ-
лыии числами, называютъ полными квадратами.
Слъд. между числами, выраженными одною и двумя
цифрами, находится только девять полныхъ квад-
ратовъ.
2)	Самое меньшее число, выраженное двумя циф¬
рами, есть 10, въ квадратъ своемъ 100, оно нмъетъ
три цифры; самое же меньшее число, выраженное
тремя цифрами, есть 100, въ квадратъ своемъ 10000,
оио имъетъ пять цнФръ; квадраты всъхъ чиселъ,
выражеииыхъ двумя цифрами и слъд. заключаю¬
щихся между 10 и 100, будутъ заключаться между
100 и 10000, н слъд. будутъ выражены тремя пли
четырьмя цифрами; также 1000 нмъетъ въ квадратъ
1000000; слъд. квадраты чиселъ, выраженныхъ тре¬
мя цифрами и потому заключающихся между 100 и

243
4000, будутъ заключаться между 4000 и 4000000,
и будутъ выражены пятью или шестью цифрами;
такимъ же образомъ можно найти, что квадраты чи¬
селъ, выраженныхъ четырьмя цифрами, будетъ вы¬
ражены семью или восемью цифрами и т. д. А от¬
сюда слъдуетъ заключить, что въ квадратъ всегда
число нулей бываетъ вдвое болъе числа нулей въ
корнъ, а вообще число цпфръ въ квадратъ бываетъ
или ровно вдвое или вдвое безъ одной болъе чи¬
сла цнФръ въ корнъ.
3)	Желая возвести въ квадратъ какое нибудь чи¬
сло, выраженное двумя цифрами, напр. 56, мы дол¬
жны будемъ, какъ сказано выше, умножить это чи¬
сло само на себя, но производя это умножеше, уви-
димъ, что для получения искомаго произведена или
искомаго квадрата, мы должны будетъ найти четы¬
ре отдъльныя произведсшя, именно: произведете
единицъ на единицы даннаго числа, произведете
единицъ на десятки, потомъ произведете десятковъ
на единицы п наконецъ произведете десятковъ на
десятки; такъ папр. умножая 56 на 56, найдемъ:
произведете 6. 6; потомъ произведете 5 десятковъ
пли 50 на 6, т. е. 50. 6; потомъ умножая множимое
на вторую цифру множителя, получимъ: произведе¬
те 5 десяткоЕъ или 50 на 6, т. е. 50. 6, и нако¬
нецъ произведете О десятковъ или 50 на 5 десят¬
ковъ или 50, т. е. 50. 50; сложивши всъ ciu четы¬
ре произведения, получимъ искомый квадратъ, т. е.
(56)* пли (50+6) 8 — 50. 50+50. 6+50 6+6.6.
Но 50. 50 есть ничто иное, какъ квадратъ десят¬
ковъ даннаго числа; произведешя 50. 6 и 50. 6
совершенно равны и слъд. вмъсто 50. 6 + 50. 6

244
можно взять одно изъ нихъ удвоенное, т. е. 50. 6+
50. 6=2. 50. 6; и наконецъ 6. 6 есть ничто иное
какъ квадратъ единицъ даннаго числа; а посему
(50+6)8 = (50)3 + 2. 50. 6+(6)3 —
Слъд. квадрата числа, соспголщаго изъ десятковъ
и единица, состоишь пза слтьдующихъ трехъ ■ча¬
стей: 1) иза квадрата дссяткова даннаго числа; 2)
изъ удвоенного произведешя десяптова даннаго числа
на единицы его; и Ъ) изъ квадрата единица дан¬
наго числа.
А поелику всякое число, яыраженное болъе не¬
жели одною цифрою, можно представить себъ со-
стоящимъ изъ десятковъ и единиц^, пршшмая во
внимаше, что десятки его могутъ быть выражены
одною пли нъеколькнмн цифрами (напр, число 526
состоптъ пзъ 52 десятковъ и 6 единицъ, слъд.
526 = 52 десятк. + 6=520 + 6; также 52746 =
5274 десятк. + 6=52740 + 6 и т. д (въ первомъ
числъ десятки выражены двумя, а во второмъ чи-
слъ четырьмя цифрами), то можно сказать, что
квадрата всякого числа, выраженного болте не¬
жели одною цифрою, состоитъ: 1) изъ квадрата
десятковъ этого числах 2) изъ удвоенного произве-
детя десятковъ этого числа па единицы его; и 3)
изъквадрата единица этого числа. Напр. (87645689)3
= (876456S0+-9)3 =(876456S0)3 +2. S7645680. 9
+ (9)3.
4)	Возмемъ квадраты двухъ какихъ нибудь по-
слъдовагельныхъ чиселъ, напр. 23 и 24; возводя 23
въ квадрат ь, получимъ: (23)3 =529; для возведе-
шя же въ квадратъ 24, представимъ его состоя-
Щимъ изъ 25+1, тогда для получения искомаго

245
квадрата должно будетъ 25-f- L умножить на 23-]-1,
т. с. умножить сначала 23 —}— 1 на I, потомъ 23—J— 1
на 23 и наконецъ сложить нанденныя произведешя
вмъстъ; но умноживши 25+1 на 1, получимъ 25+1;
умноживши 23	1	па	23,	получимъ 23 . 23 -f- 23
пли (25) 2 -j- 23, сложивши эту величину съ 23-f-i,
найдемъ:
(24)2 = (25 +1)2=(23) 2 + 25 + 25 + 1 = (23) 2-f
2 . 23	1 — 529-f- 2. 23 -f- 1, отнявши отсюда
(25) 2, получимъ: (24) 2 —(23) 2 — 2 . 25 -f-1, т. е.
разность квадратовъ двухъ поелгьдовательныхъ vп- »
селй всегда равняется удвоенному меньшему числу
съ единицею.
112.	Выразумъвши хорошо сш предварительный
замъчашя, можно уже приступить теперь и къ из-
влечен1ю квадратныхъ корней пзъ чиселъ. Пусть
напр, требуется извлечь квадратный корень нзъ 625.
Такъ какъ этотъ квадратъ выраженъ тремя циф¬
рами, то въ корни его будутъ находиться двЪ циф¬
ры (предыдущ. чл. 2 замвч.), т е. десятки и еди¬
ницы. Слъд. квадратъ 625 состоитъ нзъ квадрата
десятковъ, пзъ удвэениаго произведешя десятковъ
на единицы н нзъ квадрата едшшцъ (предыдущ. чл.
5 замвч.). Но десятки въ квадратъ дають сотни
(предыдущ. чл. 2 замвч.), слъд. въ корнв должно
быть столько десятковъ, чтобы квадратъ ихъ былъ
или ровно 6 сотенъ пли число сотенъ меньшее 6;
потому что въ 6 сотияхъ даннаго квадрата могутъ
заключаться сотпн, пронзшедипя отъ удвоеннаго
произведешя десятковъ на единицы. Но 2 десятка
въ квадратъ дають 4 сотни, а 5 десятка даютъ въ
квадратъ 9 сотенъ; слЪд. искомый корень будетъ

246
больше 2-хъ десятковъ п меньше 3-хъ десятковъ;
посему взявши въ корнъ 2 десятка или 20 единицъ,
вычтемъ квадратъ ихъ 400 изъ даннаго квадрата
625, получимъ въостаткъ 225; сей остатокъ заклю-
чаетъ въ себъ удвоенное произведете напденныхъ
2-хъ десятковъ на единицы н квадратъ единицъ; но
удвоенное произведение десятковъ на единицы даетъ
десятки; слъд. эта часть квадрата должна заклю¬
чаться въ 22 десяткахъ полученнаго остатка отъ
квадрата; и cin 22 десятка или заключаютъ въ себъ
одно только удвоенное произведете десятковъ на
единицы, или вмъстъ съ этою частно полнаго квад¬
рата заключаютъ въ себъ и десятки, пропзшеднне
отъ квадрата единицъ; какъ бы то ни было, только
удвоенное произведете десятковъ корпя на единицы
его всегда заключается въ десяткахъ даннаго квад¬
рата; слъд. если мы раздълимъ 22 десятка на удво¬
енные полученные 2 десятка, т. е. на 4 десятка, то
въ частномъ получимъ или точно искомую цифру
единицъ корня или цифру большую оной — боль¬
шую—потому что въ дълиыомъ числъ кромъ удвоен¬
на го произведешя десятковъ на единицы можетъ за¬
ключаться еще н столько десятковъ отъ квадрата
сдихшцъ, что число нхъ увеличить циФру частнаго
одною или нъсколькпмн единицами. Въ семъ случаъ
чтобы увъриться, что найденная при дълеиш иа-
шемъ въ частномъ цифра, есть точно цифра корня
или большая оной, для сего должно умножить ciio
цифру на прежде найденные удвоенные десятки, при¬
ложить къ этому произведение квадратъ сен цифры
и если cia сумма не можетъ быть вычтена изъ
остатка, иолучсняаго прежде отъ всего квадрата

247
(какъ въ настоящемъ случав 225), то это значить,
что найденная цифра для еднннцъ корня больше
надлежащей; въ такомъ случая надобно эту цифру
уменьшать до твхъ поръ, пока произведение ея на
удвоенные десятки корня съ квадратомъ ея можетъ
быть вычтено изъ остатка, полученнаго отъ даннаго
квадрата по отнятш отъ него квадрата десятковъ;
но при семъ уменьшении этой цифры, оказавшейся
большею надлежащей цифры единицъ корня, ыо-
жетъ случиться, что мы слишкомъ умеиьшимъ эту
цифру и хотя можно будетъ совершить вышеупомя¬
нутое вычнташе, но цифра въ корня, принятая за
единццы его, будетъ меньше надлежащей; въ такомъ
случая можетъ насъ вывесть изъ недоумяшя 4-е за-
мячаше предыдущаго члена, именно: если цифра въ
корня, принятая нами за единицы его, есть дВпствн-
тсльио цифра единицъ корня, то по отиятнг изъ
остатка отъ поднаго квадрата, удвоеннаго произве¬
дем.! десятковъ корня на эту цифру съ квадратомъ
ея, новый остатокъ долженъ быть менъе всего най-
деннаго удвоеннаго числа въ корня съ единицею;
если же этотъ новый остатокъ отъ квадрата будетъ
равенъ или больше всего иайденнаго удвоеннаго чи¬
сла въ корив съ единицею, то цнч>ра въ корня,
принятая нами за единицы его меньше надлежащей.
Въ настоящемъ случая разделивши 22 десятка на
4 десятка, получимъ въ частномъ 5; принимая эту
цифру за цифру единиць искомаго корня, для по¬
верки этого возмемъ удвоенное произведете десят¬
ковъ корня на эту цифру, т. е. 40 . 5 = 200, прн-
даднмъ сюда квадратъ 5, т. е. 25 и вычтемъ сумму
200 + 25 = 225 нзъ остатка прежде полученнаго

248
отъ полнаго квадрата, т. е. пзъ 225, въ новомъ ос¬
татка подучим ь нудь—это значить, что 25 есть точ¬
ный искомый квадратный корень даннаго нашего
квадрата 625.—-Все cie дънств1е расподагаютъ такъ:
т. е. отдъляютъ сначада запятою |/ 6,25 — 25
сотни даннаго квадрата, въ кото- 4
рыхъ закдючается квадратъ де- 45
сятковъ корня, находятъ, что въ
22,5
225
корнв будетъ только 2 десятка,
берутъ квадратъ сихъ двухъ де¬
сятковъ н вычнтаютъ его, т. е. 4 сотни (для крат¬
кости нулей не пишуть при 4-хъ, но подразумъва-
ютъ ихъ) изъ даннаго квадрата 625, въ остатки
подучаютъ 22 5, отдъляютъ въ семъ остаткъ десятки
н дъдютъ ихъ на удиоенные найденные десятки въ
корнъ, въ частномъ подучаютъ цифру 5, эту цнФру
записываютъ въ корень и прнннсываютъ ее также
къ д елителю 4 и потомъ помножаютъ составившееся
так. обр. число 45 на цифру корня 5 (этимъ дъй-
ств1емъ вдругъ берутъ удвоенное произведете де¬
сятковъ корня на единицы его и квадратъ единицъ
и складываютъ cin двъ части полнаго квадрата вмь-
стъ) и найденное произведете 225 вычптаютъ изъ
прежде получеинаго остатка отъ квадрата.
Возмемъ еще прнчьръ: пусть требуется извлечь
квадратный корень изъ 2104.
Отдъляемъ 27 сотенъ даннаго	1/	07 < ц _
квадрата запятою и находимъ	с;5
по соображещлмъ, подобпымъ
предыдущшгь, что въ корнъ
204
204
будетъ содержаться 5 дссят-	 ц-
ковъ; береиъ квадратъ нхъ 25

249
сотенъ и вычитаемъ нхъ изъ даннаго квадрата, въ
остаткъ получаемъ 204; отдъляемъ въ сеыъ остаткъ
20 десятковъ и дълнмъ ихъ на удвоенные найден¬
ные десятки корня, т. е. на Ю, въ частномъ нахо-
димъ для цифры единицъ корня 2, запнсываемъ ciio
цифру въ корень и въ дълнтель н помножаемъ 102
на 2, произведете 204 вычитаемъ изъ остатка 204
прежде полученпаго отъ квадрата, новый остатокъ—
нуль, показываетъ, что 52 есть точный корень дан-
иаго квадрата 2704.
Возмемъ еще примъръ:	пусть	требуется	извлечь
квадратный корень нзъ 322624.
Отдъляя въ даниомъ квад¬
ратъ сотни для опредъле-
шя десятковъ въ корнЪ,
уВПДИМЪ, ЧТО CIII СОТНН B..I-
ражаштся четырьмя циф¬
рами 3226, а потому ко¬
рень ихъ, т. е. десятки все¬
го искомаго нашего корня не могутъ быть выраже¬
ны одною цифрою (1-е замъч. предыдущ. чл.), а
должны быть выражены на основанш 2-го замъч.
предыдущ. члена двумя цифрами. А квадратъ чи¬
сла, выраженнаго болъе, нежели одною цифрою на
основанш 3-го замъч. предыдущ. члена, состоитъ
нзъ квадрата десятковъ своего корня и проч. Число
3226 сотенъ въ нашемъ даниомъ квадратъ есть квад¬
ратъ десятковъ корня всего даннаго квадрата; и какъ
выше мы замътили, что с’ш десятки-—корень числа
5226, должны быть выражены двумя цифрами, то
2d
V 32,26,24
106
1128
= 568
726
636
У02,4
9024
0

250
квадратъ ихъ, т. е. 5226 состоитъ пзъ квадрата де¬
сятковъ своего корня п проч. Слъд. чтобы получить
вс в десятки искомаго нашего корня, должно изъ чи¬
сла 3226 извлечь квадратный корень такъ, какъ
бы изъ отдъльнаго числа, подобно какъ въ преды¬
дущие примърахъ. Отдъляа въ семъ числъ сотни
для опредълешя десятковъ въ корнъ его, увидимъ,
что въ семъ корнъ будетъ находиться только 5 де¬
сятковъ, вычитая квадра!Ъ ихъ 25 сотенъ изъ 5226,
получимъ въ остаткъ 726; раздъливиш десятки сего
остатка, т. е. 72 на удвоенные найденные десятки
въ корнъ, т. с. на 10, получимъ въ частном ь для
единицъ корня числа 3226 цифру 6; взявши, какъ
въ прсдыдущихъ примърахъ, удвоенное произведе¬
те найденныхъ десятковъ на ciio цифру и квадратъ
сей цифры и вычитая сш два произведения изъ 726,
получимъ въ остаткъ 90. Теперь далъе разеужда-
емъ такъ: должно было извлекать корень изъ 322624,
а не изъ 3226 и мы стали извлекать корень изъ 5226
только для того, чтобы опредълить десятки въ корнъ
числа 522624; слъд. число 56, какъ корень числа
5226, есть ничто иное, какъ число десятковъ корня
всего числа 322624, которое посему равно (56 де-
сятк.)а 2. (56 десятк ). единицы -f- (единицы)2; до
сихъ поръ мы отняли отъ 3226 (въ которомъ за¬
ключается квадратъ десятковъ искомаго корня), квад¬
рат ь 5, принимая эту цифру за десятки корня чи¬
сла 5226, удвоенное произведшие сихъ 5 десятковъ
на 6 единицъ и квадратъ 6 единицъ; слъд. мы ни¬
что иное едълалн, какъ отняли отъ 5226 квадратъ
56; и въ самомъ дълъ квадратъ 56, есть 5156, от¬
нимая это число оть 3226, получимъ уже найден-

251
ный вами остатокъ 90; но число 56—корень числа
3226, есть относительно всего числа 322624 только
корень десятковъ, а потому квадратъ ихъ будетъ
3136 сотенъ; слъд. должно было отнять не 3136
отъ 3426, но 313600 отъ 522624; совершивши cie
вычиташе, получимъ въ остаткъ 9024; слъд. для
продолжения извлечения корня изъ всего даннаго чи¬
сла 322624, т. е. для опредЬлешя единицъ въ кор-
нъ его, послЬ опрсдьлешя десятковъ его корня,
должно только къ остатку 90, полученному нами
при извлеченш корня изъ 3226, приписать прежде
отдЪленныя двъ цифры 24 въ данномъ квадратъ;
тогда остатокъ нашъ 9024 будетъ заключать въ себь
удвоенное произведете 56 десятковъ на искомую
цифру единицъ корня и квадратъ сей цифры еди-
ннцъ корня; слъд. для опредълешя цифры единицъ
корня должно 902 десятка нашего остатка раздъ¬
лить на удвоенные 56 десятковъ, т. е. на 112, въ
частномъ получимъ для цифры единицъ искомаго
корня цифру 8; взявши потомъ удвоенное произве¬
дшие нанденныхъ уже прежде 56 десятковъ на ciio
цифру 8 и квадратъ сен цнФры н вычитая сумму
сихъ двухъ частей полна го квадрата изъ 9024, по-
лучлмъ въ остаткъ нуль, который н покажетъ намъ,
что число 568 есть точный корень даннаго квадра¬
та 522624.—Еелибы при дълеши 902 десятковъ на
удвоенные найденные десятки въ корнь, т. е. на
112, взяли мы вь частномъ цифру 7 за цифру едн-
шщъ корня, опасаясь, что цифра 8 будетъ с.шш-
комъ велика, то взявши произведшие сен цифры на
т 1127 н вычитая cie произведшие нзъ 9024, полу¬
чили бы вь остаткь отъ квадрата 1135 и корнемь

252
искомымъ было бы тогда число 507; но удвоенное
cie число съ единицею также равно 1155; слъд.
принятая нами цифра 7 за цифру единицъ корня
меньше надлежащей и потому должно было бы уве¬
личить ее единицею, т. е. вмъсто 7 взять 8, какъ
мы и нашли.
Возмемъ еще прпмъръ: пусть требуется извлечь
квадратный корень изъ 94864.
ОтдЪляя въ данномъ квадратъ
запятою сотни для опредъ-
лсшя десятковъ въ коряв,
увидимъ, что сш десятки вы¬
ражаются въ корив двумя
цифрами: ибо сотни даннаго квадрата, т. е. 948 со-
тенъ выражаются тремя цифрами; а потому для
опредълешя всъхъ десятковъ въ искомомъ иашсмъ
корнъ должно извлечь квадратный корень нзъ 948,
какъ бы пзъ отдъльнаго числа; посему отдъляя за¬
пятою сотни этого числа, т. е. 9, увидимъ, что въ
корнъ его будетъ 3 десятка, отнимая квадратъ нхъ
9 сотенъ отъ даннаго квадрата 948, получимъ въ
остаткъ 48; для получешя цифры единицъ въ кор¬
нъ числа 948-ми, отдълнмь десяткп остатка 48, т.
е. 4 десятка, и раздълнмъ нхъ на удвоенные де¬
сятки найдепнаго корня, т. е. на С, увидимъ, что
въ корнъ числа 918 не содержится ни одной еди¬
ницы, слъд. корень этого числа состоитъ только изъ
3 десятковъ или 50 единицъ; теперь далъе разсу¬
ждаемъ: мы начали извлекать корень нзъ 948 для
того, чтобы получить десятки въ корнъ даннаго
V 9,48,04 = 508
_9
608 I
I 4S64
0

квадрата 94864 и найденное нами число 50—корень
948, есть ничто иное, какъ 50 десятковъ корня
всего даннаго квадрата 94864, такъ что весь иско¬
мый корень состоит!» изъ 50 десятковъ н еще нъ-
котораго числа едшшцъ, а квадратъ его, т. е. 94864
состоитъ изъ (30 десятк.)2 -f- 2. (50 десятк.) . един, -f-
(едипнц.)9; до спхъ поръ мы отняли отъ 948 квад¬
ратъ 50, т. е. 900 н получили въ остаткъ 48; но
число 50 есть не число единицъ, а число десятковъ,
а потому и квадратъ ихъ 900 (2-е замъч. предыд.
чл.) есть не число едшшцъ, а число сотенъ, такъ
что квадратъ 30 десятковъ будетъ не 900, а 90000
и должно было вычитать не 900 изъ 948, а 90000
изъ 94864; едълавшн это вычитан ie, получимъ въ
остаткъ 4S64; слъд. и здъсь опредълившп десятки
въ корнъ, для опредълешя единицъ его должно къ
остатку 48, полученному нами при извлечеши кор¬
ня изъ 948, приписать прежде отдълеиныя двъ ци¬
фры 64; тогда остатокъ нашъ 4S64 будетъ заклю¬
чать въ ссбъ удвоенное произведете 30 десятковъ
па искомую цифру единицъ корня и квадратъ сен
цифры; отдъляя десятки сего остатка, т, е. 486,
раздълимъ ихъ на удвоенные найденные десятки
корпя, т. е. на 60, получимъ въ частномъ для циф¬
ры едшшцъ 8 н поступаемъ далъе по предыду¬
щему.
Возмемъ еще прнмъръ, болъе прсдыдущпхъ слож¬
ный: пусть требуется извлечь квадратный корень
изъ 5256500096.

254
Отделяя занятою сот¬
ни 32565000 данна¬
го квадрата для опре-
дълешя десяткоиъ въ
корнъ его, увндимъ,
что ciii десятки вы¬
ражаются болъе, не¬
жели одною цифрою
и потому для опредъ-
лснтя сихъ десятковъ должно будетъ извлечь квад¬
ратный корень изъ 32563000, какъ бы изъ отдъль-
наго числа; но отделял сотни 325650, въ семъ чи¬
сли, увндимъ, что и десятки корня сего числа вы¬
ражаются также болье, нежели одною цифрою;
а посему для опредЬлешя десятковъ корня числа
32563000 должно извлечь квадратн. корень изъ
325630, какъ бы изъ отдельного числа; такпмъ же
образомъ замътимъ, что и для опредълешя десят¬
ковъ корня числа 325630 должно будетъ извлечь
квадр. корень изъ 5256, какъ бы изъ отдельна го
числа; извлекая корень изъ сего числа подобно какъ
въ предыдущихъ прнмърахъ, получимъ въ корнь
57 и въ остаткъ 7; теперь далъе разеуждаемъ: ко¬
рень числа 3256 есть ничто иное, какъ десятки
корня числа 325630, а потому чтобы отыскать еди¬
ницы корня числа 525650 должно къ остатку 7,
полученному при извлеченш корня нзъ 3256, при¬
писать прежде отдъленныя двъ цифры 50 въ числъ
325630, тогда остатокъ нашъ 750 будетъ заклю¬
чать въ ссбъ удвоенное произведенье 57 десятковъ
на искомую циФру единицъ и квадратъ сей цифры
единицъ; поступивши, какъ въ предыдущихъ при-
V 32,56,50,00,96=57064
25
107
75,6
749
11406
114124
7300,0
68436
45649,6
456496
О

255
мТ.рахъ, для опредълешя сен цифры единицъ, уви-
димъ, что въ корн в на мъстъ ея будетъ нуль, такъ
что, корень числа 325630 будетъ состоять ровно
изъ 57 десятковъ или 570 единицъ; но корень чи¬
сла 325630 есть ничто иное, какъ десятки корня
числа 32563000, а потому чтобы отыскать единицы
корня числа 32563000 должно къ остатку 730, по¬
лученному нами при извлечены корня изъ 325650,
приписать прежде отдъленныя двъ цифры 00 въ
числъ 32563000, тогда остатокъ иашъ 73000 бу¬
детъ заключать въ себъ удвоенное произведете 570
десятковъ на искомую цифру единицъ и квадратъ
сей циФры единицъ, и т. д. разсуждая, найдемъ, что
искомый корень даннаго квадрата 32565000 96 есть
точно число 57064.
Изъ всъхъ сихъ примъровъ можно вывесть слъ-
дующее общее правило для извлсчешя квадр. корня
изъ какого-бы-то нибыло квадрата: должно данный
квадратъ разд/ълитъ запятыми на классы отъ пра¬
вой руки къ лтъвой такъ, чтобы въ каждомъ класстъ
было по деть цифры, нзключая послтьдняго къ лтъ¬
вой рукть, въ которомъ можетъ быть и одна цифра
(число классовъ равняется всегда числу цифръ ис¬
комаго корня). Потомъ изъ послтьдняго класса къ
лтъвой рукть извлепаюшъ корень и квадратъ сего кор¬
ня, вычптаютъ изъ онаго; къ остатку сносятъ слгь-
дующш классъ, онгдгьляютъ послтьдшою цифру съ
правой руки, а остальное число дтьлютъ на удвоен¬
ную найденную цифру корня, частное так. обр. по¬
лученное будетъ елгьдующая къ правой рукгъ цифра
въ корить, записавши ей о цифру въ корень, припи-
сываю/пъ ее также и къ дтьлителю к составившее-

256
сп так. обр. число помножаютъ на записанную
цифру еъ корить, произведете вычшпаютъ изъ ос¬
татка съ прпписаниымъ къ нему классомъ; по¬
томъ къ новому остатку сносятъ елтьдующш классъ
изъ даннаго квадрата, отдпляютъ опять поелтъд-
пюю цифру съ правой руки, а остальное число дгь-
лютъ на удвоенною найденную часть корил, част¬
ное записываютъ въ корень и пршшсываютъ къ Ъгь-
ли'пелю и помножаютъ составившееся так. обр.
число на записанную цифру въ корить, произведете
cie вычшпаютъ изъ 2-го остатка съ приписаипымъ
къ нему классомъ; къ сему новому остатку сносятъ
елтьдующш классъ изъ даннаго квадрата и так.
обр. далтье посшупаюшъ до тгьхъ поръ, пока не
снесутъ къ разнымъ остаткамъ вспхъ классовъ
даннаго квадрата; тогда въ поелтъдпемъ остатки?
получится пли нуль, когда данный квадратъ есть
полный квадратъ, или останется какой нибудь зна¬
чительный остатокъ, когда данный квадратъ есть
не полный квадратъ и тогда должно будетъ оты¬
скать корень приближенный. Если случится, что
по снесепш къ какому нибудь остатку (въ продол-
жеше извлечешя корня) слтьдующаго класса нзъ
даннаго квадрата и по отдгьлепш поелтъдтй циф¬
ры съ правой руки, остальное число не дтьлптся
па удвоенную найденную часть корпя, то въ корить
на мтьстть цифры, соотвтынствующей сему классу,
ставптъ пуль и къ остатку съ нриписаппымъ уже
къ нему классомъ, приписываютъ еще елтьдующш,
классъ изъ даннаго квадрата и продолжаютъ из-
влепете корпя далгье.
115. Приступая къ извлечение корней по прпб.ш-

257
«
женно, замътииъ, чго при нзвлеченш" корня нзъ
дроби должно отдЪльно извлекать корень пзъ чи¬
слителя и пзъ знаменателя: нбо при составлены квад¬
рата пзъ дроби находили отдельно, основываясь на
правнлъ умножешя дробей, крадратъ числителя п
квадратъ знаменателя. По сему = Я.
Если бы надобно было извлекать корень пзъ та¬
кой дроби, у которой числитель и знаменатель суть
числа — не полные квадраты, то вмъсто дврннаго
нрпближеннаго извлечешя корня (т. е. изъ числи¬
теля и знаменателя) нзвлекаютъ только приближен¬
но корень изъ числителя, умноживши числителя и
знаменателя дроби на знаменатель оной и слъд. сдъ-
лавши чрезъ это дънств1е знаменатель данной дроби
полнымъ квадратомъ. Напр, если бы требовалось
извлечь корень квадратн. изъ дроби -f-, то умножая
числителя и знаменателя сей дроби на 7, получимъ:
1/j-T	слъд. здъсь останется только извлечь
9 4. У	7
приближенно корень пзъ одного числителя.
Пусть теперь требуется извлечь корень квадратн.
изъ числа 57 приближенно на это значить, что
требуется отыскать такую величину, которая бы
отличалась отъ нстпннаго корня числа 57 менъе,
нежели ~ долею. Чтобы отыскать такую величину,
умножпмъ данное число 57 на квадратъ 13-ти или
вообще на квадратъ знаменателя той дроби, на ко¬
торую требуется приблизиться къ истинному корню
и произведете раздвлпмъ на квадратъ сего знаме¬
нателя, получимъ: 57 . (13)2	9G33,	число равное
13=— ШГ
57; слъд. У 57 =	9633	= j/9633; извлекая корень
•	1G9	13'
17

258
изъ 9635 по правилу, предложеннвму въ предыд.
чл, найдемъ, что |/У633 = 98 съ остаткомъ 29, ко¬
торый показывает ь, что |/ус>33 болъе 98 и менъе
99; по сему ^УОЗЗ будетъ болъе Ц и менъе ff;
13~
но У УоЗЗ = у 57; слъд. У 57 будетъ болъе f| п
~ИГ
менъе ff; но разность между f§ п ~ есть и
какъ.у 57 заключается между -Ц и ff; слъд. раз¬
ность между У 57 н ff будетъ менъе Тт- и потому
если вмъсто У 57 возмемъ величину то разность
между сею величиною и пстнннымъ квадратн. кор-
немъ числа 57 будетъ менъе доли. Слъд. У 57=
§f-=7^j приближенно на
И такъ чтобы извлечь приближенно корень квадр.
Изъ какого пибудь числа, должно умножить cie чи¬
сло на квадратъ знаменатлея той дроби, на кото¬
рую требуется приблизиться къ истинному корню,
изъ произведшая извлечь корень квадратн. такъ
точно, какъ извлекается корень изъ полнаго квад¬
рата (т. е. производить извлечете до тъхъ поръ,
пока снесутся къ остатками всъ классы изъ пред-
ложеннаго числа) и найденный так. обр. корень
раздгьлить на знаменателя помянутой дроби.
Вотъ еще прнмъръ: пусть требуется извлечь ко¬
рень квадратн. изъ 157 приближенно на
На основанш предыдущаго правила пмЪемъ:
\/Т37 = /Г'ШТЩу = У (552257= -^=il£§=
'	(65)2	(ЗУ
llff приближенно на ■—.
Извлечете корней пзъ чиселъ по приближенно
посредствоыъ десятнчныхъ дробен производится на

259
основами вышеупомянутого же правила. Пусть напр.
требуется извлечь корень изъ 73 приближенно на
ТооБ"* Для сего поступивши, какъ въ предыдущихъ
прпмЬрахъ, получимъ: 1/73=	73	. (1000)~“ =
'	(1UU0)2
/^ТШоиобО = 1/73000000; но 1/73600000=: 8544 съ
' (1000)2 1000
остаткомъ 64, который показываетъ, что \/73000000
болье 8544 ц менъе 8545; по сему 1/730бГ)000 бу-
Ш00
детъ болье и менъе	.
Слъд. п здьсь если возчемъ	вмьсто	истин-
наго корня числа 75, то разность между сего вели¬
чиною и истиннымъ корнемъ 73-хъ будетъ меиъе
Там' Т* е- 1/73= fool =8>544 приближенно на —Vo-
Здьсь еще короче можно выразить правило опре-
дълешя прпближеннаго корня, именно: въ случать
извлечешя корня изъ какого нибудь числа по при¬
ближенно посредствомъ десятичныхъ дробей дол¬
жно къ данному числу приписать двойное число
нулей противъ числа нулей вь знаменатели той
дроби, на которую требуется приблизиться, изъ со-
ставившагося так. обр. числа извлечь корень квадр.
по общимъ правиламъ и въ найденномъ так. обр.
корнть отмтытипь занятою столько десятичныхъ
знаковъ, сколько было нулей въ знаменателгь той
дроби, на которую требовалось приблизиться.
Поступая по сему правилу при опредъленш корня,
напр, числа 873456 приближенно на 1О-р0о-, полу-
чпмъ во первыхъ число 87545600000000, составив¬
шееся чрезъ пршшсашс къ данному 8 нулей; по-

2G0
томъ извлекая корень изъ сего послъдняго числа,
будетъ: ]/87345бШ00000 = 9545S86.
Отмътпвнш въ числъ 9345886 запятою четыре
знака для десятичныхъ, найдсмъ наконецъ, что
^873456 = 934,5880 приближенно на 0.
ЗдЪсь можно заметить еще, что нътъ даже на¬
добности прежде пзвлечешя корня нзъ предложен-
наго числа приписывать къ нему двойное число ну¬
лей противъ знаменателя той дроби, на которую
требуется приблизиться къ истинному корню, а про¬
сто: желая найти приближенный корень (будетъ ли
напередъ извъстна дробь, на которую требуется
приблизиться къ истинному корню, или эта Дробь
останется произвольною для насъ) какого нпбудь
числа, должно извлечь изъ него квадратн. корень
по общнмъ правиламъ п когда будутъ снесены къ
разнымъ остаткамъ всё классы изъ предложеннаго
числа, то къ каждому нзъ нослъдующихъ посл-ь
сего остатковъ, продолжая извлечете обыкновен-
нымъ образомъ, приписывать по два нуля и нако¬
нецъ въ нанденномъ корнъ отметить для десятич¬
ныхъ столько знаковъ, сколько разъ приписали ыы
по два нуля. Напр, желая найти приближенный ко¬
рень числа 8734, извлекасмъ изъ него сен корень
по прсдыд. чл. наидемъ въ корнъ число 93 и въ
остаткъ S5, къ сему остатку пришннемъ два нуля
и продолжаемъ извлечете обык. обр., найдемъ въ
корнъ цнФру 4 и въ остаткъ число 1044, къ сему

V 8734 = 93,455
8l
18
1864
18685
186Э05
634
549
850,0
7456
104 40,0
93445
10У750,0
954525
261
остатку прппишемь снова
два нуля н т. д. продол-
жаемъ; вь сечь прям Ври
мы ограничилась тремя ос¬
татками, къ которымъ при¬
писывали къ каждому по
два нуля; слъд. въ най-
денномъ корнь 93455 дол¬
жно отмътпгь три знака
для десятнчиыхъ и полу-
162975
чимъ: }/8734=95,455приближенно на—1—, т. е. что
разность между 95,455 н пстиннымъ кориемъ числа
8734 будетъ менъе тысячной доли единицы.
114.	Пусть теперь требуется извлечь корень квадр.
изъ дроби; напр. Мы сказали въ пачалъ пре¬
дыдущая члена, что для пзвлечешя квадрат, корня
изъ дроби должно извлечь оный отдълыю пзъ чи¬
слителя н нзъ знаменателя, п въ случаъ, когда оба
члена дроби пе полные квадраты, для избъжашя
двойнаго прнблнженпаго извлечешя должно знаме¬
натель сдълать полнымъ квадратомъ чрезъ умноже¬
ние числителя и знаменателя предложенной дроби
на знаменателя оной. Поступивши так. обр , полу¬
чимъ: // \'Л = /^73737=1/481; но Т7481 =21 при-
/37~	* 37.37	37
б.шжснно на единицу, т. е. что J/4S1 больше 21 п
меньше 22; посему У 481 будетъ больше ~ и мень-
__	37"
ше ff. Слъд. V-Ц- = fv приближенно на Д.
Здъсь можно гораздо болъе приблизиться къ кор-
= |/431; нзвлечемъ те¬
ню
так. обр. им г. я /Л13 — У 431;
*	"37	37
4

262
перь корень изъ 481 положпмъ приближенно на
—3, тогда' по предыдущ. чл. получимъ: \/481=:
21,931 приближенно на I0V05 посему j/481 будетъ
37
болъе 21,931 п менъе 21.932; слъд. 13=21,931 =
37	"37	'	*37	37
21931 приближенно на 1	.
37000	37000
Примтъч. Иногда случается, что знаменатель пред¬
ложенной дроби не будучи полпымъ квадратомъ за¬
ключаетъ въ себь одинъ или нъсколько множителей,
которые будутъ полные квадраты, тогда чтобы сдъ-
лать весь знаменатель полпымъ квадратомъ должно
только числителя и знаменателя предложенной дроби
помножить на тъ множители ея знаменателя, кото¬
рые будутъ не полные квадраты. Напр» пусть
требуется извлечь корень нзъ	Разлагая	знаме¬
натель 252 па производители, увндимъ, что 252 =
4 . 9 . 7; здъсь производители 4 и 9 полные квад¬
раты; слъд. надобно числителя и знаменателя пред¬
ложенной дроби помножить только на 7 п будетъ:
S   Б ■> 7 -	S	5
ЭБ2 *"252.7   17 64*
Замътпыъ здъсь, что извлекая корень пзъ дроби
■jfft пътъ надобности извлекать корень отдъльно
пзъ знаменателя; онъ уже готовъ: нбо 17G4 =
4 . 9 . 7 . 7 = 4 . 9 . 49; слъд. извлечь кореиь изъ
1764 все равно, что извлечь корень нзъ 4.9. 49;
но при извлечении корня изъ пропзведешя нъсколь-
кихъ чиселъ надобно извлекать кореиь изь каждаго
производителя отдъльно и для получешя корня всего

2G3
произведения падобно только йайдсниые так. обр.
корми перемножить между гобою; причина этого за¬
ключается въ самомъ возвышенш чпеелъ въ квадраты:
ибо пусть требуется возвысить въ квадратъ произ¬
ведете напр. трехъ чис лъ 2.5.7; тогда по чл.
110 получимъ: (2 . 5.7)а =2 . 3 . 7 . 2. 5.7; но мы
можемъ переставить производители (чл. 20) так.
обр. 2.2.5.5.7.7, тогда (2 . 5 .7)2=2.2.3.3.7.7 =
4.9. 49; слъд. при возеышенш произведешя нъ-
сколькпхъ чиселъ въ квадратъ, мы возвышали ка¬
ждый производитель въ квадратъ отдълыю, т. е.
квадратъ произведешя игъеколькихъ чиселъ равняет-
ся произведение ксадратовъ всп>хъ его производи¬
телей; а посему и корень 'квадрант, произведешя
нтъеколъкихъ чиселъ равняется произведение корней
квадрант, вегьхъ его производителей. Слъд. 5 =
/	252
^”35	Уз5	= j/зЗ; но ]/з5 = 5 прпбли-
'	4.9. 49	2.3.7	42
женно на единицу; слЬд. |/з5= ^ приближенно
~42
на т. е. /^^5” = ~г. приближенно на
Г ~252
115.	Пусть наконецъ требуется извлечь корень
квадратн. пзъ десятичной дроби; папр. изъ 2,013.
Поелику 2,015 = 2^ =	то	|/ДдШГ =
/^2013= /^20 чЗ ; слъд. чтобы едълать знамена-
/ Хобо / ХооЛо
тель полнымъ квадратомъ должно числителя и зна ■
менателй дроби	помножить	на 10, тогда бу-
дстъ: //"2ШЗ-= /^2оШ) = }/20130; но |/2оШ)=
100.10 '	10000 Too

264
141 приближенно на едииицу, а 1^20130=	при-
100
ближенно на Слъд. 1/^013= 1,41 приближен¬
но на 0,01.
Изъ этого примъра видно, что правило, изложен¬
ное въ предыдущ. чл. для извлечешя корней изъ
обыкновенныхъ дробей вполнь прпмъняется и къ
извлечений корней изъ дробей десятичныхъ, только
въ семъ случаъ оно можетъ быть выражено еще
проще, именно: замъчая, что знаменатели будутъ
полные квадраты только у тъхъ десятичныхъ дро¬
бей, у которыхъ число десятичныхъ знаковъ четное,
при извлечешь корил квадратн. изъ десятичной дро¬
би прежде всего едгьлаемъ, чтобы число десятич-
ныхъ ея знаковъ было четное; елтъд. если дана
дробь съ нечешнымъ числомъ знаковъ, то допол-
нимъ ея съ правой стороны одничъ или нисколь¬
кими нулями (чл. 58. 3.), смотря потому, на ка¬
кую долю должно приблизиться къ истинному
корню (въ той дроби, изъ которой надобно извле¬
кать корень число десятичныхъ знаковъ, всегда дол¬
жно быть четное и въ двое болъе противъ числа
нулей той дроби, на которую требуется приблизить¬
ся къ истинному корню); приготовивши так. обр.
дробь, отбросимъ въ пей запятую и извлечемъ ко¬
рень по чл. 112; и наконецъ въ пайдениомъ так.
обр. корни отдплимъ занятою для десятичныхъ
знаковъ число цифръ въ двое меньшее противъ числа
десятичныхъ знаковъ въ данной дроби, считая въ
то число и прибавленные къ пей съ правой сторо¬
ны нули. Напр, пусть требуется извлечь корень пзъ
117,03657 приближенно на	Слъд.	надобно кь

265
данной дроби прибавить съ правой ея стороны три
нули н будетъ:	117,03657000 отбросивши здъсь
запятую и извлекши корень квадратн. изъ числа
11705657000, получимъ: |/11703П57000 := 10b 185;
поелику въ данной десятичной дроби 117,03657000
находилось 8 десятнчиыхъ знаковъ, то въ найденном ь
корнъ 108183 должно для десятнчиыхъ знаковъ от-
мЪтнть 4 цифры и будетъ: ]/117,03057 = 10,8183
приближенно на 0,0001.
II въ самомъ дълъ прибавивши къ данной дроби
117,05657 съ правой стороны три нуля, мы ничто
иное сдълали, какъ не перемвняя величины данном
дроби выразили ее въ стомнллюиныхъ доляхъ; слъд.
когда пзобразимъ дробь 117,03657 въ видъ обыкно¬
венной, то будетъ: 117,03657 = 117—или
”Гоо6о”°оГ5 но Ю0000000 есть квадратъ 10000
(2-е замъч. чл. III); слъд. чрезъ прибавлеше къ
данной дроби съ правой ея стороны 3-хъ нулей,
мы сдълали знаменатель ея полнымъ квадратомъ зна¬
менателя той дроби, на которую требовалось прибли¬
зиться къ истинному корню; а по сему ]/Ii7/)3G57—
/^11703657000=У1Г703С57000; но |/ГГ703657б0б=
IOOOOOjOO	10000
108185 приближенно на единицу; a ]/l J 703657000=
10000 ‘
приближенно наСлъд. }/Г17:030о7'=
10,8185 приближенно на 0,0001.
Примтьч. 1. Иногда нужно бываетъ корень обык¬
новенной дроби выразить приближенно въ десятнч-
ныхъ доляхъ; въ такомъ случав обращаютъ данную
обыкновенную дробь въ десятичную (чл. 62) и но-
томъ поступаютъ съ нею по правилу вышснзложсн-

266
ноиу въ семъ члеиъ. Напр, требуется найти
I 20
приблнжонно на	для	сего	имъемъ ^ = 0,15
слъд. / А_= У 0,15 = |/ОД5СЮ = 0,38.
/ 20
ТТримтьч. 2. Если бы надобно было извлечь корень
квадратн- изъ перюднческой пин непрерывной дроби,
то приведя ciu дроби въ обыкновеииыя (чл. 66 и
чл. 7 0), поступить съ ними по правилу, изложсному
въ предыдущемъ членъ.
II.	о КУБАХЪ И ОБЪ ИЗВЛЕЧЕНЫ КУБНЧИЫХЪ КОРНЕИ ИЗЪ
ЧИСЕЛЪ.
116.	Кубомъ или третьего степенью какого ни¬
будь числа называется произведение, нронзшедшее
отъ умножешя этого числа самаго на себя два раза;
или кубомъ называется произведете, состоящее изъ
трехъ равны хъ производителей. Каждый нзъ сихъ
производителей называется корнсмъ кубичпымъ это¬
го произведешя или этого куба. Если по данному
числу ищется кубъ его, то это дъйств1е называется.
возведешемъ данного числа въ kj бъ ii.ni въ третью
степень. Если наоборотъ по данному кубу ищется
корень его, то это дъйств1е называется извлечешемъ
корня кубичного изъ даннаго куба. Для показания,
что такое-то число возводится въ кубъ, нзображаютъ
это такъ: напр. (7) 3 = 7 . 7 . 7 = 343, число 343
будетъ кубъ числа 7, а число 7 будетъ кубичный
корень числа 343. Для показаны, что нзъ такого-то
числа извлекаютъ корень кубичный, ставятъ данное
число подъ знакъ |/, сверьху KQToparo ставятъ число-

267
5, дабы отличить корень кубичный отъ корня квад-
3
ратнаго; слъд. J/ 343= 7.
Итакъ возвести данное число въ кубъ значить
умножить это число само на себя два раза. Извлечь
корень кубичный изъ даннаго куба значить найти
такое число, которое будучи умножено само на себя
два раза даетъ въ произведенш данный кубъ.
117.	Изъ предыдущ чл. епдно, что возведен!е
чиселъ въ кубы не представлаеть никакихъ трудно¬
стей и требуетъ также, какъ и возведете чпселъ въ
квадраты только одного дъйств!я умножешя. Сл пд.
(248)“=248. 248.248=15252992. Также (-*■ )s=?-
. s Я  ,2 7
* 9 9 7	S4-3	*
Но для извлечешя корней кубичныхъ изъ чпселъ
надобно предварительно сдълать слъдуюнця замъ-
чашя, подобный тъчъ, кашл мы сдълалн въ чл. III.
1) Взявши первыя десять чиселъ:
1, 2, о, 4, 5, б, 7, 8, 9, <0,
и кубы ихъ: 1,8,27,64,125,216, 343,512, 729,1000,
увндимъ, что если корень выражается одною цифрою,
то въ кубъ его больше трехъ цнФръ быть не мо¬
жетъ и что между числами, выраженными одною,
двумя и тремя цифрами находится только девять
полныосъ кубовъ, т. е. иыыощихъ своими кубичными
корнями цЕлыя числа; всъ же друпя числа, выра-
жеиныя одною, двумя и тремя цифрами, будутъ не¬
полные кубы н корнями своими будутъ иметь вели-
чины ирращоналъныя или песоизмтъримыя съ еди¬
ницею (1-е зам. чл. III). И слъд. корни сш надобно
будетъ отыскивать по приближенно.'
2) Кубъ 10-ти есть 1000, а куоъ 100 есть ЮООООО:
слъд. кубы чиселъ, выраженныхъ двумя цифрами

268
будутъ заключаться между 1000 и 1000000, т. е.
будутъ выражены 4-ыя, 5-ю и 6-ю цифрами; также
кубы чиселъ, выражеиныхъ тремя цифрами, будутъ
заключаться между 1000000=(i00)s и 1000000000
= (1000)* и будутъ выражены 7-ю, 8-ю и 9-ю
цифрами, и т. д. Слъд. въ кубъ всегда находится въ
трое болъе нулей, нежели въ корнъ, п вообще число
цифръ въ кубъ бываетъ или ровно въ трое, или въ
трое безъ одной, или въ трое безъ двухъ болъе
числа цнФръ въ корнъ.
5)	Возводя въ кубъ какое нибудь число, выра¬
женное двумя цифрами, напр. 55, должны будемъ
умножить это число само на себя два раза, т. е.
(55)® = 55. 55. 55; но какъ число 55 = 50+0,
то (50 + 5)® = (50 + 5). (50 + 5). (50 + 5); но
(30+5). (30+5) = (30+5)а=(50)2 + 2 (50)5 +
(5)® и потому для получения куба (50+5) должно
(30)2 + 2 (50). 5 + (5)а умножить цд (50 + 5),
т. е. умножить сначала на 50, потомъ на 5 и най-
денныя так. обр. пронзведешя сложить вмветъ; но
умножая (50)2+2 (50). 5 + (5)а на 50, получимъ:
(30)2. 30 + 2. (30). 5. 30+(5)а. 50 или 30. 50.
30+2. 50. 50. 5+(5)а. 50 или (50)®+2. (50)а.
5+(5)а. 50; умножая (50)а +2. (50). 5+(5)а на
о, получимъ: (30)а 5+2. (30). 5. 5+(5)а. 5 или (50)а.
5 + 2. 50. (5)а+(5)®; посемуг (50+5) . = (30)*
+2 (50)2 5+(5)а. 50+(50)а. 5+2. 50. (5)а+(5)*;
по 2. (30)а. 5 + (30)а. 5=5. (30)а. 5 и (5)а. 50
+2. 50. (5)2 =3. (5)2. 50; слъд. (50+5)*=(50)®+5.
(30)а. 5+3. (5)а. 30+(5)s, т. е. кубъ числа, со-
стояшаго пзъ десятковъ и едпннцъ, состоитъ изъ сл ъ-
дующпхъ 4-хъ частей: 1) Пзъ куба десятковъ даннаго

числа; 2) Изъ утроенного квадрата десятиовъ дан¬
ного числа на единицы его; 3) Пзъ утроенного ква¬
драта единицъ даннаго числа на десятки его, и 4)
Пзъ куба единицъ даннаго числа. А псе.шку всякое
число можно представить себь состояипшъ пзъ десят¬
ковъ ы едшшцъ, принимая во внпмаше, что десятки
его могутъ быть выражены одною или нисколькими
цифрами, то можно сказать, что кубъ всякаго числа
состоитъ пзъ 4-хъ вышеупомянутыхъ частей; наир.
(3847)* = (3840 + 7)з = (5840)* + 5. (5840)а.7 +
3. (7)8 . 3840 + (7)*.
4)	Возмемъ кубы двухъ поелндоватсльныхъ чи¬
селъ напр. 10 и 17; будетъ: (16)*	4096; для воз¬
ведения же 17 въ кубъ, представпмъ его состоящнмъ
пзъ 16 -f- 1, тогда (t7)s = (i6 -f- I)3 = (16 -J- 1) .
(46+!)• (16 + 1), «о (16+1) .(16+i)=(16+i)a
= (1б)2 + 2. 16. 1 + 1 (4-е замъч, чл. Ill); умно¬
жая это число на 16 + 1, получимъ: (17)* =(16+1)*
= (16)® + 3 . (16)® . 1+3.16.1+1, вычитая от¬
сюда (16)* = 4С96; получимъ: (17)*—(16)* =3.
(16)® -J- 5 . 16 + 1, т. е. разность кубовъ двухъ по¬
следовательны хъ чиселъ всегда равняется утроен¬
ному квадрату меньшого числа съ утроеннымъ симъ
меньшимъ числомъ и съ единицею.
118.	Теперь прпступичъ къ извлечение корней
кубнчныхъ изъ чиселъ. Если данное число, пзъ ко-
тораго требуется извлечь корень кубичный, будетъ
выражено не болъе, какъ тремя цифрами, то корень
его найдется или между первыми девятью числами,
если данное число есть полный кубъ, пли найдется

270
по приближению, какъ увидимъ ниже, если дацное
число не полный кубъ. А потому возмемъ число, вы¬
раженное болъе, нежели тремя цифрами; пусть наир.
требуется извлечь корень кубичный изъ 5065о. —
Такъ какъ этотъ кубъ выражень пятью цифрами,
то въ корив его Судутъ находиться двъ цифры, т. е.
десятки и единицы. Слъд. кубъ 50655 состоитъ изъ
куба десятковъ, изъ утроеннаго произведешя квадра¬
та десятковъ на сдпншщы и т. д. (предыдущ. чл.
3-е замъч.). Но десятки въ кубъ даютъ тысячи (прс-
дыдущ. чл. 2-е замъч.); слъд. въ корнЪ должно быть
столько десятковъ, чтобы кубъ ихъ былъ или ровно
50 тысячь или число тысячь, меньшее 50; потому
что въ 50 тысячахъ даннаго куба могутъ заключать¬
ся тысячи, пронзшедння отъ утроеннаго произведе¬
шя квадрата десятковъ на единицы; так. об. въ кор-
иъ будетъ находиться три десятка: ибо (50)* ==
.27000, а (40)* = 64000, число большее даннаго куба;
вычитая кубъ сихъ трехъ десятковъ, т. е. 27000 изъ
даннаго куба 50655, получимъ въ остаткъ 25655 въ
которомъ заключаются утроенное произведение ква¬
драта найдснныхъ въ корнъ 5-хъ десятковъ на еди¬
ницы корня; утроенное произведете квадрата еди¬
ницъ корня на найденные уже 5 десятка его и кубъ
единицъ корня; но утроенное произведете квалрата
десятковъ на единицы даетъ сотни (2-е замъч. чл.
III.); слъд, эта часть куба должна заключаться въ 256
сотняхъ полученнаго остатка отъ куба; въ сихъ же
256 сотняхъ могутъ заключаться еще и сотни, произ-
шединя отъ прочихъ частей куба; посему если раздъ-
лимъ 256 сотеиъ на утроенный квадратъ найденныхъ
5-хъ десятковъ въ корнъ, то въ частномъ получимъ

271
плп точно искомую цифру едншщъ корил НЛП цифру
большую оной. Чтобы увериться, что найденная въ
частномъ цифра есть истинная цмФра едшшцъ корня
нлп большая онон, то должно взять утроенное про¬
изведете квадрата напденныхъ о-хъ десятковъ на
ciio цифру единицъ, приложить къ сему произведе-
нио утроенное произведете квадрата сей цпФры
едшшцъ на 3 десятка корня п кубъ сен цпФры еди-
инцъ и если ciio сумму нельзя будетъ вычесть пзъ
остатка, полученнаго отъ куба (какъ въ настоящемъ
случаь 23655), то цнФра, полученная при дъленш
нашемъ въ частномъ будетъ больше истинной цифры
единицъ корня; въ такомъ случаъ должно будетъ
уменьшать ее до тьхъ поръ, пока можно будетъ
вычесть вышеуиомянутыя части полцаго куба изъ ос¬
татка его, наблюдая, чтобы вновь полученный оста¬
токъ былъ меньше утроеннаго квадрата всего числа,
иайденнаго въ корнъ, съ утроеннымъ симъ числомъ
п единицею (предыдущ. чл. 4-е замъч.). РаздЪляя
236 сотенъ на 27, т. е. на утроенный квадратъ най-
денныхъ въ корнъ 3-хъ десятковъ, получимъ для
единицъ корня цифру 7 и для полнаго убъждешя,
что сщ цифра 7 есть дъйствитпльно цифра едшшцъ
корня, возмемъ утроенное произведете квадрата най-
денныхъ прежде въ корнъ 5-хъ десятковъ на ciio
цифру 7, получимъ 18900, къ сему числу придадимъ
утроенное произведете квадрата 7 на найденные
прежде 5 десятка въ корнъ, т. е. 7 . 7. 3 . 30 =
49.3. 50 = 4410 и еще кубъ цифры 7, т. е. 543,
получимъ: 18900	4410 -f- 345 = 23655, вычитая
cie число изъ остатка, прежде полученнаго отъ куба,
т. е. изъ 23653, получимъ въ иовомъ остаткъ нуль—

272
это значить, что 37 есть точный искомый кубичный
корень даннаго нашего куба. Все cie д£пств1с распо¬
лагается такъ:	у	50,653 = 37
т. е. отдъляютъ сна-	27
чала запятою тыся-	27
чи даннаго куба, въ	3.	(50)2	. 7	=
которыхъ заключает-	3.	(7)а .	30	=
ся ку бъ десятковъ кор-
256,53
1S900
4410
(7)8 =	343
ня, находятъ, что въ	^	w
корнъ будетъ только	0
3 десятка, берутъ кубъ сихъЗ-хъдесятковъивычитаютъ
его, т. е. 27 тысячь (для краткости нулей не пншутъ
прн27,ноподразумъваютъ11Хъ) нзъ даннаго куба,50653;
въ остаткъ подучаютъ 23653, отдъляютъ въ сеиъ ос¬
таткъ сотни и дЪлютъ пхъ на утроенный квадратъ
нанденныхъ десятковъ въ корнъ, въ частномъ полу-
чаютъ цнФру 7, эту цифру записываютъ въ корень
и принимая ее за цыфру единицъ нскомаго корня,
составляютъ части полнаго куба, заключающаяся въ
остаткъ 23653—-какъ показано въ примъръ; складыва-
ютъ cin части между собою и сумму ихъ 25653 вычн-
таютъ изъ остатка прежде полученнаго отъ даннаго
куба, т. е. изъ 25653. Возмемъ еще прнмъръ: пусть
требуется извлечь корень кубичный изъ 15312053.
Отдъляя въ дан-	jhs,312,053=237.
номъ кубъ ТЫСЯЧИ	8
дляопредълешяде-	12|	55,12
сятковъ въ корнъ 5. (20)“. 5 = 3600
его, увидимъ, что	(°)s==	540
J	(5)==	27.
сш десятки выража-	4 '
ются болъе, иеже-	4167

273
ли одною цифрою:	1587	(11450,53
ибо тысячи данна- (250)*. 7 = 1110900
3. 250. (7)9 —	33810
го куоа выражают-	^	^
ся болье, нежели	—	,
11450оо
3-ыя цифрами; а по-	—
0
тому для опредьлешя десятковъ въ корнъ нашего
куба, надобно изъ 15512 извлечь корень кубичный,
какъ изъ отдЬльнаго числа; поступивши какъ въ
предыдущемъ прнмъръ, получимъ въ кубичномь кор¬
нъ числа 13512 число 25 и въ остаткь 1145; но
корень 15512 есть ничто иное, какъ число десятковъ
въ корнь всего даннаго куба н какъ до сихь поръ
мы, ничто иное едьлали, какъ отняли отъ 13312
кубъ 2-хъ десятковъ, утроенное произведете квадра¬
та 2-хъ десятковъ на 5 единицы, утроенное про¬
изведете квадрата 5-хъ единицъ на 2 десятка и кубъ
3-хъ единицъ, или другими словами отъ 13312 отня¬
ли кубъ 25; и въ самомъ дьлъ (25)* г= 12167, от¬
нимая cie число отъ 15512, получимъ въ остаткъ
1145; но какъ 25 суть десятки корня всего даннаго
куба, то кубъ нхъ есть не 12167 единицъ, но 12167
тысячь, т. е. 12167000 и должно было вычитать не
12167 нзъ 15512, а 12167000 изъ 13312053; со¬
вершивши cie вычиташе, получимъ: 1145055; слъд.
опредьливши 25 десятка въ корнъ, для оиредъле-
iiin единицъ корня должно къ остатку 1145, полу¬
ченному по извлеченш корня кубичнаго изъ 15512
приписать отдъленныя прежде три цнФры нашего
куба, т. е. 055; тогда въ остаткъ 1145055 будетъ
заключаться }троенное произведете квадрата 23 де-
сят' » на цифру единицъ корня; утроенное произ-
18

274
ведоше квадрата сей цифры единицъ корня на 23
десятка его п кубъ цифры едшпшъ; отдъляя въ семъ
остаткъ двк перлыя цпФры съ правой руки, осталь-
иыя раздълшгь на утроенный квадратъ 23 десятковъ,
т.*е. на 1587, получимъ въ частномъ 7; принимая
ciio циФру за цифру едшшцъ корня, составимъ части
полнаго куба, заключашицяся въ остаткъ 1145053,
какъ показано въ прнмъръ, сложимъ cie. части ме¬
жду	собою и сумму нхъ вычтемъ	изъ	остатка,	по-
лученнаго	отъ куба, въ -новомъ	остаткъ	получимъ
нуль, который и покажетъ, что число 257(^есть точ¬
ный искомый кубичный корень даннаго нашего куба.
Возмемъ еще прнмъръ, болъе предыду щн\ъ слож¬
ный: пусть требуется извлечь корень кубичный пзъ
43169672512.	^45,169,672,512	= 5508
27
27 I 161,69'
3. (30)*. 5 = 13500
3. 30 . (5)2 =	2250
(5)5 =	125
15815
367500 [ 2946725,12
5. (5500)2. 8 = 294000и00
3. (8)2 . 5500 =	672000
(8)* =	512
294672512
0 '
Отдъляя въ семъ чнелъ тысячи, увндимъ, что для
опредълешя всъхъ десятковъ въ корнъ го надобно
кзъ 43169672 извлечь корень кубичный, какъ изъ
отдъльиаго числа; отделяя и въ семъ числъ тысячи,
увндимъ, что и для опредълешя десятковъ вь корнъ
его надобно будетъ извлечь корень кубичным пзъ

275
45169, какъ иль отдъльнаго числа; извлекая нзъ
сего числа корень кубичный на основанш предыду-
щнхъ примъровъ, получимъ въ корн к его 55 и въ
остатки 294; но 35, какъ корень числа 45169 есть
число десятковъ корня кубнчнаго числа 45169672 и
потому для опредълсшя едншщъ въ корнъ сего по¬
ел г» дня го числа, должно къ остатку 294 приписать
прежде отдълеииыя три цнФры, т. е. 672, тогда
остатокъ 294672 будетъ заключать въ себъ утроен¬
ное произведете квадрата 55 десятковъ на неизвъет-
пыя единицы н проч ; раздълившн сотни сего остат¬
ка, т. е. 2946 на утроенный квадратъ 55, получимъ въ
частномъ нуль — это значить, что корень числа
45169672 состоитъ только нзъ 55 десятковъ или нзъ
550 единицъ; но 550, какъ корень числа 43169672
есть число десятковъ корня кубнчнаго числа
45169672512 н потому для опредълешя единицъ въ
корнъ сего послъдняго числа должно къ остатку
294672 приписать прежде огдъленныя три цнФры,
т. е. 512, тогда остатокъ 294672512 будетъ заклю¬
чать въ себъ утроенное произведете квадрата 550
десятковъ па иснзнЪстиыя единицы и проч. раздъ-
^ ливши сотни сего остатка, т. е. 2946725 на утроен¬
ный квадратъ 550 десятковъ, получпмъ въ частномъ
для единицъ корня цифру 8 II т. д
Изъ вскхъ сихъ прнмьровъ можно вывесть слъду-
ющее общее правило для нзвлечешя корня кубнч-
наго пзъ какого-бы-то пн было куба: должно дан¬
ный кубъ рнздгьлить запятыми на классы отъ пра¬
вой руки къ лтьвой такъ, чтобы въ каждомъ класть
было по три цифры, пзключая поелпдняго къ лтьвой
РЭкгъ, 65 копгоромъ можетъ быть двгь к одна цифра

276
(число классоьъ равняется всегда числу цнФръ иско¬
маго корня). Потомъ пзъ послгъднлго класса къ лгь-
еой рушь извлвкаютъ корень и кубъ сего корпя вы¬
читаютъ изъ оиаго, к& остатку сносшиъ слпдуюицй
классъ, отдгьляютъ послпд/йя дет цифры съ правой
руки, а остальное число д/ьлютъ на у троенный квад¬
ратъ найденной цифры въ норнгъ, цифру, полученную
отъ сего дгьлешя записываюшъ въ корень и принимая
ее за единицы корня а прежде найденную цифру за де¬
сятки его, берутъ утроенное произведете квадрант
дес/шгковъ корпя на едишщы его, утроенное произ-
ведеше квадрата единицъ корпя па десятки его и
кубъ единицъ корня, складываютъ cut произведешя
между собою и сумму ихъ вычитаютъ изъ остат¬
ка съ пршшеаниымъ къ нему классомъ; къ новому
остатку приписывшотъ елтьдуюшш классъ, отдгьлп-
ютъ опять послпд/йя двгь цифры съ правой руки, а
остальное число дгълюшъ па утроенный квадратъ
всего пайдеинаго въ корип числа, полученную цифру
въ частномъ записываюшъ въ корень и принимая ее
за единицы корня, а пайдепиыя прежде въ корип двгь
цифры за дес тки корня, берутъ утроенное произ-
ecdeuie квадрата десятковъ корня на единицы его,
утроенное произведение квадрата единицъ корня на
десятка его и кубъ единицъ корпя, складываютъ сш
произведешя мезюду собою п сумму ихъ вычитаютъ
изъ остатка съ приписаппымь къ нему классомъ; къ
новому остатку пршшсываютъ с.шдующт классъ и
щ. д. продолжаюшь до шпхъ поръ, пока не спссутъ къ
разнымъ осшаткамъ вспхъ классовъ даннаго куба
тогда съ поелпднемъ остатка получится пли
нуль, когда данный кубъ есть полный кубъ, или ос-

277
тонете я какой нибудь значительный остатокъ, ког-
да данный кубъ есть не полный кубъ и тогда дол¬
жно будетъ отыскать корень приближенный. Если
Случится, что по снесенш къ какому нибудь ос-
татку (въ продолжеше извлечешя корня) слтъдую-
щаго класса изъ даннаго куба и. по отдгьлеши по-
слгьднпхъ двухъ цифръ съ правой руки, остальное
число не дгьлится на утроенный квадратъ найден¬
ной части корня, то въ корнгь на мпсттъ цифры,
соошвтпствующей сему классу, ставятъ нуль и къ
остатку съ приписаннымъ уже къ нему классомъ
приписываютъ еще елпдующш классъ изъ даннаго
куба и продолжаютъ извлечете Корня далтье.
119.	Приступая къ извлечение корня кубичнаго по
приближенно, замЪтимъ, что при нзвлеченш корня
кубичнаго изъ дроби должно отдельно извлекать
корень кубичный изъ числителя и знаменителя оиой
и если оба члена дроби не полные кубы, то вмъсто
двоннаго приближеннаго извлечены корня, извлека-
ютъ приближенно корень только изъ числителя ея,
умноживши числителя и знаменателя этой дроби на
квадратъ ея знаменателя и слЪд. сдълавши чрезъ
это дъиете знаменатель ея полнымъ кубомъ. Напр.
еслибы требовалось извлечь корень кубичный изъ
то умножая числителя и знаменателя ея на квадратъ
^	5 	 5
знаменат&1я, т. е. на 25, получимъ: уКэ — /''"2.25=
А 5 А 525
/3	*
^50  У 50. Слъд. здъсь останется извлечь при-
125	~5
ближенно корень только пзъ одного числителя^
Пусть теперь требуется извлечь корень кубичный
изъ 35 приближенно на Д. Для сего умножимъ

данное число 35 на кубъ знаменателя 15-тн и про- .
изведете раздълнмъ на сен кубъ, тогда получимъ
35 = 35 . (15)*	= 35.^375 —	11SI25; слъд.
■ (15—.	л15)5	(15)1
\/ 35= /018125 = I 118125; но корень ку-
>	(15)*'	’	15
’ бнчный изъ 118125 найдется по правилу предыду¬
щаго члена и будетъ: у 118125 =г 49 съ остат-
комъ 476, который показываетъ, что корень кубич¬
ный числа И 8125 5 будетъ болъе 49 и менъе 50;
слъд. J/118T25 = I' 35 будетъ болъе и менпе
15
; но между • и	разность есть	^;	слъд. разность
между s у 35 и ~	будетъ менъе	~	п потому если
вмъсто |/ 35 возмемь величину то разность ме¬
жду сею величиною и мстпнпымъ корнемъ „ кубнч-
нымъ числа 55 будетъ ыенъе—долн. Слъд У1' 35 =
= 3 ^ приближенно на ~.
Итакъ чтобы извлечь' приближенно корень кубич¬
ный изъ какого ниб)дь числа, должно умножит cie
число на кубъ зш1менате.т той дроби, па котору ю
требуется приблизиться къ истинному корню, изъ
произведешя извлечь корень кубичный по общему
правилу и найденный так. обр. корень разделить
на знаменателя помянутой дроби.
Вотъ еще прнмъръ: пусть требуется извлечь ко¬
рень кубичный нзъ 215 приближенно на в Д. На
основанщ предыдущаго правила нмъемь: J/213 =
/^2l3.”(75)r= ^59375 = \\7- = 5 fJ = 5
'	(75)8	1Ъ~
приближенно на .
Желая извлечь корень кубичный изъ какого нн-
будь числа приближенно вь десятичныхъ доляхъ

279
должно поступать по ъышеупомянутому правилу.
Иапр. требуется извлечь корень кубичный изь 15
приближенно па -г^.	„	s
Для сего нмъемъ } 13 = /^13. (100)* =
5	 *	(1Ш;3
V 13000000; но |/]ЗООеООО = 235 приближенно
ioo
о /	 ___	/
на единицу; с кпд. |/13000000 =	)	13	будет	ь	бо-
100 . _
лие Щ п менъе а посему tfl'i = Щ =z 2
ioSo =	приближенно	на	.
С п.д чтобы извлечь корень кубичный пзъ какого
пибудь числа по приближенно писрдствомъ дес.ч-
тичныхъ дробей, должно къ данному числу припи¬
сать тройное число пу лей противъ числа пулей въ
знамлпателгь той дроби, на которую требуется
приблизиться; изъ систавившагося так. обр. числа
извлечь корень кубичный по общем) правилу и въ
иайдгпиомъ карнп отмтьтитъ занятою столько де-
сятичиыхъ знаковъ, сколько было пулей въ знаме¬
натели той дроби, па которую требовалось при¬
близишься.
Здт.сь можно едълагь то же замЬчашс какъ н въ чл.
115, что нътъ надобности прежде извлечена корня
кубичнаго нзъ предложеннаго числа прип бывать къ
не чу нули; а просто извлекая корень нзь даннаго
числа обыкновеннымъ образо.мъ, но снесены къ раз-
иымъ остатками всьхь классовъ онаго, должно къ
каждому изъ елпдмощихъ посла сего остатковь при¬
писывать но трл пуля н накоиедъ въ пайденпомь
корив от.гг.тпть для десятнчиыхъ столько знаковъ,
сколько раза» приписали мы но три нуля Иапр.
желая папгп приближенно корень кубичный чпсла
55 LS, нзилекаемъ пзъ него сей корень но общему

1/5,518 = 17,45
1
5 | 43,18
5. (Ю)9. 7 = 2100
3. 10. <7)3 — 1400
(7)5	543
3913
867 | 4u50,00
3. (170)2. 4 = 346800
5. 170. (4)a =	8160
(4)s =	64
35эЬ2Г4
90828 J 499760,00"
пишемъ снопа три 5. (1740)*. 5 = 45414000
ну л a « т. д. про. 5. 1740 (5)2 =	13О500
поръ, пока хотимъ)	  .
1	4431575
въ семъ примъръ
мы ограничились двумя остатками, къ которымъ при¬
писывали къ каждому7 но три нуля; слъд. въ найден-
ноиъ корнъ 1745 должно отмътить два знака для
десятичныхъ и получимъ J/ 5318-= 17,45 прибли¬
женно на
120.	Пусть теперь требуется извлечь корень ку¬
бичным нзъ дроби; Напр. |-|- умноживши числителя
и знаменателя сен дроби па квадратъ ея знамена¬
теля, сдълагмъ знаменатель oiiofi полнычъ кубомъ
И будетъ: f/ j\) — /^Т9Г~(31]= = J/' IPflTj2- ==
• з1 f (зГ/	зТ~
1 1 Sf?59; но ^/18259 = 26 приближенно на едп-
зГ~
правилу, найдемъ въ
кориъ число 17 и
въ остаткъ 405, къ
сему остатку прн-
пншсмъ три нуля
и продолжаемъ нз-
влечеше обыкновен-
нымъ образомъ, най¬
демъ вь корнъ ци¬
фру 4 н въ остаткъ
число 49976, къ
сему остатку при-

281
на -i. Желая болъе приблизиться къ истинному
корню, найдемъ болъе прпближеннын корень числа
18259, именно: V l»25U = 26,53 тогда j Ть559 =
31
26,55 ; слъд. /-''Ту = 26,55 =	приближенно
31	* "зТ 31
иа ГхТПГ-
Ирим/ьч. Здъсь то же самое должно замътнть, что
мы замътили въ прнмъч. чл. 114 относительно про¬
изводителей знаменателя данной дроби, именно: если
знаменатель данной дроби не будучи полнымъ ку-
бомь содержитъ въ себъ одинъ или нъеколько мно¬
жителей, которые будутъ полные кубы, тогда что¬
бы едълать весь знаменатель полнымъ кубомъ, дол¬
жно только числителя н знаменателя предложенной
дроби помножить на киадраты тЪ\ъ множителей ея
знаменателя, которые будутъ неполные кубы.
121.	Пусть наконец ь требуется извлечь корень
кубичный нзъ десятичной дроби. Напр. 1,1276. Дли
сего должно знаменатель данной десятичной дроби
едгълашь полнымъ кубомъ, т. е. приписать къ де¬
сятичной дроби съ правой стороны потребное чи¬
сло нулей, потомъ отбросить запятую и извлечь
корень, какъ изъ цгълаго числа и въ нийденпомъ так.
убр. корнгь ош.ишшипь для десятичныхъ знаковъ
число цифръ въ трое меньшее противъ десятич¬
ныхъ знаковъ въ данной дроби, считая въ то чи¬
сло и прибавленные къ ней съ правой стороны пули.
Въ данной дроби знаменатель есть 10UU0, т. с.
1 ООО . 10; слъд. надобно умножить его еще на 100,
что'Ъ! едълать полиыыъ кубомъ, или другими сло¬
вами приписать къ данной десятичной дроби съ нра-

282
вон ел стороны два нуля и Су деть 1,127600 отбро¬
сивши въ ней запятую, и извлекши корень, какъ
3
нзъ цълаго числа, получимъ |, 1127СОО = 104;
теперь поелику въ данной дроби было шесть дссл-
тпчпыхъ знаковъ, то иъ напдепномъ корнъ 104 дол¬
жно отмътить диъ цифры длл десятичныхъ знаковъ
5
н будетт: 1 1.127а = 1,04 приближенно на 0,01.
Длл выраженья корня кубнчнаго нзъ обыкновен¬
ной дроби приближенно вь десятичныхъ доляхъ
должно эту обыкновенную дробь пртГвесм» въ деся¬
тичную (чл. 62) н потомъ поступить съ нею по
вышеизложенному правилу.
Для извлечешя корня кубнчнаго нзъ периодиче¬
ском пли непрерывной дроби должно привести сна¬
чала cin дроби вь обыкновенный (чл. 06 и чл. 7U)
н погомь поступить съ ними по правилу нредыду-
щаго члена.
ЗАМЬЧАШЯ ОТПОСЯ1ШЯСЯ КЪ ПРОПОРЩЯМЪ.
1)	Если нензвъстень среднш членъ въ непрерыв¬
ной Геометрической пропорцш (чл. 9л нримъч. 1.),
то онъ опредъляетея с лъдутощнмь образомъ: пусть
дана ни пр. пропорщя такая: <>4 : х = х : 4 по чл.
92 нчъемь х..v = 64. 4 пли х* = 256, т. е. квад¬
ратъ нензвъетнаго средняго члена въ непрерывной
Геометрической пропорцш равняется пронзведенно
крайнихъ ея членовъ, а потому самый нсизвъгтный
среднш членъ пли х = J- 2л(> = 16, т. е. если не-
изшьстепъ среднш членъ въ непрерывной Геометри¬
ческой пропорщи, то для опрёдеълешя его должно

285
извлечь парень квадратный изъ произведете край¬
нихъ членовъ сей пропорцш.
2)	Мы сказали (чл. 63 нрпмъч. 2. 4 ), что если
нисколько прочорцш перемножутся между собою
почленно, то пол) ченмып произиедгш.т будутъ так¬
же составлять пропорцно; по сему если мы возмемъ
двъ нлн три совершенно одннакьч пропорщи, папр.
16:4 = 8:2	16:4=8:2
или
16:4 = 8:2	16:4 = 8:2
16 : 4 = 8 : 2
то изъ произведет я двухъ пропорщи получимъ но¬
вую пропорцно: (16)2 :(4)2=(8)2 : (2)“, а нзъ про¬
изведет» трехъ пропорцш получпмъ: (16)* :(4)* =
(S)> : (2)*.
Слъд, если катя пибудь четыре числа между со¬
бою пропорцюпальпы, то квадраты п к) бы ихъ
также будутъ между собою пропорцюнальны.
V
)