Теория представлений симметрических групп - Джеймс Г.

1. Необходимые сведения из теории представлений
23. Некоторые неприводимые модули Шпехта
26. Представления полной линейной группы
Приложение. Матрицы разложения симметрических групп σ_n для простых чисел 2 и 3 и n<=13
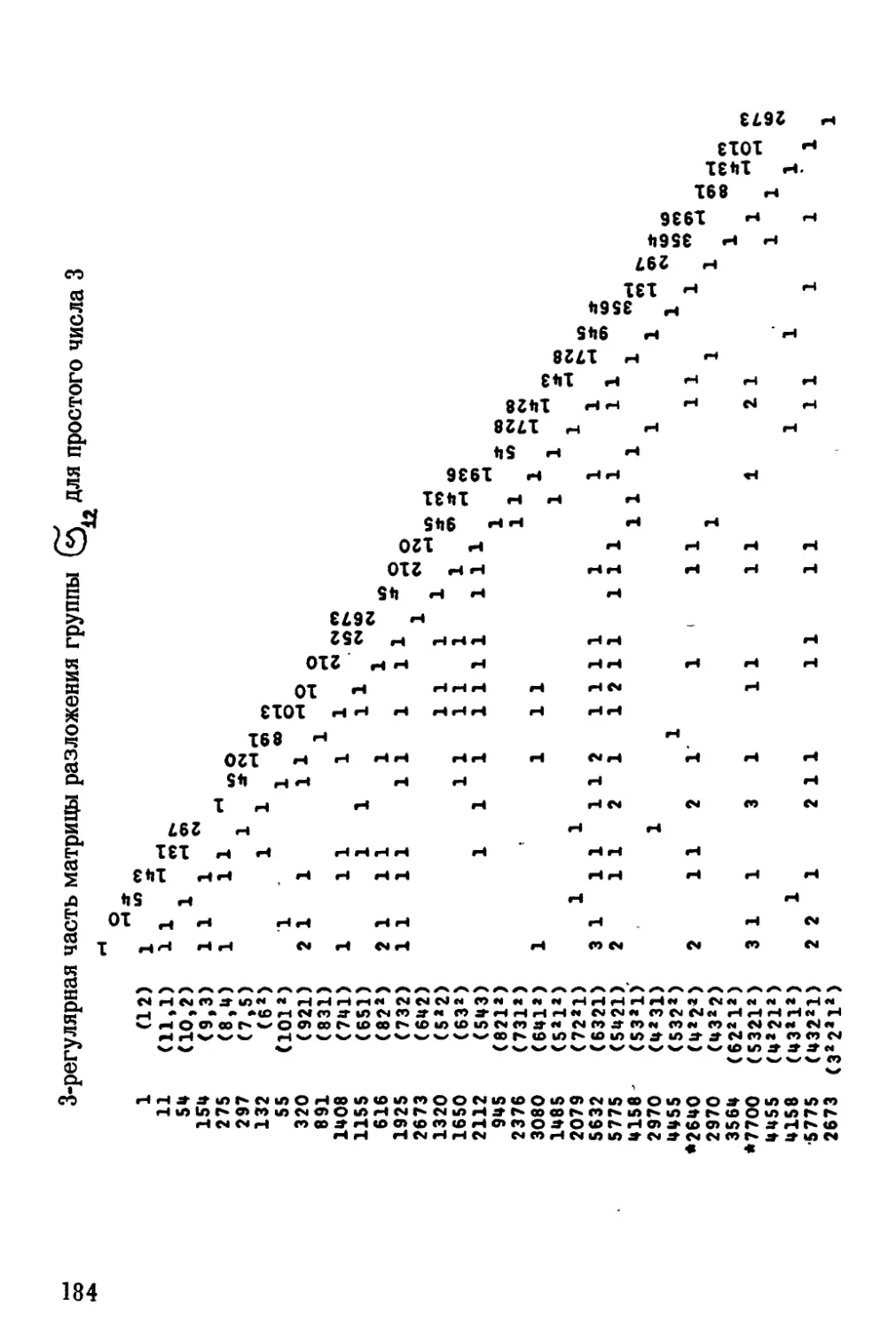
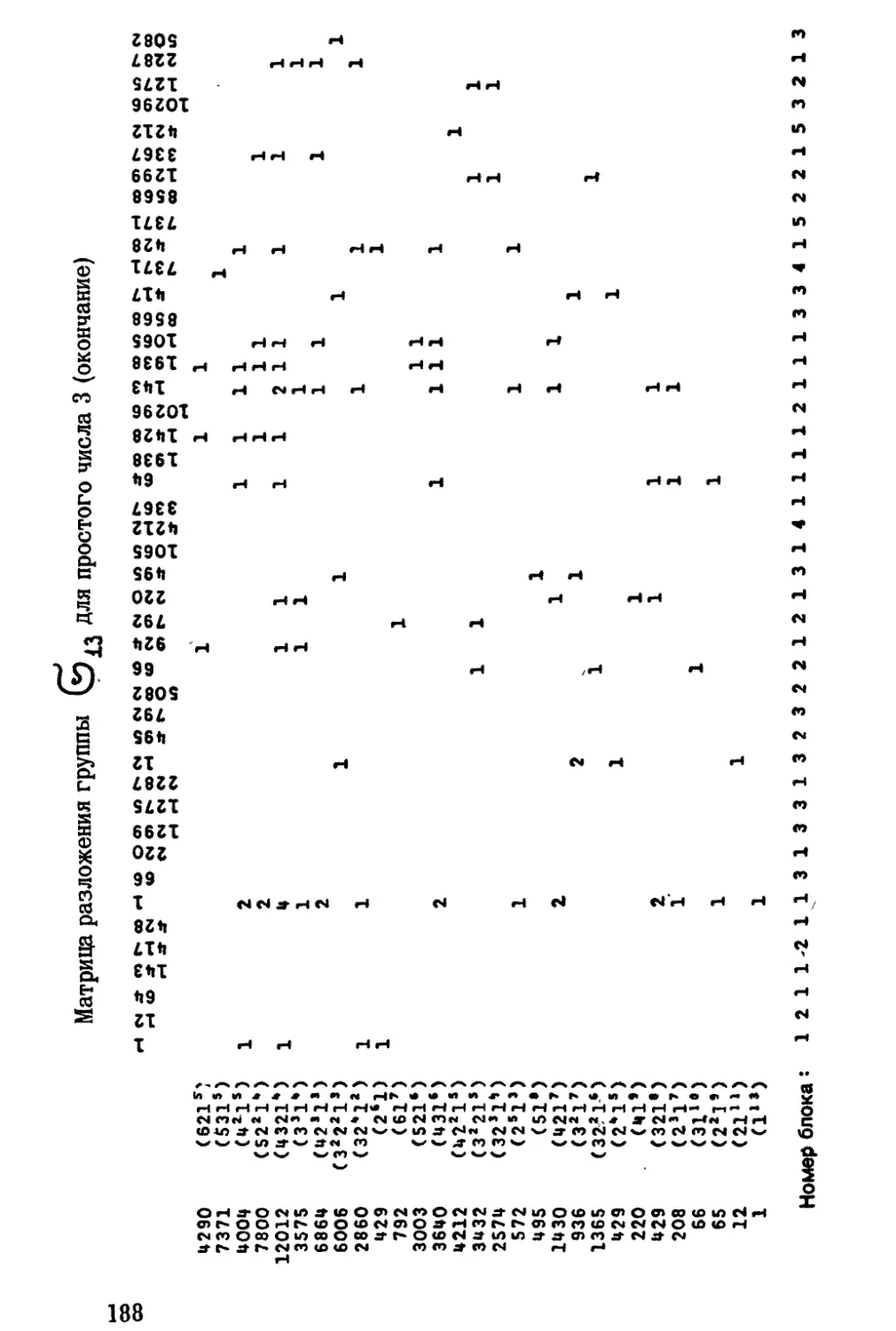
Автор: Джеймс Г.
Теги: математика физика аналитическая геометрия математическая физика высшая математика издательство мир
Год: 1982
Похожие
Графическая теория представлений ортогональных и унитарных групп
Теория групп
Классические группы, их инварианты и представления
Специальные функции и теория представлений групп
Текст
                    Lecture Notee in
Mathematics
Edited by A. Bold and B. Eclanann
682
CD. JAMBS
THE REPRESENTATION THEORY
0? THE SYMMETRIC GROUPS
SPRINGBR-VERLA6
BERLIN HEIDELBERG NEWT YORK
1978

МАТЕМАТИКА
НОВОЕ В ЗАРУБЕЖНОЙ НАУКЕ
РЕДАКТОРЫ СЕРИИ! А.Н.НОЛМОГОРОВ, С П.НОВИКОВ
Г.ДЖЕЙМС
ТЕОРИЯ
ПРЕДСТАВЛЕНИЙ
СИММЕТРИЧЕСКИХ
ГРУПП
Перевод с английского
А.В. ЗЕЛЕВИНСКОГО И
СВ. КЕРОВА
под редакцией
A.M. ВЕРШИКА
"МИР" МОСКВА 1982
32

ЕЙС 22.14
Д 40
УДК 519.46
Джеймс Г.
Теория представлений симметрических груш:Пер. с
англ. - М»: Мир, 1982. - 216с,ил.
Книга известного английского математика, содержащая
в сжатой форме большой материал о представлениях групп
подстановок - начиная с первоначальных сведений и вплоть
до современных результатов. Русское издание дополнено
новым материалом.
Для начинающих математиков и для специалистов по
алгебре, анализу, комбинаторике.
1702030000 - 201
16 - 83, ч.1.
041(01) - 82
Редакция литературы по математическим наукам
(о) Springer-Verlag, Berlin - Heidel-
^ berg, 1978.
All Rights Reserved.
Authorized translation from
English language edition published
by Springer-Verlag
Berlin - Heidelberg - tfew York.
(О) Перевод на русский язык, «Мир£>.
1982, с дополнением. ?

ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВСЩЛ
Теория представлений оимметричеоких групп была ооздана
трудами Г.Фробениуоа (1849 - 1917), И.Щура (1875 - 1941) и
А .Юнга (1873 - 1940) в самом начале этого века и вместе о
работами У.Бернсайда (1852 - 1927) легла в оонову всей теории
представлений групп* Вплоть до настоящего времени ооботвенно
теория предо тавлений групп подстановок не подвергалась какой-
либо оерьезной переработке и по существу сохраняет свой
первоначальный характер. В 30-х гг. Г.Вейль (1885 -1955) показал»
что теория представлений классических групп тесно связана о
представлениями симметрических групп» а Дж. фон Нейман (1903 -
1957) внес некоторые упрощения в первоначальное изложение.
Начиная о 40-х гг., представления оимметричеоких групп широко
используются в физике (Е.Вигнер). В ряде монографий 40 - 50-х гг.
(см. описок в конце предисловия) была несколько
усовершенствована алгебраическая и комбинаторная техника работы с этими
представлениями.
Далъяейдве впечатляющее развитие и обширные применения
общей теории представлений групп и алгебр - в первую очередь
классических групп Ли - мало коснулись теории представлений сшмет-
рических групп и даже несколько отодвинули на задний план эту
замечательную классическую область. Возможно, этим объясняется
то удивительное обстоятельство, что на русском языке до сих пор
не было систематического изложения этого предмета, да и в
мировой литературе число монографий не велико, а в учебниках этой
теме отводится незаслуженно малое место. Любопытно, что в
книгах по теории представлений для физиков можно почерпнуть
гораздо больше конкретных первоначальных сведений о представлениях
симметрических групп, чем в математической учебной литературе.
Положение начало меняться в последние годы. Среди несколь-

ких недавно вышедших книг на эту тему небольшая по размеру
книга английского математика Г .Джеймса выделяется в нескольких
отношениях^ Прежде всего, она с одержит концентрированное и
вполне элементарное изложение почти всех главных вопрооов теории
представлений симметрических групп. Кроме того, оставаясь в
рамках классических схем, Г.Джеймс вносит много упрощений и
методических новшеств; например, везде, где это возможно,
конструкции излагаются для поля произвольной характеристики.
Некоторые факты» сообщаемые автором, являются новши иди получены
совсем недавно (ом. например разд. 23). Приложения в книге
затронуты несколько меньше - им посвящен лишь последний раздел, где
излагается классическая конструкция Г.Вейля, связывающая
представления оидаетрической и полной линейной групп.
Как увидит читатель, алгебраическая сторона теории,
излагаемой в книге, неоложна и сводитоя к нескольким соылкам на
известные общие факты (см. разд. 1); в то же время комбинаторика
таблиц и диаграод Юнга по необходимости занимает много места,
она сравнительно мало известна и не столь проста, хотя и
элементарна.
Здесь следует отметить, что, начиная о работ А.Юнга,
теория представлений симметрической группы тесно связана с
нетривиальной комбинаторикой того, что сейчас называют таблицами и
диаграммами Юнга и разбиениями натуральных чисел. Эта
комбинаторика двумерных геометрических объектов составляет
обязательный остов всей теории представлений симметрических групп;
поэтому они неслучайно появляются в этой книге и не следует
удивляться обилию комбинаторных построений и понятий. В то же время
появление именно этой комбинаторики не так просто предвидеть
заранее - открытие ее есть главный вклад А.Юнга. Вкратце
неизбежность этой овязи можно пояонить так. Рассмотрим неприводимые
представления (5£ (над (Q ) и ограничим каждое из них на
($Vi > ^ ^ 1, X у, . ; мы получим схему ветвления
неприводимых представлений (ом. разд. 9), т.е. некоторый градуироваа-
ный граф. Оказывается, этот граф (возникший пока лишь в овязи
с симметрическими группами) в точности совпадает с графем, опи-
' После того, как была начата работа над переводом этой
книги, стало известно о выходе новой большой монографии (под
таким же названием) Г .Джеймс а и А.Кербера ( James G., Kerber A.
The Representation Theory of the Symmetric Group. Encyclopedia
of Mathematics. Addison Wesly» 1981.)
6

оывающим рост диаграмм (графом Юнга), ом.добавление. Этот
фундаментальный факт, котаги, имеющий до сих пор лишь апостериор-
ное доказательство, показывает, что комбинаторика таблиц и
диаграмм Юнга еоть аппарат, адекватный теории представлений
симметрических групп.
Очень скоро теория таблиц и диаграмм Юнга оторвалась от
теории симметрических групп и начала самостоятельное
существование, она даже стала одной из центральных тем в самом
комбинаторном анализе (см.fнапример, раннюю монографию Мак-Магояа и
недавние работы - Combinatolre et Representation du Groupe
dymsietrique, Strasbourg 1976* Proceedings 1976* Bd. D.Foata, -
Lecture Botes in Math., v.579, Springer, 1977)* Одним из
замечательных достижений зтой комбинаторики является алгоритм RSK
(Робинсона-Шенстеда-Кнута), первоначально возникший в связи о
правилом Литтлвуда-Ричардсона (см. разд. 16) и получивший
многочисленные применения (см. добавление).
Книга Г .Джеймса написана непринужденным, "лекционным"
языком. Автор облегчает работу читателя многочисленными примерами
и рисунками. Требования к подготовке читателя совсем скромные -
практически она доступна студентам младших курсов. Хотя в
книге отсутствуют некоторые важные темы и ссылки (симметрические
функции, операции над модулями, ASK и др. - часть из них
приведена в добавлении), она являетоя хорошим введением в предмет.
Перевод разд. d-17 осуществлен С.В.Керовым, разд. 18-26 -
А.В.Зелевинским. Мелкие погрешности в тексте исправлялись без
особых оговорок. 6 тех случаях, когда это необходимо, ну ясные
понятия определяются в сносках редактора и переводчиков, поэтому
чтение книги почти не требует обращения к другой литературе.
Отметим, что автор везде использует правую систему записи
(оператор пишется справа от элемента), мало употребительную в нашей
литературе по теории представлений, но сохраненную в переводе.
Можно ли очитать теорию представлений о «метрических групп
законченной? Скорее всего,нет. Дело не только в том, что
остаются нерешенными некоторые вопросы, например, структура
модулей ИЬехта для конечных полей. Конструкции неприводимых модулей,
базисы в них, взаимоотношения с теорией сишетричеоких функций
и геометрией пространств флагов, изучение бесконечной
симметрической группы и асимптотических проблем теории представлений,
связи о Tf-теориэй и топологией, применения к когомологиям алгебр
Ли и интегрируемым системам - связи всех этих фундаментальных
вопросов о теорией представлений симметрических групп еще ждут
дальнейшего прояснения. Ш посвящены исследования самых послед-
7

них лет. Возможно» читатель, оценивший красоту изложенной в этой
книге теории, захочет принять участие в этих исследованиях.
В заключение приведем опиоок основных монографий по теории
представлений симметрических групп, дополняющий список автора и
включающий собрания оригинальных работ (см. также литературу на
стр.2И)
Фробениуо Г. Теория характеров и представлений групп.-
Харьков; СНТИ, 1937.
Schur I. Die algebraischen Grundlagen der Darsstellungsthe-
orie der Gruppen. - Zurich, 1936.
Young A* She collected papers of Alfred Young* - Ed. G. de
B.Robinson, Toronto and Buffalo, 1977.
MacMagon P.A. Combinatory Analysis, v. 1,2.««Cambridge, 1915.
Beиль Г. Классические группы и их инварианты и
представления. - М.; ИЛ, 1947.
Itittlewood D.E/Ehe theory of group characters and matrix
representations of groups, - Oxford, 1950.
Мурнаган Ф. Теория представлений групп. - М.: ИЛ, 4950.
Robinson D.B. Representation theory of the symmetric
group* - Edinburgh, 1961.
Хамедоеш М. Теория групп и ее применения к физическим
проблемам. - М.: Мир, 4966.
Подробная библиография (120 назв.) работ последних 45 лет
имеется в Bull. Amer. Math. Soc, v. 1, N 6 (4979), 990-997*
А.М.Вердшк
8

ПРВДЮОБИБ
Теория представлений оимметричеоких груш была шврвые
построена Фробеняуосм и Щуром, а затем развита в длинной серп
работ Юнга, Хотя детальное изучение работ Юнга несомненно
окупает себя, кардай, кто пробовал проделать это,.знает, как
трудно читать его работы. Автор, например, ни разу не преуспел в
этом; поэтому в настоящей книге нет никаких оснлок на
доказательства Юнга, но, вероятно, чаоть развиваемой техники
идентична его технике.
Эти заметки оонованн на записях курса, прочитанного в
Кембридже в 1977 году, и включают вое основные теоремы о предмете,
в том числе и некоторый материал, не публиковавшийся ранее.
Многие результаты легче объяснять, стоя у доски с мелом, чем сидя
у пишущей машинки, поскольку комбинаторные аргументы часто лучше
всего излагать студенту, лишь намечая правильную линию и
предоставляя ему записать самостоятельно полное доказательство, если
он того пожелает. Во многих местах этой книги мы предваряем
доказательство рабочими примерами, оставаясь верными следующему
принципу: читателю легче продвигаться от частного к общему, чем
начинать с.громоздких обозначений, нужных для проведения
исчерпывающих доказательств. Однако вое доказательства изложены
полностью, быть может, за исключением проверки некоторых деталей,
которую читатель быстрее проведет самостоятельно. Это в
особенности важно сделать, когда он дойдет до одной из' центральных
теорем, известной как правило Литглвуда-Ричарцоона; многие, кто
читал ранние доказательства этого правила, находят его трудным
для изложения в деталях (см. [1б]* где еоть описание
встречающихся проблем).
Принятый нами подход не зависит от характеристики
основного поля, за исключением лишь таких мест, как построение таблиц
характеров симметрических групп, где сами результаты зависят от

основного поля. Читатель, не знакомый о теорией представлений
над произвольным полем» не должен пугаться этого; более того,
мы считаем, что обычную теорию представлений*' легче понять,
знакомяоь одновременно с более общей ситуацией. Не следует
думать также, что требуется техническая подготовка для понимания
"характеристически свободной" теории представлений: оимметриче-
окне группы обладают специальными свойствами, позволяющими
сделать эту книгу практически замкнутой в себе. Наиболее экономный
путь узнать важные факты, не обращаясь к общей теории, -
прочесть разд. £-5, 10-11 (замечания после примера 17.17), а затем
разд. 15-21.
Многие теоремы используют некоторую билинейную форму;
ближе к концу мы показываем» что такая билинейная форма (известная
еще Юнгу) полезна для нового варианта построения ортогональной
формы Юнга. Замечательно, что ее значение в теории представлений
симметрических групп было оценено лишь недавно.
Я благодарен миссис Робин Брингенс за тщательную и
терпеливую работу по перепечатке моей рукописи.
Г.Джеймс
*' То есть комплексных представлений - над полем (l - в
противоположность модулярным (над полем конечной
характеристики). - Прим. ред.
10

1. НЕОБХОДИМЫЕ СВЕДЕНИЯ
ИЗ ТЕОРИИ ПРОСТАВЛЕНИЙ
Мы будем предполагать, что читатель знаком с понятием
групповой алгебры FG конечной группы Q над полем Р и с наиболее
элементарными свойствами (унитадьных правых) /^-модулейЧ Для
доказательства важнейших теорем теории представлений
симметрической группы можно использовать лишь следующее:
1Л. ТЕОРЕМА. Если М - неприводимый /Т£-модуль, то он
является композиционным Фактором^ групповой алгебш РСг.
Доказательство. Пусть /п- ненулевой элемент
из М . Тогда mFCr является ненулевым подмодулем в М , а
поскольку М не приводим, то M-mF&. Легко видеть, что отобра-
есть -Р(/-гомоморфизм из F(x на ТУ. По первой теореме об
изоморфизме
FG/Шг Qq^M,
поэтому старший композиционный фактор алгебры PQ- изоморфен И.
/ Основные определения читатель может найти в книге:
Кэртис Ч., Райнер И., Теория представлений конечных групп и
ассоциативных алгебр. - М.: Наука, 1969. - Прим.ред.
'Напомним, что убывающая последовательность подмодулей
данного модуля называется композиционным рядом, если
последовательные фактормодули (композиционные факторы) неприврдимы, т.е.
каждый следующий максимален в предыдущем подмодуле; главным
композиционным Фактором называется фактор по максимальному
подмодулю (см.,например, Ф.Каш, Модули и кольца. - М.: Мир, £981, или
упомянутую книгу ЧЛСэртиса и И.Р&йнера). - Прим. ред.
II

Первая теорема об изоморфизме будет появляться неоднократно,
поскольку мы будем работать с произвольным полем, когда Рбчю-
дуль может быть приводимым, но не разложимым^.
Мы часто используем некоторые 6-инвариантные билинейные
формы, как в доказательстве частного случая теоремы Машке:
1д2. ТЕОРЕМА МАШКЕ. Если (т - конечная группа и jf7- под-
поде поля вещественных чисел, то каждый ^-модуль вполне
приводим.
Доказательство . Пусть е± ,... > ^т, есть h'-
базис FG-шщт М. Тогда имеется единственная билинейная
форма (f на М , такая, что
(е1>г{)4*1, если 1-/,и fc>$>-0> если г^\
Далее, можно определить новую билинейную форму
<^У)^У^^2(и9^)^ Для всех и>гг£/%.
Эта форда (^-инвариантна в том смысле, что
^UQyVQy^VyW} для всех £€&-
Если задан подмодуль V в М , то тге J/1 означает по
определению, что ^u>v}=0 для всех г/ из £/ . Но если vejf, то
UQ~ £ V • Поэтому
.<Ч ^> = <^~* ^>~0
благодаря тому, что наша форда ^-инвариантна. Значит, vgelft
а это и есть условие, означащее, что (7 х- подмодуль в М.
Если иФО > ?о поскольку i*7 - подполе поля вещественных
чисел, ^г/>г/>^=^,так что If/llf = О • Мы докажем ниже, что
dim V+dim U^^dimM и потому £Лявляется /Модулем,
дополняющим V в М i что и требовалось.
Теперь мы напомним читателю некоторые сведения из
элементарной алгебры, касающиеся билинейных форм.
Пусть М- конечномерное векторное пространство над F1,
Двойственное (сопряженное) к Н пространство - это векторное
У Если характеристика поля р , над которрд рассматривается
групповая алгебра F& , делит порядок группы G » то групповая
алгебра не будет полупростой, следовательно, не всякий ее идеал
будет в ней прямым слагаемым и не всякий i^-модуль будет
вполне приводимым. - Дрим. ред.
12

пространство линейных отображений из М в JF. Оно будет
обозначаться через М* • Пусть е±>•••>*/? - базис подпространства У*
дополним его до базиса е±>- -?ет ъ М . Для l^j^tn
определим Sj ЕМ* следующим образом: (еЛв.'-i , если i-J* и
(Ci)S: i 0у если %Ф1 . Рассматривая значения на et у ..., ет Р
мы видим, что каэдый элемент Ч> из -/Сможет быть единственным
образом записан как линейная комбинация &±,.. • > в ли При этом
У- ({ei)^)^i+ • • • +(Ыч>)Ет• Поэтому Si>.,,> Вт - <*азис в
itf* и
Далее, </> принадлежит Г^ аннулятору /^, тогда и только
тогда, когда fa) Ф » .. *$к)*?ш 0. Поэтому <£^,.. .> £^
порождают Г^и
afr/n V + dim К ° » с/ш i>2 •
Предположим теперь, что задана невырожденная симметричная
билинейная форма <? > на М (т.е. для каздого ненулевого т жзМ
существует некоторое т* жз М с <^т}пь'}Ф0). Определим
9: М~*М*с помощью соответствия m~*i/m> где v^« ^ —*
-*^т,эс> (осеМ).
Мы ввщим, что Vm €.M* t поскольку^, >линейна по второму
аргументу, и что # - линейное преобразование, поскольку ^ )>
линейна по первому аргументу. Далее, Kt%6={гп£Ш<гп,х}-0 Vxetfyty
поскольку билинейная форма невыроаденна. Но dim M i <?/да W *
так что 9 - изоморфизм между М и Vty*. При таком отоздествле-
нии К соответствует У0. Тем самым для каждого
подпространства V имеет место равенство
1.3. </i/n V ^ dim Vм = dim M.
Поскольку У^ V > это равенство размерностей дает
Более общо, если даны подпространства 0^1/^ УЯМ. Р то
V1" £ \J± и мы можем определить отображение
0: V~t двойственное к U^/V пространство, fl,-*vv0
+ Кх-*^*> (bcei^-y.
Если а + Vх* ос' + Vх, то а: - х' е КХи ^ ж>-фх>«$х-,х>г0
Это показывает, что v^корректно определено. Как и раньше,
Фги 0 линейны, но теперь
Кег $ -{*€. Yl<«,*> = 0 Ухе UX}= VD V1X
13

Поскольку I/ix- V^Yy то Кег 0- If .Мы получаем поэтому
мономорфизм из VУ Лет- Q=V/l/ в двойственное к
^/^пространство. Сравнение размерностей дает:
1.4. Если OsV^rV^ М, то К/// изоморфно
двойственному к V /V пространству. В частности, F изоморфно
двойственному к М jY\
Если Н - некоторый /^-модуль для группы (^ » мы можем
превратить двойственное пространство ТУ* в /1?-модуль, полагая
Заметим, что обратный элемент к 0 вводится для того, чтобы
выполнялось v($h)z:fiva)/k . Это означает, что модуль
УУ*(который мы будем называть двойственным или сопряженным к М )»
вообще говоря, не изоморфен Pi как /^-модуль. В самом деле, если
T(<j)~ матрица, представляющая £ в базисе ^,...>£/*
пространства /У, то Т'О)*1)- матрица, представляющая # в сопряженном
базисе G}?-- >*ni пространства JM* • Это значит, что характер
Pf комплексно-сопряжен с характером М, если мы работаем с
комплексными числами.
Предположим теперь, что билинейная форма ^ у является
//-инвариантной. Если V и V являются /^-подмодулями в М> то
изоморфизмы в 1.4 будут /^-изоморфизмами. Чтобы это проверить, мы
должны показать, что 9: у->^есть £?-гомоморфизм. Но (x^VxJ^r
Vva^Virfl? что и требовалось.
Ядя каадой пары подпространств V и V имеем
как можно легко вывести из определений. Заменяя V и V на £А
и У"х, мы также находим, что \)l+YL^ (VГ) V) .
На всем протяжении этой книги будет полезна следующая
картинка:
i
о
Вторая теорема об изоморфизме дает
14

Но модуль (V+V^/V^o 1.4 изоморфен двойственному к V/(V+
+ У1)\ совпадающему с двойственным к У/(УПК"9, поэтому
получаем
1.5. Для каждого /^-подмодуля /^в// V/fr/lV*!)-
самодвойственный Лг-модуль.
Всякое неприводимое представление симметрической группы
будет получаться с помощью этой конструкции.
Очень важно заметить, что Vf] Сможет для подмодуля Vиз
i^ быть ненулевым. Как можно подсчитать размерность У/(УПУ1)^
если задан базис У ? Теоретически ответ прост, но он потребует
значительных вычислений, если У тлеет высокую размерность.
Определим №ЩЩ£^!]Ш1 А относительно базиса ^,...,е/. в /г,
полагая ( г, /")-* матричный элемент ^ равным ^, ^//**
£•6. ТЕОРЕМА. Размерность r/(mvl) совпадает с рангом
матрицы Грама по отношению к некоторому заданному базису в У .
Доказательство. Как обычно, отобразим У в
двойственный к У модуль посредством
0: Г-^г,где «Vtr-^jw> (иеУ).
Пусть -е^у^е/с - заданный базис в Ки £^...^6* -
двойственный базис в Г*. Поскольку ^•^•«{ё*, ^//^ имеем
Поэтому матрица Грама относительно базиса е±,.• ^е^
совпадает с матрицей б , взятой относительно базисов е1>,..>ек в У
и е±,~.уек в Г*. Но, очевидно, #£* 9^УПУ±, так что
c/im V/fVfW^dCmltn, 0совпадает с рангом матрицы Грама.
единственные факты из общей теории представлений, которыми
мы будем пользоваться без доказательства, это результаты,
относящиеся к подсчету числа обычных и ^о-модулярных представлений
конечной группы, а также следующий хорошо известный результат о
представлениях конечной группы над полем комплексных чисел £
(ср. Кэртис и Райнер [2] , 43.18 и упражнение 46.3).
1.7. Пусть £- неприводимый ^-модуль и М- некоторый
£ч-модуль. Тогда число композиционных факторов модуля JM.,
изоморфных 5 , равно" dim Нот ~~ ($,М).
15

В действительности оказывается, что эти результаты излишни
при нашем подходе, и теорема 1Л дает все, что нам нужное, не
было бы неразумно откладывать доказательства до тех пор, пока
мы не сможем воспользоваться теоремой I.I.
Читатели, интересующиеся значениями характеров, должны быть
знакомы с теоремой взаимности Фробениуса и соотношениями
ортогональности для характеров; при обсуждении характеров мы
используем эти результаты2-!
2. СИММЕТРИЧЕСКАЯ ГРУППА
Доказательства результатов, изложенных в этом разделе, могут
быть найдены в любой элементарной книге по теории групп.
Отображение множества {i> X,..,, п} на себя называется
подстановкой п, чисел, а множество всех подстановок tl чисел, с
обычной композицией отображений образует симметрическую группу
степени п, которая будет обозначаться через (з^. Заметим, что
<?Л определена для ь*0 и что (ь^ имеет л/ элементов (где 0/=<Е).
Если /Г- подмножество в {4,%,..v$ мы будем писать 6"^-для
обозначения подгруппы в (5^ , которая оставляет неподвижным
каждый элемент вне X .
Общепринято зашсывать подстановку О? следующим образом:
/l 2 3 . . .
^ ( ix гас з*г . . .
Рассматривая орбиты группы, порозденной fir , нетрудно видеть,
что ЗГ можно записать в виде произведения непересекающихся цик-
^Имеется в виду теорема И.5. В разделах 12-17 выясняется
строение подмодулей, в частности для регулярного представления,
и непосредственно доказывается, что все его композиционные
факторы изоморфны модулям «ФЛнз теоремы II.5, Из теоремы I.I
тогда следует, что других неприводимых ^6^-модулей нет. -
Прим. дерев.
*v Эти факты также можно найти в упомянутой выше книге Кэр-
тиса и Райкера. - Прим. ред.
16

довЧ как в следующем примере:
Как правило, мы пренебрегаем 1-циклами при записи
подстановки. Например, если ЯГ меняет местами различные числа а , 6 и
оставляет остальные числа неподвижными, то (Г называется транс»
ттпяшрсйй и записывается как $Г~ (a, 6jt
Все наши отображения будут записываться слева направо: таким
образом, произведение (£ 2) (2 3) есть (I 3 2). К этому следует
отнестись внимательно, поскольку некоторые математики
интерпретировали бы это произведение, как (12 3).
Поскольку (it ix " %l*)m ft* ^х)(^± *s)"- (it i>k), каадый цикл и,
следовательно, каждую подстановку можно записать как
произведение транспозиций. Более того:
2.1. Транспозиции (*-<,а^с_ {<<xs n порождают 6^.
Это действительно так, поскольку при а< ё мы можем,
подвергнув (в- i} t>) сопряжению с помощью ($- X, & - ± ) (4-3, ё-х)...
(а> ь+±)} получить (MJ.
Если ЛГ'б^б^...^-^^ ...т^, - два способа записи ОТ в
виде произведения транспозиций, то можно доказать» что j-k четно.
Следовательно, корректно определена функция
такая» что ^anT^(-i)^} если ЙГ- произведение / транспозиций.
2.2. 0ДГРДЮ1КНИВ. Лш(51*»ал> ^ъу*-) есть разбиение Д,
если^ Я^ ^ Я^|Я^Г..- неотрицательные целые числа, Л^Я^Л^».»
f^i l , р
Говорят, что подстановка ОС имеет пикдовый тип ( cycct
type ) ft , если орбиты группы, пороаденной <Х . имеют длины
\г\*-* Таким образом, (2 5 6 8) (I 3) (4 9) (7) имеет цикло-
вый тип (4,2.2,1,0,0,...). Обычно будут использоваться сокреще-
Орбита (или траектория) точки под действием группы
отображений, и в частности группы, порожденной одним отображением,
есть совокупность всех образов этой точки относительно группы.
Циклом называется подстановка, все орбиты которой, кроме разве
лишь одной, одноточечны. - Прим. ред.
1

ния вроде следующих г
(4,2,2,1,0,0,...)=(4,2,2Д) = (4,22Д).
Это значит, что мы опускаем нули в конце Л и указываем
повторяющиеся части с помощью индекса.
Поскольку две подстановки сопряжены в (5^ тогда и только
тогда, когда они имеют одинаковый цикловый тип, то имеет место
следующее утвервдение:
2,3. Число классов сопряженности в (5^ равно числу
разбиение п^.
Далее, для любой конечной группы 6~ число
неэквивалентных неприводимых £&модулей равно числу классов
сопряженности в G , так что
2.4. Число неэквивалентных неприводимых (комплексных)
представлений группы (^я совпадает с числом разбиений п .
Мы должны поэтому стремиться к тому, чтобы построить
представление б^ дня каждого разбиения п . Рассмотрим для
начала простой пример:
2.5. ПРИМЕР. Имеется естественное ' представление,
возникающее благодаря тому, что ($^ переставляет числа 1,2,...;& ;
возьмем векторное^ пространство над F1 размерности л с
базисными элементами Г, £,...,я, и пусть действие (Г/г, на этом
пространстве определено формулой iT^ iJT (TeS^J . Мы будем
обозначать это представление через /^ (*-***) л
Можно легко выделить подмодуль в ^(п"1>^ .
пространство U , порожденное вектором { <- И + •. i- n , является
подмодулем, на котором G^ действует тривиально. Нетрудно найти
в другой подмодуль, но предположим, что мы хотим исключить
догадки. Если F- Q - поле рациональных чисел, доказательство
теореш Машке подсказывает, что мы можем построить (5^-ин-
^Это число обозначается p(aJi функция пн-^р(/г) иногда
называемая функцией Эйлера-Харди, имеет исключительное значение
в арифметике, алгебре и анализе и ей посвящено много работ, а
также недавно вышедшая специальная монография Д.Эцдрюа "Теория
разбиений" (М.: Наука, 1982). - Прим. ред.
2)
Иногда его называют натуральным. - Прим.перев.
18

вариантное скалярное произведение на J%tn'lti,s и тогда £/х
будет инвариантным дополнением к У .Здесь (f^-инвариантное
скалярное произведение на М (п~*>*1 определяется так:
(*) <Ь}> = 1, если i = j , и <i, }>в0, еслн t^.
"(п-£^?тъ ~(*-^^ &п . Тогда, несомненно,
v ' является подмодулем в £/ и легко видеть, что мы
имеем равенство. Тем самым М(л'*-*)** J ^"A^@ JJ , когда ^-(2.
Заметим, однако, что (^ дает (<£-инвариантную форму
на y^^"£»v дяя любого поля, поэтому S(n'iji^ также всегда
является подмодулем (он служит дополнением к U тогда я
только тогда, когда с/иьг ff aj- <S (п'х'0_ одан из модулей
Шпехта.
Имеются ли другие легкие способы построения представлений
Рассмотрим векторное пространство Л(п' ,v над F
порожденное неупорядоченными парами у (г j=j) # Пространство Л (п'л'^
имеет размерность ( £J и становится /^-модулем, если поло-
жить у ОС = ilCtjft . Исследовать это пространство по-видимому
нетрудно, хотя оно приводимо, поскольку JE{fjji ^ i <J; sn }
порождает тривиальный подмодуль. Ш пока не вдаемся в детали, а
просто отметим, что исследование Л Га~х'^доставляет больше
хлопот.
Более общо, ш можем работать с векторным пространством
р^(л'Щ,т) ^ порожденным неупорядоченными т-кгиж i£...im
(где ь ф1% , если /'f fc, ). Поскольку это пространство
изоморфно''пространству, натянутому на неупорядоченные (п - nv)-
наборы^ можем, не умаляя общности, считать, что /г-ж ^ m.
Это значит, что дня каждого разбиения п с двумя ненулевыми
частями в нашем распоряжении есть соответствующий (приводимый)
А7^- модуль.
Гордые этим успехом, двинемся дальше и посмотрим, что еще
можно сделать. Пусть yty (*"*'* ) - пространство, порожденное
упорядоченными парами, которые мн^ будем „обозначать через }
4- (г+j). Действие ©^ такое: j-fc- J*. . Пусть М{я ' iJ~
пространство, порожденное векторами, состоящими из
неупорядоченного 2-набора U и 1-набора -£ f где г,J _и -£ попарно
различны. Эти векторы можно обозначить через JjL , но удобно
19

изменить наша обозначения и считать базисный вектором в И
вместо
(**Ч)
Теперь долено бнть ясно, как строить ^(£Г~модуль //
дяя каждого разбиения 1 числа п . Обозначения, необходимые
для того, чтобн проделать это формально, вводятся в следующем
разделе. Модуль Мх приводим (если только Л £ ^), но
содержит модуль Шпехта S , который, как оказывается, непри-
водш, если ckaif^O.
3. ДИАГРАММЫ,
ТАБЛИЦУ И ТАБЛОИДЫ
ЗЛ. ОПЕВДЕШШ. Пусть Л . разбиение п ; диаграммой
[А] назевается множество {(*>j)J Ь/е 2> >i* i* i*j*&i}
( Z - множество целых чисел). Если (Vy^ s. [Л] , то ^,yj
называется клеткой ( ttode)[x] ; к* я строка (соответственно
столбец) диагрвшш состоит из тех клеток, у которых первая
(соответственно, вторая) координата есть к .
Изображение диаграммы иллюстрируется следующим примером:
.А Д
X X
X
Не существует никакого общепринятого соглашения о том,
как следует располагать диаграммы. Некоторые математики
изображают их, направляя первую координатную ось вправо, а вторую
вверх! Обычно, привода примеры диаграмм, опускают внутренние
скобки, так что мы пишем [4,22 , lj , а не [(&92г , l)jf.
Множество разбиений п частично упорядочено, как видно
из следующего определения.
20

3.2. ОПРЕДЕЛЕНИЕ. Если 1 и jw - разбиения п , ми
говорим, что Л доминирует м и пишем Л £ /у , если для
Бели Д £у* и Д ^ л/, мы пишем Ж £>yv .
3.3, ПРИМЕР, Отношение доминирования на множестве
разбиений числа 6 изображается графом
г
(5,0
^а. 2,1) <^
(2.1*)
О5)
Доминирование является, конечно, "правильным" порядком для
разбиений, но иногда полезно иметь линейное упорядочение, > > .
на множестве разбиений. Нужное нам линейное упорядочение зада-*
ется так:
3,4. 0ПРВДЕ21ЕНИЕ. Бели Ли/*'- разбиения п , то
будем писать Л >ft тогда и только тогда, когда для наименьшего
jу удовлетворяющего условию Л: ¥*/*•, выполняется
неравенство lj>J^i (заметим, что некоторые авторы записывают это
отношение как 1 <яс). Это называется словарным порядком на
разбиениях Ч
) Здесь %i и f*i - число клеток в г-й строке [Л] и
£jw] соответственно.- Прим.ред.
2)
Обычно используют термин "лексикографическое
упорядочение". - Прим.ред.
21

Несложно проверить» что линейный порядок > шжорирует-
ся частичным порядком /> в том смысле, что из Л/>/ч следует
Я > /ч «Но обратная импликация неверна > поскольку
^)>(5,i)>(4)X)>(4>lX)>(3lJ>(3,^ i)>(3, iV>
>(%l)>(l\lX)> (*.*')>(*')-
3.5. ОПРВДЕЛЕНИЕ. Вели /Я/ - диаграмма, то сопряженная
диаграмма [jt'J получается заменой строк [ЛJ на столбцы и
столбцов на строк*. Разбиение Л' числа ц называется
сопряженным с Д.
Единственное назначение линейного порядка > состоит в том,
чтобы зафиксировать порядок записи строк в таблице характеров
&к . Поскольку может быть более одного самосопряженного
разбиения ^ (например, (4, 2.I2) и (З2, 2) - самосопряженные
разбиения числа 8), не существует "симметричного" способа
линейно упорядочить разбиения» т.е. такого» чтобы порядок обращался
при сопряжении. Интересно заметить, однако, что
Л >ju> тогда и только тогда, когда j4'p>л' .
Следующее, что мы должны определить, это 1-таблицы.
Они могут быть определены, как биекции из [Я] на fi>%9...,ib}t но
мы предпочитаем менее формальное
3.6. 0ПРЕ5ЩЕШИЕ. Назовем Л-таблицей любой из п\
массивов целых чисел, получаемых при вписывании в каждую клетку [А]
одного из чисел i, 2,..., п$ причем повторения не допускаются.
Например,
1245 и 4573 суть (4, 3, 1\-тайляш*
3 6 7 2 18
8 6
Группа &П. действует на множестве таблиц естественным
образом; так, например, подстановка (14 7 8 6) (253)
превращает первую из приведенных выше таблиц во вторую. (Конечно,
определение таблиц как функций здесь более выигрышно. Если
задана таблица t и подстановка Ol , то композиция функций t
и ОС дает новую таблицу ЖЬ .)
Любой подход к теории представлений (Ья использует
какую-либо форму следующего результата, связывающего
доминирование разбиений с некоторым свойством таблиц.
22

3.7, ОСНОВНАЯ КСМБШТОЕНАЯ ШШ. Пусть Я J[ ft -
разбиения ъ , и предположим, что t± есть J-таблица,a £х
есть jv-таблица. Предположим, что для любого г числа из
i-й строки t^ принадлежат различный столбцам ^ . Тогда
Доказательство. Допустим, что мы можем
поместить f*t чисел из первой строки L в [Л] так, чтобы
никакие два числа не оказались в одном столбце. Тогда Г Л] должна
иметь по меньшей мере ju>t столбцов, т.е. jL^ /и . Затем
вставим j1^ чисел из второй строки ^ в различные столбцы.
Чтобы для этого хватило места, должно быть ^^^^ju^-hju^ •
Продолжая в том же духе, получаем^ что Л &/ч.
♦3.8. ОПРШШИЯ. Пусть t - таблица. Ее строчным
стабилизатором ( ъоиг-4£аёг£гхеъ) назовем подгруппу 11 ± в (3^ ,
сохраняющую строки t (как множества). Иначе говоря, Л^(хе&\
i и г'ЗГ принадлежат одной и той же строке t для всех^ %}*
Столбцовый стабилизатор Cf определяется аналогично.
Например, если i =1 2 4 5 , то Л,в<5^ , *(Г *^
36 7 l <iXh5^ ii67J #
8
И 1^1 = 4! 3! V , ^
Отметим, что л^,-# ^ ^ и Lt<j?~ % Lix '
3.9. OIPFJWEHHB. Зададим отношение эквивалентности на
множестве Я-таблщ, полагая t±^i^ тогда и только тогда, когда
ty^ - **, Д^ некоторой <%с R± . Таблоид ^Л , содержалдай £ ,
- это класс эквивалентности £ относительно этого отношения
эквивалентности.
Лучше всего рассматривать таблоид как "таблицу с
неупорядоченными строчками". В примерах мы будем обозначать -fi\$ рисуя
линии между строк £ . Так,
3 4 52 4 5 14 5 2 3 5 13 5 12 5 2 3 4 13 4 12 4 12 3
I 2 Уз *2J2 *Li }2J '3.4 ?1_5 *2J5 'з_5 Ч, g
суть различные (3,2)-таблоида, a g-£—= 4~5— '
i> п действует на множестве # -таблоидов по формуле /£j^s/ot>
Это действие определено корректно, поскольку если ft I = Т^Л*
23

wbftewm некоторой & в R± . Тогда Cl^&jcG%~1RJ%SR, »
так что* {t± Ц- {t±6tor} = f^#j . ** Ф
Мы лзшейно упорядочиваем Я-таблоиды с помощью следующего
определения:
3JQ> ОШдаШЕИЕ. Зудем писать А \ <& ), если для
некоторое i LiJ L J
(1) всякое /> <£ лежит в одной и той же строке в -ftЛ и
(2) г лежит в -Г^}в более высокой строке, чем в \^%i •
Выше мы выписали (3, 2)таблоиды в этом порядке• Имеется
много других содержательных упорядочений на Я^абловдах, но
выбранный метод достаточен для большинства наших целей.
Как и доминирование для разбиений, наилучшее упорядочение
таблоидов является частичным.
ЗЛ1. ОПРВдаЛЕНИЕ. Пусть ^-«таблица и т-г (t) обозначает
число членов, не превосходящих г , среди первых г строк £• .
Тогда пишем
[Kj^ftt,}, если и только если ntCb(tJ^m£b(^WR всех г иг.
Это есть упорядочение таблоидов всех форм и размеров, но
мы будем сравнивать лишь таблоиды, ассоциированные с одшш и
тем же разбиением.
Рассматривая сначала наибольшее г , а затем наибольшее
г , дая которых тСг(Ъ) <mi% (tx) , получаем такое
утверждение.
3.12, Дяя А -таблоидов {Ъ}ш {L} из условия {^}<{^}
бедует {t±}<{ix}.
ЗЛЗ. ПРИМЕРЫ.
(I) Вели ^= I 3 6 и /х= i 2 4 ,
2 5 7 3 5 6
4 7
то первые 7 строк и 3 столбца матриц (ml% (t±)) и (тп it (i*))
'То есть наименьшее из чисел, лежащих в строках -/^и \^х\
с разными номерами» расположено в jt^ выше, чем в {{А . -
Прим. ред. ,
24

таковы:
ill 111
12 2 2 2 2
2 3 3 2 3 3
(Ч-г(У) =2 34 (4tftJ>) = 3 44
2 4 5 3 5 5
3 5 6 3 6 6
3 6 7 3 6 7
Поэтому {tij <3 \ji].
(2) Ниже приведен граф отношения <J на (3,2)-таблоидах
Предположим, что иг<х и что кг находится в а-й,
а х в £*й строке таблицы £ . Тогда определение ml%(t)
дает
ЗЛ4. . t
I 1, если 6*1 < а и и/ < г < ОС;
™с%(ь(у**))-тс%$)= <~i> если а<ъ<ё> ж ut^i<oc,
I 0 в остальных случаях.
Поэтому
3.15. {t}<l-[t (Vrx) ^ , если аг<зс j_ or
расположен ниже, чем х jb £ .
25

При доказательстве теооемн об ортогональной форме Юнга нам
потребуется знать,когда таблоида ft} и [t(x-l,x)JnmooveR-
ственно смежны в <N порядке {вт совпадают).
3.16, ДЕША, Веди ос-4 лежит ниже ее в i и t
является Л-табдицей, то не существует Я> таблицы tt j3
№*&<}< &(*-*,*)}■
Доказательство. Сначала заметим, что доя
каждой таблицы t* с i * в t* й строке
= количество чисел, равных ? * среди первых г строк zf =
Снесли г < г*,
ij если t ^ г*".
Теперь дредположим, что x-i лежит ниже, чем а: , в t 9
и 1ЬУ^ OJ ^ # (а~* > я ) } • ь ЗЛ4 слеДУвт, что
Поэтому
И
^г®"""1*-*,*®" Wil W"" тг-*,1 (У*** 'У*'* и г'^<
Согласно первому абзацу нашего доказательства» все числа»
кроме х - I и х , появляются в ^ и t± на одних и тех
же местах. Но f и i - это .Я-таблицы. Поэтому -£i^J^
{£ j или {iij- \i(x-l }x) } , что и требовалось
доказать.
4. МОДУЛИ ШПЕХТА
С каждым разбиением // числа я мы связываем подгруппу
Юнга G^ в ©^ , полагая
26

Изучение представлений g"^ начинается с подстановочного
модуля У^Лгрулпн (3/1 относительно Gy *. Модуль Шпехта ^
является подмодулей в M^t и если основное поле - это Q,
(поле рациональных чисел), то различные модули Шпехта, когда f
пробегает разбиения и , дают все обычные неприводимые
представления 6^.
4.1. ОШЩЕШИЕ. Пусть F1 - произвольное поле, и пусть
pi^ - векторное пространство над Р , базисом которого служат
различные J4-таблоида.
Действие (3^ на таблоидах уже было ранее определено:
{tjfc^-fict} (£€.&*) • Продолжение этого действия по
линейности на М^превращает М*4 в jf7©^-модуль, а поскольку (51
действует на таблоидах транзитивно н стабилизатор одного из
ju, -таблоидов есть (Зу«, ю* имеем
4.2. 1ч является подстановочным модулем группы 61
относительно подгруппы(Sy. Это циклический Р6**~модуль,
порожденный любым таблоидом, и
4.3. ОПРЩЕЮВНИЕ. Пусть t- таблица. Тогда знакопеременная
столбцовая сумвдэ д&^ есть элемент групповой алгебры JPS^ $
полученный суммированием элементов в столбцовом стабилизаторе i
с учетом знака каждой подстановки • Короче говоря,
*t=2 (*?**) я--
xeCt
Доли таблоид в±у ассоциированный с таблицей t ,
определяется как
Модуль Шпехта для разбиения м - это подмодель
, порожденный политаблоидами.
^ Этот термин означает, что (bn, транзитивно действует на
некотором базисе М^ , причем Gju есть стабилизатор некоторого
базисного вектора. - Прим.ред.
г' М^ есть (S^-модуль, индуцированный с еданичнаго
представления подгруппы @ (см.§ 6). - Прим.перев.
27

Следует заметить, что политаблонд завися? от таблицы i ,
а не только от таблоида -fij . Все таблоида, входящие в <?^ ,
ямеют коэффициенты +1 (если VE.M^* *o гг есть линейная
комбинация таблоидов; мы говорим, что таблоид -ft} входит в
гг , если его коэффициент отличен от нуля).
4.4. ПРШЕР. Бели I- 34 t *о %= d-(2 3))(1-(4 5))
(тождественная подстановка всегда обозначается через I). Далее,
251 351 241 34 1
е i гг + .
Li • Li LE 2 5
Практический способ выписать fy , если дана Г , состоит
в том» чтобы переставить числа в столбцах t всеми возможными
способами, приписывая знак соответствующей подстановки: каждой
получаемой при этом таблице, а затем нарисовать линии между
строками каждой таблицы.
Поскольку ае^^^а^ мы получаем etOi= etT ,
поэтому
4.5. о - циклический модуль, порожденный любым поди-
таблоидом.
Если нужно привлечь внимание к основному полю F1 > мы
будем писать М£ и Sp . Многие результаты для модулей Шпехта
переносятся на области целостности, и только в теореме 4.8 и
лемме II.3 мы должны ограничиться случаем поля. Если F1
специально не указано, то основное поде произвольно. Поскольку//^ -
подстановочный модуль еДва ш Удивительно, что многие его
свойства (например, размерность) не зависят от основного поля.
Более интересно то, что многие результаты для модулей Шпехта
также не зависят от поля. Вот два частных случая. Если №~\%Х
то S^^M^ - тривиальный FtS^ модуль. Если м=(1л) * *о
Pi*4 изоморфен регулярному представлению (5к " • а & есть
знакопеременное представление (т.е. fft-+4jfti<£ ).
Используем теперь основную комбинаторную лемму 3.7 для
доказательства следующего предложения:
4.6. ЛЕША. Пусть Л j j4 - разбиения п .
Предположим, что t _есть а-таблица, a t* sctj» /f-таблида я
что {i*}*i ~ 0 . Тогда Л &м , при—этом если. Л=/г , то
28

Доказательство. Пусть о и & - два числа в
одной и той же строке t * . Тогда
Но о и 6 не могут лежать в одном столбце t , иначе мы
могли бы выбрать представителей классов смежности б^ J...,6"^
столбцового стабилизатора t по подгруппе,состоящей из I и
(Л, ^ ), и так снабдить их знаками, что
Отсюда вытекало бы, что, вопреки предположению, {i^J^i ~0 .
Мы доказали, что для каждого i числа в г-й строке t*
принадлежат различным столбцам t; лемма.3.7 дает Л£*уу .
Далее, если Л =/ч , то по построению ^^/- один из таблоидов,
входящих в -[fyXf Таким образом, в этом случае {^}-{^}^
для некоторой подстановки йГ ь Q. ш {£*}3*t**{£j3'2±ss±ft}*£
4.7. СДВДСТВИЕ. Если г/ - элемент 7Y , a t есть //-
таблица, то и£^ кратно et .
Доказательство, у есть линейная
комбинация jty-таблоидов ft*}, a ft*l*tкратно ^ по лемме.
Пусть теперь <, > - единственная билинейная фодаа на
у[Р\ для которой
(_ О, если ^, j * {^j .
Ясно, что это симметричная (Ь^-инвариантная
невырожденная билинейная форма на М^9 каким бы ни было поле. Бели
поле - это Q , то рассматриваемая фодаа является скалярным
произведением (ср. пример 2.5).
Мы часто будем использовать следующий прием: дая ц if£fll
1C£Ct C
(мы использовали (£ГЛ-инвариантность Форш).
Ключевой результат, использующий нашу билинейную форму,
таков:
29

4.8, ТЕОРЖА О ПОДМОДУЛЕ ([ч]). Если ]} есть подмодуль
М14. то либо V^S" . либо \fczS^L-
Доказательство. Предположим, что и с V и
t есть /*-таблица. Тогда по следствию 4.7 иаг± кратно е± .
Если можно выбрать и ш t так, чтобы множитель
при е^ был ненулевым, то et g; JJ . Поскольку £^
порождается et , мы получаем U^S^' •
Если же гу#£= 0 для любых г/ и ^ , то для всех v,fc
Таким образом, У Я, $^1.
4.9, ТЮРША. Модуль $ /($ (i о /является или
нулевым, иди абсолютно неприводимым *'. Если он ненулевой, то
ПсУ /е/Ь ^Ледйнственный ццмди1 ^даодуль в «3
JH i) fi f)i J самодвойствен.
Доказательство, По теореме о подмодуле
каждый подмодуль в S** либо совпадает с самим 3^', либо
содержится в $•*" Г) S^1 . Из 3.5 сразу же следуют все утверждения
теоремы, за исключением того, что 8^/(8^П S J остается
неприводимым при расширении поля. ^
Выберем базис е±>...>е^ для S , состоящий из
политаблоидов (мы увидим позже, как сделать это специальным образом)
По теореме 1.6 dim S /(S*П S^1) совпадает с рангом
матрицы Града относительно этого базиса. Но элементы матрацы
Грама принадлежат простому подполю в Р , поскольку
коэффициенты таблоидов, входящих в политаблоид, все равны ±1. Поэтому
ранг матрицы Грама над Р такой же, как над простым подполем,
так что размерность S^/1 S J41 не возрастает при расширении
F . Поскольку S^/(S^r\S^) всегда неприводим, получаем,
что он абсолютно неприводим.
ЗАМЕЧАНИЕ. Мы покажем, что все неприводимые представления
($ъ имеют вид SJ*/(S/l/)SJy; теорема 4.9 означает, что мы
можем работать над Q или над полем из о элементов.
Теперь мы сосредоточим внимание на случае cfiax F= О > хотя
оставшаяся часть этого раздела получается также из более тонких
*' То есть остается неприводимым при расширении поля. -
Прим. ред.
30

.рассмотрений разд. II. Читатель, стремящийся к более общему
результату, может перейти сразу к разд. ДО и И.
4.10. ШЖ. Воли $ есть JTG>n, ^гомоморфизм из
М' JL S Ф&1 Q 9 л Л й/v . Если Я-jt, 9 то ограничение
$ ja S вс*ь умножение на константу.
ЗАМЕЧАНИЕ. По теореме о подмодуле Ue% Q д^ £ Я-i,
поскольку Кегвф S . Позднее эта лемма будет улучшена в
различных направлениях (ср. II.3 и 13.17).
Доказательство. Предположим, что t есть
1 -таблица. Поскольку е± ф Кег О?
= (линейная комбинация р-таблоидов) а?й .
По лемме 4.6 X&J4 , а если 1=J4 , то et $ кратно et .
4.11. СЛЕДСТВИЕ. Если c/iav F= 0 ъ. @ - ненулевой эле»
мент из Kotnrc^ (Зл, М ** X то %&м .Если Я=// , .то
~~§ -умножение на константу.
Доказательство. Для -
скалярное произведение. Поэтому ранг матрица Грама по отношению к
некоторому базису в $л равен cftm$Ajwa любого поля
характеристики 0 . Тем самым
anew-*," s*nsM-o j_ m*=sa<bs*K
Любой гомоморфизм, определенный на О , можно поэтому
продолжить на Л/Л, полагая его равным нулю на S . Остается
применить лемму*
4.12. ТЕОРША (ОБЫЧШЕ НЕИРИЮДЩШЕ ПРВДСТАВШШ &Л).
Модули Шпехта над Q самодвойственны, абсолютно неприводвмы и
задают все обычные неприводимые представления (3^ .
Доказательство. Если $q = Sq , то Л £у-'
по следствию 4.II. Аналогично м й 1 , так что A =jr .
Поскольку £л П Su~ 0 9 теорема следует из теорем 4.9 и 2.4.
Так как М** вполне приводам, когда скаг А* 0 ,
следствие 4.II дает также следующее утверждение:
31

4.13. ТЕОРБМА.. Если ЫшлР** 0 , то композиционными
факторами М* служат (один раз) и некоторые из модулей
{Sxf3L Of*} (возможно» о повторениями).
Некоторые авторы предпочитают работать с групповой
алгеброй группы 6"^ , поэтому мы объясним» как построить правый
идеал в групповой алгебре, соответствующий модулю Шпехта.
Для заданной //-таблицы t положим Pt-^l & %
так что j)t €.£ Ьп , и пусть
Это, очевидно, корректно определенный /^-изоморфизм
правого идеала^ F&n, на М^ (корректность следует из того,
что J>± %=j>t<&XGRt<^{t}'£ = {i } j .Ограничение 9 на
правый идеал j>± aef FSn. задает изомолзфизм из J>± &i F&n на
5 . Используя этот изоморфизм, каждый результат можно
интерпретировать в техниках групповой алгебры. Мы предпочитаем
подход с использованием модулей Шпехта по двум причинам. Во-первых,
модуль Шпехта Зл зависит только от разбиения, yv , в то
время как правый идеал j>± зе* Р&л зависит от выбора
р-таблицы i . Более существенно, возможно, то,что вместо j>£ ,
которое является длинной суммой элементов группы, мы имеем один
объект {_t} ; это значительно упрощает обращение с конкретными
примерами, как будет видно из,следующего раздела, где мы,
откладывая дальнейшее развитие теории, рассмотрим некоторые
примеры, иллюстрирующие многие важные детали.
5. ПРИМЕРЫ
5.1. ПРИМЕР. Возвращаясь к обозначениям примера 2.5, где
первая строка таблоидов в pl^n'lti) не пишется, имеем
S(n~''iJ=(l-T)Fen=l2]aiTlaieF)a±+...+an = 0}>
У Элемент j>i GF&'n называют симметризатором Юнга.
Прим. ред.
у So - обозначение линейной оболочки. - Прим.перев.
32

Ясно, что >> £ i> тогда в только тогда,
когда сАа-г f делит п. . По теореме о подмодуле
Oc=S(ilJ1=S(i*Jc:M(ii>, если cUtF=£ и л «.г,
Ос^^^с^^сЯ^"^ еошсАагГ делит /г>^
суть единственные композиционные ряды для iv , если
сЛаг ^ делит л .
Та же теорема показывает, что если cfiai JP не делит л ,
то S<*-^ неприводим и M^^S**''*']® S <*'*'»*
Заметим, что в любом случав ок ~ £ l y и
5.2. ПРИМЕР. Рассмотрим М подробно. (3> Л)-табло-
яд определяется неупорядоченной парой чисел if ,
составляющих его вторую строку. Чтобы получить геометрическую картину
jy[ С*1*) , рассмотрим множество графов (без петель) с пятью
вершинами, ребра которых могут иметь "вес" - коэффициент из
поля. Отождествляя ij с ребром, соединяющим точку г с
точкой j , мы строим изоморфную копию М (6'х\ Например,
АН
5Ч_
- Ill
ХЧ
-AM.
35
Л5
sv
1
•
1
><
4
соответствует
• 9
4 1 3
Каждый "четырехугольник с ребрами чередующихся весов + Iм
является образующей модуля Шпехта $ &Ч
, г , i , 1 3 5 I 2 5 1 3 4
Пусть *1>г1>гз, гц >*5 — это 2 4 ? 3 4 ; 25 ?
3 5 4,4 5 соответственно. Тогда et ,...,et отвечают
33

4 1 3
соответственно.
40 ребер упорядочены согласно ЗЛО:
I 2<13<2 3<14<2 4<3 4<!5<2 5^3 5<4 5.
Последние ребра, входящие в £^ ,..., е± , суть
fi, 3~4, 2 5, ТЪ> 4~5 (что соответствует {tA->...,-[*£} )•
Поскольку эти последние ребра различны, £± 4,%., £, линейно
независимы. *
Заметим, что далеко не ясно, что они также порождают
модуль Шпехта, но мы докажем это позже. Допуская, что они
действительно дают базис, получаем, что матрица Грама относительно
этого базиса есть
Можно проверить, что
если cko,%F**0 или cka,%F^5 » то гапк Л**5>
если сколF~3 , то гал/r Я** i,
если cfiat F~ X , то галк Л « Ч*
Поэтому dim (S (3lJ°/S (SfVn S №-)- 5", если только
chat, F±£,3 . В случае ckar%F^SiJ3 эта размерность есть 4 или
1 соответственно.
34

Найдем <? (3tA^1 . Конечно,
2
и 5 градов,
ортогональны "четырехугольникам с ребрами чередующихся весов
+ 1". (Считается, что непомеченная дуга имеет вес 1 ). Это
значит, что они принадлежат S ' (Pyty определяется как
r(-i)~r(-d)(di) для i<id5).
Далее, Г^1)+Г(-1)+^+Г(;5) = ЪГ . Легко проверить,
что r(-i),...,r(-5) линейно независимы, если скалРфВ%
и что они порождают пространство размерности 4, если cka,%F*3 •
Поэтому S(5ll)L порождается Г,ГН)>1Х-1)Г..£$5)*
поскольку $&*■)-*• имеет размерность 5 (по 1.3).
Бели с/иьг Р= & , то €ti + eti+ei;H + ets-r»
Поэтому в этом случае Г принадлежит S(i,v П S(зл) ±
и по соображениям размерности порождает S(3,^D S^x.
Бели скаъР^З , то et±-hebx^P("5)^ и теперь
r(-i),~.-> Г(-5) порождают $(2,Х)П S(*'^К
Мы все еще не имеем удобного способа проверки того,
принадлежит ли некоторый граф модулю $(м\ Однако каждой такой
граф, разумеется, удовлетворяет двум условиям:
5._ЗЛг) Сумма коэффициентов на ребрах равна нулю*
(И) Валентность каждой точки равна нулю, (Формально:
сумма коэффициентов ребер в каждой точке равна нулю.)
Эти условия выполняются благодаря тому» что циклический
вектор для S&1) удовлетворяет этим условиям. Фактически эти
свойства характеризуют $&Ъ) и дают нам возможность быстро
проверить, что PeiS^'^ , если сЛаъF1^ И ( Римеет четное
число ребер, а каждая точка имеет четную валентность), и что
Г(-5)<£ S (3'*\еслк cka,iF=Z (Г(-5) имеет 6 ребер и
каждая точка имеет валентность 0 или 3;.
Пока на первый план выдвигаются две задачи, подлежащие
дальнейшему обсуждению:
35

(а) Найти базис доя модуля Шпехта общего вида» похожие на
указанный выше ( ЛВ . Не очевидно даже, что dim S^ не
зависит от поля.)
(£) найти условия, близкие к 5.3, характеризующие модуль
Шпехта как подмодуль в /^(ср. со вторым выражением для
§(*>-*>*) в примере 5.1).
Мы доказали, что 2±t?...,ets линейно независимы; здесь,
как и в общей случае, значительно труднее доказать, что они
порождают £ С***' . Мн закончим этот пример одновременный
доказательством того, что е^ ,...>et5 образуют базис в $(ЬУ 0
что условия 5.3 характеризуют 5 *3' .
Определим у0 е KomF& (М &*>, М (*)) и yL <£ Korrtf^
У/у^так: 5
а.
л
а
±
% с -
JL
~п
А
>.
а
ТГ
±
т
тг
с
с
cJ
е
е
• >
Q
е
ё
с
• ■' |'
сГ
(ty^/Y1
(т.е. Ые —fol+e').
Условия 5.3(0 или (ЯJ выполняются дая элемента гг в
pi (*>ь) тогда и только тогда, когда ^e^tv, иди хгеВг w±
соответственно. Поэтому S (3'^ Уег v>0 П Т&ъ ч± (ср. с леммой
4.10), а мы хотим доказать равенство.
Обозначим через S&**&*) пространство, порожденное
графами вида
I
+ 4Л--1 — —
С/ - Ch .
+W
J * < ■
Тогда S (3iiJ> &*><=: ¥ег v>0 _ я ^ отображает &** i(,SJ
на S &>*) (поскольку г^ * U- гк -* Г-у"- Г-* «у — Л J.
Поэтому мы имеем следующие ряда дая М &*Ji
Размерности
Кег v0 J
$0A,bt) \^c(4,i) ^ (см. пример 5.1)
О
} з* 5^
^5
36

Ho chm pi &*) - 10 f так что во всех случаях мы
получаем равенство. В частности, Ыгт S&^=5 и S ^3'*-)=*ХегъП
ПУсг у^ , что мн и хотели показать.
5.4, ПРИМЕР. S^'^порождается графами
Ясно, что первые два образуют базис.
Веди cko,iF~l , то $(%>%)с $(*»*-)±^ Это
происходит из-за того, что любой водитаблоид либо не содеркит ни одного,
либо содержит оба ребра в следующих парах ребер:
6. ТАБЛИЦА. ХАРАКТЕРОВ ГРЛШЫ ©л
Имеется много различных способов вычисления обычных
неприводимых характеров &п . Если известна таблица характеров
&n-i , то очень полезна теорема ветвления (разд. 9),но дяя
вычисления таблицы характеров <В^ этим способом пришлось бы
вычислить все предыдущие таблицы. С другой стороны, если нужно
37

узнать только несколько значений, правило Мурнагана-Накаямн
(разд. 21) является наиболее эффективным методам, но его трудно
использовать дин вычисления на компьютерах. Метод, указанный
здесь, дает все значения в таблице характеров &п
одновременно. Он принадлежит Р.Фоксу, а некоторые упрощения сделаны
Г.Муллнно.
Пусть j* обозначает обычной неприводимый характер (5Л ->
отвечающий разбиению X , т.е. характер (2С№-модуля S@ .
Через iQ. обозначается тривиальный характер группы £ .
Напомним, что &х - подгруппа Юнга; обозначим через 4<g / g^
характер модуля Мф • введенного в 4.2. (Обозначение XjtQ
означает индуцирование на (r} a / Q - ограничение на Ст. ♦)
Строки и столбцы всех матриц этого раздела
индексируются разбиениями л в словарном порядке (3.4). Поскольку
композиционный фактор S^ входит в М^ с кратностью единица,
а другие факторы отвечают разбиениям yv с yv>^ (теорема
4.13), имеет место такое утверждение:
6Л. Дусть ^я/ч^^е ?@л>/У~ скалярное произведение
характеров. Тогда матрица п^т^) является нижнетреугодь-
ной с единицами на диагонали (см. пример для 6^- ниже).
Из этого сразу же следует, что матрица в= (&Лу)%
определяемая как
веррснетреугольная.
Пусть &// обозначает класс сопряженности в
отвечающий разбиению м , и пусть А = (аяр) - матрица с
элементами
Матрицу А нетрудно вычислить, и мы утверждаем, что,
коль скоро она известна, таблица характеров С-(скЛ^ группы
&п может быть вычислена прямыми манипуляциями с матрицами.
/ / / - число элементов в конечном множестве. - Прим.
дерев. J
'~СЯм есть значение характера / на классе %м . - Прим.
перев. J ' " •
38

Прежде всего заметим, что
2 Ъ°*/,-1&,1&Ж+6,9, <&,)-*„
Но
Поэтому В = СЛ',тт» Л - транспонированная матрица Л
значение характера L, 1(5^
на элементе тнпа ju) =
^(nifaDiexMrllG-tntrh
:^;
Воля j? известна, мы можем решить эти уравнения» начиная
с левого верхнего угла В , двигаясь вниз но каждому столбцу
я перехода далее к столбцам, расположенным правее. Поскольку
£3 верхнетреугольная, на каждом шаге вычисляется только одно
неизвестное, а его можно найти, поскольку В имеет
неотрицательные элементы. Поэтому имеет место
6.2. ТЕОРЕМА. Если матрица 4=(°%и)9 где ^-/6^/1 ^Д
известна, то можно найти единственную неотрицательную верхне-»
треугольную матрицу б =* (&^ ). , удовлетворяющую уравнениям
при этом таблица характеров С трурта (5^ совпадает е
6.3. ПРИМЕР. Предположим, что п = 5. Тогда
(5)
(4, I)
(3, 2)
i«<3. I2)
(22, I)
(2, Is)
(I*)
(5)
24
(4, I) (3, 2) (3, I*) (2г, I) (2, I3) (I*1)
30
6
20
О
2
20
8
2
2
15
3
3
О
I
10
6
4
3
2
I
I
I
I
I
I
I
39

(5)
(4, I)
(3, 2)
B = (3, I2)
(2*. I)
(2, I3)
(Is)
(5)
fl20
(4, I)
24
24
(3, 2)
12
12
12
(3, I2) (22, I) (2, I3)
6
12
6
6
4
8
8
4
4
2
6
6
6
4
2
(I5)
I»
4
5
6
5
4
I
(5)
(5) f I
(4, I)
(3, 2) !
C=(3, I*)
(2a, I)
(2, I*)
(IS)
-I
0
I
0
j-I
1
(4, I)
1
0
-I
0
I
0
-I
(3, 2)
I
r
I
0
-I
I
-I
(3, i2)
I
I
-I
0
-I
I
I
(2\ I)
I
0
I
-2
I
0
1
(2, Is)
I
2
I
0
-I
-2
-I
(Ir)
ij
4
5
6
5
4
I
Столбцы таблицы характеров записаны в порядке, обратном
к обычному, в частности, степени неприводимых характеров захга-
саны сверху вниз в последнем столбце - поскольку мы выбрали
словарный порядок как для строк, так и для столбцов ^Ч
6^ ОЮЗНШ&ИЕ. Равенство типа [3][2] = [5] + [i\ -l] +
+ [3, 2] следует понимать тар: М(^ имеет композиционные
факторы, изоморфные S $Ч#рз $&*) . Вообще, если Я - раз-
бкеяие /г , то ®
МШЫ-^^^Ы
означает, что Sq является фактором Mq с кратностью т^
(т= (mftju) «_ матрица, определенная в 6*1).
^ Степень характера, т.е. размерность соответствующего
представления (над © ), есть значение характера на единичном
классе; до понятным причинам последний столбец симметричен
относительно середины, - Прим.ред.
40

Деля каждый столбец матрицы В на верхнее число этого
столбца (равное /6^/ / ) и транспонируя, получаем матрицу щ
В приведенном выше примере
[5J
[4, I] [3, 2] [3, 1г] '2\ 1] [2, 1г]
[51
[4Л1]
[3][2]
/п=[ЗК1]г
[2}г[1]
[2 НИ*
[I]5
(I
I
I
I
I
I
I
1
2
2
3
4
I
I
2
3
5
I
I
3
6
I
2
5
I
4
Заметим, что равенства JVJ [ij = [5J + [4f-ij и
[3j[2j = [5 J + [АЛ] + [3.2J согласуются с примерами
5.i я 5.2. Правило Юнга в разд. 14 показывает, как вычислять
матрицу /л, непосредственно.
Теорема 6.2 имеет интересное
6.5. СЛЕДСТВИЕ. Определитель таблицы характеров группы (%
равен произведению всех частей всех разбиений и .
Доказательство. (1Лл"П(Л1 • i)f и i^l^xh
~/./"Я. ! Поскольку Jt и В верхнетреугольные и В^СЛ',
имеем dot С=ГТГТ &l y что и требовалось доказать.
л i
Напомним, что разбиение Л ' , сопряженное с Л ,
получается "поворачиванием 1 на бок" (см. определение 3.5).
Таблица характеров группы (ь5 в примере 6.3 обладает таким
свойством:
6.6. fx'= ^л ® < (1*\
Мы докажем это в общем виде.
6.7. ТЕОРЕМА. Модуль Ъ@ -л 5 изоморфен модулю,
сопряженному с S* •
я1
ЗАМЕЧАНИЕ. Поскольку 0fi самосопряжен, можно пропустить
слова "сопряженному с" в утверждении теоремы, однако позднее мы
докажем аналогичную теорему над произвольным полем, где следует
различать 5я и его сопряженный модуль.
41

Доказательство . Цусть t - заданная £-таблж-
ца к "t1- сопряженная таблица* Например, еслк i ■ 1 2 3, то
* * 4 5
2 5
3
Цусть, как обычно,J>v=J>^<[tt \ftGЯf} и x^^EffyntfJlfteQ.
Пусть и - образующая для S&*• так что Wmfaurtfn?) u>
для Я"€б^
При помощн стандартной^ выкладки проверяем, что имеется
корректно
Ч
средством
при домищи стандартной выкладки проверяем, что имеется
корректно определенный: Й?6^ -эпиморфизм в из -Л/^'на
Ъ®®5® ' отобвпаптЛ {£'} в ф}#1/>)/^#; 0 задается по-
6.8, в: {t '%}-+({l}<X> u)fv®=({t}zt ®u)% =
в отображает ^'}ж^. в (^'}® и)^г' *i ' e
-<{*}*t>IAt№}>-lflth
Поскольку | /^ i I—ненулевой элемент
Таким образом, Кёг 0 ^ SJJ' и по теореме о подмодуле /5£г ^S
S $*'. Поэтому *"•
Лт 5^ = dim Jm в -dim (М£'/&г 6)
^
г*/п%%1\ 1, п л' 00
Точно так не dim S^'^dtm S^^dim S@ . Поэтому
dim.$>Q=ctlm Sq и в (*) выполняется равенство. Итак, *ег 0~ S^ , .
Теорема доказана, поскольку мы построили изоморфизм между
модулем М@ /S^L (изоморфным модулю, сопряженному с SU', по 1.4)
ЗАМЕЧАНИЕ. Равенство dim $л^с/ст S тривиально
получается из следствия 8.5, но это сокращает наше доказательство
только на одну строчку.
Имеется один нетривиальный характер группы (S^, который
всегда мокно быстро вычислить, а именно ^ (л"1?^ :
42

6.9. ЛШ4А. Значение /**"*'*> на подстановке £° на
единицу меньше, чем число неподвижных точек 4Г .
Доказательство. След С\ действующей на
подстановочном модуле М ^ э очевидно, совпадает с числом
неподвижных точек ct . Поскольку
И
^sSFeS'Z*0
•а = ^а
(ср. пример 5/1), тотчас же получаем доказываемый результат.
Мы можем, таким образом» выписать четыре характера грун-
сразу же. Наилучший способ найти таблицу характеров (5^ дая
малых lb состоит в том, чтобы получить оставшиеся
характеры из этих* используя соотношения ортогональности дая столбцов.
7. С00Ш0ШШЙЯ ГАШЙ
В этом параграфе t - фиксированная м-таблица.
Мы хотим найти те элементы групповой алгебры группы <S^ ,
которые обращают в нуль заданный политаблоид е+
Пусть X - поданожество
fi+d)-&o столбца таблицы t .
л
6-го, а У - подмножество
г
f i+l
Пусть б^ >. .; &к - представители вдассов смежности по
подгруппе Gr * <$y в &rUY и £rtY7k 09п ^J*5) •Элемвнт
&X,Y называ6ТСЯ элементом Гарни {[5] )«
43

Зо всех приложениях X . будет выбираться в конце /-го
столбца, a "У - в начале (i+lj-то столбца t .
Подстановки 61; .. у&ь , конечно, не определены однозначно, но
для практических нужд заметим, что 6*L >.. , б"^ можно выбрать
так, чтобы tGL r- ?б5^ пробегали все таблицы, согласованные
с t везде, кроме мест, занятых X UY % причем их элементы,
стоящие на этих местах, возрастают при чтении сверху вниз.
7Лм ПРИМЕР. Если t - 1 Л, } Х- {% зJ и Y={A, 3J,
5
то i ^i ) • • • > 4-6к можно выбрать так:
t = t±= 1 г, iti 2, tr i 2, fv= i з, 4= i з, i= i 4
43 34 35 24 25 25
5 5 4.54 3
где iqnGfi для i= If3,4,6,^/t6/=-I для z= 2f5 и #^=
= 1 - (3 4) + (3 5 4) + (2 3 4 ) - (2 3 5 4) + (2 4) (3 5).
7.2, ТЕОРЕМА. Вели \X\)Y\>j^\ , JP£et (5ry =0
(для любого основного поля).
Доказательство (см. /19]). Введем
обозначения^'^ для J>] ffign. 6$G&£&*&}* ^fuv дая
- Поскольку jXUYI >f+ i » то «DtIIH люб°го 'Г в
столбцовом стабилизаторе таблицы t некоторая пара чисел из
X UY лежит в одной строке Ьг . Следовательно, как обычно,
{bv}&xur ""' CL _ • Тем сашм /*}** (ь'то--^
далее, Gy G-y является множителем в x±t и GXUY=>
^^j&Y ^ХХ # Поэтому
Итак, {t}'£t G xy "' & надполем £ и, поскольку все
коэффициенты таблоида целые, это равенство имеет место над
любым полем.
7,3. ПРИМЕР. В примере 7.1 мы имеем
так что е±~е± -et -е* +с± . -с* .
44

8. СТАНДАРТНЫЙ БАЗИС
МОДУЛЯ ШПЕХТА
8Л, ОПРЕДЕЛЕНИЯ. Таблица t называется стандартной, если
числа в ней возрастают вдоль строк и вниз по столбцам; •[£} -
ставдартный таблоид, если в классе эквивалентности Jt}
имеется стандартная таблица; et - стандартный политаблоид, если t
стандартна .
В примере 5.2 выписаны 5 стандартных (3, 2)-таблиц и
соответствующие стандартные подитаблоиды.
Стандартный таблоид содержит только одну стандартную таблицу,
поскольку числа в стандартной, таблице должны возрастать вдоль
строк. К сожалению, политаблоид может содержать более чем один
стандартный таблоид (в примере 5.2 в ets входят 4~5 и 2 4).
Мы докажем, что стандартные политаблоиды образуют базис
модуля Шпехта над любым полем.
//-таблоиды были линейно упорядочены в силу определения ЗЛО.
Линейная независимость стандартных политаблоидов вытекает из
следующей тривиальной леммы.
8*2. ЛЕММА. Предположим, что if} > v*k Р.,., Ц^ - элементы
М^ и что {ti} - последний таблоид, входящий в г^ . Если
все таблоиды Stc } различны, то 1Г[} irx ? .. ., vtiL линейно
независимы.
Доказательство . Можно считать, что ^_}</^к...
и оv^ *'•-.*Яд,-0,то а;=0 ,поскольку {Ы входит в Vj и не
входит ни в какой г/> при k<J • Поэтому aL^ ••• =&т = 0.
Ясно, что {1'У- последний таблоид, входящий в <^ , ес-
ли f - стандартная таблица, и это все,что требуется, чтобы
заключить, что стандартные политаблоиды линейно независимы; мы,
однако, намерены получить более сильный результат, используя
порядок З.П на таблоидах:
8.3. ЛЕША. Если в t числа возрастают вниз по столбцам, то
для всех таблоидов {t,(j , "входящих в с ^ -[t'} -J {t} .
Доказательство. Если V - Ьж % рДе & - "^еДи-
ничный элемент столбцового стабилизатора t , то в некотором
столбце V имеются числа \f <* х , для которых иг располо-
45

жено ниже х . Тогда по 3.15 {£'}<* ft '(гох)}. Поскольку
{dtf(v)x)} входит в е^, аддукция показывает, что^У2^)}^^}»
Поэтому {i'}<3 {t}-
8.4. ТЕОРЕМА. Множество £ е*£ / £ - стандартная
_/У-таблица i образует базис в £/\
Доказательство (см. Д9/). Мы уже доказали, что
стандартные политаблоиды линейно независимы, а теперь используем
соотношения Гарни, чтобы доказать, что любой политаблоид можно
записать как линейную комбинацию стандартных политаблоидов -
взглдд на пример 7.3 покажет читателю, как это сделать.
Будем обозначать через [i] столбцовый класс
эквивалентности i , т.е. [t]=£t±\t±=tfl; для "ТСЕ-С^У . Столбцовые
классы эквивалентности линейно упорядочены аналогично
упорядочению 3.10 для строчных классов эквивалентности.
Предположим, что t не стандартна. По индукции мы можем
предположить, что ef можно записать в виде линейной
комбинации стандартных политабловдов, если [i'J < [i]'; нам надо
доказать то же утвервдение для е^ . Поскольку e±&=(iQn'X)et>
когда ffsCt t мы можем предположить, что элементы £
возрастают вниз по столбцам. Поскольку t не стандартна, в какой-
нибудь паре соседних столбцов, скажем в /-м и (J+-£ )-м,
находятся элементы Cti <Ql<^,<Uz>e±<iz<^.<: &d c ^U>^
для некоторого fy:
«i
>
Л
>
4
А
Л
К
Пусть 1-{оя>.. ,аг} и Y-U±y.., & Л; рассмотрим
соответствующий элемент Гарни &х,Г'^(,9п%)6'- По теоРеме
ПОСКОЛЬКУ 44 < -■•<
для 6ГФ-1 .Имеем Ц = ~S. (iQK 6')ete' •> и
доказываемый результат следует из предположения индукции.
46

8.5. СЛЕДСТВИЕ. Размерность модуля Шпехта о не зависит от
основного поля и равна числу ставдартных /У-таблиц.
ЗАМЕЧАНИЕ. Независимое доказательство теоремы 8.4 дано в
разд. 17.
Qhf*
8.6. СЛЕДСТВИЕ. _В_ о q каздый политаблоид можно записать как
целочисленную линейную комбинацию стандартных долитабловдов._
Доказательство. Этот результат следует из
доказательства теоремы 8,4, другое рассуждение см. ниже в п.8.9.
8.7. СЛЕДСТВИЕ. Матрицы представления (5^ над Q
относительно стандартного базиса в S% имеют целые коэффициенты«_
Доказательство. Имеем €t<Ji'= ё£$-^ и остается
лишь применить следствие 8.6.
8.S. СЛЕДСТВИЕ. Если гг - ненулевой элемент S^, то
каждый последний таблоид (относительно частичного порддка «з на
таблоидах), входящий в ir , стандартен.
Доказательство. Поскольку гг ~ линейная
комбинация стандартных политаблоидов, этот результат следует из леммы
8.3.
8.9. СЛЕДСТВИЕ. Если v<£ £^ и все коэффициенты
таблоидов, входящих в v , целые, то ir является целочисленной
линейной комбинацией стандартных политаблоидов.
Доказательство .Мы можем предполагать, что w
ненулевой. Пусть -££}•- последний (в смысле порядка < ) таб-
ловд, входящий в v , скажем, с коэффициентом о^Х. Согласно
последнему следствию, fe} стандартен. Лемма 8.3 показывает
теперь, что последний табловд в v-cie^ предшествует ££} , так
что по индукции v-ctet -целочисленная линейная комбинация
стандартных политаблоидов. Поэтому гг также целочисленная линейная
комбинация стандартных политаблоидов.
8.10. СЛЕДСТВИЕ. Если VG Sq и все коэффициенты таблоидов,
входящих в v , целые, то элемент, полученный приведением всех
этих коэффициентов по модулю *р , лежит в "Sp% где £' - поле
из л> элементов.
47

Доказательство. Согласно последнему следствию,
V* - целочисленная линейная комбинация стандартных
политаблоидов, скажем V=*J?Q>i el (ai<E. Ъ) ; Приводя все
коэффициенты таблоидов по модулю р , получим некоторый вектор гР . Пусть
й; обозначает а± , приведенное по модулю р . Равенство
^ {^^ а с et> показьтает» что тхс Q •£
ЗАМЕЧАНИЕ. Уже из того, что стандартные политаблоиды
порождают о ф , и из следствия 8Л0 вытекает, что любой политаблоид
можно записать в виде линейной комбинации стандартных
политаблоидов над любым полем.' Таким образом, мы можем заключить, что
стандартные политаблоиды порождают £^с над любым полем," зная
только, что это так над Q,
8.II. СЛЕДСТВИЕ. Если F* -.поле. из_ р элементов, то
с ^ есть ^-модулярное представление '(£п , полученное
из £'1 '
Доказательство. Достаточно применить последнее
следствие.
8.12, СЛЕДСТВИЕ. Существует базис в S^,
все элементы
которого содержат_лишь по одаому^тандартному таблоиду^
Доказательство. Пусть {t^ < -j^t^J-ч .. • —
стандартные у^-таблоиды. По лемме 8.3 Jt L \ ~* -
единственный стандартный таблоид, входящий в €{± . Политаблоид ct
может содержать /t£J с некоторым коэффициентом d .
Заменил <t, на Л =Ct - actl » Тогда -ftK} - единственный
стандартный таблоид,' входящий в -ft . Продолжая таким же
образом, мы построим нужный базис.
Следствие 8.12 полезно в численных выкладках.
8.13. ПРИМЕР. Все политаблоиды €tL > ••• -> et<? из пР™еРа
5.2 содержат ровно один стандартный таблоид, кроме сtt- ,
который содержит как 2~4,так и ТТ. Заменим е^ на ft,^et^et >
Тогда с+ . tt , et,*t*£ содержат соответственно 2 4, 3~4f 2ъ, !Г5,
ТЪ с коэффициентом'I и не содержат никаких других стандартных
таблоидов.

Рассмотрим следующий вектор;
V=
Вектор ir принадлежит S ' ' , поскольку суша
коэффициентов ребер нулевая и каздая точка имеет нулевую валентность
(ср. 5.3). Но V содержит -24, -34, - 3~5 , 3«4Т .
Поэтому
Далее нам понадобится техническая
8.14. ЛЕММА. Предположим, что в^Уом-ф^ №ф>^фу
и что все таблоиды, входящие в {t} Q % имеют целые
коэффициенты ({tie:М@ J > Тогда",* цриводя все эти коэффициента до
модулю -р , мы получим элемент Ъ jkl Hontp^ (М£, yM^J?
где F1 - поле из <р элементов. Если ife% в «-С**-*- s
«Г Я* Ъ э 5ДХ *
Доказательство. Тот факт, что VeHom ф1^Мр^
тривиален. л
Возьмем базис ^, • • , fa в S^ и продолжим его при
помощи стандартного базиса 5^ до базиса <f± y ..%.., -/^
в 7^/^ . Пусть ^ ^i3>,%'# > "Г^/л} -различные J?~ra6-
лоиды. Определим матрицу N-(nu):
nv-&>{*<}>■
Мы можем считать, что УГ имеет целые элементы, а после
построчного приведения первых k строк можно считать, что
первые "£ строк УГ (отвечающих базису в 5^ ) линейно
независимы по модулю о . Приводя все элементы JT по модулю ^о ,
49

мы получим множество векторов в М*9 последние л«-£ из
которых составляют стандартный базис в Sp , . а первые #
линейно независимы и ортогональны стандартному базису в $р .
Поскольку
dim S * dim M - Ы-Ст S„ ~ 'к ,
f1 г с
мы построили базис в ^ (Ц • элементы которого составляют
базис Sif , когда коэффициенты таблоида приводятся по
модулю f . х
Далее, каядый из наших базисных элементов в о^. является
целочисленной линейной комбинацией ,Я*-таблоидов и переходит
в нуль под действием 0 . Поэтому, когда все целые приводятся
по модулю -р, в 9 конечно, переводит базис Sp в нуль,
что и утверяодалось.
Мы можем теперь дополнить теорему 6.7.
8.15. ТЕОРЕМА. Над любым полем модуль $ ® S * изо-
морфен модулю, сопряженному с S*l
Доказательство. Достаточно рассмотреть случай,
когда основное поле г - поле из р элементов,
поскольку для F1** Ф мы уже этот результат доказали.
В доказательстве теоремы 6.7 мы рассмотрели
Ф&п-гомоморфизм в из t 14% в Ml 0 Sq и доказали, что
Используя приведенную выше лемму, получаем,
что $ , определяемый так:
является т бд-гомоморфизмом на $£<$ SF > ядро
которого содержит ( SpL . Сравнение размерностей показывает,
что ¥ег $ - S * *х , и теорема доказана.

9. ТЕОРЕМА ВЕТВЛЕНИЯ
В теореме ветвления говорится о том, как устроено
ограничение обычного неприводимого представления группы (9^, на S^i.
Мы используем символы I &n-t для ограничения на <3n-i
и f & п+± Дга индуцирования на <Е> п+± . Используя те
же обозначения, что в п.6.4, имеем
9Л. ПРИМЕР.
Это частные случаи следующей теоремы.
9.2. ТЕОРЕМА ВЕТВЛЕНИЯ. ft) S^f @/i+*« ®{SqI [Л] ~
диаграмма, получаемая добавлением к /j4] одной клетки ^
(И) Sq b&ri-L^^iS'cklW ~ диаграмма> получаемая
удалением из [//J одной клетки }.
Доказательство. Ввиду теоремы взаимности Фробе-
ниуса обе части теоремы эквивалентны. Часть (ii) вытекает из
более общего результата:
nJ4
9.3. ТЕОРЕМА. Если ° определен над произвольным полем,
то S**I@n-i облада'ет рядом, каждый фактор которого изоморфен
модулю Шпехта группы &п-1 • Встречающиеся при этом Факторы
указаны в части (гО формулировки теоремы ветвления, и $ль
встречается в этом ряде раньше S уесли Л1Р*ЛУ*
Доказательство (см. Д9/). Пусть it<%x< ...<ът-
такие целые числа, что при удалении клетки из Ъ;~% строки
tf-1 снова получается диаграмма (например, если /yttj =
/4,22, 'I/. то t£> *£# ; tb = <!, 3, 4). Предположим, что [Л1]
- диаграмма, полученная при удалении клетки из конца \-й
строки [р]. ^ ^
Определим 0L a HompGn-t (м>м J так:
Г о у если п<£г( -й строке {t}j
где /tjf - это {£} без клетки с номером п .
51

Если t стацдартна, то
У. г .
( е-£ у если п£ ii-& строке г f
/ ^z-*-* строке t.
Пусть 7^ - пространство, псроаденное политаблоидами ?£>
ще t - стандартная //-таблица и Л лежит в 1.,-й,
\-й ,... или ДНИ строке £ . Тогда Кг^£Я Мг &;
и ^i Mi= $ ' поскольку стандартные палита&гоидн
порождают £А* •
Для ряда
OsVtf\Ve%$tczYtSVjLnllt%$1Lc:VlS...
выполняется равенство
Но
dim (Vi/(Vi П ¥ег 9L))^dim Ft 9{ -dim SA.
Ъ> $/г/п 5 = dim S >
поскольку размерность модуля Шпехта равна числу стандартных
таблиц. Поэтому на всех местах указанного выше ряда, где это
возможно, имеет место равенство и V{/Vi-i £ (^-изоморфно $л
Это и есть доказываемый результат.
/> (Ч Л ^ d )
9,5. ПРИМЕР. Как FQS^модуль •> ' У имеет ряд с
факторами, которые, если их записывать "сверху вниз", изоморфны
соответственно £ (%*х)^ £(*>2>> *У} S &> л*> i) (ср.
пример 17.16)4
^Теорема ветвления играет важную роль в изучении всей
совокупности групп (5Гл,л^4,...,и, в частности, их индуктивного
предела - группы финитных подстановок бесконечного счетного
множества. Удобно проиллюстрировать теорему ветвления с помощью
градуированного графа, который называют графом Юнга;
соответствующий рисунок приведен в приложении. - Прим. ред.
52

10. Ч> -РЕГУЛЯРНЫЕ РАЗШЕНИЯ
Мы ввдели, что модуль либо нулевой, либо
неприводимый и что он может быть нулевым, только если основное
поле имеет простую характеристику <fi . Чтобы различать
разбиения, для которых 3 ^содержится или не содержится в S^ »
мы введем следующее
ЮЛ. 0ПРЩЕ1ЛЕНИЕ, Разбиение ft называется <р-сингулярным,
если для некоторого г
В противном случае и -^регулярно.
Например, (Q**^ «5^ 4) ^р^регул^рно тогда и только
тогда, когда sf>*5*
Класс сопряженных элементов в группе называется -f>
^регулярным классом, если порядок элемента из этого класса не делится
на ^>.
10.2. ЛЕММА. Число *р-регулярных классов в &п равно чис-
Ш ^--регулярных разбиений 71
Доказательство. Записывая подстановку (ft в виде
произведения непересекающихся циклов, видим, что порядок ОТ не
делится на <р тогда и только тогда., когда длины этих циклов
не делятся на ^о . Поэтому число -р-регулярных классов <S^
равно количеству разбиений ft числа П , у которых ни одна
часть jU; не делится на р.
Упростим теперь следующую дробь двумя способами:
(i - ее) (4. - х*) ...
I) Сократим равные множители (i- X "?) в числителе и
знаменателе. Остается
и коэффициент при х" равен числу разбиений п ,ь которых
ни одно слагаемое не делится на -f (разбиение (... 3 > Л , 1 J
53

соответствует выбору х^ из первой скобки, (х*)^ из второй
и т.д.).
2) Для каждого т разделим d. - х "Р в числителе на
1- ос171 в знаменателе, получая в результате
ft (^x^(x-)^...+ (xVfi").
Здесь коэффициент при %- - это число разбиений Л 9 в
которых никакое слагаемое не входит -р или более раз.
Сравнивая коэффициенты цри х Л , получаем нужное равенство
(читателя, которого беспокоят вопросы сходимости, мы отсылаем к
параграфу 19.3 из /3/).
ЗАМЕЧАНИЕ. Подобно большинству комбинаторных результатов,
относящихся к о -«регулярности, лемма 10.2 не требует, чтобы р
было простым, и только при переходе к теории представлений мы
не должны допускать составных р.
Мы хотим теперь исследовать целое число о^ , определенное
следующим образом: "
10.3. оА= н.о.д. {<£-*, et*yj%* et* - политаблоида в S^f-
Важность этого числа состоит в том, что это наибольший общий
делитель элементов матрицы Грама относительно стандартного
базиса модуля Шпехта. (Следствие 8.6 показывает, что каждый
политаблоид можно записать как целочисленную линейную комбинацию
стандартных политаблокдов.)
10.4. ЛЕММА (А/). Предположим, что разбиение у/ имеет 2
частей, равных / . Тогда [J % • .' делит Q*4 л_ ^делит
ГТ(г.П' Г" ' d (
ЗАМЕЧАНИЯ. Поскольку 01 ** I , бесконечные произведения не
приводят ни к каким трудностям. Некоторые целые числа,
участвующие в определении о-14 , могут быть нулевыми или отрицательными,
но мы принимаем соглашение, согласно которому, например, н.о.д.
'-3, 0> С}«3.
f
Доказательство. Определим отношение
эквивалентности ~ на множестве jw-табловдов так: {i±}r\j {t^ecm и
только если для всех г и j числа % j принадлежат одной
54

строке {£<J в точности тогда» когда они лежат в одной строке
Проще говоря, это значит, что можно перейти от -[i^j к -ftЛ,
перетасовывая строки• Класс эквивалентности имеет величину
Далее, если £t±} входит в е± и i^}^ {^л}> то из
определения политаблоида следует, что ft Л входит в е±% причем
только от {"£*} и ftx} зависит, будут коэффициенты (равные
+1) иметь одинаковые или разные знаки. Поэтому каздые два поли-
таблоида содержат общее множество таблоидов в количестве,
кратном ГТ *; Г , так что qf делится на ГТ z; ! (ср. при-
мер 5.4).
Пусть теперь t - любая уу.-таблица; получим из ~t
таблицу i* , обращая порядок чисел в каадой строке i . Например,
если t - 5 е ^ , то t* - f g s •
2 9 10 iot 9 8
ii
Я
Пусть dC - элемент столбцового стабилизатора для t *
обладающий тем свойством, что для всех i числа i и i(fc
принадлежат строкам одинаковой длины в f . (Выше, в примере, ' 0£~
может быть любым элементом группы (SV5 si * (S>fgigi^&r4f4o\^)
Тогда £i%} входит в е^ и et* с одинаковыми
коэффициентами. Легко видеть, что каждый таблоид, общий для е± и <?^* f
имеет такой вид. (В приведенном примере каадый таблоид, входящий
в €+ * , содержит единицу в первой строке. Рассматривая €-t?
ввдим, что общий таблоид не может содержать число 5 или 8 в
первой строке. Возвращаясь к С/* , получаем, что число 2 должно
быть^ первой строке общего таблоида и т.д.) Поэтому \^^Уе±лУ~'
л ГТ (% Т) </ и лемма доказана.
10.5, СЛЕДСТВИЕ. Простое число & делит д^ тогда и
только тогда, когда А/ з-сингулярна. °
Доказательство . Диаграмма J* является р-
сингулярной тогда и только тогда, когда р делит х: / при
некотором / , а это бывает как раз тогда, когда о делит ^^
<Е0.6. СЛЕДСТВИЕ. Если t * получается из //-таблицы t
обращением порядка чисел в каждой строке, то *^* щ кратно с^..
55

причем коэффициент пропорциональности не делится на р в
точности тогда,, когдаju ^-рехулярна.
Доказательство. Следствие 4.7 показывает,
4X0 €i* *t кРатно Ч > скажем е^+ $+ « ^et ♦ Далее,
*-b<4>{i}>-<**t*{t}>-
Посл§дняя строчка доказательства лемш 10,4 показывает, что
k "Д (*}•)*> а это ^сло взаимно просто с -а как раз тогда,
когда ju р-регулярна.
И. НЕЯИШОДЙМЫЕ ПРЕДСТАВЛЕНИЯ (51
Обыкновенные неприводимые представления (3^ были
построены в конце разд. г. Предположим теперь, что основное поле
имеет характеристику <р ; случай нулевой характеристики при этом
также не исключается, он соответствует -р= °°-
ИЛ. ТЕОРЕМА. Пусть модуль *> определен над полем
характеристики f> . Тогда модуль ненулевой в
том и только том случае, когда J4 ^регулярна.
Доказательство . Включение h имеет
место тогда и только тогда, когда равенство <^^У^У ^ О
выполнено для каждой пары политаблоидов et и Z-t* в £^.
Но это равносильно тому, что j> делит число ^ , которое
определено в 10.3; следствие 10.5 дает желаемый результат.
Мы вскоре докажем, что все неприводимые -^§1 -модули
эквивалентны определяемым ниже модулям J)
^Напомним, что "обыкновенными" автор называет представления
в векторном пространстве над полем характеристики нуль. - Прим.
перев.
56

-И.2. ОПРЕДЕЛЕНИЕ. Предположим, что характеристика Нравна
Ф (простому числу или с*> ) и что ju ^регулярно.
Положим
X-SZ/CS'aS?).
F F /\ Г F /'
Как обычно, мы будем опускать индекс р , если наши
результаты не зависят от поля*
Чтобы доказать» что различные модули JJ не изоморфны, нам
понадобится обобщение леммы 4Д0, утвервдавдей, что S1
переходит в нуль при любом гомоморфизме из KonvfPt^ (14 >Mj9 если
не выполнено условие Я &J4. «-
31.3. ЛЕММА. Предположим, что Л jl Н~газбиения л jg_
% -^регулярно. Пусть J/ - подмодуль ri^ Ж.предполоим^
что в - ненулевой /TS1. ~гомомотДизм из £л &Мл/У-
Тогда Я g? /и, и если jUyu, _то. /m 0c: (S^+l/J/lf.
ЗАМЕЧАНИЕ. Выбор подмодуля V не имеет значения при
доказательстве зтого результата. Существенная часть леммы состоит в
том, что для ^^регулярного разбиения Л модуль Зл
переходит в нуль при каадом гомоморфизме из Нот,^ ($ >М/4 ]; если
нарушается условие Д &р (ср. следствие 13.17).
Доказательство (см. ^Q7). Пусть t есть Д-
таблица и i* - таблица, которая получается при обращении
порядка элементов в строках t . По следствию 10.6
е^ас^-Ае^, где h±o.
Но 4ittQ = Zt**tO **ei* V *i • Поскольку #£0 и
гомоморфизм $ ненулевой, то е{* 9&t + I/ По лемме 4.6 Я &/*.
и если Л =/*
>
то
^0-A"'et# в«£-
- злемент .кратный ^ + Jf€.
Поскольку б£ поровдает £ , лемма доказана.
И.4. СЛЕДСТВИЕ. Предположим, что Л j_ у" -даЙЮИЯ. Л
к. Л^-дижияиляо. Пусть У - подмодуль Л , жлввшют
ложим. что 0 - ненулевой /TS^ -гомоморфизм из ,2? З.П /U.
~&-1 57

Tssm. 1й]ч _и HojUj _есот UsS^
Доказательство . Можно поднять $ до ненулевого
гомоморфизма из Нот^ (S^M^/lf) следующим образом:
8десь первая стрелка означает канонический гомоморфизм.
Поэтому, согласно лемме, Я ^> f^ . Если ji^ju , то
Irn в .- ненулевой подмодуль в (S^+V) IV > так что V
не содержит S **.
43.5. ТЕОРЕМА (/77). Предположим, что основное поле имеет
характеристику <р (простую или равную <=ю ). Если ft
пробегает -ft-регулярные разбиения п , то с^ пробегает полный
набор неэквивалентных неприводимых Р&х -модулей. Каждый
модуль Д) самодвойствен и абсолютно неприводим. Каждое поле
является полем разложения для ($>к .
Доказательство . Теоремы 4.9 и ИЛ показывают,
что Д)^ самодвойствен и абсолютно неприводим.
Предположим, что fJ)% ^ jO^1* Тогда имеется ненулевой
Р&п. -гомоморфизм из фл в М^/(£**П S^1) и по следствию
И.4 Л ^уи # Точно так же л/ ^ Я * так что jl-yv.
Мы показали, что различные ^ не изоморфны; остается
ответить на вопрос: почему получены все неприводимые представления
над Р ? В разд. £7 мы докажем, что каждый композиционный
фактор регулярного представления над Р изоморфен некоторому ф***
тогда теорема 4.1 дает нужный результат. Вместо того чтобы
следовать по этому искусственному пути, читатель, возможно,
предпочтет принять два результата из теории представлений, которые
мы цитируем^ по Кэртису и Райнеру /2]:
КЭРТЙС И РАЙНЕР, 83.7: если (Q - поле разложения для
группы и , то любое поле является полем разложения для Тг.
КЭРТЙС И РАЙНЕР. 83.5: если F1 - поле разложениядля (г^
то число неэквивалентных неприводимых АТ/ниодулей равно чис-
Ж -Р -регулярных классов в G .
^ Приводимые формулировки суть лишь следствия цитированных
результатов, в частности вторая есть фактически теорема Брау-
эра. - Прим. ред.
58

Так как по теореме 4Д2 Q - поле разложения, полнота
списка неприводимых представлений следует теперь из леммы 10.2.
Более подробно (для того, чтобы использовать абсолютную
неприводимость Р^); нужно соединить предложение 83.5. Кэртиса
и Райнера со следующим результатом:
КЭРТИС И РАЙНЕР,82.6: число неэквивалентных абсолютно
неприводимых JTGr -модулей не превосходит числа ^регулярных
классов в G •
Теорема 1.6 дает
И.6. ТЕОРЕМА. Размерность неприводимого представления
tyf** группы Sn над полем характеристики -р равна -р -рангу
матрицы Грама относительно стандартного базиса в £.
-И.7. ПИШЕР. Мы уже иллюстрировали применение теоремы <И.6
в примере 5.2* Рассмотрим теперь разбиение {2+2). Матрица Грама
для него равна (см. пример 5.4)
Ее f-ранг равен ОД или 29 если f« 2,3 или > 3 соответственно.
Поэтов $(*»XJ/(S(X>lJ П S(XtXjL)L0, если chaiF-X и
dim ${%'*=i или 2, если ЫшгГ^З ют > 3 соответственно.
И.8. ТЕОРЕМА. Размерность каждого нетривиального 2-модудяр-
ного неприводимого представления группы (ь^ четна.
Доказательство . Если jij* /п) и i~ _//-таб-
лица, то \еt > е-ьУ четно как порядок столбцового
стабилизатора t . Следовательно, если cfiazjr*^ Ху то <\> > - кососиын
метрическая билинейная форма. Хорошо известно, что
знакопеременная билинейная форма имеет четный ранг, так что теорема II.6
дает нужный результат.
ЗАМЕЧАНИЕ. Теорема 3/1.8 есть частный случай общего
результата, согласно которому каждое нетривиальное
самодвойственное абсолютно нецриводимое 2-модулярное представление группы
имеет четную размерность.
Гомоморфизм 9 в доказательстве теоремы 8Д5 переводит
{t'}*v в {t}xtj>t ф v и J&it-S*'1'- Таким
образом, если V ^.-регулярно, подмодуль 3я , порожденный
ftj^ij*** изоморфен $&' . В терминах групповой алгебры
59

Р&п, это означает, что правые вдеалы, пороаденше j^#f>>£
(для каждого разбиения с ^0-регулярным сопряженным разбиением
выбирается одна таблица t ) , дают все неприводимые
представления (S^ над F] скал F*= -Р ( f) цростое или равно оо ).
12. КОМПОЗИЦИОННЫЕ ФАКТОШ
Выясним теперь, что можно сказать о композиционных факторах
модулей й^ и S^ в целом. Если основное поле имеет
характеристику нуль, все композиционные факторы для У^^известны (см.
разд. 14). Задача определения композиционных факторов 3^
для поля простой характеристики все еще открыта (все опублико-
|ванные алгоритмы для вычисления полных матриц разложения для
произвольных симметрических груди дают* некорректные ответы) -
Начнем с обобщения теоремы 4.13:
12.1. ТЕОРЕМА. Вое композиционные факторы для ТУ^имеют вид
jDА _с_ %!> /и. щ за исключением случая, когда разбиение /Ч,
^р ^регулярно; в этом последнем случае модуль J)^ входит в
композиционный ряд в точности один раз.
Доказательство • Рассмотрим следующий рисунок:
S'ls"1
h
По следствию 11.4 все композиционные факторы для
имеют вид $г с % >ft . Но S-^1 изоморфен модулю,
двойственному к М*4*/ 3^ и поэтому имеет те же
композиционные факторы, но в противоположном порядке. (Cte. 1.4; следует
60

учесть, что все нецртодимые JPS^ -модули самодвойственны).
Далее, 3-^/(3 П S J отличен от нула в точности тогда,
когда ft ^регулярна, и в этом случае он равен J)^
Поскольку 0 d S^D S/USS^^VK Для К^. теорема
12Л доказана.
£2.2. СЛЕДСТВИЕ. Если разбиение ju. *#«»регудярно, имеет
единственный верхний композиционный Фактор ^)/t- S^/fS*1 Г) S^1)*
Если ^ - композиционный фактор для S^D S-^l то фО*фл
для некоторого # £>^ . Если\ JZ ^-сингулярно, то все
композиционные факторы для SJ%C имеют вид 3) л с_ .Я Рул
Доказательство . Это непосредственное следствие
теорем 4.9 и 12Д.
Матрица разложения группы содержит кратности ^модулярных
неприводимых представлений в обыкновенных неприводимых
представлениях, приведенных по модулю А) . Следствия 8.11 и 12.2 дают
12.3. СЛЕДСТВИЕ. Матрица разложения (5^ для простого ^°
имеет вид
5^ (/* f -pei-улярно) </
где ^регулярные разбиения размещены в словарном порядке перед
всеми ^.^сингулярными разбиениями.
12.4. ПРИМЕР. Вассмотрим 77=3; S] **£) - тривиальное
Т^чмодулярное представление; S(i^- знакопеременное
представление и $№ Я£ S ^ тогда и только тогда, когда f=A*
Используя пример 5Д, находим матрицы разложения для <§а :

я
d)
$®
SM
$ач>
и
1
i
J
$(U)
$(*3)
r cm *
Out)
для р= 3}
У
дляр 3
С Опущенные матричные элементы равны нулю.)
13. ПОДОСТАЕДАРШЫЕ ГОМОМОРФИЗМЫ
Картер и Люстиг Д/ заметили, что идеи, используемые при
построении стандартного базиса для модуля Шпехта, могут быть
применены для построения базиса в Уотрд (S \ М ^)> если
скол JPФ И . Мы приводим ниже их'рассуэдения с некоторыми"
упрощениями; в рдде случаев основное поле может иметь
характеристику 2.
Мы сохраняем прежние обозначения для модулей о и М ,
однако удобно ввести новое описание М ^ . Оно требует
введения таблицы 7"1 > имеющей повторяющиеся элементы; мы
используем заглавные буквы для обозначения таких таблиц. Таблица Т7
имеет тип ju , если для каадого г число г входит в
Т7 /и. раз. Например,
2 2 11
1
- это (4, 1)-таблица типа (3, 2).
13Л. ОПРЕДЕЛЕНИЕ.
^/Я^)« {Т \Т есть Л-таблица типа /*} •
62

ЗАМЕЧАНИЕ, fo может быть любой последовательностью
неотрицательных целых чисел, сумма которых равна п . Например,
если /1 = 10, можно взять /с s (4, 5, 0, 1). Определение
Р4^ как подстановочного модуля для <£>Л , построенного по
подгруппе Юнга, не требует условия J^-i^f^*/? '"*и JML &
В оставшейся части разд. 13 t будет заданной
^таблицей (типа ( in J ).
Если Т £ £Г(#,/Д пусть (i)T обозначает элемент Т,
находящийся на том же месте, на котором I стоит в таблице -£.
Пусть (В*л действует на 4T(ljju,) так:
Действие ОС , таким образом, сводится к перестановке мест;
ОС" входит в определение для того, чтобы получилось
корректно определенное (^-действие.
13.2. ПРИМЕР. Если Ц13 45 и Т= 2 2 1 I, то Т(1 2 ) =
2 1
= 12 11 и Г« 2 3) « 2 11 I
2 2 _
Поскольку Gk действует на У(1>}/*) транзитивно, а
стабилизатор точки является подгруппой Юнга (Ьу^ , мы можем взять
в качестве М^С векторное пространство над F1 , порозден-
ное таблицами из ^(2,/у . Вскоре выяснится, почему мы
определяем Pi ^ способом, зависящим как от jtc , так и
*от Я.
Если Т! и 7^ принадлежат ^Г/Я^д), мы говорим, что
7J и 7. эквивалентны по строкам (соответственно по столбшм),
если Т = Т Я Для некоторой перестановки (jf из строчного
(соответственно столбцового) стабилизатора заданной #-таб~
лицы t.
13.3, ОПРЕДЕЛЕНИЕ. Если ТС (T^j^Jy то определим
отображениеWcp так:
М {*}5-^2,{Ti/,T1 эквивалентна Т по строкам] 5 (S€R%).
63

Jfonw проверкь. что й^принадавжи- Ут.^ (М^М**) Я
13.4. ПРИМЕР. Если i~± 3 чS ж Т= Я Л ± i, то
X *
I"» Г 1 i 1 i 1 i
{t}(i x i)Q„~x i i ± + a zi . i i i a+ mxi + x ±i%±
1 r * >■ >■ <■ ',,„.
1
Заметим, что для того, чтобы выписать ft J (?т Р следует
просто сложить все различные таблицы, строки которых содержат
те же числа, что и соответствующие строки 7* •
Ясно, что
13,5» Тх± - 0 тогда и только тогда, когда некоторый
столбец Т содержит два одинаковых числа.
Если определить 9Т как ограничение 9^ на <£ , то
из 13.5 следует, что иногда $т равен нулю, поскольку
ei ^т~$}0т^± 'Что^ы исключить такие тривиальные элементы
tfomp~ (S^ M *** )> Ш в5шнимавм следующее
33+6; ОПРЕДЕЛЕНИЕ. Таблица Т7 долуотандартна, если числа
в ее Строках не убывают, а в столбцах - строго возрастают.
Цусть % fyf**) - множество полуставдартных таблиц в $Тх%н).
13.7. ПИИЕР. Вели Л=(*> О и />~(М, *)'*°%(лл)
состоит из двух таблиц 1Л 2 г и £ i 2 3.
Мы намереваемся доказать, чтв гомоморфизмы й^с Т из
^0 (Я, /О обычно задают базис в Tfom,p& (S\jyi^).
Эти гомоморфизмы мы будем называть подустандартшши гомоиор-
гзмами; так же как и в случае стандартного базиса модуля
ехта, трудная часть задачи состоит в выяснении того, будут ли
^См. ниже. -Прим. дерев.
*'Табловд -[ij - циклический вектор модуля М в
реализации 4Л; значения &? рассматриваются как элементы
модуля М4^ в реализации 13.2. Корректность определения легко
проверяется. - Прим. дерев.

полустандартные гомоморфизмы порождать Копьр^ (£л М&\%
Доказательство того, что они линейно независимы, использует
частичный порядок на классах [T*J эквивалентности по
столбцам таблиц из Ф(% ft) (ср. ЗД1 и 3.15).
3:5.8. ОПРШЛЕНИЕ. Пусть [T^j^J [71] ? если/^ J можно
получить из [TW переменой мест w и х , где их
лежит правее, чем х в Т± (не обязательно в одной строке),
и ух < х . Тогда <3 поровдает частичный порядок <3.
13,9. ПШЕР* Для %=(ВЛ) и у*/- (&>*>>i) следующий граф
указывает частичный порядок на классах эквивалентности по
столбцам:
Существенное, хотя и тривиальное, свойство этого частичного
порядка состоит в следующем:
13.10. Если Т"7 полустандартна, Т' строчно
эквивалентна Г и Т 9ФТ, то [Т']^[Т].
13.11 .ЛЕММА . Гомоморфизмы из множества /ft- /Тв^ (&>/ч>
_линейно независимы в Кот ^^ fS^M^).
Лз^ v ;
Доказательство' (ср. леммы 8.2 и 8.3). Пусть
^агр вгп - линейная комбинация гомоморфизмов с Т из
^ (jI^JUJ? в которой не все коэффициенты нулевые; выберем 7J
так, что dT ф 0 , но ат - 0 при [Tj<* [T]'. Тогда из
65

определения вт и 13,10 получаем
1*/^ ат "т *= ат± *i + линейная комбинация
таблиц 7^ , для которых [T£]^[Tt].
Поскольку столбцовый стабилизатор £ сохраняет классы
эквивалентности по столбцам и ^а?^ О, мы имеем
Поэтому ^> а^ &т — ненулевой элемент "Hom.Ps. (SlM^Jj
как и утвервдалось.-
Необходимо соблюдать осторожность в случае, когда основное
поле имеет характеристику 2:
ЗЗД2. ЛЕША. Предположим, что 0 - ненулевой элемент
F&n. (^Я> ^~^У~> и запишем
где ^ - заданная Я-таблица. Исключая случай, когда
сЖаг Р= A., и разбиение Я является 2-сиигулярным, имеем
ft) Су* * 0 для любой таблицы Т7* , имеющей
повторяющиеся элементы в некотором столбце >
(и) С + 0 для некоторой полустандартной таблицы 7^ .
Доказательство. Часть (г). Предположим,
что Ц* j находятся в одном и том же столбце i: и (г)Т*~
9 (J) Т . Мы хотим доказать, что е~,# - 0.
Поскольку яг± (i>j) =~ &± >
следует, что ^у* - 0 * когда
сАаг jP£ 5.
Если сксьг Р^ St и J? 2.-регулярно, то пусть <f
будет перестановкой, обращающей порядок чисел в каждой строке t.
По следствию 10.6
66

поэтому 2 ст Т- {*} %€ 6 ={tj э>£ eacxt =Ж% Тж^.,
Согласно -13.5, никакая таблица со столбцом, содержащим
повторяющиеся элементы, не входит в JS Ог^Тагзе^ , так что
Часть (^V • Если <f принадлежит столбцовому
стабилизатору <£ , то <t-hati'XJ'K аннулирует -fi}^ * Поэто-
откуда
СТ± * ± с Тх ? если Т^ и Тх эквивалентны
по столбцам.
Поскольку Qf 0 у мы можем выбрать таблицу 2J так,
что ст £ о » но гтя О , если [Т£]<1 [Т] •
Предыдущий абзац и часть (г) леммы показывают, что мы можем
считать числа в столбцах Т± строго возрастающими сверху вниз.
Доказательство будет закончено, если мы сможем привести к
противоречию предположение о том, что для некоторого ^
элементы (х±< ох< *.* < аг составляют ^-й столбец Т± ,
элементы в± < $%< «*• < в * составляют (j + d )-й
столбец Т± и с*ъ> & о, ЦРИ некотором ^ :
ч
л
/\
°9 > **
А
А
Пусть ее л - элемент, стоящий в ( ?•"> </)~й клетке
таблицы t , и пусть J? (^рл ауб" - элемент Гарни для множеств
1хУ'->хуУ и faw+i,. >хср,}+± }.~Тогда
Для любой таблицы Т TJSfif* б)& является линейно*
комбинацией таблиц, совпадающих с Т на всех местах, за
исключением (i.>i+i),faj+t)>->(fyj+*l fy>j)r~>(*>j) '
67

Вое таблицы,входящие в Т±21 fig* фб", имеют
коэффициенты ± Crjr у и, поскольку сумма ^>! ст TJE (4рп &)<Т
равна нулю, должна найтись таблица ТФТ± о стф 0,
которая совпадает с ^ на всех местах, кроме указанных выше.
Поскольку &±< ♦..<i^<a^<... <аг , должно быть [TJ<3
<J [Т], a это противоречит нашему первоначальному выбору Т±.
13ЛЗ. ТЕОРЕМА. Множество {6TJTe;% (lyj*,) }
составляет базис в Кош р^ ($л yjMlJ^J* за исключением случая.
когда сааг р= \ и разбиение Л 2-сингулярно,
Доказательство. Пусть £ - ненулевой элемент
tfcmF€r (3*>М^). По лемме 13.12
[t] *ь 6 =2 ст Г,где ст + 0 для некоторой 7^ еГ(л;д).
Можно предположить, что ст^^ > если ^^^efts/i)
и £7У<3 [TJ- Тогда по 13.10 {t} £± (& -Ст^ dTJ
является линейной комбинацией таблиц Т% с [Т^]^ [T^J.
По индукции 9-ст tr есть линейная комбинация
полустандартных гомоморфизмов, поэтому 0 будет линейной комбинацией
полустандартных гомоморфизмов. Теорема следует теперь из леммы
13.11.
13.14. СЛЕДСТВИЕ. За исключением случая, когда ckcL\F=%
Л ^ 2-гСингулярна, с/ып %>пгр£' (S^jftl^J совпадает с
числом полустандартных Лттаблиц типа ft.
ЗАМЕЧАНИЕ. Если 9 получается из ft переупорядочением
частей (например, Jt = (4, 5, 0, 1) и 9 = (5, 4, 1)),. то,
очевидно,
dim &» ($\ММ)= dxm Шшр&^ (S^M*) .
Иначе говоря, мы могли бы выбрать иной порядок на множестве
целых чисел в определении 13.6. Поэтому число полустандартных
таблиц данной форды и размера не зависит от порядка, который мы
выбираем на элементах таблиц. Ниже в качестве примера указаны
элементы $1((Ч,*),(*,Я, {)) для различных упорядочений мно-
68

жества £i9 %, 3j:
112 2, I I 2 3, если I<2<3,
3 2 11, 3 2 2 1, если 3<2<1,
2 I p
113 2, 1122, если К 3< 2.
2 3
13.15. СЛЕДСТВИЕ. За исключением случая, когда скаг Р^ Л
£ # 2-оингулярно, каждый элемент из Ношр^^ (S\ M*_)
можно продолжить до элемента из
Доказательство. 0^ можно продолжить до 9Т ♦
Конечно, следствие 13.15 тривиально, если с/шъ Р^ D>
но мы не знаем прямого доказательства в общем случае.
Теорема 13.13 и следствие 13.15 могут нарушаться, если
chat Р^ % и разбиение Я 2~сингудярно. Это видно из
следующего простого примера.
Т . ][ —
13.16. ПРИМЕР. Если ckw Р~ X > то формула тг + j ~*LiL
определяет элемент из Нопър^^М^который нельзяНпродолжить
до элемента из Могару (H(i'\M(i*)-
^3.17. СЛБЩСТВИЕ. За исключением случая, когда сАагР=%
и разбиение Я 2-юингулярно, 1&f<> влечет за собой
Доказательство . Имеется только одна
полустандартная % «-таблица типа /с , если Я^/t > и ничодной,
если Л Ф ft (ср. доказательство леммы 3.7). Следствие
13.11 дает нужный результат.
Следствие 13.17 уже было доказано в предположении, что
разбиение Я j4-регулярно (лемма 11.3), а теперь мы дадим
другое доказательство для случая, когда ckct% Рф%.
Пусть $eJfom,F(gn (S^M-^Jj и предположим, что t есть
% «таблица и tt есть ju -таблица. Если Л ф]^ или
если 1 ~ju и {Ь±У не входит в et , то некоторая пара
чисел а,2> лежит в одной строке 1± и в одном столбце t.
69

Поэтому
~-<<*о> ЫМ>--<ч е> {**}> <
Поскольку ска% Рф%, <(е± 0,{*±}У= 0 , Это доказывает,
что 0~ о у если Л ф уц, и что при %~fi в е± $ входят
только те таблоиды, которые входят в е± . Если Я-ft и <f
принадлежит столбцовому стабилизатору для i , то <Се± 0 ~fi}%)>-
а отсюда ввд-
но, что в^ в — <^f в , {Ь}У C-t - Таким образом; $ -
оператор умножения на константу,
13.18. СЛЕДСТВИЕ. Модуль $% неразложим, за исключением
случая, когда cka% F~ X j$_ Л есть ^юинтулярное
разбиение.
Доказательство. Если бы S был разложимым, мы
могли бы взять проектор на одну из компонент и построить
нетривиальный элемент Honvpg (S\M г J , вопреки последнему
следствию. л
ЗАМЕЧАНИЕ. Существуют разложимые модули Шпехта - см.
пример 23.10 (щ).
При исследовании теории представлений полной линейной
группы нам понадобится простая
13.19. ИОРЕМА. Множество {^т1Те^Г(^) и числа в
отроках Т не убывают } составляет базис в ^^r^Qi^M^J.
Доказательство. Наше множество
гомоморфизмов построено с помощью выбора представителей Т±,Тх,...,Ть
из каждого класса строчной эквивалентности в tTfaju) .
Линейная независимость этого множества следует из определения 9Т
Предаоложим, что 0- элемент ffomjr^n (Мл> М*).
Если Т и ^эквивалентны построкам, то Т' = 73гДО
некоторого с в Rt , так что
70

Следовательно,
и, поскольку -Мл- циклический модуль, 0 является линейной
комбинацией гомоморфизмов 9— , как и утверждалось:
i-i
Т£
-14. ПРАВИМ) ШГА
Теперь можно явно описать композиционные факторы моду-
лей Л£
14.1. ПРАВЙЙО ЮНГА. Кратность $$ как композиционного
фактора в М^ равна числу долустандартных ..Я-таблид типа
Доказательство. Поскольку (8 - поле
разложения для ®* 9 число, которое мы ищем, есть Жт Vom^^^S^M^
см. 1.7. Но оно же равно числу полустандартных Я-таблиц
типа ju , согласно следствию 13.14.
ЗАМЕЧАНИЕ. Независимое доказательство правила Юнга
появится в разд. 17.
Правило Юнга показывает, что композиционные факторы для
М $ получаются при выписывании всех полустандартных таблиц
типа м , которые имеют форму диаграммы разбиения.
ЛА (з, а, &)
14.2. ПРШЕР. Вычислим факторы для Nfi .
Полустандартные таблицы типа jit таковы:
71

1112 2 3 3 1112 2 3 1И22
3 3 3
II 1233 11123 1112 3
2 23 2
3
1112 f 1 I 2 И133
2 33 2 3 2 2
3
1113 1 I I 3 И1
223 22 223
3 3
111
2 2
3 3
Поэтому в обозначениях п. 6.4
[3] [2][2] =С7] + 216, 11+ 3[Б. 2]+2[4, 3] + [5, I2J +
+2[4, 2, 1]+[32, 1]+[3, г2].
ЗАМЕЧАНИЕ. Правило Юнге дает один и тот же ответ, каким
бы образом мы ни выбирали порядок целых чисел в определении
"подустандартностя"; не требуется также, чтобы разбиение ju,
было собственным.
м <**>
14.3. ПРИМЕР. Факторы модуля ■!■ 1@ задаются как таблицами
•13:122 1112 111,
2 2 2
так и таблицами
2 2 1 I I 2211 221.,
1 11
Поэтому[3] [2]=[б]+[4, lJ+Гз, 2] (ср. пример 5.2).
14,4» ПРИМЕР. Если mf-n/t, ,то
/"fi-m)mJ=[n.j+rit-l)lJ+[A-l>«J+... + //i-/n,/nJ.
Поскольку dim. М(л'т'":)^ (^ ) , получаем, что
dun S - \т.)~ \т- l J '
72

Согласно правилу Юнга, о^ как композиционный фактор
дяя PIq имеет кратность один, а другие модули Шпехта Si ,
которые ms получаем, удовлетворяют условию jIojh , в
согласии с теоремой 4*13. Вспоминая, что это означает, что матрица
т=(шлр) • описывающая кратности факторов для М@ с
переменным Л (см.6.1), является никнетреугодьной и имеет
единицы на главной диагонали, мы можем использовать правило Юнга и
записать модуль />] как линейную комбинацию членов вида
£**}[**.]••• №а J # (Cn0C0(J сделать это в явном виде
задается детершнантной формой, см. разд. 19 .) Следовательно, мы
можем подсчитать выражения тива
для натуральных 9± >... y ^ • Более общим образом, правило
Юнга дает возможность вычислить [f*][?] ("S^SljG^
дяя любой пары разбиений // и Р . Разложение произведения
[juj £>>J - это предает, правила Литтлвуда - Ричардсона (разд.
16), а рассуждение, которое мы только что привели, показывает,
что правило Литтлвуда-Ричардсона является чисто комбинаторным
обобщением правила Юнга.
14.5. ПРИМЕР. Вычислим [3? 2j/»S^® S(@ f G^ >
используя только правило Юнга. Согласно примеру 14.4,
[з, х]«[з][*]-[ч][1].
Для того чтобы найти /4 J [l] [2], используем правило Юнга:
Ш I 2 3 3 I I I I 2 3 1 I I I 2
3 3 3
I1II33 11113 11113
2 2 3 2
3
1111 1111
2 3 3 2 3
Поэтому
3
I?, 2][2]=[3][2l£2l-[4l[ll[2] 9
и, используя пример 14.2, получаем
?3

[З, 2][2] = [7]+2[6f 1]+зГ5, 2) + 2[4, 3] +
+ [5f 12]+2Г4, 2, fl + [32, l№, 22]-
-М-*Гб. ti-2[5f 2]-[4, 3l-[5f I2J-r4, 2, *J«
= [5f 2]+[4, 3] + [4t 2, IJ+ЕЗ2, IJ+ГЗ. 2*J
(ср. пример 16.6).
15. ШЮЛВДШАТЭДЫЮСИ!
Для того чтобы сфорафлировать в следующем разделе яра*
вяло Литтлвуда-Ричардсона, мы долгий обсудить некоторые
свойства конечных последовательностей целых чисел. Говорят, что
последовательность имеет тип ju 9 если дая каждого I число
i входит в последовательность уи^ раз.
£5.1. ШШЕР. Последовательности типа (3. 2) таковы:
22П1 212II 2II21 21112 I22II
XXV// X V V V V X V V V V X v V V V V • X V V
12I2I I2II2 II221II2I2III22
V V V V V V V V V / у V V V V V V V V V • V v • V
15.2. ОШДМШЙЕ. Ддя заданной последовательности
натуральных чисел качество ее членов определяется следующим
образом (каждый член считается либо хорошим, либо плохим):
( г ) все единицы хорошие,
( ii ) число г+£ хорошее тогда и только тогда,
когда количество предшествующая ещ хороших чисел г строго
больше, чем количество предшествующих ему хороших чисел г^1.
15.3. ПРШЕР. Мы указали выше качество членов всех
последовательностей типа (3, Вот другой пример:
< Знак v в этих примерах стоит под "хорошими", а знак
х - под "пяохими" членами. Таким образом, если выделить
подпоследовательность, состоящую из всех хороших членов
исходной последовательности, то для всякого ее члена число пред-
шествувдих ему единиц не меньше числа предшествующих ему двоек,
которое, в свою очередь, не меньше числа предшествующих ему
троек и т.д. Такие последовательности называются решетчатыми.
Подпоследовательность всех хороших чисел есть таким образом
максимальная решетчатая подпоследовательность. - Прим.ред.
74

3II233232I2
xvvvvxvvxvv
Из определения непосредственно следует, что некоторый
член последовательности г+± является плохим тогда и только
тогда, когда число предшествующих хороших г равно числу
предшествующих хороших i+ d . Ш получаем результат, которой
понадобится нам позже:
15.4. Если последовательность содержит ** хороших членов
вида с-1 подряд, то следующие за ними т членов вида с
все являются хорошими,
15.5. ОДРШШИВ. Пусть f^fo^fxr-)- последовательность
неотрицательных целых чисел, сумма которых равна л- , и пусть
/**=(Р*>/**>—) - *акая последовательность неотрицательных
целых чисел, что дяя всех г
/£**/*? v ■
Тогда yv*ji/ называется парой разбиений для л.
ЗАМЕЧАНИЕ. Как и выше, мы часто будем опускать условие
/Ч^Ла,^ — на разбиение ft, называя все же ft разбиением
л. Если условие /^з^д,^- выполняется, мы будем называть
ft собственным разбиением п . Например, в определении 15.5
ft - собственное разбиение некоторого п,1 sn . Заметим,
что модуль Шпехта 8-^ определен только для собственных
разбиений ft , но модуль М^ t порожденный ft -таблоидами,
оцределен и для несобственных ft .
15.6. ОПРВДЕШШБ. Бели дана пара ft ,ft разбиений дяя п. ,
то пусть 4 (f*>Ji) обозначает множество последовательностей типа
f , в которых для каждого г число хороших г по меньшей
мере равно ft*.
Мы обозначаем через О разбиение числа 0 , так что
-*(0if*) состоит из всех последовательностей типа ft .
Поскольку количество хороших чисел г+i в любой
последовательности не превосходит количества хороших г , мы ничего не
потеряем, предполагая, что /'г*х * ft •
15.7. Вели JL*sj4± и ^t "f^ №* i> 1 >то имеем
л (Я*/y=Tjfit*, ft) t поскольку все единицы в
последовательности являются хорошими.

Поэтому мы можем включить первое слагаемое разбиения я
в у* .
15.8, ЯШМЕ?. * (0> (3> Л)) = S ((з), &*))*
Последовательности во втором и третьем столбцах дают J ((ЗД),
(3,2)), а последовательности з последнем столбце дают 4((3,2),
(3,2)):
<5 ((3), (3,2)) zd *((ЗД), (3,2)) о Ж3,2),(3,2))
2 2 111 21211 12 121
21121 12 112
2 I I I 2 112 2 1
12211 11212
1112 2
Сравните это с примером 5.2, аде П имеет ряд
подмодулей с факторами размерностей I, 4 и 5. Это не совпадение!
Пару разбиений yv#> j4 да изображаем в виде картинки,
напоминающей диаграмму. Будем рисовать линии между строками и
окаймлять fi4 вертикальными линиями. Картинка для m$aj4*fL
всегда будет отождествляться с картинкой, получаемой при
окаймлении всех клеток первой строки (ср. 15.7).
15.9. ПРИМЕР. В примере 15.8 имеем
х XXX JXX X
X X XX 3*|Х]Т
XXX
-=><*
XXX
XX
Эти примеры указывают на необходимость введения
обозначения для операции добавления клетки из jit к /Ч *"• Мы должны
рассмотреть лишь добавление клетки, не лежащей в первой строке.
15.10. ОДтатяГВИИЕ. Предположим, что j4*f*jn. Пусть с -
целое число, большее единицы, для которогоyw^f <juc И/£*~Д..
(i) Boaaf<c_i> ft* , то f**Ac,fi - это пара
разбиений, полученная изуч*,^ заменой JH* на /ч*у- £ . Если
Р*£ "J^c * т0 Jtf'toJ14' совпадает с парой* ot 0. .
( u ) fi^JbTlc - яара разбиений, получаемая из /*Л/с
заменой /*с на уч* */*£-/ ** /'c-iVc ~A#* "
Оператор /?с просто перемещает некоторые клетки,
лежащие вне /и*, в конец расположенной выше строки ( R -
сокращение от гагзе , а Л - от <*с/Ы). В определении Лс и Лс
участвуют как /у# , так и н, напомним, что по предположению
76

/15. И.
jx хх| я>- |х х х|х х =
Гх х х х х]
хх' г
1ГТ1 «грГГТрС
|Ж ' Ш
XXXj
xxl
X X X XJ
111
Другие примеры даны в 15.13, 17.15 и 17.16.
Поскольку Ис поднимает некоторые клетки, а мы всегда
окаймляем все клетки первой строки, каждая последовательность
операций Acfic в конце концов щяводит пару разбиений к виду
%} Л (где, по необходимости, А - собственное разбиение)..
Ясно также, что
#•
15.12. Для любой пары4разбиений// >fi существует разбие-
Р и последовательность операций Лс > /^приводящая от
к//*/.
ние
15.13. ПРШЖР. Для того чтобы получить ((4, 3, 1),
(4, 5, 2*)), применим Л*х J\dRHRsR5RG^RB к (0, (4, 3,
1. 2, 1, 2))
XXX ~* ХХХ| ~* П
Ш
X X
X X X XI
х_
X X
XXXIX
X
X X
2^
XX
XX
М«
АХ XXI _RHHS
XXX
X X
X
X X
X X X XI
X X XIX X
xlx
XX
щем:
Решающая теорема о последовательностях состоит в следую-
15.14. ТЕОРЕМА» Следующее правило устанавливает взаимно
однозначное соответствие между i(/**yv)\ J (/1*ЛС)/<)Я-
3 (f1*) J4-ft с) : для заданной последовательности из первого
множества заменить все плохие числа с на числа с- i .

Доказательство. Напомним, что наше
определение операций Лс и Rc предполагает, чтоу^^-yv^f^ ,
Поэтоаду последовательность J^ из 4 (/**>/<) ^ J(/**$» /Псодер-
жит fc-iL^f1*-*. чисел с-£ (все они хорошие), //*
хороших чисел с и//с-//с плохих с . Плохие с заменяются
на с- L и получается последовательность ^ . Мы
утверждаем, что
15.15. Для всех j количество хороших чисел с-± перед
у-м членом в ^ не меньше, чем количество хороших чисел
с-£ перед J-и членом в <г^ .
Разумеется* это верно дня /W ; предположим поэтому,
что это верно для j=i . Тогда 15.15, очевидно, верно и для
/= £ + 4 , за исключением, возможно, случая,когда ?-й член
есть число с-± , хорошее в ^ , но плохое в /^ . Но в
этом случае неравенство в 15.15 (с j , замененным на I) строго^
поскольку количество членов вида с-л перед г-м членом
одао и то же как в S£ , так и в 4Х . Поэтому 15.15
выполняется для у= i+l также и в этом случав.
Из 15.15 видно, что /^ имеет по меньшей мере fte_±
хороших с-1 и что все с в jx хорошие. Тем самым, для
ifc-{y гФс число г хорошее в 4К тогда и только тогда,
когда оно хорошее в i± , так что -sx принадлежит s(f4^ftReJ9
Труднее доказать, что это отображение взаимно однозначно
и эпяморфно.
В заданной последовательности заменим все числа с- -I
левыми скобками (9 а все с - правыми скобками ).
Например, если Сз3 , то
121231233221-131 а 223
переходят в
1 ( 1 ( ) I ( ) ) ( ( 11 ) II ( ( ).
Далее, в любой последовательности, принадлежащей
*///* ju Яс J у все числа с хорошие. Поэтому каждой правой
скобке предшествует больше левых скобок, чем правых, и
последовательность выглядит как
а каждое fj - замкнутая скобочная система, содержащая^воз-
можно, (члены i с i ф с-1 1 + с.
78

Теперь" ясно, что есть только одна надежда подучить
обратное отображение, а именно изменить направление первых
fc-flt "лишвйх" скобок (именно измененные скобки должны
стать непарными правыми скобками для того, чтобы дать нам
обратный образ).
Пусть б принадлежит iff* yff^cj . Мы говорим, что
число с - 1 черное в 6 , если оно соответствует лишней
скобке, в противном случае оно белое.
Пусть t$* - последовательность, полученная из з
заменой первых fc-J4* черных c-i на с . Мы должны доказать,
что
15.16. Каждое число с~± в /* является хорошим.
Теореш 15.14 будет отсюда следовать, поскольку каждое
с , появляющееся как в 4 , так ив s* % будет хорошим и
4* будет единственным элементом в *01/Ф>/')^ *йчФЯс >/*)>
переходящим в 4 .
Мы доказываем 15.16 в два шага. Во-первых,
15.17. Для каждого члена х в 6 количество белых с-1
перед х не превосходит количества хороших с-± перед jo .
Пусть сначала се - черное число с-1 . Количество
белых чисел с-i , стоящих перед ос , равно количеству чисел
с , стоящих перед ос (по определению "черного")., и не
превосходит количества хороших чисел с-1у стоящих перед ос ,
поскольку каждое с в 4 хорошее. Это доказывает 15.17 в
случае, когда х - черное с- i .
Такое же доказательство показывает, что количество белых
с-1 ъ 4 не больше количества хороших с-1 в j . Таким
образом, мы можем начать с конца 4 и идти назад, замечая,
что 15.17 тривиально выполняется для (у- у-го члена J ,
если это верно для у-го члена, за исключением случая, когда
Q - i)-tL член - это черное с- £ 9 но этот сЬучай мы уже
разобрали.
Далее, имеем
15.18. Либо с-д, , либо для каждого с-± в j*
количество предшествующих хороших с-х больше количества
предшествующих c-i в 4*.
Для доказательства 15.18 предположим, что он . Тогда
з содержит, самое большее,f*e-f*t плохих с-1 , поскольку
79

6 принадлежит «JffW* ju.Rc'), так что для любого с-1 в s
(количество предшествующих хороших с~£)> (количество предаеству-
щих с-1 ) —QWc-Д^ )• Тем самым утвервдеяие 15.18
выполняется для числа c-if . расположенного после juc -juc черных
с- 1 в 4 .
Если член х в з* - это.с-i , стоящий перед (^с -fl£)~*&
черным числом с- ^ в 4 , то х был белым в * . Точно так же
количество чисел о- I , стоящих перед х в *$* % равно числу
белых с-1 , стоящих перед х в J , которое в свою очередь
не больше количества хороших, c-i , стоящих перед х в * • ,
по 15Л7 (причем неравенство строгое, если х - плохое число
c-i в t ,'как следует из 15.17, примененного к следующее
члену), а оно не больше количества хороших с-ь , стоящих перед
х (неравенство строгое, если х - это хорошее с-£ в 4 ),
и 15.18 в этом случае также доказано.
Из 15.18 непосредственно следует 15.16, а это завершает
доказательство теоремы 15.14.
15.19. ПРИМЕР. В примере 15.8 взаимно однозначное
соответствие между 4((3), (3,2))\ s ((3,1), (3,2)) и -J((5)t.
(5)) получается так:
2 2 1-11 —> 11111 .
X К V V У
Взаимно однозначное соответствие между s ((3,1), (3,2) )\
М ((3,2), (3,2)) и * ((4,1), (4,1)) задается так:
21211 112 11
X V V V V
2 112 1
X У V V V
2 1112
х v v v v
1 2 2 I I
V V X V v
1112 1
11112
1 2 I I I
80

те. правшю жгашд/i- ршрдсона
Правило Лвттлвуда-Ричардсона -это алгоритм для
вычисления произведения [л][^]у где Л - собственное разбиение
числа ъ-ъ и /г - собственное разбиение i . Вспомним, что
[2][ju] есть линейная комбинация диаграмм с п клетками и
интерпретируется так: если о9 - коэффициент при [*] , .то
кратность модуля Sq как композиционного фактора в S^&S^ f
t6V равна #,>. Хорошо известно, что каждое обыкновенное
неприводимое представление группы ti-xff эквивалентно представлению
£± х Sx для некоторых неприводимых представлений 2± и £л
групп G z К соответственно* Поэтому правило Литтлвуда -
Ричардсона дает нам возможность найти композиционные факторы
представления &п $ индуцированного любым обыкновенным
представлением подгруппы Юнга.
Отложим на время какую бн то ни било интерпретацию и
рассмотрим аддитивную группу, порожденную множеством {[лЦ Л —
собственное разбиение некоторого натурального числа }. Дяядан-
ной пары разбиений J4*,ft (определение 15.5) мы определяем
эндоморфизм f/4#)/^j* этой группы следующим образом:
16Д. 01РВДЕШИЕ.
где в случае, когда Я; ^ »«. при всех г> о^ есть число таких
способов заполнения клеток [»J \ [Л] натуральными числами, что
(i) числа не убывают вдоль строк,
(и) числа строго возрастают вниз по столбцам и
{"# при чтении строк справа налево, начиная с верхней,
получается последовательность из *(у**/^«
Если хоть одно из условий Л; g"Pi нарушается, то а^О~ ^
^ Разность [*]^[л] двух диаграмм называют косой (skevs)
диаграммой, а заполнение ее клеток числами, для которого
выполняются условия f^if*ii" (подустандартной) косой таблицей.
Последовательность, возникающая при чтении косой таблицы в
указанном выше порядке, называется ее канонической
последовательностью. Если jif^^jti , то условие (сгг ) означает, что
каноническая последовательность решетчатая ^см. предыдущее
подстрочное примечание). - Прим.перев.
81

Если f* =fj и, следовательно, yv - собственное
разбиение, ш пишем [juV вместо Г/ц м1*
Действие этих операторов иллюстрируется следующей леммой
и примерами 16,6 и 16.7.
16,2. ЛЕША, Если р-(р1>Рх,.*.9 J* k)y JPO- jToJ =
~ D^Jf/^J'** £ A/i» J. Вели л/ - собственное разбиение, то
Доказательство. При // « 0 условие. (*ЧЧ )
определения 16.1 просто означает, что мы имеем
последовательность типа J4 . Но /yuijf//jj««« £/"*} по определению
описывает композиционные факторы для j[^/J и первый результат
следует из правила Юнга.
Цусть /V] - диаграмма, входящая б £0j ^^ • Тогда
клетки /")>] можно заполнить уи^ единицами, J4t двойками и
т.д. так, чтобы условия (i) и (itt) из определения 16.1
выполнялись. Предположим, что некоторое t встречается в £-й
строке, причем j<i , и пусть *, - наименьшее число, дня
которого это происходит. В силу этого условия минимальности
не существует никакого i-1 , расположенного выше / ;
точно так же не может быть никакого г - 4 справа от этого I
в той же строке - в силу условия ( с ). Таким образом, при
чтении справа налево по строкам и сверху вниз этому I не
предшествует никакое i- i , так что это г плохое вопреки
условию ( Ш ). В то же время из-за условия (-ii ) никакое I
не может стоять в у-й строке при j>i . Это доказывает,
что каждое I стоит в t-й строке и [*] = [/*]<
те^ joiul. 1№ф%>Ащ+№рЪТ -
Доказательство. Допустим, что ju, есть
разбиение г и что Я и » - собственные разбиения л-г и %,
соответственно с Я^^ для всех L . Заменим каждую клетку в
£/J\[/l] f*± единицами, //д двойками и т.д. так, чтобы
при чтении последовательных строк оправа налево получилась
последовательность из 4 (j4*,jv) \ ^(^Лс)/^). Мы должны
доказать, что замена всех плохих с на c-i дает
конфигурацию натуральных чисел, удовлетворяющую IS Л (г) и (п ) тогда
и только тогда, когда мы начинаем с конфигурации, удовлетворя-
82

щей 16 Л (-i) и (?Ч ). Действительно, левша будет тогда
следовать из теоремы 15.14,
Предположим, что мы еще не заменили плохих с на с- ±
и условия 16 Л( О и (а ) выполняются для нашей конфигурации
чисел. Могут встретиться две трудности. Плохое с , возможно,
находится справа от хорошего с в той же строке» Такого на
самом деле не бывает, носкольку с , стоящее непосредственно
за плохим с , само должно быть плохим. Более сложная
ситуация встретится, если плохое с стоит на (hj)-** месте, ас-1-
на (i-l>j) -м месте. Чтобы разобраться в этом, обозначим через
тп максимальное из тех чисел, для которых на ( i,j )-м, (1у+$-
:.,(г,им- i)-vl местах стоят с . Тогда по условиям 16Л( г )
и (« ) на (i-iyj)-*. (i~l>j+*) ,...,(i-IJ+tn-d)-*
местах стоят *- i . Поскольку все с- ± в последовательности
принадлежащей *(ft*>f*)^ * (ft^ctjO) *°Р°иив» число с на
(i , j )-м месте должно быть хорошим, в конечном счете,
согласно 15.4. Это показывает, что все плохие с можно заменить на
С - ± , не нарушая условий 16 .К г ) и (гг ).
Наоборот, предположим, что после замены плохих с на
£-4 получается конфигурация, удовлетворяющая условиям
16.1(г ) и (-гг )# Исследуем конфигурацию, с которой мы начади.
Она должна удовлетворять условиям 16 Л (-г ) и (гг ), в
противном случае плохое с стоит непосредственно слева от
(хорошего) с- 4 в той же строке иди же плохое с стоит
непосредственно над хорошим с в том же столбце. Первая возможность
не реализуется согласно 15.4. Поэтому следует побеспокоиться
только о ситуации, при которой плохое с стоит на (i-i}j)-VL
месте, а хорошее с - на (i,j)-u месте. Читая
последовательные строки справа налево, видим, что число (хороших)
с- i в (г- *)-й строке слева от нашего плохого с из
(i-l>j)-i клетки больше,или равно числу хороших с ъ *-й
строке. Но для каждого *-i в (i-*)-& строке слева от
(г - i у j J)-го места должно непосредственно под ним, в i-й
строке, находиться хорошее с (поскольку на (*></)-* месте
стоит хорошее с , а в конце получается конфигурация,
удовлетворяющая условиям 16.1 (i) и (гг)). Это противоречит тоцу
факту, что на (t,j)-M месте стоит хорошее с, и
доказательство леммы завершено.
16.4» ПРАВИЛО ЛИТТЛВУДА - РИЧАРДСОНА.
83

Доказательство (£C0J ). Если У -
собственное разбиение п , то, применяя многократно операторы Лс
и Rc к паре 0,J> , получим совокупность пар разбиений со, со-
По лете 16.3 можем написать
где каждое а^ - натуральное число, о^- I и о^.-О 9 если
Следовательно, существуют такие целне числа Vй ^>з»
что
По лемме 16.2
16.5. СЛЕДСТВИЕ. [»]'[ju]'~ [f*]'fy] '= ([?][*]) '
Доказательство. Для всех £Я/
[х]С'Г№-[1][*]М-[ф][*]-
Это следствие крайне трудно доказать прямо. Более общим
образом, из правила Литтлвуда-Ричардсона следует, что дяя
каждого тождества вроде [3][1] ~[5] +[Ч>1] + [3, A J имеется
соответствующее операторное тождество [3]'[%]'** [$]'+[% i]+
Разумеется, теорема ветвления (часть ( i )) является
частным случаем правила Литтлвуда-Ричардсона (см. разд. 9).
При использовании правила Латтдвуда-гРичардсона удобно
нарисовать диаграмму [Я] > а затем дописывать f*± единиц,
f4^ двоек и т.д., следа за там,чтобы на каждом шаге [%]
вместе с добавленными числами имела форму собственной
диаграммы и одинаковые числа не оказались в одном столбце. Сохраним
в ответе только те таблицы, для которых при чтении последова-
84

тельннх строк справа налево каждому г предшествует
большее число i-d • чек I® (sfo условие необходимо в
достаточно для того, чтобн какдна иен бал хороший).
46.6. ПРИМЕР.
Действительно, имеются следующие конфигурации (ср. пример 14.5Х
XXXII XXXI XXXI XXX XXX
XX XXI XX XXI XX
I I II
16^ ПРИМЕР. f3, 2] [2] [2j=£3, 2]И*М'а
XXXII XXXII XXXII XXXI XXXI
ХХ22 ХХ2 XX XXI2XXI
2 2 2 2 2 2
XXXI
XX 2
I
2
XXXII2
XX 2
X XX I 2
XX 2
I
X XX 2
XXI
I 2
XXXI
XX
I 2
2
XXXII2
XX
2
X X XI 2
XX
I 2
X X X 2
XXI
I
2
XXX
XXI
I 2
2
XXX
XX
11
2 2
XXXI2 XXX I 2
XXI2 XXI
2
XXXI2 XXXI XXXI
XX ХХ22 ХХ2
I I 12
2
XXX
XXI
12 2
XXXII22 XXXI22
XX XXI
X X X 2 2
X X
I I
X X X 2
XX 2
II
XXX 2 XXX
XX X X 2
II II
2 2
XXXI22 XX X 2 2
XX ' XXI
I I
^ То есть возникаящая последовательность - решетчатая
(см, примечание к я. 15.3). - Дрш.перев

Мы разместили диаграммы таким образом» что при чтении их
последовательных строк справа налево диаграммы первой группы
(до первой линии) дают последовательности из *((l,x)i(i> %))>
так что
13. 2Jfe, 2j=[3> 2] .[в, 43+Ь. 3f l]+[6t 2*144*. ij+fc 3f 2>
+\Ь 3t 1*1+ [4t 2*, 1]НЗ\ 2, lH3, 2*].
Диаграммы, помещенные выше второй линии, дают [$ х]^9^ щ
Читатель может проверить, что замена плохих двоек'нэ единицы во
второй группе дает тот же ответ, что и разложение [3,Х]&*У
в соответствии с леммой 16.3.
[8. 2] [3f Ib[3.2] 3-£ ДО, 2, 1>[5, 4> 2 [5, 3t 1>
♦ p. 2*J*[5t 2f i^\ l>2[4t3, 2] +pf 3f **J +[33] +[4t2,^
+[3*, 2, 1].
Последняя группа содержит все конфигурации, где обе двойки
плохие; если заменить их на единицы, то по лемме 16.3
[3,2] [4J = [3,2] W= [7.2] + [б,з] + [б,2,</ +
+ [5,3,lJ + [5,22j + [4,3,2j ,
что нетрудно также проверить непосредственно.
17. РЯДУ ШПЕХТА № Л^
Можно получить лучшую форму правила Юнга, пригодную для
произвольного поля. В этом случае М^ имеет ряд из
подмодулей, каждый фактор которого изоморфен модулю .Шпехта. Такой ряд
будет называться рядом Шпехта. Поскольку модуль М^ над
некоторыми полями не вполне приводим, мы должны принять во внимание
порядок факторов в рядах Шпехта. Следующий пример показывает,
что порядок факторов важен.
86

VI Л. ПРИМЕР. Пусть ckaxF делит- п>ц ; рассмотрим
М^±м . Пример 5.1 показывает, что р^С*1*****) обладает
только одним композиционным радом с факторами Д) ,Д>^~**72> и что
S (n~i>lJ также обладает единственным композиционным радом -
с факторами l)^** , p)(tt) t начиная от верхнего. Таким образом,
j£(*>-i,t) He имеет рада Шпехта с факторами S^^^gto ^
начиная от верхнего. Для рада Шпехта в примере 5.1 факторы
следуют в порядке 5^> £(*-*> О
В этом важном разделе мы будем использовать только
теорему 15/14 о последовательностях и получим, с одной стороны,
правило Юнга, а с другой - стандартный базис модуля Шпехта.
В то же время мы охарактеризуем модуль Шпехта £л как
пересечение ядер некоторых FS^ -гомоморфизмов, определенных на
Pi я, если 1 - собственное разбиение. На протяжении этого
раздела F - произвольное поле.
Пусть /**>/* - пара разбиений дая п в смысле
определения 15.5. Напомним, что jit* должно быть собственным
разбиением, тогда как от ju, этого не требуется. Ш хотим
определить подмодуль $<Р >f* в М^ , а дая этого построим объект
ef *^ у "промежуточный" между таблоидом и политаблоидом.
*7.2» ОПРЩ5ВЗШШЕ. Предположим, что t есть.уч**таблица.
Пусть е^ >JU~2{4gn *Ж{Ь}%: fa^G: C± и (Г не действует на
числа вне [ft *jJ .
17.3. ПРИМЕР. Если i = u 3 5} и //*= (3,2,0), уъ=(3,4,2)
(часть t очерчена только дая того, чтобы показать, какие
числа будут двигаться), то
X Ъ 5 d 7 5 & * &
- 1 Ч Ч 9 — X 3 Ч 9 + ± Ъ Ч 9
*/**/<>
VIA. ОПРЕДЕЛЕНИЕ. Чере^ о обозначается
подпространство в Л/Л порожденное еГ ^ при различных t .
Разумеете^, Jf/'V'- это Щ-подмодуль в ЛЛ поскольку
е[ >*т « £ *+£** . Если л** 0, то $***шМ* , а если
J4*~j4 . то S^^S".
87

17.5. Волга*-//, и l?=juf мя г>{ , то ^^^V
так что первую часть разбиения /v можно включить в /чф (ср.
15.7). J
Теперь в игру вступают последовательности.
17.6. КОНСТЕ/КЦИЯ. Ддя заданной последовательности типа
ja построим сбответствующую yv- таблицу t ' следующим
образом. Рассматриваем по очереди элементы последовательности. Если
j -й член - это хорошее г , поместим J как можно левее
в £-ю строку t . ]5сли J-й член - плохое С) поместим j
в 1-4»- строку 1сак можно правее.
17.7. ПРИМЕР.
31 шзхзпиб *f(4 з, хХ (i $ ч))
XVVVVXVVXVY)/
соответствует
И 3 -/о Ы
5 $\b i
Различные последовательности в i (fyyv) соответствуют
таблицам, принадаежащим различным таблоидам, поэтому
17.8. Конструкция 17.6 дает взаимно однозначное
соответствие между 4 (0)f*) и множеством //-таблоидов.
ЗАМЕЧАНИЕ. Мы уже сталкивались с идеей рассматривать базис
М*4 как множество последовательностей, поскольку в разд. 13
таблица Т типа /w соответствует последовательности
(от, (*)т,...;(»)т.
Наша конструкция гарантирует, что последовательность из
*(Р>}*) соответствует таблице, стандартной внутри [j4*J (т.е.
числа, стоящие внутри [ff ]9 возрастают вдоль строк и вниз по
столбцам, ср. пример 17.7). Но если t стандартна внутри //^/,
то -[t} - последний таблоид, входящий в е£>> (сР .пример
<17.3); поэтому лемма 8.2 дает
17.9. {"е х / t соответствует некоторой
последовательности из <f (и * и) посредством 17.6 } - линейно независимое
подмножество в Ь J .
Мы вскоре увидим, что в действительности это базис в
5^*А . Однако наше главное намерение - доказать, что
^Vy5^^c,-/t/^5yV'//^c» гДе операторы Яс и Rc определены

в 15.10. Прежде всего заметим, что S*****^4\ ^ S*4**^.
Это тривиально, если J4*AC ,//=* 0,0 (т.е. еслиу/Д~у/* )t
поскольку мы принимаем соглашение, что S0'0- нулевой модуль.
В противном случае для заданной таблицы t мы можем взять
представителей &iy.*. >&ь классов смежности для подгруппы в
ЩИИ
17,10. ОПРЕДЕИЖЕ. Пусть //« (p±>f*&>-) и >>-(}*i >/<x-r■■
определяется так: {fcJ^i,ir~JS {*££*}/-f£ Л совпадает с -ft} во
всех строчках, кроме £-й и (i+Q-up и(л+1)-я строка {i*}—
подмножество величины v в fi<4-t строке £Ш.
ЗАМЕЧАНИЕ. Немного проще наблюдать действие V; ^ на
базисе ^f «^ , рассматриваемом как множество последовательностей:
У t, zr переводит последовательность в сумму всех
последовательностей, получаемых при замене всех, за исключением v <
штук, чисел 1> + -1 на L . Как бы мы на это ни смотрели,
У с,гг » очеввдно, есть /IS'*-гомоморфизм. Каждый таблоид,
входящий в {i} V 1,тг ) имеет коэффициент Я, так что V/ ^ "не
зависит от выбора основного поля".
17.Н. ПРШЕШ.
(I) Для /*= (3,2) V^ и Vit± - это гомоморфизмы vo
и v1 t появляющиеся в примере 5.2.
(П) Если //= (4,32,2), то
*
3
&
и
%
н
J
Лк
5 10
9
S
-1
5
1
3
6_
и
X
ч
л
ч
а
5
9
5 40
9 4 8
'
10
ь г
±
a
7
X
ч
iL
5
9
10
е
г

(Sp Если пъ 6, yv= (л,- 3,3) и *r=S 2 3 +12 4 + 1 3 4t
+ £ 3 4 (мы заменяем каздый таблоид только его второй строчкой),
то
vw,
Чо- * £Р>
-з (г+ 2 + з +?j,
irv
4Z
(l Jt + * Ъ + i H + A- 3 +1 H +3 ч).
Поэтому vcVcz iri0 n Vtx У^ц тогда и только тогда,
когда cka% р** Л, и velfez vi>j: тогда и только тогда,
когда ^сА,аг Р~Ъ.
(1У) Беря в примере (Щ) Л= 6, имеем
(ГЛ - 1 5 с)v^ij + 5+е-1-5-6 = 4-1,
(Ч 5 6 - 1 5 G - TTG + ИГд) Vfa'O.
таким образом, дая i**U £ Д) л/*« ($> i) и/4ш(д, з)
получаем
et \tmeUx , где Щ- 1 И Ъ 5 Gy
Сравните последний пример со следующим утверждением:
17.12. ЛЕША. 5 J rVc.i>f1* - 6 и
Доказательство. Пусть £ есть //-таблица;
положим а?£# ~2{(*9rtfc)4C / 4Г оставляет на месте все
числа из t , стоящие вне [f1*]). Выберем множество В ,•
состоящее из /** чисел из с-й строки "£ , и передвинем
остальные числа с-и строки i в (с- ij-ao строку. Если В
состоит из первых J4C чисел в с-й строке t , то мы получаем
таблицу, скажем ikc, и
Ддя любого другого множества /V? чисел из С-й с^оки
i мы все еще получаем /*Яе -табловд. скажем £**/. но те-
90

перь одно из перемещаемых наверх чисел, скажем х , лежит в
Г (Ц$] . Пусть у - число, находящееся над х в i . Тогда
/^ _ fxyjj - делитель а?^ и поэтому
и {^}vc-^j4* совпадает с суммой всех таблоидов, получаемых
перемещением всех, кроме yvf 9 чисел из с-й строки £ в
(с- ij-ю строку. Поэтому
Поскольку J4*JC> J4 окаймляет на одну клетку r-й строки
больше (или, если //Д-//Д S^'^-S **=* 0 ),
доказательство, которое мы использовали, чтобы вывести равенство
•{^}ае^# = 0, показывает, что е* J9*fvetmi -,# =6».
I?лз. таонмл f£<0l)
(3) SJ***/S'i*J<>J,'x$f*'/i,tei
(jjf) сЛ/n S14 ,f4=\i(j4*,J4)\> более того,,
(et>Jl4 '/ ^ соответствует посредством 17.6. последовательное
ти из _J (V/#»/w)i- базис в. ЗП^А
(1У) $/fty имев-
ветствуют
(ID S^4*^ имеет ряд Шпехта. Факторы этого ряда соот-
Доказательство. Пусть 0,р - пара разбиении,
из которой можно получить napyyv*,^ , применяя
последовательность операторов Лс и ftc (ср. 15.22); согласно 17.8,
c/Lfn S**= dimМ9~ I*(0,*) \ • Достаточно поэтому, предполагая, что
dim S***4** Ufy*>fOl 7 доказать, что dim S^**0*^ ~
91

Далее,
*l*(P*Jc*fi>l+i*(ft*P*e)h (ПО 17.9)
= / * (j4 * /() / <по морвме 15.14).
Все установлено, поскольку всюду должно быть равенство и
мы имеем (|), (П) и (Ш). '
Если j4 Kjq , то S* '■f,-SJU обладает рядом Шпехта,
факторы которого соответствуют [0]W (см. лемму 16.12). 1Лы
гл^м подтому по индукции предположить, что З^с/ч- и
rnl ЕЯ* At л?Л??т рЯДЫ Ш^а J5 Федорами, соответствующими
мы уже до-
юзшш (I) и Wpy-lfltJc.fQ-^^V^. лемму 16.3),
ГЛ7 £>*°Й^еТ РЯД°М Шпехта> £ттоРы которого соответствуют
В приведенном доказательстве глы не использовали ничего,
кроме чисто комбинаторных результатов 15.14 и 16.3 (на самом'
деле показать, что [0]№*'**У=[0]с**Ас>М*-*Р'*>/,*сУ
гораздо проще, чем доказывать лемму 16.3 в полной оощаости;.
Таким образом, мы получили другие доказательства как того, что
стандартные политаблоиды образуют базис модуля Шпехта (надо
взять ft ~fi в, части (Ш)), так и правила Юнга (взять н*=о
в части (17)).
*7Л4. СЛЕДСТВИЕ. Мн имеет шд Шпехта. Более orfmo . ,
модуль £*<££^(2).,.(%) S^&T&ii имеет ряд Шпехта.
Факторы и порядок их появления не зависят от основного поля и могут
быть найдены посредством многократного применения операторов
^с JL "-с Л [O'ftJAL&iftijyD^^ftk)] соответственно^
Факторы $л ® S(Mi)® ... g> S^f @V отвечают £Я7 ^ ^J* • • М#
(Через ( /l,ju±>^ J ju /. ) щ обозначаем разбиение
(*!>•••> Ъ )jiiyt,} >ц ^J f где 2 - последняя ненулевая часть
Л.) '
Доказательство. Нетрудно видеть, что
для построения ряда Шпехта'мы просто применяем теорему <Е7ЛЗ (П)..
92

Последнее утвервдение также сцраведаиво, поскольку,как легко
проверить, [от&>9>±Р± >-/<*)] = ft] №Л\.. [fti*.
ЗАШШИЕ. ДкеИмс и Пил недавно построили ряд Шпехта дая
модуля $^® S^f (S^ . В этом случае факторы и порядок их
появления также не зависят от основного поля. Факторы Шпехта
дает правило Литтлвуда-Ричардсона.
47 Л5. ПРИМЕР. Построим ряд Шпехта дая М ' .В
приведенном ниже графе мы всегда включаем первую строку м в
/i* (например, щЬ**йш $*>&*> О ^$*>.&%.0 ^ Ср. 17.5).
Над каждой картинкой указана размерность соответствующего
модуля.
60
fxTI1^L,lxxxxxl ft [xxxxx]_^_|xxxxxxl
XX _
X X
'а
54
м.
XXXI
У?,
Х|Х
X
* а
so
ххх!
X Х|
X
16'
хх|
я»
0,0
24
XXXI „
х_
л.
10
X X X X
14
IX XX
|х х|х
5
>А
[XXX
XXX
V
я*
XX XXX
0—
л, Д*
1 ^2.
XXX XI 4
♦ 4.
XXX XI
XX
X XX Х|
X X
XX X X XI
93

Поэтому PI (i' *' V имеет тмд Шпехта с йакторами $®sP*s№
$<Ч SM'.S*», S (зУ, S <*< л< ^ , начинаяТвержего, '
независимо от выбора основного поля.
*7Л6. ПРИМЕР. Рассглотрим S (l,'xU)t6<o~SCuU)> (ч> *> $
хххх|
XX
XX
В"
&L
_х
\
4
[х~х хх|
IX.
[Г
X
X
IX X X Х|
XX
|xjx
\J„
X X X Х|
tax
ЕТ
|хх
Яч
л
Следовательно, О / оi0 обладает рядом с
факторами, изоморфными, начиная с верхнего, S(s>x>V,S&jSj*'j
$М? $Q**l\ix) (ср. примеры 9.1 и 9.5).
17.17. ПРИМЕР. Следуя нашему алгоритму, находим, что если
M^n-tn, М (*~m>nL* имеет ряд Шпехта с факторами 3(^
£ (n-i,v>t_ > g(n~m>>m,j ^ начиная с верхнего (ср. пример
14.4).
Следует соблюдать осторожность в следующем вопросе.
Кажется правдоподобным, что М<*-*-*>™+и/£(*-*-*> т+9
изоморфен jyi(n-~m>rn) ; в конце концов, оба модуля имеют ряды
Шпехта с факторами, указанными выше. Однако это не всегда так.
Например, если cka^F1^ Si , то S &*J имеет композиционные
факторы ф ^'^ и £)(Ч>У (см. матрицы разложения в
приложении). Поскольку ф (6,х' - верхний фактор для S(CA^ , то
д) См)„ s (ы)п 5(M)la*M a,XJ/(S M+J ML).
Поэтов верхний фактор для М *' /*> изоморфен ф ' ^ ,
в то время как для М &**) это не так (см. пример 5.1).
Теорема 17.13 дает новый способ убедиться в том, что все
неприводимые представления <5^, реализуются в ввде ф* ; тем
самым, можно избежать ссылок на Кэртиса и Райнера в
доказательстве теоремы И.5. Поскольку S^M имеет те же факторе, что и
94

М**/3^ , все композиционные факторы для М*- это Д)-*
(если ju ^-регулярна) и факторы для M^/S* • Но теорема
17.13 показывает, что М / S^ имеет ряд с факторами,
изоморфными $г > Л t> J4. .По аддукции, поскольку 5Л-.ё/Л/Я. ,
каждый композиционный фактор для УУ Z4 изоморфен некоторое
^)у . Используя этот факт в случае /<=({*) , когда М1*'-
регулярное представление /^§^ > j получаем по теореме 1.1, что
каждый неприводимый^ /Т^-модуль изоморфен некоторому Д)9 .
Теорема 17.13(1) иглеет полезное
17.18. СЛЕДСТВИЕ. Если J4 - собственное разбиение /г
iL ^ • ненулевыми слагаемыми, то
Это следствие, возможно, самый важный результат этого
раздела, поскольку оно характеризует $J" как подмножество
М. ** % состоящее из векторов, обладающих определенными
свойствами (ср. пример 5.2). Оно будет обсуждаться подробнее в
разделе, относящемся к матрицам разложения для (з! .
18. КРЮКИ И КОСЫЕ КРЮКИ
Крюки играют важную роль в теории представлений групп
однако теория модулей не объясняет, почему крюки вообще должны
возникать! Например, хорошо было бы иметь прямое доказательство
формулы крюков для размерностей (разд. 20), не проделывая воей
работы,, необходимой для построения стандартного базиса модуля
ШпехтаЧ
( г , j )-крюк можно представлять себе как пересечение диаг-
i>2 настоящее время имеются, впрочем, не слишком простые,
чисто комбинаторные доказательства фор^лы крюков. См. .например:
Кнут Д.. Искусство программирования для 3BM,Ti3, Сортировка и
поиск. - М.:МирД978,с.82. - Прим, ред.
95

18Л..ПРИМЕР. X X
X X
X X
граф крюков имеет вид
X
X
X
X (2,2)-крюк есть X
X X
X
6 5 4 2
5 4 3 1
раммы с бесконечной Г=образной фигурой, имеющей ( г,j ) своей
угловой клеткой. "
XXX,
И 0 И
Ш X
2
I
3 2 1
И^ОПИдашШЕ. ф ( C,j Ьлрюк диаграммы />7 есть
подмножество [juj , состоящее из клетки ( i,\ ),u.—J
клеток справа от нее (они образуют pyjg; крюка) и /ч'-i клеток
снизу от нее (они образуют ногу крюка). J i
Ш) Дшщой (г ,j )-крюка называется число hsj-ftipUi-i-j.
(Ш) Граф крюков диаграммы [jul получается, есл4 заме-
нить каждую клетку ( г,j ) числом kg .
(Ш Косым крюком называется такая связная часть границы
диаграммы fjw] , что после ее удаления остается собственная
диаграмма.
4-крю^а^ ^Г™ ПОКаЗЭЯЫ «*■—• ^ .оснх
ХХХХ ж
XX Х-*
хн
Эта диаграмма также имеет один косой крюк дайны 6, два -
длины 5, два - длины 3, два - длины 2 и два - длины 1.
Сравнивая это с графом крюков, мы получаем иллюстрацию следующей
леммы.
£8«4.ЛЗША. Существует естественное взаимно однозначное
соответствие между крюками и косыми крюками диаграммы [/*] .
Доказательство. Крюяу кяетки (<i,j)
соответствует косой крюк,нзображенный на следующем рисунке:
**• *
t
i'-й столбец
i-я строка
96

19. ДИШИНАНТНАЯ ФОРМА
Мы знаем, что при Я^Л*^ "*
J4 Г
где матрица т* (тлм) является нижнетреугольной с единицами
по диагонали ^см. 6.4 и 4ЛЗ/. Отсюда следует, что
и матрица тп""^ также является нижнетреуголъной с
единицами по диагонали.
19Л. ПРИМЕР. Обращая матрицу
лученную в разд. 6,мы находвм,что
171 ДЛЯ ГРУППЫ О5 » П0~
15]
[4.1]
,М
[2*1 J
[2,I3J,
ДО [I
М ИИ [3jf2] МЙа [2ftg [2j[# (ijs
-1
0
1
0
-1
-i
-2
I
-I
-I
2
-2
-I
-I
3
I
-2
3
I
-4
Коэффициенты матрицы т. находятся по правилу Юнга, а
элементы матрицы т~* " могут быть найдены непосредственно с
помощью следующего утверждения:
19.2. Д31ЕНЛПШПНАЯ ФОНДА. Зсли % является
собственным разбиением числа 1Ъ , то [%] = /£Я, - i +j ] j, где мы
полагаем М= о при tn< 0.
Чтобы написать определитель для [Я] , нужно расставить
члены £Я±.]/"Лд7 ? ... в правильном порядке по диагонали, а
остальные места заполнить так, чтобы числа возрастали на
единицу прп переходе от каздого члена к следующему в той_же строке.
Предупредим читателя о необходимости различать ^OJ
(который ведет себя как мультипликативная единица) и 0 (который
дает 0, будучи умноненныгл на что угодно).
97

19.3. ПРИМЕРЫ.
|М Wl-W М-М-М + М-ВДзд],
|В>1 Р1|
[3] [4]|=[3] f2]-M[l]-[8.2]*[4.d*[6]-[4.l]-[5].
[I] [2]\ ,[3,2],
19.4. ПРИМЕР. Предположим, что мы уже доказали утверждение
о детерминантной форме для разбиений из двух частей. Тогда,
раскладывая следующий определитель по последнему столоцу, мы
имеем
Г*] - № C4JI и +
£з]
СИ
[0]
[4] [5]
[2] [3]
М И
яг
№ [4]
N й
iw га
IfoJ [«
w,
а это по индукции равно [3,2] [2] - [3,1][33 + Г^[5}=
» [3,22J + [3?, I] +[4, 2, 1] + [4 , 33+/5. 2J
-([З2. 1J+ [4, 2. U + [4, 3j+f5,2jj
диаграммы,
содержащие
XX 8
ХВ
X В
диаграммы,
содержащие
ХХВ
ХВ
+[6. iJ+£5,i2J=
дЕаграмшф
содержащие
Доказательство детерминантной
ф о рмн; Достаточно доказать результат в случае, когда Л—
- (ft±>ft%>*** > &k) с ljt>0 , поскольку нулевые части в
конце Я не меняют определителя. Результат верен, когда Л
не имеет ненулевых частей, поэтому допустим, что мы доказали
его для всех X , тлеющих меньше чем k ненулевых
частей.
^Числа-в последнем столбце матрицы ([Я; -г +-jj) есть
"дайны крюков первого столбца диаграммы [%]^41н>-к^уч Akt »
поскольку hiir^i * Л± + i - i " i * Я ^ - г * /с,
Пурть ^ - косой крюк диаграммы pi J , соответствующий

(г, i)-Kp&Ky(B примере 19.4 *з>*х и *± такош:
XXX XXX ХЛЙ
XX Xfi ХЯ
fi 8 9 9 9 В
Вычеркивание последнего столбца и t-й строки из
матрицы (рЦ - ^ + X J ) приводит к матрице с диагональными членами
М» М,..., £*i-J> frfi-ij, ...> fa*-i],
а это в точности части разбиения [X \ *^J. Таким образом,
разлагая определитель J[%i "**♦/.)/ по последнему столбцу и
используя индукцию, мы получим
[A\^J[^kJ-[a\^J^biJ+...±^\ij£^J. (*)
Рассмотрим теперь произведение [1\ ^i][^ii] . Оно
получается добавлением ^Ц, клеток к [X \ ^ J всеми способами
так, что никакие две из добавленных клеток не лежат в одном
столбце (в силу правила Литтлвуда-Ричардсона или следствии
27.14) • Диаграмма [X \ 6ij , очевидно, содерокит последнюю
клетку первой, второй, у > (i-i)~u строк [Х]9 опдда
следует, что все диаграммы в ГХ\ 4i] ["пи^ооддтяат последние
клетки первой, второй,♦♦., (г- d)-& строк /Aj , но не
содержат последних клеток AVf)-* , (Ч+Л)-Л,..., *&-f
строк [X] .
Разобьем диаграммы, входящие в [X \ i^ J [ "к {± J, на два
множества в соответствии с тем, содержат они или нет последнюю
клетку i-й строки [Я] • Ясно, что [X] является
единственной из наших диаграмм, содержащей последние клетки всех строк
Г Я J , и небольшое размышление показывает, что все остальные
множества в (* ) попарно сокращаются» Это доказывает детер-
минантную форвду.
19.5. СЛЕДСТВИЕ), dim S - til /———-р | % где считает-
ся, что —% = 0 при х< 0. г ' #
Доказательство. Уодуль f/^Jf/^J- //**7 и"861
размерность t...*!nfci (си' А'$* 0TKy© CP3^ e вытекает
наше следствие f' " •*
99

20. ФОРМШ КРЮКОВ ДОЯ РАЗМЕРНОСТЕЙ
Л. TEOP&iA (L*]J» Размерность модуля Шпехта £Л
гплглппглЯ
20
дается формулой
'*,?* Д^-*^. 1
тт 4titi и( д**®* к1ж1а)в в/*у
20.2. ПРИМЕР. Граф крюков дая /4,3,lJ есть
6 4 3 1
4 2 1
I
Следовательно, df/rt S* "** - . * 0 - 70»
Оорлула крюков является поразительным результатом. Трудно
доказать непосредственно даже то, что /if делится на
произведение дайн хрюков, не говоря ух о том, что частное есть число
стандартных Я-табяиц.
Доказательство теоремы 20.1. Ш
установим справедливость результата в случае, когда Я имеет
три ненулевые части. Яско^что то г>е доказательство проходит в
общем случае, но полное доказательство затемняет простоту
применяемых идей»
3 силу следствия 19.5
100

dim, $л
(*«-i)l (*«-0'- Ьн\
ft«-*>/ Ai-0? *&
far»! (К'*)! V
1 J £_
V V V
9 что дает
первый результат,
H&1. <kXi! AH{
^н hu &и
t
(K -VI
i
<*«-*/.
1
I 1
(*h-*)> (*H-i)l
i t
(4*1'& (*u-#
i 1
farW fan'*)1- (Ьм-4!
*« **t *« ^^""и *&*<>* »/МА"*Л"*1
<ио
TT (дпшн криков в [X])
,что ■ требуется.
101

21. правило мгащт - ншяш
Правило ЭДурнагана - Накаямы является очень красивым и
эффективным способом для вычисления одного элемента в таблице
характеров группы <SV • s следующем утвервдении длина ноги ко*
сого крэка определяется как длина ноги соответствующего крока.
ЯЛ. ПРАВИЛО НПШГАНА - НАШШ. Пусть (STJ) € 6^ ,
где ~~р является Т-диклом, а <?Г- перестановкой
остальных rt-г чисел. Тогда £л(ф)=^{(-1)1^(г) / [Я] \£>)
есть косой г-крок с длиной ноги i j-,
Как обычно, пустая сумма интерпретируется как 0. В случае
когда J3 есть 3>цикл, получаем теорезду ветвления.
21.2. ГОШШРЫ. «У Предположим, что мы хотим найти
значение характера j l * ' на классе (5,4,3,1).
XX ]Ht ХХХЫ ХХ№
x-ii *f*t х-£хх
Т Y ■ Y Y Y T Y-2UL-T
Л л л JTTV Л4Х, Д Д Д Д
Удалить косой 5-крок из £5,4,4J можно двумя способами,
и правило ЭДурнагана - Накаямы дает: /9 ,*) /л d)
+ <i№ на (3,d) ( применяя это правило снова) « / * ^ на (%:£}
(госкодьку мы не можем удалять косой 3-крюк ни *э fl} i1]9 ни
»£MJ) •"-/*» ГО--Л
(ii ) / (*»*»*) обращается в 0 на любом классе, содерва-
щем &-99-9I0-9£I-9I2-» us 13-циы, поокольку ш не можем
удалить крюки таких длин кэ{59 49 4J.
(г<0 ЗНС1THL IHHC *-Х
XXXI XXXg
^.*»*> на (7,3,3)- /^ва &3J —jt^H/^U Й/
+ ъ++*»т (o)=i,

Единственное, что требуется для конструкции таблицы
характеров по правилу ЭДурнагана - Накаямы, - это таблица характеров
группы о о • Вспомним, что (з ^ имеет порядок <Г, так что
при вычислении ее таблицы характеров можно обойтись без ЭВМ!
Наше доказательство правила Ь^урнагана - Накаямы требует
нескольких предварительных лемм. Сначала мы докажем частный
случай, когда J> есть /г*»цикд, затем посмотрим, что дает
правило Литтлвуда - Ричардсона для [?] [х, i%"oc]t и,
наконец, скомбинируем эту информацию для доказательства правила
в общем случае. По поводу другого подхода см. замечания после
п. 21.12;.
Будем называть диаграммой^крюком диаграмму вида [Ьс, iy.
ЗЛ.З. ЛЕША. Произведение [dj £j6y может содержать
диаграммы-ктжжИуЛшь если и fd ] , ji /*jS7 является диаггш-
мой-шакои. Вод febftt» I ""*- *7 lWs[^l^jfS
[*][fi]-[b+6,i*'*~L]+[Q + l-i,ln-a-*+4 + некоторые джаграши.
не явжяювдеся крюками.
Доказательство. Если клетка (2,2)
содержится в одной из диаграмм [с(] или [JZJ , то она содержится и
в [^ 1 £ А/ ~ N ~ /А/ • Это Доказывает первый
результат.
Предположим, следовательно, что fct]~ [&,1п~г~а' J и
/jAj - ££> 1%~ ] . Чтобы получить диаграмму-крюк в £^j £***
мы должны разместить € единиц на местах, указанных на
рисунке, а затем поставить 2,3,... сверху вниз в первом столбце:
/У].
X X
X
X
* *
Отсюда следует второй результат.
21.4. ТЕОРЕМА (частный случай правила Ьфрнагана - Накаямы).
Предщоложим, что J> есть /1ндш> а У - разбиение
числа W .TJaggt ф9(j>) ^равно fV)*"*, ?<ж [*]*[*jl*'^
и равно 0 в противном случае.
Доказательство, Пусть /<^J и £>£/ -
диаграммы для групп 1 ©V и £Гд-г. r^e 0< *</l- Тогда скаляР~
103

ное произведение характеров
равно 0, поскольку по лемме 21.3 fcl ] \jJ>j либо содержит
две соседние диа1$амш-крюки, каадую с коэффициентом £, либо
совсем не содержит диаграмм^кргоков. } п*
По теореме взаимности Фробениуса, характер ^i'"iA" ***•••
имеет нулевое ограничение на все подгруппы Юнга вида 6"(4>л-г*
с 0 < 1< (г ; в частности, он равен 0 на всех классах в (5^ ,
кроме, быть может, класса, содержащего наш /i-циил J* .
Следовательно, вектор-столбец, v которого на месте,
соответствующем характеру вида f,(х> * л""*■' , стоит (г 1) п~ ** , а на
остальных местах - нули, ортогонален всем столбцам таблицы
характеров группы (3^ > кроме столбца с номером j) . Поскольку
таблица харает§ров является невырожденной матрицей, этот
вектор-столбец должен быть кратен J)-столбцу. Но на месте,
соответствующем *f)7 него стоит i. Поэтому он совпадает с J>-
столбцом, что и требуется.
ШШШШ. Теорема 21.4 монет быть также доказана с помощью
детерминантной формы, но приведенное доказательство более
элегантно.
21.5. ДЕМА.. Пусть -Я - разбиение числа tx , ъ_ ? -
разбиение А-* . Тогда
( г ) Кратность ~[Л] JB [*][л> 4 %J может быть отлична
от 0, лишь если [%J \ [у] есть объединение косых крюков.
(Ц ) So ли TftJ \ fyl есть объединение 7П
дизъюнктных косых крюков, имеющих (в целом) £ столбцов (ji г кле-
тоф , то кратность [%] .в fy][Xj ^а~*/равна биномиальному-
коэффициенту / *j}~ *. ) ^#
Доказательство .В силу правила Литтлвуда-Ри-
чардсона диаграмма [%] входит в [VjL00) 1 J тогда и
только тогда, когда £?J есть подадаграмма [ЛJ , и ш
можем заменить клетки в £#J \ ^J я единицами, одной

двойкой, одной тройкой,..., одним ъ- ее так, чтобы
выполнялись следующие условия:
(г ) Каздый столбец, содержащий единицу, имеет ровно
одну единицу, причем она стоит в верхней клетке этого столбца.
(-гг) При г>1 число г + £ стоит ниже, чем % ; в
частности, никакие два числа, ббльшие единицы, не стоят в
одной строке.
(Hi ) Первая непустая строка не содержит чисел, больших
единицы.
(tV) Каждое число, большее единицы, стоит в конце своей
строки.
Предположим, что кратность [Я] в [?]&> *
./отлична от 0. Тогда [%] \ jy] не содержит четверки клеток,
Образующей квадрат.
XX
XX
поскольку ни одна из левых клеток не может быть заменена
числом, большим единицы, в силу (*V), а заменить их обе
единицами нельзя в силу ( г). Поэтому £%] \ jy] есть объединение
косых крюков.
Предположим, что [&] \ /VJ есть объединение 7П
дизъюнктных косых крюков, занимающих с столбцов. Если мы
будем пытаться заменять клетки plj \ [уJ числами, мы уввдим,
что на некоторых местах обязаны стоять единицы, а на некоторых-
числа -£ , большие единицы, как на следующем рисунке ^:
I 'I
6
ИХ
116
ь
I I X c=litrn*4
6
X
*
6
-*11 . '■ "
^Крестиком отмечены места, где могут стоять как единицы,
так и числа, большие единицы. - Прим.дерев.

Кавдый столбец содержит не более одной единицы в силу
(г ). Кроме того, каадый столбец, кроме последних столбцов
второй, третьей>..,> tn^Ti компоненты, содержит по крайней мере
одну единицу в силу ( гг), ( ггЧ) и (it/). Таким образом,
положение C-tn+d. едишщ фиксировано. Оставшиеся x-c+m-i
един ид мо1ут быть произвольным образом размещены в пг~ d
верхних клетках последних столбцов второй, третьей,..., "?гг.-й
компоненты. После того как все единицы расставлены, положение
чисел, больших единицы, определено однозначно в силу (tг ).
Таким образом, кратность [%] в /VJ£#, 1г ] равна
/ m~i \ (ггъ-± \
\х-с+т-1/ \ с-х J » что и утверждалось.
Доказательство правила Иурна-
гана-Накаямн.
Пусть *ф = ({г1б(п-г,ь)> j. MM)% где /4, -
разбиение числа % , а У - разбиение числа д-ъ .
Если Jb есть г-цикл, а ОС - перестановка
остальных -п-% чисел, то
>> а><£
Но а^ (х, ±х~х) = (l* j- [9^x>* г' * J) (по теореме
взаимности Фробениуса) = (?~%) по лемме 31.5.
Определения m и С обеспечивают, что г2С&т>
поэтому
=f(-*y-c, если ^-i,
£ 0 , если /тг^£.
Но при /n« 1 разность /ЯJ ^ £VJ является косым
г ^крюком с длиной ноги г- с . Следовательно,
jt lpf)~2{H)49fa)\ £*] 4fv]eCTb косой г-крюк с длиной ноги *£>
а это и есть правило Мурнагана - Накаяш.
21.6. СЛЕДСТВИЕ. Предположим, что Ф - простое число.
Если ни одно число в графе крюков диаграммы [Я] не делится
на ур , то характер 4, * обращается в 0 на всех
подстановках, порядок которых кратен -р .
106

Доказательство: По условию из диаграммы:
[%] нельзя удалить косой Ауэ-крюк, поэтов правилу ЭДур-
нагана - Накаямы показывает, что ф^ равен нулю на всех
подстановках, содерзсалгях &0«цикл (здесь к> 0 ).
ЗАЫЗчАНИЕ. В силу формулы крюков условие следствия 21.6
эквивалентно утвервдению, что \S^\/dtu -£Л взаимно просто
с <р . Тем самая это следствие иллюстрирует обпую теорему о
?с:л, что если ^ есть обычный непржводанкй характер группы
Gr и / Cr / /ckq j, взаимно просто с 4э , то 4,
обращается в 0 на всех ^-сшпуляркых элементах Q- (на языке
модулярной теории J лежит в блоке ^ейекта Q).
Следящая передюрдулировка правила Мурнагана - Накаяьш
полезна в численных расчетах, особенно в модулярной теории
группы G^ •
21.7. ТЕОРЕМА. Вели )> есть разбиение числа л-г ,
то обобщенный характер группы (ъ^ . сюответствукупруй <ууцм$
21 {(-$*&] lfa]\ ft] есть жтЛ г-кшк с ддгаой нога х}}
равен нулю на всех классах» креме tfxt котодае содержат t-rgyw.
Доказательство. Предположим, что диаграмма
[%] входит в
М (1>Ы*-* <К»- *»ihh -*[* "])•
Тогда по леглме 21.5 £Л] \ £yj является объединением т.
дизъюнктных косых юзюков, и коэффициент при [А] равен
2(ТХ)(-'Г-
Как мы видели выше, это равно (-1) яри /я= 1 и равно
О при -т.^ I. Следовательно,
^7f(~ i)l[3>] j[ft]\ /VJ есть косой ?~крюк с длиной ноги г}.
По определению характер £*/> tV"Cl-*»v*-± С ? <•>*
обращается в 0 на всех классах в ол , не пересекающихся с
подгруппой Ф7л,- %, %) • Одаако доказательство теоремы 21.4
показывает, что он равен нулю и на остальных классах, кроме
класса, содержащего ЗГр (где J> есть ?~цщсд).

ЗАШШИЕ. Доказатвдьотвсглока8ывавт., что "оператор [г]'-
"•p-^lJV...*^*]* приставляет косые Укрюки к границе
диаграммы".
ЯЛ. ШШШ, ( 4, ) Води 9ш (3,2) и г = 3, то на ри-
судее
поскольку это равен-
XXX... XXX. XXX XXX
+ ХХ "* XI.. ""II + 'II
показаны всевозможные способы лриставления_^осого 3-врюка к
диаграмме £3,2] . Обобщенный характер ftlbft - 4 Wh -
_ j№>i) + ^M>il) обращается в 0 на всех классах в ($^,
кроме тех, которые содержат З^-цикл. t
(гЧ ) При Л* 4 характер / ^ ^M,*L^r*-**S> обращается
< в 0 на всех классах в (5^ , кроме тех, которые содержат 2-цикл.
Эти примеры показывают, что jL (*"х) + ^ f3>*>**KJ(*y+
+ £&>*>> i) как 3-модудярные характеры, поскольку э:
-г- 7й " ' ■как ^юдуанршю характеры, отсюда сразу же следует,
что характеры /<Л~Х'*Л £(*•***} и ^ лвжат в одЬм «^^
ке группы QK . Кроме «го, характеры j, ^, <ji &>*>**)
jl&J и р*>хХ**) лежат в одном 3-блоке группы <^8 в силу-
следующей теоремы:
21.9. ТЕОРЕМА.. Пусть JS^a /. =0 является
нетривиальным соотношением между характерами на -^-регулярных классах.
Тогда коэффициент Q% отличен от 0 дия некоторого <о-ссин-
гулярного Я , а в случае, если ал отличен от 0 ровно ддя
одного *р^сингулярного Л , все характеры, входящие в
соотношение с ненулевыми коэффициентами, лежат в одном ^ог-блока.
Доказательство. Бели с ненулевыми
коэффициентами входят только ^-регулярные разбиения, то мы рассмотрим
последнее разбиение . yv , для которого коэффициент о^
отличен от 0. Характер ^ содержит неприводимый модулярный
характер iff*" , соответствующий фактору fi^1 модуля S-^ • В
силу следствия 12.2 f-^ не является компонентой никакого
другого обычного характера, входящего в наше соотношение, а это
108

противоречит тому, что модулярные нецриводимне характеры
любой группы линейно независимы.
Если разбиения с ненулевыми коэффициентами лежат более
чем в одном ^"блоке, то наше соотношение имеет два
нетривиальных подсоотношения, и, как мы только что доказали, каждое
подсоотношение должно включать ^-сингулярное разбиение.
Отсюда вытекает утверждение теоремы.
Хотя довольно просто доказать, что все соотношения мезду
обычными характерами &я , рассматриваемыми как
^-модулярные характеры, получаются путем применения теоремы 21.7, йе
видно способа, как полностью определить структуру -р -блоков
группы ($*л таким методом.
21.10. ПРИМЕР. Легко вывести из правила Мурнагана-Какаяш-,
что если /i- йтя четно, то характер
равен нулю на всех классах в 6^, содержащих цикл нечетной
дайны. Значит, по теореме 21.9 характеры -£(^А(п~*'±^...утС(П1'пУ
лежат в одном &-блоке группы &%т*
Настал подходящий момент дяя формулировки такой теоремы*
21.11^ ТЕОРШ/ (йшотеза Накаямы). Модули S1* ж
Улежат в одном «f> яблоке группы (3^ тогда и только тогра. когда
существует ^конечная) перестановка £рмножества ^1,2,..«J ,
такая, что дяя всех i
Мы не будем доказывать гипотезу Накаямы, отсылая
интересующегося читателя к |17],где приведено самое последнее
доказательство, а также ссылки на все более ранние. По мнению автора
значение этой теоремы было преувеличено; она, безусловно,
полезна (хотя не является незаменимой) при нахоадении матрицы
разложения для (5^. для маленьких значений ft , но есть лишь
немного общих теорем, где она' находит применение. В
действительности ровно один случай гипотезы Накаямы понадобится для
доказательства теоремы из этой книги; мы его сейчас докажем,
21.12. ЛЕША. Если п нечетно, то ^лежат
в различных 2^блоках группы ($>ц,.
Доказательство. Пусть Of- (1 2) (3 4) ...
«^Сл- 2, /t-i). Тогда \%<х\ нечетно, где %j - класс српря-

аднности в @я , содержащий СГ . Но -jLW(lt)=l и ft(n~ '^(ftJ-O
по лемме 6*9* Значит,
Из общей теории (см* £2], 85.12) следует, что S(n> mSl^%^
хат в различных 2-бдоках.
Данное выше доказательство правила 34урнагана~Накаяш было
проведено так, чтобы продемонстрировать, как вступают в игру
косые крюки. Это правило может быть также выведено из детер-
минантной формы, и мы закончим этот раздел кратким описанием
такого вывода.
21.IS, ЛЖДА. Пусть ЯрС&к , где J) есть г-вдкя, а
ДГ - перестановка остальных /i-г чисел> Пусть fa^/**,*-*/1*}-
разбиение числа tt . Тогда
i-i
Доказательство* ^U^**9"*- Ki(1Cj>) = число
И -таблоидов, инвариантных относительно #P-,J^ (число
ju-таблоидов, инвариантных относительно ОС и таких,., что j>
сдвигает только числа, лежащие в i~Ti строке) /поскольку
ja -таблоид 1шваркантен относительно j> тогда и только тогда,
когда каждая орбита J> со дернится в некоторой его строке )=
-2^ (число (^^х^^^^1>^1-г^и1У.^)^п)-таблошов _,ш-
вариантных относительно %)~Jst ^tP3Dld»-tfii-d[fii-x№i+il«*ff*J{£^
что и требовалось.
Как обычно, мы считаем, что [&]- 0 при к < О и
N 2JnI4. ПРИМЕР (ср. с примером 2I.2(i)). Пусть Тр €<5^з •
где р является 5-циклом, а ОС- перестановка остальных 8

чисел. Тогда
■?**(.*$'
e>iwrai
[3l[4][5]
мим!
[31Г41С6]
[21C31L41
[0][1Ц2]
значение характера
[5
Г2.
Гб] [7
[3.JC4.
С5] И [7]
,[8lMW
| Гз1 Гз] &1
(51 С6] [7]j
[3] [4] [5]
И С6] [7
[2] [31 [4]
|С-2Ы1[0]
на 5Г
в» ЙГр (в езду де-
тврминантаой форш)=
на (]С (по лемме 21.13)*
5( ^.Г5'** Н-/<5' *' °^)№) в ему детермшаютой формы.
Проанализировав этот пример, читатель,поймет, что
требуется для вывода правила Мурнагана - Накаямы из детерминантной
формы, и не испытает никаких затруднений в деталях
доказательства.
22. БШОМГШЬШЕ КОЭФФИЦИЕНТЫ
В следующих двух разделах мы будем заниматься
представлениями группы (bn, над нолем конечной характеристики -р .
Многие из возникающих проблем зависят от делимости на -р
некоторых биномиальных коэффициентов, и в этом разделе собраны
необходимые леммы.
22.1. ОПРЕДЕЛЕНИЕ. Пусть п = пр+п±р+.,.+п%р% ,где 0*п:<р
при всех I , и it* 0 . Положим
(i) Vf (п)-тах {ilnj'O при j < <} >
(ii)6f(it)^^o+,lJ.*
(ш) ег(п.)=1-и
+ п
г >
III

Для каждого положительного рационального числа п/т, пологим
$0(ь/т)-$р(п)-?р(м)* ta не определяем Vp(o) , но полагаем
ЖЛ^ШШк. ?1>(ъ1) = (г1-бр(1г))/(<р-*)>
Доказательс т'в о. Результат верен при /z.= О,
так что мы можем применить индукцию» Если &='РЬ9 то по
индукции имеем ?p£(f%-l)l}=(l>4-if>+$/(l>-l) ^ Но ^ фЧ>г+£&Х-
-1У*}=(рх-4)/(р-1)> и утвервдение в этом случае верно.
Значит, можно предположить,что 0<n>-fL<-f>L*-f>\ ПосколькуЯ(рг+х)=
~Ур(х) при 0<эс<<£>и*-рг, мы имеем
Значит, 9е (*!)=»/> (?гО+»р{(*-рУ!}=^Ч+Я-^(пМ)/Н
(по индукции), а это в есть требуемый результат.
22.3. ЛЕММА. Предположим, что а.£б>0 . Тогда *fi [ $J<
Доказательство. Мы можем применить индукцию
по a f поскольку результат справедлив при а = Я. ■
Бели <^/£ , то положим 4'=ё/<р и &'= /а-а0)/р , эде
0$Q0<43 и я н^ mod p. Используя последит лемцу, имеем
По индукции ^(^^(^-fyf^ » at постольку ^в(ф(р(л')*1
и >>(*Н(*5^ . в этом случае Л{|;<Ш-Р^^
Теперь предположим, что H»fv= О . Поскольку ( /^~ ^ -
.^ ^лмеем fy (|)- »/> (Ь-«+ 0+ ^ (£ J. Так как результат
справедлив при ё = 1* мы можем считать, что £> <Е и
>> (£*)<?/>(о)-1*)* (&- О • 0тсюда следует, что ^(?J<£(^
при ?»(<1-Ъ+±)=0 . Наконец, если )>p(d-i^ii)>0 * то
в силу сказанного в первом абзаце доказательства. &ачит,
Н2

22.4. ЛЕММА. Предположим, что а^а^йл*... + <гг р% (0Щ<р)
В частности, -р делит /|) тогда и только тогда, когдаа-1<61
для некоторого I .
Доказательство. Мы имеем равенство полиномов
над полем из -р элементов
Сравнивая коэффициенты при ее ' , получаем утвервдение леммы.
22.5. СЛЕДСТВИЕ. Пусть &z &zi . Ддя того чтобы все
биномиальные коэффициенты fi\ (fl*)>*:> ( L**J Делились на р ,
необходимо недостаточно, чтобы а-£ = -i-mocl р
Доказательство. Рассматривая треугольник
Паскаля, убеждаемся, что, f> делит все данные биномиальные
коэффициенты тогда и только тогда, когда Ф делит каждое из
чисел
(-wet'),-.('?')■
Поэтому наш результат вытекает из последнего утвервдения леммы.
23. НЕКОТОРЫЕ НЕПРИВОДИШЕ
шдш шшта
Модуль Шпехта ^ неприводам над полями характеристики
О, и поскольку любое поле является полем разложения для
группы &ь , то S^ неприводим над полем простой характеристики
ио тогда и только тогда, когда он нелриводим над полем из
-р элементов. Этим случаем мы и займемся, и в этом разделе,
если не Оговорено противное, Б1 будет полем порядка р .
Полная классификация неприводашх модулей Шпехта остается открытой
цроблемой; ниже мы разберем некоторые частные случаи.
ИЗ

23.1. ЛЕММ. Предположим, что Horrip^, (S^ S^igJP. Тогда
для неприводимости модуля £<?*- необходимо и достаточно,
чтобы он был самодвойственным.
Доказательство. Бели Ь неприводим, то он,
разумеется, является самодвойственным (поскольку его
модулярный характер веществен).
Пусть U - неприводимый подмодуль Если о^само-
двойственно, то существует подмодуль У<^S^, такой, что
. Так как композиция S^S^/V^ If, где
первая стрелка есть каноническая проекция, а вторая -
изоморфизм, является ненулевым элементом Honipg f£^} £^) , то
должно быть If^S^t так что S^* неприводим.
Условие Нотр^(Зл, StyzF не может быть опущено (см.
пример 23.10 ( UL ) ниже), но следствие Я3.17 показывает, что
оно выполняется для большинства модулей Шпехта.
Перед тем как применять лемму, мы получим один результат
о числе G*1 , которое было определено в п. 10.3 как
наибольший общий делитель чисел ^et> е£*У » где е± и ^*-
политаблоиды в Sq (здесь fc* - разбиение, сопряженное к J4 ,
а <", }'- билинейная форма на Mm ) •
Вспомним, что ае ж*? /son <fc) <JC. Положим J>± =J>7 <X-
23.2. ЛЕММА. Пусть основное поле есть Q _и_ t является
ju-таблицей. Тогда
{i ) Наибольший общий делитель коэффициентов при
таблоидах, входящих в {1}*4 Pi , равен, ft **']
Ш ) {l}*tJ>t з^ЯЧдяины крюков в [/*>]){i}%+ <
Доказательство, (г) По определению Q^ =■
-н.о.д. ^е±i у e>i dt >' при меняющейся перестановке 6Г • по
ionic<ЪьЧег%У ^ 4gn ft <{i'},{t'} xt4& я±* > =
от1суда вытекает утвервдение ( О <
114

(u ) Следствие 4.7 показывает, что {ty^ifi**1*^}3**
дая некоторого с £ Q. Чтобы вычислить с , лучше всего
рассмотреть групповую алгебру Q&n (см. замечания в конце разд. 4).
имеем ft*tfb*t - Cftxt.
Правый вдеал f^Q^ алгебры #6^ (который изоморфен
^ ) имеет дополнительный правый вдеал Ц в свду теоремы
Машке.
Умножение слева на ^ ^ задает линейное преобразование
пространства ©6^- в базисе, являющемся объединением базисов
в J*t*i @&п и в 1/ » это линейное преобразование
представляется матрицей вида
(с ■ . _ ^
dfon, ir -
О
о
J
Q другой, стороны, в естественном базисе ^Г/^Гсб^}
пространства ®&п это линейное преобразование представляется
матрицей с единицами по диагонали, поскольку единичная подстановка
входит в произведение _д#£ с коэффициентом 1.
Сравнивая следа, получаем с« dim S* =* п{. По формуле
криков для размерности модуля $* cmJJ (длины крюков в [sj ).
Поскольку {tfxtft %= &Щ*^&РъУ&я часть леммы и
следствие 8.10 позволяют дать следующее
23.3. ОПИдаГЕНИЕ. Пусть Р - поле из f> элементов.
Обозначим через в ненулевой элемент пространства
Tfontf^^ (M1*) S*)> заданный формулой
означающей, что образ элемента {t} получается из вектора
' ** в S% с помощью замени коэффициентов
всех таблоидах их вычетами по модулю f
23.4. ТВОРШ. (i ) Бет 1т $с: £Л или, эквивалентно,
/&г 6 ^ £ ^ . то модуль £* приводим**.
У Включение Е строгое. - Прш.перев.

(гг ) Если [т $ = £/*9 или, эквивалентно t/fe& O-S^,
и если Нот pQ> /£^ S^J^F1* то модуль ^ неприводим.
Доказательство. Если jP= $, то по лемме
23.2( и ) гомоморфизм ^ . определяемый формулой
действует на вектор {tfa± умножением на ненулевой скаляр.
Значит, dim Кег ч^сИт- S^t ив силу теоремы о подмодуле
Ксг^= S^q -По лемме 8Л4, перехода к полю из <р элементов,
мы получим, что Кег $ ^£^ . Значит, Кег 9 2> ^1ъ том и
только в том случае, когда 1т 0 ^S*
Первая часть теоремы теперь становится тривиальной,
поскольку в этом случае 1т $ является собственным подмодулем в £*.
Если Кег $ ^S^i то 0 дает изоморфизм между Pl/4/SJ4'L
и $& , и результат (гг ) следует из леммы 23Л.
23.5. ТЕОРЕМА. Пусть ft иррегулярно. Тогда для
приводимости <£^ необходимо и достаточно, чтобы р делило
целое число
{77 ( длины крюков в [j11])}/^
/*
Доказательство. Последняя теорема и следствие
13.17 показывают, что S^1 приводим тогда и только тогда,
когда Кеъ $ z> $№. Но, так как ju p-регулярно,
модуль J^jyS^ имеет единственный минимальный подмодуль (S**+
+ S^1) / S-^1 (по теореме 4.9). Значит, ^Л привода^
тогда и только тогда, когда ]{еъ 9 ^> S^-
Но {ifaO - (jF{t}*tJ>txJF =
JJT( длины крюков в [PjJ Л у д^ )р
в силу леммы 23.2(с г ). Поскольку £* является циклическим
116

модулем, он приводим в том и только в том случав, если Р
делит целое число ЛГ (длины ктдоков в [/*]№
Г'
23.6. ПРИМЕШ4. (г ) Если р не делит /7(дяины крюков
в Cf*l )» то б1' 7° -регулярно и) ^-^ неприводим. Это в
точности случай, когда J4 лежит в блоке дефекта 0 (ср. с
формулой крюков).
(гь ) Если и ju , и yv уэ-регулярны, то в силу
следствия 10.5 d не делит ^ . Таким образом, S**
приводим тогда и только тогда, когда -р делит /J (дайны крюков
в /jwj ). Например, £** приводим при J4=((p-i) J . где
/< л <?*
(Си ) Если ^ = (3,2) и /= 1 2 3 , то прямое
вычисление показывает, что 4 5
№*ij>t
Н.о.д. коэффициентов при всех ребрах равен 4, так что 9^~4.
Но произведение длин крюков в [*с] есть 24, так что
S^ приводим тогда и только тогда, когда скол, JT7
лавна 2 или 3. Если cha,t JP - 2, то Л J 0 - это вектор,
который обозначался через /* в примере о.2, a если сЛгьг/"7^
•го £}е = -Г(-<0-Г(-5]..
У Для дальнейшего уместно напомнить следующее
определение. Два неприводимых модуля лежат в одном, р-блоке, если
они являются композиционными факторами одного и того же
неразложимого двустороннего идеала (блока) групповой алгебры группы
над полем из -р элементов. Если эта алгебра оказывается
полупростой, то модули,лежащие в одном блоке, изоморфны. - Прим.
ред.
117

23.7. ТЕОРЕМА. Пусть ju, является разбиением-крюком,
гъ модуль £ *** определен над полем из -р злемена
и
пусть модуль ъ>J определен над полем из <р элементов.
Тогда для неприводимости" S^ необходимо и достаточно, чтобы
выполнялось одно из следующих условий:
(iijffn к fi-(*-*■> О или fc * У'
Доказательство. Поскольку
мернн, они, разумеется-, неприводимы. Таким образом, мы можем
считать, что /и= (зс, 49), где x>i>y>0 и.а:^«.
Цусть i ш ± (f*l)-- (У+сс-)>
(го
ипус» *t*21{('i9ne)&\6'eG'&.z,->y*i}}' Тогда
*^(*-(а)-(*)---(1> г'У**'
Будем временно работать над полем $ . Тогда
Значит*
* 7Г (длины крюков в Mjjft} &>£ (в силу 23,2)=
„• -(*-4tyl(*+f){*}*t-
Но 0^ ** (я- i) f в силу леммы 10.4, так что
Цусть 0 - гомоморфизм, определенный в п.23.3. Тогда
где ма работаем уже над полем из f элементов. Это
показывает, что при р/ ч имеем 1т в = S* . Таким образом,
получаем
И8

23.В. Если f^ti , то модуль S ^x,±t^ является оамо-
двойственным.
Но в силу следствия 13.17, если -р?£ или бели ^(n-i^Q
то Jfomp^ (S^) Sty^F1 • Используя лещу 23Л,
что £> 'неприводим, если т0/*1 и лийо 'Р^^> ш(*°
J4~(n--4> *) (а также если f^^fc* * л'^) по
теореме 8.15J,
Далее, предположим, что <fjib . Тогда
Пусть t*- (y+x) (у + х-0 • • (%+0 *•
X •
(я* О
Поскольку Х> dy все табловды в ?£+ имеют единицу в
первой строке. Поэтому {t}--{£*]r является единственным
таблоидом, входящим ив е±* > ив {i}&~(fa)~ »~(4д+*)]>
откуда следует,что *
Значит, ft} (l-(tX)——— (£,y+*))£7fet 9 \S^t* теорема
23.4 доказывает, что при -Р/гъ модуль 3^ в этом случае
приводим. „
Наконец, докажем, что модуль Ь-^ приводим, если
jv=(x, 1*), где оо > ± у у> 4 и -/?-£ . По
теореме 8.15 можно считать, что х ^ # • Заметим, что
- Гх+ i > i у-*> />, ! У j в СИЛУ правила Литтлвуда-Ричард-
сона. Но при ф=1 характеры ^w и ^ (*V совпадают
как 2-модулярные характеры, откуда следует равенство 2-моду-
лярных характеров
пи шу^кцши ни лучшем, чти

следовательно,
характером.
i
(х, i>)
является приводимым, 2-модулярным
Замечание . Последняя часть доказательства
показывает, что разбиения (п)> (п - 5У И)> (п ~Ч} Ч)}... лежат в одном
2-блоке, и разбиения (и ~ 4> V, (л-5, 3)> (п~5} 5) > .'•♦
также лежат в одном 2-блоке группы (S^, .(см. теорему 21.9).
Если 71 четно, то все разбиения числа п на две части
лежат в одном 2-блоке &п , поскольку пример 5.1,доказывает,
что (п) и (n-d} i) лежат в одном 2-блоке (см. также
пример 21.10). Если 1г нечетно, то разбиения п на две части
лежат в двух различных 2-блоках, поскольку лемма 21.12
показывает, что (п) и (u-iy i) лежат в различных 2-блоках.
Теорема 23.7 будет использована при доказательстве первого
результата следующего раздела о матрицах разложения групп (5^.
Для разбиений-кроков число Q*4 легкс вычисляется; к
сожалению, для других типов разбиений это не так. Например, имеет
чкесто такой результат:
. 23.9. ЛЕММА. Если J4 =■ (ос, у) , то
f-у! • Н.0Г.Л {xl,(x-$Ul, (x-i)lt!,..., (х-у)!у!}•
Доказательство. Пусть tt и ix - две f-
таблицы. Положим X;: -/ к \ к лежит в /-м столбце t± и
В /-м столбце t^}.
хних4
а
J Ги и гп
№
1Л1
и
Хц V ^u
Политаблоиды В± и е{ в S£' имеют общий
таблоид {1ь} тогда и только тогда, когда никакие два
числа, лежащие в одном из множеств Хн U Х^> Х<ц U ХЛХ >
Хн U Хн> 7У1 U Ххх. , не лежат в одной строке fay
Каадая строка {^з} должна либо не пересекаться с
XiX U Х^шбо содержать одно число из 7ffX/ и одно число
из Хн • Следовательно, f&t£ > €txy может быть отлично
от 0, лишь если / X^ /= IX^i I •
120

Предположим теперь, что \Ji%\^\Jt± \ • Для того лтобы
табловд {tbj входил и в ei± > ив etK
.необходимо и достаточно, чтобы каэдая из первых и. строк {£*}
содержала ровно одно число из Лд^ U X &^ и чтобы кавдая
строка, содержащая число из Х&± » содержала также и число
из Тц . Таким образом, е± и е± имеют y!\Xix\\%
Jx- [YjxI)I общих таблоидов.
Выберем представителя ^ для общего таблоида {^з}
таким образом, чтобы ^3 = ^*^i для некоторой <t±>
лежащей в столбцовом стабилизаторе t± . Пусть 6" -
подстановка из строчного стабилизатора {$ , которая меняет
местами каадое число из X^ с некоторым числом из Хщ и
оставляет все остальные числа на месте. Тогда ^з^^^л ^
для некоторой ИС^ из столбцового стабилизатора t^? и
^дп G~ (-i) /*/* I . Значит, i±dL± &&jf ^t^> и
(-tgn <&±)(4%к &&) зависит только от t± и от t^
а не от {*i3}.Ho f* J - f*J^ - ftj
Ж&> откуда
По определению Q является наибольшим общим делителем
таких чисел, и,поскольку 0^jX^ l^U? лемма доказана.
23.10. ПРИМЕРЫ, (г) Если yY= (5, 2), то £^ =2!»
•Н.О.Д. (5!, 4!!!, 3!2!) = 23 . 3. Но ТГСдлины крюков в
[/*]) а23*31»5 . Значившдуль S 9*х) приводим
тогда и только тогда, когда основное поле имеет характеристику
3 или 5.
(ii) Аналогично j*(5»3) приводим тогда и только тогда,
когда основное поле имеет характеристику 2 или 5. 2 ч
(itt) Если -РФ У , то в силу 23.8 модуль $ *5»* '
является самодвойственным. Пусть теперь основное поле имеет
характеристику ^ = 2. Тогда первый пример доказывает, что
$ 'неприводим, а пример 2I.8(u) показывает, что £ * J ^
имеет композиционные факторы, изоморфные 5^5|^и 5^* Так
как модуль £#»*vсамодвойственный, эти факторы мо1ут
входить в любом порядке, поэтому модуль $($>1у разложим над
полем характеристики 2.
Последний пример показывает, что условия в 13.17, 13.18
23.1 и 23.4 не могут быть опущены.
121

-?3-**-. ОПРЕДЕЛЕНИЕ. Диаграмма ^о-отеденей [и]*разбиения
м, получается из графа крюков и заменой каждого'числа
kij числом ■? ^хф.
ЖЛ2± ПРИМЕР. Если м = (g, 5, lj , то граф крюков
тлеет ввд
-10 9 * G 5 3 Я, ±>
G 5 3 X 1
Z ±
* LpJ ~ i О 1 00 ж if] ш 1 00 10
о о to
Теперь мы классифицируем неприводимые модули Шпехта,
отвечающие разбиениям на две части.
23.13. ТЕОРЕМ. Пусть разбиение ft =■ (х, у) является
хр-регулярным (это значит» что при ЛЭ= 2 мы предполагаем.
что х Ф у ). Тогда модуль £<^ , определенный над полем
из р элементов, приводим в том и только в том случае, когда
некоторый столбец [juj Рсодержит два различных числа.
Доказательство . Длины крюков /гл для [/*>]
имеют вид Aij = X - / + & при l*j < V , h^- x-J+ 1
111)11 ¥<J^X и flty"y~j+1 nP*4*J<& .Если
существует число J , такое, что ^ (^^)-г9р (ft */J,
то рассмотрим наибольшее /" с этим свойством и положим
при J*£*'i'<j+P ' Но множество {я, • /y^i </V О *}
состоит из р последовательных целых чисел, так что
9Р (h'j )*г~*/>(*ч)< , Поскольку у (к±:) ф у ау\
мы имеем* 9р (х у +х) > i>p [V-j+ i). Полагая ё> - ас ~)+ %
и замечая, что условие у>* (&j >y>p(l-x + y- l) эквивалентно
тому, что Vp fi)>$f> (х - у + i )> мы получаем следующее утвер-
23.14. Для того чтобы некоторый столбец [х, j/Jf содержал
два различных числа, необходимо и достаточно, чтобы
существовало целое число ь , такое. что & - Ч + & ^ $ $ ct + d.
*Сс

Далее, U (длины крюков в [х, ijj= (у! (X * L)\) /(х -у+±)
в силу леммы 23.9, поэтому теорема 23.5 доказывает, что модуль
S-^ приводим в том и только в том случае, если Р делит
(Х4 О \%- ijs^( / Л мы получаем
23.15а Для приводимости модуля о (°°J ^необходимо и
достаточно , чтобы существовало целое число В , такое, что
Сравнивая 23.14 и 23.15, мы видим, что если некоторый
столбец [х, ij] Р содержит два различных числа, то модуль
S (х> Ч) приводим.
С другой стороны, предположим, что ни один столбец Г*г,и]Р
не содержит двух различных чисел. Тогда для каадого 6 с
х-и + Х* $<х + ± имеем т>р (4)^ Ур (эс - <у + ij . Пусть
х - ч + l ~Ъъф*+ьх+1фх*+.Лоьрй>Ъ& О* at< о
и о.^^Офо^ . Тогда x-u+l<(a%+l*i)рг+и^
Поэтому наше предположение дает, что Х+1<(az+t+i)/о*Ч... *а*ps
Значит, х+ I - Со * ct Я* ••• «•- с% рг + Qi+t p%+i + ... + о^ ps>
где 0 $Ci< р, откуда каадое ё с X -и t L* Ьъ ос*- L
имеет вид
Следовательно, x*i-$ = c0*cip+... + c^.ip^'ii.c/^p9+...^c/ri>t
(О s cfi < р), где Ы9 р*+-+с>1г.р%=С<),рУ+...+с'%р-11'
-Sq, р&— .. - ёг рх- В силу леммы 22.2 имеем
*r (Xi<)'{&f(^6f>(^^)-ei>(:x+i)}/(p'l)=:
7> [$,, р*+...+егр*У
4 г-ср (ъ силу леммы 22.3, поскольку Oq. ф 0 )«
= *Р (*-}(+*)-**('■)•
Значит, при1 *-у+ i ^6' ^я?+ i имеем' '£ £5^77 f*A$
и модуль £(*>*' неприводим, что и требуется.
1-33

23Л6*.ПРИМЕР, Модуль О * ^ '/^ неприводим над полем
из ^ элементов тогда и только тогда; когда -рФЯ,
(ср. с примером 23.10). Этот пример интересен тем, что ранее
считалось, по-видимому^на основании случая ^р^ И 9 что
модуль S (^P'd>^ всегда имеет два композиционных фактора,
один из которых является тривиальным модулем £)&?' ^\
Поскольку dim S(*P~d,fis4inoct f>s при нечетном -f> (это
вытекает из формулы крюков), то эта ошибка дала бы
контрпримеры к гипотезе Брауэра, утверждающей, что ^(iCrj/db/ntyzo
для каждого -^-модулярного неприводимого представления ф
группы G .
Картер выдвинул следующую гипотезу:
23Л7. ГИПОТЕЗА. Условие, что никакой столбец [j4-]^ Л?
содержит двух различит чисел, эквивалентно тому, что jw >р-
регулярно и модуль S^ неприводим над полем из р> элемен-
тов.
Очевидно, что если уч ^-сингулярно, то [/*] имеет
столбец, содержащий два различных числа. Автор доказал в Д1/,
что данное условие является необходимым для того, чтобы р-
регулярный модуль Шпехта был неприводим, и что в случае Р~%,
оно также и достаточно.
Над полем из двух элементов модуль S 'XfXJ оказывается
неприводимым тогда и только тогда,когда Х=£ или 2 (только
эти разбиения на две части не рассматривались в теореме 23 ЛЗ).
Мы выдвигаем гипотезу, что (2, 2) является единственным
разбиением f-с , таким, что S^1 неприводим над полем из двух
элементов, но ни /ч , ни J4> не являются 2-регулярными.
24. О МАТРИЦАХ РАЗЛОЖЕНИЯ ГРУППЫ ^
Пока неизвестно, как вычислять композиционные факторы
произвольного модуля Шпехта в случае, когда основное поле, имеет
простую характеристику <f> . Поэтому мы не умеем находить эле-
124

менты матрицы разложения группы <5^, > содержащей кратности
всех ^-модулярных неприводимых представлений ф& (где Я
-р-регулярно) как композивдонных факторов модулей S^ $ за
исключением некоторых частных случаев. Теоремы, которые мы
приводим, дают лишь частичные результаты.
24.1. ТЕОРЕМА ( Д§/). Пусть -р нечетно.
(г ) Если pfn , то все представления (S^,,. ft^^MOT
диаграммам-крюкам, остаются неприводимыми при редукции по
модулю р> и являются попарно неизоморфными.
(1С) Если ^/ti , то часть матрицы разложения (£>^ »
отвечающая диаграммам-крюкам, имеет вид
(п) i
(n-d,d) 1 i q
(n-i,iA) i ±
(i*) 1
Доказательство. Результат верен при /i= 0,
так что мы можем предположить, что он верен для п-±. Заметим»
что
Случай (г ).4> не делит ti .
Ввиду теоремы 23.7 нужно только доказать, что представления,
отвечающие различным диаграммам-крюкам, неизоморфны.. Но это
сразу вытекает из того, что они имеют неизоморфные
ограничения на &ц- ± •
Случай (ii). иэ делит а .
Пусть сс> iy у> 0.
Ограничивая характер у.1 ' на бд.^ ,ш
видим, что он имеет не более двух модулярных компонент и,
значит, ровно две в силу теоремы 23.7. Пусть У^с -
модулярная компонента 4. (х>**)} такая, что ф£ b&n-irft*'1,
а Ц>х - такая, что </^ 4> &п.-± « ^(х>±*~1)
(положим также У^= 0 и V>/ = 0 ). ГЛы должны
показать , что </£_ 4 - у ;£ для всех ос; других равенств между
этими представлениями не может быть, поскольку остальные пары
125

представлений имеют различные ограничения на &п-± •
Следующее соотношение мезду характерами справедливо на всех
классах, кроме (ft) } и в частности па всех
-^-регулярных классах:
(это выте1шет из теоремы 21.7 или непосредственно из теоремы
21.4 с помощью обычных соотношений ортогональности для
характеров) .
В терминах модулярных характеров мы имеем
Если бы некоторое ^ac-i ^ыло отлично от *р£ • то Vjc-t
появилось бы в этом соотношении ровно один раз, что
противоречит тому факту, что модулярные неприводимые характеры группы
линейно независимы.
Всюду в дальнейшем мы будем нумеровать строки наших матриц
разложения разбиениями, а столбцы — ^-регулярными
разбиениями. Таким образом, элемент матрицы, лежащей в строке ju.
и столбце X , есть кратность J)^ как композиционного
фактора в S над полем характеристики -р . Нули мы
будем опускать. Мы будем обозначать -у&-модулярный характер
модуля 3^ через ^ *** , а -,о-модулярный характер
ф я - через if *
Я
24.2. ПРИМЕР. При р~ 3 матрица разложения (^ имеет
вид
(5) (4,1) (3,2) (3,I2) (2,2,1)
(5) I
(4,1) I
I I
(3,2)
(ЗЛ2)
<2*Л) I I
12Л3) I
(I5) I
126

Доказательство. Строки, соответствующие (5), ,
(4/Е) и (ЗД2), получаются с помощью теоремы 24 Д.
Положив [?]= [X] и 1^3 в теореме 21.7, мы получим,
что
j(9 i(2ixi) / СИ I6)
j. -fK * J+ j.K г =» 0 на 3-регулярных классах.
Ыо характеры /*' и /' ' <* неприводимы и неэквивалентны
по теореме 24.1. Значит, ji№>0 имеет ровно два фактора.
Поскольку один из них должен равняться 1р(*>0, отсюда еле-
цует, что 1&0-*<*>+*«&> и ^«.¥(»W.
Остальная часть матрицы аналогично выводится из уравнения
j (I5) ,&%) , (Н> ±) л
/ ~~ г * г = 0 на 3-регулярных классах.
24.3. ПРИМЕР. При />= 3 матрица разложения Q0
совпадает с приведенной в приложении.
Доказательство. Прежде всего заметим, что
характеры f,^*' и I '* > ^ ' неприводимы в силу примера
23.6 (t ).
По теореме 24.1 часть матрицы имеет вид
(6) (5Д) (4,12)
I
I I
I I
I I
I
Полагая % - 3, а /V/ по очереди равным [3], [гд] и
Tl3"' г, теореме 21.7, ш получим, что
на З-регуляргых классах. 3?:: уравнения, а такте уравнение
(5,1)
(4Д2}
(з,ф
(2I4)
(I6)
12^

показывают, что два последних столбца, приведенные выше» имеют
номера (3,2 Д) и (3 ) соответвтвенно и что характеры / * о
ф & *->1> и / (*У выражаются через V(0> <f><Sii\...
так, как это указано в полной матрице разложения, приведенной
в приложении.
Заметим, что примеры 24.2 и 24.3 были сосчитаны без
применения гипотезы Накаямы и не обращаясь к индукции (за исключением
того места, где это было необходимо в теореме 24.1). Мы согласны,
что быстрее было бы вывести матрицу разложения (§^ из
матрицы &5 с помощью теоремы ветвления и теории блоков, но этот
традиционный метод нахождения матриц разложения не позволяет
определить композиционные факторы модуля S &?"*•*f' даже
при <£> = 2 (ср. пример 23.16) и очень быстро приводит к
дальнейшей неопределенности.
По-видимому, если со временем будет изобретен метод для на-
хоадения матриц разложения (5^ , то он позволит получить
информацию не только о кратностях композиционных факторов в
модулях Шпехта, но и об их порядке. Наиболее полезные известные нам
теоремы в этом направлении - это теорема £3.13, дающая базис в
пространстве Hoiripg. (S%yM^) , и следствие 17.18,
описывающее $** как пересечение ядерЛС сожалению.оба этих резуль-*
тата выглядят довольно некрасиво, и обозначения затемняют
простоту их применения, но мы все же приступим к работе по их
применению.
Вернемся к обозначениям разд. 13, где /У было
описано, как пространство, породненное 2-таблицами типа /£-
Замечания, следующие за пп. 17.8 и 17.10, показывают, что
действие гомоморфизма У с ir ъ& М.^ состоит в том, что он
переводит таблицу Т"7 в сумму всех таблиц, получающихся из
Т заменой всех чисел гч- <L9 кроме гг штук, на
число г . Например:
11122 11111 11112 HI21.
^' 2 33 "^ 233 +!33 + 1 3 3
Первый результат, который мы докажем, содержится в теореме
24.6, но мы изложим этот частный случай, чтобы помочь читателю
ознакомиться с относящимися сюда идеями.
24.4. ТЕОРЕМА. Для того чтобы модуль О имел нал простым
полем характеристики -р подмодуль.» изоморфный тривиальному
128

@"jl"Модулю $(*У , необходимо и достаточно. чтобы для всех
i выполнялось сравнение М^ ~ - 1 mod уэ** , где jg. =£ fan)
Д о к а з а т е л ь с т в о . По теореме 13ЛЗ (которая в
данном случае тривиальна) существует единственный с точностью
до скалярного множителя элемент (L пространства Кот,г& (S^M**).
Здесь Т является полустандартной (п)-таблицей типа jn \ и
QT переводит {*} в сумму всех (*)-таблиц типа /4 .
Например, если J4= (3> О , то {£} 9Т =11122 +
+2IH2 + 2II2I + 2i2iI + 22ia.
Теперь решающий шаг в доказательстве состоит в том, что
если ГГ£ есть (/fcA-таблица типа (j^^J^^^^J^-i-iyf^i^
V*i+* ~ vWfittrjSP существует
таблиц, эквивалентных Т по строкам, в которых можно заменить
все числа . z+i> кроме пг штук, на / так, чтобы
получилась ПР± . Например, -11111 получается из (|)-таблиц,
перечисленных выше,заменой всех двоек единицами, а каадая из
таблице Л12,1И2-1,И2'11,121[11и211И
получается заменой всех двоек> кроме одной, единицами из (|)-
таблиц. /Ч&г*
Таким образом, fi}$T лежит в М Нс% У;}ЯГ тогда и
только тогда, когда каждое из чисел
делится на р . В силу следствия 22.5 это эквивалентно
тому, что /*£ = - d mod f>**> где ^ - {p(j4i+ i) • Значит,
следствие 17/18 показывает, что fij QT лежит в £^ в том и
только в том случае, если это сравнение выполняется для всех
24,5. ПРИМЕРЫ. С/ ). Модуль ^^8»2»2Д) содержит
тривиальный подмодуль в том и только в том случае, если основное noneS7
имеет характеристику 3.
129

(и ) Если сАаг£^Л> то модуль ^5»2' не содержит
тривиального подмодуля.
(Си) Если с/иьг flp и % менъше^чем f> f то модуль
(*(Р-Ър-*>—>(>-Ъ*') содержит тривиальный подмодуль. Положим
П*я(р-*)+ % . тогда ((ос+£)*Х ?**'*) есть разбиение
JU', сопряженное к ju=((j>~l)x't;t,) . Поскольку Кощ^ (£(п,),
S ^ )ФЪ и, 5^®яГ^) изоморфен модулю,
подряженному к £ , отсюда следует, что Tforripg (б*4', £(ltL))#Qt
В силу нашей конструкции S^1 является -^-регулярным, так
что JU есть единственное разбиение числа ti , для
которого ф** О* $(i' (напомним, что ф-?, есть единственный
верхний композиционный фактов модуля £J*). Ср. с примером
24.2, где доказано, что $(*'дхфФ^
( *V) Из матриц разложения, приведенных в цриложении,
видно, что при ^>= 2 модуль S имеет тривиальный
композиционный фактор, но по теореме 24.4 он не имеет тривиального
нижнего композиционного фактора.
Интересно отметить, что при данных Л и JH* мы можем
использовать теорему 13.13 и следствие 17.18 для определения
того, является ли пространство Jfontf^ (Зл} вл) нулевым
(кроме довольно неинтересного случая, когда cficit F1-* Л и Я
является 2-сингулярным), поскольку мы можем перечислить все
полустандартные гомоморфизмы из М^ в М**~ » а затем
проверить, переводит ли некоторая их линейная комбинация элемент
j£t J зе± в пересечение ядер из следствия 17.18. Эта работа
утомительна, но не безнадежна даже для весыла больших разбиений.
Например, после небольшой тренировки на маленьких разбиениях
для читателя не составит затруднения доказать, используя
технику теоремы 24.6 ниже, что если
Ckui F= 3 и 1= (16, 2), (13, 5) или (10, 8). С
помощью гипотезы Накаямы это доказывает, что модуль £( ' ' *'
неприводим над полями характерно тики 3 (ср. с гипотезой
Картера 23.17).
Применяя теорему 13.13 и следствие 17.18, мы обычно
интересуемся случаем, когда SJ является уО-регулярным,
поскольку в этом случае из того, что 'Нотр^ ($Л> S^)^ 0>
вытекает, что $я является композиционным фактором ^^^
К сожалению, полной классификации случаев, когда ^огпр^ (& '
5 J4 )± 0 > еще недостаточно для того, чтобы определить
матрицу разложения (3^; в примере 24.5 (izr) мы видели, что
Д) ^ есть композиционный фактор S ' ПЗД полем Jp из
ТЗО

двух элементов, но Tfomjr^^ (Sty S^¥,v)-0- Несмотря
на это; в некоторых случаях модификация этого метода позволяет
классифицировать все композиционные факторы модуля &* ; см.,
например, теорему 24.15 ниже.
В разд. 13 мы видели, что есть большой произвол в способе
определения полустандартных Л-таблиц типа /Ч . Часто
оказывается наиболее удобным рассматривать таблицы, у которых
числа не возрастают по строкам и строго убывают по столбцам; мы
будем называть такие таблицы обратными полустандартными. Вторая
часть следующей теоремы, вероятно, классифицирует все случаи,
когда Лопьр^л (S%, S^) содержит обратный полустандартный
гомоморфизм. При рассмотрении линейных комбинаций более чем
одного полустаидартиого гомоморфизма ситуация становится
чрезвычайно запутанной!
24.6. ТЕОРЕМА. Пусть Л ji _/y— (собственные) разбиения
числа /г ъ_ скм Р= р . Пусть Т* - обратная
полустандартная Л -таблица 'типа ytf , и пусть У1£0 есть
количество чисел с jb^ у-й строке Т .
( L ) Если при всех г ^ Z _и. j%> i выполняется сравне-
ние JTi-ij = -± mod <p aid ,т£& #,•/-& (Щ/Т7^о вт je-
^в Ъот.^ (М* S^JL Кеъ*вт^£Я-
(U ) Если при всех гъ% jslJ**- выполняется сравне-
m-'t
S Nm6)) У у то 0 является ненулевым элементом
пространства^ 4otnF&ft ($*, S§.
Доказательство. Поскольку I7 является
обратной полустандартной, то Кег вгг,£ S ^ в силу леммы d3.il
и замечания после следствия 53.14. Значит, Кег 0^ С 5^X
по теореме о подмодулях.
Пусть i есть -^-таблица, с помощью которой было
определено действие (Зд на р[^ . Тогда {i} От есть по
определению1 сумма Я -таблиц типа /ч , эквивалентных
Т до строкам. со
Пусть г 2 X и пусть O^iT^J^i - i . Поскольку^ 7V^ =
~f*i ? то существуют числа nr^ > v^ > ... > такие, что*
О * Vj s ST и при всех / и J>J v- =.- zr . Выберем
таблицу 7^; эквивалентную 1 по строкам, и для каждого i
заменив все числа, равные i , в у-й строке 7 ^ f за
исключением Vj штук, на г ~ I . Обозначим получившуюся
131

таблицу через 7^ . По оцределению каждая таблица 7&
входящая в {i}0^Vt-i,tr>n<WraeTCfl тайим образом, причем
вклад в коэффициент при Т* . вносят
"у
Ли - V;
различных таблиц, эквивалентных Т по строкам.
Поскольку > Лп mf*i > У=^>\ V; > существует
целое Ж , та5о1, что О zrirk <Лск • Если ^г-dj ^
s- {mod-pay для эсех у , то число
делится на -*> в силу следствия 22.5. Таким образом, если
условия части (г) теоремы выполняются, то следствие Я7.18
доказывает, что МХ6Т^ S^ t что и требуется.
В предположениях части (гг) мы снова получаем, что /Т^
не входит в -ftj^i^i-d,гг > за исключением случая, когда
m=d. *sh
оо
Но при т< г- I таблица Т^ имеет ^r ^ -fifti-i чисел,
равных /ft и расположенных в строках kft+i***. > так как
/]П получается из таблицы, эквивалентной Т по строкам.
Аналогично Т^ имеет не менее ^ ./V;-^ + JV^ - V^
чисел, равных г-I и расположенных в строках ^)^^"^
так как в £-й строке Л^ ~~ Vfc чисел, равных • г , было
заменено на i~ 1 . Следовательно, всего в строках ^, £*<,...
таблицы Т"! содержится не менее
^ -г* ^^^
чисел, не превосходящее i~~ I . Если мы предоолоотм, что это
число больше, чем ^ 1 к+т-± » то 0ТС1°Да будет следовать,
что некоторый столбец1* 7^ содержит два одинаковых числа.
132

Значит, , TJ аннулируется ЗС^ . Это показывает, что в
условиях части ( И ) теоремы {t}9T V^i>ir ъ± - 0, если
i Z ft и 0 & V$f+i - ± , таким образом, ^ £j* а?^ 6>£
лежит в $**- , что и требуется.
Поскольку М /5 изоморфен модулю, сопряженному к «£,>
и Sя Л S Л является единственным максимальным подмодулем
в 5Л , если Л ^регулярно, мы получаем
24,7. СВДСТЕИЕ. В условиях части (i ) теоремы 24.6 каждый
композиционный фактор модуля S является композиционным
фактором модуля S^ . В условиям части (ft) если 2 />-£§-
гулярно. то Д)я является композиционным Фактором g А
Следствие 24.7 имеет очень много приложений. Мы приведем
сейчас только одно из них, но используем это следствие далее
при нахождении всех композиционных факторов модулей Шпехта,
соответствующих разбиениям на две части.
24^^ПИМЕР (ср. с примером 24.3). Пусть fl= (3,2Д)
в модуля ^ S входят все
Г
в качестве
и сЛал г » 3• Тогда в число факторо:
факторы ^ » а та»же ^Z)6/ ]
Т7 нужно взять соответственно
32211, 322 и 3211.
1 111 2
1
Кроме того, теорема 24.6 дает
2^*9^ СЛВДСТВЙЕ. Если для всех i&$L выполняется
сравнение f^i-i^fti^-i mod р **, где_ %i m£p(fli f*ui)>
то модуль §& недриводим над полем характеристики р .
Доказательство . Для единственной обратной
полустандартной yV-табливд *Т типа JU имеем /fij =
"f^i+j-l^i+j* №ш условия и первая часть теоремы 24.6 пока-
зывают, что- $гр лежит в M°raf&n(M^ S^O и ^ег Q*j&* •
Учитывая размерности, получаем, что Н^/3^х^ S^L • Части
разбиения JU обязаны строго убивать, так что уч. , разу-
133

меетоя, wb-регулярно. Наше утверждение теперь вытекает из
леммы 23Л.
В случае -^?- # непосредственно проверяется, что условие
следствия эквивалентно утверждению, что никакой столбец
диаграммы 2-степеней [j11]^ не содержит двух различных чисел;
см. комментарии к гипотезе Картера 23.17.
Чтобы описать другой частный случай теоремы 24.6, введем
следующее обозначение: будем писать J4 -^-» Я , если [X]
получается из [ft] путем перемещения некоторого числа
Ы ^ 0 клеток из конца t-й строки [/*-} в конец (2~i)-&
строки fj^J , так что каждая клетка сдвигается на число мест,
кратное <pfy(*' (см. пример 24 ДЯ ниже).
24Л0. СЛЕДСТВИЕ. Пусть скаг F= f> я_уч ®ftj• »>/* —
собственные разбиения числа tl , такие, что
Если i<a<$>$% _и %^(i\j4^j4(a\ ^Hom^JSfSy^o.
Доказательство. Можно считать, что CL- Лг
и $ = X , поскольку иначе мы можем ограничиться
рассмотрением последовательности J4 —*• • • • —*J4 ^ •
Пусть ct; - число клеток,участвующих в сдвиге/*/ ^* -£-*
•*-+ fift-j+V* (если J>k mmJ<k-t + iLj то
положим d, = 0). По построению для всех с имеем ft(f}=~
^f*? + <*i+ ± ~ <* i > и ™CJl° f Cf> ^ ^ делит ///£ -
Положим -/Yfc - j(vf ~ J4(ild и rfij~f*??j-4 ~ У* $
при /<£ &>и пусть Т - соответствующая л/W-таблица
типа /Ч^ из теоремы 24.6 (легко проверить, что Т
является обратной по^устандартной^.
Ясно, что 21 (А-±~^ Ал*)Р*вно Ч' ЧРИ Г* и-
равно 0 при l> SL • Кроме того, Jf4-iyi~P<-* №. * J^-i
~Г<1г1) -di+i +di * -i mod p lPicf03 так что наше
утверждение вытекает-из теоремн 24.6 ( а г ).

1
1 1
111
24.11. ПРИМЕР. Пусть cAccvF= 3. Имеем
X 3 JL
• • • T • • • '—*• * * * X X • • •
• x x • •
X
Значит, from^ (S'f £^Ф0> если Л ^J4 и &i/i -
любые два из разбиений (7, 3, 1), (52, I), (5, З2) и (5, 3, 2, 1\
Ср. со следующей 4х4-подматрицей матрицы разложения (S^ для
простого числа 3:
j (1,3,1) ^(5ХЛ) ъ&ЪУ 1)(5.*.*>0
S (7} 3' ^
£ (5\ ±)
Заметим, что в следствии 24.10 число клеток, прднрмаемнх в
предвдущую строку на каждом шаге/^1/^--^у/*^^ не обязано
быть одним и тем же; в частности, это следствие включает случай
где i± > г ^ > ... > г % _ ^ ? поскольку на каадом шаге
разрешается никаких клеток не поднимать. Условие г± >• г*>-«#
. .. >- г 7_^ не может быть опущено, поскольку если
скьгР=%^ то
XX Д XXX ^ XX XX
и хотя прост^ства ТЬ*^ (^ 5 {*У * ?«Ъ (f *^
отличны от нуля в силу следствия, но порьрф ^5% S^Jj- О
по теореме 24.4.
Для нашей следующей теоремы нам необходимо
24 Л2, ОПРВДВЛЕНИЕ. Представим два данных неотрицательных
целых числа а и S в ввде о^а0+а^ + ... + <гг^>4 (O^ct^a^q)
и |*10+^р+... + ^ ps (О*£ 1<р9^4фф. Будем говорить, что
а содержит 6 до основанию *> , если s < г9 и при каждом i
имеем ё. = 0 или & = &.• .

24ЛЗ. ПРИМЕР. 65 « 2 + 0>3 + 1-3* + 2*3 f поэтому число
65 содержит но основанию 3 в точности числа 0,2,9 = i-З* и
И = 2 + I-8*.
24.14. ОПРЕДЕЛЕНИЕ. Определим функцию fp fas^)j полагая
fp (й>Щ) равным 1, если П.*I содержит т » по основанию -£>>
и равным нулю в противном случае.
Поскольку в силу следствия 12.2 все композиционные факторы
модуля ^^-/rt>m-/ имеют вид 7) (ЛУ>4' с J^ffl » разумным
первым шагом к вычислению матрицы разложения ©^ является
следующая
24.15. ТЕбРЕМ (37 и /В/). Кратность Д) 'nV*J' как
композиционного реактора модуля g (n-m}mj qqj^ Л fn- jj\J>
Доказательство. Поскольку результат верен
при /1= 0 или 1, мы можем считать, что он справедлив для всех
/I ' <П . Пусть £ - та Он -j* J)-таблица, с помощью
которой было определено действие о^ на jyi^"171?^) . Еассмот-
рим On —'J> 'у-таблицу Т* типа (n~tn}m) f имеющую
двойки на местах (1, I), (-1, 2),..., (I, т). Как и в
доказательстве теоремы 24.6, мы видим, что отображения 'V ,
определенные на ^V/C/l~m>mJ } обладают следующим свойством:
Кроме того, Кег втЯ S (пУ'/1?^ • - Значит, вре
композиционные факторы модуля $ (Л~М' входят в Д #ёг ^ £ -
Но по второй теореме об изоморфизме мы имеем
П'*Ь Vi(i /Л Ve-p Vi(i ас (7TW V^ + Л ft t Vijfy^ *jS
Таким образом, казгдай композиционный фактор модуля
136

fl пвъ V^ <i является фактором одного из модулей
В силу теоремы '17.13 .мы имеем
£pfa-i)
24 дб, ,8од пт m-j = -l mod f^{ , то задний
тор модуля о' ^'/^ является Фактором либо модуля jffi
либо одного из модулей SS (п~*>У1 0 ^iVг - ^J
Предположим теперь, что * тру1~^А>ГГ1~л). = ^ • Тогда
^п ^</ ^ 0 и Л- &j+i содержит /я-у по основанию **.
Если 'm>J> T0 существует единственное целое число )± ,
такое, что
и 0 ^Ji -J < m -j • Но тогда число Я~ 9.J+ 1 содер-
?ит j±~<f по основанию -Р • Значит, мы можем найти целые
числа, такие, что
В силу 24/16 каждый фактор «? u Q' есть либр фактор
$(n-Js>j*J } либо одного из . {S(n^L'iJi 0<г < j - 1 ].
Но в силу следствия 12#2 модуль ty^hD не является
фактором £(п~У г^ при 0 $ г <j - ± > поэтому J) (flW
есть фактор S 1Л7"УЧ *
Снова применяя 24.16,. мы видим, что каддый фактор S У*'***'
есть либо фактор. S<a~"^-i ></*-* )? -либо одного из
f £(*-*>>О j 0 < i ^j ~ i} • Значит, Д) (n-J>jJ есть
фактор в (n-ji-i? j i- ±) . Продолжая это рассуждение до
t 0 — ггь , ГуШ докажем следующее утверждение:
137

&^ton-fo(n-SLLm-j)~d9 jo фЪ^Ч) есть
Фактор $Tn^ni>'rk) °
Далее рассмотрим случай, когда 71 г m-± moct 4> ?* .
Пусть -'
так что п = а0 ^о±^> + ... + аъ-± рг-* + £ъ ръ+ ... ,
где 1%я 0> если /п = <> # Таким образом, 71 содержит
1U- ± по основанию <р , то есть ^ (fi-ty m-i)^ <L .
Аналогично <fp(n-l}m) = 0 ж у (-n>m)=i.
Возвращаясь к случаю общих /71 и я , мы докажем следующее:
24Л8. Если tmi nfp(n~*,™) +fp(*-*,m-0>fffc<>Jf «о
существует целое число 1 JL £^j ^?п » такое, что модуль
ф{*У*Р есть Фактор £(*-A>rri) J и ограничение
фМу^&^оолеутт тривиально фяктпр {DO1-9 с кратностью
Для доказательства 24/18 рассмотрим сдерва случай, когда пг
есть степень *Р , скажем 171-^р%. Из неравенства //>(&-4,м)+
*ff v1'*'171 V >jp(rt>m) легко следует, что ^>г делит #-*!,>
и рассуадение, проведенное выше, доказывает, что 70 г не
делит fb-tn+d. . Значит, ?p(n-m+JL) « г .По теореме
23.13 модуль «C*-*W в этом случае неприводим, и ^""''Ч
- <gC/l"4/n>^v # Поскольку по теореме ветвления ограничение
g Гл-^лУ^еЯ^ шеет Те же факторы, что и S(n~m~£'mJ&
ф §(п~^г>гп~vH3 предположения индукции вытекает, что
$^т'^^содержит Д) <п-*' с кратностью £ (*-*>«*)+jf(*-l>
in- 1) . Это показывает, что в случае, когда" пь есть
степень Ф , в 24 Л 8 можно взять j^™-
Поэтому предположим, что т не является степенью р .
Поскольку yj> (и- 4 > m) + ^ (я ~ 4> m -i) <? £ } число ti содержит
либо m , либо Tti-1 по основанию <p \ Тот факт, что 77£ ч
не есть степень <р, теперь показывает, что существует един-
138

ственное 1 , такое, что
0^J<tn и n = m+J-d moot f> fyfa).
Далее, j ^ d > ^ак как мы показали, что из сравнения
n=m-lwd4€d"\ вытекает, что fr (п-±}т) +f/>(tl~
-I)'m-l)~ fp Тп>Щ)- Указанное выше сравнение показывает, что
71+ ± содержит т (соответственно. 7г содержит тп % 71
содержит /m-i) по основанию <4Э . тогда и только тогда, корда
11+± содержит J (соответственно tl содержит У-i , tl
содержит Л ) по основанию <р . Значит,
По индукции найдется * с d ^ i <j < tn 9 такое, что
ф (п - h О является фактором £ (^J>fJ t* $ ^"^Авляетоя
фактором ф^'^Н (g^t с етмностью ^> (n-l>n$+ff(ii-±,in-k).
Но поскольку ft = Wj-lmod -Р nms , утверэдение 24Д6
показывает, что каадый фактор 5 ^"'^ является фактором ^-^«о
В частности, X)ra~si) есть фактор'$*-*>*> , и тем самым утвервде-
ние 24.18 доказано.
Кратность Д)^ как фактора в £(fl'm>m^ не
превосходит {pfc-t'toO + ff (^'^>nt"^)> так как $ (п~*у
является фактором £ (n-mtth) ^ (§*п-£ с этой кратностью по нашему
предположению индукции. Далее, 24.18 показывает, что Д?^
не является фактором ^(п-т,mj^ еош А (тг-4, m J +
+ fpUl~£)ln~l)>fp (Я;/п). Это доказывает наш следующий главный
результат:
/г\(п) О fa ^)т)
24 Л9. Кратность Д/1 у как фактора *)
Е ff (а>шУ
Наконец, мы докажем
24.20. Пви j& ± модуль ф^'М) есть фактор $(«-">»}
кратностью, не большей, чем Л у1'^)771^)'
139

Наш способ доказательства этого факта будет состоять в том,
что мы навдём подгруппу Jf группы &п и модулярное
представление ф: группы Jf , такие, что ДХ; есть фактор
$МФ l if в fy является /актором S(п'т^По
кратностью A (ti-ij) m-jj . Утверждение 24.20 будет сразу
отсюда следовать, гам бы хотелось выбрать в качестве Jf
подгруппу (S'ri'l или &n-d » чтобы можно было применить
индукцию. Поскольку простое число 2 является исключительным, мы
рассмотрим сначала
Случай I. Число р нечетно. ^
Обычные неприводаше представления группы \Э Сп-Ц^ £)
имеют вид $ J® j&f1 и fi>®®SQ \ где // пробегает
разбиения числа тг-<2 . Поскольку 4> нечетно, представлений/)
и £ZK*^ неэквивалентны. Значит, все -рмодулярные неприво-
димые представления ©f/i-д,^ шеют ВВД Ф^фЗ *j)A&&&/
где J4
по аддукции
как фактора
Далее, по правилу Литтлвуда-Ричардсона ограничение
£{ti-m>m) | Q'^i^jj имеет помимо некоторых модулей вида
S ® S ^ те же композиционные факторы, что и модуль ,
<г(п-т -1>гп~0 ф g (i V. в частности, кратность ^"V%
® ДК* J как фактора в $(Л^^1 &(п.х, xj есть
С другой стороны, ф 'аУ~ 'J"'® J) (*•' является
фактором ,? ^w J, & (n-n} sl) ° кратностью единица
(поскольку 4p(n~a'j> О) - i ), а при г <j модуль
своим фактором (поскольку /й (я-Я/> г —JJ - 0 ). Но каждый
фактор модуля 5(/tVV^> ' 'кроме Д) (^"W^ > имеет вид
Д) (Ь-п0 с i < j} откуда вытекает, чтоД)^V^® ^
является фактором Д) ^ / ^fa- £> х) ° кратностью один.
Результаты последних двух абзацев доказывают 24.20 в этом
случае.
Случай 2а. иО« Я, ж И четно.
Ограничение £(Л'т}т) ^ (Sn-i. ™еет те же факторы,
что^и $(п-т-±,т,)ф £(п-т,т-0 # В силу аддукции
этот модуль содержит фактор д) (n'd '^yJ^ с кратностью
Afa-l-iijm-jJ + flfi-i-AJjni-j-iJ.jieTKO проверить, что это
число равняется Д (л-З;, 'm~jJ> так как п четко.
В частности, при 3j <^ ^2) /~ 'i является фактором ог-
140

veanepsatJin''t>Pl(5'*,-t с кратностью единица, а
при % </ модуль $ (n -£, щ &п_£ не содершгт^у-^
в «тествв своего фактора. Как и раньше, отсюда следует, что
JJ d" 4> (Ьп-£ содершт ф (*~Г1><)) как фактор с
кратностью один, и 24.20 доказано и в этом случае.
Случай 2 ь. /Р=Я> Ж^ 71 нечетно.
Ограничение $(п~ м>пг) £(е^п* тлеет те же факторы,что и
£-(л-т-*,«; ф ^ $ (*'/п-*>т-Яф £ (л-т>т~л) Этот модуль
содержит ^)(n'J~±><l'~^ с кратностью {x(n~£j>my + t)+%fx(n-
ли 7П-/ четно. /n/'-vi *-*)
Таким образом, <£ (n"J>j) ^ &n- k, содержит j) ** V -/
в качестве фактора с кратностью 2, а при i^J-JL ограничение
£(n-i}i) ^ &п-*ц, не содержит Q (^j'^J^r1) в качестве
своего фактора. Но каждый фактор £ (пVV/, кроме ^9 (n~j><ts,
имеет вид Д) (а~1>ч с i^i~2L в силу замечания после
теоремы 23.7, так что ^) (n-j-l>j-4-) является фактором
ограничения ^2) (liV'v) / (SV*, с кратностью 2.
Результаты последних двух абзацев доказывают 24.20 в этом'
последнем случае.
Собирая вместе утверэдения 24.17, 24Л9 и 24.20, получаем
теорему 24Д5.
24.21. СЛЕДСТВИЕ. Если 1Ъ ± , то кратность <$ * У ,f ..,)
как фактора в § (а'пг>1п) совпадает с кратностью Ъ 'ai/ JJ J
как Зактора в S (n-m.-iTn^v^
Выскажем попутно гипотезу, что следствие 24.21 является
частным случаем общей теоремы об удалении первого столбца.
(Такая теорема офорвцулироваяа и доказана в работе
автора,опубликованной в Jour, of Algebra, v. 71 f N» 1,1981#p.115-122. - Дерев.)
24.22. ПРИМЕР. Пусть f = 3. В строках следующей таблицы
записаны соответственно число и , число п+1 по основанию 3
и числа, содержащиеся ъ п+± по основанию 3, для О<Г 71^13.
0 1 2 3 4 b 6 7 8 9 10 11 £2 13
1 2 10 И 12 20 21 22 100 101 102 110 111 112
0000000000 0000
12 12 12 10 12
10 10
11 12
141

Например, под числом 13 стоят 0, 2, 10, 12, представляющие
собой числа, записанные по основанию 3. Им отвечают единицы,
стоящие на местах .0+1 , 2+1 , ^Ъ& и '5+1. (считая от
диагонали) в столбце, помеченном числом 13, в приведенной ниже паре
матриц • Другой пример: число 10+1 содержит 0 и 2 по основанию
3. Им отвечают единицы на местах .0+1 и .2+1 в столбце,
помеченном числом 10.
А 1
! I
Я I I
к ii
i
12 10 8 6 4 2 0
i
I 2 1
i I
1 1
*" 13 II 9 7 5
I
I
3
I
I
i
Часть матрицы разложения о^,соо??ветствуадую
разбиениям на две части для иО = 3 и ti c< 13, можно сразу же
найти из этих матриц. Надо просто вычеркнуть из одной из них
все столбцы, предшествующие столбцу с номером п , а
оставшиеся строки и столбцы пометить разбиениями числа *TL на две
части в лексикографическом порядке. Например, при /ь = 9
имеем
(9) (8Д) (7,2) (6,3) (5|4)
(9) I-
(8Д) I I
(7.2) I
(6.3) 1 I
(5.4) I J
Для нечетных простых f> и малых п большая часть матрицы
разложения (Si дается теоремами 24.1 и 24.15.
24.23. ПРИМЕР. Пусть ^=3и Л, = 9 *. При применении
теоремы Пила 24.1 номера столбцов могут быть найдены так же,
как в примере 24.2. Кроме того, они явно приведены в /9/, с.52.
Б сочетании с информацией, полученной выше, это дает

t$) (8,1) (7,2) (6,3) (5,4) (7Д2) (6,2,1) (5.23) (4,3,2) ft2?I)
(9) 1
(8Д) I
(7,2)
(6.3)
(5.4),
(7Д2)
(6ДЗ)
(5.1*)
(4Д5)
<S.A
(I9)
1 I
I I
i I
I I
I I
I I
I 14
1 I
1
Применяя теорему 8Д5 к первым пяти строкам, получаем
другую часть матрицы разложения:
(*9)„
(22 * i
(22. ф
(23. I3)
(24, I)
(5. 4)
1
1
(4*. 1)
i
I
1
I 1
(строки, соответствующие (Я ) и (2, 1 ), уже встречались выше).
Используя теорему 21.7, мы найдем, что последние три столбца
должны быть помечены (4, 3, I2), (3 , 2, 1) и (9). Между прочим,
в общем случае мы не знаем эффективного способа нахождения
номеров столбцов при переходе к сопряженным разбиениям (хотя
теорема А в [Ъ] дает некоторые частичные ответы).
Ш объяснили 12 из те столбцов, помеченных 3-регулярными
разбиениями. Модули £®> '»*' и £'3, z , £) неприводимы
в силу примера 23.6 (г ), так что осталось найти еще два 3-мо-
дулярных неприводимых представления, соответствующих разбиениям
(4, 22,Я) и (5, 2, Я2). Но
f (*>*>)_ }(M\i)+}<*>>»*% о
на 3-регулярных классах (это вытекает из теоремы 21.7 с [у] =
-|4, ?]). Обращаясь к теории блоков дефекта <[ (или к гипотезе
Пакаямы), мы видим, что часть нашей матрицы разложения имеет

вид
(7, 2) (4, 22, i)
(7. 2) I
(4, 22Д) I I
(4, 2, I3) I
Переходя к сопряженным разбиениям, получим
(5,2, I2) (4, 3, I2)
(5, 2, I2) I
(4. 3. I2) I 1
(22, I5) 1
Теперь теорема 21.7 позволяет полностью построить матрицу-
раз ложения, поскольку на 3-регулярных классах мы можем записать
каждый обыкновенный характер, соответствующий 3-сингулярному
разбиению, в терминах обыкновенных характеров, соответствующих
3-регулярным разбиениям.
Когда #-2, теорема 24.1 неприменима. Однако при
ур = 2 все строки матрицы разложения* отвечающие разбиениям
вида (ft-/я- ± }tn>± ), известны (см. ЗУ).
Источниками матриц разложения, приведенных в приложении,
являются следующие работы: /%Z/ ( 7°= 2, п^ 9), /6/
(*«2, /* =10), Д57 ( ^> = 2, Л«И)./21/( ^> = 2,
<rt = 12, -13), Д4/ ( р = 3, 8 ^ п 3 ТО) и Д57 ( О = 3f
li ^ п, ^ 15, дополнено в {$2] )♦ Мак-Аогейн fl^J щявед
матрицы разложения для Ъ =5, а^13.
Наиболее сложными-являются случаи, когда ^о = 2, /г =£2
и 13, и при их исследовании Стокхоф использовал ЭВМ, чтобы
найти dim $ ^$ *' х% *~* и dim £) *'» *» *' с помощью
теоремы 42. 6.
25. ОРТОГОНАЛЬНАЯ ФОМА КЕГА
Обратимся теперь к проблеме нахождения матриц,
представляющих действие подстановок на модуле Шпехта S^ • Это too
отложено напоследок, чтобы подчеркнуть тот факт, что теория
144

представлений (Sa может (и, как мн считаем, должна)
излагаться без обращения к матрицам представлений.
Поскольку G^ пороздена транспозициями (х- 4, &> )
при Я < х ^ тг , достаточно определить действие этих
транспозиций на базис в £^ • Вассмотрим сначала базис иэ
стандартных политаблоидов е^. . Тогда мы имеем
25Л^ ( i ) Если числа x-^f j x лежат в одном столбце t
то. е± (ее-4, сс)=-е±.
(г г ) Я°ш #- i JL x лежат в одной строке -fc % то
С±(я-4,'х)=*е£ + линейная комбинация стандарт™*'ima^m^ffft-
ВДов е^ с, {{*}<) {j} (это получэетсд комбинацией ттеммн
8.3 и техники» примененной для доказательства одажутшт 8.9>.
(lit) Если таблшш ^ &-£> х) является стандартной, то
et(*-*>*) = ei(x-i,<t).
В случае (ii ) возникающие стандартные таблицы f * могут
быть вычислены с помощью соотношений Гарни.
25.2. ПРИМЕР. Если f4 = (3,2) и мы берем стандартные
//-таблицы в порядке *^,*3^у> ^£*
12 4,
3 5
(12)
*
2 3,
5
-I
О
О
I
V.
/1
(3 4)<
•I
-I
-I
О
О
V.
о
о
о
о
то
о
1
о
о
о
о
о
-I
-I
-I
о
о
I
о
о
о
о
о
о
I
о
о
о
I
о
о
о
о
о
ь
<М)
(4 5)»
V
13 5,
2 4
(
0 I
/I О
1 0 0
0 0
1 -I
(о о
О 0-
I 0
0 I
I 0
13 5,
34
0
0
0
I
0
I
0
0
0
-1
0
0
I
0
0
0
I
0
0
0
1 3
25
0 '
0
0
о,
У
°1
о
<°j
0
*
4,
Это представление, которое называется естественным
представлением Юнга, является во многих отношениях наилучшим способом
описания матриц, представляющих перестановки; например, oi:o не%за-
висит от основного поля."Однако мы должны принимать в расчет
три случая, второй из которых (когда x-i и х лежат в одной
строке) требует неприятного вычисления. Оказывается, этих про-
145

блем можно избежать, если раоотать над полем вещественных чисел
К t и остаток этого раздела будет посвящен случаю, когда
основное поле есть Щ.
Пусть ti<tjL<... < Ьj - стандартные у*/-таблицы,
расположенные в порядке,, предписанном определением ЗЛО. Всюду,
где возможно, мы будем использовать сокращение €± для
стандартного политабловда €±. •
Поскольку мы работаем над вещественными числами, мы можем
построить по базису е± > е% >. • > в^ ортонормированный базис
f± > £х > • • • > fd модуля £ ^ с помощью процесса ортогонализа-
ции 1^ама-Пмидта. Именно в этом новом ортонормированном базисе мы
получим "хорошие" матрицы, представляющие перестановки. Чтобы
фиксировать обозначения, мы напомним читателю процесс ортогона-
лизации Грама-Шмидта:
Предположим, мы уже построили базис /^->•••> fj
пространства, порожденного векторами £*>♦••> б/ над полем К ,
причем f±> щ%- *f] ортонорюврованы по отношению к билинейной
форме < , > . Тогда существует ненулевая линейная комбинация <f
векторов е±, ..., Си± с <(eL, fy = 0 при { ^ г ^rj. (см.
1.3). Далее в / входит таблоид faj+l} (иначе в силу
доказательства следствия 8.9 вектор 2 был бы линейной
комбинацией 6ir.., 6; , что противоречит тому факту, что
Kei > О - О ПРИ i ^ & J )• Значит, мы можем взять
где знак выбран таким образом, что l^^^j имеет
положительный коэффициент в {i+4 . Это определяет fi+± однозначно.
Разумеется, новый базис f±> Д ,..-> fd пространства
$•£ зависит от порядка векторов в исходном базисе е±>еь >•-•
•••>*«/ • °даако бУДет доказана
25.3. ТЕОРЕМА. Ортоношшхшанный базис (f&pL>--) fctj
модуля $% , достроенный по стандартному базису, не, зависит
от выбора линейного порядка на множестве стандартных таблйщ при
условии, что этот линейный порядок содержит частичный порядок
<j , определенный в З.И.
Одновременно будет доказано следующее утверждение:
146

25.4. ОРТОГОНАЛЬНАЯ ФОРМА ЮНГА. Если (Ье- £} аь) -
транспозиция в (3^ , то для всех г
где ii = tг (х- < со) , число J)± \-J>± (cc>г)) равняется
(г~к+1-J)~* > если oc-i стоит на месте (ijj ,*,х -
на месте - A/J в таблице { 'Рь^О —P£+J*ii~^
ЗАМЕЧАНИЕ. Тот факт, что если Х-1 их лежат в одной
строке или одном столбце таблицы iг \ то не существует Ь^ j
равной £г (%-4,<уупе играет роли, поскольку в этих случаях р^О.
Ортогональная"форма Юнга утвервдает, что/ (oc-ij Oc)-± jf% >
если X-i и х лежат соответственно в одной строке или одном
столбце. {„ .
Прежде чем приступать к доказательствам утвервдений 25.3
и 25.4, нам потребуется предварительная лемма.
25,5. ЛЕММА. Пусть 4 jg. i* - две yv-таблицы* и пусть
х- i лежит ниже, чем х в. I* > Тогда если Ji 1< -/Tf *!,
Доказательство. Напомним из определения
З.И, что /ft^ (У есть число элементов в первых U строках
таблицы i , не превосходящих I . Поскольку -ftl <j At*\j
^ ^tw Г^ * ^ Для B°ex i ж и .
Пусть х- ^ лежит в Я^-й строке, а Л: - в 4±^l
строке таблицы t . Пусть также Х-1 лежит в ^-й строке t
а х - в £-й строке Ь * . По условию £* < #д .
Используя ЗЛ4, мы видим, что неравенства mCu(i)^^iu(t^)
влекут за собой, что всегда tniu (t(x-l,x))f miu (t*(x-l>3>)X
за исключением, быть может, случая, когда г= се- ± и либо
4± £ г/ < /ni/г (^ , £*J , либо тоос (&±, ajzu < a±
Если 4± $ V < тгп f(X± > ^ & ) > то мы имеем:
mx~i}u ft (oc-4.,x))=z mXt u (t) (так как ос-± лежит в
Я^-й строке, а х - в 4^й строке f и 4±$и <
<0i^ ^™*,w (**) <«« как' £}<з #*}> ^mx.itU(t*(x-ija:))
(так как И < ьх< ОXJ.
Если теме (^,Ол) ^ и < at , то имеем тх_£ и(кфс-.&
x))~mx-i,v (t)+i (*аккак ^у<а±)^,тх.^и'(Ь*)*±
19-2 Г47

(так как jjtj<j {t*})= тхы/и (t*(x-i,x)) (так ^к
Значит, т iu (t (*x-i>x)j $ rn iy (£*(х-4,з)) во всех случаях.
Таким образом, ft(x-l,x)}<3 /f^x4;ocj} • Равенство
невозможно, так как {i}^ -ft*}*
Доказательства теоремы 25.3 и
ортогональной формы Юнга.
Предположим, что оба результата справедливы для всех
модулей Шпехта над Я&п^± (оба они тривиальны при /t= 0).
Доказательство будет проведено в 3 шага.
Шаг!. Матрицы, которые по нашему утверждению
представляют транспозиции ( ос - i > х ), правильны при сс< /г.
Воспользуемся обозначениями из доказательства теоремы 9.3,
так что Ус есть R @V* -модуль, порожденный теми е±<>
для которых t является стацдартной yv-таблицей, и
число П лежит в одной из строк i с номерами ^^j...^ г i *
Поскольку Vt С? V^C: ..,, наше доказательство теоремы Машке
показывает, что
где Vi есть [R&a_ ^ -модуль, порожденный теми fj. ,
для которых ti лежит в ^-й строке i (вспомним, что
наше линейное упорядочение табловдов помещает все таблоиды с
числом #- в т^-й строке перед теми, у которых ft лежит в
^-й строке, и т.д.).
В доказательстве теоремы 9.3 мы построили ft&n-d
-гомоморфизм 0L, отображающий VL на S% с ядром Ус ± .
Поско^ку ^-^©...0.2/^ и $-ЦФ...Ф Ui~>
мы, тем самым, знаем, что 9t есть US'п-±-изоморфизм между
Определим билинейную форму <^ >* на £/)• формулой
<^Х«<Н>^> ддя Ч0Г ИЗ # . ^
где вторая билинейная форма - это стандартная форда т S ^ •
Поскольку ]J^ являемся абсолютно неприводимым й
<S^«*.^-модулем, в силу леммы Щура наша новая билинейная форма на с/}
должна быть пропорциональна исходной. Это значит, что существу-
148

ет вещественная константа с , такая, что
<\U;Vy * C<(v} 1гУ для всех иут из J/i.
Поскольку обе форды являются скалярными произведениями,
константа с положительна.
Для каждой стандартной //-таблицы t , имеющей число п
в ^-й строке, обозначим через t таблицу, получающуюся_из
t вычеркиванием П , и будем писать ё± вместо е$ и А
вместо ff .Пусть tp >if>+±^~> ia, есть стандартные
jw-табливд, имеющие п в *<-й строке. Если 4>£%$ty»
то
£%=v + ater + Qjn.t */>+*+- +&гег
ддя некоторого и из J^-^и &г>0 • Значит, в силу 9.4
Поскольку последним таблоидом здесь является -ft %j , входящий
с положительным коэффициентом^ так как ^Yz0i,fz Qi}~^i%4\)
при иЬ ^2 ^ % » отсюда следует,, что " Д ^ г/^Д,
Мы предполагаем, что ортогональная фора Юнга справедлива
для $6^-модуля $я* , так что при эг <^ имеем
Здесь ij**tr(x- -i, xjy а вещественные числа ^/^ и J>^ -
это те, что входят в формулировку ортогональной формы
Юнга_(положение чисел x-i и х в таблице ^г то же, что ив t яI
Так как 0; является изоморфизмом, мы доказали результат
шага I, а именно, что
$%(x-i,x)=J>±f%+J>}.{i при х<п.
Шаг 2. Доказательство теоремы 25.3.
Мы знаем, что существуют вещественные числа ^)^>HVftT;
такие, что /rVi + Vi + ,"^i^ и <Ч>0.
Для доказательства теоремы 25.3 достаточно показать, что
коэффициент й: может быть отличен от 0, лишь если {ЧЛ^
^ \Ь г }. По индукции мы можем считать, что при {tj<{t%}
вектор / является линейной комбинацией стандартных
политаблоидов frL с {i i}^ -ft j У > и Докажем соответствующий
результат для /г .

Случай I. Для некоторого сс< п число ос лежит в^
таблице iz ниже, чем ее- 4 , и в другом столбце.
Цусть i^ (х-±,з:)=4 ь . Тогда flk}'< f *Ч } *
Значит, A =cte± + «* + ск е^ , где Г- / 0, лишь если
Используя 25.1 и применяя лемму 25.5, мы ввдим, что
^ (х-4> ж) есть линейная комбинация политаблоидов &i , для
КОТОРЫХ {^с}^ {^г}'
Так как ос < п , шаг 1 показывает, что f% есть сумма
двух векторов, цропорциональных fy и fk(x~i,oc)
соответственно. Значит, в этом случае
<£п~а е + ... + а„ е „ } где л ^ 0,лишь если
Случай 2. Для каждого #</i число ос лежит в
таблице {г либо выше, чем Х-± , либо в той же строке, либо
в том же столбце.
Поскольку таблица i% является стандартной, легко
видеть, что из условия случая 2 вытекает, что числа 1,2,..., д-1,
взятыеjb этом порядке, заполняют последовательно столбцы
таблицы Ьх , получающейся из i% вычеркиванием числа п>.
Очевидно, вектор £ имеет вид
Цусть х - наименьшее целое число, такое, что 4; ф О
для некоторого / и тли (t J</nxti(&j для некоторого и (если
такое X существует). Мы хотим получить противоречие.
Преаде всего имеем 4< ос< п \ так как при всех гс
выполняются равенства т±и (Ьг)=т±и (t)= ± (если it и //
стандартны) и tnnu (tj=ЩиЦ)у*4+-«+/'и для всех yv-таб-
лиц ^ и V: . в силу минимальности ее для всех г/
имеем mx-ii w (Ьг)& mx_i? v ,(tj ) . Пусть я находится
в t% на месте (&*) • Tor*a ^> * (иначе для всех
У мы имели бы <^^%ll^^,.iy^>i*^^
что противоречит определению х ;. поскольку числа 1,2,...
.••>/i-i идут в t% последовательно по столбцам, то х-4
находится в ^г на месте (*- i>%) . Значит, в силу шага 1
имеем
*г (а-^х>-ег и £(*-*,*>-Д'
150

При UZ-u имеем т^.. (tA=tn„ л д ), v / ^ , х
Поэтому определеше х показывает, что тх (ъТ<&vyt Г01 ^
для некоторого * < у .Но /n^w (t%)~u*u при *£<f
(так как числа 1,2,..., я-1 идут в ■£ъ
последовательно по столбцам), и первая строка i- содержит по крайней
мере % чисел, не превосходящих сх>4 (так как т^ , ,&к
^ 1Пх-±1± (t^J = г ) • Поскольку таблица i; стандартна,
это означает, что число х должно находиться в ней на
места (£,% + £) , а (ее- *) ~ лежать в столбце с
номером, не превосходящим % .
г
к-
л-4
\
00-
±
2
Z+1
сс |
Если -fy =f- ^c-i ^x j, то шаг I дает
Ij^-i^Xfj+^fa, где tf<6i<i.
Значит,
Поскольку fy £ 0 и &± ф - l, вектор / должен
появиться в правой части где-то еще. Это означает/что /*
отлично от нуля. Но nx.itl(ik)r4*i >%-i*isc.lti(kJt4tb
противоречит нашему минимальному выбору числа х .
Таким образом,мы доказали, что в выражении
коэффициент ^ может быть отличен от 0, лишь если
1^Л ^ Ъ^ъг ^ат предположение индукции в начале шага 2
показывает теперь, что Д_ есть линейная комбинация
политаблоидов eL с {t^^jt^y . Это завершает доказательство
шага 2. L J
Шаг 3, Вычисление матриц, представляющих 'Г1^ 1>к).
Выберем новый линейный порядок на таблоидах, содержащий
151

частотный порядок <? и такой, что таблоиды -ft} и H(rt-±^n)}
являются соседними, если оба они стандартны (это возможно в еж-
лу леммы 3,16), Зафиксируем наши обозначения, считая, что
{Pt}<{j:3,} <* < {t(J 1 "* это Различные стандартные таб-
ловды, упорядоченные как в определении ЗЛО, a {i^^} <&
^{~£^}^-* ^{^foj~ m воъая упорядоченность. Таким образом,
$ является перестановкой множества ^1,2,..., dJ, и
если обе таблицы ^саг ж ^с^О1^^) ставдартны, то ~£#г(п>-
Мы собираемся вычислить f^fo-l, n) . Временно
допустим, что если таблица 1 %<%■ (a-d> к) стандартна, то i^jr(a-
-17п) = ^(г+уя: ' Обозначим через & грушу ' fa (ri-lj/i)}
и через X пространство, пороаденное векторами е^>ед#о-"
••v е(г-*)я:- Пусть Y=T+entf t& Cr (так что cfvnY=dintX+Z
или dim T ■+ <£ , в зависимости от того, являются ли обе
таблицы Ъ%% я £%х (b-i>n) стандартными).
Поскольку наш новый линейный порядок содержит частичный
порядок < , то для кавдой стандартной таблицы £ векторы е^
и е±(п-£,п) одновременно входят или не входят в пространство
X (это следует из 25Л). Значит, i Т,,и У
(^-инвариантны.
В силу шага 2 векторы <f±$;>~;>f(z-i)<fir образуют
ортонормированиями базис в д,а fi£*-->f%'jc>f('i-n)<7L ортормирован-
НЫЙ базис В "Y" (если dim~Y'~ctCmT+ <L, TO £(i + i)T
нужно опустить). Пространство, пороаденное ^гж и {(ъ-и)ф>
является ортогональным дополнением к X в Т и, значит,
Сг -инвариантно, потому что наше скалярное произведение #-
инва)риантно (снова надо опустить /(г+4)яг* если ^У8
» dim T+ i)<
Далее, вектор ^г^ равен сумме некоторого элемента из X
и & г#- , где ^>0 (так-как коэффициент при •[£%&} в
-/гяг выбран положительным). Значит, если п-4 и /г лежат
в одной строке или одном столбце таблицы t %<% , то fvz (п>-£,ц)
равен сумме элемента из X и в^гяг % где £~ +1, если
1г~ { ж п лежат в одной строке t^ , и Е =-1, если
й- 4 и /i лежат в одном столбце iчзг'•
Но мы только что доказали, что в этих случаях вектор
-/W (я-4,^ пропорционален /г#г . поэтому, сравнивая
коэффициенты при €гзг , мы видим, что ^г% (a-ljnj^efzx*!
это завершает разбор случая, когда таблица ~Ьг%; (n-i><1) не
является стандартной.
152

С другой стороны, если обе таблицы i%T ni^(n-£,n) /Ц,,<^
стандартны, то £ш (n-i,n) равно сумме элемента из у и *
ее (1 + 1)^* r*e &>о • Поскольку пространство,
порожденное Д^ и ffx+iXfir • является ^-инвариантным, то
fa (Л~ *,п) =\А fa +Л f(i+4)& >
где J>± и f^ вещественны, и коэффициент при {i(Zi.^x}
показывает, что J>^ строго положительно. Имеем
X L
так что J>t +J>i - 1 и J)x > 0 • Кроме того,
откуда j^K (b-i>»>)Sbfa-J>if(x + i)**
Таким образом, остается только показать, что в нашем
случае, т.е. когда t г# (п-4>п) ^t (i+isft- ? число J>t
может быть вычислено,как в формулировке ортогональной формы Юнга.
Это будет сделано с помощью некоторых свойств группы 6^ .
Поскольку п- i и п не лежат ни в одной строке, ни в
одном столбце таблицы t гЖГ , то гь^з . Кроме того,
^ мс ^ ^iic(n~ * > /г)у так что n~ '£ лежит ниже, чем /г. ,
в i . Мы должны рассмотреть 4 случая.
( г ) Числа /г- X, п~1 и ti расположены в таблице ^
следующим образом:
(И ) Некоторые два из чисел ti-%, n- i и п лежат в
одной строке, но никакие два из них не лежат в одном столбце
таблицы tt$r •.
(ги) Некоторые два из чисел ti-£}ti-i и t лежат в
одном столбце, но никакие два из них не лежат в одной строке
таблицы i%$;>
(гИ Никакие два из чисел n-Xj/i-i и п не лежат в
одной строке или одном столбце таблицы b4& *
Мы разберем сначала случай (&); случай (ги) аналогичен
ему, а случай (i ) сравнительно тривиален. В заключение мы
займемся трудным случаем UO.
153

Случай (i i). Обозначим через Tf группу, пороаденную
элементами §±=(а-Ъ *>- l) и д^ = (-п - ± > п) . Поскольку п-1
лежит ниже, чем ft, в f^ , то таблица t г^ имеет
следующий вид:
шги
В первом случаенположим ^ =■ £ г± ,а во втором / ~
^ tvft (п-±} п) . Пространство, пороаденное векторами
/*; / *0* и /W * является //-инвариантным. В
действительности результаты, полученные к этому моменту,
показывают, что действие группы п в этом пространстве задается по
отношению к базису Д > /^а > 4to матрицами
§is(n>'A,*-i)*
к з, о)
\0 О ij
■rt о т^
\Ч 0 Tt/
где ^1 известно по шагу 'I. Осевое расстояние между ^-^
и и в таблице £ равно 1 минус осевое расстояние между п~И
ъ Ъ-'L ъ t . Таким образом, достаточно доказать, что
б"1 = i + Г~
-1
Легко видеть, что след Q±$x I^BeH '^^ "^l^^i
Значит,
* Оно по определению равно величине, обратной к у^, в
формулировке ортогональной формы Юнга. - Прим» перев.
154

Таблица характеров группы
■ft)
(i3)
i
2
1
(2, I)
0
-i
имеет следующий вид:
(3)
I
-I
i
Единственным трехмерным представлением, имеющим след I
на транспозициях и след, по модулю не превосходящий 2, на
элементах порядка 3, является представление с характером / ^ I
+ f *2, *'. Значит, Ug:Lgx=0> откуда ^=<5^ +<^,
что и требуется.
Случай (itr). Пусть Н>9± и ^ такие же, как
в случае (-гг). Можно считать, что п-Я. лет? выше, чем л-f,
а /г-4—выше, чем А в -£ , и что jf, =-£/i для
некоторого 'А из //" . Выбрав ^
и /ftf а п п в К846
мы получим, что у/ z ^ представляются матрицами
з базиса пространства -и faff
§г(ч-Х,п-1).
-со,
со,
сОх
«Л
fr-(n-l,*)-
-л
Л
-к'
А
_А
(все не выписанные элементы равны 0). Мы знаем, что каадое из
чисел У±)с0±>/%±)°/х>Рь> Xl отлично от 0. Значения Я^6^
и #^ известны, и ?~{ + в£~^= м"± в силУ шага '*• **
хотим доказать, что atL ^Ti , jB± = <^ и /^ - ^ . Для
доказательства этого не ввдно более эффективного способа, чем
приравнять (д± дх) ** к ^ д± , используя тот факт, что
9± 9ь имеет порядок 3 (ср. /§3/). Матричные элементы (4, 1),
155

(5, 2) и (3, I) соответствующих матриц дают равенства
И
Подставляя в эти равенства со ~ { -coL и о>~ =?\+iR±>
мы быстро получим требуемый результат: о1±^ж^л^>±=со1 и /^Л.
Это завершает шаг 3 и доказательство ортогональной формы
Юнга.
25.6. ПРИМЕР. На рисунке показан ортонормированный базис
модуля S ®1 ^ в терминах графов, использованных в
примере 5.2.
1 г.
*>&к* 5.
^ 5
ct iiei 3 5
Д5
156

2 «V^ ^е6г^еЧ
H H5
= 5 = I *> 5
H 5
Для большей ясности мы выбрали графы (скажем7 tr^G-j,..., G5)
так, чтобы ребра имели целые коэффициенты. Легко, проверить, что
эти графы ортогональны и что -[t[} является последним
таблоидом, входящим в Gi . Числа, на которые умножаются
векторы <fi , обеспечивают равенства {-fi> /t>e 1 (например,
<^Сг з > &ъ У ~ *2* так что вектор ( %Н?)~* Сг5 имеет
норму I). '
Следствие 8.12 было использовано, чтобы записать графы в
терминах политаблоидов. Поскольку {tx}^ {^ з } > то *х
не входит в ^3 > что иллюстрирует теорему 25.3.
• Выписав полностью матрицы, представляющие транспозиции
(1 2), (2 3), (3 4) и (4 5) в ортонормированием базисе fpfx>**>
. ) £$ у шх получим
/' ' \
(i H)<r*
fi/l ff/X \
Z^/5 '1/5 ' '
157

Интересно заметить, что последний элемент нашего ортонор-
мированного базиса всегда пропорционален вектору jtj &£ J>±у
использованному в определении 23,3 (ср. пример 23.6 (ггг)9 а
также вектор /- выше). Это так, поскольку оба эти вектора
остаются на месте под действием подгруппы Юнга (5уч » а с
точностью до скалярного множителя в^ оставляет на месте
единственный элемент S д в силу теоремы 4.13 (теорема 4.13
показывает, что dim tfotn^g (MftjSfo)**!)-
26. ПОДСТАВЛЕНИЯ
ПОЛНОЙ ЛИНЕЙНОЙ ГРУППЫ
Теория представлений групп (3^ оказывается полезной при
изучении более общих групп подстановок. Например, Фробениус
использовал часть таблицы характеров группы <5^у для нахождения
таблицы характеров группы Матье М^ . Существует другое,
менее очевидное, приложение этой теории, вытекающее из изучения
группы CrL^ (F) невыроаденных dx flf-матриц над полем F!
Вспомним, что каадая группа, имеющая представление размерности
d над Р , имеет (по оцределешаю) гомоморфный образ в &L^(fj0
Хотя результаты этого раздела будут формулироваться в терминах
полной линейной группы, они в равной степени применимы к любой
ее подгруппе. Мы собираемся построить для каздого числа /г и
каздого его разбиения представление группы CrLj (F) над полем F1
Таким образом, по каждому представлению любой группы мы сможем
построить бесконечно много новых представлений над тем же полем.
Группа GL^jpJ естественно действует на ^-мерном
векторном пространстве над полем jf1; назовем его, скажем, W''.
Пусть 1,1,..,^ - базис в W®. Если $=(gy) ~ матрица
из Glji(F) , то
Общий элемент пространства //* <g) W может быть запи-
158

сан в виде
(основание для столь, странных обозначений выяснится позже).
Действие задается, как обычно, формулой
Предположим временно, что скьгР^О* В пространстве №*%№&
есть два естественных #£^(#7-инвариантных подпространства,
а именно, подпространства, порожденные векторами вида
Они называются соответственно симметрической частью
W ® IV 'ъ второй внешней степенью W® (или кососимметриче-
ской частью W®<8 fV®). Так как сАаг р= 0 , то W(d)G)W®
равно прямой сумме этих подпространств. Запишем это разложение
в виде
w(i)®w(i)*w(i)®w(iXJ.
Менее общеизвестным является тот факт, что
для некоторых подпространств W (называемого третьей
симметрической степенью), ffl(AjV(входящего в двух экземплярах) и
W№) v(называемого третьей внеп!ней степенью).
Имеем также разложение
W(iJ® W(i)®W(i'® W&* W(i)Q3W(3,iJ9uW(l%3W(;i'%W(ij
Пи так далее". Кроме того,
Большая часть работы, необходимой для доказательства этих
159

результатов, уже проделана, поскольку они аналогичны
результатам для симметрической группы (ср.. последний цример с
разложением S<v®2b>tG4et$(if®Sbi>QSbymDm ohaxP-Oj.
Снова рассмотрим пространство W® ф W®• Как
обращаться с симметрической и кососимметрической частями, если
поле Р произвольно (включая случай ск&ъ Р= X )? Мы
приспосабливаем наши обозначения, полагая IV® равным пространству
однородных многочленов степени 2 от коммутирующих переменных f,
-м:"- • ^ 3^1ШСЫБаем моном ±/ в^ввде IJ , так что ТТ =
* Д и Ж ^ пороадено множеством ^V^' / ± /TV/ ^ of J.
Сохраним наши кладущие обозначения для W&0 Wv и для
И^^ ; мы получаем изоморфизм векторных пространств (IV ^0
0 Wto)/W(%W®,*egi как L^^ moo(W (i*J.
Другой взгляд на это состоит" в том, чтобы определит^
линейное^ преобразование vi0 : W®GD W^—^Wty переводящее у- в
^ . Тогда Лег v^'» W ^ * Если мы определим действие
Q^d(P) на ^^ естественным образом, то v^ ^ станет
^£^ (^"Г0М0М°1ФИЗМ0М:
Нашим строительным материалом в теории представлений
группы &£<a(F) будет обобщение описанной выше конструкции ИГ®
на ^-ю симметрическую степень пространства W®*
26.1. 01ШЕ1ДЕЛЕНИВ. У-й симметрической степенью проотран-
ства W® называется векторное пространство однородных
многочленов степени к от коммутирующих переменных 1,2, .„ t3
с коэффициентами из поля Р . Мы записываем моном 7± Тх •••!*•
в ш^е 11 * л • - гЧ и определяем действие группы #-£ ^ $г^
на ^(У формулой
где #~ ($ty/ н суша вврвтоя по всем индексам j±*()x>"'J<Jк
между! и а .
Для читателя, знакомого с £-й сишетричеекой степенью как
с подпространством £ymm £ (W(i0b W®®.:.®W(*) Upas),
пороаденным определенным образом симметризованными векторами,
быть может, полезно знать, что оно связано с ЦгСН) следующий
образом:
160

где обозначает взятие сопряженного пространства^
Мы рассмотрим цространство ,
соответствующее модулю М^-$°>^ в теории представлений группы
о я, . Однако преаде, чем переходить к этому, нам понадобится
еще небольшая предварительная работа. Должно быть,уже ясно, что
полезно рассматривать векторные пространства, порожденные
таблоидами с повторяющимися значениями (на время лучше всего забыть
любую подразумеваемую интерпретацию в терминах действия груп-
ш GIAF))-
Пусть Xs ос^хх ... ооа - неубывающая последовательность
положительных чисел. Если /«• есть разбиение числа п_ , a ~t
есть //-таблица (типа ( i*))9 то обозначим через IX массив
целых чисел, получаемый И£ 1 заменами г -*&i (<£<-ь <к).
Будем писать i£ X_f^ i^ X > если для всех пг и % в
г-й строке i± Х_ находится столько же чисел пг , сколько
в 2-й строке ^ X*> обозначим через {tX} класс
эквивалентности по отношению ~ , содержащий ^ j . Тогда ясно, что
есть корректно определенное отображение из множества у/-табло-
идов типа ( d* ) на множество //-таблоидов типа Щ , где
разбиение Ц определяется тем, что ^ равно числу членов
последовательности X , равных / (как и в некоторых местах ранее,
мы не требуем, чтобы J4 _ и Ц были собственными разбиениями
числа п ). Продолжим X до линейного отображения
пространства S0)J4 , пороаденного J4-таблоидами. ^
j&JLu ПРИМЕРЫ, (г) Если /T^il 2, то
порождено С2 и О. а $(*><>>(*>$ X порождено О - JUL
2 _1 2. I
(й ) Если ,Г= -I 1 I, то S '' ' ''оГ'порождено 1 I.
a50uUM)f.o. 1
В разд. 17 были определены некоторые линейные
преобразования V ^ v- на векторных пространствах 5 ^ ._Определим
соответствующие линейные преобразования на £ 0>^ X формулой
(ясно, что это определение корректно).
^См. § 1; знак # включает и структуру сопряженного модуля.-
Прим.ред.
161

26.3. ТЕОРЕМА. Пусть X - последовательность типа £ , Л -
собственное разбиение g ji*} ju - дара разбиений, такая, как в
£^15.5. Тогда #-
(О Размерность dim, Зл X равна числу полустандартных
Я-таблиц типа £ j
(uj 5 Xve.i>f4* - Ь А ;
(Ш) З^ХПКег Vc_i>ftt -S^^T.
Доказательство. В 17 .12 мы доказали, что
е v # = £ и е ^^л/#"£/#
Применяя к этим уравнениям оператор X , мы получаем, что
Из рассмотрения последних таблоидов, как и в конструкции
стандартного базиса модуля Шпехта, очевидно, вытекает, что
dim S^ Х& 1Уо&Ю1> где @l(3it^) - множество полустан-
дартннх Л-таблиц типа ^ • Если это неравенство для
некоторого Л является строгим или_если S " >* ХП Кег %-£,/<*
строго содержит S^4 *С}^ X для некоторой пары разбиений
J4 *> f^ » то выберем пару разбиений 0, )> и
последовательность операций Jc и Rc , переводящую 0,^
соответственно в Л, Я или J4*jjii (см. 15.12). Для каздого
собственного разбиения <э числа п обозначим через Q& кратность
модуля Sg как фактора в $ °^ Тогда найдется возрас-
тающая цепочка подпространств в S °^ X » имеющая по крайней
мере Q& факторов, изоморфных £*X (ср. следствие 17.14)._
Значит, число Р-табловдов типа £~с/ып S0,у>Хъ^7ОйгЫипScXz>
следствия 13.14).
По крайней мере одно из этих неравенств является строгим
(первое является строгим, если наше ядро слишком велико, а
второе - если Ыгщ 5Я>1^ №>%) I )• Напомним, что вв* есть

кратность 5 ^ как фактора в М* - S %* • Значит,
а это по теореме 13.19 равно числу Р-таблоидов типа Щ . Это
противоречие завершает доказательство.
26.4. ОПРВДШБИЯ. Обозначим_через /т_ щшмую сумму
векторных пространств £Р y^ X , где X пробегает все
неубывающие последовательности, членами которое являются числа
1,2 d . Определим действие отображений -v на Ж^^.вак
действие отдельно на каждой компоненте. Если ft - собственное
разбиение числа п , то положим W-P^W **'**.
Следующим нашим результатом является
26.5. ТЕОРЕМА. Пусть Л - собственное разбиение числа л.
Тогда
(О размерность " равна числу полуотацдартннх у?-таблиц
с элементами из множества (l .2 afj 5
(п) пространствоИ™ является пересечением ядер
-^-отображений, определенных на W 0,Л.
Доказательство. Это сразу вытекает из теоремы
26.3, поскольку W^ есть прямая сумма пространств $лХ
Отоадествим пространство W0,JU с JfC*1*) ф W^®... ® Ж^У
Мы определили действие группы GL d (F1) на симметрических
степенях, так что Gld (F) действует на ЦГ°>/* . Использование
индексных обозначений показывает, что отображения у коммутируют
с действием GL0i(F)zt значит, в силу торремы 26.5 )УЛ
является GLj (F1)-модулем, который мы назовем модулем Вейля.
Из теоремы 26.3 вытекает
#
26.6. ТЕОРЕМА. W 'J4 обладает рядом, все Факторы
которого являются модулями Вейля. Каздый модуль Жл входит в
число факторов этого рада с той же кратностью, с которой модуль
Шпехта £л входит в ряд Шпехта модуля S^4"'*4-

В частности, кратность нсоаденвя ЖЛ в ряд Вейля*'модуля
дается правилом Юнга
(заметим, что, в отличие от соответствующего случая симметрической
группы, здесь не имеет места "индуцирование"). Это обосновывает
все примеры, приведенные в начале настоящего раздела; в
действительности мы доказали их аналоги, не зависящие от характеристики
основного поля. Например, модуль W®®W®® Ж^ имеет ^^(fj
-ряд с факторами, изоморфными W(*\W(**$> /Г&^и Ж^(в этом
порядке, начиная сверху), и это верно над любым полем JT .
Теперь мы исследуем значения характеров. Пусть gcGLcf(P)
- нижнетреугольная матрица с диагональными элементами <^^a'A^•"
•••^с/ • ^от поле//*"1 алгебраически замкнуто, то каадый элемент
ОН^ (^сопряжен элементу такого вида, так что характеры
модулей Вейля достаточно вычислить только на таких Q .
26.7. ОШЩВЛЕНИЕ. Для каздого целого числа к обозначим
через /-& } fr-ю однородную симметрическую фу^тдп от ^ »•"
'-j^cl • Это значит, что
(мы принимаем соглашение, что {О } = i и г^}= 0 при к< 0).
26.8. ПРИМЕРЫ. ~[l} = c/t+ot:i + -..+e/d;
26.9. ТЕОРЕМА. Значение характера модуля на элемен- ,
те д равно {^}-
Доказательств о._ Вектор ± ^ имеет вид °£ i
+ линейная комбинация векторов j с J < г . Значит, если
1 +
VРядом Вейля автор называет ряд из теоремы 26.6.
Прим. перев.
16'*

1 £ i± ^ . - ♦ ^ i^ ^ ct . , то вектор у... -t ^ входит
в i± .. . ^ fy с коэффициентом c//£ ... e/^ Г~Поскольку
элементы вида ^ — i^ образуют базис ^^У , отсвда
вытекает наш результат.
26ДО, СЛЕДСТВИЕ. Значение на Q характера модуля W *h-~
... ® И^*1у g'* Равно ^Я J ... {#*} .
Обозначим значение на $ характера модуля через
/Я}. Напомним из 6Л, что матрица f*t = (m^) , индексированн-
ная собственными разбиениями, задается формулой
Из теоремы 26.6 вытекает, что
Поскольку детерминантная форш дает матрицу, обратную к т9
мы получаем следующую теорему.
26 Д2. ТЕОРЕМА. Если Л - собственное разбиение числа Hj
то значение /Я| характера модуля Вейля /^ на элементе ^
равно /{Я. -г+у}/.
Из определения { #} сразу вытекает
26 ДЗ. ТЕОРЕМА. Значение на Q характера модуля
есть {Я}{^}' *
Правило Литтлвуда-Ричардсона позволяет вычислить /л j {/WJ
как линейную комбинацию выражений jy} (где % - разбиение
числа 1 , уч - разбиение д-t , а >> - разбиение /г ),
поскольку мы знаем, что оно вытекает из правила Юнга.
Стоит заметить, что если бы мы определили Ч кj как
W-Z! J' ы- -ы
1^1^ • ^<*
165

где -Ы±^х >>••• J - счетное множество переменных, то
формулы
давали бы эквивалентное определение функции fa} , отвечающей
разбиению Л числа /t (поскольку наш результаты пригодны для
^± > ••• > ^d из бесконечного поля, приведенные выше
соотношения для функций -pt} должны быть алгебраическими тождествами).
Функции -pi} называются функциями Щура, и, таким образом,
алгебра функций Щура изоморфна алгебре, порожденной
представлениями [Я] , где Я пробегает все разбиения всевозможных
чисел И . Правило Литтлвуда-Ричардсона позволяет нам перемножать
функции Щура*
Следующая теорема позволяет явно вычислить функции Шура*
26.14. ТЕ0Ш1А. Если J4 - собственное разбиение числа
то
ы-%
9
>F^ "%
n
ЗАМЕЧАНИЕ. Во всем дальнейшем через 2' обозначается сумма
по всем неупорядоченным множествам из п (различных) индексов
г l>*ii-~ > г* » выбираемых либо из множества -^1,2,..., Ы^
либо из -[1,2,... у .в зависимости от того, определяем ли мы
■//*} в теР™гах переменных fet'±>^д;-',>Ч^или \°^±>о1х>"-}'
Доказательство теоремы 26.14. йиеем fa т!)л^
^Z шгетуб- = (Щ?тяе i&>2 т9r f T) (это скалярное
произведение характеров группы (5^/= A^xJ£*J.../>J j№P*J-C*iiJJ
(по определению матрицы га)« dim Tfom^ ш a (vj ^)-число
^-таблоидов типа 9 (по теореме /13.19). Вычисляя коэффициент при
d^cl£* ... dп,** в {Я^ ... {Ял} , мы уввдим, что он
равен последнему выражению.
Таким образом, о о р
{к} ■ ■ • {i.} -z (>»%z j / * £ - ^ •
166

Но в силу 26.11
что и требуется,
26.15. ОПРЕДЕЯЕНЙВ. Положим Ц=2с(1 при kz i и £-4.
Теперь мы можем доказать следующую полезную теорему.
26.16. ТЕОРЕМА. Пусть J> - подстановка из (§^ с длинами
циклов р./ >_Яа > •. - > _Р /г. . и пусть Г( Р j - централизатор Р
iT (з^. Пусть -L**(j>) - значение в точке р характера группы
&^ » соответствующего разбиению л/ . Тогда
ft) ^Ч-Ч-^ +*№{*},
Доказательство .По определению V /л/
есть число таблоидов в М^ * инвариантных относительно J) ,
т.е. это число таких У-табловдов типа ( i*1 ), что каждой
цикл J> целиком содержится в какой-либо его строке. Вычисляя
коэффициент при d ±ct£**.., е/л *- в 4р± 4j>x... Jp^ , мы
получим, что он совпадает с этим числом. Значит, учитывая теорему
26.14 и определение матрицы Пг , мы получаем
Это доказывает часть (г) теоремы.
В силу соотношений ортогональности для столбцов таблицы
характеров группы (£ мы имеем

что дает вторую часть теоремы.
26.17. СЛЕДСТВИЕ. Если £ - любая группа и $ - ее
обыкновенный характер, то для всех tiz- 0 и всех собственных
разбиений J4 числа /г функция Q№ является характером Q- , где
Здесь порядок централизатора / C(j>)j и характер j ^ относятся
к симметрической группе &к , а суша берется по всем
собственным разбиениям J> числа п ; разбиение J> записано в виде
(№>Уа>~"> J°uJ > ]^J3±?J)X^ >*.Zju.> 0 . ]&т $■ имеет
степень d , то степень Q/* равна числу полустандартных /-
таблиц с элементами из множества -{1,2,..., Ы] •
Доказательство. Характеру $ отвечает
гомоморфизм ц> из Q в б1^^ (TJ • Пусть %е(т и £/>/gJ имеет
собственные значения (=^±)<^^^' }Ы^ . Тогда ^f<2^) имеет
собственные значения d^yd^},.^ ^^ , так что 9($к)~
-J£ f ... -/• ^/j/ • - Теперь наш результат вытекает из теорем 26Л6(£ )
и 26.5 (О.
26.18. ПРИМЕРЫ. Обратимся к таблицам характеров групп 6^;<S£
Чи <$з • последняя из которых имеет вид
(Is) (2,1) (3)
Порядок централизатора 6 2 3
i i i
2 0-1
1 -I I
Мы получаем для каждого обыкновенного характера 6 любой
группы Q и каждого Q С G
в =-- тривиальный характер Q ,
в = 0
168

№%)- j(H0+o-$(f)H9)- h6'J >
Заметим, что $W®$ ®~$®+ $ M 0% в(i)-$M+qM
и т.д. (ср. с правилом Юнга).
Боли $ имеет степень с/ • то
(две последние степени проще всего вычислить с помощью
следующей теоремы).
Следующий результат аналогичен формуле крюков для dim S^
26.19. ТЕОРЕМА.
dim уу - — г * 1 \
I/Гдлины крюков в. [Л J J
. Доказательство. Сначала докажем, что
dim W™ -(^*/-~±1)> если к - неотрицательное целое число-.
Естественный базис пространства W^ состоит из (^-таб-
ловдов с элементами из /l,2,...,^j . Этот базис находится
во взаимно однозначном соответствии с последовательностями из
"палочек" (/) и "звездочек* (#), состоящими из d-i палочек
и к звездочек, например:
+*> I В Ъ Ч Ч Ч Ч 8
Таких последовательностей имеется ( гу_ у / » поэтому
такова же размерность пространства lf^kK
Поскольку {^]':\{^i +J - i } I 9 мы имеем

Обозначим этот определитель через 4(d) • Цусть разбиение Л
имеет ji ненулевых частей (так что мы берем определитель
матрицы размера А*Я). Ясно» что многочлен Ш)имеет степень X±i
+&f*»+\* старший коэффициент
\(i + '-1)и(^(яявткрюков в /Ч)(в ^^19#5 ж 20Л>#
Значит» наш результат вытекает из следующего утверждения:
Вели kz-k+i Ж i* является наибольшим целым числом о>
таким, что %i*k+i. то ф/+к)1*делит f(d) при ^ff ж(с!+№**к
делит ffit/ при л<0 (число £ измеряет, "как далеко мы
зашли вправо от диагонали", и приведенное утверждение
обеспечивает правильность числителя в формулировке теоремы).
Случаи!. £-£0.
При г^ г* мы имеем d**d + jt ^c{+ %i - г . Из третьего
приведенного выше представления ffo/J в виде определителя видно,
что при i^i* все элементы г>й строки нашей матрицы
делятся на d + -к Ц Значит, i£(d) делится на (d+k)1*
Случай 2.
Kofi этом случае мы утверздаем, что i(d)^det (Mk*d)J>
где Мк ft) - некоторая матрица, (i>j)-u элемент которой
равен
[ d+k J
для всех i и всех j^-k • Это, очевидно, верно для k=-t
(в силу нашего первого выражения для -f (d)) 9 так что
предположим, используя индукцию, что это верно для к . При всех
jZ-k вычтем 1 -й столбец матрицы М^ (£/) из (j+d)-vo
У Как многочлены от d . - Прим. дерев.

столбца . При j^-'k-t-d элемент (i,JJ новой матрица равен
%+d+j-i + k) /kt + d+J-i-i+k)_ fa +d+j -i+k-± )
ct+k J~ [ J+к J~ \ d+*-± J
Таким образом, эту нозую матрицу можно взять в качестве J4k. (°0Р
т.е. наше утвервдение'справедливо. /* ■ • \
Поскольку биномиальный коэффициент ( *%"%J равен О
при &t+j - i < 0 и равен 1 при #; */ - £ ^ О и мы имеем
Я^/-г^ О лрл г^г* и jz-fc » w матрица 7^ fyfcj
имеет вид
^*W=
единицы
нули и единицы
Следовательно, ранг M^^kj не щювосходит ^k-ij+fy-fri);
откуда следует, что размерность ядра 1%к(-к)пв меньше, чем
г * + <ic v Таким образом, ?(#)=ofe2f (?tf к fd)) делится на
(#+ к) i*+k } что и требуется.
26,20. ПИВДЕШ. (О Если Л- (£) , то aton у4 ( у;< * "<
В ча^^и, dim ff&= ^p) .
(и) Если [Х7= XXX, то граф крюков [Я] имеет ввд 4 3 'I.
XX 21
Заменяя точку ( i> i ) диаграммы [%] числом у - г , мы получим
0 12.
-I О
. , a d(d+$(d+x)(d-±)d
Наша теорема дает тогда с/г/а ^д = -> i/^.&.i.f '
Так же как и формула крюков для размерностей модулей Шпехта
5 я , формула теоремы 26.19 является гораздо более практичным
способом вычисления размерностей модулей Вейля WX* чем П°Д~
счет полубтандартннх таблиц.
171

ПРИЛОЖЕНИЕ
Матрицы разложения симметрических групп (5^ дш простых
чисел 2 и 3 и /UI3
Мы умышленно приводим матрицы разложения, не объединяя
характеры в блоки. Это облегчает угадывание закономерностей
которые могут выполняться в общем случае; сравните ,например,
часть матрицы разложения (ъ1Ъ , соответствующую разбиениям
на 3 части, с матрицей разложения Gi0 и см. замечание после
следствия 24.21.
172

Матрицы разложения групп^для простого числа 2 и п < 7.
п г о
*1 (0)
о
1
n g 2
1 (2)
1 (I1)
iH CM
n s 3
со см
1
*2
1
(3)
(2,1)
(I3)
П 5 Ц
л- со
1
3
*2
3
1
(4)
(3,1)
(22)
(212)
(1*)
1
1
1
1
n s 5
1
Ц
S
*6
5
Ц
1
(5)
(4,1)
(3,2)
(312)
(2*1)
(21э)
(Is)
1
2
1
Н Jttf Ю
•ч ш .=*-
00 О
см
Х\
1
5
9
16
10
5
10
S
9
S
1
s 6
(6)
(5,1)
(^,2)
(321)
(Ч12)
(З2)
(31»)
(2*)
(2212)
(21")
(Iе)
•■>
Ш
SmS
1
1
1
2
1
2
1
1
1
1
Н CM iH
•* •» см
to *• со
ч^ ч*» ч-*
1
1 1
1
1 1
1
1 1
1
1 1
1
п = 7
1
6
14
14
35
15
21
21
*20
35
Ш
15
14
6
1
(7)
(6,1)
(5,2)
(Ц,3)
С»21)
(512)
(321)
(322)
(tls)
(3212)
(2'1)
(31ч)
(221>)
(21*)
(I7)
■Ч CM CO iH
/-ч * * *СМ
1
1
1
1
1 1
1
1
1
1
2 1
111
1 1
1 1
1

09Т (ге*о
ff> Oil (169)
Ibj 8/. (тгэ)
- 91 (*t*S)
| « 8<i (E*9)
£ I эг (г*£)
£ S ' 8 (T*8) .
§ о Т (6) и
CM CM CM CM CO
CM
«i N » о гН* M i4«o ww м> mt r-{
iHiHiHiH* HHCMHCMH H Hn
Ч/ММ •» CM СМП *4 CO CO«4 J* CM CM
wNNwWNWvyvyW ч-> ^f if *•>
\ш* Ч-> ЧУ ГОЧУ Ч-^^Ч Уш'Уш'*
со
ч«*
,4С -
СП г-1 СМ СО .Э* Н Н СМеГ Hn *» w w
ч_, « « « »см COCO rHw CM iH iH гН
СО t>(0 U) (О 1Л d> Г^ ^ Ш Ш СМ СО
ч-/N-/ч^ ч-/%-• ч-/ч^ ч^/ч^ V-/ ч-/tO J3-
to
Чм*
»48
fHOOC^OOCMlOCMOOOOifOCMCOCPiDO
CMJfJfOlOCOCMOOCMifinOOiHr^
1H1H1H H H CM
<ГГ
iU
3
я rpyn
ожени
«=8
СО
cd
i
Матр
CMJ
числа
о
1
о
а.
е
i
0*1
♦?9
8
♦il
9
Т
<т
8*?)
(T2S)
(8
(г
(I
•9)
•9)
(8)
■Ч iH H iH
н
Н iH iH iHiH
iH H H H H гЧ CM
iHHrH 1H1H1H CMCM
iH rH CM H CM CM rH CM
• Ф * N *» H* «О *4 *
rlrlrlHHN CM rH iH r4
чу мм •» CMCMwCOw if *"n
ч^ CM CM CO CO w СО *~ч VN
Ч^ ч«* ч«* ч^ >-> CM rH
W CM
CO rf
ч^ ч^
00 H CM CO H Hn w « w
wo* ж CM CO Л* H CM rH
r^comina-wto:? m
iH
CM
•H
H
и
• •
ce
sc:
о
ё
a.
ф
X
iHt^Ooo^fO^fHiocMinO
СМСМчОГ^гНСМЮ^-СОСЯ

Матрица разложения группы \*j для простого числа 2
•Ч СО СО 00 чО О 00 СО О СО
СМ гГгЧСОСЛ СМОчО
гН Н гН СМ Гч,
1
9
35
75
90
160
315
288
450
768
42
36
225
252
210
84
350
567
300
525
126
448
(10)
(9,1)
(8,2)
(7,3)
(6,4)
(721)
(631)
(541)
(532)
(I10)
(21»)
(221«)
(2»1*>
(2"12)
(321s)
(322ls)
(3231)
(32212)
*(4321)
(52)
(812)
(622)
(422)
(432)
(71s)
(6212)
(5312)
(4*12)
(5221)
(61*)
(25).
(317)
(321ч)
(3222)
(Зэ1)
(416)
(421%)
(42212)
(423)
(4313)
(51s)
*(5213)
/^ Н N Р)
Q «к •* •
Н О) 00 Г»
1
1 1
111
1 11
1 1
1 2 1
2 11
1
2 11
1 1
2 11
2 1
2 111
2 13 1
3 13 1
2 111
3 12 1
2 12 1
л-
«»
со
1
1
i
1
1
1
2
1
1
1
гН Н
СМ СО
f* <£>
1
1
1
1
1
1
1
, 1
2
*ч
л-
ю
1
1
см см
со со
m st
1
1
1
1
1
1
1
Номер блока:
1111121213

Матрица разложения группы (!9д для простого числа 2
1
10
1*4
110
165
132
231
550
693
990
990
2310
45
330
385
660
462
120
594
1232
1155
1100
1320
1188
825
210
924
1540
252
(11)
(10,1)
(9f2)
(8f3)
(7,4)
(6,5)
(821)
(731)
(641)
(632)
(542)
(5321)
(912)
(521)
(72*)
(532)
(423)
(81*)
(7212)
(6312)
(5412)
(6221)
(4221)
(I11)
(21$)
(2217)
(2S15)
(24s)
(251)
(3216)
(3221ц)
(32312)
(3221s)
(32221)
(43212)
(31е)
(32н)
(3215)
(3S12)
(3S2)
(417)
(421s)
(422ls)
(42sl)
(431*)
(4322)
*(4321)
(52s)
(71ч)
(621s)
(531s)
(42ls)
(516)
(521")
(52212)
*(615)
Номер блока:
•ч о
(11)
(10,1)
1
1
1
1
1
2
1
1
2
3
1
1
2
2
2
2
2
3
2
2
2
3
2
2
4
2
1 2
st
st
CM
m
1
1
1
1
1
1
1
1
1
1
1
1
1
100
CO
m
00
1
1
1
2
1
3
2
1
2
2
st см eo
CO CO 00
St UO iH
* *CM
f* CO 00
1
1
1
1
1
2
1
2
1
1
1
1
1
1
1
1
1 2
1
1
1
1
1
1
1
1
2
2
1
198
H
CO
1
1
1
1
1
1
1
1
1
2
1
St
St
iH
■4
J*
CO
1
1
1
1
1
1
1
00 CO 00
St HCO
00 St rH
H
(632)
(542)
(5321)
1
1
1 1
1
1
1
1
1
1
1
1
1
2 12
176

Матрица разложения группы \Оц Для простого числа 2
Н О ^ О ^ N ОО оо «(О со см см со
гН .Э" О СО СО СМ Г* О 00 ^ Н СП СО СО
Н Н <ОЛ tf NO Jth (О (О
r-i iH гН Ю CM
см
*-ч • *CO£ft/)rHf4HrHCMC4COCMCM
WHO * • «No л- tow ^^ w d-
H rl rl O) 00 f"> CJ> 00 t«> (O N (O U) (O lA
1 (12) (l12)
11 (11,1) (21l0>
54 (10,2) (2218)
154 (9,3) (2816)
275 (8,4) (an11)
297 (7,5) (2S12)
320 (921) (3217)
891 (831) (322ls)
1408 (741) (32218)
1155 (651) (324)
1925 (732) *2S12)
2673 (642) (322212)
2112 (543) (3321)
5632 (6321) (43211)
5775 (5421) (43221)
132 (62) (26)
55 (1012) (319)
616 (822) (3216)
1320 (522) (3228)
1650 (632) (3818)
462 (4s) (3*)
165 (918) (41s)
945 (8212) (4216)
2376 (7312) (4221%)
3080 (6412) (42812)
i486 ,(5г12) (42*)
2079 (7221) (431s)
4158 (5321) (43212)
2970 (4231) (4322)
1925 (628) (421*)
4455 (5322) (42212)
2640 *(4222)
330 (81*) (517)
3696 (6318) (52218)
3520 (541s) (5281)
3564 (62212) (531%)
7700 *(53212)
462 (715) (61е)
2100 *(621ц)
1728 (7218) (521s)
1
I 1
1 1
111
II 11
1 111
1
3 1111 1
1
1 11111
3 1.111 1 1
311111 1 111
1 1
552312 1 112
1 1
111
2 1 1 ,
2 1
2 111 1
2 1
12 11
3 2 2 11
4 2 13 2 2
4 2 13 2 2
3 11
3.2 1 2 1 1
2 5 12 1
2 4 11
3 2 12 11
3 5 13 12
4 2 1
2 2 111
622322 2 111
1 1 1
622221 2 111
862423 2 122 1
2 2 12 11
422221 2 1
1 1
1 1
1 1
1
1
1 1
1 111
111
1 1
11 1
1 1
I 1
II 1
1
Номер блока:
111111212111231
177

Матрица разложения группы (*) для простого числа 2
•Н <ч jf ю л* О г* л- © cn да со О со со со о со
H(D О<0(0 Ш (О Г*. Г» СО Л" iH СЧОО О^Г
<N TO W> CO U)iA N О) 1Л Г» СМ О N ^
' Ы СЧ N HNOO О©
*•% » • **• «Л «><Ч НИ Н <М « <Ч ТО <Ч СЧО
«Ч Н Н Н СП СО f* «H СП СО Р* СО Г*. «О «О Г» (0 Ш
1
12
65
208
429
572
«129
429
1365
257»»
2860
3432
6006
5148
6435
12012
17160
15015
66
1287
936
3575
3432
2574
220
1430
4212
6864
5720
3640
8580
11440
3432
4004
12012
12870
11583
8580
495
3003
7800
10296
5005
7371
20592
21450
16016
9009
729
4290
9360
924
(13)
(12,1)
(11,2)
(10,3)
(9,4)
(8,5)
(7,6)
(1021)
(931)
(841)
(751)
(832)
(742)
(652)
(64*)
(7321)
(6421)
(5431)
(1112 )
(6*1)
(92*)
(73*)
(5*3)
(54*)
(101s)
(921*)
(831*)
(741*)
(651*)
(82*1)
(5*21)
(63*1)
(4*1)
(72*)
(632*)
(542*)
(53*2)
(I1»)
(2111)
(2*1М
(2*1т)
(2*1*)
(251*)
(2*1)
(321*)
(32*1с)
(32*1*)
(32*1*)
(3*215)
(3*2*1*)
(3*2*1)
(3*21*)
(4321*)
(432*1*)
(43*21)
(31|#)
(32*)
(3*1*)
(3*1*)
(3*2*)
(3*1)
С41»)
(421т)
(42*Is)
(42*1*)
(42*1)
(431*)
(432*)
(43*1*)
(43*)
(4*1*)
(4*21*)
(4*2*1)
(4*31*)
*(4*32)
(91*)
(821»)
(731*)
(641*)
(5*1»)
(72*1*)
(6321*)
(5421*)
(51*)
(S21«)
(52*1*)
(52*1*)
(52*)
(531*)
(5321*)
(532*1)
*(53*1*)
(62*1)
(81»)
(721*)
(631*)
(541*)
(617)
(621*)
(62*1*)
*(71«)
Номер блока:
1
1
1 1
1
111
1 1
1 11
11 1
3 11 11
4 11 11
2 11111
2 1 1
4 1 1 1 211 1
11 11
3 1 1 111 1 1
3 2 1
4 12 11
7 3 1 111 1 1
2 1
1 1111
2 11
3 1111 1
2 111
2 1
1 1
4 2 1 11
3 12 1
6 2 3 2 211 1
2 2 11
2 11 1
3 11 11
2 1
2 1
4 2 2 11 1
3,1 1
6 3 2 2 111
5 3 11 1
4 2
3 2 1
5 2 1 111
8 2 3 21311 1
8 2 3 21312 1
3 1111
7 2 2 11311 1
6 13 2 1
12 4 3 31312 2
8 4 2 2 2 12
7 2 2 11211 1
2 11
6 2 2 11211
* 1 3 2 1
4 2 2 1
12121211111212
1
1
1 1
1 1
1
1
1
i i
i
i i
i
i
i
i
i
l i '
i i
i
i
12 2 1
178

Матрицы разложения групп Q для простого числа 3 и п < 7.
п = О
*1
(О)
n g 1
*1
(1)
n g 2
(Г)
«-» ГО ft ГО
Н ^Н (О
IL
1
*2
1
п «
1
5
9
5
10
*16
9
5
10
5
1
» 3
(3)
(2,1)
(14
JB
(6)
(5,1)
(»»>?>
(3*)
(Ч12)
(321)
(221а)
(2Э)
(311)
(21М
(Iе)
*>ч •»
СП СМ
ч»* ч»/
1
1 1
1
*-*
r-t
f» *»
«О Ш
1
1 1
1
1
1 1
1
о>
/■Ч
СМ
гг
1
п
1
3
*2
3
1
|Ч СО
*■■*
*"Ч «М
м <Н
го j»
1
1
1 1
1
1
1
fJt
(Ч)
(3,1)
(22)
(21*)
(1*>
i-l fH
СМм
го м
1
1
1
1
1
f»
л- го
ч»>
1
1
ч^
1
СМ СМ
ч«* ч»*
1
1
1
n g
,1
6
14
14
15
35
21
21
35
*20
1*»
15
14
б
1
n g
1
4
5
*6
5
4
1
_2
(7)
(6,1)
(5,2)
(4,3)
(Ыг)
(421)
(321)
(32*)
(321*)
(418)
(2J1)
(31*)
(2*1J)
(21s)
(l7)
±
(5)
(4,1)
(3,2)
(31*)
(22 1)
С 21» >
(1$)
*-N
iH
/■ч *
c»» to
Ч«/ Ч^>
1
1
го
^ч.
«-4 СМ «4
о-ч л •» fH
U> 4f ГО ГО
W Ч^> Ч^ W
1
1
1 1
1
1
1
«нем
Г\ #"Ч*"Ч *"Ч
см го «• *н *н
л
(П
1
1
1
•» r-t CMf*
л- ю * го
Чм» Ч^» Ч.^ Ч^
1
1
1 1
1 1
1 1
1
1
1
1

Матрица разложения группы (3* для простого числа 3
«HftCOCDiHiHtAf** Ю сЧ © СО С©
•ч см см Л (о м фнм
1
7
20
28
Ш
21
61
70
56
*42
*Э0
56
70
3$
14
35
6>»
28
21
20
7
1
(8)
(7,1)
(6,2)
(5,3)
(I*2)
(61*)
(521)
(431)
(42*)
(3*2)
(421*)
(3*1*)
(32*1)
(51J)
(2»)
(41*)
(321»)
(2»12)
(318)
(2*1*)
(21*)
(1»)
^ч
fH
•»
во г*
1
1
1
1
1
1
1
1
С4
•»
<0
1
1
1
СО
«к
ю
1
1
1
^ч
•1
JT
1
1
1
1
«
|Ч
#ч
см
Ф Ю
1
1
1
1
1
1
Н «
еч И г4«
СО «ММ СМ* СМ
лг *■
1
1
1
1
1
1
1
1
п «пп
1
1
1
1
1
1
1
1
1
Номер блока:
1221231123U2

Матрица разложения группы (^ для простого числа 3
н г* г* #ч»ч#Н1Лмг^ю#-1агг*о*нм
СЯ * С4СО Ф (*) МШ N«^(6
1
8
27
48
42
28
105
162
84
120
168
189
216
216
168
162
*42
56
84
*70
189
120
42
56
105
48
28
27
8
1
(9)
(8,1)
(7,2)
(6,3)
(5,4)
(71*)
(621)
(531)
(4*1)
(52*)
(432)
(521*)
(431*)
(42*1)
(3*21)
(32*1*)
(3»)
(61*)
(32*)
(51*)
(421*)
(3*1»)
(2*1)
(41$)
(321%)
(2*1*)
(31*)
(2*1$)
(21т)
(1»)
^ч
Ф
1
1
1
1
1
1
1
1
Н
«
N
•
€0 Г»
1
1
1
1
1
1
1
1
1
1
«о
«•
<£>
1
1
1
1
1
1
а-
т
%Я
1
1
1
1
1
1
1
1
М
Н
г*Ы
Г* 40
1
1
1
1
1
1
1
1
1
1
1
1
1
1
гЧ
О
10
1
«Н « «Ч |Ч
« N П(Ч
a IA » 1Л
1
1
111
1
Hi
Л
St
1-1
111
1
1
1
1 1
1 1
111
1
1 1
1
1
iHH r-l
N М«
М« «Ч
st to to
1
1
1
1
1
1
1
1
1
Номер блока:
1121 1И3111М 2 15

матрица разложения группы *гэ4Лдля простого числа б
I Ш *Н О Н Ш ^ЛО»<0 <0<0*^ Г*»* d-HO I** СЛ
со л* о» го со г- счсмсооосмшсосм^о^шг-
О* Н гН CM tf) «M tf> CN
лН NCO * Л,4 гН «Н rH w CM CM «« гЧгЧгЧм «М СМ
О * * * *«*гЧСМСО.*<М«0«<« СО СМ СО м СМ ГО «,
Н Ф ООС^Ш1ЛООГ^Ш1Л*Ои>Э'^Ш4Л^1Л4ГГО
м см
см*,
J* СП
(10
(9tl
(8t2
(7,3
(52
(812
(721
(631
(541
(622
(532
U22
(Ц32
(6212
(5312
(Ц212
(5221
(Ц321
(3222
(42212
(32212
(713
(331
(Ц21
(61*
(521s
(Ц313
(3231
(25
(515
(Ц21*
(321*
(32213
(2412
Ul6
(3215
(231*
(317
(221*
(21е
(1io
1
1
1 1
11
1
1 1
1 11
1
1
1
1
i
l l
l l
l
l
l i
l l
l i
l
l
l
l l
l
l
l
li l
l l
l
l
l l
l
l
l
l
l
l
ill
l
l l
l
ill
l
l l
Номер блока
182
1211213133232114111352

Матрица разложения группы ч!3^ для простого числа 3
НО tf OIHHlAOOftOOMAOOtH,»tf?0)»HHOn
rt« ОП Л МЛв»НН4ЯЛНЛФ01(ПНН001ПО> N<J»
сЧ »Ч НАШ N N СЧ «Н (Л Г* Г>Г-сЧ*Л»ЧГ»СПСО
г% *^ **\
*"ч ^ ^4^4*"4*"4^4^4*"4W w гЧ
Н^о^^^^^^^аамаам и «HHrlH* гЧ гЧ «
^ч «N П »tft м сЧ «Ч «Ч гЧ «« N N«1 «П»Н*Н«-<*« N N« <* •« <Ч«М
rlO * * * * #4 <Ч «О Л- «* «simtftnM N«tfNW«(nrtNnN
ННО) 00 ^>tf> О» «0 Г» <0 «/) Г» (D tAlA ^ Г* 0iO(D U) & & * U) Д" С»
1
10
44
110
16S
132
45
231
SSO
693
330
38S
990
990
660
462
594
1232
1155
1100
2310
1320
*1188
1320
1540
2310
990
120
825
462
210
924
1540
825
660
1155
330
*252
924
1100
1232
990
693
132
210
594
385
550
165
120
231
110
45
44
10
1
(11)
(10.1)
(9,2)
(8,3)
(7f4)
(6f5)
(91*)
(821)
(731)
(641)
(5*1)
(72*)
(632)
(542)
(53*)
(4*3)
(721*)
(631*)
(541*)
(62*1)
(5321)
(4*21)
(43*1)
(432*)
(52*1*)
(4321*)
<3*2*1)~
(11»)
(52»)
(3*2)
(71*)
(621»)
(531»)
(4*1»)
(3*1*)
(42»1)
(32*)
(61»)
(521*)
(431*)
(42*1»)
(3*21»)
(32>1*)
(2*1)
(51*)
(421»)
(3*1«)
(32*1*)
(2*1»)
(41*)
(3214
(2»1»)
(31»)
(2*1»)
(21»)
(l11)
Номер блока :
1
1
2
1
1
2
2
2
1
1
1
1
1
1
1
1
1
1
1
1
1
2
1
1
-
1
1
1
1
1
1
2
1
1
1
1
1
1
1
1
1
1
1
1
1
2
1
1
1
1
1
2
1
2
1
2
1
1
2
1
1
2 3
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1 3
1
1
1
1
1
1
1
1
1
. 1
1
1
1
1
1
1
1
1
1
1
1
1 2 3
1
1 1
1 1
1
1 1
1 1
1
1 1
1
1 1
31241121241223

STOI H
XS*iT и.
168 ы
9E6T h *
♦i9S8 и гн
со Lbl *
cd тех и ч
§ «I9S8 н
s Stt6 н «н
0 8за н ••*
£j E*iT и н #ч r-t
g 83«iX ** гн n гч
О BZL1 «ч in ih
с liS н и
§ 9861 н гч#н «4
** T€*iT * * ы
& S*l6 * н H •"•
031 И *Ч гЧ *Н i4
0X1 Ы Н гНМ Н Ы ri
ш"
I? em ^
(т; ОТ Z н *н ih нгн
а ОТ «-« «Н «Ч г* г* «Ч СМ
^ СТО! НИ г* г-1 И i-l г4 г*М
§ 168 н
*> огт
cd
о* 9«i н^
а
I H г* *Ч Нем CM
g ТЕХ и и
1 8*il «ч-«
g 01 и н .
5Г Т г-«Н •■• гЧ
СЧ
(Я
S
а,
«
с-
а>
а,
МНМП^ЮМ «• iHfHr-trlM NWNw СО* « * « iH rH iH fH i4 «ч f* См«ч «4 « M «H«
,_,»«*« »<0 HNCO JlONfOtf « r>»HHHHM WWW CO CM CM м i4 «H «H rH «* И
W^OO>CQC*.w©O>COCt»t0eOf»<©U>t0IOCMCOa'«* N«tf«« О** CO «« NNM CSl«
i4r-t<wv^w H4/wvw4/VwwWCOM0iOMOU)U)^U)^^NC«)N «ПО <M
ww w wwvwvvvwvwwtf u)tf ^^n
ww www CO
W
iHiH^^tf>t^<N(AOlH9U>«DtO«nOOC4lO40OU>0><NU>aDOU>OO^OtA00lO««>
iHlAlac^CACniACMOftOtAiHCMr^CMiniH^f^ecOf^COr^lAr^intfr^OOtAiar^r^
iHcm cmiH «nco^r-itooxocotorHomo^O^c^f-tcn^tocnior^^r-ic^iD
•H H #-l CM iH «4 CM CM CO f-l CM t/> Ю * CM * CM CM CO I** & dt tf> CM

Х68
9C6I * -<н *
с* *i9SC
g 163
? *i9SE и
О S*i6
gtiX н r-i н
8 2*11 »И гНгНгН rH r-tiHtH
82/11 -«
tiS
98SX r^^
Xe*iX
S*»6
S 02X г-» *н .ч^^гн
>} 012 *H «4 «H сЧИгН •
I
iff
g €192 *
Я JS2 H »>4i4r4 »HH r* *H H
g 0X2 и н * гц * *м ыЛ н
gOT «H *H «H «H ^HH^iHH
Cu 168 »
5 021 «-i «ч^ч »н «-4 и
S 9*1 cH .4 H *H
i *«
л тех ^ «н
О E*iX -» -< «"<
? *iS ы ~
R OX «ч tHrHr-* »hc-iih#-« .ч
a X «*•-« NHNH i-4 iH r4fH H
n <
Г» ••n««nnilHH#»n#llM»MNH»«»««<«NN»<t<*<«b«»«tN CO
S »HNWHHHH« «4fMC4«4«4H«Hr-li-t«-4iH# M iH r-4 <-l r-4 (-1 r4 «-4 i-l«4 rH r4 tH «Hr-4 <H r-t H~ •• !£
S 4/O><OvC0Nntf Мй :? « t<» <Ч О « «4 СМ«ч м СЧ w <0 CJ СП <* СЧ*»и» ii)NNN « SN« WW #HiH О
у 4^w**»ww w w w ч^ i/) лг w Л" ** ч^ w ^ <*> СЭ w WbSttw ww ww О
CO ww ч* www w q_
Ф
Nl0tONOCOt0OONiAOMO^lA(ONO OMNNtOtnviAOl^OtfXOHWlAO^OtfHH О
(OttNttONOINNHCOMttOttNOimu) 00*ПГ«ЗШе^Г-«^<мОС»ПЭ^|-Ча»Г*>Ш«М»П«Л1Л»-1 X
»HO)«mr<>«V}iQH»<4d'H(ftOI(OU><0 0|НН*е*©СПОгГС*«ОСП«Оео01сНГО«-4
«H *H CO Л «О <S| iH r-« NnHrtlrtH CO «H »-* O» CM #-♦ #H
185

ID
Л
Z80S г
£822 «*
Й с SIZI ч
эегот и
с
с2 89S8
К
S
*
О
■ч
со
се
а.
3
s
п.
Ей
СП
S
СТЬ
cd
со
?
О
S
3*
о
is
ь
о
£
с
для
гхг*
662Х гН
вги п • #
Х£С£ *
£Х* .4 И
89S8 ,н^ и
S90T -• и г<
8Е6Х »-»•-• »* •*« •
96ZOX -« -»«-i
82*lX <н rHiHrH гн «ч f
88$Х •■*»"• «"* •"• «ч . •
£9££ •-*»-» г* «нин «н
2X2* н и
ев S90X «н н «ч#ч Нгц н гн г
§ 022 w гн гн
SL *l26 ^ гЧ И ИгНгН f
99 н н
280$ ни и н
26& «H rH iHe* fH iH
S6*i «н в-i t-i н t-i t-i
2X «H t-4 H« Иг*
$£2X н i-i i-i ih «Hf-4
662T rHi-i #-i «-tin ih
99 н н н «н ih iH
X H «H «-I *Ч «Ч WH« *f «9 *•
82*t *h*-i «-г гНгН «н «ч
LX* iH «-4 «-4 «H iHfH r4
£*»X iH iH «H «H «H v rH <H f-lf* r-tr-trH rH i4 «H
П9 «"•** ■■« **•-» r* •-<
2X н «н м «ч «н , «Mr-i c*
■J i-l i-liH lH <M «H «H «N MHMtf «ЧСОСЧ €4 CO «
CO r-t CM CO Э» «Л tO« rH fH #H «4 r-(M СЧСМСЧм «Ли ««МММ «H г* <Ч r-t «-Ч «Нм «ч NNw #•«•«« i-t rH r1«*
,4 •>•>»« * «,н *»СО Л- ШМ «ч! <П ^ Ы» СО »«• JT *Н «Ч «Ч НМ «Ч СМ СМ«« СО СЧ «М«ч СО #-| »Ч #4) »Ч «Им N МН
w «st но о» во г» *»«ч с» со г» <0 0>аэг«> «о г- <о »л»л емт ^г «л <м<п »« о л- «»> л <•>•• « счечм «nn»i я
r-t r-< rH «-* ч»/»«х f-t »^x^#^^ w vv/wwv/wv О А Г» «О СО Г» Ф %П «О «Л «О %Л W> JT «41 ГО JT **>•! «Ом СО <М
wws^ «НО wws^www^www4x4xwwr» <0«r>«A ЛЧ%* ЯГ<*>
HNtAeoCnrNOIIDCniA^OtotPtftfOlAlAM^ONJOOMO О О «flNO«OHNO»«OOM)0
Hl0ON^NФNtf^(OФmNO9^^>n^nн«DN»HlDшaин^ttc»^<яu>н•tf)^ИlD
см а- ю jt агокАо»«чс71а>0«^«Л9а>1па>счсог^<ООгН1Ла-ООвои>1ЛСо«Аа/0«А.э-в»Ог-1
f-ЧСЧСМгН СО«Л%ЯСО»ЛСО«Ч«НЯ'«в1ЛСО«Ч|Г^вО»Ч»Л«Ч«Ч1«-1вОГ*0«Н)40#Н»Н«*1«ОГ*
186

£80$
LZll
SUX
96301
me
бвгх
89S8
л XLtL
S IUL
8 tXk
*3
о
89S8
g S90I
g« 8861
^ гы
^ 96301
* 9Z*X
о
о
8861 нн
*i9
fa £988
g гхг«1
О S90I
& SSti
огг
§
ее гы
99
280$
a S6«i
л гх
13
1
1
3
LUZ
SUX
6621
огг
99
X
8г*
£X«i
*9
гх
х
Н«» «Ч ГО |Ч гЧ rH iH сЧ*» * СЧ ««< <Ч r4 iH i4 iH i4 гЧ Ы #4 «Н i-Ц* •• С^гЧ
О аг г* * о *•! о гг•« ммлол cociwa-w «ч «мм *» <ч см с* о с*
гЧ w w4^ w «О С*» <0 «Л <0 ww ^ f> wf» CD U) СМЮм W Мй д>м ww
NmO^OOOOOOt^OMOCnCAlDOUXnHd'OXON^OH
C42fOtf)^O00CMOOiOOM>JtC^C4CnO«*)inO^r<Mcrr^f4<M<P
C> Л" СЧ СО С"» О *Л СЯ CM tf> Q0 СП d-WOTOiO^HOlDlOinH*
гч сч *н /ч гч
187

cd
»
о
о
о
а
5Г
о
и
о
Е-
о
о
о,
с
19-
с
*
О
«=5
СО
со
§.
ё
2805
Z.8ZZ
SLIT
96201
гтг*
me
6621
8938
ILZL
BZb
1
r-lr4iH
r-t<4 r-l
•Н «Н
Ш£, *
an
89S8
S90I
8Е6Х r4
e*ii
эбгот
8г*?х r*
8861
ьэ
me
гхги
S90I
56*1
огг
гб£
*ге -н
99
2809
ZSL
S6t]
гх
дегг
S/.2T
6621
огг
99
X
82*1
Lib
е*х
*9
гх
X
HiH «Н
r-tiHH
H <Mr4r-l
r-tiHr-t
*4 i4
i-tr-l
•HiH
<4C* *> *H*4
•4 •-!
гЛ Ы
СЧПЫ M CM*» *• W * CM Ш M COM CM"» » U)MN «. «# Я* N« i-*«* Hr
«040 Л" CM «*> tr> <M CM NV/^ |Л Л> <"•»*• NN^jCONNwCONfONNv
OHa>0(4mtf(000)N<ooc4Md-Nu)OcDu)(noo>eo(DU)Hi
0)Г»ООгНС^ШО*ОС400^»Н<РГ*Г*<ПСПГ)«0<МС^Г>10«0«0|Н
^ r*» j* г* см го <о <о см со со j* со см r-t r-»
188

СПИСОК ЛИТЕРАТУРЫ
h] Carter R.W., busztig G., On the modular representations
of the general linear and symmetric groups, Math Z. 136
(1974), 193-242.
[2] Кэртис Ч., Райнер И, Теория представлений конечных групп и
ассоциативных алгебр. - М.: Наука,1969.
[3} Hardy G.H., Wright Е.М., An introduction to the theory of
numbers, Oxford Univ. Press, Oxford, 1960.
[4] Frame J.S., Robinson 0. de B., Thrall R.M., The hook
graphs of the symmetric group, Canad. J. Math. 6 (1934),
316-324*
£5} Garnir H., Theorie de la representation lineaire dee
groupes symetriques, Memoires de la Soc. Rovale dee So.
de Liege, (4), 10 (1950).
[б] James G.D., Representations of the symmetric groups over
the field of order 2, J. Algebra 38 (1976), 280-308.
Г7] James G.D., The irreducible representations of the
symmetric groups, Bull. London Math. Soc. 8 (1976), 229-232.
f&\ James G.D., On the decomposition matrices of the
symmetric groups I, J* Algebra 43 (1976), 42т44.
fo} James G.D., On the decomposition matrices of the symmetric
groups II, J. Algebra 43 (1976), 45-54.
FlO] James G.D., A characteristic-free approach to the
representation theory of &, J# Algebra 46 (1977), 430-450.
Phi James G.D., On a conjecture of Carter concerning irreducible
Specht modules, Math. Proc. Camb. Phil. Soc. 83 (1978),
fl2l James G.D., A note on the. decomposition matrices of (Xg and
(§^3 for the prime 3, J. Algebra, 1^78>v.53, №2, pp. 410-411.
189

J13] Kerber A. Representations of permutation groups I,"
Lecture Notes in Mathematics, no* 240» Springer-Verlag.
Г14] Kerber A., Peel M.H., On the decomposition numbers of
symmetric and alternating groups» Mitt. Math* Sem« Univ.
Giessen 91 (1971), 41-81.
ft 5] Mac Aogain В., Decomposition matrices of symmetric and
alternating groups, Trinity College Dublin Research Notes,
TCD 1976-10.
I16J McCormell J., Note on multiplication theorems for Schur
functions >,,Combinatoire et representation du groupe
syme'trique, Strasbourg» 1976,и 'Proceedings 1976, Bd. by D„
Foata, Lecture Notes in Mathematics, no. 579, Springer-
Verlag, 252-257.
[l7J Meier N., Tappe J*, Bin neuer Beweis der NeJcayama-Vermutung
uber die Blockstruktur Symmetrischer Gruppen, Bull. London
Math* Soc. 8 (1976), 34-37*
Г18] Peel M.H., Rook representations of symmetric groups,
Glasgow Math. J. 12 (1971), 136-149»
[19] Peel M.H., Specht modules and the symmetric groups, J.
" Algebra 36 (1975), 88-97.
Г20] Peel M.H., Modular representations of the symmetric groups,
Univ. of Calgary Jteseareh Paper no. 292, 1975*
Г21] Stockhofe D., Die Zerlegungsmatrizen der Symmetrischen,
Gruppen 5-J2 und ^13 zur PXlnzubl 2t Communications in
Algebra, 1979, v. 7, N*1, pp.39-45*
Г22] Specht W., Die irreduziblen Darstellungen der Symmetrischen
Gruppe. Math Z. 39 (1935), 696-711.
Г23] Thrall R.M., Young's semi-normal representation of the
symmetric group, Duke J. Math. 8 (1941), 611-624.

ДОБАВЛЕНИЕ. РЕДАКТОРА ПЕРЕВОДА
Может быть» простейшей единицей
в комбинаторике является группа
подстановок п, предметов. Эта
группа имеет различное строение для
каждого числа п. . Вопрос
заключается в том, имеется ли, однако,
некоторое асимптотическое
единообразие, преобладающее для больших п
ниш. для некоторого определенного
класса больших я. . Математика все
еще не дает ответа на такие
вопросы»
Г. Вейль "Философия математики и
естественные науки"
В этом добавлении собраны некоторые факты, имеющие
непосредственное отношение к представлениям симметрических групп и их
приложениям, однако не затронутые Джеймсом в его книге. Эти
факты относятся в основном к работам последних лет, и в их подборе
отражены интересы автора добавления. Мы остановимся на следующих
вопросах: I. Граф Юнга и комбинаторные основания. 2. Соответствие
AS7C (Робинсона - Шенстеда *— Кнута) и его применения. 3.
Предельная форма диаграмм Юнга и асимптотические вопросы. 4.
Симметрические функции и ЛГ-функтор. Наше изложение не содержит
доказательств и по необходимости является кратким; каждая из этих тем
заслуживает нескольких параграфов в книге по представлениям
симметрических групп и их применениям. Мы даем список литературы по за-.
тронутым темам, являющийся далеко не исчерпывающим (см. также
список в конце предисловия редактора перевода).
Д.1. ГРАФ КБГА И КОМБЮ&ТОНШБ ОСНОВАНИЙ
При чтении литературы по теории представлений симметрических
групп первое появление диаграмм и таблиц Юнга может оставить у
читателя впечатление чисто технического нововведения. Это ощущение
лишь усиливается, когда мы узнаем, что соответствие между
диаграммами Юнга с iv клетками и неприводимыми представлениями (§*
имеет очень сложный вид, а для построения по диаграмме
соответствующего неприводимого представления и до сих пор не найдено
прозрачного изложения (см. разд. 4 и далее).
Но все проясняется после знакомства с теоремой ветвления (см.
разд. 9) - одной из главных теорем всей этой теории. Обычно ее
191

значение. как основания всей комбинаторной 'схемы» идущей от Юнга,
недостаточно подчеркивается • В этом пункте мы остановимся более
подробно на этом, а именно опишем "изоморфизм" теории
представлений (5^ и теории диаграмм Юнга, из которого следует
принципиальный, а не технический характер этой связи.
Рассмотрим граф "У" - назовем его графом Юнга. - вершины
которого есть диаграммы Юнга (см. разд. 3)4 а ребра соединяют
всякую пару диаграмм, вторая из которых получается присоединением
одной клетки к первой. Для удобства градуируем граф по
натуральным числам, относя к вершинам степени л, (я-аду этажу) все
диаграммы £Я] с /I клетками. На рис. 1 изображено 7 этажей графа
У". Мы обозначаем, как и Джеймс, разбиения числа ti через Л ,
j flj = /г , а соответствующую диаграмму - через [Я] .
Рис.1
Обратимся теперь к теореме ветвления (см. 9.2). Презде всего
построим еще один градуированный граф, вершины /t-ro этажа
которого есть неприводимые (комплексные) представления (зп $ а
ребра (априори кратные) соединяют представления ОС и J> групп 6*,
(b^+i и имеют кратность, равную кратности вхождения вС в
ограничение j>\(g (если кратность равна нулю, то ребра нет). Теорема
ветвления фактически утверждает, что этот граф, определенный
независимо от графа Юнга, имеет лишь простые ребра (т.е. их крат-
^ В некоторых книгах диаграммы Юнга называются диаграммами
Ферре и Ферре - Сильвестра. Иногда термины "диаграмма" и
"таблица" (табло) меняют местами или употребляют слово "схема" вместо
нашего "диаграмма". Как будто бы классическая терминология,
используемая в этой книге и добавлении (см. также /Й/), теперь
стала преобладающей.
192

ограни-
ность не больше единицы) и изоморфен графу Дата, Этот изоморфизм,
единственный с точностью до единствецного нетривиального
автоморфизма графа Юнга - отражения всех диаграмм относительно
диагонали» т.е. замены строк на столбцы и наоборот» - является
фундаментом комбинаторных построений Юнга. К сожалению, до сих пор
неизвестно априорных доказательств этого глубокого факта, не
опирающихся на предварительный анализ всех представлений (5^ •
Здесь уместно отметить, что в настоящее время интенсивно
развивается теория локально полупростых алгебр, т.е. индуктивных
пределов полупростых алгебр (над© с единицей. Пример такой
алгебры ^ (ifnindC(JS**), где (f (S^)- групповая алгебра группы
(S"a f с естественными вложениями. 6 этой теории каждой такой
алгебре канонически сопоставляется градуированный граф, вершины
которого есть минимальные двусторонние идеалы допредельных
алгебр, а ребра определяются в соответствии с разложениями огг
чений модулей аналогично тому, как это описано выше для (ьЛ
Этот граф, называемый диаграммой Бтаттеди индуктивного предела,
в свою очередь и определяет локально полупростую алгебру с
точностью до изоморфизма. Тем самым, имеется эквивалентность между
категорией индуктивных пределов полупростых конечномерных алгебр
над (Си категорией градуированных графов соответствующего т**да
Vcm. £L5t 12/). По сравнению с рядом примеров, изученных в
литературе (см., напр., £l6 J ), пример графа Юнга и вгт
остается наиболее глубоким; он рассмотрен в работе [з] . Не ясно,
какие градуированные графы отвечают групповым алгебрам локальна
конечных групп; впрочем, с той же степенью подробности, как граф
Юнга, пока не изучен ни один групповой пример.
Рассмотрим чуть подробнее один аспект связи между графом Юнга
и группами -|^Л|. Граф Юнга можно рассматривать как диаграмму Хас-
се (см. Биркгоф Г. Теория структур. - М.: ИЛ, 1952, с. 22)
частично упорядоченного (по включению) множества всех диаграмм; это
частично упорядоченное множество является дистрибутивной структурой
(как множество конечных порядковых идеалов лолурешетки %+ФЁ+).
Поэтому по теореме Биркгофа (гл. 1Х,§ 5) эта структура
восстанавливается по частично упорядоченному подмножеству своих
неразложимых элементов, т.е. элементов с единственным предшествующим.
Эти элементы в нашем примере есть прямоугольные диаграммы, а их
совокупность как упорядоченное множество и есть <Z^©^£. С точки
зрения теории представлений эти диаграммы ваделены тем, что
соответствующее представление остается неприводимым при ограничении
на предыдущую группу. Таким образом, теорема Биркгофа указывает
на особую роль этих представлений в построении всех остальных
представлений.
193

По существу изомор|изм графов (см. выше) означает, что мы
могли бы изложить все факты теории представлений (ь^ на ЯЗыке
графа Юнга, используя лишь комбинаторику диаграмм. Собственно, в
этом и состоит суть работ Юнга. Опишем некоторые понятия в форле,
используемой далее.
Напомним, что диаграмма, клетки которой заполнены
натуральными числами, называется таблицей: если числа вдоль каждой строки и
каадого столбца возрастают, то таблица называется стандартной. Мы
будем рассматривать только стандартные таблицы, заполненные
натуральными числами от I до Щ , и называть их
таблицами Юнга. Таблица Шга есть дуть в графе Шга, т. е. связное
множество ребер, соединяющее одноклеточную диаграмму с данной;
действительно, таблица и есть последовательность диаграмм,
возрастающих в соответствии с возрастанием чисел, стоящих в ее
клетках, т.е. путь в графе У . Обратно, всякий путь в ~У , т.е.
последовательность диаграмм [и±],---> С1**! > определяет таблицу с
диаграммой [unJ , У которой в клетке \H^i \[v^J стоит число
"fc, £= 4 у-* к- • Число путей, ведущих в вершину [Л} , есть,
таким образ ом, число стандартных таблиц, отвечающих диаграмме
[%2 , т.е. размерность соответствующего представления (§^; мы
обозначим ее через dim, Л . Формула для dim Л - формула крюков,
см. § 20 - все еще не имеет прозрачного комбинаторного
доказательства (см. Г9 J ). Маяно пойти еще дальше и
индуктивно-построить неприводимое представление (Ьп, , соответствующее [Л] , так,
чтобы каждому пути, ведущему в [%] , отвечал элемент базиса в
нашем модуле (базис Гельфанда - Цетлина) - ср. § 25, - но такое
построение остается громоздким. В самое последнее время в £23J
предложен новый базис в неприводимых модулях, связанный с RSK
(см. далее); в целом проблема построения экономных реализаций
представлений пока остается открытой.
Назовем битаблицей пару таблиц с общей диаграммой [Л] » т.е.
петлю в графе Y" с нижней точкой в [Л] . Поскольку число таких
петель равно (dim A) *, то по теореме Бернсайда общее число
петель равно
Л (dim ajx- /<Г*/-л1
Я: Щ=п
В п. Д.2 мы опишем явное соответствие между петлями и
элементами группы (з^ (Я£Ц), дающее прямое доказательство этой
теоремы.
При переходе к группе 6^ финитных подстановок натурального
ряда удобно использовать понятие бесконечной таблицы (бесконечно-
194

го пути в графе Y" ); оно оказывается более содержательным, чем
понятие бесконечной диаграммы (см, [3] ).
Д.2. СООТВЕТСТВИЕ РОБИНСОНА - ШШСТВДА - КНУТА
И ЕГО ПРИМЕНЕНИЯ
Алгорифм Робинсон:: - Шанстеда - Кнута (Я$К) бил предложен
первоначально в «1938 г. Робинсоном [34] в связи с теорией
представлений симметрических групп, а затем был переоткрыт на чисто
комбинаторной основе Шенстедом J35J в 1961 г. ' и
усовершенствован Кнутомfe7]# Начиная со второй половины 70-х годов ему
посвящается большое число публикаций; см., например, статью Шют-
ценберже в сборнике [18J . Вероятностные его свойства и
обобщения на бесконечные таблицы, а также на другие графы
рассмотрены в [25]*
Основной вариант этого алгорифма устанавливает биекцию меяэдг
группой (S^n и множеством битаблиц (петель) порядка п , т.е.
множеством пар стандартных таблиц с одинаковой диаграммой с п
клетками,- см. п. Д.1. До сих пор остается неясным, обобщается
ли это соответствие на другие группы или оно специфично для (§^;
во всяком случае его функториальные свойства, если они имеются/
не лежат на поверхности.
Перейдем к его описанию. Зафиксируем нумерацию элементов
I. 2, ...,/г и отождествим подстановку 0£Г(§^ с
перестановкой, т.е. с последовательностью fy(l)>*-> Q(^) • Алгорифм
определяется по иццукции: мы последовательно сопоставим {$(£)>...
... > ty(k) у пару таблиц - левую и правую - с одной и той же
диаграммой из "fc клеток и, дойдя до k*n > получим нужную
пару. Обе таблицы будут стандартными (т.е. числа в строках и
столбцах возрастают), но левая заполнена числами #(2J>« •> ^{%1
а правая - числами d)...yyk> . База индукции состоит в том, что
"f? (i)} сопоставляется пара таблиц из одной клетки, в левой
таблице стоит число a(fy , а в правой * . Пусть
последовательности {%(£) v*\> Q(fy Т У*© сопоставлены две
стандартные таблицы с одной и той же диаграммой, причем левая заполнена
числами £q (i) ;.. • у Q (k)J , а правая - *£{ >.. у it} • Главное
место в алгорифме ftSftT составляет индукционный переход,
называемый "вставкой" flmevb) , состоящий в добавлении очередной
клетки. Достаточно работать только с.левой таблицей; добавив к
ней (^г+у-ю клетку опис'анным ниже способом, мы добавим ту же
клетку и к правой таблице, поместив в нее число Ж+ £ 9

Пусть все числа первой строки левой таблицы меньше чем
Q (4 + 4.) • Тогда к ее первой строке присоединяем еще одну
клетку, поставив в нее а (Ж+4.) . Бели среда чисел первой
строки есть большие, чем а(Ж + £), то наименьшее из них (оно
встретится первым при движении слева направо, так как таблица
по предположению индукции стандартна) заменяется на gft+l) 9 a
само это число • "вытесняется" во вторую строку, и процедура
повторяется с этим, вытесненным, числом и второй строкой, т.е.
либо оно вытесняет первое большее, чем оно, и занимает его место,
либо, если оно. больше всех чисел второй строки, становится
справа в эту строку. В случае вытеснения мы переходим к третьей
строке и т.д. Йроцедура заканчивается за конечное число шагов
(число строк конечно) добавлением новой клетки. Описание
вставки и тем самым Я SК закончено.
*-" f(\"ill)-
£(0,2 С*),...,£»)) «(3,6,4,1,*, 5).
Шага
I 1
2 ]
3 ' 1
4
5
6
Левая таблица
3
3 6 j
■3 4 !
6
I 4
3
6
I 2
3 4
6
12 5
1 3 4
1
Правая таблица
*
1 2
1 2
3
I 2
3
4
1 2
3 5
| 4
12 6
3 5
4
Стандартность таблиц следует из построения. Тем самым
определено отображение \5^ в множество битаблиц. Для того чтобы
установить биективность, нужно определить обратное отображение,
сопоставляющее двум стандартным таблицам с одинаковыми диаграммами
перестановку. Это отображение - оно называется стиранием
196

{d^ttttj _ действительно позволяет восстановить перестановку
"с конца"; определяем поочередно, какое число пришло последним;
для этого в правой таблице следует найти клетку с наибольшим
номером (она добавлена последней), а содержимое этой же клетки в
левой таблице переместить в предвдущую строку, в клетку, где
стоит ближайшее по величине меньшее число, и т.д. Детали
читатель легко восстановит самостоятельно.
Описанный алгоритм можно рассматривать как уточнение
формулы Берне айда: последняя выражает совпадение подсчитанной двумя
способами размерности групповой алгебры; наш алгорифм дает
фактически соответствие элементов даух базисов в групповой алгебре:
базиса из о -функций и базиса в двусторонних идеалах (см. ДЛ;
битаблица есть элемент базиса в тензорном квадрате
неприводимого модуля).
На первый взгляд кажется совершенно кеяоным, чем Ц£К ввде-
лен из других возможных соответствий, тем более что он
существенно зависит от нумерации элементов, т.е. не инвариантен
относительно автоморфизмов группы о^ . Его безусловная
плодотворность определяется большим количеством приложений, из которых мы
выбрали три: групповое, комбинаторное и вероятностное. В
указанной литературе можно найти обширный дополнительный материал.
X* Правило Диттлвуда - Ричардсона
Мы начнем с наиболее важной формулы теории представлений
симметрических групп - правила Литтлвуда - Ричардсона (см. § Я6).
Заметим, что сам алгорифм Я&К впервые появился именно в связи
с этим правилом.
Напомним, что произведением (иногда оно называется
"произведением-кружочком" и обозначается Я °/^ ) представлений
£Л] • fju, 1 . называется представление группы &п+т >
которое индуцировано с представления [Я ] ® [j11] группы
(SV * S'rn 9 естественно вложенной в §*n+rn l здесь [Л]
и [jw] - диаграммы Юнга, причем ^Я/-/г, / м, j = тп .
Представление [3L] • [f+J » вообще говоря, приводимо, и его
разложение на неприводимые и дается правилом Литтлвуда - Ричардсона:
М • М -Ц. су [*] ■
Коэффициенты С^ являются сложными функциями трех диаграмм,
а само правило имеет длинную и запутанную историю. Во всяком
случае, найденное еще в довоенных работах Литтлвудом - Ричардсоном -

Робинсоном, оно лишь недавно получило полные доказательства (Шюг-
ценберже - Ласку /18] , Томас [37] ,. Джеймс - Пил [22] , Зеле-
винский f4ljf Уайт [39] и др.). Ясное изложение имеется в
замечательной книге Макдональда [3i] (с помощью так называемых
решетчатых последовательностей, без использования RSK ). Мы
приведем здесь одну из современных формулировок этого правила,
близкую /21, 40] и принадлежащую Керову [в] .
Пусть [%] и Г/7]- дае диаграммы с п и щ клетками
соответственно. Составим из них косую диаграмму так, чтобы верхний
правый угол Пи] примыкал к нижнему левому углу Г%] (см.
рис. 2).
Рис. 2.
Рассмотрим всевозможные ставдартные таблицы, заполняющие
числами от I до 71+ m эту косую диаграмму. Запишем теперь
последовательность чисел, стоящих в такой таблице, читая их по строкам
снизу вверх (см. пример). Применим к полученной
последовательности алгорифм Я$К, в результате чего придем к двум таблицам с
одной и той же диаграммой из ft+/n клеток. Нас будет
интересовать лишь сама диаграмма. Меняя стандартные таблицы, заполняющие
данную косую диаграмму (см. выше), мы будем получать с помощью
RSK разные диаграммы. Обозначим через с» число появлений
диаграммы 9 # Правило Литтлвуда - Ричардсона теперь можно
записать так:
ы-м-2:
с>
dim, >>
М-
Приведем пример (ср. 14.4). Найдем £з] • [г] ; косая
таблица:
I | т
А
198

последовательность: С<т9 i < 1 < А . Нетрудно
убедиться в том, что £0 возможных размещений чисел 2, ..., 5 в косой
диаграмме дадут при R S К диаграммы вида £5 J , £ 4 /I J и
[3,2] с кратностями, равными I, 4, 5. Итак, [3] . [2] =.
= [5] + [4Д] + [3,2] .
Как мы увидим (см. Д.4), правило Литтлвуда - Ричардсона есть
правило умножения симметрических функций в базисе П^ра, т.е.
Я > ^ Лт у **>
где 4« - функция Шура, отвечающая диаграмме [х] . Поэтому
алгорифм RSK дает косвенным образом правило умножения этих
функций.
И. Теорема Шенстеда - Кнута и ее обобщенна
Комбинаторные свойства Я$К интересны и многообразны.
Упомянем, например, теорему Робинсона (см. [э] ): пусть QGL&n'
a v, v - левая и правая таблицы, отвечавшие а ; тогда
элементу (£~ С&п отвечает дара % и . Отсюда вытекает, что
число стандартных таблиц "равно числу инволюций в (3^ , поскольку
им и только им отвечают пары (v>v). Точное значение этого
числа неизвестно, но имеется асимптотическая формула, см. [9] .
Более важным является анализ монотонной структуры
перестановки с помощью Я$К. Теорема Шенстеда - Кнута утверждает
следующее: длина первой строки (столбца) диаграммы Юнга,
соответствующей перестановке -[$(£)>*-• > 9(п)У > равна максимально
возможной дайне монотонно возрастающей (убывающей)
подпоследовательности в этой перестановке. В качестве следствия можно подучить,
например, теорему Эрдёша и Секереша £[б] : всякая перестановка
чисел от I до n^-h l содержит монотонную подпоследовательность
длины -rw I . Действительно, длина либо первой строки, либо
первого столбца у любой диаграммы Юнга с nl+ ± клетками
больше /г . Обобщение теоремы Шенстеда - Кнута, доказанное
одновременно несколькими авторами, таково: сумма длин первых -£ строк
(столбцов) той же диаграммы равна максимально возможной длине
подпоследовательности в нашей перестановке, которую можно
разбить на ^k возрастающих (убывающих) подпоследовательностей.
Отметим, что содержимое первых -А. строк (столбцов) при
заполнении вовсе не совпадает, вообще говоря, с множеством чисел
этой подпоследовательности.
199

Эти факты использованы в [2 J и [зо] для решения проблемы
Улама (см. Д.З).
III* Вероятностные свойства.
Непосредственно из определения ЯвК следует, что образ
меры Хаара (равномерного распределения) на G^ при соответствии
Д SKпереходит в равномерную меру на парах таблиц. Если ввести
на диаграммах меру Планшереля (мера диаграммы пропорциональна
квадрату размерности соответствующего представления), то тогда
соответствие /tS#, понимаемое как отображение <J^ на множество
диаграмм, переводит меру Хаара в меру Планшереля. Вероятностные
свойства US К становятся особенно интересными, если обобщить
алгорифм на бесконечные последовательности, см. (25J . Пусть
дана бесконечная последовательность вещественных чисел (или, более
общо, элементов линейно упорядоченного множества; алгорифм RSK
можно применить и к такой последовательности, поскольку, как
легко проверить, ничего, кроме линейной упорядоченности
исходной последовательности (перестановки), мы не использовали), при
атом мы,получим две бесконечные стандартные таблицы - левая
заполнена вещественными числами (или элементами множества, где
последовательность принимает свои значения), а правая - яо-преж-
нему натуральными чисоами. Левая таблица называется
сортирующей, правая - сопровождающей (см. (25j ).
Предположим теперь, что бесконечные последовательности
вещественных чисел являются реализация»© последовательности
независимых случайно распределенных величин с распределением F1 •
Применяя к ним алгорифм Я SK, мы получим бесконечные случайные
таблицы Юнга. Если обратиться к сопровождающей таблице, которая
является бесконечной стандартной таблицей, заполненной
натуральными числами, то ей, как мы помним, соответствует путь в графе
Юнга, и мы тем самым получаем вероятностную меру на
бесконечных путях этого графа. Оказывается, что при любом распределении
f1 на прямой такие меры в определенном смысле соответствуют
характерам бесконечной симметрической группы (З^ , а при
небольшом обобщении RSK мы получаем этим способом все характеры
группы (5^. Следует заметить, что все чисто непрерывные
распределения F1 дают один и тот же характер у ц. , а мера на
путях есть мера Планшереля для (ь^ - важен лишь метрический
тип меры ОТ* f а не свойства ее носителя. Алгорифм R&Kt таким
200

образом, есть способ нахождения характеров (s^. Подробнее см.
[3, 25]
Д.З. ПРЕДЕЛЬНАЯ ФОРМА ДИАГРАММ ЮНГА
И АСИМПТОТИЧЕСКИЕ ВОПРОСЫ
Обратимся к вопросам асимптотического характера. Эта
проблематика в связи с симметрической группой, по-видимому, впервые
изучалась в работах £l, 2, 5J . Она связана с общей идеей
изучения пределов серий классических групп и соответствующей теорией
представлений (см. £*])• Такая асимптотическая теория, должно
быть, связана с некоторыми (физическими постановками (квантовая
хромодинамика), с задачами вероятностного и комбинаторного
характера и со стабилизационными проблемами алгебры и топологии
и др.
Наиболее интересная постановка вопроса для ф^ состоит в
уточнении того, как выглядят представления, характеры, таблицы
и т.п., связанные с симметрической группой, при больших п .
Другая тесно соприкасающаяся с ней проблема состоит в изучении
актуально бесконечной симметрической группы (З^» финитных
подстановок натурального ряда и ее представлений. Мы затронем здесь
лишь некоторые темы.
Рассмотрим вопрос об асимптотике регулярного представления
группы (brt • Регулярное представление (например, левое)
определяется как (левое) действие (5^ на своей групповой алгебре
£&п,У оно содержит все неприводимые представлениями
кратность вхождения каждого равна его размерности. Это
обстоятельство выделяет регулярное представление и делает интересным вопрос
о его, асимптотике*Она найдена в работе [2J и независимо, с менее
полными результатами, в [30J ; основной результат см. далее. Вы-
деленность регулярного представления видна также из следующей
простой постановки вопроса, принадлежащей В.И. Арнольду и
рассмотренной в [-7] . Рассмотрим множество всех гомоморфизмов &п
в l/(/lO-унитарную группу степени /У", JV^/l , т.е. унитарных
представлений (З^ в (£ . Это множество является замкнутым .
многообразием, а именно подмногообразием точек VS^)jL^^^\Lxil^y
удовлетворяющих необходимым соотношениям. Группа V(ffJ
естественно действует на нем (внутренними автоморфизмами) и орбиты дей-г
ствия есть классы эквивалентных представлений в (Г . Нетрудно
проверить, что орбиты наибольшей размерности состоят из пред-
ставлений, "почти" кратных регулярному, точнее, при Л ~ ^П"
201

существует единственная орбита максимальной размерности,
отвечающая представлению, которое кратно регулярному с краткостью It;
при остальных ff орбит максимальной размерности может быть
несколько, но в каждом из соответствующих представлений кратности
неприводимых представлений пропорциональны их размерностям, с
точностью до о (УУ у. Эти факты легко получаются из подсчета
размерностей. Как же устроено само регулярное представление при
больших ti ?
Перейдем к точной постановке задачи об асимптотике
регулярного представления. Будем интерпретировать меру Планшереля как
меру на диаграммах Юнга (мера диаграммы пропорциональна
квадрату размерности соответствующего представления: /ч([А])=&к!1±А1})
а саму диаграмму Юнга - как подмножество квадранта Л^ . Для
того чтобы иметь возможность сравнивать диаграммы с разным
числом клеток, нормируем их так, чтобы одна клетка п-клеточной
- i 1
диаграммы при всех /г имела размер /I * х /г" д- .В этом
случае площадь диаграммы равна единице. Обозначим граничную кривую
через У1д или просто через Л . Удобно повернуть оси координат
Рис. 3
на 45° (см. рис. 3), тогда Л есть график кусочно-линейной
функции X»—> Л (X) . Теперь можно сформулировать основной
результат [2, 30j :
202

Для всякого € > О
я.
где
Это означает, что при достаточно большом ti в соответствующем
масштабе все диаграммы Юнга, за исключением малой до мере План-
шереля доли, группируются около одной диаграммы,имеющей форму,
близкую к кривой, изображенной на рис. 3 . У.
Близость диаграмм, о которых идет речь в теореме, означает,
разумеется,и близость соответствующих характеров. Наш результат
на языке неприводимых характеров может быть уточнен так (см.
и,: , _ш, ,
где зе fo) -п - I (&) ♦ £(б) - число циклов в &\ С±>СХ-
константы.
Напомним, что нормированный характер регулярного
представления есть j- щ (б) » &е (&)> и приведенная оценка
показывает, как шшритюдимыв тярактеры. составляющие экспоненциально
подавляющую долю всех характеров, сближаются с / гед • *
Эти результаты можно рассматривать как своеобразные законы
больших чисел для представлений: сближение по мере при
надлежащей-нормировке представлений, входящих в регулярное
представление. Такая аналогия имеет более широкий смысл. В [з]
приведено доказательство теоремы, описывающей характеры (ь^ ; оно
показывает, что характеры (5^ » индуцированные с подгруппы Юнга
(см. § 16), являющиеся разложимыми, асимптотически становятся
неразложимыми за счет того, что в их разложении большая по
соответствующей мере часть неприводимых компонент сближается, когда
ft стремится к бесконечности, а подгруппы Юнга выбираются так,
чтобы! существовали предельные частоты элементов разбиения Юнга.
Случай регулярного характера, т.е. меры Планшереля, наиболее
#Для сравнения на рис. 3 дана случайная диаграмма (
= 100), полученная с помощью Я Sri на ЭВМ [2] .
203

сложен и интересен. Его доказательство опирается, в частности,
на континуальный аналог формулы крюков, состоящий в следующем.
Пусть последовательность диаграмм [Лп,] сходится (в нормировке,
указанной выше), а ее границы стремятся к кривой Ф . Тогда
размерность соответствующего представления dim Л^ выгладит так:
г
- и (diZ^y - * (i+iff*. * (*> у) *°*ч) ■> °П > (*)
где интегрирование ведется по подграфику Ф: -ffa у) :
0^ у ^ Ф(х)}- (т;е. по "непрерывной диаграмме"), ^(^у)"
"дайна крюка" в точке ( # , у ), т.е. 6(ъу)*ффс)-у+ф'*/д)-х-'
Основное дальнейшее соображение состоит в том, что искомая
функция tp^tfh должна минимизировать интеграл в ( * ), а его
значение должно быть равно - 4г . так как в силу формулы Эйлера -
Харда - Раманудаана логарифм общего числа таблиц равен ~=; YK,
и поэтому коэффициент при И в предвдущей формуле должен быть
равен нулю. Уравнение Эйлера для соответствующей несколько
необычной вариационной задачи есть уравнение Гильберта на конечном
интервале. Оказывается, существует единственная кривая,
удовлетворяющая всем нужным требованиям, она-то и дает предельную
форму диаграммы Юнга, подробности см. в ^2j и /30J .
Нахождение точного вида ненулевого члена в ( # ) -
чрезвычайно интригующая задача. Соображения, приведенные выше,
позволяют получить лишь оценку
для подавляющего (по мере Планшереля) числа диаграмм Ц&г\\ .
Иначе говоря,
Возможно, что существует предел по мере Планшереля
{ р. (dim &)z л , л
(гт -i—~ « с fr #• ^то означаю бы равенство (в
экспоненциальном масштабе) размерностей всех типичных
представлений, точнее, их равнораспределенность, как в теореме Шеннона.
Мы приведем некоторые комбинаторные следствия этих
результатов далее, а сейчас коснемся более частного вопроса, которому
посвящен ряд статей вычислительного характера.
204

Какова максимально возможная размерность неприводимого
представления группы (S'n и какова ее асимптотика? Прямая
максимизация по формуле крюков не дает результатов. Выше мы привели
оценку для типичной размерности снизу, и она пока остается
лучшей оценкой и для максимальной размерности. Маккей £32J приво-,
дат вычисления максимальной размерности представления для
ft ^ 75 , а также общую оценку снизу, основанную на неравен-
f - i,5,
где l(n)- общее число таблиц, равное (см. Д.2) числу инволюций
в (5^ , асимптотика которого известна. Оценка сверху -
тривиальное следствие формулы Берне айда. Указание на другие численные
эксперименты можно найти в £l2, 30, 32, 33[] . Гипотеза о
существовании гигантских представлений типа dun Л & //1г7 • тг >
которая оправдывается таблицей Маккея для из 75 ♦
опровергнута позже при /1= 81 (соответствующая максимальная таблица -
(15, 12, 10, 9,7 , 6, 5, 4, 3? 22, А
Какие-либо закономерности максимальных таблиц в
экспериментах не обнаружены, однако из результатов о типичной диаграмме
следует, что последовательность диаграмм, отвечающих
представлениям максимальной размерности, имеет тот же предел SL .
Расхождения мезду типичной и максимальной размерностями могут
возникнуть за счет деталей, относящихся к более тонкой структуре
диаграммы, в частности, поведения числа углов и др.
Укажем для сравнения на результат из несколько .другой
области, также относящийся к симметрической группе, где имеется
подобный разрыв. В 1909 г. Ландау [29] доказал, что
еп &(*)
Сип тъесх. - * а,
*-~ бе@Гл ГаТлл
где (/(?/- порядок элемента (Г, т.е. наименьшее общее
кратное дайн его циклов. В 1965 г. Эрдеш и Туран £l7J показали, что
относительно нормированной меры Хаара пьц на (5"^ (т.е.
равномерного распределения)
для любого & > 0 • По поводу асимптотики меры Хаара см. [5J .
Вычисление предельной формы диаграммы Юнга дает ряд
комбинаторно-вероятностных следствий; в качестве одного из примеров мы
205

приведем окончательное решение известной проблемы Улама [38~} ,
полученное в f2] , см. подробности в [25j . Вот в чем состоит
эта проблема. Пусть {£*}- бесконечная последовательность
независимых равномерно распределенных на [од] случайных величин.
Рассмотрим первые /I ее членов и какую-либо их реализацию
{£± (°°)>"> £*(">) У ; обозначим через f (п} со) мак_
симально возможную дайну монотонно возрастающей (или убывающей)
подпоследовательности. Гипотеза Улама £зв, 20] состояла в том,
что
\п —т—*
(предел по мере).
Хаммерсли [20 ] (см. также [26 ] ) показал, что этот предел
существует почти всюду, и дал двусторонние оценки; см. также
[30j . В £l2j приведены результаты многих машинных экспериментов,
подтвервдающих гипотезу Улама.
Решение этой задачи получилось как следствие приведенных
выше результатов о Я$К*ъ о предельной форме диаграмм. Любопытно,
что решение содержит информацию не только об асимптотике
максимальной дайны монотонной подпоследовательности, но и обо всей
монотонной структуре реализаций, даваемой обобщением теоремы Шен-
стеда - Кнута (см. Д.2). Редукция состоит в следующем. Применим
алгорифм RSKk реализации и рассмотрим соответствующую
диаграмму Юнга; образ равномерного распределения будет мерой Планшереля
на диаграммах, а интересующая нас длина есть длина первой строки.
Используем теперь результат о кривой SL ; хотя из стремления
диаграмм к предельной кривой еще нельзя сделать вывод о
стремлении нормированной длины первой строки к абсциссе конца кривой,
но все же можно получить оценку снизу для этой длины:
tun —TF=i £А.
Она одновременно получена этим способом Логаном и Шеппом /j30j ,
а также Хаммерсли (не опубликовано). Простые дополнительные
соображения, уже не связанные с предельной кривой и относящиеся к
мере Планшереля на таблицах, дали возможность авторам [2]
получить противоположную оценку сверху (см. подробности в [25] ),
что доказывало гипотезу. Количественные результаты, вытекающие
из обобщенной теоремы Шенстеда - Кнута, получаются точно так же.
Длина первой схроки имеет также простой групповой смысл. Пусть
диаграмма [%] имеет If клеток, а в ее первой строке п кле-
206

ток. Тогда ограничение представления (bjf, соответствующего
диаграмме £Я] , на подгруппу (ь1 имеет инвариантный вектор.
Поэтому из предыдущей теоремы вытекает, что дан почти всех по
мере Планшереля неприводимых представлений 6}у ограничение на
, имеет инвариантный вектор.
Аналогичные факты об ограничениях см. в £ 2 J .
Д.4. СМЛЕГРИЧБСКИЕ ФУНКЦИИ И 7£-ФУНКТ0Р
Связь теории представлений симметрических групп с теорией
симметрических функций у автора отмечена лишь в §26; там дана
одна из важнейших формул - формула Фробениуса для характеров
(теорема 26.16). Но роль этой связи чрезвычайно велика, и со
времен работ Фробениуса и Щура она интенсивно использовалась. Мы
приведем здесь дополнительно несколько формулировок, отсылая
читателя за подробностями к работам [24,28,31,36,41 \ ; при этом
мы используем обозначения из [31] , отличные от обозначений' §26.
Заметим, что в последние годы активно исследуются новые аспекты
этой классической темы - структуры в кольце симметрических
функций: Л-кольцо, К-функтор, полиномиальные функторы, алгебра
Хопфа и др.
Определим сначала симметрическую функцию от бесконечного
числа аргументов как формальный ряд, полученный симметризацией по
бесконечному числу аргументов симметрического полинома от
конечного числа переменных с целыми рациональными коэффициентами.
Например, x*h+2£x*, х, ДЧ*^»у>? дс; ocj и т.д.
Обозначим множество таких функций чере/ Л ; оно является
кольцом относительно естественного умножения и градуировано по
степеням полиномов. О других его структурах см. далее.
По определению 71 как Z-модуль имеет базис {тл]9
параметризующийся разбиениями Я-(*£,...,я4^;|ушщия тл получается
симметризацией одночлена ая*«... • х * * • Имеется несколько
других замечательных базисов, которые нам понадобятся:
*) -f ^я} - базис полных симметрических функций:
2) .{*а} - базис функций Шура:
3) ^Яя} ~ <5азис степенных сумм:
fя = ГТ ?%. , где <рг = m(%)-J>L ос\ .
207

Семейства {йя}я Si^ являются базисами /[ как 2-мср.
дуля, а -^Ял}- базисом А ®ч Q как векторного пространства
над Q . В^зиоы |Ад)И -[f^no определению мультипликативны.
Произведение двух функций Шура есть уже целочисленная
положительная комбинация функций 4„ (см. далее).
Я
Рассмотрим теперь А^~ группу Гротевдика группы 6^ (л-0,1,.Д
Дусть А = Ф Л к - прямая сумма. Базис в Я как 2£-модуде
по определению образуют характеры неприводимых представлений
всех групп (н . Введем умножение характеров (умножение
"кружочком"): пусть /Я/= к , jjuj^rri I 4>д о 4и, есть элемент
А п,+гя t отвечающий представлению &п,+т* индуцированному с
представления [%] ф JJ4 J группы (§*а х &^ с Q*n+m, •
Группа JI превращается в коммутативное градуированное кольцо.
Следующая фундаментальная теорема фактически принадлежит
Фробениусу.
Кольца Л ж Л изоморфны как градуированные кольца.
Изоморфизм определен единственным образом с точностью до сопряжения
диаграмм, т.е. до инволюции Я , переводящей /д в ^д' (см.
Д.1).
Этот изоморфизм состоит в сопоставлении функции Щура 1&
характера /я при всех разбиениях % .
Характеры 4 д можно воспринимать как центральные функции
на группах (Зл » т.е. функции, инвариантные относительно
внутренних автоморфизмов. Поскольку они образуют базис в
пространстве центральных функций, то можно ставить вопрос о том, какие
элементы Л соответствуют тем или иным классам центральных
функций на группах и, наоборот, что отвечает тем или иным
симметрическим функциям при этом изоморфизме. Например, пусть Я =»
= (li,"-} Ял}-разбиение и £?&- кла^° сопряженности в <§^ ,
) Я / - tl , состоящий из подстановок с цикловой структурой SL .
Характеристическая функция Е^ является центральной; оказывает-
ся , при изоморфизме ей соответствует функция Af • fJi ,где
л>я - элемент степенного базиса (см. выше). функции ^^
отвечает характер представления, индуцированного с тривиального
представления подгруппы Юнга <§я£ х ••• * ^а* ( представление
Юнга).
Эти классические утверждения дают обширную информацию о
характерах Q*a и, в частности, формулу Фробениуса для
неприводимых характеров. А именно, значение характера /А 9 отвечающего
гП8

диаграмме [Я] , на классе сопряженности £' есть коэффициент
в следующем выражении: -
где 4э 9 4^ - симметрические функции, описанные выше; ср. с
теоремой 26.16.
Знакомое нам правило Литтлвуда - Ричардсона (см. Д.2 и § 16)
также приобретает новый смысл: оно, таким образом, есть правило
умножения функций Шура:
v V2 ^ ',
dim у ^
см. [37 J . Доказательство всех этих фактов можно найти в книгах,
указанных в списке литературы. Фактически пользоваться формулой
Фробениуса трудно, но ее громоздкость - в~ существе дела;
характеры в действительности имеют весьма сложный вид. В недавно
вышедшей книге Г.Джеймса и А.Кербера, упоминавшейся в предисловии,
имеется таблица характеров для (Е>л,при П/^ Ю, полученная с
использованием ЭВМ, а также другёя численная информация.
Кольца А и Л обладают многочисленными интересными
структурами: структурой ji-кольца, операциями Адамса,
структурой алгебры Хопфа{28 , 41] (см.—также статью Гейсингера вр8Д.
плетизмами, скалярным произведением [24], [31]. В[41]дано
аксиоматическое описание А в духе теории алгебр Хоп£а, а в
[28] (см. также [31] ) - с точки зрения Л-колец.
Изучение М соответствует одновременному рассмотрению всех
представлений всех групп (з^ > tiZ { > - принцип,
обязательный при изучении серий классических групп. Однако в кольце Я
не учитываются вложения групп (Ъц в &п+±> п&*>
например, регулярные представления групп (Sk и ^л+i. различаются.
Чтобы учесть вложения и перейти тем самым к изучению прямого
предела групп, можно отождествить регулярные представления всех
(S^a с единичным представлением (5^ . Это равносильно
факторизации Я по некоторому идеалу; фактор кольцо Я9 есть, как
нетрудно показать, ftf-функтор группы Q^^t-in ind (g4^ . в
кольце Л этой факторизации отвечает факторизация по идеапу,
порозденноаду функцией к±- 1=^>1 &i - -£ . Если понимать
элементы А как неформальные ряды (придавая аргументам
вещественные значения и считая, что ряды 2 эс; сходятся), то наш
переход равносилен ограничению симметрических функций на
симплекс /х : J2 ^v= *, Xi&Oy
20Э

Профакторизованное кольцо Л ' сохраняет многие структуры,
а некоторые из них становятся более содержательными ♦ Например,
очень важен К^ - образ в Л конуса из Л 9 натянутого на
функции Шура; Я, есть конус истинных (а не просто виртуальных)
модулей в ftT-функторе группы (Ь^. Его описание, список следов
(инвариантных положительных функционалов), как и подробное
изучение К"-функтора, проведено автором и Керовым в £24J .
Наиболее интересное явление здесь в том, что Л1 следует
рассматривать как кольцо функций на дивизорах на вещественной прямой,
причем замена положительного носителя на отрицательный
эквивалентна умножению на Цк в соответствующем модуле, и поэтому
положительные и отрицательные переменные неравноправны. Дивизоры
( d ,jS ), где
появляются как мультипликативные положительные (относительно
конуса К+) К н^ункционалы на Л1 (см. [24 J ) и наша новая
модель Я* есть реализация его в виде кольца функций на
положительной части Spec Л1. Это означает,что всякой, симметрической
функции бесконечного числа переменных отвечает функция от двух
бесконечных наборов переменных, симметричная по каждому из них.
Например, степенная сумма JS ОС; переходит в сумму
%Ы*+(-1У^ lj$,r и т.д. (см. [24] ).
В заключение отметим, что симметрическая группа является
"квантом" в общей теории представлений классических групп. В
частности, гораздо более сложная теория представлений группы
GL (п у Р) - группы матриц над конечным полем JP , см.
§ 26 и [6, И, 19, 41, 4 J , в известной мере редуцируется к
теории представлений групп (5^. Любопытно, что эта и другие
подобные редукции переносятся на случай п = оо t но уже не < так
прямо, как в случае &9 (S~ Ч
п= оо
'Например, естественный аналог GL (п, F) при
есть вовсе не индуктивный предел GL (&<=> у F1 J , а более
интересная группа, введенная Л.!Л. Вершиком, С.В'. Серовым, А.В. Зе-
левинским и обозначаемая через GLB, - это есть группа всех
бесконечных матриц над JJ1 с финитной нижнетреугольной частью.
Именно эта группа обобщает то правило индуцирования, которое обычно
применяется в теории GL(fi)Pj(умножение "кружочком").
210

СПИСОК ЛИТЕРАТУШ К ДОБАВЛЕНИЮ
£ij Бершик A.M. Описание инвариантных мер для некоторых
бесконечномерных групп. - ДАН СССР, 4974, т. 218, J* 4, с. 749-
752.
[2] Вершик A.M., Херов СВ. Асимптотика меры Планшереля
симметрической группы и предельная форма таблиц Юнга. - ДАН СССР,
4977, 233, .« 6, с. 4024-1027.
[3J Вершик A.M., Керов СВ. Асимптотическая теория характеров
симметрической группы. - Функц. анализ и его приложения,
4981, т. 15,•* 4, с. 45-27.
[4J Зершик A.M., Керов СВ. Характеры бесконечной унитарной
группы. - ДАН СССР, 4982.
Гб] Зершик A.M., Шмидт А.А. Предельные меры, возникающие в
асимптотической теории симметрической группы. I, П.- Теория
вероятностей и ее примен., 4977, т. 22, J& 4, с. 72-82,
4978, т. 23, * 1, с. 42-54. * •
[б] Гельфавд СИ. Представления полной линейной группы над
конечным полем. - ГЛатем. сб., 4970, т. 83, £ 4, с. 45-41.
\у ] Карпушкин В.Н. Об асимптотике собственных чисел
симметричных многообразий и о "наиболее вероятных" представлениях
конечных групп. -4974, Вестн. МГУ, & 2, с. 9-13.
[8] Керов СВ. О правиле Литтлвуда - Ричардсона и соответствии
, Робинсона - Шенстеда - Кнута, УМН, 1983 (в печати).
[э] Кнут Д. Искусство программирования для ЭВМ, т. 3,
Сортировка и поиск. - М.: Мир, 4978.
[ю] . Стечкин Б.С. Монотонные подпоследовательности в
подстановках натуральных чисел. - Матем. заметки, 4973, т. 43, J& 4,
с. 511-514.
[ll] Фаддеев Д.К. Комплексные представления полной линейной
группы над конечным полем. - Записки научн. сем. ЛОМИ,
4974, т. 46, с. 64-88.
Fl2] Baer R., Brock P. Natural sorting over permutation spaces. -
Math. Сотр. 1968, v. 22, pp. 385-410.
[13] Bratteli 0. Inductive limits of finite dimensional C*algeb-
ras. Tians. Amer. Math. Soc. 1977, v. 171, pp. 1S5-239-
Pi4] Effros Б., Handelman D., Shen Chao-Liang. Dimension groups
and their affine representations. - Amer. J. Math., 1980,
v. 202, pp. 385-407.
2И

[15] Elliott G. On the classification of the inductive limits
of sequences of semisimple finite-dimensional algebras. -
Journ. of Algebra, 1976, v. 38, pp. 29-44.
[l6] Brdos P., Szekeres G. A combinational problem in geometry.-
Compos. Math., 1935, v. 2, pp. 463-470.
£17] Erdos p., Turan P. On some problems of a statistical
group theory I.-Z. Kahr. Verb. Geb.4, 1965, pp. 175-186.
£l8J Poata D. (edit) Combinatoi*"e et Representation du Groupe
Symetrique. Strasburg 1976. Lecture Notes in Math., v. 579,
Springer-Verlag,Berlin-Heidelberg-New York, 1977.
[19] Green J. The characters of the finite general linear
groupe. - Trans* Amer. Math. Soc, 1955, v. 80, n. 2, pp.
402-447.
[20J Hammersley J. A Pew seedlings of research.- Proc. of Sixth
Berkeley Symp. of Math. Stat, and Probability, 1970, Univ.
Calif. Press, 1972.
£21] Hillman A. Grassl R. Skew-tableau and the Insertion
Algorithm. - J. Comb. Information and Syst. Sci., 1980,
v. 5, n. 4, pp. 305-316.
[22] James G. Peel M. Specht Series for Skew Representations
of Symmetric Groups. - Journ. of Algebra, 1979, v. 56,
n. 2, pp. 343-364.
Г23] Kazhdan D., Lusztig G. Representations of Coxeter Groups
and Hecke Algebras. - Invent. Math., 1979, v. 53, pp. 165-
184.
[24I Kerov S., Vershik A. Characters, factor-representations
and Kefunctor of the infinite symmetric group.-Proc. of
OAGR Conference, 1980, 1982, Romania.
[25] Kerov S., Vershik A. The characters of the infifnite
symmetric group and probability properties of the
Robinson-Shensted-Knuth algorithm.-SIAD Journ. 1982.
[26] Kingman J. Subadditive ergodic theory.-Ann. of Prob., 1973,
v. 1, n. 6, pp. 883-899.
[27] Knuth D. Permutations, Matrices and Generalized Young
Tableaux. - Pacific J. Math., 1970, v. 34, n. 3, pp.
709-714.
[28J Knutson D. Jl-rings and the representation theory of the
symmetric group. - Lecture Notes in Math. v. 308,
Springer-Verlag, 1972.
[29] Landay E. Handbuch der Lehre von der Vertelung der
Primzahlen. - Bd. I,1909.
212

м
[36]
ГЗО] Logan В. Shepp L. A Variational Problem for Random
Young Tableaux. - Adv. in Math. 1977, v. 26, pp. 206-222.
Г31] Macdonald I. Symmetric Functions ana Hall Polynomials. -
Clarendon Press> 1979.
[32} McKay J. The Largest Degrees of Irreducible Characters
of the Symmetric Group. - Math. Comput., 1968, v. 22,
pp. 624-631.
Rasula R. On the minimal degrees of characters of Sa • -
Journ. of Algebra, 1977, v. 45, pp. 132-181.
[34] Robinson G. On the representation of $ . I. - Amer. J Math.
1938, v. 60, pp. 745-760.
Shensted C. Longest Increasing and Decreasing Subsequences.
- Canad. J. Math., 1961, v. 13, pp. 171-191.
Stanley R. Theory and Application?of Plane Partitions.
Part*!, 2, - Studies in Appl. Math., 1971, v. 1, n. 2,
pp. 167-87, n. 3, pp. 259-279.
£37] Thomas G. On Shensted's construction and the
Multiplication of Schur Functions. - Advances in Math.,
1978, v. 30, pp. 8-32.
[38] Ulam S. Monte Carlo calculations in problems of
Mathematical Physics. Modern Math, for the Engineers.
Second Series (edit. E.Bechebach). - N.Y. McGr-Hill,
1961.
White D. Some Connections between the blttlewood-
Richardson Rule and Construction of Shensted. - Journ.
of Combin. Theory., Ser. A, 1981» v, 30, pp. 237-247.
[40] Zelevinsky A. A Generalization of the Littlewood -
Richardson Rule and the Robinson - Shensted - Khuth
correspondence. - Journ.of Algebra, 1981tV.69, n.1, pp.82-94.
£41] Zelevinsky A. Representations of Finite Classical Groups.
A Hopf Algebra Approach. - Lecture Notes in Math., v.
869, Springer-Verlag, Berlin-Heidelberg-New York, 1981.
[39]
2V?

(ГДШЕНИЕ
Предисловие редактора перевода. 5
Предисловие 9
1. Необходимые сведения из теории представлений ....II
2. Симметрическая группа .16
3. Диаграммы, таблицы и таблоиды, .20
4. Модули Шпехта 26
5. примеры . .32
6 . Таблица характеров группы (ь^ 37
7. Соотношения Гарни ,43
8. Стандартный базис модуля Шпехта 45
9. Теорема ветвления 51
10* -р -регулярные разбиения 53
И. Неприводимые представления (ь^ 56
12. Композиционные факторы . . 60
13. Полустандартные гомомороизмы 62
14. Правило Юнга 71
15. Последовательности 74
16. Правило Литтлвуда - Ричардсона 81
17. Ряды Шпехта для М*4 86
18. Крюки и косые крюки 95
19. Детерминантная форма. • • • 97
20. Формула крюков дая размерностей 100
21. Правило 11урнагана - Накаямы 102
22. Биномиальные коэффициенты ***
23. Некоторые неприводимые модули Шпехта 113
24. 0 матрицах разложе:ия группы Q* J24
25. Ортогональная Форма Юнга 144
26. Представления полной линет"гноГг грушгт *58
Приложение. 'Матрицы разложения симметрических групп (5^для
простых чисел 2 и 3 и /l$i3 ±72
Список литературы 189
Добавление редактора перевода 191
214

УВМАЕМЫЙ ЧИТАТЕДЬ!
Ваши замечания о содержании книги, ее
оформлении, качестве перевода и другие просим
присылать по адресу: 129820, Москва, И-НО, ГСП, 1-й
Рижский пер., д.2, издательство "Мир".

Джеймс Г.
ТЕОРИЯ ПРЕДСТАВЛЕНИЙ СИММЕТРИЧЕСКИХ ГРУПП
Научные редакторы В.Л. Попов, г.М. Цукерман
Мл. научный редактор Э.Г. Иванова
Художник А.В. Шипов
Художественный редактор ВМ. Шаповалов
Технический редактор Н,И. Борисова
Корректор АЛ. Шехтер
ИБ№3151
Подписано к печати 06.10,82.
Формат 60x90 1/16*
Бумага офсетная № 2*
0§ъем6,75 бум. л. Печать офсетная♦
Усл. печ. л. 13,50. усл. кр. отт. 13,75»
Уч.-изд. л. 11,21. Изд. № 1/1952 •
Тираж 4000 экз. Зак. 770Ц Цена 1 р. 70 к.
Издательство "Мир"
Москва, 1-й Рижский пер., 2
Отпечатано в Производственно-издательском комбинате ВИНИТИ
г. Люберцы, Октябрьский проспект, 403

МАТЕМАТИКА
НОВОЕ В ЗАРУБЕЖНОЙ НАУИЕ
реланторы серии: а.н.нолмогоров, с.п.новинов
Г. ДЖЕЙМС
ТЕОРИЯ
ПРЕДСТАВЛЕНИЙ
СИММЕТРИЧЕСКИХ
ГРУПП
ИЗДАТЕЛЬСТВО "М И Р" МОСНВА
32

Цена 1 p. 70 к,
НОВОЕ В ЗАРУБЕЖНОЙ НАУНЕ
вышли в свет:
1. Ф. Гриффите, Дж. Кинг. Теория Неванлинны и голоморфные отображения
алгебраических многообразий.
2. Вычисления в алгебре и теории чисел.
3. П. Заде. Понятие лингвистической переменной и его применение к
принятию приближенных решений.
4. Гладкие динамические системы.
5. Л. Ниренберг. Лекции по нелинейному функциональному анализу.
6. Конструктивная теория поля.
7. К. Престон. Гиббсовские состояния на счетных множествах.
8. Д. Орнстейн. Эргодическая теория, случайность и динамические системы.
9. М. Гусман. Дифференцирование интегралов в Rn.
10. Случайные процессы. Выборочные функции и пересечения.
11. Гиббсовские состояния в статистической физике.
12. Евклидова квантовая теория поля. Марковский подход.
13. Р. Боуэн. Методы символической динамики.
14. Математические методы в теории систем.
15. Р. Харви. Голоморфные цепи и их границы.
16. К теории конечных групп.
17. О.О'Мира. Лекции о симплектических группах.
18. Исследования по метрической теории поверхностей.
19. Проблемы комбинаторного анализа.
20. Изоморфизмы классических групп над целостными кольцами.
21. Разрешимые и простые бесконечные группы.
22. Странные аттракторы.
23. Г. Крайзель. Исследования по теории доказательств.
24. Т. Спрингер. Теория инвариантов.
25. Гомотопическая теория дифференциальных форм.
26. Ж. Лере. Лагранжев анализ и квантовая механика.
27. Т. Чепмен. Лекции о Q-многообразиях.
28. Р. Мандельбаум. Четырехмерная топология.
29. Численные методы теории дифракции.
ГОТОВЯТСЯ К ПЕЧАТИ:
М. Сато, М. Дзимбо, Т. Мива. Голономные квантовые поля.
П. Вопенка. Математика в альтернативной теории множеств.
ИЗДАТЕЛЬСТВО "М И Р" МОСНВА