Автор: Бурштейн А.И.
Теги: поверхностные явления поверхностное натяжение капиллярность физика молекулярная физика
Год: 1986
Текст
АКАДЕМИЯ НАУК СССР
СИБИРСКОЕ ОТДЕЛЕНИЕ
ИНСТИТУТ ХИМИЧЕСКОЙ КИНЕТИКИ И ГОРЕНИЯ
А. И. БУРШТКЙН
МОЛЕКУЛЯРНАЯ
ФИЗИКА
Ответственный редактор
д-р физ,-мат, наук А. В, Чаплин
НОВОСИБИРСК
ИЗДАТЕЛЬСТВО «НАУКА»
СИБИРСКОЕ ОТДЕЛЕНИЕ
1986
УДК 5d2.(j,7; 533.1,7; 539.2; 541.12
Бурштейн А. И. Молекулярная физика. =
Новосибирск: Наука, 1986.
Предметом монографии являются равновесные и
кинетические свойства газов, жидкостей, твердых тел и излучения.
Доступно изложены начала статистической физики и моле-
кулярио-кинетической теории. Оригинальный подход к
уравнениям состояния реальных газов, кристаллов и жидкостей
позволяет на обширном экспериментальном материале
проследить, как изменяются свойства вещества по мере его
конденсации. Отличается оригинальностью
квазитермодинамическая теория границы раздела жидкость — пар,
описывающая ее структуру и поверхностное натяжение.
Для физиков, химиков, инженеров-теплофизиков.
Рецензенты СП. Габуда, Л. М. Вайиер
Б 17Оо'эд-"8б°° 119~87-Г © Издательство «Наука», 1986 г.
ПРЕДИСЛОВИЕ
Представление о веществе как о молекулярной среде
сформировалось еще в античные времена. Спустя два
тысячелетия это мировоззрение произвело на свет удивительный
гибрид механического и вероятностного описания большого
коллектива частиц — молекулярную физику. Ее вызвало к
жизни стремление объяснить и прогнозировать разнообразные
свойства вещества во всех его агрегатных состояниях исходя
только из тех сведений о молекулах, которые заданы их
строением. Эта задача актуальна и поныне. В ходе ее penie-
ния очень сильно развились и частично обособились такие
важные разделы молекулярной физики, как кинетическая
теория газов, физика плазмы, твердого тела, низких
температур и т. д. Однако основы этих наук, составляющих в
сущности единое целое, полезно рассматривать во взаимосвязи,
крупным планом, акцентируя внимание на главном, что
отличает разреженные среды от плотных, классические
системы от квантовых, идеальные газы от реальных. В этом и
состоит назначение молекулярной физики как части общего
курса физики или как раздела физической химии,
именуемого строением вещества. Настоящая монография
предназначена и дли первого знакомства с этими дисциплинами, и
для углубленного их изучения. Изложение материала в ней
подчинено индуктивной логике, .которая ведет читателя от
наблюдения и факта к их интерпретации, и от частных
выводов к обобщениям. Это помогает реконструировать ход
событий, которые обогатили наши представления о микромире
задолго до того, как атомы и молекулы стали доступны
прямому наблюдению.
Отбор материала в книге осуществлен по принципу:
тяжелые частицы, умеренные температуры. Это позволило
последовательно рассмотреть все агрегатные состояния
вещества, за исключением плазмы и вырожденных молекулярных
газов. Значительно более равномерно2 чем это принято в об-
Щйх курсах, распределено ьнйманйе между газообразным
и конденсированным состояниями вещества. Как
альтернатива классическому идеальному газу подробно обсуждается
чисто квантовый, фотонный, представляющий равновесное
излучение, и его фононный аналог, позволяющий описать
тепловое движение кристаллической решетки. Благодаря
этому поведение газов и твердых тел удается рассмотреть
в равной мере последовательно и строго, причем освещение
того и другого выигрывает от их сопоставления. В свою
очередь, твердые тела и жидкости сравниваются и
противопоставляются в рамках концепции свободного объема, которая
качественно или даже полуколичественно отражает
существующие между ними сходство и различие. Впервые в
монографической литературе излагается последовательная
квазитермодинамическая теория границы раздела жидкость —
пар, позволяющая самосогласованно рассчитывать ее
структуру и поверхностное натяжение по Лапласу и Ван-дер-
Ваальсу.
Чтобы достичь единообразия в описании разных
агрегатных состояний вещества — газов, кристаллов и жидкостей,
их уравнения состояния, приведенные к общему виду,
разложены на составляющие — внутреннее и термическое
давление. Для вычисления последних привлекаются надежные
сведения о некоторых компонентах воздуха или
предложенные для их описания аналитические уравнения состояния,
аппроксимирующие опытные данные в пределах
экспериментальной ошибки. Диаграммы и графики, иллюстрирующие
эти данные, могут оказаться полезными, даже если их
рассматривать вне контекста. Они позволяют сориентироваться
в том, как изменяются свойства вещества в широком
диапазоне давлений, плотностей и температур, а также в точках
фазовых переходов. Феноменологический подход, которым
объединен весь этот материал, во многих отношениях
оригинален. Он позволяет проинтерпретировать появление
узловых точек на диаграммах сжимаемости при плотностях,
соответствующих ненапряженному состоянию идеального
кристалла. Выясняется, что любое агрегатное состояние вещества
находится в сильной зависимости от конкуренции сил
притяжения и отталкивания. Геометрическое место точек, в
которых эти силы уравновешены, образует на фазовой
диаграмме ортометрическую кривую, соединяющую в шкале
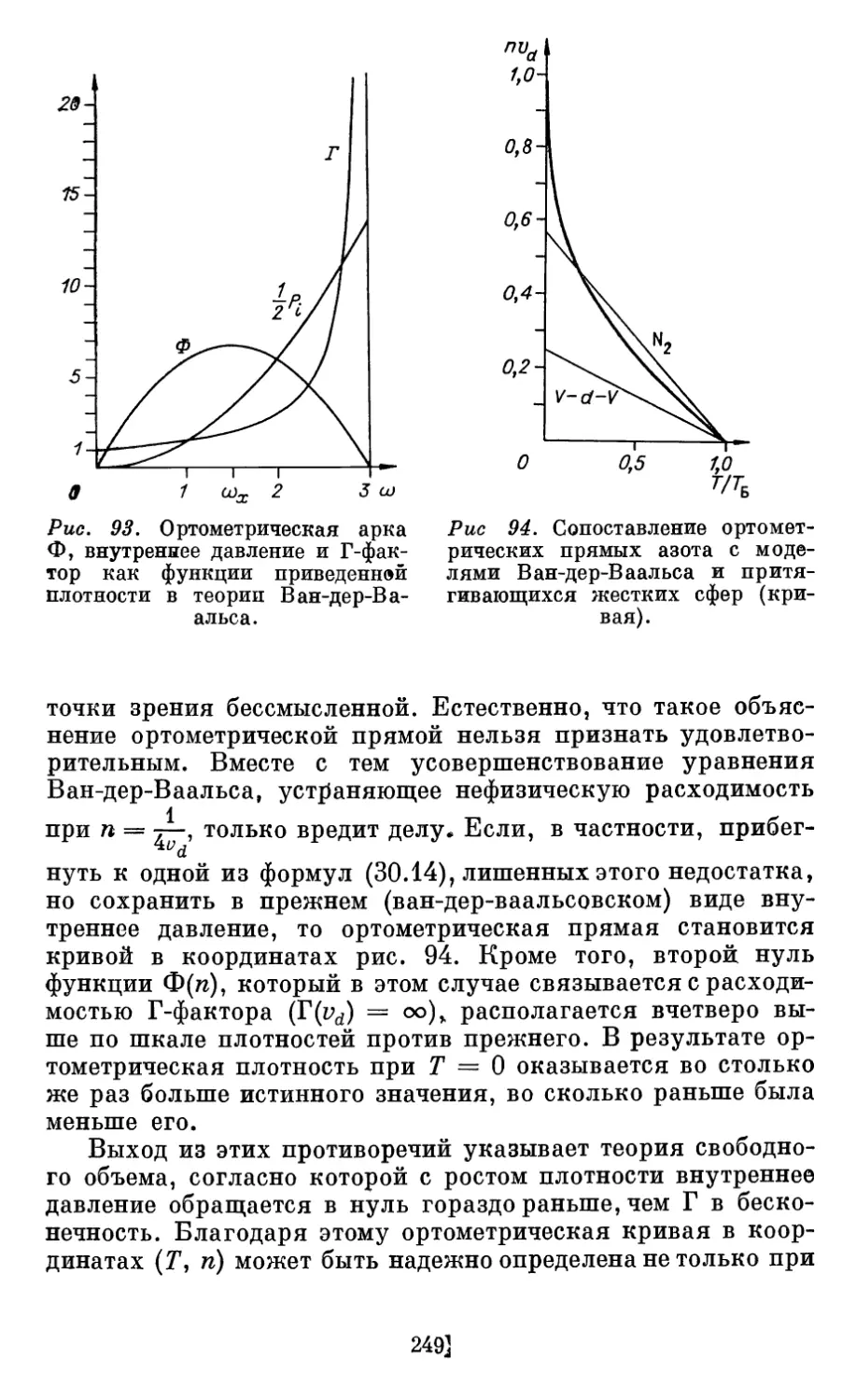
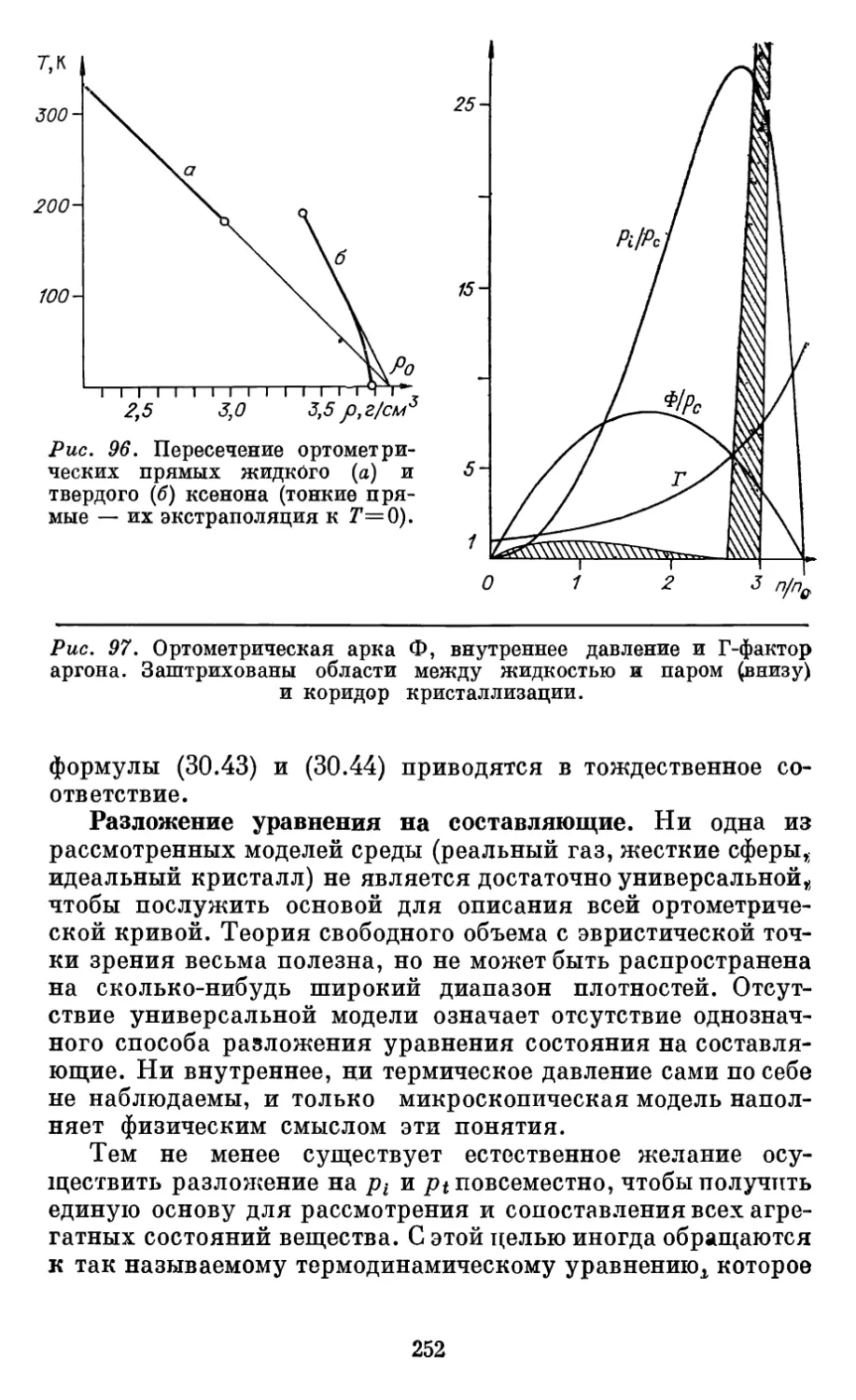
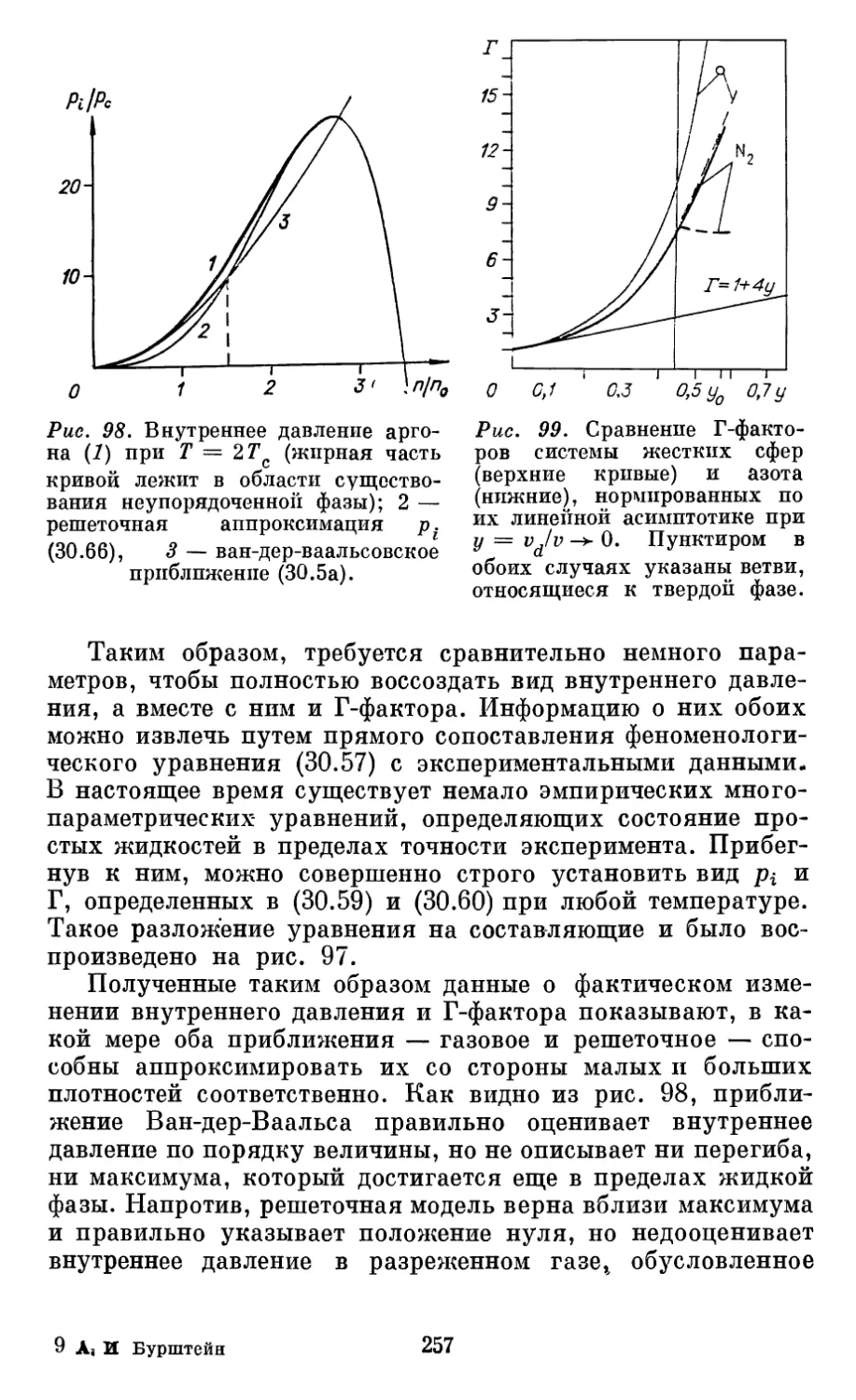
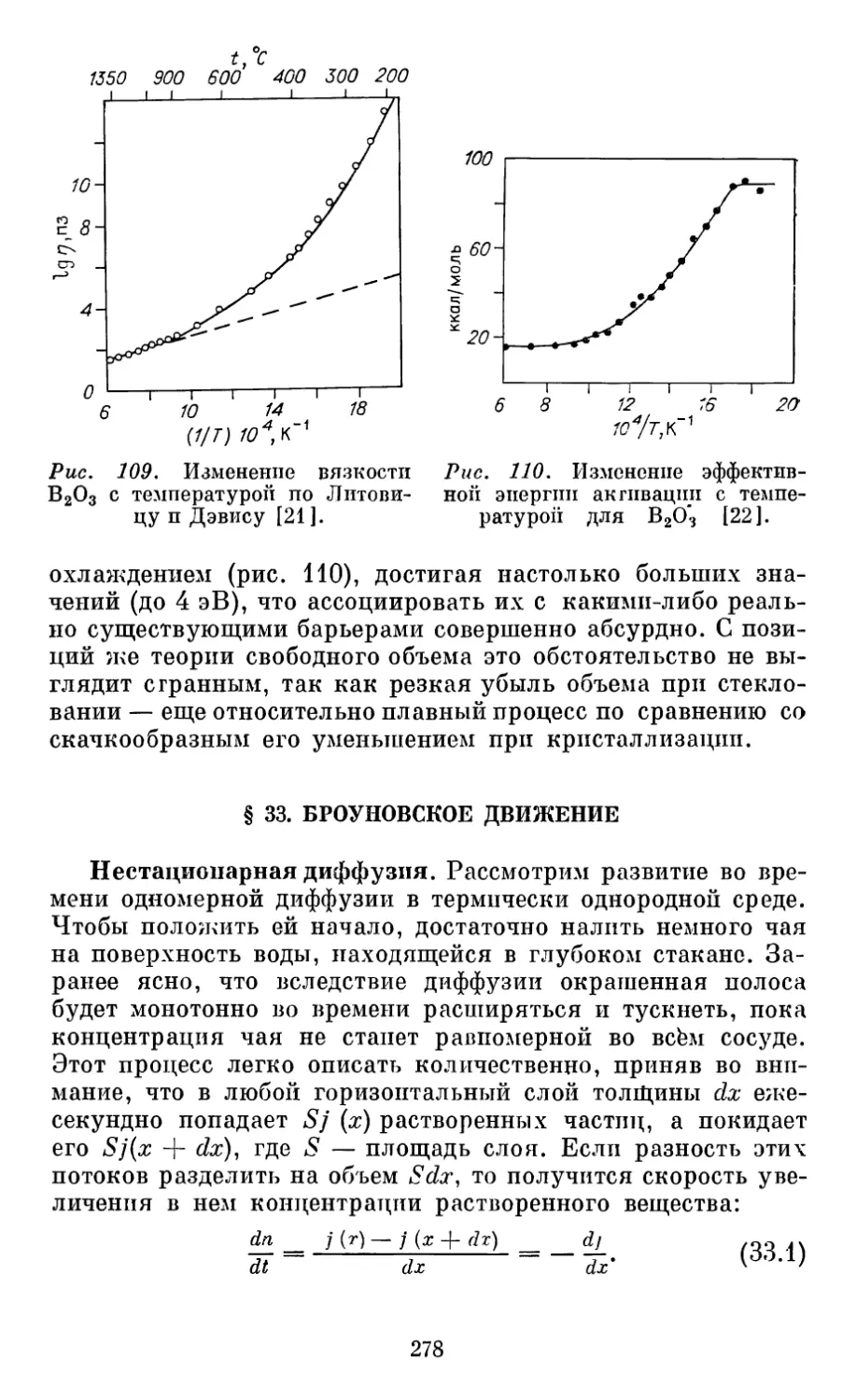
плотностей идеальный газ с идеальным кристаллом.
Используя свойства ортометрической кривой при анализе
уравнения состояния, удается установить, во что превращаются
поправки Ван-дер-Ваальса по мере уплотнения газа, при кон-
д&нсаЦий его в жидкость и после кристаллизации вещества.
Эти результаты, опубликованные в статьях разных лет,
впервые сведены воедино и могут заинтересовать не только
специалистов, но и студентов1 использующих книгу как
учебное пособие.
Рассчитанная на широкий круг читателей, книга
свободна от частностей, однако предполагает у читателя знание
основ математического анализа и механики. Автор
стремился сделать изложение по возможности замкнутым, сведя к
минимуму информацию, которую приходится заимствовать из
термодинамики и квантовой механики. Комментируя на ка,-
чественном уровне принципиально важные моменты, он
часто прибегает к образному мышлению и ассоциациям,
облегчающим усвоение идей. Этой же цели служат диаграммы,
графики и рисунки, которыми изобилует книга.
Автор выражает признательность Н. Ф. Дергачевой,
Р. И. Ратушковой, В. С. Башуровой, В. А. Морозову,
А. В. Сторожеву за помощь, оказанную в работе над
рукописью и ее оформлением,
Глава 1
ГАЗЫ
§ 1. СТАТИСТИКА МОЛЕКУЛ
Исторически «газ», газообразная фаза вещества, оказался
ранее всех других фаз понятым и изученным. Он и до сих
пор остается одной из немногих строго исследованных
систем, и поэтому успех статистической трактовки других
явлений часто зависит от возможности их сведения к модели газа.
Твердое тело, например, успешно может быть представлено
двумя газами — электронным и фононным. Жидкое
состояние, которое не моделируется газом, весьма трудно
поддается количественному описанию.
В те времена, когда существование атомов было лишь
гипотетическим, придумать молекулярную модель газа было
не так уж просто, но это единственное, что вообще можно
было сделать. Основные черты модели подсказываются всем
известными свойствами: тенденцией к беспредельному
расширению и развиваемым на стенку давлением. Совокупность
бесконечно малых твердых шариков — материальных
точек — должна была бы вести себя точно так же. Обладая
конечной массой, а следовательно, и определенной энергией
поступательного движения, эти материальные точки
(молекулы газа) безусловно разлетелись бы в разные стороны —
до бесконечности, если бы им была предоставлена такая
возможность, и оказали бы давление на всякую стенку,
которая этому препятствует. Эта качественная картина стала бы
количественной, если бы величину равновесного давления
удалось рассчитать и убедиться в том, что оно удовлетворяет
известному закону идеальных газов: pV=RT, где V — объем
одного моля газа, р — его давление^ Т — температура,
а Л — газовая постоянная.
Давление. Рассчитаем его. Если газ — это совокупность
беспорядочно движущихся точечных масс, то сила, с которой
он действует на стенку,— это суммарный импульс,
полученный стенкой в течение секунды от множества ударившихся
о нее молекул:
F = PS = 2 Дл- A.1)
г
Здесь 5 — площадь поверхности стенки, a Apt — изменение
импульса молекулы при £-м ударе о поверхность.
Величина этой силы не остается постоянной, а вследствие
случайных обстоятельств изменяется, «флуктуирует» во
времени. Также и давление в эту секунду не то, каким было
в предыдущую, и не то, каким может оказаться в любую
будущую. Черта над 2 &Р% — знак усреднения — означает,
г
что под макроскопическим давлением понимается среднее
из всех возможных его значений. Огромное число молекул,
составляющих газ,— достаточная гарантия того, что любое
измерение, когда бы нам ни вздумалось его произвести, в
условиях равновесия не может существенно отличаться от
среднего. Возможные отличия (флуктуации) в любом большом
ансамбле очень невелики. Заметные отклонения настолько
же маловероятны, как, скажем, случайное скопление всех
пассажиров в одном аэропорту Москвы при совершенной
незагруженности остальных. Кроме того, приборы с высокой
инерционностью сами сглаживают большинство отклонений,
не реагируя на слишком быстрые или небольшие флуктуации
2 ДА- Если же даже стрелка прибора «шумит», следя за слу-
г
чайными вариациями измеряемой величины, то все же
измеренное значение — это тот средний уровень, около которого
колеблются ее показания. Любая макровеличина — это
всегда среднее из различных микроскопических возможностей.
Имея это в виду, мы в дальнейшем будем опускать
знак усреднения, а слова «число ударов» о стенку, «число
молекул» с данной скоростью и т. п. употреблять только
в смысле их средних значений.
Хотя молекулы, представленные одинаковыми точечными
массами, почти лишены всякой индивидуальности, имеется
все же очень существенный признак, по которому их следует
отличать друг от друга. Это скорость движения. Если,
например, молекула летит на стенку, перпендикулярную оси
.г, то от того, какова ее скорость вдоль этой оси, зависит
величина импульса, переданного ею стенке при отражении от
нее. Если удар упругий: vy = vy\ vz = vz; vx = —vx
(штрихованные компоненты — скорость после удара, нештрихо-
ванные — до него), то очевидно
Арх = mvx — mvx = 2mvx. A.2)
Сколько случится ударов с данной величиной их в едипи-
цу времени и сколько их произойдет с меньшей или большей
скоростью,— вот во что упирается расчет давления. Знай
мы, какое количество ударов dN(vx) — из общего числа N =
= ^dN(vx), случившихся в одну секунду,— приняла стенка
от молекул, обладавших скоростью vx (т. е. не меньше их
ц не больше vx + dvx), то и силу всех ударов оценить
нетрудно:
F = pS = j 2mvxdN (vx). A.3)
Число ударов со стороны группы молекул, скорость которых
столь жестко указана, дифференциально мало в сравнении
с N. Этим оправданы обозначения (d/V, а не AN) и
интегрирование — вместо суммирования — импульсов, полученных
от столкновения с молекулами разных групп, отличающихся
скоростью «атаки».
Если мысленно выделить теперь молекулы, обладающие
какой-нибудь одной одинаковой скоростью их, то можно
заметить, что
dN(vx) = Svxdn{vx). A.4)
Усвоив принятую здесь логику обозначений, следует
«прочесть» dn(ux) как «небольшое число молекул из общего
количества п, содержащихся в единице объема, которые
движутся к стенке со скоростью, заключенной между ихжих + dvx».
В остальном оценка A.4) ничем не отличается от подсчета
числа капель дождя, падающих за одну секунду на
поверхность с площадью S. Капли, которые отстоят от поверхности
дальше, чем на vx, не успевают долететь. Попадут лишь те,
которые сосредоточены в параллелепипеде с основанием S
и высотой их (рис. 1). Их количество равно объему S*vx,
помноженному на плотность dn{vx). Косой ли дождь, или
прямой, не имеет значения, если их одно и то же. Поэтому, хотя
«молекулярный дождь» хлещет во всех направлениях: и на
стенку, и от нее, и наискосок, мы можем, классифицировав
молекулы по одному единственному признаку — величине
vx, применить к каждой группе оценку A.4), а затем,
использовав ее в A.3), найти
00 ОО
р = J 2mvxdn {vx) = 2тп J v\dW (vx). A.5)
о о
Интегрирование распространяется на все молекулы,
летящие на стенку (сух>0). Разумеется1 их не может быть
Рис. 1. Поток молекул,
налетающих с заданной скоростью v на
участок стенки площадью S.
Рис. 2. Декартово
пространство скоростей.
больше с — скорости света. Тем не менее интегрирование
можно распространить до бесконечности, если
ограничиться не слишком высокими температурами. Так как быстрых
молекул очень мало, то вклад в интеграл даже при скоростях,
значительно меньших с, уже фактически равен нулю.
Поэтому величина верхнего предела несущественна, а
математически интегрирование в бесконечных пределах значительно
более удобно.
Статистическое распределение. Равенство A.5) выражает
собой микроскопическое, молекулярно-кинетическое
определение давления. Вошедшая в него величина
представляет собой «вероятность найти молекулу, движу-
жуюся сэ скоростью vx». Она указывает, какую долю из
общею числа частиц в единице объема п составляют те из них,
которые обладают требуемым свойством, т. е. действительно
имеют скорость, укладывающуюся в пределах небольшого
интервала dvx вокруг заданной ее величины. Сохраняя
интервал dvx неизменным, легко убедиться, что число молекул,
обладающих различной величиной скорости, может быть
различно, хотя каким-то одним значением обладает каждая
из них. Поэтому, перебрав все возможности, мы
пересчитываем все молекулы в единице объема: j dn (vx) = п. Точно так
же и вероятность найти молекулу, движущуюся быстрее
или медленнее1 отнюдь не одинакова2 но вероятность найти
ее «двигающейся как-нибудь» (достоверное событие) равна
единице.
dW(vx)= J rc = 1. A.6а)
Распределения вероятности, определенные таким образом,
что \dW — 1, называются нормированными к 1. В этом
смысле dn(vx) можно рассматривать как распределение
частиц, нормированное к их плотности. Когда удобнее
пользоваться распределением вероятностей dW(vx), а когда
распределением частиц dn(vx), зависит от постановки задачи, а
иногда и от специфических свойств газа.
Если направление движения ничем не выделено — а
выделено оно может быть введением электрических, магнитных
или гравитационных полей,— то у молекул нет никаких
оснований предпочитать какое-либо направление движения
противоположному. Поэтому молекулы, летящие к стенке
или от нее, должны встречаться одинаково часто, а
вероятность их обнаружить dW(vx) не должна изменяться при
инверсии знака vx. Следовательно,
+ ОО
р = 2тп J vldW (vx) = mn ) vxdW (vx) = mnvx. A.7)
о — °°
Статистическое среднее. Обозначение vx введено в
соответствии с общим определением средней величины:
а),
которой в данном случае оказалась vx. В определении
среднего подразумевается, что интегрирование распространено
на всю область определения случайной величины: —оо ^
^ Vx ^ оо.
Принцип «невыделенности», который позволил
распространить интегрирование в A.7) на отрицательную полуось,
йГожно использовать и более широко. С тем же основанием
можно, например, утверждать — пока и поскольку дейст-
~~2
вительно отсутствуют всякие поляг— что vx ничем не отли-
10
чается от и2у и(от v\, так как все оси координат равноправны
и не имеют преимуществ друг перед другом. А значит и и2 =
= vx + t>l + v\ = 3z;£, так что равенство A.7) можно
«прочесть» и иначе:
1 —9 2 mv2 2 — / л о\
р = -g- mnv2 = -g- n —2~ = "з" ^е. A.8)
Давление определяется только плотностью газа и средней
кинетической энергией теплового движения молекул е.
Дальнейшее продвижение невозможно без выяснения
того, что же собой представляет вероятность A.6). Однако
уже сейчас можно заметить общность A.7) с уравнением со-
N
стояния, если представить п как -у:
pV = Nm7x. A.9)
Это равенство содержит постановку задачи. Левая его часть
совпадает с соответствующей частью уравнения состояния.
Правая должна быть вычислена. Но для этого необходимо,
во-первых, знать распределение и, во-вторых, с его помощью
фактически выполнить усреднение и%.
§ 2. ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ
Узнать, каково должно быть распределение,— главная
задача статистической физики. Но откуда почерпнуть
сведения об этом? В середине прошлого века, когда само
представление об атомах и молекулах было всего лишь
гипотезой, об экспериментальном исследовании распределения по
скоростям не могло быть и речи. Тем более удивительно, что
чисто умозрительных, априорных соображений, которыми
руководствовался Максвелл, оказалось достаточно для
выяснения общего вида этого распределения.
Очевидно, что число молекул, обладающих «данной»
скоростью, зависит от точности ее определения. Чем уже
интервал скоростей (vx, vx + dvx), которые мы отождествляем с
данной, тем меньше шансов найти молекулы, ему
принадлежащие. Вероятность же молекуле иметь точно заданную
скорость (dvx = 0) просто равна нулю. Учитывая эти
соображения, для изотропного пространства можно сразу же
написать:
dW(vx) = f(vx)dvxl dW(vy) =f(vy)dvyi dW(vz)=f(vz)dvz> B.1)
li
где функция распределения /(£) одна и та же независимо
от того, каков ее аргумент vx, vy, или vz — в силу
эквивалентности всех направлений.
Совершенно общее соотношение
dW(a) = f{a)da B.2)
сохраняет силу для любой непрерывно изменяющейся
случайной величины а, будь то скорость, координата, момент
количества движения, энергия или еще что-либо. Если а —
величина векторная, например скорость v, то «вероятность
найти данную скорость» — это значит найти каждую из ее
проекций в интервале dvx, dvy, и dvz около соответствующих
значений компонент. Иными словами, конец вектора
скорости должен находиться в пределах кубика со сторонами
dux, dvy, dvz, построенного около точки с координатами vx,
vy, vz (рис. 2). Чем меньше объем кубика d\ = dvxdvydvz, тем
труднее найти молекулу, чей вектор скорости был бы
направлен в столь точно указанную область пространства
скоростей. Соответственно этому
dW(w) =, g(v)dvxdvydvz = g{y)dv. B.3)
Из принципа неразличимости направлений сразу &е
следует, что функция распределения не может зависеть от
угловых переменных вектора v(9 и ф), указывающих, куда летит
молекула, а должна быть функцией лишь его модуля v =
= yvx + v\ + v\. то есть
S(v) = g(v). B.4)
Идентичность всех распределений в B.1) и ограничение,
которое накладывается B.4),— это все, что можно извлечь
из свойства изотропии пространства. Тем самым произвол
в выборе f(v) и g(v) до некоторой степени ограничивается,
хотя отнюдь не устраняется полностью. Необходима еще
какая-нибудь идея.
Эта идея подсказывается представлением о полной
беспорядочности движения молекул. Поскольку молекулы
летят во всех направлениях с любыми мыслимыми скоростями,
кажется весьма правдоподобным, что вероятность
обнаружить молекулу, движущуюся вдоль оси х со скоростью vxi
совершенно не зависит от того, какова величина проекций
ее скорости на другие оси. Если с данным значением vx
совместимы любые иу и vz и ни одно из их значений не получает
при таком совмещении преимуществ перед другими, то это
именно так. С точки зрения теории вероятностей это озна-
12
чает, что три случайных события — обнаружение различных
значений трех компонент скорости — независимы: значение
одной из них еще ничего не говорит о том1 каковы должны
быть остальные. Но в таком случае
dW{\) = dW{vx) • dW{vy) • dW(vz). B.5)
Этот результат является математическим выражением так
называемой теоремы умножения вероятностей: вероятность
случайного совпадения нескольких независимых событий
равна произведению их вероятностей. Например,
вероятность получить выпадение 1 сразу на трех одновременно
брошенных кубических игральных костях равна 1/6 X 1/6 X
X 1/6 = 1/216. Такова же вероятность выпадения вообще
любой наперед загаданной тройки чисел, например 2, 4,
или 3, 5, 2. Случайное обнаружение трех чисел — vx, vy, vz —
отличается от приведенного примера лишь тем, что
вероятности различных их значений, вообще говоря, не равны и
пока что даже неизвестны. Но оказывается, что самого
предположения о том, что они независимы, позволяющего
воспользоваться теоремой умножения B.5), достаточно для их
определения.
Действительно, подставляя в B.5) распределения B.1)
и B.3) с учетом B.4), находим
g{v)=f(vx)-f(vvH{vJ. B.6)
Логарифмируя последнее равенство и дифференцируя его
по vx, например, имеем
1 dg(v) dv 1 dg(O) vx I df(vx)
g dv dvx g dv v f (vx) dv
B-7)
X
Дифференцирование по vy и по vz приводит к аналогичным
результатам, которые вместе с B.7) могут быть представлены
в виде
1 dg(v) I df(vx) i df(yy)
g (v) vdv f (vx) vxdvx
\ df (vz\
T "w ^
4I ч ^ = -2<%,- B.8)
f{vz) vzdvz
где а — конечно, константа, так как функции различных
аргументов могут тождественно совпадать друг с другом во
всей области их определения только в том случае, если все
они равны одной и той же постоянной. Интегрируя, находим
g {v) = ^ exp (— сш2), f(l)=,~ exp (— cc£2), B.9)
где £ = vx, vy, vz. Между постоянными интегрирования Z
и Zo ввиду B.6) существует простая связь:
Z = Zl B.10)
Таким образом, если действительно движение в разных
направлениях статистически независимо, то функции
распределения должны иметь вид B.9) и никакой другой.
Важно, однако, иметь в виду, что статистическая
независимость — это лишь гипотеза и отнюдь не такая очевидная,
как может показаться с первого взгляда. Напротив, если,
например, одна из компонент скорости равна с — скорости
света, то другие заведомо равны нулю, т. е. уже отнюдь не
случайны, а строго определены. И если все же эта гипотеза
приводит к правильным результатам, то только потому, что,
как уже указывалось, релятивистские скорости при
обычных температурах практически недостижимы для атомов и
молекул. Для квантрвых газов — электронного и фотонного,
как мы увидим в дальнейшем, это уже не так:
соответствующие им плотности распределений не удовлетворяют
функциональному уравнению B.6), а значит и B.5). Поэтому в
том, что идея о независимости движения молекул в разных
направлениях оказалась все же справедливой для обычных,
нерелятивистских (не слишком горячих) газов, есть элемент
везения. Это счастливая догадка и большая удача теории
Максвелла, которая вынуждена была исходить из более или
менее произвольной предпосылки за неимением другой.
Замечательно и то, что ее привлечения оказалось
достаточно для полного определения вида /(£), равно как и g(u).
Неопределенность, которая еще сохраняется в B.9):
неизвестность Zo — устраняется, если учесть условие
нормировки:
-4-°°
y«) = 4- § f(vx)dvx-L
Из него следует, что
-j-oo
J
'Zo = J / (I) d\ = j -exp (- об») dl = Y± B.11)
— oo —oo
есть так называемый интеграл Пуассона. В том, что он
действительно равен 1/ —, убеждает следующая выкладка:
i4
, 2 +00 J to
B.12)
0 0 0
Подставляя B.11) в B.9) и B.1), находим
/(Vx)
iL exp (-
= Yt exP (-
B.13)
Остающаяся еще свобода в выборе параметра а отнюдь
не упущение теории. Эта степень свободы реально
существует и у исследуемой системы. Чем меньше а, тем чаще
(рис. 3) встречаются молекулы с большими скоростями, а
значит и большими энергиями, тем больше общий запас
кинетической энергии в веществе. Но энергетическая емкость газа
Рис. 3. Одномерное
распределение Максвелла
при разных температурах.
определяется его температурой. Значит, чем меньше а, тем
больше Т. Чтобы уточнить характер этой зависимости, надо
выполнить вторую часть программы: усреднить v\ в A.9)
и сравнить полученное таким способом уравнение с
известным уравнением газового состояния.
§ 3. УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА
Рассчитаем с помощью B.13) средний квадрат скорости:
Из этого результата видно, что искомое среднее может быть
получено простым дифференцированием B.11):
v*
л da
2a*
C.2)
15
Подстановка C.2) в A.9) дает
PF = 4£. C.3)
Если речь идет об одном моле газа, то N = No — числу Аво-
гадро. В этом случае уравнение pV = -т^- эквивалентно
уравнению pV = RT, и из тождества этих двух
формулировок одного закона вытекает искомое точное соответствие
между а и Г:
__
_
где к = -гг- = 1, 38-10~16 эрг/К. Согласно закону Авогадро,,
о
iV0 — величина постоянная. Поэтому и к — частное от деле-
лия двух мировых постоянных, тоже мировая постоянная —
константа Больцмана. Вместо C.2) мы мо&ем получить2
ввиду C.4):
^ ш7; mvl кТ
— = — = — = —'>
откуда видно, что величиной 3/2 (кТ) определяется средняя
кинетическая энергия поступательного движения газовых
молекул'. При Т = 300 К она равна 6,2-10~14 эрг =
= 4«10~2эВ. Укажем для сравнения, что энергия связи
атома в молекуле ~3 эВ, т. е. значительно больше. Еще
разительнее контраст между обычной тепловой энергией молекул
и энергией электронов в атомах, или энергией ускоренных
частиц. Тем не менее ее достаточно, чтобы обеспечить
движение молекул с весьма высокими скоростями. Например1
для О,: V7 - /Ж - /^Р- 4,8-10. с„/с-
=480 м/с, а для Н2 скорость в 4 раза больше.
В конце вывода бывает полезно оглянуться назад и
придирчиво проанализировать положенные в его основу
допущения. Такова, в частности, идеализированная модель
молекулярного движения в газе, которой мы воспользовались.
Характерную для газов чисто качественную особенность —
разлетаться во все стороны, если этому не препятствуют
стенки,— мы рассматривали как указание на то, что молекулы
газа не связаны силами сцепления (взаимодействие
отсутствует). Для этого предположения — в столь жесткой
формулировке — нет достаточного основания. Чтобы газ разлетал-
16
ся, достаточно вполне, чтобы средняя кинетическая энергия
е была больше энергии притяжения молекул при среднем
их удалении друг от друга. Действительно, энергия
межмолекулярного взаимодействия не пренебрежимо мала, ведь
именно благодаря ей совершается переход газа в
конденсированное состояние вещества, жидкое или твердое. Учет этого
обстоятельства, а также конечных размеров молекул,
которые выше считались точечными, приводит к тому, что
уравнение состояния существенно отличается от pV = RT. Этот
закон выполняется для большинства газов лишь
приближенно и только при достаточно высокой температуре. Однако
ограничения общности и применимости простой,
идеализированной модели газа не умаляют ее достоинств. Модель
точечных невзаимодействующих масс тем и хороша, что ее
простота допускает точную математическую обработку и дает
возможность составить представление о самых важных
чертах молекулярного движения в газе, выяснить основные
различия между идеальным газом молекул и таким же газом
фотонов или фононов, о которых речь впереди. Теоретический
скелет модели строен и прозрачен. И именно отправляясь
от него, лучше всего выяснять специфику реальных
объектов. Последовательно отказываясь от различных упрощений
идеальной модели, мы каждый раз будем обнаруживать
эффекты или явления, ускользающие от внимания в
простейшей схеме. С конечными размерами молекул связаны
явления переноса, с их способностью разрушаться —
химические реакции, ионизироваться — электропроводность и т. д.
Преимущество идеальной модели — красота и строгость,
а реальной — многообразие явлений к физических ситуаций,
В идеальном газе^ согласно C/3) и C.4):
р = пкТ. C.6)
§ 4. РАСПРЕДЕЛЕНИЕ МАКСВЕЛЛА
Подставляя B.9) в B.3) с учетом B.10) и B.11)i находим
где а = £^. Вероятность обнаружить скорости заданную
величиной и направлением, не может зависеть от формы
того элементарного объема в пространстве скоростей, в
который должен попасть конец вектора v. Поэтому D.1) можно
V,
Рис. 4. Элементы пространства скоростей в сферических (а) и
декартовых (б) координатах.
записать также в виде
3/2
D.2)
где под d\ (или dsv) понимается объем элемента
произвольной формы в пространстве скоростей, выделяющий ту группу
молекул, которая может нас заинтересовать. Если, в
частности, мы хотим узнать, какова вероятность найти молекулу
с данной скоростью движения v, ориентированной в
пространстве заданием сферических координат 0 и ср, то нам
необходимо рассчитать величину объема dv, заданного
приращением dv, dQ, dtp. Как видно из рис. 4, а, этот объем равен
произведению высоты сферического слоя dv на площадь его
основания: (и sin 0 dy)'VdQ, так что d\ = v2 sin QdvdQdy =
= v2dvdQ> где dQ — телесный угол, ограничивающий
разброс скоростей по направлению. Поэтому распределение
Максвелла в этих координатах имеет вид:
dW (v) = (-^) (^)
D.3)
Сложение вероятностей. Иногда условия задачи
позволяют ограничиться частью информации, которая содержится
в D.1) и D.3). Так, например, при расчете давления вполне
достаточно знать, как быстро летит молекула к стенке вдоль
оси х — вне зависимости от того, каковы проекции ее
скорости на другие оси. Все, что необходимо для расчета v%x
а следовательно, и р, заключено в распределении dW(vx).
Как получить этот частный вид распределения из общего
18
распределения Максвелла? Рецепт дает теорема сложения
вероятностей: вероятность наблюдать одно из нескольких
взаимоисключающих событий — все равно какое — равна
сумме вероятностей этих событий. Смысл теоремы
становится прозрачным, если вспомнить, что вероятность состояния —
это относительное число частиц, которые в нем находятся:
— *' y1 = dW (v). При данном значении vx все другие
проекции могут быть и одинаковыми, и различными,
большими и маленькими. Все молекулы, которые, отличаясь
лишь этими проекциями, имеют одно и то же vx, равно нас
устраивают. Чтобы найти их полное количество, надо
просто сложить вместе частицы, имеющие данное vx, но различные
vy и vz. Отношение этого числа молекул к общему числу п
дает искомую вероятность
dW (vx) = —jjdn (*>*> vy,vz) = ^ J dW (vx, vy, vz) =
—av
vyvz
2
= у — е dvx. D.4)
Подставляя сюда D.1), можно непосредственно убедиться
в справедливости этого равенства. Теорема сложения имеет
и простой геометрический смысл: dW(\) — есть вероятность
попасть концу вектора скорости в какой-нибудь один из
равновеликих кубиков объема dv, заключенных между двумя
плоскостями vx = const и vx -f- dvx = const, тогда как d\V(vx)
— вероятность попасть в любой из них, т. е. в любое
место слоя, выделенного указанными плоскостями (рис. 4, б).
Следуя этой логике, нетрудно рассчитать и вероятность
того, что молекула будет двигаться с абсолютной скоростью
v (т. е. не меньше v и не больше v + dv), безразлично в каком
именно направлении. Сформулированному таким образом
признаку удовлетворяют, очевидно, все точки шарового
слоя, заключенного между двумя сферами радиуса v и и +
+ dv. В какой бы из них ни оказался конец вектора v, его
величина будет строго соответствовать поставленному
требованию, тогда как направление может быть совершенно
произвольным. Вероятность двигаться с этой же скоростью,
но в строго заданном направлении — в пределах телесного
угла du — определена распределением D.3). Следовательно,
чтобы найти искомую вероятность, необходимо
проинтегрировать D.3) по всем углам (по всему слою), что дает
19-
2Л Я
dW (v) = j d<p j dQdW (v) = 4я (-^-K/2 e-ai)Vdi;. D.5)
0 0
Статистический вес. Полезно задуматься над
происхождением множителя и2, которого не было ни в D.1), ни в D.4).
Простая аналогия позволяет понять, что его появление
связано с различным определением «состояний», вероятность
которых ищется. Представим себе многоэтажное здание
в форме пирамиды, в котором все жилые блоки равновелики
и которое, следовательно, отличается от обычных «коробоч-
ньго> строений только готическим профилем (рис. 5).
Предположим, что это не помешало полномочным организациям
заселить его строго равномерно в соответствии с
установленной нормой жилплощади. В таком случае можно не
сомневаться, что вероятность найти в дневное время в любой
квартире какого-нибудь квартиросъемщика одна и та же
независимо от этажа и части здания, в котором квартира
расположена. Зато, если задаться вопросом, какова вероятность
обнаружить человека на определенном этаже, то сразу же
ясно, что она тем меньше, чем ближе этаж к вершине
пирамиды. Ибо, чем больше в этаже квартир, тем больше шансов,
что поиски увенчаются успехом. В обычной же конструкции
жилого дома распределение по этажам равномерно и
вероятность встречи с людьми на любом этаже одинакова.
Аналогично этому вероятность найти конец вектора v
в некоем сферическом слое возрастает при его удалении от
начала координат. Число равновеликих единиц объема
пространства скоростей, которые помещаются в нем, растет как и2.
Напротив, объем, заключенный между двумя
параллельными плоскостями, не меняется при смещении их вправо или
влево, и поэтому соответствующая вероятность инвариантна
по отношению к положению плоского слоя (см. рис. 4).
Эта аналогия не во всем точна. Вероятность заселения
равновеликих элементов объема d\ на разных сферических
«этажах» не одинакова: она экспоненциально уменьшается
А
А\
АЛ
1
г
1
1 II 1
Ik.
TV
PL
Рис. 5, Иллюстрация понятия «равновероятности».
20
по мере удаления от начала координат — как expf — -^].
Еслп бы в некоторой гостинице пустовала большая часть
номеров, а редкие постояльцы селились бы исключительно
в соответствии со своими вкусами, то несомненно, что и здесь
обнаружилось бы нечто подобное. Несмотря на равенство
площадей, низко расположенные номера — при отсутствии
лифта — обладали бы большей привлекательностью.
Чтобы отличить тяготение к нижним «этажам»
распределения от их емкости, вводится понятие статистического веса
состояния p(v). Только равновеликие элементы
пространства скоростей имеют одинаковый статистический вес. Если же
под «состоянием» понимается движение с заданной
абсолютной скоростью v, то попадание в соответствующие слои,
несмотря на одинаковую их толщину dv, неравновевоятно.
Коэффициент, указывающий, во сколько раз возрастает эта
вероятность при изменении и, есть статистический вес
состояния.
В распределении D.5) статистический вес p(v) равен inv2.
В распределении D.3) под «состоянием», вероятность
которого им описывается, подразумевается попадание вектора
скорости в элемент, указанный приращениями dv, d0, d(p.
Емкость этого состояния изменяется не только в
зависимости от и, но и от 0, так как площадь элемента сферического
слоя, заключенного между двумя близкими
меридиональными сечениями, тем больше, чем ближе он к экватору, а у
полюсов и вовсе равна нулю. 'Соответственно этому
статистический вес р(у, 0) — i/2sin 0. Если, пользуясь теоремой
сложения, определить вероятность найти молекулу,
движущуюся в заданном направлении безразлично к величине ее
скорости, то
dW(Q) = jW(v) = *^М_ = «. D.6)
Этого следовало ожидать ввиду изотропии пространства*
Из D.5) можно получить и такое распределение молекул,
когда «находиться в данном состоянии» означает иметь
кинетическую энергию не меньше е и не больше е + d&. Простой
заменой переменных и = 1/ — преобразуем D,5) к виду
D.7)
2лкТ .
21
Рис. 6. Распределение молекул по абсолютной величине скорости
движения (а) и кинетической энергии (б).
где
3/2
D.7а)
— статистический вес, показывающий, сколь много
различных состояний движения имеют одну и ту же энергию 8.
Во всех перечисленных случаях статистический вес может
быть определен общим равенством
dvx-dvy-dvz = dv = p{q)dq, D.8)
где q — любая переменная или набор переменных,
выражающихся через vx, vy, vz, a p(q) — статистический вес.
Разные средние. Таким образом, в общем случае максвел-
ловское распределение dW(q) = g(q)dq имеет плотность:
где Z — нормировочная постоянная (статистическая сумма).
Благодаря тому, что экспоненциальный фактор и
статистический вес противоположным образом изменяются в
зависимости от g, g(q) имеет явно выраженный максимум (рис. 6).
Из обычного условия у- = 0с помощью распределений D.5)
и D.7) могут быть легко рассчитаны наиболее вероятная
скорость ve и наиболее вероятная энергия ее, которые, как легко
убедиться, равны
- /"■
2кТ
И £Р =
кТ
2 '
D.9)
Обращает на себя внимание,
Этому не еле-
дует удивляться: газ представляет собой коллектив моле-
22
кул, обладающих самыми разными скоростями, и поэтому
он плохо моделируется умозрительной совокупностью
частиц, движущихся с одинаковой скоростью вдоль всех
координатных осей, которой часто пользуются для грубых
оценок. Но только в этом гипотетическом случае мы и вправе
были бы ожидать, что как для экстремальных, так и для
средних значений сохранятся те же самые соотношения, что
и для свободной частицы. На самом же деле после
усреднения по распределению Максвелла v совпадает с у и2 лишь
с точностью до постоянного множителя, как и
соответствующие экстремальные величины. Разные эксперименты
оказываются связанными с различными средними: \их\, и, и2 и т. д.
Порядок измеряемой величины может, конечно, быть оценен
при подстановке вместо v некоторого раз навсегда принятого
значения, например среднеквадратичного, но корректный
расчет всегда нуждается в фактическом усреднении искомой
величины.
Если, например, мы хотим рассчитать поток частиц,
налетающих на единицу поверхности стенки в единицу
времена то непосредственно из A.4) имеем: dj = vxdn(vx), a
Если бы ансамбль молекул состоял из частиц, летящих
только «туда» и «обратно» с одинаковой скоростью, то ее
величина должна была быть равна \vx\, чтобы поток был таким же2
как в идеальном газе. Очевидно2 что
"К | = 2 j vxdW (vx) = * = УШ. D.10а)
о v
не совпадает ни со среднеквадратичным, ни даже просто со
средним значением абсолютной величины скорости которая
равна
о у
Если же, напротив, использовать определение D.11) в
выражении D.10), то последнему можно придать вид
1 = \nv, D.12)
23
1
Шлея
пучок
Рис. 7. Положепие анализатора во время пропускания пучка (а) и
в момент адсорбции молекул на его противоположной стороне (б).
Таков же поток частиц, движущихся во все стороны с
одинаковой скоростью и.
Опыт Штерна. Опыт, подтвердивший наличие у молекул
самых различных скоростей и совпадение (количественное)
вероятности их обнаружения с распределением Максвелла,
был осуществлен Отто Штерном в 1920 г. Получить прямое
экспериментальное подтверждение теории в любом случае
важно, но оно особенно необходимо, если в ее основе лежат
совершенно новые, по существу, угаданные предпосылки:
представление об атомах, независимость движения в разных
направлениях и т. д.
В полый вращающийся цилиндр — анализатор, в
котором поддерживается вакуум, за короткий промежуток
времени, когда щель анализатора оказывалась на пути
молекулярного пучка, влетало некоторое количество молекул (рис. 7).
Продолжая лететь по инерции, эти молекулы достигали
экрана, расположенного на противоположной стороне
анализатора, за разные промежутки времени — в зависимости от
скорости, которой они обладали: At = —, где D — диаметр
цилиндра. Поскольку за это время цилиндр успевал
повернуться на некоторый угол, молекулы входили в
соприкосновение с экраном не напротив щели, а тем дальше от
противостоящей ей линии, чем меньшей скоростью они обладали
(рис. 7, б). Поддерживая экран при достаточно низкой
температуре, можно было добиться, чтобы практически все
молекулы, достигшие его, оседали в месте соприкосновения.
Осевшие молекулы серебра, из которых состоял
молекулярный пучок, создавали на экране напыленный слой, по
толщине которого можно было судить о числе осевших
молекул. С другой стороны, по углу поворота анализатора а —-
= со At можно было определить скорость, которую имели от-
D D
клонившиеся на этот угол молекулы: и = -г? = —>а>, и та-
АГ ОС
ким образом полностью восстановить распределение по аб-
24
солютным скоростям молекул, влетевших через щель.
Экспериментальное воспроизведение и исследование этого
распределения явились убедительным аргументом в пользу
атомизма и подтвердили правильность априорных положений,
послуживших отправным пунктом при выводе
распределения Максвелла.
Структура потока. Было бы, однако, преждевременно
полагать, что полученное таким образом распределение
совпадает с максвелловским. В опыте Штерна воспроизводится
распределение частиц не в сосуде, а в струе, выходящей из
него наружу. Оно должно отличаться от максвелловского
уже хотя бы потому,-что быстрые молекулы вылетают* через
открытое отверстие в большем количестве, чем за то же
самое время более медленные. Таким образом, распределение
частиц в потоке по абсолютным скоростям иное, чем в
единице объема, хотя оно и связано с максвеллойским однозначно.
В самом деле, поток частиц с данной скоростью есть
dj = vxndW (v) = v cos MW (v). n -g-, D.13)
что прямо следует из A.4), D.3) и D.5). Чтобы получить
нормированную к единице вероятность распределения частиц
в потоке, надо разделить D.13) на его интегральную
величину D.12), что дает
й- = 1. dW (v) C0S*dQ = dWj (v) dWj (Q). D.14)
J v л
Здесь
dWj (v) = | dW (v) = ± (-grJ exp (- |£) v4v D.15)
есть распределение частиц по абсолютной скорости
движения, а
dWj(Q) = / W-§-> 7(fl) = 2 cos О D.16)
— по направлениям их движения (в пределах полусферы).
Очевидно, что распределение частиц по скоростям в
опыте Штерна совпадает с D.15), так как при наблюдении вдоль
оси пучка (О = 0) в конечном, но небольшом телесном угле
АИ движется dj = jdWj (v) частиц. Помимо
несущественной постоянной это распределение отличается от
максвелловского дополнительным множителем и. Его происхождение,
как ясно уже из D.13), связано с тем преимуществом1 кото-
25
рое имеют быстрые частицы перед медленными, когда надо
за ограниченное время вылететь из сосуда. Поэтому и
средняя скорость, и средняя энергия частиц пучка оказываются
больше максвелловских:
—"" I 7ТТ7- V ЗЯ "" Ш \ a lTTT TTIV о Т /Т? 4 ~*
Vi = vdWj = — = -— у, г* = — v2dWj = -=- = 2кТ= -^е.
§ 5. БАРОМЕТРИЧЕСКАЯ ФОРМУЛА
В отсутствие внешних полей естественно считать все
точки пространства, в котором находится газ, совершенно
эквивалентными, а попадание в любые равновеликие элементы
равновероятным:
dW(x, у, z) = i^£, dW(z) = §§dW(x, y,z) = ±. dz.
x у
E.1)
Это, однако, не так, если сосуд находится в потенциальном
поле, например поле тяготения. Разные элементы
пространства отличается в этом случае величиной потенциальной
энергии молекул, в них находящихся. Из-за этого, вообще
говоря, следует положить
dW = /(*, у, z)dxdydz, E.2)
и необходимы специальные соображения для определения
/(.г, г/, z) Ф const. Если направление силы тяжести выделяет
только ось z, то отличие /(#, у, z) от константы выражается
в том, что плотность газа становится неодинаковой на
различной высоте. В силу C.6) это должно сказаться также и на
давлении.
Изменение давления с высотой должно иметь место хотя
бы потому, что газ, содержащийся в сосуде, что-то
весит, только если давление на дно больше давления на
крышку:
& = S[p@) - р{Щ] = SkT[n(O) - п{Н)]. E.3)
Но, с другой стороны, вес определяется просто общим
числом молекул в сосуде:
я
& = mgN = mgS J n (z) dz. E.4)
26
Из тождества
я
J-
О
следует1 что n(z) должно удовлетворять уравнению
dn mg /с ел
Решение этого уравнения определяет зависимость
я (z) = и (О)ехр [--£§?•]. E.6)
Плотность газа у основания сосуда может быть определена
н
из условия нормировки ]n(z)dz=N/Sl дающего при подста-
о
новке E.6) следующий результат:
ЙГ- E'7)
При mgHlkT <C 1 (не слишком длинный сосуд или
достаточно высокая температура) плотность газа n(z) « тг(О), т. е.
практически однородна по всему сосуду в соответствии с
повседневным нашим опытом. Но если mgH 3> кТ, то
уменьшение плотности с высотой становится заметным.
Условия типа
«-^w-^^1 E-8>
характерны для статистической физики. Они отражают
борьбу между детерминированным механическим воздействием
(силой тяготения в данном случае) и противостоящим ему
хаотическим тепловым движением. Сила тяжести стремится
уложить все молекулы на дно сосуда, тогда как тепловая
кинетическая энергия позволяет им, преодолевая силу
тяжести, подниматься вверх. Безразмерным показателем
экспоненты E.8) определяется относительная величина этих
усилий, измеренных величиной соответствующей энергии:
mgH и кТ. Скопление газа у дна сосуда может произойти
только, если Т < Тк, а при Я=1м Тк = -^|^ ^
3-10 К.. При этих температурах газо-
5*10~23«103 102 —2
«310
1,4-Ю-16
27
образная фаза обычно уже не существует. ЁсЛи же Т ^> Tki
то неоднородность газа в сосуде реальных размеров
незначительна и должна приниматься во внимание только в связи
с необходимостью правильного толкования веса газа.
Для обнаружения пространственной неоднородности газа'
можно было бы пойти по пути увеличения высоты сосуда.
Однако из той же формулы ясно, что заметное уменьшение
плотности (в 2,7 раза) при комнатной температуре наступит
лишь при Н=— = — ——=- = Юь см = 10 км, если
у mg 5-10~23.103
Т = 300 К. Сосуды такой величины, конечно, немыслимы,
но полученная цифра подсказывает иной способ проверки —
непосредственное сравнение с земной атмосферой.
Действительно, уменьшение плотности атмосферы с высотой —
хорошо известный факт. Если бы он описывался формулой E.6),
то соответствующее ему падение давления определялось бы
«барометрической формулой»
[] E.9)
ибо р = пк?, согласно C.6). Из E.6) следует также, что
разделение газов с высотой, которое действительно имеет место,
обусловливается различием .масс молекул (молекулярных
весов):
asW*^] <510>
Ввиду хорошего качественного соответствия этих выводов
с общеизвестными фактами, велик соблазн воспользоваться
приведенными формулами для количественного описания
состава и плотности атмосферы на разных высотах. Однако
такая экстраполяция является слишком смелой.
Приближенный закон F = —mg, которым мы описывали действие силы
тяжести, на больших высотах неверен. Его следует заменить
законом всемирного тяготения^ согласно которому
£-■*•)•
EЛ1>
Однако неясно, как это осуществить. Распределение частиц
в околоземном пространстве не является одномерным: оно
изменяется не по высоте, а вдоль радиуса, сохраняя
сферическую симметрию. Поэтому, прежде чем воспользоваться
E.11), необходимо существенно обобщить полученные здесь
результаты.
28
§ 6. РАСПРЕДЕЛЕНИЕ ЁОЛЬЦМАЙА
Так как плотность газа на высоте z равна п (z) = ' =
= —Sdz , одномерное распределение частиц dW(z) можно
представить в виде
[^]4[^]* F.1)
где Z = N/n@)S. Таково статистическое распределение,
задающее вероятность найти молекулу в слое толщиной dz.
Хотя это распределение и получено для весьма частного
случая (F = —mg), найденный вид плотности распределения
при U(z) = mgz
4[^Г| F.2)
подсказывает дальнейшие обобщения. Ясно, в частности, что
даже в рассмотренном примере система координат не
обязана совпадать с наиболее удобной, у которой ось z
параллельна силе тяжести. Поэтому распределение F.1) в общем
случае должно иметь вид
F.3)
От распределения Максвелла оно отличается лишь тем, что
роль кинетической энергии играет здесь потенциальная, а
dv — элемент объема в обычном координатном пространстве,
а не в пространстве скоростей. Это и есть распределение
Больцмана.
Для поля сил, имеющего сферическую симметрии^ оно
может быть представлено аналогично D.3) как
dW (R, 9, Ф) = 4" ехр [- -^-] R4R sin QdQd% F.4)
где Z = И j exp ^~- dR. Если нас интересует
содержание газа в околоземном слое толщины Д.Й, то естественно
пользоваться F.4). Если же интерес представляет изменение
плотности или давления, т. е. аналог барометрической фор-
мулыг то2 переходя от распределения вероятности к распре-
29
делению плотности, имеем
NdW (R) N t U \
F.5,
Знание плотности у поверхности Земли дает,
следовательно, принципиальную возможность оценить изменение ее с
высотой. К сожалению, эта возможность только
принципиальная. Любые выводы относительно плотности земной
атмосферы, вытекающие из F.5), подтверждаются только
качественно. Количественного соответствия в этом случае быть не
может хотя бы потому, что Z расходится. Кроме того,
атмосфера не находится в состоянии термодинамического равновесия.
Температура ее у поверхности Земли и на различных высотах
не одинакова, тогда как в равновесии она должна быть одна
и та же во всех точках пространства. Различие температуры
создает конвекционные токи газа (ветры), вызывает
теплообмен между слоями и другие явления, несовместимые с
представлением о равновесии. Поэтому этот пример неудачен с
точки зрения количественного подтверждения теории.
Природа, однако, позаботилась о существовании системы,
которая, будучи во многих отношениях удобнее с
экспериментальной точки зрения, в то же время является удачной
моделью идеального газа. Она представляет собой раствор
частиц твердой или жидкой фазы, взвешенных в прозрачном
растворителе. Речь идет о так называемых суспензиях или
эмульсиях. Наблюдая их под микроскопом, можно заметить,
что они непрерывно движутся случайным образом, не
взаимодействуя между собой. Это движение имеет молекулярио-кп-
нетическое происхождение: оно обусловлено различиями
в импульсах, которые получает частица в результате
столкновений с молекулами. Таким образом, в отличие от частиц
газа, которые движутся свободно, эмульсии вынуждаются
к движению некомпенсированностью ударов молекул,
налетающих с разных сторон. Для изучения таких свойств, как
распределение с высотой, это различие несущественно, важна
лишь масса растворенных частиц. Только из-за своей
внушительной массы затонувшие суда закономерно идут ко дну,
а не распределяются между дном и поверхностью. Масса
растворенных частиц не столь велика и в то же время
значительно больше молекулярной. Ее можно подобрать такой, чтобы
неоднородность распределения была легко наблюдаема в
сосуде умеренных размеров.
30
Если учесть, что вес частицы с массой т и плотностью р
mg (л Ро\
равен в растворе mg — р0 —^ = mg II I вследствие
выталкивающих свойств жидкости с плотностью р0, то
n(z) = „@)exp[--^(l - ■£•)] F.6)
представляет собой аналог барометрической формулы для
броуновских частиц (такое название получили коллоидные
частицы). Случайный характер движения броуновских
частиц, а также их распределение с высотой не поддаются
никакой иной интерпретации, кроме вышеизложенной. Поэтому
количественное исследование таких систем, выполненное
Перреном, и, в частности, точное соответствие формулы F.6)
с наблюдавшимися распределениями явились настоящим
триумфом молекулярно-кинетической теории, ее прямым
и окончательным подтверждением. Более того, измерения
Перрена позволили впервые с высокой точностью определить
число Авогадро из расчетной формулы: No = Rlk1 в которой
- И± [\ _ El
- Г V р
In,»(«,)-In д(*а)
измерялось путем подсчета числа частиц в кубике на
различных высотах и скрупулезного измерения массы частиц
несколькими методами.
Формула F.7) содержит также принципиальную
возможность определения массы частиц, коль скоро к уже известно.
Однако определение малых масс, которое только и
представляет практический интерес, ограничено размерами сосуда.
Чем меньше масса, тем большие расстояния требуются,
чтобы при заданной точности подсчета частиц обнаружить
различие. Значительный прогресс может быть достигнут лишь
усилением «силы тяжести» — заменой поля тяготения полем
центробежных сил F = ягсо2г, достигающих в современных
ультрацентрифугах огромной величины. В этом варианте
метод, основа которого была заложена Перреном, не только
не изжил себя, но даже, напротив, получил широчайшее
распространение в химии и биологии как эффективный способ
разделения близких по молекулярному весу веществ.
Так как центробежная энергия
R
-j
U = — I mwb'dr
R
31
то распределение Больцмана имеет вид
]R, F.9)
или в цилиндрических координатах
dW(R9 Ф, z) = -i-expftfi?*] RdRdydz, F.10)
где B^-^jjf- Если центрифугируется молоко, например,
и требуется определить, какое количество жирных частиц
содержится в слое толщиныДД, то ответ на этот вопрос
удобнее получить из распределения F.10) после интегрирования
по ф и по z. Но если интерес представляет плотность частиц
в кубике, позволяющая определись их молекулярный вес,
то необходимо исходить из F.9), приводя это распределение
к «барометрическому» виду
п = -^- = -£ exp [BR*] = п @) ехр [ЯД2]. F.11)
Чем больше угловая частота вращения о), тем более
неоднородно распределение частиц вдоль радиуса: плотнее у
периферии и реже вблизи оси вращения.
§ 7. КАНОНИЧЕСКОЕ РАСПРЕДЕЛЕНИЕ ГИББСА
Вероятность того, где молекула находится и как быстро
она в некотором направлении летит, задается произведением
соответствующих вероятностей — D.1) и F.3):
dW(r, v) - dW(r)-dW(v) = 4"ехР (" w)dxdydzdv*dvvdv*>
G.1)
Г U(x'v'z)
J e hT dxdydz,
-^ С — / \з/2 Г U(x'v'z)
*Td je kTdv =
где % = B + U = -^ + U(x,y,z).
Таково распределение Максвелла — Больцмана, заданное
в так называемом ^-пространстве — шестимерном
пространстве dxdydzdvxdvydvz, каждая точка которого
соответствует определенному состоянию молекулы. Распределения
Максвелла и Больцмана получаются из него как частные
32
случаи известным приемом сложения вероятностей:
dW(\) = J J j dFP(r, v) Лг, dVF (r) = J j J dJF(r, v) dv. G.2)
Таким образом, распределение G.1) наиболее полно
характеризует состояние газа, если ограничиться
рассмотрением молекулярных переменных, свяванных исключительно
с поступательным движением. Этого распределения вполне
достаточно, если мы имеем дело с одноатомным газом. Если
же речь идет о молекулах, то необходимы еще и такие
распределения, которые позволили бы определить вероятность
того или иного поворота молекулы, величины ее
вращательного момента, энергии колебаний и т. д.
Становясь на путь индуктивного обобщения G.1), можно
ожидать, что распределение, применимое к самым разным
движениям молекулярной системы, имеет вид,
отличающийся от G.1) только самым необходимым:
r, G.3)
где ЙГ—полная энергия. Эти «необходимые» изменения
должны коснуться только элемента пространства ЙГ, равного
произведению приращений тех координат, которые связаны с
данным типом движения. Однако, как мы уже убеждались
выше, в зависимости от того, какие именно координаты
выбраны для описания движения, элемент dT будет обладать
различным статистическим весом, величину которого мы и
должны теперь установить. При этом достаточно определить
статистический вес в каких-либо одних координатах, так как
в других он получится автоматически при преобразовании
переменных. Достаточно, например, указать, в каких
именно координатах статистический вес равен единице, т. е. в
каком именно пространстве попадание в изоэнергетические
элементы, определенные одинаковыми приращениями
координат, считается равновероятным. Иными словами,
необходимо указать признак, по которому можно было бы
безошибочно узнавать, в каких координатах распределение
производится по равноценным «комнатам», а в каких — по
«этажам» различной емкости. Ранее этот вопрос представлялся
очевидным: равновеликие элементы dxdydz кажется
естественным считать равноправными, тогда как равенство
приращений drdQdy никто не станет рассматривать как
достаточное основание для такого же вывода. Несмотря на
очевидность, это важная статистическая гипотеза. Она
является математическим выражением нашего убеждения в том, что
2 А. И. Бурштейн 33
не выделены именно точки реального физического
пространства и только его равновеликие элементы могут считаться
равновероятными .
К сожалению, очевидные вещи таят в себе опасность
недоразумений и путаницы, особенно в тех случаях, когда они
должны служить основой для обобщения. То, что
интуитивно кажется бесспорным, когда речь идет об обычном
координатном пространстве, уже не столь очевидно даже в случае
пространства скоростей. Когда же этот вопрос возникает при
анализе вращательного или колебательного движения,
интуитивные соображения становятся совершенно
ненадежными. Поэтому соотношение G.3) приобретает силу Закона
только после того, как дано точное определение
элементу dF.
По причине, которая будет выяснена в § 10,
равновероятным считается попадание в равновеликие элементы только
в том случае, если они заданы в пространстве канонических
переменных qt и рг — обобщенных координат и импульсов.
Из механики известно, что при произвольном выборе
обобщенных координат qt и соответствующих им скоростей qt =
dq.
= —т- обобщенные импульсы могут быть определены по
формуле
* [в
Pi ::\)
dq. dq.
Здесь е — кинетическая энергия, U — потенциальная
энергия, a L = е — U — функция Лагранжа.
Величина dV в распределении Гиббса G.3) равна
dT = dpdq = П dQidpn G.5)
i
П
i
т. е. статистический вес равен единице только в пространстве
координаты — импульсы. Следовательно, распределение
Гиббса для системы материальных точек, не
взаимодействующих между собой, имеет вид
dW = ^ ехр [--^=Д ] dqdv, G.6)
причем j dW = 1» так что
£+£
34
Подстановка рг = rnqt = тиг обнаруживает тождественность
этого распределения максвелл-больцмановскому.
Появляющийся при этом статистический вес ms как величина
постоянная не играет существенной роли и может быть
включен в нормировочную константу.
Чтобы перейти от канонических переменных, в которых
записывается распределение Гиббса, к любым иным,
достаточно прибегнуть к формуле
-ЙГ = dpdq = |/|daeft. G.8)
Якобиан этого преобразования |/| определяет
статистический вес в новых переменных. Если же мы стремимся к более
частному виду распределения, освобождаясь от не
представляющих интереса переменных, то койкретное выражение для
статистического веса получается после интегрирования по
«липшим» переменным.
§ 8. ДИЭЛЕКТРИЧЕСКИЕ СВОЙСТВА ГАЗОВ
Обобщенные координаты. В качестве примера,
иллюстрирующего применение канонического распределения к
произвольной системе, мы рассмотрим линейный ротатор —
жесткую двухатомную молекулу, атомы которой несут к тому же
разноименные заряды ±е. Такая молекулярная гантель
(рис. 8) характеризуется (кроме массы М — т1 + т2) еще
двумя константами — моментом инерции в системе центра
масс / = /71^1 + т2г\ и дипольным моментом q == е(г2 —- гх) =
= е(г2 + гх)а, где а = —2- = — —^. Соответственно этому ее
энергия (помимо энергии поступательного движения)
содержит члены, связанные с кинетической энергией вращения:
ви = =41+"#-4а. <8Л)
и потенциальной энергией, зависящей от #риентации диполя
во внешнем постоянном электрическом поле
напряжённости Е:
U = —qE = — qzE = —qE cos 9. (8.2)
Так как потенциальная энергия очень простым образом
выражается, через угол 0 между осью диполя и~полем, а
ориентация молекулы в пространстве, однозначно определяется
35
Рис. 8. Расположение масс
и зарядов в двухатомной
молекуле, обладающей ди-
польным моментом.
Рис. 9. Скорости и угловые
моменты в сферической
системе координат.
двумя сферическими координатами: 0 и ф, то именно эти
переменные естественно выбрать в качестве обобщенных
координат. В таком случае кинетическую энергию следует выражать
как функцию обобщенных скоростей 0 и ф. Координатное
пространство линейного ротатора и пространство его
обобщенных скоростей является двухмерным.
Совместив начало координат с центром тяжести системы,;
мы освободили себя от необходимости рассматривать
поступательное движение. Радиус-вектор
а = (a sin 0 cos ф, a sin 0 sinjp, a cos 0)
(8.3)
полностью представляет молекулу в этой системе отсчета.
Он описывает вокруг центра тяжести сферу, каждая точка
которой — возможное состояние изучаемой системы.
Вернее, совокупность состояний, совпадающих по положению,
но отличающихся скоростью его изменения:
а = а@ cos 0 cos ф — ф sin 0 sin ф,
0 cos 0 sin ф + ф sin 0 cos ф, — 0 sin 0).
Возведя это выражение в квадрат и подставив в (8.1), имеем
(8.4)
Используя этот результат в G.4) и принимая во внимание^,
36
что потенциальная энергия от 0 и ср не зависит, получаем
рф = / sin2 9Ф, pQ = /9. (8.5)
Обобщенный импульс /?ф отвечает вращению вокруг оеи
z, a pQ — относительно оси, перпендикулярной плоскости,
проходящей через ось z и мгновенное положение оси диполя.
Как видно из (8.5) и рис. 9, угловой момент /?ф при данной
скорости ф будет тем меньше, чем меньше 9, т. е. чем меньше
отклонение масс от оси z, а если 0 = 8, он и вовсе равен
нулю. Таким образом, между обобщенным импульсом р9 и обобл
щенной скоростью ср нет универсальной пропорции,
подобной той, которая связывает /? и 9.
Распределение. Соответственна этому и распределения
будут отнюдь не тождественными, если выразить dT через
или через координаты и импульсы, как это
требуется в каноническом распределении Гиббса:
dT = dGdcpdped/v (8.6)
Полная энергия в канонических переменных ввиду (8.2),
(8.4) и (8.5) есть
% (в, Ф, р0, рф) = |L + -jJ^ - qE cos 0. (8.7)
Теперь легко конкретизировать распределение G.3), придав
ему с помощью (8.6) и (8.7) следующий вид:
-fj- cos 9
+ -fj- cos 9 dpedpvdQdy. (8.8)
Нормировочная постоянная равна
7 _ 8п21(кТJ ,
Вероятность найти некоторое значение р^ оказывается,
согласно (8.8), зависящей от 0. Это и естественно: чем меньше
9, тем менее вероятны большие значения момента рф. При
9 = 0 невероятны какие-либо значения, кроме нулевого
(рис. 10).
37
Рис. 10. Распределения по угловым момедтам при заданной
ориентации молекулы.
Если перейти теперь к распределению молекул по
координатам и скоростям, то в силу (8.5)
+ fees 6
Р sin2 QdQdydQd'y,
(8.9)
где р@, ф, 0, ф) = Р sin20 — статистический вес, который
в этих координатах в отличие от канонических не равен
единице и едва ли мог быть угадан заранее.
Если нас не интересует скорость вращения, а лишь
ориентация диполя, то, поступая обычным образом, имеем
dW(Q, Ф) = j j dW(Q, ф, /,е, Р9)
Р0Рф
(8.10)
где а = qE/kT. При a > 1 маловероятны сколько-нибудь
существенные отклонения оси молекулы от оси z, тогда как
при а<1, напротив, все направления почти равновероятны
(рис. 11).
Электрическая поляризация. Рассчитаем равновесную
поляризацию газа, помещенного в электрическое поле, т. е.
суммарный дипольный момент всех его молекул в единице
объема при некоторой заданной температуре и
напряженности поля
Q =
(8.11)
38
Рис 11. Распределение
дипольных моментов
относительно внешнего поля
при высоких (а) и низких
(б) температурах.
oL«1
с:»/
Доля молекул, содержащихся в единице объема и
обладающих данной ориентацией дипольного момента q:
dn(q) = ndW(Q, Ф). (8.12)
Вследствие аксиальной симметрии распределения (8.10)
средние значения поперечных компонент момента равны
нулю, и дело сводится к усреднению продольной
составляющей:
Q = щ \ j cos QdW (G, Ф) = nqL (а), (8.13)
ё
где L(a) — так называемая функция Ланжевена:
1 сс>1
L(a) =
choc
shot
I
a
1 /
а \ а
т
(8.14)
Таким образом^ равновесная поляризация образца
параллельна приложенному полю, а ее абсолютная величина
является функцией его напряженности и температуры. Сразу
же можно различить две предельные ситуации:
а) при а<1 Q =
б) при а » 1
3 к
= qn.
(8.15а)
(8.156)
При достаточно высоких температурах или соответственно
низких полях связь между поляризацией и напряженностью
поля линейна, а коэффициент пропорциональности
(поляризуемость диэлектрика)
ЗкТ'
(8.16)
39
Диспропорция между числом молекул, ориентированных
по полю и против него, в этом случае еще совсем невелика
и с увеличением Е возрастает благодаря переориентации
небольшого числа молекул. В этом случае говорят, что
справедлива линейная по полю теория или линейная оптика,
если речь идет о переменных во времени полях. При удержа-
Лии в (8.15а) квадратичных по Е слагаемых появляется
возможность рассматривать эффекты нелинейной оптики.
Наконец, при очень больших полях ориентированными вдоль
направления поля оказываются почти все молекулы, и при
дальнейшем увеличении полях поляризация фактически не
возрастает («эффект насыщения»). В обычных йолях и
температурах этот случай реализуется редко. Как правило,
Q = %Е, где %, согласно (8.16), возрастает обратно
пропорционально абсолютной температуре (закон Кюри).
§ 9. РЕАЛЬНЫЙ ГАЗ
С введением распределения Гиббса задача в своей
идеальной постановке может считаться исчерпанной, так как все
свойства газа из невзаимодействующих частиц могут быть
описаны с его помощью совершенно строго, сколь бы ни была
сложна структура отдельной молекулы.
Межмолекулярное взаимодействие. Ситуация, однако, в
корне меняется, как только возникает необходимость учесть
взаимодействие молекул. А такая необходимость есть:
известно, что уравнение состояния pV== RT отнюдь не
универсальный закон, и в поведении всех реальных газов
обнаруживаются более или менее сильные отступления от него.
Фактически уравнений состояния столько же, сколько и
газов, так как взаимодействие зависит от структуры молекул.
Сколько-нибудь общую закономерность можно искать, лишь
огрубляя, идеализируя истинный характер
межмолекулярного взаимодействия. Наибольшей простотой — и поэтому
наибольшей общностью — обладает модель взаимодействия,
которая оперирует всего двумя параметрами: один из них
учитывает взаимное притяжение молекул, другой — их
отталкивание. Эта модель приводит к уравнению Дитеричи и
Вап-дер-Ваальса.
Само существование конденсированных фдз вещества —
жидкостей и твердых тел — свидетельствует о том, что между
молекулами действуют силы притяжения, связывающие их
в единое целое при низкой температуре. Однако взаимное
влечение друг к другу, которое доминирует на далеких рас-
40
стояниях, уступает место отталкиванию в случае чрезмерной
близости. Происхождение сил отталкивания, пожалуй, даже
проще понять, чем природу сил притяжения. Когда дело
доходит до «собственного объема» молекул, всякое
дальнейшее сближение означает деформацию их электронных
оболочек или атомной структуры, и поэтому встречает
решительное сопротивление. Количественная мера этого
сопротивления — потенциальная энергия взаимодействия. Она
начинает резко возрастать при переходе через минимум,
в котором силы притяжения и отталкивания взаимно
уравновешены, а затем, изменив знак, устремляется к
бесконечности (рис. 12). Продвижение одной молекулы к центру
другой требует значительных энергетических издержек, как
только расстояние между ними становится меньше d. Это
соображение позволяет упростить закон «взаимодействия, приняв,
что на расстоянии d налетающая молекула наталкивается
на потенциальную стенку. В таком случае минимальное
расстояние между центрами двух одинаковых молекул
приобретает смысл диаметра молекулы, которую следует
представлять себе как жесткий шар радиуса d/2. Такое огрубление
формы молекул и характера их взаимодействия имеет только
то преимущество, что, абстрагируясь от деталей, мы
получаем простую возможность учесть «собственный объем»
молекул, т. е. то, что они, во всяком случае, не материальные
точки, а частицы конечных размеров. Вывод уравнения Ван-
дер-Ваальса основан именно на этом упрощенном
моделировании молекул жесткими шарами, способными
притягиваться друг к другу.
Отталкивание. Обсудим вначале, какого рода уточнения
вносит учет собственного объема молекул. Будем следить за
выбранной молекулой как за материальной точкой, считая
все другие жесткими шарами радиуса d (рис. 13). Это
позволяет заметить, что если раньше точечной массе были
доступны все точки пространства, то теперь некоторая часть его
становится недосягаемой. Поскольку объем шара удвоенного
радиуса равен 8vd, где ^ == т я ' т) — собственный объем
молекулы, в каждом кубическом сантиметре, удаленном
от стенок сосуда, доля недоступного объема составляет в
общей сложности 8vdn, а доступного 1 — 8vdn. Соответственно
в сосуде объема V свободна только часть его: УA — 8vdn),
а в элементарном объеме dV — только dV(l — 8vdn) =
= dVe.
Несомненно, что равновероятными следует считать
равновеликие элементы только свободной части пространства:
41
Рис. 12. Потенциал
межмолекулярного
взаимодействия.
Избранная молекула
Рис. 13. Исключенный
(заштрихован) и
собственный объемы молекул
(иунктир).
попадание в занятые
вообще невозможно. Но
это значит, что
вероятность попасть молекулев
некоторый элемент про-
dV
странства, свободный от других молекул, есть-^-. Такое
уточнение не вносит пока ничего нового, поскольку между
номинальным объемом и его незаполненной частью существует
прямая пропорция: dW = -~ = -^-. Можно заметить, од-
нако, что для элементов, расположенных в непосредственной
близости от стенок сосуда, соотношение между dVe и dV
несколько изменяется. Каждая молекула, вошедшая в
непосредственное соприкосновение со стенкой, отсекает теперь
от свободной части пространства вдвое меньший объем, чем
раньше (рис. 14). Наша избранница — материальная
точка — все равно не может сойтись со стенкой ближе, чем
другие молекулы: ведь следует помнить, что и она в
действительности лишь центр шарика радиуса d/2. Поэтому фактически
ей мешают лишь те полусферы, которые обращены внутрь
сосуда, тогда как противоположные половинки,
оказавшиеся за его фактическими пределами, ничему уже не могут
воспрепятствовать. Вследствие этого каждая молекула,
прижавшаяся к стенке, вырезает из номинального объема
ршь 4vd, т. е. вдвое меньше, чем внутри сосуда. Если
плотность молекул непосредственно у стенки есть тг3, то в каждом
приповерхностном элементе объема только часть его 4nsvd
окажется занятой собственно веществом, а оставшийся
свободным объем будет равен dVs = dV(l — 4vdn8). СОответст-
42
и
Стенка
Рис. 14. Исключенный объем Рис. 15. Результирующая сил
у стенки сосуда: слой толщи- притяжения в объеме и у стенки
ной d/2. сосуда.
венно и вероятность найти молекулу непосредственно у
поверхности будет несколько больше, чем вдали от нее:
dV 1 — 4i;'^м fly
Ve f — Svdn V*
Это, в сущности, и объясняет, почему мы вынуждены
отличать приповерхностную плотность ns от средней по сосуду
п = N/V. Очевидно, что
NdWo 1 - 4pwrce
ns
а значит,
dV
п* =
1 — 8vd n
72,
(9.1)
1 - kvdn '
Пристеночное уплотнение частиц должно сказаться и на
давлении, которое испытывает стенка:
пкТ
р =
(9.2)
Таким образом, при vd Ф 0 давление оказывается большим,
чем в идеальной (точечной) модели газа.
43
Притяжение. К прямо противоположному результату
приводит учет взаимного притяжения молекул. Войдем в
положение молекулы, находящейся в глубине сосуда, которую
влечет к себе каждая пролетающая мимо частица. Такая
молекула обречена на непрерывные метания из стороны в
сторону, поскольку результирующая сил притяжения
непрерывно изменяет величину и направление. Ясно, однако, что
в среднем по времени эта флуктуирующая сила будет равна
нулю, поскольку молекулу влечет во все стороны, и ни
одной из них невозможно отдать предпочтение (рис. 15).
В ином положении оказывается поверхностная
молекула: находясь у самой стенки, она испытывает одностороннее
притяжение — только внутрь сосуда; извне ее ничто не
привлекает, так как стенку, как и прежде, можно считать
идеальной. Таким образом, несмотря на пульсации действующей
со стороны газа силы, среднее по времени усилие,
втягивающее молекулу внутрь газа, оказывается отличным от нуля.
Из соображений симметрии ясно, что эта средняя сила
перпендикулярна к стенке и направлена в глубь сосуда.
Направление силы сохраняется и при удалении молекулы от
стенки, тогда как ее величина, постепенно уменьшаясь,
обращаемся в нуль. В любой точке средняя сила должна быть тем
больше, чем больше плотность молекул, коллективными
усилиями которых периферийная молекула втягивается ч гущу
остальных:
? = y(z)n. (9.3)
Что жз касается коэффициента пропорциональности y(z), то
о нем можно сказать то же самое, что и о самой силе: он
равен нулю в глубине сосуда (при z-> оо), но^ монотонно
возрастает при приближении к стенке, достигая максимума
при z = 0. Как и всякому другому, этому полю сил можно
сопоставить некоторый потенциал, обращающийся в нуль
вдали от стенок:
оо
$(z)dz. (9.4)
Распределение молекул в таком поле описывается
распределением Больцмана:.
rc(z) = nexpf — -jL j y{z)dz\.
(9.5)
44
Естественно, что плотность газа уменьшается при
продвижении к стенке, но как именно — неизвестно ввиду
неопределенности y(z). Однако нам и не нужно знать столь многое.
Для оценки давления необходима лишь плотность
непосредственно у стенки:
»@) = л ехр (-■§), (9.6)
а она выражается через один-единственный (хотя и неизвест-
оо
ный) параметр у = J у (z) dz. Величина у*п имеет смысл «ра-
о
боты выхода» из газа, т. е. представляет собой энергию,
которую каждая прорвавшаяся к стенке молекула расходует
на преодоление сил сцепления, связывающих ее
(^оставшимися в глубине объема. Нововведенный параметр у призван
учесть эффект притяжения молекул в той же степени, как
vd — эффект отталкивания. И действительно, из (9.6)
следует, что давление на стенку
р = п@)кТ.= пкТехр (--§■). (9.7)
Неудивительно, что оно меньше, чем в идеальном газе: сийы
взаимного притяжения частично удерживают молекулы от
столкновений со стенкой,, которых в противном случае не
удалось бы избежать.
Уравнение состояния. Формула (9.2) справедлива для
невзаимодействующих шариков конечных размеров, тогда
как (9.7) — для точечных, но притягивающихся друг к другу
молекул. Эти результаты мгогут быть синтезированы таким
образом, чтобы одновременно учитывалось и то, и другое*
Для этого достаточно принять во внимание
приповерхностное уплотнение газа в (9.6), подобно тому, как это было
сделано в (9.1). В итоге окажется, что
щ = '*w ^ = J* ^ ехр ( — -^-1 (9.8)
и, следовательно^
Это уравнение называется уравнением Дитеричи,
Так как показатель экспоненты при обычных плотностях
много меньше единицы, то, разлагая его в ряд, легко полу-
45
Рис. 16. Жидкие (•), неустойчивые (+) и
газообразные (о) состояния на изотерме Ван-дер-
Ваальса.
чить из (9.9) следующее уравнение для
одного моля газа:
RT А
V — B
—■Т. (9-10>
где В_ = 4Novd и А =
=iVoY- Оно
широкоизвестно как уравнение
Ван-дер -Ваальса.
Сравнивая его с
уравнением состояния
идеального газа,,
можно заметить, что даже и двух параметров, которыми
учитывается межмолекулярное взаимодействие, достаточно
для проявления важных качественных особенностей
поведения реальных газов, включая их способность переходить
в жидкое "состояние.
Этот переход совершается в области, где изотерма Ван-
дер-Ваальса делает «петлю» (рис. 16). Выше и ниже ее
заданному значению давления отвечает только одно
равновесное состояние, а внутри — три. Два крайних соответствуют
устойчивым состояниям — жидкости (точки) и ее пара
(кружки). Промежуточные состояния, отмеченные крестиками,
принадлежат внутреннему участку петли, между
минимумом и максимумом, который характеризуется
положительным знаком (-$у ) . Эти состояния неустойчивы. Случись здесь
любая флуктуация объема, она имела бы тенденцию
развиваться, возвращая систему на одну из устойчивых ветвей
изотермы — левую или правую.
Неустойчивость промежуточных состояний препятствует
постепенному превращению жидкости в пар, которому
отвечало бы последовательное перемещение вдоль петли,
включая ее.внутренний участок. Вместо этого реализуется иная
возможность: гомогенная фаза распадается на жидкость
и пар, превращаясь в бинарную систему. Это случается,
когда давление на жидкость падает до давления насыщенного
пара pv, появляющегося вместе с границей раздела. Переход-
вещества через эту границу из жидкого состояния в паро-
46
образное совершается при постоянном давлении р =pv
вплоть до полного превращения его в газ. Только после этого
система снова становится гомогенной, и ее давление начинает
падать при расширении.
О гомогенной системе как до, так и после фазового
перехода известно лишь, что она разупорядочена. Только имея
дело с бинарной системой, можно судить о том, какая из
находящихся в равновесии фаз является газообразной, а
какая — жидкой. Критерием является плотность вещества,
которая претерпевает скачок на поверхности жидкости. Этот
скачок характеризуется на рис. 16 разницей молярных
объемов VL и Vv. Эта разность между ними с повышением
температуры уменьшается и при достижении критической
температуры Тс обращается в нуль. При всех Т~> Тс (закрити-
ческая область) существование бинарной системы
невозможно, и, следовательно, жидкость и газ неотличимы.
При всякой температуре ниже критической жидкость
находится в равновесии со своим паром лишь при вполне
определенном давлении pv. Величину этого давления, или высоту
«полочки Максвелла», можно определить, руководствуясь
следующими соображениями. Из-за расширения бинарной
системы в процессе испарения жидкости совершается
работа, равная pv{Vy— VL) за счет разницы в свободных
энергиях жидкости и пара:
Сг L — €Г у—Ру\* у — У £/• \v.LL8L)
Эта разница не должна зависеть от того, как совершается
переход жидкости в газ—по полочке Максвелла или по петле
Ван-дер-Ваальса. Иными словами, выражение (9.11а)
должно быть тождественно следующему:
Vy
vL
Поскольку согласно термодинамике/?= —(-^тг) ? Из этого
тождества вытекает так называемое правило Максвелла:
Vy
Pv(Vv — VL)= f p(V,T)dV.
Таким образом, величина /?v определяется из условия
равенства площадей под полочкой Максвелла и под петлей Ван-
дер-Ваальса, отсеченной от изотермы этой полочкой.
47
o-
-ю-
Рис. 17. Изотерма азота {а -
бинодаль, Ъ — спинодаль,
т = Т/Тс).
О том, насколько
хорошо теория Ван-дер-Ва-
альса передает
качественные черты поведения
реальных газов, можно
судить по рис. 17, на
котором изображено
семейство изотерм азота. Они
построены по аналитически
заданному уравнению
состояния, гораздо более
сложному, чем ван-дер-
ваальсовское, но зато
аппроксимирующему
экспериментальные данные с
точностью, не выходящей
за пределы ошибки.
Параметры этого уравнения подогнаны по данным, относящимся
к устойчивым ветвям изотермы (жидкой и газовой). В
неустойчивую область можно лишь экстраполировать эти
данные, полагаясь на аналитичность уравнений p(V) как
функций объема. При надежной экстраполяции обе ветви
сшиваются в неустойчивой области, демонстрируя поведение,
типичное для петли Ван-дер-Ваальса. Более того, определяя
положение полочки Максвелла по вышеприведенному
рецепту, можно убедиться, что получающееся значение ру
совпадает с экспериментально найденным давлением насыщающих
паров. Это свидетельствует о реальном существовании петли
В ан-дер-Ваальса.
Точки, соединенные полочками Максвелла, лежат на
кривой а рис. 17, называемой бинодалью. Восходящая ветвь
этой кривой называется линией жидкости, а нисходящая —
линией пара. Аккуратно расширяя очень чистую жидкость,
можно пересечь бинодаль и, опускаясь по изотерме вниз,
приблизиться к ее минимуму, если только он не попадает
в область отрицательных давлений. Равным образом и со
стороны пара можно в принципе продвинуться вверх по
изотерме к ее максимуму. И в том и в другом случае
реализуются гомогенные состояния, являющиеся метастабильными.
Они неустойчивы по отношению к расслоению на две фазы,,
но достижимы. Совершенно нестабильнее лишь участки изо-
терм между экстремумами — внутри соединяющей их
кривой в, называемой спинодалью (см. рис. 17). Ее восходящая
ветвь отвечает максимально расширенному
конденсированному состоянию, а нисходящая — предельно сжатому
газообразному. Метастабилып&е состояния, заключенные между
бинодалью и спинодалью, отвечают либо перегретой
жидкости, либо переохлажденному пару, если их сравнивать
со стабильными состояниями при том же давлении. Бино-
даль и спинодаль имеют общую вершину в критической
точка. Проходящая через нее изотерма испытывает в этой точке
перегиб, а при более высоких температурах \~ду) "^^
на всем протяжении изотерм.
Вся эта картина качественно правильно передается
уравнением Ван-дер-Ваальса. Положение экстремумов на
изотермах определено условием
Им определена спинодаль газа Ван-дер-Ваальса. С
повышением температуры экстремумы сближаются и, наконец,
сливаются при Т = Гс, создавая перегиб, определенный
дополнительным условием:
„ = 2RT _ 6А = Q 912
у G — Bf У4 v • /
Рассматриваемые совместно уравнения (9.12) определяют
в рамках теории Ван-дер-Ваальса координаты критического
состояния:
последняя из которых определяется подстановкой Ус и Т&
в уравнение (9.10). Совокупность этих параметров
определяет фактор сжимаемости газа Ван-дер-Ваальса в критической
точке: pcVc/RTc = Fc = 3/8 = 0,375. Он оказывается
намного больше величины, найденной экспериментально. Так,}
например, для ряда предельных углеводородов Fc = 0,267*
Значительно лучше согласуется с этой величиной значение^,
найденное из уравнения Дитеричи: 0,2706. Впрочем, любые
уравнения, оперирующие только двумя параметрами, не
могут претендовать на хорошее количественное соответствие
с экспериментом в широком диапазоне изменения р и У.
Однако с эвристической точки зрения они представляют
49
большую ценность благодаря своей простоте и физической
прозрачности.
Различие в размерах молекул и силах сцепленияу
действующих между ними, довольно сильно сказывается на
величине параметров Ван-дер-Ваальса и, следовательно, на
критических характеристиках реальных газов (9.13). Чтобы
облегчить и унифицировать сопоставление различных
молекулярных сред, Ван-дер-Ваальс ввел представление об их
соответственных состояниях, которые определяются
приведенными переменными:
Уравнение Ван-дер-Ваальса (9.10) приобретает в этих
переменных универсальный вид,.не зависящий от природы газа:
я + Зсо2 = Jm^-. (9.15)
о — со
Этот факт составляет существо «закона соответственных
состояний», согласно которому все вещества, взятые при
соответственных температурах и давлениях, имеют также
одинаковую соответственную плотность.
Оказывается, что закон соответственных состояний
находится в хорошем согласии с опытными данными, несмотря
на то что они далеко не всюду хорошо описываются
уравнением Ван-дер-Ваал'ьса. Иными словами, он имеет более
широкие пределы применимости, чем уравнение, на основании
которого этот закон был сформулирован. Изотермы
различных газов, изображенные как функции приведенных
переменных (9.14), действительно весьма близки друг к другу,
а для газов с идентичным межмолекулярным
взаимодействием практически совпадают.
Сжимаемость газов. Качественное представление о том^
как ведёт себя сжимаемость газа F = pV/RT при
изотермическом увеличении давления, можно получить из
диаграммы Хоугена и Ватсона, построенной в свое время для
семи газов (Н2, N2, CO, NH3, CH4, С3Н8, С5Н12), усредненных
в соответственных состояниях (рис. 18). Современный аналог
этой диаграммы для азота (рис. 19) позволяет судить об
изотермическом изменении F в гораздо более широких пределах
и притом не только в газообразном, но и в жидком состоянии
вещества.
Состоянию идеального газа на этих диаграммах отвечает
единственная точка: р — 0, F = 1. Все изотермы исходя
из-этой точки (бесконечно разреженного состояния), но с рос-
50
0,1
Приведенной температура- ч
Приведенная температура'=1,0
О 0,2 0,4
Интервал низких давлений,рг
0,4 0,6 1,0 2 4 6 8 10
Приведенное давление p/p-L
20
0,1 0,2
Рис. 18. Оригинальная диаграмма Хоугена — Ватсона.
40
том давления ведут себя по-разному. На высокотемпературных
изотермах сжимаемость с самого начала возрастает с
увеличением давления, тогда как при низких температурах она
сначала уменьшается, претерпевая реакий скачок вниз при
сжижении газа, и лишь затем устремляется вверх,
возвращается к исходному значению, а затем и превышает его. Эта
связано с тем, что притяжение уменьшает сжимаемость, а
отталкивание увеличивает ее. С увеличением температуры и
давления роль отталкивания возрастает и в конце концов
становится доминирующей, даже если вначале она была
относительно невелика.
Эти соображения можно уточнить, если представить
фактор сжимаемости Ван-дер-Ваал ьса в виде разложения по
степеням плотности в окрестности идеально-газового состояния:
А
А А В— от / D \2 / г> \3
Я = 1 £_ __ A j «£. i ( В | . [ В \ ,
__£ RTV — 1 "*" V + \Т) "*" \У) "г •'•
1 V
(9.16)
Представленное в таком виде уравнение Ван-дер-Ваальса
может рассматриваться как конкретный частный случай ви-
риального разложения:
тр л _| 0 ■ 0 |^ О
(9.17)
51
50 100 .750 200 250 300 350 400 р, бар
i i i I i 1 111111j
Рис. 19. Диаграмма Хоугена — Ватсона
для азота.
коэффициенты которого выражаются
через межмолекулярные силы (от vires—
лат.). Каждый из них, вообще
говоря, зависит от обеих сил, как отталки-
i так и притяжения, но в модели Ван-дер-Ваальса (и
в этом состоит ее ограниченность) они учитываются на
равных только вторым вириальным коэффициентом
Во = В~4т- (9Л8)
Конкуренция, притяжения и отталкивания определяет
не только величину, но и знак этого коэффициента, от
которого зависит наклон изотерм при р = 0:
^-«l + -j^p при |1-
(9.19)
Равенство нулю второго вириального коэффициента
определяет так называемую температуру Бойля, которая в теории
Ван-дер-Ваальса равна
Тв = 4г (9.20)
Ниже температуры Бойля при изотермическом сжатии
реального газа фактор сжимаемости сначала падает. Выше ее дело
обстоит наоборот с начала и до конца.
52
Рассматривая рис. 18 и 19, нетрудно заметить, что ниже
температуры Бойля фактор сжимаемости на любой изотерме
равняется единице в двух точках. Одна из них — общая для
всех изотерм — отвечает истинному идеальному состоянию
Т>гр
газа, в котором р = ——>-0и обе поправки Ван-дер-Вааль-
са равны нулю. Вторая точка отвечает «псевдоидеальному»
состоянию, в котором обе поправки значительны по
величине, но в точности компенсируют друг друга, благодаря чему
снова pV — RT. Псевдоидеальные состояния лежат на
пересечении изотерм с прямой F = 1, и их положение различно
при разных температурах как в шкале давлений, так и
плотностей. Геометрическое место точек, в которых газ
становится псевдоидеальным (в смысле уравнения состояния),
называется кривой идеального газа, или ортометрической
кривой. Это понятие было введено в свое время Бачинским.
Уравнение для ортометрической кривой легко получить
из (9.16), полагая F = 1 и принимая во внимание
определение температуры Бойля, данное в (9.20):
v тв*
Отсюда видно, что плотность на ортометрической кр!±±юй
линейно падает с ростом температуры:
а давление изменяется параболически:
р - „М--4£ (!-£} (9-22)
Видно, что ортометрическая кривая р(Т) представляет собой
равнобедренную параболу с вершиной в точке Гб/2 и
максимумом давления:
A-T-J^ <9'23>
Эти выводы теории Ван-дер-Ваальса как ^нельзя лучше
согласуются с экспериментальными исследованиями орто-
метрических кривых благородных и молекулярных газов,}
которые конденсируются в так называемые простые жидкости
(см. гл. 4). На рис. 20 изображена ортометрическая кривая
азота, построенная по наиболее достоверным
экспериментальным данным разных авторов. Эта кривая действительно
является параболой на всем своем протяжении: от темпера-
53
200-
Рис. 20. Ортометрическая
кривая азота и кривая
сосуществования (внизу), с —
критическая точка.
100-
туры Бойля до точки
кристаллизации,
ограничивающей снизу область
ее определения в
температурной шкале. Всюду под
этой кривой силы
притяжения доминируют над
отталкиванием, а снаружи—
наоборот. Кривая
сосуществования жидкости и пара, заканчивающаяся
критической точкой, лежит глубоко внутри области, где
притяжение играет главную роль.
То, что давление, при котором наступает вторичная
«идеализация» газа, сначала растет с температурой, а затем падает,
видно уже при внимательном рассмотрении рис. 19. Если же
учесть, что вблизи максимума ортометрической кривой
давление изменяется с температурой незначительно, то следует
ожидать, что сноп изотерм, близких по температуре к Гб/2„
должен проходить через псевдоидеальные состояния при
почти одинаковых давлениях. На диаграмме Хоугена и Ватсона
(см. рис. 18) благодаря отбору именно таких изотерм дело
выглядит так* как если бы они пересекались в общей
узловой точке. Абсцисса этой точки есть, очевидно, не что иное,
как pQ — вершина ортометрической кривой.
Приняв во внимание соотношения (9.13), можно
получить следующие оценки характерных ортоме'грическдх
параметров:
Ро = —
(9.24)
Однакэ фактическое отношение Тв/ТС1 согласно
эмпирическому правилу, близко к 2,64, а не к 3,37, как следует из^
(9.24). Именно поэтому температура ортометрического
максимума, к которой примыкают изотермы, стягивающиеся
♦в узловую точку, весьма близка к критической: Тв/2 =
= 1,3 Гс. Точно так же и максимальное давление, которое,
согласно диаграмме Хоугена и Ватсона, равно 8рс, заметно
больше значения, получающегося из (9.24): р0 = 6,8/?с. Но
лучшего и нельзя было ожидать от феноменологического
54
уравнения, оперирующего всего двумя параметрами и
количественно справедливого только при небольших давлениях
и малом отклонении F от^единицы.
§ 10. ОСНОВНЫЕ ИДЕИ
СТАТИСТИЧЕСКОЙ ТЕРМОДИНАМИКИ
Приведенный выше вывод уравнения Ван-дер-Ваальса
оказался возможен благодаря решительному упрощению
(и огрублению!) межмолекулярного взаимодействия. При
всякой попытке сделать то же самое строже и точнее
приходится снитаться с реальным взаимодействием частиц, которое
не всегда легко разделить на притяжение и отталкивание.
Поэтому теория Ван-дер-Ваальса фактически не поддается
усовершенствованию, оставаясь феноменологической
концепцией, полуколичественно описывающей реальные газы.
К счастью, существует метод, указывающий стандартный
рецепт расчета термодинамических свойств систем многих
частиц, связанных произвольным взаимодействием. Этот метод
был предложен Гиббсом.
Ансамбль Гиббса. Основная идея Гиббса состояла в ^том,
чтобы N связанных взаимодействием^ частиц рассматривать
как единое целое, а не по отдельности. Это значит, что,
задавая состояние газа, надо указать, где находятся и как
движутся все N молекул. Если раньше для определения
состояния нам вполне хватало шести координат: х, г/, z, px, py, pzf
то теперь потребуется 6N соответственно числу молекул в
образце. Задать эти 6N чисел значит указать точку в d/V-мер-
ном «Г-пространстве» координат-импульсов, которая задает
состояние всего газа, тогда как точка в 6-мерном «|х-прост-
ранстве» — только состояние одной частицы.
Переход к Г-пространству означает фактически смену
лексики: что задано одной точкой в Г-пространстве,
оборачивается распределением N точек в ^-пространстве.
Последнее, конечно, отнюдь не то распределение частиц,
которое является средневероятным, максвелл-больцмановским.
Еслп точка в Г-пространстве выбрайа произвольно, то
эквивалентное ей распределение частиц соответствует мгновенно
увиденному, молниеносно сфотографированному состоянию
газа. Спустя некоторое время его состояние станет иным и
будет представлено другой точкой в Г-пространстве или другим
распределением частиц в ^-пространстве. Механическая
система эволюционирует во времени: частицы движутся,
изменяя свое положение, а при столкновениях и скорость. Состоя-
55
Рис, 21. Изменение во времени положения точки на фазовой
траектории в Г-пространстве (а), мгновенного распределения молекул
по скоростям (б), силы, действующей нэ стенку сосуда (в).
ния, через которые последовательно проходит система,
представляют собой точки в Г-пространстве, лежащие на одной
траектории (рис. 21), или распределения в |л-пространстве„
непрерывно сменяющие одно другое во времени. Чтобы
яснее стало взаимное соответствие этих двух способов
описания газа, достаточно взять для сравнения распределение
даже не в [х-пространстве, а, скажем, по энергии (рис. 21, б)ш
Данной точке Г-пространства соответствует одно
распределение, другой — другое, и, лишь перебрав все точки
траектории, т. е. усреднив по всем возможным распределениям,,
можно рассчитывать найти максвелловское /. Легко
усмотреть в этой процедуре соответствие с определением
среднего давления, о котором шла речь в § 1. Каждому состоянию
системы соответствует какое-то давление F(t)/Sy которое
случайно осциллирует во времени около своего среднего
(рис. 21, в). Точно так же и мгновенное распределение молекул
в газе отличается, вообще говоря, от средневероятного,
которое одно только и нужно для описания равновесных
свойств системы.
Но что означает найти средневероятное? Прежде чем
усреднять распределения, надо знать, сколь часто
реализуется каждое из них, т. е. какова вероятность пребывания
системы в различных точках Г-пространства. Такова
постановка основного вопроса статистической механики. Чтобы
уяснить его, следует представить себе, как это рекомендовано
Гиббсом, совокупность совершенно одинаковых систем —
«ансамбль» одинаковых ящиков, содержащих одинаковое
56
число идентичных частиц. Нет сомнения, что
макроскопическое состояние газа в любом из них одинаково, тогда как
микроскопические состояния систем ансамбля не
обязательно совпадают: каждое из них представлено своей точкой
в Г-пространстве. Нам необходимо знать равновесное
распределение этих точек в Г-пространстве. При достаточно
большом их количестве, в выборе которого мы не стеснены,
это равнозначно установлению вероятности реализации того
или„ иного микросостояния газа.
Микрокапоническое распределение. Некоторую
информацию о виде этого распределения можно извлечь иЗ того
факта, что все точки, представляющие эти системы в
Г-пространстве, движутся по соответствующим фазовым
траекториям. Если мы хотим, чтобы результат любого усреднения
по ансамблю не зависел от времени, а именно так должно
обстоять дело в условиях равновесия, следует потребовать,
чтобы плотность точек в любом элементе Г-пространства
оставалась постоянной, несмотря на движение. Иными слова-
миг вероятность реализации любого микросостояния
должна сохраняться во времени. Если все системы ансамбля
изолированы от обмена теплом и материей с окружающей
средой, то движение их происходит с сохранением энергии
и описывается обычными законами механики. Согласно
этим законам, точки в Г-пространстве канонических
переменных (координат и импульсов) ведут себя в процессе
движения, как в потоке несжимаемой жидкости: не
уплотняются и не рассредоточиваются («теорема Лиувилля»). Чтобы
ничто не менялось во времени, достаточно распределить их
вдоль траектории равномерно. Тогда в любой элемент
объема Г-пространства будет входить столько же точек,
сколько и выходить из него за то же время. Таким образом
именно теоремой Лиувилля канонические переменные
выделяются как особые, в которых распределение по равновеликим
объемам равновероятно (см. § 7). Однако распределение
точек в Г-пространстве не задается теоремой Лиувилля
однозначно. Чтобы не погрешить против условий равновесия,
необходимо лишь равномерно распределить точки вдоль
каждой траектории. Но таких траекторий множество, и
неизвестно, как должна меняться плотность точек при
переходе от одной из них к другой.
На помощь приходит принцип неразличимости. Если
система изолирована, то в любой доступной ей точке
Г-пространства она обладает одной и той же энергией. Но если все
точки Г-пространства принадлежат гиперповерхности
одинаковой энергии, то исчезает единственный признак, по ко-
57
торому их можно было бы дискриминировать. В этих
условиях единственно разумный выход — предположить, что
все они равноправны, а следовательно, равновероятны^ т.-е„
что распределение систем в Г-пространстве совершенно
однородно. Такое усиление теоремы Лиувилля является^ конечно,,
шагом в неизвестность и должно поэтому рассматриваться
как принцип. Его окончательная формулировка известна под
названием микроканонического распределения Гиббса:
изолированная система может быть с равной вероятностью лай-
дена в любом доступном ей состоянии заданной энергии &
(от Е до Е + dE) и с нулевой вероятностью во всех
остальных. При этом вероятность, как всегда, пропорциональна
элементу объема йГ, в котором ищется система:
при £<<g><£ + dE,
АГ ^©— A01)
0 при &<Е & >Е + dEs
где АГ — полный объем фазового пространства, доступного
системе при данной энергии.
Каноническое распределение Гиббса.
Микроканоническое распределение отличается от канонического отсутствием
экспоненциального множителя. И дело не в том, что система
велика. Каноническое распределение
dJF = -£-exp — -^r \dT = <&(g)dT, 0<#<оо A0.2)
применимо не только к отдельной молекуле, но и ко всему
газу в целом. Предполагается, однако, что любые энергии
доступны системе, и устанавливается, какие из них более
вероятны, а какие менее. Энергетические флуктуации
возможны потому, что каноническое распределение Гиббса
описывает ансамбль систем, имеющих контакт с тепловым
резервуаром. В каждой из них сохраняется не энергия, а
температура — температура резервуара, в который погружены
«ящики Гиббса». Именно благодаря обмену энергией с
резервуаром, система оказывается способной то терять часть своей
энергии, то приобретать ее, соскальзывая с одной изоэнерге-
тической поверхности на другую. Изолированная же система
всегда остается на одной и той же раз и навсегда заданной
поверхности (в пределах слоя толщины dE).
То, что плотность вероятности Ф(<?Г)в A0.2) должна быть
экспоненциально убывающей функцией энергии^ вытекает
из очевидных соображений. Даже считая ее неизвестной, мы
все же должны были бы записать
dW = Ф(аГ)еЯ\
Но, если бы система состояла из двух слабо
взаимодействующих частей, так что*? = $*i + <*?2 + <^вз> N = N± + -Wa» те*
очевидно, для каждой из них имело бы место то же
соотношение: dWi&J = Ф(&г)(П\, dW(g2) = Ф(#2)<Яу. Считая их,
ввиду слабости взаимодействия, независимыми: <§ГВз < <^i> ^2»
можно определить вероятность найти совокупную систему в
некотором состоянии по теореме умножения: dW(<£) = dW(<%^) x
XdW(&2). Оба определения этой вероятности должны быть
тождественны:
а так как dT = йГ^^, то (! я) ^^) (
пренебрегается). Из этого уравнения точно так же, как из
B.6), немедленно вытекает
причем
jV^r, A0.2a)
где йГ = dq1dp1dq2dp2 . . .dq^dpn. Такое же распределение,
относящееся к отдельной молекуле, может быть получено
N
только для идеального классического газа, когда <§Г = 2 <?ч-
г=1
Действительно, только в этом случае dW = JJ dW^ и прос-
г
тым сложением вероятностей можно получить из A0.2)
)- J
N
т. е. обычное максвелл-больцмановское распределение. Этот
результат можно было предвидеть, так как каждая
классическая молекула является подсистемой, взаимодействующей
с остальным газом как с термостатом, и к ней самой
непосредственно применимо распределение Гиббса.
В случае идеального (но не классического!) газа
редукция от Г-пространства к ^-пространству достигается ценой
более значительных усилий и приводит к распределениям,
которые отнюдь не совпадают с максвелл-больцмановским.
59
Это связано с тем, что даже невзаимодействующие
квантовые частицы нельзя рассматривать как независимые нод-
N
системы dt Ф JJ dqidpi. Для классического, но реального газа
г
редукция типа A0.3) невозможна по другой причине. Если
в его полной энергии
# = 2е« +17(ft,?., ...,?*) (Ю.4)
не пренебрегать U(q^ q2, . . ., &v), то й!У =^=IJdW^ и разде-
i
лить переменные при интегрировании не удается. Стало быть,,
описать реальный газ каким-либо распределением в [х-про-
странстве не представляется возможным.
Энтропия. Это соображение возвращает нас к задаче,
поставленной в самом начале. Мы уже знаем распределения
в Г-пространстве, но еще не умеем ими пользоваться.
И раньше, при выводе уравнения состояния идеального газа,,
задача распадалась на две части: отыскание распределения
dW(\) и установление его связи с наблюдаемой величиной —
давлением: р = пт\ vtdW{\). Теперь, при новой постановке
задачи, эта вторая часть остается еще совершенно не
определенной. Если мы имеем дело с изолированной системой,,
то нам кроме A0.1) заданы объем и внутренняя энергия газа:
V ж&. Если система не замкнута, то кроме A0.2) мы знаем,
каковы ее объем и температура: У и Г. К любой из этих двух
характеристик необходимо добавить третью, чтобы состояние
газа стало полностью определенным. Совсем не обязательно,
чтобы этой характеристикой было давление, которое мы
рассчитали ранее, зная Г и У. Но, каков бы ни был этот третий
параметр, он должен рассчитываться из распределений,
относящихся ко всему газу в целом: A0.1) или A0.2) в
зависимости от ситуации.
Попробуем изменять объем газа У, сохраняя & = const,
если система изолирована, или поддерживая температуру
постоянной, если она не замкнута. Это вызовет изменение
давления газа и ряда других его характеристик. В то же
время в распределениях AЙ.1) и A0.2) ничто не изменится,
кроме нормировочных постоянных ДГ и Z, и это подсказывает,;
что именно в них заключена искомая информация.
Для идеального газа, например, АГ = j dT ~ VN.
Следовательно, увеличение вдвое объема сосуда приводит к
возрастанию доступного фазового объема АГ в 2^ раз и
соответственно уменьшает плотность вероятности Ф в 2N раз»
60
Чем больше различных состояний доступно системе, тем
меньше, естественно, вероятность каждого из них. Для
изолированной системы величина
АГ = J dT =( [_ j j^J dq
является мерой вырожденности макроскопического
состояния, числа различных способов, которыми можно разместить
молекулы в пределах сосуда, задавая им любые скорости
(энергии), не выводящие, однако, полную энергию системы
за пределы заданного интервала dE.
Если газ состоит из молекул двух сортов, то оба сорта
можно рассматривать как подсистемы с числом частиц Nt
и N2(N = iVj + iV2), каждая из которых может находиться
в одном из состояний своего фазового объема АГХ или ДГ^
соответственно. Общее число возможных состояний всей
системы мультипликативно выражается через эти объемы АГ =
= j dT± j dT2 = ДГ1АГ2, и, следовательно, взаимное
соответствие АГ с некоторой аддитивной макроскопической
характеристикой системы, например энтропией,— если оно
существует, — может быть только следующим:
S = к In АГ. A0.5)
Действительно, только логарифмическая свяэь гарантируем
аддитивность S = к In АГХ + к In АГ2 = Бг + S2 при
мультипликативности АГ = ArxAr2. Но то, что именно
энтропия связана с АГ подобным образом, было установлена
исследованиями Больцмана, которому по праву
принадлежит заслуга статистического истолкования энтропии1.
Мера хаоса, мера неупорядоченности системы — вот что
такое энтропия в свете соотношения A0.5). Чем больше
различимых микросостояний совместимо с заданными F и <g%
тем больше энтропия.
Флуктуации. Надо, однако, отметить, что не все
состояния изолированной системы можно отождествить с
макроскопическим равновесием. Если, например, не меняя
равновесного распределения скоростей, сосредоточить все
молекулы идеального газа в небольшой части сосуда, то такоа
состояние, хотя и будет относиться к числу доступных
(принадлежать АГ), должно рассматриваться как флуктуация*
Флуктуацией является и такое состояние, когда все
молекулы, равномерно распределенные по сосуду, обладают
одинаковой скоростью v = у т?-.
61
Однако можно убедиться, что эти и другие подобные
состояния, резко отличающиеся от равновесного, составляют
ничтожное меньшинство. Подавляющее же большинство
состояний таково, что соответствующее им распределение
молекул в пространстве координат и скоростей несущественно
отличается от равновесного, средневероятного. Это и
естественно: беспорядок в системе может быть осуществлен
множеством различных способов, тогда как при организации
упорядоченного состояния допустим значительно меньший
произвол. Огромное число частиц в системе настолько
усиливает это утверждение, что, как показывают конкретные
расчеты, число состояний изолированной системы,
фактически отличимых от равновесного, составляет ничтожную
долю общего числа состояний, содержащихся в ДГ. Поэтому
безразлично, определять ли энтропию изолированной
системы как логарифм числа действительно равновесных
состояний или всех вообще состояний, совместных с заданными V
ш &, как это сделано в A0.5).
Свободная энергия. Иначе обстоит дело в случае
открытой системы (канонического ансамбля). Ведь такой системе
доступны состояния с любой энергией,, т. е. фактически
неограниченный объей фазового пространства. Естественно
поэтому, что энтропия не может быть определена через
полное число состояний — оно бесконечно, а только через тот
объем, который действительно соответствует равновесию:
АГР. Несмотря на возможность обмена энергией со средой*
незамкнутая система с подавляющей вероятностью
пребывает именно в этих, квазиравновесных состояниях и крайне
редко в других.
Это связано с тем, что статистический вес р (<£) резко
возрастает с энергией. Если в случае одной частицы он растет
как <?Г1/8, то в системе N невзаимодействующих частиц
вырождение состояний с одинаковой полной энергией растет как
<gfN/2. Столь резкий рост р(<2?) оказывается способным
конкурировать с не менее резким падением вероятности
( &\ - ~
~ ехр —-г= , так что в итоге получается острейший макси-
мум вблизи & = &, и сколько-нибудь существенные
отклонения энергии от & чрезвычайно маловероятны (рис. 22)г
Поэтому по порядку величины
dW = |ф(ЙГ)йГ^ ф(#) АГР =
где ДГр = р (W)kE = ф/^ч —объем лишь той части фазового
62j
Рис. 22. Каноническое рас- Ф*1
пределение по полной энергии &
системы.
пространства, в которой
^==Ф(<Г)р(<Г)
существенно отлична от нуля.
Это вполне объясняет
необходимое здесь
усовершенствование формулы
A0.5)
АЕ
s = кы агр = -й1пФ(аг),
A0.5а>
согласно которому энтропия измеряется числом способов„
которым может быть реализовано состояние,
макроскопически не отличаемое от равновесного. Обобщенное таким
образом определение энтропии в случае изолированных
систем тождественно предыдущему, ибо Ф (Ж) = Ф (&) =-£f-
Что же касается канонического ансамбля
(термостатированных систем^ то прямая подстановка Ф(^)из A0.2) в A0.5а)
дает
gr = g _ TS:= -kT In Z. A0.6>
Здесь fF — свободная энергия (Гельмгольца), а средняя
энергия (черта над которой здесь и в дальнейшем опущена) есть
не что иное, как внутренняя энергия системы <g.
Расчетная схема. В A0.5) и A0.6) сформулированы
рецепты усреднения, которые Позволяют сразу же рассчитать
энтропию или свободную энергию системы, если известны
нормировочные постоянные соответствующих распределений
в Г-пространстве: ДГ или Z. Эти рецепты позволяют
вычислять макроскопические характеристики вещества, мину>г
распределения в [х-пространстве, которые ранее
использовались на промежуточных стадиях расчета. Благодаря этому
такая процедура применима не только к идеальным, но и к
реальным газам, а также к конденсированным средам, и в
общих чертах выглядит следующим образом.
В случае ансамбля изолированных систем, описываемого
микроканоническим распределением, основная расчетная
трудность состоит в вычислении доступного фазового объема
АГ(У, <§Г)по заданным механическим свойствам системы:
числу и массе молекул, их полной энергии <§ и размерам сосуда V9
63
Если эта задача решена, то из формулы A0.5) сразу
находится энтропия как функция заданных величин: S(V,<%).
Из этого соотношения, эквивалентного по содержащейся
информации уравнению состояния, можно теперь определить
любые термодинамические параметры, используя законы
равновесной термодинамики. В частности, из второго
начала:
TdS = dS + pdV A0.7)
следует, что
{)[)r <10-7а>
т. е. и давление, и температура определяются
дифференцированием найденной зависимости между энергией, объемом
и энтропией. Как это принято в термодинамике, параметры
состояния, которые должны считаться постоянными в
процессе дифференцирования, указаны индексами,
вынесенными за скобки.
В случае, если ансамбль описывается каноническим
распределением, расчетные трудности сосредоточиваются в
вычислении статистической суммы Z как функции объема V и
температуры Т. Эта задача немногим проще, чем
предыдущая, но если уж она решена, то с помощью A0.6) немедленно
находится свободная энергия ЗГ, являющаяся функцией тех
же переменных и удовлетворяющая уравнению
dST = —pdV — SdT, A0.8)
которое эквивалентно второму началу термодинамики. Из
него вытекает, что
Само-собой разумеется, что результаты, получаемые как
первым, так и вторым способом, совершенно идентичны, ибо
свойства равновесного состояния не зависят от того,
имеется ли у системы тепловой контакт с окружающей средой или
же она полностью изолирована. Однако с точки зрения
преодоления математических трудностей использование
канонического распределения (статистической суммы Z)
оказывается зачастую удобнее.
Идеальный газ. Простейшим критерием истинности этих
общих расчетных схем является их* непосредственная
проверка на модели идеального газа, свойства которого уже
известны. Воспользуемся, например, каноническим распре-
64
N 2
делением. Поскольку^ = ^ •=-*■, в A0,2 а) все переменные
г=1
разделяются и в результате интегрирования имеем
Z = VNBnmkTfm.
Отсюда, согласно A0.6), находим
gr = -NkT In lBnmkTL*V\t A0.9)
а из A0.8а) получается
S = kNln [V BnmkTf2] + ^kN,-
Р = ПГ. A0-10)
Если рассматривать всю проблему лишь с точки зрения
вывода уравнения состояния, то мы можем считать себя
вполне удовлетворенными; общий метод действительно приводит
к нужному результату: р = RT/V. Однако нельзя не
заметить, что ни свободная энергия, ни энтропия, которые
являются аддитивными величинами, не возрастают
пропорционально N, как это должно быть, когда объем системы
увеличивается при постоянной плотности. Это совершенно
неожиданно. В теории могут встретиться разные трудности,
но когда они обнаруживаются в конце пути, и притом весьма
успешного, возникает естественное желание избавиться от
них ценой минимальных усовершенствований.
Тождественность микрочастиц. Какими они должны быть^
позволяет осознать сравнение полученной формулы Сакку-
ро A0.10) со свободной от указанных недостатков формулой
Саккуро — Тетроде:
S = кЫ\п[^BпткТ)т] + |-ЛЛГ. A0.11)
Последняя отличается от A0.10) лишь слагаемым — kNln—.
в
Это подсказывает мысль переопределить величину Z,
разделив ее на N1:
Z = ± BnmkTKN/2VN« A0.11a)
Та же самая расчетная процедура с учетом известной форму-
TV
лы Стирлинга: lniVl^iVln— приведет в таком случае
в
3 А. И. Бурштейн 65
к аддитивной величине
gr = _ NUT In \BnmkTf2 ^], A0.12)
откуда немедленно получается правильный результат A0.11).
Последний, как и &~, зависит от удельного объема, а не
от полного, что благополучно разрешает парадокс. Но
множитель N1 мог появиться в Z только из распределения,
которое, следовательно, тоже должно иметь иной вид, чем
в A0.2), а именно:
± (§)£:. A0.13)
В равной мере относится это и д микроканоническому
распределению, которое должно быть уточнено аналогичным
образом:
Ш = ШЫГ Е^&^Е+АЕ. A0.14)
Это новшество не вызывает чувства протеста: ведь сами
распределения не претерпевают существенных изменений,
уточняется лишь абсолютный вес каждого состояния. Если
такой ценой устранимы все трудности, то ее нельзя считать
чрезмерной. Напротив, полезные нововведения, как
правило, оказываются необходимыми. И действительно,
множитель 7V!, введенный в свое время без претензии на понимание,
появляется, как потом выяснилось, из-за принципиально
важного свойства микрочастиц — их неразличимости или
«тождественности». Из-за этого свойства не имеет смысла
различать состояния системы, отличающиеся лишь
перестановкой частиц. Это отнюдь не разные, а одно и то же
состояние, ибо частицы невозможно перенумеровать: они не
поддаются маркировке и абсолютно ничем не отличаются друг
от друга.
Эта особенность обнаруживается уже в системе двух
частиц: если бы они были различимы (как биллиардные шары),
то любое состояние повторялось бы дважды — за счет
возможной перестановки, если неразличимы — только раз
(рис. 23). И действительно, всякого, переставившего
биллиардные шары, даже ненумерованные, можно уличить
в этом посредством соответствующей экспертизы. И после
обмена квартир жильцов всегда можно различить, если не
по яркой индивидуальности, то по дактилоскопическим
отпечаткам. Но электроны, протоны, одинаковые атомы
отличить нельзя. Нельзя сказать: первый атом находится здесь,
66
Рис. 23. Различные состояния
различимых A, 2) частиц (а) и
единственно возможное
состояние неразличимых (б).
О
о
другой — там, следует говорить: есть два атома,
расположенных в таких-то местах. Это особое свойство микрочастиц
игнорировалось при подсчете чиела состояний в Г-прост-
ранстве: все состояния, отличающиеся перестановкой N
частиц (всего АЛ), учитывались нами в dT как разные.
Чтобы устранить теперь эту ошибку, следует уменьшить
результат в 7V! раз. Это и сделано в распределениях A0.13)
и A0.14).
Реальный газ. Хотя принципиальная схема
сформулирована, конкретное вычисление статистических сумм
наталкивается на значительные трудности, как только
принимается во внимание неидеальность газа. Энергия
всякой реальной системы содержит помимо кинетической еще
и потенциальную часть, которая в простейшем случае адди-
*тивна по парному межмолекулярному взаимодействию
u>ik = u(qt —qk):
Статистическая сумма распределения A0.13) равна
N
2
z = 4r.
~2mkT
U
kT
A0.16)
Она отличается от своего идеального аналога £ид,
определенного в A0.11а), трудно вычисляемым множителем — обез-
размеренным конфигурационным интегралом
^.^...^. A0.17)
N
Последний можно рассматривать как результат усреднения
подынтегрального выражения по равномерному
распределению N частиц в объеме V.
Обозначая это усреднение чертой, представим
конфигурационный интеграл с учетом A0.15) в следующем виде:
67
— 2i и (qk — ^\{IкТ учитывает толькоТвза-
ft=i+i J
N
+ J
имодействие i-ц. частицы с N — i другими частицами,
имеющими более высокий порядковый номер. Все в^ —величины
одинаковой природы: они учитывают воздействие на г-ю
частицу ее более или менее многочисленного окружения.
При различных размещениях частиц в пространстве все &t
флуктуируют, пробегая доступный им ряд значений. При
небольших плотностях газа естественно предположить, что
воздействие окружения на любую из частиц независимо, т. е*
среднее от произведения равно произведению средних:
e* = II @i=lfe A0.19)
i=i i=i
Такое предположение сильно упрощает дальнейшее
вычисление статистической суммы, но ограничивает область
применимости результата сравнительно разреженными, хотя
и реальными газами.
Приняв во внимание, что
5 "(ЧЬ-Чг)
— ^ Т^г
N
b:-J...J.«
i N
N u(Tk)
= P ^ P1t^+iT^f[i+i#e#^y A0.20)
i+l JV
где rK = qK — qf, можно заметить, что это выражение
разбивается на произведение одинаковых сомножителей:
u(rh)
Для скалярных взаимодействий, зависящих только от
расстояний между частицами, возможны дальнейшие
упрощения:
A0.21)
Здесь R — радиус объема, заполненного газом, который
для простоты считается сферическим. Последнее выражение
приведено к форме, удобной для совершения предельного
перехода V -> оо (Д->оо) при неизменной плотности газа.
Такой переход оправдан тем, что число частиц в системе
макроскопически велико. Окончательный результат должен
зависеть только от плотности как от универсального
параметра, что и получается в результате перехода:
. (Ю.22)
Используя этот результат в A0.19), находим Q* =
exp to^zJ) J °r 4яЛ*г
L 2 J» |li = f(r)—уг- и, поскольку N велико^
имеем окончательно
L 0 J
(^) ^J A0.23)
где
(^) A0.24)
При удалении молекул друг от друга функция f(r) быстро
стремится к нулю, как это видно из рис. 24, чем
обеспечивается сходимость интеграла в A0.23).
Используя A0.23) в A0.16) и вычисляя свободную
энергию через статистическую сумму по формуле A0.6),
находим
оо
N кТ С
ST = ЗГЛЛ - -±- J 4яг*/ (г) dra A0.25)
о
где #"ид — свободная энергия идеального газа A0.12).
Отсюда и давление
оо
N кТ С
Ь]4«/(г) dr (Ю.26)
Рис. 24. Качественный
вид функции /(г).
Рис *25. Температурная зависимость второго вириального
коэффициента при аппроксимации межмолскулярного
взаимодействия по Ван-дер-Ваальсу (а) и Леннарду — Джон-
су {б).
оказывается отличным отрид = —т?. Приведенное к вириаль-
ной форме это уравнение состояния имеет вид
j 4яг2/ (г)
dr
A0.27)
в котором нетрудно узнать усеченное уравнение (9.19) со
вторым вириальным коэффициентом
N Г\
Бо = -£ J [e
^ 1
hT - 1J
A0.28)
выраженным в квадратурах через потенциал
межмолекулярного взаимодействия.
В использованной Ван-дер-Ваальсом модели
«притягивающихся жестких сфер» отталкивательная ветвь
взаимодействия заменена потенциальной стенкой, воздвигнутой
на расстоянии молекулярного диаметра: u(d — 0) = оо
(пунктирная кривая на рлс. 24). Принимая эту модель и
считая, что средняя кинетическая энергия частиц превышает
глубину потенциальной ямы, получаем в первом порядке
по щ1кТ из A0.28):
70
Этот результат формально совпадает с выражением (9.18),
подучившимся в теории Ван-дер-Ваальса, причем параметр
ANovd = В определен здесь идентично, а А получает более
конкретную, лишенную всякой неопределенности
расшифровку через потенциал межмолекулярного взаимодействия:
оо
А = 2nN20 j и (г) гЧг. A0.29)
о
Соответствие с теорией Ван-дер-Ваальса достигнуто здесь
ценой адекватного огрубления потенциала взаимодействия.
Это заведомо вносит ошибку в теоретическую оценку второго
вириального коэффициента. Ее вполне можно избежать,;
располагая достаточно строгой и общей формулой A0.28)%
если использовать-в ней настоящий потенциал
взаимодействия. Для благородных и простых молекулярных газов в
качестве такового наиболее часто используется так называемый
потенциал «6—12 Леннарда—Джонса»:
в котором сг и е —молекулярные константы (а ^= (З-^-б)-
• КГ8 см, е = (l-f-30)-10~15 эрг). Первое слагаемое в нем
соответствует отталкиванию, а второе — притяжению двух
частиц, находящихся на расстоянии г друг от друга.
Температурная зависимость второго вириального коэффициента,
вычисленного из A0.28) с этим потенциалом, имеет вид,
изображенный на рис. 25. Видно, что она заметно отклоняется
от линейной, ван-дер-ваальсовской, в области высоких
температур. Это объясняется тем, что при большой
кинетической энергии частиц заметно отличие от вертикальной
стенки даже столь круто возрастающего потенциала
отталкивания, как г2.
С другой стороны, как бы строго ни был определен второй
вириальный коэффициент, уравнение A0.27), как и (9.19),
все же значительно хуже описывает состояние
конденсированных сред, нежели оригинальное уравнение Ван-дер-
Ваальса (9.16). В рамках грубой модели потенциала оно
учитывает все порядки вириального разложения, тогда как
настоящий вывод позволил корректно определить только
первое, линейное по плотности, слагаемое. Впрочем,
статистическая механика позволяет однозначно выразить через и(г)
все коэффициенты вириального ряда. Однако даже это не
сильно улучшает ситуацию, так как просуммировать ряд
в общем виде, свернув его в простое выражение, подобное
71
Рис. 26. Схема зависимости фактора сжимаемости от
плотности с экстраполяцией изотерм в область между
паром и жидкостью и жидкостью и кристаллической
фй
р
фазой;
п0— плотности пара,
дого тела.
жидкости и
тверван-дер-ваальсовскому, не представляется возможным.
Когда же с ростом плотности для описания состояния
вещества приходится учитывать, наряду с линейной, также и
квадратичную, и кубическую поправки, то очень скоро для этой
цели требуется весь ряд целиком. Более того, оказывается,
что вириальное разложение вообще расходится при
приближении к критической области и для описания более
плотных сред в принципе неприменимо. Это важное
обстоятельство проясняется, если принять во внимание характер из-
72
Рис. 27. Плотная упаковка
частиц, исключающая
перестановки (а), и разреженная
среда, допускающая
многократное заполнение ячеек (б).
О
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
&=7
<о =
менения фактора сжимаемости с плотностью, схематически
иллюстрируемый рис. 26. Вириальное уравнение состояния
фактически эквивалентно разложению в ряд Тейлора в
окрестности точки с нулевой плотностью. Его линейный
вариант A0.27) заведомо непригоден даже для описания
газовых изотерм в области Тс < Т < ГБ, правее обозначенного
на них минимума. Что же касается жидкости, то
недостаточно и всего ряда, поскольку имеют место разрывы,
связанные с конденсацией, где о поведении F(n) можно судить
только предположительно (пунктир на рис. 26). В еще
большей мере все сказанное относится к твердой фазе. По этой
причине, наряду с приближением, пригодным для расчета
разреженных сред, полезно иметь и альтернативное,
специально предназначенное для высококонденсированных.
Такова, в частности, свободнообъемная теория Леннарда —
Джонса и Девоншайра, к изложению которой мы и
переходим.
Конденсат. Отправной точкой при вычислении
конфигурационного интеграла конденсированной системы является
модель плотной упаковки частиц (рис. 27, а), заполняющих
собой практически все пространство. Окруженные со всех
сторон соседями, такие частицы движутся в созданной ими
потенциальной яме с эффективным потенциалом O(qj). Они
движутся, практически не покидая ее, и центр тяжести
каждой все время остается в пределах ограниченного
«свободного объема». Это позволяет рассматривать молекулы
независимо друг от друга, ограничивая интегрирование по
пространственным координатам небольшой ячейкой —
областью порядка Д вблизи среднего положения каждой из
них. Если при этом дно ямы расположить в начале
координат, то ее глубина будет Ф@) и, следовательно,
N
A0.31)
г=1
где АФ(я) =
циал стенок,
— Ф@) есть ограждающий яму
потенпервое слагаемое — полная потенциаль-
73
ная энергия вещества в случае, когда все частицы
расположены в центре своих ячеек. Она вдвое меньше 7V<D(O), так
как энергия каждой частицы создана взаимодействием с
партнером и в равной мере принадлежит им обоим, что
необходимо учесть post factum при суммировании энергии ям»
Модельная аппроксимация U(qb . . ., q^), принятая в
A0.31), позволяет легко вычислить конфигурационный
интеграл A0.17), который становится произведением
интегралов по отдельным ячейкам, повторенным столько раз,
сколько возможно осуществить перестановок между частицами:
() A0.32)
Здесь
есть свободный объем ячейки, величина которого
складывается из доступных частице элементов пространства,
взвешенных с вероятностью ее появления в них.
Используя A0.16) совместно с A0.32) в A0.6) с учетом
формулы Стирлинга, имеем
&* = ^Ид + NkT - NkT In Ц + N ^3} A0.34)
где v = V/N — удельный объем, а £ГИД определено в A0.12).
Для среды с высокой плотностью вещества, когда миграция
частиц по ячейкам практически исключена, как, напримерs
в кристаллах, этот результат вполне надежен. Однако в
жидкости ближайшее окружение частицы не является полностью
непроницаемым для нее, а при бесконечном разрежении по-*
нятие ячеек становится совершенно условным. Это кладет
предел применимости формулы A0.34). Ее несовершенство
обнаруживается при переходе к низким плотностям. В
самом деле, при и -* оо (рис. 27, б) потенциальные барьеры
устраняются (Ф —* 0) и практически весь объем становится
доступен частице (vf -* и), но ^~оо = ^Ид + NkT все
еще отличается от идеального значения на величину NkT.
Давление идеального газа, вычисленное по этой формуле,
оказывается правильным, но энтропия иной: Soo = £ид —
— Nk. Ясно, что несовершенство формулы A0.34) связано
74
с чрезмерной упорядоченностью ячеечной структуры, т. е«
с недооценкой беспорядка, возникающего в реальной
системе при разрежении. Это несовершенство может быть
устранено введением дополнительного параметра, так
называемой «коллективной энтропии» сг, которая при увеличении
v изменяется от 1 до ей, таким образом, исправляет
асимптотическое поведение A0.34):
о
A0.35)
К сожалению, явный вид зависимости а(и) остается при этом
неизвестным. Это вносит некоторую неопределенность и в
уравнение состояния:
dlnxsvf\ 1 <|ф@) /.порч
^^ (ia36)
в котором
A0.37а)
имеет смысл внутреннего и термического давления
соответственно. Первое из них аналогично ван-дер-ваальсовско-
му члену A/V21 и зависит только от объема. Оно
представляет силы сцепления, удерживающие молекулы вещества в
конденсированном состоянии. Термическое давление,
напротив, создается тепловым движением частиц, и поэтому
зависит и от их плотности, и от температуры среды. Мы видим,;
следовательно, что в феноменологической записи уравнение
р + Pi =-pt распространяется на все фазовые состояния
вещества, но от температуры и плотности зависит
конкретный вид входящих в него слагаемых.
Теория свободного объема была впервые предложена Лен-
нардом— Джонсом и Девоншайром в 1937 г., причем
сразу же выяснилось, что, несмотря на все упрощения,
достигнутые за счет огрубления модели, она все еще слишком
сложна для выполнения конкретных расчетов. Это частично
связано с тем, что потенциал ячейки, определенный с
учетом правильного кристаллографического размещения в ней
соседних молекул, оказывается слишком громоздким для
аналитического вычисления свободного объема. Ввиду это-
75
го авторы теории и все их последователи предпочли
оперировать усредненным потенциалом
ф (q) = £ j j и ( W + g2-2a2cos0) sin ЭсШср, A0.38)
вычисленным в предположении, что равноудаленные (на
расстояние а) от центра ячейки частицы равномерно
распределены по сфере соответствующего радиуса. В A0.38) принят
во внимание вклад лишь с ближайших соседей,
составляющих первую координационную сферу, но аналогичным
образом усредняется и вклад более удаленных частиц. В
наилучшем варианте этой теории учитывался вклад трех
окружающих оболочек, что для короткодействующего
потенциала Леннарда — Джонса оказывается вполне достаточно.
Результаты расчетов представлены диаграммой на рис. 28.
В общих чертах они воспроизводят то поведение изотермы,
которое схематически было изображено на рис. 26, но
отсутствуют разрывы, связанные с кристаллизацией вещества. -
Это обусловлено тем, что коллективная энтропия, для
вычисления которой рецептов не найдено, полагалась равной
единице, что, по существу, ограничивало область
применимости теории кристаллической модификацией вещества.
Действительно, термодинамические свойства твердых тел
теория описывает количественно, а жидких сред — только
качественно. Фактически она применима только в
окрестности узловой точки, которая видна на диаграммах рис. 26
и 28. И. наоборот, вириальное разложение справедливо в
области квазилинейного изменения F(n) вблизи идеально-
газового состояния, которое тоже является узлом изотерм.
Двухфазная система. Если система расслаивается на
жидкость и пар, то возникает вопрос о положении границы
раздела и ее структуры. На первую часть этого вопроса
отвечает обычная термодинамика, на вторую.— так
называемая «квазитермодинамика», утвердившаяся благодаря
достижениям статистической физики. Рассмотрим их
последовательно.
Межфазовая граница разделяет полный объем системы
на две части: Уг и У2, содержащие iVj и 7V2 молекул
соответственно. Вообще говоря, граница может быть расположена
где угодно, и, поскольку она проницаема для молекул, их
распределение между контактирующими фазами тоже
произвольно. Эта неопределенность, однако, устраняется, если
учесть, что система стремится к минимуму свободной
энергии SF (Flf F2; N-i, N2; Г), который находится из условия
= 0. A0.39)
76
1,0
1/v*=c>5/v
1,8
Ро
Рис. 28. Диаграмма Вентора, Бюлера,
Гиршфельдера и Кертиса,
вычисленная по теории свободного объема с
учетом грех координационных сфер.
р
Рис. 29. Изменение свободной
энергии (/0), давления (р0) и химического
потенциала (jw0) при расширении веще- о
ства от жидкости до пара.
При постоянной температуре
варьироваться могут только пере- а
менные Уг и Nx, так как другая °
пара связана условием
постоянства объема системы V = Vx + V2
и числа частиц в ней N = Ni~\-
+ JVj. Поэтому
2 2 J*
г=1
= (Р2 — Pi) dV± + (^ — [х2) dNx.
A0.40)
Подставляя A0.40) в A0.39), на-
77
ходим условия равновесия между фазами:
Pi = P2 = Р A0.41а)
и
|ii = {JLa = [X. A0.416)
Первое из них обеспечивает гидростатическое равновесие
(равенство давлений с обеих сторон на границу раздела),
второе — химическое равновесие (отсутствие потока
частиц через поверхность). Если первоначально жидкость не
была в равновесии со своим паром (например,
ненасыщенным), то она вскипает и объем ее уменьшается до тех пор,
пока не установится равенство химических потенциалов и
давлений, отвечающее состоянию насыщенных паров. В этом
процессе свободная энергия бинарной системы уменьшается
до минимально возможной величины.
Система уравнений A0.41) имеет при температурах
ниже критической единственное решение, однозначно
определяющее р и [х насыщенного пара как функции Т.
В этом убеждает построение Максвелла, показанное на
рис. 29. Рассматривая его, необходимо помнить, что,
согласно A0.8а):
Pa = — т^
где /0 — свободная энергия, приходящаяся, как и у, на
одну молекулу, а
Здесь и далее индексами 0 отмечены равновесные величины,
зависящие только от Г и у, как, например, давление р0 на
изотерме Ван-дер-Ваальса, или соответствующие /0 и \i0.
Условие A0.41а) выполнено, если в точках, отвечающих
жидкости и пару, касательные к кривой fo(v) (рис. 29, а)
имеют одинаковый наклон. Это условие можно
удовлетворить многими способами, так как существует множество пар
точек, в которых касательные параллельны. Но только в
одной из них помимо условия A0.41а) выполнено также
условие A0.416). Оно требует совпадения отрезков,
отсекаемых касательными на оси ординат, которые, согласно A0.43),
равны |i0. Так как параллельные прямые, пересекающиеся
в общей точке (при v = 0), совпадают, фазовый переход
совершается по прямой, касательной сразу к двум точкам
(жидкости и насыщенного^пара). Точки касания имеют те же
аргументы, что и точки, соединенные полочками Максвелла на
петле Ван-дер-Ваальса и на изотерме \lo(v) (рис. 29, б, в).
78
Они устанавливают, каково изменение удельного объема
или плотности вещества при его переходе из жидкого
состояния в газообразное.
Хотя скачок плотности имеет конечную величину,
нельзя считать, что он совершается внезапно, на
геометрической границе жидкости. Даже при очень низких
температурах, когда поверхность мономолекулярна, она не является
геометрической, поскольку и мономолекулярный слой
размыт тепловыми колебаниями. Если же температура близка
к критической, то граница раздела между жидкостью и
паром многослойна, и в каждой ее точке можно ввести понятие
локальной плотности вещества п как функции координаты
z, перпендикулярной поверхности. Если считать, что
поверхность пересекает ось z в 0, то п(—оо) = тгь, а тг(+°°) = nv.
Одновременно с n(z) в переходной области изменяется и
давление, которое вследствие пространственной
неоднородности среды становится тензором р, имеющим две компоненты:
нормальную к поверхности pN и тангенциальную рт.
Последняя параллельна поверхности, но действует на
площадку, перпендикулярную ей. Все остальные (сдвиговые)
компоненты напряжений должны быть равны нулю, так как в
противном случае возникло бы течение жидкости,
несовместимое с понятием равновесия. Что же касается
анизотропии давления, выражающейся в неравенстве pN и рт, то '
она закономерна, и именно благодаря ей существует
поверхностное натяжение у. По определению Лапласа,
У= ){p-PT)dz. A0.44)
Очевидно, что подынтегральное выражение обращается в
нуль в глубине жидкости и газа, но может быть
значительным по величине вблизи z — 0, где тангенциальное
давление меньше внешнего или даже отрицательно.
Чтобы исследовать структуру поверхности и ее
натяжение, необходимо указать рецепт расчета n(z) и ^p(z) в
переходном слое. В первоначальной формулировке
«квазитермодинамики» предполагалось, что и давление, и свободная
энергия (на одну молекулу) / зависят от z только через
локально определенную плотность n(zI а все соотношения
между ними остаются прежними с точностью до замены р на
рт. Таким образом, получалось, как и в A0.43), что
Рт = (ii - f)n. A0.45)
79
Это соотношение и сейчас рассматривается как определение
рт, однако вторая компонента давления, pN, оставалась при
этом неопределенной, что создавало существенные
трудности. Дело в том, что истинное распределение плотности в
переходной области может быть найдено только из условий
равновесия, идентичных A0.41):
Pn(*) = Р. A0.46а)
\i{7) = ц. A0.466)
Чтобы разрешить эту систему уравнений, надо дать
непротиворечивые определения величинам рдг я |х, и в первую
очередь /.
Это было сделано сравнительно недавно Янгом,
Флемингом и Гиббсом. Идея о том, что все локальные
характеристики зависят только от п, была отвергнута. Вместо нее
предложено следующее определение свободной энергии
двухфазной системы с плоской границей раздела единичной
площади:
= J fndz = j Ln + Ъ ±! j dZm A0.47)
Величина /0, которая зависит только от тг, является
локальной термодинамической функцией в прежнем смысле этого
слова. Однако истинная свободная энергия единицы объема
fn не совпадает, с /отг, а отличается слагаемым, которое
выражается через п — dnldz. Этим фактически учитывается
нелокальность межмолекулярного взаимодействия,
связывающего частицы, находящиеся в рааных точках
пространства. Неравномерность распределения вещества между эти-
•
ми точками принимается во внимание посредством п. При
температурах, близких к критическим, к которым
адресуется квазитермодинамика, выражение A0.47) есть, по
существу, разложение ЗГ по градиенту плотности, в котором
оставлено первое неисчезающее слагаемое. Это разложение
было статистически обосновано авторами, и параметру Ъ
дано следующее определение:
—e*rJ«r(r, и)А,
где g(r, n) — так называемая радиальная функция
жидкости. Для дальнейшего существенно лишь то, что величина
Ъ зависит только от лг, а не от z и, в крайнем случае, может
рассматриваться как постоянная теории.
80
Равновесным является такое распределение плотности
72(z), при котором достигается минимум свободной энергии
A0.47). Он по-прежнему находится из уравнения A0.39)
при условии сохранения объема системы и числа частиц в
ней. В действительности надо считаться только с последним
ограничением:
§n(z)dz = N3 A0.48)
так как постоянство объема обеспечивается
фиксированными пределами интегрирования по z. Фактически дело
сводится к отысканию безусловного экстремума величины
pJV - gr = J (ц _ f) ndz = J Рт dz, A0.49)
где \х играет роль множителя Лагранжа, а рт определена
в A0.45). Ввиду A0.47) необходимо оптимизировать
«действие»
- /о (п)] п- b~P njdz, A0.50)
рассматривая его как функцию п и п. Как и в известной
задаче классической механики, это приводит к уравнению
Эйлера — Лагранжа:
Учитывая конкретный вид подынтегрального выражения в
A0.50), его можно переписать следующим образом:
(х0 (п) - Ъ (п) п - \ V (тг) п* = ,1, A0.52>
где [х0 = — [nf0 (n)], как в обычной термодинамике, а У-
= db/dn. Чтобы выяснить, как изменяется плотность
вещества при пересечении переходной области, достаточно
найти n(z), удовлетворяющее уравнению A0.52). Оно не
только конкретизирует условие химического равновесия A0.466)^
но и обеспечивает автоматическое выполнение
гидростатического равновесия — уравнения A0,46а). Действительно„
домножив A0.52) напи проинтегрировав, находим закон
сохранения для величины
Pn = [[х - /о (п)] п + ±Ъ(п)к* = р. A0.53)
81
Рис. 30 Изменение химического
потенциала (б) и компонент тензора давления
при разном его определении (а ж в) в
межфазовой области.
Коль скоро постоянство
нормального давления обеспечено, мы
можем переписать формулу Лапласа
в виде
$ A0.54)
и, подставив в нее A0.53) и A0.50),
найти
= J bn2dz.
A0.55)
Эта формула для расчета
поверхностного натяжения была
предложена еще Ван-дер-Ваальсом. Однако
до того, как был указан
вышеизложенный путь вычисления n(z),
многочисленные попытки
воспользоваться ею приводили к парадоксам:
несохранению \х или pN, или даже к
обращению знака у.
Последовательная формулировка
квазитермодинамики сделала теорию Ван-дер-Вааль-
са замкнутой, а расчет структуры
поверхности реализуемым.
Заметим в заключение, что локальная свободная энергия
ж тангенциальное давление определены в
квазитермодинамике неоднозначно. Их можно, например, ввести,
отождествив подынтегральные выражения в A0.47). В таком случае
2п
а рт, согласно A0.45), есть
A0.56)
A0.57)
В области существенного изменения этих величин (рис. 30)
свойства поверхности заметно отличаются от гомогенной
4>азы. Однако такое определение не единственное. В гл. 4
мы рассмотрим альтернативную возможность и рассчитаем
82
фактическое изменение плотности и тензора давления в
переходной области. Некоторая свобода в выборе / и рт
появляется вследствие перехода к локальному описанию
нелокального взаимодействия. Все физически наблюдаемые
характеристики межфазовой границы, такие как п, pN и у$
не зависят от этого произвола.
§11. ТЕПЛОЕМКОСТЬ ГАЗОВ
Случается иной раз, что наиболее радикальные
нововведения приходят в науку самыми прозаическими путями.
Одной из задач, стоящих перед статистической физикой,
был расчет молекулярной теплоемкости идеальных газов.
Принципиальных затруднений не предвиделось. Однако
именно эта задача оказалась одним из тех крепких орешков%
на которых проверяется на прочность новорожденная
физическая теория.
Согласно формальному определению, молярная
теплоемкость при постоянном объеме
*•& <1U>
Она выражается через полную тепловую энергию Е,
которой располагает молекула идеального газа, участвуя во
всех возможных видах движения. В простейшем случае
идеального одноатомного газа, частицы которого ни на что
иное, кроме как на поступательное движение, не способны^
Е = -^кТ, a Cv = -о-Д ~3 калДмолЬ'К). Эксперимент
подтверждает, что этот вывод верен: теплоемкость одноатомных
газов действительно не зависит от температуры и равна трем.
Однако на этом идиллическое согласие теории и опыта,
кончается. Распространение расчета на двухатомные молекулы^
способные не только поступательно двигаться, но также
вращаться и колебаться, приводит к выводам, даже
качественно не согласующимся с экспериментом.
Чтобы лучше обнажить суть проблемы, заметим, что Е
в самом общем случае однозначно выражается через Z:
A1.2)
83
Тем самым расчет теплоемкости сводится к вычислению
A1.3)
Для «обязательных» видов движения: поступательного,
вращательного и колебательного (гармонического) эти расчеты
совершенно однотипны и приводят к одинаковому
результату. Убедимся в этом.
Поступательное движение. Учитывая, что в отсутствие
п
^•, получаем
Z = VBnmkTK/*. A1.4)
С каждой степенью свободы — вдоль любой из осей: х, у,}
z — связаны равновеликие сомножители Bяттг/сГI/2, на
которые в A1.2) приходится по слагаемому кТ/2. Такова
средняя энергия, приходящаяся на одну степень свободы. Так
как поступательных степеней свободы три, полная тепловая
энергия Е = -jkT* Замечательно, что она совершенно не
зависит от массы молекул, а целиком задается температурой.
Как уже было показано, соответствующая теплоемкость
3 D
равна уд.
Вращательное движение (также в отсутствие полей).
Расчет может быть уподоблен предыдущему. Распределение
Гиббса в канонических переменных, получающееся из (8.8)
при Е = О, имеет вид
Q, рф, 9, Ф) = -1 ехр у - ggL - ^
Простой заменой p± = p0, P2 = ^~0 оно может быть
приведено к следующему:
dW (р1? ра, 9, ф) = y ехр — 2l^ — ^f\ dpx dp2 sin 0 dQ Ap.
A1.5)
В этих переменных энергия — квадратичная функция
импульсов, не зависящая от координат. Поэтому
Z = j ехР (- 2Й77) dPi J ехр f — ]
A1.6)
84
включает два равновеликих сомножителя у 2п1кГ, которые
при подстановке в (И.2) дают £" = —- + —. Следовательно^
Cv — R « 2 кал/(моль»К). Как и в предыдущем случае,;
средняя энергия не зависит от параметров самой
молекулы (/).
Наличие только двух слагаемых кТ/2 в выражении для
средней вращательной энергии связано со спецификой
двухатомной (и вообще, линейной) молекулы. Такие молекулы
обладают лишь двумя вращательными степенями свободы.
Поворот молекулы вокруг собственной оси не принимается
во внимание по причинам, которые станут ясны из
дальнейшего. Только нелинейные молекулы обладают всеми тремя
вращательными степенями свободы, причем на каждую, как
и выше, приходится к Т/2 независимо от величины
соответствующего момента инерции. В этом случае полная энергия
£г = 3'-2", а Су =-j Д.
Колебательное движение. В качестве одной из
канонических переменных, описывающих колебательное движение
двухатомной молекулы, удобно выбрать величину q =*
= х2 — хг — а (а — равновесное расстояние между
атомами, расположенными в точках хл и х2). Так как эта величина
является мерой деформации связи, разумно предположить,)
что усилие, возвращающее атомы к равновесному
положению, тем больше, чем больше q, и, конечно, обратно по
знаку:
F = -рд. A1.7)
Если такая зависимость F(q) сохраняется во всем диапазоне
возможных значений q, то осциллятор называется
гармоническим. ИЬ соответствующего уравнения движения
mq = F = —pg A1.8)
видно, что колебания носят гармонический характер, а их
угловая частота со0 = Vft/m является основной
характеристикой осциллятора.
Полная энергия гармонических колебаний
где р = mq есть импульс колебаний, вторая каноническая
85
переменная. Поэтому
Хотя в данном случае множители, появившиеся при
интегрировании по разным переменным (координатам и
импульсам), не равны друг другу, различие между ними
несущественно. После подстановки в A1.2) и дифференцирования
все не зависящие от Т параметры исчезают. В результате,
как и раньше, получаем
— Iff* TfT
"IT и v ~~
Закон равнораспределения. Можно заметить, что
идентичность всех оценок средней тепловой энергии и ее
инвариантность по отношению к форме движения обусловлены
однотипной зависимостью механической энергии от
соответствующих координат. Действительно, во всех приведенных
примерах энергия оказывалась квадратичной формой
координат или импульсов. Это подсказывает обобщение: если
энергия
Е = S yill A1.11)
1=1
то ее среднее значение в условиях равновесия при любых
yi есть
г г
2т Т
где i — число квадратичных слагаемых энергии.
Иногда это утверждение формулируется как «закон
равнораспределения тепловой энергии по степеням свободы».
При этом подразумевается, что каждый квадратичный член
в A1 11) связан с той или иной степенью свободы
механического движения, но независимо от ее специфики (величины
yi) соответствующая средняя энергия равна кТ/2. Так, на
поступательное движение всегда приходится три степени
свободы, на вращательное — две или три в зависимости от
формы молекулы. Что же касается колебательного, то здесь
необходима оговорка: как видно из A1.9), колебательному
движению соответствуют не один, а два квадратичных
члена в выражении для энергии — один, связанный с ее
кинетической частью, другой — с потенциальной. На каждый
Рис. 31. Схематическое
поведение
теплоемкости двухатомной
молекулы с изменением
температуры.
из этих членов приходится по кТ/2, и, следовательно, чтобы
сохранить вышеприведенную формулировку закона,
следует договориться приписывать каждому колебанию
молекулы две степени свободы в понимании закона
равнораспределения.
К сожалению, «удвоение» колебательных степеней — не
единственная поправка к «закону равнораспределения»,
которую следует иметь в виду. В присутствии внешних
полей на поступательные и вращательные степени свободы,}
как и на колебательные, приходится не только кинетическая,
но и потенциальная энергия. Однако появляющиеся в силу
этого дополнительные слагаемые в выражении для энергии
(например, mgz или qE cos 0) отнюдь не выражаются
квадратично через координаты и поэтому вообще не подпадают
под действие закона равнораспределения. Мы вернемся к
их рассмотрению чуть позже, а пока сосредоточим свое
внимание на газе, экранированном от любых полей, который
является вполне приемлемым объектом для проверки закона
равнораспределения.
Температурные аномалии. Если полное число степеней
свободы молекул газа есть i, то, согласно A1.12) и A1.1),}
Су = iR/2 = i кал/(моль-7£), т. е. абсолютная величина
теплоемкости численно совпадает с i.
Оказалось, что это следствие закона равнораспределения^
а по существу, самого распределения Гиббса, находится в
грубом противоречии с экспериментальными фактами,
относящимися к многоатомным молекулам. Опыт
свидетельствует, в частности, что для двухатомных молекул при обыч-
5 7
ных температурах Су = -у R, ъ не уД, как это следует цз
закона равнораспределения: из расчета 3 поступательных,
2 вращательных и 2 колебательных степени свободы- Если
бы даже предположить, что молекула не колеблется, то и в
87
этом случае согласие остается удовлетворительным
недолго: при понижении температуры теплоемкость отнюдь не
остается постоянной (рис. 31). Вследствие этого для
молекулярного водорода, например, она становится ниже 80 К
равной ЗД/2, т. е. в точности такой же, как и у одноатомных
молекул. С другой стороны, если при комнатных
температурах теплоемкость двухатомных и многоатомных газов
равна соответственно -~-R или 3i? (как если бы колебаний и вов-
се не было), то с повышением температуры она возрастает
и, если только диссоциация не наступает раньше, становится
в конце концов равной jyB точном соответствии с
требованиями закона равнораспределения.
Создается парадоксальное положение: выводы теории^
хотя и не согласуются с экспериментом во всем и полностью,,
все же отнюдь не бессмысленны и явно соответствуют в
определенной области температур и с определенными оговорками
той самой физической реальности, которую должны были бы
описывать вполне точно. Ясно ощущается необходимость
какого-то усовершенствования теории (а не коренной ее
ломки), которое позволяло бы предвидеть, в какой области
температур, какие степени свободы следует принимать во
внимание, а какие считать «вымороженными», не участвующими
в тепловом движении. Но возможна ли вообще такая
ситуация, что та или иная форма движения, дающая вклад в
теплоемкость при одних условиях, при других окажется
несущественной? Чтобы убедиться, что эта возможность вполне
реальна, вернемся к обещанному выше рассмотрению
потенциальной части энергии поступательного и вращательного
движения во внешнем поле и ее вкладу в теплоемкость.
а) Пусть сосуд с газом находится в однородном поле сил
тяготения. Тогда при интегрировании по координатам в
A1.4) вместо V — объема сосуда — появится в качестве
сомножителя следующая величина:
A1.13)
Благодаря логарифмированию в A1.2) эта часть тепловой
энергии естественно отделяется от кинетических слагаемых:
= к! ; ■ . A1Л4)
Рис. 32. Теплоемкость
идеального газа в поле
тяготения.
т. е. центр тяжести
всех молекул находится приблизительно посередине
сосуда. Теплоемкость в этой ситуации, естественно, близка
к нулю, так как изменение температуры несущественно
меняет распределение молекул по высоте, а значит, и их
полную потенциальную энергию: Су = No -т™- = т* уттА <С -й-
С возрастанием температуры Cv ~ Т~2 -> 0, так как
распределение становится все более однородным. Напротив,
при mgH > кТ U ж кТ в духе закона равнораспределения,
т. е. в том смысле, что соответствующая теплоемкость
постоянна г: Су « R. В этой ситуации теплоемкость не
зависит от Н: когда газ осел на дно сосуда, положение его
крышки не играет роли. При повышении температуры энергия
расходуется на перемещение центра тяжести всех молекул
вверх: по С7 = Д на каждый градус.
Общий характер изменения Cv от Т можно представить
себе из рис. 32: граница между областью постоянства Cv
и гиперболическим исчезновением теплоемкости
определяется критической температурой rfe = ^-.
б) Пусть теперь молекулы, обладающие дипольным
моментом, помещены в однородное электрическое поле.
Расчет соответствующей энергии (потенциальной, связанной с
поворотом на угол G) может быть проведен по общей схеме,
Однако р этом нет надобности, ибо U = —qzE, a qz = qUpt)
уже было рассчитано в (8.13). Поэтому сразу находим
-л лт dU ■
sh'a
1 В силу линейной связи f/иг, а не квадратичной, как в A1.11),
совпадения с A1 12) с точностью до численного множителя 1/2 и не
следовало ожидать.
89
где по-прежнему а = |у-^1. Анализируя это выражение
легко заметить, что теплоемкость в условиях насыщения
(qE >> кТ) равна R, тогда как^при высоких температурах
(qE <C к Т) она стремится к нулю по гиперболическому за-
кону: Су = -т (qE/kTJ, т. е. так же, как и в предыдущем
примере (см. рис. 32).
Природа дополнительной теплоемкости, которой
обладает диэлектрик во внешнем поле, достаточно прозрачна.
Повышение температуры всегда приводит к повороту части
диполей против поля, вызывая общее возрастание
потенциальной энергии, которое покрывается за счет тепла, отнятого
у термостата. Как только достигнуто равномерное
распределение диполей по всем направлениям, дальнейшее
повышение температуры уже не способно что-либо изменить и
приток тепла прекращается.
В обоих приведенных примерах теплоемкость обращается
в нуль, выше некоторой критической температуры, и дело
тут, конечно, не в том, что связь энергии с координатой
носит не квадратичный, а иной характер. Причина этого
падения теплоемкости в другом: в ограниченности фазового
пространства. Это особенно легко видеть на первом
примере: если бы сосуд был бесконечно высок (Я = оо), т. е. z
изменялось бы от 0 до оо, то теплоемкость оставалась бы
постоянной (равнялась R) во всем диапазоне температур. Во
втором случае причина та же: проекция момента на ось z%
от которой зависит энергия U = —qzE, ограничена сверху
(Ы < q)- При q = оо критическая температура также
никогда не достигается, ибо Тк — qE/k.
В случае же поступательного, вращательного и
колебательного движений соответствующие переменные
изменяются в бесконечном диапазоне, так как импульсы и моменты
импульсов могут принимать любые- значения. Кроме того»
аномальное изменение CV(T), соответствующее этим видам
движения, носит, как видно из сравнения рис. 31 и 32,
прямо противоположный характер. При высоких температурах
имеется полное соответствие с законом равнораспределения^
и лишь при достаточно низких теплоемкость уменьшается,,
стремясь к нулю. Выход из тупика мог бы быть найден»
если бы фазовое пространство этих переменных оказалось
ограниченным не сверху, а снизу. Это важное наблюдение
поможет нам осмыслить в дальнейшем действительную причину
разрешения парадокса теплоемкостей.
§ 12. КВАНТОВАНИЕ
ГАРМОНИЧЕСКОГО ОСЦИЛЛЯТОРА
Вымораживание колебаний. Трудности классической
теории теплоемкостей не могут быть устранены ни
усовершенствованием модели газа, ни ссылкой на приближенность
расчета. Закон равнораспределения является прямым
следствием распределения Гиббса, и его компрометация ставит
под вопрос либо само это распределение, либо законность
использования в нем классических механических законов,
восходящих к Ньютону. Казалось бы, тень сомнения
ложится в первую очередь на вновь введенные статистические
представления.
Но оказалось иное. Причина парадокса таилась в
неоправданном распространении законов ньютоновской
механики на атомы и молекулы — частицы чрезвычайно малые, о
которых никто не мог знать заранее, так ли они ведут себя,
как обычные тела, или совсем иначе. За неудачной
попыткой классического описания этих частиц последовали
нововведения, которые оформились в виде первых квантовых
постулатов, разрешивших парадокс теплоемкостей. Наиболее
революционный постулат механики микрообъектов удалось
сформулировать задолго до того, как экспериментаторы
получили в свои руки прямые средства исследования
элементарных частиц.
Этот постулат был введен Планком как рецепт,
благополучно ликвидирующий так называемую
«ультрафиолетовую катастрофу» — еще одно парадоксальное следствие
закона равнораспределения (см. § 19). Суть его, вкратце,
заключается в следующем: поле излучения можно
рассматривать как совокупность гармонических осцилляторов,
которые описываются так же, как и гармонические колебания
молекул. Если поле находится в равновесии с веществом, то
энергия тепловых колебаний каждого из его осцилляторов,
согласно закону равнораспределения, равна /сТ. Но так как
имеется бесконечно много различных колебаний поля (с
частотами от 0 до оо), то полная их энергия должна была бы
равняться оо! На самом деле это, конечно, не так. Планк,
анализируя экспериментальные данные по энергетическому
составу равновесного излучения, установил, что, в
действительности, средняя тепловая энергия, приходящаяся на
каждый осциллятор, при температуре Т равна
В -^ , A2.1)
91
где h = 6,6 «Ю"7 эрг»с — постоянная Планка. Это
выражение совпадает с классическим Е = кТ при малых
частотах (v <С kT/h), но обращается в нуль при больших.
Отсутствие («вымерзание») высокочастотных колебаний
разрешает ультрафиолетовый парадокс, однако в корне
противоречит закону равнораспределения, согласно которому средняя
энергия колебаний не может зависеть от их частоты.
Извлеченная из опыта формула A2.1) устраняет
трудности и в теории газовых теплоемкостей, связанные с
колебательной энергией молекул. Из нее видно, что для каждого
осциллятора с частотой колебаний v существует
критическая температура ТК — hv/k, выше которой Е = кТ, Cv =*
= Л, а ниже £ = hv exp (—hv/kT) и Cv -* 0 при Т -*0
(колебания вымораживаются). Однако пока совершенно
неясно, какой дефект в прежних выкладках нужно устранить,,
чтобы получить эту формулу теоретически.
Квантование энергии. Сталкиваясь с противоречием такого
рода, очень полезно взглянуть на него с разных точек
зрения, пусть даже равноценных. Это позволяет иногда
выделить ту из них, в которой содержится намек на источник
недоразумения. В данном случае, например, оказывается
полезным рассмотреть проблему с точки зрения
распределения, заданного не в канонических переменных, а в
энергетическом пространстве. Для этого необходимо от перемен-
ных р и q перейти к переменным Е = £^ -\ -^- и <р =
= arctg plq (энергии и фазы колебания), а затем
проинтегрировать по всем фазам (от 0 до 2я). Первый шаг выполняется^
как обычно, с помощью якобиана преобразования dEdy =5
= \I\dpdq:
(E, ф) mV + tg2
Элемент фазового пространства осциллятора в новых
переменных выражается следующим образом:
7-n j j dEdtp m dEd(p /лп г>ч
dT = dpdq = —т-^ = —0-2 2 Г^ A2.2)
^ * / mV + tg^ СОБ2ф V '
СОБ2ф
Фазовый объем, приходящийся на изоэнергетические
состояния, представляет собой полоску элдипсоидальной формы
(рис. 33), площадь которой находится прямым интегриро-
92
Рис. 33. Изоэнергети-
ческий. слой фазового
пространства
гармонического осциллятора.
ванием по <р:
2я
+ tg2 ф) cos2 ф
dE
A2.3>
Имея это в виду, мы можем выписать для Z два равноценных
определения:
е °% _е_
ftJ dpdq = J е Л —. A2.4)
О
Каким бы из них ни воспользоваться, получится один и тот
же результат: A1.10). И все же последнее выражение
обладает важным преимуществом: в самой его структуре
угадывается намек, открывающий путь для ревизии теории.
Резонно искать подсказку у самой природы, поставив
вопрос следующим образом: каково должно быть Z, чтобы
его подстановка в A1.2) приводила к правильному
результату A2.1)? Ответ можно получить, если приравнять A1.2)
и A2.1). Тогда искомая величина Z определяется простым
дифференциальным уравнением
dlnZ _ 1
da exp (a) — 1'
где а = hvlkT. Его решение имеет вид
г, С С
1 — ехр (— а) 1 — exp (— hv/kT)'
A2.5)
Теперь уже проблема обнажена до предела, доведена до
той черты, за , пределы которой может вывести лишь
незаурядная проницательность. Есть ли хоть какая-нибудь
аналогия между извлеченным из опыта выражением для
Z — A2.5) и его теоретическим аналогом A2.4) — вот как
93
теперь стоит вопрос. Усмотреть эту аналогию совсем не
просто. Еще сложнее решиться на коренное
усовершенствование механики, необходимое для устранения парадокса.
Не мудрено исчерпать всю свою смелость, став однажды на
путь таких обобщений. Но именно этот путь и привел
Планка к его знаменитому квантовому постулату.
Планк заметил;- что с помощью известной формулы
геометрической прогрессии выражение A2.5) может быть
переписано в виде
оо оо EN
z- = 2 е-" = ^ е~" , A2.6)
Л=0 N=0
причем последний результат в точности напоминает
выражение A2.4) в его последней редакции, если только принять
(постулативно!), что интегрирование следует заменить
суммированием, положив
EN = Nhv, N = О, 1, 2, . , ., оо, A2.7)
Но принять это, значит признать, что энергия системы
может принимать не любые, а лишь строго определенные
значения, что она изменяется не непрерывно, а дискретно, и
одно разрешенное значение отделено от другого
интервалом — «квантом» — величины hv. Стало быть, осциллятор
мощет колебаться не с любой энергией и находиться не в
любом состоянии, как прежде, а ему разрешены лишь
некоторые состояния движения, в которых энергия принимает
одно из значений A2.7).
Таким образом, формулой A2.7) вводится не рядовая
рабочая гипотеза, не улучшенная модель явления:
квантованием энергии устанавливается качественная
недостаточность классической механики, *ее непригодность для
описания механического поведения атомов и молекул.
Высокотемпературный предел. Возникает естественный
вопрос: почему мы раньше не сталкивались с
необходимостью усовершенствования механических представлений, в
чем специфика рассматриваемой проблемы, не позволившая
и здесь уклониться от квантования энергии. Кроме того,
необходимо показать, что вводимое таким образом новое
физическое мировоззрение отнюдь не исключает старого,
а лишь вскрывает его ограниченность. Такова сжатая
формулировка «принципа соответствия», согласно которому любая
более общая новая физическая теория должна сводиться к
старой в той области, где последняя удовлетворительно
описывала эксперимент.
94
Посмотрим же, как выполняются требования принципа
соответствия в данном случае. Чтобы подтвердить
результаты классической теории в области их применимости,
достаточно показать, что при высоких температурах
статистическая сумма A2.6) сводится к интегралу' состояний A2.4)*
Сделать это несложно:
при g«l A2.8)
суммирование в A2.6) может быть с ничтожной
погрешностью заменено интегрированием:
N—0
Нетрудно разглядеть в этой асимптотической формуле
глубокое сходство, по существу, даже тождество с той оценкой
Z, которую дает последнее выражение в A2.4). Единственное
различие — в постоянном множителе — устраняется
подходящим выбором С.
Квантовые ячейки. С этим, однако, не следует торопиться.
Нет ничего проще положить С — hn этим удовлетвориться.
Однако требования принципа соответствия могут быть
удовлетворены и иначе. Всякое распределение фактически
определялось нами с точностью до постоянного множителя G:
dW = i exp (- iL) GdT, Z = G Jexp (- ^) dr.
От выбора этой постоянной ничто не зависело, кроме
установления нуля отсчета термодинамических функций A0.5)
и A0.6). Поэтому выше всегда считалось, что 6 = 1. Теперь,,
однако, уместно вспомнить об этом элементе произвола, так
как он подсказывает другую возможность приведения в
соответствие A2.9) и A2.4): можно положить С = 1, a G —
= l/h. С введением этой поправки классическое
каноническое распределение принимает вид
Зато квантовое распределение и соответствующая статисти-
95
ческая сумма выглядят максимально просто:
WN-±. exp (- J£), Z = Д ехр (- f£). A2.11)
Это распределение, задающее вероятность каждого
состояния из разрешенного множества (N = О, 1, 2, ...),.
отличается от того, которое можно было написать сразу, глядя
на A2.6), лишь определенным выбором константы (С = 1).
Вопрос о том, как следует определить .постоянные С и
G, т. е. где, в сущности, должна появиться постоянная
Планка—в классическом или квантовом распределении, может
показаться праздным: на первый взгляд, от его решения
ничто не зависит. Однако на самом деле существуют веские
основания предпочесть то решение вопроса, которое приводит
к A2.10) и A2.11). Действительно, если измерять объем
фазового пространства в единицах А, как в A2.10), то
окажется, что
ESE^ A2.12)
Этим равенством, вытекающим из A2.3) и A2.7),
устанавливается общность лексики, т. е. соответствие классического
«фазового объема» квантовому «числу состояний». Теперь
сказать, что вероятность найти осциллятор с энергией
пропорциональна объему dT(Е),—значит выразиться не совсем
точно. Правильнее сказать, что эта вероятность измеряется
числом dN возможных квантовых состояний, оказавшихся
в пределах этого интервала (имеется в виду, что dE » hv).
Действительно, когда имеешь дело с дискретным
множеством состояний, вопрос о том, как их подсчитать, не
возникает. Если же подсчет осуществлять в пространстве
непрерывно изменяющихся переменных р и д, то для
получения идентичного результата необходимо разбить его на
ячейки объема h, в каждой из которых заключено по одному
реальному состоянию. В случае гармонического осциллятора
эти ячейки представляют собой концентрические
эллипсоидальные пояса, разделенные разрешенными траекториями
движения.
Постулат Бора. До сих пор все сказанное относилось
только к гармоническому осциллятору. Однако теперь
возможно и обобщение, которое подсказывается соотношением
A2.12). Его следует просто переписать в интегральной
форме, имея в виду, что вычисляется площадь, ограниченная
фазовой траекторией системы:
Г (Е) = ф pdq = Nh. A2.13)
8
Это соотношение вобрало в себя информацию двоякого рода:
присущее классическому осциллятору свойство A2.3),
согласно которому площадь под траекторией с энергией Е есть
ф pdq = —, и условие квантования A2.7), которым отобраны
только разрешенные значения Е = Nhv. Поэтому, как и
A2.7), оно* может служить правилом, по которому
находятся разрешенные траектории движения осциллятора. Однако
в сравнении с A2.7) оно обладает тем преимуществом, что
характерный только для осциллятора параметр — частота
колебаний v, фигурировавшая, кстати сказать, в обеих
посылках, отсутствует в окончательном выражении A2.13).
В применении к осциллятору и A2.7), и A2.13) дают,
конечно, один и тот же результат, представляют не две разные,
а одну и ту же гипотезу. Однако с точки зрения обобщения
очевидные преимущества на стороне A2.13). Поскольку это
выражение не зависит от специфики системы, велик соблазн
попытаться применить его к квантованию ротатора,
поступательного движения, наконец, к внутренним движениям
электрона в атоме. Замечательный успехг которого достиг
Бор, использовав A2.13) для отыскания разрешенных ор-
бит> а следовательно, и энергий электронов в водородоподоб-
ных атомах, подтвердил общий характер этого правила
квантования. Не останавливаясь подробно на этом вопросе,
который увел бы нас далеко в область атомной физики,
заметим лишь, что вплоть до создания строгой квантовой
механики полуклассическое правило квантования Бора A2.13)
являлось единственной надежной основой для истолкования
и расчета линейчатых спектров элементов — камня
преткновения классической, доквантовой физики.
§ 13. ВЫМОРАЖИВАНИЕ ТЕПЛОВЫХ ДВИЖЕНИЙ
Хотя квантованию подлежит любой вид движения,
прибегать к нему необходимо не всегда. Даже осциллятор при
температурах Т 3> в = hv/k можно описывать
классически. Каждый вид движения характеризуется своей
собственной характеристической температурой 6 = AEjkr где
&ЕХ — энергетическая щель между основным (наинизшим)
4 А И. Бурштейн 97
2
\\\\\
J X/ X/ \J \/N
л Д Д л л
\KKKK}
\\\\\
p
\\\\\
<YYYY4
4\XXX7
\\\\\
2
Рис, 34. Квантовые
ячейки частицы,
свободно движущейся в
потенциальном ящике.
и первым возбужденным состоянием дискретного спектра
системы. Квантование движения распространяется на все
его виды, но то новое, что оно дает в сравнении с классикой^
обнаруживается лишь в области 0 <1 Т <! в, а в может
быть самым разным. Для молекулярных колебаний, в
частности имеющих частоту v ~ 1013 Гц, критическая
температура
о hv 6,6-1СГ27-1013
1,4-10
,-16
= 471 К ^ 200°С
столь велика, что весь комнатный диапазон оказывается в
пределах квантовой области, где колебания выморожены
(подавляющее большинство молекул не колеблется).
Напротив, характеристическая температура, соответствующая
поступательному движению, неощутимо отличается от О К,
и поэтому классическое приближение оказывается вполне
удовлетворительным фактически при всех Т.
Убедимся в этом. Помещая частицу в ящик — правильный
куб с ребром S , можно заметить, что ее фазовая
траектория представляет собой прямоугольник (рис. 34), площадь
которого равна
~2~
j) pdq = 2 j pdq = 2p2>.
2~
Таким образом, импульс движения вдоль любой из осей
ввиду правил квантования A2.13) мощет быть лишь строго
определенным:
Р = ^, ЛГ-0,1,2,... A3-1)
98
Здесь q — любая из трех переменных: х, у или z, a p —
соответственно рх, ру или pz, так что фактически
тут h лт h дт h
P Jy P ]4 P M
а
р2 = ^N\ N2 = Nl + N*y +N1 = 0,1, ... A3.2)
Отеюда Ai?x = h2/8m 2?2. В сосуде с габаритами ~1 см
-=1(Г15К. A3.2а)
43-10-54
Но это чрезвычайно низкая, недостижимая температура.
Задолго до столь глубокого охлаждения практически любой
газ сконденсируется. А в пределах газообразной фазы (Т ^>
» 6) поступательное движение носит классический
характер, и это задним числом объясняет причину успешной
интерпретации свойств газа на основе распределений
Максвелла и Больцмана-
Может, правда, вызвать некоторые сомнения
правомерность сопоставления кТ именно с первым квантом. Ведь в
случае поступательного движения система термов A3.2)
не эквидистантна, как в гармоническом осцилляторе.
Ширина щели между соседними уровнями Ае^ = zN — &n-i —
= h2BN — 1)/8 S?2m возрастает при увеличении N.
Поэтому если даже кТ велико в сравнении с Де,, то все же оно
наверняка меньше некоторого достаточно большого Де^.
Легко, однако, убедиться, что это не меняет дела. В классиче-
ском пределе s = у кТ = р2/2т, а, значит, квантовый номер
терма, который соответствует, согласно A3.2), этому сред-
нему уровню энергии, есть iV« уЪкТш — = у -^-. По
мере повышения температуры этот средний уровень
увеличивается, так же как и расстояние до близлежащих к нему
термов Де^« h2N/i3?2m. Однако отношение Ае—/е— =
—— —. О
= 2N/N2» —< 1 и монотонно уменьшается при всех Т S>
>> в. Больше единицы это отношение лишь при Т <С в,
когда только первый квант и следует сравнивать с к Г, ибо
вышестоящие уровни уже опустошены.
Если колебательное движение в области комнатных
температур практически выморожено* а поступательное^ на-
против, носит вполне классический, квазиконтинуальный
характер, то вращательное движение занимает
промежуточное положение по отношению к ним обоим: его
критическая температура оказывается порядка , комнатной.
Действительно, применяя то же правило квантования A2.13)
к проекциям углового момента, получаем для каждой из них:
= 2я/?ф = Nh; /?ф = N%. A3.3)
Таким образом, угловой момент является целым кратным
величины % = hl2n. Для молекулы, способной вращаться
вокруг всех трех осей, получаем совершенно аналогично
предыдущему:
где, однако, принято во внимание, что моменты инерции
вдоль разных осей, вообще говоря, различны: /х Ф /2 Ф
Ф /3. Температура, связанная с вращением вокруг одной
из осей, равна при J{ = 100 г-см2:
в* = 5ТТ ~ ^г ттг « 30 К. A3.5)
Наименьшим моментом инерции, а следовательно, и
наибольшей в обладает молекулярный водород, у которого
вымораживание вращательного движения наступает вблизи
80 К. Чем больше молекула, тем ниже температура
вымерзания вращательного движения.
Если мы имеем дело с линейной молекулой, то момент
инерции вдоль оси молекулы, очевидно, равен нулю, а
соответствующая этой степени свободы критическая
температура отодвинута в бесконечность. Именно поэтому
средняя энергия такого вращения равна нулю, а его вклад в
теплоемкость отсутствует. Таким образом, наличие у линейных
молекул только двух вращательных степеней свободы
вместо трех имеет сугубо квантовое происхождение.
Фактически же между линейными и нелинейными
молекулами нет резкого качественного разграничения.
Рассмотрим, например, плоскую трехатомную молекулу типа Н2О —
равнобедренный треугольник, способный вращаться во всех
трех направлениях (рис. 35). Минимальный момент инерции
связан с осью, параллельной основанию треугольника Н—Н,;
так как угол у вершины тупой. Если теперь мысленно
увеличивать этот угол, то момент инерции, о котором идет речь^
100
Рис. 35. Геометрическое
строение молекулы воды (а)
и линейной трехатомной
молекулы, например СО2 (б).
будет еще более уменьшаться, пока не обратится в нуль
при угле 180°, т. е. при образовании строго линейной
молекулы. При таком предельном переходе 6 будет
постепенно возрастать и в линеаризованной молекуле обратится в
бесконечность: соответствующая степень свободы начисто
исчезнет.
Резюмируя вышеизложенное, можно видеть, что при
очень низких температурах молекулы газа участвуют только
в поступательном тепловом движении, при температурах,
сравнимых с комнатной,— в поступательном и
вращательном и лишь при заметном разогреве также и в
колебательном. Это объясняет общий характер изменения теплоемкости
с температурой, представленный на рис. 31. Однако в том,
как происходит размораживание вращательного и
колебательного движений, весьма заметны различия. При
включении колебательных степеней свободы теплоемкость
монотонно возрастает с увеличением температуры, постепенно
приближаясь к классическому пределу, тогда как при
возбуждении вращательного движения она часто переваливает через
максимум, прежде чем достигает его (см. рис. 31). Столь
тонкие детали в поведении CV(T) вблизи характеристических
температур не могут быть поняты в рамках
полуклассических представлений Бора. Правильно оценивая величину
квапта, они неточны ъ определении абсолютного положения
уровней энергии и их структуры.
Чтобы избежать этой неточности, необходимо принять
к сведению результаты последовательно квантовой теории.
Энергия вращательного движения двухатомной молекулы,
которая, согласно A3.4), есть 8 = 2/АГ2, гДе N = (N% +
\1/2
на самом деле равна
A3.6)
101
2,0 Т/в
Рис. 36. Энергетическая структу- Рис. 37. Средняя тепловая энер-
ра линейного ротатора (а) и ос- гия линейного ротатора (а) и
циллятора (б). осциллятора {б) как функции
температуры.
При этом каждый энергетический уровень, кроме
наинизшего, многократно вырожден, т. е. состоит из 27V + 1 изо-
онергетических состояний, различающихся только
пространственной ориентацией углового момента (рис. 36, а). Что же
касается гармонического осциллятора, то его спектр,
будучи строго рассчитан, ничем иным, как оказывается, не
отличается от своего полуклассического аналога A2.7), кроме
как смещением всех уровней на полкванта вверх по
энергетической оси:
Е =
4-Uv.
A3.7)
Кажущееся незначительным это отличие, однако, приводит
к тому, что даже при полном вымораживании
колебательного движения при Т = 0 энергия его в нуль не обращается.
Оказавшись в наинизшем состоянии, осциллятор не
пребывает в покое, а совершает неустранимое, чисто квантовое
движение с энергией, равной у (рис. 36, б).
Учитывая эти особенности при вычислении
статистических сумм квантового ротатора и осциллятора, можно
усмотреть происхождение отмеченных выше различий в
температурной зависимости теплоемкостей. Для системы со
спектром A3.6) статистическая сумма
Z = 2 BN + 1) е
N=0
-±N(N+1)
A3.8)
102
может быть преобразована с помощью формулы Эйлера —
Маклорена:
2 / (N) = Г / (х) dx + ф- - 1 /' @) + ± Г @)
iV=0 о
в следующий ряд по в/ Т:
Это позволяет оценить в высокотемпературном пределе
среднюю энергию вращения молекулы:
8 din Z Т 1 1 в с\ ^ т 1АЪ \<\\
Ш = - д (в/Г) =¥"¥У' «<i- (W.1U)
Она отличается от своего классическога предела г — кТ.
С ростом температуры это отклонение уменьшается, но не
исчезает вовсе, а достигает постоянного значения, равного
к&/3 (рис. 37, а). Кроме того, на кривой г(Т) существует
точка перегиба, в которой теплоемкость Cv = -^=N0
достигает максимума, показанного на рис. 31. Это видно из того,
что теплоемкость, вычисленная из A3.10), приближается к
своему пределу сверху:
Иначе обстоит дело с гармоническим осциллятором, средняя
энергия которого лишь постоянным слагаемым отличается
от найденного ранее полуклассического значения:
f|. (i3.il)
J
В высокотемпературном пределе всякая ^разница между
строго квантовым и классическим результатом исчезает:
e<7\ A3.12)
Энергия приближается к своему асимптотическому
значению сверху (см. рис. 37), так что рост теплоемкости носит
монотонный характер, как это и изображено на рис. 31.
В реальной теории теплоемкостей необходимо принять
во внимание еще и то обстоятельство, что молекулярные ко-
103
лебания па самом деле никогда не являются чисто
гармоническими. Лишь в глубине потенциальной ямы, где ее форма
близка к параболической, уровни колебаний располагаются
эквидистантно. С увеличением энергии щель между ними
становится все меньше. Но самое главное, что при
достаточно большой энергии молекулярная система вообще теряет
устойчивость и диссоциирует. В результате возрастает
общее число частиц в системе и качественно меняются степени
свободы.
При еще большем нагреве становится необходимым
принимать во внимание возбуждение атомных электронов на
вышестоящие энергетические уровни. Этим внутриатомным
движениям соответствуют кванты порядка нескольких
электрон-вольт, вследствие чего движение электронов
остается вымороженным до очень высоких температур ~ 103—
104 К. Однако при должном разогреве тепловое движение
передается и электронам, которые сначала возбуждаются
на все более высокие уровни, а затем и вовсе покидают
атомы («тепловая ионизация»).
Наконец, при температурах в миллионы, десятки
миллионов градусов, когда все молекулы диссоциировали, а
атомы ионизовались, дело доходит до возбуждения и деления
атомных ядер. Такова ситуация в недрах Солнца и других
звезд, где идут термоядерные реакции.
§ 14. ПАРАМАГНЕТИЗМ ГАЗОВ
Угловой момент молекулы или атома создается
вращением заряженных частиц — ионов или электронов. Вместе
с ним возникает и магнитный момент. Вследствие общности
происхождения между обоими моментами существует
прямая пропорция с коэффициентом у, который называют
гиромагнитным отношением. Потенциальная энергия
магнитного момента в постоянном магнитном поле Н
\U - —ул-Н =* -\izH A4.1)
точно так же зависит от угла между ними, как и энергия
диполя в электростатическом поле. Казалось бы, можно
ожидать, что здесь лишь в иных обозначениях воспроизведется
вся картина ориентационной поляризации, подробно
описанная в § 8.
В действительности дело обстоит иначе. Согласно
квантовым представлениям о вращении зарядов, магнитный мо-
104
-A I I I I
и1
Рис. 39 Распределение по
проекциям спина 1/2.
Рис. 38. Квантование
магнитного момента во внешнем поле.
мент квантуется точно так же, как и соответствующий
механический (угловой) момент A3.3):
R = 7Л> = ^. A4.2)
где N — целочисленно изменяющееся квантовое число, а
yh « 10~20 эрг/Гс. Квантование магнитного момента
является причиной дискретного изменения потенциальной
энергии:
A4.3)
Поскольку z-проекция диполя не может превышать его
самого, \\iz\ < [х = yhJ, N изменяется в конечных пределах:
ЛГ = -/, -/ + 1, ...,/- 1, /. A4.4)
Всего имеется 2/ + 1 значение проекции момента (рис. 38).
Таким образом, парамагнитная поляризация есть чисто
квантовое явление, исчезающее в классическом пределе,
при % -> 0. Квантовое число /, задающее абсолютную
величину момента, может быть целым и полуцелым. Если
магнитный момент создан только орбитальным движением
электронов вокруг атомного ядра, то / — целое. Но и сами
электроны обладают отличным от нуля моментом — «спином»,
равным 1/2. Вследствие этого полный момент атома,
складывающийся из орбитального и спинового, оказывается
целым, если число электронов четное, и полуцелым, если
нечетное.
Этих общих сведений из квантовой механики вполне
достаточно, чтобы приступить к статистическому расчету па-
105
рамагнитной поляризации. Используя A4.3), можно
видеть, что в полях доступной величины ~1О4'Гс
AU=UN — E/jv-i = уГгН ~ 106 эрг, A4.5)
т. е. при комнатных температурах много меньше кТ. Стало
быть, магнитные кванты занимают промежуточное
положение между вращательными и поступательными, но все же
не настолько малы, как последние, чтобы вовсе не быть за-
метными. При достаточно низких температурах: 0 = -т— ~
~ 1 К — парамагнитная поляризация должна приходить
к насыщению точно так же, как и диэлектрическая.
Спин 1/2. Рассмотрим сначала для конкретности чисто
спиновой магнетизм с / = 1/2. Расчет намагниченности в
этом случае даже более прост, чем в классическом. Вместо
непрерывного множества состояний теперь имеется,
согласно A4.14), только два: N = ±1/2, т. е. спин ориентирован
либо строго по полю, либо против него и имеет
соответственно только два уровня энергии (рис. 39):
Ut = -y±H и Г/2 = 7^Я. A4.6)
Частица может располагаться либо на одном уровне, либо
на другом, так что все распределение A2.11) сводится к
заданию двух чисел:
tj^ ехр (а/2) tj^ ехр (— а/2)
1 ~~ ехр (а/2) + ехр (— а/2)' 2 ~~
A4.7)
где а = у%Н/кТ. Ими определена вероятность
соответствующей ориентации момента. В условиях равновесия спины
будут распределены по проекциям в строгом соответствии с
этими вероятностями:
N± = nWu N2 = nW2i A4.8)
где п — полное число парамагнитных частиц в единице
объема. Естественно, что средний магнитный момент
образца
М = \xNx — \iN2 = \in (Wx — W2), где \i = yU/2. A4,9)
Он определяется просто избытком спинов, параллельных
полю, над теми,, которые ориентированы против него. Его
106
абсолютная величина, согласно A4.9) и A4.7), есть
В высокотемпературном пределе, при а = 2\хН/кТ <С 1,
из A4.10) простым разложением экспонент получается
закон Кюри:
^ ^Н = ХН. A4.11а)
Когда намагниченность пропорциональна приложенному
полю, восприимчивость убывает обратно пропорционально
температуре. Близкое подобие, существующее в линейной
области между магнитной и диэлектрической поляризацией,
подчеркивается и формальной близостью A4.11а) и (8.15а).
Совсем иначе дело обстоит в области низких температур,
где а ^> 1. В этом случае, как и в (8.156), наблюдается
эффект насыщения:
М = \i-n. A4.116)
При глубоком охлаждении почти все спины придерживаются
параллельной полю ориентации, а при абсолютном нуле
тех, что придерживаются противоположной ориентации,
не остается вовсе. Однако приход системы в полностью
упорядоченное состояние в парамагнетике и диэлектрике
протекает по-разному.
Это различие особенно ярко проявляется в
температурной зависимости теплоемкости, связанной с эффектом
поляризации. Энергия поляризации единицы объема есть,
очевидно, nU = —М'Н% а молярная теплоемкость, ввиду
A4.10),
Cv = -N0-§ = - §-N0H/n. A4.12)
Как видно из этой формулы, а также иллюстрирующего ее
рис. 40, теплоемкость, связанная с магнитной поляризацией,
нигде не остается постоянной. В высокотемпературном
«классическом» пределе она не равна R по той же причине, что и
теплоемкость поляризованного диэлектрика: из-за
ограниченности фазового пространства сверху. Сопоставление
рис. 32 и 40 подтверждает, что в этой области изменение
обеих теплоемкостей подчиняется гиперболической
зависимости: Cv = R(\iH/kTJ. Зато в противоположном случае —
в области насыщения, где теплоемкость диэлектрика нахо-
107
Рис. 40. Изменение
теплоемкости
двухуровневой системы с
температурой.
дится в соответствии с законом равнораспределения,
теплоемкость парамагнетика не стремится к классическому
результату, Cv = R, а обращается в нуль. Это различие
обусловлено тем, что спиновое фазовое пространство
ограничено не только сверху, но и снизу: квантованием запрещены
все промежуточные значения энергии между U2 и иг, и
поэтому Cv -> 0 как только кТ становится меньше ЛС/" =
= U2 — иг. Таким образом, если пмеется непрерывное
множество ориентации (диэлектрик), то упорядочение
системы путем охлаждения требует отнятия R калорий на
каждый градус, приближающий газ к абсолютному нулю;
когда же ориентации всего две, то на это требуется тем меньше
энергии, чем дальше зашло дело.
Общий случай. Подчеркнутое выше различие между
спиновой и диэлектрической поляризацией столь разительно
именно в случае спина 1/2, когда с непрерывным набором
ориентации сравниваются только две возможные. На самом
деле электрический диполь тоже способен принимать не
любые ориентации относительно внешнего поля, а лишь
дискретный ряд их. Пренебрежение этим обстоятельством
оправдано только большим числом и маленькой величиной
соответствующих квантов энергии. Это соображение
наводит на мысль о том, что различие между дискретно и
непрерывно ориентирующимся диполем должно исчезать при
возрастании абсолютной величины момента / и числа
различных его ориентации, если только интервал энергии,
который дробится на все большее число квантов, сохраняется
при этом неизменным.
Действительно, намагниченность единицы объема,
содержащего молекулы с моментом величины /, согласно A4.2),,
A4.3), A4.4) и A2.11), задается следующим средним:
М=п 2 ynNWN = ny%^^-. A4.13)
N=-J
108
Прямое вычисление статистической суммы, которая
представляет собой конечную геометрическую прогрессию, дает
Подставляя A4.14) в A4.13) и выполняя
дифференцирование, получаем
e 1 ,.,.кч
Этот результат представляет собой наиболее общую оценку
намагниченности, которая годится как для / = 1/2, когда
она сводится к A4.10), так и для любого другого /, целого
и полуцелого. Чисто квантовая природа парамагнетизма
обнаруживает себя в этой формуле тем, что при % -> 0
обращается в нуль и М. Однако в этой же формуле возможен и
иной предельный переход:
/->оо, Й.->-0 при [х = yfoJ = ponst, A4.16)
при котором все возрастающее число квантов укладывается
в пределах одного и того же энергетического интервала
(—[хЯ, |хЯ). В этом случае из A4.15) получается результат
кт
|f), A4.17)
совпадающий с (8.13), (8.14) с точностью до обозначений*
Предельный переход A4.16) делает энергетическое
пространство настолько мелкоструктурным, по существу
непрерывным, что результат классической теории ориентационной
поляризации восстанавливается в правах.
§ 15. РЕЛАКСАЦИЯ В ГАЗЕ
Хотя свойства равновесных состояний изучаются и
рассчитываются вне всякой связи с предысторией, способность
макросистем возвращаться к равновесию из любого
неравновесного состояния лежит в основе всех предыдущих
построений. Дело в том, что применить микроканонический
принцип равновероятности изоэнергетических состояний
можно и к одной частице, изолированной в ящике, и к сово-
109
купности материальных точек в нем. Однако ни та, ни
другая система не будет подчиняться термодинамическим
законам, полученным таким образом. Однажды оказавшись в
состоянии, отличном от равновесного, она в нем и будет
пребывать в дальнейшем, ибо, коль скоро системе
материальных точек сообщены определенные скорости, в ящике с
упругими стенками они будут сохраняться. Таким образом,,
если распределение было немаксвелловским вначале, то
таковым оно и останется.
Между тем из опыта следует, что в реальной системе
через весьма ограниченное время устанавливается максвел-
ловское распределение по скоростям, а затем и больцманов-
ское распределение в пространстве. Процесс
преобразования старого распределения в новое носит название процесса
релаксации. Для установления равновесного распределения
в координатном пространстве и в пространстве скоростей
требуются, вообще говоря, разные времена релаксации*
Почему происходит релаксация и как она происходит — вот
вопросы, на которые должна дать ответ физическая
кинетика.
Спонтанная релаксация. Решение первого из
поставленных вопросов равносильно обоснованию
микроканонического распределения с динамических позиций. Ведь если
рассматривать газ в целом как механическую систему, то
всегда остается неясным, зачем и на каком основании
привлекаются для его описания чуждые механике статистические
представления.
Разъяснение этому парадоксу дает гипотеза
размешивания Крылова. Суть ее вкратце сводится к следующему*
Любая изолированная макросистема, к которой применима
термодинамика, должна обладать способностью из почти
любого доступного ей состояния в относительно короткий
срок попадать в любой другой элемент фазового объема. Эта
гипотеза играет в физической кинетике такую *ке
основополагающую роль, как и микроканоническое распределение
в теории равновесия. Например, точка, представляющая
состояние системы в Г-пространстве, стартует из той его
области, которая доступна системе до расширения ее
объема передвижением поршня, и затем, двигаясь по сложной
и запутанной траектории, она сначала грубо, а затем все
детальнее и мельче изрешечивает, дробит фазовое
пространство. Благодаря этому через сравнительно короткое время
в относительно больших равновеликих частях его
оказывается примерно одинаковая длина попавших в них
отрезков траектории. В дальнейшем система продолжает двигать-
110
ся таким образом, как если бы ей была поставлена задача
доделать то, чего она не успела в начальной стадии
процесса. Она проходит по всем элементам пространства вновь и
вновь, оставляя в стороне лишь немногие, и дробит их все
равномернее и мельче, так что, чем больше времени прошло
с момента старта, тем с большим основанием мы вправе
считать, что во всех элементах объема равной величины
содержится равное число точек фазовой траектории. Чем
равномернее размешалась траектория системы по всему фазовому
объему, доступному ей, тем меньше отклонение от состояния
равновесия, к которому система стремится.
Действительно, если свойством быстро размешиваться
в фазовом пространстве обладает большинство траекторий,
берущих свое начало из заданного начальными условиями
исходного участка фазового пространства, то по истечении
времени релаксации тс систему, стартовавшую из одной его
точки, можно будет найти в одном месте, а стартовавшую из
другой — в совершенно ином. Но поскольку достоверно
неизвестно, из какой именно точки был произведен старт, то
спустя время релаксации мы имеем равные шансы найти
расширившуюся систему в любой равновеликой области нового
фазового объема точно так же, как до этого она могла с
равной вероятностью оказаться в одном из элементов
небольшой его части, доступной ей до расширения.
Свойством «размешиваться» обладают не все системы.
Грубо говоря, для того чтобы система размешивалась,
необходимо, чтобы она состояла из большого числа частиц,
которые были бы связаны между собой определенного вида
взаимодействием. Ясно, что ни свободная частица в ящике,
ни совокупность материальных точек этим требованиям не
удовлетворяют. Взаимодействие между частицами,
обеспечивающее размешивание, при рассмотрении идеального газа
даже не упоминалось. Однако слабые взаимодействия между
молекулами, которые почти не сказываются на равновесных
свойствах системы, должны обязательно быть приняты во
внимание, как только возникает вопрос о приходе газа к
равновесию. От эффективности этих взаимодействий зависит
время релаксации.
В. газе такие взаимодействия возможны лишь на очень
близких расстояниях и фактически сводятся к отражению
молекул друг от друга — соударениям. Столкновения
сильно запутывают траекторию движения даже отдельной
частицы, а тем более всего газа в целом, что и обусловливает
наличие у газа требуемого свойства размешивания.
111
Не любое взаимодействие и не в любой системе может
приводить к достаточно эффективному размешиванию. Для
газа существование такого свойства, обусловленного
именно механизмом соударений, было теоретически доказано
Крыловым. Оно подтверждено впоследствии машинными
экспериментами. С их помощью удается проследить за
траекторией движения системы многих частиц при условии,
что она подчиняется ньютоновским уравнениям, а
столкновения носят упругий характер. Как выяснилось, достаточно
каждой частице испытать два-три столкновения, чтобы
первоначальное распределение по скоростям
трансформировалось в максвелловское, а энтропия достигла равновесной,
т. е. максимальной величины.
Вынужденная релаксация. Встречаются, однако, системы,;
которые вовсе не обладают свойством размешивания. Их
приход к равновесию вызван не внутрисистемным
взаимодействием, а исключительно внешним воздействием. Время
релаксации в этом случае зависит от того, насколько сильно
взаимодействие системы с окружающими ее телами или
средой. Вынужденная, индуцированная релаксация, которая
происходит в этом случае, возникает только потому, что
свойством размешиваться обладает внешняя среда, с
которой система взаимодействует. Именно эта среда, все время
сохраняя состояние равновесия, постепенно заставляет
прийти в него и рассматриваемую систему.
Так, например, устанавливается равновесное
распределение по колебательным и вращательным состояниям
молекул. Роль среды играет поступательное движение, так как
возбуждение внутримолекулярных степеней свободы
производится за счет запасов кинетической энергии
сталкивающихся частиц. Равновесные свойства очень разреженного
газа также восстанавливаются не самопроизвольно, а
благодаря воздействию извне, со стороны стенок сосуда, если
они термостатированы. Свойство размешивания играет в
кинетике изолированных систем такую же роль, как
микроканоническое распределение Гиббса в теории равновесного
состояния, а способность системы испытывать внешнюю
релаксацию является кинетическим эквивалентом
канонического распределения Гиббса.
Оценка частоты столкновений. Так ли часты соударения
молекул а газе, чтобы обеспечить достаточно быстрый
приход к равновесию? Ответ на этот вопрос дает элементарный
расчет числа столкновений, которые претерпевает моле*
кула, представляющая собой жесткую сферу радиуса г1#
Идею расчета легко понять, если вообразить, что все моле-
112
кулы газа неподвижны, кроме той одной, за которой мы
наблюдаем. Она прокладывает себе путь, время от времени
наталкиваясь на другие молекулы радиуса г2. Проходя в
течение одной секунды расстояние, равное ее скорости, она
испытывает столько столкновений, сколько молекул
оказывается у нее на пути.
Последнее обстоятельство нуждается в уточнении. В
случае плавного протяженного взаимодействия между
частицами не так-то просто определить, какие молекулы считать
столкнувшимися, а какие — нет. Модель жестких сфер тем
и хороша, что в ней этот вопрос решается геометрически.
Молекулы столкнутся, если их объемы в процессе движения
пересекаются — в противном случае столкновения не
произойдет. Окружив центр летящей молекулы сферой
радиуса гг + г2 = J?, можно утверждать, что столкновение
состоится лишь в том случае, если центр молекулы-мишени
будет отстоять от траектории центра летящей молекулы не
далее, чем на R. Иными словами, за одну секунду произойдут
столкновения только с теми молекулами, центры которых
попадают внутрь цилиндра с сечением а = nR2 и
образующей v. Его объем равен ov, плотность частиц в единице
объема — тг, а значит число соударений
v = пои. A5.1)
Приведенная оценка была бы удовлетворительной, если
бы скорость налетающей частицы резко отличалась в
большую сторону от скоростей тех, с которыми ей приходится
сталкиваться. Так, например, обстоит дело, когда речь идет
об электронах, движущихся в газе: их тепловая скорость
больше молекулярной, так как меньше масса. Если же
происходят столкновения между молекулами соизмеримых масс,
а тем более между одинаковыми молекулами, то расчет
нуждается в уточнении. В этом случае не только движущаяся
частица бомбардирует мишени, но и они, в свою очередь^
атакуют ее.
Столкновения при движении с заданной скоростью*
Оказывается, что расчет и в этом случае может быть сведен
к уже проделанному. Следует лишь применить прием,
широко используемый в кинетике,— разбиение на подансамбли
коллектива соударяющихся молекул. Если перейти в
систему координат, связанную с выбранной молекулой,
которая движется со скоростью v, то все прочие молекулы могут
быть классифицированы по одному единственному
признаку — с какой относительной скоростью w они налетают на
нашу избранницу. Эта классификация задается максвеллов-
JPuc. 41. Частицы,
которым
предстоит столкнуться,
.находятся внутри
цилиндра с
образующей W.
Рис. 42. Увеличение
частоты столкновений с ростом
скорости движения сквозь
газ.
«ским распределением налетающих молекул по их
скоростям v', которое может быть переписано как распределение
по относительным скоростям w = v' — v в системе
координат, движущейся вместе с избранной молекулой со
скоростью v:
my'2 m(v+wJ
dW (▼') = 4~ e*Fdw' = -J-e i^~dw = dWy (w).
A5.2)
Здесь m — масса налетающих молекул, отличная от М-
массы избранной нами частицы.
Если теперь выделить подансамбль частиц, в котором
все молекулы имеют заданную относительную скорость
движения w (рис. 41), то все рассуждения, приведенные в
обоснование A5.1), могут быть повторены. В самом деле,
налетает ли одйа молекула со скоростью w на застывших в
ожидании членов выбранного подансамбля, или же она,
оставаясь неподвижной, выдерживает натиск молекул этого
подансамбля, надвигающихся на нее с той же относительной
скоростью, число столкновений будет одним и тем же.
Поэтому для столкновений с заданным подансамблем можно
сразу же записать
dvY = owndWY(w), A5.3)
а полное число столкновений для молекулы со скоростью
движения v будет равно
A5.4)
114
X
где интеграл вероятности Ф (х) = —^= 1 e~z dz, a a = т/2кТ*
_ о
При jAxy^l, когда налетающая частица движется со
скоростью, значительно превышающей среднюю скорость
молекул-мишеней, 0A/^аи) ж 1 и число столкновений vv ->
—*nov, как в A5.1). Зато при v -> О число столкновений не
обращается в нуль, как это было бы при неподвижных ми-
2ап -,
шенях, а оказывается равным п/— = n(JV • Оно тем больше,,
чем интенсивнее тепловое движение молекул-мишеней,
налетающих на покоящуюся частицу (рис. 42).
Средняя частота столкновений. Примем теперь во
внимание, что после каждого столкновения скорость движения
молекулы изменяется. Доля времени, которую молекула
проводит в состоянии с заданной скоростью v, определяется
распределением Максвелла dW(\), а полное число
столкновений, которое она испытывает, бывая в самых разных
состояниях, равно
v = J vydW (v) = an J f wdW (v') dW (v). A5.5)
v v'
Переходя к переменным w и v0 = —Zr~\mY •> получаем
dW(\).dW(y') = dTF(w).dVT(v0), A5.6)
где dW(vr) — Iм" 1 e 2kTdvr
есть безусловное распределение по относительным
скоростям, a dW(\0) — по скорости центра тяжести
сталкивающихся молекул (|л = mM/(m + М) — приведенная масса).
Подставив A5.6) в A5.5) и проинтегрировав по v0,
находим v = an \ wdW (w) = anw или
v = па У = 1/ —^т— паи =?= I/ —■ паи, A5.7)
где и = I/ —rp» v = *
Таким образом, полнор число столкновений получается
из A5.1) заменой и на w, а зависимость v(v) качественно
повторяет зависимость vv(у), показанную на рис. 42, если рас-
115
Рис, 43. Схема опыта по
рассеянию молекулярного
пучка в газе.
сматривать и как
функцию М при
фиксированной температуре. Когда
М = т, из A5.7)
получается
v = У2пои. A5.8)
Видно, что движение
мишеней увеличивает
число столкновений одинаковых молекул всего лишь в 1,4
раза в сравнении с тем случаем, когда они неподвижны.
Мы можем теперь оценить порядок величины времени
свободного пробега молекул при нормальных условиях:
п = 1019 1/см3, v = 105 см/с; гг = г2 = 2-10-8 см. Сечение-
столкновений равно в этом случае 50-10~16 см2, а
v = K2".50.10-16.1019.105 « 7-109 Гц. A5.9)
Следовательно, максвелловское распределение по скоростям,
если оно было каким-то образом нарушено,
восстанавливается в течение наносекунд.
Экспериментальная проверка. Когда вводится новое
физическое представление или понятие, всегда желательно
иметь прямое экспериментальное подтверждение его
существования. Оно было получено в опыте Борна и Бормана,
в котором впервые удалось определить длину свободного
пробега молекул в газе.
Для этой цели сфокусированный пучок молекул
пропускался сквозь газ не слишком высокой плотности. Все
молекулы — каждая в свое время — испытывали столкновения
и, сворачивая с траектории пучка, «выходили из ,строяк
Поэтому, по мере удаления от источника, число молекул в
пучке непрерывно убывало (рис. 43). Это число можно было
просто измерить, поставив на пути пучка перегородку.
Выяснилось, что число осевших молекул экспоненциально
убывало в зависимости от расстояния между перегородкой и
источником.
Такой характер убывания предвидел еще Клаузиус,
Число молекул, испытавших соударения и поэтому
покинувших пучок между х ж х -\- dxy должно быть пропорциональ-
116
но dx и числу молекул N(x), благополучно долетевших до
этого рубежа, т. е. не испытавших соударений в интервале @, х):
—UN = a.N{x)dx. A5.10)
Коэффициент пропорциональности не может зависеть от х,
так как нет никаких причин считать, что в каком-нибудь
интервале dx соударения случаются относительно чаще,}
чем в другом. Однако эта величина, имеющая смысл числа
соударений на единице пути, может, вообще говоря *
зависеть от скорости движения молекул, как это имело место
в A5.4).
Решая A5.10), находим число частиц1, которые прошли
без единого соударения путь х:
Щх) = Щ0)е~™. A5.11)
Этой величине и должна быть пропорциональна толщина
напыленного слоя в я-сечении. Результаты опыта
подтверждают и качественно, и количественно эту зависимость;
более того, откладывая In N от х, легко измерить по наклону
прямой величину а, которая, как нетрудно видеть, равна
обратной длине свободного пробега молекул в газе х = L
Длина пробега. Действительно, по определению
оо
I = j xdW (х), где dW(x) есть вероятность пролететь без со-
о
ударений путь х, а затем испытать столкновение в
интервале (х, х + dx). Эта вероятность определяется отношением
числа молекул, испытавших первое столкновение в
указанном интервале d£, к общему числу молекул iV@), которые
«вышли на старт» т. е.
\ dN N (х) j — ах 7
A5.12)
Поэтому
оо
—ах 1
а
= e4j-. A5.13)
Средняя длина свободного пробега I связана с временем
пробега т0 = v^:
I = vv A5.14)
117
Рис. 44. Излучение,
прерванное по фазе
столкновениями, и его спектр /(со).
Учитывая, что и х — vt, можно вывести распределение
по временам пробега, подставляя A5.14) в A5.13):
t_
dW(t)=±e 4dt. A5.15)
Оно также доступно проверке — спектроскопически.
Согласно модели Лоренца, каждое столкновение скачком
меняет фазу электромагнитной волны, которую высвечивает
возбужденный атом на своей частоте соо. Продолжительность
свечения монохроматического цуга (рис. 44) определяется
вероятностью пролететь этот интервал времени без
соударений: Wo = ехр (—1/%0). Можно показать, что форма спектра
излучения в этом случае определяется как
A5.16)
Такой контур линии называется лоренцовским или ударным.
По его ширине можно судить о времени свободного пробега
молекул газа.
В силу зависимости т0 от v длина пробега 1(и)
монотонно возрастает с увеличением скорости, стремясь к своему
верхнему пределу 1/шх, который достигается при v > i/.
Средняя длина свободного пробега может быть определена
как
7 v \ ~ v i I l/ rn
I = « — = A = V :—r-r.
\vv ] v na * m-\- M
A5.17)
Она зависит лишь от плотности газа и не превышает
величины 1/шх. Два взаимосвязанных параметра: v и X играют
фундаментальную роль в построении физической кинетики в
газовой фазе. При обычных плотностях п ~ 1019 1/см3 и а =*
= 5'10~15 см2 X ^ 2• 10"б см. Однако, откачивая сосуд,
можно существенно удлинить X: при р = 10 атм X « 0,2 смя
118
а при р = 10 атм X « 2 см. В этих легко реализующихся
условиях проще всего наблюдать эффекты, подобные опыту
Борна и Бормана, так как X становится макроскопических
размеров. При еще больших разрежениях, когда X
превышает размеры сосуда, газ превращается в так называемый
физический вакуум или ультраразреженный газ, который
по всем своим свойствам резко отличается от плотного,
обычного газа, как это будет видно из дальнейшего.
§ 16. ЯВЛЕНИЯ ПЕРЕНОСА
Локальное равновесие. Мы можем теперь приступить
вплотную к решению основной задачи кинетики —
описанию необратимых процессов. К сожалению, общие
представления о характере размешивания применить к конкретным
задачам не просто. Они лишь укрепляют нашу уверенность
в том, что одного-двух столкновений вполне достаточно*
чтобы в системе полностью восстановилось равновесное
распределение по скоростям. Практическим воплощением
этой уверенности является представление о локальном
равновесии, лежащее в основе рассмотрения большинства
необратимых, неравновесных процессов. Эта гипотеза
является крайним выражением идеи, состоящей в том, что
столкновения молекул в газе немедленно приводят к
восстановлению равновесия там, где они случаются. Считается, что
обмен энергией и импульсом между частицами происходит
таким образом, что после первого же столкновения каждая
молекула приобретает равновесные свойства, характерные
для той точки пространства, где оно произошло. Область
применимости этой гипотезы ограничена медленно
протекающими необратимыми процессами, когда в каждой точке
пространства можно ввести представление о локальной
температуре, плотности и т. п. К таким процессам относятся
прежде всего явления переноса: теплопроводность,
диффузия, вязкость и некоторые другие, которые, как это
известно из повседневного опыта, протекают достаточно медленно*
Хорошо известно, например, что если через плоский
слой газа течет поток тепла от горячей стенки к холодной,
то, хотя газу в целом, пребывающему в неравновесном
состоянии, нельзя приписать никакой температуры,
«локальная температура» — в любой точке между стенками —
может быть непосредственно измерена. Это позволяет говорить
о «локальном равновесии» при своей собственной темпера-
119
туре в каждой микрообласти с линейными размерами
порядка %. Приток частиц из других областей непрерывно
нарушает или стремится нарушить это локальное равновесие, но
оно вновь и вновь восстанавливается за времена порядка
тс = 1/v. Пространственные размеры микрообластей
определяются тем, что молекулы сохрадяют присущие им
свойства только в свободном пробеге и немедленно меняют их
после столкновения. Именно поэтому, несмотря на
огромные скорости молекул и ~ 10б см/с, перенос энергии
происходит последовательно, из микрообласти в микрообласть,,
а не непосредственно от стенки к стенке. Продвигаясь из
горячих областей в холодные, молекула после каждого
свободного пробега вынуждается столкновением отдать избыток
своей энергии, сохранив лишь столько, сколько характерно
для той микрообластиг где это столкновение произошло.
И напротив, молекулы, двигающиеся в обратном
направлении, последовательно нагреваются, так что ни в какой
области они не воспринимаются как слишком инородное
включение, а после первого же удара совершенно сливаются с
«коренным населением».
Эта качественная картина: последовательное
приспособление молекул к свойствам тех точек пространства (и
моментов времени), где их настигает очередной удар, лежит в
основе большинства кинетических расчетов явлений
переноса. Но сами эти расчеты, как оказывается, могут быть
выполнены на самых разных уровнях строгости — от очень
примитивного до весьма сложного, в зависимости от того,
насколько полно учитываются различные детали явления*
Чтобы уяснить суть метода, имеет смысл начать с самого
элементарного.
Теплопроводность. Рассмотрим передачу тепла через
некоторое сечение в газе, перпендикулярное потоку энергии.
Справа и слева через это сечение проходят потоки частиц
/+ и /_, которые в отсутствие диффузии равны друг другу:
7+ = 7_ = 7о- Однако энергия, переносимая частицами^
которые движутся в противоположных направлениях, не
одинакова. Частицы, прилетающие слева, более «нагреты»*
а те, что приходят справа, более «холодны», если dTldx < О
(рис. 45).
Какова же энергия тех и других? Здесь и начинаются
упрощения. Предположим, что все частицы испытывают
последнее (перед переходом через сечение) соударение на
расстоянии к от него — ни ближе, ни дальше. Тогда те, что идут
слева, пронесут через сечение, расположенное в точке xt
120
Х-*
а:
Л-
—"У-
Силы
^трения
сдвига
■£- Напряжение
x'
Рис. 46. Распределение
скоростей в ламинарном потоке между
плоскопараллельными
пластинами, верхняя из которых
равномерно движется относительно
нижней.
тепловую энергию
щем газе. 8(# — X), характерную для
точки х — Я, а те, что справа,
придут к этому же сечению с энергией г(х + X).
Зависимость энергии от х обусловлена тем, что е = CVT/NO (Cv —
молярная теплоемкость, No — число Авогадро), а Т =
Т{х), Поток тепла (энергии) через сечение выразится как
разность этих двух величин, которая в однородном газе
равна
q = г (х — X) /_ — е (х + X) /+ =
A6.1)
Малость X в сравнении с макроскопическим масштабом
изменения Т оправдывает разложение в ряд Тейлора Т(х —
— X) и Т(х + X) и возможность ограничиться членами
первого порядка, которые сохранены в A6.1).
То, что всем частицам в потоке приписывается
одинаковая энергия, в том числе и кинетическая, строго говоря,
неверно, так как последняя во всяком случае зависит от
скорости движения и не мо^ет усредняться отдельно от /0,
Однако эта погрешность отчасти оправдана тем, что и сам
поток оценивается методом Джоуля, в котором всем
частицам приписывается одинаковая скорость v. Считая к тому
же, что все они движутся только в трех перпендикулярных
направлениях (в каждом туда и обратно в равных
количествах), нетрудно видеть, что jQ = — vn, так что
d*
■ к-
dT
dx'
A6.2)
121
Что поток тепла пропорционален градиенту
температуры и противоположен ему по знаку, утверждалось еще
«законом Фурье». Подтверждение этой эмпирической
закономерности прямым кинетическим расчетом, конечно, ценно.
Не менее важно и то, что таким образом удается рассчитать
коэффициент теплопроводности
и т 163
х~~ з n0 - з ИГ 11ОЛЗ>
и его зависимость от различных параметров газа (М —
молекулярная масса). В частности, оказывается, сколь это ни
странно на первый взгляд, что х не зависит от плотности
газа, ибо К « 1/шх.
Вязкость. Внутреннее трение, или вязкость, газа
обнаруживается в том случае, когда газ находится в движении:
течет по трубе или обтекает какую-нибудь поверхность*
Слои, прилегающие к твердой поверхности (крылу,
стенкам трубки или сосуда), тормозятся трением об эту
поверхность и замедляются, а слои, расположенные в большем
удалении, трутся друг о друга. В результате наблюдается
постепенное замедление скорости течения при приближении к
поверхности (рис. 46).
Но как получается, что слои газа испытывают
внутреннее трение, несмотря на то, что молекулы, из которых они
состоят, большую часть времени не взаимодействуют между
собой? Дело опять-таки в столкновениях. Тепловая
скорость молекул значительно превышает по величине
макроскопическую скорость перемещения газа как целого и.
Будучи направлена в разные стороны, она выносит молекулу из
слоя, двигающегося медленно, в слой, перемещающийся
более быстро, и наоборот. Испытав столкновение на
территории соседнего слоя, молекула изменяет свою
макроскопическую скорость таким образом, чтобы стать неотличимой от
новообретенных соседей, т. е. либо ускоряется, либо
замедляется, отдавая им при этом разницу в импульсе.
Суммарный импульс, перенесенный «эмигрантами» из одного слоя
в другой (в единицу времени),— это и есть сила трения,
действующая в сечении, разделяющем слои (см. рис. 46).
Это разъяснение показывает, что расчет может быть
полностью уподоблен предыдущему. Единственное различив
состоит в том, что в данном случае переносится не энергия*
а макроскопический импульс ти(х), где и(х) есть скорость
течения: газа перпендикулярно оси х. Вместо Cv/N0 теперь
фигурирует т, а вместо Т{х) величина и(х), все же осталь-
122
ное остается прежним. Поэтому, не повторяй выкладок,,
можно сразу же написать по аналогии с A6.2):
Коэффициент вязкости
о о
как и коэффициент теплопроводности, не зависит от
плотности газа (закон Максвелла).
Из сопоставления формул A6.5) и A6.3) можно получить
важное соотношение между кинетическими коэффициентами,
из которого исключены микроскопические параметры:
^=1. A6.6)
Опыт свидетельствует о том, что и в самом деле величина
kM/v)Cv сохраняется постоянной. Если бы мы не имели
возможности с единой точки зрения разобраться в природе-
столь разных на первый взгляд явлений, как
теплопроводность и вязкость, этот факт мог бы показаться
парадоксальным.
Вместе с тем оказывается, что при переходе от одного
газа к другому численная величина kM/t\Cv может
изменяться, оставаясь по порядку величины, близкой к единице.
Этому обстоятельству не следует удивляться. Ошибка в
оценке численного множителя неизбежна в таких относительно
грубых расчетах. Информация о существе явленийг о
величине и связях между коэффициентами настолько ценное
приобретение, что на первых порах приходится мириться с
некоторой недостаточностью метода. В дальнейшем мы
рассмотрим возможные причины его несовершенства и пути их
преодоления.
Диффузия. Под диффузией понимают проникновение
одного вещества в другое, обусловленное тепловым
движением молекул. Если речь идет о газе, можно было бы
сослаться в качестве примера на то, как распространяется аромат
от человека, недавно побывавшего в парикмахерской.
Однако процесс смешения газов может быть ускорен
конвекционными токами, вызванными ветром и даже дыханием,
т. е. чисто механическим смешением, не имеющим к
диффузии никакого отношения. Поэтому в чистом виде диффузию
можно наблюдать лишь в условиях эксперимента, подобного
тому, который был осуществлен Лошмидтом —
первооткрывателем явления.
123
Две трубки, наполненные разными газами при одном и
том же давлении, приводятся в соприкосновение, после
чего кран, разделявший их, открывается и газы получают
возможность смешиваться. Проверяя состав газа через
некоторое время, можно убедиться, что возникшая смесь тем более
однородна, чем больше времени прошло с начала
эксперимента. Надо заметить, что процесс этот довольно длительный
(часы), так что на небольшом отрезке времени его можно
считать квазистационарным, т. е. таким, который идет при
почти неизменном градиенте концентраций. Это позволяет
рассмотреть его с тех же позиций, что и предыдущие два
явления. Для простоты предположим,, что мы имеем дело с
самодиффузией, т. е. с проникновением некоторых
молекул в среду, представляющую собой тот же самый газ. Этот
процесс поддается наблюдению, если диффундирующие
молекулы представляют собой изотопы одного и того же
элемента, которые удается различать соответствующими
методами.
Как рассчитать поток частиц через перпендикулярное к
нему сечение, если плотность газа в пространстве не
одинакова? Иначе говоря, что понимать под п в оценке Джоуля
■— nv = /±, в какой именно точке следует брать п(х)?
Согласно гипотезе лока ьного равновесия, плотность частиц в
колоннах молекул, направляющихся к рассматриваемому
сечению, задается плотностью газа в тех точках, где они
формировались. После каждого перехода длиной X эти колонны
перестраиваются в соответствии с плотностью частиц в
точке,, где их настигло очередное столкновение. Последний
переход перед сечением начинается на расстоянии X от него ж%
следовательно, плотность частиц в потоке, пересекающем
это сечение у должна быть п(х — X), если они движутся
слева направо, и п(х + Я), если наоборот.
Таким образом, /_ = — п(х — X), а /+ =—• п (х + X),
причем /+ =/_. Именно вследствие различия потоков справа и
слева результирующий диффузионный поток равен
/ = /- —7+в ^Ъ[п(х — Х) — п(х + *,)]= A6.7)
1 — dn ^ dn
где jD = ^.X«_i_ A6.8)
— коэффициент диффузии.
124
Из сопоставления A6.8) с A6.6) и A6.3) находим еще два
соотношения, связывающих коэффициенты переноса:
"^7 = 1. A6-9)
= 1, A6.10)
где р = пт. Более строгая теория следующим образом
уточняет эти соотношения (для газа жестких шаров):
_ ъ_ РШу _ 12
С учетом этих численных поправок можно получить:
ел / у кал В /■ г л? / Т1
О V ~М см-град-с ' * а см-с' ра у М
-^-^, где а=6,2.10-4; р=8,4.10; у = 8,3-Ю-3.
Уточнение расчета. Использованный выше метод расчета
слишком примитивизирует картину явления ради краткости
и простоты ее описания. Тем не менее найденная таким
образом расшифровка кинетических коэффициентов
правильно передает их зависимость от любых варьируемых
параметров. Чтобы удостовериться в этом, мы рассмотрим здесь
заново перенос тепла и материи, освободившись, по мере
возможности, от наиболее грубых допущений.
Пусть же молекулы движутся во всех направлениях и с
любыми скоростями, и пусть они испытывают последние
соударения и далеко, и близко от рассматриваемого сечения*
Из общего потока молекул, пролетающих сквозь это сечение„
выделим сначала те, что движутся к нему с абсолютной
скоростью и внутри телесного угла <2Q, ось которого
наклонена к оси х под углом 0 (рис. 47). Среди этих молекул
отберем лишь те, которые испытали последнее столкновение на
расстоянии jR от сечения. Сколько же таких молекул
пролетит в единицу времени через выбранное единичное
сечение? Поток равен vxdn = и cos QndW, но вероятность того?]
что мы имеем дело с молекулами, взявшими старт на
расстоянии R со скоростью и, определяется произведением
вероятностей: dW = dW(v)'dW(R). Здесь dW(R) —
распределение по длинам свободного пробега A5.13), a dW(\) =
= fo(v)d\ — обычное распределение Максвелла с плотна*
стью
/ Л , т \ 9/9. / 2 \
A6.12)
125
x+Rcosd
x-RcosO
Рис. 47. Встречные потоки частиц одинаковой скорости
с равноудаленных точек старта, где испытано последнее
столкновение.
в которой температура является функцией той точки
пространства, где произошло столкновение: Т = Т(х).
Таким образом, величина потока частиц зависит от
температуры той точки, из которой они стартуют, а также от
плотности частиц в ее окрестности п(х). Отсюда следует,
что встречные потоки частиц из двух противостоящих друг
другу точек, лежащих на сфере радиуса R (см. рис. 47),
отличаются, кроме знака, только величиной множителя nfot
задающего их абсолютную величину:
d/. = v cos Q(nfo)jd\dW(R), A6ЛЗа)
dU = v cos Q(nfo)+d\dW(R). A6.136)
Индексы ± при обозначении nf0 означают, что эта
зависящая от координаты величина берется в точках х + R cos 9
или х — R cos 6 соответственно, в которых происходит
последнее столкновение перед «финишем» на рубеже х.
Обращает на себя внимание, что d/_ Ф dj+ и при п = const,
если только в температурном отношении среда неоднородна.
Различие между (/0)_ и (/0)+ приводит к тому, что поток
высокоэнергетических частиц направляется из горячих точек
в холодные, тогда как низкоэнергетические частицы,
напротив, в большем количестве прибывают из холодных мест в
горячие. Результирующий поток частиц данной скорости есть
d] = dj_ — dj+ = v cos 6 [(тг/0)_ —
*0. A6.14)
126
Он может отличаться от нуля, даже если 7 = j dj = 0*
Этим обеспечивается перенос тепла из горячих точек в
холодные в отсутствие диффузии.
Если точки старта молекул удалены от рассматриваемого
сечения на величину порядка Я, которую можно считать
малой в сравнении с макроскопическими масштабами^ то
следует воспользоваться разложением
[(п/о)_ - (»/„)+] = - 2 ±Ш R cos 9. A6.15)
Подставляя A6.15) в A6.14), имеем
di = — 2v^ff^- v4v cos2 Qd£iRdW(R). A6.16)
Это выражение легко интегрируется по углам и длинам
свободного пробега, после чего получается
dj = -2v -^al 4nv* Z^Qldv = -^v2 -1^1 dv, A6.17)
CO
так как I = j RdW (R) = v%Q в соответствии с A5.14), a
сшзЧГ = 1/6.
Если заменить теперь то(у) на хс — 1/v, то
интегрирование по скоростям в A6.17) приводит к следующему
результату:
тс d(nu2) %ck d(nT)
-—-br = —»-sr-
A6.18)
Выполняя дифференцирование, находим
I--D%-B%, A6.19)
Z>-^=^, B-^l. A6.20,
Если принять другую зависимость то(у) в A6.18), то резуль*
тат может измениться только численно. Так, например^
при диффузии легких частиц в тяжелом газе т0 =
[nov] = X/v, и после усреднения по v получается, как
в A6,8): # = 4 vX=vHc/3, т. е. D ~ у2, а не у2. В рамках
модели жестких сфер оба результата правомерны и
находятся в удовлетворительном соответствии с простой оцен-
127
ro&D, данной в A6.8). На самом же деле зависимость хо(и)
следует рассчитывать с учетом реального
межмолекулярного взаимодействия, принимая во внимание как отталкивание
частиц, так и их притяжение.
Второе слагаемое в A6.19) описывает явление,
называемое термодиффузией. От обычной диффузии оно отличается
тем, что частицы устремляются из горячих мест в холодные
вследствие более высокой скорости передвижения, а не из-
за количественного преобладания.
С помощью A6.17) нетрудно оценить и поток тепла, т. е.
энергии, переносимой движущимися молекулами. В
простейшем случае одноатомного газа, которым мы здесь
ограничимся 2, речь идет, естественно, лишь о кинетической энергии,
так что при xo(v) = тс
iv2 ,. m\ d(n7) 5тс&2 d(nT2)
2 "J 6 dx 2т dx '
Выполнив дифференцирование,; получаем
Видно, что перенос тепла стимулируется не только
градиентом температуры,, но и градиентом концентраций» так
как вместе с материей переносится и присущая ей энергия.
Это обстоятельство затрудняет сопоставление полученного
результата с простой оценкой теплопроводности,
приведенной выше. Последняя была найдена при дополнительном
условии: п = const, тогда как формула A6.21) описывает
более общую и чаще встречающуюся ситуацию. Она
возникает, например, при истечении тепла, из жилого помещения
^ерез двойную оконную раму, внутреннее стекло которой
имеет комнатную температуру Tt, а внешнее — наружную
Те (см. рис. 45). Давление в слое воздуха между стеклами
во всех его точках нормальное. Если считать газ
идеальным, то
р = пкТ = const или 1 -g = - ± -|-г> A6'23)
2 Для многоатомных молекул q = I -^— + i-~- \ dj, где i —
^ J L 2 2 I
число всех возбужденных степеней свободы, за вычетом поступательных.
Расчет от этого не становится сложнее.
128
т. е. градиент концентраций выражается через градиент
температур. Исключая его из A6.21) с помощью A6.23),
получаем для стационарного потока закон Фурье:
T dT , Лп о/ч
= _K_ A6.24)
в котором х есть в обычном смысле коэффициент
теплопроводности. Используя в A6.24) формулы A6.20) и A6.22),,
можно убедиться, что х отличается от К всего в два раза:
я К у В - Ък2'ГХсП Ъпк~" Мб 25}
так что уплотнение молекул в направлении от горячего
стекла к холодному не очень сильно уменьшает
теплопроводность газа. Сравнивая ее величину с приближенной оцен-
кой A6.3), в которой М = Nom, Cv = -^^Nq, легко видеть,
что различие исчерпывается численным множителем.
Ввиду неопределенности самого v в A6.3) это принципиального
значения не имеет. Все же важнейшие черты процесса:
зависимость х от температуры, независимость от плотности и,,
наконец, сам порядок величины переданы простым
расчетом вполне удовлетворительно.
Теплопередача. Для демонстрации того, насколько
существенно это приобретение, приведем самый простой и уже
обсуждавшийся пример: рассчитаем поток тепла через
воздушную прослойку оконной рамы. Поскольку температуры
внутри и снаружи помещения изменяются достаточно
медленно, процесс теплопередачи можно считать, как и выше,
квазистационарным (установившимся), а в х выделить
только самое существенное — зависимость от температуры:
A6.26)
Saym
Такая расшифровка х конкретизирует выражение A6.24),
придавая ему смысл дифференциального уравнения,
определяющего зависимость Т{х) в простенке между стеклами:
где q — константа, подлежащая определению впоследствии.
Решая A6.27), находим
5 А Ж. Бгрштейн 128
Принимая во внимание, что температуры стекол равны
температуре внутренней и внешней среды соответственно,
можно сформулировать следующие краевые условия:
Т@) = Tt\ T(L) = Te. A6.29)
С помощью первого из этих условий определяется константа
интегрирования в A6.28): С = Г?/2, Затем, используя
второе условие, можно рассчитать и сам поток:
D6-30>
В этом окончательном выражении поток тепла
непосредственно выражен через заданные условиями опыта величины:
Ти Те и L. Зависимость от них могла бы быть и иной, если
бы х иначе изменялась с температурой, чем в A6.26).
Что же касается зависимости, а точнее независимости от
плотности, то она заслуживает специального рассмотрения»
В постоянстве х таится парадокс, свидетельствующий-об
ограниченной применимости полученных результатов.
Действительно, как понять то, что по мере уменьшения
плотности газа, т. е. числа частиц, участвующих в переносе
энергии, теплопроводность ничуть не ухудшается? До поры до
времени это естественно объясняется тем, что возрастающая
длина свободного пробега молекул компенсирует
уменьшение их количества. Однако в конце концов можно ведь
настолько откачать газ в сосуде, что образуется вакуум.
Тогда-то теплопроводность наверняка обратится в нуль ввиду
отсутствия переносчиков тепла. Между тем сам факт
существования этой качественно иной ситуации невозможно
усмотреть в полученных выше результатах: к = const
независимо от степени разрежения газа.
Ультраразреженный газ. Это соображение естественно
приводит нас к необходимости обсудить пределы
применимости всех расчетов — как простых, так и сложных,
опирающихся на представление о локальном равновесии.
Считается, что каждую точку газообразной среды, а точнее
микрообласть масштаба X можно рассматривать как почти
равновесную, со своими собственными локальными
характеристиками состояния: температурой и плотностью. Но всегда ли
это так? Ведь X « Una = kT/op, и, следовательно,
понижая давление (скажем, хотя бы до 1-10 мм рт. ст.), мы
можем добиться того, что длина пробега станет
макроскопической величиной, намного превышающей габариты сосуда,
В этой ситуации молекулы будут значительно чаще стал-
130
киваться с его стенками, чем с себе подобными. Такого
рода ультраразреженный газ (физический вакуум) ведет себя
совершенно иначе с кинетической точки зрения, чем
плотные газы.
Следует заметить, что отражение от стенок сосуда не
обязательно является упругим. При ударе о стенку возможно
прилипание к ней (абсорбция), позволяющее обмениваться
с пей энергией. Если стенка горячее, чем газ, то после
пребывания на ней молекулы уносят дополнительную энергию;
в противном случае энергия переходит от молекул к стенке,
т. е. во внешнюю среду. Благодаря таким неупругим
процессам осуществляется, в Частности^ теплообмен между
газом и окружением. Чтобы подогреть газг подогревают
стенки сосуда, и лишь через них — его содержимое.
В ультраразреженном газе только внешний теплообмен
и способствует восстановлению и поддержанию равновесия*
Ультраразреженный газ не обладает свойством
«размешиваться» самостоятельно, точнее обладает им в столь
незначительной степени, что воздействие внешней среды быстрее
приводит к равновесию. Это обстоятельство существенно
сказывается на всех явлениях переноса. Понятие
локального равновесия теряет всякий смысл, о внутреннее
трении также говорить не приходится: молекулы движутся,
игнорируя друг друга. Ничто не препятствует и взаимному
проникновению одного газа в другой. Что же касается
теплопроводности, то перенос тепла осуществляется
непосредственно от стенки до стенки, а не эстафетной передачей,
как раньше.
Действительно, в стационарных условиях из / молекул,
ежесекундно ударяющихся о стенку, а/ прилипает к ней, и
ровно столько же испаряется, унося с собой среднюю
энергию, соответствующую температуре этой поверхности.
Поскольку, однако, в обратном потоке имеется A — а))
упруго отраженных частиц, сохранивших свою энергию
неизменной, оказывается, что в промежутке между стенками
циркулируют два сорта частиц, движущихся в обоих
направлениях (рис. 48), причем
/ = it + it = h + 77; п = nt + nt + Щ + щ. A6.31)
Здесь знаки означают направление движения, а индексы —
номер стенки, с которой молекулы находятся в равновесии.
Поток тепла равен, очевидно,
q = ^[T2(h-Jt) + T1(h-jt)l A6.32)
5* 131
t 11 ы t t t
4V/////s
Вакуум
•
Ji
W/Z/л
•
-
\j2 •
у//
•
Рис. 48. Встречные потоки,
переносящие тепло в
ультраразреженном газе.
Плотный газ
0L
Рис. 49. Изменение
эффективного коэффициента
теплопроводности с уплотнением газа.
и для его определения необходимо составить себе
представление об относительной величине всех потоков. Из
балансных соображений ясно, что
77 = it
1? = A
it = A — «) ь\
t = h + a/7.
Левая система относится к нижней стенке, правая — к
верхней. Из них следует, что
A — ос);7 = it = /7 = A — a)/i"-
A6.33)
Каждый из этих потоков состоит только из частиц, летящих
«туда» (обратно они возвращаются в составе другого
потока). Поэтому, в отличие от D.12), получается
/* = у
A6 34)
причем все щ-, вообще говоря, различны.
Различие плотностей частиц во встречных потоках
ультраразреженного газа может быть проиллюстрировано
эффектным экспериментом. Соединив короткой трубкой два
сосуда, в которых разреженный газ поддерживается при
температурах Т± и Г2, можно убедиться^ что в конце концов
потоки через трубку в обоих направлениях станут равны
друг другу: jtl= J7' Ввиду A6.34) это возможно лишь при
—- = ^-, так как плотность газа связана с его давлением,-
132
г2 Vi (ТЛ112
то и —-= —^ == -=г- , т. е. давление в соединенных сосу-
?i T±v2 \ * 1 /
дах перестает быть одинаковым, что и наблюдается.
Используя A6.33) и A6.34) в A6.31), нетрудно найти, что
Л- B - ее) /7 = B - а) /+ = \-^U A6.35)
Учитывая этот результат при подстановке A6.33) в A6.32),
нетрудно получить
«-T^-i^-C-'J- <«••">
Величина
^-•И^-тг^'-т-^- A637)
имеет смысл и размерность коэффициента теплопроводности
вакуума и линейно выражается через число оставшихся в
нем молекул. Этот результат справедлив, пока X ^> L. Как
только знак неравенства обращается, вступают в силу
представление о локальном равновесии и прежняя оценка х
A6.25), не зависящая от плотности газа. Таким образом,
разрешение парадокса состоит в том, что эта оценка верна
в ограниченных пределах по плотности: п^—г- (рис. 49).
Ток в газе. При комнатных температурах и атмосферном
давлении любой газ — диэлектрик. Тем не менее и в этих
условиях в газообразной фазе всегда имеется небольшая
разновесная концентрация зарядов, возникающих при тепловой
ионизации молекул. Подогревая газ, можно смещать
равновесие в пользу заряженных частиц. Когда становится
возможным наблюдение электропроводности газа, концентрация
ионов в единице объема все еще много меньше плотности
нейтральных частиц. Заметим, кстати, что эта концентрация
может быть и больше равновесной, если она создается
внешними источниками — проникающей радиацией или
эмиссией электронов с катода. Независимо от их происхождения,
заряды, оказавшиеся в разрядном промежутке, подчиняясь
приложенному полю, ложатся в дрейф в направлении
действующей на них силы и, двигаясь со скоростью w,
осуществляют перенос электричества между катодом и анодом,
превращая газ в проводник.
133
Рис. 50. Среднее
смещение иона в
последовательности свободных
пробегов,
происходящих во внешнем поле.
Когда проводимость униполярна, т. е. осуществляется
носителями одного знака, плотность тока равна
i = ewn, A6.38)
где п — концентрация ионовг а е — абсолютная величина
их заряда. Если к тому же скорость дрейфа прямо
пропорциональна полю
w = иЕх A6.39)
то выполняется закон Ома:
i = вЕ, A6.40)
причем проводимость
а = еип, A6.41)
где и — подвижность носителей тока. Для доказательства
закона Ома достаточно принять, что после столкновения
иона с молекулой направление его движения меняется так,;
что вектор скорости может быть с равной вероятностью
найден в любом телесном угле независимо от того, какова была
его ориентация до столкновения. Вследствие этого среднее
значение скорости после столкновения равно нулю. Иными
словами, каждое столкновение в среднем останавливает ион,
так* что ускорение его на свободном пробеге всякий раз
начинается сызнова. Именно поэтому дрейф в поле носит
равномерный характер, несмотря на характерное для
равномерно ускоренного движения квадратичное удлинение
свободного пробега со временем (рис. 50).
В самом деле, усредненный по направлениям свободный
пробег в поле Е* равный
134
надлежит усреднить еще по распределению времен пробега
D5.15):
о
После этого становится ясно, что скорость дрейфа
пропорциональна полю:
ш= — dW(v)&—-E} A6.42)
а подвижность носителей равна
A6.43)
Естественно, что подвижность оказывается тем больше, чем
легче носители заряда и чем меньше плотность среды /г0,
сквозь которую они движутся.
Эти качественные выводы были подтверждены опытами
Резерфорда, впервые измерившего подвижность ионов в
газе. Однако вместо ожидаемого результата
и__ 50 см (В с) A6 44)
т 300-10~22
эксперимент показал величину, на порядок меньшую. Эта
аномалия отчасти связана с неточной оценкой массы
заряженных частиц. Как правило, ионы газа благодаря заряду,
который они несут, притягивают к себе некоторое число
нейтральных частиц, создавая ассоциаты, движущиеся как
единое целое. Укрупненные таким образом ионы имеют
большую массу и, следовательно, меньшую подвижность.
Другой источник ошибки в оценке подвижности связан с
грубостью модели жестких шаров. Заряженные частицы
окружены дальнодействующим кулоновским полем. Оно
искажает траектории движения частиц далеко за пределами
собственного диаметра иона, т. е. столкновения
фактически происходят на больших расстояниях, чем это следует
из простых геометрических соображений. Иными словами,
эффективное сечение иона превышает размеры нейтральных
молекул, и вследствие этого частота его столкновений с ними
больше, а интервал между столкновениями (т0) меньше, чем
это принято в A6.44). Однако такие особенности поведения
заряженных частиц послужили лишь поводом для
уточнений теории электропроводности, которая (в остальных от-
135
ношениях оказалась вполне удовлетворительной (для ионов
любого вещества и обоих знаков).
Единственным, но очень важным исключением из
правила оказался тот случай, когда можно было подозревать, что
перенос электричества осуществляется свободными
электронами. Только так можно было объяснить аномально
высокую (до 104 см2/(В-с)) подвижность отрицательных
носителей тока в некоторых экспериментах. В нейтральных
средах, а также в случае сильных полей, когда прилипания к
молекулам не происходит, электроны преодолевают
макроскопические расстояния, оставаясь свободными. В таком
случае естественно ожидать, что подвижность резко
возрастает, так как масса электрона в 105 раз меньше массы
одноименного иона. При ближайшем рассмотрении формулы
A6.43) выясняется, что за счет этого обстоятельства
подвижность м@жет возрасти в ]fM/m, т. е. примерно в 200 раз по
сравнению с ионной, что и подтверждается экспериментом.
Однако этим дело не исчерпывается. При захвате
инициативы свободными электронами меняется не только масса
носителей, но и характер их продвижения сквозь среду.
Резкое различие в массах электрона и молекул качественно
меняет характер взаимодействия между ними при
столкновениях. В силу законов механики, доля энергии, отданной
при столкновении, определяется отношением масс
сталкивающихся частиц: чем меньше масса частицы, тем меньшую
долю своей энергии она способна передать большому телу
при столкновении. В этом легко убедиться, играя
вишневыми косточками против биллиардных шаров. Энергия Де,
теряемая электроном при столкновении, составляет лишь
небольшую долю / = Де/е = т/М = 10~5 от той, которую
несет он с собой (е). Тем самым нарушается принцип
локального равновесия, на котором основывались все предыдущие
построения. Столкновения не способны корректировать
энергию электрона таким образом, чтобы она приходила в
соответствие с локальной температурой тех точек
пространства, где они произошли. Напротив, продвигаясь сквозь
газ в направлении поля, электрон последовательно
накапливает энергию* сообщенную ему в свободном пробеге,
поскольку лишь незначительная доля ее рассеивается в тепло
при столкновениях. В результате температура электронного
газа, т. е. скорость его теплового движения, заметно
возрастает, а скорость дрейфа, напротив, несколько уменьшается.
В самом деле, не будучи в силах отобрать у электрона
всю накопленную им при разгоне энергию, столкновения
тем не менее весьма эффективно изменяют направление его
136
движения. Благодаря этому работа, совершенная полем*
равномерно ускоряет движение электронов во всех
направлениях, устанавливая распределение, близкое к максвел-
ловскому, равновесному. Только температура Ге,
фигурирующая в этом распределении, не равна локальной
температуре среды Г, а определяется средней энергией е = у vl =
3
= -тг кТе, которой располагал электрон в момент столкно-
La
вения.
Пока энергия электронов невелика, а потери и вовсе
незначительны, их температура линейно возрастает по мере
продвижения к аноду:
^кТе = ^жеЕх. A6.45)
Однако этот рост не может продолжаться бесконечно,
поскольку при каждом столкновении все же теряется /-я доля
энергии электрона е. При больших 8 она не является уже
малой величиной сравнительно с той добавкой, которая
приобретается в свободном пробеге. В конце концов рост 8
полностью прекращается, и все, что заимствуется у поля,
отводится в виде тепла в окружающую электрон среду.
Накопление энергии дрейфующего электрона
описывается уравнением
— 1[е —е0],
2
в котором е0 = -х-к Т. Если пренебречь вторым слагаемым,
то в = eEwt = еЕх, как это было в A6.45). Напротив, в
стационарном режиме de/dt = О, а
eEwxc eEwTc
е0 + —J— « ——.
Используя A6.42), получаем
2 2
mw mu
ИЛИ
м> = Нт
137
Отсюда видно, что дрейфовая скорость в V7/2 раз меньше
средней тепловой. Раскрывая смысл w с помощью A6.42)
и A6.43), находим
ти
откуда
A6.46)
Таким образом, кинетическая энергия электрона в
стационарном дрейфе в //2 раз превосходит работу,
совершаемую полем в одном свободном пробеге. Их температура Те
намного превосходит температуру окружающей среды, и
именно Те следует подставить вместо Т в формулу A6.43)
для оценки подвижности электронов:
1
и = (ек VllmEf. A6.47)
Таким образом, оказывается, что вследствие зависимости
температуры электронов от поля прямая пропорция между
w и Е уступает место соотношению
1
w = иЕ = (eKE VJ/m)\ л A6.48)
Понятие подвижности вследствие этого отчасти утрачивает
свое значение, поскольку эта величина перестает быть
константой. В полях ~10В/см при нормальных условиях и ~
~ 103 см2/(В-с), Те ~ 1000 К^ а кинетическая энергия
электронов ~0,1 эВ.
Формулы A6.45) и A6.46) описывают соответственно два
крайних случая: первая — участок разгона электронов*
где потери пренебрежимо малы,, вторая — стационарный
режим, в котором приобретение и расход энергии
компенсированы. Стартуя с катода, электрон по пути к аноду
переходит из первой области во вторую. Граница между ними,
очевидно, находится в той точке, где электронная температура^
Е
согласно обеим приближенным оценкам, одинакова: =j7f
= еЕхт. Отсюда
A6.49)
138
примерно в 100 раз превышает длину свободного пробега.
При нормальном давлении это все еще достаточно малая
величина: хт ~ 10 см. Поэтому дрейф электронов почти во
всем разрядном промежутке, за исключением очень узкого
слоя, носит в нормальных условиях стационарный
характер. Но при давлениях в 1000 раз меньше атмосферного
участок разгона удлиняется до макроскопических размеров, и,
если электроды разделены расстоянием порядка нескольких
сантиметров, стационарный режим вообще не достигается.
В таком случае температура электронов измеряется просто
пройденным ими путем, как об этом свидетельствует
формула A6.45). Благодаря этому электронам можно сообщить
любую наперед заданную энергию с помощью сетки,
расположенной вблизи катода, в пределах участка разгона.
Достигшие ее электроны будут иметь энергию, заданную
разностью потенциалов между сеткой и катодом.
Итак, нарушение локального равновесия при
электронном разряде, по существу, приводит к тому, что в
разрядном промежутке сосуществуют два газа: молекулярный и
электронный, каждый при своей собственной температуре.
Разрыв температур поддерживается и регулируется
полем — источником накопления энергии. Поэтому не
составляет труда увеличить его до такой степени, что энергии
теплового движения электронов окажется вполне достаточно
для возбуждения, а затем и ионизации нейтральных частиц
среды. Перешедшие при столкновениях с электронами в
возбужденные состояния атомы и молекулы высвечивают
приобретенную энергию в видимом диапазоне. На этом, в
принципе, основана работа газоразрядных ламп, остающихся
сравнительно холодными, несмотря на создаваемое ими
дневное освещение. Наряду с возбуждением молекул при
высокой электронной температуре становится возможной и
их ионизация, вследствие которой число носителей тока
умножается. Если же после ионизации электрон способен на
коротком отрезке пути снова накопить энергию,
достаточную для повторного совершения этого акта, то число
носителей лавинообразно возрастает по мере приближения к
аноду. Свой вклад в увеличение проводимости ^аза вносят
и положительные ионы, которые, кроме того, бомбардируя
катод, выбивают из него дополнительное количество
электронов. Вследствие всего этого при определенной разности
потенциалов возникает «пробой» газа — внезапное
превращение его в высокоионизированную проводящую среду.
139
Глава 2
ИЗЛУЧЕНИЕ
§ 17. ФЕНОМЕНОЛОГИЯ
Электромагнитное излучение, рассматриваемое с
корпускулярной точки зрения, весьма напоминает газ по
целому ряду феноменологических признаков. Как и газ, поле из-
лучепия невозможно удержать в ограниченном объеме, не
поместив его в замкнутую полость. Как и газ, излучение
«давит» на стенку, оказавшуюся на его пути. Сама собой на-
шрашивается аналогия с идеальным газом: если считать свет
ансамблем фотонов, Которые, двигаясь свободно и
прямолинейно, сталкиваются со стенками полости и отражаются от
них, вышеупомянутые свойства получают качественное
объяснение.
На этом, однако, аналогия кончается. В отличие от
молекулярного газа свет обладает способностью проникать в
любые стенки и поглощаться в них. Согласно экспериментально
установленному первому закону Ламберта, при прохождении
света частоты v сквозь материальную среду интенсивность
его непрерывно падает по мере продвижения в глубь
вещества, оставаясь тем не менее отличной от нуля на любом
конечном расстоянии:
Щх) = /@) ехр (-ю). A7.1)
Здесь 1@) — интенсивность в сечении х = 0, 1(х) — в любом
другом, a e(v) — так называемый коэффициент экстинкции
или удельное поглощение на единице длины пути,
существенно зависящее от частоты проникающего света.
Кроме того, если поток света с интенсивностью /0 падает
на стенку, то часть его г]/0 отражается от нее. Оставшаяся
часть проникает внутрь (рис. 51), причем a(v) —
коэффициент поглощения связан с г] простым соотношением: а =
= 1 — т] ^ 1. Из этой оставшейся части некоторая доля
а/0 ехр(—ed), пройдя сквозь стенку, выходит наружу, а
остальное поглощается внутри нее. Поэтому тот, кто вздумал
бы изучать термодинамические свойства излучения в
прозрачном сосуде, потерпел бы неудачу: свет удалился бы
наружу, оставив о себе воспоминание в виде легкого разогрева
стенок. Чтобы удержать излучение в замкнутом объеме,
нужно поместить его в толстостенный ящик из черного
материала или, напротив, в тонкостенный прозрачный сосуд, погру-
140
51. Отражение и пропускание I
света однородной средой. ^j
женныж в практически
неограниченную газообразную среду. В
обоих этих случаях можно быть
уверенным, что излучение не
проникает за пределы окружаю-
щей полость среды. Остается лишь ""*"
поглощение внутри нее. Посколь-
ку это поглощение принципиально -*■
неустранимо, может возникнуть —
впечатление, что излучение вооб- -*-
ще удержать невозможно. Это от- —
части верно: излучение, которое
в данный момент заполняет
полость, рано или поздно будет поглощено в ее стенках и
трансформируется в тепло. Однако верно и то, что среда,
окружающая полость при всякой отличной от нудя
температуре, излучает свет, попадающий в конечном счете внутрь
полости. Наличие двух взаимно компенсирующихся
процессов: поглощения и излучения — создает условия для
установления нулевого баланса: сколько света проникает из
полости в среду, столько же и возвращается из нее обратно
благодаря тепловому излучению. В условиях равновесия
баланс должен быть детальным: количество поглощенной и
излученной энергии должно быть скомпенсировано для каждой
спектральной компоненты излучения в отдельности.
Условие детального баланса на частоте v имеет* следовательно,
вид
= a(v)/0(v)f
A7.2)
где EQ(v) — излучательная способность стенок, т. е. полная
энергжя, излучаемая в единицу времени с единицы
поверхности в единичном интервале частот во все стороны, а /0(v) —
поток световой энергии в том же интервале частот, падающим
из полости на единицу поверхности стенки.
Согласно второму закону Ламберта, количество лучистой
энергии, излучаемой в угол dQ с элемента поверхности
нагретого тела dS в интервале времени dt и в интервале частот
от у до v + dv
= E0(v)dvdQdtdS
cos О
A7.3)
141
где О — угол между направлением'излучения и вертикалью
к dS, a E0(v) — излучательная способность — характерное
свойство вещества, всегда имеющего специфическую, только
ему присущую частотную развертку (линейчатый спектр).
Физическая природа материальной среды влияет и на
частотную зависимость коэффициента поглощения а(у), которым
определяется ее прозрачность в разных спектральных
диапазонах. Казалось бы, что и /0(v) должно существенно зависеть
от того, в какой полости содержится излучение. На самом же
деле это не так: с каким бы ящиком мы ни имели дело (если
только он не прозрачен для заключенного в нем излучения),,
I0(v) всегда одно и то же. В этом можно убедиться
экспериментально, проделав в ящике небольшое отверстие и изучив
спектральный состав выходящего наружу равновесного
излучения. О том же свидетельствуют и теоретические
соображения, приведенные Кирхгофом, которые ввиду
фундаментальности факта мы специально обсудим ниже.
§ 18. ТЕОРЕМА КИРХГОФА
Рассмотрим сначала несколько идеализированную
ситуацию, когда излучение заключено в так называемый
«черный ящик» — полость с абсолютно поглощающими стенками
(а = 1). Эта ситуация проще только в том отношении, что
внутри черной полости нет отраженного света.
Содержащееся в ней излучение всегда находится на полпути между
испустившим его участком поверхности и противоположной
стороной полости, где ему суждено поглотиться. Таким
образом, плотность энергии внутри черного ящика зависит
только от излучательной способности его стенок. Она может
быть определена, если принять во внимание, что свет,
испущенный в некотором направлении за время dt, находится в
элементе конуса с образующей cdt и площадью основания
ds, перпендикулярного лучу:
Определенная таким образом плотность энергии
продолжает оставаться дифференциально малой, поскольку это лишь
та часть ее, которая попала в рассматриваемый элемент
объема с участка dS излучающей поверхности полости (рис. 52, а).
Ввиду A7.3) она равна
dE -E,{v)dvdS™*®. A8.2)
142
Рше. 52, Излучение элементов поверхности черной полости (а) и вид
этих элементов изнутри (б).
Если излучающую поверхность рассматривать из
выделенного объема полости, то ее элемент dS, спроектированный на
поверхность, перпендикулярную лучу зрения, имеет
площадь dS± = dS cos 0, а опирающийся на него телесный
dS
угол dQ' =
c2°s ■ (рис. 52, б). Поэтому полная плот-
ность энергии в частотном интервале dv может быть легко па-
лучена из A8.2) простым интегрированием по углам:
ЗХС
dv
Здесь p(v) — спектральная плотность энергии излучения,
находящегося в единичном объеме полости:
p(v)
A8.4)
Поскольку по определению черного тела а = 1, его излуча-
тельная способность E0(v) — /0(v), Исключая ее из A8.4)^
находим
J0(v)=-~q)(v). A8.5)
Этот результат легко интерпретируется: поток энергии,
как всегда, пропорционален произведению ее плотности на
скорость распространения, и только множитель 1/4 является
приобретением^ которое трудно было бы предвидеть без при-
143
веденных выкладок. Используя A8.5) в A7.2), получаем
уравнение баланса в виде
^ = ^P(v). A8.6)
Выполнение этого равенства — необходимое условие
обеспечения равновесия между излучением и стенками полости.
При а = 1 фигурирующая в нем плотность излучения p(v) —
равновесная плотность энергии в черном ящике. Будет ли
эта плотность (а стало быть, и /o(v)) точно такой же при
равновесии со стенками любой иной природы — в этом
заключается вопрос, на который дает положительный ответ теорема
Кирхгофа.
Доказательство ведется от противного. Предположим, что
в различных ящиках, термостатированных при одной и той
же температуре, устанавливается различная плотность
равновесного излучения — в прямой зависимости от того, из
какого вещества сделаны эти ящики. В таком случае,
соединив ящики с помощью окна, прозрачного для излучения,
мы создадим условия для обмена лучистой энергией. Если
в самом деле плотность излучения в одном из ящиков
больше, чем в другом, то и поток энергии, вытекающий из него,
должен преобладать над тем, который течет в обратном
направлении. В результате теплота, равная разности этих
потоков, будет ежесекундно переходить из одного ящика в
в другой, уменьшая объемную плотность энергии p(v) в
первом из них и увеличивая ее во втором. Одновременно с этим
нарушится равновесие между излучением и стенками,
которое в каждом из ящиков поддерживалось соответствующей
величиной р. В первом из них процесс излучения станет
преобладать над поглощением, а во втором наоборот, и
вследствие этого стенки первого ящика начнут охлаждаться, а
второго — разогреваться. Излучение, осуществляющее
термический контакт между ними, станет причиной
самопроизвольной передачи тепла от холодного тела к горячему, что
категорически запрещено вторым началом термодинамики.
Неосуществимость такого процесса является гарантией того,
что равновесная плотность излучения в любых средах
одинакова.
Полезно отметить, однако, следующую тонкость. Если бы
поток лучистой энергии из первого ящика Ix(v) был больше
встречного лишь для некоторых частот, тогда как для других
имело бы место обратное неравенство, то могло бы оказаться,
что полный поток энергии через окошко равен нулю, так как
144
Рис. 53. Спектр
поглощения (а), излучения
(Ео) и плотности
равновесного излучения (р).
J /х (v) dv = J /2 (v) dv. В таком случае вышеприведенные-
рассуждения показались бы неубедительными. Однако
несложно исключить и эту возможность. Вставим в окно,
соединяющее ящики, светофильтр с пропускной способностью»
|(v), прозрачный лишь для некоторых частот. В таком
случае, повторив все рассуждения, можно убедиться, что
требование баланса усложняется: ( £ (v) 1г (v) dv = J £ (v) I2 (v) dv.
Так как светофильтр может быть каким угодно, это условие
должно выполняться при любом £(v), что возможно лишь
при /х(у) = /,(v) = /0(v).
Итак, отношение излучательной и поглощательной
способности тел должно оставаться одним и тем же для любых
сред. Смысл этого утверждения проясняется, если учесть,,
что для всех реальных тел и E0(v), и a(v) имеют вид
пилообразных кривых, в которых острыми максимумами выделены
резонансные частоты данного вещества. Напротив, p(v) —
гладкая кривая, одинаковая для всех сред и изменяющаяся
только с температурой. Чтобы соотношение A8.6)
выполнялось, частотная зависимость a(v) должна в точности
дублировать спектр излучения E0(v): максимум на максимум,
минимум на минимум, причем так, чтобы отношение их, равное
p(v), изменялось монотонно (рис. 53). Опыт на каждом шагу
сталкивает нас с проявлением этой закономерности. То, что
в отраженном свете казалось темным пятном на поверхности
металла, окажется самым ярким, если металл раскалить.
Ампула с газом при комнатной температуре поглощает
именно те частоты, которые она же будет испускать, если газ
разогреть. В непрерывном спектре Солнца обнаруживаются
черные (фраунгоферовы) линии, обязанные своим
происхождением поглощению этих частот атомами водорода в
солнечной короне, и на этих же самых частотах — яркие
спектральные линии от пламени водородной горелки. Эти и другие
подобные иллюстрации закона Кирхгофа подтверждают
фундаментальный характер соотношения A8.6), в котором важней-
145
шую роль играет равновесное распределение плотности
излучения p(v). Знание этой функции дает возможность
ограничиться какой-либо одной из характеристик вещества:
a(v) или E0(v), поскольку другая определена соотношением
A8.6).
Это же соотношение наилучшим образом выражает
специфику излучения как термодинамической системы. В то время
как плотность газа однозначно задается числом молекул,
которые не покидают пределов сосуда, излучение
принципиально не сохраняется. В отдельные моменты времени оно
может нахлынуть в полость или наоборот выплеснуться из нее
в окружающую среду. Однако в среднем по времени
благодаря уравновешенному обмену со средой р = const, причем не
только частотное распределение, но и сама абсолютная
величина р целиком задаются температурой среды. Иными
словами, плотность излучения, в отличие от газа, не может быть ни
увеличена, ни уменьшена путем изменения занятого им
объема. После установления равновесия она всякий раз
оказывается одной и той же, заданной универсальной функцией
Благодаря способности излучения проникать сквозь лю-
€ые стенки точно такая же плотность излучения, как и в
полости, поддерживается и внутри равновесной среды, которая,
образно говоря, представляет собой губку, пропитанную
излучением. Обращение к полости — вакууму
макроскопических размеров — является BGero лишь методическим
приемом, позволяющим выделить излучение, так сказать, в
чистом виде. С теоретической же точки зрения безразлично,
«выжать» ли излучение в полость или рассматривать его
непосредственно в среде, которая его порождает. Последнее
даже несколько удобнее. Можно, например, представить себе
сосуд с идеальными, зеркально отражающими стенками,,
в котором заключено некоторое количество газа, а
следовательно, и уравновешенного с ним излучения. Можно
обойтись и вовсе без стенок, если газ имеет неограниченную
протяженность. В любом из этих случаев в каждой точке
пространства должно присутствовать излучение в
количестве, определяемом равновесной функцией распределения
p(v).
§ 19. УЛЬТРАФИОЛЕТОВАЯ КАТАСТРОФА
Из вышеизложенного ясно, насколько важно точно знать
vp(v). Эта информация была получена экспериментально в
жонце прошлого века путем прямого спектрального иселедо-
146
вания равновесног излучения. Однако при попытке теореаи-
чески интерпретировать полученные результаты неожиданна
обнаружились трудности принципиального характера.
Оказалось, что статистическое рассмотрение равновесного
излучения приводит к парадоксальному выводу: интегральная
(суммарная по всем частотам) плотность его энергии
бесконечна! Если бы это в самом деле было так, то равновесие
между излучением и веществом не могло бы установиться ни
при каких температурах. Обладая бесконечной
теплоемкостью, излучение «выкачивало» бы энергию из любого тела
конечных размеров, охлаждая его до абсолютного нуля. Коль
скоро этого не происходит, ясно, что парадокс возникает
из-за какой-то ошибки в теоретической оценке p(v).
Теплоемкость излучения. Чтобы найти ее, рассмотрим*
каким образом оценивается спектральная плотность энергии
равновесного излучения. Для этого достаточно знать: а)
какое число электромагнитных—колебаний dG приходится на
интервал dv в полости е иничного объема и б) какова средняя
тепловая энергия E(v), которой обладает в равновесии
каждое такое колебание.
Ответ на первый вопрос сравнительно прост. Отдельным
колебанием считается монохроматическая волна
определенной поляризации и направления движения, заполняющая
всю полость. Число таких колебаний, вообще говоря,
неограниченно, но счетно. Каждое из них задается своей
частотой v, либо длиной волны Я, либо волновым числом к = 1А»
причем
v = ск. A9.1)
Чтобы указать еще и направление движения волны, следует
превратить к в вектор к, модуль которого равен l/X = vlcr
а единичный орт к/к перпендикулярен фронту
распространения волны. Различные значения вектора к (по величине ж
направлению) маркируют возможные состояния волнового
движения и позволяют сортировать их по этому принципу
точно так же, как состояния свободного движения частицы
определяются и различаются заданием ее импульса р. Следуя
этой аналогии, можно утверждать, что число колебаний в
интервале dk пропорционально ink2dk, подобно тому как
число состояний свободного движения ~tkKp2dp. Физические
соображения, подобные приведенным в § 25, позволяют
превратить эту пропорцию в точное равенство:
dG = 2-4ккЧк. A9.2)
147
Появившаяся в нем двойка учитывает существование двух
независимых колебаний одинаковой частоты, отличающихся
поляризацией световой волны. В частотной шкале общее
число различных колебаний в интервале dv, согласно A9.1) и
A9.2a)
Энергия, приходящаяся на интервал dv в условиях
равновесия, есть просто сумма энергий всех этих колебаний:
du = E(v)dG = p(v)dv« A9.3)
Поэтому расчет
p(v) = f (V)^£ A9.3a)
rv / \ j сз \ t
целиком сводится к решению второгс вопроса: чему равна
средняя энергия E(v), приходящаяся в равновесии на одно
электромагнитное колебание.
Отвечая на этот вопрос с точки зрения классической
статистики, невозможно избежать обычного вывода закона
равнораспределения энергии по степеням свободы: на каждое
гармоническое колебание, каковым, в частности, является и
световая волна, в условиях равновесия приходится средняя
энергия, равная кТ. Полагая в A9.3) Е = кТ, получаем
распределение
-dv% A9.4)
известное под названием закона Рэлея, Но из него
немедленно следует, что
Г
\
оо
8пкТ Г
= ]
, 8пкТ Г 2 j ■
du = ] v*dvu= oo.
ч)
о
Поскольку расходимость получается на верхнем пределе,
в области высокочастотных колебаний, этот статистический
парадокс приобрел известность как «ультрафиолетовая
катастрофа».
Квантование поля. Парадокс и в самом деле носил
катастрофический характер, если принять во внимание, как
сильно были задеты основы теории и сколь радикальные
нововведения потребовались для ее усовершенствования. В по-
148
исках правильного спектрального распределения Планку
посчастливилось подобрать аналитическую формулу с одним-
единственным параметром h (постоянной Планка), которая
точно описывала частотную и температурную зависимость
плотности энергии излучения:
Интегрирование A9.5) не приводит к недоразумениям, а,,
йапротмв, позволяет получить важный результат:
A9.6)
(с/гK
который находится в согласии с термодинамическим
расчетом и(Т) и законом Стефана — Больцмана для потока
лучистой энергии:
оо
g = j/0(v)dv = lCu]=cn A9.7)
О
где <j=.-22L* =.5,67-10"' эрг/(см2-К*.с).
15с h
Однако сопоставление A9.3а) с законом Планка A9.5)
неизбежна приводит к выводу, что
ехр
\кт)
A9.8)
Этот вывод находится в противоречии с законом
равнораспределения, т. е. с основами классической теории.
Как уже было подробно разъяснено в § 12, Планк сделал
далеко идущие выводы из счастливо приобретенной таким
образом подсказки. Пытаясь обосновать формулу A9.8), он
совершенно справедливо интерпретировал ее как результат
усреднения дискретно изменяюдцейся энергии светового
колебания:
Е = ЛГе, A9.9а)
где
е = hv. A9.96)
Вскоре Эйнштейн пошел в этом отношении еще дальше,
усмотрев в квантовом постулате A9.9) возможность восстано-
149
E IN
Рис. 54. Описание излучения в волновых и
корпускулярных переменных. Черточками показано квантование
энергии электромагнитных колебаний в различных
диапазонах частот, а сплошной кривой — средняя энергия,
приходящаяся на них в тепловом равновесии.
вить в правах корпускулярное описание света (фотонную
модель).
Корпускулярная модель. В самом деле, если считать, что
кванты электромагнитных колебаний — это частицы света
с энергией е, то N = Е1г — их количество в
электромагнитной волне с энергией Е. Рис. 54 дает ясное представление
о том, что означает такая смена лексики. Вертикальные
линии на рисунке представляют собой энергетические оси
соответствующих колебаний, расчлененные квантованием на
отрезки равной длины, линейно возрастающей при
увеличении частоты. С точки зрения волновой модели N-e деление
энергетической шкалы отвечает ЛГ-му уровню возбуждения
светового осциллятора частоты v. С точки зрения
корпускулярной модели N — число фотонов, движущихся с
энергией е, или число заполнения (фотонами) состояния с
энергией е. Таким образом, по каждой из осей могут быть отйожены
либо волновые (v и £), либо корпускулярные (е и N)
переменные, поскольку е = hv, a N = Elhv. Эти модели
альтернативны. Между энергией волны и энергией фотонов нет
ничего общего: первая является ординатой, вторая —
абсциссой, и никакой связи между ними не существует. Бессмыслен-
150
Puo. 55. Среднее чиело
фотонов как функция их
энергии при
фиксированной температуре.
но поэтому пытаться представить себе квантованные волны„
как нарезанные ломтиками синусоиды. При изменении
описания образ волны должен просто уступить место другому
образу — потоку точечных частиц (фотонов), движущихся с
энергией е.
Подобным же образом разнится и статистическое
описание излучения в альтернативных моделях. С точки зрения
волновой модели область низкочастотных колебаний сугубо
классична так как Е = кТ (см. рис. 54), а квантовые
аномалии характерны только для ультрафиолетового крыла
спектра, где Ё -> 0. Напротив, с корпускулярной точки зрения
экспоненциальное убывание N в ультрафиолетовой области
вполне согласуется с классическим распределением частиц
по энергиям, в то время как распределение
низкоэнергетических фотонов существенно отличается от максвелловско-
го: они гиперболически, а не экспоненциально возрастают в
числе при г<СкТ (рис. 55). В самом деле,
N=
Gxp
(_Ne)
\ кТ/
N=0
JV=O
— -1
N
= ехр(-^
A9.10)
а при г<^кТ
так что при е>
'Jf = кТ/г -> оо при е -> 0, что вовсе не было свойственно
частицам с классическим поведением.
Таким образом, фотоны — сугубо квантовые частицы.
Их распределение во всем энергетическом диапазоне @^
<; е <! оо) никогда не сводится к классическому. В этом
смысле фотонный газ является «вырожденным»:
ненормальным, сугубо квантовым при любых температурах.
151
Выбор между волновой и корпускулярной моделью
диктуется соображениями удобства. Ни одна из них в своем
классическом виде не эквивалентна истине во всей ее
полноте. Классическому волновому движению не присуще
квантование, а корпускулярному — способность
интерферировать, дифрагировать и пр. Однако использование моделей
значительно облегчает осмысливание результатов и не
приводит к ошибочным оценкам, если не упущены из виду их
квантовые особенности и правила соответствия между ними.
При описании равновесного излучения корпускулярная
модель оказывается предпочтительнее, так как она позволяет
свести рассмотрение излучения как термодинамической
системы к модели газа. В спектре равновесного излучения
представлено множество колебаний, различных по частоте,
поляризации и фазе, и возможность проявления волновых,
интерференционных явлений сведена к нулю. Другое дело
излучение, пропущенное через монохроматор, которое
можно расчленить, а потом заставить интерферировать с самим
собой. В этом случае когерентность излучения часто делает
фотонную модель неуместной, а волновую предпочтительней *
Но при изучении равновесного излучения эти свойства не
проявляют себя, и мы можем продолжить перевод волновой
лексики в корпускулярную.
§ 20. ФОТОННЫЙ ГАЗ
Основные черты. Статистическое описание фотонного
газа задается распределением его частиц в пространстве
координат и импульсов, разделенном на ячейки объема h3:
Наряду с A9.10) здесь принято во внимание двукратное
поляризационное вырождение каждого состояния движения.
Координатная часть этого распределения, как правило, не
представляет интереса, так как потенциальная энергия
фотонов слабо меняется на расстояниях, с которыми приходится
иметь дело в земных условиях. Поэтому естественно перейти
от B0.1) к объемной плотности фотонного газа dn = ,
которая очевидно равна:
152
а после интегрирования по углам превращается в
, B0.3)
Для полной определенности теперь не хватает только
знания зависимости г(р) — главной механической
характеристики идеального газа. Для ее определения сравним с последним
результатом плотность фотонов, которую можно рассчитать
из равновесного распределения энергии йзлученияг
воспользовавшись законом Планка A9.5):
л„ __ du _ Р (v) dv __ 2*
ап ~~ Т ~~ hv ~
Эти формулы отличаются лишь тем, что последнее выражение
записано в волновых переменных, а предыдущее — в
корпускулярных. Их тождество достигается при условии, что
p = hj = hk, p = fek. B0.5)
Этими равенствами, устанавливающими соответствие между
корпускулярными и волновыми переменными, придается
необходимая замкнутость корпускулярной модели. Из B0.5)
и A9.96) следует, что
е = рс. B0.6)
Эта информация позволяет исключить одну из двух
зависимых переменных (е или р) из написанных выше
распределений. Используя B0.6) в B0.3), можно получить либо
распределение по .импульсам:
dn (p) = fpePI , B0.7)
expf-T^) —1
r* — 1
либо по энергиям:
dra (e) =
Таким образом соотношение B0.6) окончательно замыкает
модель и придает однозначность всем приведенным выше
распределениям. Из них можно теперь по обычным рецептам
рассчитать среднюю энергию, давление, поток частиц и тому
подобное в рамках чисто корпускулярных представлений.
153
Вообще, связь энергии и импульса является главной
индивидуальной характеристикой газа, определяющей
механику, которой подчиняются его частицы. Фигурирующая в
зависимости е(р) константа — характерный инвариант, при-
еущий всем частицам данного газа. В фотонном газе— это
с, скорость света, в максвелловском — /тг, масса частиц.
Сопоставление. Различия в механических и
статистических свойствах этих двух идеальных газов явственно
проступают при их прямом сопоставлении:
молекулы фотоны
т = const с — const
efcr-l
No = inv
р = mv p = me
То, что в фотонном газе сохраняется скорость, а не масса,
приводит к некоторым интересным особенностям,
качественно отличающим его от максвелловского. В частности,
исчезает случайное подобие распределений по импульсам и
скоростям, которое являлось прямым следствием постоянства
массы молекул. Поскольку с = const, распределение
фотонов по скоростям есть по существу распределение только по
направлениям движения:
^ ^ B0.9)
Оно, конечно, отнюдь не напоминает D.1), тогда как между
распределениями молекул и фотонов по импульсам имеется,,
по крайней мере, структурное соответствие.
Более того, если рассчитать из B0.9) вероятность иметь
заданную проекцию скорости, проинтегрировав это
распределение по ф, то окажется, что
dW(cx) = ^. B0.10)
Этого и следовало ожидать, поскольку для величины, от
которой энергия не зависит, мы вправе с самого начала
предполагать равнораспределение во всей области определения:
154
от — с до -{-с. В силу симметрии пространства точно такие
же распределения должны быть для су и cz. Отсюда сразу же
вытекает, что dW(c) Ф dW(cx)dW(cy)dW(cz), вопреки тому,
что имело место в максвелловском газе. Обнаружение
различных значений проекций скорости в данном случае нельзя
уже рассматривать как независимые события. Еслиа
например, сх = с, то заведомо су — сг = 0.
Специфика фотонов как квантов поля состоит еще и в
том, что их число не сохраняется. Это обстоятельство
отражено в вышеприведенной таблице тем, что No не является
инвариантом для фотонов. Что же касается массы фотона, то
она определена соотношением, формально аналогичным
классическому, но приобретающим совсем иной смысл вследствие
того, что с — const.
Интересно сравнить информацию, содержащуюся в
таблице, с тем, что мы знаем о фотоне из другого, совершенно
независимого источника — теории относительности. Такое
сравнение не только не обнаруживает никаких
противоречий, но, напротив, свидетельствует об идеальном согласии.
Соотношение B0.6) является в релятивистской механике
естественным следствием того, что масса покоя фотона равна
нулю. Кроме того, подставляя р = тс в B0,6), получаем, что
е = тс\ B0.11)
в полном согласии с общим выводом теории относительности.
Нетрудно убедиться, что в области видимого света (v =
= 1016 Гц) масса фотона ттг = — v« 107«v ~ 10~32 г.
с
Даже жесткие рентгеновские лучи (v = 1019 Гц) состоят из
частиц, масса которых раз в 10 меньше электронной. И
только кванты у-излучения (v = 1021 Гц) имеют массу, сравнимую
и даже большую, чем электрон.
Вес фотона. С понятием массы как основной
механической характеристики материальной точки связано
представление не только об ее инерционности, но и о весе. В этом
отношении фотон не отличается от других материальных тел>
и в однородном поле сил тяжести уравнение его движения
имеет вид
р = F = mg = pg/c. B0.12)
Его решение отличается от обычного только тем, что масса
фотона не сохраняется, а так же, как и импульс, экспонен-,
циально возрастает в процессе падения:
р = р@) exp (gt/c) - р@) exp {gx/c2). B0.13)
155
Поскольку gx <C с2, разлагая экспоненту в B0.13), легко
получить, что
Ар = Am-с = mgxlc, B0.14)
а прирост энергии фотона
Де = с Ар = mgx B0.15)
определяется просто разностью потенциалов на пройденном
им пути.
Этот последний результат блестяще подтвержден
прямым взвешиванием фотона. Источник строго
монохроматического 7-излУчения> получаемого методом Мессбауэра,
устанавливался таким образом, чтобы фотоны прежде чем
попасть в анализатор частоты, пролетали по вертикали
расстояние Н порядка одного метра. Каждый фотон в свободном
падении приобретал под действием силы тяжести добавочную
энергию Де = mgH. Благодаря исключительной
прецизионности метода Мессбауэра этого оказалось достаточно, чтобы
заметить смещение частоты Av = mgH/h. В анализатор
попадал свет более коротковолновый чем испускалсяг если фотон
летел вниз, и более длинноволновый в противоположном
случае. При горизонтальной траектории фотона частота света
не претерпевала изменений. Стало быть, фотон, как и прочие
частицы, испытывает на себе действие силы тяжести,
величина которой обычным образом выражается через его массу*
Из волновых соображений рассчитать гравитационный сдвиг
частоты было бы неизмеримо сложнее.
§ 21. /РАВНЕНИЕ СОСТОЯНИЯ
С точки зрения корпускулярной модели стенки полости%
в которой находится излучение, подвергаются такой же
бомбардировке фотонами, как и стенки сосуда с газом. Поток
фотонов на стенку можно легко рассчитать с помощью
B0.10) и убедиться, что он в точности совпадает с
классическим:
§) = ±-nc, B1.1)
если сопоставить скорость света средней абсолютной
скорости максвелловских частиц и. Более того, поскольку
распределение по скоростям никак не связано с
распределением по поляризациям и энергиям, плотность фотонов в
156
этой формуле может быть не только интегральной» но и
парциальной — только данного сорта. В таком случае
выражение B1.1) примет вид
dj = ±cdn. B1.2)
Простым домножением его на 8 можно убедиться,, что и
поток лучистой энергии
dq = tdj = jcp (v) dv = / (v) dv B1.3)
в точности согласуется с выражением A8.5), полученным
ранее.
Давление. Хотя часть фотонов из общего потока,
падающего на стенку, поглощается в ней, мы можем тем не менее
считать, что все они упруго отражаются, передавая еш
импульс 2рх. Это возможно, конечног только в условиях
детального равновесия, когда на каждый поглощенный
стенкой фотон приходится такой же в точности фотон,
испущенный ею в обратном направлении. Поглощенный фотон
передает стенке импульс рх, а испущенный — рх, поэтому,
рассматривая оба акта как единый процесс, можно считать, что
все фотоны отражаются упруго, как от зеркальной стенки.
Общий рецепт вычисления давления остается в таком случае-
прежним:
$ B1.4)
Однако поскольку предстоит усреднение по углам,
пользоваться в этой формуле уже усредненным по этим переменным
результатом B1.2) не следует, и выкладки должны быть_
продолжены следующим образом:
р = §2pxcxdn = ^2рс cos2 Ып = § 2е cos2 Ып (г) ^. B1.5>
Усреднение по энергиям и углам разделяется, а
интегрирование по полупространству дает
оо
р = 2 cos2 # « е-п = 1 en = ~ Jedit = 1 и. B1.6)
о
Как и следовало ожидать, давление фотонного газа прямо
выражается через объемную плотность энергии, только с
иным численным коэффициентом, чем в A.8).
157
Этот результат получается и в электромагнитной теории
свободного волнового поля независимо от его спектрального
состава. Он был впервые подтвержден очень тонким
количественным измерением давления света, выполненным в
конце прошлого века П. Н. Лебедевым, В настоящее'время
благодаря появлению мощных источников света наблюдение
этого эффекта значительно упростилось. Однако давление
равновесного излучения при температурах, близких к ком
натным, по-прежнему остается величиной, трудно
доступной измерению вследствие своей чрезвычайной малости.
В самом деле, подстановка в B1.6) равновесной плотности
энергии из A9.6) дает
Р = гТ\ B1.7)
где
^ 4а
г = 8я^ 4а= 0_15^ип_
45eV Зс см2-К4 '
При 300 К давление р = 2,5-10~15-34-108 = 2-10 дин/см2,
так что подтвердить его существование можно лишь
косвенно, например, измерением пропорционального ему потока
лучистой энергии, величина которого, согласно B1.3) и
A9.7), есть q = оТ* = 5,7-10-34.108 = 5-Ю5 эрг/(см2-с) и
легко заметна даже на ощупь% от какого бы тела радиация
ни исходила.
Уравнение состояния. Формула B1.7) представляет собой
уравнение состояния фотонного газа, физически
эквивалентное уравнению идеального молекулярного газа; р = пкТ.
Их сопоставление обнаруживает существенные различия,
обусловленные несохранением числа фотонов и иной их
статистикой. Это сказывается прежде всего в том, что число
фотонов не фигурирует в B1.7) как независимый параметр.
Если его рассчитать, проинтегрировав B0.7) или B0.8), то
окажется, что
$*£*]£ B1.9)
в такой же мере задается температурой, как и само давление.
Поэтому-то давление и оказывается функцией не двух
переменных, а лишь одной — температуры! Соответственно и на
диаграмме состояний рис. 56 мы имеем не семейство прямых,,
как в молекулярном газе, а только одну кривую р(Т) —
•единственно возможную. Более быстрое возрастание
давления с температурой обусловлено резким увеличением числа
158
фотонов в единице объема. Их средняя тепловая энергия,
видно из A9.6) и B1.9), есть
8 = —
То, что численный коэффициент q =
B1.10)
1 отличек
от 3/2t не удивительно: закон равнораспределения энергии
по поступательным степеням свободы применим только к
газам, подчиняющимся классической статистике. ' Горазда
важнее,, что по-прежнему имеет место прямая пропорция
е ~ кТ9 которой подтверждается обычный смысл
абсолютной температуры.
Вследствие того, что п однозначно задается температурой^,
состояние фотонного газа fie изменяется при изотермическом
изменении его объема. Этого можно было ожидать% поскольку
излучение присутствует не только в полости, но и в
окружающей ее равновесной среде. Увеличивая полость, мы лишь
устраняем атомы вещества, ничуть не способствуя увеличению
объема, доступного излучению. Иначе говоря,
изотермически расширить или сжать излучение невозможно.
Но его можно сжать адиабатически в том гипотетическом
случае, когда стенки полости — идеальные зеркала (а = 0fl
т) = 1). Излучение не проникает через них в окружающую
среду, а значит, и не поглощается в ней. В таких условиях
число фотонов в полости сохраняется, т. е.
nV = const или ТЪУ = const, B1.11)
как это следует из B1.9). Принимая во внимание B1.7),,
можно привести уравнение адиабаты р ,п р>
к следующему виду:
J _4
р* . V = const или pV3 = const. B1.12)
Очевидно, что при адиабатическом
сжатии фотонный газ разогревается.
Его полная энергия, согласно B1.6) и
B1.12), есть U = u-V = 3pV - У/3.
Рис. 56. Давление р и плотность фотонного
газа г] как функции температуры.
/
159
Юна возрастает обратно пропорционально \/~V. При
сохранении числа фотонов в полости это может означать лишь
увеличение их энергии (а значит, и частоты), происходящее
при отражении от стенок, которые совершают над
фотонным газом определенную работу при его сжатии.
§ 22. КОЭФФИЦИЕНТЫ ЭЙНШТЕЙНА
Поглощение и испускание. Развивая идеи фотонной
модели, легко представить себе атом как мишень, которая
подвергается обстрелу частицами света. Акт поглощения
является результатом прямого попадания, приводящего к
возбуждению атома из состояния 1 в более высокое
энергетическое состояние 2 за счет энергии поглотившегося фотона.
Для того чтобы попадание было возможно, мишень не
должна быть точечной, т. е. атом должен обладать эффективным
сечением а12. В таком случае длина свободного пробега
фотона между актом испускания и поглощением равна ^ = ~^~ •
Поток фотонов, проходя сквозь среду из невозбужденных
атомов, редеет в соответствии с законом N = N@) ехр (—х/к),
который является корпускулярным аналогом A7.1), причем
X = 1/8.
Если же так случилось, что фотон угодил в возбужденный
атом (находящийся в состоянии 2), то он способен не только
поглотиться в нем, вызвав переход на еще более высокий
энергетический уровень, но и выбить из атома
аккумулированную в нем энергию в виде нового фотона — точной копии
налетевшего. Последний удалится затем вместе с
виновником происшествия, а атом, потеряв квант hv — Е2 — Еи
вернется в более низкое состояние. Именно этот процесс
индуцированного или вынужденного высвечивания,
теоретически предугаданный Эйнштейном, позволяет извлекать из
энергетически богатой среды мощные световые потоки
одним единственным «затравочным» фотоном.
Поскольку заранее не ясно, так ли охотно атом расстается
со своей энергией, как и приобретает eet мы пока сопоставим
индуцированному процессу некоторое другое сечение сг21,
отличное от сг12. Таким образом, при прохождении света
сквозь вещество его атомы либо истребляют фотоны, либо
приумножают их количество — в зависимости от того, что
больше o12Nt или o21N2 (N± и N2 — числа атомов,
находящихся в соответствующих состояниях).
160
Рис. 57. Резонансный обмен
энергией между
двухуровневой системой (слева) и средой,
находящейся в равновесии
при температуре Т.
Р21
О ===
Помимо указанных процессов имеется еще спонтанное
(ничем не вызванное) испускание фотона возбужденным
атомом, которое является причиной теплового высвечивания
нагретых тел. Существует некоторая вероятность распада в
единицу времени А21х благодаря которой возбужденные
атомы самопроизвольно исчезают по экспоненциальному за-
dN
кону, испуская свет: ^
— A2lN2.
Возбуждение и дезактивация. Каждому атому приходится
сталкиваться не только с фотонами, но и с другими атомами,
составляющими вещество. В результате атом переходит с
уровня на уровень, либо черпая необходимую энергию у
партнера, с которым пришлось столкнуться, либо, напротив,
отдавая ему квант, от которого можно освободиться.
Скорость передачи энергии между атомом и его партнером в
обоих направлениях одинакова. Однако вероятность приобрести
энергию р12 будет во столько раз меньше вероятности отдать
ее р21, во сколько реже встречаются в веществе партнеры в
возбужденных состояниях, энергия которых больше на
величину &Е — Е2 — Е1 (рис. 57). Если вещество находится
в равновесии, то очевидно
Po
kT
B2.1)
Вероятности переходов. Чтобы достичь единообразного
кинетического описания, следует и светоиндуцированным
переходам сопоставить соответствующие вероятности, так
называемые априорные вероятности Эйнштейна. Они имеют
простой физический смысл — суммарной частоты
столкновений атома с фотонами — и различаются лишь тем, что
при этом происходит—возбуждение или дезактивация:
W
= J acdn ±= J ^-c p (V) dv.
B2.2)
А. И. Бурштейя
161
Принимая во внимание, что переходы происходят только в
том случае, если частота света оказывается очень близкой к
одной из резонансных частот атома, можно заключить, что
сечение столкновения а является острой пикообразной
функцией частоты, подобной a(v) или E0(v). Для отдельной
спектральной линии зависимость a(v) близка к б-функции, по
крайней мере, по сравнению с p(v) — весьма плавной кривой.
Поэтому
W = J В (v) б (v - v.) p (v) dv = В (v0) p (v0), B2.3)
причем неопределенность эффективного сечения а
переносится в последнем выражении в В. Если предполагать, что
процессы вынужденного поглощения и высвечивания идут
с разной скоростью, то следует еще различать
W12 = 512(vo)p(vo) и Wn = B2i(v0)p(v0). B2.3а)
Характеризующие атом постоянные В называются
коэффициентами Эйнштейна. Поскольку равновесие всегда
детально, мы вправе ограничиться рассмотрением только двух
состояний энергетического спектра атома, резонансных частоте
v0. He составляет труда записать для них основное
кинетическое уравнение, руководствуясь элементарными
соображениями баланса частиц: сколько убудет с одного уровня*
столько прибавится на другом:
llr=-d-ir= (WiJTi - WalN% - A21N2) + (p^N, - p21N2).
B2.4)
Слагаемые в первых скобках описывают взаимодействие
атома с полем излучения, а во вторых — с равновесной средой.
Соотношения Эйнштейна. В условиях детального равно-
dN9 dN,
весия не только —~ = т-= 0. но и каждая скобка.
dt at
порознь равна нулю. Это означает, что должен быть
сбалансирован обмен энергией как со средой:
B2.5а)
так и со светом:
W12NX - W21N2 - A21N2 = 0. B2.56)
Иначе говоря, количество поглощенных фотонов должно
равняться количеству испущенных. В противном случае либо
световая энергия стала бы превращаться в тепловую, либо
наоборот, но ни то,, ни другое в условиях равновесия проис-
162
ходить не должно. Из B2.5а) и B2.1) вытекает очевидный
результат:
_2 ___ 111. _ р ЬТ
N, e р21 - е '
Зато из B2.56) и B2.6) получается отнюдь не тривиальное
соотношение
Wlt = (W21 + A2i) exp (- ^l£l), B2.7)
связывающее между собой вероятности индуцированного и
спонтанного высвечивания. Преобразовав B2.7) с помощью
B2.3а) и приняв во внимание, что hv0 = Е2 — Еъ получим
B2.8)
До сих пор наше продвижение основывалось лишь на
всестороннем использовании принципа детального
равновесия. Но мы располагаем еще и знанием фактического состава
равновесного излучения, заданного законом Планка A9.5).
Уместно потребовать, чтобы формула A9.5) совпала с B2.8):
в*г-1 B19\ehT-Z21
( '
Легко видеть, что единственный способ превратить B2.9)
тождество — это признать, что между коэффициентами
Эйнштейна существуют установленные им соотношения:
В12 = 521, Ц B2.10)
£ B2.11)
Поскольку само явление индуцированного
высвечивания не было известно до Эйнштейна, можно предположить,
что первоначальный набросок теории приводил к
несопоставимым результатам. В самом деле, при В21 = 0 в правой
Л —°
части B2.9) должно было получиться _JJ e kT в противоре-
- л *12
чии с левой. Ь такой ситуации ничего не остается делать^
как постулировать существование нового эффекта.
6* 163
Эйнштейн не только ввел в физику понятие вынужденног©
испускания света, но и установил провозглашенное в B2.10)
равенство вероятностей вынужденного испускания и
поглощения. Это дает нам право не отличать в дальнейшем
вероятности вынужденных переходов, различающиеся
перестановкой индексов, а в случае двух уровней и вовсе опустить
их. Разумеется, если рассматривается не один какой-нибудь
переход, а несколько, то индексы приходится все же
сохранять, чтобы отличить В12 от 513 или В23. То же относится и к
Парциальные вероятности. Для любого стационарного
потока света, распространяющегося в данном телесном угле
и имеющего данную поляризацию а, можно ввести по
аналогии с B2.3) вероятность
dWa\= ba[(v0) p(v0) g^.. B2.12)
Такого рода вероятностное описание взаимодействия света
с резонансным ему переходом возможно, если интенсивность
излучения не слишком велика, а его спектр достаточно
широк. Если же эти условия нарушены, то понятие вероятности
перехода либо получает иное определение, либо вовсе
утрачивает смысл, становясь непригодным для описания
квантовой кинетики. Так обстоит дело при использовании мощных
монохроматических источников, когда волновая природа
фотонов проявляется в их способности интерферировать
через взаимодействие с атомом. В такой ситуации процесс
перестает быть чисто стохастическим, его течение не
укладывается в простую вероятностную схему и подчиняется
уравнениям, существенно более сложным, чем B2.4). Однако
естественные источники света, как правило, не таковы, и их
излучение вызывает переходы с вероятностью B2.12). Так как
в равновесии pa(v0, Q) = p(vo)/8n, парциальные вероятности
связаны с интегральными, фигурировавшими дышег
соотношениями
W = J'2 dWa, В (v0) = J 2 Ъа (v0) g-. B2.13)
Й ct=l a=l
Равным образом
2
S aa(vQ)dQ< B2.14)
a=l
164
Если принять во внимание, что условия баланса должны
выполняться детально, то подобно B2.11):
Отличие на 8л связано с тем, что коэффициент ba(v0)
определяет вероятность вынужденного поглощения и испускания
плоской волны определенной поляризации, а не изотропного
деполяризованного излучения. Она равна
Wa(v0) = 6a(v0)pa(v0)f B2.16)
Такова же вероятность вынужденного высвечивания
фотонов, причем они имеют такую же частоту, поляризацию и
направление движения, как и те, которые принадлежали
волне, индуцировавшей процесс.
Важность соотношений B2.11) и B2.15) состоит в том, что
они освобождают от необходимости независимо считать или
измерять оба коэффициента: Ъ и а. Достаточно определить
а из спектра испускания, чтобы простым пересчетом
установить, какова будет интенсивность спектров поглощения.
Фактически соотношение B2.15) дублирует по своему
качественному содержанию закон Кирхгофа. Но оно сыграло
важную роль еще и потому, что теоретически, на основе
квантовой теории атома удалось рассчитать прежде Ъ, чем а.
Некоторое время такой пересчет служил единственным
способом оценки а. Когда же посчастливилось развить теорию
таким образом, чтобы с одинаковым успехом рассчитывать
оба коэффициента, формула B2.15) блестяще подтвердилась.
Из соотношения B2.15) следует, что вероятность
спонтанного излучения возрастает с увеличением частоты как v3
по сравнению со способностью атома поглощать излучение.
Вследствие этого высокоэнергетические возбуждения
внутренних оболочек атомов чрезвычайно быстро распадаются,
высвечивая кванты света рентгеновского диапазона, для
которых большинство тел оказываются проницаемыми в силу
их слабой поглощаемости. В оптическом диапазоне
спонтанное высвечивание все еще доминирует над вынужденным,
которое только поэтому, вероятно, и не было обнаружено
задолго до Эйнштейна. Дневной свет, рассеянный по комнате
и дающий нам возможность видеть ее, практически не
оказывает никакого влияния на процесс высвечивания нагретых
тел, находящихся здесь же. Его интенсивность слишком
мала, чтобы индуцированные вероятности могли сравниться
165
со спонтанными. Но перейдем к радиодиапазону
(сантиметровые и километровые волны), и положение радикально
изменится. Проходят часы и сутки между
последовательными актами спонтанного высвечивания радиочастотных
квантов. Поэтому в магнитной спектроскопии, имеющей дело с
такими частотами, процессом спонтанного высвечивания
обычно пренебрегают без ущерба для результатов. Зато
индуцированное высвечивание необходимо принимать во
внимание наравне с поглощением, потому что при столь малых
энергиях hv0 <C кТ числа возбужденных и невозбужденных
состояний практически равны, и оба процесса происходят
почти одинаково часто.
§ 23. СТАЦИОНАРНАЯ ТРАНСФОРМАЦИЯ СВЕТА
Обратимся теперь к стационарному взаимодействию с
атомом излучения неравновесного состава. По-прежнему
рассматривая переходы только между двумя уровнями, мы
тем самым подразумеваем, что в действующем свете не
представлены частоты, сколько-нибудь отличные от v12 = (Е2 —
—E^/h. Иными словами, ширина спектра излучения должна
быть уже, чем Av — расстояние в частотной шкале до
соседних с v12 резонансных частот. Тогда этот свет будет
возбуждать лишь переход 1—2, не затрагивая остальных
(рис. 58). Хотя равновесное излучение, обладая
непрерывным спектром, возбуждало все переходы, в этой оговорке
раньше не было необходимости^
так как в силу детального
равновесия можно было
ограничиться рассмотрением любого из
них в отдельности.
Полагая в B2.4) -^ =
dN,
= -± = 0 и разрешая
получившееся алгебраическое
уравнение относительно NJN^
находим с помощью B2.16)
Рис. 58. Трехуровневая система и
V ее спектр /(v).
166
Всегда можно подобрать такую мощность излучения в
плоской волне, чтобы она индуцировада такое же количество
переходов в атоме, что и равновесное излучение. Необходи-
. мая для этого спектральная плотность излучения
определяется очевидным условием 6ара = Вр. Если оно
выполнено—и только в этом случае, — получаем из B3.1)
q = ехр (—Jiv12/kT). Однако больцмановское распределение
частиц по уровням не является в данном случае признаком
установившегося равновесия, как в B2.6), так как
поглощается свет строго определенного направления и поляризации,
а спонтанно испускается деполяризованный и во все стороны.
Тем не менее этот случай в некотором роде особый: свет
только рассеивается, но не поглощается.
Действительно, поглощаемая веществом энергия есть
Q = hv12(p21N2 - pM, B3.2)
а это выражение тождественно обращается в нуль при
равновесной населенности уровней, N2/N1 = ехр(—hvl2/kT) =
— PidP2i- Вместе с тем ясно, что при N2/N1 > ехр (—hv12/
IkT) Q > 0, а при N2/N± < ехр (—hvJkT) Q < 0. Таким
образом, любое отклонение q от qr = ехр (—hv12lkT) вызывает
либо излучение, либо поглощение света:
Q - hv12PnN01=± ^0(М0 = М1 + N2). B3 3)
Обе эти ситуации настолько часто встречаются и в жизни,
и в эксперименте, что трудно остановить свой выбор на
каком-нибудь из множества подходящих примеров. И факел,
и солнце, и тлеющие угли излучают свет, трансформируя
тепловую энергию в излучение. Даже человек, несмотря на
низкую температуру своего тела, способен излучать свет
(в прямом смысле, конечно). Однако с этим выводом уже
следует быть осторожным: в прохладной лаборатории любой
фотометр, чувствительный в инфракрасной области,
фиксирует приближение к нему живого существа. Но где-нибудь
в тропических широтах при температуре воздуха свыше
40°С поглощение рассеянного в пространстве света
преобладает над излучением, и только интенсивное испарение с
поверхности кожи стабилизирует ее температуру* Тем более
это верно в отношении оптических и особенно
ультрафиолетовых лучей прямой солнечной радиации, поглощение кото-
167
рых не только разогревает поверхность, но и индуцирует
сложную цепь фотохимических реакций, конечные продукты
которых обнаруживают себя в виде загара.
Дело в том, что далеко не каждый переход p2i>
дезактивирующий возникшее под светом возбужденное состояние
сложной биологической молекулы, связан с трансформацией
приобретенного кванта в тепло, т. е. в кинетическую энергию.
Суть фотосинтеза, идущего в зеленых листьях t как раз и
заключается в том, что большая часть отнятой у света
энергии трансформируется в потенциальную энергию
межатомных связей вновь образующихся органических молекул.
Поглощающая молекула является в этом процессе лишь
посредником. Ее роль сводится к преобразованию фотона в
энергию возбуждения, дальнейшая судьба которого
слишком сложна, чтобы ее здесь прослеживать. Достаточно
ограничиться пониманием того, что процесс аккумуляции в
веществе световой энергии намного сложнее ее извлечения
оттуда. Но только благодаря этому процессу существует
растительность, а следовательно, и все сущее на Земле.
Глава 3
КРИСТАЛЛЫ
§ 24. ФЕНОМЕНОЛОГИЯ
Если основополагающим свойством газов является их
способность неограниченно расширяться, то твердые тела,
напротив, стремятся сохранить свой объем и даже форму не
только в отсутствие внешних воздействий, по и вопреки им.
Столь контрастные свойства свидетельствуют о существенном
различии молекулярной структуры этих фаз. Даже древних
атомистов простое наблюдение наводило на мысль, что
твердые тела — это совокупность прочно сцепленных атомов.
Действительно, атомы твердого тела все время сильно
связаны друг с другом, тогда как в газе, проводя большую
часть времени в свободном пробеге, они практически не
взаимодействуют. Однако сильное взаимодействие не является
специфическим свойством твердых тел — это общая черта
всех конденсированных фаз, в том числе и жидкостей. Нов
168
кристаллах оно настолько сильно, что в идеальном
приближении тепловым движением атомов можно и вовсе
пренебречь, ограничившись рассмотрением их статического
взаимодействия. В этом смысле идеальные кристаллы являются
прямой противоположностью идеальному газу, в котором,
напротив, можно было ограничиться рассмотрением только
движения атомов, учитывая их кинетическую энергию, но
пренебрегая потенциальной. Чтобы это противопоставление
было яснее, укажем, забегая вперед, что в жидкости,
например, несмотря на сильное сцепление частиц, пренебрежение
тепловым движением даже в нулевом приближении
незаконно. Без теплового движения жидкость немыслима так же,
как и газ. Поэтому потенциальная энергия связей в
кристалле не просто велика, но очень велика или, выражаясь точным
языком, много больше кинетической энергии теплового
движения, тогда как в жидкости эти величины соизмеримы.
Необходимость с самого начала существенно учитывать
силы взаимодействия очень усложняет задачу. Мы уже
имели возможность убедиться, что даже в газе учет
потенциальной энергии возможен лишь при сильном огрублении модели
взаимодействия. Без детального учета специфических
особенностей взаимодействия молекул невозможно получить
реальное уравнение состояния с удовлетворительной точностью.
Еще в большей мере это относится к твердому телу.
Разнообразие атомов и молекул уже само по себе
является причиной существования очень разных по силе и
качественно отличающихся типов межцентрового взаимодействия.
Это положение еще более усугубляется тем, что при
образовании кристаллов исходные элементы зачастую меняют свое
состояние: атомы превращаются в ионы, молекулы
диссоциируют на атомы. Поэтому попытки подыскать
универсальную модель для описания свойств идеальных кристаллов
были бы не только безнадежны, но и не оправданы. Требуется
прежде всего подразделить кристаллы на группы, каждой из
которых может быть сопоставлена своя специфическая
модель, описывающая статические свойства твердых тел (их
энергии связи, строение и тому подобное). Поскольку,
однако, тепловое движение и кинетические эффекты в кристаллах
менее чувствительны к формам связи, мы можем
ограничиться самой грубой, но и совершенно необходимой
классификацией.
Типы кристаллов. Наиболее «просто» устроены так
называемые ионные кристаллы. В их образовании на
относительно равных правах участвуют два разнородных элемента:
ярко выраженный донор электрона (атом щелочного металла,
169
например) и типичный акцептор (любой галоген). При их
соединении электрон переходит с донора на акцептор и оба
заряжаются разноименными зарядами. Поэтому
возникающая связь в основном электростатического происхождения»
Взаимодействие с ближайшими соседями максимально * с
более удаленными — поменьше: полная энергия получается
суммированием по всем ионам, расположенным в правильной
последовательности (-1 1 1—). С электростатической
точки зрения, чем ближе окажутся узлы этой цепи, тем
больший выигрыш энергии будет достигнут. Однако при
чрезмерном сближении начинают сказываться силы отталкивания,
возникающие при соприкосновении электронных оболочек
ионов. Компромисс достигается при некотором определенном
расстоянии между соседними ионами а, которое называется
периодом решетки. На этом расстоянии притяжение и
отталкивание уравновешиваются и достигается минимум
потенциальной энергии.
В другом широком классе соединений: металлах и
валентных кристаллах — связь осуществляется валентными
электронами на коллективных началах. Если, например, речь идет
о кристалле чистого Na, на каждом атоме которого
находится по одному валентному электрону, то нет никакой
причины для образования разноименной мозаики зарядов — все
атомы кристалла эквивалентны. Но именно в силу этой
эквивалентности и близкого соседства атомов электрон
оказывается коллективной собственностью всех положительных
остатков, образующих решетку. В грубом приближении
можно рассматривать совокупность всех валентных электронов
металла как некоторую отрицательную жидкость, влитую в
положительный остов и цементирующую его. Рентгено-
структурные исследования показывают, что фактическое
распределение электронной плотности таково, что в
межатомных промежутках образуются уплотнения, играющие ту же
роль, что и отрицательные ионы в ионных кристаллах.
Валентные кристаллы отличаются от металлов тем, что
они строятся из атомов с четным числом электронов, каждый
из которых участвует в образовании химической (валентной)
связи. В каждой связи участвует по одному электрону от
соединяющихся атомов. В одновалентном соединении такое
соединение вызвало бы разбиение кристалла на пары атомов,
что явно противоречит высокой симметрии кристалла. Если
же валентно соединены все соседние атомы, а те, в свою
очередь, со своими соседями, то образуется очень прочный
кристалл. По этому принципу устроена, например, решетка
алмаза — одной из кристаллических модификаций углерода.
170
Четыре валентных электрона углерода образуют связь с
четырьмя соседями, расположенными по тетраэдру.
Перечисленные типы связи характерны для атомных
кристаллов. Если же происходит конденсация
молекулярных соединений, то, наряду с атомными кристаллами,
могут образоваться и молекулярные (твердый кислород, лед,
сахар). При образовании таких кристаллов вследствие очень
сильной внутримолекулярной связи (в сравнении с
межмолекулярной, кристаллической) молекулы не утрачивают своей
индивидуальности. Так как все связи в них насыщены,
межмолекулярное взаимодействие, ответственное за образование
кристаллической фазы, носит, как правило, ван-дер-вааль-
совский характер. В органических кристаллах иногда
образуются дополнительные сшивки, обусловленные тем, что
содержащийся в них водород частично ионизуется, вступая
во внутримолекулярную связь. Благодаря этому он
оказывается способным электростатически взаимодействовать с
отрицательно заряженными центрами (чаще всего
кислородом), входящими в состав соседних молекул, устанавливая
с ними так называемую «водородную связь».
Прочность. Если рассматривать различные кристаллы
с точки зрения прочности связей, то наиболее крепкими
оказываются валентные, затем следуют металлические, ионные,
молекулярные. Приведенная классификация не является
абсолютно жесткой: в ряде случаев трудно отличить валентную
связь от ионной, ван-дер-ваальсовскую от водородной.
Более того, в какой-то степени участие в образовании связи
принимают и электроны внутренних оболочек атома.
Некоторые свойства, однако, являются общими для всех
кристаллических тел. Любое растяжение или сжатие
кристалла влечет за собой возрастание энергии связей и,
следовательно, возникновение наряжений, которые направлены
противоположно приложенным внешним силам. Этим
объясняются хорошо известные механические свойства
кристаллов: упругость, твердость и др. Как правило, внешние
силы существенно меньше сил атомного сцепления и поэтому
приводят не к нарушению строения, а лишь к
деформациям, смещениям, малым по сравнению с параметром решетки.
Если же нагрузка оказывается соизмеримой с силами связи,
может наступить течение (макроскопические сдвиги
близлежащих слоев), а затем и разрыв. Последний обычно
наступает при значительно меньших нагрузках, чем можно было бы
ожидать, исходя из известной энергии связей. Это
обусловлено тем, что в реальнок кристалле всегда имеются дефекты
упаковки: отсутствует какой-либо атом в отведенном для не-
171
Рис. 59 Кубические решетки: а — простая, б — объемно
ценгрированная, в — гранецентрированная.
го узле решетки или, наоборот, присутствует другой в
неположенном для него месте — междоузлии, некоторые атомы
основного вещества замещены примесными и т. д. Эти
дефекты и их скопления (дислокации) значительно снижают
прочность твердых тел и играют важную роль во многих
явлениях переноса.
Анизотропия. Рассмотрение механических свойств
кристаллов сталкивает нас с еще одной типичной особенностью
кристаллической фазы — анизотропией. Кристалл передает
нагрузки в разных направлениях неодинаковым образом.
Именно поэтому различают деформации растяжения и
сдвига, изменение длины и ширины (вместо изменения объема).
Это означает, что в общем случае мы не можем говорить ни о
давлении, ни об объеме как об универсальных
характеристиках твердого тела. Поскольку различные направления в
кристалле не эквивалентны, необходимо указывать, как
именно распределена нагрузка: какое усилие приложено по
длине, какое — по ширине и т. д. Соответственно и реакция
на это усилие — удлинение, уширение — является разной.
Поэтому аналогом газовых изотерм (pV = const) является
в данном случае сложная связь приложенной нагрузки и
деформации кристалла. Для описания пространственной
картины напряжений используется специальный —
тензорный — математический аппарат. Чтобы не прибегать к нему,
мы не будем во всех подробностях рассматривать упругую
реакцию твердого тела и ограничимся рассмотрением
высокосимметричных, кубических решеток (рис. 59). Подвергая
их только всестороннему сжатию или растяжению, можно
полиостью избежать осложнений, связанных с анизотропией,
и на простейшем примере исследовать тепловые движения и
уравнение состояния твердых тел.
172
§ 25. ДВИЖЕНИЕ КРИСТАЛЛИЧЕСКОЙ РЕШЕТКИ
Силы взаимодействия. Атомы твердого тела образуют
жестко связанный агрегат частиц. Энергия теплового
движения слишком мала, чтобы внести заметные искажения в
их правильную упаковку. Она способна вызвать лишь
небольшие смещения около положений равновесия, малые по
сравнению с периодом решетки а. Возникающее при этом
возвращающее усилие, которое противодействует тепловому
движению, стремясь вернуть атом на положенное ему место,
является важнейшей характеристикой кристалла. Заведомо
ясно, что эта сила задается потенциалом взаимодействия
частиц, объединившихся в кристалл, и поэтому, вообще говоря,
зависит от его специфики. Тем не менее общим правилом для
всех кристаллов является линейная связь силы со
смещениями, пока они невелики.
Природу этой закономерности легко понять на примере
линейной цепочки атомов, если предположить, что каждый
из них взаимодействует лишь с двумя ближайшими к нему
соседями. Это предположение несколько упрощает реальную
физическую ситуацию? в которой межмолекулярным
взаимодействием связаны и более удаленные узлы решетки.
Однако для валентных и молекулярных кристаллов характерно
настолько резкое уменьшение взаимодействия с
расстоянием, что приближение, в котором учитываются лишь
ближайшие соседи, оказывается вполне удовлетворительным 3.
Каждый атом цепи связан со своими соседями, те — со своими,
а в конечном счете ни один из них не свободен даже от самого
удаленного звена цепи (рис. 60).
Качественное представление о потенциале, в котором
движутся атомы такой цепи, можно получить, складывая
потенциальные кривые, характеризующие взаимодействие
атома с соседом справа и с соседом слева: гг_ и и+. Каждая
из них подобна изображенной на рис. 12 и каждая имеет
свой собственный минимум (при г = а0), вблизи которого
u(r) = u0 + §(r-a0)S-§(r-aK+... B5.1а)
3 Не всякая кубическая решетка стабильна в приближении близ-
кодействия. Простую и объемно центрированную можно смять,
не встретив сопротивления, так как существует способ сделать это,
не изменив расстояния между ближайшими соседями. Единственное
исключение составляет гранецентрированная, т. е. плотно
упакованная структура, которая и присуща кристаллам, связанным
короткодействующим взаимодействием Леннарда — Джонса A0.30).
173
X»
ХП~1 Хп ^ni-1
Рис. 60. Модель гармонически связанной цепочки атомов.
Однако в сумме они дают потенциал
Ф(хп) = и-+и+= и(хп —
+ и(хп+1 — хп),
B5.16)
симметричный по смещению от положения, равноотстоящего
от обоих соседей (рис. 61).
Возвращающее усилие, приложенное к тг-му атому
B5.2)
слагается из сил, действующих на него слева и справа.
Каждая из них определена через одну и ту же производную
парного потенциала
/w-f-
B5.2а)
О ней легко составить себе представление, мысленно
дифференцируя и(г) (рис. 62). Используя разложение B5.1а),
нетрудно установить, что вблизи узла решетки, т. е. при г ж а
B5.26)
где Да = а — а0 ^ 0, a
е- Ро —4" #оДа> Р = Ро
Ясно, что, вообще говоря, АаФ 0, так как решетка может
быть как в сжатом, так и в растянутом состоянии.
Отношение А а/ао = (а— ао)/аокак раз и характеризует
относительную линейную деформацию кристалла по сравнению с
ненапряженным состоянием, когда а = а0, а минимумы и±
совпадают с минимумом Ф.
174
fiU
Рис. 61. Потенциал ячейки в
линейной цепи атомов ( ),
складывающийся из мегкмолекуляр-
еого взаимодействия с
ближайшими соседями справа и слева
{а и б) Пунктиром показан
гармонический потенциал.
Рис. 62. Межмолекулярное взаимодействие и сила как
функции расстояния между частицами.
Однако обычно — настолько мало, что несовпадение
минимумов м_ и к+ не мешает их сумме иметь при малых
смещениях атомов параболическую форму, присущую
гармоническому потенциалу — пунктир рис. 61. Силы, действующие
на атом с разных сторон, в пренебрежении квадратичными
членами в B5.26) таковы:
B5.3)
§{хп — хп^ — а) и
/+ = еДа + $(хп+1 -хп- а).
Слагаясь, они образуют общее усилие
Fn=f_ + f+ = $(хп+1 + хп_г- 2хп) =
B5.3а)
в котором постоянные напряжения, обусловленные
деформацией решетки (е Да), взаимоуничтожились, а оставшиеся
линейны по q — отклонению тг-го атома от срединного поло-
q = хп —n+1 2—2z! 1
В этом
175
смысле сила B5.3а) ничем не отличается от своего аналога
A1.7), действующего в двухатомной молекуле, разве что
вдвое больше — в результате сложения усилий обоих
партнеров по взаимодействию.
Очевидно, что слабые смещения атомов в твердом теле
должны носить характер гармонических колебаний вблизи
положений равновесия. Вместе с тем эти колебания должны
быть согласованы между собой, так как имеется вполне
определенная связь между смещениями всех атомов
кристалла. Это видно из того, что сила B5.3а) зависит не только от
индивидуальной координаты атома, но и от координат
соседей. Как отдельные звенья общей цепи, атомы в
рассматриваемой модели сцеплены только с ближайшими соседями, но
стоит лишь начать колебаться одному, как приходят в
движение и все остальные. Правильнее сказать, что колеблется
весь кристалл сразу как единое целое, а не каждый атом
порознь.
Акустические колебания. Математически это выражается
в том, что N уравнений Ньютона, описывающих движение N
атомов цепи, составляют единую систему уравнений тхп =
= Fn, где Fn определено в B5.3а). Следовательно,
тхп = р(жп+1 + **_!- 2хп). B5.4)
Решение этой системы естественно искать в виде
хп = хп + &хп = A sin [2nvt + 2ккап + б] + хП1
B5.5)
где хп = an — координата тг-го узла цепи, а Ахп —
смещение атома из него. Параметры А и б имеют смысл амплитуды
и фазы продольной волны, v — ее частоты, а к — волнового
числа. Прямой подстановкой можно убедиться, что это
решение удовлетворяет системе B5.4), если частота и волновой
вектор связаны соотношением
v = ± jj- ]/Jsin (nka). B5.6)
Так как частота не может быть отрицательной величиной,
двузначность этого соотношения означает, что волны
смещения могут двигаться как в положительном (слева направо),
taK и в отрицательном (справа налево) направлении,
различаясь знаком к. Рассматривая зависимость v(k) (рис. 63),
можно заметить также, что волновые числа всех независимых
решений B5.5) заключены в интервале (— "«рзг)* Волны с
176
Рис. 63. Частотная дисперсия колебаний различных длин
векторами fe, не принадлежащими этому интервалу,
дублируют попавшие в него решения. Всякому к' =к + — (i —
целое) отвечает точно такое же решение, как и к. Поэтому
вполне достаточно ограничиться областью определения
— 2"-^fc^ + 2~. Всюду в пределах этой области частота
колебаний монотонно возрастает с \к\ (рис» 64) и при \к\ =
= тг достигает максимума, равного
1 l/P
B5.7)
Таким образом, в связанной цепочке атомов возможны
колебания с множеством частот, спектр которых простирается
от нуля до vm. И только колебания с частотой,
превышающей vm, неосуществимы. Такие колебания не проходят по
цепи оттого, что сила, действующая на атом, слишком быстро
меняет знак. Не успевая отреагировать на ее изменения, атом
воспринимает на таких/ частотах лишь усредненное по
времени воздействие, которое, очевидно,
равно нулю. Равным образом
человек, подчиняющийся команде:
«направо» — «налево» — «направо» —
«налево» и т. д., при неумеренно
быстрой подаче команд окажется
неспособным повиноваться.
Рис. 64. Волновое и корпускулярное
описание акустической ветви колебаний
одномерной цепочки.
Ртах Р
177
Это рассуждение имеет и обратную силу:
электромагнитные колебания любой частоты осуществимы потому, что
вакуум, в отличие от твердого тела, не обладает дискретной
структурой, в которой колеблющиеся частицы разделены
конечными пространственными интервалами. В
справедливости этого легко убедиться, если, сохраняя линейную
плотность вещества, в цепочке атомов р = ml a = const устремить
?тг, а стало быть, и а к нулю. Этот гипотетический предельный
переход ко все более мелким и ближе расположенным
частицам приведет нас в конце концов к идеальной модели
непрерывной струны, механические свойства которой были
подробно изучены задолго до утверждения атомистики. У такой
струны, как и у вакуума, спектр колебаний не ограничен
\Vm = lim l/"p/tfi-— = оо), \и линейный участок зависимости
\(к) продолжен до бесконечности:
v = vo-k, 0<&< оо. B5.8)
Здесь
vo = а У м = navm B5.9)
есть не что иное, как скорость распространения звука,
заменившая с в соотношении A9.1). Эта величина остается
конечной при а ->■ 0, так как при сохранении линейной
плотности вещества — сокращение а увеличивает крутизну
потенциал as в котором находятся атомы: |3~ >-оо. Если,
однако, считаться с тем, что любая струна — атомная
структура с конечным периодом решетки, то область
применимости сплошной модели следует ограничить неравенствами
v<vm или \к\ <С 1/2а, где и в самом деле зависимость v(k)
близка к линейной. За пределами этой области скорость
звука v0 = dv/dk постепенно уменьшается, обращаясь в нуль
при v = vm (см. рис. 64).
Таким образом, аналогия между колебаниями решетки и
вакуума в этом отношении сильно ограничена. В то время
как зависимость A9.1) является совершенно строгой, ее
кристаллический аналог B5.8) справедлив лишь
приближенно и в конечном интервале частот. В этом, пожалуй,
наиболее радикальное отлдчие материальной среды как носителя
механических колебаний от вакуума — переносчика
электромагнитных волн. Забегая вперед, заметим, что в кор-
зпускулярной модели теплового движения твердого телаг
178
вводимой по аналогии со светом, это различие оборачивается
нелинейной зависимостью г(р), связывающей энергию фонона
е = hv с его импульсом р = h-k. К тому же эта зависимость
отнюдь не универсальна, и для каждого кристалла, и даже
для колебаний разной поляризации имеет свой
специальный вид.
Зная, что скорость звука в твердом теле —'3-Ю5 см/с„
можно грубо оценить vm с помощью B5.8), полагая vm ^
1 105
ж щкт = v0 yu — 3--g--108 « 1013 Гц. Таким образом,
предельная частота механических колебаний в твердом теле
лежит в инфракрасной области. Это означает, что при
исследовании акустических свойств кристаллов вполне можно
игнорировать атомную структуру, ибо вся практически важная
область колебаний, включая ультразвук, 0 < v < 109 1/с
в масштабе рис. 64 лежит неощутимо близко к нулю частот^
где отклонения от B5.8) совершенно ничтожны. Однако на
тепловых свойствах твердых тел в области высоких
температур ограниченность спектра колебаний сказывается очень
существенно и приближение сплошной среды оказывается
неприемлемым.
Число колебаний: Поскольку оценка теплоемкости
вещества всякий раз связана с подсчетом числа состояний движения,,
полезно здесь же, не порывая с волновой моделью, оценить,,
как сказывается атомная структура кристалла на числе
возможных колебаний его решетки. Для этого следует
обратить внимание на то, что любые волны из семейства B5.5)
возможны лишь в неограниченной среде. Во всяком же
реальном кристалле конечной протяженности с линейными
размерами L на смещения крайних атомов накладываются
специальные ограничения. Если, например, концы
кристалла закреплены (схвачены с двух сторон зажимом), то Ах@) =
== Ax(L) — 0. Если они свободны, то краевые условия
выглядят иначе, но в любом случае оказывается, что число
допустимых колебаний счетно?Их частоты принимают
определенный * дискретный ряд значений, и промежуточные между
ними невозможны. Следует подчеркнуть, что дискретность к
и v пространства не имеет ничего общего с квантованием.
Это классическое явление, прямое следствие атомистики. Оно
объясняется счетностью числа степеней свободы любой
системы, состоящей из дискретного числа элементов.
Действительно, при закрепленных концах цепи в ней
возможны лишь стоячие волцы, а из этих — лишь те, у
которых в концах цепи оказываются узлы, а не пучности
колебаний. Но всякая стоячая волна является суперпозицией
179
двух одинаковых бегущих волн, распространяющихся в
противоположных направлениях, и если в качестве таковых
выбрать колебания B5.5), то
Ахп = j[Axn(k) — Ахп(— к)] =
= A cos Bnvt + б) sin BnkaN). B5.10)
Из этого семейства стоячих волн следует отобрать лишь те,
которые удовлетворяют краевым условиям: Ах = 0 и Ахп =
= 0. Чтобы выполнялось первое из них, достаточно
правильно выбрать знак (—) при сложении бегущих волн в B5.10),
что там и сделано. Второе условие менее тривиально. Оно
может быть удовлетворено лишь в том случае, если
BnkaN) = 0, т. е. 2nkNa = тя или
где т — целое число. Поскольку для стоячих волн к > 0
и изменяется в интервале 0 ^ к ^ 1/2а, т принимает
последовательно все значения от нуля до N : т = 0, 1, 2, . . •
* . .,7V — 1, N. Первое и последнее представляют состояние
покоя, а все прочие т нумеруют различные независимые
колебания системы. Их общее число (N — 1) равно количеству
атомов в цепи, за вычетом крайних (закрепленных), т. е.
полному числу степеней свободы одномерной цепи, из расчета
одна на каждый атом. Число степеней свободы, стало быть,,
не зависит от того, носят ли колебания индивидуальный или
•согласованный характер. Вместо независимых движений
различных атомов возникают различные колебания цепочки как
целого, но в том же самом количестве. Поскольку все
разрешенные состояния движения, согласно B5.11), равномерно
распределены по оси fe, в интервале dk возможно dk/(l/2L)
различных стоячих волн.
Если концы цепи не закреплены и, следовательно, в ней
осуществимы бегущие волны, то и область определения к
увеличивается вдвое за счет отрицательных к. Число же
независимых колебаний, естественно, остается прежним,
равным числу атомов в цепи. Соответственно плотность бегущих
волн в /^-пространстве оказывается вдвое меньше, чем
стоячих: в интервале dk их содержится dk/(l/L) различных мод.
В трехмерном кристалле число возможных колебаний
решетки находится простым обобщением последнего резуль-
180
тата, отнести который можно к каждой из осей в отдельности.
Все три оси fe-пространства разбиты на равные интервалы
величины 1/L, и поэтому разрешенные значения образуют так
называемую «обратную решетку» с периодом 1/L. В
элементе пространства dk содержится, следовательно, (dkJL)x
X {dkylL~x)(dkzlL) = Lsdk = L34ttfc2d/c узлов такой
решетки — различных возможных колебаний трехмерной
структуры. Отсюда видно, что число таких колебаний, отнесенное
к единице объема, есть просто dk — 4nk2dk. Таким образом,
удельная плотность колебаний не зависит ни от размера
кристалла, ни от периода решетки, и поэтому в точности
совпадает с оценкой плотности световых волн,
распространяющихся в непрерывной среде: ink2dk = inp2dp/h3.
Единственное, что отличает
dG = ЪЛпкЧк = Ш B5.12)
от A9.2) — это численный множитель, который учитывает
число независимых поляризаций волны, совместимых с
данным к. В кристалле оно равно не 2, а 3, поскольку решетка
помимо двух колебаний, поперечных к к, способна также и к
продольному колебанию с тем же к. Колебания такого типа
не присущи электромагнитному полю и поэтому в A9.2) не
учитывались.
Оптические колебания. Если кристаллы состоят из
атомов различных сортов, то, наряду с колебаниями
рассмотренного типа, появляются еще и другие. Они связаны со
смещением атомов одного сорта относительно другого и подобны
колебаниям свободных двухатомных молекул.
Четкое представление об этом виде движения можно
получить, рассмотрев одномерную цепочку из чередующихся
атомов двух сортов, воспроизводящую характерную
структуру ионных кристаллов. Все четные атомы будут
описываться системой B5.4), а нечетные — точно такой же системой^
но с иной величиной массы:
х2п_2 —
B5.13)
В силу различия масс в пробном решении
Ах2п = A sin [2nvt + 2пка -2п + б], B5.14)
Л*2п-1 = В sin [2nvt + 2nkaBn — 1) + б]
амплитуды А и В могут, вообще говоря, быть разными, но к,
Vj б должны быть одинаковыми. Так как решетка типа АВ —
181
это все же одна решетка, а не совокупность двух вложенных
друг в друга решеток А и #, в ее колебания должны
согласованно вовлекаться оба сорта частиц. По этой же причине
амплитуды А и В, хотя и различны, но не независимы. У каждой
волны имеется только один произвольный параметр — ее
интенсивность, которая задана одной из амплитуд. Другая
амплитуда однозначно выражается через первую: чем
сильнее колебания частиц А, тем сильнее должны колебаться и
В, если они вовлечены в единый процесс.
Это обстоятельство сразу же обнаруживается при
подстановке B5.14) в B5.13). Выясняется, что выполнение
равенств
= 2p[5 cos Bnka) — A],
Н V ; B5.15)
-4n2v2MB = 2p[A cos Bя/ш) - В]
является обязательным условием существования решения в
форме B5.14). Но система B5.15) имеет ненулевые решения
лишь в том случае, если
Р — 2n2v2m — р cos 2лка
- р cos Bпка) р - 2n2v2M = ° B5Л6>
или
v = JL(! + !)+! i/(± + I
Двузначность этого выражения свидетельствует о
существовании двух типов колебаний, различающихся величиной
переносимой энергии. При малых к имеем из B5.17)
-=У^+ж) <25-18>
и соответственно из B5.15)
а) А = В или б) j = - £, B5.19)
где а соответствует нижней ветви спектра колебаний
(рис. 65), а б — верхней. Ясно, что нижняя ветвь
представляет собой акустические колебания, в точности подобные
рассмотренным выше. Частота этих колебаний, как и
раньше, линейно возрастает с к при v <C vm, и лишь
коэффициент пропорциональности содержит среднюю массу,
учитывающую инерцию частиц обоих сортов. Равенство амплитуд
колебаний свидетельствует о том, что это движение
специфически присуще кристаллу в целом — общему изгибу це-
182
Рис. 65. Акустическая (а) и
оптическая (б) ветви колебаний
одномерной цепи.
пп атомов, а не отдельных
ее звеньев. Рис. 66, а
иллюстрирует Это обстоятельство
на примере поперечной
волны, где оно более наглядно
выражено.
Совсем другая природа
высокоэнергетических
колебаний, показанных на
\к\
рис. 66, б. То, что атомы смещаются противофазно
и обратно пропорционально своим массам, говорит о том,
что они колеблются около общего для них положения
центра масс, периодически изменяя длину связи, как
это имело место в двухатомной молекуле такого же
типа. Специфика кристаллической структуры сказывается
здесь лишь в том, что деформация связей синхронизована,
происходит одновременно у всех атомов цепи, причем у тех
пар, которые находятся вблизи пучности волны, она
максимальна, а у тех, которые оказались в окрестности yзлaf
почти равна нулю. Частоты таких колебаний лежат в
инфракрасной области, вследствие чего они называются
оптическими.
При возрастании к энергетический разрыв между
акустической и оптической ветвью уменьшается, но не исчезает
полностью, так как даже при к = femax = 1/4а
соответствующие предельные частоты равны
Существенно, что при изменении к от нуля до ктах частота
оптических колебаний не изменяется на многие порядки,
как это имеет место для акустической ветви, а уменьшается
Рис. 66. Акустическое (а) и оптическое [б) колебания одномерной цепи.
183
лишь в (l + -^1 раз. Поэтому в грубом приближении этой
дисперсией частоты, обусловленной кристаллической
структурой, можно и вовсе пренебречь. В таком случае
специфика кристалла как единого целого исчезает. Относительные
смещения атомов теперь можно рассматривать и как
согласованные, и как независимые, ничем не отличающиеся от
совокупности колебаний N несвязанных молекул АВ. В
области же акустических частот коллективность колебаний —
существенный и неустранимый факт, который определяет
и механические, и тепловые свойства решетки.
Молекулярные колебания. В молекулярных кристаллах
помимо акустических колебаний, охватывающих единым
движением весь кристалл, возможны также и
внутримолекулярные. Оказывается, что и эти колебания принадлежат всему
кристаллу, а не отдельным молекулам. Колебание, возникшее
на одной молекуле, передается ближайшим соседям, от них—
более удаленным, и таким образом распространяется на весь
коллектив. Природа этого явления несколько иная, чем
рассмотренных выше коллективных движений решетки.
Хорошей аналогией является передача колебания одного
маятника другому, висящему на той же опоре. Если маятники
настроены в резонанс, то и небольшого взаимодействия
достаточно, чтобы энергия одного из них передалась другому.
Именно резонансная передача возбуждения и приводит к
распространению внутримолекулярных движений по твердому
телу.
Помимо колебательных движений молекул возможны
также и вращательные — для молекулы в целом или для
отдельных групп ее атомов. Однако плотная упаковка частиц в
кристаллической структуре, как правило, препятствует
свободному повороту из-за возникающих при этом стерических
трудностей (механического сцепления молекул). В таком
случае имеют место ограниченные вращения («либрации»),
частичный поворот молекулы или группы атомов в обе стороны
в пределах люфта. Такие колебания специфичны только для
молекулярных кристаллов и полимеров.
§ 26. ФОНОННЫЙ ГАЗ
Модель. Акустические колебания решетки — это
единственный общий для всех кристаллов вид теплового движения.
При низких температурах, когда оптические колебания
выморожены, этот вид движения вообще единственно возмож-
184
ный. Акустические колебания представляют собой
продольные и поперечные волны различной частоты и интенсивности,
которые распространяются со скоростью звука во всех
направлениях, отражаясь от границ кристалла.
Это подсказывает аналогию с излучением. То, что
агентом, переносящим акустические колебания, является
материальная структура кристалла, а не вакуум, сказывается
лишь на их спектре, ограниченном сверху предельной
частотой vm. Последнее обстоятельство, однако, ничуть не мешает
гармонические колебания кристалла рассматривать так же,
как и любые другие, будь то колебания молекул или вакуума.
Колебания решетки кристалла, как и всякие иные, должны
быть проквантованы. Поскольку это уже делалось
неоднократно, теперь достаточно просто условиться рассматривать
их как квантовые осцилляторы со всеми присущими им
особенностями, включая нулевую энергию.
Не повторяясь во всех подробностях, напомним лишь, что,
согласно A3.7), каждое квантованное колебание с частотой
v обладает энергией
Е = [N + 1) hv = Ne + -|. B6.1)
Оно может быть заменено эквивалентной совокупностью N
частиц с энергией, равной е = hv. Так как спектр колебаний
широк @ < v ^ vm), эти квазичастицы, названные фононами
(звуковыми квантами), могут заметно отличаться друг от
друга по энергии: 0 <! е <! 8max = hvm. Таким образомг
мы получаем обычную для газа картину: в объеме,
ограниченном поверхностью кристалла, находится множество час-
тиц-«фононов», распределенных по их энергиям е в
количестве N(e).
Само по себе только это обстоятельство еще не дает
оснований для использования лексики и расчетных методов
газовой модели. Это становится возможным, если, помимо
энергии, сопоставить каждому фонону также и некоторый
импульс, который по аналогии с фотонным газом определяется
как р = hk. Как уже было установлено при анализе
колебаний одномерной цепочки, к изменяется в пределах —1/2а^
<1 &<[ 1/2а. Так как это верно по отношению к любой из
осей кристалла, любая проекция импульса фонона
определена в интервале (—h/2a, h/2a), а его абсолютная величина р ==-
= (pl + Pi + Р2гУ/2 не превышает л/3/2а.
Основной механической характеристикой фононного газа,
как и всякого другого, является связь между энергией и им-
185
пульсом его частиц: г(р). На примере одномерной цепочки
видно, что эта зависимость, повторяющая v(k), отнюдь не
линейна. Согласно B5.6),
В трехмерном случае она еще сложнее и может оказаться
разной для колебаний различных поляризаций и
направлений движения. Однако связь ей р при малых р всегда
линейна, как в B5.8) и B5.18а):
е = voP> Р < Ртах$ B6.2)
где v0 — скорость звука.
Введением представлений фононной модели достигается
неожиданный результат: тепловое движение в твердом теле —
жестко связанном агрегате атомов — качественно сводится
к газовому феномену. Кристалл представляется просто-
напросто резервуаром для находящегося в нем газа фононов,
обладающих любыми импульсами и энергиями в допустимых
пределах и двигающихся чзо всех направлениях со скоростью
звука. Число различных состояний движения фонона в
единице объема, как было установлено в предыдущем параграфе*
определяется формулой B5.12), которая в переводе на
корпускулярный язык выглядит следующим образом:
. B6.3)
Таким образом, плотность состояний в интервале (/?, р +
+ ар) в фононном газе втрое больше, чем в максвелловском*
и в 3/2 раза больше, чем в фотонном. Это связано с тем, что
состояние классической частицы однозначно задано
указанием импульса, а фотон в аналогичном состоянии может
находиться в двух модификациях, различающихся
поляризацией. Фононы же бывают трех сортов: поперечные — двух
видов, как и фотоны, и продольные.
В статистическом же отношении фононы ничем не
отличаются от фотонов. В условиях равновесия среднее число
фононов в состоянии с данной энергией N определяется, как и
для всякого осциллятора, формулой A9.10). Поэтому
плотность фононов с энергией е такова:
~ ш*4FАт- B6-4)
186
Она лишь статистическим весом 3/2 отличается от
аналогичного распределения фотонов B0.3).
Приближение Дебая. Несмотря на такое подобие,
употребить с пользой распределение B6.4) труднее, чем его
фотонный аналог. Сложность состоит в том, что связь энергии с
импульсом, которую необходимо знать, чтобы выполнить
любой конкретный расчет, носит линейный характер лишь
при е<С £тах. При 8, близких к 8тах» эта зависимость
нелинейна даже в случае одномерной цепочки. Еще сложнее
она в реальном ^трехмерном кристалле со своей
специфической кристаллической структурой и анизотропией. Чтобы,
не вникая в детали, учесть главную особенность
кристалла — конечность спектра частот, проще всего принять, что
линейное соотношение
е = vop B6.5)
остается в силе вплоть до самых высоких энергий, а фононы
с е > z;opmax и соответственно с р > рШах яе существуют.
Таково приближение Дебая (см. рис. 64), которое, конечно,
не может претендовать на полное соответствие с
экспериментом, но качественное и даже полуколичественное согласие
обеспечивает.
В приближении Дебая главное, что отличает фононный
газ от фотонного,— это ограниченность спектра энергий и
диапазона изменения импульса. Остальные свойства и
характеристики модели те же, разве что в скорости
передвижения по кристаллу звуковые кванты не могут соперничать
с фотонами (v0 < с), да еще поляризованы они иначе: не
только перпендикулярно к направлению движения, но и вдоль
него.
Максимальные значения энергии и импульса в
трехмерной решетке, как и в линейной, определяются тем, что
плотность различных колебаний, т. е. всех возможных состояний
фонона, конечна и равна числу степеней свободы,
приходящихся на единичный объем кристалла. Так как каждый атом
может колебаться лишь в трех взаимно перпендикулярных
направлениях, то при плотности частиц п число степеней
свободы в 1 см3 есть Зтг, и оно должно быть равно, согласно
B6.3),
Рта
h *j
Ртах
%* Ъп. B6.6)
187
Поэтому в приближении Дебая
[ЗпУ
B6.7)
Не претендуя на высокую точность, эта оценка правильно
отражает суть дела и даже порядок величины вшах. Из нее
видно, что лишь при п-+ оо, когда кристалл превращается
в сплошную среду, становится возможным появление фононов
сколь угодно больших энергий. Во всяком же кристалле^
реально встречающемся в природе, плотность не больше
1023 1/см3, так что при и0 = 3-106 см/с энергия акустических
фононов не превышает етах = 5-Ю4 эрг « 0,03 эВ.
Существование энергетического потолка, обусловленного
дискретной природой кристалла, является причиной того, что
имеется качественная разница в поведении фотонного и фо-
нонного газа. Если при кТ <С етах их отличает лишь скорость
передвижения и поляризация, то при кТ ~ етах и выше фонон-
ный газ преображается и становится совсем не похож на
фотонный, который при всех температурах ведет себя
одинаковым, сугубо квантовым образом.
Несомненно также, что фононы не являются
материальными частицами в подлинном смысле слова, как фотоны. Это
видно хотя бы из того факта, что, попробовав определить
массу фонона соотношением р — mv0, даже в приближении*
Дебая получаем абсурдный результат: г = pv0 = mvl,
вместо общеизвестной формулы Эйнштейна е = тс2. Кроме
того, движение фонона как в горизонтальном, так и в
вертикальном направлении не приводив к изменению положения
центра масс колеблющейся цепочки атомов. Иначе говоря,
перемещение фонона в гравитационном поле не способно
изменить его энергии подобно тому, как это происходит при
падении фотона. Таким образом, аналогия с фотоном по
существу ограничена уже тем, что фонону нельзя
сопоставить массы как меры энергии и гравитации. Следовательно,
считать фонон частицей можно лишь чисто условно в рамках
модели, призванной описать тепловое движение в твердом
теле по аналогии с газом.
Теплоемкость решетки. Энергия движения кристалла с
волновой точки Прения есть средняя суммарная энергия всех
видов колебаний решетки, а с корпускулярной — нулевая
энергия плюс энергия всех имеющихся в наличии фононов.
Плотность ее
Етах етах
и = j EdG = uQ+ j edn, B6.8)
188
8 , дт
где Е = у + eN в соответствии с B6.1). Тепловым вкладом*
в нее является только энергия фононов. Нулевая энергия м09}
сохраняющаяся и при Т = О, имеет сугубо квантовое
происхождение. Она является мерой механического движения^
в котором неизбежно пребывают связанные взаимодействием
частицы, подчиняющиеся волновой механике.
Распределения B6.3) и B6.4), необходимые для
вычисления слагаемых энергии, в приближении Дебая B6.5) пред-
ставимы в виде
,3т,3
viK
dG =
dk = NdG = 1252-S _. B6.10)
[ехр {фТ) - 1] v30h3
Определенная в B6.8) нулевая энергия легко вычисляется*
с помощью B6.9):
етах
-»-4 J
О
Появившаяся в последнем выражении температура Дебая
B6.12)
является единственным параметром, от которого зависит
плотность энергии колебаний:
етах В/Т
0 О О
B6.13)
Полная дебаевская энергия решетки
&в = uV. B6.14>
Для одного грамм-моля вещества
в/г
Видно, что эта величина является универсальной функцией
отношения Г/6. Равным образом и молярная теплоемкость
189
решетки
Cv =
\ r (T) fii
)v = Cv(eh B6Л
поскольку в = 6(F), а дифференцирование выполняется
при постоянном объеме.
Теплоемкость кристаллов, как и свободно движущихся
молекул, ведет себя по-разному при низких и высоких
температурах. Температура Дебая играет роль
характеристической температуры, вблизи которой вымораживается
колебательное движение. Ориентируясь на типичные значения
скорости звука и плотности частиц в твердом состоянии,
можно оценить в с помощью B6.12): в ^ 360 К. Хотя это
очень грубая оценка, дающая лишь представление о
масштабе величины, для металлов она достаточно хороша: для
алюминия, например, в = 400 К, а для меди — 320 К. Для
ионных кристаллов, как правило, эти температуры ниже:
для NaCl — 280 К, для КС1 — 230 К, а для КВг — 180 К.
Но наиболее низки температуры Дебая у молекулярных
кристаллов и твердых благородных газов: для Аг — 93,3 К,
для Кг — 71,7, для Хе — 64,0 К. Необходимо отметить, что
эти данные не рассчитаны, а извлечены из сопоставления
теории и эксперимента. Отклонения от расчетных величин
всегда имеют место, но они относительно невелики и
закономерны. Теория Дебая в изложенном виде не только
огрубляет спектр колебаний кристалла, но и игнорирует различие
между продольными и поперечными колебаниями,
характеризующимися разной скоростью распространения. По этим
причинам, а также вследствие анизотропии, если таковая
имеется, в обычно оказывается функцией температуры,
изменяясь в пределах 10% своей величины, рассматриваемой
как подгоночный параметр в B6.18). Любые постоянные
значения температур Дебая являются либо ориентировочными,
либо эффективными. Этого, однако, вполне достаточно,
чтобы заметить явно выраженную тенденцию к росту
температуры Дебая с повышением прочности решетки. Она
объясняется установленной в B5.7) пропорциональностью между
0 = hvm/k и упругой постоянной |3. Последняя тем больше,
чем круче потенциальная яма, а это достигается посредством
ее углубления. Температура Дебая для решетки алмаза
равна 1860 К.
Сравним теперь состояния кристалла ниже и выше тем-
иературы Дебая. При достаточно низких температурах
интегрирование в B6.13) можно распространить до бесконеч-
190
О 0,4 0,8 1,2 1,6 2 Т/в
4-
0,8
I Г
1,6
Т/в
Рис. 67. Средняя энергия коле- Рис. 68. Фононная теплоемкость
баний кристалла в дебаевском кристаллов,
приближении.
ности без ущерба для результата:
B6.17>
и =
Так как существование потолка энергии в этом
играет роли, все отличие фононного слагаемого в этой
формуле от его фотонного аналога A9.6) сводится к множителю
3/2, учитывающему число поляризаций, да к замене с на v0.
Нетрудно видеть также, что всюду в пределах этой сугубо
квантовой области вклад нулевых колебаний соизмерим с
тепловым (рис. 67). Что касается молярной теплоемкости, то,
согласно B6.16), она возрастает по «закону Г3 Дебая»:
B6.18)
т. е. так же быстро, как и в фотонном газе.
Этот рост резко тормозится с приближением к
температуре Дебая, а при значительном превышении ее
останавливается вовсе (рис. 68). В самом деле, в высокотемпературном
пределе можно ограничиться первыми членами разложения:
-что при подстановке в B6.8) дает
B6.19)
191
£N
не
0
Т>в
Т=в
\
Рис. 69, Распределение фо-
нонов по энергиям при
разных температурах.
Когда с ростом температуры все поправочные члены
исчезают, остается классическое выражение для плотности
энергии, следующее из закона равнораспределения: &D =
= 3NTcT — по кТ на каждую из трех степеней свободы
колебательного движения N атомов. В этом пределе и
Cv = ЗЛУс = ЗД B6.20)
в точности согласуется с классическим результатом теории
теплоемкости. Он известен как закон Дюлонга и Пти:
-«молярная теплоемкость твердых тел равна 6 кал/(моль-К)
независимо от температуры».
Ничего подобного закону Дюлонга и Пти не могло иметь
места в фотонном газе. Поскольку для фотонов в = гтъл1к =
= оо, первый из рассмотренных здесь предельных случаев
распространяется на весь диапазон температур. Достижение
классического предела в случае колебаний решетки —
прямое следствие ограниченности их спектра. С волновой
точки зрения колебания решетки носят квантовый характер
лишь до тех пор, пока часть из них выморожена (рис. 69).
Но при Т ^> в даже самые высокочастотные колебания
приводятся в состояние возбуждения и могут быть описаны
классически. Благодаря этому твердое тело подчиняется
принципу соответствия в той же самой степени, что и газ (§ 13).
С корпускулярной точки зрения средняя энергия фононов
в области низких температур, при Г<С ©, порядка кТ, а
быстрое возрастание и(Т) в B6.17) объясняется уплотнением фо-
нонного газа: п ~ Г3. Это следует из рассуждений,
приводящих к B1.9), которые здесь могут быть полностью
воспроизведены. При более высоких температурах (Т S> G) рост
средней энергии фононов стремится к пределу (е ~ /ев),
а плотность фононов продолжает возрастать, но уже
линейно: п ~ тг(Г/в), как и и = гп + и0.
Иначе обстоит дело со средней энергией теплового
движения атомов, которые в отличие от фононов сохраняются
в числе при любых температурах: п = const. Их средняя
192
квадратичная скорость (а также распределение по скоростям)
правильно описывается классической статистикой только
при температурах выше дебаевской. Ниже этой
температуры, в сугубо квантовой области, средняя энергия теплового
движения атомов существенно меньше классической
величины, а ее температурная зависимость более резкая.
Согласованность колебаний. Если кристалл состоит из
атомов двух сортов, то, как было установлено в предыдущем
параграфе, на каждое акустическое колебание приходится
одно оптическое. В общей сложности из 6п степеней свободы
в кубическом сантиметре Зга приходятся на акустические и
Ъп на оптические колебания. Соответственно этому плотность
тепловой энергии двукомпонентного кристалла должна
складываться из выражения B6.13) и нижеследующего,
относящегося к оптической ветви:
и = ЪпГЁ=Ъп\ -£*- + ^|. B6.21)
Г *vo , ftvo1
ЬИ- 2Г
Поскольку частота оптических колебаний сохраняет порядок
величины при любых /с, она считается в B6.21) одинаковой,
равной v0. В таком приближении теплоемкость, связанная
с оптическими колебаниями, ничем не отличается от
теплоемкости равного количества двухатомных молекул с
частотой колебаний v0.
Небезынтересно отметить, что именно таким образом была
первоначально оценена Эйнштейном и теплоемкость,
связанная с акустическими колебаниями. Это улучшило результат
Дюлонга и Пти, продемонстрировав, что Cv ->• 0 при Т ->- 0.
Однако экспоненциальное убывание противоречило закону
Г3, который воспроизвелся лишь после того, как Дебаем был
существенно принят во внимание непрерывный спектр
акустических колебаний, начинающийся с нулевой частоты.
В этом спектре всегда находятся такие колебания, которые
могут быть возбуждены при низких температурах, в отличие
от оптических колебаний, которые возбуждаются не раньше,
чем при Т ~ hvo/k.
Любопытно, что классический результат Дюлонга и Пти
получается одинаково успешно как из B6.13), так и из
B6.21), т. е. независимо от того, рассматривается ли
движение кристаллической решетки как коллективное или как
состоящее из индивидуальных колебаний атомов в своих
потенциальных ямах. Это свидетельствует о том, что при высоких
температурах случайное наложение многих колебаний ре-
7 А. И. Бурштейн 193
шетки, в которых одновременно принимает участие
отдельный атом, придает его движению настолько
беспорядочный характер, что в нем трудно усмотреть какую-либо
согласованность с движением соседей.
Избыток индивидуальной энергии не только расстраивает
упорядоченность коллективных движений, но при
благоприятном стечении обстоятельств может даже привести к
выбросу атома из узла в междоузлие. Так создаются
термические дефекты-дислокации и вакансии, о которых речь
впереди. Пока их концентрация невелика, влиянием, которое
они оказывают на теплоемкость кристаллов, можно
пренебречь. Однако в области предплавления число дефектов
резко возрастает, и в этом случае затраты тепла на их
возникновение (частичный разрыв связей) становятся
заметными .
Теплопроводность решетки. Существование дислокаций
свидетельствует о неидеальности кристалла. Но еще задолго
до того, как это становится заметным, обнаруживается
отличие реального потенциала, в котором находятся атомыг
от гармонического. Отличие это проявляется в том, что
реальное возвращающее усилие, действующее на атомы
кристалла, нелинейно по отклонению от положения равновесия.
Степень нелинейности определяется величиной следующих
поправок в разложении потенциала. С учетом первой же
такой поправки характер колебаний решетки должен, вообще
говоря, трансформироваться. Дебай предложил
рассматривать эту поправку как слабое взаимодействие, связывающее
различные гармонические колебания, представленные в
спектре решетки. Хотя энергия такого взаимодействия мала в
сравнении с собственной энергией колебаний, его
существование все же приводит к тому, что, однажды возникнув,
колебательное движение не будет сохраняться вечно в одном и
том же виде, а с течением времени станет передаваться от
одного осциллятора решетки другим, изменяя частоту и
ориентацию волнового вектора.
С корпускулярной точки зрения передача колебательных
квантов между различными модами решетки является
свидетельством взаимодействия фононов между собой.
Происходящее при этом изменение их энергии и направления
движения может быть естественно истолковано как результат
столкновений, обусловленных этим взаимодействием. Таким
образом благодаря ангармоническим слагаемым потенциала
фононный газ превращается из идеального в реальный. Его
частицы обретают возможность сталкиваться между собой,
вследствие чего их траектории движения искривляются^
194
а передача тепла затормаживается. Если определена частота
столкновений, т. е. время свободного пробега т0, то этим
задана и его длина:
% = г;ото, B6.22)
где vQ — скорость звука, как обычно. После этого теория
теплопроводности может быть развита по аналогии с уже
построенной, так как появляется возможность исходить из
представления о локальном равновесии, существующем в
каждой точке пространства в масштабе К. Поэтому, не
повторяясь во всех подробностях, можно сразу же выписать
формулу A6.3) для коэффициента теплопроводности:
х = -^ cvvlx0 = у CvVqX, B6.23)
( дгп \
в которой cv = [ dT 1 —удельная теплоемкость кристалла.
Специфика фононного газа обнаруживается главным
образом в том, что столкновения носят несколько необычный
характер: число участвующих в них частиц не сохраняется.
Наиболее быстро осуществляются Процессы распада одного
фонона на два и, наоборот, слияния двух фононов в один,
побольше. Ангармоническое взаимодействие, благодаря
которому фононы обретают возможность сталкиваться,
разменивая свою энергию и прерывая свободный пробег, способно
не только управлять переносом тепла, но и восстанавливать
равновесие в фононном газе, обходясь без внешнего
вмешательства. Этим фононный газ существенно отличается от
фотонного, который не способен самостоятельно приходить в
равновесие. Иными словами, фотоны ведут себя как точечные
массы, тогда как фононы подобны частицам конечного
сечения.
§ 27. УРАВНЕНИЕ СОСТОЯНИЯ
Баланс сил. Изобарическое расширение твердых тел в
широком диапазоне температур едва заметно, но
противостоять ему трудно. Совершенно так же и растяжение или
сжатие легко доступными средствами не способно вызвать
сколько-нибудь заметные изменения объема и даже формы прочных
кристаллов. Поэтому если рассматривать чисто внешние
признаки изменения состояния как меру того, что происходит с
кристаллом на самом деле, то можно составить себе
превратное представление о фактическом положении вещей.
7* 195
Истина же состоит в том, что при повышении температуры
в кристалле, как и в газе, увеличивается интенсивность
теплового движения частиц, а производимое им давление pt
возрастает в еще большей пропорции. Последнее, однако,
почти полностью компенсируется в такой же мере возросшим
внутренним напряжением pt. Для грубой оценки масштаба
этих сил при высоких температурах можно воспользоваться
простейшей газовой формулой: pt ~ пкТ. Из нее видно, что
термическое давление в твердом теле, по крайней мере, во
столько же раз больше газового, во сколько больше
плотность частиц в единице объема. Нормальное давление
развивает газ с плотностью 1019 см, а плотность атомов в
твердом теле п ~ 1023 см. Следовательно, их давление при этой
же температуре в 104 раз больше. Чтобы уравновесить его,
внутреннее давление pt также должно быть ~104 атм. В
балансе этих огромных противоборствующих сил совершенно
теряется атмосферное давление, сжимающее кристалл извне.
Даже изменение его в несколько раз не может сказаться
заметным образом на форме и размерах твердого тела,
которое «замечает» лишь нагрузки, соизмеримые с pt и pt.
Сказанное в равной мере относится и к другим
конденсированным средам (жидкостям, аморфным телам, полимерам) и
объясняет, почему при характеристике их состояния
разумно отдать предпочтение внешне необнаружимым, но
огромным по величине и резко изменяющимся силам:
термическому и внутреннему давлению.
Уравнение состояния с этой точки зрения есть просто
условие баланса, которое требует, чтобы внешнее давление р
совместно с внутренним рг в точности уравновешивало
термическое давление, действующее на поверхность кристалла
изнутри:
P+Pt = Pt- B7«1)
Идеальный газ, в котором, по определению, pt = О, является
исключением в том смысле, что не возникает надобности
различать его внешнее и термическое давление, ибо р = Pt =
= пкТ. Но даже в газе, стоит лишь учесть силы
взаимодействия, как внешнее давление оказывается меньше
термического. Разница между ними как раз равна ван-дер-вааль-
совскому внутреннему давлению pt = A/V2, которое
отчасти сдерживает натиск молекул реального газа на стенки*
Но если в реальном газе pt «С р « pt, то в твердом теле
ситуация чаще всего противоположная: р <g.pt ж pt (рис. 70).
Силы сцепления настолько велики, что даже при высоких
температурах способны удержать поверхностные частицы от
196
ООоОоО
_ oooOqo
OpOOOQ OO
Газ
Твердое тело
Рис. 70. Давление газа на стенку (а) и стенки на газ (б).
активной бомбардировки среды, с которой кристалл
соприкасается. Благодаря этому не все удары и не в полной мере
достигают цели, и давление, которое передается наружу,
значительно меньше термического. Таким образом, баланс
сводится в основном между pt и ри хотя наблюдаемой
величиной продолжает оставаться р.
Эти качественные представления могут быть строго
оформлены только в том случае, если слагаемым уравнения B7.1)
даны четкие определения. В случае твердых тел это можно
сделать, расчленив полную энергию решетки на энергию
покоя Uo и энергию движения &в\
&=U0 + «ъ. B7.2)
Первое слагаемое есть не что иное, как потенциальная
энергия кристалла, все атомы которого неподвижно расположены
в узлах решетки. Очевидно, что в приближении ближайших
соседей
Nc . ч
= — " (а),
B7,3)
где с — число частиц в первой координационной сфере,
а а — ее радиус. Это в точности совпадает с первым
слагаемым потенциальной энергии A0.31), если преобразовать его
с помощью A0.38). Ясно, что UQ = U^(V) — не вся
потенциальная энергия, а лишь ее постоянная часть. Остальная
потенциальная энергия, связанная с отклонениями от
регулярной упаковки, модулируется тепловым движением
частиц. Эта часть наравне с кинетической энергией входит в де-
баевскую энергию движения <§fD, причем в гармоническом
приближении их вклад в нее равновелик.
Точно такое же разделение можно произвести и в
свободной энергии кристалла:
Т = & - TS = Uo + &~D. B7 А)
197
Между ее дебаевской частью &~D и &D сохраняется обычное
термодинамическое соотношение:
^п = &d - TS. B7.5)
Используя B7.4) в общем определенди давления A0.8а), имеем
аи
аи t oz-D \
dV \ dV Jt'
^ ^ dV
Почленно отождествляя этот результат с B7.1), получаем
следующие определения остальных слагаемых уравнения
состояния:
Pi = -^f, B7.6a)
Внутреннее давление. Поскольку U0(V) слагается из
энергии связей, объединивших атомы (молекулы) в твердое
тело, внутреннее давление, равное dUJdV, возникает как
упругая реакция решетки на ее всестороннее растяжение
или сжатие.
Если упрощенно представить себе кристалл
совокупностью параллельных атомных цепочек, то
Uo = N[ux{ax) + иу(ау) + uz(az)], B7.7)
где аХ1 ау и az — периоды простой решетки вдоль различных
осей. В пренебрежении анизотропией кристалла: их =
= иу = uz = и и ах = ау = az = a, a u(r) имеет тот же
смысл, что и в B5.1а). Используя B7.7) в B7.6а), имеем
Pi~iy1? |аЧГ + ~W + dv ) ~ 6J" 47 ; dV
Принимая во внимание, что при изотропной деформации
V = Nax-ay-az = Na3, находим
p. = JL.f(a)} B7.8)
где f(r) определена в B5.2а).
Последний результат нетрудно проинтерпретировать,
исходя из того, что каждый атом кристалла, даже находясь в
положении равновесия, испытывает действие сил B5.3),
если решетка сжата или растянута. В самом деле, даже
занимая свои места в узлах решетки (хп+1 — хп + я = #n-i +
+ 2а), соседи тг-го атома тянут его к себе с равной^
198
хотя и противоположно направленной силой
№ = /+ = -/- = еЬа. B7.9)
Действуя на атомы, расположенные внутри твердого тела,
эти силы в точности компенсируют друг друга, как в B5.3а),
и на колебаниях кристалла не сказываются. Тем не менее
решетка в целом напряжена, и это видно по состоянию
поверхностных атомов. Испытывая одностороннее
воздействие — только изнутри кристалла, эти атомы втягиваются
внутрь ^твердого тела с силой B7.9), а всего их на единице
поверхности 1/а2 штук. Растяжение периода решетки на
величину Да является причиной того, что перпендикулярно
твердой поверхности приложено давление, направленное в глубь
кристалла и равное
i ,/ \ е А г, Afl 1 AF /ОГ7 .Ач
Pi = ~7 ^ = 1*~ ~ = Г ~ш B7-10)
Это и есть внутреннее давление. Правда, такая его оценка
справедлива лишь в гармоническом приближении, когда
деформация кристалла действительно линейно возрастает с
нагрузкой и Е есть не что иное, как модуль Юнга, а к =
= 3/Е — коэффициент сжимаемости 4. Из разложения B5.26)
ясно, что это возможно до тех пор, пока
Р(я-ао)>|-(а-аоJ, т. е. Aa<2P/g
Вообще же необходимо пользоваться более общим
определением /(а), данным в B5.2а).
Очевидно,, что Pi(a) в точности повторяет зависимость
/(а), изображенную на рис. 62. Если же к рь добавляется
внешнее давление, то изобарическая силовая характеристика
просто смещается вдоль оси ординат на величину р, образуя
семейство, изображенное на рис. 71. Очевидно, что р может
принимать и отрицательные значения, поскольку
существует возможность растяжения твердого тела. Наиболее
существенное отличие внутреннего давления твердых тел от
его ван-дер-ваальсовского аналога состоит в том, что в его
формировании наравне с силами притяжения принимают
4 В действительности, х = 3A — 2о)/Е, где а — коэффициент
Пуассона, устанавливающий величину относительного поперечного
сжатия твердого тела при его линейном растяжении. В линейной
модели этот эффект игнорируется.
199
участие и силы
отталкивания. Если кристалл сильно
растянут, то доминирующую
роль играет притяжение и
внутреннее давление
положительно — направлено
внутрь твердого тела, как
это было и в реальном газе.
Но если кристалл сжат
настолько сильно, что период
решетки меньше своего
идеального значения а0 (при
котором достигается минимум
и), то внутреннее давление
отрицательно. Оно
направлено наружу, и его масштаб
определяется силами
отталкивания, Особенно важен нуль внутреннего давления, при
котором противоборствующие силы уравновешены и
решетка находится в ненапряженном состоянии с периодом,
равным а0. Только в окрестности этого нуля и применимо
квазигармоническое приближение* являющееся основой
рассмотрения твердых тел.
Термическое давление. Чтобы установить связь
термического давления с энергией колебаний, необходимо
воспользоваться известным термодинамическим соотношение^! вы*
текающим из A0.6) и A0.8):
Рис. 71. Силовая
характеристика при
разных внешних
давлениях (всестороннем
сжатии и растяжении).
которое связывает свободную энергию с полной.
Подставляя сюда B7.2) и B7.4), можно обнаружить, что точно такое
же соотношение связывает дебаевские части $F и <§\
ш
B7.12)
Воспользуемся теперь тем, что, согласно B6.15), отношение
-х~ есть универсальная функция единственной переменной
0/Г. Это позволяет, разделив B7.12) на 6 и помня о том* что
200
в = в(У), с равным правом написать
Jb _==± и\ т I d\T~
0 '~ е
d -ЗГ
Из этих тождеств прежде всего вытекает, что SF'DIT —
такая же универсальная функция 0/7\ как и <?TD/e. Стало
быть, зависимость от объема может появиться в £Гв только
через температуру Дебая S(V)V которая, согласно B6.16),
B5.9) и B5.7), равна
Она зависит от объема через р = Р(У). Ввиду этого
определение термического давления, данное в B7.66), может быть
раскрыто следующим образом:
Исключая из него (dg~D/d@)T с помощью последнего
выражения в B7.13), получаем искомое соотношение
Pt = — -§"W = ^щ B7Л5)
где и — <oBlV. Формально оно совершенно подобно A.8)
или B1.6), и с этой точки зрения постоянная Грюнайзена
^ (In О) G1G)
есть всего лишь численный коэффициент в обычной
пропорции, связывающей давление с объемной плотностью
энергии и.
Однако при ближайшем рассмотрении оказывается, что
дело обстоит не так просто. Используя в B7.16) определенно
температуры Дебая из B7.14), имеем
dV'
B7.17)
Учитывая, что при изотропной деформации -у- = 3 —, а
Р = Ро - *о(« - «о)*
B7.18)
201
как это следует из B5*2в), находим,, выполняя
дифференцирование в B7Л7):
т--£т1 = ^~T = const>0- B7Л9)
Эта оценка у свидетельствует о том, что термическое
давление, вообще говоря, не является обязательным следствием
теплового движения решетки. Оно возникает лишь в меру
ангармоничности связей. Если бы существовал кристалл,
атомы которого двигались бы в строго гармоническом
потенциале (g0 = 0), то при той же самой плотности тепловой
энергии pt равнялось бы нулю, ибо 7 = 0.
Если проводить параллель между фононным газом и
молекулярным, то факт отсутствия давления на стенку
выглядит парадоксально, и обычно истолковывается в том духе, что
фононам не присущ импульс в подлинном смысле этого
слова б. Однако если сопоставление проводить не с
молекулярным, а с фотонным газом, то объяснение парадокса
выглядит более естественно. Ведь и фотонный газ, как и фонон-
ный, не оказывает давления на свою собственную
поверхность, каковой является граница полости. Давление
испытывает лишь поверхность ящика, т. е. инородной среды, и то
лишь в той мере, в какой фотоны с ней взаимодействуют.
Опираясь на эту аналогию, поверхность твердого тела
следует считать совершенно прозрачной для идеального фонон-
ного газа. Естественно, что проницаемая в обе стороны
поверхность не испытывает давления, так как упругое
отражение от нее невозможно. Прозрачность поверхности является
естественным следствием того, что, руководствуясь
соображениями удобства, мы еще в § 25 перешли от стоячих волн к
бегущим, имеющим неограниченную протяженность.
Поэтому-то в гармоническом приближении кристалл и
представляет собой прозрачный резервуар, сквозь который во всех
направлениях и с равной силой дует фононный ветер.
Став на такую точку зрения, мы можем теперь
естественно объяснить не только отсутствие термического давления в
гармоническом приближении, но и его появление с учетом
ангармонических поправок к потенциалу. Выражаясь
лаконично х можно сказать, что поверхность твердого тела
прозрачна для идеального фононного газа, но непрозрачна или
5 Вследствие этого, а также ввиду несохранения импульса в
процессах переброса р = hk чаще называют «квазиимпульсом» фонона,
подчеркивая его несколько условный смысл.
202
1ММШШ11ШШ
ГГГГПТГГГГиТТТТм
Рис. 72. Термическое
v Pt "*"
давление фононов на ъ *J
границы кристалла
частично непрозрачна для реального. Действительно, как
выяснилось при анализе теплопроводности, учет ангармо-
низма превращает фононы в частицы конечного сечения. Ан-
гармонизм ответствен и за возникновение термического
давления, которое естественно истолковать как давление
реальных фононов на поверхность, ставшую для них частично
непрозрачной. Это позволяет представить себе твердое тело
как резервуар, наполненный фононами, которые, двигаясь
в любом направлении и упруго отражаясь от всех границ,
создают термическое давление pt (рис. 72). Можно сказать,
что поверхность кристалла так же подвержена изнутри
давлению фононного газа, как извне — газа обычного.
Величина термического давления зависит от температуры
и объема точно так же, как объемная плотность тепловой
энергии и. Используя для определения этой зависимости
B6.17) и B6.19) с учетом B7.14), находим из B7.15):
i
B7.20)
Ясно, что в изохорическом сечении термическое давление
возрастает так, как показано на рис. 67. Но рассматриваемое
как функция объема кристалла (периода решетки), оно
убывает точно так же, как в идеальном газе: pt~ п~ — ~ —=-,
v a
если, конечно, не принимать во внимание слабой
зависимости Р(а) B7.18). Поэтому изотермы pt(a), изображенные
на рис. 73, представляют собой семейство гипербол,
наинизшая из которых отвечает нулевой энергии кристалла.
Необходимо отметить, что сам факт существования нулевой
энергии, имеющей чисто механическое происхождение,
свидетельствует о том, что наименование pt не вполне соответствует
его физическому смыслу. Было бы правильнее называть pt
303
Pt
Рис. 73. Изотермы фононного газа.
Рис. 74. Устойчивый и
неустойчивый баланс сил.
«давлением движения», которое ниже температуры Дебая
лишь отчасти является тепловым. Подлинно термическим
давлением pt становится только при Г^>6, когда всеми
квантовыми поправками к классическому результату Дюлон-
га и Пти можно пренебречь.
Уравнение Ми — Гртонайзена. Теперь мы располагаем
всем необходимым для получения уравнения состояния
твердого тела. Достаточно подставить B7.6а) и B7.15) в B7.1), чтобы
получилось «го, что требуется:
Р +
dV
' = уи.
B7.21)
Это уравнение впервые было выведено Ми в классическом
варианте при Т >> 6, а затем распространено Грюнайзеном на
существенно квантовую, низкотемпературную область (Т <<
<С 0). Как уже было разъяснено в самом начале, физический
смысл его состоит в том, что внешнее давление совместно с
внутренним — деформационной реакцией решетки —
уравновешивает термическое давление, распирающее кристалл
изнутри.
В нормальных условиях внешнее давление пренебрежимо
мало. Поэтому если ограничиться этими условиями, то
можно положить р = 0 и получить вместо B7.1) pt = pt, а вместо
B7.21)
Г), B7.22)
204
где принята во внимание оценка pt через модуль Юнга,
данная в B7.10). Взятое в таком виде уравнение Ми — Грюнай-
зена описывает изобарическое тепловое расширение
кристаллов:
ЛГ = ^ = ТГи(Г>' <27-23>
Тепловое расширение — результат компромисса между
силами термического и внутреннего давления. При
увеличении температуры прибывшие в числе и прибавившие себе
энергии фононы развивают все большее давление на
поверхность кристалла, растягивая его изнутри. Решетка
кристалла реагирует на это растяжение точно так же, как ни любую
попытку внешних сил увеличить ее габариты. Оказывая
сопротивление в меру своей упругости, она вначале
развивает тем большее давление, чем значительнее деформация,
и в определенных пределах способна противостоять
термическому давлению. Более того, увеличение упругого
сопротивления вследствие деформации происходит сначала линейно
и совсем незначительных растяжений оказывается
достаточно, чтобы справиться с давлением фононов. Это соображение
может быть проиллюстрировано графически, если совместить
на одной диаграмме кривые, изображенные на рис. 71 и 73.
Такая диаграмма (рис. 74) необычна в том отношении, что
каждая точка на ней представляет собой состояние
равновесия лишь в том случае, если в ней пересекаются фононная
изотерма и силовая характеристика, представляющая собой
сумму внутреннего и внешнего давления: р + pt. Глядя на
нее, можно сделать ряд качественных выводов, являющихся
прямым следствием уравнения B7.21).
Прежде всего ясно* что устойчивое равновесие
реализуется только при пересечении фононных изотерм с восходящей
ветвью силовой характеристики. Только в этом случае любое
нарушение баланса создает усилие, возвращающее систему
в прежнее состояние. Если же изотерма пересекает
нисходящую ветвь, то стоит лишь точке отклониться вправо, как
термическое давление начинает преобладать над
сдерживающим усилием, и кристалл должен развалиться. Если же
она отклонится влево по изотерме, то, наоборот, сумма, сил,
стремящихся сжать кристалл, станет настолько
преобладающей, что процесс продолжится вплоть до пересечения с
восходящей ветвью, где и остановится ввиду достижения
равновесия.
Кроме того, очевидно, что при всяком заданном внешнем
давлении силовая характеристика имеет максимум, выше ко*
205
торого равновесие вообще не реализуется, так как изотермам
не с чем пересекаться. Это значит, что кристалл способен
выдержать не любые нагрузки и температуры. При заданном
давлении максимально возможная температура не больше
той, при которой изотерма касается максимума силовой
характеристики. А при изотермическом растяжении кристалла
максимальная нагрузка — та, при которой максимум
силовой характеристики опускается ниже изотермы процесса.
В обоих случаях предельное удлинение кристалла должно
быть порядка расстояния до максимума р£, Его нетрудно
оценить, используя разложение B5.26). Приравнивая нулю
-j- (я™), легко видеть, что максимальное Да есть
Аат = ат - а0 = Ь- = -^ « -i- а0, B7.24)
где принято во внимание определение у, данное в B7.19),
и его обычное численное значение, примерно равное двум.
Таким образом, самое большее, чего можно добиться,
подвергая кристалл растяжению,— это удлинить его на 8% в
сравнении с первоначальным размером в. При этом
приходится прикладывать тем большую нагрузку, чем большей
деформации мы желаем добиться. По мере ее увеличения
сопротивляемость решетки падает, а когда Е обращается в
нуль, наступает разрыв. Впрочем, на самом деле реальный
кристалл начинает течь и разрушаться значительно раньше,
вследствие несовершенства решетки. Однако верхнюю
оценку предельной нагрузки можно получить достаточно
надежно, используя B7.24) в B7.10):
Рт<1-Ьат = ^. B7.25)
Эта оценка максимальна еще и потому, что относится к
абсолютному нулю, когда pi « —р >> pt(O), и решетка должна
справляться в основном с усилием, приложенным к ней
извне. С повышением температуры на помощь последнему
приходят фононы, действующие изнутри, и разрушение
кристалла достигается ценой значительно меньших усилий.
Учитывая, что обычные для металлов значения Е~5-Юъ атм,
легко видеть, что рт ~ 40 000 атм. Этим, естественно, объяс-
6 Ради наглядности изображения на диаграмме рис. 74 отноше-
ние равно как и —2 превышено примерно в 5 раз.
т \ % )
206
няется, почему твердое тело подвергается значительной
остаточной деформации и разрушению только при огромных
нагрузках, соизмеримых с рт, тогда как обычными,
подручными средствами весьма трудно добиться заметных его
изменений.
С помощью B7.25) можно грубо оценить границу
температурного диапазона, в котором возможно существование
твердых тел. Исходя из равенства рт = pt = у-ЪпкТп,
определяющего наиболее высокую изотерму, находим
Е9 У
18у2пк 18-4-1023.1,4-10"
Тп = Е9 = У1^ т«<500 К. B7.26)
18у2пк 18410231410"" V '
Впрочем, настоящая точка плавления может лежать и в
2—3 раза выше по температурной шкале из-за
приблизительности оценки рт в B7.25).
Тепловое расширение. Рассмотрим теперь подробнее, что
происходит с твердым телом при его разогреве в нормальных
условиях. Прежде всего следует обратить внимание на то,
что кристаллы расширены уже при абсолютном нуле
температур. В силу квантовых свойств решетки ее движение ,не
прекращается и при Т = 0. Ему отвечает нулевая энергия
и соответствует давление pt(O), растягивающее кристалл
изнутри. Масштаб растяжения нетрудно определить из B7.23)
с помощью B6.11):
-T-b-SH*. <27-27>
При Е = 5.105 атм п = 1023, в = 300 К, относительное
удлинение равно 1 %, что не так уж мало, учитывая, что
максимальное не превышает 8%. Из B7.10) видно, что при Да/а ■=
= 10 решетка выдерживает напряжение порядка 103 атм,
созданное нулевым давлением. Это оправдывает
пренебрежение нормальным давлением, незначительным в этом
масштабе сил даже при Т = 0. Поскольку растяжение
всестороннее, увеличение кристалла в объеме втрое больше:
1
_ 21yhnl / з
где г;@) = 1/тг@) — удельный объем при абсолютном нуле
температур, а п0 = 1/и0 — плотность ненапряженного
кристалла, в котором атомы размещены в минимумах парного
потенциала и(г). Если прочность коррелирует с р, то из этой
формулы следует, что изначальное растяжение должно быть
наибольшим в молекулярных кристаллах.
207
С разогревом кристалла очень быстро увеличивается
тепловая составляющая, энергии пропорционально Г4. Пока она
мала в сравнении с нулевой, увеличение в объеме
незначительно, а когда они сравниваются, достигается классический
предел, и дальнейшее расширение становится линейным по
температуре:
Да ЗупкТ
а
B7.29)
Разумеемся, линейность соблюдается лишь в той мере, в
какой справедлива гармоническая аппроксимация сил
внутреннего давления, предполагающая, что Е = е(а)/а = const (e «
^ Ро). Итак, несмотря на значительное изменение pt в
процессе разогрева, внешним проявлением этого является едва
заметное расширение кристалла. В небольшом
температурном интервале (Тг — Т «С Т) оно всегда может быть
описано линейным законом
U — L с
в котором
У аи у /от оп\
а = If ~dT = E V B/.OU)
есть линейный коэффициент термического расширения.
Очевидно, что температурная зависимость а(Т) дублирует
зависимость Су(Т), изображенную на^рис. 68: сначала а резко
возрастает, пропорционально Г3, а затем асимптотически
стремится к классическому пределу. Вблизи комнатной
температуры он обычно уже близок, и поэтому
а = -L Зпк « 1(Г5 К. B7.31)
Таким образом, изменение размеров кристалла при
разогреве его на 1К , несмотря на противоборство сил в десятки
тысяч атмосфер, не превышает, самое большее, тысячных
долей процента от их первоначальной величины.
Если раскрыть микроскопический смысл B7.31) с
помощью явного вида Е = C0/а и у, взятого из B7.19), то
оказывается, что
а = g°*Uf = J£-. B7.32)
Эта формула имеет простое физическое объяснение,
вытекающее из самой природы межатомного взаимодействия. Дело
208
в том, что в гармоническом приближении, когда
потенциальная яма, в которой совершают свои колебания атомы, строго
симметрична, никакого теплового расширения быть не
должно. В самом делег при любой энергии колебаний
движущийся атом находится в среднем в том же положении, что и
покоящийся. Это наблюдение является иной интерпретацией*
того факта, что в гармоническом приближении фононы не^
оказывают давления на поверхность кристалла и,
следовательно, не способны вызывать его расширение. Однако если
принять к сведению ангармонизм потенциала, то, как ясно иа
рис. 62, колеблясь между двумя краями потенциальной ямы,}
атом уходит направо дальше, чем налево, и среднее его
местоположение г = а отлично от а0.
Действительно, приняв во внимание малость
ангармонической поправки, мы можем рассчитать Да = г—а = z
ъ помощью обычного распределения Больцмана с
потенциалом B5.1):
7
J
vs
Да =
Т
J
I exp I — -fnp- J dz
7
I-
— oo
Если g0 = 0, то интеграл в числителе, как и предполагалось^
обращается в нуль. И только с учетом ангармонического
слагаемого Да отлична от нуля:
4-оо
54 exp I — ^pjr I dz
4
г*
\
tja-
Вместе с ней и /(а) = |5Да Ф 0, a^ = -j/(a) = ^ находит-
а
ся в соответствии с B7.29), если принять во внимание опре-
209*
деление Е и у. Равным образом из B7.33) получается
обычный закон линейного расширения:
с коэффициентом, определенным в B7.32). Однако в свете
предыдущего ясно, что этот результат, полученный в рамках
классического и индивидуального описания колебаний
отдельных атомов, является лишь асимптотически,
высокотемпературным приближением к общей формуле B7.30).
Узел изотерм. Мы можем теперь вернуться к вопросу о
пересечении изотерм на диаграммах F(v), которое выглядит
как узел (рис. 26, 28), расположенный в области
существования кристаллической фазы. Поскольку и давление, и
температура в окрестности узла весьма высоки, в балансе сил
B7.21) ни одно слагаемое не лишнее, но зато приемлема
классическая форма этого уравнения, определяющая и в
приближении Дюлонга и Пти:
р + Pi(v) = Зт-^-. B7.34)
При гармонической аппроксимации рг B7.10) это уравнение
состояния (уравнение Ми) может быть представлено в виде
Цё* <2М5>
где v0 — удельный объем кристалла, находящегося в
ненапряженном состоянии, когда период решетки равен
равновесной длине связи а0. Отсюда с очевидностью следует, что
фактор сжимаемости всех твердых тел в ненапряженном
состоянии должен быть одинаков и равен Зу, если, конечно,
константа Грюнайзена явным образом не зависит от
температуры. Последнее условие, согласно B7.19), действительно
соблюдается, а это значит, что пересечение изотерм в узловой
точке закономерно. При такой интерпретации узла изотерм
следует ожидать, что его абсцисса должна быть равна
плотности ненапряженного состояния п0 = l/z?0, а ордината —
утроенной константе Грюнайзена, т. е. примерно 6. В том,,
что так оно и есть, нетрудно убедиться, взглянув на рис. 28.
Более того, вполне удовлетворительно объясняется также
и заметная из рисунка закономерность: убывание наклона
изотерм в узловой точке с ростом температуры. В самом деле,
210
0,01-
0,001
10
Рис. 75. Изотермы фактора сжимаемости аргона в
полулогарифмических координатах. Пунктирные участки отвечают плавлению
(переходу через коридор кристаллизации be); на пересечении изотермы 150 К
с кривой сосуществования а лежат точки, отвечающие пару и жидкости.
согласно B7.35), этот наклон, равный 1/ккТ, должен
гиперболически убывать с температурой, что и имеет место.
Впрочем, идиллическое согласие наблюдается лишь при
сопоставлении теоретических прогнозов с диаграммой рис. 28,
которая, в свою очередь, является лишь графическим
отображением численных расчетов, выполненных в рамках
теории свободного объема. Хотя и является общепризнанным,
что теория свободного объема достаточно хороша для
кристаллов, все же непосредственное сравнение с экспериментом
предпочтительнее. С этой целью на рис. 75 воспроизведена
та же диаграмма по наиболее достоверным данным,
имеющимся во всей полноте только для аргона- При сравнении ее со
211
F i
10-
8-
1,85
1,80 1,85 1,90
jo, г/см5
узловой точки, ее положение в
чено достаточно четко.
Рис. 76. Окрестность
узловой точки аргона в
укрупненном масштабе.
схемой, изображенной на
рис. 26, выясняется, что
интересующая нас
узловая точка действительно
принадлежит
кристаллической модификации
вещества, но на самом деле в
ней сходятся отнюдь не
все изотермы. Изотермы с
температурой ниже деба-
евской не попадают в нее
потому, что не
описываются уравнением Ми B7.34)^
а слишком
высокотемпературные обрываются
плавлением прежде, чем
кристалл расширяется до
ненапряженного состояния *
И все же пучком изотерм,}
пересекающих окрестность
масштабе рис. 76 обозна-
§ 28. РЕАЛЬНЫЕ КРИСТАЛЛЫ
Любые виды колебательных движений решетки, о
которых шла речь выше, способны переносить лишь энергию^
но не материю. В идеальном кристалле атомы колеблются,
оставаясь все время вблизи равновесных положений, и
диффузии вообще быть не может. Тем не менее опыт
свидетельствует, что при плотном контакте двух твердых тел
возможно проникновение одного вещества в другое.
Этот вывод, основанный на качественном наблюдении,;
возвращает нас от идеальной модели к реальности.
Напомним, что, идеализируя газ, мы считали его состоящим из
свободно движущихся частиц и лишь затем с оглядкой на
реальность учитывали их размеры и взаимодействия, стесня-
212
ющие свободу передвижения. Идеализируя же твердое
тело, мы, напротив, считали его совершенным кристаллом^
и теперь, чтобы вернуться к действительности, должны
принять во внимание дефекты решетки, которые только и
способны перемещаться в упорядоченной среде.
Точечные дефекты. Простейшим примером точечного
дефекта является примесный атом в узле решетки или
междоузлии. Не только атомы, но и молекулы легких газов, таких
как водород, кислород, азот и так далее, способны в
заметных количествах внедряться в кристаллы, в том числе и
металлические. Дислоцированными, т. е. попавшими в
междоузлие вместо узла, могут быть не только чужеродные атомыв
но и свои собственные. Оставшиеся вакантными, т. е.
незаполненными, узлы решетки тоже представляют собой дефект
структуры, и притом наиболее распространенный. В
некоторых случаях их концентрация доходит до 2% от общего
числа мест. Атомы внедрения и вакансии могут возникать
одновременно, когда в результате неизбежной термической
флуктуации в каком-либо узле решетки аккумулируется
энергия, достаточная для преодоления сил, удерживающих в нем
атом. Таким образом появляются так называемые дефекты
по Френкелю. Атом, покинувший свою потенциальную яму,,
оставляет на прежнем месте жительства вакансию, а сам
переходит в положение дислоцированного, обретая тем
самым и некоторую свободу перемещения. В результате
случайной встречи со своей или чужой вакансией он может
вернуться к оседлому образу жизни, и тогда одновременно
исчезают оба дефекта.
Чем больше мест, подходящих для оккупации, окажется
в ближайшем окружении узла решетки, тем чаще будет
достигать успеха находящийся в нем атом — претендент" на
дислокацию. Общее число переходов в единицу времени
будет очевидно равно W+ {N' 'Уо), где N' — концентрация
благоприятных для дислокации мест в единице объема^
W+ — вероятность перейти в одно из них, a Vo — объем
ячейки, включающий лишь ближайшие к данному узлу
места такого рода (рис. 77). В условиях равновесия скорость
образования дефектов (W+ V0)N'N (N — концентрация
нормальных атомов) должна уравновешиваться скоростью
рекомбинации, которая в силу аналогичных соображений
равна (WJV0)nvna (па — концентрация атомов внедрения, nv —
концентрация вакансий). Считается, что чисяо дефектов
невелико, а большая часть междоузлий, способных принять
дислоцированный атом, все еще остается пустой.
213
•
•
•
ф
•f
•>
f
f
•
•
•
•
•
Рис. 77. Атомы внедрения
и вакансии (стрелками в
сфере указаны потенциально
возможные места для
дислокации).
В соответствии с принципом детального равновесий
где Д#", грубо говоря, — разность энергии равновесного и
дислоцированного положений. Учитывая, что nv = na,
находим из условия равновесия W+V0N'N = W-^
B8.2)
Таким образом, если бы даже кристалл был собран при
абсолютном нуле вполне совершенным, то все же при
разогреве его до обычных температур какая-то часть атомов
неизбежно сместилась бы в междоузлия. Это нарушение
идеальной структуры — естественное следствие теплового
движения, и, хотя оно искажает идеальный порядок в
расположении атомов, мера этой беспорядочности находится в
строгом соответствии с температурой кристалла.
Внедрение атомов и вакансий в решетку кристалла может
происходить и порознь, независимо друг от друга.
Возникновение таких дефектов возможно благодаря конечным
размерам кристалла. С поверхности твердого тела, внешней или
внутренней, т. е. с любых трещин, пустот, дислокаций
(многоатомных искажений решетки), проще перейти в
междоузлие, чем непосредственно из регулярного узла решетки»
Какой бы дефект ни возник у поверхности кристалла, он
затем может откочевать во внутренние области, где в конце
концов скапливается в концентрации, определенной
-равновесной статистикой:
(
B8.3)
Однако если «закалить» кристалл, т. е. охладить его
настолько быстро, чтобы равновесие не успело сместиться, то он бу-
214
Рис 78. Поле одноименных зарядов
вакансии и нейтрального узла.
Рис 79. Надбарьерные переходы
между соседними плоскостями во
внешнем поле Е.
а
Я
о,
о
о
и,
/
i
р
"о
о
а
t\[
1 \J
О
wt2
О
О
дет перенаселен дефектами, исчезновение которых
заторможено трудностями возврата на поверхность,
В ионных кристаллах не редкость, когда один из ионов,
или даже оба, практически не способны покинуть
равновесное положение из-за больших размеров. В таком случае очень
вджно, что межузельные промежутки позволяют двигаться,;
если не самому иону, то, по крайней мере, его вакансии.
Вакансия в ионном кристалле несет заряд, равный, но
противоположный по знаку тому иону, который из нее удален.
Это видно из того, что точно такую же геометрию зарядов
можно было бы получить, не удаляя ион из узла, а поместив
на него противоположный заряд. Мозаика чередующихся
зарядов электростатически уравновешена, и поэтому
нейтрализация любого из них вызывает появление кулоновского
поля, центрированного на нейтральном узле (рис. 78).
Когда образование вакансий в кристаллах не связано с
появлением атомов внедрения, их называют дефектами по
Шоттки. Возникают ли они в результате диффузии вакансий
с поверхности или с самого начала в кристалле существуют
спаренные вакансии (отсутствие рядом расположенных ионов
металла и галогена), которые под действием теплового
движения диссоциируют, — в любом случае их появление не
связано с образованием равного количества дислоцированных
центров. Существование дефектов по Шоттки обнаруживает
себя весьма заметным увеличением объема кристалла,
содержащего множество пустых узлов в решетке. Между спаренны-
215
ми (ассоциированными) ионными вакансиями и
индивидуальными (диссоциированными) существует динамическое
равновесие, подобное тому, какое устанавливается между
дефектами по Френкелю. Возможны и более сложные нарушения
структуры — тройные, четверные вакансии; вакансии,
присоединившие примесные атомы или ионы, и др. Это
усложняет картину явления, но не меняет существа дела: создание
любого дефекта требует энергетических затрат, и поэтому их
концентрация всегда возрастает с температурой.
В общих чертах дело, по-видимому, обстоит так: в
металлах и электронных полупроводниках преобладают дефекты
по Френкелю, причем вдали от точек плавления их мало,,
и значение их невелико. В ионных кристаллах существенны
и те, и другие дефекты, и они играют важную роль не только
в процессе переноса материи, но и заряда. В чистых
молекулярных кристаллах преобладающим типом дефектов должны
быть вакансии (дефекты по Шоттки), поскольку большие
молекулы, значительно превосходящие своими размерами
межмолекулярные расстояния, едва ли могут найти себе
подходящие .места для дислокации, и еще меньше шансов у них
передвигаться по кристаллу в этом положении.
Диффузия. Перемещение атомов внедрения и вакансий
в твердом теле имеет мало общего со свободным,
прямолинейным движением частиц в газе, которое лишь изредка
прерывается столкновениями с молекулами или стенкой. Путь
атомов, блуждающих по кристаллу, более запутан и труден.
Перемещение даже в соседнюю ячейку требует преодоления
потенциального барьера АС/, созданного атомами,
расположенными на своих законных местах и не склонными
покидать их, чтобы облегчить задачу атому внедрения. Каждый
шаг в процессе диффузии требует энергетических затрат,
которые значительно превышают наличные тепловые
ресурсы атома (Д£/ ^> кТ). Поэтому всякий раз перед очередным
скачком атом довольно долго пребывает в исходном
положении, ожидая такого стечения обстоятельств, когда
случайно заимствованной от окружения энергии окажется
достаточно для перехода через барьер. В результате, все его
перемещения носят случайный, а не динамический характер
и могут быть охарактеризованы вероятностью перехода из
одного междоузлия в соседнее.
Рассмотрим два соседних слоя кристалла толщиной в
один период решетки а (рис. 79). Если окажется, что
плотность дислоцированных атомов чужих или собственных не
одинакова, то случайные перемещения описанного типа
будут приводить к постепенному ее выравниванию. Макроско-
216
пически это будет выглядеть как диффузия дефектов из
области высокой их концентрации в более обедненную.
Действительно, поток частиц через единичное сечение,
перпендикулярное оси х, очевидно, равен
<, = ап^и — an2W21% B8.44)
где W12 — вероятность перехода из первого слоя во второй,}
a W21 — вероятность возвращения обратно. Так как
расстояние между соседними слоями тоже а и, следовательно,
весьма мало в сравнении с макроскопическим масштабом
I/ d (In л) Л™11
I —-z—-I L на котором заметно изменение п9 можно
разложить п(х) в ряд и определить концентрацию дефектов в этих
слоях в первом приближении:
dn п , dn а,
Тогда из B8.4) получится
J-an(trla-Tr,1)-(TF»t*")«'j|- B8-6)
Если отсутствуют какие-либо причины, выделяющие
преимущественное направление, то вероятность перехода в
любое из шести соседних положений (вправо-влево, вверх-
вниз, вперед-назад) должна быть одна и та же (W), так что
Wu=Wtl~W--±, B8.7)
тде т — время жизни атома в данном междоузлии. В таком
•случае из B8.6) получается
j Z)f, B8.8)
тде
D = Wa2 = оУбт, B8.9)
а
(^) B8.10)
Структура формулы B8.10) определяется очевидными
физическими соображениями. Вероятность перехода через
барьер есть число попыток, окончившихся удачей, из числа
совершенных в единицу времени. Количество попыток равно
частоте колебаний атома в потенциальной яме и совпадает
с числом атак одной из двух противоположных ее сторон.,
217
Можно ожидать,, что такая атака наверняка окончится
преодолением барьера, если энергия колеблющегося атома
превысит At/. Таким образом, доля попыток, которые окажутся
плодотворными, равна доле возбужденных состояний,
обладающих энергией, большей At/. Отсюда следует, что процесс
диффузии в твердом теле активирован. Согласно с этим,
B8.9) и B8.10) в совокупности дают
B8.11)
Экспериментально подтверждается не только
экспоненциальная зависимость коэффициента диффузии от температуры^
но и пропорциональность его 1/У^т, вытекающая из
обычного определения частоты колебаний в потенциальной яме:
Таким образом, с увеличением размера частиц диффузия
затормаживается как из-за стерических трудностей (Atf),
так и вследствие меньшей подвижности (т), но первое
обстоятельство в этом деле является решающим. Движение
больших частиц сопряжено с преодолением высоких
барьеров и поэтому происходит очень медленно. И наоборот, чем
меньше масса и^размеры примесных атомов, тем эффективнее
внедряются они в решетку кристалла.
Так же, как диффузия дислоцированных атомов,
происходит и движение вакансий в твердом теле. Фактически,
конечно, перемещается соседняя с вакансией частица, и
притом всякий раз другая, но выглядит это так, будто движется
вакансия в направлении, противоположном реально
состоявшемуся переходу. В молекулярных кристаллах движение
вакансий организует как самодиффузию, так и диффузию
примесей, находящихся в узлах решетки. Последние
получают шанс сместиться в соседний узел только тогда, когда
в нем оказывается вакансия, совершающая миграцию по
кристаллу. По сравнению с B8.10) вероятность такого
процесса оказывается уменьшенной в ру раз, где pv — доля
пустых узлов (ру = nvv). Вследствие этого и
В = DvPv, B8.12)
где Dy — коэффициент диффузии вакансий, определенный
в B8.11). Структура этой формулы физически прозрачна:
миграция примесей за счет вакансий ограничена числом
встреч с ними. Естественно, что скорость процесса тем выше,
чем больше их концентрация.
218
Ионная проводимость. Перенос электричества в ионных
кристаллах довольно часто осуществляется тяжелыми
частицами: дислоцированными ионами или вакансиями. При
включении тока возникает направленный дрейф катионов
в одну сторону, а анионов в другую. Нейтрализуясь на
соответствующих электродах, они там же и выделяются в виде
чистой фазы. При переносе заряда вакансиями (дефектами
по Шоттки) дело обстоит точно так же: нейтрализация
анионных вакансий создает условия для образования чистого
металла, а катионных — галогена в газообразном виде.
Поэтому, в сущности, мы имеем здесь дело с электролизом
твердого состояния: разложением химического соединения на
компоненты, подобным происходящему в жидких
аккумуляторах. Однозначным доказательством ионного механизма
переноса заряда является выделение продуктов разложения
на электродах.
Как уже подчеркивалось, ионы и их вакансии
передвигаются по кристаллу не длинными свободными перебежками,
а редкими короткими перескоками — только в соседнюю
клетку* только на ближайший узел. И тепловое движение
теперь не помеха проводимости, а ее союзник. Если
свободным частицам оно лишь мешало быстрее достичь цели,
ограничивая длину пробега и сбивая скорость в конце его до
нуля, то ионы, скованные кристаллической решеткой, вообще
бы не сдвинулись со своего места, не будь термической
активации диффузии.
Но тогда, какова же роль поля? Оказывается, просто в
том, что его включение несколько облегчает перескоки в
одном направлении и затрудняет в прямо противоположном.
Так как потенциал в присутствии поля складывается из
обычного кристаллического U(x) и электростатического eV(x),
то его полная величина U(x) — еЕх непрерывно и
равномерно уменьшается в том направлении, в котором должны
следовать под действием поля дефекты, несущие положительный
заряд (см. рис. 79). Вследствие этого величина барьера,
справа и слева от дрейфующего иона, оказывается не
одинаковой, как раньше, а равна в одном случае ДС/ — e^~o^ a B
другом AU + eE-^- По этой причине равенство B8.7),
утверждавшее равновероятность переходов в любом
направлении, нарушается. В присутствии поля вероятность
перехода B8.10) в направлении оси х становится равной
(
^-^J = ^exp(|gj, B8.13а)
219
а в противоположном направлении
-2£). B8.136)
Как ни мало изменение потенциала на расстоянии порядка
периода решетки, все же при перевале через высокий барьер
даже такое его уменьшение (еЕа/2 «С АС/) воспринимается
как существенное облегчение (и наоборот). К тому же оно
может оказаться не малым по отношению к к Т, и тогда
вероятности прямого и обратного переходов, оставаясь
небольшими, могут отличаться на много порядков.
Созданная полем диспропорция барьеров немедленно
нарушает сбалансированность противоположных потоков
частиц, предпочитающих теперь более легкий путь более
трудному. В результате из B8.6) и B8.13) получается
При не слишком больших полях-^г^ 1. Разлагая на этом
основании экспоненты до первого неисчезающего члена,
находим, что ток равен
i = ej = eunE — eD т-,
J dx
где D имеет прежний вид: B8.9) или B8.11), а
eWa2 еа2 ( AU \ пл ...
и = кт == ~W v°ехр I—W)' B8.14)
При этом между uhD сохраняется общего вида взаимосвязь:
и = ^г, B8.15)
называемая соотношением Эйнштейна.
Специфика механизма передвижения заряда,
переносимого ионами, сказывается на структуре формулы,
определяющей зависимость подвижности B8.14) от температуры. В газе
повышение температуры ограничивало возможность
беспрепятственного передвижения ионов в направлении поля и этим
уменьшало подвижность. Иначе обстоит дело в данном ел у
чае: подвижность экспоненциально возрастает с ростом
температуры. Увеличение тепловой энергии облегчает перескок
через барьер, а чем быстрее ион справляется с этой задачей,
тем легче он мигрирует по кристаллу и охотнее вовлекается
в процесс электропроводности.
220
Глава 4
ЖИДКОСТИ
§ 29. ФЕНОМЕНОЛОГИЯ
Среди других фаз вещества жидкости зацимают особое
положение, промежуточное между газообразным и твердым
состоянием. Жидкости, как и твердые тела, относятся к
конденсированным средам: в состоянии равновесия они не
обладают способностью к неограниченному расширению, и их
молекулы, связанные значительными силами притяжения,
находятся в непосредственной близости друг от друга. Однако^
плотная упаковка молекул ничуть не мешает жидкости,
подобно газу, принимать без заметного сопротивления любую
форму, в какой бы сосуд она ни была налита и какое бы тело
в нее ни погрузили. Как и твердое тело, жидкость почти не
сжимаема и очень прочна на разрыв при всестороннем
растяжении, но как газ — передает давление во все стороны
одинаково, без характерной для кристаллов анизотропии.
Противоречивые свойства лишь потому мирно соседствуют
в жидкости, что это агрегатное состояние реализуется в
такой области температур, когда энергии теплового движения
уже достаточно для разрушения регулярной
кристаллической структуры, но не хватает еще для полного разрыва
связей, удерживающих молекулы в пределах конечного объема.
Рентгеноструктурные исследования показывают, что в
жидкости существует так называемый «ближний» порядок и
отсутствует «дальний». Речь идет о том, что в положении
ближайших соседей любой молекулы наблюдаются лишь
незначительные отклонения от правильной,
псевдокристаллической упаковки. Однако небольшие отклонения от
правильной упаковки быстро накапливаются, и уже на расстоянии
нескольких периодов вместо узла можно обнаружить
междоузлие, и наоборот. Так, в горке зерен пшеницы невероятно
обнаружить сколько-нибудь значительные пустоты: каждое
зерно отделено от другого лишь собственным объемом, и
поэтому можно быть уверенным, что расстояние между их
центрами примерно одинаково и приблизительно равно диаметру
зерен. Вместе с тем нет никакой упорядоченности в
положении более или менее удаленных зерен, и именно этот хаос
упаковки позволяет сыпучим телам легко перестраиваться^
расступаться при погружении в них руки, принимать форму
сосуда.
221
Кирпичная кладка, даже не скрепленная раствором,
именно в силу своей регулярности, способности к
коллективному сопротивлению не обладает свойством сыпучести. Так
устроены кристаллы — с максимальной упорядоченностью,
с минимальной энтропией. Но повышение температуры
нарушает эту гармонию. Отдельные кирпичики — молекулы —
получают возможность проворачиваться и колебаться, а при
температурах выше дебаевской это движение по существу
приобретает индивидуальный характер. Отсюда недалеко и
до полного разрушения кристаллической структуры. Если
же в результате землетрясения стены здания превращаются
в груду кирпичей или песка, то свойства конструкции,
несмотря на тот же объем и плотность, радикально меняются.
Эти аналогии позволяют понять, почему в жидкости
отсутствует или почти отсутствует сопротивление сдвигу при
столь же плохой сжимаемости, как и в твердом теле. Однако,
чтобы объяснить прочность на разрыв, необходимо принять
во внимание наряду с силами отталкивания (собственным
объемом) также и силы связи между молекулами. Если бы
песчинки или зерна притягивались друг к другу достаточно
сильно, чтобы образовать единый агрегат, но не настолько,
чтобы помешать взаимному движению, то аналогия была бы
более близкой к истине. То, что, несмотря на наличие сил
сцепления, жидкость легко дробится на части и мелкие
капли, объясняется легкостью скалывания, скольжения слоев,,
благодаря чему связи рвутся последовательно — одна за
другой, а не сразу. Поэтому судить о прочности жидкости
можно лишь в условиях всестороннего растяжения, когда
скольжение заведомо исключено. Вода, например, всего лишь
в четыре раза менее прочна на разрыв, чем свинец. Силы
сцепления проявляют себя не только тем, что почти без
посторонней помощи удерживают молекулы жидкости в конечном
объеме, но и теми особыми свойствами, которые они придают ее
поверхности, превращая ее в подобие туго натянутой пленки.
Наиболее ярким кинетическим свойством жидкости
является ее вязкость. Даже на ощупь жидкости легко отличимы
по этому свойству одна от другой. Изменяя температуру,
давление или концентрацию компонент раствора, можно
изменять вязкость на много порядков. При увеличении
вязкости некоторые жидкости постепенно твердеют, переходя в так
называемое «аморфное» состояние. Аморфные твердые тела
отличаются от кристаллов отсутствием дальнего порядка.
При не слишком большой вязкости они легко мнутся (как
глина, тесто и тому подобное), но при затвердевании
зачастую неотличимы от кристаллов по своим механическим свой-
222
ствам. Таковы многие органические растворы, полимеры,
стекла и некоторые другие соединения. Четкой грани между
жидкой и твердой фазой в этом случае не существует, а по
структуре и характеру теплового движения аморфные тела
представляют собой просто затвердевшие жидкости.
Тепловое движение в жидкости носит очень сложный,
локально коллективный характер. Движение отдельной
частицы нельзя считать свободным, так как, будучи сильно
связана с окружающими ее молекулами, она не может по
своей воле покинуть пределы ячейки, в которой находится.
Ее движение, как и в твердом теле, носит скорее
колебательный, чем поступательный характер. Но в отличие от твердого
тела, в этом движении принимают согласованное
участие лишь ближайшие соседи, а не весь коллектив молекул.
Хотя плотная упаковка и связи между молекулами
превращают их поступательное движение в некое подобие
колебательного, квантование его в большинстве случаев не
обязательно, так как при обычных температурах классическое
описание применимо к нему, по крайней мере, с тем же
основанием, что и к колебаниям решетки кристалла в области
Дюлонга и Пти. Но если молекулы ведут себя классически,
то скорости их по-прежнему распределены по Максвеллу.
В этом смысле классическая жидкость ничем не отличается
от газа, и средняя кинетическая энергия ее атомов
по-прежнему равна 3/2 кТ. Примерно столько же должно
приходиться и на потенциальную энергию колебаний и в сумме г ж
« 3&7WO, a Cv = SR = 6 кал/моль-К.
Вращательное движение многоатомных молекул в
жидкости заторможено стерическими препятствиями и этим
превращено в ограниченные (либрационные) колебания.
Исключение составляют легкие двухатомные и сферические
молекулы типа N2, CO, CH4, SF6 и т. п., которые продолжают
вращаться, правда, хаотически, и в жидкой фазе, а
молекулярный водород пребывает в состоянии свободного вращения
даже в кристалле.
Несколько огрубляя картину, можно считать, что
тепловое движение молекулы в жидкости носит характер
беспорядочных метаний в пределах одной ячейки, которые
сопровождаются сравнительно редкими перестройками структуры,
изменяющими ее местопребывание. Как всякий
промежуточный случай, равно далекий от чистых, предельных моделей,
каковыми являются газ и твердое тело, жидкость хуже
поддается точному исследованию. Модель идеального газа
бесполезна там, где взаимодействие между частицами велико и
существенно определяет поведение коллектива.
223
§ 30 УРАВНЕНИЕ СОСТОЯНИЯ
На первый взгляд кажется очевидным, что именно
следует называть жидкостью, а что газом. Однако, приступая к
количественному описанию этих фаз, следует заново
поставить этот вопрос. Термодинамические соображения
показывают, что он не праздный. Из диаграммы рис. 80 видно, что
только кристаллическое состояние вещества повсеместно
отделено от остальных. Пограничная кривая представляет
точки, в которых возможно равновесное сосуществование
фаз. Пересечение ее приводит к фазовому переходу:
в нижней части — к возгонке, а в верхней (над
тройной точкой) — к плавлению. Эта кривая монотонно и
неограниченно возрастает во всем доступном диапазоне
давлений. Напротив, кривая сосуществования жидкость — газ
обрывается в критической точке. Иными словами,
пространственное разделение жидкости и ее параг которое позволяет
безошибочно отличать их друг от друга, возможно лишь
в узком диапазоне давлений и температур, от тройной точки
до критической. Пересечение кривой, соединяющей эти
точки, приводит к фазовому переходу, в котором качественное
превращение совершается скачкообразно* посредством
испарения жидкости. Однако это же превращение можно
осуществить плавно, не пересекая кривой сосуществования, а
обойдя ее над критической точкой, и на этом пути
принципиально невозможно установить, где кончается жидкость и
начинается газ.
Таким образом, отличие жидкости от газа, очевидное в
условиях их сосуществования, становится иллюзорным,
когда мы имеем дело с одной, отдельно взятой фазой. Стало
быть, вопрос о том, является ли неупорядоченная фаза
жидкостью или газом, во всех точках диаграммы, не лежащих
на кривой сосуществования, не может быть решен
однозначно. Но так как в закритической области (р >рс, Т >ТС)
этот вопрос вообще лишен смысла, то можно условиться
считать жидким плотное состояние вещества не только на
кривой сосуществования, но и внутри заштрихованного
полуострова рис. 80.
Эта договоренность позволяет с общих позиций
сопоставить различные подходы к описанию равновесного состояния
жидкости. Несмотря на качественно правильное объяснение
конденсации, уравнение Ван-дер-Ваальса, прочитанное
буквально, с учетом микроскопического смысла констант,
непригодно для количественного описания жидкости. Это ясно
шз того, что уже при V < В = 4Nu0, т. е. еще а газообраз-
224
'Критическая
точка
\Тс
Температура ■
vc i Объем
Рис. 81. Диаграмма состояний
(рП
Рис. 80. Диаграмма состояний
(РТ).
ном состоянии, его правая часть обращает знак, лишая смые-
ла все уравнение. Гораздо шире область применимости вирм-
ального уравнения состояния (9.17). Связь всех вириаль-
ных коэффициентов с видом межмолекулярного
взаимодействия в настоящее время твердо установлена. Однако и вири-
альный ряд расходится при У> Ус. Из фазовой диаграммы
в координатах (р, У) (рис. 81) видно, что область жидкого
состояния (заштрихованный полуостров) оказывается за
пределами и этого приближения.
Более удачно описывает плотное состояние вещества
теория, развитая Кирквудом и Боголюбовым, которая
учитывает согласованность движения и местопребывания частиц
посредством корреляционных функций. Принципиально
теория способна учесть скоррелированность движения трех
частиц, и даже более многочисленных коллективов, однако
расчетные трудности быстро возрастают с увеличением числа
молекул, вовлеченных во взаимодействие. Так как теория
слишком сложна для работы с реальным межмолекулярным
потенциалом, большинство аналитических расчетов
выполнено для модели жестких сфер, т. е. при простейшем учете
отталкивания. Это вносит необходимые исправления в
правую часть уравнения Ван-дер-Ваальса, тогда как левую его
часть приходится либо просто сохранять без всяких
усовершенствований (Кац, Уленбек, Хеммер и другие), либо
учитывать притяжение как малую поправку (Цванциг). В обоих
случаях надежные результаты получаются лишь при Т >
> Тс, когда кинетическая энергия настолько велика, что
силы притяжения можно грубым образом аппроксимировать
или оценить в первом приближении по uJkT. Это позволяет
продвинуться в область весьма высоких плотностей (У <
8 А И Бурштейн
225
< Fc), но вещество в таком состоянии по-прежнему остается
газом, который лишь огромное внешнее давление удерживает
от расширения. Жидкость в обычном смысле этого слова
способна предотвратить расширение собственными силами, но
область ее существования (Т < Тс) оказывается за пределами
и этой теории.
Естественная альтернатива этим подходам состоит в том*
чтобы продвинуться в жидкофазный полуостров не из
области низких давлений или высоких температур, т. е. не со
стороны газа, а со стороны кристаллического состояния.
Последнее подобно жидкому как по плотности вещества, так ш
по условиям существования (внешнее давление мало в
сравнении с внутренним), однако решительно отделено от него
фазовым коридором (см. рис. 81). Существование этого
коридора подчеркивает принципиальное отличие упорядоченной
структуры от хаотической. Тем не менее Леннард — Джонс
и Девоншайр предприняли попытку единообразного
описания кристаллического и жидкого состояний в рамках теории
свободного объема, кратко изложенной в § 10. Эта теория
утрирует подобие твердого тела и жидкости до такой степени,
что не позволяет отличить одно от другого иначе как по
плотности вещества, и все же она дает шанс продвинуться в
область истинно жидкого состояния.
Особенно привлекательно, что границы этой теории могут
быть феноменологически раздвинуты таким образом, чтобы
уравнение состояния приобрело общий для всех фаз вид:
p + Pi=T^-. C0.1)
В такой именно форме представимо и уравнение Взде-дер-
Ваальса (9.10), описывающее разреженный реальный газ,
и уравнение Ми B7.34), относящееся к кристаллам. Коль
скоро уравнение приложимо к таким крайностям, то можно
надеяться, что оно пригодится и между ними, если
надлежащим образом определить pt и pt. В самом деле, уравнение
Цванцига, справедливое для высокотемпературного
конденсата, представимо в этой же форме, а полуэмпирические
обобщения уравнения Ван-дер-Ваальса, «натягивающие» его
на область фазового перехода, прямо исходят из нее,
варьируя лишь константы, появляющиеся в pt и pt. Место теории
свободного объема среди других определяется тем, что она
предлагает физически осмысленную оценку pt(V) и pt(Vr T)
в наиболее глубокой области фазового полуострова, вблизи
кривой плавления, по соседству с твердым телом. По мере
удаления от этой области в сторону критической точки раз-
226
личие твердой и жидкой фаз становится все более
существенным из-за появления значительного числа пустот («дырок»).
Когда рыхлость структуры приобретает принципиальное
значение, теория свободного объема уступает место более
гибкой, дырочной теории, в которую мы, однако, углубляться
не станем. Наша задача будет состоять только в том, чтобы
выяснить смысл внутреннего и термического давления в
жидкой фазе и, оперируя ими, проинтерпретировать основные
свойства жидкости, включая ее превращения в газообразное
и кристаллическое состояния.
Внутреннее давление. Согласно теории свободного
объема, это слагаемое уравнения состояния определяется
потенциальным полем, созданным окружением частицы в центре
ее ячейки. Поэтому внутреннее давление очень
чувствительно к деталям межмолекулярного взаимодействия, по виду
которого различные жидкости также можно разделить на
классы, как и соответствующие кристаллы. Поэтому,
приступая к количественному описанию жидкой фазы, необходимо
сузить задачу. Мы ограничимся здесь рассмотрением только
простых жидкостей, к которым относятся инертные газы,
большинство двухатомных молекул (водород, кислород, азот
и другие) и некоторые простые углеводороды (метан, бензол
и тому подобное).
Как объект исследования простые жидкости особенно
привлекательны тем, что межмолекулярное взаимодействие в
них определено наиболее достоверно. Оно характеризуется
потенциалом 6—12 Леннарда — Джонса, общий вид
которого
подобен изображенному на рис. 12 с минимумом в точке
а0 = 26 а. Однако одного лишь межмолекулярного
потенциала взаимодействия недостаточно для полного определения
поля ячейки. Необходимо знать еще ее структуру:
расположение соседних с данной молекулой частиц и расстояние, на
котором они находятся. При плотной кубической упаковке
частиц самые близкие соседи располагаются на расстоянии
я, следующие, во «второй координационной сфере»,
находятся на расстоянии aj/2, а в третьей — на расстоянии а~|/3.
Как уже упоминалось, эта упаковка, соответствующая гра-
нецентрированной структуре, стабильна даже в
приближении ближайших соседей. Для грубых оценок ими можно
ограничиться, но ничто не мешает учесть взаимодействие и с бо-
8* 227
лее далекими оболочками, приняв во внимание, что в первой
находятся 12 частиц, во второй — 6, а в третьей — 24.
Созданный ими потенциал в центре ячейки аддитивен по
оболочкам:
Ф@) = 12и(а) + 6и (в/2) + 24и(а/3) + .... C0.3)
Если бы речь шла о кристалле, то этот ряд можно было бы
продолжить до бесконечности. Однако в хаотизированной
структуре ошибки в расположении частиц накапливаются так
быстро, что их: отнесение к той или иной сфере очень скоро»
становится неоднозначным. Фактически только самое
близкое окружение сохраняет подобие с кристаллической
структурой («ближний порядок»), тогда как во второй и третьей
сфере координация частиц может оказаться иной, чем
ожидается в C0.3). К счастью, потенциал ячейки весьма
нечувствителен к деталям строения периферийных сфер,
поскольку взаимодействие Леннарда — Джонса очень быстро
убывает с расстоянием. Вклад частиц, находящихся во второй
сфере, по крайней мере, в (l/N раз меньше, чем ближайших
соседей, а влияние молекул третьей сферы пренебрежимо
мало.
Если ограничить рассмотрение ближайшими соседями,,
то в формуле C0.3) сохранится лишь первое слагаемое и она
станет идентичной получающейся из A0.38) при с = 12.
Это приближение является жидкостным вариантом
цепочечной модели взаимодействия, которая использовалась в § 25
для тех же целей, но в применении к кристаллам. Полная
аналогия между описанием упругой реакции твердых в
жидких сред в приближении близкодействия легко
прослеживается, если перейти от общего определения pt, данного в
A0.37), к его одномерному аналогу:
_ 1 <1Ф с du I du __ f (a)
PTr?"
Чтобы облегчить сопоставление с результатами предыдущей
главы, этот переход выполнен в предположении, что ячейка
организована как простая кубическая решетка: по одному
соседу справа и слева вдоль каждой из осей, так что с = 6,
v = а3. Полученный результат тождественно совпадает с
B7.8), и сила парного взаимодействия частиц /(а) определена
в нем совершенно таким же образом, как и в B5.2а). Из
этого сопоставления явствует, что, какая бы ни была фаза,
твердая или жидкая, ее внутреннее давление есть просто сила,
действующая на частицу со стороны заполненного веществом
полупространства1 отнесенная к занимаемой ею площади.
228
Для простых жидкостей,; однако, характерна не простая
кубическая, а гранецентрированная ячейка, внутреннее
давление в которой, вследствие более плотной упаковки частиц,
заметно отличается от C0.4) в большую сторону: в 23/2 раза.
Если к тому же учесть в этой структуре взаимодействие со
второй и третьей сферой, то и относительный вклад
притяжения и отталкивания несколько изменится. Насколько
именно, можно судить по окончательному результату,
вытекающему непосредственно из C0.3) и C0.2):
3
а Р{ Г А М 1 v a /on tr\
М f C05)
Учет внешних сфер проявляется в нем только отличием
коэффициентов X = 1,14 и [х = 1,01 от единицы. Это
свидетельствует о том, что приближение близкодействия вполне
пригодно для простых жидкостей. Следует лишь принять к све.
дению, что относительная ошибка возрастает с расширением.
Из-за несовершенства самой теории свободного объема
оценка pi по формулам C0.4) и C0.5) надежна лишь до тех пор,
пока среднее расстояние между частицами много больше его
флуктуации, т. е. в конденсированной фазе.
Для достаточно разреженной среды само понятие
«ближайшей сферы» (не говоря уже о прочих), утрачивает смысл,
уступая место «сфере действия», заполнение которой зависит
от плотности среды и ее температуры (см. § 9). Внутреннее
давление реального газа создается коллективными усилиями
частиц, оказавшихся в этой сфере, вследствие чего их
равнодействующая убывает с расстоянием гораздо более плавно,
чем каждая из них в отдельности. Поэтому при том же
потенциале C0.2) внутреннее давление в уравнении Ван-дер-Ва-
альса равно
^* _ const *± _ Л(Т)
Видно, что в газовой фазе изменение Pi(a) качественно
отлично от того, которое получается для конденсированных сред
из определения C0.4). В то же время C0.4) распространяется
не только на гармоническую область, как было в B7.10),
но и далеко за ее пределы, потому что коллективные
эффекты возникают и становятся существенными еще дальше.
Обнаружившийся резерв и использует теория свободного
объема, увеличивая а до размеров, характерных для
жидкого состояния, по крайней мере, в той области, где плотность
его все еще достаточно высока. Будучи локальной
характеристикой силовой обстановки внутри ячейки, созданной бли-
229
Рис. 82. Внутреннее
давление в теории свободного
объема. Пунктиром
показаны ангармоническая и
дисперсионная асимптотики.
жайшим окружением, внутреннее давление безразлично к
характеру упаковки остального массива молекул и может
быть непрерывно продолжено в область, где твердая фаза
превращается в жидкую. Поскольку и(г) в твердом и жидком
состоянии — одно и то же, качественное представление об
изменении pt(a) можно извлечь уже из рис. 62. Но если в
твердом теле наше внимание было привлечено только к
квазигармоническому участку этой кривой, то теперь не меньшее
значение приобретает и противоположная, ниспадающая ветвь.
Это совершенно новый аспект, попадающий в поле зрения
лишь при расширенном толковании соотношения C0.4),
которое становится возможным в теории свободного объема.
В твердом состоянии сила взаимодействия только
возрастает при удлинении межмолекулярного расстояния, как при
попытке растянуть пружину. В жидкости же способность к
сопротивлению может ослабевать по мере растяжения, если
а > ат, т. е. сила взаимодействия уменьшается при
удалении молекул друг от друга.
Об относительной протяженности восходящей и
нисходящей ветвей pi можно судить по рис. 82, на котором
изображено внутреннее давление, рассчитанное по формуле C0.5).
Квазигармоническое приближение, лежащее в основе
теории твердого тела, есть не что иное, как разложение pt(v)
в ряд в окрестности нуля этой функции с точностью до
второго порядка по отклонению от него:
*- b(v*-v*0) -Uv* -vl)
C0.6)
Все параметры этого разложения легко находятся из C0.5):
v*0 =
%
0,94, Ь = \ = 2,9, с = % = 28, C0.6а)
230
причем можно убедиться, что координата нуля pt в точности
соответствует абсциссе узловой точки на рис. 28, а Ъ
определяет угол наклона перекрещивающихся изотерм в
соответствии с B7.35). С учетом квадратичного слагаемого
квазигармоническая аппроксимация pt выглядит параболой,
показанной пунктиром на рис. 82. Максимум последней ограничивает
справа область применимости гармонического приближения.
Эта область весьма невелика в масштабе рисунка, причем
раздвинуть ее пределы путем удержания следующих членов
разложения невозможно. Как в гармонической области
неуместно вириальное разложение, так и степенной ряд C0.6)
бесполезен правее максимума pt. При удалении от него
вправо становится все более приемлемой дисперсионная
асимптотика внутреннего давления pt ->■ 24Uz;*3, изображенная
пунктирной гиперболой. При достаточном расширении среды
внутреннее давление обусловлено уже только силами
притяжения, но все еще отличается от C0.5а) быстротой
убывания. В промежутке между гармоническим и
антигармоническим изменением pt лежит область его максимума, вблизи
которого
А =/4-12E (*>*-*4J. C0.7)
Согласно C0.5),
v*m = /| _ 1,217, pi - ^ - 6,05, Р = ^ = 2,5. C0.7а)
Начиная от максимума и кончая далекой периферией pt,
где приближение близкодействия уступает место ван-дер-ва-
альсовской асимптотике C0.5а), агрегатное состояние
вещества представляет собой либо жидкость, либо газ.
Термическое давление. При переходе от твердого тела к
жидкости последовательные стадии которого изображены
на рис. 83, существенным образом деформируется
потенциальная яма, представляющая ячейку. Мысленно раздвигая
в разные стороны частицы, создающие одномерный
потенциал (см. рис. 61), нетрудно убедиться, что такая его
трансформация является неизбежным следствием теплового
расширения среды (удлинения а). Пока расстояние между
частицами близко к а0, а энергия теплового движения мала,
частица колеблется, отражаясь от потенциальных стенок в
нижней части ямы, где форма ее близка к параболической.
Гармоническая аппроксимация этой части потенциала,
принятая в теории твердого тела, становится явно недостаточной
231
Рис. 83. Трансформация потенциальной ямы ячейки при расширении
кристалла (а) и жидкости (б)
по мере теплового расширения кристалла. Амплитуду
колебаний с возросшей энергией начинают ограничивать
ангармонические участки потенциала, близкие по форме к
потенциальной стенке. Одновременно меняет кривизну и дно по-
232
тенциальной ямы в центре ячейки, поскольку, согласно
B5.2),
Как раз в тот момент, когда /(а) достигает максимума, оно
становится совершенно плоским, а вслед за тем в области
ниспадающей ветви силовой характеристики на нем
вырастает потенциальный горб, частично разделяющий яму
надвое.
Так как высота горба заведомо меньше среднего уровня
теплового движения, он не является серьезной преградой
для большинства частиц, но характер их колебаний в
деформировавшейся яме существенно изменяется, становится ан-
гармоничным. Движение молекул в таком потенциале ближе
к свободному: неровности дна ямы незначительно искажают
его, а колебательный характер оно приобретает
исключительно из-за отражений от почти вертикальных стенок
потенциала. Несколько идеализируя эту ситуацию, можно заменить
реальный потенциал моделью прямоугольной ямы (рис. 84).
В рамках этой модели каждая молекула жидкости совершает
свободное движение в пределах своей ячейки, упруго
отражаясь от ее границ.
Вообще говоря, в теории свободного объема нет
необходимости прибегать к дополнительному упрощению
потенциала. Термическое давление в ней определено выражением
A0.376) и тем разъяснением смысла «свободного объема»^
которое содержится в A0.33). Однако выполнить
интегрирование в A0.33) с учетом сложной геометрии ячейки не
просто, не говоря уже о принципиальных трудностях, которые
возникают, когда между окружающими частицами остаются
проходы через преодолимые барьеры в соседние ячейки.
Теория становится конструктивной и последовательной лишь
после того, как реальный потенциал ячейки «сглажен»,
т. е. создан статистически размазанным по сфере
ближайшим окружением, как это принято в A0.38). Некоторое
оправдание этой процедуры можно усмотреть в том, что в жидкости,
Рис 84. Гармоническая и
прямоугольная
аппроксимации потенциала ячейки.
233
в отличие от кристалла, окружающие частицу соседи не
остаются все время в узлах решетки, а, непрерывно обмениваясь
местами, появляются с равной вероятностью во всех точках
координационной сферы. В таких предположениях эта сфера
становится абсолютно непроницаемой для частицы, а взятие
интеграла A0.33) заметно упрощается. Правда, и в этом
случае результаты вычислений с потенциалом Леннарда —
Джонса получаются слишком громоздкими, чтобы
воспроизводить их здесь. Остается прибегнуть к его гармонической
и прямоугольной аппроксимации. Это не только упростит
все оценки, но и облегчит сопоставление твердых и жидких
сред с общих позиций.
Поскольку теория свободного объема должна описывать
твердое тело нисколько не хуже, чем жидкость^ полезно
прежде всего убедиться в том, что в ней воспроизводится
полученная в § 27 оценка термического давления.
Квазигармоническое усилие, возникающее при малом смещении
атома от положения равновесия вдоль одной из осей, задается
формулой B5.3а). Вызванное этим возрастание
потенциала квадратично по отклонению от центра ячейки:
где Р = Ро — go&ai причем Да = а — а0 — соответствующее
данной температуре равноверное удлинение периода решетки.
Свободный объем, вычисленный в этом приближении^ есть
( Щ j C0.8)
= n ехр (- Щ dgj =
Использованная здесь возможность распространить
интегрирование далеко за пределы ячейки появляется лишь при
таких температурах, когда ангармонический вклад в
энергию теплового движения пренебрежимо мал: кТс^^д%^>
!>1гGл. Сделанная оценка, следовательно* верна в
температурном диапазоне к@ < кТ < 9p3/g2*
При более выеоких температурах энергии теплового
движения достаточно, чтобы позволить молекуле добраться до
бортов ямы, созданных круто возрастающим отталкиванием
соседних частиц. В этой области более правомерна
прямоугольная аппроксимация потенциальной ямы:
loo, |g| =а — d.
234
Свободный объем в этом случае есть просто
Vf===^±(a-d)*. C0.9)
Представим теперь термическое давление, определепное
в A0.376), в виде
^ C0.10)
где
&) (!£f) C0.11)
есть численный коэффициент, слагаемые которого имеют
совершенно различную природу. Первое из них характеризует
изменение термического давления вследствие
взаимодействия частицы с ее локальным окружением. Второе
определено состоянием всего коллектива частиц. Если при
расширении вещества изменений в упаковке частиц не происходит,
то энтропия сохраняется, а производная от нее обращается
в нуль. Это значит, что при расширении кристаллической
структуры, когда а = 1, энтропийный вклад в Г
отсутствует, и то же самое справедливо по отношению к газу,
занимающему достаточно большой объем, когда уже а = е. Однако
в промежуточной области о(и) изменяется от 1 до е, и
пренебрегать вторым членом в C0.11), вообще говоря, нельзя.
К сожалению, способы расчета его не развиты, и мы
вынужденно ограничимся вычислением только первого
слагаемого. Что касается второго, то, будучи нулем в обеих
предельных ситуациях, оно не слишком велико и в промежутке,
но имеет принципиальное значение для понимания фазового
перехода порядой — беспорядок (плавления), к которому мы
обратимся в конце параграфа.
Подставляя в C0.11) свободный объем C0.8),
вычисленный в модели параболической ямы; имеем при а = const
где у — константа Грюнайзена, определенная в B7.19).
Используя этот результат в C0.10), находим
pt = Зу-пкТ = уи, C0.13)
где и определена законом Дюлонга и Пти. Нетрудно
установить полное тождество полученного результата с найденной
ранее оценкой термического давления B7.15). Этим подтвер-
235
ждается, что теория свободного объема вполне
удовлетворительно описывает кристаллическое состояние, по крайней
мере, при температурах выше дебаевской. В области
линейной аппроксимации внутреннего давления, определенного в
C0.6), и в границах справедливости C0.12) она немедленно
возвращает нас к уравнению Ми B7.35), полученному из
независимых соображений.
Что же касается жидкой фазы, то, исходя из
прямоугольной модели ямы, прямой подстановкой C0.9) в C0.11)
подучаем (при а = const)
L 1
г d In (а - d) a а (а2 + ad + d2) I + у3 + у3 ,оп лул
din a ~a — d a3 — d3 ~ ^~У ' ^°U<1^
Считая, что и = а3/ у 2, a vd = лсР/6, можно приближенно
получить d3la3 ж vdlv = г/. В плотной среде
Г« .—= -^. C0.15)
1 — у и— vd v >
Это выражение лишено недостатка, присущего уравнению
Ван-дер-Ваальса, в котором
Г = т^-г = \ C0.16)
1 — чу v — 4^d v '
обращает знак при v < bvd. Однако, отдавая C0.15)
преимущество в плотных средах, следует иметь в виду, что оно
утрачивается при переходе к реальному газу. Результат,
приведенный в C0.15), является не обобщением, а
альтернативой ван-дер-ваальсовского. Каждый из них описывает
различные участки изотермыpt(T, и): один при v ж vd, другой,
наоборот, при и >> vdb хотя оба принимают в расчет только
силы отталкивания.
Нельзя ли преодолеть ограниченность того и другого
подхода, избрав третий путь? Когда речь идет лишь об учете сил
отталкивания, действующих между жесткими сферами,
то преимущества теории свободного объема утрачиваются,
а недостатки остаются. В этом случае более уместно
обратиться к корреляционной теории, которая именно модель
жестких сфер описывает наилучшим образом. Ее результаты
могут быть выражены одной из равноценных формул:
C0.17)
Эти зависимости, показанные кривыми б на рис. 85, мало
отличаются друг от друга. При высоких плотностях обе име-
236
15-
10-
£-
1-
i
I i/ j
! I /
I К /
I /
У
i
i/.
86. Схематическое изменение
Г-фактора в теории свободного
объема. Пунктиром показано
приближение квазигармонической (а) и
прямоугольной (б) ям.
Рис. 85. Поведение Г-фактора по
Ван-дер-Ваальсу (а), в моделях
жестких сфер (б) и в теории
свободного объема — в приближении
прямоугольной ямы (в). Штриховкой
указана граница затвердевания.
ют особенность почти в той же точке, что и Г-фактор C0.14),
найденный в теории свободного объема (кривая 6), и хорошо
согласуются с ван-дер-ваальсовским Г-фактором (кривая а)
при у ->■ 0. С другой стороны, модель жестких сфер, даже
если она лучше описывается формулами C0.17), неприменима
к жидкостям, а тем более к кристаллам. Граница затверде-
йания показана штриховкой на рис. 85. При приближении
1С ней и особенно после пересечения гиперболический рост
Г-фактора должен прекратиться, так как вступает в силу
результат Грюнайзена C0.12). В теории свободного объема
этот переход, связанный с увеличением относительной роли
<сил притяжения, легко прослеживается на
полуколичественном уровне. При сжатии среды потенциал ячейки из
прямоугольного превращается в параболический, в результате
чего гиперболически возраставший Г-фактор выходит на
плато Грюнайзена со слабо выраженным уклоном вниз,
который обусловлен ангармонической зависимостью Р(Да)
в C0.8). Немонотонность изменения Г-фактора в зависимости
от межмолекулярного расстояния схематически показана на
рис. 86. Когда изменение коллективной энтропии
игнорируется (сг = const), второе слагаемое в C0.11) равно нулю,
а Г является непрерывной функцией, по которой нельзя
судить, где жидкость превращается в твердое тело. На са-
237
мом же деле в точке плавления имеет место разрыв
непрерывности, который мы обсудим позже.
С цзменением формы потенциала существенно
видоизменяется и характер колебаний частицы в ячейке. Пока ее
движение ограничено отражением от ветвей параболы,
амплитуда колебаний А возрастает с увеличением тепловой
энергии ($А2 = кТ), а частота остается постоянной, примерно
равной дебаевской. Иными словами, амплитуда колебаний
линейно растет с увеличением среднеквадратичной скорости
движения. Так обстоит дело, пока А <С а — d — Ао. При
более высоких температурах (меньших плотностях) средняя
энергия частиц обеспечивает им доступ к потенциальным
стенкам, где и происходит фактическое отражение. Поэтому
сохраняется «менно максимальная амплитуда колебаний
Ао = а — d = inv, C0.18)
а частота, напротив, линейно возрастает при увеличении
скорости движения:
V = 4(^)< <30-19>
Таким образом, поведение частицы в гармонической и
прямоугольной ямах носит совершенно разный характер.
В последнем случае частица мечется в ограниченном объеме,
форма и величина которого непрерывно и случайно
видоизменяются. Поэтому, несмотря на то, что движение внутри
ячейки равномерно, скорость его случайно изменяет
величину и направление при каждом отражении от границ
совершенно так же, как и при столкновении частиц в газе.
Пересечение ячейки в любом направлении есть фактически
свободный пробег, всякий раз осуществляющийся с новой
скоростью. Вследствие этого интервал времени между
последовательными соприкосновениями со стенками ячейки
приблизительно равен времени релаксации скорости:
Представление о случайно колеблющихся частицах столь
же характерно для теплового движения в жидкости, как
модель хаотического равномерного движения — для газа,
или гармонических колебаний — для решетки кристалла.
Вооружившись им, можно с помощью элементарных
соображений воспроизвести результат C0.14) подобно тому, как
было рассчитано термическое давление идеального газа в
238
§ 3 и реального — в § 9. Совершая колебания с частотой
v ~ ' __' t поверхностная молекула ударяется о стенку,
ограничивающую жидкость, передавая ей импульс 2т \ vx |.
Если к единице площади прилегает 1/а2 ячеек и в каждой
находится частица, совершающая v ударов о стенку в
единицу времени, то полное число столкновений с ней есть
1- А - Ат^г C0-21)
а 2а (а — d)
Термическое давление, которое создают эти толчки,
складываясь воедино, можно грубо оценить следующим образом:
pt = 2m\iTx\J = JT^^ ~ пкТ^. C0.22)
Действуя изнутри* оно равномерно растягивает жидкость во
все стороны, но из-за фактора Г = __ оказывается
примерно на порядок больше, чем в идеальном газе той же
плотности. Совпадение этого фактора с величиной C0.14)
показывает, что решеточная модель конструктивна. Учтя в ней
флуктуации свободного объема, как это было сделано недавно Фёрт-
лером, можно с помощью двух варьируемых параметров
добиться удовлетворительного описания модели жестких сфер
и в твердом, и в жидком состоянии.
Баланс сил. Для качественного анализа ситуации
полезно снова обратиться к графическому отображению
уравнения состояния (рис. 87). Оно позволяет видеть, как
достигается компромисс между термическим давлением,
расширяющим вещество изнутри, и противостоящей ему коалицией
сия внутреннего и внешнего давления (силовой
характеристикой). Как и прежде, термическое давление
представлено семейством изотерм, а его конкурент — изобарами,
которые суть не что иное, как внутреннее давление Pi(a),
приподнятое или опущенное на величину р ^ 0. В точках
пересечения между ними устанавливается равенство, которое
математически выражается уравнением состояния C0.1).
Баланс сил — необходимое, но недостаточное условие
существования термодинамического равновесия. Оно еще
должно быть устойчиво, а это возможно, когда
<30-23>
239
Рь+Рь
р<а
Рис. 87. Графическое При этом дополни-
иредставление баланса теЛьном условии си-
сил в жидкости (#), газе J
(О) и в неустойчивой стема непременно
области (х). возвращается в ис-
х'одную точку после
снятия небольшой
внешней нагрузки
Ар, отклоняющей ее
в ту или иную
сторону. Если же
неравенство C0.23)
обращено, то любое
нарушение баланса
создает неустойчивость,
развивающуюся в ту
или иную сторону.
Устойчивые
состояния
кристаллической фазы
возникали при
пересечении фононных
изотерм с восходящей
ветвью силовой
характеристики (см. рис. 74). На этой ветви dptlda > 0,
а так как dpjda < 0 при всех обстоятельствах, то
неравенство C0.23) естественным образом удовлетворилось. В
жидкости дело обстоит не столь просто. В ней возможно
равновесие иного типа, которое возникает при пересечении изотермы
с нисходящей ветвью силовой характеристики. Жидкостные
изотермы круче кристаллических. Около максимума рг
термическое давление убывает с расширением даже быстрее,
чем внутреннее. Благодаря этому изотерма пересекает
изобару сверху вниз, в результате чего возникают устойчивые
состояния, отмеченные точками на склоне силовой
характеристики рис. 87. Хотя призводныефг/da и dpjda имеют
одинаковый знак, условие C0.23) выполнено, поскольку
| dptlda | > | dpjda |. Однако с ростом а это неравенство
обращается, и та же самая изотерма появляется из-под изобары
после неустойчивого пересечения (снизу вверх), отмеченного
крестиком. Наконец, эти же кривые снова пересекаются
устойчивым образом (кружок) на большом расстоянии, где
изобара асимптотически приближается к прямой р = const
(ибо рг ->- 0). Это последнее пересечение осуществляется уже
в газовой фазе, где внутреннее давление —маленькая
поправка к внешнему.
240
Рис. 88. Производные от составляющих
давления.
Рис. 89. Изменение
потенциала поверхностной
ячейки в направлении,
перпендикулярном границе
раздела.
Тройное пересечение кривых не всегда возможно. Из
рис. 87 видно, что высокотемпературные изотермы имеют
лишь по одному, всегда устойчивому пересечению, как и
должно быть в закритической области, где состояния
жидкости и газа неотличимы. На рис. 88 изображены
изотермические производные от внутреннего и термического давления,
относительная величина которых, согласно C0.23),
характеризует устойчивость состояния. Область, ограниченную
отрицательной петлей dpi(a)/da, пересекают лишь
низкотемпературные изотермы, оставляя в ней участки тем большей
длины, чем меньше температура. Точки пересечения ар и
ар, в которых
d!i = (НЕ*)
da \ да /г'
C0.24)
отвечают экстремумам петли Ван-дер-Ваальса и взятые в
совокупности образуют не что иное, как спинодаль. С
повышением температуры заключенный между ними неустойчивый
отрезок изотермы стягивается в точку касания ас, в которой
не только первые, но и вторые производные от внутреннего
и термического давления совпадают:
d2Pi (d2Pt
da1
да*
C0.25)
Это и есть критическое состояние. Плотность вещества в
нем уже заведомо меньше, чем вблизи максимума pt, где
правомерна параболическая аппроксимация внутреннего дав-
241
ления C0*7). Возможно, что в околокритической области
уже приемлема асимптотическая оценка
24А, const nn 9R.
учитывающая только притяжение, а может быть даже
далекая ван-дер-ваальсовская асимптотика C0.5а). Так или
иначе, но в обоих случаях речь идет о степенной
аппроксимации внутреннего давления. Различие в показателях
степени не умаляет того факта, что и теория свободного объема,,
та теория Ван-дер-Ваальса оперируют в критической области
€ качественно близкими функциями объема, убывающими
по гиперболическому закону.
Из этого, однако, не следует, что внутреннее давление
в жидкости всегда убывает с расширением. Тройная точка
может находиться в области максимума внутреннего
давления или даже его восходящей ветви, заранее это не ясно.
Поэтому, получая уравнение состояния из C0.1) с помощью
C0.15), лучше воздержаться от каких-либо конкретных
аппроксимаций Pi(u):
^K C0.27)
Это тем более важно, что внутреннее давление гораздо
чувствительнее к деталям межмолекулярного взаимодействия,,
чем термическое. В частности, прямоугольное упрощение
потенциальной ямы, приемлемое для оценки правой части
C0.27), обращает pt в нуль, если использовать его в C0.4).
К счастью, в этом нет необходимости. Формулами C0.5)
и C0.5а) внутреннее давление определено значительно
надежнее, чем термическое, которое в любом приближении
является только оценкой.
Кипение. Рассмотрим теперь условия равновесного
сосуществования жидкости и ее пара. Граница раздела между
ними проницаема для молекул и поэтбму потоки частиц
через нее в прямом и обратном направлении (испаряющихся и
конденсирующихся) должны быть уравновешены. Но если
из газа в жидкость молекула попадает практически
беспрепятственно, то на пути из жидкости в газ воздвигнут
потенциальный барьер, обусловленный силами притяжения.
Чтобы преодолеть его, необходимо обладать энергией* заметно
превышающей средний тепловой ресурс (рис. 89). Среди
1
~ претендентов,, занимающих единицу поверхности жидко-
242
сти, найдется лишь ехР( Фо/^) таких, которые могут
справиться с этой задачей. Все они v раз в секунду атакуют
барьер, совершая обычное тепловое движение внутри ямы.
Принимая во внимание оценку v, данную в C0.19),
нетрудно установить, что поток частиц, покидающих жидкость,
равен
C0.28>
Что же касается встречного потока, то, согласно D.12),
он равен
j_ = ^nv.va C0.29)
где пу — плотность пара. Приравнивая оба выражения^
находим условие равновесия:
nv==^L-e w. C0.30)
Его физический смысл совершенно прозрачен. Две фазы,
расположенные по разные стороны потенциальной
ступеньки, находятся в равновесии только благодаря тому, что та,;
из которой труднее выбраться, более плотна.
При достаточно низких температурах, когда пар над
жидкостью можно считать идеальным, простое домножение
C0.30) на/с Г превращает это равенство в следующее:
C0.31)
где ру — давление насыщающего пара, pt — термическое
давление жидкости, определенное в C0.22), а 1 = -Л^оФо —
скрытая теплота испарения в расчете на 1 моль вещества.
Равенство C0.31) есть не что иное, как уравнение кривой
сосуществования жидкость — пар. Из него видно, что
скачок термического давления при переходе через границу
раздела фаз определяется энергией, затрачиваемой на этот
переход. Давление равновесного пара над ртутью, например,}
при нормальных условиях равно 16-10 мм рт. ст., а
термическое давление жидкой ртути приближается к 4-Ю4 атм»
Отсюда для теплоты парообразования получается,
согласно C0.31),
X = /?Г1п- = 2-273-2,31g4'10 'ША = 13,8 ккал/мольЛ
Ру 1,6-Ю £
243
что весьма близко к истине. В ограниченном интервале
температур можно считать X и pt постоянными в сравнении с
pv. Тогда прямым дифференцированием C0.31) находим
соотношение
C0.32)
dT '
известное в термодинамике под названием «уравнения
Клапейрона — Клаузиуса». Его подтверждение свидетельствует
о правомерности вышеприведенных полуколичественных оце-
лок.
Плавление. Много сложнее обстоит дело с переходом
порядок — беспорядок, в результате которого кристалл
превращается в жидкость или плотный газ. В теории свободного
объема жидкое состояние от кристаллического неотличимо.
По крайней мере, так обстоит дело, пока изменением
коллективной энтропии в C0Д1) пренебрегается. Принципиальный
характер затруднений обнаруживается даже на модели
газа, состоящего из жестких сфер. По мере увеличения
давления коллектив таких шаров должен рано или поздно
превратиться в кристалл подобно тому, как выстраиваются в
решетку биллиардные шары, стиснутые формой. Реальной
системой, весьма близкой к этой модели, является
высоконагретый газ, в котором энергия сцепления частиц
пренебрежимо мала в сравнении с кинетической, но способность
кристаллизоваться из-за этого не утрачивается. Следовательно,
дефект теории свободного объема — и не ее одной! —
состоит в том, что она не способна установить, какие особенности
возникают на изотерме C0.10) вследствие образования
дальнего порядка.
Прояснить вопрос помогает машинный эксперимент. Для
небольшого, но уже обладающего свойствами макросистемы
коллектива, состоящего из нескольких сот «биллиардных
шаров», можно предложить два способа решения этого
вопроса. Один из них состоит в том, чтобы записать
механические уравнения движения и с помощью вычислительной
машины следить за эволюцией всего коллектива во времени
при заданном внешнем объеме и полной энергии системы.
Этот метод, который можно назвать молекулярно-динамиче-
ским, воспроизводит реальную ситуацию, и поэтому все
наблюдаемые величины получаются в результате временного
усреднения. Другой способ исходит из идеи канонического
ансамбля и носит название метода Монте-Карло. Машине
поручается выбрать наугад последовательность
микросостояний, каждому из которых соответствует определенная кон-
244
Рис 90. Расчет изотермы
методом Монте-Карло (сплошная
кривая) и посредством
теории свободного объема
(пунктир). Точки — эксперимент.
5,0-
2,0 v/v0
фигурация частиц и их скоростей, и, взвесив их с больцма-
новским фактором, вычислить статсумму. Оба рецепта
позволяют определить все параметры равновесного состояния и
проследить за их изменением при вариации внешних
условий. Оказывается, что, каким бы методом ни считать,
изотерма системы «жестких сфер» получается разрывной (рис. 90).
Одна из ее ветвей принадлежит кристаллической^ а другая —
неупорядоченной фазе. Молекулярно-динамический метод
позволяет даже заметить, как система мечется между двумя
возможностями в области фазового перехода.
Если, приняв к сведению эти результаты, внести
соответствующую коррекцию в поведение термического давления
реального вещества* то объяснить кристаллизацию не
составит труда (рис. 91). В нормальных условиях это превращение
отличается от кристаллизации «жестких сфер» только тем*
что главным образом внутреннее давление, а не внешнее
сжимает жидкость до объема, в котором наступает упорядочение.
При низких температурах только кристаллическая ветвь
изотермы имеет пересечение с силовой характеристикой,
при высоких — только неупорядоченная, а при температуре
плавления Тп имеются два устойчивых пересечения: одно с
кристаллической ветвью, а другое с неупорядоченной.
Зазор между ними по оси абсцисс соответствует небольшому,
но существенному увеличению объема, сопровождающему
фазовую перестройку. Этот зазор предстает на рис. 75
фазовой щелью, повсеместно отделяющей кристаллическую
модификацию вещества от прочих.
Итак, разрыв изотермы позволяет качественно
непротиворечиво объяснить все обстоятельства, связанные с
плавлением. Чтобы согласовать эти нововведения с теорией
свободного объема, необходимо ввести в действие последнее
слагаемое в формуле C0.11). Его назначение в том и состоит,
чтобы отражать состояние всего коллектива в целом. К со-
245
P+Pi\pt
Рис. 91. Баланс сил в
твердом теле (#), жидкости @) и
газе (О)- Соответствующие
области существования в
шкале объема (S, L и G) указаны
различной штриховкой.
жалению, о нем известно достоверно только то, что а
изменяется от 1 в кристалле до е в разреженной жидкости или
газе. Создатели теории свободного объема Леннард — Джонс
и Девоншайр предполагали первоначально, что это
изменение целиком происходит при плавлении, и, исходя из этого,
оценили даже его скрытую теплоту. Однако эта точка
зрения оказалась несостоятельной. Частичное разупорядочение
кристаллов всегда предшествует плавлению, а после него
жидкость оказывается в гораздо более упорядоченном
состоянии, чем разреженная среда. Следовательно, коллективная
энтропия должна постепенно увеличиваться в конечном
интервале плотностей. Связывая это с результатами
машинных расчетов, гораздо разумнее предположить, что в точке
плавления претерпевает разрыв не одна лишь энтропия,
но и ее производная (рис. 92). Необходим именно разрыв
производной, чтобы скачком изменить термическое давление,
предоставив самой энтропии плавно возрастать по мере
последующей хаотизации системы. Если это так, тогда вполне
понятно, почему теория свободного объема, развитая для
а = const, хорошо описывает кристаллы и неплохо
жидкости, но весьма скверно узкую область около точки плавления,
Ясно также, что этот недостаток практически не
сказывается на внутреннем давлении, которое, будучи локальной
мерой силовой обстановки, нечувствительно к кооперативным
изменениям состояния всего агрегата частиц в целом.
Ортометрическая прямая. Вернемся теперь к вопросу о
происхождении ортометрической кривой, вкратце обсуждав-
246
Рис. 92. Изменение
коллективной энтропии, терпящей
разрыв в точке плавления
(жирная кривая), и ее
прямоугольная аппроксимация по
Леннарду — Джонсу (тонкие
прямые).
3-
е
2-
1-
шемуся в § 9. Она представляет собой геометрическое место
точека отвечающих псевдоидеальным состояниям вещества
с F = 1, которые лежат на оси абсцисс рис. 75. Теория
свободного объема, адресующаяся к низкотемпературным ере*
дам, в принципе может описать лишь небольшой участок
этой кривой по обе стороны коридора плавления. Но именно
в этой области — вблизи фазового перехода порядок —
беспорядок — теория свободного объема, как мы убедились,
наименее приемлема. Вириальное разложение,
удовлетворительно описывающее высокотемпературные состояния,,
ограничено по применимости областью, прилегающей к
идеально газовому состоянию — началу координат рис. 75. Что
касается модели жестких сфер, то в ее границах,
согласно C0.17), F = Г > 1 при всех р > 0, и ортометрические
состояния оказываются для нее недосягаемыми. При таком
положении вещей особенно удивительно, что теория Ван-
дер-Ваальса, несмотря на ее очевидное несовершенство,
позволяет правильно установить вид ортометрической кривой,
простирающейся от идеального газа до высококонденсиро-
ванного состояния. Исходя из того, что чудес в
естествознании не бывает, нам необходимо прежде всего убедиться, что
этот успех — случайность.
С этой целью» тождественно преобразовав C0.1),
представим уравнение состояния в виде
где
Р Рп ГГ Р
ф_ pi
Г —1
C0.33)
C0.34)
есть отношение поправок на неидеальность» появляющихся
в левой и правой частях уравнения C0.1). Согласно C0.33)ф
ортометрическая кривая* заданная соотношением F = ie
247
определена уравнением
р = пкТ = Ф. C0.35)
О том, какова она на самом деле, можно судить, лишь знаяг
что собой представляют внутреннее давление рг и
фундаментальная характеристика вещества Ф(тг, Т). Согласно
уравнению Ван-дер-Ваальса, последняя не зависит от
температуры и, рассматриваемая как функция плотности, имеет вид
равнобокой параболы:
Ф = —р^ = j A - Ъп) тг, C0.36)
1 - Ъп ~~ 1
где а = АШ\ и Ъ — B/No = Aud — удельные константы Ван-
дер-Ваальса. Один из нулей этой функции связан с более
быстрым, чем Г—1, убыванием рг(п) = an2 при тг->0, тогда
как другой обязан своим происхождением расходимости Г
в точке п = Ъ~х = т— (рис. 93), Однако из предыдущего
известно (см. рис. 85), что никакой особенности в точке п =
= т— в поведении реального Г-фактора не обнаруживается.
Ее появление в теории Ван-дер-Ваальса свидетельствует
только о несовершенстве этой модели при высоких
плотностях. Тем не менее благодаря этому уравнение ван-дер-ва-
альсовской ортометрической кривой, получающееся из
C0.35) и C0.36),
р = |, A - Ъп) п = пкТ C0.37)
линеаризуется в координатах (Г, п), превращаясь в (9.21);
T=TB(l-4vdn), ГБ = ^. C0.38)
Как уже указывалось, этот вывод теории Ван-дер-Ваальса
подтверждается опытом.
Однако при ближайшем рассмотрении оказывается, что,
хотя линейность п(Т) — экспериментальный факт, наклон
ортометрической прямой, полученной опытным путем,,
отнюдь не совпадает с тем, который вытекает из C0.38). Как
видно из рис. 94, этот наклон, задаваемый ортометрической
длотностью при Т = 0, более чем вдвое меньше
установленного экспериментально (для азота). Между тем плотность
при Т = 0 есть не что иное, как координата особенности^
присущей ван-дер-ваальсовскому Г-фактору и с физической
248
nv,
3 a>
Рис. 93. Ортометрическая арка
Ф, внутреннее давление и Г-фак-
тор как функции приведенной
плотности в теорин Ван-дер-Ва-
альса.
Рис 94. Сопоставление ортомет-
рических прямых азота с
моделями Ван-дер-Ваальса и
притягивающихся жестких сфер
(кривая).
точки зрения бессмысленной. Естественно, что такое
объяснение ортометрической прямой нельзя признать
удовлетворительным. Вместе с тем усовершенствование уравнения
Ван-дер-Ваальса, устраняющее нефизическую расходимость
при п = -.—, только вредит делу* Если, в частности, прибег-
нуть к одной из формул C0.14), лишенных этого недостатка,
но сохранить в прежнем (ван-дер-ваальсовском) виде
внутреннее давление, то ортометрическая прямая становится
кривой в координатах рис. 94. Кроме того, второй нуль
функции Ф(тг), который в этом случае связывается с
расходимостью Г-фактора (T(vd) = oo)% располагается вчетверо
выше по шкале плотностей против прежнего. В результате
ортометрическая плотность при Т = 0 оказывается во столько
же раз больше истинного значения, во сколько раньше была
меньше его.
Выход из этих противоречий указывает теория
свободного объема, согласно которой с ростом плотности внутреннее
давление обращается в нуль гораздо раньше, чем Г в
бесконечность. Благодаря этому ортометрическая кривая в
координатах (Г, п) может быть надежно определена не только при
249]
п = Ош но и при п = тг0, где рг = Ф = 0. В самом деле:
Ортометрическая прямая, соединяющая эти две точки,
должна иметь следующий вид:
C0.40)
Плотность идеально упакованной гранецентрированной
структуры
no = ^-f =^, C0.41)
при которой достигаются нули внутреннего давления и Ф-
11 3
функции^ примерно вдвое больше т- = т— == о и во столь*
ко же раз меньше —==—д, как и получилось на рис. 94
при Т = 0.
Как видно из B7.35), уравнение ортометрическои кривой
в твердой фазе
тоже описывается линейной зависимостью, если Т *Э> @-
Последнее условие не всегда выполнено, так что C0,42)
является всего лишь высокотемпературной асимптотикой
ортометрическои кривой кристалла. Для аргона, у которого
температура Дебая довольно высока (93 К), эта асимптотика
является касательной к ортометрическои кривой в точке
плавления. Она пересекается с ортометрическои прямой
жидкости при Т = 0 (рис. 95).
То, что ортометрические кривые жидкости и кристалла
должны сойтись в общей точке (при Т = 0, п = тг0), прямо
следует из сравнения C0.40) и C0.42)д если, конечно,
считать, что положение нуля внутреннего давления не зависит
от агрегатного состояния. Именно это и подтверждает
пересечение прямых в общей точке на оси ординат. О томг
насколько точным является это пересечение, лучше судить по рис. 96„
так как температура Дебая Хе лежит много ниже точки
плавления и прямолинейная асимптотика ортометрическои
кривой кристалла хорошо выражена.
250
Рис. 95. Ортометрические
кривые жидкого (а) и
твердого (Ь) аргона,
разделенные коридором
кристаллизации (пунктир — их
экстраполяция из классической
области).
1,5 р, г/см3
Наконец, в общности нулей Ф-функции и внутреннего
давления можно удостовериться, разложив уравнение
состояния C0.1) на составляющие по рецепту* который будет
обсужден позже. Сравнивая рис* 97, на котором представлен
графически результат разложения, с рис. 93, на котором
сделано то же самое для уравнения Ван-дер-Ваальса, легко
убедиться,; что отнюдь не особенности в поведении Г-факто-
ра, а только нуль внутреннего давления — причина тому,
что ортометрическая арка Ф(тг), перекинувшись через всю
область существования газа и жидкости, упирается вторым
своим концом в точку, отвечающую по плотности идеально
упакованному кристаллу. Заметим, кстати, что, имея два
нуля, эта арка обязана иметь и имеет максимум,
расположенный между ними. Величина Ф достигает в нем
максимального ортометрического давления р0, являющегося
координатой «узловой точки» на диаграмме Ватсона (см. рис. 18).
Существование этой точки — максимума Ф — является
совершенно общим фактом, равно как и вывод о том, что
вблизи нее законно разложение
ф = Ро _ А(п — Пх)\ C0.43)
Но в простых жидкостях это разложение справедливо
повсеместно — от одного нуля до другого, так как, согласно
C0.39) и C0.40),
C0.44)
и простым переобозначением параметров
кТв п.
А = —-, пх = тг, р0 = Ап*х
кТБп0
C0.45)
251
100-
3,0 3,5jD,2/cm°
Рис. 96. Пересечение ортометри-
ческих прямых жидкого (а) и
твердого (б) ксенона (тонкие
прямые — их экстраполяция к Т=0).
Рис. 97. Ортометрическая арка Ф, внутреннее давление и Г-фактор
аргона. Заштрихованы области между жидкостью и паром (внизу)
и коридор кристаллизации.
формулы C0.43) и C0.44) приводятся в тождественное
соответствие.
Разложение уравнения на составляющие. Ни одна из
рассмотренных моделей среды (реальный газ, жесткие сферьц
идеальный кристалл) не является достаточно универсальной^
чтобы послужить основой для описания всей ортометриче-
ской кривой. Теория свободного объема с эвристической
точки зрения весьма полезна, но не может быть распространена
на сколько-нибудь широкий диапазон плотностей.
Отсутствие универсальной модели означает отсутствие
однозначного способа разложения уравнения состояния на
составляющие. Ни внутреннее, ци термическое давление сами по себе
не наблюдаемы, и только микроскопическая модель
наполняет физическим смыслом эти понятия.
Тем не менее существует естественное желание
осуществить разложение на pt и pt повсеместно, чтобы получить
единую основу для рассмотрения и сопоставления всех
агрегатных состояний вещества. С этой целью иногда обращаются
к так называемому термодинамическому уравнении^ которое
252
непосредственно вытекает из второго начала
термодинамики A0.7):
Если принять к сведении^ что, согласно A0.8),
\дт)у ~ War
то «термодинамическому уравнению» состояния может быть
придан вид
Его левая часть ассоциируется с силовой характеристикой,
а правая — с термическим давлением. Если бы эта
ассоциация оказалась правильной, то термодинамические
определения
(£)E) C0-49)
послужили бы универсальной основой для определения
внутреннего и термического давления во всех фазах и в любых
условиях. К сожалению, в самой термодинамике нельзя
найти оснований для отождествления слагаемых уравнения
C0.48) с величинами, получившими смысл и определения в
рамках микроскопических моделей. Поэтому разумность
определений C0.49) можно проверить лишь по их
соответствию с теми, которые уже были введены в употребление
теориями Ван-дер-Ваальса, Ми — Грюнайзена и свободного
объема. С этой целью обратимся прежде всего к уравнению
C0.1), полагая, что pt и Г в нем зависят только от объема»
Этого единственного условия оказывается достаточно, чтобы
при подстановке C0.1) в C0.48) убедиться в тождественном
совпадении всех слагаемых:
Pi-Pi(v); Pt=T(v)^ = pt. C0.50)
Поскольку и уравнения Ван-дер-Ваальса (9.10), и уравнение
Ми B7.34) являются лишь разновидностями уравнения
C0.1), оба они определяют внутреннее и термическое
давление в соответствии с C0.49).
Однако в действительности условия применимости
«термодинамических» определений, суммированные в C0.50),
являются слишком жесткими. В частности, они полностью»
253
исключают квантовую область. При подстановке уравнения
Ми — Грюнайзена B7.21) в C0.49) выясняется, что
pt --•= 4y(w — и0) ф pt = уи, C0.51)
несмотря на то что и pt и у продолжают зависеть только от
объема. Кроме того, уже из самого определения &\ данного
в B7.2), ясно, что термодинамическое внутреннее давление
не совпадает с тем, что под этим понимается в теории твердо-
ю тела B7.6а) и свободного объема C0.4).
Можно было бы думать, что «термодинамические»
определения действительны хотя бы в классической области.
Однако и это не так. Как только допускается возможность
температурной зависимости pt или 1\ между микроскопическими
и термодинамическими определениями этих величин
немедленно возникает ничем не оправданное различие. Возьмем,
к примеру, усеченное вириальное уравнение (9.19):
C0.52)
и вычислим с его помощью «термодинамическое)) внутреннее
давление:
В таком случае «термодинамический» аналог константы Ван-
дер-Ваальса есть не что иное, как
Если второй вириальный коэффициент линейно уменьшается
« обратной температурой* как это имеет место в (9.18)t то
термодинамическое и ван-дер-ваальсовские определения
совпадают: А —А* Однако на самом деле зависимость Во ( — j
(см. рис. 25) гораздо ближе к квадратичной, чем к линейной,
и приближенно описывается формулой Вертело:
RTC Г т*21
[] C0.55)
Если использовать ее в C0.54), то оказывается, что
C0-56>
254
нигде постоянной не является и с ростом температуры
падает до нуля. В действительности же положение еще хуже,,
так как из-за небольщого экстремума, хорошо различимого
на рис. 25, при высоких температурах А даже меняет знак,,
лишая всякого физического смысла «внутреннее давление»
C0.53). Поскольку нелинейность зависимости ВоA/Т) —
опытный факт, мы с неизбежностью приходим к заключению,,
что «постоянные» в уравнении Ван-дер-Ваальса на самом
деле вовсе не постоянны, а изменяются с температурой, и
вследствие этого взаимное соответствие термодинамического и.
ван-дер-ваальсовского уравнений иллюзорно. По этой же
самой причине отождествление термодинамического
уравнения с уравнением Ми также находится в прямой
зависимости от того, постоянна ли «постоянная Грюнайзена»*
или же на самом деле у = у(Т). Таким образом, даже в
классическом диапазоне температур термодинамическое
определение рг и pt физически оправдано лишь в той мере, в какой
внутреннее давление и Г-фактор можно считать функциями
одного лишь объема.
Ввиду этого не лишено смысла попытаться разделить
уравнение состояния на составляющие, апеллируя к их
физическому смыслу, а не к термодинамике. Зная заранее, что
на ортометрической прямой Т = Т0(п) фактор сжимаемости
обращается в единицу, естественно придать уравнению
состояния следующий вид:
[^] C0.57)
где Х(п, Т) — неизвестная функция. Преимущество такой
записи состоит в том, что Х(п, Т) должна иметь гораздо
более простой вид, чем F(n, Г), и легче поддаваться
аппроксимациям. Вместе с тем эта форма записи подсказывает
простейший способ разделения
на составляющие:
Pi = Хп*кТ0 C0.59)
и
Г = 1 + Хп. C0.60)
Если Х(п, Т) остается конечной величиной при п -* 07
а Г0@) = Те, то Г и рг в разреженных газах именно так
зависят от плотности, как им положено по уравнению Ван-дер-
255
аальса с параметрами
ЦТ) = Х@, Т), а(Т) = ЦТ)-кТБ. C0.61)
Последнее соотношение является прямым обобщением (9.20).
Второй вириальный коэффициент, согласно C0.57) и (9.17),,
есть:
(^) C0.62)
Между ним и параметром А = a-Nl существует следующая
взаимосвязь:
RTKBn (T) т
А = (Г-гв) - C(Ш>
Видно, что этот параметр положительно определен во всем
диапазоне температур% так как и знаменатель, и числитель
{В0(Т)) одновременно обращают знак при Т = Т^
Убедимея теперь, что и с теорией конденсированных сред
феноменологические определения pt и Г согласуются вполне
удовлетворительно. Для этого подставим в C0.59) явное
выражение Т0(п) из C0.40). Это позволяет видеть, что pt
обращается в нуль при п = п0:
(^ C0.64)
в соответствии с его фактическим*поведением в конденсиро-
ванцой среде. При этом
Ф = j^l = пкТо - кТБп (l - ^) C0.65)
от X не зависит, а значит не зависит и от температуры, и
определена в точном соответствии с C0.45).
Естественно ожидать, что при п -* п0 выражение C0.5)
должно точно передавать зависимость рь от плотности:
Pi = COnSt.7г3 И - f 722 ~723 1 - '\ . C0.66)
L * J L ?0J
Использовав эту информацию в C0.64), мы можем судить о
поведении Х(п) не только в газе, но и в плотной среде:
(Ь(Т) при 72 = 0, C0.67а)
Х = \Ln[\ + -) прит2^тг0, C0.676)
L ~ const.
256
Pilpi
20-
Рис. 98. Внутреннее давление
аргона A) при Т = 2Тс (жирная часть
кривой лежит в области
существования неупорядоченной фазы); 2 —
решеточная аппроксимация р.
C0.66), 3 — ван-дер-ваальсовское
приближение C0.5а).
0,7 у
Рис. 99. Сравнение Г-факто-
ров системы жестких сфер
(верхние кривые) и азота
(нижние), нормированных по
их линейной асимптотике при
У = vJv _> 0. Пунктиром в
обоих случаях указаны ветви,
относящиеся к твердой фазе.
Таким образом, требуется сравнительно немного
параметров, чтобы полностью воссоздать вид внутреннего
давления, а вместе с ним и Г-фактора. Информацию о них обоих
можно извлечь путем прямого сопоставления
феноменологического уравнения C0.57) с экспериментальными данными,
В настоящее время существует немало эмпирических
многопараметрических- уравнений, определяющих состояние
простых жидкостей в пределах точности эксперимента.
Прибегнув к ним, можно совершенно строго установить вид рг и
Г, определенных в C0.59) и C0.60) при любой температуре.
Такое разложение уравнения на составляющие и было
воспроизведено на рис. 97.
Полученные таким образом данные о фактическом
изменении внутреннего давления и Г-фактора показывают, в
какой мере оба приближения — газовое и решеточное —
способны аппроксимировать их со стороны малых и больших
плотностей соответственно. Как видно из рис. 98,
приближение Ван-дер-Ваальса правильно оценивает внутреннее
давление по порядку величины, но не описывает ни перегиба,
ни максимума, который достигается еще в пределах жидкой
фазы. Напротив, решеточная модель верна вблизи максимума
и правильно указывает положение нуля, но недооценивает
внутреннее давление в разреженном газег обусловленное
9 Aj И Бурштейн
257
дальнодействием. Граница между ними лежит вблизи п =
= 720/2, т. е. примерно посередине между критической и
тройной точкой. Принимая во внимание ее положение, следует
признать, что представления решеточной модели о
характере взаимодействия молекул правильны почти во всей
области существования жидкости.
Что касается Г-фактора, то в его поведении не
обнаруживается сколько-нибудь значительных особенностей вплоть
до границы кристаллизации, где он претерпевает разрывы
(рис. 99). Если сравнить его с приближением «жестких сфер»,
подобрав vd таким образом, чтобы все асимптотики при п -*
-* 0 совпали, то оказывается, что истинный Г-фактор
возрастает с плотностью менее круто. Что же касается
кристаллической фазы (пунктирные линии), то различия не только
увеличиваются в масштабе, но и принимают качественный
характер: в модели жестких сфер Г-фактор продолжает
возрастать с уплотнением, тогда как в реальности он падает.
Это естественно объясняется тем, что нельзя учитывать
только собственный объем частиц в области, где отталкивание
и притяжение одинаково важны.
§ 31. ПОВЕРХНОСТНЫЕ ЯВЛЕНИЯ
Отличительной чертой жидкости является ее способность
свободно искривлять свою поверхность. Предоставленная
самой себе, вне сосуда pi поля тяготения, она сворачивается
в шар, принимая таким образом форму с минимальной
площадью поверхности. Этот факт хорошо известен и
объясняется тем, что поверхность жидкости подобна упругой пленке,
равномерно растянутой во все стороны, которая стремится
максимально сократить свою площадь.
Если поверхность жидкости плоская, то ее напряженное
состояние внешне никак себя не проявляет. Чтобы его
обнаружить, следует частично погрузить в жидкость пластину
(рис. 100). Тогда молекулы поверхности, непосредственно с
ней соприкасающиеся, будут испытывать одностороннее
воздействие жидкости, передающееся пластине. Очевидно, что
результирующая сил, натягивающих поверхность,
перпендикулярна линии соприкосновения, а ее величина прямо
пропорциональна длине этой линии
F = у?. C1.1)
Сила, действующая на единицу длины, и есть
«поверхностное натяжение» жидкости у.
253
Рис 100 Силы, действующие на
молекулу в поверхностном слое (а) и у его
границы со стенкой (б).
Рис. 10/. Рамка с
пленкой жидкости и
подвижной пленкой.
Если пластина, о которой шла речь, представляет собой
подвижную планку, укрепленную в рамке, заполненной
слоем жидкости, то она пересекает сразу две поверхности
(рис. 101), края которых тянут ее в одну и ту же сторону
с равной силой. Посредниками в этом деле являются
частицы, непосредственно прилегающие к планке, которые
связаны с ней межмолекулярным притяжением. Этими силами
сцепления планка как бы приклеивается к жидкости и, если
ее ничто не удерживает, приходит в движение, подчиняясь
одновременному воздействию обеих жидких поверхностей.
Остановить его можно, подвесив груз, вес которого (с
планкой включительно) равен сумме этих двух сил. Если и после
этого планка все же перемещается бесконечно медленно и
изотермически, то производится работа по поднятию груза
на высоту h:
А = —ЬТ = 2Fh = y-22'h = -y^S^ C1.2)
Она совершается исключительно за счет убыли свободной
энергии жидкости — Д#", пропорциональной сокращению
площади ее поверхности —AS = 23?h. Отсюда видно, что
y = (%)T^N C1-3)
имеет смысл избытка свободной энергии поверхностного
слоя, приходящейся на единицу его площади.
Легко понять, откуда берется этот избыток. Молекулы,
выдвинувшиеся в поверхностный слой, наполовину уже
оторвались от жидкости, так как сверху у них уже нет соседей.
Яма, в которой они совершают колебания, поперечные
поверхности, и однобока, и менее глубока, чем внутри объема
(рис. 102). При равном запасе кинетической, энергии средняя
259
Рис. 102. Потенциал ячейки С/, Ф
и тангенциальное внутреннее
давление в объеме жидкости (а) и на
ее поверхности (б).
потенциальная энергия частиц у поверхности больше, чем
в глубине жидкости, п с переходом их в объем разница
выделяется, превращаясь в работу и 1епло. Таким образом,
с энергетической точки зрения существование
поверхностного натяжения легко объяснимо.
Несколько сложнее понять происхождение сил,
создающих его. Заведомо ясно, что они складываются из сил
взаимодействия, связывающих частицы поверхностного слоя.
Однако количественная мера этого взаимодействия —
внутреннее давление, действующее вдоль поверхности, не
только не возрастает, но даже уменьшается по сравнению с вну-
трифазовым (см. рис. 102). Кроме того, в поверхности, как и
в объеме, ему противостоит термическое давление,
направленное в противоположную сторону. Если оно преобладает,
то поверхность будет не тянуть стенку, а давить на нее, как
это происходит внутри объема, где р = pt — Pi > 0.
Иными словами, необходимо с самого начала рассматривать их
разность рт — тангенциальное давление жидкости.
Вследствие анизотропии, созданной самим существованием
поверхности, давление вдоль нее /ив перпендикулярном
направлении pN не одинаково. Вдали от поверхности раздела фаз
обе составляющие давления как в газе, так и в жидкости
равны р, но с приближением к поверхности раздела
тангенциальная компонента должна уменьшиться или даже
обратить знак, чтобы создать напряжение, направленное в
сторону жидкости. Величина этого напряжения определена
260
в A0.44M
+00
V= | [p-pT(z)]dz.
— oo
Так как поверхностное натяжение определено только в
точках, лежащих на кривой сосуществования, оно является
функцией одной лишь температуры, уменьшается с ее
увеличением и обращается в нуль в критической точке.
Одновременно и поверхность раздела, очень резкая вблизи тройной
точки, постепенно размывается и превращается в широкую
область при приближении к критической точке. По этой
причине для описания ее структуры и натяжения при низких
и высоких температурах привлекаются альтернативные
модели, которые рассматриваются ниже. При низких
температурах поверхность можно считать мономолекулярной и
использовать довольно простые оценки для расчета ее
натяжения. При высоких температурах переходная область
настолько широка, что может рассматриваться как
непрерывная среда, плотность которой n(z) постепенно уменьшается
при переходе от жидкости к газу. В этом случае расчет
натяжения поверхности и ее структуры (п, рт) должен быть
самосогласован, что удается сделать с помощью
квазитермодинамики, изложенной в § 10.
Мономолекулярная поверхность. Когда граница
жидкость — пар резкая, существенной деформации подвержено
лишь несколько прилегающих к ней слоев (рис. 103). Немного
утрируя эту ситуацию, можно считать, что растяжение
испытывает только самый верхний из них, толщиной Л, и его вклад
в у определяющий. Чтобы рассчитанное у соответствовало его
наблюдаемой величине, тангенциальное давление должно
быть в этом случае большой отрицательной величиной,
намного превышающей р по абсолютному значению. В таком
случае, согласно A0.44),
y-lp-p'jha-p'ha-pjh. C1.4)
Последнее выражение следует рассматривать как верхнюю
оценку, так как \рт \ = р? — р';Г<; р J1, но термическое
давление даже при сильном растяжении не обязательно пренебре-
гр гр
жимо мало. Сделанная оценка справедлива, если р-г S> pt, р.
В глубине жидкости давление определено формулой
A0.42). .Аналогично определены и компоненты тензора
давления в поверхностном слое:
2I
Газ
/?(идхо.сть
Рис. 103. Изменение тензора давления и деформация
ячейки по мере приближения к поверхности жидкости.
где / — свободная энергия, приходящаяся на одну молекулу
в поверхностном слое, h — толщина, as — площадь
поверхностной ячейки. Компоненты внутреннего давления могут
быть определены по аналогии с его изотропной величиной
C0.4):
Считая, что число ближайших соседей в поверхностном слое
есть /п, a s = £>123 где I — расстояние до них, имеем
"Г - — ■ % C1.7)
Как уже отмечалось выше, при средних расстояниях между
молекулами, характерных для жидкой фазы, силы
притяжения доминируют над отталкиванием. Это тем более верно
для поверхности, где I > а. Пренебрегая на этом основании
отталкиванием, а притяжение считая дисперсионным,
используем в C1.7) и = — 4е(а//N. Тогда получается
бпгев
C1.8)
Подставляя этот результат в C1.4), имеем окончательно
бтеа6
248O-6 УЗ
,8 •
C1.9)
262
Последнее выражение получено в предположении, что на
поверхность выходит плоскость A11) плотноупакованной
кубической решетки, в которой плотность частиц наименьшая,
т = 6, а I = /3/2.
Формула C1.9) позволяет оценить у по порядку величины,
но оставляет нерешенным вопрос о том, каково Z, т. е.
насколько растянута поверхность по сравнению-с объемом. Чтобы
ответить на него строго, необходимо рассмотреть условия
равновесного сосуществования поверхностного слоя и объема
жидкости. Как известно из § 10, они требуют равенства
нормального давления и химического потенциала в объеме и на
поверхности. В принципе, располагая двумя параметрами
(h и s), можно подобрать их так, чтобы оба условия
выполнялись. На самом деле, однако, задача сложнее. Выясняя
структуру поверхности, нельзя исходить из того, что она мо-
номолекулярна, а надо прийти к этому заключению,
рассматривая равновесие в нескольких соприкасающихся друг с
другом поверхностных слоях. Чтобы избежать этого усложнения,
мы предположим просто, что жидкость остается
«несжимаемой» вплоть до границы раздела, т. е. ячейка, деформируясь,
не меняет своего объема:
В последнем выражении принято во внимание, что
термическое удлинение /г, которое должно оцениваться по формуле
B7.33), совершенно незначительно, и, следовательно, h ж
ж а. Используя это в C1.9), получаем
27УГ.«£ C1Л0)
Записанное в таком виде поверхностное натяжение
оказывается универсальной функцией удельного объема
жидкости. Этот вывод находится в согласии с феноменологически
установленным А. И. Бачинским «законом сохранения»
величины
C1.11)
названной Сагденом «парахором». Поскольку мы адресуемся
сейчас к низким температурам, плотностью пара nv в
формуле C1.11) можно пренебречь по сравнению с nL = 1/v. После
этого, используя в ней C1.10), получаем следующую оценку
263
парахора:
1 5
& = L?*o\ C1.12)
B7 ~|/3~\^
—|—I iV0 = 9-1023. Существование такого рода
связи между парахором и параметрами потенциала было
в свое время установлено Леннардом — Джонсом и
Корнером. Постоянная L для простых жидкостей практически
одна и та же, как видно ниже, и лишь незначительно
отличается от рассчитанного значения, которое является «оценкой
сверху» этой величины:
Вещество
Ne
Ar
N2
CO
CH4
25
54
60,4
61,6
73,2
b'lQT
7,6
7,0
7,0
6,8
7Д
Размытая граница раздела. Обратимся теперь к области
высоких температур, когда плотности жидкости и пара
сравнимы и подвержены влиянию границы раздела на довольно
больших расстояниях от нее. Чтобы установить, каково это
влияние, необходимо найти то единственное распределение
плотности в переходном слое n(z), которое обеспечивает
постоянство нормального давления A0.53), а следовательно,
и химического потенциала A0.52). С этой целью перепишем
закон сохранения A0.53) в виде дифференциального
уравнения:
^-к2 = т, C1.13)
правая часть которого
т = р — \хп + /0 (п)-п C1.14)
зависит от плотности (но не от координаты). Интегрируя
C1.13), в предположении, что Ъ не зависит от /г, находим
п
z = у ~2 ] / • C1.15)
nQ Ш Р
Начало отсчета оси z удобно расположить там, где плотность
среды равна среднеарифметическому между плотностью пара
и жидкости: п0 = (nL + nv)/2.
264
Формула C1.15) задает форму профиля плотности в виде
зависимости z(ri), для определения которой достаточно знать
функцию т(п). Учитывая, что, согласно A0.43),
Ро = (Цо -/о)", C1-16)
а |л = fi0 (nL), эту функцию можно переопределить
следующим образом:
п
-^dn- C1.17)
nL
п
Дифференцируя C1.16) и учитывая, что \х0 = п-г-- + /0,
согласно A0.43), нетрудно установить, что
dn n dn '
Подставив это соотношение в C1.17) и выполнив
интегрирование по частям, находим окончательно
' ° ' 'dn. C1.18)
П
nL
Этим выражением зависимость т(п) полностью определена
при любом заданном давлении пара /?, отвечающем данной
температуре Т. Для ее расчета требуется знять только
изотерму ро(п), отвечающую той же температуре. В простейшем
случае можно воспользоваться изотермой Ван-дер-Ваальса,
но гораздо лучше прибегнуть к современным
многопараметрическим уравнениям состояния, описывающим изотермы
конкретных газов в пределах экспериментальной ошибки.
Это позволяет рассчитывать т(п) с помощью C1.18), а затем
использовать эту информацию в C1.15) для определения
зависимости z{ri), характеризующей структуру переходной
области. Последняя параметрически зависит от константы 6,
численная величина которой неизвестна.
Чтобы устранить эту неопределенность, достаточно
учесть, что поверхностное натяжение, определенное в
теории Ван-дер-Ваальса формулой A0.55), равняется
= Ъ J ndn. C1.19)
26
-ю
10 z,A
Рис. 104. Изменение
плотности вещества (в единицах
критической) при переходе
от жидкостп к пару.
Рис. 105. Изменение тензора
давления, определенного в A0.57),
у границы раздела жидкость —
пар.
—10
Используя то, что п должна удовлетворять условию
равновесия C1.13), нетрудно преобразовать эту формулу к
следующему виду:
Vib
Пу
C1.20)
свидетельствующему о том, что не только структура
поверхности, но и ее натяжение однозначно определяются
функцией т(п). Заимствуя сведения о ней из соответствующих
уравнений или непосредственно из эксперимента, мы можем
рассчитать у по формуле C1.20) и, сравнив с наблюдаемой
величиной, определить единственный неизвестный параметр
теории — Ь. Этим окончательно и однозначно определяется
распределение плотности в переходном слое n(z).
Эта программа была реализована Бурштейном и Шохи-
ревымдля азота с помощью аналитических уравнений
состояния, которые при высоких температурах хорошо описывают
це только жидкостную и газовую ветви изотермы, но и
переходную область между ними (см. рис. 17). Результаты
приведены на рис. 104. Чем выше температура, тем ближе к
критической плотности обеих фаз и шире переходная область
между ними. Об этом же свидетельствует изменение тензора
давления вблизи границы раздела. Оно характеризуется
величиной Ар = р - рТ = PN - Рт, которая, согласно
A0.53), A0.57) и C1.13), равна
= bn2 = 2т,
C1.21)
266
Как видно из рис. 105, эта величина знакопостоянна,
достигает максимума вблизи z = 0 и обращается в нуль на
расстояниях, в несколько раз превышающих молекулярный диа-
о
метр азота C,7 А).
Заметим теперь, что описанное поведение Ар — не
единственно возможное. Как уже указывалось в § 10, локальная
свободная энергия / и тангенциальное давление рт (а
следовательно, и Ар) определены неоднозначно. Выполнив
интегрирование по частям в A0.47), можно представить
свободную энергию двухфазной системы в следующем
эквивалентном виде:
* = Л'»-!6"- i' ln2]ndz- <31-22)
Если это подынтегральное выражение отождествить с /я,
то свободная энергия окажется равной
а тангенциальная составляющая давления, найденная из
A0.45) с учетом A0.52) и C1.16), примет вид
рт = Ро(п) — ±Ь (п) п.п. C1.24)
Что касается нормального давления A0.53), то оно остается
прежним, равным р, но с помощью A0.52) может быть
представлено в сопоставимом виде:
pN = Ро(п)-Ъ{п)п^п + Ь^п* - \fjrn* = р. C1.25)
При b = const анизотропия этого тензора изменяется
следующим образом:
Ар = \ [л» - пп] = 1 [пг + р - р0]. C1.26)
В отличие от C1.21) эта величина знакопеременна (рис. 106).
Ее максимум и минимум отвечают экстремумам на петле
Ван-дер-Ваальса, а участок между ними относится к таким
состояниям, которые считались бы неустойчивыми, если бы
среда была изотропной 7. Поскольку плотность вещества
7 Так как участок изотермы, соединяющий максимум и минимум,
получается экстраполяцией эксперилшнтальных данных в
неустойчивую область, его аппроксимация тем менее надежна, чем ниже
температура. Этим, в частности, объясняется появление нефизической
особенности (перегиба) при 85 К (см. рис. 106).
267
1Q
п
рт
--10
Рис. 106.
Переопределенный тензор давления,
воспроизводящий в
координатном пространстве петлю *
Ван-дер-Ваальса.
-20
—->
"1
а
V
О z
jTllllllHli 1 .— ^_
О Z
6
Рис. 107. Разрывное изменение плотности (а) п тензора давления (б)
в межфазовоп области при исключении неустойчивого слоя по Толмену.
считается непрерывно изменяющейся от жидкостной до
газовой, такие состояния неизбежно находятся, и
соответствующий им слой вещества расположен непосредственно на
границе раздела. Его границы в шкале плотностей помечены
черточками на кривых рис. 104. Если предположить, что
состояние вещества в этом слое остается неустойчивым, и,
следовательно, нереализуемым, то вблизи границы должен
иметь место скачок плотности, которым она так же четко
обозначена, как и в случае мономолекулярного слоя, но в обе
стороны от нее плотность изменяется плавно, асимптотически
приближаясь к своим предельным значениям: nL и nv
(рис. 107). Именно таким представлял себе переходный
слой и тензор давления в нем один из пионеров исследования
поверхности Толмен.
§ 32. ЯВЛЕНИЯ ПЕРЕНОСА
Для описания процессов переноса в газе достаточно
одного лишь времени свободного пробега, т. е. времени
сохранения скорости. В модельных теориях жидкости для тех же
целей часто вводятся в рассмотрение два времени. Одно из
268
них — время корреляции скорости C0.20) — является
правопреемником длительности свободного пробега, другое
измеряет срок, который частица проводит в данном окруже
нии и в данном месте до смены того и другого. Ближайшим
аналогом последнего является время оседлой жизни
дислоцированного атома, кочующего по междоузлиям. Отличие,
однако, состоит в том, что в жидкости нет дефектов, ибо нет
порядка, поэтому и кочевой образ жизни является нормой
поведения всего коллектива, а не отдельных его членов.
Приняв во внимание, что в плотной среде ежа2, а
па? « 1, можно представить формулу C0.20) в следующем
виде:
1 па v ~ -on ,i\
— « -~nov. C2.1)
тс а — d х '
Единственное, что существенно отличает такую оценку
частоты столкновений от прежней A5.8),— это эффективная
скорость передвижения
v = v^ C2.2)
намного превышающая среднюю тепловую. Это новшество
является столь же неизбежным при правильном учете
конечного объема частиц, как и появление самого сечения
столкновения а. Последнее задает поперечный масштаб частицы,
а появление коэффициента °_ в C2.2) связано с ее
продольным размером, сокращающим на d каждый свободный
пробег, измеренный расстоянием между центрами. В разре-
женных газах поправка x_d очень близка к единице, и
поэтому не была принята во внимание. В плотной же среде,
где А, ~ а, и, по крайней мере, на порядок больше и, и этого
нельзя не учитывать.
Если кинетическая энергия частиц много больше
потенциальной, то их пробег ограничен только столкновениями.
Поэтому при высоких температурах, в закритической
области явления переноса контролируются только одним
временем — тс. Этот вывод подтверждается машинным
экспериментом, произведенным с системой жестких сфер. Движение
частиц прослеживалось во времени молекулярно-динамиче-
ским методом как в упорядоченном состоянии,
соответствующем кристаллической ветви изотермы, так и в
беспорядочном, отвечающем состоянию газа примерно такой же
плотности (рис. 108). В последнем случае возможны редкие пе-
269
#:.*
Рис. 108. Траектории теплового движения частиц в кристаллическом
(а) и жидком (б) состояниях. Цит. по [30].
ремещения и перестановки частиц, несмотря на тесноту
окружения. Однако установлено, что эти перетасовки
осуществляются последовательностью мелких шагов, подчиняющихся
обычной статистике свободных пробегов A5.13).
Иное поведение свойственно жидкости при низких
температурах, когда сцепление молекул ограничивает свободу
их перемещения. С одной стороны, ближайшее окружение
частицы способно удержать ее от перемены мест, даже если
представляется благоприятная возможность обосноваться по
соседству. С другой стороны, и сама эта возможность
возникает не часто.
Первая трудность вполне подобна той, с которой
сталкивается мигрирующий в кристалле дислоцированный атом или
вакансия. Частице жидкости также приходится
преодолевать барьер АС/, покидая ячейку, и тоже за счет тепловой
энергии. Если считать, что все дело лишь в преодолении
барьера, а за ним прием частице обеспечен, то естественно
ожидать, что частота переходов через него выразится
формулой, аналогичной B8.10). Исходя из этого, Френкель
определил время оседлой жизни молекулы следующим образом:
т = тсехр(— ^J. C2.3)
Появление экспоненты в этом соотношении приводит к тому,
что время сохранения координаты т резко удлиняется по
сравнению с временем сохранения скорости тс. Такое
соотношение времен позволяет рассматривать низкотемператур-
270
ную жидкость как квазикристаллическую структуру,
достаточно долго сохраняющуюся в масштабе ближнего порядка.
Хотя частица пересекает ячейку в среднем за время тс ~
~ 103 с, она покидает ее не чаще, чем 1010—1011 раз в
секунду-, проделывая в неизменном окружении порядка 100
колебаний. Такова же ситуация и в аморфных твердых
веществах, которые ничем принципиально не отличаются от
жидкостей, но время реорганизации ячейки т затянуто до
секунд, часов и более из-за больших AU/kT. В результате
некоторые пластические массы успешно конкурируют по
своим прочностным характеристикам с кристаллическими
твердыми телами.
Таким образом, разделение аморфных сред на жидкие и
твердые чисто условно и определено только в кинетическом
смысле. Твердыми принято считать вещества с т ~ 10 с,
поскольку именно в этом масштабе времени проверяется
пластичность вещества, когда ее испытывают человеческие
руки. Если их заменить быстродействующим механизмом,
критерий сместится в сторону меньших времен, если
длительной статической нагрузкой — в большую. Поэтому
температура стеклования, в отличие от точки плавления, есть
характеристика кинетическая, а не равновесная, и ее
положение на температурной шкале определено местом, где т
достигает условленного значения. Любая жидкость, в том числе
и такая маловязкая, как вода, обладает всеми свойствами
аморфного твердого тела при высокочастотных испытаниях.
В обычных условиях они не обнаруживаются только потому,,
что изменение нагрузки происходит медленно в сравнении
с т > 101 с. Прыгает ли человек в воду, движется ли в ней
винт парохода, время силового воздействия всегда больше т,
и жидкость успевает перемещаться в том направлении и так
быстро, как этого требует вынуждающее усилие. Но пуля
входит в жидкость быстрее, чем та способна отреагировать
на ее появление. Частицы не успевают покинуть своих ячеек
и перестроить ряды с тем, чтобы уступить ей дорогу. В
результате жидкость в целом ведет себя как твердое тело,
ломаясь п трескаясь от резкого удара.
Теплопроводность. В одноатомной жидкости, такой как
ртуть или аргон, единственно возможный вид теплового
движения — случайные колебания атомов. Энергия,
принадлежащая каждому из них, без всяких затруднений
передается от одного другому при любом столкновении. Поэтому
перенос тепла в жидкости не связан со структурными
перестройками, а ограничен только частотой столкновений C2.1).
Механизм его тот же, что и в газе, и только параметры в фор-
271
муле A6.3) должны быть переопределены соответствующим
образом:
х = knvX ->■ knva. C2.4)
Высокая плотность среды обусловливает сокращение длины
пробега до величины а и ускоренный в соответствии с
формулой C2.2) перенос энергии. Возрастание скорости, с которой
передаются энергия и импульс (звук) в плотной среде,
объясняется эстафетным характером этой передачи. Скорость
факела тоже больше скорости бегущих, так как, переходя из
рук в руки, он мгновенно преодолевает расстояние, равное
их общей длине. Используя C2.2) в C2.4), находим
х=
a— d
уш (л
У m \vj
где v и Vf в последнем выражении — удельный и свободный
объем соответственно. Эта грубая оценка, как ни странно,
очень неплохо согласуется с экспериментальными данными
по теплопроводности одноатомных жидкостей.
Вязкость. Все остальные процессы переноса, связанные
с изменением положения частиц, такие как диффузия,
электропроводность, вязкость, ограничены временем
структурной перестройки т.
Согласно Эйрингу, преимущество в скорости Аи, которое
имеет более удаленный от твердой поверхности слой жидкости
по сравнению со слоем, расположенным под ним, можно
истолковать как результат дрейфа молекул под действием
соответствующей компоненты сдвигового напряжения F:
Аи = g. (Fa2), C2.5)
где q — молекулярная подвижность, а а2 — площадь,
приходящаяся на одну молекулу в текущем слое. Если разность
скоростей отнести к расстоянию между слоями, то
воспроизводится феноменологический закон вязкого течения:
^ = qaF = F-. C2.6)
Чтобы раскрыть смысл коэффициентов подвижности или
вязкости, необходимо теперь микроскопически оценить
приращение скорости Дм, которое становится возможным
благодаря наличию и миграции вакансий в текущем слое жидкости.
Как мигрируют примеси в кристаллах, так и вакансии
(пустоты в структуре жидкости) смещаются по течению и
против него с различной вероятностью. Движение против тече-
272
ния облегчено, так как при этом атом, заполняющий
вакансию, смещается в направлении движущей силы, а в обратной
ситуации — против нее. Это приводит к тому, что высота
барьера, который приходится преодолевать в любом случае,
соответственно уменьшается и возрастает на величину
_ Fa3 = F/2n, а вероятности переходов против и по течению
приобретают вид, подобный B8.13):
F F _At7
К+е 2hTn = K-e2kTn =K = Koe kT. C2.7)
В итоге средняя скорость дрейфа вакансий, смещающихся
при каждом переходе на величину а, оказывается равной
C2.8)
Однако это отнюдь еще не скорость течения слоя Аи,
которой мы интересуемся. В отличие от вакансий,
движение которых ничем не ограничено, кроме энергетических
барьеров, молекулы стеснены в своем перемещении и
совершают перескок только в том случае, если рядом с ними
оказывается вакансия. Если последняя удалилась и строй
окружающих молекул сомкнулся, перескоки становятся
неосуществимыми. Дальнейшее движение возможно только при
следующей встрече с вакансией. Частота этих встреч
определяется, очевидно, концентрацией вакансий в среде п0 и равна
cnva2. Полагая, что при каждой встрече атом смещается
в направлении течения на величину а, мы можем оценить
Аи = a3cnv = аК-2-sh [^j) р„ C2.9)
где pv = njn есть отношение числа вакантных мест к
занятым. Этот безразмерный коэффициент, отличающий C2.9)
от C2.8), нередко упускается из виду, хотя Эйринг
принимал его во внимание и полагал, что он может быть оценен по
формуле
pv = V-^J>ttV-^<>. C2.10)
vh v
В ней и0 — удельный объем нерасширенного твердого тела,
a vh — объем вакансии, который равен z;0, если считать, что
расширение жидкости происходит исключительно за счет
проникновения вакансий в ее структуру.
Нелинейная связь скорости течения с приложенной силой,
обнаруживающаяся в C2.9), свидетельствует о том, что, во-
273
обще говоря, этот поток не является ньютоновским, а
становится таковым только при разумно малых значениях
внешней силы. При таком ограничении гиперболический синус
может быть разложен по своему аргументу, и формула C2.9)
приведена в однозначное соответствие с C2.6), причем для
коэффициента вязкости вытекает следующее определение:
Ч-1Г. C2.11)
Здесь
AU
W = KPv = Koe hTPv C2.12)
— частота перемещения частицы в соседнюю ячейку, a &W =
= 1/т есть не что иное, как частота структурных перестроек,
завершающихся изменением места «оседлого образа жизни».
Попытки вырваться из плотного окружения совершаются
частицей в любом направлении Ко раз в секунду, а во все
стороны — с частотой — = 6К0. Поэтому между временем
оседлой жизни и временем релаксации скорости сохранится
соотношение C2.3):
т = тс^- г C2.13)
но с важной поправкой, учитывающей необходимость
разрыхления структуры для организации перемещения частицы.
Из C2.6) видно, что вероятностью структурной
перестройки ограничивается не только текучесть среды, но и
подвижность частиц в ней:
1 Wa2 „0 ,7ч
Поскольку последняя связана соотношением Эйнштейна с
коэффициентом диффузии, то и он прямо выражается
через W:
D = qhT = Wa2 = DvpD. C2.15)
Здесь, как и выше, долей вакантных мест определяется
уменьшение коэффициента самодиффузии по сравнению с
коэффициентом диффузии вакансий Dv = a2K.
Равновесные свойства среды, заданные уравнением состояния, через
pv существенным образом контролируют ее кинетические
характеристики. Поскольку последние связаны между собой,
мы ограничимся анализом только коэффициента вязкости.)
274
Теория свободного объема. Вышеприведенные
рассуждения, строго говоря, относятся к упорядоченной решетке,
каковой жидкость не является. Свободный объем в жидкости
не поделен на целое число равновеликих вакансий, а диспер-
гпрован почти непрерывным образом, т. е. распределен
между всеми частицами в самых различных дозах. Тем из них,
которым не досталось ничего или слишком мало, приходится
вести оседлую жизнь, тогда как другие, расположившиеся
в сравнительно больших полостях, кочуют, используя
имеющийся в их распоряжении люфт. При последовательном
проведении этой точки зрения pv приобретает смысл доли
частиц, располагающих достаточно большим свободным
объемом z;+, равным по порядку величины объему молекулы.
Чтобы установить, насколько велика эта доля, Коэн и Терп-
белл вывели распределение частиц по доставшемуся им
свободному объему, руководствуясь одними энтропийными
соображениями, которые мы воспроизводим ниже.
Считая частицы взаимодействующими твердыми сферами,
отличающимися только объемом полости, которую они
оккупируют, можно разбить их по этому признаку на группы по
nt в каждой и подсчитать, сколькими способами это
разбиение можно выполнить при условии, что полный объем -и
общее число частиц N сохраняются. Так как перестановка
одинаковых по величине полостей не приводит к новому
состоянию системы, общее число различимых состояний равно
^ C2.16)
J I
г
причем
C2.17)
где vt = Дг- — vd — свободный объем i-ш. полости,
номинальный объем которой Дг-, а
и? = v — vd C2.18)
есть средний свободный объем, приходящийся на молекулу.
Очевидно, что полный свободный объем системы vFN = V —
— Nvd сохраняется в той же мере, что V и N. Полезно сразу
же обратить внимание, что введенный здесь «свободный
объем», по существу, является пустым объемом ячейки и
отнюдь не совпадает по определению со свободным объемом
Леннарда — Джонса и Девоншайра Vf, в пределах которого
может располагаться центр тяжести частицы, оккупирующей
275
ячейку. В случае жестких сферических молекул между
этими понятиями существует следующее простое соответствие:
Г 1 -Г v3
vf = const [v* — Vd\ « const [v — vd]3/vl = const -y, C2.19)
vd
в котором величина константы зависит от упаковки частиц
(типа решетки).
Поскольку энтропия системы пропорциональна величине
In W = N In у - ^ ^ln Т» <32-20)
задача состоит в том, чтобы найти ее оптимум при
дополнительных условиях C2.17). Действуя методом Лагранжа,
составим величину
и определим ее экстремум, варьируя число частиц в группах,
обладающих одинаковым свободным объемом:
Отсюда сразу жо получаем искомое распределение
ехр (- wt) Лг(~)
(
в котором р определена из условия нормировки ^Ni = N.
г
Принимая теперь во внимание, что свободный объем на
самом деле пробегает непрерывный ряд значений, мы должны
соответствующим образом трансформировать и
распределение C2.21), превратив его в следующее:
dN _
Интегрирование в этом выражении распространено от 0 до
оо, хотя в действительности свободный объем ограничен
по величине как снизу, так и сверху. Предполагается,
следовательно, что в жидкой фазе средний свободный объем
одинаково далек от обоих пределов, как минимального, так
и максимального. Прибегнув ко второму условию C2.17),;
276
оо
представленному в виде j vdN = VpNA легко убедиться,
о
что а = l/vF, и, следовательно, распределение по свободным
объемам
C2.22)
F
идентично по структуре распределению по временам и
длинам свободного пробега в газе. Не составляет труда
определить с его помощью долю частиц, располагающих свободным
объемом и > v+, которая равна
pv = j dW = exp ( — jji L C2.23)
Именно эта величина и должна фигурировать в выражении
C2.12), определяя в конечном счете меру вязкости среды.
Впервые на наличие важной корреляции между
свободным объемом жидкости и ее вязкостью было обращено
внимание Бачинским. Согласно «закону Бачинского», текучесть
1/г] многих жидкостей зависит исключительно от объема,
и даже более того — прямо ему пропорциональна. Эта
зависимость, как оказалось, хорошо описывает вязкость многих
соединений, исключая воду и ассоциированные жидкости
(спирты, кислоты).
В стеклующихся средах и диапазон, и масштаб
изменения вязкости шире, чем в кристаллизующихся жидкостях.,
Их поведение лучше описывается «теорией свободного
объема», учитывающей флуктуации упаковки, особенно
существенные при низких температурах и высоких давлениях.
Считается общепризнанным, что при фиксированном объеме
среды температурная зависимость текучести очень слабо
выражена, т. е. AU невелико. Когда же, нарротив,
фиксировано давление и удельный объем возрастает вследствие
теплового расширения, она приобретает весьма резкий характер.
При высоких температурах в жидкости растворено
достаточное количество пустот, так что pv ~ 1, и течение
является просто активированным процессом, каковым его считал
Френкель. Однако с понижением температуры, когда
начинает лимитировать дефицит свободного пространства,
зависимость In т] f — J искривляется (рис. 109). Это приводит к
тому, что эффективная энергия активации увеличивается с
277
900
600 400 300 200
i 1 1
wn
Рис. 109. Изменение вязкости
В2О3 с температурой по Литови-
цу п Дэвису [21].
Рис. 110. Изменение
эффективной энергии активации с
температурой для В2О [22].
охлаждением (рис. 110), достигая настолько больших
значений (до 4 эВ), что ассоциировать их с какими-либо
реально существующими барьерами совершенно абсурдно. С
позиций же теории свободного объема это обстоятельство не
выглядит странным, так как резкая убыль объема при
стекловании — еще относительно плавный процесс по сравнению со
скачкообразным его уменьшением при кристаллизации.
§ 33. БРОУНОВСКОЕ ДВИЖЕНИЕ
Нестационарная диффузия. Рассмотрим развитие во
времени одномерной диффузии в термически однородной среде.
Чтобы положить ей начало, достаточно налить немного чая
на поверхность воды, находящейся в глубоком стакане.
Заранее ясно, что вследствие диффузии окрашенная полоса
будет монотонно во времени расширяться и тускнеть, пока
концентрация чая не станет равномерной во всём сосуде.
Этот процесс легко описать количественно, приняв во
внимание, что в любой горизонтальный слой толщины dx
ежесекундно попадает Sj (х) растворенных частиц, а покидает
его Sj(x + dx), где S — площадь слоя. Если разность этих
потоков разделить на объем Sdx, то получится скорость
увеличения в нем концентрации растворенного вещества:
da _ ] (г) — / (х + dx) _ dj /QQ -П
278
Таково «уравнение непрерывности», выражающее закон
сохранения частиц в пространстве при их
перераспределении. Используя в нем формальное определение
диффузионного потока A6.7), получаем
дп Л—
D
Хотя это уравнение в частных производных, структура его
такова, что п является функцией одной универсальной
переменной z = xlYt. Проверяя это соображение прямой
подстановкой n[z(x, t)] в C3.2), легко убедиться, что оно верно,
если п удовлетворяет следующему обыкновенному
дифференциальному уравнению:
Di?+i%-0- <33-3>
Его общее решение
x/VlDt
п (х, t) = C1 J ехр (— t2) dt + C2 C3.4)
— оо
содержит константы С± и С2, выбор которых диктуется
конкретными условиями инициирования процесса.
Если, например, предположить, что в начальный момент
окрашенная жидкость занимала полупространство, а
неокрашенная — другую его половину, то размытие границы
между ними описывается следующим образом:
Если же окрашенная жидкость находится вначале в тонком
елое толщины х0 @ <х <^0)» из которого она
диффундирует в обе стороны, то
x/YISi
п = ^=. f exp(— t2)dt.
(x-xo)/Y*Dt
Уменьшая величину х0 и одновременно увеличивая исходную
концентрацию красителя так, чтобы похо = N = inv, в
пределе бесконечно узкого окрашенного слоя получим
п = ,И_ ехр (— х*/Ш). C3.5)
ybnDt
Отсюда легко получается распределение частиц красителя
279
в пространстве в любой момент времени после их старта из
начала координат при t = 0:
dW(x, t) =^ = «р(-^0 dx. C3.6)
Плотность этого распределения, оставаясь все время гаус-
совской функцией, монотонно расширяется. Его дисперсия,
характеризующая среднюю удаленность частиц от места
старта, линейно возрастает во времени:
? в j x4W(x, t) = 2£>*. C3.7)
Таким образом, ширина области, в которой частицы,
окрашивающие жидкость, распределены приблизительно
равномерно, увеличивается со временем как ]/Y Это процесс
очень длительный: при комнатных температурах
потребуются многие часы, чтобы дисперсия возросла до 1 см. Еще
медленнее он протекает, если в нем принимают участие не
молекулы, а более крупные броуновские частицы. Но этим
и исчерпывается различие между ними. Броуновское
движение есть визуализованное тепловое движение,
подчиняющееся всем установленным для него статистическим законам.
Уравнение Ланжевена. Эту истину, ставшую уже
азбучной, в свое время пришлось доказывать экспериментально.
Те, кто склонны были воспринимать уравнение диффузии
феноменологически, не усматривали ничего общего между
процессом растворения веществ и броуновским движением.
Напротив, атомисты считали, что кажущиеся
беспричинными метания броуновских частиц, их запутанные, как
клубок, траектории не могут быть объяснены ничем иным,
кроме воздействия на них случайной силы, непрерывно и
случайно изменяющейся по величине и направлению. Эта сила
есть результирующая многих ударов, обрушивающихся на
микроскопическую частицу со стороны окружающих ее
молекул. Большое тело, погруженное в жидкость,
практически не реагирует на ее флуктуации, сильно сглаженные его
инерцией. Но броуновские частицы, хотя их размеры и
больше атомных, все еще достаточно малы, чтобы
засвидетельствовать реальное существование молекул своим
собственным беспорядочным поведением, к которому
принуждает их тепловое движение. Это умозаключение
превратилось в неопровержимый довод в пользу атомистики, когда
в беспорядочном блуждании броуновских частиц удалось
усмотреть закономерности, предписанные теорией.
280
Окружающая среда двояким образом воздействует на
движение в ней броуновской частицы. С одной стороны, она
оказывает закономерное сопротивление этому движению,
возрастающее с увеличением его скорости. Сила этого
сопротивления есть F = —x/q, где q — подвижность частицы.
С другой стороны, именно молекулярное окружение и
стимулирует это движение, воздействуя на броуновскую
частицу случайно осциллирующей силой /(£), в среднем по
времени равной нулю. Флуктуации этой силы и придают
частице ускорение, направленное то влево, то вправо,
заставляя ее совершать беспорядочное движение. Подчиняясь
законам механики, она закономерно реагирует на эти
флуктуации в соответствии с уравнением Ланжевена:
Только вследствие случайной природы силы f(t) становится
случайным процессом и реакция на нее — x(t).
Между закономерным и случайным воздействиями на
частицу молекулярного окружения существует
определенная взаимосвязь. Закономерное воздействие выражается в
торможении скорости частицы, которое после усреднения
C3.8) с учетом f(t) = О описывается уравнением и = v,
где v = х, а т0 = qM есть время релаксации скорости
частицы. Согласно современным представлениям скорость этой
релаксации выражается через дисперсию случайной силы
/2 по формуле
± = fHc/kTM, C3.9)
то
где тс — время корреляции силы, совпадающее по смыслу
с длительностью столкновения. Предполагается, что
тс<т0, а *>тс. C3.10)
Если последнее условие не выполняется, то следует
прибегнуть к уравнению более общего вида, чем C3.8):
t
м'х = — ^R(t — t')x (?) ar + / (о,
о
ядром которого является так называемая функция памяти
R(t—t')=f(t)f(t')/kT. Она выражается через
корреляционную функцию силы и затухает со временем тс. При выпол-
281
нений условий C3.10) более медленно затухающую функцию
x(t') можно вынести из-под интеграла, а его верхний предел
устремить к бесконечности, после чего воспроизводится
уравнение Ланжевена с q = xJM = kTl%cf.
Опыты Перрена. Наблюдая за удалением броуновских
частиц от стартовой черты, Перрен установил, что оно
происходит равномерно в обе стороны, так что х=0, и поэтому
может быть количественно охарактеризовано только
величиной x2(t), являющейся дисперсией их пространственного
распределения. Чтобы -описать долговременное поведение
этой величины, достаточно прибегнуть к уравнению
Ланжевена C3.8), которое после домножения на х может
быть тождественно преобразовано к следующему виду:
Это уравнение позволяет при любой заданной реализации
случайной силы f(t) совершенно точно установить, по какой
траектории x(t) следовала частица, подвергшаяся ее
воздействию. Разные частицы испытывают разное воздействие и
вследствие этого оказываются в различных точках
пространства в момент наблюдения. Пути их неизбежно расходятся,
а среднее удаление от стартовой черты и друг от друга рас-
тет. Чтобы рассчитать среднеквадратичное отклонение x2(t),
необходимо усреднить уравнение C3.11) по всевозможным
реализациям f(t).
Вследствие случайного и быстрого изменения f(t)
корреляция между импульсом силы и вызванным им смещением
частицы сохраняется лишь на временах порядка т0. В более
крупном временном масштабе можно считать f(t)n x(t)
независимыми случайными величинами. В таком случае
среднее от их произведения равно произведению средних:
Учитывая это обстоятельство,
полу)() @@
чаем после усреднения C3.11)
прп^»то = ,Ж. C3.12)
до?
Здесь введено обозначение z = —-- и, кроме того, приня-
(it
то во внимание, что, согласно закону равнораспределения,
Мх2 = кТ. В этом находит выражение наша уверенность,
что броуновское движение, хотя в нем и участвуют частицы
более крупные, чем молекулы, есть тем не менее обычное
тепловое движение с положенной ему энергией.
282
Рост скорости броуновских частиц пропорционально
У^кТ/М является, конечно, прямым свидетельством его
молекулярного происхождения, но экспериментальное
измерение быстро меняющейся мгновенной скорости частицы
практически неосуществимо. Много проще следить за
положением частиц, измеряя их координаты в последовательные
N
моменты времени и усредняя по рецепту х2 = jf^xl (t). Об-
г=1
щее решение уравнения C3.12), описывающее временное
изменение этого среднего, имеет вид
z = 2kTq + const- exp(—t/gM). C3.13)
Пренебрегая экспоненциально исчезающим членом,
получаем очень простую асимптотику при t >> т0 = qM:
Р"= 2kTq-t. C3.14)
Принимая во внимание соотношение Эйнштейна D = qkT,
нетрудно видеть, что этот результат тождественно
совпадает с C3.7).
Весьма примечательно, что из динамического закона
движения, управляющего поведением частицы в среде,
получилось в конце концов решение, носящее явно выраженный
необратимый характер. Так бывает всякий раз, когда строго
детерминированную систему приводит в движение
совершенно беспорядочное усилие. Поведение системы поневоле
приобретает случайный характер, хотя она, будучи
механической, всегда делает лишь то, к чему обязывает ее
уравнение движения.
Фундаментальный закон линейного возрастания во
времени среднеквадратичной флуктуации х2 установлен
Эйнштейном, разработавшим теорию броуновского движения.
В случае, когда наблюдаются сферические броуновские
частицы радиуса Л, подвижность которых согласно Стоксу равна
q = FяДп)-\ C3.15)
из C3.14) получается х2 = kT/3nRr\-t. Эта зависимость
может быть во всех деталях проверена экспериментально, если
известны вязкость жидкости т) и радиус частиц R.
Классические опыты Перрена, измерившего х1 по положению
броуновских частиц в поле зрения микроскопа в процессе их
случайных блужданий, блестяще подтвердили теорию. Этим
был положен конец всяким сомнениям, и атомистика прочно
стала на ноги.
283
ЛИТЕРАТУРА
Цитируемые ниже первоисточпикп подразделяются на две
категории. К первой из них относятся монографии, которые могут быть
полезными для более углубленного изучения предмета, потому что
представляют-иную точку зрения на него пли более строго его излагают.
Ко второй категории относятся оригинальные статьи или редкие
издания, которые привлекались как источники информации. Ссылки на
них, встречающиеся в тексте, позволят читателю судить о степени
апробации этого материала, а при желании и получить более полное
представление о нем.
1. Бачинскнй И. Избр труды.—М : Изд-во АН СССР, 1960.
2. Блохинцев Д. И. Основы квантовой механики.— М.: Л :
ГИТТЛ, 1949.— 588 с.
3. Бурштейн А. И. Лекции по квантовой кинетике.—
Новосибирск: изд НГУ, 1968 — 236 с.
4. Бурштейн А. И. О происхождении кривой «идеального га-
за»//ЖФХ — 1974.—Т. 48, вып. П.—С. 2639—2646.
5 Бурштейн А. И. Молекулярно-кинетические аспекты
химической физики конденсированного состояния//Успехи химии.— 1978.—
Т. 47.—С. 212.
6. Бурштейн А. И. О происхождении псевдоактивационной
температурной зависимости вязкости//Докл. АН СССР.— 1973 — Т. 213.—
С. 1109.
7. Бурштейн А. И. Внутреннее давление в простых жидко-
стях//ЖФХ.— 1974.— Т. 48 — С. 2684.
8. Бурштейн А. И., Векслер Л. С, Шохирев Н. В. О
происхождении и положении экстремумов межмолекулярного взаимодействия
в простых жидкостях//ЖСХ.— 1977 — Т. 18.—С. 477.
9 Бурштейн А. И., Шохирев Н. В. Изменение плотности и
тензора давления на границе жидкость — пар//ЖФХ.— 1979.— Т. 53.—
С. 2428.
10 Вассерман А. А., Казавчннский Я. 3., Рабинович В. А. Теп-
лофизические свойства воздуха и его компонентов — М : Наука,
1966 — 375 с.
И. Гиршфельдер Дж., Кертис Ч., Берд Р. Молекулярная теория
газов п жидкостей.— М.: ИЛ, 1961.— 930 с.
12 Жарков В. И., Калинин В. А. Уравнение состояния твердых
тел при высоких температурах.— М : Р1Л, 1961 — 311 с.
13. Займан Дж. Принципы теории твердого тела.— М : Мир,
1966 — 488 с.
14. Киттель Ч. Введение в физику твердого тела.— 4.-е изд.—
М.: Наука, 1978 — 792 с.
284
15. Киттель Ч. Элементарная статистическая физика.— М.: ИЛ,
I960.- 696 с.
16. Кристи Р., Питти А. Строение вещества: введение в
современную физику.— М : ГИФМЛ, 1966.— 596 с.
17. Крылов Н. С. Работы по обоснованию статистической
физики,— М.; Л : Изд-во АН СССР, 1950.— 207 с.
18. Крокстон К. Физика жидкого состояния.— М.: Мир, 1978.—
400 с
19. Лейбфрид Г. Микроскопическая теория механических и
тепловых свойств кристаллов — М : ГИФМЛ, 1963.— 312 с.
20 Лидьярд А. Ионная проводимость кристаллов.— М.: ИЛ,
1962.- 222 с.
21 Литовиц Т., Дэвис К. Свойства газов, жидкостей и раст-
воров//Физическая акустика — 1968 — Т. 2, ч А — С. 298.
22. Macedo P. В., Napolitano A. Inadequacies of Viscosity
Theories for B2O3//J. Chem. Phys.— 1968 — V. 49.— P. 1887.
23. Маннинг Дж. Кинетика диффузии атомов в кристаллах,—
М.: Мир, 1971.—278 с.
24. Оно С, Кондо С. Молекулярная теория поверхностного
натяжения в жидкостях.— М : ИЛ, 1963.— 291 с.
25. Роулинсон Дж. Сравнение решений интегральных уравнений
для функций распределения со свойствами модельных и реальных
систем//Фпзика простых жидкостей.— М : Мир, 1971.— С. 63.
26. Румер Ю. Б., Рыбкин М. Ш. Термодинамика, статистическая
физика и кинетика.— М : ГИФМЛ, 1977.— 552 с.
27. Термодинамические свойства азота/Сычев В. В , Ваесер-
ман А. А., Козлов А. Д. и др — М \ Изд-во стандартов, 1977.— 352 с.
28. Френкель Я. И. Кинетическая теория жидкостей.— М : Изд-
во АН СССР, 1945 - 592 с.
29. Хоуген О., Ватсон К. Физико-химические расчеты в технике.—
М.; Л : Госхимиздат, 1941 — 598 с.
30. Barker T. A. Lattice theories of the liquid state The
international Encyclopedia of Physical Chemistry and Chemical Physics. V. 1.—
Oxford, London, New York, Paris. Pergamon Press.— 134 p.
31. Burshtein A. I. Simple liquid surface structure and surface
tension//Adv. in Colloid and Interface Sci.— 1979.— V. 11.— P. 315—
379
32 Cohen M. H., Turnbull D. Molecular Transport in Liquids and
Glasses//J. Chem. Phys.— 1959.— V. 31.— P. 1164.
33 Vortler H. L. Modified cell theory: equation of state for hard
sphere//Phys. Lett.— 1980 — V. 78, N 3 — P. 266.
34. Yang A. I. M., Fleming P. D. HI, Gibbs J. H. Molecular theory
of surface tension//J. Chem Phys — 1976 — V. 64.— P. 3732.
35. Глестон С, Лейдлер К., Эйринг Г. Теория абсолютных
скоростей реакций. —М.: Ил, 1948.—345 с.
ОГЛАВЛЕНИЕ
Предисловие * • 3
Глава 1. Газы 6
§ 1. Статистика молекул . —
Давление. Статистическое распределение.
Статистическое среднее.
§ 2. Функция распределения 11
§ 3. Уравнение состояния идеального газа 15
§ 4. Распределение Максвелла 17
Сложение вероятностей. Статистический вес.
Разные средние. Опыт Штерна. Структура
потока.
§ 5. Барометрическая формула .... * , 26
§ 6. Распределение Больцмана * 29
§ 7. Каноническое распределение Гиббса , 32
§ 8. Диэлектрические свойства газов 35
Обобщенные координаты. Распределение.
Электрическая поляризация.
§ 9. Реальный газ 40
Межмолекулярное взаимодействие.
Отталкивание. Притяжение. Уравнение состояния.
Сжимаемость газов.
§ 10. Основные идеи статистической термодинамики 55
Ансамбль Гиббса. Микроканоническое
распределение. Каноническое распределение Гиббса.
Энтропия. Флуктуации. Свободная энергия.
Расчетная схема. Идеальный газ.
Тождественность микрочастиц. Реальный газ. Конденсат.
Двухфазная система.
§ И. Теплоемкость газов 83
Поступательное движение. Вращательное
движение. Колебательное движение. Закон
равнораспределения. Температурные аномалии.
§ 12. Кванювание гармонического осциллятора 91
Вымораживание колебаний. Квантование
энергии. Высокотемпературный предел.
Квантовые ячейки. Постулат Бора.
§ 13. Вымораживание тепловых движений , 97
§ 14. Парамагнетизм газов , 104
Спин 1/2. Общий случай.
§ 15. Релаксация в газе 109
Спонтанная релаксация. Вынужденная
релаксация. Оценка частоты столкновений. Столкновения
при движении с заданной скоростью. Средняя
частота столкновений. Экспериментальная
проверка. Длина пробега.
§ 16. Явления переноса 119
Локальное равновесие. Теплопроводность.
Вязкость Диффузия. Уточнение расчета.
Теплопередача. Ультраразреженный газ. Ток в газе.
Глава 2. Излучение 140
§ 17. Феноменология —
§ 18. Теорема Кирхгофа 142
§ 19. Ультрафиолетовая катастрофа 146
Теплоемкость излучения. Квантование поля.
Корпускулярная модель.
§ 20. Фотонный газ 152
Основные черты. Сопоставление. Вес фотона.
§ 21. Уравнение состояния * 156
Давление. Уравнение состояния.
§ 22. Коэффициенты Эйнштейна 160
Поглощение п испускание. Возбуждение и
дезактивация. Вероятности переходов. Соотношения
Эйнштейна. Парциальные вероятности.
§ 23. Стационарная трансформация света 166
Глава 3. Кристаллы 168
§ 24. Феноменология —
Типы кристаллов Прочность. Анизотропия.
§ 25 Движение кристаллической решетки 173
Силы взаимодействия. Акустические колебания.
Число колебаний. Оптические колебания.
Молекулярные колебания.
§ 26. Фоноиный газ 184
Модель. Приближение Дебая. Теплоемкость
решетки. Согласованность колебаний.
Теплопроводность решетки.
§ 27. Уравнение состояния 195
Баланс сил. Внутреннее давление. Термическое
давление. Уравнение Ми — Грюнайзена.
Тепловое расширение. Узел изотерм.
§ 28. Реальные кристаллы 212
Точечные дефекты. Диффузия. Ионная
проводимость.
Глава 4. Жидкости 221
§ 29. Феноменология —
§ 30. Уравнение состояния 224
Внутреннее давление. Термическое давление.
Баланс сил. Кипение. Плавление. Ортометричо-
ская прямая. Разложение уравнения на
составляющие.
§ 31. Поверхностные явления 258
Мономолекулярная поверхность. Размытая
граница раздела.
§ 32. Явления переноса 268
Теплопроводность. Вязкость. Теория свободного
объема.
§ 33. Броуновское движение ...,,..,.,.... 278
Нестационарная диффузия. Уравнение
Ланжевена. Опыты Перрена.
Литература ,, * ,, , .♦«»«»,,,,,,,,,, * .. 284
Анатолий Израилевич Бурштейн
МОЛЕКУЛЯРНАЯ ФИЗИКА
Утверждено к печати
Институтом химической кинетики и горения
СО АН СССР
Редакторы издательства Л. А. Боярский, Л# В Филиппова
Художественный редактор 2V Ф# Каминипа
Художник С. Н. Машков
Технический редактор Г. Я Герасимчук
Корректоры М. П. Фомина, Н. В. Лисина
ИБ № 34011
Сдано в набор 28 05 86 Подписано в печать 01 10 86 МН-01511 Формат 84X108730
Бумага типографская № 3. Обыкновенная гарнитура Высокая печать, Уел
иеч л. 12,6 Усл. кр-отт 12,6. Уч-изд л. 15,2 Тираж 2900 Заказ № 211
Цена 2 руб.
Ордена Трудового Красного Знамени издательство «Наука», Сибирское отделение
630099, Новосибирск, 99, Советская, 18.
4-я типография издательства «Наука»*
630077, Новосибирск, 77, Станиславского, 25*