Похожие
Текст
В. И.КИРИЧЕНКО
КРУТИЛЬНЫЕ
КОЛЕБАНИЯ
В АВИАЦИОННЫХ
ДВИГАТЕЛЯХ
ЛКВВИА - 1949
В. И. КИРИЧЕНКО
USTOT-UX
к-лз
KL Y3
КРУТИЛЬНЫЕ КОЛЕБАНИЯ
АВИАЦИОННЫХ ДВИГАТЕЛЯХ
ЛЕНИНГРАДСКАЯ КРАСНОЗНАМЕННАЯ
ВОЕННО-ВОЗДУШНАЯ ИНЖЕНЕРНАЯ АКАДЕМИЯ
• Ленинград—1949
Ответственный редактор
М. В. СЕМЕНОВ
Технический редактор Павлова Т. П.
Подписано к печати 12.6.49 г. Печатных листов 11,5. Авторских листов 12,8.
В 1 печ. листе 46.400 зн. Бумага 62X94. Зак. № 674/88. Г 1334078.
Типо-литография ЛКВВИА
ОТ АВТОРА
Трудами советских ученых создана стройная общая теория
крутильных колебаний различных упругих систем. В этой книге
разбираются вопросы крутильных колебаний в авиационных дви-
гателях в объеме, необходимом для инженера, связанного с эк-
сплоатацией поршневых двигателей.
Книга представляет переработанное и дополненное изложение
материала лекций по разделу «Крутильные колебания* курса
конструкции авиационных двигателей, читаемого автором с 1944 г.
При изложении материала особое внимание обращено на объ-
яснение физического смысла рассматриваемых вопросов. Для
этих целей текст иллюстрирован рядом примеров из области
авиационного моторостроения.
Расчеты во всех случаях даются^ в форме, удобной для ре-
шения практических задач. Текст снабжен необходимым спра-
вочным материалом.
Кинга разделяется на пять глав. Первая глава посвящена
вопросам расчета свободных крутильных колебаний, вторая—за-
мене реальной упругой системы эквивалентной, но упрощенной
расчетной системой, третья—анализу крутящих моментов, вызы-
вающих крутильные колебания; вынужденным колебаниям; рас-
чету резонансных амплитуд и экспериментальному исследованию
крутильных колебаний. В четвертой главе рассматриваются спе-
циальные устройства, применяемые для гашения крутильных
колебаний—демпферы и муфты. В последней главе даются ос-
новные сведения о совместных изгнбных колебаниях винта и
крутильных колебаниях коленчатого вала.
При написании книги были использованы материалы многих
литературных источников, основные из. которых перечислены в
конце книги. Для желающих углубить свои знания в списке при-
ведены также основные работы, касающиеся крутильных коле-
баний нелинейных систем, о которых этой книге сделаны
только очень краткие замечания.
Автор считает своим долгом выразить искреннюю благодар-
ность кандидату технических наук доценту Я- С. Адрианову за
ценные указания и замечания, сделанные им при просмотре ру-
кописи, а также доктору профессору М. В. Семенову, взявшему
на себя труд редактирования этой книги.
В. И. Кириченко
н
ВВЕДЕНИЕ
Механизм авиационного двигателя состоит из ряда связанных
между собой упругих звеньев, которые во время работы под-
вергаются действию периодически меняющихся нагрузок. Перио-
дичность нагрузок вызывает вибрации элементов конструкции
двигателя.-
Как показывает опыт, из всех видов вибраций, е которыми
сталкиваются в авиационном моторостроении наиболее опасными
являются крутильные колебания системы: коленчатый вал—винт.
В различных областях машиностроения встречались с полом-
ками валов от крутильных колебаний еще в конце прошлого
столетия. Однако эти поломки были довольно редким явлением
и не привели к надлежащему исследованию и созданию общей
теории крутильных колебаний.
В авиации с крутильными колебаниями столкнулись только в
середине 20-х годов, но в связи с быстрым увеличением мощ-
ности и широким масштабом производства авиадвигателей очень
скоро крутильные колебания выросли в проблему, разрешение
которой было совершенно необходимо для дальнейшего успеш-
ного развития авиамоторостроения.
В Советском Союзе пионерами-исследователями явлений кру-
тильных колебаний явилась группа инженеров коломенского за-
вода имени Куйбышева, возглавляемая Урванцевым, и группа
инженеров завода „Русский Дизель" в Ленинграде.
Дальнейшее развитие исследовательских работ по изучению-
крутильных колебаний в авиационных двигателях возглавили
ЦИАМ им. Баранова и ГК НИИ ВВС.
Одним из результатов обширных теоретических исследова-
ний ЦИАМ в этой области явилось издание книги И. Ш. Ней-
мана „Динамика авиационных двигателей", в. которой дается
общая теория и метод расчета крутильных колебаний коленча-
тых валов авиационных двигателей.
Специальным вопросам борьбы с крутильными колебаниями
и расчетом сложных нелинейных систем посвящены работы В. Я.
Натанзона. Эти же темы явились предметом более поздних ра-
бот И. Ш. Неймана.
В области экспериментального исследования крутильных ко-
лебаний в авиационных двигателях много сделано В. К. Жито-
мирским. Ему принадлежит ряд весьма ценных статей о вибра-
4
иии моторной группы в полете, о средствах борьбы с крутиль-
ными колебаниями и других. В. К. Житомирским разработан
также вопрос о совместных изгибных колебаниях винта и кру-
тильных колебаниях коленчатого вала.
В части создания аппаратуры для экспериментального изуче-
ния явлений крутильных колебаний плодотворно работал И. И.
Попов, сконструировавший механический торсиограф, обладав-
ший лучшими качествами по сравнению с немецкими торсиогра-
фами.
Замечательные возможности по экспериментальному изучению
крутильных колебаний открылись после создания -группой со-
ветских ученых специальной электрической аппаратуры, которая
позволила в условиях полета производить запись колебаний од-
новременно во многих местах системы вал—винт.
Новым направлением в изучении развития крутильных коле-
баний в валах явилась работа И. М. Тетельбаума „Электромо-
телирование крутильных колебаний коленчатых валов поршневых
двигателей”.
Идея моделирования основывается на электродинамической
аналогии, пользуясь которой экспериментатор заменяет иссле-
дуемую упругую систему соответствующей электрической цепью
из набора емкостей и индуктивностей. ' Сообразно с порядком
работы цилиндров от специального фотоэлектрического датчика
к надлежащим элементам цепи подаются электрические импуль-
сы, в точности имитирующие крутящие моменты, вызывающие
крутильные колебания упругой системы.
Процессы, происходящие в электрической цепи, получаются
аналогичными процессам крутильных колебаний системы вал-
винт. Их можно зарегистрировать на любом участке системы.
Простым nt шротом рукояток, регулирующих величины пара-
метров элементов модели (электрической цепи), можно легко
подобрать такую комбинацию параметров цепи, что аналогичная
ей механическая система будет избавлена от опасных крутиль-
ных колебаний.
Особо видное место занимают труды В. П. Терских, работав-
шего много лег в области крутильных колебаний силовых уста-
новок морских судов.
В. П. Терских разработана теория и создана своеобразная об-
щая методика решения всех практически встречающихся крутиль-
ных систем. Профессор А. И. Лурье в предисловии к книге В. П.
Терских „Крутильные колебания силовых установок”, вышедшей
в свет в 1940 г., пишет: „... эти исследования нашего автора дают
более совершенный и более разработанный метод расчета, чем
метод германского происхождения. Поэтому выход в свет труда
В- П. Терских не только отвечает назревшей потребности, но и
является делом чести советской науки*.
В своих работах В. П. Терских дает метод, названный им „ме-
тодом цепных дробей", с помощью которого вычисляется стой-
5
\
кость или „динамическая жидкость" и решаются вопросы расчета
частот свободных и вынужденных колебаний любш линейных
систем и систем, имеющих один или два нелинейных' участка,]
разработана теория всех известных демпферов—гасителей коле-1
баний и теория колебаний систем с распределенными массами.
В настоящее время расчет крутильных колебаний является со-
вершенно обязательным разделом проекта поршневого авиацион-
ного двигателя. Этот расчет складывается из следующих этапов !
1. Замены реальной упругой системы коленчатый вал—винт
упрощенной расчетной системой. •
2. Расчета свободных колебаний системы—определения форм
и частот свободных колебаний.
3. Изучения характера внешних нагрузок, создающих вынуж-
денные колебания системы.
4. Определения возможных резонансов и подсчета амплитуд
колебаний элементов системы при резонансе.
По известным амплитудам колебаний определяют напряжения
в элементах системы и судят о ее прочности, либо сравнивая по-
лученные напряжения с принятыми предельно допустимыми, либо
вычисляя‘по одной из известных теорий прочности, учитывающей
переменный характер нагрузок, коэффициенты запаса.
В случае, когда расчет выявляет опасные резонансы крутиль-
ных колебаний, вводят запретные режимы или предпринимают
переделки самой упругой системы, или, наконец, снабжают си-
стему гасителем колебания—демпфером.
Перед внедрением двигателя в серийное производство, кроме
теоретических расчетов, обязательно проводится обстоятельное
экспериментальное исследование крутильных колебаний системы
коленчатый вал—злит на всех режимах работы двигателя.
%
ГЛлВА I
СВОБОДНЫЕ ИЛИ СОБСТВЕННЫЕ КРУТИЛЬНЫЕ
КОЛЕБАНИЯ
Свободными или собственными колебаниями упругий системы
называют такие колебания, которые происходят при наличии толь-
ко сил или моментов, стремящихся восстановить состояние рав-
новесия системы.
Практически свободные колебанья упругой системы могут
быть вызваны единократным приложением к ней внешней возму-
щающей нагрузки или быстрым разгружением упруго деформиро-
ванной системы.
Свободные колебания обычно быстро затухают благодари на-
личию сопротивлений внутри самой системы, в ее опорах и в
среде, в которой происходят колебания. На преодоление этих со-
противлений постепенно растрачивается энергия, полученная си-
стемой от приложения внешней нагрузки или содержавшаяся в
ней в качестве энергии упругой деформации.
При идеализации, состоящей в пренебрежении сопротивления-
ми, свободные колебания, раз возникнув, будут продолжаться
бесконечно.
В этой главе последовательно рассматриваются свободные
крутильные колебания систем, обладающих одной, двумя и мно-
гими степенями свободы).
В дальнейшем показывается, что реальная упругая система
коленчатый вал—винт может быть приведена к одной из таких
систем.
§ 1. Свободные колебания системы без сопротивления
с одной массой
Рассмотрим систему (фиг. 1), состоящую из массивного диска,
помещенного на конце упругого вала, другой конец которого
жестко заделан.
Жесткость вала на кручение, г. е. момент, который нужно
’) Числом степеней свободы является число независимых параметров, оп
ределяющих положение всех точек системы в каждый момент времен-i.
7
приложить к валу, чтобы закрутить его на один радиан, обозна-
чим через k
. м IPQ <
k=—=. у— (кг слг),
здесь: М— крутящий момент (кгсм\,
<р—угол закрутки вала (радиан);
G—модуль сдвига материала вала (кг/слс2);
/р—полярный момент инерции сечения вала (сл<4)
Момент инерции диска относительно оси вала обозначим
через I
mD- ~D* , 1 ,
—g— = -32~ b (кг см сек*),
здесь: т—масса диска;
Y—удельный вес материала диска;
g—ускорение силы тяжести.
Момент инерции вала относительно его оси мал по сравнению
с моментом инерции диска и поэтому нм можно пренебречь.
Если вал закрутить, прило-
жив к диску крутящий момент,
и затем внезапно снять нагрузку,
система начнет колебаться.
Обозначим угол закрутки ва-
ла в сечении у диска в момент
времени t через <р-
Составим диференциальное
уравнение движения диска, вос-
пользовавшись основным зако-
ном динамики. На диск действует
одна внешняя нагрузка—момент
сил упругости деформированного
вала, равный — k<?. Этот момент
вызывает угловое ускорение ди-
ска <р, которое пропорционально
моменту инерции диска 1.
или
— k^ = ^r
T+A’5? =o,
где
1 *
D —
8
Это же диференциальное уравнение можно составить, поль-
зуясь законом сохранения энергии. Так как мы рассматриваем
процесс, считая, что сопротивлений не существует, то рассеяния
энергии нет и при любом значении <р сумма кинетической и по-
тенциальной энергий остается постоянной
Ар’+у Лч>* = const,
диференцируя полученное равенство по времени, имеем:
/»+А(р = О. ч (1)
Уравнение (1) есть однородное линейное уравнение второго по-
рядка с постоянными коэфициентами.
Как известно, общее решение этого уравнения имеет вид
<р = Л os pt+В sin pt.
Постоянные интегрирования А и В определяются начальными
j словиями.
При £ = 0 уравнение обращается в тождество, если А = <р0—
начальное перемещение диска, измеренное от положения покоя.
Для определения В продиференцируем <р по времени, т. е.
найдем угловую скорость диска
® — — Ар sin pt+Bp cos pt.
Обозначая угловую скорость диска в момент времени t — Q
через ®0, получим: В = -^-
Уравнение движения принимает вид:
<р — <р0cospt+-^ sin/tf. (la)
Пусть ?о = О, а -ро-# 0. Это значит, что к диску! находившемуся
в покое, ударно был приложен скручивающий момент. В этом
случае закон движения диска будет (фиг. 2а)
Ч — sin pt.
Если же <рв # 0, а <р0 = 0, т. е. вал находился в закрученном
состоянии, а затем внезапно освобожден, и система предоставлена»
самой себе, то
? — ?о cos pt-
График движения для этого случая показан на фиг. 26.
9
Время Т, за которое диск совершает одно полное колебание,
называется периодом
При свободных колебаниях диска период зависит только от
свойств самой системы—момента инерции диска и жесткости
вала, но не зависит от начальных условий.
Величина, обратная периоду п, называется частотой и опре-
деляет число колебаний в единицу времени. Единицу частоты
называют Герц. Один Герц есть одно колебание в секунду
1 р 1 , /k
П~Т~'2-~2-ку Г (1в^
Величина р—называется круговой или циклической частотой
и определяет число колебаний в 2~ секунд.
Заметим, что уравнение движения диска
? = <p0cosp£+ — sinp£
может быть преобразовано.
Положим: <f0 = Osin7 и *°=<i»cos7.
Здесь
Ф= 1/^; tgT=-®—»
* \Р/ ?о
тогда
» = >I’(sin т cos pt + cos 7 sin pt)
или
? = <1> sin(p/+ ;). (lr)
10
Положим ср0 = <1>coss и --- =— «l»sins, здесь попрежнему
Ф = \ /?0’ + / 'Ро \ ,
V \ р I
но ;
tg г =----
Р*о
В этом случае уравнение движения приобретает вид:
<? = Ф (cos е cos pt — sin г sin pt),
или
<p = Ф cos (pt 4-г). (1д>
Таким образом, один и тот же закон движения может быть
записан различными способами (преобразования тождественны).
Последние две записи в явном виде показывают от чего за-
висит величина амплитуды колебания.
Рассматриваемый колебательный процесс можно геометрически
представить следующим образом (фиг. 3).
Положим, что вектор Ф вращается с угловой скоростью р
по часовой стрелке вокруг точки 0 и в начальный момент вре-
мени £ = 0 составляет с вертикалью угол s.
Проекция Ф на вертикаль:
Ф COS£ = ?0,
а проекция на горизонталь:
Очевидно,
<1> =
Ф sin е = — •
Р
И
Через промежуток времени t вектор Ф повернется на угол pt и
составит с вертикалью угол (pi 4-е).
Проекция Ф на вертикаль Фсоз (pi 4-г) и представляет собой
перемещение диска при колебаниях. При таком геометрическом
представлении колебания приобретают определенный физический
смысл названия круговая частота р и начальная фаза е.
Отчетливо видно, что форма записи колебательного процесса
зависит от времени начала отсчета. Если за начало отсчета при-
нять время, соответствующее точке /, запись колебательного
процесса содержит сумму sin pt и cos pt или сложный аргумент
(pi 4-г). Если за начало отсчета принято время, соответствующее
точке 2, то уравнение движения будет синусоида с аргументом
pt. Если, наконец, начало отсчета соответствует точке 3, то урав-
нение движения—косинусоида с аргументом pt.
Диференцируя уравнение движения по времени, получим ско-
рость колебательного процесса
<Р= — Фр sin (pi+е).
Скорость колебания можно представить в виде проекции векто-
ра, вращающегося с той же угловой скоростью, что и вектор
перемещения Ф, но длиной Фр. Так как -sin(pi+e)=cos(pi4-s4-
4- j, то вектоР скорости Фр опережает по фазе вектор пере-
мещений Ф на угол, равный (фиг. 4).
Диференцируя уравнение скорости по времени, получим ус-
корение
’« = — Фр’cos (pi4-е).
Угловое ускорение <р также можно представить в виде про-
екции вектора, вращающегося с угловой скоростью р. Величина
этого вектора равна Фр2. Так как —cos (pi + e) = cos (pi + e-p г),
то вектор ускорения Фр2 опережает вектор перемещения Ф на
угол, равный к (фиг. 4).
32
Теперь равновесие момента сил инерции и момента сил упру-
гости /<р4-А?=О можно иллюстрировать геометрически равен-
ством двух одинаковых по величине векторов, но направленных
в разные стороны (фиг. 5).
§ 2. Свободные крутильные колебания вала с двумя массами
Пусть требуется определить закон свободных колебаний без;
сопротивлений системы (фиг. 6), состоящей из двух массивных
дисков с моментами инерции и /2> соединенных валом, жест-
кость которого на кручение обо-
значим k. Момент инерции вала
пренебрежимо мал.
Система может вращаться в
подшипниках и одновременно диски
могут поворачиваться друг относи-
тельно друга при скручивании вала.
При решении задачи о крутиль-
ных колебаниях системы безраз-
лично значение угла поворота си-
стемы в подшипниках. В этом
смысле система имеет одну сте-
пень свободы. Колебания опреде-
ляются только законом изменения
угла закрутки вала во времени.
Решить поставленную задачу
можно следующим образом: для
того чтобы система пришла в ко-
лебательное движение, достаточно
к обоим дискам приложить равные
по величине, но разные по направ-
лению крутящие моменты, и затем
их удалить. После того как дефор-
Фиг. б
мированная система будет внезап-
но разгружена, оба диска начнут
совершать колебания кручения, все
время вращаясь в разные стороны друг относительно друга,
т. е. с одинаковыми периодами. Предположить противное (т. е.
что периоды колебания дисков будут не одинаковы) не пред-
ставляется возможным, так как в этом случае обязательно на-
ступит момент, когда оба диска окажутся в среднем положении
и будут иметь скорости, отличные от нуля и направленные в
одну сторону, т. е. появится вращение системы относительно
оси вала, что противоречит опыту.
Итак, диски будут колебаться с одинаковыми периодами
(одновременно проходить среднее положение и одновременно
достигать крайние свои положения), а на вале будет существо-
вать сечение, все время остающееся неподвижным.
13
Это сечение вала, не участвующее в колебаниях, называется
узлом.
Узел является как бы заделкой и делит рассматриваемую
систему на две одномассовые системы, периоды колебания кото-
рых одинаковы.
Как было установлено выше, период колебания одномассовой
системы Т = 2л1/ -т, таким образом, в рассматриваемом случае
г
условие равенства периодов колебания обоих дисков приводит
к выражению
А__ А.
k j
Здесь kv и kt жесткости валов длиной и L соответственно.
Очевидно
f k; Л2 = / k.
А А
Условие равенства периодов может быть теперь переписано
в следующем виде
АА=А4-
Очевидно также равенство /j + /3 = /.
Последние два уравнения позволяют определить положение
узла колебаний
, _ Щ _ //>
’“А+А’ *~А+А ‘
Если А = 4» то узел помещается посредине вала; если /,¥=/,—
узел распологается ближе к диску с большим моментом инерции.
Диск, момент инерции которого очень велик, практически экви-
валентен заделке.
Формула, определяющая период колебания рассматриваемой
системы, может быть представлена в следующем виде:
д/" 44
V Л(А+А) ’
Круговая частота:
/*(4+4)
р~\!
Уравнения движения дисков:
<Pi = Ф1 cos pt\
~ Ф, cos pt.
н
Амплитуды Ф( и Фг равны углам закрутки дисков относи-
тельно узла колебаний, вызванных действием статически при-
ложенного (при £ = 0) крутящего момента
ф Мкр А •
kx - rpG ’
ф МКу МКр13
А; ~ IpG •
Абсолютные величины амплитуд колебания могут быть опре-
делены только в случае, если известны начальные условия.
Относительная величина амплитуд определяется одними только
характеристиками упругой системы
‘А__А__4
ф2 ~ 4 “ л •
Знак минус в последней формуле свидетельствует о том, что
все время диски движутся в разные стороны.
Эту же задачу о колебаниях двухмассовой системы можно
решить, воспользовавшись основным законом динамики.
Пусть в произвольный момент времени t положение дисков
определяется значениями углов и отсчитанными от неко-
торой фиксированной координатной плоскости ZOY (фиг. 7).
Фиг. 7
Для определенности положим > <р2. На первый диск будет
Действовать момент упругих сил, равный — £(?!—<?,), который
вызовет угловое ускорение пропорциональное Д.
На второй диск будет действовать момент упругих сил
+ ^(?i — ??)» вызывающий ускорение пропорциональное /,.
15
Диференциальные уравнения движения дисков имеют вид:
+ ?2) = ° | (
/2<р2—£(?,—<р2) = 0 |
Решения этих уравнений ищем в форме:
-jj = Ф1 cos (pt 4- 7);
?г = Ф2СО8(/^ + 7).
Угловые ускорения:
?i = —Ф1р,С08(р/ + 7):
Ъ = — %P?cos (pt + ~i).
Подставляя <p1F <р2, »> и ®а в уравнения системы (2), получим:
—/,Ф1р2 со8(р^4--у) + Л(ф1—Ф2)со5(Х + 7) = 0;
—ДФ2ря cos (pt + 7)—k (Ф1 — Ф2) cos (pt + 7) = 0.
Чтобы решения имели силу в любо^ момент времени необ-
ходимо
—/1Ф]р2 + Л(Ф1—Ф2) =0 7
-/2Ф,р2-*(Ф1-Ф2) = 0 / ‘ ’
В этих уравнениях три неизвестных: круговая частота р и
амплитуды Ф, и Ф,.
Представляется возможным определить отношение ампли-
туд и частоту.
Складывая уравнения (2а), получим 7^*= — /,Ф2, т. е.
ф»=—Дфр
'2
Для определения р подставим вместо Ф2 его значение в первое
уравнение системы (2а), тогда получим:
-ДФ1Р2 +ЛФ /А-+1\ = 0,
\ '2 /
но Фз^О, поэтому
—/jp2 += 0
\ '2 /
„2__(Л Л)
р ~ Л4 •
]б
Примечание. Уравнения
Л?1+*(г1 — »г) = °;
4?2—* (* I — ¥2) = о
могут быть приведены к виду уравнения (1). Для этого помножим первое
уравнение на /2, второе на /] н вычтем из первого второе. Получим
А4 (+1 — ?г)+ (Л+4) к (Ф1_¥2) = °.
обозначая ij—7г = <f и р” = . получим:
7'+р*Ч,=О-
§ 3. Свободные крутильные колебания системы с тремя
массами
Пусть требуется определить закон
сопротивления системы (фиг. 8), состоящей
дисков с моментами инерции
жесткость которых на круче-
ние равна ky и А2. Моменты
инерции валов пренебрежимо
свободных колебаний бет
из трех массивных
Л 4 и 4> соединенных валами,
малы.
В произвольный момент
времени t положение дисков
относительно фиксированной
координатной плоскости ZOY
определяется значениями уг-
ЛОВ <р„ ср2 и <Р» ’).
Составим диференциаль-
пые уравнения движения дис-
ков, воспользовавшись основ-
ным законом динамики.
На первый диск действует
момент сил упругости —kx (®i—?2), вызывающий ускорение диска
71, пропорциональное 1Х.
Уравнение движения первого диска:
4<Pi + — ?-2)=0-
На второй диск действует справа момент сил упругости
— Л2(®2—?з), слева—момент сил упругости +Ai(?t—?,)• Эти мо-
менты вызывают ускорение диска <р9, пропорциональное /2.
Уравнение движения второго диска:
4'-Рз + ^2 (?2 ?з) (?1 ?г) ~ О-
*) Вращение системы в подшипниках как жесткого целого нас не инте-
ресует. В отношении крутильных колебаний данная система имеет две сте-
пени свободы, а система на п масс имеет (л—I) степеней свободы.
• rtcH’-'й И*»с итут ГВФ
rbJltf.rTEKA
На третий диск действует момент сил упругости (<&.,—з3)
вызывающий ускорение диска <р3, пропорциональное /я.
Уравнение движения третьего диска
('Р; ®з) — О-
Уравнения движения дисков
(?i—?3) = °
Лъ + *2 (?*—?з) (?|— <?2) = О
Мз~ (<Р2~ Фз) = 0
представляют систему однородных линейных диференциальньп
уравнений второго порядка с постоянными коэфициентами.
Будем искать решения в виде
?1=Ф1 cos (pZ+7)
з. = Ф, cos(pZ + 7)
?s = Ф3 cos(/rt + 7)
Постоянные Фп Ф2, Ф3, р и 7 должны быть подобраны так
чтобы удовлетворялись уравнения системы (3).
Продиференцировав дважды по времени каждое из уравне
ний (За), получим:
—Ф,р2С08 (p/ + i)
о2 = — Ф»р® cos (р£ 4-7) . (36
«Рз = -ФзР2 cos (pt+7)
Необходимо, чтобы подстановка выражений (За) н (36) в уран
нения системы (3) обращала эти уравнения в тождества, пр>
любом значении времени t.
Отсюда
— /.Ф./Я+МФ. — ф2) = о
- /2Фар2 + kq (Ф, - Ф3)—А, (Ф£- Ф2)= 0 • (Зв
~ А ФзР2— МФз—Ф.ч) = °
Сложив все уравнения (Зв) и сократив на р9^0, ’), получим
/1Ф2+/8Ф,+/3Ф3=О. (Зг
Из первого и третьего уравнений системы (Зв) найдем:
ф, —______________________А1Фг_
1 АР1—
k Ф, •
ф — _ _
/;1р2—&>
’) Условие р—0 свидетельствует о том, что система не колеблется.
16
(Зе)
(Зж)
Подставляя полученные выражения для Ф] и Ф, в уравнение
ог), получим после сокращения на Ф2^0 *):
__ г__________л'
hf-K + 2 lapa-k,
После преобразований уравнение (Зе) приобретает вид
,4гтгР'-(/1+/2+/3) = а
«1^2 у л?2 /
Это биквадратное относительно р уравнение имеет четыре
корня. Из них различных вещественных положительных корня,
которые имеют, в данном случае, физический смысл, может
быть только два.
Одновременное существование двух значений р свидетель-
•тв\ ет о том, что система совершает сложные колебания, являю-
щиеся суммой двух гармонических колебаний с различными
частотами р{ и ptt.
Уравнения движения дисков приобретают вид:
?i = Ф,! cos (pjt + fO + Ф1 п cos (pnt+iu);
= Ф,, cos (p/ + 7,) + Ф3 n cos (pnt+In);
? (= Ф. I cos (Plt + 7,) + Ф, „ cos (pnt + 7„).
Задавшись значением амплитуд одной из масс (например,
юлагая Фа । = Ф„ „ = 1), по формулам (Зд) определяют Фц, Ф, ц,
Ф31 н Фзп н строят для иллюстрации полученных результатов
формы колебаний системы.
Формой колебаний называют закон изменения амплитуд по
длине вала.
В рассматриваемом случае в соответствии с одновременным
ущесгвованием двух различных частот имеет смысл говорить
двух формах колебания: низкой и высокой частоты.
Колебания низкой частоты будут иметь один узел, колебания
высокой частоты—два узла. В общем случае узел колебания
эдноузловой формы не совпадает ни с одним из узлов двух-
головой формы так, что все сечения вала участвуют в коле-
баниях.
Пример I. Найти частоты и построить формы свободных
колебаний крутильной системы, изображенной на фиг. 9.
Подставляя заданные величины в биквадратное уравнение
(Зж), после преобразований получим:
р4—8,38- 10т-р3+0,744 10й = 0,
') Если в частном случае Ф2=0, это значит, что в сечении, где поме-
чается второй диск имеется узел, т. е. заделка, которая делит систему на две
Дномассовых и задача решается так, как это было сделано выше.
2*
19
откуда находим:
р,2 = 80-104
1
сек2
/,„»== 83-10в^
сек2
ЛЬухузлобая <рорюа р-9120^н
Фиг. 9
Положительные корни уравнения:рх = 895—*—, ри — 9120 —
С€К C€h
Задавшись Ф2 f = Ф2 и = 1, по формулам (За) находим:
ф11 =-0,163; Ф81=+1,36;
Ф1П = —0,00135; Ф1П=-0,0377
и строим обе формы колебаний системы (фиг. 9).
§ 4. Свободные крутильные колебания вала со
многими массами
Пусть требуется определить закон свободных колебаний бе
сопротивлений системы (фиг. 10), состоящей из п массивны
дисков с моментами инерции /р /2, Z8 .... соединенных валам ?
жесткости на кручение которых /?п k2 k3 .... kn. t. Момент!
инерции валов пренебрежимо малы.
Положение дисков в момент времени t определяется знач<
ниями углов <рц <р9. <р3 .... ®„.
Рассуждая так же, как и при составлении диференциальны
уравнений движения трехмассовой системы, в данном случа
получим следующую систему линейных однородных диференциаль
ных уравнений второго порядка с постоянными коэфициентам
20
/ift+Mft — ft)=°
Aft + fe«(ft—ft)—(?i—fa) = 0
4ft+kt (ft—ft)- k* (ft~ ft) — 0
/„_lft_l +fe„-l (Фп-l—ft)— fen-2 (ft-2—ft-1) = 0
4ft—Лп-i (ft-i—ft)=о
Фиг. 3
Решения этой системы будем искать в виде
?1 = Ф1 cos (pt4-7)
<Р, = Ф. COS (pt + t)
<?а~Ф3СОЯ (pt + t)
(4a)
ft-1 = Фп-i COS (pt+y)
ft — <J>„cos(/tf+7)
Здесь постоянные Фм Ф.2, Фа .... Ф„, р и 7 должны быть
подобраны так, чтобы удовлетворялись диференциальные ура-
внения движения системы (4).
Продиференцировав дважды по времени выражения (4а),
получим:
'ft = — Ф^’сов (pt + ч)
Ъ - — ф,р’ COS (pt + 7)
ft = - Фпрг cos (pt+y)
21
Необходимо, чтобы подстановка выражений (4а) и (46) в уравне
ния системы (4) обращала эти уравнения в тождества при любо»
значении времени t.
Отсюда
Лф.^2 + ^(ф1 - Ф2) = 0
- /,Фар3 + k, (Фа - Ф,)-(Ф,- Ф2) = О
—/„ 1Ф„-1Р3 + А!п_1(Фп-1 -Ф„)-Л,г_2(Ф„-2—Ф„-1)=0
- ЛфлРг-Ап-1 (Ф„_1-Ф„) = О
(4в
Вл уравнениях системы (4в) я 4-1 неизвестных: Фп Ф.Л
Ф3....Ф„ и р. Абсолютные значения всех неизвестных тольк.
из уравнений системы (4в) определены быть не могут. Для ре-
шения этой задачи необходимо знать начальные условия. Однако,
задавшись одной из амплитуд (например, Ф12=1) можно найти,
в долях этой амплитуды, величины амплитуд всех остальных
масс и значение частоты колебания р.
Для определения р необходимо путем последовательного ис
ключения величин Фа, Фя и т. д. получить из системы уравне-
ний (4в) одно уравнение, содержащее в качестве неизвестного
только р.
Заметим, что в задаче о колебаниях двух масс существовала
только одно положительное значение р; в задаче о колебаниях
трех масс уравнение, из которого определялось р, получалось
биквадратным и давало два различных положительных решения;
в рассматриваемом случае колебания п масс уравнение, из ко-
торого определяется р, будет относительно р степени 2 (я — 1) и
даст различных положительных корней (я—1).
Одновременное существование (я—1) частот свидетельствуе т
о том, что каждая из масс системы совершает сложные колеба-
ния, являющиеся суммой (я—1) простых гармонических колеба-
ний. Вал одновременно имеет (я — 1) форм колебаний: одно, двух,
трехузловую и т. д. Самая высокочастотная форма колебаний
будет иметь (л— 1) узел. Практически оказывается важным знать
частоту и форму только одно, двух и трехузловых колебаний.
Многоузловые формы колебаний обычно не определяются по-
причинам, о которых будет сказано ниже.
Решение алгебраического уравнения сильно усложняется
вместе с возрастанием порядка или степени уравнения. В общем
виде решения имеются только для уравнений, порядок которых
не выше четвертого. Для многих авиационных крутильных си-
стем число масс, участвующих в колебаниях, весьма велико
л =10 и более. В этом случае уравнение частот будет иметь
порядок 2(10—1)=18. Решение такого уравнения весьма затруд-
нительно.
22
в расчетной практике определение частот и форм колебаний
,1асто производят методом подбора корней, сущность которого
сводится к следующему.
Из первого уравнения системы (4в) выразим Ф3 через ‘I’j
п2
ф8«ф»-у
Из второго уравнения системы (4в) выразим Ф3 через Ф, и Ф3.
Во втором уравнении вместо —Ф2) подставим 1^}р2, что
справедливо по первому уравнению, тогда получим:
— (Л’М/Л)/’2 + Ла(Ф2—Ф3) = О,
откуда следует, что
• ф,=ф8 — y-W’i+W-
«2
Подобным образом получим, что
д2
ф« = Ф3 - -X- (Лф>+4ф2+W-
«3
Амплитуда колебания последней массы
Ф„=Ф„-1 - —(/1Ф1+/2фг + - • • + /л-1Фи-1).
«п-1
Положив Ф3 = 1 и задавшись значением р, последовательно
вычислим значение Ф3, Ф3,...Ф„. При выборе значения р можно
пользоваться известными данными подобных упругих систем
или найти приближенное значение р способом, изложенным ниже.
Проверка правильности выбранного значения р производится
по формуле, которая получается в результате сложения уравне-
ний системы (4в) (после сокращения суммы уравнений на
/А+/А + -.. + /А *)•
’) Физически это уравнение означает равенство нулю суммы моментов
сил инерции всех масс системы (/jWtp3 —есть максимальное значение момента
сил инерции Z-ой массы, так как /;—момент инерции /-ой массы, а — Ф,Р«2
амплитуда ее углового ускорения). Это положение сразу же вытекает из за-
кона моментов количества движения.
Момент количества движения системы, на которую внешние нагрузки не
действуют, есть величина постоянная. Момент количества движения /-го
л
(иска равен /tyi. Общий момент количества движения системы V const.
1
Отсюда, диференцируя по времени, получим
V Лр. = ° «S ЛФ.Р2=О.
i=l r=i
23
п
Если величина р была случайно выбрана правильно,
V
то
ЦФ, — О, в противном случае
необходимо
задаться новым
i=l
значением р и снова определить величины Фг, Фя,. ,.ФЯ.
Если бы мы много раз проделали расчет, задаваясь рядом
значений р, то смогли бы по точкам построить график остаточ
п
ных моментов р3£ /,Ф, в зависимости от р или р3. Этот график
»=1
или, точнее, подобный ему, изображен нафиг. 11. Точки пересе-
чения кривой с осью абсцисс, удовлетворяющие условию
п
= дают значения корней решаемой системы уравнений.
/=1
Число точек пересечения кривой с осью абсцисс соответствует
числу различных форм колебаний.
В действительности всю кривую остаточных моментов строить
нет нужды. Для определения частоты одной какой-либо формы
колебаний, например, р/ приходится:
1. Задаться ориентировочным значением р/, определить все
п
амплитуды (в долях Ф1 = 1) и составить выражение
г=1
2. Задаться новым значением pi', близким pi, снова опре-
п
делить амплитуды и составить выражение У /,<1»,..
О Все расчеты сводятся в таблицу I.
24
п
3. В координатах Х/А и рг (фиг. 12) отметить полученные
/-1
0 результате расчетов две точки
и провести через них прямую.
Пересечение этой прямой с осью рг
п
определит pi, для которого X /,Ф, ли-
i — 1
бо равна нулю, либо незначительно
отличается от нуля. Для значений р,
не сильно удаленных друг от друга,
линейная интерполяция (или экстро-
поляция) всегда дает хорошие ре-
зультаты.
4. По найденному значению pj вы-
числить окончательное значение отно-
сительных амплитуд и, составив вы-
п
\ 1
ражение /,-Фг, оценить этим точность расчета.
С - центр
тяжести масс V
Фиг. 13
Приближенное значение р, одноузловой формы колебаний
многомассовой систе-
мы, которым приходит-
ся задаваться в начале
расчета, может быть
получено путем искус-
ственного упрощения
многомассовой систе-
мы. Вместо системы
из п масс рассматри-
вается двухмассовая
система (фиг. 13), ко-
торая получена заме-
ной всех масс основ-
ной системы, кроме
массы /ь одной суммар-
п
ной массой 4 = X 4,
1-2
расположенной в цен-
тре тяжести заменяе-
Частота свободных колебаний двухмассовой си-
мых масс.
стемы
25
где k—жесткость на кручение вала длиной I, является прибли-
женным значением частоты одноузловой формы колебаний
основной многомассовой системы.
Для определения ориентировочного значения частоты двух-
узловой формы колебаний многомассовой системы рц' можно,
группируя массы, свести ее к трехмассовой, вторая частота ко-
лебаний которой и кладется в основу расчета.
При упрощении основной системы массы могут группиро-
ваться различным образом. При наличии у расчетчика некото-
рого опыта оценка частоты может быть сделана с точностью до
10% ее истинного значения.
Расчет сводится в таблицу 1. В первом столбце этой та-
блицы через строчку по вертикали проставляются номера масс.
В пятом столбце в пропущенные строки вписываются номера
участков вала. Во втором столбце против номера первой массы
ставится ее амплитуда, принимаемая равной единице. В третьем
столбце заносятся данные исследуемой системы: против номеров
масс—соответствующие моменты инерции (предварительно умно-
женные на—р2), против номеров, определяющих участки вала,—
1
соответствующие податливости этих участков —.
Aj
Далее начинается собственно расчет: амплитуду первой массы
умножают на рядом стоящую в столбце 3 цифру (— Цр2) и ре-
зультат записывают в столбце 4 рядом и строчкой ниже.
Этот результат умножают на ци
в столбце 3 и результат умножения записывают рядом в
це 2. Строчкой ниже в столбце 2 проставляется сумма
стоящих в двух верхних клетках этого столбца (1—
Сумма умножается на цифру, стоящую справа в столбце 3, ре-
зультат заносится рядом в столбце 4, складывается с цифрой,
стоящей строчкой выше, записывается строчкой ниже и так про-
должается процесс до заполнения всей таблицы.
Легко видеть, что в результате расчета во втором столбце
против номеров масс стоят их амплитуды, а в четвертом—ам-
плитуды сил инерции. Таким образом, нетрудно составить
п
сумму — р1 /|Ф/ и этим проверить правильность выбранной ча-
рядом
столб-
цифр,
стоящую
стоты р.
Еще проще можно осуществить проверку, воспользовавшись
тем, что в четвертом столбце против номеров участков ’вала
стоят моменты упругих сил этих участков.
При свободных колебаниях упругие моменты на свободных
концах вала за крайними массами должны быть равны нулю.
26
ММ масс Г4 см СО
Амплитуды X н=ф1=1
+ 5^ । .. Sk । ^.1 -1 1 1 J II СП е 1 х !
1 ♦ । и © X
е» •ьГ
?
/ 7 / /~i* — >\Р: » 4* • •ч м 7 * « — 4с 1
Амплитуды моментов си.ч упру- гости - /17’ - *- т сч =5- 1 t I I — 1 1 т i
t
1 » т
25* ГоТ ПЭ Q < * 1-2 1 04
Поэтому цифра, стоящая в таблице за амплитудой сил инерции
л-ой массы, при истинном значении р должна быть нулем.
Пример 2. Найти низшую частоту и построить соответ-
ствующую этой частоте одноузловую форму свободных колеба-
ний системы, изображенной на фиг. 14а.
Фиг. 14
•Составляем таблицу типа таблицы 1, положив ра=1---------
1 сек*
Момент за 4-й массой не ранен нулю, поэтому задаемся но-
вым значением частоты р*= 0,6 и производим пересчет..
сск
№№ участков Амплитуды мо- ментов сил упругости 2 k Амплитуды масс
— 0,6 -0,6 1 1
1-2 -0,6 1 -0,6
• -0,24 -0,6 0,4 2
2-3 — 0,84 1 -0,84
0,264 — 0,6 — 0,44 3
3-4 — 0,576 1 - 0,576
0,67 - 0,6 - 1,116 4
4 . 0,094
Момент за 4-й массой
резко уменьшился, но все еще отли-
чен от нуля.
Составляем новую таблицу при /г2 = 0,585-------;
ССК‘
— 0,585 — 0,585 1 1
1—2 — 0,585 1 -0,585
-0,243 — 0,585 0,415 2
2-3 -0,2 1 -0,2
0,242 — 0,585 0,413 3
3-4 - 0,586 1 — 0,586
0,545 — 0,585 — 0,999 4
4 . . — 0,0015
Удовлетворяясь достигнутой точностью, строим форму
банин системы при частоте р3 = 0,585 —3- (фиг. 146).
коле-
2<>
§ 5. Метод цепных дробей ')
Наиболее общим методом исследования свойств крутильных
колебаний различных систем несомненно является метод цеп-
ных дробей, разработанный лауреатом Сталинской премии про-
фессором Терских В. П. Применение этого метода особенно
эффективно при расчете сложных разветвленных систем, расщеп-
ленных или циклических систем, нелинейных систем, систем
с маятниковыми демпферами и т. п.
В дальнейшем изложении читатель найдет применение ме-
тода цепных дробей к расчету свободных колебаний сложных
разветвленных систем и к расчету совместных изгибных колеба-
ний винта и крутильных колебаний коленчатого вала.
Сначала разберем как этим методом производится расчет
свободных крутильных колебаний системы, изображенной на
фиг. 10.
Первым этапом при решении задачи по Терских является
приведение исследуемой системы (абсолютной, как ее называет
автор) к системе безразмерной (относительной).
Пользование именованными величинами, какими в уравнениях
колебаний являются: жесткость, момент упругих сил, момент
инерции и частота крайне неудобно г).
Переход к безразмерным величинам упрощает расчетные фор-
мулы и сокращает время, необходимое для производства вы-
числений.
Для осуществления такого перехода предварительно преобра-
зуем уравнение:
Af, + i) — k- i(»._i — ?,) = О,
являющееся диференциальным уравнением движения z-й массы
при свободных колебаниях (фиг. 10).
В этом уравнении первый член есть момент сил инерции
z-й массы, а второй и третий (обозначим их у, и v,-i) моменты
упругих сил участков вала ini— 1.
Таким образом.
у,- = y,-i + А?.,
но
= cos (pt + 'i), и значит <р; — — cos (pt + -;),
') См. В. П. Терских, Крутильные колебания силовых установок, Суд-
яромгиз, 1940, книга 1.
3) Обычно 1рг (кг см) величина порядка 10+® a -j- (кг 1см 1)—по-
рядка 10~”.
30
откуда
(5)
Вместе с тем по обозначению — <Рн-1),
откуда
<?.-+«=* + £ (6)
fv:
Переходя к максимальным значениям моментов упругих сил
и моментов сил инерции по формулам (5) и (6), получим:
Y, = У,.1- /Л (7>
Ф£+1 = Ф,-+-^. (8)
Выберем произвольно две величины: момент инерции / и
жесткость k1), после чего введем следующие обозначения:
ф.
1) а. = —относительная амплитуда z-Й массы;
2) = j' — относительный момент инерции z-й массы;
.а > П
3) ---------относительный момент упругих сил z-ro участка
4)
">)
вала;
k
— относительная податливость z-ro участка вала:
гь,,
Д = (-д2—частота относительной системы.
k
Уравнения (7) и (8) теперь могут быть записаны в виде:
о; = б,_| — Ь,-Дя/; (9)
а£1 i=at + о^. (10)
Эти уравнения можно рассматривать как уравнения свобод-
ных колебаний z-й массы системы (фиг. 15), полученной из си-
стемы (фиг. 10) путем деления моментов инерции всех масс на
некоторую величину / и деления некоторой величины k на жест-
кости участков системы.
Систему фиг. 15 называют относительной, потому что вели-
чины, ее характеризующие, имеют нулевую размерность, г. е.
представляют отвлеченные числа.
1) / и k следует выбирать такими, чтобы величины Э,- и е,- получились бы
одинаковой соизмеримости. Оказывается удобным взять за / и k момент инер-
ции и жесткость какой-либо массы и участка исследуемой системы.
31
Вычислим последовательно величины относительных момен-
тов упругих сил на каждом участке и величины относительных
амплитуд каждой массы. Для этого в уравнениях (9) и (10) бу-
дем придавать I значения. 1,2, 3... л. 1
^веденные здесь обозначения
1^- »,-д = м—Ц-;
1 р — —,
1%Д
е
1
м ——г
е’“ м
. . . IL "Д = НА —
л л
1
»„-1Д —
Фиг. 15
Попутно будем вычислять отношения каждой из определен-
ных величин Я| и 8; к предыдущей (соответственно о,_1 или я{).
Перед первой массой относительный момент упругих сил,
очевидно, равен нулю
Зо = 0
е1
ai — I по обозначению
si — — HjА04..
8* \М“1_.. .
я, ) а, ' 1Л
я,
я
1
м ~Е
°а — °1 — 02Да2 .. .
21
«3
— '%А — - 1 — }> д
я2
•%''А
°8 --- «2 + O2S, .
М_ Е , 21 — -_1—— .
8 оэ ~'2 va ~ 2
• (11)
1
представляют собой значения при данной А непрерывных дро-
бей, составленных таким образом, что относительный момент
инерции первой массы системы входит в последнее звено каж-
дой из этих дробей, все остальные звенья располагаются вверх
по отношению к последнему звену так же, как остальные
элементы системы расположены вправо по отношению к пер-
вому элементу, т. е. за 8jA следует е„ затем &аД и т. д.
Из последнего равенства системы (11)
о = —ял&л"Д,
л л Л J
с другой стороны, при свободных колебаниях относительный мо-
мент упругих сил за последней массой непременно должен быть
равен нулю Ьл = 0.
Таким образом, ял8л"Д = 0, я„ + 0, так как при «л=0 по фор-
мулам (11) в этом случае и = 0, что является противоречием,
ибо 04=1 по определению.
Отсюда
»Л''Д = &ЛД---
1
1
= 0. (12)
°3 -- °2 — '%Д®8
И3
V — - = М—'т, —
8 яя 8 е," 3
Ял — ап~ 1 4-6,
6n-l
°л — Зп~1— '*лАя„ •
32
-п \— UA — = ИД - = »Л"А
Я„ / я„ е"„_,
«л->Д —
Е„-2 — .
1
м-------Ц-
Последнее равенство устанавливает связь между всеми эле-
ментами системы и искомой частотой ее свободных колебаний
k
Р~~Л —. Его поэтому можно назвать частотным уравнением
свободных колебаний.
з
В. Кириченко
33
Частотное уравнение может быть записано также в виде:
а/д =а,д
= 0, (13
:____1_________
здесь величины относительных моментов инерции Н и относитель-
ных податливостей е входят в звенья непрерывной дроби в по!
следовательности, обратной той, которая имела место в первом
случае.
Наконец, можно получить еще две формы записи частотного
уравнения, осуществляя „надлом“ непрерывной дроби на звене,
соответствующем f-й массе или i-му участку вала. Тогда по-
лучим:
У/"Д = ^Д _____________________________________
У,-_ ]Д------------
si 2—
: 1
I
е* М I
---------у------------------------=0 (14)
Е'~У,+1Д
: __1______________
или
------j-----------------------.4 = 0 (15)1
У.Д----------
8,-1 —
: 1
1
/ »,д
34
где А —---------г------------------.
»,+1Д------
е,Ц —
1 J_____________
е"-’ - ~1гУ
•
При решении задачи нахождения Д можно пользоваться лю-
бой из форм частотного уравнения и предпочтение т<ьй или
иной форме дается в каждом .конкретном случае. Так, njpH рас-
чете вынужденных колебаний лучше пользоваться формой (14),
причем за следует принимать ту массу, которая будет Послед-
ней из числа масс, на которые действуют внешние моментгы.
Эта же форма (14) или форма (15) используются при решении
шдачи варьирования элементами системы.
Наиболее простой задачей варьирования является задача оп-
ределения такого значения момента инерции одной из мащс(илн
податливости одного участка вала), при котором одна из частот
свободных колебаний системы будет равна наперед заданной
величине.
При варьировании массой пользуются формой (14), при варьи-
ровании податливостью пользуются формой (15).
При определении частот собственных колебаний оказываются
более удобными первые две формы записи (12) и (13).
Разберем схему решения частотного уравнения, записанного
в форме (12) &я"Д = 0.
Задаваясь последовательно рядом значений Д, представляется
возможным подсчитать для каждой Д значение &„"Д и резуль-
таты представить в виде графика йп"Д—/(Д) (фиг. 16), П]ри этом
обнаружится, что кривая ^„''Д состоит из п отдельных ветвей.
В интервале Д, соответствующем одной ветви, функция по-
гоянно возрастает (при увеличении Д), проходя все значения
от —оо до + ^. Каждая ветвь обязательно пересекает о>сь абс-
цисс и при том только один раз.
Крайняя левая ветвь проходит через начало координат, назо-
вем ее нулевой, следующую за ней ветвь—первой и т. д.
Последняя ветвь будет называться (п—1)-й ветвью.
Точки пересечения ветвей с осью абсцисс, очевидно, являются
корнями частотного уравнения. Пересечение нулевой ветви с
осью абсцисс наступает при Д = 0, т. е. при отсутствии колеба-
ний, и представляет тривиальное решение. Таким образом, раз-
личных отличающихся от нуля решений обнаруживается п—1.
Практически отыскание решений, т. е. тех значений д, при
которых О^ДггО, проводится методом подбора. Все вычисления
проводятся в таблице 2.
з»
35
36
Верхняя строка таблицы представляет заголовок. В нее впи-
сываются слева направо звенья непрерывной дроби ,%"Д в той
последовательности, в какой они расположены в формуле.
Задавшись величиной Д = Др записывают ее в первом столб-
це в третьей строке, после чего первую под заголовком строку
заполняют значениями звеньев непрерывной дроби 0л"Д при вы-
бранной величине Дг^Др
Вторую и третью строки заполняют одновременно следующим
образом. Вычисляют величину -уу и записывают ее с обрат-
ным знаком во второй столбец второй строки, а в нижнюю стро-
ку этого же столбца — результат алгебраического сложения
- _ 1 — е "
Ml
Обратную величину найденного числа (—с обратным зна-
\ £i /
ком записывают во вторую строку третьего столбца, а алгебраи-
ческую сумму 8^-------— =&3"Д записывают в третью строку
ei
того же столбца и т. д. до заполнения всей таблицы.
В результате в третьей строке последнего столбца находится
‘интересующая нас величина в„"Д при заданном Д = Д1( а во всех
предыдущих столбцах третьей строки справа налево соответст-
венно все значения промежуточных функций е"„_г, »"„_1Де/';
М-
37
Для того чтобы установить на какой ветви кривой »Л"Д на-
ходится ПРИ заданном Ди устанавливаем сколько имеете»
в третьей строке таблицы функций е/', которые удовлетворяют
Если оказалось, что число их равно с, то это значит, что
НЯ"Д1 находится на с-й ветви кривой. Знак определяет
*) Это же условие является условием наличия узла Hat-м участке вала
если считать началом участка сечение, расположенное велел за Z-й массой,
а конец на самой Z-f-1-й массе (включая ее).
38
число корней функции 0л"Д, находящихся между Д=0 иД=Дг
Если знак положительный, то между Д = 0 й Л = Д4 находится
с корней, если же знак отрицательный, то (с—1) корней ’).
Далее, составляется аналогичная таблица для Д = Д2. Если
окажется, что при Д = Д, попрежнему ^Й"Д2 находится на с-й
ветви кривой Э„"Д, но вместе с тем знак отличается от
знака 8л"Д„ эт0 значит, что один из корней находится между
Л, и Д2.
Подсчетом двух-трех новых таблиц для значении Д, лежащих
между Д, И Д2, можно определить корень с требуемой точностью.
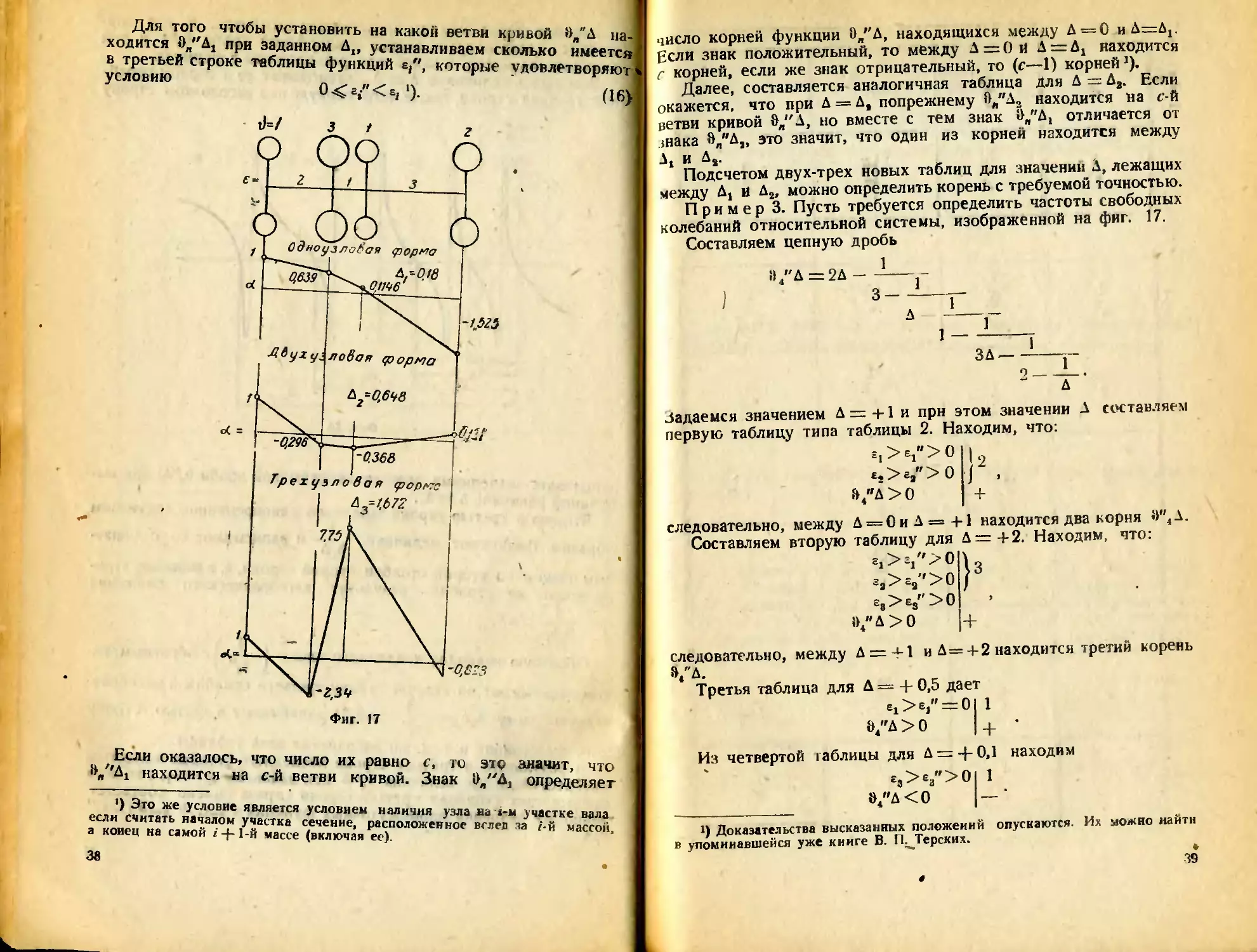
Пример 3. Пусть требуется определить частоты свободных
колебаний относительной системы, изображенной на фиг. 17.
Составляем цепную дробь
»4"Д = 2Д - ----
] з--
д
д
Задаемся значением Д = +1 и прн этом значении Д составляем
первую таблицу типа таблицы 2. Находим, что:
£.>£,"> 0 |
0 /
2
Й/'Д>0
следовательно, между Д = 0иД = +1 находится два корня И"4Д.
Составляем вторую таблицу для Д — + 2. Находим, что:
3
2-^ с2
г ез
следовательно, между Д = 4-1 и Д=+2 находится третий корень
»4"Д.
Третья таблица для Д = + 0,5 дает
Ej" —0 1
0 J- ’
&"Д
Из четвертой таблицы для Д = + 0,1 находим
es>e8">0 1
»4"Л<0 —
1) Доказательства высказанных положений опускаются. Их можно найти
в упоминавшейся уже книге В. Питерских.
39
Таким образом, 0,1<Д1<0,5; 0,5<Да<1,0; 1,0<Д#<2,0.
Подсчетом таблицы 6 устанавливаем: Aj£^0,18; подсчетом
таблиц 7 и 8: Да = 0,64 и из таблиц 9 и 10 находим Д3= 1,672.
Если частотное уравнение свободных колебаний записано в
форме (14):
8/"Д = 0,
го схема отыскания корней остается принципиально такой же,
как и при решении уравнения &я"Д = 0. В этом случае расчет
сводится в таблицу, составленную по форме таблицы 3. Здесь
, __ an-i _ 1
„-1- 8п1 — ел—1 v
Д = &Л-1Д - — - и. Т. д.
«п-1 е п—I
Для построения форм свободных колебаний воспользуемся
введенными выше обозначениями:
&/'Д = — —;
ai
„г/ а'+!
°*------V’
из которых получаются рабочие формулы для определения
амплитуд
8. — — в|&/'Д;
«i = W«
Входящие в эти формулы величины 8/'Д и «/' уже опреде-
лены й записаны в третьих строчках таблиц, составленных по
форме таблицы 2. Для определения амплитуд в таблицах, в ко-
торых 8„" = 0, добавляются еще две строчки и производятся
вычисления по схеме, показанной в таблице 4 (верхняя строка
этой таблицы является третьей строкой таблицы 2).
41
Таблица к примеру
1 2 3 4
А 2 ЗА 1 1 1 1 3 2Д
1 1 4-2 1 + 3 4-1 +1 1 +3 + 2 2 +
* — 1 — 1 — 0,5 — 2,0 + 1.0 — 0,25
| А=4-1 4-1 +2 4-0,5 -1.0 + 40 1 +1,75
2 + 2 + 2 4-6 4-1 4-2 + з 1 +4 з +
— 0,5 -0,667 — 0,1875 — 1,231 -1,300 — 0,588
Д = +2 4-1.5 4- 5,333 4-0,8125 4-0,769 + 1.7 + 3,412
3 4-0,5 + 2 1.5 4-1 4-0,5 +з + 1,00 11+
- -2,0 — CZ) 4-0 - 1 + 5
д - 4-0.5 0,0 — GO 4-1 -0,5 + 5 + 0,8
4 4-ОЛ 4-2 4-0,3 4-1 + 0,1 +3 + 0,2 1 —
* - 10 4- 0,125 — 2,353 + 0.7391 - 1,192 — 0,5531
А = 4-0,1 — 8 4- 0,425 — 1,353 + 0,8391 +1,808 - 0,3531
5 4-0,19 4-2 4-0,57 +1 + 0,19 + 3 + 0,38 1 -Ц-
-* - 5,263 4-0.3065| — 1.1409 1 + 7,097 — 0,137 - 0,3493
। А =4-0,19 - 3,263 4-0,8765 — 0,1409 4-7,287 + 2,863 + 0,0307
6 1 1 4-0,18 4-2 4-0,54 4-1 + 0,18 +3 4-0,36
1 — 5,555 4-0,2812 -1,218 4 4,587 -0,2098 — 0,3584
А =40,18 -3,555 4-0,8212 -0,218 +4,767 +2,79 0,0016 |
7 40,65 4-2 4-1.95 4-1 +0,65 +3 41.3
-* —1,538 — 2,164 4-4,673 -0,1763 — 2,111 — 1,125 2 +
Л= 4-0,65 4-0,462 — 0,214 4-5,673 + 0,4737 +0,889 +0,175
42
продолжение таблицы к примеру S
3 4
3
Д 2 ЗД 1 Д 3 *
8 4-0,648 +2 +1,944 1 +1 +0,648 + 3 +1,296 2+
- 1,543 — 2,188 +4,098 — 0,1962 - 2,213 — 1,271
Д = +0,648 +0,457 — 0,244 +5.С98 4-0.4518 +0,787 |+0,025 |
9 +1,67 +2 — 5,01 +1 +1.67 +3 +3.34 3 —
-+ — 0,5988 — 0,7138 - 0,2328 — 1,303 -2,725 — 3.636
Д= + 1,б7 +1,401 +4,896 +0,7672 +0,367 +0,275 - 0,296
10 +1.672 +2 +5,016 +1 +1.672 +3 +3,344 3 —
-* — 0,5981 - 0,7133 — 0,2324 - 1,303 — 2,71 - 3,448
А=+1,672 +1,402 +4,303 + 0,7676 +0,369 +0,29 — 0,104
Если определение частот производилось из уравнения
^0,
то амплитуды подсчитываются в таблице, составленной по фор-
ме таблицы 5.
М = д = •п = »' 1 л—1
„ -д. 8"~» _ _ 1 6П-2 n I +
о , = -^ 1
<- направление
Таблица 5
Наконец, если при определении частот было использовано
Уравнение
1>/"Д = 0,
то амплитуды подсчитываются в таблице, составленной по фор-
43
ме таблицы 6 (первая строчка этой таблицы является треты
строкой таблицы 3).
направление вычислений
II I =*5> 6"i-l — с» ъ» II о е| 20
Таблица
направление вычислений
направление вычислении амплитуд
Пример 4. Пусть требуется определить формы свободны)
колебаний системы, представленной на фиг. 17. .1
Частоты свободных колебаний этой системы были уже опре
делены (таблицы 6, 8 и 10 третьего примера).
Выписываем третьи строки этих таблиц, проводим вы-
числения и строим формы колебаний (фиг. 17).
Таблица к примеру
1 2 3 4
Л=4-О.1в1 -3,355 4- 0,8221 — 0,218 4-4,767 4-2,79 -4- 0,0016 14-
аг-4-0,639 0,1146 УЗЕЛ 04= —1,525
8t -0,18 6, = 0,525 а3 = 0,547
1 8| Д = 4-0.64 4-0,457 — 0,244 4-5,098 4-0,4518 4- 0,787 4-0,025 24-
+1 УЗЕЛ — 0,296 — 0,368 УЗЕЛ 4-0,131
— 0,648 - 0,0722 4- 0,1662
ю| a=H-j.6T2 4-1,402 4-4,303 .+ 0,7676 0,369 4-0,29 — 0,004 3-J
+1 УЗЕЛ — 2,34 УЗЕЛ 4-7,75 УЗЕЛ — 0,828
— 1,672 4- 10,09 [ — 2,855 |
44
6. Свободные крутильные колебания разветвленных систем
В настоящее время в моторостроительной практике завоевали
себе прочное место двухвальные двигатели, работающие на один
011нт. Часто также встречается применение соосных винтов про-
тивоположного вращения.J) Иногда нагнетатель или специальный
агрегат для наддува кабины приводятся не от хвостовика колен-
чатого вала, а от редуктора.
Во всех этих случаях крутильные системы двигателей не-
могут быть представлены в виде одной цепочки последовательно
расположенных масс, связь между которыми осуществляется
упругими валами,—системы получаются разветвленными. Отли-
Фиг. 18
читальная особенность разветвленных систем состоит в том, чтс-
к одной (или нескольким) ее массам присоединяется не два вала,
а три (и может быть даже больше).
Рассмотрим систему фиг. 18, имеющую только одно развет-
вление или „вилку".
Заметим без доказательств, что такая система будет иметь
различных отличающихся от нуля частот свободных колебаний
на единицу меньше числа масс.
Расчет ведется следующим порядком:
1. Задаются ориентировочным значением частоты р/, пола-
гают Ф(е) = 1. составляют таблицу типа таблицы 1 для одной
верхней ветви и определяют значение амплитуды Ф,-.
2. Полагают Ф(т)' = 1 и при той же частоте р\' определяют с
помощью такой же таблицы, составленной для нижней ветви,
значение Ф/.
В общем случае при неодинаковых ветвях окажется, что
Ф/у- Ф,.
>) Валы этих винтов располагаются телескопически и приводятся от ко-
ленчатого вала через специальный редуктор. См. Доллежаль. Редукторы числа
оборотов авиационных двигателей, Обороигиз, 1945.
45
Вместе с тем по смыслу задачи, при колебаниях дантЛ
формы, должно существовать равенство Ф/ = Ф,. т
Таким образом, следует заключить, что если амплитуд!
крайней массы одной из ветвей принята равной единице, т*
амплитуда крайней массы на другой ветви не может быть такД
равна единице
Пусть остается Ф(Н = 1, тогда амплитуды всех масс нижыЛ
ветви, найденные первым расчетом, должны быть исправлен^
Фиг, 19
ф,
лмножепием на что и даст желаемый результат Ф/ = Ф(.
3. Из диференпиального уравнения движения i-й массы
/Т1 + Л,_1 (<р, [*,-(?,. I—<р;)-Ьki= 0,*)
определяют
= i —<?;) + —yj —Л<Р/.
т. е. момент упругих сил (i—1)-го участка вала.
) Знаки моментов упругих сил в верхней и нижней ветвях k и
kr (Фщ if—<t) могут быть различными. В уравнении f-й массы стоит их
алгебраическая сумма.
46
Переходя к амплитудным значениям моментов, получим:
*.1 (Ф4 — Ф.-1) = (Ф.+l-Ф;) + А/ (Ф(. 1>' Ф/) +
Гакой же по величине, но обратный по знаку, момент действует
о стороны (i—1)-го участка вала на (г—1)-ю массу. Учитывая
* 0> заполняют таблицу типа таблицы 1, начиная от (i—1)-го
частка до конца, и проверяют равен ли нулю момент упругих
си-i за пеРВ0Й массой. Если этот момент не равен нулю, проводят
повторный расчет при новом значении частоты p"i.
Пример 5. Найти низшую частоту и построить соответ-
ствующую ей одноузловую форму свободных колебаний раз-
ветвленной системы (фиг. 19а).
Задаемся частотой = 0,151------а- и составляем таблицу
С СК
типа таблицы 1 для верхней ветви, полагая Ф-= 1.
№№ участков Амплитуды моментов сил упругости k \ Амплитуды масс
— 0,302 -0,302 1 5
5—4 -0,302 3 — 0,906
— 0,0142 - 0,151 0.094 4
4-3 -0,3162 1 -0,3162
1 —0,2222 3
Составляем такую же таблицу для нижней ветви, полагая Ф2 = 1:
— 0,302 - 0,302 1 2
2-3 -0,302 2 — 0,604
1 0,396 3
47
Исправляем значение Фа =
0,2222
0,396
0,561. Теперь:
0,1695 — 0,302 -0,561 2
2-3 0,1695 2 0,339
— 0,222 3
Вычисляем момент сил инерции 3-й массы:
73Ф3ра = — 3 • 0,222 • 0,151 = — 0,1005 кг см.
Вычисляем момент упругих сил, действующий на
массу:
первую
—Аз-1 (Ф8-Ф1) = — 0,3162 + 0,1695 + 0,1005 = —0,0462 кгсм.
Составляем таблицу для последней ветви:
— 0,222 3
3—1 — 0,0462 2 — 0.0924 *
0,0475 — 0,151 - 0,3144 1
1.... 0,0013 *
Убеждаемся, что момент за первой массой очень мал, т. е.
заданная частота р* = 0,151 —практически не отличается от
истинной.
Форма колебаний системы представлена на фиг. 196
Рассмотрим особенности расчета расщепленной системы, пред-
ставленной на фиг. 20. К этому виду приводится, например,
крутильная система двухвального двигателя, работающего на
один винт и имеющего привод нагнетателя от обоих валов
одновременно.
Расчет начинают с одной из крайних масс (допустим первой),
и дойдя до разветвления, полагают, что момент за i-й массой
равен сумме моментов упругих сил в обеих ветвях. Момент
упругих сил i'-го участка верхней ветви представляют в виде:
48
a j-Ю участка нижней ветви
— (1 — ?<и)-
Расчет каждой ветви ведут в отдельных таблицах (типа
таблицы 1), получая значения амплитуд колебания масс и
моментов упругих сил в виде двучленов ах+b, содержащих
неизвестное х. Доводя расчет до массы е, получают из одной
таблицы
Ф?: = а/.%+Ь/
и из другой таблицы
Ф, — арс 4- Ье.
Так как, очевидно, должно выполняться условие
Ф/ = Фе,
ТО
ае'х + А/ = аех+Ье,
откуда
ае -
Подставляя найденное значение х в таблицы, определяют
амплитуды колебания масс и моменты упругих сил в обеих вет-
вях, после чего продолжают расчет таким же образом, как и в
случае, разобранном выше.
Разберем применение метода цепных дробей к расчету раз-
ветвленных систем.
Будем считать, что система, изображенная на фиг. 18, при-
ведена к относительной форме. Уравнение колебания j-ой отно-
сительной массы будет
6,-1 — 8; — 8/ — >^Даг = О,
отсюда
ai ai ai
4 В. Кириченко •
49
Заменяя по формулам (11)'1 — 4—г------
«i s i-1
и по формулам (17'
, получим:
Это и есть уравнение свободных колебаний развегвленной
системы. Оно очень сходно с уравнением (14) и отличается от.
1
него только наличием в левой части дроби---, которая зна-
менует присоединение к i-ой массе ветви из группы под атл иво-1
стей и масс: а/...
Если бы к одной массе сходились не три, а сколько угодно]
ветвей, то уравнение свободных колебаний системы приняло бы
вид:
Z
где г—число ветвей.
Выделяя из под знака суммы
Обозначим:
(18)
тогда получим уравнение:
(19)
внешне ничем не отличающееся от уравнения (14). На основании
этого сходства можно сказать, что уравнение (Г9) представляет
собой уравнение свободных колебаний простой неразветвлен-]
ной системы, отличаясь только тем, что масса, на которой про-
изведен „надлом", имеет момент инерции не постоянный, но
зависящий от частоты колебаний всей системы.
Подобными рассуждениями можно показать, что уравнения
свободных колебаний простой системы являются справедливыми
и в тех случаях когда не одна, а несколько или все массы яв-
50
1Я10ГСЯ переменными, изменяющимися в зависимости от частоты
по формуле (18).
Практически составление и расчет уравнения свободных ко-
лебаний разветвленных систем удобнее делать не производя
лнадлома" следующим образом:
В системе отмечаются две крайние массы и цепочка масс и
податливостей, связывающая эти крайние массы. Для намечен-
ного таким образом .стержня" системы составляется непрерыв-
ная дробь [например, по типу (13)]. Среди звеньев составленной
дроби фиксируются те, от которых происходят ответвления и к
ним пристраиваются дроби, соответствующие этим ветвям.
4*
51
На фиг. 21а представлена система со многими разветвлениями
и схематически изображен вид уравнения свободных колебаний.
Там же даны схемы расположения таблиц для вычисления ча-
стот (фиг. 216) и форм (фиг. 21в) колебания этой системы.
Каждая таблица схемы вычисления частот составлена по типу
таблицы 2, а для вычисления форм—по типу таблицы 5.
§ 7. Свободные крутильные колебания с учетом
сопротивлений
До сих пор рассматривались свободные крутильные колеба-
ния, причем предполагалось, что сопротивления колебательному
процессу отсутствуют. В действительности сопротивления всегда
имеют место. Сопротивления могут весьма существенно влиять
на характер движения системы. Величина сопротивлений может
быть настолько велика, что свободные колебания вообще не
удастся вызвать. Например, если на весьма податливом вале
укрепить диск и поместить его в очень вязкую среду, го будучи
выведен из положения равновесия и представлен самому себе
диск медленно вернется в равновесное положение, но не будет
колебаться вокруг него.
При крутильных колебаниях систем коленчатых валов сопро-
тивления колебанию в основном складываются из трения вала
в подшипниках, трения поршней о стенки цилиндров, внутрен
него трения материала вала при деформации, сопротивления
среды, в которой происходят колебания, ударов в зазорах между
валом и подшипниками, ударов в зубьях шестерен редуктора
и т. д. Источники возникновения моментов, глушащих колебания
весьма многочисленны и разнообразны по своей природе. Оста-
новимся кратко на каждом из них.
Внутреннее трение или упругий гистерезис
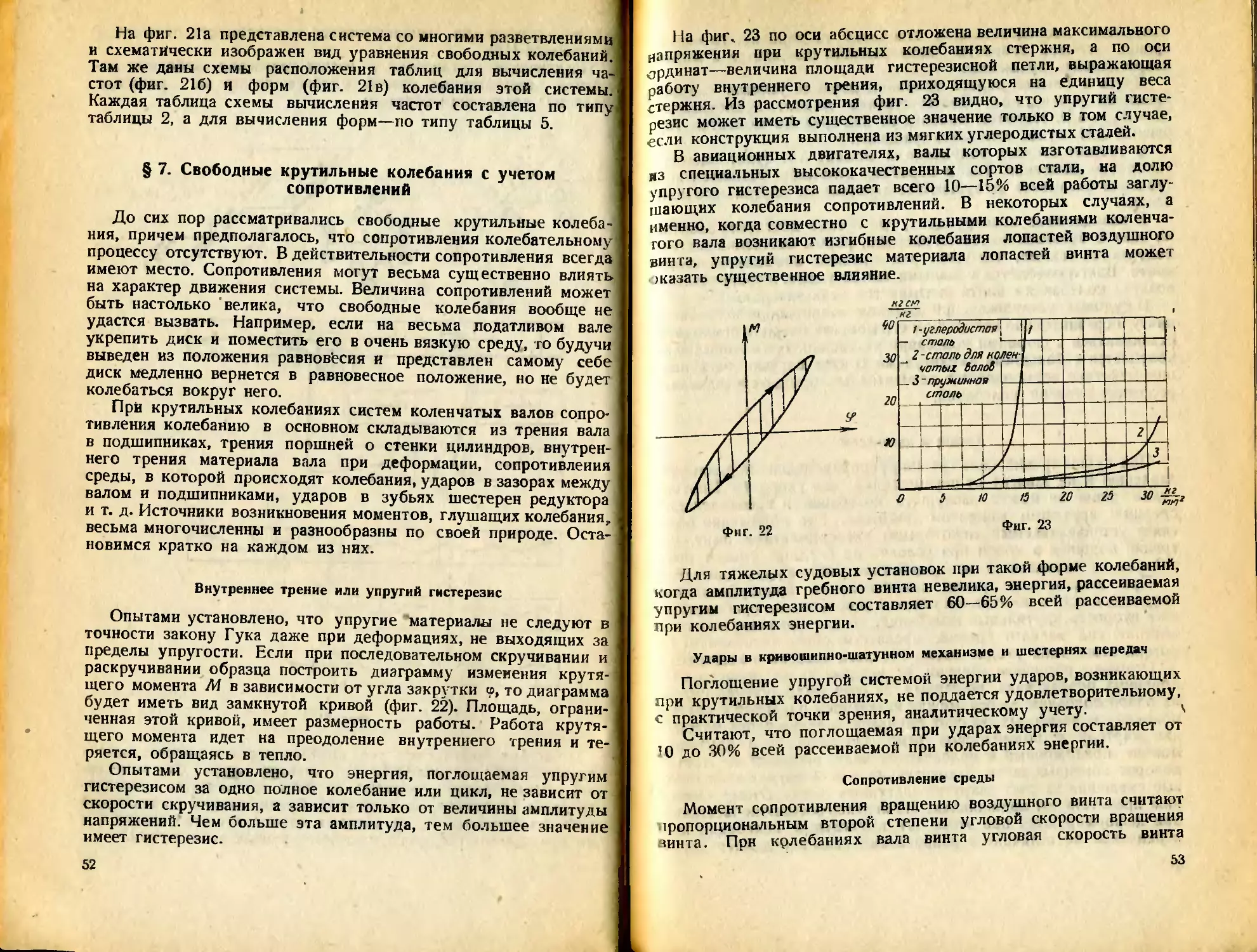
Опытами установлено, что упругие материалы не следуют е
точности закону Гука даже при деформациях, не выходящих зг
пределы упругости. Если при последовательном скручивании и
раскручивании образца построить диаграмму изменения крутя
щего момента М в зависимости от угла закрутки ®, то диаграмма
будет иметь вид замкнутой кривой (фиг. 22). Площадь, ограни
ченная этой кривой, имеет размерность работы. Работа крутя,
щего момента идет на преодоление внутреннего трения и те
ряется, обращаясь в тепло.
Опытами установлено, что энергия, поглощаемая упругим
гистерезисом за одно полное колебание или цикл, не зависит от
скорости скручивания, а зависит только от величины амплитуды
напряжений. Чем больше эта амплитуда, тем большее значени<
имеет гистерезис.
52
На фиг. 23 по оси абсцисс отложена величина максимального
напряжения при крутильных колебаниях стержня, а по оси
ординат—величина площади гистерезисной петли, выражающая
работу внутреннего трения, приходящуюся на единицу веса
стержня. Из рассмотрения фиг. 23 видно, что упругий гисте-
резис может иметь существенное значение только в том случае,
если конструкция выполнена из мягких углеродистых сталей.
В авиационных двигателях, валы которых изготавливаются
из специальных высококачественных сортов стали, на долю
упругого гистерезиса падает всего 10—15% всей работы заглу-
шающих колебания сопротивлений. В некоторых случаях, а
именно, когда совместно с крутильными колебаниями коленча-
того вала возникают изгибные колебания лопастей воздушного
винта, упругий гистерезис материала лопастей винта может
сказать существенное влияние.
Для тяжелых судовых установок при такой форме колебаний,
когда амплитуда гребного винта невелика, энергия, рассеиваемая
упругим гистерезисом составляет 60—65% всей рассеиваемой
при колебаниях энергии.
Удары в кривошипно-шатунном механизме и шестернях передач
Поглощение упругой системой энергии ударов, возникающих
при крутильных колебаниях, не поддается удовлетворительному,
с практической точки зрения, аналитическому учету. \
Считают, что поглощаемая при ударах энергия составляет от
’0 до 30% всей рассеиваемой при колебаниях энергии.
Сопротивление среды
Момент српротивления вращению воздушного винта считают
ропорциональным второй степени угловой скорости вращения
винта. При колебаниях вала винта угловая скорость винта
53
изменяется последовательно, становясь то больше, то меньш
срдней угловой скорости. Одновременно изменяется и момен
сопротивления вращению.
Пусть в течение первой половины периода угловая скорост
вращения «> = а>ср + Да>. Соответственно момент сопротивления
= + ДЛ1. Избыток момента М над средним моментом Mtf
равный Д/И, будет замедлять вращение.
В течение второго полупериода момент ДЛ1 будет вызыват
ускорение движения. Таким образом, пульсация момента сопро
тивления оказывает заглушающее действие на крутильные коле
бания.
В авиационных конструкциях, где легкий двигатель работает
на •винт с большим моментом инерции, формы колебаний систем;
получаются такими, что узел, как правило, помещается вблизи
винта. Винт колеблется с малыми амплитудами, и сопротивление
воздуха колебаниям винта оказывается незначительным.
В судовых установках при длинном валопроводе к гребному
винту и сравнительно небольшом его моменте инерции приходите
сталкиваться с формами колебаний установки, при которых вин
колеблется с большими амплитудами. В этих случаях заглушак
щее действие воды является основным фактором, определяющим
рассеяние энергий колебаний.
Трение в механизме
При сухом трении сила трения пропорциональна нормальному
давлению и не зависит от перемещений или скорости. Поэтомх
сухое трение не может заглушать колебания и преодолевается
средним крутящим моментом двигателя. Это положение объ;
сияет устанавливаемый некоторыми экспериментами факт, чт
трение поршней и колец при условии их скудной смазки npai
тически не сказывается на колебаниях работающего двигателя
При жидкостном трении сопротивления пропорциональны
скорости, и если к постоянной угловой скорости вала прибавляется
еще скорость крутильных колебаний, то это приводит к возни»
новению сил вязкого трения, препятствующих колебаниям. Н
потери этого типа уходит около 7% всей энергии колебаний.
Основное рассеяние энергии в авиадвигателях происходит
коренных опорах вала, во-первых, за счет выдавливания смазк
из одной половины зазора между вкладышем и шейкой в другую
половину и, во-вторых, за счет передачи энергии через подши!
ник картеру и подмоторной раме. Очевидно, что крутящий
момент, приложенный к коленчатому валу, вызывает не только
поворот коренных шеек относительно оси вала, но и их бок(
вые смещения за счет закрутки шатунных шеек. Этому смеще
нию препятствуют подшипники. Не являясь абсолютно жестким!
они деформируются при этом. От крутильных колебаний вал
переменные по величине и направлению силы передаются корен
54
ным опорам и приводят в колебательное состояние весь двига-
тель, о чем свидетельствуют специфический гул и вибрация
мотоустановки, которые сопровождают крутильные колебания
нала г).
Точно подсчитать величину момента сопротивления аналити-
ческим путем не представляется возможным. Обычно прини-
мают, что сопротивления пропорциональны скорости колебатель-
ного процесса <р. Коэфициент пропорциональности, учитываю-
щий все виды сопротивлений, обозначают Таким образом, мо-
мент сил сопротивления, действующий на i-ю массу системы,
принимают равным =
Моменты Mt обычно прикладывают к тем массам крутильной
системы, к которым приложены внешние возбуждающие колеба-
ния моменты. Коэфициент ? принимают одинаковым для всех
этих масс.
Численное значение коэфициента ; для различных случаев
изменяется в весьма широких пределах. По данным проф.
И. Ш. Неймана от 20 до 100 кг см сек.
В таблице 7 приводятся значения коэфициента полу-
ченные опытным путем различными авторами.
Таблица 7
Тип двигателя г
12-ти цилиндровые V-об разные двигатели 0,002 - 0,0022
То же 0,002 — 0,0023
То же 0,0016 — 0,002
Автомобильные двигатели 0,0025
1яжелые дизели (от 550 до 3000 л.с.^ 0,0136 — 0,008
То же 0,0079 - 0,0048
Различные двигатели 0,015-0,0015
Коэфициент 5’ имеет размерность—---- и является си-
лой заглушающих сопротивлений, приложенной к кривошипу и
отнесенной к 1 смг поверхности поршня и единичной скорости
шатунной шейки. Чтобы по известному коэфициенту опреде-
лить с, необходимо V умножить на площадь поршня и квадрат
радиуса кривошипа.
*) Вибрация установки при сильных крутильных колебаниях объясняется
отчасти и тем, что нарушается уравновешенность двигателя из-за того, что
при колебаниях различные кривошипы в каждый данный момент времени
имеют скорости, значительно отличные друг от друга.
55
Из приведенной таблицы видно, что для ориентировочно^
оценки заглушения при расчете крутильных колебаний двигате-
лей авиационного типа следует брать Е' - 0,002.
График, представлен-
ный на фиг. 24, позво-
ляет определить коэфн-
циент заглушения Е в за-
висимости от основных
параметров исследуемой
системы. Этот график
в аналитической записи
имеет вид:
Фиг. 24
т
Е т
здесь:/—полярный момент инерции кривошипа и связанных с
ним масс;
р—круговая частота свободных колебаний без сопроти-
вления;
а,—отношение амплитуды свободных колебаний t-ой массы
к амплитуде последней массы.
т—число кривошипов.
Не останавливаясь более подробно на определении величин
заглушающих сопротивлений, перейдем к анализу уравнения
движения при свободных колебаниях системы, на которую дей-
ствуют сопротивления, пропорциональные скорости.
Если в качестве объекта взять систему, представленную на
фиг. 1, и только добавить к условиям задачи, разбираемой в
§ 1, действие момента Л4'=- Е<р, то диференциальное уравнение
движения будет:
/<р + Еф +/кр = 0,
обозначая
k ч « п
J-=P 11 J =2п,
получим
® + 2и® + р-<р = 0. (20)
Это уравнение есть полное однородное уравнение второго
порядка с постоянными коэфициентами. Решение уравнения (20)
будем искать в виде
® = De^'.
(20а)
56
Дпфереицируя выражение (20а), найдем
о==ОСе". (206)
? = (20в)
Подставляя (20а), (206) и (20в) в уравнение (20), получим
DCW+2tiDCe<1+p2De<'=О,
и так как уравнение должно удовлетворяться при любом значе-
нии времени t, то
С2 + 2пС+р2 = 0 (20г)
и ' _______
С=—n-tyjn3 р*. •
В задачах расчета крутильных колебаний коленчатых валов
двигателей мы всегда имеем «случай малого сопротивления"
п<^ Р, поэтому можно записать оба корня уравнения (20г) в
виде комплексных чисел
С==—n^ipl ,
где
Pi =\/рг~п2-
I
Выражение (20а) приобретает вид:
(—niip.lt —n—ipAt - nt ip t —ip t
i—D^e 1 +D,e 1 =e (Dxe 1 +D,e 1). (20д)
Воспользуемся известным представлением комплексного числа
в тригонометрической форме:
е = cosp/+isinp/;
-ip *
е = cos ptt—isinp/
и перепишем выражение (20д) в следующем виде;
з — e~"f (cospf + i sin pfi+D-, (cos p^t-isin/?/)] =
= e~nt [(£>! + £>.,) cosp/ + (Dj—£>2) isin pxt\.
Обозначим
{Dx + Dz}= Ф cos 7 | !)
I {D—DJ = —Ф sin 7 / ’
') Для того чтобы можно было накисать второе из уравнений, необходимо
Положить, что постоянные интегрирования /Э1 и Ог суть сопряженные ком-
плексные числа. Если Dl=a-^-bi, а Ьг = а—Ы- то (D,+D,) - Ча и (Dx—D.^i 2b,
г- е. вещественное, а не комплексное число.
57
при этом
Ф = У<£>>+Р1«+(Р1-Па/;
Ьп = —
Теперь
<>1 + £>2
I
(D} + Ог) cospxt + (Dj—D2) i sinptt= ф [cos у cos p{t — sin 7 sin/?,<[
= Ф cos/7^+7)
и решение может быть записано в окончательном виде
у = Фе-я/со8р^+т). (21^
Движение, описываемое фор му.'ой (21), не является периоди!
ческим, так как с течением времен t последующие максималь-4
ные отклонения диска от полож-ния равновесия уменьшаются
ибо при t~»оо е~п/-»0.
Такое движение называю^
свободным затухающим ко-
лебательным движением
_ (фиг. 25).
Промежуток времени
между двумя последующи-
ми отклонениями диска и
одну сторону является по-
стоянной величиной, равной
2*
T = —______
\/p2-"2
и называется периодом условно периодического движения.
Период затухающего колебания несколько больше периода
колебаний этой же системы без сопротивлений. Однако в прак-
тически интересующих нас случаях разница в периодах или
частотах системы с сопротивлениями и без них столь невелика,
что при определении частот, сопротивлениями можно пренебречн
и считать рх=р.
Действительно, даже при п==0,1р, что соответствует очень
большому затуханию /7,220,995/7.
Сопротивлениями можно так&е пренебречь при расчете вы-!
нужденных колебаний, если частота возмущающей нагрузки!
2 ~^>р или 2 <^.р. Наоборот, ес^и 2 равняется или близка р,}
сопротивления сказываются очень сильно и ими пренебрегать ни
в коем случае нельзя.
Рассмотрим темп убывания амплитуд при свободных колеба-1
ниях с сопротивлением, пропорциональным скорости. В момент!
58
времени t амплитуда колебания равна Фе-"'. Через период Т
амплитуда будет Фе-"<'+п.
Отношение предыдущей амплитуды к последующей во все
время колебаний остается постоянным, равным:
—ntg—nT *
т. е. амплитуды убывают в геометрической прогрессии. Практи-
чески всегда колебания затухают быстро.
Произведение пТ называют декрементом затухания. Декре-
мент показывает как быстро происходит затухание. Тот факт,,
что декремент зависит не только от п, но и от периода Т, сви-
детельствует о том, что чем податливее система, тем интенсив-
нее проявляют себя при колебаниях сопротивления.
ГЛАВА II
ПОСТРОЕНИЕ ЭКВИВАЛЕНТНЫХ КРУТИЛЬНЫХ систем
Реальная крутильная система авиационного двигателя имееп
бесконечное число степеней свободы и бесконечное число частоп
и форм колебаний, так как массы системы распределены непре
рывно по всей ее длине.
Анализ движения такой системы весьма затруднителен, однако,
как показывает практика, для выявления низших форм колебани!!
реальной системы она может быть заменена упрощенной систе-
мой, которую называют приведенной или эквивалентной. Уж«
отмечалось ранее, что обычно бывает важно знать толькс
первые три частоты и формы колебаний. Для реальной и при
веденной систем они получаются практически одинаковыми.
Приведенная или эквивалентная система представляет собон
прямолинейный гладкий вал с размещенными на нем в отдель-
ных сечениях сосредоточенными массами.
Моменты инерции участков вала, расположенных между со-
средоточенными массами, считаются равными нулю.
Таким образом, построение эквивалентной системы требуе!
разрешения двух задач: первая состоит в определении длин
отдельных участков эквивалентного вала, вторая—в определении
моментов инерции эквивалентных масс.
Решение этих задач составляет содержание второй главы.
§ 8. Приведенная длина коленчатого вала
Коленчатые валы авиационных двигателей имеют сложные
в конструктивном отношении формы, однако всегда их можнс
представить себе состоящими из ряда относительно простых
элементов; полых цилиндрических участков различных диаметров,
полых конусов, щек и т. д. При построении расчетной системь
каждый такой участок заменяется участком прямолинейногс
вала, длина которого называется приведенной длиной и опре-
деляется из условия равенства жесткостей на кручение дейст-
вительного и заменяющего участков.
Равенство жесткостей одновременно означает равенство углов
закрутки этих участков под действием приложенных к ним оди-
60
наковых скручивающих моментов. Полная приведенная длина
коленчатого вала равна сумме приведенных длин составляющих
его участков. Жесткость вала Лс, состоящего из ряда участков,,
жесткости которых обозначены Л,, ^....определяется по
формуле
А°= "Т 1 Т ’
Ч+”'
Сечение эквивалентного вала может быть выбрано произ-
вольно. Обычно его берут таким же, как сечение коренной
шейки исследуемого коленчатого вала.
Перейдем к непосредственному определению приведенных
[лии отдельных участков коленчатого вала.
Ml
Полый цилиндрический вал
Пусть полый вал с наружным и внутренним диаметрами D
и d соответственно и длиной I требуется заменить валом, диа-
метры которого: £)0—наружный и d0—внутренний. Условие за-
мены: равенство жесткостей обоих валов
k0 = k или «0 — <?, но ?0 = хт-2-, а
U'p0
здесь: М—скручивающий валы момент;
(/—модуль сдвига материала валов;
1Р и /р0—полярные моменты инерции сечений валов.
Отсюда = , и так как /„ = ^n(D* — d*
ip F 32
— ^j(A>4~<V), то приведенная длина
I _ I Dy*—dp*
D^—dS '
Приведенная длина участка вала, ослабленного шпоночными
канавками, может быть определена достаточно точно только
экспериментальным путем. Приближенное значение ее может
быть подсчитано по формуле
/ —kl ^°4 ^°*
D*-d* ’
здесь сохранены старые обозначения; k—коэфициент, учитываю-
щий влияние шпоночных канавок
k=—к-’
X~Dn
где h—глубина шпоночной канавки;
п—коэфициент, зависящий от числа и расположения шпонок.
>0 —
(22>
61
По данным лаборатории ДВС ВТИ:
п
Для одной врезной шпонки..........................0,5
Дли двух ровных шпонок под углом 90°..............1,0
Для двух ровных шпонок под углом 180°............,1,2
Для двух тангенциальных шпонок под углом 120 .... 0,4
Конический вал с цилиндрической расточкой (фиг. 26а)
Рассматривая элементарный участок этого вала, соответствую
цций элементу длины dx, как полый цилиндрический вал с на
ружным диаметром Dx и внутренним о, получим, что приведен
пая длина этого участка равна
dl0=-!j*dX.
•рх
Полная приведенная длина конического вала с цилиндрическо
расточкой будет
о
После интегрирования и преобразований получим:
<*
I -
62
здесь
. 16/1 х+1 . \ ,
функция /(х) = — In + arc tgx I представлена графи-
ком, заимствованг&м у проф. Неймана И. Ш. (фиг. 266).
Цилиндрический вал с резким переходом от одного диаметра
к другому (фиг. 27)
При наличии резких изменений поперечных сечений вала при-
веденная длина участка с резкими изменениями поперечных се-
чений не может быть найдена аналитическим путем. Наличие
Фиг. 27
честных деформаций в местах резкого изменения поперечных
сечений увеличивает приведенную длину участка.
На основании опытных данных приведенную длину конструк-
ции, изображенной на (фиг. 27а), считают равной приведенной
63
длине вала с диаметром и длиной Z., — I плюс приведенна:
длина вала с диаметром О, и длиной /, + /.
, £>г
Величина I зависит от отношения и может оыть определен;
по графику (фиг. 276) лаборатории ДВС ВТИ (С. С. Зиманеню
и В. К. Житомирский).
Переход от вала к ступице
Если на вал посажена какая-либо обойма, шестерня или ма-
ховик, то приведенная1 длина перехода от вала к обойме илг
ступице (шестерни, маховика) определяется как и в предыдущей
случае. Отношение (где D—диаметр вала) ио тем же источ
никам:
Для обычной посадки .
Для прессовой посадки
0.33
0,25
Фланцевое соединение
Приведенная длина фланцевого соединения принимается рав
ной приведенной длине цилиндрического вала, длина которой
считается равной суммарной толщине фланцев, а диамет[
равен диаметру осевой окружности фланцевых болтов.
Приведенная длина колена (фиг. 28)
Пусть требуется привести колено к полному прямолинейном)
валу с наружным и
ственно. Положим
внутренним диаметрами Dt и d0 соответ
4 4« "Ь + А>ш >
длина колена;
где /0—приведенная
/Ок.—то же коренной шейки;
4ч—т0 же щеки;
—70 же шатунной шейки.
Приведенные длины коренной и шатунной шейки опреде-
ляются по формуле приведения цилиндрического полого вала
DJ-dJ . _ £>/- df ,
°* Г) 4__ Я 10Ш Г) t J 4 ‘ш-
LJK uh ‘-'ш иш
Приведенная длина щеки найдется следующим образом: ирг
скручивании колена щека изгибается, как показано на (фиг. 29)
и в результате этого шатунная шейка оказывается повернуто?
относительно коренной на угол который определяется пс
известней формуле, вполне справедливой для длинной балки, за-
деланной одним концом,
= MR
~ ЕГВ ’
64
здесь /,= -J2--момент инерции сечения щеки относительно
оси х—х;
Е — модуль упругости материала вала при изгибе.
Рш _1
Под действием того же момента /И полый вал с диаметрами
гч . М10 ~
и d0 закрутится на угол (Ро — ~г~7г' где модуль упру-
. ,го<7
5 В. Кириченко
65
гости материала вала при кручении; ~ d0*) — 11Оля
ныи момент инерции сечения вала.
Условие приведения: ‘?<ч=?0- Отсюда приведенная длина те:
/ _3-£р_Ро4-<
0Ui~ 8 '* Е bWs ‘
Приведенная длина колена
, D^~d^ , , G Dj-dj D'-dJ .
0 Z)/-rfK4 ' 4 “ Е * bWs + D^—d^ ш
(23
Выше отмечалось, что приведенная длина конструкции с рез
кими переходами поперечных сечений не может быть опреде
лена точно аналитическим путем. В формулу (23) также вво
дятся исправления в соответствии с данными опыта. С таким!
исправлениями по Картеру формула приобретает вид:
/ =(1 ’ О 8А) ^°‘ ^°4 4- — ^*4 I — Р-°- (23а
о (,. + 0,8.7) DK*—dK* +4 Z"'H 2 R bWs (23а
•
и дает удовлетворительные для практики результаты. ’)
По данным ЦИАМ средняя ошибка в величине приведенное
длины, определенной по формуле Картера против данных экспе
римента над рядом авиационных коленчатых валов, составляв'
3,3%. причем наибольшие отклонения достигают ± 10%.
Итак, складывая приведенные длины всех колен исследуемог<
вала и приведенные длины других его элементов, получаю’
длину гладкого прямолинейного вала, жесткость которого н<
IoClG
кручение Ао= , - равна жесткости коленчатого вала.
*-о
§ 9. Моменты инерции системы
При замене реальной крутильной системы упрощенной рас
четной системой требуется соблюдение равенства кинетически:
энергий, действительных масс крутильной системы и заменяющи:
их сосредоточенных масс.
Для практического выполнения этого требования необходимс
знать моменты инерции элементов исследуемой системы.
Приемы определения моментов инерции рассматривание!
ниже.
') Существует множество формул для определения приведенной длины
лена (в том числе формулы Гейгера - Дмитриевского, Зеельмана, Хольц,
Нормана и Стинсона, две формулы Тимошенко), однако для авиацией,
валов они не дают лучших результатов. I
€6
Момент инерции колена относительно оси вращения
В том случае, когда конструкция коленчатого вала известна
но чертежам, моменты инерции шеек относительно оси вала
подсчитываются аналитически, а щёк—графическим путем.
1. Момент инерции коренной шейки
4,,,= 7 rf/)4 О» см сек-),
зтесь у—удельный вес материала вала (к^сл3); .
£—ускорение силы тяжести (см/сек2).
2. Момент инерции шатунной шейки относительно оси колен-
чатого вала подсчитывается как момент инерции шатунной шейки
относительно собственной оси плюс произведение массы шейки
на квадрат расстояния от оси вала до центра тяжести шатунной
шейки.
1ШШ=~^D,2lulR2
или
U, = -g- £9 +8 Я21 •
Иногда учитывают момент инерции масла, заполняющего рас-
точку шатунной шейки.
3. Для того чтобы вычислить момент инерции щеки относи-
тельно оси коленчатого вала следует разбить щеку цилиндри-
ческими сечениями, концентричными оси вала, на отдельные эле-
менты, массу каждого элемента умножить на квадрат расстояния
то оси вала и просуммировать эти произведения.
Для этой цели:
а) выполняю^ чертеж половины йтеки в двух проекциях
(фиг. 30), (если щека несимметричная, то выполняют полный
чертеж ее);
б) из центра вала проводят ряд дуг от контура до оси сим-
метрии и прямые 1—1, 2—2, 3—3...
в) измеряют длины дуг 5 и на другой проекции соответ-
ствующие толщины щеки А;
г) определяют площадь каждого сечения щеки f=Sh (см?) и
строят кривую / (заметим, что спланиметрировав эту кривую,
мы получили бы объем половины щеки).
Для определения момента инерции щеки каждую ординату
этой кривой надлежит умножить на квадрат расстояния орди-
наты до оси Y. Для этой цели используется следующий графи-
ческий способ.
1. На произвольном расстоянии X от оси ординат проводится
Прямая АА.
67
Фиг. 30
68
/М3 9
\Х/ '
2. Через точку b кривой / проводят горизонталь до пересе-
ления ее с прямой АА в точке а'.
3. Соединяют а' с началом координат О и фиксируют точку
пересечения луча с прямой ВВ, обозначая ее Ь'.
Из подобия треугольников О а'А и ОЬ'В следует, что Ь'В —
ов '
^-а'А тгл-f но, так как ОВ = г; ОА = Х- и а'А — ЬВ, то
ОА
Ь'В = ЬВ~.
Проводя построения по пунктам 2 и 3 для точки Ь', находят
точку Ь". Из подобия треугольников Оа"А и ОЬ"В
Ь"В = Ь'В^=ЬВ
Si
Повторяя такие же построения для целого ряда точек кри-
вой /, получают кривую //.
Очевидно, что при пользовании указанным графическим ме-
тодом каждая ордината кривой 1 оказалась не только умножен-
ной на свое собственное значение г’, но и разделенной на вели-
чину X*.
Поэтому надлежит момент инерции щеки определять по фор-
муле:
Л = 2-?-№/7,
здесь F—площадь, ограниченная кривой II.
Этим же методом определяют момент инерции противовесов
1„р, если формы их сложны и не удается разбить противовес на
небольшое число геометрически простых тел, момент инерции
которых определяется аналитически.
Итак
= + + + * (24)
В том случае, когда в распоряжении имеется коленчатый вал,
можно определить момент инерции колена, воспользовавшись
прокачкой вала на двойном подвесе (фиг. 31).
Для этого выводят систему из состояния покоя, поворачивая
вал относительно его оси на малый угол а, и затем отпускают.
>) Полезно заметить, что. продолжая подобные построения, легко найти
отрезки
69
Система начинает колебаться. При повороте вала на угол
нити подвеса отклоняются от вертикали на угол 0.
Заменяя в силу малости углов синусы углами, получим
Фиг. 31
Ф=ву.
откуда
Если вес вала обозначит;
через G, то восстанавливаю
щая сила будет -у Ор.
Диференциальное урав
нение движения системь
имеет вид
24р4^_/а’
здесь /—момент инерции си
стемы относительно оси ко-
лебания, равный искомому
моменту инерции вала 1ц
плюс момент инерции пере-
кладины подвеса 1„ (известная постоянная приспособления).
Исключая из уравнения р, получим:
} г bi Г'
Т"-----ь
и окончательно
а + —
1 G _
4 I I “ = °-
(25;
Как известно, такое уравнение описывает простое гармони-
ческое колебание с периодом
4/7
Об3'
Замерив по секундомеру период колебаний подвеса с валом,,
определяют из последней формулы момент инерции 7, зная ко-
торый, находят 1в = 1—1„.
Момент инерции одного колена определяют по формуле: ’
/в—
i
70
i де 4 момент инерции носка коленчатого вала (вычисляется
аналитически);
i — число кривошипов вала.
В качестве другого способа определения момента инерции
коленчатого вала можно рекомендовать прокачку на ножах
(фиг. 32).
Пренебрегая сопротивлениями (трением в опорах и пр.), по-
лучим, что вал колеблется под действием восстанавливающего
Фнг. 32
момента Gx, равного при малых колебаниях G
Этот мо-
мент вызывает угловое ускорение пропорциональное 1В "
Диференциальное уравнение колебания вала будет:
А 4 ’
Замерив с помощью секундомера период колебаний, по послед-
ней формуле вычисляют момент инерции коленчатого вала.
Прокачкой на ножах определяют также момент инерции
винта.
71
Шатун
Для того чтобы определить момент инерции массы, которая
при крутильных колебаниях вала создает тот же эффект, что и
шатун, предварительно производят разнос масс шатуна.
Шатун совершает сложное плоское движение, при котором
возникает: сила инерции
P,~Mjs
и момент сил инерции
здесь: М — масса шатуна;
js — ускорение центра тяжести шатуна;
/, — момент инерции шатуна относительно оси, перпен-
дикулярной к плоскости движения и проходящей
через центр тяжести;
р — угловое ускорение шатуна относительно этой оси.
Очевидно, такую же силу и момент будет иметь любая систе-
ма материальных точек, жестко связанных между собой и со-
вершающих движение в плоскости движения шатуна, если вы-
полняются следующие условия:
1. Масса шатуна равна сумме масс системы.
2. Центры тяжести шатуна и системы масс совпадают во все
время движения.
3. Моменты инерции шатуна и системы масс равны, и угло-
вое ускорение шатуна относительно оси, проходящей через его
центр тяжести, равно угловому ускорению системы масс отно-
сительно этой же оси.
Заменяя шатун двумя массами (фиг. 33), одна из которых Мв
сосредоточена на оси шатунной шейки, а другая на расстоя-
нии х от центра тяжести шатуна, определяют неизвестные MBt
М„ и х из трех сформулированных выше условий, которые
в данном случае приобретают вид:
Мх + Мв — М-, (29)
Мх - х — Мв о = 0; (29а)
Мх - х* + Мва? = /= /Ир1 (296)
(Р — радиус инерции шатуна).
Система заменяющих масс расположена так, что равенство
угловых перемещений выполняется во все время движения.
Для определения х умножим уравнение (29) на а и сложим
с уравнением (29а)
| Мха 4- Мв а — Ма
Мхх — Мва — Q
Мх {а 4- х) — Ма
72
отсюда
Л1Х =
Ма
а + х
Подобным образом находим Мв =
Мх
а+ х '
Подставляя эти выражения в уравнение (296), получим
I
Мах2 Мха1 ... , р2
—; 1-------— Мрг или ах = р3 И X — —
а +х а + х г г а
Подставляя найденное значение х в уравнение (29а), получим
а3
Мх~,Мв и, наконец, подставляя последнее выражение в ура-
внение (29), находим
а2
Mt = M-P—^ ;
х а* + ра
МВ = М-^
Фиг. 33
/
Итак, шатун можно совершенно точно в динамическом отно-
шении заменить двумя массами Мх и Мв, однако практически
такая замена неудобна, так как формулы, определяющие закон
движения точки М„, сложны. Обычно шатун заменяют двумя
массами, одна из которых Мв помещается на оси шатунной шей-
73
ки, а другая М'п на оси поршневой головки шатуна. Величины
этих масс определяют из первых двух условий эквивалентности
М'п + Мв — М- ’
М'пЬ — Мв • а — 0,
откуда
М'п — М-^-\ Мв—М~.
л-t L,
При таком разносе силы инерции шатуна и заменяющих масс
совершенно одинаковы, но моменты сил инерции не равны, так
как ие удовлетворено третье уравнение.
Величина погрешности
~ {M'nb2 + Л)ва2)1? = [4- Afabjfi (31)
невелика — обычно составляет всего несколько кгм и в инже-
нерных расчетах не учитывается. »
При разносе масс механизма с прицепными шатунами сна-
чала производится разнос масс прицепного шатуна, а затем раз-
нос приведенного главного шатуна. Приведенным главным ша-
туном называют собственно главный шатун с пальцами прицеп-
ных шатунов плюс массы Мв от прицепных шатунов, отнесен-
ные к осям проушин.
Практически определение масс, отнесенных к поршневой и
шатунной головкам, можно произвести на весах для взвешива-
ния. Головки шатуна помещаются на чашки двух весов, кото-
рые одновременно при этом должны быть уравновешены. Вес
гирь, уравновешивающих весы, на которых лежит поршневая
головка, является весом частей шатуна, отнесенных к оси порш-
невого пальца. Вес гирь на других весах является весом частей,
отнесенных к оси шатунной шейки.
Другим лучшим способом в отношении точности полу-
чаемых результатов является способ определения центра тяжести
шатуна путем прокачивания на ножах. Шатун прокачивается
дважды. Сначала нож устанавливается в одной, а затем в дру-
гой головке. По данным прокачек составляются два уравнения,
из которых определяется положение центра тяжести шатуна и
момент инерции шатуна относительно оси, перпендикулярной
плоскости качания шатуна и проходящей через центр тяжести.
/' =------—-------
358000 ’
1 . X2
(30)
(32)
358000
Н*
(33)
74
здесь: Н— число прохождений шатуна при колебаниях через вер-
тикальную плоскость в минуту. Длина L' и Г в санти-
метрах (фиг. 33).
G — вес шатуна в кг.
Если имеется только чертеж, то вес шатуна приходится опре-
делять, разбивая шатун на ряд элементарных тел. Положение
центра тяжести шатуна может быть в этом случае определено,
например,методом веревочного многоугольника.
Момент инерции массы Мв, отнесенной к оси шатунной шей-
ки, относительно оси коленчатого вала равен .Му/?’; масса М'п
складывается с массой поршня.
Поступательно движущиеся массы
Суммарную массу поступательно движущихся частей в одном
цилиндре заменяют некоторой массой Мап, сосредоточенной на
оси шатунной шейки. Величина Мэ„ определяется из условия
равенства кинетической энергии этой массы Тв среднему значению-
кинетической энергии поступательно движущихся частей Г,р.
Т,= Тер;
т ы
здесь — угловая скорость коленчатого вала.
Кинетическая энергия поступательно движущейся массы равна
~2
Как известно, скорость поршня нормального кривошипно-шат> н-
ного механизма может быть определена по приближенной фор-
муле
v R&
здесь: « = и>/ — угол между кривошипом и осью цилиндра Х = у-
L — длина шатуна.
Среднее значение кинетической энергии за один оборот вала
2п 2г
1 (* v2 MnR3^ Г I , X _ * ,
I Мп 9 (1а= - Sin а + „ sm2a «7а;
f £ ft ♦* I 1 л* /
о о’
2г.
д2
insa —— sin® 2а + X sin a sin 2а
75 ►
2«
“ Г А3 Jk4 1
11 COS 2а + — COS 4а 4- к cos а — kcos3«|rfa,
но
“2 j
О
2к
/ cos па da = 0 при п любом целом числе. Поэтому
о
ср
2г
-Мп^
О
1 / к2 \
4 \ 4 /
Отсюда
^•л — 2 I 4 ) ’
(34)
1
Эта же формула обычно применяется, хотя и с меньшим
основанием, для определения Мэп в случае прицепного шатуна,
так что, если на одну шатунную шейку работает несколько ци-
линдров Z, то масса, заменяющая поступательно движущиеся
части во всех Z цилиндрах, будет ZM
Момент инерции этой массы относительно оси коленчатого
вала равен ZM^R*.
Итак, окончательно, приведенный момент инерции колена, за-
меняющий собственно колено и связанные с ним массы шатунов
и поршней
Г 7 / 12 \1
Л4В+ ~МП(1 + ~ /?а. (35)
§ 10. Редукторные системы
Если исследуются крутильные колебания редукторного мо-
тора, то редуктор и коленчатый вал приводятся к одному обще-
му валу постоянного сечения. Схема редуктора и заменяющей
его системы показаны на фиг. 34а и б.
Условием эквивалентности масс является: равенство момен-
тов сил инерции заменяющих масс моментам сил инерции фак-
тических масс редуктора.
Если при повороте коленчатого вала на угол v вал винта по-
ворачивается на vro.i <f>B (т. е. передаточное число редуктора
-
i= , то момент сил инерции винта относительно оси вала
винта равен
Л4,,=/,<р, = /,йр.
Этот же момент относительно оси коленчатого вала благо-
даря наличию редуктора будет равен MJt • i = //’<?.
76
С другой стороны, по условию Mjei должен быть равен мо-
менту сил инерции заменяющей винт массы
4b?’
отсюда
. 4о=4»2- (36)
Аналогично для ведомой шестерни редуктора / шП~ fj*.
Таким образом, приведенный момент инерции обеих шестерен
редуктора
= (37)
Длина вала между приведенными массами
/0 определяется из условия
заменяющего и действи-
тельного валов относи-
тельно оси коленчатого
вала.
Обозначим крутиль-
ную жесткость вала ре-
дуктора k,. Приложим к
коленчатому валу момент
Мкв. После шестерен ре-
дуктора возникнет мо-
лл 1
мент Мк, -j-, вызываю-
щий закрутку вала винта
на угол <р,. Отсюда
7И,, = Л/р/ = A,<pi3.
Этот же момент Мк,
закрутит заменяющий
вал, жесткость которого
обозначена на угол <р
Мкв - ^«0 ?5
отсюда
kM = k, i2 (38)
и
редуктора /,0 и
равенства моментов сил упругости
Фиг. 34
так как передаточное число редуктора авиационного двигателя
всегда меньше единицы, то /Л</,; и k^<kr
Те же самые результаты легко получить, если вместо равен-
ства моментов упругих сил и моментов сил инерции редуктора
77
и заменяющей системы потребовать равенства кинетических энер,'
гий фактических и заменяющих масс и равенства потенциальны^
энергий действительных упругих элементов редуктора и заменяю.,
ацих участков расчетной системы.
Равенство кинетических энергий: Н
/ 'L1 / 2
2 “ 2' ’ ,
о 1 куда 1л = 1.г, так как .* — г.
Равенство потенциальных энергий: I
Л,?.1 _ I
2 2’ 1
•откуда —
Редуктор с амортизационными пружинами I
(установленными без предварительной осадки) *)
В случае применения редуктора с пружинными пакетами рас-1
четная схема отличается от схемы, полученной ранее наличием
упругого участка между ведущей шестерней (к которой отно-
сят зубчатый венец ведомой шестерни) и барабаном упругой
шестерни редуктора (фиг. 35). Жесткость на кручение этого уча-
') При установке пружин с предварительной осадкой возникает совер-
шенно особый случай.
78
•тка определяется из условия равенства потенциальных энергий
дрн деформации пружин и этого участка приведенной системы.
Пусть knp кг'см— жесткость каждой пружины, п — число
пружин, р — расстояние от оси пружин до оси вала винта.
Г Потенциальная энергия пружин при повороте барабана упру-
гой шестерни редуктора относительно ее зубчатого венца на
угол <?, равнг лЛяр(р%)! _ nk„pp9i^
2 ~ 2
k„ • ф*
Потенциальная энергия заменяющего вала -"^—.отсюда
knpo=knpn?i\ (39)
Планетарйый редуктор
Совершенно таким же способом, как и в предыдущем случае,
планетарный редуктор (фиг. 36) заменяется прямолинейным ва-
лом и двумя сосредоточенными массами,
из которых одна имеет момент инерции
lti- и заменяет собой винт, а вторая
заменяет комплект шестерен редуктора.
Ее момент инерции
4 = n/ei* + lpi\
щесь: момент инерции ведущей
шестерни относительно оси
вращения;
п — число сателлитов;
1С — момент инерции сателлита
относительно своей оси;
q — передаточное число от ве-
дущей шестерни к сателлиту;
1Р — момент инерции всего ком-
плекта планетарных шесте-
. рен вместе с корпусом са-
теллитов относительно оси
вала;
i — передаточное число редук-
тора.
Действительно, кинетическая энергия
редуктора равна
4У , «4'fZ , 4®,3
~2 2 + 2
Фиг. 36
где <?, ©„ — угловые скорости коленчатого вала, вала
и сателлита относительно собственных осей. Кинетическая
г 4?’
гия массы с моментом инерции /0 равна - ,
винта
энер-
79
отсюда
/о — 4/ + И4'12 + А>*2’
так как ...
»,=»<₽; ?с —Л?-
Приведенная жесткость вала винта, как и в предыдущей 3aJ
даче, определяется по формуле (38).
Жесткость редуктора в действительности меньше жесткости,
подсчитанной по этой формуле, вследствие податливости шесте-
рен и осей сателлитов. Поэтому в формулу (38) вводится по-
правочный коэфициент ф = 0,5 -s-0,55 (по Заикнну А. Е.). учиты-
вающий податливость шестерен и опор сателлитов.
Бинт
Моторные* массы
Редуктор ,-----------Л----------.
Дг Рз Ра Ps Рв Р? Рв
J- (кг см сек2}
К- (кг см) 106
Мотор Л 7а, /«.../g ^8*^4.‘^7 Л8 /.
ВК-105 119 —3,25 1,86 13,44 0,976 13.44 0.1263 2.44
АМ-38 140 —3,5 1,694 21,9 1.465 19,0 0,266 39.61
Мерлин XX . . . 40 4,94 0,496 3.6 0,748 10,3 0,049 10,6
ДБ-601Е 175 9,32 j 0,99 1,75 1.4 17,0 0* 0*
Фнг. 37.
Приведение передачи к нагнетателю выполняется таким же
способом, как и приведение редуктора. Так как в данном слу-
чае ^нагн ^1. т° приведенная длина передачи к нагнетателю и
приведенный момент инерции нагнетателя много больше действи-
тельных величин.
Для иллюстрации ниже приводятся расчетные системы некото-
рых авиационных двигателей (фиг. 37, 38 и 39). В таблице 8
даны пределы значений чисел свободных колебаний крутильных
систем авиационных двигателей.
* Двигатели ДБ имеют нагнетатель, приводящийся через гидравлическую
муфту, <м. § 25.
Я пл и сон F-3R и E-fy
](кгск)
Винт
f-3R 866
Редуктор
0.5435
м „ „ Нагнетотел.
моторные массы
0,812 (каждая) Демпфер
ц(кг сн>)106
435 Т 298 13.05 13,05 13,05 /305 1305 247 f 0197
5.73 1 021 13.05 /305 13.05 1305 13.05 1 0197
0,812 /каждая)
0,938
[-У 138
59В
Фиг. 38
Винт
)(кгсмсек
0359
Я л п и с о н С /5
НогнетотеЛЬ
Л (кг chi)10'
Редуктор
1.42
0,1055
\!2,95 /295 t295\l295\1295\ 165
731
88,6
40 <40 <422 40 <02 QjiR
Моторные массы
О.Зчб (каждая)
Фиг. 39
&
Таблица 8
Двигатели без нагнетателей
кол cI МИИ п гп мин
5000—7500 15000-20000
Двигатели с нагнетателями
КО.1 Пс1 МИН КОЛ ЯгП мни КОЛ
700 - 1600 2600-7500 150(0—28000
двигателей с нагнетателями величина пс\ в основном опре-
^Ляется жесткостью передачи к нагнетателю.
6 В V
о. Кириченко
81
Нижний из указанных в таблице предельных значений пс[
относится к двигателям, имеющим в передаче к винту рессор
или редуктор с амортизационными витыми пружинами. Верхни]
предел значений плп относится к звездообразным двигателя*
В таблице 8а приводятся конкретные значения чисел собствен
ным колебаний крутильных систем ряда двигателей.
Таблица 8
Двигатели без нагнетателей
Дни! атечь „ кол мин кол с11 мин Примечания
М-17 5670 Двигатели ДБ имеют на- гнетатель, приводящий- ся через гидравлическую муфту (см. § 25) 1 1
АМ-34 7180 1
ДЬ-601Аа 6500 । 19900 •
ДЬ 601Е 6960 19200
Двигатели с нагнетателями
Двигатель кол "ci мин „ кол МИН кол е1П мин Примечания.
ВК-105 5500 Пружины редуктора защемлены
AI1I-82 1520 60U0 26000 Протн вовесы защемлены 1
АШ-82 <реЛ\ 1520 5160 27620
М-88 5450
Мерлин XX 705 5960 19900
Аллисон F-3R 1640 5620 20120
Аллисон Е-4 1120 2980 19900
Алжсон С-15 1035 2585 15350
12 »
ГЛАВА III
ВЫНУЖДЕННЫЕ КРУТИЛЬНЫЕ КОЛЕБАНИЯ
В этой главе рассматриваются вынужденные крутильные ко-
лебания различных систем, проводится анализ крутящих момен-
тов, вызывающих колебания, выявляются условия резонанса и
величины резонансных амплитуд. Далее кратко описываются
способы экспериментального исследования крутильных колеба-
ний и аппаратура, применяемая для этих целей.
В заключение определяются напряжения, вызванные крутиль-
ными колебаниями, и рассматриваются способы борьбы с опас-
ными резонансами. Определение резонансных амплитуд прово-
зится на основании энергитических соотношений, при подсчете
которых исходными являются формулы, данные в §11.
§11. Работа, совершаемая гармоническим моментом при
гармоническом движении
Пусть на тело, совершающее гармонические крутильные ко-
лебания <р =* Ф sin pt, действует гармонический момент М =
= С sin (pt + y) той же частоты р, что и перемещения, но со сдви-
FO.M по фазе на угол у. Вычислим работу, совершаемую момен-
* 2я
гом М за период Т= .
Элементарная работа момента
= ^±dt.
dt
Работа за период
Т 2л
о и
d<o
иодставля я значения М и = Фр cos pt, получим:
2к 2г.
W = СФ f sin (pt + у) cos pt-d (pt) = СФ j' (sinpt cos ~ +
о 0
6* 83
+ cos pt sin 7) cos pt • dipt) = СФ cos ( J sin pt cos pt • d (pt) +
0
2n
+ C'i’sin-[|"cos3p/-rf(p/),
b
HO
2n 2k
/1 1 Г
sin pt cos pt d (pt) = % I sin 2pt d (2pt) =
о о
2k
= — -r- cos 2pt । = 0,
4 |
0
2x 2k
j cos2 pt-dipt) = ^-~ I'cos 2pt• d(2pt) +
и 0
2k 2k
+ ^J d^= |Sin2p^ + =K.
о 0
Следовательно^ работа момента за период:
W= тгСФ sin 7. (40)
При 7 = 90° работа получается наибольшей и равна лСФ.
При 7 = 0° работа момента также равна нулю.
На фиг. 40а изображен график перемещения момента М,
имеющего ту же фазу (7 = 0). Когда тело удаляется от положе-
ния равновесия, что соответствует участку графика от точки А
до В, момент действует в сторону перемещения и работа мо-
мента положительна. Участок графика от В до С соответствует
обратному направлению движения тела к положению равнове-
сия. На этом участке момент сохраняет прежнее направление
действия (хотя и меняется по величине) и поэтому работа мо-
мента—отрицательна. В силу симметрии кривых М и <р относи-
тельно точки В положительная работа момента на участке А—В
равна отрицательной на участке В—С и в целом за я, а значит
и за 2к равна нулю.
На фиг. 406 изображен график перемещения и момента М,
опережающего по фазе перемещения на 90°. Из графика оче-
видно, что направление перемещения и направление действия
момента в данном случае все время совпадают, поэтому работа
получается наибольшей.
Рассмотрим другой весьма важный случай, когда на тело, со-
Фиг. 41
Фиг. 40
скоростью пр и тр
ii *1», вращающихся с различной угловой
соответственно (фиг. 41).
Периодом рассматриваемого процесса очевидно следует на-
звать время, в течение которого совершается полный поворот
одного вектора относительно другого. Это время равно част-
ному от деления 2к на относительную скорость векторов, т. е.
на разность частот пр—тр
Т—-----—-----.
(п—т)р
Вычислим работу, которую совершает момент за время 7".
Т 2г.
о о <
Подставляя значения М и = Фтр cos (mpt + е), получим:
2«
W= sin nptcos (mpt + г.) d [(« — m)pt],
0
VC-
85
и так как
то
cos {nipt + г) = cos mpt cos a — sin mpt sin a,
2x
cos ej sin npt cos mpt d[(n—m)pt)—
0
- sin s
j sin npt sin mpt-d[(n — m)pt] ,
HO
U7 — . ФтС_
п — т
о
sin npt cos mpt = у sin (n 4- m)pt + -y- sin (я — m) pt,
sin npt sin mpt = ^-cos (n—m)~ cos (nm- P*-
Произведя подстановку tf* выполняя интегрирование в указав,
ных пределах, убеждаемся, что 1Г = 0, т. е. работа гармониче-
ского момента, действующего на тело, совершающее гармони-
ческие крутильные колебания с частотой, отличной от частоты
момента, равна нулю, если промежуток времени, в течение ко-
торого работа измеряется, содержит некоторое целое число пе.
риодов изменения момента и от него отличное целое число
периодов колебания.
§ 12. Вынужденные колебания системы с одной степенью
свободы при гармоническом возмущении и отсутствии 1
сопротивлений
Пусть на систему (фиг. 42), состоящую из упругого вала,
один конец которого заделан, а другой несет диск с моментом
инерции /, все время действует гармонический момент внешних
сил
М =Ccos Qt.
Сохраняя старые обозначения, составим диференциальнос
уравнение движения диска /, считая, что сопротивления отсут-
ствуют и момент инерции вала равен нулю
В рассматриваемом случае к диску приложены два внешних
момента, возмущающий момент М и восстанавливающий момент
упругих сил — k<f, действующий всегда в сторону, противополож-
ную перемещению. Совместное действие этих моментов М *
—вызывает угловое ускорение <?, пропорциональное моментУ
инерции диска /
/И — =
(41)
>6
ИЛИ
/ф 4- A© = С cos Qt.
Разделив уравнение почленно на / и обозначив
А 2 С
-Т=Р\ У =
получим:
<р+р-^ у cos Ш.
(41а)
Общий интеграл этого уравнения, как известно из теории
швейных диференциальных уравнений, состоит из общего
интеграла уравнения ©4-р2? = О, который, как уже выяснено., имеет
вид:
<?1 = A cos pt А- В sin pt
и частного решения исследуемого уравнения (41а). При И А= р
частное решение будем искать в виде:
<f2 = FcosQt. (42)
Для определения F найдем <р2 и подставим ©2 и в уравне-
ние (41а)
ф3 = — 22Fcos
— ‘J2/7 cos S.7 + рг cos Qt — q cos 2/.
Так как требуется, чтобы по-
следнее равенство выполнялось при
любом значении времени t, то значит
— Q-F+p-‘F — — q,
откуда
р —___________________
р* _ <ja
и *
/
Итак, общий интеграл исследуе-
мого уравнения
? =Т1+?2 =
= A cos pt 4- В sin pt 4- cos
В рассматриваемом случае коле
стыми гармоническими. Они складываются из двух составляю
Щих колебаний, имеющих разные частоты.
87
Первое имеет частоту свободных колебаний р, зависящую
только от свойств самой системы. Второе—частоту возмущаю
щего момента 2.
Рассмотрим подробнее новую составляющую
с2 — f-'cos Qt.
Амплитуда F может быть представлена в следующем виде
Я
р"
F— ]_ 2а ‘
г ' Я С С
Согласно ооозначениям -~= г- в свою очередь -г- — уст по»
Р п К
определению. Теперь числитель выражения, определяющего ам-^
плитуду F, приобретает ясный физический смысл: это закрутка;,
которую получил бы вал под действием статически приложен*- !
ного момента, равного по величине амплитуде возмущающегог!
момента.
Обозначая
Ч —----~д3- г (44))
1----
Р*
получим ,
Величина т( называется коэфициентом динамичности или коэфи-
циентом нарастания амплитуд и показывает во сколько раз боль-г
шими получаются деформации системы при динамической на-
грузке по сравнению со случаем приложения статической на-
грузки.
Коэфициент динамичности (фиг. 43) зависит от отношенияс
2 „ 2
—и изменяется в очень широких пределах. При увеличении — •
от нуля до единицы т( растет от 1 до +оо. При дальнейшем узелиг-
ченни — коэфициент ц от —оо стремится к 0.
Решение (43) уравнения (41а) было получено в предположе-
нии, что 2=*ьр Пусть теперь 2 = р. Будем искать частное реше-
ние в виде
®.а = F-t cos (pt — г). (45)
Для определения Лиг найдем-
□„ = —2Fp sin (pt — г) — Fp2t cos (pt — s)
88
л подставим и <ps в уравнение (41а). Получим
— 2Fp sin (pt — = g cos pt,
откуда
r
*“ 2 ’
(45a)
Частное решение уравнения (41a) при 2=jp имеет вид
at I . к \
— Yp cos ( Pf ~ 2 )' (456)
Следовательно, прн совпадении частот возмущающего мо-
мента и собственных колебаний системы с течением времени
амплитуда колебаний неограниченно возрастает. ‘Это явление
носит название резонанса.
При сколь угодно малых возмущениях система обязательно
должна разрушиться, если ее достаточно долго выдержать
в состоянии резонанса. Этот противоречащий опыту вывод по-
лучен потому, что не учтены в действительности всегда имею-
щиеся сопротивления.
Часто явление резонанса полезно используется для разных
специальных целей. Например, на принципе резонансной на-
стройки построены приборы для измерения частоты вибрирую-
щей системы—частотомеры. На этом же принципе базируется
устройство динамических демпферов — гасителей колебания
< см. § 23 и 24).
89
При динамическом возмущении в двух предельных случаях
система не будет колебаться:
1. Когда жесткость системы k = co,
. /Л
— = ОО и
при этом т( = 1 ( таг
С v
“О £ =° И Г =
как р =
действительно равна нулю. Однако в заделке системы будет
действовать момент внешних возмущений, т. е. фундамент кон
струкции полностью воспринимает внешнюю нагрузку.
Практически построить очень жесткую систему во многиз
случаях представляется затруднительным. Если же систем
спроектирована так, что работает в дорезонансной зоне (о <—<1)
го амплитуда колебания всегда больше деформации от стати
ческого приложения нагрузки
2. Когда жесткость системы k = 0, при этом = 0 (так как
2 \
р = Ои — = ooj сколь бы велика не была величина возмущения
Этот случай имеет громадное практическое значение, так как
существенно снизить жесткость при проектировании удается до
вольно простыми приемами.
При отсутствии сопротивлений момент сил упругости строю
пропорционален деформации и при достаточном уменыпениг
жесткости (увеличении не только амплитуды колебаний сн
стемы могут быть уменьшены во много раз по сравнению с де
формацией от статической нагрузки, но и нагрузка на фунда
мент получается меньше статической. Именно это явление ис
пользуется при создании всевозможных амортизаторов и раз
личных приборов для измерения амплитуд и ускорении колеба
тельных движений — виброметров и акселерометров.
Краткое описание устройства прибора для записи амплиту/
крутильных колебаний—торсиографа дано в § 18.
§ 13. Вынужденные колебания системы, имеющей одну
степень свободы, при гармоническом возмущении
и сопротивлениях, пропорциональных скорости
Рассмотрим колебания той же системы (фиг. 42), учтя сопро
гивления и считая их пропорциональными скорости колебатель-
ного процесса.
В любой заданный момент времени t на диск действуют:
1. Возмущающий момент Л1 = С cos Qt.
2. Момент сил упругости — k<f.
3. Момент сил сопротивления—^.
Совместное действие этих моментов создает угловое ускоре-
ние диска % пропорциональное его моменту инерции /
90
Л4 — — ;<р =/» (46> ,
или
•$ 4- 2л<р + рау = q cos 9Л, '(46а )
где
Q ; з * С
2rt=j; p2=--.q=
Общий интеграл этого линейного диференциального уравне-
ния второго порядка, как известно, есть сумма общего инте-
грала этого уравнения без правой части (20) и частного реше-
ния уравнения (45а).
Общий интеграл уравнения (20) нами уже был порчен
<б1 = Ф1е-л’cosQjjf+f) и представляет закон свободных колебаний
рассматриваемой системы с сопротивлениями.
Частное решение <?2 будем искать в виде
'i2 = F3cos (S£—г), (47)
где а—сдвиг фазы возбуждающего момента относительно фазы
вынужденных колебаний.
Для определения/^ и е найдем <р2 и <р2 и подставим в иссле-
дуемое уравнение
= — /га2 Sin (2/ — г),
<р2 = —F2Q* COS (2/ — г),
—22Facos ('-It—г)—2«2Д, sin(2#—е) + р2Л2 cos (2/— г) — q cos lit
или
F„ (p2 — 22) cos (2/—$) — 2л2/2 sin (2Z—г) = q cos 2/.
Правую часть последнего равенства представим следующим
образом:
qcos Qt — qcos[(Qt — а) + sj =•= <7 cos(Qt—e)cose—
— q sin (Qt—s) sins.
Теперь
F2 (p2 — 22) cos Qt — 2nF.,Q sin Qt — q cos (Qt—s) cose —
— q sin (2/ — s)sin s.
Для того чтобы уравнение удовлетворялось нри любом зна-
чении времени /, нужно, чтобы коэфициенты при sin (2/ — е) и
cos (2/—s) в левой и правой частях уравнения были бы равны
Друг другу, т. е.
/-2(p2-22) = 9coss ( ,48)
2nF„Q — q sin s f
91
Возведя в квадрат каждое уравнение и складывая их, пол'
чим после преобразований
Ч
Д9 = ,_______________
1'(р*—Q*)a+4n*Ql
Деля второе уравнение на первое, найдем
2л2
g * р~ — 2' ’
Частное решение приобретает вид;
Ч
cos — з).
•’ | (р»_ 2«)2 + 4Я«О2
Общий интеграл исследуемого уравнения
(49]
(50)
(51)
т = Чч + ?4 = Ф1<? "'cos(/>/4-t)+ — ^_^===r-cos(2Z—s). (52).
г (Р2—22)2+4и,25!
В силу того, что первый член правой части последнего ура- i
внения быстро убывает с течением времени, интерес предста-
вляет только второй член, который иногда именуют стацио- I
парной частью вынужденных колебаний. С момента времени,
когда можно считать «]=0 колебательный процесс называют
установившимся.
Исследуем стационарную часть вынужденных колебаний не- 1
сколько подробней.
1. Частота стационарной части вынужденных колебаний равна
частоте возбуждающего момента.
2. Амплитуда F2 может быть представлена в виде
—коэфициент нарастания ампли-
туд или динамический коэфициент.
. . 2
I рафик изменения т, в зависимости от отношения частот —
при различных величинах сопротивления представлен на фиг. 44.
Из рассмотрения графика видно, что амплитуды вынужденных
колебаний сильно зависят от величины сил сопротивления. При
наличии затухания (и=#=0) коэфициент нарастания амплитуд -q
92
рСегда меньше, чем в случае, когда затухания отсутствуют (вто-
рой член в знаменателе положительная величина) ’)•
Влияние сил сопротивления на амплитуды колебания неоди-
наково при различных отношениях частот возбуждения и сво-
бодных колебаний. При 2 <<С р, что соответствует очень жесткой
системе или очень низкочастотной нагрузке, равно, как и при
что соответствует очень податливой системе или очень
высокочастотной нагрузке, даже очень большие сопротивления
практически не сказываются на амплитуде колебания. Другими
словами, вдали от резонанса силы сопротивления проявляют себя
очень слабо.
При Q&p (резонанс и область отношения частот, близких
резонансу) сопротивления становятся особейно ощутительными
/ . S« \
| член 1--=- мал .
\ Р /
При наличии сопротивлений (га=#О) амплитуды резонирующей
системы не обращаются в бесконечность и зависят от величины
возмущений, сопротивления и частоты свободных колебаний.
Действительная инженерная конструкция, в которой непре-
менно имеют место сопротивления, не обязательно должна раз-
рушиться, если мы заставим работать ее в состоянии резонанса.
Резонанс будет опасным лишь в том случае, если резонанс-
ные амплитуды превосходят допустимые из условий прочности.
Из графика (фиг. 44) видно, что максимальные амплитуды коле-
баний с сопротивлениями имеют место не при Q=p, но смещены
!) Этот вывод нельзя распространить на динамический коэфициент сил,
чередающихся от колеблющейся массы через упругую связь на фундамент.
93
р
несколько в сторону отношений <1. Однако разница в ве-
личинах максимальных и резонансных амплитуд невелика и это
дает основание считать в инженерных расчетах резонансные
амплитуды максимальными.
3. Перемещение (угол закрутки вала) сдвинуто по фазе отно-
сительно возмущающего момента на величину—г, зависящую от
частот собственных и вынужденных колебаний и от величины
сопротивлений (фиг. 45).
Положив, что сопротивления малы [в формуле (49) л=0],
получим, что до резонанса (Q<p) сдвиг г —0, после резонанса
сдвиг фаз псУчти равен при проходе через резонанс е
резко меняется. При отсутствии сопротивлений (н = 0): до резо-
нанса s = 0, после резонанса s = при резонансе s= , что
видно из формулы (456).
Очень важно отметить, что при колебаниях с сопротивле-
ниями при резонансе, вне зависимости от величины сопротивле-
ний, tgs= 4-^' И S=Q -
Все сказанное наглядно иллюстрируется векторными пред-
ставлениями (фиг. 46а)
Пусть вектор перемещений F., в данный момент времени на-
правлен вертикально вверх. На диск действуют четыре момента:
восстанавливающий момент или момент сил упругости—ky, век-
тор которого р’Р., должен быть направлен в сторону, противо-
положную перемещению; момент сил сопротивления—вектор
которого 2№F, направлен в сторону, противоположную скорости
(знак минус), т. е. составляет с вектором p2F., угол ! мо-
44
мент сил инерции—/с, вектор которого S28F, составляет с век-
jopo.M p2Ft угол к и, наконец, момент внешних сил М, вектор
которого q повернут относительно вектора перемещений F2 на
VI ол + $.
Для равновесия моментов, действующих на диск, необходимо,
чтобы сумма проекций векторов моментов на любую ось была
равна нулю.
Проектируя векторы на вертикаль, получим:
2aF3 + q cos s = p^Fv
Сумма проекций векторов на горизонталь дает:
2л2Д2 = q sin е.
Как и следовало ожидать, мы получили известные уже усло-
вия (48), из которых были определены и г.
При очень медленных колебаниях (2 = 0) момент сил сопро-
тивления, пропорциональный S, и момент сил инерции, пропор-
циональный 22, пренебрежимо малы. В этом случае на диск можно
считать действуют всего два момента М и —Ас (фиг. 466). Из
условия равновесия этих моментов е = 0.
С увеличением частоты колебаний 12 сопротивления возра-
стают и становятся заметными; еще быстрее возрастает момент
сил инерции. Очевидно, для того чтобы данный режим колеба-
ний был устойчивым, необходимо, чтобы между вектором пере-
мещений и вектором возмущающего момента был сдвиг фаз s>0.
При дальнейшем увеличении частоты 2 момент сил инерции
уравновешивает все большую часть момента сил упругости, а угол
s растет и все большая часть возмущающего момента уравнове-
шивает возрастающие сопротивления (фиг. 46в).
95
Наконец, при резонансе момент сил инерции становится рав-
ным восстанавливающему моменту, при этом сдвиг фаз е должен
, л
быть равным -g- и
возмущающий момент в точности равен и
уравновешивает момент сил сопротивления (фиг. 46г).
/2 \
При частотах более высоких I—>1 1 вектор момента сил
инерции возрастает быстрее, чем вектор момента сил упру-
гости p2F2, вследствие чего для равновесия необходимо, чтобы
сдвиг фаз е был больше (фиг. 46д).
Для очень высоких скоростей колебания момент сил
упругости ничтожен (так как мала амплитуда F3) по сравнению
с моментом сил инерции и в этом случае возмущающий момент
должен уравновешивать момент сил инерции, т. е. е = л (фиг. 46е).
Момент сил сопротивления также ничтожен, так как ничтожны
перемещения.
Для лучшего уяснения физической стороны явления приме-
ним энергетический подход к объяснению полученных результа-
тов.
При очень медленных колебаниях (2^0) возмущающий мо-
мент М находится в одной фазе с перемещением (е = 0) и, как
было показано в § 11, в этом случае за период никакой работы
не совершается.
При резонансе г = и величина работы, совершаемой воз-
мущающим моментом за период, равна ~CF2. Момент сил сопро-
тивления — сдвинут по фазе относительно перемещения на
—Амплитуда момента сил сопротивления равна и отри-
цательная работа, поглощаемая сопротивлениями за период,
равна ir£2F,a.
Остальные два момента, действующие на систему, никакой
работы за период не совершают, так как момент сил инерции
—/<? находится в одной фазе с перемещением, а момент сил
упругости—в противоположной фазе.
Отсюда следует, что при установившемся резонансном ре-
жиме необходимо, чтобы соблюдалось равенство между работой
за период моментов М и —5% т. е»
откуда
zCF2 = ^SF32,
На фиг. 47 представлено изменение работ возмущающего мо-
мента (прямая /) и сил сопротивления (парабола //) в зависи-
96
мости от амплитуд колебания. Точка пересечения прямой и па-
раболы определяет величину амплитуды, которая установится
при резонансе.
Этот энергетический ме-
тод определения резонанс-
ной амплитуды не представ-
ляет большого интереса
применительно к рассмат-
риваемой простой системе,
но оказывается чрезвычайно
полезным при расчете слож-
ных многомассовых систем.
При очень быстрых ко-
лебаниях (2~'^), как отме-
чалось выше, пренебрежимо
чалыми становятся моменты
сил сопротивления и упру-
гих сил. Остающиеся два
момента — <р 1 и М дейст-
Фнг. 47
вуют: первый — в фазе перемещения, а второй со сдвигом по
фазе, равным ~, и поэтому работы за период не совершается.
§ 14. Внешние возмущающиеТмоменты
До сих пор, разбирая задачу о вынужденных колебаниях
кручения, полагалось, что возмущающий момент меняется, сле-
дуя гармоническому закону. В действи-
Фиг. 48
тельности коленчатые валы авиационных
двигателей подвергаются действию момен-
тов, имеющих более сложный характер из-
менения во времени. Эти моменты вызы-
ваются: давлением газов в цилиндре Рг и
силами инерции поступательно-движущих-
ся масс кривошипно-шатунного механизма
Pj (фиг. 48).
Индикаторная диаграмма, полученная
экспериментальным или расчетным путем,
определяет характер изменения сил газа
во*времени или по углу поворота криво-
шипа.
Силы инерции поступательно движу-
щихся масс центрального кривошипно-ша-
тунного механизма определяются по при-
ближенной формуле:
Pj = —MnR<o2 (cos а + X cos 2a). (53)
Крутящие моменты от сил газа и сил
инерции поде штываются по формулам
7 В. Кириченко
97
MKpg = P,R,
где
т —р Sin(a+P)
3~ 3 cos р
Г =р Sin(a + p)
J 7 cos р
Как известно, всякая периодическая функция f(x), удовл<
сверяющая условиям Дирихле*), может быть представлена в вид
ряда
/(х) = Aq+Л, cos х + Д2 cos 2x+ds cos Зх+... |
Ч-А?! sinx + B2sin2x+Bssin3x+... /
или
f(x) = Ао + У, A, cos Кх+'£ВкsinКх... (55:
ь=1
Коэфнциенты ряда Ао, А, и Вк вычисляются по
Эйлера
'^0 — о
1
cos Kxdx
—к
Для получения формулы, определяющей Ао, нужно ряд п<
членно умножить на dx и проинтегрнрЪвать в пределах от I
до +«. Умножение ряда на cos Kxdx (К—произвольное целс
число) и интегрирование в пределах от —к до + к дает формул
для определения Ак, умножение ряда на sin/Cxrfx и интегрир*
ванне в тех же пределах дает формулу для определения Вк.
Подсчитав коэфнциенты Ао, Ак и Вк, обычно ряд записывал
•) Условия Дирихле состоят в том, что функция на участке, где она за*
няется рядом, должна быть ограничена и иметь конечное число экстремал
иых точек и точек разрыва непрерывности.
98
несколько более простой форме, объединяя гармоники одного
Грядка К
А к cos Кх + В„ sin Кх = Ск sin (Кх+
- г________ Ак
здесь = + tgK = -в-
Ряд приобретает вид:
f(x) = A9+-Cl sin (а: 4-рО+С’а sin (2а + Ра) + .. . + CKsin(A'A'+pK) =
I
£
= Ао + Y,Ck sin <^х+?*)•
i=i
Разложение в ряд Фурье крутящего момента производить,
пользуясь формулами Эйлера, не представляется возможным,
так как неизвестно аналитическое выражение подинтегральной
функции. Обычно крутящий момент задается в виде графика.
В этом случае интегрирование заменяется суммированием ко-
нечных разностей. Отрезок, соответствующий полному период}'
кривой крутящего момента, приравнивается величине 2~ и де-
лится на S равных частей (фиг. 49).
Коэфнциенты ряда подсчитываются по формулам Бесселя,
Чающим приближенное значение интегралов Эйлера.
I 7* 99
При выбранном значении 5 достаточно точно можно вычис-
, S
лить все гармоники до порядка A потому, что в периоде
эти гармоники будут характеризоваться шестью или больше
л
точкаvи основной кривой. Гармоники более высокого порядка
вычислять при таком делении кривой не имеет смысла,I
так как в период
2it
гармоники — попадает меньше шести точек
основной кривой и гармоника выявляется весьма грубо.
Тригонометрический ряд, заменяющий кривую крутящего мо-
мента от сил газа, сходится медленно, так как на протяжении
большем, чем половина периода, кривая моментов имеет орди-
наты, равные нулю. Это заставляет увеличивать число S; одно-
временно увеличивается объем счетной работы.
Существует большое число способов, облегчающих и уско-1
ряющих процесс анализа. Эти способы можно разделить на три
категории: механические, графические и аналитические—таблич-
ные.
Под механическими способами понимаются способы разложе-
ния с помощью специальных приборов, именуемых гармониче-
скими анализаторами.
Из графических способов следует рекомендовать, как лучший,
способ проф. Терских В. П.1). Способ основан на применении
специальных транспарантов. ,
Из аналитических—табличных способов следует выделить два:
1. Когда требуется определить коэфициенты рядал исходя не
из экспериментальной индикаторной диаграммы, а из расчетной,
удобно пользоваться таблицами, которые помещены в книге
проф. Неймана И. Ш. Эти таблицы позволяют с большей точ-
ностью определить первые 18 гармоник тангенциальной силы Г.
1) См. библиографический список в конце книги.
одного цилиндра четырехтактного двигателя с нормальным кри-
«ошипно-шатунным механизмом при степени сжатия е от 5 до 8
R 1 1
и А L °Т 3,2 Д° 4,2 ’
2. Весьма простыми и удобными являются таблицы, состав-
ленные Холмаковым И. И. Таблицы пригодны для разложения
-робой практически встречающейся кривой крутящего момента
и позволяют определить достаточно точно 8 первых гармоник.
Многочисленные результаты гармонического анализа кривых
крутящего момента от одного цилиндра показывают, что для
ориентировочного расчета могут быть использованы графики
типа, представленных на фиг. 50 или 51а и 516.
На фиг. 50 дана векторная диаграмма составляющих гармо-
нических коэфициентов сил давления газов для четырехтактных
Дизелей (диаграмма Терских В. П.). Начальные фазы векторов
приняты по отношению к ВМТ в процессе расширения. Враще-
ние векторов против часовой стрелки. На диаграмме в качестве
примера показано нахождение гармонической составляющей К —
= -g- при д = 8кг/сл2.
>01
На фиг. 51а и 516 даны коэфициенты для гармоническог
анализа кривой крутящего момента от газов в кг! см2 в завис
мости от среднего индикаторного давления pt для четырехтак
Фиг. 51а
ных двигателей легкого топлива. Для получения величин Ак и
надлежит определить по графикам значения ак
на радиус кривошипа R и площадь поршня Fn.
Для иллюстрации на фиг. 52 представлено
и Ьк
и умножит
разложение
кри
102
вой тангенциальных сил на 12 гармонических составляющих для
цилиндра четырехтактного двигателя легкого топлива.
Период кривой крутящего момента сил газа четырехтактного
дви- чтеля равен времени, соответствующему двух оборотам ко-
4 6,5
ленчатого паль. Первый гармонический член разложения имеет
период, равный периоду основной кривой. Второй гармонически!,
член имеет период, вдвое меньший и т. д.
В специальной литературе по крутильным колебаниям при-
103
104
нято порядок гармоники определять как отношение периода
чанной гармоники ко времени, соответствующему одному обо-
роту вала, а не ко времени цикла. Поэтому первый гармониче-
ский член разложения называют гармоникой половинного порядка,
второй гармоникой первого порядка и т. д. Появляются сле-
дующие обозначения гармоник /< = 0,5; 1; 1,5; 2; 2,5;...
Для двигателей двухтактных период кривой крутящего мо-
мента совпадает со временем, соответствующим одному обороту,
и поэтому дробных порядков в разложении не получается; К—
= 1, 2, 3, 4...
Период кривой крутящего момента от сил инерции поступа-
1сльно движущихся масс соответствует одному обороту вала.
Следовательно, гармоники момента сил инерции будут только
тех порядков, которые выражаются целыми числами.
Для центрального кривошипно-шатунного механизма, как из-
вестно, справедливы следующие выражения
Pj S’ — AW?“3(cosa-i-kcos 2а + ...).
Скорость массы Мн
V = —° (sin а + ^-sin 2а +.. . V
cos р \ 2 ]
Воспользовавшись этими выражениями и одним из равенств (54),
получим
— /Wn/?W(cosa + X cos 2a+., .)^sin a+ ~sin2a+.. .j
иди после преобразований
/к 1 3 Xs \
М..в . g? MnRW | -г sin a — sin 2a — к sin 3a-T sin 4a 4-... 1.
14 2 4 4 I
Подставляя вместо a его значение wt, получим
£?. MnRsw* (-^-sinwi— ^ sin2w/—Xsin3w^—^-sin4urf+... | -
14 Л 4 4 J
(58)
Приближенное выражение крутящего момента сил инерции
поступательно движущихся масс прицепного механизма имеет
вид !)
k=i
Мкр л MniRW (^А Тк cos K^t+^ВТк sin AW),
*=i
Мщ— поступательно движущаяся масса прицепного механизма.
--.-,--------
л ') Вывод формул, необходимых для подсчета Mkpji, см. И. 111. Нейман,
^•'намика авиационных двигателей, Оборонгиз, 1940.
105
Коэфнциенты АТк и ВТк, входящие в это выражение, равны
-4т> — — (AiB2—A2Bl),
STj = (Д1Д2 BlBi))
Дтг= ДА.
5Т> = -1(Д/-В?),
Дтз— 3(ДА34-ДАЪ
вт, = -з(д1д2-^А).
А Т4 = 8 Д.>В9,
bT4=-4gv-a2).
Коэфнциенты Ль Въ Д2 и В2 являются функциями угла 7,
образуемого осями главного и бокового цилиндров. При 7=7.
(7t—угол, образуемый осью главного шатуна с плоскостью, про-
веденной через ось подшипника главного шатуна и ось пальца
прицепного шатуна)
At = cos 7,
В} = sin 7 ,
. _ г 1
А а — Ра £ Pi д >
^2 — Чч.
где
_ X X3 15ХБ 35Х7
р2~4 +16+ 512 + 2048+”*’
Ра = -
1 я* х^ги
4 Я Р + 4 В + 4 В ] +
, X /?гГ ЗЯ2 X2 r2l 1 Я2
+ 2 В 1 + 8 В + 2 В C0S 7 4 В
Г. 1 Я2 3Xfr*l
[ +4 В 4 /•]
COS 27 +
х Я3г о
32TCOs3l;
ЯгГ] г21
/*[ + 8 В 4 Z’J
sin7—
X
2
1 Я2 Г. ,1 Я2 , 3 .„г21 о X Я3г . о
4 >’11 + 4 ~В + 4 1 В |sin-f+ 32 р sin37>
где /'—расстояние от оси подшипника главного шатуна до оси
пальца прицепного шатуна;
/—длина прицепного шатуна.
При 7^7,
Д! = cos 7 + fl — Хр0 + у Xp„V_sin'j/sjn7 ;
106
LI
* 1 / 1 \ п
Bi ~ Tsin + T (1 ~Zp° ~ ~2 xp’) Visin ~
-у Хр8|—sin^cosv+sin-f;
1 7”*” 1 7* 1
Д2 = ра — cos Ф+ —X — cos 2ф — -у А — cos 9 cos i + —- у cos 2; ,
7 > к t Z^ “fl
и 1 х г 1 R .
— \ J cos^sin-/ + — у Sin2i,
где
128»
до максимального
сил инерции на отношение
X ЗА3 5A5 175X*
p0— 4 + 64 +256 + '
Ф = 7о—If-
Так как при расчете крутильных колебаний вала необходимо
определить все резонансы в диапазоне рабочих режимов дви-
гателя, то необходимо иметь результаты гармонического анализа
для целой серии режимов «от минимального
числа оборотов.
При изменении режима
силы газов изменяются про-
порционально изменению
среднего индикаторного да-
вления pit а силы инерции
поступательно движущихся
масс—пропорционально из-
менению числа оборотов во
второй степени.Поэтому гар-
монический анализ кривых
Мкрг и MKpj проводят раз-
дельно и только для одного
режима—номинального. На
другом режиме, например,
крейсерском, используются
данные проведенного раз-
ложения после
ния амплитуд
от сил газа на
Pi «pew.а амплитуд гармоник от
Pi ном-
умноже-
гармоник
отношение
Для данного режима суммирование гармоник одного порядка
К от сил газов и сил инерции может выполняться либо графи-
чески (фиг. 53), либо аналитически
Скг sin(AW + ₽„) + Cx, sin^+ph>) = Qf>J<sin(A-f+Bif.J, (59)
4 107
где
Q о-= 1/ + CKf + 2CK2CK,-cos М
V
₽«»>* = ₽«.. +arc tg^
Ьл/
Г sin(pK,—ркУ) ]
[l+cos(₽r —рк/) J
Фиг. 54
В том случае, когда на один кривошип действует несколько
цилиндров, суммирование гармоник одного порядка К от раз-
личных цилиндров должно вестись с учетом их фаз, которые
определяются принятым на двигателе порядком зажигания.
Поясним сказанное примером суммирования К-й гармоники
крутящего момента, действующего на кривошип 12-цилин-
дрового четырехтактного V-образного двигателя с углом развала
между блоками 60° (фиг. 54а).
Если за начало отсчета углов а принять ось левого блока,
то К-я гармоника от цилиндра,
стоящего в левом блоке, будет
СкП sin (АЫ + ₽м).
К-я гармоника от цилиндра,
стоящего в правом блоке, при
порядке работы, показанном на
фиг. 546, будет
C^sinpO* -420°)+kn.
Величины Скл, С„„, и ₽«„
могут быть различными для
правого и левого цилиндров;
Скл = Ска и если ша-
туны центральные и массы посту-
пательно движущихся частей в
обоих цилиндрах одинаковы.
Суммирование удобнее всего
проводить графически или по
формулам (59).
В таблице 9 и на фиг. 55
приведены данные гармониче-
ского анализа крутящего мо-
мента (с учетом сил инерции)
от цилиндров, действующих на
один кривошип: V-образного
12 цилиндрового мотора, Y-образ-
ного 18-цилиндрового мотора
и 18-цилиндрового двухрядного звездообразного мотора.
Амплитуды гармоник Ск даны в процентах от среднего инди-
каторного крутящего момента двигателя.
ЮЯ
Таблица 9
результаты гармонического анализа крутящего момента от цилиндров,
работающих на один кривошип
К V-образный мотор (2 цилиндра на кри- вошип) Y-образный мотор (3 цилиндра на кри- вошип) Звездообразный мотор (9 цилиндров яа кривошип)
Ск ?° Ск ск 8°
Мкр инд ер % М л инд ср % Мкр инд ср 10
0,5 12,4 127 17,2 131 1,8 им
1 48,0 353 7,90 342 19,5 202
1.5 28.2 53 5.35 42 6.7 68
2 20.0 132 8,40 121 6,2 350
2,5 23,2 3 18,0 5 5.7 1.38
3 0,84 45 4.06 198 2,4 120
1.5 14,1 322 2,75 288 3.7 310
1 4,55 20 0.86 120 6,6 67
4.5 5,65 274 5,40 278 53,6 320
5 6,09 350 5,45 351 5,9 59
5,5 U,80 244 1.48 67 7.6 111
6 5,00 300 1,25 240 4,3 6
6,5 1,95 28 0,54 203 2.1 330
7 3.00 274,5 2.59 270 5,6 76
7,5 2,00 3,39 2.39 337 2.7 49
<s 1,10 227,5 0,75 47 1,4 21
8.5 2.46 163 0,43 274 3,5 25
9 0,35 307 0,68 189 91 302
109
не
§ 15. Вынужденные колебания многомассовой крутильной
системы
Пусть имеется система, состоящая из п масс с моментами
инерции Д, /2, . /„. Массы связаны валами, жесткость на кру-
чение которых klt k2, k3....kn „ а моменты инерции пренебре-
жимо малы.
К массам приложены внешние моменты Мг.... М„ и
моменты сил сопротивления, пропорциональные скорости $<f,.
;®а...^„(фиг. 56).
Составляя, как и раньше, для каждой массы диференциаль-
ные уравнения движения, получим систему из п линейных не-
однородных уравнений второго порядка с постоянными коэфи-
цпентами:
А?» + if, 4-AJj (?!-<?,) = /И,
4% + + k.2 (<?2—®з)—(«1—®з) = М,
(60)
4ч»,+1 (<р„- л - ?„)=м„
Фиг. 5с
Общий интеграл этой системы уравнений складывается из
интеграла этих же уравнений без правой части (однородных)^!
частных решений этих
уравнений с правой ча-
стью. Интеграл одно-
родных уравнений описы-
вает затухающие коле-
бания, поэтому интерес
представляют только част
ные решения—стационар-
ная часть вынужденных
колебаний.
В практически инте-
ресных случаях внешние
возмущающие моменты
стоящие в правой части уравнений, не являются гармони-
ческими, но имеют сложный характер изменения во времени.
Пользуясь разложением в ряд Фурье, можно представить их
приближенно в виде тригонометрических рядов
Mi — М;ср + ^ (Ahi cos + BKi sin L’/), (61)
г-i
т. е. состоящими из 5 гармонических компонентов.
111
Рассматривая последовательно действие каждой гармоники
возмущающего момента на крутильную систему отдельно, полу?
чим всего S частных решений.
Так как система состоит из п масс и на каждую массу дей-
ствует S возбуждений различной частоты, причем каждое воз-
мущение составляется из двух членов (фазовых составляющих),
то всего получим 2Sn уравнений. Если /х- момент инерции винта,.
/2—редуктора, /„—нагнетателя, то считают, что к ним приложены
постоянные во времени крутящие моменты, благодаря чему
общее число уравнений соответственно уменьшается.
Для примера напишем диференциальное уравнение движения
z-й массы, считая, что на нее действует, только одна гармоника
возмущающего момента порядка /<=1
Aft+ £ft+ А\ (ft—<Р.м)—&-i ?i) == cos ^t+Вц sin 2,/
(подобным образом можно было бы выписать всю систему п
уравнений с гармоническими возмущениями частоты 2,).
Решение будем искать в виде:
так что
и
<р(= at cos Qtt + bt sin 2Х/,
'fi — —а;2( sin Qyt 4- cos 2/
<р; = —Я;218 cos 2i/—^2/ sin 2,2
Подставляя эти выражения ft,ft и ft в диференциальное ура-
внение z-й массы, получим:
—/^2/cos 2Х/—/,^2/sin 2/—kaiQ1 sin 2!/4-^2а cos Qtt -f-
+ /% (cii cos 2/+ kjbt sin 2j/—cos 2/—i sin 2/—
—Ai-iOf-i cos 2j/—kt_\bi sin 21/4-^i-iaj cos 2j/4-sin 2XZ =
= cos Qxt 4- Ba sin 2X/.
Для того, чтобы равенство удовлетворялось при любом зна-
чении времени t. необходимо, чтобы коэфициенты при sin2x/ и
cos 2,/ в обеих частях уравнения порознь были бы равны между
собой
—4«iyi, + ^isi+^(°i—«.'4-1)—A,-i(a/-i—а}) = /4п;
(^-А;+1)-^._1 (Ь_,-Ь,) = В1г.
Подставляя вместо I его значения от 1 до п, получим систему
из 2л уравнений с 2л неизвестными: alt Ь}; а.,, Ьг-.... ап, Ьп.
В отличие от уравнений, встречающихся при расчете соб-
ственных колебаний системы, в данном случае частота колеба-
ний 2Х известна (частота вынужденных колебаний равна частоте
возмущающего момента).
112
Решая эту систему алгебраических уравнений, например,
прямым методом последовательного исключения неизвестных,
определим все амплитуды фазовых слагающих колебания а, и
Подобным же образом отыскивается второе частное решение,
т. е. проводится расчет фазовых слагающих амплитуд колебания
всех масс системы (av bt; а2, ап, Ьп) при действии на
систему только вторых гармоник возмущающих моментов. Затем
расчет проводится для третьих гармоник и т. д. до гармоник
порядка f(=S.
В результате получается, что каждая масса системы совер-
шает сложные колебания, определяемые выражением вида:
(aiK cos QKt+biK sin QKt)
(63)
или
(63a)
где
Лч = |/а8ы + b2iK ; tgSK = .
IK
Таким образом, определение амплитуд вынужденных колеба-
ний многомассовой системы при сложном характере возмущений
с математической стороны не представляет никаких затруднений.
Все дело сводится к кропотливой и долгой счетной работе.
Формально можно с любой степенью точности установить закон
перемещения каждой массы.
Однако следует заметить, что такое решение справедливо
лишь в том случае, если сопротивления пропорциональны ско-
рости колебаний. Ранее разбирались источники возникновения
сопротивлений. Они так многочисленны и разнохарактерны по
природе, что утверждение будто их суммарное действие может
быть учтено членами является весьма условным и нет на-
дежды вполне строго задать заранее значение коэфициента с.
Поэтому имеет смысл говорить только о приближенном решении.
Вполне ясно, что характер движения системы в основном
определяется лишь действием той гармоники внешнего возму-
щаюшего момента, частота которой совпадает или близка ча-
стоте свободных колебаний системы.
Перемещения, вызванные всеми остальными гармониками воз-
мущения, незначительны по сравнению с перемещениями от этой
резонирующей гармоники.
Поэтому, рассматривая только резонансные режимы работы
системы, обычно считают, что на ее массы действует только
8 В. Кириченко 113
I
одна резонирующая гармоника возмущающего момента. Соог
ветственно и перемещения масс системы получаются при это:
простыми гармоническими.
16. Расчет резонансных амплитуд
Рассмотрим задачу предыдущего параграфа в этой новог
постановке, т. е. полагая, что на массы системы действует только
гармоника К, частота которой совпадает с одной из частот
свободных колебаний системы.
Одновременно положим, что при свободных колебаниях и
при резонансе формы колебаний одинаковы в том смысле, чго
отношение амплитуд двух сечений при свободных колебания
равно отношению амплитуд этих же сечений при резонансе.
При простом гармоническом возмущении системы это поло-
жение совершенно строго и его легко представить себе на при-
мере системы с одной степенью свободы. Вспомним, что при
свободных колебаниях системы без сопротивлений (фиг. 1) на
нее все время действуют два взаимно уравновешивающих дру!
друга момента: момент сил инерции и момент сил упругости.
Вспомним также, что при резонансных колебаниях этой же
системы, но с сопротивлениями, пропорциональными скорости, в
гармоническом возмущении (§ 13) векторы действующих моме I
тов располагаются в двух взаимно перпендикулярных направле
ниях (фиг 46). В этом случае, в отличие от свободных колеба-
ний без сопротивления, имеются два новых момента: momchi
возмущающий и момент сил сопротивлений. Но вся работа
возмущающего момента за период идет на преодоление момент,
сил сопротивления и попрежнему, как при свободных колеба
ниях без сопротивления, момент сил инерции уравновешиваете}
моментом сил упругости, поэтому и формы колебаний в обои:
случаях получаются одинаковыми.
Возвращаясь к многомассовой системе, будем искать прибли
женное решение, пользуясь энергетическим методом, т. е. ис
ходить из того факта, что работа сопротивлений при резонанс»
равна работе возмущающих моментов.
1. Определим работу момента сил сопротивления, приложен
ного к i-й массе, при резонансе системы с К-й гармонико<
возмущающих моментов.
Так как условлено, что перемещения, вызванные всеми осталь
. ными гармониками возмущающих моментов, кроме К-й, не учи
тываюгся, то
и
= sin (2^+8,)
Vi=Ft^h cos(S,/ + 8x).
Так как сопротивления считаются пропорциональными
рости и равными то значит требуется определить ра
114
Момента, имеющего ту же частоту, что и перемещения и сдвиг
по фазе, равный — .
Как известно из § 11, в этом случае работа момента за
рециод равняется произведению к на амплитуду момента и на
,мплитуду перемещения, т. е. искомая работа
Работа моментов сил сопротивления всей системы, состоящей
из л масс, при резонансе с гармоникой /С-го порядка будет:
^=^9.^FiK\ (64)
ч
Суммирование распространяется на те массы, на которые дей-
ствуют моменты сил сопротивления. Условно считают их при-
ложенными только к массам, на которые действуют внешние
возмущающие моменты.
2. Определим работу момента внешних сил, действующих
на z-ю массу при резонансе системы с К-Ъ гармоникой воз-
мущения.
Работа гармоники К-vo порядка Мк = CKsin(SK^+pK) за
период колебания равна
U7, — ~CKFilt sin е,
где ч = рк — — фазовый сдвиг А'-й гармоники относительно
перемещения.
Работа всех гармоник порядка К, приложенных к различным
массам системы, будет:
L^-zC^sine,-. (65)
Следует заметить, что под знаком суммы г имеет индекс i.
Согласно обозначению е есть разность фаз возмущающего мо-
мента и перемещений. Что касается фазы перемещения то
1ля всех масс системы эта фаза является общей, так как при
резонансе, как и при свободных колебаниях, все массы должны
одновременно попадать в крайние положения и одновременно
троходить средние положения.
Фазы внешнего момента не одинаковы и определяются по-
рядком работы цилиндров, поэтому е для каждой массы имеет
свое собственное значение, что и учитывается инде ксом I.
Итак, FlTf=SU7e
’ЛИ H2KEF2/K = CKEFiKsins,..
Перепишем последнюю формулу в несколько ином виде:
F- 2 F-
sin е,,
♦ г U г1к
8* 115
где-—-^^—есть отношение амплитуды i-й массы камплитув
первой массы при резонансе системы с /<-й гармоникой крутяще^
момента.
Из условия одинаковости форм свободных колебаний
сопротивления и колебаний в резонансе это отношение оказ^
вается известным, если известна форма свободных колебаний.
Формула для определения резонансной амплитуды
массы приобретает следующий окончательный вид:
г, С„Еа, sin Е:
первоц
(66)
Амплитуды всех остальных масс легко вычисляются по най.
денному значению F1K, так как известны а2, а8.... ая.
Выражение Eosine,, входящее в формулу для определения
резонансных амплитуд, представляет собой работу, которую
совершают за период колебания все резонирующие гармоника
К-го порядка при амплитуде гармоник Ск = 1 и амплитуде коле-
баний крайней первой массы Эту величину иногда назц
вают удельной работой. При резонансе удельная работа дости-
гает максимального значения. Следовательно, задача определенжя
FK сводится к отысканию максимального значения удельной ра-
боты £а; sin г, (здесь неизвестной является величина е4).
При равномерном чередовании вспышек в многоцилиндровых
двигателях крутящие моменты, действующие на различные
кривошипы, имеют один и тот же закон изменения, но сдви-
нуты во времени. Для двух кривошипов, работающих одни
вслед за другим, этот сдвиг по углу поворота коленчатого вала
4ти
составляет угол ф = — (г—число кривошипов вала). Сдвиг по
фазе /<-й гармоники крутящего момента для этих двух криво-
шипов равен Kty.
Действительно, порядком гармоники условлено называть отно-
шение круговой частоты данной гармоники к угловой скорости
коленчатого вала, так что если гармоники порядка =
изобразить в виде векторов (фиг. 57), то эти векторы должны
вращаться вдвое медленнее вала и углы между ними должны
быть вдвое меньше угла ф.
Векторы гармоник первого порядка должны вращаться с угло-
вой скоростью вала и углы между ними должны быть равны’J'
и Т. Д.
Положим для определенности, что объектом исследований
является двигатель с шестикривошипным валом и порядков
работы цилиндров в одном блоке 1—5—3—6—2—4.
Будем считать что —относительная амплитуда первого кр*'
вошипа, аг—второго и т. д.
116
В этом случае удельная работа может быть записана следую-
щим образом:
sin г, = aj sin е 4- а5 sin (е 4- Д<]>) 4- а3 sin (г + 2/Сф) + ...
... 4-а4 sin (e-f-5Aty). (67)
Наибольшее значение суммы можно было бы установить
(1утем ряда проб, т. е. последовательно задавать ряд значений
s и вычислять Eosine., затем построить график Ss^sin е, =/(е)
и по графику определить максимальное значение интересующей
(J
Порядок работы цилиндров
Фиг. 57
нас величины. Такой примитивный метод подбора величины
практически неудобен. Лучшим способом определения znaxSa, sin е,
является графическое построение, которое иллюстрируется ниже
на конкретном примере. ,
Пример 6. Пусть исследуется 12-цилиндровый V-образ-
ный двигатель с порядком работы цилиндров в одном блоке
1—5—3—6—2—4. Для этого мотора построена эквивалентная
расчетная система и определены формы свободных колебаний
(фиг. 58 а). Положим, что 0,5-я, 2,5-я и 3-я гармоники резони-
руют с одноузловой формой колебаний системы в зоне рабочих
оборотов двигателя и требуется найти резонансные амплитуды.
В первую очередь для каждого из трех резонансов следует
определить соответственно три величины тахЪ a-sins^
Резонанс гармоники /< = 0,5
1 4к
1. Определяем фазовый угол 0,5-й гармоники —
5-=б(г.
о
2. Считая относительные величины векторами, строим
вспомогательную диаграмму, определяющую взаимное положе-
ние векторов (фиг. 58 б).
117
Фиг. 58
Действительно сумма векторов af проектируется на ось
в натуральную величину (т. е. проекция суммы ои имеет макс
мальное значение) и вместе с тем равна:
«! sin е + at Sin (е + /<ф) + а3 sin (е + 2/<Ь) + .., = max sin sjt
118
Резонанс гармоники К 2,5
Фазовый угол:
5 4~ 5
*^2-1Г=Г=30(Л
Вспомогательная диаграмма и суммирование векторов пред-
ставлено на фиг. 58 г и 58 д.
Резонанс гармоники К 3
Фазовый угол:
/ф = 3-у- = 2п = 360°.
Вспомогательная диаграмма и суммирование векторов а; пред-
ставлено на фиг. 58 е и 58 ж.
Зная величины max's,sin е{> по формуле (66) определяем
резонансную амплитуду первой массы по известной из гармо-
нического анализа величине амплитуды внешнего резонирующего
момента Ск, частоте свободных колебаний, равной SK, и заданному
коэфициенту сопротивлений 5. Величина -а/2 без труда опреде-
ляется по известной форме колебаний.
§ 17. Определение возможных резонансов
Разложение кривой крутящего момента каждого кривошипа
содержит обычно большое число гармонических компонентов.
Надлежит выяснить всели гармоники будут резонировать в диа-
пазоне рабочих режимов двигателя и все ли резонансы будут
опасными в том смысле, что вызовут недопустимые нагрузки
элементов конструкции.
Условие наличия резонанса состоит в том, что частота одной
из гармоник крутящего момента на данном режиме работы дви-
гателя совпадает с частотой свободных колебаний крутильной
системы
p — QK = Ku. (68)
30 о
Так как число свободных колебаний системы в минуту nt — — ,
' л ЗОш .. „
а число оборотов вала в минуту п=—— , то резонанс с Л-н
гармоникой наступит, когда обороты вала будут равны
« = ^. (69)
Для примера положим, что исследуется двигатель, минималь-
ные обороты которого лт;п=:400об,'мии, а максимальные птах —
119
— 3000 об/мин. Пусть известны числа свободных колебаний кру-
тильной системы этого двигателя:
пс\ — 6000 кол/мин — одноузловая форма,
пс\\ — 20000 кол/мин — двухузловая форма.
Очевидно^ с одноузловой формой колебаний будут резониро-
вать все гармоники, имеющиеся в разложении кривой крутящего
ГЛ ^/*1 _ ГЛ'
момента, начиная с д = —— до гармоники л=—-— включи-
"та* Пт1п
.. 6000 _ о _ о
телъно, т. е. гармоники К— „ппп — 2; 2,5; 3 и т. д. до гармо-
oUUU
„ 6000
ники А = -- 15.
4U0
С двухузловой формой колебаний системы в диапазоне рабо-
чих оборотов двигателя будут резонировать гармоники, начиная
п.\\ 2000() j. пец
с —-— — О_АП ~ 7 до гармоники порядка К = — — =
Птал ЗООи nmin
20000
= "400 =60'
Определение резонансных режимов можно иллюстрировать
следующим графическим построением (фиг. 59). По оси орди-
нат откладываются частоты возмущений и свободных колебаний
системы. По оси абсцисс — угловая скорость вала* 2).
Частоты свободных колебаний не зависят от угловой скорости
и поэтому изображаются в виде прямых, параллельных оси абс-
цисс. Частоты гармоник крутящего момента пропорциональны
угловой скорости и поэтому представляются пучком прямых,
выходящих из начала координат. Угол т; наклона прямой соот-
ветствующей К-й гармоники, определяется равенством tg/]=/<.
Очевидно, точки пересечения лучей с прямыми р удовлетво-
ряют уравнение р — Кш и определяют резонансные угловые ско-
рости вала.
Из всех возможных резонансов системы, выявленных рас-
четом, далеко не все будут действительно ощущаться на прак-
тике. Заведомо можно сказать, что резонансы, имеющие место
на малых оборотах двигателя, будут неопасными и даже может
быть неощутимыми, вследствие малости возбуждающих момен-
тов (следует помнить, что при уменьшении оборотов инерцион-
ные нагрузки убывают пропорционально квадрату числа оборо-
тов, а газовые — пропорционально изменению по оборотам pt
20000
’) Резонанс с гармоникой К — 6,5 наступает на оборотах п — —
6,5
= 3077, т. е больших птах.
2) Можно также по оси ординат откладывать число свободных колебаний
системы в минуту и число периодов в минуту гармоник крутящего момента,
а по оси абсцисс — число оборотов вала в минуту.
120
среднего индикаторного давления. Можно считать, что pt на-
тает с уменьшением оборотов линейно).
Резонансы, наступающие на взлетном номинальном или крей-
серском режимах двигателя, могут также оказаться неопасными.
Так будет, если удельная работа ^резонирующих гармоник Л’-го
порядка равна илн близка нулю.
Если же мала амплитуда резонирующеГг гармоники, то нель-
зя с уверенностью сказать, что резонанс неопасен.
Для многомассовой системы может оказаться, как это было
в разобранном ранее примере 6 с гармониками третьего порядка,
что для всех масс системы резонирующие гармоники находятся
в одной фазе и в этом случае их суммарный эффект может быть
ощутительным.
§ 18. Торсиографирование
Точное определение амплитуд вынужденных колебаний систе-
мы расчетным путем затруднено целым рядом обстоятельств, о
которых говорилось выше. Главным из них является неопреде-
ленность величины коэфициента сопротивлений. Поэтому перед
121
внедрением новою двигателя в эксплоатацию обязательно про»!
водится экспериментальное исследование мотора, состоящее
в непосредственном замере крутильных колебаний.
Такое экспериментальное исследование носит название горсио-
графирования.
Существует целый ряд специальных приборов, служащих для
замера и записи крутильных колебаний. Эти приборы можно
разделить на два типа:
1. Приборы, регистрирующие относительное смещение двух
сечений вала, находящихся на некотором удалении друг от друга.
2. Приборы, регистрирующие абсолютную величину амплиту-
ды колебания сечения, в котором производится замер.
Фиг. 60
Приборы первого типа неудобны тем, что требуют для уста-
новки сравнительно большего участка свободного вала. При
уменьшении базы прибора точность его показаний падает. За-
меряемая прибором величина — разность амплитуд очень мала
и для получения удовлетворительных результатов прибор дол-
жен обладать очень высокой чувствительностью. Такими прибо-
рами пользуются только в случае испытания установок, имею-
щих длинные, свободные для доступа валопроводы (например,
судовые силовые установки).
Авиационные двигатели обычно торсиографируются приборами
второго типа.
Эти приборы всегда состоят из двух частей, одна из которых
жестко присоединяется к объекту исследования и в точности
повторяет его колебания. Вторая часть является упругой систе-
мой, частота свободных колебаний которой во много раз мень-
ше частоты измеряемых колебаний. Поэтому, как известно из
§ 12, упругая система прибора практически не реагирует на вы-
сокочастотные возбуждения,.которые передаются на нее со сто-
122
роны исследуемой системы. Запись относительных смещений
основных частей прибора является записью колебаний того места
исследуемой системы, на котором установлен прибор.
На фиг. 60 изображена схема механического торсиографа.
Прибор фланцем А присоединяется к свободному концу вала
так, что вся центральная часть прибора В участвует в крутиль-
ных колебаниях вала. С центральной частью В с помощью сла-
бой пружины П соединен маховик М, посаженный на шарико-
вых подшипниках. Так как связь частей прибора В и Ж очень
податлива — маховик вращается равномерно.
Смещение маховика относительно колеблющегося диска В
записывается алмазным резцом Р на целлулоидной ленте Л,
которая во время замеров перематывается с барабана Бх на ба-
рабан Бг специальной винтовой шестерней Шх. Последняя обка-
тывается по неподвижной (зажатой от руки с помощью руко-
ятки 3) винтовой шестерне Ш2.
Если рукоятка 3 расторможена, то шестерря Ш, прекращает
вращение относительно своей оси и подача ленты также пре-
кращается.
На фиг. 61 показан примерный вид торсиограммы.
123
Параллельно записи колебаний в верхней части ленты спе-
циальный отметчик, работающий от часового механизма, делает
риски через равные промежутки времени. В нижней части ленты
другой отметчик делает риски через определенное число обо-
ротов системы. По этим отметкам определяется число оборотов,
на котором работала система во время записи колебаний.
Если отметка времени производится через каждые четверть
еекунды, а оборотов — через каждые 10 оборотов, то участок
ленты длиной 4 а-60 жж пройдет мимо резца в течение одной
минуты. За время одного оборота системы мимо резца пройдет
„ Ь ГЛ
участок ленты длиной у- мм. Отсюда число оборотов, на кото-
ром произведена запись
4а-60-10 а ..
п=-----------=2400 -- об/мин.
Выделив участок ленты, соответствующий одному обороту
исследуемой системы, по числу пик колебания определяют по-
рядок гармоники, которая на данном режиме работы определяет
характер колебания системы (находится в резонансе или вблизи
него).
Амплитуда колебаний определяется как половина размаха ко-
лебаний, записанных на ленте (фиг. 61).
Д
Е=~57,3’,
где г—расстояние от острия резца до оси торсиографа.
Значительно большую чувствительность по сравнению с ме-
ханическим торсиографом имеют электроизмерительные приборы.
Вместе с тем размеры чувствительного элемента электроизмери-
тельного прибора могут не превосходить всего 2,5 см, а вес 60г.
Благодаря этому такие чувствительные элементы—датчики могут
быть установлены при испытаниях во многих местах исследуе-
мой системы, например, в каждой коренной шейке вала.
На фиг. 62 изображена схема датчика для замера крутиль-
ных колебаний. Постоянный магнит М здесь играет ту же роль,
что и маховик в механическом торсиографе. Магнит М связан
слабой пружиной с сердечником В, благодаря чему может не-
сколько поворачиваться относительно сердечника. Сердечник
жестко крепится к валу, крутильные колебания которого жела-
тельно замерить. Этот сердечник несет на себе обмотку Е из
чрезвычайно тонкой проволоки. При всяком повороте магнита
вокруг сердечника в обмотке сердечника возникает переменное
напряжение, величина которого пропорциональна угловой ско-
рости относительного движения.
Это переменное напряжение может быть усилено специаль-
ным усилителем и записано с помощью прибора, называемого
i!2-l
осциллографом. Запись, полученная на осциллографе, будет пред-
ставлять не перемещение при колебаниях, а скорость.
Если желательно сразу же записать перемещения, а не по-
лучать их путем интегрирования кривой скорости, то применяют
так называемый „электрический интегрирующий контур" фиг. 62.
Обмотка датчика Е, напряжение в которой пропорционально
скорости колебания, создает ток i, питающий контур с последо-
вательно включенным сопротивлением 7? и емкостью С. Контур
рассчитывается так, что падение напряжения на сопротивлении
IR во много раз больше падения напряжения на конденсаторе
4- [ idt.
Поэтому можно считать, что падение напряжения на сопро-
тивлении равно полному напряжению V в обмотке датчика, а
сила тока пропорциональна V. При этом напряжение на обклад-
ках конденсатора, пропорциональное | idt, вместе с тем пропор-
ционально интегралу от скорости колебаний, т. е. амплитуде.
Осциллограмма напряжения на обкладках конденсатора одно-
временно является записью в определенном масштабе механи-
ческих колебаний исследуемой системы.
Следует заметить, что напряжение на обкладках конденса-
тора во много раз меньше полного напряжения в обйотке дат-
чика и поэтому всегда необходим дополнительный каскад уси-
ления при пользовании „интегрирующим контуром".
Обычно при экспериментальных исследованиях запись кру-
тильных колебаний производится во всем диапазоне рабочих
режимов двигателя, начиная от пт1„ до птая через каждые
50 об/мин.
• 12а
По данным торсиографирования строят график, откладывая
но оси абсцисс числа оборотов, по оси ординат амплитуды ко-
лебаний того сечения, где был установлен торсиограф. Этот
график носит название резонансной кривой. Для иллюстрации на
фиг. 63 приводится экспериментальная резонансная кривая дви-
гателя ВК-105.
По известной резонансной кривой, полученной для одного
сечения, и по известной форме свободных колебаний исследуе-
мой системы можно построить пики резонансной кривой для лю-
бого сечения системы.
§ 19. Напряжения от крутильных колебаний. Предельно до-
пустимые амплитуды
Зная из опыта или расчета величину резонансных амплитуд,
легко определить напряжения, возникающие в различных сече-
ниях вала от крутильных колебаний. Наибольшие напряжения
будут на том участке вала, где форма колебаний имеет наиболь-
ший наклон к оси вала или, что то же, где изменение амплитуд
по длине вала будет наибольшим.
Величина напряжений определяется по известной формуле
сопротивлений материалов:
-=
здесь \X'ip — момент сопротивления кручению сечения вала;
— момент, действующий на рассчитываемом уча-
стке, от крутильных колебаний;
F; и F,+i — резонансные амплитуды масс, ограничиваю-
щих рассчитываемый участок;
А, — крутильная жесткость рассчитываемого уча-
стка.
126
Если расчетным сечением является сечение вала винта (на-
гнетателя), то при определении действующего момента необ-
ходимо учесть передаточное число от коленчатого вала к валу
винта (нагнетателя), как это делалось в § 10.
Уместно поставить вопрос какие же напряжения от крутиль-
ных колебаний считать допустимыми. Нужно иметь в виду, что
при колебаниях вал испытывает высокочастотные переменные
напряжения, т. е. работает на усталость. В этих условиях проч-
ность, как известно, зависит не только от материала 'конструк-
ции и характера внешней нагрузки, но в значительной мере
определяется также формой, размерами и качеством обработки
(етали.
Обычно считают, что дополнительные напряжения только от
крутильных колебаний не должны превосходить 600 кг!см2.
Задаваясь предельно допустимыми напряжениями от крутиль-
ных колебаний, можно легко найти соответствующие этим на-
пряжениям амплитуды различных сечений вала при данной фор-
ме колебаний.
На участке, где расположен узел, форма колебаний имеет
наибольшую крутизну. Ограничивая напряжения на этом уча-
стке вала допустимыми ~доп, получим амплитуду t-й массы, бли-
жайшей к узлу
F- — М k'
где Мкр = ^ао„ W — предельный допустимый крутящий момент от
колебаний;
k'—крутильная жесткость участка вала от t-й
массы до узла.
Предельно допустимые амплитуды всех остальных масс си-
стемы легко определяются по известным, для данной формы ко-
лебаний, отношениям аа, а3, ...ал.
Определив таким образом предельно допустимую амплитуду
для того сечения вала, для которого имеется резонансная кри-
вая, устанавливают, какие из резонансов являются критическими
в том смысле, что вызывают напряжения, превосходящие допу-
стимые.
На фиг. 64 нанесена величина предельно допустимой ампли-
туды колебаний. Очевидно, что резонанс с 4,5-й гармоникой
оказывается неопасным, в то время как длительная работа на
резонансе с, гармониками 6 и 3,5-го порядков может привести
к поломке вала.
Если в диапазоне рабочих режимов двигателя имеют место
опасные резонансы, то требуется либо переделка мотора, либо
введение запретных режимов работы.
При введении запретных режимов в инструкции по эксплоа-
тации двигателя указывается, что работа на оборотах от пг до
п2 запрещается. Диапазон запретных оборотов обычно устанавли-
вается 100 об/мин (по 50 об мин в обе стороны от пкр).
127
Введение запретных режимов затрудняет эксплоатацию и пр#]
большом ресурсе двигателя не устраняет полностью опасности
поломки. Поэтому в авиамоторостроении к этой мере прибегают?
в крайних случаях.
Сам метод оценки прочности элементов крутильной системы
по предельно допустимым напряжениям в принципе является
далеко несовершенным, так как при такой оценке не учитывается
ряд конструктивных и технологических факторов, влияние кото-
рых во многих случаях может быть решающим.
Правильнее оценивать прочность элементов крутильной си-
стемы по величине запаса прочности.
Существует несколько методов определения запаса прочности
при переменных нагрузках и сложном напряженном состоянии
детали.
В своих работах, удостоенных Сталинской премии 1948 г.,
Академик С. В. Сервисен и Р. С. Кинасошвили рекомендуют для
определения запаса прочности, при асимметричном цикле, поль-
зоваться следующей формулой
где — запас прочности при работе детали только на кручение
и асимметричном цикле;
па — запас прочности при работе детали только на изгиб и
асимметричном цикле.
128
реличина nt определяется по формуле
где — предел усталости материала на кручение при симме-
тричном цикле напряжений, полученный на лаборатор-
ных образцах. Предел усталости для сталей, идущих
на изготовление коленчатых валов, лежит в пределах
3000—3300 кг/смг;
— амплитуда напряжений цикла;
— эффективный коэфициент концентрации напряжений.
Для определения пользуются экспериментальными
данными. Можно считать, что для авиационных ва-
лов с учетом поперечных отверстий для смазки
=1,8- 2,0;
г_ — коэфициент, учитывающий влияние абсолютных разме-
ров детали на предел выносливости при кручении:
Диаметр вала, мм 40 60 80 100 120
0,79 0,69 0,60 0.55 -0,53
а,ти — член, учитывающий влияние средних напряжений цикла
- -zm на предельную амплитуду. Этот член мал (ат 0,05)
и при расчете авиационных валов им можно пренебречь.
Формула для определения запаса прочности при работе вала
только на кручение и асимметричном цикле приобретает вид:
п_ = .
Величина определяется по формуле:
—•
° а + а?ат
где а_, — предел усталости материала при изгибе, полученный
для лабораторных образцов при симметричном цикле
напряжений. Величина о_х для сталей, идущих на изго-
товление коленчатых валов, лежит в пределах 5000—
6000 кг см2-, •
9 В. Кириченко
129
сЛ — амплитуда напряжений цикла:
kG — эффективный коэфициент концентрации напряжений
при изгибе.
Ает = 14-т2(Л?г—1), ]
где — коэфициент чувствительности материала к концентрации
напряжений. Для легированных сталей можно считать
71=0,9; 1
kT — теоретический коэфициент концентрации напряжений
при изгибе.
Для шейки вала с поперечным отверстием величина kT зави-
сит от отношения диаметра отверстия d к диаметру вала D.
(1 ~D~ 0,01 0,04 0,08 0,12 0,16 0,20 0,24 0,28
kT ~з 2,55 2,34 2,21 2,10 2,02 1,96 1,90
Для щеки коленчатого вала в месте перехода щеки в шейку
(входящий угол) теоретический коэфициент концентрации напря-
жений kj зависит от отношения радиуса галтели г к толщине
щеки Л
Г 0.10 0,15 0,20 0.25 0,30 0,35 0,40
kr 4,4 3,5 3,0 2,7 2,5 2,4 2,3
ес — коэфициент, учитывающий влияние размеров детали
на предел выносливости при изгибе
Диаметр вала, мм 40 60 80 100 120
Е С 0,8 0,74 0,68 0,64 0,61
°-сРт
— член, учитывающий влияние средних напряжений
на предельную амплитуду. Этот член при расчете авиа-
ционных валов может быть опущен в силу малости
(«,20,2).
Формула для определения запаса прочности при работе вала
только на изгиб и асимметричном цикле приобретает вид:
_ “1
11
130
На основании многочисленных расчетов и широко поставлен-
|.|Ь1Х экспериментов Р. С. Кинасошвили указывает, что запасы
Прочности в коренных шейках можно определять только от
Одного кручения, не учитывая изгиб. Запасы прочности с учетом
Ьзгиба получаются всего на 2—3°/0 меньшими, чем при опре-
делении их только от кручения.
I Запасы прочности коренных шеек современных авиационных
Коленчатых валов лежат в довольно широких пределах от 2 до 3.
Запасы прочности шатунных шеек от кручения, как и для
коренных, значительно меньше, чем от изгиба, и поэтому по-
следний мало влияет на величину общего запаса прочности. Так,
например, для всех шатунных шеек (кроме крайних) мотора Мер-
|лин XX п^0,93/гт. Влияние изгиба на запас прочности крайних
шеек оказывается несколько большим. Запасы прочности ша-
|тунных шеек меньше, чем коренных, и составляют 1,3—2,2.
Запасы прочности щек коленчатого вала в основном опреде-
ляются моментами, изгибающими щеку. Кручение щеки оказы-
вает малое влияние на величину общего запаса прочности.
Для современных коленчатых валов запасы прочности щек
I составляют 1,2—2,4.
сек
л
р
I
р
I
р‘
§ 20. Способы борьбы с опасными резонансами
Применяется несколько способов борьбы с опасными резо-
нансами.
Первый способ состоит в изменении частоты свободных колеба-
ний крутильной системы. При этом резонансные пики смещаются
в сторону и даже могут быть совсем выведены за пределы ра-
бочих оборотов двигателя.
При повышении частоты свобод-
ных колебаний системы резонанс-
ные пики смещаются в сторону
больших оборотов, при снижении
частоты свободных колебаний, на-
оборот, в сторону меньших оборо-
тов двигателя. На фиг. 65 это по-
ложение иллюстрируется графиком.
Частота свободных колебаний
системы зависит от соотношения
жесткостей отдельных ее участков
и моментов инерции масс системы.
Существенное изменение моментов
собой кривошипно-шатунный механизм, немыслимо без коренной
реконструкции двигателя. %
Изменение жесткости может быть получено изменением диа-
метров вала. Причем благодаря тому, что крутильная жесткость
9* 131
п
•лич
npt3 "pet "pt3
Фиг. 65
инерции масс, заменяющих
--------------------------„
Я^водки одного 12-цилиндрового V-образного двигателя. В пер-
.«Готоре'была выполнена с пружинными пакетами так же, как и
Иг --------— -V '^'ГГЛТ',\ Г’ПМРПГТСП Onuavn ия RQ
, то ее измене ilia '-----г--------- * _
пое^име возникал крйтическии резонанс с гармоникой 1,5 по-
d) пропорциональна четвертой степени ди^ ^начальном варианте ведомая шестерня редуктора на этом
— ^^тппе'пыла выполнена с пружинными пакетами так же, как и
более ранних моторах этого семейства. Однако на взлетном
(/J‘
метров, а частота свободных колебаний р =
ние пропорционально квадрату диаметров, если не учитывать Еятка. Тогда были изъяты упругие пакеты из редуктора, отчего
одновременного изменения моментов инерции системы. Фактц.
чески частота р меняется не так резко при изменении диамет-
ров, но все же существенно. Значительно проще можно достиг-
нуть желаемых результатов, варьируя моментом инерции винта
или жесткостью связи винта с валом.
В таблице 10 приведены амплитуды и напряжения от кру.
тильных колебаний коленчатого вала одного 18-цилиндрового
двухрядного звездообразного двигателя при испытании с различ-
ными винтами на взлетном режиме. В данном случае при работе
с винтом большего диаметра резонанс оказывается менее опас-
ным. |
На фиг. 66 приведены полученные на стенде эксперименталь-
ные резонансные кривые другого 18-цилиндрового двухряд*
ного звездообразного двигателя с тремя различными винтами.
Из рассмотрения графика видно, что с винтом № 1, имеющим
больший момент инерции, чем винт № 2, резонансные ампли*
0,04 л а
туды, а значит и напряжения, получаются в -» хг-х- = Ь9
раза большими. U,U17b 11
Примером избавления от опасного резонанса путем измене*
ния связи винта с коленчатым валом может служить история
132
повысилась частота свободных колебаний системы, резонанс сме-
стился вправо по оборотам и на взлете не ощущается.
Второй способ борьбы с опасными резонансами состоит в из-
менении порядка работы цилиндров.
Рассматривая формулу для определения резонансных амплитуд
_ sin
133
можно отчетливо представить себе, что, меняя порядок работ
цилиндров, в некоторых случаях удается избавиться от резонанг?
оказавшегося опасным. Действительно, при изменении nopajf»
работы цилиндров меняется величина Sa;sinej, так как при сд>5
жении векторов а, они меняются местами на вспомогательна ]
диаграмме (§ 16) и надлежащим подбором можно существен^
снизить величину удельной работы SajSinej.
На одном 12-цилиндровом V-образном моторе возника,
сильный резонанс с гармоникой 4,5-го порядка на эксплоатащ,
онных оборотах п=1600 об/мин, так что ввести запретную зОц'
не представлялось возможным.
По предложению ЦИАМ завод изготовил кулачковые валики
с порядком работы цилиндров 1—2—4—6—5—3 вместо обод.
Фиг. 67
ново 1—5—3—6—2—4
При таком изменении
удельная работа резо.
нирующей гармоники
4, 5-го порядка додж-
на была уменьшиться.
Фиг. 67 показывает, что
ожидаемый результат
был достигнут.
Рассмотрим еще
один прием борьбы с
критическими резо-
нансами, практикуе-
мый на двухрядных и
многорядных звездо-
образных двигателях.
Гармонический ана-
лиз кривой крутящего момента простого звездообразного дви-
гателя с прицепными шатунами выявляет сильную гармонику
первого порядка (см. таблицу 9). Резонанс с этой гармоникой,
если он наступает на оборотах, близких номинальным, обычно
бывает критическим.
В двухрядных звездообразных двигателях главные шатуны
из соображений наилучшей уравновешенности, как правило, рас-
полагают в противолежащих цилиндрах, благодаря чему угол
поворота вала, соответствующий времени между вспышками
в главных цилиндрах, равный фазовому углу 6 первой гармо-
ники, составляет 360° и резонанс с первым порядком становится
еще более опасным (см. пример 6).
На фиг. 68 дан график крутящего момента мотора М-85 прЯ
п = 2400 об/мин и расположении главных шатунов в первом ”
восьмом цилиндрах. На этом графике явно выражено наличие
сильной гармоники первого порядка.
Очевидно, что изменяя взаимное расположение главных шатУ
нов, можно таким образом подобрать фазовый угол перв°*
134
гармоники, что удельная работа I^sinei при резонансе сильно
уменьшится.
Однако следует иметь в виду, что при этом изменится урав-
новешенность двигателя, и удельная работа других гармоник
может возрасти.
Порядок работы цилиндров двигателя М-85: I —10—5—
— 14—9—4—13—8—3—12—7—2—11—6. При этом порядке ра-
боты цилиндров, размещая один главный шатун в цилиндре № 1,
а второй последовательно в цилиндрах №№ 8, 10, 12, 14, 2, 4 и 6,
получим соответственно фазовые углы первой гармоники ф: 360°;
51,5°; 463°; 155°; 566°; 258’ и 670’.
На фиг. 69 даны вспомогательные диаграммы для определения
Sa, sin сР Очевидно, варианты размещения шатунов 1—14 и 1—2
равноценны и дают наибольшее снижение амплитуд при резо-
нансе с первой гармоникой.
ГЛАВА IV
ДЕМПФЕРЫ И МУФТЫ
Если ни один из рассмотренных выше способов борьбы с кру-
тильными колебаниями не применим или не дает желаемых ре-
зультатов, систему снабжают специальным устройством, которое
называют демпфером, т. е. глушителем колебаний.
В авиационном моторостроении применяются демпферы раз-
личные как по идее, так и особенно по конструктивному офор-
млению. Их можно разделить на две группы: демпферы трения
(вязкого и сухого) и демпферы динамические.
Некоторые муфты, служащие для передачи крутящего мо-
мента, одновременно обладают свойствами демпфера.
Рассмотрим последовательно основные типы демпферов и
муфт.
§21. Гидравлический демпфер
(вязкого трения)
На фиг. 70 дана схема гидравлического демпфера. Цен-
тральная часть демпфера — поводок А жестко связан с ва-
лом, корпус демпфера В, являющийся маховиком, может
поворачиваться относительно поводка. Этим поворотам препят-
ствует масло, которое заполняет внутренний объем демпфера и
при относительных смещениях деталей А и В должно перетекать
через зазоры и калиброванные отверстия—катарракты К, имею-
щиеся в некоторых конструкциях на лопастях деталей А или В.
При вращении поПодка, совершающего одновременно крутиль-
ные колебания, маховик также увлекается во вращение, но в силу
инерции стремится двигаться равномерно. Так возникают отно-
сительные смещения и сопротивления, всегда направленные в сто-
рону, противоположную колебаниям поводка. На преодоление со-
противлении затрачивается энергия колебаний, поэтому они
уменьшаются, затухают. Энергия колебаний обращается демпфе-
ром в тепло. Для сохранения температуры в надлежащих преде-
лах обеспечивается непрерывная смена масла в демпфере. Обычно
на корпусе ставится расходный жиклер Ж, а к центру поводка
подводится масло от общей масляной магистрали мотора.
136
Из сказанного выше ясно как должно быть выбрано место
постановки демпфера. Наилучшим образом он будет работать
будучи установлен в том сечении системы, которое имеет наи-
большие амплитуды колебаний. Установленный в узле или около
него демпфер работать не будет.
Энергия, рассеиваемая демпфером, пропорциональна моменту
сил вязкого трения масла и амплитуде относительных смеще-
ний деталей А и В. В свою очередь обе эти величины зависят
от размеров катарракта и зазоров.
При отсутствии зазоров и катаррактов сопротивления пере-
теканию масла бесконечны, однако нельзя сказать, что одновре-
Фиг. 70
менно и работа сил сопротивления бесконечна, так как нет са-
мих смещений, и значит рассеиваемая демпфером энергия равна
нулю. В этом предельном случае демпфер обращается в жестко
закрепленную массу. При очень больших зазорах, т. е. при от-
сутствии сопротивлений, демпфер также не работает, так как
работа момента сопротивления равна нулю. Очевидно, между
этими двумя предельными случаями существует некоторый про-
межуточный, при котором работа момента сил сопротивления
максимальна и демпфер наиболее эффективен.
Элементарная теория гидравлического демпфера покоится на
двух положениях:
1. Вал в месте постановки демпфера совершает простые гар-
монические колебания
9 = Fsin
так что ,
<P = F2<cos Qht,
и
о = —FQK2 sin 2,/.
137
2. Момент сопротивления маховика относительно поводка
демпфера пропорционален скорости смещения
М6 = Ed (? —
здесь —коэфициент пропорциональности, размерность кото-
рого (кг см сек) такая же, как и коэфициента Е;
<рй—угол поворота маховика демпфера, соответствующий
моменту времени t.
При установившемся режиме работы маховик совершает гар-
монические колебания той же частоты 2К, что и колебания всей
системы
?a=^sin(2^+%),
где Fd—амплитуда колебаний демпфера;
—угол сдвига фаз маховика относительно поводка.
Скорость и ускорение маховика будут:
'?d=FdQKcos(SKt+-bdy,
<?д = — FdQK2 si п (2^ + %).
Момент сопротивления демпфера теперь может быть запи-
сан следующим образом:
Мд = ЕЙ2Л. | F cos QKt—Fd cos I- (70)
Такой же момент, но с обратным знаком, действует на махо-
вик и сообщает ему угловое ускорение пропорциональное
моменту инерции 1д
— Md=I^d = —!dFdQK- sin(2^+фД
Таким образом, уравнение движения маховика имеет вид:
7d^fc3sin(2^ + 0d) = E<,2J77cos2K/-Fd cos(2^ + %)| (71)
или
fdFaQK3 [sin QKt cos + cos QKt sin =
“Wfcos 2,/—Fd(cos2/cosO„—sin2Kf sin%)[. (71a)
Это уравнение должно удовлетворяться при любом значении
времени t. Задавая значение t, при котором 2Л/=-|-^-, полу-
чим
IdFo^^os = ^Fe sin %,
откуда
= (716)
138
Для определения зависимости между амплитудами F и F6
преобразуем уравнение движения маховика:'
Feos L\/=FJcos(2/+6J+ ^sin(2^ + -b)|=
-д
= F,} [cos (LV+%)+ ° sin {QKt + *<,)]=
COS Jd
z Feos (2/+’^) cos %+ sin (SJ-p^sin 1 _
d COS фэ
= F cos (2^4-^--^)
° cos Фа
Отсюда
Fd = Fcos'j,,. (71b)
Теперь момент, действующий на поводок со стороны махо-
вика, может быть записан следующим образом:
М, = - /^2K’sin (2Kt 4- -Ы =
— — cos Фа (sin cos + cos QKt sin'jJ =
= — IdFQ2 (cos2 Фе, sin 2Kf+i- sin 2>„• cos QKt) —
= /dCOS20d- £-/е,2к5П12фе,-?' (72)
Следовательно, демпфер действует на систему, во-первых,
как жестко закрепленная масса с моментом инерции 7dcos2,/d,
(благодаря чему снижается частота свободных колебаний си-
стемы) и, во-вторых, как сопротивление, момент которого
— i-/d2B sin 2ф<?-«р глушит колебания. Об этом свидетельствует
знак минус, указывающий на то, что момент сопротивлений
демпфера имеет фазу, противоположную скорости колебания и
значит работа этого мемеита отрицательна.
Амплитуда заглушающего момента i-4,F2/sin 2фй макси-
мальна при ф<, = 45° (если не учитывать изменения частоты сво-
бодных колебаний системы и величины F при изменении ф^) и
равна ^-/f,F2K2.
При этой наивыгоднейшей настройке демпфера
'д наив — Л>“к> (72а)
так как 1₽фе,= 1.
13S
Перейдем теперь к определению резонансных амплитуд коле-
бания системы с гидравлическим демпфером.
Для этого составим баланс подводимой и рассеиваемой энергии
при резонансе. •
как было выведено раньше в § 16, работа, совершаемая резо-
нирующими гармониками возмущающих моментов, за период
колебания
УХгв=Т.Ск^^г..
Работа моментов сил сопротивления системы за период коле-
бания
Работа, рассеиваемая демпфером за период, на основании
выводов § 11
^, = ^2^ sin 26,.
На установившемся режиме
we=w.+ wd
или
sin г, = $oKvf ,з+ sin (73)
Пренебрегая изменением формы свободных колебаний, вызван-
ных установкой демпфера, и считая, как это делалось раньше,
что форма свободных колебаний системы и форма вынужденных
колебаний при резонансе одинаковы, получим:
sin Ej = ;2KFIa'|.2 + 7,2K2f sin 26„ (73a)
, Л л
здесь a, = — известное (поскольку известна форма свобод-
ных колебаний системы) отношение амплитуды
z-й массы к амплитуде сечения вала, в кото-
ром установлен демпфер.
Отсюда амплитуда вала в месте установки демпфера
Ск?л.' sine,
F— - т .
^S«7 + J-Z,2K2sin26,
Если бы демпфера не было, то амплитуда вала в месте, где
демпфер стоит, определялась из равенства типа (66)
340
Очевидно,
(74)
Обозначая
О '3
(74а)
о
1
1 /<А О1
получим
I
(746)
Fo 1 + р sin 2''Jd
F
даиы графики показывающие во сколько раз
На фиг! 71
уменьшатся резонансные амплитуды колебаний вала в случае
постановки гидравлического демпфера при различной его на-
стройке и различном значении параметра р.
На фиг. 72 приведены резонансные кривые одного авиацион-
ного двигателя с гидравлическим демпфером и без него.
При проектировании гидравлического демпфера расчет про-
водится в следующем порядке:
1. Задаваясь требуемым, из условий прочности вала, сниже-
F'
нием резонансных амплитуд р-, определяют р при наивыгоднеи-
' о
шей настройке демпфера (% = 45 )
Hi
2. Из уравнений (72а) и (74а) определяют наивыгоднейшее
значение коэфициента
^днаив— 2piAjtt j.
3. Определяют требуемый момент инерции маховика демп-
фера
г _Hat.»
§ 22. Демпфер сухого трения
На фиг. 73 приведена схема демпфера с сухим трением.
На валу, совершающем крутильные колебания, жестко поса-
жен диск А, к торцам которого прижаты пружинами маховики В.
Характер движения маховиков зависит от сил трения на их
рабочих поверхностях. Если трения вообще нет, маховики оста-
ются неподвижными. При незначительном трении маховики увле-
каются диском и вращаются практически равномерно так, что
между ними и диском происходит скольжение, амплитуда кото-
рого может считаться равной амплитуде колебаний диска. Бла-
годаря тому, что величина грения мала, энергия, рассеиваемая
демпфером, также Ma.ia.j
142
По мере увеличения затяжки пружин растет момент сил тре-
ти и величина рассеиваемой демпфером энергии.
Начиная с некоторого предела, дальнейшее увеличение сил
(атяжки пружин приводит к уменьшению эффективности демп-
фера, так как возникает новый характер движения маховиков—
колебания с остановками относительно вала. Слишком большой
момент сил трения приводит к тому, что в течение определен-
ной части перйода колебаний маховики увлекаются диском и
следуют вместе с ним и только на остальной части периода
существует проскальзывание.
Наконец, если момент сил трения от затяжки пружйн будет
больше максимального значения сил инерции маховиков 1<?д,
скольжение совершенно прекратится и рассеиваемая демпфером
энергия будет равна нулю.
На фиг. 74 представлен график рассеиваемой демпфером
анергии в зависимости от величины момента сил трения.
Кривая построена в безразмерных координатах, причем Мд—
момент сил трения, остальные обозначения сохранены без изме-
нений.
Работа, совершаемая моментом сил трения
= (75)
здесь (э—<ti))dt — элементарное относительное угловое перемеще-
ние трущихся поверхностей.
При сухом трении момент Мд зависит от силы затяжки пру-
жин, материала трущихся поверхностей, их числа и размеров.
От относительной скорости трущихся поверхностей Мд не
зависит.
Если движение маховиков происходит без остановок относи-
тельно вала, то они все время оказываются под действием по-
стоянного по величине, но изменяющегося по направлению мо-
мента ± Мд. Так как момент сил трения всегда направлен про-
тив относительного движения, то знак момента меняется одно-
временно с изменением направления относительного движения.
Ускорение маховиков также все время остается постоянным
по величине, потому что согласно второму закону Ньютона
±
Интегрируя последнее уравнение, получим скорость махо-
виков
Постоянная интегрирования С, по смыслу должна равняться
средней угловой скорости вращения всей системы и в дальней-
шем может быть опущена.
143
Скорость колебания маховиков меняется во времени линейно
и график скорости состоит из отрезков, наклон которых к оси
абсцисс зависит от отношения . Период колебания махови-
‘д
ков, естественно, равен периоду колебаний крутильной системы.
Что касается скорости диска, то, полагая, как и раньше, что
вал совершает простые гармонические колебания, получим
<P = FSKcos(SV — ф)
(следует помнить, что форма записи гармонического колебания
может быть различной. Фазовый угол ф зависит от момента на-
чала отсчета).
На фиг. 75а представлен график скорости диска в виде ко-
синусоиды 1 и скорости маховиков в виде ломаной I]. Если за-
тяжка пружин не очень велика, то график II должен быть зер-
кально симметричен относительно ординаты точки А. Действи-
тельно, прямая не может быть продолжена, как показано на
чертеже пунктиром, потому что по разные стороны от точки А
относительная скорость, а значит и момент трения меняют знак,
т. е. меняют знак tg угла наклона прямой.
Если увеличить силу затяжки пружин, то наклон графика
скорости маховиков возрастет (фиг. 756).
В этом случае, как и раньше, прямая не может быть продол-
жена за точку А, вместе с тем график скорости не может пойти
так, как показано на чертеже пунктиром (нет изменения знака
относительной скорости). От точки А маховики будут двигаться
вместе с диском, увеличивая ускорение до тех пор, пока оно
7W
не станет равным (в точке В)—~. В точке В маховики отор-
вутся от диска.
Заштрихованная на фиг. 75а и 756 площадь, умноженная на
Mtj, представляет собой работу, которую рассеивает демпфер за
144
-g- периода. В случае колебаний с „относительными останов-
ками" заштрихованная площадь получается значительно меньшей.
Вычислим наибольшую величину Wd. За начало отсчета при-
мем момент, когда скорость колебания маховиков равна нулю.
(На фиг. 75а начало отмечено буквой С).
При == ± угловые скорости диска и маховиков оди-
наковы, т. е.
г... / . ~ , \ -к
jg-,
ИЛИ
- Л!
sin о = ± ~ -jjpy-j • (75а)
Из последнего равенства определяется начальная фаза ф.
Работа, рассеиваемая демпфером за период, равна заштрихо-
ванной на фиг. 75а площади, умноженной на 2Мд, т. е.
QK (cos !> cos QKt — sin ф sin t)-~d-11 dt.
•v J
At,;
Так как
TZ 7Г “
207 2Q? 2<7
/2 Г Г
cos2./-tfr = -„- ; I sinS);t-dt = O и it-dl = O,
J , J
" r-1 _ ~
2ё7 2QK 21-7
TO ___
U7d = 4/WdFcos ф или W^ = 4/WdF I/ 1 —
2L V
2 JdFQK2 ) •
Диференцируя последнее выражение по и приравнивая ре-
зультат нулю, найдем то значение момента трения Мд, при кото-
ром рассеиваемая демпфером энергия получается наибольшей.
Обозначим: у = а, тогда Wa=4FMd \/1 — а’7И„2
=0= /1 - nW "ТИЛ-ТТ—2-а ^-а
аМд 2 /1 _ n2Afd2
или ___
|/ 2я3— к ° к '
10 в. Кириченко 145
1 4
При этом значении момента cos<J* = p-^, a U/dmojr = —
Подобно тому, как это было сделано в предыдущем пара-
графе для системы с гидравлическим демпфером, вычислим те-
перь величины резонансных амплитуд системы с демпфером су-
хого трения, составив баланс подводимой и рассеиваемой энергии.
В данном случае, произведя подстановку, получим:
CKE«/jsin £i
4
-Q '2 4- — / ° ’
Отношение резонансных амплитуд системы с демпфером к ре-
зонансным амплитудам системы без демпфера в рассматриваемом
случае имеет вид:
F • 1
4/а^ ’
:’££а/2
О
Ооозначая —Jy-,£-= Р> получим -р- — .
Расчет демпфера сухого треиия проводится в следующем по-
рядке:
1. Задаются требуемым, из !условий прочности вала, сниже-
но
нием резонансных амплитуд -р и определяют р
2. По найденному значению р вычисляют потребный момент
инерции маховиков
д ~ 42..
3. Определяют наивыгоднейшее значение момента трения
./2"
м = У~ FIV 2
4. Определяют потребную силу затяжки пружин по формуле,
применяемой при расчете фрикционных муфт
о -___
шт ,.
[Ч/?,
146
где 'а—коэфициент трения;
I —число пар трущихся поверхностей;
2 /?:i — г1 7?+г
^ = 3-~-----------------средний радиус
трения;
А и г—внутренний и наружный' радиусы
фрикционного кольца.
На фиг. 76 даны экспериментальные резонансные кривые, ил-
люстрирующие эффективность демпфера сухого трения для од-
ного рядного 8-цилиндрового 4-тактного двигателя мощностью
Л; = 685 л. с.
При данных габаритах демпфера эффективность его может
быть увеличена за счет введения дополнительной упругой связи
(пружин) между диском и маховиками демпфера.
На фиг. 77 так же, как и на фиг. 74, в безразмерных координа-
тах построены графики энергии, рассеиваемой демпфером за пе-
риод, в зависимости от момента сил трения при различных отно-
шениях частоты свободных колебаний демпфера к частоте ко-
лебаний вала 2К.
ю<:
147
В случае 2д = 0, т. е. для демпфера без пружин, кривая со&.
падает с кривой на фиг. 79.
Резонансные амплитуды системы с таким демпфером могут
быть найдены тем же путем, что и раньше, т. е. из уравнения
величина может быть определена непосредственно по
фиг. 77.
§ 23. Динамический демпфер
Для выяснения принципа действия динамического демпфера
кРУТильных колебаний рассмотрим систему, состоящую из упру-
гого вала, один конец которого заделан, а второй несет массив-
ный диск, момент инерции которого обозначим через /. На диск
дейсТВует внешний возмущающий момент /И — Ск sin Момент
инерции вала пренебрежимо мал.
Жесткость вала на {кручение обозначим k, сопротивлениями
пренебрежем, £ = 0.
Как известно, диференциальное уравнение движения диска
имеет вид:
I <f+k<? = М.
Частное решение этого уравнения, представляющее стационар-
ную часть колебаний:
7 = Fsin QKt,
148
где F=fftmri, <pem=-^;
Если к основной системе присоединить на упругом валике k„
пополнительную массу с моментом инерции 1д (фиг. 78), то она
может быть подобрана так, что колебания
основной системы будут полностью устра-
нены. Дополнительная система будет слу-
жить демпфером. Определим каким усло-
виям должны удовлетворять при этом па-
раметры дополнительной системы.
Диференциальное уравнение движения
основной массы имеет вид:
/? + £? — — у) = Ск sin Q,,t. (76)
Диференциальное уравнение движения
дополнительной массы:
ф) = 0. (76а)
Частное решение этих уравнений будем
искать в виде:
Фиг. 78
= Fsin QKt )
= Fd sin 2^ /
(766)
Выполняя подстановку и требуя, чтобы уравнения удовлетво
рялись в любой момент времени t, получим:
- IF2К»+kF - kd{Fd -F) = CK\
-hFd^+kd{Fd-F) = Q I'
Отсюда
F- CK(kd-Id^)
(- F2K^k6+k)(kd - W)~ V
F — ________________________ I
d ~ (- W + k< + k)(kd - W)~V I
Очевидно, что при выполнении условия k6 — IdQh- — Q, ам-
плитуда основной массы F = 0, т. е. основная масса колебаний
не совершает. В этом случае
cpd= — ~ sin 2/, (76д)
т. е., работая как демпфер и полностью устраняя колебания
основной системы, дополнительная масса колеблется с частотой
возмущающего момента и амплитудой, прямо пропорциональной
149
амплитуде возмущающего момента и обратно пропорционально ft
жесткости дополнительного валика.
Знак минус в формуле (76д) обозначает, что по фазе коле-
бания демпфера смещены на 180° относительно внешнего момента.
Работу демпфера можно понимать так: параметры дополни-
тельной системы подобраны так, что при колебаниях она пере-
дает на основную систему момент все время в точности равный
моменту внешних сил, но направленный в обратную сторону.
Действительно: Л1д = <рд1гд= — С*sinQKt.
Так как Мд вовсе не зависит от того, к какой системе он
присоединяется, то можно сделать вывод, что тот же демпфер
полностью устранит колебания любой многомассовой системы,
если он будет присоединен к той же массе, на которую дей-
ствует момент 7W = Cxsin 2К£.
Если возмущающие колебания моменты, имеющие частоту *-к,
действуют на все или несколько масс многомассовой системы,
а демпфер присоединен только к одной, то система колеблется
так, как если бы в месте установки демпфера была бесконечно
большая масса, т. е. демпфер эквивалентен „заделке“ и делит
основную систему на две ветви, каждая из которых колеблется
под действием только тех моментов, которые к ней приложены.
Успех применения описываемого демпфера обеспечен лишь
в том случае, если частота внешней нагрузки не меняется
!2К = const. Если же в эксплоатации системы — var, то будучи
полезным на режиме QKpaC4, на всех остальных режимах демп-
фер эффективно не работает и может быть даже вредным. Дей-
ствительно, постановка демпфера увеличивает на единицу число
степеней свободы системы и соответственно число форм сво-
бодных колебаний. Так, система, изображенная на фиг. 78, имеет
две формы свободных колебаний и, значит, возможны два резо-
нанса, причем один наступит при QK<GKPae.„ а другой при
о >» о
“л раст
В авиационных моторах частота внешних возмущающих мо-
ментов меняется пропорционально оборотам мотора и поэтому
описываемый демпфер не применяется.
В авиационном моторостроении широкое распространение по-
лучил более совершенный тип динамического демпфера, назы-
ваемый маятниковым.
Маятниковые демпферы применяются на целом ряде авиацион-
ных двигателей в том числе на отечественных звездообразных
одно- и двухрядных двигателях семейства АШ (7, 9, и 14-цилин-
дровых моторах) и некоторых V-образных 12-цилиндровых
моторах.
§ 24. Маятниковый демпфер
На фиг. 79а изображена схема маятникового демпфера. В ка-
честве колеблющегося груза использован обычный противовес-
ов подвешен к щеке на двух роликах. Такая иподвеска позво-
150
ляет противовесу перемещаться относительно щеки поступатель-
но по дуге радиуса р—D — d.
Так как величина р, при данной подвеске, может быть легко
сделана сколь угодно малой, то этим разрешается сложная за-
дача создания массивного очень короткого маятника.
Поступательное движение противовеса дает право считать
всю его массу т сосредоточенной в центре тяжести, т. е. дела-
ет его в динамическом отношении эквивалентным простому ма-
тематическому маятнику (фиг. 796).
При вращении вала с угловой скоростью «о противовес-демп-
фер совершает колебания, частота которых пропорциональна ш
и зависит всего от двух параметров I и р.
Если на вал действует крутящий момент, частота которого
Ао>, то надлежащим подбором величин I и р можно добиться
равенства частоты свободных колебаний маятника частоте внеш-
него момента. Такой подбор называют настройкой маятника.
Очень важно, что настройка будет сохранять силу на всех ско-
ростях вращения вала.
Настроенный маятник создаст в точках подвеса давление, мо-
мент которого относительно оси вала будет все время равен
внешнему возмущающему моменту, но направлен в противопо-
ложную сторону. Благодаря этому маятник будет действовать
на вал как бесконечно большая масса, парализуя действие гар-
моники, на которую произведена настройка.
Для доказательства всего вышеизложенного рассмотрим эле-
ментарную теорию маятникового демпфера.
Пусть (фиг. 80) на равномерное вращение вала с угловой
скоростью о наложены еще малые гармонические колебания
•5 = Fsin K^t. Пусть, далее, параметры маятника подобраны так,
что масса т все время остается на оси ОД, вращающейся равно-
151
мерно. Это условие равносильно условию равенства частот ко-
лебания маятника и щеки /.
При вращении маятник разовьет центробежную силу Р, ко-
торую для малых колебаний можно считать равной /п(/ + р)ша.
Раскладывая силу Р на направление
ему, получим две составляющие Z и Т.
Р и перпендикулярное
Фиг. 80
(77)
Сила Z = PcosS передается через подвеску и создает отно-
сительно оси вала момент
Мк — Z-OC = /п(р + Z)w2 cos 6 • ОС,
плечо силы ОС = I sin <?м
Ввиду малости колебаний можно считать cos 8 = 1 и sin ?„=«„,
тогда
MR= И(р + /)ш!/?Л.
Сила Т = Р sin 5 = Р8.
Заметим, что 8 = — а. Вместе с тем ab — щ и одновремен-
но ад = <р/, гак что 8 = — = и — и'8 = —- = . Отсюда
р / + р * р-Ь/
Т = П1и^1чм.
(77а)
152
Сила Т, умноженная ина плечо р, дает момент относительно
точки подвеса.
Рассматривая движение маятника относительно точки под-
веса, получим: момент 7р вызывает угловое ускорение <pj;, про-
порциональное моменту инерции маятника относительно точки
подвеса тр3
Т р 4- тра? „ = 0 (78)
или после подстановки значения Г и сокращений
®2/<рЛ + р?Л = 0,
и окончательно
Как известно, это диференциальное уравнение описывает
простые гармонические колебания
= (786)
частота которых
р f/I- (78в)
• V Р
Приравнивая частоту колебаний маятника рм частоте колеба-
ний щеки К®, получим
K = J-- (79)
V Р
В последнюю формулу, являющуюся формулой настройки,
не входит ®, что свидетельствует о замечательном свойстве
маятника сохранять настройку при любой скорости вращения.
Для того чтобы выяснить действие маятника на вал, соста-
вим уравнение тангенциальных смещений маятника относительно
оси вала.
Тангенциальное смещение маятника относительно оси вала
можно представить состоящим из двух частей: смещения вместе
со щекой (р-Н)? и поворота относительно щеки р<рм. Соответст-
венно тангенциальное ускорение маятника (без учета малых, в
данном случае, кориолисовых ускорений) будет (р + 7)<р + руЛ1.
Это ускорение вызывается тангенциальной силой Т.
Диференциальное уравнение тангенциальных смещений маят-
ника относительно оси вала имеет вид:
/п(р + /)<р 4- mp-s „ 4- m»>3l<pM = 0. (80)
Полагая, что маятник настроен на частоту колебания щеки,
т. е., что — F sin Ku>t и = FM sin Kut, после подстановки <р и <р „
получим:
(p + l)FKa-'+pFMK3-lFM = 0,
153
откуда
(p + Z)Aa
F ~ Z-p№ •
Момент, действующий на вал, был вычислен раньше (77а)
7ИЛ = m(p+ty»2lyM.
В этом выражении угол отклонения маятника можно пред-
ставить в следующем виде:
FM с „ (р + Z)№
= —Л- F sin Kvt = -у-<— Fsin Kvt,
i I p/\ •
так что
.ИЛ=Мр + />’-/^±^’ Asin Awt,
но
AAWsin Ku>t=. — c,
поэтому
_m(p+/)L ••
p '
1 - -J- Aa
Если вместо маятника к валу жестко присоединить массу с
моментом инерции то при угловом ускорении эта масса
создаст момент, действующий на вал — /э„<р. Отсюда следует,
что при малых колебаниях маятник полностью эквивалентен
маховику с моментом инерции
= (81)
1-|№
В этой формуле числитель есть момент инерции жестко за-
крепленного „маятника", а знаменатель представляет собой ди-
намический коэфициент, величина которого зависит от отноше-
ния квадрата частоты возбуждающей гармоники к квадрату ча-
стоты колебаний маятника. < л \
При точной настройке маятника на К-к> гармонику (А =у/-|
он эквивалентен бесконечно большому маховику, так как в фор-
муле, определяющей 1ам, знаменатель равен нулю. Незначитель-
ные неточности в настройке не отражаются на эффективности
демпфера.
При резком отличии рм от частоты возбуждения Aw действие
маятника на систему становится мало заметным, так как знаме-
натель в выражении, определяющем 1ЭМ, становится по абсолют-
ной величине большим числом.
154
Как и динамический демпфер, рассмотренный в предыдущем
параграфе, точно настроенный маятник в месте постановки соз-
дает узел. Если такой демпфер поставлен на многомассовую си-
стему, то в отношении колебаний, происходящих с частотой, на
которую произведена настройка, демпфер разделяет систему на
две отдельные ветви, каждая из которых колеблется под дейст-
вием тех моментов, которые к ней приложены, а сечения, где-
стоит демпфер, „заделаны11.
Здесь кстати отметить интересный факт, с которым столкну-
лись при постановке маятникового демпфера на девятицилин-
дровый мотор АШ-62. На этом моторе наблюдался сильный резо-
нанс с гармоникой порядка К ~ 4,5. Если бы можно было уста-
новить демпфер точно в месте действия возмущающего мо-
мента, т. е. на шатунной шейке, он полностью устранил бы
колебания с частотой, на которую произведена настройка. Оче-
видно также, что маятниковый демпфер совсем бесполезен, если
он установлен в узле колебаний системы без темпфера или
близко к узлу.
В описываемом случае в качестве демпфера было решено
использовать задний противовес, как наиболее удаленный от
узла колебаний. С демпфером система имела узел на задней
щеке и благодаря податливости участка вала от места подвески
демпфера до места приложения возбуждающего момента незна-
чительные колебания с частотой, на которую была произведена
настройка, остались. Эти колебания были совершенно не опасны
для вала, но оказались разрушительными для винта. При малых
закрутках вала, вследствие значительного удаления втулки винта
от узла колебаний, ее амплитуды получались большими. Коле-
бания втулки винта вызывали изгибные колебания лопастей и
лопасти ломались.
Перестановкой демпфера на переднюю щеку кривошипа можно
было избавиться от разрушений винта, но не было гарантии
в том, что не возникнут неполадки с нагнетателем. Решение
вопроса состояло в установке двух маятников, настроенных на
один и тот же порядок /С = 4,5, на обоих щеках кривошипа.
Два демпфера дали два узла и разбили систему на три ветви,
причем крайние—нагнетатель, с одной стороны, и редуктор-
винт с другой—были совершенно свободны от вибраций с часто-
той 4.5 о.
Другое решение вопроса состояло в специальной „расстройке1*
демпфера, имеющей целью сместить узел колебании на середину
шатунной шейки.
На фиг. 81 дана кривая, показывающая на сколько нужно
укоротить маятник для того, чтобы получить желаемый эффект.
Так как потребная расстройка является функцией оборотов дви-
гателя, то этот способ борьбы с вибрацией лопастей винта хуже
первого.
Если на систему с маятниковым демпфером действует
155
ряд гармонических возмущений разных частот
, то благодаря тому, что момент инерции массы, заме-
др-уменьшение длиныр
Фиг. 81
1. 1|-,2
няющей маятник различен при различных К, ряд резонансов,
соответствующих этим возмущениям, не является просто пропор-
циональным как в обычном случае (см. § 17). Для каждого
Л
порядка К существует своя частота собственных колебаний си-
стемы, которая определяется
обычным способом, но с уче-
том изменения момента инер-
ции массы, к которой при-
соединен маятник.
Для иллюстрации этого
положения на фиг. 82 и 83
даны графики чисел собствен-
ных колебаний крутильных
систем 14 и 18-цилиндровых
двухрядных звездообразных
двигателей, у которых валы
имеют маятниковые демпферы,
настроенные на гармоники К=
i . ,.
— -И1 (I — число цилиндров,
работающих на один кривошип). На фиг. 84 и 85 даны экспери-
ментальные резонансные кривые этих двигателей.
В обоих случаях опыт обнаруживает, что резонансы гармо-
ник К — и i неопасны.
На фиг. 86 даны графики чисел собственных колебаний кру-
1 ильной системы 12-цилиндрового V-образного двигателя, вал
которого имеет маятниковые демпферы, настроенные на гармо-
ники порядка /<=4,5 и 7,5.
Расчет показывает, что без демпферов напряжения в элемен-
тах конструкции выходят за пределы допустимых. Так, при ре-
зонансе трехузловой формы с гармоникой /< = 7,5, наступающем
при и = 2680 об/мин, напряжения в щеках, примыкающих к сред-
ней коренной шейке, достигают 800 кг[см*. Маятниковые демп-
феры этот резонанс устраняют.
Элементарная теория маятникового демпфера покоится на
том допущении, что колебания маятника малы гм =- ради-
ана. Амплитуда F,, может быть определена по формуле
(82)Э
" mp/<ir(l+№)
*) См. Нейман Н III., Динамика авиационных двигателей, Оборонгиз, 1940.
156
Здесь обозначения сохранены старые.
Если радиана, маятниковый демпфер попрежнему га-
э
сит гармонику возмущения, на которую произведена настройка,
ио создает дополнительные эффекты, которые должны быть
учтены при проектировании.
Фиг. 82
157
При больших колебаниях момент, создаваемый демпфером,
не является гармоническим и разложение его в ряд Фурье со-
держит, по крайней мере, три существенных компонента (фиг. 87).
Эти обороты реактивного момента, имеющие частоту 2К<^ и ЗДш,
ПротиЫесы закреплены -______.
Фиг. 83
могут сами вызвать опасные колебания системы, к которой маят-
ник подвешен.
На звездообразных двигателях, где в качестве маятникового
груза используются тяжелые противовесы, амплитуды колебаний
маятника не превосходят нескольких градусов. Однако в некото-
.158
рых случаях роль маятника выполняет цилиндрический ролик,
помещенный в отверстие щеки вала (фиг. 88). Ролик в силу
того, что масса его относительно мала, работает на больших
амплитудах достигает 60°).
Теоретически достаточно точная настройка такого маятника
может быть получена либб при полном отсутствии сил трения
в механизме, что обеспечит скольжение ролика, либо при таком
трении, которое даст уверенность в том, что ролик катится и
не скользит.
159
Главный эффект замены скольжения вращением состоит в ка-
жущемся увеличении массы маятника на 50% вследствие допол-
нительной кинетической энергии вращения ролика. При этом
частота колебаний в ]/1,5 раза больше частоты скольжения ро-
лика и формула настройки имеет вид:
А"-0,815 (83)'>
’) См. Покорный Б. М., Расчет коленчатого вала на крутильные колебания,
Маш гиз, 1947.
160
Практически маятниковые демпферы подобного типа проекти-
руют, считая, что чистого скольжения или чистого качения в ме-
ханизме нет, и пользуются формулой настройки в виде:
/< = 0,911/-. (84)
V р
Наконец, следует заметить, что маятниковые демпферы устра-
няют колебания систем, к которым они подвешены без выделе-
ния тепла. Несмотря иа то, что мощность колебаний составляет
Фиг. 87 Фиг. 88
незначительную часть эффективной мощности мотора, она мо-
жет быть причиной значительных затруднений в том случае,
если она превращается в тепло внутри картера, как это имеет
место при применении демпферов трения.
§25. Муфты
В авиационном моторостроении часто применяются в пере-
дачах к винту и агрегатам муфты, которые предохраняют зубча-
тые зацепления и сами агрегаты от ударных нагрузок, возникаю-
щих при резком изменении режима работы мотора, смягчают
действие неравномерного крутящего момента, особенно сильное
при возможных перебоях в системе зажигания, и одновременно
являются демпферами крутильных колебаний. Конструкция и
принцип действия таких муфт весьма разнообразен. В этом па-
раграфе очень кратко рассмотрены только три типа муфт.
11 В. Кириченко 161
Маятниковая муфта (фиг. 89)
На ведущем диске А в точке 0 подвешен маятник М, стер-
жень которого охвачен поводком С, укрепленным на ведомом
диске В. Поводок С может поворачиваться относительно своей
оси.
При вращении муфты центробежная сила маятника Р дает
составляющую Т, от которой на поводок передается сила
Р— приводящая во вращение диск В. Усилие R, а значит
и „жесткость муфты®, изменяются пропорционально квадрату'
угловой скорости системы. Подбором величин М, г. а и b можно
Фиг. 89
обеспечить любую малую жесткость муфты, снизить частоту
свободных колебаний всей системы и избавить ее от опасных
резонансов крутильных колебаний.
При возникновении крутильных колебаний переменная соста-
вляющая реакции в точке подвеса маятника действует все время
в сторону, противоположную отклонению дисков от положения,
которое они занимают при равномерном вращении, т. е. муфта
действует как демпфер.
Гидравлическая муфта (фиг. 90)
Муфта состоит из ведущей части—насоса Н и ведомой—
турбины Т, между которыми жесткой связи нет. Внутренняя
полость муфты образует кольцевой канал, разделенный на от-
дельные отсеки радиальными перегородками П. Перегородки
каждой половины связаны кольцом К.
Муфта заполняется маслом, которое во время работы цирку-
лирует в каждом отсеке, как показано на схеме стрелками.
162
Циркуляция вызывается разностью центробежных сил масла
в ведущей и ведомой частях муфты.
В ведущей части центробежные силы масла больше, так как
вследствие неизбежных потерь ведомая часть вращается мед-
леннее. При полном заполнении муфты эта разность скоростей
вращения составляет всего 2—3%. При частичном заполнении
проскальзывание увеличивается и ведомая часть вращается зна-
чительно медленнее ведущей. Отсюда видно, что такая муфта
является одновременно редуктором с плавным изменением пере-
даточного числа, если обеспечена возможность постепенного
Фиг. 90
изменения наполнения муфты. Очень важно заметить, что коэ-
фициент полезного действия муфты равен ее передаточному
числу. При больших скольжениях передача становится неэконо-
мичной, и муфта требует интенсивного теплоотвода, так как вся
теряемая в ней энергия обращается в тепло.
Гидравлические муфты устанавливались в передачах к нагне-
тателям на некоторых отечественных двигателях и немецких дви-
гателях. Скольжение в муфгах не превосходило 30%.
Остутствие жесткой связи между ведущим и ведомым валами
приводит к тому, что в отношении крутильных колебаний муфта
делит систему на две независимые части, и если возмущающие
моменты действуют только на ведущую часть, то ведомая вра-
щается попрежнему равномерно. Кроме того, муфта, хотя и не-
значительно, но демпфирует крутильные колебания.
Для уяснения принципа действия муфты рассмотрим частичку
dm кольцевой струйки с сечением а. Частица dm увлекается
11*
163
во вращение и отбрасывается центробежными силами к перифе-
1, dr
рии. Обозначим ее скорость в радиальном направлении vr= ~ .
Движение вокруг оси муфты с угловой скоростью и одно-
временное перемещение в радиальном направлении вызывает
кориолисово ускорение и соответствующую ему силу инерции,
равную 2dmwVr, направленную касательно к окружности с цент-
ром на оси муфты в сторону, противоположную вращению. Мо-
мент этой силы равен 2dmw- Vr. Крутящий момент от всех ча-
стиц, расположенных на линии тока от г, до г2, равен
г2 Г1
/п I/ .> п dm с Ат . , ...
2w Vr • г • dm — 2о> —— I г dr — <о (г,— г2-),
J *
Г, г}
dm Хт
здесь ---масса жидкости, протекающая в секунду че-
рез сечение а;
Д/п— масса всех частиц кольцевой струйки;
Т — период циркуляции (в секундах).
Крутящий момент от кориолисовых сил на ведомой части
муфты будет направлен в сторону вращения и равен
(<“ — До>)—у (Г,3—Г.,*).
При переходе частички жидкости из точки 2 в точку 2' ее
окружная скорость падает на величину Ашга. Секундная потеря
соответствующей составляющей количества движения в месте
. А/л
перехода составляет Дшг, —у и равна силе действия тока жид-
кости, проходящей за секунду через сечение а, на ведомую часть
муфты. Момент силы, вызванной изменением количества дви-
. - Д/я
жения, равен До>г/ -у- и направлен в сторону вращения.
Суммарный крутящий момент, действующий на ведомую
часть муфты, равен:
2И= (<•> — Дш)-у (г,5—г23) + Дшга3 =
= Нп® — •'г) + Awr/J. (85)
При переходе жидкости из ведомой части муфты в ведущую
возникает момент Л»»/^3 действующий на ведущую часть и
направленный против вращения. Вместе с моментом от корио-
лисовых сил он равен по величине и обратен по направлению
164
моменту, приложенному к ведомой части, что и должно иметь
место по закону равенства действия и противодействия.
Крутящий момент М возникает от одной струйки жидкости,
сечение которой равно а. Полный крутящий момент может быть
найден суммированием действия всех струек, заполняющих внут-
ренний объем муфты.
При крутильных колебаниях вала угловая скорость ведущей
части муфты будет «> + <Ра(?л—угловая скорость колебания), а ве-
домой w —Дш. Если считать, что скорость циркуляции жидкости
в новых условиях сохраняется прежней, то полученное выше
выражение для крутящего момента от одной струйки сохраняет
силу и в рассматриваемом случае приобретает вид:
. , . Дот, , . „Дот
(и>—Да>)—- (г,- — Г„а)+(Д1» ?A)rj3 -у-
или .
(86)
Новый член в выражении момента пропорционален угловой
скорости колебаний и в реальных условиях всегда действует
как момент, демпфирующий крутильное колебание.
Муфта с нелинейной характеристикой
На фиг. 91а представлена схема ведомой шестерни редуктора
с пакетами из витых цилиндрических пружин, монтируемых
с предварительной осадкой.
Зависимость между силой, приложенной на окружности рас-
положения осей пружин и углом сдвига зубчатого веица относи-
тельно ведомого вала, имеет вид:
P = (kf+k^r)n,
здесь: k — жесткость каждой пружины (кг[мм\,
/—величина предварительной осадки (мм)',
₽ — угол закрутки муфты (радиан);
п—число пружин.
График этой зависимости дан на фиг. 916.
До сих пор рассматривавшиеся крутильные системы имели
восстанавливающие моменты, пропорциональные угловым пере-
мещениям. Описываемая муфта не обладает этим свойством.
Закрутка муфты начинается лишь после того, как сила Р до-
стигнет величины, соответствующей Pa — nkf — сила предвари-
тельной осадки. При .всех значениях Р<Р0 муфту можно счи-
тать абсолютно жесткой. Диференциальные уравнения, описы-
вающие колебания системы с участком, жесткость которого не-
постоянна, а является функцией перемещения, нелинейны. По-
этому такие системы также называют нелинейными.
165
Вопросы развития крутильных колебаний коленчатых валов
с муфтами, обладающими нелинейной характеристикой, разрабо-
таны советскими учеными А. И. Лурье и А. И. Чекмаревым,
И. Ш. Нейманом, В. Я. Натанзоном, Ю. А. Гопп, В. П. Терских.
Колебания нелинейных систем называют псевдогармониче-
скими. Эти колебания обладают тем свойством, что частота коле-
бания зависит от величины амплитуды.
В случае колебаний системы без сопротивлений амплитуды,
как известно, могут расти беспредельно лишь при равенстве ча-
стоты возбуждения и частоты свободных колебаний.
При колебаниях нелинейной системы рост амплитуд сопро-
вождается изменением частоты свободных колебаний и явление
резонанса исчезает.
На фиг. 92 представлены резонансные кривые системы с од-
ной степенью свободы и с нелинейной упругой связью, жест-
кость которой возрастает при увеличении перемещений.
Амплитуды колебаний такой системы могут стать бесконечно
большими (при отсутствии сопротивлений) либо при частоте
возбуждения 2 = оо, либо при частоте свободных колебаний
Р = 0.
При 2’>п каждому значению частоты возбуждения 2 соот-
ветствует три различных значения амплитуд колебания. Как по-
казывает математический анализ и экспериментальные проверки,
среднее значение амплитуд (ветвь п' — п") соответствует неустой-
ке
чивым колебаниям. Что касается относительной устойчивости
двух крайних значений амплитуд, то при имеющих место в обыч-
ных условиях работы мотора небольших нарушениях режима
колебаний весьма вероятен срыв колебаний с больших амплитуд
на малые. .
Только при очень плавном изменении частоты возбуждаю-
щего момента в сторону .увеличения может произойти .затяги-
вание" нелинейной системы на колебания с большими амплиту-
дами (ветвь т — т’).
Экспериментальные кривые вынужденных колебаний такой
нелинейной системы имеют вид, показанный на фиг. 93а для
случая системы с возрастающей частотой возбуждения, и на
фиг. 936 для случая работы системы с убывающей частотой
возбуждения.
167
ГЛАВА V
СОВМЕСТНЫЕ КРУТИЛЬНЫЕ КОЛЕБАНИЯ ВАЛА
И ИЗГИБНЫЕ КОЛЕБАНИЯ ВИНТА
До сих пор, изучая крутильные колебания коленчатых валов,
мы считали воздушный винт абсолютно твердым телом (в рас-
четах он фигурировал только как масса с моментом инерции /,).
Опыт эксплоатации винтомоторных установок показал, что
во многих случаях это допущение не оправдывается. В действи-
тельности, лопасти винта имеют ограниченную жесткость и ча
стоты свободных изгибных колебаний винта имеют тот же по-
рядок, что и частоты свободных крутильных колебаний вала.
При вовбуждении крутильных колебаний вала иногда возникают
очень сильные изгибные колебания лопастей винта, которые мо-
гут приводить к поломкам лопастей. Кроме того, опытом иногда
обнаруживаются такие опасные резонансы крутильных колеба-
ний, которые по расчету частот свободных колебаний системы
с жестким винтом не должны были бы возникнуть.
Еще в 1936 г. В. К. Житомирский при исследовании причин
тряски мотора М-34 на самолете ТБ-3 получил виброграммы,
обработка которых отчетливо выявляет два резонанса 6-й гар-
моники и два резонанса 4,5-й гармоники (фиг. 94).
Числа собственных колебаний системы пс — Кпрез, определен-
ные по пикам 6-й и 4,5-й гармоник, довольно хорошо схо-
дятся между собой1) (таблица 11).
Таблица 11
резонанс К през Об/МИН К-пре ., кол/мин
1-й 6 4.5 775 1045 4650 4700
2-й С 4,5 900 1240 5400 5500
) Несколько большее расхождение п, определенных по второй паре пи-
ков закономерно и объясняется изменением частот колебаний лопасти с уве-
личением оборотов.
168
Полученные опытом резонансы при nt 4700 и 5500 кол/ми-'
были неожиданными. Аналитический расчет частот свободных
крутильных колебаний вала с жестким винтом устанавливал
возможность появления
6-го порядка и одного —
4,5-го порядка (число
собственных колебаний
системы при двухузловой
форме пе и = 5200 кол/мин)
Наличие вторых пиков
свидетельствовало о до-
полнительных степенях
свободы системы. При-
чиной этого могла быть
податливость лопастей
винта.
В 1939 году произошло
несколько поломок вала
только одного резонанса гармоники
Фиг. 94
9-цилиндрового звездооб-
разного двигателя АШ-63. Торсиографнрование (фиг. 95) обнару-
живало два близких резонанса гармоники 3,5-го порядка на
оборотах 2280 и 2470 об/мин, в то время как по расчету вала
с жестким винтом резонанс
3,5-й гармоники (один) пред-
полагался на оборотах п —
= 2380 об/мин. .Раздвоение
пика“, наблюдавшееся при
горсиографировании мотора с
одним винтом, исчезло при
замене винта на другой.
Таким образом, экспери-
ментально доказывалось, что
появление дополнительных ре-
зонансов вызвано именно влия-
нием винта.
В описываемом случае ко-
ленчатый вал мотора имел
маятниковый демпфер, наст-
роенный на 4,5-ю гармонику
и установленный на задней
щеке. При резонансе 4,5-й гармоники узел получался в месте
подвески демпфера, вал почти не колебался, но сильно возбуж-
дались лопасти винта (см. § 24). Большой пик, нанесенный на
фиг. 95 пунктиром, представляет запись колебаний втулки винта
при резонансе 4,5-й гармоники.
Система коленчатого вала с упругим винтом колеблется так,
что на одних режимах сильно возбуждаются крутильные коле-
бания вала, а винт участвует в них как жесткое тело. На дру-
169
гих режимах возникают сильные колебания лопастей винта, а
вал почти не испытывает закруток вибрационного характера.
Наконец, на третьих режимах возникают одновременно сильные
крутильные колебания вала и изгибные колебания лопастей винта.
Частоты колебаний при резонансах третьего типа отличны как
от частот свободных колебаний коленчатого вала с жестким вин-
том, так и от частот свободных колебаний самого винта.
Все резонансы следует рассматривать как резонансы единой
системы вал—упругий винт. Однако иногда в литературе резо-
нансы первого типа называют „резонансами вала", а второго—
„резонансами винта".
§26. Расчет частот свободных колебаний системы вал—винт
Представим себе, что исследуемая система фиг. 96 рассечена
у втулки винта на две части и что к винту приложен момент
М = Mos\npt. Под действием этого момента возникнут гармони-
ческие крутильные колебания втулки винта r?, = F, sin pt с ампли-
тудой Ft. Отношение —-=~- = Кв называют „динамическая
жесткость винта". Аналогично, если на правую часть системы—
вал действует момент 7И' = Af0'sinp7, то он вызовет колебания
М' Л1'
'?M = Fмsinp't. Отношение — ==-°=/<Л( называют „динамиче-
ская жесткость вала".
При статическом приложении момента жесткость системы
определяется как отношение момента к вызванной им деформа-
ции. Поэтому, естест-
венно, отношение ди-
намически приложен-
ного момента к дефор-
мации, которая им вы-
звана, называть „дина-
мическая жесткость".
Профессор Терских
В. П., которому при-
надлежит приоритет
введения в расчетную
практику понятия „ди-
намическая жесткость"
и использования его
при расчетах сложных
систем, называет дина-
мическую жесткость
стойкостью. Стойкость, или динамическая жесткость характери-
зует сопротивляемость системы перемещениям под действием
внешних нагрузок.
При некотором значении частоты колебаний р возможно ра-
170
из расчета, на обратны и, тс
Фиг. 97
венство Kt= — К„. Тогда, при равных по величине и обратных
по знаку моментах Мо и Мо' выполняется равенство FM — F,
т. е. система может рассматриваться соединенной и колеблю-
щейся с данной частотой без воздействия внешних моментов.
При этом момент сил упругости в сечении, где система была
разделена, равен /WosinpZ.
Таким образом, задача определения частот свободных коле-
баний системы коленчатый вал—винт сводится к построению на
одном графике кривых динамической жесткости винта и вала в
зависимости от частоты колебаний р. Если одну из кривых
строить, меняя знак, получс
точки пересечения кривых,
удовлетворяющие условию
К,= —Км, определят ча-
стоты свободных колебаний
системы.
Подсчет динамической
жесткости вала Км систе-
мы, состоящей из п — 1
масс, связанных упругими
безинерционными валами,
не вызывает никаких прин-
ципиальных затруднений.
Вычисление Км = /(р) проще всего производить, пользуясь
методом цепных дробей, выполняя расчеты для различных зна-
чений р в форме ряда таблиц типа таблицы 2.
В третьей строке этой таблицы в клетке, которая заполняет-
ся предпоследней, записана величина Эта величина по оп-
ределению есть частное от деления относительной амплитуды
n-й массы (или сечения а) на амплитуду относительного момен-
та сил упругости (п—1)-го участка вала, т. е. является величиной
- обратной „относительной динамической жесткости". Таблица 2 за-
писана для относительной системы. Возврат к абсолютной систе-
1
ме, в данном случае, осуществляется умножением — на ту
жесткость k, которая была произвольно выбрана при построе-
нии относительной системы KM = k--„—v
s n-1
Для определения динамической жесткости вала может быть
также использована таблица 1. Действительно, в ней вычисляются
при заданном значении р амплитуды моментов сил упругости
всех масс. Деля амплитуду момента сил упругости («—1)-го
участка вала на амплитуду n-й массы (или, что то же, на ам-
плитуду колебаний сечения а), найдем величину Км.
Составим развернутое выражение динамической жесткости си-
стемы, представленной на фиг. 97, воспользовавшись таблицей 12,
составленной по форме таблицы 1.
171
Т а б л и ц а 12
Г
Црг _ Лр* _ 4р!
172
/ \ *1 /
Г_ /1Р2_ А _ 1>р2\
k1 k2 k2 k1)
(87)
или после преобразований
Км = —
(87а>
Выражение •
стоящее в квадратных скобках
в чи-
слителе, представляет собой обратную величину квадрата часто-
ты свободных колебаний рассматриваемой системы, не связан-
пой в сечении а. Обозначим ---у-.--= Р\ •
Выражение, стоящее в квадратных скобках в знаменателе,
будучи приравнено нулю является уравнением частот свободных
колебаний рассматриваемой системы, заделанной в сечении а.
Обозначая корни этого уравнения *р^ и *р32 и пользуясь из-
вестными свойствами корней квадратного уравнения1), получим
после преобразования следующее выражение для динамической
жесткости рассматриваемой системы:
^,=-(/i+4)A2
(876)
Распространяя эту формулу на систему с любым
масс, получим
числом
(88)
здесь / = /i + /a + /3-F ...
Если динамическая жесткость определяется на конце вала
(а не на массе), то число множителей в скобках в числителе должно
быть на единицу меньше, чем в знаменателе, так как система
из п масс имеет п—1 частот свободных колебаний, а при за-
креплении свободного конца вала п частот.
!) Первое свойство: х- + рх q - (х— .v,) (х — х.).
Второе свойство Vj-.v, q
173
Полученное в последней форме выражение для динамической
жесткости системы с любым количеством масс замечательно тем,
что динамическая жесткость может быть вычислена для всех
значений р, если известна сумма моментов инерции всех масс
системы и частоты всех форм ее свободных колебаний при сво-
бодном и заделанном сечении, для которого определяется К.
Частоты px,pv . • и .• . могут быть определены любым
способом в том числе и экспериментальным.
Именно поэтому последняя формула оказывается полезной при
определении динамической жесткости винта.
Винт, как упругая система, является очень сложным объектом.
Лопасти винта сильно закручены, их жесткость на изгиб в раз-
личных направлениях неодинакова. Кроме того, свойства винта
как упругой системы зависят от изменяемого в эксплоатации
Я V
Фиг. 98
угла установки лопасти и ог оборотов, на которых работает винт.
При увеличении оборотов жесткость лопасти как бы возрастает
.вследствие того, что к восстанавливающим силам упругости до-
бавляется восстанавливающее действие центробежных сил ло-
пасти. Все это приводит к тому, что определить частоты свобод1
пых колебаний винта просто и достаточно точно чисто аналити-
ческим путем не удается. Для этих целей существуют специаль-
ные установки, на которых частоты рх,р2... и *рх*р2... определяют
путем непосредственного замера.
Ряд частот *рх, *р2... определяется с помощью виброщупа
(фиг. 98). Виброщуп состоит из кольцевого магнита, между полю-
сами которого помещается подвижная часть прибора: катушка А,
игла В и жесткие, но легкие пружины С. Прикладывая иглу к ко-
теблющейся лопасти, заставляют катушку колебаться в поле по-
стоянного магнита с частотой колебаний лопасти. При этом в
катушке индуктируется ток, частота которого регистрируется
осциллографом. Возбуждение колебании лопасти может быть оСу-
ществленно легкими ударами руки или молотка. Втулка винта
должна быть любым способом жестко закреплена.
Для определения ряда частот рх,р2... может быть использо-
вана установка, схема котором представлена на фиг. 99а. Уста-
174
новка состоит из подставки А под плиту Б, к которой прикреплен
картер редуктора В. В картере помещается стандартный вал винта.
К нему с одной стороны прикреплен легкий вибратор Г, с
другой—испытуемый винт, посаженный как обычно на шлицы и
затянутый гайкой. Вибратор состоит из ведущей шестерни и
трех малых неуравновешенных шестерен (фиг. 996). Шестерни
вращаются электрическим мотором D, число оборотов которого
может меняться в широком диапазоне. Связь мотора с вибрато-
ром осуществляется через очень податливую муфту Е, что пол-
ностью исключает влияние момента инерции мотора на частоты
свободных колебаний испытуемой системы. Вращение неуравно-
вешенных шестерен создает гармонический момент, который пе-
редается корпусом вибратора винту и возбуждает колебания ло-
пастей.
При испытаниях винт колеблется не вращаясь. Крутильные
колебания втулки винта регистрируются осциллографом от элек-
троиндукционного датчика Ж (см. § 18), помещенного во втул-
ке. Осциллографирование проводится на ряде режимов работы
установки при различных оборотах электромотора. По получен-
ным осциллограммам строится резонансная кривая колебаний
втулки и определяются разонансные частоты.
175
Испытания проводятся при двух различных углах установки
лопастей минимальном и максимальном.
На установке описанного типа принципиально возможно оп-
ределить непосредственно Кв=f(p). Однако при этом необхо-
димо было бы записывать амплитуды перемещений. Запись ам-
плитуд не удается выполнить с той высокой точностью, с как й
записываются частоты.
Учет увеличения частот от вращения винта производится
обычно по формуле: , „ ,
* 3 Р'*=р2+аш\ (89)
здесь: рв—частота свободных колебаний вращающегося винта
7 1 \
\ сек ] ’
р—частота свободных колебаний невращающегося винта
/ 1 Y
\ сек ]’ . j
<о—угловая скорость вращения винта •
а—безразмерный коэфициент, зависящий от формы коле-
баний лопасти.
Значения *а для первых грех форм колебаний лопасти при
заделанной втулке даны в таблице 13. Коэфипиенты а для
вычисления частот при свободной втулке винта мсут быть при-
ближенно определены по формуле
а^а-Р-.
*Р
Таблица 13
Источник Форма колебаний
1 2 3
1 1,49 4,15 9,20
2 1,45 4,40 12,00
3 1,46 3,63 1?,20
4 1,45 4,40 9,20
5 1.50 4,20 7,20
6 1,50 6,00 12.00
Обычно поправки на вращение определяют для трех режимов
работы винта, соответствующих w nev и аер = <°”ПЛ- .
Зная ряд частот plt ря... и *ри*р->. . при трех скоростях
вращения и двух углах установки лопасти, а также, определив
176
Фиг. 100
12 В. Кириченко
177
ей
X. - 1 )O 200 1 1
• \ / / 161 ОС L=- --
f / М- Г 1 >₽/ OG ЕГТ- 1
/С ооог cost
S' -MT%oOOQL =9u
|| || £ О о
|| II h о
.4*’ It II 11 kJ
/|| I; Q»
/II / / ✓ . О»
— " — у_- У § §x
— _
— я —
1£к> Ij^> *?
я 1 ’>нем инт
-1^ \<Л '/ <© ь5 * 40
Cb Q>
— -—- ' \l ..
<,x Cb
SJ& ^4 Cb _
« •
Фиг. 101
<о *о •ф со о со
«О' «О' Q' О' О' О' Q «О' О' О' 1 «О' О' t О' 1 о
178
момент инерции винта I путем прокачивания, строят ряд кривых
динамической жесткости винта К, — f(p), пользуясь формулой (88)
Для лопасти, имеющей бесконечное число степеней свободы,
число множителей в формуле также бесконечно, однако влия-
ние частот высших форм на величину Кв несущественно. Чем
выше частота p-t и *рь тем при заданной частоте р ближе к
единице множители:
Поэтому оказывается достаточным знать только частоты пер-
вых двух форм свободных колебаний винта при заделанной
втулке и трех—при свободной.
Построив кривые К, на том же графике, наносят кривую ди-
намической жесткости вала—определенную табличным
расчетом. Точки пересечения кривых К, и —Км определяют ча-
стоты совместных свободных колебаний винта и вала рр рп ...
Для определения форм ^свободных колебаний системы под-
считываются таблицы типа таблицы 1, в которые вместо мо-
Ке
мента инерции винта подставляют величины — p i, соответст-
вующие различным значениям
На фиг. 100 и 101 даны
кривые -Гт- и.--г?- V-образ-
‘'Л I'M
кого 12-цилиндрового мото-
ра с „легким" и .тяжелым"
винтом при оборотах винта
nt — 1000, 1500 и 2000 об/мин.
§ 27. Вынужденные колеба-
ния системы вал—винт
По найденным значениям
частот свободных колебаний
системы коленчатый вал—винт
строят кривые частот в зави-
симости от оборотов мотора
pt = f(n) (фиг. 102). Возмож-
ные резонансы системы опре-
частот рр рп, р]П...
12*
179
деляются, как обычно, точками пересечения лучей, соответствую-
щих различным порядкам возмущающих гармоник с кривыми
pc = f(n). Нафиг. 103 и 104 представлены диаграммы возможных
Фиг 103
резонансных режимов того же V-образного 12-цилиндрового мо-
тора, для которого построены кривые на фиг. 100 и 101.
Расчет резонансных амплитуд системы вал—винт производится
известным „энергетическим методом**, который был изложен в
§ 16. Недостаточность сведений о коэфициентах заглушения Е
180
таких систем делает предпочтительней экспериментальный замер
амплитуД-
Р1а фиг. 105 дана резонансная кривая того же мотора. Тор-
сиОграфирование проводилось при работе мотора по винтовым
характеристикам с винтом, установленным на малой и большой
шаг. В таблице 14 даны значения резонансных оборотов мотора,
определенные экспериментально и расчетом. Расчет проводился
в двух вариантах с учетом податливости лойастей винта и с
„жестким* винтом.
181
Таблица 14
№ Экспери- Расчет
гармоники меит п йЬ/мш с абсолютно жестким винтом с учетом податливости лопастей
» п об/мин погреш- ность п об/мин погреш- ность %
• . Легкий винт
3 1800 1880 4,4 1900 5,5
7,5 1940 2200 18,0 1980 2,0
6,5 2190 2530 15,5 2320 5,3
6 % 2500-2600 2770 6,5 2500 0
Тяжелый винт
6 1520 1020 33,0 1430 3,3
1 3 1950 1880 3,8 1920 0,6
Из рассмотрения таблицы 14 видно насколько лучше, в дан-
ном случае, согласуются с опытом расчеты системы при учете
податливостей лопастей винта.
182
ЛИТЕРАТУРА
1. Нейман И. Ш., Динамика авиационных двигателей, Оборонгиз, 1940.
2. Заикнн А. Е. и другие, Авиационные двигатели, конструкция и расч
деталей, нзд. ВВА им. Жуковского, Оборонгиз, 1941.
-3. Терских В. П., Крутильные колебания силовых установок, Судпромгн
1940.
4. Дурье И. А . Крутильные колебания в дизельных установках, и;
НКВМ СССР, 1940.
5. С к у б а ч е в с к и й Г. С., Крутильные колебания коленчатых валов, и;
МАИ. 1942.
6. Серен сен С. В., Тетельбаум И. М. и Пригоровский Н. И., Динам
ческая прочность в машиностроении, Машгиз, 1945.
7. Покорный Б. М., Расчет коленчатого вала на крутильные колебан!
Машгиз, 1947.
8. Холма ков И. И., Динамика авиационных двигателей, Оборонгиз, 19.
9. Ден-Гарт о г. Теория колебаний, Гостехиздат, 1942.
10. А н д ро н о в А. А. и Хай кин С. А., Теория колебаний, ч. 1, OHTI
НКТП СССР, М.-Л, 1937.
11. Гопп Ю. А, Демпфирование крутильных вибраций коленчатых валов аг
амоторов, ОНТИ, НКТП СССР, 1935.
12. Гопп Ю. А., Опыты с нелинейными колебаниями, «Вестник инженер
и техников' № 1, 1937.
13. Гопп Ю. А., Графическое решение линейных и нелинейных колебав•
„Вестник инженеров и техников", № 2,1936.
14. Лурье А. И. и Чекмарев А. И., Вынужденные колебания в не;
иенной системе с характеристикой, составленной из двух прямолинейи
отрезков. Прикладная математика и механика, новая серия, т. I, вып.
1938.
15. Натанзон В. Я., Крутильные колебания коленчатых валов с муфта!
обладающими нелинейной характеристикой, Труды ЦИАМ № 40, Обор<
гиз, 1943.
16. Нейман И. Ш., Крутильные колебания многомассовой нелинейной <
стемы, ЦИАМ, Оборонгиз, 1947.
17. Кинасошвнли Р. С., Определение запасов прочности при перемени
нагрузках. Труды ЦИАМ № 55, Оборонгиз, 1943.
18. К и н а с о ш в и л и Р. С., Расчет прочности коленчатых валов рядных ав
циоиных двигателей, Труды ЦИАМ № 94, Оборонгиз, 1945.
19. Житомирский В. К., К и н а с о ш в и л и Р. С., Т е т е л ь б а у м И.
Действительные нагрузки в расчете прочности коленчатого вала, Tpj
ЦИАМ № 116, Оборонгиз, 1946-
20. Динамика и прочность коленчатых валов. Сборник статей, под ред. Сер
сеиа С. В., изд. Академии наук СССР, 1948.
Кроме того, при написании кингн были использованы многочисленв
технические отчеты и периодические издания ЦИАМ, а также, с разрешен
инженера Кирни Ю. 3., некоторые результаты его неопубликованной дисс
гации «Влияние упругости лопастей воздушного винта на частоты свободн
колебаний винтомоторной установки".
ОГЛАВЛЕНИЕ
Стр.
От автора................................. • .......... j
Введение............................................... 4
Глава I. Свободные или собственные крутил*НЬ|е колебания
§ 1. Свободные колебания системы без сопротнвлени? с одной массой 7
§ 2. Свободные крутильные колебания вала с двумя кассами........ 13
§ 3. Свободные крутильные колебания системы с тре><я кассами ... 17
§ 4. Свободные крутильные колебания вала со многими кассами ... 20
§ 5. Метод цепных дробей........................• • ................ 30
§ 6. Свободные крутильные колебания разветвленные систем....... 45
§ 7. Свободные крутильные колебания с учетом сопрогивлений ... 52
Глава II. Построение эквивалентных крутнльнь«х систем
§ 8. Приведенная длина коленчатого вала........• • •........... 60
§ 9. Моменты инерции системы...................• • • '......... 66
§ 10. Редукторные системы......................• • •........... 76
Глава III. Вынужденные крутильные к(’ле6ания
§ 11. Работа, совершаемая гармоническим моментом, ПРИ гармониче-
ском движении.................................................. 83
§ 12. Вынужденные колебания системы с одной степеНь1° Свободы при
гармоническом возмущении и отсутствии сопрот>,влеций .... 86
§ 13. Вынужденные колебания системы, имеющей одну степень свободы,
при гармоническом возмущении и сопротивлейиях пропорцио-
нальных скоростей..............................• •.............. 90
§ 14. Внешние возмущающие моменты..............• .......... 97
§ 15. Вынужденные колебания многомассовой крутильной системы . . 111
§ 16- Расчет резонансных амплитуд..............• • ........ 114
§ 17. Определение возможных резонансов.........• •......... П9’
§ 18. Торсиографироваиие.......................• •.......... 121
§ 19. Напряжения от крутильных колебаний. ПредельИ0 допустимые
амплитуды................................• 126
§ 20. Способы борьбы с опасными резонансами . . . • •.......... 131
Глава IV. Демпферы н муфть>
§ 21. Гидравлический демпфер............................... 136
§ 22. Демпфер сухого трения....................• •.......... }^2
§ 23. Динамический демпфер.....................- - lj°
§ 24. Маятниковый демпфер......................• •.......... 150
§ 25. Муфты....................................• • 1°1
Глава V. Совместные крутильные колебания »зала и изгибные
колебания винта
§ 26. Расчет частот свободных колебаний системы ва-Д винт... 170
§ 27. Вынужденные колебания системы вал—винт . .............