ЗНАКОМСТВО С ВЫСШЕЙ МАТЕМАТИКОЙ
Л. С. ПОНТРЯГИН
ЗНАКОМСТВО С ВЫСШЕЙ МАТЕМАТИКОЙ
•
МЕТОД КООРДИНАТ
ИЗДАТЕЛЬСТВО «НАУКА» ГЛАВНАЯ РЕДАКЦИЯ ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
МОСКВА 19 7 7
517.3
II 56
УДК 516
Аннотация
Эта книга является первой из четырех небольших популярных книг под общим названием «Знакомство с высшей математикой», по которым молодые читатели, начиная со школьников старших классов, смогут знакомиться с высшей математикой.
В этой, первой, книге излагается метод координат и, в основном, аналитическая геометрия на плоскости. Затрагиваются также вопросы алгебры, дается геометрическое изображение комплексных чисел и рассматриваются многочлены как комплексные функции комплексного переменного, что дает возможность'доказать основную теорему высшей алгебры. Более бегло даются декартовы координаты в пространстве и аналитическая геометрия в пространстве.
Книга может быть полезна также преподавателям средней и высшей школы.
20203—136	© Главная редакция
П	БЗ-27-32—77	физико-математической литературы
издательства «Наука», 1977
ОГЛАВЛЕНИЕ
Предисловие. ............................-. . .	4
Введение............................................. 7
Глава I. Координаты на плоскости	....	....	12
§ 1.	Прямоугольные декартовы координаты и векторы на плоскости......................... 12
§ 2.	Полярные координаты-.................... 21
§ 3.	Геометрическое изображение комплексных	чисел	25
Добавления к главе!............................. 34
1. Координаты в пространстве (34).	2. Векторы в
пространстве (36)
Глава II. Координаты и линии на плоскости ....	39
§ 4.	Графики функций и функции................... 39
§ 5.	Эллипс, гипербола, парабола................. 48
§ 6.	Параметрическое представление линий ....	60
§ 7.	Замкнутые кривые............................ 65
§ 8.	Многочлены комплексного переменного ....	73
Добавления к главе II............................... 82
1. Функции двух переменных и их графики в пространстве (82). 2. Функции трех переменных и соответствующие им поверхности (84). 3. Поверхности вращения (85). 4. Уравнение плоскости (88).
5. Поверхности первого и второго порядков (89).
Глава III. Аналитическая геометрия на плоскости 92
§ 9. Преобразование декартовых координат на плоскости.................................  94
§ 10. Линии первого и второго порядков.......... 104
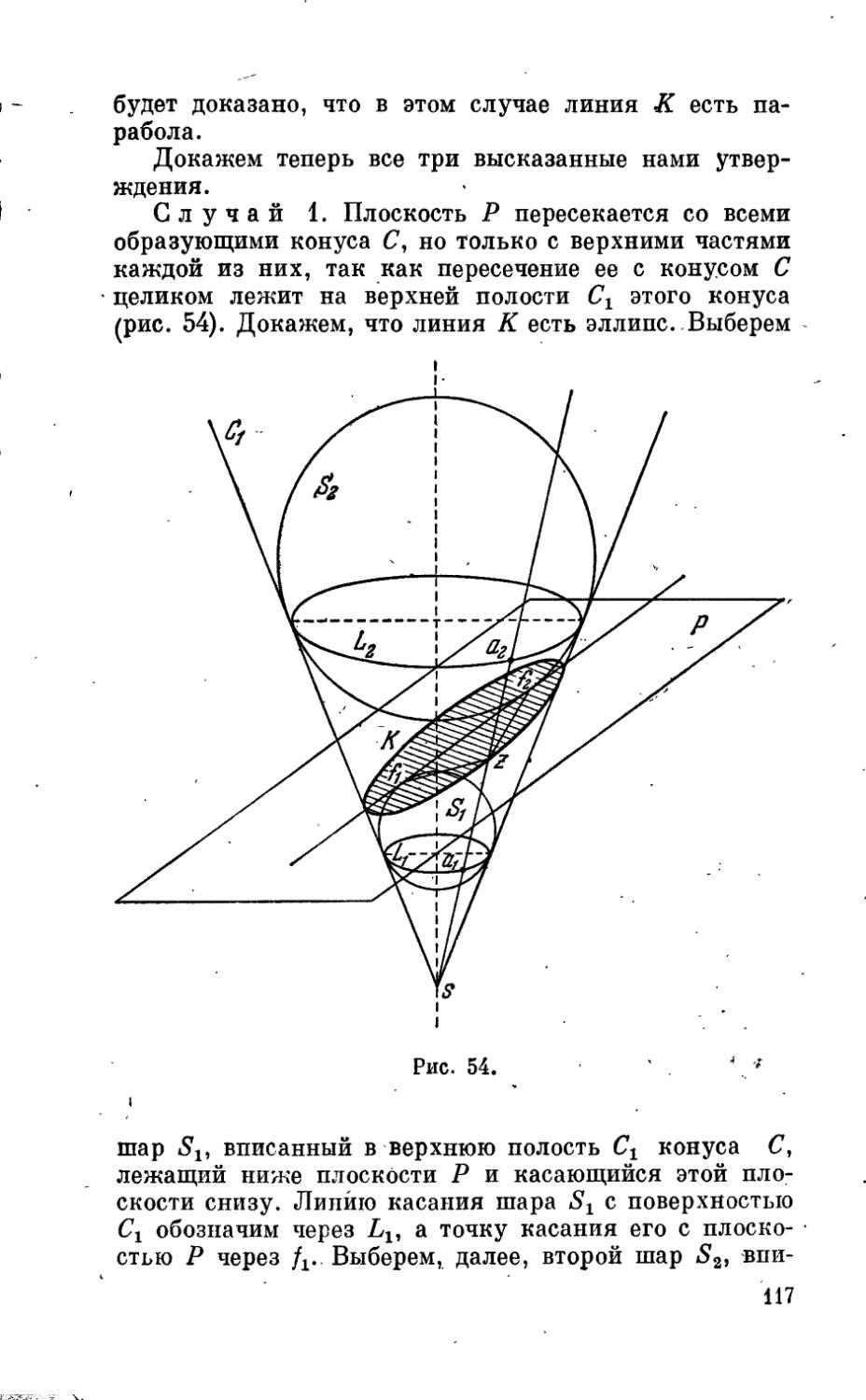
§ И. Конические сечения . . . .................. 115
Добавления к г л а в е III........................  124
1. Преобразование координат (124). 2. Классификация’поверхностей первого и второго порядков (128).
3. Конические сечения (132).
!♦
ПРЕДИСЛОВИЕ
Эта уже написанная книга — первая из четырех небольших популярных книг, которые я предполагаю написать и опубликовать под общим названием «Знакомство с высшей математикой». Предполагается, что в них будут даны важнейшие результаты классической высшей математики. Выбор материала и порядок его изложения не соответствует никакой учебной программе. Книги будут отражать мои личные вкусы и взгляды на математику, сложившиеся за много лет работы. Кроме того, они будут учитывать мои юношеские воспоминания о возможностях восприятия молодого человека, с тем, чтобы нынешнее поколение молодых людей, начиная со школьников старших классов, могло знакомиться по ним с высшей математикой и приобретать правильный здоровый вкус к ней. Внимание читателя должно быть направлено не на изощренности типа теории множеств, теории пределов и т. п., а на главные математические результаты, сложившиеся в течение тысячелетий.
В трех главах этой книги излагаются важнейшие математические применения, прямоугольных декартовых координат на плоскости. Главное место занимают краткие сведения из аналитической геометрии на плоскости: даются геометрические определения эллипса, гиперболы и параболы при помощи фокусов и директрис; далее дается классификация кривых второго порядка, т. е. доказывается, что каждая кривая второго .порядка есть эллипс, гипербола или парабола, за исключением вырожденных случаев. Ввиду исключительно большого значения комплексных чисел в современной математике, я в самом начале книги уделяю им большое внимание: дается геометрическое изображение комплексных
' 4
чисел при помощи прямоугольных декартовых координат, а затем геометрически изучаются комплексные многочлены от комплексного переменного и дается геометрическая идея доказательства основной теоремы высшей алгебры о том, что каждый многочлен степени п имеет ровно п корней. Строгое доказательство этой важнейшей теоремы невозможно без точного определения непрерывности функции. Однако я считаю, что интуитивное геометрическое доказательство ее вполне убедительно и представляет большой интерес. Потребность в точном понимании понятий предела и непре- z рывности должна возникнуть у читателя лишь в результате овладения им большим запасом конкретных математических знаний. Такие понятия, как предел и непрерывность, являются, на мой взгляд, надстройкой, уточняющей конкретные математические факты, и описание этой надстройки не должно даваться с самого начала, наводя скуку на читателя, не понимающего еще, для чего все это делается.ч
Каждая из .трех глав книги снабжена добавлениями, непосредственно следующими за самой главой. Эти до-. бавления относятся уже не к плоскости, а к пространству. В них описываются прямоугольные координаты в пространстве и простейшие применения этих координат к теории поверхностей второго порядка, именно, дается классификация поверхностей второго порядка. Добавления к главам изложены менее детально, чем сами главы, с тем, чтобы предоставить читателю материал для самостоятельных размышлений.
Вторая книга под названием «Анализ бесконечно малых» будет посвящена изложению математического' анализа. В начале будут изложены не полным и не формальным образом теория действительного числа и теория пределов. Прц__этом главное внимание будет обращено на необходимые и достаточные условия Коши сходимости для последовательности комплексных чисел. После этого будет развернута теория степенных рядов от комплексного переменного. Таким образом, можно будет определить функцию е1 комплексного переменного z и установить ее связь с тригонометрическими функциями па основе известной формулы
= cos <р + i sin ф.
5
Далее, должно следовать рассмотрение обратных функций, т. е. логарифма и обратных тригонометрических функций. Только после этого будет дано дифференцирование и интегрирование, причем интегрирование будет рассматриваться как операция, обратная к дифференцированию. Общим непрерывным функциям бу-•дет посвящено весьма мало внимания.
Третья книга с ориентировочным названием «Многомерная евклидова геометрия и теория определителей» пока что представляется мне не более полно, чем это выражено в ее заглавии.
Четвертая книга с ориентировочным названием «Обыкновенные дифференциальные уравнения» будет посвящена изложению этой теории с упором на линейные уравнения с постоянными коэффициентами с применением этих уравнений к теории электрических цепей. В этой же книге будут рассмотрены автономные системы, положение равновесия в них и предельные циклы с применением к теории регулирования (регулятор Уатта) п работе лампового генератора.
В заключение должен сказать, что вся эта серия из четырех небольших книг, рассчитана не на легкое чтение, а на серьезную напряженную работу читателя. Небольшой объем книг вовсе не указывает на их малое содержание. Изложение очень сжатое и освещает большое количество материала.
ВВЕДЕНИЕ
В настоящее время уже очень большое число специалистов из разных областей знания имеет представление о прямоугольных декартовых координатах на плоскости, так как эти координаты дают возможность наглядно-геометрически при помощи графика изобразить зависимость одной величины от другой. Так ^врач строит график температуры больного в процессе болезни, экономист — график роста производства и т. д. Название декартовы координаты наводит на ложную мысль о том, что эти координаты были открыты Декартом. В действительности прямоугольные координаты употреблялись в геометрии еще до начала нашей эры. Декарт внес в них очень важное усовершенствование, введя правила выбора знаков (см. ниже). Но главное, пользуясь прямоугольными координатами, он построил аналитическую геометрию на плоскости, связав этим геометрию и алгебру. Нужно сказать, однако, что одновременно с Декартом построил аналитическую геометрию и другой французский математик Ферма, известный широкой публике как автор (до сих пор недоказанной) великой теоремы Ферма. К 17 веку, когда жили Декарт и Ферма, развитие математики уже подготовило все для построения аналитической геометрии — синтеза алгебры и геометрии. Но последний удар был нанесен Декартом и Ферма. Однако почти все знают'только о Декарте. Такова, по-видимому, судьба всех или почти всех великих научных открытий. Они готовятся столетиями, но завершающий этап, осуществленный каким-нибудь ученым, связывается с его именем, и все открытие получает имя этого ученого. Ниже я привожу краткий и очень неполный исторический обзор
7
развития математики до 17 века для того» чтобы на примере аналитической ' геометрии продемонстрировать то явление в развитии науки, о котором я сказал выше.
Для построения системы координат мы проводим в плоскости чертежа две прямые — оси координат: горизонтальную — ось абсцисс и вертикальную — ось ординат. Пересечение их о называется началом координат.* Пусть г — некоторая точка плоскости чертежа. Опустим из нее перпендикуляр гр на ось абсцисс и перпендикуляр rq на ось ординат. Это построение дает нам возможность поставить в соответствие точке г два неотрицательных числа. Первое — длину отрезка ор и второе — длину отрезка oq. Видно, однако, что если точка г' симметрична с точкой г относительно оси ординат, то числа, соответствующие обеим точкам г и г', будут одинаковыми. То же верно и для точек, симметричных относительно оси абсцисс. Это положение исправляется правилом выбора знаков, введенным Декартом. Именно, если точка г лежит справа от оси ординат, то первое число берется со знаком плюс, а ‘если слева ——.то со знаком минус. Так полученное число называется абсциссой точки г и обозначается обычно через х. Аналогично определяется и знак второго числа, которое называется ординатой точки г и обычно обозначается через у. Числа х и у называются* декартовыми координатами точки г. Если переменные величины х и у связаны каким-либо соотношением, например, алгебраическим уравнением, то совокупность точек г, координаты которых удовлетворяют этому уравнению, образует линию на плоскости. В частности, именно таким образом строится график, если у зависит от х.
Приведенные здесь построения теперь прочно связаны с именем французского математика Декарта (1596—1650). Однако в различных, менее совершенных формах они употреблялись в математике задолго до него. Древний математик Александрийской школы Аполлоний (живший в 3—2 веках до н. э.) уже фактически пользовался прямоугольными координатами. Он определял при помощи них тщательно изучавшиеся и хорошо известные в то время кривые; параболу, ги
8
перболу и эллипс. Аполлоний задавал их уравнениями: у2 = рх (парабола);
у2 = рх -|- -у х2 (гипербола);
у2 = рх----~х2 (эллипс)
(р и а положительны).
Аполлоний, конечно, не выписывал уравнения в этой алгебраической форме, так как в те времена не существовало еще алгебраической символики. Он описывал уравнения, пользуясь геометрическими понятиями: у2 в его терминологии, есть площадь квадрата со стороной у; рх — есть площадь прямоугольника со сторонами р и х и т. д. С этими уравнениями связаны и названия кривых. Парабола по-гречески означает равенство: квадрат у2 имеет площадь, равную прямоугольнику рх. Гипербола по-гречески означает избыток: площадь квадрата у2 превосходит площадь прямоугольника рх. Эллипс по-гречески означает недостаток: площадь квадрата у2 меньше площади прямоугольника рх.
Французский математик Орезм в 14 веке, пользуясь прямоугольными координатами, строил график зависимости величины у от величины х\ при этом вместо современных терминов: абсцисса и ордината он употреблял термины — долгота и широта. Идеи Орёзма не полупили, однако, широкого распространения, потому что в те времена понятие функциональной зависимости (я имею в виду зависимость величины у от величины х) было слишком не ясным.
Таким образом, открытие декартовых координат не принадлежит Декарту, И все же тот факт, что они названы его именем, не является большой несправедливостью. Он сделал из них такое употребление, которое представляет одно из величайших достижений • математики. Декарт построил аналитическую геометрию, а в ней, как в фокусе, сошлись математические открытия медленно, с трудом слагавшиеся в течение тысячелетий. Работа Декарта «La-Geometrie», в которой излагались основные идеи аналитической геометрии на плоскости, была опубликована в 1637 г. Следует отметить, что к этим идеям одновременно пришел и другой
-	9
французский математик Ферма (1601—1665), но Соответствующая его работа была опубликована только в 1679 г. К 1637 г. идеи Ферма становятся известными его современникам по обычаю того времени только благодаря обмену письмами.
Значение аналитической геометрии состоит прежде всего в том, что она установила тесную связь между геометрией и алгеброй. Эти две ветви математики ко времени Декарта достигли уже высокой степени совершенства. Ио развитие их в течение тысячелетий шло независимо друг от друга, и ко времени появления аналитической геометрии между ними намечалась лишь довольно слабая связь. Геометрия уже незадолго до начала н. э. достигла выдающихся результатов. Тогда были детально изучены такие сложные образования, как парабола, гипербола и эллипс; в частности, было доказано, что все эти кривые могут быть получены в результате пересечения поверхности круглого конуса с плоскостью, откуда и возникло их общее название — конические сечения. Алгебра развивалась медленнее, чем геометрия. Первые ее признаки мы находим в папирусе египтянина Ахмеса, появившемся приблизительно за два тысячелетия до п. э. В этом папирусе (если применить современную терминологию) решается уравнение первой степени с одним неизвестным, причем имеется специальное иероглифическое обозначение неизвестной величины и специальные символы для обозначения действий: сложения и вычитания, а также для обозначения равенства. В дальнейшем выдающиеся достижения в области алгебры принадлежат арабам 9—15 вв., которые уже решали уравнения I и II степени, но не употребляли символики, а пользовались словесными описаниями. В конце 15 в. в Италии появляются современные знаки плюс (+) и минус (—). Быстро появляются и дальнейшие современные знаки: степень, корень, скобки- и т. д. Далее в работах французского математика Виета (1540—1603) вводятся буквенные обозначения величин, как известных, так и неизвестных. Таким образом ко времени Декарта был готов современный аппарат символической алгебры.
Важную роль аналитическая геометрия сыграла в развитии понятия числа. Отрицательные числа, известные еще индусам в 6—11 вв., европейскими математика-10.
ми долгое время не признавались считались абсурдными. Даже Виета не признавал их. Только благодаря аналитической геометрии Декарта (правило выбора знаков координат) они полностью утвердились в математике.
Точно так же комплексные числа обрели свою реальность благодаря декартовым координатам, но уже много позже Декарта. Первоначально считалось, что квадратное уравнение, не имеющее действительных решений, вовсе их не имеет. Только в 16 в., благодаря формуле Кардана решений кубического уравнения, пришлось до некоторой степени признать комплексные числа, так как оказалось, что при решении кубического уравнения, имеющего три действительных корня, в формуле Кардана при промежуточных вычислениях появляются комплексные числа. Однако и после этого комплексные числа оставались мало понятными до Гаусса (1777— 1855), который на грани 18 и 19 столетий дал при помощи декартовых координат геометрическое изображение комплексных чисел и доказал основную теорему высшей алгебры о том, что многочлен лг-й степени имеет п корней. В настоящее время комплексные числа и комплексные функции комплексного переменного играют огромную роль в теоретической и прикладной математике.
Глава!
КООРДИНАТЫ НА ПЛОСКОСТИ
В этой глав£ я описываю прямоугольные декартовы координаты на плоскости, полярные координаты на плоскости, а также изображение комплексных чисел на плоскости.
2
z
4
Рис. 1.
§ 1. Прямоугольные декартовы координаты и векторы на плоскости
В некоторой плоскости Р выберем две перпендикулярные друг другу прямые и обозначим через о точку их пересечения. Для определенности будем считать, что плоскость Р есть плоскость нашего чертежа (рис. 1), й что одна из выбранных прямых проходит горизонтально, а другая вертикально. Горизонтальная прямая называется осью абсцисс, а вертикальная — осью ор- • динат. Обе оси называются просто осями координат, а точка о — — началом координат. Выбранные оси разбивают плоскость Р на четыре четверти или квадранта. Эти четверти нумеруются в следующем порядке: первая четверть лежит над осью абсцисс и вправо от оси ор-лежит над осью абсцисс и влево от
'<3
динат; вторая
оси ординат; третья — под осью абсцисс и влево от оси ординат, и, наконец, четвертая — под осью абсцисс и вправо от оси ординат (см. рис. 1). Таким образом, четверти занумерованы в том порядке, в каком их йроходит точка, начинающая свое движение в первой
12
четверти и движущаяся против часовой стрелки вокруг начала координат.
Пусть теперь z — некоторая точка на плоскости Р. Пользуясь выбранными осями координат, поставим этой точке в соответствие два числа х и у; х — ее абсциссу, у — ее ординату. Для этого из точки z опустим перпендикуляр zp на ось абсцисс и перпендикуляр zq на ось ординат. Если точка р лежит вправо от начала координат о, то через х мы обозначим длину отрезка ор, т. е. положительное число. Если точка р лежит влево от начала координат о, то через х мы обозначим длину отрезка ор, взятую со знаком минус, т. е. отрицательное число. Если точка р совпадает с началом координат о, то х == 0. Аналогично, если точка q лежит выше начала координат, то через у мы обозначим длину отрезка oq, т. е. положительное число. Если точка q лежит ниже начала координат, то через у мы обозначим длину отрезка oq, взятую со знаком минус, т. е. отрицательное число. Если точка q совпадает с началом координат, то у = 0. Таким образом, каждой точке z на плоскости Р при помощи выбранной системы координат поставлена в соответствие пара чисел: х иу, х — абсцисса точки z, у — ее ордината. В виде формулы это записывается так:
Z = (х, у).	(1)
Числа х и у называются координатами точки z.
Начало координат о получает координаты (0, 0), z т. е. о == (0, 0). Произвольная точка z на оси абсцисс имеет ординату,* равную нулю, так что она записывается в форме
z = (х, 0) = (х).
Таким образом, положение точки z на оси абсцисс определяется одним числом х и поэтому число х естественно считать координатой точки z на оси абсцисс. Произвольная точка z на оси ординат имеет абсциссу, равную нулю, так что она записывается в форме
Z = (0, у) = (у).
Таким образом, положение точки z на оси ординат определяется одним числом у, и поэтому число у естественно считать координатой точки z на оси ординат.
•	<3
Следует заметить, что opzq (см. рис. 1) есть прямоугольник. Таким образом, длина отрезка ор равна дли-
не отрезка qz, а длина отрезка oq равна длине отрезка pz. Поэтому абсциссой точки z является не только длина отрезка ор, но также длина отрезка qz, взятая с надлежащим знаком. Точно так же ординатой точки z
является не только длина отрезка oq, но тгкже длина отрезка pz, взятая с надлежащим знаком.
Если заданы два произвольных числа х и у, то на плоскости Р легко построить ту единственную точку z, абсцисса которой
равна заданному числу х, а ордината — заданному числу у. Для этого поступим следующим образом (рис. 2): сперва построим на оси абсцисс точку р с координатой х, т. е. отложим на оси абсцисс отрезок ор, длина которого равна |х| (модуль числа х), причем точка р лежит вправо от точ-
рис> 2. ки если число хположительно, и влево от точки о, если число х отрицательно. Далее, восставим к оси абсцисс перпендикуляр pz, длина которого равна числу |j/|, причем точка z лежит над осью абсцисс, если число у положительно, и под осью абсцисс, если число у отрицательно. Конец этого перпендикуляра и является той точкой z, абсцисса которой равна числу х, а ордината — числу у* так что выполнено равенство (1). Таким образом, формула (1) устанавливает взаимно однозначное соответствие между точками плоскости Р и па
рами чисел х, у.
Если точка z движется вдоль оси абсцисс слева направо, то абсцисса ее возрастает. Поэтому говорят, что ось абсцисс направлена слева направо. Это обстоятельство можно изобразить геометрически, нарисовав на оси абсцисс стрелку, острием своим направленную в правую сторону (см. рис. 2). В том же самом смысле ось ординат направлена снизу вверх, и это можно изобразить, нарисовав на ней стрелку острием, направленным вверх. Точки, лежащие на оси абсцисс справа от начала координат, имеют положительные абсциссы. Поэтому говорят, что они составляют положительную полуось абсцисс. Точки, лежащие на оси абсцисс слева от начала координат, имеют отрицательные абсцис
14
сы и поэтому говорят, что они составляют отрицательную полуось абсцисс. В том же самом смысле точки, лежащие на оси.ординат выше начала координат, составляют положительную полуось ординат. А точки, лежащие ниже начала координат, составляют отрицательную полуось ординат.
Первая задача, которую мы решим, пользуясь методом координат, состоит в вычислении длины отрезка или, что то же самое, в нахождении расстояния между двумя точками, заданными своими координатами. •
Пусть
У1)» Z2 = (*^2’ У %)	(2)
— две точки на плоскости Р, заданные своими координатами. Расстояние между точками z± и z2, которое мы обозначим через Z(zx, z2), определяется формулой г)
Z(zx, z2) = + К(ж2 — жх)2 + (у2 — ух)\ (3)
Для доказательства этой формулы проведем через точку zx горизонтальную прямую (рис. 3), а через точку z2 вертикальную прямую. Точ-
ку пересечения этих двух прямых обозначим через г. Треугольник z1rz2 есть прямоугольный с катетами zxr, rz2 и гипотенузой ztz2. Непосредственно видно, что длина отрезка zrr равна |#2 — ^j|,a длина отрезка rz2 равна |р2 — Z/il- Таким образом, формула (3) является следствием теоремы Пифагора,
примененной к прямоугольному треугольнику ztrz2.
Теперь уместно перейти к рассмотрению векторов, при помощи которых многие формулы записываются
гораздо короче, чем при помощи координат.
Пусть а и b — две точки на плоскости Р (рис. 4). Принято говорить, что отрезок аЪ, определенным обра-
х) В дальнейшем перед корнем будет ставиться знак + пли —, если корень действительный и берется его положительное или отрицательное значение. В случае отсутствия знака считается, что берется любое из двух значений корня.
15
зом направленный, именно, от а к Ь, есть вектор аЪ. Точка а называется началом вектора, а точка b — его концом. Говорят также, что вектор ,ab приложен к точке а. Если с и d — две какие-нибудь другие точки плоскости Р, то считается, что вектор ab равен вектору cd, если отрезки ab и cd: 1) равны по длине, 2) параллельны, 3) одинаково направлены. Если отрезки ab и cd не лежат на одной прямой то все три сформулированных условия можно выразить следующим простым геометрическим способом: проведем, кроме двух отрезков ab и cd, два других отрезка ас и bd. Тогда три вышесказанных условия выражаются одним: acdb есть параллелограмм.
Очевидно, что для каждого_ вектора ab найдется равный ему вектор, выходящий из начала координат о. Обозначим его конец через z, так что векторы ab и oz равны. В основном мы будем ограничиваться рассмотрением лишь тех векторов, которые начинаются в начале координат о. Такие векторы мы будем обозначать одной буквой, а именно вектор oz будем обозначать просто буквой z. Этим самым устанавливается взаимно однозначное соответствие между векторами, выходящими из начала координат и точками плоскости Р, именно, каждому векторyj)z ставится в соответствие его конец, точка z. Тот факт, что точка и вектор, идущий из о в эту точку, обозначаются одной и той же буквой, не приводит к путанице.
Теперь определим операцию сложения двух векторов. Рассмотрим на плоскости Р два вектора zt и z2. Подразумевается, что zx и z2 есть концы векторов, начинающихся в точке о (рис. 5). Для того чтобы определить сумму векторов zt + z2, проведем из точки zt вектор ztz3, равный вектору z2. Вектор oz3 или, что то же самое, z3, есть, по определению, сумма векторов и z2:
zg = Z| z2.
В нашем построении суммы zt + z2 векторы z± a z2
16
неравноправны. Поэтому нужно доказать, что ^1 4" ^2 = ^2 "Ь %1* '
Для доказательства проведем вектор z2z3. Так как векторы oz2 и z±z3 равны, то oztz3z2 есть параллелограмм, и поэтому векторы oz± и z2z3 рав- .	г
ны. Таким образом, по определе- ‘ нию, z3 есть сумма векторов	s'/]
z2+ zv Следовательно, сумма двух	'7х/ /
векторов не зависит от порядка / /хД слагаемых.	/// 2
Разность векторов z2 — zt оп- ____s____________
ределяется как вектор z\z2 (см. о х. : рис. 5). Обозначим ее через z4. *	\
Обозначая вектор одной буквой, мы тем самым подразумеваем, что	рИо. 5.
он начинается в точке о, так что
вектор oz4 или, что то же самое, z4 равен вектору zYz2. Таким образом, согласно определению суммы мы имеем равенство
“Ь z4 = z2.
Мы видим, что разность z2 — z4 определена так, что имеет место равенство
(z8 -Zi) + Zi = z2.	(4)
Последняя формула подтверждает, что разность векторов определена нами правильно. Следует запомнить, что при построении разности векторов вектор z2 — z± начинается в точке zx и кончается в точке z2.
Среди всех векторов имеется один вектор нулевой длины, начинающийся и кончающийся в точке о. Он обозначается знаком О. Этот вектор обладает следующим свойством:
z + 0 = z.
’Длина отрезка, определяющего вектор, называется модулем этого вектора и обозначается специальным образом, именно
|z| = 1(0, z) (см. рис. 4).
Имеет место важное неравенство
IZ1 4- Z2[ [Z1I + Iz2l’	(5)
2 л. G. Понтрягин	17
Неравенство это следует из рассмотрения треугольника
OZ1Z3 (см. рис. 5). Длина стороны ozL есть |2Х|, длина
сторэны zxz3 есть |z2| и^ наконец, длина стороны oz3 есть |zx + z2|.- Таким об-
разом, неравенство (5) означает не что иное, кар то, что длина одной стороны треугольника меньше или равна сумме длин двух других его сторон.
Кроме операций ело-
Рис. 6.	жен и я и вычитания век-
торов существует еще од-
на важная операция над векторами, именно, умножение вектора на число. Если а — некоторое число, а
z — вектор, то для определения произведения
z’ = az	(6)
проведем прямую L, проходящую через точки о и z (рис. 6). Если a —число положительное, то от точки о отложим на прямой L отрезок oz', равный по длине a|z| и направленный в ту же сторону, что и отрезок oz. Конец z' этого отрезка и есть вектор az. Если число а отрицательное,то от точки о отложим’на прямой L отрезок ozr длины |a | |z], ио в направлении противоположном отрезку oz. Конец этого отрезка z' и есть вектор az. Если a = 0 или z = 0, то вектор az есть нулевой вектор.
В силу самого определения вектор z' = az лежит на прямой L. Но, очевидно, что и произвольно взятый вектор z', лежащий на прямой L, может быть записан в форме (6), если конечно z 0. Нужное число а определяется следующим образом. Если точки z' и z лежат на прямой L по одну сторону от точки о, то число а положительно и определяется формулой
a —
/
Если z' и z лежат на прямой L, но по разные стороны от точки о, то число а отрицательно и определяется формулой	4
18
Таким образом, точки вида (.6) при z 0 заполняют всю прямую L, когда а принимает всевозможные числовые значения.
Введем теперь понятие координат вектора. Так как z является у нас одновременно и точкой и вектором, то естественно считать, что координаты точки z. являются одновременно и координатами вектора z. Таким образом, мы можем записать
Z = (X, у),
где z есть вектор, а х, у — его координаты, т. е. координаты точки z.
Опишем теперь при помощи координат те операции над векторами, которые только что были определены чисто геометрически. Кроме вектора z, запишем в координатной форме еще два вектора:
ч = (ж1> У1)> z2 = («2. г/2)-
Тогда мы имеем
*1 + Z2 =	+ Ж2, У! + у2),	(7)
Z1 - z2 = («! - х2, ух - у2),	(8)
|z| = +v X2 + у2,	(9)
az = (ах. ау).	(10)
Докажем формулы (7)—(10), На рис. 7 построим сумму векторов zY + z2 как указано выше (см. рис. 5). Проведем через точку z± горизонтальную прямую, а через точку z3 вертикальную прямую. Точку пересечения этих прямых обозначим через г. Треугольники op2z2 и zLrz3 равны между собой. Из этого следует, что длина отрезка zxr. взятая с надлежащим знаком, есть абсцисса точки z2, а длина отрезка rz3, взятая с надлежащим знаком, есть ордината точки z2. Отсюда следует справедливость формулы (7). Формула (8) следует из формул (4) и (7). Формула (9) следует из формулы (3), в которой следует положить z2=z, zY = 0. Для доказательства формулы (10) рассмотрим на рис. 6 треугольники opz и op'zf. Из их подобия вытекает формула (10).
Пользуясь векторными обозначениями, мы удобно можем теперь записать расстояние между двумя точками 2»_	19
и z2. Именно, в силу формул (3) и (8) мы имеем 4ZV ^2) = 1^2 ““ 211*
Пример 1. Вычислим площадь S треугольника 02^2, где точки z19 z2 заданы своими координатами (см. формулу (2)). Треугольник этот изображен на рис. 8. Площадь названного треугольника составим
из трех частей: 1) треугольник op2z2; его площадь S2 равна х2у2/2\ 2) трапеция p2Pizizri ее площадь S3 равна (#x — x2)(z/x + z/2)/2; 3) треугольник ор^; его площадь равна Xji/x/2. Первые две площади следует сложить, а третью вычесть. Производя вычисления, получаем
S = S2 Sx S3 =	(^1^2	^1^2)»	(И)
где
= “2"	^2 “ "2“ ^2^2» ^3 ~ “g- (Ж1 Xi) (У1 “Ь У%)'
(12)
Вычисление это произведено нами при некотором довольно определенном расположении точек z± и z2 на плоскости Р относительно выбранной системы координат. Но формула (И) верна всегда, при условии, что величины Sv S2, S3 заданы формулами (12). Однако получаемая по ней площадь S положительна, если в треугольнике oztz2 направление oz2 получается из направления ozi поворотом против часовой стрелки. Если этот поворот должен быть произведен по часовой стрелке, то площадь, получаемая по. формуле (И), отрицательна.
20
§ 2. Полярные координаты
На нашей плоскости Р мы уже имеем декартову " систему крординат, т. е. ось абсцисс, ось ординат и начало координат. С этой системой координат тесно связана так называемая полярная система координат.
Пусть z = (х, у) •— произвольная точка плоскости Р, заданная своими декартовыми координатами. Поставим теперь этой точке z в соответствие два других числа ее полярные координаты.
именно, число р, равное	Рис. 9.
длине отрезка oz, р = Z(o, z), и число ф, равное величине угла в радианах между положительной полуосью абсцисс и отрезком
oz, причем угол отсчитывается в направлении против часовой стрелки (рис. 9). Мы будем писать
z = [р, ф].
(13)
Число р называется радиусом точки z, а число ф ее углом.
Радиус р точки z определен однозначно. Угол ф точки z не определен совсем, когда точка z совпадает с началом к’оординат. Но и в том случае, когда точка z не совпадает с началом координат, угол ф не определен однозначно. Именно, если ф есть угол точки z, то
Ф + 2Ьг,	(14)
% где к — произвольное целое число, так же является углом точки z. Это обстоятельство в ряде случаев имеет важное значение. С другой стороны, если задано произвольное неотрицательное число р и произвольное число ф, то всегда найдется такая точка z, что заданное число р является ее радиусом, а заданное число ф ее углом. Полярные координаты р и ф точки^г менее совершенны, чем ее декартовы координаты, так как здесь нет взаимно однозначного соответствия между точками z плоскости Р и парами чисел р, ф. Тем не менее; в ряде^ случаев полярные координаты оказываются более удобными, чем декартовы.
21
Пользуясь одновременно декартовыми и полярными координатами, мы неизбежно должны поставить вопрос о связи между теми и другими. Декартовы и полярные координаты точки z = (х, у) = [р, ф ] связаны между собой следующими формулами (см. рис. 9): z = pcosq),j у = р sin <р. J
Формулы эти следуют из рассмотрения треугольника opz. Они имеют простой геометрический смысл, когда точка z принадлежит первому квадранту плоскости. Опустим из точки z перпендикуляр zp на ось абсцисс. Так как z принадлежит первому квадранту, то абсцисса и ордината этой точки, х и у, — суть положительные числа, и мы имеем равенства
х = Z(o_, р), у = Z(p, z), р = Z(o, z).
В прямоугольном треугольнике opz op и pz являются катетами, a oz гипотенузой. Угол ф точки z равен углу этого треугольника в вершине о. И формулы (15) суть известные формулы, выражающие длины катетов прямоугольного треугольника через его гипотенузу и угол при острой вершине треугольника. В случае, если точка z принадлежит 2-му, 3-му или 4-му квадранту .плоскости, в формулах (15) следует обратить внимание на знаки левых и правых частей. Формулы (15) оказываются правильными при любом положении точки z. Но это не является случайностью, а следствием того, что правило выбора знака для абсциссы совпадает с правилом выбора знака для косинуса в тригонометрии. А правило выбора знака для ординаты совпадает с правилом выбора < знака для синуса в тригонометрии. Таким образом, правильное использование отрица-телгных чисел позволяет нам вести вычисления, не думая о знаках, входящих в вычисление величин. Если бы мы не использовали отрицательных чисел или пользовались ими неудачно, то вместо двух равенств в формулах (15) нам пришлось бы писать два соотношения для каждого из четырех квадрантов, отдельно.
Столь же большое значение имеет использование отрицательных чисел и для формулы (3). Представьте себе, что мы не употребляем отрицательных чисел. 22
Тогда мы определили бы абсциссу и ординату точки z, как соответственно длины отрезков ор и pz, и для определения положения точки z на плоскости мы, кроме пары координат (х, у), которые были бы не отрицательны, должны были бы написать еще помер квадранта, в котором эта точка находится, т. е. число 1, 2, 3 или 4. В этом случае, вместо единственной формулы (3), определяющей расстояние Z(z1? z2) через координаты точек zr и z2, мы вынуждены были бы писать 16 различных соотношений, рассматривая все случаи расположения точек zx и z2 по квадрантам. При этом ка^кдое соотношение описывало бы определенный случай: точка zx расположена в одном из 4-х квадрантов — 4 возможности; точка z2 также могла бы быть расположена в одном из 4-х квадрантов — 4 возможности. Вместе получается 16 различных комбинаций расположения. Вместо одной формулы (3) мы имели бы 16 различных формул. Также отвратительно сложно обстояло бы дело и с двумя соотношениями (15).
Пример 2. Вычислим теперь площадь S треугольника oz^ (см. пример 1; рис. 8), пользуясь полярными координатами
Z1 = tpl, Ф1], *2= [р2, ф21-	(16)
Для этого на рис. 8 опустим перпендикуляр z2r из вершины г2 на сторону ozt или на ее продолжение. Это есть высота нашего треугольника. Она равна р2 sin (ф2 — ф2). Здесь высота взята с определенным знаком. Основание же треугольника равно числу рх. Таким образом, получарм
s = —Р1Р281п(ф2 —(Pi).
Это известная формула тригонометрии. Здесь, однако, площадь S взята с определенным знаком, причем правило выбора знака то же самое, что и в примере 1. Подставляя в формулу (И) выражение декартовых координат точек z19 z2 через их полярные координаты (см. (15)), мы получаем
S = -у Р1Р2 Sin — Ф1) =
1
= 2 Р1Р> (cos Ф1 s*11 Фа—sin epi cos фг).
23
Отсюда следует:
sin (ф2 — (pj = sin ф2 cos (Pj— cos ф2 sin Фг (17)
Таким образом, мы доказали одну из основных формул тригонометрии, вычислили величину синуса разности двух углов.
Выведем из нее три другие основные формулы тригонометрии: синус суммы, косинус суммы и косинус разности. При этом мы будем пользоваться лишь следующими формулами тригонометрии, которые легко проверяются:
sin(—ф) = — sin ф, cos{— ф) == cos ф,
sin I  --ф)= соэф.
V "	/
Для получения синуса суммы подставим в формулу (17) — фг на место фг Тогда мы будем иметь
sin (ф2 + Ф1) == sin Ф2 cos (—<Pi) — cos Ф2 s*n (—Ф1) = =sin ф2 cos фх + cos ф2 sin фг,
(18)
окончательно,
sin (фх + ф2) = sin фх cos ф2 + cos фх sin ф2.	(19)
Далее, имеем в силу формул (17) и (18)
cos^Pi 4- <р2) = sin — ф2) — <Pi] = • [ л \	(л \ .
= Sin I “2-T2)COS(P1 — cosl -----Ф2 I Sin ф| ==-
= созф2созф1 — sin ф2э1п фг, или окончательно,
cos (ф1 + Ф2) = cos фг cos ф2 — sin фх sin ф2.	(20)
Заменяя в этой формуле фх на —-фп получаем
cos (ф2—ф0 = cos ф2 cos фх + sin ф2 sin фх. (21)
Пример 3. Определим скалярное произведение zr • z2 двух векторов и z2, пользуясь их полярными координатами (см. (16)). По определению,
Zj-Z2 = Pl р2 cos (ф2 — Ф1) = Р1Р2 cosy, (22)
24
где у есть угол между векторами и z2. Знак числа у не играет роли (см. формулы (18)). Но косинус положителен, когда угол у острый, и отрицателен, когда у— тупой. Пользуясь формулами (15) связи между полярными и декартовыми координатами, мы с помощью формулы (21) получаем выражение
%1*%2	^1^2 "Ь У1У2*	' '
Оно дает скалярное произведение, выраженное через декартовы координаты векторов.
§ 3< Геометрическое изображение комплексных чисел
Декартовы координаты дают еще одну возможность для установления связи между точками и числами, а именно, они позволяют геометрически изображать комплексные числа и действия над ними. .
Комплексные числа, как известно, возникли благодаря тому, что нельзя было извлечь корень квадратный из отрицательного числа. Поэтому ввели формально новое число £, удовлетворяющее уравнению
i2 + 1 = О, так что
и определили комплексное число z формулой
z = х + iy,	(23)
где х и- у — обыкновенные числа,- с которыми уже привыкли иметь дело и которые теперь, в отличие от комплексных, мы будем называть действительными. Над комплексными числами стали производить обычные действия: сложение, умножение и обратные к ним: вычитание и деление. Во всех таких вычислениях заменяли i2 на —1 и получали, таким образом, возможность производить над комплексными числами все действия так же непринужденно, как раньше над действительными.
Определим действия надч комплексными числами более формально. Пусть
'Zj = Xi + iyv Zj = x3 + iy2
25
— два комплексных числа. Тогда их сумма определяется формулой
21 + Ч = 0*1 + я2) + Z(z/L + z/2).	(24)
Произведение двух комплексных чисел и z2 определяется формулой
ад ==	+ 1У1) (х2 + iy2) = xtx2 + ix± у2 + 1у^2+
+^2УгУ2 = (ад — У1У2) + ^1У2 + УЛУ (25)
Комплексное число z, записанное в форме (23), само просится на нашу плоскость Р, па которой уже введены декартовы координаты. Его хочется изобразить в виде точки z с координатами (х, у) или, что то же самое, в виде вектора z с координатами (х, у), т. е. z — (х, у). Плоскость Р, на которую нанесены в виде точек комплексные числа z, будем называть плоскостью комплексного переменного z.
Комплексные числа z вида
z = х + J0 — х
теперь разумно называть действительными числами. Они все лежат на оси абсцисс, и поэтому ось абсцисс плоскости комплексного переменного z мы будем называть действительной осью. Комплексные числа вида
Z = о + iy = iy называются чисто мнимыми, или просто, мнимыми, и они располагаются на оси ординат. Поэтому ось ординат плоскости комплексного переменного z мы буде^м называть мнцмой осью. Комплексное число z — 0 + Ю — 0 попадает в начало координат. Действительные числа +1 и — 1 располагаются на действительной оси справа и слева от нуля на расстоянии единица. Мнимые числа ~Н-И —г располагаются на мнимой оси над нулем и под нулем на расстоянии единица от него.
Используем теперь для записи комплексного числа z полярные координаты точки z. Так как в силу формул (15)
х = р cos ср, у — р sin ср,
26
то комплексное число г, определенное формулой (23), записывается в виде
z — p(cos ф + i sin ф).	(26)
Эта запись комплексного числа z называется тригонометрической. Неотрицательное число р называется модулем комплексного числа z, а угол ф — его аргументом. Число р однозначно определено комплексным числом z и обозначается специальнььм символом
|z| = р =	4- у2.
Следует вновь напомнить, что аргумент ф комплексного числа z не определен однозначно, именно, при |z|=0 он вовсе не определен, а если |z|	0 и ф есть аргумент
комплексного числа z, то наряду с этим значением ф аргументом являются и числа
Ф + 2/т,	(27)
где к — произвольное целое число (сравните с формулой (14)).
Пользуясь формулами (24) и (25) , дадим геометрическое истолкование операциям сложения и умножения комплексных чисел.
Из формул (7) и (24) следует, что для того, чтобы сложить два комплексных числа z± и z2, достаточно сложить изображающие их векторы zx и z2. Тогда полученная сумма векторов z3 = zT + z2 изображает сумму Zj + комплексных чисел. Так как для векторов существует операция вычитания, обратная к операции сложения (см. формулу (4)), то и для комплексных чисел существует операция вычитания, обратная к операции сложения. Геометрическая интерпретация сложения комплексных чисел приводит нас к важному неравенству
ta +z2| < tai + tai
(28)
(сравните с формулой (5)).
Для того чтобы дать геометрическую интерпретацию умножения комплексных чисел z15 z2, запишем эти числа и их произведение w в тригонометрической
27
форме/ именно:
zi = Pi (cos (pi + i sin q^), ' z<> = P2 (cos Ф2 + * sin Ф2), ZjZ2 = w = о(созф + i sin Ф).
(29)
При подсчете произведения в тригонометрической форме мы используем известные формулы тригонометрии (см. (19), (20)). В силу (25,) (29), (19) и (20) мы полу- ~ чаем теперь
1V = zxza == рхр2 [(cos (pi cos ф2 — sin фг sin <р2) +
+ /(sin cpi cos ф2 + cos cpx sin (p2)] =
= PiP2lcos (фх + ф2) + i sin (<pi 4- ф2) ], или, окончательно,
a(cos ф + i sin ф )= PxP2[cos (<px + ф2) 4- i sin 1(фх+ф2) 1-(30)
Таким образом,
о = Р1Р2, Ф = <Pi + ф2.	(31)
Это означает, чтц при перемножении комплексных чисел zx и z2 их модули рх и р2 перемножаются, а их аргументы фх и ф2 складываются.
• Йз формулы (31) видно, что операция деления одного комплексного числа на другое всегда возможна, если делитель не равен нулю. В самом деле, будем считать, что w и zx — заданные комплексные числа, a z2 следует определить из уравнения w ~ zxz2. Тогда из формулы (31) мы получаем
р2==”К’ Фз^Ф-фг
Формулу произведения (30) можно распространить на произвольное число сомножителей, применяя эту формулу последовательно. Пусть
ZJ = Р/ (cos Ф/ + 1 sin Ф;)	(/ = 1» 2, ... , п)
— последовательность комплексных чисел, a w == 28
=	. . . гп. Тогда мы имеем
w = о (cos ip + i sin if) —
= Pi • • • Pnlcos (<pi+ . . . -|-ф„)Ч-гsin(фг + . . .+cpn)b
В частном случае, когда все числа zx,z2, . .\ . , zn равны одному и тому же числу z, мы получаем интересную формулу:
2п’= a (cos ф + i sin ф) = pn (cos n(p + i sin nep). (32)
При употреблении комплексных чисел часто приходится рассматривать наряду с данным комплексным числом z = х + iy число, комплексно сопряженное с ним, которое обозначается через z и определяется формулой
z = х — iy.
Если комплексное числа z записано в тригонометрической форме (см. формулу (26)), то комплексно сопряженное с ним число z записывается в форме
1 = р [cos (—ф) + i sin (—ср)]. "	(33)
Таким образом, при переходе от числа z к комплексно сопряженному числу z модуль числа сохраняется, а аргумент меняет знак.
Очевидно, что число, комплексно сопряженное с числом z, является самим числом z, т. е. z = z. Точно так же, очевидно, что комплексное число z тогда и только тогда является действительным числом, когда оно совпадает со своим комплексно сопряженным, т. е. при условии z == z.
Два комплексно сопряженных между собой числа z и z изображаются на плоскости комплексного переменного в виде двух точек, симметрично расположенных относительно оси действительных чисел.
Из формул (24), (30) и (33) непосредственно следует, что	___
4“ 22 = Zx 4“ Z2, 2XZ2 “	^2**
Первая из этих формул легко распространяется на произвольное число слагаемых, а вторая на
29
произвольное число сомножителей. Таким образом, zk = (z )k .Далее, если а — действительное число, то azn = a(z)n = a(z)n.
Следовательно, для произвольного многочлена
/ (z) = aazn +	4- ... + ап
с действительными коэффициентами мы получаем
/ (Z) = aozn + а^-1 + ... + ап = aozn +
••• + ап —	+ а1 (г)П + ••• + ar> = / (z).
Таким образом, для многочлена с действительными коэффициентами имеем
7^ = /(z).	(34)
Последняя формула приводит нас к весьма важному выводу. Именно, если у есть корень многочлена /(z) с действительными коэффициентами, т. е.
/(Y)=0, то и число у также есть корень многочлена /(z), т. е.
/(7) = о.
В самом деле, в силу формулы (34) мы имеем
/(7) = 7(7) -'о = о.
П р и м е р 4. Воспользуемся теперь формулой (32) для извлечения корня n-й степени из произвольного комплексного числа w 0. Число w — 0 не представляет интереса, так как корень n-й степени из нуля равен нулю. Для решения этой задачи нам следует решить уравнение
zn — ш,	(35)
где z — неизвестное, a w —заданное комплексное число, отличное от нуля.
Рассмотрим сперва случай w ~ 1. Тогда формула (32) дает нам вместо уравнения (35) уравнение
p”(cos nip + i sin nep) = cos 2/сл + i sin 2/сл,	(36)
20
где к — произвольное целое число (см. (27)). Здесь р и ср являются неизвестными. Из уравнения (36) следует, что
где к — произвольное целое число. Таким образом, любой корень ft-й степени из единицы записывается в виде
2/сл . . . 2кл У 1 — COS-----h t sin--,
где к — произвольное целое число. Так как к — произвольное целое число, то последняя формула дает нам как бы бесконечное множество корней из единицы. В действительности же различных корней имеется только п. Для уяснения этого обстоятельства выделим из числа *всех корней один определенный, именно:
2л ... 2л
8 = COS---г & SIH--.
п	п
Тогда произвольный корень n-й степени пз единицы записывается в форме
2кл , . . 2&л	*	/ОГ7Ч
cos----h i sm — = e\	(37)
n	n	x '
Если придать числу к два различные значения к = р, к = q, то левая часть последнего равенства представляет собой одну и ту же точку тогда и только тогда, когда
2рл_2^-==2гя
п 11
где I — целое число. Из этого следует, что для того, чтобы перебрать все различные точки, даваемые формулой (37), при различных целых значениях к. нам достаточно придать к значения 0, 1, . . . , n—1, т. е. совокупность всех корней тг-й степени из единицы перечисляется следующими комплексными величинами:
8°, е1,	(38)
Из формулы (37) видно, что все числа (38) расположены на окружности радиуса единица с центром в начале координат и составляет вершины правильного вписан-
31
ного в эту окружность n-угольника, причем одна из вершин е° = 1 есть единичная точка, лежащая на оси абсцисс. Для большей конкретности изобразим на рисунке случаи п — 3 (рис. 10), п = 4 (рис. 11) и п = 6 (рис. 12).
Вернемся теперь к вычислению корня n-й степени из произвольного комплексного числа ip Напомним опять, что аргумент комплексного числа определяется с точностью до слагаемого вида 2fcrt, где к — целое число. Принимая во внимание это обстоятельство,
выберем для числа w один вполне определенный аргумент ф0. Уравнение (35) в тригонометрической форме мы можем переписать теперь следующим образом: pn (cos пф + i sin шр) =
= a[cos(ip0 + 2&л) + i sin(ip0 + 2кл)], где к — произвольное целое число. Отсюда получаем
Пл-
Р = V а, где р есть положительное число, и Фо 2кл
где к — произвольное целое число. Положим z0 = p(cos— 4-isin— ” г \ п	п 1
83
Таким образом, произвольный корень n-й степени из w может быть записан в форме
Vх w = zoeft,
где к принимает значения к — 0, 1, ..., n-1, a есть один из корней /г-й степени из iv. Таким образом; со
вокупность всех корней n-й степени из w есть совокупность _ всех вершин правильного п-угольпика, вписанного в окружность радиуса рс центром в начале координат, причем одна из вершин находится в точке z0.
Пример 5. Соотношение
i* = - 1	(39)
является определением но-
вого числа i,позволяющего
ввести в рассмотрение комплексные числа. Таким образом, оно не может быть доказано, оно является
соглашением.
Несмотря на это, нашлись люди, пожелавшие доказать это соотношение. Сделано это было следующим образом. На рис. 13 изображена полуокружность, опирающаяся на свой диаметр г _________,__ ab. Из произвольной точки
г этой полуокружности опущен /	X перпендикуляр rs на диаметр
/	\ ab. Согласно известной теореме
I	\ элементарной геометрии длина
а-----s J "	:	2 перпендикуляра rs является
средним геометрическим меж- ' ^ис* 13*	ду длинами отрезков as и sb.
Хотя речь идет о длинах, не будет большой ошибкой сказать, "что квадрат отрезка rs равен произведению отрезков as и bs.
Вернемся теперь па плоскость комплексного переменного z. Обозначим через а точку —1, через Ъ точку +1 и через г точку i. Тогда s будет точкой о.
8 Л. С. Понтрягид	»
Автор доказательства соотношения (39) рассуждает следующим образом. Отрезок rs есть i9 отрезок as есть —1, отрезок sb есть +1. Таким образом, согласно ска-ч занной теореме элементарной геометрии/2 ==(— 1)(+ 1) = = -1.
Несмотря на чудовищную бессмысленность этого доказательства, оно было опубликовано в книге Коль-мана «Предмет и метод математики». Более того,’ оно излагалось на уроках математики в московских школах. Это было еще до второй мировой войны.
ДОБАВЛЕНИЯ К ГЛАВЕ I
Здесь строятся прямоугольные декартовы координаты в пространстве, а также определяются пространственные векторы и действия над ними, т. е. описываются для случая пространства некоторые из тех понятий, которые были даны в главе I для случая плоскости. При этом доказательство проводится менее полно, чем это было сделано для случая плоскости, в расчете на то, что читатели сами дополнят пропущенные детали. 4
1> Координаты в пространстве. Допустим, что в пространстве задана некоторая прямая R и некоторая точка х. Проведем через точку х плоскость Q, перпендикулярную к прямой R. Тогда точка пересечения р прямой R с плоскостью Q называется проекцией точки х на прямую R.
В § 1 уже была описана прямоугольная декартова система координат на некоторой плоскости Р. Она определяется двумя осями координат: осью абсцисс и осью ординат. Каждая из этих осей представляет собой прямую, проведенную на плоскости Р, причем на каждой прямой выбрано определенное направление. Оси перпендикулярны между собой, а их пересечение, называемое началом координат, обозначено через о. Для построения системы координат в пространстве будем считать, что плоскость Р расположена горизонтально. Будем называть ось абсцисс первой осью, ось ординат — второй осью, третью ось проведем через точку о перпендикулярно к плоскости Р и выберем
34
на ней направление снизу вверх. Таким образом, прямоугольная система декартовых координат в пространстве определяется тремя осями, каждая из которых есть прямая с выбранным на ней определенным направлением, причем каждые две прямые перпендикулярны между собой, и все они пересекаются в точке о, называемой началом координат. Через каждые две оси проведем координатную плоскость, именно, через оси первую и вторую проведем координатную плоскость (1, 2); через оси 2 и 3 проведем координатную плоскость (2, 3) и, наконец, через оси 1, 3 проведем координатную плоскость (1, 3).
Пользуясь выбранной системой координат, поставим в соответствие произвольной точке х пространства три числа: хъ х2,	— ее координаты,
х —	х2, х3).	(40)
Сделаем мы это следующим, образом. Проекцию точки х на первую ось обозначим через/?!, проекцию точки х на вторую ось обозначим через /?2, наконец, проекцию точки х на третью ось обозначим через р3. Через xY обозначим длину отрезка оръ если этот отрезок имеет положительное направление на первой оси, и длину того же отрезка, взятую со знаком минус, если этот отрезок имеет отрицательное направление на первой оси. Точно так, же через х2 обозначили длину отрезка о/?2, если отрезок этот имеет положительное направление па второй оси, и длину того же отрезка, взятую со знаком минус, если отрезок этот имеет отрицательнее цаправление на второй оси. Наконец, через х3 обозначим длину отрезка ор3, если этот отрезок имеет положительное направление на третьей оси, и длину того же отрезка, взятую со знаком минус, если отрезок этот имеет отрицательное направление на третьей оси. Таким образом, каждой точке х пространства соответствуют три ее координаты, числа х±, х2, х3 (см. (40)). Очевидно, что если произвольно задать числа х1У х2, х3, то существует единственная точка х с координатами х19 х2, х3. Таким образом, соотношение (40) устанавливает взаимно однозначное соответствие между точками х пространства и тройками чисел (хх, х2, х3).
8*	85
Легко доказывается, что если у  = (г/ъ у2, уз) есть какая-нибудь другая точка пространства, то расстояние /(#, у) между точками х п у определяется формулой
I {X, у) = + K(^i —*i)2 + (Уз — z2)2 + (г/з — *3)2. (41)
2. Векторы в пространстве. Так же как в случае плоскости, произвольный отрезок ab пространства, проходимый в направлении от а к Ь, называется вектором-, точка а называется его началом, точка Ь — концом. Два вектора, ab и cd, считаются равными, если существует плоскость, содержащая эти два вектора, и они равны между собой в этой плоскости (см. § 1). Таким образом, для каждого вектора ab про-" странства найдется единственный равный ему вектор ох, начинающийся в точке о. Он обозначается одной буквой х. Координатами вектора ох, или, что то же самое, вектора х, называются координаты точки х. Это записывается в виде
х = (a?i, Х2, хз).
Длина вектора х называется его модулем и имеет специальное обозначение |я|. В силу формулы (41) она определяется формулой
| х | ~ Х1 + #2 + 4
Пусть х и у — два произвольных вектора пространства. (Так как каждый из них обозначен одной буквой, то они выходят из точки о.) Проведем некоторую плоскость Q через начало координат о, содержащую векторы х и у. Таким образом, пользуясь правилами, * указанными в § 1, можно составить сумму х 4е У векторов х и у. Точно так же можно определить умножение . ве'ктора х на произвольное действительное число а, т. е. получить вектор ах. Определить сумму векторов х и у и произведение ах в пространстве можно легко, не проводя через векторы х и у плоскости. Легко доказывается, чтоесли
X = (хь х21 жз), у == (г/1, У2, Уз), &в
то мы имеем
ж + У = (*i + У\, х2 + у2, х3 4- у3), п далее
ах = (a^i, а#2, ах3).
Если х и у — два вектора пространства, то их скалярное произведение х*у определяется формулой х-у = х[у1 +х2у2 + х3у3.
Очевидно, что
х • х — х2 = | х |2.
Далее
х-у = у • х, \ах)-у = а(я-у). Кроме того, если х, у, z есть три вектора пространства, то мы имеем
(х + у)-z = x-z + y-z.	. (42)
Докажем теперь весьма важное соотношение х-у = И М cosy, '	(43)
где у — угол между векторами х и у. Формула эта была уже доказана нами для векторов х и у, лежащих в плоскости координат (1, 2), т. е. в плоскости Р. Для произвольных двух векторов х и у мы.имеем в силу формулы (42) соотношение
(х + у)2 = х2 +2х-у + у2, откуда следует
х - у = ~[(х + у)2 — х2 — у2].	(44)
Эта формула верна, в частности, и для двух векторов х и у, лежащих в плоскости Р. Но для таких векторов левая часть равна |я||#1 C0SY (см. (22)).
Таким образом, для двух векторов х и г/, Лежащих в плоскости Р, имеем равенство
| х 11 </1 cos.y =[(х + у)* — х-— у2].	(45)
Эта формула уже не содержит координат, а только длины трех векторов х + г/, х и у и косинус угла между
37
векторами х и у. Она доказана для Двух векторов х и у, лежащих в плоскости Я, но точно так же она может быть доказана и для двух векторов, лежащих в произвольной плоскости Q, а так как любые два вектора, выходящие из точки о, лежат в некоторой плоскости Q, то она верна для двух произвольных векторов. Так как равенства (44) и (4Й) имеют место для двух произвольных векторов, а правые части у них совпадают, то левые части также равны между собой, а это пока- _ зывает, что для двух произвольных векторов х и у формула (43) верна.
Из формулы (43) следует условие перпендикуляр- / пости двух векторов х и у, именно, векторы перпендикулярны между собой тогда и только «тогда, когда
х-у = 0.
Пусть е — произвольный вектор пространства, длины единица. Проведем через него или, что то же самое, через точки о и е, прямую Я. Тогда каждая точка х', или, что то же самое, вектор лежащий на прямой Я, может быть записан в виде
х' = ае.	(46)
Число а естественно считать координатой точки х' на прямой Я с выбранным на пей направлением от о к е. Пусть теперь х — произвольная точка или, что то же самое, вектор пространства. Будем считать, что х' есть проекция точки х на прямую Я. Вектор х' называется проекцией вектора х на прямую Я. Из формулы (43) следует, что
х' = (е-х)е.	(47)
Глава И
КООРДИНАТЫ И ЛИНИИ НА плоскости
В главе I рассматривались только отдельные точки пли, в крайнем случае, конечные совокупности точек, как то: треугольники, параллелограммы, многоугольники. Исключение составляла лишь прямая линия, которая получалась при определении умножения вектора на число. Эта вторая глава посвящена координатному описанию линий. В первую очередь показывается, что связь между координатами х и у в ее простейшей форме дает линию, далее вводятся понятия графика функции и самой функции Далее, по геометрическим свойствам линии строится уравнение линии. Это делается для окружности, эллипса, гиперболы, параболы, которые вначале определяются их геометрическими свойствами. После этого изучается вопрос о задании линии параметрическим способом. Для замкнутых линий определяется коэффициент зацепления линии с началом координат. В последнем параграфе дается геометрическая интерпретация поведения многочленов от комплексного переменного, в частности с использованием коэффициента зацепления, доказывается основная теорема высшей алгебры о том, что всякий многочлен n-й степени имеет п ^серией.
§ 4. Графики функции и функции
Напишем следующее равенство:
/(z) = айЛ" -f- «1хп-‘	. + ап.	(1)
• 39
Здесь справа написан многочлен степени п относительно х с коэффициентами а0,	.., ап, которые мы
будем считать действительными числами. Слева написано выражение /(#), которое мы в первую .очередь будем рассматривать как сокращенное обозначение для многочлена, стоящего справа. Таким образом, вместо того, чтобы сказать: многочлен а^хп-\-а\Хп~{-\-... ... +^п, мы можем теперь сказать коротко: многочлен /(z). Например, мы можем сказать: рассмотрим уравнение /(х) = 0, зная при этом, что j(x) есть многочлен-, стоящий в формуле (1) справа. Далее, мы можем подставлять вместо х в равенство (1) любые числа и получать опять равенство, например,, при х = О мы получаем /(0) =аЛ, при х — 1 мы получаем /(1) = = а0 4-	4- ... 4- ап. Таким образом, если коэффи-
циенты ао, «1, ..., ап нашего многочлена нам известны, томы можем вычислить значение этого многочлена/(х), подставляя вместо х любое числовое значение х. Так как х может принимать любое числовое^ значение, то говорят, что х есть независимое переменное. Тот факт, что числовое значение f(x) можно вычислить, зная числовое значение х, выражают, говоря, что f(x) есть функция независимого переменного х. Переменное х называется также иногда аргументом функции /(#). В данном случае j(x) есть многочлен, заданный равенством (1). Но могут быть и другие правила вычисления функции /(я), которые задаются какими-либо формулами или иным способом. Так мы приходим к понятию функции. Функция независимого переменного х есть такая величина /(#), которую можно узнать, когда известно значение х.
Нудем для определенности считать, что f(x) есть функция, заданная равенством (1).
Рассмотрим уравнение
У = 7(*)’.	(2)
Придавая независимому переменному х различные числовые значения, мы будем получать при помощи равенства (2J для у вполне определенные числовые значения^* поэтому у называется зависимым переменным. На некоторой плоскости Р выберем систему декартовых координат (см. § 1) и будем рассматривать на 9ЮЙ
40
ЙЛОСКОСтЙ ВСё 1ЮЧЙЙ
Z= (X, у),	(3)
где х берется произвольно, а у вычисляется по формуле (2). В результате такого построения из всех точек вида (3) на плоскости Р возникнет линия. Она описывается точкой z=(#, z/), когда х пробегает все возможные значения, а у принимает те значения, которые соответствуют значениям х в силу формулы (2). Эта линия называется графиком функции f(x). Иначе говорят, что полученная линия определяется уравнением (2). Часто вместо слова линия употребляют слово кривая. Таким образом, уравнение (2) определяет кривую на плоскости Р. Эту кривую мы обозначим буквой К. Точку (3) можно записать в форме
z=«/(x)),	(4)
подчеркивая тем самым, что ордината точки есть функция ее абсциссы.
Иногда независимое переменное обозначается н.е буквой х, а какой-нибудь другой буквой, например, буквой t. Так бывает, когда независимым переменным является время. Таким образом, мы можем рассматривать функцию ф(£) независимого переменного t и рассматривать уравнение	__
Ф = ф(0-	(5)
Здесь одна и та же буква (р использована как для обозначения зависимого переменного, так и в выражении <р(£), обозначающего функцию. Это'делается для того, чтобы сэкономить число употребляемых букв, а также для того, чтобы напомнить, что зависимое переменное <р определяется функцией <р(£). То обстоятельство, что независимое и зависимое переменные обозначены теперь не. через х и у, а через t и ф,не должно лишать нас возможности геометрического изображения функции ср (О» т. е. возможности построения ее графика. Для того чтобы построить график функции <р(/), описываемой кривой (5), мы должны принять за абсциссу точки величину t, а за ее ординату число ср, определяемое равенством (5). Говорят при этом, что мы откладываем t по оси абсцисс! а $ по оси ординат.
.41
Если вдуматься в определение графика функции, то невольно возникает сомнение. В самом деле, х принимает бесчисленное множество значений и вычислить все соответствующие значения у просто невозможно. Можно, конечно, выбрать некоторое конечное число значений х и вычислить соответствующее значение */.-Тогда мы сможем построить некоторое конечное число точек, расположенных на кривой К, и тем самым составить себе некоторое представление о ее поведении. Несмотря на это, все же говорят, что уравнение (2) определяет кривую, состоящую из всех точек вида (4).
В элементарной геометрии линию представляют себе обычно как след движения точки. Так, прямая линия описывается концом карандаша, движущегося вдоль линейки. Окружность описывается концом циркуля. Ту же интуицию движения можно привлечь для того, чтобы составить себе представление о кривой К, заданной уравнением (2). Для этого обратимся к рис. 2 и представим себе, что абсцисса х меняется в пределах от а до 6, возрастая. При этом точка р движется по осн абсцисс слева направо, а соответствующее ей значение ординаты у = f(x) отложено на перпендикуляре pz. Тогда точка z во время движения точки р описывает, двигаясь, кусок кривой К.
Рассмотрим теперь некоторые частные случаи многочлена f(x) (см. (1)} и построим соответствующие кривые К.
Пусть
f(x) — ах2,
где а — положительное число. Тогда уравнение (2) получает вид
у = ах2.	(6)
•Это уравнение определяет на плоскости Р кривую К, состоящую из всех точек вида
z = (х, ах2),
где х — произвольное .действительное число. Сразу же можно сказать, что вся наша кривая К лежит над осью абсцисс, так как ее ордината ах2 всегда неотрицательна. Далее, она проходит через начало координат, так как при х = 0 у также равно нулю. Кроме того, кривая К симметрична относительно оси ординат, так как
42
наряду с точкой’(я,у) ей принадлежит и точка (~х,у}. Ввиду этого мы можем сперва составить себе представление о поведении кривой К в первой четверти, а затем при помощи зеркального отображения относительно оси ординат получить ее также и во второй четверти. Из уравнения (6) видно, что при возрастании х от нуля и далее у также возрастает от нуля и далее, причем сперва возрастание идет медленно, а потом становится все быстрее. Таким образом, кривая К выглядит так, как это изображено на рис. 14.
Рассмотрим теперь кривую К, определяемую уравнением
у = х3 + $х,	(7)
где [J — заданное число. Здесь следует различать два случая: 1)	— неотрицательное число, и 2) £ — от-
рицательное число.
В первом случае при возрастании х функция у также возрастает. Кроме того, видно, что при отрицательном х число у отрицательно, а при положительном — положительно. Очевидно, что наряду с \	/
точкой (х, у) кривой К принад-	\	/
лежит также точка (—х, —у).	\	/
Таким образом, кривая К сим- \	/
метрична относительно начала \	/
координат. Она проходит в пер- --------------------***
вой и третьей четверти и достаточ-^ но нарисовать ее только в первой Рис. 14. четверти, чтобы затем при помощи симметрии получить и поведение ее в третьей четверти. При возрастании х, начиная от нуля, у также возрастает от нуля сперва сравнительно медленно, а затем все быстрее и быстрее, так, что кривая К имеет вид, указанный на рис. 15.
В случае, когда число отрицательно, поведение кривой К более сложно. Очевидно, что она так же симметрична относительно начала координат, но имеет не одну точку пересечения с осью абсцисс, а целых три. Для нахождения этих точек мы должны приравнять в уравнении (7) у к нулю. Тогда мы получим те значения х, в которых кривая пересекает ось абсцисс. Уравнение
ж3 _ о
43
дает иам три значения для х\ х = 0 и х — ± р. Кривая К, соответствующая отрицательному значению р, изображена на рис. 16.
Кривая К, определяемая уравнением (6), называется параболой Кривая К. определяемая уравнением (7), называется кубической параболой.
Рассмотрим теперь пример, когда функция /(я)' не является многочленом. Пусть
/(х) = sin х.
Тогда кривая К определяется уравнением
г/= sin я.	(8)
Так как sin (х + 2kn) — sin я при целом к, то для построения кривой К, определяемой уравнением (8), достаточно рассмотреть лишь ее отрезок при х, меняющемся от 0 до 2л. Из этого куска К' кривой К вся кривая К получается путем смещения куска К' вдоль оси абсцисс на величину 2&л, где к — произвольное целое число. Как видно из уравнения (8), кусок К' кривой К выглядит следующим образом. Сперва точка (х, у) движется В первой четверти, причем при возрастании х от 0 до "2“ величина у возрастает от 0 до 1. Затем при
44
возрастании х от у до л величина у убывает от 1 до 0.
3
Далее, при возрастании х от л до -у л величина у убывает
3
от 0 до — 1,и при возрастании я от у л до 2л величина у возрастает от —1 до 0. Вся кривая К имеет вид, изобра^ женный на рис. 17. Она называется синусоидой.
Пример 1. Посмотрим, какую кривую определяет на плоскости Р уравнение
У=-7’	(9)
где у—положительное число. Прежде всего видно, что уравнение (9) не ставит никакого значения у в соответствие значению х = 0, так как деление на нуль невозможно. Поэтому будем считать, что функция
/(*) = 4г	(10).
не определена при х = 0. Такие функции, которые определены не для всех значений аргумента х, в математике неизбежно приходится рассматривать. Можно встать на такую точку зрения, что уравнение (9) определяет на плоскости Р не одну, а две линии: одну при х > 0 и вторую — при х < 0. Первая линия лежит в первой четверти-плоскости Р, вторая — в третьей ее четверти. Если точка (х,у) принадлежит первой линии, то точка (— х, —у) принадлежит второй линии. Таким образом, вторая линия получается путем симметричного отображения первой линий относительно начала координат. Вторую линию легко представить себе,
45
(Y \
x, —) на первой линии неограниченно приближается к оси абсцисс, когда х неограниченно возрастает. Точно так же эта точка неограниченно приближается к оси ординат, когда х стремится к нулю, при этом у неограниченно возрастает. Обе линии вместе изображены на рис. 18,
и видно, что геометрически естественно считать, что мы имеем здесь две линии. Несмотря на сказанное, в математике принято считать, что уравнение (9) определяет одну линию, но что функция (10) в точке я=0 имеет разрыв или скачок.
Опишем еще одну функцию f(x), имеющую при я=0 разрыв. Так как эта функция играет существенную роль в математике, то она имеет специальное обозначение, именно
f(x) = sign х.
Функция эта описывается следующим образом:
sign х — 4-1 при х > 0, sign х = —1 при х < 0.
40
При х — 0 мы будем считать, что функция sign х вовсе не определяется. Таким образом, функция sign х задается двумя различными формулами: одной при х > О, другой — при х < 0. Такие случаи описания функции различными формулами на различных отрезках изменения аргумента х встречается в математике нередко. Уравнение
z/ = sign£	(И)
выделяет на плоскости Р линию, состоящую из двух различного вида кусков: при х > 0 зто прямая, параллельная оси абсцисс и про-	h
ходящая на расстоянии	- 
единица над ней, а при х < 0 это прямая, па рал-лельная оси абсцисс и про- ~~—————	**
ходящая на расстоянии -единица ниже ее (рис. 19). --------:--7
Несмотря на то, что с этой точки зрения уравнение	Рис. 19.
(И) определяет на плос-
кости Р две различные линии, в математике все-таки считают, что это уравнение определяет одну-единствен-ную линию. Точно так же и функция signa:, описанная двумя различным^ способами при х положительном и х отрицательном считается одной единой функцией, которая в точке 0 претерпевает скачок, или разрыв.
Здесь рассмотрены две функции и sign я, которые не определены в точке, х — 0 и имеют разрыв в этой точке. Таким образом, график ни одной из этих функций не может быть представлен как след движения точки по плоскости. Приведенные функции дают некоторые примеры разрывов или, что то же самое, нарушения непрерывности. В математике разрыв функции рассматривается как нарушение ее непрерывности. Так что исходным понятием является понятие непрерывности функции. Позже понятие непрерывности функции будет определено точно. Но до времени мы будем пользоваться им интуитивно, связывая его с процессом движения.
§ 5* Эллипс, гипербола, парабола
В § 4 мы исходили из уравнения */=/U), где /(#) — заданная функция, и строили кривую, определяемую этим уравнением или, что то же самое, график функции Таким образом, мы шли от алгебры к геометрии. Здесь мы выберем противоположный путь, именно, исходя из геометрических свойств некоторых кривых, мы выведем их уравнения, т. е. будем идти от геометрии к алгебре. В этом параграфе будут выведены уравнения окружности с произвольным центром и произвольным радиусом, а затем уравнения эллипса, гиперболы и параболы, расположенных вполне определенным образом относительно выбранной системы координат.
Выведем сперва уравнение окружности К плоскости Р с центром в точке z0 = Уо) и радиусом г. Здесь ^0, Уо — координаты точки z0. Точка z плоскости Р и только тогда принадлежит окружности К, когда ее расстояние до точки z0 равно г. В виде формулы это условие записывается так:
Z(z0, z) = г.
Пользуясь формулой (3) главы I расстояния между двумя точками, мы можем переписать последнее уравнение в форме /
+	— ^о)г + {у — Уо)2 = Г.
Уничтожая иррациональность возведением в квадрат обеих частей последнего равенства, получаем
(х - хи)2 + (у - у о)2 = Г3.	(12) •
Это и есть уравнение окружности К. В случае, если точка z0, центр окружности, совпадает с началом координат о, уравнение (12) приобретает особенно простой вид, именно:
з? 4- у2 = г2.	(13)
Выведем теперь уравнение эллипса и гиперболы. Соответствующие вычисления можно объединить Прежде всего дадим геометрическое определение обеих кривых. Обе они имеют фокусы^ именно две точки и /2 на плоскости Р.
48
j. f ‘ Эллипс определяется следующим условием: точка 2
I тогда и только тогда принадлежит эллипсу, когда
I	к) + Z(z, /2) = 2а,	(14)
i
i * где а — заданное положительное число {рис. 20). Иначе говоря, точка z принадлежит эллипсу тогда и только тогда, когда сумма расстояний от нее до обоих фокусов постоянна. В случае эллипса не иск-лючается совпадение точек к и /г* Тогда эллипс превращается в окруж-j ность радиуса а.
Гипербола определяется следующим услови-/	ем: точка z тогда и толь-
	ко тогда принадлежит
гиперболе, когда
fi) — Z(z, к) = 2а, (15)
где й — заданное по-‘ л ожител ьное	число *
(рис. 21). Таким, образом, точка z принад-1 лежит гиперболе тогда и только тогда, когда разность ее расстояний
I до фокусов постоянна. Наряду с условием '(15) можно написать другое аналогичное ему, условие, именно:
_Z(z. /2) — Z(z, Л) = 2а.	/16)'
Соотношения (15) и (16) определяют, в действительности, две различные кривые, но при переходе к координатам и проведении вычислений обе эти кривые объединяются в одну, так что разумно определить гиперболу условием:
,	|/(2, А) -	А)| = 2а.	(17)
|	Для того чтобы объединить вывод уравнений эл-
1 липса и гиперболы, объединим условия (14) и (17) в
4 Л. С. Понтрягин	43
ОДНО!
|Z(2, Л) + eZ(z, /2) | =2а,	<18)
где 8 равно ±1.
Для проведения вычислений выберем оси координат специальным образом, именно, проведем ось абсцисс через точки Д и /2 в направлении от fa к f%, а за начало координат примем середину о отрезка /1/2- За ось ординат примем перпендикуляр, восстановленный к оси абсцисс в точке о. Расположим чертеж так, чтобы ось абсцисс шла горизонтально слева направо, а для оси ордипат выберем направление снизу вверх. Длины равных между собой отрезков о fa и 0/2 обозначим через /. Тогда мы имеем
fa = (—7,0), /2= (АО).
Расстояния l(z, /1) и Zfz, /2) Определяются в силу формулы (3) главы I следующими формулами:
i(M1)=+vw+?;	(19)
1 (?,	= + V(x-fY + y\ '	(20)
Для того чтобы провести вычисления по возможности коротко, введем следующие обозначения:
_ и = х2 + у2 + /2, >v = xfa	(21)
При этих обозначениях формулы (19) и (20) переписываются в виде
l(z, А) = +Ku + 2p,	(22)
Дг,/2) =+/Г^21Г	(23)
Так как расстояние Z(z, /1) и Z(z, /2) выражается в виде квадратных корней, то для уничтожения иррациональности в уравнении (18) мы возведем обе его части в квадрат, после чего оно получает следующий вид (см. формулы (22), (23)):
и -J- 2р + 2е У и2 — 4v2 4- и — 2v *= 4а2,
или после сокращения и деления на 2 и перенесения части членов в правую часть, получаем
+ 8 У и2 — 4у2 = 2а2 — и.
50
Возводя обе части последнего равенства в квадрат, получаем
и2 — 4р2 = 4а4 — 4a2iz + н2.
После простых преобразований этого равенства получаем
v2 = а2и — а*.
Подставляя в полученное уравнение выражение для и и v из формул (21), цолучаем
ж2 (л2 — /2) -|- у2а2 = а* — а2/2.
Считая, что / #= а, мы можем разделить последнее соотношение на а2 (л2 — /2). Тогда мы получим следующее уравнение: U2	.
-— = 1.
j_____
«а ^аа_/а
(24)
Теперь следует различать два случая f<Za и В первом случае полагают
Ь2 = а2 — /2,
во втором случае полагают
Ъ2 = /2 - а2,
где Ъ — положительное число. Таким образом, в соответствии с этими двумя случаями мы получаем два различные уравнения:
7 + f = 1>''	(25)
(28)
Уравнение (25) есть уравнение эллипса, а уравнение (26) есть уравнение гиперболы.
На первый взгляд может показаться странным, что число е = ±1, дающее эллипс при 8 = +1 и гиперболу при 8 = — 1, исчезло в результате наших вычислений. Разница между' эллипсом и гиперболой выразилась в другой форме, именно: случай / < а — эллипс, случай / > а — гипербола. Теперь легко понять, в чем дело. Для эллипса мы имеем условие (14),и ясно, что сумма расстояний точки z до точек /ьи /2 не может быть меньше, чем расстояние между точками и /2.
4*
51
Таким образом, для случая эллипса 2а > 2/. В случае гиперболы разность между Z(.z, и l(z, /2) не может быть больше, чем 2/, и потому 2а < 2/.
Пользуясь уравнениями (25) и (26),можно составить себе представление о форме кривых, определяемых этими уравнениями, т. е. о форме эллипса и гиперболы.
Эллипс представляет собой овал, симметрично рас-
положенный относительно осп абсцисс и оси ординат
(см. рис. 20). Он пересекается с осью абсцисс в двух точках: (а,0) и (—а,0),и с осью ординат также в двух точках: (0, Ь) и (0, —6). Для эллипса число а Ь. При а = Ъ эллипс превращается в окружность.
Гипербола, определяемая уравнением (26), также симметрична относительно обеих осей (см. рис. 21): она пересекается с осью абсцисс в двух точках: (а, 0) и (—а, 0). С осью ординат она вовсе не пересекается. Таким образом, гипербола состоит из двух частей,
расположенных слева и справа от оси ординат. Эти части называются двумя ветвями гиперболы.
Дадим теперь геометрическое определение параболы и выведем ее уравнение. Парабола задается одним-единственным фокусом, который мы обозначим через /о и директрисой Z), представляющей собой прямую линию. Точка z плоскости Р тогда и только тогда принадлежит йашей параболе К, когда расстояние точки z до прямой . Z), т. е. длина перпендикуляра zr, опущенного^ на прямую Z), равно расстоянию ее до фокуса /о
(рис. 22). Для вывода уравнения параболы выберем координаты специальным образом, именно, за ось абсцисс примем прямую, проходящую через точку /о и перпендикулярную к директрисе D, направленную от ее пересечения $ с директрисой D в сторону /о. За начало координат примем середину о отрезка fas, так что ось ординат есть перпендикуляр, восстановленный к оси абсцисс в точке о. Расстояние между точкой /0 и ди
52 ,
ректрисой D обозначим через f. Тогда расстояние между точкой z = (х, у) и директрисой D дается формулой
-Z(z, г) =	+ ®|.
Расстояние между точкой г и фокусом /0 дается формулой ,	_____________
i (z, /о) ==+—-у)2+у2-
Таким образом, уравнение' параболы записывается в виде
|-L + x| = + |/^_J_)2 + j/2.
Уничтожим иррациональность, т. е. возведем обе части последнего равенства в квадрат. Это (после сокращения) дает
2/х = у2.	(27)
Это и есть уравнение параболы. Если положить 2/=^-, то мы получим уравнение
х = аг/2, которое совпадает с уравнением (6), точнее, получается из него переменой ролями осей х и у. Таким образом, вид параболы,, даваемый уравнением (27), нами был уже по-существу, рассмотрен.
Теперь я хочу сделать несколько замечаний по поводу уравнений кривых, выведенных нами здесь. Так как эти замечания относятся в равной степени ко всем уравнениям, то я остановлюсь на одном, именно, на уравнении окружности (13). Перенося все члены этого уравнения в левую часть, мы можем переписать его в виде
х2 + у2 - г2 = 0.	(28)
Напишем теперь равенство
F(x, у) = х2+у2 — Л - г(29)
В правой части этого равенства стоит вполне определенный многочлен, а в левой — выражение F(x, у). Так же, как и в случае уравнения (1), мы можем в первую очередь
53
рассматривать выражение F(x, у) как сокращенное обозначение многочлена, стоящего в правой части. Это, в частности, дает нам возможность написать уравнение (28) в виде
F(x,y)=0.	(30)
Далее, подставляя в равенстве (29) вместо х и у произвольные числовые значения, мы получаем некоторое вполне определенное числовое значение для выражения /’’(я, у). Таким образом, F(x, у) представляет собой функцию двух независимых переменных х и у . Это приводит нас к понятию функции двух переменных. F(x, у) называется функцией двух независимых переменных х, р, если, зная числовые значения этих независимых переменных, мы имеем возможность узнать значение функции F(Xf у). Равенство
z = F(x, у)
определяет в этом случае величину z как зависимую переменную, являющуюся функцией двух независимых переменных х, у. Мы можем сказать теперь, что если F(x, у) есть функция двух независимых переменных х, У, то уравнение
- F(x, у) = 0	(31)
определяет на плоскости Р некоторую кривую. Эта кривая состоит из тех точек (х, у), координаты которых х и у удовлетворяют условию (31).
Если F(х, у) и G(x, у) — две заданные функции не-завйсимых переменных х, у, то может возникнуть вопрос о решении системы из двух уравнений,
у Е(х, у) =0, у) = О,
относительно двух неизвестных величин х и у. Каждое отдельное уравнение
F(x, у) = 0,	(33)
G(x,y)=0	(34) .
определяет на плоскости Р некоторую кривую. Ясно, что пара чисел (х, у) тогда и только тогда удовлетворяет системе двух уравнений (32), когда точка (х, у) принадлежит одновременно кривой (33) и кривой (34).
54
(32),
J Таким образом, решение системы двух уравнений (32) с двумя неизвестными геометрически интерпретирует* ся как нахождение точек пересечений двух кривых (33) и (34).
*	Если уравнение (30), определяющее кривую на
плоскости Р, можно разрешить относительно т. е. переписать в форме у = }(х), то мы приходим к такой же записи уравнения кривой, какая была дана первоначально (см. формулу (2)). Однако при разрешении уравнения (30) относительно у, иногда возникают об-J стоятельства, на которые следует .обратить внимание.
Остановимся на уравнении (28) окружности. При раз-г решении его относительно у получаем
У = Vr* — ^2.	(35)
Прежде всего правая часть этого соотношения имеет смысл только при |#| г. Таким* образом, функция, стоящая в правой части, определена не для всех значений х. Далее корень- квадратный из положительного числа имеет два значения, положительное и отрицательное, так что в действительности равенство (35) следует записать в виде двух различных равенств:
У == +	— А	(36)
у » — /г2 - х\	-(37) ,
Уравнение (36) определяет полуокружность, лежащую над осью абсцисс. Уравнение (37) определяет полуокружность, лежащую под осью абсцисс. ТакихМ образом, окружность, заданная одним уравнением (28), задана теперь при помощи уравнений (36) и (37) в виде двух полуокружностей, которые вместе и составляют исходную окружность, определенную уравнением (28). Из сказанного видно, что описание окружности при помощи одного, уравнения (28) более естественно, чем описание ее при помощи двух уравнений (36) и (37).
В заключение следует отметить, что если F(x, у) — заданная функция двух, независимых переменных х и у, то уравнение (30) не всегда определяет кривую на плоскости Р. Рассмотрим уравнение
х2 + у2 + г2 = (к	(38)
Если число г положительно, то ае существует пары
55
чйсел (х. у}, удовлетворяющих $тому уравнению. Таким образом, уравнение (38) не определяет никакой кривой на плоскости Р. Если г О, то существует лишь одна точка (0,0), удовлетворяющая уравнению (38), которую также неестественно рассматривать как кривую на плоскости Р. Впрочем, иногда считают, что уравнение ж2 + У2 = 0
определяет окружность радиуса нуль, состоящую из одной точки.
Пример 2. Подвергнем эллипс, гиперболу и параболу, заданные уравнениями (25) — (27), подобному преобразованию с центром подобия в начале координат о плоскости Р. Для этого каждой точке z = (х, у) плоскости Р поставим в соответствие точку Zr= (^ri, z/i), определяемую соотношением	I
= az,
где а есть положительное число коэффициент подобия, а z и Zj понимаются здесь как векторы. Мы имеем
= (39)
Для того чтобы из кривых, определяемых уравнениями (25) —(27), получить подобные им кривые, получаемые указанным подобным преобразованием, мы должны в уравнениях (25) —(27) этих кривых вместо х и у поставить их выражение по формуле (39). Тогда мы получим следующие уравнения г для эллипса
a2a2 a2d2 ’
для гиперболы 2	2
_______= 1 a2a2 a2d2 ’ .
для параболы
4.2 - 9/ a2.“ 7 a ’
Иначе эти формулы можно переписать в виде
66
где для эллипса и гиперболы мы имеем а\ = ап, . Ъ\ == аб, а для параболы
/1 = а/.
Из сказанного видно, что кривая, подобная эллипсу, есть эллипс; кривая, подобная гиперболе, есть гипербола, причем для них имеют место условия
Легко устанавливается, что два эллипса, определяемые соответственно числами а и Ъ и (Ц и 6f, подобны, если для них выполнено условие (40). То же самое имеет место <и для двух гипербол. Что касается параболы, то всякие две параболы подобны между собой.
Пример 3. Дадим единое геометрическое определение трех кривых: эллипса, гиперболы и параболы, аналогичное тому, которое было уже дано для параболы. Для определения кривой К выберем на плоскости Р произвольную точку /о, ее фокус и произвольную прямую Dy не проходящую через точку /о, ее директрису. Далее, зададимся некоторым произвольным положительным числом к. Точка z плоскости Р тогда и только тогда принадлежит кривой К, когда ее расстояние до прямой D, т. е. длина перпендикуляра zr, опущенного на D, умноженное на число к, равно расстоянию точки z да /о- В виде формулы это записывается так:
kl(z,r)	(41)
где zr есть перпендикуляр, опущенный из точки z на прямую D. Мы уже знаем, что при к — 1 определен- -ная таким образом кривая есть парабола. Оказывается, что при k<Zi кривая К есть эллипс, а при Л>1 — гипербола. Точка же /о есть один из фокусов эллипса или, соответственно, гиперболы.
Уравнение определенной таким образом параболы нами уже было выведено. Выведем теперь уравнение кривой К при А=И=1 и убедимся, что полученное уравнение при к <С 1 дает нам эллипс, а при к > 4 гиперболу.
Из точки /о опустим перпендикуляр fas на прямую D " и примем за ось абсцисс системы координат прямую,
57
проходящую через точки $ и /о. Направление на оси абсцисс выберем по-разному при к > 1 и при к < 1, именно, при к >> 1 будем считать ось абсцисс направ-
ленной от 5 к/о, а при k<Zl—~ от /о к s. Таким образом, если повернуть чертеж так, чтобы ось абсцисс была горизонтальна и шла слева направо, то при к > 1 точка s находится левее точки /о, а при k<Z 1 наоборот (рис. 23). Так как к =/= 1, то существует такое положительное число а, что
Z(/0,s) = |afc--f4 (42)
Теперь отложим от точки /о по оси абсцисс в отрицательном направлении отрезок /0 ° Длины ак. Тогда в силу условия (42) точки s и /о обе лежат справа от точки
а ГТ
о и расстояние от точки о до s равно у- Примем полученную таким образом точку о за начало координат. Тогда директриса D параллельна оси ординат и проходит через точку s. Теперь для точки z = (х, у) мы имеем Z(z,r) = |z--£-|,
I (z, f„) = + У(х — ак)2 + у2
Подставляя эти выражения для Z(z, г) и Zj.z,/о) в равенство (41) и возведя его в квадрат для уничтожения иррациональности, мы получаем уравнение нашей кривой К в следующем виде:
к2 (я —	= (х — ак)2 + у2,
\ J
После простых преобразований мы получаем из этого равенства другое, именно:
х2(1 — к2) + у2 — а2(Д — к2).
Деля полученное равенство на а2(Г—А:2), получаем
.£1 + .... ___= 1
а2 а2 (I—к2)
58
Полагая
ак — f.
мы приводим это- уравнение к виду Х2 I У2 _______________________ А
а2 ‘ а2 — /2	’
которое совпадает с уравнением (24). Таким образом, при k<Z\ кривая К есть эллипс, а при к>1 кривая К есть гипербола. Этим самым мы доказали новое геометрическое свойство эллипса и новое геометрическое свойство гиперболы, именно, существование директрисы D.
При этом мы использовали метод координат, который в формулировке окончательных результатов не участвует.
Легко видеть, что все кривые К с данным числом к подобны между собой (см. пример 2).
Пример 4. В элементарной геометрии большую роль играют задачи на построение при помощи циркуля и линейки. Известно, что пользуясь этим методом, нельзя произвести трисекцию угла, т. е. разделить произвольный заданный угол на три равные части. Оказывается, что допустив в качестве возможных проводимых линий гиперболу с числом к = 2 (см. пример 3), мы сможем произвести трисекцию угла. Делается это следующим образом.
Будем считать, что в плоскости Р нашего чертежа выбрана прямоугольная декартова система координат так, как это сделано в § 1. Проведем в ней окружность К! произвольного радиуса с центром в начале координат о и обозначим через е пересечение окружности К' с положительной полуосью ябсцисс. Через /0 обозначим произвольную точку, лежащую на окружности К' в первой четверти нашей системы координат (рис. 24). Произведем теперь трисекцию угла Пусть а и В — две такие точки на дуге е/о окружности К', что иглы еоа, ао£ и (Jo/о равны между собой. Опустим перпендикуляр аг из точки а на ось абсцисс. Тогда очевидно, что отрезок a/о вдвое больше отрезка аг, т. е.
2Z(a, г) = Z(a, /о).	(43)
Построим теперь гиперболу К с числом к — 2, приняв за ее фокус точку /о и за директрису D ось абсцисс
59
нашей системы координат. Тогда в силу условия (43) точка а лежит на гиперболе К (см. рис. 24). Таким образом, точку а можно найти как точку пересечения
окружности К' с гиперболой К, и трисекция угла ео/о произведена. Для этого нужно иметь одно лекало гиперболы с числом к » 2. Если расстояние между фокусом и директрисой этого лекала равно у, то радиус окружности К' нужно подобрать так, чтобы длина отрезка fas была равна числу у.
§ 6. Параметрическое представление линий
До сих пор для описания линии при помощи координат на плоскости мы пользовались одним уравнением, связывающим координаты х и у. Существует другой — параметрический способ описания линии. Этот способ имеет свои преимущества. При параметрическом задании линия сразу описывается как след движения точки на плоскости. Для этого выписываем два уравнения,
# = #(£), 1 v - v (0.1
где x(t) и y(t) —две заданные функции независимого переменного t. Можно представить себе,-что они являются многочленами или .какими-нибудь тригонометрическими функциями. Когда параметр t меняется, воз
60
растая, точка
z(i) = (z(t), v(t))	'
движется по плоскости, описывая некоторую линию К. Поскольку речь идет о движении, мы, естественно, предполагаем, что точка z(f) в процессе этого движения не совершает скачков (см. пример 1), пе уточняя пока этого предположения, а считая его интуитивно ясным. Здесь z(t) есть векторная функция параметра /. Очень часто параметр / есть время. Так бывает, когда мы описываем некоторый физический процесс, протекающий во времени, а х и у есть физические величины, меняющиеся в течение времени. Например, при рассмотрении какого-нибудь электрического прибора х может обозначать напряжение, у — силу проходящего через прибор тока. Однако и при чисто геометрическом рассмотрении линий их параметрическое представление может быть очень удобным. Продемонстрируем это на примере прямой линии.
Выведем параметрическое уравнение прямой линии, пользуясь векторными обозначениями. На плоскости Р нашего рисунка, где уже заданы прямоугольные де-картовы координаты, произ- Z\ \ вольным образом проведем \ прямую линию М (рис. 25).	\
На прямой М выберем про-	X \ z
извольным образом точку _____________
zq= (#о, J/o). Напоминаю, что	0 \ у
вектор ozo, выходящий из на-	\	\
чала координат и кончаю-	\
щцйся в точке z0, мы также ’ х будем обозначать через z0.	Рис. 25.
Далее, обозначим через е век-
тор длины единица, выходящий из начала координат и параллельный прямой М. Этот вектор может быть выбран двумя различными способами в двух противоположных направлениях. Но для дальнейшего выбор направления не будет играть роли. Оказывается, что уравнение прямой М может быть записано в виде
z = z0 + te-	(45)^
Это означает, что точка z или, что то же самое, конец
61 .
вектора z описывает всю прямую М, когда параметр t пробегает все действительные числовые значения.
Докажем это. Прежде всего проведем через начало координат прямую L, параллельную прямой М, Тогда вектор е лежит на прямой L и, по доказанному ранее (см. формулу (6) главы I), каждая точка z', лежащая на прямой может быть записана в форме
z' = te.
Если сама прямая М проходит через начало координат, то L совпадает с М. В этом случае оба вектора, z0 и te, стоящие в правой части равенства (45), лежат на прямой L, и очевидно, что, откладывая от фиксированной точки z0 прямой L отрезок te произвольной длины й произвольного направления по прямой L, мы получим все точки этой прямой. Таким образом, наше утверждение в этом случае очевидно.
Рассмотрим теперь случай, когда прямые М и L ' не совпадают. На плоскости Р проведем прямую N, параллельную вектору z0, и обозначим через z' и z пересечение этой прямой соответственно с прямыми L и М. Так как oz'zz0 есть параллелограмм, то
z = z0 + z'.	(46)
Если теперь z — произвольная точка прямой М, то проведем нашу прямую N через эту точку z. Тогда найдется такое число t, что z' ~ te, и потому из равенства (46) следует, что точка z может быть записана в виде (45). Если, далее, t есть произвольное число иг' = te, то проведем нашу прямую N через эту точку z'. Тогда из равенства (46) следует, что точка z, определяемая формулой (45), принадлежит прямой М.
Выведем теперь из векторн >го параметрического уравнения прямой (45) обычное координатное уравнение прямой М. Так как вектор е имеет длину единица, то мы имеем
е =/cos a, sin а),
где а — угол между положительно направленной полуосью абсцисс и вектором е, отсчитываемый против часовой стрелки. Далее, учитывая, что z0 =	i/0),
z == (#, перепишем векторное уравнение прямой
62
(45) в скалярном виде х —	4; t cos os,
У = I/о + t sin а.
Исключим теперь из этих двух уравнений параметр £, умножив первое уравнение на sin а, второе на cos а, и вычтя одно из другого. Тогда мы получи»!
(У — Уо) cos а = (ж — До) sin а. (47)
Если прямая М не вертикальна, то cos а #= 0. Деля в этом случае последнее уравнение на cos а, мы получаем
У — Уо = (x.— Xq) tga.
Так как tg а равен tg(a+n), то последнее уравнение уже не зависит от случайностей выбора направления ' вектора е параллельного прямой М. Последнее уравнение часто переписывают в виде
У — Уо = k(x — xQ).	(48)
Число а называется углом наклона прямой М, а & = = tg а — коэффициентом наклона. Точка zo = (#о, Уо) есть произвольная точка ^рямой М.
Уравнение (48) имеет тот недостаток, что оно не пригодно для вертикальной прямой М. Для нее cos а= =0, sin ос = 1 и уравнение (47) переписывается в виде х — х0.	(49)
Дадим теперь параметрические уравнения эллипса. Они следующие:
х = x(t) — a cos t, 1
У = У(О =bsint J
Для того чтобы получить из этих уравнений обычное уравнение эллипса (см. (25)), достаточно исключить из них параметр t. Для этого разделим первое из уравнений (50) на а, второе на Ь, возведем каждое из полученных уравнений в квадрат и сложим. Тогда мы получим уравнение (25). Пара уравнений (50) не только дает эллипс как геометрическую фигуру, но и представляет его как след движения точки. Именно, когда t возрастает от нуля до 2л, точка z(t) = (x(t), y(t)) движется по эллипсу против часовой стрелки, исходя из положения (а, 0) и возвращаясь к нему же в момент
63
времени t = 2л. Так как точка z(t), движущаяся по эллипсу/ когда время t возрастает от 0 до 2л, возвращается в свое исходное положение, то кривая, описывае-_мая этой точкой, т. е. эллипс, называется замкнутой.
Она замыкается после обхода всей кривой.
Точно так же легко можно написать параметрические уравнения окружности с центром в точке z0 =' = (^о» £/о) и радиусом г. Они имеют вид
х = X (t) = Хп 4- г cos t,}
, - J (51)
У -= y(t) “ Уо + г sin t.)	'
Из этих уравнений легко получить обычное уравнение окружности, исключив из них параметр L Для этого следует перенести в левые части уравнений (51) члены х0, у0, возвести полученные соотношения в квадрат и сложить.' Тогда мы получим уравнение (12). Точка z(t) — (x(t), y(t)) пробегает всю окружность, когда t меняется от 0 до 2л, двигаясь по окружности против часовой стрелки, причем z(0) = з(2л). Таким образом, окружность также есть замкнутая кривая. Не следует исключать случая г = 0, т. е. окружности нулевого радиуса, состоящей из одной точки. В этом случае точка z(t) при изменении t от нуля до 2л вовсе не движется, а остается на месте. Но все же удобно считать, что мы имеем здесь дело с замкнутой кривой. При этом важно только то, что з(2л) =«= z(0\, что и означает замкнутость.
Пример 5. Выведем уравнение прямой Л/, проходящей через две заданные различные точ*ки z0 ==» '==	£/о) 11	= (ж1, £/1)- Если = хх, то очевидно,
что прямая М вертикальна, и уравнение ее имеет вид (49). Если я0 =Д то найдем число fc, подставив в уравнение (48) вместо z точку zx. Тогда получим следующее уравнение для к:	а
У1 — Уо =	— *о).
откуда
fc=fLZ=79-	. (52)
Таким образом, для прямой, проходящей через точки zQ и коэффициент наклона к определяется формулой (52). у 64
§ 7. Замкнутые кривые
Рассмотрим теперь произвольную замкнутую кривую К, задаваемую параметрическими уравнениями Х44)
х = #(/),
У =
когда параметр t меняется от 0 до 2л. Замкнутость этой кривой выражается в том, что она является следом движения точки з(£) = (#(£), у(£)), когда t меняется от 0 до 2л, причем начало кривой и ее конец совпадают, т. е.
z(2n)=z(0). ‘	(53)
Мы не исключаем при этом возможности, что для некоторых двух значений t\ t% параметра t имеется равенство z((2) = «(^i.). Такое явление называется самопересечением замкнутой кривой. Может даже случиться, что точка z(t) при t, меняющемся от 0 до 2л, остается неподвижной, как это было в случае окружности радиуса нуль. Важно только, чтобы имело место равенство (53), что означает замкнутость кривой К.
Относительно кривой К мы предположим дополнительно, что она не проходит через начало координат. Для такой замкнутой кривой К можно вычислить целое число /, называемое коэффициентом зацепления кривой К с началом координат. Целое число / показывает, сколько раз точка z(t) во время ее движения при возрастающем от 0 до 2л, .обходит начало координат.
Для того чтобы определить число j более формально, введем полярные коорДинаты p(t) и <р(£) точки z(t) (см. формулу (13) главы 1)л так что
z(0 = [р(0. ф(0]-
Радиус р(/) точки 'z(t) определен точкойz(t) однозначно. И так как точка z(t) при изменении t движется по плоскости Р без скачков, то функция p(t) непрерывна, т. е. также изменяется без скачков. Угол <p(J) точки z(t) определен неоднозначно, а только с точностью до слагаемого вида 2Лл, где к — целое число. Однако если выбрать для начальной точки z(0) какой-нибудь определенный угол<р(0),то функция^) определится однозначно,
Б Л. С. Понтрягин	к	65
если предъявить к ней требование, чтобы она менялась без скачков, так как изменение числа фЦ) на величину 2кл означает скачок функции фЦ). Поскольку кривая К не проходит через начало координат, то не существует таких значений аргумента t, при которых функция Ф (i) становится полностью неопределенной. Равенство (53) переписывается теперь в виде
[р(2л), ф(2л)] = [р(0), ф(0)].
Из этого равенства следует,что р(2л) =р(0),но отнюдь не следует аналогичного равенства для функции ф(^). Вместо того мы имеем
ф(2л) — ф(0) = 2/л,	(54)
где / — целое число. Так определенное целое число / и есть коэффициент зацепления замкнутой кривой К с началом координат о. Целое число / может быть определено только для замкнутой кривой К, не проходящей через начало координат. В примере 7 будет показано, что происходит, когда кривая К проходит через начало координат.
Покажем теперь, что коэффициент зацепления / кривой К с началом координат не меняется, если кривая К непрерывно деформируется в плоскости Р, не пересекая в течение этой деформации начало координат.
Для того чтобы представить себе интуитивно непрерывную деформацию кривой К на плоскости Р, материализуем эту кривую. Мы представим себе ее в виде куска нити, лежащего на плоскости Р, причем концы нити связаны между собой узлом, что означает замкнутость кривой. Непрерывная деформация кривой К означает теперь произвольное движение нити по плоскости, * при котором допустимы произвольные изгибания, растяжения и сжатия нити.
Математически непрерывная деформация замкнутой кривой К описывается следующим образом. Вводится в рассмотрение новый параметр $, меняющийся в пределах от а до &, а s Ь. Предполагается, что каждому числовому значению s соответствует некоторая определенная замкнутая кривая, которую мы обозначим через K(s). Таким образом, K(s) есть функция переменного 5. Но значение этой функции K(s) есть уже не число и даже не вектор, а целая замкнутая кри-66
вая. При фиксированном значении параметра s замкнутая кривая K(s) есть след движения точки
Z(Z, S) = [p(.f, S), <f(t, в)],
где t меняется от 0 до 2л, причем
s) = z(0, s), -
так что каждая кривая K(s) замкнута, a s — фиксированное число, определяющее кривую K(s). Предполагается при этом, что замкнутая кривая К (s) при изменении $ меняется непрерывно и ни при каком значении s не проходит через начало координат, так что коэффициент ее зацепления с началом координат определен при любом значении параметра s. Этот коэффициент зацепления вычисляется по формуле
ср(2тс, s) — ф(0, $) — 2/ ($) л. А (55)
Так как кривая деформируется непрерывно, то функции ф(2л, $) и ф(0, $) меняются при изменении 5 без скачков. А потому и j(s) при изменении s также меняется без скачков. Но так как число / (s) есть целое число, то, меняясь без скачков, оно должно оставаться постоянным.
Таким образом, в течение всей деформации замкнутой кривой K(s) на плоскости Р ее коэффициент зацепления ]'($) с началом координат не меняется, если’только эта кривая никогда в течение деформации не проходит через начало координат. Это постоянство коэффициента зацепления при деформации кривой является важным фактом, который будет нами использован в ближайщем параграфе.
Пример 6. Вычислим коэффициент зацепления окружности К параметрически заданной уравнениями (51), не проходящей через начало координат. Здесь могут иметь место два случая: состояние 1 — окружность К не содержит внутри себя начало координат, и состояние 2 — окружность К содержит внутри себя начало координат.
В первом случае из начала координат о можно провести к окружности К две касательные: оа{ и оа2, где
и а2 есть точки касания (рис. 26). Будем считать, что точки касания занумерованы так, что направление оа2 получается из направления оа{ поворотом против 5* -	ч	С7
часовой стрелки на угол а < л. Какой-нибудь угол точки обозначим через epi (имеется в виду вторая полярная координата точки «1). Тогда число ф1 + а = ф2 есть угол точки Угол ф(0) точки z(0) можно выбрать так, что ф1 ф(0)	ф2. Так как точка z(£) во время
своего движения по окружности все время находится внутри угла Л1<7Л2, то угол ф(£) все время удовлетворяет условию
Ф1 ф(0 < ф2.
Так как а < л, то-из последнего неравенства следует, что
ф(2л) — ф(0) а < л,
и потому целое число /, определяемое условием (54), есть нуль.
Во втором случае, когда начало координат находится внутри окружности А\(рис. 27), геометрически
очевидно, что вектор z(t) при возрастании t вращается , против часовой стрелки, так что угол ф(£) возрастает от значения ф(0) до ф(0) + 2л. Таким образом, в этом случае / — + 1.
Пример 7. Выясним теперь, что происходит с коэффициентом зацепления окружности К с началом координат, когда окружность К, двигаясь, переходит из состояния 1 в состояние 2 (см. пример 6). Обозначим через K(s) окружность радиуса 1 с центром на оси абсцисс в точке (1 + s, 0), где $—-малое число. При' $>0 окружность K(s) не содержит внутри себя начало координат и ее коэффициент зацепления с началом
63
координат равен нулю "(рис. 28)'. При $.< О коэффициент зацепления окружности K(s) с началом координат равен 1 (рис. 29). При малом значении s точка z(0) = = (2+$, 0) окружности K{s) лежит на положительной
полуоси абсцисс, и поэтому за угол ф(0) этой точки можно принять нуль. Исходя из предположения, что ф (0) — 0, построим угол ф(£) точки z(f), лежащей на окружности A’(s), считая эту функцию непрерывной ($ =^= 0). Для того чтобы сделать поведение функции ф(£) более наглядным, построим график этой функции сперва при фиксированном положительном малом значении 5, затем при малом. фиксированном отрицательном значении s.	*	_
При малом положительном s можно провести две касательные оа^ и оа2 к окружности К ($)(см. рис. 28). Угол точки ах обозначим через —а/2, а угол точки п2 через +а/2. Здесь а < л и близко к л при малых $. Точка z(0) есть правая крайняя точка окружности K{s). Когда точка z{t) движется при t, возрастающем от нуля, угол ее ф(£) возрастает до тех пор, пока точка z{t) не займет положения а2, при котором угол точки z{t) равен +а/2, т. е. близок к л/2. При дальнейшем движении точки z{l) от точки а2 к точке угол ф(£) стремительно убывает от 4~а/2 до —а/2, затем при движении точки z{t) от точки ai к точке г(2л) угол вновь возрастает до нуля. Таким образом, график функции ф(£) при малом положительном $ имеет вид, изображенный на рис. 30.
При малом отрицательном s окружность K{s) пересекается с осью ординат в двух точках (0, Ь) и (0, — &),
69
где Ъ — малое положительное число. Когда точка z(£)! движется по окружности K(s), исходя из своего начального положения z(0), угол ф(£) этой точки возрастает все время, но после того как точка z(t) проходит свое
положение (О, 4-Ь)', возрастание становится очень быстрым до тех пор, пока z(t) не достигнет положения (О, —Ь). За этот период времени угол возрастает на л. , После прохождения точки (0, — Ь) угол ф(£) продолжает возрастать, но уже не так стремительно. Таким образом, график функции <р(£) при s отрицательном имеет вид, изображенный на рис. 31.
При s = 0 окружность К (s), т. е. окружность К(0)’ проходит через начало координат (рис. 32). Угол (£(£),
точки z(Z) в этом случае возрастает от 0 до л/2, когда точка z(t) описывает верхнюю полуокружность окружности ^(0), и мы тогда имеем на этом протяжении
70
времени
ф(о=4-
При t=n точка z(t), т. е. точка z(л), совпадает с началом координат, и угол ф(2) не определен. После того как точка z(t) пройдет начало координат, ее угол ф(£) следует считать близким либо к —л/2, либо к Зл/2.
График функции ф(£) при t — л претерпевает разрыв и дальнейшее построение может быть проведено двумя различными способами: либо так, как это изображено на рис. 33, либо так, как это изображено на рис. 34.
Таким образом, график функции ф(£) при $ положительном и стремящемся к нулю стремится к графику функции ф(£) (при $=0), изображенному на рис. 33, а график функции ф(£) при $ отрицательном и стремя
71
щемся к нулю стремится к графику функции хр( О (при s = 0), изображенному на рис. 34.
Таков механизм, скачкообразного изменения коэффициента зацепления / ($), определяемого формулой (55),
Рис. 36.
когда в процессе изменения кривая K(s) при некотором значении s проходит через начало координат.
Пример 8. Рассмотрим кривую Кп, задаваемую параметрически следующими уравнениями в полярных координатах:
Р = Р(О = 1+ SCOSM	'
ф =	(Z) =» nt,	J	° )
где п =И= 0 есть целое число, 0^$<1 — заданное число, a t изменяется ют 0 до 2л. Так как 0 s <Z 1, то
72
p(Z) >0, и кривая Кп не проходит через начало координат. Угол ф(0, заданный формулой (56), есть непрерывная функция параметра причем <р(0) = 0, ф(2л) = 2ил. Таким образом, из формулы (54) мы получаем, что / = /г, И коэффициент зацепления кривой Кп с началом координат равен п, где п — заданное положительное или отрицательное целое число. Кривая Къ изображена на рис. 35. Кривая К$ изображена на рис. 36. Кривая К% имеет одну точку самопересечения, кривая Кз — две точки самопересечения. Эти рисунки сделаны в предположении, что s i> 0.
При s=0 точка 2(^) = [p(i), (?(£)] движется по окружности К' (р=1) радиуса единица с центром в начале координат, но <р(£) при этом возрастает со скоростью в п раз большей, чем t, поэтому, когда t изменяется от 0 до 2л, тогда z(t) п раз пробегает окружность К'.
§ 8. Многочлены комплексного переменного
Так же как и в § 4 (см. формулу (1)), выпишем равенство
/(z) =	1 + ... 4-	(57)
где ао, «1, ..ап суть комплексные коэффициенты. В правой части равенства (57) стоит многочлен степени п с комплексными коэффициентами относительно z. в левой части выражение /(з), которое мы в первую очередь рассматриваем как сокращенное обозначение многочлена, стоящего в правой части равенства (57). Так как мы умеем производить действия над комплексными числами, то, подставляя вместо z в правую часть равенства (57) какое-нибудь определенное комплексное число, получаем для /(z) определенное комплексное значение. Таким образом, /(z) есть комплексная функция комплексного переменного z.
Комплексная функция комплексного переменного z не обязательно должна быть многочленом от z. Если существует какое-то правило, по которому мы можем вычислить комплексное значение величины /(z), зная числовое значение комплексного, переменного z, то /(z) есть комплексная функция комплексного переменного z. Если мы имеем какую-нибудь комплексную
73
функцию f(z) комплексного переменного z, то, полагая ^ = /(2),	(5S)
мы получаем зависимое комплексное переменное w, определяемое как функция f(z) комплексного независимого переменного или аргумента z. В этом параграфе мы будем рассматривать только такие комплексные функции комплексного переменного z, которые задаются в виде многочлена, т. е. в виде (57).
В случае действительного многочлена /(я) действительного переменного х мы имеем простую геометрическую возможность изображения многочлена /(я) прп помощи его графика (см. § 4). Такой простой возможности геометрического изображения комплексного многочлена /(z) комплексного переменного z мы не имеем. Есть, однако, возможность геометрического подхода к изучению комплексной функции /(z) комплексного переменного z. Для этого наряду с плоскостью Z комплексного переменного z рассматривают плоскость W комплексного переменного w н ставят в соответствие каждой точке z первой плоскости точку w второй плоскости, определяемую по формуле (58). Изучение геометрических свойств этого соответствия или, как говорят, геометрических свойств отображения плоскости комплексного переменного Z на плоскость комплексного переменного W, открывает большие возможности для изучения функции /(z). Здесь мы продемонстрируем эти возможности для доказательства основной теоремы высшей алгебры.
Многочлен /(z) (см. (57)) действительно имеет степень /?, если коэффициент ао при п-й степени z в нем не равен нулю. Для того чтобы выразить это обстоятельство в совершенно отчетливой форме, мы будем рассматривать многочлен /(z) вида
/(z) = zn + a.z”-1 + ... 4- ап.	(59)
При доказательстве основной теоремы высшей алгебры доказывается прежде всего, что многочлен /(z) (см. (59)) степени п 1 имеет по крайней мере один корень, т. е. существует такое комплексное число Vi, что
/СТ1) —.0.
74
Геометрическая идея доказательства этого факта заключается в следующем. Комплексное число z записывается в тригонометрической форме, пменйо,
z = г [cos t -f- i sin t].	(60)
Здесь г есть модуль комплексного числа z, a t — его аргумент. Число г в формуле (60) будем считать постоянным положительным числом и будем считать, что t меняется отх0 до 2л. В процессе такого изменения параметра t точка z (см. формулу (60)) описывает в плоскости Z окружность радиуса г с центром в начале координат, которую мы обозначим через К (г), подчеркивая этим, что окружность зависит от выбора числа г. Пробегаемая при изменении t от 0 до 2л окружность К (г) есть замкнутая кривая, именно, при t — 0 и t = 2л z = г, т. е. начало и конец описываемой линии совпадают между собой.
Посмотрим теперь, какую линию описывает точка = /(2), определяемая равенством (58), в плоскости
IF, когда z описывает окружность К (г). Имеем
^’(0 = /(r(cos t -f- zsin£)).
Здесь написано так Как переменным мы считаем только а г — величиной постоянной. При этом t меняется от 0 до 2л. Далее, так как комплексное число z при I — 0 и при t = 2л имеет одно и то же значение г, то
п>(0) = п?(2л) « /(г).
Таким образом, линия, описываемая точкой w(t) при изменении t от 0 до 2л, является замкнутой. Мы обозначим ее через L(r), подчеркивая этим самым, что опа зависит от выбора числа г. Если замкнутая линия L(r) не проходит через начало координат, то можно вычислить коэффициент ее зацепления с началом координат (см. § 7). Оказывается, что для достаточно большого значения числа г = го этот коэффициент зацепления равен числу п, т. е. степени многочлена /(z).
Вычислим коэффициент зацепления линии L(r) с началом координат для простейшего вида многочлена /(z), именно, для случая, когда
п? = /(*) == zw.	(61)
75
Запишем число w в тригонометрической форме, положив w — р (cos ф + i sin ф).
Для случая (61) связь между полярными координатами точки w и точки z имеет вид
р = гп, ф = nt.
Когда t меняется от 0 до 2л, ф меняется от 0 до 2ял, п, следовательно, коэффициент зацепления линии L(r) в случае (61) равен п. ~
Для. вычисления коэффициента зацепления линии L(r) с началом координат в случае (59) введем в рассмотрение новый многочлен /(z, s), зависящий от действительного параметра $, 0	1, п определяемый
формулой
w = f(z, s) = zn + ^(«iz”"1 + ... + an). (62)
При s = 4-1 многочлен (62) превращается в многочлен (59), а при s = 0 он-приобретает простой вид (61). Когда z описывает окружность К в плоскости Z при ^меняющемся от 0 до 2л (см. формулу (60)),w = /(z,s) описывает замкнутую кривую L(r, $) в плоскости W.
Изучим теперь отдельно многочлен, стоящий в формуле (62) с коэффициентом 4 Мы его обозначим через g(z), так что мы имеем
g(z) = a{zn-1 + ... -г а„.
Нас интересует модуль величины g(z). Так как мы намерены рассматривать большие значения г, то заранее предположим, что г 1. Модуль суммы меньше или равен сумме модулей (см. формулу (28) гл. I). Это верно для произвольного числа слагаемых, что легко вывести из формулы (28) главы I, последовательно ее применяя. Поэтому имеем
|g(z) I ^rn-1(|a1| + |a2l+ ... +|а„|),
если г 1, или
|g(z)| ^сгп-\ -	(63)
где с = | «11 4" . • • 4“ | ап |. Мы получили то, что называется в математике оценкой модуля величины g(z), имеющей место при г 1.
76
Из формулы (62) следует, что .
f(z, s) + (-sg(z)) = zn.
Отсюда, так как сумма модулей двух комплексных чисел больше или равна модулю их суммы, вытекает, что 1Я*, $)| + s|g(z) | >rn.
Заменяя в последнем неравенстве величину s|g(z)| большей величиной в силу формулы (63), мы получаем неравенство
|/(z, s) | + с^п~х >= гп, иди, иначе
|/(z, $) | гп — сгп"<	(64)
Так Как мы намерены раорматриватйВбольшпе значения г, то можем предположить,-что rQ > с. Тогда из неравенства (64) следует, что
I/O, s)l >0
при | z | = г0. Таким образомг при $, меняющемся от 0 до 1, |и?| (см. (62)) никогда не обращается в нуль, т. е. кривая L(r, s) ни при каком значении $ не проходит через начало координат. Следовательно, (см. § 7), коэффициент ее зацепления не меняется при изменении s от 0 до 1. Но при $ = 0 этот^ коэффициент зацепления нами вычислен. Он равен п. Следовательно, и для многочлена /(z, 5) при s = l, т. е. для многочлена (59), коэффициент зацепления кривой Цг) также равен п, если г = г().
Пользуясь полученным результатом, можно легко доказать, что многочлен /(z) (см. (59)) при всегда имеет хотя бы один корень. Если свободный член ап многочлена /(z) равен нулю, то этот многочлен имеет очевидный корень yi —0. Поэтому мы рассмотрим лишь случай, когда ап 0. -
Рассмотрим изменение кривой L(r) при г, убывающем от го до 0. Н/п таком изменении г кривая L(r) деформируется и при г —0 стягивается в одну точку ш = = ап. Это значит, что iv(t) при г=0 есть неподвижная точка плоскости W, отличная от начала координат. Таким образом, аргумент этой точки ф(£) вовсе пе меняется. Мы имеем ф (2л) —-ф(0) =0, т. е. коэффициент зацепления кривой L(0) с началом координат равен нулю.
77
Так как, по ранее доказанному, коэффициент зацепления кривой L(vq) с началом координат равен п, то в процессе деформации кривая L(r) при г, меняющемся от Го ДО 0, должна при каком-то значении г пройти через начало Координат. Обозначим это значение г через г{. Таким образом,кривая проходит через начало координат. А это значит, что при каком-то значении ^которое равно Zi, мы имеем iv(ti)=O. Таким образом, получаем
w = /(гх (cos t\ + i sin t{)) = 0, и,. следовательно,
Yi = r\(cos t[ + * sin
есть корень многочлена /(z). Тем самым существование одного корня многочлена /(z) доказано.
Теперь уже легко доказать, что -многочлен /(z) (см. (59)) степени п имеет ровно п корней. Это доказательство излагается в элементарной алгебре, но я его здесь повторю. Возьмем произвольное комплексное число Y и будем делить многочлен /(z) (см. (59)) на двучлен z—у. В результате деления мы получим остаток, быть может равный нулю, который, однако, не зависит от z и который мы обозначим через Ь. Мы имеем, еле- \ довательно, f(z)—fl(z)(z — y)+b,	(65)
где многочлен /i(z) имеет уже степень п~.1 и записывается в виде
h (z) = z"-‘ + biZ’1-2 + ... + bn.
Подставляя теперь в равенство (65) вместо произвольного числа у корень Yi многочлена /(z), йолучим b *=s 0. Таким образом, многочлен /(z) делится на двучлен z— yi, если учесть корень многочлена /(z). Если многочлен /(z) имеет степень п 2, то многочлен /i(z) имеет степень п 1	1, и уже по доказанному может
быть разложен на множители
, /i(z) =/2(z)(z — у2),
где у2 — корень многочлена /i(z), а значит, и мпогочле на /(z). Продолжая этот процесс далее, мы получим для
78
многочлена, /(з) разложение
/(*) === (z — Vi) (jg — V2) ... (s- VnJ. {66) Числа
YbV2,...,Yn,	(67)
очевидно, являются корнями многочлена /(z). Однако некоторые из них могут оказаться равными друг другу. Таким образом, утверждение, что многочлен п-й степени /(z) имеет п корней, означает не то, что все эти корни различны между собой, а лишь то, что многочлен /(z) может быть представлен в виде произведения (66). Если число Yi встречается в последовательности (67) только один раз, то корень Yi называется простым корнем t многочлена f(z). Если он встречается в этой последовательности несколько раз, например, к раз, и к > 1, то корень Yi называется кратным корнем кратности к многочлена /(z).
В конце § 3 было доказано, что если многочлен /(z) является действительным, т. е. имеет действительные коэффициенты, то наряду с каждым комплексным корнем Y он имеет и корень Y, сопряженный с Y- Оказывается, что корни Y и YB этом случае имеют одинаковую кратность. Докажем это. Допустим, что_у есть комплексный (не действительный) корень. Тогда у также есть корень, притом отличный от и многочлен /(z) разлагается в произведение
/(«) = (2 -у) (Z - Т)/2(2) = ^(?)/2(2),
ГДе _ _
g(z)‘= (z — Y)(z- у) =z2- (yd-y)z + YY
есть действительный многочлен. Таким образом, действительный многочлен /(z) делится на действительный многочлен g(z), и, следовательно, проводя деление по правилам элементарной алгебры, мы получим в результате деления действительный многочлен /2(2). Если многочлен /г(з) вновь имеет корень 7,то он имеет и корень у. Продолжая этот процесс далее, мы убеждаемся, что корни у иу действительного многочлена /(z) имеют одинаковую кратность.
Пример 9. Рассмотрим более подробно простейший многочлен степени п
/(z) =» zn,
то
именно, постараемся более ясно представить себе геометрически отображение / плоскости Z на плоскость W, определяемое равенством w = zn. Для этого введем в плоскостях Z п W полярные координаты, именно, положим
z = г (cos t + /sin t),	(68)
w = p (coscp + isin ф).	(69)
Тогда имеем
p = rn, ф — nt.
Точка z при постоянном t и неограниченно возрастающем г от 0, описывает в плоскости Z прямолинейный луч A (t), наклоненный к положительной полуоси абсцисс на угол t (см. 68)).Соответствующая этой точке z точка w (см. (69)) описывает в это время прямолинейный луч Д(<р) в плоскости И7, наклоненный к положительной полуоси абсцисс на угол ф = nt. Таким образом, при фиксированном / отображение / плоскости Z b плоскость W превращается в отображение луча4(/) на луч В(ф), задаваемое формулой
р = гп. .	(70)
' Для того чтобы лучше представить себе это отображение луча A(t) на луч В(ф), можно рассмотреть график функции (70),откладывая г по оси абсцисс, а р по оси ординат (рис. 37). Заметим, что луч Л (0)
I	совпадает с положительной полу-
/ осью абсцисс на. плоскости Z, а /	луч 5(0) совпадает, с положптель-
/ ной полуосью абсцисс на _плос-/ _ кости W. Пусть теперь t возрасту , тает от 0 до 2л/п. Тогда луч A(t) '	"	г заметает угол между лучом А (0) и
Рис 37 ‘ А (2л/п) величины 2л/п. Соответствующий этому лучу A (t) луч 5(ф) совершит в это время -полный поворот на 2л и заметет всю плоскость W. Далее, при возрастании числа t от'2л/н до 4л/м луч A(t) заметет угол между лучами А(2л/п) и А(4л/п) величины 2л/п. А соответствующий ему луч 5(ф) вновь заметет всю плоскость W. Таким образом, когда t возрастает от 0
80
до 2л, луч A(t) заметает всю плоскость Z, соответствующий ему луч 5(ф) совершит п полных оборотов и п раз заметет всю плоскость W. Мы видим отсюда, что при отображении f плоскость Z п слоями накрывает плоскость W, так что в каждую точку м?=/=0 плоскости W переходит п точек плоскости Z. Исключение составляет только начало координат О плоскости W, в которое перейдет только начало координат плоскости Z. Описанное здесь отображение / плоскости комплексного переменного Z на плоскость комплексного переменного W очень типично и играет важную роль в изучении функций комплексного переменного.
Пример 10. При доказательстве основной теоремы высшей алгебры нами была взята окружность К (г) в плоскости Z комплексного переменного z радиуса г с центром в начале координат. При отображении /(z) (см. (59)) окружность(г) переходила в замкнутую кривую L(r) плоскости W. Было показано, что для достаточно большого значения г = г0 коэффициент зацепления замкнутой кривой L (го) с началом координат в плоскости W равен тг. В предположении, что свободный член многочлена (59) ап=И=0, мы рассматривали деформацию замкнутой кривой L(r) при г, меняющемся от г0 до 0. Так как коэффициент зацепления кривой Л(г0) с началом координат равен п, то естественно было бы ожидать, что в процессе изменения числа г от г0 до 0 кривая L(r) пройдет через начало координат п раз, а это означало бы, что многочлен (59) имел бы п различных корней, в действи- -тельности же он может иметь кратные корни. Для того чтобы объяснить геометрически происходящее при этом явление, сле-^ дует представить себе, что кривая L (г) может иметь при некотором значении г небольшую вокруг начала координат 0 в плоскости W (рпс. 38), причем при убывании г петля эта стягивается к началу координат. Таким образом, вместо того, чтобы пересечься и пройти через начало координат 6 Л. С. Понтрягин	S1
Рис. 38.
петлю,. обходящую
дважды, кривая L(r) проходит через него лишь один раз. Стягиванием петель такого рода и объясняется слияние корней, откуда и получаются кратные корни.
ДОБАВЛЕНИЯ К ГЛАВЕ II
Будем считать, что в пространстве задана прямоугольная декартова система координат таким способом, как это было описано в добавлении К главе I. Рассмотрим связи. между алгебраическими соотношениями и геометрическими фигурами, которые дает возможность установить эта система координат.
1.	Функции двух переменных и их графики в пространстве. Если f(x^ х2) есть функция двух независимых переменных х{ и х2, то уравнение
= /(^ь
определяет в пространстве поверхность 5, состоящую из всех точек х вида
х — (#i, х2, f(xi9 я2)).
Эта поверхность S представляет собой график функции двух переменных /(#:, х2) в пространстве, полученный при помощи выбранной системы координат (сравни § 4). Поверхность £ может быть построена следующим образом. Пусть х^ х2 — произвольная пара чисел и р = (#ь %2) — точка в координатной плоскости (1, 2) с координатами xh х2. Координатная плоскость (1, 2) и есть плоскость Р. На перпендикуляре к плоскости Р, проведенном через точку р, отложим отрезок рх длины х2) направленный вверх, если число /(^i, х2) положительно, и вниз, если число /(#i, х2) отрицательно. Поверхность S состоит из всех точек х описанного вида, когда числа х{ и х2 принимают всевозможные значения.
Если функция /(^i, х2) есть константа, т. е.
/(^1, х2) = с,
то поверхность S представляет собой плоскость Р(с), параллельную плоскости Р, проведенную на расстоянии | с| от плоскости Р над нею, если с положительно, и под нею, если с отрицательно. В плоскости Р(с) есте-
82
ствепно возникает прямоугольная декартова система координат, именно, за первую ось следует принять пересечение плоскости Р(с) с координатной плоскостью (1, 3), а за вторую ось следует принять пересечение плоскости Р(с) с координатной плоскостью (2, 3).
Рассмотрим теперь более интересную функцию /(^1, ^2), именно, функцию, определяемую равенством / (*^11 *^2)== оь (^1	*^2)»
где а — положительное число. Для того чтобы более наглядно представить себе поверхность 5, определяемую соответствующим уравнением
= а (х2 — 4),	(71)
пересечем эту поверхность плоскостью Р(с). Линия пересечения поверхности S с плоскостью Р(с) задается в плоскости Р(с) уравнением
4^4'	(72)
Прп с=0 плоскость Р(с) есть плоскость Р, а уравнение (72) определяет в ней линию, состоящую из двух
прямых — биссектрис координатных квадрантов. При с положительном линия пересечения представляет собой гиперболу, ветви которой расположены справа и слева от второй оси, а при отрицательном — гиперболу, ветви которой расположены снизу и сверху от первой
6*
83
оси. Вникая в это описание поверхности S, мы можем убедиться в том, что вблизи начала координат, через которое поверхность S проходит, она имеет форму седла (рис. 39).
2.	Функции трех переменных и соответствующие им поверхности. Если F(^i, ^2, ^з) есть функция трех независимых переменных £i, х2, хз, то уравнение
F(^i, х2, хз) = 0	(73)
определяет в пространстве поверхность 5, состоящую из всехтаких точек х = (хь x2i ^з), координаты которых удовлетворяют уравнению (73).	,
Рассмотрим теперь два специальных вида поверхностей, именно, цилиндры и конусы.
Пусть Q — некоторая плоскость пространства и L — произвольная линия на этой плоскости. Через каждую точку р линии-L проведем прямую R(p), перпендикулярную к плоскости ~Q. Совокупность всех точек пространства, лежащих на этих перпендикулярах, называется цилиндром. Линия L называется направляющей
цилиндра, а каждая прямая R (р) — образующей цилиндра (рис. 40). Если Q есть координатная плоскость (1, 2), а линия L в этой плоскости задается уравнением
F{x{, я2)=0,	(74)
то очевидно, что цилиндр с направляющей L в прост-84
ранстве задается уравнением
F(zlt х2) = 0,	(75)'
п уравнение вида (75) всегда определяет в пространстве
цилиндр с направляющей L, определяемой уравнением (74).
Пусть 5 — некоторая фиксированная точка пространства и S — некоторая поверхность. Поверхность эта называется конусом с вершиной $9 если наряду со всякой точкой х, принадлежащей S п отличной от s, поверхности S принадлежит и вся прямая, проходящая через точки s и х (рис. 41).
Если функция F(х\,Х2,Хъ) степени однородности к, т. (
Рис. 41.
есть однородная функция удовлетворяет условию
F(a^i, а#2, а^з) = ahF(x^ х2, хз),
то очевидно, что уравнение
х2, хз) = О	J76X
определяет в пространстве конус с вершиной о.
3.	Поверхности вращения. Пусть L — линия, заданная в координатной плоскости (1, 2) уравнением
F(a;i, х2) — 0.
Будем теперь вращать всю плоскость (1,2) вокруг оси 1. Тогда линия L в процессе своего движения опишет поверхность 5, уравнение которой, как легко видеть, имеет вид	,
• F fa, + %з) =0-
Ясно, что за плоскость задания линии L можно выбрать любую из трех координатных плоскостей пространства, и что вращение можно производить вокруг любой координатной оси, лежащей в этой координатной плоскости. Уравнение поверхности вращения S получит тогда соответствующий вид, который легко найти.
85
Рассмотрим несколько интересных поверхностей вращения.
Примем за линию L прямую, лежащую в координатной плоскости (2, 3) и определяемую уравнением
кх$ = х2,
где &>0. Вращение будем производить вокруг третьей оси. Уравнение поверхности вращения S в этом случае имеет вид	_______
кх3 = xj + х2.
Уничтожая иррациональность, мы получаем
12	__ 2 ।	2
«Гз — *4 “г ^2*
Поверхность > 5, определяемая этим уравнением, представляет собой круглый конус, осью которого является третья координатная ось нашей системы координат.
Зададим теперь линию L в плоскости (2,3) уравнением
-	х3 = ах2.
Уравнение это определяет в координатной плоскости (2, 3) параболу. В результате вращения этой параболы вокруг третьей координатной оси мы получим поверхность 5, определяемую уравнением
аг3 = а(ж1 +4).	'	(77)
Эта поверхность называется параболоидом вращения. Очень важно хорошо представить себе ее геометрпче-, скую форму (рис. 42).
Зададим линию L в плоскости (1, 2) уравнением ж? xi
—L Ц_ -Л = 1
Уравнение это определяет в плоскости (1, 2) эллипс. Мы не будем предполагать здесь, что а^Ь. Если то фокусы эллипса лежат не на первой оси, а на второй оси координат. Поверхность вращения S этого эллипса вокруг первой оси координат описывается уравнением
86
Поверхность S в этом случае называется эллипсоидом вращения. Если а>Ь, то эллипсоид вращения вытянут вдоль оси вращения, если же а < Ь, то он сплющен вдоль оси вращения. Следует ясно представить себе геометрическую форму этой поверхности (рпс. 43).
Рассмотрим теперь фигуру, получаемую в результате вращения гиперболы. Зададим ее в координатной плоскости (1, 2) уравнением
„2	J2.
Яч Xq	-
-г —гг = !• а2 Ъ2
Поверхность, получаемую путем вращения этой гиперболы вокруг первой оси, обозначим через Si, а получаемую при вращении вокруг второй координатной оси обозначим через S2. Уравнение поверхности Sj имеет вид
X2 X2
'а* Ь* ~~Ь*
Уравнение поверхности S2 записывается в виде X2 х2 xl
-^+^-^='1.	(80)
Очень важно хорошо себе представить обе поверхности 51 (рис. 44) и S2 (рис. 45). Они резко отличаются друг от друга. Поверхность St является двуполостным
87
гиперболоидом вращения. Она называется так потому, что состоит из двух раздельных частей. Поверхность S2 является однополостным гиперболоидом вращения. Она называется так потому, что состоит из одного куска. Уравнения этих поверхностей Sx п S2 отличаются друг
Рпс. 45.
от друга тем, что в левой части уравнения (79) имеется два отрицательных члена, а в уравнении {80) только один отрицательный член.
4. Уравнение плоскости. Пусть Q — произвольная плоскость в пространстве. Выведем ее уравнение в за-
88

данной системе декартовых координат. Для этого проведем прямую R через начало координат, перпендикулярную к плоскости Q, п*обозначпм через q пересечение прямой R с плоскостью Q. Длину отрезка oq обозначим через а. Обозначим далее через е вектор длины единица на прямой R, и имеющий направление oq, если q не совпадает с о, и произвольное направление, если q совпадает с о. Координаты вектора е обозначим через ai^a2, аз, т. е. положим
е = (ai, ао, аз).
Очевидно, что точка (х1? я2, ^з) тогда и только тогда принадлежит плоскости Q, когда ее проекция на прямую R совпадает с точкой q, т. е. когда мы имеем
е-х = а
(см. добавление к гл. I, формула (47)), или, в координатной форме,
+ as#2 + аз#з = я.	(81)
Это есть так называемое нормальное уравнение плоскости в пространстве. Коэффициенты ai, a2, аз обладают тем свойством, что
2 .	2 ।	2 л
a^ + a2 + аз = 1,
а число а неотрицательно.
Совершенно так же, пользуясь операцией проектирования, можно записать уравнение любой прямой в
-плоскости Р с координатами х, у в форме
х cos ср + У sin <р = а,	(82)
где
е = (cos ф, sin ф),
и а — неотрицательное число.
Уравнение (82) называется нормальным уравнением прямой.
5. Поверхности первого и второго порядков. Пусть F(#i, ^2, ^з) — многочлен первой или второй степени относительно переменных х\, х2, хз. Уравнение
F(x{, х2, хз) = О
определяет поверхность в пространстве. Эта поверхность называется поверхностью первого порядка, если
89
Многочлен F(rri, х2, х3) имеет первую степень, и поверхностью второго порядка, если многочлен F(xu х2, х2) имеет вторую степень. Ниже в добавлении к главе III будет доказано, что всякая поверхность первого порядка есть плоскость. Что же касается поверхностей второго порядка, то в добавлении к главе III будет дана их полная классификация. Именно, оказывается, что поверхность второго порядка либо вырождена, т. е. представляет собой цилиндр или конус, либо же в надлежащей системе прямоугольных координат имеет один из следующих пяти видов.
1)	Эллипсоид. Он описывается уравнением
гиперболоид. Он
Здесь «1, а2, «з суть положительные числа, определяю-* щие форму, эллипсоида.
2)	Двуполостный описывается уравнением
Здесь «1, а2, суть положительные числа, определяющие форму гиперболоида.'
3)	Однополости ый	гиперболоид. Он
описывается уравнением	j
2	2	2
ГГТ	ГГ"
—--------2 I	1
9	9 ’ ,9 х
“1	«2	Ь3
(85)
Здесь ai, а2? Яз — положительные числа, определяющие форму гиперболоида.
4)	Эллиптический параболоид. Он описывается уравнением
2	2
^з ~	+ “J •	(86)
а1 а2
Здесь fli и «2 - положительные числа, определяющие форму параболоида.
90
5)	Гиперболический параболоид. Он описывается уравнением
2	2
х,
а1	а2
Здесь а\ п «2 — положительные числа, определяющие форму параболоида.
Для того чтобы лучше представить себе поверхности 1), 2), 3), 4), следует сравнить их с поверхностями вращения, заданными соответственно уравнениями (78) — (80), (77). Каждая из поверхностей 1), 2), 3),4) отличается от соответствующей поверхности вращения сжатием в направлении координатной оси, перпендикулярной к осп вращения.
Для того чтобы представить себе поверхность 5), следует сравнить ее с поверхностью 5, определяемой уравнением (71), от которой она отличается сжатием либо в направлении первой оси, либо в направлении второй оси.
Глава III
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ
В § 5 было указано, что если на плоскости Р имеется декартова система координат, a F(xry) есть некоторая функция двух независимых переменных х и t/, то уравнение
У)=0	(1)
определяет на плоскости Р линию, состоящую из всех таких точек z= (х, у), координаты которых удовлетворяют уравнению (1).
Аналитическая геометрия йа плоскости изучает те линии, которые определяются уравнением (1) в случае, когда F (х, у) есть многочлен первой или второй степени относительно переменных х и у. Если многочлен F(x, у) имеет первую степень, то соответствующая линия называется линией первого порядка. Если многочлен F(x, у) имеет вторую степень, то соответствующая линия называется линией второго порядка; чаще говорят — кривой второго порядка. Доказывается, что линия первого порядка есть прямая, а линия второго порядка, или кривая второго порядка, есть эллипс, гипербола или парабола, за исключением вырожденных случаев, когда уравнение (1) второй степени определяет две прямые, одну прямую, одну точку или вообще не определяет ни одной точки. Эти факты будут установлены в § 10 настоящей главы. Напомню, что уравнения эллипса, гиперболы и параболы были выведены нами в § 5 в предположении, что декартовы координаты расположены относительно кривой спе-92
цпальным образом. Таким образом, для доказательства того, что уравнение второй степени (1) определяет эллипс, гиперболу пли параболу, нам нужно выбрать некоторую другую систему координат, отлйчную от той, в которой уравнение (1) задано. Доказательство заключается в том, что вместо заданной системы координат, в которой записано уравнение (1), выбирается некоторая другая система декартовых координат, в ко- _ торой уравнение кривой имеет специальный вид, данный в § 5.
Таким образом, первая задача, стоящая перед нами, заключается в установлении связи между двумя декартовыми системами координат, выбранными на одной и той же плоскости Р. Решению этой задачи посвящается § 9 этой главы.
Последний параграф этой главы посвящен доказательству того факта, что любое сечение круглого конуса плоскостью, не проходящей через его вершину, есть эллипс, гипербола или парабола, и что каждая из этих кривых может быть получена как такое сечение. Этот факт был известен еще древним грекам до начала нашей эры, и он дает основание для того, чтобы называть перечисленные кривые коническими сечениями. В § И настоящей главы чисто геометрическим, очень изящным методом, совершенно не зависящим от метода координат, доказывается этот результат. Приводимое в нем доказательство было получено в 19 веке и в нас- -тоящее время, как правило, не включается в высшую математику. Я привожу его только ввиду его геометрической привлекательности.
Все содержание этой главы посвящено изложению чисто геометрических фактов и не будет использоваться в дальнейшем при изложении анализа, так что читатель, интересующийся в основном анализом, а не геометрией, может без ущерба для, себя пропустить эту главу. В наибольшей степени сказанное относится к последнему §11. В то время, как в § 9 и 10 развивается метод коордицат^ весьма важный для современной высшей математики, в § 11 он вовсе не используется, между тем как результаты § 11 могут быть легко получены применением метода координат в трехмерном пространстве.
93
§ 9. Преобразование декартовых координат на плоскости
В § 1 па плоскости Р нашего чертежа довольно определенным образом была выбрана прямоугольная система декартовых координат. Ось абсцисс проходила горизонтально и была направлена слева направо. Ось ординат проходила вертикально и была направлена снизу вверх. Пересечение осей — начало координат — мы обозначали через о. Эту систему координат, в отличие от другой, которую мы будем рассматривать "на плоскости Р, мы будем называть первой. Заметим, что в этой первой системе координат положительная полуось ординат получается из положительной полуоси абсцисс путем поворота последней на угол л/2 против часовой стрелки. Это обстоятельство выражают, говоря, что первая система координат ориентирована против часовой стрелки или положительно. Представим себе теперь, что на плоскость нашего чертежа наложена прозрачная калька и на нее переведена первая система координат, т. е. оси координат и направления на них. Передвинем теперь кальку каким-нибудь обра-*	зом по плоскости чертежа,
t	не отрывая ее от плоскости
.	чертежа. Тогда мы будем ви-
’ деть сразу две системы ко-/	7.' ординат: первую сквозь прозах/ /	рачную кальку и вторую,
/,	начерченную на кальке
_ (рис. 46).
°' /	Начало второй системы
/	координат обозначим через
о'. Вторая система коорди-Рис. 46.	нат получается из первой
путем движения последней по плоскости Р. Очевидно, что вторая система координат ориентирована также против часовой стрелки или положительно.
Можно, однако, построить на плоскости Р некоторую вторую систему координат совершенно независимо от первой, т. е. не получая ее путем движения из первой. Для этого проведем на плоскости Р совершенно
94
произвольно ось абсцисс и выберем на ней совершенно произвольно направление. За ось ординат выберем произвольную прямую, перпендикулярную к проведенной осп абсцисс, и выберем на ней произвольным образом направление. Так полученную систему координат на плоскости Р будем называть второй (для ее изображения мы вновь используем рис. 46), а ее начало, т. е. пересечение оси абсцисс с осью ординат, обозначим через о'. Так как на оси абсцисс выбрано определенное направление, то точка о' разбивает ось абсцисс на две полуоси абсцисс, отрицательную полуось абсцисс и положительную полуось абсцисс. Именно, точка, движущаяся в положительном направлении, переходит из отрицательной полуоси в положительную полуось. Точно так же точка о' разбивает ось ординат на две полуоси ординат: положительную и отрицательную.
Для того чтобы найти абсциссу и и ординату и произвольной точки г в этой второй системе декартовых координат, поступают следующим вполне естественным способом. Опускают из г перпендикуляр гр' на ось абсцисс второй системы координат и перпендикуляр rq' на ось ординат второй системы координат (см. рис. 46). Если р' лежит на положительной полуоси абсцисс, то абсцисса и определяется как длина отрезка о'р'. Если р' лежит на отрицательной полуоси абсцисс, то абсцисса и определяется как. длина отрезка о'р', взятая со знаком минус. Точно так же ордината v определяется как длина отрезка o'q', если q' лежит на положительной полуоси ординат, и как длина отрезка o'q\ взятая со знаком минус, если точка q' лежит на отрицательной полуоси ординат. Для того чтобы получить положительную полуось ординат из положительной полуосп абсцисс в этой второй системе координат, нужно повернуть последнюю на угол л/2, но этот поворот может оказаться против часовой стрелки, либо по часовой стрелке. В первом случае мы говорим, что вторая система координат ориентирована против часовой стрелки пли положительно. Во втором случае говорим, что вторая система координат ориентирована по часовой -стрелке пли отрицательно. Легко указать на плоскости Р отрицательно ориентированную систему координат. Для этого, например, можно взять первую систему координат и изменить в ней направление на оси
95
ординат, именно, выбрать на осп ординат направление сверху вниз.
Напоминаю, что система координат, получаемая из первой путем ее движения/ ориентирована положительно. Легко доказать, что всякая вторая система координат, ориентированная положительно/ может быть получена из первой путем ее движения. В самом деле, выберем вторую систему координат совершенно произвольно, но будем считать, что она ориентирована положительно. Передвинем теперь нашу кальку из ее начального положения так, чтобы начало нарисованной на ней системы координат перешло в начало произвольно выбранной нами системы координат, т. е. точку о'. Будем затем вращать кальку вокруг точки о' до тех пор, пока ось абсцисс, нарисованная на кальке, не совпадет с осью абсцисс нашей вновь выбранной системы координат, причем направления у них совпадут. Это, конечно, возможно. Ось ординат, нарисованная на кальке, совпадет при этом с осью ординат выбранной нами произвольной системы координат. Направления на этих осях будут одинаковые ввиду того, что обе системы координат ориентированы положительно.
Ниже мы будем рассматривать наряду с первой системой координат некоторую вторую систему координат, ориентированную также положительно. Итак, мы будем считать, что на плоскости Р нашего чертежа имеются две системы координат. Первая — описанная в § 1 и вторая произвольная, но положительно ориентированная, с началом о'. Координаты некоторой точки г в первой системе координат обозначим через (я, у) и запишем это в виде формулы, положив
Г = («, у)1.
Координаты точки г во второй системе координат обоз-начим через (и, и) и запишем это в виде формулы, положив -
г = (u, v)2.
Если числа и и v заданы, то тем самым определена й точка г, а потому определены и ее координаты х и у. Таким образом, числа х и у можно как-то выразить через числа и и и, зная/конечно, при этом взаимное расположение обеих систем координат.
96
Очевидно, что если кривая задана уравнением (1) в первой системе координат, то для получения ее уравнения во второй системе координат нужно в функцию F(rr, у) вместо х и у подставить их выражения через и п v, В результате этой подстановки получится некоторая новая функция G(u, и) и уравнение кривой К во второй системе координат запишется в виде
G (u, v) = 0.
Вычислим теперь координаты х и у точки г в первой системе координат через координаты и п v той же точ-
ки г во второй системе координат для двух частных случаев расположения второй системы координат.
Случай 1. Вторая система координат получается'из первой системы координат ну-тем параллельного сдвига последней. Тогда ось абсцисс второй системы координат гори
зонтальна и направлена слева
направо, а ось ординат второй системы координат вертикальна и направлена снизу цверх (см. рис. 47). На плоскости Р рассмотрим три вектора:
Z = or, w = о'г, с — оо'.
Очевидно, что
Z = С + W.
12)
Найдем теперь координаты всех трех векторов z, w и с в первой системе координат. Мы, очевидно, имеем
г=(я, у)х.
Вектор с характеризует расположение второй системы координат относительно первой и "поэтому он должен быть задан так, что мы можем считать заданными его координаты в первой системе координат, именно:
.	с = (а, Ь)ь
Координаты вектора w во второй системе координат известны, именно:
_ w — (и, р)2.
7 Л. С. Понтрягин
97
Для того чтобы вычислить координаты вектора w в первой системе координат, мы должны построить вектор or', равный вектору о'г, и определить координаты точки г' в первой системе координат. Но так как первая и вторая системы координат имеют параллельные и одинаково направленные осп, то очевидно, что вектор or' имеет те же координаты в первой системе координат, что и вектор о'г во второй системе координат, так что мы имеем
о'г = or' = (и, и) ь
Таким образом, векторное равенство (2) переписывается в первой системе координат в виде двух равенств:
х = а 4- и,)
'  y = b + v.\	-
Эти два равенства выражают координаты точки г в первой системе координат через ее координаты во второй системе координат.
Случай 2. Вторая система координат получается из первой пу*гем вращения последней на угол ф против часовой стрелки вокруг начала координат, так что точки о и о' совпадают (рис. 48). Выберем теперь, в плоскости Р такую точку г', что /
z г' = (и, I?) 1.
такая точка плоскости Р, координаты которой в первой системе координат равны координатам точки г во второй системе координат. Так как вторая система координат получается из первой системы координат путем вращения на угол ф против часовой стрелки, то очевидно, что вектор or получается из вектора jor' пу-
Таким образом, г' есть
Рис. 48.	тем вращения последнего на
угол ф против часовой стрелки. Будем считать теперь, что плоскость, Р с выбранной па ней первой системой координал есть плоскость комплексного переменного. Положим
z = х -J- iy, w — и + iv.	(4)и
98
Таким образом, комплексное число z изображается точкой г, а комплексное число ш изображается точкой г'. Пусть теперь
е = cos ф + i sin ср	(5)
— комплексное число, модуль которого равен 1, а аргумент равен ср. Так как вектор or получается из вектора or' путем поворота последнего на угол ф, то, ' очевидно, имеем
z = wz	(6)
(см. формулу (30) гл. I).
Подставляя в формулу (6) выражения (4), (5) вместо комплексных чисел z, до, е, мы получаем равенство х iy = (и + (cos ф + i sin ф) —
= (и COS ф — V 8Шф) + Ц^ЗШф 4“ v COS ф).
Таким образом,
х = и cos ф — и sin ф, у = и sin ф 4- v cos ф.
Равенства (7) дают выражение координат х и у точки г в первой системе координат, через координаты и и v той же точке г во второй системе координат.
Напишем теперь формулы (7) для ф=л/2 и ф = л.
Для ф = л/2 имеем
х = — и,
У = и-
Для ф = л имеем
• w — — и
У^—и
(7)
О)
Заметим в заключение, что переход от первой системы координат к любой второй положительно ориентированной можно провести в два шага, именно, сперва произвести параллельный сдвиг (см. формулы (3)), а. затем поворот (см. формулы (7)), пли наоборот; сперва поворот, а затем параллельный сдвиг.
Пример 1. В примере 1 главы II мы рассматривали график функции	'
V
X
99
где y— положительное число пли, что то же самое, кривую, определяемую в первой системе координат уравнением
ху =?.	(10)
Введем теперь в плоскости Р вторую систему координат^ повернув для этого первую систему координат на угол л/4. Тогда в силу равенства (7) имеем
и V
Х ~ ~ у?
и . V у — —— —F — * у 2 V 2 '
Подставляя эти выражения для х и у в уравнение (10), получаем и2 V2 л 27“27=1-
Отсюда видно, что кривая, определяемая уравнением (10), есть гипербола (см. формулу (26) гл. II).
Пример 2. Разовьем теперь замечание, сделанное в этом параграфе перед примером 1. Выберем в плоскости Р некоторую произвольную положительно ориентированную систему коорди-нат, начало которой обозначим Л через о'. Ее мы будем называть ' третьей системой координат, и координаты точки г в ней обозначим через £ и т] (рис. 49):
-------1—V-	г = (£, П)зг
Перейдем теперь от первой Рис. 49.	системы координат к третьей
системе координат двумя последовательными шагами, именно: сперва параллельными сдвигом, а затем вращением. Для этого произведем такой параллельный сдвиг первой системы координат во вторую систему координат, при котором точка о перейдет в точку о'. В так полученной второй системе координат координаты точки г обозначим через (и, и) или в виде формулы запишем так:
Г = (и, и) 2.
100
Координаты точки г в первой системе координат обозначены через х и г/, т. е.
г=(х,У)1- х
Формулы (3) дают нам связь между (гг, у) и (и, р), именно:
х = а + и,
У = Ь+и.
Так Как вторая и третья системы координат уже имеют общее начало и обе ориентированы положительно, то третья система координат получается из второй путем вращения последней на некоторый угол ф. Таким образом, в силу формул (7) связь между координатами (и, и) точки г во второй системе координат и ее координатами (g, т]) в третьей системе координат дается формулами
и = g cos cp — т] sin ср, v — % sin ф + т| cos ф.
Подставляя эти выражения для и и и в равенства (11), мы получаем связь между первыми и третьими координатами точки г в следующей форме:
х = а+ geos Ф — n sin ф,1 ’	-
у == Ъ + g sin ф + ncos ф. J	' '
Так записывается связь между координатами (гг, у) в первой системе координат и координатами (g, т]) в третьей произвольной, но положительно ориентированной системе координат.. Числа а, b и ф указывают на расположение третьей системы координат относительно первой системы координат.
• Произведем теперь переход от первой системы координат к третьей системе координат так же в два этапа, но сперва произведем вращение первой системы координат на угол ф, а затем — параллельный сдвпг полученной системы координат (рис. 50). Повернув первую систему координат на угол ф мы получим вторую систему координат, координаты точки г в которой мы обозначим через .и и v. Тогда в силу формулы (7) мы имеем связь
х = и cos ф — v sin ф, 1
.	.	(13)
у = U S1D ф + V COS ф. J	' '
101
Теперь для того, чтобы получить третью систему координат из второй системы координат, нужно сдвинуть последнюю параллельно на вектор оо'. Но для того, чтобы воспользоваться формулами (3), нужно взять координаты вектора оо' во второй системе координат. Его координаты во второй системе запишем в виде оо' = (а, [3)2.
Тогда в силу формул (3) имеем
и = а + v = £ +
Подставляя выражения для и и и из последних равенств в равенства (13), получаем
х = a cos ср — р sin ф -|- S со5ф—1] sin ф, 1 у = а sin ф + р cos ф + £зшф+ т] cos ф. J
Преобразования (12) и (14), дающие переход от (?, л) к (х, У), различны лишь по форме, но совпадают между собой, так как я а = a cos ф — р sin ф, Ъ = а sin ф + р cos ф.
Итак, мы установили связь между третьей произвольной, но положительно ори-к	/// ентироваиной системой де-
\	картовых координат и первой,
\	ориентированной также по-
\	\	ложительно. Она дается со-
\	отношениями (12) пли (14).
\	Первая система координат
\	\ была выбрана в § 1 довольно
1^-—----г—*-/ определенным образом, но
\	4	' это не играет существенной
роли, так как чертеж всегда Рис- 50.	можно повернуть на некото-
рый угол. Таким образом, полученная нами связь, в действительности есть связь между двумя положительно ориентированными системами декартовых координат.
Выберем теперь в плоскости Р некоторую произвольную отрицательно ориентированную систему декарто-102
вых координат, которую будем называть четвертой (рис. 51). Обозначим через и ц' координаты- точки г в этой системе координат
Г = (V, Т]')4.
Из четвертой отрицательно ориентированной системы координат можно получить третью, положительно ориентированную, ^изменив в четвертой системе координат направление, выбранное на оси ординат. Очевидно, что связь между координатами (£, ц) точки г в так. полученной третьей системе координат и ее координатами (£', ц') в четвертой системе координат дается формулами
n = -n'J
Таким образом, в силу формул (12) и (15) связь между координатами (х, у) точки г и координатами (V, лЭ той же точки г в четвертой системе координат дается формулами
х = а + ^созф+п' sin ф, I
, .	?	(16)
у = b + S SlD(p — Ц COS ф. J	4 '
Таким образом, старые координаты (я, у) точки г выражаются через новые координаты (£, ц) в случае,
если новая система координат ориентирована положительно, при помощи формул (12); и старые координаты (х, у) выражаются через новые координаты (£', ц'), если новая система координат ориентирована отрицательно, при помощи формул (16). В обоих случаях старые координаты х и у являются многочленами первой степени относительно новых координат. Точно так же, выражая
новые координаты через старые, мы получим для них многочлены первой степени отно
сительно х и у.
Ясно, что при изучении линии, заданной уравнением (1), мы должны интересоваться только теми
103
свойствами этой линии, которые но зависят от выбора декартовой системы координат, т. е. такими, которые не меняются при замене х и у по формулам (12) пли (16). Те свойства линии, которые меняются при такой замене координат, в действительности зависят не от геометрических свойств линии, а от расположения этой линии относительно системы координат.
Если F (х, у) есть многочлен степени п относительно х и I/, то очевидно, что при замене х п у через новые координаты, по формулам (12) или (16), мы получим новый многочлен G(£, т]) или,соответственно,£?'(£'» л'), степень которого не может быть выше п, так как х и у заменяются многочленами первой степени относительно новых координат. Но степень многочленов (?(£, ?]) или, соответственно, G' (%, if) не может также и понизиться, так как при обратном переходе мы заменяем новые координаты через многочлены первой степени относительно старых координат. Таким образом, степень многочлена F(x, у) является геометрическим свойством линии или, как говорят, ее инвариантом. Степень п многочлена Е(я, у) называется порядком линии, определяемой уравнением (1). В аналитической геометрии изучаются только линии первого и второго порядков.	-
§ 10. Линии первого и второго порядков
В настоящем параграфе рассматриваются линии, определяемые уравнением
F(x, у) = 0,	:<17)
в случае, когда F(x, у) есть многочлен первой или второй степени. Если F (х^у) есть многочлен первой степени, то линия называется линией первого порядка. Если F(x, у) есть многочлен второй степени, то линия называется линией второго порядка, или кривой второго порядка. Здесь доказывается, что линия первого порядка есть прямая, а линия второго порядка есть эллппс, гипербола или парабола, за исключением вырожденных случаев, когда уравнение (17) определяет две прямые, одну прямую, одну точку, или вообще не определяет ни одной точки.
101
Если F(x, у) есть многочлен первой степени, то уравнение (17) запишем в виде
у) = акх + а2у + а0 = 0. '	(18)
Если число
а2 7^ О»
то, деля уравнение (18) на я2, мы, можем переписать его в форме
У ~ Уо = кх,	(19)
где
Мы видим, что уравнение (19) определяет прямую линию, проходящую через точку (0, yQ) и имеющую тангенс учла наклона к оси абсцисс, равный к (см. формулу (48) гл. II). В случае, если ♦
а2 = 0,
число аг не должно быть равно нулю. Тогда мы делим уравнение (18) на аи и получаем уравнение
«Г XQ,
тдэ
Таким образом, и в этом случае уравнение (18) определяет прямую (см. формулу (49) гл. II).
Таким образом, уравнение первой степени всегда определяет прямую, а по доказанному в главе II (см. формулы (48) и (49)) прямая всегда задается уравнением первой степени.
Перейдем теперь к кривой второго порядка, т. е. к случаю, когда многочлен F(x, у) ‘имеет вторую степень. Мы запишем ^го’в виде
Г(я, у) = апх2 + 2а12ху + а22у2 + а^х + а2у +
Повернем теперь исходную систему координат на угол Ф, т. е. произведем замену координат (я, у) через
105
координаты (u, v) по формулам (7). При этом многочлен F(x, у) перейдет в многочлен G(u, v). *
Поставим теперь перед собой задачу выбрать угол поворота ф так, чтобы многочлен G(u, и) не содержал произведения uv. Мы имеем
G(u, v) = up[—2uucos ф sin ф +
+ 2а12(соз2ф — sin2 ср) + 2«22cos ф sin ф] +...
Здесь выписан только тот член многочлена G(u, р), который содержит произведение uv. Для того чтобы более коротко записать полученный коэффициент при up, воспользуемся известными формулами тригонометрии для синуса двойного угла и косинуса двойного угла, именно: .
sin 2ф = 2 sin ф cos ф, cos 2ф = СО82ф — ЭШ2ф.
Пользуясь этими формулами, пбрепишем коэффициент при uv в многочлене G(u, р) в следующем виде:
(а22 — au) sin 2ф + 2u12 cos 2ф.	(20>
Будем теперь искать такой угол ф, чтобы выписанный коэффициент при uv равнялся нулю. Если
_ at2 = О, то поворот вовсе не нужен, т. е.
Ф = 0.
Если
^12 5^ 0,
то приравнивая коэффициент (20) к нулю, мы получаем для ф следующее уравнение:
ctg 2ф =~ ?22.
^12
Отсюда можно определить угол ф. Если угол ф выбран таким способом, то мы имеем
G(u, р) = Ьпи2 + Ь22р2 + bLu + Ь2р + &0.	(21)
Не может случиться, чтобы оба коэффициента и 622 были равны нулю, так как это означало бы, что многоч
106 .
лен F(x, у) при подстановке (7) превращается в многочлен первой степени, что невозможно.
Если мы произведем дополнительный поворот координат на угол л/2 (см. формулы (8)), то при. этом в многочлене б?(и, и) (см. (21)) коэффициенты Ьп и Ь22 поменяются местами, чем мы в дальнейшем и воспользуемся в случае надобности.
Подвергнем теперь выбранную систему координат параллельному сдвигу, т. е. вместо координат и и v точки введем новые координаты g, ц по формулам (см. формулы (3))
и = а
u = 0 + nJ
При подстановке (22) многочлен G(ut v) переходит в многочлен Я(£, iq), причем,
я) = Ьи12 + &22П2 + с1£ + w + Со, где
= 2Р&22 +
Из этих соотношений видно, что если
=# О, то можно выбрать число а так, чтобы = 0.
Для этого достаточно положить bi , а = -2^-
Точно так же, если
Ь22 =/= 0, то можно выбрать число 0 так, чтобы
= 0.
Рассмотрим теперь различные случаи значений чисел И ^22*
Случай!. Оба числа 6П и Ь22 отличны от нуля. Тогда выберем числа а и 0 таким образом, чтобы
107
(23)
(24)
(25) '
выполнялись равенства (24) и (25). Тогда
H(g, п) =	+ W + Со-	(26)
Если при этом число
Со =/= О,
то уравнение нашей кривой переписывается в виде
=	(27)
с0	с0
Если коэффициенты — — и — имеют различно	Но
ные знаки, то будем считать, что первый из них положителен. Этого можно достичь переменой ролей коэффициентов Ьп и Ь22, что, как было ранее сказано, возможно. Тогда положим
и уравнение (27) переписывается в виде
S1 а2 ' Ь2
Таким образом, в новых координатах (£,ц) уравнение (28) совпадает с уравнением (26) главы..!!, и поэтому наша кривая есть гипербола.
Если коэффициенты — — и — оба положи-с0	со
тельны, то будем считать, что первый из них не превосходит второго. Этого можно достичь, меняя ролями коэффициенты Ьп и Ь22, что возможно, как было сказано раньше. Тогда положим
и уравнение нашей кривой записывается в виде
Д + Л! = 1 а2 Г b2
103
Причем а Ь. В этом случае мы имеем эллипс (см. формулу (25) гл. II).
Если коэффициенты - и — — оба отрицательно	Со
ны, то не существует точки (£, ц), удовлетворяющей уравнению (27), и мы имеем вырожденный случай (наша кривая не содержит ни одной точки).
Если в равенстве (26)
~ 0,
то мы имеем вырожденный случай. Докажем это. Уравнение кривой получает вид
Ь1Л2 + W = о.
Если оба коэффициента Ьп и Ь22 имеют одинаковые знаки, то этому уравнению удовлетворяет лишь одна точка (0, 0) — вырожденный случай. Если коэффициенты Ьп и Ь22 имеют различные знаки, то будем предполагать, что Ьп положительно, а Ь22 отрицательно. Тогда положим
А _ 1 А __	1
при этом уравнение нашей кривой принимает вид
Левая часть этого уравнения может быть разложена на два множителя первой степени, так что уравнение получает вид
Каждое из уравнений
4+-1-0	(30)
определяет на плоскости Р некоторую прямую, и точка (£, ц) тогда и только тогда принадлежит нашей кривой (30), когда она принадлежит одной из
109
прямых (30). В этом случае кривая распадается па * две пересекающиеся прямые, и мы имеем вырожденный случай.
Случай 2. Предположим теперь, что только одно из чисел Ьп, Ь22 отлично от нуля. Можно предположить, что отлично от нуля число Ь22, так как эти числа можно поменять ролями. Тогда выберем число 0 так, чтобы
с2 = 0
(см. (23)), а число а примем равным 0. Тогда
1 = и, и функция
Я(и, Y]) = Ь22Ц2 + Сги + Cq.
Если число
Cj = 0, то мы ^меем вырожденный случай. Докажем это. Уравнение кривой получает вид
п2 = -г-.	(31)
°22
Если правая часть положительна, то имеем
т. е. уравнение (31) определяет две прямые, параллельные оси абсцисс. Если правая часть уравнения (31) равна нулю, то мы имеем
П2 - о, т. е. наше уравнение определяет одну прямую, именно ось абсцисс. Если правая часть уравнения (31) отрицательна, то нет точки, координаты которой удовлетворяли бы уравнению (31).
Если
q У=*0, то положим
и = а +
110
тогда уравнение кривой получает вид
й22Ц2 + ^11 +	+ с0 = °-
Можно выбрать число а так, чтобы Ci» + с0 = О,
и уравнение кривой получает вид
W+c^ = 0.	(32)
Если числа Ь32 и q имеют одинаковые знаки, то повер-нвхМ нашу систему координат на угол л; тогда обе координаты изменят знак (см. формулы (9)), и, не меняя обозначений, мы можем предположить, что числа Ь22 и q имеют разный знак. Тогда уравнение (32) переписывается в виде
или
Ч2 = 2/g,
где f — положительно, т. е. мы имеем параболу (см. (27) гл. II).
Итак, кривая второго порядка всегда есть эллипс, гипербола или парабола, за исключением вырожденных случаев.
Пример 3. Рассмотрим более внимательно гиперболу, определяемую уравнением
Так как эта кривая симметрична относительно оси абсцисс и оси ординат, то достаточно составить представление о ее поведении в первой четверти. Для этого разрешим уравнение (33) относительно у, считая х и у положительными. Тогда имеем
0 =
При х < а правая часть последнего равенства мнимая, и, следовательно, никаких точек с абсциссой х при
Ш
х < а гипербола не имеет (рис. 52). При х = а имеется одна точка (а, 0) — точка пересечения гиперболы с осью абсцисс. При дальнейшем неограниченном росте х величина у также растет неограниченно. Для того чтобы составить представление о характере этого роста, сравним его с поведением точки на прямой
у = х, (34)
проходящей через начало координат с угловым коэф-
фициентом к =	. Здесь ордината точки на прямой
обозначена через у для того, чтобы отличить ее от ординаты точки на гиперболе.
Чтобы сравнить рост величин у vs. у при одном и том же возрастающем х, составим их разность:
Умножим и разделим правую часть этого выражения t на сумму х+]Аг2—а2. Тогда получим
аЪ
Из последнего равенства видно, что у — у стремится к нулю при неограниченно возрастающем х. Прямая (34) называется асимптотой гиперболы (33). То, что обнаружено нами в первой четверти, имеет место во всех остальных четвертях. Таким образом, две прямые, определяемые уравнением
jd — л «2 ь2
являются асимптотами гиперболы, определяемой уравнением (33). Обе ветви гиперболы неограниченно при-112
ближаются к этим прямым в каждой из четвертей (см. рис. 52).	'
Пример 4. Рассматриваем функцию
= Дця2 + 2a12zrz/ + а22у2.	(35)
Эта функция двух переменных х и у называется квадратичной формой этих переменных. В алгебре и ее приложениях играют большую роль квадратичные формы многих переменных. Здесь мы продемонстрируем те свойства квадратичных форм, которые можно выявить на квадратичной форме двух переменных.
Квадратичную форму F(x, у) можно рассматривать как функцию вектора z = (х, у), т. е.
F(z) = F{x. у).	(36)
Рассматривая квадратичную форму как функцию вектора, мы ставим в соответствие каждому вектору z плоскости Р число F(z), и это соответствие уже не зависит от выбранной системы координат. Для конкретного вычисления величины F(z) следует выбрать кацую-то определенную систему координат и в ней координатным образом вычислять функцию F(z) по формуле (36). Однако вместо исходи ой системы координат, где квадратичная форма определяется формулой (35), мы можем выбрать другую систему координат, в которой
F(z) - G(u, 0 = bnu2 + Ь22р2	(37)
(см. формулу (21)). В этой второй системе координат квадратичную форму F(z) изучать легче, так как ее координатная запись проще.
Будем рассматривать квадратичную форму F(z) для векторов е длины, равной единице. Поставим перед собой вопрос о нахождении того вектора ех длины единица, при котором функция F(e) достигает, своего наибольшего значения или, как говорят, максимума^ и того вектора е2 длины единица, при котором квадратичная форма F(e) достигает своего наименьшего значения или, как говорят, минимума. Эту задачу удобно решать по второй системе координат, при которой квадратичная форма F($) имеет координатную запись (37). Произвольный вектор е длины единица во
8 Л. С. Понтрягин	113
второй системе координат записывается в следующем виде:
8 = (cos a, sin а), где а есть угол наклона вектора 8 к оси абсцисс второй системы координат. Подставляя эти значения координат (и, и) вектора 8 в формулу (37), мы получаем
F(e) = bncos2 а + b22sin2 а.	(38)
Если числа Ьп и Ь22 равны между собой, т. е. Ьп = = Ь22 = 6, то для любого вектора е длины единица мы имеем
F(8) = Ь,
т. е. величина квадратичной формы не зависит от направления единичного вектора 8; в этом случае требование максимальности и минимальности не выделяет никаких векторов.
Если числа Ьи и Ь22 различны, то мы будем считать, что
^11 > ^22*
Тогда, переписав форму (38) в виде
F(e) = bn— (bu—b2a)sin2a,
видим, что F(z) достигает своего максимума па двух векторах 8i и 8р причем для вектора 8Х a = 0 и для вектора 8j а=л, так что — 8Х. Далее, F(z) достигает своего минимума на двух векторах s2 и 82, л	'	3
причемдля вектора s2 a= у, а для 82 a =» у так что е2 = — е2.
Таким образом, для произвольной квадратичной формы F(z) двух переменных мы получаем следующий результат: эта квадратичная форма, рассматриваемая для всех векторов z == 8 длины единица, либо постоянна для всех этих векторов, либо достигает своего максимума на двух векторах 8 « ±£i и своего минимума на двух векторах 8 = ±в2, причем векторы 8Х и е2 перпендикулярны друг другу.
114
§ И. Конические сечения
Здесь мы дадим еще один подход к изучению эллипса, гиперболы и параболы. Он был изЕестен уже древним грекам до начала нашей эры. Эти кривые можно определить как линии пересечения круглого конуса, или, точнее, поверхности круглого конуса, с плоскостью, не проходящей через вершину конуса. Отсюда и происходит их название «конические сечения». Здесь будет доказано, что линия пересечения поверхности круглого конуса с плоскостью есть всегда эллипс, гипербола или парабола в смысле определений, данных для этих кривых в § 5. Доказательство это чисто геометрическое. Оно было дано в 19-м столетии.
. Прежде всего опишем, что подразумевается под поверхностью круглого конуса (рис. 53). В трехмерном евклидовом пространстве выберем какую-нибудь го-ризонтальную плоскость и	~ /
в ней окружность N с цент-рохМ в точке с. Из точки	1 \А I/
с восставим перпендикуляр	g
cs к выбранной горизон-	--------7
тальной плоскости, нап- / V\ / равленный кверху от нее*. / f /	/
Через точку s и произволь- /	j	\ /
ную точку р окружности / / !Р ;	\
N проведем прямую, прос- / /	/	; у
тирающуюся бесконечно в. обе стороны. Круглый ко-нус С состоит из всех то-	. ис. .
чек, лежащих на всех та-
ких прямых, когда точка р пробегает окружность N. Каждая из прямых называется образующей конуса С. Точка $ называется вершиной конуса С. Каждая образующая конуса С разбивается его вершиной s на две полу образующие, одна из которых направлена вверх от точки s, другая — вниз от нее. Те точки конуса С, которые лежат на верхних полуобразующих, составляют верхнюю полость конуса С, которую мы обозначим через Те точки конуса С, которые лежат на нижних его полуобразующих, составляют нижнюю полость конуса С, которую мы
8*
115
обозначим через С2. Таким образом, весь круглый конус С разбивается точкой s на две полости: верхнюю Сг и нижнюю С2.. Вертикальная прямая, проходящая через вершину s конуса С и центр с окружности 7V, называется осью конуса. Угол между образующей и осью конуса обозначим через у. Он определяет форму конуса.
Мы будем говорить, что некоторый шар S с центром, расположенным на оси конуса С, вписан в конус С, если он касается поверхности конуса по некоторой окружности L. Очевидно, что шар 5, вписанный в конус С, лежит либо внутри верхней его полости Съ либо внутри нижней его полости С2.
Проведем теперь в пространстве некоторую плоскость Р, не проходящую через вершину s конуса С, и изучим линию пересечения К плоскости Р с поверхностью С нашего конуса. Для того чтобы выяснить различные возможности расположения плоскости Р относительно конуса С, проведем через вершину s конуса С плоскость Р', параллельную плоскости Р. Могут иметь место три различных случая.
Случай 1. Плоскость Р' пересекается с конусом С только в одной точке — его вершине 5, поэтому полости Сг и С2 конуса С лежат по разные стороны плоскости Р'. Плоскость Р в этом случае пересекается только с одной полостью конуса С. Для определенности будем считать, что это есть полость С±. В то же время она пересекается со всеми образующими конуса С. Ниже будет доказано, что в этом случае линия К есть эллипс.	4	’
Случай 2. Плоскость Р' пересекается с конусом С по.двум его образующим, и поэтому плоскость Р пересекается с обеими полостями конуса С. Ниже будет доказано, что в этом случае линия К есть гипербола.
Случай 3. Плоскость Р' пересекается с конусом С по одной его образующей, -которую мы обозначим через М. Таким образом, Р' касается конуса С по образующей М, полости Сх и С2 конуса С лежат по разные стороны плоскости Р', и поэтому плоскость Р параллельна его образующей М и пересекается только с одной полостью конуса С. Для определенности будем считать, что она пересекается с полостью Cv Ниже 116
будет доказано, что в этом случае линия К есть парабола.
Докажем теперь все три высказанные нами утверждения.
Случай 1. Плоскость Р пересекается со всеми образующими конуса С, но только с верхними частями каждой из них, так как пересечение ее с конусом С целиком лежит на верхней полости Сг этого конуса (рис. 54). Докажем, что линия К есть эллипс. Выберем
Рис. 54.	' .
।
шар вписанный в верхнюю полость (\ конуса С, лежащий ниже плоскости Р и касающийся этой плоскости снизу. Линию касания шара Sr с поверхностью С± обозначим через а точку касания его с плоскостью Р через Д. Выберем, далее, второй шар S21 впи-117
санный в полость Сг конуса С, лежащий над плоскостью Р и касающийся этой плоскости. Линию касания шара S2 с полостью обозначим через L2, а точку его касания с плоскостью Р — через /2. Геометрически ясно, что вся линия К лежит между окружностями Lr и L2. Возьмем произвольную точку z линии К и проведем через нее образующую конуса С. Точки пересечения этой образующей с окружностями и L2 обозначим соответственно через а± и а2. Очевидно, что длина отрезка ага2 не зависит от выбора точки z, и мы обозначим длину этого отрезка через 2а. Таким образом, мы имеем
Z(z, аг) + Z(z, а2) = 2а.	-	' (39)
Соединим теперь точку z с точками Д и /2 отрезками. -Так как отрезки zft и zax касаются шара в точках Д и ах, то длины их равны между собой. Таким образом,
Z(z, Л) = l(z, й1).	(40)
Точно так же отрезки zf2 и za2 касаются шара S2 в точках /2-и а2, и поэтому длины их равны между собой. Таким образом,
Z(z, Д) = Z(z, а2).	(41)
Из формул (39)—(41) следует, что
Д) + Z(z, Д) = 2а,
где число а не зависит от выбора точки z на линии К. Таким образом, линия К есть эллипс (см. формулу (14) гл. II), фокусами которого являются точки Д и Д касания плоскости Р с шарами Sx и S2, и случай 1 разобран.
Случай 2. Плоскость Р пересекается с обеими полостями С± и С2 конуса С (рис. 55). Линию ее пересечения с полостью обозначим через а с полостью С2— через К2. Таким образом, линия К состоит из двух частей, и К2. Докажем, что линия К есть гипербола, а К2 и К2— две ее ветви. Для этото выберем шар Sx, вписанный в полость С± и касающийся плоскости Р. Линию касания шара S± с полостью Сг обозначим через Lj, а точку касания шара SA с плоскостью Р обозначим через Д. Аналогично выберем 118
шар S2, вписанный в полость С2 и касающийся пл о* скости Р. Линию касания шара S2 с полостью С2 обозначим через L2, а точку касания шара S2 с плоскостью Р — через /2. Легко усмотреть, что линия
Рис. 55.
лежит выше окружности а- линия К2 лежит ниже окружности L2. Выберем произвольную точку z линии Кг и проведем через нее образующую конуса С. Точку пересечения этой образующей с окружностью Lx
И9
обозначим через аг, а с окружностью £2 —через а2. Очевидно, что длина отрезка а^а2 не зависит от выбора точки z. Эту длину мы обозначим через 2а, Так как точка z лежит выше окружности Lx, то
Z(z, а2) — Z(z, aj = 2а,	(42)
Проведем теперь отрезки из точки z в точки А и /2. Отрезки zfi и zar касаются шара 3^ в точках А и следовательно длины их равны. Таким образом, имеем
Z(2, А) = Z(z, аг),	. (43)
Так как отрезки zf2 и za2 касаются шара S2 в точках /2 и а2, то они равны между собой, так что
Z(z, /2) = l(z, а2).	(44)
Из формул (42)—(44) следует, что
Z(z, А) - Z(z, А) - 2а,
где а — есть константа, не' зависящая от точки z, принадлежащей линии Кг, Точно так же доказывается, что если точка z принадлежит линии К2, то имеем
, - l(z, - l(z, f2) = 2a.
Таким образом, доказано (см. формулы (15), (16) гл. II), что линия К есть гипербола, фокусами которой являются точки А и А касания плоскости Р с шарами S1 и 32, и случай 2 разобран.
Случай 3. Плоскость Р параллельна плоскости Р', касающейся конуса С по образующей М, и пересекается с конусом С только по полости Сх (рис. 56, 57). Докажем, что в этом случае линия К есть парабола. Выберем для этого шар вписанный в полость Сх конуса С и касающийся плоскости Р. Линию касания шара 50 с полостью (\ обозначим через £0, а точку касания его с плоскостью Р через /0. Плоскость, в которой лежит окружность £0, обозначим через Q, а прямую пересечения плоскостей Рг и Q обозначим через . Легко видеть, что прямые Dr и М перпендикулярны друг другу. Прямую, по которой пересекаются плоскости Q и Р, обозначим через D. Очевидно, что она параллельна D'. Пусть теперь z — произвольная точка кривой К. Через эту точку z и образующую М конуса С 120
проведем плоскость R. Обозначим через Е прямую, представляющую собой пересечение плоскостей R и Q. Так как точка z принадлежит конусу С, то плоскость R пересекается с конусом С, кроме образующей М, еще
по одной образующей М', проходящей через точку z. Заметим, что образующие М и Mf образуют с прямой Е плоскости Q равные углы. Так как точка z принадлежит плоскости Р, то пересечение плоскости R с плоскостью Р есть прямая М", проходящая через точку z и параллельная М. Таким образом, прямые М' и М" образуют с прямой Е равные углы, и пото-
121
ка-_ их
от-
ле-
му, если обозначить через а* и ап пересечение прямых М' и М" с прямой Е, то мы получим равнобедренный треугольник za'a" с равными углами в точках а' и а", так что длины отрезков za! и za" равны между собой. Так как прямые /)' и М, лежащие в плоскости Р', перпендикулярны между собой, то параллельные им прямые D иМ", лежащие в плоскости Р, также перпендикулярны между собой. Отрезки zfQ и za' саются шара 80 в точках /0 и а!, и поэтому длины равны. А так как длина отрезка za' равна длине резка za", то мы имеем равенство
Z(z,/0) = Z(z,-а").
Равенство это выполнено для произвольной точки z,
жащей на кривой К. Таким образом, мы видим, что кривая К есть парабола с фокусом в точке /0 и директрисой D (см. § 5 определение параболы). Таким образом, случай 3 разобран.
Пример 5. Нами доказано, что любое коническое сечение есть эллипс, гипербола или парабола, но существует бесчисленное множество эллипсов; именно эллипс определяется двумя параметрами а и Ь (см. уравнение (25) гл. II). Точно так же и гипербола определяется двумя параметрами а и Ъ (см. формулу (26) гл. II). Парабола определяется одним параметром / (см. формулу (27) гл. II).
Возникает вопрос, можно ли получить каждую из этих кривых, как коническое сечение? Для того чтобы решить этот вопрос, проведем наряду с плоскостью Р параллельную ей плоскость Plt не проходящую через вершину $ конуса С. Обозначим пересечение конуса С с плоскостью Р± через Кг. Очевидно, что кривые К и Кх подобны между собой и подобно расположены, причем центром подобия является точка s — вершина конуса С. Для определения коэффициента подобия а (см. пример 2 гл. II) проведем через точку $ прямую, перпендикулярную к плоскостям Р и Рь и обозначим через р и точки пересечения этой прямой с плоскостями Р и Рх. Очевидно, что коэффициент подобия определяется формулой
__ I (s, Pi) р) ‘
122
Таким образом, наряду с кривой К, получаемой пересечением конуса С с плоскостью Р, мы можем получить любую подобную ей кривую Кг как пересечение того же конуса С с плоскостью Pv
Отсюда непосредственно видно, что каждую параболу можно получить как сечение заданного конуса С некоторой плоскостью Рх, так как все параболы подобны между собой (см. пример 2 гл. II).
Это, однако, не очевидно для эллипса и гиперболы, так как при параллельном сдвиге плоскости Р мы получаем кривую, подобную исходной, причем отношение — для эллипса и.гиперболы сохраняется. Возникает вопрос, может ли быть это отношение выбрано < произвольно путем поворота плоскости Р.
Для эллипса вопрос решается, положительно. Именно, если плоскость Р перпендикулярна к оси конуса С, то сечение К является окружностью, и отношение ~ равно 1. Поворачивая плоскость Р так, чтобы угол ее наклона к оси конуса уменьшался, мы, оче--	Ь
видно, будем уменьшать отношение — произвольным образом. Таким образом, любой эллипс может быть получен как сечение заданного конуса С некоторой плоскостью Р.
Сложнее обстоит дело с гиперболой. Легко видеть, что приближая плоскость Р к параллельной ей фиксированной плоскости Р', проходящей через вершину s конуса С, мы в пределе получаем из гиперболы К пару образующих, по которым плоскость Р' пересекается с конусом С. Таким образом, угол между асимптотами гиперболы К равен углу между образующими конуса С, получаемыми пересечением его с плоскостью Р'. Максимальную величину этого угла мы получим тогда, когда плоскость Р' проходит через ось конуса С, и она равна 2у. Таким образом, для гиперболы получаемой сечением заданного конуса С
РЬ	о
, отношение — ограничено величиной tg у, и для того, чтобы получить произвольную гиперболу, мы должны выбирать конус 4* различными способами, увеличивая угол у. Меняя таким образом
123
\
конус С, мы можем получить все возможные гиперболы.
Итак, установлено, что любая из линий — эллипс, гипербола или парабола — является каноническим сечением.
ДОБАВЛЕНИЯ К ГЛАВЕ III
Здесь мы дадим: 1) преобразование координат в пространстве, 2) классификацию поверхностей первого и второго порядков, 3) конические сечения, как пересечение круглого конуса с плоскостью при помощи координат в пространстве.
1. Преобразование координат. Прямоугольную декартову систему координат, описанную в добавлении к главе I, мы будем считать первой. Наряду с этой первой системой координат мы построим произвольную вторую. Начало этой второй системы координат мы обозначим через о', а за оси примем три произвольные прямые, попарно перпендикулярные, проходящие через точку о' с произвольно выбранными на них направлениями. Координаты произвольной точки г пространства во второй системе координат мы определим точно так же, как это было сделано для первой системы координат, именно, мы обозначим через Р1,Р2,Рз проекции точки г на три оси второй системы координат и определим координаты и2, и8 точки г во второй системе координат, как длины отрезков o'pi, о'р2, я'Рз, взятые с соответствующими знаками. В виде формулы мы запишем координаты точки г во второй системе координат так:
Г =	2^2, ^3)2*
Координаты точки г в первой системе координат обозначим через xv х2, х3, записав это в виде формулы:
Г = (Жр ^2» *£з)1 •
Перед нами стоит задача выразить координаты xt, х2, х3 точки г через координаты их, и2, и3. Решим эту задачу для двух простейших случаев.
Случай 1. Оси второй системы координат параллельны осям первой системы координат и имеют 124
те же направления, что и оси первой системы координат.
Случай 2. Точка о' совпадает с точкой о, т. е. начала обеих систем координат совпадают между собой.
Случай 1. Обозначим через с вектор оо' и положим
С = (Сц ^2» £з)1*
Это значит, что мы обозначили через сх, с2, с3 координаты вектора с в первой системе. Точно так же, как в § 9 для плоскости, здесь доказываются формулы
+ их,
3^2 == ^2 ~Н ^2»
^3 “ "Ь ^3-
Коротко это можно записать в виде
xi == ci + ut G = 1, 2, 3).
Эти формулы дают выражение координат точки г в первой системе через координаты точки г во второй системе.
Случай 2. Наряду с точкой г в пространстве рассмотрим другую точку s, для которой
= (г/i, Уз\, s = (Up v2, u3)2.
Таким образом, введены обозначения для координат точки s в первой и во второй системе. Скалярное произведение векторов г и s (см. формулу (43) в добавлении к гл. I) имеет геометрический смысл, не зависящий от системы координат, именно, оно записывается в виде r-s = ]г||s| cos у,
где у есть угол между векторами г и s. С другой стороны, то же скалярное произведение может быть записано как в первой, так и во второй системе координат при помощи координат векторов г и s. Из этого мы получаем
r-s == хгуг + х2у2 + х3у3 =	4- u2v2 + u3v3.
Это вёсьма важная формула. Из нее видно, что скалярное произведение векторов вычисляется в двух различных системах координат е общим началом одним и тем же способом.
На каждой из трех координатных Осей первой системы отложим вектор длины единица, направленный
125
в положительную сторону, и обозначим полученные три вектора через ev е2, е3. Положим*
ег = (аЬ1, а/>г, аьз\.	(45)
Таким образом мы ввели определенные обозначения для координат векторов et(i = 1, 2, 3) во второй системе координат. Очевидно, что
xt = r-et
(см. формулу (46) в добавлениях к гл. I). Записывая скалярное произведение, стоящее в правой части этой формулы, при помощи координат векторов г и взятых во второй системе координат, мы получаем
. xt = Wi + аЬ2и2 + аьзи3.	(46)
Здесь i может принимать значение 1, 2, 3. Последняя формула дает выражение координат точки г в первой системе через ее координаты во второй системе в слу-' чае 2.
В формуле (46) содержатся коэффициенты где оба индекса i и j могут принимать значения 1, 2, 3, так что общее число коэффициентов равно девяти. Зная эти коэффициенты, мы можем вычислять координаты произвольной точки г пространства в первой системе через ее координаты во второй системе. В соответствующем разделе математики — линейной алгебре — совокупность всех коэффициентов записывается в виде . квадратной таблицы
(а1,1	а1,2	а1,з\
а2,1	а2,2	а2,3 !•	(47)
а3,1	а3,2	а3,3/
Эта таблица коэффициентов	называется матрицей.
В данном случае матрица полностью описывает способ вычисления координат точки г в первой системе через координаты точки г во второй системе. Элементы первой строки матрицы (47) являются коэффициентами для выражения хх через ut, и2, и3. Точно так же элементы второй строки являются коэффициентами выражения х2 через и2, и3, а1 элементы третьей строки — коэффициентами выражения х3 через uv н2, н3. Если этот способ записи коэффициентов применить к случаю 126 _
(48)
плоскости (см. (7)), то мы получим следующую матрицу коэффициентов:
(cos. ф — sin ф sin ф • cos ф
Видно, что элементы матрицы (48) не являются независимыми числами, а все зависят от одной и той же величины ф — угла поворота. Точно так же девять элементов матрицы (47) не являются независимыми. Они могут быть выражены через три угла, но эти выражения неудобны, поэтому зависимости между элементами матрицы (47) обычно задаются другим способом — при помощи уравнений, связывающих элементы матрицы (47). Эти уравнения очень легко получить, приняв во внимание, что векторы е19 е3 не произвольны: именно, каждый из них имеет длину единица и каждые два различных вектора' перпендикулярны друг другу. Выпишем эти условия, пользуясь скалярными произведениями
2	2-	2 л 1
ei - е2 - е3 - 1,1	(49)
#1 • #2 — ^1 * ^3 — ^2 ’ ^3
Совокупность этих равенств коротко обычно записывается в следующей форме:
ej-eh = 6ЛЛ.	'	, (50)
Здесь есть так называемый символ Кронекера — число, которое равно единице, когда ] = А, и нулю, когда / =# к. Для того чтобы получить уравнения, связывающие элементы матрицы (47), следует переписать равенства (49), или, что то же самое, (50), выразив входящие в них скалярные произведения во второй системе координат (см. (45)). Предоставляем это читателю.
Пусть теперь в пространстве имеется третья система координат с произвольным началом о' и произвольно направленными осями координат, проходящими через эту точку о'. Координаты точки г в этой третьей системе координат мы введем при помощи формулы
Г в (£11 ^2» 1з)з*
Производя два последовательных преобразования координат типа 1 и 2, мы получим, очевидно, формулы
=3 Cl -|- “Ь °И,з£з 0	1» 2, 3). (51)
127
Эти формулы дают выражение координат точки г в первой системе через ее координаты в третьей системе. Следует отметить, что эти формулы выражают координаты х19 х2, х3 в виде многочленов первой степени относительно координат |2, |3. Так как обе системы — первая и третья — вполне равноправны, то координаты £1» Ёг, £з выражаются через координаты х19 х2, х3 также при помощи многочленов первой степени.
Допустим теперь, что в первой системе координат некоторая поверхность задана уравнением
^*(#1»	^з) — 0,	(52)
где F(xv х2, х3) есть многочлен степени п. При переходе от первой системы координат к третьей системе координат мы должны в многочлен F(xv х2, х3) вместо х2, х3 подставить их выражение по формулам (51). Тогда мы получим многочлен G(^x, |2, £з)> и в третьей системе координат уравнение поверхности будет иметь вид
&(il> ^2» ?з) “ 0.
Очевидно, что многочлен G(£x,	£3) также имеет сте-
пень п (сравните с § 9). Таким образом, степень п многочлена является геометрическим свойством поверхности, определяемой уравнением (52). Она называется порядком поверхности.
2. Классификация поверхностей первого и второго порядков. Будемх считать, что в пространстве задана система координат, описанная в добавлении к первой главе. Пусть F(xv х2, х3) — Многочлен первой или второй степени относительно координат xt, х2, х3. Тогда уравнение
F(xv х2, х3) == 0	(53)
определяет в пространстве поверхность. Здесь мы имеем два случая? а) многочлен F имеет первую степень и поверхность называется поверхностью первого порядкам б) многочлен имеет вторую степень, тогда поверхность называется поверхностью второ го..порядка. Мы докажем, что поверхность первого порядка есть всегда плоскость, а поверхность второго порядка либо вырождается, т. е. является цилиндром или конусом, либо имеет один из пяти видов, описанных в добавлении к главе II (см. формулы (83)—(87)).
128
С л у ч а й а). Многочлен первой степени F запишем в виде
^(•^Х’ #2» ^з) = dyX-^ 4“ $2^2 Ч~ «3^3 Ч" ^0*
Здесь не все числа av а2ч а3 равны нулю. Очевидно, существует такое число |3, что многочлен
*^2» ^з) :== Ч" ^2*^2 Ч~ Ь3Х3 4“ ^0
обладает следующими свойствами. Число Ьо = —b не положительно, т. е. Ь > 0, а числа bt, Ъ2, Ь3 удовлетворяют условию
ьиь22Ч-Ьз = 1.
Тогда уравнение (53) переписывается в виде
Ьх^х Ч- Ь2х2 Ч- Ь3х3 = Ь,
которое представляет собой нормальное уравнение (плоскости) (см. формулу (81) добавлений к гл. II).
Таким образом, доказано, что поверхность первого порядка всегда есть плоскость, а любая плоскость есть поверхность первого порядка.
Случай б). Рассмотрим сперва многочлен второй степени Ffa, х.2, х3), не содержащий членов первой и нулевой степени. Такой многочлен называется квадратичной формой от переменных xv х2, х3. Он рассматривается как функция вектора г = (жх, х2, х3),
F(r) = F(xt, х2, х3).
Будем считать, что вектор г == г есть произвольный вектор длины единица и выделим такой вектор 81? для которого функция F(e) достигает своего максимума. Построим теперь в пространстве новую систему координат с прежним началом о, приняв за первую ось прямую, проходящую через вектор и выбрав на ней направление вектора ev Две другие оси выберем произвольно так, чтобы они были перпендикулярны первой оси и между собой. В этой второй системе координат обозначим координаты вектора г через иг, и2, и3, положив
Г = ОЧ» ^2» ^3^2*
Подставляя в квадратичную форму F(xly х2, х^ выражение xv х21 х3 через uv u2, и3 (см. (46)), мы получшм для
9 Л. С. Понтрягин	129
F(r) ново© выражение.
F(r) = G(ulf u2, u3).
Будем считать теперь, что вектор г принадлежит плоскости (1, 2) второй системы координат. Тогда мы имеем
Р (г) = fcnui + 2blaU!U2 + b^uf.	(54)
Так как квадратичная форма F(s) при произвольном векторе 8 длины единица достигает своего максимума, когда 8 = 8Г, то и для векторов 8, принадлежащих плоскости (1, 2) второй системы координат, она достигает своего максимума также при 8 == ev Отсюда, в силу примера 4 главы III, следует, что квадратичная форма (54) не содержит смешанного произведения, т. е. имеет вид
#	F (г) = bnuj + b22U2,
Точно так же, рассматривая квадратичную форму F(r) для векторов, принадлежащих плоскости (1, 3) второй координатной системы, мы убедимся, что смешанный член с произведением utu3 отсутствует. Отсюда следует, что квадратичная форма F(r) для произвольного вектора г = (и19 и21 и3) имеет вид
F (г) = Ьци1 + bi2U2 + 2b23zz2u3	b33u|.
Таким образом, для векторов г, принадлежащих плоскости (2, 3) второй системы координат, квадратичная форма F(r) имеет, вид
Р (г) = ь22и2 + 2Ьг9и2и3 + Ь83из.	(55)
Мы уже знаем (см. (37)), что для квадратичной формы (55) двух переменных и2 и и3 можно так выбрать систему Координат в плоскости (2, 3), что она в новых переменных (g2, £3) получает вид
. Г(г)=,сггЙ + с8Лз.
Сохраняя первую ось второй системы координат и заменяя оси в плбскости (2, 3) указанным способом, мы получаем для квадратичной формы F(r) следующий вид:
Р(г) + с22Й+с33Гз.	(56)
Таким образом, мы доказали, что в пространстве можно .130
выбрать такую систему координат с прежним началом о, в которой произвольная заданная квадратичная форма F(r)=F(xl, х2ч х3) приобретает вид (56). Говорят, что произвольная квадратичная форма F(r) = =F(xv х2, х3) преобразованием координат может быть приведена к каноническому виду (56).
После этого, пользуясь построениями, аналогичными тем, которые были даны в § 10, мы можем доказать, что каждая невырожденная поверхность второго порядка имеет один из пяти видов, перечисленных в добавлении ко второй главе (см. (83)—(87)).
Что касается вырожденных поверхностей второго порядка, цилиндров и конусов, то их легко можно описать.
Цилиндр второго порядка в надлежаще выбранных координатах записывается уравнением
х2) = 0,	(57)
где F(xt, х2) есть многочлен второй степени относительно переменных (хх, х2), так что уравнение
F(^, х2) = 0
в координатной плоскости (1, 2) определяет кривую второго порядка. Таким образом, цилиндр (57) имеет своей направляющей кривую второго порядка, лежащую в координатной плоскости (1, 2), а все кривые второго порядка уже проклассифицированы (см. § 10).
Конус второго, порядка имеет уравнение
F (х±, х2, #з) = 0,
где F(xx, х2, х3) есть квадратичная форма второго порядка, которая, по только что доказанному, может быть приведена к каноническому виду (56). Поэтому можно считать, что конус второго порядка записывается уравнением
+ с22х% + c33xl = 0.	(58) 
Если все числа си, е22, с33 отличны от нуля и имеют один знак, то уравнению (58) удовлетворяет только начало координат. Если один или два из коэффициентов равны нулю, то мы получаем цилиндр. Если же они все отличны от нуля, но не имеют одинаковых знаков, то будем считать для определенности, ^то с33 > 0, си<0,
9*	131
c22 < 0- Тогда уравнение (58) может быть переписано в виде
Это и есть уравнение конуса с эллиптическим сечением плоскостью #3=с, с > 0.
Таким образом, мы получили полное описание всех поверхностей второго порядка.
3. Конические сечения. Будем считать, что в пространстве задана некоторая система координат, например, описанная в добавлении к главе I. Подобно тому как на плоскости мы задавали линии в параметрической форме (см. § 6), в пространстве мы можем задавать линии и поверхности также в параметрической форме. В самом деле, если x(t) есть векторная функция параметра 7, причем я? есть пространственный вектор, именно:
#(£) =	^(0»
то уравнение	< '
х = x(t)
есть параметрическое уравнение линии. Именно, когда t меняется, точка x(t) в пространстве описывает некоторую линию. Точно так же, если x(tv t2) есть векторная функция двух параметров и t2, причем t2) есть пространственный вектор, именно;
^2)	(^1(^1» ^2)» ^2(^1» ^2),	^2))»
то уравнение
£ = x(tv t2)
задает некоторую поверхность. Именно, когда и t2 принимают всевозможные значения, точка x(tv t2) описывает в пространстве некоторую поверхность S. Так как, задавая числовые значения параметров и t2, мы получаем определенную точку x(tv t2) на поверхности 5, то числа tx и 42 можно рассматривать как 'координаты точки x(tv t2) на поверхности 5. Такие координаты на поверхности имеют большое значение в геометрии, но здесь мы будем рассматривать только параметрические уравнения прямой и плоскости.
132
Пусть М — некоторая прямая в пространстве, я0— некоторая фиксированная точка на ней, а е — вектор длины единица, выходящий из начала координат и параллельный прямой М. Тогда уравнение
х = х0 + te	(59)
является параметрическим уравнением прямой М в пространстве. Когда параметр t пробегает все действительные значения, точка х, заданная уравнением (59), пробегает всю прямую М. Уравнение (59) по форме совпадает с уравнением (45) главы II и выводится совершенно аналогично.
Пусть теперь Q — некоторая плоскость в пространстве, х$ — некоторая фиксированная точка на плоскости Q и ех, е2 — два вектора длины единица, перпендикулярные друг другу, выходящие из начала координат и параллельные плоскости Q. Тогда
х = xQ + ttex + t2e2	(60)
есть параметрическое уравнение плоскости Q. Именно, когда числа tr и t2 принимают всевозможные значения, точка х, определяемая уравнением (60), описывает всю плоскость Q. Доказательство этого факта мы здесь не приводим. Оно не представляет трудности. Оказывается, далее, что числа Ч и t2 являются декартовыми координатами точки х, определяемой уравнением (60) в плоскости Q в некоторой определенной системе координат. Оси этой декартовой системы координат описываются следующим образом. Через точку xQ в плоскости Q проведем прямую Ми параллельную вектору ev и выберем на ней направление, совпадающее с направлением вектора Точно так же через точку х0 проведем прямую М2 в плоскости Q, параллельную вектору е2, и выберем на этой прямой направление, совпадающее с направлением вектора е2. Полученные две прямые Мг и М2 с выбранными на них направлениями представляют собой оси декартовых координат на плоскости Q, а числа tY и t2 являются координатами точки х на плоскости Q относительно этих осей координат. Если точка xQ лежит на прямой R, проходящей через точку о и перпендикулярной к плоскости Q, то вектор xQ может быть записан в форме
•Гц
133
где а > 0, а вектор е3 имеет длину единица и перпендикулярен к. векторам ег и е2. В этом случае векторное уравнение (60) получает вид
х = tle1 + t2e2 + ае3.	(61)
Для того чтобы от ^векторного уравнения (61) плоскости Q перейти к трем скалярным ее уравнениям, зададим координаты векторов е2, е3, положив
ei = (<Чь аг,2, аг,з)	G = 1, 2, 3).
Вместо одного векторного уравнения (61) плоскости мы можем теперь написать три скалярные уравнения, именно:
=	4"	= 1» 2, 3). (62)
Пусть теперь F(xv х2, х3) — функция трех переменных. Тогда
F(xv х2, х3) = 0	(63)
определяет в пространстве некоторую поверхность 5. Для того чтобы найти пересечение L этой поверхности S с плоскостью Q, мы должны подставить в функцию F(xv х2, х3) выражение для х1ч х2, х3 по формулам (62). Тогда мы получим некоторую функцию G(tv t2), и линия L задается в плоскости Q уравнением
G(tv t2) = 0.
Выберем теперь функцию F(xv х2, х3) специальным образом так, чтобы уравнение (63) определяло круглый конус (см. пункт 3 из добавлений к гл. II). Именно, напишем уравнение
4- xl — к2х3 = 0.	(64)
При к Ф 0 это уравнение определяет круглый конус, ось которого совпадает с третьей осью нашей пространственной системы координат. Плоскость Q мы теперь выберем также специальным образом, именно, положим = (1, 0, 0), е2 == (0, — sin у, cos у), е3 == (0, cos у, sin у), а > 0.
134
При таком задании плоскости Q ее параметрические уравнения задаются формулами
#1 =
х2 == — sin у + a cos у, я3 = £2cos у + a sin у.
(65)
Для того чтобы получить уравнение линии пересечения нашего конуса (64) с плоскостью Q, подставим выражение для х^ х2, х3 из формул (65) в уравнение (64). Тогда мы получим
11 + (sin2 у — &2cos2 у) tl — 2а sin у cos у, (1 + к2) t2 +
+ (cos2 у — к2 sin2 у) а2 =* 0.	(66)
Это есть уравнение пересечения конуса (64) с плоскостью Q, заданное в декартовой системе координат плоскости Q. Сразу видно, что уравнение (66) определяет в плоскости Q кривую второго порядка. Читателю предоставляется рассмотреть все имеющиеся здесь возможности в зависимости от значений чисел а, к и у. Следует установить, в каких случаях получается эллипс, гипербола и парабола.
Таким образом, пользуясь методом координат, мы получили результат § И почти автоматически, между тем как в § И он был получен на основании тонких геометрических построений. Это демонстрирует силу координатного метода.
Лев Семенович Понтрягин ЗНАКОМСТВО С ВЫСШЕЙ МАТЕМАТИКОЙ
•
МЕТОД КООРДИНАТ
М.» 1977 г., 136 стр. с илл.
Редакторы В. И. Благодатских, А. Ф. Лапко Технический редактор Е В. Морозова
Корректор Л. Н. Боровина
Сдано в набор 10/V 1977 г. Подписано к печати 5/IX 1977 г.
Бумага 84 х lOSVsa. Физ. печ. л. 4,25. Условн. печ. л. 7,14.
Уч.-изд. л. 5,97. Тираж 100 000 экз. Т-07083. Цена книги 25 коп. Заказ Ха 546
Издательство «Наука»
Главная редакция физико-математической литературы
117071, Москва, В-71, Ленинский проспект, 15
4-я типография издательства «Наука». Новосибирск, 77, ул. Станиславского, 25
Цена 25 коп.