Автор: Понтрягин Л.С.
Теги: анализ математический анализ функциональный анализ высшая математика
Год: 1980
Текст
ЗНАКОМСТВО
С ВЫСШЕЙ
МАТЕМАТИКОЙ
Л.С.ПОНТРЯГИН
АНАЛИЗ
БЕСКОНЕЧНО
МАЛЫХ
Л. С. ПОНТРЯГИН
ЗНАКОМСТВО
С ВЫСШЕЙ
МАТЕМАТИКОЙ
•
АНАЛИЗ БЕСКОНЕЧНО
МАЛЫХ
МОСКВА <НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
1980
22.16
П 56
УДК 517
Понтрягин Л. С.
П 56 Знакомство с высшей математикой. Анализ
бесконечно малых. — М.: Наука, 1980.—
256 с. — 45 к.
Книга посвящена изложению некоторых вопросов математиче-
ского анализа. Хотя изложение в ней не является легким, она за-
думана как книга, доступная молодым читателям, увлекающимся
математикой. Ее характерной чертой является одновременное изло-
жение теории функций действительного и комплексного перемен-
ного.
ББК 22.16
517.2
Лев Семенович Понтрягин
ЗНАКОМСТВО С ВЫСШЕЙ МАТЕМАТИКОЙ
©
АНАЛИЗ БЕСКОНЕЧНО МАЛЫХ
М., 1980 г., 256 стр. с илл.
Редакторы В. Р. Телеснин, В. В. Донченко
Технический редактор С. Я. Ш к л я р
Корректор О. М. Кривенко
ИБ № 11183
Сдано в набор 18.12.79. Подписано к печати 06.06.80. Т-08166. Бумага
84ХЮ8’/з2- Тип. № 2. Литературная гарнитура. Высокая печать. Условн.
печ. л. 13,44. Уч.-изд. л. 13,03. Тираж 100000 экз. Заказ № 464. Цена
книги 45 коп.
Издательство «Наука»
Главная редакция физико-математической литературы
117071, Москва, В-71, Ленинский проспект, 15
Ордена Трудового Красного Знамени Ленинградская типография № 2
имени Евгении Соколовой «Союзполиграфпрома» при Государственном
комитете СССР по делам издательств, полиграфии и книжной торговли.
198052, Ленинград, Л-52, Измайловский проспект, 29
© Издательство «Наука»
Главная редакция
физико-математической
литературы, 1980
ОГЛАВЛЕНИЕ
Предисловие............................................. 4
Введение................................................ 7
Глава I. Ряды........................................ . 20
§ 1. Сходящиеся последовательности чисел , .... 24
§ 2. Бесконечно малые величины...............37
§ 3. Условия сходимости Коши.................43
§ 4. Применение признака сходимости Коши г .... 57
§ 5. Сходящиеся ряды.........................65
§ 6. Абсолютно сходящиеся ряды...............72
§ 7. Функция exp(z)..........................80
§ 8. Основные трансцендентные функции ...............91
§ 9. Степенные ряды..........................98
Глава II. Дифференциальное исчисление..................103
§ 10. Производная . . . . ...........................109
§ 11. Вычисление производных.................123
§ 12. Неопределенный интеграл................132
§ 13. Вычисление некоторых неопределенных интегралов 141
§ 14. Определенный интеграл..................149
§ 15. Ряд Тейлора............................159
Глава III. Интегральное исчисление ...................171
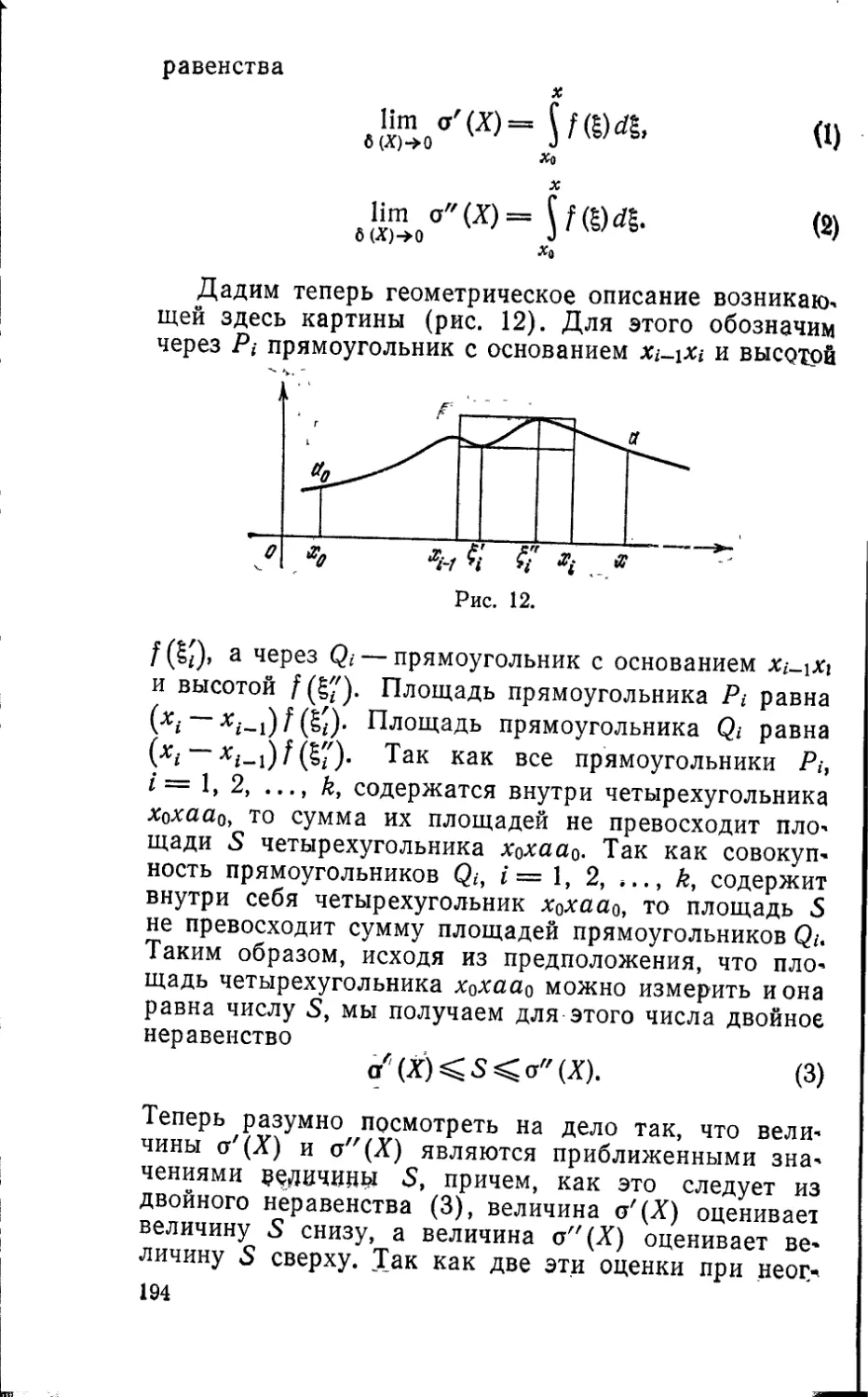
§ 16. Определенный интеграл как площадь..............171
§ 17. Определенный интеграл как предел последовательно-
сти конечных сумм..................................177
§ 18. Площадь и длина графика........................192
§ 19. Длина параметрически заданной линии ..... 197
Г л а в а IV. Аналитические функции....................206
§ 20. Интегрирование функций комплексного переменного 206
§ 21. Теорема Коши..................................218
§ 22. Ряды Тейлора и Лорана..........................231
§ 23. Вычеты........................................241
§ 24. Нахождение обратной функции ........ 247
§ 25. Целые функции и особые точки..................253
1*
ПРЕДИСЛОВИЕ
Предлагаемая книжка является второй из серии
четырех небольших сравнительно популярных книг,
издаваемых мною под общим заглавием «Знакомство
с высшей математикой». Первая книжка «Метод ко-
ординат» уже вышла в 1977 году. Эта вторая книжка
посвящена изложению основных фактов математиче-
ского анализа.
Изложение ведется так, чтобы всюду, где это воз-
можно, одновременно рассматривать как действитель-
ный, так и комплексный случай. В первую очередь
это относится к определению сходимости последова-
тельностей и рядов, в частности степенных рядов.
Точно так же определение производной дается одно-
временно для функций действительного и комплекс-
ного переменного, так как формально оно одинаково
для обоих случаев. Понятие первообразной функции
определяется одинаково как для функции действи-
тельного переменного, так и для функции комплекс-
ного переменного. Одновременно доказывается
единственность первообразной с точностью до по-
стоянного слагаемого. Такой способ изложения дает
возможность сравнительно легко включить в книгу
основные результаты теории функций комплексного
переменного, что составляет ее четвертую главу. Эта
глава является важнейшей завершающей частью кни-
ги и доведена до таких сравнительно сложных ре-
зультатов, как ряд Лорана и поведение функции
вблизи изолированной особой точки.
Те вопросы анализа, которые составляют так на-
зываемую теорию функций действительного перемен-
ного, я стараюсь отодвинуть на задний план, считая
их наименее интересными. Я не свел их вместе, а
4
разбросал по всей книжке, излагая там, где в них
возникает необходимость.
Центральное место в первой главе занимает изу-
чение функции exp(z) комплексного переменного z,
которая задается степенным рядом
exp (z) = 1 +-у +-[ту + ... +-^г+ ••• (О
Доказывается, что при действительном значении
z = х мы имеем равенство
ехр (х) = ех,
а для чисто мнимого значения z = iy имеется фор-
мула
exp (iy) = cos у + i sin у.
Таким образом, не пользуясь дифференциальным ис-
числением, мы сразу получаем разложение основных
трансцендентных функций ех, cosy, sin у в степен-
ные ряды.
Нужно обратить внимание на следующее обстоя-
тельство. Когда мы доказываем, что некоторая как-
либо заданная функция р!азлагается в степенной ряд,
то для этого достаточно доказать, что ряд сходится
к некоторому определенному числу — значению функ-
ции. Если же мы хотим определить саму функцию
при помощи ряда (см. (1)), то для этого нужно до-
казать, что ряд сходится, для чего необходимо ис-
пользовать признак сходимости Коши и дать точное
определение числа. Весь этот аппарат излагается в
первой главе.
Глава II посвящена изложению основных резуль-
татов дифференциального исчисления. Прежде всего
определяется производная одновременно "как для
функции действительного переменного, так и для
функции комплексного переменного и вводится поня-
тие интегрирования как операции, обратной к опера-
ции дифференцирования. Завершением главы являет-
ся доказательство формулы Тейлора с остаточным
членом в интегральной форме.
Глава III посвящена интегральному исчислению.
В ней интеграл определяется сперва интуитивно, как
величина площади, ограниченной графиком, и дока-
зывается, что так определенный интеграл является
первообразной для функции, задающей график.
5
Далее весьма четко и тщательно интеграл определяет-
ся как предел последовательности конечных сумм.
Таково в основном содержание книги.
Введение распадается на две части. В первой ча-
сти напоминаются некоторые простейшие понятия, ко-
торые можно почерпнуть из книжки «Метод коорди-
нат». Во второй части «Историческая справка»
дается очень краткое и неполное описание истории
развития математического анализа. Для чтения пред-
лагаемой книги нет необходимости иметь законченное
среднее математическое образование. Некоторые упо-
требляемые здесь важнейшие формулы элементарной
математики — сумма геометрической прогрессии, би-
ном Ньютона — в книге доказаны, так что она может
быть доступна и старшим школьникам, но книга не
является легким чтением и требует значительной ма-
тематической культуры. Надеюсь, что она может по-
служить также противоядием при «отравлении» тео-
рией множеств. В последнее время теоретико-множе-
ственная идеология усердно внедряется в программу
и учебники средней школы. Авторы этого внедрения
утверждают, что теория множеств важна для научно-
технического прогресса и является новейшим дости-
жением математики. В действительности теория мно-
жеств не имеет ничего общего с научно-техническим
прогрессом и не является новейшим достижением ма-
тематики. Теоретико-множественная идеология при-
водит, например, к таким уродствам, как замена тер-
мина «равенство» геометрических фигур термином
«конгруэнтность» и определение вектора как «парал-
лельный сдвиг пространства».
В заключение я выражаю благодарность В. Р. Те-
леснину за помощь, оказанную при написании и ре-
дактировании книги, а также официальному рецен-
зенту издательства Е. М. Никишину за его много-
численные замечания, значительную часть которых я
использовал.
ВВЕДЕНИЕ
Здесь в первую очередь дается напоминание тех
немногих математических фактов, которые понадо-
бятся нам и которые можно найти в моей книжке
«Метод координат». Далее дается историческая справ-
ка, в которой очень коротко и неполно излагается
исторический процесс возникновения математического
анализа.
Напоминание
ПРЯМОУГОЛЬНЫЕ ДЕКАРТОВЫ КООРДИНАТЫ
НА ПЛОСКОСТИ
В некоторой плоскости Р выберем две перпенди-
кулярные друг другу прямые и обозначим через о
точку их пересечения. Для определенности будем счи-
тать, что плоскость Р есть плоскость нашего чертежа
(рис. 1) и что одна из выбран-
ных прямых проходит горизон-
тально, а другая вертикально.
Горизонтальная прямая на-
зывается осью абсцисс, а вер-
тикальная — осью ординат.
Обе оси называются просто
осями координат, а точка о —
началом координат.
Пусть теперь г — некоторая точка на плоскости Р.
Пользуясь выбранными осями координат, поставим
этой точке в соответствие два числа х и у: х — ее
абсцисса, у — ее ордината. Для этого из точки z опу-
стим перпендикуляр zp на ось абсцисс и перпендику-
ляр zq на ось ординат. Если точка р лежит вправо
от начала координат о, то через х мы обозначим
7
Рис. 1.
длину отрезка op, т. е. положительное число. Если
точка р лежит влево от начала координат о, то через
х мы обозначим длину отрезка ор, взятую со знаком
минус, т. е. отрицательное число. Если точка р сов-
падает с началом координат о, то х — 0. Аналогично,
если точка q лежит выше начала координат, то че-
рез у мы обозначим длину отрезка oq, т. е. положи-
тельное число. Если точка q лежит ниже начала ко-
ординат, то через у мы обозначим длину отрезка oq,
взятую со знаком минус, т. е. отрицательное число.
Если точка q совпадает с началом координат, то
у = 0. Таким образом, каждой точке z на плоскости
Р при помощи выбранной системы координат постав-
лена в соответствие пара чисел: х и у, х — абсцисса
точки, у — ее ордината. В виде формулы это записы-
вается так:
z = (x,z/). (1)
Числа х и у называются координатами точки z.
Если заданы два произвольных числа х и у, то на
плоскости Р легко построить ту единственную точку
z, абсцисса которой равна заданному числу х, а орди-
ната— заданному числу у.
Если точка z движется вдоль оси абсцисс слева
направо, то абсцисса ее возрастает. Поэтому говорят,
что ось абсцисс направлена слева направо. В том же
самом смысле ось ординат направлена снизу вверх.
Пусть zi = (xi, t/i) и г2—(х2, у2) — лве точки на
плоскости Р, заданные своими координатами. Рас-
стояние между точками z\ и Z2, которое мы обозна-
чим через l(zi, z2), определяется формулой
I (zi, z2) = + V(х2 — Xi)2 + (у2 — уд2. (2)
Теперь уместно перейти к рассмотрению векторов,
при помощи которых многие формулы записываются
гораздо короче, чем при помощи координат.
Пусть а и b — две точки на плоскости Р. Принято
говорить, что отрезок ab, определенным образом на-
правленный, именно, от а к &, есть вектор ab. Точка
а называется началом вектора, а точка Ь — его кон-
цом. Говорят также, что вектор ab приложен к точ-
ке а. Если с и d — две какие-нибудь другие точки
плоскости Р, то считается, что вектор ab равен век-
8
тору cd, если отрезки ab и cd: 1) равны по длине,
2) параллельны, 3) одинаково направлены.
’ Очевидно, что для каждого вектора ab найдется
равный ему вектор, выходящий из начала координат
о. Обозначим его конец через г, так что векторы ab
и oz равны. В основном мы будем ограничиваться
рассмотрением лишь тех векторов, которые начи-
наются в начале координат о. Такие векторы мы бу-
дем обозначать одной буквой,
будем обозначать просто бук-
вой z. Этим самым устанавли-
вается взаимно однозначное
соответствие между вектора-
ми, выходящими из начала
координат, и точками плоско-
сти Р, именно, каждому векто-
ру oz ставится в соответствие
его конец, точка z.
Теперь определим опера-
а именно, вектор oz
цию сложения двух векторов.
Рассмотрим на плоскости Р
два вектора zj и z2. Подразу-
мевается, ЧТО Z] и z2 — концы
векторов, начинающихся в точке о (рис. 2). Для того
чтобы определить сумму векторов zi + z2, проведем
из точки zi вектор ziz3, равный вектору z2. Вектор
ог3, или, что то же самое, z3 есть по определению
сумма векторов Zi и z2:
«3 = Zi + z2.
В нашем построении суммы z\ + z2 векторы z\ и z2
неравноправны, но легко доказывается, что
Z\ + z2 = z2 + Zi.
Вычитание векторов определяется как операция, об-
ратная сложению.
Среди всех векторов имеется один вектор нулевой
длины, начинающийся и кончающийся в точке о. Он
обозначается знаком 0. Этот вектор обладает следую-
щим свойством: z + 0 = z.
Длина отрезка, определяющего вектор, называет-
ся модулем этого вектора и обозначается специаль-
ным образом, именно
| Z | = / (о, z).
9
Имеет место важное неравенство
I 21 + Зг I ^1 Zi | + | z21- (3)
Неравенство это следует из рассмотрения треуголь-
ника oz\Zb (см. рис. 2).
Кроме операций сложения и вычитания векторов,
существует еще одна важная операция над векто-
рами, именно, умножение вектора на число. Если
а— некоторое число, a z — вектор, то для определе-
ния произведения
г' — az
проведем прямую L, проходящую через точки о и г.
Если а — число положительное, то от точки о отло-
жим на прямой L отрезок ог', равный по длине а | г |
и направленный в ту же сторону, что и отрезок ог.
Конец z' этого отрезка и есть вектор аг. Если число
а отрицательное, то от точки о отложим на прямой L
отрезок ог' длины |а| |г|, но в направлении, противо-
положном отрезку oz. Конец этого отрезка г' и есть
вектор аг. Если а = 0 или г = 0, то вектор аг есть
нулевой вектор.
Введем теперь понятие координат вектора. Так
как г является у нас одновременно и точкой и векто-
ром, то естественно считать, что координаты точки г
являются одновременно и координатами вектора г.
Таким образом, мы можем записать
Z = (х, у},
где г есть вектор, а х, у — его координаты, т. е. коор-
динаты точки г.
Опишем теперь при помощи координат те опера-
ции над векторами, которые только что были опреде-
лены чисто геометрически. Кроме вектора г, запишем
в координатной форме еще два вектора:
Zi = (xb «/0; z2 = (x2) у2).
Тогда мы имеем
21 + z2 = (xi + х2, yi + у2), (4)
21 — г2 = (%1 — х2, уг — у2), (5)
I 2 | = + Vx2 + Z/2, (6)
az = (ах, ay). (7)
Эти формулы легко доказываются.
10
Полярные координаты. На нашей плоскости Р мы
уже имеем декартову систему координат, т. е. ось
абсцисс, ось ординат и начало координат. С этой си-
стемой координат тесно связана так называемая по-
лярная система координат. Пусть z~(x,y)— произ-
вольная точка плоскости Р, заданная своими декар-
товыми координатами. По-
ставим теперь этой точке z | 2
в соответствие два других
числа — ее полярные коор-
динаты, именно, число р,
равное длине отрезка ог, Хр
р —/(о, г), и число ф, рав-
ное величине угла между
положительной полуосью Рис. 3.
абсцисс и отрезком oz, при-
чем угол отсчитывается в направлении против часо-
вой стрелки (рис. 3). Мы будем писать
Z = [р, ф].
Число р называется радиусом точки г, а число ф —
ее углом.
Радиус р точки z определен однозначно. Угол ф
точки z не определен совсем, когда точка z совпадает
с началом координат. Но и в том случае, когда точ-
ка z не совпадает с началом координат, угол ф не оп-
ределен однозначно. Именно, если ф есть угол точ-
ки z, то ф + \kd, где k — произвольное целое число,
ad — величина прямого угла, также является углом
точки г.
Пользуясь одновременно декартовыми и поляр-
ными координатами, мы неизбежно должны поста-
вить вопрос о связи между теми и другими. Декар-
товы и полярные координаты точки z = (х, у) = [р, ф]
связаны между собой следующими формулами (см.
рис. 3):
х = р cos ф, у = р sin ф. (8)
Определим скалярное произведение Zi-z2 двух век-
торов zi= [рьф1] и г2 = [р2, ф2], пользуясь их по-
лярными координатами. По определению
Zi • Z2 = Р1Р2 COS (ф2 — Ф1) — Р1Р2 cos у, (9)
11
где 7 есть угол между векторами zi и z2. Знак числа у
не играет роли. Пользуясь формулами (8) связи ме-
жду полярными и декартовыми координатами, мы
получаем выражение
Z1 • Z2 = Х1Х2 + у1у2. (10)
Оно дает скалярное произведение, выраженное через
декартовы координаты векторов.
Геометрическое изображение комплексных чисел.
Декартовы координаты дают еще одну возможность
для установления связи между точками и числами,
а именно, они позволяют геометрически изображать
комплексные числа и действия над ними.
Комплексные числа, как известно, возникли бла-
годаря тому, что нельзя было извлечь корень квад-
ратный из отрицательного числа. Поэтому ввели фор-
мально новое число I, удовлетворяющее уравнению
/2+1=0,
так что ___
V— 1 = ± />
и определили комплексное число г формулой
z = x + iy, (11)
где х и у — обыкновенные числа, с которыми уже
привыкли иметь дело и которые теперь, в отличие от
комплексных, мы будем называть действительными.
Над комплексными числами стали производить обыч-
ные действия — сложение, умножение и обратные к
ним: вычитание и деление. Во всех таких вычисле-
ниях заменяли i2 на —1 и получали, таким образом,
возможность производить над комплексными числами
все действия так же непринужденно, как раньше над
действительными.
Определим действия над комплексными числами
более формально. Пусть
zi = Xi 4- iУ\; г2 = х2 + iy2
’—два комплексных числа. Тогда их сумма опреде-
ляется формулой
Z14- z2 = (xt 4- Х2) +1 (yi 4- у2). (12)
.12
Произведение двух комплексных чисел 2\ и z2 опре-
деляется формулой
Z{z2 = (xi + iyi) (х2 + iy2) — xtx2 + ixty2 + iy<x2 +
+ ?У\У2 = (xix2 — yiy2) + i (xxy2 + У!Х2). (13)
Комплексное число z, записанное в форме (11),
само просится на нашу плоскость Р, на которой уже
введены декартовы координаты. Его хочется изобра-
зить в виде точки z с координатами (х, у) или, что
то же самое, в виде вектора z с координатами (х,у),
т. е. z = (х, у). Плоскость Р, на которую нанесены в
виде точек комплексные числа z, будем называть
плоскостью комплексного переменного г.
Комплексные числа z вида
z = х + /0 = х
теперь разумно называть действительными числами.
Они все лежат на оси абсцисс, и поэтому ось абсцисс
плоскости комплексного переменного z мы будем на-
зывать действительной осью. Комплексные числа вида
z = 0 + i у = iy
называются чисто мнимыми или просто мнимыми, и
они располагаются на оси ординат. Поэтому ось ор-
динат плоскости комплексного переменного z мы бу-
дем называть мнимой осью. Комплексное число z =
= 0 + iO попадает в начало координат. Действитель-
ные числа 4-1 и —1 располагаются на действитель-
ной оси справа и слева от нуля на расстоянии еди-
ница. Мнимые числа -Н и —i располагаются на
мнимой оси над нулем и под нулем на расстоянии
единица от него.
Используем теперь для записи комплексного чис-
ла z полярные координаты точки z. Так как в силу
формул (8)
х = р cos <р; у = р sin ф,
то комплексное число z, определенное формулой (11),
записывается в виде
г = р(со$ф + г зтф). (14)
Эта запись комплексного числа z называется триго-
нометрической. Неотрицательное число р называется
модулем комплексного числа z, а угол ф — его аргу-
13
ментом. Число р однозначно определено комплексным
числом z и обозначается специальным символом
|z| = p = + Vx2 + у2.
Следует вновь напомнить, что аргумент <р комплекс-
ного числа z не определен однозначно, именно, при
|z|= 0 он вовсе не определен, а если | z| =£ 0 и ф есть
аргумент комплексного числа г, то наряду с этим
значением <р аргументом являются и числа <р 4- \kd,
где k — произвольное целое число.
Пользуясь формулами (12) и (13), дадим геомет-
рическое истолкование операциям сложения и умно-
жения комплексных чисел.
Из формул (4) и (12) следует, что для того, чтобы
сложить два комплексных числа zi и Z2, достаточно
сложить изображающие их векторы z\ и z2. Тогда по-
лученная сумма векторов z3 = Zi + z2 изображает
сумму Zi -I- z2 комплексных чисел. Так как для век-
торов существует операция вычитания, обратная к
операции сложения, то и для комплексных чисел су-
ществует операция вычитания, обратная к операции
сложения. Геометрическая интерпретация сложения
комплексных чисел приводит нас к важному неравен-
ству
|21 + z2|<|ziI4-|z2|.
Для того чтобы дать геометрическую интерпрета-
цию умножения комплексных чисел zi, z2, запишем
эти числа и их произведение w в тригонометрической
форме, именно:
2"i = Pi (cos «pi + i sin <pi),
z2 = р2 (cos ф2 + i sin ф2),
ZiZ2 = w — ст (cos ф + i sin ф).
При подсчете произведения в тригонометрической
форме используем известные формулы тригономет-
рии. Мы получаем теперь
W = Z1Z2 — Р1Р2 [(cos ф1 COS ф2 — sin Ф1 ЭШфг) +
+1 (sin ф1 cos ф2 + cos ф1 sin ф2)] =
== Р1Р2 [cos (ф1 4- ф2) + i sin (ф! 4- ф2)]
14
или окончательно
о (cos ф 4- i sin ф) = Р1Р2 [cos (<pi + q>2) + i sin (<p, + <p2)].
(15)
Таким образом,
a==pip2; Ф = Ф1 + ф2. (16)
Это означает, что при перемножении комплексных
чисел si и z2 их модули pi и р2 перемножаются, а их
аргументы cpi и <р2 складываются.
Из формулы (16) видно, что операция деления од-
ного комплексного числа на другое всегда возможна,
если делитель не равен нулю. В самом деле, будем
считать, что w и Z\ — заданные комплексные числа,
a z2 следует определить из уравнения w — ZiZ2. Тогда
из формулы (16) мы получаем
р2 = -^-. Фг = ф —Фь
”1
Формулу произведения (15) можно распростра-
нить на произвольное число сомножителей, применяя
эту формулу последовательно. Пусть
Z/= р/(cos ф; + г sin ф/), /=1, 2,...,я,
— последовательность комплексных чисел, a w —
= Ziz2... zn. Тогда мы имеем
а> — о (cos ф + i sin ф) ==
== Pi • • • Р« [cos (Ф1 + ... + Ф«) + i sin (ф1 + ... + ф«)].
В частном случае, когда все числа zi, z2, ..., z„ рав-
ны одному и тому же числу z, мы получаем важную
формулу
гп — о (cos ф + i sin ф) — р" (cos Яф + i sin яф). (17)
График функции. Если существует правило, по ко-
торому можно вычислить, зная число z, величину
W = f (z),
то говорят, что нам задана функция f(z) независи-
мого переменного z. Здесь w и z могут быть как дей-
ствительными, так и комплексными числами. В слу-
чае, если оба эти числа действительные, их обозна-
чают обычно через у и х, и функция y = f(x)
15
является действительной функцией действительного
переменного х. Такую функцию можно изобразить
геометрически на координатной плоскости в виде ли-
нии, которая называется графиком функции. Для
w этого каждому значению х независимого переменного
ставится в соответствие точка
г==(х,/(х)) (18)
координатной плоскости, абсциссой которой служит
х, а ординатой — величина f(x). Когда абсцисса х
пробегает все допустимые для нее значения, точка
(18) описывает линию, называемую графиком функ-
ции f(x).
Историческая справка
Математический анализ, основными понятиями ко-
торого являются производные и интеграл, прежде чем
принять современную форму, складывался и разви-
вался в течение очень длительного времени — не-
скольких столетий, а можно сказать, даже и тысяче-
летий. Во всяком случае в сочинениях Архимеда
(287—212 до н. э.) уже встречаются построения, ко-
торые можно теперь рассматривать как зачаточные
формы интеграла и производной. Архимед вычислил
площадь, ограниченную дугой параболы и куском ее
прямолинейной секущей, методом исчерпывания, т. е.
путем вписывания в эту фигуру последовательности
прямолинейных многоугольников, постепенно исчер-
пывающих всю площадь фигуры. Это построение с
современной точки зрения можно считать зачаточной
формой интегрирования. Следует заметить, что в ме-
тоде исчерпывания Архимед имел предшественников.
Архимедом также было произведено построение каса-
тельной к спирали, что с современной точки зрения
может рассматриваться как зачаточная форма диф-
ференцирования, т. е. нахождения производной.
В форме, уже содержащей основные алгоритмиче-
ские методы, дифференциальное и интегральное ис-
числение были созданы в XVII — начале XVIII сто-
летия Лейбницем (1646—1716) и Ньютоном (1643^»
1727). Лейбниц и Ньютон сделали свои открытия
почти одновременно независимо друг от друга. Но
оба они не спешили с публикациями, так как сами не
16
умели с достаточной четкостью осознать полученные
ими результаты. Созданные ими алгоритмы действо-
вали хорошо и давали надежные результаты, важные
для приложений, но не было ясного понимания того,
на чем основаны алгоритмы. Здесь имелся как бы
некоторый налет мистики. Кажется, в те времена
бытовало следующее высказывание: «Делай, вера при-
дет потом». Дело в том, что при определении скоро-
сти, т. е. производной по времени, использовалась та-
кая непонятная вещь, как мгновенный отрезок време-
ни. Этот таинственный мгновенный отрезок времени
был совершенно мал, именно, при некоторых вычис-
лениях его следовало заменять нулем, а при других
вычислениях такая замена была недопустима. Ско-
рость определялась как отношение длины пути, прой-
денного за одно мгновение времени, к протяженности
этого мгновения. Ясно, что при таком описании ско-
рости протяженность одного мгновения времени нель-
зя было считать равной нулю, так как тогда скорость
- .. о
записалась бы в виде бессмысленного выражения у-.
Но если при вычислении скорости длительность мгно-
вения времени обозначить буквой О, как это делал
Ньютон, то, проводя в этих обозначениях вычисление
отношения пройденного пути к длительности мгнове-
ния времени, в полученном результате следовало за-
менить букву, обозначающую длительность мгнове-
ния времени, нулем, и получался правильный резуль-
тат. Аналогичные трудности имелись и у Лейбница.
Выход из этих затруднений был найден Коши (1789—
1857), который ввел понятие предела. Сущность его
заключается в следующем. Рассматриваемый отрезок
времени не считается мгновенным, а имеет вполне ко-
нечную величину. Составляется отношение длины
пути, пройденного за это конечное время, к конеч-
ному отрезку времени, и в полученном выражении
длина отрезка времени начинает меняться, стремясь
к нулю. При этом смотрят, к какому пределу стре-
мится полученное отношение. Этот предел и являет-
ся скоростью, т. е. производной.
По мере того как развивалось дифференциальное
и интегральное исчисление, возникло и стало играть
очень большую роль еще одно новое понятие. Это
бесконечный ряд, т. е. сумма бесконечного числа
17
слагаемых, которую мы запишем в виде
+ %2 + • • • + + • • • (19)
Употребление таких сумм приводило большей частью
к правильным важным результатам, но иногда да-
вало и ошибочные результаты. Нужно было понять,
при каких условиях можно спокойно пользоваться
бесконечными суммами и какова числовая величина
бесконечной суммы. В качестве конкретной суммы,
вызывавшей недоумение, можно привести следующий
пример:
1-1 + 1-1 + ... (20)
Если подходить к этой сумме способом, привычным
для обычных сумм, то можно группировать члены, а
именно, можно объединить каждый член нечетного
номера со следующим за ним членом четного номера.
Каждая такая пара даст в сумме нуль, и, следова-
тельно, в результате сложения всех членов суммы
(20) мы получим нуль. Если, однако, выделить спер-
ва первый член, т. е. единицу, а затем группировать
каждый член четного номера с каждым членом нечет-
ного номера так, чтобы в результате этих комбина-
ций получались нули, то оказывается, что сумма (20)
равна единице. Существовала и такая точка зрения,
согласно которой сумма (20) равна 1/2. К этому мож-
но прийти из следующих соображений. Если считать,
что сумма (20) существует и равна s, то имеет место
очевидное равенство s= 1—s, откуда вытекает, что
s = 1/2. Вопрос с бесконечными рядами также раз-
решил Коши. Он точно определил, при каких усло-
виях сумму (19) можно рассматривать и чему равно
ее числовое значение. Именно, он составил предвари-
тельные суммы, положив
sn = 21 + z2 + ... + zn.
Таким образом, мы получаем бесконечную последо-
вательность предварительных сумм
Sl, S2> • • • > . . .
Если эта последовательность лисел стремится к не-
которому пределу $, то ряд (19) считается сходящим-
ся и сумма его считается равной числу s.
18
Роль рядов в математическом анализе особенно
подчеркивается рядом Тейлора (1685—1731). Ряд
Тейлора был получен Тейлором из одной конечно-
разностной формулы Ньютона. Огромное значение
ряда Тейлора заключалось в том, что все функции,
рассматривавшиеся в то время, могли быть записаны
в виде ряда Тейлора, так что возникло даже на неко-
торое время представление о том, что любая функ-
ция, во всяком случае по кускам, может быть пред-
ставлена при помощи ряда Тейлора. Но это представ-
ление было впоследствии полностью опровергнуто.
Новое направление в анализе возникло в связи
с рассмотрением комплексных функций комплексного
переменного. При изучении таких функций возникало
множество неясностей, но постепенно накапливался
материал при участии таких великих математиков,
как Эйлер (1707—1783) и Гаусс (1777—1855), и на-
копление этого материала привело к построению тео-
рии функций комплексного переменного или, что то
же самое, теории аналитических функций. Здесь ре-
шающие результаты принадлежат Коши. Он доказал,
что интеграл по замкнутому пути от комплексной
функции комплексного переменного равен нулю, если
внутри замкнутого пути нет никаких разрывов и осо-
бенностей рассматриваемой функции. Формулируя
эту замечательную теорему, Коши не указал на то,
что рассматриваемая функция должна иметь произ-
водную и даже непрерывную, но использовал это
предположение в процессе самого, доказательства.
Трудно предположить, что такое упущение является
ошибкой. Либо в то время считали, что дифференци-
руемость функции является столь естественным пред-
положением, что о нем даже не стоит говорить, либо
же думали, что все непрерывные функции имеют про-
изводную. Из этой теоремы Коши вывел свою ин-
тегральную формулу, позволяющую представить зна-
чение функции комплексного переменного при по-
мощи интеграла, взятого по замкнутому контуру.
Этими результатами Коши заложил основу теории
функций комплексного переменного — теорию, кото-
рая в современном анализе играет большую роль и
находит многочисленные приложения.
Глава I
РЯДЫ
В математике очень часто приходится рассматри-
вать суммы с бесконечным числом слагаемых или,
как их называют, бесконечные ряды. Такая сумма
или ряд записываются в виде
Z1 + z2 + • • • + za + . . (1)
где Zi, г2, ..., гп, ... суть действительные или комп-
лексные числа. В элементарной алгебре уже рассмат-
ривается один частный случай таких сумм. Это сум-
ма убывающей геометрической прогрессии, которая
записывается в виде
а + aq + aq1 + ... + aqn + ...,
где |^| <; 1. Устанавливается, что сумму такой гео-
метрической прогрессии можно рассматривать и она
равна
а
1 — я ’
Возникает вопрос, при каких условиях можно рас*
сматривать сумму общего ряда (1). Что здесь не все
ясно, показывает следующий пример. Рассмотрим ряд
1-1 + 1-1 + ... (2)
Если позволить себе оперировать с этой суммой, как
с обычной конечной суммой, то можно комбинировать
ее члены, образуя частичные конечные суммы, а за*
тем складывать полученные суммы вместе. Таким
образом, можно комбинировать члены ряда (2) по*
парно, складывая каждый член нечетного номера со
следующим членом четного номера. Каждая такая
20
сумма равна нулю, и, таким образом, мы приходим
к заключению, что сумма ряда (2) равна нулю. Но
если комбинировать члены по-другому, выделив пер-
вое слагаемое отдельно, а затем складывая четное
слагаемое со следующим нечетным, то каждая такая
сумма будет равна нулю, и у нас останется лишь пер-
вый член, так что сумма ряда (2) будет равна 1.
Отсюда видно, что обращаться с бесконечными ря-
дами совершенно непринужденно, как с конечными
суммами, невозможно. Необходимо прежде всего
точно определить, что следует понимать под суммой
ряда (1). Для этого точного описания составляют
так называемые предварительные конечные суммы.
Именно, полагают
Sn = Zt+Z2+ ... 4-Z„.
Сумма Зп зависит от номера п, и мы можем рассмат-
ривать ее поведение при п неограниченно возрастаю-
щем. Если при этом изменении п число sn стремится
к определенному пределу s, то считается, что ряд (1)
можно суммировать и сумма его равна s. Такие ряды
называются сходящимися. Оказывается, однако, что
и сходящиеся ряды обладают некоторыми странно-
стями, не присущими конечным суммам. Например,
может случиться, что если в сходящемся ряде (1)
расположить слагаемые в другом порядке, то мы
вновь получим сходящийся ряд, сумма которого, од-
нако, не равна сумме первоначального ряда. Для
того чтобы избежать этой и некоторых других стран-
ностей, из всех сходящихся рядов выделяют так на-
зываемые абсолютно сходящиеся ряды. Именно, ряд
(1) называется абсолютно сходящимся, если абсо-
лютные величины его слагаемых составляют сходя-
щийся ряд, т. е. если ряд
kt l + |z2|+... 4-|z„|+...
сходится. Доказывается, что сумма абсолютно сходя-
щегося ряда не зависит от порядка его слагаемых,
что абсолютно сходящиеся ряды можно перемножать
по тем же правилам, по каким перемножаются конеч-
ные суммы, и т. п. Таким образом, оказывается, что
над абсолютно сходящимися рядами можно довольно
свободно производить вычисления и получать при
этом правильные результаты.
21
Ряды важны, в частности, потому, что, пользуясь
ими, можно вычислять некоторые важные для мате-
матики числа. Так, например, известна формула
Т"1 Т • • • • + "27-1 + ••• (3)
Таким образом, пользуясь рядом (3), можно с любой
точностью вычислить число л. Следует, однако, отме-
тить, что это не есть наилучший способ вычисления
числа л, так как ряд (3) сходится очень медленно.
Не менее важно вычисление функций при помощи
рядов. Именно, если члены ряда (1) являются функ-
циями действительного или комплексного перемен-
ного z, то в случае сходимости ряда сумма его опре-
деляет некоторую функцию f(z). Именно, мы имеем
f(z) = z1(z) + z2(z) + ... +zn(z)+ ... (4)
Здесь следует отличать две существенно различ-
ные возможности. Может случиться, что некоторая
функция f(z), известная нам из каких-то других со-
ображений, разлагается в ряд (4).
Тогда этот ряд помогает нам вычислить известную
нам функцию. Вторая возможность заключается в
том, что функция f(z) сама определяется рядом (4).
Исходя из задания ее формулой (4), мы можем изу-
чать различные важные для нас свойства функции
/(г).
Особенно важным частным случаем рядов, члены
которых являются функциями переменного z, являют-
ся так называемые степенные ряды, т. е. ряды вида
а0 + a\z + a2z2 + ... + anzn + ..., (5)
где коэффициенты а0, а\, ... ап, ... суть заданные
числа, a z — действительная или комплексная пере-
менная. Было обнаружено, что очень многие играю-
щие важную роль в математике функции задаются
степенными рядами, т. е. записываются в виде (5).
Одно время существовало даже предположение, что
каждую функцию можно задать при помощи степен-
ного ряда, если не целиком, то по кускам. Это пред-
положение оказалось, однако, совершенно неверным.
В последнем параграфе этой главы тщательно
изучаются функции, задаваемые рядами вида (5) для
комплексного переменного z. Наиболее интересное
22
свойство, установленное там, следующее. Очевидно#
что ряд (5) сходится при z = 0. Может случиться,
что он сходится только в этом случае. Отбрасывая
этот тривиальный случай, рассмотрим ряд, который
сходится и при некоторых значениях z=#0. Тогда для
этого ряда определяется так называемый радиус схо-
димости г > 0. Оказывается, что для всех значений
2, для которых |z|<r, ряд (5) сходится и притом
абсолютно, а при всех значениях |г|> г ряд (5)
расходится. Таким образом, функция f(z) задается
рядом (5) для всех значений z, для которых |z|< г.
Случай г = оо не исключается. Если г = оо, ряд (5)
сходится при всех значениях z и определяет функцию
f(z) на всей плоскости комплексного переменного z.
Одна очень важная для анализа функция, зада-
ваемая степенным рядом, рассматривается и изучает-
ся в § 7. Эта функция ехр(г) комплексного перемен-
ного г задается рядом
exp(2)=l+i + -j^+....+i.+ ... (6)
Этот ряд сходится для всех значений г, так что
функция ехр(г) определена на всей плоскости комп-
лексного переменного z. На основании ее изучения
в § 7 доказываются два ее важных свойства. При
действительном значении z = х мы имеем равенство
ехр (х) — ех. (7)
При чисто мнимом z = iy мы имеем равенство
exp (iy) — cos у 4- i sin у. (8)
Из формул (6), (7) и (8) непосредственно получает-
ся разложение в степенные ряды основных транс-
цендентных функций ех, cosy, sin у для действитель-
ных значений аргументов.
При разложении некоторой функции f(z) в степен-
ной ряд мы сталкиваемся с двумя различными под-
ходами к вопросу. При первом подходе мы имеем
каким-то образом заданную функцию f(z), а затем
доказываем, что она разлагается в степенной ряд.
Для того чтобы доказать это, надо показать, что
степенной ряд при дйнном значении z сходится к
числу f(z). При другом подходе мы задаем функцию
f(z) степенным рядом. Для доказательства того, что
23
такое задание законно, мы должны доказать, что сте-
пенной ряд сходится. При втором подходе мы долж-
ны пользоваться признаком сходимости и иметь до-
вольно ясное представление о том, что называется
действительным числом. Изложению этих довольно
тонких вопросов посвящены первые параграфы
главы I.
§ 1. Сходящиеся последовательности чисел
Сходящиеся последовательности чисел играют в
математике весьма важную роль.
Говорят, что последовательность действительных
чисел
$1» • • • » ®п» • • • (О
сходится к числу s или имеет своим пределом число s,
если при возрастании номера п число sn неограни-
ченно приближается к числу s. В этом случае пишут
lim sa — s. (2)
П->оо
В частном случае, когда число s — 0, т. е. когда по-
следовательность (1) сходится к нулю, величину sn,
являющуюся функцией целого числа п, называют
иногда бесконечно малой. Было бы правильнее на-
звать ее бесконечно умаляющейся, так как речь идет
здесь о процессе приближения к нулю числа sn при
возрастающем п.
Ясно, что соотношение (2) и соотношение
lim (sn — s) = 0 (3)
П->оо
равносильны. В самом деле последовательность (1)'
сходится к s тогда и только тогда, когда последова-
тельность
s;=s2-s, ..., s;=s„-s,....
сходится к нулю. Если соотношение (3) имеет место,
то величина s' является бесконечно малой. Таким
образом, изучение процесса сходимости в значитель-
ной степени сводится к изучению бесконечно малых
величин.
24
Десятичные дроби. Для того чтобы проиллюстри-
ровать процесс сходимости на знакомых примерах,
обратимся к бесконечным десятичным дробям, изве-
стным из арифметики.
Выпишем бесконечную десятичную дробь
0,999... (4)
Здесь после нуля и запятой идет бесконечная после-
довательность девяток. Из арифметики хорошо изве-
стно, что эта десятичная дробь равна 1. Точный мате-
матический смысл этого утверждения основан на рас-
смотрении бесконечной последовательности
«! = 0,9, s2 = 0,99, ..., «„,... (5)
Здесь s„ есть конечная десятичная дробь, в которой
после нуля и запятой следует ровно п девяток. Легко
вычисляется, что для последовательности (5) мы
имеем
sn 1 Юл
Легко доказать, пользуясь обычной десятичной
1 -
записью целого числа, что —црг есть бесконечно
малая величина, а это значит, что последовательность
(5) сходится к 1. В этом и состоит точный смысл
утверждения, что бесконечная периодическая дробь
(4) равна 1.
Разберем еще один пример бесконечной десятич-
ной дроби
0,333... (6)
Здесь после нуля и запятой идет бесконечная после-
довательность троек. Эта бесконечная десятичная
дробь получается, когда мы переводим обычную
дробь -£ в десятичную дробь путем деления. В про-
цессе этого деления мы последовательно получаем
числа
Si==0,3, S2 = O,33, ...,sn, ... (7)
Здесь sn есть конечная десятичная дробь, в кото-
рой после нуля и запятой следует ровно п троек.
25
Легко вычислить, что для последовательности (7)
мы имеем
, _ 1 _ 1
sn sn з 3 • 10га *
„ , 1 л
Величина sn~ —3.10п . очевидно, является беско-
нечно малой, и поэтому последовательность (7) схо-
дится к рациональному числу у. В этом и заклю-
чается точный смысл утверждения, что бесконечная
десятичная дробь (6) равна рациональному числу -j.
Обе рассмотренные нами бесконечные десятичные
дроби (4), (6) были вполне конкретными и периоди-
ческими. Рассмотрим теперь случай общей бесконеч-
ной десятичной дроби, которую мы запишем в виде
(8)
Здесь после нуля и запятой стоят цифры fi, fz, fz,...,
каждая из которых может иметь любое значение от
О до 9. Составим последовательность конечных деся-
тичных дробей, соответствующую десятичной
дроби (8),
Si==0, fi, s2 = 0Jif2, .... s„, ... (9)
Здесь sn есть конечная десятичная дробь, в которой
после нуля и запятой стоят цифры fit ft, ..., fn- Из-
вестно, что если бесконечная десятичная дробь (8)
периодическая, то последовательность чисел (9) схо-
дится к некоторому рациональному числу s. Именно,
I I = I S I JQ« ’
так что s' есть бесконечно малая величина. В этом
и заключается смысл утверждения, что бесконечная
десятичная дробь (8) равна рациональному числу s.
Но если десятичная дробь (8) не периодическая, то
не существует рационального числа $, к которому схо-
дится последовательность чисел (9). Таким образом,
в этом случае следует поставить вопрос, можно ли
считать бесконечную десятичную дробь (8) числом.
Несомненно, что потребность в таких числах есть,
В геометрии мы встречаем такие линии, длины кото-
рых выражаются бесконечными непериодическими де-
26
сятичными дробями. Примерами могут служить: 1) ги-
потенуза прямоугольного треугольника, катеты кото-
рого равны 1; ее длина обозначается теперь через
д/2;2) длина окружности диаметра ^обозначаемая
через л. Если мы будем вычислять л/2 по обычным
правилам извлечения корней, то получим бесконеч-
ную непериодическую десятичную дробь вида (8),
причем последовательность чисел (9) в естественном
смысле сходится к л/2. Именно, последовательность
чисел
сходится к числу 2.
Аналогичное положение вещей имеет место также
и для числа л. Эти два примера показывают, что по-
требности геометрии не могут быть удовлетворены
рациональными числами. Приходится признать су-
ществование чисел, не являющихся рациональными.
Их называют иррациональными. Таких нужных для
математики иррациональных чисел можно указать,
конечно, не только два, но произвольно много. Перед
нами возникает задача описать все нужные для ма-
тематики числа. Ключом к решению этой задачи мо-
жет послужить изучение сходящихся последователь-
ностей чисел. Изучением процесса сходимости в этом
аспекте мы займемся в § 3.
Формальное определение сходимости. Сказанное
до сих пор дает достаточно полное интуитивное пред-
ставление о том, что такое сходимость. Дадим теперь
формальное общепринятое определение.
Определение. Говорят, что последователь-
ность действительных чисел
, Si, s2, ..., sn, ... (10)
сходится к числу s, если для всякого положительного
числа 8 найдется такое натуральное число v, завися-
щее от 8, что при п > v мы имеем неравенство
|s„ — s | < е. (11)
Для того чтобы лучше уяснить себе процесс схо-
димости, перейдем к геометрической интерпретации.
Каждое из чисел sn последовательности (10) изобразим
27
геометрически на оси абсцисс точкой sn, абсцис-
са которой равна числу sn. Точно так же поступим и
с числом s. Ему мы поставим в соответствие точку s,
абсцисса которой равна числу $. Обозначим теперь
через Ue совокупность всех таких точек х оси абсцисс,
для которых имеет место неравенство
|х — s| < 8. (12)
Здесь х обозначает не только точку, но и величину
ее абсциссы. Интервал Ue называется е-окрестностью
точки s. Из определения сходимости непосредственно
следует, что последовательность точек (10) сходится
к точке s тогда и только тогда, когда окрестность
при произвольном положительном в содержит все
точки последовательности (10), за исключением, быть
может, конечного их числа.
Доказательство этого утверждения не представ*
ляет трудности, и я не буду его здесь проводить. Об*
разно можно сказать, что точки последовательности
(10) скопляются в своей основной массе около точки s.
В рассмотренных нами двух примерах периодиче*
ских десятичных дробей (4), (6) числа si, «2, S3, ...
шли в возрастающем порядке и все были меньше
предельного числа s. Это, конечно, не обязательно.
Числа последовательности (10) могут частично быть
меньше s, частично больше s и частично даже совпа-
дать с самим числом s. Может случиться также, что
некоторые числа последовательности (10), имеющие
разные номера, в действительности равны между со-
бой. Крайним случаем такого рода является тот, ког-
да все числа последовательности (10) равны между
собой. В этом случае нет постепенного приближения
точки sn к точке s с ростом п, а есть стояние точки
sn на одном месте s. Но, согласно определению схо-
димости, и при этих условиях последовательность
(10) сходится к числу s.
Случай комплексных чисел. Все сказанное до сих
пор о сходимости относится к последовательностям
действительных чисел. Вопрос о сходимости последо-
вательностей комплексных чисел также важен. Од-
нако случай комплексных чисел полностью сводится
к случаю действительных чисел и в нем нет ничего
принципиально нового.
28
Переходя к комплексному случаю, выпишем по-
следовательность
ri=Si + tfi, Г2 = S2 + it2, ...» Гп — sn~}~ Мп* ••• (13)
комплексных чисел. Считается, что последователь-
ность (13) комплексных чисел сходится к комплекс-
ному числу г = s + it или имеет предел г,
Ymrn = r = s + it, (14)
п->оо
если последовательность действительных чисел
• I Г\ — Г |, I Г2 — Г I, ..., | гп — г I, . . .
сходится к нулю, т. е. если
lim| г„ — г | = 0, (15)
П-Х»
так что соотношения (14) и (15) равносильны.
Заметим, что это определение сходимости для по-
следовательности (13) комплексных чисел в случае,
если все эти комплексные числа оказываются дей-
ствительными, совпадает с определением, которое
было дано в начале параграфа для случая действи-
тельных чисел.
Если предел г последовательности (13) равен
нулю, то комплексная величина гп, зависящая от це-
лого числа п, называется бесконечно малой или, точ-
нее, бесконечно умаляющейся. Ясно, что соотношение
(14) имеет место тогда и только тогда, когда вели-
чина
г' — г„ — г
п п
является бесконечно малой.
Заметим еще, что соотношение (14) равносильно
одновременному выполнению двух соотношений
lims„ = s, lim/„ = t
rt->OO n->oo
Доказательство этого не представляет трудности, и я
его здесь не привожу. Для придания вопросу о схо-
димости последовательности (13) комплексных чисел
геометрической наглядности изобразим числа этой по-
следовательности и число г в виде точек на плоско-
сти Р комплексного переменного. Обозначим через
£/« (е > 0) круг на плоскости Р с центром г и радиусом
29
е, т. е. совокупность всех точек z плоскости Р, удовлет-
воряющих условию
| Z — Г I < 8.
(16)
Круг иг называется е-окрестностью точки г пло-
скости Р. Ясно, что последовательность (13) сходится
к г тогда и только тогда, когда при произвольном по-
ложительном 8 все точки последовательности (13),
за исключением, быть может, конечного числа их,
принадлежат окрестности UQ.
Подпоследовательность. Если из некоторой после-
довательности действительных или комплексных чи-
сел
Г1, Г2, ..гп, ... (17)
выбрать некоторую бесконечную часть ее членов и
расположить выбранные члены в том же порядке, в
котором они стоят в последовательности (17), то мы
получим новую последовательность, которая назы-
вается подпоследовательностью исходной последова-
тельности (17). Эта подпоследовательность всегда мо-
жет быть записана в следующем виде:
nf n2 nk v 7
где номера
Пь п2, ..nk) ...
составляют некоторую последовательность натураль-
ных чисел, расположенных в возрастающем порядке;
часто члены последовательности (18) бывает нужно
обозначить новыми буквами с новыми индексами так,
чтобы эти новые индексы принимали значения 1, 2,
3, ..., А, ... Для этого полагают, например,
/ — , г' = г , ..., г' = г„ , ...
Очевидно, что если исходная последовательность
(17) сходится к числу г, то и ее подпоследователь-
ность (18) также сходится к числу г. Таким обра-
зом, из
limr„ = r
П->ОО
следует, что
Пт г = limr' = r.
k-*<x> fe->oo й
30
Однако очень часто бывает, что исходная последова-
тельность (17) не сходится, но из нее можно выбрать
некоторую сходящуюся подпоследовательность. Это
обстоятельство будет играть впоследствии существен-
ную роль.
Основные правила теории пределов. Отметим те-
перь некоторые простые свойства бесконечно малых
величин. Мы будем говорить о комплексных величи-
нах, помня все время, что действительные являются
их частным случаем. Выпишем последовательность
комплексных чисел
Cj, C2t ♦ • •, Сп, . . •
Эта последовательность называется ограниченной,
если существует такое положительное число с, что
для произвольного п мы имеем
(19)
Если соотношение (19) имеет место, а гп есть беско-
нечно малая величина, т. е. такая, что
limr„ = 0,
П->°°
то и величина спгп также бесконечно мала, т. е.
lim спгп = 0.
И->оо
Доказательство этого факта не представляет никаких
трудностей. Отметим еще, что сумма и разность двух
бесконечно малых величин есть также бесконечно ма-
лая величина.
Пользуясь этими простыми замечаниями относи-
тельно бесконечно малых величин, мы можем дока-
зать пять основных правил теории пределов.
Выпишем две последовательности комплексных
чисел
zi, z2, ..., z„... (20)
wi, w2, .... wn, ... (21)
Мы предположим, что последовательности (20) и
(21) сходятся соответственно к числам г и w, т. е.
lim zn = z, lim wn = w.
n-^oo »->oo
(22)
31
Правило 1.
lim (z„ + wn) = z + w,
или словами: предел суммы равен сумме пределов.
Правило 2.
lim (z„ — wn) = z — w,
П~*°О
или словами: предел разности равен разности преде-
лов.
Правило 3.
lim znwn = zw,
П->оо
или словами: предел произведения равен произведе-
нию пределов.
Правило 4. Если до =/= 0, то
lim-
П“>оо
zn
Wn
z
w ’
или словами: предел частного равен частному преде-
лов в случае, если предел делителя не равен нулю.
Правило 5. Если величины zn и доядействитель-
ные и
2п < до„, (24)
то z до, т. е. при знаке «меньше или равно» можно
переходить к пределу. Следует подчеркнуть, что из
неравенства zn <. wn не следует z < до.
Доказательство этих правил не представляет труд-
ностей, и я приведу здесь только наиболее сложные
доказательства правил 4 и 5.
Положим
Zn = z-b^n, доп = до + доп- (25)
Здесь &п и дол являются бесконечно малыми величи-
нами. Мы составим разность
В первой дроби заменим гп и дол по формулам (25).
Тогда мы получим
z-V г ________ zw + ~ zwn ____ 2nw — zti>n
W + Wn W (w + Wn) W (W + Wn) w *
82
Числитель последней дроби есть величина бесконечно
малая, а величина -fozpa j-д, является величиной,
ограниченной при достаточно большом п, так как
w ф 0. Таким образом, вся разность (26) есть вели-
чина бесконечно малая, и, следовательно, формула
(23) доказана.
Докажем правило 5. Учитывая обозначения (25),
перепишем соотношение (24) в виде
Wa — z„ = (w + wn) — (z + 2„) > 0,
или, иначе,
(w — z) + (te>„ — 2„)>0. (27)
Так как величина u>a — zn бесконечно мала, то из со-
отношения (27) выходит, что число w — г не может
быть отрицательным. Действительно, если бы оно
было отрицательным, то ввиду бесконечной малости
числа wn — Zn число wn — zn оказалось бы отрица-
тельным при достаточно большом п.
В нижеследующих примерах даются понятия, ко-
торые используются лишь в дальнейшем. Поэтому
изучение их разумно отложить до момента, когда на
них появятся ссылки.
Пример 1. В школьном курсе математики те-
перь уже дается понятие функции.
Напомню его здесь: величина w считается функ-
цией величины z, что записывается в виде формулы
w = f (2), если, зная числовое значение величины г,
мы можем вычислить соответствующее ему числовое
значение w — f(z). Примером функции может слу-
жить многочлен w — f(z)= aozk -j- aizk~l + .., a*,
где k — натуральное число. В математическом ана-
лизе играют большую роль так называемые непре-
рывные функции. В книгах по анализу им обычно
уделящт очень много места. Не желая придавать не-
прерывным функциям чрезмерно большое значение, я
само определение непрерывной функции даю лишь в
примере, не отделяя друг от друга комплексный и
действительный случаи.
Определение. Функция f(z) называется не-
прерывной для значения z = z0 ее аргумента, если,
какова бы ни была последовательность
zb z2, .... z„, ...
2 Л. С. Понтрягин
33
значений ее аргумента, из соотношения
lim zn — z0 (28)
П->оо
следует соотношение
lim f (zn) == f (zq). (29)
П->оо
Функция f(z) называется непрерывной, если она не-
прерывна для каждого значения ее аргумента.
Из правил 1—4 теории пределов следует, что если
f(z) и g(z) — две функции, непрерывные для значе-
ния z — Zq их аргументов, то функции
f(z) + g(z), f(z) — g(z), f(z)g(z), (30)
также- непрерывны при z = Zq. Последнее из соотно-
шений (30) верно, однако лишь при условии, что
g(zo)#=0. Из непрерывности произведения функций
непосредственно следует и непрерывность степени
[f(z)]ft, где k — натуральное число.
Так как функции f(z)=z и f(z)=c, где с — по-
стоянная, очевидно, непрерывны, то из сказанного
следует, что произвольный многочлен
<p(z) = o0zft + aizft~1 + ... +ak
является непрерывной функцией. Далее, если ф(гУ
„ <p(z)
есть другой многочлен, то частное непрерывно
для каждого значения z = zq, для которого ф (zo) =# 0.
Пример 2. Приведем примеры разрывных, т. е.
не непрерывных функций.
Определим действительную функцию f(x) действи-
тельного переменного х условиями
f(x)=l при х > 0,
f (х) = — 1 при х < 0.
(График этой функции см. на рис. 4.) Этими соот-
ношениями функция f(x) не определена при х = 0.
Если считать, что она задана только для положи-
тельных и отрицательных значений, но не определена
при х = 0, т. е. значение х = 0 не является допусти-
мым значением ее аргумента, то функция f(x), со-
гласно определению, оказывается непрерывной. Это
легко проверить. Возникает вопрос, можно ли при-
34
дать функции f(x) какое-нибудь значение при х = О,
т. е. выбрать число f(0) так, чтобы полученная функ-
ция, определенная уже для всех действительных х,
была непрерывной. Ясно, что i
это невозможно. Действитель- у----;-----
НО, ПУСТЬ Xi, х2, ..., хп, ... —
последовательность положи-
тельных чисел, сходящаяся к_____________________
нулю. Тогда ?(хп)— 1 и в си- °
лу определения непрерывно-
сти мы должны были бы иметь__________
f(0)= 1. Точно так же, исхо-
дя из последовательности Рис 4
Xi, х2, ..., хя, ... отрицатель-
ных чисел, сходящейся к нулю, мы пришли бы к вы-
воду, что f(0)=—1. Таким образом, доопределить
функцию f(x) (см. (31)) для значения х = 0 так,
чтобы она стала непрерывной, невозможно.
Рассмотрим действительную функцию sin 4* дей-
ствительного переменного х. Эта функция так же, как
Рис. 5.
и предыдущая функция, определена только для поло-
жительных и отрицательных значений х. Считая из-
вестным, что функция sin <р непрерывна, легко дока-
зать, что функция sin заданная лишь для поло-
жительных и отрицательных значений х, также не-
прерывна. Но невозможно доопределить ее для х = О
так, чтобы полученная функция была непрерывна
при всех действительных значениях х. Для того что-
бы убедиться в этом, полезно представить себе гра-
фик функции у = sin -7- (рис. 5).
X
2*
35
Пример 3. Здесь мы будем говорить о комп»
лексных числах, отождествляя их с точками плоско»
сти Р комплексного переменного z. Как уже было
сказано (см. (16)), е-окрестностью точки г плоско»
сти Р или, что то же самое, окрестностью радиуса е,
где е положительно, называется множество t/8 всех
таких точек z плоскости Р, для которых имеет место
неравенство
|z — г | < е.
Таким образом, окрестность Ue есть круг радиуса в
с центром в точке г, к которому, однако, не причис»
лены его граничные точки. Если М есть некоторое
бесконечное множество точек плоскости Р, то точка г
называется его предельной точкой при условии, что
каждая окрестность точки г содержит бесконечное
множество точек из М. Если множество М содержит
лишь действительные числа, то очевидно, что пре-
дельная его точка г также есть действительное число.
В самом деле, если г = $ + it и / #= 0, то окре-
стность точки г, очевидно, не содержит действи-
тельных чисел и поэтому точка г не может быть пре-
дельной точкой для множества М, лежащего на дей-
ствительной оси плоскости Р.
Докажем теперь, что если г — предельная точка
для множества М, то в множестве М можно найти
последов ател ьн ость
П, г2, ..., гп, ..(32)
содержащую бесконечное множество различных то-
чек, сходящуюся к точке г. Для построения последо-
вательности (32) обозначим через U\/n окрестность
точки г радиуса —, где п — произвольное натураль-
ное число, и выберем из окрестности U\/n точки г не-
которую точку гп, отличную от точки г. Полученная
так последовательность точек (32) сходится к г.
Множество М называется замкнутым, если каж-
дая его предельная точка принадлежит ему. Так, на-
пример, отрезок, т. е. множество всех чисел, удовлет-
воряющих неравенству а х Ь, есть замкнутое
множество.
36
§ 2. Бесконечно малые величины
В первом параграфе разъяснялось, что означает
утверждение, что последовательность
ГЪ r2t ..., г„, ...
сходится к числу г. Это утверждение в виде формулы
записывается так:
lim rn = г. (1)
П->оо
Это было сделано как для последовательности дей-
ствительных чисел, так и для последовательности
комплексных чисел. По самому определению соотно*
шение (1) равносильно соотношению
lim | — г 1 = 0.
п->оо
Так как числа |гп — г| не отрицательны, то, для того
чтобы научиться умело и непринужденно пользовать-
ся сходящимися последовательностями, нам нужно
прежде всего научиться легко и почти автоматически
узнавать, является ли данная положительная вели-
чина sn, зависящая от натурального числа п, беско-
нечно малой или нет. Как было указано в § 1, вели-
чина sn считается бесконечно малой тогда и только
тогда, когда для нее выполнено соотношение
lim sn = 0.
П-*оо
Здесь мы рассмотрим несколько типичных, часто
встречающихся в анализе бесконечно малых величин,
которые надо научиться распознавать с той же лег-
костью, с какой мы пользуемся таблицей умножения.
Основной прием распознавания бесконечно малых ве-
личин заключается в сравнении новых, не встречав-
шихся ранее бесконечно малых величин с уже из-
вестными и хорошо зафиксированными в памяти.
Знаки Ойо. Основной прием сравнения двух ве-
личин sn и tn заключается в рассмотрении их отно-
f
шения -у- с точки зрения поведения этого отноше-
ния при п, неограниченно возрастающем. Здесь
имеются два важных случая, для которых в анализе
даже заведены специальные обозначения.
37
1. Величина — является ограниченной. Это зна-
sn
чит, что существует такая константа с, что
при произвольном п. В этом случае пишут
^п===^($/г)' (2)
2. Величина — является бесконечно малой, или,
что то же самое,
lim —= 0.
П->оо
В этом случае пишут
tn = О (sn). (3)
Ясно, что из соотношения (3) следует соотноше-
ние (2). В самом деле, если отношение стремится
к нулю при п->оо, то очевидно, что отношение это
остается ограниченным при всех значениях п.
Знаки Ойо удобны в употреблении. Ими часто
пользуются в анализе, и следует хорошо запомнить
их смысл.
Если величина sn бесконечно мала, то из соотно-
шения (2) следует, что и величина tn также беско-
нечно мала. Если величина sn бесконечно мала и
имеет место соотношение (3), то можно сказать, что
величина tn стремится к нулю быстрее, чем величина
sn. Соотношения (2) и (3) часто употребляют, когда
sn есть 1, т. е. когда последовательность чисел
<$2, • • •, sn, ... есть последовательность единиц. В этом
случае соотношения (2) и (3) записываются в виде
6г = 0(1), (4)
6. = о(1). (5)
Легко видеть, что соотношение (4) означает про-
сто, что величина tn ограничена, а соотношение (5)
означает просто, что величина tn является бесконечно
малой.
Величину tn часто сравнивают не с самой величи-
ной sn, а с ее степенью. Если имеет место соотноше-
ние
38
где sn есть бесконечно малая величина, a k — нату-
ральное число, то говорят, что величина tn имеет
порядок малости k относительно величины sn. Рас-
смотрение величин разных порядков малости относи-
тельно заданной бесконечно малой величины sn иг-
рает в анализе важную роль.
Наряду с бесконечно малыми в анализе рассмат-
риваются также и бесконечно большие величины. Ве-
личина sn называется бесконечно большой, если с
ростом п число |sn| неограниченно возрастает, т. е.
если для каждого положительного числа с найдется
такое натуральное число v, что при п > v мы имеем
1 Sn I > С.
В этом случае пишут
lims„ = oo. (6)
П->оо
Знак lim имеет здесь несколько иной смысл, чем в
случае, когда в правой части соотношения типа (6)
стоит конечное число.
Иногда бывает полезно рассматривать две взаим-
но обратные величины sn и tn, т. е. величины, свя-
занные соотношением
Sn^n = 1 •
Ясно, что в этом случае величина tn бесконечно мала
тогда и только тогда, когда величина sn бесконечно
велика. Таким образом, соотношения
lim sn = со, lim tn = 0 (7)
П->00 П->оо
равносильны, когда sn и tn взаимно обратны.
Простейшим примером бесконечно большой вели-
чины является величина sn = п. Таким образом, из
(7) следует, что — есть бесконечно малая вели-
чина. Запишем это. формулами
limn = оо, lim ^- = 0.
n->oo n->00 n
Бином Ньютона. Для установления того, что неко-
торая конкретная величина является бесконечно боль-
шой или бесконечно малой, в случаях более слож-
39
ных, чем для величин $„ = п, , приходится
употреблять некоторые алгебраические формулы,
среди которых важнейшую роль играет известная
формула «бинома Ньютона». Несмотря на то, что
формула эта входит в элементарную алгебру, я про»
веду здесь ее доказательство заново.
Прежде всего напомню обозначение:
n! = 1 • 2 • ..• п.
Таким образом, п! есть произведение всех целых чи»
сел, начиная от 1 до п. Формально считают, что
0! = 1.
Формула Ньютона дает разложение n-й степени дву-
члена z + w в виде многочлена по степеням г и w.
Она имеет вид
(*+*- Е (8)
р. 9>0
P+q-n
Здесь знак £ означает, что мы должны взять
р, <7>0
p+q-n
сумму всех членов, стоящих после него, по всем це-
лым неотрицательным р и q, для которых р 4- q » п,
Формулу мы докажем индуктивно. Прежде всего,
очевидно, что она верна при п=1. Действительно,
мы имеем
z I м 1! I Н
(2+^ = -ho|2 + W№.
Допустим теперь, что формула (8) верна для п =>
— k— 1, и докажем, что тогда она верна для n — k.
Для этого сосчитаем произведение (г4-щ)*-1(г +
+ о>). При этом подсчете мы будем предполагать,
что первый множитель (г 4- выписан по фор-
муле (8). Он содержит все члены вида
где I, j — целые неотрицательные числа, причем i 4-
+ j = k—l.
При умножении члена (9) на z мы получаем член,
содержащий множитель zi+'wi. При умножении члена
(9) на w мы получаем член, содержащий множитель
40
zlww. Для того чтобы эти два члена
между собой и содержали множитель
чтобы при умножении на z мы имели
х i — j = q,
а при умножении на w должно быть
i = q — 1.
Подсчитывая коэффициенты при обоих этих членах
и суммируя их, получаем
(k- 1)! , (k- 1)!
(p-l)lql р! (^ — 1)! *
Приводя оба члена к общему знаменателю путем ум-
ножения числителя и знаменателя первого слагае-
мого на р, а числителя и знаменателя второго ела*
гаемого на q, мы получаем в сумме
(А>-1)!р + (*?-1)1? = (fe-l)!(p + ?)^ fe!
Pty! pip! p'p! ’
Таким образом, для п = k формула (8) оказывается
доказанной, так как индуктивное доказательство ее
полностью проведено.
Выпишем теперь коэффициент в несколько
иной форме, разделив числитель и знаменатель на р\<
Тогда мы получим следующую формулу:
+ ^1~1)УУ + ... +
+ п(п - 1 b Л» - ?+ + t . + (10)
В этом виде формула Ньютона (8) обычно и дается
в элементарной алгебре.
Конкретные бесконечно малые величины. Перей«
дем теперь к рассмотрению некоторых наиболее
важных для анализа конкретных положительных бес'
конечно малых и бесконечно больших величин или,
что то же самое, последовательностей, сходящихся
к нулю, и последовательностей, неограниченно воз«
растающих. Те и другие, как уже было отмечено (см.
(7)), взаимно связаны друг с другом.
41
Первое место по значению занимает геометриче-
ская прогрессия
1, а, а2, ..., а", ..., (11)
где а — положительное число. Оказывается, что при
а < 1 последовательность (11) сходится к нулю, или,
что то же самое, ап есть бесконечно малая величина,
а при а> 1 последовательность (11) неограниченно
возрастает, или, что то же самое, а" есть бесконечно
большая величина. В виде формул это запишем так:
lima" = 0 при а<1, (12)
П->00
lim ап=оо приа>1. (13)
п->оо
Докажем соотношения (J2) и (13). Прежде всего
ясно, что они равносильны друг другу. Действитель-
но, положим 0 —и составим последовательность
1,0, 02, ..., 0V-. (14)
Последовательности (И) и (14) взаимно обрат-
ны, следовательно (см. (7)), из того, что одна из них
сходится к нулю,, следует, что другая неограниченно
возрастает. Сопоставив это с. тем. фактом, что если
одно из чисел а. или 0 меньше. 1, то другое из них
будет больше I, мы убеждаемся в том, что утверж-
дения (12) и (13) эквивалентны. Таким образом,
для доказательства соотношений (12) и (13) нам до-
статочно доказать лишь одно из них.
Докажем соотношение (13). Так как а>1, то
мы можем записать число а в. виде
а = 1 +6,
где б— положительное число. Отсюда в силу фор-
мулы (10) следует
a” = (l 4-6)"= 1+«&+ ....
где в правой части не выписано несколько положи-
тельных членов. Таким образом, мы имеем
ап > п&.
В силу положительности числа б величина п8 неог-
раниченно растет при возрастании п; то же самое
42
имеет место и для Таким образом, соотношение
(13) доказано, а вместе с ним доказано и соотноше-
ние (12).
Итак, доказано, что при 0 < а < 1 величина ап
является бесконечно малой. Эта бесконечно малая
величина очень часто служит в анализе эталоном
сравнения. Поэтому соотношение (12) нужно твердо
помнить, чтобы можно было употреблять его, не за-
думываясь.
Пользуясь тем же приемом, который был упот-
реблен нами для доказательства соотношений (12)
и (13), мы можем доказать более сильные соотно-
шения^ имеете.,
Iim^-«oo (15)
П>оо ПЯ
при а > 1, где k — произвольное натуральное число.
Переходя к обратным величинам, получаем другое
соотношение
limn*an = 0 (16)
П->оо
при а < 1, где k — произвольное натуральное число.
Словами первое из этих соотношений (15) можно
выразить, сказав, что при а > 1 величина <ха стре-
мится к бесконечности быстрее, чем величина п*,для
произвольного натурального числа k. Второе из этих
соотношений можно выразить, сказав, что при а <. 1
величина а" стремится к нулю быстрее, чем величина
—Ь, где k — произвольное натуральное число.
пя
Так же, как при доказательстве соотношений
(12) и (13), мы докажем только соотношение (15),
т. е. рассмотрим случай а > 1. Тогда мы имеем
а= 1+6,
где 6 — положительное число. Мы имеем
О"=(1 + 67 = ] + ... + ”(re~(24.‘y(”-"fe-6fe+1 +...
Здесь в правой части не выписано несколько поло-
жительных членов. Рассмотрим отдельно коэффи-
циент
п (п — 1) ... (п — /г)
а (7+Т)!
43
В числителе правой части здесь стоит k 4-1 множи-
тель. В предположении, что п > 2 k, каждый из этих
множителей больше чем , так что мы имеем
> 1 6к+'__________п 6fe+1
пк пк \ 2 ) (k + 1)! 2ft+l (й + l)t
Таким образом, при неограниченно возрастающем п
ап
величина — неограниченно возрастает, и поэтому
соотношение (15) доказано. Отсюда следует, что и
соотношение (16) также верно.
Утверждение (16) можно существенно усилить,
показав, что величина nkan не только является бес-
конечно малой, но стремится к нулю быстро, — имен-
но, быстрее, чем члены некоторой убывающей гео-
метрической прогрессии. Докажем это. Так кака< 1,
то существует число у, заключенное между а и 1, т. е.
а < у < 1.
_ ь ап ь (а х
Тогда величина п —— = п I — I является бес-
Y х Y /
конечно малой, так как < I (см. (16)). Отсюда
следует, что при 0 •< а < 1 имеем
nV = o(yn), (17)
где число у удовлетворяет условию а < у < 1.
Рассмотрим еще одну важную для анализа беско-
нечно малую величину, именно, величину
а»
nl ’
(18)
где а — произвольное положительное число. Мы дока-
жем не только то, что величина (18) бесконечно
мала, т. е. стремится к нулю при п, неограниченно
возрастающем, но что она может быть оценена че-
рез члены убывающей геометрической прогрессии.
Именно, для всякого положительного числа а можно
подобрать такое положительное число у < 1, что
имеет место соотношение
.S- = °(Yn). (19)
44
Докажем соотношение (19). Для этого прежде
всего выберем такое наименьшее целое число k, что-
бы имело место неравенство
а < k + 1.
Ясно, что k >= 0. Теперь положим
а
Y— fe + 1 •
Очевидно, что у<1. Рассмотрим значение п k.
Для этих значений п имеем п = k + I, где I 0. Мы
имеем
ап _ ak+l ____ ak ______а1_______<. ak а1 _______
п! ~~ (k +1)1 ~ Ы ' (k+ 1) ...(* + /) "" ~ki ’ (k+ Dz ~
k\ fey'' y
Таким образом, при л> J мы имеем
ап а*
— , где Ь=~^-
При п <. k рассмотрим гипотетические неравенства
(20)
где с — некоторое положительное число. Ясно, что
так как в неравенствах (20) и принимает лишь ко-
нечное число значений от 1 до k—1, то можно вы-
брать такое число с, чтобы все они были выполнены.
Принимая теперь за а наибольшее из чисел бис,
мы получаем неравенство
Отсюда следует соотношение (19).
Из соотношения (19) вытекает, что величина п!
растет быстрее, чем величина ап при произвольном
положительном а. Переходя к обратным величинам,
можно сказать, что величина стремится к нулю
быстрее, чем величина ап при произвольном положи-
тельном а < 1.
Пример. В то время, как возведение положи-
тельного числа а в целую положительную степень п
45
имеет непосредственный смысл, в алгебре определено
также возведение числа айв нулевую и в отрица-
тельную целую степень. Для этого используют обрат-
ные величины. Точно так же удается определить и
возведение числа а в рациональную степень при по-
мощи извлечения корня. Более деликатной является
операция возведения числа а в действительную сте-
пень. Однако она также определяется. Позже мы
будем говорить об этом более подробно. Однако бу-
дем считать теперь, что а
можно возводить в про-
извольную действитель-
ную степень х так, что
определена функция
г/ = а*, (21)
где х — произвольное дей-
ствительное число: отри-
цательное, положитель-
ное или нуль, а а > 0.
Будем считать, что а
здесь больше 1. Наряду
с функцией (21) рассмот-
рим функцию
у = axft, (22)
где а — положительное
число, a k — натуральное
число. Построим графи-
ки обеих функций (21) и
(22) для неотрицатель-
ных значений х. Из соотношения (15), доказанного
для целых значений х, следует, что и при произ-
вольных положительных значениях х функция
(21) при больших возрастающих х растет быстрее,
чем функция (22). Таким образом, при доста-
точно больших х график функции (21) проходит
выше графика функции (22). Если считать, что число
а > 1, но близко к 1, а число а большое, то, хотя
кривая (22) начинается в начале координат, а кривая
(21) начинается в точке 1 на оси координат, в началь-
ной стадии роста х > 0 кривая (22) поднимается
вверх быстрее, чем кривая (21), так что происходит
пересечение этих двух кривых. Но затем кривая (21)
49
постепенно обгоняет кривую (22), так что они вноеь
пересекаются (рис. 6).
В частном случае
у —2х (23)
и
У = 4х (24)
мы имеем именно такую картину. В этом случае гра-
фики функций (23) и (24) пересекаются дважды,
причем второе пересечение имеет место в точке х = 4,
у — 16. Среди нестандартных задач элементарной
математики рассматривается задача: решить уравне-
ние
2х = 4х, (25)
т. е. найти пересечение графиков функций (23) и
(24). Школьники понимают ее иногда в том смысле,
что можно найти некую формулу вроде формулы ре-
шения квадратного уравнения, из которой вытекало
бы, что решением уравнения (25) является х = 4.
Такое понимание задачи бессмысленно, так как не-
посредственно проверяется, что х = 4 является реше-
нием уравнения (25). Задачу о решении уравнения
(25) следует понимать как задачу нахождения вто-
рого решения х < 4, причем это решение можно
найти только приближенно. Его существование видно
из рассмотрения графиков функций (23) и (24).
§ 3. Условия сходимости Коши
Мы уже говорили о том, что еще древние геомет-
ры обнаружили линии, длины которых невозможно
описать рациональными числами, т. е. числами вида
, где а и b — целые. К таким линиям принадлежит,
например, гипотенуза прямоугольного треугольника,
катеты которого равны по длине единице. Длину этой
гипотенузы мы обозначаем теперь через ^2. Позже
было обнаружено, что длина окр’ужности диаметра,
равного единице, также не является рациональным
числом. Эту длину мы обозначаем теперь через л.
Оба эти числа -у/2 и л не являются рациональными.
Такого рода числа, в отличие от рациональных, назы-
ваются иррациональными. Количество иррациональ-
47
них чисел, несомненно, бесконечно. Так, все числа
видаад/2, где а — целое число, являются иррацио-
нальными. Перед математиками прошлого столетия
встала задача описать или, если угодно, создать та-
кие числа, которые необходимы для построения гео-
метрии и математического анализа. Описание этих
чисел должно, естественно, исходить из чисел рацио-
нальных, которые предполагаются при этом вполне
известными и достаточно понятными. Описание всех
чисел, нужных для математики, было сделано не-
сколькими различными способами. При любом спо-
собе описания полное доказательство всех важных
для нас свойств вновь построенных чисел представ-
ляет собой довольно громоздкое дело. В этом пара-
графе я даю один из способов построения чисел, не
входя при этом, однако, в детали доказательств их
свойств. Приводится лишь набросок доказательств,
так что читатель сможет при большом желании вос-
становить эти доказательства полностью. Однако я
не рекомендую делать это, так как доказательства
представляются мне довольно скучными.
Определение сходимости, данное в §1, отвечает на
вопрос, сходится ли последовательность чисел
И, Г2....гп, ... (1)
к заданному числу г или нет. Очень важно формули-
ровать условие сходимости в такой форме, чтобы оно
отвечало на вопрос, сходится ли последовательность
(1) к какому-нибудь числу, которого мы еще не знаем,
или нет. Этому требованию удовлетворяет условие
сходимости Коши.
Условие Коши. Говорят, что последовательность (1)
действительных или комплексных чисел удовлетво-
ряет условию Коши или просто есть последователь-
ность Коши, если для каждого положительного числа
б можно подобрать такое натуральное число v, что
при
- р > V, q > v (2)
имеет место неравенство
\rp-rq\<t. (3)
Докажем, что условие Коши является необходи-
мым условием сходимости. Допустим, что последо-
48
вательность (1) сходится к числу г. Зададимся поло-
жительным числом е = у.Тогда, согласно определе-
нию сходимости (см. § 1, (11)), существует такое на-
туральное число v, что при п > v мы имеем
К — г I < е.
Таким образом, если р, q суть числа, удовлетворяю-
щие неравенствам (2), то мы имеем два неравенства
I гр — г | < е, | rq — г | < 8.
Из этого вытекает, что
I гР — rq | = | гр — г + г — rq | < | Гр—г 1+| г—rq | < 2е=6.
Таким образом, доказано, что если последователь-
ность (1) сходится к некоторому числу г, то условие
Коши выполнено, т. е. доказана его необходимость.
Сделано это одновременно как для действительных,
так и для комплексных чисел. Разницы в доказатель-
стве для этих двух случаев нет.
Итак, мы с легкостью доказали, что условие Коши
является необходимым условием сходимости. Совер-
шенно иначе обстоит дело с достаточностью. Здесь мы
сталкиваемся не столько с трудностью доказательства,
Сколько с совершенно принципиальным вопросом о
^ом, что же такое есть число. При этом речь идет о
Действительных числах. Случай комплексных чисел
Легко сводится к случаю действительных чисел, так
как каждое комплексное число z записывается в фор-
ме z — х + iy, где х и у — действительные числа.
Хотя понятие рационального числа слагалось по-
степенно в течение веков, будем считать сейчас, что
оно совершенно ясно. Появление первых иррацио-
нальных чисел связано с теоремой Пифагора, и оно
было большим историческим событием. Само их наз-
вание «иррациональные», т. е. неразумные, указывает
на ту тревогу, которую они вызвали у древних мате-
матиков. Не останавливаясь на сложном и длитель-
ном развитии представления об иррациональном чис-
ле, скажу только, что условие Коши как достаточное
условие сходимости стало насущной необходимостью
Математики. Следовательно, числа должны быть та-
кими, чтобы всякая последовательность Коши дейст-
вительных чисел сходилась к действительному числу.
49
Построение действительного числа. Если исходить 1
из предположения, что понятие рационального числа 1
вполне ясно, то мы прежде всего приходим к выводу, I
что всякая последовательность Коши рациональных |
чисел должна сходиться к некоторому действитель-
ному числу, рациональному или иррациональному. F
Выпишем некоторую последовательность Коши .
«ь s2, ..., s„, ... (4)
рациональных чисел. Если эта последовательность
сходится к некоторому рациональному числу, то во-
прос ясен. Если же не существует такого рациональ-
ного числа, к которому последовательность (4) схо-
дится, то нам остается только признать, что суще-
ствует некоторое иррациональное число, к которому
она сходится. Признав это, мы фактически вводим
новое представление о числе, считая, что оно задает-
ся последовательностью Коши рациональных чисел.
Итак, по определению всякая последовательность
Коши рациональных чисел задает действительное
число, рациональное или иррациональное. Действи-
тельное число, которое задается последовательностью
(4), мы обозначим через s. Члены последовательно-
сти (4) мы должны теперь считать приближенными
значениями действительного числа s. При этом точ- I
ность приближения легко может быть оценена. В са- |
мом деле, согласно определению, для всякого поло-
жительного числа 6 существует такое натуральное
число v, что два любых члена sp и sq последователь- I
ности (4) с номерами, большими v, отличаются друг
от друга меньше чем на 6, и потому следует считать,
что член sn последовательности (4) с номером п > v
задает число s с точностью 6. .Так как последователь-
ность Коши (4) рациональных чисел, определяющая
действительное число $, дает нам возможность вычис-
лить это число s с произвольно высокой точностью,
то мы можем определить действия над так опреде-
ленными действительными числами и ответить на все
вопросы, возникающие в связи с этим определением.
Если наряду с последовательностью Коши (4) ра-
циональных чисел выписана другая последователь- .
ность Коши
s^, s', (5)
50
рациональных чисел, то прежде всего надо ответить
на вопрос о том, будут ли эти две последовательно-
сти задавать одно и тоже действительное число. От-
вет ясен. Мы составляем последовательность
s2-s', .... Sn-s'n, ... (6)
рациональных чисел. Последовательности (4) и (5)
определяют одно и то же действительное число тогда
и только тогда, когда последовательность (6) сходит-
ся к нулю. В этом случае последовательности (4) и
(5) называются эквивалентными.
Действительное число, задаваемое последователь-
ностью (4), положительно тогда и только тогда, ког-
да все члены последовательности (4), начиная с не-
которого номера, становятся больше некоторого по-
ложительного рационального числа.
Если наряду с последовательностью (4), опреде-
ляющей число s, имеется другая последовательность
Коши
^2» • • •, • • •
рациональных чисел, определяющая действительное
число /, то ясно, как надо определить действия над.
числами s и t. Действительное число s + t опреде-
ляется последовательностью
$1 + Л, $2 + ^2, •••, + •••
рациональных чисел, которая является последова-
тельностью Коши. Разность s — /, произведение st и
частное у определяются аналогичным образом соот-
ветствующими последовательностями Коши. Частное
$
у можно определить лишь в том случае, когда дели-
тель t не является нулем. Зная, когда действительное
число положительно, и умея вычитать действитель-
ные числа, мы тем самым знаем, что означает знак
неравенства для действительных чисел.
Оказывается, что для так определенных действи-
тельных чисел условие Коши является достаточным
условием сходимости. Доказательство этого неинте-
ресно, и я здесь его не привожу.
Если теперь объявить, что комплексное число г
задается формулой z — х + 1у, где х и у суть дей-
ствительные числа в описанном смысле, то легко до-
51
казьтвается, что последовательность Коши комплекс-
ных чисел сходится к некоторому комплексному
числу.
Итак, мы по^гроили такую систему действитель-
ных и комплексных чисел, что для нее условие Коши
является необходимым и достаточным условием схо-
димости.
Пример. Выпишем некоторую десятичную дробь
a, fif2 ... fn... (7)
Здесь после запятой стоят цифры fj2 ... fn . ., каж-
дая из которых имеет некоторое определенное зна-
чение от нуля до 9. Перед запятой стоит целое число
а, которое мы не будем записывать с помощью деся-
тичной системы, но которое может быть отрицатель-
ным, положительным или нулем. Формально выпи-
санная дробь (7) выглядит как бесконечная, но если,
начиная с некоторого номера, цифры, стоящие после
запятой, все обращаются в нуль, то она в действи-
тельности является конечной дробью. Бесконечная
десятичная дробь (7) порождает бесконечную после-
довательность конечных десятичных дробей
so —а,
Si — a, fi,
s2 = a, fif2,
(8)
sn==a, fift ••• fn,
Здесь sn есть десятичная конечная дробь, в которой
до запятой стоит целое число а, а после запятой
ровно п цифр f\f2, ..., fn. Мы уже рассматривали это
построение (см. § 1, (8), (9)), но здесь мы можем
утверждать, что последовательность рациональных
чисел (8) есть последовательность Коши. В самом
деле, если р < q суть два натуральные числа, то мы
имеем очевидное неравенство
1
sq ~ sp < iqP ’
52
Таким образом, если оба числа р и q больше на-
турального числа v, то мы имеем
I sq sp । < "iqv+i * (9)
а это и значит, что последовательность (8) есть по-
следовательность Коши. ТакИ1М образом, в силу на-
шего соглашения она определяет некоторое действи-
тельное число s — рациональное или иррациональное.
Естественно теперь считать, что действительное чис-
ло s записывается в виде десятичной дроби (7).
Остается, однако, неясным, можно ли записать любое
действительное число таким способом в виде десятич-
ной дроби. В § 4 будет доказано, что каждое дей-
ствительное число можно записать в виде десятичной
дроби.
§ 4. Применение признака сходимости Коши
Достаточность признака сходимости Коши позво-
ляет нам в ряде случаев считать существующим или,
иначе говоря, строить нужное для нас число. В этом
параграфе будет дан ряд примеров такого построе-
ния. В частности, будет точно определена длина дуги
окружности.
Верхняя и нижняя грани. Каждое действительное
число х мы можем изобразить на оси абсцисс в виде
точки, абсцисса которой равна числу х. Эту точку мы
также будем обозначать буквой х. Изображение чи-
сел в виде точек на прямой придает им некоторую гео-
метрическую наглядность. Мы будем одновременно
пользоваться как числовой, так и геометрической тер-
минологией.
Любая десятичная дробь
a, fn, (1)
в которой перед запятой стоит произвольное целое
число, положительное, отрицательное или нуль, а
после запятой стоит ровно п цифр, может быть запи-
ь
сана в виде"[^’ где Ь — некоторое целое число. На-
л * Ь
оборот, каждая дробь вида может
сана в виде десятичной дроби вида (1).
быть запи-
При п — О
53
числа вида (1) являются целыми, а изображающие
их на прямой точки называются целочисленными.
Легко представить их себе геометрически. Говорят,
что они образуют целочисленную сетку на прямой.
Числа вида изображенные геометрически, обра-
зуют уже более густую сетку, получающуюся из це-
лочисленной путем подразделения каждого ее отрезка
на десять равных частей.
Точно так же числа вида образуют на пря-
мой сетку более густую, чем предыдущая, получаю-
щуюся из нее путем подразделения каждого ее от-
резка на 10 равных частей. Таким образом, на пря-
мой мы получаем последовательность все более
ь
мельчающихся сеток, возникающих из чисел
из-
где
n = 0, 1, 2,
числа вида
... Сетки эти мы занумеруем, считая^ что
составляют сетку .
Пусть теперь М — некоторая совокупность или, как
говорят, некоторое множество действительных чисел.
Числа эти мы можем рассматривать также и как точ-
ки на прямой, так что М представляет собой одновре-
менно множество точек. Допустим, что множество М
ограничено сверху, т. е. существует такое число с, что
для всякого х, принадлежащего множеству тИ, вы-
полнено неравенство
х < с. (2),
Геометрически это значит, что все точки множества
М лежат левее точки с.
Докажем теперь, что ограниченное сверху множе-
ство М имеет верхнюю грань, именно, что существует
число g, удовлетворяющее следующим условиям. При
любом положительном е в множестве М найдется
число х, удовлетворяющее неравенству
х > g — 8,
но не существует в множестве М числа х, превосхо-
дящего число g, т. е. удовлетворяющего неравенству
x>g.
Это число g и называется верхней гранью множества
М. Геометрически верхнюю грань g можно описать
54
следующим образом. Если сдвинуть точку g сколь
угодно мало влево, т. е. взять точку g— 8, где 8
положительно, то справа от этой точки g — е най-
дется хоть одна точка множества М, но не суще-
ствует ни одной точки множества М, лежащей вправо
от точки g.
Построение верхней грани g множества М прово-
дится следующим образом. Мы будем геометрически
сравнивать множество М и точки сетки Sn. Если взять
точку р сетки 2Я, лежащую справа от точки с (см.
(2)), то все числа множества М лежат слева от этой
точки р. С другой стороны, существует такая точка
q сетки Sn, справа от которой имеются точки множе-
ства М. Так как между точками q и р сетки
имеется лишь конечное число точек этой сетки, то су-
ществует такая самая правая точка сетки S«, справа
от которой еще имеются точки множества М. Ее
мы обозначим через sn. Выполнив этот выбор точки
sn для каждого п = 0, 1, ..., мы получим последова-
тельность чисел
So, slt $п, ... (3)
Ясно, что в этой последовательности точек каждая
следующая либо совпадает с предыдущей, либо ле-
жит справа от нее. Ясно также, что не может слу-
читься, чтобы в последовательности (3) все точки,
начиная с некоторого места, повторялись, не продви-
гаясь. вправо. В самом деле, точка sn выбрана так,
что справа от нее еще имеются точки множества М.
Поэтому для достаточно большого номера п' точка
srt, лежит правее точки sn. Отсюда следует, что после-
довательность (3) конечных десятичных дробей есть
последовательность (8) § 3, т. е. может быть полу-
чена из бесконечной десятичной дроби (7), § 3. Эта
десятичная дробь в самом деле бесконечна, так как
последовательность точек (3) постепенно продвигает-
ся вправо. Последовательность Коши (3) определяет
число g, которое и является, как легко видеть, верх-
ней гранью множества М. Если множество М состоит
из единственного числа т, то g = tn, и бесконечная
десятичная дробь (7) § 3 является его записью. Та-
ким образом, мы доказали, что каждое число может
быть записано в виде бесконечной десятичной дроби
,(см. пример § 3). Отсюда видно, что множество всех
55
действительных чисел можно описать как совокупи
ность всех бесконечных десятичных дробей.
Допустим, что некоторое множество М' действи-
тельных чисел ограничено снизу, т. е. существует та-
кое число с', что для каждого числа х из ЛГ выпол-
нено неравенство
с' < х. (4)
Докажем, что для ограниченного снизу множества Л4'
существует нижняя грань g't т. е. такое число, что
при любом положительном е всегда найдется число
х из множества М', удовлетворяющее неравенству
х <. g' + е, но не существует такого числа х из М'9
что х < g'. Для доказательства обозначим через
—М' = М совокупность всех чисел вида —х, где х
принадлежит заданному множеству М'. Если множе-
ство М' ограничено снизу, то множество М — —Mf
ограничено сверху и потому имеет верхнюю грань g.
Очевидно, что число g' — —g является нижней
гранью множества Л4'.
Верхний и нижний пределы. Обозначим через М
некоторое бесконечное множество действительных чи-
сел, ограниченное как сверху, так и снизу (см. (2),
(4)). Действительное число р называется верхним
пределом множества Л4, если для всякого положи-
тельного числа е существует бесконечное множество
чисел, принадлежащих М и превосходящих число
р — 8, но существует не более конечного числа чи-
сел, принадлежащих множеству М и превосходящих
число р + 8. Аналогично действительное число р' на-
зывается нижним пределом множества М9 если для
каждого положительного числа е существует беско-
нечное множество чисел из Л4, меньших числа р' + 8,
но найдется не более конечного числа чисел из М,
меньших чем р' — е. Докажем, что множество М имеет
верхний предел. Для этого поступим так же, как при
построении верхней грани множества. Возьмем неко-
торое целое неотрицательное число и и выберем из
b t
рациональных чисел вида где о — целое число,
такое наибольшее число sn, что существует бесконеч-
ное множество чисел из Л1, превосходящих число sn<
Ясно, что последовательность
Sq, Sj, ..., sft, . • •
56
есть возрастающая последовательность десятичных
дробей типа (8) §’ 3 и потому удовлетворяет условию
сходимости Коши. Предел этой последовательности,
очевидно, и есть верхний предел р множества М. Су-
ществование нижнего предела р' множества М дока-
зывается так же, как это делалось в отношении ниж-
ней грани, при помощи рассмотрения множества — М.
Легко убедиться в том, что числа р и р' являются
предельными для множества М (см. пример 3 § 1).
Таким образом, доказано, что бесконечное множе-
ство М действительных чисел, ограниченное сверху и
снизу, имеет предельные числа. Ясно, что р есть наи-
большее из этих предельных чисел, а р' — наимень-
шее из этих предельных чисел. Может случиться, од-
нако, что р и р' совпадают между собой. В этом слу-
чае множество М имеет только одно предельное чис-
ло р = р'. Так будет, например, когда множество Л1
состоит из элементов бесконечной последовательно-
сти попарно различных чисел, сходящейся к числу р.
Ограниченные последовательности и ограниченные
множества чисел. Последовательность
И, г2....гп, ... (5)
действительных или комплексных чисел называется
ограниченной, если найдется такое положительное
число с. что для всякого номера и имеет место нера-
венство
I Гп | < с.
Аналогично множество М действительных или комп-
лексных чисел называется ограниченным, если най-
дется такое положительное число с, что для всякого
числа х из множества М имеет место неравенство
I х I < с.
Мы докажем сейчас, что из всякой ограниченной по-
следовательности чисел (5) можно выбрать сходя-
щуюся подпоследовательность (см.§ 1, (18)),и затем
докажем, что всякое бесконечное ограниченное мно-
жество М чисел имеет предельное число (см. при-
мер 3 § 1).
Мы уже отмечали, что в последовательности (5)
чисел могут под разными номерами стоять равные
между собой числа. Таким образом, может оказать-
57
ся, что последовательность (5) содержит лишь ко-
нечное число различных чисел. В этом случае в по-
следовательности (5) найдется такое число г, кото-
рое встречается бесконечное число раз под различ-
ными номерами. Выписывая все члены последователь-
ности (5), равные числу г, в том порядке, в каком
они стоят в последовательности (5), мы получим под-
последовательность
Гл2, •••» ••• (6)
последовательности (5), все члены которой равны
числу г. Таким образом, подпоследовательность (6)
последовательности (5) сходится к числу г, и наше
утверждение доказано.
Будем считать теперь, что множество М всех чи-
сел, встречающихся в последовательности (5), бес-
конечно. Разберем сперва случай, когда числа после-
довательности (5) все являются действительными,
так что и множество М состоит из действительных
чисел. Так как множество М ограничено в силу огра-
ниченности- последовательности (5), то по доказан-
ному выше (см. верхний предел) множество М имеет
хотя бы одну предельную точку р. В силу доказан-
ного ранее (см. § 1, пример 3) из множества М мож-
но выбрать последовательность
<гь <т2, ..., оя.. (7)
содержащую бесконечное множество различных чи-
сел, сходящуюся к числу р. Переставим порядок чле-
нов последовательности (7) так, что получающаяся
в результате этой перестановки новая последователь-
ность также будет сходиться к р и в то же время бу-
дет являться подпоследовательностью исходной по-
следовательности (5). Для этого поступим так. По-
смотрим на число п. Если оно не входит в последо-
вательность (7), то мы отбросим его. Если же оно
входит в последовательность (7), то мы обозначим
его через гп. Посмотрим далее на число г2. Если оно
не входит в последовательность (7), то мы отбросим
его, а если входит, то обозначим через гя?. Будем пе-
ребирать постепенно все члены последовательности
(5), и в результате этого перебора мы получим бес-
58
конечную последовательность
гПе гП2, rnk, ... (8)
Указанный процесс выбора чисел из (5) не может
остановиться, так как последовательность (7) содер-
жит бесконечное множество различных чисел. Ясно,
что полученная так последовательность (8) является
подпоследовательностью последовательности (5). Но
в то же время она содержит все числа, входящие в
последовательность (7), и потому сходится к числу р.
В самом деле, любая е-окрестность Ue числа р содер-
жит все числа последовательности (7), за исключе-
нием, быть может, лишь конечного числа их. Следо-
вательно, это верно также и в отношении последова-
тельности (8).
Рассмотрим теперь случай, когда последователь-
ность (5) содержит бесконечное множество различ-
ных чисел, но числа эти необязательно действитель-
ные, а, вообще говоря, комплексные. Каждое число
гп последовательности (5) запишем в виде
гп = sn 4” itn.
Таким образом, у нас возникают две последователь-
ности действительных чисел
$2, ..sn, ..., (9)
^2, • • •, tn> • • • (10)
Так как, по предположению, последовательность (5)
содержит бесконечное множество различных чисел,
то хотя бы одна из последовательностей (9) и (10)
также содержит бесконечное множество различных
чисел. Для определенности предположим, что беско-
нечное множество различных чисел содержит после-
довательность (9). Так как она состоит из действи-
тельных чисел, то по только что доказанному из нее
можно выбрать подпоследовательность
5/ip Sn2 •••> •••> (11)
содержащую бесконечное множество различных чи-
сел, сходящуюся к некоторому числу s. Рассмотрим
теперь последовательность
Цр • • • > Ц, • • •
59
действительных чисел. Так как она ограничена, то по
ранее доказанному из нее можно выбрать некоторую
подпоследовательность
сходящуюся к некоторому числу t. Здесь натураль-
ные числа
tnh т2, ...
идут в возрастающем порядке и составляют лишь
подпоследовательность последовательности натураль-
ных чисел
п2> .«ь
Таким образом, последовательность
S/пр S/n2> • • •, • • •
составляет подпоследовательность последовательно-
сти (11) и содержит бесконечное множество различ-
ных действительных чисел. Полагая
мы получаем последовательность
Г/Пр Лп2, •••> •••> (12)
содержащую бесконечное множество различных чи-
сел, сходящуюся к числу г = s + it и являющуюся
подпоследовательностью последовательности (5). Та-
ким образом, если исходная ограниченная последо-
вательность (5) содержит бесконечное множество раз-
личных чисел, то из нее можно выбрать сходящуюся
подпоследовательность (12), содержащую бесконеч-
ное множество различных чисел, сходящуюся к неко-
рому числу г.
Теперь перейдем к ограниченному бесконечному
множеству М и докажем, что оно имеет предельное
число. Так как множество М содержит бесконечное
множество чисел, то из него можно выбрать некото-
рую последовательность
Гь Г2, .... гп.... (13)
содержащую бесконечное множество различных чи-
сел. Согласно только что доказанному из этой после-
довательности (13) можно выбрать подпоследова-
«0
тельность, которая уже сходится к некоторому числу
f и содержит также бесконечное множество различ-
ных чисел. Отсюда вытекает, что число г является
предельным и для множества М.
Итак, наше утверждение полностью доказано.
Длина дуги окружности. После того, как объясне-
но, что такое действительное число, естественно объ-
яснить, что следует понимать под длиной кривой ли-
нии, исходя при этом из предположения, что нам
хорошо известно, что представляет собой длина пря-
молинейного отрезка. Ъе мы будем обозначать через
l(p, q), где р и q — концы отрезка. Мы рассмотрим
здесь лишь дугу окружности. Случай более общий
принципиально не отли-
чается от случая дуг
окружности и будет рас-
смотрен позже (см. § 19).
На некоторой плоскости
Р выберем окружность
К радиуса 1 с центром в
точке о и на этой окруж-
ности выберем дугу ab
такую, что угол aob, опи-
рающийся на нее, не пре-
восходит 120° (рис. 7).
Его мы обозначим через
2а. Таким образом, а
60°. Это ограничение несущественно. Будем считать
также, что, двигаясь от точки а к точке b по дуге ab,
мы идем против часовой стрелки.. Наша цель состоит
в том, чтобы дать точное формальное определение
длины дуги ab.
На дуге ab выберем последовательность точек
Oq, at, ch, ...» ak; а0 = а; ak = b. (14)
Мы будем считать, что переход от точки at_\ к точке
at осуществляется движением вдоль дуги ab против
часовой стрелки. Таким образом, точки (14) следуют
по дуге ab одна за другой и разбивают дугу do на
куски. Ломаную aoOi<*2 ... «л мы обозначим А и бу-
дем говорить, что она опирается на хорду ab. Длину
этой ломаной обозначим через 1(A). Сравним теперь
длину ломаной А с длиной хорды ab. Ясно, что
/(а&)<1(Л),
но этого нам недостаточно. Проекции точек последов
вательности (14) на хорду ab обозначим соответ-
ственно через
Яр • • •» #£•
Ясно., что
I (об) = Ца'оа') +1 (а[а') + ...+/ (a'^oQ.
Обозначим через 0,- угол наклона хорды амаг к хор-
де ab. Тогда очевидно, что
= г(а'-10^) < zK-inD
cos Р/ cos а
Суммируя последнее неравенство по всем значениям
i от 1 до k, мы получаем
/(а&)<1(Л)<^-. (15)
Положим х — l(ab) и вычислим разность
Для этого мы заметим, что х — 2sina, а потому
cos2a=l —Теперь мы имеем
Теперь неравенство .(15) переписывается .в виде
х </(Л)<х(1 +х2). (16)
Разобьем теперь дугу a4-jaz на кусочки точно так
же, как мы это сделали с дугой ab, но не будем обо-
значать точки деления никакими буквами. Получен-
ную в результате этого деления ломаную обозначим
через В, и будем говорить, что она опирается на хор-
ду ai-idi. Длину этой ломаной обозначим через l(Bi).
Объединяя вместе все ломаные Вь В2, ..., Bfc, мы
получим ломаную В, длину которой обозначим через
/(В), и будем говорить, что ломаная В опирается на
ломаную Л. Положим
62
Применяя результат (16), пригодный для любой хор'
ды ab, к хорде ai-iai, мы получим неравенство
Xi < I (В^ < Xi (1 + xl) C Xi (1 + (6 (Л))2), (17)
где 6(A) есть максимальное из чисел х,, i= 1, .k,
т. е. длин отрезков, составляющих ломаную А. Сум-
мируя неравенства (17) по всем значениям i от 1 до
k, получаем
/(А)</(В)</(А)(1+(6(А))2). (18)
Заметим еще, что все ломаные, опирающиеся на хор-
ду ab, имеют ограниченную длину, именно, мы имеем
в силу формулы (15)
где число с зависит только от хорды ab. Теперь из
неравенства (18) мы можем сделать вывод, что
| Z (В) — Z (Л) 1 < с (д (Л))2, (19)
где А — произвольная ломаная, опирающаяся на хор-
ду ab, а В — ломаная, опирающаяся на ломаную А.
Пусть теперь А и А' — две ломаные, опирающиеся
на хорду ab. Занумеровав теперь их вершины в том
порядке, в каком они встречаются при прохождении
дуги ab против часовой стрелки от а до Ь, мы полу-
чим некоторую последовательность точек, которая мо-
жет быть положена в основу некоторой ломаной В,
опирающейся на обе ломаные А и А'. Тогда наряду
с неравенством (19) мы имеем неравенство
11 (В) - Z (Л') | < с (6 (Л'))2. (20)
Из неравенств (19) и (20) следует, что
I Z (Л) — Z (Л')1 < С [(6 (Л))2 + (6 (ЛЭ)2]. (21)
Построим теперь некоторую последовательность
ломаных
Ло = ab, Ai, АП)
где каждая следующая ломаная опирается на преды-
дущую, а первая ломаная Ло является просто исход-
ной хордой ab. Предположим затем, что
Иш6(Лп) = 0. (22)
63
Из неравенства (19)' следует, что последовательность
чисел
/(Ло), W, .... 1(Аа), ... (23)
есть последовательность Коши. Ее предел мы обозна-
чим через 2s, т. е.
lim I (Ап) — 2s.
П~>оо
Легко видеть, что полученный предел 2s зависит
лишь от дуги ab, а не от случайно выбранной после-
довательности ломаных (22). Действительно, если
вместо последовательности (22) имеется другая ана-
логичная последовательность
A'o = ab, At.....А'п......
то в силу формулы (21) мы имеем
11 (Ая) -1 (А'п) | < с [(6 (Л„))2 + (6 (ЛА))2],
и потому обе последовательности (23) и
/(Л$), /(Л(), .... 1(А'п), ...
сходятся к одному и тому же числу 2s. Это число 2s
и называется длиной дуги ab. Эту длину 2s дуги ab
называют величиной угла aob, выраженной в радиа-
нах. В высшей математике обычно считают, что аргу-
мент тригонометрической функции есть угол, выра-
женный в радианах.
Из неравенства (15) следует
л • 1 / л \ % 2 SID S
х — 2 sin s < I (ДО <-----=--------.
cos s cos s
Переходя к пределу при п оо и деля полученное
неравенство на 2, получим
sin s < s < tg s. (24)
Если теперь si, Sz, ..., sn, ... — последовательность
положительных чисел, сходящаяся к нулю, то из со-
отношения (24) получаем два соотношения
!im ЛЙр. = 1,
П-»оо Stl
lim-^- = l.
П->ОО
64
Полагая tg sn — tn, мы получаем из последнего соот-
ношения
lim -?rctg--ra- = 1. (25)
П-»оо
Здесь можно считать, что последовательность
/[, ^2> • • • > tn, . . .
есть произвольная последе в ательность положитель-
ных чисел, сходящаяся к нулю.
Длина окружности радиуса 1 обозначается через
2л. Таким образом, л есть вполне определенное чис-
ло. Вычислено, что л ~ 3,1415926.
Пример 1. Пусть
«ь s2.....sn, ... (26)
— неубывающая ограниченная последовательность
чисел, т. е. такая, что srt+i sn и sn <. с, п= 1,2, ...,
где с — константа. Обозначим через g верхнюю грань
множества, состоящего из всех чисел (26). Легко ви-
деть, что
lim sn — g.
Точно так же для невозрастающей последовательно-
сти
tx, t2....tn, ..., (27)
ограниченной снизу, мы имеем
lim tn = g',
П->°о
где g' есть нижняя грань множества, состоящего из
всех чисел (27).
§ 5Г Сходящиеся ряды
Еще большую роль, чем сходящиеся последова-
тельности, играют в математике сходящиеся ряды.
Слагаемыми их могут быть как числа, так и функции.
В последнем случае ряд дает возможность, исходя из
простых, хорошо известных функций, например сте-
пеней независимого переменного, строить новые функ-
ции. Именно с этой целью ряды будут использованы
нами в первую очередь (см. § 7). Но сперва мы зай-
3 Л. С. Понтрягин 65
мемся рядами, слагаемыми которых являются дей*
ствительные или комплексные числа.
Выпишем сумму
Zi + ^2 + ... + + • • • (1)
с бесконечным числом слагаемых. Сумма эта назьь
вается рядом. Ее слагаемые п= 1, 2 ..., являют-
ся комплексными или действительными числами.
В случае, если какое-либо высказывание о ряде (1)
имеет смысл лишь при действительных слагаемых,
это обстоятельство будет оговариваться специально.
Прежде всего мы должны объяснить, что следует
понимать под суммой ряда (1). Для этого выпишем
так называемые предварительные конечные суммы
sn = zi + ^+ ... 4-z„, (2)
где п — произвольное натуральное число. Если после-
довательность
Si, S2, Sn, ... (3)
сходится (см. § 1), то говорят, что ряд (1) сходится,
и его сумма равна пределу последовательности (3).
Если последовательность (3) задана, то легко по-
лучить ряд (1), из которого она возникает, согласно
изложенному правилу. Для этого достаточно поло-
жить
21 = 31, Zz = S% Si, ..., Zn — Sn — ...
Таким образом, на первый взгляд кажется, что изу-
чение сходящихся рядов полностью сводится к изу-
чению сходящихся последовательностей, и наоборот,
изучение сходящихся последовательностей можно
свести к изучению сходящихся рядов. Но это не сов-
сем так. Прежде всего может оказаться, что при ре-
шении некоторой задачи возникает ряд, и тогда он
должен считаться первичным объектом. Если же при
решении задачи возникает последовательность, то
первичным объектом должна считаться именно она.
Бывают случаи, когда при решении задачи возникает
последовательность, но для доказательства ее сходи-
мости приходится переходить к соответствующему ей
ряду. Есть, однако, один важный вопрос, который
имеет смысл только для рядов, но не имеет смысла
для последовательностей. Хорошо известно, что сум-
66
ма конечного числа слагаемых не зависит от их по-
рядка. Но это неверно для рядов. Может случиться,
что при перестановке слагаемых ряда (1) мы полу-
чим новый ряд, сумма которого отличается от суммы
исходного ряда. Это будет показано ниже в при-
мере 1.
Важную роль в теории рядов играют условия их
сходимости или, как говорят иначе, признаки сходи-
мости. Первым необходимым и достаточным усло-
вием сходимости ряда является условие Коши, кото-
рое представляет собой простую переформулировку
на язык рядов условия сходимости Коши для после-
довательностей (см. § 3). Но очень важную роль в
теории рядов играют и достаточные условия сходи-
мости, не являющиеся необходимыми.
Условие сходимости Коши. Говорят, что ряд (1)
удовлетворяет условию сходимости Коши, если для
всякого положительного числа б можно подобрать
такое натуральное число v, что при
q>p>v
имеет место неравенство
I +zj<6. (4)
Это условие является необходимым и достаточным
условием сходимости ряда. В самом деле,
|Sp —s4( = |Zp+1 + zp+2+ ... 4-zJ. (5)
Таким образом, условие сходимости Коши для ряда
(1) в точности равносильно условию сходимости для
последовательности (3). Последнее же, как было по-
казано в § 3, является необходимым и достаточным
условием сходимости последовательности (3).
В частном случае, когда р — п—1, q — п, мы
имеем sq— sp = zn, и соотношения (4), (5) превра-
щаются в соотношение
|ze|<6,
откуда следует, в силу формулы (4),
lim z„ = 0. (6)
П->0О
Таким образом, слагаемые сходящегося ряда при не-
ограниченном возрастании их номера обязательно
стремятся к нулю.
3*
Дадим еще одно следствие условия сходимости
Коши. Если ряд (1) сходится, то ряд
+ +^+«4" ••• (7)
также сходится и для всякого положительного числа
6 можно подобрать такое натуральное число v, что
при k > v сумма ряда (7) не превосходит б.
Знакопеременный ряд. Докажем теперь один до-
статочный признак сходимости для ряда
21 + z2 + ... + zn + ... (8)
с действительными слагаемыми. Мы будем предпола-
гать, что все слагаемые этого ряда с нечетными номе-
рами положительны, а все слагаемые с четными но-
мерами отрицательны. Кроме того, будем предпола-
гать, что модуль каждого слагаемого меньше модуля
предыдущего слагаемого, т. е.
1 | < | Zn |.
Кроме того, предположим, что
lim \zn 1 = 0.
П->оо
Такой ряд (8) называется знакопеременным. Оказы-
вается, что знакопеременный ряд всегда сходится.
Для доказательства этого рассмотрим предвари-
тельную сумму S2k четного номера п = 2k, соответ-
ствующую этому ряду в силу формулы (2).Мы имеем
$26 — (21 + Z2) + (2з + 24) + ... + (22б—1 + Z2k)*
Здесь каждая из скобок, стоящих в правой части,
положительна, и поэтому число s2k возрастает вместе
с А. С другой стороны, та же предварительная сумма
s2k может быть записана в виде
s2k = 2i + (z2 + 23) + (z4 + z5) + ... +
+ (Z2k + 22fe+1) “" 226+1.
Здесь каждая из скобок отрицательна, а последний
член — z26+i также отрицателен. Таким образом,
526 <21.
Таким образом, возрастающая последовательность чи«
сел
s2, ..., s2k, ...
68
является возрастающей и ограниченной и поэтому
сходится к некоторому числу s (см. § 4, пример 1).
Так как предварительная сумма s2m-i нечетного но-
мера отличается от предварительной суммы s2k чет-
ного номера на число 22л+ь которое стремится к нулю,
то и последовательность всех предварительных сумм
сходится к тому же числу s, к которому сходится по-
следовательность предварительных сумм четных но-
меров.
Итак, доказано, что знакопеременный ряд всегда
сходится. Оказывается, однако, что если для знако-
переменного ряда (8) число
^ = 21 + 23 + ^5+ •••
неограниченно возрастает при возрастании k, то пу-
тем перестановки слагаемых ряда (8) можно полу-
чить новый ряд, сходящийся к наперед заданному
числу /. Это странное свойство некоторых сходящих-
ся рядов менять сумму при перестановке слагаемых
наводит на мысль о том, что ряды такого рода могут
обладать и другими странностями, делающими их
малопригодными для употребления. Поэтому в тео-
рии рядов основную роль играют так называемые аб-
солютно сходящиеся ряды, изучению которых будет
посвящен § 6. Эти ряды уже не имеют такого рода
странностей.
Пример 1. Для знакопеременного ряда
Z1 + ^2 + • • • + + ... (9)
составим две суммы
tk — + ••• +Z2fc-b
t'k — Z2 + %4 + • • • 4“ %2k-
Первая из этих сумм положительна и возрастает вме-
сте с k, вторая отрицательна, и модуль ее возрастает
вместе с k. Оказывается, что если tk -> 00, то модуль
t'k также стремится к бесконечности. Действительно,
мы имеем
52^ = 4 + ^-
Так как число s2k стремится к определенному пределу
при k возрастающем, то из предположения, что поло-
жительное число tk неограниченно возрастает, сле-
дует, что отрицательное число t'k неограниченно убы-
69
вает, стремясь к — оо. Зададимся теперь произвола
ным числом t и переставим слагаемые ряда (9) так,
чтобы сумма вновь полученного ряда была равна
числу Л Процесс перестройки ряда (9) следующий.
Обозначим через рх наименьшее значение натураль-
ного числа р, при котором
tp>t.
Далее, обозначим через q\ наименьшее значение чис-
ла q, при котором
tpi ~\rtq <t.
Исходя из этих начальных значений чисел pi и q\9 по-
строим две возрастающие последовательности нату-
ральных чисел
Pl, Р2...Рп, • • •> (1°)
. 4l, <?2..Яп, ••• СО
индуктивно, считая, что числа рп и qn уже заданы.
Числа Р/2+i и определим так: рп+1 есть наимень-
шее значение натурального числа р, при котором
а число qn+i есть наименьшее натуральное число q,
для которого
tpn+1
Так как ряд (9) сходится, то члены его стремятся к
нулю при п возрастающем, а отсюда легко следует,
что для полученных последовательностей чисел (10)
и (И) мы имеем
Но сумму tpn 4- tqn можно записать в виде
+ (*р2 ~ + (^2 — ^|) + ... +
+(ч-ч-.)па
Каждое из выписанных здесь слагаемых представ-
ляет собой сумму нескольких членов ряда (9), при-
чем слагаемые ряда (9) не повторяются в слагаемых
суммы (12), а при возрастании п исчерпывают все
члены ряда (9). Таким образом, если в сумме (12)'
заменить- каждое слагаемое соответствующей суммой
70
членов ряда (9), мы получим ряд, содержащий все
слагаемые ряда (9), но расположенные в новом по-
рядке. Т.ак возникающий новый ряд имеет своей сум-
мой наперед заданное число t и получается из ряда
(9) путем перестановки его слагаемых.
Пример 2. Дадим теперь конкретный числовой
ряд (9), для которого имеет место сказанное в при-
мере 1. Этот ряд есть
Так как числа tk и |/^| либо оба остаются ограни-
ченными при возрастании k, либо оба стремятся к
бесконечности, то, для того чтобы доказать, что пер-
вое из них неограниченно возрастает, достаточно до-
казать, что их сумма неограниченно возрастает, т. е.
что мы имеем
lim (tk +1 t'k I) = oo.
k->oo
Для ряда (13) нам достаточно, таким образом, дока-
зать, что ряд
1 + 4- + -т+...+-^-+..* (14)
расходится, т. е. сумма его равна + оо. Рассмотрим
отрезок ряда (14), состоящий из членов с номерами
и, удовлетворяющими условиям
2г-1 <п<2г,
где I — натуральное число. Число этих членов равно
2Z-1, а последний наименьший член равен-Ь. Таким
образом, сумма членов этого отрезка ряда больше
2z~l 1
чем —Весь РЯД (14), начиная со второго
2£ г
слагаемого, распадается на непересекающиеся отрез-
ки рассмотренного вида, где I меняется от 1 до оо.
Таким образом, сумма ряда (14) равна бесконечно-
сти.
Итак, для ряда (13) число tn неограниченно воз-
растает, и потому в силу доказанного в примере 1
.члены ряда (13) можно переставить так, чтобы сум-
71
к
i
: ма вновь полученного ряда была равна наперед за*
данному числу Л
Пример 3. Пусть
21 + z2 + ... + 2п+ . . ., (15)
Wi + а’2 + ... + wrt + ... (16)
— два сходящихся ряда. Сумму первого из них обо*
значим через s, сумму второго через t. Оказывается,
что ряды эти можно складывать почленно, т. е. ряд
(21 + 101) + (22 + W2) + ... +(2Л+&’„)+ ... (17)
сходится к числу s + t. Докажем это.
Составим предварительные суммы
Sn = Z{ + ... +zrt,
^n = Wi+ ...
Тогда в силу сходимости рядов (15), (16) для каж*
дого положительного числа 6 найдется настолько
большое натуральное число v, что при п > v имеем
I S | < у ; \tn Z I <С ~2 •
Ясно, что предварительная сумма ряда (17) номера
и равна sn + tn- Но так как при п > v мы имеем
I (sn + tn) - (5 +0 I < 6,
то ряд (17) сходится к числу s + t
§ 6. Абсолютно сходящиеся ряды
Ряд
21 + г2+ ... +зл+ ... (1)’
называется абсолютно сходящимся, если ряд, со*
ставленный из абсолютных величин, или, что то же
самое, модулей его слагаемых
|21! + |22|+ ... +|2„|+ ..., (2)
сходится.
Прежде всего следует доказать, что абсолютно
сходящийся ряд сам сходится в обычном смысле ело*
ва. Для доказательства используем признак сходимо*
сти Коши. Так как, по предположению, ряд (2) схо*
дится, то для всякого положительного числа б.су*
ществует настолько большое натуральное число v.
72
что при if ' ' мы имеем
I н- I ^р+2 I + • • • + I Zq I < <S
Так как
| Zp+д + zp+2 + ... + zj<
I I + I Zp+2 I + . . • + | Zq I < 6,
то. мы видим, что признак сходимости Коши выпол-
нен также и для ряда (1), т. е, он сходится.
К этому простому рассуждению тесно примыкает
одно важное свойство абсолютно сходящегося ряда,
которое, вообще говоря, не имеет места для ряда про-
сто сходящегося. Если ряд (1) абсолютно сходящий-
ся, то для каждого положительного числа 6 можно
подобрать настолько большое натуральное число v,
что если натуральные числа pi < Рг < • • • < рь все
превосходят число v, то имеет место неравенство
| zpx 4" zp2 + • • • + zpk | < 6. (3)
Здесь v — то натуральное число, которое соответ-
ствует положительному числу S согласно признаку
сходимости Коши для ряда (2).
Для доказательства этого свойства достаточно
* выписать неравенство
|гР1+гР2+ ... +zPfe|<|zP1| +|zP2| + ... +|zPJ<
<|zp+1| 4- |zp+2|+ ••• + IZqI < X
где p + 1 = pi, q = pk.
Независимость от порядка слагаемых. Докажем
теперь, что сумма s абсолютно сходящегося ряда (1)
не зависит от порядка его слагаемых. Для доказа-
тельства выпишем ряд
Z\ + 22 + . . . + z'n + ..., (4)
получающийся из ряда (1) перестановкой слагаемых.
Составим предварительные суммы для обоих рядов,
т. е. суммы
sn = 21 + Z2 + . . . + 2n, Sn = ZI + 22 + . . . + Zn.
Зададимся теперь произвольным положительным чис-
лом 6 и выберем настолько большое натуральное
число v, чтобы при п > v выполнялось неравенство
I sn — s | < S (5)
73
и для того же самого v имело место соотношение
(3). Зафиксируем теперь п, положив гг = v + 1. Так
как теперь сумма sn является вполне определенной,
то существует настолько большое v', что сумма sC
содержит все члены ряда (1), входящие в сумму sn.
Тогда при п' > v' сумма s'n' также содержит все
члены ряда (1), входящие в сумму sn, и потому в
силу неравенства (3) мы имеем
| Sn' — Sn | < б. (6)
Из неравенств (5) и (6) следует, что
I s'n' — s | < 26
при условии, что п' > v', где v' зависит от 6. Зада-
димся теперь произвольным положительным числом
8 и положим 6 = у. Таким образом, доказано, что,
исходя из заданного положительного числа 8, можно
найти такое натуральное число v', что при п' > v'
имеет место неравенство
I Sn' — s | < 8.
А это и значит, что ряд (4) имеет своей суммой число
s, являющееся суммой ряда (1).
Итак, доказано, что для абсолютно сходящегося
ряда сумма не зависит от порядка слагаемых.
Перемножение рядов. Для того чтобы перемно-
жить две конечные суммы, следует каждое слагаемое
первой суммы умножить на каждое слагаемое второй
суммы и полученные произведения сложить. Дока-
жем, что то же правило действует и в отношении аб-
солютно сходящихся рядов. Для доказательства этого
выпишем два абсолютно сходящихся ряда
г0 + Z[ + • • • + ^п + • • •, (7)
+ • • • + ^п + ... (8)
Здесь первые слагаемые рядов обозначены буквами
с индексами 0, а не с индексами 1. Это не имеет зна-
чения, а в дальнейшем будет удобно при примене-
ниях. Предварительные конечные суммы этих рядов
обозначим через
^ = Zo + zi + ... +z„; /п=^о + ^1+ ... + ^.
74
Предварительные суммы для рядов абсолютных ве-
личин обозначим через
= I Zo I + I Z1 | + ... +1 Zn I,
in — I w0 I + I Wi I + . . . + I Wn
Положим, далее,
lim sn = s, lim tn = t.
n->oo
Составим теперь произведения каждого члена ряда
(7) на каждый член ряда (8), т. е. произведения вида
ZpWq, и составим сумму всех этих произведений, выпи-
сав их предварительно в виде одной строки. Сделать
это можно разными способами. Укажем, например,
такой:
+ (21^0 + 2OW1) + (22Шо + 21^1 + 20Ш2) + . • .
... + (znWo + Zn-iWi + ... +z0Wn).
Здесь в одну группу собраны все произведения zpwq,
для которых р + q = п, и в этой группе слагаемые
расположены по росту индекса q от 0 до п. Этим или
другим способом расположенные в ряд произведения
вида ZpWq запишем в виде одной строки
go +gl + • • • + gm + • • • (9)
Предварительную сумму этого ряда обозначим через
hm — gb + gl + ••• + gm'
Мы докажем, что ряд (9) абсолютно сходящийся и,
следовательно, имеет сумму, которую мы обозначим
через h, так что
lim hm = h.
Далее, мы покажем, что
h = st.
Докажем это утверждение. Для этого составим
предварительные суммы для ряда абсолютных вели-
чин членов ряда (9)
hm = Igl 1 + 1^21+ ••• + I gm I-
Так как предварительная сумма hm содержит лишь
конечное число слагаемых вида [zpwql, то существует
75
для данного т такое большое п, что все члены пред-
варительной суммы hm содержатся в произведениях,
возникающих при перемножении сумм sn и 1п. Отсю-
да следует в первую очередь, что .
hm
а так как при неограниченном возрастании п оба
множителя правой части остаются ограниченными, то
ограниченной остается и предварительная сумма hm
при неограниченном росте числа т, так что ряд (9)
абсолютно сходится. Далее, очевидно, что все произ-
ведения вида ZpWq, входящие в предварительную сум-
му hm, входят в попарные произведения, возникаю-
щие при перемножении сумм sn и Таким образом,
разность sntn — hm может быть записана в виде
hm = gP{ 4- gp2 + • • •
где все номера pi < рэ < ... < pk больше m. По ра-
нее доказанному (см. (3)), для заданного положи-
тельного числа б найдется настолько большое нату-
ральное число v, что при v<pi<p2< ... < Pk
имеет место неравенство
+ Spk । < 6
и что при п > v имеют место неравенства
I sn — s | < б, | tn —-11 < б.
Из сказанного следует, что
lim hm — lim sntn — st.
m->oo
Итак, правило перемножения рядов доказано.
Одна основная формула элементарной алгебры.
Докажем здесь одну основную формулу алгебры, ко-
торая будет употребляться много раз в дальнейшем,
в частности для суммирования геометрической про-
грессии. Для записи этой формулы и ее доказатель-
ства обозначим через fk(z, w) многочлен относительно
двух переменных z и w, представляющий собой сум-
му всех произведений вида
zpwq, (10)
76
где р и q— неотрицательные целые числа, сумма ко»
торых равна k. Таким образом,
w) = zk 4- z4-1ay + zk~2w2 + ... + zwk~{ + o>fe.
Формула, о которой идет речь, следующая: 1
zn — wn = (z — w)fn^i(z, w). (11)
Для ее доказательства умножим fn_\ (z, w) на z. Оче-
видно, что это произведение содержит все слагаемые
вида (10), где k — п, кроме wn, так что мы имеем
/п-1(г, w)z — fn(z, w) — wn. (12)
Точно так же мы имеем
fn-i(z, w)w = fn(z, w) — zn. (13)
Вычитая равенство (13) из равенства (12), получаем
fn_i (z, w) (z — w) = zn — wn,
т. е. доказываемую формулу (И).
Суммирование геометрической прогрессии. Приме-
ним теперь формулу (И) для суммирования геомет*
рической прогрессии
sn = a-j-aw-j- ... -j-aw", (14)
где а и w — комплексные числа.
Ясно, что sn = afn(l, w), откуда в силу формулы
(И) получаем
a(l-wn+l)
sn 1 — w
Последнюю формулу можно применить для сум-
мирования бесконечной геометрической прогрессии
а + aw + aw2 + ... + + ... ' (16)
в случае, когда | w | < 1. Для ряда (16) сумма sn
(см. (14)) является предварительной суммой, и в
силу формулы (15) при |а>|< 1 мы имеем
lim».--(17)
П->оо 1 ш
(см. §2, (12)).
Главный признак абсолютной сходимости. Дадим
теперь один важный достаточный признак абсолют-
77
ной сходимости ряда. Выпишем ряд
zo + zi + ••• + Zn + •••» (18)
слагаемыми которого являются действительные или
комплексные числа. Наряду с ним выпишем другой
ряд
+ Щ + • • • + + • • •, (19)
слагаемыми которого являются действительные поло-
жительные числа.
Если ряд (19) сходится и выполнены неравенства
\zn n = 0, 1, 2, ...,
то ряд (18) является абсолютно сходящимся. Дока-
зательство этого утверждения настолько просто, что
нет надобности его приводить. Отметим дополнитель-
но важное соотношение. Если s — сумма ряда (18),
a v — сумма ряда (19), то имеет место неравенство
I s | < V.
Особенно важным частным случаем ряда (19) яв-
ляется геометрическая прогрессия
а + аа + аа2 + • • • + аип + ..., (20)
где а и а — положительные числа, причем а<1.
Сходимость ряда (20) нами уже доказана (см. (17)),
причем сумма v ряда (20) дается формулой
v =-т——. (21)
Таким образом, если ряд (18) удовлетворяет усло-
виям
\гп\^аа\ п = 0,1,2,..., (22)
то ряд (18) абсолютно сходится, и мы имеем
оценку его суммы в виде неравенства
ис-НЬг- <23>
Совокупность неравенств (22) можно записать ко-
ротко в виде одной формулы
г„ = О(ап) (24)
(см. § 2). Таким образом, последнее условие (24) яв-
ляется достаточным для абсолютной сходимости ряда
(18).
78
Пример I. Здесь будет дана формула, доказав
тельство которой служит хорошей иллюстрацией
только что изложенного достаточного признака аб-
солютной сходимости ряда. Сама формула найдет
важное применение в следующем параграфе. Пусть
c(k) — ограниченная функция натурального числа kt
т. е. функция, удовлетворяющая условию
| с (k} | < с,
где с — константа, не зависящая от k. Тогда имеет
место следующее предельное соотношение:
Ит(1+-Ц£-У=1. (25)
Для доказательства развернем выражение, стоя*
щее под знаком предела, по формуле бинома Ньюто*
на (см. § 2, (10)), именно, напишем
( 1 + = 1 + Zi + Z2 + • • • + 2/г + • • •,
где
__ k (k - 1) ... (k - n + 1) ( c (k) у _
Zn~ ni \ k2 J ~
= J____£. k- 1 + 1) , / c (k) у
n\ k k ' ' ' k
Эта формула верна при произвольно большом и, хотя
в биноме Ньютона содержится лишь конечное число
членов.
Непосредственно видно, что
Таким образом, при k > с мы имеем в силу формулы
(23) неравенство
с
| Z1 + 22 + ... + zn | --у• = k_ •
т
Из этого видно, что при k-^-oo сумма 21 + 22 + ...
... + 2Л стремится к нулю. Итак, формула (25) дока-
зана. Эту формулу можно переписать в виде
79
i. r м ep 2. Докажем, что ряд
1+^- + 4+ ••• +-р-+••• (26)
сходится. Для доказательства построим вспомога-
тельный ряд, слагаемые которого превосходят слагае-
мые ряда (26) и сходимость которого легко устанав-
ливается. Ряд этот следующий:
1+А+21з+ +(^Тй+--- <27>
Мы имеем
1^1 1
(п —- 1) п п — 1 п ’
Заменяя'по этой формуле каждый член ряда (27),
мы получаем новый ряд
>+('-4)+(4-4)+ - +(^т-1)+
+ (^"“7Тт)+ •••
Ясно, что сумма последнего ряда равна 2. Так как
1 1
пг (« — 1) Л *
то из сходимости ряда (27) вытекает сходимость
ряда (26), причем сумма ряда (26) меньше 2.
§ 7. Функция exp(z)
Большую роль в анализе играет функция exp(z)
комплексного переменного z, которая задается рядом
exp(2) = 4- + 44-4+ ... +4+ ... (1)
Ряд этот абсолютно сходится для произвольного зна-
чения z, так как
Ц(1 = О(¥'г). (2)
где у < 1, а это есть признак абсолютной сходимо-
сти ряда (1) (см. § 2, (19) и § 6, (24)).
Основные свойства функции exp(z). Установим те-
перь несколько свойств функции exp(z). Прежде
80
всего, ясно, что
ехр (0) = 1. (3)
Важнейшее свойство функции ехр (г/ выражается
следующей формулой:
ехр (г + w) = ехр (г) • ехр (ш), (4)
где z и w — два произвольных комплексных числа.
Для доказательства формулы (4) выпишем ряд
ехр(да) =-др + — + -2j-+ ... 4--^-+ ... (5)
Так как оба ряда (1) и (5) абсолютно сходятся, то
для получения их произведения следует перемножить
их почленно (см. § 6). Таким образом, нам следует
составить все произведения вида
W". , (6)
где р и q — целые неотрицательные числа, и просум-
мировать их. Просуммируем сперва все произведения
вида (6), для которых р + q = п, где п — фиксиро-
ванное целое неотрицательное число. Умножим эту
конечную сумму на п!. Полученная так сумма состоит
из всех слагаемых вида
Zpwq, /74
PM 7 7
где р + q = п, а числа р и q — целые неотрицатель-
ные. По формуле бинома Ньютона (см. § 2, (8))
сумма всех членов вида (7) равна
(z + w)n.
Так как в произведение рядов (1) и (5) входит сум-
ма всех произведений вида (6), а мы умножили ее на
п! для того, чтобы получить сумму членов вида (7),
то произведение рядов (1) и (5), очевидно, имеет
вид
ехр (z) • ехр (да) —
__ 1 , г + w . (г + а>)2 . (г + w)n 1 __
"ОГ ' И 2! “г • • • “г п! ~Г • •
= exp(z + w)
Хсм. (1)).
81
Таким образом, основная формула (4)' доказана.
Из соотношений (3) и (4) следует, что
ехр (— г) = —V--. (8)
н v ' ехр (г) v '
Действительно, мы имеем
1 = ехр (0) = ехр (z + (— z)) = ехр (г) • ехр (— z),
так что ехр(г)-ехр(—z)=l, а это значит, что фор-
мула (8) верна.
Из формул (4) и (8) непосредственно вытекает,
что
exp(®-z)=^-. (9)
Путем последовательного применения формулы
(4) в случае z = w мы получаем
ехр (Az) = (ехр (z))\
где k — произвольное натуральное число. Из этой
формулы и формул (3) и (8) следует, что
ехр (Az) = (ехр (z))& (10)
при произвольном целом А.
Докажем теперь, что
при |z| = a<l имеем | ехр(z) — 11 < a . (11)
Действительно,
exp(z)-1=^ + 4+ ... +^-+ ... (12)
При |z| = a<l мы имеем и, следо-
вательно, сумма ряда, стоящего в правой части ра-
венства (12), по модулю не превосходит величины
а (см. § 6, (23)). Таким образом, неравенство
(11) доказано.
Из неравенства (11) следует, что
при |ау —z| = a<l имеем |ехр(о>) — exp(z)|<
<1 ехр (г)!-!^-. (13)
82
Действительно, в силу формулы (9) мы имеем
ехр (да) — exp (z) =ехр (z) • (exp (да — z) — 1),
откуда в силу неравенства (11) следует неравенство
(13).
Из неравенства (13) следует, что функция exp(z)
есть непрерывная функция (см. пример 1 § 1). В са-
мом деле, пусть zo — произвольное комплексное число
и zi, Z2, ... zn, ... — такая последовательность комп-
лексных чисел, что
limz„ = zo.
П->оо
В силу формулы (13) мы имеем для достаточно боль-
ших п _
I exp (z„) — exp (zo) I < | exp (z0) I 1|- •
Переходя в этом неравенстве к пределу при п->-оо,
получаем
lim exp (zn) = exp (z0),
П->°°
так что функция exp (z)' непрерывна для каждого зна-
чения своего аргумента zo.
Функция exp(z) для действительных значений z=x.
Установим теперь некоторые свойства функции exp (z)
для действительных значений аргумента z = х. Преж-
де всего, ясно, что ехр(х) при действительных х всег-
да действительна и положительна. В самом деле, все
коэффициенты ряда (1) действительны и положи-
тельны, поэтому значения ехр(х) действительны и
положительны при х 0,- но они положительны и
при х < 0, что следует из формулы (8). Итак,
ехр(х) > 0.
Совершенно особую роль в математике играет
значение функции ехр(1). Число это имеет специаль-
ное обозначение е и, согласно формуле (1), оно равно
е = еХр(1)=1+± + ^+ ... +-^+ ... (14)
Благодаря своей исключительно большой роли в ма-
тематике число е вычислено с высокой точностью. Да-
дим его здесь с точностью до 5 десятичных знаков:
е « 2,71828.
83
Из формул (10) и (14) следует
exp(k) = ek (15)
для произвольного целого k. Но оказывается, что и
для произвольного рационального числа г мы имеем
ехр(г) = ег. (16)
В самом деле, полагая в формуле (10) k = l и lz —
— х, мы получаем из нее
ехр (х) = (ехр 0-)) • (17)
Так как числа ехр(х) и ехр (-у) положительны, то
из формулы (17) вытекает
ехр(т) = (exp(x))z ’
Здесь, очевидно, подразумевается, что в правой части
взято положительное значение корня из положитель-
ного числа. Полагая в этом соотношениг1 х = k, мы
получаем в силу формулы (15)
/ А 1 А
ехр (~) = (ехр 1 =(ek)1 =е1 .
гр k
1ак как — есть произвольное рациональное число,
то формула (16) доказана.
В формуле (16) справа стоит е в рациональной
степени г, определенное по всем правилам элемен-
тарной алгебры, т. е. для натуральных значений чис-
ла г обычным способом, для отрицательных и дроб-
ных степеней г, как это принято, при помощи обрат-
ных величин и корней. Таким образом, функция
ехр (г) для рациональных значений г получила ясное
с точки зрения элементарной алгебры выражение.
Можно теперь попытаться распространить функцию
определенную для рациональных значений аргу-
мента х — гу на все действительные значения х та-
ким образом, чтобы она стала непрерывной функ-
цией действительного аргумента х. Такое распростра*
некие можно дать, положив
в* = ехр(х). (18)
84
Для рациональных значений х = г' это равенство
имеет место в силу формулы (16). Но правая часть
равенства (18) определена для всех действительных
значений х и непрерывна. Таким образом, формула
(18) распространяет функцию ех на все действитель-
ные значения х.
Другого способа распространить функцию ех, оп-
ределенную для рациональных значений аргумента
х — г, на все действительные значения так, чтобы
она стала непрерывной, не существует. Это легко
проверить. В самом деле, пусть хо—произвольное
действительное число. Существует тогда такая после-
довательность
гь г2, rni ...
рациональных чисел, что
Iimrft = Xo.
П->ОО
Так как мы хотим, чтобы функция ех была непрерыв-
на в точке х = Хо, то мы должны иметь
lim еп = е\
Подставляя в левую часть этого равенства вместо еГп
выражение ехр(гп), мы получаем в силу непрерывно-
сти функции ехр (х)
lim ехр (г„) = ехр (х0)
д->оо
и, следовательно, = ехр(х0).
. Итак, доказана формула
е'=«Ры=<я-+-гг+4+ +4+ <19>
для действительных значений х. Формула эта глубоко
содержательна. Она выражает функцию ех действи-
тельного переменного х, первоначально определен-
ную чисто алгебраически, при помощи ряда (19), что
позволяет легко вычислять ее с большой точностью.
Функция exp(z) для мнимых значений z = iy. Мы
изучили функцию ехр (г) для действительных значе-
ний z — х. Изучим ее теперь для чисто мнимых зна-
чений г = iy, где у — действительное число. Оказы-
вается, что имеет место следующая замечательная
85
формула:
exp (ty) — cos у + I sin y> (20)
где cos у и sin у суть функции, определенные в триго-
нометрии и хорошо известные из элементарной мате-
матики. Здесь угол у измерен в радианах.
Проведем доказательство этой формулы. Для
этого, прежде вс^го, в ряд (1), определяющий exp(z),
подставим z = iy. Тогда ряд (1) будет содержать
члены двух типов: такие, которые не содержат в
своих коэффициентах мнимой величины /, и другие,
которые ее содержат. Собирая вместе действитель-
ные члены и чисто мнимые члены ряда (1) для z=iy>
т. е. переставляя члены этого ряда, что возможно в
связи с его абсолютной сходимостью, мы получим
„2 ,,2т
;<0-1-1+ ... +(-i)"^+ .... (2D
,,з . .2т+1
Ш = ...+(-!)“ -£ЬП)Г+ <22’
Так как ряд exp(z) абсолютно сходится, то ряды (21)
и (22) также абсолютно сходятся, и в силу результат
тов § 5 (см. пример 3) их можно почленно суммиро-
вать, и потому
exp (iy) = f(y) + ig (у).
Таким образом, доказав формулу (20), мы докажем,
что
cos y=f (у); sin у = g(y), (23)
т. е. получим для тригонометрических функций cos у
и sin у разложение в степенные ряды. Ряды эти абсо-
лютно сходящиеся для произвольного значения у,
что следует из абсолютной сходимости ряда (1).
При доказательстве формулы (20) нам придется
найти приближенное выражение функций f(y) ng(y),
исходя из рядов (21) и (22), в предположении, что
у мало. Мы будем считать, что | у | < у. Заметим, что
все слагаемые ряда (21), начиная со второго, по мо-
дулю не превосходят слагаемых,геометрической про-
грессии
1*/12+ ... + \уГ + ....
86
а все слагаемые ряда (22), начиная со второго, по
модулю не превосходят слагаемых геометрической
прогрессии
I у I3 + ... +Ы2т+1+ ...
Так как сумма первой геометрической прогрессии
равна
(см. § 6, (23)), а сумма второй геометрической про-
грессии равна
Ш3 Ш3 _4|,,р
i-Ш2 1 „1 зm
4
При I у | < у, то для функций f(y) и g(y) мы полу
чаем при | у |< у
1Ж—1 K-f-li/l2; 1g (г/) — gl<|lgl3. (24)
Идея доказательства формулы (20) следующая.
В силу формулы (10) мы имеем
ехр (tp) = (ехр (4-)У = (ехР (1а№>
где а = -|- = о(4). в пРеДположении> чт0 3 не за*
висит от k. Здесь k — натуральное число, но предпо-
ложим дополнительно, что оно четно. Выражая комп-
лексное число ехр (ta) = f (а) + ig(а) приближенно
на основании формул (24), которые справедливы, ко-
нечно, при у = а, мы получаем
/(<*) = 1+о(4г); g(a) = a + o(4-)- (25)
Возводя выражение f(a)+I’g(a) в степень k и пере-
ходя к пределу при k—>~ со, мы в результате ряда вы-
числений получим
lim (ехр (ia))fe = cos р + i sin P, (26)
£->oo
чем формула (20) и будет доказана при у = р.
87
Комплексное число ехр(ихУ запишем в тригоно-
метрической форме, т. е. положим
f («) + ig (а) = Р (cos 6 + I sin б),
где р и 6 суть функции числа а= у, т. е.‘в конеч-
ном счете, четного натурального числа k. Так как те-
перь
(ехр (Za))fe = р* [cos (&б) + i sin (йб)]
(см. введение, (14), (17)), то для доказательства со-
отношения (26) достаточно доказать два соотноше-
ния
limp^—1, (27)
Й->оо
lim kb = 0. (28)
&->оо
Пользуясь приближенными формулами (25), мы лег-
ко получаем
р’- и («)!’ + lg (»)1! = [1 + О (у)]1 + [«+ О
Далее,
* = arctgfg-.
Для приближенного вычисления отношения 4-т^г со-
ставим разность
/' + О(Н а °+0(т)~°~°,0(у)
/«) ° '+°Ш ° 1+оШ
Таким образом,
причем у = О (у) . Следовательно,
S = arctgy = -^^- • (« + 0(-р-)). (29)
88
Пользуясь полученными приближенными выраже-
ниями для р2 и 6, мы легко докажем формулы (27)
и (28). Действительно,
lim р* = lim (р2)2 = lim (1 + О =
&-»оо fe->oo &->оо > Vй ''
= 1™(1+о(^))'.
k
где В силу формулы (25) § 6
Таким образом, формула (27) доказана. Далее, мы
имеем по формуле (29)
lim £6 = lim -a-rctgY (fea-j-feO =
fe->oo k->oo Y v / •<
= lim -arctg - • lim (ka + kO (-rr)).
fe^-oo Y fe-»oA \k3JJ
В силу формулы (25) § 4
lim -*££***=!,
fe->oo Y
a
lim (4a + kO (^)) - lim (₽ + О (£)) = ₽.
Таким образом, формула (28) доказана.
Итак, равенство (26) доказано, а тем самым до-
казана и основная формула (20).
Пример 1. Определим функцию exp(z), задан-
ную рядом (1), иначе. Именно, оказывается, что
exp(z)= lim (1 +4У* (30)
&->оо ' К '
Для доказательства разложим выражение, состоящее
под знаком предела, по формуле бинома Ньютона
(см. § 2, (10)). Мы имеем
О + тУ-' + тг-Н---
... + + + ... (31)
89
Член номера т суммы (1) имеет вид
_ zm
Zm~ тГ
Член номера т суммы (31) имеет вид
z* =lm
т т х 7 т\
1 /гл k (k — I) ... (k — т + I)
где lm(k) = —±----------так что
0</т(^)<1, ' (32)
lim (33)
Л->оо
Таким образом, мы имеем
(2л+1 + гп+2 ""Ь • • •) (2л+1 + г^+2 + • • •) I
<|г„+1| + |г„+2|+ ••• =6„- (34)
Так как ряд (1) абсолютно сходится, то
lim 6П = 0. (35)
П->оо
Далее, положим
sn — 2о + 21 + ... + 2„,
sn Z0 “1“ 21 + • • • + zn‘
Из (33) и (34) следует, что
|С-«. !='.» <37>
причем при фиксированном п имеем
lim еА (га) — 0. (38)
k~> ОО
Из формул (34), (36) и (37) следует, что
|(1 +|)ft-exp(z)|<dn + eft(n). (39)
Зададимся теперь произвольно малым положи-
тельным числом а и выберем настолько большое га,
что <-£ (см. (35)). Зафиксируем это значение га
и выберем для него настолько большое число k, что-
бы было еА (га) < (см. (38)). Тогда из (39) получаем
I (1 + j)* — ехр (z) I < а. (40)
90
Таким образом, при произвольном положительном а
можно найти настолько большое k, что выполнено
неравенство (40), а это и значит, что выполнено ра-
венство (30).
Особый интерес формула (30) представляет при
z — 1. Тогда мы имеем
е= lim (1 +!)"•
jfe->OO '
Именно таким способом было первоначально опре»
делено число е.
§ 8. Основные трансцендентные функции
Основными трансцендентными функциями счи-
таются показательная функция ах, где а — положи»
тельное число, тригонометрические функции sinx,
cos х, tg х, ctg x и обратные к ним функции, т. е.
logo х, arcsin х, arccos х, arctg х, arcctg х.
В предыдущем параграфе, пользуясь функцией
exp(z), мы получили разложение функций ех, cosx,
sin х в степенные ряды, именно:
••• +^+ •••> 0)
v2 v2n
cosx=l-^+ ... +(-1)"^+ .... (2)
у3 1
*>п* = *-1г+ • +(-!>“ с£+Т)Г+ ••• <3>
(см. § 7, (19), (21) — (23)), причем ряды эти абсо»
лютно сходятся для всех действительных значений х.
Таким образом, пользуясь функцией exp(z), мы
получили разложение в ряды по степеням х трех
очень важных функций ех, cos х, sin х действительного
переменного. Каждая из этих трех функций по са-
мому своему определению имеет смысл лишь для
действительных значений аргумента.
Но так как ряды (1) — (3), при помощи которых
теперь эти функции можно вычислить, абсолютно
сходятся, то они сходятся и для комплексного значе-
ния аргумента, так что вместо действительного аргу-
мента х мы можем подставить в них комплексный
аргумент z и считать, что функции, прежде опреде-
ленные лишь для действительных значений аргумен-
91
та определены' теперь и для комплексных значений
аргумента. Таким образом, по определению мы мо-
жем написать е 1! 2! + ... • +^г+ •••’ (4)
cos z = 1 — -gj- + . . • + ( — 1)” .Л.^... 17 (2п)! 1 (5)
г3 Sin Z = Z 777" + .. ol . +( ~2п+1 — Jf—? L 7 (2п+ 1)! ~ • • (6)
Итак, пользуясь рядами, мы сумели функции, задан-
ные лишь для действительных значений аргумента,
распространить на все комплексные значения аргу-
мента. Возникает вопрос, является ли такое распро-
странение на комплексные значения аргумента слу-
чайным, т. е. можно ли его сделать для каждой из
функций е2, cos г, sin г при помощи рядов разными
способами. В следующем § 9 будет показано, что та-
кой возможности нет, что распространить на комп-
лексные значения аргумента функцию действитель-
ного переменного, пользуясь степенным рядом, мож-
но только одним способом.
Из равенства (1) § 7 и равенства (4) следует, что
ег — exp (z). (7)
Таким образом, функция ег имеет следующие свой-
ства:
е°=1, (8)
e*+w = ez-ew, (9)
е-г = 4-, (10)
его-г = -^ (И)
(см. § 7, (3), (4), (8), (9)). Кроме того, функция
ег непрерывна, так как ехр(г) непрерывна. Функции
cos г и sin z, получаемые при помощи рядов (5) и
(6), являются новыми функциями комплексного пере-
менного, но они тесно связаны с функцией е2 = exp(z). 1
Именно, подставляя в ряд (4) вместо z величину iz и j
сравнивая полученную формулу с формулами (5) и '
92
(6), мы приходим к тождеству
е1г = cos z + i sin z. (12)
Эта формула отнюдь не следует из формулы (20)
§ 7, которая доказана лишь для действительного зна-
чения аргумента, она верна для любых комплексных
значений г. Из формул (5) и (6) следует, что
cos (— z) = cos z, sin (— z) = — sin z.
Таким образом, cos z есть четная функция, a sin z
есть нечетная функция. Пользуясь этими формулами
и заменяя в формуле (12) z на —z, мы получаем
e~lz — cosz — i sinz. (13)
Разрешая соотношения (12) и (13) относительно
cos z и sin z, получаем для них следующие выраже-
ния:
eiz + e~iz ....
COS Z =----2-----’ (14)
eiz — e~iz
sin z =----%----- (15)
Таким образом, новые построенные нами функции
cos z и sin z комплексного переменного z очень про-
сто выражаются через функцию е2 комплексного пе-
ременного z.
Для функций cos z и sin z комплексного перемен-
ного теперь заново нужно доказать формулы коси-
нуса суммы и синуса суммы. Доказательство прово-
дится на основании формул (14) и (15) при помощи
формулы (9). Это я предоставляю сделать читателю.
Эти формулы указывают на сходство функций cos z
и sin z действительного и комплексного переменных.
Но есть и разница — для комплексного переменного
эти функции не ограничены.
Теперь, пользуясь формулой (9), можно более де-
тально изучить функцию ег комплексного перемен-
ного z = х + iy. Именно, мы имеем (см. § 7, (20))
= ехе1У = ех (cos у +1 sin у). (16)
Первый множитель р = ех есть показательная
функция, и ее сравнительно легко можно себе пред-
ставить. Это есть монотонная функция, которая чрез-
вычайно быстро возрастает при х->оо и очень бы-
93
стро стремится к нулю при х->—оо, оставаясь все
время положительной. График ее изображен на
рис. 8. Он пересекает ось ординат в точке р = 1. Об-
ратная функция для функции т. е. решение урав-
нения
р = ех
относительно х, называется логарифмом числа р при
основании е или натуральным логарифмом числа р.
Она обозначается через In р, так что х = In р. Дей-
ствительная функция In р определена лишь для по-
ложительных значений р. Она положительна при
р> 1 и отрицательна при р < 1. График этой функ-
ции легко себе представить, отобразив зеркально
график функции р — ех относительно биссектрисы
первой и третьей четверти координатной плоскости.
Он изображен на рис. 9.
Так как функции cos у и sin у имеют период 2л, то
из формулы (16) следует, что функция ег имеет пе-
риод 2лг, т. е.
— qZ *
Далее, из формулы (16) следует, что функция ег
не обращается в нуль ни при каком значении z, т. е.
ег=/=0.
Функция Inw комплексного переменного w. Для
того чтобы изучить функцию In w комплексного пере-
менного w, нам следует решить уравнение
ez — w = р (cos q> 4- i sin ф)
относительно z. Это уравнение перепишем в виде
е*+^ = (cos у _|_ i sin у) = р (cos ф + i sin ф).
94
Мы получаем
х = 1пр, (17)
z/= Ф 4~ 2Ъс.
Здесь в формуле (17) имеется в виду действитель-
ный логарифм действительного положительного чис-
ла р, a k — произвольное целое число. Таким обра-
зом, комплексная функция In w комплексного пере-
менного w есть многозначная функция. Она опреде-
лена лишь с точностью до слагаемого 2£jii. Это оче-
видно априори, так как функция е2 имеет период 2лг.
Натуральный логарифм действительного положитель-
ного числа также определен неоднозначно, но обычно
рассматривают лишь его действительное значение, ко-
торое определено однозначно. Здесь мы приходим к
неизбежному расширению понятия функции, именно,
функция может быть многозначной, с чем, однако,
сталкиваются уже и в элементарной алгебре при из-
влечении корня и в элементарной тригонометрии при
рассмотрении обратных тригонометрических функ-
ций.
Для того чтобы составить себе представление о
характере многозначности функции In w в комплекс-
ной области, представим себе, что точка w движется
в плоскости комплексного переменного w, описывая
некоторую кривую, не проходящую через начало ко-
ординат. Кривая эта задается уравнением
где t — действительная переменная (время), возра-
стающая от нуля. Если
w = р (cos ф + г sin ф),
то да(/) = [р(/), <p(OL гДе р(0 и ф(0 суть полярные
координаты точки w(f). Так как точка w (t) в про-
цессе своего движения не проходит через точку w =
= 0, то функция р(0 положительна и непрерывно
зависит от t, но функция ф(/) неоднозначна. Для того
чтобы сделать ее однозначной, нужно выбрать для
нее какое-либо определенное значение в начальный
момент времени t = 0, т. е. взять определенное зна-
чение ф(0), а затем следить за изменением угла ф(/)'
при изменении t так, чтобы функция ф(0 оставалась
непрерывной, т. е. не делала скачков. При этом мо-
95
жет случиться, что в некоторый момент времени
t = ti мы придем вновь в точку w (0), так что —
= w (0). При этом
Р (Л) = Р (0); Ф (/1) = Ф (0) + 2km,
здесь k может оказаться не равным нулю.
Таким образом, значение функции In w, непре-
^рывно меняющееся при возрастании t от нуля до /ь
изменится в результате движения вдоль нашей кри-
вой на число 2km, хотя значения аргумента w функ-
ции In w в начальный и конечный момент совпадают.
Легко усмотреть, что целое число k равно числу об-
ходов вокруг начала координат кривой, которая опи-
сывается точкой w(t) при своем движении. Это кон-
кретно можно себе представить в случае, когда
w (/) = cos 14- i sin t,
a t\ = 2kn, т. e. когда точка w(t) движется по ок-
ружности радиуса единица вокруг начала координат,
начиная из положения w = 1, причем мы считаем
ф(0) = 0. Так как ti = 2kn, то при таком движении
точка w(t) пробегает окружность k раз, так что кри-
вая w(t) k раз навертывается на окружность, и число
k равно числу оборотов точки w(t) вокруг начала ко-
ординат. Ввиду того, что изменение значения In w за-
висит от числа обходов кривой вокруг начала коор-
динат, начало координат называется точкой ветвле-
ния функции In w, или более полно, логарифмиче-
ской точкой ветвления.
Функции arccos w и arcsin w комплексного перемен-
ного w. Функции arccos w и arcsin w легко выражают-
ся через логарифм комплексного переменного. Для
того чтобы найти функцию arccos w, мы должны ре-
шить уравнение w = cos z относительно z. Для ре-
шения этого уравнения выразим cos г по формуле
(14). Тогда мы получим
etz + e~iz
w==-----2-----
Полагая
е1г = 1, (18).
мы имеем
£2 + 1=0,
96
откуда g = tiy+Voy2~ 1 • Здесь под функцией Vo»2— 1
подразумевается двузначная функция, и потому нет
надобности писать перед корнем оба знака. В силу
формулы (18) получаем
z = — i In (w + д/да2 — 1 )>
следовательно,
arccos w — —i In (да + — 1 )•
Точно так же получается формула
arcsin w = —i In (jw + дЛ — w2 )•
Таким образом, функции arccos w и arcsin w вы-
ражены через логарифм. Входящие в эти формулы
неоднозначные функции V” и In могут принимать свои
произвольные значения.
Пример. История логарифмов. Хорошо извест-
ное из элементарной математики понятие логарифма
возникло первоначально из сопоставления свойств
геометрической и арифметической прогрессий
..., q~n, ..., q~l, 1, q, ..., qn, ..., (19)
..., — па.....— a, 0, a, ..., па, ..., (29)
где q>l; a >• 0. Видно, что произведению чисел
первого ряда соответствует сумма чисел второго
ряда, т. е. в современном смысле числа второго ряда
являются логарифмами чисел первого ряда при неко-
тором основании. Эта зависимость между последова-
тельностями (19) и (20) была отчасти подмечена уже
Архимедом и хорошо известна математикам XV—
XVI веков. Однако это свойство не было использо-
вано для практической цели. Между тем таблица
(19), (20) дает возможность заменить операцию ум-
ножения более простой операцией сложения. Позже,
в XVI веке, потребности навигации, связанные с оп-
ределением положения корабля по звездам, вызвали
развитие различных вычислительных приемов, в ча-
стности возникновение логарифмических таблиц. Пер-
вые таблицы логарифмов были составлены швейцар-
ским математиком Бюрге и шотландским математи-
ком Непером в XVII веке. Здесь мы изложим основ-
ную идею Бюрге.
4 Л. С. Понтрягин 97
Для того чтобы составить таблицу логарифмов,
важно, чтобы числа последовательности (19) распо-
лагались достаточно густо, т. е. чтобы число q было
достаточно близко к единице. Можно положить
<7=1+-—, где k — достаточно большое натуральное
число. Если положить а = у, то вместо последова-
тельностей (19) и (20) получаем последовательности
••ОЧГ..............0+1Г'.
('+-!•).......0+В“.......... <21>
___п _________L .2. JL п
..., k> ..., k, k, ..., k, ... w
Теперь числа последовательности (22) являются ло-
гарифмами последовательности (21), взятыми при ос-
новании (1 +4) * Чем больше k, тем, гуще стано-
вится последовательность (21) и тем совершеннее
таблица логарифмов, построенная при помощи после-
довательностей (21) и (22). Бюрге взял за k число
10 000 и получил для основания логарифмов
/ 1 \ Ю 000
(1 + ^loooo J значение 2,71824, совпадающее с чис-
лом е с точностью до 4 десятичных знаков. Само число е,
как это было указано в примере 1 § 7. определяется
как предельное значение для
(+!)'
при Й->оо,
В результате этого предельного перехода соответ-
ствие между последовательностями (21) и (22) пре-
вращается в логарифмическую зависимость у — In xt
§ 9. Степенные ряды
Функция exp(z) комплексного переменного z оп-
ределяется как сумма степенного ряда (см. § 7)
exp(2)-.± + i+4+ (I)
Естественным обобщением этого является задание
функции f (z) комплексного переменного г при по-
98
моши произвольного степенного ряда
f(z) = ao + aIz + a2z2+ ... +a„zft+ .... (2)
где ао, o-i, «2, ... ап, ... — заданные комплексные
числа, определяющие ряд и тем самым функцию f(z).
Ясно, что ряд (1) является частным случаем ряда
(2), когда
Функция f(z)' может быть определена формулой (2)
лишь для тех значений аргумента г, для которых ряд
(2) сходится. Ряд (1), определяющий функцию
exp(z), сходится для всех значений z (см. § 7). Но,
конечно, произвольный ряд (2) не обладает этим
свойством. Таким образом, первой важнейшей зада-
чей, с которой мы здесь сталкиваемся, является ре-
шение вопроса о том, для каких значений z конкрет-
но заданный ряд (2) сходится или, что даже более
важно, сходится абсолютно.
Очевидно, что при z — 0 ряд (2) всегда сходится,
но существуют и такие ряды типа (2), которые схо-
дятся лишь при г = 0 (см. пример 1). Такие ряды,
конечно, не определяют никакой функции, и мы пока
будем называть их тривиальными.
Некоторые свойства нетривиального ряда. Итак,
будем исходить из предположения, что для некото-
рого значения z = zo #= О ряд (2) сходится. Тогда в
силу формулы (6) § 5
lim anzo — О,
п->оо
и потому все числа вида
a„zo, n = 0, 1, 2................
по модулю меньше некоторой константы а. Таким
образом, мы имеем |апЦг01” < а.
Отсюда мы получаем оценку для коэффициента
ап', именно, мы имеем
|a„l<-™ « = 0,1,2,...
I ^0 I
Составим теперь вспомогательный ряд из положи-
тельных членов
^)-=“+‘>та-+»т5г+ +»tS-+ ••• и
4* 99
Ряд (3), как говорят, мажорирует ряд (2), так кай
каждый его член больше соответствующего члена
ряда (2), именно:
|а„г"|<а-|Црг. (4)
Поскольку при
I z | < | z01 (5)
ряд (3) является сходящейся геометрической про-
грессией, то при выполнении условия (3) ряд (2J аб-
солютно сходится.
Отбросим в ряде (2) свободный член. Тогда мы
получим ряд
fl (z) = tzjz 4- a2z2 + ... + апгп + ...
Его мажорирует ряд
^г> = а177Г + а W+ ••• +aKl7r+ •••’ (6)
и потому мы имеем
I fl (z) I < Fl (z).
При выполнении условия (5) ряд (6), представляю-
щий собой геометрическую прогрессию, имеет своей
суммой
f Z у _ ° I г0 I - Д I * I
/1W— Izl I Z0 | - I z I
Izol
(cm. § 6, (21)). Таким образом,
Мы имеем
f(z) = ao + fi (z),
(7)
(8)
причем ft(z) удовлетворяет неравенству (7). Допу-
стим, что
Выберем теперь такое ограничение на |z|, чтобы мо-
дуль первого слагаемого суммы (8) был больше мо-
дуля второго. Тогда сумма (8), т. е. f(z), не обра-
тится в нуль. Для этого достаточно предположить,
100
что
|z|<Igi|2ol = P.
(9)
Подставляя в (7) вместо | z | его оценку (9), мы
только увеличиваем правую часть (7) и получаем
1Л(2) I <
I «о I । г ।
а 2д । г° ।
I V I _ I а° I I V I
koi 2а koi
а | а01
2а — | аа |
а I До I
а
= |Оо|-
JaKHM образом, если Яот^О, мы нашли такое поло-
жительное число р (см. (9)), что при
IZ | < р
ряд (2) сходится и сумма его f(z) отлична от нуля,
так что
при | z | < р имеем f(z)=/=O. (10)
Радиус сходимости. Оказывается, что если ряд (2)
нетривиален, то существует такое положительное
число г (случай г = со не исключается), что при
|z|< г ряд (2) абсолютно сходится, а при |z|> г
ряд (2) расходится. Число г называется радиусом
сходимости ряда (2), а круг с центром в точке 0 и
радиусом г называется кругом сходимости ряда (2).
Докажем существование радиуса сходимости не-
тривиального ряда (2). Обозначим через М множе-
ство всех действительных чисел вида |zo|, где г0
удовлетворяет условию
ряд (2) сходится при z = z0. (11)
Из условия (11) следует, что если число а принад-
лежит А1, то и любое положительное число 0 < а
также принадлежит М. Отсюда следует, что если в М
входят произвольно большие числа, то множество М
состоит из всех положительных чисел. В этом случае
положим г = оо. Если же множество М не содержит
произвольно больших чисел, то оно ограничено, и мы
обозначим через г его верхнюю грань (см. § 4).
В обоих случаях множество М содержит все числа,
удовлетворяющие условию 0 < а < г. Докажем, что
так определенное нами число г есть радиус сходи-
мости ряда (2).
101
Допустим, что 12i | < г. Тогда найдется такое чис-
ло zo, что при z = 20 ряд (2) сходится и
I | < | 20 | < Г.
Так как при z = 20 ряд (2) сходится, то в силу усло-
вия (5) он сходится абсолютно при z = Zi. Таким об-
разом, для всех точек г, удовлетворяющих условию
|г|<3г, ряд (2) сходится абсолютно. Если теперь
1211 > г, то 1211 не принадлежит множеству М, и по-
тому при 2 = 21 ряд (2) расходится. Итак, доказано
существование радиуса г > 0 сходимости для нетри-
виального ряда (2). Если ряд (2) сходится лишь при
г = 0, то мы будем считать, что его радиус сходимо-
сти равен нулю. Термин «нетривиальный ряд» в даль-
нейшем употребляться не будет.
Поведение степенного ряда вблизи точки 2 = 0.
Будем считать, что не все коэффициенты ряда (2) с
положительным радиусом сходимости равны нулю,
и докажем, что существует настолько малое положи-
тельное число р, что уравнение
И*) = 0 (12)
при |z| < р либо вовсе не имеет решении, либо имеет
единственное решение z = 0.
Пусть ak есть первый из коэффициентов ряда <(-2)„
не обращающийся в нуль. Случай k — G уже был
нами рассмотрен (см. (10)). В этом случае уравне-
ние (12) не имеет решения. Допустим теперь, что
k > 0. Запишем функцию /(z) в виде
f(2) = 2ftfft(2),
где
fk(z) ~ak + аь+12 + ... +а&+п2п+ ... (13)
Так как свободный член ряда (13) отличен от
нуля., то, согласно (10), существует такое положи-
тельное число pk9 что ^i(z)#=0 при Шким
образом, при | z| < pk функция f(z)=z*^(z) может
обращаться в нуль только тогда, когда ^обращается
в нуль ее первый множитель, т. е. при z = 0.
Теорема единственности для рядов. Пусть М — не-
которое бесконечное множество точек плоскости комп-
лексного переменного г, имеющее точку нуль своей
предельной точкой (см. § пример 3). Допустим,
102
что функция f(z)\ определяемая рядом ____
/ (z) = «о + fliZ + ... anzn..., (14)
обращается в нуль в каждой точке г множества М,
т. е.
при геймы имеем f(z) = O. (15)
Тогда оказывается, что все коэффициенты ряда (14)
обращаются в нуль. '
Докажем это. Допустим, что не все коэффициенты
ряда (14) обращаются в нуль. Тогда в силу доказан’
ного выше существует такое положительное число р,
что при |z|<p уравнение f(z) — O имеет не более
одного решения, и если оно его имеет, то это решение
есть z = 0. Неравенство | г] < р определяет окрест-
ность радиуса р точки 0. А так как точка z = О
есть предельная точка множества М, то в этой окрест-
ности содержится точка г множества М, отличная от
нуля, и для нее в силу условия (15) мы имеем f(2) —
= 0, что невозможно.
Таким образом, приходится признать, что все
коэффициенты ряда (14) равны нулю.
Сделаем теперь вывод из этого предложения, от-
носящийся уже к двум рядам
<р (г) = а0 4- сцг + ... +anzn+ • ••, (16)
ф(г) = 0о + &г+ ... +₽„zn+ ... (17)
Если теперь М — опять множество, имеющее точку О
своей предельной точкой^ то из предположения, что
для всякой точки z, нринадлежащей к М, имеет ме-
сто равенство
<р(г)=ф(2), (18)
вытекает, что коэффициенты рядов (16) и (17) сов-
падают между собой, т. е.
ая = £п, n = 0, 1, ... (19)
Доказательство этой части утверждения, относя-
щейся к двум функциям, сразу же сводится к первой
его части, относящейся к одной только функции. Для
этого сведения выпишем разность
f (2) = ф (г) — ф (z) = (во — ₽о) + (“1 — ₽1) 2 + ...
... +(ая-Рп)2,1+ ... (20)
103
Из равенства (18) следует равенство f(z) = 0 при
z&'M, так что все коэффициенты ряда (20) равны
нулю, а это значит, что имеют место равенства (19).
Итак, теорема единственности доказана.
Задание функций степенными рядами есть один из
важнейших методов высшей математики. Этот метод
ставит перед нами ряд вопросов, среди которых есть
и следующий. Может ли быть функция f(x) действи-
тельного переменного х задана двумя различными
степенными рядами
ф(х) = оо+ aix+ ... +апхп+ ..., (21)
Ш = ₽о + ₽1* + ... 4-Р„хп4- ... (22)
хотя бы на очень маленьком отрезке изменения xt
|х|< Р, где р — положительное число. Теорема един»
ственности сразу дает нам отрицательный ответ на
этот вопрос, именно: коэффициенты рядов (21) и
(22) должны быть одинаковыми, если они задают
одну и ту же функцию f(x).
В самом деле, подставляя в ряды (21) и (22) вме-
сто действительного переменного х комплексное пе-
ременное z, мы получим функции <p(z) и ф(г), кото-
рые равны между собой на множестве Mf состоящем
из всех действительных чисел, удовлетворяющих ус-
ловию |х|<р. Это множество М. имеет в качестве
своей предельной точки точку 0. Таким образом, в
силу теоремы единственности коэффициенты рядов
(21) и (22) должны быть равны между собой. Одно-
временно мы получаем решение также и другого во-
проса. Функция f(x) действительного переменного х,
которая может быть задана степенным рядом хотя
бы на очень маленьком отрезке |х|< р, может быть
превращена в функцию комплексного переменного,
задаваемую степенным рядом лишь единственным
способом. Так обстоит дело, в частности, с функ-
циями cos х и sin х действительного переменного х.
В предыдущем параграфе мы превратили их в функ-
ции комплексного переменного г, и теперь видно, что
сделать это можно было лишь одним способом.
Найдем теперь радиусы сходимости некоторых
конкретных степенных рядов.
Пример 1. Дадим прежде всего такой ряд с ра-
диусом сходимости нуль:
1 + 1!г + 2!г2+ ... + n!Z + ... (23J
104
Ряд этот расходится при любом г У= 0. Для доказа*
тельства положим jz| = ~-. Тогда мы имеем
1п!гп1 = -^,
и потому (см. § 2, (18))
1. п\
lim —уг = оо ,
п^оо <*п
Таким образом, слагаемые ряда (23) не только не
стремятся к нулю, но неограниченно возрастают, и,
следовательно, ряд (23) при z #= 0 не может схо>
диться.
Пример 2. Выпишем ряд
f(z)=l+z + z2+ ... +гп+ ... (24)
Это есть геометрическая прогрессия, при |z|< 1 она
сходится, и сумма ее определяется формулой (21) §6
/(*) = 7^7- (25)
При |г|> 1 ряд (24) всегда расходится, так как сла-
гаемые его не стремятся к нулю. Таким образом, ра-
диус сходимости ряда (24) есть единица. Следует
подчеркнуть, что-и при |z| = 1 ряд (24) всегда рас-
ходится. Здесь следует отметить очень важный и ин-
тересный факт. Ряд (24) определяет функцию f(z)\
лишь для |z|< 1, между тем как формула (25) за-
дает ее для всех значений г =# 1. Это явление очень
важно и типично в теории аналитических функций.
Первоначально аналитическую функцию можно за-
дать рядом, который определяет ее лишь в круге схо-
димости. Потом оказывается, что так заданная функ-
ция в действительности определена и для других зна-
чений аргумента — в данном случае для всех, за
исключением 2=1. Так полученное продолжение
функции, первоначально заданной на круге сходимо-
сти, на более широкую область значения аргумента
называется аналитическим продолжением исходной
функции, и это продолжение можно, оказывается,
осуществить лишь единственным способом. Типичным
для аналитических функций оказывается тот факт,
что на границе круга сходимости имеется особая
точка функции f(z), заданной формулой (25), имен-
105
но, точка z = 1, где функция f(z), заданная форму-
лой (25), равняется бесконечности или, иначе, просто
не определена. Если бы мы исходили из функции
f(z), заданной формулой (25), и захотели разложить
ее в степенной ряд, то, конечно, круг сходимости
этого ряда не мог бы содержать точку z = 1, так как
в этой точке функция, заданная формулой (25), ста-
новится бесконечной. Поэтому ряд, задающий функ-
цию (25), не может иметь радиус сходимости г > 1,
но оказывается, что он равен единице. Таким обра-
зом, препятствием к расширению круга сходимости
служит появление на его границе особой точки ис-
ходной функции (25).
Пример 3. Естественным обобщением ряда (24)
является ряд
fk(z)=l + lftz + 2*z2+ ... +nkzn+ .... (26)
где k — некоторое целое число. При k — 0 мы полу^
чаем ряд (24). Из формул (15) и (16) § 2 следует,
что радиус сходимости ряда (26) при любом k равен
единице.
При k = —1 мы получаем ряд, заслуживающий
особого внимания. Позже будет доказано (см. § 13,
пример 3), что он равен 1 — 1п(1—г), так что мы
имеем
l-ln{i-z)=l + f+ ^+ ... + ...
Заменяя здесь z на —z, мы получаем
in(i+Z)=f-4+4+ ••• •••
1 ; X О П
(27)
При 2=1 ряд (27) сходится, так как он является
знакопеременным рядом с убывающими членами (см.
§ 4). При 2 = —1 он расходится (см. § 5). Таким об'
разом, на границе круга сходимости ряд (27) в некО'
торых точках сходится, в некоторых расходится. При
k — —2 мы получаем ряд
/_2(г)=1+-^ + 4+ •• +§+ •••
Ряд этот сходится при всех значениях z на границе
круга сходимости, т. е. при |г|= 1 (см. пример 2 §6).
106
Из этих примеров видно, что на границе круга
сходимости ряд может вести себя по-разному. Ряд
/=0(г) расходится во всех точках на границе круга схо-
димости. Ряд /~1(г) в некоторых точках границы кру-
га сходимости сходится, в некоторых расходится,
И, наконец, ряд /-2(2) абсолютно сходится во всех
точках границы круга сходимости.
Пример 4. Если z0 есть постоянная комплекс-
ная величина, то некоторую функцию /(z) можно за-
дать рядом
f (z) = a0 + ai(z— z0)+ ... + (z — z0)n + ... (28)
по степеням величины г — z0. Из ранее доказанного
следует, что существует такое число г 0, что при
| z — zo < г ряд (28) абсолютно сходится, а при
[z — z0 >.гряд (28) расходится.
Глава II
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
Эта глава посвящена весьма сжатому изложению
первой основной части математического анализа, свя-
занной с понятием производной функции, вычисле-
нием производных различных функций или, что то
же самое, их дифференцированием. Для того чтобы
дать определение производной, приходится прежде
всего несколько видоизменить понятие предела, дан-
ное в главе I. Затем дается само определение одно-
временно для действительного и комплексного слу-
чая. Это делается в § 10. В § 11 даются правила вы-
числения производных. В первую очередь вычисляет-
ся производная степенного ряда, что дает возмож-
ность продифференцировать функции ez, cos г, sin 2,
разложение в степенные ряды которых уже было по-
лучено в главе I. Затем выводятся правила диффе-
ренцирования произведения, отношения и сложной
функции. Из последнего выводится правило диффе-
ренцирования обратной функции. Таким образом,
§ 11 содержит в себе правила дифференцирования
всех элементарных трансцендентных функций. Хотя
глава и называется «дифференциальное исчисление»,
в ней, однако, вводится и операция интегрирования
как обратная к операции дифференцирования. Вво-
дится понятие первообразной функции или, что то же
самое, неопределенного интеграла, также одновре-
менно для действительного и комплексного случая.
При помощи формулы Лагранжа доказывается един-
ственность первообразной с точностью до постоян-
ного слагаемого, так что предварительно приходится
доказать теорему Ролля и формулу Лагранжа для
действительных функций. Все это делается в § 12.
108
В § 13 находятся первообразные для некоторых конк-
ретных функций, а также даются некоторые правила
интегрирования, именно, интегрирования по частям и
при помощи замены переменной интегрирования.
В § 14 несколько искусственно вводится понятие оп-
ределенного интеграла как такой первообразной, ко-
торая обращается в нуль в заданной точке го. На
основе этого устанавливается ряд правил, относя-
щихся к определенным интегралам, и, в частности,
дается оценка определенного интеграла от действи-
тельной функции через ее модуль. Делается это при
помощи формулы Лагранжа.
Определенный интеграл вводится таким не вполне
естественным образом, для того чтобы в последнем
параграфе главы дать формулу Тейлора с остаточ-
ным членом в интегральной форме и для того чтобы
в ряде конкретных случаев дать оценку этого оста-
точного члена. Вычисление остаточного члена в ин-
тегральной форме делается исключительно просто.
Такого простого вычисления остаточного члена в ин-
тегральной форме я нигде не встречал.
§ 10. Производная
В математическом анализе огромную роль играет
так называемая производная функции. Представим
себе, что мы изучаем некоторую функцию f(t) дей-
ствительного переменного /. Пользуясь некоторыми
операциями, которые будут подробно описаны ниже,
мы, исходя из функции f(t), строим новую функцию
Эта новая функция называется производной
функции /(/). Прежде чем перейти к детальному опи-
санию того, как функция f'(t) получается из функции
/(/), скажем несколько слов об этой функции
Конечно, это словесное описание производной доволь-
но туманно, но все же оно даст нам некоторую воз-
можность составить себе представление о значении
производной для приложений математики, в частно-
сти для физики и других разделов естествознания.
Будем для определенности считать, что t есть время,
a f(t) есть какая-то физическая величина, меняю-
щаяся со временем. Физические величины, меняю-
щиеся с течением времени, встречаются во всех фи-
зических процессах. Так, например, абсцисса х неко-
10$
торой точки, движущейся по оси абсцисс, зависит от
времени и является его функцией, так что процесс
этого движения может быть записан в виде
х = f (/).
Это уравнение рассказывает нам о том, как положе-
ние точки меняется с изменением времени. Точно так
же температура Т некоторого тела может меняться
со временем, и тогда процесс этого изменения может
быть записан в виде уравнения
где f(t) есть какая-то определенная функция вре-
мени t. Не стараясь на первых порах определить, что
это значит точно, мы все же ясно представляем себе,
что скорость изменения величины f(t) с течением
времени t может быть разной в разные моменты вре-
мени. Таким образом, мы ясно ощущаем, что ско-
рость изменения величины f(t) зависит от момента
времени t и является функцией времени t. Эта ско-
рость и обозначается через Таким образом,
чисто словесное определение производной f'(t) сле-
дующее: f'(t) есть скорость изменения величины f(t)
в момент времени t. При изучении физического про-
цесса обычно выделяют несколько физических вели-
чин, характеризующих состояние нашего физического
объекта в данный момент времени, и эти величины,
как правило, меняются со временем, т. е. происходит
физический процесс. Например, если речь идет о сжа-
тии некоторого количества газа в цилиндре, то физи-
ческие величины, характеризующие состояние газа
в данный момент, следующие: объем газа, его давле-
ние и температура. Если происходит сжатие газа, то
все эти величины меняются со временем, и ясно, что
скорость их изменения играет существенную роль в
описании процесса сжатия газа (см. § 13, пример 1).
Оказывается, что все или почти все физические за-
коны могут быть описаны математически как неко-
торые уравнения, связывающие физические величины
со скоростями их изменения, т. е. связывающие функ-
ции и их производные. Это обстоятельство и опреде-
ляет исключительно большое значение производной
для изучения физических процессов.
110
Для того чтобы дать полное математическое опи*
сание производной, необходимо предварительно не-
сколько видоизменить операцию предельного пере-
хода, которая рассматривалась нами в § 1.
Новое понятие предельного перехода. В § 1 мы ио
ходили из некоторой последовательности чисел
52, . . Sn, . . . (1)
При этом было выяснено, какой смысл имеет утверж-
дение, что последовательность (1) сходится к некото-
рому числу s. Именно, было объявлено, что последо-
вательность (1) сходится к числу s тогда и только
тогда, когда разность sn — s неограниченно прибли-
жается к нулю при неограниченном возрастании чис-
ла л. Если это имеет место, то пишут
limsn = s. (2)
rt->oo
Напомню здесь более формальное точное описание
предельного перехода, которое принято в математике
и которое уже было дано в § 1. Соотношение (2)
имеет место тогда и только тогда, когда для каждого
положительного числа е можно подобрать настолько
большое целое число v, что при п >• v имеет место
неравенство |sn — s|<e.
Это описание предельного перехода можно легко
перефразировать, взяв за исходный объект не после,
довательность чисел, а функцию f(n) целочисленного
аргумента, которая определяется формулой
f(n) = sn, п=1,2, ... (3)
Ясно, что если мы знаем последовательность (1),
то тем самым мы знаем и функцию f(n) целочислен-
ного аргумента п, и наоборот, если известна функция
f(n) целочисленного аргумента п, то известна и по-
следовательность (1). Связь между последователь-
ностью и функцией дается формулой (3).Теперь есте-
ственно перейти от функции f(n) целочисленного ар-
гумента п к функции f(z) действительного или даже
комплексного переменного г. При рассмотрении функ-
ции целочисленного аргумента п мы считали, что этот
аргумент п неограниченно возрастает, т. е. стремится
к бесконечности. При рассмотрении функции f(z)\
комплексного или действительного переменного г мы
Ш
будем считать, что z стремится к некоторому число-’
вому значению z0, и поставим перед собой вопрос,
стремится ли значение f(z) при этом к некоторому
числу fo- Если это имеет место, то пишут
limf(z) = /0. (4)
Z->Zj
При этом мы считаем, что функция f(z) может быть
и не определена при z = z0.
Утверждение (4) имеет следующий, непосред-
ственно ясный смысл. По мере того как аргумент г
функции f(z) неограниченно приближается к неко'
торому числу г0, значение функции f(z) неограничен'
но приближается к числу fo. Точная формулировка,
принятая теперь в математике, следующая: по опре-
делению соотношение (4) имеет место тогда и только
тогда, ‘ когда для каждого положительного числа 8
можно подобрать настолько малое положительное
число б, что при |z— zo|<6 имеет место неравен-
ство \f(z)— fol < е.
Новое определение предельного перехода для
функции f(z) не только аналогично старому опреде-
лению предельного перехода для последовательности
чисел, но оно связано с ним логически, однако изу'
чать эту связь мы не будем.
Непрерывность функции. Новое определение пре-
дельного перехода для функции f (z) дает возмож-
ность дать новое определение непрерывности функ-
ции, именно, функция f(z) считается непрерывной для
значения своего аргумента zq, если имеет место со-
отношение
limf(z) = f(zo). (5)
z~>z>
Это новое определение непрерывности равносильно
старому, данному в примере 1 § 1. В дальнейшем мы
будем пользоваться лишь этим новым определением
непрерывности, и для того чтобы установить связь
с прежним определением, докажем, что функция, не-
прерывная в новом смысле (см. (5)), непрерывна и
в старом смысле. Доказательство будет дано в ниже-
следующем примере 3.
Производная функции. В математике рассматрива-
ются производные функций как действительного, так
и комплексного переменных, причем определение оди-
112
маково для обоих случаев. Поэтому будем исходить
из некоторой функции /(г) действительного или комп-
лексного переменного, не фиксируя этого заранее. За-
крепим временно некоторое значение z аргумента
функции f(z) и определим значение f' (z) производ-
ной функции f(z) для этого значения аргумента г.
Для этого наряду с закрепленным значением z рас-
смотрим произвольное значение £ аргумента функ-
ции f(z). Мы будем мыслить себе величину £ как по-
лученную из величины z путем ее изменения. Для
того чтобы подчеркнуть это, назовем приращением.
величины z величину
Дг = £ — z.
Тогда
C = z 4-Дх.
Приращению Дг независимого переменного соответ-
ствует приращение функции, определяемое формулой
Af (z) = f (С) - f (*) = f (z + Az) - f (г).
Для того чтобы вычислить производную f'(z), со-
ставим отношение приращения функции к прираще-
нию аргумента
Л.Чг) __ f(z + bz)-f(z)
Дг Z - г Дг ’ w
Это отношение определено для всякого значения £,
не равного z, или, что то же самое, для всякого зна-
чения Дг Ф 0. При t, — z числитель и знаменатель
дроби (6) обращаются в нуль, поэтому дробь не
имеет смысла. Если отношение (6) стремится к опре-
деленному пределу, когда £ z или, что то же самое,
Дг -> 0, т. е. когда
lim (7)
существует, то считают, что функция имеет про-
изводную f'(z) для своего значения аргумента z, и
эта производная определяется формулой
г (z) = lim <8>
При определении производной в точке z мы будем
предполагать, что все значения величины £, доста-
точно близкие к г, являются допустимыми значения-
113
ми аргумента. В дальнейшем мы будем считать, что
если написана производная, то она существует.
Если функция f(z) записана у нас в виде слож-
ного выражения, то при обозначении его производной
штрих ставят иногда за скобку, именно, следующим
образом:
/'(*) = (/(*))'. (9)
В дальнейшем, когда мы будем писать мы всег-
да будем считать, что производная функции f(z) су-
ществует при заданном значении z, т. е. что предел
(7) существует.
Определяя производную f'(z) функции f(z)’ при
значении аргумента z, мы, как правило, будем пред-
полагать, .что функция f(z) определена для всех зна-
чений своего аргумента, принадлежащих некоторой
окрестности U6 точки z (см. § 1, (12), (16)), так что
при вычислении предела (7) за £ можно принимать
произвольное число, удовлетворяющее неравенству
О < IS - z\< 6.
Бесконечно малые величины. В связи с новым оп*
ределением предела, данным в этом параграфе, воз-
никает и новое представление о бесконечно малых ве-
личинах. Если некоторая переменная величина т ин-
тересует нас главным образом в процессе своего
стремления к нулю, то мы будем называть ее беско-
нечно малой, В этом смысле бесконечно малой ве-
личиной является приращение Аг — S — z независи-
мого переменного при вычислении производной. Если
т в этом смысле — бесконечно малая величина и
ф(т)—ее функция, причем
lim ф(т) = 0,
т->0
то величину <р(т) мы будем также называть беско-
нечно малой. Чтобы выразить это более полно, мы
можем сказать, что величина <р (т) бесконечно мала
вместе с т. Очень часто приходится сравнивать быст-
роту убывания величины <р (т) с быстротой убывания
величины т. В первую очередь это делается при
помощи знаков О и о (см. § 2). Так, если величина
114
остается ограниченной, когда т-»-0, то пишут
Ф (т) = О (т).
Если же дробь (10) стремится к нулю при т->0,
то пишут
ф(т) = о(т).
Очень часто приходится сравнивать быстроту убыва-
ния величины ф(т) с быстротой убывания величины
тЛ, где п — натуральное число.
Если имеет место соотношение
ф(т)= О(т"),
то говорят, что ф(т) есть бесконечно малая порядка
п относительно т.
Дифференциал. Разберем теперь несколько подроб-
нее определение • производной. Она задается форму-
лой
f(z) = lim-^^^-
C-»z ® г
(см., (8)). Иначе говоря, величина
= (И)
ь *
является бесконечно малой вместе с £ — z. Равенство
(11) можно переписать в виде
f Й) — f (г) = Г (г) (? - г) + а • С - z),
причем
lim а = 0.
£->г
Если положить
а . (£ — Z) = р,
то формула (11) перепишется в виде
= (12)
причем, очевидно,
р = о(£-г). (В)
Левая часть равенства (12) представляет собой
приращение функции, а правая часть состоит из двух
членов, второй из которых удовлетворяет условию
(13). Таким образом, если f'(z)=t=O, второй член пра-
вой части равенства (12) стремится к нулю быстрее,
чем первый член. Поэтому считают, что первый член
ИЗ
правой части равенства (12) является главным во
всей сумме. Потому можно сказать, что главная
часть приращения &f(z) функции f(z) равна f'(z)Az<
Введем теперь новую терминологию. Будем называть
приращение Az независимого переменного его диф-
ференциалом и писать
Az = dz.
Главную часть приращения Af(z)’ функции f(z)' бу-
дем называть ее дифференциалом и обозначать через
df(z). Таким образом, мы получаем формулу
df(z) = f'(z)dz. (14)
Понятие дифференциала пока что мало содержатель-
но. На первых порах оно дает нам новую запись для
производной, именно, из формулы (14) следует
Г(г) = -^- (15)
Но с течением времени мы убедимся, что пользова-
ние дифференциалами полезно. Производную f'(z\
иногда записывают в виде
(16)
Запись производной в виде (15) и (16) имеет некото-
рое преимущество перед обозначением f'(z), так как
в этих записях ясно видно, по какой переменной бе-
рется производная, а это в некоторых случаях ока-
зывается очень важным. В связи с формулой (15)
операцию взятия производной часто называют опе-
рацией дифференцирования. Функция, имеющая про-
изводную в точке г, называется дифференцируемой
в точке г. Функция, имеющая производную для лю-
бого значения своего аргумента, называется диффе-
ренцируемой функцией.
Непрерывность дифференцируемой функции. Если
функция f(z) имеет в точке z производную f'(z), то
она непрерывна в этой точке. Действительно, пере-
ходя в равенстве (12) к пределу при мы полу-
чаем
Um (f (0 - f (z)) = lim (f (z) (£ - z) + о (g - z)) = 0,
116
так что функция f(z) непрерывна в точке г (см. (5)).
(Таким образом, если функция имеет производную для
каждого значения своего аргумента, то она непре-
рывна.
Частная производная. До сих пор мы говорили
только о функциях одного переменного, хотя в дей-
ствительности почти всегда имели дело с функциями
многих переменных; так, .
например, многочлен от
переменного z в действи-
тельности является и
функцией своих коэффи- 7 “
циентов. Тем не менее
при взятии производной
от многочлена мы ясно
понимали, что произвол- ——
ная берется по перемен-
ному z. В некоторых слу-
чаях, однако, имея дело
с функцией нескольких
переменных, например f(z, w)
двух переменных, нам
важно четко заявить о том, по какому из двух пере-
менных берется производная. Такая производная на-
зывается частной производной и обозначается через
(г, w).
(17)
При вычислении ее мы даем приращение только z
и считаем величину w постоянной.
Пример 1. Дадим теперь геометрическое истол-
кование производной действительной функции f(x)
действительного переменного х. Для этого начертим
график К функции f(x) на плоскости Р, в которой
выбрана некоторая прямоугольная декартова система
координат (рис. 10). Таким образом, К есть кривая,
определяемая уравнением
y = f(x). (18)
Зафиксируем некоторое значение х аргумента нашей
функции и обозначим через у соответствующее зна-
чение функции согласно уравнению (18). Тогда а —
= (х, у) есть точка плоскости Р, лежащая на кри-
вой К. Эту точку мы будем считать неподвижной. На-
117
ряду со значением аргумента х выберем произвольно
другое значение g =# х и обозначим через ц соответ-
ствующее значение функции, так что ц = f(g). Точка
a = (g, ц) лежит на кривой К, и ее мы будем считать
подвижной. Если g приближается к х убывая, то точ-
ка а движется по кривой Л, приближаясь к точке а
с правой стороны. Если величина g приближается кх
возрастая, то точка а движется по кривой Л, при-
ближаясь к точке а с левой стороны. Проведем через
точки а и а прямую L. L есть секущая кривой К.
Подсчитаем тангенс угла наклона прямой L, т. е. тан-
генс угла между осью абсцисс и прямой L. Для этого
через точку а проведем горизонтальную прямую, т. е.
прямую, параллельную оси абсцисс, а через точку
а — вертикальную прямую. Пересечение этих двух
прямых обозначим через у. Нам нужно подсчитать
тангенс угла при вершине а в прямоугольном треу-
гольнике ауа, учитывая при этом знак угла. Для оп-
ределенности будем считать, что g > х. Тогда поло-
жительное число g— х равно длине стороны ау на-
шего треугольника, а число ц — у равно длине сто-
роны уа, взятой со знаком плюс, если г) > у, и со
знаком минус, если т| < у. Таким образом, в любом
случае тангенс угла наклона прямой L равен отно-
шению • Если g < х, то тангенс угла наклона
прямой L равен тому же самому отношению. Это лег-
ко проверить, учитывая знаки обеих величин ц — у и
g — х. Если производная /'(х) функции /(х) при дан-
ном значении аргумента х существует, то это зна-
чит, что отношение стремится к пределу f (х)\
ъ х
при g.—> х. Таким образом, если производная ff(x) су-
ществует, то тангенс угла наклона секущей L стре-
мится к определенному пределу, когда точка а неог-
раниченно приближается к точке а. В этом случае
сама прямая L стремится к своему предельному по-
ложению М, причем прямая Л4 также проходит через
точку а. По определению прямая М считается каса-
тельной к кривой К в точке а. Таким образом, про-
изводная f'(x) есть тангенс угла наклона касатель-
ной М, проведенной в точке а=(х, у) к графику К
функции /(х). Это и есть геометрический смысл про-
изводной,
118
»« Г) — у
Может случиться, что отношение ' стремится
ъ X
к определенному пределу k\, когда 5->х, оставаясь
больше х, и то же самое отношение стремится к дру-
гому пределу k2, когда g х, оставаясь меньше х.
В этом случае по определению функция f(x) не имеет
производной при заданном значении аргумента х.
.Числа k\ и k2 называются соответственно правой и
левой производными. Поскольку ki и k2 не равны
между собой, обозначим через Mi предельное поло-
жение секущей L, когда а приближается к а справа,
и через ТИ2 предельное положение секущей L, когда
а приближается к а слева. Прямые М{ и М2 не сов-
падают и кривая К не имеет в точке а касательной.
Точка а в этом случае называется угловой точкой
кривой К. Простейший пример угловой точки дает
функция
f (х) = |х|.
Ее график, задаваемый уравнением у = |х|, состоит
из биссектрисы первой четверти системы координат
и биссектрисы второй четверти системы координат.
При х = 0 мы имеем &i = 4-l, k2 — —1, и термин
«угловая точка» в этом случае имеет вполне нагляд-
ный смысл.
Пример 2. Дадим еще одно очень важное при-
менение производной. Докажем, что если действи-
тельная функция f(x) действительного переменного х
имеет при заданном значении аргумента х положи-
тельную производную, т. е. f'(x)>0, то вблизи точ-
ки х функция f{x) возрастает. Более точно, суще-
ствует настолько малое положительное число б, что
при — х|<б мы имеем следующие соотношения:
если 5 < х, то f (5) < f (х);
если 5 > х, то f (5) > f (х).
Это следует непосредственно из формулы (12). Со-
вершенно аналогично устанавливается, что если при
некотором значении аргумента х производная f'(x)
отрицательна, т. е. f'(x)<Z 0, то вблизи точки х функ-
ция f(x) убывает. Именно, существует настолько ма-
лое положительное число б, что при — х| < б
119
имеют место соотношения
если £ < х, то f (£) > f (х);
если | > х, то f (I) < f (х).
Из полученных результатов можно сделать чрезвы»
чайно важный вывод. Именно, если функция /(х) при
некотором значении своего аргумента х достигает
максимума, т. е. имеет место неравенство
f (*)>/$
при произвольном значении аргумента £ функции, то
производная f'(x) равна 0.
Можно даже доказать более сильный результат,
именно, если в точке х функция f(x) имеет локаль-
ный максимум, т. е. существует такое положитель*
ное число б, что при |g — xj < б имеет место нера-
венство
(19)
Г(х) = 0.
Доказательство будем вести от противного. Допу*
стим, что Но тогда функция f(x) в точке х
возрастает, и, следовательно, существует такое зна*
чение аргумента /(х), удовлетворяющее усло-
вию | — х < б, что
f®>f(x),
а это противоречит предположению (19). Точно так
же производная f'(x) не может быть отрицательной,
так как тогда функция f(x) в точке х убывающая,
т. е. существует такое значение | < х, удовлетворяю-
щее условию | £ — х| < б, что.
f®>f(x),
а это противоречит предположению (19). Итак, до-
казано, что в точке локального максимума производ-
ная функции обращается в нуль.
Совершенно аналогично доказывается, что если
функция f(x) имеет минимум для значения своего ар-
гумента х или локальный минимум, . т. е. при
|g — х|<б выполнено неравенство то
производная этой функции обращается в нуль при
120
значении аргумента х:
f'(x) = O.
Таким образом, для того чтобы найти локальные
максимумы и локальные минимумы функции f(x),
мы должны решить уравнение
Г(х) = о
и затем уже более детально изучить все значения
аргумента х, удовлетворяющие этому уравнению.
Обычно локальный максимум и локальный минимум
функции называются просто максимумом и минимум
МОМ.
Пример 3. Докажем теперь, что если функция
f(z) непрерывна в точке г0 в смысле определения,
приведенного в этом параграфе, т. е. что если для
всякого положительного е можно подобрать такое
положительное число б, что
при | z — го I < б имеем | f (г) — f (г0) | < е, (20)
то функция f(z) непрерывна в точке го и в смысле
определения, приведенного в примере 1 § 1, т. е. для
всякой последовательности
гь г2, ... г„, ...
ее аргументов, удовлетворяющей условию
lim z„ = zo> (21)
П->оо
выполнено и соотношение
lim f(z„) = f(z0).
Д->ОО
(22)
Для доказательства зададимся произвольным по-
ложительным числом е, и пусть б — то положитель-
ное число, которое соответствует ему в силу усло-
вия (20). Из соотношения (21) следует, что суще-
ствует такое целое число v, что при п > v имеем
I гп — Zo I < б.
Тогда в силу (20) получаем
l/fe)-f(z0)l<e. (23)
Таким образом, для заданного положительного
числа е мы нашли такое целое число v, что прип >. v
121
выполнено неравенство (23), а это и значит, что вы-
полнено соотношение (22).
В дальнейшем непрерывность будет пониматься
только в смысле этого параграфа.
Пример 4. В конце § 1 были сформулированы
пять основных правил перехода к пределу в примене-
нии к последовательностям. Те же самые правила
имеют место и для предельного перехода, введенного
в этом параграфе. Формулируем их здесь.
Пусть f(z) и g(z)— две функции действительного
или комплексного переменного z, для которых выпол-
нены соотношения
lim f (z) = f0; Нт g (z) = g0.
z->z0 z~>z9
Тогда имеют место следующие правила:
Правило!, lim (f (z) + g (z)) = f0 + g0.
Z-»Zo
П p а в и л о 2. lim (f (z) — g (z)) = f0 — g0.
Z->Zq
Правило 3. lim (f (z) • g (z)) = f0 • g0.
Z-i-Za
Правило 4. Если go #= 0, то
lim
z-»z
f(z)
. g(z)
fo
go '
Правило
функции и
5. Если f(z) и g(z)~ действительные
f(zXg(z), то fo<go-
Для доказательства этих правил, так же как и в
§ 1, используем бесконечно малые величины. Для
этого положим
f (z) = fo + f (z); g(z) = go + g(z).‘
Ясно, что величины f(z) и g(z) бесконечно малы
вместе с величиной z — zq. Используя очевидные про-
стейшие свойства бесконечно малых величин, анало-
гичные тем, которые были указаны в конце § 1 перед
правилами предельного перехода, мы без труда про-
ведем доказательство пяти правил, данных здесь.
122
§ 11. Вычисление производных
Здесь мы вычислим производные некоторых'функ-
ций, в первую очередь многочленов и сходящихся сте-
пенных рядов. Пользуясь правилом вычисления про-
изводной для сходящегося ряда, мы затем найдем
производные функций cos 2, sin z. Затем будет
установлено правило дифференцирования произведе-
ния двух функций и отношения двух функций. Далее
будет установлено правило дифференцирования
сложной функции, т. е. функции вида /(z)= ^((p(z))1,
и правило дифференцирования функции, обратной к
заданной функции. Пользуясь последним правилом,
мы найдем производные обратных тригонометриче-
ских функций и логарифма.
Установим теперь некоторые простейшие правила
дифференцирования.
Отметим прежде всего, что производная постоян-
ной есть нуль. В самом деле, если f(z)=c, то
и, следовательно, f &)— f (z) = 0, так что
= (1)
Допустим теперь, что мы имеем несколько функций
fi(z), Ыг), ..•> fn(z) и столько же чисел аь а2,..., ап.
Оказывается тогда, что
(«1/1 (z) + a2f2 (z) + ... + anfn (z)Y =
= aj'(z) + a2f' (z) + ••• +«J'(z). (2)
Для доказательства этой формулы достаточно дока-
зать две другие, более простые, именно,
(f(z) + g(z)Y = f'(z) + g'(z) (3)
и
(af(z)Y==af'(z). (4)
При доказательстве мы используем правила предель-
ного перехода, данные в примере 4 § 10. Докажем
сначала первую из этих формул, именно, формулу
(3). Мы имеем
(? и + s w=«т i«>+^>--T+gM> -
= Пт(Ж^Ж + Х(^р)) =
= Нт + Нт = у (2) + (г)<
123
Так же просто доказывается и вторая из этих фор-
мул, именно, формула (4). Действительно, мы имеем
Ы (г))' = Um = а lim (г).
Докажем теперь формулу (2), пользуясь форму-
лами (3) и (4). Доказательство проведем индуктив-
но. Для п=1 формула (2) еледует из (4). Допу-
стим, что она верна для числа слагаемых, равного
п—1. Мы разобьем левую часть соотношения (2) в
сумму двух слагаемых. Именно, левую часть равен-
ства (2) мы запишем в виде
((aifi(z) + a2f2(z)+ ... + (z)) + a„f„ (z))'.
В силу формул (3) и (4) это выражение равно
(a1f,(z) + a2f2(z)+ ... +a„_tf„_I(z)), + aX(z). (5)
В силу предположения индукции мы видим, что
выражение (5) равно правой части равенства (2).
Таким образом, формула (2) доказана.
Применяя формулу (2) к многочлену
Яо + aiz + a2z2 + ... + anzn, (6)
получаем
(a0 + + a2z2 + ... +anzn)' =
— a' + a1(z)' + a2(z2)'+ ... +an(zn)'.
Таким образом, принимая во внимание формулу (1),
для того чтобы вычислить производную любого мно-
гочлена, нам достаточно научиться вычислять произ-
водную целой положительной степени переменного z,
именно, функции zfc, где k — натуральное число. До-
кажем, что
(zkY = kzk~'. (7)
Действительно, в силу формулы (И) § 6 мы имеем
= lim (S*-1-H*~2z + ••• +zft-‘) = ^zs-1
(см. правила перехода к пределу, пример 4 § 10).
Таким образом, для многочлена (6) мы получаем
124
производную в виде
(ао + «12 + a2z2 + ... + anznY =
— at + 2a2z + ... + nanzn~l. (8)
Итак, мы получили формулу производной для про-
извольного многочлена действительного или комп-
лексного переменного.
Производная степенного ряда. Докажем, что функ-
ция
f (z) = До + Д1« + a2z2 4- ... + anzn + ..., (9)
определяемая степенным рядом с радиусом сходимо-
сти г > 0, имеет производную f'(z). Положим
A (z) — Д1 + 2д2з + ... +папгп~1+ ... (10)
Тогда
f'(z) = fi(z). (11)
При этом ряды f(z) и ft (z) имеют одинаковые ра-
диусы сходимости.
Для доказательства высказанных утверждений
мы будем вычислять предварительное отношение
НС)-Hz)
С —z ’
где |z|< г. Так как в предварительном отношении
мы должны переходить к пределу при £ -> z, то мож-
но считать, что |£| < г.
Выпишем три знакоположительных сходящихся
ряда:
fo—I «о I +1 «1 к + ••• +1 «п IгП + ...»
fi = l«i 1 + 2|д2к+ ... + nl ап |гп-1 + ....
|2 = 22|д2|4-32|дзк+ ... +п2|д„кп-24- ...
Сходимость этих рядов следует из формул (17) § 2
и (4) § 9. Ряд fo мажорирует ряд f(z), а ряд Д мажо-
рирует ряд fi (z).
Запишем предварительное отношение
НС) — f (2)
С~ z
в виде ряда (см. пример 3 § 5). Мы имеем
НС) — f (z) _ До — До ।
1-г — t-z
+ «ife+ ••• ... (12)
125
Далее,
I _(£П-Л.П1|Д
I п Z-n |
= |a„||Cn-1 + r_2z+ ...
(cm. § 6, (11)). Таким образом, ряд ft мажорирует
ряд (12), так что ряд (12) сходится. Вычтем теперь
из ряда (12) ряд (10). Мы имеем
«.(4^-^)+"-)+
.. „ (|3)
Оценим величину Д1_'г-nz""1. Мы имеем
- пг— | = | - г“-')+2 (Г! - г“-!)+...
. . . + Z"-2 (g — z) + (z"-1 — Zra-1) I =
= l?-z||(cn-2 + S""3z+ ... +zn~2) +
+ г(Г“3 + ^’4г+ ... +zn-3)+ ...
... + zn-2I’d £— z|ra2rn~2.
Таким образом, ряд (13) мажорируется рядом f2,
умноженным на |£ — z|. Итак, мы имеем оконча-
тельно
|—--------и (z) <|£ —z|c,
где с — константа. Отсюда следует, что
lim 1*5^.
£-*г ? г
существует и равен величине ft(z)’. Таким образом,
формула (11) доказана.
Тот факт, что ряды f(z) и fi(z) имеют одинаковые
радиусы сходимости, следует из формул (17) § 2 и
(4) § 9.
Из формулы (10) непосредственно вытекают фор-
мулы
(ег)' = ег; (14)
sin' z = cos z, cos'z= — sinz. (15)
126
Формулы эти получаются при помощи почленного
дифференцирования рядов (1) —(3) § 8, сходящих-
ся при произвольном значении г. Таким образом,
формулы (14), (15) верны для произвольных комп-
лексных и действительных значений z.
Дадим теперь некоторые основные формулы диф-
ференциального исчисления. Именно, вычислим про-
изводную произведения двух функций, производную
отношения двух функций, а также производную
функции от функции.
Производная произведения. Если f(z) и g(z)—две
функции, то мы имеем
(f (z) • g (z))' = f' (z) • g (z) + f (z) • g' (z). (16)
Для доказательства этой формулы выпишем в удоб<
ной для нас форме разность f (£) •£(?)— f (г)-g(z)<
Мы имеем
f®-g®-f(z)'g(z) =
= f (£) -g © - f (z) • g © + f (Z) • g (0 - f (z) • g (z) =
= (f (0 - f (z)) g(S) + f (z) (g (?) - g (z)).
Деля это равенство на £ — z, мы получаем
f(£)-g(E)-f(z)-g(z)
Переходя в этом равенстве к пределу при £->z,
мы получаем формулу (16).
Производная отношения. Если f(z) и g(z)—две
функции, причем g(z)#= 0, то
( f (z) Y _ f' (z) g (z) — gz (z) f (z) ,,
k g (z) ) (g (z))2 ’ '
Для доказательства этой формулы выпишем раз-
ность
f (?) f (г) _ f (g) g (г) - f (г) g (£) nRv
g(£) g(z)“ g(£)g(z) ’ 407
Перепишем теперь по-иному числитель правой части.
Мы имеем
f($-g(z)-f(z)g® =
= f^)’g(z) — f (z) g(z) + f (z) • g (z) — g (C) • f (z) =
= (f (5) - f (Z)) g(z)-f (z) (g (C) - g (z)). (19)
127
Деля соотношение (18) на £ — z и используя при
этом равенство (19), мы после перехода к пределу
при £ —> z получаем формулу (17). Вычислим теперь
производные функций
, sin г , * cos z
tg Z =---- И ctg Z = —:-----------.
& cos z & sin z
В силу формул (17) и (15) мы получим
; = и = <2°)
Производная сложной функции f(z) = Ф(ф(г)).
Пусть ф(г) и ф(да)— две функции. Подставим во вто-
рую функцию вместо w выражение w = ф(г). Тогда
мы получим так называемую сложную функцию
7(г) = ф(ф(г)) или, как говорят иначе, функцию от
функции. Оказывается, что имеет место формула
Г (z) = ф' (®) • <р' (z) = ф' (ф (z)) ф' (z). (21)
Используя запись производной в виде отношения
дифференциалов (см. § 10, (15)), мы можем перепи-
сать формулу (21) в легко запоминаемой форме
<*Ф (Д’) _ d-ф (а>) dw ,9<?.
dz dw dz ’ - '
гдеи> = ф(з).
Докажем формулу (21). Мы имеем
Ф (ф (£)) — Ф (ф (г)) __ Ф (Ф (£)) — Ф (Ф (г)) ф (?)-ф (Z) /9<п
g-z Ф(?)-Ф(г) ’ g-z •
Чтобы получить производную (ф(ф(г)))', мы должны
в равенстве (23) перейти к пределу при £->z. Для
этого уясним себе более отчетливо, что представляет
собой первая из дробей, стоящих в правой части ра-
венства (23). Для этого вспомним, что ф (z) = w, и
положим ф(£) = (1). Ясно, что при Z-^z имеем
Таким образом, для того чтобы совершить предель-
ный переход в равенстве (23) при £->z, мы должны
подсчитать предел
]jm Ф (<о) — ф (а>)
to + w <>>-W
который по определению равен ф'(ау). Таким обра-
зом, совершая предельный переход в равенстве (23)’
128
при ?-* г. мы получаем
(Ф (ф (*)))'— Ф'М • ф'(г)»
т. е. формулу (21).
Производная обратной функции. Если равенство
z — можно разрешить относительно w, т. е.
найти такую функцию w = ф(г), что выполнено тож-,
дество
Ф(ф(г)) = г, (24) .
то функция ф(г) называется обратной по отношению
к ф(ге»). В § 24 будет доказано, что для функции, за-
даваемой степенным рядом, существует обратная
функция, которая также задается степенным рядом.
Дифференцируя (24) по г, согласно формуле (21)
получим
Ф'М,ф'(г)=1,
откуда
Подставляя в правую часть (25) t» = q>(z)’, мы полу-
чаем
ф'й=т<Ьг- да
Эта формула дает нам возможность вычислить про-
изводную q/(z) функции <p(z), обратной функции
ф(щ). Для этого нужно в функцию ф'(и') подставить
вместо w его выражение через г, т. е. положить w
= <p(z), и затем взять обратную величину получен-
ной функции ф'(ф(г)).
Сосчитаем теперь, пользуясь этим правилом, про-
изводные функций, обратных функциям е®, sin w,
cos w, tg w, ctg w, т. e. функций In z, arcsin z, arccos z,
arctg z и arcctg z. Оказывается, что
ln'z = |; (27).
arcsin'z = ,^d=, arccos'z =-------;; (28)
<1 — Z2 VI—z2
arctg' z = arcctg'z = —. (29'
Функция In z определяется как решение уравне-
ния ew — z относительно w. В силу формулы (26)
5 Л. С. Понтрягин 129
мы получаем
. ,_______1______1____1_
in z — {eWy — gW — z.
Из формул (28) докажем только первую. Функ*
ция arcsin г определяется как решение уравнения
sina> = z относительно w. Таким образом, в силу
формулы (26) получаем
. , 1 1
arcsin z = —— =------------
sin w cos w
1
1 —_____________
-\/1—sin2 W V1 — 22
Из формул (29) докажем также только первую.
Мы имеем
. , i , 1 1
arete z — -r~,— = cos w — . , . ,— = -г-;—г •
6 tg' w i + tg2ay 1 + z2
Вычислим, наконец, производную функции zr, где
г — произвольное действительное число. Для рацио-
нального г функция эта определена в элементарной
алгебре. Для произвольного действительного г мы
определим ее, положив
Zr==erlnz (30)
Для рациональных г эта формула дается в элемен-
тарной алгебре. Продифференцируем соотношение
(30), применяя к правой части правило дифференци-
рования сложной функции (2Г) и учитывая формулу
(27), положив при этом w = rlnz. Тогда мы полу*
чим
' 7 dw dz
dw 1
= e = e •'•7 =
= er In Z . r . _L = rzr . _L — rzr-1
z z
Таким образом,
(zr)' — rzr~l. (31)
Как уже говорилось в § 8, основными трансцен*
дентными функциями считаются ег, sin z, cosz, tgz,
ctg z и функции, обратные к ним. Алгебраическими
функциями здесь будем называть многочлены, ра*
циональные функции, т. е. функции, получаемые де*
лением одного многочлена на другой, и функцию, по*
лучаемую путем извлечения корня. Функции, получае*
мне путем применения основных трансцендентных
функций и алгебраических функций путем последо*
130
вательного их применения в произвольном числе и
произвольном порядке, называются элементарными
трансцендентными функциями. Приведенные в этом
параграфе правила дифференцирования дают воз-
можность вычислить производную любой элементар-
ной трансцендентной функции.
Пример 1. Дадим теперь механический смысл
производной. Представим себе, что точка движется
по оси абсцисс, так что абсцисса ее является задан-
ной функцией времени
х = (32)
Если точка движется с постоянной скоростью, то ра-
венство (32) записывается в виде
х — х0 4- vt,
где Хо — начальное положение точки при t — 0, а
v — ее постоянная скорость. Если точка движется не
с постоянной скоростью, то требуется объяснить, что
такое ее скорость в данный момент времени. Это де-
лается в механике следующим образом. Наряду с
моментом времени t рассмотрим другой момент вре-
мени т > t. За время т — t точка проходит расстоя-
ние, равное f(x) — f(t). Естественно считать, что на
отрезке времени от t до т точка имеет среднюю ско-
f (т) - f (t) ~
рость, равную Скорость точки в момент
времени t определяется как предел этого отношения
при т -*• t, т. е. как производная f' (/):
Если скорость v(f) непостоянна, т. е. меняется со
временем t, то говорят об ускорении. Среднее уско-
рение от t до т определяется как отношение
—* а УСК0Рение ° (О в момент времени t
определяется как предел этого отношения при т -*• t,
т. е. формулой и (/) = v' (/). Мы видим, что ускорение
v'(t) есть производная производной Она назы-
вается второй производной функции /(/) и обозна-
чается через f"(t). Таким образом, ускорение точки
задается формулой и.(0 = /"(Ол
б* 131
§12. Неопределенный интеграл
В §§ 10 и 11 была описана производная, именно,
для заданной функции (здесь мы ее обозначим через
й (z)) действительного или комплексного переменного
z была построена ее производная функция й'(г)того
же переменного г. Производная h'(z) функции ft (z)
имеет и другое часто употребляемое обозначение,
именно
дг____ dh (z)
Л <2) = “ЗГ“ w
(см. § 10, (15)). Операция перехода от функции ft(z)
к функции
f(z) = *'(z) (1)
называется операцией взятия производной функции
й(г) или операцией дифференцирования этой функ-
ции.
Всякий раз, когда математики рассматривают ка-
кую-либо операцию, возникает вопрос об операции,
к ней обратной. Так, в алгебре наряду с операцией
умножения рассматривается обратная к ней операция
деления, наряду с операцией возведения в степень
рассматривается обратная к ней операция извлече-
ния корня. Говоря об обратной операции, мы всегда
должны поставить перед собой два важнейших во-
проса. Первый—возможна ли обратная операция,
второй — однозначна ли обратная операция. Так, де-
ление не всегда возможно. Оно невозможно, когда
мы хотим разделить на нуль. Извлечение корня не
всегда однозначно: так, извлечение квадратного кор-
ня из числа, как правило, двузначно.
Операция, обратная к операции дифференциро-
вания, т. е. операция нахождения функции й(г) по
функции f(z)=n'(z), называется операцией интегри-
рования и имеет специальную запись
A(z)=$f(z)dz. (2)
Знак J называется интегралом и формула (2) чи-
тается следующим образом:
й(г) равна интегралу f(z)dz.
132
То обстоятельство, что операция интегрирований' яв*
ляется обратной к операции дифференцирования, оз-
начает в точности, что формулы (1) и (2) равно*
сильны;
Функцию h (z), удовлетворяющую условию (1),
часто называют первообразной функции /(z). Таким
образом, интегрирование есть нахождение первооб-
разной функции. '
На первый основной вопрос относительно опера*
ции интегрирования, — именно, на вопрос о ее воз-
можности— мы не дадим в этом параграфе сколь-
нибудь общего ответа, а лишь заметим, что в ряде
случаев операция интегрирования возможна и. ре-
зультат ее легко выписать. Так, мы имеем
coszdz = sinz, sin zdz = — cosz. (3)
Эти формулы следуют из формул (15) § 11. Точно
так же легко проверяется, что
J («0_+ a{z + a2z2 + ... 4-a„z")rfz =
= a0z + ^-z2 + ^-z3 + ... +^2"+'. (4)
Эта формула вытекает из формулы (8) § 11. Та-
ким образом, в ряде случаев операция интегрирова-
ния возможна, и, изучая ее, мы проводим вполне со-
держательные исследования.
Что касается второго основного вопроса относи-
тельно операции интегрирования, — именно, вопроса
об ее однозначности, — то мы сможем дать в этом
параграфе полный ответ на него. Прежде всего, ясно,
что операция интегрирования неоднозначна. Именно,
если имеет место равенство (2), то имеет место и ра-
венство
f (z) dz = h (z) + c, (5)
где c — произвольная постоянная. Это следует из
того, что -
(Л (г) + с)' == h' (z) + с' = hr (z)
(см. §11, (1), (3)).
133
Таким образом, интеграл определен лишь с точ-
ностью до постоянного слагаемого. Именно поэтому
f (z) dz
называется неопределенным интегралом. В этом па-
раграфе мы докажем, что этим постоянным слагае-
мым неопределенность интеграла и ограничивает-
ся,— именно, будет доказано, что если
p(z)rfz = Ai(z), (z) dz = h2 (z), (6)
то мы имеем
/г2 (z) = Aj (z) + с, (7)
где с — постоянная величина. Отметим, что это ут-
верждение верно лишь с некоторыми ограничениями,
именно, в том случае, когда функция f(z) определена
на некотором связном множестве й, т. е. совокуп-
ность всех допустимых значений аргумента z есть
связное множество й.
Сразу же нужно сказать о том, что понимают под
связным множеством Й. В случае действительного пе-
ременного связность множества й означает лишь, что
если zo и z* — два допустимых значения аргумента z
функции /(z), причем zo < z*, то и всякое число z,
удовлетворяющее неравенству Zo < z < z*, принадле-
жит к числу допустимых значений аргумента функ-
ции f(z), т. е. к множеству й. В случае комплексного
переменного z множество й есть некоторое множе-
ство на плоскости комплексного переменного г, и в
этом случае связность означает другое. Именно, если
Zo и z* — два произвольных значения аргумента функ-
ции f(z), т. е. две точки плоскости, принадлежащие
множеству й, то существует ломаная линия
zo, zi....zn = z*, (8)
целиком проходящая по множеству й. В последова-
тельности (8) указаны лишь вершины этой ломаной.
Сама ломаная состоит из всех отрезков вида
[zfZi+I], где / — 0,1.....п — 1.
Говоря, что ломаная (8) проходит вся по множеству
й, мы подразумеваем, что каждый отрезок [z/z/+i].5
j — 0, 1, ..., п—1, принадлежит множеству й.
134
Для того чтобы доказать, vro из равенств (6)
следует равенство (7), достаточно доказать, что из
равенства
Л'(х) = 0 (9)
следует
й(г) = с, (10)
где с — постоянная. Предполагают при этом, что мно-
жество О, на катором определена функция Л (г), есть
грязное множество. Полагая h(z) = h2(z)— hi (г), мы
из равенства (10) получаем равенство'(7).
Перейдем теперь к поэтапному доказательству
того, что из равенства (9) следует равенство (10).
Доказательство это непросто, и ему мы предпошлем
доказательство нескольких предложений, которые
важны сами по себе.
Максимум и минимум непрерывной функции. Пусть
й(х) — действительная непрерывная функция дей-
ствительного переменного х, определенная на отрезке
(11)
где а и b — два числа, причем а < Ь. Таким обра-
зом, аргументом х функции h(x) может служить лю-
бое действительное число, удовлетворяющее нера-
венству (11), а другие значения аргумента не рас-
сматриваются. Оказывается, что эта функция дости-
гает своего минимума и своего максимума, именно,
существуют такие значения аргумента х = а и х — р
функции й(х), что выполнено неравенство
Л(а)</г(х)</г(Р) (12)
при произвольном х, удовлетворяющем неравенству
(11). Ниже в примере 2 будет показано, что разрыв-
ная функция может не обладать этим свойством. Та-
ким образом, условие непрерывности здесь весьма су-
щественно.
Докажем прежде всего, что наша функция Л(х)’
ограничена. Доказательство будем вести от против-
ного. Допустим, что она не ограничена. Тогда для
каждого натурального числа п можно подобрать та-
кое значение ее аргумента х = уп, что имеет место
неравенство
U(Yn)l>n. (13)
135
Так как числа уп расположены на отрезке- а -^"х^
Ь, то из последовательности -
Yi. V2, •••> Уа, ... Г(Н)
можно выбрать сходящуюся подпоследовательность
й1 = УП1. Ъ2 = У„г, .... = Т (15)
так, что
lim t)k = б, ,
Л-»ОО
где б — некоторое число, принадлежащее отреййу
||аб] (см. § 4, ограниченные множества чисел, и § 1,
(18)). Так как функция h(x) непрерывна, то' мы
имеем
lim Л (б4) = й (б),
fe->oo
но это невозможно. Действительно, последователь-
ность (15) является подпоследовательностью (14), й,
следовательно, в силу неравенства (13) число |Л(б*) I
неограниченно возрастает вместе с ростом k. Итак,
мы доказали, что множество всех чисел вида Л(х)
ограничено как сверху, так и снизу, поэтому это
множество чисел имеет нижнюю грань, которую мы
обозначим через р, и верхнюю грань, которую мы
обозначим через qb Так как q является верхней
гранью множества всех чисел вида Л(х), то из этого
множества можно выбрать последовательность чисел,
сходящуюся к q, а это значит, что имеется последо-
вательность
Н1> Нг> .... |*„, ... (16)
значений аргумента х, удовлетворяющих условию
НтЛ(ц„) = ф (17)
П->оо
Так как все числа последовательности (16) при-
надлежат отрезку [аб], то из этой последовательно-
сти можно выбрать сходящуюся подпоследователь-
ность
’i = l»v ”*2 = ^.....= ••• ' ИЗ)
так, что мы имеем
lim ^ = 0.
Л->оо
ж
Но так как последовательность (18) является под-
последовательностью (16), то из формулы (17) слег
дует, что
lim ft(v*)=A(0) = <7-
Л->оо
Таким образом, верхней гранью q множества всех
чисел вида h(x) является значение функции Л(х) при
х = 0. А это и значит, что функция h (х) достигает
своего максимума при х = 0. Точно так же доказы-
вается, что функция й(х) достигает своего минимума
•при некотором значении х — а.
Следствие (теорема Ролля). Допустим
теперь, что рассмотренная выше непрерывная функ-
ция Л(х) для каждого значения своего аргумента
а < х < b имеет производную и что значения этой
функции на концах отрезка [ад] равны между собой,
т. е. Л(а)=Л(д). Оказывается тогда, что внутри от-
резка [ад] имеется число g (это значит а < % < д)
такое, что
Л/й) = 0. (19)
Докажем это. Если функция Л(х) постоянна, то
производная ее тождественно равна нулю на всем
отрезке [ад] и тогда за | можно взять произвольную
внутреннюю точку этого отрезка. Если функция Л(х)
непостоянна, то тогда имеет место по крайней мере
одна из двух возможностей. Первое — функция h(x}\
для некоторых значений своего аргумента больше,
чем Л (а). Второе — функция ft(x) при некоторых зна-
чениях своего аргумента меньше, чем ft (а). В первом
случае функция й(х) достигает своего максимума в
некоторой точке |, лежащей внутри отрезка [ад]. Во
втором случае она достигает своего минимума в не-
которой точке £, лежащей внутри отрезка [ад].
В обоих случаях производная функции Л(х) при
х = § равна нулю, т. е. имеет место равенство (19)
(см. пример 2 § 10).
Конечное приращение (формула Лагранжа). До-
пустим, что действительная непрерывная функция
Л(х) действительного переменного х, заданная на от-
резке [xoxi], имеет производную в каждой внутрен-
ней точке отрезка [xoXi]. Тогда имеет место равен-
ство
Л(х1)-й(хо) = й/(1)(х1-хо), (20)
.137
где | — некоторая внутренняя точка отрезка [xqXi],
Для доказательства рассмотрим функцию
g (х) = h (х) - х. (21)
Функция g(x) имеет одинаковые значения в точках
Хо и хь Действительно,
g(xi) — g(хо) = Л(Х1) — Л(хо) — Г" ~<Х1—х8)=0;
Л1 — ло ц
Таким образом, в силу теоремы Ролля существует
такая внутренняя точка £ отрезка [xoxi], что '
(см. (19)). Подставляя в это равенство выражение
(21) для g(£), получаем
h' (g) _ h ~ h — о
Xi ““ Xq
откуда следует соотношение (20).
Из формулы Лагранжа (20) непосредственно вы-
текает, что в случае действительной функции й(х)]
действительного переменного х имеет место наше ос-
новное утверждение, т. е. что из равенства
й'(х) —0 (22)
(ср. (9)) следует равенство
й(х) = С
(ср. (10)). В самом деле, из (22) следует, что ft'(£),
в формуле (20) есть нуль, и, следовательно, в силу
формулы (20) /i(xi)= ft(xe), где х0 и xj — два произ-
вольных значения аргумента функции й(х), заданной
на связном множестве, так что функция й(х) есть
постоянная.
Проведем теперь доказательство нашего основ-
ного утверждения для комплексной функции й(х)’
действительного переменного х. Мы имеем А(х) =
= ф (х) 4- /ф (х), где ф (х) и ф (х) — действительные
функции действительного переменного х. Из формулы
(2) § 11 следует, что й'(х)= ф'(х)+<ф'(х). Таким
образом, из равенства Л'(х) = 0 следует ф'(х)=0 и
ф'(х) = 0, так что, по доказанному, функции ф(х) и
ф (х) суть постоянные, следовательно, и функция й(х)]
также постоянная.
138
Доказательство соотношения (10) для комплекс-
ного аргумента. Рассмотрим сперва случай, когда ло-
маная (8) состоит из единственного отрезка [zozi].
Для этого на отрезке [zozi] введем действительный
параметр t, положив
z = z0(I-/) + z1#. (23)
Когда действительное переменное t изменяется от 0
до 1, точка z, заданная равенством (23), пробегает
отрезок [zoZi]. Функцию Л(г) на отрезке [гогД рас-
смотрим как функцию действительного переменного t,
положив
4(/) = Л(г0(1 — О + сД
Мы имеем
k/(t) = ht(z0(l — t) + ztt) • (z^ — z0)
(см. § 11, (21)). Так как функция ft'(z) на отрезке
[zoZj] равна нулю, и, следовательно, функция
равна нулю на отрезке 0^/^ 1, то функция #(/)'
постоянна, т. е. Й(1) = Й(0); но так как Й(0)=й(г$),
а Й(1) = Zt(zi), то ft(zi)=ft(z0). Если теперь ломаная
(8) состоит из произвольного числа отрезков, то на
концах каждого отрезка h(z) имеет равные значения.
Таким образом, мы имеем равенства
ft(zo) = A(z1),
h (z,) = h (z2),
A (4-0 &,’)=»* (A
откуда следует, что
й (z*) = Л (z0),
так что значение функции /г(г*) для любого значения
z* равно постоянной величине ft(zo) и, следовательно,
функция A(z) есть постоянная величина.
Случай функции нескольких переменных. Если под-
лежащая интегрированию функция зависит не от од-
ного переменного, а от нескольких, например двух
переменных, т. е. имеет вид то мы должны
четко указать ту из двух переменных, по которой
производится интегрирование, что, впрочем, доста-
точно ясно выражается самой формулой (2), где знак
dz означает, что интегрирование производится по z.
139
В случае функции f (г, w) интеграл •
f (г, w)dz . ,. .
сам, естественно, зависит от двух переменных г и ®,
так что соотношение (1) получает вид
f (z, w) = -^h(z,: w)'
'(см. § 10, (17)). В этом случае из соотношения
-^h(z, и») = 0
вытекает соотношение h(z,w)—c(w), где величина
c(w) есть произвольная функция w. Вместо соотно-
шения (7) мы получаем теперь соотношение
hi (z, w) — hi (z, w) -f- c (w).
Пример 1. Если множество всех допустимых
значений z функции h(z) не связно, то производная
h' (z) функции h(-z) может равняться нулю без того,
чтобы сама функция й(г) была постоянной. В каче-
стве примера приведем действительную функцию
sign* действительного переменного х, определенную
для всех ненулевых значений х, причем для поло-
жительных значений аргумента signx = 1, а для от-
рицательных значений аргумента signx =—1. Функ-
ция эта задана на несвязном множестве, именно, на
множестве всех действительных значений х, за ис-
ключением значения х — 0. Ее производная в каждой
точке равна нулю, но функция sign х непостоянна.
Пример 2. Функцию h(x) действительного пере-
менного х определим на отрезке 0 х 1 условиями
Л(0) = 0,
h (х) — 1 — х при х > 0.
Ясно, что определенная так функция h(x) разрывна,
именно, она имеет разрыв в точке х = 0 и не дости-
гает своего максимума, так как верхняя грань ее зна-
чений равна 1, а сама она этого значения не прини-
мает. .
Пример 3. Дадим формулу движения точки, пе-
ремещающейся с постоянным ускорением а (см. при-
мер 1 § 11). Если обозначить через х = f(/) коорди-
140
нату в момент времени t точки х, движущейся по оси
абсцисс, то для функции /(/) мы имеем соотношение
/"(О = а- Отсюда в силу формул (4) и (7) мы имеем
- /'(О = «о + at, (24)
где «о — скорость движения точки в момент t = 0.
В силу тех же формул (4) и (7) из равенства (24)
вытекает
/ (0 — Хо 4~ »о! + >
где хе — положение точки в момент t = 0. Это есть
известная формула равноускоренного движения точки.
§13. Вычисление некоторых неопределенных
интегралов
Дадим теперь несколько правил нахождения неоп-
ределенных интегралов. Соответствующие формулы
непосредственно вытекают из формул дифференциро-
вания, данных в § 11. В правой части каждой фор-
мулы будет стоять произвольное постоянное слагае-
мое с.
Интеграл степенного ряда. Из формулы (10) §11
дифференцирования степенного ряда вытекает фор-
мула интегрирования степенного ряда
J («о + ojz + агг2 + ... 4-a„z"4- ...)dx =
~2 ~3 1
= с4-ooz4-ai4-«2 — 4- ••• 4"опйJ 4- • • • (О
Следует заметить, что радиусы сходимости обоих ря-
дов, входящих в эту формулу, равны между собой.
Интегралы некоторых конкретных функций.
Jea4z = c4-e2; (2)
sin z dz = с — cos z, J cos z dz = c 4- sin z; (3)
Hl
Выписанные формулы вытекают непосредственно из
формул (14), (15), (20) § 11
§ = с + In z; (5)
г2 ~ c + arcsin z; (6)
Sr/ 5»
l+> = c +arctg z. (7)
Эти формулы вытекают из формул (27) — (29) § 11.
В настоящий момент мы имеем возможность выпи-
сать в виде формулы интеграл некоторой функции
лишь в том случае, когда эта функция была уже
раньше получена как производная некоторой функ-
ции. Положение с интегрированием, таким образом,
резко отличается от положения с дифференцирова-
нием. Согласно правилам, изложенным в § 11, мы
можем найти производную любой элементарной транс-
цендентной функции и выписать ее в виде другой эле-
ментарной трансцендентной функции. Оказывается,
что интеграл элементарной трансцендентной функции
не всегда можно записать в виде элементарной транс-
цендентной функции. Но и в тех случаях, когда его
можно так записать, нахождение интеграла в виде
формулы представляет большие трудности. Суще-
ствуют, однако, некоторые правила, позволяющие
преобразовать подлежащую интегрированию функ-
цию в другую функцию, которая уже является произ-
водной некоторой известной функции. Здесь мы при-
ведем два таких правила: 1) замена переменного при
интегрировании; 2) интегрирование по частям.
Замена переменного при интегрировании. Если из-
вестно, что функция f(z) является производной неко-
торой функции h (г), т. е. если
f(z)=/)'(*>
или, в другой форме,
f (z) dz = h (z),
т. e. если мы умеем выписать интеграл функции f(z),
то путем замены переменного г = ф(о>) мы можем
найти некоторую новую функцию g(w), для которой
142
интеграл тоже легко выписать. Для этого достаточно
сделать подстановку z — ty(w) в функцию h(z), по-
лучив функцию h($(w)), и вычислить производную
этой функции
(h (ф (w)))' = h' (ф (то)) • ф' {то) = f (ф (то)) ф' (то).
Пол агая
g (w) — f (ф (то)) • ф' (то), (8)
мы получаем
g (то) dw = h (ф (то)).
Таким образом, умея выписать интеграл функции
f(z), мы путем подстановки л = ф(то) получаем но-
вую функцию g(TO) (см. формулу (8)), для которой
также можно выписать интеграл. Очевидно, что из
функции g(w) можно обратно получить функцию f(z)
путем подстановки то = <р(г), где q>(z) есть функция,
обратная к функции ф(то). Описанная здесь связь
между функциями f(z) и g(w) достаточно проста, но
она становится совершенно автоматической, если под-
становку з = ф(то) делать в выражении, стоящем под
знаком интеграла, т. е. в выражении f(z)dz, заменяя
z через ф(то) как под знаком функции f(z), так и под
знаком дифференциала. Действительно, мы имеем
f (z) dz = f (ф (то)) б/ф (то)=f (ф (то)) ф' (то) dw
(см. формулу (14) § 10). Столь формальный переход
от одного подынтегрального выражения с перемен-
ным г к другому подынтегральному выражению с пе-
ременным то при замене с = ф(то) оправдывает тот
факт, что в подынтегральном выражении выписан
символ dz — дифференциал независимого перемен-
ного. Проиллюстрируем этот способ интегрирования
простым примером, именно, подсчитаем интеграл
функциигде <p(z) — некоторая заданная функ-
ция, т. е. вычислим функцию
( <р' (z) dz
J <₽(*) • W
Делая замену <р(х) = то, мы в силу наших правил
можем переписать интеграл (9) в форме
$2^p- = J^- = c + lnTO = c + ln(p(z). (10)
143
i
• ..Интегрирование по частям. Правило дифферент*- ч
рования произведения дает нам !
(и (z) и (z))' = и' (г) о (z) + и (г) о' (г) ’ • 1
(см. формулу (16) § 11). Отсюда мы получаем I
( u(z)v'(z)dz + ( v(z)u'(z)dz = c + uv. 1
- • • ' ~ 1 $
Полагая г; J
и' (z) dz — du (z), o' (z) dz = do (z), мя |
мы получаем формулу ?
u(z)dv(z)+ v(z)du(z} = c + u(z)u (z)
или, иначе,
J u(z)do(z) = c + «(z) v(z)— J u(z)rfu(z). (11)
Полученная формула называется формулой интегри-
рования по частям. Она применяется в тех случаях,
когда стоящий справа интеграл легче вычислить, чем
интеграл, стоящий слева.
Пример 1. Дадим пример применения диффе-
ренцирования и интегрирования к задаче естествозна-
ния. Для этого разберем поведение идеального газа,
находящегося в сосуде переменного объема, напри-
мер в цилиндре с подвижным поршнем. Мы будем
также считать, что газ, заключенный в цилиндр, не
имеет теплообмен с окружающей средой и что пор-
шень движется без трения, массу же газа предполо-
жим равной одной грамм-молекуле. Давление газа,
находящегося в цилиндре, обозначим через Р, его
объем через V, а абсолютную температуру через Г;
Тогда имеет место известное соотношение Клапейрона
PV — RT, (12)
где Р есть константа, не зависящая от состояния га-
за. Второе соотношение, которое мы берем из фи-
зики, дает нам величину внутренней энергии U газа,
находящегося в цилиндре, при помощи формулы
t/=C0T,
где Со есть константа, зависящая от газа, находя-
щегося в цилиндре, но не от его состояния. Для того
144
чтобыуясннтьфнзическийсмысл констант» С0,пред-
ставим себе, .что мы подогрели раз, находящийся » -
цилиндре, от температуры Tj да температуры Тг, не
меняя объема газа, т. е. не двигая* поршня. Тогда
внутренняя- энергия газа увеличится на-величину
Cv(Tz—Т\). Так как-в процессе этого нагревания газ
не произвел никакой работы (поршень не сместился),
то все тепло, приданное газу, пошло на повышение
его температуры, таким образом, С« есть теплоем-
кость нашего газа при постоянном объеме.
Обозначим через а площадь сечения цилиндра и
через / расстояние от дна цилиндра до поршня. Тогда
V = al. Сожмем теперь слегка газ, изменив положе-
ние поршня, т. е. величину /, на малую отрицатель-
ную величину 61. Тогда объем газа V изменится на
отрицательную величину 6V, определяемую формулой
6V = а61. В течение этого периода сжатия Газа сила
давления газа на поршень приблизительно равна
аР — приблизительно потому, что давление в процес-
се сжатия слегка меняется, так что сила эта в точно-,
сти равна F = <r(P+e), где е стремится к нулю вме-
сте с 61. По известному закону физики работа, затра-
ченная на сдвиг поршня, равна силе воздействия на
длину — 61 пройденного поршнем пути. Таким обра-
зом, эта работа равна
-Ра (61 + о (61))
или, иначе,
— PdV + o(dV).
Ввиду отсутствия трения и теплообмена вся эта ра-
бота должна превратиться во внутреннюю энергию
газа, т. е. внутренняя энергия газа U = С0Т должна
увеличиться на CV6T, так что мы имеем
C„6T= — P6V + o(6V). (13)
Вычисляя величину Р по формуле Клапейрона, мы
получаем
P-BL
v
Подставляя это значение величины Р в формулу (13),
получаем
У C96T = -RTy- + o(6V), (14)
145
Так как в процессе сжатия газа температура Т яв-
ляется функцией объема газа, то, деля соотношение
(14) на TGV, мы получаем
€„ ST #? , о(бП
г ’ бу “ у + nv ’
Перейдя в этом соотношении к пределу при 5У->0,
мы получаем
cv ат _ R
т av v
или, иначе,
<15>
Таким образом, в силу основного результата преды-
дущего параграфа неопределенный интеграл от левой
части соотношения (15) есть константа, так что мы
имеем
K^+4)<(V=c
или, иначе,
С C^dT л f MV
В силу формулы (10) мы получаем
С„ InT + RIn К = с.
Деля это соотношение на Со и потенцируя его, мы
получаем равенство
я
TVC* =Д
где 6 — константа, возникшая в результате интегри-
рования и потому зависящая лишь от того газа, ко-
торый находится в нашем цилиндре, но не от его со-
стояния. Подставляя в последнее соотношение Т из
равенства (12) Клапейрона, мы получаем
я+с„
PV с» =«, (16)
где с — константа, зависящая от газа, находящегося
в цилиндре, но не от его состояния.
Величина Cv, как уже отмечалось, есть теплоем-
кость газа при постоянном объеме. Величина Ср =;
=/? + СV, как легко сообразить, есть теплоемкость
того же газа при постоянном давлении, так как, если
газ нагревать, сохраняя постоянное давление, то рас-
146
ходуемое тепло частью идет на увеличение внутрен-
ней энергии (т. е. на повышение температуры) газа,
частью- превращается в механическую работу смеше-
ния поршня.
Таким образом, формула (16) записывается в виде
PVv = c, (17)
Ср
где у = тг-.
Формула (17) носит название формулы адиаба-
тического сжатия газа.
Пример 2. Применим формулу интегрирования
по частям для нахождения интеграла от функции
f(z)= u(z)ez, где и (г) есть многочлен степени п от-
носительно переменного z. Для этого положим t>(z)=
= ег, так что do(z} — ezdz. Таким образом, мы имеем
j / (г) dz — и (z)«?2 dz — и iz)dv(z) =
= е + к (г}ег — ег du (z) — с + и (г) ег — и' (г) ег dz.
Итак, мы свели нахождение интеграла от функции
u{z)ez к интегралу от функции «'(z)^. Но u(z) есть
многочлен, следовательно, и u'(z) — также многочлен,
но степени на единицу ниже. Этим открывается воз-
можность последовательного применения формулы
интегрирования по частям, в результате которого мы
можем записать искомый интеграл в форме
dz=c + u(z}ef — и' (г) ez + и" (z) е? +
... 4*(— — +
+ и" (z) + ... + (— 1)" «(я) (г)).
Здесь мы употребляем производные не только пер-
вого и второго порядков, но и произвольного поряд-
ка, естественным образом определяемые (подробно-
сти см. в § 15, (2)).
Пример 3. Пользуясь формулой (1) почленного
интегрирования степенных рядов, дадим разложение
в степенные ряды функций In (1 + z) и arctgz. В силу
формул (27) и (29) § 11 мы имеем
1п'(1+2) = у^, arctg' 2= 1^7»-»
М7
Стоящие в правых частях последних равенств функ-
ции легко могут быть разложены в степенные ряды
е-радиусом сходимости 1 на основании'формулы для
суммы геометрической прогрессии (см. (21) § 6).
Именно, мы имеем
=1’_2 + г2+ ...+(- 1)»2»+ ....
-T^=l-z24-z<+...+(-l)"*2n+... и
t 1 ГГ * 1V
•. - - - . : ?' j !
Интегрируя два последних равенства по формуле (1);
мы получим разложение функций In (1 + z) и arctg а
в степенные ряды по г с радиусом сходимости 1. Для
доведения дела до конца нам остается только вы-
брать значение константы с, входящей в правую часть
равенства (1). Для нахождения этой константы до-
статочно придать переменной г какое-нибудь опреде-
ленное значение, например z = 0, и получить значе-
ние константы с из равенства (1). Таким образом,
нам надо знать значение In 1 и arctg 0. Но так как
функции In и arctg неоднозначны, то мы имеем
in 1 — 2kni, arctg 0 — ka,
где k — произвольное целое число. Выбрав из всех
этих значений какие-либо вполне определенные: для
величин In 1 и arctg 0, мы получим те разложения в
степенные ряды функции In (1 -pz) и функции arctg z,
которые при z = 0 имеют заданные значения. Мы вы-
берем для In 1 и arctg 0 значение нуль. Тогда значе-
ние константы с в обоих случаях будет также нуль,
и мы получим. следующие разложения в степенные
ряды:
1п(1 + г)-г - 4 + т + • • • +(- l)“4j4 + • •••
Ягс182 = г-4 + 4 + •+<- 1)“4тт+-"
Следует подчеркнуть, что полученные разложения в
степенные ряды функций In (1 + z), и arctg z задают
в круге радиуса 1 те ветви многозначных функций
In(l-j-z), и arctg z, которые при z = 0 обращаются
в нуль. ’ .
148
1 §’44. Определенный интеграл *
В. § 12 мы ввели операцию интегрирования как
обратную операции дифференцирования. Именно, мы
объявили, что. интегралом заданной функции f(z) на'
зывается такая функция % (г),, которая удовлетворяет
условию
%'(z) = f(z). (1)
Любая функция %(г), удовлетворяющая условию (1).,
называется первообразной функции f(z). Соотноше-
ние (1) представляет собой уравнение, где f(z)—из-
вестная заданная функция, а %(г) — неизвестная ис-
комая функция.
Сразу же было обнаружено, что уравнение (1)
имеет не единственное решение. Очевидно, что если
функция х(г) удовлетворяет этому уравнению, то од-
новременно ему же удовлетворяет и любая функция
вида x(z)-f-c, где с—произвольная постоянная.
. Совсем не просто, а в результате довольно слож-
ных исследований был установлен и характер неодно-
значности решений уравнения (1). Было установлено,
что если множество допустимых значений аргумента
г функции f(z) связно, то вся неоднозначность реше-
ния уравнения (1) сводится к добавлению константы
с. Точнее, было доказано, что если ft(z) есть функция,
удовлетворяющая уравнению (1), т. е. условию
A'(z) = f(z), (2)
то она может быть записана в виде
A(z) = x(z) + c. (3>
Таким образом, для того чтобы из всех функций А (z),
удовлетворяющих уравнению (2), выбрать одну впол-
не определенную, достаточно придать константе с оп-
ределенное значение. Есть, однако, другой и в неко-
торых отношениях более важный способ выбора оп-
ределенного решения h (z) уравнения (2). Опишем
его.
Пределы интегрирования. Пусть f(z)—некоторая
действительная или комплексная функция действи-
тельного или комплексного переменного z, заданная
на связном множестве значений аргумента. Зада-
димся некоторым определенным значением z0 ее ар-
149
гумента и выберем такой интеграл Hz) функции
f(z) (см. (2), (3)), который удовлетворяет условию
й(за)==0. (4)
Такой интеграл всегда существует; в самом деле, для
нахождения его достаточно задать константу с так,
чтобы было выполнено соотношение ।
ОС (zo) + с = 0.
Таким образом, при
с = —X(z0)
мы получаем функцию
*(z)=*(z>—x(z0>, (5)
удовлетворяющую условиям (2> и (4). Эта функция
й(г)г называется определенным интегралом функции
f (z) и записывается в виде
Z
A(z)=Jf(?X (6)
г»
Этот интеграл ft(z) функции f(z) называется опре-
деленным интегралом, значение аргумента Zo — ниж-
ним пределом интегрирования, а значение аргумен-
та z — верхним пределом интегрирования. Величина
h(z), определенная формулой (6), зависит от исход'
ной функции f(z) и двух пределов интегрирования:
нижнего Zo и верхнего г, но не зависит от величины £,
которая называется переменным интегрирования, ее
мы можем обозначить любой буквой, например бук«
вой t, так что имеет место равенство
Ж Z
Ж о Zq
Из условий (2) и (4), наложенных на функцию
h'(z), мы вывели выражение (5) для функции й(г),
где хС2)—любая первообразная функции |(z). От«
сюда Следует, что условиями (2) и (4) функция M2)'i
определяется однозначно и что ее выражение (5) че»
рез первообразную не зависит от выбора иервооб«
разной.
150
Простейшие свойства определенного интеграла.
Если fi (г) и f2(z)— две функции с первообразными
Xi(2) и ХгХ2), а аь а2— два числа, то функция
aiXi (z) + «2X2(2) является первообразной для функ-
ции aifi(z)+ a2f2(z). Отсюда следует
J [“if 1 (?) + “2^2 (?)1 ^? =
«а
= («1X1 (2) + «2X2 (2)1 — [«1X1 (2о) + «2X2 (2о)1 =
= «1 [Xi (z) — Х1 (Zo)] + «2 [Х2 (г) — Х2 (z0)l =
Z Z
= «ipi(?M? + a2p2 (?)<*?•
2э Z}
Окончательно получаем
z 2 2
[«1/1 (?) + «2?2 (?)] Й? = «1 /1 (?) rf? + «2 /2 (?) ^?-
Zo Zp Zo
Нижний и верхний пределы го и г до некоторой сте-
пени равноправны. Для того чтобы подчеркнуть это,
обозначим верхний предел интегрирования через zi,
Йюгда мы получим
«1
J/(?M? = x(zi) —х(2о)
Zo
(7)
(см. (5)). Меняя местами пределы интегрирования,
Мы получим
Jft?)d?=X(zo)-x(2i).
Zl
Из равенств (7) и (8) непосредственно вытекает
2л 2о
p(?)rf? = -p(?)d?.
Zj Zi
(9)
15
Если заданы три значения Zo, Zi,.z2 аргумента
функции/(z), то мы имеем ч
p(fe)^ = x(zi) —х(г0),
2о •
(f(O< = X(Z2) — X(Z1),
Zi
Jf(OdC = x(z2) —Х(2о)-
г»
Из этих трех, равенств вытекает важное соотношение'
21 Z2 Zj
(к»
2® 2{ 2у
Единственность определенного интеграла. Будем
по-прежнему предполагать, что исходная функция
f (z). задана на связном множестве. Положим
21
J/(?)</? = Л (z0,zi). (11)
2- >
Тогда в силу (5)
Л(г0, Z|) = x(^i) —х(?о).
Для функции h(zo, zi) соотношения (2) и (4) перепи-
сываются в виде
h(z0, Zo) = O. (13)
Так как соотношения (2) и (4) однозначно опреде-
ляли функцию й(г), соотношения (12) и (13) одно*
значно определяют функцию ft(zo, zi).
Меняя в соотношениях (12), (13) местами z© и zi,
получим соотношения ‘ - Г *
-M£;—=f(zo)> (14)
Л(гь Zj) = O, (15)
152
которыми- функция-ft(zi, Zo) однозначно определяется.
Заметим теперь, что
Л (zj, zo) = — h (z0, zi) (16)
(см. (9) и (11)). Таким образом, величины ft(zo, Zi)
и h(zi, zo) однозначно определяют друг друга. Заме-
няя в соотношениях (14), (15) функцию ft(zi, z0) по
формуле (16), мы получаем соотношения
^^--/(Zo), , (17)
Л(гьг,) = 0 (18)
для функции Л(го, Zi), которыми она однозначно оп-
ределяется. Резюмируя, можно сказать, что функция
ft(zo, Zi) удовлетворяет как паре соотношений (12),
(13), так и паре соотношений (17), (18), причем каж-
дой парой соотношений она определяется однозначно.
Существование первообразной. Все до сих пор рас-
сказанное в этом параграфе опирается на предполо?
жение, что существует первообразная %(z) функции
f(z). Очевидно, однако, что если функция h(z0, zi),
удовлетворяющая условию (12), существует, то в
силу этого условия ft(z0. zi) есть первообразная функ-
ции f(zi), т. е. первообразная функции f(z) суще-
ствует. Точно так же, если функция ft(zo, Zi), удов-
летворяющая условию (17), существует, то функция
—h(zo,zi) есть первообразная функции f(zo), т. е.
первообразная функции f(z) существует. Резюмируя,
можно сказать, что определенный интеграл ' •>
Z,
pm
Z.
найден, если указана функция /i(z0, zi), удовлетво-
ряющая либо паре условий (12), (13), либо паре ус-?
ловий (17), (18).
Замена переменного интегрирования. Мы уже за-
нимались вопросом о замене переменного интегриро-
вания для случая неопределенного интеграла (см.
§ 13, (8)). В случае определенного интеграла тре-
буется дополнительное рассмотрение вопроса о пре-
делах интегрирования. Рассмотрим определенный
153
интеграл
z
Zi
Вместо z введем новое переменное w по формуле
2 = ф (да),
имеющей обращение, т. е. эквивалентной формуле
w = <р (z),
так что выполнены тождества
Ф (ф (w)) — w, ф(ф(г)) = г. (19)
Выясним теперь, как можно записать в виде опредв'
ленного интеграла функцию
й* (да) = h (ф (да)).
Оказывается, что это можно сделать следующим об'
разом:
h*(w) = J g(ai)da, (20)
Wd
где
g («О = f (Ф (®)) ф' (<о); (21)
дао == ф (zo), w = ф (z).
Для доказательства формулы (20) покажем, что для
функции h*(w) выполнены условия (12) и (13). Дей-
ствительно, мы имеем в силу формулы дифференци-
рования сложной функции (см. § 11, (21))
(h* (w))' — (h (ф (да)))' = h' (ф (да)) • ф' (да) =
= f (Ф (да)) • Ф' (да) = g (да)
(см. (21)). Таким образом, условие (12) для функ-
ции й*(да) выполнено. Далее, мы имеем
h* (да0) = g (®) dat = 0.
Таким образом, условие (13) выполнено. Так как для
функции Л* (да) условия (12) и (13) выполнены, то
она является определенным интегралом (20).
154
Зависимость от параметра. Если подлежащая ин-
тегрированию функция зависит не только от одного
переменного г, по которому производится интегриро-
вание, но и еще от некоторого переменного и, кото-
рое мы будем называть параметром, т. е. имеет вид
и), то ее первообразная также зависит от пара-
метра и, т. е. имеет вид x(z, и). Эта первообразная
удовлетворяет уравнению
и) = f (z, и).
Всякая другая функция h(z, и), удовлетворяющая
уравнению
~h(z,u) = f(z,u), (22)
отличается от функции %(z, и) только на величину, не
зависящую от г, но, естественно, могущую зависеть
от параметра и. Таким образом, функция h(z, и) мо-
жет быть записана в виде
h (z, и) — % (z, и) + с (и),
где с(и) — произвольная функция параметра и. Вы-
берем теперь какое-нибудь вполне определенное зна-
чение zo аргумента z и потребуем, чтобы функция
h (z, и) удовлетворяла условию
Л(г0, «) —0. (23)
Для того чтобы последнее условие имело место, мы
должны выбрать функцию с (и) параметра и так,
чтобы выполнялось соотношение
X (zo, и) + с (и) = 0,
откуда
с(м) = —x(z0, «),
и для Л (г, н)’, удовлетворяющей условию (23), мы по-
лучаем выражение
h (г, и) = % (z, а) — % (z0, и). (24)
Функция ft(z, и), удовлетворяющая условиям (22) и
(23), является определенным интегралом функции
f(г, и)] и записывается в виде
Z
h{z,u)=\f^u)dt. (25)
2а
155
Таким образом, определенный интеграл* ^2.5) имеет
вид (24). Для того Чтобы подчеркнуть некотороёрав- -
ноправие нижнего и верхнего пределов йнтегрирова-
ния, обозначим-верхний предел интегрированияче-
рез z\. Тогда мы можем записать ’ ... .
Z, •
^f^,u)d^ = h(z<i,zi,u)=^'x.(zl,u) — 'x,(20;u). (26)
Эта формула подчеркивает, что определенный интег-
рал (26) зависит от нижнего и верхнего пределов ин-
тегрирования и от параметра и. Определенный интег-
рал h(zo, zi, и) как функция своего верхнего предела
удовлетворяет условиям
^-h(zo,zi,u) = f(zl, и), (27)
Л (z0, Zb, и) — 0, (28)
которыми он и определяется однозначно. Определен-
ный интеграл h(z0, zi, и), рассматриваемый как функ-
ция нижнего предела Zo, удовлетворяет двум усло-
виям
h (z0, zl( и) = — f (zo, и), (29)
ft(zi,zb u) = 0, (30)
которыми он и.определяется однозначно. Таким обра-
зом, для того чтобы убедиться в том, что функция
Л(г0, zi, и) трех переменных является определенным
интегралом:
Zi
h(zo, zt, u) = ^f& u)d£,
Z3
мы должны убедиться в том, что функция ft(zo, Zi, «)’
удовлетворяет либо паре условий (27), (28), либо
паре условий (29), (30). Поэтому изложенный способ
нахождения определенного интеграла есть способ
проверки. Мы просто должны угадать функцию
ft(zo, Zi, и)’, которая удовлетворяет либо паре условий
(27) и (28), либо паре условий (29), (30).
Все сказанное до сих пор относительно интегри-
рования функции, зависящей от параметра и, не пред-
ставляет собой ничего интересного. Ситуация стано-
166
рится нетривиальной и требующей, осрбого внимания
в, .том случае,: .когда параметр и совпадает с одним из
пределов интегрирования, т. е. когда имеет, место
одно из двух равенств : .
или и— го, или « = Zj,
т. е. когда мы хотим найти один из двух интегралов
г,
Цг0,2ь Zj) = Jf(g, zjdt» (31)
. M • ' _
h (z0, zb z0) = J f (£, z0) d£. (32)
ZO . (
При нахождении интеграла (31) предложенный нами
способ проверки при помощи соотношений (27) и
.(28) становится негодным, но зато пригоден способ
проверки при помощи соотношений (29) и (30).Если,
наоборот, мы хотим найти интеграл (32), то предло-
женный нами способ проверки при помощи соотноше-
ний (29) и (30) становится негодным, но годится спо-
соб проверки при помощи соотношений (27) и (28).
Объясним, почему это так. Рассмотрим случай пер-
вого интеграла (31). В функции h(z0, zi, и) и заме-
нено через Zi, и функция h(z0, zt, Zi), подозреваемая
в том, что она есть интеграл (31), рассматриваемая
как функция переменного zi, уже не удовлетворяет
условию
~ h (z0, Zi, zi) = f (z0, г,). (33)
Действительно, при выведении условия (27) мы счи-
тали, что аргумент и, стоящий на третьем месте, есть
величина постоянная, а в левой части формулы (33)
при дифференцировании по г\ мы уже считаем, что
аргумент, стоящий на третьем месте, есть переменная
величина z\. В этом случае, для того чтобы убедить-
ся, что функция двух переменных h(zo, zi,zi) являет-
ся определенным интегралом (31), нужно применить
к ней условия (29) и (30), т. е. убедиться в том,, что
h (zo, zb zi) = — f (z0, Zj) (34)
и .
ft(zb Zi, Zi) = 0. (35)
157
Аналогично обстоит дело и в случае нахождения ин-
теграла (32). В этом случае мы должны убедиться
в том, что
h (z0, zh z0) = f (z0, Zi)
И
h (z0, Zo, Zo) — 0.
Интегрирование неравенств. Здесь мы будем рас*
сматривать только действительные функции действи-
тельных переменных. Мы докажем, что если для двух
функций fi(x, и) и f2(x, и) выполнено неравенство
/1 (х, и) < f2 (х, и) (36)
для всех интересующих нас значений переменных х
и и, то имеет место неравенство
х X
sign (х — xq) fi (В, и) dl < sign (х — х0) f2 и) d%,
Хо Ху
(37)
т. е. что неравенство (36) можно интегрировать в
пределах от хо до х.
Для доказательства этого утверждения составим
функцию
f(x, u) = f2(x, u) — h(x, и).
Ясно, что для того чтобы доказать, что из неравен-
ства (36) вытекает неравенство (37), нам для функ-
ции f(х, и) достаточно доказать, что из неравенства
f(x,«)>0 (38)
вытекает неравенство
sign(x-xo)p(g,«)^>O. (39)
Хо
Займемся доказательством этого свойства функции
f(x, и). Для этого прежде всего положим
h (х, и) = р (|, и) d%.
Ха
Из соотношения (23) следует, что
h (х, u) = h (х, и) — h (хо, и). (40)
158
Далее, в силу формулы Лагранжа (см. § 12, (20))
мы имеем
h (х, u) — h (х0, и) = h (i], и) (х — х0) = f (т|, и) (х — х0),
(41)
где т] — число, заключенное между хо и х. Так как по
условию (38) /(п>«)^0, то из соотношений (40) и
(41) следует
sign (х — хо) • h (х, и) 0,
т. е. неравенство (39).
Заметим, что так доказанная формула верна, в
частности, и при и = х0, так как при ее доказатель-
стве мы пользуемся соотношениями (27) и (28), за-
дающими определенный интеграл. Пользуясь соот-
ношениями (29) и (30), можно доказать, что нера-
венство (37) верно и для и = х.
Интегрирование модуля функции. Здесь мы опять
будем рассматривать действительную функцию дей-
ствительного переменного. Мы докажем, что если
IfWKM (42)
для всех значений £ на отрезке [хох], то имеет место
неравенство
<Af.|x-x0|.
(43)
Докажем это. Из соотношения (42) следует, что
-Af<f(g, Ы)<М.
Интегрируя это двойное неравенство в пределах от
хо до х, мы получим двойное неравенство
X
sign(x — Хо) • (—А1) • (х — x0)<sign(x — х0) j f (£,u)dlС
Хо
< sign (х — хо) • М • (х — Хо), (44)
из которого непосредственно вытекает неравенство
(43).
§ 15. Ряд Тейлора
Один из важнейших способов вычисления значе-
ний функции по значениям ее аргумента опирается
на разложение функции в степенной ряд. Иногда сте-
169
пенным рядом -функция и .задается. Так. мы задали-
функцию exp(z) при помощи ряда. (см. § 7). Иногда
функцию, заданную каким-либо другим способом,
удается разложить в степенной ряд и получить таким
путем средство ее вычисления. Так было с функ-
циями cos х и sin х действительного переменного х,
которые первоначально задаются геометрически, а
затем мы нашли их разложение в степенные ряды в
§ 8, пользуясь свойствами функции exp(z). Пользуясь
разложением функции в степенной ряд, можно изу-
чать ее свойства. Так это было сделано в § 7 с функ-
цией exp(z). В самом начале § 7 был установлен ряд
ее свойств. При помощи степенных рядов функция,
заданная для действительных значений переменного,,
распространяется на область комплексного перемен-
ного (см. § 9). Мы уже нашли разложение в ряды
многих трансцендентных функций. Теперь пора по-
ставить вопрос о возможности разложения заданной
функции в степенной ряд. Этим вопросом мы и бу-
дем заниматься в настоящем параграфе. Мы сразу
будем рассматривать разложение функции в ряд не
по степеням независимого переменного г, а по степе-
ням разности z — Zo, где zo есть некоторое постоян-
ное значение аргумента. При этом мы будем рас-
сматривать одновременно как действительный, так и
комплексный случай, так что рассматриваемая функ-
ция f(z) может быть как комплексной, так и дей-
ствительной, точно так же как и ее аргумент z.
Сперва мы будем исходить из предположения, что
функция f(z) разлагается в степенной ряд по степе-
ням разности z — Zo, т. е. что имеет место равенство
f(z) = a0 + ai(z — Zo)4-a2(z — z0)2 + ...
...+an(z-z0)n +... (1)
Ряд этот, очевидно, сходится при Z — Zo, но для того
чтобы^&ссмотрение его имело какой-нибудь смысл,
следует считать, что ряд сходится не только для зна-
чения аргумента z = z0, но и для других значений.
Из этого вытекает, что ряд (1) имеет положитель-
ный радиус сходимости, т. е. он абсолютно сходится
для всех значений z, удовлетворяющих неравенству
|z — z0|<r, r>0.
ЛОО
Коэффициенты ряда (1) очень легко можно вычис-
лить через производные функции f(z), правда, для
этого нужна не только первая производная, но и про-
изводные произвольного порядка функции f(z). Они
ие были еще формально определены, а потому дадим
их определение здесь.
Производйые разных порядков. Мы уже знаем, что
такое производная f'(z) функции f(z). Она называет-
ся производной первого порядка. Производная (Г(г))?
функции f' (г) называется производной второго по-
рядка функции f(z) и обозначается через f"(z). Точ-
но так же производная (f"(z))' называется производ-
ной третьего порядка функции f(z) и обозначается
через f'" (z) или f(3)(z). Производная произвольного
порядка п определяется индуктивно при помощи фор-
мулы
/,n)(z) = (f<n-1)(z))'. (2)
Мы уже знаем, что если степенной ряд сходится
в круге положительного радиуса г, то его производ-
ная, вычисленная при помощи почленного дифферен-
цирования ряда, также сходится в круге радиуса г.
Это было доказано для функции, разлагающейся по
степеням аргумента z (см. § II). Так как функция
f(z) (см. (1)) разложена по степеням аргумента
z — го, то ряд можно дифференцировать по аргумен-
ту z-—zo, сохраняя его радиус сходимости, но диффе-
ренцирование по z — Zo и дифференцирование по г
эквивалентны в силу формулы (22) § 11, так как
г°'~ ~ 1' Беря производную порядка п от обеих
частей равенства (1), мы получаем
f(n>(z) = n! ап + (n + l)n(n — 1) ... 2а„+| (г — zo) 4- ...
.;. 4- (п + k) (п + k — 1)... (k + 1) an+k (z — z0)fe 4- • • • .
причем это равенство имеет место для всех значений
|‘z —z0|<r. Полагая в нем z = z0, мы получаем
f(/t)(zo)= п\ап, откуда
Таким образом, мы выразили коэффициент аг
ряда (1) через п-ю производную функции f(z) и
6 Л. С. Понтрягин 161
можем теперь записать равенства (1) вно во ш форме:
f kz)=f(z0) + {^-{z-^)+ ....-
...+1^1^(2_го)«+... (4)
Ряд, стоящий в правой, части, последнего равенства,
называется рядом Тейлора, для функции f (z) в. тачке
z = zo. Это разложение возможна лишь при условии,
что функция f(z) имеет производные всех порядков
в точке z0. При доказательстве равенства. (3.) мы. ис-
ходили из предположения, что функция f(z) уже раз-
лагается в ряд (1.) по степеням z— гои соответствую-
щий ряд имеет положительный радиус сходимости.
Теперь возникает вопрос, разлагается ли некото-
рая заданная функция f(z) в ряд Тейлора (4). Для
решения его, очевидно, следует составить разность
Rn = Rn (Zo, z) = f (z) —
—•[/ (2o) + f' (Zo) (z — Z0) + . . . + (z&) (Z—Zo)n ]
(5)
между функцией f(z) и конечным отрезком ряда (4)'.
Ясно, что если имеет место соотношение
lim 7?„(z0, z) = 0, (6).
П->оо
то функция f(z) разлагается в ряд (4). Если соотно-
шение (6) не имеет, места, то функция f(z) не разла-
гается в ряд (4).
Оказывается, что величина Rn(zo,z) может быть
записана в виде определенного интеграла от сравни-
тельно простой функции, и эта запись в ряде случаев
позволяет решить вопрос, выполнено соотношение (6)
или нет. Для того чтобы записать функцию /?n(zo, z)’
в виде определенного интеграла, мы воспользуемся
условиями (34) и (35) § 14, считая при этом, что
Rn (zo, z) = h (z0, z, z).
Для проверки условия (34) § 14 мы должны вычис-
лить производную
R. %. 2), т
162
(8)
чтобы тем самим нейти функцию f(zo,z)', стоящую в
правой части .соотношения (34). Далее, мы должны
проверить условие (35).
Займемся вычислением производной (7), при этом
мы должны считать величину z0 переменной, а вели-
чину z—постоянной. Тогда мы имеем
^/Ы = о. =
При k > О
&
= + 4 ^+" (*о) *о)‘.
(9)
Суммируя от 1 до п равенства (9) и принимая во
внимание соотношения (8), мы получаем
Rn (z0, г) = - ± f(n+1) (г0) (г - г0)п.
Таким образом, в нашем слутае функция f(zo,z)\
стоящая в правой части равенства (34) § 14, опреде-
ляется равенством
f (г0, г) = ^-f<n+l) (г0) (г — го)"
Для проверки соотношения (35) § 14 мы должны в
равенстве (5) заменить го через г. Тогда мы, очевид-
но, волучаем
Rn (г, г) = 0.
В силу результатов § 14 мы можем теперь записать
Rn(z0,z) в виде определенного интеграла
Лп =(Zo, z) = Jj- J f+1). (&) (2 - Q" d£. (10)
Из формул (5) и (10) непосредственно вытекает ра-
венство
f (z) = f (20) +-JJ-f'(Zg) (z ~ So) + ...
г
... + fW (Zo) (2 - zQy + ± J f(n+l) (С) (г - ?)"dg. (11)
«0
6*
163
Величина (10) называется остаточным членом фор* I
мулы Тейлора. Формула Тейлора (11) имеет место ;
тогда, когда функция f(z) имеет все производные до
п + 1-го порядка включительно. Она важна не толь-
ко для разложения функции в ряд Тейлора. Для того
чтобы соотношение (6) имело смысл, необходимо,
чтобы функция f(z) имела производные сколь угодно |
высокого порядка. Таким образом, для того чтобы J
функция f(z) разлагалась в ряд Тейлора, необходимо, 1
чтобы она имела производные всех порядков и чтобы |
ряд (4) сходился. Этого, однако, недостаточно. В при-
мере 2 будет построена функция, имеющая производ-
ные произвольного порядка, причем ряд (4) сходится
при zo = 0, которая, однако, не разлагается в ряд
Тейлора при z0 — 0.
Пользуясь полученными результатами, дадим раз-
ложение в ряд Тейлора по степеням х действительной
функции
f(x) = (l+x)r (12)
действительного переменного х, где г — произвольное
действительное число (см. § 11, (30), (31)). Разложе-
ние это следующее:
|1+а)'=| +4т«+ V л*+...
... + -.!>-<'-»+') у + ... (13)
Когда г — натуральное число, формула эта совпадает
с формулой бинома Ньютона. Естественно сохранить
за ней это название и для случая произвольного г,
тем более, что формула (13) была известна Ньютону.
Мы докажем, что разложение (13) имеет место при
|х|< 1. Для доказательства этого выпишем прежде
всего производную порядка п функции (1 + х)г, поль-
зуясь формулой (31) § 11. Мы имеем
f(n)(x) = r(r-l) ... (г-п+1)(1+х/-».
Мы докажем, что остаточный член в нашем случае
стремится к нулю при |дс| < 1. Для этого мы оценим
величину
••“ТТГ (Н)
164
где g— действительное переменное, принимающее
значения из отрезка [Ох]. Именно, мы докажем, что
1р1<|х|. (15)
Если х положительно, то £ тоже положительно, и
тогда из формулы (14) сразу видно, что верна фор’
мула (15). При х отрицательном § также отрицатель’
но, и тогда из формулы
1 — —
X
Ц —х- 1 + |
также следует соотношение (15). Для функции (12)'
остаточный член Rn дается формулой
X X
Rn = А„ J (1 + gr*-1 (х - g)n dl = Аа J (1 + dl,
о oJ
где
л _ г (г — 1)... (г — п.)
п~ п! •
Так как |х|< 1, а £ меняется в пределах от 0 до х,
то величина (1 + £)Г-1 не превосходит некоторой кон-
станты б. Таким образом, в силу оценки интеграла
(см. § 14, (43)), мы имеем |/?п| 4яб|х|я+1. Вели-
чина А„ может быть записана в виде произведения
л __ г — 1 г — 2 г — п
Лп~Г' ! • 2 ••• п •
Таким образом, за исключением множителя г, вели’
чина Ап есть произведение чисел вида —j— = -^ — I.
Очевидно, что
lim(^--l) = -l. (16)
Если теперь выбрать положительное число s так,
чтобы было
|x|<s<l,
то из соотношения (16) следует, что существует на’
столько большое натуральное число /, что j
, . , I г — k I
при k > I имеем ——х < s.
165
Теперь мы имеем
Так как s < 1, то «**-*-► О при п->оо, к соотноше-
ние (6) для нашей функции /(х) доказан©. Итак, фор-
мула (13) верна при (х|< 1.
Пример 1. Выпишем теперь остаточный член
формулы Тейлора Rn для действительной функции
действительного переменного в наиболее принятой
простой форме. Для этого предположим, что функ-
ция /(л+1>(|) на отрезке от хо до х непрерывна и что
минимум ее равен р, а максимум q, так что имеет
место Неравенство
(?)<?• (17)
Оказывается тогда, что
‘ v. de)
где у — число, промежуточное между р и д. Мы мо-
жем записать числю у в виде
Y = f("+1,(n).
где t] есть число, заключенное между xq и х. Тогда
остаточный член Ra приобретает общепринятый вид
<1э>
Докажем формулу (19). Для этого воспользуемся
формулой
х
J(x-gr ^ = 7^Hj-(x-xo)n+1.
Хо
Зная, что знаки величин (х — |) и (х — х0) совпа-
дают, умножим двойное неравенство (17) на положи-
тельную величину (х — |)" sign (х — х0)п:
(х -1)" р sign (х - хо)" < (х -sign(x - ХоГ <
< (х — I)" q sign (х — ХоЛ
166
Интегрируя это двойное неравенство в пределах от
до х, мы получим (см. § 14, (44))
-ггг (х — х0)я+1 sign (х — Xe)”+1 <
п 4-1
X
< sign (х - хй)я+1 J (х - |)” fя+1) (В) rfg <
Хо
< -^Т (х — x0)n+1 sign (х — х0)я+‘.
Деля это двойное неравенство на п!, получим
-(Я+Т)Г — *о)"+1 s’Sn (х — Хо)я+1 <
< Rn sign (х — х0)я+1 < 1}!(х — x0)n+1 sign(x — хо)п+<.
Отсюда непосредственно следует формула (18). Поль-
зуясь остаточным членом в форме (19), легко полу-
чить разложение в ряды Тейлора функций ех, sinx,
cos х, но разложение функции (1 +х)г (см. (13)) при
помощи оценки (19) не получается.
Пример 2. Дадим теперь пример функции, не
разлагающейся в ряд Тейлора. Для этого прежде
всего отметим, что функция растет быстрее, чем
функция при положительном и, когда £ стремится
к оо. Действительно, мы имеем
t £2 £«+1
1 + тг + 1г+ + (я +1 )Г + ••• g
Г “
откуда непосредственно следует, что
е1
lim ттг = оо.
£->оо s
Переходя к обратным величинам, мы видим, что е-5
стремится к нулю быстрее, чем -р-, при По-
лагая В = ^г и считая, что х—>0, мы из сказанного
выводим, что если Р (~~) есть многочлен относи-
1
тельио —, то
X
limpf-Me" ~ = 0. (20)
ж->о ч * /
167
__ 1
Функция f (х) = е *2 определена для всех значений
х, отличных от нуля. При х — 0 она не определена,
но естественно считать, что f(0)= 0, ибо так доопре-
деленная функция f(x) непрерывна и в точке х — 0.
При всяком значении х #= 0 производная функции
f(x) легко вычисляется по правилам, данным в § 11,
и записывается в виде
В силу соотношения (20) мы имеем
lim fM (х) — 0.
х->0
Из этого, однако, не следует, что fw (0) = 0. Дока-
жем, что (0) = 0, по индукции. Будем считать, что
/<п-,)(0) = 0, и докажем, что и /(л)(0)=0. В самом
деле,
/“(0) = ,im = цт±Ш е- =о
х->0 х х->0 х
(см. формулу (20)). Таким образом, как сама функ-
ция f (x), так и все производные ее произвольного по-
рядка равны нулю при х = 0. Если бы эту функцию
/(х) можно было разложить в ряд Тейлора в точке
х = 0, то мы получили бы f(x)= 0, что, однако, оче-
видным образом неверно. Таким образом, эта функ-
ция f(x) = e * не разлагается в ряд Тейлора в точ-
ке х = 0.
Пример 3. Будем исходить из некоторой дей-
ствительной непрерывной функции f(x) действитель-
ного переменного х, заданной на связном множестве.
Допустим, что эта функция принимает два значения
уо и уз, т. е. существуют такие два значения ее аргу-
мента Хо И Х2, что
Уо = 1(хо), У2 = !(Х2). (21)
Тогда для каждого действительного числа уь заклю-
ченного между уо и у2, найдется такое значение аргу-
мента хъ заключенное между хо и Х2, что имеет ме-
сто равенство уг — f(xi). Коротко говорят, что дей-
168
ствительная непрерывная функция принимает все зна-
чения, промежуточные между двумя любыми ее зна-
чениями.
При доказательстве этого утверждения мы для
определенности предположим, что х0 < х2, у0 < у2.
Мы можем считать, что у{ не совпадает ни с yQi ни
е у2, так как, если бы такое совпадение имело место,
то функция f(x), очевидно, принимала бы значение
у! (см. (21)). Соберем теперь вместе все те точки
отрезка [*0X2], Для которых выполнено неравенство
ZUX i/i.
Множество всех таких точек х отрезка [хо-^2] мы
обозначим через М. Это множество непусто, так как '
оно содержит точку х0. Действительно,
f (Хо) = УО < г/1.
Верхнюю грань множества М (см. § 4) мы обозначим
через Xi и докажем, что
(22)
Доказательство равенства (22) будем вести от
противного. Именно, мы предположим, что оно не-
верно и что, следовательно,
« = I f (xi) — yi 1 > 0.
Так как функция f(x)’ непрерывна, то для этого поло-
жительного числа е найдется такое положительное
число б, что при
| х - xi | < б (23)
имеет место неравенство
lf(x) — f (xi) | < е.
Совокупность всех точек отрезка [хоХг], удовлетво-
ряющих неравенству (23), обозначим через U. Ясно,
что если f(xi)<Z у\, то все точки множества U принад-
лежат множеству М. Если же, наоборот, f(%i)> i/i,to
все точки множества U лежат вне множества М.
В первом случае любая точка х множества U, лежа-
щая справа от точки xi, принадлежит множеству М,
и потому xi не является верхней гранью множества
М. Во втором случае все точки х из множества U, ле-
жащие слева от точки xi, и еама точка xi не принад-
169
лежат множеству М, я потому течка *i не может *
быть верхней гранью множества М. Таким образом,
мы пришли к противоречию, т. е. равенство (22)
имеет место.
Пример 4. Ясно, что ряд (13) сходится и при
замене действительного числа х комплексным числом •*
z, причем радиус сходимости его не меньше 1. В дей-
ствительности он равен 1, если только г не есть нату- |
ральное число. Таким образом, мы можем определить *
функцию (1 4- z)г, где z — комплексное число, причем ।
|z| < 1, положив I
(1 + г)^1 +тГ-г+ Г(Г271)г2+-- !
+ + (24) /
Воспользуемся теперь разложением (24) для раз- I
ложения функции arcsin z в ряд Тейлора. В силу '
формулы (28) § 11 мы имеем ।
arcsin'.z = (l— z2) 2,
В силу формулы (24) мы имеем
. / 11 1 9i 1 1 1 • 3 • . , . • (2 fl I) пи •
arcsin Z = 1 + у z2 + ... +-2К-------..
(25)
Выбирая ту ветвь функции arcsin г, которая обра-
щается в нуль при z = 0, мы путем интегрирования
равенства (25) получаем
, 1 1 , .
arcsinz = z + =• • -я-z3 + ...
Z о
4- — 1 . 1 •3 • •. (2n — 1) 2П+1 I
• • • 2" 2и + 1 nl 2 + • • •
Таким образом, мы получили разложение (26) функ-
ции arcsin z в ряд Тейлора.
Гла'ва Ш
ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ
Интегральное исчисление начинается с описания
определенного интеграла действительной функции
f(x) действительного переменного х как площади, за-
ключенной между графикам функции f(x), двумя ор-
динатами и куском оси абсцисс. При этом не подвер-
гается сомнению тот факт, что площадь эта суще-
ствует. Доказывается, что описанный так определен-
ный интеграл является первообразной для функции
f(x). Таким образом, доказывается существование
первообразной, исходя из существования площади,
которое считается интуитивно ясным. Далее опреде-
ленный интеграл описывается как предел последова-
тельности конечных сумм. Здесь уже проводится
безупречно точное доказательство его существования.
В конце главы даются некоторые приложения опреде-
ленного интеграла, вычисляется, длина куска графика
функции, и длина кривой, заданной параметрически.
§. L& Определенный* интеграл как площадь
В § 14 было дано описание определенного интег-
рала функции f(z). Именно, функция h-(z) считается
определенным интегралом функции. f(z) и записы-
вается в виде
2.
*(*)= JfM,
Zo
если она удовлетворяет двум условиям:
h' (г) = f (г), h (z0) = 0.
171
Это описание определенного интеграла имеет тот не-
достаток, что оно не указывает никакого способа его
нахождения. Мы просто должны угадать какую-ни-
будь первообразную функцию %(z) функции f(z), т.е.
функцию, удовлетворяющую условию — f(2)*
Этот способ угадывания не так уж плох. Во всяком
случае, пользуясь им, мы сумели проинтегрировать
многочлены, степенные ряды и целый ряд элементар-
ных трансцендентных функций (см. § 13). Но все же
он не конструктивен: он не дает никакого определен-
ного способа для построения интегралов. Есть другой
способ описания определенного интеграла для дей-
ствительных непрерывных функций действительного
переменного, исторически более ранний, связанный
с вычислением площади. Опишем его.
Мы можем описать определенный интеграл как
площадь некоторого куска плоскости, ограниченного
частично .прямолинейными отрезками, частично кри-
вой линией. Если считать интуитивно понятным, что
такое площадь куска плоскости, то мы получаем на-
глядное геометрическое описание определенного ин-
теграла. Если дать какой-либо конкретный способ
приближенного вычисления площади, то мы получим
способ приближенного вычисления определенного ин-
теграла, но это будет сделано позже (см. § 18). Здесь
же мы установим связь между определенным интег-
ралом и площадью, исходя из чисто интуитивного
представления о площади.
Площадь графика. Будем исходить из некоторой
известной нам действительной непрерывной функции
f(g) действительного переменного Прежде всего
построим график С этой функций. Для этого на пло-
172
скости Р нашего чертежа (рис. 11) горизонтально
проведем ось абсцисс и вертикально — ось ординат.
По оси абсцисс мы будем откладывать величину а
по оси ординат величину
y = f&-
Точку на оси абсцисс, абсцисса которой равна мы
будем обозначать также через |. Выберем теперь ка-
кие-нибудь два совершенно произвольных значения
аргумента £ и обозначим их через хо и х. Через точки
хо и х проведем вертикальные прямые и точки их
пересечения с кривой С обозначим соответственно че-
рез ао и а. Если кусок аоа графика С лежит по одну
сторону от оси абсцисс, то у нас совершенно есте-
ственным образом выделяется кусок плоскости Р, ог-
раниченный с боков ординатами [хоао]; [ха], снизу
отрезком [xqx] оси абсцисс, а сверху отрезком [аоа]
графика С. Несмотря на то, что этот кусок плоскости
с одной стороны ограничен кривой линией, все же
вполне естественно считать, что он имеет площадь.
Площадь по природе своей — величина положитель-
ная или, в крайнем случае, равная нулю, например
тогда, когда хо — х. Мы алгебраизируем площадь че-
тырехугольника хохаао, придав ей определенный знак.
При х0 < х мы будем считать эту площадь положи-
тельной, если кривая аоа лежит над осью абсцисс,
и отрицательной, если кривая аоа лежит под осью
абсцисс. При Хо > х мы изменим установленный та-
ким образом знак площади на обратный. Так алгеб-
раизированную площадь четырехугольника хохаао мы
обозначим через h(xo, х).
Сравним теперь площадь h(xo,x) с площадями
двух естественно возникающих прямоугольников. Для
этого обозначим через р(хо, х) минимум функции
/(I) на отрезке [хох] и через г/ [х0, х] максимум функ-
ции на том же отрезке [хох]. Построим теперь
на отрезке [хох] как на основании прямоугольники,
один высотой р(хо, х) и второй — высотой q(xo, х).
При этом построении мы будем учитывать знак вели-
чин р(хо, х) и q(x0, х), т. е. строить прямоугольник
над осью абсцисс, если высота его положительна, и
под осью абсцисс, если высота его отрицательна.
Если кривая аоа проходит над осью абсцисс, то кри-
волинейный четырехугольник хохаао содержит внутри
173
себя первый из построенных прямоугольников и со-»
держится во втором. Из этого при условии, что
хо < х, вытекает двойное неравенство
(х — Хо) р (х0, хХ h (х0, х)< (х — хо) q (х0, х).
Если хо > х, то написанное двойное неравенство уже
неверно, и для получения правильного двойного нера-
венства мы должны изменить оба входящих в него
знака неравенств на обратные. Чтобы одной форму-
лой охватить оба случая Хо < х и х0 > х, мы употре-
бим функцию sign t, которая равна +1 при t поло-
жительном и —1 при t отрицательном. Тогда единое
неравенство, верное для обоих случаев хо <. х и х<> >
£> х, запишется в виде
(х — хо)р(Хо, х)sign(х — Хо)<h(хо, х)sign(х — ХоХ
< (х — Хо)<г(хо, x)sign(x —Хо). (1)
Эта формула, выведенная в предположении, что кри-
вая аоа лежит над осью абсцисс, верна также и в
случае, когда кривая аоа лежит под осью абсцисс,
что легко проверить.
До сих пор мы предполагали, что кривая а^а ле-
жит по одну сторону оси абсцисс. Рассмотрим теперь
и тот случай, когда она пересекает ось абсцисс в не-
скольких точках, быть может, даже в бесконечном
числе точек. В этом случае не существует четырех-
угольника хохаао, так как кривая аоа частично лежит
над осью абсцисс, а частично под осью абсцисс. Сло-
жим все площади, лежащие между верхней частью
кривой аоа и осью абсцисс, и вычтем из этого сумму
всех площадей, лежащих между нижней частью кри-
вой и осью абсцисс. Полученное так число умножим
на sign (х — Хо) и полученную величину обозначим
через ft(xo, х). Легко проверить, что и в этом случае
величина й(х0, х) удовлетворяет двойному неравен-
ству (1). Как подчеркивают это сами обозначения,
в дальнейшем мы будем считать х0 постоянной вели-
чиной, ах — переменной и положим
h (х) = h (хо, х).
Очевидно, что
Л(хо) = Л(хо, хо) = 0. (2)
174
Кроме того, мы докажем' сейчас, что
A'« = f(x). (3)
Из соотношений (2) и (3) будет следовать
Л(х) = (f(g)dg
' Хо
(4)
(см. соотношения (2) и (4) § 14). Таким образом,
будет найден геометрический смысл определенного
интеграла. Для завершения этого нам остается толь-
ко доказать формулу (3). Займемся этим.
При проведении доказательства формулы (3) ра-
зумно представлять себе случай, когда кривая аоа
проходит над осью абсцисс, помня при этом, однако,
что все выписываемые формулы верны и в самом об-
щем случае поведения этой кривой, что, конечно,
каждый раз следовало бы тщательно проверять. Для
вычисления производной функции й(х) мы выберем,
как положено, величину g, близкую к х, но не рав-
ную х. Точку пересечения вертикали, проведенной че-
рез g с графиком С, обозначим через а и составим
разность.
h (I) — h (х) = h (хо, g) — h (хо, х).
Геометрически очевидно, что
hfa* g) — h(xo, x) — h(x, g), (5)
Это вытекает из геометрического рассмотрения двух
криволинейных четырехугольников Xogaao и х^хааа
(см. рис. 11), причем равенства (б) верно как при
х < g, так и при х> g. Заменяя в неравенстве (1) х&
через х, а х через g, мы получим двойное неравен-
ство
(g — х)р(х, g)sign(g — х)<h(х, g)sign(g — x)<
< (I — x) q (x, g) sign (g — x).
Деля это двойное неравенство на положительную ве-
личину (g — x)sign(g— х), мы получим неравенство
Р(х, g)< h^~hx<xl <q(Х, I). (6)
S x
175
Так как в силу непрерывности функции f'(xf мы
имеем '
lim р (х, £) — lim q (х, I) = f (х),
£->х
то, переходя в двойном неравенстве (6) к пределу
при g-*x, мы получаем
h'(x) = f(x),
т. е. соотношение (3) доказано. Итак, нами получена
геометрическая интерпретация определенного интег-
рала как площади и одновременно дан способ вычис-
ления этой площади в том случае, когда мы можем
угадать неопределенный интеграл функции f(x). Вос-
пользуемся этим для вычисления площади куска пло-
скости, граница которого частично криволинейна.
Пример 1. В плоскости Р нашего чертежа вы-
берем горизонтально ось абсцисс и вертикально ось
ординат, начало координат обозначим через о. Рас-
смотрим в этой плоскости параболу, определяемую
уравнением
2у£ = У*,
где у — положительное число. Ось этой параболы сов-
падает с положительной полуосью абсцисс. Через не-
которую точку х положительной полуоси абсцисс про-
ведем вертикальную прямую и обозначим ее пересе-
чение с верхней ветвью параболы через а и с нижней
ветвью параболы через а'; Вычислим теперь пло-
щадь S/x), заключенную между куском параболы
аоа' и вертикальным отрезком [аа']. Осью абсцисс
эта площадь разбивается на две равные части. Вы-
числим площадь верхней части, заключенную между
отрезком [ох] оси абсцисс, вертикальным отрезком
[ха] и куском параболы [оа]. Верхняя ветвь пара-
болы задается уравнением
> = + V2vl-
Таким образом, в силу ранее доказанного (см. (4))
верхняя половина нашей площади определяется фор-
мулой
X
Л(х)= J
Непосредственно проверяется, что
/—2 -
Л(х) = У2у4х2,
О
так как для этой функции мы имеем
h (0) = 0, hf (х) =
Таким образом, вся интересующая нас площадь S(x)
равна
S (х) = 2Л (х) = у V2ух3.
§ 17. Определенный интеграл как предел
последовательности конечных сумм
В предыдущем § 16 мы вплотную подошли к кон-
структивному описанию определенного интеграла. Мы
дадим это конструктивное описание здесь. Одновре-
менно будет дано формальное определение понятия
площади, которым в предыдущем параграфе мы
пользовались чисто интуитивно. При этом мы будем
пользоваться понятием равномерно непрерывной
функции. Дадим ее определение.
Равномерная непрерывность. Мы будем рассматри-
вать некоторую действительную или комплексную
функцию f(z) действительного или комплексного пе-
ременного z. Мы должны объяснить, при каких усло-
виях функция эта считается равномерно непрерыв--
ной. Для этого каждой паре (z, £) значений ее аргу-
мента поставим в соответствие два неотрицательных
числа
Может случиться, что при всяком изменении пары
чисел (z, £), при котором |t — z|->-0, к нулю же стре-
мится |f(£)—f(z) |. Если это имеет место, то функ-
ция f(z) называется равномерно непрерывной. Более
точно, функция f(z) называется равномерно непре-
рывной, когда для всякого положительного числа 8
можно подобрать настолько малое положительное
число S, что из условия
IC-zKS (1)
следует, что
|f(C)-f(z)|<8. (2)
177
Коротко это свойство мы запишем в. виде.
Пт |/(£)-/(з)| = 0.
It—г|-*0
Если в этом определении зафиксировать величину
z, а считать переменной только величину £, то мы по-
лучим определение непрерывности функции в точке z
(см. § 10, (5)).
Как известно, функция называется непрерывной,,
если она непрерывна для каждого значения своего
аргумента. Таким образом, видно, что функция рав-
номерно непрерывная является, непрерывной. Оказы-
вается, однако, что обратное верно не всегда (см.
пример 1).
Мы докажем сейчас, что если множество М всех
допустимых значений аргумента функции f(z) замк-
нуто и ограничено, то из непрерывности функции сле-
дует ее равномерная непрерывность. Доказательство
будем вести от противного. Именно: мы предполо-
жим, что непрерывная функция f(z) не является рав-
номерно непрерывной, т. е. что для некоторого поло-
жительного числа е нельзя подобрать достаточно
малое положительное число б (см. соотношения (1)
И (21).
Таким образом, для этого положительного числа
8 можно подобрать такую последовательность пар:
21, С11 ^2» • • •»
ЧТО
lim,|£„, —з*|=Д, (3)
П->оо
НО
l/(U-f(z„)l>e>0. (4)
Так как множество М замкнуто и ограничено, а все
точки
гь За, .... z„, ... (5)
принадлежат М, то из последовательности (5) можно
выбрать подпоследовательность, сходящуюся к неко-
торой точке За множества М (см. § 4). Для того что-
бы не вводить новых' обозначений для этой подпосле-
довательности, мы будем просто считать, что сама
последовательность (5) сходится к точке зо, так что
имеет место соотношение
lim зя = з0. (6)
П->оо
178
Из соотношений (3) и (6) легко следует, что
lim ?„=Zo. (7)
В самом деле, мы имеем
I *0 I ^5 I trt I 4“ I 2q |.
Переходя в этом неравенстве к пределу при п->оо,
мы получаем соотношение (7). Так как функция f(z)
непрерывна, а следовательно, непрерывна и в точке
Zo, то мы имеем
Hm f{zn) = f(z9), (8)
П->оо
lim f(U = f(zo). (9)
n->oo
Далее, мы имеем
I f (U - f (*Л) |< I f (;„) - f (Zo) I +1 f (*„) - f (Zo) |.
Переходя в этом неравенстве к пределу при п->оо,
мы в силу соотношений (8) и (9) получаем
Hm|f(U-f(z„)l = 0,
П->оо
что противоречит соотношению (4).
Таким образом, мы пришли к противоречию и тем
доказали, что функция /(г), заданная на замкнутом
ограниченном множестве М, будучи непрерывной, яв-
ляется одновременно и равномерно непрерывной.
Перейдем теперь к конструктивному описанию оп-
ределенного интеграла
X
Л(х)=$/®^ (10)
X,
действительной непрерывной функции /(£)' действа
тельного переменного £, заданной на связном множв'
стве значений аргумента. Описание интеграла будет
опираться на вычисление его приближенных зна’
чений.
Так же, как в § 16, обозначим через
р(х0, х) и q(x0, х) (И)
минимум и соответственно максимум функции f(g);
на отрезке [хох]. Положим далее
8 (хе, х) = q (хо, х) — р (х0, х). (12)
179
Неотрицательная величина е(х0, х)' характеризует
размах колебаний функции f(g) на отрезке [х0х].Оче-
видно, что для двух произвольных точек ц и v от-
резка [хох] имеет место неравенство
lf(n)-/(v)|<e(x0, х). (13)
Подразделение отрезка. Разобьем отрезок [хох] на
отрезки некоторой монотонной последовательностью
точек
Х = (х0, Xi....х{, .... хА); хк — х. (14)
В случае хо < х монотонность означает, что
Хо < X] < ... < х{ < ... < xk. (16)
В случае хо > х монотонность означает, что
х0 > Xi > ... > х{ > ... > хА. (16)
Таким образом, в обоих случаях имеет место равен-
ство
sign (Xi — = sign (х — хо). (17)
Последовательность эта подразделяет отрезок [х©х]
на k отрезков вида
[Х/-1Х/].
Это подразделение отрезка [хох] мы будем называть
подразделением X. В частном случае мы можем иметь
подразделение, определяемое последовательностью
Х = (х0, х), (18)
т. е. отрезок вовсе не подразделен. Конструктивное
описание интеграла (10) опирается на рассмотрение
многих подразделений отрезка [хох], так что под-
разделение X мы будем в дальнейшем рассматривать
как переменную величину, значениями которой яв-
ляются произвольные подразделения отрезка [хох] на
произвольное число k отрезков, где k не фиксировано.
Переменная величина X будет в дальнейшем служить
аргументом нескольких нужных для нас действитель-
ных числовых функций. Обозначим через б(Х) наи-
большее из чисел
|х^ —Xf_i|, /=1, 2, ..., k.
Величина б(Х) есть функция аргумента X, так как
она может быть вычислена, если подразделение X за-
180
дано. Величина б(Х) характеризует мелкость подраз-
деления X. Чем меньше число в(Х), тем мельче под-
разделение X. Если подразделение X делит отрезок
[хох] на k равных отрезков, то
I X — Хо I
k
Таким образом, существуют произвольно мелкие под-
разделения отрезка Гхох], так как при k достаточно
большом величина -—-%— становится произвольно
малой.
Через е(Х) обозначим наибольшее из чисел
e(x£-i,xtj (см. 12)). Неотрицательное число е(Х)
также является функцией переменной величины X,
так как оно может быть вычислено, когда подразде-
ление X задано. Очевидно, что если р и v — два чис-
ла, принадлежащие одному и тому же отрезку под-
разделения X, то имеет место неравенство
lf(H)-f(v)l<8(X)
(см. (13)). Так как функция f(g) непрерывна, то на.
отрезке [х0 х] она равномерно непрерывна. Поэтому
для каждого положительного числа е можно подо-
брать настолько малое положительное число б, что
если подразделение X удовлетворяет неравенству
б(Х)<б, то для него выполнено и неравенство
е(Х)<е. Иначе говоря, если подразделение X ме-
няется так, что число б(Х) в процессе этого измене-
ния стремится к нулю, то число е(Х) также стремит-
ся к нулю. В виде формулы это свойство функции
в(Х) мы запишем так:
lim е(Х) = 0. (19)
Введем в рассмотрение еще одну функцию пере-
менного подразделения X, Мы положим
a(X) = (xi-Xo)f&)+ ••• + (x<-xz_l)f(^) + ...
••• +(xfe-xfe_,)f(U (20)
где. & есть произвольная точка отрезка [x<-ixz]. Та-
ким образом, в точном смысле слова а(Х) не есть
функция только подразделения X, так как для вычис-
ления суммы (20), кроме подразделения X, нужно
181
знать еще точки.
1ь &, .... (М)
и следовало бы написать
а(Х) = а(Д^..., &........U
Можно, однако, считать, что сумма (20) является не
однозначной функцией ог(Т) переменного а может
принимать любое значение, которое получается’ при
произвольном выборе последовательности (21),. при
котором, однако, каждая точка gz принадлежит от-
резку [х^х;]. Все свойства функции о(Х), которые
будут доказываться, ниже,, будут верны для любого
ее значения, т. е. для любого выбора последователь-
ности (21). Для того чтобы сократить длину форму-
лы (20), мы запишем ее иначе, именно:
k
(22)
i==l
В дальнейшем мы постоянно будем пользоваться
знаком суммирования^. Формула (22) имеет смысл
как при х > Хо, так и при х < х0, но при х = х0,от-
резок [хох] превращается в точку и никакие подраз-
деления его невозможны. Мы будем формально счи-
тать, что в этом’ случае
<т(Х) = 0. (23)
Конечные суммы or(J) будут приближенными зна-
чениями интеграла (Гб). Приближение это будет тем
точнее, чем мельче подразделение X, т. е. чем ближе
к нулю величина 6(^).
Определение интеграла. Мы покажем, что если под-
разделение X меняется так, что мелкость его б(Х)->
“>0, то величина о(Х) стремится к некоторому опре-
деленному пределу,, который мы обозначим через
/г(х). Утверждение это в виде формулы мы запишем
так:
lim а(Х) = й(х). (24)
в(Х)->0
Развернутый смысл этого утверждения следующий:
для всякого положительного числа е найдется на-
столько малое положительное число б, что из соот-
182
«ешения
& (Х) < 6
Вытекает соотношение
I <r(X) - h (х) | < г. (25)
Перейдем теперь к доказательству существования
величины Л(х), удовлетворяющей условию (25).
Заметим прежде всего, что для подразделения
(18) мы имеем
о(х0, х) = (х — х0)/ (g),
где % — произвольная точка отрезка [хох]. Докажем
теперь, что для произвольного подразделения X мы
имеем неравенство
|<т(х0, х) —о(Х) |<|х —х0|е(х0, х). (26)
Действительно,
k
а (х0, х) = Е (х{ — хг_1) f (g). (27)
Вычитая из равенства (27) равенство (22), получаем
k
а (х0, х) - а (X) = £ (х, - х^) (f (g) - f (gf)). (28)
В силу формулы (13) мы имеем
х). (29)
Из формул (28) и (29) следует, что
k
I а (хо, х) — ® (X) К £ IX/ — t |® (хв, х) =
г = 1
= |х — хо|е(хо, х),
т. е. неравенство (26) доказано.
Если монотонная последовательность
(см. формулы (15), (16)) содержит все числа после-
довательности X (см. (14)), то подразделение X' на-
зывается ыаиел&ченыаи подразделения X. Докажем,
что если подразделение X' является измельчением
подразделения Х^ то имеет место неравенство
|а(Х)-а(Х')|<|х-хв|е(Х). (30)
1S3
Те точки подразделения X', которые попадают на,
отрезок [xi-ix,], подразделяют этот отрезок на ку-
сочки. Это подразделение отрезка [x(_i, х,]. мы обо»
значим через X'i. Применяя к отрезку [х,_1Х;] и его
подразделению Xt формулу (26), верную для произ>
вольного отрезка [хох], мы получим
<|x/-xi_1|e(X). (31)
Очевидно, что
k
о(Г)=Еа(Х0 (32)
1 = 1
и
k
o(X)=Za(xj_„x<). (33),
i-1
Вычитая (32) из (33), в силу (31) получим
< Е 1х, — xi_i|e(X) = |x — х0|е(Х).
i=l
Таким образом, неравенство (30) доказано.
Пусть X и X" — два произвольных подразделения
отрезка [хох]. Докажем, что
I а(X) - о (X") |< | х - х01 (е (X) + 8 (X")). (34)
Объединим все числа, входящие в последовательно'
сти X и X", и расположим полученную так совокуп'
ность чисел в монотонном порядке. Так полученную
монотонную последовательность чисел обозначим че'
рез X'. Очевидно, что подразделение X' является иЗ'
мельчением обоих подразделений X и X". Таким об-
разом, наряду с неравенством (30) мы имеем нера-
венство
| о (X") - а (Г) | < | х - х018 (X"). (35)
Из неравенств (30) и (35) вытекает неравенство (34).
Теперь мы можем построить число й(х) (см. (24)).
Для этого выберем произвольную последовательность
Х1( Х2, ..., Х„, ...
184
подразделений отрезка [хох] , удовлетворяющую ус-
ловию
Итб(Х„) = 0. (36)
П->ос
Оказывается тогда, что последовательность
о (Х1), а (Х2), ..., о (Х„), ... (37)
сходится. Предел ее мы и обозначим через h(x), так
что
lim а(Х„) = Л(х). (38)
П->ОО
Мы докажем, что последовательность (37) удовлет-
воряет условию сходимости Коши (см. § 3). Для
этого выпишем оценку разности |о(Хг)—о(Xs) |, опи-
раясь на оценку (34). В силу (34) мы имеем
| о (Хг) - о (Xs) | < IX - х01 (8 (Хг) + 8 (JQ). (39)
Так как величина б(Хп) стремится к нулю (см. (36)),
то величина е(Х„) также стремится к нулю (см. (19)).
Таким образом, правая-часть (39) стремится к нулю,
когда натуральные числа г и s оба неограниченно
возрастают, а это и значит, что последовательность
(37) удовлетворяет условию Коши, так что суще-
ствует ее предел h (х) (см. (38)).
Теперь мы можем доказать, что полученная вели-
чина Л(х) удовлетворяет условию (24). Для этого
оценим выражение | о (X)—ft(x)|. Мы имеем
|o(X)-ft(x)|<|a(X)-<r(Xrt)| + |a(X„)-A(x)|<
<| X - Хо 1(8(Х) 4- 8 (Х„)) + I <у(Х„) - Л(х) |.
Переходя в этом соотношении к пределу при п -> оо,
мы получаем
|а(Х)-Л(х)|<|х-хо|в(Х). (40)
Из этого на основании соотношения (19) получается,
соотношение (24).
Теперь мы можем окончательно выписать опреде-
ление интеграла
X
(/(g)dg= lim <т(Х).
J в(Х)->0
185 .
Выпишем теперь одну важную оценку величины
интеграла, именно:
(х — Хо) р (х0, х) sign (х — Хо) <
< sign (х — Хо) f (|) dl < (х — хо) q (х0, х) sign (х — х0).
Хо
(41)
Для доказательства неравенства (41) выберем произ-
вольное подразделение X отрезка [хох]. Мы имеем
Р (хе, х)< f (&)< q (х0, х),
(см. (11) и (14)). Умножая это неравенство на поло-
жительное число (xi — Xi_i)sign(x« — x>-i) и сумми-
руя по i от 1 до k, мы получаем, учитывая (17), не-
равенство
(х — х0) р (хо, х) sign (х — хо) < (sign (х — х0)) о (X) <
< (х — Хо) q (хо, х) sign (х — Хо). (42)
Переходя в этом неравенстве к пределу при 6(Х)->0,
мы получаем неравенство (41).
Теперь пришло время доказать, что функция й(х)
удовлетворяет условиям
Л(хо) = О, ' (43)
h' (х) = f (х), (44)
т. е. функция Л(х) является определенным интегра-
лом функции f(g) ив смысле определения, данного
в § 14 (см. § 14, (2), (4)).
Соотношение (43) следует из формулы (23), до-
кажем соотношение (44).
Отрезок [хох] разобьем на два отрезка точкой х1,
лежащей между точками Хо и х. При этом переобоз-
начим точки Хо; х, положив хо = х°; х = х2. Выберем
некоторое подразделение X1 отрезка [х°хх] и некото-
рое подразделение X2 отрезка [х'х2]. Выписанные
подряд точки последовательностей X1, X2 составят по-
следовательность Х*Х2, подразделяющую отрезок
[х°х2]. Мы имеем очевидное равенство
<т(Х1) + <г(Х2) = а(Х,Х2). (45)
186
Переходя к пределу при б'С^У-э-О, б’(Х2)’->0, мы по*
лучаем из соотношения (45)
X1 X2 X»
J — J tifydt. (46)
Х° X1 х’
' Для вычисления производной ft'(x)’ мы, согласно
правилу, выберем точку g, близкую к х, но отличную
от нее, и составим разность ft(g) — h(x). Для вычис*
ления этой разности воспользуемся формулой (46).
Если | лежит вне отрезка [хох], то х делит отрезок
|хо£] > и в силу (46) мы имеем
с 5 5
Х° X х°
Если | лежит на отрезке [хох], то в силу (46) имеет
место соотношение
Jf(Z)d/+p(/)d/== \f(t)dt.
X* I X' *
Таким образом, в первом случае мы имеем
5 х 5
h(&-h(x) = \f(t)dt= \f(t)dt, (47)
Xq ‘ Хо X
а во втором случае
W-AW= ^f(t)dt = — \f®dt. (48)
*0 Xo £
Применяя к правым частям равенств (47) и (48)
двойное неравенство (41), мы получим в нервом
случае
(В — х)р(х, g)sign(g — х)<(sign(g — x))(h(g) — h(x))<
< (I — x) q (x, g) sign (g — x) (49)
и во втором случае
(x — £)P & x)sign(x — g)< (sign(x — g))(ft(x) — ft(g)) <
< (x — g) q (g, x) si gn (x — g). (50)
Так как p(x, g)= p(g, x)’, q(x, g)= <?(g, x)', то, деля
каждое из неравенств (49), (50) на положительную
187
величину
(g — х) sign (g — х) = (х — g) sign (x — g),
мы в обоих случаях получим одно и то же неравен*
ство
g).
Переходя в этом неравенстве к пределу при g->x,
получаем
/ (х)< А'(*)</(*)•
Таким образом, соотношение (44) доказано.
Проведем некоторое обобщение данного здесь спо-
соба интегрирования.
Кусочно непрерывная функция. Если действитель-
ная функция /(х) действительного переменного х в
некоторой точке х = а не является непрерывной, то
точка а называется точкой разрыва этой функции.
Опишем простейшие точки разрыва, именно, так на-
зываемые точки разрыва первого рода. Точка раз-
рыва а функции f(x) называется точкой разрыва
первого рода, если выполнены два следующих усло-
вия:
1) вблизи точки а нет других точек разрыва
функции f(x), это значит, что существует настолько
малое положительное число е, что на интервале
|х — а|< е нет точек разрыва функции f(x), кроме
точки а;
2) если число х приближается к а, оставаясь мень-
ше а, то функция f(x) при таком изменении х стре-
мится к пределу, который мы условно обозначим че-
рез f(a — 0). В виде формулы это записывается сле-
дующим образом:
lim f (х) = f (а — 0).
х<а
х-*а
Если число х стремится к а, оставаясь больше а, то
предел функции f(x) при таком изменении х суще-
ствует и обозначается условно через f(a 4- 0). В виде
формулы это записывается так:
lim f (х) = /(а + 0).
х>а
х-*а
188
Значение f(a,y функции в точке разрыва а обычно не
играет никакой роли и не будет рассматриваться.
Функция f(x) называется кусочно непрерывной, если
все ее точки разрыва являются точками разрыва пер-
вого рода и если на каждом конечном отрезке изме-
нения функции f(x) этих точек разрыва конечное
число. Легко определить интеграл
х
Хе
кусочно непрерывной функции f(x). Сделаем это в
предположении, что Хо < х. Предположим сперва, что
на отрезке [хох] функция f(x) не имеет других точек
разрыва кроме, быть может, его концов, каждый из
которых может быть либо точкой разрыва первого
рода, либо точкой непрерывности функции /(х).Если
хо есть точка разрыва функции f (х), то значение ее
в точке хо определим формулой f (хо)= f (хо + 0). Если
конец х есть точка разрыва функции, то значение
функции в точке х определим формулой f(x) —
— f(x — 0). Дополненная так выбранными значения-
ми в точках х0, х функция f(x) уже непрерывна на
всем отрезке [хох] и потому интеграл ее определен.
Если теперь [х©х] есть произвольный отрезок интег-
рирования, то он может быть разбит на крнечное
чйсло отрезков, внутри каждого из которых нет то-
X
чек разрыва и J f (£) di, определяется в этом случае
Ху
как сумма всех интегралов, взятых по отрезкам раз-
биения. В случае х0 > х интеграл определяется ана-
логично.
Кусочно гладкая функция. Непрерывная функция
й(х) называется кусочно гладкой, если производная
ее h'(x) есть функция кусочно непрерывная. Легко
видеть, что интеграл
X
Л(х) = \f(№
Xi
кусочно непрерывной функции f(x) есть кусочно глад-
кая функция Л(х) и что имеет место соотношение
189
h'(x)'= f(x) , верное для всех значений х, отличных от
точек разрыва функции f(x).
Интегрирование комплексной (функции f(x) дей-
ствительного переменного ». Функция f(x) может быть
записана в виде
/(х) = ф(х)4-гф(х),
где ф(х)' и ф(х)’ суть действительные функции дей-
ствительного переменного х. Пусть X — некоторое
подразделение отрезка {хох] интегрирования. Для
комплексной функции f(x) составим сумму типа а,
именно, положим
o(X)=Ei(x/-x^1)f(g/), (51)
где h — некоторая точка отрезка [x/_ix/]’.'Положим
к
/в=1
k
(X) =2 (X/ — Ху_1) ф (£/).
Очевидно, что
о.(А') = о1(1¥)Н-го2(Х). (52)
Так как для действительных непрерывных функций
ф(£) -и ф(§) имеют место равенства
X
lim o1(X)= UaX
W)-»0 J
Ха
X
Jim п2(Х)=
d(X)->Q J
то в силу формул (51) и (52) предел величины о(Х)
при Ъ(Х)~> 0 существует и может быть принят по
определению за интеграл, так что мы получим
X XX
lim <Т(Х)= U(|)dB + tUm. (53)
Если исходная комплексная функция не непре-
рывна, а кусочно непрерывна, то интеграл ее может
быть описан так же, как интеграл действительной
190
кусочно непрерывной функции, и при этом определе*
нии интеграла соотношение (53) сохраняется.
Так как для функций
равенства
J <₽(|)d| = 0,
Хо
И
X
4 $<ра)^=Ф(д
X»
ф(х) и ф.(х) имеют место
х>
J wdg=o
Хо
X
77$Ф(1)^ = Ф(Д
Хо
то для комплексной функции fix) мы имеем те же
равенства
Хо X
J f (g) dl = 0, J.f (£) (х). (54)
Хо Хи
Мы установили, что определенный в этом параг-
рафе интеграл
X,
$/(£)<£ (55)
Хо
комплексной функции действительного переменного х
удовлетворяет условиям (54), т. е. является интегра-
лом в смысле § 14-. Поэтому все результаты, полу-
ченные в § 14* имеют место и для1 интеграла (55),
в частности
Xi Xi Xi
$ f (IM& + p $ f ft) dl, (56)
Xo Xi Xo
Если в интеграле
Хо
(57)
от комплексной функции действительного перемен-
ного | подынтегральная функция удовлетворяет нера-
венству
И ft)
191
то для интеграла (57) мы имеем оценку
<m(x —х0).
(58)
Это непосредственно вытекает из равенства
х ь
= lim £(x/-x/_l)f(|/)
(см. (51)).
Пример. Приведем пример непрерывной, но не
равномерно непрерывной функции. Положим f(x)=
— — • Функцию эту будем рассматривать для всех
значений х, удовлетворяющих неравенству 0 < х 1.
Ясно, что она непрерывна, но не равномерно непре-
рывна, так как величина
ъ Л лд
при |g — х| < 6 может стать произвольно большой,
если х и g близки к нулю.
§ 18. Площадь и длина графика
В § 16 мы говорили о площади четырехугольника,
ограниченного сверху кривой линией, графиком не*
прерывной функции, как о вещи само собой понят-
ной. Для каждого здравомыслящего человека, каза-
лось бы, должно быть очевидно, что площадь может
быть измерена. Но такого рода очевидности иногда
оказываются просто неверными. Поэтому мы должны
тщательно объяснить, что следует понимать под пло*
щадью куска плоскости, ограниченного кривой ли-
нией. Точно так же обстоит дело и с длиной кривой
линии. Для того чтобы избежать недоразумений,
нужно, как говорят математики, дать строгое опреде-
ление этих понятий. Займемся этим и одновременно
вычислим соответствующие величины при помощи ин-
тегралов.
Площадь. Будем исходить из некоторой действи-
тельной непрерывной функции f(|) действительного
переменного g. График этой функции на координат-
192
ной плоскости обозначим через С. На оси абсцисс
выберем некоторый отрезок [хох] и через концы его
проведем вертикальные прямые, пересечение которых
с графиком С обозначим соответственно через Oq, а.
Для определенности будем предполагать, что хо < х
и что кусок [а0«] графика С лежит над осью абсцисс.
Тогда возникает четырехугольник х0хаао, ограничен-
ный снизу отрезком хох абсциссы, с боков ордина-
тами хойо, ха и сверху куском а^а графика С (см.
рис. 11). Поставим перед собой задачу измерить
площадь этого четырехугольника и в надежде на то,
что нам это удастся, обозначим заранее величину
этой площади через S.
Если мы имеем две точки р, v оси абсцисс, то че-
рез р(р, v) мы обозначим минимум функции f(g) на
отрезке [pv], а через z?(p, v)—максимум функции
f(|) на том же отрезке [pv]. Так как непрерывная
функция, рассматриваемая на отрезке, достигает на
нем своего минимума и своего максимума (см. § 12),
то мы имеем два равенства
рммп <7(и, v)=m
где В', — две точки отрезка [pv].
Выберем теперь какое-нибудь подразделение
X = (х0, *!, • • •. X/, ..., хД, Xk — х,
отрезка [xqx] (см. § 17, (14)). Через обозначим
точку, в которой функция f(g) достигает своего ми-
нимума на отрезке [xz-ix,], а через £•' обозначим та-
кую точку, в которой функция f(|) достигает своего
максимума на отрезке [xt—i xz]. Составим две суммы
k
k
Из этих равенств видно, что величины о'(Х), о"(Х)
являются двумя значениями многозначной функции
о(Х) (см. § 17), и поэтому имеют место два
7 Л. С. Понтрягин 193
равенства
X
lim cr'(X) =
d (X)->o J
Xo
X
lim a"(X) = \f®d$.
6 (X)->0 J
0)
(2)
Дадим теперь геометрическое описание возникаю,
щей здесь картины (рис. 12). Для этого обозначим
через Pi прямоугольник с основанием Xj-ixz и высотой
f(l'i), а через Q, — прямоугольник с основанием хг_1Х|
и высотой Площадь прямоугольника Pi равна
(х(. — f (g^). Площадь прямоугольника Qi равна
(х, — хг_1)/Так как все прямоугольники Pi,
i= 1, 2....k, содержатся внутри четырехугольника
хохаао, то сумма их площадей не превосходит пло,
щади S четырехугольника хохаао. Так как совокуп,
ность прямоугольников Qi, i= 1, 2...k, содержит
внутри себя четырехугольник хохаао, то площадь 5
не превосходит сумму площадей прямоугольников Qi,
Таким образом, исходя из предположения, что пло-
щадь четырехугольника хохаао можно измерить иона
равна числу S, мы получаем для этого числа двойное
неравенство
az'(X)<S<o"(A). (3)
Теперь разумно посмотреть на дело так, что вели,
чины <у'(Х) и о''(Х) являются приближенными зна*
чениями редичивд S, причем, как это следует из
двойного неравенства (3), величина с'(Х) оценивает
величину S снизу, а величина а"(Х) оценивает ве-
личину 5 сверху. Так как две эти оценки при неог*
194
паничеином измельчении подразделения X стремятся
к одному и тому же пределу (см. (1), (2)), то сле-
дует прийти к выводу, что наше измерение площади
четырехугольника хохаао удалось, и величина S опре-
деляется формулой
Хо
Таким образом, формальное определение площади
совпадает с интуитивным представлением о результа-
тах ее измерения.
Длина графика. Будем исходить из некоторой дей-
ствительной функции f(x) действительного перемен-
ного х, имеющей непрерывную производную. Пусть
[xqx]— некоторый отрезок оси абсцисс, причем хо<3
< х, на котором функция f(x) определена, а X— не-
которое подразделение отрезка [хох] (см. § 17). Гра-
фик функции f(x) на координатной плоскости Р обо-
значим через С (рис. 13). Пересечение вертикальной
прямой, проведенной через точку х/, с графиком С
обозначим через си. Построим ломаную
оо, ai....ak = a,
составленную из отрезков
[aoaiL [aia2], ...
Длину отрезка [ai-icu] обозначим через /(a,-i, а<).
Длину ломаной обозначим через 1(Х), т. е. положим
k
l(X)=^l{ai_b at). (4)
i=l
7*
195
Легко убедиться в том, что если |х,— >-0, то ц
/(аг_1, аг)-> 0. По определению будем считать, что
длина s(x0, х) куска [поа] графика С определяется
как предел
s(xo, х) = lim ЦХ).
„ б(Х)-»0
Нам остается доказать, что предел этот существует,
и написать его в виде некоторого определенного ин-
теграла. Займемся этим. Через точку a,-i проведем
горизонтальную прямую и обозначим пересечение ее
с вертикальной прямой, проходящей через точки xt,
at, через bi. Тогда длина отрезка [aj-iad как длина
гипотенузы прямоугольного треугольника записы-
вается при помощи формулы
I(af_b а{) = 7(/(««-» bi)r + (l(bt, at))2.
Так как
/ bi) = Xi— x^i, I (bh ai) = \f (xz) — f (xz_i) I,
то для длины /(ai-i, щ) мы получаем формулу
/(az_i, at) = ^\Xi — х,^)2 + (f (xt) — f (xz_i)A
В силу формулы Лагранжа (см. § 12) мы имеем
f (xt) — f (xz_i) = f' (h) (х, - xz_i),
где |z— некоторая точка отрезка [xz_ixz]. Таким
образом, длина /(хо, х) всей нашей ломаной задается
формулой
то = Е (Xi - хг_о VT+TW-
1 — 1
Правая часть представляет собой не что иное, как
сумму типа о (см. § 17), составленную для функции
V 1 "Ь (f' (о))2 > так что мы имеем
s (Хо, Х) = J Vl + (fW dl. (5)
Xt,
Таким образом, мы одновременно доказали, что пре-
дел суммы (4) при б(Х)->0 существует, и вычислили
этот предел в виде интеграла (5).
196 „
§ 19. Длина параметрически заданной линии
При помощи определенных интегралов описы-
ваются и определяются очень многие величины,
встречающиеся как в самой математике, так и в ее
приложениях в естествознании. При этих описаниях
интеграл чаото появляется как предел последователь-
ности конечных сумм, аналогичных суммам, рассмот-
ренным в § 17. Однако суммы эти могут иметь вид
несколько более общий, чем суммы, данные в § 17.
Для того чтобы установить связь между этими более
общими суммами и суммами, рассмотренными в § 17,
мы введем в рассмотрение суммы, так сказать, бес-
конечно малые, т. е. стремящиеся к нулю, когда под-
разделения X отрезка [хох] неограниченно измель-
чаются. Займемся этим.
Будем исходить из отрезка [хох], заданного на
оси абсцисс, и допустим, что каждому отрезку [pvj,
лежащему на отрезке [хох], поставлено в соответ-
ствие действительное или комплексное число р(р, v).
Мы будем предполагать, что число р(ц, v) стремится
к нулю вместе с числом |v — ц|. Более точно, мы бу-
дем предполагать, что для каждого положительного
числа е существует настолько малое положительное
число 6, что из соотношения
I V ~ Р I < б (1)
следует соотношение
lp(p, v)|<e. (2)
В виде формулы это свойство функции р(р, v) мы за-
пишем так:
lim р (р, v) — 0. (3)
| V-ц |->0
Функцию р(р, v) отрезка [pv], обладающую этим
свойством, мы будем называть бесконечно малой.
Допустим теперь, что задано некоторое подразде-
ление
Х = (£0, Xt....xk), xk = x,
отрезка [xox] (см. § 17, (14)). Этому подразделению
-X отрезка [хох] мы поставим в соответствие число
k
Р СП jSj 1) Р (ty—b Xi)t
197
исходя из бесконечно малой функции р (р, v)" отрезка.
Оказывается, чтр величина p(X)->0, когда подраз-
деление X неограниченно измельчается, что в виде
формулы можно записать так:
lim р(Х) = 0. (4)
в (Х)->0
Для доказательства соотношения (4) выберем
произвольно малое положительное число е и подбе-
рем для него такое малое положительное число б,
что при выполнении неравенства (1) выполняется не-
равенство (2). Будем теперь считать, что подразде-
ление X достаточно мелко, т. е. удовлетворяет усло-
вию
б(Х) < б.
Тогда для каждого отрезка подразделения X мы
имеем неравенство
\Xi— X/_i|<6.
Поэтому в силу неравенства (2) выполнено соотно-
шение
IР (лт-ь Х/)1<е.
Тогда для функции р'(Х) мы получаем оценку
k
IР W К Z I Х{ — Х/_1 11 р (Х|_1, Xi) I <
k
< Six/ —хг_1|е = |х —х0|в.
i-l
Так как е — произвольно малое число, то из послед-
него неравенства вытекает соотношение (4).
Кусочно гладкая линия. Пусть <р(/) и —две
действительные функции действительного перемен-
ного /. Полагая
* = ф(0, = (5)
мы получим параметрическую запись линии, которая
расположена на координатной плоскости Р и описы-
вается точкой
(X, 0) = (<р(/), ф(0), (6)
когда t меняется возрастая или убывая. Линия эта
называется кусочно гладкой, если обе функции <р(0'
и ф(^) кусочно гладкие (см. § 18) и производные их
198
<р'(0 и не обращаются в нуль одновременно ни
при каком значении t. Если для какого-нибудь зна-
чения t хотя бы одна из функций <р'(/)' или ф'(/) тер»
пит разрыв, то соответствующая точка t на нашей
линии называется угловой точкой. Мы будем предпо-
лагать, что при подходе к угловой точке производные
<p'(f) и if'(0 не стремятся к нулю одновременно
(точки линии, не являющиеся угловыми, называются
точками гладкости). Наша линия разбивается своими
угловыми точками на куски, каждый из которых уже
представляет собой гладкую линию. Для того чтобы
определить логически и вычислить длину кусочно
гладкой линии, достаточно вычислить длину линии
на каждом из кусков гладкости, затем сложить ме-
жду собой все эти длины. Таким образом, нам доста-
точно определить и вычислить длину линии на неко-
тором куске [W]> на котором наша линия является
гладкой.
Определим теперь логически и вычислим длину
гладкого куска линии, заданного уравнениями (5) на
отрезке [W]. Пусть
T = (t0,th ..., tk), tk = t,
— некоторое подразделение отрезка [W] (см, § 17,
(14)). Так же, как и там, мы будем считать, что по-
следовательность Т монотонна. Обозначим через аг
точку с координатами <р(/<), ф (ti), положив
а/ = (ф(^)> ФО-
Поел едов ател ьность
а0, аь ..аг......ай
определяет ломаную, составленную из отрезков вида
[амаг], i=l, 2, k. Длину отрезка [аг^аг] мы
обозначим через l(ai-\, аг), считая ее положительной,
если ti-i < ti, и отрицательной, если ti <Z tt—i. Длина
»(Т) всей нашей ломаной определяется формулой
k
aj.
Таким образом, длина ЦТ) положительна при to <Z t
и отрицательна при t <Z to- Аналогично тому, как мы
это делали в § 17, через 6(Т) мы обозначим макси-
199
мальное из чисел |Л- — ti-11, i= 1, 2, .... k. Мы до,
кажем, что при 6(Г)->0 величина ЦТ) стремится к 7
некоторому пределу, который называется длиной ли-
нии. Именно, мы покажем, что
t
lim /(Т) = ( +У(ф'(т))2 + (Ф'(т))2 dr. (7)
в(Г)-»О J
*0
Перейдем к доказательству формулы (7). Выбе-
рем какие-нибудь два значения р, v параметра t и
обозначим через р и у точки (ф(р), ф(р)) и (<₽(*)»
ф (v)). Длину отрезка [Ру] обозначим через I (р, у),
считая ее положительной при ц< v и отрицательной
при р > v. Мы, очевидно, имеем
I (Р, у) = sign (v — р) V[<p (v) — <р (р)]2 + [ф (v) — ф (р)]2.
Составим функцию р(ц, v) отрезка [pv], положив
р(р, v)= ~ V(q)'(v))2 + (^/ (V))2. (8) .
Мы докажем, что построенная так функция р (р, v)]
удовлетворяет условию
lim р(р, v) = 0, (9)
| V-H [~»0
т. е. что функция р(р, v) является бесконечно малой
(см. (3)). Из этого уже легко будет вывести фор-
мулу (7).
Приступим к доказательству соотношения (9)«
В силу формулы Лагранжа (см. § 12) мы имеем
<Р (v) — <р (ц) = (v — р) ф' (Ti), ф (v) — ф (р) = (v—р) ф' (т2),
где числа ti и т2 лежат на отрезке [pv]. Таким обра«
зом, мы имеем
“Г~= + 7(Ф'(Т1))2 + (Ф'(Т2))2.
¥ р*
Положим, далее,
® = (ф' (Т1))2 + (ф' (т2))2, W = (ф' (v))2 + (Ф' (V))2.
Таким образом, из формулы (8) следует, что
р (ц, v) = д/ю — •
200
Так как корень квадратный есть равномерно непре<
рывная функция, то для всякого положительного
числа е найдется настолько малое положительное
число 81, что при
| (0 — W I < 81
имеем _
| р(ц, V) 1 = 1 д/®~ I <8. (10)
Далее, мы имеем
I а — w К | (<р' (п))2 — (ф' (v))21 +1 (ф' (т2))2 — (ф' (v))21.
Так как
|v — tiKIv — |l|,
|v —T2|<|v —ц|,
то для заданного числа si можно найти настолько
малое число 6, что при
| v — р | < б (11)
мы имеем
I (ф' (Т1))2— (ф' (V))21 < , |(ф' (т2))2 - (ф' (v))2| .
Таким образом, для всякого положительного числа g
мы подобрали такое б, что при выполнении нера«
венства (11) имеет место неравенство (10), т. е<
функция р(ц, v) есть бесконечно малая функция. Та*
ким образом, мы получаем
k ___________________
КЛ - Z (ti - //-1) 7(ф' (ti))2 + (Ф' Vi))2 =
i=l
k _________________
= Z [/ (a/-b Of) — (ti — ti-l) л/(ф' (ti))2 + (Ф' О2] —
i==l
k
— Yi(ti — ^-i)p(6-i> ti). (12)
1=1
Так как p(p., v) есть бесконечно малая функция, то
правая часть соотношения (12) стремится к нулю при
б (Г)-»-0 (см. (4)). Таким образом, мы и получаем
соотношение
t
lim I (Т) = ^(ф'« + (Ф'« dr. (13)
6(Т)-»0 J
Итак, мы доказали, что длина кусочно гладкой ли*
нии существует и определяется интегралом (13)<
201
Пример. На линии, заданной параметрически
уравнениями (5), положение точки определяется зна-
чением параметра t (см. (6)), поэтому параметр t
естественно считать координатой, введенной на ли-
нии. Как мы это уже много раз делали раньше, мы
иногда будем называть точку линии, соответствую-
щую значению параметра t, просто точкой t. При этом
может случиться, что двум различным значениям па-
раметра t — t' и t = t", причем t’ =f* t", соответствует
на плоскости одна и та же точка. Именно, имеет ме-
сто равенство
(Ф(?), ф(/'))=(ф(п.
Такие две точки f и t" мы все же будем считать раз-
личными точками линии, а совпадение их на плоско-
сти будем рассматривать как самопересечение линии.
Длина s куска линии, заключенной между точками
и определяется формулой (13), так что длина эта
есть функция параметра t
s = s(t), (14)
причем
%= + VW+W- (15)
ds • —
при этом величина всюду положительна. Урав-
нение (14) можно разрешить относительно t, и мы
получим равенство
/ = /(«), (16)
причем
''М-ТГ>0-
dt
Я не привожу здесь доказательства того, что уравне-
ние (14) можно разрешить относительно t. Геомет-
рически это. довольно ясно, если на некоторой коор-
динатной плоскости изобразить график функции. з(/).
Подставляя в параметрические уравнения (5) выра-
жение величины t через s по формуле (16), мы полу-
чим: равенство
х = <₽(/(.$)), г/= ф (/($)). (17)
Уравнения (17) можно рассматривать как парамет-
рическое уравнение прежней линии, в котором вместо
202
параметра t введен новый параметр з. Его мы тоже
можем рассматривать как координату, введенную на
нашей линии. Точке t0 теперь соответствует точка с
координатой s = О, т. е. начало координат. Отрезок
линии от начала координат до точки $ имеет длину,
равную з. Так введенный на линии новый параметр s
является наиболее удобным. Для того чтобы не вво-
дить новых обозначений, мы будем считать, что ли-
ния задана параметрически в виде
X — ф (з), у = ф (з).
Соотношение (15) теперь получает вид
-^-=7(ф'« + (Ф'«-
Таким образом,
(Ф'(з))2+от2=1. (is)
Вектор, ведущий из начала координат в точку (<р (s),
•ф($)), мы обозначим через x(s), так что имеет место
равенство
Х(«) = (ф(з), ф(з)).
Вблизи неподвижной точки s выберем подвижную
точку о и проведем • через точки %(з), %(о) прямую
линию, секущую нашей линии. Обозначим через а
угол наклона к оси абсцисс вектора, ведущего из точ-
ки %(s) в точку % (о); тогда мы имеем, очевидно,
а — s а — з
где й— некоторый положительный коэффициент. Пе-
реходя в этих равенствах к пределу при o->s и обо-
значая предельное значение угла а через а, а пре-
дельное значение коэффициента а через а, мы полу-
чим равенство
cos а = аф' (s), sin а = оф'(s).
Из соотношения (18) следует, что а — 1, так что мы
имеем
соза = ф/(з), зта = ф'(з). (19)
Таким образом,вектор
X'(s) = (ф'(з), ф'(з))
203
имеет длину, равную 1:
Так как при проведенном предельном переходе секу-
щая переходит в касательную к нашей линии в точке
s, то вектор %'(s) есть единичный вектор, касающий-
ся нашей линии в точке s и направленный в сторону
возрастания s. Из уравнений (19) следует
tga = <£) (20)
& ф (s) '
Дифференцируя соотношение (18) по s, мы получаем
соотношение .
ф' (s) q/' (s) + ф' (s) ф" (s) = О,
из которого следует, что векторы х'($) и x"(s) пер-
пендикулярны (см. введение, (9), (10)). Обозначим
через р угол наклона вектора х"(5) к-оси абсцисс,
тогда мы имеем
ф" (5) = ь cos р, ф" (s) — b sin р, (21)
где b =|x,/(s) I — некоторая положительная величи-
на. Углы аир являются функциями параметра 5,
хотя это явно не выписано. Вычислим величину
представляющую собой скорость вращения вектора
%' относительно параметра s. Эта величина характе-
ризует крутизну поворота кривой и называется ее
кривизной. Дифференцируя по s соотношение (20),
мы получим
б/q . 1 __ гр" (s) <pz (s) — ф" (s) ipz (s) _
ds cos2 а (ф' (s))2
__ ф/Л (s) фг (s) — <pzz (s) фЛ (s>
cos2 а
Из этой формулы в силу формул (19) и (21) следует
-g- = &sin(p-a). (22)
Из того, что векторы %'($) и %"(s) перпендикулярны
друг другу, следует, что
sin (Р — а) = ± 1.
204
Таким образом, из формулы (22) следует
или же
Поэтому
da
ds
— b
Абсолютная величина скорости -т- вращения век-
тора %(s) равна Ь. Величина положительна,
если вращение вектора %($) с возрастанием s идет
против часовой стрелки, и отрицательна, если это вра-
щение идет по часовой стрелке. Величина b называет»
ся кривизной нашей линии в точке s.
Наряду с кривизной в дифференциальной геомет-
g. » 1
рии рассматривается обратная к ней величина г = -у,
называемая радиусом кривизны нашей кривой в точ-
ке s. Название это объясняется следующим: возьмем
на нашей кривой три точки si < s2 < «з, близкие друг
к другу, и проведем через три точки %(si), %(s2),
%($з) окружность, радиус которой обозначим через/1.
Оказывается, что когда все три величины $i, s2, S3
стремятся к одному пределу $, радиус ? стремится к
пределу г = -|-. Доказательство этого интересного
геометрического факта несложно, и я рекомендую
читателю провести его самому.
Глава IV
АНАЛИТИЧЕСКИЕ ФУНКЦИИ
В этой главе даются основные довольно далеко
идущие результаты теории аналитических функций.
Прежде всего определяется интеграл комплексной
функции комплексного переменного вдоль кривой,
проходящей на плоскости независимого комплексного
переменного. Далее доказываются некоторые частные
случаи теоремы Коши о том, что интеграл по замк-
нутому контуру от комплексной функции комплекс-
ного переменного, имеющей производную, равен
нулю. Это дает возможность вывести интегральную
формулу Коши и дать разложение функции комп-
лексного переменного вблизи изолированной особой
точки в ряд Лорана. В конце главы разбирается по-
ведение аналитической функции вблизи изолирован-
ной существенно особой точки. Именно, доказывает-
ся, что функция эта вблизи существенно особой точки
стремится к произвольному пределу, если надлежа-
щим образом выбрать последовательность значений
ее аргумента, сходящуюся к существенно особой
точке.
§ 20. Интегрирование функций комплексного
переменного
В § 17 было доказано, что всякая непрерывная
функция действительного переменного интегрируема,
т. е. имеет интеграл. Тот же вопрос об интегрируемо*
сти естественно поставить также и для функции комп-»
лексного переменного. Оказывается, что для интег*
рируемости функции комплексного переменного недо-
статочно ее непрерывности. Приходится предполо-
206
жить, что она дифференцируема, т. е. имеет произ-
водную в каждой точке. Но при выполнении этого
довольно скромного требования функция комплекс-
ного переменного разлагается в ряд Тейлора в каж-
дой точке, т. е. для каждого значения г0 своего аргу-
мента она разлагается в степенной ряд по степеням
;; — го с положительным радиусом сходимости. Такие
функции называются аналитическими. Аналитические
функции играют в математике очень важную роль.
Их изучению посвящен целый большой раздел в ма-
тематике. Доказательство того, что всякая дифферен-
цируемая функция комплексного переменного являет-
ся аналитической, довольно сложно. Оно произво-
дится в несколько этапов, и мы перейдем сейчас к
его подготовке.
Открытое множество. Поскольку аналитическая
функция комплексного переменного г разлагается в
степенной ряд для каждого значения г0 своего аргу-
мента, т. е. определена для всех значений аргумента,
удовлетворяющих условию
\z — z0\<r, (1)
где г — положительное число, то множество допусти-
мых значений ' аргумента аналитической функции
должно удовлетворять следующему условию. Множе-
ство G точек плоскости комплексного переменного г
является открытым, если наряду с каждой точкой го,
входящей в G, множество G содержит и все точки г,
удовлетворяющие условию (1), где г — достаточно
малое число, зависящее от выбранной точки г0.
В дальнейшем мы всегда будем предполагать, что
каждая рассматриваемая нами функция f(z) комп*
лексного переменного г задана на некотором откры-
том множестве G плоскости комплексного перемен-
ного г.
Установим теперь некоторые очень простые свой-
ства открытого множества G плоскости комплексного
переменного г, которые понадобятся нам в дальней-
шем для изучения комплексной функции комплекс-
ного переменного.
Будем исходить из некоторого замкнутого ограни-
ченного множества F плоскости комплексного пере-
менного и некоторого положительного числа г. Через
Fr мы обозначим совокупность всех таких точек £ на-
207
шей плоскости, для каждой из которых найдется
точка г, входящая в множество F и удовлетворяю-
щая условию
(2)
Оказывается, что множество Fr замкнуто и огра-
ничено. Далее, оказывается, что если множество F
содержится в открытом множестве G, то найдется на-
столько малое положительное число г, что множество
Fr полностью содержится в множестве G.
Для доказательства нашего утверждения, а вер-
нее, двух утверждений, будем исходить из двух по-
следовательностей точек
zb z2, .... zn, .... (3)
Sb ?2, .... U ... (4)
и некоторой ограниченной последовательности поло-
жительных чисел
И, г2, ..гп, ... (5)
Относительно последовательности (3) комплексных
чисел мы будем предполагать, что все они принадле-
жат множеству F, относительно последовательности
(4) комплексных чисел мы будем предполагать, что
они удовлетворяют условиям
1Сп —гп|<г„, м—1, 2, ... (6)
Мы докажем прежде всего, что из последовательно-
сти натуральных чисел
1, 2....п, ...
можно выделить такую подпоследовательность нату-
ральных чисел
«1. «2....«й, ...» (7)
что элементы последовательностей (3) и (4) с номе-
рами (7) образуют их сходящиеся подпоследователь-
ности. В отношении последовательности (3) точек,
принадлежащих замкнутому ограниченному множе-
ству F, это утверждение уже было доказано нами
(см. § 4). Для того чтобы не менять обозначений, мы
можем просто считать теперь, что последователь-
ность (3) сходится к некоторой точке zq множества F.
Так как последовательность положительных чисел
208
(5) ограничена, то существует настолько большое
число р, что все числа последовательности (5) мень-
ше чем р/2. Из этого и из того, что последователь-
ность (3) сходится к zo, легко следует, что все числа
последовательности (4), начиная с некоторого номе-
ра, удовлетворяют условию
ICn — ZoKp. (8)
Так как множество всех чисел £, удовлетворяющих
условию
I £ Zo I Р,
замкнуто и ограничено, то из соотношения (8) выте-
кает, что последовательность (4) содержит сходя-
щуюся подпоследовательность. Для того чтобы не ме-
нять обозначений, мы будем просто считать, что по-
следовательность (4) сходится к некоторому числу
Итак, исходя из двух последовательностей (3) и (4)
комплексных чисел и ограниченной последовательно-
сти (5) положительных чисел, мы можем выбрать
такую подпоследовательность (7) натуральных чисел,
что элементы последовательностей (3) и (4) с номе-
рами (7) образуют их сходящиеся подпоследователь-
ности. А для того чтобы не менять обозначений, мы
будем считать, что исходные последовательности (3)
и (4) сами сходятся к точкам z0 и £0.
Для доказательства замкнутости и ограниченно-
сти множества Fr мы предположим, что все числа
последовательности (5) равны г. Тогда последова-
тельность (4) есть произвольная последовательность
чисел, принадлежащих множеству Fr, и мы доказали,
что эта последователность (4) ограничена и из нее
можно выбрать сходящуюся подпоследовательность,
очевидно, принадлежащую Fr. Таким образом, замк-
нутость и ограниченность множества Fr доказана.
Доказательство второй части утверждения, т. е.
того, что для достаточно малого г множество Fr со-
держится в области G, мы будем вести от против-
ного. Для этого мы предположим, что последователь-
ность положительных чисел (5) сходится к нулю и
что во всяком множестве Frn найдется точка не
принадлежащая множеству G. Так как точка при-
надлежит множеству ГГ/1, то найдется точка
209
множества F, для которой выполнено неравенство
I in zn I rtl‘ (9)
Таким образом, мы пришли к двум последовательно-
стям чисел (3) и (4) и последовательности (5), схо-
дящейся к нулю. Будем считать теперь, что после-
довательность (3) сходится к точке zq, тогда из со-
отношения (9) и сходимости чисел последовательно-
сти (5) к нулю следует, что последовательность (4)
также сходится к точке zq. Но так как точка го при-
надлежит множеству F и принадлежит открытому
множеству G, то для нее существует положительное
число г такое, что если
| £ — Zo | < г,
то точка принадлежит множеству G. Таким обра-
зом, последовательность (4), сходящаяся к точке г0,
вся, начиная с некоторого номера, содержится в от-
крытом множестве G, что противоречит нашему ис-
ходному предположению. Таким образом, вторая
часть нашего утверждения доказана.
В дальнейшем роль замкнутого ограниченного
множества F будет играть у нас совокупность всех
точек, принадлежащих кривой К, параметрически
заданной уравнениями
х = <р(0, г/ = Ф(О, (Ю)
где <р (t) и ф(/)’—кусочно гладкие функции на отрезке
(11)
Поскольку у нас сейчас идет речь о плоскости
комплексного переменного z, пару уравнений (10)
естественно записать в виде одного уравнения
г = г(/) = ф(0 + *Ф(0- (12)
Так же как в § 19, мы будем считать, что пара урав*
нений (10), или, что то же самое, уравнение (12)
описывает кусочно гладкую кривую. Замкнутость мно-
жества всех точек, принадлежащих кривой К, сле-
дует из того, что множество всех допустимых значе-
ний t (см. (11)) ограничено и замкнуто, а функция.
z(t) непрерывна. В дальнейшем кривую К. мы будем
210
рассматривать как путь, проходимый точкой z(f) в
определенном направлении, когда i возрастает от р
по v. В этом смысле он ориентирован. Вместо пара-
метра t мы можем ввести другой параметр I, причем
параметры эти связаны двумя взаимно обратными со-
отношениями
(13)
так что имеют место тождества
/ = /(?(/)), ? = ?(/(?)).
Подставляя в (12) /(f) вместо t, мы получим урав-
нение
z = z (/(/)) = £(/), (14)
которое задает ту же самую кривую К, что и уравне-
ние (12). Мы будем предполагать, что производная
t'(t) на всем протяжении кривой К непрерывна и не
обращается в нуль, а потому имеет постоянный знак.
Из этого следует, что и производная t'(t) непрерыв-
на, не обращается в нуль и имеет тот же знак, что и
производная /'(/) (см. § 11, (26)). Если производ-
ные t'(I) и положительны, то кривая К при па-
раметризациях t и t (см. (12) и (14)) проходится в
одном и том же направлении. Если производные f (?)
и отрицательны, то параметризации t и t счи-
таются противоположно ориентированными, и если
путь,.описанный при параметризации t, обозначается
через К, то путь, описанный при параметризации t,
обозначается через — К. Это естественно, так как при
возрастании t кривая К проходится в одном направ-
лении, а при возрастании t кривая К проходится в
противоположном направлении.
Интегрирование функции вдоль пути. Будем исхо-
дить из непрерывной функции f(z)’ комплексного пе-
ременного г, заданной на некотором открытом мно-
жестве G, и некоторого пути К, определяемого соот-
ношением (12) и содержащегося целиком в открытом
множестве G, так что ^множество F всех точек, при-
надлежащих пути К, принадлежит множеству G. Мы
определим теперь интеграл функции f(z)' вдоль пути
211
К, обозначив его через J f (?) d?, при помощи формулы
к
V
Jf(C)rfC=$f(2(T))/(T)dT. (15>
Л И
Выясним теперь, в какой мере определенный так
интеграл функции вдоль пути зависит от параметри*
зации этого пути. Оказывается, что если две пара*
метризации пути ориентированы одинаково, то полу^
чающиеся при помощи этих двух параметризаций ин*
тегралы равны между собой. Если же параметриза-
ции ориентированы противоположно, т. е. вместо
пути К мы берем путь — К, то интеграл меняет знак.
Таким образом, интеграл зависит лишь от направлен
ния, в котором проходится путь, а не от того способа,
каким он проходится. При прохождении пути в про-
тивоположном направлении, т. е. при переходе к про-
тивоположному пути —К., мы получаем изменение
знака интеграла. Итак, в формуле
к
К есть не объект, заданный формулой (12), а дей-
ствительно геометрический путь, проходимый точкой,
z в определенном направлении, причем способ про*-’
хождения, т. е. параметризация, не играет роли. При .
изменении направления пути мы получаем вместо пути.
К путь —К и интегралы для этих путей связаны со*
отношением
p(?)d? = -Jf(g)dg. (16)
-к к
Для доказательства высказанных утверждений
рассмотрим наряду с параметризацией t параметри-
зацию I, связанную с параметризацией t соотноше*
ниями (13). При этой замене формула (12) перехо*
дит в формулу (14). Положим, кроме того,
Н = *(и). v = ?(v).
Произведя в интеграле (15) замену переменного ий«
тегрирования т на переменное интегрирования т, при*'
чем т = ((<), мы по правилам замены переменного
212
в ж; - <• ’V:. ~~:
Интегрирования (см. § 14) получае*м
V
С f (?) d'i = jj f (z (т)) z' (t) dx =
К “
t (v)
= $ f (z (* (t))) z' (t (t)) t' (t) dx =
101)
= P(W(M*))W=
a
<)
= Jf(5(t))^(t)dt (CM. (14)).
ft
Итак, мы получаем
V 'V
J f (z (t)) z' (t) dx = p (2 (t)) S'(t) dt. (17)
u A
Теперь следует напомнить, что в определении (15)
интеграла по пути предполагается, что нижний пре-
дел интегрирования ц. меньше верхнего предела ин-
тегрирования v (ц < v, см. (И)). Таким образом, не-
равенство р, < v является существенным элементом
определения (15) интеграла вдоль пути.
В случае, если t'(t) положительна, из неравенства
И < v следует неравенство Д < v. Таким образом,
равенство (17) в этом случае показывает, что две
одинаково ориентированные параметризации пути
дают одну и ту же величину для интеграла (15).
В случае ?'(/)<: О из неравенства ji < v следует
неравенство ft > v, и потому, согласно определению
(15), правая часть равенства (17) не представляет
собой интеграла по пути, так как нижний предел
интегрирования больше верхнего предела интегриро-
вания, что недопустимо. Для уяснения того, что же
стоит в правой части равенства (17), мы рассмотрим
интеграл
А .
p(^(t))i'(t)dt. (18)
213
Согласно определению интеграла по пути, формулу
(18) дает нам интеграл
-к.
Но так как
р. «
$ f (2 (т)) (t) d% = — f (2 (t)) 2' (t) rft, (19)
« А
то из соотношений (19) и (17) следует соотношение
(16). Итак, вопрос о зависимости интеграла по пути'
от параметризации полностью выяснен и наши ут-
верждения доказаны.
Если имеются два пути K.i и /С2, причем начало
пути совпадает с концом пути Ki, то, проходя по»
следовательно сперва путь Ki, затем Лг, мы получаем
новый путь К, на котором можно ввести единую па-
раметризацию, и потому в силу формулы (56) § 17
мы имеем
рм=$нм+рт. (20)
К Л1 К;
Параметризация при помощи длины. Если за па*
раметр t принять длину пути $ от точки z(D.) до точ’
ки г($) (см. § 19, пример 1)., то
|2'(s) 1=1. (21)
Действительно,
| г' (s) | = | <р' (s) + Л|/ (s) | = + У(ф'(5))2 + СФ' (s))2 = 1
(см. § 19, (18)). Это дает возможность произвести
удобную оценку модуля интеграла (15)., именно, если
на всем пути К имеет место оценка
|f(z(s))Km,
то в силу оценки (58) § 17 мы имеем
V
= J f (2 (s)) z' (s) ds </n(v —p), (22)
к
где у — p есть длина всего пути интегрирования.
214
Сравнение интеграла по пути К с интегралом по
доман°й L, вписанной в К. Подразделим путь инте-
грирования К на кусочки, введя для этого подразде-
ление
T = (tQ, Л, tk), ^О==|Л, tk = v,
отрезка [pv], изменения параметра t. Точки z(tj-i)
к z(ti) соединим прямолинейным отрезком L/ и обо-
значим через L = L(t) путь, возникающий при по-
следовательном прохождении отрезков £1, L2, .... Lk.
Ломаный путь L вписан в криволинейный путь К.
Наша задача заключается в том, чтобы сравнить ин-
тегралы, взятые по пути К и по пути L, — именно, до-
казать формулу
= (23)
J 6(T)+oJ
Таким образом, интеграл, взятый по криволинейному
пути К, может быть с любой точностью заменен ин-
тегралом, взятым по ломаной. В дальнейшем этот
результат будет играть для нас важнейшукгроль. На
прямолинейном пути Lj мы введем естественную ли-
нейную параметризацию так, чтобы путь этот про-
ходился точкой z*(t), когда t меняется в пределах от
tj-i до tj. Для этого мы положим
(24)
//-1
Непосредственно проверяется, что при t, меняющемся
от tj-y до fy, точка z*(t) проходит прямолинейный
отрезок Lj. Таким образом, при изменении t от ц. до
v точка £*(/)' проходит весь ломаный путь L. Итак,
параметризация на ломаном пути L = L(T) введена.
В определении интеграла (15) фигурирует функ-
ция z'(t), поэтому прежде всего подсчитаем вели-
чину z*'(t) на отрезке от tj-i до tj. В силу определе-
ния (24) функции z*(t) мы имеем
*'(0==
215
Далее, в силу формулы Лагранжа (см. § 12, (20)Т
мы имеем
ф(//)-ф(О-1) ~
tj — tj-i
где числа а, и 0, принадлежат отрезку //]. Таким
образом, на отрезке от t/-i до t/ мы имеем . .
г' (0 — г*' (I) = [<р' (0 — ф' (а/)] + i [ф' (/) — ф' (₽>)],
где точки t, а/, 0/ принадлежат отрезку [//-ify]1. Таи
как функция z'(t), будучи кусочно непрерывной, яв*
ляется кусочно равномерно непрерывной, то на всем
отрезке ц t <: v имеем
|z'(/)-z*'(/)l<p(T), (25)
где ;
Пт р (Г) = 0.
6(Г)->0
Здесь р(Т) есть действительное число, зависящее
от подразделения Т. Так как
t
z (I) - г* (/) = J [г' (т) - г*' (т)] dr,
и
то в силу формулы (58) § 17 мы из оценки (22) по*
лучаем
|z(/)-z*(0l<p(T)(v-p). (26)
Обозначая, как раньше, через F множество всех то*
чек, принадлежащих пути К., выберем настолько ма*
лое г, чтобы множество Fr принадлежало открытому)
множеству G, и будем считать, что при всех рассмат*
риваемых нами подразделениях Т путь ЦТ) прохо»
дит по множеству Fr. Для этого достаточно, чтобы
было
6(7X6,
где 6 — достаточно малое положительное число. Таи
как функция f(z) равномерно непрерывна на замкну*
том ограниченном множестве Fr, по которому прохо*
дят оба пути К, и L, то из неравенства (26) следует»
|/(z(/))-f(z’(0)l<Pi(7’), (27)
216
причем
lim Pi (Г) = О,
d(T)-»O
где pi (Л есть некоторое положительное число, за-
висящее лишь от подразделения Т. Из неравенств
(25) и (27) следует непосредственно
| f (z (Z)) z' (Z) - / (Z (/)) Z*' (Z) | < р2 (Г), (28)
причем
limp2(7') = 0.
д(Т)-»О
Здесь Р2(Л есть некоторое положительное число, за-
висящее только от подразделения 7\ В самом деле,
|f(z(Z))z'(Z)-f(z*(Z))z*'(Z)l =
= |[/(z(Z))z'(Z)-f(z(Z))z’'(Z)]-
-[f(Z(Z))z*'(Z)-f(z(Z))z’'(Z)]|<
< I f (z (Z)) (/ (Z) - z*' (/)) | +1 (f (z* (Z)) - f (z (/))) z*' (Z) | <
< mp (Г) 4- p! (T) • m,
где tn дает оценку модулей функций f(z(Z)) и z*'(Z),
именно
| f (z (Z)) I < tn,
\z*'(t)\<m.
Такая оценка существует, так как функции f(2(Z)) и
z*'(t), будучи кусочно непрерывными, ограничены.
Таким образом,
р2(Г) = ц1(р(Т)4-р1(Г)).
Из соотношения (28) в силу формулы (58) § 17
следует ___
Л L
= J[f(z(T))z'(t)-/(z*(T))z‘'(T)]dT <p2(Tj(v-g).
u (29)
Из соотношений (29) и (28) следует равенство (23),
которое мы должны были доказать.
Пример. При доказательстве равенства (23) я
дважды неявно воспользовался понятием равномер*
217
ной сходимости, которым нам придется воспользо-
ваться в дальнейшем уже в явной форме. Определим
это понятие здесь.
Последовательность
Л(*)> ш, ... (30)
действительных или комплексных функций действи-
тельного или комплексного переменного z считается
равномерно сходящейся к функции f(z)\ если для вся-
кого положительного числа е можно подобрать на-
столько большое число v, что при п > v для всех
допустимых значений аргумента z имеет место нера-
венство
I Ш-f(z)\< е.
Если z есть действительное число t, то из равномер-
ной сходимости последовательности (30) легко сле-
дует, что
t t
lim fn (т) dx = ( f (r) dx.
И->оо J J
Ц. U
В самом деле,
t t
$ fn^dx — ^f
Ц Ц.
Соответствующей оценкой интеграла мы пользова-
лись при доказательстве неравенств (26) и (29),
только вместо переменного номера п мы брали пе-
ременное подразделение Т.
Учитывая связь между последовательностями и
рядами (см. § 5, (2)), ясно, как следует ввести по-
нятие равномерно сходящегося ряда и как доказать,
что равномерно сходящийся ряд можно интегриро-
вать почленно.
§ 21. Теорема Коши
Теорема Коши является центральной теоремой
теории аналитических функций. Ее общая формули-
ровка и не очень педантичное доказательство приво-
дятся в примере 1. В основной части параграфа бу-
дут даны лишь особенно важные частные случаи тео-
ремы Коши.
218
Напомним прежде всего, что, согласно термияоло-
гни, введенной в § 20, уравнение
z — z (/) = <р (/) -НФ(0» (1)
причем у, t v, где <р (/) и ф(/)’ суть действитель-
ные непрерывные кусочно гладкие функции пара*
метра /, описывает некоторый путь К на плоскости
комплексного переменного г, когда t возрастает от
ц до v. Этот путь называется замкнутым, если начало
и конец его совпадают, т. е. если имеет место равен*
ство
z(p) = z(v). (2)
Так определенный путь К является путем, вдоль ко-
торого производится интегрирование заданной диф-
ференцируемой функции f(z). Именно, определен ин-
теграл
к
(см. § 20, (15)). Докажем теперь некоторые предва-
рительные результаты.
Пусть функция f(z), заданная на некотором от-
крытом множестве О, интегрируема, т. е. имеет пер-
вообразную функцию ft(z), удовлетворяющую, следо-
вательно, уравнению
Л'(г) = /(*), (3)
причем функция h (г) определена на всем множестве
G и однозначна на нем (последнее условие нужно
особенно подчеркнуть, так как хотя мы, как правило,
говоря о функции, считаем, что она однозначна, в
действительности же мы уже встречались с неодно-
значными функциями, например Inz). Так вот, если
имеет место соотношение (3), то интеграл по пути К.
от функции f (z) легко может быть вычислен. Именно,
имеет место соотношение
p(C)^ = ft(z(v))-A(z(g)). (4)
к
Докажем равенство (4). В силу правила диффе-
ренцирования сложной функции мы имеем
= h' (z (0) z’ (t) = f (z (/)) z' (t). (5)
219
Поэтому
V
Р (0 = J f (z (т)) z' (т) dx = h (z (v)) — h (z (ц))
К ;л
’(см. § 14, (20), (21)). Таким образом, равенство (4)
доказано.
В частном случае, когда путь К замкнут (см. (2)),
мы имеем
р(С)«-О.
я
Докажем теперь частный случай теоремы Коши,
который в действительности составляет ее ядро.
Теорема Коши для треугольника. Допустим, что
в открытом множестве G лежит треугольник abc.
Это значит, что не только граница То треугольника
abc, но и вся площадка То, включающая не только
границу То, но и все внутренние точки треугольника
abc, принадлежит открытому множеству G. Через Го
обозначим путь, описываемый точкой z при последо-
вательном прохождении сторон треугольника abc, т. е.
при последовательном прохождении отрезков ab, Ьс,
са. Будем считать, что путь этот проходится против
часовой стрелки. Если функция f(z) имеет производ-
ную в каждой точке z открытого множества G, то
интеграл от нее по пути То равен 0. Запишем это в
виде формулы ___ . ;
$f(M = 0. (6)
То
Равенство (6) будем доказывать от противного.
Именно, мы допустим, что имеет место неравенство
|$f(O^|>a, а > 0. (7)
Го
Середины сторон ab, Ьс и са обозначим соответствен-
но через Ci, ai, b\. Отрезками ai&i, &1С1, исход-
ный треугольник TQ разбивается на четыре треуголь-
ника, границы которых, проходимые против часовой
стрелки, мы обозначим соответственно через
г1, Г1, т], Ti. (8)
220
Каждый из треугольников (8) подобен треугольнику
То с коэффициентом подобия у. Имеет место равен^
ство •
.4
5 ад (9)
т, j-i т{
Равенство это имеет место потому, что каждый из
отрезков a\b\, b\C\, CjOi входит ровно в два из четы-
рех путей (8) и проходится при прохождении этих
двух путей в противоположных направлениях. Из не-
равенства (7) и равенства (9) следует, что среди пу-
тей (8) найдется хотя бы один путь, который мы обо-
значим через Ть для которого выполнено неравенство
Разделяя треугольник Т\ на четыре части таким же
образом, как мы поступали с треугольником То, мы
найдем такой треугольник Г2, что для него выпол-
нено неравенство
IС 1а
1ад > 45-
т,
Этот треугольник Т2 подобен исходному треугольнику
То с коэффициентом подобия (у) ’ Продолжая этот
процесс далее, мы построим последовательность тре-
угольников
То, Ть ..., Тп, ...
такую, что треугольник Тп подобен треугольнику То
с коэффициентом подобия причем имеет место
неравенство
К <10>
Тп
Обозначим через Тп треугольную площадку или,
проще, треугольник, содержащий как весь путь Тп,
так и все точки, находящиеся внутри этого пути. Оче-
видно, что треугольник Tn+i целиком содержится в
221
треугольнике tn, п — О, I, 2, Докажем теперь, что
существует точка принадлежащая всем треуголь-
никам
К К ...» Тп,... (11)
Для этого обозначим через I длину наибольшей из
сторон треугольника Tq. Тогда длина наибольшей из
сторон треугольника Тп будет равна Следователь-
но, расстояние между двумя точками в треугольнике
Тп не превосходит величины Далее, выберем в
каждом треугольнике Тп точку zn, п = 0, 1, ... Мы
покажем, что последовательность
Zo, Zu ..., zn, ... (12)
есть последовательность Коши и что ее предел z при-
надлежит всем треугольникам последовательности
(11). В самом деле, пусть v — произвольное нату-
ральное число, а р и q — два натуральных числа,
больших v. Тогда точки zP и Zq обе принадлежат тре-
угольнику Tv и, следовательно, расстояние между
ними не превосходит числа а это и значит, что
последовательность (12) есть последовательность
Коши.
Так как все элементы последовательности (12),
начиная с номера v, принадлежат треугольнику Tv,
то и предел ее принадлежит треугольнику Tv, так как
треугольник этот есть замкнутое множество. Таким
образом, точка £ принадлежит всем треугольникам
последовательности (И).
Так как производная функции f(z) существует в
каждой точке открытого множества G, то она суще-
ствует и в точке %. А это значит, что предел
llm =
z z
существует. Последнее соотношение можно перепи-
сать в виде
1^Ш-„/'^) = у(й), (13)
где | у (z) | у, причем у — число, удовлетворяющее
условию lim у = 0.
Z->2
222
Соотношение (13) можно переписать в виде
/(г)«/(^)4-Г(^)(г-^) + ?(г)(г-^). (14)
Записанную в таком виде функции f(z)~ мы будем те-
перь интегрировать по пути Тп- Сумма первых двух
членов в правой части равенства (14) интегрируема.
Действительно,
-~[f (2) (*-*) + = f (f) + f' ф (г~ £).
Таким образом, интеграл от суммы первых двух чле--
нов правой части равенства (14) по замкнутому пути
Тп в силу ранее доказанного равен нулю, Нам остает-
ся проинтегрировать лишь последнее слагаемое, т. е.
y(z)(z —2).
Величину интеграла этой функции по пути Тп мы
оценим по формуле (22) § 20. Прежде всего, длина
пути интегрирования не превосходит величины
Далее, так как обе точки г и z принадлежат треу*
гольнику Г„, то
\z — zK^.
Таким образом, мы имеем
|$ Y(z)(z — z)dz|<-^rY,
причем
limy —0. (15)
Л-»оо
Итак, мы получаем
IS (16)
1 п
Неравенства (16) и (10) противоречат друг другу в
силу соотношения (15). Итак, мы пришли к противО’
речию, и равенство (6) имеет место.
Отметим, что при доказательстве равенства (6)
мы использовали лишь существование производной
f'(z) заданной функции f(z), но не использовали не'
прерывность производной, т. е. непрерывность фуак»
ции/'(г)._
223
Выведем теперь из равенства (6) два следствия
оба являющиеся частными случаями теоремы Коши.
Следствие 1. Будем считать, что в открытом
множестве G, на котором определена дифференцируем
мая функция f(z), задан замкнутый путь К, опреде-
ляемый уравнением (1) и условием (2). Выберем в
открытом множестве G некоторую точку а и предпо-
ложим, что прямолинейный отрезок [dz(/)], прове-
денный из точки а в произвольную точку z\t) пути
К, целиком проходит в открытом множестве О. Ока-
зывается тогда, что интеграл функции f(z) по замк-
нутому пути К равен нулю, или в виде формулы
$ f(Odg = O. . (17)
к
Для доказательства впишем в заданный путь К.
ломаный путь L, определяемый подразделением
T = (t0, tlt ..., tk\ ta==v, tk = v,
так, как это было сделано в предыдущем параграфе.
Если подразделение Т достаточно мелко, т. е. если
8(Т) мало, то ломаный путь L проходит очень близко
от криволинейного пути К; из этого следует, что каж-
дый отрезок, исходящий из точки а и ведущий в точ-
ку z*(t) ломаного пути L, проходит внутри открытого
множества G. Таким образом, каждый треугольный
путь /С/, составленный из отрезков
[azfy-OJ, [z (//.О z (//)], [z(//)a],
ограничивает треугольную площадку Я/, целиком ле-
жащую в открытом множестве G. Таким образом,
для каждого треугольника К/ верно соотношение (6),
что в виде формулы записывается так:
J f(g)dg = O. (18)
Суммируя это1 равенство (18) по / от 1 до k, мы по-
лучаем
k
£p©d$ = 0. (19)
/-1 Kj
224
Так как каждый отрезок [яг(//) ] входит в два сосед-
них треугольника К, и Ki+i и при интегрировании по
этим треугольникам проходится в противоположных
направлениях, то интегралы по этим отрезкам взаим-
но сокращаются при суммировании (19). Из замкну-
тости пути К это же верно и для отрезка, идущего
из точки а в точку z(/0) = z(^). Таким образом, в
результате суммирования (19) мы получаем лишь
интеграл по пути L, что в виде формулы можно запи-
сать так:
$f(M = 0.
L
Так как в силу доказанного в предыдущем параграфе
(см. § 20, (23)) мы имеем равенство
p(gm = lim р(?)с??,
К б(П->0£
то формула (17) доказана.
Ясно, что замкнутый путь /(, заданный уравне-
нием (1) и условием (2), можно пройти, начав дви-
жение из произвольной его точки, отчего интеграл по
замкнутому пути не изменится. Таким образом, ин-
тегрируя функцию по замкнутому пути, мы не долж-
ны указывать начало замкнутого пути, а должны
указывать только сам замкнутый путь.
В частном случае, когда К— окружность, лежа-
щая вместе со всеми своими внутренними точками
в открытом множестве G, то, приняв за а центр этой
окружности, мы получаем для нее равенство
= (20)
к
Следствие 2, Допустим, что в открытом мно-
жестве б, на котором задана дифференцируемая
функция f(z), лежат две концентрические окружности
Ki и Кг с общим центром о2, причем К\ больше Кг-
Допустим далее, что в кольце, заключенном между
окружностями К\ и Кг, лежит окружность К$ с цент-
ром в о3, все внутренние точки которой также принад-
лежат кольцу. Мы будем считать, что все точки, ле-
жащие на окружности Ki и внутри нее, за исключе-
нием, быть может, двух точек о2 и Оз, принадлежат
8 Л. С. Понтрягин 225
открытому множеству G. Будем считать окружности
Ki, Кч и Кз путями интегрирования функции f(z)',
проходимыми против часовой стрелки. Тогда оказьь
вается, что имеет место равенство
(21)
Ki Кг Кз
При доказательстве равенства (21) будем пользо-
ваться чертежом (рис. 14). Для того чтобы было
удобнее словесно описывать чертеж, предположим,
что прямая Р, проходящая через точки о2 и Оз, гори-
зонтальна и что точка о2 лежит левее точки о3. Это
предположение никак не связано с расположением
осей координатной плоскости комплексного перемен-
ного г. Мы просто временно повернули чертеж для
удобства описания. Прямая Р делит каждую из трех
окружностей Ki на половины — верхнюю K't и ниж-
нюю К". Каждая из окружностей Ki пересекается с
прямой Р в двух точках — правой bj и левой с/. Часть
открытого множества G, заключенную между окруж-
ностью Ki и двумя окружностями Кч и Кз, обозначим
226
через R. Эта часть делится прямой Р на два куска}
верхний R' и нижний R". Замкнутый путь, составляю-
щий границу куска R', проходимый против часовой
стрелки, обозначим через С', а замкнутый путь, со-
ставляющий границу куска R", проходимый против
часовой стрелки, обозначим через С". Пусть а' — не-
которая точка, лежащая внутри куска R', а а''—не-
которая точка, лежащая внутри куска R". Каждый
отрезок, идущий из точки а' в любую точку пути С',
очевидно, лежит в открытом множестве G. Точно так
же каждый отрезок, идущий из точки а" в точку пути
С", лежит в открытом множестве G. Таким образом,
в силу следствия 1 мы имеем два соотношения
$ДМ = 0, (22)
С'
Jf(C)dC = O. (23)
С"
Замкнутый путь С' состоит из нескольких кусков —
трех полуокружностей и трех отрезков. Выпишем
этот путь с учетом направления его прохождения
против часовой стрелки:
C' = (Kf, С1с2,-К£ Ь2с3, - К'з, Mi).
Точно так же запишем путь С":
С" = (КГ, bib3, - КГ, с3Ь2, - К.”, С2С1).
Заметим, что прямолинейные отрезки, входящие в
пути С' и С", проходятся в противоположных направ-
лениях, полуокружности Ki и КГ проходятся против
часовой стрелки, а полуокружности К/ и К"» / = 2,3,
проходятся по часовой стрелке. Таким образом, скла-
дывая равенства (22) и (23), мы получаем, учитывая
формулу (20) § 20,
f(C)^+$ f(C)^ = O,
откуда в силу формулы (16) § 20 непосредственно
следует равенство (21).
Обозначим через г/ радиус окружности К/, / = 1,
3. Формально каждый из трех интегралов в фор-
муле (21)' зависит от радиуса соответствующей ок-
ружности и не зависит от радиусов двух других ок-
8* 227
ружностей, но так как равенство (21)v сохраняется
при любых радиусах окружностей, то ясно, что каж-»
дый интеграл, входящий в (21), в действительности
не зависит от радиуса соответствующей окружности.
Интегральная формула Коши. Обозначим через
и комплексное число, которое соответствует точке о2,
и рассмотрим функцию
g (г) == (г — и)п,
где п — целое число. Таким образом, перед нами
стоит задача вычислить интеграл
h (и)=\
Параметризуем окружность К2, положив
z (/) = и + г2еа.
Когда t меняется от 0 до 2л, точка пробегает
ьсю окружность К2. Далее, мы имеем
zf (/) = ir2ea.
Таким образом, в силу формулы (15) § 20 мы имеем
2л 2л
h(и) = J r&nxir2eix dr = iri+x J el (n+1)x dx.
0 0
В случае, если n + 1 Ф 0, первообразная функция
функции, стоящей под знаком последнего интеграла,
есть e*(n+i)T Поэтому при п+1=/=0 имеем
2л
( е(п+1)/т rfT==_J—ei(«+i)-2« -—J- =0. Таким
J i \ti -f* 1) i [n -h 1)
о
образом, при «¥= — 1 мы получаем
$($-«)" d£ = 0. (24)
к,
В случае, когда п = —1, имеем
2я
A(u) = r£i^ dx — 2ni.
о
228
Таким образом,
( К
к^~и
— 2ш.
(25)
Последняя формула имеет весьма важное обобщение.
Пусть f(z)— функция, дифференцируемая во всем
круге /Сь Мы положим
g(z) = ^L •
6 V 1 Z — U
и подсчитаем интеграл
к, 6 “
Мы имеем
g (г) = 7ГТ + = тМ" + (и> + Y (г), (26)
где | у (z) | < у и при г, принадлежащем К2, lim у = 0.
Гг->0
Так как интеграл по окружности /С2 от левой ча-
сти равенства (26) не зависит от г2, точно так же
как интегралы от первых двух слагаемых правой ча-
сти равенства (26) не зависят от г2, то и интеграл от
последнего члена правой части (26) не зависит от г2.
Мы имеем
|5у(О^|<у2лг2.
№
Таким образом,
lira $ у(М = 0, (27)
П->0 д2
но так как интеграл, стоящий в левой части (27), не
зависит от г2, то он равен нулю, и мы получаем
S -F%^ = f(u)$ + Н«)$ rfs = 2«zf(«)
(см. (25)).
Перепишем эту формулу заново, обозначив через
К окружность с центром и, ориентированную против
часовой стрелки
J 1^Ь^==2л«7(«). (28)
k s “
Здесь предполагается, что окружность К и все лежа-
щие внутри нее точки лежат в открытом множестве
229
G, в котором 'функция f(z)' дифференцируема. Фор-
мула (28) есть интегральная формула Коши, играю-
щая в теории аналитических функций исключительно
важную роль.
Пример. Дадим теперь общую формулировку
теоремы Коши и ее не вполне педантичное доказа-
тельство. Допустим, что в открытом множестве G, на
котором задана дифференцируемая функция f(z),
имеются замкнутые кусочно гладкие, не пересекаю-
щие друг друга и не имеющие самопересечений пути
Kj, j = 0, 1, т, ориентированные против часовой
стрелки. Эти пути мы будем просто называть замкну-
тыми кривыми. Мы будем предполагать, что замкну-
тые кривые
Кь К2.....Кт (29)
все лежат внутри замкнутого пути Ко и что ни одна
из кривых (29) не находится внутри другой из этих
кривых. Обозначим через R ту часть плоскости, кото-
рая содержится внутри Ко и лежит вне кривых (29).
Будем считать, что часть плоскости R содержится в
открытом множестве G. Оказывается тогда, что
т
$ = f(№. (3°)
К. 7-1 К]
Для доказательства разобьем всю плоскость комп-
лексного переменного z на мелкие квадраты верти-
кальными и горизонтальными прямыми. Размер квад-
ратов будем предполагать настолько малым, что
каждый из них, пересекающийся с множеством R, це-
ликом содержится в открытом множестве G. Пусть
^1» ^2, .... Сп
— совокупность всех квадратов, которые пересекают-
ся с множеством R. Пересечение каждого квадрата
Ck с множеством R обозначим через В*, а границу
куска Bk обозначим через Л*. Если квадрат С* це-
ликом лежит в множестве R, то граница Л* куска
Bk есть просто граница квадрата С*. Если же квад-
рат Ck не полностью помещается в множестве R, то
Ak частично состоит из прямолинейных отрезков, вхо-
дящих в границу квадрата Ck, частично же — из ку-
сков кривой, ограничивающей множество R, т. е. при-
230
надлежит одной или нескольким кривым /С/, / = О,
f( ..., т. Внутри каждого куска В* выберем произ-
вольно точку аь и соединим эту точку а* прямолиней-
ным отрезком с каждой точкой границы Ак куска Вь.
Все такие прямолинейные отрезки, очевидно, принад-
лежат открытому множеству Q. Таким образом, мы
имеем
J f(M = 0. (31)
лк
В этом интеграле мы будем предполагать, что замк-
нутая кривая Ак ориентирована против часовой стрел»
ки. Каждый прямолинейный отрезок границы Ак,
принадлежащий квадрату Ск, принадлежит одновре-
менно и другому квадрату Ci и проходится при ин»
тегрировании по кривым Ак и А/ в противоположных
направлениях. Каждый криволинейный отрезок гра-
ницы Ак принадлежит одной из кривых К/, / = О,
1, т. При этом, если он принадлежит кривой Ко,
то проходится в том же направлении, что и кривая
Ко. Если же он принадлежит одной из кривых (29),
то проходится в направлении, противоположном про-
хождению этой кривой. Таким образом, суммируя все
соотношения (31) по k от 1 до я, мы получим в ре-
зультате
т
$ /м+Е $ км=о.
К. /“1 -К}
Из этого соотношения следует равенство (30),
Доказательство это формально не безупречно, так
рак, например, предполагается очевидным, что замк-
нутая кривая разбивает плоскость на две части: внут-
реннюю и внешнюю, что доказывается отнюдь не про-
сто, а здесь принимается как очевидное. Кроме того,
некоторые из линий А/ могут быть. устроены не так
Просто, как это может показаться на первый взгляд,
Например, они могут содержать бесконечное множе-
ство криволинейных кусочков.
§ 22. Ряды Тейлора и Лорана
Здесь будет доказано, что дифференцируемая
функция f(z), заданная на открытом множестве G, в
каждой точке Zo этого открытого множества разла-
231
гается в ряд Тейлора, т. е. может быть записан#'
в виде
(г) == а0 + al (z — z0) + а2 (z — z0)2 + ...
• •• + (z — ZoY1 + ••• (1)
(см. § 15), причём ряд этот имеет положительный ра*
диус сходимости г. Будет также дана оценка вели-
чины г снизу. Именно, будет показано, что если все
точки z вида
| z — z01 < г'
содержатся в открытом множестве О, то радиус схо«
димости г не меньше, чем г':
г г'.
Далее будет рассмотрен случай, когда сама точка
Zo не принадлежит к открытому множеству G, но вся*
кая точка z, удовлетворяющая условию
О < | z — z01 < г', г' > О,
принадлежит открытому множеству G. Это случай
так называемой изолированной особой точки функции
f(z). Функция f(z) не определена в точке z0, но опре-
делена во всех других точках некоторого круга с цен-
тром в точке Zq. В этом случае функция f(z) разла-
гается в так называемый ряд Лорана, Именно, она
может быть разбита в сумму двух функций
f(z) = f+(z) + f_(z), (2)
где f+(z) разлагается в ряд вида (1) по неотрица*
тельным степеням величины z— г0, а функция f_(z)]
разлагается в ряд по отрицательным степеням вели*
чины z — Zo, т. е. записывается в виде
М*)=1^ + (^+(3)
причем ряд этот сходится при любом ’
z¥=z0. (4)
Сразу же приведем пример такой функции, кото*
рую мы уже теперь можем разложить в ряд Лорана.
Это есть !
/(г) = е“. (5)
232
Действительно, мы имеем
е* =1 + т + ^-?+ ••• ••• <6>
(см. § 8, (4)). Для функции (5) a f-^z)]
равна сумме всех членов ряда (6), содержащих отри-
цательные степени z.
Мы видим, что ряд Тейлора есть частный случай
ряда Лорана, при котором точка го принадлежит от-
крытому множеству G; тогда, как мы увидим, функ-
ция /_(г) тождественно равна нулю.
Для доказательства того, что функция /(г) разла-
гается в ряд Лорана по степеням величины z — го,
мы выберем прежде всего окружность К* с центром
в точке г0, целиком, со всеми своими внутренними
точками, за исключением, быть может, точки г0, со-
держащуюся в открытом множестве G. Далее, Пусть
w — некоторая точка, лежащая внутри окружности
Ki, отличная от г0(^=#^о)« Выберем две окружности
А2 с центром в точке го и Аз с центром в точке w
так, чтобы они целиком лежали внутри окружности
Ki и находились каждая вне другой. Теперь мы по-
ложим
К этой функции g\z) мы применим -формулу (21)'
§21, считая, что Zo = 02 и w = 03. Для удобства вы-
числений мы для каждого из трех интегралов, входя'
щих в формулу (21) § 21, введем особое обозначение,
положив
*•(“’) = уН ">=1. 2. 3-.
тогда формула (21) § 21 может быть переписана в
виде
Л3 (w) = hl (w) — h2 (w). (7)
Вычислим теперь последовательно функции /гз(ау)1,
hi(w) и hi(w). h3(w) непосредственно задается ин*
тегральной формулой Коши (см. § 21, (28)). В силу
этой формулы мы имеем
h3 (w) — f (w). (8)
233
Вычислим теперь функцию /г^даУ. Для этого мы за-
пишем выражение, стоящее под знаком соответствую-
щего интеграла, в виде
= НЕ) НО , 1 =з
g — ан (£ — zo) — (w — 20) С — zo . _ w — гй
?-г0
= и
Мы разложили здесь в ряд в виде геометрической
прогрессии выражение
И> — Zp~ *
5-Z0
что возможно, так как величина
где
Действительно, точка £ лежит на окружности К\, а
точка w — внутри этой окружности.
Ряд, стоящий в правой части формулы (9)', рав-
номерно сходится по переменному £ (см. пример 1
§ 20) и потому допускает почленное интегрирование,
так что мы имеем
n=0 X,°'
Итак,
fti(ay) = ao + a1(w —20)+ ... + (u> — z0)" + ...,
(Ю)
(1П
п 1 f
Al
и мы полагаем
t+ (w) = hl (w).
В случае, если точка zo принадлежит открытому мно-
жеству G, функция hi(w) тождественно равна нулю,
так как мы интегрируем по окружности Къ, которая
вместе со своей внутренностью принадлежит области
дифференцируемости функции f (г). В этом случае мы
234
имеем равенство
f (w) = hl (w) = f + (ay)
(cm. (7) и (8)).
Вычислим теперь функцию h2(w) в случае, если го
не принадлежит открытому множеству G. Функцию,
стоящую под знаком соответствующего интеграла, за-*
пишем в виде (
I (£) =____________Ш = _ НО . I =
g — Ш (ш — Zq) — (g — zo) w — Zq ’ j g ~ Z0
W — Zo
00 ь
= (12)
k~L
Здесь мы применили разложение в виде геометриче-
ской прогрессии выражения
1
! £ —го ’
W — Zo
так как величина
Действительно, точка £ лежит на окружности а
точка w вне ее. Вследствие этого ряд, стоящий в пра-
вой части равенства (12), равномерно сходится по £
и допускает почленное интегрирование. Таким обра-
зом, мы получаем ' 4
а 1
— h2 (w) = —
W — Zq
a-2
(W — Zq)2
. J————
(ay — z0)k
где
Теперь мы положим
(13)
(14)
f_ (w) = — h2 (w).
Несмотря на то, что число го не принадлежит к от»
крытому множеству G дифференцируемости функции
f(z), может случиться, что все коэффициенты a~i,
а~2....a~k, ... ряда (1.3) обращаются в нуль. В этом
случае функция f-(w) тождественно равна нулю, и
235
тогда следует положить
f (ay) = f+ (w),
доопределяя тем самым исходную функцию f(z) в
точке z0 так, чтобы она стала аналитической и в
точке zq.
Итак, мы разложили функцию f(w) в сумму двух
функций
f (о>) = f+ (w) + f _ (w).
Правда, здесь в виде аргумента стоит буква w, а не
г, но w может быть заменено буквой г, и мы получим
результат, который был сформулирован вначале (см.
(2)). Заметим, что ряд (13) для функции схо-
дится при всех значениях w го. Согласно построе-
нию он сходится для всех значений w, удовлетворяю-
щих неравенству
Г2 < | W — Zo | < <
Но, как уже . отмечалось, коэффициенты a_k (см.
§ 21) не зависят от радиуса г2 окружности /С2. Та-
ким образом, для построения ряда (13) и его сходи-
мости достаточно, чтобы было выполнено неравен-
ство
О < | w— г0| < и.
Что касается w, находящихся вне круга /Сь то
сходимость этого ряда вытекает из того, что при вы-
ходе из круга /С члены ряда (13) по модулю ста-
новятся меньше. Таким образом, ряд (13) сходится
при произвольном w zQ, так что достаточность ус-
ловия (4) для сходимости ряда (3) доказана.
Точка го, не входящая в открытое множество G,
называется изолированной особой точкой функции
f(z). Различают три различных типа особых точек.
Если ряд (3) содержит бесчисленное множество чле-
нов, то точка го называется существенно особой точ-
кой функции f(z). Если ряд (3) содержит лишь ко-
нечное число членов, однако отличное от нуля, то
точка г называется полюсом функции /(г). Если ряд
(3) вовсе не содержит членов, то точка называется
устранимой особой точкой функции f (г), так как, при-
дав этой функции в точке г0 значение /(го)=ао, мы
получаем разложение функции f(z) в ряд Тейлора
в точке г0.
236
Подытоживая полученный результат, мы можем
записать разложение функции f(z). в ряд Лорана в
точке zo в следующем виде:
f (z) = Е ап (z — z0)", (15)
где п принимает всевозможные целые значения, как
отрицательные, так и положительные. Теперь возни-
кает вопрос, определяются ли коэффициенты ап, вхо-
дящие в разложение (15), самой функцией f(z).
Иначе говоря, не может ли функция f(z) быть раз-
ложена в точке Zo в ряд Лорана двумя различными
способами, т. е. с разными коэффициентами. Дока-
жем, что это невозможно, т. е. покажем, что коэффи-
циенты ап разложения (15) определяются функцией
f(z). Заметим прежде всего, что ряд (15) сходится
равномерно на всякой окружности К с центром в zo
положительного радиуса, не превосходящего г\. Ум-
ножим равенство (15) на величину (z— z0)-<A+I>,
где k — произвольное целое число. Тогда мы полу-
чим равенство
f(z).(z-Zo)-(ft+I) = San(z-zo)"",fc+1). (16)
tl
Так как ряд, стоящий в правой части равенства (15),
равномерно сходится на окружности К, то и ряд (16)
также сходится равномерно на окружности К. Таким
образом, при интегрировании равенства (16) по ок-
ружности К мы можем правую часть интегрировать
почленно. В результате этого интегрирования мы по-
лучаем равенство
$ f (О (£ - Zo)-(*+1) dl - £ ап $ (S - Zo)"-<fe+,) dl. (17)
К. п К
В § 21 (см. (24), (25)) было доказано, что
(С —Zo)"-<*+l)rfg=^O только в том случае, когда
к
показатель степени п —(k 1) = —1, т. е. этот интег-
рал отличен от нуля лишь в том случае, когда n = k.
Таким образом, мы из соотношения (17) получаем
й*=1НШ(?_го)’<6+1) (18)
к
237
Формула эта в явном виде выражает коэффициент
ak через функцию f(z). Тем самым все коэффициенты
разложения (3) функции f(z) в ряд Лорана в точке
г0 однозначно определяются самой функцией f(<).
Займемся теперь еще одним вопросом единствен-
ности.
Пример 1. Связное открытое множество G мы
будем называть областью. Напоминаю, что множен
ство G называется связным, если каждые две его
точки можно» связать ломаной линией, проходящей в
этом множестве (см. § 12). Пусть G — некоторая об’
ласть, на которой заданы две аналитические функ-
ции fi (г) и f2(^). Допустим, что существует такое бес-
конечное множество М точек области G, имеющее
своей предельной точкой точку го области G, что
функции fi (г), и /2(г) совпадают во всех точках мно-
жества М. Оказывается тогда, что функции fi(z) и
f2(z) тождественно равны между собой на всей об-
ласти G. Докажем это.
Пусть г* — произвольная точка области G и z =
— z(t) — путь, соединяющий точку г0 с точкой г*, це-
ликом проходящий в области О, так что
г(/о) = го, г(Г) = г*, (19)
причем точка г (О принадлежит области G. Как уже
было доказана в § 9, из того, что функции fr(z) и
f2(z) совпадают на множестве М, следует, что в точке
го их разложения в ряды Тейлора совпадают. Так как
радиуб сходимости г этого ряда Тейлора положите-
лен, то часть пути (19), начинающаяся в точке г (/о),
проходит внутри круга радиуса г с центром в го, и
на этом отрезке пути имеем
Л(г(0) = Мг(0). (20)
Пусть теперь ti — верхний предел множества всех зна-
чений t, для которых имеет место равенство (20). Так
как функции fi(z(O) и f2(z(f)) переменного t непре-
рывны, то в точке t\ мы также имеем равенство
fi(z(6)) = M*(O). (21)
Таким образом, в точке zi — z(ti') функции fitzf и
/г(г)^ совпадают. Далее, так как точка t\ является
предельной для точек it удовлетворяющих условию
£38
(20), то и точка Zi является предельной для точек z,
для которых выполнено равенство
Л(2) = Ш-
Из последнего следует, что ряды Тейлора для функ-
ций fi(z) и /2(2) в точке z\ совпадают. Радиус схо-
димости этого ряда Тейлора мы, обозначим через г\.
Если теперь допустить, что t\ #= t*, то окажется, что
имеется целый отрезок пути (19) при t, принадлежа-
щем отрезку t\ t f2, целиком лежащий в круге
радиуса г\ с центром в zi, и поэтому точка ii не яв-
ляется верхним пределом тех точек, для которых
имеет место равенство (21). Итак, мы доказали, что
Л = t* и, следовательно, в точке z* = z(t*) функции
fi(z) и f2(z) равны между собой. Так как точка z*
есть произвольная точка области G, то функции fi(z)'
и /г(г) совпадают во всех точках области G.
Из доказанного непосредственно вытекает, что
если некоторая функция f(z) обращается р нуль во
всех точках множества М области G, то функция эта
тождественно равна нулю на всей области G.
Пример 2. Хотя определение производной дей-
ствительной функции действительного переменного и
определение производной комплексной функции комп-
лексного переменного формально совершенно одина-
ковы (см. § 10), что и дает возможность формулиро-
вать их одновременно, реальное содержание этих пр-,
нятий весьма различно. Предположение, что дей-
ствительная функция действительного переменного
дифференцируема, т. е. имеет производную в каждой
точке, является сравнительно слабым ограничением
на функцию. Предположение же, что комплексная
функция комплексного переменного дифференцируе-
ма, т. е. имеет производную в каждой точке, является
требованием чрезвычайно сильным. Это глубокое раз-
личие видно, в частности, в том, что действительная
функция действительного переменного, имеющая про-
изводную произвольно высокого порядка, может це
разлагаться в степенной ряд (см. § 15, пример 2),но
комплексная функция комплексного переменного,
имеющая лишь производную первого порядка, разла-
гается в каждой точке в степенной ряд. Эта глубо-
кая разница объясняется тем, что когда мы опреде-
ляем производную f' (х) действительной функции f (х),
239
действительного переменного x, т. e. изучаем отно.
шение
Hg)-f(x)
1-х
при то £ может приближаться к х только с двух
сторон, убывая или возрастая. При определении же
производной f'(z) комплексной функции f(z) комп»
лексного переменного z мы изучаем отношение
ш-ш.
и ищем предел этого отношения при £ -> z, причем £
может приближаться к z по бесконечному множеству
направлений, так как £ находится не на прямой, а на
плоскости комплексного переменного. Так, точка £
может приближаться к точке z, двигаясь горизон-
тально, или же это приближение может осуществлять-
ся при движении точки £ по вертикальному направ-
лению. В обоих случаях в пределе должна получить-
ся одна и та же величина, а это уже налагает на
функцию f(£) весьма сильные ограничения. Для того
чтобы разобраться в этом, разобьем величину г на ее
действительную и мнимую части, положив z = х + iy.
Величину f(z) также разложим на действительную
и мнимую части, положив f (г) = и (х, у) + iv (х, у) •
Положим далее
£ = £ +
тогда отношение (22) запишем в виде
U (g, ч) + (В. Ч) — « (х, у) — iv (х, у)
(23)
(24)
(£ — *) + г (п — у)
Если теперь £->z горизонтально, то в формуле (23)
следует положить tj — у = 0, и предел отношения
(23) при £ -> z получает вид
ди (х, у) , . ду (х, у)
дх ~rl дх
Если £->-z вертикально, то в формуле (23) сле-
дует положить £ — х — 0, и предел (23) получает вид
1 ди (х, у) . ду (х, у) .
i ду ду *
Так как выражения (24) и (25) должны быть равны
240
кмк-
между собой, то мы получаем дна соотношения
ди (х, у) ___ dv (х, у) ди (х, у) _ ди (х, у)
дх ду ' ду дх '
Соотношения эти называются условиями Коши — Ри*
мана. Из этого видно, насколько велики требования,
которые мы налагаем на комплексную функцию комп-
лексного переменного, требуя, чтобы она имела про-
изводную.
§ 23. Вычеты
Будем исходить из некоторой аналитической функ-
ции /(z), заданной на некоторой области G. Как мы
уже говорили в предыдущем параграфе, может слу-
читься, что некоторый круг с центром в точке zq пол-
ностью, за исключением лишь своего центра zo, при-
надлежит области G. В этом случае точку z$ мы на-
зывали-изолированной особой точкой функции /(г).
Мы различали три вида особых точек: существенно
особые точки, полюсы и устранимые особые точки.
В случае устранимой особой точки можно придать
функции f(z) определенное значение f(z0) в этой
точке и тем самым сделать функцию f(z) аналити-
ческой функцией в точке zo. Таким образом, устра-
нимую особую точку zo функции f(z) естественно
включить в множество G. В двух других случаях,
говоря, что точка zo является существенно особой
точкой или полюсом функции /(z), мы тем самым как
бы включаем точку zo в число тех точек, в которых
функция f(z) рассматривается. Поэтому естественно
включить все изолированные особые точки функции
f(z) в область G, и так расширенное множество сно-
ва обозначить через G. Это расширенное множество
G также является связным открытым множеством, т. е.
областью. Мы будем говорить теперь, что аналитиче-
ская функция f(z) задана на области G, хотя в дей-
ствительности в особых точках она не определена.
Следует отметить, что множество М особых точек
функции f(z) может быть бесконечным, но оно не
может иметь предельной точки в области G. В са-
мом деле, для любой точки zo области G функция/(г)
Дифференцируема в некотором круге, с центром в
точке zo, за исключением, быть может, самой точен
241
z0, и потому внутри этого круга функция f (гУ не мен
жет иметь особых точек, отличных от Zo- Таким обра*
зом, точка zo не может быть предельной для множе-
ства М.
Поведение функции вблизи полюса и неособой
точки. Пусть f(z)—аналитическая функция, заданная
на области G, и zq — некоторая точка области G, не
являющаяся существенно особой точкой функции
f(z) (случай полюса не исключен). Тогда в некото-
ром круге с центром в zQ функция /(г) может быть
записана в виде
f (г) = (z — Zof 7 (z), (1)
где
f (z) = aQ+al(z — z0)+... + dn(z — z0)n + (2)
причем d0 = f (zo) =# 0.
Докажем это утверждение. Так как z0 не является
существенно особой точкой функции f(z)., то функция
f(z) в окрестности точки zq может быть записана
в виде
f (z) = X ап (z — ZoT, (3)
где йц =# 0. Таким образом, функция f (z)' может
быть записана в виде
/(z)=(z—гоГЕац+ацч-!(z—г0)+.. .+«ц+й<г—z0)“+...].
(4)
Тем самым формула (2) доказана.
В случае отрицательного ц говорят, что функция
f(z) имеет в точке z0 полюс порядка В случае
положительного ц говорят, что функция f(z) имеет
в точке г0 нуль кратности р.
Отношение двух функций. Пусть ф (z) и ф (z)-^ две
аналитические функции, заданные в области G., л точ-
ка Zo — неособая точка этих функций, и пусть
ф (z) =«о + й1 (z — Zo) + ... + dra (z — Zof + ..., (5)
4>(z) = ₽o + ₽i(z — Zo) + ... +|ft(z — ZO)"+ ... ;(6)
— разложения этих функций в ряды Тейлора в точке
Zo, причем
ао = Ф (z0) ¥= 0, р0 = ф (z0) 0. (7)
242
Пусть р — радиус сходимости ряда (5), о — радиус
сходимости ряда (6) и о' — расстояние между точкой
zo и ближайшим к ней нулем функции ф.(г)'. Наи-
меньшее из чисел р, а, а' обозначим через а". Тогда
отношение % (z) = , разлагается в ряд Тейлора
ф(г)
-^ + у1(г-2о)+...+у„(г-го)п+..., (8)
Ро
причем радиус г сходимости этого ряда не меньше
чем ст".
Докажем это утверждение. Отношение ф(г)/ф(г)
имеет производную в каждой точке z (см. § И, (17))„
удовлетворяющей условию |z — Zo|<o", и потому
является аналитической функцией в области G, оп-
ределенной условием |z—г0|<Г о". В силу резуль-
татов предыдущего параграфа она разлагается в
точке г0 в ряд Тейлора с радиусом сходимости, не
меньшим чем а". Первый член %.(zo)' ряда Тейлора
(8), очевидно, равен отношению
,Ф = А. =£= 0. (9)
Ф(*о) Ро
Таким образом, наше утверждение доказано.
Пусть теперь <p(z) и ф(г) —две функции, задан-
ные в окрестности точки Zo формулами
ф (z) = (z — z0)p ф (z), ф (z) = (z — z0)’ ф (z)
(cm. (4)), где функции ф (z)’ и ф(г) разлагаются в
ряды Тейлора по степеням (г — zo), причем
ф («о) =5^ 0, ф (z0) ¥= 0.
Тогда отношение
Ш = = (10)
где £(z)T разлагается в ряд Тейлора в точке z0 и
(11)
Это утверждение вытекает непосредственно из фор-
мул (8) и (9),
243
Вычеты. Пусть f(z)—аналитическая функция, за?
данная на области G, и га — некоторая точка этой;
области. Положим г
= (12)
К
где К есть окружность с центром в г0 настолько ма«
лого радиуса, что правая часть (12) уже не зависит
от этого радиуса. Величина v (го) называется выче*
том функции /(г) в точке г0. Если г0 не является
особой точкой функции /(г), то вычет и(г0) функциц
/(г) в точке г0, очевидно, равен нулю (см. § 21, (20))*
Если го есть особая точка функции /(г), то величина
ц(го) определяется формулой
е(г0) = а_ь
где а-i есть коэффициент ряда Лорана при (г — го)’1
(см. §22, (14)).
Пусть /Со — такая замкнутая кривая, что все точ-
ки, лежащие на ней и внутри нее, принадлежат об-
ласти G. Тогда внутри этой кривой и на ней самой
может быть лишь конечное число особых точек, та»
как предельная точка множества всех особых точек
не может принадлежать области G. Мы будем пред-
полагать, что на самой кривой Ко нет особых точек
функции f(z). Обозначим через гь г2, zm сово-
купность всех особых точек функции /(г), лежащих
внутри кривой /Со. Тогда имеет место формула
2^- V (С) di = v (г,) + V (z2) + .., + V (zm). (13)
Для доказательства этого утверждения окружим каж*
дую точку Zj окружностью К/ достаточно малого ра«
диуса. Тогда в силу формулы (30) § 21 мы имеем
Ко /=1 Ку /=1
Таким образом, формула (13) доказана.
Логарифмические вычеты. Пусть /(г)—функция,
заданная на области G. Функция
244
называется логарифмической производной функции
f(z). Действительно, мы имеем
5(2)=-^-111/(2).
Впрочем, последняя формула нам вовсе не нуж-
на. Она.только объясняет название функции g(z).
Пусть zo — произвольная точка области G, не яв-
ляющаяся существенно особой точкой функции f(z).
Тогда в окрестности точки Zo функция f(z) записы-
вается в виде (4). Мы имеем, далее,
f' (z) = pd3 (z — Zo)11"1 + (ц + 1) di (z — Zof + ...
...+(p + n)dn(z-zor+n-i + ...
Таким образом,
g &== и _ z°)_1+Y <14)
(cm. (10)), где y(z) есть ряд по неотрицательным
степеням z— zo, имеющий положительный радиус
сходимости. Тогда вычет o(zo) логарифмической про-
изводной g(z) (логарифмический вычет) функции
f(z)' определяется формулой g(t>)dt,~ р.
к
Пусть теперь Ко—некоторая замкнутая кривая,
проходящая в области G, в которой задана функция
f(z). Мы предположим, что все точки, лежащие внут-
ри кривой Ко, принадлежат области О и что на самой
кривой и внутри нее нет существенно особых точек
функции f(z). Кроме того, мы будем считать, что на
кривой Ко нет ни нулей, ни полюсов функции f(z).
Пусть теперь Zi, z2....zp — совокупность всех ну-
лей функции f(z), лежащих внутри кривой Ко, при-
чем Z/ имеет кратность р,. Пусть, далее, zT, z2, ..., z*q—
совокупность всех полюсов функции f(z), лежа-
щих внутри кривой Ко, причем z'k имеет порядок v*.
Пусть h(z)—некоторая функция, аналитическая в
области G, не имеющая в этой области никаких осо-
бенностей, т. е. ни полюсов, ни существенно особых
точек. Оказывается, что тогда имеет место следую-
щая очень важная формула;
г / р 4
i*/" <2Р - 2 «> <15>
К.ч i~i fe-i
245
Обозначим через К; Ъкружность малого радиуса
с центром в точке г/, а через L* — окружность малого
радиуса с центром в точке zl. Тогда мы имеем
2ш’ J h ® f (?) — 2лг J h ® £ - z, ~ Pih
Kl - Ki
(см. (14) и § 21, (28)). Точно так же имеем
1 1 z./«x
2ш J h ® f (С) 2ш J h ® ~t—7“-------------vkh (zk)
Lk 5 A
(cm. (14) и § 21, (28)). Из формулы (30) § 21 еле»
дует, что
„ р q
$h ® -ТТЕГ1 “ 2 Ы “ Z v‘ft (г'К
Ко /=1 fe=l
В частном случае, когда h(z) = 1, мы получаем
важный результат:
<ls>
Ко
где у.— общее число нулей функции f(z)\ содержа»
щихся внутри кривой Ко, с учетом их кратностей, а
v — общее число полюсов функции f (z), содержащих»
ся внутри кривой Ко, с учетом их порядков.
В другом важном случае, когда h(z) — z, мы
имеем
- р я
1 С if __ v .. _ V.. „♦ ™
2да’ J f&) к2к' (17'
Ко i=i *=i
Пример. Пользуясь логарифмическим вычетом,
докажем основную теорему алгебры, т. е. докажем,
что многочлен f (z) = za u+ aiz”-1 + ... _+ an имеет
ровно n корней с учетом их кратностей. Для этого
составим логарифмическую производную
f' (^1 _ П,га-Х + (и— l)ai2®-2+ ... +a«~i ,,8ч
g[Z,~ 7W~ zn + a12«-‘ + ...+a„
и докажем, что
2л« 5 п>
к
246
где К есть окружность достаточно большого радиуса
г с центром в точке z — 0.
Так как стоящий в левой части последнего равен-
ства интеграл берется по окружности К большого ра-
диуса г, то заменим величину z, положив
2==1/и. (19)
Тогда для больших значений величины z величина и,
обратная ей, будет мала. Сделаем подстановку (19)
в формулу (.18), и после этого умножим числитель и
знаменатель полученной дроби на ип. Тогда мы по-
лучим.
где функции ф(ы) и ф(и) являются многочленами по
степеням и, делящимися на и (т. е. конечными рядами
без свободных членов). Тогда g(l/u) разлагается в
следующий ряд по степеням а:
§(1/и) = п« + у!«2+ ... +Yn«rt+1+ (21)
с положительным радиусом сходимости р.
Подставляя теперь 1/г вместо и, мы получим в
силу формул (20) и (21)
g(z)=~ + ~г + • • • + . •
Ряд этот по отрицательным степеням z равномерно
сходится при | z | = г > и допускает потому почлен-
ное интегрирование по окружности К радиуса г, и
мы получаем
1 Г f' (£) rfg _ „
2л/1 KS) “
К
Так как многочлен f(z) не имеет полюсов, то
последняя формула указывает на то, что в круге К.
имеется ровно п нулей многочлена f (z)’.
§ 24. Нахождение обратной функции
Используем результаты, полученные в § 23, для
нахождения обратной функции (см. § 11) .
Рассмотрим уравнение
ф(йи) = 2, (1)
247
где ф^ку)* есть аналитическая функция переменного
w, разлагающаяся в ряд Тейлора в точке w = u>0, т. е.
по неотрицательным степеням величины w — w0, при-
чем для этой функции выполнены условия ф (Шо) = ?о,
ф'(га>о)=#О. В уравнении (1) величину w мы будем
считать искомой неизвестной величиной, a z—извест-
ной величиной. Мы докажем, что уравнение (1) имеет
решение ау = ф(г), где <p(zo)=o>o, причем <р(г) —»
аналитическая функция переменного z, разлагающая-
ся в ряд Тейлора в точке z = z0, т. е. по неотрица-
тельным степеням величины z — z0.
Для доказательства выберем в плоскости комп-
лексного переменного w окружность К настолько ма-
лого радиуса, чтобы уравнение ф(ш)—ф(ауо)=О
имело внутри этой окружности лишь один корень
w = о>о кратности 1 (см. § 9) и чтобы функция
ф(да)—ф(о’о) не обращалась в нуль на этой окруж-
ности, так что для точки w, принадлежащей окруж-
ности К, имеет место неравенство
| ф (w) — ф (ау0) | > б > 0. (2)
Таким образом, в силу формулы (16) § 23
1 С Ф7 (<») da _ 1
2 л/ J ф(со) — ф (Wq) ’ ‘°'
К
В силу формулы (17) § 23
1 С соф' (со) do . .
2л/ J ф (со) — ф (z0o) W
К
Будем теперь искать нуль <p (z) функции
ф (о>) — z = (ф (w) — ф (щ>Л)) — (г — z0), (5)
находящийся в круге Д’ при достаточно малом зна-
чении величины |z — Zol- В силу формулы (16) § 23
величина
1 С ф7 (а>) da
2ni J ф (®) — z
К
является целым числом, а так как при z = zq она
равна 1 (см. (3)), то и для достаточно малых значе-
ний z — Zo она также равна 1 в силу соображения не-
прерывности, так что уравнение (1) при достаточно
малых значениях |z — Zo| имеет лишь один корень
248
внутри круга К. В силу формулы '(17)' § 23 нуль
функции ф(ш)—z, который мы обозначили через
<p(z), задается формулой
<n М = — ( «>Ф'(<»)*0_______
2ni J (ф (ш) - ф (©„))-(z - z0) W
(CM. (5)).
Функцию, стоящую под знаком интеграла в пр а-
вой части равенства (6), можно записать в следую»
щем виде:
_________юф7 (со)__________
(Ф (СО) — Ф (w0)) — (2 ~ Zo)
________________________соф' (со)____________
(ф (®)-ф (®о)) [1—гА—¥т—т!
т L ф (со)—ф (w0)J
оо
= 2 (®) (<0) - ф (!„) р+1 • (7)
Здесь мы разложили функцию
___________________________1_______
1 _ z — zq
ф (со) — ф (w0)
в геометрическую прогрессию, которая сходится при
|г — z0|<S и о, принадлежащем окружности Д’ (см«
(2)). Ряд (7) сходится равномерно на окружности
и его можно проинтегрировать по этой окружности,
так что мы получаем
Ф (z) = £ (z — Zo)" • 2^7 j [ф (о) - ф (w0) ]»+« • <8)
n=0 Я
Этот степенной ряд по неотрицательным степеням
г —Zo сходится при |z — z0|<6. Следует заметить,
что свободный член этого ряда равен wo в силу фор»
мулы (4). Таким образом, мы нашли решение урав-
нения (1) в форме степенного ряда по неотрицатель-
ным степеням z— z0. Допустим, что функция ф(о>),
заданная в точке w0 при помощи ряда Тейлора, в
действительности определена на некоторой области Н
плоскости комплексного переменного w, а функция
q>(z), заданная разложением (8) в точке z0, в дей-
ствительности определена на некоторой области G
плоскости комплексного переменного z, причем для
249
всякой точки z из области G выполнено условие, что
ф(г) принадлежит Н. Составим теперь функцию
1р(ср(г)). Она является аналитической для всех зна-
чений z, принадлежащих области G, так как имеет
производную по г для всех этих значений. Для всех
значений z, близких к z0, мы имеем тождество
Ф (ф (z)) = z. (9)
Но так как левая и правая части этого равенства яв-
ляются аналитическими функциями в области О, то
они тождественно равны для всех значений z, при-
надлежащих области G определения обеих функций
(см. § 22). Таким образом, для всех значений z из
области G мы имеем тождество
t(<p(z))sz. (10)
Пример 1. Решение ш = ф(г) уравнения
eE'=l+z (11)
по определению есть натуральный логарифм вели-
чины 1 + z: ф(гУ= ln(l + z). Дифференцируя тож-
дество
еФ(г)=14-г, (12)
получаем ф'(г)е*>><г) = 1. Заменяя в этом соотноше-
нии величину е^г\ взятую из равенства (12), мы
сразу получаем
ф'(г)=1/(1+г).
Разлагая правую часть последнего равенства в сте-
пенной ряд как геометрическую прогрессию, полу-
чаем
ф'(г) == 1 — z + z2 + ...+(-1)»г»+ ... (13)
Интегрируя это равенство и принимая во внимание,
что ф(0)= 0, мы получаем
T(z) = z-4 + ^+...-H-l)nT+T+... (14)
Этот ряд для функции ф(г)' имеет радиус сходимо-
сти 1. На первый взгляд кажется, ^то мы уже полу-
чили разложение функции ln(l-|-z) в ряд (14). Од-
цако это не так. Мы исходили из предположения, что
функция ф(г)’ есть решение уравнения (12), но это
250
предположение не обосновано в том смысле, что мы
вообще не знаем, существует ли функция ф(г), удов-
летворяющая уравнению (12). Мы только доказали,
что если ф(гУ удовлетворяет уравнению (12), то она
разлагается в ряд (14). Теперь нам остается дока-
зать, что если в уравнение (12) вместо ф(г) подста-
вить ряд (14), то мы получим тождество. Однако сде-
лать это вовсе не легко.
Легко сделать нечто другое. Исходя из предполо-
жения, что 1п(1+’г) задается рядом (14), мы сразу
получаем, что In' (1 +‘z) задается рядом (13) и что,
следовательно, 1п'(1 + г) = 1/(1 + г). Таким обра-
зом, легко доказывается, что если функция In (1 + z/
задается рядом (14), то мы имеем In' и = \/и. Отсю-
да легко вывести, что In ew = w. Действительно, най-
дем производную функции In и, считая, что и = ew^
Мы имеем
(I I 1 f dll 1 d mt 1 «
7-lnu = ln = = — «=!.
Таким образом, мы имеем
-^-lnew = l,
aw
откуда следует, что In ew = w + с.
Полагая в этом равенстве w — 0, мы получаем
для с значение с = 0. Таким образом, соотношение
In ew = w
вытекает из предположения, что ln(l"+z) задается
рядом (14). Из этого, однако, никак не следует, что
функция <p(z), заданная рядом (14), удовлетворяет
уравнению (12), так как мы вообще не знаем, су-
ществует ли решение этого уравнения. Этот пробел
восполняется результатом настоящего параграфа.
Существование решения уравнения (11) относи-
тельно w в виде w = <р (г) вытекает из доказанной
в этом параграфе разрешимости уравнения (1). Дей-
ствительно, положим ifi(w)=ew — 1. Тогда уравне-
ние (11) переписывается в виде
ф(ш) = 2, (15)
причем ф(0)=0, ф'(0)= 1. Построенное решение
этого уравнения (см. (8)) w = cp(z) при малых
251
значениях z записывается в виде ряда
(p(z)==alz + a2z2+...+anzn+... (16)
Так как для этих малых значений z функция, заданная
рядом (16), удовлетворяет уравнению — 1 + г,
то, по доказанному ранее, функция эта разлагается
в ряд (14) при малых значениях г, и, следовательно,
коэффициенты ряда (16) равны коэффициентам ряда
(14). Следовательно, функция ф(з), определенная ря-
дом (16), определена во всем круге |z|< 1. Так как
ряд, определяющий функцию ф(о0, сходится при
всех значениях w, то, подставляя в (15) функцию, оп-
ределенную рядом (14), мы получаем тождество
ф(<р(з))=з (см. (10)). Таким образом, мы доказали,
что ряд (14) действительно дает функцию In(l-f-z)'
при z| < 1.
Пример 2. Совершенно аналогичным образом
обстоит дело с функцией arcsin z, которая опреде-
ляется как решение t0 = cp(z) уравнения sinw = z.
Исходя из предположения, что функция ф(г)', удов-
летворяющая уравнению
sin<p(z) = z, (17)
существует, мы с легкостью доказываем, что
<p' (z) = 1 / V1 — £2
(см. § 11, (15)). Отсюда легко получается разложе-
ние функции ф(з) в ряд по z с радиусом сходимости
1 (см. § 15, (26)). Но для доказательства того, что
функция ф(г), удовлетворяющая уравнению (17),
действительно существует, мы должны воспользо-
ваться результатами настоящего параграфа, а затем,
точно так же как это было сделано для логарифма,
мы докажем, что функция ф(г), заданная рядом (26)
§ 15, действительно удовлетворяет тождеству
sin<p(z) = 2 (18)
для всех |z| < 1.
В то же время очень легко доказать аналогично
тому, как это сделано для функции In и, что для
функции ф(г) выполнено тождество <p(sinw)=^,
что в действительности эквивалентно тождеству (18):
однако не видно никакого простого доказательства
эквивалентности этих тождеств.
252
§ 25. Целые функции и особые точки
Функция f(z)\ область G существования и диффе-
ренцируемости для которой совпадает со всей пло-
скостью переменного z> называется целой. Как это
следует из результатов § 22, она разлагается в ряд
Тейлора в каждой точке zo плоскости с бесконечным
радиусом сходимости. В частности, это имеет место
для точки z — 0. Таким образом, она записывается
в виде
f (z) = #0 + a^z + ... + anzn + ..., (1)
где ряд (1) сходится при всех значениях z. В частном
случае, когда ряд (1) имеет лишь конечное число
членов, функция f(z) является многочленом. Но мы
имели и более сложные примеры целых функций. Это
были ez, sin z, cos z (см. § 8).
Ограниченные целые функции. Докажем прежде
всего, что если целая функция f(z) ограничена во
всей плоскости комплексного переменного г. т. е. для
нее выполнено неравенство \f(z) | < с, где с — поло-
жительная константа, az — произвольное значение,
то функция эта является константой:
Дг) = С1. (2)
Для доказательства воспользуемся формулой (18J
§ 22. Мы имеем
К
где К есть окружность радиуса г. Тогда
lf(Or(n+1)l <-£?,
и в силу оценки (22) § 20 получаем
' 2»=Z (3)
К
Так как ап не зависит от г и при 1 правая часть
неравенства (3) стремится к нулю при г-*оо, мы
получаем ап = 0 при п 1. Таким образом, f(z)—ao
(см. (2)).
253
Поведение многочлена при z—>сю. Если ряд ’(1у
содержит лишь конечное число членов, т. е. функция
f (г) есть многочлен, то мы имеем
f (z) = а0 + агг + ... + anzn,
где ап 0. Будем считать, что п > 0. Тогда мы
имеем
f^==z*(an + -^+... +»•
Из этого равенства ясно, что f(z)->oo при z->oo
или в виде формулы
lim f (z) = оо.
Z->oo
Случай целой функции, отличной от многочлена.
Если ряд (1) содержит бесконечное множество чле-
нов, т. е. функция /(z) не является, многочленом, то
она обладает следующим замечательным свойством:
каково бы ни было комплексное число а, всегда най-
дется такая бесконечная последовательность
z2, zn, ...
значений аргумента z, неограниченно возрастающая,
т. е. удовлетворяющая условию
lim ]zn | = оо, (4)
П->оо
что имеет место равенство
lim f(z„) = a. (5)
П->оо
Утверждение это мы будем доказывать от против'
ного. Его отрицание можно формулировать в следую'
щей форме. Найдется настолько малое положитель’
ное число е и настолько большое положительное
число р, что
при |z| > р имеем \f(z) — а|>е. (6)
Рассмотрим теперь функцию g(z) = \/(f(z)'—а)\ Из
условия (6) следует, что при | z | > р имеем g(z)C
< 1/е, т. е. что функция g(z) вне круга радиуса р
ограничена. Однако внутри круга радиуса р она мо-
жет иметь полюсы, а именно в тех точках, где функ-
ция f(z) — а обращается в нуль. В ограниченном кру-
ге радиуса р функция а может обращаться в
254
нуль лишь в конечном числе точек. Обозначим их че-
рез ои, аг, ат. В точке а/ функция g(z) имеет
полюс, так что в ее разложении в ряд Лорана в точ-
ке се/ имеются отрицательные степени величины
z — а/. Сумму всех их обозначим через <р/(г). Функ-
ция <p/(z) есть многочлен относительно величины
l/(z — а/). Таким образом, при неограниченно воз-
растающем z величина <p/(z)->0. Положим теперь
h (2) = g (z) — <Р1 (z) — ф2 (z) — ... — <pm (z).
Функция h(z) уже не имеет полюсов в круге радиуса
р и остается в нем ограниченной. В то же время она
ограничена и вне круга радиуса р. Таким образом,
функция h(z)\ есть целая функция, ограниченная на
всей плоскости переменного г, и потому она является
константой (см. (2)). Таким образом, мы имеем
-f (г)1, а ~ Ф1 (г) — ф2(г) — ... — <Рт (Z) = Ср
Отсюда получаем
/ (г) = ф(г),
где ф (z)’"есть рациональная функция, т. е. дробь от
двух многочленов по z. Тдк как функция f(z) не
имеет полюсов, то функция ф(г), которой она равна,
в действительности является просто многочленом.
Итак, мы пришли к противоречию, так как предпола*
гали, что функция f(z) не является многочленом, И
наше утверждение (см. формулу (5)) доказано.
В этом рассмотрении выпал случай а — оо, Вос-
полним этот пробел. Отрицание утверждения (5) в
случае а = оо означает, что функция f(z) ограничена
во всей плоскости и потому является константой.
Таким образом, мы опять пришли к противоречию.
Поведение функции вблизи изолированной особой
точки. Пусть F(z) имеет изолированную особую точку.
Тогда она, согласно результатам § 22, представима
в виде
F(z) = F_(z)4-F+(z). (7)
Разложение в сумму (7) функции F(z) мы сделаем
несколько иначе, чем в § 22. Именно, член а0, не со-
держащий степени г — zo, мы отнесем к функции
T’-(z), так что функция F+fz), разлагается в ряд по.
положительным степеням величины z — z$, и потому
F+ (z0) = 0. (8)
Как было доказано в § 22, ряд
F- (г) = а0 + a_i (z — z0)-1 + ... + a_n (z — z0)_" + ...
сходится при всяком значении z Ф z0, так что функ-
ция
/ («) = ао + fl-iW 4“ • • • + + ...
есть целая функция. Если точка z0 есть полюс функ-
ции F(z), то функция f(«) есть многочлен. Если точ-
ка Zo есть существенно особая точка функции F(z),
то функция f(w) есть бесконечный ряд по степеням*
и. Пусть теперь а — произвольное комплексное чис-
ло. Согласно ранее доказанному результату (см. (4)
и (5)) можно подобрать такую последовательность
• • •, • • •
значений аргумента функции что
lim | ип | = оо (9)
Д-»<х>
И
lim f(un) = а. - (10)
Положим теперь z„ — z0 4---. Тогда из условия
Мд
(9) следует limz„ = z0, а из соотношения (10) еле-
Д->оо
дует lim F_(zn) = a. Так как F+(zo)=O (см. (8)), то
Д->оо
для функции Г(г)мы получаем lim/’(z„) = a. Это
М->ОО
имеет место в том случае, когда точка zq является
существенно особой точкой функции F(z). В случае,
если Zo есть полюс, мы имеем lim F (zn) = оо. Таким
гп-*го
образом, поведение функции F(z) вблизи ее изоли-
рованной особой точки z0 совершенно различно в
случае полюса и в случае существенно особой точки.
45 коп.