О кривых определяемых дифференциальными уравнениями - Пуанкере А.

Автор: Пуанкере А.

Теги: математика дифференциальные уравнения

Год: 1947

Похожие

Методы интегрирования обыкновенных дифференциальных уравнений

Курс математики для студентов-физиков. Том 2

Обыкновенные дифференциальные уравнения Т.1

Лекции по теории обыкновенных дифференциальных уравнений

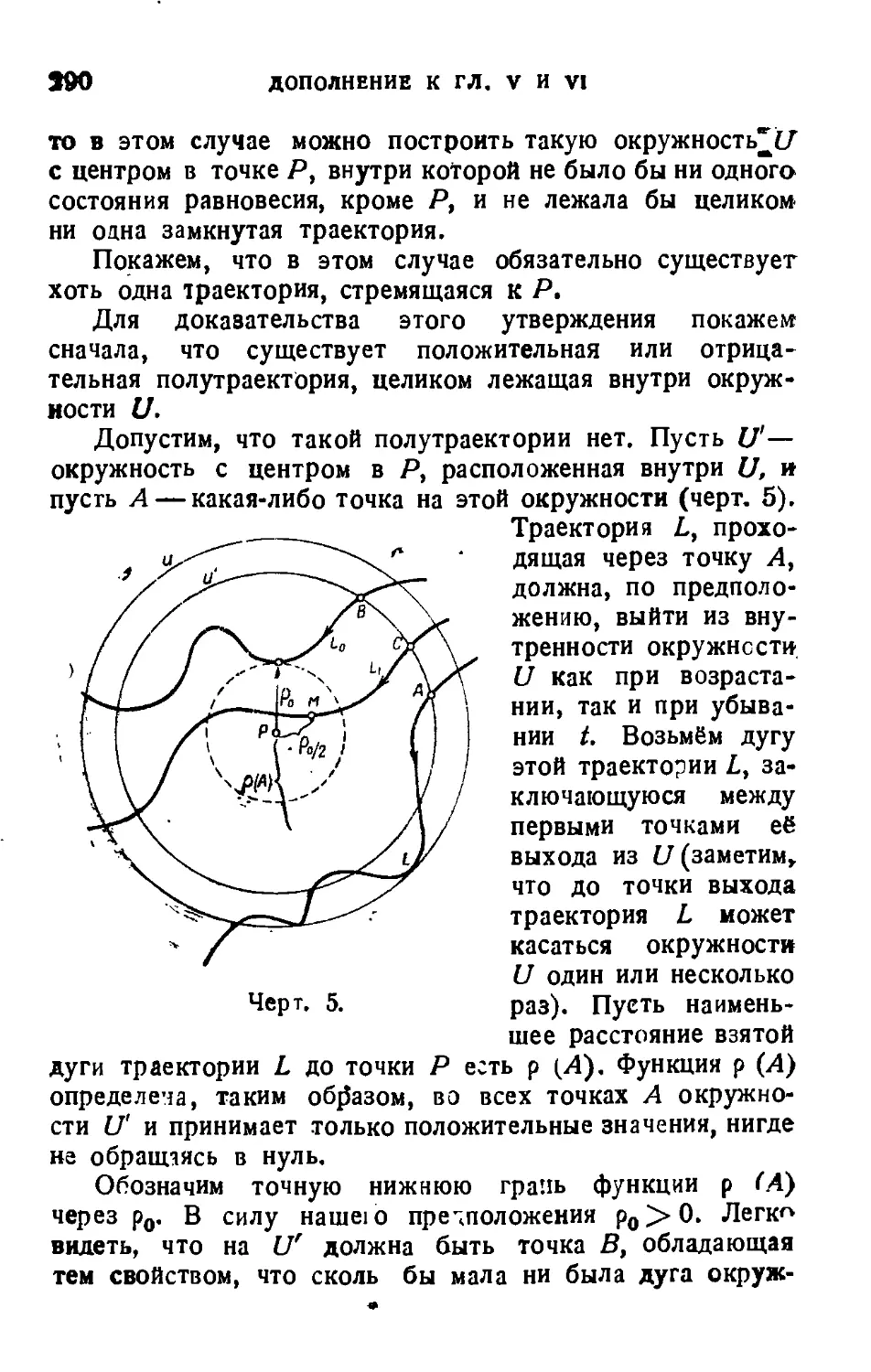
Текст

КЛАСС И КИ
ЕСТЕСТВОЗНАНИЯ
МАТЕМАТИКА
МЕХАНИ КА
ФИЗИКА
АСТРОНОМИЯ

АНРИ ПУАНКАРЕ
О КРИВЫХ,
ОПРЕДЕ ЛЯЕМЫХ
ДИФФЕРЕНЦИАЛЬНЫМИ
УРАВНЕНИЯМИ
ПЕРЕВОД
С ФРАНЦУЗСКОГО
ЖЛеонтовиг и А.Мийер .
ПОД РЕДАКЦИЕЙ
и
С ПРИМЕЧАНИЯМИ
t Л.Л.ЛпЭронова
И С ДОПОЛНЕНИЯМИ
Ж.Леонтових, Л."Майср
^.Степанова,, "ИЖетрооского
uJO.fPootcaHCRQU
о:
о г и з
«ГОСУДАРСТВЕННОЕ ИЗДАТЕЛЬСТВО
ТЕХНИКО-ТЕОРЕТИЧЕСКО И
к - ЛИТЕРАТУРЫ
МОСКВА ЛЕНИНГРАД 194Т

ПРЕДИСЛОВИЕ
Классический период развития математического ана-
лиза— XVIII век — оставил в наследство математике так
называемые элементарные методы интегрирования диффе-
ренциальных уравнений; тогда же был в основном выде-
лен тот класс уравнений, в котором нахождение общего
решения сводится к квадратурам или алгебраическим
операциям. Первая половина XIX в. проходит под знаком
критики этого наследства в двух направлениях. С одной
стороны, Коши ставит и для достаточно широкого класса
уравнений разрешает задачу о существовании решения.
С другой стороны, Лиувилль доказывает невозможность
нахождения в квадратурах общего решения специального
уравнения Риккатн, за исключением известных случаев,
когда это решение выражается в виде комбинации пока-
зательных и рациональных функций. Это открытие зна-
чительно обесценило отыскание новых случаев элемен-
тарной интегрируемости.
Теоремы существования открыли теоретическую дорогу
для приближённых и численных методов, которые, впро-
чем, начали развиваться, независимо от всякой теории,
ещё в предыдущий период, под влиянием настоятельных
требований прикладной математики, в особенности небес-

б ПРЕДИСЛОВИЕ
ной механики. Однако приближённые методы не могли
удовлетворить теоретическую мысль математика, а также
оказались недостаточными и для натуралиста, применяю-
щего математические методы. Основное неудобство
здесь состоит в том, что приближённое решение изобра-
жает с достаточной точностью только одно частное
решение в заданном интервале изменения независимого
переменного.
Чтобы остановиться на примере, укажем, что прибли-
жённое интегрирование уравнений небесной механики
даёт прекрасные результаты при вычислении положений
тел солнечной системы на любой, даже весьма большой,
в смысле исторической хронологии, конечный промежу-
ток будущего времени; но эти методы отказываются
служить, когда дело идёг о проблемах космогонии, где
надо знать характер решения в течение неопределённо
большого, т. е. практически бесконечно большого про-
межутка времени.
Новые, так называгмые «качественные методы иссле-
дования дифференциальных уравнений» появились в по-
следней четверти XIX в. и связаны с именем Пуанкаре
и Ляпунова. Ляпунов поставил и в очень широком классе
случаев разрешил с полной строгостью одну частную
задачу качественной теории — задачу устойчивости дви-
жения. Заслугой Пуанкаре является постановка общей
задачи качественного исследования дифференциального
уравнения. Эту задачу можно сформулировать так: не
интегрируя заданного дифференциального уравнения, по
свойствам правой части его дать возможно более полную
картину расположения кривых, удовлетворяющих, этому
уравнению, во всей области их существования. Анало-
гичная постановка применима к системе дифференциаль-
ных уравнений. Например, если дело идёт о динамиче-

ПРЕДИСЛОВИЕ 7
ской системе, где независимое переменное интерпретируется
как время, а зависимые переменные рассматриваются
как координаты движущихся точек фазового пространства,
то задача становится о поведении этих точек по крайней
мере в течение того промежутка времени, пока движу-
щиеся точки не оставляют данной области пространства,
в частности и для бесконечного в обе стороны проме-
жутка времени.
Первым большим исследованием Пуанкаре в осуще-
ствлении этой программы был ряд мемуаров «О кривых,
определяемых дифференциальными уравнениями», кото-
рый даётся русскому читателю в настоящем переводе.
В некоторых вопросах, сюда относящихся, результаты
Пуанкаре являются фундаментальными и служат основа-
нием для ряда последующих работ. Таково исследова-
ние интегральных кривых на плоскости; здесь следующий
существенный вклад принадлежит Бендиксону (перевод
его мемуара помещён в «Успехах математических наук»,
1941, вып. IX); таково исследование траекторий на торе,
впоследствии существенно дополненное • Данжуа (об иссле-
дованиях последнего сообщается в дополнении к настоя-
щему изданию). Общий вопрос об интегральных кривых
в «-мерном пространстве только поставлен Пуанкаре,
и полученный им ряд результатов носит предваритель-
ный характер; но сколько-нибудь полного развития эта
теория не получила и до настоящего времени, указывая
путь новым исследованиям.
В противоположность Ляпунову, Пуанкаре не всегда
строг в доказательствах своих теорем; некоторые его
утверждения являются ошибочными. С другой стороны,
за 60 лет, протекших со времени появления в свет
мемуаров Пуанкаре, прогресс других отделов математики
(топологии, теории функций) позволяет по-новому осве-

8 ПРЕДИСЛОВИЕ
тить ряд результатов автора. Дополнения к переводу
ставят своей целью исправить указанные недочёты и уси-
лить некоторые результаты основного текста.
Мечта Пуанкаре — довести качественную теорию до
того уровня, когда она позволит решать основные кос-
могонические проблемы — осталась неосуществлённой и
до сих пор; но качественные методы, связанные с имене»
Пуанкаре, всё глубже проникают в исследования не
только в области математики и механики, но и в области
физики и техники. Большая заслуга в применении этих
методов в физике принадлежит московской школе физи-
ков Л. И. Мандельштама.
В. Степанов*

АНРИ ПУАНКАРЕ
О КРИВЫХ,
ОПРЕДЕЛЯЕМЫХ
ДИФФЕРЕНЦИАЛЪН ЫМИ
УРАВНЕНИЯМИ

ПЕРВЫЙ Л1ЕМУАР
олиая теория функций, определяемых диф-
ференциальными уравнениями, была бы чрез-
вычайно полезна для большого числа вопро-
сов математики и механики. К сожалению,
сразу видно, что в громадном большинстве
случаев, с которыми нам приходится иметь дело, эти
уравнения не могут быть проинтегрированы с помо-
щью уже известных на~м функций, например, с по
мощью функций, определяемых квадратурами. И если бы
мы захотели ограничиться только тени случаями, которые
можно изучить при помощи определённых или неопреде-
лённых интегралов, то область наших исследований ока-
залась бы чрезвычайно суженной, и огромное большинство
вопросов, встречающихся в приложениях, осталось бы
нерешённым.
Необходимо, следовательно, изучать функции, опре-
деляемые дифференциальными уравнениями сани по себе,
не пытаясь сводить их к более простым функциям, так
же, как это было сделано по отношению к алгебраическим
функциям, которые сначала пытались свести к радикалам,
а теперь изучают непосредственно, так же, как это было
сделано по отношению к интегралам от алгебраических
дифференциалов после долгих попыток выразить их
в конечном виде.
Таким образом, исследование свойств функций, опреде-
ляемых дифференциальными уравнениями, — задача, пред-
ставляющая величайший интерес. Первый шаг. на этом

12 ПЕРВЫЙ МЕМУАР
пути уже был сделан, когда было изучено поведение-
функции, определяемой дифференциальным уравнением,
в окрестности какой-либо данной точки плоскости*
Задача, стоящая теперь перед нами, — это пойти дальше
и изучить поведение этой функции на всём протяжении
плоскости. В этом исследовании нашей отправной точкой,
очевидно, будут служить уже известные результаты,
относящиеся к поведению такой функции в некоторой
области плоскости. ^
Полное исследование функций состоит из двух частей:
1) качественной (если можно так выразиться) части,
или геометрического изучения той кривой, которая опре-
деляется этой функцией;
2) количественной части, или вычисления численныг
значений функции.
Так, например,» для того чтобы исследовать алгебраи-
ческое уравнение, мы сначала определяем, с помощью
теоремы Штурма, число действительных корней — это
качественная часть; затеи находим числовые значения
этих корней — в этом заключается количественное изуче-
ние .уравнения. Точно так же, для того чтобы изучить
алгебраическую кривую, мы начинаем с построения этой
кривой (как принято выражаться в соответствующих
математических курсах), т. е. определяем наличие замкнутых
ветвей, бесконечных ветвей и т. д.
После этого качественного изучения кривой можно
точно определить некоторое число её точек.
Естественно, что именно с качественной части должно-
начинаться исследование всякой функции, и поэтому про-
блема, которая в первую очередь встаёт перед нами, — это
построение кривых, определяемых дифференциальными
уравнениями^.
Это качественное исследование, когда оно будет пол-
ностью выполнено, будет очень полезно для вычисления
численных значений искомой функции и позволит более
просто установить сходящийся ряд, изображающий иско-
мую функцию в некоторой части плоскости, и главная
трудность заключается именно в отыскании надёжного
критерия для перехода от одной области, где функция

ПЕРВЫЙ МЕМУАР 13
определена одним сходящимся рядом, к другой области,
где она выражается с помощью другого ряда.
С другой стороны, это качественное исследование и
само по себе представляет первостепенный интерес. К нему
могут быть сведены различные, исключительно важные
вопросы анализа и механики. Возьмём в качестве примера
задачу трёх тел. Разве" нельзя поставить вопрос, будет ли
одно из этих тел всегда оставаться в некотором участке
неба или оно сможет удалиться в бесконечность? Или
вопрос о том, будет ли расстояние между двумя из этих
тел неограниченно убывать, или, напротив, это расстояние
будет всегда заключено в определённых пределах? Разве
нельзя поставить тысячу вопросов такого рода, и все
эти вопросы будут разрешены, как только мы сумеем
качественно построить траектории этих трёх тел. И если
рассматривать большее число тел, то чем иным являете»,
вопрос о неизменности элементов планет, как не подлинным
вопросом качественной геометрии? Так как показать, что
большая ось не имеет вековых изменений, это значит
обнаружить, что она постоянно колеблется между некото-
рыми определёнными границами.
Таково обширное поле открытий, простирающееся
.перед взорами математика. Я не имел претензии пройти
«го полностью, но я хотел по крайней мере переступить
«го границы; я ограничился одним весьма частным случаем,
тем, который естественно представлялся первым, — именно,
изучением дифференциальных уравнений первого порядка
и первой степени.
Таким образом, во всём последующем я рассматриваю
кривые, определяемые дифференциальным уравнением вида
?дг йу
где X и Y—многочлены, целые относительно х и у.
Я называю эти кривые характеристиками.^.
Рассматривая две части одной и той же характеристики,
находящиеся по Одну и по другую сторону от какой-нибудь
из её точек, мы разделяем эту характеристику (если только
она не является замкнутой кривой) на две различные

14 ПЕРВЫЙ МЕМУАР .
полухйрактеристики; эти две полухарактеристики будут
в дальнейшем играть довольно существенную роль. Напри-
мёр, предположим, что характеристика есть лбгарифмиче-
ская спираль р = ем; её можно разделить на две полу-
характеристики, допустим, так, чтобы одна полухаракте-
ристика состояла бы из точек,-для которых
а другая из точек, для которых
Для того чтобы обойти те трудности, которые могут
возникнуть при изучении бесконечных ветвей, мы будем
предполагать, что кривые спроектированы при помощи
гномоничёской проекции на сферу. Именно, пусть мы
имеем плоскость Р и точку (х, у) на ней; рассмотрим
сферу, разделённую на две полусферы плоскостью, парал-
лельной плоскости Р,— мы будем называть эту плоскость
плоскостью экватора. Если соединить прямой линией
центр сферы с точкой (х, у), то эта прямая пересечёт
сферу в двух точках, лежащих на разных концах одного
и того же диаметра; мы будем обозначать через (х,у, 1)
ту из этих точек, которая лежит в одной полусфере, и
через (х, у, 2) ту, которая лежит в другой полу-
сфере.
Всякая прямая плоскости Р проектируется в большой
круг этой сферы. Когда в дальнейшем мы будем говорить
о касательной в какой-нибудь точке характеристики, та
это будет означать, что речь идёт о большом круге,
касающемся характеристики в этой точке.
Всякий большой круг пересекает экватор в двух точ-
ках: coj и ша; угол, определяющий положение большого
круга, проходящего через эти диаметрально противопо-
ложные точки »! и <о2 экватора, измеряется дугой эква-
тора, заключённой между coj и некоторой фиксированной
точкой экватора. Угловой коэффициент прямой, соот-
ветствующей такому большому кругу, будет тангенсом
этого угла.

ПЕРВЫЙ МЕМУАР 15
Наконец, точки перегиба характеристики •—это те
точки, в. которых она пересекает, переходя с одной
стороны на другую, соприкасающиеся большие круги.
Очевидно, что при этих условиях через все точки
сферы, за исключением некоторых особых точек, прохо-
дит одна и только одна характеристика, причём угловой
коэффициент касательной к характеристике даётся урав-
нением
их йу
Кроме того, [очевидно, что расположение характеристик
симметрично по отношению к центру сферы.

ГЛАВА I
ОПРЕДЕЛЕНИЯ И ОБЩИЕ ЗАМЕЧАНИЯ
Прежде чем итти дальше, необходимо дать некото-
рые определения и привести некоторые общие теоремы,
которые окажут нам .большую пользу при качественном
изучении кривых на сфере.
Рассмотрим сначала кривые на сфере, не имеющие ни
двойных точек, ни точек остановки!8).
Мы будем называть кривую на сфере сферическим
циклом, если, выйдя из некоторой её точки и пройдя
конечную дугу этой кривой, мы снова вернёмся в исход-
ную точку 1*1. Сферическим циклом будут, например,
малый или большой круги на сфере.
Мы будем называть сферической спиралью кривую,
которая пересекает какой-нибудь сферический цикл
только в одной точке. Примером сферической спирали
может служить локсодрома, которая пересекает каждый
параллельный круг в одной точке.
Сферический цикл разделяет поверхнэсть сфзры на
две области—одну из них мы будем называть внутрен-
ней, другую внешней; невозможно перейти из одной
такой области в другую, не пересекая цикла.
Если соединить две точки характеристики при помощи
дуги какой-нибудь кривой, которая, кроме этих двух
конечных точек, не имеет никаких других общих точек
с характеристикой, то дуга кривой и дуга характеристики,
заключённые между этими точками, составят в совокуп-
ности сферический цикл. Так, например- если мы соедл-

ГЛ. I. ОПРЕДЕЛЕНИЯ И ОП1Ц11Е ЗАМЕЧАНИЯ .17
ним дугоИ большого круга два конца какой-нибудь дуги
малого круга, то эти две дуги вместе образуют зам-
кнутый цикл.
Однако здесь могут представиться цве возможности.
Первый случай. Две вегви характеристики,
являющиеся её продолжениями за те две точки, которые
соединены дугой. произвольной кривой, лежат либо обе
внутри, либо о5е ьнё сферического цикла, образованного
двумя дугами — дугой криЕОй и дугой характеристики.
Мы .будем говорить в этом случае, что дуга кривой
поддерживает (sous-tend) дугу характеристики.
Этот случай как раз имеет, месго, например, когда
концы дуги малого круга соединены дугой большого
круга.
Второй случай. Из двух ветвей характеристики,
являющихся её. продолжениями га те две точки, которые
соединены дугой Произвольной кривой, одна лежит внутри,
а другая вне цикла, образованного дугой кривой и дугой
характеристики.
В этом случае мы будем говорить, что дуга кривой
перехватывает (sur-tencf) дугу характеристики.
Предположим, например, что рассматриваемая харак-
теристика есть локсодрома; она пересекает какой-нибудь
меридиан в бесчи:ленном множестве точек. Рассмотрим
среди этих точек пересечения какие-нибудь две последо-
вательные точки; они соединены с одной стороны дугой
локсодромы и с другой стороны — дугой меридиана;
очевидно, что дуга меридиана перехватывает дугу локсо-
дромы.
Из самого определения цикла непосредственно выте-
кают следующие предложения:
1) Два цикла пересекаются либо в чётном, либо в бес-
конечном числе точек 1Б1, -
2) Всякая алгебраическая кривая состоит из одного
или нескольких циклов!6].
3) Всякая алгебраическая кривая пересекает любой
цикл либо в чётном, либо в бесконечном числе точек.
Теорема 1. Если мы разделим характеристику,
не имеющую ни двойных точек, ни точек остановки,
2 А. Пуанкаре.

18 ПЕРВЫЙ МЕМУА!»-
на две полухарактеристики и если одна из этих полу-
характеристик пересекает всякий алгебраический цикл
только в конечном числе точек, то характеристика
сама является циклом.
Действительно, построим плоскую кривую С, опре-
делённую следующим образом: абсцисса каждой точки ${
кривой будет равна длине дуги характеристики, отсчиты-
ваемой от некоторой фиксированной точки сс0 до той
точки at, которая соответствует C4; ордината точки |3,-
будет равна углу между касательной к характеристике
в точке at и осью х.
1) Каждой точке |3, кривой С соответствует одна и
только одна точка at характеристики.
2) Так как характеристика не имеет точек остановки,
то и кривая С также их не имеет.
3) Точке at характеристики соответствует ил1Т одна
точка ^ кривой С, если характеристика не является
циклом, или же бесчисленное множество точек р<, если
характеристика является циклом.
4) Кривая С пересекает всякую прямую, параллельную
оси у только в одной точке.
5) Одной из двух полухарактеристик соответствует
часть кривой С, расположенная справа от оси у, другой —
часть кривой С, расположенная слева от этой оси.
Предположим для определённости, что та полухаракте-
ристика, которая по условию пересекает всякий алгебраи-
ческий цикл, только в конечном числе точек соответ-
ствует полукривой С, которая расположена справа от
оси у.
Первая гипотеза. На полукривой С существует
бесчисленное множество точек $о соответствующих
точкам ait лежащим на экваторе.
Так как по условию рассматриваемая полухаракте-
ристика может пересекать экватор (который является
алгебраическим циклом) только в конечном числе точек,
то на экваторе может находиться только конечное число
точек а,. Но тогда хотя бы одной точке а< должно соот-
ветствовать бесчисленное множество точек $(, и, следо-
вательно, характеристика является циклом.

ГЛ. 1. ОПРЕДЕЛЕНИЯ И ОБЩИЕ ЗАМЕЧАНИЯ 19
Вторая-гнпотеза. На полукривой С существует
бесчисленное множество точек {3<, в которых касательная
к кривой С параллельна оси лг.
Это значит, что существует бесчисленное множество
точек $и соответствующих таким точкам аь которые
являются точками перегиба характеристики. Но геометри-
ческое место точек перегиба характеристик есть алге-
браическая кривая, а следовательно, в силу сделанного
предположения, у рассматриваемой характеристики может
быть только конечное число точек перегиба. Отсюда
опять следует, что' хотя бы одной точке о^ должно соот-
ветствовать бесчисленное множество точек ф{; т. е.
характеристика есть цикл.
Если предположить, что ни первая, ни вторая гипо-
тезы не выполняются, то тогда всякой точке {3<, абсцисса
которой больше некоторой определённой величины л;0,
будет соответствовать точка а,, остающаяся всегда в одной
и той же полусфере, например, в первой полусфере;
ордината же такой точки {3< будет, при возрастании
абсциссы, либо всё время возрастать, либо всё время
убывать — например, возрастать.
Мы приходим, таким образом, к третьему случаю,
который в свою очередь содержит в себе две возмож-
ности.
Третья гипотеза. При изменении х от л:0 до
бесконечности ордината точки р<, т. е. угол наклона
касательной к характеристике, всё время увеличивается,
но всегда остаётся меньше некоторой определённой
величины.
Пусть
^! — точка кривой С, абсцисса которой равна л:0;
«1 — соответствующая точка характеристики;
а1ш1 — касательная к характеристике в точке otjj
«! — точка, в которой касательная otjCOj пересекает
экватор; »
*< — какая-нибудь точка характеристики, соответствую-
щая точке р<, лежащей справа от {Зх;
ai<»i — касательная в этой точке;
<°< точка, в которой эта касательная пересекает экватор.
2»

ПЕРВЫЙ МЕМУАР
Когда точка а< будет продвигаться вдоль полухарак-
теристики, о>< будет перемещаться вправо, всё время
оставаясь на некоторой дуге экватора ш^, полухарак-
теристика не может пересечь экватора, не имеет, по
предположению, точек перегибами заключена вся целиком
внутри сферического треугольника а^юд (черт, ^следова-
тельно, её сферическая длина меньше, чем а1ш1 -j-^i^g, т. е.
конечна; но это абсурдно t7l. Таким
образом, третья гипотеза неприемлема.
Четвёртая гипотеза. При
изменении х от х0 до бесконечности
ордината точки ${, т. е. угол наклона
касательной к характеристике, неогра-
ниченно возрастает.
Это значит, что угол наклона каса-
тельной к характеристике может при-
нимать все значения
<^i ' где^ — некоторая заданная постоянная
Черт. 1. и я— любое целое положительное
число.
Следовательно, угловой коэффициент касательной
к характеристике для бесчисленного множества различ-
ных точек р< равен tgy0.
Но геометрическое место точек, в которых угловой
коэффициент касательной к характеристике равен tgy0,
есть алгебраическая кривая и значит, по предположению,
может пересекать рассматриваемую полухарактеристику
только в конечном числе точек сс<. Отсюда снова следует,
что хотя бы одной точке at соответствует бесчисленное
множество точек р<, т. е. что рассматриваемая характе-
ристика есть цикл.
Резюмируя, мы можем сказать, что из тех четырёх
гипотез, которые вообще возможны, первая, вторая и
четвёртая приводят нас к выводу, что характери-
стика есть цикл; третья гипотеза приводит к противо-
речию.
Следовательно, теорема доказана.

ГЛ. I. ОПРЕДЕЛЕНИЯ И ОБЩИЕ ЗАМЕЧАНИЯ 21
Опр еделение. Мы будем называть полициклом
замкнутую кривую, имеющую двойные точки Р1.
Пример. Кривая, получающаяся при пересечении
сферы' с круговым цилиндром, касающимся этой сферы
в некоторой точке, есть полицикл W.
Топографическая система. Проведем на сфере такую
систему циклов и полициклов, чтобы через каждую точку
сферы, за исключением некоторых особых точек (через
которые не проходит ни один цикл) проходил бы один
и только один цикл или полицикл. Мы будем называть
такую систему циклов топографической системой вслед»
ствие еб сходства с системой кривых уровня земной
поверхности.
Двойные точки полициклов будут тогда соответство-
вать седловинам земной поверхности, а особые точки,
через которые не проходит ни один цикл, будут соот-
ветствовать вершинам и котловинам земной поверхности;
в связи с этим мы будем называть эти точки сёдлами,
вершинами и котловинами.
Так, например, семейство кривых
f(x, у) = const.,
где f(x,y) многочлен, целый относительно хну, будет
представлять собой топографическую систему, если эти
кривые не пересекают экватора. Сёдлами этой системы
являются те точки, в которых мы имеем одновременно
д1~д1—п ( -У ^L^l
дх~ду~и> \дхду) дх*ду*
вершины — это те точки, в которых
и, наконец, котловины (впадины) это те точки, в которых
дх~ду~ ' \дхду)
Точно так же, если х, у и z связаны алгебраическим
соотношением

22 ПЕРВЫЙ М1ИУАР
причем ? никогда не обращается в нуль и z нш можде
оставаться конечным и действительным, когда х к у бес-
конечно велики и действительны, то семейство кривых
2= COnSt.
есть топографическая система.
Пусть, например,
/(*, У, *) = B — *)» — 2 (*• -f.y» + 1) = 0;
~ может обратиться в нуль только если
9
что невозможно.
Далее, если мы будем рассматривать г как постоян-
ную, то члены наивысшей степени имеют вид
Иначе говоря, кривые г = const, не пересекают экватора
и, следовательно, образуют топографическую систему.
Мы будем называть кривой контактов геометри-
ческое место точек, в которых характеристики касаются
циклов топографической системы.
Если топографическая система — алгебраическая, то и
кривая контактов будет алгебраической кривой.
Если мы имеем топографическую систему и рассмотрим
один из полициклов, соответствующий какому-нибудь
седлу этой системы, то одна часть вершин и котловин
будет находиться вне этого полицикла, а другая часть внутри
него; так что каждый полицикл некоторым определённым
образом распределяет вершины и котловины системы.
Две топографические системы мы будем называть
подобными, если они имеют одни и те же сёдла, одни и
те же вершины и котловины и если вершины и котловины
одинаковым образом распределяются при помощи поли-
циклов, проходящих через сёдла.

ГЛАВА II
ИЗУЧЕНИЕ ХАРАКТЕРИСТИК В ОКРЕСТНОСТИ
ДАННОЙ ТОЧКИ СФЕРЫ
Прежде чем приступить к исследованию характеристик
на всей сфере в целом, необходимо напомнить получен-
ные ранее результаты, относящиеся к изучению этих
кривых в некоторой ограниченной области сферы. Основ-
ные теоремы, относящиеся к этому изучению, сформу-
лированы и доказаны в различных мемуарах Коцш, оза-
главленных «Мемуары об исчислении пределов»*) и
напечатанных в томах XIV, XV и XVI «Докладов Париж-
ской Академии наук»**'), а также в знаменитом мемуаре
Брио и Буке, напечатанном в XXXVI томе «Журнала
политехнической школы»***).
Я сам занимался этим вопросом в заметке, помещён-
ной в XLV тетради «Журнала политехнической школы»
и в докторской диссертации, которую я защищал перед
Факультетом наук в Париже****).
Пусть точка, вокруг которой мы хотим изучить
поведение характеристик, есть
*) Memolressur lecalcul des liraltes.
**) Comples rendus des seances de l'Academle des Sciences,
t. XIV. XV et XVI.
**•) Journal de l'Ecole Polytechnique, t. XXXVI.
****) Journal de i'Ecole Polytechnique, t. XLV.

24 ПЕРВЫЙ МЕМУАР
Мы можем рассматривать X и Y, которые являются
многочленами по х и у, также и как многочлены по
х — а ну— р, так что ¦
ЛГ= а0 -f- «I (* — <0 + «2 (У - Р) -f • • •»
Первый случай. а0 и #0 не равны одновременно
нулю; предположим, например, что
ао>О.
Дифференциальное уравнение может быть записано в виде
dx x
где / есть ряд, расположенный по возрастающим степеням
л:—л и у — р.
Тогда в силу теоремы, доказанной Коши (Доклады,
т. XIV), у может быть выражено в виде ряда, располо-
женного по возрастающим степеням л: — а и обращаю-
щегося в р при х = а.
Следовательно, че: ез точку (a, fj) проходит одна и
только одна характеристика.
Второй случай. ао= fro = O. Но av аа, Ь1 и Ь2
не равны нулю одновременно.
Тогда точка (а, C) есть обыкновенная особая точка.
Напомним прежде всего одну теорему, касающуюся этих
особых точек, теорему, которую я доказал в своей дис-
сертации.
Если уравнение
(«! — X) (Ь2 — X) — bfa = О
имеет два различных корня Xt и Я2 и если отношение
этих корней положительно или мнимо, то общий ин-
теграл уравнения
dx _ dy
lf-'zY ¦
имеет вид
Z\*Z a-->.--= const.,

ГЛ. П. ИЗУЧЕНИЕ ХАРАКТЕРИСТИК В ОКРЕСТНОСТИ ТОЧКИ 25
где Zi. и 2а—ряды, расположенные по возрастающим
степеням разностей x—z, у—$ и обращающиеся в нуль
при - .
х = а и у = $.
Предположим, -что точка (л;, у) неограниченно при-
ближается к точке (а, |3) таким образом, что
х — а г
Угловой коэффициент касательной в точке (х,у) будет
иметь своим пределом
«1 + «а I* *
Следовательно, предельноэ положение прямой, соеди-
няющей точки (х,у) и (а, р) и предельное положение
касательной к характеристике, проходящей через точку
(х, у), образуют томографическую связку.
Двойные прямые этой связки даны уравнением
V- (ai + аз V-) •= bi + h V-
Пусть jij и \i2 — два корня этого уравнения; легко
выразить Xj и Яа в виде рациональных функций от а^,
а2, bu b2, {I.J и ji8.
Теперь можно разбить второй случайна четыре основ-
ных по делу чая.
Первый подслучай. Двойные прямые томографи-
ческой связки действительны, и всякие две сопряжённые
прямые связки или обе лежат в остром углу, образованном
двумя двойными прямыми, или обе в тупом углу.
В этом случае >.j и Х2 действительны и их отношение
положительно; следовательно, теорема, которую мы на-
поминали вначале, применима, и общий интеграл может
быть записан в виде
Z^Z-**= const.,
где Zj и Z2 — действительные функции от х и у, обра-
щающиеся в пуль при
х = а и _у = р,

26 ' ПЕРВЫЙ МЕМУЛР
тогда как \х и Х2—два действительных положительных
числа.
Отсюда следует, что все характеристики проходят че-
рез особую точку (a, f3), если только они попадают
в столь близкую к этой точке область сферы, что ряды
Zj и Za сходятся. Такая особая точка будет называться
узлом.
Пусть, например, требуется изучить характеристики,
удовлетворяющие уравнению
dx dy
~х~~2у
в окрестности точки х=у = 0.
Общее уравнение этих характеристик имеет вид
где k — постоянная. На плоскости это уравнение изобра-
жает семейство парабол, имеющих общую ось и общую
вершину вначале; на сфере это же уравнение изображает
линии пересечения сферы с конусами, имеющими центр
сферы вершиной, а параболы направляющими. Все эти
линии пересечения проходят, очевидно, через точку
х=у = 0.
Второй подслучай- Двойные прямые пучка дей-
ствительны, но две сопряжённые прямые пучка лежат по
разные стороны от двойных прямых.
В этом случае -г-1 действительно и отрицательно; тео-
рема, о которой мы говорили, не приложима.
Но Врио и Буке в мемуаре, напечатанном в «Жур-
нале политехнической школы», XXXVI теградь, показали,
что через точку (а, Р) проходят две и только две харак-
теристики l:°J.
Такая особая точка будет называться седлом.
Пусть, например, требуется изучить поведение харак-
теристик, определяемых уравнением
dx dy
х - — •
В окрестности начала координат.

ГЛ. II. ИЗУЧЕНИЕ ХАРАКТЕРИСТИК В ОКРЕСТНОСТИ ТОЧКИ 27
Общи! интеграл будет
ху = const.,
м единственными характеристиками, проходящими через
начало координат, будут два больших круга
л; = 0, у = 0.
Третий подслучай. Двойные прямые связки мнимы,
и связка не сводится к системе прямых в инволюции.
В этом случае Х1 и Х2 — две комплексные сопряжён-
ные величины и их отношение мнимо. Общая теорема
может быть приложена, и общий интеграл имеет вид: \
Zjx> Z2-'-i = const.,
где Zx и 22, Хх и Ха — комплексные сопряжённые вели-
чины.
Пусть
Тогда общий интеграл можно записать в виде:
i-^ ) = const.
Кривые P-f- xia = const, (где 5 и т) — ряды, располо-
женные по возрастающим степеням разностей х — а и
у — C и обращающиеся в нуль при х = а и у = ф), оче-
видно, являются циклами, нигде не пересекающими друг
друга и образующими в окрестности точки (а, Р) топо-
графическую систему с вершиной в точке (а, |3).
Если обратить внимание на то, что уравнения
дают для 5 и т), а следовательно, и для х и у только одну
систему действительных вначений, то станет ясным, что
характеристики пересекают циклы

28 ПЕРВЫЙ МЕМУАР
лишь в одной точке; следовательно, характеристики яв-
ляются спиралями; точка, пробегающая любую из этих
спиралей в некотором определённом направлении, будет
неограниченно приближаться к началу. Такая особая точка
будет называться фокусом.
Пусть, например, нам дано уравнение
dx dy
х—у х-\-у'
общим интегралом которого является
/x+ly\i
(*+>¦> (figI=«>"*¦
При переходе к полярным координатам этот интеграл
примет вид:
p2g-2g> _ const.
Это уравнение даёт нам на плоскости логарифмическую
спираль и, следовательно, на сферг сферическую спираль.
Четвёртый под случай. Двойные прямые томо-
графического пучка мнимы, и этот пучок сводится к си-
стеме прямых в инволюции.
В этом случае Xt и Ха — комплексные сопряжённые,
но отношение их равно — 1. Теорема, о которой мы гово-
рили вначале, не приложима. v
Этот четвёртый случай является более частным слу-
чаем, чем все предыдущие, и он, вообще говоря, не бу-
дет иметь места, когда X и Y—многочлены самого об-
щего вида данной степени. Поэтому мы ограничимся
только некоторыми замечаниями.
Прежде всего, очевидно, что в этом случае ни одна
ветвь характеристики не может пройти через точку (а, В),
так как тогда касательной к ней в этой точке должна
была бы быть одна из двойных прямых в инволюции,
а эти прямые мнимы.
Но в силу того, что мы увидим дальше *), все харак-
теристики суть спирали, и тогда двигающаяся по ним
•) См. главу XI.

ГЛ. п. Изучение характеристик в окрестности точки 29
точка будет закручиваться вокруг точки (а, р>, неограни-
ченно приближаясь к ней: в этом случае точка (а, Р) есть,
как и "раньше, фокус; или же все характеристики обра-
зуют топографическую систему, для которой точка (а, р)
является вершиной; тогда точка (а, Р) есть центр.
Последнее как раз имеет место в том случае, когда
теорема, о котор'сй мы. говорили вначале, применима,
несмотря на отрицательную величину отношения ^.
Аа
Действительно, общий интеграл запишется тогда в виде
где
или иначе
'¦=А.
Очевидно, что в этом случае характеристики образуют
топографическую систему циклов.
Так, например, уравнение
dx dy
имеет общий интеграл
Частные случаи, оставленные в стороне.
Во всём предыдущем мы оставили в стороне те частные
случаи, когда
лх = ла или лх = 0.
Эти случаи, вообще говоря, не имеют места, если X и
Y—многочлены самого общего вида данной степени.
Рассмотрим сначала случай, когда
Aj = Ха.
Для этого- необходимо^ достаточно, чтобы

30 ПЕРВЫЙ МВМУЛР
Брио и Буке показали, что в этом случае через точку
(а, Р) проходит бесчисленное множество характеристик,
т. е. что мы снова имеем узел.
Пять предыдущих случаев исчерпывают все те случаи
особых точек (а, р); при которых точка (а, р) является
простой, однократной точкой пересечения кривых
а не слиянием нескольких простых точек. Мы будем на-
зывать такие особые точки особыми точками первого
рода. Как мы видели, существует четыре типа таких
особых точек: узлы, сёдла, фокусы и центры.
Остаётся рассмотреть те случаи, когда
Aj = 0
или когда
a1 = ai = 0,
или
Это как раз те случаи, когда кривые' X=Y=0 имеют
в точке (а, |3) несколько слившихся точек пересечения.
Действительно, если
то кривая Х=0 имеет в точке (а, Р) кратную/точку.
Если
*i = *a = 0,
то кривая К=0 имеет в точке (а, р) кратную точку.
Если
Л=°.
то это значит, что
и, следовательно, кривые Х=0, Y=0 касаются друг
друга в точке (а, Р).
М« будем называть такие особые точки особыми
точками второго рода; на основании предыдущего их

ГЛ. II. ИЗУЧЕНИЕ ХАРАКТЕРИСТИК В ОКРЕСТНОСТИ ТОЧКИ 31
можно, очевидно, рассматривать как результат слияния
нескольких особых точек первого рода.
.Различные особенности, которые могут представить
такие особые точки, слишком многочисленны и разнооб-
разны, для того чтобы мы стали их здесь подробно изу-
чать. Заметим только, что такие особые точки не могут
существовать, когда X и Y многочлены самого общего
вида данной степени [11'.
Точки, расположенные на экваторе. Во всём преды-
дущем мы неявно предполагали, что а и Р остаются ко-
нечными, т. ё., что точка (а, C) не лежит на экваторе.
Но случай, когда точка (а, р) лежит на экваторе, может
быть очень легко приведён к уже изученным случаям.
Рассмотрим сначала точку на экваторе, не лежащую
на большом круге,
х = 0.
Мы положим
х*= г , у— г .
Если мы будем затем рассматривать г и t как координаты
некоторой точки на плоскости, то эта точка будет не чем
иным, как гномонической проекцией точки (*, у), сферы
на плоскость, параллельную плоскости большого круга
х = 0. Для рассматриваемой точки (а, Р) сферы коорди-
наты г и t будут конечны, и, таким образом, мы прихо-
дим к тем случаям, которые были рассмотрены в начале
этой главы.
Если бы мы хотели исследовать характеристики вблизи
точки пересечения экватора и большого круга л: = 0, то
мы положили бы
t 1
и стали бы рассуждать совершенно так же.

ГЛАВА III
РАСПРЕДЕЛЕНИЕ ОСОБЫХ ТОЧЕК
Теорема II. . Всякая система характеристик
имеет особые тонки.
Первая гипотеза. Кривые Х=0 и К=0 пере-
секаются в точках, не лежащих на экваторе.
Тогда эти точки пересечения будут, очевидно, осо-
быми точками..
Вторая гипотеза. Кривые Х=0 и К = 0 пере-
секаются в точке, лежащей на экваторе.
Предположим, что эта точка не лежит на большом
круге
х = 0;
мы положим
г ' •* г
и введём обозначение
где т есть степень того из многочленов X и Y, кото-
рый имеет наивысшую степень. Дифференциальное урав-
нение принимает тогда вид:
dz dt ,ri
По предположению, при t — a и z = 0 мы имеем

ГЛ. III. РАСПРЕДЕЛЕНИЕ ОСОБЫХ ТОЧЕК 33
и, следовательно,
^ = 0, Y1 — tXl = 0,
т. е. точка
t = a, г = 0
есть особая точка данного уравнения.
Третья гипотеза. Кривые Х=0 и У = 0 нигде
не пересекаются: Степень многочлена X выше степени
многочлена Y.
В этом случае по крайней.мере один из многочленов
X и- Y имеет чётную степень. .Кроме того, Yl делится
на г так, что
Y^zY*
. Ясно, что при
г = *.= 0
мы будем иметь
zX1=^zYfi — tX1 = 0,
и, следовательно, точка
есть особая точка.
Четвёртая гипотеза. Кривые Х = 0 и У=0
нигде не пересекаются. Степень X ниже степени Y.
Положив в этом случае
х г ' у г
и рассуждал так же, как и в предыдущем случае, мы
покажем, что точка
• z = t = O
есть особая точка.
Пятая гипотеза. Кривые Х=0 и F=0 нигде
не пересекаются. Степень X и У одна и та же. Кроме
того, если Ха и. Ка суть члены наивысшей степени в X
и в У, то ¦
не равно тождественно нулю.
3 а. Пуанжаре.

34 ПЕРВЫЙ МЕМУАР
В этом случае, если т есть степень (необходимо
чётная) X и У, то функция xYt—уХ% однородна отно-
сительно х и у и степени т-\-1, т. е. нечётной степени.
Следовательно, она обращается в нуль либо при х = 0,
либо при некотором конечном значении *-.
Если она обращается в нуль при некотором значе-
нии а отношения ^-, то, полагая
мы будем при t = а и г = 0 одновременно иметь:
это значит, что точка
ts=a, г = 0
есть особая точка.
Если функция xY%—уХ% обращается в нуль при
X = О, ТО МЫ ПОЛОЖИМ
г ' •* г
и увидим, как и выше, что точка
есть особая точка.
Шестая гипотеза. Кривые Х=0 и У=01м1
нигде не пересекаются. Степень X та же, что и степень У.
Кроме того, если -Ха и У9 суть члены наивысшей сте-
пени в X и в У, то мы имеем тождественно:
«
д;Уа—уХйг=0.
Эта гипотеза недопустима.
В самом деле, если мы имеем тождество
=yX 2,

ГЛ. III. РАСПРЕДЕЛЕНИЕ ОСОБЫХ ТОЧЕК 35
то Х% делится на а; и равно хХ9, Ка делится на у и
равно уУъ, так что мы имеем тождественно
или
Но У9 = Хд. есть однородная функция от л: ну нечётной
степени; следовательно, она обращается в нуль либо при
х = 0, либо при некотором конечном значении а отноше-
ния —. Следовательно, либо при x = Q, либо при
— =i а мы необходимо имели бы
т. е. кривые Х = 0, К=0 пересекались бы в некоторой
точке экватора, что противоречит предположению.
В общем, из шести, гипотез, которые можно сделать, '
шестая гипотеза приводит к противоречию; если же
осуществляется одна из остальных пяти гипотез, то диф-
ференциальное уравнение имеет особые точки либо на
экваторе, либо вне экватора 11Б1.
Общий случай.. Можно, не нарушая общности,
предположить:
1) что многочлены X п У одинаковой степени;
2) что если А"а и Ка— члены наивысшей степени в X
и К, то
не равно тождественно нулю;
3) что кривые Х=У=0 не имеют слившихся точек
пересечения и не пересекаются на экваторе;
L 4) что уравнение
не имеет кратных корней.
В этом случае экватор всегда является характе-
ристикой, и все особые точки суть простые особые
точки. Более того, можно, . не ограничивая общности^
предположить", что все особые точки суть узлы, сёдла и
фокусы.
3*

36 ПЕРВЫЙ МЕМУАР
Число особых точек, очевидно, четно, так как всё
симметрично относительно центра сферы. Минимальное
число особых точек равно, следовательно, двум, и этот
случай может осуществиться двумя способами:
1) Кривые
Х=0, К = 0
нигде не пересекаются, но однородное уравнение
имеет действительный корень и только один I16'.
Тогда мы будем иметь на экваторе две особые точки,
лежащие на концах одного и того же диаметра. Я утвер-
жцаю, что эти особые точки всегда будут узлами.
Чтобы доказать это, надо рассмотреть общие свойства
особых точек, расположенных ца экваторе.
Предположим, что при
t = a и г = 0
мы имеем
Положим
и пусть
где \х и i)j — многочлены, целые относительно г и и 1171
и \ и ji — постоянные. Полагая
получим
отсюда находим
\ - Хоа)-j- (^ - Aja — *о) и,

ГЛ. III. РАСПРЕДЕЛЕНИЕ ОСОБЫХ ТОЧЕК 37
где Oj и 0а—многочлены, целые относительно гни.
Замечая, Что ц0 = А.оа, мы можем написать дифференци-
альное уравнение в таком виде:
_dz_
da
(ц, — XiO — ).вч) ц + «Bj
Тогда корни.уравнения E) будут:
[18]
Оба эти корня действительны.
Следовательно, веяная особая точка, лежащая на
экваторе, либо узел, либо седло (это можно было пред-
видеть, так как экватор есть характеристика).
Для того чтобы такая особая точка была узлом, необ-
ходимо и достаточно, чтобы:
Но левая часть этого неравенства есть "в точности то
значение, которое принимает выражение
при
Мы не изменим его знака, написав
ду \Xt х
Следовательно, особая точка
будет седлом, если при изменении — От а — е до a -j- e
выражение -^ 2- переходит от отрицательных значе-
Л2 X
3*

38 ПЕРВЫЙ МЕМУАР
ний к положительным, и узлом, если при изменении -^-
от а — е до а-1-е выражение -=г— ¦"- переходит от поло-
жительных значений к отрицательным.
Установив это, мы ваедём новое понятие, которое
окажет нам очень большие услуги. Пусть мы имеем цикл,
целиком лежащий в одной из полусфер. Этот цикл делит
сфе на дчэ области, одна из которыт, расположенная
целиком в одной полу-
сфере, называется вну-
тренностью цикла.
Если цикл лежит
целиком в первой по-
лусфере, то мы скажем,
что подвижная точка
обходит цикл в поло-
жительном направле-
церт 2. нии, если внутренность
цикла лежит всё время
налево от неё; если же наоборот цикл лежал бы во
второй полусфере, то точка описывала бы цикл в по-
ложительном направлении, если внутренность была бы
всё время направо от неё.
Предположим, что подвижная точка описывает неко-
торый цикл в положительном направлении, и рассмотрим
у
изменение выражения — . Пусть А есть число скачков,
А.
совершённых этим выражением, от —со до -}- со; пусть k
есть число скачков этого выражения от -\- со до —со.
Пусть
2 '
число i мы назовём индексом цикла.
Если мы соединим две точки А и С цикла ABCDA
дугой АМС, лежащей целиком внутри цикла, то цикл
ABCDA будет разложен на два цикла АВСМА и AMCDA]
очевидно,
инд. ABCDA = инд. Л5С7ИЛ + инд. AMCDA.

ГЛ. III. РАСПРЕДЕЛЕНИЕ ОСОБЫХ ТОЧЕК 39
Так что подсчёт индекса какого-либо цикла можно при-
вести к подсчёту индексов, различных составляющих его
бесконечно малых циклов 1211.
Теорема III. Индекс бесконечно малого цикла, не
содержащего внутри никакой особой тонки, равен
нулю.
В самом деле," если кривая Х= 0 не пересекает этот
цикл, то
Если кривая Х = 0 пересекает цикл, то кривая К=0
его не пересекает; Y имеет один и тот же знак и X
переходит один раз от положительных значений к отри-
цательным и один раз от отрицательных значений к поло-
жительным, откуда
A = l, k = \, i = ^- = 0.
Таким же образом, если бы кривая Х=0 имела
внутри цикла кратную точку порядка т, то мы имели бы
, , . h — k n
я = т, к = т, i ^ —^— ^ "•
Теорема IV. Если бесконечно малый цикл содержит
внутри особую точку, то его индекс равен ±1.
Он равен -\-\, если особая точка есть седло; —1,
если особая точка есть узел или фокус.
В самом деле, прложим
у — р = р sin ш, . х — а = р cos ш.
Предположим, что рассматривается цикл
где р есть бесконечно малое.
Для того чтобы обойти этот цикл в положительном
направлении, надо менять ш от 0 до 2тс.

40 ПЕРВЫЙ МЕМУАР
Пренебрегая бесконечно малыми и возвращаясь к обо-
значениям предыдущей главы, мы имеем
При изменении ш от 0 до 2тс X обращается в нуль дважды,
так как
обращается в нуль дважды при двух значениях ю, кото-
рые мы обозначим ш0 и дао-|-я. При м=аш0— е, где е> 0
бесконечно мало, имеем
tga> = tga>0— S,
где С положительно и бесконечно мало. Следовательно,
У
X ei + «2 'g шо — <h^'
Заметим, что tgo>o= —^; пренебрегая по сравнению
i tg-coo величиной b?, мы получим
Yа^
_ ^__
X— а\ С '
у
Следовательно, если ахЬ^ — aa#i<0, то -^ при да =
= да0 и при ш = дао-|-1: делает скачок от —с» до -j0!
тогда
у
Если, напротив, atb2 — a2*i>0, то ^r при в> = «>0 и
при да=дао-}-гс делает скачок от -}-оо до —с»; тогда

ГЛ. III. РАСПРЕДЕЛЕНИЕ ОСОБЫХ ТОЧЕК 41
При каком же условии
afa — aa*i>0?
Возьмём опять уравнение E), которое имеет вид:
. (а,-*)(*„ —X)-0^=0.
Очевидно, что мы будем иметь
афъ — аФ\ > 0|
если оба корня уравнения мнимы или имеют одинаковые
знаки, т. е., если особая точка есть узел или фокус.
Наоборот, .
если оба корня действительны и имеют разные знаки,
т. е., если особая точка есть седло.
Следовательно, теорема доказана.
Проблема I. Вычислить индекс цикла, лежащего
целиком в одной из полусфер. "
Пусть N. есть число узлов, F—число фокусов, С—
число сёдел, находящихся внутри .цикла. Если разложить
данный цикл на бесконечное множество бесконечно малых
циклов у, то бесконечное множество циклов у будет
иметь индекс 0;
N-\-F циклов у будут иметь индекс —1;
С ' » » » • » -f-1.
Следовательно, индекс данного цикла будет
-Q.
Проблема II. Вычислить индекс экватора.
Пусть 2Nr есть число узлов, 1С' — число сёдел, лежа-
щих на экваторе.
Пусть t as — = tgco. Будем менять ю от — -^ до -f- — ,
т. е. tg ш от — со до -J- с». Так как веб симметрично

42 ПЕРВЫЙ МВМУЛР
V V
по отношению к центру сферы, то ^ = т^"
ш+тс jro же значение, что и для ш; когда мы будем
менять ш от -й- -до -к , то -р будет принимать те же зна-
чения, что и при да, меняющемся от —-н- ло -J- -г- Сле-
я . я Y
довательно, при да, меняющемся от —-к до -f- -^ , -^
h . k
сделает -j скачков от — со до -f- с» и -д- скачков от
-\- со до — с».
Установив это, рассмотрим выражение
При ш = — -J имеем Я = -f- °° >" ПРИ ш = ~\"о имеем И =
= — с».
Пусть X есть число переходов Н от отрицательных
значений к положительным, ц — число переходов от поло-
жительных значений к отрицательным; мы будем, оче-
видно, иметь
jj, — Л=-1.
Но Н может перейти от отрицательных значений к поло-
жительным или. через 0, что соответствует седлу, или
через с», что соответствует одному из тех -к значений да,
у
при которых -г: делает скачок от —с» до 4-с».
Следовательно, мы имеем
Точно так же
!
Отсюда
.Л/' — С

ГЛ. III. РАСПРЕДЕЛЕНИЕ ОСОБЫХ ТОЧЕК 43
ИЛИ
- . i = Nt — С — 1.
Примечание. Если число узлов, расположенных
вне экватора, есть 2N, число фокусов, расположенных
вне экватора, 2F, число сёдел, расположенных вне
экватора, 2С, . число узлов, лежащих на экваторе,
2N', число сёдел, лежащих на экваторе, 2С", то имеет
место соотношение
В самом деле, для того чтобы получить этот результат,
достаточно приравнять два значения индекса экватора,
полученные в двух предшествующих проблемах.
Следствие I. Полное число узлов и фокусов равно
полному числу сёдел плюс 2. ¦
Следствие II. Полное число особых точек есть
кратное 4- плюс 2.
Следствие III. Если число особых точек сводится
к 2, то эти точки — узлы или фокусы; они непременно
являются узлами, если лежат на экваторе.
Кривая Х=0 и кривая К=0 слагаются из некото-
рого числа циклов. Рассмотрим какие-нибудь два из этих
циклов: они пересекутся в чётном числе точек 1221.
Пусть <*!, ... , а8и будут 2я точек пересечения этих
двух циклов, расположенных в том порядке, в котором
они встречаются, если обходить один из циклов, напри-
мер цикл ЛГ = О, в положительном направлении.
Т е о.р е м а V. Предположим, что две последователь-
ные точки ак и ак+1 лежат в одной и той же полу-
сфере; я утверждаю, что если ак есть узел или фокус,
то ак+1 есть седло и наоборот I83'.
Для этого достаточно показать, что всякий цикл, кото-
рый охватывает ак и a#fi, имеет индекс 0.
В самом деле, пусть (черт. 3) АВ есть дуга цикла,
на которой находятся точки ак и а*+1; пусть CD и EF—
дуги цикла К = 0, пересекающие АВ в точках ак и ah+1
соответственно.

44 ПЕРВЫЙ МЕМУАР
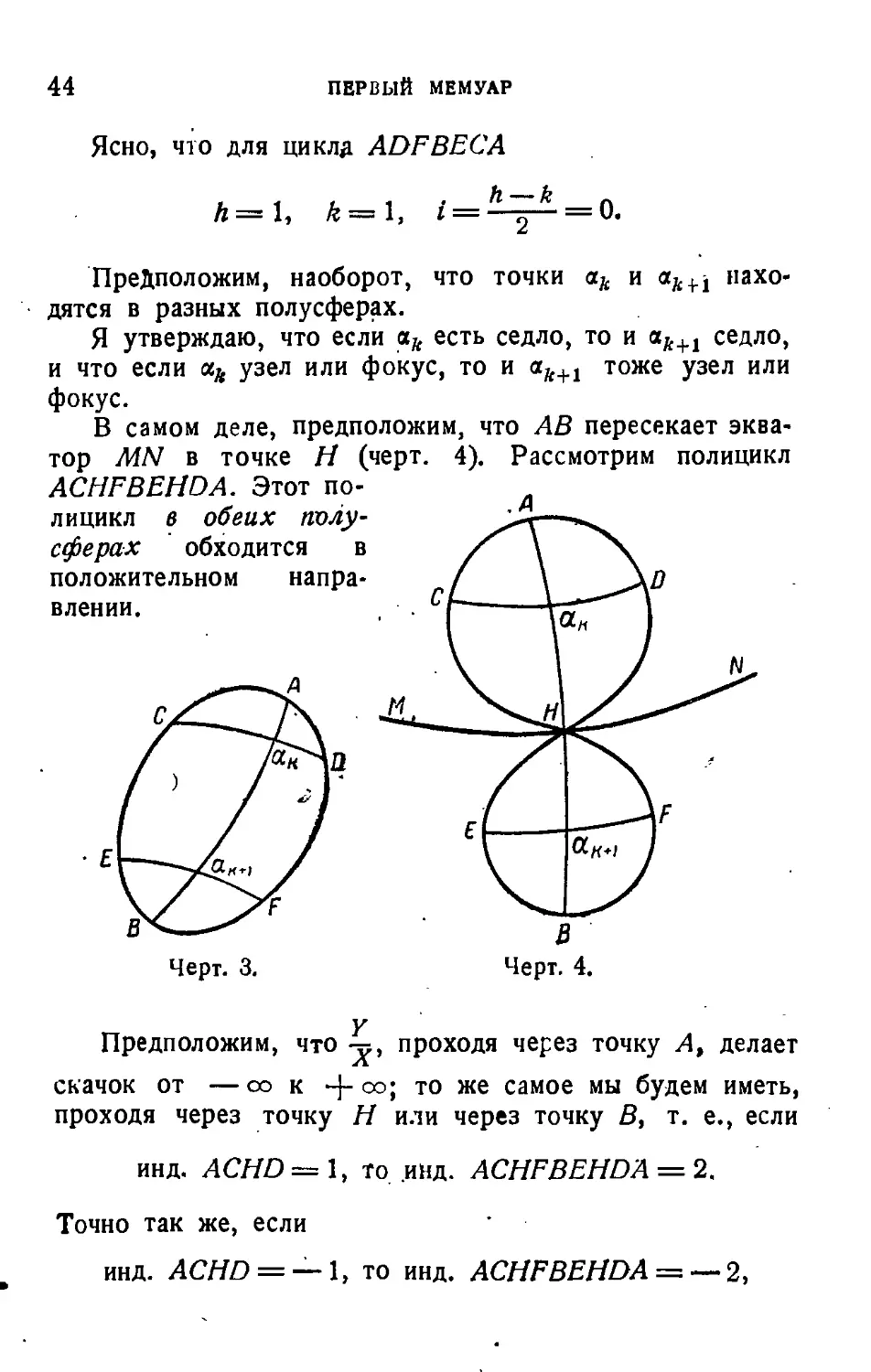
Ясно, что для циклд ADFBECA
Предположим, наоборот, что точки ак и <хк+1 нахо-
дятся в разных полусферах.
Я утверждаю, что если ак есть седло, то и ак+1 седло,
и что если аА узел или фокус, то и ак+1 тоже узел или
фокус.
В самом деле, предположим, что АВ пересекает эква-
тор MN в точке Н (черт. 4). Рассмотрим полицикл
ACHFBEHDA. Этот по-
лицикл в обеих полу-
сферах обходится в
положительном напра-
влении.
Черт. 3.
Предположим, что -^, проходя через точку А, делает
скачок от —со к -j- oo; то же самое мы будем иметь,
проходя через точку Н или через точку В, т. е., если
инд. ACHD =1, то .инд. ACHFBEHDA = 2.
Точно так же, если
инд. ACHD = — 1, то инд. ACHFBEHDA = — 2,

ГЛ. III. РАСПРЕДЕЛЕНИЕ ОСОБЫХ ТОЧЕК 45
т. е. во всех случаях
инд. ACHDA в инд. HFBEH.
Чго и требовалось доказать.
Особый случай 1241. Во всём предшествующем мы
предполагаем, что ЛГ2 и Ка одной и той же степени, при-
чём .
не равно тождественно нулю.
Мы не исследовали, что было бы, если бы мы имели
тождественно
С некоторой точки зрения, изученный нами случай есть
случай более общий, чем тот, который иы оставили
в стороне.
С другой точки зрения, — наоборот: действительно,
любые два многочлена X и Y можно рассматривать как
частные случаи многочленов
X-\-XxZ, Y+kyZ,
где \ тюстоянно и Z есть многочлен той же степени, что
и X и Y.
Итак, предположим, что мы имеем тождественно
«Yg = XZ, Уд = yZ,
где Z есть однородная функция от х и у.
В этом случае экватор не является характеристи-
кой и, следовательно, особые точки на экваторе могут
быть и узлами, и фокусами, и сёдлами.
Правило, позволявшее в предшествующем случае найти
индекс экватора, не приложимо; с другой стороны, если
экватор содержит особые точки,, то кривые
пересекаются на этом большом круге (экваторе), и он,

46 ПЕРВЫЙ МЕМУАР
следовательно, уже не имеет индекса в точном смысле
этого слова.
Итак, предположим, что на экваторе нет особых то-
чек, и посмотрим, каков индекс, этого большого круга.
Мы найдём, что вдоль эквзтора
L-У.
Х~х '
т. е., что индекс экватора будет равен — 1; замечая,
что, с другой стороны, индекс равен
-(ЛЧ-F-C),
где 2N, 2F,'2С есть число узлов, фокусов и сёдел, мы
получим
т. е. теорема, доказанная нами в предыдущем случае,
остаётся справедливой.
Предположим теперь, что на экваторе есть особые
точки, именно: 2N' узлов, 2F' фокусов и 1С сёдел, и
посмотрим, как можно обойти возникающую здесь труд-
ность.
Пусть au:-{-Cy-|-T = 0 есть какой-нибудь большой
круг, не проходящий ни через одну особую точку.
Положим
х> — х v/_ У
дифференциальное уравнение обращается в
dx' _ dy1
Х'~ Y '
где X' и Y[ суть целые многочлены по х' и у'.
Можно выбрать круг ах -f- $у -{- Y ='0 таким образом,
чтобы
1) X* и У были бы одной и той же степени;
2) большой круг ах -}- $у 4- Y ^ 0 не являлся бы харак-
теристикой, т. е. члены наивысшей степени в у'X' — х'У
взаимно уничтожались бы.

ГЛ. 1П. РАСПРЕДЕЛЕНИЕ ОСОБЫХ ТОЧЕК 47
Если (а, Ь) есть особая точка уравнения
dx dy
~~v — v »
то точка (a', b'), где
,/ ¦ a
a'
¦¦aa + pb+i '
есть особая точка уравнения
dx'
у •
Если точка (a, b)t была узлом, седлом или фокусом,
то (а', Ь') тоже будет узлом, седлом или фокусом, так
что число узлов, сёдел и фокусов будет 2{N-\-N'),
2 (С+ (У), 2 (F-f- F'), и так как мы пришли к случаю, когда
экватор не содержит ни одной точки, то можно написать

Г Л А В А IV
ТЕ0РИЯ1К0НТАКТОВ
Изучение особых точек, которое мы только что про-
вели, позволяет нам, наконец, приступить к рассмотрению
вопроса о том, каковы возможные геометрические формы
характеристик на всей поверхности сферы.
Это рассмотрение должно начаться с фундаментального
вопроса о числе тдчек, в которых данная дуга или данный
цикл касаются характеристики, т. е. с вопроса о числе
контактов данной дуги или цикла.
Число контактов алгебраической дуги или цикла всегда
конечно.
Предварительные замечания. Мы видели, что алгебраи-
ческая кривая бэз двойных точек состоит из некоторого
числа циклов; точно так же алгебраическая кривая с двой-
ными точками состоит из некоторого числа циклов и поли-
циклов. Но сами полициклы в свою очередь можно рас-
сматривать как распадающиеся на некоторое число циклов,
соприкасающихся в двойных точках и имеющих в них
угловые точки.
Так, кривая
состоит из двух диаметрально-противоположных полицик-
лов, каждый из этих полициклов состоит в свою очередь
из двух циклов, соприкасающихся в точке

ГЛ. IV. ТЕОРИЯ КОНТАКТОВ 49
и имеющих в ней угловую точку с углом между касатель-
ными в 90°. •
Мы видели, что алгебраическая кривая С пересекает
всякий 'алгебраический цикл в конечном и чётном числе
точек. Это требует некоторых пояснений.
Если в какой-либо данной точке алгебраическая кри-
вая С проходи* из внутренней части цикла во внзшнюю,
или наоборот, то мы скажем, что кривая пересекает цикл,
и эта точка будет считаться за одну точку пересечения
или за нечётное число слившихся точек пересечения. Если,
напротив, в окрестности данной точки, являющейся общей
точкой кривой С и цикла, кривая С остаётся целиком вне
или целиком внутри цикла, то мы скажем, что кривая
касается цикла, и эта точка будет считаться ?а чётное
число слцвшихся точзк пересечения 1261.
Предположим, например, что данный цикл имеет угло-
вую точку в начале и что его уравнение имеет вид
0=(у — Щ(у—ц*)-Н„
где 68 есть многочлен, содержащий только члены третьей
или более высокой степени.
Предположим, что некоторая бесконечно близкая к на-
чалу точка находится внутри цикла всякий раз, как
х>0 и (.у — Щ(у —11*)<0 РЧ,
и вне цикла, если
*<0 или если *>0, (у— Ьх)(у — цл:)>0.
Пусть
0=у — тх-\-Ь2
есть-уравнение кривой С, где 62 есть многочлен, содер-
жащий только члены второй или более высокой степени.
Легко видеть, что кривая С пересекает цикл всякий
раз, как
(/и
и касается, в противном случае:
4 А. Пуанкаре.

50 ПЕРВЫЙ МВМУАР
Теорема VI. Число контактов алгебраического
цикла, не имеющего угловых точек, не имеющего с ха-
рактеристикой точен соприкосновений высшего порядка
и не проходящего ни через одну особую точку, всегда
конечно и четно.
В самом деле, пусть уравнение этого цикла будет
мы найдём его контакты, отыскивая его точки пересечения
с кривой
Так как эта кривая есть алгебраическая кривая, то число
её точек пергсечения с данным циклом всегда четно, если
считать за два пересечения те точки, в которых кривая
касается цикла. Но в этих точках цикл имел бы с некото-
рой характеристикой контакт чётного порядка в против-
ность предположению.
Следовательно, слившихся точек пересечения у кривых
<р = 0, F = 0
вообще не существует. Следовательно, число контактов
чйтно.
Что и требовалось доказать.
Примечание I. Теорема остаётся верной ив том
случае, когда данный цикл имеет контакт высшего по-
рядка с какой-либо характеристикой, при условии, что мы
будем считать контакт л-го порядка за п контактов.
Примечание II. Предположим теперь,что алгебраи-
ческий цикл имеет угловую точку. Предположим для опре-
делённости, что эта угловая точка находится в начале
координат, что уравнение цикла, как и выше, имеет вид
0 = О — he) (у —
и что внутренняя часть цикла определяется условиями

ГЛ. IV. ТЕОРИЯ КОНТАКТОВ 51
Тогда многочлен о запишется в виде
<? = Х012к?х — (X -f tf у] + Yo [2у — (X + ц) *] + в>,
где Л'о и Уо-^ значения ЛГ и Y при лс = ^ = О, и 62 —
многочлен, содержащий лишь члены второй и более высо-
кой степени.
Угловой коэффициент касательной к кривой ср = О
в начале координат будет тогда
Для того чтобы кривая ф = 0 пересекала цикл, нужно,
чтобы выражения
имели бы разные знаки.
Упрощая, можно написать
и, следовательно, для того что5ы а и р имели бы разные
знаки, нужно, чтобы Yo — 1Х0 и Ко — \iX0 имели бы одина-
ковые знаки.
Другими словами, условием пересечения данного цикла
кривой ф = 0 является то, что характеристика, прохо-
дящая через начало, не пересекает его.
Следовательно, угловая точка должна быть сосчитана
за один контакт, если характеристика, проходящая через
эту точку, не пересекает цикла, и за два контакта в про-
тивном случае.
Примечание III.Предположим теперь, что начал),
через которое попрежнему проходит цикл, есть особая
точка. Пусть •
«2,
4*

52 ПЕРВЫЙ МЕМУАР
где Ь'7 и 6, — многочлены, члены которых второй или более
высокой стецени.
Мы будем иметь:
Кривая <р = 0 проходит через начало. Если она не
касается кривой /г = 0, то особая точка должна быть
сосчитана за один контакт: но если она имеет с циклом
F = 0 контакт я-го порядка, то особая точка должна быть
сосчитана за п -\-1 контакт.
Но, для того чтобы она касалась цикла F = О, необ-
ходимо и достаточно, чтобы
Л °
т. е. необходимо и достатоано, чтобы цикл F = О касался
бы характеристики, поскольку угловой коэффициент т
касательной к одной из характеристик, проходящих через
начало, даётся уравнением
— т (а -\- pm) -f a' -f P'm = 0.
Точно так же легко видеть, что цикл F = 0 будет иметь
в начале контакт л-го порядка с кривой-ев = 0, если он
имеет контакт л-го порядка с одной из характеристик,
проходящих через начало.
Следовательно, особая точка, через которую проходит
данный цикл, но которая не является угловой точкой этого
цикла, будет сосчитана за л -)-1 контакт, если цикл
имеет в этой точке контакт л-го порядка с характери-
стикой.
Примечание IV. Предположим, наконец, что начало
есть особая точка и угловая точка данного цикла.

ГЛ. IV. ТЕОРИЯ КОНТАКТОВ 53
Пусть попрежнему
и внутри .цикла
V -v>0, (^ — Хлг) О; — 11.x) < 0.
Мы будем иметь
. <р = (a* -f fty) 12Хадг - (к -\- И-XVl +
+ (а'дг + Р» [?^ -(* + V) *1 + °3>
где 03— многочлен, содержащий лишь члены третьей или
более высокой степени.
Черей' начало проходят, следовательно, две ветви кри-
вой <? = 0. Следовательно, начало будет сосчитано за
чётное число контактов, если обе ветви касаются или обе
ветви пересекают цикл, и за нечётное в противном случае;
другими словами, для того чтобы начало должно было бы
быть сосчитано за нечётное число контактов, необходимо
и достаточно, чтобы две касательные в начале к кривой
в = 0 не содержались бы обе вместе в одном из углов,
образованных касательными в начале к кривой F = 0, т. е.
необходимо и достаточно, чтобы выражения
¦ в = I (а' + Э'Х>СХ + & — 2Х,а (а + ?*)] -
- М2(а' + р'Х) - (а
имели бы разные знаки.
Упрощая, можно написать:
а =
Если особая точка есть фокус, уравнение
0 [

54 ПЕРВЫЙ МЕМУАР
имеет лишь мнимые корни. Левая его часть имеет, следо-
вательно, всегда один и тот же знак, а кЬ имеют разные
-знаки и особая точка считается за нечётное число кон-
тактов.
Если особая точка есть седло или узел, то ола счи-
тается иногда за чётное, иногда за нечётное число контактов,
смотря по положению касательных в начале к циклу F = 0.
Резюме. Число контактов алгебраического цикла
всегда четно при условиях:
1° соприкосновение л-го порядка считается за л кон-
тактов;
2° угловая точка данного цикла рассматривается как
один или два контакта, смотря по тому, касается ли в ней
цикла, характеристика, проходящая через эту точку, или
пересекает его;
3° особая точка считается за л-j-l контакт, если цикл
имеет в этой точке соприкосновение л-го порядка с ха-
рактеристикой;
4° фокус, являющийся угловой точкой данного цикла,
считается за один контакт;
5° седло или узел, являющиеся угловой точкой дан-
ного цикла, считаются за один или за два контакта,
смотря по положению касательных к циклу в угловой
точке.
Следствие. Если две алгебраические кривые имеют
одни и те же концы, то число их контактов может быть
одинаковой или различной чётности, если эти концы не
являются фокусами; они всегда одинаковой чётности, если
оба конца являются фокусами.
Теорема VII. Если между двумя точками сферы
можно провести какую-либо дугу без контакта, то
между этими жг точками можно провести алгебраи-,
ческую дугу без контакта.
В самом деле, пусть уравнения данной дуги будут:
где t — подходяще выбранный.параметр. Параметр гсегда
можно выбрать так, чтобы концы дуги соответствовали
значениям f = Q и *=тг.

ГЛ. IV. ТЕОРИЯ КОНТАКТОВ 55
Если данная дуга не пересекает экватора, то х и у
остаются конечными и непрерывными функциями от t при
изменении t от 0 до тс; то же относится и к их произ-
водным.
Пусть ,xv ух и л:а, уа —значения х и у для / = 0 и для
/ = 7г; функции
¦ X A^COSy— X^Sltl-^ »
обращаются в нуль при / = 0 и при / = тг.
Следовательно, функции х и у могут быть разложены
в сходящиеся ряды по sin mt следующим образом:
m$inmt-\-x1 cos ^-{-x^sin-^,
«1=1
4n^. [«4.
y=
Точно так же будут сходящимися и ряды
т=оо
т
T *2 "?л cos т/ ~ Ysin Y + Т cos
m = l
m ~ oo
, cos mt—Q sin ^ +^- cos -^
Й
« d*
Если подставить эти величины вместо х, у, -г? ,
в выражение
dy vdx
то получится функция от t, которая при t, ¦ меняющемся
от 0 до те, не обратится в нуль 1301 и квадрат которой
остаётся, следовательно, веб время большим некоторой
данной величины и9.

56 ПЕРВЫЙ МЕМУАР
Пусть
А^~ 2 Am%\nmt-\-xlzos-^-\-x2s\n^
т = 1
m^V- t t
Sh. = 2 Bm sln mt +^i cos 2- -f- _y2 sin ^
Дуга ¦
есть алгебраическая дуга и имеет те же концы, что и
данная дуга.
Кроме того, всегда можно взять jj. столь большим,
чтобы Ар, Вр, —J-, —¦ сколь угодно мало отличались
<*? di> dB. dA.
бы от ?@, ^(О. ~dl' If и чтобы X-dt~Y'dT> ГДе
л; и _у в ЛГ и К заменены через А^ и S^, сколько угодно
мало отличались бы от Х-% — К-^,гдел:и.увЛТи К
заменены через « и iji, В частности, можно взять jj. столь
dB. dAp
большим, чтобы выражение Х-~- — К ~ отличалось бы
от Х-77 — Y ~Jf меньше чем на s и, следовательно, чтобы
мы имели всё время
dB, dAu. <
Но в этом случае дуга
х
будет алгебраической и без контакта.
Что и требовалось доказать.
Если бы Данная дуга пересекала экватор, но не пере-
секала большой круг

ГЛ. IV. ТЕОРИЯ КОНТАКТОВ 57
S •
то мы сделали бы замену переменных, полагая
и теорема была бы доказана тем же способом.
Если бы данная дуга пересекала все большие круги
сферы, то мы разложили бы её на некоторое число вспо-
могательных дуг, ни одна из которых не пересекала бы
всех больших кругов сферы, и теорема, доказанная после-
довательно для всех этих вспомогательных дуг, была бы
справедлива и для дуги в целом.
Теорема VIII. Если АВ есть алгебраическая дуга
без контакта и ААи ВВХ— две дуги характеристик,
/по между точками Ах и Вх можно провести дугу без
контакта. ¦
В самом деле, пусть
есть уравнение дуги АВ, где <р и ^ — непрерывные функ-
ции от t, принимающие лишь одно значение для каждого
значения t. Пусть i и р —'значения t, соответствующие
точкам А и В.
Каждому значению t соответствует одна и только
одна характеристика, так что значениям а и р соответ-
ствуют характеристики ААХ и ВВУ Пусть t0, t{, i.?, .. .
будут значения t, которым соответствуют характеристики,
проходящие через сёдла.
Рассмотрим характеристику, соответствующую некото-
рому данному значению L Пусть 5 есть длина дуги этой
характеристики, отсчитываемая от той точки, в которой
она пересекает дугу АВ. Обе величины Sat определяют
точку сферы и образуют, так сказать, новую систему
координат. Пусть
/ = а, s = if — координаты точки Ах\
t=$, s = 3—координаты точки Sjj
i = t0, s — s0 | координаты сёдел;

53
ПЕРВЫЙ ЫЕЫУАР
Уравнение
s = F(t),
где F есть непрерывная функция t, имеющая лишь одно
значение при каждом значении t, изображает непрерывную
кривую, не имеющую контактов при всех значениях t, не
равных ни /0, ни (и ..., а при t = i0, например, непре-
рывную и без контактов, если при этом значении s<s0.
Но всегда можно выбрать F таким образом, чтобы
при t = a F = T,
при t = p F = b;
при t = t0 F<s0;
при t = ty
tB'
т. е. можно провести от
А1 до Ву дугу без кон-
тактов и, следователь-
но, алгебраическую ду-
гу без контакта 1811.
Что и требовалось
доказать.
{черт. 5) — две ха-
дае алгебраические
Черт. 5.
Теорема IX. Если АВ и /ijfi
рактеристики и если ААХ и ВВ^
дуги, не пересекающие АВ и AtBy ни- в одной точке
отличной от точек А, А1 и В; Ви то числа контактов
дуг АА1 и ВВ^ одинаковой чётности.
Пусть А' есть точка, столь близкая к Л, что дуга
АА' не имеет контакта и что характеристика А'В' пере-
секает дугу ВВХ в такой точке В', что дуга ВВ' не
имеет контакта.
Предположим также, что а[в[ есть дуга характери-
стики и что дуги i4jAi и SjSi также без контакта.
По предыдущей теореме можно провести алгебраи-
ческие дуги без контакта АВ' и AiBr
Число контактов алгебраического цикла
АВ'ВХА\А
должно быть чЗтно.
t_ Но характеристики АВ, А%Ву касаются этого цикла

ГЛ. IV. ТЕОРИЯ КОНТАКТОВ 59
в А и в В, характеристики А'В' и AiBi пересекают ею
в В' и в А[. Следовательно, четыре угловые точки счи-
таются за чётное число контактов. Следовательно: число
контактов АВ' -\- число контактов В'В^ -\- число контактов
В1А'1-\-часло контактов а[а^зО (mod 2) или, что то же,
число контактов ААХ -\- число контактов ВВ1 = 0 (mod 2).
Что1, и требовалось доказать.
Теорема X. Если дуга некоторой кривой поддер-
живает Характеристику, не проходящую ни через одну
особую точку, то число контактов на этой ду?е кри-
вой нечётно I32!.
В самом деле, пусть F = 0 есть уравнение поддержи-
вающей дуги. Рассмотрим функцию F; эта функция пере-
ходит,, например, от положительных значений к отрица-
тельным, когда точка (л:, у), описывающая характеристи-
ку, проходит через один из концов поддерживающей дуги,
и or отрицательных к положительным, когда она прохо-
дит через другой конец этой дуги. Это значит, что функ-
ция F проходит через нечетное число максимумов и ми-
нимумов, когда точка (л:, у) описывает данную дугу харак-
, теристики. Но эти максимумы и минимумы даются урав-
нением .
дх ' ду '
значит, дуга характеристики пересекает кривую о = 0 в
нечётном числе точек.
Но эта кривая, являясь алгебраической, пересекает в
чётном числе точек цикл И, образованный дугой харак-
теристики и поддерживающей дугой; следовательно, она
пересекает поддерживающую цугу в нечётном числе точек.
Следовательно, число контактов этой дуги нечётно.
Что и требовалось доказать.
Примечание I. Как нужно изменить теорему, если
дуга характеристики проходит через седло?
Седло принадлежит, очевидно, кривой о = 0, но оно
является максимумом или минимумом функции F лишь
при условии, что дуга; характеристики имеет в нём угло-
вую точку.

60 ПЕРВЫЙ МЕМУАР
В самом деле, предположим сперва, что там нет угло-
вой точки. Кривые р=р{х0, у0) и <? = 0 обе пересекут,
вообще говоря, цикл Н, т. е. седло будет точкой простого
пересечения цикла и о = 0, не соответствуя ни макси-
муму, ни минимуму функции F.
Если, наоборот, седло является угловой точкой, то одна
из кривых: ® = 0, /г = 0, пересечёт цикл Н, а другая—
коснётся его, так что седло окажется или же точкой про-
стого пересечения Н и <э = 0 и в то же время точкой макси-
мума функции F, или же оно будет двойной точкой пересе-
чения Н и ер = 0, не являясь точкой максимума функции F.
Следовательно, если дуга характеристики проходит
через седло и не имеет там угловой точки, то число кон-
тактов поддерживающей дуги четно.
Если дуга характеристики проходит через седло и
имеет в нём угловую точку, число этих контактов нечетно.
ПримечаниеII. Точно так же можно показать, что
если дуга характеристики не проходит ни через одну осо-
бую точку, то на" дуге, которая ее перехватывает, число
контактов четно.
Контакты топографической системы. Если мы рас-
смотрим какую-нибудь алгебраическую топографическую
систему, то геометрическое место точек контакта такой
системы есть алгебраическая кривая.
Будем различать внутренние и внешние контакты топо-
графической системы, смотря по тому, остаётся ля харак-
теристика в окрестности контакта внутри того цикла
топографической системы, которого она касается, или,
наоборот, остаётся вне этого цикла.
Кривую контактов можно таким образом разделить на
определенное число дуг, которые будут соответственно
дугами внутренних и дугами внешних контактов.
Эти дуги будут разделены:
1° особыми точками;
2Э точками, в которых кривая контактов касается
одного из циклов топографической системы.

ВТОРОЙ МЕМУАР
ГЛАВА V М
ТЕОРИЯ ПОСЛЕДУЮЩИХ
сновное соглашение. Рассмотрим какую-либо
полухарактеристику', мы будем продолжать
неограниченно, если это можно сделать, не
встретив ни одной особой точки. Если, напро-
тив, двигаясь по этой полухарактеристике,
мы придём в" узел, то мы остановим её в узле; если
мы придём в седло, то нам представятся три возможных
пути, по которым мы можем продолжить характеристи-
ку: первый — по прямому про-
должению пути, которым мы
шли до сих пор, и два дру-
гих — направо и налево; кы усло-
вимся следовать одному из пу-
тей, ведущих направо или нале-
во, никогда не выбирая того,
который прямо ' перед нами.
Например (черт. 6), продолжением АО мы будем считать
либо ОВ, либо OD, но не ОС 121. Таким образом,
можно сказать, что в окрестности седла есть четыре
характеристики, склеенные друг с другом и имеющие
попарно общую ветвь; это характеристики АОВ, ВОС,
COD, DOA.
Черт. 6.

62 ВТОРОЙ МЕМУАР
Определение последующих. Пусть .
— алгебраическая дуга без контакта; о и-^ — алгебраические
функции от t, имеющие лишь по одному значению для
каждого значения t. Пусть концы дуги соответствуют
значениям t:
Такая дуга без контакта будет иметь две стороны, кото-
рые мы назовём её прайЬй и левой сторонами; действи-
тельно бесконечно близкая к дуге АВ точка может лежать
еправа или слева от этой дуги. Например, точка т лежит
Черт. 7. Черт. 8.
слева от дуги АВ (черт. 7), точка/я' —.справа от дуги АВ,
потому что нельзя перейти от одной из этих точек
к другой, не пересекая дугу АВ или не удаляясь от этой
дуги на конечное расстояние или не проходя через окруж-
ность бесконечно малого радиуса, начерченную вокруг А
или В как центра 1*1.
Установив это, рассмотрим какую-либо точку Мо
дуги АВ (черт. 8). Из этой точки выходят две полу-
характеристики — одна налево, другая направо от
дуги АВ', рассмотрим ту, которая идет налево. Может
представнеиться сколько случаев.
1° Эту полухарактеристику можно неограниченно про-
должать, не пересекая снова дугу АВ.
2° Эта. полухарактеристика, не пересекая более
дугу АВ, накручивается на фокус.

ГЛ. V. ТЕОРИЯ ПОСЛЕДУЮЩИХ 63
3° Не встретив снова дугу АВ, она кончается в узле,
где мы и должны её остановить согласно основному со-
глашению. В этих трёх первых случаях мы скажем, что
точка Мо не имеет последующей.
; 4° Полухарактеристика снова пересекает дугу АВ
в точке Mv не пройдя ни через одну особую точку. Мы
скажем тогда, чтЬ точка М1 есть последующая точки Мо.
i 5° Полухарактеристика кончается в седле, не встре-
тив снова дугу АВ. В этом случае в силу основного
соглашения надо свернуть направо или налево, и каждый
из этих путей может нас привести или не привести к.
пересечению с дугой АВ. Точка Мо может иметь тогда
О, 1 или 2 последующих.
Может, наконец, случиться, что полухарактеристика
встречает два седла или даже больше; в этом случае
точка Мо может иметь больше двух последующих.
Если, отправляясь от точки Мо, мы рассмотрели бы
вместо левой полухарактеристики правую, то мы могли
бы придти к некоторой точке М', лежащей на дуге АВ.
Мы будем называть эту точку М' предшествующей
точке Мо.
Таким образом, точка Мо будет предшествующей для
своей последующей Mv
Если значения t,. соответствующие Af0 и Ми суть /0
и tlt то соотношение, связывающее t0 и tu есть закон
последования.
Теорема XI. Если to = tlt то характеристика
есть цикл. Если же to^tlt то характеристика есть
спираль.
В самом деле, первая половина утверждения .есть просто
тавтология. Вторую легко доказать следующим образом.
Заметим прежде всего, что дуга M0DM1 (черт. 9)
перехватывает (sur-tend) дугу характеристики М0СМи
так как она не имеет контактов (теорема X). у
Кроме того, эта дуга М^рМ-^ не пересекает характе-
ристику ни в одной точке, отличной от Мо и М^. В про-
тивном случае дуги MiM%, M0M3 поддерживали бы
(sous-te'ndus) дуги М^М^ М0НМ3, что невозможно,
так как они, по предположению, не имеют контактов.

64
ВТОРОЙ ЫЕМУАР
Установив это, проведём через точку No, бесконечно
близкую к Мо и находящуюся слева от неё дугу харак-
теристики NqEN^, она пересечет дугу,М0М1 в точке Л^,
бесконечно близкой к М1 и «аходящейся слева от неё,
так как перейти на правую сторону она могла, бы лишь
пересекши характеристику M0CMlt что невозможно. Цикл
Afj/WoNofTVj пересекается с характеристикой М0СМ1 в
одной лишь точке Мо. Следовательно, эта характеристика
есть спираль.
Что и требовалось доказать.
Теорема XII. Всякая характеристика, которая
не кончается в узле, есть цикл или спираль М.
В самом деле, если эта ха-
рактеристика не пересекает ни
один алгебраический цикл в
бесчисленном множестве точек,
то она является циклом в силу
теоремы I.
Если, напротив, она пере-
секает алгебраический цикл в
бесконечном множестве точек,
то, так как этот цикл состоит
из конечного числа дуг без
контакта, она пересечёт одну
из этих дуг более чем в одной точке, т. е. одна из точек
пересечения будет иметь последующую.
Если эта точка пересечения совпадает со своей после-
дующей,— характеристика является циклом; если она не
совпадает со своей последующей, — характеристика явля-
ется спиралью в силу теоремы XI.
Следовательно, теорема доказана.
Теорема XIII. Пусть точка Мо определяет харак-
теристику, не проходящую через седло, и пусть Мо
имеет последующую Мх; если ^ = 0^^ есть закон по-
следования, то функция <f1 голоморфна для значений t0,
близких к тому, которое соответствует точке Мо.
В самом деле, мы предположили с самого начала, что
в уравнении дуги без контакта:
Черт

ГЛ. V. ТЕОРИЯ ПОСЛЕДУЮЩИХ 65
к
функции 9 и «J* — голоморфные функции от t для значений t,
близких к тому, которое соответствует Мо, а также
для значений t, близких к тому, которое соответствует Mv
, Предположим, что мы имеем то решение уравнения
в частных производных
которое обращается тождественно в t0, если в нбм поло-
жить
(*) и у =
Эго решение даёт поверхность, проходящую через про-
странственную кривую
В окрестности точки Мо это решение будет голоморф-
ной функцией от Jt и у, так как дуга
не касается характеристики.
Но она будет голоморфна по х и но у также й вдоль
всей характеристики, проходящей через точку УИ0, если
только эта характеристика не проходит ни через одну
особую точку. Но мы предположили, чго эта характери-
стика доходит до точки Mlt не встретив ни одной осо-
бой точки. Следовательно, в окрестности точки Мх пере-
менная г есть голоморфная функция от х и у; и если
положить
то z становится голоморфной функцией от tx в окрестно-
сти того аначения tu которое соответствует М1.
Но z есть не что иное,» как t0. Следовательно, t0
есть голоморфная функция от tv Точно так же можно
доказать, что tx есть голоморфная функция эт t0 в окрест-
ности значения t0, соответствующего Мо..
Следствие I. Функция tK = Ь,(/0), выражающая
закон последования, может иметь разрывы только при
5 А. 11уанкар»

66 ВТОРОЙ МЕМУАР
*
тех значениях t0, которые соответствуют характеристикам,
проходящим через сёдла.
Следствие II. Если дугу АВ без контактов разде-
лить на части, так что точки каждой части или все имеют
последующие, или все нз имеют их, то 'граница каждой
части будет иметь своей последующей конец дуги без
контакта АВ или будет соответствовать характеристике,
проходящей через седло.
Следствие III. Пусть концы д;ти без контакта
соответствуют величинам
t = a и * = Р;
пусть ни при каком t из промежутка
отвечающая ему характеристика не проходит через седло;
пусть при данных постоянных otj и Pj для всех значений t
из промежутка
соответствующая характеристика есть цикл.
Тогда харак геристики, определяемые любым значениемt,
содержащимся между аи^, всегда являются циклами.
Теорема XIV. Величина ~ всегда положительна.
В самом деле, пусть АВ есть дуга без контакта
(черт. 10), М0М1 — характеристика и No — точка, беско-
нечно близкая к М6 и лежащая справа от неё. Пусть
7У0Л^ есть характеристика, проходящая через эту точку.
Точка Nl бесконечно близка к Mt; я утверждаю, что Л^
лежит справа от М1. Действительно, если бы она лежала
слева, то характеристика Л/^Л^ при продолжении своём
за точку. Л/2 выходила бы из цикла MqHM^qMq, т. е.
дуга характеристики N0N[ была бы поддержана дугою
NONU что невозможно, так как эта дуга без контакта.
Изучение кривой последования И. Если рассматри-
вать величины t0 и tx как координаты точки, то закон
последозания

ГЛ. V. ТЕОРИЯ ПОСЛЕДУЮЩИХ
67
даёт некоторую кривую. Эта кривая лежит целиком
в квадрате
Первый случай. Ни одному значению t из проме-
жутка не соответствует характеристика, проходящая через
седло.
, В этом случае крияая последования непрерывна; пря-
мые, ¦параллельные осям, пересекают её лишь в] одной
точке; двигаясь по этой кривой в подходяще выбранном
Л F В п
Черт. 10.
направлении, мы будем ?всё_»время удаляться от осей
координат. Это значит, что" если KLCD есть (черт. 11)
квадрат
= а>
«.
то кривая имеет вид, подобный кривым
АВ, CD, EF, ОН.
Она будет иметь вид CD, если значения ta, равные а
и J3, соответствуют циклам, тогда как никакое другое значе-
ние tf0, содержащееся между аир, не соответствует циклу.
Второй случай. Предположим, что некоторым
значениям t '

68 6Т0<»0Й МЁМУЛР
содержащимся между а и 8, соответствуют характеристики,
проходящие через седло; что, кроме того, значениям а
и В соответствуют циклы и что никакому промежуточному
значению не соответствует цикл.
Из каждого седла выходят четыре ветви характе-
ристик; некоторые из этих ветвей пересекают дугу без
контакта, другие не пересекают.
Предположим сначала, что все те Еетви, которые пересе-
кают дугу без контакта, выходят из одного и того же
седла.
1° Невозможно, чтобы все четыре ветви, вышедшие
из одного седла, пересекли' дугу без контакта. Пусть,
в самом деле, данная дуга без Контакта есть АВ (черт. 12).
Пусть С есть данное седло; пусть СМ0, CMlt CNQ,
__. _^ . СЛ^— четыре ветви ха-
"*" рактеристик, выходящие
из этого седла, такие, что
M^Mq, N^Nq не имеют
угловых точек.
По теореме X, приме-
чанию I, часть MQMt ду-
ги АВ поддерживает ха-
рактеристику МоСМ^Обе
дуги АМ0, МХВ находят-
ся, следовательно, по
iCM0; назовём эту сторону
внешней частью цикла. Из двух ветвей кривых CN0, СЛ^
одна находится вне, другая внутри цикла MqMjCMq. Пусть
CNX находится • внутри; она не может пересечь дугу АВ
иначе, как между Мо и М1 и с той же стороны, что и
ветви кривой СМ0, CMt; таким образом, алгебраическая
дуга М^ поддерживает дугу характеристики M^CN^ что
невозможно по теореме X.
Таким образом, сделанное нами вначале предположе-
ние невозможно.
Что и требовалось доказать.
2° Может случиться, что три ветви, выходящие из
одного и того же седла, пересекаютfдугу без контакта.
В этом случае либо существует точка, имеющая две по.
У >
/
/
A/ No С \
Черт. 12.
одну и ту же сторону
S
В
^>
цикла .
\
4
/
Mi

ГЛ. V. ТЕОРИЯ ПОСЛЕДУЮЩИХ
69
следующих, причём точки, лежащие между этими по-
следующими, не имеют предшествующих; либо существует
точка, имеющая две предшествующих, причём точки,
лежащие между этими предшествующими, не имеют по-
следующих.
Таким образом, кривая последования имеет вид или
CHFD, или CABD (черт. 13).
3° Не может случиться, чтобы только две или только
одна ветвь, выходящая из седла, пересекли бы дугу без
Черт. 13. ¦ Черт. 14.
контакта. В самом деле, предположим сначала, что две
ветви характеристик СМ0 и СМ1 пересекают АВ и что
MfiCM1 имеет угловую точку в С (черт. 14). Бесконечно
близкая к уИ0 точка будет иметь последующую, если она
лежит справа от Мо, и не будет иметь последующую,
если она лежит слева от Мо. В силу следствия II тео-
ремы XIII, точки дуги М0А не имеют последующих. Точка,
бесконечно близкая к А, не будет иметь последующей,
чго невозможно, так как А есть своя собственная после-
дующая. Точно так же, предполагая, что М^СМ^ не имеет
угловой точки или что СМ1 не пересекает дугу ABt
мы пришли бы к невозможному следствию, что беско-
нечно близкая к А точка не имеет последующей. Следо-
вательно, предположения, сделанные вначале, невозможны.
Что и требовалось доказать.
Мы не будем детально исследовать те случаи, когда
ветви характеристик, пересекающие дугу без контакта,
выходят из нескольких различных сёдел. Рассмотрение

70
ВТОРОЙ МЕМУЛР
основывается на тех же принципах и является только
более длинным. Приведём только несколько примеров
возможных комбинаций.
Кривая CABD (черт. 15). Дуга без контакта пере-
сечена двумя ветвями характеристик, вышедшим из одного
седла \, и двумя ветвями, вышед-
шими из другого седла (а. Каждая
из этих двух систем из двух ветвей
характеристик имеет угловую точ-
ку— одна в А., другая в ja.
Если менять t0 от а до значе-
ния, соответствующего точке А и
характеристике, проходящей через \,
,.уо .последующая существует; далее,
при t0, меняющемся от значения, со-
ь L ответствующего точке А, до значе-
Черт. 15. ния, соответствующего точке В и
характеристике, проходящей через р,
последующей нет; а когда tQ меняется от значения,
соответстьующего точке В до C, последующая снова
существует 161.

ГЛАВА VI
ТЕОРИЯ ПРЕДЕЛЬНЫХ ЦИКЛОВ
В силу того, что мы видели выше, характеристики
могут быть разделены на четыре класса:
1° циклы;
2° спирали, которые можно неограниченно продолжать
в оЗе стороны, не останавливаясь в узле, не приближаясь
к фокусу и не возвращаясь в исходную точку;
3° характеристики, которые можно неограниченно про-
должать в одну сторону, не встречая узла и не прибли-
жаясь к фокусу, но которые при продолжении в другую
сторону кончаются в узле или неограниченно прибли-
жаются к фокусу;
4° характеристики, которые и в ту и в другую сто-
рону кончаются в узле или в фокусе.
По тем же принципам полухарактеристики делятся
на четыре класса:
1° циклы;
2° полуспирали, вдоль по которым можно пройти
бесконечную дугу, не приходя в узел или фокус и не
возвращаясь в исходную точку;
3' полухарактеристики, кончающиеся в узле;
4°полухарактеристики, неограниченно закручивающиеся
вокруг фокуса.
В силу теоремы I пол/характеристики второго класса
пересекают некоторые алгебраически г циклы и, следова-

72
ВТОРОЙ МЕМУАР
тельно, некоторые алгебраические дуги без контакта
в бесчисленном множестве точек.
Пусть АВ—одна из этих дуг без контакта.
Пусть Мо (черт. 16) —та точка, из которой выходит
рассматриваемая полухарактеристика. Пусть Mt — по-
следующая точки MQ и пусть Mi лежит справа от Мо.
Пусть УИа — последующая
точки Mv /W3— последующая
точки УИа и т. д.; Ма лежит
справа от Мх, Мъ — справа от
Ма и т. д.
Вообще М„ и лежит справа
от Мп и так как при сколь угод-
но большом п точка Мп лежит
на дуге АВ, то Мп стремится
к некоторому пределу, когда п
неограниченно растёт. Пусть
этот предел есть Н.
. ^Последующая точки Мп,
когда п бесконечно велико,
бесконечно близка к Мп. Сле-
довательно, Н есть своя собственная последующая 171.
Следовательно, характеристика, проходящая через Я,
есть цикл; мы назовём её предельным циклом данной
полухарактеристики. Пройдя по характеристике, прохо-
дящей через Мо, достаточно большую дугу, можно как
угодно близко подойти к точке Н.
Пусть НК—дуга характеристики, проходящей через
точку Н. Пусть CD — алгебраическая дуга, проходящая
через К.
Можно взять п столь большим, чтобы дуга характе-
ристики, вышедшая из Мп, пересекла бы CD.
Предположим, например, что Дуга, вышедшая из УИ2,
пересечёт CD в ЛГ2; дуга, вышедшая из М3, пересечёт CD
в Ns; дуга, вышедшая из Мп, — в точке Nn. Точка ЛГ3 будет
лежать направо от Af2,..., Л^+1 — направо от Nn. Таким
образом, данная полухарактеристика пересечёт CD в'бес-
конечном множестве точек Afa, N3,..., Nn,... и Nn будет
стремиться к К при неограниченно возрастающем п.
Черт. 16.

ГЛ. VI. ТЕОРИЯ ПРЕДЕЛЬНЫХ ЦИКЛОВ 73
Таким образом, всякая полухарактеристика второго
класса имеет предельный цикл.
Каждая алгебраическая дуга, сколь бы мала она ни
была, пересекающая этот цикл, пересечёт и полухарак-
теристику в бесконечном множестве точек.
На полухарактеристике можно найти точку, которая
будет сколь угодно близка к какой-либо точке её пре-
дельного цикла.
Пусть АВ (черт. 17) есть алгебраическая дуга без
контакта. Предположим, что ни одной точке М, лежащей
между А и В, не соответствует характеристика, про-
ходящая через седло; что точке Мо соответствует пре-
дельный цикл и что ни одной точке М, отличной от Мо
и лежащей между А и В, не соответствует предельный
цикл. Каждая характеристика, пересекающая АВХ будет
иметь предельным циклом тот цикл, который проходит
через Мо.
<В
д -в
Черт. 17. Черт. 18.
Рассмотрим предельный цикл С (черт. 18), не прохо-
дящий через седло и проходящий через точку Мо\ через
MQ можно провести столь малую алгебраическую дугу АВ,
чтобы она была без контакта и чтобы между Мо и А
или между Мп и В нз было бы ни одной точхи,
которой соответствовал бы предельный цикл или характе-
ристика, проходящая через седло. Тогда все характе-
ристики, пересекающие АВ, будут иметь С предельным
циклом, так что С будет предельным циклом для двух
систем характеристик, лежащих одна внутри цикла, дру-
гая вне него.

74
ВТОРОЙ МЕ.МУЛР
Посмотрим, что происходит, когда С проходит через
седло. Пусть Н—седло и НА, НВ, НС, HD — чэтыре
ветви характеристик, выходящие из этого седла. Пред-
положим, чго две из этих ветвей, например, НА и НВ,
кончаются в одной и той же точке М таким образом,
что образуют цикл НАМВН; этот цикл будет предельным
циклом для кривых вида аа, что доказывается исследо-
ванием чертежа (черт. 19) 181._
Рассмотрим, напротив, кривую рр; легко видеть, что
если ветви, кривых НС, HD не кончаются в одной и той
же точке N, то цикл НАМВН не является предельным цик-
лом для pp. Если, напро-
тив, НС и НВ соединяются
в N, то кривые рр имеют
предельным циклом поли-
цикл
HAMHDNCH.
N
Теорема XV. Внутри
и вне любого предельного
цикла находится по край-
ней мере один фок\х или
узел М.
При доказательстве этой теоремы мы будем называть
касаниями цикла те точки, в которых он касается одного
из больших кругов л: = const.
Касания будут прямые, если и окрестности точки
соприкосновения касающийся большой круг остаётся вне
цикла. Они будут обратными в противном случае.
Мы докажем сначала две следующие леммы:
Лемма I. Если точки пересечения экватора с боль-
шим кругом х = 0, которые мы обозначим через т, т\
обе находятся вне некоторого цикла, то избыток числа
прямых касаний этого цикла над число л его обратных
касаний равен 2.
Если точки т, т' лежат обе внутри цикла, то этот
избыток равен — 2.
Если одна из точек лежит вне, а другая внутри цикла,
то этот избыток равен 0.

ГЛ. VI. ТЕОРИЯ ПРЕДЕЛЬНЫХ ЦИКЛОВ 75
В самом делг, от любого цикла А к любому другому
циклу В можно перейти путём непрерывных деформаций,
т. е. переходя от цикла А к циклу А', бесконечно мало
от него отличающемуся, и затем через серию циклов С,
бесконечно мало отличающихся друг от друга, приходим'
к циклу В', бесконечно мало отлячающемуся от В.
При этих последовательных деформациях прямое каса-
ние никогда не перейдёт в обратное касание и обратное
касание не перейдёт в прямое, так как это могло бы
наступить лишь тогда, когда одни из больших кругов
имели бы касание высшего и притом нечётного порядка
¦ с одним из циклов; но в этом случае слились бы два
касания, одно прямое и одно обратное, и они, вообщэ
говоря, должны были бы исчезнуть для одного из циклов,
бесконечно близких к С.
Избыток, который оценивается в этой лемме, может
меняться при непрерывных изменениях цикла только тогда,
когда сливаются и затем исчезают два касания. Но эго
может наступить в двух случаях:
1° Когда один из циклов С проходит через одну из
точек /я, /и', но мы предположим: 1) что обе точки т
и п! находятся внутри Л и вне В; или 2) что обе точки m
и /и' находятся вне А и вне В; или 3) что m находится
вне А и вне В, тогда как /и' находится внутри обоих
этих циклов. Следовательно, всегда можно найти серию
циклов С, позволяющих перейти от цикла А к циклу В
таким образом, чтобы ни один из циклов С не проходил
бы ни через m ни через /и'.
2° Изменение избытка может произойти ещё и тогда,
когда один из циклов С соприкоснётся с одним из боль-
ших кругов х = const. Но в этом случае сливаются и
исчезают одно прямое и одно обратное касания. Следо-
вательно, оцениваемый избыток не изменяется.
Следовательно, этот избыток один и тот же для А и
для В.
Предположим теперь, что А есть какой-либо
выпуклый цикл, aS — данный цикл.'
Избыток, о котором идёт речь, будет для А равен 2,
если m и /и' лежат вне А; он будет равен — 2, если обе

76 ВТОРОЙ МЕМУАР
точки /ии/»' лежат внутри А, и нулю, если одна лежит
внутри, другая вне А.
Избыток, о котором идёт речь, будет для В равен
2,—2 и 0 при тех же условиях.
Следовательно, лемма доказана. .
Лемма II. Если обходить цикл таким образом,
чтобы внутренняя его часть была всё время слева,
то при каждом прямом касании -^ делает скачок от
-\- оо до — оо, если мы находимся в нижней полу-
сфере, и от — то до -f- то, если мы находимся в верх-
ней полусфере; для обратных касаний наоборот.
Доказательство теоремы. Предположим сна-
чала, что предельный цикл таков, что обе точки /и и /»'
находится по одну и ту же сторону цикла, которую мы
будем называть внешней.
Пусть:
v есть число узлов и фокусов, находящихся внутри
цикла;
v' есть число узлов и фокусов, находящихся вне цикла;
Т и^у'—числа сёдел, расположенных внутри и вне цикла.
' Имеем
•v^_v' —f —f = 2.
Цикл пересекает экватор в нескольких точках, так
что его можно разложить на некоторое число вспомога-
тельных циклов, одни из которых лежат целиком в ниж-
ней полусфере, другие — целиком в верхней полусфере;
эти циклы образованы из дуг первоначального цикла и
дуг экватора.
Пусть, для определённости, данный цикл есть
ALDKCGBHA и пусть он пересекает экватор в точках
А В, С; D (черт. 20). Цикл разлагается на три вспомо-
гательных цикла
АЕВНА, CFDKC, CGBEALFC.
По теореме IV имеем:
L " — (v — т) •= инд. АЕВИА + инд. CFDKC +
-f инд. CGBEALDFC.

ГЛ. VI. ТЕОРИЯ ПРЕДЕЛЬНЫХ ЦИКЛОВ 77
Пусть теперь <х, а', а", а!" есть число прямых каса-
ний дуг АНВ, CKD, CGB, ALD; ft р', р", р'" —число
обратных их касаний; пусть X и
X' — число скачков от—то до-f-
:-j-'oo, которые делает -тт» когДа
мы проходим дуги ЛЕВ и CFD;
пусть |л и ji' — число скачкбв от -}-
. -|- то до — то, которые делает -rz,
когда мы проходим дуги АЕВ Чгрт. 20
и CFD.
Замечая, что вдоль всего данного цикла
в силу леммы II имеем:
2 инд. АЕВНА = — а-\-Ъ —ji
2 инд. CFDATC =-a' + X'— ji
2 инд. COBEAL** — а' — а"+р' + р"-V— X'
откуда
— Bv — 2"г) = р + р' + р" + р'" — а — а' — а" — а
или по лемме I
— Bv — 2f) = — 2, v — -у = 1.
Следовательно, мы имеем также
откуда
v>0, v'>0.
Чго и требовалось доказать.
Если /п и т' находятся по разные стороны цикла, то
эту трудность легко преодолеть.
В самом деле, всегда можно найти на сфере две
диаметрально-противоположные точки, находящиеся по

78 ВТОРОЙ МЕМУАР
одну и ту же сторону цикла, и достаточно сделать за-
мену переменного, для того чтобы придти к только что
рассмотренному случаю.
Если нельзя наЧти на сфере две диамзтрально-проти-
воположные точки, находящиеся по одну и ту же сторону
цикла, то точки дикла попарно диаметрально-противо-
положны, т. е. цикл сам симметричен по отношению
к центру сферы; но тогда теорема очевидна.
Теорема XVI. Алгебраический цикл, проходящий
через все узлы и все фокусы, пересекает все предельные
циклы. ' '
В самом деле, пусть С—какой-либо предельный цикл;
¦ одни узлы и фокусы находятся внутри него, другие узлы
и фокусы вне него.
Следовательно, одни точки алгебраического цикла
лежат вче С, а другие внутри С, т. е. данный алгебраи-
ческий цикл пересекает С.
Что и требовалось доказать.
Следствие. Всякий алгебраический цикл, проходя-
щий через все узлы и все фокусы, пересекает все харак-
теристики Р°1.
Теорема XVII. Если ни один предельный цикл не
проходит через седло, то предельных циклов конечное
число.
В самом деле, проведём алгебраический цикл С через
все узлы и все фокусы. Пусть
— уравнения этого цикла.
Если бы предельных циклов было бесконечное мно-
жество, то цикл С должен был бы иметь с ними бес-
конечное множество точек пересечения, так как он пере-
секает все предельные циклы. Тогда на цикле С должна
была бы существовать точка, сколь угодно близко от
которой находились бы такие точки пересечения С с пре-
дельными циклами, и, следовательно, если

ГЛ. VI. ТЕОРИЯ ПРЕДЕЛЬНЫХ ЦИКЛОВ 79
есть закон последования на некоторой дуге без контакта
цикла С, то должно было бы существовать значение
t0 = т, такое, что при /0, меняющемся в промежутке
(т — е, г-f-e), переменное tx бесконечное множество раз
становилось бы равным t0.
Но если г не соответствует характеристика, прохо-
дящая через седло, то <р(^о) голоморфно при /0 = т. и
мы не можем, следовательно, бесконечное множестло
раз иметь (при t0, меняющемся от г—е до т-{-е):
Это невозможно также и в том случае, когда т не
соответствует предельный цикл.
Таким образом, бесконечное множество циклов может
существовать лишь в том случае, когда один из циклов
проходит через седло.
Теория предельных колец. Пусть попрежнему алге-
браический цикл С проходит через все узлы и фокусы.
Можно разделить этот цикл на некоторое число дуг без
контакта, содержащих все точки, соответствующие пре-
лельным циклам, и не содержащих точек, соответствую-
щих характеристикам, проходящим через сёдла.
Пусть t1 = <р (/0) есть закон последования на одной
из этих дуг и пусть t0 меняется от а до C; пусть точки
/0 = а, /о==Р имеют последующие tl = a', ^=C'. Пусть
Л, — толка дуги без контакта, соответствующая to = x.
Предположим, что мы рассматриваем на сфере точку,
находящуюся на характеристике, проходящей чпрез А1У
и отделенную от Ах дугой характеристики длины s, и
поставим в соответствие этой точке точку плоскости
с координатами s и t (черт. 21).
Дуге без контакта будут соответствовать:
1° отрезок АВ (черт. 21) прямой s = 0, заключённый
между точками
х — а, т = Р;
2° некоторая дуга кривой CD, определённая уравне-
нием

80 ВТОРОЙ МЕМУАР
где А (г) есть та длина дуги характеристики, проходящей
через Av которую нужно пройти, чтобы снова попасть
на дугу без контакта.
Каждая точка дуги без контакта будет изображаться
некоторой точкой Bt отрезка АВ и некоторой точкой Dt
дуги CD. Всякая дуга кривой, идущая из Dt в Bt, изо-
бражает некоторый цикл; этот цикл будет без контакта,
если дуга кривой DtSt- не касается ни одной из прямых
т = const.
f* Ясно, что можно соединить прямыми точки А к С,
В и D, а затем покрыть криволинейный четырёхугольник
ABCD дугами кривых, не касающих-
ся ни одной из прямых т = const,
и нигде не пересекающихся.
Следствие. Вокруг каждого
предельного цикла существует коль-
цевая область, ограниченная двумя
циклами без контакта, которые мы
! L '—L""g gf з будем называть граничными цик-
п ' лами, и которая сплошь заполнена
нигде не пересекающимися циклами
без контакта.
Эти кольцевые области существуют в конечном числе;
мы назовем их предельными кольцами.
Вокруг узлов и фокусов также можно провести ряд
циклов без контакта, охватывающих друг другз, так что
узлы и фокусы также имеют свои предельные кольца.
Мы неявно предположим, что ни один из предельных
циклов не проходит через седло, так как мы рассматри-
вали на алгебраическом цикле С дуги, на которых нахо-
дились все точки, соответствовавшие предельным циклам,
и не было ни одной точки, которой соответствовала бы
характеристика, идущая через седло.
Предположим теперь, что предельный цикл проходит
через седло;'мы знаем, что могут быть два случая:
1° Такого рода характеристика является предельным
циклом лишь для характеристик, достаточно близких
к ней и лежащих внутри цикла (см. черт. 19)- В этом случае
мы вырежем на С дугу без контакта, ограниченную точ-

ГЛ. VI. ТЕОРИЯ ПРЕДЕЛЬНЫХ ЦИКЛОВ 81
кой, соответствующей предельному циклу, проходящему
через седло, и не содержащую никакой другой точки,
соответствующей характеристике, проходящей через седло.
Рассуждая, как в общем случае, нетрудно видеть, что
цикл, проходящий через седло, также имеет предельное
кольцо, но он сам является ,гля него одним из граничных
циклов.
2° Циклы НАМВ'Н, HCNDH (черт. 19) являются пре-
дельными циклами для характеристик, лежащих внутри
этих- циклов, тогда как полицикл HAMBHDNCH является
предельным циклом для внешних характеристик.
Рассуждая, как в предыдущем случае, нетрудно видеть,
что каждый из эти» трёх циклов имеет предельное кольцо,
для которого он сам является граничным циклом; таким
образом, эти три предельных кольца образуют в своём,
сочетании одно предельное кольцо.
Междукольцевые области. Граничные циклы разби-
вают сферу на два класса областей: 1) предельные кольца;
которые мы только что изучили; 2) междукольцевые
области.
"Подвижная точка, пробегающая характеристику с по-
стоянной скоростью, выйдя из какой-нибудь точки между-
кольцевой области, через конечное время пересечёт один
из граничных циклов и войдёт в предельное кольцо.
Ибо междукольцевые области не содержат ни узла, ни
фокуса, ни какой-либо точки предельного цикла.
Я утверждаю, что, подобно предельным кольцам,
междукольцевые области сплошь можно покрыть циклами
без контакта. В самом деле, предположим для определён-
ности/ что междукольцевая область ограничена тремя
граничными циклами Л, В и С и разделена на две части,
покрытые: одна — характеристиками, идущими из A t S,
другая — характеристиками, идущими из Л в С. Обе части
области должны быть разделены характеристикой, про-
ходящей через седло D (черт. 22). Пусть <хД a'D, J3D,
|3'D—.четыре ветви характеристик, выходящие из D.
Пусть т есть какой-нибудь параметр, определяющий
точку Х2 ка цикле А. Пусть (х, у) — точка характе-
ристики, вышедшей из кх, a s — длина дуги характери-
6 А. Пуанкаре.

82
ВТОРОЙ МЕМУАР
стики, отделяющая (х, у), от ^. Изобразим точку (х, у)
сферы точкой плоскости с координатами s и t. Прямая
A1ClB1 (s = 0) (черт. 23) изобразит цикл А; Ах и Вг
изобразят точку о; С\ изобразит точку а'; дуги ?4Е3>
6
?-ь
p. ¦
-_— D,
У
В,
С,
Черт. 23.
E2Et изобразят соответственно циклы В и С; Dlt D2, Da
изобразят точку D; Et и Ea изобразят Р; Еа и Et иза-
бразят Р'.
Кроме того, мы будем иметь:
Дуги кривых офк, 8s, C9, для которых
изобразят циклы; эти циклы будут без контакта, если
дуги apf, 8e, СИ не имеют касательных, параллельных оси s.
Ясно, что можно покрыть многоугольник A1B1E1E2EaEi
дугами, удовлетворяющими этому условию. Таким обра-
зом, междукольцевую область можно покрыть циклами
без контакта, что позволяет высказать следующую теорему:
Теорема XVIII. Всегда существует топографи-
ческая система, образованная циклами без контакта,
полициклами без контакта и предельными циклами-

ГЛ. VI. ТЕОРИЯ ПРЕДЕЛЬНЫХ ЦИКЛОВ. 83
Эта топографическая система покрывает всю поверх-
ность сферы. Вершины и впадины её являются узлами,
и фокусами данного уравнения. Седловины являются
сёдлами данного уравнения I11!. •
Знание топографической системы позволяет полностью
изучить 1121 вид кривых, определённых данным диффе-
ренциальным уравнением. Впрочем, это будет ещё яснее
из нижеприведённых примеров.

: Г Л А В А VII
ПРИМЕРЬГПОЛНОГО ИССЛЕДОВАНИЯ ™
Первый пример. Рассмотрим уравнение (черт. 24):
dy dx
ху—\ 1 — xi ~у~'
Заметим прежде всего, что кривые Х = 0, К = 0,
одна из которых естьху = 1, другая х2-\-у7=\, не
пересекаются ни в одной точке, ни вне экватора, ни на
экваторе.
Если, далее, Х2 и У2 СУ1Ъ члены второй степени
в X и Y, то
Выражение хК2—уХ2 обращается в нуль лишь при^ = 0.
Следовательно, уравнение не имеет ни одной особой
точки вне экватора, а на самом экваторе оно имеет две
особые точки, которые представляют собой точки пере-
сечения экватора с большим кругом ^ = 0 и являются,
очевидно, узлами.
Экватор, проходя через нее особые точки, пересекает
Fee пгедельные циклы; но так как он является характе-
ристикой и не проходит ни через одно седло, то он
может пересекать другие характеристики только в узлах N
и N1. Значит он не пересекает предельных циклов; еле-

ГЛ. VII. ПРИМЕРЫ ПОЛНОГО ИССЛЕДОВАНИЯ
85
довательно, предельных циклов не существует, и таким
образом все характеристики выходят из N и кончаются в Л/'.
Черт. 24 изображает
стереографическую проек-
цию нижней полусферы;
NBN1 В ' — экватор; N, N -
узлы, NAN', NA'N' — хара-
ктеристики.
Второй пример.
Врзьмбм уравнение (черт. 25)
йу
их
Ьху — Ь ~ х*+у*—1 •
Здесь кривые ЛТ = О,
У = 0 также не пересе-
каются; но выражение xY2 — yX2 представляет собой
так что оно обращается в нуль при
Черт. 25.
преобразуем уравнение к виду
у = 0, у = 2х,
у = — 2х.
Отсюда следует:
1° что вне экватора
нет особых точек;
2° что на экваторе
есть шесть особых
точек; из них четыре
являются узлами и
две — сёдлами.
Полагая
1 t
х — -, у = ~,
dt
/D-=г flf^z'Xb^

86 ВТОРОЙ МЕМУАР
Полонам последовательно / = 0, / = 2, / = — 2; коэф-
фициент, при z в знаменателе под dz остаётся всё время
отрицательным:
Рассмотрим производную по / от знаменателя дроби
с числителем dt; она будет
отрицательна при t = — 2;
положительна при / = 0;
отрицательна при / = 2.
Следовательно, точки 2 = 0, / = ±2 являются узлами;
точка z = t = 0 является седлом.
Черт. 25 изображает, как и раньше, стереографи-
ческую проекцию нижней полусферы' А и В— два седла;
С, О,. Е и F—четыре узла.
Топографическая система циклов без' контакта имеет
своими впадинами и вершинами точки С, D, Е, F, а сед-
ловинами— точки А и В.
Рассмотрим теперь большой круг
Этот большой круг проектируется в СН; ни в однсй
его точке мы не будем иметь
и, следовательно, не будем иметь dx = 0. Следовательно,
это есть цикл без контакта. Следовательно, если С—ка-
кая-нибудь впадина топографической системы циклов без
контакта, то Е тоже является впадиной, тогда как D и F —
вершины.
Сплошные линии чертежа (черт. 25) изображают топо-
графическую систему циклов без контакта. Можно пока-
зать, как и в предыдущем примере, что предельных
циклов не существует.
Значит характеристики, выходящие из С, кончаются
или в F или в D; область, заполненная характеристиками,
идущими из С в F, отделена от области, заполненной
характеристиками, идущими из С в D, характеристикой,
идущей из С в-А: . ¦ . .

бесконечнее множество
характеристик идёт
ГЛ. \И. ПРИМЕРЫ ПОЛНОГО ИССЛЕДОВАНИЯ 87
Следовательно, если есть характеристики, идущие из
С в D, то есть и характеристика, ". идущая из С в Л.
В этом случае существует и характеристика, идущая
из О в В,
Таким образом, возможны две гипотезы:
Первая гипотеза Вторая гипотеза
из С в F, из С в F,
из С в D, из Е в F,
из Е в D, из Е в D,
одна характеристика |из С в А, из ? в Л,
идёт (из D в В, из F в В.
Для того чтобы решить, какая из этих гипотез пра-
вильна, отметим, что дуга большого круга у = 0, идущая
из А в В, есть дуга без контакта. Следовательно, харак-
теристика, идущая из А, не может её пересечь и находится
целиком в одной из двух четвертей сферы: в AOBCGF
или в AOBDHE,
В окрестности точки А дифференциальное уравнение
имеет;вид
dt At — Р — 5*a + fea
где <р4 — ряд, начинающийся с членов четвёртой степени
по г и f; отсюда получаем
* = |.гЭ + г39 [И],
гдз 0 — голоморфная функция от г.
Значит характеристика, проходящая через точку Л
в окрестности этой точки, проходит через точки, соот-
ветствующие ^>0, т. е. эта характеристика лежит
в четверти сферы AOBDHE. Следовательно, она целиком
лежит в этой четверти сферы и не может кончиться
в узле С; следовательно, она кончается в узле Е.
Таким образом, мы должны остановиться на второй
гипотезе; характеристики будут иметь вид, изображённый
пунктирными линиями на черт. 25.

88
ВТОРОЙ МЕМУАР
Третий пример. Возьмём уравнение (черт. 26)
их .
йу
Существует только по одной особой точке в каждой
ф
полусфере; это — точка лг =
у = 0, являющаяся фо-
кусом. Нет ни одной осо-
бой точки на экваторе,
который является харак-
теристикой и, следова-
тельно, предельным цик-
лом.
Рассмотрим топогра-
фическую систему, со-
стоящую из окружностей,
имеющих центр в начале
координат, т. е. из циклов
:2+у = const.
Кривая контактов
этой топографической
системы есть
Черт. 26.
т. е. окружности не имеют контактов нигде, кроме
окружности радиуса 1, являющейся предельным циклом.
Следовательно, система характеристик имеет "вид,
изображённый на черт. 26AБ1.
Четвёртый пример Aб1. Возьмём уравнение (черт. 27)
dx ^ _
х (xi -\-у"-— 1) (;са -\-у"~ — 9) — у (л:2 +у2 — 2х — '8)
= У С*2 + У2 — 1) С*2 + Jr— 9) + х № +3'У—72х~^Щ "
Нетрудно видеть, что существуют три особые точки*.
1" точка О
х=у = о:

ГЛ. VII. ПРИМЕРЫ ПОЛНОГО ИССЛЕДОВАНИЯ
89
2° точки А и В, в которых пересекаются окружности
— 2х — 8 = 0.
Точка О— фокус; точка А есть узел, а точка В—седло.
В настоящем примере экватор есть цикл без контакта;
как и в предыдущем примере, окружности с центром
в начале будут циклами без контакта, за искиючением
окружностей
лгЗ-f У —1=0, л:24-У>— 9 = 0,
являющихся характеристиками.
Первая окружность, не проходящая ни через одну
особую точку, является предельным циклом; вторая про-
ходит через узел и седло.
Таким образом, суще-
ствуют 3 типа характери-
стик: одни закручи-
ваются вокруг фокуса
(черт. 27) и имеют пре-
дельным циклом
—1 = 0;
другие кончаются в узле А
и имеют предельным цик-
лом
х*-\-у*— 1=0;
Черт. 27.
третьи кончаются в А и
в точке, симметричной с А', они пересекают экватор.
Следующие характеристики будут исключительными:
М71;
3° характеристика, выходящая из седла В и пересекаю-
щая экватор;
4° характеристика, выходящая из седла В и имеющая
предельным цикэдм
1° окружность л:94-У*=
2° окружность л;2

90
ВТОРОЙ МЕМУАР
Если t изображает время, то подвижная точка, двигаю-
щаяся по закону
-9)Н- х(х*+у*-2х-8),
не сможет выйти из ок-
Г ужности
Черт. 28.
если она находилась
внутри её.
Пятый пример
1181. Возьмём уравнение
(черт. 28)
dx dy
АС — В~ ВС + А*
где
Л = ^Bдг»+2У4-1),
В=уBх*-\-2у'*— 1),
2 + л;9 —
У+ 0,1.
Особые точки даются уравнениями
АС— 5 = 0, 5С+Л = 0,
откуда
Л = 5 = 0.
Следовательно, существует по три особые точки в каждой
полусфере, а именно:
1° два фокуса
2° седло
рели мы рассмотрим кривые
f =
—У
с" nst.,

ГЛ. VII. ПРИМЕРЫ ПОЛНОГО ИССЛЕДОВАНИЯ 91
то кривая их контактов будет:
— (АС— В) -\-j-r (ВС -}- А) = 0.
Но
А~~2'дх' В = ~2"ду'
и предыдущее уравнение обращается в
или" С=0.
Но кривая С=0 сама является одной из кривых
F = const.
Все кривые F = const, состоят из циклов без контакта
за исключением С = 0,' которая состоит из предельных
циклов.
Экватор также является циклом без контакта.
Остаётся построить алгебраические кривые
При АГ<—-j- кривая будет мнимой.
При АГ= — -j она сводится к двум особым точкам
При 0>АГ> — -т- она состоит из двух циклов. Это
относится, в частности,. к кривой С = 0, состоящей из
двух предельных циклов.
При К= 0 она обращается в полицикл, имеющий
двойную точку в начале.
При /е>0 она состоит из одного цикла. ч
Система характеристик имеет, следовательно, вид,
показанный на черт. 28.

ГЛАВА VIII
ОТЫСКАНИЕ ЦИКЛОВ БЕЗ КОНТАКТА
Лёгкость, с которой нам удалось полностью исследо-
вать примеры предыдущей главы, имеет две причины:
во-первых, предельные - циклы были алгебраическими
и поэтому топографическая система циклов без контакта
и предельных циклов также была алгебраической; во-вто-
рых, по самому виду дифференциального уравнения можно
было сразу найти топографическую ристему. В общем
случае, очевидно, этого не будет.
Если предельные циклы не являются алгебраическими,
то полное решение, очевидно, невозможно, так как мы
никогда ке сможем найти уравнение предельных циклов A91
в конечной форме. Но можно добиться разделения сферы
на следующие области: 1) области без циклов, или
ациклические, в которых заведомо нет ни одной точки
предельного цикла; 2) моноциклические области, в кото-
рых находятся все точки одного из циклов и нет ни одной
точки никакого другого предельного цикла.
Такое разделение предельных циклов всегда возможно,
если предельных циклов конечное число !201.
В дальнейшем мы будем предполагать: 1) что суще-
ствуют только две особые точки, лежащие вне экватора
и соответственно являющиеся фокусами или узлами;
2) что эти точки имеют координаты: х=у — 0.
В тех случаях, когда существует более двух осо-
бых точек, рассмотрения будут более длинными, и. саж-
ными.

ГЛ. VIII. ОТЫСКАНИЕ ЦИКЛОВ БЕЗ КОНТАКТА 93
В том случае, которым мы ограничиваемся, заведомо
существует лишь конечное число предельных циклов;
поэтому разделение циклов всегда возможно.
Мы будем рассматривать лишь то, что делается
в первой" полусфере. В самом деле, всё повторяется
по другую сторону экватора, который, вообще говоря,
является предельным циклом B11.
Мы разделим эту полусферу:
1° на области ациклические, не пересечённые ни одним
предельным циклом;
2° на области моноциклические, содержащие целиком
один из циклов и не пересечённые никаким другим;
3° на области циклические, заведомо содержащие одни
предельный цикл целиком и, может быть, пересечён-
ные одним или несколькими другими предельными циклами;
4° на области сомнительные, которые, может быть,
содержат один предельный цикл целиком, может быть,
несколько, а может быть, не пересечены ни одним
предельным циклом.
Рассмотрение можно продолжать, пытаясь расширить
ациклические области с тем, чтобы теснее зажать пре-
дельные циклы во всё более и более узких моноцикли-
ческих областях и заставить исчезнуть циклические и со-
мнительные области. Можно, если угодно, окончить рас-
суждение тогда, когда нет других областей кроме ацикли-
ческих и моноциклических; можно также продолжить его
с тем, чтобы ещё расширить ациклические области
и провести ещё больше циклов без контакта.
Общий метод f22l. Рассмотрим алгебраическую функцию
1° которая остаётся конечной и вполне определённой,
так же как и её производные, когда х и у принимают
конечные действительные значения, и обращается в бес-
конечность, когда х или у обращается в бесконечность;
2° которая равна нулю при х =у = 0 и положительна
при х или у, отличном от нуля;
3° у которой производные первого порядка обращаются
одновременно в нуль лишь при лг=в^ = 0;

94 второй j
4° которая такова, что при лг=^ = О имеет место
неравенство 1231
')*?.- Y
х
х Гу)дхду
5° которая такова, что кривая
дх * ду
не пересекает экватор.
Уравнение
где /(^ — произвольная постоянная, даёг топографическую
систему, имеющую вершину в начале, для которой эква-
тор является одним из циклов.
Уравнение кривой контактов будет:
она не пересекает экватор в силу пятого условия и имеет
изолированную точку в начале в силу четвёртого условия.
Значит циклы Ft = Кх будут без контакта, если Кх
очень мало и если Кх очень велико. Будем менять Кх
от 0 до оо и предположим, например, что при
цикл Fi7=Kl не имеет контакта;
» » имеет контакт;
» » не имеет контакта;
» » имеет контакт;
эо » » не имеет контакта.
Тогда области сферы, определённые неравенствами
будут ациклическими; области, определённые неравенствами
будут сомнительными.

ГЛ. VIII. ОТЫСКАНИЕ ЦИКЛОВ БЕЗ КОНТАКТА 95
Первая проблема. Узнать, циклично, ли сомни-
тельная область.
Для этого мы дадим способ, которым можно опреде-
лить, проходит ли в данной области чётное или нечёт-
ное число циклов. Ясно, что если мы устанозили, что
число циклов, пересекающих сомнительную область, не-
чётно, то это будет означать, что эта область циклична.
Чтобы решить проблему, которую мы пергд собой поста-
вили, необходимо ввести новее понятие.
Пусть ABC— дуга цикла без контакта, EBD — дуга
большого круга у = 0. Пусть (черт. 29) ЕВ есть та часть
этой дуги, которая лежит вне цикла ABC', BD — часть,
лежащая внутри цикла; ВС — та часть дуги ABC, которая
лежит .направо от наблюдателя,
стоящего на сфере в точке В и смо-
трящего в сторону Е; В А — та часть
этой дуги, которая лежит налево
от этого наблюдателя. Мы скажем,
что цикл ABC положителен по отно-
шению к дуге большого круга у <= 0,
если характеристика, проходящая
через точку В, лежит- в угле ЕВС,
как, например, FB, и отрицателен,
если эта характеристика лежит в угле ЕВА, как, напри-
мер, F'B.
Установив это, заметим, что если менять цикл ABC,
то он меняет знак: 1) всякий раз, как он становится пре-
дельным циклом; 2) всякий раз, когда FB касается ЕВ.
Теперь мы в состоянии решить предложенную про-
блему. Для этого рассмотрим сомнительную . область,
заключающуюся между циклами
Fx = a, F1 = p.
Пусть дуга большого круга у = 0 пересекает эти
циклы в точках А и В. Пусть X есть число- предельных
циклов, лежащих в сомнительной области; пусть ja есть
число контактов большого круга у = 0, лежащих между
А и В; пусть v — число, которое четно, если циклы FY = а,
Ft=rp одного знака, и нечётно—в противном случае;

96 ВТОРОЙ МЕМУАР
пусть 9 — число перемен знака циклов без контакта топо-
графической системы, определённой в теореме XVIII, при
переходе от цикла F1 = а к циклу F1 = р. Мы будем
иметь
0 = X 4-1*» 9 = 4mod- 2).
откуда
X = v-J-ji.(mod. 2),
что и позволяет судить, четно или нечётно число пре-
дельных циклов I9*!.
Вторая проблема. Узнать, является ли данная
область моноциклической.
При решении этой проблемы мы будем опираться на
следующую теорему:
Теорема XIX. Положим
х = р cos <о, у = р sin <о,
и пусть дифференциальное уратение обращается в
Если <{>(р) есть какая-нибудь функция от р, имеющая
лишь одно конечное значение для каждого конечного
значения р, то .между любыми двумя предельными ци-
клами всегда существуют точки, в которых
либо —-¦= оо, либо <р(р> <о)= оо,
В самом деле, пусть а>0 — некоторое значение а>, р0 и
р^—значения р, соответствующие точкам пересечения
рассматриваемых предельных циклов и дуги большого
круга
О) = 0H.
. Рассмотрим функцию
и посмотрим, как она меняется, когда ш0 меняется от О

ГЛ. Vitl. ОТЫСКАНИЕ ЦИКЛОВ БЕЗ КОНТАКТА 97
до 2гс. Ясно, что эта функция меняется непрерывно,
что она остаётся конечной и возвращается к прежнему
значению.
Следовательно, она проходит через максимум и для
некоторого значения a>j величины о>0, соответствующего
значениям pt и ро величин р„ и р? мы будем иметь:
или
Следовательно, если рассматривать ш как постоянное,
равное <ov и менять р от pt до р^, то функция
или обратится в бесконечность, или пройдёт через ма-
ксимум, т. е. мы будем иметь либо
либо
Ф= СО,
лцбо
Обобщённая'теорема XIX. Пусть <р (лг, у) и
^(, у) — две функции от х и у, такие, что каждой
системе значений х и у соответствует одна, и только'
одна, система значений у и ty и каждой системе значе-
ний <р и ty соответствует одна, и только одна, система
значений х и у. Если положить
и если после этого преобразования уравнение обра-
щается в
А. Пуанкаре.

98 второй ыемуар
то в области, заключённой между двумя предельными
циклами, всегда будут точки, в которых либо
9 = оо,
либо
В самом деле, пусть С и С—два данных предель-
ных цикла. Предположим, что ни в одной точке области R,
заключённой между этими двумя циклами, 6 не обращается
в бесконечность; я утверждаю, что в этой области есть
точки, где
S
В самом деле, пусть т—точка цикла С и пусть
тH—соответствующее значение функции ty(x, у); дуга
кривой
Ф (*> У) = Чо,
проходящая через т, пересечёт цикл С в точке т', так
как, если бы она не пересекала цикл С, то она должна
была бы выйти из области R, пересекши цикл С; следо-
вательно, она в этой области касалась бы одной на
характеристик (в силу теоремы X). Но это невозможно,-
так как мы предположим, что в R нет точек, где
6 = оо.
Пусть ?0 и Ъ'о — значения I, соответствующие точкам
и /»'.
Когда точка т обходит цикл С, функция
т и /»'.
проходит через максимум, т. е. для некоторого значения*),
величины "»}д, которому соответствуют значения St и 5Х
величин ?0 и ?0, мы будем иметь:
в 01. 4i) = в (Si. Ча-
йными словами, при 1A = 11! и при изменении I от Sj до

ГЛ. Vltl. ОТЫСКАНИЕ ЦИКЛОВ БЕЗ КОНТАКТА 99
^ функция 6 проходит через максимум или минимум, т. е.
Что и требовалось доказать.
Решение второй проблемы. Для того чтобы доказать,
что какая-нибудь сомнительная область моноциклична
(или ациклична), достаточно показать, что можно найти
две функции 5 и •»}, удовлетворяющие условиям предыду-
щей' теоремы, и такие, что ни в одной точке области мы
не имели бы
НИ в = 00, НИ з| = 0.
Продолжение исследования. Если топографическая
система
не достаточна для полного разделения предельных циклов,
то можно рассмотреть сколь угодно большое число систем,
удовлетворяющих тем же условиям
1° ясно, что некоторые части областей, оставшихся
сомнительными при употреблении системы Ft = Kv будут
пересечены теми новыми циклами без контакта, которые
даются системами /7а = /B, ••• и станут, следовательно,
ациклическими;
2° среди областей, остающихся сомнительными при
употреблении всех этих систем, будут такие, в которых
нельзя провести цикл, окружающий начало, и которые,
следовательно, также являются ациклическими (см. при-
мер II следующей главы);
3° сомнительные области, сжимаясь всё более и более,
вообще говоря, станут, наконец, все ациклическими или
моноциклическими, чем и закончится разделение предель-
ных циклов; это разделение всегда возможно, и если не
*) Ср. примечание
7*

100 ВТОРОЙ МЕМУАР
существует слившихся предельных циклов, то всегда можно
обнаружить, когда оно закончено;
4° так как циклические области всё более и более
сжимаются, то предельные циклы можно будет определить
с любой степенью точности.
Примечание. Теория разделения предельных циклов
имеет некоторую аналогию с теми способами, которые
служат для разделения корней алгебраического уравнения.
С этой точки зрения способ, которым решается первая
проблема, напоминает метод подстановок, позволяющий
узнать, имеет ли алгебраическое уравнение чётное или
нечётное число корней в данном промежутке.
Теорема XIX эквивалентна теореме Ролля.
Что же касается случая слившихся предельных циклов,
который аналогичен случаю кратных корней, то он пред-
ставляет некоторые специальные трудности, которые я ещё
не разрешил 1*1.

Г Л А В А IX
ПРИМЕРЫ НЕПОЛНОГО ИССЛЕДОВАНИЯ
Пример I. Рассмотрим дифференциальное уравнение
?
* — 2х — Z)— у~у(х*-\-у* — 2-е
которое при
х = р cos ш, у = р sin ш
обращается в
dp = р (р2 — 2р cos ш — 3)d(o.
В качестве топографической системы возьмём систему
кругов
Кривая контактов для этих кругов обращается в сфе-
рический эллипс j "
j>2—2p coso» —3 = 0,
охватывающий начало. Следовательно, области
Р<1, Р>3
будут ацикличны, тогда как область
.yj.ll ¦. : 1<р<з
сомнительна; однако, обращая внимание «а то, что циклы
р = 1 и р = 3 имеют разные знаки, мы заключаем, что
она циклична.

102 ВТОРОЙ МБМУАР
Воспользуемся теперь теоремой XIX, полагая
4»(р) = 1пР, <р(Р, ш) = Р(р3 — 2pcosm — 3),
откуда
Кривая 2р — 2 cos о» = 0 есть сферический эллипс, проходя-
щий через начало и касающийся окружности р = 1. Значит
ни в одной точке области 1<р<3 мы не имеем
ни ~ н= оо, ни Ф = оо ни т I tf—) = 0.
dp ' т ' dp\rdpj
Следовательно, эта область моноциклична.
Следствие. Кроме экватора, в каждой полусфере
существует один и только один предельный цикл. Этот
цикл лежит целиком в области
Если подвижная точка двигается по закону {t — время)
— 2х — 3)— y]dt, -
— 2х — 3) + х] dt
и если при / = 0 мы имеем р<1, то подвижная точка
заведомо выйдет из окружности р = 1 и заведомо не выйдет
из окружности р = 3 1271.
Пример II. Рассмотрим уравнение
dx_ dy
_
—у + 2х (jc2 + J» — 4х + 3) ~ х + 2у (jc» +j» - 4х + 3)'
откуда
Рассматривая снова окружности р = /A, мы увидим,
что области р<1, р>3 ацикличны, тогда как область
1<р<3 сомнительна. Но теперь циклы р = 1 и р = 3-^
одного знака; поэтому нельзя утверждать, что эта область
цйкличиа.

ГЛ. IX. ПРИМЕРЫ НЕПОЛНОГО ИССЛЕДОВАНИЯ 103
Рассмотрим цикл
<р(р, ш) = р2 — 3,5 р cos (в — 2 = 0.
Для того чтобы он имел контакт, нужно, чтобы
Но вдоль по циклу <р = 0 мы имеем:
JL.I.*t
dy p da*
щ
и
ра —4р cos ш-|тЗ> 1,25.
Следовательно, соотношение (X) не может быть выполнено,
и цикл <р = 0 есть цикл без контакта. То же будет иметь
место и для циклов ? = .Ка, лишь бы —е<ЛГа<-)-*> где
е достаточно мало.
Область — е<<р< -J- е ациклична. Остаются, следова-
тельно, дре сомнительные области:
Iе область 1<р<3, <р>4~е>>
2° область 1<р<3, <р<—г.
Но ни в одной из этих областей нельзя провести цикл, окру-
жающий начало. Значит они также ацикличны.
Следствие. Кроме экватора, других предельных
циклов нет. Подвижная точка, двигающаяся по закону
dx =. [—у 4- 2х (*• -\-у\— 4х 4- 3I dt,
dy = [х 4- Ь (*а 4- У2 ~ 4* + 3I dt,
может как угодно близко полойти к экватору.
Пример III. Рассмотрим уравнение
^ = р(ра — 2pcos ш — 3) (р2-г-2р cos ш — 8).
Рассмотрение циклов р = const, показывает нам, что:
Iе области р<1 и р>4 ацикличны;
2* область 1<р<4 сомнительна.
Кроме того, так как циклы р«1 и р = 4 одного
знака, то в этой области должно быть чётное число npt-
лмьных циклов.

ВТОРОЙ МБМУАР
Рассмотрим цикл: . /
6 (р, ш) = ра —" 2р cos ш — 5,5 = 0.
Этот цикл целиком лежит в сомнительной области; он н^
имеет контактов, так же как и циклы
Р2—2р cos со — 5,5 =. К2, где АГа < + *, *а > ~ «,/
причём е очень мало. Кроме того, эти циклы имеют зНак,
противоположный знаку циклов р = 1 и р = 4.
Таким образом, мы имеем следующие области:.
1-я область р<1 ациклична;
2-я область 1<р<4, 6<—е циклична;
3-я область 1<р<4, — е < 6< -f в ациклична;
4-я область 1<р<4, e>+e циклична;
5-я область р>4 ациклична.
Воспользуемся теперь теоремой XIX, полагая
? (р, <в) = р (р2 — 2р cos ш — 3) (ра — 2р cos ш — 8),
откуда
( 5^) = 4 (Р — cos ш) ^РЯ ~2Р cos ш — 5>5)-
Кривая _ Ы J=iJ = 0 сводится, следовательно, к двум
циклам
р = cos ш, "ра = 2р cos ш -}- 5,5,
которые лежат целиком в ациклических областях — один
в первой, другой в третьей. Так как, с другой стороны,
ни <рни jb не обращаются в бесконечность, то вторая и
четвёртая области моноцикличны.
Заключение. Вне экватора, в каждой полусфере,
лежат два, и только два, -предельных цикла.

ервые две части этой работы были напечатаны
в этом же журнале; первая — в ноябре и де-.
кэбре 1881 г. C-я серия, т. VII\ вторая —
в августе 1882 г. C-я серия, т. VIII). В после-
дующем я сохраняю, несмотря на замечания,
которые можно сделать против них, те же названия, что
и в первых двух мемуарах, чтобыне вводить новых опре-
делений.
ТРЕТИЙ МЕМУАР
ГЛАВАХ»)
УСТОЙЧИВОСТЬ И НЕУСТОЙЧИВОСТЬ
Всякий, читавший первые две части этого мемуара, не
мог не поразиться сходством, существующим между рас-
смотренными в них вопросами и важнейшей астрономи-
ческой проблемой об устойчивости солнечной системы.
Конечно, эта проблема гораздо сложнее, чем те вопросы,
которыми мы занимались, так как дифференциальные урав-
*) Journal de~"Matheraatlques pures.et appliquees, 4-e serie,
t. \\mSf. v. 167-244.

106 ТРЕТИЙ МЕМУЛР
нения движения небесных тел очень высокого порядка.
Более того: в этой проблеме встретится новая трудность,
существенно отличная от тех, которые мы преодолели,
изучая уравнения первого порядка, и я намерен отчётливо
её выявить, если не в этой, третьей части, то по крайней
мере в следующих частях этой работы.
Но как бы там ни было, хотя решение этой проблемы
и требует величайших усилий и новых методов, тем не
менее аналогия между вопросами, подлежащими решению,
очевидна. При изучении дифференциального уравнения
dx dy
X~Y
можно положить:
dx у dy у
dt~ • Л™
Рассматривая затем хну как координаты движущейся
точки, t как время, мы должны найти движение точки,
скорость которой задана в функции её координат. Именно
это движение мы и изучали и искали решение вопросов
такого типа: описывает ли подвижная точка замкнутую
кривую? Остаётся ли она всегда внутри некоторой части
плоскости? Другими словами, употребляя язык, принятый
в астрономии, мы исследовали, устойчива или неустойчива
орбита этой точки.
Мы могли бы поставить перед собой аналогичные
вопросы также и в том случае, когда X и Y являются
уже не многочленами по х и у, а алгебраическими функ-
циями этих переменных или же когда дифференциальное
уравнение порядка выше первого.
Но предварительно необходимо точно определить, что
нужно понимать под устойчивостью и неустойчивостью.
Для этого мы изучим пять следующих уравнений, ко-
торые дадут нам примеры всех могущих представиться
случаев.
1° Пусть сперва
ж У'

ГЛ. X. УСТОЙЧИВОСТЬ И НЕУСТОЙЧИВОСТЬ 107
уравнения траекторий 41 будут:
х9-\-у9=ч const.
Так как все траектории замкнуты, то устойчивость
является полной.
2° Пусть теперь, в полярных координатах,
-(р —2)« ,
где h — какая-либо постоянная. Нетрудно было бы пе-
рейти' от этого уравнения в полярных координатах к соот-
ветствующему уравнению в прямоугольных координатах;
. тогда мы увидели бы, после приведения уравнения к виду
dt^*' dT=psY*
что А" и Y являются уже не многочленами, целыми отно-
сительно х к у, а алгебраическими функциями от этих
переменных. Дифференциальное уравнение будет первого
порядка, но степени выше первой.
Решение находится непосредственно:
где С— постоянная интеграции.
Если А соизмеримо с 2тс, то траектория будет замкну-
той кривой, и мы возвращаемся к предыдущему случаю.
Предположим, что это не имеет места.
Тогда траектория не будет замкнутой кривой; но, тем
не менее, сна будет обладать известной устойчивостью;
можно было бы даже сказать — некоторой ссобого рода
периодичностью. В самом.деле, пусть М есть точка траек-
тории, в которой находится изображающая точка в мо-
мент времени /; опишем вокруг -М окружность сколь
угодно малого радиуса г. Изображающая точка, вышедшая
из точки М, должна будет, очевидно, выйти из этой окруж-
ности; но она снова пересечёт эту малую окружность и
притом бесконечное Множество раз, сколь бы мало ни
|било г. Другими ¦ словами, подвижная точка, вышедшая

108 ТРЕТИЙ МЕМУАР
из точки М, никогда не вернётся. в М, но будет попа-
дать в точки, бесконечно близкие к М.
С другой стороны, точка М всегда остаётся внутри
кольца, ограниченного двумя окружностями
р ¦= 1 и р = 3.
Её траектория полностью заполняет это кольцо, не оста-
вляя никаких просветов. Я хочу сказать, что в каждой
сколь угодно малой плоской области, лежащей внутри
кольца, есть точка траектории 131. Немцы сказали бы, что
Punktmenge *), образованное различными точками траек-
тории, является uberall dicht **) внутри кольца.
Этот второй случая не может иметь места для диф-
ференциальных уравнений первого порядка и первой сте-
пени. Поэтому мы его до сих пор ни 'разу не встречали.
3° Пусть теперь, в полярных координатах:
или, в прямоугольных координатах:
dt Yx*+y*
Общий интеграл есть
<^-т- постоянная интеграции.
Ив этом случае также, если А несоизмеримо с 2гс,
то подвижная точка не может вернуться к отправному
положению, но может притти в бесконечно близкие к нему
точки. Отличие от предыдущего случая заключается в том,
что подвижная точка не должна теперь оставаться в неко-
торой определённой части плоскости, но траектория её
заполняет всюду гмотйй (iiberall dicht) всю плоскость PI.
Этот третий случай';! так же как и второй, не может
иметь места для уравнений первого порядка и первой
степени. ''¦•¦ '¦'''..
*) Точечное множество.
¦*) Всюду^плотным.

ГЛ. X. УСТОЙЧИВОСТЬ И НЕУСТОЙЧИВОСТЬ 109
4° В качестве четвёртого примерами возьмём логариф-
мическую спираль, дифференциальное уравнение которой
имеет вид
¦J- = та,
аа> г
или же
^=шс—у, О-ш=ту4-х.
Общий интеграл, как известно, есть
р = Сежш.
Пусть М есть начальное положение подвижной точки;
если ми опишем вокруг точки М окружность достаточно
малого радиуса, ми увидим, что подвижная точка, начав
двигаться, выйдет из этой окружности и, выйдя, больше
уже никогда в неё не возвращается. Это прямо противо-
положно тому, что имело место в трёх изученных выше
случаях, когда подвижная точка, выйдя из очень малень-
кого круга, возвращалась в него затеи бесконечное мно-
жество раз. С этой точки зрения, можно сказать, что
траектория неустойчива.
Известно,. что окружности р = const, являются для
наших траекторий циклами без контакта. Вся плоскость
покрыта этими циклами без контакта, так что на ней
нет предельных циклов. Именно вследствие наличия этих
циклов без контакта траектории неустойчивы.
5° Пусть, наконец, дано уравнение
Окружности р = const, являются попрежнему циклами без
контакта, за исключением окружностей р = 1 и р = 2,
которые являются предельными циклами. Так как общее
решение есть
_ Се»—2
р ~~ О» - 1'
то легко видеть, что траектория неустойчива, т. е., что,
выйдя из окружности достаточно малого радиуса с центром
в начальной точке, она никогда более в неё не возвращается.

НО Третий мймУар
Отличие от предыдущего случая заключает я в наличии
предельных циклов. Отсюда следует, что если подвижная
точка находилась в начальный момент в точке, лежащей вну-
три кольца, ограниченного двумя окружногтями р = 1 и
р = 3, то она всё время остаётся внутри этого кольца.
Мы можем теперь, отправляясь от этих примеров,
дать точное определение устойчивости. Мы скажем, что
траектория подвижной точки устойчива, если, сколь бы
мал ни был радиус г окружности (или сферы), описанной
вокруг начальной точки, подвижная точка, выйдя из этой
окружности (или сферы), вновь войдёт в неё-бесконеч-
ное множество раз. Это как раз то, что имеет место
в первых трёх примерах №.
Траектория будет неустойчива, если, выйдя из этой
окружности или сферы, подвижная точка уже больше
в неё не вернётся. Это то, что' имеет место в последних
двух примерах.
Определённая таким образом устойчивость имеет лишь
теоретическую важность. Для приложений следовало бы
определить ту часть пространства, из которой не выходит
подвижная точка. Но как рлз для случая устойчивости
определение подобной области гораздо более трудно, чем
для случая неустойчивости. Здесь существует трудность,
на которой я не хочу сейчас останавливаться, но кото-
рая в дальнейшем развитии настоящей работы будет пред-
метом достаточно долгих обсуждений.
В тех случаях, которые мы изучали до сих пор, т. е.
в случаях уравнений первого порядка и первой степени,
траектории являются циклами, т. е. замкнутыми кривыми,
или спиралями (см. гл. V, теорему XII). В первом случае
они устойчивы; во втором — неустойчивы. Таким образом,
мы не могли встретить ничего, подобного тому, что мы
имели во втором и третьем примерах.
Вообще говоря, плоскость могла быть покрыта бес-
конечным множеством циклов без контакта и предельных
циклов (гл. VI, теорема XVIII). За исключением предель-
ных циклов, все траектории являются спиралями 1Б1.
Таким образом, неустойчивость является правилом,
устойчивость — исключением.

ГЛ. X. УСТОЙЧИВОСТЬ И НЕУСТОЙЧИВОСТЬ 111
В особо исключительных случаях может также слу-
читься, что плоскость покрыта не бесконечным множе-
ством циклов без контакта, но бесконечным множеством
замкнутых кривых, удовлетворяющих данному дифферен-
циальному уравнению и образующих одну из тех систем,
которые мы назвали топографическими (см. гл. I). Тогда
имеет место устойчивость. Этот случай наступает в окрест-
ности тех исключительных особых точек, которые я назвал
центрами. К более углублённому изучению их мы теперь
и перейдем.

ГЛАВА XI
теория:центров
* *
Напишем наше дифференциальное уравнение в таком
виде> чтобы*оно изображало движение некоторой подвиж-
ной точки:
dt A> dt r'
Предположим, что Хп У являются многочленами степени я
по х и у. Предположим, кроме того, что за начало коор-
динат мы взяли ту особую точку, которую мы хотим изу-
чить, так что Хи Y обращаются в нуль вместе с х и у. Мы
можем тогда написать
где Х{ и Yt — однородные многочлены от х и у степени i.
Посмотрим теперь, можно ли построить многочлен F от-
носительно х и у, такой, чтобы в выражении
которое также является многочленом от х и у, исчезли
бы все члены, степени которых по х и у ниже р.
Предполагая, что F не содержит членов степени 0 и 1,
что для нас необходимо, мы можем написать
(F(—однородный многочлен по х и у степени i)

ГЛ. XI. ТЕОРИЯ ЦЕНТРОВ
Положим затем
113
dFi
dFi
Ф1к будет однородный многочлен степени i-\-k — 1.
Если мы запишем, что в Ф обращаются в 0 все члены
степени ниже р, то мы получим:
О)
= — Ф„о Ф0
Фр_Ы = —Фр-2,2 —Фр-3,3— • • ¦ — Ф2,р_2.
Первое из этих уравнений даст нам Fa, второе Fu,..., и,
наконец, (р — 2)-е даст нам Fp_t при условии, конечно,
что все они могут быть удовлетворены.
Рассмотрим сначала первое уравнение.
Пусть
Fu = ах* + 2Ьху + су\
так что
i- Фа1 = {ах + by) (ах
су) (fx + 8у);
тогда пергое из уравнений A) влечёт за собой следующие
три:
B)
Эти уравнения совместны только тогда, когда
а Т О
C) Р а + 8 Ч =°-
О р 8
8 А. Пуанкаре.

114 третий мемуа?
Мы предположим, кроме того, что величины а, Ь, с, полу-
чаемые из уравнений B), таковы, что форма F2 является
положительно-дефинитной.
Если оба эти условия соблюдены, то мы приходим
к четвёртому подслучаю, о котором мы сказали несколько
слов в гл. II, но который мы пока ещё не исследовали
до конца.
Если бы они не были выполнены, то особая точка
была бы узлом, фокусом или седлом, и мы ничего не могли
бы добавить к тому, что уже было сказано по поводу
этих точек. Мы предположим, следовательно, что оба эти
условия выполнены. ta
Так как форма F2 является положительно-дефини ой,
то мы всегда можем записать её в таком виде:
Если мы сделаем затем замену переменных, полагай
to получим
fa = X
Следовательно, мы всегда можем предполагать, что
так как, если бы это было не 'так, то линейной замены
переменных было бы достаточно для того, чтобы привести
Fq к такому виду. В дальнейшем мы будем считать выпол-
ненной эту гипотезу.
Какие следствия вытекают для Х^ и Kj?
Уравнения B) обращаются в
а = 0, 8 = 0, р + т = О,
откуда
*1-ЙУ, Yt = -$x.
Остальные уравнения A) напишутся в виде:

ГЛ. XI. ТЕОРИЯ ЦЕНТрОВ 115
где Fq— однородный многочлен степени q, который
нужно определить, тогда как Hq— однородный многочлен
степени q, который можно рассматривать как данный, так
как он зависит лишь от многочленов Л'и К и от однородных
многочленов Fq,Fu,..., Fq_u которые должны были
быть вычислены до нахождения F9.
В каком случаа возможно удовлетворить уравнению
вида D)?
Для того чтобы ответить на этот вопрос, мы перейдём
к полярным координатам, полагая
, _y=psin<o.
Мы получим
У дх ду дш
Кроме того, мы будем иметь
о (ш) = 2-^fc cos ?ш -f- 2^л sin k®,
(Ji (a>) = 2<^л cos ^ш ~\~ 2^* sin Ы.
В этих выражениях k может принимать только значения
меньшие или, в крайнем случае, равные q и одной чётно-
сти с q. В частности, если q нечёгно, то в них не может
быть постоянных членов (т. е. членов, где k = 0).
Уравнение D) запишется тогда в виде:
-Й-to.
Для того чтобы ему можно было бы удовлетворить, необ-
ходимо и достаточно, чтобы функция ty(u>) не имела по-
стоянных членов, т. е. чтобы
Это условие, как мы только что видели, выполняется само
собой, когда q нечётно. Наоборот, если q четно, то оно,
вообще говоря, не выполняется.
8*

116 ТРЕТИЙ МЕМУАР
Таким образом, если q нечётно,- то уравнению D)
можно удовлетворить одним и только одним способом;
для этого достаточно положить
А —5* Я — Як
Если q четно и если притом Со = 0, то нашему уравне-
нию можно удовлетворить бесчисленный множеством спо-
собов; можно попрежнему положить
л —^ Я, Як
Ак— k' °к— k
при k, не равном нулю, и можно взять Ао произвольно.
Что же, в конце концов, мы получаем, когда q четно
и Со не равно нулю? В этом случае удовлетворить урав-
нению D) невозможно, но можно выбрать Fq так, что-
бы было
¦* дх ду
при всех значениях х и у, если Со положительно.
Наоборот, если Со отрицательно, то можно выбрать
Fq таким образом, чтобы мы всегда имели
Для этого достаточно положить
для всех значений k, отличных от нуля, причём Ао
остаётся произвольным. Тогда мы получим
или же
Пусть, например,
q^=4, Яд = рд;4 — 2*гУ-f" &У4

ГЛ. XI. ТЕОРИЯ ЦЕНТРОВ 117
Мы будем иметь
Положим тогда
Мы получим
Если 3C = а, то левая часть этого уравнения равна нулю
и уравнение D) удовлетворено. Если 3C > а, левая часть
положительна, каковы бы ни были х и у. Если 3C < а,
левая часть отрицательна, каковы бы ни были х и у.
После этого легко видеть, что можно сделать две
гипотезы.
1° Предположим сначала, что можно определить F2,
Fa, •.., Fq-i так, чтобы первые q — 2 уравнения A) были
бы удовлетворены, но что невозможно затем определить
Fq так, чтобы было удовлетворено (q— 1)-е уравнение
A). В этом случае q необходимо четно, и мы определим
F , как только что было сказано, таким образом, чтобы
Мы положим затем
Я утверждаю, что если А есть положительная, достаточно
малая постоянная, то уравнение
изобразит замкнутую кривую, которая будет циклом без
контакта.
В самом деле, если р достаточно мало (меньше, напри-
мер, р0), то функция F при постоянном ш будет убывать,

118 ТРЕТИЙ МЕМУАР
когда р убывает от р0 до jO, так как при очень малом р
знак j- определяется членом .-— = 2р.
Пусть k0 есть наименьшее положительное значение,
которое может принимать FHa окружности р = ро> и пусть
k<k0.
Ясно, что F = k есть замкнутая кривая, или, точнее,
среди ветвей, из которых состоит эта алгебраическая
кривая, есть замкнутая ветвь, окружающая начало и ле-
жащая в круге р=Ро- Именно эту ветвь, исключая все
остальные, мы и будем рассматривать.
Для того чтобы между этим циклом и одной из наших
траекторий был контакт, нужно, чтобы
л у dF i vdF п
Но многочлен Ф, по предположению, не имеет членов
степени ниже q, и его члены степени q приводятся к виду
Когда р меньше некоторой определённой границы (а мы
всегда можем считать, что р0 меньше этой границы), знак
Ф определяется как раз членами степени q, а так как они
сохраняют постоянный знак, то Ф не может обратиться
в нуль.
Следовательно, между двумя нашими кривыми контакта
быть не может.
Таким образом, . внутренность цикла F = k0 покрыта
бесчисленным множеством циклов без контакта, охваты-
вающих друг друга и окружающих начало.
Пгедположим, для определённости, что Со отрица-
тельно; мы будем иметь внутри круга р = р0:
dF ydF ±Уа
Х+У
Следовательно, когда t будет стремиться к-{-<х>, по-
движная точка будет удаляться от начала до тех пор, пока

ГЛ. XI. ТЕОРИЯ ЦЕНТРОВ 119
не выйдет из кривой F = A0; и, выйдя из этой кривой,
она уже не сможет в неё вернуться. Когда t стремится
к —со, подвижная точка будет неограниченно и асим-
птотически приближаться к началу координат, описывая
бесконечное множество витков ¦ вокруг этой точки. Сле-
довательно, траектория является спиралью Iе!. Другими
словами, имеет место неустойчивость, и начало коор-
динат является фокусом.
Если бы Со было положительно, то "достаточно было бы
переменить знак у /, и мы получили бы те же результаты.
Пусть, например,
dx P*3 dy . 2ахгу— $у3
If—у Т' Tt~~x~\ 2 *
Мы положим F2 = х2 -f-_y3, F$ — 0; третье из уравнений
A) напишется в виде:
Мы видели, что, вообще говоря, удовлетворить этому
уравнению невозможно. Мы возьмём
и, как мы видели, мы будем иметь
Как мы видели, если 3C — а не равно нулю, то кривые
являются ликлами без контакта, если только k доста-
точно мало. Мы будем иметь неустойчивость, и начало будет
фокусом.
Предположим теперь, что Зр = а. Третье из уравнений
A) будет тогда удовлетворено. Мы возьмём F6 = 0, и
пятое из уравнений A) напишется

120 ТРЕТИЙ МЕМУАР
Кроме того, полагая C = 1, а = 3, мы найдём: /
и нетрудно видеть, что первому из уравнений A) можно
удовлетворить, полагая t7l
Мы возьмём затем F1 = 0, и седьмоз из уравнений A)
напишется
где
или
Положим x = pcos<o, ^ = psin<o; разложим затем по
синусам и косинусам дуг, кратных ш, и посмотрим, обра-
щается ли в нуль постоянный член
Мы находим
-o--f = — 24 cos8 <o + 4O cos6<o — 19cos4<o -\-2 cosa<o,
г
откуда
r 9^
°~ 64"
Таким образом, седьмому из уравнений A) удовлетворить
невозможно; следовательно, начало опять является фоку-
сом. Мы должны отсюда заключить, что если движение
подвижной точки определено уравнениями
dx рл-з dy _ , , 2a*i

ГЛ. XI. ТЕОРИЯ ЦЕНТРОВ 121
то траектория этого движения будет неустойчива, каковы
бы ни были аир.
Таким образом, мы должны попытаться решить после-
довательно все уравнения A), и если мы будем вынуждены
остановиться, то это будет означать, что траектория
неустойчива.
2° Но может случиться, что мы никогда не будем
вынуждены остановиться, что требует соблюдения беско-
нечного множества условий. Эти условия, очевидно, необ-
ходимы для того, чтобы траектория была устойчивой,
т. е. для того, чтобы начало было центром. Являются ли
они достаточными? Этим мы теперь и займёмся. Обра-
зуем последовательно, с помощью уравнений A), много-
члены F2, F3,..., Fq и рассмотрим бесконечный ряд
Если этот ряд сходится, то никаких трудностей не воз-
никает, так как он удовлетворяет уравнению
Кривые F = k будут, следовательно, траекториями по-
движной точки; они будут замкнутыми кривыми, если k
достаточно мало.
Остаётся исследовать, сходится ли ряд F. Положим
— psin<o, K = i?sin(o-|-pQcos<o И.
Предыдущее уравнение принимает вид:
R
Мы можем разложить функцию —тт по .возрастающим
степеням р, причём это разложение начинается с члена,
содержащего р3; мы получим

122
ТРЕТИЙ МЕМУАР
где 62, 83,... являются функциями от ш. Предыдущее
уравнение обращается в"
и если положить
где гд являются функциями от ш, то можно последовательно
найти zq с помощью следующих уравнений, заменяющих
теперь уравнения A):
A bis)
Если уравнениям A) можно удовлетворить многочленами
по х и у, то уравнениям A bis) можно удовлетворить
чисто тригонометрическими функциями (т. е. многочле-
нами по cos со и sin со).
Но если, наоборот, уравнениям A) удовлетворить
невозможно (т. е. если величины Со не все равны нулю),
то тем не менее можно решить уравнение A bis) и вы-
числить последовательно функции г'й\ но эти функции
не будут уже содержать только тригонометрические члены;
они будут содержать члены, где ш будет входить не под
знаками синуса и косинуса, быть может, в первой, быть
может, в более высокой степени.
Невозможно не поразиться аналогией между таким
образом вводимыми членами и членами, которые астро-
номы называют вековыми. Однако между ними есть су-
щественная разница, которую необходимо отметить. В обыч-
ных методах небесной механики, когда встречается векд>

ГЛ. XI. ТЕОРИЯ ЦЕНТРОВ 123
вой член, то это ещё не позволяет заключить, что орбита
неустойчива; может случиться, что ряд расходится или же,
что полученный таким образом член является лишь пер-
вым членом разложения, сумма которого всегда остаётся
конечной. Так, аш может быть первым членом разложения
81паш = а<о _ + __-„.
Совсем не то имеет место в занимающем нас случае
с тем'методом, который я только что изложил. Если
в ходе вычислений встречается вековой член, то можно
немедленно заключить, что налицо неустойчивость; для
этого даже нет необходимости, чтобы ряд
был сходящимся.
Мы можем поставить вопрос о сходимости также и
в том случае, когда функции га содержат вековые члены,
так как хотя этот вопрос представляет гораздо меньше
интереса, тем не менее целесообразно освободиться от
ненужных ограничений, для того чтобы легче притти
к решению.
Скажем сначала несколько слов по поводу следующих
трёх простых случаев Ш-.
мы находим тогда,в качестве общих интегралов уравне-
ний движения:
у—? = *, у + ^Гн"?^' }+arctg ?—v = k>
где k — постоянная интеграции. Попробуем построить F.
В первом случае легко находим
>— Р1 [10]
В третьем случае положим
l+parctgP I'

124
ТРЕТИЙ МЕМУАР
левая часть этого равенства есть голоморфная функция
от р при р = 0, которая- обращается в нуль вместе с р,
но производная от которой не обращается в нуль вместе
с р. По известной теореме мы выводим отсюда
где ty — голоморфная функция от vj. Тогда мы будем иметь
Эта функция, как и в. первом случае, голоморфна по р
и по cpi если только эти переменные достаточно малы.
Во втором случае этот способ уже нельзя приложить,
так как функция
•р р+1
неголоморфна. Разлагая F не по степеням р, но по степе-
ням ср, положим тогда
пЧп i_
Функции Н можно будет тогда определить последова-
тельно с помощью следующих уравнений ЧЧ:
(Iter)
Определённые таким образом функции Н будут много-
членами по р, и нетрудно видеть, что все коэффициенты
их положительны, что степень Нп есть 2 (« -J- 1) и что
полином Нп не содержит членов степени ниже и+ 2

ГЛ. XI. ТЕОРИЯ ЦЕНТРОВ 125
. Пусть Sn — сумма коэффициентов многочленов Нп,
a S'n — сумма коэффициентов производной -~ • так как
Нп — степени 2(п-\-\), то
С другой стороны, формулы A ter) дают нам
с ос'.
°тсюда
5„
Предположим, что р положительно и меньше единицы и
рассмотрим общий член ряда, определяющего F; мы бу-
дем иметь
Следовательно, если ро положительно и меньше -г, то
ряд сходится и притом абсолютно.
Отсюда мы заключаем, что F есть голоморфная функ-
ция от р и ф, если только
1
Этот результат легко было предвидеть. Положим, в са-
мом деле,
E) ' I-j-ln-L —<p = JL-f 1Пт-?-.
' р ' р + 1 т 1 .' 1+1
¦
Я утверждаю, что ч\ есть голоморфная функция от р и
в окрестности точки р = <р = (Н121. Чтобы доказать это
нужно доказать две вещи:
1° Что т) стремится к нулю, когда р и <р одновременно
стремятся к нулю.

126 ТРЕТИЙ МЕМУАР
В самом деле, если р и <р стремятся к 0, то обе части
уравнения E) неограниченно растут. Но, для того чтобы
неограниченно росло, необходимо, чтобы ч\ стремилось бы
к 0 или к 1. Но если начальное значение т) достаточно
близко к нулю, то ?) будет стремиться к 0, а не к 1.
Достаточно проверить, что нетрудно сделать, что когда
<р и аргумент р постоянны, модуль р стремится к нулю.
Этого будет достаточно, так как мы немного дальше
покажем, что т) есть однозначная функция от р и <р [J81.
2° Нужно показать далее, что yj возвращается к началь-
ному значению, когда р и <р описывают каждое в своей
плоскости достаточно малые контуры, окружающие точку
нуль. Но при этом левая, а следовательно, и правая
части уравнения возрастут на кратное 2лг, откуда сле-
дует, что yj описывает замкнутый контур, окружающий
точку нуль1и1. Следовательно yj, а значит и
являются голоморфными функциями от р и<р, если эти пере-
менные достаточно малы.
Предположим теперь, что
Р(р) есть ряд, расположенный по степеням р и сходя-
щийся, когда р достаточно мало. Общий интеграл диффе-
ренциальных уравнений будет
С другой стороны, мы получим
гДе Q(p) есть голоморфная при р = 0 функция от р.

Гл. xl. теория центров 127
Положим теперь
E bis) i + pinp + Q(p)-(o = I + pinT1 + Q(T1).
Рассмотрим ту из функций % удовлетворяющих этому
уравнению, которая обращается в р при ш = 0. Я утвер-
ждаю, что это будет функция от р и ш, голоморфная
при достаточно малых значениях этих переменных.
Для этого нужно показать, что т), при достаточно
малых р и ш, есть однозначная функция от р и ш, стре-
мящаяся к нулю, когда эти переменные одновременно
стремятся к нулю. Рассуждение остаётся абсолютно тем
же, что и в предыдущем случае. Из него следует, что
есть голоморфная функция от р и от ш.
С другой стороны, легко найти коэффициенты разло-
жения F по степеням р и ш. В самом деле, напишем:
Мы предположим (это нам будет полезно для дальней*
шего), что все ар положительны, и, кроме того, можно
найти два числа \>. и а, такие, что
Функции Н будут даны уравнениями:
Введём Следующее обозначение: неравенство

128 ТРЕТИЙ МЁМУАР
с двойным знаком неравенства, которое будет означать
(в том случае, если коэффициенты разложений функций /
и <р по степеням р положительны, что мы и предполагаем),
что каждый коэффициент разложения функции / меньше
соответствующего коэффициента разложения функции <р.
Тогда мы можем написать:
p
Я утверждаю, что всегда можно найти число Мп, такое,
чо
что
В самом деле, предположим, что это верно для Нп;
я утверждаю, ¦ что то же будет верно и для Ип+1. При
сделанном предположении мы получим
отсюда
dHn ~,
ельно,
^ tfno>»
Мпап\ Bя +
ан
dp
= 2ау-Мп и
^, vi Afj Ba
*-^J(l—др
1)ПЧ
+ 2 "^
^2аМп\
** A-
• >ИП =
. 2дЛ1п(п •
др)»я+3
: Мо Bв|1
1-др
f D1.
1
¦)"•
Тогда
Из этого неравенства мы заключаем, что ряд F схо-
дится, когда, например,
1вК
Но легко видеть, что разложение Но начинается с члена
содержащего р2, Нг — с члена, содержащего р8,..., Нп —
с члена, содержащего р'»+а. Значит, функция F есть голо-

ГЛ. XI. ТЕОРИЯ ЦЕНТРОВ 129
морфная функция не только от р и со, но и от р и рсо.
Разложение функции F сходится, таким образом, при
Следовательно, этот ряд сходится для всех значений со,
содержащихся между 0 и 2тг, если только
Вот каким образом всё предшествующее связано
с принципами, изложенными Врио и Буке в XXXVI тетради
Журнала политехнической школы.
Предположим, что а> постоянно; длл переменных Сир
мы будем иметь дифференциальное уравнение
или
где ф есть совокупность членов, степень которых по С и
р по меньшей мере равна двум. Положим
Мы получим
причём функция ty содержит множителем р9.
Это и есть тот тип уравнений, который, по теореме
Бр>ю и Буке, имеет бесчисленное множество голоморфных
интегралов, обращающихся в нуль вместе с р. Следова-
тельно, С есть голоморфная функция от р.
Что и требовалось доказать.
Перейдбм теперь к общему случаю,.
Необходимо прежде всего напомнить уже употреб-
лявшееся выше обозначение ^ и уточнить его смысл. Когда
9 А. Пуанкаре.

130 ТРЕТИЙ MI-МУЛР
я буду писать в дальнейшем
/(p. <°)<С'т>(р. °>),
то я буду предполагать, что .функции / и ср разложены по
возрастающим степеням р. Коэффициенты обоих разложе-
ний будут функциями от со, которое я в данное время
считаю постоянным и предполагаю действительным и за-
ключённым между 0 и 2тт. Написанное выше неравенство
означает тогда, что при всех действительных значениях со,
содержащихся между 0 и 2ъ, все коэффициенты разло-
жения функции ф положительны и превышают абсолют-
ные величины соответствующих коэффициентов разложе-
ния функции /.
Пусть
2 = 1 +g1p+egp«+...+ Qqp*.
Коэффициенты Rt и 24- полиномов R и Q будут триго-
нометрическими функциями от со. Предположим, что все эти
тригонометрические функции остаются всё время по абсо-
лютной величине меньше некоторой положительной вели-
чины L. Мы будем иметь
Функция ^ . , зависящая лишь от р, разла-
гается в ряд по степеням р, если только р достаточно мало.
Отсюда вытекает, что существует ряд Fv расположенный
по возрастающим степеням р и со, сходящийся, если только
р достаточно мало, для всех действительных значений
со, содержащихся между 0 и 2тт, и удовлетворяющий
уравнению
do) ~~ dp I— .p (Z. + 1) "
Кроме того, Z7! обращается в р2 при со = 0. Положим,
как и выше,

ГЛ. XI. ТЕОРИЯ ЦЕНТРОВ 131
. Функции zq определены урарнениями A bis), а фугк-
ции «а — аналогичными уравнениями
«2=1.
G) ^ = (,7-1)^ +
-\-{q — 2)йа_Х+...+2«^-., .
где
Теперь я утверждаю, что, когда со действительно и меньше
чем 2тт, мы всегда будем иметь:
(8) !*,!<«,.
Для того чтобы показать это, я предположу, что не-
равенства (8) имеюз- место для г2, г8,..., za_lt и докажу,
что они имеют место и для zq.
В самом деле, в силу сделанного предположения,
сравнивая соотношения A bis), F) и G), мы будем иметь:
О) . . . К1«4
Функция га не полностью определена уравнениями
(Ibis); действительно, эти уравнения дают нам только,
производную от zq как функцию z2, zs,.. ., zq_1] отсюда
следует, что zq известно лишь с точностью до постоян-
ной интеграции. Мы выберем эту постоянную так, чтобы
za обращалось в нуль вместе с со.
А тогда из неравенства (9) следует неравенство
(8) ' К1<«3-
Что и требовалось доказать.
Следовательно, мы имеем
и так как для малых значений р ряд F1 сходится при лю-
бом значении со, содержащемся между 0 и 2тс, то то же
имеет место и для F.
Но по самому способу определения га все zq являются
тригонометрическими функциями от со (в случае, когда Со
9*

132 ТРЕТИЙ МЕМУАР
все равны нулю). Значит, если F- сходится для всех зна-
чений со, содержащихся-между нулём и 2тг, то этот ряд
будет сходиться и для всех действительных значений со.
Следует заметить, что если бы, отправляясь от ряда
F, который мы только что определили, мы перешли бы
от полярных координат р и со к прямоугольным коорди-
натам х и у, то F не было бы уже рядом, расположен-
ным по возрастающим степеням х и у. Это связано с тем,
что мы выбирали Постоянные интеграции таким образом,
чтобы г^ обращалось бы в нуль вместе с со.
Тогда могло бы, например, случиться, что мы полу-
чили бы
Р=?* + P3(l- cos со) -f...,
что дабт
В самом деле, если требовать, чтобы F была голо-
морфной функцией от х и у, то постоянной интеграции
(которую мы выше назвали Ао) можно располагать, когда
q четно, но ею уже нельзя располагать, когда q нечётно.
Следовательно, вообще говоря, невозможно добиться того,
чтобы zq обращалось в нуль вместе с со.
Хотя это и не имеет особой важности с точки зрения
интересующих нас вопросов, но, тем не менее, эту труд-
ность легко обойти. Мы имеем
dF _ R dF
da> U dp
Пусть F при замене р на — р и со на со-{-те обращается
в F3. Тогда, как легко проверить, мы будем иметь
dF? _ R dFz
dco Q dp '
• p
так как — — меняет знак, если заменить в нбм р на — р
и со на со -f- к. Следосательно, будем иметь ещё
d(F+Ft) __ /? d(F + Fs)
дш Q dp '

ГЛ. XI. ТЕОРИЯ ЦЕНТРОВ 133
причём ряд F -f- F9 будет сходиться для всех действитель-
ных значений со, лишь бы р было достаточно мало. Еслц
вернуться к прямоугольным координатам х и у, то F -f- F%
будет голоморфной функцией от х и у. Мы видим, таким
образом, что когда все Со равны нулю, то всегда суще-
ствует сходящийся ряд F, расположенный по степеням х и
V и удовлетворяющий уравнению:
дх ' ду
Итак, для того чтобы начало координат было цен-
тром, т. е. для того чтобы все траектории подвиж-
ной точки были устойчивы, необходимо и достаточно,
чтобы все величины, которые мы обозначили через Со,
были бы одновременно равны нулю 1Щ.
Однако часто бывает трудно узнать, выполнено ли
одновременно всё это бесчисленное множество условий
или нет. Поэтому представляет интерес указание некото-
рых случаев, в которых заранее можно быть уверенными,
что все Со равны нулю.
Я укажу только два простейших.
Предположим, что когда мы меняем у на—у, не меняя
х, то X обращается в — X, а Уне меняется. Я утверждаю,
что траекторий" подвижной точки будут замкнутыми кри-
выми, симметричными относительно оси х.
В самом деле, выйдем в момент / = 0 из некоторой
начальной точки, лежащей на оси х. В силу сделанных
гипотез начальная скорость подвижной точки будет пер-
пендикулярна к этой оси. Если заменить t на —t, у
на—yt то уравнения движения и начальные положения не
изменятся. Значит, подвижная точка в моменты t и — t
будет находиться в точках, симметричных относительно
оси х. По самому виду уравнений можно заключить, что
если начальное положение подвижной точки достаточно
близко к началу, то наступит такой момент /0, в кото-
рый её траектория снова пересечёт ось*!"!. Таким обра-
зом, в моменты t0 и—/0 подвижная точка будет нахо-
диться в одной и той же точке на оси х. Слеювагельно,
её траектория есть замкнутая кривая и из' предыдущего

134 ТРЕТИЙ МЕМУАР
ясно, что она симметрична по отношению к оси х. Сле-
довательно, заранее можно быть уверенным в том, что
все Со равны нулю.
Тиссеран (Tisserand) обратил моё внимание на одну
астрономическую проблему, дающую пример только что
указанного нами; случая. Делоне (Delaunay) встретил
в своей теории луны уравнения:
|? = М A + М^ + М^) sin О,
-ff A+/>,«¦ +/>8«*) cos 0..
Предполагается, что е очень мало при f=0 и что
коэффициент М имеет порядок квадрата этой малой вели-
чины, тогда как другие коэффициенты конечны (Мемуары
Академии наук, т. XXVIII, стр. 107) *). ' ¦
• Делоне даёт следующие выражения:
е cos 0 = 2 Atcos' (а* "I" c)>
e sin 8 = 2
но он не рассматривает вопросы сходимости и возмож-
ности разложения.. •
• Эти уравнения имеют тот вид,' который мы рассматри-
вали. Положим, в самом деле
е cos 8 =.х, е sin 8 = у;
•мы получим
~ = Мху (Мх — Л + М&* —Р^) -
- Ny A + N^ + Njfi -Ь N^) = X,
Л = м + My* (Ж, + М^) + Ж*2 (Р, + ^ae2j -f
+ Nx (.1 + ^ + ^
*) M^aolres de l'Academle de Sciences, t. XXVIII, p. 107.

ГЛ. XI. ТЕОРИЯ ЦЕНТРОВ 135
где
X и Y обращаются в нуль при у = 0, если
A0) МA+/>,*»-f-Яа**)+
+ Me (I -f N^ + /V2v4 + AVk6) = О-
В силу предположений, сделанных относительно коэф-
фициентов, уравнение A0) удовлетворяется при х = х1,
где х1 есть весьма малая величина того же порядка, что
и М. Точка x = xv у = 0 является центром, так как X
меняет знак, а К не меняется, если вместо у поставить —у.
¦ Заранее можно быть уверенным в том, что все величины,
которые мы обозначили через Со, равны нулю.
Отсюда следует, что х и у являются периодическими
функциями времени t, которые могут быть представлены
рядами того вида,, которым пользуется Делоне.
Если мы тем или иным способом узнали, что все вели-
чины Со равны нулю, то мы можем быть уверены в том,
что вокруг центра- есть' некоторая плоская область /?,
покрытая замкнутыми кривыми или циклами, окружаю-
щими центр и являющимися траекториями подвижной точки
в рассматриваемой области. Вне области R траектории
будут, вообще говоря, спиралями. Эта область будет огра-
ничена некоторым граничным циклом, который явится
последней замкнутой траекторией. Я утверждаю, что этот
граничный цикл должен проходить через особую точку.
В самом деле, мы всегда можем провести дугу без
контакта, пересекающую граничный цикл, а также и те
замкнутые кривые, которые достаточно близки к нему,
и продолжающуюся по другую сторону граничного цикла,
вне области R. Мы определим положение точки на этой
дуге с помощью некоторого параметра t, который будет,
например, равен нулю на граничном цикле, отрицателен
в области R и положителен вне этой области.
Вернёмся теперь к главе V (второй мемуар) и к тому,
что мы назвали законом последования:
*! = <?! Со)-

136 ТРЕТИЙ МЕМУАР
При отрицательных значениях t0 мы находимся. вну-
три JR; траектории замкнуты, и мы имеем
Наоборот, при положительных значениях t0 мы находимся
вне R; траектории уже не замкнуты, и мы имеем
Таким образом, невозможно, чтобы функция <pi была голо-
морфна при *0 = 0. Следовательно, в силу теоремы XIII,
граничный цикл должен проходить через особую точку.

ГЛАВА XII
УРАВНЕНИЯ СТЕПЕНИ ВЫШЕ ПЕРВОЙ
Мы перейдём теперь к изучению дифференциальных
уравнений первого порядка и степени выше первой, т. е.
уравнений вида
A)
dy
где F — многочлен, целый по х, у и -— .
Воспользуемся следующей геометрической интерпрета-
цией: рассмотрим поверхность
B) F(x, у, г) = 0
и запишем уравнения движения изображающей точки на
этой поверхности следующим образом:
,п .. , dx dF
Bbis) Ъ = -Тж,
y.
dF dz dF
'Tz' Tt — ~dx"
dx dy
dz
dt
так что -п, -й, —t равны многочленам, целым по х,
у и г.
Этот способ представления является наиболее простым
во всех тех случаях, когда поверхность F (х, у, г) не
имеет бесконечных полостей или каких-либо особенностей.
Но в' некоторых случаях бывает удобнее пользоваться

138 ТРЕТИЙ МЕМУАР
более общим способом изображения. Положим
C) 5 = ?!(*, У, г), <*] = ?а(*. у, г), С = ?8(*, У, г),
где «j, <р2, <р3— рациональные функции переменных х,у иг.
За исключением особых случаев, которые мы оставим
в стороне, из уравнений B) и C) можно вывести урав-
ьения:
D) FUi, % С)=*0
E) х - 6, ($, -г], С), .у = 82 ($, ч, С), г = 83 E, ц, С),
где Z7! — полином и функции Ь1г б2, б3 рациональны. Тогда
точки поверхностей B) и D) будут поставлены во взаимно-
однозначное соответствие при помощи бирационального
преобразования, и мы будем иметь
где функции фц Фа и "Ь рациональны.
Можно использовать -произвол в бирациональном пре-
образовании C) так, чтобы поверхность D) не имела бы
бесконечных полостей, а также для того, чтобы дости-
гнуть разных других целей, например, для того, чтобы за-
ставить исчезнуть какие-либо мешающие особенности.
Итак, вот каким образом мы поставим проблему диф-
ференциальных уравнений высших степеней. Дана поверх-
ность S, не имеющая бесконечных полостей, уравнениз
которой есть
F^x, у, г) = 0;
требуется изучить движение изображающей точки на этой
поверхности, если уравнения движения суть
Ё?— у ЁУ — v ^.— 7
где X, Y u Z—многочлены, целые относительно х, у и г,
удовлетворяющие условию

ГЛ. XII. УРАВНЕНИЯ СТЕПЕНИ ВЫШЕ ПЕРВОЙ 139
• Изучим сначала траектории изображающей точки
в окрестности какой-либо точки М поверхности. Мы бу-
дем отличать случай, когда точка М есть обыкновенная
точка поверхности 5 (хотя и могущая быть особой точкой
дифференциальных уравнений), от случая, когда точка М
есть особая точка поверхности S.
В первом случае мы можем в окрестности точки М
представить х, у и z как голоморфные функции двух'
параметров и и v таким образом, чтобы три функцио-
нальных детерминанта
д(у,г) . д{х,г)
д (и, v) ' д (и, v) д (a, v)
не обращались бы одновременно в нуль. Тогда можно
написать •;
' —~п Ё? I/
dt~~u' dt~Vt
где U и V — голоморфные функции от а и л. Мы при-
ходим, таким образом, к исследованию плоских кривых,
определённых дифференциальным уравнением первого по-
рядка и первой степени, так как в окрестности рассма-
триваемой точки функции U и Vимеют.все свойства по-
линомов.
Если рассматриваемая точка есть обыкновенная точка
дифференциального уравнения, то через неё проходит одна
и только одна траектория. Если-же эта точка есть осо-
бая точка дифференциального уравнения, т. е. если
в ней U= V=0, то она может быть седлом, фокусом,
узлом или центром и будет иметь те же свойства, что
и точка того же наименования, определённая в первой
части *). !
Особые точки дифференциального уравнения типа B)
и B bis) даются уравнениями-
' дг ==я дх "•" Z ду
*) Т. е. в первом мемуаре.

140 ТРЕТИЙ МЕМУАР
Предположим теперь, что рассматриваемая точка есть
особая точка самой поверхности, т. е. что мы имеем
дх ~ ду ~~ дг ~~ и'
¦ Этот случай приводится к предыдущему. Так, напри-
мер, предположим сначала, что поверхность S имеет двой-
ную линию, что рассматриваемая точка есть точка этой
двойной линии и что две касательные плоскости в этой
точке различны. Тогда можно представить х, у и г в окрест-
ности рассматриваемой точки как голоморфные функции
двух параметров и притом двумя способами, одним — отно-
сящимся к одной из полостей поверхности, проходящей че-
рез двойную кривую, и другим — ко второй полости. Мы
приходим, таким образом, к предыдущему случаю.
Точно так же, предположим, что рассматриваемая
точка, которую мы можем взять за начало координат, есть
коническая точка второго порядка. Пусть, например,
где F{—однородный многочлен степени I по х, у и г.
Рассмотрим часть этой поверхности вблизи начала,
т, е. вблизи конической точки. Я утверждаю, чтб мы
. можем, при помощи бирационального преобразования,
преобразовать эту часть поверхности в часть' другой по-
верхности, которая уже не будет иметь особой точки.
Для этого достаточно положить -
$ = |A_г), ^ = ^A_г), ..;С«а.Г—г;
откуда \ •..-.'' -:
Таким образом, это бирациональное преобразование
обратимо, в результате чего поверхность F переходит
в следующую:
A—• zf F^ ...
..+A—*)«-?¦„ = 0.

ГЛ. XII. УРАВНЕНИЯ СТЕПЕНИ ВЫШЕ ПЕРВОЙ 141
Эта преобразованная поверхность пересекается с пло-
скостью г =1 по кривой 2-го порядка
и не имеет особых точек вдоль этого сечения.
Кроме того, та часть поверхности S, которая была
близка к конической точке, после преобразования перей-
дёт в ту часть преобразованной поверхности, которая
близка к этой кривой второго порядка, т. е. в часть по-
верхности, лишённую особых точек 1181.
Таким образом, мы опять пришли к предыдущему
случаю. Однако в дальнейшем мы будем предполагать,
что поверхность S не имеет особых точек.
В силу сделанных предположений алгебраическая по-
верхность S не имеет бесконечных полостей; следова-
тельно, она состоит из некоторого числа замкнутых
полостей SltS2 Sn, лежащих отдельно друг
от друга. С той точки зрения, которая нас интересует,
нам достаточно изучить вид траекторий на одной
из этих полостей в отдельности, например, на по-
лости Si-
Во всём дальнейшем основную роль будет играть по-
нятие рода полости St, рассматриваемое с точки зрения
геометрии положения 1181.
Вот определение рода. Если на замкнутой поверхности Sj
можно провести р замкнутых циклов, не имеющих общих
точек, не разбивая при этом поверхность на две отдель-
ные области, и если больше циклов с теми же свойствами
провести нельзя, то мы скажем, что поверхность SY есть
поверхность рода р (или, что то же, что она 2р -f-1-связна).
Так, сфера имеет род 0, так как на сфере нельзя провести
ни одного замкнутого цикла, не разбивая её поверхность
на две области. Тор имеет род 1, так как меридиан
или параллель не разделяют его на две области, и если
на поверхности мы провели, например, меридиональную
окружность, то уже нельзя провести никакой другой замк-
нутый цикл, не пересекающий первый, не разбивая тор
на две области.

142 Третий мемуар
В заключение этой главы распространим на интересую-
щий нас случай одну важную теорему первого мемуара *).
Мы сохраним соглашение, сделанное в начале второго
мемуара **), т. е. мы будем считать, что каждая траекто-
рия, проходящая через'узел, кончается в узле и что каждая
тр?ектория; проходящая через седло, продолжается либо
направо, либо налево по одной из ветвей кривой, прохо-
дящей через это седло.
Тогда ясно, что траектории могут быть разбиты на
четыре класса:
1° циклы, или замкнутые кривые;
2° траектории, кончающиеся в узле;
3° траектории, асимптотически стремящиеся к фокусу,
неограниченно закручиваясь вокруг него;
4° траектории, которые можно неограниченно продол-
жать, никогда не возвращаясь в начальную точку, никогда
не встречая узла, но не приближаясь асимптотически
к фокусу.
Ясно, что последние траектории имеют бесконечную
длину, будем ли мы отсчитывать дуги на самой поверх-
ности S: или на проекции этой кривой на какую-нибудь
плоскость 1а°1.
Рассмотрим теперь траекторию, которая пересекает
всякий алгебраический цикл лишь в конечном числе точек.
Очевидно, что она не может принадлежать к третьему
классу, так" как всякая алгебраическая кривая, проходя-
щая через фокус, пересечёт в бесчисленном множестве
точек всякую траекторию, закручивающуюся вокруг этого,
фокуса. Я утверждаю, что она не может принадлежать
и к четвёртому классу. Для этого я покажу, что если
мы предположим, что траектория четвёртого класса пере-
секает всякий алгебраический цикл в конечном числе
точек, то отсюда будет следовать, что проекция траекто-
рии на некоторую плоскость имеет конечную длину, а это
противоречит тому, что мы только что видели. В самом
деле, рассмотрим часть траектории, описываемую подвиж-
*) См. главу I, теорема I.
**) См. главу V, основное соглашение.

ГЛ. XII. УРАПИЕПИЯ СТЕПЕНИ ВЫШЕ ПЕРВОЙ 143
ной точкой, начиная с некоторого момента t=t0, кото-
рый мы в дальнейшем определим точнее, до t = -j-co.
Мы разобьём поверхность Sj с помощью некоторого
числа алгебраических циклов на некоторое число таких
областей, чтобы прямая, параллельная оси г, могла пере-
сечь каждую из них только в одной точке. Рассматривае-
мая траектория пересекает эти алгебраические циклы
лишь в конечном числе точек. Значит, мы можем взять
/0 достаточно большим для того, чтобы, начиная с мо-
мента , t0, подвижная точка не пересекала бы ни одного
из этих циклов и, следовательно, оставалась внутри одной
из тех областей, которые мы только что определили.
Отсюда следует, что, начиная с момента t0, проекция
подвижной точки на плоскость (х, у) остаётся всё время
внутри некоторой конечной области R этой плоскости.
Рассмотрим на поверхности 5 геометрическое место
таких точек, что проекция на плоскость (х, у) траекто-
рии, проходящей через какую-нибудь из этих точек, имеет
в ней точку перегиба. Это геометрическое место будет
алгебраической кривой и, следовательно, может быть пе-
ресечено рассматриваемой траекторией лишь в конечном
числе точек. Мы можем взять t0 столь больщим, чтобы,
начиная с этого момента t0, проекция нашей траектории
на плоскость (х, у) не имела точек перегиба и была,
следовательно, выпуклой кривой.
Геометрическое место точек поверхности Sv в которых
— = 0 или в которых ~ = 0, также является алгебраи-
ческой кривой. Отсюда можно заключить, рассуждая так
же, как и выше, что можно взять tQ достаточно большим,
для того чтобы, начиная с этого момента, —тт и —^
оставались одного и того же знака, например, положи-
тельными,
Пусть теперь Ма есть проекция подвижной точки
в момент to,'M1 — проекция этой точки в момент <i(*i>*0)-
Через точку Мо я провожу прямую, параллельную оси х;
через точку Mt — прямую, параллельную оси у, пересе-
кающую первую прямую в некоторой точке Р.

144 ТРЕТИЙ МЕМУАР
Пусть R' есть прямоугольник, стороны которого па-
раллельны обеим осям и который'выбран так, что область,
определённая выше, лежит внутри него. Криволинейный
треугольник МаМхРг образованный дугой траектории
MqM^ и двумя прямыми М0Р и МХР, будет выпуклым и
лежащим целиком внутри R'. Его периметр будет, следо-
вательно, меньше, чем периметр R'. Значит, дуга МОМХ
всегда меньше периметра R', какова бы ни была точка Mv
Следовательно, длина проекции нашей траектории будет
конечной, что невозможно и что заставляет нас отбросить
предположение, будто траектория относится к четвертому
классу.
Отсюда следующий вывод: всякая траектория, пере-
секающая каждый алгебраический цикл лишь в конечном
числе точек, есть или замкнутый цикл или оканчивается
в узле, где она должна быть остановлена.

ГЛАВА XIII
РАСПРЕДЕЛЕНИЕ ОСОБЫХ ТОЧЕК
Возьмём снова полость S1 рода р и предположим, что
эта полость не имеет ни конических точек, ни кратных
линий.
Пусть С есть число сёдел, лежащих на этой полости
N—число узлов, F—фокусов; я утверждаю, что мы
будем иметь соотношение '211
N-\-F — С=2 — 2р.
Проведём на поверхности S1 какой-нибудь цикл. Этого
цикла будут касаться в некоторых точках различные
траектории; одни будут касаться его извне, другие изнутри.
Пусть Е есть число внешних контактов, /—число вну-
тренних контактов; число
._ E—I—2
J — . 2
будет называться индексом цикла. Если цикл имеет угло-
вую точку, то может случиться, что траектория, прохо-
дящая через эту точку, пересекает цикл, проходя из внеш-
ней части во внутреннюю; в этом случае эта точка не
должна считаться точкой контакта. Но может случиться
также, что'эта траектория не переходит и» внешней части
цикла во внутреннюю, а остаётся или во внешней части,
если угловая точка есть вершина выступающего угла, или
во внутренней, если угловая точка есть вершина входящего
угла. Тогда угловая точка должна считаться или внешним,
Ю А. Дуаикаре.

146
ТРЕТИЙ МЕМУАР
или внутренним контактом (см. первый мемуар, глава IV).
Мы будем предполагать, что цикл выбран таким образом,
что он разбивает полость St на две области, из которых
по крайней мере одна односвязна.
Если полость St рода 0, то обе области будут одно-
связными, и нужно сделать специальное соглашение, для
того чтобы определить, какую из двух областей надо счи-
тать внутренностью цикла.
Если полость St рода > 0, то одна
из областей будет односвязна, а дру-
гая многосвязна, и внутренностью цикла
нужно считать именно первую область.
Соединим теперь две точки А и В
тремя дугами кривых АМВ, ANB,
АРВ (черт. 30). Мы получим таким
образом три цикла:
C1 = ANBMA,
CS = APBMA.
Из них третий можно рассматривать как сумму двух
других:
С3 == Q 4" '-а-
Я утверждаю, что
Ind С, — ind Cj-J-ind Cj
или, что то же,
A) ?8_/8_
где Elt Ev Еа — число внешних контактов, Iv /2, /8 —
число внутренних контактов траекторий с рассматривае-
мыми тремя циклами.
Эти контакты разбиваются на 5 классов:
1° Те, которые расположены на АМВ.
2° Те, которые расположены на АРВ.
Первые принадлежат только циклам Ct и С8, вторые —
только циклам С, и С8. Контакт, принадлежащий к одному
из этих двух классов, дважды войдёт в левую часть ра-

ГЛ. XIII. РАСПРЕДЕЛЕНИЕ ОСОБЫХ ТОЧЕК • 147
венства A): один раз со знаком-(-, другой раз со зна-
ком —; соответствующие члены взаимно уничтожаются.
3° Те, которые расположены на ANB. Контакт этого
класса будет внешним для Ct и внутренним для Са или
наоборот. Значит он дважды войдет в левую часть
равенства A): один раз со знаком-}-, другой раз со
знаком —. Соответствующие члены взаимно уничто-
жаются.
4° Те, которые могут быть в точке А. В зависимости
от положения траектории, проходящей через точку Л, мы
можем иметь; или внешний контакт для всех трёх циклов,
или же внешний контакт только для цикла Cv или только
для цикла Са, или же (но только в том случае, когда
точка А есть вершина входящего угла для Са) — вну-
тренний контакт для цикла С3, или же, наконец (но только
в том случае; когда точка А есть вершина входящего
угла для циклов Ct и С8) — внутренний контакт для
циклов С, и С3 и внешний для цикла Са.
Во всех случаях сумма соответствующих членов левой
части A) обращается в —1.
5° Контакты, расположенные на В.
В силу тех же соображений сумма соответствующих
членов обращается в —1.
Левая часть A) обращается, следовательно, в —2,
так что это равенство справедливо. Следовательно, индекс
составного цикла равен сумме индексов отдельных соста-
вляющих его циклов.
Найдём теперь индекс бесконечно малого цикла.
Если бесконечно малый цикл не окружает ни одной
особой точки, то мы всегда можем считать его выпуклым,
так как в противном случае его всегда можно было бы
разложить на несколько ещё меньших выпуклых циклов.
Но тогда черт. 31 показывает, что цикл имеет всего два
контакта, и притом внешних, с траекториями МР и М"Р".
Следовательно, индекс равен нулю.
Если цикл охватывает седло, мы попрежнему будем
предполагать его выпуклым, и черт. 32 показывает, что он
будет иметь четыре внешних контакта и что его индекс
равен 1.
W

148
ТРЕТИЙ МЕМУАР
^Если^цикл окружает узел и фокус, то я утверждаю,
что индекс его равняется —1. В самом деле, в окрест-
ности узла или фокуса всегда можно провести цикл без
контакта, лежащий внутри рассматриваемого цикла. Тогца
рассматриваемый нами цикл может быть разложен на
несколько циклов, а именно:на цикл без контакта, о кото-
ром мы только что говорили, и на другие выпуклые
циклы, не охватывающие особые точки. Индекс цикла
без контакта будет равен — 1;
индекс остальных есть 0. Ин-
декс исходного цикла есть,
следовательно, — 1.
Черт. 31.
Черт. 32.
Из предыдущего следует, что индекс какого-либо
цикла равен числу сёдел, лежащих внутри него, минус
число узлов и фокусов.
Центры, являющиеся исключительными особыми точ-
ками, с этой точки зрения эквивалентны фокусам; в са-
мом деле, вокруг центра можно провести замкнутый цикл
с двумя внутренними и двумя внешними контактами; этот
цикл будет тогда иметь индекс —1.
Мы разобьём теперь поверхность полости St на не-
которое число односвязных областей, проведя некоторое
определённое число циклов.
Сумма индексов этих циклов будет, очевидно,
C—F—N.
Для того чтобы оценить эту сумму индексов другим
способом, будем рассматривать фигуру, образованную
полостью Sv разбитой на односвязные области, как много-

ГЛ. ХП1. РАСПРЕДЕЛЕНИЕ ОСОБЫХ ТОЧЕК 14S
гранник. Всем известна теорема Эйлера, по которой, если
л, р, "у—-число граней, рёбер и вершин выпуклого много-
гранника, то мы должны иметь
Эта теорема легко обобщается на тот случай, когда много-
гранник, не будучи уже выпуклым, образует поверхность
рода р\ тогда мы находим
«-р-Н-2 — 2р.
Но в геометрии положения можно не беспокоиться о форме
граней и рёбер; следовательно, нам нет нужды предпола;
гать, что грани плоски, а рёбра прямолинейны. Отсюда
вытекает, что фигура, образованная полостью Slt разби-
той на односвязные области, есть настоящий криволиней-
ный многогранник, к которому приложима теорема Эйлера.
Гранями будут тогда сами односвязные области; ребром
будет часть границы одной из этих областей, являющейся
одновременно общей границей с одной из соседних обла-
стей; вершиной будет конец ребра, т. с. точка, общая
границам трёх или более областей.
Предположим, что вершина является общей для гра-
ниц v областей; она будет тогда эквивалентна вершине
многогранного угла с v-гранями прямолинейного много-
гранника. При этом мы будем иметь
Кроме того, мы можем предполагать, что все углы,
образуемые различными рёбрами, сходящимися в одной и
той же вершине, являются выступающими.
Нам нужно оценить для совокупности наших циклов
избыток числа ?? внешних контактов над числом 2/
внутренних контактов.
Мы можем не заботиться о контактах, имеющих место
в какой-либо точке ребра; действительно, если такой кон-
такт является внешним по отношению к циклу, образую-
щему границу одной из тех двух областей, для которых
ребро служит общей границей, то он же будет внутреи-

150 ТРЕТИЙ МЕИУАР
ним контактом для цикла, образующего границу второй
из этих областей, и наоборот.
Следовательно, нам нужно рассмотреть лишь контакты,
имеющие место в вершинах. Пусть мы имеем вершину,
общую v-циклам. .Траектория, проходящая через эту точку,
пересечёт два из этих циклов и будет иметь внешний
контакт с (v — 2)-мя остальными. Следовательно, мы бу-
дем иметь:
С другой стороны, искомая сумма индексов равна
т. е. равна
Р_<х — f = 2p— 2.
Отсюда
C—F—N=2p — 2.
Что и требовалось доказать.
Из этой формулы непосредственно вытекает, что только
поверхности -рода 1 могут не иметь ни одной особой
точки.

ГЛАВА XIV
ОБОБЩЕНИЕ ПЕРВЫХ ДВУХ ЧАСТЕЙ *)
Мы рассмотрим теперь снова каждую из изложенных
теорем в главах IV — VI, для того чтобы выяснить, при-
ложимы ли они к интересующему нас случаю и в какой
мере они должны быть изменены.
Теорема VI, согласно которой каждый алгебраический
цикл имеет чётное число контактов, остаётся верной, но
только по отношению к циклам, разбивающим поло:ть 5,
на две области,- из которых, по крайней мере, одна
является односвязной.
В самом деле, индекс подобного цикла, зависящий от
числа особых точек, содержащихся в нём, есть число не-
пременно целое. Следовательно^ ?Е—?/, а значит и
2E-J-S/ есть число четно*, т.е. число контактов будет
всегда чётным IJ21.
Теорема VII, согласно которой между двумя точками
можно провести алгебраическую дугу без контакта, если
только между этими точками можно провести какую-
нибудь дугу без контакта, остаётся справедливой и для
уравнений более высокой степени. Чтобы убедиться в этом,
достаточно только сослаться на доказательство, приведён-
ное в мемуаре первом. Нам нужно ввести одно
только видоизменение; дугу без контакта мы изобразим
*) Подразумевается: результатов двух первых мемуаров

152 ТРЕТИЙ МВМУАР
уравнениями
*«=?@, У*~Ш F(x, у, г) = 0,
причём концы этой дуги соответствуют t = О, t = я. Дока-
зательство проводится так же, как и в первом мемуаре.
Важно отметить, что ряды
cos m*_ Ц sin | +^ cos -|-
tie только сходятся, но сходятся равномерно, что необ-
ходимо для дальнейшего хода рассуждения; в самом деле,
сумма ряда
2 mAmcosmt,
принимая одинаковые значения при t и 2ir — t, будет не-
прерывной функцией от t, когда t возрастает от — оо
до -fool*»!.
Теорема VIII и её доказательство также, остаются в силе
без всяких изменений.
Таким образом, если А и В можно соединить дугой
без контакта и если А1 и Вх являются двумя точками
траекторий, проходящих через А и В, то Ах и Bt также
можно соединить дугой без контакта 1а41.
Теорема IX формулируется так:
Если АВ и А1В1 — две дуги траекторий и если ААЬ
ВВ^ — две алгебраические дуги, не пересекающие АВ и
^jB, ни в одной точке, отличной от точек А, В, А1
и Ви то числа контактов дуг ААХ и ВВ1 одинаковой
чётности.
Эта теорема остаётся справедливой и в интересующем
нас случае, если только цикл АВА1В1 разбивает полость
на две области, одна из которых односвязна.
Теорема X. Если дуга некоторой кривой поддержи-
вает (sous-tendu) дугу траектории, не проходящую
ни через одну особую точку, то число контактов на
этой дуге нечётно.

ГЛ. XIV. ОБОВЩКНИЕ ПЕРВЫХ ДВУХ ЧАСТЕЙ 153
Эта теорема также остаётся в силе, если цикл, обра-
зуемый этими двумя дугами, разбивает полость St на две
области, одна из которых односвязна Iя5).
Таким образом, теоремы главы IV, образующие то,
что я назвал теорией контактов, распространяются, с не-
которыми изменениями, на интересующий нас случай.
Я перейду теперь к теории последующих.
Пусть
есть алгебраическая дуга без контакта и пусть Мо,
Afj—две последовательные точки пересечения этой дуги
с одной и той же траекторией. Тогда М1 есть последующая
для Мо, Мо — предшествующая для Mt; если^и^ — зна-
чения t, соответствующие этим двум точкам Мо и М1У то
соотношение, связывающее t0 и iit есть закон последования.
Теоремы XI и XII справедливы лишь после существен-
ных изменений, к которым мы вернёмся в дальнейшем.
Теорема XIII, наоборот, остается справедливой и для
уравнений высших степеней.
Если /1 = ^1(^0) есть закон последования, то функ-/
ция <pj голоморфна. Исключение может представиться лишь
для тех значений /, которые соответствуют траекториям,
кончающимся в особой точке до нового пересечения
с дугой без контакта, а также для значений *0 или tlt
соответствующих концам дуги без контакта.
Теорема XIV также остаётся справедливой, но дока-
зательство должно быть изменено, так как цикл
М0НМiN0M0, о котором идёт речь в доказательстве,
приведённом в главе V, может не разбивать полость St
на две области. Но пусть Ро будет точка, лежащая на
дуге без контакта между No и Мх (см. мемуар второй,
черт. 10), на конечном расстоянии от No. Пусть
Рх—точка, лежащая на дуге без контакта, направо от
Mj и на конечном расстоянии от этой точки. Соединим
Р0Рг такой дугой кривой, чтобы вамкнутый цикл
MqM^PqMq ограничивал бы односвязную область. Траек-
тория A^o^i не может выйти из этой области, не удаляясь
от траектории М0М1 на конечное расстояние или же не

154 ТРЕТИЙ МЕМУАР
пересекая ей, что невозможно." Значит точка Л^ должна
быть справа от точки Mv
Что и требовалось доказать.
Я утверждаю, что всегда можно провести на полости
St циклы без контакта. В самом деле:
1° В окрестностях узлов и фокусов можно провести
циклы без контакта, охватывающие эти особые точки.
2° Если MQ и М1—две последовательные точки пере-
сечения некоторой траектории МйРМ1 с дугой без кон-
такта M0QMlt то цикл MqQM^Mq можно считать циклом
без контакта. В самом деле, пусть No—точка, беско-
нечно-близкая к Мо и лежащая справа от неб, как на
черт. 10, на который мы только что ссылались, а Л^ — по-
следующая No. В бесконечно-узкой области, содержащейся
между траекториями М0М1 и Лу^, мы можем провести
дугу NqRM^ пересекающую каждую траекторию только
один раз. Цикл NqRM^QNq, отличающийся бесконечно
мало от цикла MqPM^QMq, будет тогда без контакта.
Таким образом, если полость St содержит узел или
фокус, то заведомо можно провести цикл без контакта;
если же она их не содержит, то каждая траектория
должна пересечь, по крайней мере, один алгебраический
цикл в бесчисленном множестве точек (если только она
не сводится к замкнутому циклу, как мы видели в главе
XII). Этот алгебраический цикл можно разделить на
конечное число дуг без контакта. Следовательно, по
крайней мере, одна из этих дуг будет пересекать-я
с траекторией в бесчисленном множестве точек. Из этих
точек мы выберем две последовательные Мо и Mlt и
они дадут нам, как мы только что видели, цикл без
контакта. Следовательно, всегда существуют циклы без
контакта, если только не все траектории обращаются
в замкнутые циклы.
Если цикл без контакта делит полость Sx на две
области, одна из которых односвязна, то эта последняя
содержит по крайней мере один узел или фокус.
В самом деле, индекс цикла без контакта рапен — 1.
Следовательно, если N, F и С обозначают число узлов,
фокусов и сёдел, лежащих внутри нашей односвязной

ГЛ. XIV. ОБОБЩЕНИЕ ПЕРВЫХ ДВУХ ЧАСТЕЙ 155
области, то
N + F— С=»1,
что и доказывает высказанную нами теорему.
Предположим теперь, что цикл без контакта делит
полость St на две области, обе могущие быть много-
связными. Я утверждаю, что в каждой из этих областей
есть особые точки.
Пусть R есть одна из этих областей, которую я буду
предполагать ^-связной. Требуется найти индекс цикла
без. контакта С, рассматривая область R как внутрен-
ность цикла. Мы можем построить односвязную поверх-
ность /?!, имеющую границей цикл С. Совокупность обеих
областей R и Rt образует тогда замкнутую поверхность
рода 2~> что ПОПУТНО доказывает, что q должно быть
нечётно (ср. Riemann, Gesammelte mathematische Werke,
lre ed., p. 12; Leipzig, Teubner, 1876). Положим
Если мы разложим область R на некоторое число
односвязных областей, то мы можем рассматривать за-
мкнутую поверхность /? —|— /?а как многогранник. Прилагая
к этому многограннику теорему Эйлера и рассуждая,
как в предыдущей главе, мы найдём
индекс С= 2г'.—2Л,
где V/ обозначает сумму индексов циклов, при помощи
которых область R была разбита на односвязные области. Но
если N, F и С—число узлов, фокусов и сёдел области R, то
2г = С— N— F.
Кроме того, так как цикл С не имеет контактов, то
индекс С = — 1; отсюда
С— N—F = 2h— 1
или
N+F-\-Ceal (mod. 2),

156 ТРЕТИЙ МВМУАР
что и доказывает, что N, F и С не могут одновременно
обращаться в нуль.
С интересующей нас в данный момент точки зрения,
всякую замкнутую траекторию, не проходящую через
особую точку, можно рассматривать как цикл без кон-
такта; л хочу этим сказать, что её индекс будет ра-
вен —1. Замкнутая траектория не имеет, собственно говоря,
индекса 12°1, но бесконечно-близкие к ней циклы имеют
индекс, и я утверждаю, что он равен—1.
В самом деле, могут представиться два случая:
Пусть MqPMq есть замкнутая траектория; пусть
AMQB — дуга без контакта; пусть t— параметр, опре-
деляющий положение точки на этой дуге; пусть значение /,
соответствующее Мо, есть 0. Пусть
есть закон последования на нашей дуге. Мы будем
иметь
Может случиться, что функция <pj — *0 не обращается
тождественно в нуль. Пусть в этом случае /0 — беско-
нечно малое значение переменной./, No — соответствую-
щая ему точка, Л^ — ее" п ^следующая и t1 —соответствую-
щее точке Л^ бесконечно малое значение переменной t.
Пусть NgQNi — дуга траектории, соединяющая No и Nt;
цикл NqQ^Nq, бесконечно мало отличающийся от MqPM0,
может быть, согласно тому, что мы видели выше, упо-
доблен циклу без контакта. В этом случае замкнутая
траектория MQPM0 является предельным циклом и имеет
свойства, доказанные для таких циклов во втором мемуаре.
Может также случиться, что функция <р: — /0 то-
ждественно обращается в нуль. В этом случае траектории,
близкие к М0РМ0, будут замкнутыми, охватывающими
друг друга циклами.
Если провести цикл, бесконечно мало отличающийся
от М0РМ0, то число его внешних контактов будег то
же, что и число его внутренних контактов, и его индекс
будет попрежнему ранен-г-1.

ГЛ. XIV. ОБОБЩЕНИЕ ПЕРВЫХ ДВУХ ЧАСТЕЙ 157
Что и требовалось доказать.
Таким образом, если замкнутая траектория разбивает
полость St на две области, то в каждой из них есть
особые точки.
Следовательно, всякий алгебраический цикл, про-
ходящий через все особые точки, пересекает все те
циклы без контакта и все те замкнутые траектории,
которые делят полость St на две области.
Это и есть обобщение теоремы XVI из второго мемуара.
Перейдём теперь к обобщению теоремы XVIII, что и
является главной задачей настоящей главы.
Эта теорема в обобщённом виде формулируется так:
полость St можно покрыть семейством циклов и поли-
циклов {замкнутые кривые с двойной точкой) таким
образом, чтобы через каждую точку этой полости
проходил бы один и только один цикл; исключение
составляют фокусы и узлы, которые считаются бес-
конечно малыми циклами. Среди этих циклов одни
являются циклами без контакта, другие — замкну-
тыми траекториями.
Если род р полости Si ;равен 0, то обобщение совер-
шается непосредственно. В самом деле, при доказатель-
стве теорем от X до XVIII первых двух мемуаров мы
опирались только на одно свойство сферы — на её одно-
связность, или, что то же самое, на то, что она имеет
род 0.
Есть ещб один случай, когда -это обобщение может
быть сразу .же сделано. Предположим, что на полости
Sj вырезана двусвязная область R, ограниченная двумя
циклами без контакта С и С. Предположим далее, что
эта область R не содержит никаких особых точек. Я
утверждаю, что теорема XVIII прилагается к этой области,
т. е., чго эту область можно покрыть бесконечным
множествэи циклов К, являющихся или циклами без
контакта, или замкнутыми траекториями.
Кроме того, ясно, что циклы К должны быть распо-
ложены таким образом, что каждый из них разделяет
область R на две: одну*—ограниченную циклами К и С,
и другую — циклами К и С. Другими словами, невоз-

158 ТРЕТИЙ МЕМУАР
можно, чтобы цикл К сам по себе был границей области
R', целиком содержащейся в R. В самом деле, индекс
такого цикла был бы равен — 1, тогда как R, а следова-
тельно, и R' не содержат никаких особых точек.
Разобьбм теперь с " помощью какой-либо точки М
каждую траекторию на полутраектории, аналогичные
полухарактеристикам первых двух мемуаров. Одна из
этих полутраекторий содержит те точки, которые
подвижная точка пробегает, пройдя точку М, а другая —
те точки, которые были пройдены подвижной точкой
до её прибытия в точку М. Полутраектории разделяются
тогда на три типа:
1° замкнутые траектории, остающиеся целиком внутри R;
2° _ полутраектории, которые продолжаются неогра-
ниченно, не замыкаясь и- не выходя из области R\
3° полутраектории, которые выходят из R, пересекая
цикл С или С.
Мы начнём с построения предельных колец вокруг
замкнутых траекторий, так же, как мы это сделали во
втором . мемуаре. Для этого соединим точку цикла
С с точкой цикла С' какой-либо алгебраической
дугой. Эта алгебраическая дуга может быть разложена
на конечное число дуг без контакта. Через каждый
конец этих дуг я проведу маленькую дугу без контакта.
Таким образом, я провёл внутри R некоторое число дуг
без контакта, и я могу быть уверенным, что каждая
полутраектория первого типа пересечёт, по крайней мере,
одну из них.
-Возьмём одну из этих дуг без контакта и рассмо-
трим, какие из точек взятой дуги имеют последующую.
Для этого мы условимся считать, что точка Мо дуги
без контакта нг имеет последующей, если траектория,
проходящая через точку Мо, выходит из области R или
если она не пересекает снова дугу без контакта. Наобо-
рот, если траектория, проходящая через Мо, не выходя
из R, снова пересечёт дугу без контакта в точке М1У
то точка Л-fj будет последующей для Мо.
Среди тех дуг без контакта, которые я в конечном
числе провел в области R, одни не будут пересекаться

ГЛ. XIV. ОБОБЩЕНИЕ ПЕРВЫХ ДВУХ ЧАСТЕЙ 159
ни с одной замкнутой траекторией первого типа и должны
быть отброшены, другие же будут пересекаться, по
крайней мере, с одной замкнутой траекторией; я назову
их вспомогательными дугами.
Рассмотрим какую-либо вспомогательную дугу; на
этой дуге всегда можно найги точки, допускающие после-
дующую, так как точка, в которой её пересекает замкнутая
траектория, есть своя собственная последующая. Кроме
того, никакая траектория, проходящая через точку вспо-
могательной дуги,, не проходит через седло, так как
в области R сёдел нет. Кривая последования будет, сле«
довательно, иметь один из видов, которые изображены
на черт. 11 (второй мемуар, глава V).
Мы видели, что если мы соединим дугой траектории
М0РМх точку MQ дуги без контакта с её последующей Мх,
то цикл MqPMxMq можно рассматривать как цикл без
контакта. Само собой разумеется, нужно сделать исклю-
чение для того случая, когда обе точки Мо и Мх совпа-
дают; в этом случае цикл без контакта обращается
в замкнутую траекторию. Мы проведён получающиеся
таким образом циклы без контакта для всех тех точек
вспомогательной дуги, которые имеют последующую.
Совокупность всех этих циклов образует тогда предель-
ное кольцо, подобное тем, которые мы рассматривали во
втором мемуаре.
Это предельное кольцо будет покрыто семейством
циклов без контакта, из которых некоторые вырождаются
в замкнутые траектории; кроме того, это предельное
кольцо разбивает область R на две другие, аналогичные
ей по свойствам, области R' и R", заключающие мень-
шее число вспомогательных дуг.
Продолжая те м.е рассмотрения с областями R' и R",
мы разобьём, наконец, область R на некоторое число
предельных колец и на некоторое число межкольцевых
областей, внутри" которых нельзя провести ни одной
замкнутой траектории.
Рассмотрим одну из этих межкольцевых областей;
она будет вполне подобна области R с той лишь разницей,
что в ней нельзя будет провести полутраектории первого

160 ТРЕТИЙ МЁМУЛР
типа. Я утверждаю, что нельзя также провести полу*
траекторию второго типа.
В самом деле, для каждой полутраектории второго
типа существует предельный цикл, который должен быть
полутраекторией первого типа, так как внутри области R
георемы главы V верны .без ограничений; следовательно,
полутраектория не может всё время оставаться внутри
такой межкольцевой области, которую не пересекает ни
одна полутрасктория первого типа.
Таким образом, любая межкольцедая область может
содержать лишь полутраектории третьего типа; отсюда
следует, что каждая траектория, пересекающая такую
область, должна в обе стороны окончиться в точках,
лежащих на циклах f и f', ограничивающих область.
Невозможно, чтобы оба конца были на одном и том же
цикле т» так как дуга" без контакта не может поддер-
живать (sous-tendre) дугу траектории.
Следовательно, всякая траектория, проведённая в меж-
кольцевой области, идёт от некоторой точки цикла f
к некоторой точке цикла к'; это и доказывает возможность
покрытия этой области циклами без контакта.
Теорема XVIII таким образом доказана для области R.
Заслуживающим внимания частным случаем является
тот, когда закон последования на какой-нибудь вспомо-
гательной дуге имеет вид tx = tQ. Тогда можно, принимая
во внимание, что в области R нет особых точек, про-
вести рассуждение, аналогичное употребленному в конце
главы XI, и показать, что все траектории, пересекающие
эту область, замкнуты.
Если оставить в стороне этот особенный случай, то
все замкнутые траектории являются предельными цик-
лами; теорема XVII, согласно которой предельных циклов
конечное число, легко распространяется на этот случай
(до сих .пор, само собой разумеется, речь идёт только
о предельных циклах и замкнутых траекториях, лежащих
целиком внутри R).
Теоремы XVII и XVIII остаются в силе и тогда, когда
циклы С и С, ограничивающие область R, являются за-
мкнутыми траекториями, а не циклами без контакта. Исклю-

ГЛ. XIV. ОБОБЩЕНИЕ ПЕРВЫХ ДВУХ ЧАСТЕЙ 161
чение для теоремы XVII может быть в том случае, когда
цикл С сводится к замкнутой траектории, проходящей
через седло.
Для того чтобы доказать теоремы XVII и XVIII во-
всей их общности, мне остаётся показать, что полость
St можно разбить на конечное число областей, подоб-
ных R.
Для этого' мы сделаем сперва несколько предвари-
тельных замечаний.
Мы видели, что если соединить дугой траектории
M0PMt две точки Мо и Мх дуги без контакта, то цикл
MqM^Mq можно считать циклом без контакта, т. е.
через каждую из его точек можно провести цикл без
контакта, бесконечно мало отличающийся от цикла
Предположим далее, что дуга траектории A0:
пересекает цикл без контакта М1РМ1 в точке Mv
Я утверждаю, что цикл MlPMiQMQQM1 можно считать
циклом без контакта.
В самом деле, пусть M'0Q'M[, MQ"M[, . . . ,
M^Q'^M^—дуги траекторий, бесконечно мало отли-
чающиеся от M0QM1 P'l. Мы всегда можем провести дугу
кривой, встречающую цикл без контакта М1РМ1 в точке
М[, пересекающую каждую из указанных выше дуг
траекторий в одной только точке, проходящую через
точку Мо и снова достигающую- цикл без контакта
в точке М*\ Замкнутый цикл А/^РМ^М^мФ, беско-
нечно мало отличающийся от M^M^MqQM^ будет без
контакта.
Представим себе теперь, что на полости St прове-
дено некоторое число циклов без контакта (или замкну-
тых траекторий) и что таким образом на этой полости
определена некоторая область Р, ограниченная этими цик-
лами без контакта. (Может случиться, что область Р
совпадает со всей полостью St; так, например, предпо-
ложим, что Sx есть тор и что на торе проведён мери-
диональный круг С, являющийся циклом без контакта.
Вся лолость целиком образует тогда одну область Р,
И А. Луашс&р».

162 ТРЕТИЙ МЕМУАР
ограниченную двумя циклами, так как надо будет раз-
личать два края разреза, сделанного на торе.)
Теперь я утверждаю, что через каждую точку Мо
области Р можно провести цикл без контакта, лежащий
внутри этой области. Рассмотрим в самом деле полу-
траекторию, проходящую чергз MQ. Вот какие случаи
могут иметь место:
1° Может случиться, что полутраектория замыкается,
не выходя из области Р. Это — единственный исключи-
тельный случай; через точку Мо нельзя провести цикл
без контакта, а только замкнутую траекторию.
2° Может случиться, что полутраектория MQQMl
выходит из области Р в точке Mt через один из огра-
ничивающих эту область циклов, например, через цикл
MXHMV В этом случае цикл M^M^QMqQM^ как мы
только что видели, можно рассматривать как цикл без
контакта.
3° Или же полутраектория кончается в узле или
в фокусе. Этот случай приводится к предыдущему, так
как узел или фокус можно окружить малым циклом без
контакта, который траектория должна будет пересечь,
для того чтобы окончиться в узле *или в фокусе.
4° Или же полутраектория неограниченно продол-
жается, не замыкаясь, не кончаясь в узле или в фокусе
и не выходя из области Р. Тогда можно найти
в области Р дугу без контакта, пересекающую полутра-
екторию в двух точках NQ и Nv Отсюда следует, по
теореме VIII, что можно соединить точку Мо с другой
точкой полутраектории Му дугой без контакта. В этом
случае цикл, образованный дугой без контакта МйМ±
и дугой траектории М0М1} можно рассматривать как
цикл без контакта.
Таким образом, всегда можно провести через точку
Мо в области Р цикл без контакта, который в некото-
рых случаях может обращаться в замкнутую траекторию.
Если точка Ма является седлом,, то в ней кончаются
не две, а четыре полутраектории. Тогда можно провести
через точку Мо два • цикла без контакта, вместе обра-
зующих замкнутую кривую с двойной точкой.

ГЛ. XIV. ОБОБЩЕНИЕ ПЕРВЫХ ДВУХ ЧАСТЕЙ 1бЗ
Вот теперь каким образом мы будем поступать, для
того чтобы разбить полость Sj на области, аналогичные
R. Мы начнём с того, что окружим все узлы и фокусы
бесконечно-малыми циклами без контакта. Пусть в так
определённой области Р есть какое-нибудь седло; че-
рез это седло я проведу два цикла без контакта 1281;
таким образом, я разделил полость Sl на меньшие
области Р. Я поступлю таким же образом с осталь-
ными сёдлами; в конце концов, полость Sl окажется
разделённой на некоторое число областей R, ограничен-
ных циклами без контакта и не содержащих никаких
особых точек.
Я утверждаю, что каждая из этих областей двусвязна
и ограничена лишь двумя циклами.
Предположим в самом деле, что область R дГ'связна
и ограничена «-циклами.
Мы имеем, во-первых (см. Riemann, loc.' clt., стр. 12),
7>я>0, 9 — «(mod. 2).
Кроме того, каждый из этих циклов имеет индекс—1,
и в области нет особых точек. Если мы замкнём
область' R, строя на каждом из ограничивающих её
циклов С односвязную поверхность, и если мы затем
разделим саму область R на односвязные области цик-
лами С, то мы получим подобие криволинейного много-
гранника рода ч~^п*. Теорема Эйлера даст нам тогда
где 2* обозначает сумму индексов циклов С, а 2'' —
сумму индексов циклов С". Но мы имеем
-2*--п, 2'' = о,
откуда
7 = 2, я = 2.
Что и требовалось доказать.
И*

164 ТРЕТИЙ МЕМУАР
Г" Таким, образом, все наши области являются'двусвяз-
ными и ограничены двумя циклами; следовательно, мы
можем покрыть каждую из них циклами без контакта,
что и доказывает теорему XVIII во всей её общности.
После того как на полости 5t построено семейство
циклов без контакта и предельных циклов, охватывающих
друг друга, то это семейство можно использовать для
построения самих траекторий.
Если цикл без контакта разбивает S1 на две области,
то каждая траектория может пересечь его только в одной
точке.
Напротив, это уже неверно, если цикл без контакта
ке разделяет St на две области; но даже и в этом слу-
чае рассмотрение циклов без контакта остаётся не менее
важным, чем раньше. Это станет понятнее после тех
примеро.в, которые я дам в следующей главе.

Г Л А В А XV
ДЕТАЛЬНОЕ ИЗУЧЕНИЕ ТОРА
Как мы видели, поверхности рода 1 являются един-
ственными, на .которых может не быть особых точек.
После, случая поверхностей.рода 0, по существу изучен-
ного в первых двух частях, поверхности рода 1 без
особых точек являются простейшим случаем. Его мы
и рассмотрим теперь подробно.
Для большей определённости я .предположу, что
поверхность St является тором
г2 + (R — Vx* +.у2 )а = /а.
Однако всё то, что будет сказано о торе, относится
также к любой поверхности рода. 1, иЗо, с точки зре-
ния геометрии положения, она не отличается от тора.
Мы положим;
х = (/?-{- г cos со) cos tp,
у =в (R -|- r cos со) sin tp,
z = rs\n со.
Дифференциальные уравнения мы запишем в таком
виде:
^L = Q JS. = Ф
dt Ъи' dt '¦

166 ТРВТИЙ МЕМУАР
где Q и Ф являются многочлйнами, целыми относительно
cos», sinm, coscp и sin «p.
С другой стороны, находим:
, z дгсовч>4- у sin» — R
81П@ = , COS CO = 1 ? i .
Отсюда следует, что если Q и Ф являются полиномами, целы-
ми по cos ш, sin со, cos ср и sin ср, то -J-., jj и — булут
рациональными функциями от х, у и г.
Для лучшего понимания дальнейших рассуждений
надо припомнить главы VIII и IX (второй мемуар). В самом
деле, мы приложим те же методы и разделим тор на аци-
клические области (покрытые циклами без контакта,
среди которых нет предельных циклов), на области ци-
клические (покрытые циклами без контакта, среди которых
заведомо есть предельные циклы), на области моноци-
клические (где есть один и только один предельный цикл)
и на области сомнительные (относительно которых нельзя
утверждать ни того, что в них отсутствует предельный
цикл, ни того, что в них имеется предельный цикл).
Исследование будет закончено, если останутся только
ациклические и моноциклические области.
Задача, следовательно, состоит в том, чтобы узнать,
является ли область циклической и является-ли она моно-
циклической. Правила, которые мы применим здесь для
ориентации, будут те же, что и изложенные в VIII главе.
1° Пусть дана двусвязная область R, ограниченная
двумя циклами без контакта С и С, и пусть АМВ есть
какая-либо алгебраическая дуга, пересекающая эти дпа
цикла в точках А и В. Рассмотрим наблюдателя, двигаю-
щегося по этой дуге и попадающего в область R через
точку А. Если полутраектория, идущая в область R из
точки А, находится направо от наблюдателя, то мы ска-
жем, что цикл С положителен; в противном случае он
будет отрицателен. Предположим, что наблюдатель, дви-

ГЛ. XV. ДЕТАЛЬНОЕ ИЗУЧЕНИЕ ТОРА 167
гаясь по нашей дуге, выходит из области R через точку
В. Через эту точку проходят две полу траектории: одна,
идущая внутри R, и другая, идущая вне этой области.
Эту последнюю мы и рассмотрим. Если она находится
направо от наблюдателя, то цикл С будет положителен
(см. мемуар второй, гл. VIII).
Если оба цикла одного и того же знака, то число
предельных циклов, лежащих в области /?, будет той же
чётности, что и число контактов дуги АМВ\ оно будет
иной чётности в противном случае.
В частности, предположим, что оба цикла С и С
являются двумя меридиональными окружностями ср = ср0
и <p = <pi. Предположим, что в области R и на еб границе
функция Q имеет один и тот же знак; предположим, что
вдоль цикла С мы имеем
dt
и что вдоль цикла С мы имеем
§<"¦
Возьмём за дугу АМВ Дугу параллели ш = О, которая
будет дугой без контакта. Оба цикла будут иметь проти-
воположные знаки. Число предельных циклов, содержа-
щихся в R, будет, следовательно, нечётно. Следовательно,
эта область заведомо циклична.
2° Пусть р и 6 — полярные координаты точки в неко-
торой плоскости. Предположим, что устанавливается соот-
ношение между m и ср, с одной стороны, р и 6, с другой,
такое, что область R на торе и некоторая двусвязная
плоская область Rl точечно соответствуют друг другу
и притом это соответствие взаимно однозначное. Предпо-
ложим, что по выполнении всех преобразований данное
дифференциальное уравнение принимает вид
*) Для ясности изменено обозначение автора «? (р, 0)» для
правой части уравнения. — Прим. ред.

168 ТРЕТИЙ МЕМУАР
Если в области R находится более двух предельных
циклов, то в этой области непременно будут точки,
в которых либо
^ = 0, либо F=oo
. op
(см. гл. XIII, теорему XIX).
Пусть, в частности^
где К—какая-либо постоянная.
Если в области R ни функция Q, ни функция j- не
обращается в нуль, то область R заведомо ациклична
или моноциклична.
Мы рассмотрим сначала следующий пример:
д~ — а -\- b cos со — cos <?, jj = с,
где а, Ь, с — такие постоянные, что
а>Ь>0, а + Ь<1,
Положим
а 4- b = cos <?„, а — ft =
где углы «ро и ?i заключены между 0 и у.
Так как ^ никогда не обращается в нуль, то все
параллели ю = const, являются циклами без контакта.
Вот, следовательно, первая система циклов без контакта,
среди которых нет ни одного предельного цикла.
Но легко видеть, что когда да заключено между <fl и
2тг — cpj, то -^ положительно, и что когда <р заключено
между —о0 и -f-<?0, то ~ отрицательно. Таким образом,
тор разбивается на четыре части: области cpj <<р < 2тг —
— fi> —?о<?<?о» где все меридианы являются ци-

ГЛ. XV. ДЕТАЛЬНОЕ ИЗУЧЕНИЕ ТОРА 169
клами без контакта (это будут ациклические области), и
области #(<po<?<<Pi) и /?'(—<Pi<»< — <Po)> являю-
щиеся сомнительными.
. Рассмотрим, в частности, область R. Прежде всего я
утверждаю, что она является циклической, так как мы
имеем
57 >° для цияла <? = ?!,
-jj<0 для цикла <? = 'fo
и, кроме того,
dta
Следовательно, оба цикла без контакта ср = cpt и «р =
= ср0, ограничивающие область /?, имеют противополож-
ные знаки, если за дугу АМВ, о которой мы говорили
выше, взять дуг} без контакта ш =» 0. Следовательно,
область R содержит, по крайней мере, один предельный
цикл.
Но она не может содержать больше одного цикла,
так как если бы она содержала два, то внутри R мы должны
были бы иметь или 2 = 0, или д- = 0. Но Q никогда не
0<f
дФ
обращается в нуль, a v- = sin «p может обращаться в нуль
только при ср = ттг, т. е. вне /?. *
Следовательно, в области R можно провести один и
только один предельный цикл, который я назову С.
По той же причине в области /?' можно провести
один и только один предельный цикл, который я назову С".
Мы пришли таким образом ко второй системе циклов
без контакта, среди которых есть два предельных цикла
С и С' и бесчисленное множество меридианов.
Два цикла С к С' разбивают тор на две области Р
и Р'\ обе покрыты циклами без контакта. Рассмотрим
подвижную точку, движение которой определено нашими
дифференциальными уравиениами. Если в начальный момент
эта подвижная точка находится в одной из областей Р

170 ТРЕТИЙ МЕМУАР
или .Р', то она никогда не может выйти из неё. Следо-
вательно, если её координата ср в начальный момент за-
ключена между «pj и 2тг — <?i» то она всегда останется
между ср0 и 2тг— ср0.
Кроме того, если подвижная точка однажды пересе-
чёт один из циклов без контакта второй системы, то она
больше уже не сможет снова его пересечь. При неогра-
ниченном возрастании времени подвижная точка будет
асимптотически приближаться к одному из двух циклов
С и С. Другими словами, возвращаясь к языку главы X,
мы скажем, что орбита подвижной точки неустойчива.
Второй пример, который мы рассмотрим, ещё проще
первого. Я напишу просто
йч> dv .
где а и b—две положительные постоянные. Непосред-
ственно видно, что все параллели и все меридианы являются
циклами без контакта и что общий интеграл имеет вид
--f = const.
Если отношение у рационально, то все траектории
замкнуты; следовательно, ыы имеем устойчивость.
Предположим теперь, что отношение -г иррациональ-
но; устойчивость всё же буцет иметь место в том смысле,
что если взять какую-нибудь сколь угодно малую часть
р тора, то любая траектория будет пересекать эту часть
бесконечное множество раз.
Если подвижная точка в начальный момент находится
в некоторой точке А, то она не попадает вновь в эту
точку, но она будет бесконечное множество раз прохо-
дить через бесконечно-близкие точки.
Рассмотрим кривую
со = сер -f- d,
где с—рациональная постоянная, a d—какая-либо по-
стоянная величина. Эта кривая будет замкнутым циклом

ГЛ. XV. ДЕТАЛЬНОЕ ИЗУЧЕНИЕ ТОРА 171
и легко видеть, что это непременно цикл без контакта.
Следовательно, на торе можно построить бесконечное
множество систем циклов без контакта, среди которых
не будет ни одного предельного цикла.
Двух вышеприведённых примеров достаточно, чтобы
показать, что наличие предельного цикла является при-
знаком неустойчивости, а отсутствие подобного цикла —
признаком устойчивости. Но, для того чтобы лучше дать
себе отчет в етом важном факте, необходимо глубже
проникнуть в сущность вопроса.
Мы предположим для дальнейшего, что ю и ср моно-
тонно растут вместе со временем, т. е. Q и Ф всегда
положительны, и что, кроме того, на торе нет особых
точек.
Рассмотрим меридиан ср = 0, являющийся циклом без
контакта*. Пусть М@) есть некоторая точка на этом мери-
диане, в которой подвижная точка находится в началь-
ный момент. Эта точка будет иметь координаты
(ср = О, (о = соо).
При возрастании времени величины ю и ср также будут
расти, так что ср, наконец, станет равный 2ir; тогда под-
вижная точка придёт в точку Af(l), которая будет лежать
на цикле без контакта ср = 0, от которого мы отправля-
лись; эта точка будет последующей для точки /И@) и
будет иметь координаты
Две величины ш0 и ш1 будут связаны некоторым со-
отношением, которое является ничем иным, как законом
последования главы V. Я напишу этот закон в двойной
записи:
Сделанные предположения позволяют высказать по
поводу этого закона последования следующие принципы:
Первый принцип. Функция <|» непрерывна.

172 ТРЕТИЙ МЕМУАР
Второй принцип. Функция <|» возрастает вместе
с (оо, так что
и, кроме того,
Третий принцип. Функция <|» голоморфна при всех
действительных значениях ш0.
Кроме того, ясно, что функция в имеет те же свой-
ства, что и функция ty-
Пусть теперь МA), МB),... ,М(i) — последователь-
но взятые последующие точки М@) и М{—1),
М ( — 2), ..., М (— /) — последовательно взятые пред-
шествующие -точки М @). Их координаты а>1( а>2,... , ш_1У
(o_a, ... будут нам даны уравнениями:
•-1 = вЫ «.« = 8(8(«о». а)-8=
Точки Ж образуют множество точек, которые я назову
Р согласно обозначениям, принятым Кантором I29). Через
Р' буду обозначать производное множество от Р, т. е.
множество точек, в окрестностях которых находится бес-
конечное множество точек, принадлежащих Р. Наконец,
через
D(P, Q)
я обозначу множество точек, общих двум множествам Р
и Q. По различным вопросам теории множеств и упо-
треблению предшествующих обозначений я отсылаю инте-
ресующихся к ряду мемуаров Кантора, появившихся на
немецком языке в Mathematische Annalen (т. 15, 17, 20, 21),
а на французском — в Acta Mathematica (т. 2, стр.
340—408 13°1).
Я могу поставить перед собой следующие вопросы:
1° Каковы свойства множества Р точек М и его про-
изводных?

ГЛ. XV. ДЕТАЛЬНОЕ ИЗУЧЕНИЕ ТОРА 173
2° В каком круговом порядке распределены точки М
на меридиональной окружности ср = О?
Я докажу, что либо
D(P,P') = 0,
либо
Другими словами, если множество Р имеет общую точку
со своим производным Р', то все его точки будут точ-
ками этого производного множества.
В самом деле, пусть М (г) есть точка множества Р,
принадлежащая Р'; по определению множества Р' в окрест-
ности точки М (г) находится бесконечное множество точек,
принадлежащих Р. Следовательно, мы можем найти мно-
жество точек
M{kA), M(k2), .... M{kp),...,
принадлежащих Р, таких, что
llm M (kp) = М (г) при р = оо.
Пусть теперь М (у) есть какая-нибудь точьа Р. Рассмо-
трим точки
M(kt — /-fv), Af(A9—/-f-v) M(kp — г-tv), ...
В силу непрерывности функции ty мы будем иметь:
WinM(kp — i-\~v) = M{y) при р=со.
Следовательно, М (у), а, значит, и всякая точка множества
Р принадлежит Р'.
Что и требовалось доказать.
Условие D(P, Р') = о, переведенное на язык главы X,
означает, что траектория неустойчива. В самом деле, если
точка М @) не принадлежит Р', то подвижная точка
никогда не придёт в окрестность своего начального поло-
жения. Исключением, однако, является тот случай, когда
все траектории замкнуты.
Теорема XX. Если для всех траекторий D (Р, Р') =
= 0, то заведомо существует предельный цикл, или
же все траектории замкнуты.

174 третий мемУаР
Пусть, в самом деле, N@) есть точка множества Р\
в окрестности которой находится, по определению, бес-
конечное множество точек из Р. Пусть Q есть множе-
ство точек N(i), т. е. множество всех предшествующих
и последующих точки N@).
Невозможно, чтобы в каждом интервале, содержащемся
между двумя какими-нибудь точками из Р, находилась бы
точка из Q. В самом деле, в окрестности точки N@)
есть бесконечное множество таких интервалов; следо-
вательно, в этой окрестности находилось бы бесконечное
множество точек из Q, что невозможно в силу предпо-
ложения
D(Q,Q') = 0.
Итак, пусть М @) и МA)— две точки из Р, между
которыми нет ни одной точки из Q. Тогда их нет и
между М (i) и МB1), так как, если бы точка N(k) была
между М@) и М @, то точка N(k— i) была бы между
М@) и М (i), потому что функция ф монотонно растёт.'
Точно так же их не будет в интервале, содержащемся
между М (pi) и М (pi -f- /). Кроме того, если точка М (/)
лежит, например, справа от М@), то точка M(pi-\-i)
лежит справа от M(pi). При возрастании р вторая коор-
дината ш. точки М (pi) будет меняться всё время в одном
направлении; она будет, например, всё время расти, но
она не может возрастать неограниченно, иначе точка N@)
попала. бы в одни из вышеуказанных интервалов. Эта
координата а» будет, следовательно, стремиться к пределу,
который будет соответствовать некоторой точке Р@)
меридиональной окружности. Следовательно, мы будем
иметь
llm M (pi) = Р @) при р — со.
Отсюда выводим
Vim M (pi-\-i) ==P(/),
P@) =

ГЛ. XV. ДЕТАЛЬНОЕ ИЗУЧЕНИЕ ТОРА 175
Итак, z-я последующая точка Р@) есть эта же точка.
Следовательно, траектория, проходящая через эту точку,
замкнута, и легко видеть, что она является предельным
циклом.
Условие D (Р, Р') = Р означает, что траектория устой-
чива. В самом деле, сказать, что исходная точка М@)
принадлежит к Р'—это значит сказать, что подвижная
точка бесконечное множество раз возвращается в окрест-
ность этой точки. Следовательно, если мы для всех траек-
торий имеем D(P, P') = P, то устойчивость несомненна.
Именно это имеет место, например, во втором из приве-
дённых выше примеров.
Но следует поставить вопрос, не может ли случиться,
что мы имеем для одних траекторий D (Р, Р') = 0, а длч
других —D(P, Р") = Р] это и будет началом всех тех
трудностей, которые мы в дальнейшем встретим.
Прежде чем итти дальше, я установлю .следующую
лемму: пусть Af(O) и N@) — две какие-нибудь тонки;
M(i) и N{1) — их 1-е последующие. Я утверждаю, что
если обе эти последние точки находятся в интервале
(Ж@), N@))j то существует предельный цикл.
В самом деле, если это так, то две точки М B0 и
JVBz) обе содержатся в интервале 0И (/), N@)> две точки
М{Ъ!) и NCi)B интервале (MBi), NBi)),... Следо-
вательно, при возрастании р вторая координата а» точки
M(pi) будет меняться всё время в одном направлении и
никогда не сможет превзойти некоторую границу*). Отсюда,
как и выше, следует существование такой точки Р@), что
\\тМ(р/) = Р(р) при р=оо,
и, следовательно, существование предельного цикла.
Займёмся теперь изучением того кругового порядка,
в котором расположены точки M(i), оставляя в стороне
тот случай, когда существует предельный цикл и когда
этот порядок легко определяется.
Пусть а„. есть длина дуги М@)МA), а1—длина дуги
МA)М{2),... и вообще at—длина дуги МA)МA~\- 1).
*) Точнее, этим свойством будет обладать вычет коор-
динаты <о по модулю 2 я. — Прим. ред.

176 ТРЕТИЙ МЕМУАР
Я утверждаю, что отношение
при неограниченном возрастании п будет стремиться
к определённому конечному пределу, не зависящему от /
и несоизмеримому с 2кг.
Возьмём, начиная от точки Мф), дугу L меридио-
нальной окружности, равную k целым окружностям, т. е.
равную 2Awr, и предположим, что
A) <Xo + ai+•••+av<2?w<a0 + ai+ •••+«>+!•
В силу этого неравенства на дуге L есть v + 2 точки из Р,
а именно: М@), М A),... ,М (у-\-1) и не больше.
Чтобы правильно понять это предложение и избежать
всяких недоразумений, существенно сделать следующее
замечание: вторая координата ш точки М меридиональной
окружности «р «= 0 определена не однозначно, так как мы
получаем ту же точку, увеличивая а» на кратное 2тг. Но
если, однако, мы задались значением ш0, то координата
ю^ последовательных последующих Ж(г) уже определена
однозначно уравнениями
<°i = Ф W» <*< = Ф К-1)-
Мы предположим, следовательно, что мы задали ю0 и
тогда мы можем рассматривать ш< как вполне определён-
ные величины.
В некоторых случаях бывает удобно рассматривать не
сами координаты ш{, но величины, сравнимые с ш< по
модулю 2л и содержащиеся между а и а + 2тс (где а есть
вторая координата некоторой точки N на меридиональной
окружности). Мы будем обозначать эту величину через
(ш{, а) и будем называть её координатой точки M(i),
приведённой по отношению к точке N.
Так, например, при доказательстве теоремы XX мы
говорили, что при возрастании р вторая координата со^
точки M(pi) изменялась всегда в одном и том же напра-
влении, никогда не превосходя при этом некоторой опре.

ГЛ. XV. ДЕТАЛЬНОЕ ИЗУЧЕНИЕ ТОРА 177
делённой границы. Речь шла не о самой величине ш{,
которую мы выше определили, но об этой координате,
приведенной по отношению к точке N@).
Напротив, во всём дальнейшем речь будет итти, при
отсутствии прямых указаний на обратное, о самих коор-
динатах ш{.
Так, когда я говорю, что дуга L содержит v + 2 по-
следовательные последующие М @), М A),... ,М (v-{- 1),
то я хочу сказать, что координаты соо, coj, ..., cov+1 содер-
жатся между ю0 и соо-[-2?тг.
Неравенства A) написаны в предположении, что все
дуги а„, Oj,... , а{ положительны. Это на самом деле
имеет место. Я всегда могу предположить, что
«I > «О-
Действительно, мы не можем иметь <о1 = а>0) так как это
равенство влечет существование замкнутой траектории,
чего нет по предположению, а если бы мы имели a>j < ш0,
то мы стали бы отсчитывать дуги ю в другую сторону.
После этого второй принцип даёт
или
Что и требовалось доказать.
Пусть теперь N@) — какая-нибудь точка, содержа-
щаяся между М @) и М A), (о'0 — её координата, так что
@0<@0<аI-
Пусть (о^—г координата /-й последующей N(i). Я утвер-
ждаю, что
действительно, если бы мы имели
12 А. Пуанкаре.

178 ТРЕТИЙ МЕМУАР
то обе точки N@) и N(i) содержались бы между точ-
ками М@) и М{1), а если бы мы имели
то обе точки ЖA)и M{i-\-\) содержались бы между
точка-ми N@) и N{i). В обоих случаях в силу доказан-
ной выше леммы существовал бы предельный цикл, чего
нет по предположению.
Точно так же, если бы мы имели
то мы отсюда вывели бы
Далее из неравенства A) мы получаем
и, так как
то
Если, следовательно, мы возьмём, начиная от точки М(\),
лугу длины Ik кг, т. е. L, то на этой дуге будет лежать
v-j-2 точки из Р, а именно Af(l), AfB), ..., Af(v-f-2).
Теми же рассуждениями можно было бы показать, что
если взять дугу, равную L, начиная от некоторой-точки
из Р, то на этой цуге будет лежать v -J- 2 точки из Р.
Если теперь взять- на дуге а0 некоторую точку N и,
начиная с этой точки N, дугу, равную L, то эта дуга
будет заведомо содержать точки М A), М B),..., М(у-\- 1);
может содержать или не содержать точку М (v -J- 2) и за-
ведомо не будет содержать точку Af(v + 3).
То же рассуждение можно было бы провести, если
бы точка N лежала на какой-нибудь дуге ait откуда сле-
дует вывод: число точек из Р, лежащих на какой-либо
дуге, равной 2kкг, равно или v-j-1, или v-J-2.

М. XV. ДЕТАЛЬНОЕ ИЗУЧЕНИЕ ТОРА 179
Если дать k другое значение k', то для v получится
другое значение v'. Я рассмотрю два интервала, содержа-
м+1 v + 2 „ •/ ¦+ 1
щихся один между —j— и —¦?—, другой между —р— и
—ту—. Я утверждаю, что эти интервалы имеют общую
часть. Рассмотрим в самом деле дугу, равную 2kk' it r,
на которой лежит М точек множества Р. Получаем:
что и доказывает высказанное предположение. То же будет
иметь место, если мы рассмотрим вместо двух значений
k и двух интервалов три или больше.
Так, если давать k все целые положительные значе-
ния, то все интервалы (—4— , —г~) будут иметь общую
часть и, кроме т-го, длина интервала будет стремиться
к нулю. Следовательно, Т^ и Т стремятся к общему
пределу, который я обозначу через -
Число — не является рациональным.
В самом деле, если бы оно было, например, равно 2,
то мы имели бы
v + 1 = 2k, или v-f-2 =
Пусть, при k = 1
v-fl=2, v-f-2 = 3.
Тогда, при ?>1 мы имели бы
втсюда
12*

180 ТРЕТИЙ МЕМУАР
Отсюда легко было бы вывести, что круговой порядок точек
M(i), где индекс / положителен, обратен следующему:
Ш@), МB), МA), ... ad inf.; Af(l), AfC), ... ad inf.],
откуда следовало бы существование предельного цикла.
Если бы было, наоборот, v -f- 2 = 2 при k — 1, то при
мы получили бы
откуда
v + 2 = 2?.
Круговой порядок был бы обратен предшествующему
и опять существовал бы предельный цикл.
Следовательно, иррационально.
Очевидно, мы будем иметь
= 2irni при п =
что мы и утверждали.
Мы можем теперь сказать, что круговой порядок точек
Р характеризуется некоторым иррациональным числом
- ; этот результат мы попробуем теперь выразить более
точным: образом.
Чтобы сделать очевидным, чтр v зависит от k, я буду
писать v{k) вместо v> Я рассмотрю затем v(yfe)-(-2 точки
B) Af(O), M(l), AfB) Af[v(A)+U.
Посмотрим, в каком круговом порядке они располо-
жены. Нужно будет сперва поместить точки М @),
МA), ..., М [v(l) -f-1] на меридиональном круге в порядке
их индексов. Затем Aftv(l)-J-2] поместится между Мф)
и ЖA) и так далее до М [v B) -j- I ], которая поместится
между М [v A) -f 1 ] и Ж @). Следующая точка М [v B) -f 2]
будет помещаться между М@) и ЖA); остаётся устано-
вить, будет ли она до М [v(l)-)-2] или после этой точки.
Она будет раньше, если
vB)-f-2«2v(l)-f-3,

ГЛ. XV. ДЕТАЛЬНОЕ ИЗУЧЕНИЕ ТОРА 181
и после, если
Это и есть единственные возможные случаи.,
Можно таким образом продолжать, и никогда не будет
затруднения в помещении новой точки, если известны k
чисел:
v(l), vB), .... v(A).
Таким образом, круговой порядок точек B) зависит только
от этих k чисел, иначе говоря, от у., и он будет такой
же, как порядок чисел j«—E(pt) №2h Но k можно взять
сколь угодно большим.
Следовательно, круговой порядок точек M(i) зависит
только от иррационального числа ц и совпадает
с круговым порядком чисел («'—E(pi) [E(x) обозначает,
как обыкновенно,, наибольшее целое число, содержа-
щееся в jc]. •
Из этой теоремы непосредственно следует, что между
каждыми двумя точками множества Р находится беско-
нечное множествэ других точек; следовательно, между
каждыми двумя точками множества Р всегда есть точка
множества Р'.
Пусть N есть какая-нибудь точка множества Р'. По
определению в окрестности этой точки находится беско-
нечное множество точек из Р; между каждыми двумя из них
всегда есть точка из. Р'. Следовательно, в окрестности N
лежит бесконечное множество точек из Р', т. е. N принад-
лежит к Р" — производному множеству от Р''.
Следовательно, можно написать v :
-1\ D{P', Р") = Р'. С*
С другой сторрны, одна из теорем общей теории множеств
даёт ' :'5.'-'
"., D(P', р«) = р" т, г
откуда ,
Р'=Р". Jji
Итак, Р' севщйает со своим прэяэводным; значите это

182 ТРЕТИЙ MEM У АР
есть одно из тех множеств, которые Кантор называет
совершенными.
Но известно, что Кантор различает два класса совер-
шенных множеств: одни — множества неплотные ни в каком
интервале и другие — плотные в некотором интервале.
Мы можем, следовательно, сделать три гипотезы,
в формулировке которых мы снова употребляем обычный
язык:
1° Мы можем предположить, что все точки меридио-
нальной окружности 9 = 0 принадлежат f.
2° Мы можем затем предположить, что на этой окруж-
ности есть некоторые дуги, все точки которых принад-
лежат Р', причём, однако, это имеет место не для всех
течек нашей окружности.
3° Мы можем, наконец, предположить, что на нашей
окружности нет ни одной дуги, все точки которой при-
надлежали бы Р'.
Я хочу сначала показать, что вторая гипотеза должна
быть отброшена. В самом деле, приняв её, мы могли бы
найти на окружности дугу АВ, все точки которой щ~и-
надлежат Р1, но притом такую, что если продолжать её
за А или за В, то не все точки продолжения принадлежали
бы Р.
Пусть At и Bt суть /-е последующие точек Аи В; /-ми
последующими различных точек дуги АВ будут различные
точки дуги А{В{, и все они должны, очевидно, составлять
часть множества Рг.
Я утверждаю, что две дуги АВ и А{В{ не могут иметь
общей части; в самш деле, если бы А и В были располо-
жены на дуге А{В{ или если бы А{ и В{ были располо-
жены на дуге АВ, то существовал бы предельный цикл,
в противность предположению. Если бы точка А{ лежала
на дуге АВ и Bt вне этой дуги (или если бы В{ лежала
на дуге АВ, a At вне этой дуги), то все точки дуги BBt
(или дуги АА{), которые образуют продолжение дуги АВ
за точку В (или за точку А), принадлежали бы Р', что
противоречит сделанному предположению.
Пусть Ж@) — точка из Р, лежащая на дуге АВ; точка
Af(O будет лежать на дуге AtBt и, следовательно, вн#

ГЛ. XV. ДЕТАЛЬНОЕ ИЗУЧЕНИЯ ТОРА 188
АВ. Так как число / произвольно, то, значит, на дуге
АВ нет ни одной последующей или предшествующей для
Ж@), т. е. нет нл одной точки из Р, кроме Ж@). Но,
для того чтобы все точки дуги АВ принадлежали Р',
необходимо, чтобы на этой дуге было бесконечное мно-
жество точек из Р.
Следовательно, вторая гипотеза должна быть отбро-
шена и нам остаётся изучить первую и третью.
Первая гипотеза, несомненно, может осуществиться;
именно, мы видели, что она действительно имеет место
для уравнений
dm d<t ,
если отношение г- иррационально.
Я утверждаю прежде всего, что если все точки окруж-
ности принадлежат Р', то это имеет место, какова бы
ни была та траектория, с помощью которой построены
множества Р и Р'. В самом деле, рассмотрим другую траек-
торию, пересекающую меридиональную окружность в не-
котором числе точек, образующих множество Q.
Я утверждаю, что производное множество Q' от Q
состоит, как и Р1, из всех точек окружности. В самом
деле, пусть N@)—какая-либо точка этой окружности,
N(i)—её 1-я последующая, Q — множество точек N(i).
В окрестности точки N@) есть, по предположению, бес-
конечное множество точек из Р:
M(k^), уИ(&2), ..., уИ(?п), ...
Если п неограниченно возрастает, то выражение
\>.kn — E((i&n) стремится к некоторому пределу h. Этот
предел характеризует положение точки N@) на окруж-
ности.
Я хочу сказать, что три точки M(J), M(k) и N@)
будут при любых j и k иметь тот же круговой порядок,
что и три числа j*/ — ?(jy), \& — E&k) и h.
Легко убедиться, что положение точки N(i) такгм же
образом определяется числом h-j-\u~? (Л-j-j«), а отсюда

184 ТРЕТИЙ МЕМУАР
вытекает, что на каждой дуге окружности находится бес-
конечное множество точек из Q,, что равносильно тому,
что все то'^ки окружности принадлежат Q'.
Как мы только что видели, любая точка окружности
характеризуется числом Л. Это число Л равно j*/ — Е (pi)
для точки М (/), принадлежащей Р и имеющей координату
mt. Оно равно нулю для точки М @), имеющей коорди-
нату oig. Кроме того, если щ изменяется от ш0 ад ед0 -|— 2тг,
то h монотонно растёт от 0 до 1. Это следует из того,
что точки окружности следуют друг за другом в том, же
круговом порядке, что и характеристические числа.
Следовательно, h есть возрастающая функция от ш
для значений о> между пределами <о0 и оо0 -f- 2те; значит,
её мржно представить в виде сходящегося тригонометри-
ческого ряда
2чгЛ = 2 Ат cos /»ш -4- 2 Вт sIn /яш ¦
или же
C) 2чгЛ — ш = 2 А'т cosmio-f 2 В'т sin /»ш =^0 (ш).
Функция 9 (ш), изображаемая рядом C), будет непре-
рывной и периодической функцией ш. Закон последования
может тогда быть написан в риде
«14-9 К) = <°о+е Ы
Пусть Л/^@) — точка меридиональной окружности,
имеющая характеристическое число Л; построим траекто-
рию, прохрдящую через N@), и будем продолжать её до
тех пор, пока она снова в точке NA) пересечёт меридио-
нальную окружность. Если мы припишем всем точкам этой
дуги траектории Af(O), NA) (кроме точки NA)) харак-
теристическое число Л, то все точки тора будут иметь
одно и только одно характеристическое число. Выражение
2чгЛ — ш -}- ji'f
будет непрерывной и периодической функцией от ш и ю,
допускающей разложение в тригонометрический ряд такого
вида: ...
4) Я («, да) = 2 Amv cos (шо -}- Щ + >¦««)•

ГЛ. XV. ДЕТАЛЬНОЕ ИЗУЧЕНИЕ ТОРА 185
Общий интеграл данных уравнений напишется тогда так:
ш = (i'f -J- И (со, о) -f- const.
Следовательно; мы заранее уверены в том, что общий
интеграл может быть выражен с помощью тригонометри-
ческого ряда, но. у нас нет никаких методов вычисления
коэффициентов этого ряда.
В рассматриваемом случае
для всех траекторий, и на торе нельзя найти сколь угодно
малую область, которую бы не пересекали бесконечное
множество раз все траектории.
Перейдём теперь к третьей гипотезе, которая, как мы
увидим, равносильна предположению, что D (Р, Р') = Р
для одних траекторий и что D (Р, Р') = 0 для других.
Итак, представим себе, чтоР' образует совершённое,
нигйе не плотное множество, или, говоря на обычном
языке, представим себе, что на окружности нельзя найти
ни одной дуги, все точки которой принадлежали бы Р'.
Так как Р' есть совершенное множество, то на окружно-
сти заведомо можно найти дугу А @M@), концы кото-
рой принадлежат Р1, но никакая другая точка которой не
принадлежит Р' (см. Кантор, Ada Mathematica, т. IV,
вып. 4).
Тогда все дуги А (/) В (/) будут иметь то же свойство;
отсюда следует, что две дуги A (i) В {I) и A (k) В (Jt) при--
1фк не имеют ни одной общей точки. • ^
Кантор доказал, что если на ойружности, например,
мы имеем совершенное, нигде не плотное множество, то
точки окружности разделятся на три класса:
1° точки некоторых дуг I84!, у которых ни одна точка
не принадлежит множеству;
2° концы этих дуг, которые, очевидно, принадлежат
множеству;
3° наконец, точки множества, не являющиеся концами
такого рода дуг.
В,;идтересующем нас случае дугами, точки которых
не принадлежат множеству, являются дуги A (i) В (/) Г 351;

186 ТРЕТИЙ М1МУАР
концами этих дуг служат сами точки А {С) к В (/); накв-
нец, другие точки множества получатся, если искать точки,
в окрестности которых есть бесконечное множество то-
чек A {t) и 5 к.1).
Следовательно, существует и три рода траекторий:
1° Прежде всего, я укажу на те две траектории, одна
из которых проходит через точку Л@), другая — через
точку В @) и которые я буду называть траекториями
Ли В. Для этих двух траекторий имеем, очевидно:
D (Р, Р') шш Р.
2° Затем следуют траектории, которые пересекают
одну из дуг А (/) В (/) и, следовательно, пересекают их
все. Если точка С @) одной из этих траекторий находится
на дуге А @) В @), то ее /-я последующая С (/) будет на
дуге А @ В (/). В окрестности какой-либо точки из Р'
находится бесконечное множество точек А (/) и В (/),
следовательно, и бесконечное множество точек С (/). Зна-
чит, если Q обозначает множество точек С(/) и Q' — его
производное множество, то
<?' = />'.
Отсюда ясно, что
D(Q, Q') = 0.
3° Наконец, существуют траектории, проходящие через
точки третьего рода и, следовательно, не пересекающие
ни одной дуги A(i)B(i). Для этих траекторий множество
Р' также остается прежним, и ясно, что
Следовательно, множество Р1 одно и то же для всех
траекторий, и мы имеем
D [Р,Р')=Р или 0,
смотря -по тому, какую траекторию мы взяли.
Дуги А (/) В (I) следуют одна за другой в,тем же кру-
гввом порядке, что и числа ji/ — Е ({«').

ГЛ. XV. ДЕТАЛЬНОЕ ИЗУЧЕНИЕ Т«РА 1S7
Формулы
+ 9 Ы
ш = [if -f Я (а>, ») -f- const.,
где 6 чсв) и Я (се, <р) означают тригонометрические ряды,
изображающие непрерывные и периодические функции,
остаются в силе и здесь, но не сохраняют полностью своё
значение.. В саном деле, функция о> —J- в (ш) является
постоянной вдоль всей дуги А (/) В (Д и можно было бы
также найти на торе области, где функция Я (со, <р) -f-
>— w сохраняет постоянное значение.
Остаётся посмотреть, совместима ли эта третья гипо-
теза, некоторые следствия которой мы только что развили
с тремя принципами, сформулирозанными нами по поводу
закона последования
- <°i = т1 (шо\
и с тем частным видом дифференциальных уравнений,
который мы рассматриваем.
Я могу утверждать,. что она совместима с первыми
двумя принципами, в силу которых функция ¦ф есть непре-
рывная и возрастающая функция.
Совместима ли она с третьим принципом, по которому
: функция ф голоморфна? Это неясно. Нужно было бы-или
найти пример, в котором осуществлялась бы третья гипо-
теза,-чего я до сих пор не смог сделать, или же доказать
невозможность её во всех случаях, — и этого я не смог по-
лучить. Я думаю, что третья гипотеза действительно может
осуществиться; однако есть частные случаи, относительно
которых можно доказать, что она не имеет места и что,
следовательно, нужно принимать первую гипотезу.
Пусть С @) есть какая-либо точка меридиональной
окружности, СA), С{2),..., С (г) — её i первых после-
дующих; мы остановимся, когда (/ —|— 1)-я последующая
будет лежать на дуге А @) А A). Пусть тепе;ь Мо и /п0,
Мх и /»!,..., Mi_l и /«,-_!, Mt и /я< — наибольшее и
наименьшее значения, которые, производная -~- может
принимать соответственно на дуге С@)СA), на дуге

188 ТРЕТИЙ МЕМУАР
С A) С B),..., на дуге С («'.— 1) С (/) и, наконец, на дуге
С(/)С@). Если
или же если
то можно быть уверенным, что третья гипотеза должна
быть отброшена.
Тем же процессом можно найти и верхний предел для
любой, из определенных выше дуг А (г) В (г). Если Месть
максимум, т — минимум производной -r-V, то все дуги
АA)ВA) меньше, чем
1 i —: at —¦ ¦
1~"Ж
Можно сделать ещё одно замечание; возьмём точку
А @) и траекторию Л* проходящую через эту точку. Пусть
С @) и D @) — две точки, очень близкие к А @) и лежа-
щие одна направо, другая налево от этой точки. Пусть
С и Dt— траектории, прЪходящие через эти точки. Мы
можем"яредставить себе подвижные точки a, cud, одно-
временно-описывающие эти три траектории таким обра-
зом, ""гго «сегда. все они находятся на.одной и той же
меридиональной окружности. Тогда при возрастании вре-
мени окажете^ что расстояние ас будет стремиться' к нулю
и что расстояние ad не бр|ет стремиться к нулю, сколь
бы близки ии были точки'С@) и •?)(()) к точке А @).
Напротив^ в случае первой гипотезы невозможно, чтобы
расстояние между двумя подвижными точками вис, опи-
сывающими две различные траектории, стремились к нулю.
Я не ^сомневаюсь в том, что можно с пользой применить
это замечание, хотя я сам ничего не смог из него извлечь.
Bte эти рассмотрения не дали мне возможности решить
основной вопрос и не позволили мне строго доказать, что
третья гипотеза действительно может иметь место.

ГЛ. XV. ДЕТАЛЬНОЕ ИЗУЧЕНИЕ ТОРА 189
Возникает много других вопросов, тесно связанных
с предыдущим. Так, можно спросить себя, как меняется
характеристическое число ц, определённое выше при изме-
нении коэффициентов дифференциальных уравнений. Можно
доказать, что это изменение числа р.непрерывно. Но мы
можем предположить, что при некоторых значениях ко-
эффициентов существует предельный цикл; число jj. можно
тогда рассматривать как рациональное. Если при других
значениях коэффициентов число |х иррационально (или \i
рационально, но предельного цикла не существует) и если
менять коэффициенты непрерывным образом так, чтобы
пройти через значение, дающее предельный цикл, то число |г
для этих значений будет иметь или максимум, или минимум.
В этом—отправная точка для целого ряда работ, которые
бесспорно будут плодотворными и на которые я, мне
кажется, должен указать исследователям.
Я надеюсь, что буду иметь возможность в одной из
последующих глав этого мемуара дать более полные ре-
зультаты по этим вопросам. А именно, я вернусь к ним
после того, как в следующих частях этой работы
поставлю ряд проблем, аналогичных предыдущим, но ещё
более тонких, которые тесно, связаны с важным вопросом
сходимости тригонометрических рядов и, в частности,
с рядами, употребляемыми в небесной механике.
Прежде чем кончить, я хочу в нескольких словах пока-
зать, в чём состоит только что указанная связь между
интересующей нас проблемой и методами небесной меха-
ники.
Мы видели, что общий интеграл данных нам уравне-
ний может быть записан в виде:
ш — jj,^ — // (Ш) <р) — const.,
где Н—тригонометрический ряд. Предположим, что наше
дифференциальное уравнение имеет вид
где {j.o — постоянная, а — очень малый коэффициент, & F —

190 ТРЕТИЙ МЕМУАР
многочлен от cos со, sin o>, cos <р, sin cp, или же тригоно-
метрический ряд
Р = 2 А*п cos («о> 4- пер -f Ьтп)-
Мы получим
Л <Э//\ . дН
j^ +
Предположим, что jj. и Я могут быть разложены по сте-
пеням а, так что
Я = Я,ос-j-Яаос9 + Я3а3-f ...
Твгда мы будем 1'меть:
*^Г + ~д^ = ~1кГ F~
Постоянные jj-j, jj.a, jig,... надо выбрать так, чтобы пра-
вые части предыдущих равенств были тригонометрическими
рядами без свободных членов. Тогда (если ji.o иррацио-
нально) возможно найти тригонометрические ряды Нь
#2,..., формально удовлетворяющие предыдущим уравне-
ниям.
Нельзя не заметить аналогии между этим мэтодо-i
приближений и методом Линдштедта в небесной механике.
Нельзя не понять, что вопрос о сходимости только что
изложенного мною процесса тесно связан со сходимостью
рядов, употребляемых этим учёным астрономом из Дерпта.
Но рассматриваемый здесь вопрос, очевидно, много проще,
чем аналогичные вопросы небесной механики; хотя труд-
нвсти имеют ту же природу, но они менее многочисленны
и их, несомненно, легче преодолеть. В силу этого сообра-
жения я и занимался вопросом, составляющим предмет

ГЛ. XV. ДЕТАЛЬНОЕ ИЗУЧЕНИЕ ТОРА 191
изучения настоящей главы, и в силу него же я, несо-
мненно, вернусь к этому вопросу, как только найду но-
вые результаты.
В 4-й части настоящей рдбэты я приступаю к изуче-
нию дифференциальных уравнений 2-го порядка. Я оставлю
на короткое время уравнения 1-го порядка, намереваясь,
однако, в дальнейшем вгрнугься к проблемам, связанным
с этими уравнениями и пока ещё не разрешённым; я объ-
единю их с аналогичными проблемами, которые возникают
для уравнений высшего порядка.
Париж, 15 января 1885 г.

ЧЕТВЁРТЫЙ МЕМУАР
ГЛАВА XVI
УРАВНЕНИЯ 2-ГО ПОРЯДКА; ОСОБЫЕ '"ТОЧКИ
ы займемся теперь изучением дифференци-
альных уравнений высшего порядка.
Пусть х, у и г—координаты движу-,
'цейся точки в пространстве и t — вспо-
могательное переменное, которое мы бу-
де м считать представляющим время. Запишем уравнения
в таком виде:
A)
dx у dy__Y dz _ 7
dt ' dt ~ ' dt ~ '
где X, Y и Z—многочлены, целые относительно перемен-
ных х, у и г. Ясно, что всякое уравнение второго порядка
и первой степени легко может быть приведено к такому
виду[Ч.
Точно так же всякое уравнение п—1-го порядка и
первой степени можно представить в следующей форме:
B)
dxx
dt
dx%
dt
где Xlt X%,..., Xn—многочлены, целые относительно
переменных хи л;а,..., хп. Если мы имеем уравнение

гл. xvi. уравнения 2-го порядка; особые точки 193
п—1-го порядка по степени выше первой, то можно запи-
сать его в следующее виде:
dx\ у dx% у •¦ dXn __ у
~d~t~— lJ ~~di 2' "'"' dt — п'
гдеЛ^, Х%, ..., Хп—^^многочлены, целые относительно
переменных хи лга, ...,хп, г и г —функция от хь х2,..,
..., хп, связанная с этими переменным соотношением
r (xv х%, ..., хп, z) = и,
левая" часть которого есть полином.
Вводя новое переменное т, мы можем написать:
dxi_x dF dx2x=x д_ ^Ь — х —
dz „ dF v dF v dF
Правые части этих новых уравнений — многочлены, целые
относительно хг и г; таким образом, наши уравнения
приведены к форме B); только порядок системы увеличился
на единицу.
Если мы хотим для случая уравнений B) пользоваться
геометрическим изображением, аналогичным тому, которым
мы пользовались до сих пор, то мы должны рассматривать
хи л:8, ..., хп как координаты точки в пространстве п
измерений. Но это геометрическое изображение будет
теперь, вообще говоря, лишь языком иногда более, иногда
менее удобным, но уже ничего не будет давать для непо-.
средственного, наглядного представления. Тем не менее,
нам придётся иногда пользоваться этим языком.
Напротив, для случая уравнений второго порядка
в форме A) — как раз этот случай будет нами исследован
более подробно — геометрическое изображение сохраняет
все свои преимущества, и мы всё время будем им пользо-
ваться.
В дальнейшем, мы будем иногда рассматривать траек-
торию движущейся точки (лг, у, г), не всю целиком, а
только те её- части, которые расположены в некоторой
13 А. Пуанкаре.

194
ЧЕТВЕРТЫЙ МЕМУАР
определённой области пространства. Тогда уже не нужно
будет предполагать, что X, Y, Z—целые многочлены,
а достаточно только, потребовать, чтобы они вели себя
как целые многочлены внутри рассматриваемой области.
Нетрудно видеть, что в случае системы A) через, ка-
ждую точку пространства проходит одна и только одна
траектория. Исключением являются лишь те точки, в кото-
рых три функции \Х, Y и Z одновременно обращаются
в нуль, т. е. особые точки 14.
Три уравнения
Х=0, К=0, Z=0
геометрически изображают три алгебраические поверхности.
Может случиться, что эти три поверхности проходят через
одну и ту же кривую. Все точки этой кривой будут тогда
особыми точками, а сама эта кривая будет особой линией.
Мы вернемся ниже к этому важному случаю.
Рассмотрим сначала только изолированные особые точки.
Здесь возможны два случая:
,ч дХ дХ дХ дУ дУ дУ
1) не все производные: ^, Ту , ^j^, ^, ш;
7Г'~д~' <Г °бРаЩаются в особой точке в нуль — этот
случай мы рассмотрим подробно;
2) все эти девять производных одновременно обра-
щаются в нуль — этот случай приводится к предыдущему
при помощи приёма, указанного Брио и Буке (Журнал
политехнической школы, XXXVI тетрадь) 1*1.
Итак, предположим, что эти девять частных производ-
ных не обращаются в нуль одновременно, и составим
уравнение относительно S
C)
дХ
дх
дУ
дх
dZ
дх
с дХ
S Ъ
кдУ
dj-
dZ .
Ту
дХ
Тг
с дУ
Ъ. д!
dZ
дг
= 0.

гл. xvi. уравнения 2-го порядка; особые точки 195
Если X, Y, Z — многочлены самого общего вида дан-
ной степени, то это уравнение, вообще говоря, не будет
иметь ни корней, равных пулю, ни кратных корней. Я ничего
не буду говорить здесь о том частном случае, когда урав-
нение относительно S имеет корни, равные нулю, или
кратные корни; я ограничусь только тем, что отошлю
читателя к сказанному мною по поводу аналогичных слу-
чаев в первой части этой работы.
Оставляя в стороне этот исключительный случай, мы
должны рассмотреть следующие пять гипотез:
Первая гипотеза. Три корня уравнения относи-
тельно S действительны и одинаковых знаков (мы всегда
можем предполагать их положительными).
В этом случае общие интегралы уравнений A) могут
быть представлены (вблизи особой точки) в следующей
форме:
И1,1 Н'п% Но'
Здесь #!, Я9 и /73 — функции от х, у и *, голоморфные
в окрестности особой точки и обращающиеся в нуль в этой
особой \очке; St, 5а', 53 — корни уравнения C); Аи Ла,
Л3—постоянные интеграции. Эта теорема была доказана
в моей диссертации (Paris, Gautier-Villars. A875),
стр. 70) Ш.
Нетрудно видеть, что все кривые семейства, пред-
ставляемые уравнениями D), проходят через особую точку.
Таким образом в рассматриваемом случае все траектории,
проходящие достаточно близко от особой точки, будут
стремиться к этой точке.
Такая особая точка называется узлом.
Вторая гипотеза. Три корня уравнения относи-
тельно 5 действительны, но неодинаковых знаков. Пред-
положим, например, что корни Sj и 52 положительны,
a Ss отрицателен.
В этом случае, вообщг говоря, невозможно предста-
вить интегралы уравнений A) в форме D). Но, на осно-
вании теоремы Врио и Буке, доказанной в мемузре,
13*

196 ЧЕТВЕРТЫЙ МЕМУАР
упомянутом выше, для уравнений A) существуют три част-
ных интеграла, которые имеют следующий вид:
где cpi. ?2 и ?з — голоморфные функции от одной и той
же переменной и, обращающиеся в нуль, если особая точка
выбрана за начало координат при и = 0. У Врио и
Буке эта теорема высказана в несколько иной форме; но
переход от формулировки этих двух геометров к той,
которая приведена выше, не представляет никакого труда.
В рассматриваемом нами случае эти три интеграла
действительны; таким образом, нам уже заведомо известно,
что три траектории, которые я назову 7\, Т2 и Г3, про-
ходят через особую точку.
Для того чтобы продолжить дальше наше исследова-
ние, сделаем линейную замену переменных, или, другими
словами, сделаем преобразование координат, выбирая за
начало координат особую точку, а за оси координат —
касательные к трём траекториям Tv Га и Г3. После этого
преобразования уравнения A) сохранят ту же форму, и
корни уравнения относительно 5 не изменятся. Только
члены первой степени в многочленах X, Y и Z соответ-
ственно примут вид:
Я утверждаю теперь, что уравнение в частных произ-
водных
X— -4- V — — 7
дх ' ду
имеет голоморфный интеграл, обращающийся в нуль при
х ' ' 0 и v "~~ О
Действительно, всегда существует ряд, расположенный
по возрастающим степеням х и у, который формально
удовлетворяет этому уравнению. Для того чтобы найти
коэффициенты этого ряда, положим

гл. xvi. уравнения 2-го порядка; особые точки 197
и посмотрим, существует ли ряд
удовлетворяющий рассматриваемому уравнению, которое
мы запишем в виде:
Коэффициент атп при хту" в искомом ряде мы получим
из уравнения
(т Sx -j- п 5а — 53) атп = р,
где р — совокупность членов, зависящих от коэффициентов
многочленов X', V, Z' и от коэффициентов apq, где р и q
меньше тип (один из индексов р или ? может быть
соответственно равен т или л; но не может быть одно-
временно: р== mt q = n).
Остается показать, что полученный таким образом ряд
сходится. Это не представляло бы никаких затруднений,
если бы .S3 так же, как 5t и 5а, было бы положительно.
Действительно, в этом случае нужно былобы только ото-
слать читателя к теореме, доказанной в моей диссертации,
о которой я уже говорил выше. Но в нашем случае 53
отрицательно, и нам приходится пользоваться вспомога-
тельным уравнением:
E bis) S0& % %^
В этом уравнении ?з — положительная величина мень-
шая, чем St и S2; X", Y", Z" — многочлены, которые мы
получим, заменяя в X', Y-'. и 2' коэффициент при каждом
члене его абсолютной величиной. „.,.,.,,
Мы будем иметь ряд
формально удовлетвордющиЛ уравнению (-5 bis), и э.г^т
ряд будет сходиться,»так как 2з положительно.

198 ЧЕТВЕРТЫЙ МЕМУАР
Коэффициент а'тп получается из уравнения
где р' составлено из коэффициентов X", Y", Z", и из а'
так же, как р составлено из коэффициентов X', Y1 и Z1
и из apq. Все а'тга положительны. Действительно, если это
верно для всех a'pq, то Р' булет положительно,, так как
все коэффициенты X", Y" и 2" положительны. Кроме того
т Sj-{- п 52 — S3
тоже всегда положительно.
Я утверждаю теперь, что
\<*тп\<<*тп-
В самом деле, если это верно для индексов, меньших т
и меньших п, то
IPKP'-
Кроме того, мы имеем
так как S3 положительно, а 53 отрицательно. Следова-
тельно, мы получаем
lam»I<a'mn-
Это доказывает, что ряд
2 «wry
сходится.
Таким образом, уравнение E) действительно имеет
голоморфный интеграл.
Геометрически это означает, что через особую точку
проходит поверхность U, на которой расположено бес-
конечное множество траекторий. На этой поверхности
лежат траектории 7\ и Га, но траектория Ть не лежит на
ней.
Если в уравнениях A) мы заменим г рядом 2 аи1»*и!Уп»
то эти уравнения примут вид:
/йч dx Y dy _у

гл. xvi. уравнения 2-го порядка; особые точки 199
где X и Y—голоморфные функции от х и у, обращаю-
щиеся в нуль вместе с этими переменными. Члены первой
степени в X и Y, соответственно, будут Stx и Say.
Таким образом, мы приходим к случаю уравнений пер-
вого порядка, когда мы имеем только две переменные,
координаты изображающей точки на плоскости. Кривые,
определяемые уравнениями F), будут проекциями траекто-
рий, расположенных на поверхности U. Легко убедиться,
что для этих плоских кривых особая точка х = 0, у = 0
является узлом; отсюда вытекает следующее заключение:
все траектории, расположенные на поверхности U, пере-
секаются в особой точке.
Кроме того, нетрудно 1*1 показать, что никакие другие
траектории не проходят через особую точку; подойдя более
или менее близко к этой точке, они затем снова удаляются
от неё и выходят из её окрестности.
Итак, бесконечное множество траекторий, образую-
щих поверхность, а также одна отдельная, изолированная
траектория проходят через особую точку; все другие
траектории остаются на конечном расстоянии от этой
точки. Такая особая точка называется седлом.
Третья гипотезJ. Уравнение C) имеет один дей-
ствительный корень и два комплексных сопряжённых корня,
сумма которых имеет тот же знак, что и действительный
корень.
Пусть
Sfp/ S = a — $t и
— это три корня. Общий интеграл уравнений A) так же,
как и в случае первой гипотезы, может 0ыть записан в виде:
Кроме того, мы можем положить
где К и К' — голоморфные и действительные функции от
х, у и г.

200 ЧЕТВЕРТЫЙ МЕ^УАР. . ./
Рассмотрим общее уравнение /
G)--. /Уз3+ ^ + < = const. ./. '
Это уравнение изображает бесконечное -множество
замкнутых поверхностей, вложенных друг в друга, и со-
держащих внутри себя особую точку. ... . -. ¦
Нетрудно показать, что «ни одна траектория не может
пересечь ни одну из этих поверхностей более, чем в одной
точке, если постоянная в правой части достаточно мала/
Действительно, уравнения всякой траектории могут быть
записаны в такой форме.; .... •
где Су D,;.- у и 8¦•— четыре"'действительные постоянные
(заметим, что для одной и той же траектории Н3 должно
веб время сохранять один'и тот~жё знак). Таким' образом,
поверхности G) — эт*о поверхности без контакта, анало-
гичные циклам без контакта, рассмотренным в предыду-
щих частях. '¦
Всякая траектория, раз попав внутри одной из поверх-
ностей G), будет итти, в?б время приближаясь тк особой
точке; но она может приближаться к ней только асимпто-
тически (как в случае фокуса в первой-части этойработы);
действительно, нетрудно видеть, что она не может пройти
через особую точяу с определённой касательной."
Однако есть одно исключение. Мы видели, на основа-
нии теоремы Врио и Буке, что существуют три траектории
7\, 7 и Та, уравнения которых имеют вид:
где cpi> Ъ и ?з — голоморфные функции одной и той же
переменной в. В наЬем случае две из этих траекторий -ч-
мнимые, но третья действительна,, и еб уравнения имеют
вид: ' ¦¦'-¦'¦ '•
Эта траектория проходит через особую точку с опреде-
лённой касательной. ' '','.'

гл. xvi. уравнения 2-го порядка; особые точки 201
Кроме того, бесконечное множество траекторий рас-
положено на поверхности; . '
Эти траектории — спирали, аналогичные тем, с которыми
мы встречались в первой части. Все другие траектории
тоже имеют вид'спиралей и лежат на поверхностях, общее
уравнение которых
?+*?^const. :. ¦ ,.
В зависимости от величины 53 эти поверхности будут
или обычными поверхностями с единственной касательной
плоскостью, или же они будут похожи на ту поверхность»
которая получается при вращении параболы вокруг каса-
тельной в её верцвдне. - г .;-.-
-, Во втором случае траектории, .можно было бы скорее
сравнить со штопором, а не со спиралью. ^-,.
¦ Рсрбая точка этого типа может бытьфазван&ъфокусом.
. Четвёртая гипотеза. Уравнение-С.C) имеет один
дейстйительный корень и два комплексных^ сопряжённых,
сумма'-которых имеет знак, противоположный знаку дей-
ствительного корня. ,
В этом случае интегралы уравнений A) не:мргут быть
представлены в форме D). Три траектории Tlf-*T2 и Т3>
которые были определены выше, всё ещё существуют, но
только одна из них Jx — действительна. -.¦¦¦-¦
Мы всегда можем сделать такое преобразование ко-
ординат, чтобы, начало было передесено в особу» точку,
а члены первой степени X, Y и Z были бы приедены,
к виду: .. - г
*«•.¦+ЙУ» V-rrty и 53г.
Тогда уравнение
дх ' ду
будет иметь голоморфный относительно х к у интегрдл

202 ЧЕТВЁРТЫЙ МЕМУАР
обращающийся в нуль вместе с этими переменными (это
можно показать совершенно так же, как во втором
случае).
Следовательно, существует поверхность, проходящая
через начало координат, на которой расположено беско-
нечное множество траекторий. Пусть
*¦— уравнение этой поверхности. Если мы заменим г в X
и Y через <р (*, у),. то уравнения A) приведутся к уравне-
нию первого порядка и будут изображать плоские кри-
вые, являющиеся проекциями на плоскость (х, у) траек-
торий, расположенных на поверхности г = у(х, у). Не-
трудно видеть, что для этих .плоских кривых начало
координат является фокусом.
Таким образом, в рассматриваемом случае существует
поверхность, проходящая через начало координат, и на
этой поверхности расположено бесконечное множество
траекторий, которые, как спирали, закручиваются вокруг
особой точки, асимптотически приближаясь к ней. Кроме
того, существует траектория Ти проходящая через особую
точку. Все другие траектории остаются на конечном рас-
стоянии от особой точки.
Такая особая точка может быть названа седло-фокус.
Пятая гипотеза. Уравнение C) имеет один дей-
ствительный корень и два комплексных сопряжённых, сумма
которых равна нулю.
Этот пятый случай можно считать предельным и исклю-
чительным случаем потому, что он, вообще говоря, не
имеет места, когда X, Y и Z — многочлены самого общего
вида данной степени.
В этом, пятом, случае интегралы уравнений A), вообще
говоря, не могут быть представлены в форме D). Но
если бы всё-таки случилось так, что интегралы могли бы
быть представлены в этой форме, если бы мы положили
= ia,

гл. xvi. уравнения 2-го порядка; особые точки 203
то нетрудно было бы видеть, что все траектории лежат
на поверхностях
К* + К'2 = const.
Мы имели бы тогда одну действительную траекторию Tv
проходящую через начало координат, уравнение которой
было бы
Мы имели бы также проходящую через особую точку
поверхность /78 = 0, на которой расположено бесконеч-
ное Множество траекторий. Эти траектории — замкнутые
кривые, ' охватывающие особую точку. Поверхности
К* -\-К'2 = const, являются как бы своего рода футлярами,
внутрь которых вложена траектория Ти так что их можно
было бы сравнить с цилинДрами, имевшими общую ось,
которые были согнуты и деформированы одновременно
с этой осью; деформированная ось и есть траектория.
Траектории, расположенные на этих поверхностях, похожи
на винтовые линии, шаг которых всё время уменьшается,
так что они не про:тираются в бесконечность, а асимпто-
тически приближаются к поверхности Hs — 0.
, Такая особая точка назыпается центром.
Если же, напротив; интегралы не могут быть пред-
ставлены в форме D), то особая точка будет иметь или
такой же характер, как фокус, или такой же характер,
как седло-фокус.
Я не буду здесь останавливаться дольше на этом
исключительном случае, рассчитывая вернуться к нему
позже, если мне встретится в этом необходимость для
каких-нибудь приложений. Сейчас я ограничусь только
тем, чго отошлю читателя к главе XI, где подробно были
рассмотрены аналогичные особые точки уравнений первого
порядка.
Таким образом, если оставить в стороне тот предель-
ный случай, который мы только что рассматривали, то
уравнения второго порядка могут иметь четыре тиаа особых
точек: сёдла, узлы, фокусы, сёдла-фокусы.
* Легко распространить эту теорию на уравнения по-
рядка п, Заметим только, что при возрастании а число

204 ЧЕТВЕРТЫЙ МЕМУАР '
типов особых точек растёт очень быстро. Действительно,
мы видели, что для я=1 число типов равно 3; .для
я = 2 число типов равно 4; нетрудно было бы видеть,
что для я = 3 число типов равно 8,' а для я = 4
равно 10.
-•• Рассмотрим-теперь тот частный случай, когда все три
поверхности Л"=0, ^=0, Z = 0 пересекаются вдоль
некоторой кривой; эта кривая является тогда особой
линией.
Сделаем замену переменных
* = <Pi(*'> У, *')> У = Ъ(.Х'> У. Л * = <?8(*', У, А
где <pi» ?а и ?з.— функции, голоморфные внутри рассма-
триваемой нами области.
Мы всегда можем выбрать эти голоморфные функции
таким образом, чтобы уравнения особой линии в новых
переменных были бы:
, Действительно, пусть
/(*, у, г) = 0, Л (л-, у, г) = 0
—уравнения особой линии и пусть
— координаты какой-нибудь точки М особой линии; пусть
/а (Х'У>г) — какая-нибудь голоморфная функция, обращаю-
щаяся в нуль в точке М. Положим:
| х'=/(х, у, г),
(8) \ . ' У=/г(х,У, Z),
[ г' =/2(х, у, г). •
Мы можем выбрать функцию /2 таким образом, чтобы
функциональный детерминант функций/,/! и/2 не обращался
бы нуль в точке М и, следовательно, чтобы уравнения (8)
могли бы быть разрешены относительно х,.у и г. Это
возможно всегда, за исключением того случая, когда

гл. xvi. уравнения 2-го порядка; особые точки 205
особая линия в точке М имеет двойную точку или
ещё какую-нибудь особенность; мы предположим, что
этого нет.
Отсюда следует, что мы всегда можем считать, что осо-
бая линия есть ось г и что такая точка особой линии,
которую мы рассматриваем, есть начало координат.
Тогда X, Y и Z должны обращаться в нуль при х
и у, равных нулю одновременно.
Теперь сделаем ещё одну замену переменных, которая
на этот раз будет линейной и будет, следовательно,
простым преобразованием координат.
В силу предыдущего ясно, что члены первой степени
в X, Y и Z должны иметь вид
ах + а'у, px-j-p'jf, чх + ч'У-
Я оставлю в качестве оси особую линию, но изменю
плоскость ху и выберу новую плоскость ху так, чтобы 7
и у' обратились бы в нуль.
Составим теперь уравнение, аналогичное уравнению C),
но уже только второй степени
Р
=0.
В том случае, когда это уравнение имеет два действи-
тельных корня одинаковых знаков или два комплексных
сопряжённых корня, сумма которых не равна нулю, урав-
нение в частных производных
дх ' ду
имеет голоморфный интеграл, обращающийся в нуль
при x = j = 0.. Чтобы убедиться в этом, достаточно
повторить то рассуждение, которое мы проводили в случае
второй гипотезы.
Существует, следовательно, поверхность, проходящая
через особую точку, на которой расположено бесконеч-
ное множество траекторий. При изучении траекторий,
лежащих на этой поверхности, мы приходим к случаю

206 ЧЕТВЕРТЫЙ МЕМУАР
уравнений первого порядка; для этого' достаточно в урав-
нениях A) заменить z его' выражением, найденным из
уравнения поверхности.
Нетрудно показать, что для траекторий, лежащих
на этой поверхности-, особая точка является узлом, если
корни уравнения (9) действительны и одинаковых знакоз,
и фокусом, если корни комплексные и сопряжённые.
В узле так же, как и во всех достаточно близких к нему
точках особой линии, пересекается бесконечное множество
траекторий. Вокруг фокуса, так же, как и вокруг всех
достаточно близких к нему точек особой линии, закручи-
вается бесконечное множество траекторий, асймптотл-
чески приближающихся к нему.
Остаётся рассмотреть случай, когда уравнение (9)
имеет действительные корни разных знаков. В этом
случае, на основании теоремы Врио и Буке, о которой
говорилось выше, можно показать, что в.сё ещё существуют
две траектории, проходящие через особую точку с опре-
делённой касательной. Это те траектории, которые мы
обозначали 7\ и 78; что же касается траектории Тй, то
она вырождается в саму особую линию. Все другие
траектории остаются на конечном расстоянии о г особой
точки. Такая особ*я точка называется седлом.
Итак, через седло и через все достаточно близкие
к нему точки особой линии будут проходить две траек-
тории; всв' другие траектории остаются на конечном рас-
стоянии от особой линии.
Таким образам, на особой линии будут: дуги, все
точки которых — узлы, дуги, все точки которых — фокусы,
и, наконец, дуги, все точки которых — сёдла.
Точки, которые отделяют эти дуги друг от друга,
а также кратные точки особой линии, будут иметь более
сложную структуру, о которой я здесь говорить не буду.
Я закончу эту главу, приведя очень простые примеры
на каждый из случаев, разобранных выше.
Изолированные особые точки 14.
1) Узел. Пусть
dx dy dz ,,

ГЛ. XVI. УРАВНЕНИЯ 2-ГО ПОРЯДКА; ОСОБЫЕ ТОЧКИ 207
Траектории — прямые, проходящие через начало.
2) Седло. Пусть
dx dy dz j.
На поверхности г = 0, проходящей, очевидно, через
начало, лежит бесконечное множество траекторий, которые
являются прямыми, проходящими через начало.
Кроме того, сама ось г тоже является траекторией,
проходящей через начало.
Все другие траектории, уравнения которых
xz*= const., уг = const.
— гиперболы, остающиеся на конечном расстоянии от
начала.
3) Фокус
dx dy dz__j.
х +у ~ — х+у ~~ г ~~
Траекторией 7\ является здесь ось г, а поверхностью
Нъ = О плоскость' ху. Все другие траектории распо-
ложены на конусах вращения; их проекции на плоскость
ху — логарифмические- спирали; таким образом, все эти
траектории асимптотически приближаются к началу ко-
ординат.
Заметим, что поверхности, общее уравнение которых
мы писали в виде
д 7Г= const.,
здесь являются круглыми конусами. Они не имеют, следо-
вательно, ни одной из тех двух форм, о которых я говорил
выше как о характерных для этих поверхностей; но это
исключительный случай.
Если бы мы рассматривали дифференциальное уравне-
ние
dx __ dy _dz
х+у ~~ —х+у ~~ аг ' .

208 ЧЕТВЕРТЫЙ МЕМУАР
то при а < 1 эти поверхности имели бы единственную
касательную плоскость, а при а > 1 имели бы форму
поверхности, которая получается от вращения параболы
вокруг касательной в её вершине. Следовательно, исключи-
тельным случаем является случай о = 1.
4) Седло-фокус. Пусть
dx __ dy =dL—dt
х+у — х+у —г
Одна траектория — именно ось г — проходит через
начало. Бесконечное множество траекторий лежит в пло-
скости ху\ эти траектории-^логарифмические спирали,
асимптотически приближающиеся к началу. Остальные
траектории лежат на поверхности (х2-\-у2) z* = const.
и остаются, следовательно, на конечном расстоянии от
начала.
5) Центр. Пусть
djc__ dy <1г ...
у —х г
Общее уравнение траекторий
у2 = ла, arctang ? = In г -f A,
где А и г9—две постоянные интегрирования.
Траектории лежат на круглых цилиндрах. Единствен-
ная среди них — именно ось г — проходит через начало. Бес-
конечное множество траекторий лежит в плоскости ху;
эти траектории — окружности с центром в начале.
Все остальные траектории, делая на цилиндрах бес-
конечное множество витков, асимптотически прибли-
жаются к плоскости ху.
Точки особой линии.
6) Узлы.
dx dy dz
~х"~~ У~~ W
Траектории—прямые, параллельные плоскости ху,
пересекающие ось z; ось г и есть особая линия.

гл. xvl. уравнения 2-го порядка; особые точки 209
7) Сёдла.
dx dy rfz
Прямые г = const., х = 0 и прямые г = const., у «= О—
это траектории, пересекающие ось г, т. е. особую линию.
Все другие траектории лежат на гиперболических цилин-
лрах ху = const, и остаются на конечном расстоянии
от оси г.
8) Фокусы.
dx dy dz
х+у e — х+у 0" "
Траектории — логарифмические спирали, расположен-
ные в плоскостях, параллельных плоскости ху; они за-
кручиваются вокруг особой линии, асимптотически при-
ближаясь к ней.
14 Д. Пуанкаре.

глав;ахуп
интегрирование рядами
Мы видели, что всякое дифференциальное уравнение,
[при известных условиях], может быть представлено в форме
m dx* _ v dxi v dxn_ у.
К1) ~dt v J л» •••» ~dT пг
где все Х{ — целые многочлены. Если рассматривать пара-
метр t как время, то эти уравнения будут определять
движение точки в пространстве в измерений.
При неограниченном возрастании времени движущаяся
точка может:
1) или оставаться всё время в конечной части про-
странства и в то же время не приближаться неограниченно
ни к одной особой точке;
2) или удаляться в бесконечность;
3) или по истечении конечного промежутка времени
пройти через особую точку 171;
4) или неограниченно приближаться к особой точке
типа фокус;
5) или же движущаяся точка через конечные проме-
жутки времени, бесконечное множество раз возвращается
в окрестность особой точки так, что её расстояние до
особой точки становится меньше любой напербд заданной
величины, оставаясь конечным в промежутках времени
между двумя последовательными возвращениями в эту
окрестность.

ГЛ. XVII. ИНТЕГРИРОВАНИЕ РЯДАМИ 211
Другими словами, расстояние от движущейся точки до
особой точки может или оставаться ббльшим конечной
[положительной] величины A-й и 2-й случаи), или стре-
миться к нулю C-й и 4-й случаи), или же, наконец,
это расстояние может колебаться, становясь меньше любой
наперёд заданной величины, но не оставаясь всё время
меньше этой величины и, следовательно, не стремясь
к нулю E-й случай).
Таким образом, существует пять типов траекторий;
нетрудно построить примеры всех этих пяти типов.
Представляло бы большой интерес нахождение выра-
жений для xlt xit ..., хп в виде рядов, разложенных
по разным функциям времени и сходящихся для всех
действительных значений t, от—сю до-|-оо. Эта вадача
всегда может быть решена, и я дам здесь одно из ев
решений. Но по самой природе этой задачи она может
быть решена бесконечным множеством способов. Ничто
не доказывает, что решение, данное мною, — самое удач-
ное; как раз наоборот, весьма мало вероятно, что ояно
и то же решение этой задачи одинаково целесообразно
во всех частных случаях. Поэтому для всякого уравне-
ния, которое нужно будет интегрировать, следует искать
решение, аналогичное тому, которое дано мною, но во-
обще не совпадающее с ним, стремясь всегда выбрать
это рещение, учитывая специальные особенности данной
задачи.
Введём новое переменное S, полагая
A\ dXl а. V dXi = У ^2 в У
так что
ds Х± Хъ Хп
При этом Yt — функции от хи xi% ..., х„, удовлетво-
ряющие следующим условиям: при всех действительных
значениях переменных х, а также при всех значениях л\
при которых их мнимые части заключены между —- р и -|-р,
функции Y голоморфны и их модуль меньше М.
14*

212 ЧЕТВЕРТЫЙ МЕМУАР
Таким образом, если одновременно
| Im х, |< р •),
I Im *9 | < р,
I Im xn К р, _
то мы будем иметь также одновременно:
\УЛ\<М, \Yi\<M, .... \Yn\<M.
Пусть теперь
JLO) „(о) @)
— система действительных значений переменных
При всех значениях хи х9, ..., хп, удовлетворяющих
неравенствам
функции У голоморфны и модули их меньше М.
Следовательно, если мы разложим функции Y в ряды,
расположенные по степеням
„ „@) ,. „(О) „@)
*i~"*ii -*j л а, • • •, Ля~~Л»>
то коэффициенты этих рядов будут по абсолютной вели-
чине соответственно меньще коэффициентов разложения
функции
Щ ' у
Мы запишем, пользуясь обозначениями главы XI,
предполагая при этом, что функции Y и Z разложены
по степеням xi—х{*\
*) Im х обозначает — мнимая часть числа х.

ГЛ. XVII. ИНТЕГРИРОВАНИЕ РЯДАМИ 213
Пусть s0—действительное значение s, соответствующее
значениям x'f переменных х{. Отправляясь от уравне-
ний B), мы можем разложить переменные
по степеням разности s—s0.
Предположим теперь, что мы имеем другую движущуюся
точку, координаты х которой удовлетворяют уравнениям
О Ый d*l — dx* =, — dx" = 7
4 ' ds ds ds
Мы можем написать разложения для координат этой но-
вой движущейся точки
по степеням s—s0. Все коэффициенты рядов 41 положи-
тельны и по абсолютной величине больше соответствен-
ных коэффициентов рядов <р.
Найдём функций <}», т. е. проинтегрируем уравнения
B bis). Прежде всего мы получим
Обозначим общую величину х{ — х^ через и. Тогда
уравнения B bis) сведутся к уравнению
du M
ds"
отсюда
и, наконец,
им =
Подкоренное выражение обращается в нуль, когда
Ж
Следовательно, ряды для функций «j» будут сходиться при
всех значениях s, удовлетворяющих неравенству

214 ЧЕТВЕРТЫЙ МВМУАР
То же справедливо и для разложений функций <р.
Таким образом, функции 9 (s) голоморфны внутри кру-
Q
га радиуса -^~ с центром в любой точке s0 действитель-
ной оси.
Если мы проведём с обеях сторон действительной оси,
на расстоянии -J^r от этой оси, две параллельные пря-
мые, уравнения которых
то эти прямые будут ограничивать полосу В плоскости,
внутри которой функции <р голоморфны.
Будем искать конфррмное отображение этой полосы
на круг. Пусть
pl причём s = s1
Посмотрим, при какой условии
Мы имеем
_^ «*"' (cos
V = eaBi (cos a^ + i sin as2) +1 '
или
Для того чтобы эта величина была меньше 1, необ-
ходимо и достаточно, чтобы cos asa был положителен, т. е.
чтобы
Другими словами, точка s должна находиться внутри по-
лосы, ограниченной двумя прямыми

ГЛ. XVII. ИНТЕГРИРОВАНИЕ РЯДАМИ 215
Если мы возьмём
пМп
то эта полоса будет как раз полосой В и зависимость
между v и s будет давать конформное отображение
полосы В на круг радиуса 1 с центром в начале.
Если мы будем рассматривать хи л:2, ..., хп уже
не как функции от s, а как функции от v, то они будут
голоморфны внутри этого круга; следовательно, эти пере-
менные могут быть разложены в ряды, расположенные по
возрастающим степеням v, и сходящиеся при всех значе-
ниях, модуль которых меньше 1. Коэффициенты этих рядов
могут быть вычислены последовательно.
Действительно, существует одна и только одна система
рядов, расположенных по возрастающим степеням величины
и формально удовлетворяющих уравнениям B). Эти ряды
сходятся при всех действительных значениях s, так как при
действительных значениях s модуль v меньше единицы.
Я покажу теперь, что всегда можно выбрать перемен-
ное s так, чтобы оно удовлетворяло всем требуемым усло-
виям. Для этого достаточно положить
Во-первых, я утверждаю, что функция
Y == **
*
будет голоморфна при всех действительных значениях пере-
менных х. В самом деле, эта функция может перестать
быть голоморфной только в том случае, когда
а это невозможно при действительных значениях пере-
менных х.
Во вторых, Yt всегда будет меньше -ц по абсолютной
величине, когда Х( — действитель ы.

216 ЧЕТВЕРТЫЙ МЕМУАР
Пусть теперь х^, х(°ъ, ..., х$ —какая-нибудь си-
стема действительных значений переменных х, и пусть Д —
область, определённая неравенствами
\х1—JCi|<p, |дга — *2|<р, •••» \хп — хп |<Р«
Величина р может быть названа радиусом, а система
значений лг(?, х^, ..., х®п — центром области Д.
Всегда можно взять радиус А столь малым, чтобы внутри
этой области функции Y были бы голоморфны и по аб-
солютной величине меньше 1; мы всегда будем выбирать
в качестве р наибольшую из величин, удовлетворяющих
этим условиям.
Я утверждаю теперь, что каков бы то ни был центр
области Д, число р всегда будет больше некоторой по-
стоянной величины р0. Действительно, когда центр области Д
непрерывно смещается, р тоже изменяется непрерывно; при
этом р не может обратиться в нуль ни для какой конечной
системы значений лг{?, х^, ..., х„\ так как в противном
случае, функции Y не были бы голоморфны в этой точке.
Остаётся показать, что р не Стремится к нулю, когда
центр области удаляется в бесконечность. Предположим,
например, что х(^ — неограниченно возрастает, в то время
как другие величины х^р могут либо оставаться конеч-
ными,, либо тоже неограниченно возрастать. Сделаем за*
мену переменных, полагая:
X =— X =^ . X —22-
тогда
Х1 == То)» "*2 ^ ~Щ> • • •> хп === "(oj*
Мы можем предположить, что в то время как х^ не-
ограниченно возрастает, величины^0-, у'з\ • • •, Уп* стре-
мятся к конечным пределам; действительно, в противном
случае мы моглн бы достигнуть этого путём линейной
замены переменных.
Мы всегда можем предположить: 1) что все много-
члены Хг, Х9, ..., Хп — одинаковой степени т\ 2) что

ГЛ. XVII. ИНТЕГРИРОВАНИЕ РЯДАМИ 217
члены /и-ой степени этих я многочленов могут обратиться
в нуль одновременно только в том случае, когда все пере-
менные xv х3 хп обращаются в нуль. Действительно,
в противном случае нам достаточно было бы сделать линей-
ную замену переменных (я подразумеваю здесь дробно-
линейную подстановку).
Сделав все эти предположения, положим
мы получим
у _
Эта функция, как функция переменных у, может перестать
быть голоморфной (при действительных значениях пере-
менных у), только в том случае, когда одновременно
А это невозможно в силу сделанных нами предположений.
Таким образом, если yf* = 0, yf\ ..., у^ — система
действительных значений переменных у, то всегда можно
найти такую величину р', чтобы при всех значениях пере-
менных у, удовлетворяющих неравенствам
Ы<р'. Ь'з-^'Кр', •-., \Уп-уТ\<?\
функции Y были бы голоморфны и по модулю меньше 1.
Этого достаточно для того, чтобы показать, что р не
стремится к нулю.
Отсюда следует, что р всегда больше некоторой вели-
чины р0 и, следовательно, при всех значениях х, модуль
мнимой части которых меньше р0, функции Y будут голо-
морфны и по модулю меньше 1.
Что и требовалось доказать.
Таким образом, определяя $ так, как мы это делали
выше, мы можем разложить переменные х по степеням

218 ЧЕТВЕРТЫЙ МЕМУАР
и эти разложения будут годиться для всех действитель-
ных значений s или t.
Мы видели, однако, что некоторые затруднения возни-
кают в том случае, когда члены наивысшей степени в много-
членах X могут одновременно обращаться в нуль; как мы
уже говорили, в этом случае достаточно сделать замену
переменных. Однако проще поступать следующим образом:
мы всегда можем найти такой многочлен Z степени т,
чтобы члены от-ой степени всех п-{-1 многочленов Xlt...
..., Хп и Z могли бы одновременно обращаться в нуль
только в том случае, когда все переменные х одновре-
менно обращаются в нуль. Мы можем тогда положить
'< = •
и можно показать так же, как и раньше, что при всех
значениях х, модуль мнимой части которых меньше некото-
рой заданной величины р0, функции Y голоморфны и по
модулю меньше 1.
Найденные нами ряды, расположенные по степеням
будут в совокупности изображать всю траекторию. При
этом нужно заметить, что если эта траектория проходит
через особую точку, то мы должны рассматривать её как
кончающуюся в этой особой точке, которая будет, таким
образом, точкой остановки траектории. В самом деле,
движущаяся точка (по самой форме уравнений) может
достигнуть особой точки только при бесконечно больших
значениях s к t.
Среди уравнений, к которым можно попытаться при-
ложить этот метод, можно назвать уравнения задачи трёх
тел, к которым этот метод действительно приложим. В этом
случае разложения по возрастающим степеням
будут годиться для всех значений времени.

ГЛ. XVII. ИНТЕГРИРОВАНИЯ РЯДАМИ 219
Исключение возможно только тогда, когда начальные
условия взяты так, что два из рассматриваемых трёх тел
должны столкнуться по истечении конечного промежутка
времени; действительно, в момент столкновения 5 делается
бесконечно большим ВД. Все формулы будут, следова-
тельно, справедливы только до момента столкновения. Но,
с другой стороны, очевидно, что для значений времени,
следующих за моментом столкновения, проблема становится
иллюзорной.
Пусть теперь t есть время (речь идёт здесь о подлин-
ном времени, а не о том, которое я несколько произвольно
ввёл в уравнения A)).
Если бы мы были заранее уверены, что расстояние
между любыми двумя из рассматриваемых трех тел все время
остаётся ббльшим некоторой определенной величины (при
этом это расстояние может неограниченно увеличиваться),
то мы могли бы утверждать, что координаты этих трёх
тел могут быть разложены в ряды по степеням
сходящиеся при всех значениях времени.
Я не думаю, однако, что применение этого метода
к небесной механике может принести много пользы. Я хотел,
я это повторяю, привести только некоторый пример, а не
давать метод, который нужно применять во всех случаях.
Переменное s можно выбрать бесчисленным множеством
способов; выбор, сделанный мной, был совершенно произ-
волен и ничто не мешает умножить до бесконечности число
методов, аналогичных только что изложенному.

ГЛАВА XVIII
РАСПРЕДЕЛЕНИЕ ОСОБЫХ ТОЧЕК
Эта глава вся целиком является приложением одной
теоремы Кронекера, изложенной в двух его мемуа-
рах, озаглавленных: Ueber Systeme von Functlonen meh-
rerer Varlabeln, которые напечатаны в Monatsberichte
Академии Берлина (март 1869, август 1869) t»l.
Пусть
F(x,y,z) = 0
— некоторая поверхность, 'котбрую я буду предполагать
замкнутой.
Пусть diso — элемент этой поверхности. Положим
Интеграл
0 dF
дх
дХ
ХТх
у дУ
* дх
' dZ
Z дх
dF
dj
дХ
ду
дУ
ду
dZ
ду
1 С Rdw
dF
dz
дХ
dz
дУ
dz
dZ
dz

ГЛ. XVIII. РАСПРЕДЕЛЕНИЕ ОСОБЫХ ТОЧЕК
221
распространённый на всю рассматриваемую поверхность,
или на какую-нибудь замкнутую полость этой поверхно-
сти, называется индексом этой поверхности или этой
замкнутой полости.
Пусть, например,
Х = х, Y = y, Z = z,
\-z* — а2.
В этом случае наша поверхность есть сфера, которая
содержит внутри себя начало координат, являющееся
узлом.
Мы имеем
S =
= а, 2 = V^*2 -j- 4уа -+¦ 4га «= 2а,
О 2х 2у 2г
л: 1 О О
jV 0 1 О
г О О 1
Тогда индекс равен
1 г — a dw 1 г ,
но Г dw есть площадь поверхности нашей сферы и, значит
равен 4iraa. Следовательно, индекс равен 1.
Если Х = х, Y*=y, Z = — z, то начало есть седло
и индекс равен — 1.
Если Х = х, К=—yt Z== — г, то начало опять
седло, но индекс равен +1.
Если Х= — х, Y = —у, Z= — г, то начало—узел
и индекс равен — 1.
Изложим теперь общую теорему, которую нетрудно
вывести из теоремы Кронекера.

222
ЧЕТВЕРТЫЙ МЕМУА1»
Мы будем различать два типа особых точек: положи-
тельные особые точки, для которых детерминант
0)
дХ, дХ дХ
дх ду dz
дУ дУ дУ
дх ду дг
dZ dZ dZ
дх ду дг
положителен, и отрицательные особые точки, для которых
этот детерминант отрицателен.
Нетрудно видеть, что существуют положительные
узлы, фокусы, сбдла и сёдла-фокусы, и, с другой сто-
роны,— отрицательные узлы, фокусы и сёдла и сёдла-
фокусы.
Здесь мы имеем положение, как раз обратное тому,
которое наблюдалось в случае уравнений первого порядка:
dx
dy
T
Действительно, в этом случае все узлы и фокусы
были положительны, а все сёдла — отрицательны.
В силу теоремы Кронекера, индекс замкнутой поверх-
ности равен разности между числом положительных осо-
бых точек и числом отрицательных особых точек, распо-
ложенных внутри этой поверхности.
Предположим теперь, что рассматриваемая нами по-
верхность есть поверхность без контакта, т. е. что ни
в одной действительной точке этой поверхности не имеет
места равенство
X —Л~ Y — 4-Z — = О
Я буду различать два типа поверхностей без контакта:
поверхности положительного типа, для которых
dt
dz

ГЛ. XVIII. РАСПРЕДЕЛЕНИЕ ОСОБЫХ ТОЧЕК 223
и поверхности отрицательного типа, для которых
dF dF ,vdF
Чтобы иметь возможность отличать эти два типа, мы
должны условиться выбирать функцию F таким образом,
чтобы вне рассматриваемой нами замкнутой поверхности
значения функции F были бы больше, чем внутри неё.
Я .покажу теперь, что индекс поверхности без кон-
такта зависит только от её типа и от её рода (рода
с точки зрения Analysis Situs, ср. мемуар III, гл. XII).
Я покажу, что индекс поверхности положительного
типа не меняется от замены X, К, Z на г, г , г, а ин-
' ' ох ду dz'
деке поверхности отрицательного типа не меняется от
замены X, Y, Z **-'?,-'?,-%.
Действительно, будем изображать скорость движущейся
точки вектором, проекции которого на три оси коорди-
нат равны соответственно X, Y, Z. Через каждую точку
нашей поверхности будет, следовательно, проходить один
такой вектор; все эти векторы будут направлены во
внешнюю область поверхности, если поверхность поло-
жительна, и внутрь поверхности, если она отрицательна.
Будем теперь непрерывно менять X, Y, Z и F так,
чтобы поверхность деформировалась, а векторы изменялись.
Индекс не будет меняться, если только ни в какой момент
деформации скорость не обращается в нуль ни в одной
из точек поверхности. Как раз это и имеет место, если
поверхность всё время остаётся поверхностью без кон-
такта и сохраняет свой род и свой тип flol.
Таким .образом, индекс поверхности без контакта
зависит только Iй! от её рода и типа, а потому, в част-
ности, можно заменить X, Y, Z через rt-^, —-g- • — -^ .
выбирая знак4" или —, смотря по тому, положительна
или отрицательна данная поверхность.

224 ЧЕТВЕРТЫЙ МЕМУАР
Рассмотрим, в частности, сферу без контакта в при-
мере, разобранном выше:
Х=х, Y=y, Z = z\ F = xa+^2 + ^2 —a2.
Мы видели, что индекс такой сферы равен -|-1, если
сфера положительна; но та же сфера будет иметь индекс,
равный—1, если она отрицательна, как нетрудно видеть,
полагая
Х=^-х, Y=—y, Z = — 2) F = *2-Kya + .?a—a2.
Таким образом, индекс поверхности без контакта
рода 0 будет равен г±г 1, в зависимости от того, положи-
тельна она или отрицательна. В случае уравнений первого
порядка
dx __ у dy_v
dt~~A> dt~r
индекс цикла без контакта всегда был равен -j-1, незави-
симо от того, был ли этот цикл положителен или отри-
цателен.
Отсюда вытекают такие следствия:
Внутри поверхности без контакта рода 0 число поло-
жительных особых точек на единицу больше числа отри-
цательных, если поверхность положительна и число поло-
жительных особых точек на единицу меньше числа
отрицательных, если поверхность отрицательна.
Внутри поверхности беа контакта рода 0 всегда нахо-
дится по крайней мере одна особая точка.
Совершенно аналогичные рассмотрения привели нас,
в случае уравнений первого порядка, к соотношению
между числом сидел, фокусов и узлов. Здесь мы не можем
ожидать ничего подобного. Действительно, в случае урав-
нений первого порядка, мы имеем соотношения между
числом положительных особых точек (именно — узлов
и фокусов) и числом отрицательных особых точек
(именно — сёдел). Но в рассматриваемом нами теперь
случае узел, седло, фокус или седло-фокус могут быть
как положительными, так и отрицательными. Это и мешает
обобщать соотношение, о котором я только что говорил>

ГЛ. XVIII. РАСПРЕДЕЛЕНИЕ ОСОВЫХ ТОЧЕК 225
Пусть теперь мы имеем положительную поверхность
без контакта рода 0 и другую, отрицательную поверх-
ность без контакта рода 0, лежащую внутри первой
поверхности. Пусть Е—часть пространства, заключённая
между этими двумя поверхностями. Разность индексов *)
равна 2. Следовательно, число положительных особых
точек, находящихся в пространстве Е, на две единицы
больше числа отрицательных особых точек (число поло-
жительных особых точек было бы на две единицы
меньше числа отрицательных, если бы положительная
поверхность лежала внутри отрицательной).
Итак, между двумя поверхностями без контакта рода О
и различных типов всегда находится по меньшей мере
две особые точки.
Найдём теперь индекс поверхности без контакта
рода 1. Пусть
где с — произвольный параметр, уравнение семейства
поверхностей (эти поверхности получаются от вращения
семейства овалов Кассини).
Поверхности F = с4 будут, рода О, если с > а, и рода 1,
если с<а. При с = а поверхность F=a* имеет кони-
ческую точку.
Дифференциальные уравнения траекторий, ортогональ-
ных к этим поверхностям, будут
f ^
dt~dx* dt~ ду' dt~dz '
У этих траекторий есть только одна '12' особая точка,
именно —начало координат, и эта особая точка положи-
тельна, в чём нетрудно убедиться. Кроме того, для этих
траекторий поверхности F = с4 будут положительными
поверхностями без контакта.
Пусть мы имеем две поверхности
*) Этих двух поверхностей.
15 А. Пуанкаре.

226 ЧЕТВЕРТЫЙ МБМУАР
Первая^из этих поверхностей будет рода 1, а вторая
рода of индекс второй равен-J-1 I18J; пусть J — индекс
первой поверхности. Разность между индексами должна
равняться разности между числом положительных и отри-
цательных особых точек, заключённых, между этими двумя
поверхностями. Но между ними находится только одна
положительная, особая точка и нет отрицательных. Мы
будем, следовательно, иметь
1—У=1, откуда У=0.
Таким образом индекс положительной поверхности
без контакта рода 1 равен нулю; то же самое справед-
ливо и для отрицательной поверхности без контакта
рода 1.
' Таким же рассуждением можно было бы показать,
что индекс поверхности без контакта рода р равен
— {р—1), если она положительна и -\-(р — 1), если она
отрицательна.
Отсюда, непосредственно следует, что внутри всякой
поверхности без контакта всегда есть особые точки, если
только эта поверхность не первого рода; в последнем
же случае ничего сказать нельзя.
Пусть даны две повгрхности без контакта, лежащие
одна вне другой, и пусть Е—часть пространства, за-
ключённая между этими двумя поверхностями.
Если эти поверхности обе положительны, или обе
отрицательны,* то в пространстве ? всегда будут находиться
особые точки, за исключением того случая, когда поверх-
ности одинакового рода.
Если одна из двух поверхностей положительна, а дру-
гая отрицательна, то в пространстве Е всегда будут
находиться особые точки, за исключением того случая,
когда одна из этих поверхностей рода 0, а другая — рода
2, или когда обе поверхности рода 1.
Нетрудно распространить асе предыдущие результаты
на общий случай уравнений
dxi _ с1хг dxn _
Л1 л, Хп

ГЛ. XVIII. РАСПРЙДЕЛЕНИЕ ОСОБЫХ ТОЧЕК ' 227
Действительно, пусть
F (хх,х2, ... ,лгп) == О
— уравнение многообразия я— 1 измерения (Mannigfal-
tigkett), которое в пространстве я измерений играет ту
же роль, что и поверхность в обычном пространстве.
Пусть dw— элемент этого многообразия. Положим
2
Пусть Д — детерминант, у которого первый элемент
первого столбца равен 0; (/4- 1)-й элемент первого столбца
dF
равен Xt; (*-}-1)-й элемент первой строки есть-^— и
наконец (А-[-1)-й элемент (t-\- 1)-го столбца есть
Пусть ш есть интеграл
Г dw,
взятый по всему многообразию
Интеграл
Д dw
взятый по всему многообразию F = 0, будет индекс этого
многообразия.
Так же, как и в уже рассмотренном частном случае,
мы будем различать положительные и отрицательные
особые точки; можно было бы показать, что индекс
многообразия равен разности между числом положитель-
ных и числом отрицательных особых точек, лежащих
внутри этого многообразия.
15*

228 четвертый мемуар
Но здесь необходимо сделать одно важное замечание.
Для того, чтббы классифицировать особые точки, мы
составляем уравнение относительно 5*.
dXt о d-Xi дХп
дх\ х дх3 ''' dxi
dxt дх$ '' ' дхп
дХп дХ». . дХ» S
dxi дх2 ''' дхп
Предположим, что- это уравнение я-й степени имеет р
действительных положительных корней, q действительных
отрицательных корней, 2г комплексных корней с поло-
жительной действительной частью, 25 комплексных корней
с отрицательной действительной частью. Имеем
Четыре числа p,q,r,s характеризуют особую точку
и позволяют судить о форме траекторий вблизи этой
особой точки. Но при этом точки (p,q,r,s) и (q,p,r,s)
должны рассматриваться как точки одинакового типа;
иными словами — форма траекторий одна и та же в обоих
случаях.
Так, например, если мы положим п = 3, то нетрудно
видеть, что для уравнений
dx dy dz
~X ЧГУг ~dt~Z
начало координат, являющееся особой точкой, характе-
ризуется четырьмя числами C, 0, 0, 0) и есть узел так
же, как и для уравнений
dx dy dz
It *' 41 -y> ~dl~~z>
у которых эта особая точка характеризуется четырьмя
числами @, 3, 0, 0).

ГЛ. XV1H. РАСПРЕДЕЛЕНИЕ ОСОБЫХ ТОЧЕК 229
Далее, особая точка положительна, если q четно, и
отрицательна, если. q нечётно. Нетрудно видеть, что
когда и четно, то
p = q (mod. 2),
и. когда и нечётно, то
p = q-\-\ (mod. 2).
Следовательно, когда я четно, особые точки (р, q, r, s)
и (?. Р, ris) или обе положительны, или обе отрицательны.
Наоборот, если я нечётно, то эти особые точки разных
знаков.
Отсюда следует, что при чётном я две точки одина-
кового типа имеют также и одинаковые знаки и что это
не имеет места при нечётном я. Так, например, при й = 2
фокусы и узлы всегда положительны, а сёдла всегда
отрицательны, а при я = 3 узлы (так же, как и фокусы,
сёдла и сёдла-фокусы) могут быть и положительными и
отрицательными.
Мы определим подобно тому, как мы это сделали
выше для поверхностей, многообразия (я— 1)-го измере-
ния без контакта, которые могут быть разделены на два
типа: тип положительный и тип отрицательный.
Многообразие (л— 1)-го измерения характеризуется
с точки зрения геометрии положения своими (л — 2)
порядками связности, которые определены Риманом (Rie-
mann, Gesammelte Werke. Leipzig. Teubner. 1876, p. 448)
и Бриоши (Anriall di Matematica, t. V).
Индекс многообразия без контакта будет зависеть
только от порядка связности этого многообразия и от
его типа.
Рассмотрим теперь два многообразия без контакта
с одинаковыми порядками связности и пусть одно из них
будет положительным, а другое — отрицательным; их
индексы будут одинаковы по величине и по знаку, если л
четно, и одинаковы по величине, но противоположны по
знаку, если л нечётно.
Индекс положительного односвязного многообразия
без контакта равен -f-1: Число положительны* особых

230 • ЧЕТВЕРТЫЙ МЕМУАР
точек, лежащих внутри такого многообразия, на единицу
больше числа отрицательных особых точек.
Если п четно, то особые точки одинакового типа
всегда будут одинакового знака и мы получим таким
образом соотношение между числом особых точек раз-
личных типов. Мы не получим подобного соотношения,
когда п нечётно. Так, например: мы получим такое соот-
ношение при я = 2 и не получим при л = 3.
Пусть М и М' будут два многообразия без контакта
одинакового порядка связности, из которых одно по-
ложительно, а другое отрицательно, и пусть второе
лежит внутри первого. Пусть Е— часть пространства
между М и М'.
При нечётном п в пространстве Е всегда будут нахо-
диться особые точки, если индекс М не равен 0, в част-
ности, когда М односвязно. Но мы "ничего не можем
сказать, когда п четно.

ГЛАВА XIX
ИССЛЕДОВАНИЕ ЗАМКНУТЫХ КРИВЫХ
Среди траекторий подвижной точки, определённых
уравнениями
dx dy dz ..
~~Х— ~Y"=~Z~ — Clt'
могут встретиться замкнутые кривые. Мы увидим, что для
траекторий, подходящих достаточно близко к замкнутой
траектории, можно дать теорию, совершенно аналогичную
той, которую мы развили в XVI главе для траекторий,
проходящих достаточно близко от особой точки; таким
образом замкнутые траектории в известной мере играют
ту же роль, что и особые точки.
Прежде всего нужно было бы уметь устанавливать —
существуют ли замкнутые траектории. Однако в настоя-
щее время я очень мало могу сказать по этому поводу.
Рассчитывая вернуться к этому вопросу позднее, я огра-
ничусь сейчас только тем, что у приведу"* один простой
пример.
Пусть мы имеем'тор без контакта,1 внутри которо-
го нет ни одной особой точкн. Разрежем его меридио-
нальными плоскостями и предположим, что эти пло-
скости тоже не имеют контактов с траекториями вну-
три тора.
Введём специальную систему координат. Прежде всего
предположим, что ось г есть ось вращения тора, а пло-
скость (х, у) есть плоскость симметрии тора, так что

232 ЧЕТВЕРТЫЙ МЕМУАР
уравнение тора имеет вид
(*9 +.У3 + «*+#а—г2K
Положим затем
гг = т), лс = (/? -|- ?) cos со, у =
так что уравнение тора примет вид
Так как плоскости меридиана ш = const, являются
плоскостями без контакта, то —гт сохраняет всё время
один и тот же знак, например, всё время положительно.
Что же касается тора, то я буду предполагать для опре-
делённости, что он является отрицательной поверхностью
без контакта, так что движущаяся точка, войдя внутрь
тора, уже не сможет выйти из него.
Через точку Мо с координатами
лежащую внутри тора, я проведу траекторию; подвижная
точка, вышедшая в начальный момент из точки Мо, по
истечении некоторого времени t будет находиться в точке Мх
с координатами
лежащей внутри тора.
Положим
Е и Н "будут голоморфными функциями от ?0 и тH.
Если мы имеем
Е = Н = 0,
то траектория, проходящая через точку Ма, будет зам-
кнута.
В плоскости меридиана ю = 0 назовём индексом какой-
нибудь кривой
Г F )

ГЛ. XIX. ИССЛЕДОВАНИЕ ЗАМКНУТЫХ КРИВЫХ 233
интеграл
\_CRds
распространённый на все элементы ds этой кривой.
В этом выражении, так же как и в интеграле Кронекера,
«-!¦
dF
в %:-
н
дЗ
дЯ дН
Рассмотрим в частности кривую
т. е. меридиональную окружность тора. Принимая во вни-
мание, что вдоль этой кривой мы имеем всегда
dF
и следовательно
мы легко покажем, что индекс нашей меридиональной
окружности равен 4-1- Следовательно, внутри этой окруж-
ности существует по крайней мере одна точка (&0, тгH),
в которой S и Н обращаются в 0; отсюда следует, что
внутри тора существует" йо крайней мере одна замкнутая
траектория. . (
Что и требовалось доказать.
Я напомню, кроме того, что в ноте, напечатанной
в 1-ом томе ^Bulletin astronomique* и озаглавленной^

234 ЧЕТВЕРТЫЙ МЕМУАР
«5мг certaines solutions particulieres du ргоЫёте des •
trols corps» («О некоторых частных решениях задачи трёх
тел»), я показал, что уравнения небесной механики могут
иметь частные интегралы, которые с некоторой точки
зрения можно считать представляющими замкнутые траек-
тории.
Итак, предположим, что тем или иным способом мы
установили существование замкнутой траектории.
Обозначим через s дугу этой траектории, отсчитывае-
мую от некоторой фиксированной точки, и через / — длину
всей кривой. Мы будем пользоваться специальной систе-
мой координат.
Пусть О — начало отсчёта дуг и М — какая-нибудь
точка замкнутой траектории. Пусть s — дуга ОМ. Я про-
веду в точке М нормальную плоскость к траектории и
в этой плоскости проведу через точку М две прямоуголь-
ные оси. Пусть х и у координаты относительно этих
осей какой-нибудь точки нормальной плоскости. Положение
любой точки пространства будет определяться этими тремя"
координатами х, у и s. Такая система координат удобна
для изображения точек, очень близких к замкнутой траек-
тории.
Пусть Ро — точка с координатами х0, у0 и 0, лежа-
щая в нормальной плоскости s = 0. Если х0 ну0 достаточно
малы, то траектория, проходящая через точку Ро, пересечёт
последовательно все нормальные плоскости, соответствую-
щие постоянно возрастающему значению s. В конце концов
она пересечёт в точке Р1 с координатами xv уи I нор-
мальную плоскость s = l, которая совпадает с плоскостью
s = 0. Если \к0, у0 достаточно малы, то jc1? yt есть
голоморфные функции от переменных х0 и у0, обращаю-
щиеся в 0 вместе с этими переменными. Пусть
где R и R'M обозначают совокупности членов порядка
выше первого относительно х0 и у0.

. ГЛ. XIX. ИССЛЕДОВАНИЕ ЗАМКНУТЫХ КРИВЫХ 235
Положим
и ¦ .
дифференциальные уравнения тогда могут быть записаны
в виде
dx _ у аУ — v
Функции X и У являются здесь рядами, расположенными
по возрастающим степеням х и у и сходящимися при
достаточно малых значениях х и у. Коэффициенты этих
рядов — тригонометрические ряды, расположенные по сину-
сам и косинусам дуг, кратных t. Кроме того, X и Y
обращаются в нули при х и у, равных 0. Пусть
hx + ky, h'x + k'y
—члены 1-й степени в X и Y. Как мы уже говорили, A, k,
A', k'—тригонометрические ряды. Рассмотрим уравнения:
Интегралы этих уравнений имеют следующую форму
В этих выражениях Л, и Л2 — постоянные интеграции,
9,, <ра> 4*1 и 4*2 — тригонометрические ряды. Что же ка-
сается постоянных^ и Х2, то они определяются из уравнения
= 0
или
B) 53 —
Рассмотрим теперь те различные случаи, которые
могут вдесь представиться.

236 ЧЕТВЕРТЫЙ МЕМУАР
Первый случай. Может случиться, что корни уравне-
ния, определяющего 5, — комплексные, сопряжённые,
и модуль их не равен единице. Мы получим тогда
Ха = Х — /X', А1 =
где X, X', А, 6, ®, <р',ф и ? — действительны. Кроме того X
не равно 0. Предположим для определённости, что
Х>0.
Уравнения A) принимают вид
90(
_^'^ sln(x'
Положим
Поверхности
при достаточно малых х и _у, а следовательно, и С,
будут поверхностями рода 1, содержащими внутри
замкнутую траекторию.
Если в выражении для F мы заменим х и у их зна-
чениями A bis), то получим
откуда
Принимая во внимание, что уравнения A bis) суть
интегралы дифференциальных уравнений
мы получим

ГЛ. XIX. ИССЛЕДОВАНИЕ ЗАМКНУТЫХ КРИВЫХ 237
Следовательно, мы имеем
Но если х и у достаточно малы, то hx-\-ky
и h'x-\-k'y будут очень мало отличаться от ^ и Y, так
что мы будем иметь
dF л у dF л v dF
Следовательно, при достаточно малых значениях С
поверхности F=C будут поверхностями без контакта.
Если А>0, то эти поверхности положительны и под-
вижная точка всё время удаляется от замкнутой тра-
ектории.
Если же, наоборот, А<0, то наши поверхности отри-
цательны и подвижная точка асимптотически прибли-
жается к замкнутой траектории.
Второй случай. Может случиться, что уравнение
относительно 5 имеет корни, действительные и положи-
тельные, причём оба корня больше 1. Тогда Хх и Ха
действительны и положительны.
Положим
— Ъ'к
Можно было бы показать, как в предыдущем случае,
что при достаточно малых значениях С поверхности
F = C суть поверхности рода 1, содержащие внутри
замкнутую траекторию, и что, кроме того,
т. е. что поверхности /7 = С являются положительными
поверхностями без контакта.
Отсюда следует, что подвижная точка, бесконечно
близкая к замкнутой траектории при / = — со, при
возрастании t будет удаляться от неё.

238 ЧЕТВЕРТЫЙ МЕМУАР
Если, наоборот, оба корня уравнения относительно 5
были бы действительны, положительны и оба меньше 1,
то совершенно такое же исследование показало бы нам,
что поверхности F = C—отрицательные поверхности
без контакта. И, следовательно, подвижная точка асимп-
тотически приближалась бы к замкнутой траектории.
Третий случай. Оба корня уравнения относи-
тельно 5 действительны и положительны, но один больше,
а другой меньше 1.
Тогда оба значения А действительны, но разных
знаков.
Я утверждаю, что в этом случае в нормальной пло-
скости s=0 можно провести такие две кривые /Си К1,
которые пересекали бы замкнутую траекторию в точке
х = 0, у = 0, s = 0 и, кроме того, обладали бы следую-
щими двумя свойствами:
1. Уравнения этих кривых могут быть представлены
в форме
* = ?(«), У = ^(и),
где <р и $ — голоморфные функции одной и той же
переменной и, обращающиеся в 0 при и = 0.
2. Если точка (х0, у0) лежит на одной из кривых К
или К', то и точка (хи ух), соответственно, тоже лежит
на одной из них.
Действительно, мы всегда можем путём линейной
замены переменных привести соотношение, связывающее
хи У1 с хо> Уо к следующему виду.
C) *о. Л).
*i = SqX0 -f Фа (*о> Уо)>
где <&i и Фа — ряды, расположенные по возрастающим
степеням х0, у0 и начинающиеся с членов второй степени.
Пусть
у = аа*а -{-
— уравнение кривой К. Мы будем иметь тождество:

ГЛ. XIX. ИССЛЕДОВАНИЕ ЗАМКНУТЫХ КРИВЫХ 239
Сравнивая обе части этого равенства, мы найдём ряд
соотношений, которые дадут последовательно
яа> яз» • • •» яп» • • •
Предположим, что Si>l>s2. Всегда можно найти
две такие положительные величины М и C, чтобы, поль-
зуясь обозначениями главы XI, мы имели бы
ф (Х V) <
Рассмотрим теперь наряду с уравнениями C) уравнения
v -с v МР
Проводя для уравнений C bis) те же рассуждения, что
и для уравнений C), мы увидим, что существует ряд
. у = аа'я<» + а3'**+ ... + «
удовлетворяющий условию
При этом мы имеем
Но ряд ф' (лг) сходится; действительно, решая полученное
уравнение, найдем 116J
Следовательно, ряд ф тоже сходится.
Что и требовалось доказать.

240 ЧЕТВЕРТЫЙ Ы ЕМУ АР
Совершенно так же можно доказать существование
кривой К, уравнение которой будет
Установив существование кривых К и К', нетрудно
видеть» что все траектории разбиваются на три типа:
1. Траектории, пересекающие кривую К, — подвижные
точки, описывающие такие траектории, будут беско-
нечно-близки к замкнутой траектории при t = — со и
будут удаляться от неё при растущем времени.
2. Траектории, пересекающие К'; они асимптотически
приближаются к замкнутой траектории.
3. И, наконец, все остальные траектории, остающиеся
на конечном расстоянии от замкнутой траектории.
Нам остаётся рассмотреть случай, когда один или два
корня уравнения, определяющего S, — отрицательны; но
случай, когда только один из корней отрицателен, невоз-
можен !161; если же отрицательны оба корня, то мы воз-
вращаемся к формулам первого случая, полагая в них 1171
Нельзя не поразиться той аналогии, которая суще-
ствует между только что проведённым исследованием и
теорией особых точек. Первый случай (когда оба значе-
ния к комплексны) соответствует случаю фокуса; второй
случай (когда оба значения к действительны и одинако-
вых знаков) соответствует случаю узла и третий случай
(когда оба значения к действительны и разных знаков)
соответствует случаю седла.
Нам остаётся ещё исследовать тот исключительный
случай, когда оба корня к — комплексные, сопряжённые
и модули их равны 1. Этот случай соответствует тому,
который мы подробно рассмотрели в главе XI. Мы
увидим, что аналогия сохраняется до некоторой поры,
и мы получим результаты, совершенно сходные с теми,
которые мы имели в этой главе. Но, углубляя наше

ГЛ. XIX. ИССЛЕДОВАНИЕ ЗАМКНУТЫХ КРИВЫХ 241
исследование, мы найдём существенные отличия и встре-
тим совершенно новые трудности.
1 Запишем дифференциальные уравнения в "следующем
виде:
где Х{ и Y{ — однородные многочлены степени i отно-
сительно х и у, коэффициенты которых тригонометри-
ческие ряды, расположенные по синусам й косинусам дуг,
кратных t.
Положим теперь
где F есть многочлен, целый относительно х и у,
коэффициенты которого тригонометрические ряды по t,
a Ft— совокупность членов степени /относительно х и у.
Многочлен F не содержит, следовательно, ни членов
нулевой, ни членов первой степени.
Мы будем стараться определить F9, F8, ..., Fp_t
таким образом, чтобы в выражении
все члены степени, меньшей р относительно х и у, обра-
щались бы в 0. Полагая
Ф =ЛГ -^-Ч-К iS.
'* * дх * к ду '
мы получим
-jf + $21 =0,
= —ф22,
16 А. Пуанкаре.

242 ЧЕТВЕРТЫЙ МЕМУАР
Первое из этих уравнений даст нам Fa, второе— Fs
и (р—1)-ое даст нам Fp_t при условии, конечно, что
эти уравнения могут быть удовлетворены.
В силу сделанных нами предположений по поводу
корней уравнения, определяющего 5, первое из уравне-
ний D) всегда может быть удовлетворено.
Действительно, интегралы линейных уравнений
так же, как и в первом случае, могут быть представлены
в форме A bis) с той только разницей, что здесь X
равно 0. Таким образом интегралы уравнений E) будут
х = А[? (/) cos (X't -f 9) — ?' @ sin (X7 -f в)],
y=A[if@cos (X't-И) — f @sin(X't + в)].
Если вместо х и у за новые переменные взять
е_ xtf—уч' xty— у?
(что является линейной заменой переменных по отноше-
нию к х и у, но нелинейной по отношению к (\ то
уравнения E) примут вид;
Мы всегда можем предполагать, что эта замена пере-
менных уже произведена и что, следовательно,
Xi = l'y, У1= — Ух.
Итак мы возьмём
тогда остальные уравнения D) запишутся в виде:
где Fq — искомый однородный многочлен степени q,
а Я3 — многочлен той же степени, который мы можем

ГЛ. XIX. ИССЛЕДОВАНИЕ ЗАМКНУТЫХ КРИВЫХ 243
считать известным, потому что он зависит только от
Fq, F8, ..., Fq_u которые должны быть определены
раньше, чем Fq. Коэффициенты полинома Hq так же,
как и коэффициенты полинома Fq — тригонометрические
р;ды по /. Если мы положим
x=pcosa>, _y = psina>,
то мы будем иметь
где <р(а>, t) и <К<о,/) — тригонометрические ряды, завися-
щие от двух аргументов ш и t.
Уравнения ф) принимают тогда вид
Если тригонометрический ряд ^ (<о, /) не содержит
члена Со, не зависящего от / и а>, и если, кроме того,
У — иррациональное число (что мы будем предполагать
выполненным), то мы всегда можем найти тригономе-
трический ряд,, зависящий от <о и /, удовлетворяющий
этому уравнению t18l. Если Со не равно 0, то удовлетво-
рить уравнению F) невозможно; но можно выбрать Fq
таким образом, что при положительном Со мы будем
иметь
(знак неравенства меняется нЪ обратный, когда Со отрица-
тельно).
Для этого достаточно положить
Если мы рассмотрим теперь многочлен
F=F2 + F8+...4-F3,
то выражение
лч dF vdF . v dF
16*

244 ЧЕТВЕРТЫЙ МЕМУАР
будет рядом, расположенным по степеням х и у, коэф-
фициенты которого — тригонометрические ряды по /.
Члены наинизшей степени в Ф обращаются в
Рассмотрим теперь поверхности F = /С, где К— постоян-
ная. При достаточно малых значениях К эти поверхности
будут поверхностями рода 1, содержащими внутри замк-
нутую траекторию; они будут положительными поверх-
ностями без контакта при отрицательном Со и отрица-
тельными поверхностями без контакта при положитель-
ном Со.
Таким образом, когда не . все Со для q = 2, 3,...
обращаются в 0, мы приходим к первому случаю, и имеет
место неустойчивость t19l.
Случай, когда все Со обращаются в 0, может с первого
взгляда показаться совершенно исключительным, так как
для того, чтобы он имел место, нужно, чтобы выполня-
лось бесконечное множество условий; тем не менее этот
случай чрезвычайно важен не только вследствие тех
специфических трудностей, которые представляет его
исследование, но также и потому, что это как раз тот
случай} который встречается при исследовании общих
уравнений динамики.
Так как мы не можем удовлетвориться непосредствен-
ной проверкой того, что все Со обращаются в 0 — что
потребовало бы проверки бесконечного множества усло-
вий,— то мы должны в первую очередь решить следую-
щую задачу: как можно узнать a priori, что все Со
обращаются в 0? Вот для этой цели одно простое правило:
если существует функция М, голоморфная относительно
хх у и /, действительная, положительная и определён-
ная во всех точках замкнутой траектории, и если,
кроме того, мы имеем
то мы можем быть заранее уверены, что все Со равны 0.

ГЛ. XIX. ИССЛЕДОВАНИЕ ЗАМКНУТЫХ КРИВЫХ 245
Действительно, я покажу, что при этом условии не
может существовать поверхность без контакта
F = K
рода 1, содержащая внутри замкнутую траекторию. ;
В самом деле, будем временно рассматривать х, у и /
как прямоугольные координаты точки в пространстве.
Точки, для которых выполняются условия
F<K, 0<*<2ir,
заполняют некоторый объём V, ограниченный, во-первых,
поверхностью F=K, представляющей собой своего рода
цилиндрическую поверхность, и, во-вторых, двумя пло-
скостями: /=*= 6 и 1=2ъ. Пусть dm — элемент поверх-
ности F = К. Положим
Теорема Грина даёт нам:
-f Г JMdxdy — j JM dxdy
Первый интеграл в левой части этого равенства берётся
по поверхности F=K,- второй nj плоскости / = 0
и третий по плоскости /=2тс; интегралов правой части
распространён на весь о5ъём V. " '
Интеграл в правой части равен 0 в силу соотнесе-
ния G). Второй и третий ийтегралы в левой части взаийно
уничтожаются, так как функция М возвращается "к преж-
кему значению, когда t увеличивается на 2те. Следовательно,
первый интеграл должен был бы быть равен 0. Но это
М
невозможнр, так как -=- всегда полежителвно и
ij . . ¦.
всегда сохраняет один и тот же знак.

246 ЧЕТВЕРТЫЙ МЕМУАР
Таким образом, поверхности без контакта не может
существовать, следовательно, все Со равны нулю.
Что и требовалось доказать.
Рассмотрим в частности уравнение
где <р< — тригонометрические ряды, расположенные по
синусам и косинусам дуг кратных t (мы ограничиваемся
сейчас случаем одного аргумента). Такое уравнение было
изучено Гильденом (Gylden), Линдштедтом (Lindstedt),
Калландро (Callandreau). Мы можем записать это урав-
нение в таком виде:
т. е. как раз в том виде, который мы сейчас рассматри-
ваем. Нетрудно видеть, что
дх ' ду
и, следовательно, все Со равны 0.
Отсюда следует, что если мы будем интегрировать
уравнение
YdFJ- vdF-X- dF о
X-dx-TY!y'+—t=0>
пользуясь методом последовательных приближений, пре-
небрегая сначала третьими степенями х и у, потом
четвертыми степенями и т. д., то у нас никогда не
появятся вековые члены. Линдштедт смог доказать это
предложение только при определённых ограничениях, от
которых мы теперь можем освободиться.
Если все Со равны 0, то существует ряд
расположенный по возрастающим степеням х и у и по
синусам и косинусам дуг кратных /, формально удовле-
творяющий уравнению

ГЛ. XIX. ИССЛЕДОВАНИЕ ЗАМКНУТЫХ КРИВЫХ 247
Если этот ряд сходится, то будет существовать
семейство F=K замкнутых поверхностей рода 1, на
которых и будут расположены траектории.
До сих пор мы имели полную аналогию между нашим
исследованием и исследованием главы XI, но теперь она
прекращается. В главе XI ряд F всегда был сходящимся;
здесь этого может и не быть. Это связано с тем, что
интеграл уравнения
Fbis) Д2 — A'|j = $ =
.имеет вид
т — пк
и делитель т — пк' может быть очень малым.
Отсюда следует, что траектории не всегда будут
лежать на поверхностях семейства F=K. Для того
чтобы лучше дать себе в этом отчёт, рассмотрим частный
пример.
Мы будем пользоваться особой системой координат.
Именно, пусть
далее положим
р = 1пС—1Я + *1, ? = ardg_i__arctg_?_.
Каждой системе значений р, а> и <р соответствует одна
и только одна точка М пространства; точки,, для которых
(о или <р различаются на кратное 2тс, совпадают.
Поверхности р = const, представляют собой семейство
вложенных друг в друга торов. Поверхность р = — оо
вырождается в окружность г=1, 2 = 0; при этом поло-
жение точки М не зависит от <р. Поверхность р = -\- оо
вырождается в ось z; и при этом положение точки М
не зависит от со. Поверхности со = const, являются
плоскостями, проходящими чфез ось z. Поверхности
<р = const, сферы, центры которых лежат на оси z.
Рассмотрим теперь дифференциальные уравнения:

248 ЧЕТВЕРТЫЙ МЕМУАР
Я буду предполагать, что ряд 0 сходится абсолютно
и равномерно для всех значений юи<р. При этом тип
могут принимать всевозможные целочисленные значения
как положительные, так и отрицательные.
Общий интеграл этих уравнений есть:
— sin (отаH 4- и<»0 -f 6mn)],
где аH, <р0 и р0—постоянные интеграции. Мы подразуме-
ваем, что в последней формуле неявно содержится член A^t.
Мы всегда можем предположить, что начало отсчёта
времени, начало отсчёта переменного ш и единица длины
выбраны так, что <о0 = «р0 = р0 = 0. Кроме того,- для
упрощения формул я буду предполагать, что все Ьтп
равны 0, рассчитывая вернуться к общему случаю позднее.
Тогда мы получим
Может представиться несколько случаев:
Первый случай. Отношение-| иррациональное
число и Aqq не равно 0.
Я утверждаю, что в этом случае можно найти функцию
F(a>, ?)» допускающую разложение в тригонометрический
ряд, и такую, что поверхность
будет поверхностью без контакта; другими словами, для
всех значений ш и <р мы будем иметь или неравенство
«о . в>«?
или обратное неравенство.
Я могу написать

ГЛ. XIX. ИССЛЕДОВАНИЕ ЗАМКНУТЫХ КРИВЫХ 249
где 6j «одержит только конечное число членов O^i 6a
сколь угодно мало (эю всегда возможно ввиду того,
что ряд б сходится абсолютно и равномерно).
Я возьму
Пусть теперь
так что будем иметь
г. dFJRdF
Неравенство (8) обращается в
ИЛИ В
или же в противоположное неравенство; одно из этих
неравенств очевидно, так как абсолютная величина первого
члена больше, чем абсолютная величина второго.
Мы приходим, таким образом, к уже рассмотренному
нами случаю, когда вокруг замкнутой траектории суще-
ствуют поверхности без контакта, т. е. к тому случаю,
в котором имеет место неустойчивость. .,
Второй случай. Отношение -— рационально и Лоо
равно нулю.
Предположим для определённости, что Р=1, а а —
целое положительное число.
Здесь уже нецелесообразно считать начальные значе-
ния Шц, <р0 и р0 переменных а>, <р и Р равными нулю.
Положим для сокращения "
|х = та -)- лр = та -\- п\
|i — будет целым числом, и мы получим одно и то же
значение ja для бесконечного множества- систем значе-
ний тип. При п= — am мы будем иметь: i». = 0.

250 ЧЕТВЕРТЫЙ МЕМУАР
тогда получим
Р = Ро + i 2 A»' cos т («о — а?о) +
lT Isln (^ + ота)о + л<Ро) — sln
где Ат' = Атп, при « = — <ш, или при |х = 0.
Так как |х всегда является целым числом, то тригоно-
метрический ряд, дающий р, будет равномерно сходящимся.
Что же касается коэффициента при t
2^mCOS(@0 — а<р„),
то он может быть положительным, или отрицательным,
в зависимости от значений a>Q и <р0. Отсюда следует, что
в зависимости от выбранной траектории р будет стре-
миться к-}-оо или к—со при неограниченном возра-
стании t.
Следовательно, мы опять имеем случай неустойчивости,
так как р .не остаётся конечным, но характер этой
неустойчивости совсем иной, чем в первом случае; дей-
ствительно, здесь мы уже не можем построить поверх-
ность без контакта.
Движущаяся точка приближается асимптотически либо
к оси г, либо к окружности г = 0, г=\, в зависимости
от своего начального положения. Существуют также и
замкнутые траектории, которые соответствуют тому слу-
чаю, когда
2 Ат' cos т ((о0 — а<?0) = о.
Третий случай. Отношение у — иррациональное
число и Аоо равно нулю.
Мы снова предположим, что
так что мы будем иметь

ГЛ. XIX. ИССЛЕДОВАНИЕ ЗАМКНУТЫХ КРИВЫХ 251
Может случиться, что ряд, дающий р, сходится равно-
мерно для всех значений t, т. е. что ряд с положитель-
ными членами
(9)
сходится; тогда траектория вся целиком будет лежать на
поверхности
Эта поверхность рода 1 и аналогична тору. Форма траек-
торий на этой поверхности совершенно сходна с той,
которую мы рассматривали в главе XV.
Четвёртый случай. Мы сделаем те же предпо-
ложения, что и в предыдущем случае, с той только
разницей, что ряд
(Ю)
хотя и будет сходиться, но уже неравномерно, так что
ряд (9) будет теперь расходящимся. , .
Этот случай может осуществиться. Предположим,
например, что
111 + 1
тогда ряд
заведомо сходится абсолютно и равномерно.
Далее, превратим а в непрерывную дробь:
а = а1-\г -
Р
Пусть -*?— n-ая подходящая дробь; мы предположим,
Vn
что
Рассмотрим ряд
т2
2т2

20Z ЧЕТВЕРТЫЙ МЕМУАР
такой, что коэффициент при sin(Pra — (?„*)/ в этом ряду
есть
/1 \р„ + Q 1
V2/ Pn-Q^cc-
Мы будем иметь
Но числа ап я могу взять какими угодно, я положу
например,
где Я—целое число. Коэффициент при sin (Рп — Qn<x)t
будет тогда больше, чем:
М
1—Чп*
Нетрудно видеть, что при Н больше, чем 2Л+1, это
выражение неограниченно возрастает при возрастании п.
Следовательно, коэффициенты ряда A0) возрастают
неограниченно и ряд не может быть равномерно сходя-
щимся. .
Итак будем предполагать, что этот ряд сходится
неравномерно.
Я буду называть регулярной поверхностью рода один
непрерывную поверхность, удовлетворяющую условиям,
аналогичным условиям Дирихле (в теории рядов Фурье);
уравнение такой поверхности может быть, следовательно,
записано в виде
Р = 2 Вшп COS (ОТО) + Л'-Р) 4- 2 Стп sin (ma) "f "?)•
Невозможно, чтобы регулярная поверхность была бы
в нашем случае поверхностью без контакта.
Действительно, если бы она была положительной
поверхностью без контакта, то во всех её точках мы

ГЛ. XIX. ИССЛЕДОВАНИЕ ЗАМКНУТЫХ КРИВЫХ 253
должны были бы иметь
dp dp du> dp d
dt~T~ d<o dt ~> df dt
или - .
— 2 S""» (arn + P") sf n (OT0) ~^~ '
+2 Cmn (am + P«) cos (me -j- no) > о
и следовательно
2>c 2к
Jda) Г A'rf<p>0.
о о
Но этот интеграл равен нулю, так как мы предположили,
что Аоо равно нулю.
Точно так же не может случиться, чтобы какая-нибудь
траектория вся целиком лежала бы на какой-нибудь
регулярной поверхности.
Действительно, на такой поверхности мы должны
были бы иметь:
и следовательно
но тогда ряд
2 Стп sin (ma) + л?)
не был бы сходящимся 1211.
Более того, мы имеем
р = 2 тй^х^р-sin (та + ЛР)л
Если ряд, стоящий в правой части, не является равно-
мерно сходящимся, то (как я показал, в одной заметке,
напечатанной в Bulletin Astronomique, t. 1, p. 319 I221)
сумма его может стать больше любого наперёд заданного
числа. Таким образом, р может неограниченно возрастать,
хотя и не существует поверхностей без контакта I28'.

254 четвертый ивмулр
Но мы можем спросить себя, стремится ли р к бес-
конечности, при t-*oo; другими словами, можем ли мы
взять такое достаточно большое значение t, чтобы, начи-
ная с этого значения, р оставалось бы больше любой,
наперёд заданной величины? Или же р всё время колеб-
лется, причём амплитуда этих колебаний неограниченно
возрастает, а наибольшее и наименьшее значения, дости-
гаемые при этих колебаниях, стремятся соответственно
к 4~°°и — оо?В последнем случае р будет принимать
всякое заданное значение бесчисленное множество раз.
Нетрудно видеть, что оба эти случая возможны. Дей-
ствительно, пусть D — какое-нибудь целое число, не
являющееся полным квадратом; пусть и и v — два целых
положительных числа таких, что
Пусть
. (« —
где ип и vn также целые числа. Мы возьмём тогда
оо
й = ° = 2 (А1Уcos («»" - v?)
л = О
так что
о = "V Ап sin \nt.
Если |Л|>1, |/U|<1, то этот ряд будет сходиться,
но сходиться неравномерно.
Если А положительно и достаточно велико, но вс5
же меньше, чем у., то р будет стремиться к бесконеч-
ности; если же, напротив, А отрицательно и заключено
между — 1 и—у, то р будет совершать колебания,
разнахи которых будут неограниченно возрастать.

ГЛ. XIX. ИССЛЕДОВАНИЕ ЗАМКНУТЫХ КРИВЫХ 255
По поводу доказательства я отошлю читателя к моей
заметке, которую я представил Парижской Академии
Наук (Comptes Rendus des seances de VAcademie des
Sciences, seance du 7 decembre A885)).
Итак, возможны два случая: или р изменяется от — оо
до-{-оо,и тогда всё происходит совершенно так же, как
если бы А00 не равнялось нулю; или же р принимает
бесчисленное множество раз любое наперёд заданное
значение.
Очевидно мы будем иметь
где М соответственным образом выбранная положитель-
ная величина. Мы будем иметь, следовательно,
\%\<М, \?\<\Mt\.
Положим теперь а = 1; тогда через одинаковые про-
межутки времени, равные 2тг, координата а будет при-
нимать значения 0, 2^ 2/пг а движущаяся
точка будет возвращаться к плоскости- ш = 0; кроме того,
в эти моменты мы будем иметь <р = 2|3/иг.
Положим
где т.—'целое число, выбранное таким образом, чтобы
R (<р) было заключено между 0 и 2тс.
Если мы рассмотрим окружность С, уравнение которой
р = 0, @ = 0,
то положение точки на этой окружности будет опреде-
ляться величиной R (<?), так как
Уравнения нашей траектории дают нам

256 ЧЕТВЕРТЫЙ МЕМУЛР
Для ?=2/пг, a>5=0(mod2ir), <р=2|3як имеем
р=ФBтш).
Каждой точке окружности С, для которой.
f}(<p) = B|3n — 2т) тс (л и т — целое)
будет, следовательно, соответствовать величина р, равная
ФBшг). Будем рассматривать эту величину р, как функ-
цию взятой нами точки на окружности, т. е. как функ-
цию R(<?), и обозначим её через
Эта функция разрывна и определена только в точках
Прежде всего я покажу, что на всякой дуге окруж-
ности С, сколь бы мала она ни была, всегда найдутся
точки, в которых наша функция F определена и при-
нимает сколь угодно большие значения.
Действительно, рассмотрим точку, которую я обозначу
через Р'.
Для нашей движущейся точки и для точки Р значе-
ния (о и <р одинаковы. Но точка Р всё время остаётся
на торе р = 0.
Пусть АВ — рассматриваемая дуга окружности С.
Нетрудно видеть, что, сколь бы мала ни была эта дуга,
всегда можно указать такое достаточно большое h, что
имеет место следующее свойство: пусть t0—какое-нибудь
произвольно выбранное значение t; при нзкотором зна-
чении t, содержащемся между tQ и tQ-\-h, точка Р попадёт
на дугу АВ. Другими словами, промежуток времени
между двумя последовательными моментами пересечения
дуги АВ точкой Р не превосходит А.
Пусть теперь мы имеем некоторое значение /, для
которого
Р-ф@

ГЛ. XIX. ИССЛЕДОВАНИЕ ЗАМКНУТЫХ КРИВЫХ 257
положительно и очень велико; обозначим это значение t
через t0. Мы видели выше, что такое значение всегда
существует.
Именно существует такое ft, меньшее, чем А, что
точка Р
лежит на дуге АВ. Тогда мы будем иметь
Ф (*0 + k) > Ф (*0) — Mk > Ф (/0) - Mh.
Так как Ф(*о) положительно и очень велико, а М и
h конечны, то &(to-{-k) тоже будет положительно и
очень велико. Следовательно, в точке окружности С
лежащей на дуге АВ, величина F [R (в)] будет положи-
тельна и очень велика.
Что и требовалось доказать.
Совершенно так же можно было бы показать, что
F[R (?)] на ДУге АВ может стать отрицательным и очень
большим по абсолютной величине; действительно, Ф (t)
может становиться отрицательным и очень большим по
абсолютной величине либо для положительных, либо для
отрицательных значений t.
Пусть теперь
?1. ?2>- ••>?«>•••
бесконечная последовательность значений <р такая, что
UmR(<fn) = A,
»->оо
1»->СО
Мы скажем, что Fl есть одно из предельных зна-
чений функции F для точки
/?(?) = А
Предположим теперь, что функция F определена
в двух точках:
4
17 А. Пуанкаре.

258 ЧЕТВЕРТЫЙ МЕМУАР
и имеет соответственно значения Fo и F'o. Кроме того, я
буду предполагать, что в точке /?(<р)=/10 функция F
имеет п;едельное значение Fv Я утверждаю, что в точке
/? (<р) = А'о она будет иметь предельное значение F'^ и
что это значение есть
Действительно, в силу сделанных предположений
существует два целых числа X и X', таких, что
Ф Bfor)~/>0> ФBХУ) = /^.
Кроме того, существует последовательность целых чисел
V-i, Ъ V-w-
таких, что
) = ,40; lim Ф BjvO = F,.
Рассмотрим бесконечную последовательность целых
чисел
Очевидно, мы будем иметь
Я утверждаю, что
lim Ф [27Г (^ + Х'-Х)] = ^ =
Действительно, мы имеем
(И) Ф [2* (h, + X' - X)] _ ф B*tv) = J -g- Л.
Или, принимая во внимание два условия:
Я-^оо
lim R [2p Ci*» + X' — X) тг] = /? BpX'ir) ,
п*оо

ГЛ. XIX. ИССЛЕДОВАНИЕ ЗАМКНУТЫХ КРИВЫХ 259
мы получим как предел правой части равенства A1) —
и как предел левой части его —
Р i р
Отсюда
Что и требовалось доказать.
Функция F[R(<f)] была однозначна, но была опреде-
лена не для всех точек окружности С. Наоборот, функ-
ция Ft [R (<?)], которая отныне будет обозначать какое-ни-
будь предельное значение функции F вблизи точки R (<р),
будет определена во всех точках окружности С, но уже
не будет однозначной.
Пусть теперь *•
Av Aj,..., An,...
— бесконечная последовательность точек окружности С,
стремящаяся к точке В.
Пусть
F F F F
' 1» * 2> * 3> • • '» * п> • ' •
— некоторая последовательность предельных значений
функции F, соответствующих точкам At, Л2)... Положим
llm Fn = О.
n
Я утверждаю, что О будет одним из предельных зна-
чений функции F в точке В.
Действительно, в силу сделанных нами предположе-
ний, всегда можно указать бесконечное множество точек
Ап, таких, чтобы расстояние их до точки В и разность
О — Fn были бы сколь угодно малы и чтобы в окрестно-
сти каждой из этих точек Ап можно было бы найти бес-
конечное множество точек М, расстояние которых до
точки А„ и разность Fn — F (М) были бы сколь угодно
17*

260 ЧЕТВЕРТЫЙ МЕМУАР
малы. Отсюда следует, что точка В является пределом
точек М и что G есть предел F (/И), так что О есть одно
из значений функции Fx (В), определённой выше. Что и
требовалось доказать.
Я утверждаю теперь, что если в некоторой точке М
функция F [В (<р)] принимает значение Fo, и если в то же
время Fl есть одно из предельных значений функции F
в той же точке М, то 2Fi—Fo тоже будет предельным
значением.
Действительно, мы имеет бесконечную последователь-
ность точек
А\, -^Si • • •» ™ni • • •»
в которых функция F принимает соответственно значения
F{A1),F(Aa) F(An),...,
и, в силу сделанных предположений, расстояние АпМ
стремится к нулю, a F(А„) стремится к./7,, когда я не-
ограниченно возрастает. В силу предположения, доказан-
ного выше, одно из предельных значений функции F
в точке Ая будет
В пределе, ври неограниченном еоэрастанни п,. точкд Ап
совпадает с точкой М, a F (А^ обратится ft Ft; слвдова.-
тельно, 2^ — Fo также будет предельным зиаченивй функ-
ции F в точке М.
Таким образом, если мы рассмотрим определенную
выше функцию Fl [R{y)\, то может представиться один
из следующях случаев:
1) функция Ft может принимать только значения ±<х>;
2) функция Fx принимает только в точке М значения
± оо. и F(M)\
3) функция Ft в каждой точке М будет принимать
всевозможные значения и будет не только неоднозначна,
но и полностью не определена;
4) функция Fx будет принимать в точке М бесконеч-
ное множество различных значений, отличающихся одно
от другого на постоянный период. Другими словами, это
будет многозначная функция, аналогичная арксинусу.

ГЛ. XIX. ИССЛЕДОВАНИЕ ЗАМКНУТЫХ КРИВЫХ
Первая из "этих гипотез заведомо может осуществляться
(действительно, как мы видели выше, может случиться,
что функция Ф (/), стремясь к бесконечности, принимает
всякое данное значение только конечное число раз),
Я имею все основания думать, что третья гипотеза тоже
может осуществляться, но что, напротив, четвёртая гипо-
теза никогда не может быть "осуществлена.*
Однако всего предшествующего достаточно дла того,
чтобы понять, как велико разнообразие могущих предста-
виться случаев: ;
1) Может случиться, что р принимает всякое данное
значение только конечное число раз, и стремится к zt со,
когда время неограниченно возрастает (это имеет место,
когда /Iqq не равно нулю, или /1(^ = 0, но-r- рационально;
•¦г
или же когда при А^, равном нулю, и -g- иррациональном
ряд'Ф (t) сходится неравномерно или стре*митс"я к беско-
не%бсти). • ¦•¦¦¦¦•¦.
2) Но может также случиться", что р всё время коле-
блется между некоторыми определёнными границами, при-
нимая бесконечное множество раз всякое значение, заклю-
чающееся между этими границаии (это имеет Место, когда
Аоо равно нулю, ^ иррационально и,ряд АФ (t) сходится
равномерно).
3) Наконец, может случиться, что р принимает любое
значение бесконечное множество рад (это имеет место,
когда Аоо равно нулю, -g- иррационально и ряд Ф (Q не
: ^ ¦ * г ¦ * - - .* • iff''
сходится равномерно и не стремятся к бесконечности).
В первом случае движущаяся- точка или лс&^время
удаляется от замкнутой траектории р = — с© (еслц р стре-
мится к 4-со) или асимптотически приближаете», к «ей
(если р стремится к —со), Д1ожет даже слуднться, что,
двигаясь по одним траекториям^ точка всё время удаляется
от замкнутой траекторину!вто время как двигаясь по
другим траекториям, он^ ¦ асимптотически ггр'иближается
K-4ffl (-е*сли Afo равно нулю и *-

262 ЧЕТВЕРТЫЙ МЕМУАР
Во всех этих случаях имеет место неустойчивость, т. е„
другими словами, если в момент t = 0 движущаяся точка
находилась очень близко о'т замкнутой траектории, то
либо для очень больших положительных значений t, либо
для очень больших по абсолютной величине отрицательных
значений t она не будет более близка к замкнутой траек-
тории.
Наоборот, во втором случае имеет место устойчивость,
т. е., другими словами, если движущаяся точка была очень
близка к замкнутой траектории в момент 1 = 0, то
она всё время будет оставаться очень близкой к ней
как при положительных, так и при отрицательных зна-
чениях t. ,
Наконец, в третьем случае мы имеем неустойчивость
в том смысле, что движущаяся точка, очень близкая
к замкнутой траектории в начальный момент, может сильно
удаляться от неё в некоторые другие моменты времени.
Но мы имеем, наоборот, устойчивость в том смысле, что
движущаяся точка, удалившись от замкнутой траектории
на большое расстояние, будет вновь приближаться к ней,
подходя в некоторые моменты времени сколь угодно близко
к замкнутой траектории 1а*1.
Тот простой пример, который мы так долго рассма-
тривали, позволяет нам теперь вернуться к общему слу-
чаю и сказать: из того, что все Со равны нулю, еще"
нельзя заключить, что определённый выше ряд
сходится и что точка, очень близкая к замкнутой траек-
тории, всё время будет очень близка к ней, и даже нельзя
заключить, что точка, удалившись от замкнутой траекто-
рии, вновь приблизится к ней.
Может случиться, что точка, очень близкая к замкну-
той траектории, так и останется очень близкой к ней или
будет бесконечное множество раз удаляться от , неё, но
затем каждый раз снова подходить сколь угодно близ-
ко к ней; или же, наконец, может случиться, что Tq4-
ка, удалившись от замкнутой траектории, .так н оста-
нется на большом расстоянии of неб. Эги три логиче-

ГЛ. XIX. ИССЛЕДОВАНИЕ ЗАМКНУТЫХ КРИВЫХ • 263
ски возможных случая могут действительно осущест-
вляться.
В силу предыдущего, легко понять, в какой мере труд-
ности, встречающиеся в небесной механике вследствие
существования малых делителей и приблизительных соизме-
римостей средних движений, связаны с самой природой
вещей и не могут быть обойдены. Чрезвычайно вероятно,
что каких бы методом мы ни пользовались, мы всегда
будем встречать те же трудности.
Париж, 13 декабря 1885.

ДОПОЛНЕНИЯ

ДОПОЛНЕНИЕ К ГЛАВАМ V и VI
ОБЩАЯ КАЧЕСТВЕННАЯ ТЕОРИЯ
Е. Леонтович и А. Майер
Результаты, полученные Пуанкаре о возможном пове-
дении и формах характеристик уравнения первого порядка
и их соотношении между собой, изложенные в первых
двух его мемуарах, были обобщены в работе норвежского
математика Бендиксона *), применившего методы теории
множеств.
При этом выяснилось, что основные результаты Пуан-
каре о ходе характеристик на плоскости являются в сущ-
ности следствиями двух теорем: теоремы о существовании
и единственности решения и теоремы о непрерывности
зависимости решения от начальных условий.
В настоящем дополнении излагаются важнейшие резуль-
таты работы Бендиксона
Мы будем рассматривать систему
(А) -§Г%
*) Sur les courbes de finies par des equations diffirentiel-
les, Ada Mathem. т. 24 A901), стр. 1—30.
**) Напомним, что, начиная с 3-го мемуара, Пуанкаре также
придерживается, этого способа записи, но при этом он вообще
сохраняет предположение, что Хи К яйляются многочленами,
целыми ао х я у.

268 ДОПОЛНЕНИЕ К ГЛ. V И VI
где функции X (х, у) и Y (х, у) предполагаются одно-
значными и непрерывными функциями от х и у в некото-
рой конечной односвязной области G значений х и у и
удовлетворяющими в окрестности любой точки этой обла-
сти условиям Липшица. '
В силу этих условий, какие бы значения х0, у0 из
области G мы ни задавали, и какое бы значение t0 мы
ни взяли, существует одно и только одно решение
системы (А):
удовлетворяющее условиям'
и определённое в некотором промежутке t0 — S< /< to-{- 5
(теорема Коши).
Повторным применением теоремы Коши можно, вообще
говоря, расширить промежуток (/0 — 5, ^0 —|— 5), в котором
определено решение. Нижеследующая теорема, которую
мы приведён без доказательства*), устанавливает, в каких
границах это расширение возможно:
Теорема о продолжении решения. Пусть
О'—какая-нибудь область, лежащая целиком вместе
с границей внутри области G. Пусть решение х = <? (f),
у = tj» (/) может быть продолжено лишь для значений
t, меньшах Т (или больших *:). Тогда существует такое
значение е>0, что все точки х'= <р (t), у= <]* (t), для
которых Т— е < t < Т (или соответственно т"< t < т ~\~ е),
лежат вне G'.
В дальнейшем, говоря о решении, системы (А), мы бу-
дем подразумевать какое-либо решение:
(а) . *-?(/). y-=*t(t\
продолженное на максимальный возможный промежуток
значений нерешенной /. .
, „ «у Ci(f.: От е п а нГр v, Курс • Дифференциальных уйв'нен'ий,
гон1"й (\Щ, стр. ез.

ОБЩАЯ КАЧЕСТВЕННАЯ ТЕОРИЯ 269
Так как t не входит в правые части системы (А), то
наряду с решением
.(а) *=«?(*). J'e*4p@
существует бесконечное множество других решений
(a') * =
где С—любая постоянная.
Решение системы (А) можно геометрически интерпрв'.
тировать в пространства (х, у, I) кривыми, лежащими
в цилиндрической области, образованной прямыми, парал-
лельными оси t, пересекающими плоскость (х, у) в точках
области О. Через каждую точку этой цилиндрической
области проходит одна и только одна кривая; причём кри-
вые (а) и (а') получаются друг из друга сдвигом по оси
t на расстояние С.
В дальнейшем нас будут особенно интересовать два
частных типа решений:
а) периодические решения; они изображаются в про-
странстве (х, у, I) винтовой линией, с шагом, равным
периоду; Ь) стационарные решения
гже Xq и у0 — кйнстанты. Последние (гевкний, <Ие*идн&,
будут получаться при задании таких начальных значений
•*ч>> Уо> которые являются решением системы уравнений
*(*JO —0, У(х,у)=шО.
Геометрически таким решениям соответствуют прямые,
параллельные оси t.
Для нас будет более интересна другая интерпретация
системы (А). Именно, мы будем рассматривать t как время,
а систему (А) как систему дифференциальных уравнений,
определяющих закон движения точки, помещённой в на-
чальный момент времени t0 в одну из точек (х0, у0) обла-
сти G плоскости (х, у).
Каждому решению системы (А) на плоскости (х, у)
соответствует кривая-—траектория движения.

270 ДОПОЛНЕНИЕ К ГЛ.. V И VI
Двум решениям
(a)
и
(а') * =
соответствует одна и та же траектория; изображающие
их в пространстве (х, у, t) кривые имеют одну и ту же
проекцию на плоскость (х, у). Механически, решения (а)
и (а') определяют движения, отличающиеся друг от друга
началом отсчёта времени. Нетрудно видеть поэтому, чтб
решения системы (А) могут быть записаны в виде:
= *(t — V хо,уо).
Здесь х0, у0, t0—начальные значения и х, у — коорди-
наты движущейся точки.
При этой интерпретации периодическим решениям
соответствуют замкнутые траектории. Стационарным реше-
ниям
соответствуют траектории, выродившиеся в точку; такие
точки мы будем называть состояниями равновесия.
Определим некоторые термины, которыми нам в даль-
нейшем придётся пользоваться, и уточним те, которыми
мы уже пользовались выше.
Траекторией мы будем называть кривую
x = <?(,t — t0, x0, yo)=>x(t),
y = ty(t — t0, х0, уй)=уA),
где пара функций х (t), у (t) является решением системы
(А), продолженным на максимальный возможный промежу-
ток значений переменной t.
Положительной полутраекторией мы будем называть
ту часть траектории, для которой, при определённом движе-
нии, соответствующие значения t больше некоторо-
го выбранного значения t0. Отрицательной полутраек-

ОБЩАЯ КАЧЕСТВЕННАЯ ТЕОРИЯ 271
торией мы будем называть ту часть траектории, для ко-
торой, при определённом движении, соответствующие
значения t меньше некоторого выбранного значения t0.
Для единообразия мы будем обозначать траекторию
буквой L, а положительную и отрицательную полутраекто-
рии, соответственно.буквами Z.+ и L_.
В дальнейшем мы для краткости будем пользоваться
выражениями «траектория (или полутраектория) при 1 =
«=т проходит через заданную точку»; страектория (полу-
траектория) при t > tQ остаётся в данной области» и
т. д.; подразумевая под этим, что движущаяся точка
x = x(t), ys=ay{t) при t = i совпадает с заданной точ-
кой; что движущаяся точка при t>t0 остаётся в данной
области и т. д.
Введённые, таким образом, понятия траектории, полу-
траектории, состояния равновесия для системы:
находятся, очевидно, в тесной связи с понятиями харак-
теристики, полухарактеристики, особой точки, введённы-
ми Пуанкаре для уравнения:
dy Y(x, у)
dx X(x,y)'
В частности, особые точки уравнения
dy _ Y{x, у)
dx X(x, у)
определяются как точки, в которых имеют место равен-
ства
Х{х, У) = О, Y(x, у) = 0,
т. е. так же, как состояния равновесия системы
Вообще же соотношение между характеристиками
(полухарактеристиками) и траекториями (полутраекто-

272 ДОПОЛНЕНИЕ К ГЛ. V И VI
риями) не вполне определено, так кяк Пуанкаре, как
уже было отмечено (ср. примечание 2 и 10 к «первому
мемуару»), не даёт точного определения понятия харак-
теристики. Во всяком случае, из самого определения
траектории следует, что состояние равновесия («особая
точка» по Пуанкаре) само является траекторией и что
никакая другая траектория через состояние равновесия
проходить не может (в силу единственности решения!),
тогда как Пуанкаре не причисляет особые точки к харак-
теристикам, и характеристика может проходить через
особую точку (ср., в частности, «основное соглашение»,
гл. V). Траектория же, отличная от состояния равнове-
сия, может стремиться к состоянию равновесия в том
" смысле, что сколь бы мала ни была окрестность состоя-
ния равновесия все точки траектории, начиная с некото-
рого значения /< лежат в этой окрестности. При этом,
как вытекает из теоремы Коши, значения t должны не-
ограниченно возрастать (или неограниченно убывать).
Наряду с теоремой Коши, основную роль в дальней-
шем играет также следующая известная .теорема *).
Теорема о непрерывной зависимости ре-
шения от начальных условий. Пусть мы имеем
решение системы (А)
x = <((t—t0, х0, у0), y = ^(l — t0, х0, у0),
и пусть оно существует при всех значениях t, удовле-
творяющих неравенству to-^.t^ Т(или *„>-*>- 7), где
Т—некоторая определённая величина **). Тогда для
всякого в > 0 можно указать такое 8 > 0, что если
\х—хо\<Ь, |_у-}0|<8,
то решение
x = <?(t—t0, х0, у0), у = <К/—'о>Я
^Доказательство этой теоремы см., например, Гурса.
Курс математического анализа, т. III, ч. I, ГТТИ, 1923, стр.
19-22.
•*) Если решение определено при всех значениях
4) то за Т можно взять любое число.

ОбЩАЯ КАЧЕСТВЕННАЯ ТЕОРИЯ 273
также определено для всех значений t из промежутка
*о-^.*-*СТ (или *<,>¦/>" Г), и при этих значениях t
имеют место неравенства
\х—х\<в, \у—J|<e.
Этой теоремой нам придётся часто пользоваться в та-
кой геометрической форме:
Пусть (*„, у0) и (хи yt)—две точки одной и той
же траектории, соответствующие значениям t0 и tv Тогда,
каково бы ни было в>0, всегда можно указать такое
8>0, что всякая траектория, проходящая при t = tQ через
8-окрестность точки (д;0, уо\ проходит при t = t1 через
некоторую точку е-окрестности точки (xlt yt).
Мы будем в дальнейшем рассматривать только такие
положительные (отрицательные) полутраектории
x = (f(t —10, xot yQ),
y = ^(t — tQ, x0, y0),
которые постоянно остаются внутри некоторой ограничен-
ной области G', целиком (вместе с границей) лежащей
в области G. Такого рода полутраектории мы будем соот-
ветственно называть положительно (отрицательно) устой-
чивыми в смысле Лагранжа. Из теоремы о продолжении
следует, что такие полутраектории определены для всех
значений *>*0(/<*0).
Одним из важнейших понятий для дальнейшего является
понятие «предельной точки полутраектории».
Точка М называется предельной для положительной
полутраектории L+ (отрицательной полутраектории L_),
если сколь бы мало ни было е>0 и сколь бы велико
ни было Г> 0, в круге радиуса е с центром в точке М
всегда будут лежать точки полутраектории L+ (L_), соот-
ветствующие значениям ^>Г(^< — Т).
Таким образом, на положительной (отрицательной)
полутраектории, имеющей предельную точку М, можно
указать бесконечную последовательность точек, соответ-
18 А, Пуанкаре.

274 ДОПОЛНЕНИЕ К ГЛ. V И VI
ствующих неограниченно возрастающим (убывающим) зна-
чениям t, которая стремится к точке М. Наоборот, пре-
дельная точка М такой последовательности точек есть
предельная точка полутраектории.
Очевидно, что если точка М есть предельная точка
данной полутраектории при определённом, выбранном на
ней движении, то она будет предельной точкой этой
полутраектории и при всяком другом выбэре движения.
Кроме того, если мы имеем две положительные (отрица-
тельные) полутраектории, выделенные из одной и той же
траектории, • го они имеют, очевидно, одни и те же пре-
дельные точки.
Из принципа Больцано-Вейерштрасса следует, что вся-
кая положительно (отрицательно) устойчивая в смысле
Лагранжа полутраектория имеет хотя бы одну предельную
точку.
Мы будем говорить, что точка М есть предельная
точка траектории L, если М есть предельная точка
либо для полутраектории L+, либо для полутраекторйи
?_, произвольно выделенных из траектории L. В первом
случае мы будем говорить также, что М есть предельная
точка траектории L при t -*¦-\- с», во втором — при
t-* — <x>.
Все дальнейшие теоремы и рассуждения, относящиеся
к полутраекториям, мы будем для краткости формулиро-
вать только для положительных траекторий; с очевидными
изменениями они будут справедливы, конечно, и для
отрицательных полутраекторий.
Теорема I. Множество всех предельных точек
положительной полутраектории замкнуто.
Теорема является очевидным следствием определения
предельной точки полутраектории.
Теорема II. Множество всех предельных точек
положительно устойчивой в смысле Лагранжа полу-
траектории состоит из целых траекторий, целиком
лежащих внутри или на границе той области, внутри
которой лежит данная полутраектория.
Для доказательства этой теоремы, очевидно, доста-
точно показать, что:

ОБЩАЯ КАЧЕСТВЕННАЯ ТЕОРИЯ 275
1) если точка Afo(Sio, ?]0) является предельной для
рассматриваемой полутраектории L+, то и любая точка
М(?, ¦»)), лежащая на траектории V, проходящей через
точку т0, — также является предельной для полутраекто-
рии L+;
2) все точки траектории L' содержатся внутри или
на границе области О', внутри которой лежит полутраек-
тория L+.
Докажем сначала первое утверждение.
Пусть Mt (Si, 7)j) — какая-нибудь точка траектории L',
отличная от Мо. Отметим, прежде всего, что какое бы
движение на V мы ни выбрали,
разность значений t, соответству-
ющих данным точкам Мо и Ми
всегда одна и та же; обозначим
эту разность через Т.
Возьмём любое е>0 и по-
строим круг радиуса е с центром
в точке Мj (черт. 1). В силу тео-
ремы о непрерывной зависимости
от начальных условий, для вся-
кого в>0, можно указать такое
8>0, чтобы всякая траектория,
при t = x, проходящая через ка-
кую-либо точку в круге радиуса Черт. 1.
8 с центром в точке Мо, прохо- , .
дила бы при значении t = ?-\- Г-через некоторую точку в
круге радиуса е с центром в точке Mt. Так как точка Мо —
предельная для полутраектории L+, то на L+ существует
бесконечнее множество точек (xiy yt), соответствующих
неограниченно возрастающим значениям tt и находящихся
в круге радиуса 8 с центром в Мо. Следовательно, на
L+ существует также и бесконечное множество точек
(*<» У{)> соответствующих тоже неограниченно возра-
стающим значениям tt' — tt -f- T и лежащих в круге радиуса
е с центром в Mt. Следовательно, М1 есть предельная
точка для L+.
Для доказательства второго утверждения предполо-
жим, что существует хоть одна точка Mt траектории L',
18*

276 ДОПОЛНЕНИЕ К ГЛ. V И VI
не принадлежащая ни области О', ни её границе. Выби-
рая в предыдущем рассуждении е меньше расстояния
точки Мг до границы области О', мы придём к заключе-
нию, что полутраектория L+ имеет точки вне G', что
противоречит предположению.
Теорема III. Множество всех предельных точек
положительно устойчивой в смысле Лагранжа полу-
траектории связно *).
Для доказательства предположим противное, т. е.
допустим, что это множество несвязно. Так как оно
замкнуто, то его можно разбить на два замкнутых непу-
стых множества А и В, не имеющих общих точек, и, сле-
довательно, лежащих на положительном расстоянии друг
от друга. Обозначим это расстояние через а.
Если мы возьмём 8 = -^ и построим 8-окрестности
множеств А и В, то эти 8-окрестности также не будут
иметь общих точек.
В силу определения предельной точки полутраектории
мы можем, при выбранном движении на данной полу-
траектории, указать две неограниченно возрастающие по-
следовательности значений t:
tu t2l ...,tn... (tn->-\-co),
^такие, что tt <t[<t!i<ft< ... <*n<*n<-- • и, кроме
'того, такие, что точки полутраектории L+, соответствую-
щие значениям tn, лежат в 8-окрестности множества
А, а точки, соответствующие значениям t'n — в 8-окрест-
ности множества В. Но тогда, очевидно, существуют зна-
чения t — xnt удовлетворяющие неравенствам ^ж<хп<^,
для которых соответствующие точки полутраектории L+
лежат вне 8-окрестностей множеств А и В.
В силу принципа Больцано-Вейерштрасса, множество
этих точек будет иметь хотя бы одну точку сгущения М,
*) Понятие связности множества — см. Хаусд'орф,
сТеория множеств», ОНТИ (Ю37), стр. 118—120.

ОБЩАЯ КАЧЕСТВЕННАЯ ТЕОРИЯ 277
которая будет, очевидно, предельной точкой для полу-
траектории L+. Так как точка М не лежит внутри
8-окрестности множеств А к В, к, следовательно, не при-
надлежит ни А, ни В, то мы получаем противоречие
с предположением, что множество А-\-В содержит все
предельные точки рассматриваемой полутраектории. Таким
образом, теорема доказана.
Заметим, что свойства множеств предельных точек,
описанные в теоремах I, II и III, сохраняются и в том
случае, если рассматриваются траектории на замкнутой
поверхности любого жанра или в многомерном эвклидов-
ском пространстве. Следующие же теоремы о характере
множества предельных точек полутраектории, вообще
говоря, уже неверны для поверхностей любого жанра
или в многомерных пространствах.
Для дальнейших рассмотрений, уточняющих характер
множества предельных точек полутраектории, нам пона-
добится ряд лемм, связанных с так называемым «.отрез-
ком без контакта» *).
Мы скажем, что отрезок АВ, лежащий целиком в об-
ласти G, есть отрезок без контакта, если:
a) на нём не лежит ни одно состояние равновесия;
b) ни в одной своей точке он не касается никакой
траектории.
Если мы возьмём ту прямую Д на которой лежит
данный отрезок без контакта АВ, то плоскость (л:, у)
будет разбита этой прямой на две части; мы скажем, что
точки этих частей лежат по разные стороны от-
резка АВ.
Некоторые из формулируемых ниже лемм мы оставим
без доказательства ввиду их геометрической очевидности
(хотя строгое доказательство некоторых из них весьма
кропотливо).
Лемма I. Пусть траектория Lo при t=tQ прохо-
дит через какую-нибудь точку М отрезка без кон'
такта АВ. Тогда всегда можно указать значения tt и
'a ifi < 'о < 'а) такие, что все точки траектории Lo,
*) Дуга без контакта у Пуанкаре.

278 ДОПОЛНЕНИЕ К ГЛ. V И VI
соответствующие значениям t, удовлетворяющим нера-
венству /j</</0> лежат по одну сторону отрезка
АВ, а все точки, соответствующие значениям t, удо-
влетворяющим неравенству ^0</</2> — п0 другую сто-
рону отрезка АВ.
Лемма вытекает из непрерывности правых частей си-
стемы (А).
Лемма II. Если траектория Lo пересекает отрезок
без контакта АВ, переходя при возрастании t с одной
стороны АВ {«.левой») на другую сторону (*правую»),
то и все другие траектории, пересекающие отрезок
АВ, переходят при возрастании t с той же стороны
отрезка АВ («левой») на другую («правую») его сто-
рону.
Мы будем говорить короче:
«Все траектории пересекают отрезок без контакта
в одном и том же направлении».
Лемма III. Пусть АВ — отрезок без контакта, и
М—точка на нём, отличная от его концов А и В.
Каковы бы ни были е > 0 и Д > 0, всегда можно ука-
зать такое 8>0, чтобы всякая траектория, проходя-
щая при t — i через какую-нибудь точку ^-окрест-
ности точки М пересекла бы, не выходя из е-окрест-
ности точки М, отрезок АВ при значении t, удовле-
творяющем неравенству:
Лемма IV. Пусть траектория Ьй, проходящая при
t=t0 через точку Мо, при t = tt пересекает отрезок
без контакта АВ в точке, отличной от его концов А
и В. Тогда, сколь бы малы ни были е > 0 и Д > 0, всегда
можно указать такое 8 = 8(е, Д)>0, что всякая траек-
тория L, проходящая при t — tQ через какую-нибудь
точку Ь-окрестноспш точки Мо, пересечёт, при t=T,
отрезок АВ, причём:
|Д
*) Доказательство см. Камке, Differentialgleichungen reel-
ler Funktionen, стр. 205—210.

ОБЩАЯ КАЧЕСТВЕННАЯ ТЕОРИЯ 279
Ь) точки траектории L, соответствующие значе-
ниям t из промежутка [t0, Т), находятся на расстоя-
нии, меньшем е, от точек траектории Lo, соответ-
ствующих тем оке значениям t.
Эта лемма является следствием теоремы о непрерыв-
ной зависимости от начальных условий и леммы III.
Лемма V. Всякая часть траектории, соответ-
ствующая значениям t, лежащим в некотором конеч-
ном промежутке [а, |3], может иметь лишь конечное
число точек пересечения с любым отрезком без кон-
такта.
Доказательство поведём от противного. Предположим,
что траектория Lo имеет бесконечное множество точек
пересечения с некоторым отрезком без контакта /, и все
эти точки соответствуют значениям t между а и |3. Из
бесконечного множества значений t, соответствующих
этим точкам пересечения, мы можем выбрать последова-
тельность
сходящуюся к некоторому значению т(а<Р)
Точка траектории Lo, соответствующая t=t, является
точкой сгущения для множества точек пересечения LQ
с отрезком без контакта / и поэтому должна лежать на
/. Но в силу леммы I, при значениях t, достаточно близ-
ких к т, в частности, при значениях tn с достаточно
большим номером л на Lo не может быть точек, которые
лежали бы на отрезке без контакта /.
Таким образом, мы приходим к противоречию, и лемма
доказана.
Лемма VI. Если траектория L пересекает какой-
нибудь отрезок без контакта I в двух точках Мо и
Ми соответствующих значениям t, равным t0 и tt
(/0</j), и если при значениях t, заключённых между
t0 и tu нет точек траектории. L, лежащих на отрезке
I, то на части Мо Мх отрезка I не может лежать
вообще ни одной точки траектории L.
Действительно, если бы на части Мо Л|, отрезка /
лежала бы точка траектории L, то она могла бы соот-

280 ДОПОЛНЕНИЕ К ГЛ. V И VI
ветствовать либо значению f>tu либо значению t<t0
(так как, по условию, между t0 и tl нет уже больше зна-
чений t, соответствующих точкам пересечения траектории
L с отрезком /). Но при t = t^ траектория L входит
внутрь (или выходит из) области, ограниченной замкну-
той кривой MqIkM^q (черт. 2), составленной из дуги
МотМ1 траектории L и отрезка MQMV Для того чтобы
она могла бы ещё раз пересечь отрезок MQMU она должна
выйти из (или войти внутрь) этой области. Это невоз-
можно, так как траектория L не может при t>t1 пере-
сечь ни кусок траектории МотМи
ни отрезок MQMit так как тогда она
должна была бы пересечь последний
в направлении, противоположном
первоначальному вопреки лемме II.
Отсюда следует, что на отрезке М0М1
не может лежать точек траектории L,
соответствующих/>/г Совершенно
так же можно показать, что на от-
резке"? М0М1 не может быть точек
• Черт 2. • пересечения с траекторией L, соот-
ветствующих /</0.
Доказанное предложение можно сформулировать и так:
последовательные точки пересечения траектории L
с отрезком без контакта I, располагаются на отрезке
I в порядке возрастания t.
Аналогичным рассуждением доказывается и следующая
лемма:
Лемма VII. Замкнутая траектория может иметь
с любым отрезком без контакта только одну точку
пересечения. •
Лемма VIII. Если через точку М (отличную от
состояния равновесия), предельную для полутраектории
L+, проведён отрезок без контакта I, содержащий М
внутри себя, то на I будет находиться бесконечная
последовательность точек траектории L, расположен-
ных в порядке возрастания t, стремящаяся к М.
Эта лемма непосредственно следует из лемм 111 и VI
и самого определения предельной точки.

ОБЩАЯ КАЧЕСТВЕННАЯ ТЕОРИЯ
281
Нижеследующая теорема описывает одно из важней-
ших свойств траекторий на плоскости. В других случаях
этого свойства уже, вообще говоря, нет (например — для
траекторий на торе, или в трёхмерном пространстве),
благодаря чему взаимное расположение траекторий в этих
случаях может быть гораздо более сложным, чем на пло-
скости.
Теорема IV. Если траектория L не замкнута и
имеет хотя бы одну предельную точку, отличную от со-
стояния равновесия, то траектория L сама не может
быть "предельной ни для какой траектории.
Предположим противное: пусть траектория L сама
является предельной для некоторой полутраектории L',.
Пусть М — предельная точка траектории Z., отличная от
состояния равновесия — такая по услозию существует.
Проведём через М отрезок без контакта /, содержащий М
внутри себя. Тогда на отрезке/будет лежать бесконечное
множество точек траектории L,
расположенных в порядке возра-
стания (убывания) t (лемма VIII).
Пусть Ри Р2, Рй— три после-
довательные точки пересечения
траектории L с отрезком / (черт. 3).
Так как мы предположили, что
L сама является предельной для по-
лутраектории L+, то в частно-
сти предельной для Z.+ будет
точка />2. Тогда на основании
леммы VIII либо на отрезке Pt P2, либо «а отрезке Р2 Р3
должна находиться последовательность точек полутраекто.
рии L+, стремящаяся к точке Р2. Но нетрудно видеть, что
это невозможно, так как полутраектория Z.+ может пересечь
каждый из отрезков Р^Р^ и Р$РЯ только по одному разу.
Действительно, пусть L+ пересекает Р1 Р2 при значении
t = Т; тогда при значениях /¦> Г она либо выйдет из конеч-
ной области, ограниченной замкнутой кривой PlmPsP1 —
образованной дугой Р^пР^ траектории L и отрезком без
контакта Pt P%, либо войдёт внутрь этой области. Пусть
Черт. 3.

282 ДОПОЛНЕНИЕ V. ГЛ. V И VI
для определённости L', выходит из области Pj
тогда L' уже не может войти в неё, так как она не
может войти ни через дугу PLmP2 (траектории не пере-
секаются), ни через отрезок РгР2 (в силу леммы II),
и, следовательно, L' больше уже вообще не может пе-
ресечь отрезок РХР2. Совершенно так же можно провести
рассуждение для того случая, когда L\ входит в область
Р1т»РаР1. Ясно,_ что такое же рассуждение справедливо
для отрезка Р^Ра. Таким образом, предположение, что
траектория L есть предельная для полутраектории L'
приводит к противоречию, и теорема доказана.
Следствие. Ни одна точка незамкнутой траектории
L не может быть предельной для самой L.
Теорема V. Если полутраектория L+ не имеет среди
своих предельных точек состояния равновесия, то либо
полутраектория L+ замкнута, либо она имеет замкну-
тую предельную траекторию.
Действительно, если хоть одна предельная точка L+
принадлежит L, то, в силу теоремы IV, траектория L за-
мкнута. Если же траектория L не замкнута, то предельные
точки L± не принадлежат L. Траектория Z.o, проходящая
через какую-нибудь из этих предельных точек, не может
иметь среди своих предельных точек состояний равно-
весия— так как тогда и Z.+ имела бы среди своих пре-
дельных точек состояния равновесия. В силу теоремы IV
траектория Lo замкнута, так как в противном случае она
не могла бы быть предельной для полутраектории Z.+.
Теорема VI. Если полутраектория L+ имеет
замкнутую предельную траекторию Lo, то Lo является
единственной предельной траекторией для L+.
Если сама полутраектория L+ замкнута, то все её
точки являются предельными для неё самой, и ясно, что
никаких других предельных точек у неё быть не может.
Предположим теперь, что L+ не замкнута. Покажем
сначала, что сколь бы малог е>0 мы ни взяли, все
точки полутраекгории Z.+. начиная с некоторого значения
t = t0 (зависящего от е), будут находиться внутри е-окрест-
ности траектории Lo.

ОБЩАЯ КАЧЕСТВЕННАЯ ТЕОРИЯ 283
В самом деле, так как траектория Ьй замкнута, то
в соответствующем ей движении
* = *(/), y—yy.t)
функции x(t) и у {{) будут периодическими функциями от t,
т. е. существует А(Л>0) такое, что:
Возьмём теперь какую-нибудь точку М A,ч\) траектории
Z.o, соответствующую t = x; эта же точка будет соответ-
ствовать значениям т-]— А, т-f-2A, ... Напомним, кроме
того, что мы всегда можем выбрать движение по траекто-
рии Lo так, чтобы число х, которому соответствует
точка Af($,7i), имело бы любое выбранное значение.
Проведём в точке МA,ч\) отрезок без контакта /,
целиком лежащий внутри рассматриваемой е-окресгности
траектории Lo. В силу леммы IV, для всякого е>0 и Д>0
(Д < -я- А) мы можем указать такое 8 = 8(е,Д)>0, чтобы
всякая траектория при t = г, проходящая через какую-
либо точку 8-окрестности точки М(ъ,т\) за время от/ = г
до i = Г, не выходила бы из е-окрестности траектории Lo
и в момент /== Т, где \Т—(г-|-А)|<Д, пересекла бы
отрезок без контакта /.
Так как точка М ($,ti) — предельная для полутраек-
тории Z.+, то на отрезке / — сколь угодно близко
к М ($,¦»!) и, следовательно, внутри 8-окрестности точки
Af(E,Ti) находится бесконечное множество точек полу-
траектории Z.+. Пусть точка Яд, соответствующая t = tQ,—
одна из таких точек. Тогда, на основании сказанного
выше, полутраектория L+ пересечёт отрезок / ещё раз
в точке- Я1? отличной от Ро, соответствующей значению
t = tv где |/( — (/0-|-Л)|<Д; причём, в силу выбора
числа полутраектория L+ при t0 <^t ^.t1 будет содержаться
в s-окрестности траектории Lo (черт. 4). Так как ti > t0,
то, очевидно, точка Pt лежит на отрезке / ближе к точке
Af($,7i), чем Ро (это следует из того, что точка М(Ь,т\)
есть предельная точка для /.-)_, и точки пересечения L+

284
ДОПОЛНЕНИЕ К ГЛ. V И VI
с отрезком / должны быть расположены на / в порядке
возрастания t (см. лемму VIII). Следовательно, точка Р1
лежит в 8-окрестности точки М (?,•»]). Применяя к точке
Я, то же рассуждение, что и к точке Ро, мы придём
к заключению, что полутраектория Z-j. пересекает отрезок
/ в точке Р2, при значении/2, где |/а —(/, +А)|<Д; при-
чём Z.+ за время от t1 до ta не выходит из е-окрестности
траектории Lq. Продолжая
такое же рассуждение даль-
ше и замечая, что после-
довательно получаемые зна-
чения /0,^,/2,...,/„,... неогра-
ниченно возрастают, мы
видим, что вся часть полу-
траекгории Z.+, соответ-
ствующая значениям />/0,
целиком лежит в е-окрестно-
сти траектории Lo.
Покажем теперь, что
замкнутая траектория Lo
содержит все предельные
точки полутраектории L+.
Предположим противное,
т. е. предположим, что у
полутраектории L+ суще-
ствует предельная точка Q,
не лежащая на замкнутой
траектории Lo, и, следова-
<¦ тельно, находящаяся на не-
котором расстоянии с?>0 от LQ. В любой близости точки Q
должны находиться точки полуграектории L+> соответствую-
щие сколь угодно большим значениям t. Но в силу до-
казанного выше, для любого е>0, в частности для е<-н-,
существует такое t0, что все точки полутраектории L+,
соответствующие f>*0, будут лежать в е-окрестности
траектории Lo. Но еслие<-2", то точка Q будет лежать
вне г-окрестности траектории До; и следовательно, сколь
ЧеРт< 4>

ОБЩАЯ КАЧЕСТВЕННАЯ ТЕОРИЯ 285
угодно близко от точки Q не могут находиться точки полу-
траектории L+, соответствующие сколь угодно большим
значениям t.
Таким образом, мы приходим к противоречию, и тео-
рема доказана.
Мы сделаем теперь дополнительное предположение, что
в области О находится лишь конечное число состояний
равновесия.
Всюду в дальнейшем мы это предполо-
жение сохр аня ем.
Теорема VII. Если среди предельных точек полу-
траектории. L+ могут быть только состояния равнове-
сия в конечном числе, то всё множество предельных
точек полутраектории L+ состоит из одного и только
одного состояния равновесия.
Мы будем говорить в этом случае, что полутраекто-
рия L+ стремится к состоянию равновесия или что
траектория L стремится к состоянию равновесия при
Эта теорема непосредственно вытекает йЪ сделанного
нами предположения о конечном числе состояний равно-
весия и теоремы III о связности множества предельных
точек полутраектории.
Результаты произведённого исследования множества
предельных точек полутраектории могут быть резюмиро-
ваны следующим образом. Положительная полутраектория
при наших ограничениях может иметь множество предель-
ных точек одного из следующих типов:
I. Одно состояние равновесия.
II. Одна замкнутая траектория.
III. Некоторое множество, состоящее из целых траек-
тррий, одни из которых являются состояниями равновесия,
а другие — траекториями, отличными от состояния равно-
весия и стремящимися к состояниям равновесия как при
t -+ _J- oo, так и при t ->• — oo*J.
*) Заметим, что каждая из этих траекторий может стремить-
ся как к разный состояниям равновесия при /-»+оо и при
/->—оо,так и к одному н тому же.

286 ДОПОЛНЕНИЕ К ГЛ. V И VI
Последний тип возможного множества предельных то-
чек полутраектории мы разберём подробнее и выясним,
каковы отличительные свойства тех траекторий, отличных
от состояний равновесия, которые могут входить в состав
предельного множества.
Ответ на этот вопрос вытекает из нижеследующих тео-
рем о взаимном расположении траекторий.
Лемма IX. Незамкнутая траектория L не может
иметь одну и ту же, отличную от состояния равнове-
сия, предельную точку, одновременно как при t ->• -J- °°>
так и при t ->• — оо.
Предположим противное: пусть М есть предельная
точка траектории L и при /->-I0 и при t-+ — со,
причём М не является' состоянием равновесия. Проведём
через точку М отрезок без контакта /, содержащий точку
М внутри. Тогда (лемма VIII) на /должна находиться как
стремящаяся к точке М последовательность точек L, соот-
ветствующих неограниченно возрастающим значениям t,
так и стремящаяся к точке М последовательность точек L,
соответствующих неограниченно убывающим значениям t.
Нетрудно видеть, что эти точки не могут быть распо-
ложены на отрезке / в порядке возрастания t, что проти-
воречит лемме VI.
Лемма X. Пусть L — Незамкнутая траектория,
имеющая среди своих предельных точек не только со-
стояния равновесия, и пусть Р — какая-нибудь точка на L.
Всегда можно взять столь малую окрестность точки Р,
чтобы все пересекающие эту окрестность траектории
также не были бы замкнуты.
Пусть Ро— какая-нибудь, отличная от состояния равно-
весия, предельная точка траектории L. Проведём через Ро
отрезок без контакта /, и пусть Р1 и Яа — две последо-
вательные точки пересечения траектории L с отрезком /
(в силу леммы VIII такие точки существуют).
Возьмём ех>0 и е2> 0 столь малыми, чтобы е^окрест-
ность точки Р1 и еа-окрестность точки Р2 не имели бы
общих точек.
Выберем затем Ь1 > О так, чтобы:
а) всякая траектория, проходящая через точку из

ОБЩАЯ КАЧЕСТВЕННАЯ ТЕОРИЯ 287
^-окрестности точки Pv пересекала бы отрезок /, не вы-
ходя, из Sj-окрестности точки Р1 (лемма III);
Ь) всякая траектория, проходящая через точку из
8х-окрестности точки Plf пересекала бы отрезок /в точке,
принадлежащей еа-окрестности точки Р2 (лемма IV).
Но тогда всякая траектория, проходящая через точку,
принадлежащую Sj-окрестности Plt будет пересекать отре-
зок без контакта / по крайней мере в двух различных
точках, одной — лежащей в Sj-окрестности Plt и другой—
лежащей в еа-окрест.чости Р2. В силу леммы VII такая
траектория не может быть замкнутой.
Таким образом, лемма доказана для точки Р1 траек-
тории L; из теоремы о непрерывной зависимости от началь-
ных условий сразу следует справедливость леммы и по
отношению ко всякой другой точке этой траектории.
Лемма XI. Пусть L — замкнутая траектория, М—
точка на ней, А — точка внутри L. Если сколь угодно
малую .окрестность точки М пересекают замкнутые
траектории, отличные от L, то всегда можно указать
столь малое 8>0, чтобы все замкнутые траектории,
пересекающие Ь-окрестность точки М, содержали бы
точку А внутри. .
Эта лемма, в силу непрерывной зависимости от началь-
ных условий, геометрически совершенно очевидна; поэтому
мы её доказательства пгиводить не будем.
Теорема VIII. Внутри всякой замкнутой траек-
тории есть по крайней мере одно состояние равновесия.
Предположим противное; именно, что внутри некоторой
замкнутой траектории Lo нет ни одного состояния равно-
весия. Обозначим через g область, лежащую внутри Lo.
Пусть L — траектория, проходящая через какую-либо точку
области g. Если L незамкнута, то, в силу теоремы V, она
и при t~+-\-co и при t-* — оо имеет замкнутые предель-
ные траектории, которые в силу леммы IX различны.
Следовательно, внутри g непременно есть ещё хотя бы
одна замкнутая траектория. То же рассуждение показывает,
что и вообще внутри каждой замкнутой траектории, ле-
жащей внутри g, непременно будет находиться ещё хотя
бы одна замкнутая траектория.

288 ДОПОЛНЕНИЕ К ГЛ. V И VI
Определим теперь внутри g и на Lo функцию F (х, у)
следующим образом: если через точку (х, у) проходит
замкнутая траектория, то значение F (х, у) равно площади,
заключённой внутри этой замкнутой траектории; если
через точку (х,у) проходит незамкнутая траектория, то
функция F (х,у) равна площади /0, заключённой внутри Lo.
Значения, принимаемые определённой таким образом
однозначной функцией F (х, у), будут иметь точную нижнюю
грань С, причём С неизменно должно быть меньше /0,
так как внутри Lo, как было указано выше, непременно
должна находиться ещё хотя бы одна замкнутая траек-
тория.
При этом возможны следующие два случая: 1) либо
F{x,y) принимает значение С в некоторой точке (а, Ь)
области g или на Lo; 2) либо существует последователь-
ность точек (хп, уп) (л= 1, 2,...), для которой значения
F(x,y) стремятся к С при п-*-\-оо. Во втором случае
последовательность точек (хп,уп) будет иметь хотя бы.
одну предельную точку в области g или на Lo, которую
мы также обозначим через (а, Ь). В обоих случаях точка
(а, Ь) будет обладать тем свойством, что в любой, сколь
угодно малой ей окрестности нижняя грань значений F(x,y)
будет равна С.
Рассмотрим траекторию Lv проходящую через точку
(а, Ь). Если траектория Lx — незамкнута, то, в силу леммы
X, вокруг точки (а, Ь) можно построить столь малую окрест-
ность, что все пересекающие эту окрестность траектории
также будут незамкнуты. Но тогда значение F(x,y)
в любой точке этой окрестности будет равно /0, и точная
нижняя грань значений F (х,у) в этой окрестности не
может быть равна С < /0, что противоречит определению
точки (а, Ь).
Следовательно, траектория L^ замкнута. Но тогда
внутри L1 непременно лежит ещё хотя бы одна замкнутая
траектория. Пусть La—такая замкнутая траектория, лежа-
щая внутри Lj, и пусть /а — площадь, заключённая внутри
?2. В силу леммы XI, всегда можно взять столь малую
окрестность точки (а, Ь), что всякая пересекающая эту
окрестность траектория либо не замкнута, либо замкнута

ОБЩАЯ КАЧЕСТВЕННАЯ ТЕОРИЯ 289
и содержит Lg внутри. Но тогда значения функции F(x, у)
в этой окрестности будут больше /2, и, следовательно,
С>./а. Но внутри 1а непременно будет находиться еще1
хоть одна замкнутая траектория —L3. Пусть /8 — площадь,
ограниченная Lg. Тогда значения функции F (х, у) в точках
L8 равны /8</2 <С, в противовес определению С. Таким
образом, предположение, что внутри Lo нет состояния
равновесия, приводит к противоречию, и теорема до-
казана.
Следствие. Если траектория L пересекает отре-
зок без контакта / более чем в одной точке, и если
М1 и MQ — две последовательные точки пересечения
траектории L с отрезком / (так что на части AftAf3
отрезка / больше уже нет точек траектории L), то
внутри замкнутой кривой К, образованной частью
MtM% отрезка / и дугой М^тМ^ траектории L,
непременно находится хотя бы одно состояние равно-
весия.
Действительно, рассмотрим какую-нибудь траекторию L,
пересекающую, при t = t0, отрезок М^М^. Нетрудно ви-
деть, что либо полутраектория L±, соответствующая />/0,
либо полутраектория L_, соответствующая t<t0, должна
целиком лежать внутри К. Пусть для "определённости
это есть полутраектория L+* Если среди предельных, то-
чек L+ (которые, очевидно, все лежат внутри К) нет со-
стояний равновесия, то множество предельных точек
состоит из замкнутой траектории, целиком лежащей вну-
три К. Но в силу только что доказанной теоремы внутри
этой замкнутой траектории непременно должно находиться
хотя, бы одно состояние равновесия. Таким образом, наше
утверждение доказано.
Теорема IX. Пусть Р — состояние равновесия.
Тогда либо в каждой сколь угодно малой окрестности
точки Р лежит замкнутая траектория, содержащая Р
внутри, либо существует траектория, стремящаяся к Р.
Предположим, что вокруг состояния равновесия Р суще-
ствует окрестность, не содержащая целиком ни одной зам-
кнутой траектории, заключающей Р внутри себя. Так как
состояний равновесия, по предположению, конечное число,.
1Q А. Пуанэаре.

390
ДОПОЛНЕНИЕ К ГЛ. V И VI
то в этом случае можно построить такую окружность^?/
с центром в точке Р, внутри которой не было бы ни одного
состояния равновесия, кроме Р, и не лежала бы целиком
ни одна замкнутая траектория.
Покажем, что в этом случае обязательно существует
хоть одна траектория, стремящаяся к Р.
Для доказательства этого утверждения покажем
сначала, что существует положительная или отрица-
тельная полутраектория, целиком лежащая внутри окруж-
ности U.
Допустим, что такой полутраектории нет. Пусть U'—
окружность с центром в Р, расположенная внутри U, и
пусть А — какая-либо точка на этой окружности (черт. 5).
Траектория L, прохо-
дящая через точку А,
должна, по предполо-
жению, выйти из вну-
тренности окружнсст»
U как при возраста-
нии, так и при убыва-
нии t. Возьмём дугу
этой траектории L, за-
ключающуюся между
первыми точками её
выхода из U (заметим»
что до точки выхода
траектория L может
касаться окружности
U один или несколько
раз). Пусть наимень-
шее расстояние взятой
дуги траектории L до точки Р есть р {А). Функция р (А)
определена, таким обр*азом, во всех точках А окружно-
сти U' и принимает только положительные значения, нигде
не обращаясь в нуль.
Обозначим точную нижнюю грань функции р (А)
через р0. В силу нашею предположения р0 > 0. Лет*
видеть, что на U' должна быть точка В, обладающая
тем свойством, что сколь бы мала ни была дуга окруж-
Черт. 5.

ОБЩАЯ КАЧЕСТВЕННАЯ ТЕОРИЯ 291
кости U', содержащая точку В внутри себя, точная нижняя
грань значении р (Л) на этой луге есть р0*).
Нетрудно видеть, что р {В) = р0.
Действительно, пусть р (В) ф. р0; тогда р (В) = р0 -}-
4-а>р0. Пусть траектория Lo, проходящая через точку Б
при t — t0, рыходит из внутренности окружности U
при t = t1<Ct0 (впервые, при убывании t, начиная от /0)
и при t = ta>tQ (впервые, при возрастании t, начиная
от t0). Возьмём столь малое т > 0, чтобы точки ?0,
соответствующие значениям t между t1 и ti—т, а также
между <2 и /а~Нт лежали бы вне U. Из теоремы о непре-
рывной зависимости от начальных условии следует, что>
всегда можно указать столь малую окрестность точки В,.
чтобы:
а) точки всех траекторий, пересекающих при t = t0.
ету окрестность, соответствующие t = t1 — т nt = t2-\-?t.
лежали бы вне U;
Ь) точьи этих траекторий, соответствующие значе-
ниям t, заключённым между ^ — т и /2~ЬТ> лежали бы
в Y'0KPeCTH0CTH отрезка траектории Lo, соответствующего
тем же значениям t.
Но тогда нетрудно видеть, что длЪ выходящих ив
так построенной окрестности точки В траектории имеем:
р (А) ^- р0 ~\- а ?- —р0-}-" чт0 противоречит предпо-
ложению, что точная нижняя грань функции р (А) в любой
окрестности точки В есть р0.
Следовательно, р (В) = р0, и так как функция р (Л) не
обращается в нуль, то ро>О.
Но тогда можно взять точку М, лежащую внутри U'
на расстоянии Ц- от точки Р; траектория Lit проходящая
через точку М, должна, по предположению, выйти иа
внутренности окружности U и, следовательно, обязана
пересечь U' в некоторой точке С. Значение функции р [А)
*) Заметны, что в гышецитированной книге Kamke «Differen-
tlalgleichui.gen reeller Funkiioner.» — в доказательстве этой теоре-
vu имеется ьеточносгь.
19*

292 ДОПОЛНЕНИЕ К ГЛ. V И VI
в точке С не превосходит -^<р0, что противоречит опре-
делению р0 как точной нижней грани значений функ-
ции р (А).
Полученное противоречие доказывает, что непременно
существует положительная или отрицательная полутраек-
тория, остающаяся целиком внутри U. Пусть для опре-
делённости это есть положительная полу траектория L+.
Все предельные точки полу траектории L+ должны, сле-
дояательно, также лежать внутри U. Так как, по предпо-
ложению, во внутренности окружности U нет ни одной
замкнутой траектории, то множество предельных точек
траектории L+ либо состоит из одной только точки Р,
либо из точки Р и траекторий, стремящихся к Р (см.
теорема VII, случай III). В обоих случаях теорема доказана.
Пусть Р—состояние равновесия, и пусть полутраекто-
рия L+ сремится к Р. Окружим Р столь малой окруж-
ностью С, чтобы на L+ заведомо была бы точка R вне С,
и, сверх того, окружность С не содержала бы внутри ни
одного состояния равновесия, отличного от Р. Обозначим
через Е последнюю (в сторону возрастания t) точку
пере;ечения полутраектории L+ с С, и пусть Q — точка,
лежащая на L+ после Е, и следовательно, внутри С.
Прове чём в точке Q отрезок без контакта QA, не пере-
секающий L+ ни в одной точке, отличной от Q. В таком
случае имеет место следующая теорема.
Теорема X. Либо все траектории, пересекающие
отрезок QA (.в точках, отличных от точки Q), покидают
при возрастании t внутренность окружности С, либо
на QA существует часть QQ', такая, что все пересекаю'
щие QQ' траектории стремятся к Р, оставаясь внутри С.
Для доказательства допустим, что на отрезке QA
нашлась точка В такая, что траектория V, проходящая
через точку В при t = t0, при *>/0 остаётся внутри С;
покажем, что траектория V стремится к Р при t-*--\- оо.
Для этого достаточно показать, что L+' при t-*--\-oo
не имеет предельных точек, отличных от состояния равно-
весия.

ОБЩАЯ КАЧЕСТВЕННАЯ ТЕОРИЯ 293
Допустим противное; пусть N есть предельная точка
полутраектории L' + и пусть N не является состоянием
равновесия. Точка N не может быгь предельной для L + ,
так как L+ имеет единственной своей предельной точкой
точку Р. Также точка N не может лежать hi L+, так
как тогда все точки полутраект^-ии L+, в том числе и
точка R, лежащая вне С, были бы предельными для U
при t—>-j-oo, и полутраектория L'+ должна была бы
покидать внутренность окружности С вопреки предпо-
ложению. Следовательно, через точку N можно про-
вести отрезок без контакта /, не пересекающий L+.
Полутрэектория L+, ос агаясь внутри С, должна пересечь
этот отрезок в бесконечном множестве точек; пусть Pt
и Ра — какие-нибудь два последовательных из эгих точек
пересечения. Мы получили замкнутую кривую D, обра-
зованную дугой PjPa траектории L и частью Р,Ра
отрезка /, лежащую целиком внутри С. Внутри этой
замкнутой кривой D, в силу следствия из теоремы VIII,
непременно должно лежать хоть одно состояние равнове-
сия. Полутраектория L+, имеющая точки вне С, не может
лежать целиком внутри D; она не пересекает D (т^к как
по самому построению отрезка / она не пересекает этот
отрезок) и поэтому не может стремиться к юму состоя-
нию равновесия, которое лежит внутри D. След< вате ьно,
это состояние равновесия отлично от Р, что противоречит
предположению, что внутри С нет состояний равновесия,
отличных от Р.
Следовательно, траектория L' при *-* + оо стремится
к Р. Ио тогда и всякая другая траектория, пересгкак^щая
отрезок без контакта QB, будет, при /->-}-«э, остават ся
в области, ограниченной простыми дугами QP, ВР и
отрезком QB, лежащей целиком внутри С. К каждой из
этих траекторий приложимо то рассуждение, кото-
рое было только что проведено для L', т. е. каждая
из этих траекторий будет при /-¦ -f- °° стремиться
к точке Р.
Таким образом теорема доказана.
Пусть Р, L+, E, С и QA имеют те же значения,
что и в теореме X.

294 ДОПОЛНЕНИЕ К ГЛ. V И VI
Теорема XI. Пусть все траектории, пересекающие
некоторую часть QQ' отрезка QA при возрастании t,
покидают внутренность окружности С. Тогда на С
существует такая точка S, что траектория Z/, про-
ходящая при / = т через точку S, обладает следую-
щими свойствами:
1) при t-+ — оо траектория L' стремится к Р,
причём все точки траектории V, соответствующие t < т,
лежат внутри С;
2) какую бы точку N траектории V соответствую-
щую *<z (и следовательно, лежащую внутри С), мы
ни взяли, всегда можно через эту точку провести отрезок
без контакта NN' такой, что всякая траектория,
при t — t0, пересекающая отрезок QA, достаточно
близко к Q (но в точке, отличной от точки Q), пере-
сечёт при t —ti > ta отрезок NN' сколь угодно близко
к точке N, не выходя за время от t0 до t^ из внутрен-
ности окружности С.
Дш доказательства возьмём на отрезке QQ' последо-
вательность точек Q( (/ = 1,2 ,...), стремящуюся к точке Q.
По пред-'оло-кэнию, траектория, проходящая при t = t0,
чер>з любую из точек Q{, при некоторых значениях />f0
должна лежать вне окружности С; пусть S{ — первая
точка её выхода из внутренности окружности С, соот-
' вегствующш t>t0. Точки 5< различны; следовательно,
на окружности С лежит бесконечное множество точек Sit
которое должно иметь на С хоть одну точку сгущения.
П/сть S — оша из этих точек сгущения. Выберем из
последовательности точек Q{ такую подпоследователь-
ность Qt (ft = 1,2,...), чтобы соответствующая после-
довательность точек* Si ¦ (k = 1, 2,...) стремилась бы
к точке 5 (черт. 6). '
Рассмотрим траекторию L', проходящую при / = т через
точку S, и докажем, что Lr при /<т остаётся внутри С
Д йствительно, пусть на L есть точка, соответствую-
щая / = /,<¦:, лежащая вне С. Тогда и все траектории,
проходящие при значениях / = т через достаточно близкие
к точке S точки St окружности С, при некоторых зна-

ОБЩАЯ КАЧЕСТВЕННАЯ ТЕОРИЯ
295
чениях t < х также будут находиться вне окружности С.
Траектория L' при некотором значении 1, лежащем между tt
и т, должна пересечь отрезок без контакта QQ', так как
в противном случае траектории, проходящие при t = x
через достаточно близкие к 5 точки St , выходили бы
при некотором значении t < x из внутренности окруж-
ности С, не пересекая отрезок QQ', что противоречит
определению точек S{ . Пусть М есть точка пересечения
траектории L с отрезком QQ'. Нетрудно видеть, что
точка М, в силу непрерыв-
ной зависимости от началь-
ных условий, должна быть
предельной для точек Q
т. е. должна совпадать с
точкой Q. Но это невоз-
можно, так как, по усло-
вию, траектория L, прохо-
дящая при/= ~i через точ-
ку Q, не имеет при t >7
уже никаких точек на С,
и, следовательно, не может
при tf=ax>j, пройти через
точку S, лежащую на С.
Следовательно, при зна-
чениях <<х траектория 11
целиком лежит внутри С. Рассуждениями, совершенно
аналогичными теи, которые были проведены при дока-
зательстве теоремы X, нетрудно показать, что LJ имеет Р
своей единственной предельной точкой. Таким образом,
первое утверждение теоремы доказано.
¦¦-* Для доказательства второго утверждения теоремы
возьмём на части траектории L, соответствующей <<t
и, следовательно, лежащей внутри С, какую-нибудь точку Л
и проведём отрезок без контакта N'N", содержащий
точку N внутри себя. Нетрудно видеть, что траектория /.<„
проходящая при f = х через какую-либо точку S{ , доста-
точно близкую к точке 5,[при <<х, не встретив отрезка QQf
Черт. 6.

296 ДОПОЛНЕНИЕ К ГЛ. V И VI /
пересечёт отрезок N'N" в некоторой точке A/*ft. При
дальнейшем убывании t, траектория L{ пересечёт отре-
зок QQ' в точке Q<-. Рассмотрим область D, лежащую
целиком внутри С, ограниченную дугами QP и NP траек-
торий L и L', самой точкой Р, отрезками QQt и NNt
и дугой N{ Qi траектории L{ . Всякая траектория, пере-
секающая при возрастании t отрезок без контакта QQ4
(в точке, отличной от Q'), входит в область D. Так как
по условию теоремы она должна в дальнейшем выйти из
окружности С, а следовательно, и из области D, то всякая
траектория, пересекающая отрезок QQi^, пересечёт также
и отрезок NNf (так как траектория может выйти и»
Области D только через этот отрезок).
Кроме того, точка Nt (/»>/*) будет лежать на
отрезке AW сколь угодно близко к точке N, если соот-
ветствующую точку S{ взять достаточно близко к точке 5.
Отсюда нетрудно видеть, что все траектории, пересекаю-
щие отрезок QQ{k достаточно близко к Q, пересекут
отрезок NN^ при возрастании t сколь угодно близко
к точке N*). Таким образом теорема доказана.
Заметим, что, обратно, все траектории, проходящие
ири t = t0' через точки отрезка NNt (отличные от точки
N), при убывании t пересекут отрезок QQt (и затем, при
дальнейшем убывании t, выйдут из С). Действительно,
если бы на NN{ существовала такая точка М, через
которую при t = t0' проходила бы траектория, не пере-
секающая при /</(/ отрезок QQtk, и, следовательно>
при всех t<C.t0' остающаяся внутри D (а значит и внутри
окружности С), то, в силу теоремы X, эта траектогия,
а также все траектории, пересекающие отрезок NM, не
выходя из D, при t-*- — оо стремились бы к точке Р.
*) Отсюда нетрудно также вывести, что все точки Ы1щ
#«»>•'*) лежат иа отрезке NihN по одну и ту же сторону точ-
ки//и образ_\ют последовательность, расположенную в порядке
возрастания номеров 1т и стремящуюся к точке N.

общая качественная т еория 297
Но это противоречит тому, что на отрезке NNt сколь
угодно близко к точке N есть точки N{ , через которые
проходят траектории, пересекающие отрезок QQt. в точ-
ках Q{ и таким образом выходящие из области D.
Относительно траектории L, обладающей указанным»
в теореме XI свойствами, мы будем говорить, что траек-
тория V есть продолжение траектории L относительна
окружности С; саму траекторию L мы назовём продол-
жаемой относительно окружности С. И, наоборот, траек-
тория L есть продолжение траектории L' относительна
окружности С*).
- Пусть, попрежнему, внутри окружности С лежит только'
одно состояние равновесия Р.
Теорема XII. Существует только конечное числа
траекторий, стремящихся к Р и продолжаемых отно-
сительно окружности С.
Предположим противное; пусть существует бесконеч-
ное множество :
траекторий, продолжаемых относительно С.
Без ограничения общности можно считать, что все
эти траектории стремятся к Р при t—»--)-оо. Пусть Alt
Ла,... их последние (при возрастающем /) точки
пересечения с окружностью С**). Возьмём одну из
предельных точек множества \Ап) и обозначим её через А.
Не i рудно видеть, что траектория L, при / = т, прохотяща*
через точку А, при всех значениях ?>* остаётся внутри С;
действительно, в противном случае все траектории, про-
ходящие при t = -c через достаточно близкие к точке А
точки Ап окружности С, тоже покидали бы внутренность
*) Если ни через одну точку одной из областей, на которые
простая дуга, образованная дугами т( аекюрий L и Z/ и точ-
к< й Р, делит внутренность «пружи сти С, не проходит траек-
тория, стремящаяся к Р, то Бендиксои говорит, что ривая,.
ссста ленная из L, Р и Z/,есть «характеристика, пере-
секающая точку Р».
•*) При этом так же, как и в теоремах X и XI, предполагается,,
что на всех траекториях, Ln есть точки, лежащие вне С.

298 ДОПОЛНЕНИЕ К ГЛ. V И VI
окружности С, при ?>i:, что противоречит выбору этих
точек.
Покажем, что траектория L при t-y -\- оо не может
иметь предельных точек, отличных от точки Р, и, следо-
вательно, стремится к Р.
В самом деле, пусть ?+ — полутраектория, выделенная
•из L, соответствующая значениям /^>т, и, следовательно,
кроме точки А, целиком лежащая внутри С.
Предположим что ?+ имеет предельную точку Q,
отличную от Р (и следова-ельно, не являющуюся состоя-
нием равновесия). Пусть Ln —одна из трагкторий Ln.
Через точку Q можно провести отрезок без контакта /,
«е пересекающий траекторию ?„. Полутраектория L+
должна п.ресечь отрезок / в бесконечном множестве
точек; пусть Pt и Р9 — две последовательные точки пере-
сечения полутраектории L+ с отрезком /. Рассмотрим
•целиком лежащую внутри С простую замкнут/ю кривую К,
образованную дугой Р^ полутраекюрии Z,+ и отрез-
ком Р{Р%. В силу сл-дсвия из теоремы VIII, внутри этой
заикнугой кривой непременно должно содержаться хотя
¦бы одно сое ояние равновесия, и, следовательно, там
должна находиться точка Р, так как, но предположению,
внутри С нет других состояли равновесия. Траектория^ ,
очевидно, не пересекает кривую К и так как онл имеет
точки вне кривой К, то траектория L- лежит вне области,
ограниченной кривой К. Следовательно, Lni не может
стремиться к Р, что противоречит нашему предположению.
Та;<им образом L? стремится к Р.
В >зьмём теперь на ?+ какую-нибудь точку В и проведём
•чер нзё отрезок без контакта В'В", содержащий точку В
внутри себя. Тогда бесконечное множество траекто-
рий Ln пересечет либо отрезок В'В, либо отрезок ВВ".
Пусть, например, тр,1е<тории ?„ и Ln пересекают отре-
зок В'В, соответственно в точках Bt и Ва, и пусть 5а
лежит ближе к й, чн Bv
В силу TejpeMU X, все траектории, пересекающие
о.резок BtB, будут при возрастании t, не выхлдя

OBUUI КАЧЕСТВЕННАЯ ТЕОРИЯ 299
изнутри С, стремиться к точке Р. Но это противоречит
предположению, что траектория ?„г продолжаема отно-
сительно окружности С.
Таким образом, теорема доказана.
Отметим, что при уменьшении радиуса окружности С
число продолжаемых относительно С траекторий может
неограниченно возрастать*).
* Теоремы X и XI в известной мере освещают вопросы
взаимного расположения траекторий; с помощью них мы
можем уточнить строение множества предельных точек
данной полутраектории, в том бэлее сложном случае,
когда оно не сводится к одному состоянию равновесия,
«ли к замкнутой траектории.
Теорема XIII. Множество всех предельных точек
полутраектории L+ состоит либо: а) из одного состоя-
ния равновесия; либо б) из одной замкнутой траекто-
рии; либо в) из состояний равновесия и траекторий,
стремящихся к ним и продолжаемых по отношению
к некоторым окружностям.
Случаи а) и б) содержатся в теоремах VI и VII.
Если же не имеет место ни случай а), ни случай б), то
в силу теоремы IV множество предельных точек L+ состоит
из состояний равновесия и траекторий, стремящихся
к состояниям равновесия.
В самом деле, возьмем одну из этих предельных тра-
екторий ?j, и пусть при f-*--)-00 она стремится к состоя-
нию равновесия Pv Построим окружность С с центром
в Pj, не содержащую внутри ни одного состояния
равновесия, кроме Ри и пересекающую Lv Возьмем на Lx
точку Q, лежащую после последней (при возрастающем t)
точки пересечения траектории Lt с С и проведём в Q
отрезок без контакта Q'Q?, содержащий точку Q внутри
себя. Так как точка Q — предельная для полутраектории ?+,
то либо на Q'Q, либэ на QQ" (пусть, например, на QQ')
•) Бендиксон показал (Acta Mathem., 1900), что в том случае,
когда правые части рассматриваемой системы — аналитические
функции от х ну, число траекторий, продолжаемых относитедьно
любой окружности, всегда конечно.

300 ДОПОЛНЕНИЕ К ГЛ. V И VI
лежит бесконечное множество точек полутраектории L+.
Ни через одну точку отрезка QQ', достаточно близкую
к Q, не может проходить траектория при t— -j- oo, стре-
мящаяся к Ри не выходя из С. Действительно, в противном
случае, в силу теоремы X и полутраектория L+, которая
пересекает QQ' в точках, сколь угодно близких к Q,
должна была бы при t-*--\-oo, не выходя из С, стре-
миться к Pj и, следовательно, имела бы в качестве своей
предельной точки единственную точку Ри что противоре-
чит предположению. Но тогда из теоремы XI вытекает,
что Lt продолжаема по отношению к С.

ДОПОЛНЕНИЕ К ГЛАВЕ XI
ЦЕНТР
А. Майер
Мы даём здесь теорию центра в том виде, как она
была разработана Ляпуновым в 1892 г. в работе «Общая
задача об устойчивости движения» *). Рассуждения Ляпу-
нова далеко перекрывают не только теорию центра, дан-
ную Пуанкаре в 3-ем мемуаре, но частично и более
поздние работы Бендиксона (Acta Mathematica, т. 24
A901), стр. 1—30) и Фроммера (Mathem. Annalen, т. 99
A928).
1. Необходимые и достаточные условия центра.
Следуя Пуанкаре, мы скажем, что состояние равно-
весия Р является центром для системы дифференциаль-
ных уравнений
если существует окрестность точки Р, не содержащая
других состояний равновесия, такая, что все траектории,
пересекающие её в какой-либо точке (кроме точки Р),—
замкнуты.
*) Ляпунов, Общая задача об устойчивости движения,
изд. 2 е, ОНТИ A935), стр. 128-=-! 70.

302
ДОПОЛНЕНИЕ К ГЛ. XI
Мы предположим, что X и Y—голоморфные функции
от х и у в некоторой окрестности состояния равновесия;
перенося в него начало координат, мы будем иметь
к=2
где Хк(х, у) и Yb(x, у)—однородные многочлены
степени k.
В настоящем дополнении мы ограничиваемся рассмотре-
нием случая, когда
а ь
с d
фО.
Как показано Пуанкаре (гл. XI настоящего издания\
необходимым условием центра в этом случае является
следующее условие: уравнение
а — [a b
с d — [
= 0
должно иметь чисто мнимые корни: ^ = X/, (ла=^ — \t,
где А>0. Мы предположим это условие выполненным.
Линейной заменой всегда можно привести в этом
случае систему к виду:
ft =2
где Хк(х,у) и Yh(x,y\ как и прежде,—однородные
многочлены степени k по х и у, и ряды сходятся в неко-
торой окрестности начала, так что правые части суть
голоморфные функции от х и у при |х|<л0 и |.yK.)V
Перейдём к полярным координатам р и ф, пэложиа:

ЦЕНТР
Тогда, после несложных вычислений, получим систему
со
-gl = У]р* [Хк (cos <p, sin <p)cos <p -j- Yk (cos tp, sin tp) sin <pj
fc=2
(A,)
Рй"] < ^ (cos <?, «rin ®) cos T-
ft =2
— A^cos?, sin<p)sin<p),
где ряды, стоящие в правых частях, сходятся в области:
0<<s<2ir, 0<p<po.
Так как А>0, то из второго уравнения без труда
видим, что существует такое pt>0, что при 0<]р.<р,
и 0^y^2it будем иметь:
2
Поэтому, ограничиваясь этой областью значений р и
мы будем иметь р однозначной функцией от <р.
Исключая t, получим уравнение:
00
S р* {Х]( (cos <p, sin <p) cos ср -}- yk (cos <p, sin !f) sla у}
2
оо
Х+ S p*-1{Kj(cos<f,sincp)cos<p—-Yt(cos<f, sin<f)sitif}
где знаменатель правой части в рассматриваемой области
не обращается в нул>. Следовательно, правая часть этого
уравнения есть голоморфная функция от р в области:
О <; р ^ pi, 0 < <р < 2п, и её можно представить в виде
ряда по степеням р, сходящегося в указанной области.
Таким образом, будем иметь
(Б) Щ- = ра \]aft (cos ?, sin
Jt=2

304 ДОПОЛНЕНИЕ К ГЛ. XI
где коэффициенты afr(cos<p, sin да) суть многочпены по
<ros» и sinср и притом степени чётной — при нечётном
Jt и нечётной — при чётком k.
В самом деле, уравнение (А/) имеет вид:
d<r
еде ай(ср) — многочлен по cos<p и sin да, все члены ко-
торого имеют степень, чётную при нечётном k, и. нечёт-
кую — при чётном k. a pft (в) — многочлен по cos о и sin <p,
¦степени членов которого одной чётности с k. Следова-
тельно, если мы напишем
ОО ОО
- т.
1
m = o[k = l J n=o
т0 T?t (?) будет многочлен по cos да и sin <p, степени
членов которого одной чётности с л.
ОО ОО
pm_m_vr; и > р»^п(ср), полу-
т=0 »=0
1
чим многочлен aft('f) = я* (cos <p, sin да) =
т+пк
Хт»(?)> каждое слагаемое которого есть многочлен по
¦cos » и sin cp, степени членов которого обратной чётности с k.
Таким образом, пользуясь тождеством cosyo -j- sin'?o = 1,
мы можем считать коэффициенты aft(?) однородными
многочленами по cos о и sin о, степени которых обратной
чётности с k.
Будем искать решение, определённое начальными
значениями: р = с (с>-0) при <р = 0.
Мы утверждаем, что это решение может быть при
достаточно малых значениях параметра с и всех <р из

центр
305
промежутка 0<с?<;2тг представлено в виде ряда
B) Р= S«*(?)'S
причём Hj(cp)= 1.
. Доказательство распадается на 2 части: а) формаль-
ное нахождение ряда и б) доказательство сходимости
ряда в области: 0 ^ с < с0, О < о ^ 2я, где с0 — доста-
точно малое положительное число.
Обращаясь сперва к формальному нахождению рядаB),
заметим, что в силу начальных условий: при <р = 0,
р = с, будем иметь:
C)
= 0 при*>1.
Внеся выражение B) в уравнение (В) и сравнивая
коэффициенты при одинаковых степенях величины с, по-
лучим систему уравнений для последовательного нахожде-
ния коэффициентов «л(?):
¦ «/(?) = О,
и/(в) = ао
иаа) 4" в1«
Вообще:
D)
где
есть многочлен с целыми положительными
ak
k_2
и
коэффициентами от величин а0, av.
«я, .... «*-!•
Существенно для дальнейшего отметить, что если
все ап и ип заменить в этом выражении /?*(<?) положи-
тельными числами ап, ип такими, что | ап\ ^ ап, \ип\ < и,,,
то новое Rk будет также положительным числом, причём
20
- Пуанкаре.

306^ ДОПОЛНЕНИЕ К ГЛ. XI
В силу у слови,'I C) из выражений для ик' получаем
1ф) -f
и вообще, в силу D);
E) «*(?
Таким образом, ряд B) формально построен. Остаётся
1 ассмотреть вопрос о его сходимости.
Хотя сходимость этого ряда вытекает из общих
теорем о зависимости решения дифференциального уравне-
ния от параметра *), но мы изложим здесь доказательство
сходимости ряда B), так как эти теоремы не входят
в оэычный курс дифференциальных уравнений.
Для доказательства сходимости ряда B) отметим, что ряд
00
2 ак(<р) рк, стоящий, в правой части уравнения (В), изобра-
/.=0
жает функцию от р, голоморфную при всех значениях
¦р,и <р из замкнутой области: 0^®^2ir, O^p^pj.
Следовательно, эта функция ограничена при всех значениях
р и <р из указанной области, т. е.
S
<М. В силу
о
известной теоремы теории аналитических функций
отсюда получаем
K(cos<p, sin<p)[< -?.
*) Ср., напр., Г у р с а. Курс математического анализа
т. 3, § 463, стр. 24, ГТТИ A933).

центр 307
у^ '
Обозначим — через ак и положим:
p
Вообще, найдя ut, ..., ик_и_мы определяем Rk, заменяя
в Rk все ат и ит через ат и ит, а затем полагаем
ак =
В • силу соотношения E) и ранее сделанного заме-
чания о функции Rk(f), мы при 0<]ф<]2те будем иметь
Отсюда следует, что для доказательства "сходимости
ряда B) достаточно доказать сходимость ряда
F) J
Чтобы доказать сходимость последнего ряда, заметим,
что мы получим Rk, как коэффициент при ск, если мы в ряд
ОО * 00
2 ajtPfc+a подставим ряд р = 2%с* и соберём вместе
члены с одной и той же степенью переменной с.
Таким образом, будем иметь
оо М I т — \*+3 °° _
Sl*(S«>) =2 я**
Так как ut = 1 и afc = 2ir 7?^ при А > 2, то отсюда
следует
оо _ оо 1 / оо __ \ft+2
2 eiC* = c + 27uAf 2Т* 2«.с» •
оо _
Обозначив 2"ftcfc через г», получаем для v квадратное
20*

308 ДОПОЛНЕНИЕ К ГЛ. XI
уравнение: _
G) ' г» = с-[-2т:М--^=
Pi
Таким образом, остаётся доказать, .что квадратное
уравнение G) имеет корень v, обращающийся в нуль
вместе с с и голоморфный при малых значениях с.
Решая уравнение G), находим для искомого корня
выражение:
— _ с + р!— Y (c + Pil2 — 4cp1(J"+2r>Afp1)
Отсюда следует, что v есть голоморфная функция па-
раметра с при достаточно малых значениях его. Следова-
тельно, всевда существует столь малое с0, что при
0<с<г0 ряд F), а следовательно, и ряд B) сходятся.
Таким образом, доказано, что решегие уравнения(В),
удовлетворяющее' начальным условиям: <э = 0, р = с, где
!с0, можно представить в виде ряда
причём этот ряд сходится при всех значениях <э из
области 0^ ср ^ 2т:, а коэффициенты его определятся по
формулам E).
На основании этого результата легко решить
вопрос об условиях существования центра.
Рассмотрим функции ик(?). Так как ао(?) есть
однородный многочлен от cose? и sin», все члены кото-
рого нечётной степени, то его можно записать как ли-
нейную, функцию от cos «<? и sin ив, причём п будет
принимать только нечётные значения; следовательно, при
такой записи в йо(?) свободного члена не будет. Отсюда
вытекает, что
9
о
будет также линейной функцией от cos и о и sinn®.

центр 309
Но тогда подинтегральное выражение для %(<р) можно
представить также в виде линейной функции от cos лев
и sin л», причём теперь уже п будет принимать только
чётные значения. Таким образом, для иа^р) есть две воз-
можности:
а) подинтегральная функция не имеет свободного
члена — тогда и3(?) есть линейная функция от cos «ев и
sin nv;
б) подинтегральная функция имеет свободный член
g — тргда и3{о) = g's -\- v3('f), где г>3(<?) — периодическая
функция от «р.
Если имеет место случай а), то мы рассмотрим
дальнейшие коэффициенты: и4(<?), иБ(«р), .. . Допустим,
что по отношению к каждому uk(z>) при k < m имеет
место случай а), так что все ик (<р) при ?</и являются
периодическими функциями от <р, тогда как для ит(<р)
наступает случай б), так что ит(<р) =g<o-\- vm(<?), где
vm(<a) — периодичгская функция от <р*).
При этом предположении мы будем иметь
оо
р@) = с, pBir) =*c-\- 2izgcm -\- 2 ^B^N*.
Отсюда, при 0<с^С!, где с1 — достаточно мало,
получим
00
2
т + 1
так что при ьтих значениях будем иметь:
|рB*)-<
Отсюда следует, что все траектории, соответствующие
достаточно малым значениям параметра с, не замкнуты.
Следовательно, в достаточно малой окрестности начала
координат нет ни одной замкнутой траектории.
*) Можно было бы показать, что«т» есть необходимо не-
чётное число; однако мы настом не б_удем останавливаться.
так как это нам для дальнейшего ие нужно.

310 ДОПОЛНЕНИЕ К ГЛ. XI
Допустим теперь, что случай б) никогда не наступает,
так что все /?/;(<?) не имеют свободного члена. Тогда все
и*(?) СУТЬ периодические функции от ф и при всех* с,
из промежутка 0 <; с < са, имеем
р(О) = с/ рB*) = с.
Следовательно, все траектории, пересекающие отрезок
оси абсцисс между точками @, 0) и (с0, 0), замкнуты и
притим лежат целиком в сколь угодно малой окрестности
начала координат при достаточно малом значении пара-
метра с, т. е. имеет место случай центра.
Таким образом, случай центра имеет место лишь
тогда, когда выполнено бесконечное множество
условий — именно, условий равен:тва нулю свободных
членов во всех /?*(»). Так как составление функций /?^(ф)
требует вычисления всех ит (о) при т < k, то в боль-
шинстве случаев практически невозможно непосредственно
по этим условиям исследовать те случаи, когда в дей-
ствительности имеет место центр.
2. Теорема Ляпунова.
Ляпуновым была впервые доказана нижеследующая
теорема:'
Необходимое и достаточное условие существования
центра для системы
(А*)
где коэффициенты а, Ь, с, d таковы, что уравнение
а — ji b
с d — ]
имеет чисто мнимые корни, заключается в том,
что система (А*) должна иметь не зависящий от t

ЦЕНТР 311
действительный голоморфный интеграл F{x,y) =
= С*).
Докажем предварительно 3 леммы, которые будут нам
нужны в дальнейшем.
Л е мма .1. Пусть Fm(х, у) ф'О — однородный много-
член, от х и у степени т:
и пужъ xF' —yF'==0. Тогда: 1) т есть число чет-
нов, т. е. т = 2р, где р — целое положительное число;
2) Fm(x,y) = a(x'i-\-y*)P, где а — постоянное число.
Доказательство. Составим выражение:
ту
т —1
Условие тождественного равенства нулю даёт:
при
Из последних соотношений видно., что равенство нулю
а\,т-\ влечёт за собой равенство нулю всех коэффициен-
тов с нечётным первым индексом, и что при нечётном т
из flm_t,i = 0 следует равенство нулю всех коэффициен-
тов с чётным первым индексом, т. е. тождестпенное ра-
венство нулю многочлена Fm (x, у), вопреки предполо-
жению.
*) Ляпунов, Общая задача об устойчиоости движения.
Отметим, что эта теорема осталась неизвестна Фроммеру
(см. цит. работу), который говорит, что вопрос о существовании
голоморфного интеграла в рассматриваемом случае не решён.

..(pk + l) „
2. ..? "о,
312 " ДОПОЛНЕНИЕ К ГЛ. XI
При т чётном, равном 2р, коэффициенты ап т_п
с нечётным индексом я попрежнему равны нулю. Коэффи-
циенты же an> m_n с четным индексом я выражаются через
а0>от следующим образом:
_т(т — 2)...(т — 2&-I-2)
а2к,т-2к— 2-4...BЙ) а0, т'
Полагая т = 2р и обозначая а0>т через <х и внося эти
выражения в Fm(x, у), получаем*
и, следовательно,
где а = а0>т.
т
Лемма П. Пусть Fm(x, y)= ^аПт
« = о '
причём коэффициенты аП(„,_п действительные числа,
и пусть Fm(x, у) не делится на х^-\-у^. Тогда и
хР' —yF'mx также не делится на х2-\-у\
Доказательство этой леммы столь же элементарно,
как и предыдущей леммы. Достаточно заметить, что не-
обходимое и достаточное условие делимости многочлена
на х2-\-у"* заключается в том, что этот многочлен обра-
щается в нуль при x~*iy. Тогда без труда убеждаемся,
- что условие обращения в нуль при х = iy многочлена
х-^ту ~~У^'тх совпаДаеТ с условием обращения в нуль при
x = iy многочлена Fm(x, у).
Лемма III. Пусть U(х, у)<= ~^, где Fm{x,у)-
однородный многочлен с действительными коэффициен-
тами, не делящийся на х*-\-у*. Тогда, при рфО, вы-
ражение xUy —yllj не может быть многочленом.
Лемма эта вытекает непосредственно из леммы II.
Перейдём теперь к доказательству теоремы.

ЦЕНТР 313
Предположим, что система
(А)
эквивалентная, системе (А*), имеет центр, и докажем,
что существует действительный голоморфный интеграл:
F(x,y) = C этой системы, не зависящий от t.
Для доказательства рассмотрим ряд
B) Р = *+2 «*(?)**,
ft = 2
изображающий решение системы (А) в полярных коор-
динатах. Так как, по предположению, система (А) имеет
центр, то, по доказанному выше, каждый из коэффициен-
тов ик(<о) есть многочлен по cos<р и sine-
Из известных теорем о неявных функциях следует,
что из соотношения B) можно выразить с как функцию
от р, в виде ряда, сходящегося при достаточно малых
значениях р. Обращение ряда B), производимое обычным
путём, позволяет увидеть, что ряд для с имеет вид:
00
(8) с = р+2 **(?)>*,
где vk(o) есть многочлен по costs и sin <в> и г яд (8) схо-
дится в области: 0 ^ <э <^ 2т:, 0 ^ р <^ р *).
*) Ср. Гурса, Курс математического анализа, т. I,
стр. 80-Ь2. ,
Формальное нахождение коэффициентов ряда (8) не пред-
ставляет затруднений. Для этого внесем выражения (8) для с
в правую часть равенства B) и сравним коэффициенты при
одинаковых степенях р. Получатся формулы, позволяющие по-
следовательно определить ffc(<p), как многочлены по cos?
и sin <p:
l/j (<р) = — н2 (if),
v-д (?) = — "а ('¦?) — «г'?) ¦ 2w.. (<p),

314 ДОПОЛНЕНИЕ К ГЛ. XI
Если мы обе части равенства (8) возведём в квадрат,
то будем иметь:
Нетрудно усмотреть, что в общем выражении vk (tp) =
в правую часть будут входить только щ, ..,, ил, »2,.... Wj_i
и чго подобно тому, как это было в предыдущем -случае
(см, выше), мы получим вместо #&(?) положительную вели-
чину Rk, причём | Rk (tp) | < Rjc, если вместо —щ, —и3,...,
— Ufa v2, v3,..., ffc_i подставим положительные числа ~йп. vn
такие, что
Это обстоятельство позволяет доказать сходимость ряда (8)
тем же методом, каким была доказана сходимость ряда B).
В самом деле в силу того, что ряд B) сходится при всех
значениях f и саз области: 0 << у < 2я, 0 < с < с0 и изобра-
жает ограниченную при этих значения! tp и с функцию, то для
коэффициентов и^(ср) будем иметь неравенства:
_ д|___ __ _
Положив затем, ик = —-, v2 = и* v3 = иа + и2 • 2i/2> ...
Cg*
и Еообще V]c = Rji, мы без труда заметим, что
к=2 Л = 2 п=2
оо
Отсюда для г = р + ^j vnfl получаем уравнение
оо
г = р +
или
1—-
со

ЦЕНТР 315
Переходя затем от полярных координат обратно к декар-
товым, полагая x = pcos«) _у = р sin «p, получим, что
соотношение (9) изображает интеграл системы (А),
причём ряд, стоящий в правой части этого равенства,
будет сходиться при в?ех значениях х и у из некоторой
области, окружающей начало координат.
Однако ещё нельзя утверждать, что'мы получим, таким
образом, искомый голоморфный интеграл системы (А).
В самом деле, при переходе к декартовым координатам
член dft(<p)p* хотя и даст однородную функцию от х к у
степени А, но эта функция может не быть голоморфной
в окрестности начала координат, так как она, вообще
говоря, имеет вид
где С/ъ (х, у) = —т , причём F есть однородный
(х*+у*)Р
(+у)
многочлен степени m = 2p-\-k и, следовательно, Uk(x,y)
есть однородная функция степени k, a Vk(x, у) имеет
аналогичное выражение, но степень однородной функции
Vk(x>У) есть k — Ь
Таким образом, мы получим интеграл
Ф(х,у)за
S V^T v*(*, y)\ = с, ¦
где ряд, стоящий в правой части, сходится в круге
+ >?
Чтобы получить голоморфный интеграл, заметим, что
если бы мы перешли в системе (А) к полярным коорди-
Легко видеть, что это уравнение имеет решение, Ыэращаю-
щесся в нуль при р = 0 и голоморфное при 0 < р < р.
оо
Следоватетьно, ряд р = 2 ^пРп сходится при 0 < р < р,
*=а _
а так как npi 0<<р-^2л имегм: \vn(<?)_\^vn, то и ряд (8)
будет сходиться при 0 < ч < 2™( 0 ¦< р < р.

316 ДОПОЛНЕНИЕ К ГЛ. XI
натам, полагая х =— р cos (<р -\- тс), у =— р sin
то все предыдущие формулы останутся в силе, если в них
заменить всюду р на —р и <р на со -\-тт. При обратном
переходе по тем же формулам к декартовым координатам
мы получим те же функции Uk(x, у) и Vk (х, у), но
вместо Yx<i-{~y* будет стоять —Vx2-{-y2.
Поэтому функция
A0) Р(х,у) = х*+у1* + %ик{х,У),
fc = 3
приравненная постоянной, есть также интеграл системы (А),
причём ряд y\U/t(.x, у) сходится попрежнему в круге
, +> P
Чтобы доказать, что F(x, y) = C есть голоморфный
интеграл, достаточно показать, что Uk {x, у) есть целый
многочлен, т. е. что показатель р равен 0.
Для этого напишем тождество:
ОО
A1) ~ = Fx'[-
ИЛИ
со оо
(и') х 2 W*v-yu[») г 21
к=3 Л=
Легко убедиться, что xUk —УЩХ есть однородная
функция той же степени k, как само Uk. Поэтому то-
ждество (И') распадается на систему тождеств:

ЦЕНТР 317
Вообще b{xU'—yU'vx) выразится многочленом, соста-
вленным из Хи, У к и частных производных по х и по у
от Uk при k < п.
В силу леммы III, Us (x, у) есть целый многочлен,
ибо в правой части соответствующего тождества стоит
многочлен 2xX2-\-2yY2. Если доказано, что все Uk при
?<я — многочлены, то из выражения для xU' —yU'nJ1
и леммы III вытекает, что Un есть также многочлен *).
Следовательно, каждая из функций Uk (х, у) есть
многочлен. В силу сходимости ряда A0) отсюда следует,
что соотношение F(x, y) = C есть действительно голи-
морфный интеграл системы (А), что и требовалось доказать.
Покажем теперь, что из существования голоморфного
интеграла, не зависящего от t, следует, что- для си-
стемы (А) имеет место центр.
В самом деле, пусть система (А) имеет голоморфный
интеграл:
A3) F{x,y)=%Fk{x,y) = C,
к-0
где каждая функция Fk(x, у) есть однородный многочлен
оо
степени k и ряд 2 ^к (х> У) сходится в круге д:2 -\-у*
А
2
Без ограничения общности можно считать, что F0 = 0.
Далее из тождества A1) и леммы I следует, что если
Fm(x> У) есть первый член ряда A3), не равный тожде-
ственно нулю, то /я = 2/> и Fm{x, y) = a{xi-\-yi)P, при-
чём без ограничения общности можно считать, что а= 1.
Итак, вдоль каждой траектории мы имеем тождество:
A4) ({у)+
к = m +1
*) Заметим, что мы не ставим перед собой вопроса о воз-
можности удовлетворить всем равенствам (!2). Из предыдущего
следует, что эти равенства удовлетворяются теми функциями
Uji(x, у), которые получаются из dk(<f)^—в случае, когда
имеет место центр.

318 ДОПОЛНЕНИЕ К. ГЛАВВ XI
Из последнего равенства очевидно, что для всякого
е>0 можно выбрать столь малое ^Х', что если мы
рассматриваем траектории, пересекающие ^-окрестность
начала координат, то С будет положительно и меньше е.
Перейдём к полярным координатам, полагая
х = р cos <р» У = р sin «p.
Тождество A4) при этом перейдёт в тождество
00
A5) p2P-f- 2 P*fft(cos<p, sln«)i=C.
к + 1
Заметим, что ряд, стоящий в левой части равенства A5),
сходится при р^Л 0^<p-C2ir и притом равномерно
относительно св. Поэтому изображаемая им функция огра-
ничена в указанной области.
Чтобы показать, что из равенстпа A5) вытекает, что
система (А) имеет в достаточно малой окрестности начала
координат только периодические решения, извлечём из
обеих частей равенства A5) арифметический корень сте-
пени 2р. Обозначая для краткости ct= j/C, будем иметь
A6)
2р/
i/ 1+
Очевидно, что существует столь малое Р!>0, что
при р^р, и 0<C<p<|2ir стоящий слева корень есть голо-
морфная функция от р. Поэтому равенство A6) можно
записать так:
A6') Р [1 + 2 Р"-Ч, (?)] = <!.
а
п=а
Коэффициенты dn(<?) легко находятся по методу не-
определённых коэффициентов, причём, подобно тому, как
это было и раньше, rfn(<p) есть многочлен от cos<p
и sin <p.
Повторяя рассуждения, проведённые в разборе пре-
дыдущего случая, мы без труда убедимся, что ряд A6')

центр 319
можно обратить, т. е. существует такое со>О, что при
0^с^с0 и 0^<р<^ 2тг, имеем
A7) . р-С1
причём /„(<?) — многочлены от cos о и sin cp *).
Отсюда следует, что р есть периодическая функции
от <р, т. е. что траекторил в достаточно малой окрест-
ности начала координат замкнуты. Таким образом,
система (А) имеет центр.
Теорема Ляпунова доказана полностью.
В заключение сделаем два замечания.
1. Изложенный в 3-м мемуаре Пуанкаре метод есть
по существу попытка решить вопрос о центре отыска-
нием голоморфного интеграла путём нгпосредственного
подбора функций Uk(x, у), удовлетворяющих уравне-
ниям A2). Этот путь был также исследован Ляпуновым.
Ляпунов доказал, что если коэффициенты ик(<?) ряда
B) получатся из уравнений D) "как периодические функ-
ции <в при k < /те, тогда как «„,(<?) уже не будет перио-
fl функцией:
um(<P) =
то и Uk(x, у) при A</re-j-l можно найти из равенств
A2), тогда как подобрать Um+1(x, у), удовлетворяющее
соответствующему уравнению, уже невозможно. Но воз-
можно в этом случае выбрать Umvl (х, у) так, чтобы левая
часть этого уравнения отличалась от правой на величину
m+I
(напомним, что можно доказать, что т есть число нечёт-
ное). Величина G связана с величиной g простым соот-
ношением
*) Отметим, что в отличие от ряда (?), в ряд A7) входит
постоянное cv не являющееся, вообще говоря, начальным зна-
чением р.

320 ДОПОЛНЕНИЕ К ГЛАВЕ XI
где А— коэффициент, входящий в члены первой сте-
пени системы (А)*).
2. Из обшей качественной теории (см. доп. 1) сле-
дует, что состояния равновесия разбиваются на 2 класса.
Именно, пусть Р— состояние равновесия. Тогда есть две
и только две возможности: или вокруг Р можно построить
окрестность, не содержащую целиком никакой замкнутой
траектории, окружающей Р, или такой окрестности
вокруг Р построить нельзя.
В последнем случае, очевидно, любая окрестность Р
будет содержать целиком бесконечное множество траек-
торий, окружающих Р.
Можно дать два определения понятия центра. Согласно
Пуанкаре, состояние равновесия Р называется центром в
том и только в том случае., если все траектории, пере-
секающие некоторую окрестность U точки Р, замкнуты
и лежат целиком в U, причём U можно взять сколь
угодно малой.
Согласно Бендиксону, центром называется такое состо-
яние равновесия Р, в' любой- окрестности которого
лежат замкнутые траектории, окружающие Р (хотя может
быть и не существует окрестности точки Р, сплошь
заполненной замкнутыми траекториями, окружающими Р).
Возникает, естественно, вопрос: в каких случаях оба
определения центра эквивалентны. Иначе: каковы должны
быть условия, наложенные на правые части системы,
чтобы каждое состояние равновесия, являющееся центром
в смысле Бендиксрна, было необходимо и центром
в смысле Пуанкаре.
Для исследованной здесь системы (А) имеет место
эквивалентность обоих определений. В самом деле, если
не выполнены условия центра (т. е. не все коэффи-
циенты ик (<р) ряда B) являются периодическими функ-
циями от о), то, как мы видели, в некоторой окрестности
начала координат нет ни одной замкнутой траектории.
Если же условия центра выполнены (все мА(<р) перио-
дичны), то, как мы видели, все траектории, пересекающие
*) Ср. Ляпунов, циг. сочинение, стр. 165—169.

ЦЕНТР 321
достаточно малый отрезок полярной оси: ? = 0,
0<!р<!с0 — замкнуты. Так как из уравнения (В) следует,
что каждую прямую <р = <р0 можно путём замены пере-
менных р = р, <р = «! — <Ро взять за полярную ось, не
нарушая предпосылок, лежащих в основе рассуждений,
то в некоторой окрестности начала нет ни одной точки,
через которую проходила бы незамкнутая траектория,
т. е. имеет место центр в смысле Пуанкаре.
Дюлак доказал, что если только правые части
системы
голоморфны в некоторой окрестности исследуекого
состояния равновесия Р (хотя бы младшие члены разло-
жений Л' и К в окрестности состояния равновесия были
степени выше первой), то оба определения центра экви-
валентны, т. е. из существования бесконечного мно-
жества замкнутых траекторий, стягивающихся к Р, сле-
дует, что некоторая окрестность U точки Р сплошь
заполнена замкнутыми траекториями, стягивающимися к Р.
В случае же, если правые части X и Y не голоморфны,
то можно построить примеры, когда имеет место центр
в смысле Бенликсона, но не в смысле Пуанкаре. Напри-
мер, это имеет место для системы
где замкнутыми являются траектории хй-\-у2 = —
/Z7C
(k — целое) и только они.
21 А. Пуанкаре.

ДОПОЛНЕНИЕ К ГЛАВЕ XV '
ИНТЕГРАЛЬНЫЕ КРИВЫЕ НА ПОВЕРХНОСТИ ТОРА
В. В. Степанов
Исследования Пуанкаре о расположении интегральных
кривых на поверхности тора были впоследствии приведены
в систему и в одном пункте существенно дополнены
французским математиком Данжуа *).
Рассматривая систему дифференциальных уравнений
A) -%=Ш°), 4г = ф(?' т>.
Данжуа не предполагает, что функции Q и Ф — тригоно-
метрические полиномы или даже аналитические функции.
Кроме того, при наличии условия ФфО допускается
обращение в нуль функции Q. Таким образом, система A)
может быть сведена к уравнению
B) 1% = Мъ<»).
где функция А предполагается непрерывной и однознач-
ной на поверхности тора, т. в. непрерывной периоди-
ческой функцией от двух аргументов <р и ш, с периодом
2тс по каждому из них. Кроме того, требуется, чтобы
через любую точку тора (<р0, ш0) проходила единственная
интегральная кривая уравнения B); для этого достаточно
*) Denjoy, Journal de Mathematiques, IXC, t. 11, 1932.

ИНТЕГРАЛЬНЫЕ КРИВЫЕ НА ПОВЕРХНОСТИ ТОРА 323
предположить, что функция А удовлетворяет по аргу-
менту ш условию Липшица
(?. — положительное постоянное). В частности, это послед-
нее условие выполняется, если существует непрерывная
ал
производная —т— .
Так как функция А не обращается в бесконечность,
то меридиан <р = 0 является, как и у Пуанкаре, циклом
без контакта, и каждое решение дифференциального
уравнения может быть продолжено для —оо<<р< -J-oo,
причём интегральная кривая бесконечное множество раз
пересечёт меридиан <р = 0. Решение, определённое началь-
ными значениями: <р = 0, а> = ш0, может быть записано
в виде.
C) ш = ы(<р, ш0).
При увеличении аргуменга <р на 2ir функция и, вообще,
возвращается к прежнему значению; если при-возраста-
нии <р на 2q-n функция и возрастает на 2ртс (р — целое
число, д —натуральное), то уравнения представляют
цикл, т. е. замкнутую кривую, делающую q оборотов
в направлении меридиана и р оборотов вдоль оси тора.
Рассмотрим далее и как функцию от а>0. Начальным
условиям <р = 0, ^ ш = оH -\- 2ir удовлетворяет кривая
ш=:м(<р, ш0 -J- 2те); но геометрически, в силу однознач-
ности решения уравнения B), это та же кривая C) на
торе, только начальной точке и всем следующим припи-
саны увеличенные на 2тс координаты ш.
Итак, мы получаем:
" (?» °»о + 2ir) = и (<р, ш0) -f 2т.
Вводя функцию
»(?, »о) = в(Ч). шо)— <°о>
мы заключаем, что V, как функция от ш0, допускает период
2и, и при <р = 0 она обращается в нуль при любом и>0.
21*

324 ДОПОЛНЕНИЕ К ГЛ. XV
Если мы рассмотрим два решения уравнения A)
C') ш = ы(<р, ш0), ш' = и (?, ш0'),
причём ш0' — ш0 не является кратным 2ir, то ш' — ш тоже
не может стать кратным 2тс, иначе две характеристики C')
имели бы общую точку; следовательно, разность
и(?. то) —и (?) шо) заключена всегда между теми же
последовательными кратными 2ir, что и разность ш0' — ш0.
В частности, если ш0 — шо'<О, то
для любого <р; таким образом, и япляется при постоян-
ном <р возрастающей функцией от ш0.
Обозначим через C (<р) минимум функции v (<р, ш0)
при изменении ш0 в интервале @,2тг), а через т(<р) её
максимум на том же интервале, и пусть
Очевидно, Д@) = 0. Докажем, что A(<p)<2ir.
В самом деле, в противном случае нашлись бы три
числа о', ш0', а>0" (причём в силу периодичности v можно
считать Шд < аH" < ш0' -f-2ir) такие, что
Но тогда функция
"(Т. %) — «(?,%) = <•)"—о/
принимала бы при (р = 0 значение ш0" — ш0', а при <р —?'
значение Шц — Шд±2тг; следовательно, для некоторого
значения ср", среднего между 0 и ср', разность ш" — ш'
была бы равна 0 или 2тг, что противоречит единствен-
ности.
При помощи функции C) легко написать закон
последования:
ш, = и Bir, ш0) = ш, (ш0)
и вообще
шп = иBл1г, шо) = ш„ (ш0).

ИНТЕГРАЛЬНЫЕ КРИВЫЕ НА ПОВЕРХНОСТИ ТОРА 325
В наших теперешних предположениях легко вицеть,
что о)! является непрерывной возрастающей функцией
от ш0 (см. Гурса, т. III, гл. XXIII); но мы уже не вправе
утверждать, что ш1 есть голоморфная функция от ш0.
Более того, лишь при существовании непрерывной про-
дА
изводной -^— функция o)j допускает непрерывную про-
изводную по ш0.
Однако, условие голоморфности функции а^ = а^ (ш0)
не входит в рассуждения Пуанкаре, и его выводы
остаются справедливыми и в наших предположениях.
Можно вместе с Данжуа доказать в общем случае,
как при наличии, так и при отсутствии предельных
циклов, существование числа вращения ц (рационального
или иррационального).
В самом деле, для шп мы получаем, в силу доказан-
ного: 1) шп есть возрастающая функция от ш0; 2) если
<»оОо'Оо + 27Г> т0 а^Ои'О^ + Зтг; 3) ш„—шо =
= и Bлтс, ш0) — шо = г>Bлтг, ш0) имеет период 2тг по ш0.
Обозначая минимум и максимум функции v Bлтг, а>0),
соответственно, через п$п и щп, имеем
я (Т«-?„)¦< 2*.
Возьмём теперь целое число /?!>1, и пусть n = pr-\- s,
л>-1, 0^5^/7—1. Мы имеем:
, Ph<<»тр — »(»-«р<PV » = 1, 2, .... г;
Pi<mi — m*-i < Tfi» k — rp = l, 2, ..., s; s<p —1.
Отсюда получаем:
ГРРр + s?! < л?» < «Тп < /"РТр + *Ti-
Оставляя р постоянным и неограниченно увеличивая л,
находим:
Р, < llm Р» < lim Tn < Тр-
Но по предыдущему у — Рр< —, следовательно, -|fn
и р„ при я -¦ оо имеют общий предел 2itji, причём
<

326 ДОПОЛНЕНИЕ К ГЛ. XV
Итак,
П
П-ЮО П
Заметим, что эта же формула легко доказывается
и для п < 0.
Очевидно, число ц. есть то самое, которое определено
Пуанкаре в случае отсутствия предельных циклов.
Допустим теперь, что на торе существует замкнутая
траектория, проходящая через точку @, ш0), причём она
приходит снова в эту точку при © = 2^ir и mg=:a>0-f-2pir;
очевидно, что при y = 2rqiz приращение ш0 будет 2rpir
(г — любое целое). Таким образом, для этой частной
последовательности точек имеем
Um «*Г—»д?.
г* оо rq q
В силу доказанного существования предела ц. получаем
!. = .
r q
Итак, при наличии замкнутой траектории число
—рациональное.
. = —
Обратно, пусть jj. = — рационально (дробь дана
в несократимом виде), тогда по определению чисел $q
и т3 мы имеем
Вычитая из этих неравенств величину 2ir— =2ic[t и заме-
чая, что рв-^ 2-rcii. ^ ув» получаем
где 0<^' = 2/;- —^а, 0<тгв'-=^в —2рт. Но— ря'
и Yj' являются минимумом и максимумом непрерывной
функции vBqv, a>0) — 2pir, следовательно, они достигаются
в интервале 0 ^ а>0 <; 2ir и, значит, найдётся такое значе-
ние ш0', что 2piz = vBqiz, шо') = ш?' — ш0'. Соответствую-

ИНТВГРАЛЬНЫ! КРИВЫВ НА ПОВЕРХНОСТИ ТОРА 327
щая характеристика ш ¦- и (<р, <»о') является замкнутой
траекторией.
Для дальнейших рассуждений нам будет полезно
следующее отображение меридиана С тора, соответ-
ствующего <р = 0 на круг- Г радиуса I. Пусть закон
последования на меридиане С будет wt = wl (ш0) и вообще
ш„ = о)„ (о)о). Точке Мо с координатой ш0 на С поставим
в соответствие произвольную точку Мо с угловой коор-
дчнатой t0 на Г; после этого точке Мп [ш„ (ш0)] ставим
в соответствие точку Мп (*0 -}- 2nitu). Точки М„ всюду
плотны на Г; геометрический порядок точек Мп на С
совпадает с геометрическим порядком точек М„ на Г;
если точка Мг лежит на наименьшей дуге М^М^, то
точка Мг лежит на дуге MpMq (см. Пуанкаре, гл. XV).
Мы можем далее дополнить уже установленное соот-
ветствие. Выбросим точку Мо из С и точку Мо из Г
и назовём оставшиеся круговые интервалы соответ-
ственно С и Г'. Любая точка М ? Г', не совпадающая с М„,
делит точки всюду плотного множества {М„}—Мо на
два класса: I — точки Мр, предшествующие М,
и II—точки Мд, следующие за М. В силу устано-
вленного соответствия все точки Мп на С тоже разобьются
на два класса: \Мр\ и {MQ}, причём каждая точка Мр
предшествует любой точке Мг Заметим, что верхняя
грань М' точек Мр не следует ни за какой точкой Mq\
нижняя грань М" точек Мй не предшествует никакой
точке Мр. Если М' = М", то этой точке М' и ставим
в соответствие точку М; если же М' Ф М", то точку М
ставим в соответствие целому сегменту to = [M', M").
Наконец, точке Мо или' же сегменту /=[УИ0', Мо"\,
где Мо' есть верхняя грань, а Мо" — нижняя грань всех Мп
на С, если Мо' Ф Мо", ставим в соответствие точку Мо.
Таким образом, каждой точке с угловой координа-
той t на Г поставлено в соответствие: или точка М, или
сегмент i=[M'% M"\ на С. Предельные точки для мно-
жества \Мп\ суть либо точки М, не принадлежащие
сегментам /, либо концы М', М" сегментов /; ни одна
внутренняя точка этих сегментов не является предельно:;
для точек Мп.

328 ДОПОЛНЕНИЕ К ГЛ. XV
Таким образом, множество Р, рассмотренное Пуанкаре,
является меридианом С, из которого выброшены смеж-
ные интервалы (ЛГ, М"), если таковые существуют. Ото-
бражению o)j = o)j (ш0) меридиана С на себя соответствует
отображение окружности Г на себя, осуществляемое пово-
ротом всех точек этой окружности на угол 2тгц.
Пуанкаре показал, что логически возможны два случая:
либо множество Р' совпадает с С, либо Р нигде не
плотно на С. Данжуа установил, что при требовании
одной только непрерывности функции а^ (ш0) множество Р
может совпадать с любым совершенным неплотным
множеством Е на С, причём смежные интервалы к Е или
составляют один ряд из предшествующих и последующих
интервалов, или же распределяются на конечное или
счётное количество таких рядов.
дА
Если мы введём ограничение: -г- существует" и непре-
рывна, то функция ш1 = ш1 (ш0) = и Bтг, ш0) также допу-
скает непрерывную производную —-(см. Гурса, т. III,
гл. XXIII). Данжуа показывает, что при этих условиях
может быть осуществлён случай нигде не плотного мно-
жества Я', опять с любым числом рядов, на которые
распадаются смежные интервалы; при этом структура
совершенного множества Е, с которым совпадает мно-
жество Р, подчинена определённым ограничениш.
Наибольший интерес представляет, однако, следующий
результат Данжуа. Если -."^ есть Функция ограничен-
ной вариации, то случай всюду разрывного Р не может
иметь места.
Приведём доказательство этой теоремы.
дА
В предположении, что -з— существует, производная
ди
от решения по параметру, -г—, удовлетворяет урав-
нгнию:
d / да \ , i, , ч ч да

ИНТЕГРАЛЬНЫЕ КРИВЫЕ НА ПОВЕРХНОСТИ ТОРА 329
Отсюда, считая решение и (<р, ш0) известным, имеем
, J Аш' (9, и (9, ш,)) d?
В частности,
2л
j" Л'ш (т, я (9,
Отсюда, в силу наших предположений о непрерывности
функции AJ, получаем
Рассмотрим функцию
Эга функция ограничена: In k ^ А (а>0) ^ Jn /С. и, сверх
того, в силу монотонности логарифмической функции, имеет
ограниченную вариацию одновременно с -~-. Пусть пол-
ная вариация функции А (ш0) (по сказанному конечная) есть
V; по определению полной вариации имеем
Допустим, что осуществлён случай всюду разрывного
множества Р'; пусть его смежным интервалам соответствует
на Г счётное множество: { т)}. Пусть X ? {-г)}, и пусть
её последующие будут klt X2 >.„,... Рассмотрим
дугу Un, причём п выбрано равным Qm, где-^ —одна
¦) Постоянный множитель при показательной функции
/ д \ d
равен I. так как ( -
й мно
/ да \ dwa .
-г— = -—- = 1.

330 ДОПОЛНЕНИЕ К ГЛ. XV
из подходящих дробей разложения иррационального числ!
(А в непрерывную дробь. Дуга М„ в тригонометрическом
смысле имеет длину 2irQraji; наименьшая геометрическая
/^
длина дуги АХ„ есть 2ir|Qmn — Рт\.
Докажем, что ни одна из точек Хо, если — л<<7<2я,
, дфп, не попадает в отрезок ХХП.
В самом деле, для — л < 0 < л, q фО и при любом целом
р' имеем kkq=*2iz\p\g\ — p'j > 2tiJ (aQto — Pm\ = dm, так
как |^|<<2m = n. Аналогично для л < q < 2л, при лю-
бом целом р", имеем
так как g—в<л = <?т *).
*) Мы ссылаемся на следующее свойство подходящих дро-
бей непрерывной дроби (см. Хинчин, Цепные дроби, стр. 29—34).
Назовём наилучшим приближением второго рода числа ц такую
дробь— @>О), что для всякой другой дроби -у с положи-
тельным знаменателем 6<д мы имеем: | Ьу. — а |>| efA—р |. Тео-
ремг, о которой идёт речь, такова: всякая подходящая дробь
к иррациональному числу jx есть наилучшее приближение
второго рода.
Вот краткое доказательство этой теоремы. Рассмотрим две
Р Р
последовательные подходящие дроби "' ] и тт2- к бесконеч-
Чт-1 Чт
ной непрерывной дроби, представляющей число ц. Допустим,
что дрсбь -г- (*< Q^) даёт для числа ц лучшее приближение
р
2-го рода, чем дробь -— . В таком случае мы докажем прежде
Чт
а Рт-\ Рт
всего, что -г- не может лежать между п н т»- В самом
' ° Р™-> \-\аЧт-1 — ЬРт-1
деле —--7Г-"Ч= """Т' m х >-гтг1—. так как
I b Чт-1 I I *Qm-l
р числителе стоит целое число :?0; с другой стороны.

ИНТЕГРАЛЬНЫЕ КРИВЫЕ НА ПОВЕРХНОСТИ ТОРА 331
Отметим, что наше утверждение справедливо для лю-
бой начальной точки X.
Рассмотрим теперь два ряда точек:
А = Ад, А1, •••, Ар, • . •> »п-1>
Каждая из геометрических дуг АрХ_п+;, имеет длину, рав-
ную 2irrfm, где dm = \Qmp—Рт\, причём направления
этих-дуг одинаковы и они не содержат внутри себя ника-
кой точки обоих рядов. Следовательно, точки верхнего
ряда чередуются с точками нижнего ряда; также, как и
интервалы 1к, соответствующие на С точкам кк.
Заметим, что если интервал i{ есть последующий для
интервала /0, то, обозначая длины интервалов теми же
символами, что самые интервалы, будем иметь
«о)
так как, в силу предположения, b<^Qm, то
а Рт-1
К I Р" Р™~1 1
Qm-l\^\Qm Qm-lV
чем наше утверждение доказано. Отсюда следует, что числа
ЬРт — aQm и в bPm_t— aQm_x имеют одинаковые знаки.
Покажем теперь, что допущение | Ь\>. — а |< | Qm|x — Рт |
приводит к противоречию. Подставим в предполагаемое нера-
венство выражение ц через, остаточное частное
и, за
Qmrm+\-\- Qm-1
где rm+1>l. Получаем
Qmrm+1 + Qm-1 ¦ I Qmrm + 1+ Qm-1'
Но последнее неравенство абсурдно, так как в левой части его
оба члена числителя одного знака, а, следовательно, весь числи-
тель по абсолютной величине>2. Теорема доказана.

332
ДОПОЛНЕНИЕ К ГЛ. XV
где i(°) есть некоторая средняя точка интервала i0. Иначе,
для этой точки х(°) имеем: h (z^) = In j- . Вообще, беря
аналогичные точки х(«> в интервалах iq, мы получим
V / > откУда h
Составляя абсолютную величину суммы колебаний функ-
ции h между п точками т(«5 в построенных нами чередую-
щихся интервалах, имеем:
n-1
2/
п —1
n-l
или
i4a—in
/o
Отсюда, для данного i0 и для n — Qmi получим:
-у
е
v
Но это неравенство приводит к противоречию, так как
1п -*¦ 0 при п -*¦ ± оо. Теорема доказана.
Функция-^1 имеет ограниченную вариацию, если -^
имеет равномерно относительно ср ограниченную вариа-
цию.
В самом целе, имеем
Поэтому, если полная вариация функции Лш(ср, со) по пе-
ременному со меньше или равна 1^ для любого ср, то

ИНТЕГРАЛЬНЫЕ КРИВЫЕ НА ПОВЕРХНОСТИ ТОРА 333
т. е. вариация функции h (св0), а следовательно, и функ-
ции -~ конечна.
и">0
В частности, это имеет место, если существует непре-
рывная производная Аы, и подавно, если А — аналити-
ческая функция от со и «. Таким образом, вопрос, поста-
вленный Пуанкаре, разрешён; исключительный случай
не может представиться, если А есть аналитическая
функция.
Остаётся добавить об исследовании более общей си-
стемы уравнений A) на торе, предполагая только, что
функции Q и Ф не обращаются одновременно в нуль и
что начальные значения переменных со, <р, при ?=0,
определяют единственную интегральную кривую (это будет
иметь место, в частности, если Q и Ф удовлетворяют
условиям Липшица по переменным <о и ср).
Кнезер *) поставил себе ещё более широкую задачу, со-
держащую исследование кривых, удовлетворяющих на торе
дифференциальному уравнению A), как частный случай,
а именно — исследовать регулярное распреде-
ление кривых на поверхностях двухсторон-
него и одностороннего тора. Если в работе Кне-
зера ограничиться тем, что относится к кривым на двух-
стороннем (обычном) торе, то задача ставится так: иссле-
довать регулярные семейства кривых на
торе. Под регулярным, на поверхности F, семейством
кривых понимают семейство кривых, обладающих следую-
щим свойством: через каждую точку Р поверхности F
проходит единственная кривая, при этом для любой точки
Р существует окрестность, которую можно так отобра-
зить на квадрат, что кривые семейства перейдут в семей-
ство прямых, параллельных стороне квадрата.
Основной результат Кнезера заключается в следующем.
В случае отсутствия замкнутых кривых самое общее регу-
лярное семейство является топологическим образом одного
из двух видов семейств, изученных Пуанкаре, т. е. путём
*) Н. Kneser, Regulure Kurvenscharen аи/ Ringflachen,
Math. Ann., 91 A923).

334 ДОПОЛНЕНИЕ К ГЛ. XV
взаимно однозначного и непрерывного преобразования
поверхности тора общее семейство может быть приведено
в уже изученные нами; таким образом, этот случай топо-
логически не даёт ничего нового.
При наличии замкнутых кривых поверхность тора
разделяется этими кривыми на полосы в конечном или
счётном множестве. Не больше как на конечном числе из
этих полос распределение кривых может быть топологи-
ческим образом семейства интегральных кривых дифферен-
циального уравнения:
dy х
в прямоугольнике |je|<[a, 0<!j/<;i, в котором ото-
ждествлены точки (х, 0) и (х, 1); следовательно, обра-
зами прямых х = —а и х = а являются замкнутые кри-
вые на торе. Далее, может быть конечное или счётное
множество полос, в которых заполняющие их кривые
являются топологическими образами семейства кривых
при условии (х, 0) == (х, 1). Или, наконед, топологическими
образами семейства параллельных прямых х = const.
В первом случае каждая кривая асимптотически прибли-
жается к ограничивающим линиям х= — а кх = а, причём
оба конца кривой приближаются к этим линиям (напом-
ним, что их образами на торе являются предельные циклы)
в одинаковом направлении, например, в направлении
у -»¦ -J- оо. Во втором случае Один конец кривой асимп-
тотически приближается к одной ограничивающей кривой
в направлении у -*•-(- оо, а другой приближается ко вто-
рой прямой в.направлении у-*- — оо. Наконец, в третьем
случае вся поверхность тора между циклами, соответ-
ствующими граничным прямым, заполнена замкнутыми
кривыми.
Только первый случай даёт картину, не предусмотрен-
ную в условиях Пуанкаре и Данжуа (у них в уравнениях
A)Ф не обращается в нуль). Этот случай на поверхности
тора 0 <^ со < 2тг, 0 ^ ср ^ 2тс осуществляется, например,

ИНТЕГРАЛЬНЫЙ КРИВЫЕ НА ПОВЕРХНОСТИ ТОРА 335
при помощи интегральных кривых системы дифферен-
циальных уравнений
~-^= sin ш, -37- = — cos о).
На торе мы имеем предельные циклы ш=0 и ш = тг.
Остальные траектории имеют уравнения
ш = 2 arctg(e'tg-^-),
Из формул видно, что точка на поверхности тора уда-
ляется при /-»¦-{- со и при / -¦ — оо в направлении
ср —>- —{— сзо, если 0 < <в0 < тг, ив направлении <?-*¦ — со,
если 7г<шо<2тг.

ДОПОЛНЕНИЕ К ГЛАВЕ XVI
О ПОВЕДЕНИИ ИНТЕГРАЛЬНЫХ КРИВЫХ СИСТЕМЫ
ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ
УРАВНЕНИЙ ВБЛИЗИ ОСОБОЙ ТОЧКИ
(Обзор современного состояния вопроса)
И. Г. Петровский
Пусть
п
(О ^¦« 2 «<***+.?«(*!. *», -, *п) ('=1. 2,..., Я),
где а1к — постоянные, a <ft—функции, имеющие в некото-
рой окрестности U начала координат О, ограниченные
частные производные первого порядка; в точке О, как
сами функции, так и все их эти производные должны быть
непрерывны и обращаться в 0. Совокупность такого рода
условий мы будем для краткости называть «условиями А».
Кроме того, мы будем иногда предполагать существо-
вание таких положительных чисел М и а, что в- U имеют
место неравенства:
=!. 2, .... я).
В последнем случае мы будем говорить, что система A),
или функции <ft, удовлетворяют «условиям В».

О ПОВЕДЕНИИ ИНТЕГРАЛЬНЫХ КРИВЫХ 337
Система A), очевидно, эквивалентна системе
dxt ^__ с1хя dxn
2 а2кхк + «2
для которой начало координат О является особой
точкой. Мы будем всюду в дальнейшем говорить о повз-
дении интегральных кривых этой системы при /-*-|-оо.
Случай, когда t-+ — оо сводится к этому заменой /на — t
в системе A).
Условимся характеристической матрицей для системы
A) называть Х-матрицу
B) *Я--ИЛ
где Е—единичная матрица, а X — некоторый параметр.
Из теории Х-матриц *) известно, что при помощи
линейного, с постоянными коэффициентами, неособенного
преобразования
=1' 2> •••> ")•
систему A) всегда можно привести к такому канониче-
скому виду
(/=1, 2, .... я),
что характеристическая матрица для системы C)
•) См., например, Бохер, Введение в высшую алгебру,
главы XX и XXI.
22 А. Пуаскаре.

338 ДОПОЛНЕНИЕ К ГЛ. XVI
будет иметь
мп
где Mlsr-некоторые матрицы нормальной формы, структура
которых выяснится ниже, а вне квадратов Мк стоят
только нули.
Нелинейные, члены в новых уравнениях, которые мы
обозначили через <^ (Ур Уъ, •••> Уп)> обладают по отношению
к переменным у$ такими же свойствами, какими обладали
функции ср4 (х1г х2, ..., хп) по отношению к переменным
Xj. В частности, если функции ф{ удовлетворяли «условиям
А» (соответственно «условиям В»), то и функции «^ будут
удовлетворять «условиям А» (соответственно «усло-
виям В»).
Заметим, что если оси Охи Олг2, ..., Охп считать
взаимно ортогональными, то оси Oyv Oy8, ..., Оуп бу-
дут образовывать, вообще говоря, некоторую косоуголь-
ную систему.
Пусть ХЛ — корень характеристического уравнения
-
||
= о.
Каждая матрица Мк соответствует одному какому-нибудь
элементарному делителю (X—Xft)Pft матрицы B), если
\к — действительно, и одной паре сопряжённых элемен-
тарных делителей (к — Х^'ц и (X — Xfc)Pft, если Хй—ком-
плексно.

О ПОВЕДЕНИИ ИНТЕГРАЛЬНЫХ КРИВЫХ 339
В первом случае будем иметь
X — кк, 1 0 0 ... О О
О X — Хл 1 О... О, О
о о л — xft 1 . . . о о
о о о о . . . х—хл 1
о о о о ... о х—хА
причём порядок матрицы равен рк\ в частности, если
рк=\, то матрица Мк состоит из одного элемента
х—хл.
Во втором случае паре сопряжённых элементарных
делителей [к — (ак + /,3Л)]Р* и [к — (ак — /3Л)Р* соответ-
ствует матрица
X — ак —рл ОООО.
рл л — аА 1 0 0 0 .
О О X— ак — рл О О .
О 0 Рл X — ак 1 0 .
О О О ОХ — ак — рл .
О О О О рл X — ак .
порядок которой равен 2ре.
В дальнейшем мы будем предполагать, что матрицы-
Мк расположены так, что действительные части корней
Хл при увеличении k не убывают; а из тех матриц, кото-
рые соответствуют элементарным делителям (X — k^fk и
(X — \kfk, сначала идёт та, которой соответствует мень-
шее из чисел рк и рк".
При дальнейшем изложении мы будем предполагать,
что действительные части всех Х,? отличны от 0, если не
сказано явно обратное.
22*

340 дополнение к гл. xvi
Через A*), соответственно через C*), мы будем обо-
значать линейные системы, полученные из A), соответ-
ственно из C), зачёркиванием функций <pt (соответственно
зачеркиванием функций <]><), т. е.
dt _
A*) ¦**¦= 2а«Л (/=1' 2> •••' п^ "
C*) аа = %Ь<ьУъA=1, 2, ..-,«).
Каноническая система C*) легко интегрируется. В самом
деле, предположим сначала, что все корни Хк действи-
тельны и различны и ни один из них не равен 0. Последнее
условие будет выполнено, если определитель |a<ft| Ф 0.
Корни kt будем считать расположенными в порядке воз-
растания их.
Тогда система C*) имеет вид
&?-Х<у< (/=1, 2 я).
Её решениями будут
D) у(=С^ (/=1, 2, .... я).
Нас будут интересовать те интегральные кривые D),
которые при t->-\-co приближаются к началу координат
О. Такие кривые мы будем называть О-кривыми. Ясно,
что для таких кривых в уравнениях D) могут быть отлич-
ными от 0 только те Q, которым соответствуют отрица-
тельные корни Х<; пусть число таких корней будет nv
Тогда все О-кривые системы C*) распадутся на следую-
щие п14~ 1 классов.

О ПОВЕДЕНИИ ИНТЕГРАЛЬНЫХ КРИВЫХ 341
В «j-й класс мы относим все те О-кривые, у которых
при t-> -\- оо медленнее всех *) стремится к 0 координата
уп1, которые, следовательно, касаются оси Оупх в начале
координат. Этот класс кривых мы получим, если в урав-
нениях D) будем считать
Ст равным любому действительному числу^ отличному
от 0, а все остальные С< будем выбирать совершенно
произвольно. В этот «ласе входят все О-кривые, за исклю-
чением только тех, для которых СПх = 0 и которые обра-
зуют («! — 1)-мерное многообразие в пространстве (уи
У* •••» Уп)-
В (ях—1)-й класс входят все те О-кривые, у которых
медленнее всех стремится к 0 при t -*¦ -(- °° координата
уп -1 и которые, следовательно, касаются в начале коор-
динат оси Oyni_v Для таких кривых
^-1 равно любому отличному от 0 числу, а все осталь-
ные Ct произвольны. К этому классу относятся все те
исключительные О-кривые, о которых говорилось в конце
предыдущего пункта, за исключением тодько тех, у кото-
рых Gni_1 = 0 и которые образуют .(«i — 2)-мерное мно-
гообразие.^ "... , ¦ .,-.
Вообще, в s-й класс мы относим все те О-кривые,
у которых при f->-f-°° медленнее всех стремится к О
координата уа и которые, следовательно, в начале коор-
динат касаются оси Оув.. Эти кривые целиком покрывают
в окрестности U некоторое s-мерное многообразие, за
исключением находящегося на нём некоторого (* — 1)-мер-
ного многообразия.
Первый класс состоит только из двух О-кривых: пра-
вой и левой полуосей Oyv
*) Мы говорим, что величина а медленнее стремится к 0>i
величина b, если

342 дополнение к гл. xvi
Наконец, 0-й класс состоит только из тривиального
решения системы C*), когда все
Основным результатом в изучении поведения интеграль-
ных кривых вблизи особой точки является то, что факты,
отмеченные выше для системы C*), а, следовательно, и
A), у которой все ^ = 0, имеют место и для общей сис-
темы A), у которой функции <р« удовлетворяют «усло-
виям Л». Это можно сформулировать так:
Пусть система A)удовлетворяет «условиям А», а её
характеристическая матрица \Е — ||а<л|| имеет только
действительные и различные элементарные делители
1-й степени; пусть сверх того |а<л|-т^0- Тогда: 1) каж-
дая О-кривая такой системы имеет в точке О определён-
ную касательную;-^) все О-кривые распадаются на п1-\- 1
классов, где поесть число отрицательных корней детер-
минанта характеристической матрицы B), причём
О-кривые, входящие в s-й класс, имеют общую касатель-
ную и покрывают целиком некоторую s-мерную поверх-
ность за исключением только лежащей t в, ней некото-
рой (s — 1)-мерной поверхности*).
Допустим теперь, что среди элементар-
ных делителей матрицы B) имеются'ком-
плексные, сверх того мы будем сначала предполагать,
что действительные части всех корней детерминанта этой ма-
трицы различны и отличны от 0. Паре комплексных элемен-
тарных делителей [X — (а-^-ф)) и [К — (а — ip)] соответ-
ствуют в системе C*) уравнения;
Умножая первое из этих уравнений на yt, а второе на
У(.п, и складывая их, мы получим
1г=д?>--где
•) О. Perron, Math. Zeitscfirtfi, 1930.

О ПОВЕДЕНИИ'ИНТЕГРАЛЬНЫХ КРИВЫХ 343
и, следовательно,
Поэтому и теперь все О кривые системы C*) можно
разбить на классы совершенно так же, как и в предыду-
щем случае. Те, из, величин yit которым соответствуют
действительные .элементарные делители, а также те из
yt >У{+1 > которым соответствуют пары со-
пряжённых комплексных элементарных делителей, обозначим
соответственно через
При этом нумерацию-величин /у произведем так, чтобы
соответствующие им диагональные члены системы C*J
возрастали при увеличении номера J. Тогда, как легко
видеть, , все Окривые системы C*), а,- следовательно
и системыA*) распадаются на mt-\- 1 классов, где тх есть
число тех Tj, которым соответствуют корнц детерминанта
характеристической .матрицы с .отрицательными действи-
тельными частями. В s-й класс входят все те О-кривые,
у котррых при t ->• + °° из величин rj медленнее всех
стремится к 0 величинам га. Если г8 равно некоторому ук,
то это кривые -касаются; в начале координат оси Оук.
Если же га = У У к'--\-Ук+л, то эти интегральные кривые
касаются в О'"двумерной плбскостй (yh, yjc+i). Соответ-
ственно этим ;двумг возможностям интегральные кривые $-го
класса покрывают' некоторую поверхность' А-го" или
(A -f- 1)-го измерений с выпуском каждый "раз некоторой
поверхности (А—1)-го измерения.
То же сацре имеет место а для систем A) общего
вида, еслЩтолько предположить, что функции ср4 удо*
влетворЪют «условиям А». ' '*'
Дале|, оказывается, чтощ при этих предположениях
у кривых s-го класса поведение, выражения

344 ДОПОЛНЕНИЕ К ГЛ. XVI
при t-*-\- eo также не зависит от функций <р«. Именно
при р>0 и при /->-J-oo имеем
arctg Ш1. _> 4- оо *).
6 Ук ' '
Что касается других arctg ^Ш-, то на их поведение
функции <р< могут влиять очень сильно, какой бы быстроты
приближения к 0 у последних мы ни потребовали, когда
точка (хи х2 хп) приближается к началу координат.
Допустим теперь, что среди элементарных де-
лителей матрицы А?—||а<4| есть несколько
элементарных делителей 1-й степени, соот-
ветствующих корням детерминант а матрицы
B) с одинаковыми действительными частя ми.
Для упрощения изложения мы будем предполагать, что
все элементарные делители матрицы B) действительны.
Если все <р< —0, то из уравнений D) легко видеть, что
при Х<+1 = ... = А<+я> все кривые, которые при неравных
корнях Хк образовывали B-}-1)й, ...\ (г-J-/»)й классы,
теперь сливаются в один класс. Он состоит из О-кривых,
у которых касательные в начале координат лежат в гипер-
плоскости 0><+1 Л+м)- В этом классе есть крявые,
приближающиеся к О по любому направлению, лежащему
в этой гиперплоскости. Все они целиком покрывают неко-
торую {I -|- /»)-мерную поверхность, за исключение^ только
некоторой лежащей на ней t-мерной поверхности/
Чтобы всё это сохранило силу и для общих систем
A) достаточно потребовать, чтобы функции у( удо-
влетворяли «условиям В» **). Что «условий А» для этого
недостаточно, показывают следующие примеры ***):
*) О. Perron, !ос. cit.
**) Для п = 2 см. О. Perron, Uber die Gestalt der Integral-
kurven einer Dlfferentlalgleichung erster Ordnung lif der Uragebung
eines singularen Punktes, Math. Zeitscbrifli Bd. 15 A922), pp.
121—146. В дальнейшем мы будем коротко обозначать, эту ра-
боту О. Perron II. Для любого п см. I. P«trowsky, Ober das
Verhalten der Integralkurven нпЛ Systems gewOhnllcner Differen-
tialgleichungen In der Nahe eines singularen Punktes. Математ.
Сборник, т. 41 A934), стр. 108—166. .
**•) О. Perron II, p. 1311

О ПОВЕДЕНИИ ИНТЕГРАЛЬНЫХ КРИВЫХ 345
П р-им ер 1. Все интегральные кривые (за исключением
оси О*а) системы
dt
dx%
_
~ a
_
~dt~ . a In I.jci I •
около начала координат даются уравнением ,
Отсюда видно, что все ' они касаются в О оси Ох2.
Между тем у системы
**%
по каждому направлению к О подходит одна и только
одна интегральная кривая; ~
Пример 2. У систем»
^-— х
dt ~ Хи,
1
111 \Ху\
It ** lnUJ '
интегральные кривые (за исключением оси Ох2) даются
уравнением
( elnlnln—). . ,.
Отсюда следует, ^tTO
p^^C-^.l и Hminf^=C—1. '.
Xi -> 0 ¦ '.: *| -Ю
Значит, теперь у этих интегральных кривых в начале
координат вообще нег касательных.

346
ДОПОЛНЕНИЕ К ГЛ. XVI
Аналогично обстоит дело и в том случае, когда
матрица ХЕ—||я<й|| имеет несколько комплексных элемен-
тарных делителей 1-й системы с одинаковыми действи-
тельными частями. '
Перейдём, наконец, к тому случаю, когда матрица
ЬЕ— ||вй|| имеет элементарные делители выше
1-й степени. При этом мы ограничимся случаем, когда
одному и тому же корню детерминанта этой матрицы
соответствует не больше одного такого элементарного
делителя, и этот элементарный делитель действителен,
так как в общем случае дело обстоит подобным же
образом.
Элементарному делителю (к — /й)Р соответствуют в си-
стеме C*) уравнения
E)
Интегрируя эти уравнения, получим
Ы.Л + Q V),;
)¦
Отсюда видно,' что при t-+-\-co и ^<0 величина
yi+1 стремится к 0 медленнее: всех других у$, где
j.= t-^-l, ..., t-\-p, если только не все Cj = 0
(J=i-\- 1, ... , i -\-p). Поэтому все О-кривые, которые при
неравных >rj-+1.1'.;, A.i+JD образовывали бы различные
классы, соответствующие уравнениям E), теперь сольются
в один класс О-кривых, касающихся в О оси Оуц.р. Они
будут покрывать целиком некоторую (i -}- /?)-мерную

О ПОВЕДЕНИИ ИНТЕГРАЛЬНЫХ КРИВЫХ 347
поверхность, за исключением только некоторой, находя-
щейся на ней г-мерной поверхности.
Подобным же образом можно разобрать случай, когда
имеется несколько действительных или комплексных эле-
ментарных делителей, соответствующих одному и тому же
корню матрицы B).
Чтобы сохранился неизменным характер поведения
интегральных кривых вблизи точки О и для общих
систем A), опять достаточно потребовать, чтобы
функции <?( удовлетворяли «условиям В»*).
До сих пор мы предполагали, что ни у одного корня
детерминанта характеристической матрицы B) действитель-
ная часть не обращается в нуль. В противном случае
легко построить примеры, показывающие, что функции <р<
весьма сильно влияют на поведение интегральных
кривых системы A) вблизи точки О. Но даже в этом
случае можно показать *'*), что вблизи О всегда суще-
ствует «j-мерная поверхность, целиком заполненная О-кри-
выми; здесь п1 есть число тех ' уравнений канонической
системы A), у которых на главной диагонали стоят
отрицательные коэффициенты. Эти О-кривые при t -* -\- со
ведут себя совершенно так же, как если бы ни у одного ^
действительная часть" lie обращалась в О: они распадаются
на,такие же классы; функции arctg-^il. в , случае ком-
плексных корней ведут себя опять попрежнему и т. д.
*) Для п — 1 см. О. Perron II. Для любого я см. /. Pet-
гоwsky, loc. cit.
**) /. Petrowsky, loc clt.

ДОПОЛНЕНИЕ К ГЛАВЕ XVIII .
ОСОБЫЕ ТОЧКИ ВЕКТОРНЫХ ПОЛЕЙ
Ю. Рожанская
ВВЕДЕНИЕ
Исследования этой главы основаны на понятии индекса
особой точки, введенного впервые Кронекером *). Анали-
тическое определение индекса заменено после исследова-
ний Броуэра **) и Гопфа ***) чисто топологическим поня-
тием индекса особой точки векторного поля.
Освобождённая от аналитического аппарата теория
векторных полей играет в 'настоящее время большую
роль, как в топологии, так и в качественной теории
дифференциальных уравнений. Мы не имеем возможности
да^гь здесь полное изложение этой теории, но излагаем
в современных, чисто топологических, терминах лишь
{латЪриал, относящийся к XVIII главе мемуара Пуанкаре,
а также теоремы Кронекера и Гопфа, на которых он
основан. Теория векторных полей опирается на теорию
непрерывных отображений. Из этой последней мы при-
водим необходимые определения и- формулировки теорем.
*) Kronecker, Gber Systeme von Functionen mehrerer Varla-
beln, Monatsberichte de l'Academle de Berlin A869).
**) В г о u w e r, Ober Abbildung von Mannlgfaltigkelten, Math.
Ann. Bd. 71 A912).
***) H. H opf, Vektorfelder In n-dimensionalen Mannigfaltig-
kelten, Math. Ann. 95 A926), p. 225-250.

ОСОБЫЕ ТОЧКИ ВЕКТОРНЫХ ПОЛЕЙ 349
В конце мы указываем на связь современного опреде-
ления индекса с аналитическим определением Кронекера.
§1. Вводные замечания. Рассмотрим л-мерное евкли-
дово пространство /?". Пусть в каждой точке р ? Rn вадан
вектор v(p), длина и направление которого являются
непрерывными функциями точки. Такое векторное распре-
деление называется непрерывным векторным полем.
Если в некоторой точке векторного поля вектор по
длине обращается в нуль, то направление его в этой точке
становится неопределённым, и следовательно непрерыв-
ность направлений в окрестности этой точки нарушается.
Определение 1. Точка с исчезающим вектором
называется особой точкой векторного поля.
Во всём дальнейшем мы будем, рассматривать вектор-
ные поля с конечным числом особых точек.
§ 2. Степень отображения. Пусть 5" есть поверх-
ность достаточно малого я-мерного шара с центром в дан-
ной особой точке, не содержащего ни внутри, ни на
границе других особых точек, кроме* центра. На S",
как на части /?", определено частичное векторное поле
и притом непрерывное. Рассмотрим другую сферу 5"",
так называемую сферу направлений. Перенесём векторы,
определённые на 5», параллельно самим себе в центр
сферы направлений и продолжим их, если это необходимо,
до пересечения с этой сферой. Каждой точке p^S"
будет соответствовать единственная точка пересечения
направления параллельного вектору v(p) со сферой
направлений. Так как сверх того векторное поле на S»-1
непрерывно, то полученное таким образом соответствие
между точками *сферы S* и точками сферы направлений
5"-1 будет однозначным в одну сторону и непрерывным
отображением:
5'*-1 на 5", или на её часть *).
•) Отображение / (S*-1) = S"-1 называется непрерывным
в точке р g 5я-1, если для всякого е>0 существует такое 6>0,
что коль скоро расстояние.от переменной точки х до точки р

350 ДОПОЛНЕНИЕ К ГЛ. XV11I
Полученное нами отображение /Eп-1)=>5'1-1 есть
непрерывное отображение самого общего вида. Из теории
непрерывных отображений известно, что всякое непрерыв-
*
ное отображение f(Sn~1) = Sn-1 может быть с любой
точностью аппроксимировано симплициальным (кусочно*
аффинным) отображением fm (Sn-1) = Sn-1.
При этом, отображение fm E") есть приближение
* 1
отображения / (Sn~1) = -S"" с точностью до — , если
Р (fm (p)»/G°)X~ Л"" любого p^S"-1. Отображение
fm OS") = 5"~1 — симплициальное, если каждый сим-
плекс 7 некоторого симплициального подразделения по-
верхности 5'1 отображается целиком на симплекс х
симплициального подразделения сферы 5". Совокупность
всех симплексов, отображающихся при помощи /т на х,
называется полным прообразом /„-1 (x) симплекса т.
Среди симплексов /„,-* (x) есть, вообще говоря, такие,
которые отображаются на симплекс х с той же индика-
трисой (порядком обхода вершин, или ориентацией). Эти
симплексы мы называем положительными. И возможно
есть такие, которые отображаются с обратной индикатри-
сой. Последние мы называем отрицательными.
Пусть р есть внутренняя точка симплекса х.
Определение 2. Разность между числом положи-
тельных и числом отрицательных симплексов из S"-1,
отображающихся на содержащий точку р симплекс х,
называется степенью отображения /т в точке р.
Степень отображения одна и та же для всякой точки
p^S*-1. Это — число, зависящее от отображения в целом.
Поэтому имеет смысл говорить просто о степени
отображения.
удовлетворяет неравенству р (р, -*)<С &• т0 расстояние между их
образами удовлетворяет неравенству р (/ (p),f (•*))< е. Отобра-
жение, непрерывное в каждой точке из S"-1, называется
непрерывным на S»-1.

ОСОБЫЕ ТОЧКИ ВЕКТОРНЫХ ПОЛЕЙ 351
Пусть
/1E»-1) = 5»-i)/aE»-1) = 5»-1,...,/mE»-1) = 5»-1,. ..
есть последовательность симплициальных отображений, при-
ближающих заданное непрерывное отображение/^»-1) =
*= 6'»-i с точностью до — (/и =1, 2,...). Для каждого из
приближающих отображений мы можем вычислить его
степень. Полученные числа gv g2,.. ,,gm,... обладают тем
свойством, что они совпадают между собою, начиная с неко-
торого достаточно большого числа N.
Определение 3. Степенью отображения / назы-
вается ЧИСЛО g = gN =g7H-i = • • •
Определение 4. Индексом особой точка вектор-
ного поля называется степень отображения f(Sn-1) = Sn~1
сферы, окружающей эту точку, на сферу направлений.
Отметим без доказательства некоторые установлен-
ные Броуэром факты, относящиеся к степени отображе-
ния.
1. Степень отображения/(S"-1) в одну точку поверх-
ности S'1-1 равна нулю. Такое отображение получается,
если векторы параллельны между собой.
2. Степень отображения является инвариантом непре-
рывной деформации отображения, т. е. отображения, кото-
рые можно непрерывно перевести друг в друга, имеют
одну и ту же степень.
3. При умножении (т. е. последовательном применении)
двух отображений их степени перемножаются.
§ 3. Теорема" Кронекера. В дальнейшем мы будем
изучать индексы п-м ерных областей Мп с ^»
ограниченных (и—1)-мерными многообразиями ЛР»-1.
Определение 5. Индексом многообразия Мп
называется степень отображения его границы Мп~1 на
сферу направлений Sn-1; в частности, индексом симплекса
Тп называется степень отображения его границы 5"-1 на
сферу направлений.
Теорема 1. Если внутри симплекса нет особых
точек, то его индекс равен нулю.

352 ДОПОЛНЕНИЕ К ГЛ. XVIII
Доказательство. Действительно, такой симплекс
можно стянуть непрерывным преобразованием в одну
точку, не задевая при этом особых точек. В этой точке
задан вектор, отличный от нуля. В силу непрерывности
векторного поля, векторные распределения на каждой из
промежуточных поверхностей дают нам непрерывную
деформацию первоначального отображений, в отображение
в одну "точку сферы направлений. Степень первоначаль-
ного отображения равна степени окончательного отобра-
жения, т. е. равна нулю.
Теорема 2 (Кронекера). Индекс многообразия
MnaRn, ограниченного (и — 1)-мерным многообразием
М"-1, равен сумме индексов, входящих в Мп особых
точек.
Доказательство. Подразделяем многообразие
Мп на столь, малые- симплексы Tt (/=1,2 k):
чтобы внутри каждого из них было не более одной осо-
бой точки. Кроме того, совокупность границ этих сим-
плексов— граничный комплекс — выбираем так, чтобы на
них также не было особых точек. Заметим, что (л — ^-мер-
ные грани симплексов Tt, не лежащие на граничном
многообразии /И"-1, входят каждая в два и только два
симплекса Ti и Tj, причём, если в Г< эта грань входит
с положительной индикатрисой, то в 7) — с отрицательной.
Пусть 5J1—*, S%~1 S%~1 — границы симплексов
*
= Sn-1 — симплициальные отображения границ симплекса
Т{ на. сферу направлений. Степени отображения S^"*1,
SJ-1 52~'и Мп~1 на 5"-1 соответственно будут:
Si=Pi — «i,Sr2 = /7a — «a gu — Pu—Ч g = P—N,
где р^ Р, nt, N. (/= 1,2 k) — числа положительных
и отрицательных симплексов этих многообразий. Пусть
далее pt, n{ — числа тех положительных и отрицательных
симплексов из 51"-1, которые являются общими гранями
двух симплексов: Т{ и Г, (у = 1,2 k\ j ф i).

ОСОБЫЕ ТОЧКИ ВЕКТОРНЫХ ПОЛЕЙ 353
Заметим, прежде всего, что
О) Л+/С+--- + А = «*+«*+ ••• + «!•
Действительно, если некоторый симплекс из Sf-1,
не входящий в Л1'*-1, входит в границу симплекса 7^ со
знаком плюс, то он же в границу некоторого симплекса 7},
и только одного, войдёт со знаком минус и, следова-
тельно, каждая единица, составляющая р*, войдёт не-
пременно в одно и только в одно из слагаемых правой
части. Отсюда следует, что левая часть равна правой.
Далее легко видеть, что
— (я* + «2 + г-«*).
Следовательно, на основании A)
р _ N = (Pi — «i) 4- (Pa — я2) + ... + (рк — я4)
или
Итак, степень отображения многообразия Мп равна
сумме степеней отображений отдельных симплексов, на
которые оно подразделено. Но для тех симплексов, в ко-
торых нет особых точек, степени отображений равны
нулю, а для симплексов, содержащих особые точки —
равны индексам этих точек. Следовательно, для случая
симплициальных отображений теорема доказана.
Если отображения /4 не симплициальные, мы прибли-
жаем их симплициальными и получаем, в силу упомянутых
определений, тот же результат.
Следствие. Если все особые точки, расположенные
внутри Мп, простые, т. е. их индексы равны + i, то
индекс Мп равен числу положительных особых точек без
числа отрицательных.
В этой форме теорема формулирована у Пуанкаре.
Замечание. При доказательстве теоремы Кроне-
кера мы не пользовались нигде тем, что Мп~1 — связное
многообразие. Теорема справедлива и для области, огра-
ниченной конечный числом связных многообразий.
23 Зав. 471. А. Пуанкаре.

354 ДОПОЛНЕНИЕ К ГЛ. XVIII
§ 4. Многообразия без контакта. В дальнейшем будем
предполагать, что граничное многообразие М1"—1 диффе-
ренцируемо, т. е. имеет непрерывно изменяющуюся каса-
тельную гиперплоскость. "
Определение 6. Многообразие М"—1 называется
многообразием без контакта, если среди векторов не-
прерывного поля, определённого на нём, нет ни одного
касательного вектора.
Теорема 3. Для многообразия без контакта все
векторы либо направлены внутрь этого многообразия,
либо наружу.
Доказательство. Действительно, в противном
случае при переходе от внутреннего вектора к наруж-
ному, в силу непрерывности направления векторов, был бы
по крайней мере один касательный вектор.
Определение 7. Многообразие без контакта, все
векторы которого направлены наружу многообразия, на-
зывается положительным (d'espece positive), а все векторы
которого направлены внутрь — отрицательным (d'espece
negative).
Теорема 4. Индекс многообразия без контакта
зависит только от топологической структуры много-
образия и от его знака (для и = 2, в частности, — от рода
поверхности и от её знака).
Доказательство этой теоремы у Пуанкаре только" на-
мечено и не может быть признано достаточным. Она
является частным случаем более общей теоремы Гопфа,
которую мы приводим далее.
Определение 8. Отображение f~(M'l~1) = Sn-1
называется диаметральным к отображению /(Мп~1) =
* —
= Sn~1, если для любой точки х^М"—1 её образ / (х)
есть точка сферы, диаметрально противоположная точке
Теорема 5. Диаметральное к отображение
»
многообразия Лг*-1 на сферу направлений S"—1 есть,
произведение данного отображения f на диаметральное.
отображение d сферы Sn~l самой на себя.

ОСОБЫЕ ТОЧКИ ВЕКТОРНЫХ ПОЛЕЙ 355
Доказательство. Действительно, положим
* — *
и f(x)=y? S"-1, и пусть у есть точка сферы 5"-1,
диаметрально противоположная точке у. Тогда f(x)=y
и с другой стороны d/(x) = d(y) = у. Следовательно,
Теорема 6. Степень диаметрального отображе-
*
ния сферы S"-1 на самоё себя равна (— 1)".
Д-оказательство. Для и = 2 имеем диаметральное
отображение окружности самой на себя. Оно имеет сте-
пень, равную 1 = (— 1)а, так как любая дуга аЬ пере-
ходит при этом в дугу ab, имеющую ту же индикатрису.
Таким образом, для я —1 = 1 теорема верна.
Предположим теперь, что теорема доказана для
(и — 2)-мерной сферы, т. е. что интересующая нас сте-
пень в этом случае равна (— I)»-1. Докажем утверждение
4 *
теоремы для (и — 1)-мерной сферы S"-1.
- *
Рассмотрим на сфере S»-' экватор 5"-а. Построим
симплекс 7*-1, одна из (и — 2)-мерных граней которого
Г"~а лежит на экваторе и одна вершина а вне экватора.
Далее, пусть 71-1—симплекс, составленный из сим-
плекса Т "-2, диаметрального к Г"-2 и лежащего, следо-
вательно, на том же экваторе, и точки а', диаметральной
к точке а. Индикатрисы симплексов Г"-2 и 7"п-2 будут
одинаковы, если п—1—чётное число, и противоположны,
если и — 1—нечётное. Рассмотрим симплекс Г""-1, по-
лучающийся из Т "-1 зеркальным отражением в эква-
торе 5"-а. Пусть а" — зеркальное отображение точки а'.
Тогда, так как точки а к а" лежат в одном и том же
полушарии, то можно перейти от Г"-1 к т"" с той же
индикатрисой, с которой (и — 2)-мерные грани, лежащие
в плоскости экватора, переходят друг в друга, т. е. с ин-
дикатрисой равной, согласно предположению, (—I)"-1;
переходя затем от Т''п~1 к Г'"-1, мы изменим индика-
трису. Степень отображения окончательно будет равна
(—1) (—1)»-1 = (—1)», что и требовалось доказать.
21*

356 дополнение к гл. xvm
Теорема 7. Если векторное поле на многообра-
зии Мп заменить диаметральным *), то его индекс
изменится на (— 1)п, т. е. не изменится для п чёт-
ного и переменит знак для п нечётного.
Доказательство. Диаметральное векторное поле
на Мп влечёт за собой и диаметральное отображение
границы многообразия Мп, т. е. М"-1 на сферу напра-
влений S»-1. Пусть f {Mn-l)=-Sn-1 — первоначальное
— *
отображение, a f (Mn-1) = Sn~1—диаметральное к нему
отображение. Тогда, на основании теоремы 5, f = df.
Отсюда, в силу упомянутого в § 2 результата, из общей
теории непрерывных отображений имеем: g(f)—g(d) • g(f).
Но на основании предыдущей теоремы: g(d) =ж(—1)п.
Следовательно, g(f) = (—l)n'g(f)> чт0 и требовалось
доказать.
Пусть мы имеем непрерывное отображение/. (М'1-1)^
* * *
= 5"-х многообразия Мп-1 на сферу Sn~i. На 5"-1
задано касательное векторное распределение, многознач-
ное для точек сферы S"-1, но являющееся однозначной
непрерывной функцией от точек Мп-1.
Определение 9. Полученное векторное распреде-
ление называем векторным полем, отнесённым к много-
образию Мп-1.
Предполагаем, как и прежде, что интересующее нас,
отнесённое к М"-1 векторное поле допускает на М*-1
конечное число особых точек, т. е. имеется конечное
*
число прообразов точек из S"-1, в которых по крайней
мере один из приложенных к ней векторов обращается
*
в нуль. Если в некоторой точке из S"-1 более одного
вектора обращается в нуль, то соответствующую точку
из М"-1 мы считаем за кратную.
*) Под диаметральным по отношению к данному вектор-
ному полю' понимается векторное поле, где каждой точке р
отнесен вектор, заданный в точке, диаметральной относительно
точки р.

ОСОБЫЕ ТОЧКИ ВЕКТОРНЫХ ПОЛЕЙ 357
Теорема 8. Сумма индексов особых точек каса-
*
тельного к 5»-1, отнесённого к Мп~1 векторного поля
равна ?i[l+(—1)"], где g^— степень отображения
f1(Mn-1) = Sn~1 многообразия Мп~1 на сферу Sn-1.
Доказательство. Сумма индексов особенностей
нашего векторного поля равна, по определению, сумме
степеней отображений на соответствующие сферы напра-
влений границ симплексов некоторого подразделения
многообразия М"-1. Рассмотрим, для её подсчёта, на 5"-1
лве диаметрально-противоположные точки q и q. В этих
точках проведём (и — 1)-мерные касательные гиперплоскости
га_2 п—8
и в них построим сферы направлений Sq и S- ,
Пусть точка q покрыта, при нашем отображении, Р по-
ложительными и N отрицательными (и—1)-мерными сим-
плексами, где Р — N=gv Пусть Tv /2 Гр, Т[, 7^...,
Т^ — эти симплексы. Заметим, что, беря достаточно мелкое
*
симплициальное подразделение на S4'1 и выбрав точку q
не на границе его, можем предположить все эти сим-
плексы без общих точек в прообразе.
Для симплексов Г4 G=1, 2 Р) и Г/ (/ = 1, 2,. .^ Л/)
производим стереографическую проекцию из точки q на
касательную плоскость в точке q. Для остальных покры-
вающих сферу симплексов произведём стереографическую
проекцию из точки q на касательную плоскость в точке q.
В обоих случаях мы пользуемся стереографической проек-
цией из внешней точки, которая не меняет индика-
трису. Степень отображения границы какого-нибудь из
симплексов Т или Т на 5"~"а равна соответственно 1
или —1 (так как поле, полученное на касательной пло-
скости, есть весьма малая деформация первоначального).
Степень отображения той же границы (как вошедшей
в один из симплексов, отличных от Ti или TJ) на S~ ,
в силу теоремы 6, равна соответственно (— 1)" или
— (—1)п. Таким образом, для симплекса Т сумма степе-
ней отображений на обе сферы равна 1+(— 1)п, для

358 ДОПОЛНЕНИЕ К ГЛ. XVIII
симплекса Т равна —[1+(—1)П1- Отсюда для совокуп-
ности всех симплексов Т{ и 77 сумма степеней отобра-
жения границ есть g1 [1 -)-(— 1)п]. Для всех границ
симплексов подразделения, которые не принадлежат сим-
плексам Т{ и Т-, все отображения будут производиться
по два раза, оба раза в касательную плоскость в q,
и следовательно, так как каждый (и — 2)-мерный симплекс
этой границы входит один раз с плюсом, а другой раз
с минусом (в соседний симплекс), то соответствующие
степени взаимно уничтожаются. Итак, теорема доказана.
Определение 10. Эйлеровой характеристикой
п-мерного комплекса называется альтернированная сумма
с = а° — а1-f-ct2 + <*3-Ь .. . -j- ( — 1")™ а», где а0 —число
вершин, а1 —число ребер, ..-., а"— число «-мерных
симплексов комплекса. Эйлерова характеристика — один
из основных топологических инвариантов комплекса.
Теорема 9 (Гопфа). а) Индекс многообразия
Afczi?", ограниченного отрицательным многообразием
без контакта, равен (— 1)п • с *), где с есть эйлерова
характеристика многообразия Мп; Ь) индекс многообра-
зия М", ограниченного положительным многообразием
без контакта, равен (— 1)" • (— 1)п • с = с *).
Доказательство. Прежде всего заметим, что до-
статочно доказать лишь первую часть теоремы (случай а).
Действительно, если векторное поле на. М"—1 таково,
что Мп~х есть положительное многообразие без контакта,
то, рассмотрев диаметральное векторное поле, мы полу-
чим отрицательное многообразие Мп-1. Тогда случай Ь)
нашей теоремы следует из случая а) и теоремы 7.
Итак, пусть векторное поле в Мп задано таким обра-
зом, что на граничном многообразии Мп~х все векторы
направлены внутрь Ж™-1. Устраиваем из Мп комплекс,
разбивая Мп на конечное число симплексов таким обра-
зом, чтобы на граничном комплексе, составленном из
граней подразделения, не было ни одной особой точки
нашего векторного поля. Для граничного комплекса опре-
*) Последний индекс есть так называемая «Curvatura Integra»
многообразия М\

ОСОБЫЕ ТОЧКИ ВЕКТОРНЫХ ПОЛЕЙ 359
делено непрерывное векторное поле {v (р)}. На границе
каждого из симплексов отбираем те точки, векторы из
которых направлены внутрь симплекса, или в крайнем
случае лежат на границе (для тех граней, которые лежат
на М1*-1, все векторы направлены внутрь единственного
прилегающего к ним симплекса, в силу условий теоремы).
Для всех этих точек строим вспомогательное непрерывное
векторное распределение {и(р)}, которое будет играть
роль поля «внутренних нормалей», удовлетворяющее сле-
дующим условиям:
1) все векторы и (р) направлены внутрь своего сим-
плекса; ^
2) на всех гранях <> — 2 измерений векторы и(р)
и v (р) не совпадают по направлению;
3) на гранях п—1 измерения совпадение векторов
и(р) и v(p) возможно не более, чем в конечном числе
точек.
Рассмотрим полуплоскость, определённую диаметраль-
ным к и(р) вектором и(р) и вектором v(p). Она пере-
секает (и — 1)-мерную грань нашего симплекса, в которой
лежит точка р, по некоторому вектору w(p); причём,
если v(p) лежал сам в этой (и — 1)-мерной грани, то w(p)
совпааает с v(p). Если мы рассмотрим теперь два сим-
плекса из нашего комплекса, примыкающих к одной и
той же (я—1)-мерной грани, то мы видим, что совокуп-
ность всех точек р этой грани разбивается на 3 катего-
рии: I — точки, векторы которых v (p) направлены внутрь
первого симплекса, II — точки, векторы которых v(p)
направлены внутрь второго, и III — точки, для которых
векторы v (р) лежат на общей границе. Образуя векторы
w{p) для обоих симплексов, мы получим векторное рас-
пределение на всей (и—1)-мерной их общей грани, при-
чём, в силу непрерывности векторов и(р) и v(p\ будет
непрерывным и вектор w (p) всюду, за исключением того
конечного числа точек, в которых направления векторов
и (р) и v (р) совпадают между собой. В этих последних
построенная полуплоскость имеет неопределённое напра-
вление, и следовательно для поля {w (p)} получится
особая точка.

360 ДОПОЛНЕНИЕ К ГЛ. XVIII
Поле ['w(p)), определённое на всём граничном ком-
плексе, называется «проекцией» поля [v (p) } при помощи
и (р) на граничный комплекс.
Установим связь между суммами индексов особенно-
стей поля {v(p)} и его проекции {«/(/>)}..
Пусть J? (&= 1, 2, ..., <хп) — симплексы многообра-
зия М*\ 5™ — сумма индексов особенностей поля { v(p)},
«га
лежащих внутри 7^; sn = 2 *? — сумма индексов всех
особенностей поля {я С0)} и s"-1 — сумма индексов осо-
бенностей поля \w(p)\. Особые точки поля {'«;(/?)} рас-
пределяем по разным симплексам, относя особую точку
границы к тому из и-мерных симплексов, внутри кото-
рого произошло совпадение направлений и(р) и v(p).
Определим теперь касательное к S"-1 (сфере напра-
влений) поле w*(p), отнесённое к 'границе S"-1 сим-
плекса Т? следующим образом. Векторные поля и(р)
и v{p) на 5"-1 дают отображения /1(Sn~1) = Sn~1 и
/2{Sn-1) = S'1-1 на Sn~K Соединяем на S"-1 точки f^p)
и /й(р) дугами больших кругов и направляем вектор
/i (Р)> /а (/О по касательной к такой дуге. Каждой точке р
отнесён однозначно некоторый вектор w*(p). Это вектор-
*
ное распределение на 5"-1 многозначно. Совокупность
векторов w*(p) и называется векторным полем { w* {p)},
отнесённым к 5"-1. Особыми точками этого последнего
поля будут те точки р, где совпадают направления век-
торов и(р) и v(p), т. е. как раз особые точки нашей
проекции w(p).
Деформируем границу 5"-1 симплекса Т% вместе с по-
лем { w (р)} в метрическую (л — 1 )-мерную сферу, а поле
{и (р) } в поле внутренних нормалей в этой сфере. Тогда
за сферу направлений может быть взята сама сфера 5"-1,
причём из построения параллельного переноса и(р) и v(p)
в центр S"-1 и пересечения с S"-1 видно, что векторное
поле { w* (/?)} будет зеркальным отражением в экваторе

ОСОБЫЕ ТОЧКИ ВЕКТОРНЫХ ПОЛЕЙ 361
деформированного поля { w (p)}. Так как при деформации
индекс сохраняется, а при зеркальном отражении меняет
знак, то, если обозначим сумму индексов поля w* (р)
на S"-1 через ajj, получим, что сумма индексов w(p) на
S"-1 будет также равна а% и, следовательно,
«»
sn-i _ 2 а"
Для вычисления afcn вводим ещё одно касательное к Sn~x
поле \w**(p)). Выберем на Sn-1 некоторую фиксиро-
ванную точку О* и проведём через точки О*, ft (р), /а(р)
малый круг на S"-1. Строим вектор Л (/0/а (/О по каса-
тельным к этому кругу. Наши круги становятся неопре-
делёнными, когда вместо трёх определяющих их точек
мы имеем только две точки, т. е. когда или /х (р) = О,
или /2(р) = 0 или /, (р)—/а(/0* Таким образом, мы
получаем для нового поля три типа особенностей:
1) точки совпадения направлений и (р) и v(p), где
2) точки, где /j(/?) = 0;
3) точки, где /2(/0 = 0.
Прежде всего, легко видеть, что в окрестности точек
первого типа поле {in** (p)
деформацией поля {w* (p)
является сколь угодно малой
. так как соответствующие
дуги малых кругов сколь угодно мало отличаются от дуг
больших кругов. Поэтому сумма индексов этих особых
точек поля {w** (р)} равна сумме индексов особых то-
чек поля {w* (р)}, т. е. интересующему нас числу а?.
Для вычисления этой суммы индексов, а также суммы
индексов всех особенностей поля { w** (p)} каждой осо-
бой точке р с S11-1 ставим в соответствие касательную
плоскость в /х (р). В этой касательной плоскости рассма-
триваем (л — 2)-мерную сферу направлении S"-8, с цен-
тром в /j (p). Берём столь мелкое¦симплнциальное под-
разделение 5"-1, чтобы в каждый симплекс попало не
более одной особой точки и на границе не было бы осо-

362 ДОПОЛНЕНИЕ К ГЛ. XVIII
бых точек. Рассматриваем векторы fx (x)f^{x) на S"-1
для всех точек jeoSn~a границы симплекса подразделе-
ния, содержащего в себе особую точку р, и переносим
их в центр Sn~2, т. е. в ft (р), стереографически проек-
тируем на касательную плоскость и рассматриваем полу-
ченное отображение Sn~2 на Sn~2. Степень его и есть
индекс точки р.
Вычислим 2 Д/0> т- е> сумму индексов всех особых
р g го**
точек поля \w**(p)}. Обозначим особые точки 1-го
типа через q, 2-го — через г, 3-го—через s.
Тогда
1) 2^(9) = а*> как мы Уже указывали.
2) Индекс одной точки г равен zt 1, смотря по тому,
будет ли симплекс, содержащий эту точку, отображаться
при помощи /j на S"-1 с положительной или с отрицатель-
ной индикатрисой.
Всего мы получим число положительных симплексов,
покрывающих точку О, без числа отрицательных симпле-
ксов, покрывающих ту же точку, при отображении fv
Обозначая степень отображения fx (p) через gt, имеем
2'(/•)= Si-
3) Если бы подсчёт индекса для точек 3-го типа про-
изводился при помощи отображения в касательную плос-
кость в точке /2(s), то мы получили бы для суммы инде-
ксов число ?2 — степень отображения /2. Но так как сфера
направлений 5га~9 лежит в касательной плоскости k/x(s),
для которой /3 (s) — внешняя точка, то ориентация ме-
няется на обратную, и мы имеем
2/(*) = -?2.
Итак, объединяя полученные результаты, имеем:
2/(/»)=e"-f-ft-ft-
р
С другой стороны, мы видели, что по теореме 8

ОСОБЫЕ ТОЧКИ ВЕКТОРНЫХ ПОЛЕЙ 363
Следовательно,
Так как отображение /х соответствует полю { и (р)},
которое можно перевести непрерывно в поле векторов,
смотрящих в одну точку, т. е. в поле «внутренних
нормалей», то его степень, по теореме 6, равна (—1)га.
Отсюда
«*=(- i)ra-x • (-1)" 4-^2=-1 +g* = -1 + Л
так как, по определению: g2 = s%.
Суммируя по всем симплексам Т? (k—l, 2, ..., ап),
получаем
— s"-1 =—a4-\-sn, .
или
Предположим теперь, что теорема Гопфа верна для
(я— 1)-мерного граничного комплекса, т. е. допустим,
что
я—1
Sn-I _(_!)»-! V (
Тогда
2(
i=0
Остаётся проверить справедливость нашзй теоремы для
п=\. Мы имеем в этом случае конечное число отрез-
ков, разбитых на конечное число а1 подотрезков, с по-
мощью а0 вершин! Если в окргстности особой точки
(которая по условию не совпадает с вершинами) все
векторы направлены к неч, то её индекс равен —1, если
от неё, то он равен +1.
Пусть s\—сумма индексов особых точек комплекса
Тр — а1к — число векторов в вершинах) смотрящих внутрь

' 364 Д0П0Л1ЕНИЕ К ГЛ. XVIII
своего симплзкса. Тогда:
если — я? = 2, то sxk=—1;
если — ai = 0, то sxk=-\-1;
если — а1 = 1, то s{ = 0.
к к
Отсюда во всех трёх случаях
Но, с другой стороны, 2( — а1) есть число векто-
ров в вершинах, направленных внутрь своего симплекса,
а каждый вектор в вершине направлен внутрь только
одного из симплексов, которые к этой вершине примы-
кают, т. е. число таких векторов равно числу вершин:
Отсюда, суммируя A), получим: s1 = а1 — а0, что и тре-
бовалось доказать.
Следствие 1. Так как эйлерова характеристика
есть топологический инвариант многообразия Мп, то то
же самоз справедливо для суммы индексов особен-
ностей многообразия Мп.
Следствие 2. Дчя поверхности М2 года р, в част-
ности, имеем, что сумма индексов особенностей в
многообразии М3, ограниченном Мя, равна р—1,
если Ж9—отрицательная поверхность без контакта, и
равна 1—р, если уИ2 — положительная поверхность без
контакта.
Примечание. Так как в доказательстве мы нигде
ке пользовались связностью многообразия М"—1, огра-
ничивающего Мп, то та же формула справедлива и для
случая Мп, ограниченного конечным числом замкну-
тых Мп-1.
§ 5. Аналитическое определение индекса много-
образия. Индекс многообразия Мп~1, или степень отобра-
жения Мп~1 на сферу направлений, можно определить
аналитически, предполагая существование непрерывно

ОСОБЫЕ ТОЧКИ ВЕКТОРНЫХ ПбЛЕЙ 365
изменяющейся касательной гиперплоскости к этому мно-
гообразию. Мы покажем, как это можно сделать для
многообразия М2; для общего случая рассуждения ана-
логичные.
Пусть уравнение многообразия Мэ есть
A) F{x,y,z)~01
где F (а:, у, г) непрерывно дифференцируема. Функции
B) X (х, у, z), Y (х, у, z), Z (х, у, г),
которыми заданы компоненты векторного поля по пря-
моугольным декартовым осям координат х, у, г, мы
тоже будем предполагать непрерывно дифференцируемыми.
¦ Когда точка (я, у, z) описывает поверхность A), кон-
цы векторов B), перенесённые в начало коорлинат про-
странства (?, 1}, ?), описывают поверхность
C) 1 = Х(х,у,г), -ц = У{х,у,г), <.=Z(x,y,z).
Определение индекса, как степени отображения, в
существенном сводилось к подсчёту того числа, кото-
рое показывает, сколько раз (в алгебраическом смысле,
т. е. учитывая ориентацию) поверхность сферы напра-
влений покрыта образами точек поверхности.
Вычислим, какую элементарную площадку dm на сфере
направлений I2 -\- тJ -f- С2 = 1 описывают векторы B),
концы которых образуют элементарную площадку dQ на
поверхности C). Очевидно,
. dQ cos (v, p)
^шта ^>>
где (v, р) есть угол нормали к поверхности с радиусом-
вектором, a S = YX*-{-Y*-\-Z2. Вычисляем далее
COS (V, р) = COS (V, 6) COS (p, I) -f COS (V, T)) COS (p,Tj) -f
+ cos (v, t) cos (РД) -
Таким образом, имеем
D) da> =
v, С)]

366
ДОПОЛНЕНИЕ К ГЛ. XVIII
Мы выразили алгебраическую площадь элемента
единичной сферы через элементарные площадки поверх-
ности C). Остаётся отнести da> к элементарной площадке
dw поверхности A). Эта связь выражается формулой*):
E) cos (v, \) dQ =
cos
D (г, x)
cos (л, у) +
x) v ' ¦" '
D (x, y)
cos
(n,z)]
dw
и двумя аналогичными формулами, получаемыми круго-
вой заменой \, % С Здесь (л, х) есть угол внешней нор-
мали к поверхности A) с осью х, и аналогичное значе-
ние имеют (л, у) и (л, г). Мы предполагаем, что вну-
тренности поверхности A) соответствует область, где
F<0; тогда косинусы углов внешней нормали к поверх-
ности A) с осями координат будут соответственно:
F)
где
1 Лр _1_ dF I dF
"S дх' Иду' "S дг'
jL V \дх
Подставляя значение F) в E), а эти послгдние в D),
и используя формулы преобразования C), находим
f. ur иг иг
шг Vs\ f л\ • f 4\
dF
дХ
дх
дУ
dZ
дх
dF
%
дХ
Ту
дУ
5у
dZ
ду
dF
dz
дХ
дг
дУ
дг~
dZ
дг
1
dw= g
*) В а л л е-П у с с е н, Курс анализа бесконечно малых,
т. 2, гл. I, § 5, 33, или Гу рса, Курс математического анализа,
т. 1, § 137.

ОСОБЫЕ ТОЧКИ ВЕКТОРНЫХ ПОЛЕЙ 367
Покрытая площадь сферы выразится интегралом от dm
по всей поверхности A), а индекс, т. е. число раз, ка-
кое сфера покрыта, получится делением на 4чг, т. е.
индекс равен
— -г- \ — dw.

ПРИМЕЧАНИЯ
24 Зав. 474 А. Пуанкаре,

к мемуару первому
14 'Более точное определение того, что такое качественное
исследование дифференциального уравнения содержится в до-"
полнеиии «Общая качественная теория».
R] Понятие отдельной характеристики, таким образом, не
вполне определено, поскольку не вполне выяснено понятие
кривой, определяемой дифференциальным уравнением. По смыслу
дальнейшего, автор под характеристикой понимает кривую,
изображающую решение уравнения -р = -у (существующее по
теореме Коши, при условии, что начальная точка (х0, у0)
не является «особой», т. е., что Х(х0, у0) и К(х0, у0) не обра-
щаются одновременно в нуль), и продолжения этого решения
(существование которых доказывается с помощью теоремы
Коши) как для этого уравнения, так и для уравнения -т- = у #
В случае, если такое продолжение приводит нас к особой точке,
то специальным соглашением устанавливается, когда характе-
ристика останавливается в этой точке и когда она должна
быть продолжена через особую точку (сравните начало V главы).
В настоящее время более принято пользоваться понятием «траек-
тории», определение которой дано в дополнении «Общая каче-
ственная теория».
Р1 Здесь и всюду в дальнейшем под «кривой» подразуме-
вается кривая, имеющая, за исключением, быть может, конеч-
ного числа точек, непрерывно вращающуюся касательную. —
М Приводимое определение сферического цикла не вполне
точно. Из дальнейшего ясно, что под словами «сферический
цикл» автор подразумевает простую замкнутую кривую, имеющую,
за исключением конечного числа точек, непрерывно вращающуюся
касательную. Аналогично под термином «дуга» подразумевается
простая дуга, имеющая непрерывно вращающуюся касательную,
н лишь в редких случаях допускается существование одной
или нескольких угловых точек.

372 примвч&ния
М Ввиду того, что рассматриваемые циклы могут иметь
угловые точки, вопрос о числе точек пересечения нуждается
в уточнении. Это уточнение автор делает н гл. V.
[*] Утверждение автора, что всякую алгебраическую кривую
на сфере Пуанкаре можно рассматривать как состоящую из
циклов, — нуждается в доказательстве. Это доказательство) хотя
и совершенно элементарное, весьма громоздко, и потому мы
его здесь не приводим. Отиетим» что вопрос о числе этих
циклов становшея вполне определенным лишь в предположении,
что алгебраиче. кая кривая не имеет особых точек. В этом случае
из теоремы Хариака (Mathematische Annalen, Bd. -10 A876)) сле-
дует, что число таких циклив на сфере Пуанкаре не пре-
вышает (я — 1) (л — 2) + 2, если л — степень алгебраической
кривой.
171 В сил/ третьей гипотезы, дуги больших кругов, каса-
тельных к рассматриваемой части характеристики,пересекают
экватор в точках некоторой дуги, одним из концов которой
является точка шх, другой конец этой дуги в тексте обозначен
через и;, так что все точки ш< лежат между щ и ш5. Конец
рассуждений, которыми устанавливается невозможность третьей
гипотезы, заключается по существу просто в ссылке на гео-
метрически очевидные факты.
Р1 Уточним это определение. Заметим, прежде всего, что
под двойными точками автор понимает двойные точки с раз-
личными действительными касательными. Как явствует из даль-
нейшего, полициклом Пуанкаре называет замкнутую самопере-
секающуюся аналитическую кривую, не имеющую других особых
точек, кроме точек самопересечения, которое являются двой-
ными точками. Ьолее сложные особые точки кривых исключаются
нз рассмотрения, пото,\у что в дальнейшем полициклы
используются исключительно для построения так называемой
топографической системы (см. ниже) в предположении, что
дифференциальное уравнение имеет лишь простые особые
точки — узлы, фокусы и сёдла.
Iе! Предполагается! конечно, что ось цилиндра пересекает
поверхность шара и что радиус поперечного сечения цилиндра
меньше радиуса шара.
1101 Здесь автор, в отличие от остальных частей мемуара,
пользуется аналитическим продолжением через особую точку,
в которой дифференциальное > равнение не определено, и через
которую, следовательно, продолжение по теореме Коши невоз-
можно. Поэтому сделанные здесь высказывания о ходе харак-
теристики находятся в некотором противоречии с дальнейшими
соглашениями о продолжении характеристики через особую
точку (см. начало главы V).
1Ц] По поводу таких особых точек «второго рода» см. ра-
боту Фро м м ер а, Интегральные кривые дифференциального
уравнения 1-го порядка..., Успехи Математических наук, вып. IX
A941), стр. 212—253.

ПРИМЕЧАНИЯ 373
I1'] Если бы точка лежала на большом круге х = О, то
/ 1
мы сделали бы подстановку: х = —, у = —, и провели бы со-
вершенна такое же рассуждение.
1131 В тексте знак — отсутствует.
["] В тексте: «Кривые X и Y»
1Щ Заметим, что теорема II непосредственно вытекает из
следствия II на стр. 41, которое выводится независимо от
предыдущих рассмотрений.
1161 Начатую здесь классификацию тех случев, когда на
сфере существуют только две особые точки, Пуанкаре не до-
водит до конца. Поставленный здесь вопрос о том, каковы
должны быть эти особые точки, Пуанкаре решает на стр. 41
(следствие IU).
A71 Степени которых не превышают т—1.
[is] Формула и предшествующий текст помещаются с испра-
влениями, внесёнными редактором трудов Пуанкаре /. Drach.
РЧ Так как
?! + Хох»> + hx™-1 (У—ах) +
-* Су-"*I + •. • 4- хю Су — ах)»
то
-l (y-ax) + Xaxr"»-' (у—ах)' + • • •
+ *« Су-«*)".
1-1 (У - ах) + (Н*«-« (у-ах)* +
н, следовательно,
Отсюда, при y=s ax, учитывая, что
имеем
что и доказывает утверждение текста.

374 примвчания
Щ Так как
у ж аи ''О
то будем иметь
Таким образом, утверждение текста справедливо, если пред-
полагать, что *>0.
РЧ Ввиду того что при изложении теории индекса автор
допускает некоторые неточности (в частности, например, поль-
зуется ие вполне определённым понятием бесконечно малого
цикла), в дополнении «Особые точки векторных полей» даётся
строгая теория индекса.
Щ Предполагается, что учитывается кратность точек пе-
ресечения.
Ш Необходимо иметь в виду, что речь идёт об особых
точках, лежащих на одном из циклов л— 0. На кривой А"=0
могут быть 2 узла или 2 седла, разделённых кратной точкой, на-
пример:
[ЗЦ Рассматривается в противопоставление «общему случаю»
(сы. стр. 33).
[Щ Эта формула может быть получена иным путём, сравните
главу XIII.
1*0] Это соглашение о подсчёте точек пересечения алгебраи-
ческой кривой с алгебраическим циклом ие охватывает целого
ряда случаев (лежащей на цикле изолированной особой точки
алгебраической кривой, точки заострения цикла и т. д.). По-
этому и доказательство теоремы VI, основанное на этом согла-
шении н резюме, которое Пуанкаре делает ниже, верно

ПРИМЕЧАНИЯ 375•
лишь при "известны! оговорках. Мы не даём здесь нужных
уточнений (которые не трудно сделать), потому что в дальней-
шей теория контактов применяется преимущественно лишь при
простейших предположениях.
I*7) Здесь и в дальнейшем, согласно I. Drach. изменены
знаки некоторых неравенств.
РЧ Здесь I. Drach исправлена ошибка, имеющаяся в перво-
начальном тексте.
Iм) Для справедливости дальнейших рассуждений ну ж.
ио сделать предположение, что эти ряды, так же как и ря-
dx dy
ды для х, у, -7J- и —, сходятся равномерно на отрезке
[О, 2яТ.
ро] В силу отсутствия контакта.
[Щ Отметим, что тут Пуанкаре фактически стронт ие дугу
без контакта, а дугу, пересекающую каждую характеристику
лишь в одной точке. Такие дуги могут быть названы «дугами
однократного пересечения» и в некоторых случаях могут играть
ту же роль, что и дуги бее контакта.
Iй) Настоящая теорема сформулирована Пуанкаре в весьма
общем виде; относительно дуги подхватывающей кривой ие
делается никаких предположений, ие считая того очевидного до-
пущения, что она имеет непрерывно вращающуюся касательную.
Доказательство же, даваемое Пуанкаре этой теореме, содержит
ряд предположений, сильно суживающих общность теоремы
(подхватывающая дуга предполагается алгебраической, функ-
ция F меняет знак при переходе через неб и т. д.). Поэтому мы
изложим здесь вкратце идею другого доказательства, без труда
распространяющегося на случаи, рассмотренные в примечаниях
I н II.
Пусть точки пересечения дуги траектории (см. дополне-
ние к гл. V) и поддерживающей дуги будут точки А и В. На
поддерживающей дуге установим определенное направление
движения, например, от Л и Д. Тогда в каждой точке поддер-
живающей дуги существует вектор касательной. Так как эта
дуга не проходит через особые точки дифференциального урав-
нения, то в каждой её точке получается определённый, с точ-
ностью до целократиого 2я, угол между векторами—вектором,
касательным к траектории, проходящей через эту точку,
и вектором, касательным к поддерживающей дуге. Будеммерить
этот угол против часовой стрелки. Тогда, опираясь на опреде-
ление поддерживающей дуги, нетрудно показать, что если
в точке А этот угол меньше я, то в точке В он больше к (или
наоборот). Следовательно, при движении от А к В по поддержи-
вающей дуге, угол этот нечётное число раз будет делаться
кратным числу п,—а каждая точка, в которой этот угол кратен я,
будет, очевидно, точкой касания поддерживающей дуги и траек-
тории.

. 376 ПРИМЕЧАНИЯ
К МЕМУАРУ ВТОРОМУ
I1! Этой главой начинается второй мемуар «О кривых,
определяемых дифференциальным уравнением* (Journal de
Matbematlque, pure et appllquee C-е ser. L VIII A88?)).
PI Ср. по этому поводу дополнение «Общая качествен-
ная теория».
Р] Для уточнения понятия правой и левой сторон дуги/У?
можно поступить следующим образом: соединим точки А и В
простой дугой АСВ, не имеющей с данной дугой АВ, кроме
А н В, никаких других общих точек. Тогда мы получим простую
замкнутую кривую, разбивающую плоскость на две части (по
теореме Жор дана). Точки одной из этих частей будем считать
лежащими справа от данной дуги АВ, а точки другой—слева от
неё.
М Повидимому, название сспираль» автор применяет лишь
к кривым, не имеющим точек остановки. Поэтому пол харак-
теристику, кончающуюся в узле, Пуанкаре не называет спи-
ралью, хотя онан будет пересекать некоторый цикл в одной
только точке.
ГО Последующие, до конца главы, рассуждения Пуанкаре
представляют собою просто разбор нескольких частных примеров,
иллюстрирующих предыдущую теорию.
Щ Из текста следует, что автор имел в виду ещё второй
пример, соответствующий кривой CHFGHD, В втом случае
дуга без контакта пересечена тремя ветвями характеристик,
выходящими из одного седла, и тремя ветвями, выходящи-
ми из другого седла. Собрания трудов Пуанкаре Драша
(/. Drach).
PI Все последующие рассуждения Пуанкаре (до теоремы XV)
хотя и совершенно ясны по идее, но нуждаются в некоторых
уточнениях. Мы не будем приводить их здесь, так как по суще»
ству эти уточнения даны в соответствующих частях дополнения
сОбщая качественная теория».
W Нетрудно уточнить, на основании высказываний, де-
лаемых автором, что здесь понимается под спредельным ци-
клом»: именно, пользуясь понятием траектории, можно ска-
зать, что Пуанкаре называет предельным циклом множество
всех предельных точек незамкнутой полутраектории, если
среди этих предельных точек есть отличные от состояний рав-
новесия.
Iе] Приводимые здесь рассуждения можно рассматривать
лишь как намётку того пути, которым могла бы быть доказана
эта теорема. Смотрите тго этому вопросу дополнение сОбщая
качественная теория».
'« Ш Как уже отмечалось, понятие характеристики у Пуан-
каре .'не вполне определённо. '

ПРИМЕЧАНИЙ 377
Если особая точка, в которой кончается характеристика,
причисляется к этой характеристике, то данное утверждение
очевидно.
Если же эту особую точку не причислять к характе-
ристике (что соответствует и более употребительному те-
перь понятию траектории), то это утверждение, очевид-
но, неверно; характеристики могут итти из узла в узел,
не пересекая алгебраического цикла, проходящего через эти
узлы.
lul Предыдущие рассмотрения не могут, очевидно, счи-
таться доказательством теоремы XVIII. Можно считать доказан-
ным существование спредельного кольца»; легко доказать также,
что вблизи узла или фокуса существует семейство циклов без
контакта, но совершенно нельзя считать очевидным, что между-
кольцевые области можно заполнить циклами и полициклами*
без контакта. Приведённое автором рассуждение является лишь
примером такого заполнения для одного частного случая меж-
ду кольцевых областей. Следует также отметить, что, вообще
говоря, для одного и того же дифференциального уравнения мо-
жет существовать несколько различных, не полосных между
собой топографических систем, удовлетворяющих условиям тео-
ремы XVIII.
Таким образом, теорема XVIII до настоящего времени
остаётся недоказанной.
[ц] Эти слова ии в коем случае нельзя понимать в том
смысле, что топографическая система, удовлетворяющая усло-
виям теоремы XVIII, всегда однозначно определяет качественную
картину характеристик; наоборот, можно построить примеры
качественна различных картии характеристик, допускающих
одну и ту жг топографическую систему кривых без контакта.
Однако знание такой топографической системы всё же весьма
существенно помогает при качественном нсследованин диффе-
ренциального уравнения.
1181 См. примечание 19.
Р*1 В этом месте автор допустил ошибку в вычисле-
ниях, заставившую его (ошибочно) остановиться на первой
гипотезе. Ошибка эта здесь исправлена, согласно вычисле-
ниям редактора. — Собрания трудов Пуанкаре Драша
(J. Drach).
[Щ В этом чертеже была допущена неточность — неверно
дано закручивание спиралей; мы помещаем чертёж в испра-
вленном виде.
\Щ При рассмотрении этого примера Пуанкаре ошибочно
считал экватор предельным циклом. В тексте сделаны необхо-
димые поправки.
[Щ Такое перечисление противоречит основному соглаше-
нию; если считать, что характеристика кончается в седле, то
окружность лг* + _у2 = 9 состоит из двух характеристик; иначе
оиа состоит из двух ветвей характеристик.

378 ПРИМЕЧАНИЯ
I18! При рассмотрении этого примера Пуанкаре ошибочно
считал экватор предельным циклом. В тексте сделаны необхо-
димые поправки.
1191 Пуанкаре точно не определяет, что он понимает под
«полным исследованием», а также не вполне ясно, какой смысл
н содержание он вкладывает в слова: «нахождение уравнения
в конечном виде». Можно думать, судя по примерам предыду-
щей главы, что под «уравнением в конечном виде» пони-
мается алгебраическое уравнение, а под «полным исследова-
нием» — знание уравнений предельных циклов в «конечном
виде» (т. е. в виде алгебраических функций, если, конечно,
8то возможно) и знание качественного хода остальных харак-
теристик.
Очевидно, что в рассматриваемом вопросе нет никакой
принципиальной разницы между алгебраическим и неалгебраи-
ческим уравнением. Это понимание «полного исследования»
имеет смысл и без нужного ограничения вида функций, дающих
уравнения предельных циклов.
Кроме того, очевидно, что «полное исследование» в смысле
Пуанкаре не является только качественным исследованием в со-
временном понимании (см. доп. к гл. V), так как включает в себе
отыскание точного уравнения некоторых траекторий, илн, по
терминологии Пуанкаре, характеристик.
В главе IX Пуанкаре фактически (за исключением сравни-
тельно мелких деталей, которые нетрудно дополнить) проводит
исчерпывающее качественное исследование; с его точки зрения,
однако, оно является «неполным».
[Щ Ло сих пор не известен регулярный метод для каче-
ственного исследования заданного дифференциального уравнения
и, в частности, неизвестен регулярный метод решения той задачи
разделения предельных циклов, о которой говорит Пуан-
каре. Слова Пуанкаре, что такое разделение предельных циклов
всегда возможно, можно, понимать лишь в том смысле, что
это разделение теоретически возможно путём конечного чи-
сла шагов.
РЧ В силу сделанных предположений, на экваторе нет
особых точек.
РЧ Поскольку не указан способ построения функции Fj(x,y)
• (а также и других функций, вводимых Пуанкаре в этой главе,
например, функций Ft,FH,..., илн функций, о которых ои гово-
рит при решении «второй проблемы», см. ниже) для заданного
дифференциального уравнения, — этот метод нельзя считать
регулярным методом, позволяющим решить вопросы о суще-
ствовании и числе предельных циклов. Поэтому «общий метод»
Пуанкаре, равно как и дополняющие его в дальнейшем рассу-
ждения, нужно рассматривать лишь как некоторые приёмы, ко-
торые иногда удаётс использовать, и границы приложимости ко-
торых не установлены. Практически, отыскание функции Fx{x,y),
удовлетворяющей поставленным требованиям (как и отысца-

ПРИМЕЧАНИЯ 379
ние остальных функций, вводимых вдесь), столь затруднительно,
что его обычно не удаётся выполнить даже в том простейшем
случае, которым ограничивается автор. Вопросы, связанные,
с установлением числа и расположения предельных циклов,
вообще остаются и до настоящего времени одними из трудней-
ших вопросов качественной теории дифференциальных уравне-
ний.
W Смысл етого неравенства — кривая контактов имеет
в начале изолированную особую точку; левая часть его была
неправильно вычислена у Пуанкаре. Здесь она приведена в ис-
правленном виде, даняом редактором «Собрания трудов Пуан-
каре», Драшем (J. Drach).
[Щ Всё это рассуждение (касающееся решения первой про-
блемы) может быть уточнено, и в то же время становится на-
гляднее, если использовать понятие траектории (см. дополнение
к гл. V) и ввести параметр /. Тогда, если Ft (х, у) = а и
ft (*,У) = Р — уравнения циклов без контакта, ограничивающих
«сомнительную» область, то, как легко видеть, в точках этих
циклов мы будем иметь
Если —7J имеет равные знякн на циклах ^адв Fi = $, то,
как легко видеть, траектории, пересекающие эти циклы, или
входят в область, ограниченную ими, или все выходят из нее.
Отсюда можно заключить (опираясь на теоремы дополнения
«Общая качественная теория»), что внутри этой области суще-
ствует хотя бы один предельный цикл.
&F\
Если же -— имеет один и тот же знак на циклах Fi = а и
Fi = р, то все траектории, пересекающие один из этих циклов,
входят в ограниченную етнми циклами область, а пересекающие
другой — выходят из неё.
Предполагая, как это неявно делает Пуанкаре, что нет пре-
дельных циклов чётной кратности (см. примеча«не в конце
главы), отсюда уже нетрудно получить, что число предельных
циклов нечВтио в первом случае и четно во втором.
РЧ Повидимому, под «простыми, ие слившимися» и «сливши-
мися* предельными циклами, Пуанкаре понимает следующее:
Пусть С—предельный цикл и АВ— отрезок без кснтакта,
пересекающий его в некоторой точке Р Пусть Si = <f (So)"!—
функция послегования на отрезке АВ. Будем рассматривать
?» к 8%, как прямоугольные декартовы координаты. Тогда кри-
вая Si="f(st) при значении ijj, соответствующем предельному
циклу С, имеет общую точку р с прямой *! = s6. Если <р' (sc) ф 1г
ТО кривая последдвания пересекает прямую st = s0 в точке р\

380 ПРИМЕЧАНИЯ
Мы скажем, по определению, что в этом случае цикл С—про-
стой (однократный) предельный цикл.
Если же ?'(?«) = Ь то кривая st = <p (s$) касается прямой
sl = sn в точке;;, и мы скажем, что цикл С есть кратный
предельный никл (кратности к, если точки р есть А-кратная
точка пересечения кривой последования и прямой ^ = sn) или
же, пользуясь терминотогией Пуанкаре, мы скажем, что имеем
несколько слившихся циклов. Очевидно, С будет четно-кратным,
если вблизи точки р кривая Si = <р <s0) лежит по одну и ту же
сторону прямой s± = So, и нечётно-кратным, если эта кривая
лежит по разные стороны этой прямой.
Введём параметр /, перейдя от одного уравнения к системе,
и будем говорить о траекториях (см. лополнение 1). Условимся,
для определённости, при построении функции последования
двигаться по траектории в сторону возрастающего /, так что
точке Мь последующей для Мв, будет соответствовать большее
значение /, чем точке Afn. Тогда, как легко видеть, при <р'($о)<1
подвижная точка, находящаяся при 1 = 0 на отрезке бга кон-
такта АВ (и не совпадающая с точкой Р), будет при t-*- + re
приближаться к предельному циклу. Иначе можно сказать, что
все траектории, как лежащие вне С, так н лежащие внутри С,
и достаточно близкие к предельному циклу С, неограниченно
приближаются к нему при t ->¦ -\- оо. Точно так же при <р' fij))>l все
траектории, достаточно блиакие к циклу С, удаляются от него
при <-»- + оо (или приближаются при *"-»¦—оо).
Нетрудно видеть, что один из этих двух случаев будет
иметь место по отношению и к нечётно-кратному циклу. В слу-
чае же чбтно-кратного цикла положение иное: если траектории,
лежащие внутри пгедельного цикла С, приближаются к нему
при /->¦ + 00, то траектории, лежащие вие С, должны удаляться
от него при t ->¦ + оо н наоборот.
Построения Пуанкаре теряют силу в- случае чётно-кратного
цикла, подобно тому, как аналогичное алгебраическое построе-
ние теряет силу для четно-кратных корней.
N См. примечание Щ,
I*7] Прн /-»¦ — оо; прн <->-+оо она будет стремиться
к началу координат.
К МЕМУАРУ ТРЕТЬЕМУ
I1] Термин «траектория» Пуанкаре употребляет в смысле,
отличном от того, в котором он употребляется в примечаниях
и в дополнениях. Именно: а) в согласии с «основным соглаше-
нием» Пуанкаре продолжает траекторию через седло (см. гл. V);
б) хотя у Пуанкаре и не сформулировано отчётливо, причисляет

ПРИМ1ЧЛНИЯ 381
лн он нлн нет узел к той траектории, которая кончается в этом
узде (т. е. к бесконечному множеству траекторий), но неко-
торые места заставляют думать, что он неявно это причисление
делает.
PJ Очевидно, что в точках окружностей р= 1 н р=3 тео-
рема единственности решения неверна. Поэтому естественно
было бы считать эти окружности особыми линиями и не про-
должать траекторию, идущую от точки одной из этих окруж-
ностей к точке другой из них. Пуанкаре же опирается на ана-
литическую форму общего решения, и поэтому называет «тра-
екторией» целое множество траекторий в нашем смысле. Кроме
того, не определен знак перед корнем, и, как ясно из дальней-
шего,.он считается то положительным, ю отрицательным. Только
поэтому и получается всюду плотное заполнение кольца одной
«траекторией».
И Здесь, как и в предыдущем примере, Пуанкаре опи-
рается на аналитически ю.'форму общего решеиия и под «траекто-
рией» подразумевает кривую, изображающую функцию, получен-,
иую из данной записи общего решения при определённом зна-
ченди произвольного постоянного интеграции. Только поэтому
в данном примере «траектории», являясь совокупностью разо-
мкнутых кривых, и заполняют всюду плотно всю плоскость.
Вопрос о геометрическом изображении отрицательных зна-
чений раднуса-вектора р остается открытым.
М Словом «устойчивость» пользуются для обозначения
весьма различных понятий. Мы перечислим здесь вкратце не-
которые наиболее важные определения устойчивости траекторий
(употребляя термин «траектория» в смысле дополнения к главе
V). Существуют определения устойчивости, характеризующие
поведение данной отдельной траектории. Таково определение
Пуассона (изложенное в тексте Пуанкаре) и гораздо более
широкое определение Лагранжа, уточнённое Биркгофом, кото-
рый называет траекторию устойчивой, если она не уходит
в бесконечность и не стремится к точкам пространства, где
правые части дифференциальных уравнений имеют особенности.
Наряду с этим существуют определения устойчивости траек-
тории, связанные с тем, как ведут себя соседние траектории
по отношению к исследуемой. Таково определение Ляпунова.
Траектория х ¦» <f(t), у = ty (t) называется устойчивой по Ля-
пунову в данной точке jco= <pft0), _Уо = <Н<о). если при любом
*>0 найдётся такое S>0, что длл всякой траектории х =<р(/),
из неравенств ' .
следуют неравенства
для всех значений U

382 примечания
I51 Таким образом, здесь Пуанкаре причисляет к спиралям
также н траектории, кончающиеся в узле, — которые он, повндн-
мому, раньше к спиралям не причислял^
М Тот факт, что траектория делает бесконечное множе-
ство витков, не вытекает непосредственно из этих рассмотрения.
Это утверждение является непосредственным следствием извест-
ной теоремы Бенднксона (см. дополнение «Общая качественная
теория»).
171 Здесь была допущена ошибка в вычислении; в тексте
даны исправленные вычисления по Драшу (J. Drach).
•PI Легко видеть, что если в системе
dx _ dy
ЧГ~Л' ~ШяаУ
перейти к полярным координатам р, ш, то мы получим:
где Д и Q те самые, которые вводит Пуанкаре.
М Принимая во внимание (см. предыдущее примечание),
что
dp R
33"=""
эти три примера запишутся так:
dm * dm ' dm (? +Пdm ' dm W-trt dut
или, что то же:
. Таким образом, здесь Пуанкаре по неясным причинам фак-
тически просто изменил обозначение полярного угла.
lio] Выбор F совершается на основании следующих трёх
условий:
1) /7=rortst. есть общий интеграл;
2} F{?, <P) есть голоморфная функция от р н <р в окрест-
ности р = 0 при ограниченном ?;
3) разложение F(p, <?) по степеням р должно начинаться
с члена р> (с коэффициентом 1).
Именно поэтому Пуанкаре в третьем примере и делает та-
кой1 выбор Ft со введением вспомогательной функции ф.

ПРИМЕЧАНИЯ 383
1Ц1 Уравнения (ter), кроме первого из них, получаются,
очевидно, из тождества
й dp ^ дч
Функция Но остается при этом неопределённой и находится из
общего требования, чтобы разложение F начиналось бы с членов
х* -{-у* = р* (ср, предыдущее примечание).
[Щ Правильнее было сказать: многозначная функция С (р, ср),
определяемая уравиеннем E), имеет ветвь, голоморфную в точке
р = о, <f = 0 и обращающуюся в этой точке в нуль. Эта ветвь
и удовлетворяет условиям 1° и 2°.
Даже в такой формулировке дальнейшие рассуждения текста
ие доказывают этого утверждения.
1Ш1 Это утверждение также не доказано (ср. примеча-
ние P4J.
1 Это утверждение было бы справедливо, если бы было
доказано, что уравнение
определяет ? как одиозначную функцню от а. Между тем, это
неверно; обозначая j =*— 1, можно без труда убедиться, что
уравнение
х — In х = и,
•квивалентиое предыдущему, определяет х как многозначную
функцню от и.
I15J В силу очевидного свойства: что если /(р)<Сл (?)< то
df dj
1*4 Резюмируем положение.
Достаточность условий «все Со => 0» Пуанкаре доказывает,
устанавливая существование голоморфного, при малых значениях
х и у интеграла системы F{x,y) = k, дающего при малых k
замкнутые кривые. Само доказательство существования голо-
морфного интеграла совершается по методу мажорантных функ-
ций через доказательство существования голоморфного ните*
грала уравнения
Где Я(р) голоморфно при малых р. Это последнее рассужде-
ние, однако, не вполне убедительно (ср. примечания [и], [14]).

384 примечаний
Адамар (Rice Institute Pamphlet, XX, №1,1933 г.) показал, видо-
изменяя рассуждения Пуанкаре, что вспомогательное уравнение
действительно имеет голоморфный интеграл, и что, следова-
тельно, утверждения Пуанкаре правильны. Мы иг будем здесь
останавливаться на этом подробнее, так как с лучай центра разо-
бран в дополнении.
1171 Следует иметь в виду, что Пуанкаре говорит об урав-
нениях вида -л =у-\-..„ -?г =—* + ...,для которых доста-
точно близкие к началу траектории являются либо замкнутыми
кривыми, либо спиралями, закручивающимися вокруг начала.
РЧ В последних двух равенствах под х, у и г подразуме-
ваются новые координаты ?, •») и С. Производимый Пуанкаре
разбор того случая, когда на поверхности 5 есть особые точки*
ввиду своей неполноты является лишь указанием иа то, как
в некоторых случаях задача построения траектории на поверх-
ности, имеющей особую точку, может быть сведена к задаче
преобразования поверхности без особой точки (и траектории
на ней) на поверхность с особой точкой. Мы не останавливаемся
на этом вопросе подробнее ввиду того, что Пуанкаре всюду
в дальнейшем предполагает поверхность не имеющей ни особых
точек, ни уходящих в бесконечность полостей.
[Щ Топологии, по принятому ныне наименованию.
1*°1 Это утверждение нетрудно доказать, если заметить, что
траектория конечной длины, лежащая иа замкнутой поверхно-
сти, может иметь лишь одну предельную точку при t-*-\-<x>
и одну предельную точку при t-t-—оо.
РЧ Современная теория индекса изложена в дополнении
«Особые точки векторных полей». Рассуждения же Пуанкаре
страдают целым рядом неточностей.
РЧ Поскольку определение индекса и все рассмотрения
с внешними и внутренними контактами были у Пуанкаре про-
ведены не строго, это утверждение нельзя считать строго дока-
занным.
Р31 Равномерная сходимость рядов для <р'@ и <}/@ необ-
ходима не только в настоящем случае, ио и в прежде рассмо-
тренном (см. примечание РЧ к мемуару 1).
Заметим, кроме того, что непрерывность суммы ряда есть
лишь необходимое условие для равномерной сходимости ряда.
; Р*1 Как уже было отмечено (см. примечание 1811 к ме-
муару 1), рассуждение Пуанкаре доказывает существование «дуги
однократного пересечения», а не дуги б#з контакта.
РЧ Условие односвязности одной из областей неявно вхо-
дит в самое понятие «поддерживает».
Iм] Принятое теперь определение индекса (см. дополнение
«Особые точки векторных полей») прилагается и к замкнутым
траекториям. Таким образом, рассмотрение траекторий, близких,
к замкнутым, является излишним.

383
$ц Чтобы яснее представить себе построение Пуанкаре,
следует провести в точке Мо отрезок АВ дуги цикла без кон-
тактаЛ^РЛ*! так, чтобы внутренней точкой отрезка Л В являлась
бы точка Мй. Точку Мо' следует взять иа части АЩ этого от-
резка и точку MW — иа М0В (см. чертеж, где М0Ми М'М'
М—дуги траекторий, а М0М[РМ^М0 — построенный
цикл без контакта).
РЧ Из последующего видно, что Пуанкаре не проводит
фактически полициклов через седла, ограничиваясь ссылкой на
совсем ие очевидную возможность такого построения. Поэтому
здесь остаются в силе замечания, сделанные по поводу тео-
ремы XVIII во втором мемуаре.
РЧ Георг Кантор, знаменитый немецкий математик, созда-
тель теории множеств.
[*>] На русском языке основы теории множеств изложены
в книге: Александров и Колмогоров, Введение в тео-.
рию функций действительного переменного.
I31! Здесь мы в целях единства обозначений пишем —,
вместо того, чтобы писать (л, как это было у Пуанкаре.
Щ Здесь Е(х) обозначает целую часть числа х. т. е.
Е(х) есть целое число, удовлетворяющее неравенствам
, как производное множество, является замкнутым.
РЧ Этн дуги носят название «смежных дуг».
Щ Все смежные дуги могут не исчерпываться одной после-
довательностью A(l) B(i); может существовать конечное или
даже счетное множество таких последовательностей.
К МЕМУАРУ ЧЕТВЁРТОМУ
И1_Очевидно, конечно, что ие для всякого уравнения вто-
рого порядка после приведения его к системе трех уравнений
X, Y, Z будут многочленами.
W Заметим, что точки, координаты которых д:0, jo, zu, одно-
временно обращают в нуль X, У и Z, для системы A) ие
представляют никаких особенностей; в них условия теоремы
Кошн выполняются, и единственное решение, удовлетворяющее
начальным условиям
х (*о) = -«о. У D>) = _Уо. г D>) =* г0, при t = t0,
очевидно, будет
х — хо,у = уо, г = 20.
Таким образом, если под траекторией понимать (как это теперь
принято) кривую, изображающую решение системы (I), то ка*
25 Зав. 474. А* Пуанкаре,

386 ПРИМЕЧАНИЙ
ждая такая точка сама по себе есть траектория (состояние р"ав»
новесия).
Щ Брио и Буке рассматривали случай одного уравнения
первого порядка; поэтому при ссылках, делаемых Пуанкаре,
следует иметь в виду, что положения, указываемые Пуанкаре,
не содержатся в мемуарах Брио к Буке. Пикар (Malhemallschc
Annalen, том 46) уточнил доказательства теории Брио и Буке,
ио опять-таки только для системы
dx dy
ах-{-by -f-... а'х + b'y +...
Наконец Дюляк (Dulac, Bulletin de la Soclete mathematlque
de France, t.XL, № 4, 1912 г.) доказал следующую теорему:
Пусть X<(i' = 1, 2, .... ri) — корни векового уравнения для
системы B).
Пусть далее прямая D проходит через начало, не встре-
чает ни одной точки 1{ и оставляет р точек Х1( Ха \р,
по одну сторону, а п—р точек Хр+ь .... Х„ по другую сто-
рону. Мы всегда можем предположить, что числа Xp+i Х„
имеют положительные действительные части, а кр+1.... Хп —
отрицательные действительные части. Тогда можно выразить
переменные Х\, х% хп через переменные гъ гг zp таким
образом, что если z\ удовлетворяют системе р уравнений
J zh гг, .„, zj-t) (/=1, 2 р),
то соответствующие значения х{ удовлетворяют системе
B). Многочлены <?j содержат лишь члены вида:
г?» ,4% " г?'"
где <7i, fa, «•> qi~i~-целые положительные или равные нулю
Числа, удовлетворяющие равенству
I4I Приводим точную формулировку теоремы Пуанкаре.
Пусть X], Х2, ...,ХП — кории векового уравнения,
Предположим, что выполнены следующие гипотезы:
Гипотеза 1. Если действительные и мнимые части корней
Хь \i,...,\n рассматривать как координаты точек плоскости, то
эти п точек должны лежать по одну сторону от некоторой
прямой, проходящей через начало, или, что то же самое, выпуклый
полигон, внутри которого находятся эти точьн, не должен
содержать начала координат.

ПРИМЕЧАНИЯ
38?
Гипотеза 2. Величины \lt X, \п не должны удовле-
. творять ни одному соотношению вида:
где /n:, mit...,mn — целые положительные числа.
Гипотеза 3. Вековое уравнение не имеет кратных корней.
Теорема. Если гипотезы 1, 2 и 3 выполняются, то
уравнения
йхл dx-i dxn
Хч (xi, x% xn) Xn (xi, x% .
имеют интегралы, 'вида
где T{ — голоморфные функции от x\, xit. ..,xn и kt — no'
стоянные интеграции.
Если сравнить эту формулировку с формулировкой текста,
то мы видим, что
I6) Изложение расположения кривых около особых точек
для уравнений высших порядков представляется иам во многих
местах недоказательным, опирающимся только на анализ урав-
нений, у которых X, У и Z лниейиы.
Полное изложение этого вопроса читатель сможет най-
ти в работе И. Г. Петровского «О поведении интегральных
кривых системы обыкновенных дифференциальных урав-
нений вблизи особой точки», Математический сборник,
том 41, М 1.
Iе) Полный анализ случая трёх лииейиых дифференциальных
уравнений с тремя неизвестными читатель найдёт в статье
Кочиной сКритические точки линий тока колниеарного движения
в пространстве», Известия Главной Геофизической Обсерватории,
1929 г., № 1.
Р1 При выполнении условий единственности движущаяся
точка ие может вейтн в особую точку за конечный промежуток
времени. Случай 3) нужно понимать в том смысле, что движу-
щаяся точка достигает особой точки по прохождении конеч-
ного пути.
М Вопрос о реальном значении этих рядов после столкно-
вения анализирован в работах Леви-Чивнта (см. Lev i-C I v i t a
25* ^

388 ПРИМЕЧАНИЯ
«Fralettorle slngolari ed utri nel probleraa rfstretto del tre corpl»
Annall dl Mathemattea, ser. 3, vol. 9, 1903).
Ш Современные основания этой теории изложены в допол-
ненни «Особые точки векторных полей».
1101 Если поверхность во всё время деформации остаётся
без 7 контакта, то угол между нормалью и вектором скорости
не может иерейти через значение-^. Следовательно, тип поверх-
ности не меняется.
Нарушение рода поверхности может произойти только при
нарушении взаимной однозначности соответствия точек перво-
начальной поверхности и деформированной поверхности. При
этом должны были бы слиться точки противоположной ориеи*
тации, что невозможно, есдн ие допускать контактов в проме-
жуточные моменты.
№1 Нам кажется не доказанным это утверждение.
( Вычисление показывает, что, кроме отмеченной особой
точки, таковыми являются все точки окружности: jcj + у* «= а\
г = 0.
РВ1 Можно, например, с помощью геометрических соображе-
ний проверить, что этот индекс равен 1, однако это ие следует
из положительного характера начала координат ввиду наличия
внутри поверхности других особых точек (см. предыдущее
примечание).
1141 По поводу формы решений линейных дифференциаль-
ных уравнений с периодическими коэффициентами см., напри-
мер, Гурса, Курс математического анализа, т. 2, §§ 416, 417,
423, 424.
Р51 В формулах C bis) так же, как и формулах до конца
страницы, нужно всюду заменить s^ большей величиной Sj, что
так же, как и употребление усиливающих функций для — <t>i
и Ф?, увеличивает модуль коэффициентов ф (х).
Тогда функция 'У(х) выбрана таким образом, что кривая
остаётся инвариантной по отношению к преобразованию:
Положим:
и будем сначала искать кривую
X ш ф (г) =з 71* + ?*** + Ь 1ц*п +

ПРИМЕЧАНИЯ 389
инварнаитную по отиошению к преобразованию
Отсюда получаем
Полагая, что | «о |<~о".и приравнивая коэффициенты при оди-
наковых степенях z0 в обеих частях равенства, мы непо-
средственно получаем
• ¦
Ti w 1 и т« (*i — Sjn) ¦»
Тогда, вводя переменные хо, у& уравнение -«о = Ф (^е) можно
записать так:
где ряд в правой части сходится, потому что s± > 1.
Так как _ув = 41' (¦*•)• т0 эт0 и есть уравнение текста; следо-
вательно, неявная функция Уо также может быть разложена
в сходящийся ряд по степеням ха.
Изучение кривых, инвариантных по отиошению к точечному
преобразованию от двух переменных в окрестности двойной
точки, было продолжено в следующих работах:
Т. Levl-Civlta, Sopra alcunl criteri di Instabillta (Annali di
Matematlca, 3e serie, t. V, 1901).
I.-Hadamard, Sur l'lteratlon et les solutions asymptotlques
des equations differentielles (Bulletin de la Soc. Math, de France,
t. XXVI, 1901).
S. Lattes, Sur les equations fonctionnelles qui definlssent
une courbe ou une surface invariante par une transformation
(AnnaH di Matematica. 3e selr, t. XIII, 1906). Собрания трудов
Пуанкаре Драша (J. Drach).
И В исследуемом уравнении свободный член ар — »т>0.
так как он является значением детерминанта преобразования,
который при t=t0 равен +1, а при дальнейшем изменении
не обращается в 0.
РЧ См. Гурса, Курс математического анализа, том II,
§ 416, примеч. 2.
РЧ Ряд может получиться расходящимся. Решение, найден-
ное квадратурами, не будет периодическим по <о и /.
Р91 Неустойчивость в одну сторону. В другую кривые
асимптотически приближаются к периодическому решению.

390 примечания
[*>) В тексте было: «cos(mm -f mp), sin(mu>+п<р)»
РЧ Можно только утверждать, что ряд
am + p,
расходится. Это противоречит лишь абсолютной сходимости
ряда для р.
РЧ В этой заметке допущена ошибка в доказательстве. —
Р31 Это утверждение соответствует тому факту, что инте-
грал от почти периодической функции без постоянного члена
не ограничен, если он не почти периодичен.
РЧ Этот вид устойчивости Пуанкаре назвал устойчи-
востью по Пуассону.

Оглавление
Предисловие • . . 5
ПЕРВЫЙ МЕМУАР
Глава I. Определения и общие замечания 16
Глава II. Изучение характеристик в окрестности дан- •
ной точки сферы 23
Глава III, Распределение особых точек 32
Глава IV. Теория контактов 48
ВТОРОЙ МЕМУАР
Глава V. Теория последующих 61
Глава VI. Теория предельных циклов • . 71
Глава VII. Примеры полного исследования 84
Глава VIII. Отыскание циклов без контакта 92
Глава IX. Примеры неполного исследования 101
ТРЕТИЙ МЕМУАР
Глава X. Устойчивость и неустойчивость .... . . . 105
Глава XI. Теория центров 112
Глава ХИ. Уравнения степени выше первой 137
Глава XIII. Распределение особых точек 145
Глава XIV. Обобщение первых двух частей 151
Глава XV. Детальное изучение тора 165
ЧЕТВЁРТЫЙ МЕМУАР
Глава XVI. Уравнения 2-го порядка; особые точки . . . 192
Глава XVII. Интегрирование рядами 210
Г л а в aXVIH. Распределение особых точек 220
Глава XIX. Исследование замкнутых кривых ..... 231
Дополнение к главам V и VI. Общая качественная
теория (Е. Леонтович и А. Майёр).. .-. .-. ...-.-.-. 267
Дополнение к.главе XI. Центр (А. Майер) . .... 301

Ш бглавйЁЙйй
Дополнение к главе XV. Интегральные кривые на
поверхности тора (В. В. Степанов) 322
Дополнение к главе XVI. О поведении интегральных
кривых системы обыкновенных дифференциальных
уравнений вблизи особой точки (Обзор современного
состояния вопроса) (И. Г. Петровский) 336
Дополнение к главе XVIII. Особые точки векторных
полей (Ю. Рожанская) 343
Примечания 369
Редактор B.'Jt. Демадович. Гехн. редактор М. С. Бондарев.
19,7 уч.-изд, л.
Тираж 8003 а кз,
Закаа а 474.
4-я типография им. Евг. Соколовой треста сШнгаграфвншга» ОГИЗа
при Совет* Министров СССР. Ленинград. Ивмайловсвий пр., 89.
Подписано i
< печати
ч 321 СО тип. зн. в печ.
. Цена книги
12 руб.
J8/IX
л.
1947 г.
241Д печ. л.
А 06691
Переплет 2 руб.