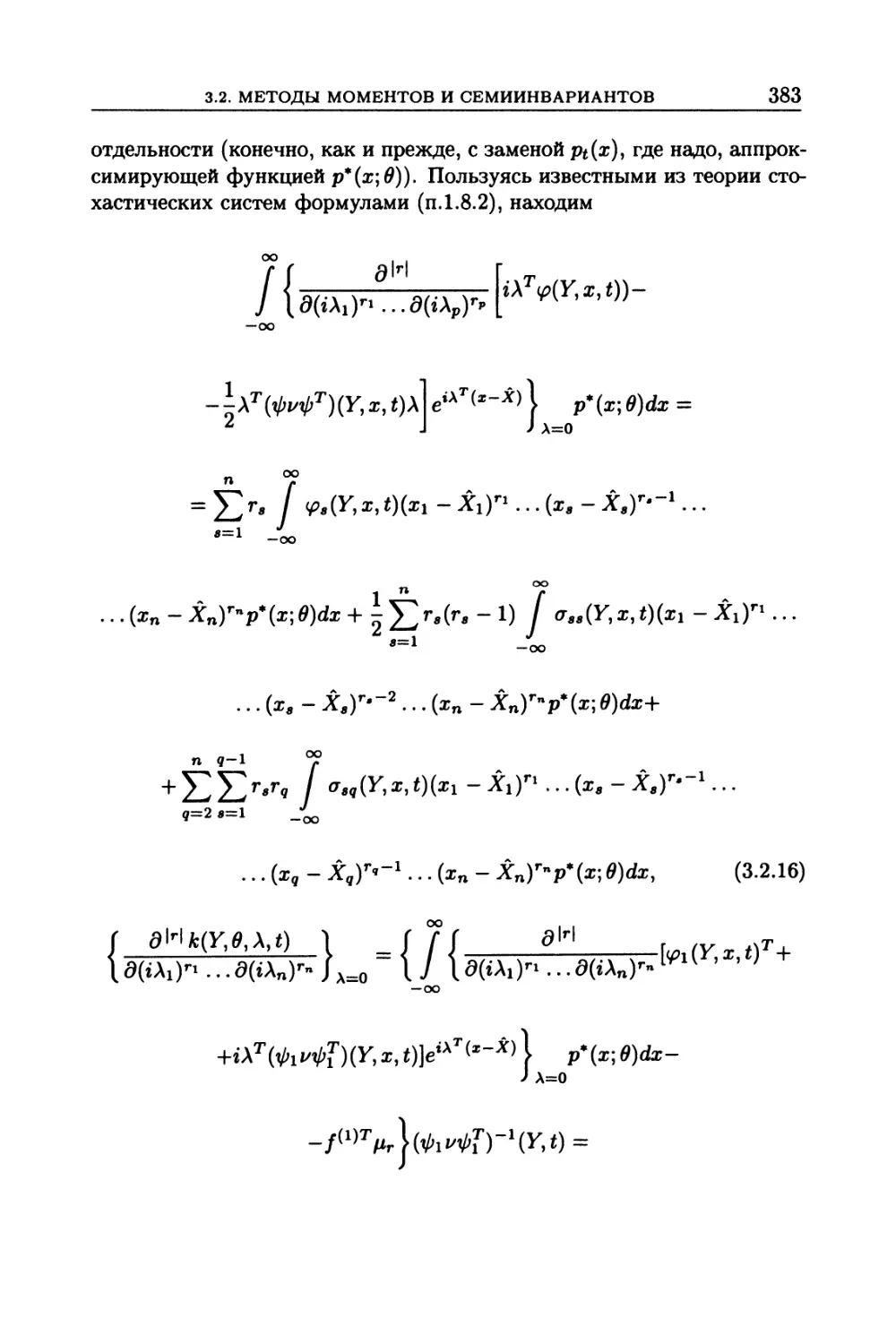Автор: Синицын И.Н.
Теги: вычислительная математика численный анализ математика информатика высшая математика прикладная математика
ISBN: 5-98704-058-2
Год: 2006
Текст
И.Н. СИНИЦЫН
ФИЛЬТРЫ КАЛ
И ПУГАЧЕВА
ФИЛЬТРЫ
КАЛ МАНА
И ПУГАЧЕВА
И.Н. Синицын
И.Н. Синицын
ФИЛЬТРЫ
КАЛМАНА И ПУГАЧЕВА
К
Москва
«Логос»
2006
УДК 519.62
ББК 22.193
С38
Издание осуществлено при поддержке
Российского фонда фундаментальных исследований
Издательский проект 05-01-14043
Синицын И.Н.
С38 Фильтры Калмана и Пугачева: Учеб, пособие. - М.: Универ-
ситетская книга, Логос, 2006. - 640 с.: ил.
ISBN 5-98704-058-2
Дается систематическое изложение теории линейного оценивания
(фильтрации, экстраполяции и интерполяции) процессов в непрерыв-
ных и дискретных стохастических системах на основе фильтров Калма-
на и их обобщений. Подробно излагается теория нелинейного условно
оптимального (по Пугачеву) оценивания. Фильтры Калмана и Пугаче-
ва лежат в основе современных методов оперативной обработки ин-
формации. Для усвоения излагаемых методов приводятся необходимые
сведения из теории стохастических систем и библиографические заме-
чания, а также свыше 300 примеров и задач для упражнений.
Для математиков, физиков, специалистов в области информатики,
радиотехники, теории управления и связи, радиолокации, навигацион-
ной аппаратуры. Может использоваться в учебном процессе высших
учебных заведений при подготовке специалистов и магистров по на-
правлению и специальности «Прикладная математика и информатика».
ББК 22.193
ISBN 5-98704-058-2
© Синицын И.Н., 2006
© «Университетская книга», 2006
© «Логос», 2006
ОГЛАВЛЕНИЕ
Предисловие............................................. 9
Г л а в а 1. Сведения из теории стохастических систем ... 15
1.1. Математические модели систем и их характеристики . 15
1.1.1. Математические модели непрерывных систем (15). 1.1.2. Линейные диффе-
ренциальные системы (25). 1.1.3. Соединения систем и их характеристики (26).
1.1.4. Стохастические дифференциальные системы (31). 1.1.5. Дискретные сто-
хастические системы (33). 1.1.6. Устойчивость, управляемость и наблюдаемость
линейных систем (45).
1.2. Случайные функции ............................................. 53
1.2.1. Вероятностные пространства (53). 1.2.2. Случайные величины (55).
1.2.3. Условные вероятности (56). 1.2.4. Вероятности в конечных произведени-
ях пространств (60). 1.2.5. О вероятностях в бесконечных произведениях про-
странств (65). 1.2.6. Определения и вероятностные меры случайной функции (67).
1.2.7. Некоторые типовые случайные процессы (70). 1.2.8. Вероятности событий,
связанных со случайными функциями (77).
1.3. Моменты, характеристические функции и функционалы ... 78
1.3.1. Математическое ожидание случайной величины (78). 1.3.2. Моменты вто-
рого порядка (80). 1.3.3. Моменты высших порядков (86). 1.3.4. Характеристи-
ческие функции и функционалы (88). 1.3.5. Ортогональные разложения одно- и
многомерных плотностей. Семиинварианты и квазимоменты (91). 1.3.6. Условные
моменты (103).
1.4. Элементы стохастического анализа.............................. 109
1.4.1. Операции анализа над случайными функциями (109). 1.4.2. Интегрирование
случайной функции по неслучайной мере (115). 1.4.3. Интегрирование функций
по случайной мере (118). 1.4.4. Стохастические интегралы (121). 1.4.5. Стохасти-
ческие дифференциалы (132).
1.5. Распределения процессов в стохастических системах.......... 137
1.5.1. Стохастические дифференциальные уравнения (137). 1.5.2. Приведение
уравнений непрерывной стохастической системы к стохастическим дифференци-
альным уравнениям (140). 1.5.3. О численном интегрировании уравнений стоха-
стических дифференциальных систем (144). 1.5.4. Одно- и многомерные распре-
деления в стохастических дифференциальных системах (145). 1.5.5. Одно- и мно-
гомерные распределения в дискретных и непрерывно-дискретных системах (154).
1.6. Методы теории линейных стохастических систем ................. 156
1.6.1. Методы спектрально-корреляционной теории линейных стохастических си-
стем (156). 1.6.2. Методы общей теории линейных стохастических систем (163).
1.7. Методы теории нелинейных стохастических систем (I).
Нормальная аппроксимация и эквивалентная линеаризация .. 169
1.7.1. Моменты вектора состояния. Линейные системы с параметрическими шу-
4
Оглавление
мами (169). 1.7.2. Методы нормальной аппроксимации и эквивалентной линеари-
зации (175).
1.8. Методы теории нелинейных стохастических систем (II).
Параметризация распределений .............................. 182
1.8.1. Вводные замечания (182). 1.8.2. Метод моментов (182). 1.8.3. Методы ор-
тогональных разложений к квазимоментов (193). 1.8.4. Структурная параметри-
зация распределений. Методы эллипсоидальной аппроксимации и линеаризации
(203).
1.9. Дополнения и задачи .................................. 210
Г л а в а 2. Оптимальное оценивание. Фильтры Калмана 237
2.1. Задачи оценивания в стохастических дифференциальных
системах................................................... 237
2.1.1. Оценивание состояния системы (237). 2.1.2. Оценивание неизвестных па-
раметров системы (239). 2.1.3. Экстраполяция состояния системы (240). 2.1.4.
'Постановка математических задач оценивания и экстраполяции в стохастических
дифференциальных системах (240). 2.1.5. Особенности постановок задач интер-
поляции в стохастических дифференциальных системах (242).
2.2. Оптимальная фильтрация в стохастических
дифференциальных системах ...................................... 243
2.2.1. Общая формула для оптимальной оценки (243). 2.2.2. Вспомогательная за-
дача (244). 2.2.3. Преобразование уравнений (245). 2.2.4. Стохастический диф-
ференциал оптимальной оценки функции состояния системы (247). 2.2.5. Урав-
нения для апостериорной характеристической функции (248). 2.2.6. Уравнение
для апостериорной плотности (249). 2.2.7. Стохастический дифференциал апосте-
риорного математического ожидания (250). 2.2.8. Стохастический дифференциал
апостериорного момента второго порядка (251). 2.2.9. Стохастический дифферен-
циал апостериорной ковариационной матрицы (253). 2.2.10. Применение теории
оптимальной фильтрации для оценивания параметров в уравнениях стохастиче-
ских дифференциальных систем (255). 2.2.11. О возможности решения задач
оптимальной фильтрации при автокоррелированной помехе в наблюдениях (255).
2.2.12. Об уравнениях с.к. оптимальной фильтрации в случае винеровских и
пуассоновских шумов (256).
2.3. Оптимальная линейная фильтрация в стохастических
дифференциальных системах .................................... 258
2.3.1. Уравнения линейной фильтрации (258). 2.3.2. Обновляющие процессы (261).
2.3.3. Случай уравнений, линейных относительно вектора состояния (261)
2.4. Линейные фильтры Калмана-Бьюси .......................... 263
3,4.1. Вводные замечания (263). 2.4.2. Об одной форме уравнений фильтра Кал-
мана-Бьюси (266). 2.4.3. Фильтры Калмана-Бьюси для стационарных систем
(267). 2.4.4. Связь между стационарными фильтрами Винера и Калмана-Бьюси
Оглавление
5
(268) . 2.4.5. О некоторых свойствах матричного уравнения Риккати для ковари-
ационной матрицы ошибки фильтрации (268).
2.5. Оптимальная линейная фильтрация при автокоррелированной
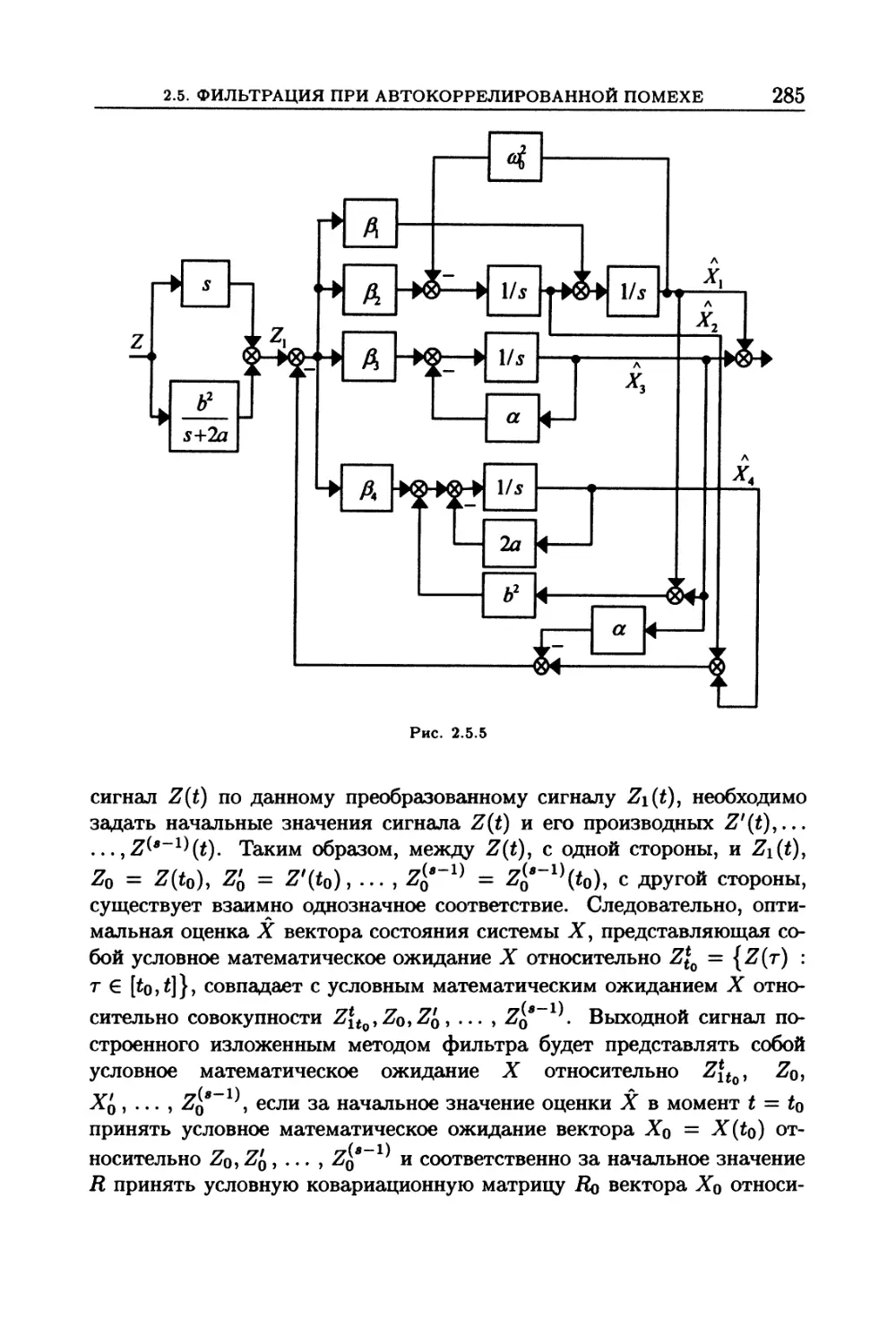
помехе в наблюдениях.............................................. 271
2.5.1. Метод Гулько-Новосельцевой (271). 2.5.2. Метод Брайсона-Йохансена (279).
2.5.3. Начальные условия в случае автокоррелированной помехи (284). 2.5.4. Диф-
ференцирующие свойства оптимального фильтра в случае автокоррелированной
помехи (289).
2.6. Оптимальная линейная экстраполяция и интерполяция ... 290
2.6.1. Оптимальная линейная экстраполяция (290). 2.6.2. Оптимальная интерпо-
ляция (294).
2.7. Фильтрационные уравнения для ненормированных
распределений в стохастических дифференциальных
системах.......................................................... 298
2.7.1. Уравнения ненормированной одномерной плотности (298). 2.7.2. Уравнение
для ненормированной характеристической функции (300). 2.7.3. Об уравнениях
с.к. оптимальной фильтрации для ненормированных распределений в случае ви-
неровских и пуассоновских шумов (301).
2.8. Дискретное оптимальное оценивание ........................... 302
2.8.1. Задача дискретного оценивания (302). 2.8.2. Задача интерполяции в дис-
кретных стохастических системах (303). 2.8.3. Дискретная оптимальная филь-
трация (304). 2.8.4. Дискретная с.к. оптимальная линейная фильтрация (304).
2.9. Дискретные фильтры Калмана................................... 308
2.9.1. Случай некоррелированных шумов (308). 2.9.2. Дискретный фильтр Кал-
мана для коррелированных шумов (313). 2.9.3. Дискретный фильтр Калмана для
автокоррелированных шумов в наблюдениях (314). 2.9.4. Дискретный фильтр
Калмана при линейных преобразованиях (314). 2.9.5. Связь между непрерывны-
ми и дискретными фильтрами Калмана (315).
2.10. Дискретные линейные оптимальные экстраполяторы
и интерполяторы................................................... 316
2.10.1. Дискретные линейные экстраполяторы (316). 2.10.2. Дискретные линейные
интерполяторы (317).
2.11. Устойчивость, управляемость и наблюдаемость
стохастических систем и фильтры Калмана .......................... 320
2.11.1. Вспомогательные утверждения (320). 2.11.2. Основные теоремы (322).
2.11.3. Линейные стохастические дифференциальные системы с автокоррелиро-
ванными помехами в наблюдениях (325). 2.11.4. Дискретные линейные стохасти-
ческие системы (326).
2.12. Оценивание и распознавание в стохастических
системах. Адаптивные фильтры Калмана ............................. 329
6
Оглавление
2.12.1. Задачи оценивания и распознавания (329). 2.12.2. Стохастические диффе-
ренциалы апостериорных вероятностей в задаче распознавания (330). 2.12.3. Оп-
тимальное распознавание в линейных системах (333). 2.12.4. Оптимальное рас-
познавание в случае уравнений, линейных относительно вектора состояния (335).
2.12.5. Адаптивное дискретное оценивание. Адаптивные фильтры Калмана-
Лайниотиса (336).
2.13. Дополнения и задачи ................................. 338
Г л а в а 3. Субоптимальное оценивание.
Обобщенные фильтры Калмана................................. 371
3.1. Субоптимальное оценивание. Метод нормальной аппроксимации 371
3.1.1. Общая характеристика приближенных методов оптимального оценивания
(371). 3.1.2. Метод нормальной аппроксимации апостериорного распределения
(373).
3.2. Методы моментов и семиинвариантов для приближенного
решения фильтрационных уравнений.............................. 378
3.2.1. Метод моментов. Начальные моменты (378). 3.2.2. Метод моментов. Цен-
тральные моменты (381). 3.2.3. Метод семиинвариантов (387).
3.3. Методы ортогональных разложений и квазимоментов
для приближенного решения фильтрационных уравнений ........... 391
3.3.1. Метод ортогональных разложений (391). 3.3.2. Метод квазимоментов (394).
3.3.3. Сокращение числа уравнений (396).
3.4. Уравнения субоптимальной фильтрации для ненормированных
распределений ................................................ 397
3.4.1. Модифицированный метод нормальной аппроксимации (397). 3.4.2. Моди-
фицированный метод моментов (402). 3.4.3. Модифицированный метод ортого-
нальных разложений (404).
3.5. Методы, основанные на упрощении фильтрационных
уравнений .................................................... 409
3.5.1. Способы упрощения уравнений оптимальной фильтрации (409). 3.5.2. Обоб-
щенный фильтр Калмана-Быоси (409). 3.5.3. Фильтры второго порядка (412).
3.5.4. Гауссов фильтр (416). 3.5.5. Априорная оценка точности фильтрации (417).
3.6. Дискретное субоптимальное с.к. оценивание и
распознавание. Адаптивные обобщенные фильтры Калмана .... 418
3.6.1. Дискретное субоптимальное оценивание и распознавание (418). 3.6.2. Суб-
оптимальное адаптивное оценивание (419). 3.6.3. Дискретный субоптимальный
адаптивный фильтр на основе МНА (419). 3.6.4. Дискретный субоптимальный
адаптивный фильтр на основе ОФК (422). 3.6.5. Субоптимальная адаптивная
идентификация (423). 3.6.6. Адаптивное распознавание (426).
3.7. Дополнения и задачи ...................................... 428
Оглавление
7
Г л а в а 4. Условно оптимальное оценивание.
Фильтры Пугачева .................................. 437
4.1. Задачи условно оптимального оценивания в стохастических
дифференциальных системах......................... 437
4.1.1. Основная идея условно оптимальной фильтрации (437). 4.1.2. Классы допу-
стимых фильтров (439). 4.1.3. Классы допустимых фильтров при автокоррелиро-
ванной помехе в наблюдениях (440). 4.1.4. Постановка задач условно оптимальной
фильтрации и экстраполяции (442).
4.2. Решение задач условно оптимальной фильтрации ................ 446
4.2.1. Определение коэффициентов уравнения условно оптимального фильтра
(446). 4.2.2. Случай винеровского процесса и линейного фильтра (449). 4.2.3. Слу-
чай винеровского процесса и нелинейного фильтра (451). 4.2.4. Уравнения для
оптимальных коэффициентов в общем случае (454). 4.2.5. Уравнения, определя-
ющие фильтр Пугачева (458). 4.2.6. Формула для производной ковариационной
матрицы ошибки фильтров и экстраполяторов Пугачева (469). 4.2.7. Применение
условно оптимальной фильтрации к задачам распознавания (470).
4.3. Фильтрация при автокоррелированной помехе в наблюдениях 471
4.3.1. Преобразование уравнений (471). 4.3.2. Определение коэффициентов урав-
нения фильтра Пугачева (474). 4.3.3. Оптимальные коэффициенты уравнения
линейного фильтра (475). 4.3.4. Оптимальные коэффициенты уравнения нелиней-
ного фильтра Пугачева (476). 4.3.5. Уравнения, определяющие фильтр Пугачева
(477). 4.3.6. Формула для производной ковариационной матрицы ошибки (485).
4.4. Условно оптимальная линейная фильтрация ..................... 486
4.4.1. Фильтрация (486). 4.4.2. Фильтрация при автокоррелированной помехе
(492).
4.5. Условно оптимальная экстраполяция............................ 498
4.5.1. Постановка задач условно оптимальной экстраполяции (498). 4.5.2. Урав-
нения, определяющие условно оптимальный экстраполятор Пугачева (499). 4.5.3.
Уравнения, определяющие экстраполятор Пугачева при автокоррелированной по-
мехе в наблюдениях (504).
4.6. Линейная условно оптимальная экстраполяция...................... 509
4.6.1. Экстраполяция (509). 4.6.2. Экстраполяция при автокоррелированной по-
мехе (514).
4.7. Дискретное условно оптимальное оценивание,
распознавание и адаптация ........................................... 518
4.7.1. Постановка задач дискретного условно оптимального оценивания (518).
4.7.2. Классы допустимых фильтров (519). 4.7.3. Дискретный фильтр Пугачева
для нелинейных регрессионных уравнений (520). 4.7.4. Фильтры Пугачева для не-
линейных авторегрессионных уравнений (526). 4.7.5. О двух трактовках дискрет-
ных фильтров Калмана и Пугачева (528). 4.7.6. Применение дискретной условно
8
Оглавление
оптимальной фильтрации к задачам распознавания, идентификации и адаптации
(529). 4.7.7. Дискретный линейный фильтр Пугачева для дискретных линейных
стохастических систем (529). 4.7.8. Дискретный фильтр Пугачева для дискретно
линейной системы с параметрическими шумами (534).
4.8. Дискретная условно оптимальная экстраполяция
и интерполяция .................................................... 537
4.8.1. Дискретная условно оптимальная экстраполяция для нелинейных регресси-
онных уравнений (537). 4.8.2. Дискретные условно оптимальные экстраполяторы
Пугачева для нелинейных авторегрессионных уравнений (539). 4.8.3. Постановка
задачи дискретной условно оптимальной интерполяции (540). 4.8.4. Условно оп-
тимальная интерполяция (540). 4.8.5. Условно оптимальная интерполяция с фик-
сированной задержкой (541). 4.8.6. Условно оптимальная обратная интерполяция
(542). 4.8.7. Линеаризованные дискретные условно оптимальные интерполяторы
(543).
4.9. Эллипсоидальные субоптимальные и условно
оптимальные фильтры ............................................... 546
4.9.1. Эллипсоидальные субоптимальные фильтры, основанные на приближен-
ном решении фильтрационных уравнений (546). 4.9.2. Модифицированные эл-
липсоидальные субоптимальные фильтры, основанные на прибилженном решении
фильтрационных уравнений для ненормированных апостериорных распределений
(552). 4.9.3. Эллипсоидальные субоптимальные фильтры, основанные на МЭЛ
(563). 4.9.4. Эллипсоидальные условно оптимальные фильтры и экстраполято-
ры (565). 4.9.5. Дискретные эллипсоидальные условно оптимальные фильтры и
экстраполяторы (569).
4.10. Условно оптимальное оценивание по бейесовому критерию 571
4.10.1. Постановка задачи (571). 4.10.2. Уравнение для оптимальных коэффи-
циентов (572). 4.10.3. Уравнение для оптимального коэффициента OL при огра-
ничениях (575). 4.10.4. Определение моментов вектора (577).
4.10.5. Уравнения фильтра Калмана-Быоси по бейесовому критерию (577). 4.10.6.
Условно оптимальные фильтры по сложным статистическим критериям (579).
4.10.7. Фильтр Калмана-Быоси по сложному статистическому критерию (582).
4.10.8. Дискретные условно оптимальные фильтры по бейесовому и сложному
статистическому критериям (583).
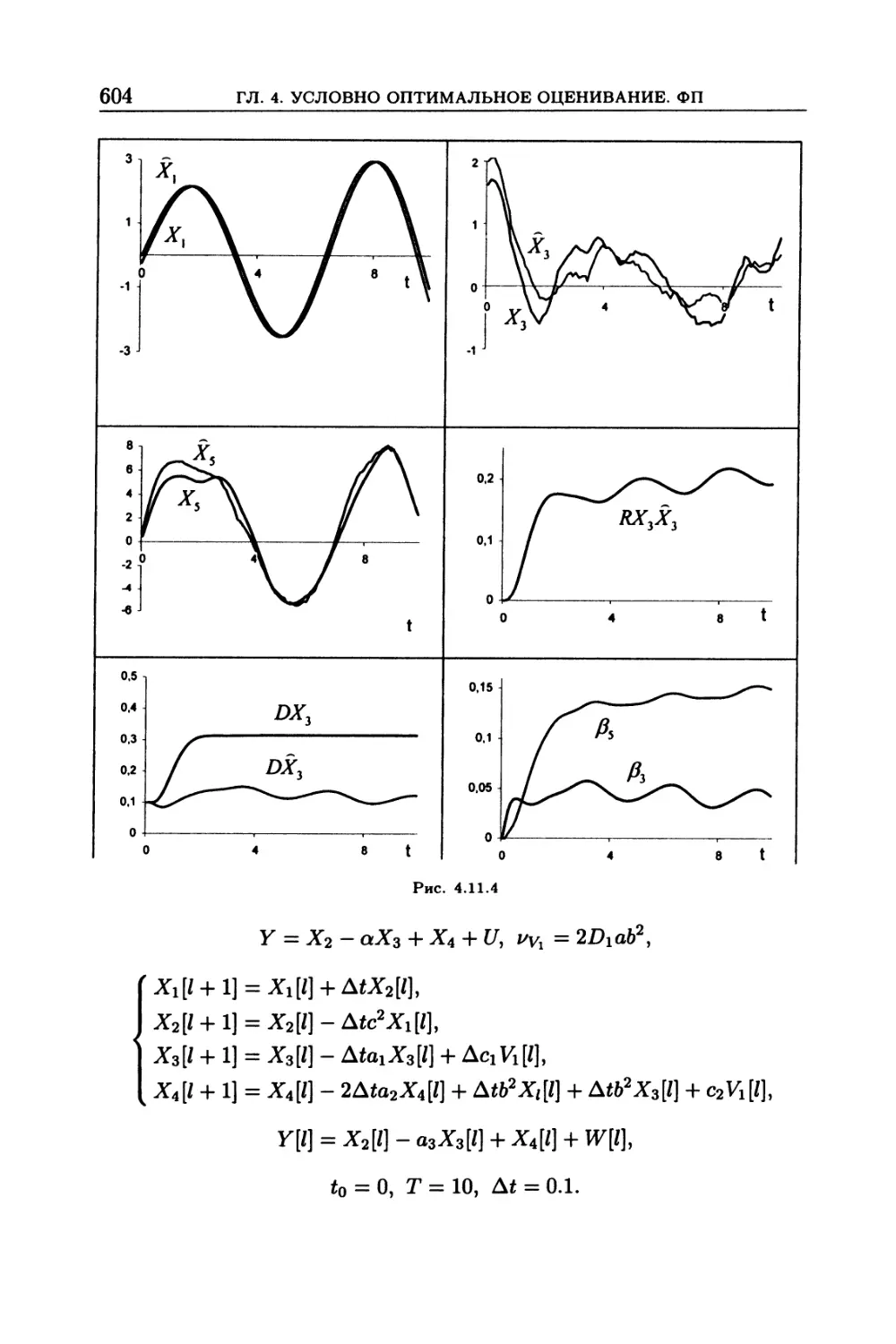
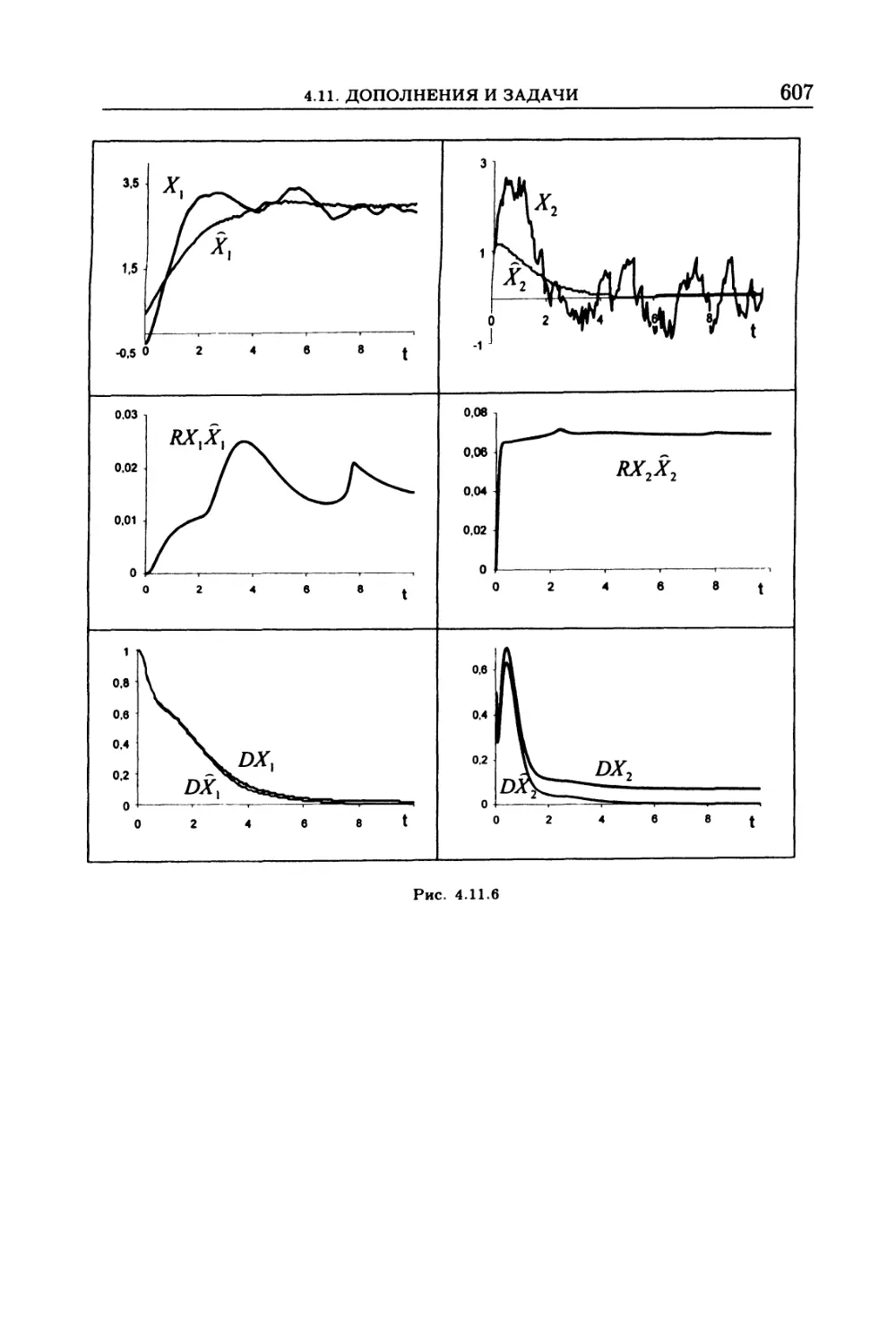
4.11. Дополнения и задачи .......................... 587
5. Рудольф Эмиль Калман ............................ 608
6. Пугачев Владимир Семенович ...................... 611
7. Библиографические замечания ..................... 616
Список литературы................................... 620
Предметный указатель................................ 632
Памяти академика
Владимира Семеновича Пугачева
посвящается
ПРЕДИСЛОВИЕ
В монографии дается систематическое изложение теории
фильтров Калмана и Пугачева для обработки информации в сложных
стохастических системах, а также приводятся новые результаты фун-
даментальных работ, выполненных в Институте проблем информатики
Российской академии наук в рамках научного направления “Стохасти-
ческие системы и стохастические информационные технологии”. В кни-
ге впервые в полном объеме описываются непрерывные и дискретные
фильтры Пугачёва.
Книга предназначена для научных работников и инженеров в об-
ласти прикладной математики, теории управления и информатики, а
также в других областях науки и техники, связанных с обработкой
информации в системах, поведение которых описывается стохастиче-
скими дифференциальными, интегральными, интегродифференциаль-
ными, разностными и другими уравнениями (стохастические системы).
Книга может представлять интерес для математиков, специализирую-
щихся в области стохастических уравнений и их приложений. Она мо-
жет быть полезна студентам высших учебных заведений, обучающихся
по специальности “Прикладная математика”. Единая методика, тща-
тельный. подбор примеров и задач (их свыше 300) позволяют использо-
вать книгу широкому кругу студентов, аспирантов и преподавателей.
Монография состоит из четырех глав. В конце каждой главы в виде
специального раздела даны дополнения и задачи для упражнений.
В главе 1 приводятся необходимые сведения из теории стохасти-
ческих систем. Рассматриваются математические модели динамиче-
ских систем в условиях случайных возмущений и их характеристики.
Излагаются основные понятия теории распределений случайных вели-
чин и случайных функций. Изучаются различные вероятностные меры
случайных функций и вероятности событий, связанные со случайны-
ми функциями. Обсуждаются вопросы устойчивости, управляемости и
наблюдаемости линейных систем. Излагаются основные понятия, свя-
занные с математическим ожиданием случайных величин в линейных
10
Предисловие
пространствах, рассматриваются свойства операторов моментов второ-
го и высших порядков, устанавливаются свойства характеристических
функционалов, а также соответствие между вероятностными мерами
и характеристическими функционалами. Особое внимание уделяется
теории ортогональных разложений одно- и многомерных плотностей.
Изучаются условные операторы моментов и их свойства. Приводят-
ся элементы теории регрессии. Рассматриваются вопросы сходимости,
непрерывности и дифференцируемости случайных функций. Обсуж-
даются вопросы интегрируемости случайных функций как по неслу-
чайной, так и по случайной мере, излагаются элементы теории стоха-
стических интегралов Ито, симметризованного интеграла Стратонови-
ча и 0-интеграла. Рассматриваются стохастические интегралы по ме-
рам Винера и Пуассона. Устанавливается связь между общей формой
процесса с независимыми приращениями и интегралом Ито. Приво-
дятся формулы Ито для дифференцирования нелинейных функций в
случаях винеровского, пуассоновского и общего случайного процесса с
независимыми приращениями. Описываются методы приведения урав-
нений непрерывной стохастической системы к стохастическим диффе-
ренциальным уравнениям и их численного интегрирования. Даются
сведения по теории одно- и многомерных распределений в непрерыв-
ных, дискретных и непрерывно-дискретных системах в конечномерных
пространствах. Приведены известные уравнения (Фоккера-Планка-
Колмогорова, Феллера-Колмогорова, Пугачева и др.), описывающие
одно- и многомерные распределения. Рассмотрены основные методы
теории линейных стохастических систем применительно к непрерыв-
ным, дискретным и непрерывно-дискретным системам. Последние два
раздела главы 1 посвящены приближенным методам теории нелиней-
ных стохастических систем, основанным на параметризации распреде-
лений. Рассматриваются методы нормализации, нормальной аппрокси-
мации и статистической линеаризации, методы начальных и централь-
ных моментов, ортогональных разложений и квазимоментов, эллипсо-
идальной аппроксимации и линеаризации, а также их модификации.
Глава 2 посвящена теории оптимального (в смысле минимума сред-
ней квадратической) оценивания состояния и параметров стохастиче-
ских систем по результатам наблюдения (теория оптимальной филь-
трации) и фильтрам Калмана для стохастических дифференциальных
и дискретных систем. После постановки задач оценивания (фильтра-
ции, экстраполяции и интерполяции) выведены общая формула для оп-
тимальной оценки вектора состояния, уравнения, определяющие одно-
мерно апостериорное распределение вектора состояния системы, и фор-
Предисловие
11
мулы для стохастических дифференциалов апостериорных средних и
моментов второго порядка, а также формулы для стохастических диф-
ференциалов апостериорных вероятностей в задаче распознавания. За-
тем излагается точная общая теория оптимальной линейной фильтра-
ции. В этом случае уравнения оптимальной фильтрации допускают
точное решение. Излагаются свойства уравнений Риккати. После по-
дробного изложения теории стационарных и нестационарных фильтров
Калмана-Быоси подробно изучается случай автокоррелированной по-
мехи в наблюдениях, которая может быть представлена как результат
преобразования белого шума линейным формирующим фильтром. Изу-
чаются дифференцирующие свойства оптимальных фильтров. Дает-
ся точное решение задачи оптимальной экстраполяции и интерполяции
вектора состояния линейной системы. Затем рассматривается случай,
когда уравнения системы и наблюдения линейны только относительно
вектора состояния и нелинейны относительно наблюдаемого процесса.
Особое внимание уделено уравнениям оптимальной фильтрации для не-
нормированных распределений. Далее излагается теория оптимального
оценивания и дискретных фильтров (экстраполяторов и интерполято-
ров) Калмана. Рассматриваются вопросы устойчивости, наблюдаемо-
сти и управляемости непрерывных и дискретных стохастических си-
стем и фильтров Калмана. В последнем разделе изучаются вопросы
оптимального оценивания, распознавания и адаптации.
Глава 3 содержит изложение теории нелинейного субоптимального
(приближенного) оценивания с помощью обобщенных фильтров Кал-
мана для нелинейных непрерывных и дискретных стохастических си-
стем. Рассмотрены две группы методов субоптимальной нелинейной
фильтрации. К первой группе относятся методы, основанные на при-
ближенном решении уравнений оптимальной нелинейной фильтрации:
метод нормальной аппроксимации апостериорного распределения, ме-
тод моментов, метод семиинвариантов и методы, основанные на ор-
тогональных разложениях апостериорных распределений, в частности
метод квазимоментов. Все эти методы, кроме метода нормальной ап-
проксимации, принципиально позволяют получить решение задачи оп-
тимальной фильтрации с любой степенью точности. Однако возможно-
сти практической реализации соответствующих фильтров сильно огра-
ничены из-за сложности получающихся алгоритмов. Ко второй группе
относятся методы, основанные на упрощении уравнений оптимальной
нелинейной фильтрации. Фильтры, даваемые этими методами: обоб-
щенный фильтр Калмана-Бьюси, фильтры второго порядка и гауссов
фильтр, по сложности реализации равноценны фильтру метода нор-
12
Предисловие
мальной аппроксимации. Однако ввиду произвольности допущений,
лежащих в основе этих фильтров, вопрос о точности их приближения к
оптимальному фильтру остается неясным. Изложен метод априорного
исследования точности субоптимальных фильтров. Особое внимание
уделено уравнениям нелинейной субоптимальной фильтрации для не-
нормированных распределений. Рассмотрены модифицированные ме-
тоды нормальной аппроксимации, моментов и ортогональных разло-
жений. Заключительный раздел главы 3 содержит изложение методов
дискретного субоптимального оценивания и распознавания. Рассматри-
ваются неадаптивные и адаптивные обобщенные дискретные фильтры
Калмана.
Глава 4 посвящена теории нелинейного условно оптимального оце-
нивания (фильтрации, экстраполяции и интерполяции) вектора состоя-
ния системы и условно оптимального оценивания параметров системы
(теория условно оптимальной фильтрации Пугачева). Теория Пугаче-
ва позволяет строить фильтры минимальной сложности, сравнительно
легко реализуемые в задачах практики. Кроме того, она дает возмож-
ность получать фильтры, равноценные по сложности любому данному
субоптимальному фильтру, но обладающие более высокой точностью.
В этом состоит существенное преимущество методов условно оптималь-
ной фильтрации Пугачева по сравнению с методами субоптимальной
фильтрации главы 3. После изложения основной идеи условно опти-
мального оценивания, постановки соответствующих задач даются об-
щие методы построения фильтров и экстраполяторов. Рассматривается
применение теории условно оптимальной фильтрации для решения за-
дачи распознавания в случае линейного уравнения наблюдения. Затем
эти методы распространяются на случай автокоррелированной помехи
в наблюдениях, представимой в виде выходного сигнала формирующе-
го фильтра, описываемого стохастическим дифференциальным уравне-
нием (не обязательно линейным). Дается применение теории условно
оптимальной фильтрации и экстраполяции к линейным системам с па-
раметрическими шумами. Подробно рассматривается теория дискрет-
ного условно оптимального оценивания, распознавания и адаптации.
Излагается теория эллипсоидальных субоптимальных и условно опти-
мальных фильтров и экстраполяторов Пугачева.
В заключительном разделе получены основные уравнения услов-
но оптимальной фильтрации по бейесовым и сложным статистическим
критериям. Рассмотрены фильтры Калмана-Бьюси и Пугачева по та-
ким же критериям. Приведены уравнения фильтров Калмана и Пуга-
Предисловие
13
чева для трех задач интерполяции процессов в дискретных стохастиче-
ских системах.
Современное алгоритмическое и программное обеспечение филь-
тров Калмана реализовано в виде универсального программного обеспе-
чения в большинстве стандартных научных и научно-технических биб-
лиотек, пакетов прикладных программ, специлизованного программно-
го обеспечения для различных средств вычислительной техники (см.
библиографию).
В разделах 5 и 6 автор счел необходимым привести портреты и
краткие биографические сведения о Р.Э. Калмане (р.1930) и В.С. Пуга-
чеве (1911-1998).
Биографические замечания и список литературных источников
приведены в конце книги. Автор ни в коей мере не претендует на пол-
ноту списка. В нем указаны только те источники, на которые даются
ссылки в тексте.
Книга разбита на главы, разделы и пункты. Формулы (примеры)
нумеруются с указанием номеров главы и раздела, например, (1.2.3)
означает, что формула (3) принадлежит разделу 2 главы 1.
Для удобства читателей формулировки основных результатов и вы-
делены в виде предложений. Начало и конец выводов, доказательств
и рассуждений, приводящих к определенным результатам, отмечены
треугольными указателями о и <1.
Книга может использоваться разными категориями читателей.
Для усвоения изложенного в ней материала в полном объеме необхо-
димо знание основ теории вероятностей, например книги В.С. Пугаче-
ва “Теория вероятностей и математическая статистика” (Наука, 1979,
2002), В.С. Пугачев и И.Н. Синицын “Теория стохастических систем”
(Логос, 2000, 2004), а также основ функционального анализа в объе-
ме книги В.С. Пугачева “Лекции по функциональному анализу” (Изд.
МАИ, 1996).
Как показывает многолетний педагогический опыт автора, книга
может быть использована для чтения стандартных и специализирован-
ных курсов по теории вероятностей и стохастическому анализу, стати-
стическим основам системного анализа, информатики, радиотехники,
теории управления и связи, теории надежности конструкций, динамике
машин и механизмов, а также фрагментов в специализированных кур-
сах, например, аналитической механики стохастических систем, стати-
стической теории колебаний и устойчивости и др. (Синицын 1996).
14
Предисловие
Многие дополнения и задачи, приведенные в конце каждой из глав,
имеют самостоятельный интерес, носят комплексный характер, а пото-
му и могут быть использованы для курсовых и дипломных работ.
Раздел 4.10 и пп.2.12.5, 3.6.1-3.6.6, 4.8.3-4.8.7 написаны на базе сов-
местных работ с В.И. Шином (Gwangju Institute of Science and Tech-
nology, South Korea), а также разработанных им специально для на-
стоящей книги дополнений и комментариев. Раздел 4.9 и п. 1.8.4 под-
готовлены совместно с В.И. Синицыным. Дополнения 4.11.20-4.11.22
разработаны совместно с Э.Р. Корепановым. Б.Г. Доступов, И.Е. Каза-
ков, А.В. Добровидов, Р.А. Ивановский, А.В. Борисов, В.В. Белоусов,
Э.Р. Корепанов, В.И. Синицын, А.В. Босов, М.Е. Шайкин, О.С. Ушмаев
предоставили автору материалы для задач и дополнений.
Список литературы и предметный указатель составлен совместно
с И.В. Синицыной и Хоанг Тхо Ши. Считаю своим приятным долгом
выразить им благодарность за неоценимую помощь.
Автор благодарен В.В. Белоусову за помощь в подготовке рисун-
ков, Е.Н. Федотовой - за подготовку нескольких вариантов оригинал-
макета, а редакторам Е.В. Комаровой и Н.А. Власовой за большой труд
по подготовке рукописи к печати.
Без помощи Российского фонда фундаментальных исследований
и издательства “Логос” этот многолетний труд, посвященный памяти
академика В.С. Пугачева, не был бы издан.
Москва 1998 — 2005 гг.
ГЛАВА 1
СВЕДЕНИЯ ИЗ ТЕОРИИ
СТОХАСТИЧЕСКИХ СИСТЕМ
Глава 1 содержит необходимые сведения по моделям непрерывных
и дискретных систем (раздел 1.1) и по теории случайных функций (раз-
делы 1.2 и 1.3). Основы стохастического анализа изложены в разде-
ле 1.4. Элементы общей теории стохастических систем рассматривают-
ся в разделе 1.5. Методы теории линейных и нелинейных стохастиче-
ских систем кратко описаны в разделах 1.6-1.8. В конце главы даны
дополнения и задачи для упражнений.
1.1. Математические модели систем и их характеристики
1.1.1. Математические модели непрерывных систем. Как
известно (ТСтС, раздел 1.1), в практических задачах системой обыч-
но называют любую совокупность взаимодействующих предметов лю-
бой природы. Первым шагом к построению математической модели
системы является математическое описание того, что система получа-
ет на входе и выдает на выходе. Это описание состоит в определе-
нии двух множеств величин, связанных однонаправленной причинно-
следственной зависимостью, с помощью которых можно определить
внешние воздействия на систему и то, что она дает на выходе в каждый
данный момент времени. Величины, определяющие внешние воздей-
ствия на систему, называются входными сигналами. Величины, опре-
деляющие действие системы на окружающую среду и, в частности, на
другие системы, называются выходными сигналами системы. Обычно
входные сигналы (причины) не зависят от выходных сигналов, в то вре-
мя как выходные сигналы (следствия) принципиально зависят от своих
причин, т. е. от входных сигналов.
Кроме входных и выходных сигналов, для построения математи-
ческой модели системы часто приходится вводить еще некоторые вспо-
могательные величины, в число которых могут включаться величины,
характеризующие действия различных частей системы друг на друга
(внутренние взаимодействия частей системы). Все эти величины, ха-
рактеризующие положение (состояние) системы в каждый данный мо-
мент времени, обычно называются переменными состояниями систе-
мы.
16
ГЛ. 1. СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
В дальнейшем мы будем называть входным сигналом системы всю
совокупность ее входных сигналов, выходным сигналом - всю совокуп-
ность ее выходных сигналов и вектором состояния - всю совокупность
переменных состояний системы.
Множество всех возможных входных сигналов системы будем на-
зывать ее пространствам входных сигналов, множество всех возмож-
ных выходных сигналов системы - ее пространством выходных сиг-
налов, а множество всех возможных векторов состояния системы - ее
пространством состояний. Входной и выходной сигналы системы как
определенные функции времени, а также изменение вектора состояния
со временем характеризуют функционирование или, как часто говорят,
состояние системы.
После определения входного и выходного сигналов и вектора состо-
яния системы для получения ее математической модели остается уста-
новить соотношения между этими величинами. Эти соотношения могут
быть детерминированными или содержать некоторые элементы неопре-
деленности. В последнем случае обычно пользуются вероятностным
подходом, приписывая случайный (стохастический) характер и соот-
ветствующие распределения всем неопределенным величинам. Таким
образом, мы приходим к следующему определению математической мо-
дели системы.
Математической моделью системы называется совокупность
четырех элементов: 1) пространства состояний, 2) пространства вход-
ных сигналов, 3) пространства выходных сигналов и 4) соотношений,
связывающих входной и выходной сигналы и вектор состояния системы.
Понятия входного и выходного сигналов и вектора состоя-
ния относятся не к самой системе, а к ее математической модели.
В действительности состояние любой системы, все внешние воздействия
на нее и все ее действия на окружающую среду и, в частности, на дру-
гие системы невозможно охарактеризовать никаким обозримым и тем
более конечным множеством величин. Поэтому, говоря о входном и вы-
ходном сигналах и о состоянии системы, мы всегда имеем в виду вход-
ной и выходной сигналы и состояние принятой математической модели
системы.
Модель системы называется детерминированной, если каждой ре-
ализации ее входного сигнала соответствует одна определенная реали-
зация выходного сигнала. Модель системы называется стохастиче-
ской, если каждой реализации ее входного сигнала соответствует вполне
определенное вероятностное распределение ее выходного сигнала. Для
одной и той же системы можно построить много различных моделей.
1.1. МАТЕМАТИЧЕСКИЕ МОДЕЛИ СИСТЕМ И ИХ ХАРАКТЕРИСТИКИ 17
В зависимости от степени детальности характеристики поведения си-
стемы и количества учитываемых факторов одни модели будут проще,
другие - сложнее. Чем больше факторов учитывает модель, тем она
сложнее, тем полнее и в принципе точнее она описывает поведение си-
стемы. Однако точность сложной модели может оказаться иллюзорной.
Из-за ограниченности и неточности исходных данных, используемых
при ее построении, чрезмерно сложная модель может оказаться менее
точной, чем более простая. Поэтому степень сложности модели долж-
на быть согласована с доступной информацией, используемой для ее
построения.
Что касается сложных систем, то, как правило, никакая модель не
может с достаточной точностью воспроизвести все функции. Одни мо-
дели будут лучше по одним показателям, другие - по другим. Поэтому
для сложных систем строят не одну, а несколько моделей и в зависи-
мости от цели применяют ту или иную. При этом одни модели могут
быть детерминированными, а другие - стохастическими.
Входной и выходной сигналы любой системы представляют собой
функции времени. Если они определены для всех моментов времени,
начиная с некоторого начального момента, то модель системы назы-
вается непрерывной. Соответственно и саму систему называют в этом
случае непрерывной. Если реализации входного и выходного сигналов
определены только на дискретных множествах моментов времени, то
модель системы называется дискретной. В этом случае и саму систе-
му обычно называют дискретной (импульсной). Впрочем, дискретные
модели часто применяются и для описания поведения непрерывных си-
стем. Для расчетов на цифровых ЭВМ всегда применяются дискретные
модели, независимо от того, являются ли соответствующие системы не-
прерывными или дискретными.
Общие характеристики непрерывных систем. Будем счи-
тать, что математическая модель изучаемой системы построена. По-
этому, говоря о характеристиках системы, будем иметь в виду харак-
теристики ее математической модели. Основной характеристикой си-
стемы является ее оператор, определяющий механизм формирования
выходного сигнала по данному входному сигналу. Оператор детерми-
нированной системы отображает пространство входных сигналов в
пространство выходных сигналов. Оператор стохастической системы
ставит в соответствие каждому входному сигналу определенное рас-
пределение выходного сигнала (конечно, зависящее от входного сигна-
ла). Другими словами, оператор стохастической системы отобража-
ет пространство входных сигналов в пространство всех возможных
18
ГЛ. 1. СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
распределений на пространстве выходных сигналов.
Рассмотрим непрерывную систему с конечномерными входными и
выходными сигналами, представляющими собой, как правило, непре-
рывные ограниченные функции времени. Оператор детерминирован-
ной системы отображает пространство непрерывных функций в такое
же пространство. Пусть x(t) - входной сигнал детерминированной си-
стемы, представляющий собой непрерывную скалярную или п-мерную
векторную функцию времени y(t) - выходной сигнал, представляю-
щий собой непрерывную скалярную или m-мерную векторную функ-
цию t. Обозначим буквой А оператор системы. Соотношение между
входным и выходным сигналами детерминированной системы можно
записать в виде операторного уравнения
y(t) = Ax(t). (1-1.1)
Эта краткая запись включает всю совокупность математических one-
раций, которые надо выполнить над функцией ar(t), чтобы определить
функцию y(t).
Детерминированная система называется физически возможной,
если значение ее выходного сигнала y(t) в каждый момент t не зависит
от значений входного сигнала х(т) при т > t. Таким образом, значе-
ние выходного сигнала физически возможной системы y(t) в каждый
момент t является функционалом от входного сигнала х(т}, заданно-
го в интервале to < т < t. Строго говоря, y(t) представляет собой
m-мерный вектор, компоненты которого являются функционалами от
х(т), т G Для краткости мы называем векторную величину y(t)
функционалом, имея в виду m-мерный векторный функционал.
Стохастическая система называется физически возможной, ес-
ли распределение значения ее выходного сигнала Y(t) в любой мо-
мент t не зависит от значений входного сигнала х(т) при т > t.
Пусть задан некоторый невозмущенный входной сигнал x(t)
системы и пусть y(t) - соответствующий ему выходной сигнал, кото-
рый также назовем невозмущенным. Всякий другой входной сигнал
x'(t) будем называть возмущенным входным сигналом, а соответству-
ющий ему выходной сигнал y'(t) - возмущенным выходным сигналом.
Отклонения входного и выходного сигналов от невозмущенных опреде-
лим как Дя(£) = x'(t) — x(t) и Д?/(^) = y'it) — y(t). Детерминированная
система (1.1.1) называется устойчивой относительно заданного невоз-
мущенного сигнала, если отклонение Д?/(^) остается сколь угодно ма-
лым при любом достаточно малом отклонении Дзг(^) входного сигнала,
1.1. МАТЕМАТИЧЕСКИЕ МОДЕЛИ СИСТЕМ И ИХ ХАРАКТЕРИСТИКИ 19
т. е. для любого е > 0 существует такое 6 = 6(e) > 0, что | Ay(t) | < е
при t > to, когда | Ax(t) | < 6 при всех t > to.
Стохастическая система называется устойчивой относительно за-
данного невозмущенного сигнала почти наверное (с вероятностью 1),
если отклонение ее выходного сигнала ДУ (t) сколь угодно мало с веро-
ятностью 1 при любом достаточно малом отклонении входного сиг-
нала Дя(£). Стохастическая система называется устойчивой отно-
сительно заданного невозмущенного сигнала по вероятности, если при
любом е > 0 существует такое 6 = 6(e) > 0, что lim Р\ sup |ДУ (t)| >
t-*00 \t>t0
> е I = 0 при всех Ax(t), удовлетворяющих условию sup | Ax(t) | < 6.
/ t>t0
Стохастическая система называется устойчивой относительно за-
данного невозмущенного сигнала в р-среднем, р > О, если математи-
ческое ожидание М| ДУ (t) |р остается сколь угодно малым при всех
достаточно малых отклонениях входного сигнала Дя(£).
Стохастическая система устойчива по вероятности, если она
устойчива в р-среднем. Точно так же из устойчивости почти на-
верное вытекает устойчивость по вероятности. Из р-устойчивости
при данном р следует р\ -устойчивость при всех р\ < р. Обратное в
общем случае неверно.
Говоря об устойчивости системы, в прикладных задачах всегда име-
ют в виду устойчивость всех реализаций происходящих в ней процессов.
С этой точки зрения наибольшее значение для приложений имеет по-
нятие устойчивости почти наверное. Однако в практических задачах
часто приходится ограничиваться устойчивостью в среднем (р = 1) или
в среднем квадратическом (р = 2). Класс систем, устойчивых в сред-
нем квадратическом (с.к. устойчивых), и класс систем, устойчивых
почти наверное (п.н. устойчивых), являются подклассами класса си-
стем устойчивых по вероятности, причем пересечение этих подклассов
непусто.
Система называется линейной, если при любых числах N,
Ci , ... , с/у и при любых функциях Xi(t) , ... , Xl\f(t)
N
' N
Л< ^2cuxu(t) ► = y^ cuAxu(t).
(1-1.2)
Это определяющее свойство линейных систем обычно называется прин-
ципом суперпозиции. Поэтому линейные системы можно определить
как такие системы, для которых справедлив принцип суперпозиции
(1.1.2).
20
ГЛ. 1. СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
Система называется нелинейной, если принцип суперпозиции
(1.1.2) для нее не выполняется или выполняется только при некоторых
вполне определенных N, xi(t), ... , x^(t), ci, ... , с^.
В прикладных задачах обычно удается представить модель любой
системы с конечномерными векторами входного и выходного сигналов,
а также вектора состояния в виде соединения конечного числа типовых
линейных систем и безынерционных нелинейных звеньев. О послед-
них говорим, имея в виду, что практически любая нелинейность дает
на выходе определенную функцию текущего значения ее входного сиг-
нала. А именно значение выходного сигнала нелинейного звена в лю-
бой момент t представляет собой определенную функцию значения его
входного сигнала в тот же момент t и не зависит от значений входного
сигнала до момента t:
y(i) (1.1.3)
где через x(t) и y(t) обозначены входной и выходной сигналы нели-
нейного звена. Функция р полностью характеризует безынерционное
нелинейное звено и поэтому принимается за его характеристику. Вход-
ной сигнал нелинейного звена в общем случае представляет собой век-
тор, компонентами которого служат некоторые переменные состояния
системы и, может быть, некоторые ее входные сигналы.
Большую часть непрерывных линейных систем, встречающихся на
практике, составляют системы, поведение которых описывается обык-
новенными дифференциальными уравнениями. При этом обычно все-
гда эти уравнения можно представить в стандартной форме Коши,
т. е. в виде системы уравнений первого порядка, решенных отно-
сительно производных. Добавив к уравнениям всех линейных частей
системы зависимости между входными и выходными сигналами всех
нелинейных звеньев, получим систему нелинейных дифференциальных
уравнений в форме Коши, описывающую нелинейную систему. Обо-
значим через z{f) = [zi(£).. .zp(£)]T вектор состояния системы, через
x(t) = [яДг)... xn(t)]T - векторный входной сигнал, а через y(t) =
= [з/i (£) • • • Ут(1)]Т ~ векторный выходной сигнал (здесь и в дальнейшем
Т - оператор транспонирования). Тогда дифференциальные уравнения,
описывающие поведение системы, в общем случае запишутся в виде
z = f{z, x,t), у = g(z, t), (1-1-4)
где f - р-мерная векторная функция векторов z, х и времени t, а
д - m-мерная векторная функция вектора z и времени t. Систему с ко-
нечномерными вектором состояния и значениями входного и выходного
1.1. МАТЕМАТИЧЕСКИЕ МОДЕЛИ СИСТЕМ И ИХ ХАРАКТЕРИСТИКИ 21
сигналов, описываемую обыкновенным дифференциальным уравнени-
ем и формулой для выходного сигнала вида (1.1.4), будем для краткости
называть дифференциальной системой.
При данном начальном состоянии системы zq = z(£o) уравнения
(1.1.4) полностью и однозначно определяют оператор системы. Заме-
тим, что от начальных условий всегда можно избавиться, включив их в
вектор входного сигнала. В самом деле, уравнения (1.1.4) с начальным
условием z(fo) = zq можно написать в виде
z = /(г, х, t) + z06(t - tQ), у = g(z, t) (1.1.5)
и интегрировать их при нулевых начальных условиях z = 0 при t = to+e
и при сколь угодно малом е > 0. Приняв zq за дополнительную компо-
ненту вектора входных сигналов, т.е. за входной сигнал (п +р)-мерный
вектор x(f) = [^o"rEi(f)... xn(f)]T, можем утверждать, что уравнения
(1.1.5) с нулевыми начальными условиями полностью определяют опе-
ратор системы.
Рассмотрим линейную многомерную систему с п входами и т вы-
ходами. На основании принципа суперпозиции действие каждого вход-
ного сигнала на многомерную линейную систему можно рассматривать
отдельно, а затем результаты действия отдельных входных сигналов на
каждом выходе просуммировать.
Для нахождения реакции на А;-м выходе линейной системы на сиг-
нал, действующий на одном только Л-м входе, можно рассматривать
эту систему как систему с одним входом и одним выходом. Тогда для
вычисления реакции на А;-м выходе системы на любой сигнал, действу-
ющий на Л-м входе, при отсутствии сигналов на остальных входах, до-
статочно будет знать соответствующую весовую функцию gkh(t> т)- Эта
весовая функция представляет собой реакцию на к-м выходе системы на
единичный импульс, действующий на h-м входе в момент т, при отсут-
ствии сигналов на остальных входах. Совокупность весовых функций
9kh(t, г) (к = 1, ... , m; h = 1, ... , п), соответствующих всем входам и
выходам, является исчерпывающей характеристикой многомерной ли-
нейной системы.
Зная весовые функции многомерной линейной системы, соот-
ветствующие всем входам и выходам, и суммируя полученные резуль-
таты для каждого отдельного выхода по всем входам, найдем все вы-
ходные сигналы рассматриваемой линейной системы, соответствующие
одновременному действию всех входных сигналов. Таким образом, вы-
ходные сигналы 2/i(t), ... , ym(t) линейной системы с п входами и т
22
ГЛ. 1. СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
выходами выражаются через ее входные сигналы zi(£), ... , xn(t) фор-
мулой
УМ = f
Л=1
9kh(t,r)xh(r)dr (k = l, ... ,m).
(1.1.6)
-оо
Вводя матрицу
’ 9п (t,r) 9l2(t,T) 9in(t,r) '
9(1,т) = 92i(t,r) 922(t,T) . 92n(t,T) (1.1.7)
- 9ml (^, Т) 9т2^,т) . • • 9mn(t, t) -
можно записать формулу (1.1.6) в виде
оо
y(t) = Ax(t) = J g(t,T)x(r)dT, (1.1.8)
—ОО
где x(t) = [ rci (t)... xn(t) ]T, y(t) = [yi(t)... ym(t) ]T - векторные входной
и выходной сигналы, представленные в виде матриц-столбцов. Матрич-
ная функция <?(t, т), определяемая формулой (1.1.7), называется весовой
функцией линейной системы с п входами и т выходами.
Для физически возможной линейной системы согласно определе-
нию имеем <?(£,т) =0 при т > t и формула (1.1.8) принимает вид
у(0
(1.1.9)
где to _ момент начала работы системы.
Для асимптотической устойчивости конечномерной линейной си-
стемы в целом необходимо и достаточно, чтобы все элементы матрицы
g(t, т) удовлетворяли условию:
оо
/ \dkh(t) т)| dr < оо (к = 1, ... , тп] h = 1, ... , п). (1.1.10)
—оо
1.1. МАТЕМАТИЧЕСКИЕ МОДЕЛИ СИСТЕМ И ИХ ХАРАКТЕРИСТИКИ 23
Для случая N раз непрерывно дифференцируемого входного сиг-
нала, причем в этом случае g(t, т) может содержать и линейную ком-
бинацию производных J-функций до порядка N включительно, необхо-
димое и достаточное условие (1.1.10) устойчивости линейной системы
заменится условием
(т - a)N 1g(t,a)da
dr < оо.
(1.1.11)
Стационарные системы. Стационарной называется такая си-
стема, у которой при любом сдвиге входного сигнала во времени без
изменения его формы (т.е. при замене x(t) на x(t — А) при любом А)
выходной сигнал претерпевает тот же сдвиг во времени, также не изме-
няя своей формы (т.е. y(t) заменяется на y(t- А)). Система, описывае-
мая дифференциальными уравнениями (1.1.4) или (1.1.5), стационарна
тогда и только тогда, когда правые части этих уравнений, т.е. функ-
ции f(z,x,t) и g^Zjt), не зависят явно от времени: f(z,x,t) = f(z,x),
9(z,t) = g(z).
Из определения стационарной системы следует, что весовая функ-
ция стационарной системы зависит только от разности ее аргумен-
тов. Основной особенностью физически возможных стационарных ли-
нейных систем является то, что любая асимптотически устойчивая
стационарная линейная система усиливает неограниченно долго дей-
ствующий входной сигнал, представляющий собой показательную
функцию est, без изменения его формы. Обозначив коэффициент уси-
ления показательного входного сигнала через
оо
Ф(в) = у w(a)e~s<rdcr, (1.1.12)
О
получим y(t) = Ф($)ев*. Эта формула показывает, что коэффициент
усиления Ф($) показательной функции зависит от параметра s. Этот
коэффициент называется передаточной функцией Ф($) стационарной
линейной системы.
Передаточная функция многомерной системы определится как т х
xn-матрица, элементами которой служат передаточные функции от
всех входов ко всем выходам, рассматриваемым по отдельности.
Формула (1.1.12) показывает, что передаточная функция стацио-
нарной линейной системы Ф($) является преобразованием Лапласа ее
24
ГЛ. 1. СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
весовой функции. Пользуясь терминами операционного исчисления,
можно сказать, что передаточная функция стационарной линейной си-
стемы представляет собой изображение ее весовой функции. Это об-
стоятельство дает возможность определять передаточные функции ста-
ционарных линейных систем по их весовым функциям (и наоборот) и
при этом пользоваться готовыми таблицами формул операционного ис-
числения (ТСтС, приложение 3), чтобы избежать вычисления интегра-
лов (1.1.12).
Ограничиваясь чисто мнимыми значениями параметра s, s = icu,
получаем передаточную функцию системы Ф(гси) как функцию кру-
говой частоты гармонических колебаний егиН. В случае многомерной
системы элементы матрицы Ф(гси) определяют коэффициенты усиле-
ния амплитуд и сдвиги фаз при прохождении гармонических колебаний
от каждого входа к каждому выходу системы. Поэтому передаточная
функция линейной стационарной системы, рассматриваемая как функ-
ция чисто мнимого параметра s = ш (т.е. суженная на мнимую ось
комплексной плоскости), называется частотной характеристикой ста-
ционарной линейной системы.
Свойство стационарных линейных систем пропускать гармониче-
ские колебания без изменения их формы путем умножения амплитуды
на |Ф(го>)| и сдвига фазы на — arg Ф (геи) лежит в основе метода ча-
стотных характеристик. В его основе лежат следующие формулы:
оо
g(t,r) =w(t-T) = ^~ [ $(iw)e<u,(‘-T)dw (1.1.13)
27Г J
—оо
ИЛИ
оо
w(u) = -L f . (1.1.14)
27Г J
—оо
Весовая функция w(u) физически возможной стационарной линей-
ной системы равна нулю при отрицательных значениях аргумента и.
Так как любой ограниченный непрерывный входной сигнал, действу-
ющий на конечном интервале времени (а только такие сигналы при-
ходится рассматривать в практических задачах), можно представить
интегралом Фурье, то с помощью частотных характеристик можно вы-
числять установившиеся выходные сигналы устойчивых стационарных
линейных систем практически при любых входных сигналах.
1.1. МАТЕМАТИЧЕСКИЕ МОДЕЛИ СИСТЕМ И ИХ ХАРАКТЕРИСТИКИ 25
1.1.2. Линейные дифференциальные системы. В случае ли-
нейной системы уравнения (1.1.4), естественно, линейны и, следователь-
но, имеют вид
z — az + а^х + ао , = + (1.1.15)
где а - квадратная матрица порядка р; ai - р х n-матрица; ао ~ вектор
размерности р; b - тп х р-матрица; 6о -вектор размерности тп. В общем
случае а, ах, ао, Ь и &о могут зависеть от времени t. В частном случае
стационарной линейной системы a, ai, ao, Ь и &о постоянны.
В некоторых случаях вектор состояния можно исключить из урав-
нений системы (1.1.15). Тогда получится линейное дифференциальное
уравнение выше первого порядка, связывающее выходной сигнал у с
входным сигналом х. При этом поведение системы можно изучать, не
интересуясь ее состоянием. Однако для исследования систем всегда
удобно представлять описывающие их дифференциальные уравнения в
форме Коши. Для этого приходится приводить эти уравнения к системе
уравнений первого порядка путем ввода дополнительных переменных.
Эти дополнительные переменные обычно и принимаются за переменные
состояния системы.
Пусть u(t, to) - решение однородного уравнения
й = аи (1.1.16)
при начальном условии u(t,to) = I, т.е. фундаментальная матрица
решений уравнений (1.1.16).
Тогда, учитывая, что при любых to> т, t, to <т < t,
u(t, to) = a(t, t)u(t, to). (1.1.17)
получим общее решение (1.1.15)
t
z(t) = u(t,to)zQ + У u(t,r) [ai(r)z(r) + ao(r)]dT, (1.1.18)
to
t
y(t) = b(t)u(t,to)zo + У 5(f)u(f,T)ai(r)a:(T)dT+
( ‘° (1-1.19)
+ b(t) У u(t, т)ао(т)4т 4- &o(O •
to
26
ГЛ. 1. СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
Отсюда видно, что рассматриваемая система (1.1.15) представляет со-
бой линейную систему с аддитивным дополнительным выходным сиг-
налом
t
Уо(*) = tQ)zQ + b(t) / u(t, т)ао(т)(1т + bQ(t) (1.1.20)
to
и весовой функцией
g(t, т) = b(t)u(t, r)ai (т)1(£ - т), (1.1.21)
где l(s) - единичная ступенчатая функция, равная 1 при s > 0 и 0
при s < 0. Формула (1.1.21) показывает, что весовая функция линей-
ной дифференциальной системы легко находится, если известна фун-
даментальная матрица решений соответствующего однородного урав-
нения (1.1.16).
Для нахождения передаточной функции стационарной линейной
системы, описываемой уравнениями (1.1.15), необходимо: положить
а0 = 0, Ьо = 0, вместо каждой компоненты входного сигнала Xh по
очереди подставить в (1.1.15) показательную функцию e8t, а вместо вы-
ходного сигналаг/ подставить функцию Ф/1(«)е4’^, где Ф/1(§) - Л-й столбец
матричной передаточной функции системы Ф($) (Л = 1, ... , п). При
этом следует положить z = Фь^е8*. Сократив полученные уравнения
на sst, найдем Ф/^з) и Ф/1(«). Однако проще найти Ф/^з) и Ф/^з), поло-
жив в (1.1.15) х = Ie8t, у — $e8t, z = Ф($)е5*. В результате получим
Ф($) = —(а - sl)-1^ , ф(5) = -Ь(а - sl)"1^ . (1.1.22)
Отсюда видно, что передаточная функция стационарной линейной си-
стемы, описываемой дифференциальными уравнениями (конечно, ли-
нейными с постоянными коэффициентами), представляет собой ра-
циональную функцию комплексной переменной s.
1.1.3. Соединения систем и их характеристики
Соединения систем. Каждая сложная система состоит из ряда
более простых систем, взаимодействующих между собой определенным
образом. В зависимости от характера взаимодействия они могут быть
связаны между собой различными способами. Основными типами со-
единений простых систем в сложных системах являются последователь-
ное соединение, параллельное соединение и обратная связь.
1.1. МАТЕМАТИЧЕСКИЕ МОДЕЛИ СИСТЕМ И ИХ ХАРАКТЕРИСТИКИ 27
Последовательным соединением систем называется такое соедине-
ние, когда выход каждой системы связывается с входом следующей си-
стемы, т.е. когда выходная переменная каждой системы служит вход-
ной переменной для следующей системы. При этом предполагается, что
соединяемые системы обладают направленным действием.
Параллельным соединением систем называется такое соединение,
при котором входная переменная подается одновременно на несколько
систем, а их выходные переменные суммируются.
Обратной связью называется соединение выхода системы с ее вхо-
дом. Если выходная переменная системы непосредственно подается на
ее вход без какого-либо преобразования, то обратная связь называется
жесткой. Жесткая обратная связь может быть положительной или
отрицательной в зависимости от того, суммируется выходная перемен-
ная системы с ее входной переменной или вычитается из нее. Если в
цепь обратной связи включена некоторая система, преобразующая вы-
ходную переменную основной системы, то такая обратная связь назы-
вается гибкой.
Для удобства мы всегда будем рассматривать отрицательную гиб-
кую обратную связь, что, очевидно, не нарушает общности, так как пе-
ремену знака всегда можно включить в преобразование, выполняемое
системой, включенной в цепь обратной связи. Очевидно, что жесткую
обратную связь можно рассматривать как частный случай гибкой об-
ратной связи, когда система, включенная в цепь обратной связи, пред-
ставляет собой идеальную следящую систему (отрицательная жесткая
обратная связь) или безынерционное усилительное звено с коэффици-
ентом усиления, равным —1 (положительная жесткая обратная связь).
Применяемые на практике методы описания систем в виде операто-
ров, весовых, передаточных, частотных и других описывающих функ-
ций позволяют строить удобные графические представления математи-
ческих моделей линейных систем, которые сами могут рассматриваться
как изобразительные модели, эквивалентные аналитическим. Обычно
выделяют два вида графических моделей: структурные схемы и графы.
Структурной схемой называется графическое изображение
структуры системы или ее части. При этом под структурой понима-
ется совокупность частей и связей, изображающих каналы, по которым
передаются воздействия от одной части к другой. Элементами струк-
турной схемы являются:
• Линейные динамические звенья, изображаемые прямоугольника-
ми, которым соответствуют операторы, описывающие функции, про-
ставляемые на схеме или в прилагаемом описании.
28
ГЛ. 1. СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
• Безынерционные функциональные преобразователи, также
изображаемые прямоугольными, которым соответствуют безынерцион-
ные линейные и нелинейные преобразования.
• Сумматоры, изображаемые разделенными на секторы кру-
жочками; к некоторым секторам подходят стрелки, изображающие сла-
гаемые, а от других, наоборот, отходят стрелки, изображающие сумму.
Вообще сумматоры реализуют алгебраическое сложение и для удобства
операций сложения и вычитания обычно отмечаются соответствующи-
ми знаками у концов стрелок или зачеркиванием секторов, в которых
осуществляется вычитание. Наконец, иногда просто в кружочках пока-
зывают знаками +, — соответствующие операции.
• Связи, передающие воздействия без изменения, изображаемые
прямыми линиями со стрелками, указывающими направление воздей-
ствия. Такими же линиями со стрелками изображаются сами воздей-
ствия.
• Узлы или точки разветвления на линиях связи; значения пере-
менных на стрелках, подходящих к узлу и отходящих от него, равны
между собой.
В настоящее время наметилась тенденция к использованию на-
правленных графов. Элементами графа служат отрезок линии - дуга
или ребро, которому сопоставляется оператор, описывающая функция,
безынерционный функциональный преобразователь и пара изображае-
мых кружками вершин на концах ребра, которым сопоставляются зна-
чения входной и выходной величин. Направления передачи воздействия
на графе отмечаются соответствующими стрелками. От вершины мо-
гут исходить несколько ребер, в этом случае входные величины для всех
отходящих ребер одинаковы. Направленные графы в отличие от струк-
турных схем не требуют специальных обозначений для сумматоров и
точек разветвления и все графы изображаются с помощью лишь трех
элементов: ребер, вершин и стрелок.
Правила преобразований структурных схем и графов ли-
нейных систем. Часто бывает полезно структурную схему преобразо-
вать к более удобному для исследования виду путем расчленения слож-
ных систем на более простые (декомпозиция), объединения простых си-
стем в одну (агрегирование) и различных преобразований с целью упро-
щения структуры при сохранении числа и порядка входящих систем.
Основной принцип структурных преобразований состоит в том, что
все преобразования структурной схемы линейной системы и, в частно-
сти, перестановки соседних элементов, агрегирование и декомпозиция
нескольких последовательно (параллельно) соединенных систем, пред-
1.1. МАТЕМАТИЧЕСКИЕ МОДЕЛИ СИСТЕМ И ИХ ХАРАКТЕРИСТИКИ 29
ставление системы и замыкающей ее обратной связи одной системой и,
наоборот, декомпозиции сложной системы на более простую, замкну-
тую обратной связью должны производиться так, чтобы все входные и
выходные сигналы каждого преобразуемого участка схемы оставались
неизменными. Основные правила структурных преобразований произ-
вольных линейных систем приведены (ТСтС, п.1.3.7).
Весовые функции соединений линейных систем. Весовая
функция двух последовательно соединенных систем определяется фор-
мулой
t
g{t,r) = У (1.1.23)
Г
Рассмотрим теперь параллельное соединение линейных систем,
имеющих известные весовые функции д\ и р2- При параллельном со-
единении линейных систем их весовые функции суммируются'.
g(t,r) = gi(t,r) +£2(*,т). (1.1.24)
Весовые функции двух взаимно обратных линейных систем удовлетво-
ряют двум интегральным соотношениям
оо оо
g~(t, a)g(a, г) da = 6(t — т), J* g(t,a)g~ (а^т) da = 6(t — r). (1.1.25)
—oo —oo
Системой, обратной по отношению к системе с обратной связью,
является параллельное соединение системы, обратной по отношению к
системе, стоящей в прямой цепи, и системы, стоящей в цепи обратной
связи. Таким образом, последовательное соединение этих систем дает
идеальную следящую систему. Такие системы являются взаимно обрат-
ными. Применяя формулу (1.1.24) для весовой функции параллельного
соединения линейных систем, находим
p~(t,r) =9i(t,r) +g2(t,T). (1.1.26)
Соединения стационарных линейных систем. Рассмотрим
сначала последовательное соединение двух стационарных линейных си-
стем с передаточными функциями Ф1($) и Фг(з). Тогда, последователь-
ное соединение стационарных линейных систем дает стационарную
30
ГЛ. 1. СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
линейную систему, передаточная функция которой Ф($) равна произ-
ведению передаточных функций соединяемых систем’.
Ф($) = Ф1($)Ф2($). (1.1.27)
Если передаточные функции п соединяемых последовательно си-
стем равны Ф1($),..., Фп(з), то передаточная функция соединения Ф($)
определяется формулой
п
Ф(«) = Ф1(в)Ф2(5) • • • Фп(в) = П (1Л-28)
к=1
Результат последовательного соединения стационарных линейных си-
стем не зависит от порядка их соединения.
Имеют место следующие формулы для амплитудно- и фазо-частот-
ной характеристик последовательного соединения:
п
|ф(^)| = П 1^(^)1> (1.1.29)
k=l
1g |Ф(гш)| = 1g |Ф*(го>)|, arg Ф (го;) = 57 arg Ф^ (геи). (1.1.30)
к=1 /г—1
При последовательном соединении стационарных линейных сис-
тем их фазо-частотные характеристики и логарифмические ампли-
тудно-частотные характеристики суммируются.
В результате последовательного соединения двух взаимно обрат-
ных стационарных линейных систем получается идеальная следящая
система, передаточная функция которой равна единице. Передаточные
функции двух взаимно обратных стационарных линейных систем яв-
ляются взаимно обратными величинами. Если данная система имеет
передаточную функцию Ф(§), то передаточная функция обратной си-
стемы будет 1/Ф($).
Передаточная функция параллельного соединения стационарных
линейных систем равна сумме передаточных функций соединяемых си-
стем:
Ф($) = Ф1(«) + Ф2(«). (1.1.31)
Эта формула распространяется на любое число параллельно соединен-
ных систем:
п
Ф(а) = £фк(в). (1.1.32)
к=1
1.1. МАТЕМАТИЧЕСКИЕ МОДЕЛИ СИСТЕМ И ИХ ХАРАКТЕРИСТИКИ 31
Рассмотрим систему, состоящую из стационарной линейной систе-
мы с передаточной функцией $i (s), замкнутой отрицательной обратной
связью, содержащей стационарную линейную систему с передаточной
функцией Для определения передаточной функции Ф($) этой
системы рассмотрим обратную систему, которая имеет передаточную
функцию 1/Ф($). Эта обратная система представляет собой параллель-
ное соединение системы с передаточной функцией 1/Ф1 (s) и системы с
передаточной функцией Ф2($). Поэтому, пользуясь формулой (1.1.32),
получаем
*(») ф,(»)+!' Ф,(.)
Отсюда находим передаточную функцию интересующей нас системы с
обратной связью:
ф(” = гттажы- <1133>
При жесткой отрицательной обратной связи в формуле (1.1.33) следует
положить Ф2(«) = 1.
Таким образом, при любых соединениях стационарных линейных
систем всегда получаются стационарные линейные системы, пере-
даточные функции и частотные характеристики которых определя-
ются при помощи элементарных алгебраических действий по данным
передаточным функциям (соответственно частотным характерис-
тикам) соединяемых систем,
1.1.4. Стохастические дифференциальные системы. Стоха-
стические модели систем учитывают действие различных случайных
факторов. При применении моделей, описываемых дифференциальны-
ми уравнениями, учет случайных факторов приводит к уравнениям,
содержащим случайные функции (раздел 1.2).
Дифференциальные уравнения (1.1.4) для стохастической системы
должны быть заменены в общем случае уравнениями
Z = F(Z,x,t), Y = G(Z,t), (1.1.34)
где F(z,x,t) и G(z,t) - случайные функции р-мерного вектора z,
n-мерного вектора х и времени t (при этом, как правило, G от х не зави-
сит). Вследствие случайности правых частей уравнений (1.1.34) и, воз-
можно, также начального значения вектора состояния Zq =
= Z(to) вектор состояния системы Z и выходной сигнал Y в каждый
данный момент t представляют собой случайные величины. Поэтому
мы обозначаем их, так же как и случайные функции в правых частях
32
ГЛ. 1. СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
уравнений (1.1.34), большими буквами. Рассматриваемые как функции
времени t, вектор состояния системы Z(t) и ее выходной сигнал Y(t)
представляют собой случайные функции времени t (в общем случае век-
торные). В каждом конкретном опыте случайные функции F(z,x,t) и
Gfat) реализуются в виде некоторых конкретных функций f(z,x,t) и
g(z,t) и этим их реализациям соответствуют вполне определенные ре-
ализации z(t), y(t) вектора состояния Z(t) и выходного сигнала
которые, очевидно, определяются дифференциальными уравнениями
(реализациями уравнений (1.1.34)) z = f(z,x,t), у = g(z,t). Таким
образом, мы приходим к необходимости изучать дифференциальные
уравнения со случайными функциями в правых частях.
В том случае, когда все неопределенные величины в правых частях
уравнений можно считать случайными функциями времени, уравнения
(1.1.34) запишутся в виде
Z =/(Z, я, (*),*), Y = g(Z,N2(t),t), (1.1.35)
где f и g - вполне определенные функции, в число аргументов ко-
торых входят случайные функции времени JV’i(t), N2(t). Начальный
вектор состояния системы Zq в практических задачах всегда являет-
ся случайной величиной, независимой от случайных функций Ni(t) и
N2(t) (от действующих на систему случайных возмущений). Каждой
реализации [пх(£)тП2(£)т]Т случайной функции [Nx(*)TN2(t)T]T
соответствуют реализации /(z, я, ni (£),£), g(z,n2(t),t) функций
f(z,x, М(£), t), g(z,N2(t'),t'), и согласно этому уравнения (1.1.35) дают
реализации z(t) и y(t) вектора состояния системы Z(t) и ее выходного
сигнала Y (£).
Линейные стохастические дифференциальные системы.
Дифференциальные уравнения линейной стохастической системы от-
личаются от уравнений детерминированной линейной системы (1.1.15)
дополнительными аддитивными случайными слагаемыми:
Z — aZ 4- d\x 4- clq 4- d2N\(t), Y — bZ 4- 4~ b\N2(t}. (1.1.36)
В этих уравнениях M (t) и N2(t) - случайные функции времени, в общем
случае векторные. Вводя составную векторную случайную функцию
N(t) = [2Vi(t)TN2(£)т]Т и блочные матрицы d2 — [аг 0], Ь[ = [0Ьх ], где
0 означает матрицу, все элементы которой равны нулю, представим слу-
чайные слагаемые в (1.1.36) в виде a2MW = a2N(t), = b2N(t).
Поэтому без потери общности можно отбросить индексы у случайных
функций и записать (1.1.36) в виде
Z = dZ + dYx + a0 4- d2N(t), Y = bZ 4- b0 + bxW(t). (1.1.37)
1.1. МАТЕМАТИЧЕСКИЕ МОДЕЛИ СИСТЕМ И ИХ ХАРАКТЕРИСТИКИ 33
Линейные системы с параметрическими шумами. В при-
ложениях иногда приходится встречаться с линейными системами, в
которых шумы зависят линейно от вектора состояния системы. В та-
ких случаях приходится пользоваться для описания поведения систе-
мы линейными дифференциальными уравнениями с флуктуирующими
параметрами. Флуктуации параметров уравнений линейной системы
обычно называются параметрическими шумами. Для таких систем
матрицы а2 и bi в уравнениях (1.1.37) зависят не только от времени, но
являются также линейными функциями вектора состояния системы.
Таким образом, уравнения (1.1.37) в случае параметрических шумов
заменяются следующими уравнениями:
(р \
0-20 4" a2k^k j Af(£) ,
7 Рк=\ (1Л-38)
Y = bZ + ь0 + ко + X blkZk] N(t).
\ Л=1 /
Билинейные стохастические дифференциальные системы.
Так называются системы, в которых векторы Z, У, М, N2 в уравнениях
(1.1.35) допускают декомпозицию вида
Z = [z,TZ"T]T , Y = [у'ТУ"Т]Т , М,2 = 2То] ,
причем компоненты Z' и У' удовлетворяют линейным уравнениям вида
(1.1.36), а составляющие Z" и Y" удовлетворяют билинейным уравне-
ниям:
Z' — aZ' 4“ Qix 4" do o>2^i , Y1 — bZ1 4" bo 4" biN^ ,
/ p ' \ / p ' \
Z" = Ao + 22 AkZ'k z" > Y" = + 52 BkZ'k Z" (L1-39)
у k=l J у k=l J
Здесь a, ai, 02, Ao? Afc, bo, bi, Bq, Bk - матрицы, Qq, bo - векторы
соответствующей размерности.
Билинейные стохастические системы являются важным частным
случаем стохастических систем со случайными параметрами.
1.1.5. Дискретные стохастические системы. Известно (ТСтС,
раздел 1.5), что для дискретного ввода входных сигналов в систему не-
обходимо в зависимости от их значения изменять некоторые параметры
2 Фильтры Калмана и Пугачева
34
ГЛ. 1. СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
входных импульсов. Процесс такого изменения называется модуляцией
импульсов входным сигналом. Устройство, формирующее последова-
тельность импульсов, зависящую от входного сигнала, называется им-
пульсным элементом. Обычно форма импульсов сохраняется при мо-
дуляции неизменной. При этом в принципе возможно изменять в зави-
симости от значений входного сигнала один из трех параметров импуль-
са: амплитуду, длительность или момент начала действия импульса. В
соответствии с этим различают три основных вида модуляции импуль-
сов:
• амплитудно-импульсная модуляция (АИМ), при которой
амплитуда импульсов аь линейно зависит от значения входного
сигнала в момент начала действия импульса tk, аь — aktyk) =
= Саим^(^);
• широтно-импульсная модуляция (ШИМ), при которой длитель-
ность импульса Тк линейно зависит от значения входного сигнала в
момент начала действия импульса: Ти(^) = Сшим^(^);
• временная импульсная модуляция (ВИМ), при которой
временной сдвиг Тс (запаздывание) импульса линейно зависит от
значения входного сигнала в определенный момент времени Тс —
— ^вим^(^)-
При АИМ и ШИМ модулирующий сигнал изменяет площадь (т.е.
интенсивность) импульсов, а при ВИМ площадь импульса остается по-
стоянной.
Зависимость модулируемого параметра импульсов, вырабатывае-
мых импульсным элементом от соответствующих дискрет-
ных значений входной переменной, называется характеристикой им-
пульсного элемента. Последняя может быть линейной или нелинейной.
Импульсный элемент с линейной характеристикой является линейным,
а с нелинейной характеристикой - нелинейным.
Импульсные элементы различаются также по форме и характеру
модуляции импульсов, по частоте импульсов и их относительной дли-
тельности. Обычно импульсные элементы работают периоди-
чески, вырабатывая по одному импульсу за каждый период. Период
следования импульсов Тп называется периодом повторения (тактом)
дискретной системы. Величина cjn = ^/Тп представляет собой часто-
ту повторения импульсов. Отношение длительности одного импульса
(средней в случае ШИМ) Ти к периоду повторения импульсов 7 = Т^/Тп
называется относительной длительностью импульсов. Величина 1—7
называется скважностью импульсов элемента.
1.1. МАТЕМАТИЧЕСКИЕ МОДЕЛИ СИСТЕМ И ИХ ХАРАКТЕРИСТИКИ 35
Характеристики дискретных линейных систем. Обозначим
реакцию дискретной линейной системы на кратковременное входное
возмущение, равное единице и действующее только в течение времени
действия к-го импульса, через Qkif). Тогда ее реакция на кратковремен-
ное возмущение, равное x(tk) и действующее только в течение времени
действия к-го импульса, будет равна gk(t)x(tk)- Реакция дискретной
линейной системы на всю последовательность импульсов, модулирован-
ных входным возмущением x(t), определится формулой
оо
yW= 52 9k(t)x(tk). (1.1.40)
к=—оо
Здесь функции gk(t) называются весовыми коэффициентами дис-
кретной линейной системы.
Для любой физически возможной дискретной системы gk(t) — 0
при t < tk (к = 0, ±1, ±2,...). Поэтому физически возможной дискрет-
ной линейной системы, находящейся в покое до момента to, формула
(1.1.40) может быть переписана в виде
y(t) = 52 9k(t)x(tk), (1.1.41)
где неравенство под знаком суммы показывает, что суммирование рас-
пространяется только на моменты действия импульсов tk, заключенные
в интервале [£о,£]-
Весовая функция любой дискретной линейной системы представ-
ляет собой линейную комбинацию 6-функций
оо
9М= ^2 9h(t)6(tk-r). (1.1.42)
k=—oo
И, наоборот, всякая линейная система, весовая функция которой яв-
ляется линейной комбинацией 6-функций, дискретна.
Рассмотрим дискретную линейную систему, представляющую со-
бой последовательное соединение импульсного элемента (ИЭ) и непре-
рывной линейной системы с весовой функцией gi(t,r). Обозначим
функцию, описывающую форму импульсов, вырабатываемых импульс-
ным элементом, через r)(t). В случае АИМ выходной сигнал линейного
импульсного элемента z(t) выразится формулой
оо
z(t)= 52 x(tk)T)(t - tk). (1.1.43)
36
ГЛ. 1. СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
Эта функция является входной переменной непрерывной линейной си-
стемы с весовой функцией pi(t, т). Выходная переменная рассматрива-
емой дискретной системы определяется формулой
7 °° 7
y(t) = I :9i(t,T)z(r)dT = / 91^,т)г1(т - tk)dr.
— Ж) k=~ ОО — ОО
Функция if(r — tk) отлична от нуля только в интервале tk < т <
< tk + Ти, где Ти - длительность импульса, поэтому последную фор-
мулу можно переписать в виде
оо ^+ти
у(4) = z(tk) J Pl(t, 7)77(7 — tk)dr. (1.1.44)
*=-00 4
Сравнивая формулу (1.1.44) с (1.1.40), получаем:
th +Ти ТИ
9k(t) = У 9i(t,r)r)(r - tk)dr = у pi(t,f* + . (1.1.45)
tk о
Следовательно, весовые коэффициенты последовательного соединения
импульсного элемента и непрерывной линейной системы зависят от
формы импульсов, вырабатываемых импульсным элементом, и весо-
вой функции непрерывной части системы.
В случае ШИМ для простоты будем считать, что импульсный эле-
мент вырабатывает прямоугольные импульсы постоянной величины а,
длительность которых пропорциональна значениям входного сигнала
в соответствующие моменты времени. Тогда входной сигнал z(t) не-
прерывной части системы будет равен а в интервалах времени [£*,£* +
-b^(tjb)], где 4 = £шим, и нулю вне этих интервалов. Следовательно,
получим следующее выражение для выходной переменной рассматри-
ваемой дискретной линейной системы:
th+t-x(th)
y(t) = a / 9i(t,T)dr. (1.1.46)
*=-oo 4
При малой длительности импульсов зависимость (1.1.46) принимает вид
y(t) » а£ У #1(М*)®(**), £ = €шим, (1.1.47)
k=—7ЯО
1.1. МАТЕМАТИЧЕСКИЕ МОДЕЛИ СИСТЕМ И ИХ ХАРАКТЕРИСТИКИ 37
где величина а£, представляющая собой произведение амплитуды им-
пульса на его длительность при единичном входном сигнале, определяет
интенсивность импульсов. Таким образом, при ШИМ последователь-
ное соединение импульсного элемента и непрерывной системы с весо-
вой функцией gi (t, т) можно считать линейной дискретной системой,
весовые коэффициенты которой определяются формулой
9k(t) = С = Сшим- (1.1.48)
При ВИМ в произвольной форме последовательное соединение им-
пульсного элемента и непрерывной линейной системы лишь прибли-
женно можно рассматривать как линейную дискретную систему, если
максимальный возможный временной сдвиг импульса достаточно мал,
чтобы весовая функция непрерывной части системы была бы
приблизительно линейной функцией г в диапазоне возможных значе-
ний временного сдвига.
Рассмотрим особенности дискретных линейных систем, содержа-
щих цифровые вычислительные устройства. Пусть выходная перемен-
ная такой системы интересует нас лишь в определенные моменты вре-
мени t] (I = 0, ±1, ±2,...). Полагая в формуле (1.1.40) t = найдем
значения выходной переменной системы в интересующие нас моменты
времени (I = 0, ±1, ±2,...):
оо
= 52 9k(ti)x(tk)
k=—oo
или, полагая xk = x(tk), yi = = 9ik, to
OO
У1= 22 3ikxk (1 = 0, ±1, ±2,...). (1.1.49)
—OO
В случае, когда последовательность моментов фиксации выходной пере-
менной системы совпадает с последовательностью моментов
действия импульсов = ti (I = 0, ±1, ±2,...), формула (1.1.49) при
t = ti даст следующее выражение значений выходной переменной фи-
зически возможной дискретной линейной системы:
38
ГЛ. 1. СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
I
yi = ^9ikXk (/ = 0,1,2,...). (1.1.50)
к—О
Формула (1.1.50) и аналогичные формулы для дискретных
систем с несколькими входами и выходами описывают, в частности,
работу цифрового устройства в случае, когда результаты вычислений
линейно зависят от исходных данных. В этом случае исходные дан-
ные для вычислений, вводимые на каждом шаге вычислений, являются
входными сигналами, а результаты вычислений - выходными перемен-
ными. Весовые коэффициенты gik определяют программу вычислений
(1.1.49). Свойства цифрового устройства полностью характеризуются
программой вычислений.
При достаточно малом Тп дискретную линейную систему мож-
но приближенно рассматривать как непрерывную линейную систему
с весовой функцией g(t,tk) = 9k(t)/Tn. Последовательное соединение
импульсного элемента и непрерывной стационарной линейной системы
можно считать непрерывной стационарной линейной системой, если пе-
риод повторения импульсов достаточно мал по сравнению с постоянны-
ми времени непрерывной части системы.
Стационарные дискретные линейные системы. Дискретная
система называется стационарной, если при сдвиге во времени входно-
го возмущения без изменения его формы на интервал времени, крат-
ный периоду повторения импульсов, выходная переменная сдвигается
во времени на такой же интервал без изменения своей формы. Из этого
определения следует, что дискретная система может быть стацио-
нарной только в том случае, когда действующие на систему значения
входного возмущения следуют друг за другом через равные промежут-
ки времени. Если значения входной переменной вводятся в систему
через неравные интервалы времени, то дискретная система нестаци-
онарна.
Весовые коэффициенты стационарной дискретной линейной систе-
мы представляют собой одну и ту же функцию, сдвинутую во времени
на интервалы, кратные периоду повторения импульсов:
9k(t) =go(t-kTn) (fc = 0,±l,±2,...). (1.1.51)
Весовые коэффициенты gik для стационарной дискретной линейной
системы зависят только от разности индексов:
9ik = 9k(ti) — 9о((1 ~ *)ТП) (k,l = 0, ±1, ±2,...).
(1.1.52)
1.1. МАТЕМАТИЧЕСКИЕ МОДЕЛИ СИСТЕМ И ИХ ХАРАКТЕРИСТИКИ 39
Будем обозначать их wm (m = 0,±1,±2,...). Для физически возмож-
ных стационарных дискретных линейных систем go(t) = 0 при t < 0 и
wm = 0 при т < 0.
Весовые коэффициенты wm последовательного соединения им-
пульсного элемента и непрерывной стационарной линейной системы оп-
ределяются формулой
ти
wm — w(mTn - a)r}(a)da (m = 0, ±1, ±2,...). (1.1.53)
о
Формула, выражающая последовательность значений выходной пе-
ременной через последовательность значений входной переменной, для
стационарной дискретной линейной системы принимает вид
оо оо
У1 = 52 Wl~kXk = 52 w™x‘~™ (1.1.54)
к= — оо т= — оо
Реакция стационарной дискретной линейной системы на показа-
тельное возмущение est в момент t = 1ТП равна значению этого возму-
щения в тот же момент, умноженному на функцию
оо
Ф(«)= 52 w-e-smT", (1.1.55)
т= — оо
зависящую только от параметра s. Функция Ф($) является передаточ-
ной функцией стационарной дискретной линейной системы.
Полагая в (1.1.55) s = iuj, находим частотную характеристику
системы:
Ф(гш) = jP wme~imTn“. (1.1.56)
тп——оо
Формула (1.1.56) показывает, что частотная характеристика стационар-
ной дискретной линейной системы является периодической функцией
частоты ш с периодом П = 2тг/Тп. Формула (1.1.56) определяет ча-
стотную характеристику стационарной дискретной линейной системы
в виде ее ряда Фурье. Коэффициентами этого ряда являются весовые
коэффициенты системы
Q 27г/Тп
Wm = 1 [ $(w)eimTn“du = [ $(w)eimTnUdu. (1.1.57)
П J 2тг J
о о
40
ГЛ. 1. СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
Для физически возможной стационарной дискретной линейной си-
стемы формула (1.1.55) принимает вид
оо
ф(в) = 12 wme~emTn .
т=0
(1.1.58)
Формулы (1.1.55) и (1.1.56) показывают, что передаточные функ-
ции стационарных дискретных линейных систем являются функциями
величины z = еаТп. Обозначая через Ф(з) передаточную функцию фи-
зически возможной стационарной дискретной линейной системы и рас-
сматривая ее как функцию параметра z, можем переписать формулу
(1.1.58)
оо
Ф(з)= £wmz~m. (1.1.59)
m=0
При этом по определению
Ф(а) = Ф (е‘Тп) , Ф(г) = Ф .
\ П /
(1.1.60)
Функция Ф(г) называется z-преобразованием весовых коэффициентов
wm.
Для вычисления значений выходных переменных стационарных ли-
нейных систем с непрерывно изменяющимися выходными переменными
в промежутке между импульсами можно пользоваться общей
формулой (1.1.40), заменив в ней весовые коэффициенты gk(t) их вы-
ражением (1.1.51). При этом практически удобно определять момент
времени t между двумя соседними импульсами относительным прира-
щением времени после каждого импульса е. Иными словами, любой
момент времени в интервале между импульсами 1ТП < t < (I + 1)ТП
удобно определить формулой t = 1ТП -I- еТп (0 < е < 1). Полагая
у(1Т„ + еТ„) = yi(e),
► ,
дк(1Т„ + еТп) = д0((1 - к)Т„ + еТ„) = wz_*(s) ,
(1.1.61)
получим для физически возможной стационарной дискретной линейной
системы
оо
У,(е) = £ wm(e)xz_m (0 < е < 1; I = 0, ±1, ±2,...). (1.1.62)
т=0
1.1. МАТЕМАТИЧЕСКИЕ МОДЕЛИ СИСТЕМ И ИХ ХАРАКТЕРИСТИКИ 41
В случае показательного входного возмущения x(t) = eet, xi~m =
_ es(i-m)Tn и фОрМуЛа (1.1.62) дает
ОО
!/«(£) = е“Тп 22 wm(e)e~‘mTn . (1.1.63)
m=0
Входящая в эту формулу функция при 0 < е < 1, I = О
оо
Ф(в,£) = 22 wm(£)e-’mT" (1.1.64)
m=0
называется передаточной функцией стационарной дискретной ли-
нейной системы с непрерывным выходом. При з = геи формула
(1.1.64) определяет частотную характеристику стационарной дискрет-
ной линейной системы с непрерывным выходом. Зависимость переда-
точной функции и частотной характеристики от е отражает тот факт,
что дискретная система может быть стационарной лишь по отношению
к сдвигам во времени, кратным периоду повторения импульсов, и не мо-
жет быть стационарной в полном смысле, т.е. по отношению к любым
сдвигам во времени. При Е = 0 передаточная функция стационарной
дискретной линейной системы совпадает с ранее введенной передаточ-
ной функцией, определяемой формулой (1.1.58): Ф(з,0) = Ф(з).
Рассматривая передаточную функцию стационарной дискретной
линейной системы с непрерывным выходом как функцию параметра
z = еаТп, можно переписать формулу (1.1.64) с учетом (1.1.60) в виде
оо
Ф(г,е) = 22 (0 < е < 1). (1.1.65)
тп=0
Стационарные дискретные системы, описываемые раз-
ностными уравнениями. В случае, когда поведение дискретной ли-
нейной системы описывается разностным уравнением, это уравнение
всегда может быть написано в виде
йпЗ/л+п + ап-1Ук+п 4--F ai3/fc+i + аоУк —
— Ьт^к+т 4" Ьт—1 4- • • • 4- biXk+i 4" •
(1.1.66)
42
ГЛ. 1. СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
Для того чтобы дискретная линейная система, описываемая разност-
ным уравнением (1.1.66), была стационарной, необходимо и достаточно,
чтобы все коэффициенты уравнения были постоянными.
Разностное уравнение (1.1.66) может быть записано в оператор-
ной форме. Для этого введем оператор сдвига V, определяющий сдвиг
функции на период повторения Тп: V/(£) = /(£ 4- Тп). Полагая t = кТп,
получим Vlfk = fk^-i (I = 1,...,п). Значит уравнение (1.1.66) можно
представить в полиномиальной относительно V форме:
F(V)yk = Н(У)хк ,
(1.1.67)
где
F(V) = anVn 4~ an_i Vn 1 4~ • • • 4~ czi V 4~ , 1
H(V) - bmVm + dm_! Vя1-1 + . •. + h V + do . J
Передаточная функция стационарной дискретной линейной систе-
мы, поведение которой описывается разностным уравнением (1.1.67),
всегда является дробно-рациональной функцией переменной z = esTn
вида
Ф(г) = F(z) / H(z). (1.1.68)
Передаточные функции стационарных дискретных линейных си-
стем, описываемых разностными уравнениями, определяются совер-
шенно так же, как и передаточные функции непрерывных стационар-
ных линейных систем, описываемых дифференциальными уравнения-
ми. В случае непрерывной системы оператор дифференцирования в
дифференциальном уравнении заменяется параметром показательной
функции з, а в случае дискретной системы оператор сдвига в разност-
ном уравнении заменяется величиной z — esTn. В обоих случаях в ре-
зультате получается алгебраическое уравнение для передаточной функ-
ции системы. Операторы дифференцирования D и сдвига V связаны
тем же самым соотношением, что и величины з и z\ V = e7nD и z —
— (>sTn
Дискретные линейные системы, описываемые разностны-
ми уравнениями. В приложениях для математического описания мо-
делей дискретных линейных систем обычно используются следующие
разностные уравнения
%к+1 — / ^гк^к+г 4" у O'lsk'tk+s 4“ ?
1.1. МАТЕМАТИЧЕСКИЕ МОДЕЛИ СИСТЕМ И ИХ ХАРАКТЕРИСТИКИ 43
Ук = bkZk + bok , 1>1, (1.1.69)
ИЛИ
Zk+1 - CkZk +qkXk + С0к,Ук = bkZk + bok (1.1.70)
соответственно для векторов состояния z и выходного сигнала у. В
(1.1.69) и (1.1.70) принято, что векторы х, г, у имеют размерности п, р,
т соответственно; агк - (р х р)-матрица; aisk - (р х п)-матрица; аок и
Ъ$ь ~ векторы размерности р и т соответственно.
Для стационарных систем входящие в уравнения (1.1.69) и (1.1.70)
коэффициенты не зависят от к: агк — ar> &isfc = &is> Ьк — 6,
bok — b. Модель (1.1.69) называется линейной дискретной порядка I
(/ = 1,2,...); модель (1.1.70) - дискретной линейной первого порядка.
Дискретную линейную систему (1.1.69) любого порядка можно при-
вести к линейной модели первого порядка (1.1.70). При этом ограни-
чимся рассмотрением уравнения для вектора состояния z.
Введем новые величины zik , • • • , zik, определив их следующими
соотношениями:
Zk — %ik Qikxk , ^r,n+i — %r+i,k Qr+i,kxk (^ — !,...,/ 1). (1.1.71)
Входящие сюда величины определяются из уравнений
1-1
zi,k+i — ^rk^r+i,k qi+i,kxn) (1.1.72)
г=0
1-1
Qi+i,k — bok ? (1.1.73)
г—о
i-1
Qik — + У? ai-i+h,k-l+i-lQhk • (1.1.74)
h=l
Положим теперь
Zk = Zlk ' Z2k , Ck = 0 0 I 0 0 I o - 0 , qk = q*k q3k
- Zlk - 0 0 0 I - qk+l,k -
- O,0k Olk 0,2k ak — l,k -
(1.1.75)
44
ГЛ. 1. СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
где 0 - квадратная матрица той же размерности, что и aQk, au,...
... все элементы которой равны нулю, а I - единичная матри-
ца той же размерности. Тогда уравнения (1.1.71) и (1.1.72) с учетом
(1.1.75) запишутся в виде уравнения (1.1.70).
Для дискретных линейных систем аналогично формулам (1.1.18)и
(1.1.19) находим
к
Zk = Ukozo + ^2 UhrairXr + aor , (1.1.76)
r=0
к к
Ук = bkukozo + 52bkUkralrxr +bk^2ukraOr + bok , (1.1.77)
r=0 r=0
где матрица весовых коэффициентов дкг связана с матрицей фундамен-
тальных решений икг формулой
9кт = bkukralrl(k - г). (1.1.78)
Дискретные нелинейные системы, описываемые разност-
ными уравнениями. Для описания дискретных нелинейных систем
применяют следующие два основных типа нелинейных разностных
уравнений:
Zk+i = fa(zk, ••• , гк+1-1,хк), ук = gk(zk,xk), 1 = 1,2,..., (1.1.79)
zk = fk{zk,xk), ук = gk(zk,xk), (1.1.80)
где zk и ук - векторы размерности р и тп соответственно; fk -
р-мерная векторная функция отмеченных переменных, а дк - т-мер-
ная функция. Для стационарных дискретных нелинейных моделей име-
ем fk = f, дк = д независимо от к.
Нелинейная модель (1.1.79) приводится к модели (1.1.80) (ТСтС,
п.1.5.5).
Дискретные стохастические системы. Уравнениям (1.1.34),
(1.1.35) в дискретном случае отвечают стохастические разностные урав-
нения
Zk+1 = Fk(Zk,xk), Yk = Gk(Zk), (1.1.81)
Zk+i = h{Zk,xk,Nlk), Yk = gk(Zk,N2k). (1.1.82)
1.1. МАТЕМАТИЧЕСКИЕ МОДЕЛИ СИСТЕМ И ИХ ХАРАКТЕРИСТИКИ 45
Следовательно, уравнения для дискретных систем с параметрическими
шумами Nik и Nik записываются в виде:
(р \
^20* + y^Q2ikZik I Nik ,
/ р 7 (1.1.83)
Yk = bkZk + bok + I bwk + 5? I Nik >
\ t=l /
где Zk = [ Zik • • • Zpk ]T.
Для дискретных билинейных стохастических систем имеем следу-
ющую систему уравнений:
Z'k+1 = akZ'k + OikXk + во* + Я2к^2к >
Y^bkZi + bok + buNb,
ZL+1 = (Au + Е Aikz;k) Z4, Yk = (B0k + £Btkz'lk ) z1;,
\ »=1 J У i=l J
(1.1.84)
где Zk = [ziTZ'k'T]T, Yk = [rZIX"T]T> M,2* = [M,2T0].
1.1.6. Устойчивость, управляемость и наблюдаемость ли-
нейных систем
Устойчивость линейных систем. Для линейных асимптотиче-
ски устойчивых систем (пп. 1.1.1, 1.1.5) можно использовать понятие
устойчивости не процессов, а всей линейной системы в целом. В даль-
нейшем будем пользоваться общей теоремой Ляпунова об асимптотиче-
ской устойчивости, а также частными критериями, подробно рассмот-
ренными, например, в (Воронов 1979, 1985).
Управляемость стационарных систем. Рассмотрим сначала
линейную стационарную систему
х = Ах 4- Ви, (1.1.85)
где х = x(t) и и = u(t) векторы состояния и управления размерности п
и г соответственно; А - квадратная (п х т)-матрица; В - прямоуголь-
ная (п х г)-матрица. Следуя Калману (Калман 1961) будем называть
дифференциальную систему (1.1.85) вполне управляемой, если для лю-
бых моментов времени to и ti, (ti > to) и любых заданных состояний
46
ГЛ. 1. СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
хо и xi существует управление u(t) (to < t < £i), переводящее началь-
ное состояние x(to) = xq в конечное состояние x(ti) = х^. Аналогично
определяется управление для дискретной системы
= Axi 4- Bui.
(1.1.86)
Условие полной управляемости дается следующей теоремой Калмана
(Калман 1961).
Теорема 1.1.1. Линейная дифференциальная система (1.1.85) или
дискретная (1.1.86) полностью управляема тогда и только тогда, ко-
гда матрица
КУ = [В АВ А2В ... АП-1В] (1.1.87)
размерности (п х пг) имеет ранг, равный п, rank/Cy = п.
Для г — 1 (В - вектор-столбец) из теоремы следует, что для пол-
ной управляемости векторы В, АВ, ... , Ап-1 В должны быть линейно
независимыми.
Наблюдаемость стационарных систем. Теперь рассмотрим ли-
нейную стационарную систему вида
х = Ах 4- Ви, у = Сх 4- Du.
(1.1.88)
Здесь размерности векторов х,у,и соответственно равны п,щ,г', раз-
мерности матриц A,B,C,D - равны соответственно (п х п), (п х г),
(nt х п), (их х г). По определению состояние x(t) называется наблюда-
емым, если в момент наблюдения t = to можно однозначно определить
x(to) по данным измерениям y(t) и u(t) на конечном интервале времени
£о < £ < £1, £1 > £о- Система (1.1.88) полностью наблюдаема, если на-
блюдаемы все ее состояния в любые моменты времени. Условия полной
наблюдаемости системы (1.1.88) даются следующей теоремой Ройтен-
берга (Воронов 1979, 1985, Ройтенберг 1971).
Теорема 1.1.2. Для того чтобы линейная стационарная диффе-
ренциальная система (1.1.88) была полностью наблюдаемой, необходи-
мо и достаточно, чтобы матрица
КУ = [ст АТСТ АттСт ... (1.1.89)
имела ранг п, rank/Cn = п.
1.1. МАТЕМАТИЧЕСКИЕ МОДЕЛИ СИСТЕМ И ИХ ХАРАКТЕРИСТИКИ 47
Принцип двойственности для стационарных систем. Для
управляемости и наблюдаемости линейных систем Калманом установ-
лен следующий принцип двойственности. Пусть даны две линейные
дифференциальные системы
х — Ах 4- Ви, у = Сх 4- Du, (1.1.90)
£ = AT£ + CTv, r] = BTfi + DTv. (1.1.91)
Такие системы называются двойственными или сопряженными . Оче-
видно, что условие rank [В АВ ... АП-1В] = п является условием
управляемости (1.1.90) и одновременно условием полной наблюдаемо-
сти системы (1.1.91), а равенство rank [СТ АТСТ ... — п
является условием полной наблюдаемости системы (1.1.90) и одновре-
менно условием полной управляемости (1.1.91). Иными словами, систе-
ма (1.1.90) полностью управляема тогда и только тогда, когда полно-
стью наблюдаема сопряженная с ней система (1.1.91), и наоборот.
Аналогично рассматривается принцип двойственности для дис-
кретных систем вида
xi+i = Axi 4- Вщ, yi = Cxi 4- Dui,
6+1 = ATb + CTvh тц = + DTvt. (1.1.92)
Управляемость и наблюдаемость нестационарных систем.
Применительно к нестационарным линейным системам
х = A(t)x 4- B(t)u, (1.1.93)
xi+i = Aixi 4- Btui, (1.1.94)
имеют место следующие определения и утверждения (Калман 1961,
Ройтенберг 1971).
Система (1.1.93) или (1.1.94) называется вполне управляемой в мо-
мент времени или 10, если из любого состояния, которое она занимает
в момент времени или Iq, ее можно перевести в нулевое состояние за
конечный промежуток времени, выбирая надлежащим образом закон
управления и = u(t) или (щ).
Теорема 1.1.3. Пусть — ^(Z)^”1 (t), где d(t) - фундамен-
тальная матрица системы х = A(t)x, а через И\(£о,£) обозначена
матрица
W1(W)= Г Ф(1о,т)В(т)Вт(т)Фт(1о,т)</г. (1.1.95)
48
ГЛ. 1. СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
Тогда линейная нестационарная система (1.1.93) управляема в мо-
мент времени to, если и только если для некоторого конечного ti мат-
рица Wi(to,ti) является положительно определенной матрицей, т.е.
квадратичная форма (f, Wif) (где £ - п-мерный вектор) положитель-
на для всех £ / 0.
Для дискретной системы роль матрицы Wi(t0, А) играет
h
(1.1.96)
p=/o
Рассмотрим теперь задачу восстановления начального значения
x(to), по найденной из наблюдений вектор-функции y(t) (to < t < tk)
для линейных систем
x = A(t)x, y — C(t)x. (1.1.97)
Следуя (Бьюси и Джозеф 1968, Калман 1963), можно сформулировать
следующие утверждения.
Если любое известное начальное состояние х(to) может быть опре-
делено по известной на отрезке [to, tfc] вектор-функции y(t), то система
называется вполне наблюдаемой на отрезке [to, t*].
Система (1.1.97) вполне наблюдаема на отрезке [to,t*], если и
только если матрица
rth
W2(to,tk)= / $T(t,t0)C'T(t)C(t)$(t,t0)d« (1.1.98)
Ao
является неособой, det W2(to, tk) 0.
Для дискретной линейной системы
xi+i = Aix, yi = C1X1 (1.1.99)
в качестве матрицы W2(to,tfc) принимается следующая:
U
(iiioo)
P=h
Система (1.1.90) или (1.1.92) называется равномерно вполне наблю-
даемой, если существуют фиксированные постоянные a,ai,a2, такие,
что
О < a\I < W2(t - a,t) < аъ! Vt > to + а
1.1. МАТЕМАТИЧЕСКИЕ МОДЕЛИ СИСТЕМ И ИХ ХАРАКТЕРИСТИКИ 49
И
О < аД < < 012I V& > 0.
Система (1.1.90) или (1.1.92) называется равномерно вполне управ-
ляемой, если
0 < otil < Wi(t - a, t) < «2-^ Vt > tQ 4- а
и
О < оц! < Wijj-h < 012I Vh > 0.
Управляемость систем с подвижными концами. Рассмотрим
сначала стационарную дифференциальную систему (1.1.88) при D = 0:
х = Ах 4- Ви, у = Сх. (1.1.101)
Целью управления является приведение вектора y(t) к моменту
времени tnK в заданное состояние 3/(tnK) = 3/пк- Условия, при которых
такое приведение является возможным, следуя (Бьюси и Джозеф 1968,
Калман 1963), называется условиями управляемости по у.
Справедливо следующее утверждение.
Теорема 1.1.4. Для того чтобы система (1.1.101) была управля-
емой по у, необходимо и достаточно, чтобы ранг матрицы
Р= [СВ С АВ СА2В ... CA”1"1!?] (1.1.102)
был равен Hi, rankP = щ.
Для нестационарного случая, когда
х = A(t)x 4- D(t)u, y = C(t)x (1.1.103)
справедлива теорема.
Теорема 1.1.5. Пусть Ф(£,т) = ^(^(t)”1, где ti(t) - фундамен-
тальная матрица решений системы х = A(t)x, а через
rh
W3(to,ti)=/ C(ii)$(ti,T)B(T)BT(r)$T(ti,T)C'T(ti)dT. (1.1.104)
j to
Тогда нестационарная система вполне управляема по у на отрезке вре-
мени to < t < ti, если и только если матрица УУз(йьМ является
положительно определенной.
50
ГЛ. 1. СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
Для стационарных дискретных систем вида
xi+i = Axi 4- Вщ, yi — Cxi (1.1.105
имеет место предыдущая теорема. А для нестационарных систем
= Aixi 4- Btui, yi = Cixi (1.1.106)
в этой теореме матрица УУз(£о Д1) должна быть заменена на следующую:
h
Wo.h = 52 Ch*h,pBpBTp$h,p. (1.1.107)
P—Iq
Неполностью управляемые и наблюдаемые системы. Си-
стема с одним входом и одним выходом (непрерывная или дискретная)
полностью управляема и наблюдаема только в том случае, если переда-
точная функция Ф(з), получаемая из уравнений sx — Ах 4- Ви, у = Сх,
невырожденная, т.е. невозможно сократить полюсы Ф(з), представив
ее в виде отношения многочленов со степенью знаменателя меньше чем
п. Если Ф($) вырождена, то система либо неполностью управляема,
либо неполностью наблюдаема, либо неполностью управляема и непол-
ностью наблюдаема (Воронов 1979, 1985).
Для сложных линейных систем со многими входами и выходами
различают неполностью управляемые и наблюдаемые системы. Пусть
задана линейная система
х = Ах 4- Ви, у — Сх (1.1.108)
с базисом е = {ei , ... , еп}. Базис е представляет собой совокупность
линейно независимых векторов, например, единичных ортов евклидова
n-мерного пространства Вп, при этом
х — eiXi. (1.1.109)
г=1
Если ввести управляемые и неуправляемые группы переменных, то
может оказаться, что для некоторого Xj все функции чувствительности
1.1. МАТЕМАТИЧЕСКИЕ МОДЕЛИ СИСТЕМ И ИХ ХАРАКТЕРИСТИКИ 51
обращаются в нуль (£ - преобразование Лапласа). Тогда Xi совершенно
не зависят от иj (j = 1, ... , г 1). В этом случае говорят, что Xi полно-
стью инвариантна по отношению к воздействиям и/или неуправляе-
ма. Если же все координаты Xi при всех возможных базисах ё управля-
емы по всем воздействиям, то система будет полностью управляемой.
Можно также рассмотреть случай, когда при некотором базисе ё,
какая-либо из координат Xi будет неуправляемой по одному из воздей-
ствий Uj, но управляемой по другим воздействиям, остальные же коор-
динаты управляемы по всем воздействиям. Тогда система будет также
полностью управляемой, поскольку можно выбрать вектор и, переводя-
ющий систему в заданное состояние, но она уже будет частично инва-
риантной по координате Xi и управлению Uj. Если же при некотором
базисе ё некоторая координата Xi окажется совершенно неуправляемой,
то система будет полностью неуправляемой.
Для неполностью управляемой системы (1.1.108) всегда можно най-
ти такое преобразование х = Sx, det S 0, при котором исходная си-
стема преобразуется к виду
З;1 — Ли#1 4- А12х2 + Вй,
X2 = Л22^2, у = Сх. (1.1.110)
Здесь х2 - это совокупность тех я*, которые оказываются полностью
независящими от управлений и как непосредственно, так и через ком-
поненты векторов х1, характеризующих управляемую часть системы.
Критерий полной управляемости позволяет установить, будет ли систе-
ма полностью управляемой при всех возможных базисах. Размерность
управляемой части системы (dim#1 = ти) совпадает с рангом матрицы
К,у. В полностью управляемой системе = п, если 0 < п± < п система
не полностью управляема; при п± — 0 система полностью неуправляе-
ма.
Назовем величины, характеризующие полностью или частично со-
стояние системы и допускающие непосредственное измерение, наблюда-
емыми выходами системы. Переменные состояния я*, полностью опи-
сывающие состояние системы, могут не совпадать с наблюдаемыми вы-
ходами и число их может быть больше, чем число выходов. Но если
любая из переменных состояния может быть выражена через значения
наблюдаемых выходов при и = 0, то система будет полностью наблю-
даемой. Если же некоторые из переменных состояния не могут быть
выражены через наблюдаемые выходы, то система будет неполностью
наблюдаемой.
52
ГЛ. 1. СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
Для неполностью наблюдаемой системы (1.1.108) после преобразо-
вания х = Sx соответствующую систему можно разбить на следующие
группы:
= Ли#1 + В1й, i2 = А21Х1 + А22Х2 + B2U, y = Cix1. (1.1.111)
Идентифицируемость систем. Предположим, что при помо-
щи измерений определено состояние х(ЛД) в моменты t = hA (h =
= 0,1, ... , п) (Д - некоторая фиксированная величина) для стацио-
нарной линейной системы
х = Ах. (1.1.112)
Обозначим через /ДД) и /2(Д) следующие (п х п)-матрицы:
Л(Д) = [ж(Д) х(2Д) ... ж(пД)], (1.1.113
/2(Д) = [х(0) х(Д) ... х((п-1)Д)}. (1.1.114)
При этом в силу известного разложения
A2t2
eAt = I + At+ — + --- (1.1.115)
при <1е1/2(Д) 0 0 справедливо следующее соотношение:
7(<) = еЛ{ = /1(Д)/2-1(Д). (1.1.116)
Формула (1.1.116) выражает собой тот факт, что матрица eAt может
быть определена по измеренным (п х п)-матрицам /ДД) и /2(A)- Это
свойство системы (1.1.112) называется свойством идентифицируе-
мости. Если записать матрицу /2(Д) в виде
/2(Д) = [х(0) /(Д)х(0) /2(Д)х(0) ... /^(ДИО)], (1.1.117)
то условие идентифицируемости системы (1.1.112) состоит в том, что
ранг матрицы (1.1.117) должен быть равен п, гапк/2(Д) = п.
1.2. СЛУЧАЙНЫЕ ФУНКЦИИ
53
1.2. Случайные функции
1.2.1. Вероятностные пространства. В теории вероятностей
(ТСтС, раздел 2.1) всегда рассматривается некоторый опыт, результа-
ты которого при соблюдении заданного одинакового комплекса условий
могут быть различными вследствие действия случайностей. Любой ка-
чественный результат опыта, о котором можно сказать, что он появился
или не появился, называется событием. С каждым опытом связано не-
которое множество возможных событий. Каждое из этих событий имеет
вполне определенную вероятность. Вероятности всех возможных в дан-
ном опыте событий образуют распределение вероятностей, связанное
с данным опытом.
В случае, когда множество всех возможных в данном опыте собы-
тий счетно, каждое событие фактически представляет собой множество
некоторых простейших событий. Среди множества всех возможных в
данном опыте событий всегда можно выделить так называемые “неде-
лимые” события, каждое из которых не содержит никаких подсобытий,
кроме невозможного события и самого себя, и из которых любое собы-
тие может быть получено операцией объединения. Такие простейшие
“неделимые” события называются элементарными событиями. Вводя
понятие элементарного события, мы получаем возможность рассматри-
вать любое событие как некоторое множество элементарных событий и
таким путем установить полную тождественность событий и множеств.
При этом множество всех элементарных событий представляет собой
достоверное событие П, а пустое множество 0 - невозможное событие.
Множество Q всех элементарных событий называется пространством
элементарных событий. Каждое элементарное событие си представля-
ет собой точку пространства элементарных событий Q.
При построении вероятностных моделей в случае несчетных П за-
даются не всеми возможными подмножествами Q, а некоторыми систе-
мами подмножеств, замкнутыми относительно счетных объединений и
счетных пересечений элементов системы. Таким путем приходят к по-
нятию а-алгебр событий. Разумеется, и в этом случае можно условно
называть П пространством элементарных событий.
Вероятностные пространства. Как отмечалось выше, множе-
ство 5 событий, для которых необходимо определить вероятности,
должно представлять собой алгебру в случае конечного числа элемен-
тарных событий и а-алгебру в случае бесконечного множества элемен-
тарных событий. Только в этом случае можно пользоваться основными
законами теории вероятностей - законом сложения и законом умно-
жения при решении задач теории вероятностей. Вероятность события
54
ГЛ. 1. СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
Р(А), А е 5, при этом представляет собой неотрицательную аддитив-
ную (в конечном случае) или «7-аддитивную функцию множества в про-
странстве элементарных событий. Чтобы определить распределение ве-
роятностей, необходимо задать пространство элементарных событий Q,
а-алгебру множеств 5 (алгебру в конечном случае) в этом пространстве
и определить на этой «7-алгебре (алгебре) вероятность Р(А).
Пространство элементарных событий Q с выделенной в нем
(7-алгеброй множеств 5 и заданной на этой «7-алгебре вероятностью
Р(А) называется вероятностным пространством и обозначается
(Q,5,P). При этом постулируется, что вероятность Р(А) представля-
ет собой нормированную неотрицательную меру, т.е. неотрицатель-
ную (7-аддитивную функцию множества, удовлетворяющую условию
Р(П) = 1.
Пусть в измеримом пространстве (9,5) определена неотрицатель-
ная конечная или «7-конечная мера I/, тогда вероятность Р = Р(А) мо-
жет быть представлена в виде суммы ^-непрерывной и 1/-сингу-
лярной мер, причем ^-непрерывная часть представляет собой интеграл
по мере и от некоторой функции /(cv),
Р(А) = I f&Mdu) + Р,(А). (1.2.1)
А
Когда вероятность Р(А) ^-непрерывна, PS(A) = 0 и
Р(Л) = У/(w)p(dw). (1.2.2)
А
В этом случае функция /(о?) представляет собой производную Радо-
на-Никодима вероятности Р по мере v и называется плотностью ве-
роятности по мере и в пространстве (Q,5, Р).
Любое подмножество N множества Nq € 5, для которого
P(7V0) — 0, называется нулевым множеством. Если нулевое множе-
ство N принадлежит «7-алгебре 5 вероятностного пространства
(9,5,Р), то, очевидно, P(N) — 0. Однако нулевое множество может
и не принадлежать 5 (если Nq С 5, то подмножества множества No мо-
гут и не принадлежать 5). На таких нулевых множествах вероятность
P(N) не определена. Вероятностное пространство (9,5,Р) называет-
ся полным, если «7-алгебра 5 содержит все нулевые множества этого
пространства. Если вероятностное пространство (9,5,Р) не полно, то
его всегда можно пополнить, добавив в 5 все нулевые множества и все
1.2. СЛУЧАЙНЫЕ ФУНКЦИИ
55
объединения нулевых множеств с множествами из 5 и определив соот-
ветствующим образом вероятность Р на добавленных множествах.
1.2.2. Случайные величины. В элементарной теории вероят-
ностей (ТСтС, раздел 2.2) случайной величиной называется величина,
которая принимает в результате опыта какое-нибудь одно из множества
возможных значений, причем заранее (до опыта) невозможно предви-
деть, какое именно значение она примет. При этом предполагается,
что в пространстве возможных значений каждой случайной величины
существует распределение вероятностей. Следуя (ТСтС, раздел 2.2),
приходим к следующему определению случайной величины. Случай-
ной величиной со значениями в измеримом пространстве (X, Л) назы-
вается (5, Л)-измеримая функция точки в вероятностном пространстве
(Q,5, Р), отображающая Q в X и определенная всюду в 0, за исключе-
нием, быть может, множества нулевой вероятности Р. Значение случай-
ной величины в любой данной точке cv пространства Q (т.е. значение,
которое она принимает, когда в результате опыта появляется элемен-
тарное событие о?) называется реализацией этой случайной величины.
Очевидно, что любая случайная величина в (X, Л) является в то же
время и случайной величиной в (X, Л'), где Л' - любая а-алгебра в X,
содержащаяся в Л, Л' С А.
Мы часто будем обозначать случайную величину той же бук-
вой, что и пространство ее значений. При рассмотрении множества
случайных величин со значениями в одном и том же пространстве, обо-
значения этих величин будут дополняться индексами. Так, например,
X, Ха представляют собой случайные величины со значениями в про-
странстве X. Если X, Ха - случайные величины в (X, Л), то согласно
определению X — х(ш), Ха = жа(си), где rr(cv), rra(cv) - (5, Л)-измеримые
функции, отображающие Q в X.
Вероятностная мера. В силу (Л, 5)-измеримости случайной ве-
личины X = х(ш) в (X, Л) вероятность того, что она примет значение
из множества А, определяется следующей формулой:
Р(Х е А)-Р(х-Х(А)), Ае Л,
где, как всегда, ж”1 (А) - прообраз множества А в пространстве Q.
Формула
/1ДА) - Р(Х е А) = Р(х-1(А)), А € Л, (1.2.3)
определяет вероятность индуцированную случайной величиной X =
— x(lj) в пространстве ее значений. Тройка (Х,Л,//х) представляет
56
ГЛ. 1. СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
собой вероятностное пространство, индуцированное в (X, Л) случайной
величиной X = х(си).
Пространство X значений случайной величины X = х(ы) называет-
ся ее фазовым пространством или пространством реализаций. Веро-
ятность дх в фазовом пространстве называется вероятностной мерой
или распределением случайной величины X. Вероятностное простран-
ство (Х,Л,дх) называется фазовым вероятностным пространством
случайной величины X = х(и). Очевидно, что любое вероятностное
пространство можно рассматривать как фазовое пространство некото-
рой случайной величины. Если случайная величина X = х(си) рас-
сматривается в ее фазовом вероятностном пространстве, аргумент ш в
ее обозначении, естественно, не указывается. В таких случаях мы ее
будем обозначать просто через X, а ее реализации через х.
Если в пространстве (X, Л) определена неотрицательная конечная
или a-конечная мера I/, то вероятностная мера дх случайной величины
X может быть представлена формулой
дх(А) = у /(x)i/(dx) + д;(А), А е А, (1.2.4)
А
где ДХ(А) - ^/-сингулярная мера. В частном случае, когда мера дх у-
непрерывна, д£(А) = 0 и
дх(А) = у* f(x)v(dx), А е А. (1.2.5)
А
Здрсъ f(x) как производная Радона-Никодима вероятностной меры дх
по мере v называется плотностью вероятности случайной величины
X по мере у.
В задачах, связанных с одной случайной величиной, всегда удоб-
но за вероятностное пространство принимать ее фазовое вероятностное
пространство, что обычно и делается в элементарной теории вероятно-
стей. Однако в задачах, связанных с множеством случайных величин
(возможно, с различными фазовыми пространствами), целесообразно
изучать их все в каком-нибудь одном вероятностном пространстве.
1.2.3. Условные вероятности. Как известно из теории вероятно-
стей, если Р(В) 0 О, В Е 5, то условная вероятность любого события
А Е S относительно события В (при данном событии В) определяется
следующей формулой:
Р(Л|В) = ^. (1.2.6)
1.2. СЛУЧАЙНЫЕ ФУНКЦИИ
57
Событие А называется независимым от В, если Р(А\В) =
= Р(А). Если Р(А\В) Р(А), то А зависит от В. Два события всегда
зависимы или независимы взаимно.
События Л1, ... , Ап называются независимыми, если каждое из
них не зависит от любого из остальных и любых пересечений остальных.
Необходимым и достаточным условие независимости событий Ai,...
..., Ап служит равенство Р(А\, ... , An) = P(AJ... Р(АП).
Пусть {Bk} С S - произвольная последовательность попарно не-
пересекающихся (несовместных) событий, В - порожденная этой по-
следовательность а-алгебра, В С 5. Очевидно, что любое событие
В Е В представляет собой объединение некоторого множества событий
Bk, В = UВк{. Поэтому для любых событий А € 5 и В Е В
i
Р(АВ) = P(U ABki) = ^Р(АВк{) = £Р(В*;)Р(Л|В*(). (1.2.7)
i
Введем теперь функцию точки в пространстве элементарных собы-
тий Q при фиксированном А Е S, определив ее равенством
Ря(А|си) = Р(А\Вь) при cu С Вк
на тех множествах В^, для которых Р(Вк) 0 0, и оставив ее неопреде-
ленной на тех множествах Bk, для которых Р(Вк) = 0, Р#(А|си) пред-
ставляет собой Р-интегрируемую элементарную функцию си при любом
фиксированном событии А, определенную на Q почти всюду относи-
тельно Р. Последняя часть формулы (1.2.7) представляет собой инте-
грал по множеству В от элементарной функции Р#(А|си) по мере Р.
Поэтому формулу (1.2.7) можно представить в виде
Р(АВ) = У P5(A|cu)P(du), В Е В. (1.2.8)
в
Для вычисления интеграла в этой формуле нет необходимости знать
вероятность Р на всей а-алгебре 5. Достаточно задать Р на меньшей
а-алгебре В. Поэтому, обозначив через Рв сужение вероятности Р на
а-алгебру В, Рв(В) = Р(В)> В Е В, можем переписать формулу (1.2.8)
в виде
Р(ЛВ) = У* P5(A|cu)P5(du), В Е В. (1.2.9)
в
58
ГЛ. 1. СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
Формула (1.2.6) показывает, что при любом фиксированном собы-
тии В, Р(В) 0, условная вероятность Р(А\В) обладает всеми свой-
ствами вероятности, т.е. сама представляет собой вероятность на 5.
Отсюда следует, что (А|со), рассматриваемая как функция множе-
ства А, является а-аддитивной функцией.
Свойства условной вероятности. Предположим, что В - произ-
вольная а-алгебра, содержащаяся в 5, В С 5. Так как Р(АВ) < Р(В) =
= Рв(В) при любых А € 5, В € В, то Р(АВ) — 0, если Рв(В) = 0. Это
значит, что вероятность Р(АВ), рассматриваемая как функция множе-
ства В при фиксированном А, Pg-непрерывна. При любом фиксирован-
ном А существует Pg-интегрируемая функция Pg(A|cv), через которую
Р(АВ) выражается интегралом (1.2.9). Эта функция определена на Q
почти всюду относительно Pg. Следовательно, Pg (A |cv) представляет
собой а-аддитивную функцию множества на 5 со значениями в про-
странстве Pg-интегрируемых функций Li(Q, В, Pg). Функция Pg(A|cv)
называется условной вероятностью относительно а-алгебры В. Она
определена для всех событий А € 5 и при каждом А представляет со-
бой Pg-интегрируемую функцию точки в Q, определенную почти всюду
относительно Р. Функция Рд(А | о?) является непрерывной функцией
множества со значениями в пространстве Li(Q,5,Pg).
Регулярная условная вероятность. Если условная вероятность
Pg(A|o/) представляет собой вероятность на 5 почти при всех о/, то она
называется регулярной. В общем случае, когда условная вероятность
Pg(A|cv) не регулярна, регулярной условной вероятностью в простран-
стве (0,5) относительно а-алгебры В называется функция перемен-
ной cv и множества А Е 5, совпадающая с Pg(A|o?) почти всюду при
любом фиксированном событии А и представляющая собой вероятность
на 5 почти при любом фиксированном cv. Если регулярная условная
вероятность существует, то мы всегда будем рассматривать именно ре-
гулярную условную вероятность. Поэтому особого обозначения для нее
вводить не будем.
Условная вероятность при любом А представляет собой скалярную
случайную величину, так как она является числовой измеримой функ-
цией точки в П. Она принимает определенное числовое значение толь-
ко после опыта, когда появляется определенное элементарное событие
cv (или в предположении, что в результате опыта появилось данное эле-
ментарное событие о;). Если А Е В, то
Р(АВ) = Рв(АВ) = I PB(du>) = I l4(w)PB(dw). (1.2.10)
АВ В
1.2. СЛУЧАЙНЫЕ ФУНКЦИИ
59
Имеют место утверждения (ТСтС, раздел 2.3):
• сужение условной вероятности Ря(А|а?) на а-алгебру В всегда
представляет собой регулярную условную вероятность.
• условная вероятность относительно полной а-алгебры 5 вероят-
ностного пространства регулярна и представляет собой индикатор мно-
жества.
• условная вероятность относительно В = {0,0} совпадает с веро-
ятностью Р и, следовательно, тоже регулярна.
Условное распределение случайной величины. Рассмотрим
теперь случайную величину Z = z(a>) в некотором измеримом простран-
стве (Z,C), определенную на вероятностном пространстве (Q,5, Р).
Функция
Мв№) - Рб^-^С)^) , С е С , (1.2.11)
называется условным распределением случайной величины Z = z(w)
относительно а-алгебры В. Если /i^(C|cj) представляет собой регу-
лярную условную вероятность (т.е. вероятность на С почти при всех
cv), то она называется условной вероятностной мерой или регулярным
условным распределением случайной величины Z = z(uj) относительно
а-алгебры В.
Пусть X — x(cv) - случайная величина в (Х,Л), Sx - индуциро-
ванная ею а-алгебра, Sx — £-1(Л). Рассмотрим Psx(A|o?) условную
вероятность относительно этой а-алгебры. Она представляет собой из-
меримую относительно а-алгебры А числовую функцию случайной ве-
личины X:
PsA^) = Qx(A\x^)). (1.2.12)
Условная вероятность любого события в этом случае определяется зна-
чением ж, которое принимает в результате опыта случайная величина
X, и не зависит от того, какое именно из элементарных событий о/,
реализующих это значение гг, при этом появляется.
Условной вероятностью относительно случайной величины X —
= rr(cv) в пространстве (0,5) называется условная вероятность от-
носительно (j-алгебры 5Х, индуцированной этой случайной величиной.
Пусть теперь Y = ?/(cv) - случайная величина в (5,В), функция
fiv(B\x) = Qx(y-1(B)\x), В ев, (1.2.13)
называется условным распределением случайной величины Y относи-
тельно случайной величины X. Условное распределение /^(Bl#)
случайной величины Y относительно величины X = x(cv) и условное
60
ГЛ. 1. СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
распределение Mse(B|a>) величины Y относительно а-алгебры 5Х, инду-
цированной случайной величиной X = х(си), связаны соотношением
(Вк) = (В|хк)), в е в. (1.2.14)
Если ду(В|х) представляет собой регулярную условную вероят-
ность (т.е. вероятность на В почти при всех ж), то она называется услов-
ной вероятностной мерой или регулярным условным распределением
случайной величины Y относительно X (при данном значении х вели-
чины X). Если существует регулярная условная вероятность Qx(A|x),
то существует и регулярное условное распределение ру(В\х) случайной
величины Y относительно X (ТСтС, раздел 3.2).
1.2.4. Вероятности в конечных произведениях пространств.
Рассмотрим измеримое пространство, представляющее собой произве-
дение (Qi xfi2,5i х52) измеримых пространств (Qi,5J, (Пг,^)- Пред-
положим, что в этом произведении пространств определена вероятность
Р(А), А е 51 х 52. Сужение Pi(Ai) вероятности Р(А) на а-алгебру
51 х (12 представляет собой вероятность в пространстве (Qi,5i). Точно
так же сужение Р2(А2) вероятности Р(А) на а-алгебру Qi х 52 пред-
ставляет собой вероятность в пространстве (П2>52). Таким образом,
вероятность, заданная на произведении пространств, индуцирует опре-
деленную вероятность в каждом из этих пространств.
Вероятности Pi(Ai), Ai 6 5i, и Рг(А2), А2 6 52, индуцирован-
ные в пространствах (Qi,5i) и (П2,52) вероятностью Р, заданной на
произведении пространств (S7i х Q2,5i х 52), называются проекциями
вероятности Р на подпространства (Qi,5i) и (^2,52). Условная веро-
ятность в произведении пространств относительно а-алгебры Qi х 52
зависит только от координаты си2 точки этого пространства
Р(ЛП(П! х Д2)) = /pnixS2(4|w2)P2(dw2), A2eS2. (1.2.15)
А2
Точно так же условная вероятность относительно а-алгебры 51 х П2
зависит только от координаты cui.
Сужение условной вероятности PQ1Xs2(Ak2), равной рассматрива-
емой как функция множества А, на а-алгебру 51 х П2
Pi(Aik2) =Pqix52(Ai х Пгкг) (1.2.16)
называется условной вероятностью в пространстве Пр Аналогично
формула
-^(Агкх) = P5ixQ2(Hi х A2|cvi) (1.2.17)
1.2. СЛУЧАЙНЫЕ ФУНКЦИИ
61
определяет условную вероятность в пространстве П2.
Имеют место формулы
Р(А, х А2) = У Pi(Ai|w2)P2(dw2), (1.2.18)
Аз
P(Aj х А2) = I(1.2.19)
Ai
Таким образом, вероятность, заданная на произведении прост-
ранств, однозначно определяет вероятности и условные вероятности
в этих пространствах, и наоборот, заданные вероятность в одном
пространстве и условная вероятность в другом пространстве одно-
значно определяют вероятность в произведении этих пространств.
В том случае, если условная вероятность Pi(Ai|си2) регулярна, то
продолжение вероятности Р в произведении пространств Qi х П2> за-
данной на классе измеримых прямоугольников формулой (1.2.18), опре-
деляется формулой
Р(С} — J* p2(dw2>) J* lc(^i,^2)Pi(^i|^2), С Е х • (1.2.20)
Точно так же, если условная вероятность Рг(^2|^1) регулярна, то
продолжение вероятности Р, имеет вид
Р(С) = j'Pi^dwi) J* 1с(^1,^2)^2(dw2|^i)> С € х <?2 . (1.2.21)
Вероятностные меры в произведении двух пространств.
Проекции вероятности р на подпространства (Х,Л) и (У, Б) простран-
ства (X х У, Л х В) совпадают с вероятностными мерами случайных
величин X и У соответственно:
1*х(А) = Р>(А х У), А € А, 1 (io
ру(В) = р(Х х В), В € В. f
Условные вероятности, порождаемые в (Х,Л) и (У, В) вероятностью р,
совпадают с условными распределениями случайных величин X и У.
Значения вероятностной меры р на измеримых прямоугольниках
произведения пространств {X х У, Л х В) выражаются через распреде-
ления и условные распределения случайных величин X и У формулой
д(А х В) = У p,x(A\y)ny(dy) = У . (1.2.23)
в А
62
ГЛ. 1. СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
Если существуют регулярные условные распределения /лх(А\у) и
цу(В\х), то продолжение меры д на сг-алгебру С — А х В выражается
формулой
д((7) = JHx(dx) jlc(x,y)iiy(dy\x) = J^y(dy) j lc(x,y)fix(dx\y), С&C .
(1.2.24)
Значение условной вероятностной меры дж(А|т/) при любом А Е
Е А представляет собой производную Радона-Никодима меры д(А х В),
рассматриваемой как функция множества В по мере ^У(В\ а значение
условной вероятностной меры р,у(В\х) при любом В Е В представляет
собой производную Радона-Никодима меры д(А х В), рассматриваемой
как функция множества А, по мере дж(А):
z J( х dud A XT/) ч du,(x x В) z_
Дя(А|т/) = - — , р,у(В\х) = - — . (1.2.25)
<Wy(y) d/j,x(x)
Предположим теперь, что в пространствах (X, А) и (У, В) опреде-
лены неотрицательные сг-конечные меры vx и иу и что вероятностная
мера д в произведении пространств (X х У, А х В) абсолютно непрерыв-
на относительно произведения мер иу, определяемого формулой
^(С) = f Vx(dx) j\c(x,y)vy(dy) = У Vy(dy) j lc(x,y)vx(dx).
(1.2.26)
В этом случае для любого множества С Е С — А х В
№ = I
f(z)v(dz),
(1.2.27)
где f(z) = f(x,y) - плотность вероятности случайной величины Z, т.е.
совместная плотность вероятности случайных величин X, Y по мере v.
Интеграл по произведению пространств в предыдущей формуле равен
любому из двух повторных интегралов по мерам их иру:
р,(С)= I vx(dx) lc(x,y)f(x,y)vy(dy)= vy(dy)
^c(x,y)f(x,y)i/x(dx),
C EC.
1.2. СЛУЧАЙНЫЕ ФУНКЦИИ
63
Применив эту формулу к случаю, когда С представляет собой измери-
мый прямоугольник С — АхВ,Ае А, В ЕВ, будем иметь
х В) = У vx(dx) I f(x,y)vy(dy) = j vy(dy) j f(x,y)vx(dx).
AB BA
(1.2.28)
Отсюда видно, что вероятностная мера случайной величины X
vx-непрерывна и плотность вероятности fx(x) случайной величины
X по мере vx определяется формулой
fx(x) = У f(x,y)vy(dy). (1.2.29)
Вероятностная мера случайной величины Y vy-непрерывна и плотность
вероятности fy(y) случайной величины Y по мере иу определяется фор-
мулой
А(У) = У f(x,y)vx(dx). (1.2.30)
Условное распределение случайной величины X vx-непрерывно, ре-
гулярно и существует условная плотность вероятности случайной вели-
чины X относительно Y по мере vx
= (1.2.31)
Условное распределение случайной величины Y также регулярно,
Ру-непрерывно и условная плотность вероятности величины Y относи-
тельно X по мере иу определяется формулой
Ш*) = • (1-2.32)
Jx{X)
Таким образом, если существует совместная плотность вероят-
ности случайных величин X, Y по некоторому произведению мер, то
их условные распределения регулярны и существуют их плотности
вероятности, определяемые формулами (1.2.29) и (1.2.30), причем их
условные плотности вероятности, определяются формулами (1.2.31)
и (1.2.32). Объединив (1.2.31) и (1.2.32), получаем соотношение, выра-
жающее теорему умножения плотностей вероятности:
f(x,y) = fx(x)fy(y\x) = А(у)А(х|г/). (1.2.зз)
64
ГЛ. 1. СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
Независимость случайных величин. Случайная величина Y
называется независимой от случайной величины X, если ду(В|х) =
= ру (В) почти при всех х относительно рх. Если мера рх множества
тех z, для которых py(B\z) 0 РУ(В), отлична от нуля, то величина Y
зависит от X. Если случайная величина Y не зависит от X, то
д(Л х В) = цх(А)1лу(В) = У fix(A)fiy(dy), (1.2.34)
В
ц(А х В) = у nx(A\y)ny(dy). (1.2.35)
в
Так как обе эти формулы справедливы для любого множества В ЕВ,
то рх(A|j/) = Дх(А) почти при всех у относительно ру.
Таким образом, если случайная величина Y не зависит от X, то
и случайная величина X не зависит от Y. Две случайные величины
всегда взаимно зависимы или взаимно независимы. Необходимым и до-
статочным условием независимости случайных величин X и Y служит
равенство
р(А х В) = рх(А)ру(В) или р = рх х ру (1.2.36)
для всех А Е Л, В € В. Если существует совместная плотность ве-
роятности случайных величин X и У, то необходимым и достаточным
условием их независимости может также служить равенство
f(x,y) = fx(x)fy(y). (1.2.37)
Случайные величины , ... , Хп называются независимыми, ес-
ли каждая из них не зависит от любой из остальных. Необходимым и
достаточным условием независимости случайных величин Х±, ... , Хп
служит равенство
д(Л1 х ...х Ап) = д(А1)...Дп(Ап), Ак еАь (к = 1, ... ,п), (1.2.38)
где Hk(Ak) - вероятностная мера случайной величины Хь (к = 1,...
..., п), а р - совместная вероятностная мера случайных величин
Х\, ... , Хп. В случае, когда существуют плотности вероятности, не-
обходимым и достаточным условием независимости случайных величин
Xi, ... , Хп является также равенство *
/(*1, .... хп) = /1(ц)... /„(хп), (1.2.39)
1.2. СЛУЧАЙНЫЕ ФУНКЦИИ
65
где fk (х) - плотность вероятности случайной величины Xk (к =
= 1, ... , n), a f(xi, ... , хп) - совместная плотность вероятности слу-
чайных величин Xi, ... , Хп. Для независимости случайных величин
Xi, ... , Хп недостаточно их попарной независимости.
Замечание. Аналогично определяются вероятности и веро-
ятностные меры в конечных произведениях пространств (ТСтС, раз-
дел 2.4).
1.2.5. О вероятностях в бесконечных произведениях прост-
ранств. Пусть {П«}, t Е Т - произвольное семейство пространств.
Если из каждого пространства 0$ выбрать точку cut, то совокупность
выбранных точек, соответствующих всем t Е Т, принимается за точку
си произведения пространств = f] ш = {cut,Z e Т]. Если = R
teT
для всех t E T, то числа cu$ при фиксированных t представляют собой
координаты точки си.
Если в каждом из пространств , ... , выбрать некоторое
множество Ath С то множество всех точек си произведения про-
странств координаты си«х , ... , cu$n которых удовлетворяют усло-
виям cutfc 6 Ath (к = 1, ... ,п), представляет собой прямоугольный
цилиндр в пространстве Пт с основанием А^ х • • • х Atn в произве-
дении (ltl х • • • х Sltn. Любой цилиндр с основанием А^ х • • • х Atn
в 0^ х • • • х fitn можно рассматривать как прямоугольник с основа-
нием Atl х • • • х Atn х Qtn+1 х • • • х Sltm в Slti x • • • x при любом
m > n. Аналогично множество точек произведения пространств Пт,
удовлетворяющих условию {cutx , ... , cu*n} Е В, где В - произвольное
множество в Qtj х • • • х (ltn, представляет собой цилиндр с основанием
В в х • х (ltn.
Пусть в каждом пространстве fit задана а-алгебра множеств St,
тогда произведение а-алгебр ST = П определяется как минималь-
ter
ная а-алгебра, содержащая все измеримые прямоугольники произведе-
ния пространств Пт, т.е. прямоугольники с измеримыми сторонами
Ath (к = 1, ... , п), соответствующие всем n, ti, ... , tn Е Т и
всем множествам Atk Е Stk (к = 1, ... , п). Таким образом, произведе-
ние а-алгебр ST представляет собой а-алгебру, порожденную классом
прямоугольников с измеримыми сторонами в
Основные свойства а-алгебры ST изучены в (ТСтС, разделы 2.5 и
2.6), там же рассмотрен вопрос существования распределений в Пт.
Предположим, что в каждом пространстве (О*, 5*) заданы вероят-
ность Pt(At) и регулярные условные вероятности ,... ./«(AJou^,...
...,cu/n), соответствующие всем Zi,...,/n СТ (п = 1,2,...). Тогда веро-
66
ГЛ. 1. СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
ятности во всех возможных конечных произведениях пространств
х Л*2) — j >
Ati
^.....иСЧ X x Atn) =
Pt„,ti |wj,
Atl x • xAtn_1
x X X ^n-1)
(t!, ... ,ineT; n = 3,4,...).
Определив по первой формуле (1.2.40) вероятность Ptltt2 сначала на из-
меримых прямоугольниках пространства Яц х П$2, продолжим ее на а-
алгебру 5^ х St2. Найдя после этого по второй формуле (1.2.40) при п =
= 3 вероятность Р^^Лз на измеримых прямоугольниках пространства
х х Q*3, продолжим ее на а-алгебру 5^ х St2 х St3. Продол-
жая этот процесс, определим последовательно вероятности Ptlt...ttn
при п = 4,5,.... Легко понять, что условные вероятности
Pt.h ,... Jn) (Mi, • • • , € T; n = 1,2,...) должны быть со-
гласованными таким образом, чтобы они любыми способами давали од-
ну и ту же вероятность Ptl в произведении пространств х • •
х Qtn (п = 2,3,...). Тогда полученное в результате семейство ве-
роятностей во всех конечных произведениях пространств (П*,5*) будет
удовлетворять условиям согласованности и симметрии.
Зададим теперь функцию множества Р на множестве всех измери-
мых прямоугольников бесконечного произведения пространств Пт фор-
мулой
P(R) = Ptl,...,t„(Ati x-xAJ, (1.2.41)
где R - прямоугольник со сторонами Atl , ... , Atn, лежащими соот-
ветственно в пространствах , ... , Sltn • Эта функция а-аддитивна.
Функция P(R) является вероятностью на множестве всех измеримых
прямоугольников пространства (QT,5T), имеющих основания в одном
и том же конечном произведении пространств Яц х • • • х $ltn. Она может
быть однозначно продолжена на а-алгебру 5^ х
• • • х Stn всех измеримых цилиндров пространства Пт с основаниями в
х • • • х Sltn. Согласно
P(G1,...,tn)=Ptl....(1.2.42)
1.2. СЛУЧАЙНЫЕ ФУНКЦИИ
67
где ~ цилиндр в QT с измеримым основанием в
х • • • х х • • • х <Stn). Более того, (1.2.41) определяет вероят-
ность в пространстве QT на множестве всех измеримых прямоугольни-
ков С. При этом существует однозначное продолжение вероятности Р,
определяемой формулой (1.2.41), на а-алгебру ST, порожденную мно-
жеством С всех измеримых прямоугольников.
Вероятность Ptlt.,.,tn представляет собой проекцию вероятности
Р на подпространство (Qfl х • • • х fttn, Stl х • • • х Stn) пространства
(QT,5T). Отсюда следует, что определенная таким же путем вероят-
ность Pl в подпространстве (Q£,<S£) пространства (QT,5T), L С Т,
является проекцией вероятности Р на (Q£,<S£).
Таким образом, вероятности и все возможные регулярные условные
вероятности в каждом из пространств (Qt,St), t е Т, однозначно опре-
деляют вероятность Р в бесконечном произведении этих пространств
(ПТ,5Т)= (п Пь П <St)-
мет ter /
Наконец, отметим, что вместо того чтобы задавать вероятность и
согласованные регулярные условные вероятности в каждом простран-
стве (Q*,5t), а потом находить по формулам (1.2.40) согласованное се-
мейство вероятностей во всех конечных произведениях пространств
(Qt,5t), можно непосредственно задать согласованное семейство веро-
ятностей Рц ,..., tn в конечных произведениях пространств. Если в каж-
дом из пространств (Qt,5t) существуют все регулярные условные ве-
роятности Р^1г ,...,in(At\wh , - • • , win) (h, ••• ,ln £ T, n — 1,2,...), to
согласованное семейство вероятностей Ptlt...,tn во всех конечных про-
изведениях пространств (Qt,5t) однозначно определяет вероятность в
бесконечном произведении пространств (QT,5T)
Определение и свойства условных функций распределения рас-
сматриваются аналогично (ТСтС, раздел 2.6).
1.2.6. Определения и вероятностные меры случайной
функции. В элементарной теории вероятностей случайной функцией
называется такая функция, значение которой при каждом данном зна-
чении аргумента является случайной величиной. Из этого определения
следует, что случайная функция представляет собой множество случай-
ных величин, соответствующих всем значениям аргумента из области
его изменения (области определения случайной функции). В результате
опыта случайная функция при каждом значении аргумента принимает
некоторое конкретное возможное значение. Совокупность этих значе-
ний, соответствующих всем значениям аргумента, представляет собой
некоторую конкретную функцию. Таким образом, при наблюдении слу-
68
ГЛ. 1. СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
чайной функции в каждом опыте получается некоторая функция. В
разных опытах получаются разные функции. Каждая функция, кото-
рая может быть получена в результате наблюдения случайной функции,
называется реализацией этой случайной функции. Каждая реализация
случайной функции представляет собой конкретную функцию того же
аргумента.
В книге будут изучаться скалярные и конечномерные функции ска-
лярной независимой переменной. Такие случайные функции обычно
называются случайными процессами, а аргументом является время t.
Определение случайной величины, данное в п. 1.2.2, охватывает и
случайные функции. Согласно этому определению случайная функция
представляет собой случайную величину со значениями в некотором
функциональном пространстве. Однако для конструктивного опреде-
ления вероятностной меры случайной функции удобно рассматривать
ее как семейство случайных величин со значениями в достаточно про-
стых пространствах (на числовой оси, на комплексной плоскости или в
конечномерном пространстве). Поэтому обычно в приложениях прини-
мают следующее определение случайной функции (ТСтС, п.1.2.6).
Случайной функцией в измеримом пространстве (X, Л) называет-
ся бесконечное семейство случайных величин {Xt,t € Т} в (X, Л), т.е.
семейство (5,Л)-измеримых функций точки {я*(си),£ е Т} в некото-
ром вероятностном пространстве (Q, ,Р). Иными словами, случайной
функцией в (X, Л) называется такая функция x(t,a>), отображающая
произведение пространств Т х П в X, сечение которой в любой точке
t е Т (S, Л)-измеримо.
В зависимости от характера исследования целесообразно пользо-
ваться различными обозначениями случайных функций. Если на-
иболее существенно то, что значения случайной функции при фиксиро-
ванных значениях аргумента t € Т представляют собой случайные вели-
чины, мы будем обозначать случайные функции Xt = St(cu), Yt = yt(w)
и т.п. (t рассматривается как параметр). Если же более существен-
но то, что реализации случайной функции являются функциями аргу-
мента t е Т, мы будем обозначать случайные функции Х(£) = z(£,cu),
У (О = y(t,w) и т.п.
Измеримые случайные функции. Определение случайной
функции требует лишь измеримости сечений при любом t функции
x(t,cu) и не требует ее измеримости как функции двух переменных.
Случайная функция X(t) = x(t,w) называется измеримой, если в про-
странстве Т определена а-алгебра Т7 и функция x(t,w} представляет
собой (Т х 5, Л)-измеримую функцию, отображающую Т х Q в X.
1.2. СЛУЧАЙНЫЕ ФУНКЦИИ
69
Многомерные распределения случайной функции. Если
при каждом значении t € Т задана вероятностная мера дДА) зна-
чения случайной функции Xt при этом t и согласованное семейство
регулярных условных вероятностных мер Mt,/1,...,/n(A|z/lj...i/n) относи-
тельно ее значений ,..., Xin при всех других значениях аргумента
£, • Jn € Т, п = 1,2,..., то, как известно из (ТСтС, раздел 2.6),
однозначно определяется вероятностная мера д случайной функции Xt
на а-алгебре Ат пространства Хт. Для этого надо сначала опреде-
лить по формулам (1.2.40) многомерные распределения слу-
чайной функции Xt, т.е. совместные вероятностные меры ее значений
Xtl,..., Xtn при всех п, ti,..., tn:
х Л2) = У
х-хЛ<ж) =
= ! Vtn,ti.....t„_1Htn|a:i,...,a:n_i)x
лчх-хл1п_1
(1.2.43)
x Дй....tn-i(dxi x ••• x <£гп-1),
потом определить вероятностную меру д случайной функции Xt на из-
меримых прямоугольниках пространства (ХТ,АТ) по формуле (1.2.41):
м(Я) = Мй.......е„(Л1 X ••• х Atn), (1.2.44)
а затем продолжить эту вероятностную меру на ст-алгебру Ат (в форму-
ле (1.2.44) R — прямоугольник со сторонами А^,...,А^, R =
= {х : xtl € Atli...yxtn € Atn,). Формула (1.2.44) определяет про-
должение вероятностной меры д случайной функции Xt на а-алгебру
А^ х • • • х Atn всех цилиндров пространства Хт с измеримыми осно-
ваниями в одном и том же конечном произведении пространств
(Xtl х ••• х Xtn,Atl х ••• х Atn):
..............tn(Btl,...,(J> (1.2.45)
где Вц,.,.4п 6 Atl x • • • x Atn — основание цилиндра Ct!t...,tn) лежащее
в Xtl х • • • х Xtn.
Вместо того чтобы задавать распределения и регулярные ус-
ловные распределения значений случайной функции, можно не-
70
ГЛ. 1. СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
посредственно задать согласованное семейство многомерных распреде-
лений € Т (п = 1,2,...). По теореме Колмогорова
(ТСтС, п.2.6.2) согласованное семейство многомерных распределений
скалярной или конечномерной векторной случайной функции X(t) все-
гда полностью и однозначно определяет вероятностную меру этой
случайной функции в ее функциональном фазовом пространстве ХТ
на а-алгебре Ат, порожденной всеми борелевскими прямоугольниками
(т.е. прямоугольниками, стороны которых являются борелевскими
множествами пространства значений случайной функции X).
Естественно возникает вопрос: всякое ли согласованное се-
мейство многомерных распределений определяет некоторую
случайную функцию? Теорема Колмогорова дает на него положитель-
ный ответ. В самом деле, по теореме Колмогорова любое согласованное
семейство многомерных распределений однозначно определяет вероят-
ность р в пространстве (ХТ,ЛТ). Тройка (Хт,АТ,р) представляет со-
бой вероятностное пространство, любая случайная величина в котором
является измеримой функцией точки данного пространства, т.е. функ-
ционалом или оператором.
1.2.7. Некоторые типовые случайные процессы
Случайные процессы с независимыми значениями. В об-
щем случае ни одно из многомерных распределений случайной функции
не определяет ее многомерные распределения высших размерностей.
Однако существуют случайные функции, для которых какое-нибудь
из многомерных распределений определяет всю последовательность ее
многомерных распределений. Для случайной функции X (t) с независи-
мыми значениями случайные величины Xtl , ... , Xtn независимы при
любых ti, ... , tn 6 Т и при любом натуральном п. Поэтому имеет
место следующее соотношение:
yn(xi, , x^tr, ... ,tn) = fi(x1;t1)fi(x2\t2). • ./i(zn;tn) (1.2.46)
(n = 1,2,...).
Таким образом, все многомерные распределения случайной функции с
независимыми значениями однозначно определяются ее одномерными
распределениями.
Марковские случайные процессы. Другим примером случай-
ных функций, у которых все многомерные распределения определяют-
ся одним из них, являются марковские случайные процессы. Дадим
сначала определение марковской последовательности случайных вели-
чин. Последовательность случайных величин {Хр} называется марков-
ской случайной последовательностью, если при любых натуральных
1.2. СЛУЧАЙНЫЕ ФУНКЦИИ
71
Pi < • • • < рп условное распределение величины ХРп относительно вели-
чин ХР1 , ... , ХРп_г зависит только от ХРп_г, т.е. совпадает с условным
распределением величины ХРп относительно ХРп_1.
Случайная функция Xt = X(t) непрерывно изменяющейся ска-
лярной переменной t называется марковским случайным процессом,
если при любом выборе последовательности значений аргумента {£р},
£р-1 < tp, последовательность случайных величин {Х^р} является мар-
ковской. Марковский случайный процесс X(t) обладает тем свойством,
что при данном его значении х в какой-нибудь момент г, Х(т) = х,
распределение его значения Xt в любой последующий момент t > т
однозначно определяется его значением х в момент т и совершенно не
зависит от его реализации до момента т. Иными словами, всем реализа-
циям марковского процесса X(t), принимающим одно и то же значение
х в данный момент г, Х(т) = х, соответствует одно и то же услов-
ное распределение X(t) в любой момент t > г, не зависящее от хода
реализации до момента т.
Различают следующие пять видов скалярных марковских случай-
ных процессов (Тихонов 1977):
• дискретная случайная последовательность (марковский дискрет-
ный процесс с дискретным временем, или цепь Маркова). В таком слу-
чае параметр t пробегает дискретный ряд значений hlo, hl i ... (Д - шаг
дискретности) и случайная величина X(t) = Xi может принимать дис-
кретное множество значений xi;
• непрерывнозначная случайная последовательность (марковская
последовательность или непрерывный процесс с дискретным временем).
Такой процесс отличается от дискретного процесса с дискретным време-
нем тем, что случайная величина Xi может иметь континуум значений;
• дискретный (разрывный) случайный процесс (марковский дис-
кретный процесс с непрерывным временем). В этом случае процесс
X(t) принимает дискретные значения, время t - континуум значений;
• непрерывнозначный случайный процесс (непрерывный марков-
ский процесс). В данном случае X(t) принимает значения из некоторого
непрерывного пространства и аргумент t изменяется также непрерыв-
но;
• дискретно-непрерывный процесс. В этом случае при непрерыв-
ном изменении t случайный процесс X (£) в некоторые моменты времени
имеет скачки (дискретные или непрерывные), а на интервалах времени
между скачками ведет себя как непрерывнозначный случайный про-
цесс.
Имеется обширная литература, посвященная теории и приложени-
72
ГЛ. 1. СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
ям марковских процессов (см. библиографические замечания к разделу
1)-
В прикладных задачах пользуются также следующими общими оп-
ределениями марковского процесса.
Случайный процесс X(t) называется марковским, если для любых
п моментов времени ti < < • • • < tn условная функция распре-
деления “последнего” значения X(tn) при фиксированных значениях
xi = X(ti), Х2 = X(t2), ... , яп-1 = X(tn-i) зависит только от X(tn-i),
т.е. при заданных х^, х2 , ... , хп справедливо следующее соотношение:
Р {X(tn) < Хп | X(ti) = Xi , . . . , X(tn—1) = %п— 1} =
= P{X{tn) < Хп | X(tn-1) = Sn-i} . (1.2.47)
Для трех моментов времени t> > tj > tk соотношение (1.2.47) принимает
вид
P{X(ti) < Xi | X(tk),X(tj) = Xj} = P{X(ti) < Xi | X(tj) = Xj} .
(1.2.48)
Замечание!. Последнее соотношение позволяет утверждать, что если
известно состояние марковского процесса (при tj), то будущее состояние (при tj) не за-
висит от прошлого (при tk)- Очевидно, что, если настоящее состояние известно не точно,
будущее состояние марковского процесса будет зависеть от прошлых состояний.
Для симметричного вида относительно времени определения мар-
ковского процесса имеет место соотношение:
Р{Х(М < Xi,X(tk) < xk I X(tj) = Xj} =
= Р{Х&) < Xi | X(tj) = Xj}P{X(tk) < xk | X(tj) = Xj}. (1.2.49)
Замечание 2. Определения (1.2.48) и (1.2.49) эквивалентны. При этом
(1.2.49) выражает тот факт, что при фиксированном состоянии процесса в настоящий
момент (при tj) будущее (при ti) и прошлое (при tk) независимы.
Приведем необходимые соотношения для векторных непрерывных
и дискретных марковских процессов для случая, когда существуют пер-
вая и переходная плотности вероятности.
По теореме умножения плотностей n-мерная плотность марковско-
го случайного процесса X (t) определяется формулой
fn(x!, ... , хп; «1, ... , tn) = fi(xr,ti)fz(x2-,t2 I Xi;ti)x
х/з^з; ^3 I , X2\ tl j ^2) • • • fn(Xnt tn I , • • • > 11 > • • • > tn—1),
(1.2.50)
1.2. СЛУЧАЙНЫЕ ФУНКЦИИ
73
где fk(xk\tk(xi, ... , Xk-Г, ti, • • • , th-1) - условная плотность значения
Xtk процесса X(t) при данных его значениях , ... , Xk-i, при
t = ti, ... , tk-i (к = 2,3,...). Но по определению марковского про-
цесса его n-мерная плотность выражается формулой:
/п(^1 , • • • , , • • • , tn) = /1 (*^1 i tl )/з (*^2) t2 | 2*1 > tl) • • •
• • • /2(^п5 tn I Хп—1 > tn_1)* (1.2.51)
Отсюда, положив п = 2 и выразив условную плотность /2(я2; t2 | #i;ti)
через одномерную и двумерную плотности, получим
/n^l » • • • > Хп; ti , ... , tn) =
= /1(^15 ti)/2(x2*, t2|xi; ti)... /2(^71» tnlxn_ 1; tn_ 1) =
_ /2(^i, а:2; f 1, ^2)/2(х2, ж3; t2, t3)... /2(xw i, жп; tn-1, tn) и 9 52)
fdx2;t2)fl(<X3;t3) . . ./l(*n-i;tn-l)
(n = 3,4,...)
Таким образом, все многомерные распределения марковского процесса
однозначно определяются его двумерным распределением.
В прикладных задачах условная плотность ЛСг*; 1; tjh-i) =
= f(^kitk I Xk-i]tk-i) (к = 2,3,...) называется переходной плотно-
стью.
Многомерные распределения случайной функции Xt с заданны-
ми первой плотностью вероятности /i(x;f) и переходной плотностью
f(x;t\y;s) определяются согласно (1.2.43) формулой
x - xAtn) = У dxi У dx2... j fi(.xi,ti)f(x2;t2\xi;ti)x
х/(^з> ^з|х2; t2) • • • f(xn] tn|xn_ 1’, tn_\)dxn. (1.2.53)
Продолжение на все измеримые множества n-мерного простран-
ства (Xtl х • • • х Xt^Ah х • • • х Xtn) выражается формулой
Дй...У /i(a:i;ti)/(a:2;^2|2:i;ti) --
в
’ ’ * f (^nj tn|#n-i j tn—i)dxi ... dxn. (1.2.54)
74
ГЛ. 1. СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
После нахождения многомерных распределений вероятностная ме-
ра случайной функции Xt определяется на множестве измеримых пря-
моугольников пространства (ХТ,АТ) формулой (1.2.54). Обозначим
Ctly...ytn цилиндр в Хт с основанием в n-мерном пространстве
(Xtl х • х Xtn). Формула определяет
продолжение вероятностной меры случайной функции Xt на множе-
ство всех измеримых цилиндров функционального пространства Хт.
На основании теоремы о продолжении меры для любого множества
А 6 Ат при любом е > 0 можно найти такой цилиндр С а D А (с конеч-
номерным основанием), что ~~£ < /1(А) < и(Сл)- Таким образом,
известная из функционального анализа теорема о продолжении меры
дает возможность с любой степенью точности аппроксимировать зна-
чение вероятностной меры случайной функции на любом измеримом
множестве функционального пространства (ХТ,АТ) ее значением на
некотором цилиндре, которое вычисляется по приведенным формулам.
Замечание 1. Как следствие теоремы полной вероятности, первая плотность
/1(зт;С и условная плотность /(зт; t | Х\ t) связаны соотношением:
/i(x;t)= [ | x';^)dx' (1.2.55)
J — оо
(уравнение Смолуховского-Чепмена-Колмогорова).
Замечание 2. Полагая в формулах (1.2.47)-(1.2.54) t = hl (h - шаг
дискретизации), получим соответствующие соотношения для дискретного марковского
процесса.
Нормальные случайные процессы. Приведем сначала необхо-
димые для дальнейшего известные из элементарной теории случайных
функций формулы для многомерных нормальных (гауссовских) плот-
ностей распределений.
Рассмотрим прежде скалярную случайную функцию Xt = X(t)
с нулевым математическим ожиданием, у которой все многомерные
распределения нормальны и, следовательно, определяются плотностя-
ми вероятности следующими плотностями fn и характеристическими
функциями дп:
fn = = [(27г)п|/Сп|]“1/2ехр|-|а:7’Л'г;1х|,
9п = 9п(^1 , • • • , ^ni й > • • • > tn) = ехр ( ——Л КПЛ j (п = 1,2,...),
(1.2.56)
1.2. СЛУЧАЙНЫЕ ФУНКЦИИ
75
где
Ш,*2) ... K^tjl
^(^2,^1) ^(^2,^2) ••• K(t2,tn)
Кп = .
.^n,^i) ••• #(*„,*„)-
(1.2.57)
K(t, s) - ковариационная функция случайной функции Xt = X(t), а
|/fn| - определитель матрицы Кп. Такие случайные функции называ-
ются нормально распределенными. Семейство нормальных многомер-
ных распределений согласовано. Формула (1.2.45) определяет вероят-
ностную меру скалярной случайной функции Xt на множестве всех из-
меримых цилиндров функционального пространства (ХТ,ДТ):
M(Ctl...tj = [(27ГГМ-1/2 I exp{-^xTK-1x}dx, (1.2.58)
где - основание цилиндра Выражением такого вида
можно аппроксимировать значение вероятностной меры рассматрива-
емой случайной функции на любом измеримом множестве А 6 Ат с
любой степенью точности.
Для векторной случайной функции нормальное распределение
удобно определять характеристической функцией:
5ti (Ai, ... , Ап) = exp (iArmn - ^АтАГпа) (п = 1,2,...).
(1.2.59)
Здесь
А = [AfAf...An]T , mn = [mx(t1)Tmx(t2)T ...mx(tn)T]T , (1.2.60)
Kn
"^(^1,^1) ••• Kx(ti,tn)
^z(^2,^l) -Кж^гДг) •••
- Kx(tn>ti) Kx(tnyt2) ... Kx(tnAn) •
(1.2.61)
где матрицы-столбцы Л и mn и матрицу Кп следует понимать как блоч-
ные матрицы. Если все матрицы Кп невырожденные, то можно также
определить нормальное распределение случайной функции с помощью
многомерных плотностей вида:
/п(*1 , . . . , Хп, «1 , . . . , tn) = [ (27r)”|Kn| Г1/2 X
76
ГЛ. 1. СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
хехр -mn)| (n = l,2,...), (1.2.62)
I z J
где в дополнение к обозначениям (1.2.60)»и (1.2.61) ип = . х„ ]Т.
Аналогично проверяется согласованность многомерных функций
распределения конечномерной случайной функции. Общие свойства
нормальных распределений даны в (ТСтС, раздел 3.8).
Обобщенные нормальные процессы. Рассмотрим важный для
практики класс обобщенных нормальных процессов, для которого пер-
вая плотность вероятности /i(x;f) случайной функции Xt = X(t) и
условные плотности вероятности fn = t\yi,..., уп; «i,. • •, sn) ее
значения при данном t относительно ее значений при всех других зна-
чениях t нормальны и заданы формулами
fi(x]t) = (2тгсо)"1/2ехр|-|сох2|, (1.2.63)
/п(ж; t|?/i,..., уп\si,..., sn) = (2тгсп)“1/2 ехр{-^-сп(х - ап)2}, (1.2.64)
(п = 1,2,...).
Здесь со = [K(t,t)]-1; сп = | /<„1/1 A"n|, где Кп - матрица, опреде-
ляемая формулой (1.2.59), в которой переменные заменены
переменными Zi,... ,1п; Кп - окаймленная матрица Кп, равная
г K(t,t) K(t,h) ... K(t,Zn)l
K(h,t) K(h,h) ... Ш,/п)
Kn= . . . ; (1-2.65)
-K(ln, t) K(ln,h) ... K(ln,ln).
an = 23£=1 gkUk > где коэффициенты gi,..., gn удовлетворяют линейным
уравнениям
п
K(sm,8k)gk = K(sm,t) (m = 1,... ,п). (1.2.66)
*=1
Легко проверить, что формулы (1.2.43) дают нормальные те же мно-
гомерные распределения случайной функции Xt. Следовательно, слу-
чайная функция Xt распределена нормально и ее вероятностная мера
определяется формулой (1.2.58).
1.2. СЛУЧАЙНЫЕ ФУНКЦИИ
77
Случайные процессы с согласованным семейством много-
мерных плотностей. Полученные результаты для обобщенных нор-
мальных случайных процессов легко распространяются на случайные
функции с любым согласованным семейством многомерных плотностей
вероятности /п(^1, •, хп\*1, • • •, М (или с любым согласованным се-
мейством условных распределений /n(a;;f|yi,...,s/n;si,...,sn); в
этом случае fn(xi,....,tn) = /i(xi;ti) ...
... /n-i(^n!^nl^i,...,tn-i))- Вероятностная мера случай-
ной функции на множестве всех измеримых цилиндров в функциональ-
ном пространстве (Хт, Ат) определяется в этом общем случае форму-
лой
,...,tn ) = J* ... j* (1.2.67)
..<п
Формулой такого вида можно аппроксимировать с любой степенью точ-
ности и значение вероятностной меры случайной функции на любом
измеримом множестве пространства (ХТ,ЛТ).
1.2.8. Вероятности событий, связанных со случайными
функциями. Многомерные распределения случайной функции опре-
деляют ее вероятностную меру только на а-алгебре Ат. Если случайная
функция является случайной величиной не только в (ХТ,АТ), но и в
измеримом пространстве (Хт,77) с более широкой а-алгеброй 7* D Ат,
то многомерные распределения в общем случае не определяют вероят-
ностную меру случайной функции на множествах из Т7, не принадле-
жащих Ат. Результаты изучения структуры а-алгебры в бесконечном
произведении пространств в (ТСтС, разделы 2.5 и 2.6) показывают, что
любое множество из а-алгебры Ат в фазовом пространстве случайной
функции представляет собой множество функций x(t), на которые на-
ложены ограничения не более чем в счетном множестве точек t. По-
этому а-алгебра Ат достаточно богата и охватывает все практически
интересные события только в случае счетного множества Г, когда слу-
чайная функция может быть представлена в виде последовательности
случайных величин. Если же множество Т несчетно, то многие важные
для практики события не входят в а-алгебру Лт, и их вероятности в
общем случае нельзя вычислить с помощью многомерных распределе-
ний случайной функции. Для решения подобных задач а-алгебра Ат
оказывается слишком бедной.
Чтобы можно было аппроксимировать с помощью многомерных
распределений вероятности событий, ограничивающих значения слу-
78
ГЛ. 1. СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
чайной функции в несчетном множестве точек t, необходимо сузить
класс изучаемых случайных функций, наложив определенные ограни-
чения на поведение их реализаций (ТСтС, разделы 2.8-2.10).
1.3. Моменты, характеристические функции
и функционалы
1.3.1. Математическое ожидание случайной величины. Рас-
смотрим сначала случайную величину X с конечным множеством воз-
можных реализаций xi , ... , xn в произвольном линейном простран-
стве. Обозначим pi, ... , pn вероятности реализаций Xi, ... , хм соот-
ветственно. Математическим ожиданием случайной величины с ко-
нечным множеством реализаций называется сумма произведений всех
ее реализаций на их вероятности. Условимся обозначать математиче-
ское ожидание случайной величины X символом MX или тх. Тогда
получим для математического ожидания случайной величины X фор-
мулу
N
mt=MX = £xkpk. (1.3.1)
k=l
Теперь рассмотрим случайную функцию X(£), t е Ту. Предполо-
жим, что при любом значении аргумента t € значение случайной
функции Xt = X(t) имеет конечное математическое ожидание MXt.
Множество математических ожиданий величин Xt, соответствующих
всем t е Ti, образует функцию mx(t). Эта функция в элементарной
теории случайных функций называется математическим ожидани-
ем случайной функции X(t). Таким образом, математическое ожи-
дание случайной функции X(t) представляет собой функцию mx(t),
значение которой при каждом данном t € Т\ представляет собой ма-
тематическое ожидание значения случайной функции X(f) при этом t,
MX(t) = mx(t). Математическое ожидание действительной случайной
функции X (t) выражается через ее одномерную плотность формулой
сю
mx(t) = MX(f) = У xfi(x-,t)dx. (1.3.2)
—сю
Теория распределений вероятностей, изложенная в разделе 1.2,
применима к случайным величинам со значениями в любых измери-
мых пространствах. Для дальнейшего развития теории вероятностей
1.3. МОМЕНТЫ, ХАРАКТЕРИСТИЧЕСКИЕ ФУНКЦИИ И ФУНКЦИОНАЛЫ 79
необходимо наложить некоторые ограничения на фазовые пространства
случайных величин. Ограничимся теперь случайными величинами в
линейных пространствах.
Если случайная величина X = х(ш) с конечным множеством ре-
ализаций определена в вероятностном пространстве (Q,5, F), то х(о?)
представляет собой простую функцию элементарного события о;,
N
= 52 я*1®* ’ (1.3.3)
к=1
где Ei, ... , Едг - попарно непересекающиеся измеримые множества,
Efc е 5, причем F(|jEfc) = 1. В этом случае Pk — Р(Е*) (к =
= 1, ... , N) и поэтому можем переписать формулу (1.3.1) в виде
тх=МХ = I x(w)P(dw). (1.3.4)
Таким образом, математическое ожидание случайной величины
X = х(о?) с конечным множеством возможных реализаций, опреде-
ленной в вероятностном пространстве представляет собой
интеграл от этой случайной величины по мере Р, распространенный
на все пространство элементарных событий Q.
Математическим ожиданием случайной величины X = х(о?)
в В-пространстве X, определенной в вероятностном пространстве
(Q,5,P), называется вектор тх = MX € X, определяемый формулой
(1.3.4).
Для существования математического ожидания случайной вели-
чины X = х(си) необходимо и достаточно, чтобы функция х(си) была
Р-интегрируемой, т.е. принадлежала пространству Li(Q,5,P) функ-
ций со значениями в X. Каждой функции х(о?) 6 Li(Q,5,P) формула
(1.3.4) ставит в соответствие вектор тх 6 X. Таким образом, можно
говорить об операторе математического ожидания М, отображающем
Li(Q,5, Р) в фазовое пространство случайной величины X. В частном
случае, когда X - комплексная плоскость, оператор математического
ожидания представляет собой функционал в Li(Q,5,P).
Заменой переменных х = х(ш) с учетом формулы (1.2.3) для веро-
ятностной меры рх случайной величины X формула (1.3.4) приводится
к виду
тх = MX = / xpx(dx). (1.3.5)
80
ГЛ. 1. СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
Если существует плотность вероятности /Х(х) случайной величины X
по некоторой мере р, формула (1.3.5) принимает вид
тпх = MX = У xfx(x)v(dx). (1.3.6)
Основные свойства математических ожиданий подробно рассмот-
рены в (ТСтС, разделы 3.1 и 3.2).
1.3.2. Моменты второго порядка. В элементарной теории ве-
роятностей момент второго порядка Гх и ковариационная матрица Кх
случайного вектора X определяются следующими формулами:
Гх = [?;д] = МХХ*, (1.3.7)
Хх = та=МХ°Х0*, XQ = X—mx. (1.3.8)
Здесь звездочка означает операцию транспонирования матрицы с заме-
ной всех ее комплексных элементов соответствующими сопряженными
числами. При этом между тх, Гх и Кх имеет место зависимость
Гх = Кх 4- mxm* . (1.3.9)
Для двух случайных векторов X и Y вводят понятия взаимного момен-
та второго порядка (матрицы) Гху и ковариации (взаимной ковариаци-
онной матрицы) Кху:
Гх, = = мхг*, (1.3.10)
Кху = ВД] = МХ°У°* , (1.3.11)
причем
Гху = Кху -I- тпхту . (1.3.12)
Момент второго порядка случайной функции X(f), t 6 (матри-
ца) Гх(^, ^) и ковариационная функция (матрица) Хх(^1,^2) определя-
ются следующими формулами:
Цм) = , t2) ] = 1ВДХ(«2)‘, (1.3.13)
Kx(tlyt2) = [K^(ti,t2)] = MX°(ti)X°(t2)* , (1.3.14)
причем
r^ti,^) = ^(ti,t2) + mI(ti)mx(t2)‘. (1.3.15)
LXMOMEHTH, ХАРАКТЕРИСТИЧЕСКИЕ ФУНКЦИИ И ФУНКЦИОНАЛЫ 81
Для двух случайных функций X(t) и Y(t), t 6 Ti, взаимный момент
(матрица) второго порядка Га;у(<1, <г) и ковариационная функция (мат-
рица) Kxy[ti,t2) определяются формулами
rI!Z(ti,t2) = [?₽Ж*2)] = MX(t!)y(t2)*, (1.3.16)
Kiy(t!,t2) = [t2)] = MX°(ti)y0(t2)*, (1.3.17)
при этом
ГЖ!/(^1,^2) = KXy(ti,t2) + mx(ti)my(t2)* • (1.3.18)
Предположим теперь, что фазовое пространство X случайной вели-
чины X = определенной на вероятностном пространстве (Q, 5, Р),
является В-пространством или слабо полным топологическим линей-
ным пространством. Возьмем произвольный линейный функционал /
в X. Он принадлежит сопряженному с X пространству F, Fc = X*.
Рассмотрим случайную величину XfX. Ее фазовым пространством,
очевидно, также служит пространство X. Если существует математи-
ческое ожидание этой случайной величины, то оно представляет собой
вектор тпх € X, зависящий от f € F. Таким образом, формула
Гж/ = MXjX = У (1.3.19)
определяет оператор Гж, отображающий F в X. Областью определе-
ния Drx этого оператора, очевидно, будет некоторое подпространство
пространства F.
Оператор Гж, определяемый формулой (1.3.19), называется опера-
тором момента второго порядка случайной величины X. Оператор
момента второго порядка центрированной случайной величины Х° =
= X — тх называется ковариационным оператором случайной величи-
ны X. Ковариационный оператор Кх случайной величины X опреде-
ляется формулой
#ж/ = мх°7хо = у [ -mx]f[x(u)-mx ]P(dcv). (1.3.20)
Формулы (1.3.19) и (1.3.20) приводятся соответственно к виду
rxf = MXjX = Ixfrpx(dx), (1.3.21)
Kxf = MXQ~fX° = [ (x — mx)f(x — mx)px(dx),
(1.3.22)
82
ГЛ. 1. СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
причем
Kxf = rxf-mJ^. (1.3.23)
Формула (1.3.23) показывает, что для существования ковариационного
оператора случайной величины необходимо и достаточно существова-
ние операторов математического ожидания и момента второго по-
рядка и что область определения Dkx ковариационного оператора сов-
падает с областью определения Drx оператора Гх.
В частном случае, когда величина X имеет конечное или счетное
множество реализаций {хк }, формулы (1.3.19) и (1.3.20), определяющие
операторы Гх и АГХ, принимают вид
гг/ = 52 xkfxkPk , Kxf = ^хк - mx)f(xk - mjpjt, (1.3.24)
к к
где рк = Р(Е>к) ~ вероятность того, что X примет значение Хк (к =
= 1,2,...). Областью определения операторов Гх и Кх в этом случае
служит все пространство F.
Моменты второго порядка конечномерного случайного
вектора. Рассмотрим n-мерный случайный вектор X. Условимся пред-
ставлять векторы в виде матриц-столбцов, операцию транспонирова-
ния отмечать знаком Т, а операцию транспонирования с одновременной
заменой всех комплексных элементов соответствующими сопряженны-
ми числами - звездочкой. Тогда результат действия любого линейного
функционала f на вектор X можно будет записать в виде произведения
транспонированного n-мерного вектора f на вектор X, fX = fTX, где
в левой части f означает функционал, X - вектор, а в правой части f
и X - соответствующие матрицы-столбцы. Формула (1.3.20) при этом
даст Kxf = МХ°(/Т X0). Отсюда следует, что Kxf представляет собой
п ___________________________________________ _____
матрицу-столбец с составляющими (Kxf)p = 52 fqMXpX%. При этом
9=1
Kxf можно рассматривать как произведение ковариационной матрицы
Кх вектора X, Кх = [fcpg], kpq = МХрХ° (р, q = 1, ... , п) на матрицу-
столбец /, Kxf — Kxf. Таким образом, ковариационный оператор слу-
чайного вектора определяется его ковариационной матрицей. Совер-
шенно так же приходим к заключению, что оператор момента второго
порядка случайного вектора X определяется матрицей моментов второ-
го порядка его составляющих Гх = [7рд], где ypq = MXpXq (p,q = 1,...
... , п). Гх/ представляет собой произведение матрицы Гх на матрицу-
столбец /. Формула (1.3.23) дает в этом случае известное соотноше-
ние между центральными и начальными моментами второго порядка
1.3. МОМЕНТЫ, ХАРАКТЕРИСТИЧЕСКИЕ ФУНКЦИИ И ФУНКЦИОНАЛЫ 83
и математическим ожиданием случайного вектора. Это соотношение
в матричной форме имеет вид Кх = Гх — тхт*. Легко видеть, что
все эти результаты справедливы и для случайного вектора со счетным
множеством составляющих.
Если Хр = Хр(си) (р = 1, ... , п) - скалярные случайные величины,
заданные в вероятностном пространстве (Q,5, Р), то их моменты вто-
рого порядка существуют тогда и только тогда, когда функции хр(ш)
принадлежат //-пространству £2 Р), так как
= MXpXq = J xp(u)xq(u)P(du) = (xp,xq). (1.3.25)
Таким образом, множество всех скалярных случайных величин с конеч-
ными моментами второго порядка, определенных в одном и том же ве-
роятностном пространстве, представляет собой гильбертово простран-
ство (//-пространство) со скалярным произведением (X, У) = МХУ. В
частности, множество всех центрированных скалярных случайных ве-
личин с конечными дисперсиями является //-пространством, в котором
скалярным произведением служит ковариационный момент случайных
величин.
Определитель матрицы моментов второго порядка конечномерного
случайного вектора есть действительное неотрицательное число, равное
нулю тогда и только тогда, когда некоторая линейная комбинация со-
ставляющих вектора эквивалентна нулю. Этим же свойством обладает
ковариационная матрица.
Моменты второго порядка случайных процессов. Рассмот-
рим сначала случайную функцию X — X(t), все реализации которой
принадлежат некоторому линейному пространству скалярных функций
X. Определим в этом пространстве слабую топологию с помощью мно-
жества Fc линейных функционалов. Тогда для любого f € Fc будем
I __ ______
иметь Kxf = 52 AMX°(t)X°(tfc). Ковариационный оператор случай-
k=i
ной функции X (£) полностью определяется ее ковариационной функци-
ей = MX°(*)X°(f).
Оператор момента второго порядка случайной функции X (£) пол-
ностью определяется ее начальным моментом второго порядка
Гж(£, f) = MX(t)X(f). Формула (1.3.23) дает в этом случае известное
соотношение между ковариационной функцией, начальным моментом
второго порядка и математическим ожиданием случайной функции.
При существовании функций Кх(1,1') и Гж(££') область определения
операторов Кх и Гж содержит Fc.
84
ГЛ. 1. СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
Если X — X(t) - случайная функция, все реализации которой
принадлежат некоторому линейному пространству n-мерных вектор-
ных функций X, то за множество линейных функционалов Fc, опре-
деляющее слабую топологию в X, можно принять множество всех ко-
нечных линейных комбинаций функционалов fqs (g = 1, ... , n; s G
G 7i), fqsx(t) = xq(s), т.е. функционалов, сопоставляющих любой
векторной функции x(t) G X значение какой-нибудь ее составляющей
при каком-нибудь значении s аргумента t. Тогда будем иметь Kxf =
i _____ ______
= 52 fkMXQ(t)X°k(tk). Таким образом, Kxf представляет собой век-
k=i
торную функцию из пространства X с составляющими (Kxf)p —
I _____ ____________
— 52 fkMXp(t)X® (tk). Ковариационный оператор векторной случай-
k=i
ной функции X (t) определяется матрицей ковариационных и взаимных
ковариационных функций ее составляющих
[Kn(t,t') K12(t,t') ... Kln(t,t')i
К ^) — TC2i(^,f) K22(t,tf) ... K2n(t,t’)
-Knl(t,t') Kn2(t,t') ... Knn(t,t‘).
где _______
Kpq(t, t’) = MX°(t)X°(t') (p,q = 1, ... , n).
Оператор момента второго порядка векторной случайной функ-
ции X(t) определяется матрицей rx(t,t') начальных моментов второ-
го порядка ее составляющих. Формула (1.3.23) дает в этом случае
известное соотношение между ковариационными функциями, началь-
ными моментами второго порядка и математическими ожиданиями.
Это соотношение в матричной форме имеет вид Kx(t)t') = Гд.^,^) —
-mx(t)mx(t')*, где mx(t)* = |^7П1(£)... mn(t) ], mp(t) = MXp(t) (p —
= l,...,n). При существовании матричных функций Kx(t,t') и
rx(t,t') область определения операторов Кх и Гж содержит Fc.
Моменты второго порядка случайных величин в В-прост-
ранстве. Пусть X = х(си) и У = у (си) - случайные величины в про-
странствах X и Y соответственно, определенные в вероятностном про-
странстве (Q,<S,P). Если каждое из пространств X и Y представляет
собой В-пространство (ТСтС, раздел 3.3), a F и G - соответствующие
сопряженные пространства линейных функционалов, то формула
Гхуд = MXgY = [ x(cj)^)P(dw) (1.3.26)
1.3. МОМЕНТЫ, ХАРАКТЕРИСТИЧЕСКИЕ ФУНКЦИИ И ФУНКЦИОНАЛЫ 85
определяет оператор ГЖ!/, отображающий G в X, Оператор ГЖ!/, опреде-
ляемый формулой (1.3.26), называется взаимным оператором момента
второго порядка случайных величин X и У.
Взаимный оператор момента второго порядка центрированных слу-
чайных величин X® = X — тх и У0 = У — ту называется взаимным
ковариационным оператором случайных величин X и У. Взаимный ко-
вариационный оператор Кху случайных величин X и У определяется
формулой
Kxyg = M.X°gY° = - тх]д[у(ш) - my]P(du), (1.3.27)
при этом
Кхуд ~ Гху9 пахдтПу . (1.3.28)
Для существования оператора Кху необходимо и достаточно существо-
вание тж, ту и Гж2/, причем области определения операторов ГЖ2/ и Кху
должны совпадать.
Если X и У - случайные величины с конечным или счетным мно-
жеством реализаций {х^ у к}, то
Гхуд = 52 ХМУЬРЬ > К*«9 = 52^* " mk)9(.yk ~ ту)рк , (1.3.29)
к к
где Рк - вероятность появления к-й пары реализаций (хкУк) (к =
= 1,2,...) величин X, У.
Случайные величины X и У называются некоррелированными, ес-
ли Kxyf = 0 для всех f е F (т.е. Кху = 0). Если Kxyf 0 хотя бы для
одного f € F, то величины X и У называются коррелированными.
Предположим, что случайные величины X и У независимы. В
этом случае вероятностная мера pz составной случайной величины Z =
= (X, У) равна произведению вероятностных мер рх, ру величин X, Y.
Пусть U = ip(x) - произвольная скалярная рх-интегрируемая функция
в пространстве X, а V = - произвольная /^-интегрируемая функ-
ция в пространстве У со значениями в некотором В-пространстве. В
этом случае, если случайная величина U представляет собой функцию
случайной величины X, а случайная величина V - функцию случайной
величины Y, причем одна из величин U, V скалярная, то в случае не-
зависимых величин X и У математическое ожидание произведения
величин U и V равно произведению их математических ожиданий,
т.е.
М(/?(Х)^(У) = / <p(x)^(y)pz(dx х dy) =
86
ГЛ. 1. СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
= j px(dx} = j ip(x)px(dx) J iKy)py(dy) =
= М<р(Х)Мф(У). (1.3.30)
Независимые случайные величины всегда не коррелированы. Об-
ратное не всегда верно. Некоррелированные случайные величины могут
быть зависимыми.
Основные свойства моментов второго порядка рассмотрены в
(ТСтС, п.3.3.2).
1.3.3. Моменты высших порядков. В элементарной теории
вероятностей для более полной характеристики (действительных) ска-
лярных и векторных случайных величин вводят следующие начальные
и центральные моменты высших порядков:
дг = М(Х°)Г , аг = МХг, (г = 1,2,...), (1.3.31)
аг = аГ1,...,Гп = MXp...XJ’,
Mr = Мп ,..., rn = М(Х?)Г1 • • • (*п)г" , (1-3-32)
(И =Г1 + ---+т„, |г| = 1,2,...).
Величина г = (п , ... , гп) в формуле (1.3.31) называется векторным
индексом или мультииндексом. Для скалярных случайных величин
между начальными и центральными моментами имеют место следую-
щие формулы связи:
аг = 57 C'r Mpmz ₽ (тх = «1), (1.3.33)
р=0
Mr = £(-1Г-₽С₽артГ₽ • (1.3.34)
р=0
Аналогично в элементарной теории случайных функций опреде-
ляются высшие моменты для действительных скалярных случайных
функций X(t), t е Т\:
ar(ti , ... , tr) — MX(^i)... X(tr) —
OO oo
— j ''' j • • • xrfr(^i, ... , xr; й , ... , tr}dxi ... dxr , (1.3.35)
—oo —oo
1.3. МОМЕНТЫ, ХАРАКТЕРИСТИЧЕСКИЕ ФУНКЦИИ И ФУНКЦИОНАЛЫ 87
... ,tr) = MX°(t1)...x°(tr) =
оо оо
— J*' * J* [^i гММ] • • • mr(tr)]x
— оо —оо
Х/Г(Ж1, ... , xr;ti, ... , tr)dxi.. .dxr . (1.3.36)
Смешанные начальные и центральные моменты порядка г, (|г| =
= Г1 + • • • + гп) для действительных скалярных случайных функций
Xi(t), ... , Xn(t) вычисляются по формулам
= м{х1(?;))...Х1(^))...Х„(^п))...Х„(^))} , (1.3.37)
= м { [ X. (t^) - mi (t^) ] ... [^i (£>) - ] ...
... [xn(t'n)) -mn(t<n))] ... [xn(tW) -mn(t("))]} . (1.3.38)
Операторы моментов высших порядков определяются так же, как
оператор момента второго порядка и ковариационный оператор. При
этом для простоты мы ограничимся случайными величинами в дей-
ствительных линейных пространствах. Пусть X = х(си) - случайная
величина в действительном линейном пространстве X. Формула
тг(Л , ... , /г_!) - МХ(ЛХ)... (А-1Х) =
= rr(cj)/irr(cd)... fr~ix(w)P(dw) =
= У xfax... fr-ixpx(dx) (1.3.39)
определяет оператор mr, отображающий произведение пространств
Fr-1 в X. Здесь /1 , ... , /г_1 G F - произвольные линейные функ-
ционалы на X. Этот оператор называется оператором момента г-го
порядка случайной величины X. Оператор тп® момента r-го порядка
центрированной случайной величины XQ = X — тх называется опе-
ратором центрального момента г-го порядка случайной величины X.
88
ГЛ. 1. СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
Функционал (/1 , ... , fr) R на произведении пространств Fr, опре-
деленный формулой
Лтг(/1, ... , /г_1) = М(ЛХ)... (/ГХ), (1.3.40)
называется моментной формой г-го порядка случайной величины X, а
функционал
Л-О = М(ЛХ°)... (/ГХ°) (1.3.41)
- центральной моментной формой г-го порядка случайной величины
X. При г = 1 моментная форма первого порядка совпадает с вели-
чиной fmx, f 6 Fc. Очевидно, что оператор момента r-го порядка
является (г — 1)-линейным оператором, а моментная форма г-го поряд-
ка - г-линейным функционалом. Напомним, что функция т перемен-
ных /1, ... , fm называется т -линейной, если она линейна по каждой
переменной при фиксированных значениях остальных.
1.3.4. Характеристические функции и функционалы. Как
известно, характеристическая функция действительного случайного
вектора X определяется формулой (ТСтС, раздел 3.4)
<?(А) = Ме<лТх = У eixTxf(x)dx. (1.3.42)
—сю
Размерность вектора А совпадает с размерностью вектора X.
Основные свойства характеристической функции изучены в
(ТСтС, п.3.4.2).
В элементарной теории случайных функций для действительной
случайной функции X(t), t Е Ti, определяют семейства одномерных и
многомерных характеристических функции gi = gi (A; t) и gn =
= Pn(Ai , ... , An; ti , ... , tn) с параметрами t и ti , ... , tn соответствен-
но:
gi(X;t) = MeixTxw, (1.3.43)
9n(Xi, ... , An; ti, ... , tn) =
= Mexp{iAfX(/i)+ - + iA^X(t„)} (n = 2,3,...). (1.3.44)
Пусть теперь X = x(cj) - случайная величина в действительном
линейном пространстве X и F - сопряженное с X пространство всех
непрерывных линейных функционалов на X. Функционал
JZx(/) = Mei/X = [ eifx^P(daj) = [ eifxp.x(dx) (1.3.45)
1.3. МОМЕНТЫ, ХАРАКТЕРИСТИЧЕСКИЕ ФУНКЦИИ И ФУНКЦИОНАЛЫ 89
на пространстве F (f Е F) называется характеристическим функцио-
налом случайной величины X. Характеристический функционал суще-
ствует у любой случайной величины в любом действительном линейном
пространстве, так как для такой величины fX является действительной
случайной величиной и \ег^х | = 1.
Основные свойства характеристического функционала рассмотре-
ны в (ТСтС, п.3.4.2).
Связь между характеристической функцией и моментами.
Для скалярной случайной величины X n-мерного случайного вектора
в элементарной теории вероятностей в предположении, что существуют
моменты г-го порядка, выводятся следующие формулы (ТСтС, п.3.4.3):
аг = Гг5<г>(0) г = 1,2,.. (1.3.46)
«м = 1+R-’ г—1 (1.3.47)
Дг = i-r [ £-е~“т’д(Х) алг , (1.3.48) А=0
e~<Am’5(A) = 1 + £ г~^ХГ + ’ г=2 (1.3.49)
OraW
dAf1... дх^
Oihi
Ph!
(1.3.50)
(1.3.51)
</(А) = 1 + £г $2 ^^А^...А^+Я„ (1.3.52)
e-ixTm’g(X) = l + jy £ ГТ
Пл I .
r=2 hid-----y-hn-=r
^A^.-.A^+K,
/In*
(1.3.53)
где Ru и R'u - остаточные члены в формуле Маклорена.
Разложение характеристического функционала. Предполо-
жим теперь, что случайная величина X имеет операторы моментов до
90
ГЛ. 1. СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
порядка п + 1 включительно. В этом случае имеем (ТСтС, п.3.4.4):
<М/) = [= [ (1+ ££(/*)” +
' \ г=1 ' (1.3.54)
;п+1 \
+ T—W}wn+Iefx]^dx^
(п + 1)! /
где в - постоянная в формуле Лагранжа. Отсюда, принимая во внима-
ние (1.3.40), получаем
п .г
g*(f) = 1 + Е >•••>/) + Рп(/), (1-3.55)
Г=1
где fmr{f, ... , /) - моментная форма r-го порядка случайной величи-
ны X, в которой все аргументы Д , ... , fr равны /, a Pnfj) ~ остаточ-
ный член, для которого справедлива оценка
|pn(/)| < I |/x|n+1^(dx). (1.3.56)
Если случайная величина X имеет операторы моментов всех поряд-
ков и интеграл в (1.3.56) при всех f € F растет медленнее, чем (п + 1)!
при п -» оо, то pn(f) -» 0 при п -> оо и формула (1.3.55) принимает вид
ОО т
р«(/) = 1+Е^т’-(/>•••’/)• (ъз-57)
Г=1
Соответствие между вероятностными мерами и характери-
стическими функционалами. Каждая случайная величина в дей-
ствительном топологическом линейном пространстве имеет характери-
стический функционал. Данной вероятностной мере в действительном
линейном пространстве соответствует единственный характеристиче-
ский функционал. Естественно возникает вопрос: в какой мере характе-
ристический функционал определяет распределение случайной величи-
ны, соответствует ли данному характеристическому функционалу един-
ственная вероятностная мера? В (ТСтС, п.3.4.5) доказаны следующие
утверждения.
• Характеристическая функция конечномерного случайного век-
тора интегрируема тогда и только тогда, когда существует плот-
ность вероятности этого вектора по лебеговой мере.
1.3. МОМЕНТЫ, ХАРАКТЕРИСТИЧЕСКИЕ ФУНКЦИИ И ФУНКЦИОНАЛЫ 91
• Характеристический функционал любой случайной величины X
в любом действительном линейном пространстве однозначно опреде-
ляет ее вероятностную меру на минимальной а-алгебре, содержащей
все множества вида {ж : f\x Е Ai, ... , fnx € Ап}. В частности, ес-
ли в фазовом пространстве случайной величины X определена слабая
топология с помощью множества линейных функционалов F, это будет
а-алгебра, порожденная базой топологического пространства X. Таким
образом, существует взаимно однозначное соответствие между вероят-
ностными мерами в действительном линейном пространстве и харак-
теристическими функционалами. Распределение вероятностей в дей-
ствительном топологическом линейном пространстве можно задать как
вероятностной мерой, так и характеристическим функционалом (разу-
меется, если за а-алгебру в этом пространстве принимается а-алгебра,
порожденная рассмотренным классом множеств).
• Когда существуют операторы моментов всех порядков случай-
ной величины X и моменты случайных величин \fX\ при всех f Е F
растут с увеличением порядка г медленнее, чем факториалы г!, после-
довательность операторов моментов однозначно определяет харак-
теристический функционал, а следовательно, и вероятностную меру
случайной величины X. Таким образом, распределение вероятностей в
действительном линейном пространстве можно задавать и с помощью
неограниченной последовательности операторов моментов.
1.3.5. Ортогональные разложения одно- и многомерных
плотностей. Семиинварианты и квазимоменты. Пусть ш(х) - не-
которая плотность в г-мерном пространстве Rr, для которой су-
ществуют все моменты. Система пар полиномов pv(x), qv(x) (и =
= 0,1,2,...) называется биортонормальной с весом w(x), если
сю
[ w^p^q^dx = J ® “Р" (1.3.58)
/ 1± при р — I/.
— сю
Система пар полиномов р„(х), q„(x) (1/ = 0,1,2,...) называется биор-
тогональной, если условие (1.3.58) выполнено только при р р. Вся-
кая биортогональная система пар полиномов {р„ (х), q„ (х)} может быть
сделана биортонормальной путем деления полиномов р„(х), qv(x) со-
ответственно на множители а„, произведение которых равно инте-
гралу (1.3.58) при соответствующем v и р — v. Когда qy(x) = р„(х)
92
ГЛ. 1. СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
(р = 0,1,2,...), условие (1.3.58) принимает вид
сю
У* w(x)pl/{x)ptl(x)dx = . (1.3.59)
— сю
В этом случае система полиномов {pv(x)} ортонормальна, если она
удовлетворяет условию (1.3.59) при всех р, р, и ортогональна, если она
удовлетворяет условию (1.3.59) только при р / р. Всякая ортогональ-
ная система полиномов {рДа;)} может быть нормирована путем деления
р„(х) на корень квадратный из интеграла (1.3.59) при соответствующем
у и р = V.
Существование всех моментов плотности ш(х) необходимо и доста-
точно для существования всех интегралов (1.3.58) и (1.3.59).
Часто для удобства целесообразно пользоваться векторной (муль-
тииндексной) нумерацией полиномов р^х), q„(x) так, чтобы сумма ко-
ординат |р| = 4- • • • 4- у г векторного индекса у = [у^ .. .уг]Т была
равна степени полиномов р1/(ж) и qu(x). Тогда число линейно независи-
мых полиномов данной степени т = |р| будет равно числу независимых
одночленов степени т, т.е. числу С^.т_1 = (г 4- т — 1)!/ [m!(r — 1)!].
В случае векторных индексов у и р величина 6у^ в (1.3.58) представля-
ет собой единицу, если р = у, и нуль, если хотя бы одна из координат
векторного индекса р не совпадает с соответствующей координатой ин-
декса У.
Пусть /(ж) - плотность некоторого r-мерного случайного векто-
ра X, для которого существуют моменты всех порядков. Попытаемся
представить плотность /(ж) разложением
оо
/(ж) = U)(x) Cvpv(x). (1.3.60)
i/i ,... , i/r =0
Тогда су будет определяться согласно
оо
Су = У f(x)qy(x)dx = Mqy(X) = дДа),
(1.3.61)
где Qi/(q) представляет собой линейную комбинацию моментов случай-
ной величины X, полученную из qy(x) заменой всех одночленов х1^ ...
... Хуг соответствующими моментами , . •. , &kr- Таким образом, все
ЬЗ^МОМЕНТЫ, ХАРАКТЕРИСТИЧЕСКИЕ ФУНКЦИИ И ФУНКЦИОНАЛЫ 93
коэффициенты с„ выражаются через моменты случайного вектора X.
При этом в силу того, что Pq(x) и Qo(^) - взаимно обратные постоянные
(полиномы нулевой степени), всегда соро(я) — 1-
В некоторых случаях плотность w(x) для построения разложения
(1.3.60) удобно выбирать так, чтобы ее моменты первого и второго по-
рядков совпадали с соответствующим моментами плотности f(x) (слу-
чайного вектора X).
f(x) = w(x) 1 + 52 С>'Р’'(Х) ’
к=3 |i/|=Jfe
(1.3.62)
где
с„ = [qv(d/id\)g(X)]x=0 . (1.3.63)
Формула (1.3.62) определяет ортогональное разложение плотности
/(ж). Конечным отрезком этого разложения можно практически поль-
зоваться для приближенного представления f(x) даже тогда, когда f(x)
не имеет моментов выше некоторого порядка. В этом случае достаточно
заменить распределение /(ж) усеченным распределением
fo(x) = f(x)lD(x) / У f(x)dx,
(1.3.64)
аппроксимирующим f(x) с достаточной точностью, и затем аппрокси-
мировать /в(^) отрезком ряда (1.3.62). Ограничиваясь в (1.3.62) по-
линомами не выше У-й степени, получим приближенную формулу для
плотности f(x):
/(*) « Г(х) =w(x)
п
1 + 5212
к=3 |i/| =к
(1.3.65)
Функция /*(ж), аппроксимирующая плотность /(ж), полностью оп-
ределяется моментами случайной величины до У-го порядка включи-
тельно. При этом моменты функции /*(ж) до У-го порядка включи-
тельно совпадают с соответствующими моментами величины X:
оо
У Г(х)дц(х)(1х = с^ = q^(a)
—ОО
(1.3.66)
94
ГЛ. 1. СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
при |Д| < Af. Таким образом, математические ожидания всех поли-
номов Qi/(X) не выше N-й степени, вычисленные с помощью аппрокси-
мирующей функции /*(#), совпадают с математическими ожиданиями
соответствующих полиномов qu(X), вычисленными с помощью истин-
ной плотности /(ж). А так как полиномы qu(x) любой данной степени
к линейно независимы и число их совпадает с числом моментов к-го
порядка, то из совпадения математических ожиданий полиномов qv(X)
следует и совпадение моментов функции /*(#) и плотности f(x) до TV-го
порядка включительно. Обозначив моменты аппроксимирующей функ-
ции /*(ж) через ,,кг и Длх кг’ можем записать*полученный ре-
зультат в виде
=aki,...,kr, Рк11...,кг = Рк1,...,кг при fci +--- + fcr <2V.
(1.3.67)
Что касается моментов высших порядков аппроксимирующей
функции /*(#), то они выражаются через моменты до TV-го порядка
включительно из уравнений
дд(а*) = 0 при |р| >7V. (1.3.68)
Для дальнейшего нам понадобятся следующие формулы, выража-
ющие моменты случайной величины X до TV-го порядка через коэффи-
циенты приближенного выражения (1.3.65) ее плотности:
N
akl,...,kr =aklt.-,кг +52 12
к=1 11/| =к
(klt ... , кг =0,1, ... , N; fci + • • + = 3, ... , N), (1.3.69)
где сверху индексом w отмечены моменты плотности w(x),
р„,кг,...,кЛх) =*1* ...x^py(x), (1.3.70)
ар^,... ,fcr(a!w) получается изр^ ,... ,кг(х) так же> как из Qv(x) в
(1.3.61) (т.е. заменой всех одночленов xf4 ... х^г соответствующими мо-
ментами Лг плотности w(x)). Формула (1.3.69) с учетом (1.3.70)
дает выражения моментов величины X до N-ro порядка включительно
через моменты плотности ш(х) и коэффициенты приближенного пред-
ставления /*(ж) плотности f(x) величины X.
Функции р„(х) и q„(x) не обязательно должны быть полинома-
ми. Они могут быть любыми функциями, удовлетворяющими условию
1.3. МОМЕНТЫ, ХАРАКТЕРИСТИЧЕСКИЕ ФУНКЦИИ И ФУНКЦИОНАЛЫ 95
биортонормальности и условию существования всех интегралов (1.3.61).
Все сказанное о разложении (1.3.62) справедливо и в этом более общем
случае. Однако, если функции ^(ж) не являются полиномами, то, не-
смотря на совпадение моментов первого и второго порядков распреде-
лений w(x) и /(ж), коэффициенты с„ не будут равны нулю при |р| = 1
и 2, вследствие чего суммирование по fc в (1.3.62) будет начинаться с
к= 1.
Иногда применяется разложение по производным некоторой
плотности w(x), имеющей производные и моменты всех порядков:
сю
/(х) = (1.3.71)
1/=0
Здесь в случае n-мерного вектора х = [ яч ... хп ]т индекс у представ-
ляет собой вектор той же размерности, у — [pi ...рп]т, производная
w^\x) понимается как частная производная dM wfxj/dx"1...
... dx^n , а суммирование производится по всем координатам вектора
v от 0 до оо. При этом ри(х) = w^)(a:)/w(a:), а функции qu{x) являют-
ся полиномами. Эти полиномы в случае скалярного х определяются
следующей рекуррентной формулой:
qv(x) = (-1)^ - , (1.3.72)
д=0 '
где Шд ~ моменты плотности м(я), равные
оо
«А = У xxw(x)dx (Л = 1,2,...). (1.3.73)
— ОО
Разложение плотности по полиномам Эрмита. Биортого-
нальной системой полиномов, построенной с помощью нормального рас-
пределения с нулевым математическим ожиданием, является система
полиномов Эрмита {ЯДя),С„(х)} (ТСтС, приложение 2). Чтобы по-
лучить биортонормальную систему полиномов, соответствующую нор-
мальной плотности с математическим ожиданием m и ковариационной
матрицей К, можно на основании формулы (6) приложения 1 (ТСтС)
принять
Pv(x) = —Г“------Ни(х-тп), qu(x) = G„(x - т). (1.3.74)
У\!... yr!
96
ГЛ. 1. СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
Тогда формула (1.3.65), принимает следующий вид:
/(ж) S3 /‘(я) = wN(x)
N
k=3 |i/| =k
с„Н„(х — т)
i/J... i/r!
(1.3.75)
где
оо
с„ = У f(x)G„(x — m)dx = MGv(X -т) = G^p),
—оо
(1.3.76)
где G„(p) - линейная комбинация центральных моментов X, получен-
ная в результате замены каждого одночлена вида (Хх — mi)hl...
... (Xr — mr)hr соответствующим моментом При этом все
моменты (как начальные, так и центральные) функции /*(ж), аппрок-
симирующей плотность f(x), до порядка N включительно совпадают с
соответствующими моментами плотности /(ж), а моменты высших по-
рядков функции /*(ж) выражаются через моменты до порядка N из
соотношений
СД/Г) = 0 при р| >N, (1.3.77)
где звездочкой отмечены моменты функции /*(х).
Коэффициенты с„ при Н„(х — m)/(i/i!... i/r!) в разложении плот-
ности /(х) по полиномам Эрмита называются квазимоментами слу-
чайной величины X. Число |р| = Pi + • • • + vr называется порядком
квазимомента с„. Квазимомент порядка к представляет собой линей-
ную комбинацию центральных моментов до порядка к включительно.
Связь между моментами, квазимоментами и семиинвари-
антами. В этом случае используются следующие формулы (ТСтС,
п.3.5.3):
М(А) = £г £ bV" ’^А^.-.А^+Д», (1-3.78)
где семиинварианты /сл = , • - • , Khn и центральные моменты рь —
= i • • • , связаны между собой соотношениями
Э и lng(A)
dAj*1 ..Ж"
1.3. МОМЕНТЫ, ХАРАКТЕРИСТИЧЕСКИЕ ФУНКЦИИ И ФУНКЦИОНАЛЫ 97
[(Ai+--+A„)/2] . у
= Да1,...,а„- У к^-Л1!...Лп’х
«'ll+’-’+^np k=l
, •• , «'nfe
Vlk'- • • • I'nk'-
(1.3.79)
(Л1 + • • + hn = |r|),
[(A.+ ’+Ap)^]
An + У
p=r
Да,
M! •••/»»!,.
p!
A„ = Kht
(Л1,... , Лп = 0,1,2, ... ,Л1+ -ЛП>4). (1.3.80)
Здесь прямоугольными скобками отмечена целая часть соответст-
вующего числа. Однако в общем случае результат достигается ценой
очень сложных и громоздких выкладок. Поэтому обычно непосред-
ственно выражают квазимоменты су через семиинварианты кг по сле-
дующим формулам:
су = ку (р| =3,4,5), (1.3.81)
[ 1И/3] !
-А-[= Ё А £ (И =6,7,...), (1.3.82)
где Qi = [ди ... qlr ]Т , ... , qp = [qpl... qpr ]T, так же как и и = [pi...
...i/r]T, - r-мерные векторные индексы и внутренняя сумма распро-
страняется на все значения Qi , ... , qp, |gi| , ... , |gp| > 3, дающие в
сумме вектор и — [*л... i/r]T. Первый член в правой части формулы
(1.3.99), соответствующий р = 1, равен к,у.
Ряд Эджуорта. Слагаемые в формуле (1.3.82), соответствую-
щие различным р, часто оказываются различными по величине, причем
наибольшее значение имеют слагаемые, содержащие наибольшее число
множителей, т.е. соответствующие р = [ |р| /3], а наименьшее значе-
ние имеет первое слагаемое ку. Чтобы понять это, рассмотрим случай,
когда величина X представляет собой сумму большого числа п незави-
симых случайных величин. В этом случае все семиинварианты имеют
порядок п (семиинварианты суммы независимых величин равны сум-
мам соответствующих семиинвариантов слагаемых). Поэтому первое
4 Фильтры Калмана и Пугачева
98
ГЛ. 1. СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
слагаемое в выражении (1.3.82) для квазимомента си имеет порядок
п, в то время как р-е слагаемое - порядок пр. Это дает возможность
приближенно вычислять квазимоменты пренебрегая семиинвариан-
тами высших порядков, в отличие от формулы (1.3.76), которая требует
знания момента (а следовательно, и семиинварианта для вычис-
ления с„. В связи с этим возникает мысль перегруппировать слагаемые
в разложении f(x) по полиномам Эрмита так, чтобы собрать вместе
члены одного порядка относительно п. В результате придем к извест-
ному разложению Эджуорта (ТСтС, п.3.5.4):
/(ж) = wN(x)x
сю 2s-+-l
£ L
s=0 p=l r |i/|=2s+2p+l
91Н---\-qP—y
_ m)+
gii!...<Zpr!
oo 2s -
E S "'г-уЛ1'-' <L3-83>
s=lp=lP* |r/|=2s+2p <71+- -+qp=v 911' ‘ "qPr' J
В формуле (1.3.83) каждый член первой суммы по s представляет собой
сумму всех слагаемых порядка п-5-1/2, а каждый член второй суммы
по s - сумму всех слагаемых порядка n~s.
Разложение (1.3.83) называется рядом Эджуорта - по имени уче-
ного, впервые получившего это разложение для скалярной случайной
величины. Ряд Эджуорта (1.3.83) представляет собой асимптотическое
разложение плотности /(ж) относительно п-1. В случае скалярной ве-
личины X погрешность конечного отрезка ряда (1.3.83) имеет порядок
первого отброшенного члена существующей суммы по «о- Применение
ряда Эджуорта позволяет включить в отрезок разложения значитель-
но большее число полиномов Эрмита при учете моментов до данного
порядка, чем обычное ортогональное разложение. А именно, учитывая
моменты (или семиинварианты) до TV-го порядка включительно, полу-
чим в отрезке ряда Эджуорта полиномы Эрмита до степени 37V — 6
включительно. В результате повышается точность приближения к ис-
тинному распределению. Поэтому рядом Эджуорта часто пользуются
на практике. Это тем более обоснованно, что большая часть случайных
величин, встречающихся в приложениях, относится к классу величин,
которые можно считать суммами большого числа независимых слагае-
мых.
Так же, как в случае ортогонального разложения, при аппрокси-
мации плотности /(ж) отрезком /*(ж) ряда Эджуорта с учетом момен-
тов до TV-го порядка моменты аппроксимирующей функции /*(ж) до
1.3. МОМЕНТЫ, ХАРАКТЕРИСТИЧЕСКИЕ ФУНКЦИИ И ФУНКЦИОНАЛЫ 99
TV-го порядка включительно совпадают с соответствующими момента-
ми плотности /(ж), а моменты порядка выше 3N - 6 определяются из
соотношений G„(jj,*) = 0. Моменты же порядков от N + 1 до 3N — 6
получаются из уравнений G„(p*) — где - сумма всех коэффици-
ентов при Н„(х — т)1(у\ \... i/r!) в отрезке ряда Эджуорта.
Согласованные биортогональные системы полиномов. Для
одновременного приближенного представления всех многомерных рас-
пределений случайной функции целесообразно пользоваться согласо-
ванными биортогональными системами полиномов.
Пусть {wn(xi, ... , xn;ti, ... , tn)} - согласованная последователь-
ность многомерных плотностей, где Xi, ... , хп - r-мерные вектор-
ные переменные. С каждой плотностью wn свяжем биортонормаль-
ную систему полиномов {pU1,..., Уп (xi , ... , хп\ti , ... , tn) и
q^i,(iei , ... , хп;, ... , tn)}. Конечно, предполагается, что для
каждой плотности шп существуют все моменты. Эти полиномы, есте-
ственно, будут зависеть от переменных ti, • • • как от параметров, что
и отражено в наших обозначениях.
Биортонормальные системы полиномов {рУ1,..., „п (яч , ... , хп;
ti, • • • ? ^п), , ип (#1 ) • • • , хп? ^п)} — 1,2...) будем назы-
вать согласованными, если они удовлетворяют условиям:
1) f Wn(^l > ••• ? j ^1 , ••• ? ^n)Pl^l , ... , ип (*^1 ч • • • ч хп"ч ч • • • ч ^п)
xdxn — Wn—1 , . . . , Хп—1, ti , ... , tn_ 1 )Pi?i , ... , i/n_i (^-1 ч • • • ч *^n—1 ч
ti, ... , *n-i)<5o,i/n ч где <5о,о = 1, = 0 при vn 0 0;
2) Qi/J 1,0 (*^1 ч • • • Ч ХП Л Ч • • • Ч ^n) ч • • • ч ^n—l (*Г1 ч • • •
• • • , хп— 15*1 ч • • • ч ^п—1} ч
^тг-1
3) Ри\ , . . , ип-1 — к,к (*Г1 ч • • • ч хп—1 ч *Гп—1 ч ^1 ч • • • ч ^п—1 ч ^n—1)
к=0
~ Р^1 , ••• ,Vn-l (*^1 ч • • • ч хп—1ч*1ч • • • ч ^п—1) ч
4) Qu} , ... , vn_ j ,i/n (ЗЧ , . . . , Xn—1, Xn—1, ti , . . . , tn — i, tn_ 1)
~ , ... , Vn-l+Vn (*Г1 ч • • • ч xn— 1 j^l 4 • • • ч ^n—1)-
Так как полиномы pu и q„ определены только с точностью до взаим-
но обратных постоянных множителей, то, умножив рУ1 на произ-
вольный множитель 71/1,... ? „п и разделив qU1 ?... ? Un на тот же множитель,
можно заменить условия 3) и 4) условиями:
^тг-1
3 ) Ри\ , , vn-i—k,k (*Г1 ч • • • ч ^п—1 ч ^п—1 ч ч • • • ч ^п—1 ч ^п— 1)
/с=0
Х'К*, ... , i/n_1-k,k ~ Р^1 , ... , i/^-i (Ж1 ч • • • ч хп-1ч tl ч • • • ч ^n-l)li/i ,...,уп-1'ч
4 ) 7l/j , ... , vn-l ,^п (х1 ч • • • Ч Xn—1 Ч ХП—1 Ч ^1 Ч • • • Ч ^п— 1 Ч
£п-1) — 7^1 , , yn-l+ynQyi , ••• , ^тг-1-Ь^тг (Ж1 Ч ’ ' ’ Ч ХП~1ч ^1 Ч ' ’ * Ч ^П~1)‘
100
ГЛ. 1. СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
Согласованные в этом смысле биортонормальные системы поли-
номов существуют. Примером таких систем могут служить системы
полиномов:
,... ,ип (яч , ♦ • • ч Хп, Й ч • • • ч ^п) =
= -m(*i), ••• ч хп -т(^п))/(1/ц!...1/пг!), (1.3.84)
Qi/i ,... , vn (#1 ч • • • , Хп, t} , ... , tn) —
= G»i ,...,1/п(ж1 -mfa), ... ч xn -т(1п))ч
где , !/n (^i , ... , хп)ч GU1,...,i/n (xi , ... , xn) ~ полиномы Эрмита
(п = 1,2,...) (ТСтС, приложение 2). Согласованной последовательно-
стью плотностей wn в случае (1.3.84) служит последовательность мно-
гомерных нормальных плотностей
^п(х\ , . . . , Хп’ч tl ч • • • •) ^п) =
= [(2тг)гп |ЯП| ]1/2 ехр {Ц(*(П)Т - - тп)} ,
®(п) = [а?Г...Яп]7 , тп = [т(^)т...тп(«п)Т]Т , (1.3.85)
где
К(£1,<2) ••• K(ti,tn) '
„ _ K(t2,t2) ... K(t2,tn)
— 4
.K(t!,tn)T K(t2,tn)T ... K(tn,tn) .
a m(t) и K(t, t') - математическое ожидание и ковариационная функция
некоторой случайной функции.
Согласованные ортогональные разложения многомерных
плотностей. Пусть {/n(^i , • • • , хп, ti, ... , tn)} ~ согласованная пос-
ледовательность многомерных плотностей r-мерной векторной функ-
ции X(t), имеющей моменты всех порядков, а {р^ ,... ,i/n (a?i , ... , хп,
ti, ... , tn)}, {Qi/i , a;n;ti, ... , tn)} (n = 1,2,...) - согласо-
ванные биортонормальные системы полиномов, соответствующие согла-
сованным многомерным плотностям wn(xi, ... , x^ti, .. • , tn), имею-
щим те же моменты первого и второго порядков, что и случайная функ-
ция X(t). Представив каждую многомерную плотность fnfxi, — • > хп'ч
ti, ... , tn) случайной функции X(t) ортогональным разложением
(1.3.62) по полиномам ри ,..., Уп (х\ 9..., хп; ti, ... , tn), получим согласо-
1.3. МОМЕНТЫ, ХАРАКТЕРИСТИЧЕСКИЕ ФУНКЦИИ И ФУНКЦИОНАЛЫ 101
ванные ортогональные разложения всех ее многомерных плотностей:
/п(*1 , • • • , ^1 ) • • • , ^п) — Wn(Xl Ч ' ' ‘ Ч Я'П) Ч • • • ) ^п) X
х 52 c,/i
3 |pi | Н----1- |рп | =k
vn (^1 ? • • • ? ^n)*
, ... , Vn (^1 ) • • • 5 %П j tl 5 • • • ? ^n) 5 (1.3.86)
где коэффициенты си ,..., Уп (ti , ... , tn) определяются следующей фор-
мулой:
оо оо
—оо —оо
хqyi,,vn (*^i j • • • , ^П, ^1 , • • • » • • • dxn —
= [&/i ,...,i/n(d/*dAi, ... , d/idX^ti, ... , tn)x
*9n(Xi, ... , An; ti, ... , tn) Jaj—...—Дп~о • (1.3.87)
Здесь <?n(Ai , ... , An; ti, ... , tn) - n-мерная характеристическая
функция случайной функции X(t).
Из условия 2) согласованности систем полиномов
{.Ри , ... , Уп (*^1 > * * * > *^п5 ^1 , • • • , ^n), Qvi , ... , Уп (яч ч • • • » Хпч ^1 Ч • • • ч ^п)}
при п = 1,2,... и из условия 1) согласованности плотностей fn следует,
что
G/1 ,... , i/n_i,o(^l ч • • • ч ^n) ~ Cpj ,... , i/n_1 (tl ч • • • ч ^п—1)
при всех Pi, ... , рп-1- После этого из условия 1) согласованности си-
стем полиномов следует, что интегрированием разложения (1.3.86) для
плотности fn по хп получается разложение (1.3.86) для плотности fn_\.
Отсюда по индукции для любого п следует, что разложения (1.3.86)
согласованы в том смысле, что интегрированием (1.3.86) для fn по
a:m+i, ... , хп при любом т получается разложение (1.3.86) для fm.
Далее, примем во внимание условие 4) согласованности систем по-
линомов и то, что X(tn) = X(tn_i) при tn — tn-i и, следовательно,
102
ГЛ. 1. СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
условная плотность случайной величины Xtn при Xtn_r = xn-i равна
8(хп — xn-i). Тогда будем иметь
fn(xi , • • • , Хп] , ... , tn—i, 1) —
“ fn—i(a?i )••••) xn—i*, ti, ... , tn—i)fi(xn ~ xn—i). (1.3.88)
Отсюда вытекает следующее условие:
, i/n_! ,l/n (tl , . . • , tn—l , tn — 1 ) — CU1 , (tl , . . . , tn—1) .
(1.3.89)
После этого из условия 3) и из формулы (1.3.88) для плотностей шп
и wn_i следует, что при tn = tn-i формула (1.3.86) дает выражение
(1.3.88) для плотности /п, где fn-\ представлена соответствующим раз-
ложением (1.3.86). Таким образом, разложения (1.3.86) многомерных
плотностей случайной функции согласованы и в том смысле, что для
них справедлива формула (1.3.88), которую также можно рассматри-
вать как одно из условий согласованности многомерных распределений.
Ограничиваясь в (1.3.86) полиномами не выше N-n степени, полу-
чим согласованное приближенное представление многомерных
распределений случайной функции X(t). Этим приближенным пред-
ставлением можно практически пользоваться, если случайная функция
X(t) имеет конечные моменты до ЛГ-го порядка включительно, неза-
висимо от того, существуют или не существуют ее моменты высших
порядков.
Согласованные разложения многомерных плотностей по
полиномам Эрмита. Взяв в качестве плотностей wn нормальные
многомерные плотности (1.3.85), получим согласованные разложения
многомерных плотностей случайной функции X(t) по полиномам Эр-
мита (ТСтС, приложение 2):
fn(.X\ , . . . , Хп\ tj. , . . . , tn) —
= [(2тг)гп |КП| ]"1/2 ехр -mn)| х
1 J
F„(rri -m(Zi),...
> • • •
^11! • I'nr'-
• • •, хп ? (п — 1,2,...).
(1.3.90)
1.3. МОМЕНТЫ, ХАРАКТЕРИСТИЧЕСКИЕ ФУНКЦИИ И ФУНКЦИОНАЛЫ 103
Формула (1.3.87) для коэффициентов cU1,... jt/n (ti , ... , tn) принимает
при этом следующий вид:
Cpi (^1 , • • • , tn}
ОО оо
fn&l , • • • > t\ , ... , tn)GU1 ,... , уп (#i TTl(ti), . . .
—оо —оо
... ,хп - m(tn))dxi .. .dxn = [G^ ,...,рп(5/г5А1 - m(£i), ... , д/1дХп-
~т(1пУ)9п(Х\ , ... , An; , ... , tn) ]а1==...==ап—о —
= [<^1,...,Рп(дДдА1, ... , d/idXn)9n(Xi , ... , Xn]tr, ... ,tn)x
xexp {-z'Afm(ti)---------iX^m(tn)} ]Л1= .=ап=о • (1.3.91)
1.3.6. Условные моменты. В элементарной теории вероятностей
широко применяются различные условные характеристики случайных
величин и векторов. Так, условное математическое ожидание дан-
ной функции </?(^0 случайной скалярной или векторной величины X
при данном значении случайной скалярной или векторной величины Y
определяется формулой
оо
Ж'/’РОИ = У ‘P(.x)f2(x\y)dx, (1.3.92)
—ОО
где /2(^1?/) - условная плотность величины X при данном значении у
случайной величины Y.
Из (1.3.92) как частный случай вытекает формула для условного
математического ожидания случайной величины при данном значении
величины X:
оо
M[X|j/]= I xf2(x\y)dx. (1.3.93)
— ОО
Обозначение /2(^1?/) применяется для плотности случайной вели-
чины X, зависящей от параметра у, и в том случае, когда у не явля-
ется значением некоторой случайной величины Y. Формулы (1.3.92) и
(1.3.93) при этом определяют математические ожидания ц>(Х) и X как
функции параметра у. Математическое ожидание случайной величи-
ны X как функция параметра у, от которого зависит распределение X,
называется регрессией X на ?/. В частном случае, когда параметр у -
104
ГЛ. 1. СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
возможное значение некоторой случайной величины У, регрессия X на
у представляет собой условное математическое ожидание X при У = у.
Зная условное математическое ожидание, можно определить все
условные моменты случайных величин.
Условное математическое ожидание случайной величины Z =
= (р(Х), рассматриваемое как функция случайной величины У,
М[</?(Х)|У], называется условным математическим ожиданием
случайной величины Z — <р(Х) относительно У. Так как условные
математические ожидания и условные моменты различных порядков
случайных величин относительно случайной величины У сами являют-
ся случайными величинами, то для них, в свою очередь, можно опреде-
лить математические ожидания и моменты различных порядков. Нако-
нец, приведем часто применяемую в элементарной теории вероятностей
формулу полного математического ожидания
М<р(Х,У) = М[М[(Х,У)|У]] . (1.3.94)
Отсюда при 9?(Х, У) = X находим
МХ = М[М[Х|У]] . (1.3.95)
Предположим теперь, что на вероятностном пространстве (П,
5, Р) задана случайная величина X = ®(и), фазовым пространством ко-
торой служит измеримое линейное пространство (X, Л). Введем слабую
топологию в X с помощью достаточно полного множества линейных
функционалов Fc и допустим, что X полно в этой топологии (т.е. явля-
ется слабо полным топологическим линейным пространством). Пред-
положим, что условная вероятность Pj-(A|o;), A G S, относительно не-
которой а-алгебры 7 С 5, регулярна. Условным математическим
ожиданием случайной величины X = х(ш) относительно а-алгебры У
называется слабый интеграл
Mjr(X|w) = У a:(w')PF(da/|w). (1.3.96)
В частном случае, когда X - сепарабельное В-пространство, a Fc -
сопряженное с X пространство непрерывных линейных функционалов
на X, интеграл в (1.3.96) можно понимать как сильный интеграл (если,
конечно, х(а)') является Ртг(А|а>)-интегрируемой при данном значении
си (Е Q).
Мера Pf(A|q;) при всех А € 5 определена почти для всех ш отно-
сительно меры Р и является относительно F измеримой функцией ш.
1.3. МОМЕНТЫ, ХАРАКТЕРИСТИЧЕСКИЕ ФУНКЦИИ И ФУНКЦИОНАЛЫ 105
При этом (ТСтС, раздел 3.6) доказано, что функция Mj-(X|cu), а вме-
сте с ней прообразы всех множеств а-алгебры Л', порожденной этим
классом множеств, принадлежат а-алгебре У. Это значит, что функ-
ция Mj-(X|cu) (^, Л^-измерима, т.е. является случайной величиной в
(Л',Л/), определенной на вероятностном пространстве где
Рр ~ сужение вероятности Р на У.
Если а-алгебра У индуцирована некоторой случайной величиной
У — y(w), то У = Sy, т.е. представляет собой прообраз соответствую-
щей а-алгебры В множеств фазового пространства величины У. Тогда
формула (1.3.96) определяет условно математическое ожидание слу-
чайной величины X относительно случайной величины У. В этом слу-
чае Pjr(A|cu) является измеримой относительно В функцией случайной
величины У = у(ш). Следовательно, условное математическое ожида-
ние случайной величины X относительно У представляет собой (Б,Л')“
измеримую функцию случайной величины У. Поэтому мы будем обо-
значать условное математическое величины X относительно У симво-
лом М(Х|У) или, короче, тх\у- Заменой переменных х = x(ti) для
условной вероятностной меры формула (1.3.96) в этом случае приво-
дится к виду
mx\Y = М(Х|У) = jx/j.x(dx\Y). (1.3.97)
Эта формула определяет условное математическое ожидание случай-
ной величины X относительно величины У в случае существования ре-
гулярного условного распределения рх(А|?/). Заменив в (1.3.97) случай-
ную величину У ее реализацией у, получим условно математическое
ожидание тх\у = М(Х|1/) величины X при данном значении у величи-
ны У.
Свойства условных моментов. Условные математические ожи-
дания обладают всеми свойствами безусловных математических ожи-
даний с той лишь разницей, что каждое из приведенных там утвержде-
ний справедливо только почти для всех си (или у) относительно меры
Р (соответственно ру) и может не быть справедливым для некоторого
нулевого множества значений си (соответственно у). Наряду с этими
общими свойствами условные математические ожидания обладают и
рядом специфических свойств.
1) Если условное математическое ожидание Mj^Y|cu) представля-
ет собой слабо Р?-интегрируемую функцию и случайная величина X
106
ГЛ. 1. СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
имеет математическое ожидание, то для любого множества Е Е У
У = у a:(w)/’(dw).
Е Е
(1.3.98)
Формулу (1.3.98) можно переписать в виде
= / x(cj)P(dw), Е € У. (1.3.99)
В частности, положив Е — Q, получим
М [М^(Х» ] = MX. (1.3.100)
Эта формула называется формулой полного математического ожи-
дания. Если сг-алгебра У индуцирована случайной величиной У, то
Mjf(X|cj) — М(Х|У) и формула (1.3.100) принимает вид
М[М(Х|У)] =МХ. (1.3.101)
Рассмотрим теперь частный случай, когда функция ie(cj) измери-
ма относительно сг-алгебры У, т.е. (JT, Д) измерима. В этом случае,
если функция х(ы) является (JT, Д)-измеримой, то почти при всех си
существует условное математическое ожидание случайной величины
X = x(cj) относительно У, совпадающее с этой случайной величиной:
Mjt(X|cj) = х(щ) почти при всех си. (1.3.102)
2) Если скалярная случайная величина Z = z(cj) измерима отно-
сительно У, то для любой случайной величины X = х(а)), для которой
существует Mjr(ZX\cj),
M^(ZXfcj) = г(о,)М^рф) = ZM^(X|cj) (1.3.103)
почти при всех си.
В частности, когда а-алгебра У индуцирована случайной величи-
ной У — у (си) в (У, 23), измеримая относительно У скалярная случайная
величина Z представляет собой измеримую относительно сг-алгебры В
функцию случайной величины У, Z = <р(У). А так как Mj?(X | си) =
— М(Х | У), то формула (1.3.103) принимает вид
М(^(У)Х|У) = ^(У)М(Х|У),
(1.3.104)
1.3. МОМЕНТЫ, ХАРАКТЕРИСТИЧЕСКИЕ ФУНКЦИИ И ФУНКЦИОНАЛЫ 107
причем это равенство справедливо с вероятностью 1.
3) Если дважды применить к случайной величине операцию услов-
ного математического ожидания: один раз относительно а-алгебры
Т, а другой - относительно более бедной а-алгебры Т* С Т, то ре-
зультат будет равен условному математическому ожиданию отно-
сительно , независимо от порядка этих двух осреднений:
= М7(Мр(Х|а>) = M^(Mjt(X|cj)|cj) = M^(X|cv). (1.3.105)
Свойства условных моментов случайного вектора, образо-
ванного частью компонент нормально распределенного векто-
ра Пусть X - нормально распределенный случайный вектор, т - его
математическое ожидание, К - его ковариационная матрица. Разобьем
вектор X на два блока Xi и Х2, X — [Х^Х/1] , и в соответству-
ющем блочном виде представим его математическое ожидание m —
— [ ] , ковариационную матрицу К и обратную матрицу С:
Хы Х12
Х21 К22
С = К-1 =
с12
С*21 С22
Как известно, распределения и условные распределения векторов Xi и
Х2 в этом случае нормальны, причем условная плотность вектора Х2
при данном значении xi вектора Xi определяется следующей формулой
(Пугачев 1979):
/2(^2 | ®i) = [(2тг)п | К | / | Кп |]-1/2 exp|-i [U2C22U2 +u^C2iUi +
+ и[С12и2 + uftCn - J , (1.3.106)
где n - размерность вектора X2; | К | и | Хц | - определители матриц
К и Хц соответственно; и = [и? и?]Т = х — т. Из условия СК — I
вытекают соотношения
С11Хц + С12Х21 — I, С11Х12 + С12Х22 ,
£>21Хц 4“ С22Х21 — 0 , £>21X12 + £>22X22 — 7 ,
из которых следуют формулы
Си = (Kn - ад^)-1, С12 = ~СпК12К^ ,
С22 = (К22 - К21К^К12Г1, С21 = -С22К21К^ ,
Кп = (Си - C12C^1C2i)-1, Ki, = -КцСпС^1,
К22 = (С22 — C2iC111Ci2)-1, К21 = —АГггСггСц1.
108
ГЛ. 1. СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
Подставив вытекающие отсюда выражения Кпг и C22C2i в (1.3.106) и
учитывая, что С12 = С21, получим
/2(^2 |*1) = [(2тг)” I К I / I Кп |]-1/2 х
X exp < [u2C22U2 + U2C22(C22C21U1) + (С22 C21U1)TC22U2 +
I &
+ j = [ (27г)” I К | / I Kn |]~1/2 x
x exp < — - [uf + (P22 ] C22 [иг + C,221C,2iUi ] | =
I z J
= [(2ТГ)” I К | / I Кп |Г1/2 x
x exp [u^ - (K21Ki11U1)T] C22 [«2 - KnK^U! ] I.
i z J
Отсюда видно, что условное математическое ожидание m2|i и услов-
ная ковариационная матрица K2|i вектора Х2 при данном значении х\
вектора Xi определяются формулами
m2|i = m2 -F - mi), (1.3.107)
K2|i = С22 = К22 - К21К^К12 . (1.3.108)
Попутно получается следующее соотношение между определителями
матриц Ку Кп и /<2|1•
|К2ц| = \К22-К21КГ11К12\ = 1^1 / 1^111 . (1.3.109)
При mi = m2 = 0 имеют место следующие формулы:
тМ2 = К12К£Х2, т2ц = K2iK^X1 (1.3.110)
Условные моменты высших порядков вектора Х2 при Xi = Xi вы-
ражаются через условное математическое ожидание m2\i и условную
ковариационную матрицу K2\i обычными для нормального распреде-
ления формулами (Пугачев 1979).
Замечание!. Пусть У — Xi — Ki2K22 Х2, тогда Ку — Кц —
—Ki2K22 K2i. При этом У и Х2 независимы и М [ У ^2* ] — Независимость
Ку от Х2 является свойством нормально распределенных векторов.
1.4. ЭЛЕМЕНТЫ СТОХАСТИЧЕСКОГО АНАЛИЗА
109
Замечание 2. Пусть заданы векторы Xi,X2,-Хз, такие, что МХ1 =
= МХ2 = МХз = 0, М [Х2Х2Т] = К22 > 0. М [Х3Х3Т] = #зз > 0,
М [ Х2 Х^ ] — 0. Обозначим через Z = [ X? X? ] . Тогда имеют место следующие
соотношения:
M[X1 I Z] = M[X1ZT] {M[ZZT]}~1 Z, (1.3.111)
Kz = М [ZZT] = diag(tf22,tfzz), K~l = diag^1,^1),
KXlz = [KX1Xi,KXlZ], (1.3.112)
KX1ZKzlZ = KX1XiK^X2 + KX1zK^Z, (1.3.113)
M[X1 |X2,Z] = M[X1 I X2] + M[X1 \Z].
О свойствах условных операторов моментов. Опираясь на
понятие условного математического ожидания, можно определить ус-
ловные операторы моментов различных порядков, условные момент-
ные формы и условные характеристические функционалы случайных
величин. Из свойств условных математических ожиданий следует, что
все свойства операторов моментов второго порядка, установленные в
п.1.3.3, с вероятностью 1 (почти для всех си) справедливы и для услов-
ных операторов моментов второго порядка. Из полученных формул
вытекают соответствующие специфические свойства условных момен-
тов второго и высших порядков.
1.4. Элементы стохастического анализа
1.4.1. Операции анализа над случайными функциями. Сле-
дуя (ТСтС, раздел 4.1), приведем необходимые определения для случая
случайных величин со значениями в В-пространстве. Пусть {Хг}, Хг =
= жг(си) - произвольное множество случайных величин со значениями
в В-пространстве, зависящее от параметра г, принимающего значения
из некоторого множества R. Говорят, что Хг сходится в среднем квад-
ратическом (с.к. сходится) к случайной величине X, Хг X, если
М||Х||2, М|| Хг II2 < оо и
М|| Хг - X II2 -> 0 при г —> г0. (1-4.1)
Применительно к скалярным случайным функциям Xr(t), задан-
ным на произвольном множестве Т\, справедливы следующие утвер-
ждения.
ПО ГЛ. 1. СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
• Для с.к. сходимости Xr(t) к случайной функции X(t) необходи-
мо и достаточно существование предела
lim r„(t,t)= lim MXr(f)X(Z) (1.4.2)
Г,8—>ro r,S—>ro
при каждом фиксированном t ETi, и при этом существует также
предел
lim ГГ,(М') = MX(t)X&) = Г(М'), (1.4.3)
r,S—>Го
• Для с.к. сходимости Xr(t) к X(t) необходима и достаточна
сходимость математических ожиданий mXr (f) к тх(t) для всех t € 7\
и сходимость взаимных ковариационных функций КГ8(1,1') к Kx(t,t')
для всех t, t‘ eTi.
Для множества n-мерных векторных случайных функций,Хг(^), t €
€ Ti, имеют место теоремы.
• Для с.к. сходимости Xr(t) к некоторой векторной случайной
функции X(t) необходимо и достаточно существование предела
lim tiTrs(£,t) = lim trMXr(^)Xs(t)*, teT\. (1-4.4)
r,S—>To r,S—>Fo
При этом существует предел
lim rrs(f,t') = MX(t)X(t'y = t,t' e Ti. (1.4.5)
r,S—>Fo
• Для с.к. сходимости Xr(t) к векторной случайной функции X(t)
необходима и достаточна сходимость математических ожиданий
mXr(t) ка также ковариационных и взаимных ковариационных
функций Kr8(t,t') к ковариационной функции Кх(1,1*), t, t* € 7\.
Средняя квадратическая непрерывность случайной функ-
ции. Случайная функция X(t) со значениями в В-пространстве на-
зывается непрерывной в среднем квадратическом (с.к. непрерывной) в
точке t €71, если при любом е > 0 существует такая окрестность Vt (е)
точки что
М|| X(t') - X(t) ||2 < е при всех t' е Vt(s). (1.4.6)
Случайная функция X (t) называется непрерывной в среднем
квадратическом (с.к. непрерывной) на если она с.к. непрерывна
при всех t € Ti.
1.4. ЭЛЕМЕНТЫ СТОХАСТИЧЕСКОГО АНАЛИЗА
111
Необходимые и достаточные условия с.к. непрерывности согласно
(ТСтС, раздел 4.2) формулируются следующим образом. Для с.к. не-
прерывности скалярной случайной функции X(t) в точке t еТ\ (на Ti)
необходима и достаточна непрерывность ее момента второго порядка
Гх(£, t') в соответствующей точке (£, t) еТ\ х7\ (во всех диагональ-
ных точках (t,t) произведения пространств Т\ х Т\; причем функция
Vx(t,t') непрерывна на Т\ х Ti).
Процессы С некоррелированными приращениями. Пусть
Xv - Xt - приращение случайного процесса Xt = X(t) на интервале [t, ^), t < t1.
Случайный процесс X(t} называется процессом с некоррелированными приращения-
ми, если для любых непересекающихся интервалов [ij, [^3, ^4)> ^1 < ^2 < ^3 < ^4
соответствующие приращения xt, - xti и xt4 - xf3 процесса X(t) не коррелиро-
ванье Из этого определения следует, что приращения процесса с некоррелированными
приращениями на любых конечных интервалах имеют конечные моменты второго (а сле-
довательно, и первого) порядка. При этом сам процесс X (t) может и не иметь конечных
математического ожидания и момента второго порядка.
Однако если в некоторый момент to значение процесса с некоррелированными при-
ращениями X (t) почти наверное равно нулю, xto = 0. то процесс X (i) имеет конеч-
ные математическое ожидание и момент второго порядка, так как его значение в любой
момент Xt совпадает с его приращением на интервале [to, 0 ПРИ t > Й) и с ег0 прираще-
нием на интервале [Мо). взятым с обратным знаком, при t < to. В дальнейшем будем
рассматривать только такие процессы с некоррелированными приращениями. Любой про-
цесс с некоррелированными приращениями X (t) сводится к такому процессу. Приведем
основные свойства процессов с некоррелированными приращениями (ТСтС, п.4.2.3) .
1) Пусть X(t) - процесс с некоррелированными приращениями и Xto = 0. То-
гда значение Xt процесса X (t) в любой момент t не коррелировано с его будущими
приращениями на интервалах, следующих за моментом to, и с его прошлыми при-
ращениями на интервалах, предшествующих моменту tg: MX® (Х®2 — Хц ) — 0
при t < t\ < t%, ti > to и t\ < ^2 < t> ^2 < *0-
2) Введем функцию
0
k(t) = <
при t > to ,
при t = to ,
при t < to •
M(X° - xt° )(*£ - О = fc(t2) - fc(ti),
fc(min(ti, t2))
0
-fc(min(ti, t2))
Kx{t\,t2) = <
при t\, ^2 > ^0 ,
при t < to < ^2? ^2 < to < ,
при ti, ^2 < to •
112
ГЛ. 1. СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
3) Если ковариационная функция случайного процесса X(t) определяется соглас-
но свойству 2), где k(t) - неубывающая функция, неотрицательная при t > to, не-
положительная при t < to и равная нулю при t ~ to, то X(t) представляет собой
процесс с некоррелированными приращениями, значение которого в момент to равно
нулю почти наверное.
4) Для того чтобы случайный процесс X(t) был процессом с некоррелирован-
ными приращениями и его значение при t = to было равно нулю почти наверное,
необходимо и достаточно, чтобы его ковариационная функция определялась соглас-
но свойству 2), где k(t) - неубывающая функция, неотрицательная при t > to,
неположительная при t и равная нулю при t — to.
5) Случайный процесс с некоррелированными приращениями с.к. непрерывен то-
гда и только тогда, когда функция k(t) непрерывна. Мы будем считать в дальнейшем,
что k(t) не только непрерывна, но и дифференцируема. В этом случае
Кс(*1Лг) = У i/(r)dr,
to
где 1/(t) - неотрицательная функция, называемая интенсивностью процесса с некорре-
лированными приращениями X(t).
Случайный процесс W (t) с плотностями
= (2тг£)~1/2ехр {— w2/2t} ,
/n(wi, ... , wn;ti, ... , tn) = - tn-i)]-1/2 X
x exp {— wl/2ti — (w2 — wi)2/2(t2 — ti)------
• • • — (wn — wn_i)2/2(tn — tn—i)} (n = 2,3,...)
при ti < ^2 < • • • < tn и с непрерывными реализациями называется стандартным
винеровским процессом. Этот процесс является процессом с независимыми приращени-
ями, так как при любых ti < ^2 < ’ * ’ < tn совместная плотность случайных величин
У1 = , 1г = Wt2 — Wtx,. .. , Yn = Wtn — Wrtn_1 определяется формулой
p(yi, • • • , yn) = [(2тг)п£1(*2 - ti) • • • (fn - tn-i)]"1/2 exp {-yl/2ti~
— ti) — • • • — y^/2{tn — tn-l)} ,
т.е. представляет собой произведение плотностей величин Yi , . . . , Yn. Но независи-
мые случайные величины с конечными моментами второго порядка не коррелированы.
1.4. ЭЛЕМЕНТЫ СТОХАСТИЧЕСКОГО АНАЛИЗА
113
Следовательно, стандартный винеровский процесс является процессом с некоррелирован-
ными приращениями. Ковариационная функция такого процесса определяется формулой
Kw(ti,t2) = min(ii,t2) , а его интенсивность тождественно равна 1.
Случайный процесс P(t)> скачком возрастающий на единицу в случайные моменты,
образующие пуассоновские потоки, называется пуассоновским процессом. Так как числа
скачков пуассоновского процесса в неперекрывающихся интервалах времени по определе-
нию независимые случайные величины, то пуассоновский процесс является и процессом
с независимыми приращениями
t t
ц = MP(t) = У i/(r)dr, Dp(t) = k(t) = У i/(r)dr = д.
to to
Здесь через v(t) обозначена в общем случае переменная интенсивность пуассоновского
потока скачков процесса P(t).
Скалярный или векторный ступенчатый случайный процесс X (t) с независимыми
одинаково распределенными скачками, происходящими в случайные моменты времени,
образующие пуассоновский поток, называется общим пуассоновским процессом. Так
как суммы независимых случайных величин, не содержащие одинаковых слагаемых, не-
зависимы, то общий пуассоновский процесс представляет собой процесс с независимыми
приращениями. Если скачки имеют конечные математическое ожидание TTIq и ковариа-
ционную матрицу (дисперсию в случае скалярного процесса X[t)) Kq, то он является
также процессом с некоррелированными приращениями. При этом
mx(t) = MX(t) = то V = тпод,
т=1
ГС дГП
rx(t) = (Kq + тотТ) > пг^—ге-’' = (Ко + тот? )ц,
ТП=1
t
fc(t) = rx(t) - mx(t)mx(t)T = Kofi = Ko f vo(r)dr,
to
v(t) = Kovo(t).
Таким образом, процесс X(t) имеет конечный момент второго порядка, а значит
является процессом с некоррелированными приращениями.
Дифференцирование случайных функций. Случайная функ-
ция X(t) скалярной переменной t G Ti со значениями в В-пространстве
114
ГЛ. 1. СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
называется дифференцируемой в среднем квадратическом (с.к. диффе-
ренцируемой) в точке € Тх, если при данном t существует с.к. предел
X(t + r)-X(t) ,лл^
lim — ---------—. (1.4.7)
г—>0 Г
Случайная функция X (t) называется дифференцируемой в среднем
квадратическом (с.к. дифференцируемой) на Т\, если она с.к. диффе-
ренцируема при всех t G 7i.
Случайная функция X’(t), определяемая из условия
lim М
г—>0
X(t + r)—X(t)
г
X'(t)
2
= 0,
(1.4.8)
называется средней квадратической (с.к.) производной случайной
функции X(t).
Пусть функция X (t) - скалярная случайная функция скалярной пе-
ременной t G Ti. Справедливы следующие теоремы (ТСтС, раздел 4.3).
1) Скалярная случайная функция X(t) с.к. дифференцируема на
Т\ тогда и только тогда, когда существует конечная производная
d2rx(t,t')/dtdt' во всех диагональных точках t' = t G Ti.
В результате получаем следующие формулы для взаимных момен-
тов второго порядка случайной функции X(t) и ее с.к. производной и
для момента второго порядка с.к. производной X'(t):
= (1-4-9)
rX'(t,t') =
d2Vx(t,t')
dtdt'
(1.4.10)
2) Скалярная случайная функция X(t) с.к. дифференцируема на Ti
тогда и только тогда, когда ее математическое ожидание тх (t) диф-
ференцируемо наТ\, а ее ковариационная функция Kx(t,t') имеет ко-
нечную вторую смешанную производную d2Kx(t,t,)/dtdtl во всех диа-
гональных точках t' = t G Т\. При этом математическое ожидание
с.к. производной X’(t) равно производной математического ожидания
mx(t) случайной функции X(t):
mx>(t) = MX'(t) = m'x(t),
(1.4.11)
а формулы (1.4.9) и (1.4.11) остаются справедливыми, если заменить
в них начальные моменты Г соответствующими ковариационными
функциями К.
1.4. ЭЛЕМЕНТЫ СТОХАСТИЧЕСКОГО АНАЛИЗА
115
Таким образом, взаимные моменты второго порядка случайных
функций Х'(£) и Y(t) выражаются через соответствующие взаимные
моменты второго порядка случайных функций X (t) и Y(£) формулами
= Г>,.(М') = 8Г-;’,‘'''). (1.4.12)
3) Для существования с.к. производной скалярной случайной
функции X(t) до порядка N включительно необходимо и достаточно
существование конечной смешанной производной d2NTx(t, t')/dtNdt,N
во всех диагональных точках t' = t Е Т\ (или существование ко-
нечной производной mxN\t) на Т\ и конечной смешанной производной
d2NKx{t,tly/dtNdt,N во всех диагональных точках t' = t Е Ti). При
этом всюду существуют конечные производные dp+qrx(t,t,)/dtpdt,q и
dp+qKx(t,t'}ldtpdt,q (p,q = 0,1,N) и справедливы следующие фор-
мулы для математических ожиданий и моментов второго порядка
производных X(p\t)
= MX(p\t) = m(p\t), (1.4.13)
(i-4-i4)
(!,!') = (1-4.15)
Для конечномерных векторных случайных функций следует, что
векторная случайная функция X(t) с.к. дифференцируема на Т\ тогда
и только тогда, когда выполнено одно из следующих двух равноценных
условий:
• существует конечная производная 52 tr во всех
диагональных точках t' — t Е
• математическое ожидание mx(t) дифференцируемо на Т\ и су-
ществует конечная производная д2 tr Kx(t,t,)/dtdt/ во всех диагональ-
ных точках tl = t Е Ti.
При этом всюду на Ti х существуют производные drx(t,t')/dt,
drx(t,t,y)/dtf, d2rx(t,t')/dtdtf, dKx(t,t’)/dt, dKx(t,t'}ldt',
d2Kx(t,t')ldtdtl и справедливы формулы (1.4.9)-(1.4.12).
1.4.2. Интегрирование случайной функции по неслучайной
мере. Рассмотрим теперь случайные функции, заданные на простран-
стве с мерой (Ti, 3,р), где 9 - некоторая сг-алгебра множеств простран-
ства Ti, а р - заданная на Т\ неотрицательная мера (ТСтС, главы 4
и 5) .
116
ГЛ. 1. СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
Назовем простой случайной функцией случайную функцию с ко-
нечным множеством значений, все реализации которой измеримы отно-
сительно а-алгебры 3 (и соответствующей а-алгебры мно-
жеств пространства L значений случайной функции). В соответствии с
этим определением простая случайная функция X(t) имеет вид
N
X(t) = ^XplBp(t),
Р=1
(1.4.16)
где Лд,...,Хм ~ случайные величины, a Ед,...,Ем € 3 - измеримые
множества пространства (71,3).
Простая случайная функция называется р-интегрируемой, если
она отлична от нуля только на множестве конечной меры р. Инте-
грал от простой случайной функции X(t) по множеству A G 71 х Т\
выражается как сумма
С С к
Y{A) = / = I Xdp = ^Хр^АЕр). (1.4.17)
A A P=1
Эта формула определяет интеграл от простой случайной функции со
значениями в любом линейном пространстве L. При этом интеграл
Y (А) представляет собой случайную функцию множества со значени-
ями в том же линейном пространстве L, определенную на а-алгебре
Ti х ТУ
Математическое ожидание, момент второго порядка и ковариаци-
онная функция случайной функции Y (А) для линейных функций слу-
чайных величин определяются следующими формулами:
Шг/И) = J mx(t)p(dt),
А
(1.4.18)
Г„(А,А') = KV(A,A') = ИKx(t,t')^dt)^dt').
ЛА1 А А'
(1.4.19)
Для взаимного момента второго порядка случайной функции Y(А)
и любой случайной функции Z(v), v G V:
ryz(A,v) = j rxz(t,v)p(dt).
A
(1.4.20)
1.4. ЭЛЕМЕНТЫ СТОХАСТИЧЕСКОГО АНАЛИЗА
117
При V = Ti, v = f € Ti, Z(^) = X(t') формула (1.4.20) дает
Гуж(А,*') = I Vx(t,tf)p(dt). (1.4.21)
A
Предположим теперь, что случайная функция Z(v) является ин-
тегралом от простой случайной функции Xi(u), и € 17, по некоторой
мере I/, определенной на а-алгебре U множеств пространства 17. В этом
случае V — U.v — B^U,
Z(B) = У* Xi(u)i/(du),
в
Гуг(А,В) = 1 j rXX1(t,u)p.(dt) v(du). (1.4.22)
А В
Формулы (1.4.20)—(1.4.22) остаются, конечно, справедливыми, если
заменить в них функции Г соответствующими ковариационными функ-
циями К,
Перейдем теперь к общему определению интеграла от случайной
функции. Случайная функция X(t) называется р-интегрируемой в
среднем квадратическом (с.к. р-интегрируемой), если она предста-
вима почти при всех t Е Т как с.к. предел последовательности д-
интегрируемых простых случайных функций {Xn(t)} и если существует
с.к. предел последовательности интегралов УП(А) = f Xndp, независи-
А
мый от выбора последовательности {Хп(£)}. Этот с.к. предел называ-
ется средним квадратическим (с.к.) интегралом от случайной функции
X(t):
У(4) = [ X{t)n(dt) = [ X dp = l.i.m. УП(А). (1.4.23)
J J n—>oo
A A
Далее рассмотрим важный случай, когда интегрируемая случайная
функция имеет вид g(s, t)X(t), где X(t) - конечномерная векторная слу-
чайная функция, представленная, как всегда, в виде матрицы-столбца,
a g(s, t) - неслучайная матрица. Случайную функцию такого вида мож-
но считать случайной функцией переменной t со значениями в линейном
пространстве L функций переменной s. В данном случае следует, что
при любом s е S с.к. интеграл
y(s)= [ gMX^dt) (1.4.24)
118
ГЛ. 1. СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
существует тогда и только тогда, когда существует интеграл
= Уу tr[g(s,t)rx(t,t')g(s,t')*]n(dt)n(dt'). При этом справедливы следующие формулы: (1.4.25)
my(s) = У g(s,t)mx(t)p(dt), (1.4.26)
ry(s,s') = Уу g(s,f)rx(f,f')g(s',t')Xdt)/z(dt'), (1.4.27)
Гуг(«,и) = У g(s,t)rxz(t,v)ii(dt), (1.4.28)
ryx(s,t) = У g(s,t')rx(t,t')p.(dt'). (1.4.29)
Если случайная функция Z(v) представляет собой с.к. интеграл
Z(y) = j h(v,u)Xi(u)/2(du), (1.4.30)
то
= У rxxi(^,u)/i(v,u)*i/(du),
ryz(s,v) = Уf g(s,t)rxxi(t,u)h(v,uyfi(dt)i/(du). (1.4.31)
Формулы (1.4.27)—(1.4.31) справедливы также и для соответствую-
щих ковариационных операторов.
1.4.3. Интегрирование функций по случайной мере. Слу-
чайной мерой в измеримом пространстве (Ti, 9) называется случайная
функция множества Z(A), определенная на а-алгебре 3 и обладающая
свойством а-аддитивности:
Wn) = Z(An) почти наверное (1.4.32)
для любой последовательности попарно непересекающихся множеств
{An} С 3. Случайные меры могут иметь значения в любых линейных
пространствах. Мы будем рассматривать только скалярные случайные
меры, в общем случае комплекснозначные с конечными моментами вто-
рого порядка.
1.4. ЭЛЕМЕНТЫ СТОХАСТИЧЕСКОГО АНАЛИЗА
119
Пусть Z(A) - скалярная случайная мера, М | Z(A) |2 < оо для всех
А € Ее математическое ожидание mz(A) в силу (1.4.32) представ-
ляет собой числовую меру (в общем случае комплекснозначную), опре-
деленную на а-алгебре 3. Момент второго порядка случайной меры
Z(A), определяемый как Г2(А,А') = MZ(A)Z(A') и рассматриваемый
как функция множества А при фиксированном А1 € $9, тоже представ-
ляет собой числовую меру на а-алгебре &. Если задавать Гг(А, А') как
функцию прямоугольного множества А х А' в произведении измеримых
пространств (Ti х^^хЭ), то
оо
r,(U^n,UBm)= £ гг(лп,вт)
П,7П=1
для любых последовательностей попарно непересекающихся прямо-
угольных множеств {An х Вп} С 9 х 9, А^А^ = 0, BkBh = 0 при
h к.
Таким образом, момент второго порядка случайной меры пред-
ставляет собой а-аддитивную функцию множества на классе всех
измеримых прямоугольников пространства (71 хТ^ЗхЗ). Иными
словами, ГДА, А') представляет собой в общем случае комплекснознач-
ную функцию множества на классе измеримых прямоугольников про-
странства (Ti х Ti, 9 х S). Она может быть однозначно продолжена до
меры на а-алгебре 9x9.
Интеграл от простой случайной функции (1.4.16) со значениями в
любом линейном пространстве L по случайной мере Z(A) имеет вид
Г г N
Y(A) = / X(t)Z(dt) = / XdZ = ^XpZ^AEp).
a A P=1
При этом интеграл представляет собой случайную функцию множества
со значениями в том же пространстве L, определенную на ст-алгебре г.
Предположим теперь, что случайные функции X(t) и Z(A) неза-
висимы, т.е. что их значения при любых t € Т\ и А € Э являются
независимыми случайными величинами. В этом случае справедливы
следующие равенства:
MXPZ(AEP) = МХр • MZ(AEp),
MXpXgZ(AEp)Z(A'Eg) = MXpXq • MZ(AEp)Z(A'Eg)
120
ГЛ. 1. СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
и, следовательно,
n г
ту(А) = У^МХртг(ЛДр) = / mx(t)mz(dt),
Р=! JA
(1.4.33)
N Г Г
Г„(А,А') = ГР,ГZ(AEP, А'Еч) = / / Tx(t,t')rz(dt,dt'). (1.4.34)
₽-«=1 А А'
Условимся, что некоторый факт имеет место почти при всех t € Т\
относительно случайной меры Z, если он не имеет места только при
£, принадлежащих некоторому множеству N е SJ, на котором мера Z
равна нулю почти наверное. Очевидно, что это равноценно тому, что
данный факт имеет место почти при всех t G 2i относительно меры
mz(A) и всех мер Гг(А, А'), соответствующих различным фиксирован-
ным A' G Э.
Случайная функция X(t) называется интегрируемой по случай-
ной мере Z, если она представима почти при всех t€l\ относительно
Z как с.к. предел последовательности простых случайных функций
{Xn(t)} и если существует с.к. предел последовательности интегралов
УП(А) = J XndZ, независимый от выбора последовательности {Xn(t)}.
А
Этот с.к. предел называется интегралом по случайной мере Z от слу-
чайной функции X(t)t
Y(A) = / X(t)Z(dt) = / XdZ = l.i.m. УП(А).
(1.4.35)
A A
Необходимые и достаточные условия с.к. интегрируемости по слу-
чайной мере формулируются следующим образом (ТСтС, раздел 4.5) .
Для существования интеграла от случайной функции X (t) по случай-
ной мере Z необходимо и достаточно существование интеграла
Jx(A) = jj Xrx(t,t')XTz(dt,dt') (1.4.36)
А А
для всех А € Л. При этом для всех А, А' € Л существуют пределы
ПтМ[АУп(А)] = Ату(А), ИтМ[АУп(А)] [А'Ут(А')] = АГУ(А, А')А'.
Для простых случайных функций из (1.4.33) и (1.4.34) вытекают
следующие формулы:
ту(А) = У mx(t)mz(dt) = j mxdmz, (1.4.37)
А А
1.4. ЭЛЕМЕНТЫ СТОХАСТИЧЕСКОГО АНАЛИЗА
121
Гу(л,л') = у у ГЖ(^Г)Г2(Л,Л'). (1.4.38)
А А'
Рассмотрим теперь частный случай с.к. непрерывной скалярной
или конечномерной векторной случайной функции X(t). Для такой
случайной функции интеграл по случайной мере Z существует, если
ее момент второго порядка rx(t,t') ограничен и полная вариация ме-
ры Г2(Л,Л') на классе измеримых прямоугольников произведения про-
странств (Ti х Т\, 9 х 9) конечна.
1.4.4. Стохастические интегралы. Случайная мера Z(A) назы-
вается стохастической мерой, если ее математическое ожидание равно
нулю, а ковариационная функция зависит только от пересечения мно-
жеств аргументов:
KZ(A, А') = М7(Л)Щ9 = а(АА'). (1.4.39)
Функция (У (А) представляет собой неотрицательную меру, так как при
любом А 6 3
а(4) = KZ(A,A} = TZ(A,A) = М | Z(A) |2 > О
и для любой последовательности {А*} С 9 попарно непересекающихся
множеств
= ГДЩ*, Т1) = £r2(4fc>7i) = £<7(40-
Значения стохастической меры на непересекающихся множествах не
коррелированы.
Интегралы от случайных функций по стохастической мере назы-
ваются стохастическими интегралами. Формула (1.4.34) для стоха-
стического интеграла от простой случайной функции X(t) принимает
вид
N Г
ГУ(А,А') = 52^(44%)= / ra(t,t')cr(dt)- (1-4 40)
P=1 А А'
Стохастический интеграл
У(А) = У X(t)Z(dt) = I XdZ (1.4.41)
А А
122
ГЛ. 1. СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
при независимых X(t) и Z(A) существует тогда и только тогда, когда
при любом А € Л существует интеграл
Л(А) = I XTx(t,t)Xa(dt) = I M\XX(t)\2a(dt). (1.4.42)
А А
В частности, стохастический интеграл (1.4.41) от скалярной или ко-
нечномерной векторной случайной функции X(t) существует тогда и
только тогда, когда существует интеграл
7д(Л) = j rx(t,t)a(dt) = f M\X(t)\2a(dt). (1.4.43)
A A
Для теории стохастических систем важны стохастические интегра-
лы при определенном виде зависимости случайной функции X(t) ска-
лярного аргумента t от стохастической меры Z(A). А именно интегра-
лы в случае, когда X(t) при любом t € [£о,оо) представляет собой не-
которую (неслучайную) функцию значений меры Z(A) на борелевских
множествах интервала [^о, £)• Пусть St - а-алгебра множеств простран-
ства элементарных событий Я, индуцированная случайными величина-
ми Z(A), соответствующими всем борелевским множествам А С [£о,£)«
Функция X(t) является при любом t € [*о,оо) измеримой функцией
значений меры Z(A) на измеримых множествах интервала [to,£) тогда
и только тогда, когда X(t) при любом t € [£о,оо) представляет собой
случайную величину, измеримую относительно а-алгебры St. Таким об-
разом, мы должны определить интеграл по стохастической мере Z(A)
от случайной функции X(t) = x(£,cj), значение которой при любом
t G [£q,oo) представляет собой функцию cj, измеримую относительно
а-алгебры St-
На стохастическую меру Z (А), определенную на борелевских мно-
жествах интервала [fo,oo), наложим дополнительное ограничение, а
именно, будем предполагать, что условные математические ожидания
случайных величин Z(A) и Z(A)Z(A') относительно а-алгебры St совпа-
дают с их безусловными математическими ожиданиями в случае, если
A(J[ t0,t) — Ш^) = 0 , т.е. если борелевские множества А и А'
расположены целиком правее интервала [£о,£):
MSt(Z(A)|o>) = MZ(A) = 0 при Ap|[t0,t) = 0 , (1.4.44)
MSt (Z(A)Z^\u) = MZ(A)Z(A^ = сг^АА1) при
1.4. ЭЛЕМЕНТЫ СТОХАСТИЧЕСКОГО АНАЛИЗА
123
АП[*о,*) = А'П[*о,О = 0 • (1.4.45)
Эти условия всегда выполняются, в частности, когда значения стоха-
стической меры Z на непересекающихся множествах независимы, так
как в этом случае условные распределения случайных величин Z(A) и
Z(A)Z(A') относительно а-алгебры St, порожденной значениями меры
Z на борелевских множествах интервала не пересекающихся с А
и А1, совпадают с их безусловными распределениями.
Пусть X(t) - простая случайная функция, значение которой при
любом t € [fo,oo) представляет собой случайную величину, измеримую
относительно а-алгебры St-
N
X(t) = (1.4.46)
Р=1
В этом случае формулы (1.4.40) остаются справедливыми.
В (ТСтС, раздел 4.6) доказано, что для существования стохасти-
ческого интеграла (1.4.41) от случайной функции X(t), представимой
в виде с.к. предела последовательности простых случайных функ-
ций рассмотренного вида, необходимо и достаточно существование
интеграла (1.4.42) при любом А € Л. В частном случае скалярной
или конечномерной векторной случайной функции X(t), значение ко-
торой при каждом t G [to,oo) измеримо относительно о-алгебры St,
для существования стохастического интеграла (1.4.41) необходимо и
достаточно существование интеграла (1.4.43).
Процессы С независимыми приращениями. Случайный процесс
X(t) называется процессом с независимыми приращениями, если при любых N,
*0 < *1 < ’ ’ ’ < случайные величины xt0, xtl - xta, ... , XtN - XtN_t
независимы. При этом, как всегда, за пределами теории, основанной на моментах пер-
вого и второго порядков, будем считать процесс X(t) действительным (скалярным или
конечномерным векторным). Обозначим через pi (Л; t) одномерную характеристическую
функцию X(t), а через fo(Aj t, s) - характеристическую функцию его приращения на
интервале (t, з). Тогда при любых ti < ^2
Л(А; ti, t2) = , Vtx < t2. (1.4.47)
Pi (A; h)
Таким образом, характеристическая функция приращения процесса с независи-
мыми приращениями полностью определяется его одномерной характеристической
функцией. Более того, все многомерные распределения процесса с независимыми при-
ращениями однозначно определяются его одномерным распределением.
Рп(А1 , . . . , Лп; ti , ... , tn) =
124
ГЛ. 1. СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
— -----Aw;fj)^i(A2 d-------h Anifrz) - - - <7i(Aw;*n) (1 4 48)
<71(^2 + • • • + Ап;^1)^1(Аз d---F An;^2) • • • <7i(An;£n-i)
Процессы с независимыми приращениями относятся к классу случайных функций,
все многомерные распределения которых полностью определяются одним из них. Одна-
ко в отличие от случайных функций с независимыми значениями и марковских процес-
сов, для которых любое одномерное или двумерное распределение однозначно определя-
ет все многомерные распределения, для процессов с независимыми приращениями одно-
мерное распределение не может быть произвольно задано. Формула (1.4.47) показывает,
что характеристическая функция (A; t) может быть одномерной характеристи-
ческой функцией процесса с независимыми приращениями только в том случае, когда
при любых t < 8 отношение <71 (А; $)/<71(А; t) тоже является характеристической
функцией, т.е. непрерывной неотрицательно определенной функцией, равной 1 при
А = 0.
Если процесс с независимыми приращениями X (t) имеет конечный момент второго
порядка, то он является процессом с некоррелированными приращениями. Следователь-
но, ковариационная функция процесса X (t) с независимыми приращениями определяет-
ся формулой
Kx(ti, t2) = fc(min(£i,£2)), (1.4.49)
где k(t) - неубывающая неотрицательная функция, представляющая собой ковариацион-
ную матрицу (дисперсию в случае скалярного процесса X(t)) значения процесса X(t)
при данном t. Мы будем в дальнейшем считать, что функция k(t) непрерывна и диф-
ференцируема, вследствие чего ковариационная функция процесса X(t) определяется
формулой:
min(ti ,ta)
Kx(h,t2) = k(t0) + J v(r)dr. (1.4.50)
to
Любой процесс с независимыми приращениями представляет собой марковский слу-
чайный процесс.
БеЛЫЙ Шум. Любой процесс с некоррелированными приращениями и диф-
ференцируемой ковариационной функцией имеет слабую с.к. производную, представля-
ющую собой белый шум. В частности, любой процесс с независимыми приращениями,
обладающий дифференцируемой ковариационной функцией, имеет слабую с.к. производ-
ную, которая представляет собой белый шум. Белый шум, полученный дифференцирова-
нием процесса с независимыми приращениями, называется белым шумом в строгом
смысле, в отличие от белого шума, получаемого дифференцированием процесса с некор-
релированными приращениями (п.1.4.1).
Винеровские процессы и меры. Действительный скалярный
или векторный случайный процесс с независимыми приращениями
1.4. ЭЛЕМЕНТЫ СТОХАСТИЧЕСКОГО АНАЛИЗА
125
W(i), t > 0, называется винеровским процессом, если он удовлетворяет
условиям:
• все реализации w(f) процесса W(t) непрерывны и w(0) = 0;
• одномерное распределение процесса W(f) нормально;
• математическое ожидание процесса W (t) тождественно равно ну-
лю, а его ковариационная функция определяется формулой
min(h,t2)
, ^2) ~
0
где u(t) - неотрицательная функция, интенсивность винеровского про-
цесса W(t). Непосредственно из этого определения следует, что лю-
бой винеровский процесс представляет собой нормально распределен-
ный случайный процесс. Его одномерная характеристическая функция
и все многомерные характеристические функции определяются форму-
лами:
t
= exp j — ^АТА:(£)АI , k(t) = [ v(r)dr,
I A I J
0
(1.4.51)
Pn(^l J • • • > -^n> ^1 fc(tl) , . . • , tn) — k(ti) ... fc(ii) ] "Ai I '
= exp < -ifW- *’1 fc(tl) fc(t2) • • k(t2) A2 >.
- fc(ii) k(t2) ... k(tn) J - ‘
(1.4.52)
Винеровский процесс как процесс с независимыми приращениями, об-
ладающий нулевым математическим ожиданием, конечным моментом
второго порядка k(t) для каждого момента t, порождает стохастиче-
скую меру с независимыми значениями на непересекающихся интер-
валах. Эта стохастическая мера определяется формулой £((£1,^2]) =
= Ж(^) - ИГ(й). Стохастический интеграл (1.4.41) по винеровской сто-
хастической мере Z и по любому интервалу [а,5), А = [а,5), а > 0,
может быть записан в виде интеграла Стилтьеса:
ь ь
У([а,ЬУ) = / X(t)Z(dt) = I X(t)dW(t).
(1.4.53)
126
ГЛ. 1. СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
Формулы (1.4.40), (1.4.42) и (1.4.43) в случае винеровской стохасти-
ческой меры Z принимают соответственно вид
ГУ(А,А') = j rx(t,t)dt,
А А'
/д(Л) = IМI XX(t) \2dt,
A
M | X(t) \2dt.
(1.4.54)
(1.4.55)
(1.4.56)
В частном случае скалярной или конечномерной векторной слу-
чайной функции X(t), измеримой при каждом t € [0, оо) относительно
St, последовательность простых случайных функций {Хп(£)} такого же
класса, с.к. сходящаяся к X(t), всегда существует. В этом случае сто-
хастический интеграл (1.4.54) называется стохастическим интегралом
Ито.
Пуассоновские процессы и меры. Случайный процесс P(t)
называется простым пуассоновским процессом, если его значение в
любой момент времени t равно числу скачков пуассоновского потока
на интервале времени [0, £]. Простой пуассоновский процесс является
процессом с независимыми приращениями, причем его одномерное рас-
пределение - пуассоновское. Скалярный или векторный ступенчатый
случайный процесс
P{t)
W(f) = ^Xk, (1.4.57)
где {Л*} - последовательность независимых одинаково распределен-
ных случайных величин, называется общим пуассоновским процессом.
Общий пуассоновский процесс является процессом с независимыми при-
ращениями.
Скалярная случайная функция Р(А,А), определенная на прямо-
угольных множествах ДхА произведения пространств [0,оо) х Rq,
где Д - элемент о-алгебры В+ борелевских множеств [0, оо), А - эле-
мент о-алгебры Во, порожденной всеми прямоугольниками простран-
ства Rq с выколотым началом, называется пуассоновской мерой. Ес-
ли Р(Д, А) для любого Д G В-|_, A G Во представляет собой случайную
1.4. ЭЛЕМЕНТЫ СТОХАСТИЧЕСКОГО АНАЛИЗА
127
величину, распределенную по закону Пуассона, то центрированная слу-
чайная функция
Р°(Д,А) = Р(Д,А)-Др(ДМ), тпР(Д,А) = МР(Д,А) (1.4.58)
является стохастической мерой с независимыми значениями на попарно
непересекающихся множествах. При этом, очевидно, др(Д,А) - неот-
рицательная мера.
Стохастический интеграл Ито. Пусть Ж(£) - скалярный про-
цесс с независимыми приращениями, имеющий нулевое математическое
ожидание и конечный момент второго порядка fc(f); X(t) - некоторая де-
терминированная или с.к. непрерывная скалярная случайная функция
с конечным моментом второго порядка, значения которой для каждого t
не зависят от приращений процесса W (£), т.е. W(t2)-W(ti),t <ti <t2\
{Pn} - последовательность разбиений интервала (а, 6]
N
Рп : (а,ь]= U - №=а, t{^ = b,
к=1
такая, что max(^n^ — 4-\) О ПРИ п °0- Средний квадратический
предел Y последовательности сумм {Уп},
Nn
Yn = £ ^(<ln_)1)[^(dn)) - ^(4”А)], (1-4.59)
Л=1
если этот предел существует, называется стохастическим интегралом
Ито от X (t) по отношению к процессу с независимыми приращениями
W(t) на интервале (а, Ь]:
Ь Nn
Y= f X(t)dW(t) = l.i.m. 52 - Иф^,)]. (1.4.60)
/ n—>oo *
a *=1
Справедливо следующее утверждение. Стохастический интеграл
(1.4.60) существует тогда и только тогда, когда интеграл Рима-
на-Стилтьеса
ь
М IX(i)I2 dk(t) = М IУ|2 = DY (1.4.61)
128
ГЛ. 1. СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
существует и равен дисперсии стохастического интеграла Ито.
Определение стохастического интеграла Ито легко распрост-
раняется на случай матричного процесса X(t) и векторного процесса
Ж(£). Векторный интеграл Ито (1.4.60) существует тогда и толь-
ко тогда, когда скалярные интегралы Ито, входящие в (1.4.60), суще-
ствуют. Необходимое и достаточное условие существования вектор-
ного интеграла (1.4.60) совпадает с условием существования интегра-
ла Римана-Стилтьеса
ь
I MX(t)dk(t)X(ty = МГУ*,
а
равного ковариационной матрице векторного процесса Y.
Пусть Y(i) - случайный процесс, определяемый формулой
t t
Y(t) = У(i0) + У Xi(r)dT + У X2(r)dW(r), (1.4.62)
to to
где первый интеграл представляет собой с.к. интеграл от случайной
функции Xi (t), а второй - интеграл Ито от случайной функции по про-
цессу с независимыми приращениями W(£). Функции Xi(t) и Хг(0
предполагаются удовлетворяющими условиям, при которых оба инте-
грала существуют при любом t на некотором интервале времени Т. Да-
лее, пусть X(t) - некоторая случайная функция. Интегралом Ито от
случайной функции X(t) по процессу Y(t) в пределах (а, Ь] называется
сумма интегралов
ъ ь ь
У X(r)dY(r) = j X(r)Xi(r)dr + j Х(т)Х2(т)<П¥(т) , (1.4.63)
a a a
где первый интеграл представляет собой с.к. интеграл, а второй -
интеграл Ито. При этом, конечно, предполагается, что случайные
функции X{i)X\(t) и X(t)X2(i) должны удовлетворять условиям, при
которых интегралы в правой части формулы (1.4.63) существуют.
Остановимся подробнее на стохастических интегралах по пуассо-
новской мере. Пусть теперь Р°(Д,Л) - центрированная пуассоновская
мера (1.4.58); Y(t, и) - действительная скалярная с.к. непрерывная слу-
чайная функция переменных t, и с конечным моментом второго порядка
1.4. ЭЛЕМЕНТЫ СТОХАСТИЧЕСКОГО АНАЛИЗА
129
и независимая от P((ti,t2],A) для любых t < ti < t2, и € Я? = Я’\{0},
А € Bq. Пусть {Рп} - последовательность разбиений интервала (а, 5] и
множества 0 < |u| < R,
N
Рп • (о,ь] = и (4Д, 4 ~а» = ъ>
*= „ (1.4.64)
{ч : 0< |«| <Я}= U 4jn). ^"’еВо,
J=1
где max(t^ -t£”\) -> 0, max sup |u' - u| -> 0 при n -> оо. Средний
* j и,и'ел^
квадратический предел ZR последовательности интегральных сумм
Nn Мп
zn =EEy^nA>«?))p°((4n-)i>4n)]Min)). (1.4.65)
Jb=l j=l
если он существует, называется стохастическим интегралом Ито от
случайной функции Y (2, и) относительно пуассоновской меры
Р(А,А) распространенным на интервал (а, 5] и множество {и : 0 <
< |u| < R}:
ь
ZR = у у Y(t,u)P°(dt,du) =
а 0< |u| <R
Nn Мп
= l.i.m.££r(41)pujn)P0)((41)1,t<n)],Ain)). (1-4.66)
fc=l j=l
Справеливо следующие утверждение. Стохастический интеграл
Ито (1.4.66) существует тогда и только тогда, когда существует
интеграл Римана-Стилтьеса
ъ
У у My2(t,u)MP(dt,du) = М(3Й)2 = DZr, (1.4.67)
а 0< |u| <R
равный дисперсии стохастического интеграла Ито ZR.
Теперь обобщим определение стохастического интеграла Ито по
пуассоновской мере, распространив его на множество (а,Ь] х
хЯ9\{0}. Стохастический интеграл Z случайной функции Y(t,u) по
5 Фильтры Калмана и Пугачева
130
ГЛ. 1. СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
пуассоновской мере Р(Д,Л), распространенный на интервал (а, Ь] и
пространство Я9\{0} = 1?q, определяется как с.к. предел стохасти-
ческого интеграла (1.4.65) при R —> оо, если этот предел существует:
ь ь
Z= [ [ Y(t,u)P°(dt, du) = l.i.m. [ f Y(t,u)P°(dt,du). (1.4.68)
J J R-^ooJ J
a Rq a o< |u| <R
Стохастический интеграл Ито (1.4.68) существует тогда и
только тогда, когда существует интеграл Римана-Стилтьеса
ь
У У MY2(t,u)pP(dt,du) = MZ2 = DZ. (1.4.69)
а Я’
Определение стохастического интеграла по пуассоновской мере лег-
ко обобщается на случай векторных с.к. непрерывных случайных функ-
ций Y(t,u). В этом случае формула (1.4.69) заменяется на
ъ
Kz = MZZT = j I My(Z,u)y(i,u)TMp(dt,du). (1.4.70)
° я?
Другие виды стохастических интегралов. Построив инте-
гральные суммы Yn при других выбранных в интервалах
точках, в которых берутся значения случайной функции X(t), полу-
чим другие определения стохастического интеграла. Взяв, в частности,
значения X(t) в правых концах интервалов определим сто-
хастический интеграл
Ь Nn
Г1 = /X(r)diW(r) = lim.£X(tW) [ж(«(") - Ж(41\)] .
{ П^°°Р=1
После этого для любого в € [0,1] можно определить стохастический
0-интеграл следующим образом:
ь
Yo = J X(r)d0W(r) = (1 - 6)Y 4- 0У1 =
1.4. ЭЛЕМЕНТЫ СТОХАСТИЧЕСКОГО АНАЛИЗА
131
’ 71
= 1-bIS;E[(1-+ [w^-WS)] • (1-4.71)
Очевидно, что интеграл Ито является 0-интегралом при в = 0, а
интеграл Yi - 0-интеграл при 0 = 1. При 0 = 1/2 стохастический инте-
грал (1.4.71) представляет собой симметризованный стохастический
интеграл, или интеграл Стратоновича.
Интеграл Ито обладает большим преимуществом перед другими
видами стохастических интегралов. Это преимущество заключается в
простоте вычисления моментов интеграла. Для интеграла Ито матема-
тическое ожидание и дисперсия (ковариационная матрица в векторном
случае) вычисляются, как мы видели, совершенно элементарно. Вычис-
лить же математическое ожидание 0-интеграла при 0 0 в общем слу-
чае очень трудно вследствие зависимости X(tp^) от W (4^) ~ ^(4-\)-
Процессы с независимыми приращениями и интеграл Ито.
В прикладных задачах за общую форму процесса с независимыми приращениями X (£)
часто принимают выражение (ТСтС, п.4.4.10):
X(t) = WoW + / c(x)P(t,dx), (1.4.72)
я’
где Wq(^) _ винеровский процесс; j4) - пуассоновский процесс как функция t и
пуассоновская стохастическая мера как функция множества А\ с(х} - векторная функ-
ция, отображающая R^ в пространство значений процесса X (£) при каждом t. Одно-
мерная характеристическая функция </i(A; t} процесса X(£), имеет следующий вид:
In дг (A; t) = -1XTk(t)X + / [ eixTc<x) - 1 ] n(t, x)dx , (1.4.73)
где p(t, x} определяется формулой
I д(<, x)dx = MP(t, A). (1.4.74)
A
При этом имеем
MI(t) = / c(x)n{t,x)dx. (1.4.75)
Rq0
132
ГЛ. 1. СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
Характеристическая функция pj(A;t) центрированного процесса X°(t) = X(t) -
равна
In<?i(A;i) = — ^ATfc(£)A + J Je‘ATc^) — 1 — iATc(i)] p(t,x)dx. (1.4.76)
«3
Приращение процесса с независимыми приращениями на любом интервале облада-
ет тем свойством, что его можно представить в виде суммы любого числа независимых
случайных величин. Для этого достаточно разбить данный интервал на соответствующее
число частей и представить приращение процесса на этом интервале в виде суммы его при-
ращений на выбранных частных интервалах. Это значит, что распределение приращения
процесса с независимыми приращениями безгранично делимо. Из теории безгранично
делимых распределений известно, что всякое безгранично делимое распределение можно
представить в виде композиции нормального и пуассоновского распределений.
1.4 '5. Стохастические дифференциалы. Случайный процесс
Z(t) называется процессом Ито, если его можно представить в виде
Z(t) = Z(t0) + I X(j)dr + I Y^dW^
t t0 t0 (1.4.77)
+ j J u)P°(dr, du),
to Я’
Здесь t > 0; W(t) - винеровский процесс; Р°(Д,А) - независимая от
JV(t) центрированная пуассоновская мера; первый интеграл понимает-
ся как с.к. интеграл; второй интеграл - как стохастический интеграл
Ито; третий - как стохастический интеграл относительно пуассоновской
меры Р(Д,Л); случайные функции X(t), У1(£) и удовлетворяют
условиям существования интегралов. В этом случае принято говорить,
что случайный процесс Z(t) имеет стохастический дифференциал Ито:
dZ = X(t)dt^Yx(t)dW(t) + I y2(t, u)P°(dt,du). (1.4.78)
В частном случае, когда в (1.4.77) У2(^,и) = 0 и У1(£) = Y(t) с
вероятностью 1, стохастический дифференциал процесса Ито
Z(t) = Z(t0) +
t t
I X(r)dt + j Y(r)dW(r),
to to
(1.4.79)
1.4. ЭЛЕМЕНТЫ СТОХАСТИЧЕСКОГО АНАЛИЗА
133
если опустить аргумент t, выражается формулой
dZ = Xdt + YdW.
(1.4.80)
Формула Ито для стохастического дифференциала нели-
нейной функции. Пусть задан процесс Ито (1.4.79), где случайная
функция Y (t) имеет конечные абсолютные моменты четвертого поряд-
ка. Тогда стохастический дифференциал скалярной действительной
непрерывной функции U(t) = обладающей ограниченными
первыми и вторыми производными, причем вторые производные удо-
влетворяют условиям Липшица с постоянной b
d2<p(z',t) d2(p(z,t)
dzpdzq dzpdzq
<ь52 izr~zri»
r=l
(1.4.81)
определяется следующей формулой Ито:
dU = l<pt(Z, t) + <pz(Z, t)TX + Itr [ v>zz(Z, t)Y vYT ]| dt+
+<pz(Z,t)TY dW. (1.4.82)
Здесь n - размерность вектора z; ^(z,t) = dip(z,t)ldt\ tpz =
= d4>(z,t)/dz - матрица-столбец первых производных по компонентам
вектора z; y>zz(z,t) = (д/dz)(d/dz)T\p{zyt) - квадратная матрица вто-
рых производных по компонентам z\ v(t) - интенсивность винеровского
процесса Ж(£). Эта формула отличается от обычной формулы диф-
ференцирования сложной функции последним слагаемым в фигурных
скобках.
В частном случае при z € Rn и <£>(z,t) = ^1^2» из формулы (1.4.82)
вытекает формула для стохастического дифференциала произведения
двух процессов:
d(Zi Z2) = ZidZ2 + Z2 dZi + Y^Y/ dt. (1.4.83)
Формулу (1.4.82) можно записать и для векторной функции
скалярного аргумента (p(z, t) = [(z, t)... (pn(z, t) ]т. С этой целью
обозначим через ipzz : А матрицу-столбец, элементами которой служат
следы произведений матриц вторых производных соответствующих эле-
ментов ipp(z,t) матрицы-столбца (p(z,t) по компонентам вектора z на
матрицу А:
4>zz : А = [tr(<pi„A)...tr(y>nzzA)]T. (1.4.84)
134
ГЛ. 1. СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
Пользуясь этим обозначением, из (1.4.82) получаем следующую форму-
лу для стохастического дифференциала векторной случайной
функции U(t) = ip(Z(t),t):
dU = \<pt(Z,t) + pz(Z,t)TX + ^zz(Z,t) :П/УТ| dt+
+4>z(Z,t}TYdW, (1.4.85)
где = (d/dz)<p(z,t)T; ipzz = (d/dz)(dT/dz)<p(z,t).
Обобщенная формула Ито для стохастического дифферен-
циала нелинейной функции. Теперь рассмотрим процесс Ито, опре-
деляемый (1.4.77). Положим, что случайная функция У1(£) в (1.4.77)
имеет конечные абсолютные моменты четвертого порядка. Если ска-
лярная функция непрерывна и имеет ограниченные первые и
вторые производные, а ее вторые производные удовлетворяют условию
Липшица (1.4.81), тогда случайная функция U(t) = (p(Z(t),t) являет-
ся процессом Ито и ее стохастический дифференциал вычисляется по
обобщенной формуле Ито:
dU = ^t(z,t) + 4>z(Z,f)TX + |tr [^(7,4)^^])^+
+ У [<p(Z + Y2,t)T - 4>(Z,t) - <pz(Z, t)TY2] np(dt,du)+
«о
+¥>2(7)4)TYidW + I [<p(Z + Y2,t) - <p(Z,t)]P°(dt,du). (1.4.86)
В частности, в случае центрированного пуассоновского процесса
t
Ж(£) = P(t) ~ MF(£), MP(Z) = /ц = f i/(r)dr, когда
о
dZ = Xdt + YdW, (1.4.87)
формула (1.4.86) имеет следующий вид:
dU = + <pz(Z,t)T(X - Yv)+
+[<p(Z + Y,t)~ <p(Z, t) ]iz} dt + [tp(z + Y, 4) - <p(Z, 4) ] dW. (1.4.88)
1.4. ЭЛЕМЕНТЫ СТОХАСТИЧЕСКОГО АНАЛИЗА
135
В случае, когда процесс с независимыми приращениями W(t) в
(1.4.79) определяется формулой (1.4.72), то (1.4.86) приводит к следую-
щему результату:
dU — t) 4- <pz(Z, t\^ X(t)-h
+^г[^Д7Ж(*>оЖ(г)Т] +1[<p(Z+ Y(t)c(x),t) — <p(Z,t)~
-ipz(Z, t)TY(t)c(x) ]up(£, x) dz} dt 4- tpz(Z, t)TY(t) dWo4-
+ J[tp(Z + Y(t)c(x),t) - <p(Z, t)] P°(dt, dx). (1.4.89)
Пользуясь обозначением (1.4.84), получаем из (1.4.89) соответству-
ющую формулу для стохастического дифференциала векторного слу-
чайного процесса U(t) = ip{Z(t\t)\
dU = {v>t(Z,t) 4- vz(Z,t)TX(t)4
+ 1-4>zz(Z, t) : У(*>оЖ (*)T + j[<p(Z + Y(t)c(x), t) - <p(Z, t)-
—<pz(Z, t)TY(t}c(x) ]i/p(t,x) dx} dt 4- t)TY(t) dWo4-
+ У MZ + Y(t)c(x), t) - <p(Z, i) ] PQ(dt, dx). (1.4.90)
Rq
n0
Стохастические в-дифференциалы. Теперь рассмотрим дру-
гие виды стохастических дифференциалов. В зависимости от того, как
понимается стохастический интеграл в (1.4.79), можно ввести разные
виды стохастических дифференциалов. Так, если стохастический инте-
грал в (1.4.79) представляет собой 0-интеграл, то формула, аналогичная
(1.4.80),
deZ = Xdt + Yd0W (1.4.91)
определяет стохастический 0-дифференциал.
Если один и тот же случайный процесс Z(t) может быть определен
с помощью формулы (1.4.79) при двух различных толкованиях стоха-
стического интеграла, отвечающих 01 и 02,
t t
Z(t) = Z0 + I Хвг(т) dr + I Yei(r)deiW(r) =
to to
136
ГЛ. 1. СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
t t
= Zo + JX02(r)dr + I ^2(т)^2Ж(т), (1.4.92)
to to
то соответствующие стохастические дифференциалы d01Z и d02Z будут
равны:
Х01 dt + Y01 d01 W = X02 dt + Y02 d02W. (1.4.93)
Таким образом, разные стохастические дифференциалы одного и того
же случайного процесса различаются лишь по форме представления
этого процесса в виде (1.4.79).
Формула Ито (1.4.82) позволяет установить соотношения между
различными видами стохастических дифференциалов, а следователь-
но, и стохастических интегралов в частном случае, когда скалярный
случайный процесс U(t) представляет собой определенную функцию
винеровского процесса U(t) = <p(W(t),t). При этом имеем
dU = ( <pt(W, t) + h;r [<pww(W, t)v(t) ] I dt + <pu,(W, t)TdW, (1.4.94)
1 £ I
d9U = (^(^,4)+ dt + <pw(W,t)T]dffW.
(1.4.95)
Эта формула определяет в-дифференциал U(t) = <^(lV(t),t) в слу-
чае винеровского процесса Ж(£). В частности, при 0 = 1/2 получаем
стохастический дифференциал Стратоновича
d1/2U = dt + <pw(W, t)Td1/2W. (1.4.96)
Замечание. Для дифференциалов Стратоновича функции винеровско-
го процесса справедлива обычная формула дифференцирования сложной функции. В
этом состоит некоторое преимущество сим метризованных стохастических интегралов и
соответствующих дифференциалов Стратоновича перед другими видами стохастических
интегралов и дифференциалов. Однако для функций более сложных процессов и, в част-
ности, для функций пуассоновского процесса формулу для 0-дифференциала вывести не
удается, в то время как для дифференциала Ито это не представляет, как мы видели, ни-
каких трудностей. В этом состоит одно из многочисленных преимуществ стохастических
интегралов и дифференциалов Ито.
Имеет место следующее соотношение между 0-интегралом функции
<Pw(Wr,r)T и интегралом Ито:
Еб^РАСПРЕДЕЛЕНИЯ ПРОЦЕССОВ
137
t
I il>(Wr,T)deW(r) =
to
t t
I il>(WT,r)dW(r) + 01 tr
to to
[ awr ' 'J
(1.4.97)
dr.
1.5 . Распределения процессов в стохастических системах
1.5.1. Стохастические дифференциальные уравнения. Век-
торное дифференциальное уравнение вида
X = <p(X,t)+il>(X,t)V (1.5.1)
называется векторным стохастическим дифференциальным уравнени-
ем, если обобщенная случайная функция V = V(t) представляет собой
белый шум в строгом смысле. Пусть Xq - случайный вектор той же
размерности, что и случайная функция X(t). Уравнение (1.5.1) с на-
чальным условием X(to) = Xq определяет случайный процесс X(t).
Чтобы придать уравнению (1.5.1) и высказанному утверждению точ-
ный смысл, проинтегрируем уравнение (1.5.1) в пределах от ДО t при
начальном условии X(t0) = Xq. В результате получим
t t
X(t) = Х0 + j ^(Х(т),т)йт + j ^X{r),T)V(r)dT, (1.5.2)
to to
где первый интеграл представляет собой с.к. интеграл, а второй - сто-
хастический интеграл. Вводя процесс с независимыми приращениями
W (t), производной которого служит белый шум V(t), перепишем преды-
дущее интегральное уравнение в виде
t t
X(t) = Хо + У* <p(X(r),r)dT + У* ^X(r),r)dW(r). (1.5.3)
to to
Стохастическое дифференциальное уравнение (1.5.1) или эквивалент-
ное ему уравнение
dX = 9р(Х, t)dt + ф(Х, t)dW
(1.5.4)
138
ГЛ. 1. СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
представляет собой сокращенную запись уравнения (1.5.3).
Уравнение (1.5.3), в котором второй интеграл - стохастический
интеграл Ито, называется стохастическим интегральным уравнени-
ем Ито, а соответствующее дифференциальное уравнение (1.5.1) или
(1.5.4) - стохастическим дифференциальным уравнением Ито.
Случайный процесс X(t), удовлетворяющий (1.5.3), в котором инте-
гралы представляют собой с.к. пределы соответствующих интеграль-
ных сумм, называется средним квадратическим или, короче, с.к. ре-
шением стохастического интегрального уравнения (1.5.3) и соответ-
ствующего стохастического дифференциального уравнения (1.5.1)
(или (1.5.4)7 при А(^о) = Ао. Если интегралы в (1.5.3) существуют для
каждой реализации процессов TV(Z) и X(t) и равенство (1.5.3) справед-
ливо для каждой реализации, то случайный процесс X(t) называется
решением в реализациях уравнения (1.5.3) и соответствующего сто-
хастического дифференциального уравнения (1.5.1) (или (1.5.4),) при на-
чальном условии X(Iq) = Xq.
3 а М е Ч а Н И е. К уравнению вида (1.5 4) приводится и более общее стохасти-
ческое дифференциальное уравнение Ито, в котором функции ф и 'ф зависят от процесса
W = W(t).
dX = у>(Х, W, t)dt + W, t)dW. (1.5.5)
В этом случае, положив A(i) = W(£), приведем это уравнение к системе двух уравне-
ний:
dX = p(X,X,t)dt^-^X,X,t)dW, dX=dW. (1.5.6)
Вводя составной векторный процесс [%(t)TX(i)T] , получим стохастическое диф-
ференциальное уравнение Ито вида (1.5.4):
X 1 _ Г <p(X,X,i)
X ~ О
dW.
I
Это уравнение с начальными условиями А(^о) = Ао, А(^о) ~ Ао, где Aq - случай-
ная величина, независимая от Ао, распределением которой служит одномерное распре-
деление процесса IV(t) при t — to, эквивалентно исходному стохастическому диффе-
ренциальному уравнению с начальным условием А(*о) = Ао.
Стохастическое дифференциальное уравнение Ито (1.5.1) (или
(1.5.4)) при начальном условии А(^о) = Ао, где Ао - случайная ве-
личина, независимая от будущих значений белого шума V(s), s > to
(будущих приращений Ж($) — Ж(£), s > t > to, процесса W), определя-
ет марковский случайный процесс.
1.5. РАСПРЕДЕЛЕНИЯ ПРОЦЕССОВ
139
При решении задач, связанных со стохастическими дифференци-
альными уравнениями, часто целесообразно предварительно упростить
дифференциальные уравнения подходящей заменой переменных. Од-
нако замена переменных в стохастических дифференциальных урав-
нениях в общем случае отличается от обычной замены переменных в
дифференциальных уравнениях тем, что требует применения формулы
Ито или обобщенной формулы Ито вместо обычной формулы диффе-
ренцирования сложной функции (п.1.4.5).
Если второй интеграл в (1.5.3) понимать как стохастический
0-интеграл, то уравнение (1.5.1) (или (1.5.4)) будет стохастическим диф-
ференциальным уравнением другого вида. В этом случае будем назы-
вать уравнение (1.5.1) (или (1.5.4)) стохастическим дифференциаль-
ным уравнением с в-дифференциалом.
Стохастическое дифференциальное уравнение с 0-дифференциа-
лом, соответствующее случаю, когда второй интеграл в (1.5.3) пред-
ставляет собой 0-интеграл, будем записывать в виде
^=<p(X,t)+^X,t)V (1.5.7)
at
или
deX = <^(Х, t)dt 4- ^(Х, t)d0W . (1.5.8)
При 0 = 1/2 уравнения (1.5.7) и (1.5.8) являются стохастическими диф-
ференциальными уравнениями Стратоновича.
Замечание. В силу несовпадения стохастических интегралов разных видов
уравнение (1.5.1) (или уравнение (1.5.7)) при разных 0 и при одних и тех же функциях
и *0(Х, t) определяют различные случайные процессы. Это необходимо всегда
помнить и соответственно всегда указывать, в каком смысле понимается стохастическое
дифференциальное уравнение. В дальнейшем мы почти всегда будем пользоваться урав-
нениями Ито, не оговаривая этого специально. И только в тех редких случаях, когда нам
придется рассматривать стохастические дифференциальные уравнения других видов, бу-
дем указывать, в каком смысле они понимаются.
Для нормального распределенного белого шума в уравнениях
(1.5.7) (или (1.5.8)) справедливо следующее утверждение.
Если случайный процесс X (t) определяется векторным стохасти-
ческим дифференциальным уравнением с 0-дифференциалом
deX = (X, t)dt 4- V>(X, t)deW , (1.5.9)
а диффузионная матрица cr(X, t) = ^(X, t)i/(£)^(X, t)T невырождена и
дифференцируема по X, то стохастическое дифференциальное урав-
нение Ито, определяющее тот же процесс X(t), имеет вид (1.5.4),
140
ГЛ. 1. СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
где
<p(x,t) = (1-5.10)
Это утверждение относится и к уравнениям (1.5.1) и (1.5.7):
deX/dt = (X, t) + ^(Х, t)V. (1.5.11)
В общей теории стохастических систем изучаются более
сложные стохастические дифференциальные уравнения. Будем рас-
сматривать в конечномерном пространстве Rp следующее векторное
стохастическое дифференциальное уравнение:
dX = <p(X,t) + ^'(X,t)dW0 + j 4l>"(X,t,v)P°(t,dv). (1.5.12)
«о
Здесь ip = <p(X,t) и V»' = t[>'(X, t) - соответственно векторная и матрич-
ная функции X и t; Wo = IVo(t) - тп-мерный винеровский случайный
процесс интенсивности i/0 = i/o(t); Ф" = - векторная функция
X, t и вспомогательного g-мерного векторного параметра v; f dP^^t^A)
A
- центрированная пуассоновская мера, причем
J dP°(t,A) = У dP(t, А) - У vP(t,A)dt; (1.5.13)
AAA
f dP(t, A) - число скачков пуассоновского процесса в интервале време-
А
ни Д; vp(t, А) - интенсивность пуассоновского процесса F(t, А); А -
некоторое борелевское множество пространства Rq с выколотым нача-
лом. Начальное значение Xq вектора X представляет собой случайную
величину, не зависящую от приращений винеровского процесса VKo(t)
и пуассоновского процесса P(t, А) на интервалах времени Д = (ti, tz],
следующих за to, to < ti < для любого множества А.
1.5.2. Приведение уравнений непрерывной стохастической
системы к стохастическим дифференциальным уравнениям.
Все случайные функции в уравнениях, описывающих реальные явле-
ния, отличаются от белого шума. О непосредственной замене случай-
ной функции в дифференциальном уравнении белым шумом можно го-
ворить только в том случае, когда эта случайная функция входит в
1.5. РАСПРЕДЕЛЕНИЯ ПРОЦЕССОВ
141
уравнение линейно. Поэтому рассмотрим сначала непрерывную нели-
нейную стохастическую систему, состояние которой, характеризуемое
вектором Y, описывается уравнением
K = (1.5.14)
где 99(2/, t) и ^(2/, 0 ~ известные функции вектора у и времени t Функ-
ция представляет собой вектор той же размерности р, что и
вектор состояния системы У, а |^(у, t) является (р х т)-матрицей, где
т - размерность векторной случайной функции X(t). Если интер-
вал корреляции случайной функции X(t) достаточно мал, то ее мож-
но считать практически белым шумом. Вопрос о том, в каком смысле
следует понимать стохастическое дифференциальное уравнение, полу-
ченное заменой в (1.5.14) случайной функции X(t) белым шумом, в
практических задачах можно решать только одновременно с построе-
нием математической модели системы с учетом всех принимаемых до-
пущений. А так как при построении модели системы часто бывает не-
возможно даже просто перечислить все неучитываемые запаздывания,
не говоря уже об оценке их величин, то легко прийти к выводу, что
простая замена случайной функции в дифференциальном уравнении
белым шумом не может быть рекомендована. Поэтому для приведения
дифференциальных уравнений применяют другой способ.
Метод формирующих фильтров. Этот метод приведения диф-
ференциальных уравнений, описывающих состояние системы, к стоха-
стическому дифференциальному уравнению состоит в замене случай-
ной функции (в общем случае векторной), входящей в дифференциаль-
ное уравнение, некоторой другой случайной функцией, которую можно
представить как результат безынерционного преобразования решения
стохастического дифференциального уравнения. Этот метод применим
и в тех случаях, когда случайная функция входит в дифференциальное
уравнение системы нелинейно. Рассмотрим дифференциальное уравне-
ние, описывающее эволюцию состояния системы, в общей форме:
Y = f(Y, X, t), У (t0) = Го , (1.5.15)
где X = X(t) - случайная функция. Если случайную функцию X(t)
можно представить в виде X(t) = w(U(t),t), где cu(E7, t) - некоторая
функция вектора U(t) и времени t, a U(t) - случайный процесс, опреде-
ляемый стохастическим дифференциальным уравнением вида (1.5.1):
(1.5.16)
142
ГЛ. 1. СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
0
при начальном условии С7(£о) = Uq, тогда составной векторный случай-
ный процесс Ki(t) = [У(t)TU(t)T]Т будет решением системы векторных
стохастических дифференциальных уравнений:
У = /(К,си(С7,0»О» U = 4- ЖЖ (1.5.17)
при начальном условии У(£о) = У(Ь U(to) = Uq. Эту систему векторных
уравнений можно записать в виде одного векторного уравнения для Ух:
У1 = ЖьО + ЖЖ, (1.5.18)
где
У _ Г Y1 , } _ Г f(Y,w(U,t),t) 1 _
(1.5.19)
Это векторное стохастическое дифференциальное уравнение всегда по-
нимается в том же смысле, что и уравнение (1.5.16), определяющее
процесс U(t). В частности, если уравнение (1.5.16) представляет со-
бой уравнение Ито, то и уравнения (1.5.17) или (1.5.18) для составного
процесса У1(£) = [ У (t)TU(t)т ]Т будут уравнениями Ито.
Уравнения X(t) = cu(£7(£), £) и (1.5.16) можно рассматривать как
модель некоторой системы, формирующей случайную функцию X(t)
из белого шума V. Такая система называется формирующим фильт-
ром для случайной функции X(t), а изложенный метод приведения
уравнения непрерывной системы к стохастическому дифференциаль-
ному уравнению - соответственно методом формирующих фильтров
(ТСтС, раздел 5.1).
Уравнения стохастических дифференциальных систем. В
дальнейшем всегда будем предполагать, что эволюция состояния систе-
мы (в общем случае расширенного вектора состояния У) описывается
векторным стохастическим дифференциальным уравнением Ито вида
(1.5.1):
Y = tp(Y,t) +i(>(Y,t)V, (1.5.20)
где <p(y,t) и ^(y,t) - известные функции у и t размерности р х 1 и
р х т соответственно. Белый шум V в (1.5.20) будем понимать как
m-мерный векторный белый шум в строгом смысле. Начальное значе-
ние У (to) = Уо вектора состояния всегда будем считать независимым от
белого шума V(£), t > to-
1.5. РАСПРЕДЕЛЕНИЯ ПРОЦЕССОВ
143
Для некоторых сложных стохастических дифференциальных
систем в конечномерных пространствах используется векторное стоха-
стическое дифференциальное уравнение Ито вида (1.5.12):
dY = f <(r,t,v)P°(t,dv). (1.5.21)
Здесь ip = и ф1 = - известные (p x 1)-мерная и (p x m)-
мерная функции вектора Y и времени t; Wo = Ио(2) - m-мерный ви-
неровский случайный процесс интенсивности i/q = ^o(t); i/>"(y,t,v) -
(рх 1)-мерная функция у, t и вспомогательного (дх 1)-мерного парамет-
ра щ f dPQ(t,A) - центрированная пуассоновская мера, определяемая
д
(1.5.13), где f dP(t,A) - число скачков пуассоновского процесса в ин-
д
тервале времени Д; vp(t,A) - интенсивность пуассоновского процесса
F(t,A); А - некоторое борелевское множество пространства 7?q с вы-
колотым началом координат. Интеграл (1.5.21) в общем случае рас-
пространяется на все пространство с выколотым началом коорди-
нат. Начальное значение Yq вектора Y представляет собой случайную
величину, не зависящую от приращений винеровского процесса Ио(£)
и пуассоновского процесса P(t,A) на интервалах времени Д = (ti,^],
следующих за tOi t0 < ti < для любого множества А.
Для вычисления вероятностей событий, связанных со случайны-
ми функциями, в прикладных задачах достаточно знания многомер-
ных распределений. Поэтому центральной задачей теории стохасти-
ческих дифференциальных систем является задача вероятностного ана-
лиза многомерных распределений процессов, удовлетворяющих вектор-
ным стохастическим дифференциальным уравнениям Ито вида (1.5.20)
или (1.5.21) при соответствующих начальных условиях.
В теории стохастических дифференциальных систем различают
два принципиально разных подхода к вычислению распределений. Пер-
вый общий подход основан на статистическом моделировании, т.е. на
прямом численном решении стохастических дифференциальных урав-
нений (1.5.20) или (1.5.21) с последующей статистической обработкой
результатов. Второй общий подход основан на теории непрерывных
марковских процессов и предполагает аналитическое моделирование,
т.е. решение детерминированных уравнений в функциональных про-
странствах (уравнений Фоккера-Планка-Колмогорова, Феллера-
Колмогорова, Пугачева и др.) для одно- и многомерных распределе-
ний (п. 1.5.4). В практических задачах часто используют и комбини-
144
ГЛ. 1. СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
рованные методы. При этом наряду с общими методами теории сто-
хастических систем выделяют специальные методы, ориентированные
на линейные стохастические системы (разделы 1.6 и 1.9) и нелинейные
стохастические системы (разделы 1.7-1.9).
1.5.3. О численном интегрировании уравнений стохасти-
ческих дифференциальных систем. Численное интегрирование стохасти-
ческих дифференциальных уравнений имеет некоторые особенности (ТСтС, раздел 5.2).
Дело в том, что все численные методы интегрирования обыкновенных дифференциаль-
ных уравнений, кроме простейшего метода Эйлера, основаны на вычислении прираще-
ний искомых функций на каждом шаге путем применения интегральной теоремы о сред-
нем значении. В соответствии с этим правые части уравнений (производные искомых
функций) берутся в средних точках интервалов. Различные методы численного инте-
грирования отличаются один от другого, по существу, только способом приближенного
нахождения средних значений правых частей уравнений. К стохастическим интегралам
теорема о среднем значении неприменима. Однако для стохастических интегралов от не-
случайных функций справедлив некоторый аналог теоремы о среднем, показывающий,
что наилучшую аппроксимацию стохастического интеграла от непрерывной неслучайной
функции дает произведение значения данной функции на приращение процесса, по кото-
рому производится интегрирование, на этом интервале. Поэтому, например, все методы
численного интегрирования обыкновенных дифференциальных уравнений можно приме-
нять к стохастическим дифференциальным уравнениям (1.5.20), у которых коэффициент
при белом шуме является детерминированной функцией времени t, т.е. ^(У, 0 ~ ^(^)-
Если же функция ^(У, t) в (1.5.20) зависит от У, то метод численного интегрирования
таких уравнений должен выбираться в зависимости от того, в каком смысле понимается
стохастический интеграл.
При моделировании стохастических дифференциальных уравнений с помощью ана-
логовых вычислительных устройств для функции ^>(У, зависящей от У, необходимо
предварительно привести уравнения к форме Стратоновича. Объясняется это тем, что
при таком моделировании белый шум приходится заменять процессом с малым, но все
же отличным от нуля интервалом корреляции, так как белый шум физически нереали-
зуем. А в этом случае моделируемый процесс будет близким к решению стохастическо-
го дифференциального уравнения только тогда, когда данное уравнение понимается как
уравнение Стратоновича. При моделировании процессов, определяемых стохастическими
дифференциальными уравнениями (1.5.20), необходимо моделировать случайные величи-
ны или случайные процессы. При численном интегрировании стохастических дифферен-
циальных уравнений на ЭВМ требуется на каждом шаге моделировать приращение AIV
случайного процесса IV(t). В случае моделирования с помощью аналоговых устройств
необходимо генерировать широкополосные случайные процессы. Само собой разумеется,
что в результате численного интегрирования стохастического дифференциального урав-
нения, так же как и при его моделировании с помощью аналоговых устройств, всегда
1.5. РАСПРЕДЕЛЕНИЯ ПРОЦЕССОВ
145
получается реализация решения, соответствующая использованной при интегрировании
реализации процесса W(£) с независимыми приращениями или широкополосного процес-
са, моделирующего белый шум V(£) (ТСтС, раздел 5.2).
1.5.4. Одно- и многомерные распределения в стохастиче-
ских дифференциальных системах. Уравнение для одномер-
ной характеристической функции случайного процесса У(0, заданного
нелинейным стохастическим дифференциальным уравнением (1.5.21),
имеет следующий вид (ТСтС, п.5.3.1):
= м{[гАту>(Г,0 + Х(А;Г,О] е<АТу} , (1.5.22)
где
X(W) = -lxT^'(Y,t)u0(t)i>'(Y,t)TX+
£
+1 _ iAV'(r,t,u)} vP{t,du). (1.5.23)
я?
Обозначим через po(A) характеристическую функцию величины Yq.
Тогда начальное условие для уравнения (1.5.22) будет иметь вид
Pi(A;to)=Po(A). (1.5.24)
Таким образом, уравнение (1.5.22) и начальное условие (1.5.24) полно-
стью и однозначно определяют одномерную характеристическую
функцию gi (A; t) вектора состояния нелинейной стохастической диф-
ференциальной системы (1.5.21) в любой момент времени t > to.
Уравнение (1.5.22) представляет собой однородное линейное диф-
ференциальное уравнение с неограниченным оператором в бана-
ховом пространстве C(RP) ограниченных непрерывных функций
р-мерного вектора А. Начальным условием для уравнения (1.5.22) слу-
жит условие (1.5.24).
Для стохастического дифференциального уравнения (1.5.20) как
частный случай получаем известное уравнение Пугачева для характе-
ристической функции:
3si(A;tp = M{[tA^(y,<)+x«,iA«)]eiATy} . (1.5.25)
Здесь функция х — х(р; определяется формулами
х(м;<) = h = ^1пМд;*), (1.5.26)
Д1 (Д, t) ot ot
146
ГЛ. 1. СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
х(д;0 = [dh(n;t,s)/ds]s=t , (1.5.27)
где hi (д; t) - одномерная характеристическая функция процесса с не-
зависимыми приращениями W, V = W, h(p;t,s) = hi(p;s)/hi(p;t).
Уравнения для многомерных характеристических функ-
ций. Пусть
^П(А1, ... , An;fi, ... ,tn) = Мехр
< i£xTkY(tk) >
. к=1
1.5.28)
- п-мерная характеристическая функция вектора состояния системы
Y. Тогда имеем следующее уравнение (ТСтС, п.5.3.2) для п-мерной
характеристической функции процесса Y(t):
• ч An; ti, ... , tn)
dtn
= М< [iXn<p(Yt„,tn) + x(An;ytn,Zn)] exp
i^XlYtk
. k=l
(1.5.29)
где функция x(Xn\Yn,tn) определяется формулой (1.5.23) при А = Ап,
Y = Ytn, t = tn. При этом начальное условие для уравнения (1.5.23)
имеет вид:
^n(Ai , ... , An; ti , ... , tn—i, tn—i) =
= 9п—i (Ai , ... , An—2, An_i 4- An; t\ , ... , tn—i) (n = 2,3,...). (1.5.30)
Для нахождения pn(Ai , ... , An; ti,... , tn) при любых ti, ... , tn пред-
положим, что tS1 < ts2 < '" < tSn_1 < t8n для некоторой перестановки
(«1, ... , sn) чисел (l,...,n). Тогда в силу условия согласованности
многомерных распределений дп, что выражаются следующим образом:
^n(Ai , ... , An; t\ , ... , £n) — ^n(Asi , ... , Х8п 5 tsi » • • • » tsn) • (1.5.31)
Это равенство выражает gn(Xi , ... , An; ti, ... , tn) при всех Ai , ...
... , An; t\ , ... , tn, если эта функция известна для любого упорядо-
ченного набора п моментов времени.
Таким образом, уравнение (1.5.29) с начальными условиями
(1.5.24), (1.5.30) и условие согласованности распределений (1.5.31) при
п = 2,3,... последовательно определяют все многомерные распределе-
ния вектора состояния нелинейной стохастической дифференциаль-
ной системы (1.5.21).
1.5. РАСПРЕДЕЛЕНИЯ ПРОЦЕССОВ
147
По теореме Колмогорова (п. 1.2.6) многомерные распределения слу-
чайной функции однозначно определяют ее распределение в соответ-
ствующем функциональном пространстве. Следовательно, уравнения
(1.5.22) и (1.5.29) с начальными условиями (1.5.24) и (1.5.30) полно-
стью определяют распределение вектора состояния системы в соответ-
ствующем функциональном пространстве. Это пространство в слу-
чае нормально распределенного белого шума V всегда будет простран-
ством непрерывных функций на любом конечном интервале времени, а
при наличии пуассоновских компонент - пространством ограниченных
кусочно- непрерывных функций с не более чем счетным множеством
разрывов первого рода. Наконец, отметим, что если решение Y(t)
уравнения (1.5.21) является сильным и единственным и имеет конеч-
ные моменты второго порядка, то оно всегда удовлетворяет уравнениям
(1.5.22), (1.5.29) с соответствующими начальными условиями.
Конкретная форма уравнений для характеристических
функций. Предположим, что существует одномерная плотность
/1(2/; t) вектора состояния системы (1.5.21). Тогда математическое ожи-
дание в (1.5.25) легко вычисляется и уравнение Пугачева (1.5.25) для
одномерной характеристической функции принимает вид
оо
d91&t’^ = / [ixT^y't) + xWy,t')T^t)]eixTyfi(y,t>)dy. (1.5.32)
—ОО
Здесь
оо
Л (г/; 0 = (7^ У е~^Туд1 (у, t)dp,,
—оо
(1.5.33)
где р - размерность вектора состояния У, а интеграл по каждой компо-
ненте р-мерного вектора р понимается как главное значение интеграла
(в смысле Коши в случае, когда <?i(/x; t) неабсолютно интегрируема) или
в разрешенном относительно <?i(A;£) в виде:
е’(дТ ^g^^dfidy.
dt (2тг)Р J J
—оо —оо
(1.5.34)
Совершенно так же, предположив, что существуют все многомер-
148
ГЛ. 1. СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
ные плотности процесса У(0, приведем уравнение (1.5.29) к виду
q
Q, 9п(^1 ? • • • , j) ••• , ^n) =
oo oo
= 7^ / "7
—оо —оо
' п
х exp < i ^2
. k=i
(1.5.35)
Mfc )Ук * 5п(Д1 , • • , Дп! tl > • • j tn) X
х d/ii...dp,ndyi ...dyn.
Уравнения для многомерных плотностей. Заменив в уравне-
ниях (1.5.32) и (1.5.35) переменную интегрирования у на т/, умножив это
уравнение на (2тг)_ре“*Л у и проинтегрировав по А, получим интегро-
дифференциальные уравнения для одно- и многомерных плотностей:
оо оо
= (2^F / /{ixT^t} + x(V’(7/)*)TA;O]eiAT(’’-y)/i(7/;t)d^A,
—оо —оо
(1.5.36)
'д^~/п(У1 > • • • > Уп] , • • • > —
ОО оо
[гАп<р(т?п,^п) + x(iKih,tn)Tbn;tn)] х
—оо —оо
{п >
- Ук) ? /п(Ш, ... , T)n-,ti, ... , tn)x
Jt=l J
xdr]i • • • dr]ndXi ... dXn . (1.5.37)
Начальные условия для уравнений (1.5.36) и (1.5.37) имеют вид
fi(y, to) =fo(y),
(1.5.38)
fn(yi j • • • > Уп— ij 2/n> ti, , tn—i, tn_i) —
= fn-i(yi, , yn-r,ti, ... , tn_i)6(yn -yn-i), (1.5.39)
где fo(y) - плотность начального значения Yq вектора состояния.
1.5. РАСПРЕДЕЛЕНИЯ ПРОЦЕССОВ
149
Формулы ДЛЯ фуНКЦИИ X9 Конкретный вид функции X ~ в
уравнениях для характеристических функций определяется видом процесса с независимы-
ми приращениями W (t). Если процесс с независимыми приращениями
W(f) - винеровский, то его одномерная характеристическая функция h\ t) и
х(м;«) = д/dt in Мм; О определяются как
' * 1
Мм;0 = ехр < [ у(т)<1тц > , *(м;*) = ~МТМ)м/2- (1-5.40)
J I
. о )
Если процесс с независимыми приращениями W(t) - общий пуассоновский, то
х(м;0 = [э(м) - i]M),
(1.5.41)
где </(м) - характеристическая функция скачков; 1/(т) - интенсивность потока скач-
ков процесса W(t). В частном случае простого пуассоновского процесса с единичными
скачками ^(/х) —
Для процесса с независимыми приращениями W(t), представляющего собой линей-
ную комбинацию независимых винеровского и пуассоновских процессов, имеем
N
Ж(0 = W0(t) +12СкРк W ’ (15-42>
*=1
1 N
х(м;0 = -«М^оЮм + ^З [Ыс*М) — 1 ] *ъ(0 , (1.5.43)
к=1
где 1/q(t) - интенсивность винеровского процесса Wo(^); ~ характеристическая
функция скачков общего пуассоновского процесса - интенсивность потока
его скачков.
Если вектор W(t) состоит из N независимых подвекторов, т.е. W(t) =
= [^1(г)т...^(г)т]7 , то, разбивая вектор /X на соответствующие блоки, /X —
= [ /X. [l/tf ] , получим
Мм;*) = .. .hiN(p.N-,t)] , (1.5.44)
N
x(M) = 52х*(м*;*)>
*=i
(1.5.45)
150
ГЛ. 1. СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
где hik(pk',t) и Xk(^k’,t) - одномерная характеристическая функция процесса И^(£)
и соответствующая функция Отсюда, разбивая матрицу в уравнении (1.5.21)
на соответствующие блоки, {у, t) — [ £) • • • 0 ]» находим
N
*=1
(1.5.46)
В общем случае для процесса с независимыми приращениями РИ(t), когда
W(t) = W0(t) + j ip"(x)P(t,dx),
я?
(1.5.47)
имеем
х(р; t) = -|ртЦ)(Ср + У JevT^"(a!) - 1 - ipTt[)"(x) ] vP(t,x)dx.
я?
(1.5.48)
Здесь Ц)(0 ~ интенсивность винеровского процесса Wq(^)» a lSp(tyx}dx —
— \dp>(t^x)/9t]dx - интенсивность пуассоновского потока скачков процесса W).
равных с(ж).
Уравнение Фоккера-Планка-Колмогорова. Рассмотрим те-
перь случай чисто винеровского процесса Ж(^). Тогда уравнение
(1.5.36) принимает вид известного уравнения Фоккера-Планка-Колмо-
горова:
+ ^tr [0(У, t')‘/(t№(y,t)Tfl(y, t) ]) . (1.5.49)
2 (оу ду )
Это линейное однородное уравнение в частных производных второго по-
рядка параболического типа. Начальными условиями для него служат
условия (1.5.38).
Уравнение (1.5.40) и условие (1.5.39) справедливы и для п-мерной
плотности fn(yi,-" ,Уп\1\, ••• , tn).
Замечание!. Уравнение (1.5.49), если ввести обозначения дифференци-
руемой матрицы <т(?/, t) и вектора плотности потока вероятностей 7г(?/, t):
t) = ^(.У, t)T,
1.5. РАСПРЕДЕЛЕНИЯ ПРОЦЕССОВ
151
1 ГАТ -|т
принимает следующий вид:
где
дт
dxvir(y,t) = —n(y,t).
Замечание 2. Уравнения (1.5.49) допускает также следующую запись:
dfi,t =
где L* - сопряженный оператор для оператора
г Т/ ч д 1 Г , ч д дт
L = v l-«’‘>ay + 2tI
Уравнение для переходной плотности в случае винеровско-
го процесса. В условиях допущений п.1.2.7, написав уравнение (1.5.49)
для двумерной плотности и заменив в нем /2(2/1,2/25 h, £2) ее выражени-
ем через одномерную плотность и плотность перехода, /2(2/1,2/2 5 ti, h) =
/1 (2/15 £1 )/(2/2; £212/15 £1), получим после сокращения на /1(3/1; ^i)
д/(у2^2\уг,^ дт t
-----dt2-----= дуг +
1 ( д дт 1
+ 2tr \ <Э?/2 <Эг/2 [V’(y2,t2)l'(t2)V’(y2,t2)T/(?/2;<2|?/i;tl)] J • (1.5.50)
Это уравнение совпадает с (1.5.49). Таким образом, плотность пере-
хода f(y,t\rp,r) марковского процесса, определяемого стохастическим
дифференциальным уравнением (1.5.20), рассматриваемая как функция
двух первых аргументов у и t, t > т, определяется уравнением (1.5.49).
Начальное условие для переходной плотности, очевидно, имеет вид
f(y; т\у, т) = д(у-т]).
(1.5.51)
Определив одномерную плотность /1 (?/; t) и переходную плотность
/(2/, ^l7/;т) марковского процессса Y(t) путем интегрирования уравнения
152
ГЛ. 1. СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
(1.5.49) при соответствующих начальных условиях, можно найти все
многомерные плотности процесса Y (t) по формуле
fn(yi, ... , Уп'Л , ... , tn) = fi(yr,t1)f(y2]t2\yi\t1)...
• ../(3/n;*n|j/n-i;*n-i) при ti < t2 < ••• < tn.
(1.5.52)
Если t81 < t82 < • • • < t8n для некоторой перестановки (si, ... , sn)
чисел (1,.. .p), то n-мерная плотность fn(yi, • • • , yn\h , • . • , tn) выра-
жается той же формулой с заменой всех индексов 1, ... , п соответству-
ющими индексами si, ... , sn.
Случай полиномиальной правой части и независимого от
состояния системы коэффициента при белом шуме. В том слу-
чае, когда функция <p(y,t) в уравнении (1.5.20) представляет собой по-
лином относительно р, а коэффициент при белом шуме ^(y^t) не зави-
сит от у, i/>(y,t) = уравнение (1.5.25) сводится к линейному опе-
раторному уравнению в частных производных, порядок которого равен
степени полинома <p(j/,t):
dgi(X,t) _ iXT^ + xW(t)T*;t) (1.5.53)
ut [ \ гол j
Это уравнение в частных производных записано в операторной фор-
ме. Чтобы привести его к явной форме, необходимо заменить вектор
у в полиноме <р(р,£) оператором дифференцирования д/гдХ и получен-
ный в результате линейный дифференциальный оператор применить к
функции р1(Л;£), рассматриваемой как функция А. Иными словами,
каждый одночлен ук1 ... урр полинома ip(y, t) следует заменить соответ-
ствующим оператором (d/idXi)kx ... {d/idXp)k^.
Ясно, что (1.5.53) - линейное однородное уравнение в частных про-
изводных относительно pi, порядок которого равен степени полинома
Совершенно так же уравнение для n-мерной характеристической
функции перепишется в этом случае в виде
ддп
dtn
f д \
\idX~’tnJ 9п-
(1.5.54)
Это уравнение отличается от (1.5.53) только обозначениями.
Случай полиномиальной правой части и нормального бе-
лого шума. Уравнение (1.5.25) приводится к линейному уравнению в
1.5. РАСПРЕДЕЛЕНИЯ ПРОЦЕССОВ
153
частных производных тогда, когда функции t) и t) в стохасти-
ческом дифференциальном уравнении (1.5.20) обе представляют собой
полиномы относительно у, если белый шум V распределен нормально.
В результате получим следующее операторное уравнение:
dgi(A;Q
dt
.*т ( ® ±
А ПйА’'
2 ylC/A J yZC/A J
Si О; t)-
(1.5.55)
К этому же уравнению приводится в данном случае и уравнение
для п-мерной характеристической функции дп. Уравнение (1.5.55)
представляет собой линейное однородное операторное уравнение в част-
ных производных порядка max(P, 2Q), где Р - степень полинома <^(р, t);
Q - степень полинома
Стационарные процессы в стохастических дифференци-
альных системах. Для теории стохастических дифференциальных систем большое
значение имеет вопрос о существовании стационарных процессов в стационарных диффе-
ренциальных системах, когда процесс Y(t) в системе стационарен в том или ином смысле.
Рассмотрим стационарную дифференциальную систему (1.5.21) в условиях стационарно-
го белого шума V. В этом случае функции <^(1/, £), ^(ЗЛ 0» 'Ф"(У, ^)» Х(ДЧ 3/? 0 не
зависят явно от времени, уЧМ) = <?(у). ^'(М) = <(!/,*,*>) = V’" (!/,*>)>
= Х(М>!/)- Если » такой системе процесс Y (t) стационарен по отношению
к одномерному распределению, то его одномерная характеристическая функция pi (A; t)
тоже не зависит от времени, pi(Ajt) = pi(A), $pl(A)/dt = 0, и уравнение (1.5.22)
принимает вид
м{[гЛт<р(У)+х(А;К,0)]е<АТу} = 0. (1.5.56)
В случае, когда уравнение (1.5.56) имеет нетривиальное решение pi (А) 0 0, pi(0) = 1,
в системе возможен стационарный в узком смысле по отношению к одномерному распре-
делению процесс Y (t).
В случае нормально распределенного белого шума одномерное распределение ста-
ционарного процесса в стационарной системе можно найти интегрированием уравнения
(1.5.39) при df\/dt = 0:
ЛТ 1 Г Я ЯТ 1
[¥’(j/)/i(j/)] + 2tr j = 0- (1-5-57)
154
ГЛ. 1. СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
1.5.5. Одно- и многомерные распределения в дискретных и
непрерывно-дискретных системах. Рассмотрим сначала нелиней-
ные дискретные системы, описываемые следующими стохастическими
разностными уравнениями вида:
(fc = l,2,...),
У*+1 =^k{Yk)^^k(Yk)Vk (А; = 1,2,...),
(1.5.58)
(1.5.59)
где функции Vk(yk,Vk), У>к(Ук) и 1^к(Ук) имеют размерности (р х 1),
(р х 1) и (р х т) соответственно. Характеристические функции hk =
= hk(p) векторных случайных величин Vk и соответствующие им плот-
ности = Pfc(v) будем считать известными.
Применительно к уравнению нелинейной регрессии (1.5.58) имеют
место следующие рекуррентные формулы, определяющие одно- и мно-
гомерные плотности и характеристические функции:
Л(у) = 7Д7 f e~'XTy9kWdX, дк(Х) = Mexp{iXTYk} , (1.5.60)
^9ki,..., kn (^i ? • • • ? • • • dAn ,
gkl ,...,kn(Ai, ... , An) = Mexp< AfV*,
I z=i
(1.5.61)
5*+i(A) = Mexp {iXTwk(Yk, Vfc)} =
OO oo
e^T^Mfk(y>)hk(V)dydv,
(1.5.62)
— oo —oo
1.5. РАСПРЕДЕЛЕНИЯ ПРОЦЕССОВ
155
{n—1
г 52 VYk, + iA„ ujk„ (Ykn, Vkn)
1=1
oo oo
—oo —oo
exP < « 52 y/l + гАп (Уп, Vn)
. h=l
xfkt,...,k„(yi, , yn)dyi ...dy„dvn, (1.5.63)
причем
ffki ,fcn_i,fen-1 (Al > • • • > An) — ffki ,... ,kn-i (Al ? • • • ? ^n — 1 4" An),
9ki,..., kn (Ai , ... , An) = gk31,..., k3n (AS1 , ... , ASn), (1.5.64)
где ($! , ... , sn) - любая перестановка чисел (1 , ... , n), причем kSl <
< kS2 < • • • < kSn.
Таким образом, одно- и многомерные характеристические функ-
ции и плотности {У*} в нелинейной дискретной стохастической си-
стеме (1.5.58) определяются рекуррентными формулами (1.5.60)-
(1.5.64).
Общие рекуррентные формулы для распределений в нелинейной
авторегрессионной дискретной стохастической системе (1.5.59) немед-
ленно получаются из соответствующих формул (1.5.60)-( 1.5.64).
Замечание. Полученные в п.1.5.4, уравнения для одно- и многомерных рас-
пределений непрерывных марковских процессов принципиально могут быть использованы
(п.1.2.7) для получения рекуррентных уравнений для плотностей /1 (?//’,/) и } Ik |
?//,/) различных порядков приращений марковской последовательности {У/}, определя-
емой уравнениями (1.5.58) или (1.5.59). В этом случае достаточно применить известные
методы численного анализа функциональных уравнений Фоккера-Планка-Колмогорова,
Пугачева и др.
Для непрерывно-дискретных систем, в которых марковские про-
цессы допускают разрывы и описываются смешанными уравнениями
(1.5.20) и (1.5.59) нахождение распределений представляет весьма слож-
ную задачу (ТСтС, п.5.3.13). Применительно к стохастическим систе-
мам со случайной структурой соответствующие стохастические уравне-
ния и уравнения для распределений даны в задачах 1.9.59-1.9.64.
156
ГЛ. 1. СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
1.6. Методы теории линейных стохастических систем
1.6.1. Методы спектрально-корреляционной теории линей-
ных стохастических систем. Рассмотрим линейную дифференци-
альную стохастическую систему вида:
Y = aY + a0 + 5V, (1.6.1)
где у - вектор состояния системы размерности р\ а = a(t), clq = ao(t),b =
= b(t) - коэффициенты соответственно размерности (р х р), (р х 1),
(р х ти), которые в общем случае могут быть функциями времени
V - белый шум размерности т, интенсивность которого i/ = то-
же в общем случае может быть функцией времени t. Для нахождения
моментов первого и второго порядков случайного процесса Y (2), опреде-
ляемого линейным дифференциальным уравнением (1.6.1), достаточно,
чтобы он был белым шумом в широком смысле. Поэтому везде в этом
разделе будем считать V произвольным белым шумом с интенсивно-
стью I/ = i/(t).
Выразим вектор состояния системы Y формулой
t t
Y(t) = u{t,to)Yo + У и(£,т)Ь(т)У(т)сЬ" 4- J и(1,т)ао(т)с1т, (1.6.2)
to to
где u(t, т) - матрица, определяемая как функция t однородным диффе-
ренциальным уравнением du/dt = a(t)u и начальным условием и(т, т) =
= I. Математическое ожидание, ковариационная функция и момент
второго порядка вектора состояния системы Y(t) определяются соот-
ветственно формулами
t
m(t) = u(t, to)mQ 4- J u(t,r)ao(r)dr , (1.6.3)
to
min(ti Д2)
/ЦйЛ) = u(ti,to)Kou(t2,to)* + / u(ti,T)b(r)v(r)b(r)Tu{t2,T)*dT,
to
(1.6.4)
r(ti,t2) = K(ti,t2) + m(ti)m(t2)T, (1.6.5)
где mo - математическое ожидание начального значения Yq вектора со-
стояния Y; Kq = К (to, to) - его ковариационная матрица. При выводе
1.6. МЕТОДЫ ТЕОРИИ ЛИНЕЙНЫХ СТОХАСТИЧЕСКИХ СИСТЕМ
157
этой формулы учитывалось, что начальное состояние системы Yq не
зависит от белого шума V(t) при t > to и что u(t,r) = 0 при т > t.
Последним обстоятельством объясняется то, что верхний предел инте-
грирования равен min(ti,t2)- Кроме того, учитывалось, что коэффи-
циенты уравнений реальных систем всегда действительны, в то время
как элементы матрицы u(t,r) могут быть комплексными даже в этом
случае.
Дифференциальные уравнения для моментов второго по-
рядка. В практических задачах обычно бывает достаточно найти веро-
ятностные характеристики вектора состояния системы Y в каждый дан-
ный момент t (определяемые одномерным распределением), т.е. только
значения ковариационной функции K(t, t) = К (t) и момента второго
порядка Г(£, t) = T(t). Само собой разумеется, что все эти величины
для линейной системы можно определить по формулам (1.6.3)-( 1.6.5)
при ti = t2 = t. Однако в случае линейной стохастической системы
их можно вычислить значительно проще, а именно - интегрированием
соответствующих линейных дифференциальных уравнений:
m = am + ao, m(to) = m0, (1.6.6)
К = аК + Кат 4- bvbT, K(tQ) = KOi (1.6.7)
Г = аГ + Гат 4- bvbT 4- а^тт 4- mog , r(to) = Го, (1.6.8)
dK(t\, t2)/9t2 = -K(ti, ^2)о(^2)^, ti < ^2» -K(ti,ti) = K(ti) (1.6.9)
при t2 < h, K(ti,t2) = K(t2^ti)T.
Стационарные процессы в непрерывных стационарных ли-
нейных системах. Рассмотрим асимптотически устойчивую стацио-
нарную линейную систему (1.6.1), находящуюся под действием стацио-
нарного белого шума с постоянной интенсивностью у. В этом случае а,
оо, Ь постоянны, функция u(t,r) зависит только от разности аргумен-
тов, u(t, т) = w(t — т), и полученные формулы при to —оо принимают
соответственно следующий вид:
сю
т = У w(£)aod£,
о
ОО
к = I wtt)bvbTw(g)*d£,
(1.6.10)
(1.6.11)
О
158
ГЛ. 1. СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
ОО
к(т) = K(t 4- T,t) = у* w(£ + r)bi/6Tw(£)*d£ (т > 0). (1.6.12)
о
Таким образом, с течением времени в асимптотически устойчивой
стационарной линейной дифференциальной системе под действием
стационарного белого шума устанавливается стационарный в широ-
ком смысле процесс. Условие асимптотической устойчивости систе-
мы является не только достаточным, но и необходимым для суще-
ствования стационарного процесса.
Поскольку т и К в стационарном режиме постоянны, то, полагая
в уравнениях (1.6.6) и (1.6.7) т = 0, К = 0, получим линейные алгеб-
раические уравнения для т и К:
ат + ао = 0, аК 4- КаТ + bubT = 0. (1.6.13)
Если начальные значения то и Kq удовлетворяют уравнениям
(1.6.13), то уравнения (1.6.6) и (1.6.7) имеют очевидное решение m =
= mo, К = Ко- В этом случае при любом to процесс Y(t) будет стацио-
нарным в широком смысле (приложение 5).
Уравнения для ковариационной функции к(т) стационарного про-
цесса У(^) в линейной стационарной системе (1.6.1),
dk(r)/dT = ак(т), г > 0, fc(0) — К, (1.6.14)
где к(т) = к(—т)т при т < 0.
Полученные результаты распространяются на нестационарные ли-
нейные системы (1.6.1) при постоянных а, Ь, и и произвольной функ-
ции времени ao(t). В этом случае полученные уравнения для К и к(т}
остаются справедливыми, a m представляет собой функцию времени,
определяемую уравнениями (1.6.6). Процесс Y(t) в системе, для кото-
рого m определяется уравнением (1.6.6) при любом начальном условии,
а К и к(т} находятся изложенным здесь способом, будет ковариационно
стационарным.
Спектральная теория стационарных процессов в стацио-
нарных линейных дифференциальных системах. Рассмотрим
асимптотически устойчивую стационарную линейную дифференциаль-
ную систему уравнений с передаточной функцией Ф(«). Предположим,
что входной переменной системы служит стационарный случайный про-
цесс X(t), обладающий плотностью sx(w). Следовательно, он предста-
вим спектральным разложением:
оо
X(t) = mx(f) + У e^V^du. (1.6.15)
— ОО
1.6. МЕТОДЫ ТЕОРИИ ЛИНЕЙНЫХ СТОХАСТИЧЕСКИХ СИСТЕМ
159
Спектральному разложению X(t) соответствует спектральное разложе-
ние Y(t):
ОО
Y(t) = my(t) 4- у* elu,^(icd)V(td)cfcj, (1.6.16)
— оо
причем случайный процесс Y(t) стационарен. Его ковариационная
функция и спектральная плотность равны:
оо
ку(т) = / 8у(ш)е1ШТdw, (1.6.17)
— оо
оо
Зу(ш) = [ ку(т)е~гигг dr = Ф(гси)в1(си)Ф(га;)*. (1.6.18)
2тг J
— оо
Взаимная спектральная плотность входного и выходного сигналов
системы определяются по формулам:
51/х(^) = в1(си)Ф(га;), зХу(и) = зх(и)Ф(гшУ = . (1.6.19)
Приведенные формулы справедливы только для асимптотически
устойчивых стационарных систем, работающих в установившемся ре-
жиме, т.е. при бесконечно долго действующем стационарном входном
сигнале. Практически эти формулы применимы, когда время действия
входного сигнала превышает время переходного процесса. Если система
описывается дифференциальным уравнением и, следовательно, ее пере-
даточная функция рациональна, то выходной сигнал может быть ста-
ционарной случайной функцией и при любом времени работы системы
и специальных начальных условиях. А именно, случайное начальное
значение У(£о) = Yq следует выбрать так, чтобы ковариационная мат-
рица случайного вектора Z(t) = [Х(£)ТУ(£)Т]Т не зависела от t. Для
этого достаточно взять случайное начальное значение Yq, для которого
оо оо
Kyo = fc!z(0) = /, Kxoyo = kxy(0) = jsx(w)$(iu)*dw.
— оо —оо
(1.6.20)
Для вычисления дисперсий и ковариаций компонент выходного сиг-
нала устойчивой стационарной системы, работающей в установившемся
160
ГЛ. 1. СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
режиме под действием стационарного входного сигнала (практически
при достаточно долгом действии входного сигнала), в каждый данный
момент времени t достаточно положить в формуле (1.6.20), определяю-
щей ковариационную функцию выходного сигнала, = t2 = t Тогда
получим следующую формулу для ковариационной матрицы значения
выходного сигнала в момент t:
оо
Ку = ky(O) = У $(icu)Sa;(cu)$(icd)*dLU .
—оо
(1.6.21)
Для нахождения дисперсий и ковариаций компонент выходного
сигнала по формуле (1.6.20) на практике приходится вычислять инте-
гралы от рациональных функций. Для вычисления таких интегралов
удобно пользоваться следующей формулой:
Г Ьр(га>)2п 2 + bl(icj)2n 3 + • • • + fan-i (^) + &2n-2
J |ao(iw)n + ai(tw)n-1 4- • • • + an_i(tw) 4- an|2
-oo
= (-l)n+1 —(1.6.22)
a0
Здесь
Си С12 • • • Cin Ьо С12 • С1п
д„ = С21 С22 • • • С2п , Dn = Ь2 С22 • • • с2п
Сп1 Сп2 • • Спп Ь2п-2 Сп2 • • спп
где cpq = a2p-q при 0 < 2p-q < n\ cpq = 0 при 2p-q < 0 или 2p-q > n.
Для применения формулы (1.6.22) необходимо представить числи-
тель в (1.6.21) в виде полинома относительно геи, а знаменатель выра-
зить как квадрат модуля полинома относительно геи с положительными
коэффициентами ao, ai, • • , ап.
Формулой (1.6.22) можно также пользоваться и для вычисления ко-
вариаций компонент входного сигнала с компонентами выходного сиг-
нала по формуле
сю
Кху = кху(0) = / sx(w)$(iw)*du>.
(1.6.23)
1-6. МЕТОДЫ ТЕОРИИ ЛИНЕЙНЫХ СТОХАСТИЧЕСКИХ СИСТЕМ
161
Для уравнения (1.6.1) основные формулы получаются, если поло-
жить: — -(а - iu/Z)-1b.
Спектрально-корреляционные методы для дискретных ли-
нейных стохастических систем. Рассмотрим сначала дискретную
линейную стохастическую систему, описываемую следующим разност-
ным уравнением первого порядка:
Г/+1 = atf + btVt + аш (1 - 1,2,...), (1.6.24)
где Yi - вектор состояния размерности р; Ц - независимые векторные
случайные величины размерности т с нулевыми математическими ожи-
даниями и ковариационной матрицей щ, bi и - коэффициенты
размерности (р х р), (р х 1) и (рх т) соответственно.
Для математического ожидания mi — МУ/, ковариационной мат-
рицы Ki = M(Y/ — mi)(Yi — mi)T и ковариационной функции K(l,h) =
= М(У/ — mi)(Yk — mh)T имеем рекуррентные уравнения:
тп/+1 = aimi + аы , mi = МУ1, (1.6.25)
Kt+i = aiKiaf + , Кх = МУУ/, (1.6.26)
K(l,h+ 1) = K(l,h)al, l<h, = (1.6.27)
При I > h имеем K(l,h) = K(h, l)T.
В случае стационарной дискретной линейной системы (1.6.24) мат-
рицы щ, bi и вектор oqi не зависят от дискретного времени I: сц — а,
bi — 5, aw = а и уравнение (1.6.24) принимает вид
У/+! = aYi + оо + bVt. (1.6.28)
Величины Vi имеют одно и то же распределение, а следовательно, и
одну и ту же ковариационную матрицу у. Если в системе (1.6.28) су-
ществует стационарный дискретный случайный процесс {У/}, то посто-
янны его математическое ожидание m = mi — m^i и ковариационная
матрица К — Ki = A'/yi- Причем они удовлетворяют алгебраическим
уравнениям:
т = ат 4- oq , К — аКаТ 4- ЬуЬт . (1.6.29)
При этом ковариационная функция К{1 4- h, /) = k(h) определяется ре-
куррентным соотношением:
k(h 4-1) = k(h)aT. (1.6.30)
Ь Фильтры Налмана и Пугачева
162
ГЛ. 1. СЪЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
Для асимптотически устойчивой дискретной линейной системы с
передаточной функцией Ф(го>) формулы (1.6.15)—(1.6.23) приобретают
вид
27Г
Xt = mf + fe”lK(u)du), (1.6.31)
О
2тг
Yi =myi+ I e^,$(iw)Vd(w)dw,
О
2тг
ky = = I e^hsvd<kj,
sdv (ш) = sd(u)$(iu)*,
«Г» = ^(W)$(icv),
oo
Ky = &q = j
OO
Kxy = k£v= У sS(w)$(iw)‘dw.
—OO
(1.6.32)
(1.6.33)
(1.6.34)
(1.6.35)
(1.6.36)
(1.6.37)
(1.6.38)
Аналогично выписываются формулы спектрально-корреляционной тео-
рии дискретной линейной системы, заданной передаточной функцией
ф(2).
Корреляционная теория линейных преобразований. Пусть
даны математическое ожидание mx(f) и ковариационная функция
Kx(t, t') входного сигнала Х(£), поставим задачу найти my(s) и Ky(s, s')
выходного сигнала Y(з) для линейного преобразования
У(з) = AX(t),
(1.6.39)
где А - произвольный линейный оператор. Эта задача решается просто,
если допустить, что операция математического ожидания и оператор А
переместительны. В этом случае справедливы формулы
ту(з) = Amx(t),
(1.6.40)
Ky(s,s') = AtAvKx(t,t') = At. AtKx(t,t'), (1.6.41)
1.6. МЕТОДЫ ТЕОРИИ ЛИНЕЙНЫХ СТОХАСТИЧЕСКИХ СИСТЕМ 163
Vy(s,s') = AMrFx(t,t') = At'Atrx(t,t'). (1.6.42)
Здесь индекс у оператора А указывает, что этот оператор действу-
ет над функцией данного аргумента при фиксированных значениях
всех остальных переменных. Таким образом, в основе корреляционной
теории линейных преобразований случайных функций лежат формулы
(1.6.40) и (1.6.42).
1.6.2. Методы общей теории линейных стохастических си-
стем. В случае линейной системы (1.6.1) уравнения (1.5.63) для одно-
мерной и (1.5.64) для n-мерной характеристической функции принима-
ют следующий вид:
= ХТа-^ 4- [г*Атао + x(bTA;t)] д\, <7i(A; to) = <?о , (1.6.43)
= An°(<n)^f2 + [^n°o(^n) +x(b(<n)TAn;tn)] дп (1.6.44)
С/Cn ОЛп
9n(Xi , • ’ • , An; ti , ... , tn__i, tn—i) =
= 9n—i (Ai , ... , An—2, An—i 4" An j ti, ... , tn—i) > n = 2,3,...
Уравнения (1.6.43) и (1.6.44) как уравнения в частных производных
первого порядка, линейных относительно производных, интегрируются
на основе стандартных алгоритмов (ТСтС, п.6.2.2).
Явные формулы для одно- и многомерных характеристи-
ческих функций. Имеют место следующие выражения для одно-,
двух- и n-мерных характеристических функций (ТСтС, раздел 6.2)
t
#i(A;t) — 0o(ti(t,to)TA)exp{iATy и(1,т)ап(т)(1т+
t t0 (1.6.45)
+ У х(Ь(т)ти((,г)тА;т)1/т),
to
<7г(А1, A2‘,ti,t2) = ^o(^(ti, to)TAi 4-u(t2, to)TA2)x
tl t2
x exp/iAf У u(ti,T)aQ(r)dr 4- iX? J*и(^2,т)ав(т)(1т+
to to
164
ГЛ. 1. СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
+ у х(Ь(т)Т + u(t2,r)TA2)] ;т)(1т+
to
х(Ь(т)ги(12, т)тХ2; r)d.T
(1.6.46)
Un(^l ? ’ • - » h ) • • • ? ^n) —
= 9o I 52 “<**’ *o)TAfc I expl i
to
+ 52 [ xWr)T±u(ti,r)TXi;r)dT
*=4<. '=*
(n=l,2,...).
(1.6.47)
Формулы (1.6.47) дают явные выражения одно- и многомерных
характеристических функций случайного процесса Y(t), определяемо-
го линейным стохастическим дифференциальным уравнением (1.6.43).
Если Y представляет собой расширенный вектор состояния системы,
включающий все дополнительные переменные, векторы состояния и
выходные сигналы всех формирующих фильтров, введенных в систе-
му для приведения ее уравнений к стохастическим дифференциаль-
ным уравнениям, то для нахождения многомерных характеристических
функций вектора состояния системы следует положить в (1.6.47) рав-
ными нулю компоненты всех векторов Ai, ... , АЛ, соответствующие не
интересующим нас компонентам вектора У. Таким образом, форму-
ла (1.6.47) дает полное решение задачи определения одно- и многомер-
ных распределений вектора состояния любой линейной системы, пове-
дение которой описывается линейным стохастическим дифференциаль-
ным уравнением (1.6.1).
Случай нормального распределения состояния. В частном
случае нормально распределенного белого шума V, когда —
— —/хГ1/(£)д/2, и формула (1.6.47) принимает вид
1.6. МЕТОДЫ ТЕОРИИ ЛИНЕЙНЫХ СТОХАСТИЧЕСКИХ СИСТЕМ 165
9n(^i>»•••> An;ti,f tn) —
/ п \ ( 1 *f
= 9о ( 52 “(**» *о)тА* I «ПК * 52 А* / “(**>T)°o(T)dT“
\t=i / 1 *=i 4
1 n n 1
-2^212Л«Т и(и,т)Ъ(т)и(т)Ъ(т)ти^к,т)тЛгхА (1.6.48)
к=1л=* 4
ИЛИ
9п(А1 > > — > AnJ ti , ... , tn) =
/ " X f »
= 9o I 52 “(**> I exp{ * 52 A* / и(*к,т)ао(т)Лт-
\*=i / 1 t=i 4
-1 52 [ u(tl' тЖт)*'(т)ьСг)Т«(*А> r)TdT\h | (n = 1,2,...).
'•*=1 i J
(1.6.49)
Формула (1.6.49) симметрична относительно nap ,(Ап,^п).
Поэтому она справедлива при всех , ... , tn.
Если начальное распределение нормально, то
до(Х) = ехр |iXTmo - ^АтКоа) (1.6.50)
I ЛВ I
и формула (1.6.49) принимает следующий окончательный вид:
Pn(Ai, , ... , Хп\Ч , ... , tn) = ехрр52л* »(t*><o)mo+
t=i L
У 1 1 п Г
+ / u(tfc,T)ao(T)dr -- 52 V “(t«>fo)^o«(tfc,<o)T+
to f’fc==1
mm(t|,U)
+ J u(ti, т)Ъ{т)и(т)Ь(т)тu(th, r)Tdrj Ал} (n = 1,2,...). (1.6.51)
to
166
ГЛ. 1. СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
Формула (1.6.51) показывает, что в рассматриваемом случае все
многомерные распределения случайного процесса Y (t) нормальны с па-
раметрами
t
m(t) = u(t, to)mQ 4- jи(1,т)ац(т)(1т, (1.6.52)
to
min(ti ,$2)
^(^1,^2) = w(Zi,^o)^ow(^2,^o)* + У и(^1,т)Ь(т)р(т)Ь(т)ти(^2,т)*йт.
to
(1.6.53)
Таким образом, при нормальном распределении начального состо-
яния системы Уо и нормально распределенном белом шуме V в урав-
нении (1.6.1) состояние системы, рассматриваемое как функция вре-
мени, представляет собой нормально распределенный случайный про-
цесс. Для асимптотически устойчивой линейной системы распреде-
ление процесса Y(t) асимптотически нормально, если белый шум V в
уравнении (1.6.1) распределен нормально.
Стационарные в узком смысле процессы в стационарных
линейных системах. Рассмотрим устойчивую стационарную линей-
ную систему (1.6.1) под действием стационарного в строгом смысле бе-
лого шума. В этом случае а, ао> и Ь постоянны; функция u(t,r) зависит
только от разности аргументов, u(t,r) = w(t — т)\ функция х не зави-
сит от времени: х(/М) = х(м)- Полагая в формуле (1.6.45) = —00,
u(t,r) = w(cr), а = t — т, u(t,to) — w(oo) = 0, приходим к следующей
явной формуле для одномерной характеристической функции процесса
У(«):
(71(A) — ехр гАт
(1.6.54)
о о
Отсюда видно, что одномерная характеристическая функция векто-
ра состояния стационарной линейной дифференциальной системы при
tQ = —00 не зависит от времени t (именно вследствие этого она обо-
значена просто pi(A)). Следовательно, при неограниченном времени
работы такой системы в ней устанавливается стационарный по отноше-
нию к одномерному распределению процесс. Одномерная характери-
стическая функция этого процесса, конечно, удовлетворяет уравнению
(1.6.43) при dg\/dt = 0. Формула (1.6.54) показывает, что в случае
1.6. МЕТОДЫ ТЕОРИИ ЛИНЕЙНЫХ СТОХАСТИЧЕСКИХ СИСТЕМ
167
нормально распределенного белого шума, когда х(м) = од-
номерное распределение стационарного процесса в системе нормально,
причем математическое ожидание т и ковариационная матрица К зна-
чения процесса Y(t) при любом t определяются формулами (1.6.13).
Полагая в (1.6.47) to = —оо, и(£,т) = w(a), а = t — т, находим при
^1 < ' * ’ < следующее выражение для многомерной характеристиче-
ской функции:
9п(^1 ,)•••) AnJ tl J • • • > ^n) —
n tk—tk-1 / n \
+ f *\T [ w(tl ~ + j ‘kf (n = l,2,...). (1.6.55)
*=2 о \ dk ) ’
Таким образом,с течением времени в асимптотически устойчивой
стационарной линейной дифференциальной системе под действием
стационарного белого шума устанавливается стационарный в узком
смысле случайный процесс.
При произвольном начальном моменте to процесс в системе будет
стационарным в узком смысле, если его начальное распределение опре-
делить характеристической функцией
0о (А) = exp iXT
I w(a)aoda + j* x(bTw(a)TX)da ► .
о о
(1.6.56)
Для нормально распределенного белого шума V и нормально распреде-
ленного начального значения процесса Y(£) многомерные характеристи-
ческие функции стационарного в узком смысле процесса определяются
формулой
оо
5п(А1, , ••• , An;ti, ••• , tn) = expp'2^Afc у
1 k=i о
w(tj - tk + <y)bvbTw(<y)TdoXi
(n = l,2,...).
(1.6.57)
168
ГЛ. 1. СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
Методы общей теории линейных дискретных стохастиче-
ских систем. Представим уравнение (1.5.62) для дискретной линейной
системы, описываемой (1.6.24), с учетом независимости Уд и 14 в виде
Л+1(А) = ехр {<Атао*} hk(b{ Х)дк(а[Х). (1.6.58)
Отсюда следует явная формула для одномерной характеристической
функции:
Як+1 (А) = ft (of... af А) ехр {»Атво*} А*(6* А)х
к-1
х JJ ехр {*Ата*... e,+iao,} h,(bja^+1... a* А). (1.6.59)
Ж=1
Аналогично находим разностное уравнение n-мерной характеристиче-
ской функции:
9кг(Ai, ... , Хп) —
= exp{iAjaok.}fcJt_(5^An)ftI,..,fc.(Ai, ..., Ап-пв^А,). (1.6.60)
Его решение при начальных условиях (1.5.64) дает рекуррентную фор-
мулу для многомерных распределений:
9къ C^i, — ,Лп)=рд11...1дж_1(А1,... jXn-i + <>д^_1>Од'1 - --<*д^Ап)х
х ехр {iA^aofc. } *n)x
х П “Р {iA^a*- • • • a«+i°o»} л«(ьГвГ+1 al,Ап) - (1.6.61)
Ж=1
Конечная формула (1.6.59) и рекуррентная формула (1.6.61) дают яв-
ные выражения для всех многомерных характеристических функций
дискретной линейной стохастической системы (1.6.24).
При нормальном распределении величин 14 и Y± все величины Уд
и их линейные функции, в частности векторы [*£ ••*£] > Распре-
делены нормально. Таким образом, при нормальных распределениях
величин 14 и У1 уравнения (1.6.59)-(1.6.61) полностью определяют все
многомерные нормальные распределения последовательности {Уд}.
Если в стационарной дискретной системе существует стационарный
процесс, то он стационарен в узком смысле. Одномерные распределения
определяются уравнениями (1.5.62) при pi(A;t) = pi (А).
1.7. МЕТОДЫ ТЕОРИИ НЕЛИНЕЙНЫХ СТОХАСТИЧЕСКИХ СИСТЕМ (I) 169
1.7. Методы теории нелинейных стохастических систем (I).
Нормальная аппроксимация и эквивалентная
линеаризация
1.7.1. Моменты вектора состояния. Линейные системы с
параметрическими шумами. Формула для производной по времени
математического ожидания т = m(t) = MY(t) процесса Y(t), опре-
деляемого (1.5.21), имеет вид
т = М<р(УД). (17.1)
Эта формула не является замкнутым уравнением, определяющим
математическое ожидание процесса Y(t), так как математическое ожи-
дание в правой части зависит от неизвестного одномерного распределе-
ния процесса Y(t), а не только от ш.
Формула для производной момента второго порядка. Обо-
значим через 7^- = MYi(t)Yj(t) компоненты матрицы моментов второго
порядка Г = МУ(t)Y(t)T. Существует два подхода к выведу форму-
лы для производных в силу уравнения (1.5.22). Согласно первому
методу достаточно дважды продифференцировать уравнение для одно-
мерной характеристической функции (1.5.22) по (»А*) и (tAj):
7‘J [ 3(t’Afc)d(»Aj) ]А=0- ( 7 )
По второму методу следует вычислить по обобщенной формуле Ито
стохастический дифференциал произведения Yk(t) х Yj(t), приняв во
внимание Г = [7^] (fc, j = 1, ... , р). В результате придем к искомой
формуле для производной по времени момента второго порядка про-
цесса Y(t) в (1.5.21):
Г = М {^(Г,t)YT + Y<p(Y, t)T + а(Г, t)} . (1.7.3)
Здесь
а(У, t) = i/>'(Y, t)T + У t, u)tl>"(Y, t, u)Tvp(t) du),
(1.7.4)
Формулы (1.7.1) и (1.7.3) в общем случае не являются замкнутыми
уравнениями для т и Г, так как правые части их зависят от одномер-
ного распределения процесса Y(t), а не только от т и Г.
170
ГЛ. 1. СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
Формула для производной ковариационной матрицы. Из
формулы (1.7.3) легко выводится формула для производной по времени
ковариационной матрицы К вектора Y системы (1.5.21):
К = М {<p(Y,t)(YT - тТ) + (У - m)<p(Y,t)T + a(Y,t)} . (1.7.5)
Для системы (1.5.20) в формулах (1.7.3) и (1.7.5) следует а(У, t)
заменить на
сг(У, t) = гр(У, t)v(t)il>(Y, t)T , p(t) = р0 W • (1.7.6)
Формулы для производных момента второго порядка и ко-
вариационной функции. В дальнейшем нам понадобятся еще фор-
мулы для производных момента второго порядка Г($1, ti) и ковариа-
ционной функции K(t\^ti) процесса Y(t) по второму аргументу при
ti < t?:
ЗГ(Ь,«2)/^2 = MYtl<p(Yt2,t2)T, (1.7.7)
dK(tlyt2)/dt2 =M(ytl -mt,MYt2,t2)T. (1.7.8)
Бесконечная система уравнений для моментов. Предполо-
жим, что функция (p(y,t) в уравнении (1.5.20) представляет собой по-
лином относительно у, а функция ^>(у, t) — не зависит от у. Пред-
ставив компоненты вектора ip(y, t) в явной форме полиномов
N
4>r(y,t)= 52 Vr<h.......hpy^ •Урр (г = 1, ... ,р) (1.7.9)
hi ,..., /ip=0
с коэффициентами, в общем случае зависящими от времени t, и вклю-
чив функцию ^(t) в состав белого шума V, придем к следующей беско-
нечной системе уравнений для начальных моментов:
р N
&ki ,, кр = 52fcr 52 , hpGhi+k! ,..., hr+kr-l ,..., hp+kp +
r=l hi ,...,hp=0
Л1 kp
+ 52 • • 52 .../.раА1_Л1,...1кр_Лр (1.7.10)
/ц=0 hp=0
(fci , ... , kp = 0,1,2,...; fci + • • • kp = 1,2,...),
1.7. МЕТОДЫ ТЕОРИИ НЕЛИНЕЙНЫХ СТОХАСТИЧЕСКИХ СИСТЕМ (I) 171
где
Xhi
dhl....л,,х(А; t)
d(iXi)hl... d(iXp')h”
(1.7.11)
л=о
Уравнения (1.7.10) можно записать компактнее, пользуясь вектор-
ными индексами k = [ fci ... кр ]т, h = [ hi... hp ]T:
p TV ki ^p
&k = 52fcr 52 (Pr,h&h+k—er + @ki * ’ ’ Л
r=l /11 ,,/ip=0 /ii=0 /ip=0
(1.7.12)
(fci, ... , kp = 0,1,2,...; |fc| =ki + --- + kp = 1,2,...),
где er - вектор, все компоненты которого равны нулю, кроме r-й, равной
единице:
ег = [0.. .010.. .0]Т ,
&к = ,..., кр , фг'к, = ar,/ii ,..., hp j Xh = Xh\ ,..., hp •
Очевидно, что Xh — 0 при |Д| = hi 4- • • • 4- hp < 2 и Xh = "rs при
h — вр 4" .
Если в белый шум в (1.5.20) включен множитель то интен-
сивность v заменяется произведением vi = ‘фи'фт и величины Xh при
h = ег 4- е8 равны соответствующим элементам матрицы vi = 'фи‘фт.
В уравнениях (1.7.12) величина а8 равна нулю, если хотя бы одна
компонента векторного индекса s отрицательна, и равна единице, если
все компоненты векторного индекса s равны нулю, «о = 1- В случае,
когда функции <p(y,t) и a(y,t) = представляют со-
бой полиномы относительно у, а белый шум V распределен нормально,
т.е. координаты вектора <£>(з/, t) определены (1.7.9), а элементы матрицы
а(у, t) в форме:
N
<ТгЛу^)= 52 , .,Лр2/11 Ур” (r>s ' !> ••• ,Р), (1-7.13)
Л. 1 ,... , /ip=0
получим искомые уравнения:
р N
«*1,... ,кр = 52kr 52 ¥>Г,Л1...ЛраЛ1+*1 .....Л.+fcr-l, - ,ЛР+*р +
г=1 /11 ,..., hp=0
1 Р N
+ й kr(kr — 1) O’rr.hi , •••, hp&hi+ki ,..., hr+kr— 2 ,..., /1р4-Л4-р +
г=1 /ii ,..., hp=Q
172
ГЛ. 1. СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
р г-1 N
+ 52 52 52 °r8,hi ,..., hp х
r=l e=l hi,...,hp=O
ХаЛ1+*1 ,..., Л.+Ъ-1,..., hr+kr-1,..., hp+*p (1.7.14)
(*i, , кр = 0,1,2,. ..;|fc| = fc1 + ... + tp = 1,2,...).
Уравнения (1.7.14) также можно переписать в компактной форме, поль-
зуясь векторными индексами при к±, ... , кр = 0,1,2,...; |fc| =
= fci + • —F кр = 1,2, —:
р N
OLk = Е ¥’r,fcah+t-e,+
г—1 /ii,...thp=0
1 Р N
+ 2 52^г(^г52 &rr,h&h+k—2er 4“
г—1 Л1,...,ЛР=О
р г-1 N
4" кгк8 Ог8,К&К+к—ег—е, •
г—1 в=1 Л1 ,...,Лр=0
(1.7.15)
В уравнениях (1.7.15), так же как в (1.7.12), величина а8 равна
нулю, если хотя бы одна компонента индекса з отрицательна, и равна
единице, если все компоненты векторного индекса з равны нулю, «о = 1-
Линейные системы с параметрическими шумами. Вектор
состояния линейной системы с параметрическими белыми шумами оп-
ределяется уравнением:
(р \
Ьо 4" V. (1.7.16)
h=l /
Уравнения для тп, Г, К и K(ti,t2) в этом случае имеют вид
тп = атп + ап, m(tQ) = mQ. (1.7.17)
Г = аГ + Гат 4- аотпт 4- та? 4- Ьо^Ь?4-
р р
+ ^(.bhubo +b0^b[)mh+ Г = [7ы], Г(«о) = Го, (1.7.18)
Л=1 h,l=l
1.7. МЕТОДЫ ТЕОРИИ НЕЛИНЕЙНЫХ СТОХАСТИЧЕСКИХ СИСТЕМ (I) 173
Р
К = аК + Кат + + У ''J&hi'bQ 4- ЬорЬд )m^+
А=1
р
+ 52 bhV^(”**”*» + *Ы)» к = [*ы]» #(*о) = ко,
л,1=1
(1.7.19)
dK(t,,t2)/&t2 = K(ti,t2)a(t2)T, t2>ti, K(ti,ti) = K(ti). (1.7.20)
При нормально распределенном белом шуме V в (1.7.16) моменты
вектора состояния Y системы определяются бесконечной системой урав-
нений (1.7.15), которая в этом случае разделяется на независимые систе-
мы уравнений для моментов каждого данного порядка k (fci, ... , кр =
= 0,1,2,...; |fc| = fcj+ - +fcp = l,2,...):
р / р \
Otk = У2 I °г,0аЛ-ег + °г,е,аД;+е,—I +
r=l X д=1 /
1 Р / Р
+ 2 У ^г(^г “ 1) ( ^гг,0Од._вг. + У ^0rr,e«aJb+eq-eI.+
г=1 ' 9=1
Р \ Р Р“Х /
4" У ^гг,е,4-еш^Д:4-е,4-еш--2е,. J У У"^ krka I ОудДОЦг—ег—е« 4“
9,u=l ' г=2 8=1 '
Р Р х
+ 5Z<Trs»e«a*+e«~er“e* + ' аг8,еч+е„ак+еч+е„-ег-ев ) •
9=1 9»u—1
(1.7.21)
Стационарные процессы в линейных системах с парамет-
рИЧеСКИМИ Шумами. Рассмотрим стационарную линейную систему (1.7.16) со
стационарными параметрическими шумами. В этом случае О, CLq, Ьо, Ь^, и Р постоянны.
Поэтому, положив в (1.7.14) и (1.7.19) Ш = 0 и К = о, получим алгебраические уравне-
ния для математического ожидания и ковариационной матрицы значения стационарного
процесса в любой момент t:
атп + ао = 0, (1.7.22)
Р р
аК 4- Кат + 4- )rnh + bhub{(rnhmi + км) = 0.
h-l htl=l
(1.7.23)
Для нахождения ковариационной функции стационарного процесса к(т), где Т =
= Й — Й,
dk{r)/dr = afc(r), fc(0) = К (1.7.24)
174
ГЛ. 1. СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
При Т < 0 ковариационная функция определяется формулой к(т) = к^—т)^.
В случае нормально распределенного белого шума V можно также определить мо-
менты высших порядков одномерного распределения стационарного процесса в системе.
Для этого следует положить в уравнениях для моментов вектора состояния
ак =0 (Ал , ... , кр = 0,1,2,...; |fc| = кг + • • • 4- кр = 1,2,...). (1.7.25)
Стационарный процесс в линейной системе с параметрическими шумами физиче-
ски может существовать только тогда, когда системы, описываемые детерминированными
уравнениями (1.7.12) и (1.7.19), устойчивы. Однако это условие в общем случае недоста-
точно для существования стационарного в узком смысле процесса в системе.
Формулы для моментов в нелинейных дискретных стоха-
стических системах. Формулы для моментов первого и второго по-
рядков применительно к дискретной системе (1.5.58) имеют следующий
вид:
m/+i =М^(УЬУ/), (1.7.26)
Кк+1 = М Vi) - m,+1 ] Vt)T - mf+1 ] . (1.7.27)
Для нелинейных систем формулы (1.7.26) и (1.7.27) не являются зам-
кнутыми уравнениями.
Уравнения для моментов дискретной линейной системы с
параметрическими шумами. Рассмотрим следующую дискретную
линейную систему с параметрическими шумами:
(р \
boi -I- bijYij I Vi,
J=i J
(1.7.28)
где boi, Ьц, ... , bpi - матрицы того же размера, что и матрица ao/J
У/1?... ,Yip - компоненты вектора У/, тогда получим искомые разност-
ные уравнения для вектора mi
7Л/+1 = aimi + aoi, mi = МУ1,
(1.7.29)
1.7. МЕТОДЫ ТЕОРИИ НЕЛИНЕЙНЫХ СТОХАСТИЧЕСКИХ СИСТЕМ (I) 175
и матрицы Кц
р
#/+i = aiKiaf 4- М? 4-
r=i
р р
+bjivib^)mji 4- 52 52 bjivibu^mijmih 4- . (1.7.30)
}=l h=l
K1 = M(Y1-m1)(Y1-m1)T.
Уравнение
К(j, h 4-1) = K(j, h)c% (1.7.31)
с начальным условием = Kj полностью определяет K(j,h) при
h > j. При h < j имеем K(j,h) = K(h,j)T.
Распределение процесса {У/} не будет нормальным при нормаль-
ных распределениях Vi и Yi вследствие нелинейности уравнения (1.7.28)
относительно Yi и Vi.
1.7.2. Методы нормальной аппроксимации и эквивалент-
ной линеаризации. В общем случае точное решение уравнений, опре-
деляющих многомерные распределения вектора состояния нелинейной
стохастической дифференциальной системы (1.5.21), невозможно. Про-
стейшим приближенным методом нахождения многомерных распреде-
лений вектора состояния является метод аппроксимации распределения
состояния системы нормальным распределением.
Аппроксимируя одномерное распределение процесса Y (£) в системе
(1.5.21) нормальным, будем иметь
Pi(A; Z) « exp (iATm - ^ХТКЛ| , (1.7.32)
I л I
» [(2тг)р |#|Г1/2exp |-|(ут -тт)К~1(у - т) j ,
где т и К - неизвестные математическое ожидание и ковариацион-
ная матрица вектора состояния системы Y. Вычислив математические
ожидания в формулах (1.7.1) и (1.7.5) для производной математическо-
го ожидания т = МУ(t)
m = M^Y,t) (1.7.33)
и производной ковариационной матрицы К
К = М [^(Г, t)(YT - тТ) 4- (Г - t)T 4- a(Y, t)] , (1.7.34)
176
ГЛ. 1. СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
а(Г,4)=ао(У,«) + У ^'(Y,t,uW{Y^u)TvP{t,du),
(1.7.35)
<70(У, t) = f(Y, t)ib(t№X, t)T (1.7.36)
для нормального распределения N(m, К), получим искомые обыкновен-
ные дифференциальные уравнения метода нормальной аппроксимации
(МНА), приближенно определяющие т и К (ТСтС, раздел 7.2):
т = <pi(m, К, t), m(to) = , (1.7.37)
<pi (т, К, t) = MN<p(Y, t), (1.7.38)
К = К, t), K(to) = Ko, (1.7.39)
<рг(т,К,1) = <p2i(m,K,t) +^>2i(m,K, t)T + <pn(m,K,t) ,(1.7.40)
¥>21 (m, A, t) = MNtp(Y, t){YT - mT), (1.7.41)
¥>22(m,K,t) = MNo(Y,t) =
+ Mjv У <(У, t, u)<(r, t, u)Ti/p(t,du). (1.7.42)
*4
Здесь индекс N у знака математического ожидания означает, что оно
вычисляется для нормального распределения N(m, К) вет-
чины Y:
оо
М"( )=(2^ / ( )еХ₽
—ОО
-^(УТ-™Т)К Чу-т) dy.
Число уравнений, позволяющих определить m и ТС, Qmha = р(р +
+3)/2.
Таким образом, в основе метода нормальной аппроксимации од-
номерного распределения (1.7.31) и (1.7.32) в нелинейной стохасти-
ческой дифференциальной системе (1.5.21) лежат уравнения (1.7.37) и
(1.7.39) при (1.7.38), (1.7.40)-(1.7.42) и соответствующих начальных
условиях,
В частном случае единичной матрицы ^'(K,f), ^'(У, t) = I,
i//'(Y)t,u) = 0, имеем <^22(^1» ^>0 = ^(0- Изложенный метод прибли-
женного определения моментов т и К дает те же уравнения, что и
1.7 МЕТОДЫ ТЕОРИИ НЕЛИНЕЙНЫХ СТОХАСТИЧЕСКИХ СИСТЕМ (I) 177
метод статистической линеаризации (МСЛ) Казакова. Действитель-
но, МСЛ основан на приближенной формуле:
^(У, 0 « + fci (У - т), (1.7.43)
где = pi (т, К, 1) и fci = fci (m, К, t) = p?i (m, К, 1)К-1, определяемые
из условия минимума средней квадратической ошибки при допущении о
нормальности распределения У. Заменив функцию p(Y, t) полученной
линейной функцией У, приведем уравнение (1.5.21) в случае ^(У, t) = I
к линейному стохастическому дифференциальному уравнению
Y = pi + fci (У - т) + V. (1.7.44)
Уравнения (1.7.37) и (1.7.39) позволяют получить в этом случае следу-
ющие приближенные уравнения для т и К:
т — pi, (1.7.45)
К = kiK + Kk[ + и. (1.7.46)
Если подынтегральная функция ^"(Y,t, и) в уравнении (1.5.21) до-
пускает представление:
^"(У, 1, и) = 0'(У, t)d(u), (1.7.47)
тогда уравнение (1.5.27) принимает вид (1.5.20):
У = а(У,1) + 6(У,0И\
где
W(t) = W0 + j c'(u)P°(t,du) (1.7.48)
- процесс с независимыми приращениями. Входящие в уравнения
(1.7.37) и (1.7.39) функции (1.7.41), (1.7.42) будут иметь следующий вид:
^(m.tf.t) = [(d/dm)rf]Ttf = ktK, (1.7.49)
<^22(m, К, t) = t)p(W(Y, t)T,
v(t) = vq(1) + J c'(u)c'(u)Ti/p(t,du). (1.7.50)
«S
178
ГЛ. 1. СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
Таким образом, применительно к нелинейной стохастической
дифференциальной системе (1.5.20) в основе метода нормальной ап-
проксимации лежат уравнения (1.7.37) и (1.7.39) при (1.7.38), (1.7.40),
(1.7.49), (1.7.50) и соответствующих начальных условиях.
Для практического применения методов составлены таблицы фор-
мул и fci = [(д/дт)(рТ] применительно к типовым скалярным и
векторным нелинейным функциям (ТСтС, приложение 6).
Многомерные распределения. Аналогично находятся нормаль-
ные аппроксимации всех остальных многомерных распределений про-
цесса Y(t). Так как нормальное распределение полностью определяется
моментами первого и второго порядков, а последние - двумерным рас-
пределением, то достаточно найти нормальное приближение двумерной
характеристической функции ^(Ai, Аг;^!,^)- Для этого следует найти
ковариационную функцию /Г(£1,£2) процесса Y(t). Она определяется
из уравнения
dK(ti,t2)/dt2 = K(ti,t2)K(t2)~1V2i(.m(t2),K(t2),t2)T. (1.7.51)
Это уравнение при любом фиксированном ti представляет собой линей-
ное обыкновенное дифференциальное уравнение, определяющее
К(£1,$2) как функцию t2, ti < t2, при начальном условии K(ti,ti) =
Таким образом, обыкновенные дифференциальные уравнения
(1.7.37), (1.7.39), (1.7.51) определяют последовательно математиче-
ское ожидание m(t), ковариационную матрицу K(t,t) = К (t) и кова-
риационную функцию K(ti, t2) процесса Y(t) в нелинейной стохастиче-
ской дифференциальной системе (1.5.21). Многомерные распределения
(приближенно нормальные характеристические функции и плотнос-
ти) процесса Y (t) имеют вид:
gti...t„ (Ai, • • • , An) = exp (iATmn - |атКпа| (n = 1,2,...),
(1.7.52)
fn(yi 5 • • • ? Уп, tl ? • • • J tn) =
= [(2тг)п|Л'п]-1/2ехр -т^)Л'п1(Уп-’п„)| (n = l,2,...),
I Л J
A= [AfA^...An]T , mn = [my(t1)Tmy(t2')T .my(tn)T]T,
rK(ti,ti) K(t!,t2) ... K(ti,tn)l
t> _ AT(t2,£i) K(t2,t2) ... K(t2,tn)
ЛЛ-п —
K(tn,t2) ... K(tn,tn).
1.7. МЕТОДЫ ТЕОРИИ НЕЛИНЕЙНЫХ СТОХАСТИЧЕСКИХ СИСТЕМ (I) 179
гдеуп = [уТу% ...уТ]т.
Уравнение (1.7.51) применительно к нелинейной стохастической
дифференциальной системе (1.5.21) удобно записать в следующем виде:
dK(ti,t2)/dt2 = £2), £1,^2),
(1.7.53)
где обозначено
оо оо
<P3(K(t1,t2),t1,t2) = [(2тг)2р |К2| ]-1/2 у у (У1 — mtl)<p(y2,t2)T х
— ОО —оо
хехр [-([j/ft/Г] 1([У1’у2’]Т - m2)l dyidy2 ;
zn2 = К2 =
K(t2,t\) K{t2,t2)
(1.7.54)
Определение стационарных процессов. Для приближенного нахо-
ждения характеристик стационарного в узком смысле процесса в нелинейной стохастиче-
ской дифференциальной системе (1.5.20) при стационарном белом шуме V также можно
применить совместно методы статистической линеаризации и нормальной аппроксимации.
В этом случае </?(У, t) = 9?(У), ^(У,£) = ^(У), = У не зависят от времени t,
вследствие чего функции (fli и , определяемые формулами (1.7.38) и (1.7.40), также не
зависят от t.
Для нахождения математического ожидания и ковариационной матрицы значения
стационарного процесса при любом t получим уравнения
=0, ^2(т,7<)=0.
(1.7.55)
Если существуют постоянные вектор ТП и неотрицательно определенная матрица К, удо-
влетворяющие этим уравнениям, и это частное решение уравнений асимптотически устой-
чиво по Ляпунову, то можно предположить, что данное решение характеризует стационар-
ный процесс в системе. Для определения ковариационной функции fc(r) стационарного
процесса из (1.7.51) получим уравнение
dk(r)ldr = у>21(ш, К)К 1к(т).
(1.7.56)
Уравнение (1.7.56) при начальном условии Aj(O) = К определяет ковариационную
функцию стационарного процесса при Т >0. При Т < 0 ковариационная функция
удовлетворяет условию к^т) — к(—т)^\
180
ГЛ. 1. СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
Для стационарной нелинейной системы (1.5.21), когда ^(У, 0 = (р(У),
^(У.О = ^(У), = <(У.и), . vP не зависят от времени, урав-
нения (1.7.54) и (1.7.56) сохраняют вид.
После нахождения Ш, К, к(т) все приближенно нормальные многомерные рас-
пределения стационарного в узком смысле процесса в системе определяются формулами
(1.7.52).
Использование спектрально-корреляционной теории случайных функций для урав-
нения (1.5.20), понимаемого как уравнение Стратоновича, позволяет заменить совместное
решение системы конечных уравнений (1.7.54) и (1.7.55) на решение системы конечных и
интегральных уравнений:
sy = *>(<*>; К) = Ф(гш;m, K)sv(oj)$(wj;m, К)* , (1.7.57)
оо
К — У sv(u;m,K)dw. (1.7.58)
—ОО
Здесь = 1//2ТГ - спектральная плотность стационарного белого шума V;
К) - эквивалентная передаточная (описывающая) функция статистически ли-
неаризованной системы для У°:
Y° = $(s,m,K)V, Y° = Y — m, (1.7.59)
равная
Ф(я;тп,К) = - [а(тп, К) - si]1 Ь(тп, К), (1.7.60)
ГЯеа(т,К) = MN4>(Y,t)Y0T = ^(m./C)^1! b(m,K) = MNil>'(Y,t).
О других методах эквивалентной линеаризации. Задача экви-
валентной линеаризации детерминированной векторной нелинейной функции U =
при использовании критерия минимума средней квадратической ошибки, очевидно, сов-
падает с классической задачей линейного регрессионного анализа. В этом случае опти-
мальная линейная с.к. регрессия вектора U на вектор Y определяется формулой:
mu(Y) = gY, д = ГиуГ~1 (1.7.61)
или, с учетом смещения Q,
mu(Y) =gY + а, д = КиуК~1, а = ти- дту . (1.7.62)
Если векторы U viY действительны и их совместное распределение нормально, регрес-
сии всегда линейны. Поэтому эти формулы определяют регрессию проекции U нормально
распределенного вектора [ JJ^Y^ ] на его проекцию У* в дополнительное подпростран-
ство.
1.7. МЕТОДЫ ТЕОРИИ НЕЛИНЕЙНЫХ СТОХАСТИЧЕСКИХ СИСТЕМ (1) 181
Пусть f (11, у) - совместная плотность случайных векторов U н Y; Шу н Ку - ма-
тематическое ожидание и ковариационная матрица вектора Yy det |Ау | 0. Формула
(1.7.62) для д при этом принимает вид
оо оо
д = КиуК~х = У I (u - mu)(l/ - ту)тK~lf (и, y)dudy =
—оо —оо
оо
“ «»и] (У ~ mv)T К~* fi(y)dy, (1.7.63)
—оо
где fl(y) ~ плотность случайного вектора Y. Эта формула вместе с приближенной
формулой
mu(Y) g(Y - ту) (1.7.64)
дает статистическую линеаризацию регрессии Ши(Уг) по Казакову. Аналогично в случае
(1.7.61) имеем
оо оо оо
^ = Ги„Г“1=У у «фТГ~1/(«*>»Мы4|' = У
—оо —оо —оо
(1.7.65)
Формула (1.7.65) вместе с приближенной зависимостью
ти(У)«дУ (1.7.66)
дает статистическую линеаризацию TTlu(Y) по Бутону.
В случае, когда распределение в (1.7.63) и (1.7.65) является эллипсоидальным, при-
ходим к эллипсоидальной линеаризации (п.1.8.4).
Метод нормальной аппроксимации для дискретных нели-
нейных СТОХаСТИЧеСКИХ систем. Основные уравнения метода нормальной
аппроксимации для нелинейной системы (1.5.58) имеют следующий вид:
7П/+1 = Mn(jJi(Yi, Vi) , mi = MjvYi , I = 1,2,
Kl+1 = MNui(Yt, У«М(УЬ и)т - VfiMNCJifYt, Vt)T,
Ki=MN(Yi-mi)(Yi-mi)T, 1 = 1,2,...,
K(l, h) = MNYiuh(Yh, Vh)T - miMNuh(Yh, Vh)T,
K(l, I) = Ki при I < h, I, h = 1,2,... ,
K(l,h) = K(h,l) = K(h,l)T при I >h,
OO oo
где Мдп(-) = f f (-)fNl(y)riNl(y)dydV't fNl(y) и T}m(v) - нормальные плот-
—oo —oo
кости величин Y) и V|. Отсюда немедленно получаются уравнения для дискретной авто-
регрессионной стохастической системы (1.5.59).
(1.7.67)
(1.7.68)
(1.7.69)
182
ГЛ. 1. СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
1.8. Методы теории нелинейных стохастических
систем (II). Параметризация распределений
1.8.1. Вводные замечания. Обобщением метода нормальной
аппроксимации распределений являются различные приближенные ме-
тоды, основанные на параметризации распределений. Аппроксимируя
одномерную характеристическую функцию д± (A; t) и соответствующую
плотность известными функциями #1(А;0), /1(?/;0), зависящими
от конечномерного векторного параметра 0, мы сводим задачу прибли-
женного определения одномерного распределения к выводу из уравне-
ния для характеристических функций обыкновенных дифференциаль-
ных уравнений, определяющих 0 как функцию времени. Это относит-
ся и к остальным многомерным распределениям. При аппроксимации
многомерных распределений целесообразно выбирать последовательно-
сти функций {5*(Л1, , АП;0П)} и ,уп;^п)}, каждая пара
которых находилась бы в такой зависимости от векторного параметра
0п, чтобы при любом п множество параметров, образующих вектор 0п,
включало в качестве подмножества множество параметров, образую-
щих вектор 0n-i- Тогда при аппроксимации n-мерного распределения
придется определять только те координаты вектора 0п, которые не были
определены ранее при аппроксимации функций Л , ... , gn-i, fn-i-
В зависимости от того, что представляют собой параметры, от кото-
рых зависят функции /*(т/1 , ... , уп; 0п) и #* (Ai , ... , Ап ; 0п), аппрокси-
мирующие неизвестные многомерные плотности /п(т/1,...
..., уп‘, ti , ... , tn) и характеристические функции gn(Xi , • • • , Ап;
^1, - ^п), получаются различные приближенные методы решения
уравнений, определяющих многомерные распределения вектора состо-
яния системы У(£), в частности методы моментов, семиинвариантов,
ортогональных разложений и др. (п.1.3.5).
1.8.2. Метод моментов. Предположим, что параметр 0, от ко-
торого зависят функции g£(A;0), /Г(?/;0), аппроксимирующие одномер-
ную характеристическую функцию #i(A;£) и соответствующую плот-
ность /1(?/;0), представляет собой совокупность моментов вектора Y до
определенного порядка N включительно. В качестве аппроксимирую-
щей плотность функции /*(?/;0) удобно взять конечный отрезок
ее ортогонального разложения вида (п.1.3.5):
h(y,t) « /Г(у;0) = Wi(j/)
N
1 + ЕЕ с^рЛу)
1=3 |р|=/
(1.8.1)
Коэффициенты ср здесь - линейные комбинации моментов случайного
1.8. МЕТОДЫ ТЕОРИИ НЕЛИНЕЙНЫХ СТОХАСТИЧЕСКИХ СИСТЕМ (II) 183
вектора Y (t) до порядка N включительно:
cv - qv{a) (vi, ... , i/p = 0,1, ... , N; |i/| = Ч-к vp = 3, ... , N).
(1.8.2)
Здесь qv (а) представляет собой результат замены всех одночленов
?/р ...урр в выражении полинома qv(y) соответствующими моментами
аГ1 Коэффициенты полиномов ри(у) и qy(y) в общем случае за-
висят от моментов первого и второго порядков вектора Y (t), поскольку
плотность wi(y) в (1.8.1) имеет те же моменты первого и второго по-
рядков, что и fi(y;t).
Для стохастической дифференциальной системы (1.5.21) получим
следующую систему уравнений для моментов аг (ТСтС, п.7.3.1):
N
«г = (1.8.3)
к=3 |р| =к
(гг , •.. , гр) = 0,1 , ... , ЛГ; |r| = 1 , . .. , N) ,
где
Р Г
<Py!r(m,K,t) = £> / Vi • -Ув'-1 ypv,P»(.yyt)wi(.t)Pr(y)dy+
s=l J
р 00
Ч-| Vt'ski's - 1) / • • • У?~2 • • • Ург^(у,t)wi(y)pr(y)dy+
P S-l °°
+ Y,YVsVt / ^i1 yi‘~1........y"’~l yp’asi(.y,t)wipi(y)dy+
s=2 1=1 J™
OO
+ У У([У1 +‘Ф1(у4,и)]‘'1 ... [yp + ^p(y,t,u)],'p -
— oo
p 1
-У11 Урр - 52Vsy^ Уз’~1 Урр‘Ф"(.У>u) Уx
xi/p(t,du)wi(?/)pr(i/)dy. (1.8.4)
При этом функции ^г,о(^? Kjt) получаются из последней формулы при
Рг(у) =Ро - 1.
184
ГЛ. I. СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
Интегрируя систему уравнений (1.8.3) при начальных условиях
= (n,---,rp = O,l,...,TV;|r| =1,...,7V), (1.8.5)
найдем все координаты вектора 0 как функции времени t (а° - моменты
начального значения Yq вектора У(t) при t = to).
Уравнения (1.8.3), очевидно, линейны относительно моментов аг
выше второго порядка, |г| = 3, ... , N, и нелинейны относительно мо-
ментов первого и второго порядков, поскольку плотность wi(^) и ко-
эффициенты полиномов и qv(y) зависят от моментов первого и
второго порядков, вследствие чего и коэффициенты <рг,о? 4>т*и уравне-
ний (1.8.3) зависят от указанных моментов.
При составлении уравнений (1.8.3) в конкретных задачах полезно
иметь в виду, что число N? моментов r-го порядка, а также полное
число моментов порядков, не превосходящих TV, р-мерного случайного
вектора определяются формулами
Qr _Сг _(р + г —1)!
^2р - - °*+р 1 - N\p\ 1
(1.8.6)
Разложение (1.8.1) может быть, в частности, разложением fi(y;t)
по полиномам Эрмита. Можно также пользоваться для аппроксимации
/i(j/;t) отрезком ряда Эджуорта (п. 1.3.6). В этом случае число слага-
емых в сумме (1.8.1) при учете моментов до TV-го порядка возрастает
до 3TV — 6, вследствие чего можно рассчитывать на большую точность
аппроксимации.
Для нелинейной стохастической дифференциальной системы
(1.5.20) основные уравнения для начальных моментов имеют вид:
f { Э(»Х1 )г>... d(iXp)Tr Х
—ОО
х [ iХт<р(у, t) + «) ] е,А v ? fi (у; O)dy
(1.8.7)
или вид (1.8.3) при
оо ^|г|
^•° = / { d(ixly....d(ixpyr
—со
1.8. МЕТОДЫ ТЕОРИИ НЕЛИНЕЙНЫХ СТОХАСТИЧЕСКИХ СИСТЕМ (II) 185
х [:AT¥>(j/,t) + x(^(y,t)TA;t)]etAT’> Wi(y)dy, (1.8.8)
J А=0
00
= / { х
—оо
х [tAT¥>(y, t) + х(Ф(у, *)ТА; t)] е‘*Т,1 Р^у) «Ъ (y)<fy • (1.8.9)
) А=В
Одномерное распределение. Центральные моменты. Для
стохастической системы (1.5.21) уравнения метода центральных момен-
тов могут быть записаны в следующем виде:
N
т = У2 *)?»,(<*), (13.10)
1=3
N
К = ¥>2,о(пг, ЗГ, t) + У2 У? y>2,F(w*>^,0^(a) » (1.8.11)
1=з м=1
где
оо
f <p(y,t)v}!(y)pr(y)dy, (1.8.12)
—сю
оо
^2,„(m, К, t) = У {<р(у, t)(yT - mT) + (у - шМ», t)T+
+ ^(У, * )}wi (y)Pr(y)<hh (1.8.13)
коэффициенты и у>2эо(т, K^t) определяются формулами
(1.8.12) и (1.8.13) при pv = Ро(у) = 1 с заменой р наО;
N
Mr = <Pr,o(m,K,t) + $2 52 ¥>’-.F(m,K,t)ft,(a)-
<=з m=i
(|r| =3, ,N), (1.8.14)
186
ГЛ. 1. СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
где функции </?r>p(m, К, J определяются согласно (1.8.4) путем замены
произведений ... ур на (тд — mJ ... (ур — тр), a es - вектор, все ком-
поненты которого равны 0, кроме s-й, равной 1.
Начальными условиями служат
m(i0) = то, Hr(t0) - (п, ... ,тр = 0,1,...,N; |г| = 2, ... , N).
(1.8.15)
Для стохастической дифференциальной системы (1.5.20) уравне-
ния (1.8.10) и (1.8.14) имеют следующий общий вид:
mh= У ip(y,t)fi(y,e)dy (h = 1, ... ,р), (1.8.16)
—ОО
. _ 7 ( дН-1
J \ d(iXi)ri ... (гХр)гг Х
—ОО
X [гХт<р(у, t) + х(^(у, t)TX; t) ] | х
) Л=0
р 7
*fi(y,6)dy ~Zr^r-eh / <f>h(y,t)ft(y;0)dy (1.8.17)
-oo
(n , ... , rp = 0,1,... , AT; |r| = 2,... , IV)
или в подробной записи
N
m1M> = <Pi,o,h(m,K,t) + У У (h = l,...,p),
k=3 |i/| =k
(1.8.18)
p
pr = frfifrn,, K,t) - У K, t)p.r_eh +
Л=1
1=3 |1/|=Z
p
<pr>v(m,K,t) -^2гк>р1>и>11(т,К,^р.г^ек
h=l
(1.8.19)
(n , ... , rp = 0,1, ... , N; |r| = 2, ... , N),
1.8. МЕТОДЫ ТЕОРИИ НЕЛИНЕЙНЫХ СТОХАСТИЧЕСКИХ СИСТЕМ (II) 187
где обозначено
= У Ph(yA)wi(y)dy, (1.8.20)
—оо
оо
= У <ph(y,t)p„(y)wi(y)dy, (1.8.21)
—ОО
°° д । ।
у,,о(та,к,() = / {a(iA1)/.3(iA[p-*MM)+
— ОО
+ xW’(’M)TA;£)]e,AT(y-m)| Wr(y)dy, (1.8.22)
J л=о
оо
— ОО
+ xWy,t)T^t)]eixT{y-m)] pA.y)wi{y)dy. (1.8.23)
) л=о
Начальные моменты в qp(q) должны быть выражены через цент-
ральные. Очевидно, что уравнения (1.8.10) и (1.8.16), (1.8.18) и (1.8.19)
всегда нелинейны из-за наличия слагаемых вида /zr_ehQI/(a). При при-
менении ортогональных разложений по полиномам Эрмита qy(a) =
— (п.1.3.5) и, следовательно, qp(q) автоматически получаются
как линейные комбинации центральных моментов. При аппроксимации
/1 (?/; t) отрезком ряда Эджуорта (п.1.3.5) следует в коэффициентах ряда
Эджуорта заменить семиинварианты их выражениями через централь-
ные моменты.
Многомерные распределения. Начальные моменты. Для
стохастической системы (1.5.21) многомерная аппроксимация распре-
деления начальными моментами
,..., rip ,... , rni ,... , Гпр (^1 ? • • • ) tn) —
= MYf11 (^)... у;^(^)... Yf"1 (tn)... у;-(tn), (1.8.24)
согласно п. 1.3.5 определяется следующими формулами:
/п(?/1 , • , ?/п;*1 , • •• , *п) ~ /п(?/1 , • •• > Упу^п) = ™п(?/1 , • •• , Уп)*
188
ГЛ. 1. СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
{N I
>+Е Е .................... Pi/i,..., (j/i, - • - j Уп) / ? (1.8.25)
i=i ki|4—и I"» I —i J
J *n /dtn = <pM,...
> &п,0 (mn, Kn, tn)+
N
+52 52 ,«n)x
/=3 pi|4-h|i/n|=Z
XiPK1 ,..., кп,и ,..., pn (^> Km ^n) J
(KI ,..., K| = 1, ... , N, |M| + ••• + K| = n,...,AT), (1.8.26)
где введены следующие обозначения
*P*i ,... , , ... , i/n (й^п-^п? tn) —
on nn
- • • »n-l*p »nl* • • •»«:' 1 • • • Упр’Ч’АУп, tn) X
xwn(»i, , Уп)р^ ,..., (»i, • - - , yn)dyi... dyn+
oo oo
- • • ffnl’i'i* • • • sC-i’p у™ 2 • - »n7a«(s«> *«)x
xtOn(jft , - • , Уп)Рп.............«/.(»!, • • • , yn)dyi... dyn+
+У2 52 i/»«iZnr
OO
—oo
--Уп-1,1 • • • Уп-ljp 9nl*-УпгГ • Упз' УпрГ0*г(Уп> tn) X
XWn(»l , - - • , Уп)р^ , -- ynjdyi ...dyn+
oo oo
-oo -oo h;
1-8- МЕТОДЫ ТЕОРИИ НЕЛИНЕЙНЫХ СТОХАСТИЧЕСКИХ СИСТЕМ (И) 189
• |[»П1 +^'(Уп,*п,«)Г“ •••
• • [Упр + tn,«)]"”’ — Уп“* Упр”-
_ • • у™'-1 • Уп;'#Ч»п,*п,«)}м*п,<Мх
«=1 '
xwn(jd , ... , , yn)dyi .dyn (1.8.27)
(|*i| + • + |*n| = 3, ... , TV; |i/i| +•--+ |vn| =0,1, ... , TV;
KI +•• •+ K| — 3, ... , N).
При этом функции ^«1, —,ж«,о в (1.8.25) определяются (1.8.27) при
Pv!, ,vw(l/i, , Pn) = Ро,...,оЮ = 1 И 1/1, ... , vn = 0. Начальные
условия для (1.8.26) имеют вид
®Г1 , ... , Гж (^1 э - - - , ^п— 1» In—1) — , ... ,Гж-1+гж (^1 J - - - , ^п—1)- (1.8.28)
При составлении уравнении для моментов n-мерного распределе-
ния следует ограничиться только теми моментами, которые зависят
от всех п переменных ti, ... , tn, т.е. для которых ни одна из сумм
|Г1| , ... , |гп| не равна нулю, так как моменты, зависящие только от
части переменных ti, ... , tn, например, от tr+i,... , представля-
ют собой моменты (п — 1)-мерного распределения и, следовательно,
определены раньше при аппроксимации (п — Ас)-мерного распределе-
ния. Естественно, что уравнения (1.8.26) при |ri| = • - — (rn| = 0
совпадают с соответствующими уравнениями для моментов (п — к)-
мерного распределения. Если при всех п аппроксимирующая функция
/*(t/i, ... , Уп,0п) зависит от моментов не выше N-ro порядка, то при
п = N придется составлять уравнения (1.8.26) только для моментов,
соответствующих |ri| = • - - = |гп| — 0, и после определения TV-мерного
распределения все остальные многомерные распределения будут опре-
делены однозначно. В частности, при аппроксимации всех многомер-
ных плотностей, например, согласованными ортогональными разложе-
ниями (п. 1.3.5), с учетом моментов не выше TV-го порядка все многомер-
ные распределения процесса Y(t) будут однозначно определены после
нахождения моментов N-мерного распределения. Уравнения (1.8.26)
при п > 2 являются линейными обыкновенными дифференциальными
уравнениями.
190
ГЛ. 1. СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
В случае нелинейной стохастической дифференциальной систе-
мы (1.5.20) имеем следующую систему уравнений для начальных мо-
ментов при < • • • < tn:
даГ1
гп(*1, , tn)/dtn
—оо —оо
х +х(^(з/п,*п)ТАп;г„)] егХ"Уп > х
J Ап=0
хуГГ • • • у?р” • • • УпГ^1 • • • yrnn-^f*(yi, • • • , Г„;0n)dyi ...dyn (1.8.29)
(Гц , ... , гпр = 0,1, ... , АГ; In I , ... , |rn | = 1, ... , N - п + 1;
|ri| +----1- |гп| = п, ... , N)
или в подробной записи - в виде (1.8.26) при отсутствии пуассоновых
компонент в функциях (1.8.27).
Многомерные распределения. Центральные моменты.
Уравнения для центральных моментов n-мерного распределения слу-
чайного процесса Y (£) при ti < • • • < tn имеют вид
, ... , Гп (^1 ? • • • > ^п) / 9tn = , ... , rn,0 (^п, ^711 ^п) +
N
+£ Е Qpi ,... , Vn (оц , , an)x
fc=3 |pi| ч----------h |pn| =k
P
, ... , rn ,P1 , ... , Vn (jnn, Kn,tn) L'nsP'n , ... ,rn-ea ^s^n)
S=1
(|n| , ... , |rn| = 1, ... , TV; |ri| +••• |rn| =max(3,n), ... , N).
(1.8.30)
Здесь функции срГ1 t... )Гп>Р1,..., pn (™m> Kn, tn) определяются формула-
ми (1.8.27) с заменой степеней т/ц , ... , у±р , ... , уп\ , • • • , Упр на т/ц —
—mi(^i), ... , yip — Шр(^1), ... , yni — Trii(tn), ... , упр — rrip(tn), а на-
чальные моменты в qP1 ,..., Un (qi , ... , оп) заменяются их выражениями
через центральные моменты. Начальные условия для (1.8.30) имеют
вид
Mri , ... , тп (tl , . . • , tn— 1 , tn—l ) = р,Г1 } ... } Гп-14-Гп (^1 > • • • > tn— 1 ) . (1.8.31)
1.8. МЕТОДЫ ТЕОРИИ НЕЛИНЕЙНЫХ СТОХАСТИЧЕСКИХ СИСТЕМ (II) 191
Для двумерного распределения (п = 2) необходимо к уравнениям
(1.8.30) добавить следующее уравнение для ковариационной функции:
9K(ti^t2)/dt2 = <£30(^2, Л2, £2)+
N
+Е Е (а1 > ^2)^3,1/1 ,1/2 (ш2> ^2, £2), (1.8.32)
1=3 |1/1| + |1/2| =1
где
сю сю
¥’з,р1,р2(’п2,К'2,<2) = У ... У [j/i - m(t1)]a(y2,t2)Tх
—сю —сю
Xw2(j/1, y2)pV1,u2(yi, y2)dyidy2 (1.8.33)
(И1,Н1 HI + HI =3,...,N).
При этом функция (рзо определяется (1.8.33) при (2/1,2/2) —
— РодО/ьЗ/г) = 1- Уравнения (1.8.32) и (7.3.45) для п — 2 с началь-
ными условиями K(ti,ti) = Mn,r2(^i?^i) — Mri+r2W определяют
искомое двумерное распределение.
Для стохастической системы (1.5.20) уравнения для центральных
моментов имеют вид
, ... , Гп (^1 1 • • • > ^n) / 9tn —
00 00
= [[{ Q( \ 'г \----------д( \ y~{iXn4>(yn, tn) +
J J (9(%Xni) n • • • 9(iXnp) np
— OO — OO
+x(^(yn,tn)T Xn]tn) exp{i\^[yn — m(tn)]} } [2/11 - m1(t1)]ri1 ... x
J An=0
X [yip -mp(*1)]rip ...[з/п-1,1 “ mi(in_i)]rn~1’1 ... x
x [Уп—i,p mp(^n—i) ] ,p fn(2/1 > • • • ? Уп5 ^n)dyi... dyn
p
rnhPri ,..., rn— eh (1.8.34)
h=l
(rn , ... , rnp = 0,1, ... , N; |n| , ... , |rn| =1, ... , N -n + 1;
|nI 4--+ |rn| =n, , N).
192
ГЛ 1 СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
Приближенное определение стационарных процессов. Для
приближенного определения одномерного распределения стационарного в узком смысле
процесса в стацноварво* веливейно* стохастяческо* дифференциально* системе мето-
дом моментов следует положить 6tr — 0 пли Ду- = 0. Если полученные таким путем
уравнения имеют решение, которое может служить множеством моментов некоторой слу-
чайно* величины, то можно предположить, что стационарный в узком смысле процесс в
системе существует. Для определения других многомерных распределений этого стаци-
онарного процесса следует заменить в уравнениях производные no t„ производными по
Tn—i — tn — tj, а начальные условия записать соответственно в виде
аГ1,.. ,г„(л , ... , т„_2,тв_2) =«n,...,r._i+r.(Ti , - , т„_2) (1.8.35)
ИЛИ
Мп , ...Г.(Т1 , , Т„_2,тп_2) = рг, , ...,г__,+гя(Т1 , ... , Тп_2). (1.8.36)
Метод моментов для нелинейных дискретных систем. Для
нелинейной дискретной стохастической системы (1.5.58) уравнения для
начальных и центральных моментов, определяемых формулами
о? ’ 7’ = MKrV ... Кг7 ... У7\г ... кг;р,
•1 ,---,«ж <11 <1Р <ж1 '»Р
. ;Г: = М(ум - .. (Yhp - mhpY'r
- - (У.1 - mi.iY-1 (У.Р - ’ЧрГ” , (1 8 37)
имеют следующий вид (ТСтС, п.7.3.9):
«Г', = (1.8.38)
<»’u.+l = му?? <у'- -v'- )•••
(1-8-39)
= м[«п(у,у)-мШ|1(у,у)Г1 х ---
. . . х MYhVt) -Мм,(У,У,)Г' , (1.8.40)
Mh,д_+1 = М(У. - тцГ" (1/.-1Р - »»»!._,,)’-*•’>X
X j (у., У.) - м^ж! (У., У.) Г’1 х • •
х [^1_Р(У.,У.)-М^ЖДУ.,У.)]Г-’ , (1-8.41)
1.8. МЕТОДЫ ТЕОРИИ НЕЛИНЕЙНЫХ СТОХАСТИЧЕСКИХ СИСТЕМ (II) 193
где
h < • • • < ln-i <ln] rn , ... , rnp = 0,1, ... , N - n + 1;
Гц , ... , Пр = 0,1, ... , N; |n I = Гц d-F rlp = 1, ... , N;
|n| ,..., |rn| = 1,...,ЛГ-nd-1;
|n | d---F |rn| = n, ... , N] n = 2, , N.
Заменяя неизвестные истинные распределения в формулах
(1.8.38)—(1.8.41) их аппроксимирующими функциями, получаем замкну-
тую систему разностных уравнений, последовательно определяющую
все многомерные распределения процесса {V/}. Уравнения (1.8.38) и
(1.8.40) при начальных и определяют и для всех I > 1.
Уравнения (1.8.39) и (1.8.41) при начальных условиях
“«‘й.,4т- ("-2............") (*•’•«)
определяют соответствующие моменты для всех ln > ln-i-
1.8.3. Методы ортогональных разложений и кваэимо-
ментов. При аппроксимации распределения конечным отрезком ор-
тогонального разложения естественно (п. 1.3.6) принять за параметры
распределения математическое ожидание т, ковариационную матрицу
(от которых зависит эталонное распределение, а следовательно, и по-
линомы рДр), Qi/(p)) и коэффициенты разложения су\
N
1=3 |«z|=/
= Wl(y)
(1.8.44)
Тогда для стохастических систем (1.5.20) будем иметь систему уравне-
ний (ТСтС, п.7.5.1):
N
т = </?io(m,K,t) + ,
1=3 н =i
N
К = ^P2Q(rn,K,t) -F У2 У2
1=3 |i/|=z
(1.8.45)
(1.8.46)
7 Фильтры Калмана и Пугачева
194
ГЛ. 1. СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
cK = <pK0(m,K,t) 4- <p10(m,K,t)Tq™(a) 4- tr [<p2o(m, K, t)q^(a) ] 4-
N
+ 52 52 {y’«v(m,A',t)4-^ilz(m,A',t)Tg™(a)+ tr [q>2v(m, K,t)q*(a)] 4-
/=з 1^1=1
+ 52 12 V>2^m,K,t)}cv (|iz| =3, ... , N),
(1.8.47)
где введем следующие обозначения:
ОО
<pl0(m,K,t)= У <р(у, t)wi (y)dy,
—ОО
OO
—OO
oo
q>2o(m,K,t) = j\<p(y,t)(yT-mT)+
—OO
+(y - rn)<p(y, t)T + iHy, i)T]W! (y)dy,
<^2и(пг, К, t) = У [<p(jz, t)(j/T ~ тт) + (у - т)<р(у, t)T+
—ОО
+ -ф(у, t)r]p„(i/)wi (y)dy,
х
—oo
x [iXTtp(y, t) 4- х(^(1/, t)]etxTy | Wi (y)dy,
) A=0
(1.8.48)
(1.8.49)
(1.8.50)
(1.8.51)
(1.8.52)
(1.8.53)
+ xWy, t)]e,xTy > p„(.y)wi (y)dy-
) x=o
1.8. МЕТОДЫ ТЕОРИИ НЕЛИНЕЙНЫХ СТОХАСТИЧЕСКИХ СИСТЕМ (II) 195
В (1.8.47) начальные моменты аГ1 , ... , аГр в д™(а) и q* (а) долж-
ны быть заменены их выражениями через коэффициенты су в соответ-
ствии с формулами п.1.3.5.
При этом за начальные значения тп, К, си ( |р| = 3, ... , N) при
t = to следует принять соответствующие параметры ортогонального
разложения, аппроксимирующего плотность fo(y) величины Уо:
m(t0) = m0, К= Ко, cy(to) = с„о • (1.8.54)
Замечание!. Уравнения (1.8.45)-(1.8.47) справедливы и в том случае,
когда только qy(y) представляют собой полиномы, а Ри(у) не являются полиномами.
В частности, эти уравнения справедливы тогда, когда правая часть формулы (1.8.1) яв-
ляется отрезком разложения fl(y', t) по производным плотности Wi(y). В этом случае
РЛ.У) = w^^/w^y), a q„(y) есть полиномы.
Замечание2. Если qy(y) не являются полиномами, то предыдущие
выкладки в части вывода уравнений (1.8.47) неприменимы. В этом случае, чтобы выве-
сти уравнения для коэффициентов Су, следует вычислить стохастический дифференциал
функции qy(Y, t) процесса У(t) по формуле Ито и взять математическое ожидание по-
лученного выражения. В результате при нормальном белом шуме получатся уравнения,
аналогичные (1.8.47).
Для стохастической системы (1.5.21) входящие в уравнения (1.8.45),
(1.8.46) функции 92ю(т,К, t) и <piy(m, К, t) определяются формулами
(1.8.48), (1.8.49), а функции </?2о(ттг.,К,t), (p2v(^,K,t) и ipKy(m,K,t) -
формулами
сю
<P2o(m, K,t)~ У [</?(у, t)(yT - тт') + (у - m)ip(y, t)T + а(у, £)]wi(y)dy,
—сю
(1.8.55)
ОО
<p2v(m,K,t) = У [<p(j/)(j/T — mT') + (,y — m)<p(y,t)T + &(y,t)]pvwi(y)(y)dy,
— ОО
(1.8.56)
ОО
= У + |tr +
—ОО
Я?
яЛу) + ^"(У, t, u)) - qK(y) -
оу J
х Vp(t,du) >wi(y)pu(y)dy (|«| , |р| =
(1.8.57)
196
ГЛ. 1. СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
где и имеют вид (1.7.35) и (1.7.36). Уравнение для ск при
этом приобретает следующий вид:
ск = <рко(т, К, t) + t[>™0(rn, К, t)Tm 4-1 tr ^(т, К, t)K j +
N
[ (т, к, t) + VC (т, К, t)Tm ] +
1=з м =1
+ |tr [vA(m,tf,i)k] (|«| = 3,...,N). (1.8.58)
Здесь ipKy(m, К, t) определяется формулой (1.8.57), а
^(m.K.t) = У 9™(г/>1(у)рЛу)Ф (|к| , И =3, ... , N),
(1-8.59)
^(т,К,«) = [ q* (y)w1(y)pv(y)dy ( |«| , М == 3, ... , N).
Замечание. Уравнения (1.8.53) нелинейны относительно коэффициентов
Су. Если отказаться от требования совпадения моментов первого и второго порядков
распределения (у} с соответствующими моментами распределения Л(у;<) и задать
моменты для Wi(?/) априори, то получатся линейные уравнения для Су. Однако при
этом придется взять большее количество членов разложения.
Метод квазимоментов. При аппроксимации плотности t)
отрезком разложения по полиномам Эрмита (ТСтС, приложение 1)
р„(у) = Н„(у - m)/(i/i!, ... , i/p!), q„(y) = Gv{y - m), вследствие не-
го имеем:
су = qvipc) = Gy(jj,), (1.8.60)
Q О
q™ = ~т) = ~'a~GK{y — т} = —KrGK—er(y - т), (1.8.61)
(УПЪр Оуг
q“ = -J^GK(y — т} = -i«r(«r - l)GK_2er(y - т), (1.8.62)
OJS. у? Z
q*rs = G*(y -т) = -KrKaGK-er-e, {у-m}, (1.8.63)
q^r(a) = -кгск-ег. (r = 1, ... ,p; |«| = 4, ... , N}; (1.8.64)
qKrr(a) = -|кг(кг - l)cK_2er, ?£,(«) =-«r«<>c(c_e,._e, (1.8.65)
Xi
1.8. МЕТОДЫ ТЕОРИИ НЕЛИНЕЙНЫХ СТОХАСТИЧЕСКИХ СИСТЕМ (II) 197
(г, s = 1, ... , р; s > г; |я| = 5, ... , 7V),
где ег - вектор, все координаты которого равны нулю, кроме r-й, рав-
ной единице. При |я| = 3 имеем q™(a) = 0 и q^(a) = 0. Таким образом,
при аппроксимации плотности /i (р; t) отрезком разложения по полино-
мам Эрмита элементы матриц q™(a) и q£ (а) пропорциональны соответ-
ствующим квазимоментам. Уравнения (1.8.45)-(1.8.47) для нелинейной
стохастической системы (1.5.20) определяют математическое ожидание
т, ковариационную матрицу К и квазимоменты сД |р| = 3, ... , N).
Согласованные ортогональные разложения многомерных
распределений. Для стохастической дифференциальной системы
(1.5.20) многомерные распределения случайного процесса можно искать
в виде конечных отрезков согласованных ортогональных разложений
многомерных плотностей fn = fn(yi, ••• , yn,ti, • • • , ^n)’
fn = /п(У1, , yn',ti, ... , tn) a f*(yi, ... , yn;0n) = wn(yi, ... , yn)x
где wn = {wn(yi, ... , Уп)} (ft — 1? 2,...) - согласованная последова-
тельность плотностей, имеющих те же моменты первого и второго по-
рядков, что и соответствующие плотности fn, вследствие чего каждая
из плотностей wn зависит, как от параметров, от значений математиче-
ского ожидания m(t) и ковариационной функции K(tyt') процесса У(£)
при t, t* = ti, ... , tn (n = 1,2,...). При этом уравнение для ковариа-
ционной функции процесса У(£), если заменить двумерную плотность
/2(3/1,3/2*, £1,^2) аппроксимирующим ее отрезком ортогонального разло-
жения (1.8.66), имеет вид
dK(t^t2')ldt2 =
N
= </>2o(7ft,/f,ti,£2) + Е Е ^2i/ii/2 ^1, ^2)с1/11/2 (£1,t2) ,
/=3 |*/1 |-+- |ж^2 | =/
(1.8.67)
где
оо оо
(p2o(m,K,ti,t2) = У У [3/1 ~m(ti)](p(y2,t2)Tw2(yi,y2)dyidy2,
—00 —оо
(1.8.68)
198
ГЛ. 1. СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
<P2V^(m,K,t1,t2) =
ОО оо
[j/1 - m(tiy)]<p(y2,t2)Tpl,iu2(yi,y2')W2(yi,y2')dy1dy2 (1.8.69)
—оо —оо
Эти функции </>20 и <£>2i/ii/2 зависят от значений т^2, Kf2 мате-
матического ожидания m(t) и ковариационной матрицы K(t) вектора
Yt и от ковариационной функции K(£i, £2) процесса Y(t).
Уравнения для коэффициентов согласованных ортогональных раз-
ложений многомерных распределений процесса Y (£) приводятся к виду
, /сп (^1 ? ? tn} / dtn — , *п,0 ••• 5 ^п)Н“
{N 1
ЕЕ Cp(tn)<Pi^(mt„, Ktn, tn)T L™ t...,Kn (a)+
1=3 |jz| =i -*
+ tr
N
< ЙоКАЛН YY cv(tn)<P2V(mtn,Ktn
1=3 |i/|=i
tr
V2(mtn,Ktn,tn')T+
N 1
+ 52 52 (th’ (m, K, th, tn)T
/=3 |i/i| 4- |i/2| =1
*n(«) +
N
+E E ^Ki,...,/Cn,i/i,...,i/n ^n)Ci/i,...,i/n (tl, • • • j tn),
1=3 |vi | 4-}- |p„ | =1
(1.8.70)
где |«i | , ... , |«n| = 1, ... , N - n + 1; |/ci| d----------F |«n| — n, , N).
Здесь в дополнение к предыдущим обозначениям принято
<pKi о(тп,К,ti , ... , tn) =
сю оо
/ д \
Q/C1 , ... , Кп ( У1 > • • • > Уп—1> • ) [^П^(3/7М ^n)-h
—оо —оо
+ x(Tp(Vn, ^п)]егА" Уп > wn(j/i, ... , yn)dyx, ... ,dyn,
J A„=0
-f /
(1.8.71)
1.8. МЕТОДЫ ТЕОРИИ НЕЛИНЕЙНЫХ СТОХАСТИЧЕСКИХ СИСТЕМ (П) 199
У3»! , ... , «П,И , ... , (т> ^1 > • • • 1 tn) —
ОО оо
= / ' " / {9ki’ •••’*" (У1’ ” [’An^(l/n3n) +
—оо —оо
4” х(^(?/п? ^n) j ^п)]е п Уп Г Р1?! , ... , Vn (yi , • • • ? Уп) *
j Ап=о
х wn(?/i, ... , yn)dyx , ... ,dyn. (1.8.72)
Эти функции зависят от значений mth = m(th) и K(th,ti) (h,l =
= 1, ... , п) математического ожидания m(t) и ковариационной функ-
ции K(t,t') процесса Y(£), что для краткости показано буквами т, К,
ti, ... , tn в качестве аргументов.
На основании свойства коэффициентов согласованных ортогональ-
ных разложений (п.1.3.5) начальные условия для уравнений
(1.8.70) имеют вид
, ... , Кп (^1 ? • • • ? ^n—1 ? ^n —1 ) — , ... , /Сп-14-/Сп (£1 ? • • • , ^п— 1) • (1.8.73)
Таким образом, для нелинейной стохастической системы
(1.5.20) согласно методу ортогональных разложений сначала следу-
ет проинтегрировать уравнения (1.8.45)-(1.8.47) для приближенного
определения параметров т, К, с„ (\v\ = 3, ... , IV) отрезка разло-
жения одномерной плотности /1 (?/;£) как функции времени t. По-
сле этого, проинтегрировав уравнения (1.8.70) с начальными услови-
ями (1.8.73) при п — 2, t2 > t\ совместно с уравнением (1.8.67) при
начальном условии — K(t±), определим приближенно кова-
риационную функцию K(ti,t2) процесса Y(t) и все оставшиеся неиз-
вестными коэффициенты cU1 V2 отрезка разложения двумерной плот-
ности /2 (?/i, 2/2; ^1, ^2) • Интегрируя далее уравнения (1.8.70) с началь-
ными условиями (1.8.73) для ti < • • • < tn последовательно при п =
= 3, ... , N, приближенно определим коэффициенты сУ1 у...уип отрез-
ков разложения (1.8.66) плотностей fn(yi , • • • , Уп\ ti , • • • Зп) (п =
= После этого коэффициенты отрезков разложений всех
остальных многомерных плотностей процесса Y(t) определятся со-
гласно п.1.3.5, так как при п > N по меньшей мере п — N индексов
равны нулю у всех коэффициентов сУ1 y.„yVn в (1.8.66).
Для нелинейной стохастической системы (1.5.21) уравнения (1.8.70)
имеют следующий вид:
,..., кп (й > • • • ? ^n)/dtn = ,... уКп ,o(mn, Кп, tn)+
200
ГЛ. 1. СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
,..., кп ,o(^n> Кп, ^п) Уп(^п) ~Ь tr ..., кп,о(^^> Кп, tn)K(tn) j +
n-1
кп,о(тп> *n, tn)
dK(tn,th) '
din
N (
+E £ C«1 , ... , Kn,0> ^«1 , ... , Kn,^l , •• , (mn, ^n> ^n)“b
i=3 Ы+ -+ |v„|=/ 1
+CJ ,... ,к„,щ ,...,„„ (™n, кп, t„)ih(tn)+
+ tr [^„...«.^„.„.-.(йпЛпЛ)^)] +
Э/С(tn, th)
dtn
(1.8.74)
/1=1
(kil , • • • , knl = 1, ... , TV; |/€i| 4-h |/€n| = max(3,n), ... , TV),
где
(?71n,/fn? tn) —
сю
—oo
, ... , Kn,H ,
7 f dTqKl,..., Kn (yi, • • • , 2/n) , . v
• J t------------
1
+ 2tr
—oo
d dT
Я д qK1,...,Kn(yi, ••• , yn)o{yn,tn) 4-
. oyn uyn
J qKl(yi, •••,уп-1,уп + ^"(з/п,*п,«))-
-qKt,(3/1 , !/n) - dT<1Ki.К"{У1”",Уп\"(Уп, tn, u)l x
@Уп
xi/p(£n,du)}wn(2/i , ••• , Уп)Риг ,,izn (z/i, ••• , yn)dyx ...dyni (1.8.75)
c,
oo oo
I I qZ, .,^(yi^ >з/п)х
—oo —oo
XWn(i/1, • • • , yn)pV1 (j/i ,••• , yn)dyi ...dyn,
(1.8.76)
1.8. МЕТОДЫ ТЕОРИИ НЕЛИНЕЙНЫХ СТОХАСТИЧЕСКИХ СИСТЕМ (II) 201
ОО оо
V’ki , ... , , ... , Vn (™П, ^n, tn) = J* • • • j Qki , ... , Кп (1/1 > • • • > Уп) X
—оо —оо
xwn(j/i, , yn)Pvlt...,vn(yi > ••• , yn)dyi ...dyn, (1.8.77)
oo oo
... ,Kn,Pi ,... = f /
—oo —oo
xwn(j/i, , 2/п)Рр1,...,рп(2/1 , , yn)dyi... dyn , (Л = 1, ... , n - 1).
(1.8.78)
Функции <pM,...,Kn.o, ^м,...,кл,о, ^£,...,кл,0, ^...,кл,о определя-
ются формулами (1.8.75)-(1.8.78), a pV1,, j,n (j/i, ... , уп) =
= Ро,... ,o(j/i, •• • , Уп) = 1 для i/i, ... , vn = 0.
В частности, для п = 2 уравнение для К(ti,^) должно быть до-
бавлено к (1.8.74). Оно имеет следующий вид:
N
dK(ti,t2)/dt2 = £30(^2, ^2, ^2) + У2 Ct,lt,2(p3^1^2(m2^2it2) ,
/=3 ||?11 + |1/2| =1
(1.8.79)
где функции <рзо, <рз,>/1,1/2 определены формулами (1.8.70).
В (ТСтС, п.7.5.4) выписаны уравнения согласованных разложений
по полиномам Эрмита.
Замечание. Как и уравнения для моментов (п. 1.8.2), уравнения для коэф-
фициентов ортогональных разложений многомерных плотностей процесса Y (t) в практи-
ческих задачах удобно получать дифференцированием случайной функции
Qki ,..., кп (^(tl) • • • (tn)) по tn согласно формуле Ито или общей формуле диффе-
ренцирования сложной функции и вычислением математических ожиданий полученных
выражений с помощью приближенного представления соответствующих плотностей от-
резками их ортогональных разложений.
Приближенное определение стационарных процессов. Для
приближенного определения одномерного распределения стационарного в узком смысле
процесса в стационарной нелинейной стохастической дифференциальной системе метода-
ми, основанными на ортогональных разложениях, следует положить
т = 0,К = 0,ск = 0. (1.8.80)
Если полученные таким путем уравнения имеют решение, которое может служить век-
тором параметров соответствующего отрезка ортогонального разложения одномерного
распределения, то можно предположить, что стационарный в узком смысле процесс в
202
ГЛ. 1. СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
системе существует. В данном случае для определения других многомерных распределе-
ний этого стационарного процесса следует заменить производные по tn производными по
Tn—i = tn — ti, а начальные условия принять в виде
С«1 , • ••, «п (Т1 > • • • > тп—2» Лг-2) = c«i ,..., кп-i+«n (Т1 > • • • > ^п-2) • (1-8.81)
Методы, основанные на ортогональных разложениях, для
дискретных нелинейных систем. Применительно к дискретным
нелинейным стохастическим системам (1.5.58) имеем следующие рекур-
рентные уравнения метода ортогональных разложений:
/п(У1 > • • • > Уп, , ... ,уп,т,К)х
с?1 = MqMYhVt)) =
Мехр{гЛтш/(У1,У/)} ,
\гол/ ]Л=0
(1.8.83)
. (1.8.84)
Здесь
Г Ktl Kkh
т = [т/1...т'[п]Т, К = Khl2 Kh
кТ.,.
Killn -I
Kl2ln
Kln .
(1.8.85)
l/l
d
idXi
{p^ ,,i/n»Q^i, • , ~ биортогональные полиномы, причем
•=An=0
(1.8.86)
ОО оо
У ••• у w(yi, , yn,m,K)pV1 ,...,p„(yi, , Уп)х
—оо —оо
(з/i > • • • > Vn)dyx ... dyn — буцп ... ^»/пдп ,
1.8. МЕТОДЫ ТЕОРИИ НЕЛИНЕЙНЫХ СТОХАСТИЧЕСКИХ СИСТЕМ (II) 203
где I// = I = 1,2,..., , ... , vin = 0,1,..., N;
Ы ,•••, Ы = 1, ••• , N - п + 1, |i/z| = КI + • • • + НР| = п,...
Замечание. В (ТСтС, разделы 7.3-7.5) приведены уравнения модифици-
рованных методов параметризации распределений, позволяющих эффективно находить
распределения для частных классов нелинейных систем.
1.8.4. Структурная параметризация распределений. Ме-
тоды эллипсоидальной аппроксимации и линеаризации. Для
структурной аппроксимации плотностей вероятности случайных векто-
ров будем использовать плотности, имеющие эллипсоидальную струк-
туру, т.е. плотности, у которых поверхностями уровней равной вероят-
ности являются подобные концентрические эллипсоиды (эллипсы для
двумерных векторов, эллипсоиды для трехмерных векторов, гиперэл-
липсоиды для векторов размерности больше трех). В частности, эл-
липсоидальную структуру имеет нормальное распределение в любом
конечномерном пространстве. Характерная особенность таких распре-
делений состоит в том, что их плотности вероятности являются функ-
циями положительно определенной квадратичной формы и = и(у) =
(ут — mT)C(y — т), где m - математическое ожидание случайного век-
тора Y, С - некоторая положительно определенная матрица (ТСтС,
раздел 7.6).
Для нахождения эллипсоидальной аппроксимации плотности ве-
роятности г-мерного случайного вектора будем пользоваться конечным
отрезком разложения по биортонормальной системе полиномов
{рг?Ди(т/)), дг>1/(и(т/))}, зависящих только от квадратичной формы и =
= и(у), функцией веса для которых служит некоторая плотность веро-
ятности эллипсоидальной структуры w(u(t/)):
оо
У w(u(y))pr^u(y))gr,M(u(7/))<fy = <5„м. (1.8.87)
— ОО
Индексы и и // у полиномов означают их степени относительно пере-
менной и. Конкретный вид и свойства полиномов определены ниже.
Однако без потери общности можно принять, что gr>o(u) = pr>o(u) = 1.
Тогда плотность вероятности вектора Y может быть приближенно пред-
ставлена выражением вида
N
f(y) » /*(«) = w(w) 52 сг,«/Рг,^(м), (1.8.88)
1/=0
204
ГЛ. 1. СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
где коэффициенты crjl/ определяются формулой
ОО
Сг,1/ = У f(y)qrAu)dy = МдГ1„(17), (р = 1,...,N).
—оо
(1.8.89)
Поскольку pr,o(u) и qr,o(u) - взаимно обратные постоянные (полиномы
нулевой степени), то всегда сг>орг,о = 1 из (1.8.88) приходим к результа-
ту:
/(р) « /*(и) = w(u)
N
1 Н" ^Г,рРг,1/(ц)
и=2
(1.8.90)
Формула (1.8.90) выражает сущность эллипсоидальной аппрокси-
мации плотности вероятности случайного вектора Y.
Для приложений большое значение имеет случай, когда за распре-
деление w(u) выбирается нормальное распределение
w(u) = w(xTCx) = -/===== ехр(—xTK’_1a:/2); (1.8.91)
учитывая, что С = /С-1, приведем условие биортонормальности (7.6.6)
к виду
оо
2г/2Г(г/2) / РгЛи)ЧгАи)иГ/2~1е~и/2(1и =
7 о
(1.8.92)
Задача выбора системы полиномов {pr,i/(^)> Qf,m(w)}> используемой при
эллипсоидальной аппроксимации плотностей (1.8.88) и (1.8.89), сводит-
ся к нахождению биортонормальной системы полиномов, для которой
весом служит х2‘РаспРеДеление с г степенями свободы. При этом ис-
пользуются следующие формулы:
pr,„(u) = Sr,„(и), (1.8.93)
9г,Л«) = (r+ 2i/-2)!!(2i/)!!'Sr’‘'^’ Г~2' (1-8.94)
8г,Ли) = Srv/2~\u) = (1-8.95)
д=0 '
1.8. МЕТОДЫ ТЕОРИИ НЕЛИНЕЙНЫХ СТОХАСТИЧЕСКИХ СИСТЕМ (II) 205
При разложении по полиномам 5r>I/(u) плотности вероятности слу-
чайного вектора Y и всех его возможных проекций согласованы.
Эллипсоидальная аппроксимация одномерного распреде-
ления. Уравнения метода эллипсоидальной аппроксимации (МЭА) для
нахождения одномерной плотности вероятности р-мерного слу-
чайного процесса Y (t), определяемого стохастическим дифференциаль-
ным уравнением Ито (1.5.20), имеют вид (ТСтС, п.7.6.2):
= Wi(u) N i/=2 , (1.8.96)
ОО Ср,„ = У fl (у; t)qp>v(u)dy = Mqp,v(U) (v = 1,.. -,N), (1.8.97)
N тп = cP,i/9?ii/(m, K, t), i/=2 (1.8.98)
N К = (Р2о(тп,к, t) + У^Ср^2и(.ТП,К, t), v—2 (1.8.99)
где oo
ipio(m,K,t) = У <p(2/,t)wi(u)dy, OO (1.8.100)
OO K,t)= У <p(y, t)pp,v(u)wi (u)dy, —OO (1.8.101)
оо
<p2o(.m,K,t) = У [<p(y,t)(yT-тт) + (у-тп)<р(у,^т+ a(y,t)]wi(u)dy,
—ОО
(1.8.102)
ОО
<p2v(m,K,t) = У [<p(y,t)(yT -тт) + (у- m)<p(y,t)T+
— ОО
+а(2/, t) ]PpAu)wi(u)dlh (1.8.103)
• _ (ср,к-1 КСр,к\
Ср,к — I п Iх
\ 2р р )
206
ГЛ. 1. СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
' N
xtr< АГ-1</?2о(т,+ К~х y^Cp|t/y2y(7n, АГ,<) ► +
< р=2
N
+V>ko(™, к, t) + СруФкЛтп, K,t), к = 2,... ,N, (1.8.104)
р=2
где введены следующие обозначения:
оо
фк0(т,К,г) = У [<?р>к(и)(2(у + tr K~xa(y,t))+
—ОО
+2<7"(u)(y~m)T^ 1ст(М)(г/-"»)+у {9Р,к[(?/Т-Н/’"Т-”гТ)-К' 1(у+^"-7п)}-
-Qp,k(u) ~ 29р,к(и)(У “ т)ТK~1ip"}i/P(T,dv)]w1(u)dy, (1.8.105)
^KV(m,K,t) = У [9р,к(«)[(2(у - т)тK~xip(y,t) + trA'-1<r(i/,t)]+
—ОО
+2q"(u}(y - m)TK~xa(y,t)K~x(y - m)+
+ У {9р,«((уТ + ’Ф"1’ ~ mT)K~l(y + -ф" - т))-
-9Р,к(и) - 29р,к(и)(т/ - m)TK~x^''}i/P(t,dv)]pp<v(u)wi{u)dy. (1.8.106)
Уравнения (1.8.98), (1.8.99), (1.8.104) при начальных условиях
m(t0) = m0, K(t0)=K0, cPiK(t0) = CpK (k = 2,...,N) (1.8.107)
определяют m, К, ср^,..., cp,n как функции времени. Для нахождения
величин Ср к следует аппроксимировать плотность начального значения
¥о вектора состояния системы формулой (1.8.96).
Эллипсоидальная аппроксимация многомерных распреде-
лений. Представим n-мерную плотность вероятности процесса Y (f) в
форме
« /пА(и) =
= W„(u)
N
1+Спр,1/Рпр,1/ (^)
i/=2
Сир,»/ — МдПр, t'(^)*
(1.8.108)
1.8. МЕТОДЫ ТЕОРИИ НЕЛИНЕЙНЫХ СТОХАСТИЧЕСКИХ СИСТЕМ (II) 207
Здесь использованы следующие обозначения:
U = (Уп - mn)TCn(Yn - rhny, Сп = К~\
Yn = [Y1T Y^ ...Y^]-, Yk = Y(tk); (1.8.109)
mn = [mf ml ... m?]; mk = m(tk);
' K(ti,tz) ... K(tM '
К(<2,<1) K(t2,t2) ... K(t2,tn)
.K(tn,«l) ^(^n>^2) ••• K(.tn>tn} .
(1.8.110)
где K(ti,tj) - ковариационная функция процесса У(£);
Г г/п) Ь11 ✓Чп) Ь12 г*(п) 1 • * °1п
Сп = Z^(n) °21 г^(«) ь22 ху(п) • • Ь2п (1.8.111)
р(п) L Gnl ^(п) Ьп2 z-r(n) Lznn J
- матрица, состоящая из блоков cffl размерности р х р; Ck =
= [ ^ki • • • ^kn ] ~ ее ^‘Я блочная строка.
В качестве wn(u) возьмем нормальную плотность вероятности
wn(u) = [ (2тг)п|К„| ]-1/2е-“/2. (1.8.112)
Полиномы рПр,и (м) и Qnp,p(^) определим формулами
Р„р,Л«) = SnPtV(u) = L(-l)t,-M^^l^ - (1-8.113)
~ (пр+2д —2)!!
9п₽,Л«) = (np +(2^_ 2)!!(2i/)!!Pnp’,'(u)' (1-8.114)
Символ п в индексе коэффициентов разложения и полиномов означает
принадлежность к n-мерному распределению.
Уравнение для коэффициентов разложения спр,к примет вид
208
ГЛ. 1. СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
&Спр,к
dtn
Спр,к,—1
2пр
К>Спр,к,
пр
ЭКп
. dtn
ОО оо
+ / / {2?пр,к(и)(Уп -тп)ТСпЧ>(.Уп,1п)+
—оо —оо
+29пр,«(“)(&> - mn)TC^a(yn,tn)Cn(yn - mn)+
+9пр,к(и') ’ ’ [^ПП а(Упь tn) ] + У [9пр,к(й) — ?пр,к(и) —
Я?
-29пр,к(«)(Уп “ ™п)ТСп ^"(уп, tn, v)vp(t, dv) ]wn(u) X
N
1 4" ' Cnp,«/Pnp,|z(«)
i/=2
dyi ...dyn,
(k = 2,3,...,2V),
(1.8.115)
Будем требовать согласованности n- и (n — 1)-мерного распределений
при tn = tn_i + тп, где тп - малая величина, достаточная для обес-
печения существования матрицы Сп. Тогда начальные условия для
уравнений (1.8.115), определяющих коэффициенты разложения, можно
записать в виде
Спр,р(^1» ^2» • • • » ^n—1» ^п— 1 “Ь Тп) — С(п—1)р, 1/(^1» • • • » ^п-1)* (1.8.116)
В случае двумерного распределения п = 2 к уравнениям для коэф-
фициентов разложения (1.8.115) следует добавить уравнение для кова-
риационной функции процесса Y(t):
оо оо
— = У У (yi -mi)(p(y2,t2)TffA-(u)dyidy2, (1.8.117)
—оо —оо
где
/^А(«) = w2(u)
N
1 “Ь С2р,у(й, ^2)Р2р,у(ц)
„=2
(1.8.118)
w2(u) = [ (2тг)2| JCn| ] 1/2exp{-(yn-mn)TKn1(yn-mn)}, (1.8.119)
(2р + 21/-2У'
P2p,,(u) = S2p.,(u) = V?.t. . 1..|Цм. (1.8.120)
д — Q \^P '
1.8. МЕТОДЫ ТЕОРИИ НЕЛИНЕЙНЫХ СТОХАСТИЧЕСКИХ СИСТЕМ (II) 209
К этому уравнению следует добавить начальное условие K(ti, ) =
= Ввиду вырожденности двумерного распределения при t2 = ti
уравнение для ковариационной функции до момента ti + т2 интегриру-
ется при вырожденном распределении
N
и Wi(u) 1 + 52ciPip(ti)plp,F(u) 6(yi - у2),
и—2
(1.8.121)
а начиная с момента ti + т2 - совместно с уравнениями (1.8.117). Ве-
личина т2 определяется в процессе интегрирования, когда матрица JC2
станет невырожденной.
В основе метода эллипсоидальной аппроксимации многомерных
плотностей в нелинейной стохастической системе (1.5.20) лежат уравне-
ния (1.8.98), (1.8.99), (1.8.104), (1.8.115), (1.8.117) с соответствующими
начальными условиями.
Определение стационарных процессов. Для приближенного опре-
деления одномерного распределения стационарного в узком смысле процесса в стационар-
ной нелинейной стохастической системе методами, основанными на эллипсоидальной ап-
проксимации распределений, следует положить в уравнениях (1.8.98), (1.8.104), (1.8.115)
т = 0, К = 0, Ср,к - 0, k = 1,...,N.
(1.8.122)
Если полученные таким путем уравнения имеют решение, которое может служить векто-
ром параметров соответствующей эллипсоидальной аппроксимации одномерного распре-
деления, то можно предположить, что стационарный в узком смысле процесс в системе
существует. В этом случае для определения других многомерных распределений этого
стационарного процесса следует заменить в уравнениях (1.8.115) производные по tn про-
изводными по Tn—i — tn — £1, а начальные условия (1.8.116) принять в виде
^пр,к(^1» • • • » ^п—2, Тп—2 "Ь Д) — С(п—1)р,к(^1 , • • • , 7"п—2), (1.8.123)
где Д - малая величина, обеспечивающая невырожденность матрицы С в уравнениях
для параметров распределения. *
Замечание. Метод эллипсоидальной аппроксимации переходит в ме-
тод эквивалентной линеаризации для эллипсоидального распределения, если принять в
(1.8.90) известную зависимость СК = Ск(т?1,/С, t) и ограничиться уравнениями (1.8.98)
и (1.8.99).
210
ГЛ. 1 СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
1.9. Дополнения и задачи
1.9.1. Показать, что для устойчивой стационарной линейной системы
у =ау + Ьх, у = [7/13/2]Т , X = [a:iX2 ]Т ,
где а, Ь - постоянные квадратные матрицы, у - выходной сигнал, матрица передаточных
функций имеет следующий вид:
Ф(8) = -(а-5/)-1Ь=-^-[-(a22-s) ai2 lb,
Д(«) [ в21 -(an - s) J
Д(в) — s2 — (ац + 022)5 + 011022 — 012021 .
1.9.2. Показать, что для устойчивой стационарной системы задачи 1.3 при Оц =
— ^22 — &12 — ~&21 = > 0) матрицы фундаментальных решений
u(t,T) и передаточных функций Ф($) определяются формулами
u(t, т) = е т)
COS w(t — т) sin Cj(t — T)
— sincu(f — r) coscu(f — т)
1.9.3.
Показать, что для стационарной линейной механической системы с одной
степенью свободы (Булгаков 1954)
я
р
О 1/А 1 [Я 1 .Г О
-С -В/А ] [ р ] + [ Q
где обобщенная координата Q — 1/1 и обобщенный импульс р = Aq — У2 ~ компоненты
вектора состояния У — [ 2/12/2 ] ; Ж = [ О, Q ] “ входной сигнал; у - выходной сигнал
системы; А(А > 0) В, С - постоянные коэффициенты, определяющие инерционную,
диссипативную и позиционную силы, матрицы фундаментальных решений ?1(£,т) и пе-
редаточных функций Ф($) имеют вид
u(t,r) = е т)х
coswc(t - г) + sin wc(t - г)
Аа$ . , ч
-т)
-г— sinwc(t — г)
Ашс >
coswc(t - г) - sinwc(t - т)
Ф(з) =
1
As2 + Bs + C
As2 +Bs + C
(2e = В/A ,cj2 = o)q — e2 ,a)g = C/A).
О
О
1.9. ДОПОЛНЕНИЯ И ЗАДАЧИ
211
1.9.4. Показать, что для линейной нестационарной системы
3/1 = 2/2 , У2 = -Ct 2yi+x, t > 0,
элементы матрицы фундаментальных решений и(£,т) при 27 = \/|1 - 4с|, с < 1/4,
определяются формулами (Михайлов 1986):
1 /i\ 1/2 Г /т\7 //\7
un(t,r) = — pi + 27)(-) -(1-27)^-J
/. ч (т«)1/2[ру /П71
^,r) = —~(?) ] ,
1 / f \ /т\У
Найти u(tj Т) при С > 1/4.
1.9.5. Доказать, что для нестационарной линейной системы
У1 = J/2 , У2 = -t 2yi-t гу2 + X , t > 0 ,
матрица фундаментальных решений u(t, т) равна (Михайлов 1986)
COS 1П у: Т Sin 1П у:
— | sin In у COS In .
1.9.6. Доказать, что весовая функция нестационарной линейной механиче-
ской системы
У + t~Ly + (1 - n2t~2)y = х, y = z,
имеет вид (Свешников 1961):
д(!,т) = [ Jn(r)Nn(*) - Nn(t)Jn(t)]r,
где <7п(т) и Nn(t) - функции Бесселя первого и второго рода соответственно.
1.9.7. Показать, что для стационарной линейной системы
z — az-^bx, y = Z, Z = [ZiZ2Zs]T , X = [х±Х2Хз]Т
212
ГЛ. 1 СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
где Q, и - постоянные квадратные матрицы, у - выходной сигнал, элементы матрицы
передаточных функций Ф(з) = — (<1 “ з!))~^Ь при Д($) — |<1 — з/| определяются
формулами:
Фи ($) = — b [s2 — 3(0,22 4- <133) + <122<1зз ~ <123<132 ] /Д($),
Ф12($) = 6(-sai2 4- 012^33 ~ <132<11з)/Д(з),
Ф13($) = —bfsais 4- 012^23 ~ 0,13022)/Д($),
Ф21(Ю = Ь(-Зй21 4- ^21^33 - <131<12з)/Д($) ,
Ф2г(з) = — Ь [$2 — $(<1ц 4- азз) 4- <1ц<1зз — <113<131 ] /Д($),
Фгз($) = &(—$<123 4- <1Ц<123 “ <121<11з)/Д($) 1
Фз1 ($) — —Ь(заз1 4- <121<132 — 0,31022)/^(з) ,
Фзг($) = Ь(—зоз2 4- ацаз2 — <*12^31)/Д(5),
Фзз($) — ~Ь [$2 — $(<1ц 4- 022) 4- Оцй22 — <112<121 ] /Д($) •
1.9.8. Показать, что для стационарной системы задачи 1.9 при Оц — O31 =
— <113 ~ O32 — 0, <112 ~ <123 ~ 1» <121 = —а22 ~ —2в, О33 = ~<* элементы
матрицы передаточных функций определяются следующими формулами:
$п(з) = — b [з2 + (2е 4- a)s + 2ае] /Д(з),
$12(3) = -b(s + а)/Д(з), Ф1з(з) = -Ь/Д(з),
$21 (з) = Ьшо(з + а)/Д(з), $22(3) = -6з(з + а)/Д(з),
$23 (3) = —6в/Д(з) , $31 = $32 = 0,
$зз(з) = -b(s2 + 2es + о»о)/Д(з), Д(з) = -(з + а) [ц, + (2е + з)з] .
Проверить, что элементы матрицы и(^,т) фундаментальных решений равны:
ui3(i,r) = (-l/w2)[un(t,r) +a/uou2i(t,r) -u33(i,r)] ,
«31 = «32 = 0, «зз(^т) = ехр {-a(t - т)} ,
«2з(*,т) = (- 1/w2) {«2i(t,T)(l - 2ea/oio) - a[un(t,r) - «зз(*,т)]} ,
а функции Иц, 1112, и2Ъ и22 определены в задаче 1.5.
1.9.9. Показать, что для стационарной линейной механической системы с 71 степе-
нями свободы дифференциальные уравнения движения имеют следующий вид (Булгаков
1954):
а) в лагранжевых переменных
Aq+(B + B')q + (С + C')q = Q ,
1.9. ДОПОЛНЕНИЯ И ЗАДАЧИ
213
где q = [ Qi . . . qn ]- вектор обобщенных координат, Q = [ Qi . . . Qn - вектор
обобщенных сил; в данном случае вектор у — q представляет собой выходной сигнал,
а вектор X = Q - входной сигнал, А - симметричная матрица инерционных коэф-
фициентов, В - симметричная матрица диссипативных или ускоряющих сил, Bf - ан-
тисимметричная матрица гироскопических сил, С - симметричная матрица позиционно
консервативных сил, С1 - антисимметричная матрица позиционно неконсервативных сил;
б) в канонических переменных
где q и р = Aq - вектор обобщенных координат и вектор импульсов; в данном случае
Г Т TVT
при тех же входном и выходном сигналах [Q р J - вектор состояния системы.
1.9.10. Показать, что нелинейное уравнение
п — 1
У(П)+ 52 =
к=п—тп
тп
= 52 bh(y’у' ’ • • • ’ J/(n~m-1), t)xw , (m<n)
n=0
заменой переменных
Z1 = У, Zk+1 = z'k, (k = 1, ... , п - m - 1),
zjt+i = z'k - , ... , zn_m, t)x, (k = n-m, ... , n - 1)
приводится к системе уравнений
zk = Zk+1, (к — 1, ... , n - m - 1),
z'k = Zk+i + qk(zi, , zn-m,t)x , (fc = n - m , ... , n - 1),
n
z'n = - 52 a«-l(zl > ••• > zn-m,t)zi ->p(zi, ... , zn_m,t) +
l=zn—m—l
4" Qn(zl ? • • • > zn—тч ?
где функции qn—m > • • • > Qn ПРИ an — I определяются формулами (1.2.37).
1.9.11. Рассмотрим функционально-дифференциальную систему
y = f(yt0,i), y(.to) = Уо- (I)
214
ГЛ. 1 СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
Пусть функция f — f (?/|0, t) представима в виде
t
f = f(y,U)t})U = j F(t,T,y(r),u(r))dT) F(t,r,y,u) = w(t)T)(p(y,u,T).
to
(П)
Здесь - весовая функция физически реализуемой асимптотически ус-
тойчивой линейной системы
С = аС + «199, Г] = /3(,
где Ot, /3, Qi - некоторые матрицы. В этом случае функция U определяется из уравнений
и = Ру', у' = ay' + aiip(y,и,t), y'(t0) = О,
и системы (I), (II) приводятся к дифференциальной системе вида (Синицын 1986):
У = У (to) = Уо, ,п„
у' = ау' + ацр(у,&у',t), у'(to) - 0.
1.9.12. Пусть при условиях задачи 1.9.11 в (II) функция при F(t, т, у, и) =
— где - известная матричная функция времени, а
<р(у,и, т) - известная векторная функция указанных аргументов, если принять
и = il>(t)y', у' = <p(y,u,t), у'(to) = 0,
тогда исходная система (I) задачи 1.9.11 приводится к дифференциальной системе (Си-
ницын 1986)
У = f(y,^y',t), y(t0) = Уо, у' = ip(y,i/ry',t), у'(to) = 0.
1.9.13. Показать, что если в условиях задач 1.9.11 и 1.9.12 принять соответственно
N
F(t,r,y,u) = ^wi(t,rypi(y,u,r\ (I)
Z=1
N
F(t,T,y,u) = «>т), (П)
1.9. ДОПОЛНЕНИЯ И ЗАДАЧИ
215
то уравнения и (11) приводятся к уравнениям задач 1.9.11 и 1.9.12, если ввести блоч-
ные матрицы
w(t,r) = [wi(f,r)...wjv(t,r)], V’(i) =
Ч>(.У, и, т) = [</?! (у, U, т)Т ... <PN(y, и, т)Т]Т.
1.9.14. Показать, что интегродифференциальные уравнения движения системы с
одной степенью свободы под действием переменной силы в среде, подчиняющейся
закону наследственной вязкоупругости
t
У1=У2, У2 = -СУ1- j $(t-r)<p(i/i(r),T)dT + a:(t), (I)
to
при экспоненциальном ядре влияния Ф(£ — т) = Ьв~^~т^ и у± (£q) — 2/10> £/2(^0 ) ~
— t/20 ? приводятся к трехмерной дифференциальной системе:
У1 = У2, У2 = -СУ1 - (Ь/А)у3 + x(t), Уз = A(j/1 - Уз),
У1М = У10, Уг(«о) = У20, 2/з(«о) = о. (II)
Здесь Т/l ~ обобщенная координата, У2 - обобщенная скорость, С - коэффициент упру-
гости, Ф(£ — т) - ядро, отражающее влияние наследственной вязкоупругости среды,
<р(г/1, т) - зависимость силы от обобщенной координаты 2/1» в общем случае нелинейная.
1.9.15. Доказать, что для приводимости скалярной случайной функции
Y(t) = bo(t) + &i(t)X(t) к стационарной линейным преобразованием необходимо
и достаточно, чтобы ее ковариационная функция зависела от разности аргументов:
Kx(t,t') = Kv(t,t')/y/Dv(t)Dv(t>) = ry(t - t').
Дать обобщение на случай функций в конечномерных и бесконечномерных пространствах.
1.9.16. Доказать, что для приводимости к стационарной случайной функции
У(«) = bo(t) + bi(t)X(<p(t)) путем линейного преобразования с одновременной за-
меной аргумента, необходимо и достаточно, чтобы отношение £ частных производных ее
корреляционной функции могло быть выражено в виде взятого с обратным знаком отно-
шения значений некоторой функции ((/9 — *0) при значениях аргумента, равных tut1
соответственно:
dRy(t,t')/dt = = Ky{t,t')
dRy(t,t')/dt‘ > y/Dy(t)Dy(t')
216
ГЛ. 1 СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
Дать обобщение на случай случайных функций в конечномерных и бесконечномерных
пространствах.
1.9.17. Пользуясь результатом задачи 1.9.16, доказать, что случайная функция Y(t)
с ковариационной функцией
Kv(t,t') = <? exp{-ft2(t2 + t'2) - l\t - t')2[a + b{t +1') ]2}
приводится к стационарной при (/>(£) — dt 4- Ы?.
1.9.18. Пользуясь результатом задачи 1.9.16, доказать, что случайная функция Y(t)
с ковариационной функцией
= Dexp{/i(t + t') - - f|}
приводится к стационарной преобразованием Jf(s) = 6~~^Y(t}, 8 = , где A^(s) -
стационарная случайная функция с экспоненциальной ковариационной функцией
Rx(a) = De~a\a\, а — з — s'.
1.9.19. Пусть функция tZ), t, t' € 71, является ковариационной функцией
случайного процесса, a -R('u) - полиномом с положительными коэффициентами. Дока-
зать, что функция = R{K(t^t')) также является ковариационной функцией
некоторого случайного процесса.
1.9.20. Показать, что скалярные стохастические дифференциальные уравнения с
0-дифференциалом первого порядка:
1)У = -E(l + V2)Y + kVi,
2) Y = (1 + V2)<p(r) + kVi,
з)У = ЫМ+£Ж0И
1=1
приводятся к следующим стохастическим дифференциальным уравнениям Ито:
I) Y = —е(1 - 2051/22 + V2)Y + fc(-20ei/2i + Vi),
2) Y = [ 1 + 20ei/22<p'(Y) + V2 ]</>(У) + 20i/12<p'(^) + Vi ],
з) У = <p0(Y,t) + в £ i/pqtpp(Y,t)<p'q(Y,t) + £ <pi(Y,t)Vi,
p,g=l 1=1
где ip = dip/dy -, V = [ Vi ... Vn ] T - нормально распределенный белый шум интен-
сивности I/. При каких условиях уравнения Ито совпадают с исходными уравнениями?
1. 9.21. Пусть Y(t) - такой 72 — 1 раз с.к. дифференцируемый случайный процесс,
что его (?2 — 1)-я с.к. производная имеет дифференциал Ито
= <р(У, Y,..., У<п-1>, *)<ft + i/>(Y, Y,..., y(n-1), t)dW.
Это соотношение называется стохастическим дифференциальным уравнением Ито П-го
порядка относительно процесса Y(t). Его можно также записать в виде
У(п> = у>(У, Y,...,у(”-1>, t) + V>(y, Y,..., У*”-1), t)v,
1.9. ДОПОЛНЕНИЯ И ЗАДАЧИ
217
где V = dw/dt — белый шум в строгом смысле. Доказать, что это уравнение при-
водится к стандартной форме стохастического дифференциального уравнения Ито для
некоторого ft-мерного векторного процесса. Более общее стохастическое дифференци-
альное уравнение ft-го порядка
п—1
k—n—т
т
= 52 М*', у, • • •, уС”-"»-1), t)yw
Л=1
при 0 <2 ТП <2 ft понимается как эквивалентная система стохастических дифференциаль-
ных уравнений первого порядка. В случае винеровского процесса W (£) вывести формулы
перехода от уравнения Ито ft-го порядка к уравнению в 0-дифференциалах ft-го порядка,
и наоборот.
1. 9.22. Показать, что скалярным стохастическим дифференциальным уравнениям
второго порядка с ^-дифференциалом:
1) У + 2^о(1 + Уз)У + ш§(1 + У2)У = fcVi,
2)У = <ро(У,У,0 +Е^(У,У,«)И
1=1
соответствуют следующие стохастические дифференциальные уравнения Ито:
1) У + 2£о?о(1 ~ 201/зз£а>о + Уз) У + Ц>(1 “ 201/2з£Н) + Уг)У =
= к(—20^1/13^0 4- Ц),
/,/1=1 1=1
где </>д(У, У, t) = diph(Y\ У, £)/dY, V = [ V1 ... Vn ]Т — нормально распределен-
ный белый шум интенсивности I/. Найти условия, при которых уравнения Ито совпадают
с исходными уравнениями.
1.9.23. Проверить, что для нелинейной системы второго порядка
У + 2еУ + <р'(У) = V (е > 0),
где V - стационарный нормально распределенный белый шум интенсивности 1/; (р(у) -
нелинейная функция; (р1 (?/) — Bip(y}/By. Одномерная плотность и характеристиче-
ская функция стационарного в узком смысле процесса определяются формулами
fi(y>y) = сехр{-Л2[у>(г/) + у2/2]} (ft2 = lev),
__ оо
51(Д',Д«) = [ eiX’v~h^dy,
h J
—оо
218
ГЛ. 1 СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
где С - нормирующая постоянная. Рассмотреть частные случаи: а) ф'(у) —
= СЧУ + азу3; б) <р'(у) = asgnj/; в) ip'(y) = a sin у.
1.9.24. Показать, что одномерная плотность стационарного в узком смысле процесса
в 71-мерной нелинейной системе
Y = ^(У) - 2еаГ + bV, е > О,
где V'(y) = [V’i(y) ••• ‘Фп(.у)]Т, дфк^/дук. = 0 (к = 1,...,п),
п
УТф(у) = £ УкФк = 0; V - нормально распределенный 71-мерный стационарный
к=1
белый шум с независимыми компонентами одной и той же интенсивности 1/; Ь - по-
стоянная П X Ш-матрица; CL - постоянная П X 71-матрица, удовлетворяющая условию
а 4- ат = 2ЬЬТ , определяется формулой (Пугачев, Синицын 1985):
/1(3/) = \/ап/'ппе~ауТу, а = 4е/к
Для случая единичных матриц CL и Ь эта формула получена в (Должанский и др. 1974).
1.9.25. Показать, что одномерная плотность стационарного в узком смысле процесса
в системе
Y = atp'(Y) + bV,
где - нелинейная функция ф1 (?/) = ^^(?/)/tty', Ъ - постоянная (прямоугольная в
Т
общем случае) матрица; а - постоянная матрица, удовлетворяющая условию CL 4- CL =
= 2bbT-, V - стационарный нормально распределенный белый шум с независимыми
компонентами одной и той же интенсивности 2/, определяется как (Пугачев, Синицын
1985): /1(1/) — Св^^у^и, где С - нормирующая константа.
1.9.26. Показать, что одномерное распределение стационарного в узком смысле про-
цесса Y(t) = [ Y\ (t) Уз (£) в нелинейной стохастической системе
Yi= asgn(V2 -PYk), Y2 = -Yr + V,
где Ot и (3 - постоянные коэффициенты; V - стационарный нормально распределенный бе-
лый шум интенсивности Р, определяется по формуле Фуллера (Баррет 1960):
/1(У1,У2) =сехр{-0(у? + 2а|7/2-0У1|)Л}- Здесь С - нормирующая константа.
Найти соответствующую характеристическую функцию.
1.9.27. Показать, что одномерное распределение стационарного процесса в нелиней-
ной механической системе
q = дН/др, р = -dH/dq - 2ер + b(q)V, b(q) = Л(д)1/2,
где q = [qi . .. qn и р — A(c[)q = [pi .. . рп]^ - векторы обобщенных ко-
ординат и импульсов; Н — H(q,p) — рТ^р/2 4- Щд); Щ#) - потенци-
альная энергия; V = [И ... Vn]T - вектор обобщенных сил, компоненты которого
1.9. ДОПОЛНЕНИЯ И ЗАДАЧИ
219
представляют собой независимые нормально распределенные стационарные белые шу-
мы одинаковой интенсивности Р, определяются формулой (Пугачев и Синицын 1985):
/х(<7,р) — се~аН, а — te/v, где С - постоянная нормировки. Отсюда, в частности,
для 6(q) = I получаем известную формулу Гиббса (Гиббс 1928).
1.9.28. Показать, что функция /1 = fi (?/; t) будет решением уравнения Фокке-
ра-Планка-Колмогорова для уравнения (1.5.20) с нормальным белым шумом V тогда и
только тогда, когда векторная функция CL = в(1/, t) допускает представление (Мощук,
Синицын 1992а,б)
а(т/, t)=a{(y,t) +а^(у, t) (I)
такое, что функция fl является плотностью инвариантной меры обыкновенного диффе-
ренциального уравнения
y = a}(r,i), (II)
т.е. удовлетворяет условию
% + = °- <ш>
а соответствующая функция ~ определяется формулой
lz 1Г ain/i (дт /nn
1.9.29. Предположим, что для уравнения (1.5.20) при нормальном белом шуме V
известны представление векторной функции t) в виде (I) задачи 1.9.28 и неотри-
цательная скалярная функция являющаяся плотностью интегрального
инварианта (II) задачи 1.9.28. Пусть, кроме того,
1) существует обратная матрица диффузии (Т \ det |(Т | 0;
2) векторная функция "Ух — 'ух (1/, Z), где
71 (.У,*) = ° 1
1 1 Г д ( t А
удовлетворяет условию отсутствия вихря
д^и/дУз = d^j/dyi (i,j = 1,... ,р);
3) скалярная функция Fl — Fi (у, t), где
Fi(y,t) = / y{(y,t)dy,
220
ГЛ. 1 СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
является первым интегралом уравнения (11) задачи 1.9.28;
4) выполнено условие нормировки
J (у, (у, t)dy = 1.
Тогда существует случайный процесс Y = V(i), для которого одномерная плот-
ность fi(y, t) определяется формулой (Мощук, Синицын 1992а,б):
= Mi(y;i)expFi(y,t). (I)
Соответствующие формулы для переходной и многомерной плотностей даны в (Синицын
1993).
1.9.30. Показать, что функция f), являющаяся плотностью интеграль-
ного инварианта уравнения (II) задачи 1.9.28, будет плотностью одномерного распределе-
ния случайного процесса Y — Y(t), определяемого уравнением (1.5.20) при нормальном
белом шуме с невырожденной матрицей диффузии О (det |(71 0) тогда и только тогда,
когда существует матричная функция = {у, t), такая, что
= (дА1/ду)т, Ai + = CT/л, (I)
где ~ —а} (Мощук, Синицын 1992а,б). Соответствующие формулы для переходной
и многомерной плотностей даны в (Синицын 1993).
1.9.31. Показать, что решение задачи 1.9.29 для системы с вырожденной полной
матрицей диффузии, когда
У' = Q(y',y",t), Y" = P(y',y'U) + 6о(К,,У,,^)Уо, (I)
где Y = [Y'tY"t]T, Y' «Y" - S-мерные векторы, 2s — р, Vo - Г-мерный нор-
мальный белый шум интенсивности Ц) — ^о(^)» Р ~ размерностьь вектора У; Oq —
= bQ{Y\Y\t)yQ(t)bQ{Yl,Yn,t)T - невырожденная (частная) матрица диффузии
белого шума Vo, дается следующими формулами (Мощук, Синицын 1992а,б):
/i(j/',2/",*) = Д1(у' ,У" ,t)expFi(y' ,у" ,t), (II)
W,y",t) = frfdy'dy", (III)
7i(y',y",t) = Сто ^2 , дун/ду, = d^ij/dyi, (IV)
+ + = °' <V)
1.9. ДОПОЛНЕНИЯ И ЗАДАЧИ
221
P = Pl + Pl. (VI)
иу
1.9.32. Показать, что решение задачи 1.9.30 для системы с вырожденной полной
матрицей диффузии возможно тогда и только тогда, когда выполнены условия (Мощук,
Синицын 1992а,6):
= (дВ1/ду")т, Bi+B{ = (I)
где Рг = Р- Pi; - плотность конечного интегрального инварианта уравнений:
У' = Q, Y" = Р}. При этом h(y',y",t) = (Л1(у',у",у).
1.9.33. Показать, что для любых векторов Q, р и любых векторных функций
Q(q»P)» Pisi^P) той же размерности, что и векторы Q, р соответственно, при условии
существования функции 7V(q), удовлетворяющей уравнению в частных производных
дт дт
-^-[N(q)Q(q,p)] + N(q&-P(p,q) = О,
oq op
одномерное распределение процесса в системе
Я ZT
9 = <2(9>Р), Р = Р(9.Р)-2е(Я)а(д)-д- + г>(д)У, (I)
ор
где Ь(</) - произвольная прямоугольная матрица; £1(q) - произвольная квадратная мат-
рица, удовлетворяющая условию o(q) = 2Ь(^)Ь(^)^; Н = H(q,p) - первый
интеграл уравнений (I) при o(q) = b(q) = 0; 2е(Н) - коэффициент вязкого трения;
V = y(t) - нормально распределенный векторный белый шум с независимыми компо-
нентами одной и той же интенсивности I/, может быть представлено формулой (Пугачев,
Синицын 1985):
Я
/1(9,Р) =cN(q)e~0^H\ = j e{rj)dq, р = 1/и. (II)
о
В частном случае одинаковой размерности векторов q и р при Q^q^pj —
= dH(q,p)/dp, P(q,p) = -dH(q,p)/dq, N(q) = 1 и из формулы (II) следует
формула задачи 1.9.27. При € = COBSt формула (II) принимает вид (Мощук, Синицын
1990): fi(q,p) = cN(q)e~aH(q'p\ а = 4б/к
1.9.34. Показать, что для одномерной нестационарной стохастической системы
У = a0(t) + a(t)y + 6(У, t)V, b(Y, t) = y/C(t)Y, Y(t0) = Yo, (I)
222
ГЛ. 1 СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
где V - нормальный белый шум интенсивности l/(i)), уравнение Пугачева для одномер-
ной характеристической функции имеет вид (Силуянова 1981):
5i (A; t) = g0(ip(t,X) !)ехр
•ф(т, A))a0(r)dr
Здесь
ехр
ф(т, <p(t, Л)) =
fa^^dri
*0
i/2f i/(ti)c(ti) ехр
*0
f a(a)da
to
dn + t)
При постоянных CLq, CLt С и V — 1 и начальном условии ро(А) ~ (1 “ 2lJDo)
9i(X\t) = [exp(a^) — zcA(exp(at) — l)/2a]~2aa° x
X [ 1 - 2iDor(t) Г1/2 exp (2^) , (III)
где r(^) = A[exp(a^) —icA(exp(a£) — 1)/2а] \ Найти стационарные решения
(III). Дать обобщение на случай векторного уравнения (I), когда b(y,t) =
= diag [bx{y,t).. .bp(y,t)\b2j(y,t) = Cj(t)Ty.
1.9.35. Показать, что в условиях предыдущей задачи многомерная характеристиче-
ская функция определяется рекуррентной формулой (Силуянова 1981):
9п(^1 > • • • j j ^1 > • • • j ^п) = 9п-1 (А1 , . . . , An-i 4-
+<р 1 (tn, Лп); tj, ... , tn-i) ехр
Ап))оо(т)<1т
(I)
где П — 2,3,...,
/ \ ч if
<p(*n, An) = т-s ехр
I
to
1.9. ДОПОЛНЕНИЯ И ЗАДАЧИ
223
exp tn — J a(a)d<r tn — 1
r'K1 ? An/J — i/2 f "(SMC) exp - f a(a)da tn — 1 t^ + ^n.An)
1.9.36. Показать, что для стационарных случайных процессов с ковариационными
функциями De -f- Of|T"|) и De ^1 -+• 4- интенсивности экви-
валентного белого шума соответственно равны 47?/01 и 161?/Зп. Вычислить интервалы
корреляции.
1.9.37. Показать, что для процесса, приводимого к стационарному и определяемого
формулой Y — ^о(^) 4" bi(t)X(t), где X(t) - стационарная случайная функция,
интенсивность эквивалентного белого шума и интервал корреляции соответственно равны
оо
v(t) = 6i(t) У bi(t + т)кх(т)<1т,
— ОО
_ 1 _ I/(t)
Тк ~ 2™?* bl(t)kx(Oy
Вычислить v(t) и Tfc для процесса, определяемого формулой Y (t) — ^о(^) 4“
+WW , где <p(t) является монотонно возрастающей функцией.
1.9.38. Доказать, что для уравнений Ланжевена Y\ — У2, Y2 — —2бУ2 4“ V,
где 6 > 0 - постоянная; V - белый шум постоянной интенсивности I/, дисперсии и
ковариация процессов Yi (t) и Y% (t) при нулевых начальных условиях определяются
формулами (Чандрасекхар 1943):
кц = v(4et - 3 + 4e~2£t - e~i£t)/16e3,
кп = i/(l - 2e~2£t + e-4et)/8e3, fc22 = i/(l - e~4£t)/4£.
1.9.39. Показать, что в условиях задачи 1.9.3 при обобщенной силе Q в виде белого
шума интенсивности I/ уравнения для дисперсий, ковариации и ковариационных функций
имеют вид
кц = Ък^/А, к\2 — ~Скц — (B/A)ki2 4- (1/А)к22,
к>22 — ~2Ск±2 ~ (2В/А)к22 4" *6
97^11(^1, ^)/^2 = 7<12(£1, t2)/A,
dKi2(tl,t2)/0t2 = —С7<11(^1, t2) — BKi2(tl,t2)/A,
97<21(^1,^2)/dt2 = 7f22(^l, h)/A,
224
ГЛ. 1 СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
^^22(^1, ^2)/^2 = “671^21(^1 > ^2) BK22(tl, ^2)/^*
1.9.40. Доказать, что ковариационные и взаимные ковариационные функции ста-
ционарных и стационарно связанных процессов примера 1.1.9 при входном
сигнале X (t) в виде стационарного белого шума интенсивности V определяются форму-
кц(т) = —(cos шст + 7sinwc|r|),
^22(т) - тг—e-ita'0,T|(coswcr -7sinwc|r|),
4^w0
*12(т) = -77-^—е-<“'о|т| sinwc|r| (7 = </х/1 - с2, шс = а?ох/1 - С2)-
4(,а>са>о
1.9.41. Показать, что в условиях задачи 1.9.39 дисперсии и ковариационные мо-
менты координаты и импульса в режиме стационарных случайных колебаний, т.е. когда
колебания представляют собой двумерный стационарный случайный процесс, определя-
ются формулами = U/2ВС, к\2 — 0, к>22 = Av/2В. что при наличии
сильного демпфирования (jE?^ > 4АС7), процесс установления стационарных колебаний
происходит в две стадии: сначала устанавливаются колебания импульса, а после этого -
координаты (Чандрасекхар 1943).
1.9.42. Показать, что уравнения для ковариации выходных переменных системы
(задача 1.9.1) при Xh = J2l=l bhlVl (Л = 1, 2), где V = [ Vi ... Vn - белый шум
интенсивности I/; bfoi - коэффициенты, зависящие от времени, имеют вид
п
Лц = 2(ацкц +<212&12) + 52 "rhblrblh,
r,h=l
п
&12 = «21&11 + («11 + «22)^12 + «12&22 + 52 Urhblrb2h,
г,h=l
п
к22 = 2(^21 &12 4-«22^22) 4- 52 yrhb2rb2h-
г, h=l
1.9.43. Показать, что для линейной системы с одной степенью свободы задачи 1.9.3
при обобщенной силе Qt представляющей собой стационарный случайный процесс со спек-
тральной плотностью Sx(cj) = Dol/t^(p? 4“й/^), уравнения для ковариаций компонент
Yi = Q, Y2 = Р> К3 = Q/A вектора состояния, если положить CJq = С/А, 2б =
= B/A> имеют вид
fell = 2fci2, &12 = ^23 ~ <*&13,
1.9. ДОПОЛНЕНИЯ И ЗАДАЧИ
225
fcl2 — &22 ~ ^0^11 ~ 2б&12 "Ь fcl3, &22 — — 2(а>о&12 4- 2бА?22 ~ ^2з),
^23 = ~^о^1з — (а + 2б)&2з + &зз, &зз = —2а(&зз — D).
Рассмотреть стационарные решения в случаях: a) Ol, € < О>о; 6) £ > CU,UJo;
в) О>о = 0, б, а > 0.
1.9.44. Показать, что уравнения для ковариаций стационарной линейной системы
задачи 1.9.9 при Q = IV, где I - постоянная ТП X 71-матрица, V - 71-мерный белый шум
интенсивности 1/, имеют вид
кп =а-1к21+к21а-\
К12 = А~'К22 - Кп (С - С) - К12А-\В - В'),
к21 = К22А~г - (С + С')Кп - (В + В'^А^Кц,
К22 = -(С + С')К12 - К21(С - С") - (В + В'УА-'Кл-
-К22А~\В - В') + Ыт.
Здесь КП и &22 ~ ковариационные матрицы векторов канонических переменных Yj =
= 9, у2 = р, а блоки К12 и -^21 ~ взаимные ковариационные матрицы Y\ и
Рассмотреть частные случаи: а) С = С1 — 0, В = 2бА; б) С — С = 0, В = Т)С\
в) | С| < 0, В — 2бА. Написать уравнения для блоков ковариационных и взаимных
ковариационных функций канонических переменных системы задачи 1.9.44 в условиях
стационарных случайных колебаний.
1.9.45. Показать, что в условиях задачи 1.9.38 для стационарного белого шума с
любой функцией х(д) одномерное стационарное распределение процесса опреде-
ляется характеристической функцией (Пугачев и Синицын 1985):
{А
Л [
J fjl
о
1.9.46. Показать, что многомерные распределения векторного случайного процесса
У(£), определяемого дифференциальным уравнением Y = Од + oY ЬХ(1), где
X(t) - случайная функция, представляющая собой решение линейного стохастического
дифференциального уравнения X — Q(j 4" OlA + (3V при независимых начальных
значениях Yq и Xq, определяются формулой (Пугачев и Синицын 1985):
(п \ / п \
^U11(*Mo)TA)5o I 52u12(*Mo)Ta) X
*=1 / \*=1 /
8 Фильтры Калмана и Пугачева
226
ГЛ. 1 СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
х ехр <
/?('г)т 52 и^(и,т)т>ч',т
i=k
dr\, A = (A1...An)T,
где р, q ~ размерности Y(f) и ffo(p)>3o(<:r) - характеристические функции на-
чальных значений Yq , Xq процессов Y(t)t X (t); Мц (£, т) - фундаментальная матрица
решений уравнения du\\/dt — = 1р\ 1212 (£>7") - решение уравнения
du\2/dt = ащ2 + bu22 при нулевом начальном условии Ui2(T) т) — 0; U22(t^ т) -
фундаментальная матрица решений уравнения du22/dt — OtU22\ и22(т,т) = Iq (Ip,
Iq - единичные p X рид X д-матрицы).
1.9.47. Показать, что установившаяся дисперсия Dy выходной переменной систе-
мы, состоящей из импульсного устройства, вырабатывающего прямоугольные импульсы
длительности Т*и (с периодом повторения Тп) и линейного звена с передаточной функ-
цией Ф($) под действием импульсного белого шума с дисперсией D каждого импульса
определяются по формулам:
1) при *(s) = k/s Dy = kD/(k + 2),
2) при Ф(в) = k/(Ts + 1) Dy = k2Dp(zi).
Здесь p(zi) - zl(ziy - 1)2/(1 - zj), Zi = e~Tn/T, 7 = T„/Ta.
1.9.48. Показать, что линейной системе с параметрическими шумами
Aq + (1 + V3)(B + B')q + (1 + V2)(C + C')q = (1 + VJQ.,
где g = [ gi • • • qn ]и Q* = [ Qi • • • Qn — 72-мерные векторы; А, В, С - симмет-
ричные, а В', с - антисимметричные П X 72-матрицы; V — [ Vi V2 V3 ] — нормально
распределенный белый шум интенсивности 1/, соответствует уравнение Ито
Aq + (1 + V3)(B + B')q + (1 + V2)(C + C")g =
= (1 + V1)Q. + e[-y13Q.A~\B - B')+
+p23(C + C')qA~1(B - B') + v33(B + B'jqA-^B - B')].
1.9.49. Показать, что для линейной стохастической системы с параметрическим шу-
мом задачи 4.6 уравнения для математического ожидания, дисперсии и ковариационной
функции имеют вид
772 = -б(1 - 20ei/22)m - 2e0kv\2,
Ь = -2б(1 - 20£U22)D + к2Уц -F б27/22(7722 + D) - 2£kmvi2,
1.9. ДОПОЛНЕНИЯ И ЗАДАЧИ
227
dK(t^t2)ldt2 = -е(1 - 2^22)АГ(^^2).
Найти стационарные значения ТП и D, а также условия их существования.
1.9.50. Показать, что для линейной стохастической системы с параметрическими
шумами задачи 1.9.20 уравнения для математического ожидания и ковариаций имеют
вид
mi = m2, m2 = -т1и>о(1-20СиоЬ'2з)-2т2Си>о(1-20(и>О1/зз)-20К^о1/1з;
fell = 2fci2, ki2 = —Wq(1 — 20£а>о1/2з)&11 — 2£a>o(l — 20£о?о1/3з)&12 + &22,
fc22 = -2wq(1 - 20(o>oi'23)fci2 - 4<WO(1 - 20(сиоРзз)А:22 + к21>ц~
-2mikwQi>i2 - 4m2£woA:i'i3 + ^ор2г(т2 + &n)+
+4Cw^i/23("ii"i2 + kl2) + 4(2WQi/33(m2 + k22)-
1.9.51. Математическое ожидание ТП и дисперсия D в системе
TY + Y = b(X — aY3), X = тх + V,
где V — стационарный белый шум интенсивности I/, согласно методу нормальной ап-
проксимации приближенно определяются уравнениями
Тт = Ьтх — т[ 1 + ab(m2 -F 3D) ], Т2Ь = b2v — 2DT[ 1 + Заб(т^) ].
Найти приближенные значения ТП и D для стационарного режима колебаний. Пользуясь
методом моментов (до четвертого порядка), проверить, являются ли найденные'ТП и D
“лишним” решением.
1.9.52. Применяя метод нормальной аппроксимации, показать, что дисперсии и ко-
вариация переменных состояния в нелинейной системе
TYi + Yi—b sgn(y2 - У1), У2 + аУ2 = V2D^V,
где V — белый шум единичной интенсивности, определяются приближенно уравнениями
Ткп = 2/Зк12 + 2(1 + /3)кц, Tki2 = 0к22 - (1 + аТ + £)fc12,
fc22 = 2а(Р - fc22), 0 = b[(kn + fc22 - 2fc12)7r/2]-1/2.
Найти кц, k\2, ^22 Для стационарного режима. Пользуясь методом моментов (до чет-
вертого порядка), проверить, является ли найденная дисперсия кц для стационарного
режима “лишним” решением.
228
ГЛ. 1 СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
1.9.53. Пользуясь методом нормальной аппроксимации, показать, что для системы
TY + Y = 6sgn(X-y), X + аХ = y/WaV,
где V — нормальный белый шум единичной интенсивности, дисперсии и ковариации
переменных Yi — Y, У2 = ^3 = X имеют вид
кц = 2ki2, Tki2 = Тк22 — ^12 + — &ц),
ki3 = к2з ~ afci3, кзз = 2a(D - fc33),
Тк22 = %к22 + 2/?(&23 ~ ^12), Тк2з = ~(1 4- аТ)к2з 4- @(кзз ~ &1з),
/3 = Ь[(кц + к33 — 2ki3)ir/2]~1^2.
Найти стационарные значения дисперсий и ковариаций.
1.9.54. Показать, что для нелинейного осциллятора
Y+ tp(Y,Y)+u%Y = V,
где V — белый шум интенсивности I/, дисперсии и ковариации переменных Y} — Y,
Y% — Y в соответствии с методом нормальной аппроксимации определяются уравнения-
ми
fell = 2fci2, fcl2 = к22 - (Ц) + ^1)^11 “ &2&12,
fc22 = “2(о>о + fci )ki2 — 2к2к22 + У,
где ki и А?2 — коэффициенты статистической линеаризации функции 1/2 )• Мате-
матические ожидания начальных значений Y\, Y2 равны нулю.
1.9.55. Пользуясь результатами предыдущей задачи, убедиться в справедливости
следующих приближенных формул для дисперсий и ковариаций стационарного процесса
в системах:
а) осциллятор с сухим трением, = bosgnj/2.
Ли = 7rv2/8wQbo, Л12 = О, Л22 = wofcn;
б) осциллятор Рэлея, = —^11/2 4" ^35/2’
кп = (1/6шоЬ3)(Ь1 + y/b1+6vb3), Л12 = 0, к22 =
в) осциллятор Ван-дер-Поля, ^(^1,^2) = ^(?/1 ~ 1)^2,
Ли = (1 + у 1 + 2iz/w^b)/2, Л12 = 0, Л22=^оЛц.
1.9. ДОПОЛНЕНИЯ И ЗАДАЧИ
229
1.9.56. Доказать, что для двумерной стохастической системы
Yi=ao- aYi + /цЦ , У2 = -У1У2 + h2V2
(flo, ^1» ^2 > 0, Vi и V% - независимые нормальные белые шумы с единичными
интенсивностями) уравнения семиинвариантного метода с точностью до первых четырех
семиинвариантов (i, j — 0,1,2, 3, 4) имеют вид
* 4и = 4- а>о , /^ю = ^lo^oi> ^oi — — 2ая20 4- ,
/€ц = — ак,ц — K,QiK,20 — *40*41 ~ *^21 >
* ^20 = “2(/€ц/€о1 + *^10*^02 + *42 ) 4" Л-2 >
/€зо = — Задсзо , «40 = — 4ак4о ,
* >21 = ~2а«21 — *4)1 *й0 ~ 2/420*41 ~ *40*>21 ~ *^31 >
/€12 = “в/€12 ~ 2(/€01 /€21 4" *420*4)2 4" *€2j + *^10*^12 4“ *€22) ,
* 4)3 = ~3(/€о1/€12 4- 2/€ц/€02 4“ *^10*^03 4" 3/€1з) ,
/€31 = —За/€з1 — /€01/€40 ~ 3/€зо/€ц — 3/€20*^21 ~ *40*4)1 ?
/€22 = -2а/€22 - 2(/€01 /€31 4- /€30«02 4- 3/€21/€ц + 2/€20«12 4" /€10^22) ,
* 43 = —а/€1з ~ 3(/€о1/€22 4" 2/€21/€q2 4“ /€20*4)3 4“ 3/€ц/€12 4" *4о*4з) >
* 4)4 = — 4(/€о1*€13 4- 3/€12*€о2 4“ /€ю*4)4 4“ 3/€ц/€оз) •
Показать, что при CLq hfa, различие между значениями Z€q2\ *»02^» **02^» вычислен-
ными с точностью до семиинвариантов второго - четвертого порядков, пропадает.
1.9.57. Составить уравнения для первых двух моментов задач 1.9.34 и 1.9.35. Пока-
зать, что решение этих уравнений при начальных условиях Шо = AfYo, Do =
имеет вид (Силуянова 1981):
«1(0 = «ю 4- «и exp(-af),
«2(0 = «20 4- «21 exp(-at) 4- «22 exp(-2at),
где «ю = «11 = ^0 ~ «ю; «20 = (14- 2ao^i)<4)/2aia2; «21 — «11 (1 4-
4-2(Zoal)/aai; «22 = Do — «20 ~ «21- Найти стационарные решения.
1.9.58. Показать, что уравнения метода эллипсоидальной аппроксимации нелиней-
ной стохастической системы (понимаемой в смысле Ито):
У1 = Y2, У2 = -еУ2 - wgyx - aY? + Fcoswt + V(t) (I)
при учете моментов до четвертого порядка имеют следующий вид (Пугачев и др. 1995):
ТГЦ = 7712, ТП2 = —67712 ~ U/q771! “ «(^1 4* Зт^кц) 4" D COS Wt, (II)
230
ГЛ. 1 СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
fcn = 2fci2, fci2 = к22 - eki2 - о^и “ 3akn(ml + А?ц) - 24ac2,2k^,
&22 = ~ek22 ~ 2cjQfci2 - 6afci2(mi + fcn) - 48ac2i2knki2 + (HI)
• ^2,2r/» i2/i xi i 3otki i z_ .
C2.2 = j^ieafculfcn + ВД) - knv] + -^p(fci2 + ВД),
(IV)
где 6, Q, U>o» и й?о — некоторые положительные константы; V — интенсивность нор-
мального белого шума V(^); |/f| — ку\к22 — &12-
1.9.59. Рассмотрим систему со случайно изменяющейся структурой (1.1.35), в кото-
рой, в частности, TVj (£) представляет собой ступенчатую случайную функцию с одним
и тем же при всех t конечным множеством возможных значений {S1, . . . , Sn}. Каждо-
му фиксированному значению Sfc случайной функции N\ (t) соответствует определенная
структура системы, которая описывается следующими уравнениями:
Z = f(Z,sk,N2(t),t), Y = g(Z,sk,N2(t),t), (I)
где N2(t) — векторная случайная функция, образованная всеми компонентами TV(^),
кроме 7Vi(£). При переходе TVj (t) в случайный момент от одного значения к другому
структура системы изменяется. При этом вектор состояния системы может претерпевать
скачкообразное случайное изменение. Задачи исследования таких систем возникают в
условиях, когда отдельные устройства систем выходят из строя, вследствие чего уравне-
ния, описывающие работу системы, изменяются.
Другим типом систем со случайно изменяющейся структурой являются стохастиче-
ские системы, которые описываются различными уравнениями в разных областях про-
странства состояний. К изучению таких систем сводятся задачи потери управления, сры-
ва слежения вследствие ограниченности диапазонов изменения переменных состояния, в
которых система может функционировать. Допустим, что пространство состояний си-
стемы разбивается на П попарно непересекающихся частей А.\, . . . , А.п, так что при
переходе из одной части в другую структура системы изменяется. При этом уравнения
стохастической системы имеют вид
Z = f(Z,sk,N(t),t), Y = g(Z,sk,N(t),t). (II)
Здесь
п
S = '£sklAh(Z),
к=1
где 1аЛу) — индикатор множества. Ясно, что эти уравнения принципиально не отли-
чаются от уравнений (I).
1.9.60. Рассмотрим систему задачи 1.9.59, которая в каждой структуре описывается
стохастическим дифференциальным уравнением Ито:
Y = a(Y,sk,t) + b(Y,sk,t)V (к = 1, ... , N), (I)
1.9. ДОПОЛНЕНИЯ И ЗАДАЧИ
231
где Si , ... , Stf - возможные значения ступенчатого случайного процесса i5(t), описы-
вающего случайные изменения структуры системы.
Сначала рассмотрим случай, когда переходы системы от одной структуры к другой
образуют пуассоновские потоки событий. Обозначим пуассоновский процесс переходов в
к-ю структуру через Pfc (t), а его интенсивность через S, £), имея при этом в виду,
что она зависит от случайного значения процесса S, от которого он переходит к значению
S&, и может зависеть также от состояния системы в момент перехода. Легко видеть, что
процесс S(t) определяется стохастическим дифференциальным уравнением Ито:
N
dS = ^sk - S)dPk . (II)
к—1
Предполагая, что при изменении структуры системы ее вектор состояния может скач-
ком получать случайное приращение, напишем искомое стохастическое дифференциаль-
ное уравнение системы со случайно изменяющейся структурой в виде
N
dY = a(Y, S, t)dt + Ь(У, S, t)dW + dQk , (III)
k=l
где Qk(t) ~ общий пуассоновский процесс с переменным распределением скачков, по-
рождаемый простым пуассоновским процессом Pk(t) (& = 1 , ... , TV). Распределение
каждого скачка процесса Qfc(t) может зависеть не только от времени, но и от векто-
ра состояния системы К и ее структуры в момент перехода в к-ю структуру. Таким
образом, добавив к вектору состояния системы Y значение процесса S, определяющего
ее структуру, мы получим систему стохастических дифференциальных уравнений Ито,
описывающую поведение системы со случайно изменяющейся структурой. Ее вектором
состояния естественно будет вектор Y = [ S Y^ ]
Уравнения системы со случайно изменяющейся структурой (I) и (II) при пуассонов-
ских потоках изменений структуры можно записать в общей форме уравнений Ито:
dY = a(Y, t)dt + b(Y, t)dW . (IV)
Здесь Y = [S YT]T - вектор состояния системы; IV(t) - процесс с независи-
мыми приращениями, состоящий из N 4- 1 независимых блоков W(Z);
[PnQJ,]1 ; 0>(у, £), Ь(у, t) - блочные матрицы, равные
232
ГЛ. 1 СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
1.9.61. Составим уравнение Ито для случая задачи 1.9.60, когда изменения струк-
туры процесса представляют собой эрланговские потоки событий. Эрланговский поток
событий получается из пуассоновского потока путем пропуска подряд 71—1 событий и от-
бора каждого события, имеющего номер, кратный данному числу 71. Натуральное число 71
будем называть параметром эрланговского потока. Ясно, что в случае эрланговских пото-
ков изменений структуры системы, перед дифференциалами dPfc и dQk в стохастических
дифференциальных уравнениях системы следует ввести множитель (/?£ (.Pjfe, S), пред-
ставляющий собой периодическую функцию Pfc с периодом, равным параметру
соответствующего эрланговского потока, равную 1 при Рк = TIS (в = 1, 2,. ..) и 0 при
всех остальных (целочисленных) Р^. В результате стохастические дифференциальные
уравнения системы примут вид
N
dS = Y,(sk - S)<pk(Pk,S)dPk , (I)
к=1
N
dY = a(Y, S, t)dt + b(Y, S, t)dW + ^<pk(Pk,S)dQk. (II)
fc=l
Аналогично можно привести к общей форме уравнения Ито, уравнения системы
со случайно изменяющейся структурой при эрланговских потоках изменений структуры.
Однако в этом случае коэффициенты при dPk и dQk зависят от Р^. Поэтому вектор
состояния системы следует расширить добавлением к нему вектора Y1 с компонентами
Y( = PX,... ,Yb = PN> определяемыми уравнениями dYy — dP\ , . . . , dY^ —
= dPN
1.9.62 Составить уравнение для одномерной характеристической функции векто-
ра состояния системы со случайно изменяющейся структурой. Для этого найдем сна-
чала функцию соответствующую процессу W(t\ /1 = [/1/11 , ••• , Pn] •
Функция х(/1‘, t) в этом случае представляет собой сумму функций X, соответствующих
независимым блокам 1У(£), [7*1 (t)Qi , . . . , [Pn(1)Q n(1)T]T, составляющим
процесс W(fy
N
Y,S,t) = x(& t) + 52 Xk &k Ф
k=i
где Xk(P>k\YyS,t) - функции X процессов W(t), [Pk(t)Qk(t)T]T соответ-
ственно (A? = 1 , . . . , TV); p P? Pl . . . рм j - разбиение вектора p на соответ-
ствующие блоки; ph = [/1£0 ~ разложение вектора рк на блоки, соответствующие
процессам Pk(t) и Qk(t)- Здесь мы учли, что интенсивность потоков скачков процессов
.Pfc(t) и распределения скачков процессов Qk(t) могут зависеть от вектора состояния
системы Y = Пользуясь формулой для характеристической функции прира-
щений пуассоновского процесса и порождаемого им общего пуассоновского процесса на
1.9. ДОПОЛНЕНИЯ И ЗАДАЧИ
233
бесконечно малом интервале Sj, согласно которой
hkffik] Y, S, t) =
= 1 + [ е*”дк (цк; Y, S, t) - 1 ] vk (Y, S, t)(s -1) + o(s - t), (II)
находим
- 1] ^(Y,S,t), (III)
где ffk(Pk] У, в» 0 - характеристическая функция скачков процесса Qjfe(t) в момент t,
зависящая также от Y(t), S(t). Таким образом,
N
x(fi>Y,S,f) = хМ + £ [ei(ik°gk^k;Y, S,t) - l]vk(Y,S,t) (IV)
к=1
и соответственно
x(b(Y, S, t)TX-, Y, S, t) = x(b(Y, S, t)TX-, i)+
N
+ Z [ei{’k~S)Xo9k(X-,Y,S,t) - 1] i/k(Y,S,t), (V)
k=l
где A — [AoAT]T - разбиение вектора А на блоки, соответствующие блокам S, Y век-
тора состояния системы Y. В результате получим уравнение для одномерной характери-
стической функции процесса в системе со случайными изменениями структуры:
д91^ = м(гАга(У, S, t) + x(b(Y, S, t)TX-, t)+
ot [
N 1
+ 12 [ei(’‘-S)4(W>t) - 1] vk(Y,S,t) le<Ao$+«ATr (VI)
k=l L J
1.9.63. Основываясь на уравнениях для одномерной характеристической функции
задачи 1.9.62, можно вывести уравнения для условных характеристических функций в
различных структурах и для вероятностей этих структур. Имея в виду, что S(t) = St
- дискретная случайная величина с возможными значениями Si , . . . , S/y и вероятно-
стями этих значений Pi(t) , . . . , Pn(J^) при каждом t, по формуле полного математи-
ческого ожидания находим
N
<h(A;i) = Me<AoS(t)+iATy(t) = Y,PieiXoS‘gi(X-,t\ st), (I)
к=1
234
ГЛ. 1 СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
где </i(A;t | S/) - условная характеристическая функция вектора состояния системы
Y в 1-й структуре. Аналогично вычисляется математическое ожидание в правой части
уравнения для (Aj Z). В результате уравнение примет вид
dt
N
= ^2PielX°Sl[{*Ата(У, $/,£) + еглТу | +
i=i
N N
+ [eiX°^Sh~Sl^Mgk(X]Y1si1t)i>k(Y1si1t)eixTY | -
i=i k=i
N Г N
~^PieiX°SlM 53° vk(Y,8ht)eixTY | si
i=i Lfc=i
(П)
Здесь индекс (/) у сумм по к указывает, что слагаемое, соответствующее к — I, в сумму
не входит. А не входит оно потому, что при отсутствии изменения структуры процессы
Pl (t) и Qi (t) сохраняют постоянные значения, вследствие чего gi(X;Y,sht) = 1.
Изменив порядок суммирования в первой двойной сумме, получим
N N
^eiX<>Sk ^PlM [gk(X-,Y,Sl,t^k(Y,Sl,t)eixTY | *] . (III)
к=1 1=1
Поменяв в (III) местами индексы к и I (от этого двойная сумма не изменится) и подставив
полученное выражение в уравнение (II), будем иметь
N
^VAoS'
1=1
dpigi(X-,t | st)
dt
N
= Y PieiX°S‘M [ {гЛТа(У- si, t) + XWY, st, t)TA; 0} eiATy | s, ] +
1=1
N N
+ YPie,X°S' Ul)PkM sk,t)ezXTY | sk j -
Z=1 Jt=l
- 52 pieiXo3‘M [ *(y’ *)eiATY ।si ] ’ (IV>
1=1
1.9. ДОПОЛНЕНИЯ И ЗАДАЧИ
235
где для краткости положено f) — Sfc, t) • Сравнив коэффициенты при
к=1
одинаковых показательных функциях и обозначив через fl (?/', t | S[) условную одномер-
ную плотность процесса V(Z) в l-й структуре, из (IV) составим систему уравнений
оо
dplg1(X;t\si) Г т ( ,ч.
---------------=Pi / {гА2а(т/, $/,£)+
— оо
+x(b(y,si,t)TX\t)elxTy}fi(y-,t | st)dy+
N °?
+ Y}l}pk / 5,z(A;j/,sfc,t)i//(j/)sfc)<)e,ATy/1(j/;t | sk)dy-
*=i -oo
OO
-pi У I Si)dy = ()V
— OO
Положив здесь A — 0 и имея в виду, что 3i(0;t | si) = 1 , x(O;t) = О, получим
уравнения для вероятностей структур (/ = 1 , ... , 7V) системы в момент t:
N ОО оо
Pl = / i'i(y,Sk,t)fi(y,t\sk)dy-pi / i/[(y,t)f1(y,t\si)dy.
k—1 J J
— L —OO —oo
1.9.64. В условиях задачи 1.9.63 выведем уравнения для условных плотностей из
уравнений для условных характеристических функций в случае винеровского процесса
IV(£). Изменим обозначение переменной интегрирования у на Т], умножим уравнение
для pigi(X;t | si) на е,АТу/(2тг)р и проинтегрируем по А. Учитывая формулы
оо
77ТГ [ gi(X;’n,sk,t)ezXT<'y-y)dX = qi(y-y,T),sk,t), (I)
№)р J
— ОО
где qi(y,T],Sk,t) - плотность скачков процесса при данных ту, и t,
оо
qi(y - I sk)dr). (II)
— oo
В результате для (/ — 1 , ... , TV) имеем
236
ГЛ. 1 СВЕДЕНИЯ ИЗ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ
dpifi(y;t\ Si) дт r , , Ч1
------dt------= ~Pl ду а^У’31 ’ । s<) 1+
{д дт 1
дуду I St)] J +
N °?
+ X)l)pk / q‘(y -W’s*’ tV'i(Tl,Sk, t)fi(r?;i I Sk)d7]-Pii/i(y; ttf^y; 11 sz).
*=1 -oo
(III)
В важном частном случае, когда при переходе от одной структуры к другой вектор
состояния системы Y не получает случайного приращения, слагаемые с dQk в уравнении
для Y отсутствуют (Qjfe(^) = 0). При этом в уравнении для одномерной характеристи-
ческой функции gi (A; t) и в уравнениях для условных одномерных характеристических
функций gi (A; t | S/) при разных структурах gi (А; ?/, Sfc, £) ЕЕ 1. Соответственно в
уравнениях для условных одномерных плотностей | S/) при разных структурах
Ql (у — 7)\ g, Sk,t) = 8(у — 7]), и уравнения для /1 (?/; t | Si) (I — 1 , . . . , N)
принимают вид
dpifi(y,t | s{) дт . .
------dt------= ~Р‘ ду а(у’ S‘ ’ । +
N
+ «М) [рШу; И *!«<)] G = i, •••, at), (iv)
k=l
Для систем co структурой, изменяющейся при переходе из одной области простран-
ства состояний в другую, случайный процесс S(t) изменения структуры представляет co-
TV
бой функцию вектора состояния Y(t): S(t) — SfcIa*, (Y(t)) , где Xi, ... , An -
k=i
попарно непересекающиеся области, на которые разбито пространство состояний. Вслед-
ствие этого стохастическое дифференциальное уравнение системы представляет собой
уравнение вида (5.1.27). Если при попадании на границу одной из областей, скажем
An, процесс останавливается (поглощается), то функции d и Ь в этой области следует
принять тождественно равными нулю: SN^t) = 0, ^(.У) SN-> — 0-
ГЛАВА 2
ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ.
ФИЛЬТРЫ КАЛМАНА
Глава 2 посвящена теории с.к. оптимального (в смысле минимума
средней квадратической ошибки) оценивания состояния (фильтрации,
экстраполяции и интерполяции) и параметров в стохастических диффе-
ренциальных и дискретных линейных и нелинейных системах. В раз-
деле 2.1 дается постановка типовых задач оценивания в стохастических
дифференциальных системах как с винеровскими, так и с пуассонов-
скими шумами. Раздел 2.2 содержит вывод основных уравнений оп-
тимальной фильтрации и экстраполяции. Теория линейной оптималь-
ной фильтрации изложена в разделах 2.3 и 2.4 как частный случай об-
щих уравнений оптимальной фильтрации. Центральное место занима-
ет теория стационарных и нестационарных фильтров Калмана-Быоси.
В отдельном разделе 2.5 приведено изложение линейной оптимальной
фильтрации при автокоррелированной помехе в наблюдениях. Вопросы
линейной оптимальной экстраполяции и интерполяции обсуждаются в
разделе 2.6. Уравнения оптимальной фильтрации для ненормирован-
ных распределений получены в разделе 2.7. Раздел 2.8 посвящен теории
с.к. оптимального оценивания в дискретных стохастических системах.
В разделе 2.9 подробно изучены свойства дискретных фильтров Кал-
мана для линейных стохастических систем. В разделе 2.10 изложена
теория дискретных линейных с.к. оптимальных экстраполяторов и ин-
терполяторов. Вопросы устойчивости, наблюдаемости и управляемо-
сти стохастических систем и фильтров Калмана рассмотрены в разде-
ле 2.11. Там же обсуждаются проблемы с.к. оптимальной фильтрации
в сингулярных стохастических системах, а также вырожденных шумов
в уравнениях наблюдения. В разделе 2.12 применительно к линейным
и нелинейным стохастическим дифференциальным и дискретным си-
стемам получены основные уравнения теории совместного оценивания
и распознавания состояния и параметров. Рассматриваются гибрид-
ные фильтры Калмана. В конце главы даны дополнения и задачи для
упражнений.
2.1. Задачи оценивания в стохастических
дифференциальных системах
2.1.1. Оценивание состояния системы. На практике часто воз-
никают задачи непрерывного определения состояния системы по ре-
238
ГЛ. 2. ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФИЛЬТРЫ КАЛМАНА
зультатам непрерывных наблюдений. Так как наблюдения всегда со-
провождаются случайными ошибками, то следует говорить не об опре-
делении состояния системы, а об его оценивании (фильтрации, экстра-
поляции, интерполяции и т.д.) путем статистической обработки резуль-
татов наблюдений.
Будем рассматривать задачи оценивания состояния систем, моде-
лями которых могут служить стохастические дифференциальные урав-
нения (п.1.5.1). Предположим сначала, что поведение системы описыва-
ется следующим векторным стохастическим дифференциальным урав-
нением Ито (1.5.20):
X = (^(X,Z)+V>(X,t)V, (2.1.1)
где X - n-мерный вектор состояния системы; V - r-мерный векторный
белый шум; ^(Х, £), *ф(Х, t) - известные функции состояния систем и
времени. Значениями функции ip(X,t) служат n-мерные векторы, а
значениями функции iplX, t) - п х г-матрицы.
Если непрерывно измеряется вектор состояния системы X, то ре-
зультатом наблюдений будет n-мерный случайный процесс Y(t) =X(t)+
+U(t), где U(t) - ошибка наблюдения, представляющая собой случай-
ную функцию времени. Однако на практике обычно наблюдаются не
компоненты вектора состояния, а некоторые функции вектора состоя-
ния. Впрочем, могут наблюдаться некоторые компоненты вектора со-
стояния. Эти компоненты также можно рассматривать как функции
вектора состояния.
В общем случае результат наблюдения определяется формулой
Y = У(*) = ^0(X,L/,i), (2.1.2)
где Y - П1-мерный вектор; U - ошибка наблюдения, представляющая
собой векторную случайную функцию времени размерности г > п\\
= ipQ(X,U,t) - известная функция состояния системы, ошибки на-
блюдения и времени. Функция <ро в общем случае не линейна как от-
носительно вектора состояния, так и относительно ошибки наблюде-
ния. Размерность П2 вектора ошибки U на практике не может быть
меньше числа наблюдаемых величин П2 < ni, так как каждое наблюде-
ние сопровождается ошибкой и ошибки разных измерительных средств
обычно независимы (или, по крайней мере, содержат независимые сла-
гаемые). В некоторых случаях измерения производятся инерционными
приборами или же результаты измерений пропускаются через различ-
ные фильтры. Таким образом, достаточно общей моделью наблюдений,
2.1. ЗАДАЧИ ОЦЕНИВАНИЯ В СТОХАСТИЧЕСКИХ ДИФ.СИСТЕМАХ 239
производимых в системе, можно считать дифференциальное уравнение
Y = lpi(Y,X,U,t).
(2.1.3)
Итак, мы пришли к задаче непрерывного оценивания вектора со-
стояния системы X в каждый момент t > Iq по результатам непрерыв-
ного наблюдения процесса У, определяемого стохастическим диффе-
ренциальным уравнением (2.1.3) со случайными функциями X и £7, в
интервале времени [to, t].
2.1.2. Оценивание неизвестных параметров системы. В не-
которых случаях дифференциальные уравнения модели изучаемой си-
стемы могут содержать неизвестные параметры и, как правило, всегда
содержат параметры, известные с ограниченной точностью. Поэтому
возникает задача непрерывного оценивания неизвестных параметров
системы (точнее, ее модели) по результатам непрерывных наблюдений.
Предположим, что функции в уравнении (2.1.1) зависят от
конечного множества неизвестных параметров, которые мы будем рас-
сматривать как компоненты вектора 0. Тогда уравнение (2.1.1) можно
переписать в виде
x = <^(x,0,t) + V>(AW)Vi,
где <^(Х,0, t), ^(А',#, t) - полностью известные функции указанных ар-
гументов. В таких случаях обычно применяют следующий прием: не-
известный векторный параметр 0 считают случайным процессом 0(t),
который определяется дифференциальным уравнением 0 = 0, и вклю-
чают компоненты этого векторного процесса в вектор состояния систе-
мы (“расширяют” вектор состояния путем включения в него неизвест-
ных параметров в качестве дополнительных компонент). В результате
получается дифференциальное уравнение, определяющее расширенный
вектор состояния системы X1 = [ХТ0Т] :
£ Г X 1 _ Г <^(X,0,t) Г ip(X,Q,t) '
dt 0 J [ 0
У1,
(2-1.4)
0
ИЛИ
X'= ^(X,,t)+^'(X,,t)V1.
Таким образом, задача непрерывного оценивания неизвестных пара-
метров модели системы сводится к задаче непрерывного оценивания
состояния системы с расширенным вектором состояния.
240
ГЛ. 2. ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФИЛЬТРЫ КАЛМАНА
От неизвестных параметров может также зависеть функция в
уравнении наблюдения (2.1.3). Эти параметры также следует включить
в вектор 0 и, следовательно, в расширенный вектор состояния.
Построение модели какой-либо системы или процесса обычно на-
зывают идентификацией этой системы или процесса.
2.1.3. Экстраполяция состояния системы. Во многих зада-
чах практики важно не только оценивать текущее состояние системы,
но и прогнозировать будущее состояние системы по результатам на-
блюдения ее поведения. Задача прогнозирования, т.е. экстраполяции
состояния системы, по существу представляет собой задачу оценивания
ее будущего состояния. Эта задача отличается от задачи п.2.1.1 только
тем, что вместо оценивания вектора Xt = X(t) требуется в каждый мо-
мент t > to оценивать вектор Xt+& = X(t 4- Д) при некотором Д > 0.
Можно также поставить задачу одновременного оценивания векторов
-Xt+Ai, • • • , ^е+Дп Д™ 0 < Д1 < • • • < Дп-
2.1.4. Постановка математических задач оценивания и экс-
траполяции в стохастических дифференциальных системах
Задача 1. Векторный случайный процесс [УТХТ]Т определяется
векторными стохастическими дифференциальными уравнениями Ито:
dY = (У, X, t)dt 4- (У, X, t)dW,
dX = <p(Y, X, t)dt 4- X, t)dW, (2.1.5)
где У - ni-мерный наблюдаемый случайный процесс; X - п-мерный не-
наблюдаемый процесс; W - r-мерный процесс с независимыми прира-
щениями (п.1.4.4), причем V = dW/dt; <pi(Y,X,t) и ip(Y, X,t) - извест-
ные векторные функции, отображающие пространство Rni х Rn х R
соответственно в пространства 7?П1 и 7?п, а и ^х(У,Х,<) —
известные матричные функции, отображающие 7?П1 х Rn х R в 7?П1Г и
Rnr соответственно. Требуется найти оценку X(t) вектора состояния
X (может быть расширенного) системы в любой момент t > to по ре-
зультатам непрерывного наблюдения процесса У в интервале времени
[W], У/о = {У(т) : to < Т < t}.
Задача 2. Векторный случайный процесс [УТХТ] определяется
векторными стохастическими дифференциальными уравнениями Ито
dY = (У, X, t)dt 4- (У, X, t)dW,
dX = <р(Х, t)dt 4- ^(Х, t)dW, (2.1.6)
где, в отличие от задачи 1, процесс 1У(£) состоит из двух независимых
блоков, один из которых входит только в первое уравнение (2.1.6), а
2.1. ЗАДАЧИ ОЦЕНИВАНИЯ В СТОХАСТИЧЕСКИХ ДИФ.СИСТЕМЛХ 241
другой - только во второе уравнение (2.1.6). Требуется найти оценку
X(t + Д) будущего состояния системы Xt+& = X(t + Д), Д > 0, в
любой момент t > to по результатам наблюдения процесса Y в интервале
времени [to, t], У/о = {У(т) : to < т < t}.
Замечание. Само собой разумеется, для этого необходимо, чтобы матрицы
и имели соответствующую блочную структуру = [0^[], t/> = [^>z0] так,
чтобы было
ipidW = [0$]
dWi '
<ПУ2
= ^<ПГ2) i/)dW = [i/>'0]
t/ТУ1 / / птт
Задача 1 в приложениях обычно называется задачей фильтрации,
так как она технически решается путем пропускания наблюдаемого сиг-
нала через устройство, называемое фильтром, предназначенное для то-
го, чтобы “отфильтровать” помеху и получить на выходе сигнал, с воз-
можно большей точностью воспроизводящий процесс X(t), Задача 2
обычно называется задачей экстраполяции или прогноза.
Развивая общую постановку задачи 1 оптимального оценивания на
случай стохастических дифференциальных уравнений с винеровскими
и пуассоновскими шумами (1.5.21), придем к следующему результату.
Пусть векторный случайный процесс [У(£)ТХ(£)Т]Т определяется си-
стемой векторных стохастических дифференциальных уравнений Ито:
dY = + ^(Y,X,t,v)P°{dt,dv), (2.1.7)
я?
dX = <p(Y, X, t)dt 4- ф'(Х, X, t)dWQ 4- ф"(Х, X, t, v)P°(dt, dv). (2.1.8)
Здесь Y = Y(t) - ni-мерный наблюдаемый случайный процесс; X =
= X(t) - n-мерный ненаблюдаемый случайный процесс; ТУо = ТУо(^)
- r-мерный винеровский процесс (г > ni); Р°(Д,Л) - центрированная
пуассоновская мера, независимая от винеровского процесса Wo(0> а ин”
тегрирование распространяется на все пространство Яд с выколотым
началом координат; = ^(Y^X^t), <р = <p(Y,X,t)-, ф{ = ф[(У,Х,1),
ф' = ф*(у,Х,1) - известные функции, отображающие Rni х Rn х R
соответственно ЯП1, Rn, Rn>r-, ф”(Х,Х,1,и), ф" = ф"(у,Х,1,и) - из-
вестные функции, отображающие ЯП1 х Rn х Rq в ЯП1, Rn, Требу-
ется найти оценку X(t) процесса X(t) в каждый момент времени t по
242
ГЛ. 2. ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФИЛЬТРЫ КАЛМАНА
результатам наблюдения процесса У(т) до момента t, — {У(т) :
to < т < t}.
Уравнения задачи 2 включают как уравнение (2.1.7), так и уравне-
ние
dX = (p(X,t)dt + ^(X,t)dWo + I ^”(X,t,v)PQ(dt,dv). (2.1.9)
Замечание. Стохастические дифференциальные уравнения определя-
ют марковский случайный процесс. Следовательно, поставленные задачи представляют
собой задачи непрерывного оценивания и экстраполяции одних компонент марковского
процесса по результатам наблюдения остальных его компонент.
Кроме того, будем считать выполненными достаточные условия су-
ществования одно- и двумерных распределений (ТСтС, задачи 5.1 и
5.2). В некоторых случаях будет достаточно существования конечного
числа статистических моментов.
2.1.5. Особенности постановок задач интерполяции в сто-
хастических дифференциальных системах. Будем различать три
типовые оптимальные задачи интерполяции:
• интерполяция на закрепленном (фиксированном) интервале, или
интерполяция с фиксированной задержкой;
• прямая интерполяция, или интерполяция в закрепленной (фик-
сированной) точке;
• обратная интерполяция, или интерполяция с постоянным (фик-
сированным) сдвигом.
Рассмотрим эти задачи подробнее применительно к стохастическим
дифференциальным системам (п.2.1.4).
Задача 1. Предположим, что для стохастической дифференциаль-
ной системы (2.1.5) решены задачи с.к. оптимальной фильтрации, т.е.
найдена с.к. оптимальная оценка Xt\t состояния системы X(t) по реа-
лизации функции У (г) (to < т < t) Поставим задачу, основываясь на
оценке Xs\s состояния системы X(s) по реализации У($) на последую-
щем отрезке времени t < s < ti, улучшить оценку состояния системы
X(t) для момента времени t < Обозначим через Xt\tl, где t<ti, оцен-
ку состояния X(t) по реализации У(т) на отрезке to <т <ti. Моменты
времени to и ti будем считать закрепленными.
Задача 2. Пусть закреплена точка причем t\ > to- Требуется
дать оценку Xtl\t по реализации У(т) на отрезке ti < т < t. Оцен-
ка состояния X(t\) по реализации У(т) на отрезке t0 < т < t\
предполагается известной.
2.2. ОПТИМАЛЬНАЯ ФИЛЬТРАЦИЯ
243
Задача 3. Выберем некоторый постоянный временной сдвиг Д (Д >
> 0). Требуется найти Xt\t+& (* > £о), представляющую собой оценку
состояния X(t) по реализации Y(т) на отрезке to < т < t -I- Д.
Замечание. В большинстве практических задач реального времени основное
внимание уделяется вопросам оценивания состояния и параметров, т. е. фильтрации и
экстраполяции.
2.2. Оптимальная фильтрация в стохастических
дифференциальных системах
2.2.1. Общая формула для оптимальной оценки. Постав-
ленные в п.2.1.4 задачи можно решать различными способами в за-
висимости от того, какие оценки желательно получить. Естественно
потребовать, чтобы оценки процесса Y(t) или его будущего значения
Y(t -I- Д) были в некотором смысле оптимальными. Если задать кри-
терий оптимальности, то задачи, поставленные в п.2.1.4, станут вполне
определенными. Естественным критерием оптимальности во многих
задачах математической статистики служит критерий минимума сред-
I2
него квадрата ошибки (с.к.о.), М X — X — min. Такие оценки будем
называть с.к. оптимальными или просто оптимальными.
Если принять этот критерий, то общее решение задач п.2.1.4 и дру-
гих более общих задач оценивания немедленно получается из известного
свойства моментов второго порядка: из всех моментов второго порядка
скалярной случайной величины наименьшим является ее дисперсия -
центральный момент второго порядка (п.1.3.2). Отсюда следует, что
наилучшее приближение случайной величины (как скалярной, так и
векторной) неслучайной величиной с точки зрения критерия минимума
с.к.о. дает ее математическое ожидание. В частности, наилучшее при-
ближение случайной величины по результатам наблюдения дает апо-
стериорное математическое ожидание этой величины, т.е. ее условное
математическое ожидание относительно результатов наблюдений.
Обозначим через У/о совокупность значений наблюдаемого процес-
са в интервале времени [£о,£], У/о = {^(т) • т € [£о,£]}- Оптимальная
оценка вектора Хи = Х(и), дающая решение задачи 1 при и = t и
решение задачи 2 при и = t + Д, определяется формулой
Х< = М[Хи|У/0]. (2.2.1)
Эта формула определяет оценку значения Хи любой случайной функ-
ции X(t) по результатам наблюдения другой случайной функции Y(t)
в интервале [ t0, t ].
244
ГЛ. 2. ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФИЛЬТРЫ КАЛМАНА
Для практического применения формулы (2.2.1) в общем случае
необходимо найти апостериорное распределение Хи. Эта задача очень
сложна и в общем случае пока не решена. В частном случае, когда
процессы Y(t) и X(t) определяются уравнениями (2.1.5) или (2.1.6),
она может быть решена при некоторых дополнительных ограничени-
ях. Однако даже в этих случаях практическое применение формулы
(2.2.1) представляет большие, часто непреодолимые трудности. При-
чиной этого является то, что непрерывное определение апостериорного
распределения в нелинейных стохастических дифференциальных систе-
мах всегда требует очень громоздких вычислений, которые могут быть
выполнены только после наблюдений. Это приводит к большим затра-
там времени на вычисление оценок после наблюдений. Практически же
во многих случаях оценки необходимо получать в реальном масштабе
времени по мере поступления результатов наблюдений. Трудности при-
менения формулы (2.2.1) не снижают значения теории с.к. оптимально-
го оценивания и экстраполяции. Эта теория необходима для изучения
потенциальной точности оценок, т.е. предельно достижимой точности
оценивания.
2.2.2. Вспомогательная задача. В основе теории с.к. оптималь-
ной фильтрации лежит общая формула для стохастического дифферен-
циала оптимальной оценки данной функции вектора состояния систе-
мы (1.4.82). Пусть f(X, t) - некоторая скалярная функция п-мерного
вектора состояния системы и времени. Ее оптимальная оценка по ре-
зультатам наблюдения Y/ согласно (2.2.1) определяется формулой
f(t) = М [/(X,t) I у/о] . (2.2.2)
Оценка (2.2.2) представляет собой функционал от случайного про-
цесса Y(t) на интервале времени [ to, t ] и, следовательно, сама представ-
ляет собой случайный процесс. Поставим задачу найти стохастический
дифференциал Ито этого процесса.
Эта задача может быть решена при условии, что W(£) в уравнениях
(2.1.5), (2.1.6) представляет собой винеровский процесс, размерность
которого г не меньше размерности п\ наблюдаемого процесса Y(t), и
что функция ^1 в (2.1.5) не зависит от X. Уравнения (2.1.5) в этом
случае имеют вид
dY = <^i (У, X, t)dt -1- rfa (У, t)dW,
dX = cp(Y, X, t)dt + ^(У, X, t)dW. (2.2.3)
Замечание. Применительно к уравнениям (2.1.7), (2.1.8) и (2.1.7), (2.1.9)
соответствующая задача будет рассмотрена в п.2.2.12.
2.2. ОПТИМАЛЬНАЯ ФИЛЬТРАЦИЯ
245
2.2.3. Преобразование уравнений. Для получения основных
уравнений с.к. оптимального оценивания важно уметь приводить урав-
нения (2.2.3) к виду, в котором фигурируют независимые белые шумы,
образованные г — ni и п\ последними компонентами шума W(t).
> Чтобы упростить задачу нахождения стохастического дифферен-
циала процесса /(£), преобразуем уравнения (2.2.3) к более простому
виду. Сначала заметим, что для винеровского процесса W(t) интенсив-
ности р(т) при любом ортогональном преобразовании r-мерного про-
странства Rr случайный процесс
t
W'{t) = I Sl(y,T)i/-^2(T)dW(T), (2.2.4)
О
где П(2/,т) - матрица ортогонального преобразования, возможно, зави-
сящая от у и t, представляет собой винеровский процесс с независимыми
компонентами.
Замечание. Степень симметричной неотрицательно определенной мат-
рицы У определяется формулой У§ = AA.SAT, где Л = diag {Al, ... , Ад} -
диагональная матрица, к которой У приводится ортогональным преобразованием А, а
Л5 = diag {Af, ... , Af}.
Действительно, ковариационная матрица значения процесса W' (t)
при данном t определяется формулой
t
= У (1(у1т)у~1^2(т)у(т)у~1^2(т)С1(у,т>)Т(1т = Irt,
о
(2.2.5)
так как Q(j/, t)Q(j/,t)t = Ir в силу ортогональности матрицы 0(1/, т).
Компоненты процесса W'(t) не коррелированы, а следовательно, и не-
зависимы, так как винеровский процесс распределен нормально. При
этом каждая компонента процесса Wf(t) представляет собой стандарт-
ный винеровский процесс.
Заменим процесс IV(£) в уравнениях (2.2.3) процессом При
этом дифференциал dW заменится величиной ^1/f2(t)O(y, t)TdW'. Вы-
берем теперь ортогональную матрицу Q(j/, t) так, чтобы привести мат-
рицу V>i (j/, t) к блочному виду [0 tp"(y, t) ], где первый блок представляет
собой ni х (г — ni )-матрицу все элементы которой равны нулю, а второй
- ni xni-матрицу. Это при некоторых условиях возможно, так как орто-
гональная ni х ni-матрица Q имеет г(г — 1)/2 произвольных элементов,
которые должны удовлетворять ni(r — гц) условиям, и г(г—1)/2 > г2/4
246
ГЛ. 2. ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФИЛЬТРЫ КАЛМАНА
ПРИ г > 2, П1(г — ni) < г2/4. В результате такого преобразования будем
иметь
dW =
vl/2(t)tt(Y,t)TdW' =
_^Y,X,t)
“ iMY,X,t)vV2(t)(l(Y,t) ] aVV ~
0 ^(Y,t)
J>'(Y,X,t) ^"(Y,X,t)
M(Y,t)dW2
ф'(Х, X, t)dWi + <(У, X, t)dW2
dW' -
где Wi (t) и W2 (t) - независимые винеровские процессы, образованные
соответственно г—ni первыми и ni последними компонентами процесса
VK'(t). При этом уравнения (2.2.3) приводятся к виду
dY = (Y, X, t)dt + ф"(У, t)dW2,
dX = <p(Y, X, t)dt + ф'(У, X, t)dWi + ф"(Х, X, t)dW2. (2.2.6)
Чтобы найти матрицы ф', ф", ф” и выяснить условия, при кото-
рых приведение уравнения (2.2.3) к виду (2.2.6) возможно, вычислим
условную ковариационную матрицу случайного вектора
^(У,<)
V>(y,x,t)
АРУ =
о
ф'(У,Х,е>
ф"(Х,Х,1)
AW'
(2.2.7)
относительно величин Y, X, где Д1У = W(t + At) — W(t), АРУ' = W'(t+
+Д£) — W'(t). Имея в виду, что АРУ и Д1У' независимы от Yt, Xt и их
ковариационные матрицы равны соответственно v(t)At -1- о(Д£) и IrAt,
по формуле преобразования ковариационной матрицы при линейном
преобразовании случайного вектора находим для (2.2.7), опуская для
краткости аргументы функций ^i, Ф' Ф”, Ф",
* ] v at + »(At) = [ “ *1 ] [ J.T ] Д1. (2.2.8)
Отсюда, разделив обе части на Д^, при At —> 0 получаем
’ Ф1УФ1 Ф^Ф7 1 _ Г Ф"Ф"Т ф'(ф"Т 1 /'9 9 0'1
фиф{ фифт ] [ ф"ф'{т ф'фт + ф"ф"т ’
2.2. ОПТИМАЛЬНАЯ ФИЛЬТРАЦИЯ
247
или
V’lV"7 = Ф^ФТ, Ф"Ф"Т = V’H’i'. ф'ф'Т + ф"ф"Т — фифт. (2.2.10)
Определяемая этой формулой матрица ф" не зависит от X, так как
не зависит от X. Второе уравнение (2.2.10) имеет решение тогда и
только тогда, когда матрица обратима при всех у, t. Для этого
необходимо, чтобы матрица была обратимой при всех у, t, так
как на основании первого уравнения (2.2.10) |^Г|2 — • В этом
случае второе уравнение (2.2.10) дает ф" = 'фи'ф?• После этого
третье уравнение (2.2.10) приводится к виду
'ф,'ф,Т — ,фу'фт — 'фуфТ (<ф" 1)Т(^1/ 1)'Ф1^'фТ
или, так как в силу первого уравнения (2.2.10) (V,i,1)T(V,i,1)T —
= (V’l^?')-1, 'ф,'ф,Т = 'фу'ф1'—фуф^('ф1уф'[)~1ф1уфт. Правая часть это-
го уравнения представляет собой симметричную неотрицательно опре-
деленную матрицу. <
Таким образом, доказано следующее утверждение.
Лемма 2.2.1. Уравнения нормальной стохастической дифферен-
циальной системы (2.2.3) приводятся к виду (2.2.6), где IVi(£) и W2(t) -
независимые винеровские процессы, образованные соответственно
г — П\ первыми и ni последними компонентами процесса опре-
деляемого ортогональным преобразованием (2.2.4), тогда и только то-
гда, когда матрица обратима при всех
У, t.
2.2.4. Стохастический дифференциал оптимальной оценки
функции состояния системы. Теперь по формуле Ито для стохасти-
ческого дифференциала нелинейной функции (1.4.82) мы можем найти
стохастический дифференциал с.к. оптимальной оценки данной ска-
лярной функции вектора состояния системы (2.2.3) и времени.
Справедливо следующее утверждение.
Лемма 2.2.2. Стохастический дифференциал с.к. оптимальной
оценки f известной скалярной функции f{X,t) вектора состояния X
и времени t нормальной стохастической дифференциальной системы
(2.2.3) вычисляется по следующей формуле:
df = M[/t (X, t) + А (X, t)T<p(Y, X, t)+
+ |tr {fxx(X, ЩфифТ)(Г, X, t)} | Y/0]dt + M[/(X, t) (У, X, t)T- +
248 ГЛ. 2. ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФИЛЬТРЫ КАЛМАНА
+fx(X,t)T(^)(Y,X,t) I - fadt), (2.2.11)
где для краткости положено
(фуфТ)(Х, X, t) = ^(У, X, t)v(t)^{Y, X, t)T,
Wvtf)(Y, X, t) = i/>(Y, X, (У, t)T,
oo
<Pi = У <piPt(x)dx = M[y>i(Xt,Yt,t I y/0)J. (2.2.12)
—OO
При этом предполагается, что матрица о^ = невырождена,
существуют производные ft, fx, fxx и все условные математические
ожидания в правой части (2.2.11).
2.2.5. Уравнения для апостериорной характеристической
функции
> Положив в (2.2.11) f(x,t) = etX х, получим стохастическое урав-
нение для апостериорной характеристической функции вектора Xt:
5t(A) = М [е*лТх‘ |У/0].
Имея в виду, что в данном случае
Л = 0, fx = iXeixTx, fxx = -XXTeixTx
И что
tr {ААТ(^^Т)(2/,^,С} =
из (2.2.11) получаем
dgt(X) = М
|iXT<p(Y, X, t) - |ат(тМ’Т)(У, X, 0а! eixTx
I А \
dt+
+М[{у>1(У,Х,£)т -ф^ + iXT(iln'il>i)(Y,X,t))} х
хе<АТх | У/0](^1^)_1(У,«)(^ - (2.2.13)
Правая часть здесь представляет собой функционал от характери-
стической функции (А), рассматриваемой как функция А, поскольку
^^ОПТИМАЛЬНАЯ ФИЛЬТРАЦИЯ
249
апостериорное распределение вектора Xt полностью и однозначно опре-
деляется этой характеристической функцией. Поэтому (2.2.13) пред-
ставляет собой стохастическое дифференциальное уравнение для апо-
стериорной характеристической функции р$(А). Это уравнение нели-
нейно, поскольку в силу (2.2.12) ф\ = М[<^1(У,Х,£) | У^] тоже явля-
ется функционалом от р<(А). В начальный момент to функция р«0(А)
представляет собой условную характеристическую функцию величины
Xq относительно Yq. Это служит начальным условием для уравнения
(2.2.13). <
Таким образом, доказано следующее утверждение.
Теорема 2.2.1. Пусть матрица невырождена и су-
ществуют условные математические ожидания в правой части
(2.2.13). Тогда уравнение для апостериорной характеристической
функции gtW вектора X нормальной стохастической дифференциаль-
ной системы (2.2.3) имеет вид (2.2.13) при начальном условии р*0(А)
величины Xq относительно Yq,
Решив уравнение (2.2.13), можно легко вычислить с.к. оптималь-
ную оценку Xt вектора состояния системы X, определяемую формулой
(2.2.1). Для этого достаточно вспомнить (п.1.3.4), как выражается ма-
тематическое ожидание через характеристическую функцию. Тогда по-
лучим
Xt =М [Xt I УД] =
(2.2.14)
. - А=0
2.2. в. Уравнение для апостериорной плотности
> Из уравнения (2.2.11) совершенно так же выводится стохастиче-
ское уравнение для апостериорной плотности pt(x) вектора Xt:
dpt(x) = -— [y>(y,a:,t)Pt(z)]dt+
ох
[ (^И’Т) (У> M)Pt (*)])<** + ([vi(Y,x,t)T-<ff]pt(x)-
£» I \JJb I I
[(^Г)(Ух.«)я(а:)]}(^^Г)-1(Г,0(ЙУ -^di). (2.2.15)
Имея в виду, что в силу (2.2.12)
оо
<Э1 = м [ (У, X, t) I УД ] = У ч>1 (У, х, t)pt (x)dx,
—ОО
(2.2.16)
250
ГЛ. 2. ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФИЛЬТРЫ КАЛМАНА
заключаем, что (2.2.15) представляет собой нелинейное стохастическое
интегродифференциальное уравнение относительно апостериорной
плотности pt(x). В начальный момент to функция р*0(х) представляет
собой условную плотность величины Xq относительно Уо- Это служит
начальным условием для уравнения (2.2.15). <
Таким образом, имеем следующую теорему.
Теорема 2.2.2. Пусть матрица = ф1УфТ невырождена и су-
ществует условное математическое ожидание фг. Тогда стохасти-
ческое интегродифференциальное уравнение для апостериорной плот-
ности pt(x) вектора X нормальной стохастической дифференциаль-
ной системы (2.2.3) имеет вид (2.2.15) при начальном условии pto(x)
величины Xq относительно Yq.
Решив уравнение (2.2.15), можно найти по формуле (2.2.1) с.к. оп-
тимальную оценку X вектора состояния X системы:
оо
Xt = M[Xt|y/0] = J xpt(x)dx. (2.2.17)
— оо
Однако реализовать эту возможность, так же как вычислить X по фор-
муле (2.2.14), чрезвычайно трудно. Как уравнение (2.2.13), так и урав-
нение (2.2.15) можно решить только после получения результатов на-
блюдений Y/, что невозможно выполнить непрерывно в реальном мас-
штабе времени в процессе работы системы.
2.2.7. Стохастический дифференциал апостериорного ма-
тематического ожидания
> Формула (2.2.1) определяет с.к. оптимальную оценку как апосте-
риорное математическое ожидание соответствующей случайной величи-
ны. Точность оптимальной оценки при данных результатах наблюдений
характеризуется апостериорной ковариационной матрицей оцениваемой
случайной величины. Поэтому для теории с.к. оптимального оцени-
вания необходимо вывести формулы для стохастических дифференци-
алов апостериорных математического ожидания X и ковариационной
матрицы R вектора состояния системы. Эти формулы легко выводят-
ся из общей формулы (2.2.11). Так как формула (2.2.11) определяет
стохастический дифференциал скалярной функции состояния системы,
необходимо применять ее для каждого элемента матриц X и R по от-
дельности.
Положив в (2.2.11) /(X, t) = Xk, будем иметь ft = 0, fx =
= [0... 1... 0]т, fxx = 0, и формула (2.2.11) даст
k
dXk = <Pkdt + M[Xfc(<Pi’ - <pl)+
2.2. ОПТИМАЛЬНАЯ ФИЛЬТРАЦИЯ
251
+(^МГ)* I ’(dK - <f>idi) (k = 1, ... , n), (2.2.18)
где в соответствии с общим обозначением (2.2.16)
фк = M[(pk(Y,X,t) \У/о],
(фифТ)к ~ к-я строка матрицы фиф? и аргументы функций уц, фиф?
и Для краткости опущены.
Из (2.2.18) вытекает матричная формула для стохастического диф-
ференциала оптимальной оценки X (апостериорного математического
ожидания) вектора состояния X системы (2.2.3):
dX = ipdt 4- М[Х{<^1 (У, X, t)T -$}+
+W>vtf')(Y,X,t) | Y^u^-^Y^dY - ^dt). о (2.2.19)
Таким образом, доказана теорема.
Теорема 2.2.3. Пустпъ матрица = Фт^фТ невырождена и су-
ществуют условные математические ожидания в правой части
(2.2.19). Тогда стохастический дифференциал апостериорного мате-
матического ожидания вектора состояния X нормальной стохасти-
ческой дифференциальной системы (2.2.3) определяется формулой
(2.2.19).
2.2.8. Стохастический дифференциал апостериорного мо-
мента второго порядка
t> Найдем стохастический дифференциал апостериорного момен-
та второго порядка вектора состояния системы. Положив в (2.2.11)
/(X, t) = ХкХц будем иметь при к <1
ft = o, fx = [0...Xl...Xk...0]T,
k I
и формула (2.2.11) даст
252
ГЛ. 2. ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФИЛЬТРЫ КАЛМАНА
drki = М [Хкщ + Xt<pk + {фуфт)к1 | Г/о ] dt+
+М[Х*Х/(<р?’ - <tf) + Хк(‘фи'ф{)1+
+XtW>vtf)k I - frdt) (Л, I = 1, ... , n). (2.2.20)
Здесь в дополнение к прежним обозначениям Гы = М [Л^Х/ | УД], а
~ соответствующий элемент матрицы фифт.
Для вывода соответствующей матричной формулы перепишем
(2.2.20) в виде
dTki = М [Xk<pi + Хцрк + (V’pV’7)*/ I ] dt+
П1
+ £ M[X*Xtar + Xkblk + X,bkr | Y*0](dYr - <plrdt)
r=l
где ar - r-й элемент матрицы-строки a hr ~ эле-
мент Л-й строки и r-го столбца матрицы Тогда, обо-
значив через Ьг r-й столбец матрицы V’W’i'(V’iW’i')-1 > h = [&ir • • • bPr]T
(r = 1, ... , nJ, получаем следующую формулу для стохастического
дифференциала апостериорного момента второго порядка Г вектора со-
стояния X системы:
dT = МрМУ, X, t)T 4- ^(У, X, t)XT+
+(^T)(Y, X, t) | У/Jdt + M[XXTar(Y, X, t)+
r=l
+Xbr(Y, X, t)T + br(Y, X, t)XT | У/0К</Гг - <£1г<Й)- < (2.2.21)
Следовательно, имеем следующий результат.
Теорема 2.2.4. Пусть матрица ai = невырождена и су-
ществуют условные математические ожидания в правой части
(2.2.21). Тогда стохастический дифференциал апостериорного момен-
та второго порядка вектора состояния X нормальной стохастиче-
ской дифференциальной системы (2.2.3) определяется формулой
(2.2.21).
2.2. ОПТИМАЛЬНАЯ ФИЛЬТРАЦИЯ
253
2.2.9. Стохастический дифференциал апостериорной кова-
риационной матрицы
о Для нахождения стохастического дифференциала апостериорной
ковариационной матрицы R вектора состояния системы известной фор-
мулой, связывающей математическое ожидание, момент второго поряд-
ка и ковариационную матрицу случайного вектора R = Г - ХХТ, или,
в скалярной форме, Rm = I'm - XkXi. Из этой формулы следует, что
dRkl = сСГы ~ d(XkXT).
Для нахождения d{XkX^) применим формулу Ито для стохастического
дифференциала произведения двух случайных процессов в случае ви-
неровского процесса W (1.4.83). Имея в виду, что на основании (2.2.18)
роль матриц-строк Yi и Уг в данном случае играют
м | у/0 ]
М [-XjGpi’ - ¥>i) + (V’l'V’D/ I Yt0 ]
находим
d(XkXt) = XkdXi + XtdXk+
+M [xk(<p[ + (i/>vipi)k | У/о] (V4^n-1V’iW’i’W’iW’?')~lx
xM - ф[) + | Г/о ] dt.
Подставив сюда выражения dXk и dXk из (2.2.18), будем иметь
d(XkXt) = {Xk<pi + Х,фк + - ^)+
+(V’W’i')* I - ^1) + I Vj}dt+
+М[(ад + XiXk)(rf - + xk(№tf)i+
+Х1(фу‘ф[)к I Y^^y^dY -<pidt).
Вычитая эту формулу из (2.2.20) и добавляя нулевое слагаемое
М[ШГ - ф?) I у/0] = хМ - ф{) = о,
получим
254
ГЛ. 2. ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФИЛЬТРЫ КАЛМАНА
dRkl = {М[(Хк - Xk)<Pi + (X, - Xt)Vk + (Wf)kl I У/J-
-M[x*(^f - <£f) + ftWi’)* I ^/0](^I/V’iiT)_1M[x/(^1 - ^)+
+(’М’Г)Г I rt‘0]M + - xk)(xt - xt)(rf - ФТ)+
+(Xk - XkMvtf), + (Xt - Xt)(^T)k I Y*0](Mf )-'(<!¥ - frdt)
(2.2.22)
(k,l = 1, ... , n).
Преобразуя последнее слагаемое в (2.2.22), получаем матричную фор-
мулу для стохастического дифференциала апостериорной ковариацион-
ной матрицы R вектора X состояния системы:
dR = {М[(Х - X)<p(Y, X, t)T + <p(Y, X, t)(XT - Хт)+
+(^T)(Y,X,t) | УД] - M[X{V1 (Y,X,t)T - фТ}+
+(^T)(Y,x,t) I ^(мГИ^ММВД -<pt}xT+
+(^T)(Y,X,t) I y/0]}dt+
+ ^M[(X - X)(XT - XT)ar(Y,X,t) + (X- X)br(Y,X,t)T+
r=l
+br(Y, X, t)(X - X)T | У/0](йУг - <pirdt). <i (2.2.23)
Таким образом, доказана следующая теорема.
Теорема 2.2.5. Пусть матрица = 'фги'фТ невырождена и
существуют все условные математические ожидания в правой ча-
сти (2.2.23). Тогда стохастический дифференциал апостериорной ко-
вариационной матрицы R вектора состояния X нормальной стоха-
стической дифференциальной системы (2.2.3) определяется формулой
(2.2.23).
Замечание!. Средний квадрат ошибки оптимальной оценки X при дан-
ных результатах наблюдений т.е. апостериорное математическое ожидание квадрата
модуля ошибки, очевидно, равен следу апостериорной ковариационной матрицы вектора
состояния системы:
М[|Х - if I У/J = tr R. (2.2.24)
2.2. ОПТИМАЛЬНАЯ ФИЛЬТРАЦИЯ
255
Замечание 2. Ясно, что формулы (2.2.19) и (2.2.21) или (2.2.19) и (2.2.23)
в общем случае не являются стохастическими дифференциальными уравнениями относи-
тельно ТП и Г или ТП и /?, так как их правые части зависят от неизвестного одномерного
апостериорного распределения. Тем не менее, как будет показано дальше (глава 3), эти
формулы могут служить основой для различных приближенных методов фильтрации.
2.2.10. Применение теории оптимальной фильтрации для
оценивания параметров в уравнениях стохастических диффе-
ренциальных систем. Все доказанные теоремы справедливы также
для случая, когда X является расширенным вектором состояния стоха-
стической дифференциальной системы, в который включены все неиз-
вестные параметры, входящие в уравнения (2.2.3). При этом в соответ-
ствии с очень существенным для всей теории с.к. оптимальной филь-
трации условием независимости функции V>i в первом уравнении (2.2.3)
от вектора состояния она не может также зависеть от неизвестных па-
раметров, поскольку они входят в расширенный вектор состояния. Та-
ким образом, теорию с.к. оптимальной фильтрации можно применять
для решения задач одновременного оценивания вектора состояния сто-
хастической дифференциальной системы и неизвестных параметров, от
которых могут зависеть функции у>, ¥>1 в уравнениях (2.2.3).
2.2.11. О возможности решения задач оптимальной филь-
трации при автокоррелированной помехе в наблюдениях. Все
выведенные формулы в пп.2.2.4-2.2.9 справедливы, только если ^(y^t)
не обращается в нуль ни при каких у и t, так как только при этом
условии матрица V'lW'f может быть обратимой. Поэтому решение за-
дачи с.к. оптимальной фильтрации при V’iGM) = 0 в общем случае
невозможно. Однако в некоторых частных случаях эта задача может
быть сведена к случаю V>i (з/, t) 0 0, если помеха в наблюдениях может
быть представлена как результат преобразования белого шума форми-
рующим фильтром (п. 1.5.2), описываемым дифференциальным урав-
нением. Это, во-первых, случай линейной фильтрации, который будет
рассмотрен позже. Во-вторых, это случай, когда задача сводится к
уравнениям:
X = <^(Х, £) + V>Vi, Ui = <^2(^1,0 + *02^2?
Z = ^Х + b2U1+b0. (2.2.25)
При этом в последнее уравнение могут входить не все компоненты век-
тора [71, а только некоторые из них, образующие вектор помехи U.
Дифференцируя третье уравнение (2.2.25), приведем его к виду
256
ГЛ. 2. ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФИЛЬТРЫ КАЛМАНА
И — Ь\(р{Х, t) + Ь1Х + b2^P2{Ui, t) + l)2Ui + bo“h
+ [bn/ЛМ [V1TV2T]T. (2.2.26)
Исключив из этого уравнения и уравнения формирующего фильтра по-
мехи все компоненты вектора CZi, которые могут быть выражены через
X и Z из уравнения наблюдения Z = biX + £>2^1 + Ьо, получим урав-
нение типа первого уравнения (2.2.3), если хотя бы одна из величин
Ьгф и Ь2^2 отлична от нуля. Поэтому решение задачи оптимальной
фильтрации в этом случае принципиально возможно при условии, что
размерность векторного белого шума [ ] не меньше размерности
ni наблюдаемого сигнала Y и матрица
q1
О i!)Tb^
^2 j [ ^2^2 ,
= b^u^b} 4- b2^2^lbz,
играющая роль матрицы ‘фхУ'ф'^ в общей теории с.к. оптимальной филь-
трации, обратима при всех t. В этом случае, расширив вектор состояния
X добавлением к нему всех оставшихся компонент вектора C7i, можем
написать для данной задачи все выведенные формулы и уравнения тео-
рии с.к. оптимальной фильтрации.
2.2.12. Об уравнениях с.к. оптимальной фильтрации в слу-
чае винеровских и пуассоновских шумов. Формула (2.2.12) и вы-
текающие из нее уравнения с.к. оптимальной фильтрации могут быть
обобщены на случай, когда уравнение наблюдения (2.1.7), во-первых, не
содержит пуассоновских шумов и, во-вторых, функция <ф" не зависит
от X, т.е.
tf(Y,X,t,v) = 0, xp[{Y,X,t) = ^{Y,t), (2.2.27)
а уравнение состояния имеет вид (2.1.8).
Замечание. В случае, когда функция ^"(Y^X, t, v) в (2.1.8) допускает
представление вида
V>"(r, X, t, v) = X, t)jr(v), (2.2.28)
аР°(Д,Л) = P°([0,t),dv) , тогда уравнение (2.1.8) принимает вид
dX = v>(Y, X, t)dt + X, t)dW, (2.2.29)
где W(t) = W(t) 4- f 7r(v)P°([0, t), dv). Поэтому уравнение (2.1.8) охватывает все
уравнения вида (2.2.29) с любыми процессами с независимыми приращениями.
2.2. ОПТИМАЛЬНАЯ ФИЛЬТРАЦИЯ
257
> Для обобщения формулы (2.2.12) на случай уравнений (2.1.7),
(2.1.8) при условии (2.2.27) заметим, что в п.2.2.4 при вычислении раз-
ности М [ /(Х*+де, 14- Д/) - f(Xt) t) | Y* ] следует применить обобщен-
ную формулу дифференцирования (1.4.86). В результате появится до-
полнительное слагаемое
j{f(X 4- ^(Y, X, t, v), t) - /(X, t)-
-/4x,oV4^^v)}i/P(t,dv) dt,
где i/p(t, А) - интенсивность потока событий, порождающего пуассонов-
ский процесс Р([0, t), А). Это же слагаемое добавится в правой части
формулы (2.2.12). В результате вместо (2.2.12) получим следующую
формулу, обобщающую лемму 2.2.2:
df = dM [ f(X, t) I УД ] = M ft(X, t) + fx(X, t)T<p(Y, X, t)+
fxx(X, t)(^T)(Y, X,t)+ {f(X + i/>"(Y, X,t,v),) —
-f(X,t) - fx(X,t)T^"(Y,X,t,v)^P(t,dv) | Г/Ор«+
+M [/(X,t) MY,X,t)T + fx(X,t)T(^T)(Y,X,t) | У/J x
x (^!iz^)(y, t)(dY — <pdt)
(2.2.30)
(лемма 2.2.3).
Положив в (2.2.30) = e'x7\ находим уравнение для апосте-
риорной характеристической функции обобщающее уравнение (2.2.13)
с.к. оптимальной фильтрации:
dpt(A) = М \iXT<p(Y,X,t) - ±XT(№T)(Y,X,t)X+
+ f [e‘*T^"(yx,t,v) _ ! _ jxT^,(Y,X,t,v)] i/p(t,dv)|e<ATl | У/о dt+
9 Фильтры Калмана и Пугачева
258
ГЛ. 2. ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФИЛЬТРЫ КАЛМАНА
4-М — фТ + i\Tfyv^T)(Y,X,t>)x
xeixTx | У/о " ^idt) (2.2.31)
(теорема 2.2.6) . <
2Л. Оптимальная линейная фильтрация в стохастических
дифференциальных системах
2.3.1. Уравнения линейной фильтрации. Задачу оптималь-
ной фильтрации удается решить до конца в случае линейных уравнений
(2.1.5):
dY = (bY 4- ЬХ 4- b0)dt 4- ifadW, dX = (aY 4- arX 4- a0)dt 4- xpdW, (2.3.1)
где коэффициенты a, ai, ao, &i, 'Ф и в общем случае зависят
от времени t и соответственно имеют размерности п х ni, п х n, п х 1,
щ х ni, ni х п, ni х 1, п х г, ni х г. В этом случае распределение
процесса [У(£)ТХ(£)Т]Т нормально при нормальном распределении его
начального значения Следовательно, и апостериорное рас-
пределение вектора состояния системы X относительно наблюдаемого
процесса Y/ нормально, и для его определения достаточно найти апо-
стериорные математическое ожидание X и ковариационную матрицу
R = М(Х - Х)(Х - Х)т. Для этого обратимся к формулам (2.1.19) и
(2.1.23) для стохастических дифференциалов величин X и R.
t> Подставив в (1.12.19) и (2.1.23) выражения функций у? и <^i,
</?(У,Х,*) =аУ+ aiX + a0, ¥>1(У, X, t) = bY 4- brX 4- 60,
получим
dX = (aY + ахХ + a0)dt + {М[Х(ХТ - Хт) | +
+ - (bY + biX + bo)dt], (2.3.2)
dR = M[(X - X)(YTaT + + aj)+
+ (aY + aiX + a0)(XT - XT) + | Y}0]dt-
- M[(X - X)(YTbT + XTbl + bl) + V-^Г I Y}0] X
2.3. ОПТИМАЛЬНАЯ ЛИНЕЙНАЯ ФИЛЬТРАЦИЯ
259
X + biX + bo)(XT - Хт) + Мт I УД]Л+
+ ElE^'W^ - *ь)(Х - X)(XT - Хт) | У^]+
/=1 '•fc=l
+ М[Х - X I у/Х + ДМ[ХТ - Хт I УД] | X
X
^ - (Е b*Yk + Е + to j dt
\Jfe=l Р=1 /
(2.3.3)
где ahr ~ элементы матрицы а = Ь^{ф\уф^) х, а $ - /-й столбец мат-
рицы фиф? (фъуфТу'1. Учитывая, что
М[Х(ХТ - Хт) I УД] = М[(Х - Х)ХТ I УД] =
= М[(Х-Х)(ХТ-ХТ)|УД] = Л,
М[Х - X I УД] = X - X = о,
М[(Х - Х)УТ I УД] = М[Х - X I УД]УТ = о
и что апостериорные центральные моменты третьего порядка равны ну-
лю вследствие нормальности апостериорного распределения, приведем
полученные формулы (2.3.2) и (2.3.3) к виду:
dX = (аУ 4- X 4- ао)сЙ4-
+ (Rb[ + фуфТУф^фТ)-1^ - (ЬУ + ЬГХ + 60)<й], (2.34)
dR = [«17? + Ra[ 4- фифт-
— (Rb? + фиф?+ ф11/фт)^1. < (2.3.5)
Таким образом, формулы (2.1.19) и (2.1.23) в данном случае дают
систему уравнений, определяющую оптимальную оценку X вектора со-
стояния системы X и его апостериорную ковариационную матрицу R,
характеризующую точность оценки X.
Матричное уравнение Риккати (2.3.5) для апостериорной ковари-
ационной матрицы R не содержит X и, следовательно, может быть
проинтегрировано отдельно. Определив R, можно после этого найти
величину
Р = (Rb{ + фи'ф^'фхи'ф^) \
(2.3.6)
260
ГЛ. 2. ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФИЛЬТРЫ КАЛМАНА
называемую матричным коэффициентом усиления и определить оцен-
ку X вектора состояния системы X интегрированием уравнения (2.3.4),
которое можно теперь переписать в виде:
dX = (аУ 4- + a^dt + 0[dY - (bY + bYX + b0)dt]. (2.3.7)
Уравнение (2.3.5) не содержит результатов наблюдений. Поэтому
апостериорная ковариационная матрица вектора состояния X совпада-
ет с априорной ковариационной матрицей вектора ошибки X = X — X
оценки X. Это дает возможность определять R и вычислять коэффи-
циент Р в уравнении (2.3.7) заранее, до получения результатов наблю-
дений. Тогда определение оценки X сведется к интегрированию урав-
нения (2.3.7) по мере получения результатов наблюдений, что можно
выполнять на практике в реальном масштабе времени непосредственно
в процессе работы изучаемой системы.
Уравнения (2.3.5) и (2.3.7) при начальных условиях
Х(*о) = Хо = М[Х0 | Уо], R(to) =Ro = М[(Х0 - ХО)(ХОТ - Хот) | Уо]
(2.3.8)
определяют с.к. оптимальную оценку X вектора X и его ковариаци-
онную матрицу R при всех t > tQ. Эта оптимальная и несмещенная
оценка X при t > to, так как в силу формулы полного математического
ожидания (п.1.3.6) и формулы (2.2.1)
М(Л - Xt) = М{М(Л - Xt) I у/0]} = М(Л - Xt) = 0.
Таким образом, доказано следующее утверждение (Липцер и Ши-
ряев 1968).
Теорема 2.3.1. Уравнения (2.3.5)-(2.3.7) тогда и только тогда ре-
шают задачу с.к. оптимальной несмещенной оценки состояния линей-
ной нормальной стохастической дифференциальной системы (2.3.1),
когда матрица оч = невырождена.
В случае, когда коэффициенты a,a^a^b,61?5о»Vs V’i и интенсив-
ность белого шума и не зависят от времени t, то в уравнениях (2.3.5)-
(2.3.7) следует принять R = 0, т.е.
aiR + Rai + -I- + Ф1^Ф1)] = 0-
(2.3.9)
Теорема 2.3.2. Уравнения (2.3.9), (2.3.6) и (2.3.7) тогда и только
тогда решают задачу с.к. оптимальной несмещенной оценки стаци-
онарного состояния линейной нормальной стационарной стохастиче-
ской системы (2.3.1), когда матрица ai = Ф1кф1 невырождена.
2.3. ОПТИМАЛЬНАЯ ЛИНЕЙНАЯ ФИЛЬТРАЦИЯ
261
ЗямбЧ&НИб. Как будет показано в разделе 2.4 в случае Q = О, Ь — О,
теорема 2.3.1 дает известный результат (Калман и Бьюси 1960).
2.3.2. Обновляющие процессы. Случайный процесс
t
Y^t) = Y(t) - I(bYT 4- ЬгХт 4- b0)dr, (2.3.10)
to
дифференциал которого входит в уравнение (2.3.7) для оптимальной
оценки, обладает тем свойством, что его приращение на любом интер-
вале [t, s] не коррелировало со значениями YT процесса Y(t) при т <t.
Если случайный процесс Yi(t) обладает свойствами:
1) при любом t > to его значение представляет собой функционал
от процесса У(т), т € [to, t];
2) при любых а < t < s приращение У1($) — Ух(£) не коррелирова-
на с У (а), то процесс У1(£) называется обновляющим по отношению к
процессу Y(t).
Таким образом, в уравнение (2.3.7) для оптимальной оценки состо-
яния системы входит не дифференциал наблюдаемого процесса У(£),
а только дифференциал (конечно, стохастический) соответствующего
обновляющего процесса У!(£).
Оказывается, что это общее свойство всех уравнений с.к. опти-
мальной фильтрации. Процесс
t
Yi(t) = Y(t) - j<pi(r)dr, (2.3.11)
to
дифференциал которого входит во все уравнения теории с.к. оптималь-
ной фильтрации (раздел 2.2), всегда является обновляющим по отноше-
нию к Y(t).
При оптимальной линейной фильтрации в любой момент времени
используется лишь та часть поступающего в этот момент приращения
наблюдаемого процесса, которая не коррелирована с его прошлыми зна-
чениями, несет существенно новую информацию. Этим и объясняется
название “обновлящий” процесс.
2.3.3. Случай уравнений, линейных относительно вектора
состояния. Рассмотрим теперь более общий случай уравнений (2.1.5),
линейных только относительно вектора состояния X системы
dY = [bi(У, t)X 4- Ьо(У, t)]dt 4- ^1(У, t)dW,
dX = [щ (У, t)X 4- оо(У, t)]dt 4- Ж t)dW. (2.3.12)
262
ГЛ. 2. ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФИЛЬТРЫ КАЛМАНА
В этом случае при каждой реализации y(t) наблюдаемого процесса Y(t)
второе уравнение (2.3.12) линейно относительно X. Поэтому можно
сделать вывод, что при нормальном начальном распределении X услов-
ное распределение вектора Xt нормально для каждой реализации yfQ =
= {Ут • т 6 [£о,£]} наблюдений Y при всех t > to.
о Приняв условное распределение Xt относительно У/о нормаль-
ным, напишем для этого случая формулы (2.2.19) и (2.2.23) для сто-
хастических дифференциалов оптимальной оценки X и апостериорной
ковариационной матрицы R вектора состояния системы. Подставив в
(2.2.19) и (2.2.23) выражения
¥>(Г, X, t) = аг (У, t)X + оо(У, t), (Y, X, t) = br (Y, t)X + Ь0(У, t),
учитывая независимость ф от X и принимая во внимание, что для нор-
мального распределения все центральные моменты третьего порядка
равны нулю, получим:
dX = [ai(y,^)X + ао(У,0]^ + [Rbi(Y,t)T + (^Г)(^,0]х
х ^^y^Yt^dY - [&1(У,^)Х + д0(У,ОН), (2.3.13)
dR = {ai(Y,t)R + fiax(y,0T + ^^T)(Y,t) - [Rbi(Y,t)T+
4- (xp^)(Y,t)]}dt. <i
(2.3.14)
Таким образом, справедливо утверждение (Липцер и Ширяев 1968).
Теорема 2.3.3. Фильтрационные уравнения (2.3.13) и (2.3.14)
тогда и только тогда решают задачу с.к. оптимального линейного
оценивания состояния нелинейной нормальной стохастической диф-
ференциальной системы (2.3.12), линейной относительно вектора со-
стояния, когда матрица <?i = невырождена.
Аналогично п.2.3.5 выписываются уравнения для стационарного
фильтра в случае стационарных уравнений (2.3.12).
Как и в случае линейной фильтрации п.2.3.1, фильтрационные
уравнения представляют собой замкнутую систему уравнений, опреде-
ляющую X и R. Поэтому оптимальную оценку X вектора состояния
системы X и его апостериорную ковариационную матрицу R, характе-
ризующую точность оптимальной оценки X, можно вычислять по мере
получения результатов наблюдений совместным интегрированием урав-
нений (2.3.13) и (2.3.14).
В противоположность линейной фильтрации, основанной на урав-
нениях (2.3.1), в случае (2.3.12) нельзя вычислить R заранее, до получе-
ния результатов наблюдений, так как от результатов наблюдений зави-
2.4. ЛИНЕЙНЫЕ ФИЛЬТРЫ КАЛМАНА-БЬЮСИ
263
сят коэффициенты уравнения (2.3.14). Поэтому оптимальный фильтр
в данном случае должен выполнять интегрирование обоих уравнений
(2.3.13) и (2.3.14). Это приводит к существенному повышению порядка
оптимального фильтра. Если линейный фильтр (2.3.7) всегда описыва-
ется уравнениями того же порядка п, что и второе уравнение (2.3.1), то
в рассматриваемом более общем случае оптимальный фильтр описыва-
ется уравнениями порядка n + n(n + 1)/2 = п(п + 3)/2.
Пример 2.3.1. Процесс У (£) определяется скалярным стохастическим диф-
ференциальным уравнением Ито
dY = [ (Y, t)0 + b0(Y, t) ] dt + i/a (y, t)dW, (I)
где 0 - неизвестный векторный параметр. Найти оптимальную оценку 0 при каждом
t > to по результатам наблюдения процесса Y в интервале времени [М-
Заменив в (I) 0 случайным процессом ©(*). определяемым дифференциальным
уравнением dQ(t) = 0, и приняв О за вектор состояния X соответствующей системы,
получим дифференциальные уравнения вида (2.3.11) при Gi (У, f) = 0, Оо(У, £) = О,
^(У? £) = 0- Уравнения (2.3.13) и (2.3.14) в этом случае принимают следующий вид:
d© = flb1(J/,t)T(V>i^i’)-1(^O {dY - [ bi (Г, t)Q + Ьо(У,0] <й} > (П)
dR = -Rbi (Y, t)T(ipi vtf)-\Y, t)bi (Y, t)Rdt. (Ill)
Поскольку параметр 0 неизвестен и может в действительности не быть случайным, на-
чальные условия для © и R приходится брать произвольно. Полученные уравнения (II),
(III) дадут в этом случае оценку О, оптимальную в предположении, что параметр 0
случаен и имеет нормальное распределение с математическим ожиданием ©о и ковариа-
ционной матрицей Rq.
2.4. Линейные фильтры Калмана-Бьюси
2.4.1. Вводные замечания. Предположим, что в уравнениях
(2.3.1) а = b = 0. Это соответствует практической задаче фильтрации
полезного сигнала X, определяемого вторым уравнением (2.3.1) при а =
= 0, в случае, когда наблюдается сигнал Ь1Х + Ьо с аддитивной помехой,
представляющей собой нормальный белый шум. Уравнения (1.4.1) в
этом случае можно переписать в виде:
X = + + Z = brX + bQ 4- faV, (2.4.1)
где X - вектор состояния размерности п х 1; Z - вектор наблюдения раз-
мерности их х 1, а V = dW/d(t), W - винеровский процесс. Уравнение
оптимального фильтра (2.3.7) в этом случае имеет вид
к = ахХ + а0 + 0(Z - brX - bQ). (2.4.2)
264
ГЛ. 1. ТЕОРИЯ ОПТИМАЛЬНОГО ОЦЕНИВАНИЯ
Уравнение (2.4.2) определяет структуру оптимального фильтра. А
именно, оптимальный фильтр получается из данной системы (систе-
мы, формирующей полезный сигнал X (рис.2.4.1а) установкой перед ее
входом усилителя с коэффициентом усиления 0 и замыканием получен-
ной системы отрицательной обратной связью, содержащей усилитель с
коэффициентом усиления bi (рис.2.4.1б). При подаче на вход получен-
ного таким путем фильтра наблюдаемого процесса Y с вычтенной из
него функцией времени Ьо на выходе фильтра будет получаться опти-
мальная оценка X вектора X.
Рис. 2.4.1
Таким образом, получен следующий результат (Калман и Бьюси
1960).
Теорема 2.4.1. Уравнения (2.4.2), (2.3.5) и (2.3.6) тогда и только
тогда решают задачу с.к, оптимальной несмещенной оценки состо-
яния линейной нормальной стохастической дифференциальной систе-
мы (2.4.1), когда матрица ai = фгиф? невырождена.
Оптимальные фильтры, построенные согласно этой теореме, будем
называть фильтрами Калмана-Бьюси для системы (2.4.1).
2.4. ЛИНЕЙНЫЕ ФИЛЬТРЫ КАЛМАНА-БЬЮСИ
265
Замечание. В п.2.4.2 будет рассмотрен случай, когда белые шумы разные
в уравнениях состояния и наблюдения, а также независимы.
Так как процесс У(£), представляющий собой интеграл от наблю-
даемого процесса, при построении оптимального фильтра не использу-
ется, то за начальное значение оценки X при t = to следует принять
априорное математическое ожидание вектора Хо, Хо = МХо, а при
интегрировании уравнения (2.3.5) для определения коэффициента уси-
ления /3 за начальное значение матрицы R следует принять априорную
ковариационную матрицу вектора Хо, Яо = М(Хо — МХо)(Хо’ — МХ^).
Однако обычно эти априорные характеристики неизвестны. Это вы-
нуждает брать произвольные начальные значения X и R. Конечно, при
этом X не будет оптимальной оценкой вектора X, а может быть лишь
асимптотически оптимальной, если только первое уравнение (2.3.7) и
уравнение (2.3.5) описывают асимптотически устойчивый процесс (т.е.
если система, описываемая первым уравнением (2.3.7) и уравнением
(2.3.5), асимптотически устойчива). Вопросы устойчивости, управляе-
мости и наблюдаемости будут рассмотрены в разделе 2.11.
Пример 2.4.1. Найти оптимальный фильтр для фильтрации синусоидального
сигнала данной частоты CJq, наблюдаемого с аддитивным нормально распределенным
белым шумом.
Синусоидальный сигнал Xi (t) и его производную X2(t) = Xi(t) можно рас-
сматривать как компоненты вектора состояния системы, описываемой дифференциаль-
ным уравнением
d_ Г Xi 1 = О
dt Х2 . —wo
11 Г %!
оJ [х2
(I)
Наблюдаемый процесс определяется
Y = Z = Xi + V = [1 0]Х + V.
(П)
Следовательно, в данном случае а — йо = Ъ = Ъо = ф = 0, bi — [1 0], l/>i — 1,
а, =
о
. -“о
1
о
Уравнение (2.3.5) представляет собой систему уравнений
R11 — 27?12 — Р-17?п, Я12 = + ^22 —
Я22 = -2ш2Я12 - (Ill)
Определив Яц> R12 и Я22 интегрированием этих уравнений при начальных условиях
Яц(М = М(Х§!)2, Я12(«о) = МХ&Х&, R22(t0) = М(Х°2)2, найдем средний
266
ГЛ. 1. ТЕОРИЯ ОПТИМАЛЬНОГО ОЦЕНИВАНИЯ
квадрат ошибки фильтрации Х\, 7?ц = M[(Xj — A\)2 | Yfg] и его производной Х2,
R22 — М[(А^2 — Х2)% | и матричный коэффициент усиления
/3 = у lRb[ = у 1
Я11 Я12 1
т?12 R22 О
Rn = Pi
R12 /?2 в ’
(IV)
= у 1
Уравнение (2.3.7) для оптимальных оценок Х\, Х2 имеет в данном случае вид
_d ГХ
dt Х2 J ” -Uq
О 1
'п О
-1
Яц
Я12
(Z-XJ.
(V)
Структурная схема найденного оптимального фильтра показана на рис.2.4.2.
Рис. 2.4.2
2.4.2. Об одной форме уравнений фильтра Калмана-
Бьюси. При ао = Ьо — 0 вместо уравнений (2.4.1) часто принимают
следующие:
X = aiX + V>Vi, Z = bxX + V2, (2.4.3)
где Vi и V2 - некоррелированные нормальные белые шумы с интенсив-
ностями У\ и у2 соответственно, причем ai,^ и bi имеют размерности
п х п, п х г, ni х п. В этом случае, повторяя вывод п.2.3.1 и используя
легко проверяемые равенства
(2.4.4)
p = Rblv^,
(2.4.5)
2.4. ЛИНЕЙНЫЕ ФИЛЬТРЫ КАЛМАНА-БЬЮСИ
267
получим следующие уравнения Риккати для R:
R = aiR + Ra? + фих'ф1' — \ (2.4.6)
R = a\R 4- Ra{ - Rh^u^l^R + . (2.4.7)
Таким образом, получен следующий результат.
Теорема 2.4.2. Для линейной нормальной стохастический диф-
ференциальной системы (2.4.3) в случае невырожденности матрицы
шумов 1/2 в уравнении наблюдения фильтр Калмана-Бьюси определя-
ется уравнениями (2.4.5), (2.4.6) или (2.4.5), (2.4.7) и
k = ахХ + 0(Z - ЬгХ). (2.4.8)
Замечание. В ряде практических задач удобно принять в (2.4.3) ф = I,
тогда основные уравнения фильтра Калмана-Бьюси примут следующий вид:
X = aix + VI, Z = ЪхХ 4- V2,
X = aix + 0(Z - biX), p = Rb{v^1,
R = aiR + Ra{ + pi - Pv2PT (2.4.9)
2.4.3. Фильтры Калмана-Бьюси для стационарных систем.
Полагая в (2.4.6) R = 0 и принимая в (2.4.3)
«1 = aj, ф = bi = b*lt Ф1 = Ф1, pi,2 = Pi,2,
0 = 0’, R = 0, R = R*, (2.4.10)
получим следующую систему уравнений для стационарного фильтра
Калмана-Бьюси:
Я = a;x + 0*(z-b;x), 0* = R'bf ,
0 = a*iR* + R’a*iT + - 0*v20*T. (2.4.11)
Следовательно, имеем следующее утверждение.
Теорема 2.4.3. Для стационарной линейной нормальной стоха-
стической системы (2.4.3) при условиях (2.4.10) в случае невырож-
денности матрицы шумов 1/2 в уравнении наблюдения стационарный
268
ГЛ. 1. ТЕОРИЯ ОПТИМАЛЬНОГО ОЦЕНИВАНИЯ
фильтр Калмана-Бьюси определяется уравнениями (2.4.11).
Аналогично выписываются уравнения стационарного фильтра
Калмана-Бьюси для уравнений (2.4.1).
2.4.4. Связь между стационарными фильтрами Винера и
Калмана-Бьюси. Возьмем преобразование Лапласа (ТСтС, приложе-
ние 3) от обеих частей уравнений (2.4.10) при нулевых начальных усло-
виях. Тогда получим следующее выражение для передаточной функции
[ si - 4- ] X(s) = /3Z(s), (2.4.12)
где £X(t) = X(s) и £Z(t) = Z(s) - преобразования Лапласа X(t) nZ(t).
Отсюда находим
X(s) = Ф($)2($). (2.4.13)
Здесь Ф($) - передаточная функция, равная
Ф(5) = [s/-aj + /3*b*l]~l/3*, (2.4.14)
а /3* - стационарное значение матричного коэффициента /3, определяе-
мое согласно (2.4.11). Передаточная функция Ф($) соответствует стаци-
онарному фильтру Калмана-Бьюси, который в рассматриваемом слу-
чае идентичен фильтру Винера.
2.4.5. О некоторых свойствах матричного уравнения Рик-
кати ДЛЯ ковариационной матрицы ошибки фильтрации. Рас-
смотрим дифференциальное уравнение (2.4.7). Введем обозначения
х = R, Xq = Rq, а = a(t) — ai,
b — b(t) = c = c(t) = ,фу\'фТ (t\ <t < tk)> (2.4.15)
Тогда уравнение (2.4.7) примет следующий вид:
х = ах + хат — xbx + с, (2.4.16)
где X - симметричная (п X ?1)-матрица; G, 6, С - (п X 71)-матрицы, представляющие
собой функции независимой переменной t. По аналогии со случаем скалярного уравнения
Риккати уравнение (2.4.16) называется матричным уравнением Риккати.
Как и аналогичное скалярное уравнение, матричное уравнение Риккати приводится
к системе линейных дифференциальных уравнений удвоенного порядка, и, следовательно,
его решение в общем случае выражается через фундаментальную матрицу решений этой
системы линейных уравнений.
2.4. ЛИНЕЙНЫЕ ФИЛЬТРЫ КАЛМАНА-БЫОСИ
269
Введем две новые переменные квадратные матрицы у и Z, положив
У = XZ.
(2.4.17)
Дифференцируя эту формулу, будем иметь
У = XZ + XZ.
Подставляя сюда выражение X из (2.4.16), получим
у = axz + cz + x(z + aTz — bxz),
или
у = ay + cz + x(z -by + aTz).
Так как мы ввели две неизвестные функции у, Z вместо одной X, то имеем право свя-
зать их каким-либо соотношением. Приняв выражение в скобках нулю, получим систему
однородных линейных дифференциальных уравнений для у, Z
у = ay + cz, z = by — aTz> (2.4.18)
Решив уравнения (2.4.18), можно найти решение X уравнения (2.4.16) из (2.4.17).
Обозначим через Ф(£,7~) фундаментальную матрицу решений системы уравнений
(2.4.18), т.е. решение уравнения
удовлетворяющее начальному условию U — u(t,T) — /271 ПРИ — Т- Тогда общее
решение уравнений (2.4.18) определится формулой
[утгт]Т = Ф(Мо) [j/o*oJT, (2.4.19)
где Уо и %0 - начальные значения у и Z при t — to- Разбив (2п X 2п)-матрицу Ф(£, г)
на блоки размера (п X п),
Ф(<,т) =
Фц(«,т)
$21(t,T)
Ф12(<,Т)
Ф22(*,Т)
перепишем (2.4.19) в виде
!/= Ф11(Мо)УО + $12(Mo)*O, * — $21(Mo)2/O + $22(Mo)*(b (2.4.20)
270
ГЛ. 1. ТЕОРИЯ ОПТИМАЛЬНОГО ОЦЕНИВАНИЯ
Теперь можно найти решение X уравнения (2.4.16) из (2.4.17), выразив уо и Zq через
начальное значение Xq матрицы X. Из (2.4.17) видно, что, приняв Zq = Z, получим
J/0 — Zq. Подставив эти значения в (2.4.20), из (2.4.17) находим
я = [$n(Mo)zo +$i2(^fo)][$2i(Mo)£o + ^22 *о) ] 1 • (2.4.24)
Следуя (Ройтенберг 1992), рассмотрим важный для аналитического синтеза филь-
тров Калмана-Бьюси итерационный метод решения уравнения (2.4.16). Определим по-
следовательные приближения (2.4.16) Z^(t), Z^^(t), . . . , посредством следу-
ющих линейных дифференциальных уравнений:
а;(°) = ах^ + х^ат + с, a/°\to) = ®о,
а/1) = а/1) + а/1) ^аг — а/°Ч| + а/°Ча/°> + с, x^l\to)=xo,
х<2> = Ja — х^Ь j х^ 4- х^ [ат — bx^ j + x^bx^ + с, x^(t0) = a?o,
i<") = [а - x(n-1)b] а/"> + х^ [ат - Ьх(п~^ ] + x^-^bxin~^ + с,
(2.4.25)
х(п)(«о) = ж(«о) > 0.
Обозначим
Д„ = ж(п) - х{п~1\ ап = а- х<п~»Ь. (2.4.26)
Так как Х^п^ и Х^п - симметрические матрицы, то и Дп " симметрическая матрица.
При этом Дп (п > 2) в силу (2.4.25) удовлетворяет уравнению
= + Дп<£ ~ ^n-i^^n—ь Дп(^о) = 0* (2.4.27)
Заметим, что (2.4.25) на основании (2.4.26) и (2.4.27) могут быть представлены в виде
х<"> = ах^ + х^ат + ДП6ДП - xMbx^ + с, х™ (t0) = х0. (2.4.28)
Обозначим через $^(t) и l9^(t) фундаментальные матрицы решений следующих систем
линейных обыкновенных уравнений:
х = az, рп = апрп. (2.4.29)
Тогда в силу п.1.1.2 общие решения уравнений (2.4.16), (2.4.28) и (2.4.27) можно предста-
вить в виде
х = x(t) = Фх(<,т)а;о [Ф®(£,т)]Т+ / Фх(4,т)(ст -хтЪтхт) [Фх(<,т)]Т</т,
Ло
(2.4.30)
2.5. ФИЛЬТРАЦИЯ ПРИ АВТОКОРРЕЛИРОВАННОЙ ПОМЕХЕ
271
^(n) = х(п)^ = $*(t,t0)x0&X(t,t0)T+
+£ $x(t,t0) [ст - х^Ьтх^ + ДПТ5ТДПТ] $x(t,r)dr (п > 2), (2.4.31)
Д„ = - f ф£(*,т)Д„_1>т5тДп_1>г [$^(t,r)]Tdr < 0 (п > 2). (2.4.32)
Jto
Здесь индексами Т снизу отмечена зависимость функций от Т,
$x(t,r) = 0x(t) [^(т)]-1, фД(*,т) = ew [^(т)]-1. (2.4.33)
В силу (2.4.32) уравнение (2.4.31) можно записать также в виде
х(п) _ фД(^ ^)д.о [фД(г,*0)]т +
/•f
+ / $^(t,r) |ст+x$n-1>&Tx<n-1)l [Ф^(г,т)] dr. (2.4.34)
Jto L J
Справедливо следующее утверждение.
Лемма 2.4.1. Пусть матрица > 0 для всех t и
дифференцируема по времени t. Тогда на каждом конечном интервале
времени (to,tk) имеет место соотношение x^n\t) < a?(n-1)(£) при п >
> 1, а при п —> оо последовательность равномерно сходится
к решению x(t) уравнения Риккати (2.4.16).
2.5. Оптимальная линейная фильтрация при
автокоррелированной помехе в наблюдениях
2.5.1. Метод Гулько—Новосельцевой. Теория линейной филь-
трации Калмана-Бьюси была распространена Брайсоном и Йохансе-
ном, Гулько и Новосельцевой на случай произвольной помехи в на-
блюдениях, для которой существует линейный формирующий фильтр,
описываемый дифференциальным уравнением. Мы изложим сначала
метод Гулько-Новосельцевой (Гулько и Новосельцева 1966а, 19666) как
более естественный и простой.
о В случае, когда помеха в наблюдениях U не является белым шу-
мом, второе уравнение системы (2.4.1) заменяется уравнением
Z = ЬгХ+ ^ + ^17.
(2.5.1)
272
ГЛ. 2. ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФИЛЬТРЫ КАЛМАНА
Предположим, что помеха U может рассматриваться как выходной сиг-
нал формирующего фильтра, описываемого дифференциальным урав-
нением
I h
£ а»и{к) = Е -h < (2.5.2)
л=о л=о
где Vi - белый шум. Идея Гулько и Новосельцевой состоит в том, что-
бы преобразовать наблюдаемый сигнал системой, обратной формиру-
ющему фильтру (ТСтС, п.2.2.4), и получить в результате сигнал Zi с
помехой, представляющей собой белый шум. Тогда задача сведется к
построению фильтра Калмана-Быоси для преобразованного наблюдае-
мого сигнала. Само собой разумеется, наблюдаемый сигнал Z(t) следу-
ет умножить слева на перед пропусканием через систему, обратную
формирующему фильтру. Для этого необходимо, чтобы функция ^1 ни
при каком t не обращалась в нуль (в случае скалярных Z(t) и U(t))
или была обратимой квадратной матрицей (в случае векторных Z(t) и
Это построение показано на рис.2.5.1.
Рис. 2.5.1
Как показано в (ТСтС, п. 1.2.4), система, обратная по отношению к
системе, описываемой дифференциальным уравнением (2.5.2) (т.е. к
формирующему фильтру), в общем случае при h > 0 представляет
собой параллельное соединение системы, осуществляющей линейную
дифференциальную операцию
l—h
L = ^kDk, D = d/dt,
k=0
и системы, описываемой дифференциальным уравнением
h h—l
Е&^Е^’ (2.5.3)
fc=O л=о
2.5. ФИЛЬТРАЦИЯ ПРИ АВТОКОРРЕЛИРОВАННОЙ ПОМЕХЕ
273
где
7<-h = Ph 'оц,
7* = Ph 1
h—l h—т
ah+k — ^2 52 ^r+sPr+jlh+k-r
r=max(O,fc—Z+2/i) j=0
(k = 0,1, ... ,1 - h - 1),
k h—r
ak = «k- £ £c;+/r+np2r (* = о,1,...,л-1).
r=max(0,fc—l+h) j=0
Эта система обведена штриховой линией в левой части рис.2.5.1, где
буквой L отмечена система, выполняющая дифференциальную опера-
цию, а буквой К - система, описываемая дифференциальным уравне-
нием (2.5.3).
Пропустив наблюдаемый сигнал Z через систему, состоящую из
усилителя с коэффициентом усиления ^j”1 и системы, обратной фор-
мирующему фильтру, получим на выходе сигнал
Z\ = L^r^iX) + Х[ + L^bo) + Vi, (2.5.4)
где Х{ - выходной сигнал системы, описываемой дифференциальным
уравнением (2.5.3) при Z = t^j"1 {Ь\Х 4- &о),
h h—l
Y^pkX[{k} = ^ак [^l(brX + b»)]W . (2.5.5)
fc=0 fc=0
Приведя это уравнение к системе уравнений первого порядка подстанов-
кой Х'к+г = Хк — qkil>il(biX 4- &о) (fc = 1, ... , Л - /), как это показано
(ТСтС, п.2.2.3), получим дифференциальное уравнение, определяющее
вектор X'= [Х{Т...ЛХТ] :
X' = схХ + с2Х' + со- (2.5.6)
Так как Х{ входит в выражение (2.5.4) преобразованного наблюдаемого
сигнала Zi, то необходимо расширить вектор состояния системы X,
добавив к нему вектор X'. Тогда получим для расширенного таким
путем вектора состояния уравнение
274
ГЛ. 2. ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФИЛЬТРЫ КАЛМАНА
Чтобы сигнал Z\ имел требуемую для применения теории линей-
ной фильтрации форму, т.е. был суммой линейного преобразования
расширенного вектора состояния [хтх,т] и белого шума, необхо-
димо, чтобы выражение не содержало производных белого
шума Vi. Для этого необходимо, чтобы матрицы Ь\ и гр имели соответ-
ствующую структуру. Физически это соответствует требованию, чтобы
фильтруемый полезный сигнал X был более гладким, чем помеха (имел
производные более высокого порядка, чем помеха). В этом случае, под-
ставляя после каждого дифференцирования X из первого уравнения
(2.4.1), получим Цгр^ЬгХ) как линейную функцию Ь2Х вектора X.
Тогда будем иметь
Zi = ь2х + х{ + ь'о + Vi = ь; [хгх,т]т + ь'о + =
= Ь'х [ ХТХ[Т... X'hT ] + Ь'о + V1, (2.5.8)
где b{ = [ &2 I • • • 0 ]. Здесь единичный блок представляет собой коэф-
фициент усиления блока Х[ в выражении преобразованного наблюда-
емого сигнала Zi, а нулевые блоки - коэффициенты усиления блоков
Х'2Т, ... , X'hT (рис.2.5.1). <1
Таким образом, имеем следующую теорему.
Теорема 2.5.1. Задача с.к. оптглмальной линейной фильтраг^ии
прогресса X(f) при автокоррелированной помехе в наблюдениях, опре-
деляемой (2.5.1) и (2.5.2), приводится к задаче с.к. оптглмальной ли-
нейной фильтраг^ии составного прогресса [X(i)TX'(^)T] , где вектор
X'(t) удовлетворяет уравнению формируюгцего фильтра (2.5.6) в слу-
чае, когда помеха в наблюдениях представляет собой белый гиум. По-
строив для этой задачи фильтр Калмана-Бьюси, получим оптималь-
ный фильтр для первоначальной задачи в виде последовательного со-
единения усг/лителя с коэффициентом усиления гр^1, системы, обрат-
ной формируюгцему фильтру, и фильтра Калмана-Бьюси для расгии-
[1
XTX,J (рис.2.5.1).
Замечание. В частном случае при h — 0 уравнение (2.5.2) дает непо-
средственно обратную формирующему фильтру систему как систему, осуществляющую
! I
дифференциальную операцию L — Ьр Ot^D^. В этом случае преобразованный на-
fc=O
блюдаемый сигнал Z\ определяется формулой
Zx = L^r^iX) + LW^&o) + Vi = b2X + b'o + Vi,
(2.5.9)
2.5. ФИЛЬТРАЦИЯ ПРИ АВТОКОРРЕЛИРОВАННОЙ ПОМЕХЕ
275
и расширять систему не приходится. Оптимальный фильтр в этом случае представляет
собой последовательное соединение усилителя с коэффициентом усиления 1, системы,
выполняющей линейную дифференциальную операцию L, и фильтра Калмана-Бьюси
для преобразованного наблюдаемого сигнала Zi.
Пример 2.5.1. Построить оптимальный фильтр для выделения полезного сиг-
нала, представляющего собой сумму синусоиды данной частоты й?о со случайными или
неизвестными амплитудой и фазой и стационарной случайной функции с ковариационной
функцией
к(т) = De~a^ ( cosojit + — sino>i |т|
\
из аддитивной смеси его с помехой, имеющей показательную ковариационную функцию
*1(т) = Pie-“lTl.
Обозначив синусоидальный сигнал и его производную соответственно через Х\ (t)
И x2(t) , получим дифференциальные уравнения
Xi = Х2, Х2 = -u%Xi.
(I)
Стационарная случайная функция X^(t) (ТСтС, п.2.5.3) может рассматриваться как
выходной сигнал формирующего фильтра, описываемого уравнениями
Х3 = Х4, Х4 = -Ъ2Х3 - 2аХ4 + V, (II)
где Ь2 = О? + (л>2, а V - белый шум интенсивности V — t2Ddb2. Наблюдаемый сигнал
по условиям задачи определяется формулой
Z = Xi+X3 + U, (III)
где U - помеха с ковариационной функцией &1(т) = а^г1 . Таким образом, мы
имеем систему (1)-(Ш) с четырехмерным вектором состояния, описываемую первым урав-
нением (2.4.1) при CLq — 0:
Г 0 1 о
—Ц) 0 0
L о о -б2
О'
о
о
0.
Формирующий фильтр для помехи U (ТСтС, п.5.1.3) описывается уравнением U+OtU —
= Vi, где Vi - белый шум интенсивности — 2D\Ol. Обратная система представляет
собой форсирующее звено первого порядка с передаточной функцией 3 4" Ot. Пропустив
наблюдаемый сигнал Z через это звено, получим преобразованный наблюдаемый сигнал:
Zi — Z-\-olZ — Xi 4~ctA\ 4"Аз4"оАз4"^1 = скА14"А24"СкАз4"А44"16>. (IV)
276
ГЛ. 2. ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФИЛЬТРЫ КАЛМАНА
Таким образом, преобразованный наблюдаемый сигнал определяется второй формулой
(2.4.1) при 61 = [ а 1 а 1 ], &о = 0, ^1 = [01].
Применив изложенный метод, получим оптимальный фильтр, схема которого пред-
ставлена на рис.2.5.2. Имея в виду, что в данном случае фильтр должен давать оценку
сигнала Xi + Х$, необходимо на выходе полученного фильтра поставить сумматор, вы-
полняющий сложение оценок сигналов Х\ и A3. На рис.2.5.2 в средней части обведена
штриховой линией система формирования сигналов А\, А2, Х$, Х4, справа внизу об-
веден штриховой линией усилитель с матричным коэффициентом усиления 61, а слева
вверху - усилитель с матричным коэффициентом усиления f3.
2.5. ФИЛЬТРАЦИЯ ПРИ АВТОКОРРЕЛИРОВАННОЙ ПОМЕХЕ
277
Уравнение (2.3.5), определяющее ковариационную матрицу ошибки R, в данном случае
имеет вид:
Г 0 1 0 ОН -о 0 0 1
R = О ГН О О О О «о 3° R 4“ R 10 0 0 0 0 0 —ь2 —
L 0 0 —Ь2 -2а J .0 0 1 -2а.
' а2 а а2 а 1 о 0 0 0
R а 1 а 1 р 1 0 0 0 0
2D\a а2 а а2 а it 4- 0 0 0 0
_ а 1 а 1 . .0 0 0 2Dab2 .
(VII)
Средний квадрат ошибки равен дисперсии суммы ошибок на первом и третьем вы-
ходах оптимального фильтра, т.е. 4“ 2Я1з 4~ Язз-
Пример 2.5.2. Рассмотрим задачу предыдущего примера в случае помехи U с
показательно-косинусной ковариационной функцией к\ (т) — alTl COSCU2T. Слу-
чайную функцию с такой ковариационной функцией можно рассматривать как результат
преобразования белого шума Vi интенсивности Vi = 2Z?iQ формирующим фильтром с
передаточной функцией (s 4~ 7)/4" 2aS 4~ 7^)> где *у2 = Ot2 4~ й>2 (ТСтС, п.5.1.3).
Дифференциальное уравнение этого фильтра имеет вид U 4" 2&V 4“ y2U — Vi 4" 7^1-
Обратная система представляет собой параллельное соединение форсирующего звена пер-
вого порядка с передаточной функций S4~2q — у и апериодического звена с передаточной
функцией 27(7 — Ol)/(s 4" 7) (рис.2.5.3). В результате преобразования наблюдаемого
сигнала Z — Х± 4~ Х$ 4" U этой системой получится сигнал
Zi = (2а - 7)(%! 4- Хз) 4- Xi 4- Х3 4- Х5 4- Ц =
= (2а - 7)(Xi 4- Х3) 4- Х2 4- Х4 4- Х5 4- Vi, (I)
Рис. 2.5.3
278
ГЛ. 2. ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФИЛЬТРЫ КАЛМАНА
где Х$ определяется дифференциальным уравнением
Х5 = 27(7-«)№+^з)-7^5.
(П)
Расширив систему (I)—(III) предыдущего примера добавлением величины Х§, получим
систему с пятимерным вектором состояния, описываемую первым уравнением (2.4.1) при
а0 = 0:
г 0 1 0 0 о - о О'
-Wq 0 0 0 0 0 0
ai = 0 0 0 1 0 , V* = 0 0
0 0 -ь2 -2а 0 1 0
. 27(7 - а) 0 - а) 0 “7- .0 0.
и преобразованный наблюдаемый сигнал, определяемый второй формулой (2.4.1) при
bl — [ 2а (3 1 2а [3 1 1 ], = О, ф\ — [01]- Построив для этой системы фильтр
Калмана-Бьюси, получим оптимальный фильтр, показанный на рис.2.5.4. Штриховой ли-
нией обведена система предыдущего примера и соответствующая расширенная система.
Матричный коэффициент усиления /3 представляет собой матрицу-столбец с элементами:
(2а — 7)(Яр1 + Rps) + Rp2 + Rpi 4- ЯР5
2 D^a
(р = 1, ... , 5).
(П1)
Уравнение (2.3.5) для ковариационной матрицы ошибки фильтрации имеет в данном слу-
чае вид
л = Г 0 — Wq 0 0 . 27(7 - а) 1 0 0 0 0 27 0 0 0 0 0 1 —Ь2 —2а (7 — а) 0 0 ' 0 0 0 -7- R+
' 0 -wjj 0 0 27(7 “ «) ‘
10 0 0 0 D
+R 0 0 0 0 0 1 -ь2 -2а 27(7 - «) - 0 2Z>ia
.0 0 0 0 -7
2.5. ФИЛЬТРАЦИЯ ПРИ АВТОКОРРЕЛИРОВАННОЙ ПОМЕХЕ
279
’ (2а - 7)2
2а - 7
(2а - 7)2
2а - 7
. 2а - 7
2а - 7
1
2а — 7
1
1
-о
О
+ О
О
.0
О
о
о
о
о
(2а - 7)2
2а — 7
(2а - 7)2
2а — 7
2а — 7
О
О
О
О
О
2а - 7
о
о
о
2Dab2
О
2а — 7
1
1
°1
О
О .
О
0.
2а - 7
1
1
Я+
(IV)
2а — 7'
х
2.5.2. Метод Брайсона-Йохансена. Изложенный в п.2.5.1 ме-
тод, как уже было сказано, применим только в том случае, когда ре-
зультат применения линейной дифференциальной операции L к
280
ГЛ. 2. ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФИЛЬТРЫ КАЛМАНА
с заменой производной X после каждого дифференцирования ее выра-
жением из первого уравнения (2.4.1) не содержит производных белого
шума, т.е. если все компоненты случайного процесса X(t), входящие
в уравнение наблюдения, не менее гладки, чем помеха U(t). Если это
условие не выполнено, то наблюдаемый сигнал нельзя преобразовать
системой, обратной формирующему фильтру помехи, и метод Гулько-
Новосельцевой неприменим. В этом случае можно применить метод
Брайсона-Йохансена (Брайсон и Йохансен 1965), основанный на диф-
ференцировании наблюдаемого сигнала и исключении помехи и ее про-
изводных, не содержащих белого шума, из уравнений формирующего
фильтра с помощью уравнения наблюдения и уравнений, полученных
из него дифференцированием.
> Приведем уравнение формирующего фильтра помехи (2.5.2) к
системе уравнений первого порядка, приняв U\ = 17,
Uk = UM (fc = l,...,/-ft-l),
Uk = ик+1 + gM (k = l-h,... , z- 1),
Z-l
Ui = -of1 £ + «Vi. (2.5.10)
i=l
Дифференцируя уравнение наблюдения в (2.4.1), умноженное слева на
V’f1 до появления в полученном уравнении белого шума, будем иметь
±j.^Z) = ~[^\b1X + bQ)}+Uk+1 (fc = 0,1, ... , s), (2.5.11)
at* at*
если
d* [V,i~1(biA' 4- bo] /dt8 при s < I — h
содержит белый шум, и
dk
[^(btX + 6о)] + ик+1 (к = 0,1, ... , I - h - 1),
jl-h jl-h
[^(ЬгХ + Ьо)] +ut-h+l + qi-hVi, (2.5.12)
если ни при каком s < I - h производная d8 [^fx(biX 4- bo)] /dt8 не
содержит белого шума. В первом случае исключим из уравнений фор-
мирующего фильтра помехи Ui, ... , U8 с помощью уравнения наблю-
дения и уравнений, полученных из него (з — 1)-кратным дифференци-
рованием. Во втором случае исключим из уравнений формирующего
2.5. ФИЛЬТРАЦИЯ ПРИ АВТОКОРРЕЛИРОВАННОЙ ПОМЕХЕ
281
фильтра помехи U\, ... , Ui-h-i и белый шум Vi с помощью уравнения
наблюдения и всех уравнений, полученных из него дифференцировани-
ем. В обоих случаях получим для ,...,[7/ (s < I — h) линейные
дифференциальные уравнения, в правых частях которых будут линей-
ные функции вектора состояния X и линейные комбинации наблюда-
емого сигнала и его производных. Расчленив каждую из переменных
C7s+iна две части, одна из которых порождается линейными
функциями вектора X в правых частях уравнений, а другая - линейной
комбинацией наблюдаемого сигнала и его производных, будем иметь
Us+k = X,k-Yk (fc = l,... J-s), (2.5.13)
где Х{, ... , X[_s определяются дифференциальными уравнениями с
линейными функциями вектора X, a Yi, ... , Y/_s определяются теми
же уравнениями с линейными комбинациями наблюдаемого сигнала и
его производных в правых частях. Расширив вектор состояния систе-
мы X добавлением к нему блоков Х±, ... , X[_s и написав последнее
уравнение, полученное дифференцированием уравнения наблюдения, в
следующем виде:
Н8 d8
+ Yr = — [V-Г1 (Ъ1Х + M] + (2.5.14)
Ul CLL
при s < I — h и в виде
dl~h (f~h
—№lZ) + Y1 = -^ [^4brX + M] +*{ +qi-hVr (2.5.15)
при s = I — h, проведем задачу к построению фильтра Калмана-Бьюси
для наблюдаемого сигнала
d8
Zl = —^~1Z)+Yl. <i (2.5.16)
Таким образом, имеем следующий результат.
Теорема 2.5.2. Задача с.к. оптимальной линейной фильтрации
процесса X(t) в системе (2.4.1) при условии (2.5.1) при автокоррелиро-
ванной помехе в наблюдениях, если все компоненты X (t) более гладкие,
чем помеха U(t), то путем дифференцирования наблюдаемого сигнала
и исключения помехи и ее производных, не содержащих белого шума,
из уравнений формирующего фильтра с помощью уравнения наблюде-
ния и уравнений, полученных из него дифференцированием, приводит-
ся к построению фильтра Калмана-Бьюси для наблюдаемого сигна-
282
ГЛ. 2. ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФИЛЬТРЫ КАЛМАНА
ла Zi. Оптимальным фильтром в этом случае будет последователь-
ное соединение системы, формирующей сигнал Zi(t) из наблюдаемого
сигнала Z(t), и фильтра Калмана-Бьюси с расширенным вектором со-
стояния . .Х'Т_8]Т и наблюдаемым сигналом
Пример 2.5.3. В условиях примера 2.5.1 дифференцирование наблюдаемого
сигнала дает
Z = X1+X3 + U = X2+Xi-aU + V1.
Подставив сюда выражение U из уравнения наблюдения, получаем
Z = Х2 + Х4 - a(Z - Xr - Х2) + Vi = + X2 + aX3 + X4 - aZ + Ц.
Как и в примере 2.5.1, задача сведена к построению фильтра Калмана-Бьюси для наблю-
даемого сигнала Z\ — Z -j- ttZ.
Пример 2.5.4. В условиях примера 2.5.2 представив уравнения формирующего
фильтра в виде U = t7i,
Ui = U2 •+* Vi, U2 = —y2Ui — 2otU2 + (т — 2a) Vi,
и дифференцируя наблюдаемый сигнал, получим
Z = Хг + Х3 + и = Х2 + Х4 + U2 -f- Vx.
Исключив помеху U — U\ и белый шум Vi из второго уравнения формирующего филь-
тра с помощью уравнения наблюдения и уравнения, полученного из него дифференциро-
ванием,
U1=Z-X1-X3, V1=Z-X2-X4- и2,
будем иметь
= -7^2 + 72(*1 + Х3) — (7 — 2а)(Х2 + Х4) - 72^ + (7 - 2а)Й.
Положив U2 — X1 +* Y2, где X1 и Y2 определяются соответственно уравнениями:
X' = -7Х' + 72(%! + Х3) - (7 - 2а)(Х2 + Х4),
У2 = -7У2 - 72Z + (7 - 2a)Z,
приводим задачу к построению фильтра Калмана-Бьюси для наблюдаемого сигнала
Z1 = Z - У2 = х2 + Xi + X' + V!.
2.5. ФИЛЬТРАЦИЯ ПРИ АВТОКОРРЕЛИРОВАННОЙ ПОМЕХЕ
283
Чтобы убедиться в том, что полученный фильтр совпадает с фильтром приме-
ра 2.5.2, положим X' = (2а - 7)(Хх + Хз) + х5, У2 = -(2а - 7)Z - У'.
Тогда после элементарных преобразований получим для Х$ и Y1 уравнения
Х5 = 27(7 - <*)(Х1 + Х3) - ?Х5, Y' = —7У' + 27(7 - a)Z.
а преобразованный наблюдаемый сигнал Z\ выразится формулой:
Zi = Z + (2а - 7)Z + Г = (2а - 7)(Хх + Х3) + Х2 + Х4 + Х5 + Ц.
Отсюда непосредственно видно, что Z\ представляет собой результат преобразования
наблюдаемого сигнала системой, обратной формирующему фильтру, а уравнение для Х5
совпадает с соответствующим уравнением примера 2.5.2.
Пример 2.5.5. Найти оптимальный фильтр для фильтрации сигнала, пред-
ставляющего собой сумму синусоиды известной частоты CUq с неизвестными амплитудой
и фазой и случайной функции с ковариационной функцией &(т) — De а , в случае
помехи с ковариационной функцией
= Die~a^T^ ( cosO7iт + — sina>i |т| ) .
\ U>1 /
В этом случае за вектор состояния системы принимаем трехмерный вектор, опреде-
ляемый уравнениями
X1=X2, х2 = -u$Xi, Хз = -аХз + V.
где V - белый шум интенсивности V — 2Dot. Формирующий фильтр для помехи опи-
сывается уравнением
и + 2aU + Ь2и = V1,
где Ь2 — й2 + Ш2, a V1 - белый шум интенсивности fi = 2Di<lb2. Система, обрат-
ная формирующему фильтру, выполняет линейную дифференциальную операцию вто-
рого порядка L = Z?2 -+* 2aD -+* Ь2. Наблюдаемый сигнал определяется формулой
Z = Xi -j- Х3 -j- U. Следовательно,
Z = Х1 + х3 + й = Х2 - аХ3 + й + V,
и Z содержит производную белого шума V. Поэтому операция X/ неприменима к Z, и Z
не может служить входным сигналом системы, обратной формирующему фильтру. Метод
же дифференцирования наблюдаемого сигнала применить можно. Для этого заменим
уравнение формирующего фильтра системой уравнений первого порядка, положив (71 —
= (7,
(71 = (/2, (/2 = -b2Ui - 2aU2 + Ц.
284
ГЛ. 2. ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФИЛЬТРЫ КАЛМАНА
Продифференцируем наблюдаемый сигнал Z = Х\ -j- Х3 + Uy
Z = Х1 + Х3 + их = Х2 - аХз + U2 + V
и исключим из второго уравнения формирующего фильтра U\ с помощью уравнения
наблюдения, U\ = Z — Х\ — Х3. В результате приведем это уравнение к виду
U2 = —2aU2 + b2(Xi + Х3) - b2Z +
Положив U2 = Х4 — Y и определив Xi и Y уравнениями
Xi = -2aXi + b2(Xi + Х3) + Ц, Y = ~2aY + b2Z,
будем иметь
Z = X2 - aX3 + Xi - Y + V.
Расширив вектор состояния добавлением компоненты X±t приводим задачу к построению
фильтра Калмана-Бьюси для преобразованного наблюдаемого сигнала Z\ = Z -j- Y.
Этот сигнал получается как результат преобразования наблюдаемого сигнала Z систе-
мой, представляющей собой параллельное соединение дифференциатора и системы с пе-
редаточной функцией I?/(з 4- 2g). Оптимальным фильтром в данном случае служит
последовательное соединение системы, преобразующей наблюдаемый сигнал Z и дающей
на выходе сигнал Zy и фильтра Калмана-Бьюси для расширенного вектора состояния
[ Xi JV2-X3 Х4 ] и наблюдаемого сигнала Zy Схема этого фильтра представлена на
рис.2.5.5.
2.5.3. Начальные условия в случае автокоррелированной
помехи. Фильтры, найденные изложенными в пп.2.5.1 и 2.5.2 метода-
ми, оптимальны только при определенных начальных условиях. Чтобы
понять это, напишем выражение для преобразованного наблюдаемого
сигнала в виде
Г
Zi(t) = LZ(t) + / w(t,r)Z(r)dr = ^2ckZ^(t)+
L fc=°
t
+ У w(t,T)Z(r)dr, (2.5.17)
to
где w(t, т) - весовая функция той части системы, преобразующей на-
блюдаемый сигнал, которая описывается дифференциальным уравне-
нием. Эта формула однозначно определяет Zi(t) по данному наблю-
даемому сигналов Z(t). Чтобы однозначно определить наблюдаемый
2.5. ФИЛЬТРАЦИЯ ПРИ АВТОКОРРЕЛИРОВАННОЙ ПОМЕХЕ
285
Рис. 2.5.5
сигнал Z(t) по данному преобразованному сигналу Zi(t), необходимо
задать начальные значения сигнала Z(t} и его производных Z'(t),...
..., Таким образом, между Z(t), с одной стороны, и Zi(t),
Zq = Z(to), Zq = Z'(t0), c другой стороны,
существует взаимно однозначное соответствие. Следовательно, опти-
мальная оценка X вектора состояния системы X, представляющая со-
бой условное математическое ожидание X относительно Z%0 = {Z(r) :
г 6 [to, t]}, совпадает с условным математическим ожиданием X отно-
сительно совокупности ZftQ,Zo,Zo, ... , Zq8-1). Выходной сигнал по-
строенного изложенным методом фильтра будет представлять собой
условное математическое ожидание X относительно Zq,
Xq, ... , Zq8-1), если за начальное значение оценки X в момент t = to
принять условное математическое ожидание вектора Xq = X(to) от-
носительно Zq, Zq , ... , Zq8-1) и соответственно за начальное значение
R принять условную ковариационную матрицу Rq вектора Xq относи-
286
ГЛ. 2. ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФИЛЬТРЫ КАЛМАНА
тельно Zo, Zq , ... , Zq8~^. При таких и только при таких начальных
условиях выходной сигнал фильтра будет оптимальной оценкой век-
тора состояния системы X. Это было показано (Бьюси 1967), кото-
рый независимо от Гулько и Новосельцевой получил тот же фильтр
и начальные условия, обеспечивающие его оптимальность, в частном
случае, когда формирующий фильтр помехи описывается уравнением
(2.5.2) при I = 1, h = 0, ai = /3q — 1.
о Чтобы найти условные математическое ожидание и ковариаци-
онную матрицу вектора Xq относительно Zq, Zq , ... , Zq~^ вспомним,
что теория п.2.3.1 была развита в предположении, что совместное рас-
пределение процессов Y(t) и X (t) нормально. Поэтому мы естественно
предположим, что распределения процесса X(i) и независимой от не-
го помехи U(t) нормальны. Тогда совместное распределение величин
XqZq, Zq , ... , ZqS~^ будет тоже нормальным и условное математиче-
ское ожидание и ковариационная матрица величины Xq относительно
Zq, Zq, ..., Zq8~^ полностью определяются математическим ожиданием
и ковариационной матрицей составного вектора [Xj* Zq Z'q ...
...z<s-1)T]T
Для нахождения математического ожидания и ковариационной
матрицы вектора [ Xq Zq Z'q ... Zq8~^ j напишем выражение для на-
блюдаемого сигнала и его производных при t — tQ, имея в виду, что
каждое дифференцирование произведения Ь±Х по условию дает линей-
ную функцию вектора X без белого шума:
к
z(ok} = blkX0 + + Y, Ck^io~i}U^ (fc = 0,1, ... , s - 1), (2.5.18)
г=0
где дю, &и , • • • , 6i,s-i ~ значения матрицы Ь± и полученных в резуль-
тате дифференцирования матриц-коэффициентов при Xq для t = to;
боо, 6q0 , ... , бдо1) - значения вектора bo, и его производных при t =
= *о; V’io, V’lo > • • • > ^о-1) “ значения матрицы V>i и ее производных при
t = t0- Введя матрицу Bi = [bfo^Ti • • • ]Т> вектор Bq —
чт
и матрицу Ф с блоками V’o = при > j; = О
ЪТЪ,Т
°оо° оо • • •
• • •0 00
для i < j (г, j = 1, ... , s), можем переписать полученные равенства в
виде
[... Z^"1)T]Т = BiXo + Во + Ф [U^U'o ... ]Т.
2.5. ФИЛЬТРАЦИЯ ПРИ АВТОКОРРЕЛИРОВАННОЙ ПОМЕХЕ
287
Отсюда, считая математическое ожидание помехи тождественно рав-
ным нулю, находим математическое ожидание вектора
z^z1*...
,(в-1)Т
'о
т
[MZjMZ'o ...]Т = BlМХ0 + Во,
(2.5.19)
его ковариационную матрицу
Кх = BiKoBl + ФХиФт
(2.5.20)
и взаимную ковариационную матрицу векторов Xq и
г(8-1)Т
О
т
Kxz = K0Bf,
ZfZ'T...
(2.5.21)
где Kq - ковариационная матрица вектора Хо, а Ки - ковариацион-
ная матрица вектора начальных значений помехи и ее производных
. U^T j . Полученные формулы полностью определяют
математическое ожидание и блоки Кх = Хо, Kxz, Kzx и Kz ковариаци-
онной матрицы вектора [X?Zq Z'q ... Zq8~^T j .
Пользуясь известными формулами для условных математического
ожидания и ковариационной матрицы проекции нормально распреде-
ленного вектора относительно его проекции на дополнительное подпро-
странство (п.1.3.6), находим:
М [х0 | Z'Q, ... , Z^‘~1} ]Т =
= МХо + KXZK^ ([ Z0TZ'l... ] -
- [MZjMZ'o ...MZ<S-1)T]T) , XX|2 = Ko - KXZK-'KZX, (2.5.22)
где Kx\z - условная ковариационная матрица вектора Xq относитель-
но I ZqZ'q ... . Подставив в (2.5.22) полученные выражения
288 ГЛ. 2. ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФИЛЬТРЫ КАЛМАНА
. MZq* J , Kz, Kxz и Kzx = Kzz, найдем искомые на-
чальные значения оценки X и ее апостериорной ковариационной мат-
рицы R:
Хо = МХо + К0В? (BtKoB? + ФХиФт)-‘ х
х ...Z^~1)T]T-BiMXo-Bo) , (2.5.23)
Ro = Ко - K0Bf (BiKoB? + ФХиФт)-1 BiBo- < (2.5.24)
Только при этих начальных условиях фильтр, построенный мето-
дами п.2.5.1 или п.2.5.2, будет оптимальным.
Пример 2.5.6. Чтобы найти начальные условия для фильтра примеров 2.5.1
и 2.5.3, будем считать коэффициенты при SHlCUot и COSCUgt в выражении синусоидаль-
ного сигнала Х± независимыми нормально распределенными случайными величинами с
нулевым математическим ожиданием и дисперсией Dq. Тогда, пользуясь формулами для
вычисления ковариационных функций производных случайных функций Х± и Х% и их
взаимных ковариационных функций с их производными Х2 и Х4 (ТСтС, п.4.3.2), полу-
чим МХю — МХ20 = МХ30 = МХ40 = О, Kz — Dq Ч~ D Ч~ Z?i, KXlZ = Dq,
Kxiz ~ 0» KX3z — £>3, *x<z — 0»
- Dq 0 0 O’
K _ K _ 0 w%Do 0 0
° “ x “ 0 0 DO
.0 0 0 b2D.
Учитывая, что в данном случае Bj = bi — [1010], Во = 0, по формулам (2.5.5) и
(2.5.6) находим:
Хю = DqZq/(Dq Ч- D 4- Z?i), Х20 = 0»
Хзо = DqZq/(Dq Ч- D Ч- Di), X4Q = 0,
Япо = Dq — Dq/(Dq Ч- D Ч- Pi), Я220 — WqDq,
R33Q — D — D2/(Dq Ч- D Ч- Z?i), Я440 — b2D,
Rij = 0 i / j.
Пример 2.5.7. В условиях примеров 2.5.2 и 2.5.4, принимая во внимание, что
начальное значение переменной Х$ в условиях задачи не определено, вследствие чего его
можно взять произвольно, в частности положить Х50 = 0, получаем те же начальные
значения Х1,Хг,Хз,Х4, Rij (j>-j = 1,2,3, 4), что и в предыдущем примере, и,
кроме того, Х50 = 0, Я150 = ^250 — ^350 = ^450 = ^550 = 0-
2.5. ФИЛЬТРАЦИЯ ПРИ АВТОКОРРЕЛИРОВАННОЙ ПОМЕХЕ
289
Пример 2.5.8. В условиях примера 2.5.5 при А40 — 0 формулы (2.5.5) и
(2.5.6) дают те же значения Аю> Азо> А30, А40> -R110, -^220» -^330» что и в примере
2.5.6, и кроме того, /?140 = -^240 = -^440 = 0.
2.5.4. Дифференцирующие свойства оптимального филь-
тра в случае автокоррелированной помехи. Сначала отметим,
что если система предварительного преобразования наблюдаемого сиг-
нала, в частности система, обратная формирующему фильтру помехи,
выполняет s-кратное дифференцирование этого сигнала, то на вход со-
единенного с ней фильтра Калмана-Бьюси поступают производные на-
блюдаемого сигнала до порядка s включительно. При этом выходной
сигнал фильтра будет содержать линейную комбинацию наблюдаемого
сигнала и его производных до порядка s — 1 включительно. Эту линей-
ную комбинацию можно выделить, применив метод в (ТСтС, п.2.2.4)
к дифференциальному уравнению фильтра Калмана-Бьюси, входной
сигнал которого содержит производные наблюдаемого сигнала. В ре-
зультате фильтр Калмана-Бьюси заменится параллельным соединени-
ем системы, выполняющей дифференциальную операцию порядка з — 1
над наблюдаемым сигналом, и фильтра Калмана-Бьюси, получающего
на вход сам наблюдаемый сигнал с некоторым (в общем случае матрич-
ным) коэффициентом усиления и выходной сигнал той части преобразу-
ющей системы, которая описывается дифференциальным уравнением.
Это преобразование можно также выполнить структурными преобра-
зованиями оптимального фильтра (ТСтС, п.1.3.7). Для этого следует
представить фильтр Калмана-Бьюси (рис.2.5.6а) схемой, показанной
на рис.2.5.66, объединив обе обратные связи, а затем каждый диффе-
ренциатор последовательно перенести по ходу сигнала через объеди-
ненный усилитель (с коэффициентом усиления а = у/3) (рис.2.5.7а,б),
потом через сумматор (рис.2.5.76,в), затем перенести сумматор по ходу
сигнала через точку разветвления (рис.2.5.76,в,г,д) и перенести усили-
тель с коэффициентом усиления ai = — /3bi против хода сигнала
через сумматор (рис.2.5.7д,е) и, наконец, поменять местами получив-
шиеся рядом сумматоры (рис.2.5.7е,ж). Если перед входом фильтра
Калмана-Бьюси есть еще дифференциаторы, то при повторении пре-
образования они все попадут в прямую цепь, параллельную фильтру
Калмана-Бьюси (рис.2.5.7е).
В результате такого преобразования s-кратное дифференцирова-
ние входного сигнала перед входом фильтра Калмана-Бьюси заменяет-
ся (s — 1)-кратным дифференцированием в цепи, параллельной этому
фильтру.
10 Фильтры Калмана и Пугачева
290
ГЛ. 2. ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФИЛЬТРЫ КАЛМАНА
а
б
Рис. 2.5.6
2.6. Оптимальные линейная экстраполяция
и интерполяция
2.6. Г. Оптимальная линейная экстраполяция. Для линейной
системы (2.3.1) при а = 0 в соответствии с общей постановкой задачи 2
в п.2.1.3 легко решается задача оптимальной экстраполяции состояния
системы на данное время Д. Для этого достаточно выразить Х*+д
через Xt по формуле для решения линейного стохастического диффе-
ренциального уравнения (п.1.1.2).
г> В обозначениях (2.3.1), приняв за начальный момент а за ко-
нечный t 4- Д, получим
*+Д
Xt+д = u(t 4- Д, t)Xt 4- У u(t 4- А,т)ав(т)с1т+
t
t+д
4- У u(t + Д,r)V>(r)dir(г), (2.6.1)
t
2.6. ОПТИМАЛЬНАЯ ЛИНЕЙНАЯ ЭКСТРАПОЛЯЦИЯ И ИНТЕРПОЛЯЦИЯ 291
Рис. 2.5.7
292
ГЛ. 2. ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФИЛЬТРЫ КАЛМАНА
где u(t, т) - решение однородного уравнения ut = а^и при условии
и(т, т) = I. Взяв условное математическое ожидание относительно У/о в
(2.6.1), найдем оптимальную оценку будущего состояния Х*+д системы:
Х<+дИ = М[Х<+д|ГД] =
t+д
= u(t + Д, t)Xt + у* u(t +Д,т)ао(т)с1т). <з (2.6.2)
t
Таким образом, справедливо следующее утверждение.
Теорема 2.6.1. Оптимальный экстраполятор нормальной ли-
нейной стохастической дифференциальной системы (2.3.1) при а = О
представляет собой последовательное соединение оптимального филь-
тра с усилителем с коэффициентом усиления е = u(t + Д, t) и сум-
матором, добавляющим вырабатываемый соответствующим устрой-
ством детерминированный сигнал - второе слагаемое в правой части
формулы (2.6.2) (рис.2.6.1).
Рис. 2.6.1
Пример 2.6.1. В условиях примера 2.4.1
u(t + Д,£) =
созсиоД ~8то?оД
—о?о sin а>о Д cos cjq Д
(I)
и формула (2.6.2) дает
X2t
-Xu+ait = Хм cos «о А +----sinw0A,
Wo
X2t+a|t = -XitwosinwoA + X2tcosw0A.
Пример 2.6.2. В условиях примера 2.5.1 оптимальный экстраполятор пред-
ставляет собой последовательное соединение оптимального фильтра с усилителем с коэф-
фициентом усиления, представляющим собой матрицу u(t + Д, t) с элементами
Un(t + Д, t) = U22(t + Д, t) = С08 0>оД,
2.6. ОПТИМАЛЬНАЯ ЛИНЕЙНАЯ ЭКСТРАПОЛЯЦИЯ И ИНТЕРПОЛЯЦИЯ 293
ui2(f + Д,£) = —sincjoA, U2i(t + A,t) = -а?о8та>оД,
о>о
изз(£ + Д, t) = е (созо^Дч---------зто^Д
\
U34(t 4- Д, t) = —е“аЛ sino>i Д,
_ * ( (L
U44U 4- ДЛ) = е а | coscjiД--------зта^Д
\ CJ1
д2
М4з(£ 4- Д,£) =-----е“аЛ зта^Д,
а>1
Ui3(t "Ь Д» 0 ~ 4” Д, t) ~ U23(t 4" Д, t) = U24(t 4- Д, t) =
= U3i(t 4- Д, t) = l^32(t 4- Д, t) = U4i(t 4" Д, t) = U42(t 4- Д, t) = 0.
Пример 2.6.3. В условиях примера 2.5.2 оптимальный экстраполятор пред-
ставляет собой последовательное соединение оптимального фильтра с усилителем с коэф-
фициентом усиления, представляющим собой матрицу, элементы которой определяются
формулами предыдущего примера и формулами:
U51 (t 4” Д, t) —
27(7 - а)
wg +72
(7 cos wo Д + wq sin wo Д - 76 7Л
U52(t + Д,«) = ^-4-^—^(7sinwoA — wo cos wo Д + woe '|'д),
wg + 72
27(7 — а)е-аД
“53<1+A’f)=ц,7(7'-о7+ц?1(м(7~2°) [“s“,a
+ (Wj -
wi [(7 — a)2 + w2]
х< (7 - a)sinwiA — wj coswiA + wie^“
u55(t + Д,г) = е"7Д
U15(t + Д, t) = U2s(^ + Д) t) = U35(t + Д, t) — U4s(t + Д, t)) — 0.
294
ГЛ. 2. ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФИЛЬТРЫ КАЛМАНА
Для линейной стохастической системы (2.4.3) справедливо следую-
щее утверждение.
Теорема 2.6.2. Несмещенная с.к. оптимальная оценка Х$+д|$ со-
стояния линейной нормальной стохастической дифференциальной си-
стемы (2.4.3) является решением дифференциального уравнения
-X’t+Alt = °1^+д|* (А > 0) (2.6.3)
с начальным условием
[*^]д=0 = ^ (2.6.4)
При этом ковариационная матрица Rt+&\t ошибки является решением
матричного дифференциального уравнения
Я*+Д|* = а1Я*+Д|* + -й«4-Д|«аГ + 'фщ'ф1' (2.6.5)
с начальным условием
[^+Д|*]д=о = Rt, (2.6.6)
где матрица Rt предполагается известной.
2.6.2. Оптимальная интерполяция. Как известно (п.2.1.5),
интерполяция состояния стохастической дифференциальной системы в
момент времени t основана на наблюдениях как до момента времени t,
так и после. Обычно точность интерполяции выше точности фильтра-
ции, поскольку используется больше наблюдений.
Интерполяторы с закрепленным (фиксированным) интервалом ис-
пользуют все наблюдения на всем фиксированном интервале для оцен-
ки состояния для всех моментов времени из этого интервала.
Интерполяторы с закрепленной (фиксированной) точкой оценива-
ют состояние системы в прошлом на основе текущих наблюдений вплоть
до текущего момента. Такие интерполяторы обычно используются при
оценке состояния для некоторого фиксированного момента времени.
Интерполяторы с постоянным (фиксированным) сдвигом предна-
значены для оценки состояния системы на фиксированном интервале
относительно текущего наблюдения. Этот тип интерполяторов служит
для повышения точности за счет отказа от оценки скрытых свойств.
Уравнения описанных с.к. оптимальных интерполяторов могут
быть получены на основе комбинации уравнений линейной с.к. опти-
мальной фильтрации в прямом и обратном времени. Интерполяторы с
2.6. ОПТИМАЛЬНАЯ ЛИНЕЙНАЯ ЭКСТРАПОЛЯЦИЯ И ИНТЕРПОЛЯЦИЯ 295
фиксированным сдвигом и фиксированной точкой предназначены для
работы в реальном масштабе времени. Интерполяторы с фиксирован-
ным интервалом могут быть сначала использованы на основе фильтра-
ции всех наблюдений, а затем их интерполяции.
Применительно к стохастической дифференциальной системе
(2.4.3) справедливы следующие утверждения (Калман 1963).
Теорема 2.6.3. Несмещенная с.к. оптимальная оценка на за-
крепленном (фиксированном) интервале состояния линейной нор-
мальной стохастической дифференциальной системы (2.4.3) является
решением векторного дифференциального уравнения:
+ & [^|ti “ ^|t] (*о < t < *i) (2.6.7)
с условием в конце ti интервала интегрирования
=^1й- (2-6-8)
Здесь
Rt = V'l уц'ФТ Rt\ti > (2.6.9)
ait = ai(t), Vt = ^(t), "it = ^i(t).
При этом ковариационная матрица ошибки является решением
матричного дифференциального уравнения:
= (ait 4- 4- Rtfa (ait 4- Bt)T - (to < t < ti) (2.6.10)
с условием в конце ti интервала интегрирования
[^|h]t=tl = (2-6.11)
Замечание. Проверкой нетрудно убедиться, что матрица > входящая в
формулу (2.6.9), удовлетворяет следующему матричному дифференциальному уравнению
^Rt\ti = - auR^ + Ь&мЬц - (to < t < h)
(2.6.12)
с условием в конце ti интервала интегрирования
<2в13>
296
ГЛ. 2. ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФИЛЬТРЫ КАЛМАНА
где 7?^^ предполагается известной.
Теорема 2.6.4 (Язвинский 1970). Несмещенная с.к. оптималь-
ная оценка в закрепленной (фиксированной) точке Xt\tl (t > ti) состо-
яния системы (2.4.3) является решением векторного дифференциаль-
ного уравнения
dX
—- bltxt\t) (i > h) (2.6.14)
ас
с начальным условием
[xhJ (2.6.15)
Матрица Вц является решением матричного дифференциального
уравнения
= — Вц(ац + Bt) (* > ti) (2.6.16)
at
с начальным условием
Bltl = 7, (2.6.17)
где Bt определена (2.6.9); B2t равна
B2t = (2.6.18)
I - единичная матрица. При этом ковариационная матрица ошибки
Rtlt является решением матричного дифференциального уравнения
— -BuB2tU2tB2tB^t (t>tj (2.6.19)
at
с начальным условием
(2.6.20)
Теорема 2.6.5 (Медич 1963). Несмещенная с.к. оптимальная
оценка «Хф+д состояния системы (2.4.3) с постоянным (фиксирован-
ным) сдвигом является решением векторного дифференциального урав-
нения
2.6. ОПТИМАЛЬНАЯ ЛИНЕЙНАЯ ЭКСТРАПОЛЯЦИЯ И ИНТЕРПОЛЯЦИЯ 297
^X|t+A — в1Дф+д + Взд+дВг.ц-д (2<+д - Ь1,«+д-Хе+д|е+д) +
(^ф+д — Хф) (t > to) (2.6.21)
с начальным условием
[х4|(+д](=(о = Х4оИо+д. (2.6.22)
Здесь Bt определена (2.6.9), а входящая в (2.6.9) обратная матрица
Яф1 удовлетворяет (2.6.12) и (2.6.13). Матрица Взд+д удовлетворя-
ет матричному дифференциальному уравнению
d
-^В^+л = (ait + Ве)В3,е+д — В33+д(ам+д + В*+д) (t > to) (2.6.23)
с начальным условием
В3д0+д = ВМо+д, (2.6.24)
где ВМо+д определяется из аналогичного (2.6.16) дифференциального
уравнения
= -Ви(аи + Bt) (t > to) (2.6.25)
at
с начальным условием
Ви. = I, (2.6.26)
где I - единичная матрица. При этом ковариационная матрица ошиб-
ки Rt\t+& является решением матричного дифференциального уравне-
ния
^Я*|*+д = (ait + В*)/?ф+д + Rtit+biO'U + Bt)T-
~В3^4.дВ2Д4-Д1/2Д4-дВ^4-Д^^Д ~ Ф^иФ? (* > ^о) (2.6.27)
с начальным условием
[ Вф_|_Д ] £__£о В$0|£0-|_Д.
(2.6.28)
298
ГЛ. 2. ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФИЛЬТРЫ КАЛМАНА
2.7. Фильтрационные уравнения для ненормированных
распределений в стохастических дифференциальных
системах
2.7.1. Уравнения ненормированной одномерной плотности
о Рассмотрим сначала задачу оптимальной фильтрации по крите-
рию минимума с.к.о. применительно к уравнениям (2.1.5). Введем не-
нормированную плотность вероятности pt — pt(x) посредством следую-
щего соотношения:
pt(x) = MPt(x). (2.7.1)
Здесь функция д не зависит от х (но, конечно, может зависеть от Yt,
YtlQ) и определяется дифференциальным уравнением
dp = $dt + $dY, (2.7.2)
где <р и ф - некоторые функции Kt, Yt0, правила выбора которых будут
определены позже.
Используя формулу Ито для дифференцирования произведения
двух функций (1.4.83), удовлетворяющих стохастическому дифферен-
циальному уравнению, представим коэффициенты при dW в
уравнениях (2.2.11) и (2.7.2) в виде
{(¥>Г - ^Г)р< - [^Tpt] j wwi")-1^
и V'V’i- Следовательно, получаем
dpt = pdpt+
+ptdp + - <pT)pt - [V’W’fpt] |
(2.7.3)
После подстановки выражений для dpt и dp в (2.7.3) и (2.7.2) из (2.2.11),
принимая во внимание независимость р от х, получим
dpt = L*pptdt - {(tpl - <Pi)ppt - ^[Фу'ФТ pPt](^i^T)~1‘Pi}dt+
+{(¥>?" - ‘Pi'lPPt - dY + (pptdt+
ox
2.7. УРАВНЕНИЯ ДЛЯ НЕНОРМИРОВАННЫХ РАСПРЕДЕЛЕНИЙ 299
+4>ptdY + {</>f - <pf)pt - pt]}^Tdt, (2.7.4)
OX
где L* - сопряженный оператор для оператора (замечание 2 на стр.151)
L = <p(Y,x,t)T^~ + |tr
OX 2 ox ox
Из (2.7.4) следует, что если принять (р = 0,
тогда в силу (2.7.1) придем к линейному стохастическому дифференци-
альному уравнению для pt в частных производных с параметрическими
шумами (Закаи 1969):
dpt(x) = L*pt(x) + {y>i(y,a:,t)Tpt(a:)-
ят
о (2.7.5)
OX
Заме Ч а Н И е 1. Независимость р от X обеспечивается тем, что ф =
= РФ1(Ф1^Ф1)~1(У^) зависит от У и Г/О «Я зависит только от Y иУ/0).
После интегрирования уравнения (2.7.5) при начальных условиях
Pt(x) = Pt0(x) = ръ(х | 1о) коэффициент при р в (2.7.1) будет опреде-
ляться формулой
оо
р = У pt(x)dx, (2.7.6)
— ОО
при этом формула (2.2.14) для оптимальной оценки примет вид
оо
Xt = м-1 У xpt(x)dx. (2.7.7)
— ОО
Замечание 2. Коэффициент р в (2.7.1) можно определить и путем
интегрирования стохастического дифференциального уравнения (2.7.2) при начальном
условии р — 1 и при t = to. В результате получим
( 1
р = ехр < У ^(^1Р^Г)-1(^т,т)йУ(т) ►,
vo <
где интеграл представляет собой стохастический интеграл Ито (п. 1.4.4). Однако это бу-
дет лишней (проверочной) операцией, поскольку р определяется значительно проще по
300
ГЛ. 2. ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФИЛЬТРЫ КАЛМАНА
формуле (2.7.6), вытекающей из условия нормирования апостериорной плотности вероят-
ности.
Таким образом, имеем следующее утверждение.
Теорема 2.7.1. В основе теории с.к. оптимальной фильтра-
ции, основанной на ненормированной апостериорной одномерной плот-
ности для нормальной стохастической дифференциальной системы
(2.1.5), лежат уравнения (2.7.5)-(2.7.7) при условиях невырожденно-
сти матрицы = V’iW'o существования условных математических
ожиданий и соответствующих начальных условиях.
2.7.2. Уравнение для ненормированной характеристиче-
ской функции. Теперь обозначим ненормированную апостериорную
характеристическую функцию, соответствующую р* (я), через р*(А). Со-
гласно этому определению имеем
оо
Л(А) = У eixTхnpt{x)dx = pgt(X), (2.7.8)
— ОО
где (А) - апостериорная характеристическая функция процесса Xt.
Покажем, что р«(А) удовлетворяет следующему уравнению:
dgt(X) = / iXTip(Y,x,t) — ^ХТ{^yij)T}{Y,x,t}X}etXTх х
— оо
оо
xpt(x)dxdt + У {(pi(Y,x,t)T+
— оо
+iXTх, t)}etxTхpt^dx^i/ipi^1 (Y, t)dY. (2.7.9)
о Действительно, используем формулу для дифференциала произ-
ведения двух процессов (1.4.83) и примем во внимание, что коэффици-
енты при dW в уравнениях (2.2.11) и (2.7.2) равны соответственно
оо
У (¥>Г - Ф\ +iXipi'ipT)e,xTxpt(x)dx^ivi/)i)~1ip1
— ОО
И 'ф'фх = (^1^Г)-1^1> мы получим
2.7. УРАВНЕНИЯ ДЛЯ НЕНОРМИРОВАННЫХ РАСПРЕДЕЛЕНИЙ
301
dgt(X) = ndgt(X) + gt(X)dp,+
ОО
+ У (у’Г ~ФТ + iXT7/>i/i/>l)etxTxpt(x)dx(i/>ii'^)~1 p,<pidt. (2.7.10)
—ОО
Подставляя в (2.7.2) выражение для dgt(X) из (2.2.10), выражение для
dp из (2.7.2), примем во внимание формулы (2.7.1) и (2.7.8), а также
соотношения 92=0, ^ = /z(^(^ii/^r)-1, найдем:
оо
dgt(X) = f (iXT\р - ^Атфи'ф1'Х)е'хТхpt(x)dxdt+
J £
—оо
+ У (<Р1 - Ф1 +i^T^^T)e'xTxPt(x)(tl>ivtl>i) '(dY -<p!dt)+
+9t(X)a[ (ipivip’[)~1dY+
OO
+ У - Ф1 +iXT^vi/>T)e'xTxpt(x)dx(^ii^i1)T<pidt. (2.7.11)
—OO
Отсюда с учетом (2.7.1) приходим к искомому уравнению (2.7.9). При
этом (2.2.14) для оптимальной оценки дает
Л = М[Х|У/о]=д[^
(2.7.12)
Таким образом, имеем следующий результат.
Теорема 2.7.2. В основе теории с.к. оптимальной фильтрации,
основанной на ненормированной апостериорной одномерной характери-
стической функции для нормальной стохастической дифференциаль-
ной системы (2Л.5)% лежат уравнения (2.7.6), (2.7.8), (2.7.9) и (2.7.12)
при соответствующих начальных условиях.
2.7.3. Об уравнениях с.к. оптимальной фильтрации для
ненормированных распределений в случае винеровских и пуас-
соновских шумов. Уравнение с.к. оптимальной фильтрации для не-
нормированной одномерной характеристической функции (2.7.8) про-
цесса X(t) в условиях теоремы 2.2.6 (п.2.2.12) имеет вид:
302
ГЛ. 2. ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФИЛЬТРЫ КАЛМАНА
ОО
<2<7г(А) = У |гАт</>(У, х, t) - ^XT^'i>otp'T)(Y,x,t)X+
—ОО
+ I JeiATV-"(r,M,v) _ 1 _iXTi()”(Ytx,t,v)] vP(t,dv)Jx
Я?
oo
x e'xTxpt(x)dxdt -I- У -I-x
—oo
x (2.7.13)
Таким образом, справедливо утверждение.
Теорема 2.7.3. В условиях теоремы 2.2.6 уравнение с.к. опти-
мальной фильтрации для ненормированной апостериорной одномерной
характеристической функции (2.7.8) имеет вид (2.7.13).
2.8. Дискретное оптимальное оценивание
2.8.1. Задачи дискретного оценивания
Задача 1. Векторный дискретный случайный процесс [YJTXZT]
определяется стохастическими разностными уравнениями нелинейной
регрессии вида (1.5.58):
yz=cvlz(yz,Xz,Vz),
Xz+1 = u;l(Yl,Xl,Vl) (1 = 0,1,2,...), (2.8.1)
где yz - П1-мерный наблюдаемый случайный процесс; Xi - n-мерный не-
наблюдаемый случайный процесс; Vi - r-мерные случайные величины с
известными характеристическими функциями hi = hi(p) и плотностя-
ми гц = rji(v)\ шц и wi - известные векторные функции, отображаю-
щие пространство Rni х Rn х R соответственно в пространства Rni и
Rn. Требуется оценить вектор состояния системы Xi в любой момент
I > /о по результатам наблюдения процесса Yi в интервале времени [Zo, /],
vj = {У9, J = 0,1,, 0.
Задача 2. Векторный дискретный случайный процесс [У;ТХ;Т]
определяется стохастическими уравнениями нелинейной регрессии вида
у =Wlz(yz,xz,vz),
Xl+1 = wz(Xz, Vz) (1 = 0,1,2,...), (2.8.2)
2.8. ДИСКРЕТНОЕ ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ
303
Требуется оценить вектор состояния системы т > 0 в любой мо-
мент I > /о по результатам наблюдения процесса Yi в интервале времени
КоД Го'= = 0,1,..., 0.
Аналогично ставятся задачи 1 и 2 для дискретных стохастических
систем, описываемых уравнениями авторегрессии вида (1.5.59). В этом
случае уравнения (3.7.1) и (3.7.2) имеют соответственно вид
у^ЫГЛО + ЫУЖ,
Xl+l=<pl(Yl,Xl) + il>l(Yl,Xl)Vl (/ = 0,1,2,...); (2.8.3)
У< = ¥’и(У/,Х/) + ^1г(У/)У<,
xz+i =^Z(XZ) + ^(XZ)VZ (/ = 0,1,2,...). (2.8.4)
Замечани e. Пусть имеет место случай зависимых ошибок наблюдения,
когда первое уравнение (2.8.1) следует заменить на Yi = U)n(Xi, И^), {И^} - после-
довательность независимых случайных величин, причем W; удовлетворяет разностному
уравнению вида (2.8.1), V[), где {V/} - последовательность незави-
симых случайных величин с известным распределением (без потери общности V/ могут
совпадать с V/ во втором уравнении (2.8.1). Тогда, если расширить вектор состояния
X, = [ЛТИ'.Т] , то уравнения соответствующих задач фильтрации и экстраполяции
сводятся к уравнениям (2.8.1)-(2.8.4).
Задачи с.к. оптимальной фильтрации будут рассмотрены в насто-
ящем разделе (пп.2.8.3 и 2.8.4) и разделе 2.9.
2.8.2. Задачи интерполяции в дискретных стохастических
системах. Предположим, что векторный дискретный случайный про-
цесс [1^ГХ/Т]Т определяется разностными уравнениями (2.8.2). Ана-
логично п.2.1.5 будем различать три типовые задачи с.к. оптимальной
интерполяции.
Задача 1. Интерполяция с фиксированной точкой (прямая интер-
поляция): момент времени оценивания фиксирован, т.е. I = S, а интер-
вал наблюдения к = I > S растет.
Задача 2. Интерполяция с фиксированной задержкой: в этом слу-
чае ни I, ни к не фиксируются, но их разность остается постоянной, т.е.
к - I = г, (г — постоянное время задержки).
Задача 3. Интерполяция с фиксированным интервалом (обратная
интерполяция): интервал наблюдения фиксирован к = N (N — посто-
янная величина), а время оценивания I изменяется от 0 до N.
Эффективные решения задач интерполяции случайных последо-
вательностей, описываемых разностными уравнениями, известны для
304
ГЛ. 2. ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФИЛЬТРЫ КАЛМАНА
линейных уравнений и для специального класса нелинейных уравне-
ний (обобщенные гауссовские последовательности). В общем случае
для нелинейных уравнений (2.8.2) или (2.8.4) эффективного решения
поставленных задач интерполяции не найдено. Задачам экстраполяции
и интерполяции посвящен раздел 2.10.
2.8.3. Дискретная оптимальная фильтрация. Формула
(2.2Л) для с.к. оптимальной оценки Xi процесса Х[ для дискретного
случая имеет вид
(2.8.5)
(u = I для задачи фильтрации и и = I 4- т для задачи экстраполяции).
При произвольных нелинейных функциях си/ и сиу не удается получить
замкнутую систему рекуррентных уравнений относительно с.к. опти-
мальной оценки Xi = М [X/ | Yq ] вектора состояния X/ системы (2.8.1)
по результатам текущих наблюдений Yq = {Yi, i = 0,1, ... , I}, а так-
же ковариационной матрицы Ri = М JX/XZT | Yq j ошибки оценивания
Xi = Xi — Х[. Основная трудность связана с нахождением одномерных
фильтрационных плотностей ЛДя/ I !/о) и характеристических функ-
ций pi,/(A | ylQ).
Среди методов дискретного оценивания наибольшее распостране-
ние получили в первую очередь регрессионные методы.
2.8.4. Дискретная с.к. оптимальная линейная фильтрация.
Пользуясь формулами пп.1.1.5 и 1.5.3, можно показать, что дискретным
аналогом уравнений (2.3.1) являются стохастические уравнения вида
У/ = Я/Х/ + ^1/И, Х/+1 = Ф/+1./Х/ 4- гМ.
Поэтому в качестве наиболее общей модели дискретной линейной нор-
мальной стохастической системы примем следующую:
У/ = Я/Х/4-У2./, Xt+^QwXi+^V^ (Z = 0,1,2,...), (2.8.6)
где X/, У/ - векторы (n х 1), (ni х 1)-матрицы состояния и наблюдения;
Ф/+1,/ - (п х п)-матрица; ifa - (п х Г1)-матрица, Vi,/, V24 - нормальные
некоррелированные белые шумы с нулевыми математическими ожида-
ниями и интенсивностями vij, 1/2,/-
Справедливо следующее утверждение (Бьюси и Джозеф 1968),
обобщающее известный результат Калмана (Калман 1960а, 19606).
2.8. ДИСКРЕТНОЕ ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ
305
Теорема 2.8.1. Пусть 1/2,1 > oil, где а > 0, единичная (гг х гг)-
матрица. Тогда уравнения дискретного фильтра Калмана для дис-
кретной линейной нормальной стохастической системы (2.8.6) име-
ют следующий вид:
хН? + j/г,»)"1 W - ВД|/-1), (2.8.7)
Xi\, = Лк-! + ft (Yi - Вдц-i) , (2.8.8)
Xl0|-i = Ко = 0, (2.8.9)
ft = + i/2.,)-1, (2.8.10)
#j+i|j = Фн-иЯфФн-и + $,T+I|t “ Ф»+1|Л|»-1x
xH? (HlRl\l_1H?’ + 1/2>|)-1Н<Я/|<-1ФГ+1|/ + (2.8.11)
Ящ = (7-ft^)fl/|J_1(7-ft^)T+fti/2,/ftT = Я^-Шц-ъ (2.8.12)
fliol-i = Rh = kXo- (2-8.13)
ЗАеСЬ Ящ = МХфД, Яф-i = МХф-i Д-i, (2.8.14)
X^Xt-X^. (2.8.15)
Следуя (Бьюси и Джозеф 1968), дадим прямой вывод теоремы 2.8.1.
> Первая часть уравнения (2.8.7) вытекает из (2.8.6), так как
МГц = 0. Соотношение (2.8.11) выводится следующим образом. Со-
гласно (2.8.14), (2.8.15) имеем
Я|+1|/ = M-Xi+in-Xj+JH = M(Xz+i — Х|+1ц)(Х|+1 — Xj+1p)T.
Но в силу (2.8.6), (2.8.7), (2.8.15):
-Xj+1 ~ + inVu - — &i+i,iXiц + i/>iVu.
Значит,
Л|+1р = М(Ф|+1,<-Хщ + +i>iVu)T =
= + ilnMVuVfrtf,
306
ГЛ. 2. ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФИЛЬТРЫ КАЛМАНА
что совпадает с первой частью уравнения (2.8.11). Обозначим
Yi = Yt - ЪХщ-! (2.8.16)
обновляющий дискретный случайный процесс, тогда очевидны следую-
щие соотношения:
М[Х,|У'] = (2.8.17)
Yt = Hi(Xt - ХфЩ + V2l = Ht {X, - M [X, | У'’1 ]} , (2.8.18)
M [xz | У'"1,!,] = М[Х|У'"1]+м[х/|У/]. (2.8.19)
В силу (2.8.12) и (2.8.18) тождества
М[Х I У] = М[ХУГ] {М[УУТ]}-1У (2.8.20)
справедливы следующие формулы:
Х,|/ = + м [xz I У,] = XZ|z-i + MXiYtT {м [yzyzT] }_1 У,.
(2.8.21)
Учитывая, что согласно (2.8.14)
Ri\i-i = MX/p-iX/p-j,
получим
МУ/У^ = 4-1/2,z, (2.8.22)
MXzyzT = M [ Х1Ц_1 ] Hf. (2.8.23)
Замечание1. Формула (2.8.16) вытекает из следующих равенств:
Yi = HiXi 4- V21 - HiXi\i-i = HiXiy-x 4- V^z,
MXZ|Z_zyzT = МХф-^7, = 0, MXZ|Z-1V2T = 0.
Замечание 2. С учетом замечания 1 формула (2.8.23) выводится на основе
следующих соотношений:
м [XZV2TZ] = о, м [Хщ-iX^! ] = о,
2.8. ДИСКРЕТНОЕ ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ
307
М [х,У(т] = М [ВДи-1 ] НТ = М (Хф-! + Хф-г) =
= 7?/Ц_1Н;Т + М [Хф-1-Хф_1 j Я,т.
Из формул (2.8.21)-(2.8.23) и (2.8.16) вытекает формула (2.8.8).
Наконец, выведем уравнение (2.8.12).
Согласно (2.8.8), (2.8.15), (2.8.16) имеем равенства
Хщ = Xi - Хщ = Xi - X/jz-i - PiYi = Хщ-! — fliYi. (2.8.24)
Отсюда вытекает, что
м [ хЦ1х^ ] = м [(x^j - - тт ]
или согласно (2.8.14)
Я/р = Л/н-1 - ДМ [у,Х^ ] - М ] 0Т 4- AM [ YY? ] Дт.
(2.8.25)
Так как М [Xz|z-i V2T ] = 0, то в силу замечания 1 имеют место следу-
ющие соотношения:
ДМ [^X/p-i ] = ДМ [вд^Х-Г.! ] = ДЯ,Я/ц_1> (2.8.26)
М [Xz|z-iYtT] Дг = М [Xjiz-iXz]h ] НТДт = R^H? ff. (2.8.27)
Но согласно (2.8.22):
ДМ [YiYtT] Дт = Д(Я,Я,|/_1Я,Т + Р2)<)ДТ.
Отсюда, в соответствии с (2.8.10) находим:
дму,у,тдт = (2.8.29)
Подставляя (2.8.26)-(2.8.29) в (2.8.25), получаем (2.8.12). <
Подробному изучению фильтра Калмана посвящен раздел 2.9.
В разделе 2.11 будут рассмотрены вопросы устойчивости, управляемо-
сти и наблюдаемости фильтров Калмана.
Задачи с.к. оптимальной дискретной экстраполяции и интерполя-
ции будут рассмотрены в разделе 2.10.
308
ГЛ. 1. ТЕОРИЯ ОПТИМАЛЬНОГО ОЦЕНИВАНИЯ
2.9. Дискретные фильтры Калмана
2.9.1. Случай некоррелированных шумов. Рассмотрим нор-
мальную стохастическую линейную систему (2.8.3), записанную для мо-
мента времени I в следующем виде:
Yt = btXt + V2.z, + Vu_i, (2.9.1)
где и V2j - дискретные нормальные некоррелированные белые шу-
мы, удовлетворяющие условиям:
= MV2,i = о, = vVi6ij,
= V2MV1(iv£. = 0 (i/2< > a/r2). (2.9.2)
Обозначим через X/(+) апостериорную оценку X/, основанную на дан-
ных наблюдений Yi и априорной оценке Х}(—); через lfy(+) =
= MXi(=F)Xi(qF)T - априорную (—) и апостериорную (-+-) ковариаци-
онные матрицы ошибок фильтрации, где Х/(^=) = Х/(^) — X/, тогда в
силу результатов п.2.8.4 уравнения дискретного фильтра Калмана для
(2.9.1) примут следующий вид (рис.2.9.1):
Xz(-) = az_1XZ-i(+), (2.9.3)
/?/(—) = a/-i^/_i(4-)ajC_i 4-Pij-i, (2.9.4)
Л(+) = *<(-) +ft [У/ -6(Л-1(-)] , (2.9.5)
/?,(+) = (/ - МЩ-) = (I- (2.9.6)
ft = Ri(-V>T [btR^bf + z/2,,]’1. (2.9.7)
при начальных условиях:
MX0 = Хо, MXoXj’ = Rq. (2.9.8)
Теорема 2.9.1. Пусть а > 0, I = 1Г2 - единичная
матрица, тогда дискретный фильтр Калмана для дискретной линей-
ной нормальной стохастической системы (2.9.1) с некоррелированны-
ми шумами определяется рекуррентными уравнениями (2.9.3)-(2.9.7)
при начальных условиях (2.9.8).
2.9. ДИСКРЕТНЫЕ ФИЛЬТРЫ КАЛМАНА
309
1^ Вычислить !?/( — ), используя Rl — l ( + ), Qi-1 и V1J — 1
2° Вычислить Д, используя /?/(—) (шаг 1^), Ь/ и V2J
3° Вычислить 71/(4-), используя Pi (шаг 2°) и fli(-) (шаг 1®)
4° Последовательно вычислить uV/(4“), используя Pl (шаг 2®), начальные
условия JVq и результаты наблюдений У/
Рис. 2.9.1
о Следуя (Греваль и Эндрюс 1993), дадим независимый от п.2.8.4
вывод уравнений дискретного фильтра Калмана. Будем искать линей-
ную оценку Х/(4-) в виде линейной комбинации априорной оценки Х/(—)
и данных наблюдений У/, т.е.
Xi^=PlXt{-)^piYh (2.9.9)
где Pl и Pi находятся согласно п.1.3.6 исходя из следующих уравнений
линейной регрессии (уравнения принципа ортогональности):
m[(Xz-Xz(+))Y)t] =0 0 = 1,2,... ,1-1), (2.9.10)
m[(Xz-Xz(+))V] =0. (2.9.11)
Подставим в (2.9.10) формулу для Xi из второго уравнения (2.9.1) и
Х/(+) из (2.9.9), а также учтем, что шумы Viti и Уг,/ некоррелированы
и М [ Ум У/] = 0 для 1 < j < I. В результате получим
М [ (а,-!^-! + У,.,-! - #%,(-) - тут]= О 0 = 11).
(2.9.12)
310
ГЛ. 1. ТЕОРИЯ ОПТИМАЛЬНОГО ОЦЕНИВАНИЯ
Далее подставим первое уравнение (2.9.1) в (2.9.12), тогда будем иметь:
М [ (а,-!X,-! - tfXf(-) - 0М - /3tV2,i)Yf ] = 0 (j = 1, ... , I - 1).
(2.9.13)
Очевидно, что уравнение (2.9.11) справедливо и на предшествующем
шаге I — 1:
М [ (Xt-г ~ Л-1(+))У/ ]= 0 (j = 1,21) (2.9.14)
и MV2,z^jT = 0, i = 11. Выполним, с учетом уравнения (2.9.13),
следующие несложные преобразования:
ai^MX^Y? - ^МЛ(-)У/ - /31Ьга/_1МХ/_1Г/’-
-ДМЦ,iYT = ацММ/ - ^MXt{-)YT - pfya^MX^Y^ =
= M [ (X, - fabiXi - flxt) - /3}(Xt(-) - Xi)Y^ ] =
= (I - p} - 0ibi)MXtYT = 0. (2.9.15)
Уравнение (2.9.15) для любого Xi будет выполняться только при усло-
вии
13} = -fftb,. (2.9.16)
Для ошибок
Xz(t) = Л(Т) - Xh = УД-) - Yi - biXi{-) - Yi (2.9.17)
уравнения принципа ортогональности (2.9.11) принимают следующий
вид:
М(Х, - Л(+))У7 = о. (2.9.18)
Подставляя Xi, АД+) и Yi из уравнений (2.9.1), (2.9.9) и (2.9.17), полу-
чим
М [а,-!*,-! + Ц,,-! - flXt(-) - ftYj] [б,Х,(-)-у]Т = 0. (2.9.19)
Учитывая равенства (2.9.4) для /?/(—) и соотношения
MV^Y? = MVi,/X/(+)T = 0,
(2.9.20)
2.9. ДИСКРЕТНЫЕ ФИЛЬТРЫ КАЛМАНА
311
М [а,-!*/-! - #Х{(-) - ^Yj ] [^(-) - Yj ]Т = 0, (2.9.21)
получаем следующее уравнение для определения /?/(—):
(/ - fabWt-W - fav2,i = 0. (2.9.22)
Отсюда немедленно следует формула (2.9.7).
Аналогично получается формула (2.9.6) для Л/(+)
[Х/(+)Х/т(+)]. Подставляя (2.9.16) в (2.9.9)
, находим
= М
й(+) = (I - + I3M, (2.9.23)
Хг(+) =%,(-) + ft [^-Ь/Лн]. (2.9.24)
Вычитая Xi из обеих частей уравнения (2.9.24), получаем следующие
соотношения:
Л(+) - Xt = Л(-) + /ЗМ + fav2,i - ftbtXtt-) - xh
Xz(+) = Xz(-) - fabtXtt-) + faV2,h Xz(+) = (Z -/3tbtm-) + faV2,i.
(2.9.25)
Наконец, принимая во внимание определение /?/(+), условие
MXz(-)y2j = 0, а также последнее соотношение (2.9.25), находим
Я/(+) = М (7 - АЬ<)Х/(-Й1г(-)(/ - ftbt)T + ftv2J
= (I- ftbi)Rt(-)(I - ftbi)T + (2-9.26)
Из (2.9.7) и (2.9.36) имеем следующее выражение
7?z(+) = fiz(-) - fabiRit-) - Ri(-)bTff + ftbiR^-W
+ftv2,i/3? = (.1 - Pibi)Ri(-) - Ri(~)bl^ + [jM-tf + p2,z]}^t.
(2.9.27)
Ho
ЬЛ(-)ЬТ + P2,< = Rt(-)bT, (2.9.28)
поэтому приходим к следующему результату:
/?,(+) = (7-^)Я/(-). (2.9.29)
312
ГЛ. 1. ТЕОРИЯ ОПТИМАЛЬНОГО ОЦЕНИВАНИЯ
Формула (2.9.29) очень удобна для рекуррентных вычислений ошибок
фильтрации.
Наконец, для вывода формулы (2.9.4) заметим, что в силу соотно-
шений
= &i-1Xi-1(+), Xi(-) - Xi — ai-iXi-i(-\-) — Xi,
й(-) = az-1 [й-1(+) - Xi-г ] - =
= aJ_1Xz_1(+) - V^-!, MXz-iV^-j = 0. (2.9.30)
имеем для /?/(-) = MX/(-)Xf(-) следующее уравнение:
ft(-) = MXz(-)Х,г(-) = aj-ifli-1 (+Xi + «'I.i-I- о (2.9.31)
В некоторых практических задачах вместо уравнений (2.9.1) ис-
пользуют следующие:
Yt = btXt + V2J, Xt = a^Xi^ + Vi,/-!. (2.9.32)
В этом случае уравнения дискретного фильтра Калмана имеют вид
Xz(-) = az-iA'z-i(-l-), /?j(-) =
%,(+)= %,(-)+ft [r« -bzXz(-)] , pl = Rt(-)bf[biRi(-)bT + u2<i]~1,
Я,(+) = Я,(-) - ftbtRil-) (2.9.33)
при начальных условиях (2.9.8).
Теорема 2.9.2. Пусть 1/2>/ > <*1> а > 0, где I = 1Г2 - единич-
ная матрица. Тогда дискретный фильтр Калмана для дискретной
линейной нормальной стохастической системы (2.9.32) с некоррелиро-
ванными шумами Vij, V2>/, определяется рекуррентными уравнениями
(2.9.33) при начальных условиях (2.9.8).
Как отмечалось в разделах 2.3 и 2.4, для стохастических диффе-
ренциальных систем вычисление матричного коэффициента усиления
/3i и ковариационной матрицы ошибки фильтрации не требует текущих
данных измерений и может быть выполнено уже во время проектиро-
вания дискретного фильтра Калмана.
В уравнения (2.9.5) и в третье уравнение (2.9.33) входит вектор
[У/-6/А'/(-)], который аналогично п.2.3.2 называется обновляющим дис-
кретным случайным процессом (п.2.8.4).
2.9. ДИСКРЕТНЫЕ ФИЛЬТРЫ КАЛМАНА
313
Пример 2.9.1. Рассмотрим линейную дискретную систему второго порядка
(Греваль и Эндрюс 1993):
Xt = XZ-! + VX./-1, Yt = Xt + V2,t. (I)
MV11Z = MV2>/ = О, МУ2)>УМ = 6ij, MV2,jVld = 26ij, (II)
MX(0) = Xo, M [ X(0) - Xo ]2 = -Ro. (III)
Yt = 2, Y2 = 3, Уз = I- (IV)
Найдем X$ и Rqq. Имеем СЦ — Ь[ = 1, =1,1/2 =: 2, тогда согласно (2.9.4) и (2.9.7)
находим
Я,(-) = Я,_1 + 1, (V)
о Ri(-) R/-i(+) + l /vn
А = ЯЙЙТ2 = «,->(+) + !' (VI)
я<(+) = [ 1 *№->(+) +1) = TXV'' (VII)
Я/-1(+) + 3] Я/-1(+) + 3
Х,(+) = Х/_1(+) + д [у - х((+)]. (VIII)
Пусть I = ОО, тогда Я/(+) = .R/-i(+) — R*, причем
R* = (1Х)
гС то
Отсюда, решая уравнение Я* + R* —2 = 0, находим R* = 1. Для I = 1 по (2.9.5)
находим
Х1(+) = Хо + ^^(2-Хо). (X)
Для I = 2 вычисляем Х2(+) И Т.д.
2.9.2. Дискретный фильтр Калмана для коррелированных
шумов. Теоремы 2.9.1 и 2.9.2 допускают обобщения на случай корре-
лированных шумов pij и 1/2,ь когда в (2.9.2)
МУИУ2? = v12,iiij, vi2,i/0. (2.9.34)
В этом случае в формулах для Д и /?/(+) следует положить
/3i = [/?/(—+ 1/12,1 ] [biRi(—)bf + i/2,i + Ь/^12,/ + ^12 ify] , (2.9.35)
314
ГЛ. 1. ТЕОРИЯ ОПТИМАЛЬНОГО ОЦЕНИВАНИЯ
я«(+) = Ri(-) ~ Pl [ W~) + рГ2>1 ] • (2.9.36)
Теорема 2.9.3. В условиях теоремы 2.9.1, но для случая (2.9.34)
коррелированности шумов Vij и V2,i уравнения дискретного фильтра
Калмана определяются уравнениями (2.9.3)-(2.9.5), (2.9.35), (2.9.36)
при начальных условиях (2.9.8).
Аналогично формулируется обобщение теоремы 2.9.2 для уравне-
ний (2.9.32).
2.9.3. Дискретный фильтр Калмана для автокоррелиро-
ванных шумов в наблюдениях. Теперь рассмотрим обобщение дис-
кретного фильтра Калмана для автокоррелированных шумов в наблю-
дениях, когда
Yl = blXl+X2,h (2.9.37)
где
V2j=a{_1V2,i_1+V3tl_1 (2.9.38)
и Уз,/-1 - дискретный нормальный белый шум, МУ3д = 0. Введем рас-
ширенный вектор состояния Xi = > удовлетворяющий раз-
ностному уравнению вида второго уравнения (2.9.1):
=а/_1Х/_1+УМ-1, (2.9.39)
где
Г ai-i 0 1.-, Г Vij-i
ty-i = п • , vij-i = т7
О at_x J [ V3J-1 .
Тогда уравнение (2.9.37) примет следующий вид:
Yi=biXh (2.9.40)
где обозначено bi = [bi I].
Очевидно, что для уравнений (2.9.39) и (2.9.40) условия теорем
Калмана выполняются только до тех пор, пока det [б/Л/(—)bf] 0.
2.9.4. Дискретный фильтр Калмана при линейных преоб-
разованиях. Рассмотрим линейное преобразование переменных У/ и
Xi в уравнениях (2.9.1):
У/=В/У/, Xt^AtXt,
(2.9.41)
где Ai - невырожденная (п х п)-матрица; Bi - матрица, состоящая из ni
столбцов, так что произведение Bi bi имеет смысл, размерность У/ произ-
вольна и может зависеть от I. Тогда после несложных преобразований,
2.9. ДИСКРЕТНЫЕ ФИЛЬТРЫ КАЛМАНА
315
получаем следующие уравнения линейно преобразованного дискретно-
го фильтра Калмана:
X^a^Xj-i+V^, (2.9.42)
У/ = Ь(Х1+К2>/, (2-9.43)
Rl(+) = Rl(-) + Rl(-)bl[blRl(-)^ + и2>1] &&(-), (2.9.44)
Ri+i(—) = alRl(+)a[ + vlt. (2.9.45)
Ri(±) = AtRi(±)A{, (2.9.46)
где введены следующие обозначения:
at = AiaiA^1, = B/fyAf1,
H.1,1 = ^iVi,iA'i, v2l = (2.9.47)
2.9.5. Связь между непрерывными и дискретными филь-
трами Калмана. Пользуясь формулами п. 1.1.5 и уравнениями пп.2.4.2
и 2.9.1, получаем следующие результаты:
= ax(t)X(t) + Vx(t), (2.9.48)
at
Xt+1 = atXi + [ g(ti+i,r)w(r)dT, (2.9.49)
ftl+1
Ri+i = aiRta{ + Pi,; = aiRiaf + / g(ti+i,r)v1(r)gT (ti+^rjdr,
Jti
(2.9.50)
= f'+1 5(‘')(iJ+1,T)I/i(r)ff(‘')T(tt+1,T)dT (i = 1,2), (2.9.51)
Jt,
Ri= ft,+t giR4tl+1,T)R(r)g^T(tl+l,T)dT. (2.9.52)
r> Пользуясь полученными формулами, выведем уравнения филь-
тра Калмана-Бьюси (п.2.4.2) из уравнений дискретного фильтра Кал-
мана (п.2.9.1). Обозначим At = ti - t/__ i. В силу определения весовой
функции для дискретной системы (п. 1.1.5) имеем
g(ti, ti—i) = ai = I + o-i (t/—i)At + O(At2). (2.9.53)
316
ГЛ. 2. ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФИЛЬТРЫ КАЛМАНА
Из свойства интенсивности белого шума находим
vyj = V’(t|)i,i(<<)V’(tj)TAt + O(At2), v2,i = р2(^)(Д<)-1- (2.9.54)
Проверкой убеждаемся в следующих формулах:
Я,(-) = [/ - ai(t)At] [I - ] х
xRi-i (-)[/ + ai (t)At ]Т + + 0(А«2), (2.9.55)
Д<(~)-^-1(~) = aim-i(-) + Ab-KnW7, +
+O(At2), (2.9.56)
AhM>%? = aJ5o+ p2(t)]-1} =
= Rb{^1=/3. (2.9.57)
Это уравнение совпадает с (2.4.6). Подставляя (2.9.52) в (2.9.53) и пе-
реходя к пределу, получаем уравнение Риккати (2.4.6). <
2.10. Дискретные линейные оптимальные экстраполяторы
и интерполяторы
2.10.1. Дискретные линейные экстраполяторы. Рассмотрим
задачу дискретной с.к. оптимальной экстраполяции (п.2.8.1) примени-
тельно к линейным уравнениям вида (2.9.32):
Yt = btXt + V2J, ХИ1 = atXt + (2.10.1)
Применяя теорию дискретной с.к. оптимальной линейной фильтрации
раздела 2.9, приходим к следующему результату (Калман 1963).
Теорема 2.10.1. В условиях теоремы 2.9.2 уравнения дискретного
линейного экстраполятора имеют вид:
Xj+rp = ajXi+j-ij. (2.10.2)
При этом ковариационная матрица ошибки Ri+T\i является решением
уравнения
Rt+T\i = ai+TRi+Ta[+T + ai+rV’z+ri'i,z+r’/’z+rai+r- (2.10.3)
2.10. ДИСКРЕТНЫЕ ЭКСТРАПОЛЯТОРЫ И ИНТЕРПОЛЯТОРЫ
317
Замечание!. Пользуясь формулами п.2.9.5, нетрудно вывести уравнения
непрерывной экстраполяции (теорема 2.6.2) из уравнений теоремы 2.10.1.
Замечание2. В условиях п.2.9.1 линейную экстраполящию можно рассмат-
ривать как линейную фильтрацию, когда нет данных наблюдения или их затруднительно
получить. Тогда следует положить /?/ = 0 и уравнение экстраполятора будет имет вид
А}(-|-) = ai-iXi—i (”F). Предыдущие значения оценок будут начальными условиями
для этого уравнения.
Замечание 3. В условиях, когда на определнных интервалах времени li
и /2 могут отсутствовать данные наблюдений, допустимо применение алгоритмов п.2.9.1,
при этом на этих интервалах времени не следует проводить уточнение оценок и принять
ai = 0.
Как показано в (Калман 1963), применительно к уравнениям (2.8.6)
основные уравнения теоремы 2.10.1 имеют следующий вид:
Л+т|/ = (2.10.4)
где
Ф/j = •• • $j+2,j+i$j+i(2.10.5)
I
Ri\j = (2.10.6)
»=j+i
(I = j+ l,j+ 2,...).
Здесь Xj\j и Rj\j предполагаются известными (теорема 2.8.1). Таким
образом, справедливо утверждение.
Теорема 2.10.2. В условиях теоремы 2.8.1 уравнения с.к. опти-
мального несмещенного экстраполятора имеют вид (2.10.4)-(2.10.6).
2.10.2. Дискретные линейные интерполяторы. Аналогич-
но непрерывному случаю (п.2.6.2) выводятся основные уравнения с.к.
оптимальной интерполяции, решающие поставленные в п.2.8.2 задачи.
Следуя (Язвинский 1970), приведем основные результаты.
Теорема 2.10.3. В условиях теоремы 2.9.2 несмещенная с.к. оп-
тимальная оценка Хцр/ на закрепленном интервале (обратная
интерполяция) определяется рекуррентным уравнением;
Xl\N = xiv + At (x/+1|„ - X/+1|Z) (I = N - 1, • • • , 1, o), (2.10.7)
с условием в конце интервала N
= (2-10.8)
318
ГЛ. 2. ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФИЛЬТРЫ КАЛМАНА
Здесь
Ai — Ища? (2.10.9)
При этом ковариационная матрица ошибки интерполяции (I =
= 0,1,...,ЛГ — 1) определяется рекуррентным уравнением:
Run = R,v + Ai (Л/+1|„ - Яицг) А? (I = N - 1, ... , 1,0) (2.10.10)
с условием в конце интервала N
[#f|N]Z=jV = Rn\N- (2.10.11)
Замечание. Теорема 2.10.3 распостраняется и на случай уравнений
(2.8.6), только при этом в формулах (2.10.7), (2.10.9) и (2.10.10) А[ следует заменить на
А|Н1 ~
Теорема 2.10.4. В условиях теоремы 2.9.2 несмещенная с.к. оп-
тимальная оценка X^j в закрепленной точке (прямая интерполяция)
определяется рекуррентным уравнением:
Xiy = + A, (2.10.12)
(I - фиксировано, j = I + 1,1 + 2,...) с начальным условием
= (2.10.13)
Здесь
Ai = RjljaiR^iy. (2.10.14)
Ковариационная матрица Ri\j ошибки интерполяции определяется ре-
куррентным уравнением:
Ri\j — + Aj (Rj\j ~ Rj\j-i) Aj (2.10.15)
(I - фиксировано, j = I + 1,1 + 2,...) с начальным условием
= (21016)
Замечание. Теорема 2.10.4 распостраняется и на случай уравнений (2.8.6),
если в (2.10.11), (2.10.14) и (2.10.15) А/ заменить Ajj+i:
J-1
AjJ+1 — JJ ^i+l|i’
i=l
2.10. ДИСКРЕТНЫЕ ЭКСТРАПОЛЯТОРЫ И ИНТЕРПОЛЯТОРЫ
319
Основные уравнения дискретной с.к. оптимальной обратной ин-
терполяции в обозначениях раздела 2.9 имеют вид (Греваль и Эндрюс
1993):
= %i(+) + Ai ^Xj+iipv] , (2.10.17)
(2.10.18)
Xv|pv] = ^w(+)> (2.10.19)
Ri\[N] = #f(+) + Ai [/?j+i|pv] - l?/+i(-)] A{. (2.10.20)
Алгоритм обратной интерполяции на первом этапе использует фильтра-
цию Калмана, сохраняя Л}(т), Л/(т) для каждого L На втором этапе,
начиная с момента N последнего измерения, проводится интерполяция
промежуточных данных, сохраненных в памяти на первом этапе.
В основе дискретной с.к. оптимальной прямой линейной интерпо-
ляции лежат рекуррентные уравнения:
Хф- = Ли-1 + AjPj [Yi - bjXi(-) ] , (2.10.21)
А, = Aj.1Ri-1(+)aJ_1R-1, (2.10.22)
Ri\j = Rm-i+Ai [Ri(+) - ЛД-)] Af. (2.10.23)
Алгоритм прямой интерполяции основан на использовании фильтра
Калмана для фильтрации Xi на каждом Z, использует наблюдения до
момента Z, затем реализует интерполяцию для I < j. Значения X,/3j,Yj)
ajR и R получаются с помощью фильтра Калмана при Aj = I в начале
работы алгоритма. Ковариационная матрица ошибки прямой интерпо-
ляции (2.10.23) не требуется для работы алгоритма.
Для дискретной с.к. оптимальной интерполяции с фиксированной
задержкой т применяются следующие рекуррентные уравнения:
-fy/+l+r - а1+тХц1+т + t/iti+Taf+TRi+T(+) (xZ|i+T - Xj+1|/+t) +
+Ai+i0i+i [li+i — i>j+iajXi+1|/(+) j , (2.10.24)
Az+1 = AlRl(+)a{R^1(-). (2.10.25)
320
ГЛ. 2. ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФИЛЬТРЫ КАЛМАНА
Алгоритм интерполяции с фиксированной задержкой оценивает состоя-
ние системы в момент l+т на основе наблюдений до момента I. Задерж-
ка —т равна разности интервалов времени между оценкой и наблюде-
ниями. Требуется запоминать промежуточные данные работы фильтра
Калмана для моментов i + т < г < L. Кроме то-
го, фильтр Калмана используется для оценки в момент I -I- т согласно
(2.10.24). Первые т шагов рассматриваемого интерполятора основаны
на использовании прямого интерполятора с фиксированной точкой в
начальный момент времени. На этом же этапе вычисляются А/.
2.11. Устойчивость, управляемость и наблюдаемость
стохастических систем и фильтры Калмана
2.11.1. Вспомогательные утверждения. Рассмотрим линей-
ную нормальную стохастическую дифференциальную систему (2.4.3)
на конечном отрезке времени:
X = aiX + ^Vlt Z = blX + V2 (tQ<t<tk). (2.11.1)
Здесь Vi и V2 - некоррелированные нормальные белые шумы с нулевы-
ми математическими ожиданиями и интенсивностями, заданными мат-
рицами i/i и 1/2- Следуя п.1.1.6, рассмотрим также сопряженную для
(2.11.1) систему:
X = -а^Х+ 1ртУг, Z = b{X + V2, (2.11.2)
где Vi и V2 - некоррелированные белые шумы с нулевыми математиче-
скими ожиданиями и интенсивностями Pi = i/f \ i>2 = i/^-1.
Обозначим через i?(t) и i?c(t) фундаментальные матрицы решений
уравнений х = а^х и х — —а^х. Согласно п.1.1.2 имеют место следую-
щие соотношения между $(£) и dc(t):
= I, (2.11.3)
0T(t) = [^(t)]"1, tfcT(t) = tf-1(*)> (2.11.4)
рЧгЦ’ПМГ1]7 = {[tfWr1}T[’?c(0]T =
= foWt)-1 =i(tk,t), (2.11.5)
#c(t) [t?c(t*)]-1 = [tr1(t)]TtfT(M = [i?(t*)i?-1(t)]T = $T(t*)t)-
(2.11.6)
2.11. УСТОЙЧИВОСТЬ, УПРАВЛЯЕМОСТЬ И НАБЛЮДАЕМОСТЬ 321
Согласно п.1.1.6 для того, чтобы система (2.11.2) была вполне на-
блюдаемой, необходимо и достаточно, чтобы была положительно опре-
делена матрица
wom*) = f" {ihorw1}7
(2.11.7)
которая с учетом (2.11.5) и (2.11.6) может быть записана в виде
fth
Wi(t0,**)= / Ф(^,^(^)^1М^(0ТфТ(^,^. (2.11.8)
Jta
Другими словами, систему (2.11.1) будем называть вполне управ-
ляемой, если сопряженная система (2.11.2) вполне наблюдаема.
Справедливо следующее утверждение (Калман 1963, Бьюси и Джо-
зеф 1968).
Теорема 2.11.1. Система (2.11.1) вполне управляема, если и
только если матрица Wi(to,^)> определяемая (2.11.7), является по-
ложительно определенной матрицей.
Введем еще две матрицы: Wi(t - a, t), определяемую согласно
(2.11.7) при to = t — а, и новую матрицу
и
W2(t-a,t)= / Фт(£,т)Ь^ (т)1/2\т)Ь1(т)Ф(т,$дг. (2.11.9)
J t—a
Согласно п.1.1.6 система (2.11.2) будет равномерно вполне наблю-
даемой, если существуют такие фиксированные положительные посто-
янные (7,01,02, что
О < oil < W2(t - a,t) < a2I V* > t0 4- a. (2.11.10)
Согласно п.1.1.6 система (2.11.1) будет равномерно вполне управля-
емой, если
О < oil < Wi(t-M) <о27 Vt>tQ + a. (2.11.11)
Прежде чем сформулировать условия устойчивости фильтров Кал-
мана-Бьюси, следуя (Ройтенберг 1992), приведем четыре вспомогатель-
ных утверждения, касающихся решения уравнения Риккати (2.4.7):
R = aiR + Raf-RbTv^iR + №1il>T, R(t0) = Ro- (2.11.12)
11 Фильтры Калмана и Пугачева
322
ГЛ. 2. ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФИЛЬТРЫ КАЛМАНА
Лемма 2.11.1. Решение R = jR^j-Ro^o) уравнения Риккати
(2.11.12) с начальным условием Rq > 0 для всех t > Iq удовлетворя-
ет условиям:
О < jRf^flo,^) < Ф(£, to)Ro$T(t, £о)+
+ [ Ф(г,т)^(т)1/1(т)^т(т)Фт(г,г)б/т = $(t,to)Ro$T(t,t0) + Wi(to,t),
Jto
(2.11.13)
где Ф(<, to) = i?(t)j?-1(t), i?(t) - фундаментальная матрица уравнения
х — а^х.
Лемма 2.11.2. Если Rq - положительно определенная матрица
(Rq > 0), то решение уравнения Риккати (2.11.12) Я(£;/?о,£о) для1 > to
будет положительно определенной матрицей. Если же Rq неотри-
цательно определенная матрица (Rq > 0), но система (2.11.1) рав-
номерно вполне управляема, то решение уравнения Риккати (2.11.12)
R(t;RQ,t0) будет положительно определенной матрицей для всех t >
> tQ + (У .
Лемма 2.11.3. Если система (2.11.1) равномерно вполне наблю-
даема и равномерно вполне управляема и если Rq - неотрицательно
определенная матрица, то матрица R(t',RQ,tQ) равномерно ограниче-
на для всех t > to + а и удовлетворяет условию
R(t\Ro,to) > W2_1(Z-a,Z)4-Wi(Z-a,Z) Vi > t0 + a. (2.11.14)
Лемма 2.11.4. Если система (2.11.1) равномерно вполне управля-
ема и равномерно вполне наблюдаема и если Rq - положительно опре-
деленная матрица, то матрица R(t-,RQ,t0) удовлетворяет условию.
[W1-1(t-a,t)4-W2(t-CT)t)]_1 <R(t;Ro,t0) Vt>t0 + a. (2.11.15)
2.11.2. Основные теоремы. Наоснове лемм 2.11.1-2.11.4 в (Кал-
ман и Бьюси 1961) доказаны следующие утверждения.
Теорема 2.11.2. Если система (2.11.1) равномерно вполне наблю-
даема и равномерно вполне управляема, то фильтр Калмана-Бьюси
^-=aiX + 0(Y -biX), $ = (2.11.16)
at
равномерно асимптотически устойчив, т.е. тривиальное решение
(2.11.16) при Y = 0 однородного дифференциального уравнения
^ = (а1-/3)Х (2.11.17)
at
2.11. УСТОЙЧИВОСТЬ, УПРАВЛЯЕМОСТЬ И НАБЛЮДАЕМОСТЬ
323
равномерно асимптотически устойчиво.
Теорема 2.11.3. Пусть система (2.11.1) равномерно вполне на-
блюдаема и равномерно вполне управляема. Тогда матрицы RW(t-
являются решением уравнения Риккати
(2.11.12) при начальных условиях (to) = R^ uR^(to) = R^ соот-
ветственно, где R^ и R^ - неотрицательно определенные матрицы,
удовлетворяющие условию
||R™ (t + а; Я*1’, t0) - R™ (t + ст; R™, to) || <
< cfe-2c2<7 ||/г(1)(«;^х)Ло) -7?(2)(t;^2),to)|| (2.11.18)
для всех t > to. Здесь ci и С2 - положительные постоянные величины,
входящие в следующее условие равномерной асимптотической устой-
чивости решения (2.11.17):
||Фс(*,г)т|| = ||ФС(* + а,С|| <Cie"C2a, (2.11.19)
Фс(£,т) — 19с(С^с(т)_1, 19(С - фундаментальная матрица решений
(2.11.17).
Теорема 2.11.4. Пусть система (2.11.1) равномерно вполне на-
блюдаема и равномерно вполне управляема. Тогда решение уравнения
Риккати (2.11.12), соответствующее начальному условию R(to) = О,
имеет при to ~> —сю предел
lim R(t;0,to) =R(t), (2.11.20)
to—>—oo
который существует для всех t .
Теорема 2.11.5. Пусть система (2.11.1) равномерно вполне на-
блюдаема и равномерно вполне управляема и пусть R ограничена свер-
ху и снизу
0 < —-------1 < R(t) < (2.11.21)
1 + 0102
Тогда последовательность решений уравнения Риккати (2.11.12)
|R+(t;Ro+n\oJ, где R^n^ < монотонно возрастая, равно-
мерно сходится к матрице R(t), определенной (2.11.20). Аналогично,
последовательность {R-(CRo~n\o}, где r!q^ > монотонно
убывая, равномерно сходится при t —> сю к матрице R(t), определенной
(2.11.20).
324
ГЛ. 2. ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФИЛЬТРЫ КАЛМАНА
Теорема 2.11.6. Пусть сстема (2.11.1) стационарна, т.е. а*,Ь*,
i/j* - постоянные матрицы, а матрицы v* и - постоянны и положи-
тельно определены. Предположим, что система (2.11.1) равномерно
вполне управляема и равномерно вполне наблюдаема, т.е. выполнены
следующие условия (п.1.1.6):
rank = rank j = n.
(2.11.22)
Тогда справедливы следующие два результата.
1) Решение R(t;O,to) уравнения Риккати (2.11.12) имеет при t0 ->
— оо предел
lim R(t-,0,to) = R*, (2.11.23)
to~+ — ОО
который существует при всех t, причем R* есть постоянная симме-
тичная положительно определенная матрица, являющаяся решением
алгебраического уравнения Риккати:
a]R* + R*d[T — — °- (2.11.24)
2) Каждое решение уравнения Риккати (2.11.12) R(1',Rq,Iq), удо-
влетворяющее начальному условию R(to) = Rq, где to -> — оо, a Rq
неотрицательно определенная матрица, стремится равномерно к R*
при t —> оо, т.е. матрица R* представляет собой единственное поло-
жительно определенное состояние, удовлетворяющее дифференциаль-
ному уравнению Риккати (2.11.12).
В условиях теоремы 2.11.6, если, следуя п.2.4.5, ввести обозначения
(2.4.15)
а* = ai, 6* = с* = фУгф'1',
то уравнения Риккати (2.11.12) и фильтра Калмана-Бьюси (2.11.16)
можно записать в виде
R = S(fi), 5(Я) = a*R 4- Ra*T - Rb*R 4- с*, (2.11.25)
X = (а* - Rb*)X 4- &*Y. (2.11.26)
Отсюда, согласно п.2.4.5, система векторных уравнений для уравнений
Риккати (2.11.25) имеет следующий вид:
SI — 'll si
ш ы
—а*Т
с*
ь*
а*
(2.11.27)
, н =
2.11. УСТОЙЧИВОСТЬ, УПРАВЛЯЕМОСТЬ И НАБЛЮДАЕМОСТЬ 325
где размерности векторов & и & равны п. В (Бьюси и Джозеф 1968)
доказано следующее утверждение.
Теорема 2.11.7. Симметричная положительно определенная
матрица R*, удовлетворяющая алгебраическому уравнению Риккати
S{R*) = О
(2.11.28)
(5(7?) - определена в (2.11.25)), находится из соотношения
[-7?’/] Д(7?) =0
(2.11.29)
или из эквивалентного соотношения:
I
R*
= 0.
(2.11.30)
Здесь - полином, аргументом которого является матрица Л.
Соответствующий скалярный полином Д(А) определяется из соотно-
шения
det(AZ - Н) = (—1)ПД(А)Д(-А),
(2.11.31)
причем Д(А) - полинолс степени п, а нули этого полинома имеют
отрицательные действительные части.
2.11.3. Линейные стохастические дифференциальные си-
стемы с автокоррелированными помехами в наблюдениях. Сле-
дуя (Бьюси и Джозеф 1968, Ройтенберг 1992), рассмотрим линейную
нормальную стохастическую дифференциальную систему вида
X=a1X + i{>Vll X(t0) = X0,
Z = bxX + U, U = C1U + V2, U(t0) = U0.
(2.11.32)
Здесь Vi и V2 - некоррелированные нормальные белые шумы размерно-
сти и и г2 с нулевыми математическими ожиданиями и интенсивностя-
ми i/i и v2; X,Z,U - векторы, имеющие размерности n, ni, г2; а\, , с\,
- матрицы размерности п х n,r2 х n,r2 х r2,n х п соответственно. На-
чальные условия Xq и Uq будем считать, во-первых, независимыми от
Vi, V2 и, во-вторых, нормально распределенными величинами с нулевы-
ми математическими ожиданиями и ковариационными матрицами Кх°,
Ки°.
Далее введем следующие обозначения:
ai = ai — 1bi, 'ф = 'ф, b\ = b\a\ — c\b\,
326 ГЛ. 2. ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФИЛЬТРЫ КАЛМАНА
Pi = Pi - i>2 = 2?,
Т> = Ьц/л^Ь? + и2, U = biKXobl + Ки°,
N = :FV -Uci-V, F = ax- Vbxax + Vcibi,
V = - bfcx) + i/>v1i/>Tb[] V-1, (2.11.33)
a E - представляет собой решение следующего уравнения Риккати:
Ё = ахЕ + Еа[ + VDVT + ^1г1>т, £(t0) = Ео = Кх° - KXob{QUQXbxOKXo.
(2.11.34)
Здесь и далее значения функций ai, bx, сх, vx, v2, U, V при t = to отме-
чены нуликом снизу. Наконец обозначим
X = X - VY, X(t0) = Хо = (K^bfoUo1 - Vo) *о,
Уо = Y(t0), Vo = V(t0) = [£o(«iobio “ ьГосю) + V’o^ioV’o&io] Do1-
(2.11.35)
Тогда уравнение фильтра Калмана-Бьюси для системы (2.11.32) при-
мет следующий вид:
X = (ax-Eb{'D~1bx)X + MY, X(t0) = Хо. (2.11.36)
Справедливо следующее утверждение.
Теорема 2.11.8. Фильтр Калмана-Бьюси для системы (2.11.32)
имеет вид классического уравнения фильтра Калмана-Бьюси с заме-
ной параметров задачи ai,i/>,bi,Vi,V2 на ai,ij>,bi,Pi,p2f определенные
(2.11.33), и описывается уравнениями (1.11.34)—(1.11.36).
Замечани е. Теоремы 2.11.1-2.11.7 немедленно распространяются и на слу-
чай автокоррелированной помехи в наблюдениях, описываемых уравнениями (2.11.32).
2.11.4. Дискретные линейные стохастические системы.
Аналогично случаю линейных стохастических дифференциальных си-
стем (пп.2.11.1-2.11.3) рассматриваются вопросы устойчивости, наблю-
даемости и управляемости дискретных линейных нормальных стоха-
стических систем (2.8.6) на конечном интервале времени
Yl = HlXl-^V2th X/+i 1 = /о, 1,2,..., lk. (2.11.37)
Здесь Xi и Yi - векторы состояния и наблюдения размерностей п и
ni; Viti и V23 - некоррелированные нормальные белые шумы размер-
ности гх и Г2, и + Г2 = г с нулевыми математическими ожиданиями
2.11. УСТОЙЧИВОСТЬ, УПРАВЛЯЕМОСТЬ И НАБЛЮДАЕМОСТЬ 327
и интенсивностями i/ij и 1/2,/; Ф/+13,^i,Hi - (п х п),(п х Г1)-матрицы.
Начальное условие X(Iq) = Хо будем считать, во-первых, независимы-
мой от Vij и V23, и, во-вторых, нормально распределенной случайной
величиной с математическим ожиданием Xq и ковариационной матри-
цы Кх°, Л/\Х0,Кх°). В таких предположениях уравнения фильтра
Калмана получены в п.2.8.4 и определяются теоремой 2.8.1.
Следуя п.1.1.6, для интервала 1,1 — h введем следующие матрицы:
1-1
Wi,l,l-h = 52 Фи+1^1.,^ГФ&+П
j=(—ft-i
I
= 52 (2.11.38)
j=l—h
Тогда система (2.11.37) будет называться равномерно вполне наблюдае-
мой, если существуют фиксированные постоянные а 1,02 и целое поло-
жительное число h, такие, что
О < ail < W2,i,i-h < а21 V/ > h. (2.11.39)
Система (2.11.37) называется равномерно вполне управляемой, если
О < ad < Wi,i,i-h < а21 V/ > h. (2.11.40)
В (Дейст и Прайс 1968) доказаны следующие утверждения.
Теорема 2.11.9. В условиях теоремы 2.8.1, если система
(2.11.37) равномерно вполне наблюдаема и равномерно вполне управляе-
ма, а Кх° - неотрицательно определенная матрица, то матрица Ящ
равномерно ограничена для всех I > 2h и удовлетворяет следующим
условиям:
< (Ий-*+ww-i>) < <2n-4i>
Теорема 2.11.10. В условиях теоремы 2.8.1 тривиальное решение
однородного разностного уравнения (2.8.7) при Yi = О,
Л|» = ^ф-1фМ-1Л-и-1 (2.11.42)
328
ГЛ. 2. ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФИЛЬТРЫ КАЛМАНА
равномерно асимптотически устойчиво .
Теорема 2.11.11. Пусть система (2.11.37), во-первых, удовле-
творяет условиям теоремы 2.8.1, и во-вторых, равномерно вполне на-
блюдаема и равномерно вполне управляема. Тогда решение уравнения
Риккати (2.8.11) Ri+i,i> соответствующее начальному условию
jR/o+i|/o = 0, имеет при Iq —> —оо предел
/0^оо [ЯжИН/о+И'о = °] = (2.11.43)
который существует VI.
Теорема 2.11.12. В условиях теорем 2.11.9 и 2.11.11 последова-
тельность J решений уравнения Риккати при начальных усло-
виях R<+S) < монотонно возрастая, равномерно сходится при
I -> оо и матрице jR/+i|z, определяемой (2.11.43). Аналогично, после-
довательность решений уравнения Риккати при начальных
условиях < Rqмонотонно убывая, равномерно сходится
при I —> оо и матрице Ri+i\i, которая определена (2.11.43).
Для стационарных систем (2.11.37), когда
ФИц/ = Ф*, = = = ЛИ1|,=Л*,
(2.11.44)
уравнение Риккати переходит в следующее алгебраическое уравнение
Риккати:
R* = Ф*Я*Ф*Т - Ф*Я*Я*Т(Я*Я*Я*Т + I/;)"1 + Я*Я*Ф*Т +
(2.11.45)
В этом случае имеет место следующая теорема (Пейн и Сильверман
1974).
Теорема 2.11.13. Пусть с* - матрица, удовлетворяющая соот-
ношению
ф'1^ф*Т = CJCJT. (2.11.46)
Если пара матриц (Ф*,Я*) наблюдаема, т.е.
rank [Н*Т,Ф*ТН*Т, , (Ф‘Т)П~1Я‘Т] =п, (2.11.47)
а пара матриц (Ф*,С*) управляема, т.е.
rank [с;, Ф’с; . Ф*<”-1)СТ ] = п, (2.П.48)
2.12. ОЦЕНИВАНИЕ И РАСПОЗНАВАНИЕ
329
то алгебраическое уравнение Риккати (2.11.45) имеет единственное
постоянное частное решение R*, где R* - постоянная симметриче-
ская положительно определенная (п х п)-матрица.
3 а М е Ч а Н И в. Для одномерной стационарной системы, когда — 1,
ДГ = 1. ф«+1|/ = ф* ', уравнение Риккати имеет вид
о , -Ф*2 Р2Дф-1 .
Стационарное решение R* этого уравнения приводит к квадратному уравнению
Я’2 + (i/2‘ - Ф’2р2‘ - 1^) R* - I'M = 0.
Так как Р* > 0, то уравнение имеет положительное постоянное решение.
2.12. Оценивание и распознавание в стохастических
системах. Адаптивные фильтры Калмана
2.12.1. Задачи оценивания и распознавания. Как известно,
во многих задачах распознавания наблюдаемой случайной величиной
является некоторая функция случайного процесса, определяемого сто-
хастическими дифференциальными или разностными уравнениями, за-
висящими от того, к какому из распознаваемых классов относится этот
случайный процесс. В этом случае задача тоже сводится к оцениванию
неизвестного параметра в стохастических уравнениях (2.1.5), (2.1.6) и
(2.1.7), (2.1.8). Предположим, что входящие в эти уравнения функции,
зависят от неизвестного параметра 0, который может принимать одно
значение из конечного множества значений 01, ... , 0?v, соответствую-
щих распознаваемым классам Ai , ... , А^. Тогда задача распознава-
ния сведется к решению вопроса о том, какое из значений 01, ... , 0дг
имеет параметр 0 для данного наблюдаемого сигнала. Но значение па-
раметра 0, выдаваемое системой распознавания, можно рассматривать
как оценку параметра 0. Для решения задачи распознавания можно
применить прием расширения вектора состояния системы, включив па-
раметр 0 = 0 (0 = 0) в вектор состояния X. Единственное отличие
состоит в том, что в задаче оценки неизвестных параметров (п.2.1.2)
параметр 0 неизвестен и априори может принимать любые значения,
а в задаче распознавания 0 может принимать лишь одно из конечного
множества заранее известных значений 01, ... , 0уу. В частном случае
когда 0 может принимать лишь два значения и одному из них соответ-
ствует X = 0, задача распознавания представляет собой задачу обна-
ружения сигнала, определяемого стохастическим уравнением.
330
ГЛ. 2. ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФИЛЬТРЫ КАЛМАНА
2.12.2. Стохастические дифференциалы апостериорных
вероятностей в задаче распознавания. Решение о том, к како-
му из N классов Ai, ..., An относится наблюдаемый сигнал, обычно
принимается по максимуму апостериорной вероятности: за значение
параметра в принимается то из значений , ... , 0#, которое имеет
наибольшую апостериорную вероятность. Иными словами, модель рас-
познавания принимает 0 = 0^, если апостериорная вероятность 0^ боль-
ше (или по крайней мере не меньше) апостериорных вероятностей всех
остальных значений , ... , 0/i-i,0/i-i, ... , On параметра в. Поэтому
модель распознавания должна вычислять апостериорные вероятности
всех классов (всех значений , ... , On параметра в).
В случае распознавания процессов, определяемых стохастически-
ми дифференциальными уравнениями, можно пользоваться формула-
ми для стохастических дифференциалов апостериорных вероятностей
классов, которые можно вывести из общего уравнения для апостериор-
ной характеристической функции вектора состояния системы (п.2.2.5).
о Чтобы вывести эти формулы, напишем уравнение (2.2.13) для
расширеного вектора состояния [ХТ0Т]Т. Предположим, что от 0 за-
висят функции </>, в уравнениях (2.2.3). Напомним, что все уравне-
ния теории оптимальной фильтрации справедливы только при условии,
что грх в (2.2.3) не зависит от X, а следовательно, и от 0. Тогда учи-
тывая, что d0 = 0 получим
dpt(A,/x) = M <iXT<p(Y,X,Q,t)-
,iXT
-^XT(^T)(Y,X,Q,t)}eixTx+^Te | У/о dt+
+m {<fil(Y,x,e,t)T -tf+
+»Лт(^Г)(Г,Х,е,О}е<АТх+'мТ0 I r/0 - y-'dt).
(2.12.1)
Положив здесь A = 0, найдем стохастический дифференциал апостери-
орной характеристической функции pj(/i) вектора 0,pj(/i) =
= М [е<дТе | У/о ] =Л(0,м):
2.12. ОЦЕНИВАНИЕ И РАСПОЗНАВАНИЕ
331
dg'M = М [ (У, X, 0, t)T - tf} Xе | У/о ] х
x^iV^)-l(Y,t}(dY - <ркЙ). (2.12.2)
Но 0 - дискретная случайная величина с возможными значениями
6\, ... , 0^. Поэтому, обозначив апостериорные вероятности этих зна-
чений соответственно через Qi(t), ... , Qn(£),
qk(t) = P(Q = 6k | У/о) (k = l,...,N), (2.12.3)
будем иметь следующие равенства:
N
Ш = ^к^Тв”, (2.12.4)
к=1
м[^(У,Х,0,4)ге^е|У/о] =
N
= [^(У,Х,^,0Т I Г/о ] , (2.12.5)
к=1
N
VI = Y,4k(t)M [<p1(Y,X,0k,t)T I У/о]. (2.12.6)
к=1
Подставив выражения (2.12.3)-(2.12.6) в (2.12.2) и положив для крат-
кости
£1Л = М[^1(У,ХА,0|К/о] (h = l,...,N), (2.12.7)
придем к равенству
N z N
^e^'dqyt) = 5>(t)^T9‘-
k=l ^=1
—5Z 5Z l(V’i*zv,F)-1 (dY - 52^(0^^) •
k=l h=l \ h=l /
(2.12.8)
332
ГЛ. 2. ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФИЛЬТРЫ КАЛМАНА
Сравнив коэффициенты при одинаковых показательных функциях в
левой и правой частях этого равенства, получим
(N \ / N
^Tk - 52 I 1- 52 ^^Thdt
h=l / \ h=l
(2.12.9)
(fc = l,...,7V). <
Эти формулы нельзя рассматривать как стохастические дифферен-
циальные уравнения для апостериорных вероятностей (Zi (£), ... , <7w(t),
так как величины
£х* = М[^(У,ХА,0|17о] (k = l,...,N) (2.12.10)
зависят от распределений процесса X при 0 = . , On. Лишь после
решения уравнения (2.2.13) относительно апостериорных характеристи-
ческих функций или уравнения (2.2.15) относительно апостериорных
плотностей процесса X при 0 = , ... , 0N и вычисления величин фи
как функций Y и t равенства (2.12.9) становятся уравнениями, опреде-
ляющими (71 (2), ... ,
Таким образом, задача оптимального распознавания решается
лишь после решения уравнений (2.2.13) или (2.2.15) при соответствую-
щих условиях. При этом уравнения (2.2.15) определяют апостериорные
вероятности классов qi (t), ... , qN(t) при всех t > to, если за их началь-
ные значения при t = to взять соответствующие условные вероятности
классов относительно величины Yq.
Ясно, что задачу оптимального распознавания можно решать с од-
новременным оцениванием вектора состояния системы X. При этом
оптимальная оценка X в соответствии с (2.2.1) определяется формулой
N
X = Y/qk(t)Xk, (2.12.11)
к=1
где Хк ~ условная оптимальная оценка вектора X в предположении,
что 0 = вк (к = 1, ... , N). При этом в вектор X могут входить и
неизвестные параметры, от которых могут зависеть функции <£, ф и <pi
в уравнениях (2.2.3).
Таким образом, имеем следующий результат.
Теорема 2.12.1. Если выполнены условия теоремы 2.2.1, то зада-
чу оптимального распознавания можно решать с одновременным оце-
ниванием вектора состояния системы и всех неизвестных парамет-
ров, входящих в уравнения стохастических дифференциальных систем
2.12. ОЦЕНИВАНИЕ И РАСПОЗНАВАНИЕ
333
(2.2.3) на основе уравнений (2.2.13) или (2.2.15), (2.12.9), (2.12.11) при
соответствующих начальных условиях.
Замечание. Аналогичное предложение устанавливается и для дискретных
стохастических систем (см. раздел 2.13).
2.12.3. Оптимальное распознавание в линейных системах.
Точное решение задачи оптимального распознавания легко получается
для линейных уравнений (2.2.3), а также в более общем случае, когда
уравнения (2.2.3) линейны только отностельно X,
о В случае линейных уранений (2.2.3) сигналы Y и X определя-
ются для различных классов сигналов, т.е. для значений 01, ... ,
параметра в, уравнениями
dY [ b(0k, t)Y + (Ok,t)X + bQ(0k,t) ]dt +fa (t)dW,
dX = [a(0k,t)Y + a1(0k,t)X + a0(Oklt)]dtfaOk,t)dW (fc = 1, ... , N).
(2.12.12)
В этом случае
fak = b(0k,t)Y + b, (6к^Хк + bQ(0k, t) (k = 1, ... , N),
где Xi, ... , Хм - условные оптимальные оценки вектора состояния X
при О = , ... , вк, определяемые уравнениями типа (2.3.4):
dXk = [a(0fc,£)y + ai(0к, t)Xk + о>о(0к, t) j dt+
+Pk{dY- [&(МтММЫМ]<й) (2.12.13)
(fc = 1, ... , N),
где в соответствии с результатами п.2.3.1
Рк = [Rkbi(0k,t)T + ('фуф[У'1 (9к,0] W’iW’?’)-1 (к = 1,... , N),
(2.12.14)
Rk = а(вк, t)Rk + Rka(0k,t)T + (^^Т)(^, 0 ~ (0*, <)Т+
[biftk^Rk + ^iwpT)(0k,t)] (2.12.15)
(к = 1, ... , N).
Уравнения (2.12.9) для апостериорных вероятностей классов при этом
принимают вид
334
ГЛ. 2. ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФИЛЬТРЫ КАЛМАНА
dqk(t) = { YTb(0k,t)T + Xkbi(0k,t)T + b0(Ok,t)T-
N x
- W [ YTb(0k, t)T + fl bi (0*, t)T + bo (ek, t)T ] 1X
h=l '
x (dY
N
- [ b(6k W + bi (Ok, t)Xk + bo(0k, t) ]
h=l
dt ►
(2.12.16)
(k = 1, ... , N).
Уравнения (2.12.13) и (2.12.16) представляют собой замкнутую си-
стему уравнений, определяющую Х\, ... , Xn, Qi(t), ... , Q/v(£) при со-
ответствующих начальных условиях. Оптимальная оценка вектора со-
стояния X определяется после этого формулой
N
X = ^qk(t)Xk. <
fc=l
(2.12.17)
Таким образом, имеем следующий результат.
Теорема 2.12.2. Если выполнены условия теоремы 2.12.1, то
уравнения (2.12.13) и (2.12.16) полностью и точно решают задачу оп-
тимального распознавания для линейных систем.
П р и м е р 2.12.1. Найти оптимальную систему обнаружения несущего информа-
цию сигнала X, определяемого линейным уравнением X = 0>1Х 4- O,q 4- "фУ в случае
приема сигнала Z — Ь\Х 4“ 6g 4" ^61V, где V - белый шум интенсивности I/. В этом
случае параметр 0 имеет два возможных значения 0i — 1 (сигнал X присутствует в
принимаемом сигнале) и 02 = 0 (принимается один шум). Уравнение, определяющее
сигнал X, запишется в виде
X = 0(агХ 4- а0) 4- 0фхУ. (I)
Уравнения (2.12.13), определяющие условные оптимальные оценки сигнала X при гипо-
тезах 0 — 1 и 0 — 0, имеют вид
Л = aiXi 4- а0 + - biXi - Ьо), (П)
^2 =02(Z-blX2-bo). (Ill)
2.12. ОЦЕНИВАНИЕ И РАСПОЗНАВАНИЕ
335
Апостериорная вероятность (ft присутствия сигнала X в силу (2.12.16) определяется
уравнением (напомним, что Q1 Ч" <?2 = 1 ПРИ всех t)
<71 = (Xf-X2T)bfg1(l-g1)(V>ii/V’i’)"1 [z - 9151 (Х1 - X2) - &1Л - b0] •
(IV)
Оптимальная система обнаружения в данном случае представляет собой последователь-
ное соединение двух параллельно соединенных фильтров Калмана-Бьюси, вырабатываю-
щих соответствующие условные оценки Xi и Х% сигнала X, устройства, интегрирующе-
го дифференциальное уравнение, определяющее апостериорную вероятность Qi сигнала
X, и порогового устройства, выдающего сигнал тревоги (сигнал о присутствии X) в
случае, когда Qi становится больше 1/2.
2.12.4. Оптимальное распознавание в случае уравнений,
линейных относительно вектора состояния. Задача оптимального
распознавания легко решается также в более общем случае системы,
линейной только относительно вектора состояния X (п.2.3.3).
о В этом случае Y и X для различных классов сигналов определя-
ются уравнениями вида (2.3.13):
dY = [ 61 (У, 6к ,t)X + bo (У, 0к, t) ] dt + (V, f)dW,
dX = [ai{Y,ek,t)X^ao{Y,ek,t}]dt^^Y,6k^)dW (2.12.18)
m = + (fc = l,...,^), (2.12.19)
где оптимальные оценки Xi, ... , Хц вектора X при 0 = 0i, ... , 0jv,
определяются уравнениями (2.3.13) и (2.3.14):
dXk = [ ai (У, вк, t)Xk 4- а>о (Y, 0к, t) ] dt-Ь
+ [Rb1(Y,0k,t)T +
x {dV - [b1(y,0fc,t)TXt +M1S0M)] dt} , (2.12.20)
Rk = ai(Y,ek,t)Rk + Rkai (Y, 0k,t)T + (№T)(Y,0k,t)-
- [ял (y, ek,t)T + ek, t)] x
х^и^ГГ1^,*) [bAY,Ok,t)Rk + (MT)(Y,ek,t)] (2.12.21)
(fc = 1, ... , N).
336
ГЛ. 2. ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФИЛЬТРЫ КАЛМАНА
Уравнения (2.12.9) для апостериорных вероятностей классов при этом
принимают вид
dqk = J Xlbi(Y, 6к, t)T + bo(Y, 0к, t)T-
n 1
-£gfc(i) [ед(У,^,4)т + bo(Y,0h,t)T] lx
h=l '
N
dY [ bl (Y, 0h, t)Xh + Ьо(Г, M ] dt
h=l
(2.12.22)
(k = 1, ... , N). <
Итак, имеем следующее утверждение
Теорема 2Л2.3. Если выполнены условия теоремы 2.3.2, то урав-
нения (2.12.20)-(2.12.22) представляют собой замкнутую систему
уравнений, определяющую Хг,. .. , Х^, qi(t) , ... , qN(t), Ri , . .. , Rn .
Они полностью и точно решают задачу оптимального распознава-
ния в рассматриваемом случае. После решения уравнений (2.12.20)-
(2.12.22) оптимальная оценка вектора состояния системы или рас-
ширенного вектора состояния X, включающего все неизвестные пара-
метры, линейно входящие в уравнения (2.2.3) наряду с вектором X,
находится по формуле (2.12.17).
2.12.5. Адаптивное дискретное оценивание. Адаптивные
фильтры Калмана—Лайниотиса. Теория адаптивной фильтрации
процессов, восходящая к работам Лайниотиса (Лайниотис 1971а, 19716,
1973, 1975), к настоящему времени получила широкое развитие и при-
менение (см.библиографию к разделу 2.12). Конструктивный характер
и простота реализации обусловили популярность точных адаптивных
фильтров Калмана-Лайниотиса в линейных непрерывных и дискрет-
ных системах с неизвестными параметрами. Однако для нелинейных
непрерывных и дискретных систем точное построение оптимального ко-
нечномерного адаптивного фильтра невозможно вследствие известных
в теории нелинейной фильтрации трудностей, связанных с определени-
ем фильтрационной плотности.
Рассмотрим нелинейную дискретную стохастическую систему вида
(2.8.1) с различными шумами Vij и V2,/:
Yi =cvi/(Xz,0,V2,/), / = 0,1,2, ... ,
Х/+1 =tv/(X/,0,Vi>/), / = 0,1,2, ... ,
(2.12.23)
(2.12.24)
2.12. ОЦЕНИВАНИЕ И РАСПОЗНАВАНИЕ
337
где I - дискретный момент времени; Xi € Rn - вектор состояния си-
стемы; Yi 6 Rni - вектор наблюдения; 0 € Rh - вектор неизвестных
постоянных параметров системы; Vij 6 Rri и 14,/ 6 Rr* — случай-
ные шумы в системе и канале наблюдения соответственно; и о?/ —
известные нелинейные векторные функции отмеченных аргументов.
Предполагается также, что шумы Vij и V^i — взаимно независи-
мые случайные векторы с известными плотностями вероятностей р1 (vn)
и p2(v2/) соответственно, начальное значение Xq не зависит от { Vi,/} и
{V2,/}, а условная плотность p(xq | уо) может быть вычислена на осно-
вании априорной информации об уравнениях (2.12.23) и (2.12.24).
Требуется по результатам текущих наблюдений
У'= {Уо,У1, (2.12.25)
получить с.к. оптимальную оценку фильтрации Х[ вектора состояния
Xi в условиях статистической неопределенности относительно действи-
тельного значения вектора параметров 0 в системе и канале наблюде-
ния.
Модель системы (2.12.23) и (2.12.24) определена с точностью до
неизвестного вектора параметоров 0, который может быть как непре-
рывным, так и дискретным. Согласно бейесовому подходу, используе-
мому в теории адаптивной фильтрации, будем рассматривать параметр
0 как случайный вектор с известной априорной плотностью распреде-
ления р(0). Далее, всюду будем предполагать, что параметр 0 - дис-
кретный, принимающий конечное множество значений 0 = 0\, ... , с
вероятностями р(0\), , p(&n) соответственно. Полученные в работе
результаты могут быть легко обобщены на случай, когда параметр 0 -
непрерывный (см. раздел 2.13).
Известно (Лайниотис и Парк 1976), что оптимальная среднеквад-
ратическая оценка Xi = M(Aj | Y1) вектора состояния Xi, ее ковари-
ационная матрица Ri = М - Xi)(Xi — Xk)T | У*] и условные веро-
ятности
Р& I У'),..., p(eN I У')
определяются следующими рекуррентными уравнениями:
N
Xt = Y/Xi(0i)p(Oi\Y‘), (2.12.26)
i=l
N ( ТЛ
Ri = '£i\Ri(<М + [X,(Oi) - Xt ] [Xt(Oi) - Xt ] [ p(6i I У'), (2.12.27)
i=l '
338
ГЛ. 2. ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФИЛЬТРЫ КАЛМАНА
р(0< I У'+1) = -----P(y,+1 । Г'Л)-----р(0< | У'), (2.12.28)
ЕЙ+i | | У')
J=1
р(0; |У°)=р(0<) (г = 1, , 2V). (2.12.29)
Здесь через
Xi(6i) = M(X, I Yl,0i),
Ri(0i) = M [(Л(0<) - XMXtWi) - Xi)T I r',^]
обозначены с.к. оценка вектора состояния и ее ковариационная мат-
рица при фиксированном значении 0 = 0^, ap(t/j+i | Yl,6i) - условная
плотность. Величины Х/(0{), Ri(6i) и p(t//+i | определяются из
решения задачи дискретной фильтрации (2.12.23) и (2.12.24) при каж-
дом фиксированном значении параметра 0 = (г = 1, ... , N).
В случае линейных уравнений (2.12.23), (2.12.24), нормально рас-
пределенных шумов {Vi,/}, {Уг,/} и начального вектора [ вели-
чины Х/(0<), Я/(0г), p(v/+i | Xi и Ri в (2.12.26)- (2.12.29) опреде-
ляются известной замкнутой системой уранений адаптивного фильтра
Калмана-Лайниотиса (раздел 2.13).
В нелинейном случае (2.12.23) и (2.12.24) при произвольных не-
линейных функциях и шц не удается получить замкнутую систему
рекуррентных уравнений относительно X/(0f), Ri(6i) и p(^+i I Yl,0i)
в (2.12.26)-(2.12.29). Основная трудность определения этих величин
Х/(0г),Я/(0г) и p(v/+i I Yl,0{) связана с нахождением фильтрационной
плотности p(xi | yz,0i), эффективное определение которой возможно
для систем с аддитивными шумами {Vi,/}, {V2,/}• Такие системы будут
рассматриваться в дальнейшем в главах 3 и 4.
2.13. Дополнения и задачи
2.13.1. Вывести уравнения (2.2.6) для стохастических дифференциальных уравне-
ний п.1.1.4: а) линейных; б) линейных с параметрическими шумами; в) билинейных.
2.13.2. Вывести уравнения для апостериорных одномерных плотности и характери-
стической функции для линейных, линейных с параметрическими шумами и билинейных
стохастических дифференциальных систем п.1.1.4.
2.13.3. Вывести уравнения для апостериорных моментов первого и второго поряд-
ков для линейных, линейных с параметрическими шумами и билинейных стохастических
систем п.1.1.4.
2.13. ДОПОЛНЕНИЯ И ЗАДАЧИ
339
2.13.4. Вывести уравнения для апостериорных одномерных плотности и характери-
стической функции для уравнений систем (2.3.1) и (2.3.12).
2.13.5. Вывести фильтрационные уравнения в случае винеровских и пуассоновских
шумов для системы (2.3.1).
2.13.6. Выписать уравнения фильтра Калмана при наличии аддитивных компонент
a0(t) И Ьо(£) в первом и втором уравнениях (2.4.3).
2.13.7. Дать обобщение метода Гулько-Новосельцевой (п.2.5.1) на случай профиль-
трованных винеровских и пуассоновских шумов.
2.13.8. Рассмотреть обобщение метода Брайсона и Йохансена (п.2.5.2) на случай
профильтрованных винеровских и пуассоновских шумов.
2.13.9. Вывести уравнения с.к. оптимального экстраполятора для системы (2.3.1).
2.13.10. Выписать уравнения с.к. оптимальных прямого и обратного интерполято-
ров для системы (2.3.1).
2.13.11. Пусть задана нелинейная дискретная стохастическая система
У/ = У’п(Х0 + У2,/,
Xl+1 и
Здесь Vij и V2 I ~ взаимно независимые случайные векторы размерностей Г1 и Г2 с
известными одномерными плотностями. Будем считать, что случайные шумы не зависят
также от начального состояния -Vo, задаваемого условной плотностью
f(xo | Уо}. Функции и Ipi предполагаются непрерывными и достаточное число
раз непрерывно-дифференцируемыми (по V/). Считая известными результаты наблю-
дения YJ = {У<(т), г = 0,1,2, ... ,вывести уравнения для фильтрационной
плотности /(®i I г/о) <Аоки 1971)-
Согласно формуле Байеса имеем для фильтрационной плотности
// I ,J+1\ _____ f (^+1 >У1+1 I Ув) /тт\
где f(yi+i I Vo) - условная плотность. Далее можно написать для f(xi, Я/4-l, У1+1 |
Уо):
f(xi,xi+i,yi+i I у£) = f(xi I yo)f(xi+1 I Xi)f(yi+1 I Xl+1). (Ill)
Интегрируя уравнение (III) no Xi, получим
f(xl+i,yi+i I Уо) = У f(xi I Уо)/(х1+1 I xi)f(yi+i I xi+i)dxt. (IV)
я»
340
ГЛ. 2. ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФИЛЬТРЫ КАЛМАНА
Из уравнений (П) и (IV) получим искомую рекуррентную формулу для f (х, | J/q (l =
= 0, 1 , .. . ,
f f(xi I yl0)f(xi+1 I Xi)f(yi+1 I xt+i)dxi
f(xl+l | !/o+ ) = г f[ i IX f/ j \~ff i \7j j \> (V)
J f(xi I ylo)f(xi+i I xt)f(yi+i I xi+i)(dxi,dxt+i)
Rn
где (dxi, dxi+i) = dxo ... dxidxo ... dxi+i.
2.13.12. Показать, что если в условиях задачи 2.13.11 отказаться от условия неза-
висимости шумов Vlj и 1^,2» то вместо плотностей f(xi+i | Xi) и f {уl-^-l | ^Z-f-l)
придется вычислять плотности /(^+1 I X1) и f(yi+i I Ii+1). В этом случае имеем
следующие соотношения (Аоки 1971):
/(®о+1>Уо+1) = /(^+1,4>У«+1,!/о) =
= f(ylo)f(xo I y‘o)f(xi+i I хо,Уо)Л(У1+1 I хо,Уо) (0
f(xl+1 v‘+1} - ^^хо+1’Уо+1^ -
Л° ’У0 )- f(y‘o+1) ~
_ f(xb I y‘o)f(xi+i I хо,Уо)ЛУ1+1 I Др+1.Уо) _
f(yi+i I Уо)
= f&o I !/o)/(s<+i I хо,Уо)ЛУ1+1 I ^о+1,Уо) zjp
f f(xb I ylo)f(xi+i I Xo,ylo)f(yi+1 I xo’1,ylo)dxo'1
Rn
2.13.13. В условиях задачи 2.13.11 и 2.13.12 выписать выражения для одномерных
фильтрационных и условных характеристических функций.
2.13.14. Вывести уравнения метода Гулько-Новосельцевой (п.2.5.1) для линейных
дискретных фильтров (раздел 2.9), экстраполяторов и интерполяторов (раздел 2.10).
2.13.15. Получить уравнения метода Брайсона и Йохансена (п.2.5.2) для линейных
дискретных фильтров (раздел 2.9), экстраполяторов и интерполяторов (раздел 2.10).
2.13.16. Показать, что оптимальный линейный фильтр для сигнала Х\ == Аес*
(А - случайный коэффициент), наблюдаемого с аддитивным нормально распределенным
белым шумом V интенсивности У, Y — Z — Х\ + V, определяется уравнением
= сХ\ + (Z — X\)R/v,
где R находится из уравнения R = 2с7?. Написать уравнение оптимального линейного
фильтра для векторного случайного коэффициента А.
2.13. ДОПОЛНЕНИЯ И ЗАДАЧИ
341
2.13.17. Показать, что оптимальный линейный фильтр для сигнала X = Xq 4“ At
(Xq, А - случайные величины), наблюдаемого с аддитивным нормально распределенным
белым шумом V интенсивности I/, Y = Z = X + V, определяется уравнением
к = X + (Z - X)R/v,
где R находится из уравнения R = —R?lv. Написать уравнение оптимального линей-
ного фильтра для векторных Xq и А.
2.13.18. Написать уравнение оптимального линейного фильтра для сигнала X =
N
= У2 Aptp, наблюдаемого с аддитивным нормально распределенным белым шумом.
р=1
Рассмотреть случай векторных случайных коэффициентов Ар.
2.13.19. Написать уравнения оптимального линейного фильтра для сигнала X в
линейных системах задач 1.9.1-1.9.9, наблюдаемого с аддитивным нормально распреде-
ленным белым шумом. Входной сигнал считать постоянным.
2.13.20. Пользуясь уравнениями примеров 2.4.1 и 2.4.2, написать уравнения линей-
ного оптимального фильтра для выделения сигнала Xi = Xq -t~At (Хо» А - случайные
величины) и стационарной случайной функции с ковариационной функцией
А;(т) = De а ( coscjo't +
из аддитивной смеси его с помехой с ковариационной функцией к\ (т) в случаях:
а) A?i(r) = iaJ(t); б) A?i(r) = D\e~ai в) к\(т) — D\e~ai coster.
2.13.21. Построить оптимальный фильтр для выделения полезного сигнала, пред-
ставляющего собой сумму синусоиды данной частоты CJq со случайными амплитудой и
фазой и стационарной случайной функции с ковариационной функцией к(т), из адди-
тивной его смеси с помехой с ковариационной функцией к\ (т) в случаях, когда функ-
ции &(т) и (т) представляют собой линейную комбинацию типовых ковариационных
функций (ТСтС, п.5.1.3).
2.13.22. Общая задача фильтрации скалярного сигнала известной формы в слу-
чае, когда помеха - белый шум. Следуя (Пугачев 1957, 1960, 1962), предположим, что
требуется выделить из входного сигнала X (t) полезный сигнал S(t) известной формы,
которая определяется некоторой функцией ^(t), но неизвестной амплитуды при адди-
тивной помехе типа белого шума. В этом случае входной сигнал системы определяется
формулой
X(t) = S(t) + AT(i) = u<p(t) + JV(t), (I)
где U - неизвестная амплитуда полезного сигнала - случайная величина с начальным
моментом второго порядка уи, a 7V(£) - помеха.
342
ГЛ. 2. ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФИЛЬТРЫ КАЛМАНА
Для получения минимума средней квадратической ошибки необходимо преобра-
зовать входной сигнал таким образом, чтобы получить максимальное отношение сиг-
нал/шум. Очевидно, что для этого следует умножить входной сигнал на известную функ-
цию полезного сигнала - функцию </>(£) и интегрировать полученное произведение. При
этом полезная часть сигнала будет как бы накапливаться за счет интегрирования суще-
ственно положительной функции, и за счет этого отношение сигнал/шум будет увеличи-
ваться.
Обозначим через to момент начала работы системы; t - текущий момент времени,
в который рассматривается выходной сигнал системы; Т - текущее время в интервале
(^О, t). Тогда, умножив входной сигнал системы %(т) на функцию (£>(т) и проинтегри-
ровав в пределах от to до t, получим
t t
Z(t) = U j <p2(T)dT + У ^(т)ЛГ(т)(/т. (II)
to to
Полагая для краткости
t t
b(t) = I<p2(r)dr, Zm(t) = J<p(r)N(f)dr, (III)
to to
приведем полученную формулу к виду
t
Z(t) = I lp(r)X(r)dr = Ub(t) + ZUI(t). (IV)
to
Докажем, что преобразование входного сигнала, определяемое формулой (IV), обес-
печивает максимальное отношение сигнал/шум по сравнению с любой другой линейной
системой при любом возможном значении U случайной величины U. Если заменить ве-
личину U ее возможным значением It, то полезная часть сигнала будет равна
s(t) = ub(t).
Дисперсия шумовой части сигнала (IV) на основании второй формулы (III) и из-
вестной формулы для дисперсии интеграла от белого шума определяется соотношением
t
Рш(0 = D [ Zm(t) ] = и I <p2(j)dr = vb(t), (V)
to
2.13. ДОПОЛНЕНИЯ И ЗАДАЧИ
343
где У - интенсивность белого шума 7V(t). Отношение сигнал/шум на выходе фильтра,
осуществляющего преобразование (IV) входного сигнала X(t), обычно принимают рав-
ным отношению абсолютной величины реализации полезной части сигнала (IV) к средне-
му квадратическому отклонению шумовой части этого сигнала. На основании предыду-
щих результатов это отношение определяется формулой
7 =
|s(t)l = М = |ц| дт-
л/О) 1'
(VI)
Рассмотрим теперь фильтр, который выполняет те же операции, но умножает вход-
ной сигнал Х(т} не на функцию (£>(т), а на другую функцию ^(т). Полезная часть
выходного сигнала такого фильтра и дисперсия шумовой части определяются формулами
t
S\(t) = и j il>(r)ip(T)dr,
to
(VII)
(VIII)
to
На основании неравенства Буняковского-Шварца
t
2 t
t
(IX)
to
to
to
имеем
l51(t)l < l«l
(X)
to
Из (IX) и (X) получаем следующую оценку отношения сигнал/шум на выходе рас-
сматриваемого фильтра:
1*1 «)|
у/ ^ш 1 (О
1^1(01
I t
у f ^2(т)(/т
to
(xi).
Сравнив правую часть этого неравенства с выражением (VI), видим, что < 'у.
Таким образом, отношение сигнал/шум на выходе любого линейного фильтра не может
превзойти такое же отношение на выходе фильтра, осуществляющего преобразование
344
ГЛ. 2. ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФИЛЬТРЫ КАЛМАНА
(IV). Фильтр, осуществляющий это преобразование, обычно называют согласованным
фильтром. Согласованный фильтр преобразует выходной сигнал таким образом, что в
результате на выходе получается наибольшее возможное отношение сигнал/шум.
Сравнивая выражение (IV) для выходного сигнала согласованного фильтра с вы-
ражением (I) входного сигнала системы, видим, что для воспроизведения полезного сиг-
нала S(t) = U<p(t) без систематической ошибки следует умножить выходной сигнал
согласованного фильтра на Иными словами, следует подключить к выходу
согласованного фильтра усилитель с переменным коэффициентом усиления </?(t)/6(t).
Выходной сигнал на выходе такой системы
у(0 = (хп)
Ошибка системы
У(<) = У(<) - YTp(t) = Y(t) - U<p(t) =
Имея в виду, что математическое ожидание белого шума, а следовательно, и ма-
тематическое ожидание случайной функции Zui(t) равно нулю, а также принимая во
внимание формулу (V), определим средний квадрат ошибки найденной оптимальной си-
стемы:
п* = м [у2(0] = ^Р[ИШ(«)] = (XIII)
Найденная система обеспечивает минимум дисперсии ошибки при нулевой систе-
матической ошибке, или, что то же самое, условный минимум средней квадратической
ошибки при нулевой систематической ошибке.
Если взять меньший коэффициент усиления выходного сигнала согласованного
фильтра, то появится систематическая ошибка, а дисперсия шума на выходе уменьшится.
Естественно ожидать, что при этом можно получить некоторое уменьшение суммарной
средней квадратической ошибки. Это вполне согласуется с известным положением, что
абсолютный минимум не может быть больше условного минимума. Обозначим неизвест-
ный коэффициент усиления выходного сигнала согласованного фильтра А и найдем такое
значение А, при котором средний квадрат ошибки системы имеет минимальное возмож-
ное значение. Ясно, что коэффициент А зависит от времени t. Однако, имея в виду,
что момент t является фиксированным, не будем указывать эту зависимость. Умножив
выходной сигнал согласованного фильтра (IV) на А, найдем выходной сигнал системы:
У(0 = XZ(t) = XUb(t) + AZm (t). (XIV)
Вычитая из этого выражения требуемый выходной сигнал У-(£) — Uнайдем
ошибку системы:
У (О = и [ А&(0 - <p(t) ] + AZm(t).
2.13. ДОПОЛНЕНИЯ И ЗАДАЧИ
345
Отсюда, принимая во внимание формулу (V) для дисперсии ошибки шума на выхо-
де согласованного фильтра, получаем следующее выражение среднего квадрата ошибки
системы:
т? = М [У2(О] = 7u [A6(t) - y(t)]2 + A2p6(t). (XV)
Дифференцируя эту формулу по А и приравнивая результат нулю, получаем урав-
нение для определения А:
= 27u [ Xb(t) - <p(t) ] b(t) + 2Ai/b(t) = 0.
ил
Отсюда находим
7ufe(t) + v'
(XVI)
Подставив найденное выражение А в формулу (XV), находим минимальный средний
квадрат ошибки оптимальной системы:
7цр<р2(0
7ub(t) + и
= i/A(t)y>(t),
(XVII)
где показана явно зависимость А от времени t. Сравнивая эту формулу с (XIII), видим,
что найденная оптимальная система дает средний квадрат ошибки в
7uft(t) + V V
+ 7иЬ(0
(XVIII)
раз меньший, чем система, обеспечивающая минимум дисперсии ошибки при нулевой
систематической ошибке.
Итак, с.к. оптимальная система для фильтрации сигала известной формы в
случае, когда помеха - белый шум, представляет собой последовательное соединение
согласованного фильтра и усилителя с коэффициентом усиления A(t), определяемым
формулой (XVI). Согласованный фильтр представляет собой последовательное соеди-
нение усиления, коэффициент усиления которого численно равен значению полезного
сигнала и интегратора.
Замечание. Изложенный метод дает возможность определять оптимальные
системы как с бесконечной памятью, так и с конечной памятью Т. В последнем случае
следует во всех формулах заменить нижний предел интегрирования to на t — Т.
В некоторых практических задачах форма полезного сигнала неизвестна, но извест-
но линейное дифференциальное уравнение, определяющее полезный сигнал:
S = a(t)S.
(XIX)
346
ГЛ. 2. ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФИЛЬТРЫ КАЛМАНА
Интегрируя это уравнение при случайном начальном условии S(to) — U, получаем
S(t) = U exp
a(r)dr ►
(XX)
Из (XIX) и (XX) видим, что неизвестный полезный сигнал <p(t) связан с коэффи-
циентом (l(t) уравнения (XIX) формулами
n(t\ _ У’ЧО
(’ -
<p(t) = exp <
(XXI)
to
Определив таким путем функцию <^(£), можно рассмотренным выше способом най-
ти оптимальную систему. Однако в таких случаях целесообразнее непосредственно найти
дифференциальное уравнение оптимальной системы с бесконечной памятью. С этой це-
лью запишем выражение для выходного сигнала системы:
У(0 = A(t) I ^T)X(r)dr.
to
(XXII)
Дифференцируя уравнение (XXII) по времени t и опуская для краткости обозначе-
ние аргумента t, получим
t
Y = Х^ (p(j)X(j)dr +
to
(XXIII)
Умножив это выражение на А, вычтем из него выражение (XXII), умноженное на
А, в результате получим
XY-XY = Х2<рХ или Y = уУ + ХрХ. (XIV)
А
Последнее уравнение есть искомое дифференциальное уравнение для оптимального
фильтра. Однако оно содержит неизвестные функции А и <р. Чтобы исключить эти
функции, перепишем формулу (XVII) для минимальной средней квадратической ошибки
оптимальной системы, опуская для краткости аргумент t и звездочку, в виде Х<р = Т}/V,
откуда находим
1п А = Ат/ - 1пу> - Ini/. (XXV)
2.13. ДОПОЛНЕНИЯ И ЗАДАЧИ
347
Из формулы (XVII) следует также, что
In т) = In 4- In v - ln(7ub 4- и) 4- 2 In <p. (XXVI)
Подставив это выражение в формулу (XXV), будем иметь
In А = Х<р — ln(7u6 4-f) 4-1п7и. (XXVII)
Отсюда дифференцированием получаем
А Ф 7и<Р2 т)
— =--------------= а------.
Л <р УиО + и и
(XXIII)
Подставив это выражение в уравнение (XXIV) и учитывая, что Xtp = Т}/иприхо-
дим к следующему уравнению:
Y = (а - Y 4- ^Х.
\ у J V
(XXIV)
Как следует из уравнения (XIX), в данном случае полезный сигнал S(t) формирует-
ся с помощью системы, представляющей собой интегратор, охваченный обратной связью
с усилителем, коэффициент усиления которого равен о(^), при подаче на вход нулево-
го сигнала и установке случайного начального значения на интеграторе. Из сравнения
уравнений (XIX) и (XXIV) следует, что оптимальная система в данном случае отличается
от системы формирования полезного сигнала только тем, что на ее вход вместо нулевого
сигнала подается сигнал Т](Х — V), а на интеграторе устанавливается нулевое началь-
ное условие вместо случайного. Таким образом, оптимальная система в данном случае
получается из системы формирования полезного сигнала путем включения предвари-
тельного усиления с переменным коэффициентом усиления Tjifyy, замыкания отри-
цательной обратной связью и подачи на вход входного сигнала системы X(t). Этот
результат впервые получен Калманом для дискретных систем и Калманом и Бьюси для
непрерывных систем (разделы 2.4 и 2.9). Поэтому оптимальная система, описываемая
дифференциальными уравнениями, в случае, когда полезный сигнал также формируется
системой описываемой дифференциальными уравнениями, называется фильтром Калма-
на.
Величину минимальной средней квадратической ошибки оптимальной системы Т] —
= 7/* в данном случае также можно получить интегрированием дифференциального
уравнения. Действительно, дифференцируя (XXVI) и принимая во внимание формулу
(III) для функции Ь и формулу (XVII) для минимальной средней квадратической ошибки
оптимальной системы, получаем
5 = 7иУ>2
т] -fub 4- и
.суФ
+ 2— =--------F 2а.
(р I/
(XXX)
348
ГЛ. 2. ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФИЛЬТРЫ КАЛМАНА
Отсюда вытекает следующее дифференциальное уравнение для минимального сред-
него квадрата ошибки Т] оптимальной системы:
Л
fi = 2ат) - (XXXI)
Отметим, что изложенным способом можно получить только оптимальную систему
с бесконечной памятью, так как никакая система с конечной памятью не может быть
описана дифференциальными уравнениями.
2.13.23. Общая задача фильтрации сигнала неизвестной формы. Дадим обобще-
ние задачи 2.13.22 на случай скалярного сигнала неизвестной формы. Следуя (Пугачев
1957, 10960, 1962), будем считать, что полезный сигнал неизвестной формы можно при-
ближенно представить в виде полинома
N
= (I)
Г=1
где Ui , ... , Un - случайные коэффициенты, a (t) , . . . , - известные функ-
ции времени t. Для простоты рассмотрим сначала случай, когда N — 2. При этом
входной сигнал системы определяется формулой
(П)
Фиксируем начальный момент времени to и текущий момент времени t, а любой
момент времени в интервале (to,t) обозначим Т. Предположим сначала, что
t
У <Р1(т)<р2(т)</т = 0.
to
(П1)
Рассуждая так же, как в задаче 2.13.22, приходим к выводу, что в данном случае
следует пропустить входной сигнал через два параллельных согласованных фильтра, со-
ответствующих двум составляющим полезного сигнала. Выходные сигналы этих двух
согласованных фильтров выражаются формулами
t
ZAt) = I <pi(r)X(r)dT = Utbn(t) + Zlui(t),
to
t
Z2(t) = <P2(r)X(r)dT = U2b22(t) + ^2ш(0,
to
(IV)
(V)
2.13. ДОПОЛНЕНИЯ И ЗАДАЧИ
349
где для краткости положено
t t
bu(t) = у^i(r)dr, 622(0 = /¥’2(T)dr> (VI)
to to
t t
21ш(0 = У<pi(r)N(r)dr, = I<p2(r)N(r)dr, (VII)
to to
На основании формул (IV) первый согласованный фильтр не пропускает второй ком-
поненты полезного сигнала, а пропускает лишь первую компоненту и шум, причем обес-
печивает для первой компоненты максимум отношения сигнал/шум на выходе. Второй
согласованный фильтр пропускает лишь вторую компоненту полезного сигнала и шум,
причем также дает на выходе максимальное отношение сигнал/шум.
Из формул (IV) и (II) видно, что для воспроизведения полезного сигнала без систе-
матической ошибки при любых возможных значениях Ui, U2 случайных величин U\ , U2
достаточно умножить выходной сигнал первого согласованного фильтра на ip\ (t)/t>H (t),
а выходной сигнал второго согласованного фильтра на <р2 (0/^22 (£) и полученные ре-
зультаты сложить. Тогда выходной сигнал системы будет равен
У(0 = u^{t) + t72^(t) + Уш(0, (VIII)
где
Г»(0 = И2ш(0. (IX)
on (t) 022(4
Имея в виду, что математическое ожидание белого шума N(t), а следовательно, и
математические ожидания шумов на выходах согласованных фильтров 2/1ш(£)’ ^2ш(^)
равны нулю, приходим к выводу, что в данном случае средний квадрат ошибки равен
дисперсии выходного шума Уш (О- Для нахождения дисперсии этого шума заметим, что
дисперсии шумов на выходах согласованных фильтров и ^2ш(^) определяются
формулами, аналогичными формуле задачи 2.13.22 (V):
t
£>1ш(0 - £>[^1ш(0] = v ! 4%(rdr = 1/611(0,
to
t
£>2ш(0 = £>[^2ш(0] = У ! ¥’2('rdr = ^2(0,
to
(X)
(XI)
350
ГЛ. 2. ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФИЛЬТРЫ КАЛМАНА
Кроме того, заметим, что в данном случае выходные шумы согласованных фильтров
не коррелированы, так как в силу условия
t
M[Zlui(Z)Z2111(t)] = " У ‘/’iCO^CO =0.
to
(ХП)
Вследствие этого дисперсия шума на выходе найденной оптимальной системы равна
среднему квадрату ошибки:
??(*) , у!(0
611(0 &2г(0
(хш)
Найденная таким путем оптимальная система, очевидно, обеспечивает условный ми-
нимум средней квадратической ошибки при нулевой систематической ошибке для любых
возможных значений IQ, V>2 случайных величин t/j, U2.
Чтобы найти оптимальную систему, обеспечивающую абсолютный минимум средней
квадратической ошибки, заменим коэффициенты усиления (t)/Ьц (^) и ^2(^)/^22(^)
коэффициентами Ai и А2 соответственно. Тогда выходной сигнал системы
y(Z) = A1Z1(t) + A2Z2(0 =
= XiUMt) + A2I72622(0 + AiZllu(t) + A2Z2ui(Z). (XIV)
Вычитая отсюда требуемый выходной сигнал
УтР(0 = ^т (0 + ^(0. (xv)
найдем ошибку системы
У(0 = Ui [Ai6ц (0 ~ 9’1(0 ] + ^2 [А2622(0 — ^2(0 ] +
+А1£1Ш(0 + А222ш(0. (XVI)
Отсюда вытекает следующее выражение для среднего квадрата ошибки системы:
= 711 [А16ц(0 — <Р1 (0] 2 + 722 [А2622(0 — <Рг(О]2 +
+2712 [Aii>i 1(0 - У’ЛО] [Лг522(0 _ 9’г(0] +
+ФМ)+аЫ)]> (XVII)
где 711,712,722 _ начальные моменты второго порядка случайных величин t/i, U2
ypq = M[UpUq] (p,g = l,2).
(XVIII)
2.13. ДОПОЛНЕНИЯ И ЗАДАЧИ
351
Дифференцируя выражения для Т) по Ai и Аг и приравнивая производные нулю,
получим следующие уравнения для определения неизвестных коэффициентов усиления
Ai и Аг:
ди
= 27ц6ц(t) [ AiЬц(t) — <^i(t) ] + 2712611(f) [ АгбггМ ~ (f) ] +
ил\
+2i/6n(f)Ai =0, (XIX)
On
у — 2712622W [А16ц(£) — <^i(t)] + 2722622(С [Аг622(£) — ^2(0] +
0Л2
+21/622 (*)А2 =0, (XX)
[711611 (0 + I/] Ai + 712622(^)^2 = 711^1 W + 712^2^), (XXI)
712бц(£)А1 + [722622(t) + 1/] Аг = 7i2<^i(С + 722^2(0- (XXII)
Определив из этих уравнений Ai и А2 и подставив полученные выражения в фор-
мулу для среднего квадрата ошибки системы, получим следующее выражение для мини-
мального среднего квадрата ошибки оптимальной системы:
т?* = V [ Ах (t)^i (t) + А2 (t)^2 (t) ], (XXIII)
где явно выражена зависимость Ai и Аг от t.
Таким образом, с.к. оптимальная система в данном случае представляет собой
параллельное соединение двух цепочек, каждая из которых состоит из согласованного
фильтра и усилителя.
Отбросим теперь условие (III) и введем обозначение
t
W) = у (XXIV)
to
Введем вместо функций (т) и (/?2 (т) функции
Wl(r) = <£1(т), W2(r) = С21Ш1(т) + <рг(т),
где С21 - неизвестный пока коэффициент. Тогда будем иметь
t
У wxM^Mdr = c21bn(t) + d12(t). (XXV)
to
352
ГЛ. 2. ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФИЛЬТРЫ КАЛМАНА
Отсюда видно, что если принять
21 611(0’ (XXVI)
то получим
t
У о,1(т)а>2(т)йт = 0.
to
(XVII)
Подставив выражения функций (г) и (02 (т) через (Vi (т) и С^2 (?) в выражение
для входного сигнала системы, будем иметь
Х(т) = (171 - c21U2)wx(t) + и2ы2(т) + 2У(т). (XXVIII)
Вводя новые случайные величины
получим
V1 = U1 - C21CZ2, v2 = U2, (XXIX)
Х(т) = V1W1 (т) + V2w2(r) + N(r). (XXX)
Таким образом, общий случай сводится к только что рассмотренному, так как функ-
ции Wl(r) и С^2(т) удовлетворяют условию (III). Поэтому оптимальная система может
быть найдена с помощью изложенного метода. В результате, обозначив коэффициенты
усиления выходных сигналов согласованных фильтров и Д2> получим следующее вы-
ражение для выходного сигнала с.к оптимальной системы:
t t
Y(t)=pi У 4- дг У с^(т)Х(т)</т.
to to
(XXXI)
Заменив здесь функции CUi (т) и (л)2 (т) их выражениями через функции (т) и 102
получим
t t
Y(t) = (Д1 4- С21Д2) I <pi(r)X(r)dT 4- М2 У <М2(т)Х(т)</т. (XXXII)
to to
Наконец, полагая
Ai = Mi + c2iM2, Аг = Дг,
(XXXIII)
2.13. ДОПОЛНЕНИЯ И ЗАДАЧИ
353
найдем
t t
Y(t) = Ai У tp^X^dr + A2 У ¥>2(т)Х(т)</т. (XXXIV)
to to
Отсюда видно, что оптимальная система в рассматриваемом случае имеет ту же
структуру, что и в предыдущем случае. Иными словами, и в случае, когда условие (II) не
выполняется, оптимальная система состоит из параллельного соединения согласованных
фильтров с усилителями их выходных сигналов. Для непосредственного определения ко-
эффициентов усиления выходных сигналов согласованных фильтров в этом случае запи-
шем выражения выходных сигналов согласованных фильтров. Пользуясь обозначениями
(VI) и (XXIV), находим
t
Z^t) = У (pitfXtfdr + UMt) = U2b122(t) + Zim(t), (XXXV)
to
t
z2(t) = у 9?2(r)X(r)dT + Uib12(t) = U2bn(t) + Z2iu(i), (XXXVI)
to
Выходной сигнал оптимальной системы выразится в данном случае формулой
y(t) = Ai [С71Ьц(t) 4- Uibntt)] +
4-Аг [£7161г(О 4- (/2^22(£) ] 4- AiZiin(t) 4- Аг^гш(0’ (XXXVII)
Вычитая из (XXXVII) выражение
yTp(t) = S(t) = + U2<p2(t) (XXXVIII)
для требуемого выходного сигнала, найдем ошибку системы:
У(^) = I7i [ Aidn(t) 4- Аг&1г(О — ^1(0] +
4-172 [Ах612(t) 4- A2&22W ~ <^2(£)] 4-
4-А1Я1Ш(^) 4- Аг^гшСО* (XXXIX)
Найдем средний квадрат ошибки. Для этого учтем, что шумы на выходах согласо-
ванных фильтров коррелированы и их корреляционный момент определяется формулой
t
М[21Ш(г)И2ш(*)] = v У Vi(r)y2(T)dT = vbi2(t). (ХХХХ)
to
12 Фильтры Калмана и Пугачева
354
ГЛ. 2. ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФИЛЬТРЫ КАЛМАНА
Принимая во внимание (ХХХХ) и формулы (X), (XI) для дисперсий шумов на вы-
ходных согласованных фильтров и опуская для краткости аргумент t, получаем средний
квадрат ошибки на выходе системы:
7/ = М [PW] = 711(А1&ц 4- А2&12 — <^1)2 +
+722(А1&12 + А2&22 “ ^г)2 + 2712(А1&11 4- А2&12-
—</2i)(AiЬ12 4- А2622 — ^2) 4- ^(АгЬц 4- 2А1А2612 4- А^Ьгг)- (XXXXI)
Дифференцируя выражение (XXXXI) по Ai и А2 и приравнивая производные нулю,
получаем следующие уравнения для определения оптимальных значений коэффициентов
усиления Ai и А2:
Of)
хт— ~ 2711^11 (А1Ьц 4- А2&12 — <^i) 4- 2722612^1612 4- А2622 — <^2)4-
оЛ1
4-2712^11 (Ai612 4- А2&22 — <£>2) 4- 27i2&i2(Ai6ii 4- А2612 — <Р1)4-
4-2i/(Ai&h 4- А2612) = О
0^ = 2Ац612(А1&ц 4- А2612 — <Р1) 4- 2722622^1612 4- А2622 — <£2)4-
4-27i2&i2(Ai6i2 4- А2622 — ^2) 4- 2712622(Ai6ц 4- А2612 — ^1)4-
4-2i/(Ai6i2 4- А2622) = О (ХХХХП)
или
6ц [7и(А16ц 4- А2612 — 4- 71г(А1612 4- А2622 - <^2) 4- vXi ] 4-
4-612 [712(А16ц 4- А2612 - 4- 722(Ai6i2 4- А2622 - <£2) 4- 1/А2 ] = О,
612 [7и(А16ц 4- А2612 - <^1) 4- 7i2(Ai6i2 4- А2622 - ^2) 4- vX\ ] 4-
4-622 [712(А16ц 4- А2612 — <£i) 4- 72г(А1612 4- А2622 — ^2) 4- иХ2 ] = О,
(ХХХХШ)
Заметим, что на основании неравенства Коши-Буняковского
&12 —
’ t
У (г)(р2(т)йт
-to
t t
< У ‘Pi^d.T у
to to
tpl(r)dr = 611622,
(XXXXIV)
2.13. ДОПОЛНЕНИЯ И ЗАДАЧИ
355
причем знак равенства может иметь место только тогда, когда функции (т) и (т)
линейно зависимы. Однако этот случай, очевидно, сводится к случаю сигнала известной
формы. Поэтому &12 < ^11^22 и рассмотренные уравнения представляют собой одно-
родные линейные уравнения относительно выражений в квадратных скобках с неравным
нулю определителем. Следовательно,
7ii(Ai&ii + ^2^12 — <^1) + 712(А1&12 + АгЬзг - <£2) + — О,
712(А1Ьц 4- А2612 — ^2) + 722(Ai&i2 4- Аг^гг — ^2) + ^Аг — О
или
[Ти&п(0 + 712^12(0 + + [711612(0 +712б22(0]^2 =
= 711^1(0+ 712^(0; (xxxxv)
[712611(0 + 722612^] Ai + [712612W + 722622(0 + И Аг =
= 712^1 (0 + 722^2 (0 • (XXXXVI)
Определив из уравнений (XXXXV) и (XXXXVI) коэффициенты усиления Ai и А2 и под-
ставив полученные результаты в выражение (XXXXI), получим формулу (XIII) для ми-
нимального среднего квадрата ошибки оптимальной системы.
Совершенно так же доказывается, что и в общем случае фильтрации полезного сиг-
нала (I) при произвольном N оптимальная система представляет собой параллельное
соединение согласованных фильтров, к выходам которых подключены усилители. Опти-
мальные значения коэффициентов усиления Ai , ... , Ajv выходных сигналов согласо-
ванных фильтров Z\ (t) , . . . , Z/^(t) определяются системой уравнений, аналогичных
уравнениям (XXXXV) и (XXXXVI):
N Г N
УТ УТ 7грЬр8 (0 4- 6rsV
s=l _р=1
где 6га - символ Кронекера,
N
Ав = У^р^рМ (г = 1, ... , TV)
Р=1
(XXXXVII)
t
bpq(t) = bqp(t) = У ^p(r)^(r)dr (p,q = 1, ... , TV),
to
Минимальный средний квадрат ошибки оптимальной системы
N
*Г = у J2Ap(t)^p(t)-
Р=1
(XXXXVIII)
356
ГЛ. 2. ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФИЛЬТРЫ КАЛМАНА
Изложенный метод применим для оптимальных фильтров как с бесконечной, так и с ко-
нечной памятью Т. В последнем случае следует заменить нижний предел интегрирования
to на t — Т.
Если функции неизвестны, но известно линейное дифференциальное уравне-
ние (в данном случае уравнение IV-го порядка), определяющее полезный сигнал S(t),
то, как и в задаче 2.13.22, можно решить задачу нахождения оптимальной системы с
бесконечной памятью.
2.13.24. Задача совместной с.к. оптимальной фильтрации сигнала известной
формы и сигнала неизвестной формы, состоящего из нескольких компонент (Пуга-
чев 1957, 1960, 1962). Для вывода дифференциальных уравнений оптимальной системы с
бесконечной памятью в общем виде рассмотрим задачу воспроизведения векторного сиг-
нала S(£) с составляющими Si(t) , . . . , Sn(t), определяемого системой обыкновенных
линейных дифференциальных уравнений
п
Si = 0>ij Sj (г = 1 , . . . , п) (I)
.7=1
со случайными начальными условиями Si(to) — Ui (i — 1 , . . . , 71). Как известно из
теории дифференциальных уравнений, общий интеграл системы уравнение (I) представ-
ляет собой линейную комбинацию 72 линейно независимых частных интегралов этой си-
стемы уравнений. Обозначим Ipik (t) (£ = 1 , ... , 71) частный интеграл системы урав-
нений (I), удовлетворяющий начальным условиям 'фцс (£о) = 0 при 2 A;, — 1-
Частные интегралы такого вида, соответствующие k = 1 , . . . , 72, линейно незави-
симы. Поэтому требуемый выходной сигнал со случайными начальными значениями
Yrpi(to) = -S'»(to) = Ui (i = 1, ... , n) определяется формулой
n
YTpi(t) = Si(t) = £ UkT/>ik(t) (i = 1, ... , n). (II)
fc=l
Предположим, что этот сигнал необходимо с наибольшей точностью воспроизвести
по резульатам наблюдения векторного входного сигнала Х(£) с составляющими
п п п
xp(t) = 5?ср»^»(^)+^р(^) = 5?ср«5?+^р(0 (р = 1, ,т),
i=i i=i *=1
(ni)
где Ni(t) , . . . , Nm(t) - некоррелированные один с другим белые шумы, интенсивно-
сти которых соответственно равны , . . . , 1/т. Положив для краткости
п
<PPk(t) = $2СР*^«*:(0 (р=1, ... ,т;к = 1, ... ,п), (IV)
1=1
2.13. ДОПОЛНЕНИЯ И ЗАДАЧИ
357
будем иметь
п
Xp(t) = ^Ukppk(t) + Np(t) (р = 1,...,т). (V)
к=1
Рассматриваемая задача представляет собой задачу одновременного линейного ал-
гебраического преобразования ТП сигналов в 71 сигналов в случае, когда функции 'фък (£)
связаны с функциями фрк(1) формулами (IV). Оптимальная система для воспроизведе-
ния каждой составляющей требуемого выходного сигнала представляет собой параллель-
ное соединение согласованных фильтров с усилителями выходных сигналов. Обозначим
коэффициент усиления h-й компоненты р-го входного сигнала в выражении i-й компо-
ненты выходного сигнала через . Тогда i-я компонента выходного сигнала
W = Ш2ХрИ <Ppfl(r)Xp(T)dT.
Р=1 Л=1 /о
(VI)
Подставив сюда выражение (V) входного сигнала .Хр(т) и вводя для краткости
обозначение
t
bkh = У Vpk(r)<PPh(r)dT (к,h = 1, ... , п\р = 1, ... , m),
to
получим
n т п
Yi(t) = £uk£^X%№+
к=1 р=1 Л=1
+ Ё12Ай [ ‘Pph(r)Np(r)dT.
р=1 л=1 /о
(VII)
(VIII)
Вычитая из этой формулы выражение (II) для требуемого выходного сигнала, найдем
ошибку на 2-м выходе системы:
п / т п \
г<(<) = Ё Е Ё ХЖ - Н +
Л=1 \р=1 Л=1 /
+ЕЕА2/^л(г)ад</г <i = 1’•••>")• (к)
р=1 Л=1 /0
358
ГЛ. 2. ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФИЛЬТРЫ КАЛМАНА
Отсюда получаем следующее выражение для среднего квадрата ошибки на 2-м выходе
системы:
п / тп п \ / т п \
% = 52 (52 £ А₽М - ) (52 52 хч‘ь^ - ^.) +
r,s=l \р=1 h=l / \g=l 1=1 /
т п
+£>, SWi’M- m
р=1 h,l=l
где 7rs (Г, S - 1 , .. . , п) - вторые начальные моменты случайных величин U\, . . .
Аналогичной формулой определяются смешанные начальные моменты второго по-
рядка составляющих вектора ошибки системы:
п / т п \ / т п \
ла = 52 8 (52 52 Л2ьгл - V’ir 1 (52 52 AS’)+
K,s=l \р=1 h=l / \<7=1 t=l /
ТП П
+52 "₽ 52 ASASW (*, з = 1,..., n). (Xi)
р=1 h,l=l
Дифференцируя выражение (X), соответствующее данному фиксированному значе-
нию £, по параметрам (р = 1 > • • • > т>h - 1 > • • >п) и приравнивая производ-
ные нулю, получим после преобразований следующую систему линейных алгебраических
уравнений для определения неизвестных коэффициентов усиления :
п тп п
(XII)
(u = 1, ... , т\ s — 1, ... , п).
Заметим теперь, что левые части этих уравнений не зависят от индекса U. Следова-
тельно, и правые части не зависят от U. Это дает возможность ввести новые неизвестные:
(i,s = l, ... ,n;u = l, ... ,m). (XIII)
Определив из (XIII) величины Лрд и подставив в предыдущие уравнения, получим
п т п
52v>ir - 52 52 xphvv lPihb(rh
r=l L Р=1 Л=1
= Mis (s - 1 , . . . , n).
(XIV)
2.13. ДОПОЛНЕНИЯ И ЗАДАЧИ
359
Обозначим через элементы матрицы, обратной по отношению к матрице вторых
начальных моментов 'yrs случайного вектора U. Тогда, решив предыдущие уравнения от-
носительно выражений в квадратных скобках и выполнив элементарные преобразования,
получим следующую систему уравнений:
п / т \
S ГЕл'М +7г"л) Pih = ipir (Г = 1, ... , n). (XV)
h=l \p=l /
С помощью полученных уравнений для формулы (X) и (XI) приводятся после
преобразований к виду
п п
•Па = 52 ^я^зя = $2 ^зя (м = 1 > • • • , р)- (XVI)
9=1 9=1
Это формула является очевидным обобщением формулы (XXXXVIII) задачи 2.13.23.
Выведем дифференциальные уравнения оптимальной систем с бесконечной памя-
тью. При этом чтобы избежать громоздких выкладок, представим все полученные фор-
мулы и уравнения в матричном виде. Вводя вектор-столбец S и матрицу А:
/$1 (t)
S = 5г(<)
\Sn(t)
/ aii«i2 • • -ain
д _ [ &21&22 • • -fl2n
anlan2•••апп
(XVII)
представим уравнения (I) в виде
S = AS.
(XVIII)
Матрица
V’liV’n ..•V’in
^21^22 • • • ^2n
V*nlV*n2 • • • 'Фпп
представляет собой фундаментальную матрицу решений уравнения (XVIII). Поэтому мат-
рица Ф удовлетворяет следующим уравнению и начальному условию:
(XVIII)
Ф = АФ, Ф(*о) = 1,
(XX)
где I - единичная матрица, диагональные элементы которой равны 1, а остальные - 0.
Вводя случайный вектор-стобец U и матрицу Ф:
<^11^12 • • • <^1п
<^21^22 • • -<^2п
9?т1У?т2 • • • фтпп
(XXI)
360
ГЛ. 2. ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФИЛЬТРЫ КАЛМАНА
представим выражение (V) вектора-столбца входных сигналов системы Х(£) в виде
X(t) = Фи + N(t).
(XXII)
На основании формулы (IV) матрица Ф выражается через матрицу фундаменталь-
ных решений Ф уравнения (XVIII) соотношением
Ф = СФ,
(XXIII)
где С - матрица коэффициентов в формуле (IV) с элементами Cpi (р = 1 , 771JI —
= 1 , . . . , п).
Введем матрицу М = M(t) решений уравнений (XV), соответствующих различ-
ным выходам системы, с элементами (t, к — 1 , ... , 71), зависящими от t. Тогда
формула (VI) для выходных сигналов системы на основании формулы (XIII) примет вид
t
Y(t) = M(t) У Ф(т)тр-1Х(т)</т,
to
(XXIV)
где У - диагональная матрица, обратная матрице интенсивностей белых шумов
... ,Nm(t), а индексом Т обозначена операция транспонирования матрицы.
Матрица Н вторых начальных моментов Tfaj вектора ошибки системы на основании
(XVI) выразится формулой
н = ФМТ = МФТ. (XXV)
Вводя обозначение Г для матрицы вторых начальных моментов урд составляющих
случайного вектора U, перепишем уравнения (XV), определяющие элементы матрицы М,
в виде
М ( +Г"1 ) = Ф,
\р=1 /
где (р = 1 , ... , 771) - матрицы, определяемые формулой
(XXVI)
Л'М-.-й’Х
В(р) =
(р = 1, ... , тп).
(XXVII)
l(p)Jp) «,(₽) /
X°nl °п2 •• • °пп /
Продифференцируем формулу (XXIV) по времени t. Опустив для краткости обо-
значение переменной t, получим
t
У = М j Ф(т)Т1/-1Х(т)б/т + МФТ1/-1Х.
to
(XXVIII)
2.13. ДОПОЛНЕНИЯ И ЗАДАЧИ
361
Подставив сюда выражение интеграла
t
Ф(т)Г1/-1Х(т)</т = M-1Y,
(XXIX)
из уравнения (XXIV), получим
Y = MM-1Y + МФТ1/-1Х.
(XXX)
Это и есть дифференциальное уравнение оптимальной системы с бесконечной па-
мятью. Однако в таком виде это уравнение не показывает, как можно реализовать оп-
тимальную систему. Чтобы привести это уравнение к виду, непосредственно дающему
реализацию оптимальной системы, исключим из уравнения (XXX) неизвестные матрицы
МиФ, выразив их через матрицы коэффициентов А и С уравнений (XVIII) и (XXIII).
Для этого продифференцируем (XXVI) по времени t. Тогда, учитывая соотношения (VII)
и (XXII), получим
М nTv/B^+r-1
\р=1
т
(.<pph<pPk)h,k^i
p=i
= Ф = АФ.
(XXXI)
Но из формулы (XXVI) следует
= М"1Ф,
Р=1
(XXXII)
а из соотношения (XIII) получаем
т / m \
52 vp 1 (w* )м=1 »»= (52 vp 1 )
P=1 'P=1 ' h,k=l n
= ФЛ/^Ф = ФТСТ1/-1СФ. (XXXIII)
Подставив эти выражения в (XXXI), будем иметь
ММ-1Ф + МФТСТ1/-1СФ = АФ. (XXXIV)
Умножая уравнение (XXXIV) справа на матрицу Ф 1 и учитывая формулу (XXV),
приведем его к виду
ММ"1 = А - HCT1/-1C. (XXXV)
362
ГЛ. 2. ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФИЛЬТРЫ КАЛМАНА
Из (XXXV) следует, что
М = AM-НС7’г/"1 СМ. (XXXVI)
Подставляя выражение (XXXV) в уравнение (XXX) и учитывая, что на основании
формул (XXIII) и (XXV) МФТ = МФТСТ = НСТ, приведем уравнение (XXX) к
виду
Y = (А - HCTi/-1C)Y + HCTi/-1X. (XXXVII)
Это уравнение непосредственно указывает путь реализации оптимальной системы.
Сравнивая его с уравнением (XVIII), видим, что оптимальная система получается из си-
стемы формирования полезного сигнала путем подачи на вход входного сигнала X(t) с
коэффициентом усиления (матричным) и замыкания отрицательной обратной
связью с коэффициентом усиления (тоже матричным) НС^Г'-*С.
Чтобы получить дифференциальное уравнение для матрицы начальных моментов
второго порядка ошибки оптимальной системы Н, продифференцируем (XXV). Тогда,
принимая во внимание формулы (XX) и (XXXVI), получим
Н = МФТ + МФТ = (AM - НСТ1/-1СМ)ФТ + МФТАТ. (XXXVIII)
Отсюда, пользуясь формлой (XXXV), получим искомое уравнение
Н = АН + НАт-НСтр-1СН. (XXXIX)
Это матричное уравнение Риккати определяет матрицу моментов второго порядка
вектора ошибки оптимальной системы (раздел 2.4). Уравненияя (XXXVII) и (XXXIX)
определяют оптимальный фильтр Калмана для оценки векторного полезного сигнала
S(t), задаваемого дифференциальным уравнением (XVIII) в случае, когда входной сигнал
системы представляет собой линейную функцию (XXII) этого полезного сигнала, адди-
тивно смешанную с векторным белым шумом N(t).
Выясним, какие преобразования можно осуществлять с помощью фильтров Калма-
на. Очевидно, что если требуемый выходной сигнал не совпадает с полезным
сигналом S(t), а есть результат некоторого линейного преобразования S(t), то вместо
функций Ipik (t) в формулу для ошибки системы войдут соответствующие преобразован-
ные функции При этом из всех полученных формул изменятся только формулы
(X), (XXI), (XV), (XVI), куда войдут функции вместо функций Соответствен-
но в матричных формулах изменятся только формулы (XXV) и (XXVI): в них вместо
матрицы Ф будет матрица Q. Дифференциальное уравнение (XXX) по-прежнему бу-
дет справедливо. Однако в общем случае оно не преобразуется к виду (XXXVII), хотя
2.13. ДОПОЛНЕНИЯ И ЗАДАЧИ
363
формально и можно получить оптимальную систему из системы формирования полезно-
го сигнала путем ее замыкания отрицательной обратной связью и подачи на вход соот-
ветственным образом усиленного входного сигнала. Для этого достаточно представить
уравнение (XXX) в виде
Y = ^А - (А - ММ-1) j Y +МФТ1/-1Х. (ХХХХ)
Однако выразить коэффициенты усиления в цепях обратной связи и входного сиг-
нала оптимальной системы через матрицы коэффициентов А и С и получить диффе-
ренциальное уравнение для матрицы начальных моментов второго порядка ошибки опти-
мальной системы в общем случае не удается. И лишь в частном случае, когда требуемый
выходной сигнал связан линейной алгебраической зависимостью с полезным сиг-
налом S(t), можно построить оптимальный фильтр Калмана для оптимального воспро-
изведения сигнала Yj1p(t).
Предположим, что требуемый выходной сигнал Yj’p(t) связан с полезным сигналом
S(t) формулой
YTp(t) = QS(t), (XXXXI)
где Q - некоторая неособенная матрица, которая может зависеть от времени. В этом
случае матрица Ф в формуле (XXV) и уравнениях (XXVI) заменится матрицей Q = С^Ф
и вместо формул (XXV) и (XXVI) получим
Н = Q$MT = МФТ<ЭТ, (ХХХХП)
М ( £ + Г-1 j = Qtf. (ХХХХШ)
\р=1 /
При этом, если матрица Q перестановочная с матрицей A, AQ = QA, то формулы
(XXXV) и (XXXVI) заменяются соответственно формулами
ММ"1 = А + QQ"1 - HCfi/-1 Cl, (XXXXIV)
М = AM + QQ-1M - HC^i/-1CiM, (XXXXV)
где C^CQ"1. (XXXXVI)
Уравнения (XXXVII) и (XXXIX) заменяются в этом случае уравнениями
Y= [ А - - QQ-1)] Y + HCfi/-1X,
(ХХХХ VI)
Н = (А + QQ-1)H + Н(АТ - QT-1QT) - HCft^CiH. (XXXXVII)
364
ГЛ. 2. ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФИЛЬТРЫ КАЛМАНА
Замечание 1. К алгебраическому преобразованию вида (XXXXI) приводят-
ся и некоторые операции анализа. Однако определить матрицу Q в этом случае можно
сравнительно просто только для оптимальных систем, предназначенных для дифферен-
цирования полезного сигнала. Так, например, для дифференциатора первого порядка
YTp(t) = S(t) = AS(t) и, следовательно, Q = А. Для дифференциатора второго
порядка
YTp(t) = S(t) = [ AS(t) ] = AS(t) + AS(t) = (A + A2)S(Z)
и, следовательно, Q = А + А^. Аналогично определяется матрица Q для дифферен-
циаторов более выского порядка.
Замечание2. Рассмотрим частный случай, когда матрица коэффициентов
уравнения (XVII) А постоянная. В этом случае для дифференциатора любого порядка
YTp(t) = S<”>(t) = ApS(t) и, следовательно, Q — А^. Для экстраполятора
°° А* °° А*
YTp(t) = S(t + Д) = £ = £ =rA*S(t).
fc=O fc=O
Вводя матрицу
00 A*
= E 1ГА*’
k=0
преобразуем предыдущую формулу к виду
YTp(t) = eAAS(f).
Сравнивая эту формулу с (XVIII), видим, что для экстраполятора
Q = еДА.
Таким образом, если матрица коэффициентов уравнения формирования полезного сиг-
нала (XVIII) постоянная, то с помощью фильтров Калмана легко можно осуществлять
оптимальную оценку и прогнозирование любых линейных комбинаций полезного сигнала
и его производных. При этом уравнения (XXXXVII) и (XXXXVIII) отличаются соответ-
ственно от уравнений (XXXVII) и (XXXIX) только тем, что вместо матрицы С в них
входит матрица Ci = CQ
2.13.25. Задача с.к. оптимального преобразования стационарного случайного
сигнала (Пугачев 1957, 1960, 1962). В задачах 2.13.22-2.13.25 полезный сигнал S(t)
представляет собой регулярную функцию времени, зависящую от случайных параметров
Ui , ... , U. Однако в некоторых практических задачах полезный сигнал содержит
2.13. ДОПОЛНЕНИЯ И ЗАДАЧИ
365
наряду с регулярной функцией времени и нерегулярную часть, представляющую собой
случайную функцию, которую нельзя аппроксимировать линейной комбинацией сравни-
тельно небольшого числа детерминированных функций со случайными коэффициента-
ми. Чтобы научиться находить оптимальные системы и для таких полезных сигналов,
рассмотрим задачу определения оптимальной стационарной линейной системы в случае,
когда входной сигнал X(t), представляющий собой сумму полезного сигнала S(t) и по-
мехи 7V(t), является стационарной случайной функцией времени, а требуемый выходной
сигнал Урр(£) есть стационарная случайная функция, стационарно связанная с входным
сигналом X(t). Обычно в практических задачах требуемый выходной сигнал Yrp(t)
представляет собой результат некоторого линейного преобразования полезного сигнала
S(t), содержащегося во входном сигнале X(t). При этом ограничимся рассмотрением
оптимальной системы с бесконечной памятью, время работы которой достаточно вели-
ко, чтобы можно было его считать бесконечным, и предположим, что математическое
ожидание ТПХ входного сигнала X (t) равно нулю.
Допустим сначала, что входной сигнал X(t) представляет собой белый шум, ин-
тенсивность которого равна V и, следовательно, спектральная плотность Sq =
Обозначим через р(т) искомую весовую функцию оптимальной стационарной линейной
системы. Тогда выходной сигнал этой системы У (t) выразится формулой
оо
Г(0 = I g(r)X(t - r)dr. (I)
О
Ошибка системы
оо
Г(0 = j 9(r)X(t - r)dr - YTp(t). (II)
О
Отсюда находим средний квадрат ошибки системы
оо оо
Т] = м [у2(о] = V ! g2(r)dT -2 ! g(r)kyTrX(j)dr + DyTp, (III)
О о
где кутРх(т) - взаимная корреляционная функция требуемого выходного и входного
сигналов, a DyTp - дисперсия требуемого выходного сигнала. Дополним первые два
слагаемых в предыдущем равенстве до полного квадрата. В результате получим
Л ~ DyrP
оо оо
-^/*yrps('r)dr + 1'/ 9(т)~
о о
-Л
^^УТрХ
2
dr.
(IV)
366
ГЛ. 2. ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФИЛЬТРЫ КАЛМАНА
Отсюда непосредственно видно, что средний квадрат ошибки будет иметь минималь-
ное возможное значение, если весовую функцию </(т) оптимальной системы определить
формулой
0(т) = ^kyTpX(r). (V)
Заменив здесь взаимную корреляционную функцию требуемого выходного и вход-
ного сигналов ее выражением через взаимную спектральную плотность тех же сигналов
§утрХ
оо
кУТрХ(т) = I SyTpX{^Tdwy (VI)
— ОО
получим
оо
р(т) = 1 у 8УТрХ(ш)е™<Ь). (VII)
— ОО
Эта формула определяет весовую функцию оптимальной системы только при Т > 0.
При Т<0 </(т) = 0. Ограничимся случаем дробно-рациональной взаимной спектраль-
ной плотности требуемого выходного и входного сигналов. Чтобы найти выражение </(т)
при всех Г, разложим рациональную дробь »SyTpa.(a;) на элементарные дроби и обо-
значим через [ SyTpx (^) ] । сумму всех дробей с полюсами в верхней полуплоскости
комплексной переменной (J, а через [ &утРх (^) ] ” СУММУ всех элементарных дробей с
полюсами в нижней полуплоскости. Тогда получим
$утрх(ш) — [‘S'l/TpzG^) ]+ + [ $УТрХ (")]_• (VIII)
Подставив это выражение в формулу (VII), получим
оо
9(т)= I [8УТрХ(Ш)]+е^^, (IX)
—ОО
так как
оо
У [Sj/TpiCw)]-= 0 ирн т > 0.
—ОО
Формула (IX) определяет весовую функцию оптимальной системы </(т) при всех
значения Т, так как
оо
У [ SyTpX (w) ] + = 0 при т < 0. (X)
— ОО
2.13. ДОПОЛНЕНИЯ И ЗАДАЧИ
367
Заменив интенсивность V входного сигнала ее выражением через спектральную
плотность V = 2тГ$о» приведем формулу (IX) к виду
оо
-оо
(XI)
Наконец, сравнив эту формулу с известным выражением весовой функции стацио-
нарной линейной системы через ее частотную характеристику
оо
<?(т) = ^- / (XII)
Z7T J
—оо
находим частотную характеристику оптимальной линейной системы
ф(М = |[М")]+- (XIII)
Таким образом, для нахождения частотной характеристики оптимальной стацио-
нарной линейной системы в случае, когда входной сигнал представляет собой белый шум,
следует разложить взаимную спектральную плотность требуемого выходного и входного
сигналов на элементарные дроби, отбросить все дроби с полюсами в нижней полуплос-
кости комплексной переменной U) и разделить полученное выражение на спектральную
плотность входного белого шума.
Найдем средний квадрат ошибки оптимальной системы. Для этого подставим в
формулу (IV) выражение (V) весовой функции оптимальной системы. Тогда, принимая
во внимание известное из теории интегралов Фурье равенство Фурье-Планшереля, на
основании которого
оо оо
О —оо
(XIV)
получим
оо
H* = DVTr-± I |[S„TpI(cu)] + |2^. (XV)
—ОО
Отсюда с помощью формулы (XIII) получаем
оо
^=DVTp -So I |ФМ|2^.
— ОО
(XVI)
368
ГЛ. 2. ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФИЛЬТРЫ КАЛМАНА
Эта формула обычно и служит для вычисления минимального среднего квадрата ошибки
оптимальной системы.
Рассмотрим теперь общий случай, когда входной сигнал X(t) представляет собой
производную стационарную случайную функцию с дробно-рациональной спектральной
плотностью Sx(fd). Выразив эту спектральную плотность в виде
Sx(w) = |Ф(гш)|2, (XVII)
найдем передаточную функцию Ф(з) формирующего фильтра, преобразующего белый
шум V(t) с единичной спектральной плотностью Sq — 1 во входной сигнал X(t).
Система с передаточной функцией 1/Ф(з) преобразует входной сигнал в белый
шум V(t). Поэтому для определения оптимальной системы можно использовать прием,
рассмотренный в предыдущей задаче. Оптимальная система будет представлять собой
последовательное соединение системы с передаточной функцией 1/Ф(з) и оптимальной
системы для случая белого шума V(t) на входе. Согласно формуле (XIII) частотная
характеристика 9v(ibd) оптимальной системы для белого шума V(t) с единичной спек-
тральной плотностью на входе определяется формулой
9,(ш) = [SPTl>I(w)]+. (XVIII)
Следовательно, частотная характеристика оптимальной системы для входного сиг-
нала X (t) выразится формулой
*'•“>=Ж? (Х1Х)
Заметим теперь, что
s—<“>=(хх)
где - взаимная спектральная плотность сигналов Yrip(t) и X(t). Подста-
вив это выражение в предыдущую формулу, получим следующее выражение частотной
характеристики оптимальной линейной системы:
ф<^ = • (XXI)
Ф(гси) [ Ф(—гш) J +
Минимальный средний квадрат ошибки оптимальной системы на основании (X)
определяется формулой
2.13. ДОПОЛНЕНИЯ И ЗАДАЧИ
369
Но на основании формул (XVII) и (XXI)
[ ] + = 1ф(МФ(М12 = I ф(^) I2 sx(u). (XXII)
Подставив это выражение в предыдущую формулу, получим следующее окончатель-
ное выражение для минимального среднего квадрата ошибки оптимальной системы:
оо
n*=DVTr- I |Ф(гш)|2 Sx(w)du>. (XXIII)
—ОО
Замечание. Функция (Дт) удовлетворяет интегральному уравнению
оо
I кх(£ - rfigtfW = кУТрХ^) (ц > 0). (XXIV)
О
Задача определения оптимальной стационарной линейной системы с бесконечной
памятью для стационарных и стационарно связанных входного и требуемого выходно-
го сигналов впервые была решена Н.Винером. Несколькими годами ранее такая зада-
ча для дискретных систем была решена А.Н.Колмогоровым. Интегральное уравнение
(XXIV) обычно называют уравнением Винера-Хопфа, а решенную задачу - задачей Ви-
нера. Аналогичная задача для систем с конечной памятью Т приводит к интегральному
уравнению
Т
I кх(£ ~ чШ = кУТрХ(т)) (0<ri< Т). (XX)
о
Ее решение подробно изучено В.С.Пугачевым (Пугачев 1957, 1960, 1962).
2.13.26. Написать уравнения линейного с.к. оптимального фильтра для выходного
сигнала в линейных системах с параметрическими шумами задач 1.9.20, 1.9.22, 1.9.48-
1.9.50, наблюдаемого с аддитивным нормальным белым шумом.
2.13.27. Выписать уравнение с.к. оптимальной фильтрации раздела 2.7 для:
а) линейных нормальных стохастических систем; б) линейных нормальных систем с пара-
метрическими нормальными шумами; в) билинейных нормальных стохастических систем.
2.13.28. Написать уравнения дискретной с.к. оптимальной фильтрации, пользуясь
ненормированными распределениями (раздел 2.7).
2.13.29. Найти оптимальный фильтр и оценить точность фильтрации в примере 2.4.1
с помощью стандартного программного обеспечения при следующих значениях парамет-
ров:
370
ГЛ. 2. ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФИЛЬТРЫ КАЛМАНА
1) cjo = 1? v — 1? Ли (to) = 1? -Ri2(^o) — R22^q) = 0;
2) CJo = 1? V = 10? Ли (to) = 1? Л12^о) = ^22(^0) = 0;
з) cjo — 1? и — 1? Яц(^о) — -^12(^0) — 0,7?22(£о) = 1;
4) 0,0 = 1? = 10, Й11 (to) = Л12(£о) = 0, 7?22(to) = 1-
2.13.30. Найти оптимальный фильтр и оценить точность фильтрации в примерах
2.5.1 и 2.5.4 с помощью стандартного программного обеспечения при следующих значе-
ниях параметров:
1) О,0 = 1,« — а = 10“1, 0,1 = 10, D = 1,-Di — 10—1;
2) о,0 = 1,а = а = 10“х,cji = 10, D = 1, Z?i = 1;
з) 0,0 = 1,а = а = 10“1, сих — 10, D = 10“1, D\ = 1;
4) о,0 — 1,а = а = 10“1, tJi = 10,-D = 10“1, Z?i = 1.
2.13.31. Найти оптимальный фильтр и оценить точность фильтрации в примерах
2.5.2 и 2.5.7 с помощью стандартного программного обеспечения при следующих условиях:
1) 0,2 — ^о; 2) 0,2 = 10о,о; з) 0,2 = 10—1cuq-
2.13.32. Найти оптимальный фильтр и оценить точность фильтрации в примерах
2.5.5 и 2.5.8 с помощью стандартного программного обеспечения при следующих значе-
ниях параметров:
1) о,0 — 1,^1 — 10о,0,а = а = 10-1, Di = D = 1;
2) о;о = l,o;i = Юо,о,а = а = l,Di = D = 1;
з) 0,0 = l,o,i = 10o,o,Q! = а = 100, D\ = D = 10-1;
4) 0,0 = l,o,i — 10о,о,а = а = l,Di = 10-1,Z) = 1;
5) 0,0 = l,o,i — Юо,о,а = а = l,Z>i — 1,Z) = 10“1;
6) 0,0 = l,o,i — 10о,о,а = а = l,.Di = 10, D — 10-1.
2.13.33. В условиях задач 2.13.29-2.13.32 с помощью стандартного программного
обеспечения найти оптимальные экстраполяторы и оценить точность экстраполяции для
примеров 2.6.1-2.6.3.
2.13.34. Найти дискретные оптимальные фильтры (экстраполяторы) и оценить точ-
ность фильтрации (экстраполяции) для дискретизированных уравнений систем в задачах
2.13.29-2.13.33 с помощью стандартного программного обеспечения.
ГЛАВА 3
СУБОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ.
ОБОБЩЕННЫЕ ФИЛЬТРЫ КАЛМАНА
В главе 3 излагается теория приближенных (субоптимальных) ме-
тодов оценивания состояния и параметров в стохастических системах.
В разделе 3.1 дается краткая характеристика субоптимальных методов
оценивания для стохастических дифференциальных систем. Подроб-
но рассматривается метод нормальной аппроксимации апостериорного
распределения. В разделах 3.2 и 3.3 изложены методы моментов, се-
миинвариантов, ортогональных разложений и квазимоментов для при-
ближенного решения фильтрационных уравнений. Раздел 3.4 содержит
вывод уравнений для модифицированных (для ненормированных рас-
пределений) методов нормальной аппроксимации, моментов и ортого-
нальных разложений. В разделах 3.6. и 3.7 для дискретных стохасти-
ческих систем рассматриваются дискретные субоптимальные фильтры,
основанные как на приближенном решении фильтрационных уравне-
ний, так и на их упрощениях. Особое внимание уделяется дискретным
обобщенным фильтрам Калмана. В разделе 3.8 получены фильтраци-
онные уравнения на основе стандартного и модифицированного мето-
дов эллипсоидальной аппроксимации. Раздел 3.9 содержит изложение
теории субоптимального совместного оценивания и распознавания. Рас-
сматриваются адаптивные субоптимальные фильтры Калмана. В конце
главы даны дополнения и задачи для упражнений.
3.1. Субоптимальное оценивание. Метод нормальной
аппроксимации
3.1.1. Общая характеристика приближенных методов оп-
тимального оценивания. Точное решение задач оптимального оце-
нивания возможно только в случаях, когда уравнения нормальной сто-
хастической системы (2.2.3)
dY = (У, X, t)dt + (У, t)dW,
dX = ip(Y, X, t)dt + ^(У, X, t)dW. (3.1.1)
линейны (п.2.3.1) или линейны только относительно вектора состояния
X при независимой от состояния функции <ф (п.2.3.3). Конечно, уравне-
ние (2.2.13) и формула (2.2.14) или уравнение (2.2.16) и формула (2.2.17)
372
ГЛ. 3. СУБОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ОФК
дают точное решение задачи оптимальной фильтрации в общем случае
для любых уравнений (2.3.1), удовлетворяющих условиям, при которых
была выведена формула (2.2.11). Однако это решение не может быть
реализовано практически. Для нахождения оптимальной оценки век-
тора состояния необходимо решить фильтрационное уравнение (2.2.16)
для апостериорной характеристической функции или фильтрационное
уравнение (2.2.16) для апостериорной плотности вектора состояния X
после получения результатов наблюдений, и лишь потом можно вычис-
лить оптимальную оценку вектора X по формуле (2.2.14) или (2.2.17).
Но методов точного решения уравнений (2.2.16) и (2.2.17) в общем слу-
чае пока еще не существует. Численное решение этих уравнений в зада-
чах реального времени тоже невозможно, так как для этого требуется
много времени, а решать их необходимо каждый раз после получения
результатов наблюдений. Кроме того, практическое применение тео-
рии оптимальной фильтрации раздела 2.2 имеет смысл только в тех
случаях, когда оценки можно вычислять в реальном масштабе време-
ни по мере получения результатов наблюдений. Действительно, теория
раздела 2.2 дает оптимальные оценки в каждый момент t по резуль-
татам наблюдений, полученным к этому моменту, без использования
последующих результатов наблюдений. Если эти оценки не могут быть
вычислены в тот же момент t или хотя бы с фиксированным приемле-
мым запаздыванием и их вычисление приходится откладывать на буду-
щее, то нет никакого смысла отказываться от использования наблюде-
ний, получаемых после момента t, для оценивания состояния системы
в момент t. Поэтому для статистической обработки результатов после
окончания наблюдений целесообразно применять известные из матема-
тической статистики методы постобработки информации.
Необходимость обрабатывать результаты наблюдений в реальном
масштабе времени непосредственно в процессе эксперимента привела к
появлению ряда приближенных методов оптимальной фильтрации, на-
зываемых обычно методами субоптимальной фильтрации. Одни при-
ближенные методы основаны на приближенном решении фильтрацион-
ных уравнений (2.2.13) или (2.2.15), а другие - на превращении фор-
мул (2.2.19) и (2.2.23) для стохастических дифференциалов оптималь-
ной оценки X и апостериорной ковариационной матрицы ошибки R в
стохастические дифференциальные уравнения для X и R путем разло-
жения функций </>, ipi и V’i в степенные ряды и отбрасывания остаточ-
ных членов.
Для приближенного решения уравнения (2.2.13) для апостериорной
характеристической функции #i(A) вектора Xt можно применить ме-
3.1. СУБОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. МН А
373
тоды, основанные на параметризации одномерных распределений слу-
чайного процесса, определяемого стохастическим дифференциальным
уравнением (разделы 1.7 и 1.8). Эти методы дают стохастические диф-
ференциальные уравнения для параметров апостериорного распределе-
ния. Простейшим таким методом является метод нормальной аппрок-
симации (МНА) апостериорного распределения (раздел 1.7). Другие
методы основаны на использовании в качестве параметров апостери-
орных распределений моментов, семиинвариантов или коэффициентов
ортогонального разложения апостериорной плотности вектора состоя-
ния системы (раздел 1.8).
3 а М е Ч а Н И е. Все получаемые дальше стохастические дифференциальные
уравнения, так же как и уравнения раздела 2.2, представляют собой уравнения Ито. Ха-
рактерной чертой уравнений Ито в теории оптимальной фильтрации, отличающей их от
других форм стохастических дифференциальных уравнений, является то, что дифферен-
циал наблюдаемого процесса Y всегда входит в них в комбинации dY — ipidt. Иными
словами, в уравнения Ито всегда входит дифференциал соответствующего обновляющего
процесса (п.2.3.2).
3.1.2. Метод нормальной аппроксимации апостериорного
распределения
о Так как нормальное распределение, аппроксимирующее апосте-
риорное распределение вектора X, полностью определяется апостери-
орными математическим ожиданием X и ковариационной матрице R
вектора X, то при аппроксимации апостериорного распределения век-
тора X нормальным распределением все математические ожидания в
правых частях формул (2.2.19) и (2.2.23) для dX и dR будут определен-
ными функциями X, R и t, т.е. (2.2.19) и (2.2.23) будут представлять
собой стохастические дифференциальные уравнения, определяющие X
и R:
dX = f(Y, X, R, t)dt + h(Y, X, R, f)dt [ dY - (Y, X, R, t)dt ] , (3.1.2)
dR = {/(2)(У, X, R, t) - h(Y, X, R, t)^^)(Y, t)h(Y, X, R, Z)T} dt+
где
+
r=l
f{Y,X,R,t) =
(3.1.3)
= [(2тг)" |Я|]~1/2 У V(Y,x,t)wp{-(xT - XT)R~\x - X)/2jdx,
—OO
(3.1.4)
374
ГЛ. 3. СУБОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ОФК
fw(Y,X,R,t) =
= [(2тг)п |7?| ]-1/2 у <р!(У, х, t)exp (хт — XT)R~1(x — X)/2j dx,
— ОО
(3-1.5)
h(Y,X,R,t) = |[(2тг)п |Я| ]~1/2 У [х<р^,х,1)т + ^(Y,x,t)] х
—ОО
х ехр { - (хт - XT)R-1 (х - X)/2} dx- Xfw(Y, X, R, t)T J x
xfMiW,*), (3.1.6)
fM(Y,X,R,t) = [(2ir)n \R\]~1/2 I ^x-XMY,x,t)T+
—OO
+</р(У, x, t) (xT — XT) + СИ я, 0 } x
x exp |-(xT - XT)R-\x - X)/2} dx, (3.1.7)
pr(Y,X,R,t) = [(2тг)" |Я|Г1/2 У {(* - X)(xT - XT)ar(Y,x,t)+
—ОО
+(х - X)br(Y,x,t)T(xT - Хт) + br(Y,x,t)(xT - Хт)}х
х ехр (хт — XT)R~l(x — Х)/2^ dx (г = 1, ... , ni). < (3.1.8)
Таким образом, доказано следующее утверждение.
Теорема 3.1.1. Пусть уравнения нормальной стохастической
дифференциальной системы (3.1.1) допускают применение МН А. Тогда
в основе МН А апостериорного распределения лежат уравнения (3.1.2)
и (3.1.3) при соответствующих начальных условиях.
За начальные значения X, R при интегрировании уравнений (3.1.2)
и (3.1.3), естественно, следует принять условные математическое ожи-
дание и ковариационную матрицу величины Хо относительно Yq:
Хо = М[Х0 | Го], Яо = М [(Хо -ХО)(ХОТ-ХОТ) | Го] •
3.1. СУБОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. МНА
375
Если нет информации об условном распределении Xq относительно Уо,
то начальные условия можно взять в виде Xq = МХо, Rq = М(Хо ~
—МХ0)(Х^ — MXj^). Если же и об этих величинах нет никакой инфор-
мации, то начальные значения X, R приходится задавать произвольно.
Из формулы (3.1.8) видно, что если функция pi линейна относи-
тельно X, функция *ф не зависит от X, то при нормальной аппрок-
симации апостериорного распределения все матрицы рг равны нулю,
вследствие чего уравнение (3.1.3) не содержит dY.
В случае, когда функции ^1(У, О и il)(Y,X,t) зависят только от
времени, т.е.
Ш = Ш = Ш (3.1.9)
а процесс W является винеровским то, как известно (раздел 1.7), МНА
приводит к тем же уравнениям, что и метод статистической линеариза-
ции (МСЛ). В практических задачах целесообразно сначала заменить
уравнения (3.1.1) при условии (3.1.9) на статистически линеаризован-
ные, а затем формально применить уравнения линейной теории филь-
трации (раздел 2.3).
Пример 3.1.1. Найти алгоритм оценивания состояния нелинейной системы
X = -X3 + XV1, (I)
по результатам наблюдения величины X с аддитивной помехой р2> представляющей со-
бой нормально распределенный белый шум, независимый от У}.
Наблюдаемый процесс в этом случае определяется уравнением Z = Y — X 4" У}.
Процесс W(i) в уравнениях (3.1.1) состоит из двух независимых скалярных винеровских
процессов Wl(0» ^2 (О» слабыми с.к. производными которых служат белые шумы Vi
и V2 соответственно. Соответствующую структуру имеют в этом случае матрицы
^(y,X,t) = [X0], ^1(V,^) = [01], v =
где и V2 - интенсивности белых шумов Vi и У соответственно. Функции ip и pi
определяются формулами p(Y, X, t) = —Х^, pi (У, X, t) = X. Уравнения (3.1.2) и
(3.1.3) имеют вид
к = -Х(Х2+ 3R) + t'21R(Z - X), (II)
R = (izi - 6Л)(Х2 + R) - р2-1Я2. (Ш)
Эти уравнения приближенно определяют оптимальную оценку X состояния системы (I)
и апостериорную дисперсию ошибки. За начальные значения X и R следует взять апри-
орные математическое ожидание и дисперсию величины Xq, поскольку Yq не задано и
может быть взято совершенно произвольно, независимо от Xq.
Ul 0
0 V2
376
ГЛ. 3. СУБОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ОФК
Пример 3.1.2. Найти алгоритм приближенной оптимальной фильтрации про-
цесса, определяемого уравнением
X = -X3 + V1, (I)
если аддитивная помеха в наблюдениях представляет собой нормально распределенную
случайную функцию с ковариационной функцией к(т) = Dc~~a , Z — Y = X 4- U.
Дифференцируем уравнение наблюдения и подставляем в полученное уравнение значение
U из уравнения формирующего фильтра помехи
и = -aU + V2i (II)
и значение U из уравнения наблюдения. В результате получаем
Z = -aY+ аХ-X3+ V1+V2. (Ill)
Заменив уравнение наблюдения этим преобразованным уравнением наблюдения, сводим
задачу к задаче оптимальной фильтрации (раздел 2.2) при (р\ (Z, X, t) — —OlZ+OlX —
—Х\ = [1 1]. Уравнения (3.1.2) и (3.1.3) имеют в этом случае вид
к = -Х(Х2 + ЗЯ) + (i/i + t/2)-1 Н + aR-
—3R(X2 + R)][z+ aZ-аХ + X(X2 + ЗЯ) ] , (IV)
л Г л "12
Я = 1/1 - 6Я(Х2 + Я) - (IZ1 4-1/2)-! + ай - ЗЯ2(Х + Я)] -
-6(1/1 + 1/2)-1ХЯ2 [ Z + aZ - аХ + Х(Х2 + Я) ] , (V)
где интенсивность У2 белого шума V2 равна 2Da.
Чтобы найти начальные условия для полученных уравнений, воспользуемся прие-
мом п.2.5.3 для нахождения условных математического ожидания и дисперсии начального
значения Xq процесса X относительно Уо- Так как Y0 = X0 + Ut и помеха U распре-
делена нормально и независима от X, то безусловные дисперсии и ковариация величин
Xq и Yq равны соответственно Dq, Dq + D и Dq. Допустив, что Xq - нормально
распределенная величина, пользуясь известными формулами для условных математиче-
ского ожидания и дисперсии одной компоненты нормально распределенного случайного
вектора относительно другой, находим начальные значения величин X и R:
3.1. СУБОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. МНА
377
Хо = м [Хо I Zo ] = DoZo/(Do + D), (VI)
Ro = M [ (Xo - Xq)2 I Zo ] = D0D/(D0 + D). (VII)
Пример 3.1.3. Найти приближенно оптимальный алгоритм оценивания состо-
яния X системы, описываемой скалярным уравнением
X = -0X + Vi,
(I)
и неизвестного параметра 0 по результатам наблюдения процесса Z = Y = X + Vjj»
где V2 - белый шум, независимый от Vp
Заменим параметр 0 случайным процессом e(t), определяемым уравнением О —
= 0, и примем за расширенный вектор состояния пару [ X0 ] . Тогда уравнения (3.1.1)
будут иметь вид
Z = Y = Х + [01][И V2]T,
X
ё
хе
о
10 Vi
0 0 v2
(П)
Таким образом, в данном случае h — 2, y>(V, X, 0, t) — [ —Х0 0 (V, X, 0, t) =
= х,
i[>(Y,X,0,t) = q Q
<MY,X,0,t) = [01].
Уравнения (3.1.2) и (3.1.3) имеют вид
i = -XQ - R12 + <1Яц(2 - X), ё = j/2_1Z?i2(Z - X),
Rix =vx~ 2(ёЯц + ХЯ12) - R2n, (Ш)
Я12 = — QRx2 — XR22 — 1'i1R11R12, R22 = — I'l 1Rx2> (IV)
где 72ц, 7212 , 7222 ~ апостериорные дисперсии и ковариация ошибок оценок X и О
соответственно. За начальные значения Ху О, 72ц, 7212 , 7222 следует принять соот-
ветствующие априорные величины, причем 0о, 72220 и 72120 всегда приходится брать
произвольно, так как априорной информации о параметре 0 обычно иет, за исключением,
может быть, информации о возможном диапазоне его значений.
378
ГЛ. 3. СУБОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ОФК
3.2. Методы моментов и семиинвариантов для
приближенного решения фильтрационных уравнений
3.2.1. Метод моментов. Начальные моменты. Если аппрок-
симировать апостериорную плотность pt(x) вектора состояния Xt систе-
мы некоторой функцией р*(я; 0), зависящей не только от апостериорных
математического ожидания X и ковариационной матрицы R вектора
X, но и от его апостериорных моментов до порядка N включительно,
то в силу п. 1.8.2 к уравнениям для X и R придется добавить уравне-
ния для апостериорных начальных моментов аг или центральных дг
(гх, ... , гр = 0,1, ... , 2V; |г| = 3, , АГ).
о Чтобы вывести уравнения для апостериорных начальных момен-
тов аг, положим в (2.2.11) f(X) = Х[х ... Х„п. Тогда будем иметь
А = df/dt = о, df/dxs = TSx?... х;--1... х^ (s = i,..., п),
a^f/oxl = rs(r, - i)xp... хр-2... х;» (s = 1,..., n),
d2f/dxsdxq = rsrqx?... xp -1 ... xp-1...xp (3.2.1)
(s = 1, ... , q — 1; q = 2 , ... , n),
n
tr [AS(VH>T)] = 12 (O2f/dXsdXq)asq(Y,X,t) =
s,q=l
n
= £x> W • • • x;--2... xp+
S=1
+2 Z Z rw^Y’ W • • • x;--1... xp-1 ...x?,
q=2 s—1
где asq(Y,X,t) - элементы матрицы a(Y,X, t) = (il>vi/>T)(Y,X,t). Под-
ставив эти выражения в (2.2.11), получим следующие стохастические
дифференциальные уравнения для апостериорных начальных момен-
тов вектора X:
dar = (}rdt + T]r(dY — f^dt)
(П , ... , rn = 0,1, ... , N; |r| = 1, ... , TV), (3.2.2)
где
3.2. МЕТОДЫ МОМЕНТОВ И СЕМИИНВАРИАНТОВ
379
п °г
= 52г» / ^,(У,ж,г)жр ...xrs,~1...x%‘p*(x;9)dx+
8=1 -оо
1 п т
+ ^Yr»(.rs - 1) / ао(У,®,«)а:р ...xrs‘~l ...xT*p*(x\&)dx+
*=> -Уоо
п V-1 °°
+ ^52rarq / а,д(У,®,0®р ...х^-1 ...х^-1 ...x^p*(x;ff)dx,
«=2«=1 4,
(3.2.3)
т)г = pT(Y,O,t) =
<Pi (У, х, 4)атр .. ,x%‘p*(x;ff)dx - f^Tar+
—ОО
оо
• • -я?”1 • • х
°-л -оо
у(1) = fW(Y,e,t) = I tpi(Y,x,t)p*(x’,0)dx, (3.2.4)
—ОО
а ('фъ''фТ)8 - s-я строка матрицы Интегрирование уравнений
(3.2.2) при начальных значениях моментов аг при t = to, равных соот-
ветствующим условным моментам вектора Xq относительно Yq, прибли-
женно определяет все апостериорные моменты аг (и , ... , гп =
= 0,1, ... , N] |г| = 1, ... , 2V), составляющие вектор параметров в.
При аппроксимации апостериорной плотности pt(x) отрезком орто-
гонального разложения вида (п. 1.3.5):
N
pt(x) =р*(х;в) = Wi(x)
1 + 52 12
к=3 М=*
(3.2.5)
380
ГЛ. 3. СУБОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ОФК
функции /Зг, т)г и представляют собой линейные функции момен-
тов аг( И = 3, ... , N) с коэффициентами, зависящими от моментов
первого и второго порядков:
N N
Рт — Рв,г + Цг = ^0,г “Ь ^1/,г9р(^)»
*=3|iz|=* k=3 |г|=*
N
/(1) = /о(1) + Е Е (3.2.6)
k=3 |r|=fc
так как cv = qv{a), а величина qv(a) при |i/| > 3 представляет собой ли-
нейную функцию моментов аг (|г| = 3, ... , TV |i/|) с коэффициентами,
зависящими от моментов первого и второго порядков (п.1.3.5).
При аппроксимации плотности pt(x) отрезком ряда Эджуорта
(п. 1.3.5) с учетом начальных моментов до TV-го порядка число слагае-
мых в сумме по к увеличится до 3N — 6 и коэффициенты с„ при |i/| > N
не будут равны qv(a) = а будут функциями семиинвариантов до
TV-го порядка, которые надо будет заменить их выражениями через на-
чальные моменты. <
Таким образом, имеем следующий результат.
Теорема 3.2.1. Пусть уравнения нормальной стохастической
дифференциальной системы (3.1.1) допускают применение метода на-
чальных моментов. Тогда в основе метода начальных моментов для
аппроксимации апостериорного распределения (3.2.5) лежат уравне-
ния (3.2.2) при соответствующих начальных условиях.
Пример 3.2.1. Для задачи примера 3.1.1
Y — Z = X + V2, X = -X3 + XVi, (I)
уравнения (3.2.2) имеют вид (d!i — X, а2 = X2 + R)
X = -а3 + (а2 - X2)(Z - X), (II)
а2 = -2а4 + 1^а2 + ^(аз - Xa2)(Z - X), (III)
а3 = 72ХЪ - 180Ха2 + 3(^ + 20Х2)а3 - + 90Ха% - ЗОа2а3+
+^\a4-Xa3)(Z-X), (IV)
а4 = 256Х® - 480Х4а2 + 160Х3а3 + б^сц + 120а| - 60а2а4+
3.2. МЕТОДЫ МОМЕНТОВ И СЕМИИНВАРИАНТОВ
381
+Р2’1(4Ха4 - 20Х2а3 + 60Х3а2 - ЗОХс^ + 10а2а3 - 24X5)(Z - X). (V)
При аппроксимации апостериорной плотности отрезком ряда Эджуорта с учетом момен-
тов до четвертого порядка в правой части последнего уравнения добавится слагаемое
Юмз = Ю(огз - ЗХа2 + 2Х3)2.
3.2.2. Метод моментов. Центральные моменты. Уравне-
ния для апостериорных центральных моментов выводятся значительно
сложнее, чем для начальных. Их можно вывести дифференцирова-
нием формулы, выражающей /1Г через характеристическую функцию
(п.1.3.4).
> Напишем сначала уравнения для апостериорных математическо-
го ожидания X и ковариационной матрицы R. Заменив в выражени-
ях математических ожиданий в (2.2.19) и (2.2.23) апостериорную плот-
ность pt(x) аппроксимирующей ее функцией р*(я;0), получим уравне-
ния
dX = fdt + h(dY - fwdt), (3.2.6)
dR = (/(2) - hihvip[hT)dt + ^pr(dYr - f^dt), (3.2.7)
r=l
где
oo
f = f(Y,e,t)= У <p(Y,x,t)p*(x-,e)dx, (3.2.8)
— OO
y(D = = У <pi(Y,x,t)p*(x;O)dx, (3.2.9)
— OO
/(2) = /(2) (У, 0, t) = I [(z - X)<p(Y, X,t)T +
— OO
+<^(У,x,t)(xT — XT) 4- ^i/^T)(Y,x,t)]p^(<x;e)dx, (3.2.10)
oo
h = h(Y,0,t) = | У [z^1(y,z,t)T+
—OO
+(^i/^jr)(y,z,t)]p*(z;0)dz - X/^^T|(^ii/^i’)-1(y,t)> (3.2.11)
382
ГЛ. 3. СУВОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ОФК
pr = Pr(Y,e,t) = I [(х - Х)(хт - XT)ar(Y,x,t)+
—ОО
+(х - X)br(Y,x,t)T + br(Y,x,t)(xT - XT)]p*(x;0)dx (3.2.12)
(г = 1, ... , П1),
а 0 - совокупность моментов X, Я, /1Г (и , ... , гп = 0,1, ... , 7V; |г| =
= 3, ... , N).
Для вывода уравнений для остальных моментов /1Г продифферен-
цируем формулу (п. 1.3.4)
Г 3|г|
Mr = Я6.А ” е~*Л ХЛ(А) , (3.2.13)
[д(гА1)Г1 ...д(гАп)г» ]л=0
выражающую апостериорные центральные моменты через апостериор-
ную характеристическую функцию pt (Л). В результате получим
Q 1Г1 •\т V
dpr = ЯГП V! (3-2.14)
[d(iAi)ri ...0(гАп)г» ]А=0
По формуле Ито (1.4.82) с учетом (2.2.13), (3.2.6) находим
de-ixT*gt(X) = -iXT e~ixT * gt(X)dX + e~ixT * dgt(X)+
+ 5 ] 52 (*Ae)(iAg)e_‘AT*gtWhtihvifihT - ^iX'kihvtf h? I di,
le,g=l e=l )
где hs - s-я строка матрицы h, определяемой формулой (3.2.11), a
oo
к = k(Y, 0, A, t) = | У bl (У, x, t)T+
— OO
+iXT (‘ф1/‘фг)т (Y, x, t)]e~xT(x~*)p*(z; 0)dx-
-fWTe-xTji9tW } (V’^V’D-1 (X, t). (3.2.15)
Подставим полученное выражение de~xTgt(X) и дифференциалы dX
и dpt(A) из (3.2.6), (2.2.13) в (3.2.14) и вычислим каждое слагаемое по
3.2. МЕТОДЫ МОМЕНТОВ И СЕМИИНВАРИАНТОВ
383
отдельности (конечно, как и прежде, с заменой pt(x), где надо, аппрок-
симирующей функцией р*(я;0)). Пользуясь известными из теории сто-
хастических систем формулами (п. 1.8.2), находим
/{д(»А1)-Л..а(гАр)-яРЛ:Г*>(К’:С’<))
—ОО
“ Аг (У, х,$) А
2!
,»АТ(® X) I p*(x-,ff)dx =
J а=о
¥>,(У, X, i)(xi - Xi)ri ... (х, - Х,)"-1
...(хп~ XnYnp*(x-,9)dx +
2 J
хв)г--2... (х„ - X„)r"p*(z; 9)dx+
п 9-1 °?
+ Z52r‘r« / ^{Y^tYxx-X^ ...^s-X,Y‘~l...
q=2 »=1 -oo
... (x, - X,p-‘... (x„ - X„)r-p'(x;S)<fc, (3.2.16)
a|r|^A‘) 1 =(7l[И(Г,х,0Т+
—oo
+iAT (V’li'V’DO'')x, £)]e,AT(®-*) 1 P*(x', 0)dx-
) A=0
384
ГЛ. 3. СУБОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ОФК
ОО
| У ¥>i(y,a:,t)T(a:i -Xi)r' ... (хп - Xn)r"p*(x;0)dx+
—со
...(xn-Xn)rnp*(x;O')dx-ft‘^Tpr^^1^i) l(Y,t), (3.2.17)
{5(»A1)r> ...9(iXnyn (iA«We“A %d<(A)}A=0 = T,rqpr-e.-',,
(3.2.18)
a(iAi)n ...9(iAn)-"(iAe)e-‘A Xd‘(A)}A=0 = r’(r’ " 1)Mr-2e” (3219)
J d|r| .. .1
'/A=o
~ • I d(iX^ ... (iXty-~i... d(iXn)r« JA=0 ’
где e8 - вектор, все компоненты которого равны нулю, кроме одной $-й,
равной единице. В результате получим окончательные уравнения
dpr = ]Br ~^r,fapr.e. + X 52г»(г» “ 1)^^1^?'ЛГДг-2е.+
' в=1 S=1
+ 5252r,r9fteV’l«/V’ir^Mr-e,-e, - g ^rtTh-e.^lV^Thtjdt+
q=2 s=l s=l '
+ Иг - £ г*л^г-е. ) (dY - f^dt) (3.2.21)
\ S=1 /
(n, ... ,rn = 0,l, ... , N-, |r| = 3, ... , N),
где
3.2. МЕТОДЫ МОМЕНТОВ И СЕМИИНВАРИАНТОВ
385
п 7
0r = /3r(Y,e,t) = ^re / iPs(Y,x,t)T(X1-X^ ...
8=1 -оо
...(х,-Х.у--1...(хп -Х„)г"р*(*;№+
1 п 7
+5?^,-!) / -Х1)п ...(xs-Xs)r’~2...
«=1 л
...(х,- Х,У‘~*... (х, - Х,)г’-1... (in - Xny~p*(x;0)dx, (3.2.22)
<va.\ / 9^k{Y,9,X,t) | .
T)r = 7?Г(У, 0,t)= < ----Я,.Л Г
(a(iAi)ri ...5(tAn)r" J A=o
= | J ^(Г,х,0Т(®1 - *i)n •• .(x„-X„)r"P*(x;0)dx+
— OO
n 7
+ ^rs / x,t)(xi -Х1У1 ... (xs - ХаУ‘~г...
S=1 -oo
• • • (X„ - X„)r"p‘(x;(?)dx - f^Pr-e,}(^i^D_1(^t), (3.2.23)
fs - s-й элемент матрицы-столбца /, определяемый формулой (3.2.8).
За начальные значения моментов /хг при t = to следует принять
соответствующие условные моменты величины Xq относительно Уо-
Уравнения (3.2.6), (3.2.7) и (3.2.21) определяют приближенно все
моменты, от которых зависит аппроксимирующая апостериорную плот-
ность pt(x) функция р*(я;0). В качестве р*(х;0) обычно берут отрезок
ортогонального разложения (3.2.5) плотности pt(x), в частности разло-
жения по полиномам Эрмита, или отрезок ряда Эджуорта. В последнем
случае можно рассчитывать на более точную аппроксимацию плотно-
сти pt(x) при данном наивысшем порядке учитываемых моментов. <
Следовательно, имеем следующий результат.
13 Фильтры Калмана и Пугачева
386
ГЛ. 3. СУБОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ОФК
Теорема 3.2.2. Пусть уравнения нормальной стохастической
дифференциальной системы (3.1.1) допускают применение метода
центральных моментов. Тогда в основе метода центральных момен-
тов для аппроксимации апостериорного распределения (3.2.5) лежат
уравнения (3.2.6), (3.2.7) и (3.2.21).
Пример 3.2.2. В задаче примера 3.2.1
Y = Z = X + V2, X = -X3 + XVi, (I)
при аппроксимации Pt(x) отрезком разложения по полиномам Эрмита с учетом моментов
до четвертого порядка уравнения (3.2.6), (3.2.7) и (3.2.21) имеют вид
А' = -Х(Х2 + ЗЯ)-дз + ^"1Я(2-Х)) (П)
Я = (i/i - 6Х2)Я - i/21R2 - 6Хр3 + 1/2“1дз(2 - X) - 2д4, (III)
Дз = 9ХЯ2 - 9(Х2 + ЗЯ)д3 - 9Хд4 + 31/1(2ХЯ + д3)-
--^Ядз + ^Ч/М-ЗЯ^И-Х), (IV)
Д4 = 120Я3 - 108ХЯдз - 12(Х2 + 5Я)д4 + 4д| + 6^ (X2R + 2Хд3 + /м)~
-2^1R(H4 - ЗЯ2) + б1/2_1Ядз(^ - X). (V)
При аппроксимации Pt(x) отрезком ряда Эджуорта с учетом моментов до четвертого
порядка в правой части последнего уравнения добавится слагаемое 10д|.
Пример 3.2.3. В задаче примера 3.1.3
Y = Z = X + V2, Х = -XQ + Vi, 0 = 0, (I)
при аппроксимацииPt(x) отрезком разложения по полиномам Эрмита или отрезком ряда
Эджуорта с учетом моментов до четвертого порядка уравнения (3.2.6), (3.2.7) и (3.2.21)
имеют вид
Я = -хё - Я12 + i/f/Rn(z-х), ё = 1/2-1Я12(^-х), (п)
Яц = i/i — 20Яц — 2ХЯ12 — 2д21 — v2 1 R2i + i/2 1Дзо(^ ~ X), (III)
Я12 = — ёЯ12 — ХЯ22 — pi2 — i/2 1ЯцЯ12 + i/2 1д21 (Z — X), (IV)
я22 = -v^Rh + ^2-1Д12(Z - X), (V)
3.2. МЕТОДЫ МОМЕНТОВ И СЕМИИНВАРИАНТОВ
387
Дзо — ЗЯ11Я22 — 30/хзо — ЗХд21 — 3/хз1 —
3
-^2-1Я11Мзо + ^2-1(М40 - 3R2n)(Z - X), (VI)
к!
Д21 = 2Ri2 ~ 20Д21 - 2ХД12 - 2/222 - ^1/2^1Л12ДзО ~ V1#11Д21 +
+^2_1(М31 - ЗЯиЯ12)(2 - X), (VII)
Д12 — R12R22 — ©М12 — Х/203 — Д13 — 1'^'1Я12Д21 ~ Х*/2^1/*12 +
+^2-1 (Д22 - Я11Я22 - 2Rj2)(Z - X), (VIII)
3
ДОЗ = “9^2 1-^12Д12 + ^2 1 (Д13 ~ ЗЯ12Й22)(^ ~ X), (IX)
Д40 = — 12/?12Дзо — 24.Rn/Z2i — 40/мо — 4Х//31 —
—2р2 1Лц(д4о - ЗЛп) + 6р^’1ЛцДзо(^ — X), (X)
Д31 = -”ЗЙ22Д30 “* 15R12M21 ~ 9R11/X12 — 30Д31 — ЗХ/Х22 +
+3lAf1 RnR12~ ^21 - 9^Г1^11М31+31/^1(Д12Дзо+ЯцД21)(^~Х),
(XI)
Д22 — — 67?22Д21 — 10-R12M12 — 2Д11Д03 — 20Д22 — 2Х/Х13 +
4-1/1 1/?11/?22 4- 5l/2 1ЛцЛ12 — и2 1(^12Д31 4- #11Д22)4-
4-1/^1(7?22Дзо 4- 4Л12Д21 4- ЛиДп)^ — (ХП)
Д13 = —6R22M12 — ЗД12Д03 — ®Д13 “ Х^Д04 4" 3l/2 1R12(R11R22 4" ^12)“*
3 1
_ 9^2 1Й12Д22 - ^^1-R11M13 4- 3l/jf 1(/?22Д21 4- Я12Д12)(^ “ (ХШ)
До4 = — 2i/^”1R12(M13 — 3R12-R22) 4- 6l/2 XR22M12(^ — X). (XIV)
3.2.3. Метод семиинвариантов. Если параметрами функции
р*(я;0), аппроксимирующей апостериорную плотность pt(x) величины
X, служат семиинварианты, то можно вывести стохастические диффе-
ренциальные уравнения, приближенно определяющие эти апостериор-
ные семиинварианты (ТСтС, п.7.4.1).
388
ГЛ. 3. СУБОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ОФК
о Для этого продифференцируем по формуле Ито (1.4.82) выраже-
ние семиинварианта \г через характеристическую функцию
(ТСтС, п.3.5.3)
Хг = [а(гА1)п ...а(гАр)’-»1пл(А)] А=о • (3 2 24)
В результате получим
Г д|г|
<3-2-25)
Стохастический дифференциал Лпр* (А) находим по формуле Ито
(1.4.82). Пользуясь обозначением (3.2.15) коэффициента к при dY—$\dt
в выражении стохастического дифференциала (2.2.13) характеристиче-
ской функции (А), будем иметь
dlnpt(A) = exp{-lnpt(A)}dpt(A)+
+ | ехр 12гХтX — 2 In gt (А)} kt/ti ктdt.
Подставив это выражение в (3.2.25), заменив стохастический диффе-
ренциал dpt(A) его выражением (2.2.13), пользуясь формулами (п. 1.8.2)
и учитывая, что согласно (3.2.23)
г a,r|fc 1
ia(iA1)n...a(»A„)’-- /А=0-т?г’
получим уравнения для апостериорных семиинвариантов вектора X со-
стояния системы (3.1.1):
dXr = 0rdt + Tfr(dr -
n!...rn! Пу](-1Г
gi=o
, f f}r_qdt+
+T)r_q(dY - fwdt] +
3.2. МЕТОДЫ МОМЕНТОВ И СЕМИИНВАРИАНТОВ
389
"Уну
___________Хи • • • X*.
и+^.=9 1,111
ri-qi rn-qn
(3.2.26)
(П .... , rn = 0,1, ... , N; |r| =3, ... , N),
где /3r, r]r - определяются формулами (3.2.9), (3.2.22) и (3.2.23).
При этом мы учли, что, во-первых, в силу (3.2.15) к = k(Y,0,O,t) =
= 0, во-вторых, первые производные функции exp {iXTX — lnpt(A)}
по г’А равны нулю и, в-третьих, производные функции ехр{2гАтХ -
—2Ingt(Л)} по гЛ отличаются от производных функции ехр{гЛт —
— In <7Г(Л)} только тем, что все семиинварианты удваиваются. При этом
мы воспользовались векторными индексами г = [ri...rn]T, q =
= [ Qi ... qn ] , i/д. = [ i/fci ... i/kn ] , I = [ li ... ln ] . <
Добавив к (3.2.26) уравнения (3.2.6) и (3.2.7), получим полную си-
стему уравнений, приближенно определяющую апостериорные семиин-
варианты вектора X, от которых зависит функция р*(я;0).
За начальные значения семиинвариантов Хг при t = to следует при-
нять соответствующие семиинварианты условного распределения вели-
чины Xq относительно Уо-
Таким образом, получен следующий результат.
Теорема 3.2.3. Пусть уравнения нормальной стохастической
дифференциальной системы (3.1.1) допускают применение метода се-
миинвариантов. Тогда в основе метода семиинвариантов для аппрок-
симации апостериорного распределения (3.2.5) лежат уравнения
(3.2.6), (3.2.7), (3.2.26) при соответствующих начальных условиях.
Обратим внимание на то, что при |r| = 1 матрицы-строки т)г сов-
падают с соответствующими строками матрицы h в уравнении (3.2.6),
r]ek = *7о... ,1 ,...,о = hk (к = 1, ... , п),
к
а при |г | = 2 их элементы представляют собой соответствующие эле-
менты квадратных матриц рг в уравнении (3.2.7),
^2efc — [ Р1 кк • • • Ртпкк ] , qek+ei — [ Plkl • • • Pmkl ] {к, I — 1,..., п).
390
ГЛ. 3. СУВОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ОФК
Пример 3.2.4. В задаче примеров 3.2.1 и 3.2.2
Y = Z = X + V2, х = -X3 + XVi, (I)
при аппроксимации Pt(x) отрезком разложения по полиномам Эрмита с учетом моментов
до четвертого порядка уравнения (3.2.16), (3.2.7) и (3.2.26) имеют вид
£ = -X(X2 + 3R)-k3 + v21R(Z-X), (II)
R = i/i - 6(Х2 + R)R - 6Хк3 - 2к4 - 1/2_1Я2к3(2 - X), (III)
к3 = -18ХЯ2 - 9(Х2 + ЗЯ)к3 - 9Хк4 + 3v4(2XR + к3)-
+ (IV)
к4 = 12R3-72XRk3-12(X2+4R)k4+4kI+6^[(X2+2R)R+2Xk3+k4)]+
Ч-l/"1 (6Я3 - Зк>1 - 2Rk4). (V)
При аппроксимации р^(х) отрезком ряда Эджуорта с учетом семиинвариантов до
четвертого порядка в правой части последнего уравнения добавится слагаемое 10к|.
Пример 3.2.5. В задаче примера 3.2.3
Y = Z = X + V2, Х = -XQ + Vi, 0 = 0, (I)
при аппроксимацииPt\Х) отрезком разложения по полиномам Эрмита или отрезком ряда
Эджуорта с учетом семиинвариантов до четвертого порядка уравнения (3.2.6), (3.2.7) и
(3.2.26) имеют вид
к = -XQ - R12 + рГ/Яп (И - X), (II)
ё = ъ^12(г-х), (ш)
Rn = —2©Яц — 2ХЛ12 — 2к21 — У2 ^2 1^зо(^ — -^)» (IV)
Я12 = —0Я12 ~ XR22 — К12 — v2 1R11R12 "I" ^2 1к21(^ — -V)> (V)
«22 = -^Rb + «/2-1«12(2 - X), (VI)
кзо — — 6ЯцЯ12 ~ 30кзо — ЗХк24 — Зкз1 —
3
-l/2 1Rllli30 + ^2 ГК4о(^ — ^)>
(VII)
3.3. МЕТОДЫ ОРТОГОНАЛЬНЫХ РАЗЛОЖЕНИЙ
391
«21 — —2(7?ii7?22+^12) —20«21 —2^V«12 —2«22—lj^12«30—^2 lI?ll«21 +
&
+p2-1«3i(2-X), (VIII)
«12 = —2jR12jR22 — ®«12 — -Х«03 ~ ^2 1^12«21 ~ «13 — Z^2 X^?ll«12 +
&
+1^2 ^22(2-X), (IX)
3 _
«03 = ~qI/2 1-R12«12 + ^2 Х«1з(^ ~ X), (X)
«40 = -12(7?12«ЗО 4" -йц«21) *“ 4(©/€40 4" Х/€31)4-
+21/2-1Лц(ЗЛ?1-«4о), (XI)
/^31 = —ЗЯ22/сзо — 9J?i2k2i — 37?ц/€12 — 3(0кз1 4- JV/€22)4“
13 3
4-3i/2 1R11R12 — ~У2 1Я12«40 ~ К^17?Ц«31 “ X «30«21> (ХП)
4U
«22 — —47?22«21 6/?12«12 ~ 27?цКоз ~ 2(0^22 + Х«1з)"“
—1/2 1(-й12«31 4-Яц«22)4-
+vi4Rn(RnR22 + 5Я?2) - 2^к221, (XIII)
«13 = “3(7?22«12 4" Я12«оз) — ®«13 — -Х«04 4" Зр2 1R12(RuR22 4" Я12) —
-“^Г1д12«22 ~ (XIV)
4U £л
^04 = 21/2 2 (67212^22 — «1з) — 31/2 1«12- (XV)
3.3. Методы ортогональных разложений и квазимоментов
для приближенного решения фильтрационных
уравнений
3.3.1. Метод ортогональных разложений. При аппроксима-
ции апостериорной плотности отрезком (3.2.5) ее ортогонального разло-
жения (п. 1.8.3) естественно принять за параметры, образующие вектор
апостериорные математическое ожидание X, ковариационную мат-
рицу R вектора X и коэффициенты си (|1/| = 3, ... , N) в (3.2.5).
392
ГЛ. 3. СУБОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ОФК
t> Для вывода стохастических дифференциальных уравнений для
коэффициентов су при у = к воспользуемся формулой (п. 1.8.3), выра-
жающей ск через характеристическую функцию pt (А):
Ск = [qK(d/idX)gtW]x=0
(3.3.1)
Чтобы найти стохастический дифференциал величины ск, применим
формулу дифференцирования Ито (1.4.82), учитывая, что полином qK(x)
зависит от апостериорных математического ожидания X и ковариаци-
онной матрицы R вектора X. Предварительно перепишем уравнения
(3.2.6) и (3.2.7) в скалярной форме:
dX, = f,dt + hs(dY - fwdt) (s = 1, ... , n), (3.3.2)
dR,4 = (f^-h^^h^dt+q^dY-f^dt) (s,g = 1, ... , n), (3.3.3)
где rjsq - матрица-строка, элементами которой служат соответствующие
элементы матрицы р\ , ... , рП1,
“Пвд — 1]ea+eq — [Pleg • • • Pmsq ] (5, Qi — 1 , • • • > Л-). (3.3.4)
Теперь по формуле дифференцирования Ито (1.4.82), учитывая (3.3.2),
(3.3.3) и первое уравнение (3.1.1), согласно которому dY = (pidt+^idW,
находим
dc»[d{(g«(5/i5A)pt(A)}]A=0 =
= £ [dqK(d/idX)dXs • gt(X)] А=о dXs+
8=1
+ [dqK(d/idX)dR,u gt(X) ]A=0 dRsu + [ qK(d/idX)dgt(A) ]A=0 +
s,u=l
Г1 ra2qK(^A)-gt(A)'
дХядХи
hs^iv^ih^+
A=0
d2qK(d/idX) gt(X)
dRsudRki
T],u^l^TTlkl +
A=0
8,k,l=l
д2дк(д/г9Х) gt(X)-
9XadRki
A=0
hsipivipigiki
(3.3.5)
3.3. МЕТОДЫ ОРТОГОНАЛЬНЫХ РАЗЛОЖЕНИЙ
393
Подставив сюда выражения (3.3.2), (3.3.3) и (2.2.13) дифференциалов
dX8, dR8q и dpt (А), вспомнив, что для любого полинома Р(х)
Р [\d/idX)gt(X)]x=Q = P(ot), получаем стохастические дифференциаль-
ные уравнения:
^а?.Мл+ _ „,й^)+
Огь8-ц
'8U
d2qK(a) т т 1
s,k,i=i uXsoRki
dqK(a)',
---х—п8+
дХ,
+ L - f^dt) (И =3,...,ДГ),
S,U=1 8и '
где в дополнение к прежним обозначениям принято
(3.3.6)
оо
s-1-oo
ох8
оо
I asu(Y,x,t)^^p*(x;0)dx,
/ их 8иХ\л
—оо
оо
Нк = HK(Y,0,t) = ( У <pi(Y,x,t')TqK(x)p*(x;0)dx+
—ОО
(3.3.7)
ОО
8~ Х-оо
*4"^Р*(р;0)<Ь - с.
их8
(3.3.8)
Здесь через (V’W’Ds обозначена s-я строка матрицы ipvTp'i- Для вывода
формул (3.3.7) и (3.3.8) достаточно вычислить
(gK(d/idA)<zt(A) ]
с помощью (2.2.13), учитывая, что = ст(у,х, t).
ti м.
8,U,k,1=1
т т .
и
394
ГЛ. 3. СУБОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ОФК
На основании формулы (3.2.5) для р*(х;0) функции Д,
t/su, Fk и Нк в уравнениях (3.3.2), (3.3.3) и (3.3.6) представляют
собой линейные комбинации величин су (|i/| = 3, ... , N) с коэффи-
циентами, зависящими от X и R. Величины дц^о^/дХ^ dqK(pt)/dR8U,
d2qKt{a)/dX8dXu. d2qn(a)/dR8udRkh d2qn{a}ldX8dRki после замены
моментов их выражениями через су тоже будут линейными комбина-
циями величин cv с коэффициентами, зависящими от X и R. Таким
образом, уравнения (3.3.2), (3.3.3) и (3.3.6) представляют собой полную
систему стохастических дифференциальных уравнений, приближенно
определяющую все величины X, R, су (|i/| = 3, ... , N), составляющие
вектор параметров в.
За начальные значения коэффициентов су при t = Iq следует при-
нять соответствующие коэффициенты ортогонального разложения
условной плотности величины Xq относительно Yq. <
Таким образом, получен следующий результат.
Теорема 3.3.1. Пусть уравнения нормальной стохастической
дифференциальной системы (3.1.1) допускают применение метода ор-
тогональных разложений. Тогда в основе метода ортогональных раз-
ложений для аппроксимации апостериорного распределения (3.2.5) ле-
жат уравнения (3.3.2), (3.3.3) и (3.3.6) при соответствующих началь-
ных условиях.
3.3.2. Метод квазимоментов
t> В частном случае разложений (3.2.5) по полиномам Эрмита ко-
эффициенты Су представляют собой квазимоменты (п. 1.8.3). В этом
случае на основании (ТСтС, приложение 1) для производных полино-
мов Эрмита Gy формулы (3.3.7) и (3.3.8) приводятся к виду
у>8 (У, Ж, t)GK-e, (я - т)р* (^; 0)dx +
8=1
и=2 8=1
—оо
оо
I У (У, X, t)Gк~2е, (х - т)р* (х; 0)dx+
—ОО
<Xsu(Y,x,t)GK-e,-eu(x - т)р*(x,0)dx, (3.3.9)
3.3. МЕТОДЫ ОРТОГОНАЛЬНЫХ РАЗЛОЖЕНИЙ
395
ОО
Нк = | У у>1 (У, х, t)TGK(x - т)р*(х; 0)dx+
—ОО
п 7
+ к» I (‘<l>^il>T')(Y,x,t)GK-e,(x - m)p*(x;0)dx-
S=1 -оо
(3.3.10)
На основании (ТСтС, приложение 1) для производных полиномов Эр-
мита Gy с учетом того, что qK(х) = GK(x — m), производные dqn(a)/dX8,
dqK(a)/ORsu, д2Чк(а)/дХадХи, d2qK(a)/dRaudRki, d2qK(a)/dXs9Rki в
этом случае пропорциональны соответствующим квазимоментам:
^О.к{р}/^Х8 — К3Ск—еа) (3.3.11)
dqK(a)/dR,a = -^-dqK(a)/dX2 = -^к.а(ка - 1)ск-2е., и (3.3.12)
/&Rsu — д /дХ8ЭХи — К>8^и^к—ел—еи1 (3.3.13)
d2qK(a)/dR2a = - 1)(кв - 2)(к, - 3)ск_4е,, (3.3.14)
d2qK{a)/9RaadRkk = i«8(«s - 1)«,(к8 - l)cK_2e,_2efc, (3.3.15)
& О.к{р)/^^88^^81 = 2)/€/Сл_Зел_ef, (3.3.16)
qK,{^)/QRasdRkl = ^^8^8 2ee —efe —е/, (3.3.17)
qn^/ORsudRsl = K'aiP'S 2ел —eu —e/, /0R8udRkl —К'8КиК'кК'1Ск—еа—еи—ек—е1) (3.3.18) (3.3.19)
d2qn(a)/dX8dR88 = - 1)(«, - 2)cK_3ej, (3.3.20)
q^ip)/^X8dRsl = 2еа — ei > (3.3.21)
396
ГЛ. 3. СУБОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ОФК
/dXgdRkk ~ п^з^к^к ~ 1)ск—ев-2е&, (3.3.22)
$ /dX8dRki — K>8K>kK>icK—€a—ek^ei. < (3.3.23)
Следовательно, получаем следующий результат.
Теорема 3.3.2. Пусть уравнения нормальной стохастической
дифференциальной системы (3.1.1) допускают применение метода ква-
зимоментов. Тогда в основе метода аппроксимации апостериорного
одномерного распределения посредством квазимоментов лежат урав-
нения метода ортогональных разложений (теорема 3.3.1), при усло-
вии, когда в уравнениях (3.3.6) функции Fn и Нк определяются согласно
(3.3.9), (3.3.10).
Пример 3.3.1. Уравнения (3.3.6) для апостериорных квазимоментов в задачах
примеров 3.2.4 и 3.2.5 совпадают с уравнениями для семиинвариантов, так как квазимо-
менты до пятого порядка включительно совпадают с соответствующими семиинвариан-
тами. Различие получится только при аппроксимации Pt(x) отрезком разложения по
полиномам Эрмита с учетом моментов (семиинвариантов) по меньшей мере до шестого
порядка.
3.3.3. Сокращение числа уравнений. Изложенные выше ме-
тоды дают принципиальную возможность получить приближение к оп-
тимальной оценке с любой степенью точности. Чем выше максималь-
ный порядок N учитываемых моментов, семиинвариантов или квази-
моментов, тем выше будет точность приближения к оптимальной оцен-
ке. Однако число уравнений, определяющих параметры апостериор-
ного распределения, быстро растет с увеличением числа учитываемых
параметров. В табл.3.3.1 и 3.3.2 (ТСтС, п.7.3.7) показана зависимость
числа уравнений в системе, определяющей параметры апостериорного
распределения, от размерности р вектора состояния системы и наивыс-
шего порядка учитываемых моментов, семиинвариантов или квазимо-
ментов. Из этой таблицы видно, что даже для вектора состояния си-
стемы сравнительно небольшой размерности, порядка 10, число уравне-
ний, определяющих параметры апостериорного распределения, дости-
гает 1000 при учете моментов, семиинвариантов или квазимоментов до
четвертого порядка. При необходимости учета моментов, семиинвари-
антов или квазимоментов до 10-го порядка число уравнений достига-
ет 1000 для четырехмерного вектора состояния. Вследствие этого из-
ложенные приближенные методы решения уравнений оптимальной не-
линейной фильтрации практически реализуемы только при невысокой
размерности расширенного вектора состояния системы, включающего
3.4. СУБОПТИМАЛЬНАЯ ФИЛЬТРАЦИЯ ДЛЯ НЕНОРМИР. РАСПРЕД. 397
все переменные состояния и неизвестные параметры. Между тем число
подлежащих оцениванию неизвестных параметров во многих задачах
практики оказывается больше 100. Для таких задач практически реа-
лизуемы только методы нормальной и эллипсоидальной аппроксимации
апостериорного распределения (раздел 3.8).
Таблица 3.3.1
Максим, порядок момента N Размерность вектора состояния 71
1 2 3 4 5 6 7 8 9 10 20
2 2 5 9 14 20 27 35 44 54 65 230
4 4 14 34 69 125 209 329 494 714 1000 10625
6 6 27 83 209 461 923 1715 3002 5004 8007
8 8 44 164 494 1286 3002 6434
10 10 65 1000 3002 8007
Таблица 3.3.2
Максим, порядок момента N Размерность вектора состояния П
10 20 30 40 50 100 150 200
2 65 230 495 860 1325 5150 11475 20300
4 85 270 555 840 1425 5350 11475 20700
6 105 310 615 1020 1525 5550 12075 21100
8 125 350 675 1100 1625 5750 12375 21500
10 145 390 735 1180 1725 5950 12675 21900
3.4. Уравнения субоптимальной фильтрации
для ненормированных распределений
3.4.1. Модифицированный метод нормальной аппроксима-
ции. Введем моменты для ненормированной плотности pt(x):
TTtp — 7Tlf^
xr^pt(x)dx,
(3.4.1)
где г = [ и ... гп ]Т - векторный индекс. В силу (2.7.8) они выражают-
ся через ненормированную характеристическую функцию <jt(A) той же
398
ГЛ. 3. СУБОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ОФК
формулой, которая определяет обычные моменты случайной величины
через ее характеристическую функцию
тг —
d|r|flt(A)
9(гА1)Г1 .. . 9(гАп)Гп
(3.4.2)
А=0
где |г| = п + • • • + гп. Вследствие (2.7.1) эти некоррелированные мо-
менты выражаются через обычные начальные моменты аг случайного
вектора Xt = X(t):
Trip — potp, (3.4.3)
Аппроксимируя неизвестную ненормированную плотность какой-либо
функцией, зависящей от конечного числа моментов, можно вывести из
(2.7.9) соответствующие стохастические дифференциальные уравнения
для моментов тг. Добавив к этим уравнениям уравнение (2.7.2) для
нормирующего множителя д с той же аппроксимацией pt{x) при вы-
числении фх:
dp = рфТ (^хИ/'Г)-1 (Y,t)dY, (3.4.4)
получим замкнутую систему уравнений, которая дает приближенное
(субоптимальное) решение задачи оптимальной фильтрации.
t> Простейший метод приближенного решения уравнений оптималь-
ной фильтрации получается при нормальной аппроксимации апостери-
орного распределения:
gtW « ехр |г'АтХ — ^Ат7?а| ,
I 4U J
где X = X(t) и R = R(t) - апостериорные математическое ожидание
(т.е. оптимальная оценка X(t)) и ковариационная матрица фильтрации:
Х = М[Х(*)|У/0], R = М [{%(*) - х} X(t)T I У/о] . (3.4.5)
На основании формулы (3.4.3) и известной формулы, связывающей ма-
тематическое ожидание, ковариационную матрицу и начальный момент
второго порядка, имеем
X = т/р, R = Г/р - ттТ/р2, (3.4.6)
где т - вектор с компонентами те1 , ... , m€n; еп - n-мерный вектор,
все компоненты которого равны нулю кроме s-й, равной 1; Г - матри-
ца с элементами m€a+€h (з,Л = 1, ... , п). При такой аппроксимации
апостериорного распределения будем иметь
3.4. СУБОПТИМАЛЬНАЯ ФИЛЬТРАЦИЯ ДЛЯ НЕНОРМИР. РАСПРЕД. 399
й(1) ” w = 7WWехр Н(*т ’ *Т)Л-,(1 “ *’} ’
9tW « 9*tW = дехр [iXTXT - |атДА)) . (3.4.7)
I л I
Дифференцируя уравнение (2.7.9) по iAs, получим
оо п
d 1г 1Л = / (*’• + 52 + х> (^Т<р - |ат<70а) ) +
°Чглв/ J I ..-1 \ * / J
—оо
оо
4- У {cti, + + i'ATCTi)} e,xTxpt{x)dxff21d,Y, (3.4.8)
—ОО
где аргументы функций для краткости опущены и введены обозначения
(То = 'фи'ф1', О’! = 'фУ'фТ, (72 = V'lW'F, (3.4.9)
а (71в “ 5-я строка матрицы (71. Продифференцировав (3.4.8) по iXh,
будем иметь
оо
d л/д\ = [ la°ah + Xs^h + Xh<^^ eixTxpt(x)dxa21dY + o( |A|).
O\iX8)u\iXh) J
—oo
(3.4.10)
Полагая A = 0 в (3.4.8) и (3.4.10) и пользуясь аппроксимацией (3.4.7),
получим следующие уравнения для m и Г
оо оо
dme, = У <pspl(x)dx -dt+ (crla + (a:)^1 • dY,
—oo —oo
oo
dme,+eh = У {CToeh + xa<ph + xhips}p*(x)dx dt+
—OO
oo
+ У (xaffih + xhffia + xaxh<Pi )Pt (xjdxcrz1 dY. (3.4.11)
—OO
400
ГЛ. 3. СУБОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ОФК
Для того чтобы получить из (3.4.11) матричные уравнения для т
Г, заметим, что произведение crih&z1 представляет собой - h-ю строку
матрицы &2 = ^1^2 Поэтому
П1
•^s^l/1^2 ^s^lhr^Yf
г=1
и x8d\hr представляет собой ($,Л)-й элемент (п х п)-матрицы
•^1 . . . Xl&lnr
: [^iir • • • ^inr] — ••• ••• •••
Xn . _ xn&nlr • • • xn&lnr
Далее обозначим через br = briY^x^t) r-й столбец матрицы Тогда
получим
[<711Г • • • ^Inr ] — хЬ^.
Аналогично,
’ ^llr '
- &lnr -
[Xi ...xn] = brxT.
Вводя обознчение ar = ar(Y,x,t) для r-го элемента матрицы - строки
придем к заключению, что + х3хь<рТ) пред-
ставляет собой (з,Л) - элемент матрицы xbf + brxT + ххТаг. Поэтому
уравнения (3.4.11) дают
оо
dm — <ppt(x)dx
—оо
оо
—оо
+ Wi)p*t (ж)<72 1
dY,
ОО
>т + 4>xT)pt (x)dx • dt+
°°
П1 г
Y
’-i-co
(хЬ? + brxT + xxTar)p* (x)dx dYr.
(3.4.12)
3.4. СУБОПТИМАЛЬНАЯ ФИЛЬТРАЦИЯ ДЛЯ НЁНОРМИР. РАСПРЕД. 401
Здесь
= 0q(Y,x,1) = (^^T)(Y,x,t). (3.4.13)
Эти уравнения допускают следующую запись:
dm = uh (У, X, R, t) • dt + м 52 h^Y *> R> *>'dYr’
r=l
dT = fj,h3(Y, X,R,t) dY, (3.4.14)
где введены следующие обозначения:
fi(Y,X,R,t) =
= 7 ^(У.х.Оехр |Ьхт - XT)R-\x - X)| dx, (3.4.15)
i/(27r)n \R\ J (2 J
— oo
/11 (У, X, R, t) = — [ [ CT1 (у, x, t) + xtpi (У, X, t) ] x
V(27r)" 1Д1 J
— OO
x exp |^(жт — Хт)Я-1(а: — X)) dx, (3.4.16)
f2(Y,X,R,t) =
= У [ [ху>(У, X, £)T + <p(Y, X, t)xT + <7о(У, X, R, t)]x
У(2тг)п Я| J
—OO
x exp (|(zT - XT)R-l(x - X)J dxa2(Y,t)-1, (3.4.17)
h2r(Y,X,R,t) =
OO
= 1 —== У [жа;таг(г/, ж, t) 4- xbr(Y, x, t)T 4- dr(Y, a:, t)xT ] x
। -oo
x exp “ XT)R~l(x — X)| dx, (r = 1, ... , n), (3.4.18)
402
ГЛ. 3. СУБОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ОФК
h3(Y,X,R,t) =
оо
= /,о <_|рГ /^1(у>М)Техр/|(;гт-Хт)/Г1(а:-Л')| dxa2(y,t)~1.
у(2тг)п |Я| J U J
—ОО
(3.4.19)
Уравнения (3.4.14) с учетом формул (3.4.6) образуют замкнутую
систему уравнений, приближенно определяющую тп, Г, д, X, R. На-
чальными условиями для (3.4.14) служат
m(t0) — — Хо, Г(^о) — Го — Ro 4" Мот, д(^о) — 1, (3.4.20)
где Хо и Rq - условное математическое ожидание и ковариационная
матрица вектора Хо относительно Yq. <
В результате получено следующее утверждение.
Теорема 3.4.1. В условиях теоремы 2.7.1 в основе модифициро-
ванного метода нормальной аппроксимации ненормированного апосте-
риорного распределения в нормальной стохастической дифференциаль-
ной системе (3.1.1) лежат уравнения (3.4.14) при начальных условиях
(3.4.20).
Замечание. Уравнения (3.4.14) несколько проще, чем уравнения метода
нормальной аппроксимации, получаемые из уравнения (2.2.13), хотя и содержат на одно
уравнение больше.
3.4.2. Модифицированный метод моментов
о Совершенно так же из уравнения (2.7.9) получаются уравнения
для ненормированных моментов тг до заданного порядка г = 1,...
...,7V:
dmr =
д и
д(г\х^ ...d(ixny-
iXT<p — ^ХТаоХ \ е*хТх
pt(x)dx • cft+
A=0
* I I "
+ f [ (rf + e“T‘ ]
— oo
(3.4.21)
Выполнив в (3.4.21) дифференцирование, положив после этого А = 0 и
заменив pt(x) на р^(ж,а), рЦх,а) - аппроксимирующая апостериорная
3.4. СУБОПТИМАЛЬНАЯ ФИЛЬТРАЦИЯ ДЛЯ НЕНОРМИР. РАСПРЕД. 403
плотность pt (ж)~ функция, зависящая от моментов аг до порядка N
включительно), получим
dmr = р
•Х” +
+ | V п(п - 1)<70н(У> ху 0®? • • • 2 • • • *пП +
2 1=1
+ 52 52 r‘rhaolh(Y, X, t)xrhk 1
1=2 h=l
X/' 1... х„п Pf (х, a)dx dt+
у>1 (К, X, t)'1'!? ... + 52 П<?п(К X, t)xp
t=l
xpt (x, a)dxff2 (Y,t) 1 • dY
(3.4.22)
(n , • • • , rn = 0,1, , ... , N, r = 1, ... , N).
Добавив к этим уравнениям уравнение (3.4.4), при той же аппрок-
симации pt(x)-.
ОО
dp = д f (pi(YyXyt)Tp*(x^a)dxa2(Yyt)~1 • dY (3.4.23)
— оо
получим с учетом (3.4.3) замкнутую систему уравнений для тпг (г =
= 1, ... , N) и р, которая приближенно определяется тпг, р, аг и, в
частности, оптимальную оценку X и ковариационную матрицу ошибки
фильтрации R. Начальные значения моментов mr, mr(to) равны аг(*о),
где аг(£о) - соответствующие условные моменты Хо вектора X относи-
тельно Yq вектора У, и p(to) = 1, как всегда. <
Итак, имеем следующий результат.
Теорема 3.4.2. В условиях теоремы 2.7.1 в основе модифициро-
ванного метода начальных моментов апостериорного ненормирован-
ного распределения в нормальной стохастической дифференциальной
системе (3.1.1) лежат уравнения (3.4.21) и (3.4.23) при соответству-
ющих начальных условиях.
404
ГЛ. 3. СУБОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ОФК
Что касается выбора функции р£(т,а), то заранее можно принять
конечный отрезок ортогонального разложения р*(т), в частности, раз-
ложения по полиномам Эрмита или конечный отрезок ряда Эджуорта
(п.1.3.5).
Пользуясь любой ортонормальной системой полиномов (п. 1.3.5):
оо
{pv(x)qv(x)} , У w(x)pv(x)qv(x)dx = <5МД
— ОО
(3.4.24)
(некоторая эталонная плотность), можно выбрать в качестве функции
Я (я, а)
pt*(T,a) = w(t)
N
1+22 52
k—3 |i/| =Ас
Здесь
ОО
С|/ = / ql/(x)pt(x)dx = М^(т) = ф,(а),
(3.4.25)
(3.4.26)
q„ (а) - результат замены в полиноме qu (я) всех одночленов яр ...
соответствующими моментами аг = аГ1„,Гп. В частности, при нормаль-
ной плотности w(x) с параметрами X и R имеем
р,(х) = q„(x) = G„(x - X), (3.4.27)
Уг- • •
где Н„(х) и Gj/(a:) - полиномы Эрмита (ТСтС, приложение 1).
3.4.3. Модифицированный метод ортогональных разложе-
ний
о Аппроксимируем отрезком ортогонального разложения вида
(3.4.25) ненормированную плотность pt(x\
(3.4.28)
где согласно (2.7.1) и (3.4.26)
оо
с„ = У qv(x)Pt(x)dx = [q„ (д/OiX) gt(X) ]A=0,
— OO
(3.4.29)
3.4. СУБОПТИМАЛЬНАЯ ФИЛЬТРАЦИЯ ДЛЯ НЕНОРМИР. РАСПРЕД. 405
qy (д/дгХ) - результат замены в полиноме qy(x) всех одночленов х[г ...
... xrj соответствующими дифференциальными операторами:
дг /д(гХ)Г1 ...д(гХ)Гп. В разложении (3.4.28), в отличие от (3.4.25), на-
чинается суммирование по Л, начиная с к = 1, так как мы предполага-
ем, что моменты первого и второго порядков, соответствующие w(x), не
совпадают с неизвестными апостериорными моментами случайного век-
тора X. Такое допущение ведет к зависимости полиномов pv(x) и qv(x)
от значений случайных процессов X(t), 7?(t), которые определяются
стохастическими дифференциальными уравнениями, что чрезвычайно
усложняет уравнения для коэффициентов су.
Пользуясь аппроксимацией (3.4.28) и формулой (3.4.29), получим
следующие уравнения для коэффициентов си\
dCy
оо
= [ Яи(- |ат<т0а| eixTxpl (х)
J \огл/ 2 )
—оо
dx •
оо
+ гАТ(Т1) eixTxpt(x)
dx - а2 1 dY,
А=0
где аргументы функций <р, сто, 04, 02 Для краткости опущены. Вы-
полнив дифференцирование подынтегральных функций совершенно
так же, как при выводе (3.4.22), положив после этого А = 0, приняв
во внимание, что
Г1Х? ...х[‘ 1.. .хр* = Д- (хр .. ,
г, (г, - 1)хр ... хр-2 ... хр* = А (хр ... х**), (3.4.30)
д2
ТЫХ? ... xp'1... хр-1... X'- = (хр ... хр)
и заменив р%(х) ее выражением (3.4.28), получим
406
ГЛ. 3. СУБОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ОФК
de.
N
LifvotX) £) 4- (y,t) dt+
k=l ||/| =k
N
4- phuo(Y, t) 4- EE cKhUK(Y,t) dY
к=1 |k| =k
(3.4.31)
(i/j,...,^ = 0,1,. ..,N, M
Здесь введены обозначения
ОО
fvo(Y, t) = У |<р(У, х, t)Tqvx(x) + |tr [q„xx(х)а0(У, х, t) ]} w(x)dx,
—ОО
f„K(Y,t) =
(3.4.32)
ОО
= j {<р(У,М)Т9|/а:(20 + |tr [9„„(i)ai)(Y,i,t)] j w(x)pK(x)dx,
—oo
оо
hvo(Y,t) = У {q>i(Y,x,t)Tqv(^x) + qvx(x)Tai(X,x,t)}w{x)021(Y,t)dx,
— ОО
(3.4.33)
hVK(Y,t) =
oo
= у {(p1(Y,x,t)Tqv(x) + qvx(x)Ta1(Y,x,t)}w(x)pK(x)dxa2(Y,t)~l,
— OO
(3.4.34)
где qvn{x) - матрица-столбец производных полинома qv(x) по компонен-
там вектора х\ qvxx(%) ~ матрица вторых производных qy(x) по компо-
нентами х. К уравнению (3.4.31) надо добавить уравнение (3.4.4) для
р, в котором фг вычисляется с помощью аппроксимации (3.4.28) ненор-
мированной плотности pt(x) = др^(а;). Это уравнение имеет вид
N
dp = pho(Y,t) + ЕЕ cuhv{Y,t) dY,
k=i м=л
(3.4.35)
3.4. СУБОПТИМАЛЬНАЯ ФИЛЬТРАЦИЯ ДЛЯ НЕНОРМИР. РАСПРЕД. 407
где
оо
йо(У,t) = У <p(Y,x,t)Tw(x)dxff2(Y,t)~1,
—ОО
(3.4.36)
ОО
hvtY't) = У 9?1(У,ж, t)Tw(x)pv(x)dxa2(Y) t)'1-
— оо
(3.4.37)
Начальные условия для (3.4.31) и (3.4.35) имеют вид
c„(to) = с°, Pi, ... , i/n = 0,1, ... , N, |р| = 1, ... , N, /z(t0) = 1,
(3.4.38)
где с£ - коэффициенты разложения (3.4.28) плотности pt0 = ро(х | 1о)
начального значения Хо процесса X (t) относительно начального значе-
ния Yq процесса Y(£) :
Ро(х | Уо) = w(x)
N
1+52 52
Л=1 |i/| —k
(3.4.39)
В частности, взяв за w(x) нормальную плотность с параметрами х
и К, определим производные полинома дДя) = G„(x — х) в (3.4.32)-
(3.4.34) по известным формулам для производных функций (ТСтС,
приложение 1):
= uiGv-e, (х-х), (3.4.40)
= *("I - l)G>-2e, {X - х), (3.4.41)
0X7
d2q„(x) _ .
dxldxh~VlVhGv-e,-eh{'x xY
(3.4.42)
После интегрирования уравнений (3.4.31) и (3.4.35) оптимальная
оценка X вектора X и апостериорная ковариационная матрица R ошиб-
ки фильтрации определяется приближенно по формулам
408
ГЛ. 3. СУБОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ОФК
оо
X = X(t) = x+ — f xpv(x)w(x)dx, (3.4.43)
М=1 ^4
оо
R = R(t) = у* (х - Х)(хт - XT)w(x)dx+
—оо
2 °?
4- ~ I (х ~ Х)(хт - XT)w(x)pv(x)dx (3.4.44)
м=* V {°
(каждый полином р„(х) ортогонален с весом w(x) по всем одночленам
х\* .. .xjf ПрИ |г| = п + • • • + гп < |р| ). Все интегралы в (3.4.43) и
(3.4.44) выражаются через моменты распределения w(x) до четвертого
порядка включительно. В частности, при нормальной плотности w(x)
с параметрами х, К все интегралы (3.4.43) и (3.4.44) выражаются через
х и К. <j
Таким образом, получен следующий результат.
Теорема 3.4.3. В условиях теоремы 2.7.1 в основе модифици-
рованного метода ортогональных разложений для ненормированного
апостериорного распределения в нормальной стохастической диффе-
ренциальной системе (3.1.1) лежат уравнения (3.4.31) и (3.4.35) при
начальных условиях (3.4.38) и (3.4.39).
Замечание 1. Вектор X и матрицу К в выражении плотности w(x),
в частности нормальной, можно в принципе выбрать произвольно, например, положить
X = 0, К — 1п. Однако для повышения точности аппроксимации (3.4.28) при данном
N или для уменьшения N при данной точности аппроксимации (3.4.28) следует выби-
рать X и К как можно ближе к X и R. Для достижения этой цели можно рекомендовать
выбирать X и К равными в каждый момент времени t соответственно априорному услов-
ному математическому ожиданию тх\у и априорной условной ковариационной матрице
Кх\у вектора X относительно Y, полученным, например, методом нормальной аппрок-
симации.
Замечание 2. Уравнения (3.4.31) и (3.4.35) в отличие от (3.4.22) и
(3.4.25) линейны относительно Су и р (точнее, являются линейными с параметрическими
шумами). Однако число уравнений в (3.4.31) и (3.4.35) при данном N в (3.4.25) и (3.4.28)
одинаково, а именно равно
3.5. МЕТОДЫ УПРОЩЕНИЯ ФИЛЬТРАЦИОННЫХ УРАВНЕНИЙ
409
3.5. Методы, основанные на упрощении фильтрационных
уравнений
3.5.1. Способы упрощения уравнений оптимальной филь-
трации. Теперь изучим другие методы получения субоптимальных
фильтров. Первые попытки распространить линейную фильтрацию
Калмана на нелинейные стохастические дифференциальные системы,
естественно, основаны на линеаризации их уравнений (3.1.1). Наибо-
лее удачными следует признать два способа линеаризации этих урав-
нений. Первый способ основан на линеаризации уравнений (3.1.1) от-
носительно вектора состояния X в окрестности его оценки X. Этот
способ приводит к так называемому обобщенному фильтру Калмана-
Бьюси. Другой способ основан на статистической (или эквивалентной)
линеаризации уравнений (3.1.1). В обоих случаях порядок фильтра ра-
вен п(п 4- 3)/2 вместо п в случае линейных уравнений (3.1.1). Число
уравнений первого порядка в системе уравнений фильтра называется
порядком фильтра. Это происходит из-за того, что уравнение для R
в этих случаях зависит от результатов наблюдений, вследствие чего
это уравнение не может быть заранее проинтегрировано отдельно и его
приходится интегрировать совместно с уравнением для оценки X.
Желание повысить точность оценивания вектора состояния систе-
мы X ведет к различным попыткам получить из (2.2.19) и (2.2.23) зам-
кнутые приближенные уравнения для X и R с помощью разложения в
ряд функций ip(y,x,t), 4>\{y,x,i) и ^{y^x^i) относительно х и отбрасы-
вания членов высших степеней, которые не могут быть выражены через
X и R. Все методы, полученные таким способом, дают фильтры того
же порядка, что и метод нормальной аппроксимации.
3.5.2. Обобщенный фильтр Калмана-Бьюси
о Естественно возникает мысль применить для приближенного ре-
шения задач нелинейной фильтрации теорию линейной фильтрации
к линеаризованной системе. Конечно, при этом возникает вопрос: в
окрестности какой функции x(t) производить линеаризацию уравнений
системы (3.1.1)? Ясно, что однозначного ответа на этот вопрос быть
не может. Однако стало общепринятым линеаризовать уравнения в
окрестности неизвестной оценки X(t}. При этом придется линеаризо-
вать только коэффициенты при dt в (3.1.1), т.е. функции (/?(г/,я;,£) и
9?i(i/,a;, t) относительно ж, а функцию ^(y,x,t) принять равной
^(г/,Х*,£), так как если этого не сделать, то второе уравнение (3.1.1),
не будет линейным относительно X и dW.
На основании приведенных рассуждений заменим уравнения (3.1.1)
410
ГЛ. 3. СУБОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ОФК
приближенными уравнениями
dY = [^(У, X,t) + <plx(Y, X,t)T(X - X) ] dt + ipi(Y,t)dW, (3.5.1)
dX = [<p(Y,X,t)+y>x(Y,X,t)T(X — X)]dt+ i/>(Y,X, t)dW, (3.5.2)
где <Px(X, X, t) и <£1а;(У, X, t) - как всегда, матрицы производных компо-
нент векторных функций и по компонентам вектора х,
¥>*(Y,X,t) = -^-<p(Y,X,f)T, 4>lx(Y,X,t) = ^-^(Y,X,t)T.
OX OX
Если рассматривать оценку X как известную функцию времени t, то
полученные уравнения представляют собой частный случай уравнений
(2.3.12).
Оптимальная оценка X и апостериорная ковариационная матрица
R ошибки в этом случае определяются уравнениями (2.3.13) и (2.3.14)
при
а(У, t)X + ao(Y, t) = <p(Y, X, t) + <px(Y, X, t)T(X - X),
b(Y,t)X + b0(Y,t) = <fi(Y,X,t) + <pix(Y,X,t)T(X - X). (3.5.3)
Подставив выражения (3.5.3) в (2.3.13) и (2.3.14), получим приближен-
ные уравнения для X и R:
dX = <p(Y,X,t) + h(Y,X,R,t) [dy-^rXtytt] , (3.5.4)
dR = [<px(Y, X,£)TR + Rtpx(Y, X, R, t) + (^T)(Y, X, t)-
—h(Y, X, R, t)^ivil>{)(Y, t)h(Y, X, R, t)T|dt, (3.5.5)
где
h(Y,X,R,t) = {R<plx(Y,X,t) + (tP^)(Y,X,t^^i^)~1(Y,t). <
(3.5.6)
Теорема 3.5.1 Если уравнения нормальной стохастической диф-
ференциальной системы (3.1.1) допускают линеаризацию в окрестно-
сти неизвестной оценки X и матрица невырождена, то
уравнения (3.5.4) и (3.5.5) определяют фильтр, обычно называемый
обобщенным фильтром Калмана-Бьюси.
3.5. МЕТОДЫ УПРОЩЕНИЯ ФИЛЬТРАЦИОННЫХ УРАВНЕНИЙ
411
Так же, как и уравнения (2.3.13) и (2.3.14), уравнения (3.5.4) и
(3.5.5) должны интегрироваться совместно при начальных условиях
X(t0) = Хо = М[Х0 | Го], R(t0) = Ro = М[(Х0 - *о)(ХГ ~ *о) I Го].
(3.5.7)
Обобщенный фильтр Калмана-Бьюси имеет порядок п(п+3)/2, тот же,
что и приближенно оптимальный фильтр метода нормальной аппрок-
симации апостериорного распределения (п.3.1.2).
В приложениях обычно рассматривается более простая задача, ко-
гда функции и в уравнениях (3.1.1) не зависят от У и про-
цесс W(£) состоит из двух независимых блоков, один из которых входит
только в первое, а другой - только во второе уравнение (3.1.1). В этом
случае = [ф‘ 0], ф± = [O^J], W = [VK1TH<f]T, так что
фбЖ = ф'(П¥1у
fadW = ф'(1№2, фиф1, = ф'1/1ф,Т, фиф? = 0, фтуфТ = ф'^Ф'Т•
Уравнения (3.1.1) при этом принимают вид
X = <p(X,t) + ф’(Х,1)У1, Z = Y = <^i(X,t) (3.5.8)
Эти уравнения сводятся в результате линеаризации функций ip, ipi и
замены X в выражении ф' оценкой X к уравнениями задачи Калмана-
Бьюси. В этом случае вид уравнения (3.5.4) и (3.5.5) обобщенного филь-
тра Калмана-Бьюси принимают вид
i = <p(X,t) + /?¥>i;c(X,i)(V’iMi’)~1W [z-¥>i(Xo], (3.5.9)
R = <px(X,t)TR + R<px(X,t) + (^^T)(X,t)-
-R^X^^T^W^X^R. (3.5.10)
Теорема 3.5.2. Если уравнения нормальной стохастической диф-
ференциальной системы имеют вид (3.5.8), допускают линеаризацию в
окрестности неизвестной оценки X, матрица (?2 = ф\У2фТ невырож-
дена, то уравнения обобщенного фильтра Калмана имеют вид (3.5.9),
(3.5.10).
Замечание. Уравнения (3.5.9) и (3.5.10) можно также вывести из общих
формул (2.2.19) и (2.2.23) при принятых предположениях, подставив в них выражения:
<р(х, t) = <p(X,t) + <px(X,t)T(x - X),
<pi(x,t) = <pi(X,t) + (f>ix (X, t)T(x — X),
i/>ki(x, t) = 4>ki(X, t) + i/>kix(X, t)T(x - X)
(fc = l,...,n; l = l,...,g) (3.5.11)
412
ГЛ. 3. СУБОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ОФК
и отбросив получившийся в результате в качестве коэффициента при dY — (p^dt =
= dY — ,t)dt третий центральный момент, который должен быть малым, если
система (3.5.8) близка к линейной. Этот второй путь предпочтительнее, так как он дает
возможность строить более точные фильтры, учитывая члены высших порядков малости.
Обобщенный фильтр Калмана-Бьюси иногда называют также
фильтром первого порядка, поскольку он основан на учете только чле-
нов первого порядка малости в разложении функций в ряд Тейлора.
Конечно, слово “порядок” понимается в данном случае не как порядок
системы дифференциальных уравнений, описывающей фильтр.
Пример 3.5.1. В задаче примера 3.1.1
Y = Z = X + V2, X = -X3 + XVi, (I)
обобщенный фильтр Калмана-Бьюси описывается уравнениями
k = -X3 + v^R(Z - X), (II)
R = -6Х2Я + i/i X2 - 1/2-1Я2. (III)
Пример 3.5.2. В задаче примера 3.1.2
y = z = х + v2, х = -хе + xvlt ё = о (i)
обобщенный фильтр Калмана-Бьюси дается уравнениями
к = -Xe + v;lRn(Z -X), (II)
ё = 1/2-1Л12(2-Х), (III)
Rn = -2(ёЛц + ХЯ12) - v^R^ + 1/1, (IV)
•R12 = —ё/?12 — XR22 — V2 1ЛцЙ12, (V)
R22 = —V2lR12R22- (VI)
3.5.3. Фильтры второго порядка
> Введем следующее обозначение
<pxx(X,t) : (х - Х)(хТ - ХТ) = [tr[<plxx(X,t)(x-X)(xT-XT)j...
• • • tr {<рП1ХХ(Х, t)(x - Х)(хт - Хт)}]Т.
(3.5.12)
3.5. МЕТОДЫ УПРОЩЕНИЯ ФИЛЬТРАЦИОННЫХ УРАВНЕНИЙ 413
Тогда, учитывая члены второй степени относительно х—X, будем иметь
<р(х, t) ъ <р(Х, t) + <рх(Х, t)T(x -Х) + ±<рхх(Х, t) : (х — Х)(хт - Хт),
(3.5.13)
<pi(х, t) & <pi(X,t) + /pix(X, t)T(x - X)+
+±4>ixx(X, t) : (x - X)(xT - XT), (3.5.14)
A
+ X^X,t)(xk-X'k)^ £ ^^(X^x.-X^-Xt)- (3-5.15)
“ oxk 2 “ dxkdxi
K=L K,l=l
Вычислим для этого случая по отдельности все слагаемые в правых
частях формул (2.2.19) и (2.2.23), которые при принятых допущениях
имеют вид
dX = + М [X {¥>i(X,t)r - ф!} 1Vo] - frdt),
(3.5.16)
dR = (м[ (X - X)tp{X,t)T + tp(X,t){XT - XT)+
+(V-W'T)PU) I Vo] - M [X {¥>i(X,t)T - Ф1} I Vo ]
xM [ ЫХ,0Т - tf} XT I Vo ] U + M[(X - X)(XT - XT)X
x {^i(X,t)T - #} I Vo] WW'fr1 («W - (3-5.17)
В результате в формулах (3.5.13)-(3.5.15) и правых частях (3.5.16) и
(3.5.17) будем иметь
p*rtX,t) + ^pxx(X,t) : R, (3.5.18)
^1 к‘f’li.X,t) +-<fixx(X,t) : R, (3.5.19)
м[хЫх,*)т-О Vo] =
= M [(X - X) {¥>i(X,t)T - I Vo ] « R<Pix(X,t), (3.5.20)
M [(X - XMX,0T I Vo] » R<px(X,t), (3.5.21)
414
ГЛ. 3. СУБОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ОФК
м[*ыадт -tf} | у/0] =
= М [Wi^'T)(X,t) | УД ] « ^'^'T)(X,t)+
i( (JXk dxi 2 dx^uX[
i - d2ib,T - 1
+/(X,t)V^-(X,t) \Rkl =
2 OXkOXi )
= (^V1^T)(X,t) + j [<»(%,<) : л] u^'(X,t)T+
+^'(X,t>i [<x(X,t) : flf + £ I ) ^,t)Rkl, (3.5.22)
2 L J \dxk dxi I
Kyl=l \ /
M [(X - X)(XT - XT) {<plr(X,t) - ф1г} I У/о ] «
a 5 £ S£(*-'><M<X - W ~ *T)(X‘ - *‘>x
(3.5.23)
Если в выражении (3.5.23) пренебречь центральными моментами чет-
вертого порядка, то неизбежно придется пренебречь и произведением
моментов второго порядка RRki, так как в силу известного неравенства
теории вероятностей
Rh = {М [ (Хк - Хк)(Х, - Xt) | У/о ] }2 <
< М [ (X* - Xk)2(Xi - Xt)2 I yt‘ ] . (3.5.24)
Таким образом, последним слагаемым в правой части уравнения (3.5.17)
следует пренебречь. Тогда, подставив полученные выражения в (3.5.16)
и (3.5.17), приходим к уравнениям
£ =4>(X,t) + Kpxx(X,t) : R+
+R>plx(X,t)(^2^)-1(t) Z-4>x(X,t)- \yixAt) : R ,(3.5.25)
3.5. МЕТОДЫ УПРОЩЕНИЯ ФИЛЬТРАЦИОННЫХ УРАВНЕНИЙ
415
R = R<px(X, t) + </>х(Х, t)TR + ^v^'T){X, t)+
4 4 ^'(X,t)T + ^'(X,t)V1 : я]Т +
n
+ £
k,l=l
^Lv
dik 1 dxi
(X,t)Ru-
< (3.5.26)
Таким образом, получен следующий результат.
Теорема 3.5.3. Если уравнения нормальной стохастической диф-
френциальной системы (3.5.8) допускают представления второго по-
рядка (3.5.23), матрица = ф^Ф^ невырождена, то уравнения
фильтра второго порядка имеют вид (3.5.25) и (3.5.26)
Фильтр, определяемый уравнениями (3.5.25) и (3.5.26), обычно на-
зывается модифицированным фильтром второго порядка. В отличие
от этого фильтра, усеченным фильтром второго порядка называется
фильтр, который получается, если, пренебрегая моментами четвертого
порядка в фигурных скобках в (3.5.23), учесть слагаемое RRki- Этого
нельзя делать, так как это может привести к изменению знака сла-
гаемых в уравнении (3.5.17). Неудивительно поэтому, что в задачах
практики усеченный фильтр второго порядка дает плохие результаты.
Поэтому мы будем рассматривать только модифицированные фильтры
второго порядка и называть их просто фильтрами второго порядка.
Пример 3.5.3. В задаче примера 3.1.1
Y = Z = X + V2, Х = -X3 + XVi, (I)
уравнения фильтра второго порядка (3.5.25) и (3.5.26) имеют вид:
£ = -X3-SXR + ^RCZ-X), (II)
R = -6X2R + Vi(X2 + R)-i^1R2. (Ill)
Пример 3.5.4. В задаче примера 3.1.2
Y = Z = X + v2, х = -хе + V1, 0 = О (I)
уравнения фильтра второго порядка (3.5.25) и (3.5.26) имеют вид:
X = - хе - Я12 + i^Rn (Y-Х), (II)
416
ГЛ. 3. СУБОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ОФК
ё = 1/Г1Я12(2-Х), (III)
Rn = -2(0Яц + ХЯ12) - v^Rh + "I, (IV)
Я12 = ~0Я12 — XR22 ~ ^2 1R11R12> R-22 = ~^2 1R12R22- (V)
3.5.4. Гауссов фильтр
> Точность приближения второго порядка к оптимальному можно
повысить, если; оставаясь в рамках второго приближения в разложе-
ниях функций (pi и в ряд Тейлора, сохранить в уравнении (3.5.17)
слагаемые с центральными моментами четвертого порядка в коэффи-
циенте при dY — (pidt и в выражении 'фг/'фт. При этом, естественно,
предполагая систему близкой к линейной, и, как следствие этого, апо-
стериорное распределение вектора ее состояния близким к нормально-
му, допускается возможным заменить центральные моменты четвертого
порядка их выражениями через элементы ковариационной матрицы Я,
соответствующими нормальному распределению. Тогда, принимая во
внимание, что для нормального апостериорного распределения
м [ (Хг - Хг)(Ха - Хв)(Хк - Xk)(Xi - Xt) I ] =
= RrsRki + RTkRai + RriRsk, (3.5.27)
получим в уравнении (3.5.26) дополнительные слагаемые
i[^(X,t) : Я] 1/1 : й]Т +
+ Y, ^-(X,t)u1^-(X,t)RkTRla+
dxkdxi дхгдх8
X,l ,r,s=l
+ Е : Я],
дхкдх1 2
к,1=1
(3.5.28)
где Rk - к-й столбец матрицы R. Полученный таким путем фильтр
называется гауссовым фильтром. <
Таким образом, доказано следующее утверждение.
Теорема 3.5.4. Если в условиях теоремы 3.5.3 сохранить сла-
гаемые с центральными моментами до четвертого порядка и заме-
нить их эквивалентными нормальными, то уравнения гауссова филь-
тра имеют вид (3.5.25) и (3.5.26) с учетом слагаемого (3.5.28).
3.5. МЕТОДЫ УПРОЩЕНИЯ ФИЛЬТРАЦИОННЫХ УРАВНЕНИЙ
417
Пример 3.5.5. В задачах 3.5.3 и 3.5.4 гауссов фильтр совпадает с фильтром
второго порядка вследствие того, что функции <р\ и линейны и их вторые производные
равны нулю.
3.5.5. Априорная оценка точности фильтрации. Все субоп-
тимальные фильтры описываются стохастическими дифференциальны-
ми уравнениями, которым удовлетворяет оценка X и вспомогательные
переменные, которые мы объединим в вектор S. Компонентами вектора
S в уравнениях метода нормальной аппроксимации, обобщенного филь-
тра Калмана-Бьюси (п.3.5.2), фильтра второго порядка (п.3.5.3), гаус-
сова фильтра служат независимые элементы матрицы R. Компонента-
ми вектора S в уравнениях метода моментов (пп.3.2.1, 3.2.2) служат все
моменты от второго до ДГ-го порядков; метода семиинвариантов - все
семиинварианты от второго до TV-го порядков; метода ортогональных
разложений (в частности, метода квазимоментов (пп.3.3.1, 3.3.2)) - не-
зависимые элементы матрицы R и коэффициенты с„ (|i/| = 3, ... , TV)
отрезка ортогонального разложения, аппроксимирующего апостериор-
ную плотность
Если подставить в уравнение приближенного оптимального филь-
тра выражение dY из первого уравнения (3.1.1), то уравнения филь-
тра вместе с уравнениями (3.1.1) будут представлять собой систему
стохастических дифференциальных уравнений, определяющую состав-
ной векторный случайный процесс [У(£)ТХ(£)ТХ(£)Т5'(£)Т]Т. Для этой
системы уравнений можно написать, например, уравнение Пугачева
(п. 1.5.4), определяющее одномерную характеристическую функцию, т.е.
одномерное распределение процесса [У(t)TX(t)TX(f)TS(t)T]T. Зная это
распределение, можно найти совместное распределение Xt и Xt и сред-
ний квадрат ошибки фильтрации М |х — х| 2, и доверительные обла-
сти для вектора X при любом t > to. Таким образом, уравнение Пу-
гачева для характеристической функции, соответствующее уравнениям
фильтра, рассматриваемым совместно с уравнениями системы и наблю-
дения, принципиально точно определяет безусловное математическое
ожидание квадрата модуля ошибки, которое характеризует точность
фильтрации. Методы параметризации распределений дают возмож-
ность решать уравнение Пугачева для характеристической функции с
любой степенью точности. Поэтому точность любого субоптимально-
го фильтра и вообще любого фильтра, описываемого стохастическими
дифференциальными уравнениями, можно априорно оценить методами
14 Фильтры Калмана и Пугачева
418
ГЛ. 3. СУБОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ОФК
параметризации распределений. При этом точность фильтрации можно
характеризовать как средним квадратом ошибки, так и доверительны-
ми областями, которые всегда можно определить, зная совместное рас-
пределение X и X. Вычисления, необходимые для такой оценки, конеч-
но, очень сложны. Но они не включают результатов наблюдений, и для
их выполнения необходимы только априорные данные. Поэтому эти
вычисления приходится выполнять для каждого фильтра только один
раз.
Имея возможность априорно оценивать точность любого метода
приближенно оптимальной (субоптимальной) фильтрации, можно вы-
брать подходящий фильтр для каждой конкретной задачи в процессе
проектирования фильтра или алгоритма фильтрации.
Замечание. Полезно заметить, что матрица R в уравнениях субоптималь-
ных фильтров может и не быть близкой к апостериорной ковариационной матрице ошиб-
ки фильтрации. Конечно, можно рассчитывать на то, что при достаточно большом N
методы моментов, семиинвариантов и квазимоментов (или более общий метод ортогональ-
ных разложений) позволяют приблизиться к решению задачи оптимальной фильтрации
с любой степенью точности. При этом матрица R будет близка к апостериорной кова-
риационной матрице ошибки фильтрации и будет характеризовать точность фильтрации
при данных результатах наблюдений. Однако это не дает возможности оценивать точ-
ность фильтрации заранее. Вычислять апостериорную ковариационную матрицу ошибки
R можно каждый раз только в процессе фильтрации. Кроме того, как уже неоднократно
отмечалось, повышение порядка фильтра, особенно в многомерных задачах, приводит к
невозможности реализации фильтра. Поэтому возможности методов п. 1.7.2 не могут быть
практически использованы для апостериорной оценки точности фильтрации. Пользуясь
же фильтрами невысоких порядков, нельзя рассчитывать на близость матрицы R к апо-
стериорной ковариационной матрице ошибки. В уравнениях фильтров низких порядков
матрица R скорее играет роль вспомогательной переменной.
3.6. Дискретное субоптимальное с.к. оценивание
и распознавание. Адаптивные обобщенные фильтры
Калмана
3.6.1. Дискретное субоптимальное оценивание и распозна-
вание. Приведенная в п.3.1.1 общая характеристика субоптимальных
методов с.к. оценивания естественно переносится и на дискретные сто-
хастические системы, описываемые уравнениями нелинейной регрессии
(2.8.1), (2.8.2) и авторегрессионными уравнениями (2.8.3), (2.8.4).
Аналогично тому, как было выполнено в разделах 3.1-3.4 для за-
дач обработки результатов наблюдений в реальном масштабе време-
ни и приближенного определения одно- и многомерных апостериорных
3.6. ДИСКРЕТНОЕ ОЦЕНИВАНИЕ И РАСПОЗНАВАНИЕ. АОФК
419
характеристик (плотностей, характеристических функций, моментов и
др.) путем приближенного решения фильтрационных уравнений, могут
быть использованы методы параметризации распределений (разделы
1.7 и 1.8). Простейшими такими методами являются МНА и МСЛ. Из-
вестны применения методов моментов, семиинвариантов, ортогональ-
ных разложений, квазимоментов. В разделе 4.14 будут рассмотрены
субоптимальные и условно оптимальные аппроксимации апостериор-
ных распределений, основанные на методах эллипсоидальной аппрок-
симации и линеаризации.
Аналогично разделу 3.5 рассматриваются вопросы субоптимально-
го оценивания путем упрощения фильтрационных уравнений в дискрет-
ных стохастических системах. В разделе 6 приведена обширная библио-
графия работ по с.к. субоптимальным фильтрам, построенным путем
упрощения фильтрационных уравнений.
Поставленные в разделе 2.12 задачи оптимального совместного оце-
нивания и распознавания в стохастических дифференциальных систе-
мах также легко обобщаются на случай дискретных стохастических си-
стем, описываемых нелинейными авторегрессионными уравнениями.
3.6.2. Субоптимальное адаптивное оценивание. Задачи с.к.
субоптимальной адаптивной фильтрации, т.е. субоптимального оце-
нивания состояния с неизвестным вектором, естественно, можно было
бы решать с использованием описанных выше методов субоптималь-
ной фильтрации. Однако этот подход резко повышает размерность
фильтрационной задачи. Поэтому наряду с этим подходом в разде-
ле 2.12 применен так называемый “partitioning approach” (Лайниотис
1968). Согласно этому подходу совместная задача фильтрации и оце-
нивания параметров подразделяется на две подзадачи: первая - оцени-
вание состояния, вторая - оценивание параметров. Полное и детальное
описание подхода содержится в (Ватанабэ 1991).
Как отмечалось в п.2.12.5, для дискретных нелинейных стохасти-
ческих систем (2.12.23) и (2.12.24) при произвольных нелинейных функ-
циях си/, cuiz не удается получить замкнутую систему рекуррентных
уравнений относительно Ri(6i) и p(t/z+i | yoz,0i) в уравнениях
(2.12.25)—(2.12.28). Основная трудность связана с нахождением филь-
трационной плотности p(xi | Воспользуемся подходом Лайнио-
тиса (п.2.12.5) и рассмотрим два важных частных случая.
3.6.3. Дискретный субоптимальный адаптивный фильтр
на основе МНА. Рассмотрим применение МНА для адаптивной суб-
оптимальной фильтрации. Пусть уравнения (2.12.23), (2.12.24) имеют
420
ГЛ. 3. СУБОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ОФК
ВИД
Xz+1 + / = 0,1,2..., (3.6.1)
= + I = 0,1,2,.... (3.6.2)
Функции <pi = = 'il)i(Xi)O) и tpu = <pu(Xi,()) предполага-
ются непрерывными и достаточное число раз непрерывно-дифферен-
цируемыми (по х). Проверкой нетрудно убедиться (задача 2.13.11), что
фильтрационная плотность p(xi | Yj,^) и условная плотность р(з/л-х |
yj,0i) при каждом фиксированном значении параметра Qi (г = 1,...
... ,N) удовлетворяют следующим рекуррентным уравнениям дискрет-
ной нелинейной фильтрации (Аоки 1971):
p(xl+1 I У0'+1Л) = P(z<+1 /Р(х, I Y^pfa+I I xi,0i)dxt,
PW+1 I Yo^i) j
Rn
(3.6.3)
p(yi+i I Yo,0t)= J J p(xt | Y^,0i)p(xi+1 | xi,9i)p(yi+i | xl+i,0i)dxidxi+i.
RnRn
(3.6.4)
В теории дискретной субоптимальной фильтрации по МНА исполь-
зуются замкнутые уравнения для оценок Xifjk) и определяющие
фильтрационную плотность
p(Xl I У0‘Д) ~ V(X(^),RitOi). (3.6.5)
Подчеркнем, что в задачах адаптивной фильтрации недостаточно
нормальной аппроксимации фильтрационной плотности p(xi | Fj,^), а
необходимо при фиксированном осуществить нормальную аппрокси-
мацию И условной ПЛОТНОСТИ p(t/Z+l I Уо,0г),ОТ которой зависят услов-
ные вероятности p(0i | 1g) в (2.12.26)-(2.12.28),
р(уг+1 I Уо', ffi) ~ Af(Yl+1 (0i),Si+1 (W, (3.6.6)
У+1(^) = М(У,+1 |У01,^),
(3.6.7)
z др
= М j [у+1(<М - У/+1 ] [У1+1(^) - У+1 ]
У0'^Л. (3.6.8)
о Рассмотрим случай, когда уравнение наблюдения (3.6.2) линейно:
^ = ^(^+^(^2/.
(3.6.9)
3.6. ДИСКРЕТНОЕ ОЦЕНИВАНИЕ И РАСПОЗНАВАНИЕ. АОФК
421
Применяя к уравнениям (3.6.1) и (3.6.9) уравнения дискретной субоп-
тимальной фильтрации, основанные на нормальной аппроксимации, по-
лучаем уравнения раздела 2.9 для Х/(0») и Ri(0i) (Сейдж, Меле 1976):
^/+i(0i) = Xi+i\i(0i) 4- A+i(#i) - ^+i(^)X/+1p(^) j , (3.6.10)
(3.6.11)
0i+i(Oi) = Ri+i\iHi+i(0i)T x
x [^/-hl(^t)^-hl|/(^t)^-hl(^i)T + ^1,/-Ь1(^)йн1^1,/+1(^)Т] > (3.6.12)
Яж|/(<М = cov{^,^ | yj,^} +cov{V>/Vu,^Vu | yj,^} , (3.6.13)
= Rw\i(0i) - /WW^W+^i)- (3.6.14)
Здесь Xi(0i) - с.к. оценка фильтрации; Х/+1|/(^) - одношаговый про-
гноз; Ri+i\i((k) - матрицы, аппроксимирующие ковариационные матри-
цы оценок X/+1|/(^i). Условные математические ожидания и условные
ковариации
ф1 = м I Го'Д)], cov {<phV>t I У0'Л)} , cov {^Vu,i>iVu | Г0'Л} ,
(3.6.15)
входящие в правые части уравнений (3.6.10)-(3.6.14), вычисляются для
нормальной плотности. Начальными значениями для уравнений
(3.6.10)-(3.6.14) служат
Хо(»г) = МХо, Яо(0г) = cov{Xo,Xo} (3.6.16)
для любого вг, i = 1, ... , N.
Далее, учитывая, что Vi,/+i и У/ - независимы из (3.6.9), получаем
для yz+i(0i) и следующие соотношения:
У+1(#г) — М [Hi+i(0j)Xi+i 4- ^н(0*Ж2,Ж |
(3.6.17)
= Я/+1(^)7?/+1|/(^)Я/+1(^)т 4-
(3.6.18)
где оценка X/+i|/(^i) и матрица Я/+1|/(#г) определяются из уравнений
(3.6.10)- (3.6.14). о
В результате получаем следующее утверждение.
422
ГЛ. 3. СУБОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ОФК
Теорема 3.6.1. Пусть уравнения нормальной авторегрессион-
ной стохастической системы (3.6.2), (3.6.9) с аддитивным шумом в
наблюдениях допускают применение МН А. Тогда уравнения (3.6.6)-
(3.6.8), (3.6.10)—(3.6.14) и (3.6.17), (3.6.18) совместно с (2.12.26)-
(2.12.28) полностью определяют субоптимальный адаптивный
фильтр на основе МНА.
3.6.4. Дискретный субоптимальный адаптивный фильтр
на основе ОФК
о В тех случаях, когда найти явные аналитические выражения для
(3.6.15) трудно, вместо уравнений (3.6.10)—(3.6.14) можно использовать
уравнения дискретного ОФК. В самом деле, подставим (3.6.15) вместо
<pi ее разложение в ряд Тейлора в окрестности Х/(0г), получим
Ф1 = М Ых,,е^ I У‘,0г] = ^(Х/;^). (3.6.29)
Далее примем
COV {frVu, V4V1.1 I Y^di} = (3.6.20)
В этом случае уравнения дискретного адаптивного ОФК (АОФК) для
и примут следующий вид (Сейдж, Меле 1976):
Л+1№) = Xz+ihW) + A+1W) [г<+1 - Яг+1(ад+1|«(0<)] , (3.6.21)
xl+1\l(ei) = ^xl(ei),ei), (3.6.22)
A+iW) = fll+1|l(0i)H<+1(6»i)r X
х [Я<+1(₽<)Я/+ц/(^)Я/+1(^)т + V’i,I+i(^)^+iV’i,/+i(^)T]“1,
(3.6.23)
= д^х.^еу+
+1 dXi dXt
+^Xi(ei),ei)^Mei),ei)T, (3.6.24)
Я<+1(<М = Rl+1^i) - /WWhi(W+i|/(<M. о (3.6.25)
В результате приходим к утверждению.
Теорема 3.6.2. Если в условиях теоремы 3.6.1 нелинейная функ-
ция (pi в уравнении (3.6.1) допускает разложение в ряд Тейлора в ок-
рестности оценки фильтрации Xi(Qi), тогда уравнения дискретного
субоптимального АОФК имеют вид (3.6.21)-(3.6.25).
3.6. ДИСКРЕТНОЕ ОЦЕНИВАНИЕ И РАСПОЗНАВАНИЕ. АОФК
423
Замечание!. Если уравнение наблюдения (3.6.2) нелинейное, то мож-
но применить линеаризацию фц в окрестности оценки прогноза X/_|_q/(0i). В таком
случае, положив 77/_|_i(0i) = 9</?i/(X/_|_ip (0j), 0{))/ЭХ[, допустимо воспользоваться
уравнениями теорем 3.6.1 и 3.6.2.
Замечание 2. Для того чтобы построить адаптивный фильтр для
дискретных нелинейных стохастических систем (2.12.23) и (2.12.24) можно применить
адаптивный линейный фильтр Калмана-Лайниотиса (раздел 2.12) к линеаризованным
уравнениям системы и наблюдения (раздел 3.7).
3.6.5. Субоптимальная адаптивная идентификация. За-
дача адаптивной фильтрации может быть рассмотрена как задача сов-
местной фильтрации вектора Х[ и идентификации неизвестного вектора
параметров в Е Rh. В этом случае в качестве оценок 0i параметра 0 по
наблюдениями могут быть выбраны оптимальные оценки по различ-
ным вероятностным критериям: минимума среднего квадрата ошибки,
максимума апостериорной вероятности и др.
Пример 3.6.1. Рассмотрим дискретную аппроксимацию уравнений Ван-дер-
Поля с неизвестными параметрами (задача 1.9.55). Тогда вектор состояния Xi Е R? я
наблюдение У/ G R определяются уравнениями:
^1,Z+1 = Х\%1 + 01X2,/, (I)
Х2,/-|-1 = 02X1^ + 01Х2,/ + ^Xf1X2,1, (П)
Yt = Xu + 02Хх3 z + Vi (I = 0,1,2,...), (Ill)
где Xi = [ХМХ2,/]Т, Xi’O и Х2,о -независимые нормально распределенные слу-
чайные величины, Xito ~ «Л/*(?711, <^i), Х2,о ~ «Л/*(Ш2, </2), V/ Л/\0, (Ту), О>1,
О>2, О3, Ю1, <^1> ТП>2, (TV ~ известные постоянные. Неизвестные параметры 01 и 02
изменяются в следующих диапазонах:
01 G [1,075; 1,225], 02 G [—0,275; 0,475 ]. (IV)
Так как параметры 01 и 02 - непрерывные, то проведем предварительное кванто-
вание интервалов (IV) для N = 3. Положим
01 = 011, 012? 013 И 02 = 021,^22,023, (V)
где
0ц = 1,1; 012 = 1,15; 01з = 1,2;
021 = -0,15; 022 = 0,1; 023 = 0,35. (VI)
424
ГЛ. 3. СУБОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ОФК
Вычисления оценок X\ti, ^2,/ переменных состояния Xltl, x2tl, среднеквадратиче-
ских оценок 0102,1 независимых параметров 01,02 и условных вероятностей р(0 —
= Oij I *о) (i = 1,2; J = i, 2,3) были проведены с использованием трех адаптив-
ных фильтров на основе МНА, ОФК и на основе метода статистической линеаризации
нелинейной системы (1)-(Ш).
Моделирование системы (1)-(Ш) проведено при следующих значениях неизвестных
параметров:
01 = 012 = 1,15, в2 = в22 = о, 1, (VII)
Щ = 0,05; 02 = —0,05; Оз = —0,15; Ш1 = 1,5; d\ = 0,3; ТП2 = 0; = 5;
(Ту = 2.
На рис.3.6.1 представлены результаты расчетов среднеквадратических отклонений
_МНА _ОФКЛ _МСЛ * . уМНА уМНА у уОФК _
I » I ° ^1 I ошибок фильтрации А| z , А^ z — Aij, Aj z —
= Х1°/ФК - Xij, Х1с/тл = Х^сл - Xi. I с использованием адаптивных филь-
тров на основе МНА, ОФК и СТЛ соответственно, и среднеквадратическое отклонение
6Г1Д сигнала X^j. Величины (Т^СЛ и были вычислены методом
статистического моделирования. При этом усреднение было проведено по 1800 реализа-
циям. Аналогичные графики среднеквадратических отклонений ^2^^» ^2^*^
и СГ2д для сигнала X2j представлены на рис.3.6.2.
Рис. 3.6.1
На рис.3.6.3 приведены результаты расчетов условной вероятности pi — р(0\ —
— $121^2 == $22 | -Н/Э» соответствующей моделируемым значениям неизвестных пара-
метров (VII) в уравнениях (1)-(Ш) с использованием фильтров на основе МНА
ОФК (р°ФК) и МСЛ (pzMCJ1) соответственно.
3.6. ДИСКРЕТНОЕ ОЦЕНИВАНИЕ И РАСПОЗНАВАНИЕ. АОФК
425
Рис. 3.6.2
Рис. 3.6.3
На рис.3.6.1 и 3.6.2 видно, что фильтр на основе МНА имеет более высокие точ-
ностные характеристики по сравнению с фильтром на основе ОФК. Анализ условных
вероятностей pi на рис.3.6.3 показывает, что фильтр на основе МСЛ не позволяет распо-
знать истинные значения параметров системы (VII) при I > 60. Следствием этого яв-
ляются достаточно большие значения среднеквадратических отклонений (уМСЛ, ^.МСЛ
(к > 60), приведенные на рис.3.6.1 и 3.6.2 соответственно. Таким образом, в данном
примере статистически линеаризованные уравнения являются грубым приближением не-
линейных уравнений (1)-(Ш). Отметим также, что затраты машинного времени на ре-
шение уравнений фильтрации на основе МНА практически одинаковы с затратами на
426
ГЛ. 3. СУБОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ОФК
решение аналогичных уравнений на основе ОФК и МСЛ.
3.6.6. Адаптивное распознавание. Предложенные в п.3.6.2-
3.6.5 уравнения адаптивной фильтрации могут быть использованы в
задачах распознавания классов, к которым относится наблюдаемый сиг-
нал (состояние системы) Х[. В этом случае модель системы имеет вид
(2.12.23), (2.12.24), где неизвестный скалярный параметр 0 принимает
одно из значений 01, ... , 0/v, соответствующих распознаваемым клас-
сам сигналов Ai, ... , An- Решение о том, к какому из N классов
Ai, ... , An относится наблюдаемый сигнал Xi в каждый фиксирован-
ный момент времени I, принимается по максимуму условной вероятно-
сти, т.е. Xi е Aj при
ptfi I У0‘) = max {р(0! I У0‘), ... , p(0N | У')} .
В частном случае, когда N = 2, задача распознавания сигналов пред-
ставляет собой задачу обнаружения.
Пример 3.6.2. Пусть сигнал Xi определяется уравнением
Xl+1 =Xi+ai+ a2Xte-a3Xl + Wi (I = 0,1,2...), (I)
а наблюдение Yl задается в виде
Yt =eXt + Vi (I = 0,1,2...)- (П)
Здесь Xi € R1, Yl e R1, Wi ~ АГ(0,ст2), Vi ~ У(0,а2), Xo ~ X(0,ag), ax,
0,2, G3, (Tw, crv и a0 - известные постоянные. Параметр (индикаторная переменная) 0
принимает два значения: 0 = 0 и 0 = 1 с априорными вероятностями р± — Р(0 — 0)
иР2 = Р(0=1) соответственно (Pl +Р2 = 1).
Задача обнаружения состоит в проверке гипотезы (Т/q или ^1) ° том, какой модели
наблюдения соответствуют наблюдаемые данные Yq ,
Но : У/ = X, + V/,
Hi : Y( — V[ (наблюдения генерируются одним шумом). (III)
Вычисляя условные вероятности р(0 — 0 j Yq) и р(0 — 1 | Yq), получаем известную
бейесову процедуру принятия решения о том, какому значению параметра 0(0 = 0 или
0 — 1) в (II) соответствуют текущие наблюдения Y^. Численные расчеты проведены при
следующих значениях параметров: G1 = 0,0001; О>2 ~ 0,01; G3 — 2; (Jw — 0,01;
<Т„ = 0, 02; 0-0 = 0, 01.
На рис.3.6.4 представлены графики условной вероятности р(0 — 1 | Yq), соответ-
ствующие наблюдаемым данным (II) при 0 — 1 и вычисленные при различных значени-
ях априорных вероятностей: Pi — 0, 15", 0, 3} 0, 5. На рис.3.6.5 представлены графики
3.6. ДИСКРЕТНОЕ ОЦЕНИВАНИЕ И РАСПОЗНАВАНИЕ. АОФК
427
Рис. 3.6.4
р(0 = ОI Го'), соответствующие наблюдаемым данным (II) при 0 — 0 и вычисленные
при таких же значениях априорных вероятностей р2 — 0, 15; 0, 3; 0, 5.
Из рис.3.6.4 и 3.6.5 видно, что использование адаптивного фильтра на основе МНА
позволяет достаточно быстро распознать, какой из двух моделей наблюдения yi = Х[ 4"
4-VJ, р(0 = 1 | Y1) > 0,8 (рис.з.б.4) или Yi = V/, р(0 = 0 | Y1) > 0,8 (рис.з.6.5)
соответствуют наблюдаемые данные Y^ в (II).
Рис. 3.6.5
428
ГЛ. 3. СУБОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ОФК
3.7. Дополнения и задачи
3.7.1. Вывести уравнения МНА апостериорного распределения для винеровских и
пуассоновских шумов в уравнениях стохастической дифференциальной системы (3.1.1).
3.7.2. В условиях задачи 3.7.1 вывести уравнения методов: моментов; семиинва-
риантов; ортогональных разложений; квазимоментов для аппроксимации апостериорного
распределения.
3.7.3. В условиях задачи 3.7.1 вывести уравнения модифицированных методов: мо-
ментов; семиинвариантов; ортогональных разложений; квазимоментов для аппроксима-
ции апостериорного распределения.
3.7.4. Пользуясь МНА, найти алгоритмы оценивания состояния нелинейных одно-
и двумерных стохастических дифференциальных систем в задачах 1.9.20, 1.9.22, 1.9.23,
1.9.26, 1.9.34, 1.9.38, 1.9.49-1.9.56, 1.9.58 по результатам наблюдения величины X с адди-
тивной помехой, представляющей собой нормально распределенный белый шум, незави-
симый от V.
3.7.5. В условиях задачи 3.7.4 найти алгоритмы оценивания состояния стохастиче-
ских систем на базе методов: моментов; квазимоментов; ортогональных разложений.
3.7.6. Найти алгоритмы оценивания нелинейных многомерных стохастических диф-
ференциальных систем в задачах 1.9.24, 1.9.25, 1.9.27-1.9.33, 1.9.48 по результатам наблю-
дения вектора состояния с нормальной аддитивной помехой.
3.7.7. В условиях задачи 3.7.6 построить алгоритмы оценивания состояния на базе
методов: моментов; квазимоментов; ортогональных разложений.
3.7.8. Построить субоптимальный алгоритм экстраполяции в задачах 3.7.4-3.7.7.
3.7.9. Построить субоптимальные алгоритмы оценивания состояния систем со слу-
чайной структурой в задачах 1.9.59-1.9.64 методом нормальной аппроксимации апостери-
орного распределения (Казаков 1977, Артемьев и Казаков 1980).
3.7.10. Вывести уравнения квазилинейной фильтрации для стохастической диффе-
ренциальной системы:
X = <р(Х, t) + u(t) + V’(f)Vi, X(to) = Xo, (I)
Z = b(t)X + V2, (II)
где Xq, Vi,V2 ~ некоррелированы и имеют нормальное распределение; (fl = (^(У, £)
- нелинейная функция; u(t) - известная векторная функция. Показать, что в случае,
когда уравнение (I) допускает применение МСЛ:
<р(Х, t) = (PQ(тх, Кх,t) 4- <^1 (тх,КХ,t)(X - тх), (III)
фильтрационные уравнения имеют вид (Казаков и Гладков 1987):
i = ^4^X4 u(t) 4- b'(t)(Z - b(t)X), Xq = mXQ, (IV)
3.7. ДОПОЛНЕНИЯ И ЗАДАЧИ
429
R = ipiR + Rip? — Rb(t)v2 1bT(t)R + (V)
где Ь1 (f) = RbT (t)v2 1; ¥>0 = 9^0 — (plTZl1. Входящие в коэффициенты МСЛ (£>q =
— (ро(тпх, Rx, t) и — (pi(mx, Kx, £) переменные ТПХ и Kx находятся из следу-
ющих уравнений:
тх = сро (тх, Кх ,t) +u(t), (VI)
Кх = <pi(mx,Kx,t)Kx + Kx<pi(mx,Kx,t)T + ^H(t)T. (VII)
Рассмотреть вопрос о несмещенности и устойчивости оценки фильтра путем рас-
смотрения уравнения для ошибки X — X — X фильтрации
X = [ - b'(t)b{t) ] X + Ь' (i)V2 - V>(t)Ц, Хо = -Хо°. (VIII)
3.7.11. В стандартной схеме использования МСЛ в задачах нелинейной фильтрации
для вычисления коэффициентов статистической линеаризации, зависящих от моментов
вектора состояния, применяется МНА. И такой фильтр, согласно (Казаков и Гладков
1987), называется квазилинейным фильтром. Окончательно, в квазилинейном филь-
тре его коэффициент усиления зависит только от времени и вычисляется на основе нор-
мальной аппроксимации. В работе (О, Шин 1997) предлагается модифицировать этот
фильтр. То есть вычислять коэффициенты статистической линеаризации и соответствен-
но коэффициент усиления линеаризованного фильтра с помощью метода параметризации
распределений. В результате использования параметризации распределения более точно
вычисляются коэффициенты МСЛ и, как следствие, точнее вычисляется коэффициент
усиления квазилинейного фильтра, что в конечном счете уменьшает с.к. ошибку оцени-
вания (как и показали результаты моделирования). Кроме того, усложнение (громозд-
кость) вычисления коэффициентов МСЛ за счет моментов старшего порядка не влияет
на время вычисления самой оценки состояния, так как коэффициенты МСЛ и коэффи-
циент усиления квазилинейного фильтра не зависят от наблюдений и могут быть заранее
найдены.
3.7.12. Обобщить результаты пп.3.6.2-3.6.4 на случай субоптимальной адаптивной
непрерывно-дискретной фильтрации (Ли, О, Шин 2003).
3.7.13. Решить пример 3.1.1 в случае, когда уравнение (I) имеет вид: X — —Х% 4-
+XV1 + и, где U - постоянная величина. Найти условия с.к. устойчивости фильтра.
3.7.14. Решить пример 3.1.2 в случае, когда уравнения (I), (II) имеют вид: X —
= -X3 + V!+u,U= -aU + V2 + и2, где Hi, ^2 “ постоянные величины. Найти
условия с.к. устойчивости фильтра.
3.7.15. Решить пример 3.1.3 для случая, когда уравнение (I) имеет вид: X —
= -ОХ + V1 + и, где U - постоянная величина. Найти условия с.к. устойчивости
фильтра.
3.7.16. Решить пример 3.2.1 для уравнений: Z — X 4" V2 4" ^2> X — —Х% 4"
+XV1+U1 , где 111,2 “ постоянные величины. Найти условия с.к. устойчивости фильтра.
430
ГЛ. 3. СУБОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ОФК
3.7.17. Решить пример 3.2.2 в условиях уравнений задачи 3.7.16. Найти условия с.к.
устойчивости фильтра.
3.7.18. Решить пример 3.2.3 для уравнений: % — X + V2, X — —Хд + Vl + U,
0 = 0 , где U - постоянная величина. Найти условия с.к. устойчивости фильтра.
3.7.19. Решить пример 3.2.4 для уравнений задачи 3.7.16. Найти условия с.к. устой-
чивости фильтра.
3.7.20. Решить пример 3.2.5 для уравнений задачи 3.7.15. Найти условия с.к. устой-
чивости фильтра.
3.7.21. Модифицированным МНА (п.3.4.1) решить примеры 3.1.1-3.1.3 и 3.2.1-3.2.5,
а также задачи 3.7.13-3.7.20. Найти условия с.к. устойчивости фильтров.
3.7.22. Модифицированным методом моментов (п.3.4.2) решить примеры 3.1.1-3.1.3
и 3.2.1-3.2.5, а также задачи 3.7.13-3.7.20. Найти условия с.к. устойчивости фильтров.
3.7.23. Модифицированным методом ортогональных разложений (п.3.4.3) решить
примеры 3.1.1-3.1.3 и 3.2.1-3.2.5, а также задачи 3.7.13-3.7.20. Найти условия с.к. устой-
чивости фильтров.
3.7.24. Модифицированным методом квазимоментов решить примеры 3.1.1-3.1.3 и
3.2.1-3.2.3, а также задачи 3.7.13-3.7.20. Найти условия с.к. устойчивости фильтров.
3.7.25. Решить пример 3.5.1 для уравнений задачи 3.7.13. Найти условия с.к. устой-
чивости фильтра.
3.7.26. Решить пример 3.5.2. для уравнений задачи 3.7.14. Найти условия с.к.
устойчивости фильтра.
3.7.27. Решить пример 3.5.3 для уравнений задачи 3.7.13. Найти условия с.к. устой-
чивости фильтра.
3.7.28. Решить пример 3.5.4 для уравнений задачи 3.7.14. Найти условия с.к. устой-
чивости фильтра.
3.7.29. Показать, что для нормальной стохастической дифференциальной системы
X = -П(Х) + V1 + и, МХ0 = 0, МХ02 = а%, (I)
Z = X + V2 (II)
(Vi, v2 - независимые белые шумы с интенсивностями и 1^25 ~ постоянная вели-
чина), если провести статистическую линеаризацию функции: “h
+Пх(Х,Я)(Х -X), то субоптимальный гауссовский фильтр будет описываться сле-
дующими уравнениями:
Я = Qo(X,R) + Rv^Z - X) + и, Уо = О, (III)
R = -2Я1(Х,Я)Л - v^R2 + i/i, Ro = сто- (IV)
3.7.30. Показать, что для нелинейной нормальной стохастической дифференциаль-
ной системы:
Х = П(и-Х) + У1, Z = X + V2 (I)
3.7. ДОПОЛНЕНИЯ И ЗАДАЧИ
431
квазилинейный фильтр описывается следующими уравнениями:
X = -П1Х + 7?i/2-1(Z - X) - Slimx, Хо = тХо, (II)
R = -21)17? - Т?2^"1 + i/i, 7?(?0) = <710, (Ш)
тх = По(« ~ тпх,Кх), mx(t0) = тХо, (IV)
Кх = -21)1 (и - тх, КХ)КХ + !/i, КМ = а2Хо. (V)
Здесь По = По (и — ТПХ,КХ) и П1 = Пх(и — ТПХ,КХ) - коэффициенты МСЛ
нелинейной функции П(11 — JC) в первом уравнении (I); X - оценка; R - дисперсия
оценки; l/j и 1^2 ~ интенсивности белых шумов V]. и р2- Оценить смещенность и с.к.
устойчивость фильтра.
3.7.31. Показать, что для нелинейной нормальной стохастической дифференциаль-
ной системы:
Т0Х + Х = П(« - X) + Vi, Z = X + V2, Х(?о) = Хо (I)
квазилинейный фильтр описывается следующими уравнениями (Казаков и Гладков 1987):
Л = х2 + - Х1), Х1(?о) = (II)
Л = ад"1 Xi - Т~хХ2 + RiMiZr - Xi), Х2(?0) = rn20, (III)
Rn = 2/?12 - рГ1/??!, Rn (t0) = К^о, (IV)
•Й12 — Т?22 + QiT0 1 Rn ~ То 1/?12 — f2 17?ц/?12, 7?i2(?o) = К^о, (V)
Я22 = Ь + 2П17'0 xT?i2 — 2Т0 lR22 — f2 1T?J2, 7?22(?о) = Tf220, (VI)
mf = = -To-1™2 + Г0-11)0(и - , K^), (VII)
&x __irx __________ ifx rr~^ t^x « t1-i icx
Лц — 2Л12, Л12 — A22 — ^0 A12^"J0 Л11>
^2 = -2To-1^22 + 2To^1K^2 + To-21/!, (VIII)
где По = По (и — и П1 = П1(и — ТП^К^) - коэффициенты МСЛ
нелинейной функции П(и — X}. Оценить смещенность и с.к. устойчивость фильтра.
3.7.32. Требуется отфильтровать сообщение содержащееся в модулирующей
функции амплитудно-модулированного сигнала Ф(-^1 > — (®0 4“ (£)) COS((Jq£ 4“
где ” априорно известные значения амплитуды, частоты и фазы;
А - постоянный коэффициент. Сигнал принимается на фоне аддитивного белого шума
V-2, имеющего нулевое математическое ожидание и интенсивность 1^2»
= (°о 4“ AXi(t)) cos(cdo£ 4- 'фо) 4- V2. (I)
432
ГЛ. 3. СУБОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ОФК
Полезный сигнал Х\ (£) описывается уравнением
X^-aXi+V^
(П)
где Ot - постоянная величина; Vi - центрированный белый шум интенсивности У\, неза-
висящий от V2 и начальных условий. Показать, что уравнение субоптимального гауссова
фильтра имеют следующий вид (Казаков и Гладков 1987):
Xi = —&Х1 + Япу21 [^1 - (ао + AXi)cos(cj0t + V\))] Acos((j0£ +Vto),
(HI)
Ri = vi + - R%v2 1 A2 cos2(cdo£ 4" V’o), (IV)
где X\ - оценка, a 7?i - дисперсия ошибки оценки. Для t 2?Г/CJq из (IV) находим
уравнение для стационарного значения Ry
R*2X2/2v2 ~ 2aR{ - vx = 0. (V)
Отсюда получаем
R* = 2i/iaA-2 + (4i/12a2A-4 + 2i/ii/2A-2)1/2. (VI)
Следовательно, подставляя (VI) в (III), получаем приближенное уравнение фильтра (Ти-
хонов и Кульман 1975):
Xi — —о.Х\ •+ Я*у2 ХА
Zi cos(w0£ + ф0) - |(ао + АА1)
(VII)
Рассмотреть случай широтно-импульсной модуляции и временной импульсной мо-
дуляции (Тихонов и Кульман 1975).
3 7.33. Показать, что уравнения субоптимального гауссова фильтра для нелинейной
стохастической дифференциальной системы
Xi = Qi(X1,X2,t) + ui + Vi (г = 1,2), (I)
Zi = Xi + V3 (II)
(Q^ - нелинейные функции; Vy2 -центрированные белые шумы с интенсивностями У\ —
— ^11 j ^12) ^2 = ^22; ^3 ~ центрированный белый шум, независимый от Уу2, с интен-
сивностью Уз) имеют вид (Казаков и Гладков 1987)
Xi = Пю + x(Zi — -Xi) 4- щ,
(П1)
3.7. ДОПОЛНЕНИЯ И ЗАДАЧИ
433
%2 = Q20 + -Й12^з Х(^1 — Х1) 4“ ^2, (IV)
Ru = J'l 4- 27?цП'1Од 4- 27?12^1о|2 4- Яп^з"1, (V)
R12 = ^12 4- 7?цЯ'10д 4- Л12(П'10,2 + ^20,1) + ^22^20,2 + ^11^12^3 \ (VI)
R22 = ^2 4~ 2Л12П20Д + 2^22^20,2 4" -Rj2^3 *• (VII)
Здесь введены следующие обозначения: Х{ - оценки; Rjj - элементы ковариационной
матрицы ошибок оценки; fl^o = fljo(Xi, -R11,-Й12,-^22)» j = / 9Xj.
3.7.34. В (О и Шин 1996) рассматривается специальный, но достаточно широкий
класс динамических систем, для которых удается построить субоптимальный фильтр су-
щественно меньшего порядка, чем ОФК. В этом классе систем вектор состояния и век-
тор наблюдения описываются произвольными нелинейными уравнениями при следующих
типичных ограничениях: начальное состояние должно быть не случайным, а точно из-
вестным числом (вектором) и размерность вектора-шума системы (system noise) должна
быть меньше, чем размерность вектора состояния (т. е. шумов в системе должно быть
меньше, чем степеней свободы). В этом случае удается построить фильтр существенно
ниже размерности, чем у ОФК. Порядок нового фильтра равен 71 4“ г(г 4" 1)/2, где 71 -
размерность вектора состояния, а Г - размерность вектора-шума системы, в отличие от
порядка ОФК, Т1 4" 7l(7l 4“ 1)/2.
3.7.35. Основываясь на уравнениях дискретного МНА (п.1.7.2), вывести уравнения
дискретного МНА апостериорного распределения для дискретных стохастических систем
(2.8.1) и (2.8.3).
3.7.36. Решить дискретным МНА апостериорного распределения задачи 3.7.13-
3.7.15 для дискретных версий уравнений системы и наблюдений.
3.7.37. Основываясь на уравнениях дискретного модифицированного МНА апосте-
риорного распределния, решить задачи 3.7.13-3.7.15 для дискретных версий соответству-
ющих уравнений системы и наблюдений.
3.7.38. Основываясь на уравнениях дискретных методов начальных и центральных
моментов (п.1.8.2), вывести уравнения методов начальных и центральных моментов для
аппроксимации апостериорного распределения для стохастических систем (2.8.1) и (2.8.3).
3.7.39. Решить дискретными методами начальных и центральных моментов задачи
3.7.16-3.7.18 для дискретных версий уравнений системы и наблюдений.
3.7.40. Основываясь на уравнениях (п. 1.8.3), вывести уравнения дискретных ме-
тодов ортогональных разложений и квазимоментов для аппроксимации апостериорного
распределения для дискретных стохастических систем (2.8.1) и (2.8.3).
3.7.41. Решить дискретными методами ортогональных разложений и квазимоментов
задачи 3.7.16-3.7.18 для дискретных версий уравнений системы и наблюдений.
3.7.42. Вывести уравнения дискретного ОФК для дискретных систем (2.8.1) и (2.8.3)
(Аоки 1970, Ройтенберг 1992, Чен 1994).
434
ГЛ. 3. СУБОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ОФК
3.7.43. Вывести уравнения дискретного фильтра второго порядка для дискретных
систем (2.8.1) и (2.8.3) (Аоки 1970, Ройтенберг 1992, Чен 1994).
3.7.44. Вывести уравнения дискретного гауссова фильтра для дискретных систем
(2.8.1) и (2.8.3) (Аоки 1970, Ройтенберг 1992, Чен 1994).
3.7.45. Вывести уравнения дискретного ОФК, фильтра второго порядка и гауссова
фильтра из дискретных уравнений для ненормированных распределений (см. раздел 4.9).
3.7.46. Фильтры Калмана-Бьюси и Калмана при вырожденной помехе в на-
блюдениях. Существенным предположением, использованном при получении уравнений
фильтра Калмана-Бьюси (разделы 2.4 и 2.8), является предположение о невырожденно-
сти матрицы интенсивности белого шума V2 (или V^z) в уравнении наблюдения. Среди
основных подходов к синтезу фильтров Калмана-Бьюси при вырожденной помехе в на-
блюдениях следует отнести следующие.
1) Метод линейного преобразования вектора состояния (возможно, расширенного),
при котором часть компонент преобразованного вектора фильтруется абсолютно точ-
но, а для оценки оставшихся компонент используется обычный фильтр Калмана-Бьюси
(см.раздел 2.5), а также (Колмановский 1973, Квакернак и Сиван 1977).
2) Метод регуляризации уравнения наблюдения, например, в (2.4.1), путем добавле-
ния малой величины — /17П1 (/X - малый параметр), далее записываются обычные
уравнения фильтра Калмана-Бьюси, в которые в качестве аргумента вводятся исходные
наблюдения, наконец, используются получаемые из этих уравнений предельные соотно-
шения (при /1 —> 0) на математические ожидания и ковариационную матрицу ошибки
фильтрации (Липцер 1974, Липцер и Ширяев 1974, Серебровский 1975, Ляшко, Диденко,
Цитрицкий 1979).
3) Метод согласованного вырождения ковариационной матрицы шума в наблюдени-
ях и матрицы, определяющей “наблюдаемую” часть вектора состояния (Миллер и Сереб-
ровский 1979, Бутов 1980, Миллер и Рубинович 1995).
4) Метод специальных дифференциальных преобразований уравнений исходных на-
блюдений такой, что для новых наблюдений имеет место согласованное вырождение ко-
вариационной матрицы шума в наблюдениях и матрицы, определяющей “наблюдаемую”
часть преобразованного вектора состояния (Борисов 1998).
Отдельные вопросы линейной фильтрации при вырожденной помехе в наблюдениях
получены в работах (Лифшиц, Виноградов, Голубев 1969, Брайсон и Хо Ю-Ши 1972,
Кайлат 1974, Моулан 1974, Миямото и Такеда 1976, Черноусько и Колмановский 1978,
Ройтенберг 1978, 1992, Симкин 1980).
3.7.47. Дать обобщение уравнений ОФК (п.3.5.2) на случай, когда в качестве опор-
ной траектории X — X[t^ выбирается решение детерминированной системы уравнений
3.1.1 при ф — ф\ — 0. Оценить влияние отклонения параметров на смещение нуля и
коэффициента усиления ОФК. Дать обобщение на дискретный случай (Вуллок и Мурман
1993).
3.7.48. Выписать уравнения дискретных методов нормальной и эллипсоидальной
3.7. ДОПОЛНЕНИЯ И ЗАДАЧИ
435
аппроксимации (разделы 3.1 и 4.9), моментов и семиинвариантов (раздел 3.2), методов ор-
тогональных разложений и квазимоментов (раздел 3.3) для случая негауссовского белого
шума, представляющего собой конечную сумму гауссовских шумов. Результаты сравнить
с (Аоки 1965, Камерсон 1969, Соренсон и Алспаш 1971, Масрелиез 1975, Мартин и Масре-
лиез
By и
1975, Масрелиез и Мартин 1977, Фугерсон 1983, Тзаи и Курц 1983, By и Чэн 1993,
Кунду 1989).
3.7.49. Решить задачу 3.7.48, используя ненормированные распределения (раздел
3.4).
3.7.50. Применительно к уравнениям (3.1.1), в которых функции , *01 явля-
дифференциальными функциями малого скалярного параметра, ф —
ются
= (£>(У, X, = гр(¥\Х^ц\ (£1 = гр = гр^У^ц) вы-
писать уравнения для первых и вторых функций чувствительности ЭХ/Эц, Э2 X/Эц2,
dR/d^R/dp2 для методов нормальной аппроксимации и статистический линеари-
зации (п.3.1.2). Рассмотреть случай линейных уравнений (раздел 2.4) с малым парамет-
ром (Ивановский и Игнатов 1986).
3.7.51. Решить задачу 3.7.50 для: а) методов моментов и семиинвариантов; б) мето-
дов ортогональных разложений и квазимоментов; в) методов эллипсоидальной аппрокси-
мации и линеаризации.
3.7.52. Решить задачи 3.7.50-3.7.51 для модифицированных методов на основе не-
нормированных распределений (раздел 3.4).
3.7.53. Для сингулярной стохастической дифференциальной системы вида
X1 = <p1(X,t,p) + ^1(X,t,p)V, х = [х1Тх2Т]т,
рХ2 = ц? (X, t, д) + V-2 (X, t, р) V, (I)
Y1 = у?}(У, t,р) + </>}(Г, t,p)V, Y = [ Y'TY2T]T,
pY2 = V2(Y,t,p)+tf(Y,t,p)V, (II)
(/1 - малый параметр; V - нормальный белый шум) вывести уравнения методов разде-
лов 3.1-3.4. Получить уравнения сингулярного ОФК (п.3.5.2).
3.7.54. Решить задачу 3.7.53 для соответствующей дискретной сингулярной системы.
3.7.55. Решить задачу 3.7.10 с помощью стандартного программного обеспечения
ОФК для кубической нелинейности (р(Х, f) = Ot^X^ 4“ С^Х2 4“ Ot^X 4“ OtQ при
следующих значениях параметров:
1) U = 0, гр = 1, Pi = Р2 = 1, «3 = 1, «2 = «1 = «0 = О, Ь = 1, (То = 1;
2) и = 0, гр = 1, 14 = р2 = 1, аз = — 1, ot2 = (*i = «о = о, b = 1, (То = 1;
з) и = 0, гр = 1, Pi = 1, 1/2 = 10-1, а3 = 1, а2 = «1 = «о = О, Ь = 1,
(Т0 = 1;
436
ГЛ. 3. СУБОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ОФК
4) и = 0, гр = 1, Pi = 10 \ V2 = 1, «з = 1» q2 = «1 = «о = 0- b = 1,
а0 = 1;
5) и = 1, гр = 1, i/i = i/2 = 1, «з = -1, «2 = Qi = Qo = О, b = 1, а0 = 1,
6) и = 1, гр = 1, i/i = 1, i/2 = 10-1, «з = -1, «2 = «1 — «о = 0, b = 1,
ао = 1;
7) и = 1, гр = 1, i/i = 10"1, 1/2 = 1, «3 = -1, се2 = «1 = «о = 0, 6 = 1,
а0 = 1.
3.7.56. Решить задачи 3.7.29 и 3.7.20 с помощью стандартного программного обеспе-
чения ОФК для кубической нелинейной функции Q(X) — Ot$X^ -j-O^X? 4“Q1% 4“О?0
при следующих значениях параметров:
1) и = 0, гр = 1, i/i = i/2 — 1» Q3 = 1, «2 = «1 = од = 0, ао = 1,
2) U = 0, гр = 1, 1/1 = 1/2 = 1, «з = -1, «2 = Q1 = Qo = О, ао = 1;
3) и = 1, гр = 1, 1/1 = 1/2 = 1, «3 = 1, «2 = «1 = а0 = 0, ао = 1;
4) U = 1, гр = 1, 1/1 = 10"1, 1/2 = 1, «з = 1, «2 = Q1 = Q0 = о, ао = 1;
5) U = 1, гр = 1, 1/1 = 1, 1/2 = 10-1, «3 = —1, «2 = «1 = «О — 0, ао = 1;
3.7.57. Решить задачу 3.7.31 с помощью стандартного программного обеспечения
ОФК для кубической нелинейной функции — X} — —(и — Х}^ При следующих
значениях параметров:
1) То = 1, 1/1 = 1/2 — 1, г! = 0, /Cfio — -^220 ~ 1’ -^120 ~ 0;
2) То = 1,1/1 = 1, 1/2 — Ю \ и — 0, .KTio = -^-220 “ 1> К12О ~ 0;
3) То = 1, 1/1 = 10 \ 1/2 — 1» и — 0, = А22О — 1» К120 = О»
4) То = 1, i/i = i/2 = 1, гл = 1, Af10 = К$2О = 1» К12о = 0;
5) То = l,i/i = 1,1/2 — Ю \ г1 = 1, Af10 = А22о = 1» К120 = 0;
6) То = 1, 1/1 — Ю 1, 1/2 — 1» и — 1» К11О = ^220 = 1’ К12О = О-
ГЛАВА 4
УСЛОВНО ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ.
ФИЛЬТРЫ ПУГАЧЕВА
Глава 4 посвящена теории условно оптимального оценивания, вос-
ходящей к работам В.С.Пугачева. В разделе 4.1 изложен принцип ус-
ловно оптимальной фильтрации и постановки основных задач для сто-
хастических дифференциальных систем. Раздел 4.2 содержит решение
задач фильтрации и распознавания. Фильтрация при автокоррелиро-
ванной помехе в наблюдениях рассмотрена в разделе 4.3. В разделе 4.4
изучается линейная фильтрация Пугачева. Вопросы условно оптималь-
ной экстраполяции изложены в разделах 4.5 и 4.6. Раздел 4.7 посвя-
щен дискретному условно оптимальному оцениванию, распознаванию
и адаптации. Дискретная условно оптимальная экстраполяция и ин-
терполяция рассматриваются в разделе 4.8. Теория эллипсоидальных
субоптимальных и условно оптимальных фильтров дается в разделе
4.9. В разделе 4.10 дается развитие теории непрерывных и дискретных
фильтров Пугачева на случай бейесовых критериев. В конце главы 4
приводятся дополнения и задачи для упражнений.
4.1. Задачи условно оптимального оценивания
в стохастических дифференциальных системах
4.1.1. Основная идея условно оптимальной фильтрации.
Практическое применение приближенных методов оптимальной филь-
трации (глава 3) ограничивается высоким порядком фильтров, особен-
но в задачах большой размерности, в которых даже применение про-
стейшего метода нормальной аппроксимации п.3.1.2 и методов разде-
лов 3.2-3.5 приводит к необходимости интегрировать систему уравне-
ний высокого порядка. Поэтому единственным способом получения
практически реализуемых фильтров в задачах большой размерности
является понижение порядка фильтров. Чтобы понять, как это мо-
жет быть достигнуто для непрерывных систем, проанализируем струк-
туру уравнения для субоптимальной оценки в методах разделов 3.1-
3.5. Легко видеть, что все эти методы дают для оценки X уравнение
вида
dX = а<(У, X, t)dt + /Зт?(У, X, f)dY + 7<ft, (4.1.1)
где £(У, X, Z), т/(У, X, t) - некоторые функции текущих значений наблю-
даемого процесса У, оценки X и времени а о, Р и 7 - некоторые
438
ГЛ. 4. УСЛОВНО ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФП
функции времени. То, что они становятся известными вместе с R толь-
ко после интегрирования полной системы уравнений, определяющей все
неизвестные параметры функции р*(я;0), аппроксимирующей апосте-
риорную плотность pt(x), для дальнейших рассуждений не имеет зна-
чения. Так, например, в методе нормальной аппроксимации (п.3.1.2)
£ = [fT - f^ThT] , rj = h. Соответственно, коэффициент а име-
ет блочную структуру а = [1п 1п ], где 1п - единичная п х п-матрица,
/3 = /п, 7 = 0. Чтобы определить функцию £ в методе ортогональных
разложений п.3.3.1, подставим в уравнение (3.2.6) выражения:
N
f = /о+52 52
к=з н=к
N
fm = А" + Е Е
к=з и=л
N
h = ho -j- 52 52 h-c-
k—з |И=*
функций /, h и перепишем это уравнение в виде
N
dX= f0- hof™ + 52 J2 (Л - hofP - hvf^})cv-
k=3 |v\ =k
N \
h0+52 52 IdY-
k=3\v\=k J
Отсюда видно, что компонентами векторной функции £ в этом случае
служат все компоненты n-мерных векторных функций /о, ~ hof^,
- hofy1), - - hyf^ (|i/| , |/i| = 3, ... , N) и соответственно мат-
рица а состоит из горизонтально расположенных диагональных блоков,
первые два из которых представляют собой единичную матрицу 1п, а
остальные - произведения 1п на соответствующие коэффициенты cv и
на произведения срсм. Если некоторые компоненты векторых функций
/о, - fy, - hofy1^, - hyf^, - hyf^ не зависят от X, то линейную
комбинацию этих компонент с соответствующими столбцами матрицы
4.1. ЗАДАЧИ УСЛОВНО ОПТИМАЛЬНОГО ОЦЕНИВАНИЯ
439
а можно выделить и принять за вектор 7 в (4.1.1). Матричная функция
rj представляет собой блочную матрицу, состоящую из всех расположен-
ных по вертикали п х п\-матриц До, hy ( |i/| = 3, ... , АГ), а матрица Р
состоит из горизонтально расположенных блоков, первый из которых
представляет собой единичную матрицу /п, а остальные - произведения
1п на соответствующие коэффициенты су ( |р| = 3, ... , N). Аналогич-
но можно привести к виду (4.1.1) уравнение (3.2.6) и при применении
метода моментов или метода семиинвариантов.
Если бы коэффициенты а,/3,7в(4.1.1) были известными функция-
ми времени, то уравнение (4.1.1) определило бы фильтр того же порядка
п, что и второе уравнение (3.1.1), описывающее поведение системы. По-
этому естественно возникает мысль попытаться непосредственно опре-
делить коэффициенты а, /3, 7 в уравнении (4.1.1) как функции времени
I - I2
из условия минимума среднего квадрата ошибки, М LX* — = min,
при всех t > to. Это приводит к теории условно оптимальной фильтра-
ции Пугачева, в которой уравнение фильтра задается заранее и опти-
мизируются только коэффициенты этого уравнения.
Выбор функций £ и т] в (4.1.1) при применении методов разделов
3.1-3.5 не единственен. Так, например, в методе ортогональных разло-
жений (п.3.3.1) можно принять так же, как и в методе нормальной ап-
проксимации (п.3.1.2), £ = [fT — f^ThT]T, т] = h, а = [In In], Р = In,
7 = 0. То, что при этом функции ( и т/ получаются зависящими от
неизвестных параметров R, су (|р| = 3, ... , АГ), как будет показано
дальше, не имеет существенного значения. Чем больше компонент бе-
рется у вектора £ и чем больше строк у матрицы т/, тем точнее будет
фильтрация.
4.1.2. Классы допустимых фильтров. Итак, мы пришли к
идее решения задач 1 и 2 п.3.1.1 путем нахождения оптимального филь-
тра в некотором классе допустимых фильтров, определяемом условием,
чтобы поведение фильтра описывалось дифференциальным уравнени-
ем заданного порядка и заданной формы. Таким образом, мы отказы-
ваемся от абсолютной оптимизации и ограничиваемся условной опти-
мизацией в заданном ограниченном классе фильтров.
В п.4.1.1 класс допустимых фильтров был определен уравнением
(4.1.1) того же порядка п, что и второе уравнение (2.1.5). Определив
оптимальные коэффициенты а, /3, 7 в уравнении (4.1.1), можно оце-
нить точность полученного условно оптимального фильтра. Если точ-
ность фильтрации оказывается недостаточной, можно повысить поря-
док допустимых фильтров, например, взять за основу уравнения (3.1.2)
440
ГЛ. 4. УСЛОВНО ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФП
и (3.1.3) метода нормальной аппроксимации и соответственно ввести
дополнительную неизвестную матрицу R. Тогда к уравнению (4.1.1)
добавится уравнение, определяющее матрицу R, и порядок фильтра по-
высится до п(п + 3)/2. Компонентами векторной функции £ будут все
компоненты векторных функций /, -hf^ и все независимые элемен-
ты матриц , - pif^ , ... , - Pmfni (число которых у
каждой такой матрицы равно п(п + 3)/2), а матричная функция т/ будет
состоять из П1 + 1 вертикально расположенных блоков, представляющих
собой п х пх-матрицы h, р±, ... , рП1. Само собой разумеется, фильтр
метода нормальной аппроксимации будет в этом случае допустимым
фильтром, у которого элементы матриц а и /3 равны 1 и 0 в зависимо-
сти от того, входят или не входят в соответствующие уравнения данные
элементы матрицы-столбца £ и матрицы tj, а 7 = 0. Оптимизация ко-
эффициентов а, /3, 7 в уравнениях такого фильтра даст в общем случае
лучший фильтр, чем фильтр метода нормальной аппроксимации. Если
точность такого условно оптимального фильтра тоже окажется недо-
статочной, то можно снова повысить порядок допустимых фильтров,
например, добавив к уравнениям (3.2.16) и (3.2.7) уравнения (3.2.2),
или (3.2.21), или (3.2.26), или (3.3.6) при некотором N, и внести соот-
ветствующие дополнительные неизвестные. При этом полученные диф-
ференциальные уравнения будут определять вектор U = [ XTST j , где
S - вектор, компонентами которого служат все добавленные к X вспо-
могательные переменные, а оптимальная оценка вектора X определит-
ся формулой X = AU, где А = [1п 0] (как всегда, в таких случаях 0
представляет собой матрицу, все элементы которой равны нулю.).
Эти соображения приводят к следующей общей схеме построения
классов допустимых фильтров.
Задаются порядок N > п фильтров, постоянная п х ДГ-матрица
А ранга п, функция значения которой представляют собой
q х 1-матрицы, функция 77(2/, u, t), значения которой представляют собой
s х П1-матрицы, и дифференциальное уравнение
dU = a£(Y, U, t)dt 4- /Зд(У, U, t)dY + <ydt (4.1.2)
при любых функциях времени а, /3, 7 в качестве коэффициентов (оче-
видно, а представляет собой N х g-матрицу, /3 - N х s-матрицу, а 7 -
N х 1-матрицу). Оценка вектора X определяется формулой X = AU.
В частном случае N = п, А = 1п уравнение (4.1.2) имеет вид (4.1.1).
4.1.3. Классы допустимых фильтров при автокоррелиро-
ванной помехе в наблюдениях. В случае, когда помеха в наблю-
4.1. ЗАДАЧИ УСЛОВНО ОПТИМАЛЬНОГО ОЦЕНИВАНИЯ
441
дениях получается в результате преобразования белого шума форми-
рующим фильтром, задачи фильтрации и экстраполяции приводятся к
уравнениям (2.1.5) и (2.1.6) при ^1=0. В таком случае теория опти-
мальной фильтрации неприменима. В этих случаях задачи фильтра-
ции и экстраполяции приводятся к случаю белого шума в наблюдениях
преобразованием наблюдаемого сигнала системой, обратной формиру-
ющему фильтру, или дифференцированием уравнения наблюдения.
В соответствии с этими результатами и в теории условно оптималь-
ной фильтрации будем вводить в уравнения допустимых фильтров про-
изводные наблюдаемого сигнала до s-го порядка включительно, если
его s-я производная содержит белый шум. При этом производные, не
содержащие белого шума, могут входить в уравнения фильтров нели-
нейно. В этом случае задачи условно оптимальной фильтрации удается
решать при произвольных уравнениях наблюдения и формирующего
фильтра помехи, не требуя их линейности, как это приходится делать
в теории оптимальной линейной фильтрации.
На основании сказанного определим класс допустимых фильтров в
случае автокоррелированной помехи в наблюдениях уравнением
dX = a£(Y, Y, ... , r(s), X, t)dt+
+frl(Y, Y, ... , У w, X, t)dY(s) + 7dt (4.1.3)
или более общими формулами X = AU и уравнением
dU = a£(Y, У, ... , y(s), U, t)dt+
+/Зт?(У,У, .... Y^,U,t)dY^ +ydt, (4.1.4)
где матрица А определяется так же, как и в случае белого шума в
наблюдениях.
Можно и не вводить производные наблюдаемого сигнала в уравне-
ния допустимых фильтров или вводить производные до порядка h <
< s. Для этого достаточно взять функцию £ независимой от .
..., Yи положить rj = 0. Однако качество фильтрации значительно
улучшается при вводе производных наблюдаемого сигнала до порядка
з включительно.
Функции £ и т] в (4.1.3) и (4.1.4) можно взять произвольно. Одна-
ко целесообразно их выбирать, руководствуясь соображениями п.4.1.1,
приведя сначала задачу к случаю белого шума в наблюдениях путем
s-кратного дифференцирования уравнения наблюдения и исключения
442
ГЛ. 4. УСЛОВНО ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФП
некоторых компонент помехи с помощью уравнения наблюдения и урав-
нений, полученных из него (з - 1)-кратным дифференцированием.
4.1.4. Постановка задач условно оптимальной фильтрации
и экстраполяции. Определив класс допустимых фильтров, следует
решить вопрос о том, какой фильтр в этом классе считается оптималь-
ным. В соответствии с общей постановкой задач фильтрации и экстра-
поляции в п.2.1.4, требующей нахождения оптимальной оценки теку-
щего или будущего состояния системы в каждый момент t > to, следуя
Пугачеву В.С., будем считать оптимальным такой фильтр, который да-
ет в известном смысле наилучшую оценку при всех t > to. Однако в
общем случае нелинейной системы в классе допустимых фильтров мо-
жет не быть такого фильтра, который давал бы наилучшую оценку при
всех t > to. В самом деле, такой фильтр был бы оптимальным одно-
временно по множеству критериев. В каждый данный момент t > to
I - I2 H I2
условие M Xt — XJ = min или M Х*+д = min представляет
собой один определенный критерий оптимальности. Требование, чтобы
это условие выполнялось для некоторого множества значений t, равно-
сильно требованию оптимальности фильтра одновременно по соответ-
ствующему множеству критериев. Иными словами, задача оптимиза-
ции фильтра при всех t > to представляет собой задачу многокрите-
риальной оптимизации. Такие задачи, как правило, не имеют реше-
ния. Фильтр Калмана-Бьюси, дающий оптимальную линейную оценку
состояния линейной системы в каждый момент t > to, представляет
собой исключение (раздел 2.4). Значит, оптимальность фильтра надо
определить так, чтобы решение задачи было возможно.
Исходя из приведенных соображений, будем считать оптимальным
такой фильтр из класса допустимых фильтров, который при любом
совместном распределении величин У, X, X в момент t > to дает наи-
лучшую оценку Х8 вектора Х8 или вектора Xs+д, Д > 0, в бесконечно
близкий момент s > t, s -> t, реализующую минимум среднего квадрата
ошибки М |xs - Xs| или соответственно М |xs — Хв+д| . Иными сло-
вами, будем считать оптимальным такой допустимый фильтр, который
на каждом бесконечно малом интервале времени совершает оптималь-
ный переход из того состояния, в котором он оказался в начале этого
интервала, в новое состояние. Такой допустимый фильтр будем назы-
вать условно оптимальным. Тогда задачи фильтрации и экстраполя-
ции сведутся к нахождению оптимальных значений а, /? и 7 в (4.1.1),
или (4.1.2), или (4.1.3), или (4.1.4) в любой момент t > to, обеспечиваю-
4.1. ЗАДАЧИ УСЛОВНО ОПТИМАЛЬНОГО ОЦЕНИВАНИЯ
443
I - I2
щих минимум среднего квадрата ошибки фильтрации М I или
экстраполяции М |xs — Х8±д | , Д > 0, в бесконечно близкий будущий
момент s > t, s —> t.
Условно оптимальный фильтр обладает тем свойством, что в дан-
ном классе допустимых фильтров не существует фильтра, который при
данном начальном распределении У, X и X в момент to был бы лучше
условно оптимального при всех t > to- Это значит, по терминологии
теории многокритериальной оптимизации, что условно оптимальный
фильтр представляет собой один из множества допустимых фильтров,
оптимальный по Парето.
Замечание!. В классе допустимых фильтров могут существовать фильтры,
лучшие, чем условно оптимальный, при некоторых значениях t > to- Так, например,
если бы удалось определить функции Q, в (4.1.1), (4.1.2), (4.1.3), (4.1.4) из условия
минимума среднего квадрата ошибки в некоторый данный момент Т > to (такие Q, /?,
'У, конечно, будут зависеть не только от t, но и от Т), то соответствующий допустимый
фильтр может оказаться лучше условно оптимального в некотором интервале времени,
включающем точку Т. Такой фильтр тоже будет оптимальным по Парето, так как в
классе допустимых фильтров не существует фильтра, лучшего, чем этот, при t — Т.
ЗамечаНИб2. В теории многокритериальной оптимизации система называ-
ется оптимальной по Парето (парето-оптимальной), если в классе допустимых систем
не существует лучшей системы одновременно по всем критериям. Парето-оптимальная
система может быть оптимальной по какому-нибудь одному критерию или по нескольким
критериям или не быть оптимальной ни по какому из принятых критериев.
При решении поставленных задач можно отказаться от тех огра-
ничений, которые приходится накладывать на уравнения (2.1.5) в тео-
рии оптимальной фильтрации. Поэтому в задаче условно оптимальной
фильтрации возьмем уравнения (2.1.5) в самой общей форме:
dY = (У, X, t)dt + fa (У, X, t)dW,
dX = faY, X, t)dt + faY, X, t)dW (4.1.5)
и будем предполагать, что W(t) представляет собой процесс с независи-
мыми приращениями с нулевым математическим ожиданием и конеч-
ной ковариационной функцией
t
&w(*i,*2) = A:(min(ti,t2)), &(С = &(*о) + j v(r)dr. (4.1.6)
to
444
ГЛ. 4. УСЛОВНО ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФП
Для задачи экстраполяции необходимо ограничиться, как и в
п.2.1.4, случаем, когда функции р и не зависят от наблюдаемого век-
тора Y, процесс Ж(£) состоит из двух независимых блоков IVi(t),
и соответственно матрицы имеют блочную структуру
= [^'0], = [0V4]> так что ^dW = 'i/j'dWi, 'ifadW — 'ip{dW2- В
этом случае, отбрасывая штрихи у функций и напишем уравне-
ния (2.1.6) в виде:
dY = (У, X, t)dt + fa (Y, X, t)dW2,
dX = faX,t)dt + faX,t)dWi, (4.1.7)
где VFi(t), ТУг(£) - независимые процессы с независимыми приращени-
ями с нулевыми математическими ожиданиями и конечными ковариа-
ционными функциями
t
= A?i(min(£i,f2)), ki(t) = ki(to) + j Vi(r)dr (i = 1,2). (4.1.8)
to
В случае автокоррелированной помехи в наблюдениях, имея в виду,
что оценивать необходимо только состояние и параметры системы, но
не помеху, будем рассматривать отдельно n-мерный вектор состояния
системы X (может быть, расширенный путем включения в него неиз-
вестных параметров системы) и Л-мерный вектор помехи 7V, причем
будем предполагать, что h > щ.
Замечание. Размерность вектора помехи не может быть меньше размер-
ности наблюдаемого вектора, так как никакая линейная функция наблюдаемого вектора
не может быть свободной от ошибок измерений.
В задачах практики состояние системы и помеха определяются раз-
личными, независимыми одно от другого стохастическими дифферен-
циальными уравнениями (уравнением системы и уравнением форми-
рующего фильтра помехи). Однако для общности целесообразно при
построении теории рассматривать случай, когда X и N определяются
совместными стохастическими дифференциальными уравнениями. Та-
ким образом, для задачи фильтрации при автокоррелированной помехе
в наблюдениях будем записывать уравнения наблюдения, системы и
формирующего фильтра помехи (2.1.5) в виде
dr = ^i(r,X,N,t)dt,
dX = у>(У, X, N, t)dt + faY, X, N, t)dW,
4.1. ЗАДАЧИ УСЛОВНО ОПТИМАЛЬНОГО ОЦЕНИВАНИЯ
445
dN = <p0(Y, X, N, t)dt + ^о(К, X, N, t)dW. (4.1.9)
Для задачи экстраполяции будем записывать (2.1.6) в виде
dY = <p1(Y,X,N,t)dt,
dX = <р(Х, t)dt + t)dW!,
dN = <p0(N, t)dt + iMN, t}dW2. (4.1.10).
В практических задачах обычно наблюдается сигнал
X = y>i(X,N,t)dt (4.1.11)
с помехой N, а исследуемая система и формирующий фильтр помехи,
как уже было сказано, описываются независимыми уравнениями. В
этом случае функции <р и ф в уравнениях (4.1.9) не зависят от Y и N,
функции 9?о и ‘фо не зависят от Y и X, a W состоит из двух независимых
блоков W\ и Wg, один из которых входит только в уравнение системы,
а второй - только в уравнение формирующего фильтра. Матрицы ф
и фо при этом имеют соответствующую блочную структуру ф = [*0'0],
фо = [0Фо], так что фс/W = ф'сПУг, фо(1№ = фойМ^
Ясно, что в результате решения поставленных задач можно полу-
чать фильтры значительно меньших порядков, чем фильтры, даваемые
методами приближенного решения уравнений оптимальной фильтра-
ции (глава 3). При этом низший порядок фильтров есть п(п + 3)/2, в
то время как условно оптимальные фильтры могут иметь любой поря-
док, не меньший, чем п (и меньший, чем п, только в случае оценивания
части компонент вектора X).
Что же касается точности фильтрации, то следует отметить, что
методы параметризации распределений дают возможность оценивать
по априорным данным точность любого фильтра, описываемого конеч-
ным числом стохастических дифференциальных уравнений, независимо
от того, каким методом получен этот фильтр. Это позволяет сравни-
вать по точности методы теории условно оптимальной фильтрации с
методами субоптимальной фильтрации. Кроме того, принятый в тео-
рии условно оптимальной фильтрации метод построения классов до-
пустимых фильтров позволяет построить класс допустимых фильтров,
содержащий любой наперед заданный фильтр, описываемый конечным
числом дифференциальных уравнений. Оптимальный фильтр этого
класса будет, как правило, лучше и уже во всяком случае не хуже,
чем данный фильтр.
446
ГЛ. 4. УСЛОВНО ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФП
Таким образом, теория условно оптимальной фильтрации Пугаче-
ва обладает двумя несомненными преимуществами по сравнению с ме-
тодами субоптимальной фильтрации. Во-первых, она позволяет полу-
чать фильтры более низкого порядка и, следовательно, более простые
в реализации. Во-вторых, она дает возможность получать фильтры не
меньшей, а при желании и большей точности, чем фильтры, даваемые
методами субоптимальной нелинейной фильтрации (глава 3).
4.2. Решение задач условно оптимальной фильтрации
4.2.1. Определение коэффициентов уравнения условно оп-
тимального фильтра. Для нахождения оптимальных коэффициен-
тов а, /?, 7 в уравнении (4.1.2) рассмотрим два момента времени t > to
и s > t. На основании (4.1.2) для бесконечно малого At = s — t можем
написать с точностью до бесконечно малых высших порядков
Us-Ut = o£tAt 4- Цт1У AY + 7 At, (4.2.1)
где ДУ = Y8 — Yt, а через rjt для краткости обозначены £(У*, £7*, t),
T](Yt, Ut,t). Точно так же на основании первого уравнения (4.1.5) имеем
с точностью до бесконечно малых высших порядков
ДУ = (ри At 4- *01* АРИ,
где AW = Ws - Wti (pit = 4>i(Yt,Xt,t), <фц = ^i(YtiXtit). Подставив
это выражение в равенство (4.2.1), умноженное слева на А, будем иметь
Х8 - Xt = Aa^At + A^rjt^itД* + ^itAW) + A7At. (4.2.2)
Очевидно, что Х8 будет оптимальной оценкой Х8 тогда и только тогда,
когда Х8 — Xt будет оптимальной оценкой Х8 - Xt, так как Х8 - Х8 —
= (Х8 - Xt) - (Xs - Xt). Таким образом, требуется определить а, /3,
у так, чтобы величина Х8 — Xt была оптимальной оценкой Х8 — Xtl
I ~ I2
обеспечивающей минимум с.к.о. М — Х8 . Формула (4.2.2) задает
структуру допустимой оценки величины Х8 - Xt, а именно, при любом
t > to в каждый момент s > t, бесконечно близкий к t, оценка должна
быть линейной функцией случайных векторов
£tAt = ttYt,Ut,t)At
4.2. РЕШЕНИЕ ЗАДАЧ УСЛОВНО ОПТИМАЛЬНОЙ ФИЛЬТРАЦИИ
447
и
rjtAY = Tjt(ipuAt 4- 'i/iuAW) =
= n(Yt, Ut, t) [ (Yt, Xt, t)bt + (Yt, Xt, t) Д W ].
Этим определяется использование информации, получаемой до момен-
та t. Она влияет на оценку в момент s только посредством значения
величины Ut под знаком функций £ и т] в (4.2.2). В этом состоит ограни-
чение, накладываемое на класс допустимых оценок требованием, чтобы
они определялись формулой X = AU и уравнением (4.1.2) при каких-
нибудь а, /?, 7. Но для того, чтобы линейная функция случайных векто-
ров £tAt и T)t ДУ была оптимальной оценкой случайного вектора Х8 — Xt,
необходимо и достаточно, чтобы она была линейной средней квадрати-
ческой регрессией Xs - Xt на &At и ту* ДУ. Поэтому для определения
оптимальных коэффициентов Аа, А/?, Ау в (4.2.2) можно применить
теорию линейной регрессии (ТСтС, п.3.6.1).
t> Согласно теории линейной регрессии для оптимальности оценки
Х8 — Xt величины Х8 — Xt необходимо и достаточно, чтобы оценка была
несмещенной и ошибка Х8 — Х8 была не коррелирована со случайным
вектором [(£tAt)T(r)tAY)T]T.
Условие несмещенности оценки дает
M(XS - Xt) = M(XS - Xt).
А так как это равенство должно быть справедливо при любом s > t, то,
положив s -> Z, после сокращения получим
= MXt. (4.2.3)
Чтобы это условие было выполнено при всех t > £о> необходимо и до-
статочно, чтобы оно было выполнено при t = to и чтобы при всех t > to
дифференциал dM(Xt - Xt) был равен нулю. Для вычисления это-
го дифференциала воспользуемся формулой Xt = AUt и уравнениями
(4.1.2) и (4.1.5). Тогда, учитывая, что величина ДЖ не зависит от Yt,
Xt,Ut и что МДЖ = 0, получим
AaM£t 4- А/ЗМщрн 4- Ay - M<pt)dt = 0.
Это дает уравнение, связывающее а, /3, у:
Aami 4- А/Зт2 4- Ау = то,
(4.2.4)
448
ГЛ. 4. УСЛОВНО ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФП
где для краткости положено
m0 = M^(y,Xt,i), mi
т2 =Mrf(Yt,Utit)ip1(Yt,Xtlt). (4.2.5)
Таким образом, Xt будет несмещенной оценкой Xt при всех t > to, если
Хо = X(to) является несмещенной оценкой Xq = X(to) и коэффициенты
а, 0, У уравнения (4.1.2) удовлетворяют уравнению (4.2.4) при всех
t > t0.
Условие некоррелированности ошибки Xs - Xs со случайным век-
тором [ (£Д£)т(т/ДУ)т] в силу несмещенности оценки Xt дает
M(XS - Х,)&М = О, М(Х, - Х,)ДУ w = 0. (4.2.6)
Подставив во второе из этих равенств выражения
As — Xt + (Aoi^t + А7)Дг -Г A(3i]t{^n
Xs = Xt + <ptДГ = ^ + ^ДЖ,
вытекающие из (4.1.2) и (4.1.5) и формулы X — AU с точностью до
бесконечно малых высших порядков, приняв во внимание, что Yi, Xt,
Ut независимы от ДРК и МДРИ = 0, МДТУДИ^ = vt Д£+о(Д£), получим
{м(Аг - + A^Mrit^uVt^uTlT - j At + o(At) = 0.
Отсюда после сокращения на At и перехода к пределу при At —> 0
находим
А/3 = ^02^22 , (4-2.7)
где
«02 = M(Xt - AUt)V1(Yt,Xt,t)TT](Yt,Ut,t)T+
+M^(Yt, Xt, t>(t) (Yt, Xt, t)T7j(Yt ,Ut,t)T,
k22 = (4.2.8)
Само собой разумеется, формула (4.2.7) справедлива только в том слу-
чае, когда матрица к22 обратима. Если это условие не выполнено, то
решение задачи невозможно.
Замечание. Условие обратимости матрицы /€22 значительно слабее условия
обратимости матрицы в теории оптимальной фильтрации (раздел 2.2). Матрица
4.2. РЕШЕНИЕ ЗАДАЧ УСЛОВНО ОПТИМАЛЬНОЙ ФИЛЬТРАЦИИ 449
/€22 может быть обратимой даже в том случае, когда матрица ф\ Wlff необратима ни при
каких Y, X, t. Для обратимости матрицы /^22» представляющей собой ковариационную
матрицу случайного вектора J](Yt, Ut, t)^i (У^, Х^ деленную на dt, необходимо
и достаточно, чтобы компоненты этого вектора не были связаны никакими линейными
зависимостями.
Сократив первое равенство (4.2.6) на At и перейдя к пределу при
8 —> t, ПОЛУЧИМ
M(Xt - Xt)& = 0. (4.2.9)
Это условие будет выполнено при всех t > to, если оно выполнено при
t = to и дифференциал dM(Xt ~ Xt)f£ равен нулю при всех t > to- Что-
бы вычислить этот дифференциал, достаточно найти стохастический
дифференциал функции (Xt - Xt)tf — (AUt - Xt)^ случайных про-
цессов Yt, Xt, Ut по формуле дифференцирования сложной функции и
взять математическое ожидание полученного выражения. <1
Таким образом, для определения оптимальных коэффициентов а,
/3, 7 служат уравнения (4.2.4), (4.2.7), (4.2.8).
4.2.2. Случай винеровского процесса и линейного фильтра.
Сначала мы вычислим дифференциал dM(Xt — для частного слу-
чая винеровского процесса W(t) и линейного уравнения фильтра (4.1.2),
когда
£(у,М) = [yTuT] , q(y.M) = I-
В этом случае
d(Xt - Xt)& = d(AUt - Xt) •
> По формуле дифференцирования Ито (1.4.82), опуская для крат-
кости индексы t, находим элементы матриц d(AUt - Xt}Y^ и d(AUt —
-Xt)Uf:
(N \ / N \
CLkhUh - Xk У = l^akhdUu-dXk +
/1=1 / \/l=l /
(N \ / N \
52 akhUh - xk j dYi + I 52 a/M'iihrfu - Фк^Фи I dt,
h—l / \h=l /
(N \ / N \
52 akhUh - Xk \U{ = 52 akhduh - dXk j Ut+
/1=1 / \/l=l /
15 Фильтры Калмана и Пугачева
450
ГЛ. 4. УСЛОВНО ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФП
(N \ / N \
^akhUh - Хк I dUi + I j dt,
h=l / \h=l /
где akh ~ элементы матрицы A, (/h/'i)/», V’u, V’a ~ h-e строки матриц ,
фг и ф. Из этих формул вытекают следующие матричные равенства
dM(AU - X)YT =
= M(AdU - dX)YT + М(АС/ - X)dYT + (А/ЗМфц'ф? - Мфцф{^,
dM(AU - X)UT =
= M(AdU - dX)UT + M(A17 - X)dUT + (АрМф^фТ - Ы.фифТ)0т dt.
Подставив сюда dY, dX и DU из (4.1.2) и (4.1.5), будем иметь
<M(AU - X)YT = M(Ao£ + A^ + A7 - y)YT+
+ {M(A17 — X)y?T А/ЗЪАфууфТ — Мфиф^у dt,
dM(AU - X)UT = M(Aa£ + A^ + A7 - <p)UT+
+M(AU - X)(£TaT + 7T)dt + {M(AJ7 - X)<p{+
+АрМф1УфТ — МфифТ}/!}1^.
Но в силу несмещенности оценки и' неслучайности 7М(АС7 — Х)-ут =
= М(Х — Х)"ут = 0, а выражение в фигурных скобках равно нулю
в силу (4.2.7), (4.2.8) при т] — I. Поэтому, подставив в полученные
равенства выражение 7 из (4.2.4), будем иметь
dM(AU - X)YT =
= {АоМ(£ — mi)YT + A/?M(</?i — m2)YT — М(</? — то)Ут} dt,
dM(AU - X)UT =
= { АаМ(е - mY)UT + АрМ(<рг - m2)UT - М(<р - m0)UT} dt+
+M(AU - X)£TaTdt
ИЛИ
dM(AU - X)CT = {AoM(e - mi)£T+
+A/?M(y>i - m2)CT - M(<p - m0)eT}dt + M(AC/ - X)eT[OoT]dt,
4.2. РЕШЕНИЕ ЗАДАЧ УСЛОВНО ОПТИМАЛЬНОЙ ФИЛЬТРАЦИИ 451
где нулем обозначена (пх хТУ) хпх-матрица, все элементы которой равны
нулю. Таким образом, мы получили линейное дифференциальное урав-
нение для М(Л{7 — Х)£т = МХ(Х — Х)£т. Для выполнения условия
(4.2.9) необходимо, чтобы интеграл этого дифференциального уравне-
ния был тождественно равен нулю. Но интеграл линейного дифферен-
циального уравнения равен тождественно нулю тогда и только тогда,
когда он равен нулю в начальный момент t = to и уравнение однородное.
Это дает условие
Асжп + Л/3/€21 - «01 = О,
где
«п = м [e(yt, Ut, #Yt, Ut, t)T,
«21 = M[<p1(Yt,Xt,t)-m2]^Yt,Ut,t)T,
koi = M[<p(Yt,Xt,t)-m0]£(Yt,Ut,t)T. (4.2.10)
Отсюда находим
Аа — (kOi - < (4.2.11)
Для того чтобы можно было определить Аа по этой формуле, не-
обходимо, чтобы матрица яц была обратимой при всех t > to- Из пер-
вой формулы (4.2.10) следует, что это условие всегда будет выполнено,
если компоненты векторной функции £ не связаны линейными зависи-
мостями («и представляет собой ковариационную матрицу случайного
вектора £(Yi,L^,£)). Таким образом, в случае линейной фильтрации
процесса, определяемого нелинейным стохастическим дифференциаль-
ным уравнением, условие (4.2.9) будет выполнено при всех t > to тогда
и только тогда, когда оно выполнено в начальный момент t = to и ко-
эффициенты о, Р уравнения (4.2.6) удовлетворяют уравнениям (4.2.7)
и (4.2.11) при всех t > to- После определения Аа и Ар по формуле
(4.2.7) и (4.2.11) величина Ау находится из уравнения (4.2.4). О том,
как определяются математические ожидания в (4.2.8)- (4.2.10), будет
сказано дальше.
4.2.3. Случай винеровского процесса и нелинейного филь-
тра. Рассмотрим теперь случай произвольной функции £(t/, u, t), непре-
рывной вместе со своими первыми и вторыми производными по компо-
нентам векторов у, и и первой производной t, и любой функции т?(г/, и, t).
> В этом случае для винеровского процесса W (£) в (4.1.5) по фор-
муле дифференцирования Ито (1.4.82) находим
(n \ ( N \
^ksVs Хк 1^=1 aksdUs dXk j £tA
s=l / \s=l /
452
ГЛ. 4. УСЛОВНО ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФП
, (V' тт у (&& 9& д£,1
+ П aksus-xk I—+ dyr + ^ «ад
\s=l / \ г=1 а s=l
+ - x‘) {£> ^&'1''Г''ФТ,+
ni >
+2££^Д('’*).<4<,1+
+152 «|j!-(0’nMr‘'(Wi)r+
9£i
/ , / , afcs n
дУг
~12aks^^iri'^k - 52 ^—(^1)5^ pt
Здесь (/877^1 )/i> 'Фгн и представляют собой h-e строки матрицы /377^1,
'ipi и'ф соответственно. Производные функции ^(y,u,t) по компонентам
векторов у и и, так же, как и сама функция £(y,u,t), здесь и везде
дальше берутся при у = Y, и = U. Теперь запишем это выражение в
матричной форме:
d(AU - Х)^т = (AdU - dX)£T+
+(AU - Х)С (^dt + dYT^+ duT^f-} +
\9dt 9y 9u J
+ - ’Ф^’ФТ) + TiTl3T^~^ £Tdt+
н|(Л17-Х)ЛгЬ1^1’ + 2r)T9T^\ ^-]d
2 IL \vy °u / .
+tr 0ттф1уф{т]Т9т^-^-
OU OU
f?dt.
4.2. РЕШЕНИЕ ЗАДАЧ УСЛОВНО ОПТИМАЛЬНОЙ ФИЛЬТРАЦИИ 453
Подставив сюда выражения dY, dX, dU из (4.1.5) и (4.1.2), будем иметь:
d(AU - Х)^т - (Аа£ -I- А/Зтщ)! + Ay - ip)£T+
+ + 7-С] +
д
ду
+ Лт/-)«тл+
ди J
+|(AC/-X)(tr
V’l^f (тр +2т]Т0т-^Л
\ду ди)
+tr /3уф1^ф{ут13т^-^-
ди ди
T\dt + HdW,
(4.2.12)
где через Н обозначена сумма всех получившихся коэффициентов при
dW. Подставим в правую часть выражения Ау из (4.2.4) и приравняем
нулю математическое ожидание полученного выражения d(AU — Х)£т.
Тогда, принимая во внимание независимость Н, dW и МсЛ/Г = 0, полу-
чим уравнение для а и у:
лет
Аакц + M(AU - Х)(£тат + = 41 - 4М1> (4.2.13)
ди
где /сп определяется первой формулой (4.2.10), a
41 (4.2.14)
4i = «01 + M(x -AU)^- + M{(X - AU)rf+
(JL
АфуфТ - A^i^f} (тг- + T1T^T-^-} £T+
\dy du)
+ ^M(X-AC/)(tr
+2’т'зт^)
du )
dy
+tr
}tTdt.
(4.2.15)
Ф^Т
+
454
ГЛ. 4. УСЛОВНО ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФП
В формуле (4.2.15) Koi определяется последней формулой (4.2.10). Все
функции без указания аргументов представляют собой значения со-
ответствующих функций в момент t, например £ = £(Yt,Ut,t), ipi =
= (pi(Yt)Xtjt). Уравнение (4.2.13) совместно с (4.2.4) определяет а и 7
после вычисления ft по формуле (4.2.7). <
4.2.4. Уравнения для оптимальных коэффициентов в об-
щем случае. Наконец, перейдем к общему случаю произвольного про-
цесса W (£) с независимыми приращениями с нулевым математическим
ожиданием и конечной ковариационной матрицей. Такой процесс в об-
щем случае выражается следующей формулой (1.4.72):
W(t) = W0(t) +1 c(p)P°(t,dp),
где Ио (С - винеровский процесс; с(р) - некоторая векторная функция
(той же размерности г, что процесс W(£)) g-мерного векторного аргу-
мента х, а интеграл при любом t > to представляет собой стохастиче-
ский интеграл по центрированной пуассоновской мере Р°(£,В), незави-
симой от процесса Wo(£) и имеющей независимые значения на попарно
непересекающихся множествах.
Для дальнейшего нам понадобится вычислить интенсивность про-
цесса ИД£). Для этого воспользуемся формулой для одномерной харак-
теристической функции (Л; t) процесса W(t) (1.4.73),
t
1п/ц(Л;£) = -|лтУ vo(r)drX + j [еглТс(р) _ i _ г'Лтс(р)] p(t,p)dp,
0 *1
где vq — vn(t) - интенсивность винеровского процесса TVo(£); а д(*>Р)Ф*
- математическое ожидание числа скачков процесса W (£), равных с(р)
(точнее, для любой бесконечно малой области Др, содержащей точку
ж), р(£, рДр-Ь 0( Др) представляет собой математическое ожидание чис-
ла скачков процесса W(t), принадлежащих множеству {у : у = с(р),р е
е Др}. Но математическое ожидание простого пуассоновского процес-
са, порождаемого потоком скачков процесса W (t), равных с(р), равно
интегралу по времени от интенсивности vp(t,p)dp этого процесса:
t
p,(t,p)dp = У vp(r,p)drdp.
о
4.2. РЕШЕНИЕ ЗАДАЧ УСЛОВНО ОПТИМАЛЬНОЙ ФИЛЬТРАЦИИ
455
Подставив это выражение в предыдущую формулу, будем иметь
t
ln/ii(A;t) = j {"Ati/o(t)cJtA+
o
-by [егА — 1 — iXTc(p) j p)dpjdr. (4.2.16)
Для нахождения интенсивности процесса W (£) вычислим ковариацион-
ную матрицу k(t) его значения Wt при данном t. Так как
Г д дт
(JIa. (У1а д____q
то для нахождения k(t) достаточно дважды продифференцировать
формулу (4.2.16) по Л и положить после этого Л = 0. В результате,
учитывая, что fti(0; t) = 1, получим
—-InftHAjt) =
1 dTh1(A-,t)
diA
У|iAti/o(t) + У c(p)T [etATc^ - 1 j vp(r,p)dpjdr,
0 RJ
d dT
^-f-lnhl(A;t) =
1 9 1 dhi(A;t) dThi(A;t)
/ц(А;«) diAdiA^ ’ ' h^t) diA diA
/b»w+/
0 R?
с{р)с{р)тегХТvp(r, p)dp >dr
и
5/n(A;t)
diA
fc(t)
c(p)c(p)Te,xTvp(r, p)dp >dr.
0 Ri
456
ГЛ. 4. УСЛОВНО ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФП
Отсюда видно, что интенсивность р(£) процесса TV(£) определяется фор-
мулой
i/(f) = i/0(<) + j c(p)c(p)TetxTc^i/p(r,p)dp. <
R%
(4.2.17)
c> Вычислим теперь стохастический дифференциал d(AU — Х)£т.
Согласно обобщенной формуле дифференцирования Ито (1.4.86) в этом
случае в правой части формулы (4.2.12) вместо и будет интенсивность
I/O винеровского процесса и добавятся интегральные члены
С7 4- frrpl>]c(p) ] - X - #(р)} х
х£(У + ^1с(р),[/ + &тгф1с(р),1)т -
-(AU - Х)(? -(AMi - Ф)с(р)£Т-
vp(t, p)dpdt+
+ J {A[U + 0T]i//ic(p)] - X - tl>c(p)} х
яо
x£(Y + i(>ic(p),U + fiipl>ic(p),t)T-
~(AU - Х)£т dP°(t,dp) =
[ AU - X + (Afrrpl/i - ip)c(p) ] x
x [£(V + i/>ic(p),U + firppic(p'),t)T - £T] -
-(AU - X)c(p)Ttf
d p o‘
a~ +
dy
>i/p(t,p)dpdt+
[AU - X + (Afirpp! - il>)c(p)]£(Y + tl/c(p),U + 0rpJ>1c(p),t)T-
4.2. РЕШЕНИЕ ЗАДАЧ УСЛОВНО ОПТИМАЛЬНОЙ ФИЛЬТРАЦИИ
457
-(AU-X)£T \dP°(t,dp).
Математическое ожидание первого интеграла добавится к выражению
dM(AU — Х)£т, найденному для случая винеровского процесса W(t)
в п.4.2.3, а математическое ожидание второго интеграла равно нулю.
В результате условие ЙМ(Л{7 — Х)£т = 0 даст уравнение (4.2.13), в
котором «о! определяется формулой:
^01
= к01+М(Х -AW&- + М
oat
(X-AU)x
c(p)T^p(t, Ptfptf
- Aprrfavoifl| (+ r>T^T'^l
+|м(х - лс/)Лг (^- + 2т1т0Т7г} +
2 [ [ \oy ou / oy
+tr
М11'оФТт]Т13т^-^-
OU OU
+ j M[X-Аи + (1/>-07рМс(р)]х
x [£(У + ipc(p),U + /3rpl>ic(p),t)T - £T]Ti/P(t,p)dp. (4.2.18)
Эта формула отличается от (4.2.15) двумя дополнительными интеграль-
ными членами в правой части. <
Таким образом, в случае любого процесса с независимыми прира-
щениями W(t) в (4.1.5) с нулевым математическим ожиданием и ко-
нечным моментом второго порядка коэффициенты а и 7 определяются
теми же уравнениями (4.2.4) и (4.2.13) после нахождения А/3 по фор-
муле (4.2.7).
> В частном случае при £(y,u,t) = [утит]Т, £(y,u,t) = I,
лет
£(У + ^ic(p),l7 + ^ic(p),t)T -£т = c(p)T«/>f[7nij8T], = [0Zjv],
458
ГЛ. 4. УСЛОВНО ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФП
и формула (4.2.18) дает
«и =«oi +MUX-A17)
c(p)Tvp(t,p)dpil^
j [Ли 0Т]+
+ У М[Х - AU + (чр - Pr)i/)1)c(p)]c(p)Ti/p(t,p)dpx
Л?
xtf[Ini/3T] = «01 + м((Х - AU)rf+
"о
гд
У c(p)c(p)TvP(t,p)dp
-Aftyi
c(p)c(p)TvP(t,p)dp
Отсюда на основании (4.2.17), пользуясь обозначениями (4.2.8), нахо-
дим
«01 = «01 + («02 - А(}к,22)\1п1РТ]]
или в силу (4.2.7), = kqi- Таким образом, уравнение для о, полу-
ченное для случая £(y,u,t) = [ утит ]Т, r](y,u,f) = I при винеровском
процессе TV(t) в (4.1.5), справедливо при любом процессе с независи-
мыми приращениями РИ(£) с нулевым математическим ожиданием и
конечным моментом второго порядка. <
Итак, оптимальные коэффициенты о, /?, 7 в уравнении фильтра
(4.1.2) в общем случае определяются формулой (4.2.7) и уравнениями
(4.2.4) и (4.2.13), в которых величины mo, mi, m2, «22, ^02, «11, ^21 и
Kqj определяются формулами (4.2.5), (4.2.8), (4.2.10), (4.2.14) и (4.2.18).
4.2.5. Уравнения, определяющие фильтр Пугачева. Для
вычисления математических ожиданий в (4.2.5), (4.2.8), (4.2.10),
4.2. РЕШЕНИЕ ЗАДАЧ УСЛОВНО ОПТИМАЛЬНОЙ ФИЛЬТРАЦИИ 459
(4.2ДЗ)-(4.2.15), (4.2.18) в общем случае необходимо знать совместное
распределение векторов Yt, Xt, Ut при любом t > to, т.е. одномер-
ное распределение составного случайного процесса Z(t) =
= [У(^)ТА'(^)ТС7(^)Т] . Это распределение определяется уравнением
Пугачева для характеристической функции, соответствующим системе
стохастических дифференциальных уравнений (4.1.2) и (4.1.5).
> Подставив в (4.1.2) выражение dY из (4.1.5), приведем эту систе-
му уравнений к виду:
^i(y,X,t)
¥>(У,Х,0
a£(Y, U, t) + ^(У, U, t)^ (У, X, t) 4- 7
dt+
4>i(Y,X,t)
<p(Y,X,t)
^(Y,U,t)^(Y,X,t)
dW.
(4.2.19)
Роль матрицы a(x,t) и b(x,t) в общей теории в нашем случае игра-
ют соответственно первая и вторая матрицы в правой части уравнения
(4.2.19). Подставив эти матрицы в уравнение Пугачева для характери-
стической функции (п. 1.5.4) и соответственно положив А — [ А^А^X? ] ,
получим уравнение для совместной одномерной характеристической
функции <71(Л1,Л2, Аз;£) процессов У(£), X(t) и U(t):
(Ai, Аг, Аз;£)/dt = М{гА^<^1(Уг,Л7,£)-|-
+iX^(Yt,Xt,t) +iAf[a£(K,tfM)+
+/3T](Yt, Ut,t)V1 (Yt, Xt, t) + 7] +
(Yt,Xt, t)TAi + i/>(Yt, Xt, t)TA2+
+^i(Yt, Xt, t-)TT)(Yt, Ut, t)TflTX3-, t)} exp{iA?yt+
+iX%Xt+iXlUt}. (4.2.20)
К этому уравнению следует добавить начальное условие
<7i (Ai, А2, Аз;£0) = </о(А1, Аг, Аз), (4.2.21)
где </о(А1, Аг, Аз) - совместная характеристическая функция начальных
значений Уо = У(^о), Xq = X(to), Uo = U(to) процессов У(£), X(t), U(t).
460
ГЛ. 4. УСЛОВНО ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФП
Само собой разумеется, начальное распределение определяемого урав-
нением (4.1.2) процесса U(t) не может быть известным. Поэтому его
неизбежно надо задавать более или менее произвольно. Единственное
требование, которому следует подчинить это распределение, состоит в
том, чтобы в начальный момент t = t0 удовлетворялись условие несме-
щенности оценки (4.2.3) и условие (4.2.9). Как мы видели, только в этом
случае фильтр, определяемый формулой X = AU и уравнением (4.1.2)
при а, /8, 7, удовлетворяющих (4.2.4), (4.2.7) и (4.2.13), будет условно
оптимальным. <
Таким образом, имеем следующий результат.
Теорема 4.2.1. Пусть уравнения стохастической диффренциаль-
ной системы (4.1.5) допускают существование одномерных моментов.
Тогда в основе теории условно оптимальной фильтрации для допу-
стимых фильтров (4.1.1) или (4.1.2) лежат уравнения (4.2.4), (4.2.7),
(4.2.13) и (4.2.20), (4.2.21) при условии невырожденности матрицы «22-
Теорема 4.2.2. В условиях теоремы 4.2.1 в случае винеровского
процесса и линейного фильтра, невырожденной матрицы «22 уравне-
ния фильтра имеют вид (4.2.4), (4.2.7), (4.2.11) и (4.2.20), (4.2.21).
В важном частном случае, когда функции ip, Ф, в уравне-
ниях (4.1.5) не зависят от У, величина Y обычно не включается и в
уравнение (4.1.1) или (4.1.2), определяющее класс допустимых филь-
тров, т.е. функции и rj принимаются также не зависящими от У. В
этом случае для определения всех математических ожиданий в (4.2.5),
(4.2.8), (4.2.10). (4.2.13)-(4.2.15) и (4.2.18) достаточно знать совместную
одномерную характеристическую функцию <?i(Ai, Л2, t) процессов X(t)
и U(t). Чтобы получить уравнение Пугачева для этой характеристиче-
ской функции, достаточно положить в (4.2.20) Ai = 0. Тогда, изменив
нумерацию величины А2, Аз, т.е. обозначив Ai и А2 соответственно,
получим
dc/i(Ai, А2;£)/д£ = М{гА^(Л*,£)+
+iX2[a£(Ut,t) + fr](Ut,t)4>i(Xt,t) +7] +
+x(i/>(Xt, i)TAi + (Xt, t)TT](Ut, t)T(3TX2-, t)} exp{iAf Xt + iX%U}.
(4.2.22)
Уравнения (4.2.20) можно решить совместно с (4.2.5), (4.2.7) и
(4.2.13) любым приближенным методом (разделы 1.6-1.8). При этом,
взяв достаточно большое 2V, можно найти решение с любой степенью
точности. Вычисления, необходимые для определения коэффициентов
а, /3, 7 в уравнении (4.1.2) условно оптимального фильтра и совместно-
го распределения У*, Xt, Ut при любом t > to, конечно, очень сложны,
4.2. РЕШЕНИЕ ЗАДАЧ УСЛОВНО ОПТИМАЛЬНОЙ ФИЛЬТРАЦИИ 461
особенно в многомерных задачах. Однако эти вычисления использу-
ют только априорные данные и не опираются на результаты наблюде-
ний. Поэтому их надо выполнять для каждой конкретной задачи (или
класса задач) только один раз при синтезе фильтра (алгоритма филь-
трации). Практическое применение фильтра при каждом конкретном
эксперименте требует только решения уравнения (4.1.2) при известных
функциях времени а, /3, 7.
Уравнения (4.2.4), (4.2.7) и (4.2.13) (или (4.2.11) в случае линейно-
го фильтра), связывающие N х ^-матрицу /3 и N х 1-матрицу 7, дают
nq 4- ns 4- п = n(q 4- s 4- 1) скалярных уравнений. Эти уравнения од-
нозначно определяют а, /3, 7 в уравнении (4.1.1) фильтра n-го поряд-
ка, для которого N = п, А = 1п (конечно, в случае обратимых при
всех t > to матриц кц и «22)- Однако они недостаточны для опреде-
ления N(q 4- s 4- 1) элементов матрицы а, /3, 7 при N > п. Поэтому
(7V — п)(^ 4~ s 4" 1) элементов матриц а, /3, 7 можно задать произволь-
но. В частности, взяв за основу для определения класса допустимых
фильтров какой-нибудь субоптимальный фильтр, можно оставить урав-
нения для вспомогательных переменных (образующих вектор S) неиз-
вестными и ввести коэффициенты а, /3, у, подлежащие оптимизации,
только в уравнение для оценки, приняв при этом, конечно, А = [10].
Тогда уравнения всех допустимых фильтров будут содержать только
n(g4-$4-1) неизвестных скалярных коэффициентов, которые можно од-
нозначно определить из уравнений (4.2.4), (4.2.7) и (4.2.13) (или (4.2.11)
в случае линейного фильтра). Можно также попытаться определить
оставшиеся неопределенными (TV — ri)(q 4- s 4- 1) элементов матриц а,
/3, у путем дополнительной минимизации среднего квадрата ошибки
М |х — х| 2 на каждом шаге процесса численного решения уравнения
(4.2.10).
В некоторых случаях функции £ и q в (4.1.1) или (4.1.2) могут
зависеть от неизвестных параметров. Так, например, взяв за основу
определения класса допустимых фильтров уравнения МНА, получим
функции
£(y,x,t) = [f(y,x,R,t)T - f{1\y,x,R,t)Th(y,x,R,t)T] ,
т)(у, x, t) = h(y, x, R, t), (4.2.23)
зависящие от неизвестной матрицы R. Взяв за основу уравнения како-
го-нибудь другого метода главы 3, можно получить функции £, ту, зави-
сящие и от других неизвестных параметров - апостериорных моментов,
462
ГЛ. 4. УСЛОВНО ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФП
семиинвариантов или квазимоментов. В таких случаях можно заменять
эти параметры соответствующими априорными параметрами и опреде-
лить их вместе с а, /3, 7 в процессе решения уравнений (4.2.4), (4.2.7),
(4.2.13) и (4.2.20) (или (4.2.22)). Само собой разумеется, это касается
только параметров, от которых £ и т/ зависят нелинейно. Параметры,
входящие в £ и т] линейно, можно принять за элементы оптимизируемых
матриц а и /3.
Теория условно оптимальной фильтрации (оценивания состояния и
параметров систем) не дает абсолютно оптимальные фильтры, удовле-
творяющие уравнениям теории оптимальной фильтрации раздела 2.2,
а дает только условно оптимальные фильтры, которые, конечно, в об-
щем случае хуже оптимальных, но зато легко реализуемы. Однако,
если абсолютно оптимальная оценка X вектора X удовлетворяет урав-
нению допустимого фильтра (4.1.1) или (4.1.2) при X = AU при каких-
либо функциях времени а, /3, 7, то уравнения (4.2.4), (4.2.7), (4.2.13) и
(4.2.20), конечно, определяют именно эти а, /3, 7 и условно оптималь-
ный фильтр будет абсолютно оптимальным (абсолютно оптимальный
фильтр будет в этом случае допустимым и, следовательно, оптималь-
ным в классе допустимых фильтров). Точно так же, если оптимальный
фильтр в каком-нибудь классе, содержащем класс допустимых филь-
тров, удовлетворяет уравнению (4.1.2) при каких-нибудь а, fi, то
теория условно оптимальной фильтрации даст именно этот фильтр.
Наконец, подчеркнем, что теория условно оптимального оценива-
ния дает возможность оценивать не все компоненты вектора состояния
системы (в общем случае расширенного), а только некоторые из них.
Для этого достаточно взять функции £ и т/ в (4.1.1), зависящие только
от соответствующих компонент вектора X. Так, например, взяв £ и т/
в (4.1.1) зависящими только от Y, t и оценок неизвестных параметров
системы, можно оценивать только параметры системы, не оценивая ее
состояния. В таких случаях будут получаться фильтры, порядок кото-
рых меньше размерности п расширенного вектора состояния.
Пример 4.2.1. Для задачи примера 2.1.1
y = z = x + v2, х = -X3 + XVt, (I)
найдем фильтр Пугачева, удовлетворяющий уравнению первого порядка
X =aix3 +а2Х + pz + y. (II)
г _ iT
За основу для выбора функций £(^Y,f) — X Х% и 1 мы приняли
уравнение субоптимального фильтра метода нормальной аппроксимации, в котором ко-
эффициенты — R(3 -|- 1^2 * ) и ^2 1 ПРИ XhZ заменены подлежащими оптимизации
4.2. РЕШЕНИЕ ЗАДАЧ УСЛОВНО ОПТИМАЛЬНОЙ ФИЛЬТРАЦИИ
463
функциями времени Q2» Р и, кроме того, введены также подлежащие оптимизации ко-
эффициент Qi при X3 и свободный член 'у.
Сначала находим по формулам (4.2.8)
«22 — "2, «02 — М(Х - Х)Х = т2о - тп, (III)
где 77lrs = M.Xr Xs. После этого формула (4.2.7) дает /3 = ^(ТВ2О —
-шц), и уравнения (4.2.4) и (4.2.13) принимают вид:
m03ai + m0iO!2 + 7 = -т30 - /Зтю,
(IV)
(4тОб - ЗгП15 - тоз)»! + (4m04 - Зт13 - тО1тоз)а2 + 3(тоз - mi2)7 =
= -тпзз + тзошоз + ^(Зт22 - 4mi3 + mwm03) - 3i/2^2(mi2 - тоз), (V)
(2тО4 - т13 - тО1тоз)а!1 + (2т02 - тп - n^i)a2 =
= -тз1 + т3отпо1 + /3(т2о - 2тц + тютщ). (VI)
Уравнение (4.2.22), определяющее совместную характеристическую функцию слу-
чайных величин Xt и Xt, имеет в нашем случае вид
dgi (Ai, А2; t)/dt = М { -г Ai X3 + i А2 («i X3 + а3 X + /ЗХ + 7) -
-i^AfX2 - \v2/32X2}eiX'x+iX'*. (VII)
Z Z
Так как
Лг+s
M(iXY(iXye^x+i^x =
U Л-yU Л2
то уравнение (VII) сводится к линейному уравнению в частных производных
dgi _ . d3gi
dt 1 dXl
1 d3ffi _i_ xd91.L.
~aiX2~d^ +012X2 dX2 +
+PX2~^T + 91'1Х^~й\^ + ~ o"2^A2) 91'
C/Ai 2 uA^ \ 2 J
Интегрируя это уравнение c OL — [Q1Q2], Р и 7’ определяемыми полученными алгеб-
раическими уравнениями, найдем оптимальные Q и у. Для этого можно, конечно, при-
менить любой приближенный метод интегрирования уравнений в частных производных.
При этом придется учесть, что моменты TTlrs в уравнениях для Ot и у выражаются через
характеристическую функцию Qi формулой
TTlrs
dr+sgi
d^iXrYdiiXrY
Ai =A2=0
464
ГЛ. 4. УСЛОВНО ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФП
Однако практически лучше всего применить для приближенного решения уравнения для
один из методов параметризации распределений, независимо от того, сводится это
уравнение к уравнению в частных производных или нет.
Пример 4.2.2. Если в предыдущем примере определить класс допустимых
фильтров второго порядка, содержащий обобщенный фильтр Калмана-Бьюси приме-
ра 3.6.1, то следует положить А = [10], U = [U1U2]T = [ХЯ]Т и соответствен-
но принять
= [uj Uj Щ U2 U2 U2], — U2>
Тогда уравнения допустимых фильтров запишутся в виде
X - AU = [1 0][С71С72]т = Ui
И
Ur — OtriU^ -}-0tr2Ui + Olr^UiU2 -\-0tr^UyU2 +Olr§U2 + Pr^Z + 7r (r — 1? 2).
Формулы (4.2.8) в этом случае дают
0
1
к22 =М172[01]
1/1 0
0 V2
U2 = ^2тоо2;
К02 — М(Х — U\)X — ТП200 “ ш110,
где ТПГ31 — После этого (4.2.7) дает
& =Л/? = [01]
_ Ш200 ~ ^110
^г^оог
Уравнения (4.2.4) и (4.2.13) в этом случае имеют вид
77l030<2il+Ш020<212+^021^13+^021*214+7ПоО2<215+71 — ~ ?™300 ~ Лш102,
(4тобо ~ 3mi5o — mQ30)cvii + (4moso ~ Зтио — ^о2ошозо)<^12 +
(+4mo4i ~ 3mi3i — ШоцШозо)<^1з + (4mosi ~ 3mui — Ш021 ^030)^14+
+(4тоз2 ~ 3mi22 ~ ^002^030)^15 + 3(тозо ~ ^120)71 ~
— —^ЗЗО + ШЗООШОЗО+Л (Зш221 ~4mi3i +тю1Шозо) + 3^1 ^f(mii2 —Ш022),
(I)
(ЗШо5О “ 2771140 — Шо2ОтОЗо)<^11 + (Зто4О “ ш020 “ 2mi3o)Qi2 +
+ (Зто31 “ m020m0U “ 2mi21)«13 + (3mo41 ~ ^020ш021 “ ^-131)^14 +
4.2. РЕШЕНИЕ ЗАДАЧ УСЛОВНО ОПТИМАЛЬНОЙ ФИЛЬТРАЦИИ 465
4-(3mo22 “ m020m02)^15 4“ 2(mo2O “ шпо71 — ~ш320 + 7ПзОО7ПО2о4-
+/?1(2т2и — ЗШ121 4-шо2ОшЮ1) 4- ^2(^102 ~ 3moi2, (II)
(2mo4i ~ Шозотпои ~ Ш131 )ац 4- (2тоз1 — ^020^011 ~ ^121)^124-
4-(2mo22 “ Ш0П “ ш112)О!13 4- (2тоз2 — Ш011Ш021 “ ^122)^144"
4-(2moi3 — шоцтоог — тюз)^15 4- (mon — mioi)7i 4- (moso ~ mi4o)Q2i4-
4-(т040 - т1зо)«22 4- (т031 - mi2i)Q23 4- (m04i — mi3i)a24 4-
4-(то22 — mi2i)Q25 4- (того - тц0)72 = —т3ц 4- т3оотоц4-
4-Л(т202 - 2тц2 4- тОцтю1) - /^2тОоз 4- ^2(т2ц - mi2i)4-
4-Л^2^2(тю2 — 2то12), (III)
(3mo5i — тозото21 — 2mi4i)an + (3mo4i — тоготог! ~ 2mi3i)ai24-
4-(Зт032 - т0цт021 - 2т122)а13 4- (Зт042 - mQ21 - 2т132)а14 +
+ (Зто23 — mo2imoo2 ~ 2тцз)а15 4- 2(то21 — ^111)71 + (moeo ~ mi5o)o!2i +
4-(то5о - тио)«22 4- (mo4i — rni3i)a23 4- (m05i - mi4i)a24 4-
4-(тоз2 ~ mi22)^25 4- (тозо ~ mi2o)72 = -m32i 4- т3оото214-
+/?i(2m2i2 ~ 3mi22 4"mo2imioi) 4-/?f ^(тюз ~ Зто1з) 4-^г(т221 — mi3i)4-
4-/?1/?2*/2(2тц2 — Зтогг), (IV)
(тозг “ тозотоог)^!! 4- (то22 ~ mo2omoo2)Qi2 4- (тогз ~ топтоог)£*1з4-
4-(то23 ~ mO2imoo2)«i4 4- (тоо4 ~ mQ02)Qi5 4- 2(mo4i ~ mi3i)a2i4-
+2(тоз1 — mi2i)oi22 4- 2(то22 — тц2)а23 4- 2(тоз2 ~ mi22)<^24 4-
4-2(moi3 — тюз)^25 4- 2(топ — mioi)72 = ~^3Q2 4- т3оотоо24-
4-2/?2(m202“mii2)—2^1^2^2тооз4-^2д/2(тю2~то12)4-/?1 (тоогтю!—тюз)-
(V)
Уравнение (4.2.22) для совместной характеристической функции </1(А1, А2, A3 J t}
величин X, Ui, U2 имеет в данном случае вид
dgi (Ai, А2, X3\t)lddt = M{-iAiX3+
+iX2(otiiUi 4- 0112^1 4" °lisUiU2 4- oti^U^ U2 4- ot^U^ 4- 0iXU2 4- 71)4"
4-гАз(<221 t/f 4- ot22Ui 4- ot23UiU2 4- Oi24U^U2 4- 0:25^2 4" &2XU2 4- 72)“
466
ГЛ. 4. УСЛОВНО ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФП
-i/iA?X2/2 - i/2(AА2 + £2А3)2/2} ехр {гД2X + гХ2иг + iX2U2} . (VI)
Решив уравнение (VI) совместно с уравнениями (I)-(V), определяющими Q, /3, 'у, любым
приближенным методом параметризации распределений, найдем 7 из 14 неизвестных эле-
ментов матриц Q, /3, у. Остальные 7 можно или взять произвольно, или выбирать на каж-
дом шаге численного решения задачи так, чтобы средний квадрат ошибки был минималь-
ным на этом шаге. Если избрать первый путь, то целесообразно взять те же значения Q21,
Q22» 61(23, 6124, 6^25, /?2 и что и в уравнениях обобщенного фильтра Калмана-Быоси
примера 3.6.1 0(22 — Р1, 6124 ~ “6, Q25 = ~^2 а21 ~ ^23 — Л ~ 71 = О-
Таблица 4.2.1
t 1 2 3 4
0,0 0,5000 0,5000 0,5000 0,5000
0,4 0,1584 0,1704 0,1587 0,1584
0,8 0,0930 0,1076 0,0943 0,0930
1,2 0,0652 0,0789 0,0660 0,0652
1,6 0,0497 0,0618 0,0504 0,0497
2,0 0,0399 0,0508 0,0408 0,0402
Рис. 4.2.1
В таблице 4.2.1 (рис.4.2.1) приведена зависимость ошибки фильтрации от времени
для данной задачи для МНА апостериорного распределения (столбец 1), обобщенного
4.2. РЕШЕНИЕ ЗАДАЧ УСЛОВНО ОПТИМАЛЬНОЙ ФИЛЬТРАЦИИ
467
фильтра Калмана-Бьюси (столбец 2), фильтра Пугачева первого порядка (столбец 3) и
условно оптимального фильтра второго порядка в классе допустимых фильтров, содержа-
щем обобщенный фильтр Калмана-Бьюси, при 0*21 ~~ £*23 — /^1 ~ 71 ~ 0, £*22 ~ ^1,
0(24 — —6, Q25 ~ —^2 1 (столбец 4). Расчеты произведены для — 0,01, V2 — 1-
Анализ результатов расчетов показывает, что даже фильтр Пугачева первого по-
рядка дает существенно более высокую точность фильтрации, чем значительно более
сложный обобщенный фильтр Калмана-Бьюси, и приближается по точности к фильтру
нормальной аппроксимации. Результаты расчетов показывают также, что оптимизация
(даже частичная) в классе фильтров, содержащем данный фильтр (в нашем случае обоб-
щенный фильтр Калмана-Бьюси), может существенно повысить точность фильтрации.
Пример 4.2.3. Найдем фильтр Пугачева для задачи примера 3.1.3,
y = z = x + v2, X = -XQ + Vi, 0 = 0. (I)
За основу класса допустимых фильтров примем первые два уравнения метода нормальной
аппроксимации и соответственно положим
e(X,0,t) = [x©,x]\(X,0,t) = 1.
Тогда уравнение (4.1.1), определяющее класс допустимых фильтров, будет представлять
собой систему двух уравнений
X = ctuXQ + Qi2^V + 0iZ + 7i, (II)
0 — 0(21 XQ “I" 0(2%X -|- 02% +72- (Ш)
Формулы (4.2.8) и уравнение (4.2.7) в этом случае дают
«22 = ^2, (IV)
«02 — М [ (X — Х)Х(0 — 0)Х j — [m2000 — 7711010 7711100 “ 771Ю01 ]Т ,
01 — ^2 1 (777-2000 “ TTiioio), 02 — ^2 1 (ш1100 “ 777-1001),
где Tn,pqrs = MXpQqXrQs. Уравнения (4.2.4) и (4.2.13), определяющие оптимальные
коэффициенты (Иц, Q12, £*21, £*22, 71, 72, имеют вид
TTlQOll£*11 + 777«оО1О£*12 + 71 — ~777цоО “ /?1Т77ю00, (V)
7770011 £*21 + 771оО1О£*22 + 72 = “^17771000, (VI)
468
ГЛ. 4. УСЛОВНО ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФП
(2тоО22 ~ ЛТ-Ю12 — ш0011 )Q11 + (2moO21 “ ш1012 ~ ^0010^0011)^12 +
+ (л10031 — Л2ю21)^21 + (ТПООЗО “ ™ОО2о)(*22 + (^iQOll “ ш1001)71 +
+(тоо2о — ^1010)72 — — Шип — 2тцоошоо11 + /?i(m2ooi — 2тпюп +
+miooomoou) + /Мш2ою - тюго) “ ^/^moooi + ^гЛ/Ыткюо - 2mooio),
(VII)
(2moo2i ~ mion — mooiomoon)niii + (2moo2O ~ тюю ~ mooio)Qi2+
+(mooio ~ тюоо)71 — ~шпю + mnoomioio+
+/?i(m2ooo ~ 2тюю + ^ioooWoio) — ^2/^1, (VIII)
(mooi3 ~ ^0112)^11 + (mooi2 ~ moin)^i2 + (2moo22 ~ moi2i — moon)a2i +
+ (2moo2i “ moi2o ~ ^0010^0001)^22 + (mOoo2 ~ moioi)7i +
+(moon — mono)72 — Л(тцо1 ~ ^1002) + ft(^ino ~ 2тюп +
looomooi 1) 4-г'г/УгКюо — 2moooi) — ^2/^2 Шоою, (IX)
(mOoi2 — wioin)«n + (moon — mOno)«i2 + (moo2i ~ mOonmooio)«2i +
+ (moo2O — тоою)«22 + (moooi — moioo)7i —
= ft(mnoo ~ miooi) — ^2 (тюю ~ тюоотоою) “ ^2Л^2- (X)
Наконец, напишем уравнение (4.2.22), определяющее совместную характеристическую
функцию величин X0, X, 0:
dgi (Ai, А2, A3, А4; £)/ ddt — М{— iAi JC0 -F iA2(ctii-X0 + Q12-X fl\X + 71)+
+iA4(a2i^0 + OL22X + P2X + 72) — ^iAj/2—
—^2(^1 A3 + ^2A4)2/2} exp |гА1 X + гАг© + 4A3X 4- zA4©} . (XI)
Решив уравнение (XI) совместно с уравнениями, определяющими матрицы Q, /?, 7, лю-
бым приближенным методом параметризации распределений, найдем коэффициенты
уравнений условно оптимального фильтра, предназначенного для оценивания состояния
системы х = -ex + Vi и неизвестного параметра в, и совместное распределение X,
0, X, 0, с помощью которого можно определить точность оценивания и найти довери-
тельные области для X и 0.
Пример 4.2.4. Построим теперь для задачи предыдущего примера фильтр
Пугачева для оценивания одного только неизвестного параметра 0. Для определения
класса допустимых фильтров включим неизвестную функцию времени X в уравнении
4.2. РЕШЕНИЕ ЗАДАЧ УСЛОВНО ОПТИМАЛЬНОЙ ФИЛЬТРАЦИИ 469
для 0 предыдущего примера в оптимизируемые коэффициенты. Тогда получим следую-
щее уравнение класса допустимых фильтров:
0 = а© + fiZ + 7.
(I)
Таким образом, функции £ и Т] определяются в этом случае формулами
£(0,*) =0, 77(0,0 = 1.
Поскольку все допустимые фильтры линейны, для определения Q, /3, у надо пользоваться
формулами (4.2.4), (4.2.5), (4.2.7), (4.2.8), (4.2.10) и (4.2.11). Эти формулы последователь-
но дают
Р = - 771101), (П)
_ +шцотоо1 +/3(mioi -^ioo^ooi) /ТТТч
а ~ г?2 2 ’ V111/
ш002 ш001
7 = -amooi - pm100. (IV)
Уравнение (4.2.22) для совместной характеристической функции величин X, 0, 0 имеет
в данном случае вид
^01 (Ai, А2, Аз; 0/ddt — — 2А1 А?0 4~ 7А3 (q0 4- РХ 4- 7) —
—7^1 Aj/2 — УъРъ^/^} ехр |iAi X 4- гАг0 4- г Аз©} . (V)
Решив уравнение (V) при Q, Р, 'у, определяемых полученными формулами, любым при-
ближенным методом параметризации распределений, найдем оптимальные коэффициен-
ты Q, Р,^ и совместное распределение X, 0, 0, с помощью которого можно определить
точность оценивания, в частности найти доверительные интервалы для 0.
4.2.6. Формула для производной ковариационной матри-
цы ошибки фильтров и экстраполяторов Пугачева. Из общей
формулы для производной по времени ковариационной матрицы зна-
чений случайного процесса, имеющего стохастический дифференциал
(п. 1.7.1), можно вывести формулу для производной по времени ковари-
ационной матрицы ошибки условно оптимального фильтра.
> Вычитая из уравнения (4.1.2), умноженного слева на матрицу А,
второе уравнение (4.1.5), находим стохастический дифференциал ошиб-
ки фильтрации X — X — X:
dX — 4- APr]ipi 4- А'у — ip)dt 4- (АР’Ц'фу — 'i/jjdW.
470
ГЛ. 4. УСЛОВНО ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФП
Подставив отсюда выражения коэффициентов при dt и dW, получим
R = (мХ^ат + МХ^7]Т/3Т + МХ7Т) Ат-
-МХ<рт + А!а№Хт + рЩ^Хт + 7МХТ)-
—М(рХт + M(A^T/i^i — т]Т /ЗтАт —
Эта формула справедлива для любого допустимого фильтра. Для ус-
ловно оптимального фильтра выполняются условие несмещенности
оценки (4.2.3) и условие некоррелированности ошибки со случайным
вектором £ (4.2.9), вследствие чего MX = MX — MX = 0, МХ£Т —
= М(Х — Х)£т = 0. Кроме того, в силу формул (4.2.7) и (4.2.8):
MXip^TiT - Mi/h/'i/jT'qT -I- т)Т =
= M(X - X)^r]T - М'фи'фгТ)1' 4- АрМт)'ф\У'фТт)Т —
= “^02 4" А/Зк>22 — 0-
Поэтому для фильтра Пугачева формула для производной ковариаци-
онной матрицы ошибки принимает вид
R - M[(Xt -XtMYt, Xt, t)T + <p(Yt, Xt, t)(X? - X?)-
-A^Yt, Ut, 4)^1 (Yt, Xt, (Yt,Xt,t)Tr)(Yt, Ut,t)T/3TAT+
+^(Yt,Xt,t)v(t)^(Yt,Xt,t)T]. <i (4.2.24)
Таким образом, имеем следующее утверждение.
Теорема 4.2.3. В условиях теоремы 4.2.1 всегда справедлива фор-
мула (4.2.24) для производной по времени матрицы ошибки фильтра
Пугачева (4.1.2).
4.2.7. Применение условно оптимальной фильтрации к за-
дачам распознавания
> Теорию условно оптимальной фильтрации можно применить для
задачи распознавания сигналов в случае, когда функция ipi в первом
уравнении (4.1.5) линейна относительно вектора состояния X,
(У, X, 0, t) = b(Y, 0. t)X -4- 60(У, 0, i),
а функция не зависит от X. В этом случае
<Pik = м [(У,X,0k,t)\ У4‘ ] = b(Y,0k,t)Xk + b0(Y,0k,t)
и уравнения (2.12.9) принимают вид
4.3. ФИЛЬТРАЦИЯ ПРИ АВТОКОРРЕЛИРОВАННОЙ ПОМЕХЕ
471
dqk(t) = X%b(Y,0k,t)T + bo(Y,0k,t)T-
N 1
-[xfb(y,0ft,z)r + г»о(У,0М)т] \qk(t)Wivipi'r1(Y,t)x
h=l '
x <dY
N
- E[6(y>№ + WGh'V ]
h=l
dt >
(4.2.25)
(k = 1, ... , N).
Заменив здесь оптимальные оценки Х\, ... , Xn вектора состояния си-
стемы для разных классов сигналов соответствующими условно опти-
мальными оценками и добавив уравнения типа (4.1.1) или (4.1.2), опре-
деляющие эти оценки, Хк = AUk,
dUk = ak£(Y, Uk,ek, t)dt 4- /3kTj(Y, Uk,Ok,t)dY 4- ^dt (4.2.26)
(k = 1, ... , N),
получим замкнутую систему уравнений для Xi, ... , Хдг и
• • • <
Итак, имеем следующий результат.
Теорема 4.2.4. Если выполнены условия теоремы 4.2.1, то при
линейной относительно X функции ipi в первом уравнении (4.1.5) и не
зависящей от X функции ф\ теория условно оптимальной фильтра-
ции дает возможность решать задачи распознавания сигналов раз-
личных классов при любых функциях ср и ф во втором уравнении
(4.1.5).
4.3. Фильтрация при автокоррелированной
помехе в наблюдениях
4.3.1. Преобразование уравнений. При решении задач теории
условно оптимальной фильтрации при автокоррелированной помехе в
наблюдениях ограничимся для простоты случаем винеровских процес-
сов W(f), Wi(£) и Wz(t) в уравнениях (4.1.9), (4.1.10).
Согласно сказанному в п.4.1.4 для приведения задачи фильтрации
к случаю белого шума в наблюдениях будем дифференцировать урав-
нения наблюдения до появления белого шума (члена с dW) в правой
части по формуле Ито (1.4.85).
472
ГЛ. 4. УСЛОВНО ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФП
t> Дифференцируя первое уравнение (4.1.9) по формуле Ито полу-
чаем, опуская для краткости аргументы функций,
dK = + <pTv<Pi + vLf + <pfn<Po + : ФП«ФТ) dt+
+(<Ри^1 + rfn'MdW,
где, как обычно, ipu = dip^/dt, ip\y = (d/dY)^, <pix = (д/дХ^р^, <pin =
= (9/dN)<pT, матрица Ф определяется формулой Ф = [0 i/jt 'фТ]т, а
Ф1 : ФрФт согласно обозначению (1.4.85) представляет собой матрицу-
столбец ni х 1, элементами которой служат следы произведений матриц
вторых производных соответствующих компонент векторной функции
ipi по всем компонентам векторов У, X, N и матрицы Фг/Фт. Если
фТг'Ф + / 0, то s = 1 и полученное уравнение представляет собой
стохастическое дифференциальное уравнение, определяющее процесс
У(£). Если же (рТг'Ф + ФгпФо — О’ то полученное уравнение представ-
ляет собой обыкновенное дифференциальное уравнение. В этом случае
дифференцирование надо продолжать.
Предположим, что отличное от нуля слагаемое в dW появляется
только после 5-кратного дифференцирования первого уравнения (4.1.9),
так как первое уравнение (4.1.9) не может содержать меньше ni неза-
висимых компонент помехи, то это может быть только при h > sni.
Тогда, положив У<°) = У, У<*+1) = dY^/dt (fc = 0,1, ... , 5 - 1), будем
иметь
У<*+1> = <pk+1(Y^,X,N,t) (fe = 0,1, ... , s-1), (4.3.1)
где функции tp2, , <Ps определяются рекуррентной формулой
<pk+i(Y,X,N,t) =
= 4>kt(Y, X, N, t) + <pky(Y, X, N, t)7^ (У, X, N, t)+
+<pkx (У, X, N, t)T<p(Y, X, N, t) + pkn (У, X, N, tf<p0 (У, X, N, t)+
+ ^(Ф* : Ф1/ФТ)(У, X,N, t) (k = 1, ... , s - 1). (4.3.2)
В этой формуле $k • Фг/Фт - n\ х 1-матрица, элементами которой
служат следы произведений матриц вторых производных соответству-
ющих компонент векторной функции по всем компонентам векторов
4.3. ФИЛЬТРАЦИЯ ПРИ АВТОКОРРЕЛИРОВАННОЙ ПОМЕХЕ 473
У, X, N и матрицы ФрФт. Дифференцирование последнего уравнения
(4.3.1), соответствующего к = s — 1, дает
dY^ =<ps+l(Y^\X,N,t')dt + ^1(Y^,X,N,t>)dW, (4.3.3)
где
<^+i (У, X, N, t) = ?st (У, X, N, t) + psy(Y, X, N, t)T<pi (Y, X, N, t)+
+<p„(У, X, N, t)T<p(Y, X, N, t) + <pan(У, X, N, t)T<p0(Y, X, N, t)+
+|(Ф, : №T)(Y,X,N,t),
tyx{Y,X,N,£) =
= ^„(У, X, N, t)TiKY, X, N, t) + <pin(y, X, N, <)т^о(У, X, N, t).
Таким образом, в результате s-кратного дифференцирования урав-
нения наблюдения первое уравнение (4.1.9) заменяется уравнениями
(4.3.1) и стохастическим уравнением (4.3.3). Эти уравнения можно пе-
реписать в виде
dy(fc) = y(*+1Mt (Л = 0,1, ... , s - 1),
У<’) = <ps+i (У(о), X, N, t)dt + (У(о), X, N, t)dW. о (4.3.5)
Уравнение (4.3.5) вместе со вторым и третьим уравнениями (4.1.9)
с Y = представляют собой систему уравнений вида (4.1.5) с расши-
ренным вектором состояния X’ = [XTNT]T вместо X и расширенным
наблюдаемым вектором Y* = [Y^T ,Y^T .. .Y^T]T вместо Y. Поря-
док этой системы уравнений, как правило, можно понизить, исключив
некоторые или все компоненты вектора помехи N с помощью уравнений
(4.3.1).
Пример 4.3.1. Для уравнений вида
dY = (pi(Y,Xi,Ni,t)dt (У — скалярная величина),
dXk=Xk+1dt (к = 1, ... J-1),
dXk = 4>k(Y, X, N, t)dt + ^(У X, N, t)dW (k = l, ... , n),
dNk = Nk+ldt (fc = l,...,r-l),
dNk = 4>Qk (У, X, N, t)dt + V’o* (У, X,N,t)dW (k = r, ... ,k),
474
ГЛ. 4. УСЛОВНО ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФП
где Х\ , . . . , Хп, Ni , . . . , Nfi - компоненты векторов X и TV, S = ГПш({, г) и
формулы (4.3.2) и (4.3.4) дают
к
<Pk+l = <Pkt + VkyVl +
t=l
' 94>i v . 9V>i дг
dXi Xk~,+2 + dNi Nk~,+2
ж---О
(k = 1, ... , s - 1)
5<pi . dtpi .
Vs+l — Vet + ‘PsyVl + 'dN^>Ol,+
diPi V , v
дхг Xa~t+2 + QNi Na~t+2 •
dX^e + dN^Oa'
<p'a = Xs+i, il)'s = 0 при s - r < I,
V’Os = Ns+1> ^Qs=° ПРИ s = l < r-
Компоненты помехи TV} , . . . , N8 могут быть исключены из уравнений системы с по-
мощью уравнений (4.3.1), которые последовательно дают
Ni =¥31-1(y(°),y(1>,Xi,t),
р р
у(р+1) _ <ppt _ tppytpi — 52 V’izi-^p-t+2 — 52 <Pini^p-i+2
Np+1 =--------------------------------------------------------
Vln,
(p= 1, ... , s- 1),
~ dxv Vin' 1)-
Точно так же, заменив первое уравнение (4.1.10) уравнениями (4.3.5), приведем
уравнения (4.1.10) в задаче экстраполяции к уравнениям вида (4.1.7) с расширенным век-
тором состояния X' = [XTNT]T вместо X и расширенным наблюдаемым вектором
у/ = рл(0)ТГ(1)Т Г(»)Т]Т вмест0 Y.
4.3.2. Определение коэффициентов уравнения фильтра
Пугачева. Совершенно так же, как в п.4.2.1, теория линейной ре-
грессии дает для определения оптимальных а, /3 и 7 в (4.1.4) условие
4.3. ФИЛЬТРАЦИЯ ПРИ АВТОКОРРЕЛИРОВАННОЙ ПОМЕХЕ
475
несмещенности оценки X (4.2.3) и условия некоррелированности ошиб-
ки со случайными векторами &AZ и
М(Д14+д, - Xt+^ff = 0, M(AUt+±t - Xt+^Y^Tr]l = О,
где 6 = e(rf(0), Vt(1), • • • , Yt(>\ Ut,t\ m = rf(Yt(0\ Kt(1), ... , Yt(s}, Ut, t).
Из условия несмещенности оценки вытекает уравнение (4.2.4), в
котором
т0 = MV(Yt(0},Xt,Nt,t), mr = M£(YtW,Yt(1} , ... , Yt{‘}
т2 = Mr,(Ytw,Yt{1}, ... , Yt(e},Utlt)<ps+l(Yt(0},Xt,Nt,f). (4.3.6)
Из условия некоррелированности ошибки со случайным вектором
совершенно так же, как в п.4.2.1, выводится формула (4.2.7) для
оптимального А/?, в котором
«02 = М [ (Xt - AUt^s+1 (Ytw,Xt,Nt, t)T + (^)(YtW,Xt,Nt, t) ] ,
«22 = Мт?(У<(0),у/1), ... , Yt{s\Ut,t)^1v^)(YtW,Xt,Nt,t)x
XT)(YtW,YtM Yt(s\ut, tf. (4.3.7)
Из условия некоррелированности ошибки со случайным вектором
&AZ при AZ —> О вытекает условие (4.2.2), которое должно быть вы-
полнено при всех t > to. Из этого условия совершенно так же, как и
в разделе 4.2, выводится второе уравнение, связывающее оптимальные
а и 7. Сначала выведем это уравнение для случая линейного фильтра
(4.1.4).
4.3.3. Оптимальные коэффициенты уравнения линейного
фильтра. В случае линейного фильтра функция £ в уравнении (4.1.4)
линейна
(Л»1.........<)=[smV|T.-.sWT«’']T.
а г) представляет собой единичную матрицу порядка m, ...
..., у^ ,u,t) = I, При этом из (4.2.9) вытекает з + 2 условий Х[М(А(/ -
—Х)у(*)т] = 0 (к = 0,1, ... , s), M(AJ7 — X)UT = 0. Вычислив стоха-
стические дифференциалы величин (AU — X)Y^T к = 0,1, ... , з) и
476
ГЛ. 4. УСЛОВНО ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФП
(AU — X)UT по формуле Ито (1.4.85) с учетом уравнений (4.3.5) и фор-
мул (4.2.4) и (4.2.7), получим систему линейных дифференциальных
уравнений для M(AU — X)Y^T (к = 0,1, ... , з) и M(AU — X)UT:
dM(AU - X) [ YWTY(1)T... Y^U7 ] =
= {AaM(£ - 7П1)^Г + - m2)£T - M(</> - mo)aT} dt+
+{M(A17 - X) [у<1)Т... Г(я)т00]Т +
+M(At7-X) [y<°)Ty(1)T...yMTt7'r] [0.. .0aT] }dt.
Для выполнения условия (4.2.9) при всех t > to необходимо, чтобы эта
система была однородной и условие (4.2.9) было выполнено в начальный
момент to. Условие однородности уравнения дает для оптимального Аа
формулу (4.2.11), где
«01 = М [<р(У/0), Xt, Nt, t) - mo ] <(У((0), rt(1), ... , YtM, Ut, t)T,
«и = M [С(У/О), У/0, • • •, Yt(s}, Ut, t)-mt ] £ (Уе(0), Уе(1),..., ytW, Ut, t)T,
«21 = M [^+i(yf(o),Xt)M,0 -m2] e(yt(0),yt(1), , Yt(s},Ut,t)T.
(4.3.8)
Таким образом, условие (4.2.9) в случае линейного фильтра будет
выполнено при всех t > to тогда и только тогда, когда оно выполнено
в начальный момент to, и а при всех t > to определяется формулами
(4.2.11) и (4.3.8).
4.3.4. Оптимальные коэффициенты уравнения нелинейно-
го фильтра Пугачева. Приравняв нулю дифференциал dM(AU —
—Х)£т, получаем уравнение (4.2.13), в котором
«'i = М [i?(yf(0),yf(1), ... , YtM,Ut,t)<pe+t(YtW,Xt,Nt,f) -m2] х
х<(У/0),yt(1), ... , У/в), Ut, t)T, (4.3.9)
«oi = M(<p - mo)(T + M(X - AU)-^—+
Ol
+ £ M(X - AU)Y^T^ + M{(X - AU)rf+1 +
4.3. ФИЛЬТРАЦИЯ ПРИ АВТОКОРРЕЛИРОВАННОЙ ПОМЕХЕ
477
£Т+
+|м(Х-А17)Лг (я^ + 2т1Т0Туг} +
2 ( [ \оу\8) OU/ иу{8'
+ tr /Зг)1р1и-ф'[т]Т0т^-^- |<т. (4.3.10)
OU OU J J
Здесь как и в п.4.2.3, все функции без указания аргументов представля-
ют собой их значения в момент Z, например, £ = £(у/°\у/х) , ... , у/*\
Из (4.2.13), (4.3.8)-(4.3.10) при £(у^\у(1>>, ... , y<8\u,t) =
= [f(2/(O)T,3/(1)T, ••• , 2/(в)Т}«Т)]Т, Т7(3/(О\3/(1), ••• , y(8\u,t) = I следу-
ет, что к21 = «21, ^oi = Яо1 и уравнение (4.2.13) дает формулу (4.2.11).
Само собой разумеется, формулы (4.3.9) и (4.3.10) можно полу-
чить из (4.2.14) и (4.2.15), если заменить Y составным вектором У' =
= [y(°)T,y(1)T,...,y(s^r+i]7 , a <£>i, V*i и rj - блочными матрицами
$ = [y(1)T...yWT¥>f+1]r, [0...0^ПТ и 7?' = [О...О77].
4.3.5. Уравнения, определяющие фильтр Пугачева. Для
определения математических ожиданий в (4.3.6)-(4.3.10) и
(4.2.13) достаточно знать совместное однозначное распределение про-
цессов yW(t),y^)(^), ... , yW(^),X(^),2V(t) и U(t). Одномерная ха-
рактеристическая функция этого распределения определяется уравне-
нием Пугачева (п. 1.5.4), в котором a(x,t) и Ь(х,£) должны быть замене-
ны блочными матричными функциями
[ Г™... + V^UT + 7Т]Т
соответственно. В результате получим для одномерной характеристиче-
ской функции <71 (Ai, ... , As+4; t) процесса [У(°)(£)т, Y^(t)T ...
.. ,Y^a\t)T,X(t)TiN(t>)TU(<t>)T]T уравнение
dgi(Ai, ... , As+4j i)/dt =
= A*K(fc) +iAf+1<^s+i + iAf+2<p + iAf+3<po+
it=i
+iAf+4(a£ + Pri<p,+i + 7) + x(iplXa+i + ^ТАя+2+
478
ГЛ. 4. УСЛОВНО ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФП
+‘ФоЪ+з + Ф1 ilT0TXs+4-, i)| ехр | i ^2 \Г+1К(А:)+
' k-0
+iXl+2X + iXT+3N + iXT+4U
(4.3.11)
Здесь, как и в (4.3.10), все функции без указания аргументов понима-
ются, как их значения в момент t.
Начальным значением характеристической функции pi (Ai,...
..., As+4 ; t) при t = to служит характеристическая функция начальных
значений векторов у(°\у(х), ... , Y^8\X,N,U. При этом начальное
распределение U следует задавать так, чтобы при t = to были выпол-
нены условия несмещенности оценки и некоррелированности ошибки
со структурной функцией
Замечание!. Уравнение (4.3.11), конечно, может быть выведено из обще-
го уравнения (4.2.20) путем замены У расширенным вектором У1 = ,
...y^Yx - расширенным вектором X1 = [ Х^NT ] , (/?, Чр, ipi, Чр\ , T] соответ-
ствующими блочными матрицами [фГ(рТ J , £'фТ'фо' ] , [У^0^... ] ,
[o...ovl] [0...07?] и векторов Al, А2, A3 векторами [аГ---аГ+2а^+3] ,
Ав_^-4 соответственно.
Замечание2. Если некоторые компоненты помехи N исключены с помо-
щью уравнений (4.3.1), то эти компоненты помехи должны быть заменены в <р, Чр, р8^.-[,
Чр\ в (4.3.6)-(4.3.11) их выражениями через у(0)у(Х) . . . y(s\ a N в (4.3.11) следует
понимать как вектор, составленный из оставшихся компонент помехи. Однако можно
поступить и наоборот, исключить из (4.3.6)-(4.3.10) У(Х) . . . y(s) с помощью уравне-
ний (4.3.1). В этом случае для вычисления математических ожиданий в (4.2.13), (4.3.6)-
(4.3.10) достаточно знать совместное распределение векторов У^®\ X, N, U в каждый
момент t. Характеристическая функция этого распределения определяется уравнением
(4.3.11) при А2 = • • • = As+i = 0.
ЗамеЧЯНИеЗ. В задачах практики функция <pi в первом уравнении
(4.1.9) обычно не зависит от У = У^\ функции (р и Чр во втором уравнении (4.1.9) не
зависят от У и N, а функции <Pq и 4pQ в третьем уравнении (4.1.9) не зависят от У, X.
В этом случае функции £, Т] в (4.1.3) или (4.1.4) обычно берутся не зависящими от У,
и для определения всех математических ожиданий в (4.2.13), (4.3.6)-(4.3.10) достаточно
знать совместное распределение векторов X, N, U в каждый момент t. Чтобы получить
уравнение для характеристической функции pl(Ai, А2, A3J t) этого распределения, до-
статочно положить в (4.3.11) Ai = • • • = As+i = 0 и переименовать векторы Ав+2,
А$+з, As+4 в Ai, А2, A3 соответственно. Тогда получим уравнение
4.3. ФИЛЬТРАЦИЯ ПРИ АВТОКОРРЕЛИРОВАННОЙ ПОМЕХЕ
479
5р1(А1, л2, Аз;0/3* = M{iAf^ + iA2Vo + гА^(а£ + £77^+1 + 7)+
+xW>TAi + <А2 + ^TriTpTX3’t)} exp{iAfX + 1X2N + iXjU}. (4.3.12)
Таким образом, имеем следующий результат.
Теорема 4.3.1. Пусть уравнения стохастической дифференци-
альной системы (4.1.9) допускают существование одномерных момен-
тов. Тогда уравнения (4.2.4), (4.2.7), (4.2.13), (4.3.11) (или (4.3.12))
полностью и точно решают задачу нахождения условно оптимально-
го фильтра при автокоррелированной помехе в наблюдениях, постав-
ленную в п.4.1.4.
За мечание1. Для решения уравнения (4.3.11) или (4.3.12) совместно с
(4.2.4), (4.2.7), (4.2.13) (или (4.2.11)) можно применить любой из приближенных методов
параметризации распределений (разделы 1.7, 1.8).
Замечание2. В частном случае, когда класс допустимых фильтров
определяется уравнением (4.1.1) А — 7, U — X и во всех формулах, определяющих
условно оптимальный фильтр, следует заменить AU и U величиной X.
Замечание 3. Все сказанное в конце п.4.2.5 о нахождении коэффициентов
уравнения условно оптимального фильтра, остающихся неопределенными после расчета
изложенным методом, о практическом применении фильтра и о возможности оценивать
только часть компонент вектора состояния системы, в частности только ее параметры,
полностью относится и к только что полученным уравнениям для случая автокоррелиро-
ванной помехи в наблюдениях.
Пример 4.3.2. В задаче примера 3.1.2,
Y = Z = X + N, Х = -X3 + Vi,N = —aN + V2, (I)
где TV - стационарная помеха с показательной ковариационной функцией —
= Ре-в1г1 , а vltv2 - независимые нормально распределенные белые шумы, возьмем
за основу для построения класса допустимых фильтров уравнение для X, полученное в
примере 3.1.2 методом нормальной аппроксимации:
i = -Х(Х3 + 37?) + (i/i + i/2)_1 [i'l + aR - 3(X2 + R) ] x
x [z + aZ-aX + X(X2 + 3T?)] . (II)
Правая часть этого уравнения представляет собой полином относительно Z, X, Z, со-
держащий члены Z у ZX2, X, X3, X3, Z, ZX2. Заменив коэффициенты при этих
480
ГЛ. 4. УСЛОВНО ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФП
величинах подлежащими оптимизации функциями времени Qi, &2, <*3, <*4> <*5> 01 > 02
и вводя свободный член 7» также подлежащий оптимизации, получим уравнение допу-
стимых фильтров в виде
к = «1Z + a2ZX2 + а3Х + а4 X3 + а5 X5 + (ft + P2X2)Z + 7. (Ill)
Таким образом, в данном случае
<p(X,t) = -X3, <po(N,t) = -aN, <pi(X,N,t) = X + N,
<P2(X,N,t) =—X3 — aN,
ЩХ, t) = <MN, t) = 1, <01 (X, N, t) = [11],
V представляет собой диагональную матрицу с элементами l/j, 1/2,
= [zzx2xi3x5]T, = [ix2]T.
Формулы (4.3.7) и (4.2.4) после исключения помехи выражения функции (/?2 дают:
Р1 — ТПО4О + ш031 — ^(Шпо — 772101 ~ ТПо2О + ТПои)
^177^002 “ 771Q42 + ТПоЗЗ ~ й(771ц2 ~ ТПюз ~ ТПо22 + 7По1з)
«22 = (У1 + ^2)
1 771002
771002 771004
0 = [Л Z?2 ] = «02W221,
(IV)
(V)
где TTlijk = . Уравнения (4.2.4) и (4.2.13) в этом случае имеют вид
771100^1 + 771102^2 + 771оО1<*3 + Т71оОЗ<*4 + Т71оО5<*5 + 7 “
= —771030 + 01 (тпозо — атпюо + атпою) + /?2(тП032 — <7771102 + <*771012)) (VI)
(771200 “ 771iqo)c*1 + (Т712О2 “ 7711ОО7711О2)<*2 + (771101 “ ТПюоТПоО! )<*з +
+ (771103 ~ 771100771003)<*4 + (Т71105 ~ 77lioo77loO5)<*5 =
= —771130 + 771юо771оЗО + /?1(т71130 — ТПюоТПоЗо) + 02^132 ~ 771ю2771озо) +
+/?1<7(Т712ОО ~ 771цо — TTI^qq + 771юо771о1о) +
+/?2й(7П202 — 771ц2 — 77lioo77lio2 + ТПюгТПою)) (VII)
4.3. ФИЛЬТРАЦИЯ ПРИ АВТОКОРРЕЛИРОВАННОЙ ПОМЕХЕ
481
(3171202 — 2171211 — 772100^102)^1 4“ (3171204 — 2171213 — ^102)а2 +
-Ь(ЗгП103 — 2тП112 “ 771102771001 )<*3 + (3171Ю5 — 2171Ц4 — 771Ю2771оОз)а4 +
+ (3771107 ~ 2Т71Ц6 — 771102771005)^5 + 2(771Ю2 — 771Ц1)? = 771132 — 21711414-
“ЬТ71102 771030 — 2а(7712Ц — 771202 — 771121 + ТПцг) + /31(171132 — 771Ю2 771030 ) +
-hy82(771134 ~ 771104771030) 4“ /?1 <^(771202 — 771Ц2 — 771юо771Ю2 4“ 771Ю2771010)4“
4-/?2й(т71204 — ТТ1Ц4 — 771юо771Ю4 4“ 771ю4771ою)4-
4-1/1 [ 771002 4" 2()8i771Ю1 4- ^2771103) ] 4"
4-(т/1 4- 1/2) [Л (2171011 — 3771002) 4- ^2(2771113 — З771004) 4- /?1 (771110 — Зт71Ю1)4-
4-2/?1/?2(771Ц2 - Зтпюз) 4“ ^2(я1Ц4 - Зтпюб)], (VIII)
(2771101 — Шцо — Tn\QQmQQi)ot± 4- (2тпюз — 171112 — 177-102177-001 )^2 4"
4" (2171002 — 771011 — 771ooi)<*3 4" (2171004 — 771013 ~ 771001771003)<*4 4"
4-(2771006 — 771015 ~ 771001771005)^5 4" (171001 — TTIqio)? =
= 771031 ~ 771030771001 4" /31 (171031 “ 771030771001)4"
4-^2(771033 ~ 771030771003) 4" /?1О(т?1101 ~ 7Т10Ц — 771100771101 4" 771010771001)4"
-4-^2<1(7711ОЗ — 771013 — 771юоТ71ООЗ 4" 771оюТ71ООз) ? (IX)
(4171103 — 3?71112 — 771100771003)а1 4" (4Т71Ю5 — ЗТПЦ4 ~ 771ю277100з)<*24“
+ (4171004 — 3171013 — 771001771003 )^3 4" (4171006 ~ 3171015 — 771QO3)a44"
4"(4171008 — 3171017 ~ 771003771005)а5 4" 3(Т71ООЗ ~ 771012)? =
= 2171033 ~ 3171042 4" 171030771003 — За(771ц2 — 771ЮЗ — 771022 4" 771013)4-
4-/31 (771033 ~ 771030771003) 4" /?2(т71035 — 771030771005)4"
4-^10(771103 ~ 771013 — 771100771103 4" 771ою771ооз)4-
4"^2О-(Т71105 ~ 771015 ~ ТПюО771005 4" 771010771005)4"
4"3l/i()8i 171002 4- /32171004) 4" 3(l/i 4- 1/2) [/31 (171011 4" 2171002)4-
4-2/31/32(171013 — 2171004) 4- /3f (171015 ~ 21Т100б], (X)
16 Фильтры Калмана и Пугачева
482
ГЛ. 4. УСЛОВНО ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФП
(6тП105 ~ 5тПц4 — 771юо771005 )а1 + (6т71ю7 ~ 5771Ц6 — пг 102^1005)^2 +
+"(6771006 — 5771015 — 771001771005 )<^3 + (6т71оо8 5т71017 ~ 771ОО3771ОО5)^4 +
+ (бТ71оо,1О ~ 5m019 - m005)Q5 + 5(тП005 ~ ^014)7 =
= 4тП035 — 5тП044 + *71030**1005 “ 5а(т71ц4 — 771105 ~ 771024 + *™015) +
+/?1(Т71О35 ” 772030^77005) + ^(771037 ” 771030*71007) +
+/31(1(771105 ~ *71015 ~ **1100*71105 + *71010*^005) +
+/?2в(*71107 ~ 771017 ~ *71ЮО**^ОО7 + *71010*71007) +
+5l/i (/31771004 + /ЗгТПоОб) + 5(l/i + 1/2) [)31(771О13 ~ ЗТ71ОО4) +
+2/31/?2(2771015 — Зтпооб) + /?2 (2771017 ” 3771008)] • (XI)
Уравнение (4.3.12), определяющее характеристическую функцию вектора £ X IV X j ,
имеет вид
(Aj, А2 , А3; t) /dt = М{ —iAj X3 — IX2clN+
+iA3 [ai(X + N) + a2(X + N)X2 + a3X + a<X3 + a5X5 + 7] -
— [t'lA2 + ^2 A2 + (i/i + + /?2*2)2A2 j /2—
-(Л + /32X2)(^iXi + i/2A2)A3} exp{iAiX + iX2N + iA3X}. (XII)
Решив уравнение (XII) совместно с уравнениями, определяющими Ot = [ Ct 10(2^3^4^5 ]>
0 = [Лтй] и '7', найдем коэффициенты уравнения условно оптимального фильтра.
При этом следует иметь в виду, что необходимые для решения уравнений, определяющих
оптимальные Ct, моменты TTlijjfe = Ш?Х’Хк при i = 0,1,2 выражаются через
моменты OLpqr = ЪЛ.Х^Хг вектора [X NХт] формулами
TnQjk = oijok, Tnijk = otjik + а>+1,о,ь
Tri2jk = otj2k + 2aj+i,i,fc + aj+2,o,b (XIII)
Пример 4.3.3. Обобщая задачу примера 4.1.3, найдем фильтр Пугачева для
оценивания неизвестного параметра 0 в уравнении системы
X = -ОХ + V1 (I)
4.3. ФИЛЬТРАЦИЯ ПРИ АВТОКОРРЕЛИРОВАННОЙ ПОМЕХЕ
483
по результатам наблюдения состояния X системы с аддитивной помехой, представляю-
щей собой независимую от X нормально распределенную стационарную случайную функ-
цию N(t) с ковариационной функцией кп(т) = Ре~а'т' .
В данном случае напишем уравнения (4.1.9) в виде:
Y = Z = X + N, X = -Xe + Vi, ё = 0, N = -aN + V2, (II)
где Vi и V2 - независимые нормально распределенные белые шумы, причем интенсив-
ность белого шума V2 равна 1/3 =
Чтобы найти подходящий класс допустимых фильтров, приведем задачу формально
к случаю белого шума в наблюдениях и применим МНА п.3.1.2. Дифференцируя уравне-
ние наблюдения, заменим его уравнением
Z = -Х& -aN + Vi+ V2. (Ill)
Это уравнение вместе с уравнениями, определяющими расширенный вектор состояния
X' = [ X 0 N ] , образует систему уравнений вида (3.1.1) с ^>{Z, X, 0, N, t) =
= [ -хе О — aN ]т, (Z, X,e,N,t) = -хе- aN,
^{z,x,e,N,t) =
10 0
0 0 1
, V-i(Z,i) = [!!],!/ =
i/j о
0 i*> ’
для которой справедливы уравнения теории оптимальной фильтрации раздела 2.2. Урав-
нения для х, е, полученные МНА п.3.1.2, имеют в данном случае вид
Jc = -хе - Я12 - (и +1/2)-1 (XRl2 + 0Яц + аЯ1з)(2 - Хё - Я12 - aN),
(IV)
ё = -(^ + + 0Я12 + aR23)(Z - хё - Я12 - aN), (V)
где Rij (i,j — 1,2,3) представляют собой элеметны ковариационной матрицы векто-
ра [XOJV]' относительно Z^Q. Правая часть уравнения для 0 представляет собой
полином второй степени относительно О и Z, содержащий члены ©, 02, z и ez с ко-
эффициентами, зависящими от других неизвестных функций времени X, 7V, 1?12» ^22,
/?23- Согласно основной идее теории условно оптимальной фильтрации все эти вели-
чины следует включить в подлежащие определению коэффициенты уравнения. Тогда,
добавив еще член с Z (очевидно, это не может ухудшить качество фильтрации), получим
уравнение класса допустимых фильтров
0 = «1© + Q2©2 + OL3Z + (/?1 + ^2&)Z + 7. (VI)
Формулы (4.2.7) и (4.3.7) с учетом того, что в данном случае (/?2 6, ^) =
= — X0 — (1N = аХ — X0 — dZ (при нахождении класса допустимых фильтров эта
484
ГЛ. 4. УСЛОВНО ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФП
функция ф2 играет роль функции в уравнениях теории оптимальной фильтрации),
дают для оптимальных Р\ и ($2 уравнения:
(^1 + ^2) (А + 7ПооО1/?2) =
— шош — 7По12о + о(тпюо1 — tnioio + mono ~ moioi) + ^i?
(1/1 + ^2)(тооО1Л + ТПООО202) =
= ТП0112 — moi2i + а(тюо2 — тюп + mom ~ тоюг) + i/imoooi, (VII)
где = . Формулы (4.2.13), (4.3.8)-(4.3.10) дают для оптимальных
«1, &2 и «3 уравнения
(тооог - moooi)ai + (шоооз - тооозтооо1)«2 + (miooi ~ тюоотооо1)«з =
= /31 [moiи + amoioi — (mono + оттгюоо ~ O77ioioo)moooi ] +
-4-^2 [moi 12 + «7711002 — 07710102 “ (тош 4“ CLTriiQQi — OTTloiOl )moooi ] J
(VIII)
(тоооз — moooimooo2)tti + (З7П0004 — 2tti0013 — тоооз)аг+
+(3тпюо2 — 2ТП1011 — m 1000mooo2)^3 = Pi [moi 12 4- оттгюог — omoio2~
-(mono + flmiooo — omoioo)mooo2] + P2 [3(топз + оттгюоз ~ оттгоюз)-
—2(тпо122 + ОТП1012 — 07710112) + (2i/i — тош — ottiiooi 4“ отоюi)тоооз] 4-
4-2(i/i4-1/2) [Pi (mooio-moooi)+PiP2(2тпооп -Зтпооо2)4-/?|(mooi2-Зтпоооз)],
(IX)
(miooi — miooomoooi )«i 4- (тюог — тюоотоооз)^ 4- (тгооо — т1Ооо)аз =
= Pl [mino 4" 07712000 — ОТПцоо ~ (mono 4" 07711000 — O77ioioo)miooo ] 4-
4-/?2 [mill! 4- 07712001 ~ 07711101 ~ (moill 4- 07711001 — 07710101 )miooo] • (X)
Оптимальное значение у определяется в силу (4.2.4.) и (4.3.6) формулой
7 = — «17710001 — «гтоооз — «зтюоо 4- /?i (mono 4- оттгюоо — отпоюо)4-
4-^2 (moi 11 4- 07711001 — 07710101)- (XI)
Уравнение (4.3.12), определяющее одномерную характеристическую функцию процесса
^X(t) Q(t) N(t) 0(t) j , имеет вид
4.3. ФИЛЬТРАЦИЯ ПРИ АВТОКОРРЕЛИРОВАННОЙ ПОМЕХЕ
485
, А2, A3, А4; t)/dt = M{-iAiX0 — iX3aN+
+i'A4 [aj© + a202 + a2(X + N) - (fa + faQ)(XQ + aN) + 7] -
—Vl Al + (/?! + /?2©)A4 j /2 — 1<2 1^ Л3 -F (/31 + y820)A4 j /2} X
x ехр{г’А1Х + гАг© -I- iXzN + гЛ4©}. (XII)
Решив уравнение (XII) совместно с уравнениями, определяющими оптимальные О, /$, у,
найдем коэффициенты уравнения фильтра Пугачева.
4.3.6. Формула для производной ковариационной матрицы
ошибки. Совершенно так же, как в п. 4.2.6 была выведена формула
(4.2.24), выводятся формулы для производной по времени ковариаци-
онной матрицы ошибки условно оптимального фильтра в случае ав-
токоррелированной помехи в наблюдениях. В результате получается
формула для производной по времени ковариационной матрицы ошиб-
ки фильтра Пугачева
R = М[(Х*+Д - Xt)<p(Xt+&,t + Д)т + <p(Xf+A,t + Д)(Х£д - Хт)+
+il>(Xt+^,t + Д)^1(< + W>(Xt+b,t + Д)т—
-faffi, Ut,t)ih (Yt, Xt, Nt, t)v2(t)^i (Yt,Xt, Nt,t)TTi(Yl, Ut, t)T].
(4.3.13)
Замечание. Формулу (4.3.13) можно также получить из (4.2.34) чисто
формально как частный случай, заменив аргумент X функций (£>, парой X, N,
аргумент Y функции Т) блочным вектором Y1 = [ Y^TY^T ... Y^8^ ] и матрицы
7/, 01 блочными матрицами [ 0 . . . О 7/ ], [ 0 ... О 0^ ]
Таким образом, приходим к следующему результату.
Теорема 4.3.2. В условиях теоремы 4.3.1 всегда имеет место
формула (4.3.13) для производной по времени от ковариационной мат-
рицы ошибки фильтра Пугачева.
486
ГЛ. 4. УСЛОВНО ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФП
4.4. Условно оптимальная линейная фильтрация
4.4.1. Фильтрация. Рассмотрим частный случай линейных отно-
сительно У, X уравнений (4.1.5),
dY = (a^Y + + О1о)<й + (сю -I- У^С1ГУГ 4- У^С1>П14-ГХГ j dW,
\ r=l r=l /
dX = (<121У + CL22X + O2o)d£ + I C20 + C2rYr + С2>П1+г^г j dW,
\ r=l r=l /
(4-4.1)
где ar8 и Cr8 - функции t, не зависящие от У = [У1 ...УП1 ]т, X =
= [Xi... Хп ]т. Класс допустимых фильтров определим уравнением
dX = a[YTXTjTdt + ^dY + ydt. (4.4.2)
t> В этом случае
pi (У, X, t) = ап У + ахгХ 4- аю,
<£>(У, X, t) = 021У 4" CL22X 4” 020,
<1>1 (У, X, t) = с10 + 22 drKr + £ d,„1+rXr,
r=l r=l
П1 n
ip(Y,X,t) = C20 4" 2 c?rYr 4" 2 ^2,п1+гХГ1
r=l r=l
£(У, X, t) = [ YTXT ]т, Ti(Y, X, t) = I,
Подставив эти выражения в (4.2.8) и (4.2.10), находим следующие вы-
ражения для матриц
KOI = [021 Ку 4“ d22Kxy ашКух 4- 0>22КХх ],
Ко2 = (КХу — Kxy)dn 4- (Кх •“ Kxx)di2~^
(П14-П \ / ni+п \ П1+п
с2о + 22С2гГПг Iv I cio + 52 cirmr) + 52
Г=1 / \ Г=1 / г,в=1
4.4. УСЛОВНО ОПТИМАЛЬНАЯ ЛИНЕЙНАЯ ФИЛЬТРАЦИЯ
487
«11 —
11/
iy
К ух
Кх
«21 — «12 — [ацКу + а^Кху ацКух + а^Кхх ],
(ni+n \ / ni+n \ П14-П
сю + 52С1тТПт)" I сГо + 52 cirmr) + 52 c^cukrs,
r=l / \ r=l / r=l
(4.4.3)
где Ky, Кx, Кх, КуХ = Кху, Кхх = К?х, КУх = К?у - ковариационные и
взаимные ковариационные матрицы случайных векторов Yt,Xt,Xt,mr
- математическое ожидание компоненты Qr случайного векторо Q =
= [У1... YniXi... Хп ]т, a kr8 - ковариация компоненты Qr, Qa вектора
Q. Учитывая, что согласно (4.2.3), (4.2.9) Кх = Кхх, Кху = Кху и,
следовательно, Кх — КХх — Кх ~ К% = R, получаем
«01 = [<121^ + Л22Кху ОшКуй -F 022^4 ] ,
(П1+П \ / П1+П \ П1+п
С20 + 52 С^гГПг I У I С?о + 52 CTrmr I + 52 С2гУсТ9кг8,
г=1 / \ г=1 / г,в=1
«11 =
л\ух
ху КА
«21 = [оц^у + ^пКху а\\Ку% + а^Кх ]. (4.4.4)
Подставив эти выражения в (4.2.11), (4.2.7), получим
а = [ai«2 ] = [(<121 — Ро>п)Ку + (а22 — 0^21)К±У
(02! - MKvi + (022 - 0O21)KS]
= [<121 — /?<111 <122 ~ /?<112 ] ?
z / ni+n \
Р = < Яа?2 + I с20 + 52 C2rmr I «/(С1о +
\ г=1 /
ni+n m+n х
+ £2 cfrmr) + ^2 С2г"с[вкг*\к22
Г=1 Г,в=1 )
(4.4.5)
488
ГЛ. 4. УСЛОВНО ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФП
Оптимальное значение 7 находится из уравнения (4.2.4) с помощью
формулы (4.2.5):
7 = а21тпу -I- а22тх + а2о - а [тут?]Т -
-Р(ацтпу + ai2mx 4- аю) = а20 - /Заю- (4.4.6)
При этом уравнение (4.4.2) принимает вид
dX = (а21К + а22Х 4- o>2o)dt 4- (5 ^dV — (апУ + CL12X + aio)dt j . (4.4.7)
Для определения /3 необходимо найти математическое ожидание тп
и ковариационную матрицу К случайного вектора Q = [У1... УП1Х±...
.. . Хп]т, ковариационную матрицу R ошибки X = X — X. Для этого
воспользуемся выведенными в (п.1.7.1) уравнениями (1.7.17) и (1.7.19).
Эти уравнения в нашем случае имеют вид
тп- — am -f- do,
(4.4.8)
П1+п
к = аК + Кат + соис^ + (cqi/c? + crvco)mr+
r=l
ni+n
+ У Сг^с^тПгГП, + kr,), (4.4.9)
г,«=1
где
а = ап аю ? ао = <110 , Сг = С1г
. а21 а22 . а20 . . а2г
(г = 0,1, ... , П1 + п).
Уравнения (4.4.8) и (4.4.9) с соответствующими начальными условия-
ми определяют все элементы mr, kr8 матрицы-столбца тп и матрицы К
г, s = 1, ... , П1 + п).
Уравнение для матрицы R вытекает из формулы (4.2.31):
R = a22/? + Ra? —
(П1+п \ / П1+п \
С20 + У2 C2r^r I У I Сп, + У2 Clrmr I +
Г=1 / \ Г=1 /
П1+п
+ уз ^rs
К22
(ni+n
Сю 4- Cirmr
г=1
4.4. УСЛОВНО ОПТИМАЛЬНАЯ ЛИНЕЙНАЯ ФИЛЬТРАЦИЯ
489
П1+П
+ ^2
Г, 8-1
(Ш+п \ / П14-П \
С20 + 52 C2rmr I V I + 52 ^mr I +
Г=1 / \ Г=1 /
П1+п
+ 52 с^<^вкгв, (4.4.10)
г,в=1
где К22 определяется последней формулой (4.4.3). Уравнение (4.4.10)
представляет собой матричное уравнение Риккати. о
Итак, получен следующий результат.
Теорема 4.4.1. Пусть уравнения стохастической дифференци-
альной системы (4.4.1) допускают существование одномерных момен-
тов. Тогда уравнение фильтра Пугачева имеет вид (4.4.7). После на-
хождения mr, kr8 (r,s = 1, ... , ni + п) и R путем интегрирования
уравнения (4.4.8)-(4.4.10) оптимальный коэффициент (} в (4.4.7) опре-
деляется по формуле (4.4.5).
Докажем, что фильтр, определяемый уравнением (4.4.7), оптима-
лен в классе всех линейных фильтров. Для этого достаточно показать,
что ошибка фильтрации не коррелировала с любым результатом изме-
рения Y8, s е [to, t]. Чтобы сделать это, напишем уравнение для ошибки
фильтрации Xt = Xt — Xt. Вычитая второе уравнение (4.4.1) из (4.4.7),
находим
dXt = (022 — /Ja^Xtdt +
n+m
/Зсю - С20 + 52 (fair - C2r)Qr
r=l
dW.
Умножив это уравнение почленно справа на Угт, взяв математическое
ожидание и учитывая, что случайный вектор QT = [ Y^X? ]Т не кор-
релирован с dW, при т < t, получим
dMXtYf = (а22 - /3a12)^XY^dt при т < t.
Но в силу (4.2.9) MXTY? = 0, Vr е [to, t]. Следовательно, MXTY? =
= 0 при всех t > т. Таким образом, мы имеем пример, когда условно
оптимальный фильтр является оптимальным и в более широком классе
всех линейных фильтров.
В частном случае линейной системы (4.4.1), когда сг = 0 (г =
= 1, ... , ni +п), уравнения (4.4.7) и (4.4.10) совпадают с уравнениями
теории оптимальной линейной фильтрации (раздел 2.3). Следователь-
но, в частном случае винеровского процесса W(t) в (4.4.1) при сг = О
490
ГЛ. 4. УСЛОВНО ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФП
(г = 1, ... , ni + п) условно оптимальный фильтр оказывается опти-
мальным и в классе всех возможных фильтров. Заметим, что в рассмот-
ренном случае нет необходимости использовать уравнение (4.2.20). Это
объясняется тем, что оптимальные а, /3, 7 зависят в этом случае толь-
ко от первых и вторых моментов случайных векторов Q = [ YTXT ] и
X = X — X, которые определяются уравнениями (4.4.8)-(4.4.10).
Для того чтобы найти доверительные области для X*, достаточно
знать совместное распределение величин X*, Xt. Это распределение
полностью определяется характеристической функцией <7i(Ai, А2, A3; t)
случайного вектора £ytTXtTXtTj , которая находится из уравнения
(4.2.20). Это уравнение в данном случае принимает вид
_ (А^ац -F A^(i2i + Ajfa2i)7n~ + (Afai2 + А^агг + •+
Ot UAl ОЛ2
+ Аз^(«22 -Ь + ^°20 АГа2о)<71 +
х ехр
{lAfy+ iA£X + iA3x}.
(4.4.11)
Для винеровского процесса W(t) (4.4.11) представляет собой ли-
нейное уравнение в частных производных второго порядка. В частном
случае линейной системы (4.4.1) уравнение (4.4.11) представляет собой
линейное уравнение в частных производных первого порядка, которое
легко интегрируется стандартным методом (ТСтС, п.6.2.2). В резуль-
тате можно получить явное выражение характеристической функции
ошибки фильтрации X = X — X. Определив распределение ошибки,
можно находить доверительные области для X.
Тот же условно оптимальный фильтр (4.4.7) получится и в том
случае, когда класс допустимых фильтров определяется формулой X =
= AU и уравнение (4.1.2) при
£(У, и, t) = [ YTUT ]т, T}(Y, и, t) = Ini.
4.4. УСЛОВНО ОПТИМАЛЬНАЯ ЛИНЕЙНАЯ ФИЛЬТРАЦИЯ
491
при любом N > п и любой постоянной п х TV-матрице А ранга п. Это,
конечно, прямое следствие того, что фильтр (4.4.7) оптимален среди
всех линейных фильтров.
Пример 4.4.1. Рассмотрим случай скалярных уравнений (4.4.1) с независимы-
ми белыми шумами Vj, V2
Y = ОцУ + О12Х + О10 + (сю + С11У + C12-XJV1,
X = П21У 4- CL22X 4- П20 + (его + С21К 4- С22Х)р2,
£] (г = »'^).-=[о £] (1)
Обратим внимание на то, что Cjr и С2г в этой задаче не те, что в общем случае в уравне-
ниях (4.4.1). Они представляют собой соответственно первые и вторые элементы матриц-
строк, на которые умножается вектор в (4.4.1). Для простоты мы оставляем
для них обозначения С\г и С2т- Тогда в формулах (4.4.3) и (4.4.5) имеем
«22 = I'l (сю + СЦ7П1 + С12т2)2 + ^2(Cnfcll + 2СцС12й12 + Ci2fc22), (II)
0 = K^auR. (Ill)
При этом уравнения (4.4.8)-(4.4.10), определяющие , Ш2, &Ц, &12? &22 и -R» имеют
вид
mi = anmi 4- ai2W 4- аю, (IV)
Ш2 = П21П21 4- О>22^2 4~ 020? (V)
fcn = 2(ацА;11 4- 012^12) 4- (сю 4- cnmi 4- С12тг)24-
4-^2 (с?1&11 4- 2сцС12&12 4- 0^2^22)? (VI)
&12 = (оц 4- 022)^12 4- O21&11 4- O12&22? (VII)
А?22 — 2(О21&12 4- 022^22) 4- 1^1 (его 4- C2imi 4- С22П1-2)24-
4-1/2(^21^11 4- 2С21С22Л12 4- 622^22)? (VIII)
R = 2022^ — к'22а12^2 4- 1/1 (С20 4~ С21ТП1 4~ С22П12)24-
4-1/2(^21 fell 4- 2С21С22^12 4- £22^22)- (IX)
492
ГЛ. 4. УСЛОВНО ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФП
4.4.2. Фильтрация при автокоррелированной помехе. При-
меним теорию к частному случаю линейной системы с параметрически-
ми шумами, линейного уравнения наблюдения и линейного фильтра. В
этом случае уравнения (4.1.9) имеют вид
Y = bnY + b12X + b13N + b1(h
dX = (ап У 4- Oi2-^ 4" о>1з^ 4- аю)сЙ4-
(ni n h \
с10 4- CirYr + У2 с1,П1-|-г-^г 4- Cl.m+n+rM» 1 dW>
Г=1 Г=1 Г=1 /
dN — {q>21Y 4~ (L22X 4~ (I23N 4~ О2з)^4~
4- fС20 4- С2ГУГ + ^.ги+Л + (4.4.12)
\ Г = 1 Г=1 Г=1 /
> На основании формулы (4.3.2) и первой формулы (4.3.4) уравне-
ния (4.3.1) и последнее уравнение (4.3.5) имеют в данном случае вид
У(*> = bklY + Ък2Х 4- bk3N 4- bkQ, (fc = 1, ... , s)
dY^ = (Ьв-ыдУ 4-i>e+i,2X 4Лц,з^ + Ьж,о)Л4
4- Гсзо 4- сЗгУг 4- У2 c3,ni+r-^r 4- У2 сз,п14-п+гМ-j dW, (4.4.13)
\ г=1 г=1 г=1 /
где функции времени bki определяются рекуррентной формулой
bfc+i,i = bkibu 4-bk2&u 4-bk3a2i 4-bki (/= 0,1,2,3; k = 1, ... , з), (4.4.14)
а
с8Г — b82Cir 4- bs3C2r (г = 0,1, ... , п\ 4- п 4- h). (4.4.15)
Уравнение допустимых фильтров (4.1.3) имеет вид
dX = а [ Y. y^tYtXt ]Т dt + 0dYM + ydt.
Положив для краткости Z = перепишем первые s
уравнений (4.4.13) в виде одного уравнения
Z = biY 4- Ь2Х 4- b3N 4- bo,
(4.4.16)
4.4. УСЛОВНО ОПТИМАЛЬНАЯ ЛИНЕЙНАЯ ФИЛЬТРАЦИЯ
493
где
Ь« = [Ьц.- Ь5]Т (/ = 0,1,2,3). (4.4.17)
При этом уравнение допустимых фильтров примет вид
dX = а [ ZTYTXT ]Т dt + 0dY<•> + ydt. (4.4.18)
Подставив выражения функций y^+i, Ф1 из второго уравнения
(4.4.12) и последнего уравнения (4.4.13) в (4.3.7) и учитывая несме-
щенность оценки X и вытекающие из (4.2.9) равенства Кху = К^у,
КХх — Кь, находим
«02 = ,2 + (Кхп — K^n)bJ^13 4- 013, «22 = <^33,
где R = Кх — - ковариационная матрица ошибки фильтрации, бук-
вой К с индексами обозначены, как всегда, ковариационные и взаимные
ковариационные матрицы соответствующих случайных векторов
ni+n+Л ni+n+h
CTjj: = CiQUCjo + ^2 (ctri'cjo + CiOi/cJr)mr + CiTvcJq(mrmg + krq)
r=l r=l
(4.4.19)
(i,j = 1,2,3),
mr и krq (r,q = 1, ... , ni + n + h) - математические ожидания ком-
понент случайного вектора Q = [УТХТЛГТ]Т и элементы его ковари-
ационной матрицы. После этого по формуле (4.2.7) можно вычислить
оптимальное значение /3:
(3 = 4- (Кхп — Kznjb^ 3 4-<Т1з] ^зз1. (4.4.20)
Для нахождения оптимальной матрицы а в (4.4.18) подставим вы-
ражения функций <£>, и £ из (4.4.12), (4.4.13) и (4.4.18) в (4.3.8).
В результате, учитывая (4.3.6) и равенства Kzx = K$z, Кху = К&у,
Кхх = Кх, находим
«и =
Kz
Kyz
K£z
Kzy KZi
Ky Kyi
Kiy Ki
«oi = [anKyz 4- a^Kiz 4-
494
ГЛ. 4. УСЛОВНО ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФП
аиКу + а^Кху 4- о>1зКпуацКУх 4- аггКх 4- ахз^пя],
«гх = [bs+i,iKyZ 4- b8+iy2Kxz 4- Ъ8+1узКпг
Ьз+гдКу 4- b8+iy2Kiy 4- Ь8+1узКпу Ь8+1у1КУ£ 4- b«4-i,2Кх 4- Ья+хд^пя]-
Вследствие этих формул (4.2.11) дает для оптимального а = [ахаг^з]
систему уравнений
(*\KZ 4~ Ot2KyZ 4" ОСзКхг —
— (ахх — 0b8+iyi)Kyz 4- (ах2 — /3bs+iy2)Kxz 4- (ахз — @Ь8+1уз)Кпг,
a\KZy 4- (У-2Ку 4- азК%у =
= (^хх — 0Ь8+1у1)Ку 4- (ах2 — Pb8^2)Kiy 4- (ахз — /ЗЬ8+1уз)Кпу,
&1KZ£ 4- с^Кух 4- а3К£ —
= (ац - 0Ь8+1у1)КУх 4- (ахг - 0Ь8^у2)Кх 4- (ахз - 0Ь8+1уз)КПх- (4.4.21)
На основании соотношений
Kzy = biKy 4- b2Kxy 4- ЬзКпу,
Kz± = bxKyx 4- b2Kt 4- ЬзКПх, (4.4.22)
вытекающих из (4.4.16), второе и третье уравнение (4.4.21) можно пе-
реписать в матричном виде:
(#2 4- otibi — ахх 4- 0b8+iyi аз 4- Qx&2 ~ ^Х2 4- /?Ьв+х,2 ] «хх —
— (ахз 0Ь8+1уз) [ Кпу КПх ],
«хх =
Ку
Кху
Кух
Кх
(4.4.23)
- ковариационная матрица случайного вектора . Так как
компоненты случайных векторов У и X не могут быть связаны линей-
ными зависимостями, то матрицу «и можно считать обратимой. Тогда
будем иметь
[tt2 4-axbx <*з + «х&2] = [ахх -/?Ь«+х,х) ^Х2 - &s+x,2] 4-
4-(ахз — ах^з — /?£>в+х,з) [Кпу Кп± ] «ц1.
(4.4.24)
4.4. УСЛОВНО ОПТИМАЛЬНАЯ ЛИНЕЙНАЯ ФИЛЬТРАЦИЯ 495
Вычитая из первого уравнения (4.4.21) второе, умноженное справа
на bf, и третье, умноженное справа на Ь?, на основании соотношений
(4.4.19) и соотношений
K2 = Kzyb[ + K2ib^ + Kznb^
Kyz = Kyb[ + Kyibl + Kynbl,
Ki2 = Kiyb? + Kibl + Kinbl,
Kn2 — Knyb? + Knzb^ + KnbJ,
также вытекающих из (4.4.16), и равенств Kzx = KZXi Кух = Kyi,
Кхх = К±, получаем
(ttlKsn 4- Ot2Kyn 4- ot3Kin)bl =
= [ (an — 0b8^-iyi)Kyn 4- (ai2 — fib8+iy2)K£n] Ъз +
4-(ai3 — /3b8+iyz) [(/Gi® — Knx)bz + /Gifyf ] ,
а1[«>2(^п-ад + ЬзКп]ЬГ+
4-[a2 4-aibi a3 4- 0162] [Kyn K?n] ^2 ~
= [an - /?bs+ijai2 - /3b8+iy2] [KynKin] b%+
4-(ai3 — /ЗЬ8+1уз) [(/fn® ~ Kn£tf 4- /fnfyf] .
Подставив сюда выражение [a2 4- Qibi a3 4- aib2 ] из (4.4.24), получим
а1[Ь2(К®п-^п)4-Ь3/<п]ЬГ4-
4-(ai3 — /ЗЬ8+1уз — aib3) [Kyn Kxn] к111 [/f^ К^п ] bj =
= (ai3 - 0Ь8+1уз) [(/fn® ~ Knx)bz 4- ЫпЬГ] .
Отсюда на основании вытекающего из равенств Kzx = Kzx, Кух = Кух,
Кхх = Кх соотношения
Ь3(Кпх - Кпх) = -Ъ2(КХ - Кх) = -b2R (4.4.25)
получаем уравнение
а1(Ь3^пЬГ-Ь2ЯЬ^) =
496
ГЛ. 4. УСЛОВНО ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФП
= (а13 - /?Ь,+1.з [Knbl + (Кпх - Knx)bJ ], (4.4.26)
где для краткости положено
кп = Кп - [ Куп Kin ] «П1 [ К?п ктп ]т. (4.4.27)
Замечание. В случае нормального распределения вектора [ Y? X? N? ] ,
что возможно, конечно, только при Cir = 0, С2г == 0 (г — 1 , . . . , П\ 4" П 4" Л-), Шп и
Кп представляют собой условные математическое ожидание и ковариационную матрицу
помехи N относительно Y и X.
Так как компоненты помехи N не связаны линейными зависимостя-
ми и h > nis, то П1$ х П1$-матрица b^KnbJ всегда обратима (матрица
ПРИ n < nis необратима). Поэтому уравнение (4.4.26) всегда
определяет оц.
Формулы (4.3.6), (4.2.4) и (4.4.24) дают следующую формулу для
оптимального 7:
7 — аю — ^a+i,o + («13 — /36«4-1,з — а16з)тп, (4.4.28)
где
mn - тп - [Куп Кin] «й1 [my ml]. (4.4.29)
Для нахождения /3, а = [ахаг^з] и 7 по формулам (4.2.7), (4.4.19),
(4.4.20), (4.4.23), (4.4.24), (4.4.26)-(4.4.29) необходимо знать математи-
ческое ожидание тп = [гПут^т^]7 и ковариационную матрицу
ху
пу
Л ух
кх
кпх
ХуП
Кхп
Кп
случайного вектора Q = [УТХТ2УТ], а также матрицы R и Кхп =
= Кпх. Для нахождения тп и К воспользуемся уравнениями (1.7.17) и
(1.7.19) из п. 1.7.1, которые в данном случае имеют вид
m — Am 4- Aq ,
К — АК 4- KAT 4- cqi/c^ 4- (co^c^ 4- crpc^)mr4-
r=l
ni+n+h
+ 5? Сгис^ (mrmq + krq),
r,g=l
(4.4.30)
(4.4.31)
4.4. УСЛОВНО ОПТИМАЛЬНАЯ ЛИНЕЙНАЯ ФИЛЬТРАЦИЯ
497
где
£>и £>12 £>1з £>ю 0
А = Оц 012 G13 , ^0 = ^10 , Ст = С1г
021 ^22 023 ^20 С2т
— — — — — —
(г = 0,1, ... , 711 4- п 4- h).
Уравнения (4.4.30) и (4.4.31) с соответствующими начальными услови-
ями определяют т и К,
Для нахождения уравнения для ковариационной матрицы ошибки
воспользуемся формулой (4.3.13). Подставив в нее выражения tp, ф, V’l
из (4.4.12) и (4.4.13), получаем уравнение
R — a^R 4- Ra^2 4- агз^Кпх — КПх) 4- (Кхп — 4- оц,
(4.4.32)
где <тц, озз определяются формулой (4.4.19).
Для нахождения уравнения для Кхп следует составить уравне-
ние (п. 1.7.1) для ковариационной матрицы составного вектора
= [VTXT.ZVTA'T J . Из этого уравнения получается сле-
дующее уравнение для Кхп\
Кхп — &зКхп 4~ 4~ (Кх R)a22 4* ^ij/^214'
4-(<12 4- ai&i 4- /ЗЬв+1,1 Куп 4- («1&2 4- РЬа+\2)Кхп+
4-(охЬз 4- &Ь8+\^)Кп 4- /Зсг22- (4.4.33)
При выводе этого уравнения учтено, что Кх = Кх — Я, Кху = Кху. <
Таким образом, доказано следующее утверждение.
Теорема 4.4.2. Пусть уравнения стохастической дифференци-
альной системы (4.4.12) допускают существование одномерных мо-
ментов. Тогда уравнение линейного фильтра Пугачева имеет вид
(4.4.18). При этом, интегрируя уравнения (4.4.32) и (4.4.33) при соот-
ветствующих начальных условиях с /3 и а, определяемыми формулой
(4.4.20) и уравнениями (4.4.24), (4.4.26), найдем оптимальные а и 0,
после чего оптимальное значение у определится по формуле (4.4.28).
За мечание. В отличие от случая п.4.4.1, построенный таким путем услов-
но оптимальный фильтр в общем случае не будет оптимальным в классе всех линейных
фильтров. И лишь в частном случае, когда помеха в первом уравнении (4.4.12) представ-
ляет собой 711-мерную векторную случайную функцию, определяемую линейным стоха-
стическим дифференциальным уравнением S-ro порядка, не содержащим производных
белого шума в правой части, Ьхз — 1щ> & производные S-ro порядка компонент вектора
498
ГЛ. 4. УСЛОВНО ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФП
состояния, входящих в первое уравнение (4.4.12), не содержат белого шума. Найден-
ный изложенным методом условно оптимальный линейный фильтр будет оптимальным в
классе всех линейных фильтров. В этом случае даваемый изложенным методом фильтр
совпадает с фильтром п.4.4.1 для наблюдаемого сигнала, преобразованного системой, об-
ратной формирующему фильтру помехи.
Пример 4.4.2. В задаче примера 4.1.2 условно оптимальный линейный
фильтр, найденный изложенным методом, совпадает с абсолютно оптимальным филь-
тром примера 4.1.2.
4.5. Условно оптимальная экстраполяция
4.5.1. Постановка задач условно оптимальной экстраполя-
ции. Развивая постановку задачи условно оптимальной фильтрации
(п. 1.2.4), будем считать оптимальным такой экстраполятор из класса
допустимых экстраполяторов, который при любом совместном распре-
делении величин У, X, X в момент t > to в стохастической дифферен-
циальной системе дает наилучшую оценку вектора Х^+д, Д > 0, в бес-
конечно близкий момент s > t, s —> t, реализующую минимум с.к.о.
М |хв--Хв+д| . Тогда задача оптимальной экстраполяции (п.2.6.1)
сведется к нахождению оптимальных значений а,/3,7 в (4.1.1), (4.1.2)
или (4.1.3), (4.1.4) в любой момент времени t > to, обеспечивающих
I ~ ~ |2
минимум с.к.о. экстраполяции М Xs — Хв+д , Д > 0, в бесконечно
близкий будущий момент s > t, s -> t.
Для задачи экстраполяции необходимо ограничиться, как и в
п.2.6.1, случаем, когда функции и гр не зависят от наблюдаемого век-
тора У, процесс W(t) состоит из двух независимых блоков Wi (t) и W2 (t)
и соответственно матрицы гр и ^1 имеют блочную структуру гр = [гр10],
гр\ = [0гр*1 ], так что = гр'дЖх, гр\<1№ = гр\д№2- В этом случае,
отбрасывая штрихи у функций гр1 и V4 > запишем уравнения задачи 2 в
следующем виде:
dY = у>(У, X, t)dt 4- грх (У, X, t)dW2,
dX = у>(У, X, t)dt 4- гр(Х, f)dWx, (4.5.1)
где Wi = Wi (t), 1У2 = py2(t) - независимые процессы с независимыми
приращениями с нулевыми математическими функциями
^(ti,t2) = ki(min(ti,t2)),
t
ki(t) = fci(t0) 4- У Vi(r}dr.
to
(4.5.2)
4.5. УСЛОВНО ОПТИМАЛЬНАЯ ЭКСТРАПОЛЯЦИЯ
499
В случае автокоррелированной помехи в наблюдениях, имея в виду,
что оценивать надо только состояние и параметры стохастической диф-
ференциальной системы, но не помеху, будем рассматривать отдельно
n-мерный вектор состояния X и h-мерный вектор помехи АГ, причем
h > ni, пх = dim У. Уравнения задачи условно оптимальной экстрапо-
ляции будем записывать в виде
dY = (У, X, N, t)dt, dX = у>(Х, t)dt + ^(Х, t)dWr,
dN = <p0(N, t)dt 4- V>o(W, t)dW2. (4.5.3)
4.5.2. Уравнения, определяющие условно оптимальный
экстраполятор Пугачева. Совершенно так же, как в случае условно
оптимальной фильтрации, решается задача условно оптимальной экс-
траполяции, поставленная в п.4.5.1. Разница будет лишь в том, что в
случае экстраполяции Xt представляет собой оценку будущего состоя-
ния системы Х*+д, Д > О, которое в силу (4.5.3) определяется стоха-
стическим дифференциальным уравнением
dXf+д = ^(Х^+д, t 4- A)dt 4- ^(X^-f-д, t 4- A)dIV(t 4- Д).
Заменив этим уравнением второе уравнение (4.1.5) и повторив все вы-
кладки пп.4.2.1-4.2.5, получим уравнения, определяющие коэффициен-
ты уравнения условно оптимального экстраполятора. Приведем полу-
ченные таким путем результаты.
Условие некоррелированности ошибки с rft ДУ дает, как и в п.4.2.1,
формулу (4.2.7) для А/?, в которой
«02 = M(Xt+A - AUt)<pi(Yt,Xt,t)Tr)(Yt,Ut,t)T,
«22 = (4.5.4)
Условия несмещенности оценки и некоррелированности ошибки с &Д£
принимают в этом случае вид
MXt = мх(+д, М(Л - Хд+д)еГ = 0.
Из этих условий получаются уравнения (4.2.4), (4.2.11) и (4.2.13) для
Аа и Ау и формулы (4.2.5) (4.2.10) и (4.2.14) для mi, m2, «и, «21, «21,
а вместо первой формулы (4.2.5) для то, последней формулы (4.2.10)
для «01 и формулы (4.2.18) для получаются формулы
m0 = M(p(Xt+&,t 4- Д),
(4.5.5)
500
ГЛ. 4. УСЛОВНО ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФП
/СО! = М [^(Х4+д, t + A) - то ] £(Yt, Ut, t)T,
d£T
«oi = «01 4- М(Х*+д — AU)-jr-- +
ot
(4.5.6)
<Pi ~ fc2{p)Tv,p(t,p)dpil)l
я?
X £т + i^MPG+д - ЛС7)^ tr X
у оу ои / z [ [
/д тптд\дт] Г. тт.тЗа7']],
х (яГ + 2,? я^) л7 +tr ^1Р2°^ Р aZaZ (£
у оу ои / оу [ ди ои J
+М (Xt+A - AU)
- APrFl)iV2<ri>T > X
djr
ди ди
4- f M [Х*+д - AU - A/Jt/V'ioHp) ] x
X [£(^ 4-^ic2(p),U + 0тгф1с2(р),1)т - CT]^2p(t1p)dp1 (4.5.7)
где C2(p), i/2o и У2Р - соответствующие величины в представлении ин-
тенсивности 1/2 процесса W2 (t) формулой вида (4.2.17).
В случае винеровского процесса И^) сг(р) = 0,1/20 = ^2 и формула
(4.2.26) принимает вид
дЕт
«01 ~ «01 4- М(Х*+д — AU}-^-—Ь
+М [ (Xt+A - AU)<p{ - APtji/ji^i] £Т+
+^М(Х(+д -Л(7)<1г V’l^V’fx
.1 <
’ 2 ' - II"
( д птотд\ ат]
х ( — + 2т?т/Зт— ) д-
\at/ ouj оу
+tr ртгфхV2IpTГ)тРт
ои ои
В качестве пояснения ко второй формуле (4.2.23) и формулам
(4.5.7) и (4.5.8) заметим, что роль матриц ^1,
траполяции играют соответственно
(4.5.8)
i/, vq в задаче экс-
[V’t+AO], [OV’t+A],
0
0 1/2
"IO
о
о
У20
4.5. УСЛОВНО ОПТИМАЛЬНАЯ ЭКСТРАПОЛЯЦИЯ
501
и величинам Ф^ФТ соответствуют
о
^20 .
о
[O^i]
V1
О
[0^1]
^10
О
[V’t+aO]
"ю О
О
= •фг^о'ФТ,
= 0,
О
р2
= [V’t+aO]
О
Р2
= 0.
О
0
"20 J ФТ .
^1
О
о
j ы
> Для вычисления математических ожиданий в первой формуле
(4.5.4), а также в (4.5.6)-(4.5.8) недостаточно знать одномерное распре-
деление составного случайного процесса [ Y(t)TX(t)TU(t)T ]Т, а надо
знать совместное распределение величин Yti Хд+д, при каждом t.
Чтобы найти это распределение, напишем уравнение Пугачева, опреде-
ляющее двумерную характеристическую функцию 0г(А1, Аг, Аз,Д1,дг,
Дз;£, s) процесса [Y(t)TX(t)TU(t)T ]Т при s > t. Совершенно так же,
как в п.4.2.5, получаем
#02 (Ai, А2, А3, /Z1, д2, Дз; М) /дз = М {(Ув, Х8, s) + г/z % <р(Х8,з)+
+ipl[a,£(Ya,Ua,s) + 0aTi(Ya,Xa,s) + 7,] +
+х(^1(^»,^»>з)ГД1 + ^(X„,s)/22+
+if)i(Ya,Xa, s)TT)(Y„ Ua, s)Tftц3;«)} x
x exp {iX^Yt + iXjXt + iX^Ut + inT^t + гдТ-Х, + ifJ^Ua} . (4.5.9)
К этому уравнению следует добавить начальное условие
0г(А1, Аг, Аз, ди, Дг, Дз; С = 01 (Ai Ч- Д1, Аг Ч- /хг, Аз Ч- Дз; t, s). (4.5.10)
Распределение Uq при этом следует выбрать так, чтобы условия =
= MXt4-/,M(Xt — Xt+д)^/1 = 0 удовлетворялись при t = fo- <
Таким образом, получено следующее утверждение.
Теорема 4.5.1. Пусть уравнения стохастической дифференци-
альной системы (4.5.1) допускают существование одно- и двумерных
моментов. Тогда уравнения (4.2.4), (4.2.7), (4.2.13), (4.2.20), (4.2.21),
(4.5.9) и (4.5.10) полностью и точно решают задачу нахождения ус-
ловно оптимального экстраполятора Пугачева.
502
ГЛ. 4. УСЛОВНО ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФП
Замечай И е 1. В частном случае, когда функции и в уравнени-
ях (4.5.1) не зависят от для решения задачи достаточно знать двумерное распределе-
ние процесса , определяемое двумерной характеристической функцией
52(А1,А2,Д1,Д2,;«,8) этого процесса:
552(A1,A2,,/21,/22,;^s)/9s = <р(Ха, s) + s) +
+Psq(Ua,s)4>i(X - s,s) +7,]+
+x(V’PG, s)T/n + (X, s)Ti](Ua, s)T/3f fj,2; s)} x
xexp{iAfXt + iX^Ut + ifj.{Xa + i/zf(7s} . (4.5.11)
Для приближенного решения уравнений (4.2.20) и (4.5.9) или (4.2.22) и (4.5.11) сов-
местно с уравнениями (4.2.5), (4.2.7) и (4.2.13) можно применить один из приближенных
методов параметризации распределений (разделы 1.7 и 1.8).
Замечание 2. Все замечания п.4.2.5 относительно уравнений (4.2.5), (4.2.7),
(4.2.13) и (4.2.20) и функций £, 7] полностью относятся и к задаче условно оптимальной
экстраполяции.
Теория условно оптимальной экстраполяции случайных процессов
дает возможность строить экстраполяторы Пугачева для одновремен-
ного оценивания состояния и параметров системы и экстраполяции ее
состояния на несколько различных интервалов времени в реальном мас-
штабе времени. Все сложные расчеты, необходимые для проектирова-
ния таких экстраполяторов, не опираются на результаты наблюдения
и могут быть выполнены по априорным данным в процессе проекти-
рования. Практическое применение таких экстраполяторов сводится к
одновременному интегрированию уравнений (4.1.1) или (4.1.2) для оце-
нок текущего и будущих состояний системы.
Пример 4.5.1. Найти экстраполятор Пугачева для прогнозирования процесса,
определяемого уравнением
X = (а + Ы}Х* + XV (I)
на время А > 0 по результатам его наблюдения с аддитивной помехой, представляющей
собой белый шум р2> независимый от Vj. Белые шумы Vi и V2 будем считать нор-
мально распределенными. Класс допустимых фильтров для экстраполяции определяется
уравнением
к = Q1X3 4- a2X + PZ+ <>(. (II)
Уравнение наблюдения в данном случае имеет вид К — Z — X + р2- Формулы
(4.2.7) и (4.2.23) дают /€q2 — 7Пцо ~ ГП101. ^22 — ^2 и Р ~ у2 1(т1Ю ~ ^101),
4.5. УСЛОВНО ОПТИМАЛЬНАЯ ЭКСТРАПОЛЯЦИЯ
503
где ТПГ8и — МХ^ Х*+дХ*. После этого уравнения (4.2.4) и (4.2.13) в силу (4.5.6) и
(4.5.8) принимают вид.
771QO3 <21 + 771001 <22 + 7 = (fl + W + 6Д)?71оз(Ь (Ш)
(4?Пооб “377215 — 772оОз)а14-(4тоО4 ~ЗтТ1013 ~ 771003771001)<22+3(771003 — 771012 )7 =
= (а + б£ + 6Д)(т033 — 771оЗО771ООз)+^(2771ц2 —4?П1оз+771100771003 “"^2^771002))
(IV)
(2771004 “771013 —771003771001 )<21 + (2т71002 ~771011 + 771qO1 )а2 + (Т71ОО1 ~ТПою)? =
= (а+ М + 6Д)(т71031 —771030771001 )+/?(771цо —2771101 +772100771001 —Т'г/?)- (V)
Уравнения (4.2.22) и (4.5.11) имеют в этом случае вид
9д\ (^1, ^2 j t)/9t — М{гА1 (а + Ы)Х^ + iA2(<2i Х^ + 0L2X + (ЗХ + 7) —
-i/iX2A?/2 - 1/2^2А1/2)} ехр{гА1Х + iА2Х}, (VI)
9д2 (Ai, А2, /11, Д2; t, s)/ds =
= M{i/ii(a + bs)X% + i/i2(aieX’ + а28Х8 + /38Х8 + 7J-
-ViX^l/2 - U2/328l4/2)} exp{iAiXf + iA2Xt + i^X8 + i^X*}- (VII)
Решив уравнения (VI) и (VII) совместно с уравнениями (III)-(V) для Q, /?, 7> найдем
оптимальные Q, /?, 7> определяющие экстраполятор Пугачева. Для этой цели надо сна-
чала решить задачу фильтрации, пользуясь уравнением для д\ и уравнениями для Q, /3,
7 с заменой ТПГ8и величинами 771r-|-Sjo,u- Подставив найденные таким путем Q, /?, 7 в
уравнение для р2, можем решить это уравнение относительно д2 и таким образом найти
@2 в первом приближении. После этого можно определить коэффициенты уравнений для
а, (3> 7 в первом приближении. В результате эти уравнения определят О', /3, 7 во втором
приближении. Решив уравнения для д\ и д2 с этими Q, /?, 7, найдем pi, Р2 во втором
приближении, и так далее. Уравнения для pi, р2 можно решить на каждом шаге любым
из приближенных методов параметризации распределений (разделы 1.7 и 1.8).
Совершенно так же, как и в п.4.2.6, выводится формула для про-
изводной по времени ковариационной матрицы ошибки экстраполятора
Пугачева:
R = M[(Xf+A - XiMXt+^t + Д)т + <p(Xt+A,t + Д)(х^д - Xf)-
-A/3r}(Yt, Ut, t)v2{t)^(Yt,Xt, t)T7](Yt, Ut,t)T0TAT+
+^(Х<+д,< + Д>1(« + Д)Ж4+Д,« + Д)Т]- < (4.5.12)
504
ГЛ. 4. УСЛОВНО ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФП
Таким образом, имеем следующее утверждение.
Теорема 4.5.2. В условиях теоремы 4.5.1 формула для произ-
водной по времени ковариационной матрицы ошибки экстраполятора
Пугачева имеет вид (4.5.12).
4.5.3. Уравнения, определяющие экстраполятор Пугачева
при автокоррелированной помехе в наблюдениях. Решение по-
ставленной в п.4.5.1 задачи экстраполяции состояния системы при авто-
коррелированной помехе в наблюдениях возможно только в том случае,
когда компоненты вектора состояния, входящие в уравнение наблюде-
ния, имеют с.к. производные более высокого порядка, чем компоненты
помехи, входящие в то же уравнение наблюдения, т.е. когда при диффе-
ренцировании уравнения наблюдения появляется сначала белый шум,
входящий в уравнение формирующего фильтра помехи. Физически это
значит, что полезный сигнал в уравнении наблюдения более гладок, чем
помеха.
> Допустим, что белый шум, входящий в уравнение формирую-
щего фильтра помехи, появляется после s-кратного дифференцирова-
ния уравнения наблюдения. Тогда первое уравнение (4.1.10) заменится
уравнениями (4.3.5), причем функция V’l в последнем уравнении (4.3.5)
определяется формулой
V>i(y, X, N, i) = <p,n(Y, X, N, t)T^N, t), (4.5.13)
а функции , ... , по-прежнему определяются формулой (4.3.2) и
первой формулой (4.3.4). Уравнения (4.3.5) вместе со вторым и третьим
уравнением (4.1.10) образуют систему уравнений вида (4.1.7) с расши-
ренным вектором наблюдения Y' — [у(°)ту(1)т .. . у(«)т] вместо У и
расширенным вектором состояния X1 = [ XTNT ]Т вместо X. Порядок
этой системы уравнений, как правило, можно понизить путем исклю-
чения некоторых или всех компонент помехи N с помощью уравнений
(4.3.1).
После преобразования уравнения наблюдения задача условно оп-
тимальной экстраполяции решается совершенно так же, как и задача
фильтрации. Разница будет лишь в том, что X будет представлять со-
бой оценку будущего вектора состояния системы Д > 0, стохасти-
ческий дифференциал которого определяется в силу второго уравнения
(4.1.10) формулой
dXt+д = 9?(Аг+д,£ + Д)<Й + + A)dWi(t + Д).
4.5. УСЛОВНО ОПТИМАЛЬНАЯ ЭКСТРАПОЛЯЦИЯ
505
Заменив этим уравнением второе уравнение (4.1.10) и повторив все вы-
кладки пп.4.3.2-4.3.4, получим уравнения, определяющие коэффициен-
ты уравнения условно оптимального экстраполятора (4.1.3) и (4.1.4).
Приведем полученные таким путем результаты.
Условие некоррелированности ошибки с rjtAY^ дает формулу
(4.2.7) для оптимального значения А/?, в которой
«02 = М(Х<+Д - Yt{>\ut,t)T,
(4.5.14)
а «22 определяется второй формулой (4.3.7).
Условия несмещенности оценки и некоррелированности ошибки со
случайным вектором & дают уравнения (4.2.4) и (4.2.13) ((4.2.11) в слу-
чае линейного экстраполятора) для оптимальных а и 7, в которых
ТПо — М<£>(Хг+д,£ + Д),
«01 = м [ <p(Xt+&, t + Д) - то ] £(Уе(0), У((1), ... ,Yt(a\ut,t)T,
41 = М(у><+Д - mo)eT + М(Х - AU) + £ М(Х - AU)y^T +
+М [(X - AU)<pJ+1 - АрггфгУг^] (^у + СТ+
1 ( Г rf д rj. ,г д \ дт
+-M(X-At7)|tr[^^ (^)+2’/ +
+tr (4.5.15)
ami, m2, /сц, «22, *>2 определяются второй и третьей формулами (4.3.6),
второй и третьей формулами (4.3.8) и формулой (4.3.9). Как и в (4.3.10),
все функции без указания аргументов в (4.5.15) представляют собой их
значения в момент t, а = <£>(Хг+д,£ -I- Д).
Для вычисления математических ожиданий в (4.5.14) и (4.5.15)
необходимо в общем случае знать совместное распределение величин
Yt^0\Y^ , ... , Yt*\ Xti Xt+д, Nt,Ut в каждый момент времени t. Что-
бы найти это распределение, напишем уравнение Пугачева для двумер-
ной характеристической функции <72(^1, ... , А«+4, Д1, • • , Дв+4^1^2)
объединенного случайного процесса [У(°)(£)т, Y^(t)T,...
..., Y^ (t)TX(t)TN(t)TU(t)T]T. Для этого достаточно подставить в это
506
ГЛ. 4. УСЛОВНО ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФП
уравнение при п = 2 вместо а(Х, t) и b(X, t) соответствующие блочные
матрицы
y(i)
у(»)
<p,+1(Y™,X,N,t)
t)
L a£(YU, t) + 0rfY', U, t)<ps+1 (Y(°), X,N, t) + ч J
0 0
о
t) о
о ^o(^t)
0 I3t}(Y', U, t)iMYW,X, N, t).
где Y' = [y(0)r у(1)Т...Г(.)Т]3 , и соответственно заменить векторы
Ai, Аг блочными векторами [ Af ... Af+4 ]Т, [/if ... /if|_4 ]Т. В результа-
те получим уравнение
дд2(Ai, .. • , Ав+4,/11, ... , /is-+-4;^i,^2)/^2 —
= м{* £ fiY™ + фГ+1^+1 (у/20) , xt2, м2, t2) + фТ+2¥>№2 , t2)+
fc=l
+фГ+з¥’о(М2,*2) + мТ+4[а«2^(К2>^2>(2) +
+А27?(У/2 , Ut2, У2)^.+1 (Y<?, Xt2, м2, t2) + 7t2] +
}f »+1
exPS i 52 A* + iXT+2Xt, + »АГ+зМ, +
fc=l
s+l 4
+iAf+4l/tl +г52^У/2*-1) +»дГ+2^г +фв+зМ2 +фГ+4^2 k (4-5.16)
fc=l )
где для краткости через р, обозначена матрица-столбец, состоящая из
двух блоков
4.5. УСЛОВНО ОПТИМАЛЬНАЯ ЭКСТРАПОЛЯЦИЯ
507
Pl =^(Xt2,t2)TIJ.,+2,
М2 = ^l(Xt2\Xt2,Nt2,t2)Tlle+l + Д»+з+
+^(Yg\xt2,Nt2,^^
Начальное условие для уравнения (4.5.16) имеет вид
д<?2(А1 , . . . , Ав+4,/11 , . . . , /1в+4^1,^1) =
= Ogi(Ai + , ... , As+4 + /is+4;^i)- (4.5.17)
Если некоторые компоненты вектора помехи N исключены с по-
мощью формул (4.3.1), то N в (4.5.16) следует понимать как вектор,
составленный из оставшихся компонент помехи.
Если , ... , в функциях £ и г? заменяются их выражени-
ями (4.3.1), то для вычисления математических ожиданий в (4.5.14) и
(4.5.15) достаточно знать двумерное распределение процесса
[У(°)(t)TX(t)TN(t)TU(t)T]T. Чтобы получить уравнение для двумер-
ной характеристической функции этого процесса, следует положить в
(4.5.16) Аг = • • • = Ав+1 = /12 = • • * — Ms+i 0-
В практически важном частном случае, когда функции </?i, £, т/, а
следовательно, и </?e+i, V’l не зависят от У = у(°\ для вычисления мате-
матических ожиданий в (4.5.14) и (4.5.15) достаточно знать двумерное
распределение процесса [X(t)T2V(£)Ti7(t)T]T. Уравнение для характе-
ристической функции этого процесса получается из (4.5.16), если по-
ложить Ai = • • • = Ae+i = /11 = • • • = /1в^1 = 0. Тогда, заменив Ав+г,
Аз+з, As+4, /1в+з, /is+4 соответственно величинами Ai,Аг, Аз,/ii,/1г,/13,
получим
ддъ (Ai, Аг, Аз, /11, /12, /13; ^1, ^2) = M{i/if ip(Xt2, £2)+
+i 1^2 (М2, ^2) + фГ[а*2£(К2, ^2»^2)+
+A2^(K2,^2^2)^s+i(^t2,M2,^2) + т«2] + х(Д; ^2)} х
х exp {iAfXtl + гА^Мг + iXjUtl + i$Xt2 + 1Д2Х + Фз^2} ,
(4.5.18)
где /i - матрица-столбец, состоящая из двух блоков
508
ГЛ. 4. УСЛОВНО ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФП
Д1 =
Д2 — ^o(M2i^2)TM2 + ^l(^t2,Nt2,t2)TT)(Yt",Ui2,t2)TpTli3,
а У" = [<p!(X,N,t)T ...<ps(X,N,t)T]T. <
Таким образом, имеем следующий результат.
Теорема 4.5.3. Пусть уравнения стохастической дифференци-
альной системы (4.1.10), (4.3.5) допускают существование одно- и дву-
мерных моментов. Тогда уравнения (4.2.4), (4.2.7), (4.2.13), (4.3.11),
(4.5.16), (4.5.17) полностью и точно решают задачу условно опти-
мальной экстраполяции в случае автокоррелированной помехи в на-
блюдениях.
Изложенная теория позволяет строить условно оптимальные экс-
траполяторы Пугачева для одновременного оценивания текущего со-
стояния и неизвестных параметров системы и прогнозирования ее со-
стояния на любое число заданных интервалов времени Ai, ... , Дуу.
Замечание. Формулы (4.5.14) и (4.5.15) и уравнения (4.5.16)-(4.5.18) могут
быть получены из соответствующих формул и уравнений п.4.2.6 заменой векторов Y и
X в качестве аргументов функций (/9, , £ и 7] соответствующими блочными
матрицами У7 = [у(0)Ту(1)Т ...YW]T И X' = [Х^Т]Т и матриц ¥>1,^1,
Т] соответствующими блочными матрицами [ У , [0...0 ,
[0... От?].
Аналогично п.4.5.2 выводится и формула для производной по вре-
мени ковариационной матрицы ошибки экстраполятора Пугачева
R = М[(Х,+Д - Xt)<p(Xt+±,t + ^T + <p{X{+^t + Д)(Х4д - ХТ)+
+lp(Xt+^.,t + Д)^! (t + Д)^(^<+Д, t + Д)7” —
-^(У/, Ut, tMYt,Xt, Nt, (Yt,Xt, Nt, Ut, t)T],
(4.5.19)
где У' = [У(°>ГУ(1>Г...ГМГ]Т, У<°) = У.
Таким образом, получим следующий результат.
Теорема 4.5.4. В условиях теоремы 4.5.3 формула для произ-
водной по времени ковариационной матрицы ошибки экстраполятора
Пугачева имеет вид (4.5.19).
4.6. ЛИНЕЙНАЯ УСЛОВНО ОПТИМАЛЬНАЯ ЭКСТРАПОЛЯЦИЯ 509
4.6. Линейная условно оптимальная экстраполяция
4.6.1. Экстраполяция. Аналогично п.4.5.2 решается задача ус-
ловно оптимальной экстраполяции состояния системы с параметриче-
скими шумами. Уравнения (4.4.7) в этом случае имеют вид
(П1 п \
Сю + с1г^г + У7 cl,ni+n-^r j dW2t
г—1 г=1 /
dX — (оуъХ + аго)^ + I с20 “I" (4.6.1)
\ г=1 /
где VKi(t), W2(t) - независимые процессы с независимыми приращени-
ями.
> Для нахождения оптимальных коэффициентов а, /?, 7 в (4.4.2)
сначала найдем для этого случая mo,Koi,«o2- Подставив в (4.5.4)-
(4.5.6) выражения функций 9?, , £ и 77 = Z, находим
Шо — О>22 (^ + Д)тПж(£ + Д) + d20 (J' + Д)>
«01 = [a22(t + Д)А"ху(^ + Д, t) CL22(i И" &)KXx(t + Д, t) ] ,
«02 = [ Kxy(t + Д, t) “ Kxy ] aH + [^«(^ + Кхх ] a12’ (4.6.2)
где Kx(s,t), KxyM, Kxi(s,t) - ковариационная функция процесса
X(t) и его взаимные ковариационные функции с Y(t) и X(t). Для вы-
числения Kx(s,t) обратимся к формуле (1.7.8), которая дает уравнение
dKx(t,s)/ds = Kx(t, s)a22(s)T при s > t.
Но нам необходимо значение Kx(s,t) при s > t. Поэтому вспомнив,
что Кх(з^) = Kx(t,s)T, транспонируем полученное уравнение. Тогда
будем иметь
dKx(s,i)lds = a22(s)Kx(s,t) при s > t.
Решение этого однородного линейного уравнения при начальном усло-
вии Kx(t,t) = Kx(t) = Кх определяется формулой
Кх(з^) = u(s,t)Kx при s > t,
510
ГЛ. 4. УСЛОВНО ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФП
где u(s,t) - фундаментальная матрица решений уравнения du/ds =
= ^22(5)11, т.е. решение этого уравнения, удовлетворяющее условию
u(t, t) = I (п.1.1.2). Положив е = u(t + A,t), будем иметь Kx(t +
+A,t) = еКх. Кроме того, приняв во внимание, что в силу (4.2.3) и
(4.2.9)
M(Xt+A - X) = О, M(Xt+A - X)YT = 0, M(Xf+A - Х)ХТ = о,
находим
Kxy(t + A, t) = КХу, KXx(t + A, t) = Kx.
Подставив найденные выражения Kx(t+A, t), Kxy(t+A, t), Kxx(t+A, t)
в последние две формулы (4.6.2), получим
Koi = [a22(t + А)Кау 0,22(1 + A)Kf ],
^02 — (ёКх “ Кхх) а12'
Для нахождения а и 7 по формулам (4.2.11) и (4.2.4) выразим величины
тж(£+А), Кху, Кхх в формуле (4.6.2) для то и в формуле (4.4.3) для «21
соответственно через тж, Кху, Кх. Для этого проинтегрируем второе
уравнение (4.6.1), приняв за начальный момент t, а за конечный t + А:
н-д
Xt+д = u(t + A,t)X* + h(t) + j u(t + ^ir)c2(r)dW1(r)y
t
где
Н-Д
h(t) = / u(t + Д,т)а2о('г)^Л (4.6.3)
t
а через C2 обозначен весь коэффициент при dWi в (4.6.1). Отсюда, учи-
тывая что n(t + A, t) = е и что Yt и Xt независимы от dW\ и MTVi(t) —
— 0, получаем
mx(t + А) = Emx(t) + h(t) — етпх + h,
Kxy(t + A, t) = еКху) Kxi(t + A, t) = eKx&,
Подставив найденное выражение mx(t + А) в первую формулу (4.6.2),
будем иметь
mo = a22(t + A)(emx + h) + a2o(t + A).
4.6. ЛИНЕЙНАЯ УСЛОВНО ОПТИМАЛЬНАЯ ЭКСТРАПОЛЯЦИЯ 511
Сравнив полученные выражения Kxy(t+Д, t) и Kxx(t+A, t) с найденны-
ми раньше, получим Кху = еКху, Кх = еКх&. Отсюда, имея в виду, что
матрица е = u(t + Д,£) обратима, находим Кху = е~1Кху, Кх± = е~хК%.
Подставив эти выражения в формулу (4.4.3) для «21, будем иметь
«21 = [йиКу + 0>12^ху ацКух 4- 0>12КХх ] =
= [ацКу 4- с&12£ i^xy П]лКух + Кх\ -
Наконец, подставив найденные выражения тпо, «oi, «02, «21 в (4.2.4),
(4.2.7) и (4.2.11), находим оптимальные а, /?, 7 в (4.4.2):
а = [aia2] = \-РапКу 4- {а22^ 4- Д) - Рапг~1} Кьу-
~Ра\\Кух 4- {<122(1 4- Д) — /fai2£~X} =
= [ —/fan «22^ 4- Д) — /fai2£~X ] ,
P — xx)a\2K,22 ">
у = а2о(* 4- Д) - PaiQ 4- /fai26-1/i, (4.6.4)
где «22 определяется последней формулой (4.4.3), а все величины без
указания аргументов берутся в момент t.
Подставив выражения (4.6.45) в (4.4.2), получаем уравнение экс-
траполятора Пугачева
dX = £<122 (^ 4" Д)Х 4" <120 (^ 4" Д) j 4"
+Р - (апУ 4- ai2e-1X 4- flio - < (4.6.5)
Таким образом, получен следующий результат.
Теорема 4.6.1. Пусть векторный случайный процесс [УТХТ]
удовлетворяет системе линейных стохастических дифференциальных
уравнений с параметрическими шумами (4.6.1). Тогда уравнения ли-
нейного экстраполятора Пугачева имеют вид (4.6.5). Необходимые
для вычисления «22 по формуле (4.4.3) и Р по формуле (4.6.1) момен-
ты второго порядка можно найти из уравнений вида (4.4.8) и (4.4.9)
для составного вектора £yTXTXTj . Роль матриц cir, С2Г играют
[Ocir ] и [с2Г0], а матрица и диагональна.
Докажем теперь, что найденный экстраполятор Пугачева можно
представить в виде последовательного соединения фильтра Пугачева,
512
ГЛ. 4. УСЛОВНО ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФП
усилителя с коэффициентом усиления е = (t + Д, t) и сумматора, вводя-
щего неслучайное слагаемое Л(£), определяемое формулой (4.4.11), т.е.
что
X = eXi + Л, (4.6.6)
где Xi - выходной сигнал условно оптимального фильтра - условно
оптимальная оценка текущего состояния системы X. Чтобы доказать
это, достаточно показать, что (4.6.6) удовлетворяет уравнению (4.6.5)
условно оптимального экстраполятора.
> Из (4.6.6) находим стохастический дифференциал величины X:
dX = edXr 4- (eXx 4- h)dt.
Ho Xi как выходной сигнал условно оптимального фильтра удовлетво-
ряет уравнению (4.4.7), которое в нашем случае имеет вид
dXi = (^22-^1 4- a2o)dt 4" Pi [sK (®11У 4" 012-^1 4" o,io)dt j ,
где Pi = Ria^2K22 a = Kx — Kx - ковариационная матрица ошибки
условно оптимального фильтра. Чтобы найти Л, продифференцируем
формулу (4.6.3). Имея в виду, что u(t 4- Д,£ 4- Д) = 7, u(t 4- Д,0 = е,
du(t 4- &,r)ldt = «22^ + Д)и(* 4- Д,т), находим
h — 0>2q(1 4- Д) — €6120 4- 6122(^ 4- Д)Л.
Чтобы вычислить б, вспомним, что на основании результатов п.4.1.2
du{s,f)lds = 6122(s)^(s>0, 9u(s,t)/9t = —u(s, t)6122(0-
Тогда будем иметь
€ = d22(t 4- Д)б - €0,22 •
Подставив найденные выражения dXi, h,e в формулу для dX, получим
dX = б(б122-^1 4- a2o)dt 4- cPi [б/У — (&цУ 4- ^12-^1 4~ a>ioi)dt j =
= [б12г(£ 4- Д)бЛ1 — €0,22X1 4- 6120(^ 4” Д) — £&го 4- 0,22^ 4- Д)Л j dt =
= £ 6I22 (t 4- Д) (ёХл 4- Л) 4- 6120 (t 4- Д) j dt+
4.6. ЛИНЕЙНАЯ УСЛОВНО ОПТИМАЛЬНАЯ ЭКСТРАПОЛЯЦИЯ 513
+601 [<^У — (ацХх 4> (iio)dt j .
Вычислим теперь правую часть уравнения (4.6.5) для X, определяемого
формулой (4.6.6). Учитывая, что 0 в (4.4.2) зависит от выходного сигна-
ла фильтра X, из (4.6.6) находим Кхх = еК^хХ = еКХх. Подставив это
выражение в формулу (4.6.4) для /?, получаем 0 = е(Кх — =
= €01. Подставив это выражение 0 и выражение (4.6.6) в правую часть
уравнения (4.6.5), убеждаемся в том, что она совпадает с найденным из
(4.6.6) выражением dX. Следовательно, выражение (4.6.6) удовлетво-
ряет уравнению (4.6.5), что и доказывает наше утверждение. <
Таким образом, мы распространили полученный в п.2.6.1 для ли-
нейных систем результат на значительно более широкий класс задач
условно оптимальной экстраполяции состояния как линейных систем,
так и линейных систем с параметрическими шумами. Впрочем, этот
результат ясен интуитивно, поскольку математическое ожидание (как
априорное, так и апостериорное) члена с dW в уравнении Ито всегда
равно нулю, вследствие чего основную роль для прогнозирования состо-
яния системы играет линейная часть ацХ + azo в правой части второго
уравнения (4.4.10).
Докажем, что найденный условно оптимальный экстраполятор оп-
тимален в классе всех линейных экстраполяторов. Для этого доста-
точно показать, что его ошибка в любой момент t не коррелирована со
значениями наблюдаемого процесса Уа при всех а < t.
> Из формулы для Х«+д, полученной путем интегрирования вто-
рого уравнения (4.6.1), и формулы (4.6.6) следует, что ошибка условно
оптимального экстраполятора Xt = X* — Х*+д связана с ошибкой услов-
но оптимального фильтра Хи формулой
t+д
Xt=eXu~ f u(t + Д,^)с2(т)с/Ж1(т).
t
Умножив это равенство справа на Y? при а < t, взяв математическое
ожидание и учитывая независимость Ya и c2(t) от dWi, находим
MXtYj = еМХпУат, а < t.
Но по доказанному в п.4.4.1 МХ^У/^ = 0 при всех а < t. Следователь-
но, и MXtY? — 0 при всех а < t, что и доказывает наше утвержде-
ние. <
17 Фильтры Калмана и Пугачева
514
ГЛ. 4. УСЛОВНО ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФП
В частном случае линейных уравнений (4.6.1), когда сг — 0 (г =
= 1, ... , Th + п), найденный условно оптимальный экстраполятор сов-
падает с оптимальным экстраполятором п.2.6.1. Следовательно, в слу-
чае линейных уравнений (4.6.1) и винеровских процессов 1У1(£) и W2(t)
условно оптимальный экстраполятор оказывается оптимальным среди
всех экстраполяторов.
Для оценки точности экстраполяции можно воспользоваться фор-
мулой (4.5.12) для производной ковариационной матрицы ошибки экс-
траполяции, которая дает уравнение
7? — CL22^ “I” A)jR 4~ Rd22(t “I” Д)^“
ni+n
cirmr
ni+n
4- Ciri/2c^skrs
r=l
C2o(t + A) +
+ У C2r(t + A)mr(t + A) Px(t + A)x
П1+1
c2o(^ 4- Д)"^ 4" c2r(t 4- Д)ттг(/: 4- Д)
r— 1
ni + l
4- У2 c2r(t 4- Д>1(£ 4- Д)с2«(* 4- A)Tkrs. (4.6.7)
r,S —1
Пример 4.6.1. В задаче примера 4.4.1 при d2i = d2Q — C2i = 0 и по-
стоянном d22 условно оптимальный экстраполятор представляет собой последователь-
ное соединение условно оптимального фильтра и усилителя с коэффициентом усиления
б = еа22Л.
4.6.2. Экстраполяция при автокоррелированной помехе.
Применим теорию п.4.5.3 для нахождения условно оптимального линей-
ного экстраполятора состояния линейной системы с параметрическими
шумами. Уравнения (4.1.10) имеют в этом случае вид
4.6. ЛИНЕЙНАЯ УСЛОВНО ОПТИМАЛЬНАЯ ЭКСТРАПОЛЯЦИЯ
515
У — 6цУ 4- 612Х 4- bi^N 4- bio,
dX = (ai2^ 4" ciio)dt 4" I Сю 4" CjrXr j dWi,
\ r=l /
(h \
c20 4- C2r^Vr j dW2, (4.6.8)
r=l /
а класс допустимых экстраполяторов определяется уравнением
(4.4.18), в котором 61,62,63,60 находятся по формулам (4.4.14), (4.4.17)
при ац = 0, 012 — О, С121 = 0, 022 — 0- Коэффициенты csr (г —
= 0,1, ... , h) определяются в этом случае формулой сзг = 65зс2г, а
Ъ82С1г - о (г = 0, , ... , п)
о Подставив выражения функций (/?, ^s+i, Ф1 из (4.6.8) и (4.4.13) в
(4.5.14) и (4.3.7), находим, как и в п.4.6.1,
^02 — (^хп -K^in)6s_|_i 3,
^22 = Ь 82(У22Ь^2^
где eu(t 4- Д,£), u(i,r) - решение однородного уравнения du/dt = 0120
при начальном условии о (г, г) = /, а
h
<722 = С2О^2С^о + 52(С2О^2<^Г + C2QV2($0)mni+n+T +
r=l
h
4~ Qsr^c^gO^ni+n+r 4~ А;П1_|_п_|_Г)П1_|_п_|_д). (4.6.9)
r,g=l
После этого (4.2.7) дает следующую формулу для оптимального значе-
ния /3:
Р = {(^^Се — 2 + (ёКхп ~ ^±71)6^1-1,3} /(652^226^2) (4.6.10)
Подставив выражения функций 4>s+i, ф из (4.6.8), (4.4.13) и
(4.4.18) в (4.5.15) и учитывая вытекающие из условия несмещенности
оценки и условия некоррелированности ошибки
XXz ~~ кху — sKXy, — еКХХ1
516
ГЛ. 4. УСЛОВНО ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФП
получаем из (4.2.11) систему уравнений для оптимального значения а:
otiKz 4- ot2^yx 4- а3КАх —
— —0Ь8+1дКуг 4- {ai2(* + Д) - Х} KxZ - &b8+iy3Knz,
oi\KZy 4- oizKy 4- ot3Kiy =
= — /ЗЬ8+1дКу 4- {ai2(£ 4- Д) — /3be+i,2£-1} Кху — /ЗЬ8+1>3Кпу,
°tiKzx 4- c^Kyi 4- а3Кх —
= -/3l)8+itiKyi 4- {ai2(* 4- Д) - ^be+i.2^-1} К± — ftb8+ii3Kni. (4.6.11)
Эта система уравнений получается из (4.4.21), если заменить ац, ai3
нулями, a ai2 и /?«+1,2 ~ величинами a^t 4- Д) и be+i,2£-1- Поэтому
оптимальные ai,a2,<*3 определяются формулами (4.4.26) и (4.4.24) с
такой же заменой. Чтобы найти оптимальное значение 7, заметим, что
в рассматриваемом случае
mx(t 4- Д) = emx(t) 4- h(t) = етх 4- h,
t+д
h(t) = / u(t 4- Д, r)aio(r)dr.
(4.6.12)
Тогда, пользуясь формулами (4.2.4), (4.3.6), (4.5.15), (4.4.24), найдем
7 = аю(^ 4- Д) — (aiЬ3 4- f3b8+\'3}fhn 4- [Л12(£ 4- Д) — ot3 ] h, (4.6.13)
где тп определяется формулой (4.4.29).
Для нахождения а,/3,7 по полученным формулам необходимо
знать, как и в п.4.4.3, т,К,Я,К±, и Kin.
Математическое ожидание т и ковариационная матрица К слу-
чайного вектора Q = [УТХТЛГТ] определяются уравнениями (4.4.30)
и (4.4.31), в которых
А =
bi 62
0 ai2
0 0
Ь3
о
0 агз
Г Ьо 1 Г о о
, Aq = flio , С30 = Сю 0
&20 0 С20
Q20
Сзг = 0 (г = 0, 1 , . . . , П1),
4.6. ЛИНЕЙНАЯ УСЛОВНО ОПТИМАЛЬНАЯ ЭКСТРАПОЛЯЦИЯ 517
СЗг = 0 Cl.r—П1 0 О' 0 0 (г = П1 + 1, ... ,П1 + п),
'0 0
СЗг = 0 0 ( г = П1 4- п 4-1, ... , П1 4- п 4- Л).
_ 0 ^2,г—П1— п
Чтобы получить уравнение для Я, воспользуемся формулой (4.5.19). В результате, имея в виду, что mi(t) = mx(t 4- Д) и
М [Xt+д - mx(t + Д)] Af+д = еКхет,
М(Х - т4)Х£д = KixeT = Кх = eKxi,
R = еКхет - eKxi - KixeT + Kt = еКхет - Kit
получим
jR = ai2(J 4- A)-R 4- ^aX2(t 4- А)?1 — РЪ82(У22Ь82РГ 4- 4- Д), (4.6.14)
где 0*22 определяется формулой (4.6.9), а
п
<ТЦ = Cio^icfo 4- 52(cio^icfr 4- Ciri/icfo)mni+r4-
r=l
n
+ 52 ClrI'lCl«(mn1+rnini+9 + fcni+r,ni+9). (4.6.15)
r,g=l
Матрица К^п определяется в рассматриваемом случае уравнением
Кхп = a3Kin 4- КхПа2з 4- («2 4- Qibi 4- /3ba+iti)Kyn+
4-(а1Ьг 4- /ЗЪ^Кхп 4- (с*1Ьз 4- /3b8+ij)Kn. < (4.6.16)
Таким образом, имеем следующий результат.
Теорема 4.6.2. Пусть векторный случайный процесс [УТХТ]
удовлетворяет системе линейных стохастических уравнений (4.6.8).
Тогда экстраполятор Пугачева имеет вид (4.4.18), в котором Ьо, bi, &2,
Ь3 находятся согласно (4.4.14), (4.4.17) при ац = ai2 = 021 = ^22 = 0 и
сзг = ЪазС2г, Ь82С1г = 0. При этом интегрирование уравнений (4.4.30),
(4.4.31), (4.6.14), (4.6.16) при соответствующих начальных условиях
с найденными коэффициентами а, /3 и у полностью решает задачу
нахождения условно оптимального экстраполятора.
Замечание. Из доказанного в конце п.4.4.2 следует, что найденный
условно оптимальный экстраполятор может быть представлен в виде последовательного
соединения фильтра Пугачева с усилителем (с коэффициентом усиления €) и сумматором,
вводящим неслучайное слагаемое h.
518
ГЛ. 4. УСЛОВНО ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФП
4.7. Дискретное условно оптимальное оценивание,
распознавание и адаптация
4.7.1. Постановка задач дискретного условно оптимально-
го оценивания. Те же рассуждения, которые привели нас в п.4.1.3
к классам допустимых фильтров, описываемых дифференциальными
уравнениями, подсказывают мысль использовать дискретные фильтры,
описываемые разностными уравнениями, и дискретные наблюдения в
задачах 1 и 2 (п.2.8.1). Для решения этих задач в реальном масштабе
времени рассмотрим принцип дискретного условно оптимального оце-
нивания Пугачева. Этот принцип состоит в отказе от абсолютной оп-
тимальности и ограничении оптимальными оценками для некоторых
ограниченных классов допустимых оценок, удовлетворяющих некото-
рым простым в реализации разностным уравнениям, которые могут
быть вычислены на основе результатов наблюдений в масштабе реаль-
ного времени. Главная трудность при синтезе условно оптимальных
фильтров состоит в выборе класса допустимых фильтров. Обычно в
практических задачах за класс допустимых дискретных условно оп-
тимальных фильтров принимают множество фильтров, описываемых
конечномерными разностными уравнениями с некоторыми неизвестны-
ми коэффициентами. В этом случае проблема оптимизации сводится к
определению оптимальных значений всех неизвестных коэффициентов,
которые в общем случае зависят от времени.
Первой особенностью нелинейного условно оптимального оценива-
ния служит то обстоятельство, что такое оценивание является мно-
I л I2
гокритериальным, поскольку требуется минимизация М IX/ — Х/1 для
любого момента времени I из некоторого интервала. Как известно, фор-
мула (2.8.5) дает абсолютно оптимальную оценку для любого момента
времени I. Однако, ограничивая класс допустимых оценок, трудно на-
деяться на то, что получаемая таким образом оценка будет оптимальной
для любого момента времени I. Ясно, что так будет всегда в линейном
случае. Таким образом, надлежит воспользоваться известными парето-
оптимальными оценками.
Второй особенностью нелинейного условно оптимального оценива-
ния является то, что оптимальные коэффициенты фильтров должны
определяться только априорными данными без использования текущих
наблюдений, как это имеет место в фильтрах Калмана (раздел 2.9).
Данные текущих наблюдений используются только в процессе филь-
трации при рекуррентном решении уравнений фильтра.
4.7. ДИСКРЕТНОЕ УСЛОВНО ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ
519
Поставим задачу найти условно оптимальную оценку Xt для лю-
бого момента времени I случайных величин Хц используя наблюдения
случайных величин У/ = {Yi, ... , в классе допустимых фильтров.
4.7.2. Классы допустимых фильтров. Рассмотрим сначала
систему уравнений (2.8.1):
Yl=cjll(YhXhVl),
Х^^УцХцЦ) (/ = 1,2,...). (4.7.1)
Определим класс допустимых фильтров формулой
Xt = AUt (4.7.2)
и разностным уравнением
(4.7.3)
Здесь А - некоторая постоянная (п х 7У)-матрица, N > п, ранга n; Q -
некоторые известные, так называемые структурные функции
(в общем случае векторные функции размерности g); 6i - произволь-
ные (N х д)-матрицы коэффициентов фильтров; а 7/ - произвольные
(N х 1)-матрицы столбцы смещений нуля. Каждому выбору значений
6 ц yi соответствует определенный допустимый фильтр, а все возможные
значения 6ц yi определяют класс допустимых фильтров для данных
функций Различные последовательности функций {£/} определяют
различные классы допустимых фильтров. Каждому выбору {0} соот-
ветствует определенный класс допустимых фильтров.
Последовательность функций {0} в (4.7.3) может быть в принципе
произвольной. Но точность фильтрации зависит от выбора {0 } - Таким
образом, встает вопрос о рациональном выборе {(/}. Априори можно
только сказать, что чем больше размерность структурных векторных
функций £/, тем выше может быть точность фильтрации. Некоторые
указания на то, как выбрать функции £ц могут быть получены путем
замены уравнений раздела 3.6, определяющих субоптимальные оценки,
соответствующими разностными уравнениями.
Следуя Пугачеву, примем за оптимальный такой допустимый
фильтр, который минимизирует средний квадрат ошибки M|X/+i —
—Xt+i |2 на каждом шаге (при каждом I) путем выбора 6ц 7/ в (4.7.3) при
данных значениях 7д, h < I, найденный в результате предыдущих
шагов. Такой фильтр называется дискретным условно оптимальным
520
ГЛ. 4. УСЛОВНО ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФП
фильтром или дискретным фильтром Пугачева. Значения Si и 7/ в
(4.7.3), соответствующие условно оптимальному фильтру, принимают-
ся за оптимальные значения Si, 7/.
Само собой разумеется, что все, что было сказано в п.4.1.4 о харак-
тере задач непрерывной условно оптимальной фильтрации, относится
также и к задачам дискретной условно оптимальной фильтрации.
Уравнение (4.7.3) показывает, каким образом допустимый фильтр
использует в каждый момент времени (/4-1) информацию, содержа-
щуюся в предыдущих результатах наблюдений Ух, ... , У/. А именно,
эта информация используется только через Ui. И только текущий ре-
зультат наблюдения У/ используется непосредственно при формирова-
нии оценки Х/+1 в момент времени I. Таково условие, при котором
М |х/+1-Х1+1| минимизируется в каждый момент времени (/4-1)
условно оптимальным фильтром.
Таким образом, задача синтеза фильтра Пугачева сводится к нахо-
ждению оптимальных последовательностей {<?/} и {7/} в (4.7.3).
4.7.3. Дискретный фильтр Пугачева для нелинейных ре-
грессионных уравнений. Рассмотрим уравнения нелинейной регрес-
сии (4.7.1).
> Записав (4.7.3) в форме
Х1+1 = ASiCi(YhUt) 4- Ayh (4.7.4)
I - I2
видим, что средний квадрат ошибки М LXi+i — будет минималь-
ным тогда и только тогда, когда правая часть уравнения (4.7.4) пред-
ставляет собой линейную с.к. регрессию случайной величины X/+i на
случайный вектор С(У/,С//).
Из теории линейной регрессии следует, что правая часть (4.7.4)
представляет собой с.к регрессию на ^(У/,17/). Таким образом,
имеем следующие два уравнения для нахождения оптимальных значе-
ний 61 и 7/:
A6iMQ(Yh Ui) 4- Ац = MXz+i, (4.7.5)
M(AUl+1 - Xl+MYhU{)T = 0. (4.7.6)
Полагая в (4.7.5)
mJ+1 = MXI+I) Pl = MQ(YhUt), (4.7.7)
получаем
Ayi = mi+i - A6ipi.
(4.7.8)
4.7. ДИСКРЕТНОЕ УСЛОВНО ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ
521
Подставляя в (4.7.6) выражение (4.7.3) для Ui+i, приходим к уравнению
для 6f.
ДйМ [С(ГЬ Ut) - pt ] Ct(Yt, Ut)T - M(XZ+1 - mt+MYt, Ut)T = 0.
Отсюда, обозначая
Bi = м (G(yh Ui) - pi ] <z(yz, Ut)T,
rr (4.7.9)
Di = M(Xi+1-mi+MYhUi)T,
находим
A6t = P/Bf1. (4.7.10)
Формула (4.7.10) определяет А<5/, если матрица Bi обратима, det В/
0. Последнее всегда имеет место, когда компоненты вектора 0(1/, Ui)
линейно независимы
Вычислим математические ожидания в (4.7.7)-(4.7.9). Для этого
следует сначала подставить в (4.7.7) и (4.7.9) выражения для X/+i и Yi
из (4.7.1). В результате получим
mz+1 = Mwz(Xz,Vt), pi = MCz(wlz(Xz,Vt),Ui),
Bl = Щ(1ШХ1,У1),и1) -pi]CiMXi,Vi),Ui)T,
D, = M [WZ(XZ, Vt) - mi+i ] G(wlz(Xz, Vt), Ui)T.
Для вычисления по формулам (4.7.11) достаточно знать распределение
случайной величины Vi и совместное распределение случайных величин
Xi, Ui (напомним, что из-за независимости случайной величины Vi от
Vi, ... , Vi-i составной случайный вектор [XfUf]T независим от Vi).
Для того чтобы найти это распределение, запишем (4.7.3) в виде
А+1 =ШМ*ь^),С//)+7/. (4.7.12)
Тогда одномерная характеристическая функция
<71,/(A,р) = Мехр {iXTXi + ififUi] (4.7.13)
определится уравнениями п. 1.5.5, которые в данном случае имеют сле-
дующий вид:
Р1,<+1(А,д) = Мехр {iXTcji(Xi,Vi) + ip,T [6iCi(uu(XhVi),Ui) + 7Z ]} .
(4.7.14)
522
ГЛ. 4. УСЛОВНО ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФП
Начальным условием для рекуррентного уравнения (4.7.14) служит на-
чальное значение характеристической функции
01,1(А,д) = Mexp{iATXi + ipTUi} (4.7.15)
вычисляемое для начальных значений Xi и U\. <з
Таким образом, имеем следующий результат.
Теорема 4.7.1 Пусть уравнения дискретной стохастической си-
стемы (4.7.1) допускают существование одномерных моментов. То-
гда, если матрица Bi невырождена, фильтр Пугачева определяется
рекуррентными уравнениям (4.7.2), (4.7.3), (4.7.8), (4.7.10) с (4.7.11) и
уравнением (4.7.14) при условии (4.7.15).
Замечание!. Чтобы начать рекуррентный процесс, необходимо задать
совместное распределение Xi и Ui (начальное распределение). Если распределение ве-
личины Xi (независимой от V\) известно и определяется характеристической функцией
fci(A), можно принять за оценку Xi математическое ожидание Х1 — МА\ — 7711 и
определить совместную характеристическую функцию Х± и Xi формулой <71 д (А, /1) =
= fci(A)e*M mi. Можно также определить оценку Х\ как случайную величину с вы-
бранным произвольно распределением и принять <71,1 (А,/1) = hi (A)Zi (/1), где /1(/1)
- характеристическая функция величины АГ1. В том случае, когда распределение не
известно, то его приходится задавать произвольно. После этого начальная характеристи-
ческая функция определится так же, как и в предыдущем случае.
ЗамечанИб2. Так как величины У/ не входят в уравнения (4.7.10), (4.7.14),
то все последовательности величин W. {?/}. {Р1Л можно вычислить изложенным
методом заранее. Тогда процесс оценивания последовательности величин {АГ/} сведется
к применению рекуррентной формулы (4.7.3).
ЗамечаНИбЗ. Точность оценки можно характеризовать вторым моментом
ошибки
К = М(Х, - - Xt)T
или средним квадратом ошибки
€1 = М(Х, - Xi)T(Xi - Xi) = tr Rh
которые определяются характеристической функцией Qi j (А, /1). Можно также находить
доверительные области для АГ/, поскольку <71,/(А, /1) полностью определяет совместное
распределение АГ/ и АГ/.
Замечание 4. Уравнения (4.7.10)-(4.7.12) могут быть решены любым при-
ближенным методом параметризации распределений (разделы 1.7 и 1.8). Взяв достаточно
большое N\ можно надеяться найти решение с любой степенью точности.
4.7. ДИСКРЕТНОЕ УСЛОВНО ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ
523
> В задачах прямого оценивания, когда в (4.7.2) следует принять
Xi = Ui, уравнения фильтра Пугачева имеют следующий вид:
Х,+1 = 6&ШХ,, V^Xt) + 71, (4.7.16)
7« = m«+i — $iPi> (4.7.17)
6i = ABf1, (4.7.18)
где
mi+i = Ma>i(Xi,Vi),
Pl = M<j(uu(Xi, Vt),Xi),
Bt = M [ct(cuu(X(,Vt),Xt) -P«]
Dt = M[^XhVi)-ml+1]Ci(wu(Xl,Vl),Xl)T. (4.7.19)
Для вычисления по формулам (4.7.19) достаточно знать совместное
распределение Xi и Xi и распределение Vi, которое по предположению
известно. При этом в силу (4.7.14) и (4.7.15) имеем
5i,j+i(A,m) = Мехр |гАта>((Х(, VJ) + »дт [5<С("н(^,И),Х0 +7i] } ,
(4.7.20)
Р1,1(А,д) = Mexp|iATXi+t/4TXiJ . < (4.7.21)
Таким образом, справедливо следующее утверждение.
Теорема 4.7.2 В условиях теоремы 4.7.1 фильтр Пугачева прямо-
го оценивания определяется уравнениями (4.7.16)-(4.7.18) при (4.7.19)
и уравнением (4.7.20) при условии (4.7.21).
Для зависимых ошибок наблюдения, когда вместо первого уравне-
ния (2.8.1) имеет место Yi = wn(Xi, Wi), где {И7/} - последовательность
независимых случайных величин, задача сводится к рассмотренной вы-
ше задаче, если {И7/} определить некоторым стохастическим разност-
ным уравнением
W+1=4'+iW,v,).
где {И} - последовательность независимых случайных величин, с из-
вестным распределением (без потери общности Vi могут совпадать с
величинами Vi во втором уравнении (4.7.1)). В этом случае, во-первых,
следует ввести расширенный вектор наблюдения Yi = [1|ТИ^Т]Т, и во-
вторых, обратить внимание, что оценке подлежат не все компоненты
У/, а только те, которые соответствуют Y[.
524
ГЛ. 4. УСЛОВНО ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФП
Пример 4.7.1. Рассмотрим дискретный двумерный случайный процесс, удо-
влетворяющий уравнениям
Yt = Xi+Wh Xl+1 = (Xt + Vt)2, (I)
где Vi и W] - назависимые случайные величины с нулевыми моментами первого и тре-
тьего порядков. Найти условно оптимальные оценки Х[, выбрав уравнение фильтра Пу-
гачева в виде разностного уравнения первого порядка:
Л+1 = 6, [х,2 X,(Yh -X,) (Yt - Xt)2 f + 7ь (П)
Выбор в качестве 6/^/ квадратичной формы переменных Xi и Y-Xt в данном случае
естественен, так как при этом уравнение для оценок получается похожим на уравнение,
определяющее величины Xi, вследствие чего можно ожидать получения достаточно точ-
ных оценок величин Х[.
Оптимальные коэффициенты фильтра 6/ и 'У/ определяются согласно (4.7.7),
(4.7.10), (4.7.11), причем
Dl = [4'W],
d(p = МХ,2Х,2 - МХ,2МХ,2.
4° = МХ,3Х< - MX,2MX,Xt - 4°,
4° = MX,4 - (mx(2)2 - 4Z) - 24°; (ni)
= MX,4 - (MX2)2,
42 = MX,X,3 - МВДМХ,2 - 41.
K13 “ “1 *11 z*12>
42 = MX,2X,2 - (MX,X,)2 + HiM.Xf - K^l - 24г,
«23 = 4° + 4'f - «и - 3«i2 - «13 " 2«22 + 2H;MX;X;,
42 = 4‘)+24j)+4') - - 44) - 242-
- 44'2 - 442 + я; - + 4HiMx12, (iv)
mt = Xt2 + G/; (V)
pi = [MXf MX1X1 - MX,2 MX,2 + MX,2 - 2MX|X, + Ht ] . (VI)
4.7. ДИСКРЕТНОЕ УСЛОВНО ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ
525
Здесь Hi и Gi - дисперсии величин Wi и Vi соответственно, Н[ - четвертый момент
Wi. Для нормально распределенных величин Wt H'l = ЗЯД Для вычисления вто-
рых и четвертых моментов величин Х{ и Х[ в (III)-(VI) достаточно знать совместное
распределение Xi и Х{. При этом моменты можно вычислять дифференцированием ха-
рактеристической функции Xi и Xi или интегрированнием, считая известной плотность:
оо оо
/1.'М = 4^2 / / (VII)
—оо —оо
величин Xi и Xi,
оо оо
MX,2 = " (^) = / / x2fuMdxdi, (VIII)
° —оо —оо
оо оо
МХ(Х, = -(^^ = У У x^fu(x,^dxd^, (IX)
О —оо —оо
оо оо
МХ2 = -(^) = [ [ efu(x,£)dxd£, (X)
\ и г" /0 * *
—оо —оо
оо оо
=11 x'fuMdxdt, (XI)
О —оо —оо
оо оо
MX<3X,= (feL) = f / ^UuMdxd^, (XII)
yaA ufi/Q J J
—oo —oo
oo oo
МХ^=(^Л = f [ x2efuMdxd^, (XIII)
yaA dp? / 0 J J
—co —co
oo oo
МХ1Х1=(^Л = [ [ xefuMdxdt, (XIV)
у и AU fl J Q J J
—co —oo
oo oo
= = [ [ ffuMdxdt, (XV)
\ /о J J
—oo —oo
526
ГЛ. 4. УСЛОВНО ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФП
где индексом 0 внизу отмечены значения величин в круглых скобках при А = fl = 0.
Уравнение (4.7.20) для характеристической функции имеет в данном случае вид
Р1,«+1(А,д)
= I I1
—оо —оо —оо —оо
+ v)2+
+ifi (ii [£2 - £ + u) (z - £ + u)2 ]Т + } х
x fl ,i (x> (v)Qi (u)dudvdxd£, (XVI)
где Pi (v) и Qi (u) - плотности V/ и Wi соответственно.
Полученные формулы определяют рекуррентный процесс для последовательного
вычисления /1J, $1 и 7f.
4.7.4. Фильтры Пугачева для нелинейных авторегрессион-
ных уравнений.
> Применительно к уравнениям нелинейной авторегрессии (2.8.3),
когда
У = ¥’п(У,Х/)+^п(У)Ч,
Xl+1 = ^(У^Н^Оь^М (i = 1,2,...), (4.7.22)
функции Q следует взять линейными относительно У/, т.е. положить
b(Yh X,) = [б(й)тУЛй(й)Т]Т • (4.7.23)
Тогда, разбив матрицу коэффициентов <5/ на блоки, <5/ = [«/А], пред-
ставим уравнение фильтра Пугачева в виде
ХН1 = a^i(Xi) 4- ^(Xi)Yi 4- 7ь (4.7.24)
Здесь & = £i(Xi) и T]i = Tfi(Xi) - известные структурные функции филь-
тра; а/, 7/ - коэффициенты фильтра. В этом случае из (4.7.19),
имеем
= Мб (Л), Р{2} = M^Xi^uiXi), (4.7.25)
4.7. ДИСКРЕТНОЕ УСЛОВНО ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ
527
В/ =
к(/)
«и
«21
К(0 1
«12
«22 J
det |В,| / О,
«</1) = м[ыхо-М')]б(й)т,
«12 = «21Т = М [б(Х() - р<? ] <pu(Xi)T7ti(Xi)T,
«й = М [тИХОЫ*») - 4°] <Ри(Х1)ттП(Х1)т+
+ M7]l(Xl^u(Xl)^u(Xl)T7ti(Xl)T,
(4.7.26)
Dl = [«01 «02 ] >
«й = М[^(Х,)-т,+1]6(Х/)т,
«02 = М[<#(л)) - mi+i]pu(Xl)T7]i(Xl)T+
+ (4.7.27)
ml+1 = р(01), р(01) = MW(Xt), (4.7.28)
где MV/ = 0, = ui - ковариация белого шума Vi.
Из (4.7.17) и (4.7.18) следует, что матрица коэффициентов фильтра
5i = [aiPi] определяется следующими уравнениями:
а««и + ^«21 = «01 > а««12 + А«22 = «02 > (4.7.29)
а вектор смещения ц - формулой
71 = Ро} - ОЧР1} - 01Р2}- (4.7.30)
Замечание. Из (4.7.5), (4.7.6) при А = I, Xi = Ul с учетом (4.7.23)
имеем из линейной регрессии соотношения:
М(Х< - X/)6(*1)T = 0, М(Х, - X^Y^Xi)7, = О, М(Х( - Xt)Xf = 0.
Подставив (4.7.22) и (4.7.23) в (4.7.20), получим рекуррентное урав-
Г ~ 1т
нение для одномерной характеристической функции X?X? :
528
ГЛ. 4. УСЛОВНО ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФП
01,ьн(А,м) = м|гАт [^t(Xt) + ^Xt)Vi ] +
+фт[а,б(Х<) + + 7<]}. (4.7.31)
Но величины Xi и Xi независимы от Vi. Следовательно, условное ма-
тематическое ожидание
Мехр{[гАт^(^) + Л(^п(^)] И | *i,Xi}
совпадает с безусловным математическим ожиданием, представляю-
щим собой значение характеристической функции hi (А') случайной ве-
личины Vi при
А' = ^(Х,)ГА + ^u(Xi)TrU(Xi)Tti.
учитывая это, представим (4.7.31) в виде
= M/l/(V-J(XJ)TA + ^и(^)т%(Х,)х
х^тд) ехр{гАт^/(Х() + гмт[а/й(Х<)4-
+^(Л)¥’1|(Х|)+7<]}. (4.7.32)
Уравнения (4.7.29), (4.7.30) и (4.7.32) определяют рекуррентный про-
цесс вычисления 0i,/+i, a/+i, Д+i, 7/+i по известным pij, оц, fr. Для на-
чала процесса необходимо задать характеристичесую функцию
0i,i(A,/x) величин Xi и Х\. <
Таким образом, получен следующий результат.
Теорема 4.7.3. Пусть уравнения дискретной стохастической си-
стемы (4.7.22) допускают существование одномерных моментов. То-
гда, если матрица Bi невырождена, то дискретный условно опти-
мальный фильтр Пугачева прямого оценивания определяется рекур-
рентными уравнениями (4.7.24), (4.7.29), (4.7.30) при (4.7.25)-(4.7.28)
и уравнением (4.7.32) при условии (4.7.21).
Аналогично выводятся уравнения фильтра Пугачева для авторе-
грессионных уравнений (4.7.22) при Xi = AUi.
4.7.5. О двух трактовках дискретных фильтров Калмана и
Пугачева. Следует обратить внимание, что в своих работах В.С.Пуга-
чев трактовал дискретный фильтр Калмана не так, как это принято
4.7. ДИСКРЕТНОЕ УСЛОВНО ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ
529
большинством авторов. Он принимал за дискретный фильтр Калмана
обычный одношаговый линейный предсказатель и так же построил, из-
ложенную выше, нелинейную дискретную условно оптимальную филь-
трацию. В западной литературе делают различие между алгоритмами
фильтрации и одношаговыми предсказателями. А В.С.Пугачев отож-
дествлял их. Это просто разная трактовка, как понимать, что такое
термин фильтрация. В.С.Пугачев понимал под дискретной фильтра-
цией то, что невозможно в один и тот же момент времени I одновре-
менно и получать наблюдение, и тут же (мгновенно в этот же момент
времени) оценивать состояние. Поэтому, например, структуру линей-
ного дискретного фильтра он записывал в следующей форме:
Xz+1 =azXz 4-/^4-7< (4.7.33)
и таким образом получался либо фильтр Пугачева, либо “одношаговый
предсказатель”:
(XZ,KZ) прогиб ХИ1, (4.7.34)
который В.С.Пугачев называл дискретным фильтром Калмана (Пуга-
чев 1979, 2002). В западной литературе (и Калман сам) записывают
дискретную версию фильтра Калмана “по определению”, когда в один
и тот же момент времени I мы и получаем наблюдение, и тут же (мгно-
венно) производим оценку состояния. Тогда уравнение для оценки за-
пишется в следующем виде:
Xl+1 = atXi + + 7/. (4.7.35)
Вследствие разницы форм (4.7.33) и (4.7.35) получаются разные урав-
нения для коэффициентов фильтров.
4.7.6. Применение дискретной условно оптимальной филь-
трации к задачам распознавания, идентификации и адаптации.
Полученная в п.4.2.7 теорема 4.2.4 путем перехода к дискретной версии
уравнений в (4.2.25) и (4.2.26) переносится на случай условно оптималь-
ного распознавания сигналов, принадлежащих к N классам (пп.2.12.5,
3.6.2-3.6.4).
Аналогично пп.3.6.4, 3.6.5 решаются задачи условно оптимальной
адаптивной идентификации и распознавания.
4.7.7. Дискретный линейный фильтр Пугачева для дис-
кретных линейных стохастических систем
о Рассмотрим как частный случай уравнений (4.7.1) систему ли-
нейных уравнений
Y[ = biXi 4- bio 4- ipuVi, Xi^-x = aiXi 4- o>iq 4- ФМ. (4.7.36)
530
ГЛ. 4. УСЛОВНО ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФП
Согласно п.4.7.4 в этом случае оценка Xi векторов Х[ определяется
уравнением (4.7.24)
Х+1 =аЛ+/^+7г (4.7.37)
Для нахождения оптимальных значений оц, fa, yi надо положить в
формулах (4.7.26) ipi(X) = сцХ 4- аю, = ЬХ 4- Ью, &(Х) = X,
rji(X) = I, a и фц считать постоянными. Тогда получим
= О/М(Х - МХ,)Х^ = aiKXlil,
= aiM(Xt - MXi)(X^ + bf0) + VwV-u =
= aiKXlbf + VwV’n, (4.7.38)
= M(X, - MXi)XT = Ki„
*(12 = «21)T = - МХ,)(Х,ТЬ,Т + bfo = KilX.bT,
4г = btM(Xt - MX^Xfbf + bf0) + =
= biKXlbf + thii'iil’u,
mi = aiMXi + at0, p{‘} = MXb = btMXi + bl0, (4.7.39)
где KXl,KXl,KXt±l и KXlXl - ковариационные и взаимные ковариацион-
ные матрицы Xi и Xi.
Если учесть легко проверяемые равенства
М(Л+1 - Xi+1)Xf = 0, М(Х1+1 - Xi+1)YtT = о,
М(Х<+1 - Xi+1)Xf+1 = М(Х°+1 - Х?+1)Х?+1 = Kil+l - KXl+lil+1 = 0,(4.7.40)
а также симметричность матриц KXli.1,Kil+1Xl+1 = X’’ f = Xfl+1,
то уравнения (4.7.29) после замены I 4- 1 на I принимают следующий
вид:
otiKXl 4" fabiKXl = о>[КХ1,
aiK^bf + 0i(biKXlbf + V’n^V’n = <4^ + ‘Ф^и- (4.7.41)
Уравнения (4.7.41) легко решаются. Вычитая первое уравнение (4.7.41),
умноженное справа на bf, из второго, получаем
ft [bl(КХ1 - Ki,)b[ + VwV’n ] = ai(KXl - Kijbf + VwV’h- (4.7.42)
4.7. ДИСКРЕТНОЕ УСЛОВНО ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ 531
Заметим теперь, что в силу равенств KXlil = KX,XI, MXt = МХ( вели-
чина КХ1 — Кх> представляет собой второй момент ошибки Ri, т.е.
R, = М(Х, - Xl)(Xl - Xt)T = М(Х° - Xt°)(Xz - Xi)T =
= Kii Kxixt Kxixi "I" KXl — KXI (4.7.43)
Следовательно, уравнение (4.7.42) для оптимальных значений Pi имеет
вид
PitbiRibl + VwV’n) = aiRitf + 1/тФи- (4.7.44)
Решая уравнение (4.7.44), находим
Pi = (aiRibf + ^it'i^ii^biRib'i' + VwV’u)-1- (4.7.45)
ЗамечаНИе1. Матрица biRibJ всегда обратима, так, ее необрати-
мость равноценна существованию линейной функции вектора ошибки Х[ — Х[ с нулевой
дисперсией. То есть это означало бы, что соответствующая линейная функция вектора
Xi могла быть оценена абсолютно точно, что невозможно. Тем более обратима матрица
(.biRibf + i(>iuixl>{l).
После определения Pi по формуле (4.7.46) из первого уравнения
(4.7.41) имеем
оц = ai ~ Pibi- (4.7.46)
Замечание 2. Уравнение (4.7.46) получается только при условии об-
ратимости матрицы К£г Это условие тоже всегда выполняется, так как в случае его
невыполнения существовала бы линейная функция вектора Xi, оценка которой имела бы
нулевую дисперсию, что невозможно.
Подставив полученные выражения в (4.7.30) и учи-
тывая МХ/ = МА/, находим оптимальное значение уг.
yi = aiMXi 4- аю — оцMX/ — /?/(Ь/МХ/ 4- Ь/о) = a/о ~ Plbio. (4.7.47)
Наконец, подставив найденные значения а/ и 7/ в (4.7.37), приведем
его к виду
X/+i = aiXi 4- а/о 4- /?/(У/ - Ь/Х/ - Ь/о). < (4.7.48)
о Осталось написать уравнение (4.7.32) для характеристической
функции ^ij(A,/z). В данном случае оно имеет вид
532
ГЛ. 4. УСЛОВНО ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФП
0i,H-i(A, д) = + ^>у^гд)Мехр{1Ат(а/Х/ + а<0)+
+inT(aiXi + /3ibtXi + at0)} = hi^f A + ц) ехр{г(Аг + дт)а(0} x
хМехр |г(Ага/ + дт/3ibi)Xi + ipfaiXi j
или
3i,«+i(A, д) = hi($fX + {г(Аг + дт)аю} x
х^ДаГА + Ь^/З^д.а^д). (4.7.49)
Из (4.7.49) легко выводится рекуррентная формула для характеристи-
ческой функции д[ /+1 ошибки Xi — Xi. Заметим, что
Р1,/+1(м) = Мехр {гдт(Х( - А))} = Р1,/+1(-д, д). (4.7.50)
Положим в (4.7.50) Л = —д. Тогда, учитывая соотношения
-а/ц + bfpfiJ. = -ащ, gi,i(-a[n,afц) = д'и{а[ц), (4.7.51)
находим
01,/+1(д) = hl ц) д'и(а[ ц). (4.7.52)
Формула (4.7.52) полностью определяет распределение ошибки Xi — Xi
на каждом шаге I и, следовательно, дает возможность находить дове-
рительные области для X/. <
о Выведем из формулы (4.7.52) рекуррентное уравнение для вто-
рого момента Ri ошибки Xi - Xi. В самом деле, продифференцируем
(4.7.52) дважды по д и положим после этого д = 0. В результате полу-
чим
Ri+i = (ai ~ PMRiaf + (фи - < (4.7.53)
Таким образом, получен следующий результат.
Теорема 4.7.4. Пусть векторный дискретный случайный про-
цесс [XZT1^T]T удовлетворяет дискретным линейным авторегресси-
онным уравнениям (4.7.36). Тогда уравнениями дискретного линейного
фильтра Пугачева служат рекуррентные уравнения (4.7.44), (4.7.45) и
(4.7.49). При этом с.к. точность фильтрации определяется согласно
(4.7.53).
4.7. ДИСКРЕТНОЕ УСЛОВНО ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ
533
Замечание!. Уравнение (4.7.53) можно проще вывести следующим образом.
Вычитая второе уравнение (4.7.36) из (4.7.48), получаем для ошибки Х[ = Х[ — Xi
уравнение
= (а/ - Pibi)Xi + {Ми - (4.7.54)
Из (4.7.54), принимая во внимание, что Х{ и Х[, а следовательно, и Х{ не зависят от
Vi и, применяя формулу для ковариационной матрицы линейной функции случайного
вектора, получим
R/+1 = (а{ - /3tbi)Ri(a{ - bffif) + (Ми - $i)vi(il>ufii - iff).
Отсюда, раскрыв в каждом слагаемом скобки и пользуясь формулой (4.7.45), получим
искомое уравнение (4.7.53).
Замечание 2. Определяемая (4.7.54) оценка х1+1 при каждом I опти-
мальна в классе линейных функций (со сдвигом) величин Xi и У/. Докажем, что она
оптимальна в более широком классе линейных функций величин Xi, Y± , . . . , У/. Для
этого достаточно показать, что для Xi выполняются следующие соотношения:
М(Л+1 - Х|+1)ХГ = О М(Х(+1 - Xl+1)Y? = 0 (р = 1,2, ... , /).
(4.7.55)
Подставив в формулы (4.7.55) выражение Х/-ц — Х/-|-1 = Х/4-1 из (4.7.54) и приняв
во внимание независимость Vi от , получаем
М(Х(+1 - Х,+1)Л+х = (а, - M)M(Xi - Xi)Xl,
М(Х/+1 - ХЖ)ГРТ = (а, - M)M(Xi - Xi)Yf (4.7.56)
(р=1,...,/-1).
Из (4.7.56) и второго соотношения (4.7.40) следует, что Х/_}-1 оптимальна в классе линей-
ных функций величин Xi, У1 , ... , У/, если оценка Х[ оптимальна в классе линейных
функций величин Xi, Ух , ... , У/—1- А так как оценка
Х2 =01X1 4- Ом 4- 0l(Yl ~ biXi — 610)
оптимальна в классе линейных функций величин Xi, Ух, то и при любом I оценка X/_|_i
оптимальна в классе линейных функций величин Х1, У1 , . . . , У/. Более того, если все
величины Vi и величины Xi и Xi распределены нормально, то величины Xi+u Хи
У1 , ... , У/+1 при любом I имеют совместное нормальное распределение. В этом случае
оценка Х/4-i совпадает с регрессией Х/4-1 на Xi, Ух , ... , У/4-1 и, следовательно, оп-
тимальна в классе всех функций величин Xi, Ух , . . . , У/+1 (абсолютно оптимальна).
534
ГЛ. 4. УСЛОВНО ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФП
4.7.8. Дискретный фильтр Пугачева для дискретно линей-
ной системы с параметрическими шумами. С этой целью рас-
смотрим стохастическую дискретную систему:
X/+i — aiXi +аы + few 4- j V/, (4.7.57)
\ г=1 /
(п \
dot + ^drtYir \vt. (4.7.58)
r=l /
Здесь Х[г и Yir - r-е компоненты векторов Xi и Yi\ -
постоянные коэффициенты. В качестве класса допустимых фильтров
Пугачева выберем класс линейных фильтров следующего вида (п.4.7.3):
-V/+1 = Sub + 621Y1 4- 7/.
(4.7.59)
Здесь принято 6t = [<SUJ2<], Л = Uh А = I, Q(XhYt) = [А'/ТУ/Т]Г.
Учитывая, MXj = MXi = ггц, а также независимость Xi,Xi от Vi, по-
лучим с помощью формул (4.7.11) следующие уравнения:
mj+i = aimi + oqi, pi = [mf m[b[ + 5^]T, (4.7.60)
Bi =
h к hkKh ’ Dl = tа‘Кх>*> blKx‘b> + H‘22 ’
OlKx'Xi t>lKXlbl + Л122 J
(4.7.61)
n
Bill = Coi^l + 52"lir(eo/lZ/C^ + CrjP/Co/)
r=l
n
+ + klrs^CrlVlCrt,
Г,8 = 1
П
Нц2 = coiuid^t + '^2,mir(cfiivid^i + cTividh)
n r=1 (4-7.62)
+ 52 +kiT»)crivi^
Г,Л=1
n
H122 = doividu + ^2Tnir(doiVidri +
r=l
n
+ 52 + kirs)driuid^,
Г,8=1
4.7. ДИСКРЕТНОЕ УСЛОВНО ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ
535
Из (4.7.6) имеем:
М(Х/+1 - Х«+1)Х,Г = 0, (4.7.63)
М(Х/+1 - X/+1)rzT = 0. (4.7.64)
Умножая обе части (4.7.63) на <5^ и обе части (4.7.64) на <5^, добавляя
равное нулю слагаемое M(Xj+i — = 0 и учитывая несмещен-
ность оценки получаем равенство M(X/+i — Xi+i)Xi = 0. По-
скольку это равенство выполняется для любого момента времени /, то
и M(Xi—Xi)Xi = 0. Отсюда следует несмещенность Xi и следующие со-
отношения: KXl = KXlXn К±1Х1 = = КХг Таким образом, с учетом
(4.7.61) приходим к следующим уравнениям для матричных функций
Ju и 62Г
fiiiKxi + $i2ibiKXl = aiKXl, (4.7.65)
SiiKirf + + Я(22) = aiKXlbT + Я(12. (4.7.66)
Умножая (4.7.65) на bf и используя (4.7.66), находим
62i[bt(KXl - KSl)bf + Hl22] = at(KXl - Kit)bT + Hll2. (4.7.67)
Наконец, замечая KXl±l = K±lXl = K±t и учитывая несмещенность Xi,
получаем
XXl = KXl KXixi ” Kxtxt 4" KXl
= M(X, - Xi)(*«T -*/T)-
Формула (4.7.67) представляет собой ковариационную матрицу ошибки
Xi = Xi — Xi. Обозначая ее через Я/, получаем (4.7.67) в форме
^2i(biRibf 4- Н122) = cuRibJ 4-Н/12- (4.7.68)
Решая (4.7.68), находим
62i = (аЛЬТ + Hn^biRtf + НтУ1. (4.7.69)
После этого с учетом (4.7.69) уравнение (4.7.65) дает соотношение
= (4.7.70)
Очевидно, что формулы (4.7.69) и (4.7.70) справедливы при условии не-
вырожденности матрицы biRibf + Н 122, т.е. когда компоненты векторов
Xi и Xi линейно независимы.
536
ГЛ. 4. УСЛОВНО ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФП
После определния 6ц, &21 по формуле (4.7.8) при А = I находим
7/ — aoi ~ faboi.
(4.7.71)
В результате уравнение (4.7.59) фильтра Пугачева приобретет сле-
дующий вид:
Xw = aiXt 4- aol 4- <52zСИ - hXt - bol). (4.7.72)
Подчеркнем, что уравнение фильтра Пугачева (4.7.72) по форме совпа-
дает с уравнением дискретного фильтра Калмана (п.4.7.5).
Для получения уравнения для ковариационной матрицы ошибки
фильтрации 621 Xi = Xi - Xi перепишем уравнение фильтра Пугачева
(4.7.72) с учетом (4.7.69)-(4.7.71). В результате получим
^z+i — (и/ — 62ibi)Xi +
п
tizidoi - cqi 4- - cri)Xir
r=l
Vt.
(4.7.73)
Отсюда, учитывая независимость X/, Xi от V/, имеем следующие урав-
нения для mi. К[ и Riz
7П/+1 = aimi 4- ащ. (4.7.74)
Kw + (4.7.75)
Ri+\ — tyRiaf - 62i(biRia[ 4- #h2) + Hui, (4.7.76)
где Hln и Нц2 определены (4.7.62). <з
Таким образом, получен следующий результат.
Теорема 4.7.5. Пусть векторный дискретный случайный про-
цесс [ ] удовлетворяет дискретным линейным стохастиче-
ским разностным уравнениям с параметрическими шумами (4.7.57),
(4.7.58). Тогда дискретный линейный фильтр Пугачева при условии
невырожденности матрицы bi Ri bf 4- Н122 определяется уравнениями
(4.7.73)-(4.7.76) при условии (4.7.69) и соответствующих начальных
условиях.
Замечание!. Уравнения (4.7.74) и (4.7.75) линейны относительно Ш/ и
в то время как (4.7.76) нелинейно относительно Ri в силу зависимости &21 от Rl-
Замечание2. Как это принято в теории фильтров Калмана и Пугачева,
mi.Ki.Ri и &21 могут быть вычислены заранее во время синтеза фильтра, поскольку
(4.7.74), (4.7.73) и (4.7.69) не содержат результатов наблюдений.
4.8. ДИСКРЕТНАЯ ЭКСТРАПОЛЯЦИЯ И ИНТЕРПОЛЯЦИЯ
537
Замечание 3. Линейный фильтр (4.7.72) в случае, когда Х± , . . . , Xi—\
входят в него только посредством Xi, является оптимальным фильтром среди всех воз-
можных линейных фильтров. При этом уравнение (4.7.14) потребуется только для оценки
точности фильтрации, например, посредством вычисления доверительных областей, а не
только средней квадратической ошибки.
4.8. Дискретная условно оптимальная экстраполяция
и интерполяция
4.8.1. Дискретная условно оптимальная экстраполяция
для нелинейных регрессионных уравнений
о Рассмотрим сначала нелинейные регрессионные уравнения
(2.8.2):
Yi=uu(YhXhVi), (/ = 1,2,...). (4.8.1)
Задача экстраполяции отличается от задачи оценивания (раз-
дел 4.7) только величиной, которая должна быть оценена. В зада-
че экстраполяции вместо Xi+i должно быть оценено будущее значение
Л}+т+1 дискретного процесса Xi в момент времени 14-1 по результатам
наблюдения Yq,Yi, ... ,Yi, где т - некоторое натуральное число. Со-
ответственно, для того чтобы была оптимальной оценкой
минимизирующей средний квадрат ошибки М |X/+i — | , правая
часть уравнения экстраполятора
(4.8.2)
должна быть линейной средней квадратической регрессией случайной
величины Xj+t+i на случайный вектор 0(Yi, Ui). Применяя теорию
линейной регрессии, мы снова получаем уравнения (п.4.7.3):
A6i =
(4.8.3)
Ayi = m/+r+i - A6ipi.
(4.8.4)
Здесь
m/+r+i = MXf+r+i,
Pz=M0(Xz,Uz),
Di = M(JG+t+i - m/+r+i)0(X/,U/),
Bi = M [ Cl (Xt, Ut) - Pl ] Cl (Xt, U,)T.
(4.8.5)
(4.8.6)
(4.8.7)
(4.8.8)
538
ГЛ. 4. УСЛОВНО ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФП
После подстановки в (4.8.5) и (4.8.7) второго уравнения (4.8.1) для мо-
мента времени I + т + 1, получим
m/+r+i = Mcvj+TpQ+r, V/+r), (4.8.9)
D, = М [ш1+т(Х1+т, Vl+T) - ml+T+l ] Ut))T. (4.8.10)
Из формул (4.8.6), (4.8.7) следует, что для вычисления математических
ожиданий достаточно знать распределения Vi и совместное одномерное
распределения Xi и Ui. Совместное одномерное распределение Xi и Ui
можно определить характеристической функций (4.7.13) <?i,z(A, д), удо-
влетворяющей рекуррентному уравнению (4.7.14) при начальном усло-
вии (4.7.15). Для вычисления математических ожиданий в (4.8.9) и
(4.8.10) потребуется совместное распределение Xi,Xi+r,Ui. Зададим
его следующей характеристической функцией:
!?2,/,<+*(А1,А2,д) = Мехр{гА1’Х/ + iXlXi+T +ifiTUi} . (4.8.11)
Эта функция в силу второго уравнения (4.8.1) будет удовлетворять ре-
куррентному уравнению:
<?2,«,н-т+1(А1,А2,д) = Mexp{iAfX< + iX%ui+T(Xi+T, V/+r) + ipTUi}
(4.8.12)
при начальном условии
02,м(^1,Аг,д) = <7i,z(Ai + Лг,д). < (4.8.13)
Таким образом, имеем следующее утверждение.
Теорема 4.8.1 Пусть векторный дискретный случайный процесс
[ Y^X? ] удовлетворяет стохастическим разностным уравнениям не-
линейной регрессии (4.8.1). Тогда, если матрица Bi невырождена, то
условно оптимальный экстраполятор Пугачева определяется рекур-
рентным образом уравнениями (4.8.3), (4.8.4), (4.7.48), (4.7.49), (4.8.12),
(4.8.13).
Замечание. Уравнения теоремы 4.8.1 могут быть решены только итеративно,
поскольку $1,^1 зависят от <?2,/,/+т(Al, А2, д), которое в силу (4.8.12), (4.8.13) зависит
от • Можно предложить следующий итеративный процесс вычислений: сначала
находятся Р1,/ Аля Т = 0, а затем ^2,/,/4-т определяется в первом приближении,
далее строится второе приближение и т.д.
о Аналогично разделу 4.7 получаются уравнения прямой экстрапо-
ляции. Полагая Xi = Ui, А = /, получим искомую систему уравнений:
(4.8.14)
4.8. ДИСКРЕТНАЯ ЭКСТРАПОЛЯЦИЯ И ИНТЕРПОЛЯЦИЯ
539
7/ = mi+r+i - 6ipi, (4.8.15)
32,/,j+t+i(Ai,A2,m) = Mexp{iAfX/ + гА^и>г+г(Х^т,i7t+T) + »/%(} ,
(4.8.16)
а также (4.8.6), (4.8.8)-(4.8.10), (4.8.13). <
Таким образом, получен следующий результат.
Теорема 4.8.2. В условиях теоремы 4.8.1 прямой условно опти-
мальный экстраполятор Пугачева определяется уравнениями (4.8.6)-
(4.8.10), (4.8.13), (4.8.14), (4.8.16).
4.8.2. Дискретные условно оптимальные экстраполяторы
Пугачева для нелинейных авторегрессионных уравнений
о Применительно к нелинейным авторегрессионным уравнениям
(2.8.4)
У, = <pu(YhXi) + V-n(Wb Х/+1 = <л(Х/) + ^(Х,)И (4.8.17)
аналогично пп.4.7.4 и 4.8.1 получаем следующую рекуррентную систему
уравнений прямого дискретного условно оптимального экстраполятора
Пугачева:
Х1+т+1 = ai^Xi) + far^X^Yi + 7b (4.8.18)
«/«и + = K$,aiK$ + 0ik$ = k$, (4.8.19)
7i = ^'+r+1) - (4-8.20
p</+T+1) = M^+r(Xl+r),
Pl = [ЛГ]Т,
= мый), p(2} = ЩЫМ
(4.8.21)
(4.8.22)
где Bi = ] определены в (4.7.26). При этом одно- и двумер-
ные характеристические функции удовлетворяют уравнениям (4.7.32)
и (4.8.13), (4.8.16).
В результате имеем следующее утверждение.
Теорема 4.8.3. Пусть векторный дискретный случайный про-
цесс [ Y^X'f ]Т удовлетворяет нелинейным стохастическим разност-
ным уравнениям авторегрессии (4.8.17). Тогда, если матрица В[ не-
вырождена, то дискретный прямой условно оптимальный экстрапо-
лятор Пугачева определяется уравнениями (4.8.18)-(4.8.22), (4.7.32),
(4.8.13), (4.8.16).
540
ГЛ. 4. УСЛОВНО ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФП
4.8.3. Постановка задачи дискретной условно оптимальной
интерполяции. Предположим, что векторный случайный дискретный
процесс [ ] определяется разностными уравнениями нелинейной
регрессии (2.8.2):
(4.8.23)
Xz+1 =(vz(X/,Vz) (Z = 0,1,2,...). (4.8.24)
В п.2.8.2 были рассмотрены три постановки задачи дискретной интер-
поляции.
1. Интерполяция с фиксированной точкой (прямая интерполяция):
момент времени оценивания фиксирован, т.е. I = S, а интервал наблю-
дения к = I > S растет.
2. Интерполяция с фиксированной задержкой: в этом случае ни Z,
ни к не фиксируются, но их разность остается постоянной, т.е. к — I = т,
(т — постоянное время задержки).
3. Интерполяция с фиксированным интервалом (обратная интер-
поляция): интервал наблюдения фиксирован к = N (N — постоянная
величина), а время оценивания I изменяется от 0 до N.
Эффективные решения задач интерполяции случайных последо-
вательностей, описываемых разностными уравнениями, известны для
линейных уравнений и для специального класса нелинейных уравнений
(условно-гауссовские последовательности). В общем случае для нели-
нейных уравнений (4.8.23), (4.8.24) эффективного решения поставлен-
ных задач интерполяции не найдено. В случае, когда возможен выбор
структуры интерполятора на базе априорной информации о частично
наблюдаемой случайной последовательности (4.8.23), (4.8.24), эффек-
тивное решение задач дискретной интерполяции может быть получе-
но на основе принципа дискретного условно оптимального оценивания
(Синицын и Шин 1991).
4.8.4. Условно оптимальная интерполяция. Обозначим че-
рез Xs\i оценку вектора Xs по текущим наблюдениями Yq — {Уг, г —
= 0,1,...,/}, I > S. Согласно принципу условно оптимального оце-
нивания определим класс допустимых оценок XS\i следующим разност-
ным уравнением условно оптимального прямого интерполятора
(УОПИ):
Xsn=6iCi(Yi^Xsli^^ 1>S (4.8.25)
при заданной последовательности функций {£/} и при всех возможных
значениях структурных коэффициентов 6i и 7/ размерности п х q и
4.8. ДИСКРЕТНАЯ ЭКСТРАПОЛЯЦИЯ И ИНТЕРПОЛЯЦИЯ
541
п х 1 соответственно. Начальное условие для уравнений (4.8.25) име-
ет вид Xs = Xs\s и находится из решения известной задачи условно
оптимальной фильтрации (п.4.7.3).
Пусть ковариационная матрица Kq случайного вектора Q =
= 0(^+1, %5|/) - положительно определенная матрица при всех I > S.
Относительно функций (J/, шц и Q будем в дальнейшем предполагать,
что они обеспечивают существование всех моментов конечного порядка
составного случайного вектора [Х/л J|JT при всех I > S.
Принимая уравнение (4.8.25) как уравнение линейной регрессии
случайного вектора Xs на случайный вектор 0(^+1, Asp), получаем.
Теорема 4.8.4. Пусть дискретный векторный случайный про-
цесс [1|ТЛ’|Т] удовлетворяет уравнениям (4.8.23), (4.8.24) и услови-
ям теоремы 4.5.1, а оценка Xs\i вектора Xs по наблюдениям Yq, I > S
ищется в классе оценок, определяемых уравнением нелинейного УОПИ
вида (4.8.25). Тогда оптимальные значения коэффициентов 5[ и ц для
УОПИ существуют и определяются уравнениями
6[Ri = Li, yi = rs — dipt, (4.8.26)
где введены следующие обозначения:
п = мхь = 0 = С(У+1,Х|/),
С? = G - тп<( = й - рь Rt = Lt =
Для вычисления Ri, Li, ri и pi достаточно знать одномерное рас-
пределение случайного вектора в каждый момент времени
1>S.
4.8.5. Условно оптимальная интерполяция с фиксирован*
ной задержкой. Обозначим через Хщ^т оценку вектора Xi по на-
блюдениями = {Yi, г = 0,1, ... , I + т}, т > 0. Так же, как в
п.4.8.4, определим класс допустимых оценок Хщ+Т следующим разност-
ным уравнением условно оптимального интерполятора с фиксирован-
ной задержкой (УОИФЗ):
А/4-1|л-14-г = йС(А/+г|/+1+г) -1-7/, I > Iq (4.8.27)
с начальным условием Х/о|/о+г, которое находится из решения зада-
чи условно оптимальной прямой интерполяции. Принимая уравнение
(4.8.27) как уравнение линейной регрессии случайного вектора X/+i на
542
ГЛ. 4. УСЛОВНО ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФП
случайный вектор £/(У/+1+г, Хщ+т) и используя уравнения (4.8.26), ана-
логично теореме 4.8.4 получаем.
Теорема 4.8.5. Пусть векторный случайный дискретный процесс
[yfTXfT]T удовлетворяет уравнениям (4.8.23), (4.8.24), а оценка Xq/+r
наблюдаемого вектора Xi по наблюдениями Y^T ищется в классе оце-
нок, определяемых уравнением (4.8.27). Тогда оптимальные значения
коэффициентов 6[ и ц для ОИФЗ существуют и удовлетворяют урав-
нениям (4.8.26) с функциями
Ri = МС<Т = К<„ Ц = г{ = МХ{+1 = тХ1+1)
С? = С - Pi, Pl = MG, G = G(r(+i+r,X{|t+T). (4.8.28)
Для нахождения R[, Li,ri и pi достаточно знать распределение слу-
чайного вектора j при I > Iq и распределения величин
И, I > Iq, которые по предположению известны. Распределение на-
чального значения этого вектора находится из решения задачи условно
оптимальной прямой интерполяции.
4.8.6. Условно оптимальная обратная интерполяция.
Можно также строить рекуррентные алгоритмы оценивания по фик-
сированным наблюдениям, т.е. после завершения эксперимента. Приве-
дем уравнения условно оптимального обратного интерполятора
(УООИ). С этой целью обозначим через Хцм оценку вектора Xi по
наблюдениям Y^ и определим класс допустимых оценок следующим
разностным уравнением УООИ:
Хцк = 6/0(^+i|n) + 7/ (4.8.29)
с граничным условием Х^ — которое находится из решения за-
дачи дискретной условно оптимальной фильтрации.
Теорема 4.8.6. Пусть векторный случайный процесс [У^Х^]7^
удовлетворяет уравнениям (4.8.23), (4.8.24), а оценка Хц^ вектора
Xi по наблюдениям Y^ ищется в классе оценок, определяемых урав-
нением (4.8.29). Тогда оптимальные значения коэффициентов 6i и
yi для УООИ существуют и удовлетворяют уравнениям (4.8.26) при
О = й(Л+1Цу) для УОФ.
Для нахождения Ri, Li, ri и pi достаточно знать распределение слу-
чайного вектора ^XiTX^1|Nj в каждый момент времени I = 0,1,...
... ,Ni. При этом распределение граничного значения
4.8. ДИСКРЕТНАЯ ЭКСТРАПОЛЯЦИЯ И ИНТЕРПОЛЯЦИЯ
543
находится с использованием уравнений дискретной условно оптималь-
ной фильтрации.
4.8.7. Линеаризованные дискретные условно оптимальные
интерполяторы. Основываясь на линеаризованных уравнениях
Yt = biXi + &/о + buVh (4.8.30)
Х/4-1 = Q>iXi 4- (Liq 4- biVi (4.8.31)
и линейном уравнении (4.8.25)
XS|/4-1 = 0tiXS\i 4- ЙК/+1 + 7b (4.8.32)
и линейной теории фильтрации (раздел 2.3), придем к следующим ли-
неаризованным уравнениям УОПИ:
а«4х + = 41, a«4i + Ас22 = 4*; (4.8.33)
7/ = rs - &iP\ys - PiP2,i- (4.8.34)
Здесь введены обозначения
cii — ci2 = C2i = bi-^iaiKXi xsy1 (4.8.35)
с22 = bi+iaiKx^Tbf^ 4- Ь1Д4-11//+1Ь^/+1,
coi = ^Xs,xS|/> с02 = К^х^, (4.8.36)
П = MX/, rs = MXS, (4.8.37)
Pi,s = MXs|/,
P2,i = Ь/4-1П-ь1 + Ь/4-i,о = bi+i(airi 4- a/o) 4- &/4-i,o. (4.8.38)
Г iT
При этом 2п-мерный вектор Zi = X? X$\i , компоненты вектора ма-
тематического ожидания и ковариационной матрицы в силу линейной
теории определяются при I > S следующими уравнениями:
Z/4-i = AiZi 4- Аю 4- BijVi 4- B2,/V/4-i; (4.8.39)
= AiTnzt 4- Аю, (4.8.40)
^zt+1 = AiKztA[ 4- 4- B2,M4-i^2j (4.8.41)
544
ГЛ. 4. УСЛОВНО ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФП
с соответствующими начальными условиями. В (4.8.39)-(4.8.41) введе-
ны обозначения
(4.8.42)
. 0ibi+iai
. fiibi+ibi
В2,1 =
О
fiibi+i
Таким образом, имеем утверждение.
Теорема 4.8.7. Если в условиях теоремы 4.8.4 уравнения для
[У|ТХ|Т]Т} содержат аддитивные шумы, а нелинейные функции wi и
шц допускают эквивалентную линеаризацию, то УОПИ определяется
уравнениями (4.8.32) при условиях (4.8.33)-(4.8.42).
о Для УОИФЗ имеем уравнения (4.8.30), (4.8.31) для [YJTXIT]T и
следующее уравнение ОИФЗ:
X/+i|i+i+r — а/Хф+г 4- АУ/+1+г 4-7/, I > /о,
где оц, 0i и 7/ определяются согласно системе
а,с(0 4- в,с{1} - 4- вЛ1) -
а/сц -г Р/С12 — Cq! , СХ/С2! “Г Р/<-22 “ 4)2 >
7/ = Г/ - Q/P1,/ - 01Р2.1-
(4.8.43)
(4.8.44)
При этом имеем вспомогательные уравнения для Зп-мерного вектора
Z/+1 — AiZi 4- А/о 4- BijVi 4- В2,/У/+т 4- Вз,/У/+1+т>
где для li = I 4- т,
Ai = ai 0 . 0 : 0 : 0 an : 0 Pibh+ian : ai . , A/o = ai «/jo 7/ (4.8.45)
ви = bi 0 0 , В2,1 = 0 bh Pibii+ibih , Вз,1 — 0 0 (4.8.46)
4.8. ДИСКРЕТНАЯ ЭКСТРАПОЛЯЦИЯ И ИНТЕРПОЛЯЦИЯ
545
Отсюда вместе с соответствующими начальными условиями находим
mZl+x = AiTnzt + A/о; (4.8.47)
= AiKztA[ -I- 4- Вг./Р^В^ 4- B3ji//1+iB^z
(/i = I + r, I > /о). (4.8.48)
Далее введем обозначения
41 = МХф!, С|2 = 41 = ^14-Iah^xbxi|/+1,
с22 = + ^l.h+l^i^hh+l’
41 = ^хьх/М1> 4г —
Г[ = МХ/4-1 = а/МХ/ 4- а/о,
PU = МХфг, Р2.1 = 5/1+1П 4- &h+i,o. < (4.8.49)
Таким образом, имеем следующее утверждение.
Теорема 4.8.8. Если в условиях теоремы 4.8.5 уравнения для
]¥? Х?]Т содержат аддитивные шумы, а нелинейные функции щ и
tdn допускают эквивалентную линеаризацию, то УОИФЗ определяет-
ся уравнениями (4.8.43) при условиях (4.8.44)-(4.8.49).
Замечание. Рассмотренные три вида эллипсоидальных условно опти-
мальных интерполяторов требуют для своей реализации трех различных алгоритмов и
при этом каждый из этих интерполяторов должен проектироваться совместно с УОФ.
Как и в теории дискретной условно оптимальной фильтрации все сложные вычисления,
связанные с нахождением Ri, Li, ri, pi, 5i, 7ь основаны только на априорной инфор-
мации о модели уравнений (4.8.23)-(4.8.25), (4.8.27), (4.8.29) и не используют результатов
наблюдений. Поэтому они могут быть выполнены заранее в процессе проектирования
дискретного интерполятора с использованием программных средств для решения задач
статистического анализа случайных процессов, описываемых разностными уравнениями.
Кроме того, изложенная теория позволяет в процессе проектирования определять сред-
ний квадрат ошибки оценивания и, например, исходя из этого, выбирать подходящий
дискретный условно оптимальный интерполятор. Сам же процесс оценивания (прямой
интерполяции или интерполяции с фиксированной задержкой) может быть осуществлен
в реальном масштабе времени непосредственно в процессе проведения экспериментов.
18 Фильтры Калмана и Пугачева
546
ГЛ. 4. УСЛОВНО ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФП
4.9. Эллипсоидальные субоптимальные и условно
оптимальные фильтры
4.9.1. Эллипсоидальные субоптимальные фильтры, осно-
ванные на приближенном решении фильтрационных уравне-
ний
> Применим метод эллипсоидальной аппроксимации (МЭА), из-
ложенный в п. 1.8.4, для приближенного решения задачи оптимальной
нелинейной фильтрации. Для этого аппроксимируем апостериорную
плотность pt (х) формулой
и = (хт - Хт)С(х - X),
(4.9.1)
pt (ж) =р*(я;0) = wi(u)
1 +
i/=2
где С - матрица, обратная по отношению к ковариационной матрице
ошибки фильтрации R, С — Л”1.
На основании формулы (п.1.8.4) имеем
оо
ск = У fx(x\t)qK(u)dx = MqK(U) =
— ОО
= [qK((dT/idX - тпт)С(дт/idX - m)<Zi(A;Z)]A=0 . (4.9.2)
Чтобы найти стохастический дифференциал ск, применим формулу Ито
(1.4.82), учитывая, что ск представляет собой функцию трех случайных
процессов X(t), R(t), gtW, стохастические дифференциалы Ито кото-
рых определяются формулами (3.3.2), (3.3.3) и (2.2.13). В результа-
те получим уравнение (3.3.6), которое на основании равенства qK(a) =
= MqK(U) перепишем в виде
de. = к + ±
I дх> 3=1 °Kau
2 3^1 эхадхи 2,ДГ=1
+1 м
8,к,1=1
d2gK(U)
dX.dRki
4.9. ЭЛЛИПСОИДАЛЬНЫЕ ФИЛЬТРЫ
547
dgK(U)
9Хв
hs+^M
8,U=1
dgK(U)
dRau
"Леи
(dY - f^df).
(4.9.3)
Вычислим входящие сюда математические ожидания производных по-
линома qK(U). Имеем
М^^ = Мд;^- = М^(С/) (| =0. (4.9.4)
@Х3 дХ8 I j=1 j
Далее находим
п
/rfO -
дХ.ЯХ.
\ / п
= М 4д"(£/) - Xj) - Л) + 2я'к(и)сви ,
V=1 J V=1 J
(4.9.5)
оо
0
Мд"(С/)С(Х - Х)(ХТ - ХТ)С =
N _ °?
/ q^(u)py(u)un/2wi(u)du С,
о )
1/=2
(4.9.6)
где нормирующий множитель а определяется соотношением
ОО
а'1 = I
о
(4.9.7)
Вводя обозначения
ОО
Ско = - / gK(u)un/2wi(u)du, £KV =
п J
о
оо
= - [ q”(u)py(u)un^2wi(u)du (4.9.8)
п J
о
и заметив, что вследствие ортогональности pv(u} ко всем функциям их
при X < и' величина £КУ обращается в нуль при и > к - 1. В результате
получаем
(к—1 \
(4-9-9)
</=2 /
548
ГЛ. 4. УСЛОВНО ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФП
На основании (4.9.9) имеем
4Мд"(С7)
(к-1 \
СкО 4~ j cew. (4.9.10)
и—2 /
Математическое ожидание во втором слагаемом в (4.9.5) определяется
формулой
—оо
Г N
^(u)un/2-1wi(u) 1 + 52c^(u) du-
v—2
(4.9.11)
Вводя обозначения
Ско = “У^(u)un/2-1wi(u)du, £„ = ауg^(u)pr(u)un/2-1Wi(u)du
О о
(4.9.12)
и заметив, что вследствие ортогональности рУ(и) ко всем функциям их
при А < г/ величина QKy обращается в нуль при и > к - 1, получаем
Mq'AU) = Со + £ (4.9.13)
1/=2
На основании (4.9.10) и (4.9.13) формула (4.9.5) принимает вид
=2 (с*» + 52 с-> <4-914)
uXec/Au у у_2 у
где для краткости положено
Ско ~ 2£«о 4“ Ско> С**7 = 4” Ску
Вычисление производных dqK(U)ldR8U дает
= ~Cse I 7к0 + 52С"7»" ) > (4.9.15)
dR» \ ^2 )
4.9. ЭЛЛИПСОИДАЛЬНЫЕ ФИЛЬТРЫ
549
М
dgK(U)
9Rau
(К
7«о +
i/=2
(4.9.16)
з 0 и,
где 7ло, 7*2 , • • • , 7кк определяются формулами
оо
7«о = - / q'K(u)un/2wi(u)du,
п J
о
оо
7^ = - / g«(u)p!/(u)un/2wi(u)du.
n J
о
(4.9.17)
(4.9.18)
Дифференцируя эти формулы по компонентам вектора X и эле-
ментам матрицы R и имея в виду, что
dcij dcij
dRrr = ~CriCri' QRrs
(crjCej 4” CejCrj),
(4.9.19)
получаем
M 92qK(U) = = j п) (4.9.20)
дХкдЯаи
MdRaKBdRrr = (7к0 + §’ (4-921)
= Чс1аска ( 7*о + £ cv^KV ) , к / I, (4.9.22)
uH88uKkl у v_2 )
Мяв9”лв ~ = 2(c*»c/u+c«»c*«) I 7к0 + ^.Cv'Ikv J ,з±и,к±1. (4.9.23)
OK8UUiXkl У у=2 /
Подставив выражения (4.9.4), (4.9.19)-(4.9.23) в уравнение для сто-
хастического дифференцала величины с*, приведем его к виду
{/ К \
FK - I 7*о + 52^7^ 1 tr [ё(/(2) - hil>ii/^ihT)] +
\ i/=2 /
(к—1 \
Cd) + ^c„CKV j tr [Chipi^hT] +
i/=2 /
550
ГЛ. 4. УСЛОВНО ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФП
1 I v-
п I 7«о + /
\ V=2
п 'I
A»ukl1]su^l^TT){i pt+
8,U,k,l=l '
+ {HK
n
7«0 4" У Ci/Ykv
, v=2
п
У СзиЦзи ►
s,u,=l ,
(dY - fMdt)
(4.9.24)
(к = 2, ... , TV),
где
Assrr — Car' A-sskl — ^CksCts) & ф I,
A-sukl — ^(CksClu 4" Ci8Cku)i S U,k 2,
c8U - элементы матрицы С, определяемой формулой
(4.9.25)
\
7«о+52 м™ )с-
v=2 )
(4.9.26)
Формулы (3.2.8)-(3.2.12) для /, /(1), /(2), h и рг при аппроксимации
(4.9.1) апостериорной плотности принимают вид
/ = /(К,^, t) = У ¥>(K,a:,t)wi(u)
— ОО
N
1 + Yc^'P^'^
и=2
dx,
(4.9.27)
N
/14
^(Y,x,t)wi(u) l + 52<W>>/(u) dx, (4.9.28)
,7—9
ОО
i/=2 J
\т 4- <^(У,ж, t)(xT — .
— ОО
N
+{'ф1/'фт)(¥, x,t)] wi(u) 1 4- СуРу(и) dx,
I V=2
oo
h = h(Y,O,t) = | У [x^i(y,x,i)T + (ilwil>T)(Y,x,t)] x
—oo
—ОО
oo
(4.9.29)
XWi (u)
N
1+52^w
p=2
dx - Xf^T
(4.9.30)
4.9. ЭЛЛИПСОИДАЛЬНЫЕ ФИЛЬТРЫ
551
оо
pr = pT(Y,6,t) = I {(х — Х)(хт - XT)ar(Y,x,t)+
—оо
+(* - X)br(Y,x,t)T + br(Y,x, t)(xT - XT)}Wl(u)
N
1 +
i/=2
Формулы (3.3.7), (3.3.8) для FK и Нк преобразуются к виду
dx.
(4.9.31)
ОО
FK = FK(Y,0,t) = I q'K(u){2<p(Y,x,t)TC(x — Х)+
—ОО
+ tr [ Ca(Y, х, t) ]} wi (u)
N
1 + J2crPr(u)
i/=2
dx+
oo
—oo
N
— XT)Ca(Y,x,t)C(x — X)wi(u) 1 + ct/pt/(u) dx,
u=2
(4.9.32)
N
1 4- У^с^рДи) dx+
i/=2
oo
HK = HK(Y,e,t) = | У q>i(y,x,t)TqK(u)wi(u)
— OO
oo
+2 У q'K(u)(xT - XT)C(ilHsipT)(Y,x,t)wi(u)x
—OO
N
1 + y^cFpF(u)
i/=2
dx-fwTcK И^^Г) <
(4.9.33)
Таким образом, получен следующий результат.
Теорема 4.9.1. Пусть уравнения нормальной стохастической
дифференциальной системы (3.1.1) допускают применение МЭА. Тогда
фильтрационные уравнения эллипсоидального субоптимального филь-
тра (ЭСОФ) имеют вид (4.9.1), (3.3.2), (3.3.3), (4.9.24) при условиях
(4.9.27)-(4.9.33).
552
ГЛ. 4. УСЛОВНО ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФП
4.9.2. Модифицированные эллипсоидальные субоптималь-
ные фильтры, основанные на приближенном решении филь-
трационных уравнений для ненормированных апостериорных
распределений
о Рассмотрим сразу уравнения с винеровскими и пуассоновскими
шумами (2.1.7) и (2.1.8). Будем считать выполнеными условия теоре-
мы 2.7.3. Пусть w(u) — некоторая плотность вероятности п-мерного
случайного вектора, зависящая только от квадратической формы и =
= (хт — хт)С(х - я), например, нормальная плотность Х(ж,К), С =
= К~1 (п.1.8.4)), {рДи), qy(u}} — биортогональная система полиномов
с весом w(u), причем ру(и) = pn,v(u), q^u) = Qn>M(u). При нормаль-
ной плотности w(u) полиномы ру(и) и QM(u) определяются формулами
(п. 1.8.4). В этом случае МЭА апостериорной плотности pt(x) имеет вид
(1.8.96), а коэффициенты cv = сп>1/ определяются формулой (1.8.97) при
р = п.
Замечание. При данных векторе X и матрице С — К неизвестными па-
раметрами распределения в (1.8.96) являются только коэффициенты С\ , ... , C]\j. Для
приближенного решения уравнений оптимальной фильтрации аппроксимация (1.8.96) при
произвольно заданных X и К не годится, так как при такой аппроксимации апостериор-
ной плотности Pi (х) апостериорное математическое ожидание вектора состояния всегда
будет равно X и задача фильтрации решена не будет. Поэтому за вектор X в (1.8.96) не-
обходимо взять неизвестную оптимальную оценку X вектора состояния системы X. Что
касается матрицы К, то ее можно, конечно, принять равной неизвестной ковариационной
матрице ошибки фильтрации R (апостериорной ковариационной матрице вектора состо-
яния X). Уравнения субоптимального фильтра будут при этом сложными (вследствие
того, что X и R сами определяются стохастическими дифференциальными уравнениями)
и число их (порядок фильтра) всегда будет на N — 1 больше порядка фильтра метода
нормальной аппроксимации.
Аппроксимируем ненормированную апостериорную плотность ве-
роятности формулой
Pt(x) ^р'(и) = w(u)
N
p + ^cvpv(u)
l/=l
(4.9.34)
Здесь согласно (1.8.96) имеем
OO
C„= I q„(u)pt(x)dx = = [<7v(^)ftM3A(A)]A=0 , (4.9.35)
— OO
4.9. ЭЛЛИПСОИДАЛЬНЫЕ ФИЛЬТРЫ
553
причем
и = (хт - Хт)С(х - X); U = (Хт - ХТ)С(Х - X);
Ux = (dT/idX - X)C(d/idX - X). (4.9.36)
Для того чтобы составить стохастические дифференциальные
уравнения для коэффициентов надо согласно (1.4.83) найти стоха-
стический дифференциал Ито произведения дх(и)р*(А), имея в виду,
что и зависит от X = тп/рп что тп и д определяются стохастическими
дифференциальными уравнениями. Потом следует заменить перемен-
ные х и и операторами d/idX и С7д, выполнить диффренцирование и
после этого положить А = 0.
Уравнения для m и д с функцией £i, определяемой формулой
оо
фг = У Vi(Y,x,t)pt(x)dx
(4.9.37)
при аппроксимации (4.9.34) плотности pt(z) имеют вид
ОО
<pw(u) /1 + У2 dxdt+
-оо L
°? Г N 1
+ / (ai + ^i’)w(u) д + У^ cvpu(u) dxa^dY, (4.9.38)
-оо I-
°Г Г N
dp — I <pTw(u) p + cl/pt/(u) dx&2
-oo I- "=1 -I
1/=1
Г N
L v=l
N
i/=l
ldY, (4.9.39)
N
где w(u) определена согласно (1.8.91). Если обозначить для краткости
оо
/о - fo(Y,X,t) = у <p(Y,x,t)w(u)dx,
—ОО
оо
fv = Л(У, X,i) = у* Ч)(У\х> t)w(u)pv(u)dx,
—оо
(4.9.40)
(4.9.41)
554
ГЛ. 4. УСЛОВНО ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФП
ОО
ho ho(Y,X,t) = f [<7i (У, х, f) + x<pi(y,x, t)T] x
—oo x w{u)dxa2(Y,t)~1, oo (4.9.42)
h„ = hjAXiX't) = I [<71(У,x,t) + axpi(y,:r,f)T] x
— OO x w(u)dxa2(Y,t)~1, oo bo = bo(Y,X,t) = У Vi(y,x,t)Tw(u)dx02^X,t)~l, — CQ OO (4.9.43) (4.9.44)
b„ = by(X,X,t) = J cpi(Y, x,t)w(u)pl/(u)dxa2(Y,t) x, (4.9.45)
— oo
можем записать уравнения (4.9.38) и (4.9.39) в виде
dm = N f,f0(Y,X,t) + Y,c. 1 ,fv(Y,X,t) dt~\~
+ L i/— i N >Ло(^Д>*) + ]>> 7 1 ,hv(Y,X,t) dY, (4.9.46)
dp = — x N liboiYX^ + ^c, ,bv{Y,X,t) dY. (4.9.47)
Запишем коротко уравнения (4.9.46) и уравнение для ненормированной
характеристической функции (2.7.13) в виде
dm = fdt + hdY, dp = bdY, (4.9.48)
dgt = Adt + BdY. (4.9.49)
Здесь обозначено
N N N
f = pfo + 52 Cufu' h ~ + У2 cvhi,, b = pb0 + 52
i/=i p—i i/=i
4.9. ЭЛЛИПСОИДАЛЬНЫЕ ФИЛЬТРЫ
555
А = У |{АТ^(У,ж, t) - ^Ат(^Уо'ф,Т)(¥^х^>)Хх
—оо
х у [e‘ATV>"(»,M _ ! _ iXT^"(Y, X, t,v) ] vp(t,dv)eixTxpt(x)dx,
«?
OO
В = j x,t)T + гА^^Ро^'ГХ^я^)] x
—oo
хе^йСг^ММ'Г )-1(^, t)dY. (4.9.50)
Вычислим дифференциал Ито полинома qx(u), и = (хт — тпт/д)х
хС(х — т/р) по формуле (1.4.82). Имея в виду, что У определяется
уравнением (2.1.7) и что X = m/д, находим
<WU) = {q'x(u)(xT - Хт)С(х - Х)+
+ 2q"(u) tr [С(х - Х)(хт - XT)Cha2hT} /д2+
+ Q*(u)tr [СЛстгЛ7] /д2 — 4g"(u)XTC'(a: — Х)(хт — Хт)х
х Cha2bT/д2 — 2q'x(u)XTCha2bT/1?+
+ 2q'x(u)(xT - XT)Chff2bT/p2+
+ 2qx(u)XTC(x - x)(xT - XT)CXba2bT/i?-
— 2q'x(u)XTC(x — X)ba2bT /1? + qx(u)XTCXba2bT/i?}dt-
- 2q'x(u)(xT - XT)Cdm/p + 2q'x(u)XTC(x - X)dp/p. (4.9.51)
Далее найдем дифференциал Ито произведения qx(u)gt(X). По
формуле для дифференциала Ито произведения двух процессов
(1.4.83); имея в виду, что коэффициенты при dWo в уравнениях (4.9.47)
и (4.9.51) равны в силу уравнения (2.1.7) соответствующим (2.1.9) ко-
эффициентам при t/У, умноженным на матрицу ^1 и что V'lW'f — а2,
получаем
d[9x(u)^(A)] = 4x(u)d9tW + dqx(u)gt(X)+
+ 2q'x(u)(xT - XT)C(h + Xb)(T2BTdt/ii. (4.9.52)
Вычислим каждое из трех слагаемых по отдельности в (4.9.52), заме-
нив предварительно переменные х и и операторами d/idX и Ux соответ-
ственно.
556
ГЛ. 4. УСЛОВНО ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФП
Сначала находим первое слагаемое
[Qx(u)dpt(A)]A=0 = У |^(u)[2v?TC'(x-X)+
—ОО
+ tr (Cao) + 2<z"(u)(a;T - Хт)Са0С(х - Х)+
+ У [?х(«) - ?х(«) - 2^(и)(а:Т - *TW"] х
я?
ОО
xvp(t, dv)}p*t(u)dxdt + j {gx(u)<pf+
—оо
+q'x(u)(xT - X^Caijpj^dxa^dY, (4.9.53)
где <т0 = bi/QbT и
й = (ят + 'ф"Т - Хт)С(х - X). (4.9.54)
Для вычисления второго слагаемого в правой части (4.9.52) заме-
тим, что для любого полинома р(х) в силу (4.9.35) имеем
[р(Э/гЭА)^(А)]л==0 = У p{x)pt{x)dx.
— CQ
Пользуясь аппроксимацией (4.9.34) ненормированной плотности
Pt(x), получаем
[<^а)Й(А)]л=0 = J {[q'x(.u')(xT - Хт)С(х - Х)+
— ОО
+ 2q"(u) tr ^С(а: - Х)(хт - XT)Ch<T2hT] /р?+
+ q'x tr {Ch02hT)/i^ - 4qx(u)XTС(хт - Хт) х
х СЛа2&т//х2 - 2q'x(u)XTChff2bT/ц2 + 2q'x(u)(xT — Хт)х
х Ch02bT/iJ? + 2?"(u)XTC(x - Х)(хт - XT)CXba2bT/д2-
- 2q'x(u)XTC(x - Х)Ьа2Ьт/ц2 + q'x(u)XTCXba2bT/p.2]dt-
- 2q'x{u)(xT — XT)Cdm/ц+
+ 2q'x(u)XTC(x - X)dn/p\p*tdx. (4.9.55)
4.9. ЭЛЛИПСОИДАЛЬНЫЕ ФИЛЬТРЫ
557
Имея в виду, что р и матрицы С, Л, Ь, аг = ‘Фг^'ФТ, X от х не зависят
и (хт - Хт)С(х - X) = tr [С(а: - Х)(хт - Хт)] , приходим к выводу,
что при аппроксимации (4.9.34) функции pt(x) необходимо вычислить
четыре типа интегралов (напомним, что ро(^) = 1):
оо
h = У qx(u)(x — X)w(u)pv(u)dx, (4.9.56)
— ОО
оо
Ь, = У qfx(u)(x - Х)(хт - XT)w(u)pl/(u)dx, (4.9.57)
—оо
оо
/з = у* qx(u)(x - Х)(хт - XT}w(u)pv(u)dx^ (4.9.58)
—оо
оо
Ц = J qx(u)(x — X)w(u)pu(u)dx. (4.9.59)
—оо
Нетрудно проверкой убедиться, что Ii = 0, а
h = У q'x(u)(x - Х)(хт — XT)w(u)pv(u)dx =
— ОО
оо
= 2п/2+1Цп/2Т1) / <Wp^u)u^e-^du (4.9.60)
— ОО
(для нормальной плотности w(u)). Так же вычисляется интеграл
оо
11 = У qx(u)(x — Х)(хт - XT)w(u)py(u)dx =
—оо
оо
= / WP-Mu’^du. (4.9.01)
— ОО
Вследствие ортогональности степеней их полиному ру(и) с весом
U)(u\ — ----------1g u/2
ww - 2п/2Г(п/2)и e
(4.9.62)
558
ГЛ. 4. УСЛОВНО ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФП
при А < у интеграл в (4.9.60) равен нулю при всех и > х- Нормальному
распределению Х(0, К), К = С”1, п-мерного случайного вектора X
соответствует ^-распределение с п степенями свободы квадратичной
формы U = ХТСХ (ТСтС, приложение 2). По той же причине и в
силу биортонормальности полиномов pv(u), при и = х находим из
(4.9.61)
12 = Кх/п. (4.9.63)
Аналогично, интегрированием по частям убеждаемся в том, что инте-
грал в (4.9.60) равен нулю при всех у < х ~ 1> а ПРИ у = X ~ 1
13 = К/2п.
(4.9.64)
Точно так же убеждаемся в том, что интеграл в (4.9.60) равен нулю при
всех у > х “ 1 и ПРИ у == X ~ 1
К(х-Г)
2п(п + 2х ~ 2) ’
(4.9.65)
При у < х ~ 1 интегрированием по частям находим
У Qx7w)p4u)un/2c U^2du = - У ^х{и)р'и(и)ип^2е u/2du~
о о
оо оо
f q'x(u)pv(u)un^2~le~u^2du + [qx(u)pv(u)un^2e~uf2du —
2 J J
о о
= Jqx(u)p"(u)un/2e u/2du+^ J qx(u)p'v(u)un/2 ге u/2du-
О о
оо оо
qx{u)p'v(u)un/2e~u/2du - qx(u)pv(u)un/2~1e~u/2du+
О о
оо
+ | j qx(u)pv(u)un/2e~u/2du.
о
Первые три интеграла в последней части этих равенств равны нулю
вследствие ортогональности qx(u) степеням их при X < у — 1 < х — 2.
Последний интеграл тоже равен нулю при у < х - 1-
4.9. ЭЛЛИПСОИДАЛЬНЫЕ ФИЛЬТРЫ
559
Следовательно, при и < х — 1
h = = ~1П- <«“)
Отсюда при подстановке в (4.9.55) выражения (4.9.34) функции р£(и)
все выражения, содержащие интегралы 1% и Д, сократятся, кроме со-
ответствующих значению и = х ~~ 1- При у = х ~ 1 интеграл Ц равен
Ц = ~2"/2Г(п/2) /Wft-= —2(n + 2y —2)'
О
(4.9.67)
В результате формула (4.9.55) примет вид
[<*<7х(СШ(А)]а=0 = + *с*) tr<d*)+
I 71 х Z /
+^- (tr [Cha2hT] - 2XTCha2bT + XTCba2bT) /д2)<ft. (4.9.68)
Вычислим последнее слагаемое в (4.9.52) при х = З/гЗА, и = С7д,
А = 0. Учитывая, что от А в этом слагаемом зависит только
оо
В= У -F a1)etxTxpt(x)dxo21,
— оо
и выполнив дифференцирование, совершенно так же, как при выводе
формулы (4.9.53), получим при аппроксимации (4.9.34) функции pt(x)
следующие выражения:
[q'x(Ux)(dT/idX - XT)C{h + ХЬ)а2Вт]л_о =
ОО
I {q'x(u)(xT - XT)C(h + ХЬ)<рг +
—ОО
560
ГЛ. 4. УСЛОВНО ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФП
+2q"(u)tr [(h + Xb)alC(x - Х)(ХТ - ХТ)С^ +
+^(u)tr p/i + }pt(u)dxdt/p.. (4.9.69)
Подставив выражения (4.9.53), (4.9.68) и (4.9.69) в (4.9.52) при
х = д/idX, и = Ux и учитывая (4.9.2), заменив индекс р на х, при-
ходим к уравнению
оо
dcx = У {q'x(u)(2<pTC(x - X) + tr [Ссто ])+
—ОО
+2q"(u)(a;T - Хт)Са0С(х - Х)+
+ У [?х(й) -Qx(u) -2qx(u)(xT -ХТ)С^"] vP(t,dv)-
—q'x(u)(xT - XT)C(h + Xb)<pi/p+
+q'x(u)t,r [(h + /p + 2qx(u)x
xtr [(h + Xb)aTC(x-X)(xT-XT)C] /д}х
xp[(u)dxdt + |-^-(cx_i + 2^cx) tr [CK1 +
I £Tl u J
+^-(tr [Cha2hT] - 2XTCha2bT + XTCXba2bT)/p2\dt+
£Tl j
+ У + Qx(u)(xT ~ XT)Cai} p^ujdxa^dY. (4.9.70)
— oo
Примем в дополнение к обозначениям (4.9.44) и (4.9.54) следующие:
7х0 = 7xo(K,X,t) = j {q'x(u)(2<p(Y,x,t)TC(x - X) + tr [Ca0(Y,x,t)])+
— OO
+ 2q'^u)(xT - XT)Ca0(Y,x,t)C(x - X) +
4.9. ЭЛЛИПСОИДАЛЬНЫЕ ФИЛЬТРЫ
561
+ j [?x(u) _ 9x(w) “ 2g^(u)(a:T - XT}C$"(K,a:,<,v)] x
«o’
x vp(t,dv)}w(u)dx, (4.9.71)
7Xu = IxAY.XA) = I {q'x(u)(2<p(Y,x,t)TC(x - X) + tr [Ca0(Y, x, t) ])+
+ 2g"(u)(a:T - XT)Ca0(Y, x, t)C(x - X)+
+ У [?х(й) - gx(u) - 2qx(u)(xT - XT)Ci/>"(Y,x,t, v)] x
x i/p^t^dv^w^py^dx, (4.9.72)
oo
£xo = Exo(Y,X,t) = У (гл) <ti(У,x, t)T - tpi(Y,x,t)(xT - XT) j +
—OO
+ 2q^{u)(T\{Y^x,t)T C(x — X)(xT — XT)}w(u)dx, (4.9.73)
oo
£XF = exv(y,X,t) = У {g^.(u) ^CTi(y,x,t)T - <pi(y,x,t)(2:T - XT) j+
+ 2qx{u)<yi(Y,x,t)TC(x — X)(xT — XT)}w(u)pv(u)dx, (4.9.74)
t?xo = qxo(YX,t) = J {qx(u)<pi(Y,x,t)T + q'x(u)(xT - XT)x
x CaitYx^w^dx^Y,^-1, (4.9.75)
= qxAYX,t) = У {qx(u)<pi(Y,x,t)T + qx(u)(xT - XT)x
x C,cri(y,x,^)}w(u)pI/(u)d2TCT2(y,0_1- (4.9.76)
Тогда, имея в виду, что uTFv = tr [ FvuT ] для любой квадратной мат-
рицы F и векторов и, v, можем переписать уравнения (4.9.70) в виде
{N
4- У^с1/7Х1/(У,Х,р4-
i/=i
+ tr
{д(/ю(У, X, t) + Xbo(Y, X, t)} +
562
ГЛ. 4. УСЛОВНО ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФП
N
+ X, t) + Xb„(Y, X, t)) х
|/=1
+^(cx-i + 2Хсх)tr [(Ж] +
&TL L J
' г N
tr C(h0(Г, X, t) + cvhv(Y, X, t)/n
(N
h0(Y, X, t)T + 52 cvhv(Y, X, t)T/p.
l/=l ,
(N \
l/=l /
(N \
b0(Y, X, t)T + 52 c„b,,(Y, X, t)T/n j +
l/=l /
(N \
bo(Y, X, t) + 52 cvbv(Y, X, t)/n I x
l/=l /
(N \ 1
bo(Y,X,t) + ^2c^(^X,t)T/n \ >dt+
^=1 / J
{N 1
n4xo(Y,X, t) + 52с^х„(У,X,t) \dY (x = 1, • • • , N). (4.9.77)
l/=l J
Два уравнения (4.9.47), система уравнений (4.9.77) и соотношение
X = т/р при начальных условиях
m(to)=M[Xo|rob М = 1, cx(t0)=cx0 (х = 1,...,ДГ), (4.9.78)
где схо (х = 1, ... , N) - коэффициенты разложения (4.9.34) условной
плотности вероятности Pt0(x) — pq(x | Уо) вектора Xq относительно
Yq, определяют модифицированный эллипсоидальный субоптимальный
4.9. ЭЛЛИПСОИДАЛЬНЫЕ ФИЛЬТРЫ
563
фильтр (МЭСОФ). После решения уравнений (4.9.47) и (4.9.77) опти-
мальная оценка вектора состояния и ковариационная матрица ошибки
фильтрации в МЭСОФ определяются приближенными формулами:
X = т/р,-, (4.9.79)
—оо
N / \ / Т \
+ 52 ~ / (ж-—) \ Т ~ ~~ ) w(u)P«'(u)^a:- * (4.9.80)
1 д у \ д / \ м /
х -оо
Таким образом, доказано следующее утверждение.
Теорема 4.9.2. МЭСОФ в условиях теоремы 2.7.1 определяется
уравнениями (4.9.47) и (4.9.77). При этом с.к. оптимальная оценка
вектора состояния и ковариационная матрица ошибки фильтрации
МЭСОФ определяются согласно (4.9.79) и (4.9.80).
Из теоремы 4.9.2 вытекают частные результаты для нормальных
стохастических дифференциальных систем при ф” = 0.
Замечание. Порядок МЭСОФ особенно при большой размерности П
вектора состояния системы (2.1.8) значительно ниже порядка других субоптимальных
фильтров. Так, при учете в разложении (4.9.47) моментов до десятого порядка, N = 5 и
Tl + TV+l < П(п4-3)/2 уже при П > 3. ЭСОФ при П > 3, N = 5 дает фильтры более
низкого порядка, чем фильтр метода нормальной аппроксимации, обобщенный фильтр
Калмана—Бьюси, фильтры второго порядка и гауссовский фильтр.
4.9.3. Эллипсоидальные субоптимальные фильтры, осно-
ванные на МЭЛ
> В качестве субоптимальных методов второго класса (п.3.1.1) рас-
смотрим случай, когда выполнены условия теоремы 2.2.1 для уравнений
(2.1.7) и (2.1.8) при ф” = 0. Тогда после эллипсоидальной линеариза-
ции функций У, t) и (X, У, t) придем к следующим нелинейным
уравнениям для математических ожиданий
7hv = aft, (4.9.81)
тх = aft (4.9.82)
и линейным уравнениям для У0 = Y — ту и Х° = X — тх:
Y° = + «12, tX° + V’l.tV, (4.9.83)
X° = a^ltX° + a^tX° + V. (4.9.84)
564
ГЛ. 4. УСЛОВНО ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФП
Здесь ад ag t, ot^t, o^t* Qi2,t — коэффициенты МЭЛ, парамет-
рически зависящие от неизвестных первых и вторых моментов (тх, ту,
Кх, Ку, Кху), а также от известных структурных коэффициентов citX,
city, citXy, задающих эллипсоидальную структуру распределения.
Очевидно, что в силу линейности уравнений (4.9.83) и (4.9.84)
ЭСОФ согласно линейной теории фильтрации (раздел 2.3) будет опи-
сываться следующим линеаризованным уравнением для оценки Х° от-
носительно центрированных переменных:
к о л г . л 1
X = («Г1Л0 + ai2,tx°) + А [г° - №,tY° + а^Х0) ] • (4.9.85)
Здесь коэффициент усиления Д определяется уравнением
Pt = [Rt(af2\t)T + VWit] (V’u^V’u)-1, (4.9.86)
а матрица ошибок — матричным уравнением Риккати следующего ви-
да:
Rt = «П, tRt + («12,t)T +
- [-^(«n.t)7^ + ‘Ф^'Фи ] (V’lt^u)-1^!,*Rt + ’ФиУ'фТ) (4.9.87)
при соответствующих начальных условиях.
При использовании нецентрированных переменных X, X, Y урав-
нение линеаризованного ЭСОФ будет иметь вид
X = (an,t^ + + ao,t — а11^ту ~
+Pt [ Y - (а^У + а^Х + - a^tmy - a^tmx) ] . (4.9.88)
Входящие сюда /3t и Rt определяются уравнениями (4.9.86) и (4.9.87).
В качестве начальных условий для линеаризованного ЭСОФ следует
принять
X(t0) = хо = ммэл [ Хо I Го ]; (4.9.89)
R(t0) = Ro = Ммэл [ (Хо - ХО)(ХОТ - X?) | Yo ] . < (4.9.90)
Таким образом, имеем следующий результат.
Теорема 4.9.3. Пусть векторный случайный процесс [УТХТ]
определяется линеаризованными по МЭЛ уравнениями (4.9.81)-
(4.9.82). Тогда уравнения линеаризованного МЭСОФ имеют вид
4.9. ЭЛЛИПСОИДАЛЬНЫЕ ФИЛЬТРЫ
565
(4.9.85) (или (4.9.88)) при условиях (4.9.86), (4.9.87), (4.9.89),
(4.9.90).
Замечание 1. Вследствие нелинейности исходных уравнений уравнения
ЭСОФ параметрически связаны между собой и в отличие от линейной теории (раздел 2.3)
принципиально не могут быть проинтегрированы до получения результатов наблюдений.
Замечание 2. Полагая в линеаризованных уравнениях = 0,
__ (у ’
I = и, получим линеаризованные уравнения ЭСОФ в форме уравнений Калмана-
Бьюси (раздел 2.4).
ЗамечаниеЗ. В практических задачах обычно экстраполяция проводится
в рамках линейных или линеаризованных исходных стохастических дифференциальных
уравнений. Поэтому немедленно используются соответствующие результаты главы 2.
4.9.4. Эллипсоидальные условно оптимальные фильтры и
экстраполяторы. Рассмотрим задачу условно оптимального оценива-
ния, когда требуется в каждый момент t > to найти оптимальную оцен-
ку X(t) значения процесса X(t) в тот же момент t (задача фильтрации)
или его будущего значения X(t 4- Д), Д > 0 (задача экстраполяции) по
результатам наблюдения процесса Y(i) до момента t (т.е. в интервале
[^о,0) в классе допустимых оценок, определяемом формулой X = AU
и стохастическим дифференциальным уравнением вида
dU = [ а£(У, С7, t) 4- 7 ] dt 4- /?7?(У, С7, t)dY (4.9.91)
при заданных векторной и матричной структурных функциях £, т/ и
при всех возможных функциях времени а, /?, 7 (а и /? - матрицы,
7 - вектор). При этом А представляет собой (п х АГ)-матрицу N >
> п ранга п. За критерий оптимальности возьмем критерий минимума
средней квадратической ошибки оценки X(t) от оценки величины X(t)
или X(t 4- Д).
Как отмечалось в п.4.1.2, самым сложным вопросом в практиче-
ских применениях теории условно оптимальной фильтрации является
вопрос о выборе класса допустимых фильтров, определяемого задани-
ем структурных функций ( и г/ в уравнении (4.9.91). В принципе их
можно задать произвольно. При желании можно выбрать (иг/ так,
чтобы класс допустимых фильтров содержал произвольно заданный
условно оптимальный фильтр. В этом случае такой фильтр будет прак-
тически всегда точнее заданного субоптимального. С другой стороны,
выбрав в качестве компонент векторной функции £ и элементов мат-
ричной функции т/ конечный отрезок некоторого базиса в соответству-
ющем гильбертовом пространстве L2, можно получить приближение с
любой степенью точности к неизвестным оптимальным функциям £,
т/. По-видимому, это наиболее рациональный способ выбора функций
566
ГЛ. 4. УСЛОВНО ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФП
£, т/, основанный на уравнениях теории субоптимальной фильтрации
(пп.4.9.1-4.9.3). При этом новые возможности открывают уравнения
субоптимальной фильтрации, полученные из уравнения для ненорми-
рованной апостериорной характеристической функции (п.4.9.2).
Для применения уравнений ЭСОФ, полученных из ненормирован-
ных уравнений для апостериорного распределения, необходимо изме-
нить постановку задач условно оптимальной фильтрации так, чтобы
использовать уравнение для множителя д (п.4.9.2).
Определим класс допустимых модифицированных эллипсоидаль-
ных условно оптимальных фильтров (МЭУОФ) (4.9.91) уравнением
dp = pX(Y,U,t)dY (4.9.92)
и формулой
X = AU/p, (4.9.93)
где x(Y, X, t) - некоторая заданная матричная функция, р - матрица-
строка коэффициентов (зависящих от £), подлежащих оптимизации на-
ряду с коэффициентами а, /3, 7 в уравнении фильтра (4.9.91).
Основываясь на результатах п.4.9.2, рассмотрим подробнее четыре
класса допустимых МЭУОФ.
1-й класс. Важный класс допустимых МЭУОФ можно получить,
положив U = тп, А = 1пи определив функции £, т/, х в (4.9.91) и (4.9.92),
руководствуясь уравнениями (4.9.46) и (4.9.47). Это дает следующие
выражения для структурных функций:
(4.9.94)
т] = r](Y, U, t) = [ дЛо (К, U/р., t)T hi (У, U/ц, t)T...hN(Y, U/ц, t)T ]Т;
(4.9.95)
X = X(Y,U,t) = [f^(Y,U/iM,t)Tb1(Y,U/fi,t)T bN(YtU/ii,t)T]T.
(4.9.96)
При этом порядок МЭУОФ, определяемого уравнениями (4.9.91) и
(4.9.92) будет равен n + 1.
2-й класс. Для получения более широкого класса допустимых
МЭУОФ перепишем уравнения (4.9.77) в виде
4.9. ЭЛЛИПСОИДАЛЬНЫЕ ФИЛЬТРЫ
567
( N
dcx = j Fx0(Y, X, t) + 22 CvFx„(Y, X,t)+
l/=l
N N ч
+ 22 cac„FxA>/(K,X3) + cx_i 22 CACFF^Ar(y,X,i)l(ft+
A,i/=1 A,i/=1 '
' N 1
+ wxo(Y, x, t) + 22 X, t) J dY.
(4.9.97)
Здесь введены обозначения
Fx0(Y, X, t) = Д7хо(У, X, t) + ц tr [(Ло(Г,X, t)+
+Xb0(Y, X, t))Ex0(Y, X, t)]; (4.9.98)
Fx„(Y,X,t) = yx0(Y,X,t) + tr [(h„(Y,X,t)+
+Xbv(Y,X,t))ex0(Y,X,t) + (ho(Y,X,t) + Xbo(Y,X,t))Ex.,(Y,X,t)] +
+^<Jx_i,v{tr [bl/K + Ch0(Y,X,t)a2(Y,t)h0(Y,X,t)T^ -
-2XTCho(Y, X, t)a2(Y, t)bo(Y, X, t)T+
+XTCXb0(Y,X,t)a2(Y,t)b0(Y,X,t)T} + [ctf] ; (4.9.99)
FxX„ = tr [c(hx(Y,X,t) + Xbx(Y,X,t^exl/(Y,X,t)] /^+
+i<5x_1>A{ tr [с'/ю(УД,0<72(Г,<)Лг(У)Х,()т] -
-XTC(h0(Y,X, t)<T2(y, t)b„(Y, X, t)T+
+h„(Y, X, t)a2(Y, t)bo(Y,X, t)T+
+XTCXb0(Y, X, t)a2(Y, t)b„(Y, X,t)T}/^ (4.9.100)
^А„ = ^{tr [c(hx(Y,X,t) + a2(Y,t)hv(Y,X,t)T] -
-2XTChx(Y, X, t)ff2(Y, t)bv(Y, X, t)T+
+XTCXbx(Y, X, t)a2(Y, t)bv(Y, X, t)T}/fi2. (4.9.101)
568
ГЛ. 4. УСЛОВНО ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФП
Взяв за основу для построения класса допустимых МЭУОФ уравне-
ния (4.9.46), (4.9.47) и (4.9.97), мы должны будем принять за компонен-
ты вектора U все компоненты вектора тп и коэффициенты ci, ... , сдг,
так что U = [ттС1.. .сдг] . Порядок всех допустимых фильтров при
этом равен п 4- N 4-1.
3-й класс. Наиболее широкий класс допустимых фильтров, даю-
щий МЭУОФ максимальной доступной точности, можно получить, ес-
ли принять за функцию £ в (4.9.91) вектор, компонентами которого
служат все компоненты векторных функций су/Ху (х,у = 1,...
в (2.7.44), (2.7.45) и все слагаемые, входящие в состав скаляр-
ных функций Fxo, cvFXy, c\CyFx\y (х, А, и - 1, ... , N), cx-icxCyF^Xt/
(X — 1,А, v = 1, ... , N) в (4.9.97), а за функцию т] в (4.9.91) при-
нять матрицу, строками которой служат все строки матриц CyhXy
(х, у = 1, •. • , АГ) в (4.9.97) и все матрицы-строки, дт/хо, СуТ)Ху (х,и =
= 1,..., N) в (4.9.98). Что же касается функции х в уравнении (4.9.92)
то мы определим ее формулой (4.9.96), так же, как и в случае простей-
шего класса допустимых фильтров. Полученный таким путем класс
допустимых фильтров содержит ЭСОФ, определяемый уравнениями
(4.9.46), (4.9.47) и (4.9.98), и ЭУОФ будет, как правило, более точным,
чем этот ЭСОФ.
4-й класс. Заметим, что 3-й класс допустимых фильтров может
дать слишком сложный ЭУОФ из-за большой размерности структур-
ной векторной функции %. Поэтому может оказаться целесообразным
сузить этот класс, взяв его подкласс, в котором за компоненты век-
торной функции £ приняты все компоненты векторных функций
CyfXy (х,у = 1, • •• ) У) и все скалярные функции Fxq, cuFXy, cxcuFxXy
(X, А, у = 1, ... , АГ), Cx-iCACpF*^ (х ~ 1, А, у = 1, ... , N) без разбие-
ния их на отдельные слагаемые. Этот класс допустимых фильтров так-
же содержит ЭСОФ (4.9.46), (4.9.47), (4.9.98) и, следовательно, ЭУОФ
в нем будет, как правило, более точным, чем ЭСОФ (4.9.46), (4.9.47),
(4.9.98).
Таким образом, справедливо следующее утверждение.
Теорема 4.9.4. Пусть векторный случайный процесс [УТХТ]
удовлетворяет нелинейным стохастическим дифференциальным урав-
нениям (2.1.7), (2.1.8). Тогда МЭУОФ вида (4.9.91), (4.9.92) будет сов-
падать с МЭСОФ, если структурные функции фильтров выбрать со-
гласно одному из четырех описанных выше классов.
Для нахождения коэффициентов а, /?, 7 уравнения МЭУОФ
(4.9.91) необходимо знать совместное одномерное распределение слу-
чайных процессов X(t) и X(t). Это распределение находится путем
4.9. ЭЛЛИПСОИДАЛЬНЫЕ ФИЛЬТРЫ
569
решения задачи анализа системы, описываемой стохастическими диф-
ференциальными уравнениями (4.9.91) и (4.9.92).
Как всегда в теории условно оптимальной фильтрации, все
сложные вычисления, необходимые для нахождения оптимальных ко-
эффициентов уравнения МЭУОФ (4.9.91) или (4.9.92), основаны толь-
ко на априорных данных и поэтому могут быть выполнены заранее в
процессе проектирования МЭУОФ. При этом может быть определена и
точность фильтрации для каждого допустимого МЭУОФ. Сам же про-
цесс фильтрации сводится к решению дифференциального уравнения,
что дает возможность производить фильтрацию в реальном времени.
Замечание. Определение коэффициентов уравнения эллипсоидального
условно оптимального экстраполятора (ЭУОЭ) предусмативает знание совместного эл-
липсоидального двумерного распределения процессов X(t) и X(t). Аналогично разде-
лам 4.5 и 4.6 формулируются соответствующие предложения.
Предложенные алгоритмы синтеза ЭУОФ и ЭУОЭ, основаны на
структурной параметризации посредством МЭА и МЭЛ (п.2.5.4) апо-
стериорных распределений. В этом случае математические ожидания в
уравнениях предложений 4.2.1-4.2.5, 4.3.1-4.3.4, 4.4.1-4.4.4 и 4.5.1-4.5.4
следует вычислять для соответствующих одно- и двумерного эллипсо-
идальных распределений.
4.9.5. Дискретные эллипсоидальные условно оптимальные
фильтры и экстраполяторы. Задача построения дискретного эллип-
соидального условно оптимального фильтра (ЭУОФ) для непрерывной
системы, описываемой уравнениями, отличается от рассмотренной за-
дачи построения непрерывного фильтра (экстраполятора) только тем,
что процесс Y(t) наблюдается в дискретные (как правило, равноотсто-
ящие) моменты времени № (I = 0,1,2, = to). В этом случае
требуется найти оценку Xi значения процесса X(f) в каждый момент
№ (задача фильтрации) или его будущего значения X(t 4- Д), Д > 0,
(задача экстраполяции) по результатам наблюдений процесса Y(t), по-
лученным до момента №:
Уо' = : Yh = У(«(л)), h = . (4.9.102)
Класс допустимых фильтров в этом случае естественно задать раз-
ностным уравнением
l//+1=J/</(X/)l7/)+7/ (4.9.103)
и формулой
Х<+1 = AUl+1,
(4.9.104)
570
ГЛ. 4. УСЛОВНО ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФП
где Xi = Х(№), А, как и в случае непрерывной фильтрации, матрица
размера п х /V, N > п, ранга n, 6i и 7/ - соответственно матричные коэф-
фициенты и векторные свободные члены. Задача оптимизации филь-
тра в этом случае состоит в нахождении оптимальных <5/, 7/ в (4.9.103)
для каждого I по данным наблюдениям Yq = {У/ : I G {I : № <
и значениям 6i, yi при I < s. Для оптимизации можно пользоваться
теми же критериями, что и в случае непрерывного фильтра, положив
X = X = Xi+i в случае фильтрации и X = Xi+^+i в случае
экстраполяции.
В случае дискретной фильтрации определим класс допустимых
ЭУОФ уравнением (4.9.104), а также уравнением для д, полученным
заменой дифференциального уравнения (4.9.92) соответствующим раз-
ностным уравнением:
«-Н = щ + pixfXiM^Y, - ^-1) (4.9.105)
и той же формулой Xi = AUi/nh что и в случае непрерывной фильтра-
ции.
В случае дискретной фильтрации для определения класса допусти-
мых фильтров можно заменить дифференциальные уравнения фильтра
(4.9.91) и (4.9.97) соответствующими разностными уравнениями:
Uw = Ul + al^Yl,Uht^)h+
+Pn]{Yi,Ui,tW){Yi - Yi-i) + (4.9.106)
W+i = щ + - У-i), (4.9.107)
где h = — t№ (к = 0,1,2,...). В этом случае структурные вектор-
ные функции Q в (4.9.103) будут зависеть еще от У/-1 и определяются
как векторы, компонентами которых служат все компоненты векторов
Uh ^i(Yi — У/-1), а роль структурной матрицы 6i и вектора 7/ играют
[la'fhff]7' и yih соответственно.
Выбрав класс допустимых фильтров для непрерывной фильтра-
ции, определим соответствующие функции £, ту, х, после чего уравне-
ния (4.9.106), (4.9.107) определят соответствующий класс дискретных
допустимых фильтров.
4.10. ОЦЕНИВАНИЕ ПО БЕЙЕСОВОМУ КРИТЕРИЮ
571
4.10. Условно оптимальное оценивание по бейесовому
критерию
4.10.1. Постановка задачи. Рассмотрим векторный случайный
процесс [ XTYT ] , определяемый стохастическими дифференциальны-
ми уравнениями Ито вида (2.1.7) и (2.1.8):
dX = <p(Y, X, t)dt + ф'(У, X, t)dW0+
+1^,(Y,X,t,v)P°(<dt,dv),t > t0, X(t0) = Хо, (4.10.1)
dY = acpi (У, X, t)dt + (К, X, t)dW0+
+1 ^(Y, X, t, v)P°(dt, dv), Y (to) = Yo. (4.10.2)
Здесь X = X(t) - случайный процесс co значениями в Rn,X e
€ Яп; У = Y(t) - случайный процесс со значениями в Rni , Y е Rnt \
W = W(t),W е Rr - винеровский процесс с интенсивностью и = v(t)\
P^ti^A) - центрированная пуассоновская мера: А - некоторое бо-
релевское множество в Rq с выколотым началом координат; v G Rg
-вспомогательный параметр; <р = (p(Y,X,t), ф* = ф'(Х, X,t), =
= ip\(Y,X,t) и V’J = ^i(Y,X,t) - заданные функции, отображающие
ДП14-П4-1 в дп дпк рпх рпгк соотвегСТВеННО; ф" = ф" (Y, X,t,v), ф" =
= ф"(у,Х,^у) - заданные функции, отображающие Rn*+n+4+* в 7?п,
7?П1 соответственно; [ X?Yq ]Т - случайный вектор с известным распре-
делением. Винеровский процесс IV (t) и пуассоновский процесс P°(t, А)
для любого множества А предполагаются взаимно независимыми и не-
зависимыми от начального значения [Х^УОТ ] . Интегральные члены в
(4.10.1), (4.10.2) представляют собой функции У, X, t, v и характеризуют
скачкообразные изменения правых частей уравнений (4.10.1), (4.10.2).
Требуется по результатам наблюдений У/о = {У(т) : to < т < t}
найти наилучшую оценку X = X(t) процесса X(t) в классе допусти-
мых оценок, определяемых уравнением фильтра Пугачева
dX = a(t)C(y, X, t)dt + 0(t)ri(Y, X, t)dY + y(t)dt (4.10.3)
при заданных структурных функциях £(У, X, t) и rj = т/(У, X, t), отобра-
жающих Дп1+п+1 в Rq и R8ni соответственно. Неизвестные коэффици-
енты усиления фильтра (4.10.3) а = a(t), (3 = (3(t), у = y(t) представ-
ляют собой матрицы размерности nxg, пхзипх!.
572
ГЛ. 4. УСЛОВНО ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФП
По определению будем считать условно оптимальным такой фильтр
из класса допустимых (4.10.3), который минимизирует дифференциал
di по времени t бейесова критерия /,
di = min, I = ML(X(t), Х(*)) (4.10.4)
при достаточно гладких положительных функциях потерь L(X, X), L е
е c\Rn х яп).
4.10.2. Уравнения для оптимальных коэффициентов а,/7,7.
> Для нахождения неизвестных коэффициентов усиления а = a(t),
/7 = /7(£), 7 = 7(f) фильтра (4.10.3) выпишем выражение для диффе-
ренциала di, используя обобщенную формулу Ито (1.4.86). Имеем
di = М 4- 4- ртщп) + ; ^12 + ^хх • 0п +
А
1 г
+ 2Lxx ' а22
dt+ I [L(X + ф", X + - ЦХ, X)-
«3
- £?(/3^")]мЯ^,</и),
(4.10.5)
где
<7ц = ф'иф, (Т12 = ф'и(0Т]ф'1)Т,
<Т22 = (0Г)ф{)и(Рт1ф{)Т,
ti
Др((й,<2],-4) = MP((ti,t2],Л) = Уvp(s,A)ds, AcR4,
h
Тт -
Lxx —
~ dL
dXi ’
dL2
dXidXj
Тт -
’ Lx ~
d2L
dXidXj
dL
dXi
> LXX -
pl '
’ dXn J ’
d2L
fzz : D = [ tr (fij,zzD) ], f = [ fi}J , fij,zz -
dXidXj J ’
д2/ц 1
. dXkdX, J ’
7? = [l?y] (i,j,k,s = l, ... ,n), (4.10.6)
dL '
’ dxn_
, Ъхх =
vp(t,dv) - интенсивность пуассоновского процесса P([0,t),A).
В (4.10.5), (4.10.6) производные Lx,L^,Lxx,L^^, вычисляются в точ-
ке (X(t),X(t)); функции <р,вычисляются в точке (T(t),X(t),^;
4.10. ОЦЕНИВАНИЕ ПО БЕЙЕСОВОМУ КРИТЕРИЮ
573
'Фг ~ вычисляются в точке (Y(t), X(£), и), а £, ту вычисляются в точ-
ке (Y(t),X(t),t).
Из (4.10.5) видно, что выражение для дифференциала di содержит
линейные и квадратичные по /? слагаемые в ai2, &22, а также линейные
по а слагаемые. Поэтому, предполагая, что положительно опреде-
ленная матрица для всех Х,Х, коэффициент [3 определим из условия
минимума di по (3:
г дцх + г,х + ^)
J др
Я’ L
— L^i/)”TTiT fjLp(dt,dv) t= 0,
(4.10.7)
где
d^x + y/z,x + /M") = Г дь(х + ф",х + 0т№)
д/З dPij
- матрица размерности п х з (г = 1, ... , n, j = 1, ... , ni).
Определить коэффициенты а из условия минимума дифференциа-
ла в di по а (аналогично тому, как это сделано для /3) нельзя, так как
этот минимум не существует для а Е Rnq. Здесь будет рассмотрен слу-
чай, когда а лежит в некотором компакте. Так же будет показано, что
при некоторых типах ограничений на а величина будет рав-
номерно стремиться к нулю для любого конечного интервала времени.
Поэтому коэффициент а в (4.10.3) будем определять из условия
М(£^т) = 0,
(4.10.8)
которое должно выполняться в каждый момент времени t. Для этого
необходимо и достаточно, чтобы условие (4.10.8) выполнялось в началь-
ный момент времени to и производная M(L^CT) по t в каждый момент
времени тождественно равнялась нулю. В результате после дифферен-
цирования (4.10.8) по обобщенной формуле Ито (1.4.86) для коэффици-
ента а получаем следующее уравнение:
M(L^etT) + + М +
+М[Ь*(а£ + ^1)т^] +М(Ьх^г) + |м[(Ь^Т)*» : ст] +
574
ГЛ. 4. УСЛОВНО ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФП
«0
- Lx(p^)T^]Vp(t,dv) = 0, (4.10.9)
U= [ХТГТХТ]Т, a = BvBT, В = [v>'T^T(/Ml)T] •
Для простоты записи в (4.10.9) использованы такие же сокращен-
ные обозначения для функций и производных, как и в (4.10.8) (4.10.6).
При отсутствии скачкообразных компонент в уравнениях (4.10.1),
(4.10.2), т.е. когда ф" = ф" = 0, уравнения (4.10.7), (4.10.9) для коэф-
фициентов а и /3 упрощаются. А именно
м [bjfViV’ + (.Lxx^' + = 0 (4.10.10)
M(L^etT) + м(ь*х&т) + м +^w)eT] +
+М[^(ае + ^1)те5] +М(^^т) + ^М[(^ет)^ : а] =0.
(4.10.11)
Коэффициент 7 в (4.10.3) может быть определен из условия несме-
щенности оценки MX(t) = MX(t) в каждый момент времени, т.е.
7 = - аМ£ - /3M(Wi). (4.10.12)
Коэффициенты a, /3, у, определяемые уравнениями (4.10.7),
(4.10.9)—(4.10.12), называются коэффициентами условно оптимального
фильтра по бейесовому критерию. <
Таким образом, имеем следующий результат.
Теорема 4.10.1. Пусть векторный случайный процесс [ХТУТ]
удовлетворяет стохастическим дифференциальным уравнениям
(4.10.1), (4.10.2). Тогда значения матричных коэффициентов усиления
а, (3, у условно оптимального фильтра (4.10.3) по бейесовому крите-
рию (4.10.4) определяются уравнениями (4.10.7), (4.10.9) и (4.10.12).
Замечание. Из (4.10.7), (4.10.9), (4.Ю.12), как частный случай для
критерия минимума средней квадратической ошибки, Z/(A\ JV) — (X — Х)^* (X — X),
получаются уравнения условно оптимального фильтра Пугачева (раздел 4.2).
4.10. ОЦЕНИВАНИЕ ПО БЕЙЕСОВОМУ КРИТЕРИЮ
575
4.10.3. Уравнение для оптимального коэффициента а при
ограничениях
> Пусть теперь матричный коэффициент а лежит в некотором ком-
пакте
aeQcRnq, а = [а<;] (i = 1, ... , n, j = 1, ... , q), (4.10.13)
Его будем по-прежнему определять из условия минимума дифферен-
циала di в каждый момент времени t. В этом случае коэффициент а
определяется из условия
а = argminM(L^a^). (4.10.14)
aeQ
Коэффициенты (3 и 7 определяются по-прежнему уравнениями (4.10.7),
(4.10.10). <1
Таким образом, приходим к следующему результату.
Теорема 4.10.2. Пусть векторный случайный процесс [ XTYТ ]
удовлетворяет стохастическим дифференциальным уравнениям
(4.10.1), (4.10.2). Оценка X описывается уравнением (4.10.3) с огра-
ничением (4.10.13) условно оптимального фильтра (4.10.3). Тогда зна-
чения матрицы их коэффициентов усиления а, (3, у по бейесовому кри-
терию (4.10.4) определяются уравнениями (4.10.7), (4.10.12), (4.10.14).
о В частности, если коэффициенты усиления а^, а = [а$у ] ограни-
чены по модулю,
|«0| <а™, а™ > 0 (г = 1, ... , n; j = 1, ... , д), (4.10.15)
т.е. компакт Q представляет собой параллелепипед, то решением зада-
чи (4.10.14) будет
а = -nsignM(L^^T), ajj = [а™] . <з (4.10.16)
Замечание!. Рассмотрим предельный переход, когда N = ШШ а?? ~>
ij J
—> ОО. Из (4.10.5), (4.10.6) получаем
di - A*dt + (4.10.17)
V
где
576
ГЛ. 4. УСЛОВНО ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФП
А —А (£)— М
1Г 1г \
: ^12 + -Ьхх : Яп + т^хх : а22) +
л» L )
+М J [l(X + X + ^') - ЦХ,X) - LTX^' - ] vP(t,dv),
Lx, = ^~, «=[« •«,1Т.
(/Al
В силу (4.10.16) и (4.10.17) следует, что
^<л‘(«)-лг$2|м(^1е>)|
ij
для любого t и
t t
о < I(t) < /(to) + у Л*(т) - N^f |м(^хЛ>)| dr.
to to
Отсюда
I(t0) + I A*(r)dr
to
t
> L / dr
to
и если при N —> сю,
t t
jj / A*(f)dr-+0, to J |M(L^)| dr->0.
to to
Последнее, при дополнительном условии непрерывности М(£/^£у) для любых Z, j озна-
чает, что lim =0 на интервале (to, t), если M(ij^ £j) =0 при t = to-
N—>oo 1 1
Рассмотренный предельный переход проясняет смысл условия (4.10.8): коэффици-
ент Q, определяемый (4.10.8), удерживает значение вблизи нуля при доста-
точно больших диапазонах изменения Ot. В связи с этим можно рекомендовать подбирать
оптимальную структуру фильтра, исходя из формул (4.10.16), (4.10.7) и (4.10.10), так как
расчет коэффициента Ot существенно проще осуществить по формуле (4.10.16), чем по
4.10. ОЦЕНИВАНИЕ ПО БЕЙЕСОВОМУ КРИТЕРИЮ
577
формуле (4.10.9). Однако отобранный таким образом фильтр будет обладать недостат-
ком - коэффициент усиления Q будет часто менять знак. Поэтому в заключение для
отобранного фильтра коэффициент усиления Q следует пересчитать по формуле (4.10.9).
При этом следует убедиться в том, что зависимость критерия I(t) почти не изменится.
Замечание 2. Уравнение (4.10.8) имеет простой геометрический смысл.
Рассмотрим сужение функций L и £ на пространстве Rn оценок X. В любой точке
X этого пространства вектор £ должен быть ортогонален (в смысле скалярного произ-
ведения, задаваемого оператором математического ожидания) вектору нормали к
поверхности уровня функции i, проходящей через эту точку X, т.е. вектор £ должен
касаться поверхностей уровня функции L.
4.10.4. Определение моментов вектора . Зада-
ча определения коэффициентов а = a(t)f/3 = /?(£), 7 = y(t) сводится
к нахождению математических ожиданий составного случайного век-
тора X = j , определяемого уравнениями (4.10.1)—(4.10.3).
Для этого необходимо знание одномерного распределения (одномерной
плотности вероятности fi(x, у, X; t) или одномерной характеристиче-
ской функции <71 (А,д,p\t) случайного вектора X. В частности, при
<фп = ^'' = 0 одномерная плотность X; t) описывается уравнени-
ем Фоккера-Планка-Колмогорова (ФПК) с коэффициентами а, 0 и 7,
удовлетворяющими уравнениям (4.10.10)—(4.10.12). Отметим, что усло-
вия существования оптимальных коэффициентов а, f3 и 7 совпадают
с условиям существования и единственности решения уравнения для
одномерной плотности вероятности составного случайного вектора X,
описываемого уравнениями (4.10.1)-(4.10.3), в которые вместо а, (3 и 7
подставлены их выражения из (4.10.7), (4.10.9), (4.10.12). Полученное
таким образом уравнение для одномерной плотности будет уже инте-
гродифференциал ьным. Заметим, что если условия существования и
единственности решения уравнения для одномерной плотности процес-
са, описываемого уравнениями (4.10.1)—(4.10.3), выполнены для доста-
точно гладких функций времени а, /3, 7, £ G [ОТ], то тогда и оптималь-
ные коэффициенты а, (3 и 7 также существуют и единственны.
4.10.5. Уравнения фильтра Калмана-Быоси по бейесовому
критерию
> Получим уравнения фильтра Калмана по бейесовому критерию
для линейных уравнений (4.10.1)—(4.10.3):
dX = aXdt + 'il>'dWl, dY = axXdt + ^[dW2, dX = aXdt + pdY + 7,
(4.10.18)
где a = a(t), b = b(t), ai = ai(t), bi = bi(t) - известные матрицы;
19 Фильтры Калмана и Пугачева
578
ГЛ. 4. УСЛОВНО ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФП
W = [Wr1TWr7’]T, Wi = JVi(£) и W2 = W2(t) - независимые винеровские
процессы с матрицами интенсивности 1/1, 1/2 соответственно; [Х^УОТ ]Т
- нормально распределенный случайный вектор. В этом случае соглас-
но теореме 4.10.1 оптимальные коэффициенты а, {} и 7 определяются
уравнениями
M(L^x.aXXT) + Щ1^яаХХт) + Щ1^^0а1ХХт)+
+M(LxXT)a?/3 + |м [(LxXT)vv : a] = 0,
7 = (a - fan )MX - aMX, (4.10.19)
где
M[(L*XT)W : <r] =[/0 ], U = [XTXT]T, a = diag [<Ti<T2],
fij = trM <ti 4-trM <72,
<7i = bvibT, <72 = b^vibf. (4.10.20)
В силу линейности уравнений (4.10.18) все математические ожидания
в (4.10.19) и (4.10.20) полностью определяются нормальным законом
распределения случайного вектора U = [хтХт| . Компоненты его
математического ожидания тп = Mt7 и ковариационной матрицы
К = M(t/ — m)(U — m)T, = MX, m2 = MX,
Kn =M(X-mi)XT, Хп =M(X-mi)XT, K22 = M(X - m2)XT,
m =
7П1
ТП2
Kn K12
K?2 K22
(4.10.21)
находятся путем решения следующей системы линейных обыкновенных
дифференциальных уравнений с соответствующими начальными усло-
виями:
mi — ami, m2 = am2 + 0aimi, Кц = аК^ 4- К\\ат 4- ai,
К12 = О>К\2 + Kud?рт 4- Q^X12,
X22 = ctX22 + X22Q^ + /3a>iKi2 4- 0? 4- 0(Т20^• (4.10.22)
4.10. ОЦЕНИВАНИЕ ПО БЕЙЕСОВОМУ КРИТЕРИЮ
579
При наличии ограничений (4.10.13) согласно теореме 4.10.2 опти-
мальное значение коэффициента усиления а определяется формулой
а = —ат sign M(L^XT), ат = [а£]. < (4.10.23)
Таким образом, доказано следующее утверждение.
Теорема 4.10.3. Пусть векторный случайный процесс [УТХТ]
удовлетворяет линейным стохастическим дифференциальным урав-
нениям (4.10.18), тогда уравнения фильтра Калмана-Бьюси по бейе-
совому критерию (4.10.4) определяются (4.10.19)-(4.10.23).
4.10.6. Условно оптимальные фильтры по сложным стати-
стическим критериям. Рассмотрим векторный случайный процесс
[ XTYT ] , определяемый стохастическими дифференциальными урав-
нениями (4.10.1) и (4.10.2). В соответствии с принципом условно оп-
тимальной фильтрации будем считать, что наилучшей оценкой X(t)
процесса X(t) является такая оценка, которая при каждом данном t
минимизирует в бесконечно близкий момент t' > t, t' —> t заданный
функционал от вектора математического ожидания = MX и мат-
рицы вторых моментов ошибки фильтрации = М(ХХТ):
7 = /(т*,Гх) =min, X = X(t) = X(t) - X(t). (4.10.24)
Следуя (Андреев: 1980), критерий (4.10.24) будем называть сложным
статистическим критерием. Примерами таких критериев могут слу-
жить:
• критерий минимума среднеквадратической ошибки
h = tiT* = trM(XXT) = min;
• критерий максимума отношения сигнал/шум
/2 = m^(trr^)”1/2 = max;
• критерий максимума вероятности невыхода ошибки из заданных
допусков П
I3 = р {х С п} = / f(X)dX = max,
П
где /(X) - нормальная плотность распределения ошибки, /(X) =
= ЛГ(т^,г*).
580
ГЛ. 4. УСЛОВНО ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФП
Требуется по результатам наблюдений У/о = {У(г) : to < т < £}
найти наилучшую оценку X (t) процесса X (t) в классе допустимых оце-
нок, определяемых следующим уравнением фильтра:
dX = a(t)£(Y, X, t)dt + /3(t)rj(Y, X, f)dY (4.10.25)
при заданных функциях £ = £(У,Х,£) и т/ = ?/(y,X,t), отображающих
ДП1+п+1 в дг и двщ соответственно. Здесь а = a(f) € MnXr и /3 =
= /3(t) € МпХ8 - матрицы коэффициентов, подлежащие определению;
МпХГ - пространство вещественнозначных матриц размерности п х г.
Добавив к вектору £ еще одну координату, равную 1, т.е. положив
= [Ст1]т и введя матрицы а' = [017], получим следующий условно
оптимальный фильтр (4.10.25) со сдвигом:
dX = а(*)£(У, X, t)dt + 0(*)т?(У, X, t)dY + 7(t)dt (4.10.26)
c> Определение оптимальных коэффициентов a(£), f3(t) в (4.10.25)
осуществляется в два этапа. Первый этап решения задачи состоит в
определении коэффициентов aet\ = a(0,A, t) и /Зод = f3(0,X,f), обеспе-
чивающих минимум приведенного критерия:
1в,х = Pm* + tr (АГ*), (4.10.27)
где 0, А - вектор и матрица (симметричная, положительно определен-
ная), элементами которых являются произвольные множества 0i и А^
(i,j = 1, ... , п) соответственно, 0 Е Ад С /?п, A G A# С RN, N =
= n(n + 1)/2. А на втором этапе, выбрав конкретный вид критерия
(4.10.24) и подставив в него значения а^д, ^,д, определяются опти-
мальные значения 0о, Ао, соответствующие минимуму принятого кри-
терия (4.10.24). В результате, следуя п.4.2.1, придем к следующему
утверждению.
Теорема 4.10.4. Если векторный случайный процесс [ХТУТ]Т оп-
ределяется стохастическими дифференциальными уравнениями
(4.10.1), (4.10.2), тогда значения коэффициентов а = a(t) и /3 = /3(t)
условно оптимального фильтра (4.10.25) находятся из решения задачи
^(0 — /^(0 —
(0о, Ао) = argmin/ (т»(аМ11Зу),Г^(ав,х,(в>|х)),
(в,л)ел
Л = х Лд,
(4.10.28)
4.10. ОЦЕНИВАНИЕ ПО БЕЙЕСОВОМУ КРИТЕРИЮ
581
где функции aetx^Pe,x удовлетворяют следующим уравнениям:
А/?0,А«22 = «02,
(4.10.29)
<ЧА«11 + М (х - X + Ь) = «01 - &,А*21, (4.10.30)
V / оХ
при этом коэффициенты в (4.10.29) определяются по формулам
«02 = АМ(АГ — X)tp[riT + AM(V»' уф'^г)7) — |0M(<pfr/T),
(4.10.31)
«11 = М(е - Ш1)£Т, «22 = М(г)ф'11/ф'1ТГ]Т),
«21 = M(w>i - т2)ст, «01 = М(у> - m0)CT,
41 = |6О1+М(Х-Х)^+м((х-.¥-10) X
or IV 2 j
(4.10.32)
(4.10.33)
+ - ^,А^1^[Т| х
+|м| (х-х-^е
— 4- 2пТ/?Т —
dY +2л Рв'хдх) дУ,
х
«3
1
2
+ tr
ОЛ оХ .
Л’
-&,A»^i) [^Y + ^,X + pe,XT]^,t)T-С] up(t,v)dv, (4.10.34)
где тпо = М^, т\ = М£, m2 = и = u(t) - интенсивность винеров-
ского процесса; up([tQyt),D) - интенсивность пуассоновского процесса
Р([Ьо,1),П). Аргументы у функций в (4.10.29)-(4.10.34) опущены.
Для вычисления математических ожиданий в (4.10.29)-(4.10.34) до-
статочно знать характеристическую функцию pi = pi (Л, д, p; t) процес-
Т
са [хтгтхт1 , которая, согласно п.4.2.1, определяется уравнением
582
ГЛ. 4. УСЛОВНО ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФП
о
—= М{гАт<р + ifiT<pi + ipT(ae<>£ + 0e,xTWi)+
+х(А, fi, р', X, Y, X, t)} exp (iXTX + ipTY + ipTX^ , (4.10.35)
Х(А,м,р;Х,У,Х,0 =-|C1K1T + У [exp(iC2) - 1 - i&]vp(t,dv),
(4.10.36)
G = ф,тХ+ф[тp+ip'j7'T)T0lAp, G = XT^"+p.T^i+pT0etXTpl>" (4.10.37)
с соответствующим начальным условием
дю = Мехр (гАтХ0 + ifiTY0 + ipTX0 j
для Y = Yq,X = Xq,X = Xq при t = to-
4.10.7. Фильтр Калмана-Бьюси по сложному статистиче-
скому критерию
t> Из теоремы 4.10.24 получается фильтр Калмана-Бьюси по слож-
ному статистическому критерию, когда уравнения (4.10.1)-(4.10.3) ли-
нейные
dX = A(t)X(t)dt 4- B(t)dW. dY = A^Xtydt 4- B^dW, (4.10.38)
dX = a(t)Xdt 4- P(t)dY. < (4.10.39)
Теорема 4.10.5. Если векторный случайный процесс [ХТУТ]Т
определяется линейными стохастическими дифференциальными урав-
нениями (4.10.38), то оптимальные значения коэффициентов a(t),
/3(t) фильтра (4.10.39) находятся из решения задачи (4.10.38) с функ-
циями сцд и /3ot\, удовлетворяющими следующим уравнениям:
ae,x= (A- 0e,xAi)KXx + ^(Х 1 - А^/3^
£
(4.10.40)
К^
где
00,х =
— ^Огп^х 4- Кх\ А? 4- ВиВ?
Кх = Кх — КХх — гПхТПх, тх ~тх ~ тх'
(4.10.41)
(4.10.42)
(BivBT)-1,
4.10. ОЦЕНИВАНИЕ ПО БЕЙЕСОВОМУ КРИТЕРИЮ
583
При этом математическое ожидание тх и ковариации Кх,
КХх, Кх векторов X и X удовлетворяют линейным дифференциаль-
ным уравнениям:
dm Л dm v л ,
— = Атх, —rf- = ав>хт% + Pe,\Aimx, (4.10.43)
ai di
^ = АКх+КхАТ + ВиВТ,
dt
= АКХХ + + аИ,\КХХ + ВуВ1&0,Х>
UL
= Ро,х^\КХх + + ао,хКх + Кха?,х + Po>xBivB\ Ро,х-
(4.10.44)
Полагая в (4.10.41)-(4.10.44) 0 = 0, А = 1, получаем фильтр Кал-
мана-Бьюси.
4.10.8. Дискретные условно оптимальные фильтры по бей-
есовому и сложному статистическому критериям. Уравнения
дискретных условно оптимальных фильтров, соответствующих непре-
рывным фильтрам (теоремы 4.10.1 и 4.10.3), получаются предельным
переходом. Уравнения теоремы 4.10.2 требуют дополнительного иссле-
дования в дискретном случае.
Остановимся сначала на дискретном условно оптимальном филь-
тре по сложному статистическому критерию. Пусть дискретный про-
цесс [XZTY^T]T удовлетворяет следующим стохастическим разностным
уравнениям:
= ^1/(*ь Ш = 0,1,2,...). (4.10.45)
Здесь Xi G Rn - случайный процесс (вектор состояния) в дискретный
момент времени I = 0,1,2...; Yi 6 Rni - случайный процесс; {V/} -
последовательность независимых r-мерных случайных векторов с не-
известным распределением; {иц}, {cuiz} - последовательности заданных
функций, отображающих Яп+г в Яп, Rni соответственно. Требуется
по результатам наблюдений Yq = {Уо,У1, ... , У/} найти наилучшую
оценку Xi+i процесса Xj+i в классе допустимых оценок, определяемых
разностными уравнениями
Xl+1 = 6iCi(XhYi), / = 0,1,...,
(4.10.46)
584
ГЛ. 4. УСЛОВНО ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФП
где Q = Q(X,y) - заданная функция, отображающая Rn+k в R8; 6i 6
€ Afnxs - неизвестная матрица коэффициентов условно оптимального
фильтра (4.10.46), подлежащая определению.
Аналогично уравнению фильтра (4.10.46), добавив к вектору Q еще
одну координату, равную 1, т.е., положив £/ = [^Т1Т]Т и введя матрицу
= [<5/7/], получим условно оптимальный фильтр (4.10.46) со сдвигом
7Г
Хж=(5/0(Х/,У/)+7ь / = 0,1,.... (4.10.47)
В качестве критерия оптимальности оценки X/+i принимается сле-
дующий сложный статистический критерий:
Л+1 = 7 = min, X/+i = X/+i - X/+i. (4.10.48)
Определение оптимальных коэффициентов <5/ в (4.10.48) осуществ-
ляется в два этапа. Первый этап состоит в определении функций
й(0,А), обеспечивающих минимум приведенного критерия:
^.А = + tr (АГ*-+1) = min’ (410-49)
(0,А)€Л, Л = A# х Ад, W = n(n + l)/2,
где в G A# С Rn и Л 6 Ад С RN - неопределенные множители. Далее
определяются оптимальные значения 0о,Ао, соответствующие миниму-
му сложного статистического критерия (4.10.48).
Таким образом, приходим к утверждению.
Теорема 4.10.6. Если дискретный случайный процесс [ХТУТ]
определяется уравнениями (4.10.45), то значения коэффициентов ус-
ловно оптимального фильтра (4.10.47) по критерию (4.10.48) находят-
ся из решения задачи
6i = (5/(0о, Ао), (0о, Ао) = argminl (^ (<5/(0, А)) , Г* (<S/(0,A)),
(0,х)ел 4 1+1 7 +
(4.10.50)
в которой функции 6i(0,X) удовлетворяют следующим уравнениям:
б1(в,Х)К1 = Ь1, (4.10.51)
где
h = МуДХь Г,)т - iА- 1вг1Т, (4.10.52)
4.10. ОЦЕНИВАНИЕ ПО БЕЙЕСОВОМУ КРИТЕРИЮ
585
n = MCi(Xi,Yi), Kl = MQ(XhYl)Q(XhYl)T, / = 0,1,2,....
t> Следуя разделу 4.7, для нелинейных уравнений авторегрессии,
когда (4.10.45) линейны по Vr.
Xw = y>i(Xi) + ^Xt)Vh Yt = ipukXt) + (4.10.53)
уравнение фильтра (4.10.46) выбирается в виде
Х/+1 = + PirimYh (4.10.54)
где М) и T)i(Xi) - заданные функции, MV/ = 0, M(V/VjT) = vi.
В условиях теоремы 4.10.6, положив (/(X,i/) = [&(X)Tt/T?ft(X)]T,
J/ = [а/ft], имеем следующий результат. <з
Теорема 4.10.7. Если дискретный векторный случайный процесс
[ХТУТ]Т определяется уравнениями (4.10.53), то оптимальные зна-
чения коэффициентов оц, Pi условно оптимального фильтра (4.10.54)
по критерию (4.10.48) определяются из решения задачи (4.10.50) при
8i(9,X) = [ai(e,X)^e,X)], СКХ,у)= [&(X)V»7/WT]T- (4.10.55)
При этом уравнения для оц(0,Х), Pi(0,X) имеют вид
оц(0, А)кц + ft(0,A)«12 = «оь а/(0,А)«21 + ft(0,A)«22 = «02, (4.10.56)
где
«и = М(66т), «12 = «Г1 =
«22 = ЩгПФиФиЧп) + tyT),
«01 = М(у>и^г) -
£
«02 = М(у>п^17,т) + М(^н^п»?1Т) - |а-10М(¥>п»йг). (4.10.57)
Для сокращения записи аргументы у функции в (4.10.57) опущены.
При определении 1С/,£/,г/в (4.10.51), (4.10.52) и в (4.10.56),
(4.10.57) достаточно знать совместное распределение случайных век-
торов Xi и Xi при каждом I и распределение величин V/, которые по
предположению известны.
586
ГЛ. 4. УСЛОВНО ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФП
Замечание. Чтобы определить совместное распределение векторов Х[ и
Xi, достаточно знать их характеристическую функцию
9i = = Мехр(гАтХ/ +ifj.TXi] (I = 0,1,2,..., (4.10.58)
которая в случае теоремы 4.10.6 описывается следующим уравнением:
9i+i = Мехр {iXTul(Xl,Vl)+ifiT } (4.10.59)
с соответствующим начальным условием
до = So (А, д) = М ехр { iXT Хо + гцтХ0
(4.10.60)
Правая часть уравнения (4.10.59) полностью определяется характеристической
функцией gi в силу независимости векторов Х[ и Xi от V/. Аналогично рассматри-
вается вопрос о нахождении совместного распределения в условиях теоремы 4.10.7.
t> Теперь найдем дискретный фильтр Калмана по сложному ста-
тистическому критерию. С этой целью рассмотрим задачу линейного
оценивания состояния линейной системы. В этом случае (4.10.53) и
(4.10.54) имеют вид
= aiXt + фМ, Yt = btXi + Vh
(4.10.61)
Xw=aiXi+piYi,
(4.10.62)
где сЦ'Ьцфцфи ~ известные матрицы, зависящие от I; Pi - неизвестные
коэффициенты фильтра, определяемые по сложному статистическому
критерию (4.10.48). Тогда из теоремы 4.10.7 немедленно получаем сле-
дующий результат. <з
Теорема 4.10.8. Если векторный дискретный случайный процесс
[YJTX<T]T определяется уравнениям (4.10.61), то значения коэффици-
ентов оц, Pi условно оптимального фильтра (4.10.62) по критерию
(4.10.48) находятся из решения задачи (4.10.50) при
6(ff, X) = [«/(0, А)А(0, А)], Q(X,Y) = [%/тУ/т]Т. (4.10.63)
При этом &i(0, А) и Pi(d, А) определяются по следующим формулам:
4.11. ДОПОЛНЕНИЯ И ЗАДАЧИ
587
Ж А) = (at - Ж А)ЮГХ1ЛГт; - Ia"1^ ГТ1,
А(0,А) = (aiRtb't' + ^tvt^u - |a-10x
\ **
х (тЕ( + |ТП5|Г^0ГП^()) + V’n^iJ) 1, (4.12.64)
где Ri = Г%. — Гу у Г^ГТ^ * , а математические ожидания тх, =
• Xi Л/,Л/ ’
= МХ/, т^{ = MXj и моменты второго порядка векторов Xi и Xi\
Гх, = MX/XZT, ГХ/ Х/ = ^^Х?, = MXiX? удовлетворяют си-
стеме линейных уравнений:
mXl+1 =а1тХп = ai(9.X)m^ + /3i(0,X)bimXi, (4.10.65)
Гх/+1 =airXlaf
гх,+1>х,+1 = А)т + О|Гх, btPt(0, Х)Т + VwV’n/W А)т,
Гх1+1 = ЖА)Г*,ЖА)Т + 0t(0,X)btrXi^ at(0,X)T+
+а,(0, X^^bf 0,(0, А)т + ft(0, X^u^lMO, A)T. (4.10.66)
В частном случае теоремы 4.10.8 при в = 0,А = Z, поскольку
ГХ/Х/ = Г^ = ГХ/, Ri = Ге,, уравнения (4.10.62)-(4.10.66) опре-
деляют дискретный фильтр Калмана.
4.11. Дополнения и задачи
4.11.1. Сформулировать постановки задач условно оптимального оценивания, экс-
траполяции и интерполяции для стохастических дифференциальных систем, описывае-
мых уравнениями (2.1.7) и (2.1.8).
4.11.2. В условиях задачи 4.11.1 сформулировать теоремы 2.2.1-2.2.3, 2.3.1 и 2.3.2.
4.11.3. Построить фильтр Пугачева в условиях задач 3.7.4, 3.7.6, 3.7.9.
4.11.4. Построить фильтр Пугачева в условиях задач 3.7.10, 3.7.29-3.7.33 для случая
кубических нелинейных функций.
4.11.5. Построить фильтр Пугачева в условиях задач 3.7.13-3.7.20, 3.7.36 и 3.7.39.
588
ГЛ. 4. УСЛОВНО ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФП
4.11.6. Вывести уравнения линейного фильтра Пугачева для уравнений (2.9.1) и
(2.9.2) с некоррелированными шумами. Решить задачу для коррелированных шумов
(п.2.9.2).
4.11.7. Решить задачу 4.11.6 для автокоррелированных шумов в наблюдениях
(п.2.9.3).
4.11.8. Вывести уравнения п.2.9.4 для линейного фильтра Пугачева.
4.11.9. Вывести уравнения п.2.9.5 для непрерывных и дискретных линейных филь-
тров Пугачева.
4.11.10. Пользуясь результатами п.4.8.2, получить уравнения дискретного линейного
условно оптимального экстраполятора Пугачева. Решить задачу для уравнений п.4.7.8.
4.11.11. Вывести уравнения теорем 4.8.4-4.8.6 дискретной условно оптимальной ин-
терполяции для нелинейных авторегрессионных уравнений (4.8.17).
4.11.12. Получить из уравнений предыдущей задачи уравнения дискретных линей-
ных условно оптимальных интерполяторов. Сравнить результаты с уравнениями п.4.8.7.
4.11.13. Вывести уравнения эллипсоидальной субоптимальной фильтрации для ав-
торегрессионных уравнений п.4.7.4.
4.11.14. Получить уравнения эллипсоидальной условно оптимальной экстраполяции
для авторегрессионных уравнений п.4.7.4.
4.11.15. Найти уравнения эллипсоидальной условно оптимальной интерполяции в
условиях пп.4.8.4-4.8.6. Рассмотреть случай авторегрессионных уравнений п.4.7.4.
4.11.16. Покажем, что теория условно оптимальной фильтрации процессов при ав-
токоррелированной помехе в наблюдениях (раздел 4.3) распространяется на задачи филь-
трации по сложным статистическим критериям, представляющим собой функционалы от
математического ожидания и матрицы вторых моментов ошибки фильтрации (Синицын
и Шин 1991, Синицын, Шин, Корепанов 1993, Синицын 1996).
Рассмотрим векторый случайный процесс [ XТуТ ] , определяемый стохастиче-
скими дифференциальными уравнениями Ито:
dX = <?(У, X, N, t)dt + ^'{Y, X, N, t)dW + I ^"(Y, X, N, t, v)P°(dt, dv),
(I)
dY = <pi(Y,X,N,t)dt.
(П)
Здесь X = X(t) - ненаблюдаемый случайный процесс co значениями в яп,
X Е Rn; Y = Y(t) - наблюдаемый случайный процесс, Y е Rni-, W = W(t)
- винеровский процесс, W Е Яг; /^((^1,^2),^) ~ центрированная пуассоновская ме-
ра, 1? С RQ’t V Е Rq - вспомогательный параметр. Примем, что помеха N = N(t\
4.11. ДОПОЛНЕНИЯ И ЗАДАЧИ
589
NeRk также удовлетворяет уравнению вида (4.10.24),
dN = <p0(Y, X, N, t)dt + i/>'0(Y, X, N, t)dW + ^(Y, X, N, t, v)P°(dt, dv).
(П1)
в (1)-(Ш) принятой = <p(Y,X,N,t), = il>'(Y,X,N,t), tpi = <pi(Y,X,N,t),
<p0 = <p0(Y,X,N,f), = %(Y,X,N,t) - заданные функции, отображающие
дп1+п+*+1 в Rn Rn.T Rn, Rk Rkr соответственно, = ^"(Y,X,N,t,v),
Щ = itf(Y,X,N,t,v) - заданные функции, отображающие Дп1+п+^+9+1 в Дп и
R^ соответственно. Требуется по результатам наблюдений = {У(т) : to < Т < t]
найти наилучшую оценку X (t) процесса X (t) в классе допустимых оценок, определя-
емых уравнением фильтра (4.10.25). В соответствии с принципом условно оптимальной
фильтрации п.4.1.1 будем считать, что наилучшей оценкой X(t) процесса X (t) является
такая оценка, которая минимизирует в бесконечно близкий момент t1 > t, tf —> t функ-
ционал (4.10.24) от вектора математического ожидания = MJV и матрицы вторых
моментов ошибки фильтрации = NL{X Х^).
Следуя п.4.10.6 для приведения задачи фильтрации (1)-(Ш) к случаю процесса с
независимыми приращениями в наблюдениях будем дифференцировать по обобщенной
формуле Ито (1.4.86) уравнение (II) до появления процесса с членами, содержащими dW
или P°(dt, dv) в правой части. Предположим, что отличные от нуля слагаемые с dW и
с P°(dt,dv) появляются только после 8-кратного дифференцирования уравнения (II).
Положив У (°) = У, У<*+1> = dY^/dt, к = 0,1, ... , s - 1, имеем
dy(*) = y(*+i)dt) fc = о, 1, ... , з - 1, (IV)
</У<*> = (У, X, N, t)dt + fa (Y, X, N, t)dW+
+ У fa (У, X ,N, t, v)P° (dt, dv). (V)
Здесь введены следующие обозначения:
<?i+i = fit + + <^£1 + : BvBT-
~ I P°(t, dv), i = 1, ... , s, (VI)
«3
590
ГЛ. 4. УСЛОВНО ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФП
Ai : BvBT = [tr (<pii,uuBi/BT).. .tr (<pini<uuBvBT) ]T,
B=WTOpoT]T, U=[XTYTNT]T, +
= <pa(X + ф",Y,N + $,t) <& = <fi(Y,X,N,t),
tt=ft(Y,X,N,t), ^ = ^(Г)ХЛД)«),й = [й1...^п1]Т,
Фи = d<pi/dt, <pix = (d/dx)<pT, <piv = (d/dy}$,
<Pn,uu = (д/ди)(д/ди)т<ра , ... , <pini,uu = (д/ди) (д/ди)т <pini.
После 3-кратного дифференцирования наблюдений расширим класс допустимых
фильтров (4.10.25), введя в правые части уравнения (4.10.25) продифференцированные
наблюдения (IV), (V):
dX = a(t)£ (у<°),У(1), ••• , Y<'\X,t)dt+
+0(t)rj (Y^ ,Y^,... , Y^, X, t) dY^, (VII)
где £ = £ (y(0),l/(1) , , y(*>,X,i) нТ) = T) (y(0),I/(1) , . .. , y(*>,X,t^ - не-
которые заданные функции отмеченных аргументов, отображающие Д(*+1)п1+п+1 в
R1 и Rhni соответственно, OL = Ot(t) Е А4пхЬ Р — Е ~ матрицы
коэффициентов фильтра, подлежащие определению по критерию (4.10.24).
Применим уравнения условно оптимальной фильтрации по сложному статистиче-
скому критерию, полученные в п.4.10.6, к расширенному частично наблюдаемому слу-
чайному процессу [Х'ТУ'Т]Т где X' = [(ХТУТ]Т Y' = [у(0)Т у(1)Т
. . . , В результате получаем следующее утверждение.
Если векторный случайный процесс определяется стохастически-
ми дифференциальными уравнениями (1), (II), то значения коэффициентов Ot = Oi(t)
и /3 = /3(t) условно оптимального фильтра (4.10.25) по сложному статистическому
критерию (4.10.24J находятся из решения следующей задачи:
“(О = <*0O,AO(*)> 0(f) = &о,Ао(0>
(0о,Ao) = argmin/ (7П^(ао>А,^>л),Г^(а(>1А,^>А)), (VIII)
(0,А)€Л
4.11. ДОПОЛНЕНИЯ И ЗАДАЧИ
591
0 6 A# С Яп, А € Ал С Rn х Rn, A = А$ х ЛА.
Здесь 0 и А - неопределенные параметры, а функции Ct0tx == Ot0tx(t) и /Зф,Х —
= PojJfy удовлетворяют следующим уравнениям:
А/?0,А«22 = «02,
(IX)
(1 \ В£Т
X “ X + -0 ) — «01 “ /?М«21> (X)
z / аХ
при этом коэффициенты в (IX) и (X) определяются по формулам
«22 = + М
V’lVl TVp(t,v)dv I 7}Т
«02 = АМ(АГ - X)<pJ+1riT + AM(V>'^JT»7T) - |вМ(уз^+1»7Т)+
Zi
+м
V’lVl^P^,1')^ •
(ХП)
«11 = М(е - ТП1)£Т, k'21 = М(т,<р<+1 - m2)CT, (XIII)
/ ж 1 \ д£т
41 = M(v-mo)eT + M Х-Х--0)-|-+
\ ЛЛ 1 ОЪ
+gM(x-x-l«)r"«>T^) +
-Л.лЧЙ"'ЙТ (д^7 + ’ТЛТ»^) f-‘ ( +
if/ 1ХГ/- -7’/ д т „г О \ \
+2М (* - х - 2е) Г (*!* (акй + 2” ) дай) +
592
ГЛ. 4. УСЛОВНО ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФП
+tr +
\ о л о л / J
м( (х - х -(е(к(0),...
I у. " /
..., у(') + х + 0в,хТ]$, t)T - £т)\vpdv, (XIV)
то = М</?, mi = М£, m2 = ,
V = y(f) - интенсивность винеровского процесса; Up — l/p([to, t), 1?) - интен-
сивность пуассоновского процесса аргументы у функций в (X)-(XIV)
опущены.
Для линейных уравнений (1)-(Ш), (4.10.25) получается фильтр Калмана-Бьюси при
автокоррелированной помехе в наблюдениях по сложному статистическому критерию.
4.11.17. Показать, что в случае автокоррелированной помехи в наблюдениях, т.е.
если уравнение (4.10.2) имеет вид
dY = <pi(Y,X,N,t)dt,
(I)
а помеха N — N(t) удовлетворяет уравнению формирующего фильтра
t)dW + У M(Y,X,N,t,v)P°(dt,dv),
(П)
dN = <p0(Y, X, N, t)dt + V>o(y. X, N,
то путем дифференцирования наблюдаемого процесса Y до появления членов, содержа-
щих dW, можно привести полученную систему уравнений (4.10.1), (I), (II) к уравнени-
ями вида (4.10.1), (4.10.2) с расширенным вектором, а затем применить полученные в
пп.4.10.2-4.10.5 результаты (Синицын, Шин, Мощук 1993, 1995).
4.11.18. Условно оптимальные фильтры по бейесовым критериям (4.10.3) позволя-
ют также оценивать состояние стохастической дифференциальной системы в условиях
неопределенности, когда функции ч/)Г, ч//1, <^1, ч/)" в (4.10.1), (4.10.2) зависят от
неизвестных параметров. С этой целью нужно расширить вектор состояния X включе-
нием в него неизвестных параметров в качестве дополнительных компонент (Синицын,
Шин, Мощук 1993, 1995).
4.11.19. Требование гладкости функции потерь L(X, X) можно ослабить. Для на-
хождения оптимальных коэффициентов Q, /Зу у необходимо лишь, чтобы существовали
математические ожидания в формулах (4.10.7)-(4.10.12), т.е. чтобы функции, стоящие
под знаком математического ожидания, были суммируемыми по некоторой вероятност-
ной мере. Поэтому функции Lg, , L^X МОГУТ иметь и разрывы. На практике
4.11. ДОПОЛНЕНИЯ И ЗАДАЧИ
593
неизвестная одномерная плотность /1 (х, у, XJ t) аппроксимируется отрезком некоторо-
го разложения. Это означает, по существу, что и функция L(X, X) вместе с ее произ-
водными будет аппроксимироваться отрезком разложения в некотором пространстве Iq.
I л I3
Например, если X) — , то функция L (а также
может быть заменена рядом
оо
L= £ (I)
iJ=O
(Hi - классические полиномы Эрмита), сходящимся в среднеквадратическом к этой
функции по мере Д
exp{-a:2/2£>i -Х2/2Р2)
=-----!=--о .............-dxdX,
(П)
2iry/Did2
оо оо
так как < ОО и / <Z ОО (Синицын, Шин, Мощук 1993, 1995).
—ОО —оо
4.11.20. Пусть последовательность {А/} 71-мерных случайных векторов состояния
дискретной нелинейной стохастической системы с памятью определяется стохастическим
разностным уравнением нелинейной регрессии порядка 1\-.
Х1+1=Ш1(Х,,... , Xt+t^Vi), / = 0,1,2,... ,h >1. (I)
Уравнение (I) при l\ > 1 в общем случае приводится к уравнению вида (1.5.58)
путем расширения вектора состояния. Будем предполагать, что такое приведение осу-
ществлено.
Предположим, что наблюдается последовательность 711-мерных случайных векто-
ров {V/}, удовлетворяющих уравнению
У»=Уи(ХьУ,)> / = 0,1,2,...,
(П)
где — последовательность известных нелинейных функций. Требуется по ре-
зультатам измерения случайных векторов Yq * = {Yo> • • • yXi—i] найти оптималь-
ную оценку Yn вектора Yn по критерию минимума средней квадратической ошибки
м I Yl-Х, I2 для каждого момента времени I в классе допустимых фильтров, определя-
емых следующим разностным уравнением условно оптимального фильтра с памятью,
или, короче, фильтром Пугачева с памятью к:
Yi+i = WW-i, ... , , ... , У-fc+i) + 7„ (HI)
594
ГЛ. 4. УСЛОВНО ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФП
для заданной последовательности структурных функций {£/} фильтра:
Ь = Q(YhYi-i, • • • , ,YhУ/-1, ... , Yt-k+1), (IV)
любых матриц коэффициентов усиления 5/ и векторов смещений 'Yi, (/ = 0,1,...).
Число fc, 1 < fc < / 4~ 1 учитывает память условно оптимального фильтра.
Используя необходимые и достаточные условия оптимальности линейной средней
квадратической регрессии случайного вектора Х[ на £/, определяемого (IV), доказать
следующие утверждения (Корепанов 1992, 1998):
1) Пусть векторный дискретный случайный процесс [ X^Y^ ] удовлетворя-
ет уравнениям (I) и (II). Тогда оптимальные значения матричного коэффициента
усиления 5i и векторного коэффициента смещения фильтра Пугачева с памятью
(III) определяются следующими уравнениями:
&iKi — Li, — mi- &1S1,
(V)
mi = Mwi(XhVi), Si = MQ(XhYi),
Li = M((ui(Xi,Vi)-mi^(Xi,Yi), K, = M(G - Si)tf. (VI)
Аргументы у функций для краткости опущены.
Замечание. Для определения Ш/, S/, /С/, L/, входящих в (V), необходимо
знание совместного распределения векторов Xi = [«Х^ • • • и
V[ = [ ] Для каждого I. В самом деле, совместная характеристическая
функция
Р/(Ао , • • • , Ajb-1,/10 > • • • , Д*-1,РО , • • • > Рк-1) =
'fc-1
fc-1
к-1
= М ехр <
12 «Aj Yi-j + 52 Yi-i + 12
(VII)
составного вектора
[W]T
определяется рекуррентно следующим уравнением:
Р/+1(Ао > • • • > Ajb-i,/lo > • • • , Mfc-bPO > • • • > Рк-1) —
к-1
7=1
, ••• ’ ^-*+1>^1<(ж/,^), ••• , ^i,/-fc+i(zi-iHi>vi-*+i))+
4.11. ДОПОЛНЕНИЯ И ЗАДАЧИ
595
k~l к-1 X
+?/]+52 +52 гх
j=i j=i }
, ... , xi-k+i)Yi, ... , Yi-k+i,VI, • • • , vj_fc+i)x
xdxidxi-i • • • dxi-k+i<%dYi-i • • • dYi-k+i x
xdvidvi-i... d^-fc+i/u+itpo) • (VIII)
Здесь fl(xi , . . . , Xi—k+1, Yi , . . . , , . . . , - совместная плот-
ность объединенного вектора > полностью и однозначно определяемая ха-
рактеристической функцией
Pt(Ao , .. • , А*-1, До J • • J Цк-1,р0 , • • • > Рк-1) , (IX)
Л/+1(Ро) — известная одномерная характеристическая функция шумов . В каче-
стве начального условия для Qk—1 используются совместные характеристические функ-
ции следующих составных случайных векторов:
Г»-1 = [ПТ_,...И1ЧТ]Т. (X)
Характеристическая функция (}k—1 может быть определена в силу исходных уравнений
из известных распределений векторов Xq и Yq и последовательности шумов {V[}.
Для определения совместной характеристической функции составного вектора
[XL,v,T,]' достаточно записать уравнения условно оптимальных фильтров Пуга-
чева с памятью (Ш) для к — 1 шагов, I = 1 , . . . , к — 1:
Yi = Si-iCi-AYt-iУо,2,-1, Zo) + 7,-1, 1 = 1,...,к-1,
(XI)
где Cl—1 — известные структурные функции, а i и "у— неизвестные коэффици-
енты фильтра (XI), удовлетворяющие (V). Тогда начальное распределение векторов Xq
и Yq, распределения {V/} и уравнения (I)-(III), (XI) полностью определяют совместное
распреДеление
2) Пусть векторный дискретный случайный процесс удовлетворя-
ет уравнениям
Yi =^u(Xi)^MXl)Vi, 1 = 0,1,2,...
(XII)
596
ГЛ. 4. УСЛОВНО ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФП
Тогда матрицы коэффициентов СЦ, 01, фильтра Пугачева с памятью
У+1 = a&(YhУ/_1......fU+i,У-i, • • • , y-fc+i)+
+ lfyln(YhYi-i > ••• , У-*+ьУ1-1, ••• , yi-k+i)Xi +7/,
6 = б(У,У-1, • • • , У/-к+1,У|-1, • • • , У-*+1),
Vi = m(Yi,Yt-iУ/-*+1,У-1,... , У/-*+1)
определяются следующими уравнениями:
ацг^+01^ = 41 . ац^1+рцг^ = , 7t = , (XIV)
= = (XV)
41)=M(¥>/-tf))6T,
42 = M(v>i - lo ^(МРи)7 + ^iVi^urii ,
4? = M(& - , 4> = 4)T = M(6 - l^ni‘Pu)T, (XVI)
42 = M(j»¥>u -1{2 •
Аргументы у функций для сокращения записи опущены.
Замечание. В случае, когда уравнение фильтра (III) имеет вид
У1+1 = 6О(У,У-1..... У-*+1,У) + 71, (XVII)
т.е. не содержит “памяти” относительно наблюдений, рекуррентное уравнение (VII) суще-
ственно упрощается. При этом определение коэффициентов 5/ и 'У/, согласно (V), пред-
полагает для каждого П знание распределений векторов Х[ =
и V[ в силу их независимости. Рекуррентная формула для характеристической функции
Х[ может быть записана в следующей форме:
д/+1(Х,до , • • • , M*-i) = Mexp|iXTw/(X/,У)+
к-1 ч
+»4 [^(y.y.i,..., y(-*+i,yt) + 7i] + } • (xviii)
j=l J
4.11.21. В условиях предыдущей задачи получить уравнения дискретных фильтров
Пугачева с памятью по сложным статистическим критериям (Синицын, Шин, Корепанов
1993).
4.11. ДОПОЛНЕНИЯ И ЗАДАЧИ
597
4.11.22. В условиях задачи 4.11.2 получить уравнения дискретных фильтров Пуга-
чева с памятью по бейесовому критерию (Корепанов 1998).
4.11.23. В (Шин 1998) решена задача условно оптимальной комплексной фильтрации
для стохастической дифференциальной системы
X = /(X, t) + д(Х, t)W, XeRn (I)
в предположении, что измерительная система состоит из нескольких подсистем
у(») = я«(Х,t) + V(i), ERm, u = 1, ... , N. (II)
Очевидный подход, состоящий в объединении всех измерений в один вектор Y =
— ж
— Т ' 7 . . . I v ’ с последующим применением стандартных фильтрационных
уравнений, имеет ряд недостатков. Предлагается декомпозировать на 7V локальных под-
задач с вектором состояния X и локальным вектором наблюдения с последующим
применением фильтров Пугачева к локальным подзадачам (первый этап). А на втором
этапе - объединить полученные “локальные” условно оптимальные оценки (в виде линей-
ной комбинации) по критерию минимума среднего квадрата ошибки и тем самым полу-
чить “глобальную” условно оптимальную оценку исходного вектора состояния. В частном
калмановском случае линейных уравнений (I) и (II) эта задача имеет точное решение
Аналогичные задачи (I), (II), но для дискретных и непрерывных линейных и нели-
нейных систем с применением фильтра Калмана и обобщенного фильтра Калмана решены
в работах (Шин и Шевляков 2004, О, Шин, Ли, Чой 1998).
4.11.24. В (Ли, Чо, О, Шин 1997) дано развитие стандартного итерационного обоб-
щенного фильтра Калмана (ИОФК) применительно к дискретным стохастическим систе-
мам на условно оптимальные фильтры (УОФ). Достоинством ИОФК (а также итераци-
онной версии УОФ) по сравнению со стандартным ОФК (или УОФ) является улучшенная
точность оценки в каждый дискретный момент времени к за счет возможности улучшать
оценку Xk путем небольшого количества дополнительных итераций (по 2) в каждый
момент времени к, а недостатком является увеличение времени,необходимого для выпол-
нения дополнительных Tlk итераций (как правило не больше 3, т.е. в каждый момент
времени к. Если обычная структура УОФ имеет вид
Хк+1 = ак£к(Хк) + 0kT]k(Xk)Yk + Ук,
к = 0,1,2,..., Хо = М(Хо), i = 1,2, ... , М*, М* < 3 (I)
или
Хк+1 = ai6k(Xk,Yk), (II)
то дополнительная итерационная по 2 схема, введенная в УОФ, где на каждом дискретном
шаге к, определяется следующим образом:
Х*,<+1 = ak£k(Xkti)0kYk + Vk, i = 0,1, ... , пк, Xkio = Xk_i,
598
ГЛ. 4. УСЛОВНО ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФП
Xk=Xk,nk, к = 1,2,... , Хо = *о,о = М(Х0). (1П)
4.11.25. В (Синицын, Шин, О 1997) решена классическая задача нелинейной ин-
терполяции с фиксированной точкой с помощью интерполяторов Пугачева. Эта задача
описывается следующими уравнениями:
Xt = f(Xt, t) + g(Xt, t)Wt, Yt = + Vt, t > 0. (I)
Требуется оценить Xi по результатам текущих наблюдений Yq = \YU I 0 < U < Z},
где t - фиксированное время, a t - текущее (переменное) время.
Оценка фильтрации Хщ может быть определена стандартным фильтром Пугачева
(“вперед” по времени). А именно
dX
+ Vs, 0 < s < t, ХО|о = М(Х0). (П)
Оценка интерполяции Хщ может быть определена аналогично, но уже интерполятором
Пугачева (“назад” по времени):
= au^(Xllu, Xulu) + Xu|u)K + Vu, (III)
t < и < t, Xi^u=zf = X^f.
Решением “вперед” уравнения (II) служит оценка фильтрации X^f, которая далее
выступает как начальное значение для интерполятора “назад” (III). Интересен частный
случай, когда интерполятор (III) не зависит от текущих наблюдений Yq, потому что они
уже учтены фильтром (II). В этом случае ~ 0-
4.11.26. Вывести уравнения фильтров Пугачева для билинейных стохастических
систем. Сравнить результаты с (Шайкин и Шин 1997, 2001, Чой и Шин 1999).
4.11.27. Основываясь на непараметрических методах оценивания дискретных и не-
прерывных сигналов (Добровидов и Кошкин 1997, Васильев, Добровидов, Кошкин 2004),
вывести уравнения условно оптимального оценивания.
4.11.28. На рис.4.11.1-4.11.6 даны решения шести задач синтеза линейных и нели-
нейных фильтров Пугачева с помощью программного обеспечения “СтС-Фильтр”.
1) Уравнения системы:
' Xt(i +1) = %i(z) + д*х2(0,
\х2(1 + 1) = Х2(!) + Atao + ^ta2Xl (Z) + bV(l),
У (О = Xi(l) + cW(l);
4.11. ДОПОЛНЕНИЯ И ЗАДАЧИ
599
уравнения фильтра:
' Л(/ + 1) = ац(0й(0 + а12(/)Х2(0 + ВДВД + 71(0.
1. Х2(/ + 1) = а21 (0Л(0 + а22(0%22(0 + /МОВД + 72(0;
начальные условия:
мЛ(0) 4- MXi(O) = 4000, МХ2(0) = МХ2(0) = -20,
DXi(0) = 160000, PXi(0) = 10000, £>Х2(0) = DX2(0) = 1.
Рис. 4.11.1а
600
ГЛ. 4. УСЛОВНО ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФП
Рис. 4.11.16
2) Уравнения системы:
1X1 = х2>
Х2 = ~Ц)Х1,
Хз = х4,
Х4 = -Ь2Х3 - 2аХ4 + V,
Y = Х4 + Х2 + U, vy = 2Dab2,
кх3 = De-“ITI (coswit + — sinwi |т|), b2 = a2 + ш2,
4.11. ДОПОЛНЕНИЯ И ЗАДАЧИ
601
' ХД1 + 1] = Xi И + Д*Х2[1],
X2[l + 1] = Х2[1] - Д«с2Х1[1],
< Хз[/ + 1] = ХзИ + Д*Х4И,
к Х4[1 + 1] = Х4[1] - Д«Ь2Х3[1] - 2Д*аХ4[/] + ClV,
Начальные условия: MXi (0) = 0,5, MJV2(0) = 3,3, МХз(О) = 3,0,
DXi(O) = 0,01, РХ2(0) = 0,5, РХз(О) = 0.
Уравнения фильтра
' ХхР + 1] = «иИХхИ + ai2[/]X2[/] + Д[/]Ур] + 71Ш,
Х2[1 + 1] = a2i [1]Х1 [/] + а22[/]Х2[/] + /32 [/]У [Z] + 72[/],
Х3[1 + 1] = азз[/]Хз[1] + а34ИХ4И + 0з[/]У[1] + 7зИ,
. Х4[1 + 1] = а4з[1]Х3[1] + О44[ТО] + 04ИКр] + 74[/].
Результаты вычислений представлены на рис.4.11.2.
3) Уравнения системы
Х1 = х2,
Х2 = —UqXi,
х3 = х4,
Х4 = -b2X3 - 2аХ4 + V,
Y = Xi+X2+U, vy = 2Dab2, кх3(т) = De “1^ (coswir+ — sinwi |т|),
0>1
Ъ2 = а2 + и>2, u>i = Wo, Ь2 = 1.
Начальные условия: МУ(0) = 0,5» МУз(О) = 3,3, МУз(О) = 3,0,
DYi(0) = 0,01, РУ2(0) = 0,5, РУ3(0) = 0, t0 = О, Т = 10, Д* = 0,1.
Уравнения фильтра
1X1 [I + 1] = СГ11ЮХ1И + аиИХзИ + /31 ИУ[1] + 71И>
+ 1] = «21И^1И + «22р]^2^] + ^2р]^р] + 72[/],
-ХзР 4-1] = сгззР]-Х’зШ 4" а34И-^4И 4" Рз+ 7зр],
%4р + 1] = 0143[/]-Хзр] 4- a44p]^4p] 4- ^4р]^р] 4- 74И.
602
ГЛ. 4. УСЛОВНО ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФП
Результаты вычислений даны на рис.4.11.3.
4) Уравнения системы
' Л = х2,
Х.2 = —UqXi,
< Х3 = Х4,
Х4 = -b2X3 - 2аХ4 + V,
кХ8 = 27(7-а)(Х1+Хз)-7*з,
У = Х4 “I” Х% 4" i/y = 2Dab2 у ^Vi = 2^iQ,
4.11. ДОПОЛНЕНИЯ И ЗАДАЧИ
603
*i/(r) = Die °cosw2r, b2 = а2 + ш2, 72 = а2 + ш2
X1[/ + 1] = Xi[/] + AZX2[/],
X2[Z + 1] = X2[l]- &tc2Xi[l\,
X3[l + 1] = ХзИ + д*х4[/],
Х4[1 + 1] = X4[Z] - Д<Ь2ад - 2Мс2аХ4[1] + dV,
ад +1] = ад] + д«с2Х1 р] + Atc2x3[i] - д«с3ад/],
У [/] = a2Xi И + X2[Z] + агХзИ + Х4[1] + Х5[/] + Иф],
t0 = 0, Т = 10, Д4 = 0.1.
Начальные условия: МУ1 (0) = 0,5, MY^O) = 3,3, МУз(О) = 3,0,
РУ1(0) = 0,01, РУ2(0) = 0,5, РУз(О) = 0.
Уравнения фильтра
' Хх[/ + 1] = ап [/]Х1Ю + “1ЖИ + /МОТ*] + 7i[*],
Х2[/ + 1] = «21 [*]Х1 [*] + «22р]Х2[/] + ^г[/]УИ + 72р]>
* x3[l + 1] = азз[/]Хз[/] + садЗД + адип + 7з[П.
Х4[/ + 1] = а4з[/]ХзР] + «44 И%4 R] + /МОТ] + 740,
, X3[l + 1] = а51ИХ1И + а5з[#зр] + «55ИЗД + /МОТ] + 7бИ,
Результаты вычислений представлены на рис.4.11.4.
5) Уравнения системы
1X1 = Х2,
Х2 = — а>дХ1,
X3 = -aX3 + V1,
Х4 = b2(Xi + Х3) - 2аХ4 + V2,
604
ГЛ. 4. УСЛОВНО ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФП
Рис. 4.11.4
Y = Х2 - аХ3 + Х4 + U, Wi = 2D4ab2,
1A7i[Z 4-1] = Xi[/] + AtX2[/],
X2[l + 1] = X2[/] - Aic2Xi[/],
X3[/ + 1] = X3[Z] - ДйцХзИ + ДС1Ш
X4[l + 1] = - 2&ta2x4[l] + Atb2Xt[Z] + Д^2Х3[/] + caV^Z],
K[J] = X2[Z] - азХзР] + *4p] + Иф],
t0 = 0, T = 10, At = 0.1.
Рис. 4.11.5
606
ГЛ. 4. УСЛОВНО ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ. ФП
6) Уравнения системы
'Ху = Х2,
Х2 — —Л — 2X2X3cu + 12 + У,
. Х3 = 0,
Y = Xi 4- U, w = 2,
Х1[14-1] = Xi[/] 4- Д«Х2[1],
Х2[1 4-1] = Х2[1] - Д*ш2Xi[/] - 2wAty2[/]y3R] 4- 12Д* 4- ci V[l],
Хз[/ + 1] = ХзИ,
г И = хф] 4- Иф],
to = 0, Т = 10, Д4 = 0.05.
Начальные условия: МХх(О) = 0,5, МХ2(0) = 1, МХ3(0) = 2, DХг (0) =
= 1, РХ2(0) = 0,5, №(0) = 1.
Уравнения фильтра
Xi[l + 1] = ац[/]Х1[/] + a12[l]x2[l] + ^[l]Y[l] + 7i[Z],
x2[l 4- 1] = «21 р]^1 И + tt22R]^2p] 4- «23^2p]^3p] 4- /?2p]^R] 4- 72^],
Хз[/ 4-1] = «зз[/]Хз [/] 4- /?зр]^Р] 4" 7зШ>
Результаты вычислений представлены на рис.4.11.6.
4.11.29. Решить задачи 3.7.47, 3.7.50-3.7.52 с помощью фильтра Пугачева.
4.11.30. Получить уравнения условно оптимального оценивания для задач 3.7.48 и
3.7.49.
4.11.31. Решить задачи 3.7.53 и 3.7.54 на основе теории условно оптимального оце-
нивания (Белоусов 2004, Синицын, Синицын В, Корепанов, Белоусов 2004)
4.11.32. Решить задачи 3.7.55-3.7.57 на основе программного обеспечения фильтров
Пугачева “СтС-Фильтр”.
4.11. ДОПОЛНЕНИЯ И ЗАДАЧИ
607
Рис. 4.11.6
КАЛМАН
Рудольф Эмиль
(1930 года рождения)
5. Рудольф Эмиль Калман
Рудольф Эмиль Калман родился 19 мая 1930 года в Будапеште (Венгрия). Сын
инженера-электрика он решил пойти по стопам отца. Он иммигрировал в США, там по-
лучил образование бакалавра, а затем в 1953-1954 гг ему присвоена степень магистра по
электротехнике в Массачусетском технологическом институте (MIT). Позже Калман по-
кинул MIT и продолжил свое образование в Колумбийском университете, где в 1957 году
получил ученую степень доктора наук под руководством профессора Дж.Р.Рагаццини.
Ранний интерес к системам управления появился у Калмана еще во время учебы в
MIT и особенно в Колумбийском университете. Его первые исследования обладали мате-
матической новизной и были основаны на применении дифференциальных и разностных
уравнений в переменных состояния. Источником этих исследований были практические
задачи. Уже в эти ранние годы Калман проявил свой яркий оригинальный подход к ис-
следованию динамических систем, который он развивал на протяжении своей блестящей
научной карьеры.
В период 1957-1958 гг. Калман работал штатным инженером в исследовательской
лаборатории известной фирмы IBM. В течение этого времени он внес существенный вклад
в создание теории анализа и синтеза дискретных линейных систем управления по квадра-
тическому критерию качества, в том числе и на основе применения теории Ляпунова. Он
предвидел значение цифровых вычислительных машин для анализа и синтеза больших
систем и был одним из пионеров их использования для анализа и моделирования процес-
сов в них, а также оптимального синтеза структур больших (крупномасштабных) систем
управления.
В 1958 году Калман начинает работать в исследовательском институте перспек-
тивных разработок (RIAS) в Балтиморе, который позже возглавил известный профессор
С.Левшец. Здесь Калман прошел путь от математика-исследователя до заместителя ди-
ректора по научной работе. Именно в этот период (1958-1964 гг.) Калманом были выпол-
нены пионерские работы, внесшие существенный вклад в современный системный анализ
и теорию управления. Его лекции и публикации того времени говорят о его огромной
плодотворной деятельности в области общей теории управления. Полученные Калманом
5. КАЛМАН РУДОЛЬФ ЭМИЛЬ
609
результаты позволили подвести прочный фундамент общей линейной теории управления
на основе таких понятий, как управляемость и наблюдаемость и создать структурную
теорию сложных управляемых систем, важную для инженерной практики. Особенно яр-
кие результаты получил Калман в области синтеза по квадратическому критерию каче-
ства линейных дискретных и непрерывных управляемых систем. Калман сыграл важную
роль во внедрении работ Каратеодори в теорию оптимального управления, впервые вы-
явил связь между принципом максимума Понтрягина и уравнением Гамильтона-Якоби-
Беллмана, а также с вариационным исчислением в целом. Его работы подчеркивали не
только математическую общность, но и были нацелены на широкое использование ЭВМ
как неотъемлемую часть процесса анализа, синтеза и эксплуатации систем управления в
различных областях науки, техники и производства.
Именно в эти годы (1958-1959 гг.) Калман сделал одно из самых своих извест-
ных изобретений - так называемый “фильтр Калмана”. Калман писал, что в 1958 году
он предложил свой фильтр для дискретных динамических систем, обобщив известные
результаты Винера, Колмогорова, Бодэ, Шеннона, Пугачева и др. на случай систем, за-
данных в пространстве состояний. В 1960-1961 гг. Калман в сотрудничестве с Бьюси
разработал непрерывную версию своего фильтра (“фильтр Калмана-Бьюси”).
Фильтр Калмана по критерию минимума средней квадратической ошибки и его обоб-
щения на случай гауссовских нелинейных непрерывных и дискретных динамических си-
стем являются, пожалуй, самыми известными результатами современной теории управ-
ления, которые нашли практическое приложение. Круг областей применения фильтров
Калмана необычайно широк. Это космическая навигация и инерциальное управление ле-
тательными аппаратами (проект “Аполлон”), радиолокационная техника и связь, анализ
и синтез систем управления и регулирования технических и социально-экономических
систем. Фильтры Калмана предполагают непременное использование ЭВМ, что позво-
ляет эффективно решать задачи анализа и синтеза систем на всех этапах разработки,
производства, испытаний и эксплуатации изделий. С теоретической точки зрения Кал-
ман подвел единый фундамент под теорию фильтрации и управления в виде принципа
“дуальности”.
В 1964 году Калман начал работать в Стенфордском университете, сотрудничая с
департаментами электротехники, механики и исследования операций. Здесь его иссле-
дования сместились в область теории реализации и алгебраической теории систем. Он
открыл новые пути в известных и новых областях и построил доныне неизвестную об-
ласть современной теории системного анализа.
В 1971 году Калман стал директором Математического центра системного анализа и
профессором университета Флорида. Он ведет активную научно-исследовательскую и пе-
дагогическую работу с департаментами математики и электротехники, инженерии и про-
мышленности. Он также работает консультантом в исследовательских центрах Франции.
В период 1973-1997 гг. Калман возглавлял кафедру в Швейцарском федеральном инсти-
туте технологий в Цюрихе. Последние 15 лет Калман посвятил исследованию вопросов
20 Фильтры Калмана и Пугачева
610
ГЛ. 5. КАЛМАН РУДОЛЬФ ЭМИЛЬ
построения математических моделей динамических систем (идентификации) по экспери-
ментальным, зашумленным данным, применительно к задачам эконометрики, статистики
и теории вероятностей.
Заслуги Калмана в развитии теории управления, прикладной математики и инже-
нерном деле получили широкое признание. В 1985 году Калман стал одним из первых
лауреатов Kyoto Prize - аналог японской Нобелевской премии в области новых техноло-
гий (фонд Inamori Foundation, Japan). Калман является обладателем многих почетных
наград, таких как IEEE Medal of Honor (1974) и IEEE Centennial Medal (1984), премия
(Steel Prize), премии Веллмана (1997). Калман является иностранным членом Американ-
ской академии наук, Французской, Венгерской и Российской академий наук. Калман -
член национальной инженерной академии (США) и американской академии искусств и
наук. Калман также является почетным доктором университетов многих стран.
Подробную информацию о Калмане, его работах и последователях, конференциях и
семинарах, учебных курсах, практических применениях программного обеспечения филь-
тров Калмана можно найти на многочисленных сайтах, см. например, сайт “The Kalman
Filter”.
РУДОЛЬФ
ЭМИЛЬ
КАЛМАН
(1930 г. рождения)
Выдающийся ученый, инженер и педагог, автор
фундаментальных работ в области анализа и
синтеза дискретных линейных систем, теории
вероятностей и эконометрики, теории фильтра-
ции и управления, системного анализа и иден-
тификации.
ВЛАДИМИР
СЕМЕНОВИЧ
ПУГАЧЕВ
(1911-1998)
Выдающийся ученый и замечательный педагог,
основоположник статистической теории управ-
ляемых систем, автор фундаментальных работ
в области авиационной баллистики и динами-
ки полета, теории управления и информатики,
теории дифференциальных уравнений и теории
вероятностей.
ПУГАЧЕВ
Владимир Семенович
(1911 - 1998 гг.)
6. Пугачев Владимир Семенович
Владимир Семенович Пугачев выдающийся русский ученый и замечательный педа-
гог, основоположник статистической теории управляемых систем, автор фундаменталь-
ных работ в области авиационной баллистики и динамики полета, теории управления и
информатики, теории дифференциальных уравнений и теории вероятностей. Научные ис-
следования В.С.Пугачева включают свыше 300 работ по авиационной баллистике и дина-
мике полета, теории дифференциальных и интегральных уравнений, теории вероятностей
и математической статистике, теории управления и информатике.
В.С.Пугачев родился 25 марта 1911 г. в Рязани. Следуя традициям семьи, В.С.Пуга-
чев решил стать инженером-путейцем и в 1928 г. поступил в Московский институт инже-
неров транспорта. Откуда спустя год был переведен на второй курс инженерного факуль-
тета ВВА им.Н.Е.Жуковского. Вся постановка обучения в академии способствовала быст-
рому формированию инженера и ученого в области авиации, чему помогала и практика,
которую В.С.Пугачев проходил в конструкторских бюро А.Н.Туполева и С.В.Ильюшина.
В.С.Пугачев окончил академию за два года и был оставлен в ней адъюнктом. Однако
через пол года В. С. Пу гачев был назначен начальником вычислительного бюро в Научно-
испытательном институте ВВС ввиду необходимости усилить практические работы для
обеспечения быстрейшего развития авиационной техники.
В 1935 г. В.С.Пугачева назначают начальником кафедры воздушной стрельбы ВВА
им.Н.Е.Жуковского. В короткий срок он разрабатывает основы теории воздушной стрель-
бы - новой отрасли авиационной науки, создает учебный курс, пишет учебник и готовит
научно-педагогические кадры. Впоследствии первоначально изданный ВВА им.Н.Е.Жу-
ковского учебник лег в основу книги В.С.Пугачева “Теория воздушной стрельбы”. В это
время В.С.Пугачев выполняет работу по комплексной оценке эффективности стрельбы в
воздушном бою, впервые применив методы исследования операций и системного анали-
за для научного обоснования направлений развития авиационной техники, и остановится
основоположником исследований операций и системного анализа в нашей стране, на не-
сколько лет опередив аналогичные исследования за рубежом.
612
ГЛ. 6. ПУГАЧЕВ ВЛАДИМИР СЕМЕНОВИЧ
В условиях нараставшей угрозы нападения со стороны фашистской Германии
В.С.Пугачев участвует (в качестве руководителя и ответственного исполнителя) в выпол-
нении работ, направленных непосредственно на совершенствование отечественной авиаци-
онной техники. В годы Великой Отечественной войны В.С.Пугачев вместе с коллективом
ВВА им.Н.Е.Жуковского продолжает работу по подготовке авиационных инженеров для
фронта.
Для решения ряда важных задач, связанных с повышением эффективности стрель-
бы и бомбометания, потребовалось изучение процессов управления в условиях случайных
возмущений. В то время в мировой литературе для подобных задач не существовало ме-
тодов решения. В поисках их В.С.Пугачев разработал общую теорию систем, описывае-
мых стохастическими дифференциальными уравнениями. Работой “Случайные функции,
определяемые обыкновенными дифференциальными уравнениями” (1944 г.) были зало-
жены основы нового научного направления - статистической теории процессов управле-
ния (статистической динамики) задолго до появления публикаций в этой области науки
за рубежом.
В послевоенный период научная деятельность В.С.Пугачева была связана с даль-
нейшей разработкой статистической теории процессов управления и ее применений в
различных областях науки и техники. В 1947 г. им были завершены исследования по
общей статистической теории линейных систем и приближенных методов исследования
точности нелинейных систем. Разработанные В.С.Пугачевым методы теории управления
послужили основой его последующих работ в области динамики управляемого полета,
выполненных в период с 1947 по 1952 гг. В эти годы В.С.Пугачев в качестве научно-
го консультанта ведет работу в специализированном КБ по созданию систем управления
авиационным оружием и становится одним из руководителей разработки системы ПВО
Москвы. В 1948 г. за теоретические исследования в области баллистики В.С.Пугачеву
была присуждена Государственная премия СССР.
В 1956 г. В.С.Пугачев был приглашен в Институт автоматики и телемеханики АН
СССР (впоследствии переименованный в Институт проблем управления) для организации
лаборатории и работ в области статистических методов в теории управления. Продолжая
работы А.Н.Колмогорова, Н.Винера, Л.А.Заде, Д.Р.Рагаццини, Р.К.Бутона, Л.Дэвиса,
В.С.Пугачев разработал общую теорию оптимизации линейных систем по критерию ми-
нимума среднего квадрата ошибки. Им впервые выведено общее необходимое и доста-
точное условие минимума средней квадратической ошибки системы, дающее уравнение
для определения оптимальных систем различных классов с любым числом входов и вы-
ходов. В.С.Пугачевым впервые было дано решение уравнений, определяющих оптималь-
ную линейную систему, методом канонических разложений случайных функций. Следует
подчеркнуть, что работы В.С.Пугачева, в которых были впервые заложены основы тео-
рии оптимизации многомерных линейных систем и линейных систем с распределенными
параметрами, опередили работы зарубежных ученых.
6. ПУГАЧЕВ ВЛАДИМИР СЕМЕНОВИЧ
613
Развивая идеи статистической теории оптимизации линейных систем, В.С.Пугачев
построил с помощью метода канонических разложений статистическую теорию оптимиза-
ции нелинейных систем. Развитая В.С.Пугачевым теория может применяться для реше-
ния широкого класса задач обработки информации, где встречаются различные задачи
обнаружения, воспроизведения и оценивания сигналов. Эта теория была распростране-
на на случай условно нормально распределенной помехи с математическим ожиданием
и ковариационной функцией, зависящими от конечного множества неизвестных или слу-
чайных параметров, и на случай входного и требуемого выходного сигналов, зависящих
от счетного множества случайных параметров.
В цикле работ, выполненных в 50-е годы, В.С.Пугачев создает методы статистиче-
ской теории оптимальных систем. В этой области В.С.Пугачев развивает общие методы
определения оптимальных линейных систем, основанные на разработанной им же теории
канонических разложений случайных функций. Кроме того, им создаются общие ме-
тоды оптимизации динамических систем по любым статистическим критериям. Работы
В.С.Пугачева в области статистической теории оптимальных систем заняли ведущее место
в мировой науке и получили широкое распространение. Всего в области статистической
динамики управляемых систем В.С.Пугачевым опубликовано свыше 70 работ. Результа-
ты его работ в области статистических методов теории процессов управления обобщены
в монографии “Теория случайных функций и ее применение к задачам автоматического
управления” (1957 г.). Эта монография была переиздана в 1960 и 1962 гг. и переведена в
Англии, Франции, Польше и ГДР.
В начале 60-х годов В.С.Пугачев создает новый курс теории автоматического управ-
ления, который читает в ВВИА им. Н.Е.Жуковского. В 1963 г. В.С.Пугачевым совмест-
но с его учениками опубликована монография “Основы автоматического управления”, в
которой впервые систематически излагались применявшиеся в то время методы исследо-
ваний автоматических систем, включая статистические методы. В 1968 и в 1974 гг. книга
была переиздана.
В период с 1965 по 1970 гг. главным направлением научной работы В.С.Пугачева
была разработка статистической теории обучающихся автоматических систем. В 1976 г.
за участие в создании адаптивной системы управления сложным технологическим про-
цессом (горячая прокатка труб) В.С.Пугачев удостоен Государственной премии СССР.
При создании этой системы использовались методы теории обучающихся систем, разра-
ботанные В.С.Пугачевым.
К концу 70-х годов стало необходимым распространить нашедшей широкое приме-
нение калмановской теории линейной фильтрации на нелинейные системы. Многочислен-
ные попытки получить решение этой задачи путем линеаризации исходных уравнений с
различными уточнениями на протяжении 20 лет не привели к удовлетворительным ре-
зультатам, а методы субоптимальной фильтрации часто приводили на практике к про-
тиворечивым результатам. В.С.Пугачев предложил принципиально новый подход, осно-
ванный на идее условно оптимального оценивания и применении хорошо разработанной к
614
ГЛ. 6. ПУГАЧЕВ ВЛАДИМИР СЕМЕНОВИЧ
этому времени теории нелинейных стохастических дифференциальных систем. Им была
разработана теория условно оптимальной оперативной (в реальном масштабе времени)
фильтрации процессов в стохастических дифференциальных системах. В этих публи-
кациях дан метод нахождения оптимального по Парето фильтра в классе допустимых
фильтров, описываемых дифференциальными уравнениями заданного вида. Разработан-
ный метод позволяет оценивать не только состояние системы, но и неизвестные параметры
в ее уравнениях. Для решения уравнений, определяющих неизвестные функции в диф-
ференциальном уравнении условно оптимального фильтра, было использовано уравнение
для одномерной характеристической функции. В этом случае все неизвестные функции
определяются заранее в процессе проектирования фильтра, а не во время его оператив-
ной работы. Для проектирования фильтра используется только априорная информация.
При практическом применении теории для получения требуемых оценок необходимо лишь
интегрирование дифференциального уравнения фильтра в темпе получения текущей ин-
формации.
Метод условно оптимальной фильтрации был распространен на задачи экстраполя-
ции процессов в стохастических дифференциальных системах. Метод условно оптималь-
ной фильтрации и экстраполяции был обобщен В.С.Пугачевым на системы со случайно
изменяющейся структурой, а также на любые марковские системы, как непрерывные, так
и дискретные с известным переходным распределением.
Все прикладные работы В.С.Пугачева всегда были ориентированы на применение
вычислений. В ЗО-е годы он сам выполнял большие вычислительные работы в области
авиационной баллистики, для него были характерны доведенные до числа научные ре-
зультаты, так необходимые практике. В.С.Пугачев был одним из первых ученых, на-
чавших применять вычислительную технику в своей практической работе. Развитие
ЭВМ значительно расширило возможности практического применения разработанных
В.С.Пугачевым статистических методов, которые в задачах теории управления и инфор-
матики вследствие своей большой сложности могут быть реализованы практически толь-
ко с использованием вычислительной техники.
С 1984 г. и до последних дней В.С.Пугачев работал в Институте проблем информа-
тики Российской академии наук. В эти годы под его руководством и при непосредствен-
ном участии впервые создано программное обеспечение для анализа и моделирования,
фильтрации и экстраполяции процессов в сложных стохастических системах. Наряду с
линейными фильтрами Калмана нелинейные фильтры Пугачева прочно вошли в инже-
нерную практику.
Результаты многолетних работ В.С.Пугачева по теории вероятностей и теории стоха-
стических систем обобщены и систематически изложены в учебнике “Теория вероятностей
и математическая статистика” (1942, 1979, 1982, 1984, 2002) и в монографиях “Стохасти-
ческие дифференциальные системы”, “Анализ и фильтрация” (1985, 1987, 1990 гг.) и
“Теория стохастических систем” (1997, 2000, 2004), написанных совместно с И.Н.Сини-
цыным. В 1990 г. за цикл работ по статистической теории управляемых систем В.С.Пу-
6. ПУГАЧЕВ ВЛАДИМИР СЕМЕНОВИЧ
615
гачев был удостоен Ленинской премии. Незадолго до смерти В.С.Пугачевым совместно с
И.Н.Синицыным были написаны учебники для специалистов в области прикладных ма-
тематических методов “Lectures on Functional Analysis and Applications” (World Scientific,
1999 г.) и “Stochastic Systems. Theory and Applications” (World Scientific, 2001).
Более подробная информация об академике В.С.Пугачеве содержится на сайте ИПИ
РАН (htpp://www.ipiran.ru).
7. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ
По главе 1
В основу главы 1 положены материалы (Пугачев и Синицын 2000, 2004). Там же
содержится обширная библиография по теории непрерывных и дискретных стохастиче-
ских систем. П.1.1.6 написан на основе материалов (Калман 1961, 1963, Пугачев 19626,
1966, 1974, Бьюси и Джозеф 1968, Ройтенберг 1978, 1992, Воронов 1979, 1985). Обширная
библиография по прикладной теории марковских и условно марковских процессов содер-
жится в (Стратонович 1966, Тихонов и Миронов 1977, Королюк и др 1985). Задачи и
дополнения 1.9.1-1.9.53 составлены на основе (Гиббс 1928, Ченхдрасекхар 1943, Булгаков
1954, Баррет 1960, Свешников 1961, Силуянова 1982, Пугачев и Синицын 1985, 1990, 2000,
2004, Михайлов 1986, Мощук и Синицын 1992а, б, Синицын 1993, Пугачев и др. 1995).
Дополнения 1.9.54-1.9.64 составлены на основе результатов (Казаков и Артемьев 1980,
Красовский 1987, Пугачев и Синицын 1990).
Программное обеспечение задач автоматического составления уравнений для пер-
вых и вторых моментов и анализа нормальных стохастических дифференциальных си-
стем для ПЭВМ описано, например, в (Пугачев и Синицын 1990), а пуассоновских - в
(Пугачев и Синицын 1997). Примеры решения линейных и нелинейных задач на осно-
ве диалоговых пакетов “СтС-АНАЛИЗ” и “СтС-ФИЛЬТР” и обширная библиография
даны, например, в (Пугачев, Синицын и др. 1995, Синицын и др. 2004а, б).
По главе 2
Глава 2 написана на основе (Пугачев и Синицын 1985, 1987, 1990). При этом были
также использованы источники (Бьюси и Джозеф 1968, Кайлат и др. 1968, 1971, 1973,
Липцер и Ширяев 1968, 1974, Язвинский 1970, Аоки 1971, Кайлат 1974, 1997, Гелб 1974,
Ройтенберг 1978, 1992, Андерсон и Мур 1979, Мейбек 1979, 1982, Пугачев 1979, 1984,
2002, Соренсон 1985, Левис 1986, Красовский 1987, Чу и Чен 1987, Греваль и Эндрюс
1993, Сэйд, Хассиби 2000, Бар-Шолом, Ли, Кирубараджан 2001, Хайкин 2001).
Разделы 2.1-2.6 по непрерывной фильтрации изложены, следуя (Пугачев и Синицын
1985, 1987, 1990). Известные уравнения Кушнера-Стратоновича для апостериорных плот-
ностей выведены на основе (Кушнер 1964а, б, 1967, Стратонович 1966). При этом допол-
нительно написаны пункты, посвященные стохастическим дифференциальным системам,
содержащим и винеровские, и пуассоновские шумы. Добавлен раздел 2.7, содержащий
фильтрационные уравнения для ненормированных распределений в стохастических диф-
ференциальных системах. В его основу положены (Уонхэм 1965, Закаи 1969, Пугачев и
Синицын 2001).
В основу теории дискретной фильтрации (разделы 2.8-2.10) положены ( Калман
1960а, б, 1963, Бьюси и Джозеф 1968, Язвинский 1970, Аоки 1971, Сейдж и Меле 1976,
Ройтенберг 1992, Греваль и Энрюс 1993).
7. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ
617
Вопросы устойчивости, управляемости наблюдаемости линейных непрерывных и
дискретных стохастических систем изложены на основе ( Калм ан и Быоси 1961, Калман
1963, Бьюси и Джозеф 1968, Дейст и Прайс 1968, Ройтенберг 1992).
Раздел 2.12 написан на базе (Пугачев и Синицын 1985, 1987, 1990) в части тео-
рии совместного оценивания и распознавания. Адаптивная фильтрация изложена, следуя
(Лайниотис 1971а,б, 1973, 1975, Лайниотис и Парк 1976, Азаров и др 1998, О и др. 1998,
Синицын и Шин 1998).
В основу дополнений 2.3.11, 2.3.12 положены работы (Язвинский 1970, Аоки 1971,
Гелб 1974, Соренсон 1985). Дополнения 2.13.22-2.13.25 разработаны на базе (Пугачев
1957, 1960, 19626).
Вопросам алгоритмического и программного обеспечения фильтров Калмана для
различных применений посвящена обширная литература. Текущее состояние можно про-
следить, например, на сайте “Kalman Filtering”, а также на сайтах стандартных библиотек
и программных средств. Систематическое изложение принципов и подходов к алгоритми-
зации фильтров Калмана, их аналитическому и статистическому моделированию, тести-
рованию и диагностике можно найти (Бьюси и Джозеф 1968, Балакришнан 1984, 1987,
Чен 1985, Чу и Чен 1987, Харвэй 1989, Чен и Чу 1991, Греваль и Эндрюс 1993, Кэрр
1993) , а также в материалах Kalman Filtering Software: User Guide 1984. Special Issue on
Applications of Kalman Filters 1983).
По главе 3
Материал главы 3 базируется на работах (Липцер и Ширяев 1968, 1974, Аоки 1971,
Ройтенберг 1978, 1992, Мейвек 1979, 1982, Пугачев и Синицын 1985, 1987, 1990, Красов-
ский 1987, Греваль и Эндрюс 1993, Хайкин 2001). При этом основное внимание уделено
обобщенным фильтрам Калмана, основанным на двух подходах. Разделы 3.1-3.3, 3.5 из-
ложены, следуя (Пугачев и Синицын 1985, 1987, 1990). При этом добавлен новый раздел
3.4, посвященный уравнениям для ненормированных распределений (Пугачев и Синицын
2001). Раздел 3.5 основан на (Пугачев 1985, 1987, 1990, Греваль и Эндрюс 1993, Чен 1993).
Раздел 3.6 содержит изложение дискретных субоптимальных адаптивных и неадаптивных
фильтров Калмана. В этом же разделе рассмотрены вопросы субоптимальной адаптив-
ной идентификации и распознавания. В основу раздела положены работы ( Азаров и др.
1998).
Дополнения 3.7.10-3.7.12 написаны на основе работ (Казаков и Гладков 1987, О и
Шин 1997, Ли, О, Шин 2003), 3.7.29-3.7.31, 3.7.33 - (Казаков и Гладков 1987), 3.7.32 -
(Тихонов и Кульман 1975, Казаков и Гладков 1987), 3.7.46 - (Колмановский 1973, Липцер
1974, Липцер и Ширяев 1974, Серебровский 1975, Кванернак и Сиван 1977,Ляшко, Ди-
денко, Цитрицкий 1979, Миллер и Серебровский 1979, Бутов 1980, Миллер и Рубинович
1995, Борисов 1998).
Материал главы 3, с одной стороны, необходим для уяснения теории обобщенных
фильтров Калмана, а с другой стороны, для получения важных классов нелинейных
условно оптимальных фильтров Пугачева, например - эллипсоидальных (глава 4). В
618
ГЛ. 7. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ
главе 3 в качестве критерия оптимизации был принят критерий минимума средней квад-
ратической ошибки. Теория субоптимальных фильтров по другим критериям для ком-
пактности и единства изложения отнесена в главу 4.
По главе 4
В главе 4 сделаны попытки впервые дать полное и систематическое изложение не-
прерывного и дискретного условно оптимального оценивания и распознавания. В осно-
ву положены, во-первых, оригинальные работы В.С.Пугачева (Пугачев 1978, 1979а,б,
1980, 1981, 1982а,б, 1984), во-вторых, книги и обзоры работ, сделанные под руководством
В.С.Пугачева (Пугачев и Синицын 1985, 1986, 1987, 1990, 1993, Пугачев, Синицын, Шин
1986, 1987), в-третьих, работы отечественных и зарубежных авторов, непосредственно
примыкающие к теории неадаптивной и адаптивной фильтрации Пугачева по критерию
минимума средней квадратической ошибки, бейесовому и сложно статистическому кри-
териям.
Панкову А.Р. и его ученикам принадлежат важные результаты по дискретному ми-
нимаксному оцениванию в классе условно оптимальных оценок в дискретных и непре-
рывно-дискретных стохастических динамических системах (Панков 1990, 1992, 1993, 1994,
Панков и Босов 1992, 1994, 1995а,б, 1996, 1997, Босов, Панков, Овсянко 1996).
Важное значение для уяснения связи между теорией условно оптимальной филь-
трации и управления в области синтеза условно оптимальных фильтров и регуляторов
заданной сложности имеют работы Казакова И.Е. (Казаков 1987, 1988, Казаков и Глад-
ков 1987, Шатин 1994).
Принципиальное значение для практического выбора структурных функций филь-
тров Пугачева имеют работы (Дашевский 1981, Раол и Синха 1986а,б, Руденко 1988, 1990,
1991, 1992, Хоанг и др. 1997а,б).
Создание программных средств, реализующих фильтры Пугачева, представляет со-
бой нетривиальную задачу. Сложность задачи заключается в том, что программное
обеспечение должно автоматически по исходным нелинейным стохастическим уравне-
ниям составлять и решать систему уравнений высокого порядка для опредления неиз-
вестных параметров распределения переменных состояния и их оценок, а также вычис-
лять коэффициенты фильтра Пугачева. Известное программное обеспечение для синтеза
фильтров Пугачева представляет собой как отдельные программы в библиотеках NALIB,
TRANSSTATLIB и др., так и интеллектуализированные пакеты прикладных программ,
реализующие информационные технологии быстрой (оперативной) обработки информа-
ции в сложных нелинейных стохастических системах на основе методов параметризации
распределений и эквивалентной линеаризации (Пугачев и Синицын 1989, 1990, 1993, Си-
ницын и др. 1991, Синицын и Корепанов 1995, Синицын, Корепанов, Шин 1998, Корепа-
нов 1998, 2001, Синицын и др. 2004а,б).
Значительный объем известного программного обеспечения синтеза фильтров Пу-
гачева представляют отдельные программы, предназначенные для решения конкретных
прикладных задач фильтрации измерений в морской, авиационной, ракетно-космической
7. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ 619
и медицинской технике. Проблема разработки информационной технологии и базового
программного обеспечения синтеза фильтров Пугачева для ПЭВМ впервые была постав-
лена и решена в ИПИ РАН в 1986-1993 гг. Известны алгоритмические и программные
реализации неадаптивных и адаптивных фильтров Пугачева для высокопроизводитель-
ных параллельных средств вычислительной техники (Синицын 1995, Синицын и Карпен-
ко 1996, Синицын, Синицын В., Степанов, Ушмаев 2003, Синицын, Степанов, Ушмаев
2003, 2004).
СПИСОК ЛИТЕРАТУРЫ
Азаров С.В., Менхо О., Синицын И.Н., Шин В.И. (1998). Метод нормальной аппрокси-
мации в задачах адаптивной дискретной фильтрации и распознавания // Автоматика и
телемеханика. Nil. С.21-31.
Андерсон Б. и Моор Дж. (b.D.Anderson and J.В.Moore 1979). Optimal Filtering. New
Jersey: Prentice-Hall, Inc.
Антоулас А. (ред.) (A.C.Antoulas 1991). Mathematical System Theory. The influence of
R.E.Kalman. Springer-Verlag, Berlin.
Аоки M. (1971). Оптимизация стохастических систем. - M.: Наука.
Еалакришнан A. ^Balakrishnan A.V. 1987). Kalman Filtering Theory. Optiminzation Soft-
ware, Inc., New York.
Баррет Д.Ф. (1960). Применение уравнений Колмогорова для исследования систем автома-
тического управления со случайными возмущениями// Тр. I Международного конгресса
ИФАК, Москва, СССР, 1960. Статистические методы исследования. Теория структур,
моделирование, терминология, образование. - М.:Изд-во АН СССР. С.84-89.
Белоусов В.В. (2004). Информационная технология синтеза фильтров Пугачева для быстрой
обработки информации в сингулярных стохастических системах. Кандид, дис. на соиск.
уч. ст. к.т.н. - М.: ИПИ РАН.
Библиотека программ "NALIB” для решения научно-технических задач на ПЭВМ типа
IBM PC, PS/2 и совместимых с ними. Руководство Пользователя (1993). Т.1. 2, 3. - М.:
Изд. ИПИ РАН.
Богуславский И.А. (1969). Оценка условной плотности вероятностей фазовый координат по
неполной информации // Автоматика и телемеханика. Nil. С.44-58.
Борисов А.В. (1998). Оптимальная фильтрация в системах с вырожденными шумами в
наблюдениях // Автоматика и телемеханика. Nil. С.32-45.
Борисов А.В., Панков А.Р., Овсянко Д.Е. (1996). Алгоритмы нелинейной фильтрации
процессов в линейных системах случайной структуры // Космические исследования. Т.34.
N5. С.18-25.
Босов А.В. (1998). Условно-минимаксные алгоритмы оценивания и управления для нели-
нейных стохастических систем // Автоматика и телемеханика. Nil. С.46-59.
Брайсон А. и Йохансен Д. ( Bryson А.Е., Johansen D.E. 1965). Linear filering for time-
varying systems using measurements containing coloured noise // IEEE Trans, on Automat.
Contr. V.AC-10. NI. P.4-10.
Брайсон А. и Хо Ю-Ши (1972). Прикладная теория оптимального управления. - М.: Мир.
Браммер К. и Зиффлинг Г. (1982). Фильтр Калмана-Бьюси. - М.: Наука.
Булгаков Б.В. (1954). Колебания. - М.: Гостехиздат.
Бутов А.А. (1980). Оптимальная линейная фильтрация при вырождении шума в наблюде-
ниях // Автоматика и телемеханика. Nil. С.33-39.
Список литературы
621
Бхаруха-Рейд А.Т. (A.T.Bharucha-Reid 1960). Elements of the Theory of Markov Processes
and Their Applications. - McGRAW-HILL Book COMPANY. New-York - Toronto - London.
Бьюси P. (вису R.S. 1967). Optimal filtering for correlated noise // Journal of Mathematical
Analysis and Applications. V.20. Nl. P.1-8.
Бьюси P. и Джозеф П. (Вису R.S., Joseph Р. 1968). Filtering for Stochastic Processes with
Applications to Guidance. New-York. Wiley Interscience Publishers.
Васильев В.А., Добровидов А.В., Кошкин Г.М. (2004). Непараметрическое оценивание
функционалов от распределений стационарных последовательностей. -М.: Наука.
Вилски A (A.S. Willsky 1979). Digital Signal Processing and Ccontrol and Estimation Theory:
Points of Tangency. Areas of Intersection and Parrallel Directions. MIT Press, Cambridge.
Воронов A.A. (1979) Устойчивость, управляемость наблюдаемость. - M.: Наука.
Воронов А.А. (1985). Введение в динамику сложных управляющих систем. - М.: Наука.
Гелб А. ( A.Gelb 1974). Applied Optimal Estimation, MIT Press, Cambridge, MA.
Гиббс Дж. (j. W. Gibbs 1928). The Collected Works of J. Willard Gibbs: in two volumes. - New
York: Longmans, Green and Co. [Рус. пер.: Термодинамика. Статистическая механика. -
M.: Наука, 1982].
Гревалъ М. и Эндрюс А. ( M.S. Grewal and А.Р.Andrews 1993). Kalman Filtering: Theory
and Practice. New Jersey: Prentice-Hall.
Гулько Ф.Б. и Новосельцева Ж.А. (1966а). Решение нестационарных задач фильтрации и
упреждения методами моделирования // Автоматика и телемеханика. N4. С. 122-141.
Гулько Ф.Б. и Новосельцева Ж.А. (19666). Решение нестационарных задач фильтрации и
упреждения при произвольной помехе методами моделирования // Автоматика и телеме-
ханика. N10. С. 153-168.
Дашевский М.Л.и Липцер Р.Ш. (1967). Применение условных семиинвариантов в задачах
нелинейной фильтрации марковских процессов // Автоматика и телемеханика. N6. С.12-
25.
Дашевский М.Л. (1968). К проблеме существования решений в задачах субоптимального
оценивания // Автоматика и телемеханика. N12. С.29-34.
Дашевский М.Л. (1981). Синтез условно оптимальных фильтров на основе уравнений оп-
тимальной нелинейной фильтрации // Автоматика и телемеханика. N10. С.35-42.
Дейстп Дэю. и Прайс К. ( J .J .Deyst, С.F.Price 1968). Conditions for asymptotic stability of
the discrete minimum-variance linear estimator // IEEE Trans. Autom. Control. V.AC-13,
N6. P.702-705.
Добровидов А.В., Кошкин T.M. (1997). Непараметрическое оценивание сигналов. -М.:
Наука. Физ.мат.лит.
Закаи М. (Zakai М. 1969). On the optimal filtering of diffusion processes // Ztschr. Wahrs-
cheinichkeitstheor. verm. Geb. Bd. P.230-243.
Ивановский P.H. и Игнатов A.A. (1982). Теория чувствительности в задачах управления
и оценки. -Л.: Изд-во ЦНИИ “РУМБ”.
622
Список литературы
1\.азаков И.Е. (1987). Синтез условно оптимального управления по локальному критерию
в нелинейных стохастических системах // Автоматика и телемеханика. N12. С.72-80.
Казаков И.Е. (1988). Условно оптимальное управление в нелинейных дискретных стохасти-
ческих системах // Изв. АН СССР. Техническая кибернетика. N3. С. 165-169.
Казаков И.Е. и Артемьев В.М. (1980). Оптимизация динамических систем случайной
структуры. - М.: Наука.
Казаков И.Е. и Гладков Д.И. (1987). Методы оптимизации стохастических систем. - М.:
Наука. Гл. ред. физ.-мат. Лит.
Казаков И.Е. и Мальчиков С.В. (1981). Приближенное построение фильтров Пугачева за-
данной сложности // Автоматика и телемеханика. N12. С.48-55.
Кайлат Т. (T.Kailath 1974). A View of Three Decades of Linear Filtering Theory, IEEE Trans.
Inf. Theory. V. IT-20. N2. P.146-181.
Кайлат T. (T.Kailath 1997). Linear Least-Squares Estimation, Stroundsburg: Dowden, Hut-
chinson and Ross.
Кайлат T. и dp. (T.Kailath and others 1968, 1971, 197з). An innovations approach to least-
squares estimation. Pts I-VII // IEEE Trans, on Automat. Contr. V.AC-13. N6. P.646-660;
V.AC-16. N3. P.217-226; N6. P.720-727; V.AC-18. N5 P.435-453; N5. P.588-607.
Кайлат T, Сэйд А., Хассиби В. (T.Kailath, A.Sage, V.Hassibi 2000). Linear Estimation.
New Yersey: Prentice Hall.
Калман P. (Kalman R.E. 1960a). A new approach to linear filtering and prediction problems
// J. Basic Eng. (ASME Transactions). V82D. P.35-45.
Калман P. (Kalman R.E. 19606). Contributions to the theory of optimal control // Boletin de
la Sociedad Matematica Mexicana. V.5 Segunda seria. Nl. P. 102-119.
Калман P.E. (Kalman R.E. 1961). Об общей теории систем управления // Труды 1 контр.
ИФАК. Т.2.. - М.: Изд-во АН СССР. С.521-547.
Калман P.E. (Kalman R.E 1963). New methods in Wiener filtering theory // Proceeding on the
First Symposium on Engineering Applications of Random Function Theory and Probability
New York. Y. Wiley. P.270-388.
Калман P. и Бьюси P. (Kalman R.E. and Bucy R.S. 1961). New results in linear Entering and
prediction theory // Trans. ASME. Journ. Of Bfsic Engineering. V.83D. P.95-108 [Новые
результаты в линейной фильтрации и теории предсказания // Техническая механика: -
Сб. переводов. 1961. Т.83. Серия Д. Nl. С. 123-133].
Катлин Д. (Katlin D.E. 198в). Estimation, Control, and the Discrete Kalman Filter. Springer-
Verlag. New-York.
Квакернак Г. (Kwakernaak H. 1970). Sensitivity analysis of discrete Kalman filters // Interna-
tional J. Control, 12. P.657-669.
Квакернак Г. и Сиван Р. (1977). Линейные оптимальные системы управления. - М.: Мир.
Колмановский В. Б. (1973). О выборе законов наблюдения при произвольной помехе // Изв.
АН СССР. Техн. Кибернетика. N4. С. 110-114.
Список литературы
623
Корепанов Э.Р. (1992). Дискретные условно оптимальные фильтры с памятью // ДАН.
Т.324. N1. С.50-55.
Корепанов Э.Р. (1998). Разработка и реализация информационной технологии синтеза
фильтров Пугачева. Канд. Дисс. на соиск. уч. ст. к.т.н. -М.: ИПИ РАН.
Корепанов Э.Р. (2001). Развитие алгоритмического и программного обеспечения для син-
теза фильтров Пугачева // Системы и средства информатики. Спец.вып. - М.: Наука.
Физматлит. С.37-42.
Королюк В.С., Портенко Н.И., Скороход А.В. Турбин А.Ф. (1985). Справочник по теории
вероятностей и математической статистике. - М.: Наука.
Красовский А.А. (ред.) (1987). Справочник по теории автоматического управления. - М.:
Наука.
Кушнер Г. (Kushner H.J. 1964). On the dynamical equations of conditional probability density
functions with applications to optimal stochastic control theory // J.Math. Anal. Appl. V.8.
P.332-344.
Кушнер Г. (Kushner H.J. 1967). Dynamical equations of optimal nonlinear filtering // J.Dif-
ferential Equations. V.3. P. 179-199.
Кэрр T. (Kerr Т.Н.. 199з). Numerical approximations and other structural issues in practical
implementations of Kalman filtering // Guanrong Chen (Ed.) (1993) Approximate Kalman
Filtering. World Scientific, Singapore.
Лайниотис Д. ( Lainiotis D.G. 1971a). Optimal adaptive estimation. Structure and parameter
adaptation // IEEE Trans. Automat.Control. V.AC-16. N2. P.160-170.
Лайниотис Д. ( Lainiotis D.G. 19716). Optimal nonlinear estimation // Int. J.Control. V.14.
N6. P.1137-1148.
Лайниотис Д.и Парк С. ( Lainiotis D.G., Park S.K. 1973). On joint detection, estimation
and system identification discrete data case // Int. J.Control. V.17. N3. P.609-633.
Лайниотис Д.и Парк С. ( Lainiotis D.G., Park S.K. 1975). Patitioned linear estimation
algorithms discrete case // IEEE Trans. Control. V.AS-20. N3. P.255-257.
Лайниотис Д.и Парк С. ( Lainiotis D.G., Park S.K. 1975). Patitioning. A unifying framework
for adaptive systems, I:Estimation// IEEE Proceedings. V.64. N3. P. 1126-1143.
Левис Ф. ( Lewis F.L. 1986). Optimal Estimation with an Introduction to Stochastic Control
Theory. New York. John Wiley & Sons.
Ли У., О. M., Шин В.И. ( Lee Y., Oh М. and Shin V.I. 2001). Adaptive nonlinear conti-
nuous-discrete filtering // Applied Numerical Mathematics. N47. P.45-56.
Ли У., Чо Ю., О М., Шин В.И. (Younghee Lee, Yonggun Cho, Oh Myoungho and V.I.Shin
1997). Iterated Conditionally Optimal Filters // Automation and Remote Control. V.58. N6,
P.961-968.
Липцер Р.Ш. (1974) Уравнения почти оптимального фильтра Калмана при особенной ма-
рице ковариаций шума в наблюдениях // Автоматика и телемеханика. NI. С.35-41.
Липцер Р.Ш. и Ширяев А.Н. (1968) Нелинейная фильтртация диффузионных марковских
процессов // Тр. Мат. ин-та им.В.А.Стеклова АН СССР. Т.104. С.135-180.
624
Список литературы
Липцер Р.Ш. и Ширяев А.Н. (1974) Статистика случайных процессов. -М.: Наука.
Лифшиц Н.А., Виноградов В.Н., Голубев ГА. (1969) Линейная фильтрация при особенной
матрице ковариаций шума в наблюдениях // Изв. АН СССР. Техн. Кибернетика. N3.
С.127-135.
Лъюнг Л. (1991) Идентификация систем. Теория для пользователя: Пер. англ. Под ред.
Я.3.Цыпкина. -М.: Наука. Гл.ред. физ.-мат.лит.
Ляшко И.И., Диденко В.П., Цитрицкий О.Е. (1979) Фильтрация шумов. Киев: Наукова
Думка.
NZIedus Дж. (1973). Статистически оптимальные линейные оценки и управление. - М.:
Энергия.
Мейбек П. (Maybeck P.S. 1979, 1982). Stochastic Models, Estimation and Control. V.l, 2, 3.
Academic Press. San Diego.
Мендели Дж. (Mendel J.M. 1987). Kalman Filtering and other Digital Estimation Techniques
// IEEE Individual Learning Package. IEEE Press, Piscataway. New York.
Менхо О., Чангхи Хан, Синицын И.Н., Шин В.И. (1998). Рекуррентная фильтрация в
дискретных нелинейных системах с неизвестными параметрами // Автоматика и телеме-
ханика. Nl. С.44-63.
Миллер Б. и Рубикович Е. (Miller В.М., Rubinivich E.Ya. 1995). Regularizaton of a gener-
alized Kalman filter // Math. Comput. Simul. V.39. P.87-108.
Миллер Б.М. и Серебровский А.П. (1979). Задача оптимального управления линейной си-
стемой с вырожденным квадратичным критерием качества // Автоматика и телемехани-
ка.N7. С.33-34.
Михайлов Ф.А. (1986). Теория и методы исследования нестационарных линейных систем.
- М.: Наука.
Мияллото Я. и Такеда Г. (Miyamoto Y., Takeda Н. 1976). Optimal filter for coloured mea-
surement noise // Technol. Repts. Tohoku Univ. V.41. Nl. P.83-104.
Моулан П. (Moylan P.J. 1974). A Note on Kalman - Bucy filters with zero measurement noise
// IEEE Trans. Automat. Control. V.19. P.263-264.
Мощук H.K., Синицын И.Н. (1992a). Распределения с инвариантной мерой в механических
стохастических системах // Докл. АН России. Т.322. N4. С.662-667.
Мощук Н.К., Синицын И.Н. (19926). Приближенный метод анализа стохасти-
ческих механических систем // ПММ. Т.56. Вып.6. С.907-917.
О М., Шин В.И., Ли У., Чой В. (M.Oh, V.l. Shin, Y. Lee and U.J.Choi 1998). Suboptimal
discrete filters for stochastic systems with different types of observations // Computer and
Mathematics with Applications. V.35. N.3. P. 17-27.
О M., Хан И., Синицын И.Н., Шин B.H.(Myoungho Oh, Changhee Han, Sinitsyn I.N. and
Shin V.l. 1998). Recursive filtering in discrete nonlinear systems with unknown parameters
// Automation and Remote Control. V.59. Nl. P.36-43.
Панков A.P. (1990). Рекуррентное оценивание траекторий динамических систем с помощью
регрессионных нелинейных фильтров // Статистические методы в теории управления ЛА:
Список литературы
625
Тем. сб. научи, тр. МАИ. -М.: Изд. МАИ. С.45-53.
Панков А.Р. (1992). Рекуррентная условно-минимаксная фильтрация процессов в разност-
ных нелинейных стохастических системах // Изв. АН СССР. Техническая кибернетика.
N3. С.63-70.
Панков А.Р. (Pankov A.R. 1993). Conditionally - minimax nonlinear filter for differential system
with discrete observations // Advances in Modelling & Analysis. Ser.B.AMSE Press. V.28.
Nl. P.31-39.
Панков А.Р. (1994). Стратегии управления в линейной стохастической системе с негауссо-
выми возмущениями // Автоматика и телемеханика. N6. С.74-83.
Панков А.Р. и Борисов А.В. ^Pankov A.R., Borisov А. V. 1994). Optimal filtering in stochastic
discretetime systems with unknown inputs // IEEE Trans. Autom. Control. V.AC-39. N12.
P.2461-2464.
Панков А.Р. и Борисов А.В. (1992). Робастное рекуррентное оценивание процессов в сто-
хастических системах // Автоматика и телемеханика. N9. С. 102-110.
Панков А.Р. и Босов А.В. ( Pankov A.R., Bosov A.V. 1994). Conditionally - miminax al-
gorithm of nonlinear system state estimation // IEEE Trans. Autom. Control. V.39. N8.
P.1617-1620.
Панков А.Р. и Босов А.В. (1995). Конечномерные алгоритмы оценивания состояний нели-
нейных стохастических систем // Вестник МАИ. Т.2. N2. С.44-51.
Панков А.Р. и Босов А.В. (1996). Алгоритмы управления в системах с переключающимися
каналами наблюдения // Изв. РАН. Теория и системы управления. N2. С.98-103.
Панков А.Р. и Босов А.В. (1997). Алгоритмы управления для дискретных систем случайной
структуры // Автоматика и телемеханика. N10. С.113-125.
Пейн X. и Сильверман Л. ( Payne H.J., Silverman L.M. 1974). On the discrete-time algebraic
riccatic equation // IEEE Trans. Automat. Control. V.AC-18. N2. P.226-234.
Прохоров М.Б. и Саулъев В.A. (1977). Метод оптимальной фильтрации Калмана-Бьюси и
его обобщения // В кн. Математический анализ (итоги науки и техники).-М.: ВИНИТИ
АН СССР. Т.14. С.167-207.
Пугачев В.С. (1957, 1960, 1962). Теория случайных функций и ее приложения к задачам
автоматического управления. -М.: Наука.
Пугачев В.С. (19626, 1966, 1974г). Основы автоматического управления. -М.: Наука. 1-3-е
изд.
Пугачев В.С. (1978). Оценивание переменных и параметров в стохастических системах,
описываемых дифференциальными уравнениями // Докл. АН СССР. Т.241. N5. С. 1031-
1034.
Пугачев В. С. (1979а). Оценивание состояния и параметров непрерывных нелинейных систем
// Автоматика и телемеханика. N6. С.63-79.
Пугачев В.С. (19796, 2002). Теория вероятностей и математическая статистика. -М.: Наука
[Англ. пер. Probability Theory and Mathemetical Statistics. Oxford, Pregamon Press, 1984].
626
Список литературы
Пугачев В.С. (Pugachev V.S. 1980). Estimation of Markov processes // In: Time Series Pro-
ceedings of the International Conference. Nottingham, March 1979. Amsterdam etc.: North
Holland. P.389-400.
Пугачев B.C. ^Pugachev V.S. 1981). The finite-dimensional distributions of a random process
determined by a stochastic differential equation and their application to control problems //
Пробл. упр. и теории информ. V.10. N2. P.95-114.
Пугачев B.C. (Pugachev V.S. 1982a). Conditionally optimal estimation in stochastic differential
systems // Automatica. V.18. N6. P.685-696.
Пугачев B.C. (19826). Обобщение теории условно оптимального оценивания и экстраполя-
ции // Докл. АН СССР. Т.262. N3. С.535-538.
Пугачев В. С. (1984). Условно оптимальная фильтрация и экстраполяция непрерывных про-
цессов // Автоматика и телемеханика. N2. С.82-89.
Пугачев В.С. (1996). Лекции по функциональному анализу. - М.: Изд. МАИ.
Пугачев В.С., Синицын И.Н. (1985). Направления развития теории условно оптимальной
фильтрации // В кн. “Перспективные методы планирования и анализа экспериментов
при исследовании случайных полей и процессов”. Тез. докл. II Всесоюзн. Конф. Сева-
стополь, 2-4 октября 1985 г. -М.: 4.1. С.168-170.
Пугачев В.С., Синицын И.Н. (1985, 1990). Стохастические дифференциальные системы.
Анализ и фильтрация. - М.: Наука, 1 и 2-е изд. [Англ, пер.: Stochastic Differential
Systems. Analysis and Filtering. - Chichester, New York: John Wiley, 1987].
Пугачев B.C., Синицын И.Н. (1986). Направления развития математического обеспечения
для исследования стохастических систем //В кн. Информатика: проблемы, перспективы.
- М.: Наука. С.30-38.
Пугачев В.С., Синицын И.Н. (1989). Современное состояние и перспективы развития ма-
тематического обеспечения для исследования стохастических систем // Тез. докл. Все-
союзного совещания “Проблемы управления-89”. Ташкент. Т.1. С.504-505.
Пугачев В.С., Синицын И.Н. (1991) (Ред.). Принципы разработки интеллектуализирован-
ных ППП для построения условно оптимальных фильтров. Пакет прикладных программ
“СтС-Фильтр” // Г.К.Алдушин, Р.Н.Бабкина, В.Ф.Бурлака, В.Ю.Вигдерович, Б.И.Тер-
щиков, Э.Р.Корепанов, О.А.Куленко, В.С.Пугачев, В.И.Синицын, И.Н.Синицын,
А.П.Хатунцев. В.И.Шин. Препринт. - М.: ИПИ АН СССР.
Пугачев В.С., Синицын И.Н. (1993). Стохастические системы. Теория и программное обес-
печение // Юбилейный сборник трудов институтов Отделения информатики, вычисли-
тельной техники и автоматизации РАН. - М.: Т. 1. С.75-93.
Пугачев В.С., Синицын И.Н. (1994). Прикладные методы анализа стохастических систем
// Вестник МАИ. NI. С.39-47.
Пугачев В.С., Синицын И.Н., Хатунцев А.П., Шин В.И., Корепанов Э.Р., Синицын В.И.
(1992). Проблемы разработки математического обеспечения для проектирвоания дискрет-
ных условно оптимальных фильтров // В кн. Системы и средства информатики. -М.:
Наука. Вып.З. С.3-19.
Список литературы
627
Пугачев В.С., Синицын И.Н., Хатунцев А.П., Шин В.И., Корепанов Э.Р., Синицын В.И.
(1992). Математическое обеспечение для проектирования условно оптимальных фильтров
и анализа процессов в дискретных стохастических системах // Автоматика и телемеха-
ника. N6. С.78-85.
Пугачев В.С., Синицын И.Н., Чередниченко А. А., Шин В.И., Синицын В.И. (1991). Ма-
тематическое обеспечение для анализа многомерных нелинейных стохастических систем
// Автоматика и телемеханика. Nl, С.87-97.
Пугачев В.С., Синицын И.Н., Шин В.И. (Pugachev V.S., Sinitsyn I.N., Shin В.I. 1986).
Problems of analysis and on-line conditionally optimal filtering of processes in nonlinear sto-
chastic systems // Second IFAC Symposium on Stochastic Control, Vil’nius, USSR, 19-23 May
1986. Moscow. Preprints. Part 1. P.4-18.
Пугачев B.C., Синицын И.И., Шин В.И. (1987). Проблемы анализа условно оптималь-
ной фильтрации в реальном масштабе времени процессов в нелинейных стохастических
системах // Автоматика и телемеханика. N12. С.3-24.
Раол Дж. и Синха Н. (Raol J.R., Sinha N.K. 1986). On Pugachev’s filtering theory for
stochastic nonlinear systems // Second IFAC Symposium on Stochastic Control - Reprints. -
Vilnius. USSR, May 1986. Part 1. P.195-200.
Раол Дж. и Синха Н. (Raol J.R., Sinha N.K. 1986). A nonlinear filter for estimation of
state of a continuous-time systems with discrete measurements // Second IFAC Symposium
on Stochastic Control - Reprints. - Vilnius. USSR, May 1986. Part 1. P.211-216.
Ройтенберг Я.Н. (1978, 1992). Автоматическое управление. -M.: Наука. Гл. ред. физ. мат.
лит.
Руденко Е.А. (1988). Оптимальные дискретные конечномерные алгоритмы идентификации
состояния и параметров движущихся объектов при дискретных измерениях // Теория и
методы идентификации и управления движущимися объектами: Тем. сб. науч. тр. МАИ.
-М.: Изд. МАИ. С.43-52.
Руденко Е.А. (1990). Оптимальная структура дискретных нелинейных фильтров произ-
вольного порядка // Статистические методы в теории управления ЛА: Тем. сб. науч. тр.
МАИ. —М.: Изд. МАИ. С.53-60.
Руденко Е.А. (1991). Адаптивный дискретный нелинейный фильтр для реализации на борту
ЛА // Управление и навигация ЛА в условиях параметрических неопределенности: Тем.
сб. науч. тр. МАИ. -М.: Изд. МАИ. С.23-30.
Руденко Е.А. (1992). Оптимальная структура дискретных алгоритмов конечно-мерной
непрерывно-дискретной нелинейной фильтрации при марковских помехах // Оптимиза-
ция алгоритмов обработки информации и управления: Тем. сб. науч. тр. МАИ. -М.:
Изд. МАИ. С.62-70.
Румгарт П. и Сонг Т. (Ruymgaart Р.А., Soong Т.Т. 1988). Mathematics of Kalman-Bucy
Filtering. Springer-Verlag, Berlin.
Свешников A.A. (1961). Прикладные методы теории случайных функций. - Л.: Судпром-
гиз.
628
Список литературы
Сейдж Э. и Меле Дэю. (1976). Теория оценивания и ее применение в связи и управлении.
-М.: Связь.
Серебровский А.П. (1975). О регуляризации дискретного фильтра Калмана // Автоматика
и телемеханика. N3. С.70-74.
Силуянова И.Д. (1982). The finite-dimensional distributions of the outputs of one class of
nonlinear systems // Пробл. упр. и теории информ. V.ll. N6. P.407-418.
Синицын В. И. (1992). Метод эллипсоидальной аппроксимации в задачах анализа и филь-
трации процессов в стохастических системах // Системы и средства информатики. - М.:
Наука. Вып.2. С. 154-160.
Синицын И.Н. (1986). Stochastic hereditary control systems // Пробл. упр. и теории информ.
V.15. N4. Р.287-298.
Синицын И.Н. ( Sinitsyn I.N. (1990). Problems of signal analysis and conditionally optimal
processing in stochastic differential systems // Proceedings: Latvian Signal Processing Inter-
national Conference, Riga. V.2. P.60-64.
Синицын И.Н. ( Sinitsyn LN. 1991). Ill Problems of on-line conditionally optimal filtering //
Ill-posed Problems in Natural Sciences: Proceedings of the international Conferrence, Moscow
August, 19—25, 1991. eds F.N.Tilhonov et al. - Utercht. VSP. Moscow: TVP Sci Publ.
P.174-183.
Синицын И.Н. (1993). Конечномерные распределения с инвариантной мерой в стохастиче-
ских механических системах // Докл. АН СССР. Т.238. N3. С.308-310.
Синицын И.Н. ( Sinitsyn I.N. 1995). Parallel simulation technologies for stochastic systems //
In Lectures Notes in Computer Science, 1277. Parallel Computing Technologies, 4th Intern.
Conf., PACT-97, Proceedings. Springer. P.383-388.
Синицын И.Н. (1996). Из опыта преподавания статистических основ информатики в тех-
нических университетах //В кн. Системы и средства информатики. Спец, вып., по-
священный П-му международному конгрессу ЮНЕСКО “Образование и информатика”.
-М.: Наука. Физ.мат.лит. Вып.8. С.68-73.
Синицын И.Н. (1997). Условно оптимальная фильтрация и распознавание сигналов в стоха-
стических дифференциальных системах // Автоматика и телемеханика. N3. С. 124-130.
Синицын И.Н. и Карпенко А.П. (Sinitsyn I.N., Karpenko А.Р. 1996). Combined parallel
statistical and analysis modeling methods, algorithms and software for dynamical stochastic
systems research // Proceedings of EUROSIM 10996 International Conference. L.Dekker,
W.Smit and J.C.Zuidervaat (editors). Elsevier Science B.V. P.187-194.
Синицын И.Н., Карпенко А.П., Чередничено, Корепанов Э.Р. (1989). Диалоговый ком-
плекс для исследвоания и моделирования стохастических систем на базе ПЭВМ //В
сб. трудов 3-й Всесоюзной школы “Прикладные проблемы управления макросистемами”,
Апатиты. -М.: Изд. ВНИИСИ. С.237-239.
Синицын И.Н. и Корепанов Э.Р. (1995). Теория и программное обеспечение условно опти-
мальной фильтрации и распознавания сигналов в стохастических системах // Тезд докл.
Список литературы
629
2-й Всероссийской конференции “Распознавание образов анализ изображений: новые ин-
формационные технологии” (РОАИ-2-95). Ульяновск. Часть 2. С.8-9.
Синицын И.Н., Корепанов Э.Р., Шин В.И (Sinitsyn I.N., Korepanov E.R., Shin V.I. 1998).
Methods, algorithms and software tools for CAE of stochastic control systems // Proceedings
EUROSIM’98 Congress, Helsinki university of Technology, Espoo, Finland, April 14-15, 1998.
P.200-205.
Синицын И.Н., Маишева Е.Ю., Корепанов Э.Р., Мощук Н.К., Огнева О.С., Синицын
В.И., Шин В.И., Хатунцев А.П. (1991). Программные средства для анализа и модели-
рования случайных процессов, проектирования фильтров и идентификаторов на ПЭВМ
// Тез. докл. IV Всесоюзной научно-технической конференции “Перспективные методы
планирования и анализа экспериментов при исследовании случайных полей и процессов”.
Петрозаводск, сентябрь, 1991. -М.: Изд. МЭИ. С.82-83.
Синицын И.Н., Мощук Н.К., Шин В.И. (1993). Условно оптимальная фильтрация в сто-
хастических дифференциальных системах по бейесовым критериям // ДАН. Т.ЗЗО. N4.
С.436-439.
Синицын И.Н., Петрова Е.В., Шин В.И. (1988). Алгоритмическое и программное обеспе-
чение для фильтрации случайных процессов с использованием ПЭВМ // Тез. докл. 3-го
межведомственного семинара по актуальным вопросам вычислительной техники и инфор-
матики “Электронный офис для научных исследований”, Москва. ИАЭ им.Курчатова.
С.20-23.
Синицын И.Н., Синицын В.И., Корепанов Э.Р., Белоусов В.В., Ильясов Д.Ф., Ушмаев
О. С. (2003). Субоптимальные обучающиеся информационные технологии и системы //
Материалы межрегиональной научно-технической конференции “Интеллектуальные ин-
формационные системы” (Интеллект - 2003). Тула. Изд. Тульского государственного
университета. С.25-27.
Синицын И.Н., Синицын В.И., Корепанов Э.Р., Белоусов В.В. (2004а). Современное мето-
дическое и программное обеспечение анализа качества и моделирования стохастических
систем управления // Труды III международной конференции “Идентификация систем и
задачи управления” (SICPRO’04). CD-ROM. С.17-43.
Синицын И.Н., Синицын В.И., Корепанов Э.Р., Белоусов В.В. (20046). Информационные
технологии синтеза параметризованных фильтров Пугачева. -М.: Наукоемкие техноло-
гии. N7. С.50-79.
Синицын И.Н., Синицын В.И., Степанов А.М., Ушмаев О.С. (2003). Проблемы реали-
зации вычислительных методов обработки и анализа сигналов и изображений на архи-
тектурах с ассоциативной памятью // Труды 1-й Всероссийской конференции “Методы и
средства обработки информации”. -М.: Изд. МГУ им.М.В.Ломоносова. С.137-141.
Синицын И.Н., Степанов А.М., Ушмаев О.С. (2004). Проблемы синтеза фильтров и иден-
тификаторов с ассоциативной памятью // Труды III международной конференции “Иден-
тификация систем и проблемы управления” (SICPRO’04) CD-ROM.ISBN5-201-14966-9.
С.1896-1911.
630
Список литературы
Синицын И.Н. и Шин В.И. (1991). Условно оптимальная фильтрация процессов в стоха-
стических дифференциальных системах по сложным статистическим критериям // Докл.
АН СССР. Т.320. N4. С.813-817.
Синицын И.Н., Шин В.И., Корепанов Э.Р. (1993). Теория условно оптимальной фильтра-
ции стохастических процессов по сложным статистическим критериям //В кн. “Системы
и средства информатики”. Ежегодник. -М.: Наука. Вып.5. С.106-120.
Синицын И.Н. и Шин В.И. (1994). Условно оптимальная интерполяция случайных после-
довательностей, определяемых разностными уравнениями // ДАН. Т.336. N4. С.453-456.
Синицын И.Н. и Шин В.И. (1998). Распознавание процессов, определяемых стохастически-
ми дифференциальными уравнениями // ДАН. Т.359. N2. С. 1-5.
Синицын И.Н., Шин В.И., О М. (Sinitsyn, I.N., Shin, V.I. and Myoungho Oh 1997). Услов-
но оптимальная интерполяция случайных процессов с фиксированной точкой в стохасти-
ческих дифференциальных системах // Автоматика и телемеханика. N2. С.224-233.
Соренсон X. (Sorenson H.W. (ред.) 1985). Kalman filtering: Theory and Application. New
York: IEEE Press.
Стратонович P.JI. (1966). Условные марковсккие процессы и их применение к теории оп-
тимального управления. -ML: Изд. МГУ.
Тихонов В.И. и Миронов М.А. (1977). Марковские процессы. - М.: “Советское радио”.
У онхэм М. ( Wonham М. 1965). Some application of stochastic differential equations to opti-
mal nonlinear filtering // J.Soc. Industr. Appl. Math. Control. V.2. P.347-369.
Фильтр Калмана. Применения (1983). Special Issue on applications of Kalman filters of
IEEE Trans. On Autom. Control. 28(3).
Фильтр Калмана. Программное обеспечение (1984). Kalman Filtering Software: User’s
Guide, Optimization Software. Inc. New York.
Фишер И. ( Fisher I.R. 1967). Optimal nonlinear filtering // Advances in Control Systems.
Theory and Applications (ed. Leondes C.T.). V.5. P. 199-300. New York, London: Academic
Press.
Хайкин C. (Haykin S. 2000). Unsupervised Adaptive Filtering. Vol 1; Blind Source Separation.
Vol 2: Blind Deconvolution. John Wiley & Sons. New York.
Хайкин C. (Haykin S. 2001). Kalman Filtering and Neural Networks. New York. John Wiley
& Sons.
Харвэй A. (Harvey A.C. (1989). Forecasting, Structural Time Series Models and the Kalman
Filter. Cambridge University Press. Cambridge. UK.
Хоанг С., Нгуен T, Баралле P., Талагранд О. (Hoang S., Nguyen T.L., В arail le R., Tala-
grand O. 1997a). Approximation approach for nonlinear filtering problem with time dependent
noises. Part 1: Conditionally optimal filter in the minimum mean square sense // Kybernetika
V.33. N4. P.409-425.
Хоанг С., Нгуен T, Баралле P., Талагранд О. (Hoang S., Nguyen T.L., Baraille R., Tala-
grand O. 19976). Approximation approach for nonlinear filtering problem with time dependent
noises. Part II: Stable nonlinear filters // Kybernetika V.33. N5. P.557-576.
Список литературы
631
Я.андрасекхар С. (s. Chandrasekhar 1943). Stochastic Problems in Physics and Astronomy //
Reviews of Modern Physics. V.l5. Nl. P.1-89. [Рус. пер.: Стохастические проблемы в
физике и астрономии. - М.: ИЛ, 1947].
Чен X. (Chen H.F. 1985) Recursive Estimation and Control for Stochastic Systems. John Wiley
& Sons. New York.
Чен X. и Чу C. (Chen H.F., Chui С.К. 1991). A modified adaptive Kalman filter for real-time
applications // IEEE Trans, on Aero. Electr. Sys.27. P. 149-154.
Черноусъко Ф.Л. и Колмогоров В.Б. (1978). Оптимальное управление при случайных воз-
мущениях. -М.: Наука.
Чу С. и Чен X. (Chui С.К., Chen H.F. 1987). Kalman Filtering with Real-Time Applications.
Springer-Verlag. New York.
Чой В. и Шин В. И. (1999). Точные уравнения оптимальной нелинейной фильтрации для
одного класса билинейных систем // Автоматика и телемеханика. N8. С.114-126.
Шатин А.С. (1994). Программная реализация теории условно оптимальной фильтрации и
условно оптимального управления в задачах анализа и синтеза линейных стохастических
управляемых систем // Техническая кибернетика. N4. С.64-70.
Шайкин М.Е. и Шин В.И. (2001). Декомпозиции нелинейных стохастических дифферен-
циальных систем // Автоматика и телемеханика. N3. С.409-421.
Шин В.И. (Shin,V.I. 1995) Statistical analysis and suboptimal filtering of random processes
in nonlinear stochastic systems // Intern. Workshop on Advanced Electronics Technology-95,
Moscow, Russia. P. 11-15.
Шин В.И. (Shin V.l. 1995) Statistical analysis and filtering of processes in nonlinear stochastic
systems // The Korean Mathematical Society, Seoul, Korea, vol. 32, Nl, P.4-8, April, 1995.
Шин В.И. (1998). Фильтры Пугачева для комплексной обработки информации // Автома-
тика и телемеханика. Nil. С. 195-206.
Шин В.И. и Шевляков Г. (Shin V.l. and G. Shevlyakov 2004). An Optimal Mean Square
Combination of Estimates with Application to Filtering Problems // Proc. 7th International
Conf, on Pattern Recognition and Image Analysis (PRIA-7-2004). St.Petersburg, Russia.
V.2. P. 394-397.
Язвинский A.(jazwinski A.H. 1970). Stochastic Processes and Filtering Theory. New York:
Academic Press.
предметный указатель
Агрегирование 28
Анализ стохастический 109
Апостериорная характеристическая
функция 248
— математическое ожидание 250
---ковариационная матрица 253
---момент второго порядка 251
— плотность 249
Биортогональная система 91
Биортонормальная система 294
Вероятностная мера 55, 67
Вероятностное пространство 54
Вероятность 53
— в бесконечных произведениях-
пространств 65
— в конечных произведениях про-
странств 60
— событий, связанных со случайной
функцией 77
— условная 56
Вход системы 15
Выход системы 15
Вычислительная техника 619
Годограф 30
Граф 28
Двойственность (дуальность) 47
Дельта-функция (J-функция) 35
Дифференциал стохастический
Ито 139
— Стратоновича 136
— в- дифференциал 135
Длительность импульса 34
Идентификация 240
Идентифицируемость 52
Интеграл
— по мере неслучайной 115
— по мере случайной 118
— средний квадратический (с.к.) 109
— стохастический 121
-----Ито 121
-----общий (^-интеграл) 130
-----симметризованный
(Стратоновича) 130
Интегрирование
— по неслучайной мере 115
— по случайной мере 118
— численное стохастических уравне-
ний 144
Интерполяция 242,540
— оптимальная 294
— прямая (с фиксированной точкой)
242, 540
— обратная (с фиксированным интер-
валом) 242, 540
— с фиксированной задержкой 292,
540
Интерполятор условно оптимальный
-----прямой 540
— с фиксированной задержкой 541
— обратный 542
Информационная технология 618, 619
Квазимомент 91, 96
Ковариационная функция 83
Ковариационный оператор 84
Критерий минимума с.к.о. 579
— максимума отношения сигнал/
шум 579
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
633
— максимума вероятности невыхода
ошибки допусков 579
— парето 443
Кумулянт (семиинвариант) 96
Лемма Лоэва
Линеаризация статистическая 181
--- эквивалентная 175
]\4^атематическая модель системы 15,
16
Математическое ожидание
случайной величины 78
Мера вероятностная 54, 55
Метод квазимоментов 193
— моментов (ММ) 182
— нормальной (гауссовской)
аппроксимации (МНА) 175
— ортогональных разложений 193
— эллипсоидальной аппроксима-
ции 205,206
Метод статистической линеари-
зации Бутона 181
-------Казакова 181
— формирующих фильтров 141
— частотных характеристик 24
— Эйлера 144
— эллипсоидальной аппрок-
симации (МЭА) 203
— эллипсоидальной линеариза-
ции 203
Модель системы дискретная 17
---непрерывная 16
— детерминированной системы 16
Модуляция амплитудно-
импульсная (АИМ) 34
— временная импульсная (ВИМ) 35
— широтно-импульсная
(ШИМ) 34
Момент начальный второго
порядка 80
— условный 103
— порядка Т1 86
— смешанный 86
— центральный второго порядка 80
---порядка Т1 86
---смешанный 86
Наблюдаемость 46
— вполне 48
— неполная 50
— полная 46
— равномерная вполне 48
Нормальное (гауссовское)
распределение 74
Оператор 17
— детерминированной системы 17
— ковариационный 81
---взаимный 85
— математического ожида-
ния 79
— момента второго порядка 81
---------взаимный 81
— системы 17
— стохастической системы 17
Оценивание 237
— адаптивное 336
— априорное 417
— оптимальное 237
— субоптимальное 371
— условно оптимальное 336
Параметризация распределе-
ния 182
— структурная 203
Переменные состояния системы 15
Период повторения 34
634
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Полиномы биортонормальные сог-
ласованные 91, 92
— Эрмита 95
Помеха 271
— автокоррелированная 271
— вырожденная 434
— коррелированная 271
Потери 572
Поток пуассоновский 231
Преобразование 28
— Лапласа 268
— линейное 314
— структурных линейных систем 28
Преобразователь линейный 28
— функциональный 28
Программное обеспечение 67, 618, 619
Пространство 16
— вероятностное 53
— входных сигналов 16
— выходных сигналов 16
— состояний 16
— фазовое (реализаций) 56
— элементарных событий 53
Процесс случайный 70
--- винеровский 111
---марковский 70
---обновляющий 261
---общий пуассоновский 112, 113
---простой пуассоновский 112, 113
---пуассоновский 112, 113
-------стандартный 112, 113
-------с независимыми прираще-
ниями 123
-------с некоррелированными
приращениями 111
Разложение ортогональное 91
— согласованное ортогональное 100
Распределение процессов 137
— ненормированное 298
— 71-мерное 145
Распознавание 329
— адаптивное 426
— оптимальное 330
Связь 28
— обратная 27
---гибкая (жесткая) 27
---отрицательная (положи-
тельная) 27
Семиинвариант (куму-
лянт) 91
Сигнал входной 15
— выходной 15
Система 15
— дискретная (импульсная) 17
— дифференциальная 21
---линейная 19, 25
— непрерывная 17
— стационарная 23
---физически возможная 18
Скважность импульсвного элемента 34
Случайная величина 53, 55
— функция 53
Событие 53
— элементарное 53
Соединение 26
— параллельное 27
— последовательное 27
— систем 26
Состояние системы 15
Стохастический анализ 109
Стохастическая система 16
--- билинейная 33
---дискретная 33, 44
---дифференциальная 31
--- линейная 32
---с параметрическими
шумами 33
Структура 27
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
635
Суперпозиции принцип 19
Структурная функция фильтра Пуга-
чева 440
Теория стохастических систем 15
— линейных 156
— спектрально-корреляционная 156
— общая 163
— нелинейная 169
Управляемость 45
— неполная 50
— полная 46
Уравнение
— Винера-Хопфа 369
— разностное 44
— Риккати 268
— сопряженное 49
— стохастическое дифферен-
циальное 137
--------Ито 138
Условная вероятность 56
-----регулярная 58
Условный момент 103
— оператор момента 109
Устойчивость 18, 115
— асимптотическая 19
— в данном режиме 19
— в среднем 19
— в среднем квадратическом
(с.к. устойчивость) 19
— в р-среднем 19
— почти наверное (п.н. устой-
чивость) 19
Формула Ито 133
-----обобщенная 134
Фундаментальная матрица
системы 47
Функционал характеристический 286
Функционирование 16
Функция весовая 22
— передаточная стационарной систе-
мы 23
Фильтр
— адаптивный 419
— Винера 268
— второго порядка 412
— гауссов 416
— допустимый 439
— квазилинейный 429
— оптимальный по сложному стати-
стическому критерию 579
-----по бейесовому критерию 571
— первого порядка 410
— с памятью 593, 596, 597
— с.к. оптимальный 437
— формирующий 141
— эллипсоидальный субоптимальный
546, 563
-----условно оптимальный 565
Фильтры Калмана (ФК) 237, 308
— адаптивный Калмана-Лайниотиса
329, 336
— адаптивный обобщенный Калмана
(АОФК) 418
— итерационный обобщенный фильтр
Калмана 597
— Калмана по бейесовому крите-
рию 583
— Калмана по сложному статистиче-
скому критерию 583
— Калмана-Бьюси 263, 266, 267
— Калмана-Бьюси по бейесовому
критерию 577
— Калмана-Бьюси по сложному ста-
тистическому критерию 582
— обобщенный Калмана (ОФК) 371,
409
— обобщенный Калмана-Бьюси 409
636
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
— согласованные 351
Фильтры Пугачева (условно оптималь-
ные) 437
— дискретные линейные 529
— дискретные нелинейные 520, 526
— линейные 475, 486
— нелинейные 476
— нелинейные при автокоррелиро-
ванной помехе 492
— с памятью 593, 596, 597
— эллипсоидальные дискретные 569
— эллипсоидальные непрерывные 565
Фурье интеграл 24
— преобразование 25
Характеристика амплитудно-
фазовая (годограф) 30
— импульсного элемента 35
— частотная 24
-----стационарной линейной систе-
мы 24
Характеристический функционал 88
Характеристическая функция 88
Цилиндр 69
— с измеримым основанием 69
Частота повторение импульсов 34
Шум белый 141
-----в строгом смысле 142
— некоррелированный 308
— автокоррелированный 314
----нормально распреде-
ленный 142
Эджуорта ряд 17
Экстраполяция 240
— дискретная с.к. оптимальная ли-
нейная 316
— с.к. оптимальная линейная 290
— условно с.к. оптимальная 498, 504
— условно с.к. оптимальная линей-
ная 509, 514
Электронно вычислительная маши-
на (ЭВМ) 17
— персональная ЭВМ (ПЭВМ) 616,
619
Элемент импульсный 34
Эллипсоидальный экстраполятор 569
— субоптимальный 552
— условно оптимальный 569
----модифицированный 569, 570
Эллипсоидальная аппроксимация (ЭА)
— многомерных распреде-
лений 206
— одномерных распреде-
лений 205
Эллипсоидальный фильтр
— субоптимальный 546
----модифицированный 552
— условно оптимальный 565, 569
----модифицированный 569
Эрланговский поток 332
Эрмита полиномы 95
Научное издание
Игорь Николаевич Синицын
Фильтры Калмана и Пугачева
Монография
Редактор НА. Власова
Переплет Т.Ю. Хрычевой
Компьютерная верстка Е.Н. Федотовой
Подписано в печать 07.11.2005. Формат 60x90/16
Печать офсетная. Бумага офсетная. Печ. л. 40,0
Тираж 1000 экз. Заказ № 6630
По вопросам приобретения литературы
обращаться по адресу:
105318, Москва, Измайловское ш., 4
Тел./факс: (095) 369-5819, 369-5668, 369-7727
Электронная почта: universitas@mail.ru
Дополнительная информация на сайте:
http://logosbook.ru
Издательская группа «Логос»
105318, Москва, Измайловское ш., 4
Отпечатано в полном соответствии с качеством
предоставленных диапозитивов
в ОАО «ИПК «Ульяновский Дом печати»
432980, г. Ульяновск, ул. Гончарова, 14