Автор: Неганов В.А. Яровой Г.П. Табаков Д.П.
Теги: электротехника общая радиотехника электроника антенны свч
ISBN: 978-5-88070-222-0
Год: 2009
Текст
Неганов В.А., Табаков Д.П., Яровой Т.П.
Современная теория
и практические применения
антенн
Под редакцией
Неганова В. А.
Издательство «Радиотехника»
Москва, 2009
УДК 621.396.67
ББК 32.845
Н41
Рецензенты:
С.Б. Раевский (Нижегородский технический университет)
Ю.Б. Нечаев (Воронежский государственный университет)
Неганов В.А., Табаков Д.П., Яровой Г.П.
Н41 Современная теория и практические применения антенн. / Предисловие
академика Ю.В. Гуляева, под ред. В.А. Неганова. — М.: Радиотехника, 2009.
— 720 с.: ил.
ISBN 978-5-88070-222-0
Рассмотрены основные разделы теории и техники антенн. Освещены
вопросы расчета и построения различных типов антенн (от вибраторных до
рупорных и антенных решеток, включая фазированные). Основное внимание
уделено антеннам СВЧ и расчетам их электромагнитных полей в ближней
зоне, т.е. вопросам электромагнитной совместимости.
Принципиальное отличие книги от известных заключается в последова-
тельном применении метода физической регуляризации (самосогласованного
метода) к расчету электромагнитного поля антен, позволяющего осуществлять
непрерывный переход с излучающей поверхности антенны к пространству
вне ее. С помощью самосогласованного метода получены новые результаты
по теории антенн: установлены связь между поверхностной плотностью
тока на вибраторной антенне и напряженностью электромагнитного поля,
однонаправленный режим излучения для кольцевой (рамочной антенны),
режимы стоячих и бегущих волн в цилиндрической спиральной антенне,
входное сопротивление практически для всех типов антенн. Теоретический
материал подкреплен примерами применения многолучевых антенн.
Предназначено для разработчиков антенно-фидерных устройств,
аспирантов и докторантов, занимающихся вопросами проектирования
антенных систем различного назначения, студентов радиотехнических
специальностей высших учебных заведений.
УДК 621.396.67
ББК 32.845
ISBN 978-5-88070-222-0
© Радиотехника, 2009
© Неганов В.А., Табаков Д.П., Яровой Г.П., 2009
Предисловие
Основным недостатком практически всей литературы по антеннам является
некорректное описание электромагнитного поля в ближней зоне антенн. Например,
для вибраторных антенн отсутствует связь между током проводимости и напря-
женностями электрического и магнитного полей излучения. Поэтому в литературе
даже появились работы, ставящие под сомнение уравнения Максвелла. Негановым
В.А. разработан метод физической регуляризации некорректно поставленных по
Адамару электродинамических задач (иногда он называется самосогласованным
методом) [1]. Суть метода заключается в записи сингулярных интегральных пред-
ставлений (СИП) электромагнитного поля, позволяющих осуществлять непрерыв-
ный переход от напряженностей электромагнитного поля излучения к поверхнос-
тному току проводимости на антенне. Таким образом удовлетворяются граничные
условия электродинамики, устанавливающие связь между токами и напряжен-
ностями электрического и магнитного полей. Из СИП, записанных для самосо-
гласованных физической и математической моделей задачи, легко получаются
сингулярные интегральные уравнения (СИУ) относительно токов на поверхности
антенн. Таким образом, подход позволяет устранять некорректные формулировки
краевых задач для антенн в виде интегральных уравнений Фредгольма перво-
го рода. Метод физической регуляризации позволил выявить ряд новых свойств
электромагнитного поля: на примере вибраторной антенны показано, что в про-
межуточной зоне электромагнитное поле не является чисто поперечным; уста-
новлены условия однонаправленного режима излучения для кольцевой (рамоч-
ной) антенны; установлены условия возникновения режимов стоячих, бегущих
и смешанных волн в цилиндрической спиральной антенне; определены входные
сопротивления для многих типов антенн. Одна из основных идей книги - разумное
использование приближений в физических моделях. Например, тонкопроволоч-
ное приближение для вибраторной антенны приводит к интегральному уравне-
нию Фредгольма первого рода (интегральные уравнения Поклингтона и Халлена),
а модель вибраторной антенны в виде идеально проводящей полой трубки - к СИУ
с гиперсингулярным ядром.
Другая особенность книги - сведение задач дифракции к СИУ. В частности,
решена задача дифракции плоской электромагнитной волны на разомкнутом иде-
ально проводящем кольце, представляющем собой киральный элемент, что поз-
волило получить новое конформное малоотражающее покрытие объектов.
Надеюсь, что книга даст новый надежный математический аппарат для оценки
антенн с точки зрения их электромагнитной совместимости и электромагнитной
экологии.
1. Неганов В.А. Физическая регуляризация некорректных задач электродинами-
ки. — М.: «Сайнс — Пресс», 2008.
Академик РАН
Ю.В. Гуляев
Предисловие авторов
В последнее время не ощущается недостатка в литературе по антеннам. Вслед
за книгой В.В. Татаринова [90] в 1936 году вышел целый ряд книг по антенно
- фидерным устройствам. Появились систематические курсы А.А. Пистолькорса
[122, 88], С.И. Надененко [103], Г.Т. Маркова [69], А.Л. Драбкина и В.Л. Зузенко
[105,10], А.З. Фрадина [74], А.С. Никольского [124], Д.И. Воскресенского [95, 112,
102] и др. В последнее время появились учебники Д.М. Сазонова [2] под редакцией
Г.А. Ерохина [27], под редакцией Д.И. Воскресенского [3,4], а также монографии
В.Ф. Кравченко [58—60].
Основной недостаток практически всей литературы по антенно — фидерным
устройствам - некорректное описание электромагнитного поля в ближней зоне
антенн. Например, для вибраторных антенн отсутствует связь между током про-
водимости на антенне и напряженностями электрического и магнитного полей. В
результате даже появились работы [15], ставящие под сомнение уравнения Мак-
свелла. Практически все результаты, приведенные в литературе, справедливы
только для дальней зоны антенн. Поэтому в книге обращено особое внимание на
проблему вычисления электромагнитных полей (ЭМП) в ближней зоне излучаю-
щих структур, которая является основой в задачах электромагнитной совмести-
мости. В учебной и даже научной литературе эта проблема ранее практически не
рассматривалась: считалось, что математический аппарат, использующий интег-
ральные соотношения с традиционно регулярными функциями Грина, и мощные
ЭВМ позволяют определить ЭМП в любой точке пространства, в том числе и в не-
посредственной близости от антенны. Другой недостаток связан с формулировкой
краевых задач для антенн в виде интегральных уравнений Фредгольма первого
рода. В этом случае возникают некорректно поставленные задачи по Адамару
задачи [7]. Один из авторов книги, В.А. Неганов, ввел в электродинамику понятие
самосогласованной физической и математической моделей задач [13]. Оказалось,
что только для такой физической модели, использующей самосогласованный ме-
тод, включающий в себя сингулярные интегральные представления (СИП) ЭМП,
содержащие обобщенные функции и сингулярные интегральные уравнения (СИУ)
для определения ЭМП на поверхности излучающей структуры, можно корректно
определить ЭМП в ближней зоне. В книге на примерах электрического вибратора,
рамочной и цилиндрической спиральной антенн показана суть проблемы. В час-
тности, введение для вибраторной антенны физической модели в виде идеально
проводящей полой трубки, диаметр которой обязательно имеет конечное значе-
ние, приводит краевую задачу для антенны к СИУ с гиперсингулярным ядром.
Поэтому при использовании самосогласованного метода (метода физической регу-
ляризации) указанные выше проблемы не возникают.
Метод физической регуляризации удобен и для решения задач дифракции
электромагнитных волн. В частности, решена задача дифракции плоской электро-
магнитной волны на разомкнутом идеально проводящем кольце, представляющем
собой киральный элемент [129], что позволило предложить новое конформное ма-
лоотражающее покрытие объектов.
Что касается учебников [2,3,4,27], то в них опущен некоторый важный, с на-
шей точки зрения, материал, подробно описанный в [17], [18]. Поэтому в кни-
Современная теория и практические прилипилшя QJWMiHH 5
ге применительно к дальней зоне подробно излагается материал, изложенный
в [17, 18] (которые в настоящее время трудно найти) с учетом новых результатов
[2, 3]. Ближняя зона антенн в книге описывается с помощью СИУ (метод физичес-
кой регуляризации)
Книга написана на основе прочитанных авторами курсов лекций в Поволжском
государственном университете телекоммуникаций и информатики и Самарском
государственном университете.
Авторы выражают благодарность своим ученикам за помощь в проведении от-
дельных совместных исследований и численных расчетов на ЭВМ: кандидатам
физико — математических наук И.В. Матвееву и А.А. Сарычеву.
Авторы благодарны аспиранту И.М. Градинарю за верстку книги, аспирантам
А.А. Вороному, Ю.В. Соколовой, Т.А. Панферовой, М.И. Лемжину за помощь при
оформлении рукописи книги.
Авторы благодарны проф. С.Б. Раевскому (Нижегородский государственный
технический университет) и проф. Ю.Б. Нечаеву (Воронежский государственный
университет) за рецензирование книги, советы и ценные замечания, способствую-
щие улучшению качества книги.
Самара, январь 2009 года
6
Современная теория и практически^ примене^шя ашпенн
Список основных сокращений
АП — автоматизированная система
АР — антенная решетка
АФАР — активная фазированная антенная решетка
АФР — амплитудно — фазовое распределение
БММ — блок математической модели
БФМ — блок физической модели
БЭ — базовый элемент
ВУ — входное устройство
ВЩР — волноводно - щелевая решетка
ДА — диэлектрическая антенна
ДН — диаграмма направленности
ДОМ — диаграммообразующая матрица
ДОС — диаграммообразующая система
ДОУ — диаграммообразующее устройство
ИС - излучающая система
ИУ — интегральное уравнение
КБВ — коэффициент бегущей волны
КВЧ — крайне высокие частоты
КИП — коэффициент использования поверхности
КНД — коэффициент направленного действия
КПД — коэффициент полезного действия
КСВ — коэффициент стоячей волны
КУ — коэффициент усиления
МА ~ многолучевая (многоканальная) антенна
МАР - многолучевая антенная решетка
МФР - метод физической регуляризации
PC - распределительная система
СИП — сингулярное интегральное представление
СИУ — сингулярное интегральное уравнение
СЛАУ - система линейных алгебраических уравнений
СУ — согласующее устройство
УБЛ - уровень боковых лепестков
ФАР - фазированная антенная решетка
ЦСА — цилиндрическая спиральная антенна
ЭИ — элементарный излучатель
ЭМП — электромагнитное поле
Современная теория и практические применения джпенн
Список основных обозначений
7
ZA - внутреннее (собственное) комплексное сопротивление антенны
относительно точки А
Ra - активная часть внутреннего (собственного) сопротивления
ХА - реактивная часть внутреннего (собственного) сопротивления
It - сопротивление излучения
Znp - комплексное сопротивление приемника
Rnp - активная часть комплексного сопротивления приемника
Хпр - реактивная часть комплексного сопротивления приемника
е - комплексная амплитуда ЭДС
I - комплексная амплитуда тока
F(0, ф) - нормированная амплитудная ДН по полю
К2(0,ф) - нормированная амплитудная ДН по мощности
р - единичный вектор поляризации
^(0,ф) - векторная нормированная ДН по полю
/(0,ф) - ненормированная амплитудная ДН по полю
f 10, ср) - ненормированная амплитудная ДН по мощности
20о(2фо) - ширина ДН по нулевому уровню мощности
20О 5(2фО5) - ширина ДН по нулевому уровню половинной мощности
О(0,ф) - коэффициент направленного действия (КНД)
i.eA - базисный (единичный) вектор главной поляризации
in3 - базисный (единичный) вектор паразитной поляризации
ф(ф,0) - фазовая характеристика ДН антенны
- мощность излучения антенны
С(ф,0) - коэффициент излучения антенны
ц - КПД излучения антенны
Pim - мощность реактивных потерь антенны
10 (1д) “ модуль тока на входе (в точке А) антенны
1п - модуль тока в пучности тока
1д - действующая длина антенны
Аэ - эффективная площадь антенны
q - коэффициент использования площади антенны
ТА - шумовая температура антенны
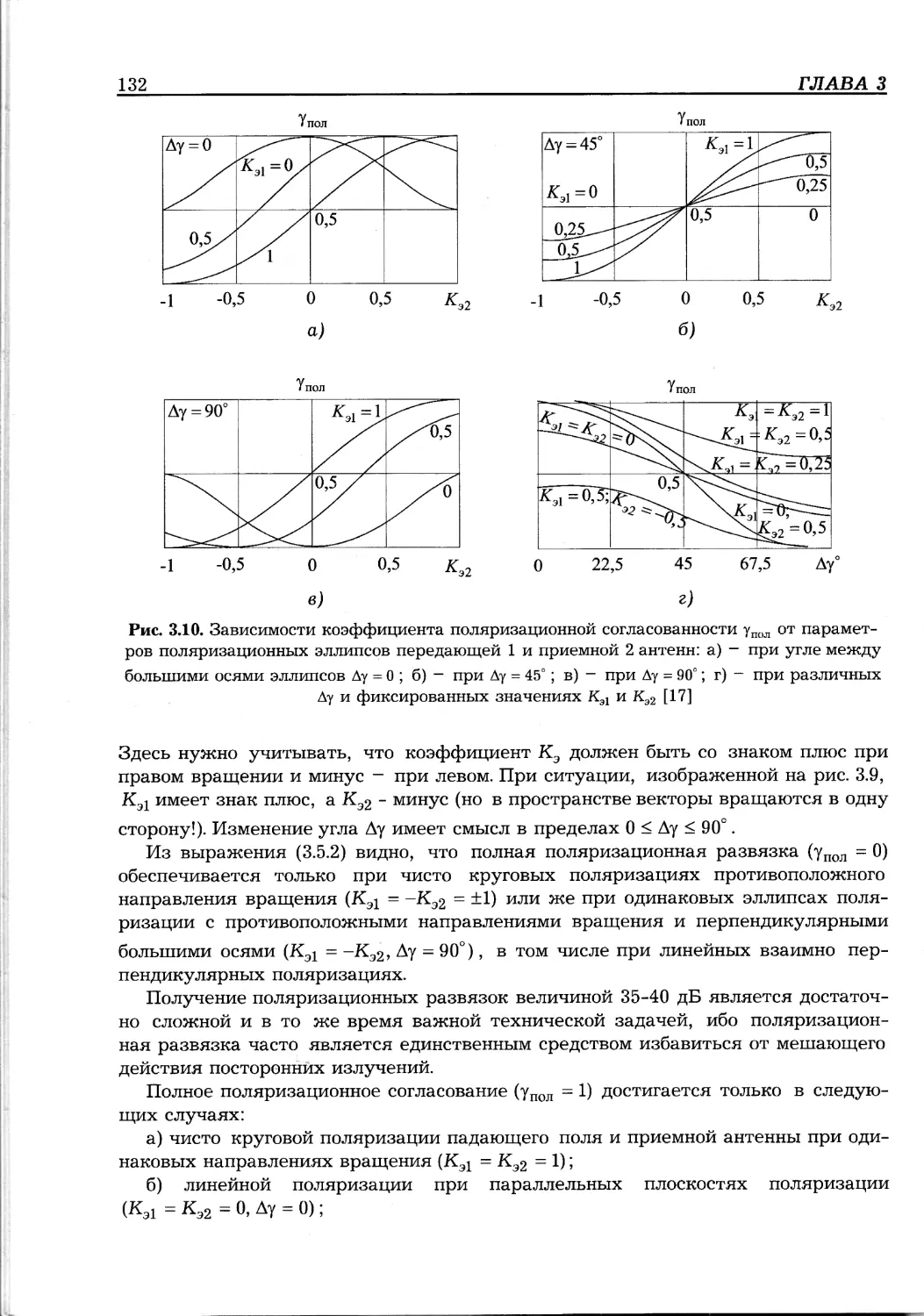
Упол ~ коэффициент поляризационной согласованности антенны
50,р0,г0 - орты декартовой системы координат
р0,ф0,20 - орты цилиндрической системы координат
го,0о,фо - орты сферической системы координат
Wc - характеристическое сопротивление среды
= [no, Н] - вектор поверхностной плотности электрического тока
Zo - комплексное входное сопротивление антенны
Ro - активная часть входного сопротивления антенны
Хо - реактивная часть входного сопротивления антенны
Рп - мощность потерь
РА - мощность антенны, отнесенная к току в точке А
8
Современная теория и практические применения антенн
D(6,cp) - КНД антенны в направлении 0,<р
Do -КНД антенны в направлении максимального излучения Оо,<ро
- сопротивление излучения диполя Герца
п0 - единичная нормаль к поверхности
£(6,ф) - вектор Умова - Пойнтинга в направлении 0, ср
Введение
9
Введение
В.1. Назначение и классификация антенн
Антенны являются неотъемлемым и существенным элементом любой радиоли-
нии.
Радиолиния есть комплекс приборов, осуществляющих передачу информации
(сообщений) через окружающее пространство с помощью свободно распространя-
ющихся электромагнитных волн (радиоволн). Радиолиния включает в себя среду,
в которой распространяются радиоволны. Наиболее общее и существенное, что
отличает радиотехнику от других областей техники передачи сообщений, заклю-
чается именно в использовании окружающего пространства для передачи элект-
ромагнитных колебаний, несущих информацию.
На распространение радиоволн в окружающем пространстве определяющее
влияние оказывают характеристики земной поверхности и атмосферы. Возмож-
ности человека в управлении этими характеристиками крайне ограничены. Эти
радиоволны отличаются от направляемых электромагнитных волн, процессом
распространения которых можно управлять в широких пределах, в том числе по
желанию изменять направление их распространения.
Общий вид схемы радиолинии показан на рис. В.1. Передатчик 1 формирует
высокочастотные сигналы, соответствующие передаваемой информации. От пере-
датчика эти сигналы с помощью фидера 2 подводятся к передающей антенне 3,
которая излучает электромагнитные волны в окружающее пространство 4. Иногда
антенна может быть подключена к передатчику и непосредственно, без фидера.
От передающей антенны радиоволны расходятся во все стороны, их удельная
энергия на единицу объема с расстоянием быстро уменьшается. Поэтому в пункте
приема приемной антенной 5 улавливается лишь небольшая доля излученной
энергии. Принятые электромагнитные колебания по фидеру 6 поступают на вход
приемника 7, в котором после усиления и ряда преобразований восстанавливается
исходный сигнал.
Основное назначение антенны - излучение или прием электромагнитных
волн. Поэтому антенну часто определяют как устройство, предназначенное для
излучения и приема электромагнитных волн. Можно также сказать, что антен-
ной называется устройство, осуществляющее преобразование (трансформацию)
4 ^5
Рис. ВЛ. Схема радиолинии [2]
10
ВВЕДЕНИЕ
направляемых электромагнитных волн в радиоволны,и,наоборот, радиоволн - в
направляемые электромагнитные волны. Если антенна непосредственно подклю-
чается к выходу передатчика, то об антенне говорят как об устройстве, преобра-
зующем энергию токов высокой частоты в энергию радиоволн.
Антенны осуществляют непосредственный контакт с окружающим пространс-
твом и поэтому не должны экранироваться. Габариты антенн, как правило, долж-
ны быть соизмеримы или много больше длины волны, поэтому они обычно вели-
ки, зачастую больше габаритов всех других блоков данного радиотехнического
устройства.
Другие элементы радиолинии (фидер, согласующие, разделительные и пере-
ходные устройства, выходные каскады передатчика и входные элементы прием-
ника) в некоторых случаях также могут излучать и принимать электромагнитные
волны. Однако в них эффект излучения или приема является вредным, трудно
контролируемым, и его стремятся свести к возможному минимуму.
Кроме собственно излучения и приема радиоволн, другим назначением антенн
является пространственное распределение электромагнитной энергии при излуче-
нии и пространственная избирательность при приеме. Поэтому важной и неотъ-
емлемой характеристикой любой антенны является ее направленность. Действие
многих радиотехнических устройств и систем (радиолокационных, радионавига-
ционных и др.) основано на использовании направленных свойств антенн.
Таким образом, антенны делятся на передающие и приемные. Основные харак-
теристики приемных антенн, в том числе направленность, могут быть найдены,
если известны аналогичные характеристики в случае, когда эти же антенны рабо-
тают в передающем режиме, поэтому нет необходимости изучать отдельно теории
передающих и приемных антенн. Обычно изучать свойства антенны более просто
в передающем режиме. По этой причине всюду ниже, если не будет оговорено
особо, подразумевается, что антенна работает в передающем режиме.
Возможность использовать любую передающую антенну для приема электро-
магнитных волн и наоборот не означает, что передающие и приемные антенны
всегда идентичны по конструкции. Даже для одного и того же типа для антенн в
передающем режиме в отличии от приемного необходимо решать специфические
проблемы, связанные, например, с высоким уровнем мощности, поступающей от
передатчика и имеющей возможность вызвать пробой антенны.
При изучении свойств антенн принято считать (кроме случаев, когда излучате-
ли расположены непосредственно у поверхности Земли), что антенна находится
в свободном пространстве, т.е. в неограниченной однородной среде без потерь с
относительными диэлектрической ( £) и магнитной ( ц) проницаемостями, равны-
ми единице, что соответствует вакууму. Влияние факторов, связанных с особен-
ностями влияния среды на процесс передачи энергии от передающей антенны к
приемной антенне, изучается в теории распространения радиоволн.
Антенно-фидерное устройство есть соединенные вместе высокочастотные
элементы радиотехнической станции. Антенно-фидерные устройства включают
в себя антенны, линии передачи, узлы коммутации и распределения электро-
магнитной энергии, селекции ее по частоте и поляризации. Антенны и элементы
линий передачи имеют как конструктивную общность, так и общность методов
расчета, основанных на теории электромагнитного поля и теории линейных цепей
переменного тока. Эта общность и обусловила выделение теории и техники антен-
но-фидерных устройств в отдельную самостоятельную область радиотехники.
Введение 11
Необходимость в классификации антенн вызвана тем, что освоение современ-
ной радиотехникой чрезвычайно широкого диапазона частот электромагнитных
колебаний (от длинных радиоволн частотой в единицы килогерц до частот оптичес-
кого диапазона) и широкое практическое применение радиотехнических устройств
обусловили создание большого количества типов антенно-фидерных устройств.
В соответствии с действующими ГОСТами антенны классифицируют по диа-
пазонам радиоволн:
1. Антенны мириаметровых или сверхдлинных волн (СДВ), т.е. антенны, рабо-
тающие в диапазоне длин волн X > 10 км. Этот диапазон волн соответствует очень
низким частотам (ОНЧ), т.е. частотам меньше 30 кГц.
2. Антенны километровых или длинных волн (ДВ) ( Z=10...1 км). Это диапазон
низких частот (НЧ) — 30...300 кГц.
3. Антенны декаметровых или средних волн (СВ) ( X =1000...100 м). Это диапа-
зон средних частот (СЧ) - 300...3000 кГц.
4. Антенны декаметровых или коротких волн (КВ) ( X =100...10 м). Это диапазон
высоких частот (ВЧ) 3...30 МГц.
5. Антенны метровых волн ( Х=10...1 м). Это диапазон очень высоких частот
(ОВЧ) - 30...300 МГц.
6. Антенны дециметровых волн ( X =100... 10 см). Это диапазон ультравысоких
частот (УВЧ) - 300...3000 МГц.
7. Антенны сантиметровых волн ( А,=10...1 см). Это диапазон сверхвысоких час-
тот (СВЧ) - 3...30 ГГц.
8. Антенны миллиметровых волн ( Х=10...1 мм). Это диапазон крайне высоких
частот (КВЧ) - 30...300 ГГц.
9. Антенны субмиллиметровых волн или децимиллиметровых волн ( Х=1...0,1
мм). Это диапазон гипервысоких частот (ГВЧ) — 300...3000 ГГц.
10. Антенны оптического диапазона ( Х< 0,1 мм).
В приведенной выше классификации, как и в ГОСТе, диапазон СВЧ соответс-
твует сантиметровым волнам, однако в существующей практике этот термин име-
ет более широкие границы, а именно — он включает волны от дециметровых до
миллиметровых. В зарубежной (и переводной) литературе СВЧ-антеннам (техни-
ке) соответствует термин микроволновые антенны (техника).
Такая классификация вызвана особенностью распространения радиоволн в раз-
личных диапазонах и разными возможностями в реализации требуемых характе-
ристик, размеров антенн и точности их изготовления. При этом конструктивные
и электрические особенности антенны разных диапазонов имеют существенные
различия.
В данной книге основное внимание будет уделено антеннам диапазона СВЧ (300
МГц - 300 ГГц), в котором функционирует подавляющее большинство радиоло-
кационных систем, систем наземной и космической радиосвязи, радионавигации,
радиотелеметрии и телевидения.
В зависимости от конструктивного оформления антенные структуры подразде-
ляются на две группы. К первой относятся антенны, повторяющие форму объек-
та, на котором они расположены (конформные антенны), ко второй — выступаю-
щие антенны, не следующие за изменением формы объекта. Конформные антенны
весьма важны с точки зрения аэродинамических или гидродинамических свойств
объекта (самолета, ракеты, торпеды, подводной лодки и т.д.).
Классификацию антенн удобно проводить по геометрии излучателей, выделяя
12
ВВЕДЕНИЕ
о)
п)
Рис. В.2. Простые излучатели: а) — диполь, или вибратор Герца; б) — симметричный
вибратор; в) — конический диполь; г) — дискоконусная антенна; сЗ) — вертикальный вибра-
тор (монополь); е) — конический вибратор; ж) — однопроводная антенна бегущей волны с
нагрузкой; з),и) — уголковые вибраторы; к) — чашечный излучатель; л) — петлевая антен-
на; м) ~ вибратор Пистолькорса; н) — четырехугольная рамка; о) — щелевой излучатель;
п) — микрополосковый излучатель [57]
следующие четыре класса антенн [57].
1. Излучатели небольших размеров ( I < X) для диапазона частот 10 кГц — 1 ГГц.
К числу антенн этого класса относятся простые, или элементарные, излучате-
ли, которые показаны на (рис. В.2). К ним относится и изотропный излучатель,
создающий равномерное поле по всем направлениям. Такой излучатель создать
нельзя, но удобно использовать как модель для сравнения. На концах простей-
шего элементарного излучателя (ЭИ) - вибратора Герца (рис. В.2,а) размещаются
емкостные диски длиной I < X. Иногда его называют элементарным электрическим
вибратором в отличие от элементарного магнитного вибратора (рис. В.2,л).
К простейшим излучателям принято относить линейные, фигурные, рамоч-
ные, щелевые, активные и выпрямительные антенны.
К линейным антеннам относят антенны с прямолинейными элементами. Про-
стейшей линейной антенной с симметричным питанием является диполь с синусо-
идальным распределением тока в плечах, представляющий собой открытый конец
двухпроводной линии передачи. Он может быть полуволновым ( I = Х/2 ), волновым
( I = X) или иметь длину I = 1,28Х . К широкополосным вибраторам относятся кони-
ческий диполь (рис. В.2,в) и уголковый вибратор (рис. В.2,з).
К рассматриваемой категории простейших антенн относятся вибраторы с не-
симметричным питанием: монополь (рис. В.2,д), полу диполь с синусоидальным
распределением тока. Эти антенны имеют длину I = Х/4. Используются также вер-
тикальные излучатели длиной I = Х/2 и I = 5Х/8.
К широкополосным линейным антеннам относятся конические и плоские веер-
ные излучатели, а также антенны, в конструкции которых используется длинный
( I > X) провод.
К линейным антеннам принадлежат и различные антенны бегущей волны, про-
стейшей из которых является провод с согласованной нагрузкой (рис. В.2,ж), с
Введение
13
противовесом (Бевережда), антенна Харченко и др.
Антенны с изменяющимися образующими (фигурные). К таким простей-
шим антеннам относятся излучатели с непрямолинейной формой образующих. Два
из них показаны на рис. В.2, и, к. В эту группу можно включить и так называемую
антенну Вивальди на основе симметричной щелевой линии, обладающую огром-
ным перекрытием диапазона.
Рамочные антенны. Такие антенны выполняются в виде замкнутых провод-
ников. Простейшими из них являются: малая рамка (показанная на рис. В.2,л маг-
нитная антенна периметром I » Л ; обычно I - Х/10 ); большая рамка (та же антен-
на периметром Z « X); петлевой вибратор Пистолькорса (рис. В.2, м); дисковая и
квадратная антенны и др.
К рамочным антеннам можно отнести и показанный на рис. В.2, п микрополос-
ковый излучатель (МПИ), у которого удалена центральная часть.
Щелевые антенны. Простейший вариант щелевой антенны (рис. В.2, о): узкая
щель (ширина kw « 1) в плоском экране длиной Х/2...Х. Щель может располагать-
ся на цилиндрической, сферической или более сложной поверхности и иметь раз-
личную ширину. Щелевой излучатель иногда выполняют с крестообразной щелью.
Такие излучатели широко используются в технике СВЧ и КВЧ — диапазонов.
Активные антенны. Под активной антенной понимают обычный пассивный
излучатель со встроенным в него активным элементом (усилителем). Такое соче-
тание позволяет получить малогабаритную широкополосную антенную структуру
с повышенной чувствительностью. Наличие активного элемента делает такую ан-
тенную систему условно устойчивой, для нее не выполняются принципы сложения
и взаимности. Класс активных антенных систем весьма широк. К нему относятся
приемные и передающие антенны с активными элементами, адаптивные, много-
функциональные, самонастраивающиеся антенные системы и др. В таких системах
одновременно с приемом радиосигнала может происходить пространственно-вре-
менная обработка сигнала в целях существенного улучшения характеристик всей
радиотехнической системы.
Выпрямительные антенны (ректенны). Разработка таких антенн связана с
проблемой получения электрической энергии от Солнца, но не непосредственно, а
после преобразования солнечной энергии на космических спутниках, находящихся
на геостационарных орбитах, в СВЧ энергию и передачи ее на Землю. Такие сис-
темы пока не созданы по причинам технического, технологического, финансового,
экологического характера и ряду других.
2. Структурные формы излучателей (иногда их называют антеннами бегу-
щей волны) размерами от А до 10 А для диапазона частот 3 МГц — 10 ГГц. Сюда
относятся спиральные, диэлектрические, директорные, импедансные антенны, а
также антенны «вытекающей» волны.
Обычно по структурной форме излучатели подразделяют на две категории:
плоские и пространственные.
Плоские излучатели имеют следующие подвиды: прямолинейные, согнутые,
складные, с изгибами, закрученные и плоскостные. Схемы таких излучателей
приведены на рис. В.З, а-з.
К подвиду прямолинейных относятся антенны, ЭИ которых располагаются
вдоль прямых линий. Примером может служить логопериодическая вибраторная
антенна (см. рис. В.З, а). Логопериодическая V-образная антенна (см. рис. В.З, б)
является примером согнутых излучателей. К подвиду складных излучателей от-
14
ВВЕДЕНИЕ
dlW
в)
ШАЛ
Рис. В.З. Схемы плоских и пространственных излучателей: а) - логопериодическая виб-
раторная антенна; б) - логопериодическая V-образная антенна; в) — меандровая антенна;
г) - зигзагообразная антенна; б) - логопериодическая вибраторная антенна с контуром
оптимизации усиления; е) - антенна - архимедова спираль; ж) — антенна - логарифми-
ческая спираль; з) - логопериодическая плоскостная антенна; и) - две логарифмические
соприкасающиеся антенны; к) - цилиндрические спиральные антенны; л) — конические
спиральные антенны [57]
носятся антенны в виде меандра или зигзага (см. рис. В.З, в, г). Логопериодическая
вибраторная антенна с контуром оптимизации усиления (см. рис. В.З, д) является
примером излучателей с изгибами. К закрученным антеннам относятся архимедо-
ва спираль (см. рис. В.З, е), логарифмическая спираль (см. рис. В.З, ж), спирально-
щелевые антенны и др. К подвиду плоскостных излучателей относится, например,
логопериодическая плоскостная антенна (см. рис. В.З, з).
К пространственным излучателям относятся структуры с изломами, а
также цилиндрические и конические спиральные антенны. Примером структуры
с изломами могут служить две соприкасающиеся антенны (см. рис. В.З, и). Ци-
линдрические спиральные антенны (см. рис. В.З, к) отличаются наличием двух
существенно разных режимов излучения: нормальным и аксиальным. Нормаль-
ный режим, или режим всенаправленного излучения, реализуется, если раз-
мер спирали I мал по сравнению с длиной волны k(l/X « 1). Излучение при этом
направлено перпендикулярно оси спирали. Коническая спиральная антенна (см.
рис. В.З, л) при малой длине также является всенаправленным излучателем. Если
Введение
15
размер спирали соизмерим с длиной волны X(l/X ~ 1), то и цилиндрическая, и
коническая антенны излучают вдоль своих осей.
3. Групповые излучатели или антенные решетки с размерами от X до 100 X
и более для диапазона частот 3 МГц — 30 ГГц. Антенное полотно образуется из
одинаковых или разных элементарных излучателей (ЭИ), объединенных системой
питания (диаграммообразующей матрицей - ДОМ). Поле излучения антенны опре-
деляется расположением ЭИ и особенностями их питания — амплитудами и фаза-
ми токов, образуемых системой питания в ЭИ. Положение главного луча (или, в
общем случае, нескольких лучей) и его перемещение (сканирование) в пространс-
тве, т.е. управление им, осуществляется изменением амплитуд и фаз токов в ЭИ.
Сама ДОМ состоит из нескольких групп ЭИ. Такие группы могут быть линей-
ными, плоскостными и пространственными. Некоторые примеры групповых излу-
чателей показаны на рис. В.4.
Линейные группы излучателей. Эти группы образованы расположенными
в линию параллельными или продольными излучателями. Синфазно возбужда-
емая последовательность параллельных излучателей (см. рис. В.4, а — г) созда-
ет излучение по нормали к плоскости, в которой они расположены (рис. В.4, а).
Продольные излучатели составляют группу ЭИ, возбуждаемых в противофазе и
потому излучающих преимущественно в одном направлении (рис. В.4, б). Одним
из наиболее распространенных излучателей этой группы является волновой канал
(рис. В.4, д).
Плоскостные группы излучателей. Группы образуют излучатели, распола-
гающиеся в одной плоскости. Плоскостная группа может состоять из нескольких
подгрупп (2x2, 4x4, 6х8и т.д.). Такими подгруппами могут быть полотна, ре-
шетки, плоскостные антенны, суммирующие излучатели.
к)
Рис. В.4. Групповые излучатели, расположенные в плоскости: а) — г) - зигзагообразные
излучатели; д) - волновой канал; е) - два вибратора; ж) - двухствольное полотно вибрато-
ров; з) - V-образный излучатель; и) — ромбическая антенна; к) - квадрантный излучатель
[57]
16
ВВЕДЕНИЕ
Для работы в КВ диапазоне строятся полотна из волновых ( I = 1) или полувол-
новых (I = л/2) вибраторов (см. рис. В.2, б, в, п). Для УКВ связи и телевизионного
вещания используются антенные решетки (АР) из волновых или полуволновых
вибраторов, например в виде четырех- или восьмизначных матриц. В микроволно-
вом диапазоне для спутниковых систем строятся плоскостные антенны. В качестве
одиночных ЭИ в плоскостных антеннах используются плоскостные прямоугольные
(см. рис. В.2,п) или скрещенные ЭИ, а также щелевые ЭИ (см. рис. В.2, о). В под-
группу суммирующих излучателей входят излучатели в виде одиночных вибрато-
ров или длинных проволочных антенн (см. рис. В.2, ж). Примерами суммирующих
излучателей являются АР из V - образных (рис. В.4, з, к), ромбических (рис. В.4,
и), турникетных, рупорных (рис. В.4, з-л) антенн.
Пространственные группы излучателей. Такие группы образуют не распо-
ложенные в одной плоскости излучатели (рис. В.5, в), к которым могут относиться
кольцевые, направленные и всенаправленные излучатели, а также конформные
группы.
Кольцевой излучатель строится из одиночных ЭИ, располагающихся по ок-
ружности или в вершинах правильного многоугольника.
По способу формирования излучаемого поля различают четыре класса антенн
[2,3]:
1. Излучатели небольших размеров ( I < X). Это одиночные вибраторные и ще-
левые излучатели, полосковые и микрополосковые антенны, рамочные антенны и
др. Обычно используются в диапазоне ЮкГц — 1ГГц.
2. Антенны бегущей волны размерами от Л до Юл для диапазона 3МГц — ЮГГц.
Это спиральные, диэлектрические директорные, импедансные антенны, антенны
«вытекающей» волны.
3. Антенные решетки размерами отХ до 100л для диапазона частот 3МГц —
ЗОГГц. Это антенны, состоящие из большого числа отдельных излучателей. Не-
зависимая регулировка фаз (иногда и амплитуд) возбуждения каждого элемента
Рис. В.5. Группы излучателей, расположенные в объеме: а,б) - линейные группы соот-
ветственно поперечных и продольных излучателей и их диаграммы направленности;
в) — пространственная группа из антен типа волнового канала; г) — четырехлучевая
рупорно-волновая антенная решетка [57]
Введение
17
антенной решетки обеспечивает возможность электрического управления диа-
граммой направленности. Применяются линейные, плоские, кольцевые, выпуклые
и конформные (совпадающие с формой объекта установки) антенные решетки. На
основе антенных решеток выполняются системы с обработкой сигнала, в том числе
и адаптивные антенные решетки к изменяющейся помеховой обстановке.
4. Апертурные антенны размерами от X до 1000 X для диапазона 100МГц —
ЮОГГц и выше. Это зеркальные рупорные и линзовые апертурные антенны. К
апертурным антеннам примыкают и «гибридные» антенны, представляющие соче-
тание зеркал и линз с облучающей системой в виде антенной решетки. Апертурные
антенны строятся по оптическим принципам и обеспечивают наиболее высокую
направленность излучения.
Наиболее просто описываются физические и математические модели одиноч-
ных излучателей небольших размеров (рис. В.2). Особенность нашей книги - при-
менение сингулярных интегральных уравнений для описания электромагнитного
поля (ЭМП) таких антенн в любой точке пространства, причем поля, переходяще-
го в ток на металлической части антенны или в тангенциальное электромагнитное
поле на апертуре антенны. Поэтому такой метод описания антенны мы называем
самосогласованным способом.
Простейшая антенна бегущей волны может быть получена с помощью экви-
дистантной двумерной антенной решетки (рис. В.6). В случае возбуждения линей-
ной решетки токами равной амплитуды с линейно нарастающим вдоль решетки
фазовым сдвигом получаем распространяющуюся вдоль решетки волну, которая
излучает в окружающее пространство (см. главу 9).
Рассмотрим простейший случай двумерной АР, состоящей из одинаковых ЭИ,
расположенных на одном и том же расстоянии d друг от друга (рис.В.6). Такая
решетка называется линейной эквидистантной АР. В качестве ЭИ в этой АР ис-
пользуются бесконечные (по оси у ) проводники, поэтому от угловой координаты
ср поле не зависит, так как d/dy = 0.
Предположим, что диаметр проводников АР а сколь угодно мал ( ka « 1)
Рис. В.6. Эквидистантная двумерная антенная решетка
18
ВВЕДЕНИЕ
и, следовательно, ток можно считать сосредоточенным в геометрическом центре
каждого проводника. Учитывая, что ЭИ имеет широкую ДН, множитель АР пред-
ставим в следующем виде:
N
/(С)(0) = In exp {ikzn cosG}, (В.1)
П=1
где п — номер ЭИ в АР; N — общее число ЭИ; 1п — комплексная амплитуда
тока в п - м ЭИ; zn — расстояние от начала координат до n-го ЭИ; 0 — угол меж-
ду осью z и направлением в точку наблюдения.
Поскольку точка наблюдения находится в дальней зоне, лучи от каждого ЭИ
показаны на рис. В.6 в виде системы параллельных линий. Пусть ЭИ возбуждаются
токами с одинаковой амплитудой 10 , а фаза от одного ЭИ к другому нарастает
по линейному закону. Тогда ток в п -ом ЭИ будет In - Iq exp {i(n - 1)АФ}, где АФ
— разность фаз между соседними ЭИ.
Подставив это значение тока в уравнение (В.1), определим нормированную ДН
такой равноамплитудной эквидистантной АР:
/(с) = |sin ф/pV sin((p/N)], <р = (fcZ3K/2)(cos 0 - £), (В.2)
где 1ЭК — эквивалентная длина АР, 1ЭК =Nd ; S, = АФ/(/сй).
Как следует из выражений (В.2), множитель решетки f' 7 есть периодическая
функция, которая при значениях своего аргумента <p/N = тл ,где т — ±1,± 2,..., об-
ращается в единицу в силу свойств замечательного предела (при х —>0 функция
х/х—>1). Это означает, что помимо своего основного максимума (лепестка) при
Ф = 0 ДН такая АР имеет еще и так называемые боковые лепестки.
ДН рассматриваемой АР в прямоугольной системе координат показана на
рис. В.7. Это типичный вид ДН эквидистантной АР конечной, на достаточно боль-
шой длины 1ЭК = Nd . Ширина ДН по уровню половинной мощности
де = 2де1/2 =5ix/(z3K sine0), <в.з)
где 0q - угол отклонения главного лепестка ДН от плоскости АР.
Данной формулой можно пользоваться уже при 1ЭК > ЗХ. Как следует из вы-
ражения (В.З), при неограниченном увеличении длины АР ( 1ЭК —> оо) ширина ДН
стремиться к нулю. Таким образом, для увеличения разрешающей способности АР
необходимо повышать ее длину, т.е. увеличивать число ЭИ в ней.
Другим существенным обстоятельством является зависимость положения глав-
Рис. В.7. Диаграмма направленности периодической антенной решетки конечной длины
1Ж = Nd в прямоугольной системе координат [3]
Введение
19
а) б)
Рис. В.8. Схемы стержневых диэлектрических антенн: а) — при большом замедлении и
широкой ДН; б) — при малом замедлении и узкой ДН; 1 — питающий волновод; 2 — согла-
сующая вставка; 3 - антенна [17]
ного максимума ДН решетки от разности фаз ДФ между ЭИ cos0-£, = АФ/(ксГ).
Так, при ДФ = 0, когда ЭИ решетки возбуждаются синфазно, 0О = 90°, т. е. направ-
ление максимума ДН перпендикулярно плоскости решетки. Изменяя разность фаз
между ЭИ, можно обеспечить качание луча (сканирование) АР в необходимых
пределах. Управление ДН антенн осуществляется с помощью диаграммообразую-
щих матриц (ДОМ), рассматриваемых в книге.
Другим примером антенны бегущей волны являются стержневые диэлектри-
ческие антенны (рис. В.8), которые формируют поверхностные вдоль диэлектри-
ческого стержня бегущие волны.
На практике используются диэлектрические антенны (ДА) двух типов: короткая
и протяженная. Короткая ДА имеет примерно одинаковые продольный и попереч-
ный размеры и по существу представляет собой линзу. Протяженная ДА может
быть выполнена в виде стержня постоянного диаметра или сужающегося к концу,
полой диэлектрической трубки - отрезка диэлектрического волновода, составно-
го стержня из отрезков стержней разного диаметра и т.п.
Схемы простых стержневых ДА с изменяющимся по длине I диаметром при-
ведены на рис. В.8. Принцип действия ДА основан на использовании свойств по-
верхностной волны, интенсивность которой убывает по радиальной координате г
согласно экспоненциальному закону: Е (г) = ехр{-ос
ризующее скорость убывания интенсивности по г .
, где а - число, характе-
Распределение интенсивности поля по г показано на рис. В.8 горизонтальной
штриховкой. Падающая волна г, распространяющаяся по волноводу 1,через со-
гласующую вставку 2 возбуждает в ДА поверхностную волну. При большом замед-
лении волны (рис. В.8, а) протяженность поля (по сути, апертура ДА) сущест-
венно меньше, чем при малом замедлении (рис. В.8, б): < О2. Это означает, что
при малом замедлении ДН уже, т.е. разрешающая способность такой ДА выше.
Большую группу антенн бегущих волн образуют щелевые антенны. Их основу
составляют ЭИ в виде щелей с продольными (рис. В.9, а) или поперечными (рис.
В.9, б) гофрами в волноводах.
К этому же подклассу излучателей на основе частопериодических структур,
период р которых намного меньше длины волны ( р « X ), относятся гофрирован-
ные антенны (рис. В.9).
20
ВВЕДЕНИЕ
Рис. В.9. Периодические направляющие структуры: а) - щель над гофрированной плоскос-
тью с поперечными канавками; б) - щель над гофрированной плоскостью с продольными
канавками; в) - щель над двумерной гофрированной поверхностью [25]
Варианты таких структур, осуществляющих замедление волны, показаны на
рис. В.9. Эти структуры оказались удобными при создании антенн для космических
аппаратов, имеющих тяжелый температурный режим.
Во-первых, в антеннах этого класса отсутствует диэлектрик, не стойкий к рез-
кой смене температур (-12О...12О°С), во-вторых, частопериодические структуры
обеспечивают резкую частотную зависимость, что позволяет при относительно
малом изменении частоты А//f0 обеспечить сканирование лучом антенны в боль-
ших пределах.
Для эффективного теле- и радиовещания на больших территориях, устойчи-
вой работы некоторых других радиотехнических систем желательно иметь ан-
тенные структуры, обеспечивающие возможно более равномерное излучение в го-
ризонтальной плоскости. В то же время в ряде случаев, например при передаче
больших объемов информации по радиорелейным линиям связи, требуются ан-
тенные системы, обеспечивающие максимальную концентрацию энергии в нужном
направлении. Аналогичная задача возникает в радиолокации: требуется узкая ДН
для точного определения местоположения объекта. Особенно высокие точности
необходимы в радиоастрономии, когда принимаются радиосигналы от весьма уда-
ленных источников. Во всех этих случаях антенны, например зеркальные или
линзовые, должны удовлетворять условию D/Х »1. Это требование достаточно
просто обеспечить в видимом, субММ, ММ и СМ диапазонах, но оно практичес-
ки невыполнимо в диапазонах более длинных волн.
Имеется иной путь получения узкой ДН — применение сложных антенных
структур — антенных решеток (АР). Для этого может быть использована антен-
на типа «волновой канал» (см. рис. В.4, д) или АР из таких антенн (см. рис. В.5, в).
Возможно построение АР и из других отдельных (см. рис. В.З) или групповых (см.
рис. В.4) излучателей. Для получения остронаправленного излучения широко при-
меняются АР, состоящие из совокупности отдельных, как правило, одинаковых,
излучателей. В качестве элементов АР могут использоваться направленные и сла-
бо направленные излучатели (симметричные вибраторы, щели, открытые концы
волноводов, рупоры, диэлектрические стержни, спирали).
Разработка современных антенн основывается на сочетании теоретических и
экспериментальных методов. Это связано со сложностью построения достаточно
точных математических моделей, адекватно описывающих поле излучения и дру-
гие характеристики антенн. Зачастую для проведения строгих расчетов антенн не
Введение
21
хватает ресурсов даже мощных ЭВМ. Поэтому расчеты, выполняемые на разумном
уровне математической строгости, дополняют и сочетают с экспериментальными
исследованиями. При этом широко используют имитационные модели антенн, ос-
нованные на принципе электродинамического подобия (одновременное изменение
физических размеров антенны и рабочей частоты при сохранении электрического
размера). Имитационные модели значительно ускоряют и удешевляют проведение
экспериментальных исследований. В последнее время широкое распространение
получают автоматизированные стенды для антенных измерений, в которых снятие
характеристик антенн производится с помощью ЭВМ, ведущей также обработку
результатов и оформление протоколов измерений.
Антенные решетки принято классифицировать в зависимости от распо-
ложения излучателей в пространстве, характера их размещения в решет-
ке, шага решетки, типа применяемых излучателей, способа их возбуждения и
сканирования и т.д.
Использование АР позволяет существенно повысить эффективность современ-
ных бортовых и наземных радиосистем благодаря возможности осуществления
быстрого безынерционного обзора пространства путем перемещения луча АР в
нем электрическими методами (электрическое сканирование), увеличения коэф-
фициента усиления (КУ) антенны, формирования ДН с требуемыми шириной и
уровнем боковых лепестков путем создания соответствующего амплитудно-фа-
зового распределения по раскрыву АР, увеличения излучаемой мощности и
снижения потерь в фидерном тракте за счет размещения в каналах излучателей
решетки независимых генераторов или усилителей высокочастотной энергии, осу-
ществления многофункциональной работы радиосистемы, т.е. совмещения в ней
нескольких функций, например поиска, обнаружения и сопровождения цели,
увеличения помехозащищенности путем пространственной обработки сигналов
(подстраивающиеся, адаптивные АР) и т.д. При этом АР может служить пер-
вичным звеном обработки (в общем случае пространственно-временной) радиосиг-
нала и поэтому в значительной мере определяет основные характеристики всей
системы.
Использование устройств СВЧ и КВЧ с электронными приборами и электри-
чески управляемыми средами позволяет не только создать управляемое фазовое
распределение в АР и тем самым осуществить электрическое сканирование для
обеспечения высокой скорости обзора пространства и увеличения объема, инфор-
мации о распределении источников излучения или отражения ЭМВ в окружающем
пространстве, но и обеспечить первичную обработку поступающей информации
(просуммировать поля, преобразовать частоты, усилить сигнал и т.д.) непосредс-
твенно в СВЧ или КВЧ тракте антенны.
Применение АР обусловлено также необходимостью в широких пределах элек-
трическим способом управлять положением ДН в пространстве. Наиболее быстрого
перемещения луча (сканирования) в АР можно добиться изменением амплитуд и
фаз токов (полей) в отдельных ЭИ конкретной АР. Это и осуществляется в фа-
зированной антенной решетке (ФАР). Время установки луча в заданную точку
пространства определяется быстродействием фазовращателя. Обеспечить необ-
ходимое амплитудно-фазовое распределение в ФАР, составленной из отдельных
ЭИ, существенно проще, чем в зеркальных, линзовых, волноводно-рупорных и
других антеннах. Большая степень свободы при управлении элементами ФАР поз-
воляет создать нужную ДН, например, обеспечить минимальный уровень ее боко-
22
ВВЕДЕНИЕ
вых лепестков, осуществить ДН с «провалом» в некотором диапазоне углов и т. п.
Таким образом, ФАР дает возможность получить наилучшие характеристики из-
лучения, иными словами, оптимизировать ДН по заранее заданным требованиям.
Предположим, что ЭМП системы пассивных линейных излучателей представ-
ляет собой сумму полей отдельных ЭИ. Пусть эти ЭИ одинаковые (имеют одни и те
же размеры, форму и т.п.), расположены в пространстве одинаковым образом (на-
пример так, как показано на рис. В.5, а или В.5, б), характеризуются одним и тем
же законом распределения токов. В этом случае ЭМП в дальней зоне определится
как произведение функции, описывающей ДН каждого ЭИ, ГЭЛ(0,ф) и некоторо-
го скалярного множителя /^(0,ф) системы точечных изотропных излучателей,
размещенных в местах нахождения элементов рассматриваемой АР. Множитель
/<с'(0,ф) называется множителем решетки. ЭМП системы излучателей можно опи-
сать выражением
Е(т, 0, ф) = АЕЭЛ (0, ф)/(с) (0, ф) ехр{г/сг} / г (В.4)
Множитель ехр{г?сг} / г описывает поведение ЭМП в дальней зоне, т.е. поведе-
ние сферической волны, по фронту которой ( г - const) поле неоднородно. Ампли-
тудный множитель А зависит от мощности генератора, питающего АР.
Примером направленного излучателя на основе АР может служить кольцевой
вибратор при правильном выборе фаз ЭИ, составляющих кольцо.
Все направленные излучатели используются при обеспечении строго синфазно-
го питания ЭИ, что позволяет получить почти равномерное распределение излуче-
ния во всех направлениях. Примерами таких излучателей являются квадрантная
антенна (см. рис. В.4, к), дипольная рамка (из двух размещенных крест-накрест
диполей типа вибратора, показанного на рис. В.2, б) и др. Конформная группа
составляется из ЭИ, размещенных на поверхности конуса, цилиндра или сферы.
Для примера на рис. В. 10 показана коническая спиральная антенна для разведы-
вательного ИСЗ.
На основе антенных решеток выполняют антенные системы с обработкой сигна-
ла, в том числе адаптивные к изменяющейся помеховой обстановке.
Апертурные излучатели размерами от X до 1000 X для диапазона частот 100
МГц — 100 ГГц и выше. Апертурой (от лат. aperture — отверстие) называется
поверхность раскрыва (например, АА' на рис. В.10) антенны либо отверстие в
электродинамической или оптической антенной системе. Разрешающая способ-
Рис. В.10. Коническая спиральная антенна для разведывательного ИСЗ: 1 - точки пита-
ния; 2 ~ высокотемпературная диэлектрическая пленка; 3 - печатные ЭИ [3]
Введение
23
^y/z/zl
п)
У)
Рис. В.11. Апертурные излучатели: а - ж) - зеркальные (рефлекторные) антенны (точкой
показано положение облучателя относительно зеркала); з - л) - рупорно-волноводные
антенны; м),н) — линзовые антенны соответственно с ускоряющей и замедляющей лин-
зами; о),п) — короткая и стержневая диэлектрические антенны; р) — щелевая антенна на
коаксиальной линии; с),т) - щелевые антенны на прямоугольном волноводе; у) - гофри-
рованная антенна [57]
ность антенны, т.е. минимальное расстояние между двумя удаленными точками,
при котором они все еще «видны» отдельно, обратно пропорционально величине
(линейному размеру) ее апертуры. ДН апертурного излучателя зависит от его
формы, размеров и распределения тока на нем. К классу апертурных излучателей
относятся зеркальные, рупорно-волноводные, линзовые, диэлектрические антен-
ны, а также антенны бегущей волны.
Зеркальные (рефлекторные) антенны. Эти антенны имеют самую разно-
образную конструкцию. Принцип их работы состоит в отражении зеркалом волн,
приходящих от возбудителя (облучателя). В качестве зеркала могут использовать-
ся плоская поверхность (рис. В.11,а), уголковая поверхность, или внутренняя по-
верхность конуса (рис. В. 10, б), осесимметричное параболическое зеркало (рис.
В.10, в), параболических рупор (см. рис. В.11, г, д) т.п. Широко используются
зеркальные антенны с переотражением от рассеивающего (рис. В.11, е) или фоку-
сирующего (рис. В.11, ж) зеркал.
Большинство зеркальных антенн при приеме радиоволн фокусирует падающие
на них лучи в одной точке - фокусе антенны, а при работе на передачу созда-
ет пучок параллельных лучей от облучателя, падающих на зеркало (рис. В. 12).
Размер основного зеркала D обычно очень большой ( О/л »1), поэтому при рас-
смотрении принципа работы зеркальных антенн можно использовать законы гео-
24
ВВЕДЕНИЕ
Рис. В.12. Двухзеркальная параболи-
ческая антенна: 1 - основное зерка-
ло; 2 ~ облучатель; 3 — волнопровод;
4 ~ вспомогательное зеркало [17]
Рис. В.13. Схема, поясняющая принцип действия
линзовой антенны: фг - первоначальный фронт; ф2
- итоговый фронт (плоский); 1,2 - лучи, прохо-
дящие разные пути в воздухе и теле линзы, но к
фронту ф2 приходящие в одной и той же фазе [17]
метрической оптики. Благодаря большому значению коэффициента D зеркальные
антенны обладают высокой разрешающей способностью, поскольку ширина диа-
граммы направленности 0 « X/D « 1.
Ру порно-волноводные антенны. Простейшие из этих антенн представляют
собой регулярный волновод (коаксиальный, прямоугольный, круглый и т.п.), из
открытого конца которого осуществляется излучение. Для лучшего согласования
излучателя со свободным пространством и увеличения разрешающей способности
используются Е - плоскостные (рис. В.11, з) и Н -плоскостные (рис. В.11, и) секто-
риальные рупоры, а также пирамидальный (рис. В.11, к) и конический (рис.В.11,
л) рупоры.
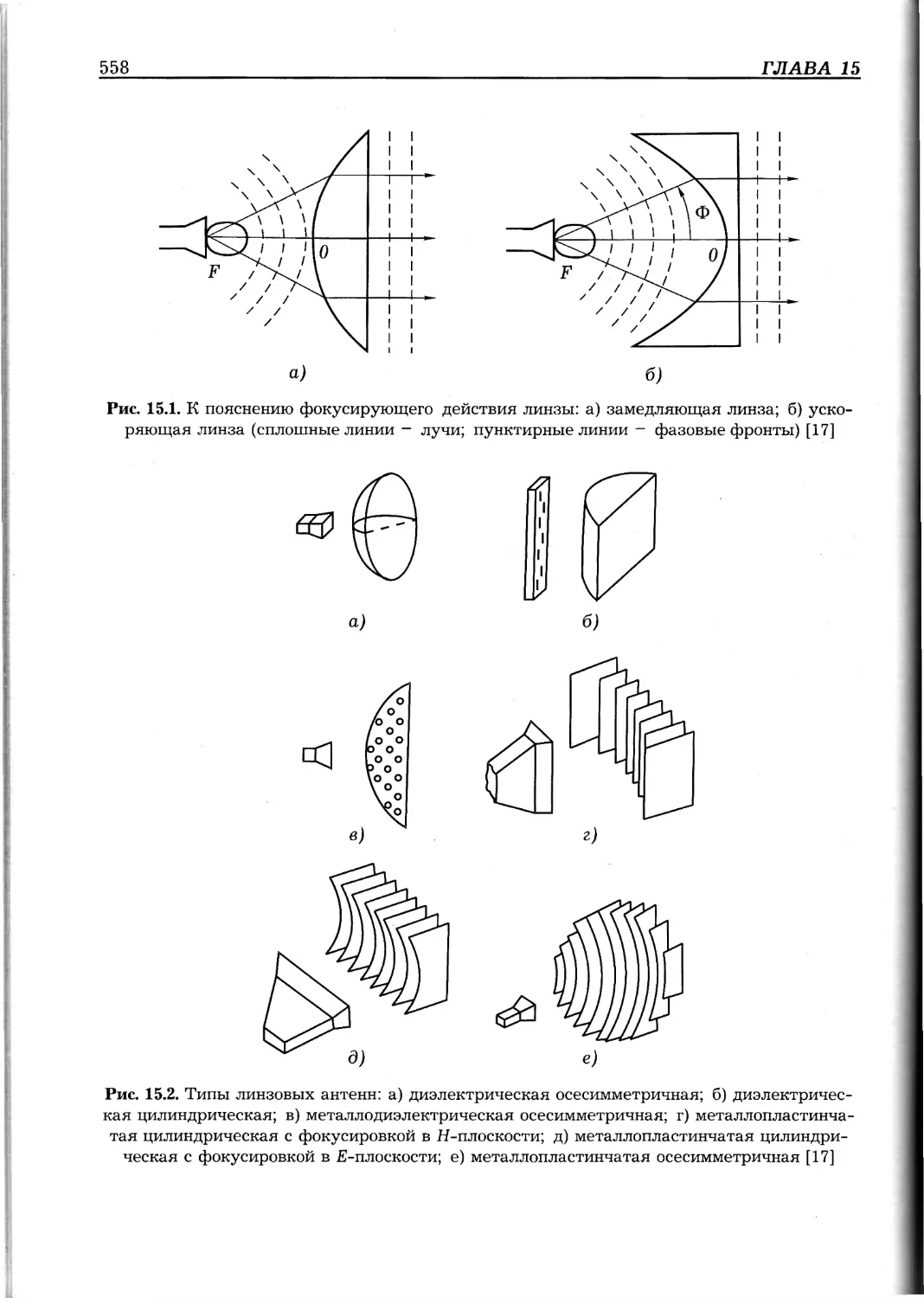
Линзовые антенны. Эти антенны применяются для преобразования (исправ-
ления) фазового фронта волны. При этом используются как ускоряющие (рис. В.11,
м), так и замедляющие (рис. В.11, н) линзы. Для рассмотрения принципа их дейс-
твия достаточно знания законов геометрической оптики и простой схемы, приве-
денной на рис. В.13. Волна, распространяющаяся от некоторого источника О (не
обязательно точечного), имеет расходящийся, допустим, сферический или почти
сферический фронт . После призмы, в которой каждый луч проходит свой, от-
личный от других путь, получается плоская или почти плоская волна с фронтом
Ф2, распространяющаяся вдоль оси z . На практике используется большое число
линз разных размеров и форм.
В.2. Структурная схема однолучевой антенны [2]
В схеме конкретной антенны можно выделить следующие элементы: вход, со-
гласующее устройство, распределитель и излучающую систему (рис. В. 14). Под
входом антенны обычно понимают сечение линии передачи с волной заданного
типа. Положение этого сечения должно быть указано точно, что необходимо для
однозначного электрического расчета тракта. Современные антенны могут иметь
несколько, а иногда сотни и тысячи входов. Эти входы могут использоваться для
одновременной работы антенны на различных частотах или же для независимого
Введение
25
Рис. В.14. Структурная схема однолучевой антенны
формирования нескольких различающихся характеристик направленности.
Согласующее устройство предназначается для обеспечения режима питающей
линии, как можно более близкого к бегущей волне. Наряду с обычными схемами
узкополосного и широкополосного согласования в антеннах часто используются
возможности согласования входа путем рационального выбора ряда конструктив-
ных размеров в распределителе.
Распределитель антенны представляет конструкцию из проводчиков и диэлек-
триков и предназначен для создания нужного закона распределения излучающих
токов, обеспечивающего формирование требуемой характеристики направленнос-
ти.
И наконец, излучающая система представляет собой область пространства, в
которой протекают токи, возбуждающие электромагнитные волны. В силу принци-
па обратимости антенн такое же название может быть сохранено и для приемных
антенн. В качестве излучающей системы могут фигурировать как реальные элек-
трические токи, текущие по металлическим поверхностям, так и эквивалентные
фиктивные электрические и магнитные токи на замкнутых поверхностях, окружа-
ющих антенну, а также токи электрической и магнитной поляризации в объемах,
занимаемых магнитодиэлектриками.
Выделение распределителя и излучающей системы связано с традиционным
подходом, согласно которому расчет антенны разделяется на две части: внутрен-
нюю задачу и внешнюю задачу. Внутренняя задача состоит в нахождении фун-
кций распределения высокочастотных токов в излучающей системе. Во внешней
задаче по известному распределению токов определяются электромагнитное поле
антенны и характеризующие его параметры (ширина луча, уровень бокового из-
лучения, коэффициент направленного действия и др.). Разделение расчета антен-
ны на внешнюю и внутреннюю задачи целесообразно в двух случаях:
- при создании приближенных методов анализа характеристик антенн извес-
тной конструкции, основанных на угадывании предполагаемого решения более
сложной внутренней задачи;
- при построении методов синтеза антенн с заданными характеристиками поля
излучения. В этом случае предварительное определение требуемого распределения
токов в излучающей системе облегчает конструирование соответствующего распре-
делителя.
26
ВВЕДЕНИЕ
В.З. Многолучевые антенны [3]
В.3.1. Классификация и схемы построения
Многолучевые антенны (МА) представляют собой устройства, способные форми-
ровать в пространстве несколько диаграмм направленности, каждой из которых
соответствует определенный входной канал антенны [3]. Многолучевые антенны
применяются как самостоятельные передающие или приемные устройства и как
элементы сложных антенн, например, фазированных антенных решеток (ФАР).
Такие антенны имеют большие функциональные возможности и позволяют осу-
ществлять параллельный обзор пространства в широком секторе углов с высокой
степенью разрешения, одновременное сканирование несколькими независимыми
лучами, расширение сектора однолучевого сканирования ФАР, управление фор-
мой ДН антенны и т.п.
Структурная схема МА представленная на рис. В. 15, состоит из излучающей
части 1 (которая может быть выполнена в виде решетки излучателей или раскры-
ва апертурной антенны); диаграммообразующего устройства (ДОУ) 2 (основной
элемент функциональной схемы, предназначенный для создания требуемых амп-
литудно-фазовых распределений (АФР) поля в излучающей части МА) и входов
антенны 3, представляющих собой поперечные сечения линий передачи с единс-
твенным распространяющимся типом волны.
При подключении генератора к какому-либо входу МАв пространстве формиру-
ется соответствующая этому входу ДН. На рис. В. 16 приведен пример соответствия
возбуждаемых входов МА и формируемых при этом ДН. При работе МА в режиме
приема часть энергии плоской волны, падающей из направления, соответствую-
щего максимуму какой-либо ДН МА, собирается на соответствующем входе ан-
тенны. При этом, если на остальных входах электромагнитные колебания отсутс-
твуют, то входы такой МА считаются развязанными.
Критерии классификации МА (рис. В. 17) условно можно разделить на две груп-
пы: в первую входят общие системные и антенные критерии, такие, как функ-
Рис. В.15. Структурная схема
МА [17]
Рис. В.16. Пример соответствия входов МА
и формируемых ДН [17]
Введение
27
Критерий клас-
сификации
МА
пассивные
активные
приемные МА
Функциональное
назначение
приемно-
передающие МА
Динамика лучей
Способ форми-
рования лучей
Способ реализа-
ции излучающей
частицы
Способ возбуж-
дения излучаю-
щей части
Расположение
излучателей в
пространстве
Тип ДОУ
Практические
схемы МА
самостоятельное
антенное уст-
ройство
неподвижный
веер лучей
апертурные МА
элемент
сложной
антенны
(ФАР)
переизлучение
волн
сканирующий
веер лучей
цифровой
последовательный
линейные
выпуклые
реактивные ДОУ
на несущей частоте
на основе лин-
зовых антенн
на основе мат-
рицы Бласса
сложение
мощности
нескольких
генераторов
независимое ска-
нирование лучами
частотный
гибридные МА
криволинейные
кольцевые
дуговые
синхронизация
автогенераторов
широкоугольное
сканирование од-
ним лучом
амплитудный
МА решетки
параллельный
цилиндрические
ДОУ с тепловыми потерями
на промежуточной частоте
на основе зеркальных
антенн
на основе многовол-
новых линий передач
на основе RC-матрицы
смесительные матри-
цы
конические
эфирный
матричные
на сходящихся
линиях задерж-
ки
матрицы Батле-
ра
Рис. В.17. Классификация МА[3]
28
ВВЕДЕНИЕ
а)
б)
Фокальная линия
Рис. В.18. МА апертурного типа на основе: а) - замедляющей линзы; б) - линзы Люне-
берга; в) — зеркально-параболической антенны; г) - зеркально-параболической антенны с
вынесенными облучателями; д) - двухзеркальной антенны; е) - параболического отра-
жателя типа «песочные часы» [3]
циональное назначение МА в системе, динамика и способы формирования лучей;
вторую составляют критерии, определяющие способы схемного построения МА.
Можно выделить два крупных класса МА по способу реализации излучающей
части: апертурные и решетки. Апертурные МА обычно реализуются на основе ан-
тенн оптического типа - линзовых или зеркальных антенн. На рис. В.18 приведены
возможные схемы построения таких антенн.
ДОУ апертурных антенн представляет собой совокупность облучателей с зер-
калом или линзой. Входам облучателей, вынесенным из фокуса зеркала или лин-
зы, соответствуют ДН, отклоненные от нормали к апертуре антенны. Чем больше
смещение облучателя из фокуса, тем больше отклонение соответствующей ему ДН
от нормали. Достоинством МА оптического типа является простота конструкции
и возможность формирования ДН с низким уровнем боковых лепестков. К недо-
статкам относятся низкий уровень пересечения соседних лучей, малое значение
коэффициента использования поверхности (КИП), громоздкость конструкции и
большой вес.
В состав МА с излучающей частью в виде решетки излучателей входит ДОУ в
виде диаграммообразующей схемы (ДОС) матричного типа. Известно множество
практических схем МА решеток (МАР). Наиболее распространенными являются
МАР на основе параллельной ДОС (матрица Батлера) и последовательной ДОС
(матрица Бласса).
На рис. В. 19 представлены электрические схемы таких антенн. Отличительным
признаком и достоинством МАР на основе матрицы Батлера (рис.В.19,а) является
возможность составления ДОС из одинаковых восьмиполюсных делителей мощ-
ности (например, волноводно-щелевых мостов) и набора статических фазовраща-
Введение
29
а) б) в)
Рис. В. 19. МА на основе матричных ДОС: а) - четырехлучевая антенна на основе ДОС
Батлера; б) - четырехлучевая антенна на основе ДОС Бласса; в) - четырехлучевая ан-
тенна на основе модифицированной ДОС Бласса [3]
телей. Это предопределяет и ряд недостатков такой антенны: отсутствие возмож-
ности реализации на решетке амплитудных распределений специальной формы,
обеспечивающих формирование ДН с низким уровнем боковых лепестков; исполь-
зование только бинарного числа излучающих элементов (т.е. количество излуча-
телей должно определяться целой степенью числа 2); частотно-зависимое поло-
жение лучей в пространстве. Некоторые недостатки таких антенн не свойственны
МАР на основе матрицы Бласса (рис. В.19,б), которая позволяет формировать веер
оптимальных в каком-либо смысле ДН при произвольном числе излучателей и
входных каналов антенны. Направления лучей, формируемых МАР этого типа,
могут быть независимыми от частоты.
Наличие диссипативных (тепловых) потерь позволяет обеспечить развязку вход-
ных каналов МАР за счет уменьшения КПД. Если количество излучателей МАР
последовательного типа совпадает с количеством ее входов, то можно исключить
из схемы поглощающие нагрузки (рис.В.19,а). В такой МАР диаграммообразующую
схему называют модифицированной матрицей Бласса. Различные фазовые рас-
пределения в МАР с ДОС последовательного типа реализуются за счет различных
углов наклона горизонтальных линий передачи (рис.В.19,б) или за счет статических
фазовращателей (рис.В.19,в). Общим недостатком МАР на основе матричных ДОС
является наличие большого числа мостовых устройств, статических фазовраща-
телей и сложной разветвленной фидерной схемы. Количество мостовых устройств
Мм в зависимости от числа формируемых лучей N определяется следующими
выражениями: для полной и модифицированной матрицы Бласса соответственно
Мм = N2,Mm = (А2 - N) / 2; для матрицы Батлера Мм = (N / 2)log2( А). Количест-
во статистических фазовращателей для матрицы Батлера определяется со-
отношением Мф = (log А -1) / 2. На рис. В.20 эти зависимости проиллюстрированы
графически. Из графиков следует, что ДОС параллельного типа при одинаковом
числе входных каналов имеет наименьшее количество элементов по сравнению с
ДОС последовательного типа. В этом преимущество матрицы Батлера перед мат-
рицей Бласса.
Недостатки перечисленных МА препятствуют их реализации в диапазоне край-
не высоких частот (КВЧ). Это связано с тем, что непосредственное применение
30
ВВЕДЕНИЕ
Рис. В.20. Количество мостовых устройств для МА при использовании различных ДОС [3]
метода электродинамического подобия к построению МА матричного и оптическо-
го типов в диапазоне КВЧ ограничено конструкторско-технологическими трудно-
стями и большими погонными потерями в одноволновых линиях передачи. Одно из
возможных решений задачи построения МА в этом диапазоне состоит в использо-
вании в качестве ДОС линий передачи с несколькими распространяющимися ти-
пами волн. Антенны на основе таких линий передачи называются многомодовыми.
Управление формой и положением ДН в таких антеннах, а также формирование
веера ДН происходит за счет изменения амплитуд и фаз волн, распространяю-
щихся по многоволновой линии передачи. Многомодовые антенны состоят из от-
резка многоволнового волновода и устройства возбуждения волн в нем; излучаю-
щая часть выполняется в виде открытого конца многоволнового волновода. Анализ
показывает, что электромагнитные процессы в многоволновых линиях передачи
без потерь имеют почти периодический характер, т.е. поперечные АФР поля на
продольной оси многоволновой линии передачи повторяются с определенной степе-
нью точности через определенные расстояния, называемые почтипериодами. При
этом чем более высокую точность требуется обеспечить между повторяющимися
АФР, тем дальше на продольной оси волновода они находятся друг от друга, т.е.
тем больше значение почтипериода. Кроме того, в многоволновых линиях пере-
дачи происходит фокусировка полей, т.е. синфазное сложение полей отдельных
распространяющихся волн.
На рис. В.21 представлены упрощенные конструкции трех- и четырехлучевых
антенн на основе прямоугольных волноводов с волнами Нп0. Многоволновый вол-
новод в таких антеннах выполняет роль фокусирующей линзы и преобразует пос-
ледовательность АФР поля в раскрыве, соответствующую вееру ортогональных
лучей, в последовательность сфокусированных распределений поля возле метал-
лических перегородок. Каждое сфокусированное распределение из этой последова-
тельности определяет амплитуду волны на соответствующем этому распреде-
лению входе антенны. Главный недостаток таких антенн — быстрое увеличение их
продольного размера с ростом числа лучей.
Введение
31
Входы
Металлические
перегородки
Апертура
антенны
Многоволновый
волновод
а)
Входы
Металлические
перегородки
Апертура
антенны
Многоволновый
волновод
б)
Рис. В.21. МА на основе прямоугольных многоволновых волноводов: а) - трехлучевая ан-
тенна; б) - четырехлучевая антенна [3]
В.З.2. Исторический обзор [2]. Истоки современной теории и техники ан-
тенн и трактов СВЧ восходят к XIX в. Возникновение первых серьезных науч-
ных представлений об электромагнитном поле принято связывать с известными
экспериментами М. Фарадея (1791 - 1867). Строгую математическую основу элек-
тромагнетизма заложил в 1864 г. Д. К. Максвелл (1831 - 1879) в виде системы уни-
версальных уравнений. Вслед за этим наиболее значительные теоретические и эк-
спериментальные исследования структуры полей элементарного диполя и других
простейших излучателей электромагнитных волн были выполнены Г. Герцем (1857
- 1894), не усмотревшим, однако, практического значения в наблюдаемых
им явлениях. И только в 1895 г. нашим великим соотечественником А. С. Попо-
вым (1859—1906) были созданы первые технически оформленные антенны: излу-
чающая (в виде квадратных металлических листов, закрепленных на концах
герцевского вибратора) и приемная (в виде вертикального проводника и систе-
мы заземления). Теоретическая трактовка вибраторной антенны как совокупности
диполей принадлежит немецкому ученому М. Абрагаму, сформулировавшему в
1900 г. понятие о сопротивлении излучения антенны.
В конце XIX в. Дж. Дж. Томсоном (1893) и Рэлеем (1897) были также высказаны
соображения о теоретических перспективах передачи электромагнитных волн по
металлическим трубам, однако практическая реализация этих идей задержа-
лась почти на 35 лет.
Подлинное становление антенной техники и техники устройств СВЧ произош-
ло в 40—50-е годы нашего столетия. Условно можно выделить следующие основ-
ные периоды развития антенн и высокочастотных трактов.
1. Период проволочных антенн длинноволнового и средневолнового диапазонов
(1900—1925 ).Размеры антенн были малы по сравнению с применявшимися рабочими
длинами волн, и основная трудность состояла в обеспечении приемлемого КПД из-
лучения. В наиболее совершенных антеннах того времени использовались мачты
высотой до 150 м и разветвленные системы заземления. Очень плодотворной
оказалась идея Александерсена о построении вертикальной антенны с несколь-
кими синфазно настроенными снижениями и развитой горизонтальной частью.
В 1917—1918 гг. М. В. Шулейкиным был разработан и опубликован метод рас-
чета емкости и индуктивности сложных длинноволновых радиосетей.
2. Период коротковолновых антенн (1920—1935). С освоением диапазона ко-
32 ВВЕДЕНИЕ
ротких волн размеры антенн стали не только соизмеримыми, но и могли су-
щественно превышать рабочую длину волны. Поэтому появились возможности
реализовать направленное действие антенн. Среди многих достижений антенной
техники этого периода следует отметить появление многовибраторных синфаз-
ных антенн (прообраз современных антенных решеток), созданных под руко-
водством М. А. Бонч-Бруевича и В. В. Татаринова (радиолиния Москва—Таш-
кент, 1926 г.).
3. Начало освоения УКВ связано у нас с работами Б. А. Введенского и А. И.
Данилевского и относится к 1921 г. Однако периодом становления антенн УКВ
и трактов их питания следует считать десятилетие с 1930 по 1940 гг. В этот пе-
риод появились эффективные источники непрерывных колебаний дециметрового
и сантиметрового диапазонов длин волн, что дало мощный импульс практи-
ческой реализации волноводов и стимулировало поиски технических решений
различных элементов волноводного тракта. Развитие техники телевидения и
УКВ-вещания привело к необходимости построения широкополосных антенн.
Зародилась техника рупорных антенн и антенн квазиоптического типа - зер-
кальных и линзовых.
4. Революционизирующее влияние на антенную технику и технику уст-
ройств СВЧ периода 1940—1960 гг. оказало стремительное внедрение радиоло-
кационных систем сантиметрового и дециметрового диапазонов. Именно в это
время были заложены теоретические основы инженерных расчетов наиболее рас-
пространенных остронаправленных антенн: зеркальных, рупорных, линзовых.
Особо следует отметить широкое внедрение разнообразных щелевых антенн
(резонаторных и в виде решеток на прямоугольных волноводах) и появление
сверхширокополосных излучателей (логопериодические и логоспиральные антен-
ны). В 1950—1960 гг. получила определенное завершение и теория пассивных
элементов тракта на прямоугольных и коаксиальных волноводах, появились
невзаимные ферритовые устройства и управляемые ферритовые фазовращатели.
Зарождалась техника полосковых линий передачи и диэлектрических волно-
водов.
5. Совершенствование и развитие антенн и устройств СВЧ в настоящий
период оказались тесно связанными со следующими ключевыми событиями:
выходом человека в космическое пространство, немыслимым без соответствую-
щего радиотехнического обеспечения; бурным прогрессом вычислительной техни-
ки на основе достижений интегральной технологии; быстрым освоением области
миллиметровых волн и волн оптического диапазона; созданием технологии по-
лосковых, микрополосковых и волоконно-оптических линий передачи, что приве-
ло к миниатюризации и улучшению качественных показателей трактов СВЧ и
соответствующих антенн.
Наиболее значительными достижениями этого периода в области антенной
техники являются практическая реализация фазированных антенных решеток с
быстрым электрическим сканированием луча (время перемещения луча порядка
единиц и долей микросекунды), создание развертываемых в космосе остронаправ-
ленных зеркальных антенн и решеток, предназначенных для глобальных систем
радиосвязи и радиовещания и для систем исследования природных ресурсов Зем-
ли, создание гигантских наземных полноповоротных антенн с диаметром зеркал
60—100 м для радиоастрономических исследований и радиосвязи с объектами в
глубоком космосе.
Введение
33
Становление современной теории и техники устройств СВЧ и антенн потре-
бовало усилий многих тысяч инженеров и ученых разных стран. Мы можем гор-
диться вкладом нашей страны в этой области. Еще в 1927 г. чл.-корр. АН СССР
А. А. Пистолькорсом была создана основополагающая теория однопроводных и
многопроводных линий передачи. Эта теория в 1930—1940 гг. была существенно раз-
вита проф. В. В. Татариновым, предложившим наиболее распространенный метод
измерения комплексных входных сопротивлений в линиях передачи по продоль-
ному распределению напряжения или тока и создавшим ряд классических схем
согласования нагрузок с линией передачи.
В 1939 г. А. А. Пистолькорс и М. С. Нейман разработали теоретические основы
и первые конструкции направленных ответвителей — основных «строительных
элементов» современных разветвленных трактов СВЧ. Применение направленных
ответвителей в качестве рефлектометров — приборов для измерения коэффи-
циента отражения в линиях передачи — было предложено в 1940 г. советским
ученым А. Р. Вольпертом. Им же в 1939 г. была предложена круговая номограмма
для линий передачи, существенно облегчившая инженерные расчеты режимов
линий и согласующих устройств. Л. Д. Бахрахом и Д. И. Воскресенским разработа-
ны основы многолучевых антенн.
Сложные теоретические вопросы возбуждения волноводов были впервые раз-
работаны в 1940—1950 гг. советскими учеными А. Л. Драбкиным, И. И.
Вольманом, Г. В. Кисунько, Г. Т. Марковым, Е. М. Студенковым. Теория невза-
имных устройств с ферритами была создана А. Л. Микаэляном, А. Г. Гуревичем и
В. В. Никольским (60-е годы), теория переключающих и фазирующих устройств
с полупроводниковыми диодами — Б. В. Сестрорецким (70-е годы), теория
синтеза фильтров и направленных восьмиполюсников— А. Л. Фельдштейном и А.
М. Моделем (60—70-е годы).
Значителен вклад советских ученых и в области антенной техники. До сих
пор в инженерных расчетах многоэлементных антенн применяется метод наво-
димых электродвижущих сил, основанный на работах Д. А. Рожанского, И. Г.
Кляцкина, А. А. Пистолькорса и В. В. Татаринова (1922—1928). Повсеместное
признание получило понятие коэффициента направленного действия антенны,
предложенное А. А. Пистолькорсом в 1928 г. Советский ученый М. С. Ней-
ман (1935) впервые применил к изучению приемных антенн принцип взаимнос-
ти, чем были заложены основы теории приемных антенн. М. С. Нейман также
первым выдвинул в 1938 г. идею щелевой антенны. Фундаментальные основы
теории этих антенн были заложены А. А. Пистолькорсом, который сформулиро-
вал принцип двойственности, устанавливающий соответствие характеристик
проволочных и щелевых антенн (1944). Окончательное завершение теория ще-
левых антенн получила в 1945—1948 гг. в работах проф. Я. Н. Фельда. Важное
значение в теории апертурных антенн (в частности, рупорных) имело строгое
электродинамическое решение задачи об излучении из открытого конца волново-
да, полученное в 1958 г. чл.-кор. АН СССР Л. А. Вайнштейном.
Особенно велик вклад советских ученых в теорию синтеза антенн по задан-
ной форме диаграммы направленности. Первые фундаментальные результаты
в этом направлении были получены А. И. Узковым еще в 1945 г. В дальнейшем
теория синтеза антенн получила развитие в трудах Л. Д. Бахраха, Я. Н. Фельда,
Е. Г. Зелкина, В. И. Поповкина, В. П. Яковлева и других ученых.
Советские ученые явились также пионерами использования ЭВМ в элект-
2 — Непнов
34
ВВЕДЕНИЕ
родинамических расчетах сложных излучающих систем и антенн. В частности,
Е. Н. Васильевым еще в 1960 г, был использован метод интегральных уравнений
для расчета с помощью ЭВМ характеристик излучения антенн, размещенных
вблизи металлических тел вращения. В 1970—1980 гг. В. В. Никольским и его
сотрудниками был создан ряд оригинальных методов электродинамического рас-
чета на ЭВМ волноводных и микрополосковых устройств и линий передачи.
Среди результатов, полученных советскими учеными в 70-е годы, следует от-
метить успешную разработку и внедрение методов восстановления на ЭВМ ха-
рактеристик излучения крупногабаритных антенн по замерам амплитуд и фаз
ближнего электромагнитного поля. Основоположниками этого перспективного
направления исследования характеристик антенн явились чл.-кор. А. Н. Армян-
ской ССР. П. М. Геруни и чл.-кор. АН СССР Л. Д. Бахрах.
Заканчивая краткий обзор развития техники антенн и устройств СВЧ, можно
с удовлетворением отметить, что в быстром историческом развитии антенны из
простого средства увеличения дальности радиосвязи в первых приборах А. С. По-
пова превратились в определяющее звено радиосистем. Предельные возможности
современных радиолокационных станций по дальности и точности пеленгации
целей, предельные чувствительность и разрешающая способность радиотелеско-
пов, предельные дальности радиосвязи в космосе с удаленными объектами и мно-
гие другие характеристики разнообразных радиосистем определяются технически
достижимыми параметрами антенных устройств, в первую очередь — шириной
луча, т. е. направленностью действия. Наиболее сложные современные антенные
системы в сочетании с многоканальными трактами по своему функциональному
назначению превратились в своеобразный технический аналог глаза, обеспечи-
вающий «радиовидение».
Электродинамические основы теории антенн 35
Глава 1. Электродинамические основы теории антенн
1.1. Передающая и приемная антенны
Электрический ток, расходующий энергию источника, рассматривается как не-
посредственная причина существования электромагнитного поля. В задачах элект-
родинамики он обычно заранее задан и называется «сторонним» током. Уравнения
Максвелла в терминах комплексных амплитуд для однородной изотропной среды,
включающие объемную плотность стороннего тока)ст, записываются в виде:
rot Н = + jcm,
А/ 7
—► —►
rot Е = -йярН,
(1.1.1)
где = £ — io / со.
Г1 А/ 7
Величины Е и Н будем понимать как векторные функции, в принципе опре-
деленные во всем пространстве. Область V (внутри которой распределен сторон-
ний ток с объемной плотностью jcm), создавая электромагнитное поле Е,Н, излу-
чает энергию во внешнее пространство, причем плотность потока энергии выра-
жается вектором Умова-Пойнтинга
—► —► —и-
S = Е,Н
(1-1.2)
Излучает всякий переменный ток, но излучение в обычных цепях переменного
тока — явление вредное, поскольку это увеличивает потери энергии. Например,
в случае колебательного контура, который должен накапливать энергию при ма-
лых потерях, излучение может препятствовать достижению требуемой добротно-
сти. Однако, пока размеры L области тока очень малы в сравнении с длиной
волны, потери на излучение составляют лишь малую часть общих потерь энергии.
Иными словами, излучение незначительно, если выполняется условие квазиста-
ционарности:
L « X. (1.1.3)
Однако по мере ослабления условия (1.1.3) излучение быстро возрастает и еще
для квазистационарного объекта может превышать джоулевы потери. Тогда рас-
сматриваемая область V с прилежащим пространством (если она не экранирова-
на) непригодна, например, для накопления электромагнитной энергии, но зато она
может быть использована в качестве излучателя — передающей антенны. Важно
отметить, что от антенны требуется не просто излучение, а передача энергии
в пространство, отвечающая определенным практическим задачам. Так, напри-
мер, радиовещательная станция обслуживает одновременно целый район, нахо-
дясь чаще всего в его центре, и потому её антенна должна излучать более или
менее равномерно в разных направлениях. При двусторонней же связи, особенно
при дальней, нерационально рассеивать энергию во всех направлениях, и ее уз-
36
ГЛАВА 1
ким лучом направляют на приемный пункт. Особенно узок должен быть луч
в радиолокации, где это обусловлено необходимостью точного обнаружения объекта.
Луч радиолокационной антенны обычно должен еще периодически перемещаться,
совершая «обзор» пространства. Итак, важнейшим фактором является направлен-
ность действия антенны (в литературе встречается также термин «направленные
свойства»). Для осуществления требуемой направленности излучения нужно в каждом
конкретном случае иметь вполне определенное строение источника электромаг-
нитного поля, поэтому значительное место в теории антенн отводится анализу
различных распределений тока.
Рассмотрим теперь приемную антенну. Процесс приема заключается в преоб-
разовании радиоволн, пришедших в пункт расположения приемной антенны,
в направляемые электромагнитные волны, воздействующие на входное устройство
приемника. Это преобразование выполняется приемной антенной. Электромагнит-
ное поле Е,Н, распространяясь в виде волны того или иного рода, наводит токи
с объемной плотностью
j = <зЁ
во всех несовершенных диэлектриках (о cde) и проводниках (о » сое). В уравне-
ниях Максвелла (1.1.1) эти вторичные токи учтены с помощью комплексной диэ-
лектрической проницаемости ек , мнимая часть которой пропорциональна плотно-
сти тока проводимости. В проводниках ток проводимости более существен, чем
в несовершенных диэлектриках, поэтому для дальнейших целей его удобнее выне-
сти из выражения электрической индукции
со
в первой строчке (1.1-1) и соответственно считать £ в проводящих областях веще-
ственной величиной. Уравнения Максвелла при этом принимают вид
rotH = i(£>EE + j + f™,
- - а (1.1.1а)
rot Е = -мяцН.
На рис. 1.1 область Vj, где распределен сторонний ток jcm (возбужденный генера-
тором), играет роль передающей антенны. Она создает поле Е,Н, которое наводит
а) б)
Рис. 1.1. Передающая (объем ) и приемная (объем V2 ) антенны
Электродинамические основы теории антенн
37
в проводящей области V2 ток j . Если этот ток заставить течь через полезную нагруз-
ку (входное устройство приемника), то область V2 будет служить приемной антен-
ной.
Поскольку желательно уменьшение потерь, проводящие элементы приемных
антенн (область V2) обычно выполняют из металлов с высокой проводимостью (медь,
латунь, алюминий и др.); в анализе же их часто можно принимать за идеально
проводящие (с —> оо). В этих же условиях при изучении распределения тока при-
емной антенны полезны следующие соображения.
Ранее (рис. 1.1) имелось в виду электромагнитное поле, существующее в про-
странстве при наличии передающей и приемной антенн, каждая из которых в той
или иной мере определяет его строение. Теперь же будем рассматривать электро-
магнитное поле излучения как заданное, а приемную антенну как возмущающий
его фактор. Пусть сначала передающая антенна излучает в пространство, свобод-
ное от проводящих тел, и создает в области V2, где пока нет приемной антенны,
поле Ё,Н, (например, однородное), электрические силовые линии которого пока-
заны на рис. 1.2, а. Если теперь поместить сюда идеально проводящее тело (объем
V2) (рис. 1.2, б), то прежнее поле Е,Н не сможет существовать, так как оно
не удовлетворяет граничным условиям на поверхности внесенного тела, которое
будем считать моделью приемной антенны. Поле деформируется (рис. 1.2, б), как
можно полагать, благодаря тому, что на «первичное» поле Ё,Н, налагается до-
полнительное поле Ё', Н', возбуждаемое наведенными токами. Это «переизлучен-
ное» поле таково, что суперпозиции Ё + Ё', Н + Н' удовлетворяет требуемым
условиям на поверхности, ограничивающей V2, и, в частности, при о —> оо тан-
генциальная компонента электрического поля Ё + Ё' на указанной поверхности
обращается в нуль.
Вторичное поле распространяется во все стороны от возбудившего его метал-
лического тела — происходит процесс переизлучения электромагнитных волн. Если
в проводнике нет потерь, то энергия возбуждения токов полностью переходит
в энергию переизлученного (вторичного) электромагнитного поля.
Если к рассмотренному металлическому телу присоединить волновод или дру-
гой фидер, то наведенные токи возбудят электромагнитные волны и в фидерной
линии. Энергия возбуждения токов расходуется как на создание вторичного поля
Рис. 1.2. К пояснению принципа работы приемной антенны: а) — неискаженное падающее
плоское электрическое поле; б) — структура электрического поля вблизи металлического
тела; в) — схема включения приемной антенны (1 - проводник, 2 - фидер, 3 - приемник)
38
ГЛАВА 1
излучения, так и на создание в фидерной линии направляемых волн, которые
поглощаются в приемнике. При этом металлическое тело становится приемной
антенной (рис. 1.2, в).
Заметим, что как бы тщательно не конструировались антенны, фидерная ли-
ния и приемник, энергия возбужденных токов в реальных условиях не может быть
полностью передана в приемник. Часть энергии этих токов неизбежно рассеивает-
ся на переизлучение, так как процесс приема обязательно связан с искажением
поля, т.е. с возникновением вторичного поля.
При оценке приемной антенны, как и передающей, существенна ее направлен-
ность действия. Например, антенна радиовещательного приемника должна быть
ненаправленной, чтобы улавливать сигналы, поступающие с различных направ-
лений, а при двусторонней связи желательно иметь приемную антенну, эффек-
тивно действующую в одном нужном направлении и нечувствительную к посто-
ронним сигналам, идущим отовсюду.
Одна и та же антенна (выполненная, например, в виде проводника заданной
формы) может функционировать как в качестве приемной, так и в качестве пере-
дающей. На основании теоремы взаимности [1], можно показать, что направлен-
ность действия антенны одинакова при приеме и при передаче, если выполнены
некоторые условия, приведенное ниже. При более детальном подходе будет уточ-
нено, как именно понимается «направленность действия» при приеме и при пере-
даче.
В заключение раздела вернемся снова к самой постановке задачи об излучении
в виде уравнений Максвелла (1.1.1), (1.1.1а). Вначале было подчеркнуто, что сто-
ронний ток, будучи заранее заданным, выражает причину существования поля
излучения. Однако при определении поля можно использовать эквивалентные элек-
трические и магнитные источники.
На рис. 1.3 область стороннего тока окружена мысленной поверхностью S.
Если известно тангенциальное электромагнитное поле на S , то этого достаточно,
чтобы найти поле во всем пространстве. В данном случае можно не знать объемной
Рис. 1.3. К вопросу вторичных эквивалентных источников на
поверхности S от передающей антенны
Электродинамические основы теории антенн
39
плотности стороннего тока jст, так как распределение поля на S можно истолко-
вывать как совокупность эквивалентных электрических и магнитных поверхност-
ных токов [1], которые полностью определяют излучение. При такой постановке
задачи справедлива следующая теорема эквивалентности.
Теорема эквивалентности. Под «теоремой эквивалентности» понимают совокуп-
ность результатов, получаемых при замене заданного на некоторой поверхности
электромагнитного поля эквивалентным распределением поверхностных токов —
электрического и магнитного [1]. Поле в окружающем пространстве (обычно в дальней
зоне) определяется затем как якобы созданное этими эквивалентными источ-
никами.
Пусть «истинные источники» — сторонние токи jcm, распределенные в области
Vl (рис. 1.3), — неизвестны, но известно поле Es, Hs , созданное ими на замкну-
той границе S рассматриваемой области V • Этих данных достаточно, чтобы оп-
ределить электромагнитное поле вне области V • Применяемый метод состоит
в том, что поле внутри объема V мысленно отбрасывается, а на поверхности
S вводятся фиктивные поверхностные электрические fje и магнитные токи.
Плотность поверхностного электрического тока при этом равна
п‘
(1.1.4)
а плотность поверхностного магнитного тока
fjm = -|_n0,E5J. (1.1.5)
Поле Ё,Н вне V в силу принципа суперпозиции находится суммированием
двух полей, одно из которых возбуждено электрическим поверхностным током
(Е',Н'), а другое (Ё",НЯ) — магнитным:
Ё = Ё' + Ё",
Н = Н' + Н".
(1.1.6)
Таким образом в уравнения Максвелла можно ввести сторонние объемные плот-
ности электрического je,cm и магнитного ymcm токов, которые связаны с поверхно-
стными плотностями фиктивных электрических и магнитных токов следующим
образом:
Г’ст =ne(W1,u2)8(n-n'),
Г'- =nTO(u1,u2)5(n-n'),
(1-1.7)
где т]е’т заданы на поверхности S (рис. 1.3) как функции координат их,и2\ п —
нормальная координата (по отношению к поверхности £ ), определяющая при п = пг
поверхность £ ; 5(п - п') — одномерная функция Дирака. Тогда уравнения Макс-
велла для комплексных амплитуд записываются в виде:
rot Н = йоа J? + Г’™,
rv '
rot Ё = -ie>pKH - jm’cm,
(1.1.8)
где ц?. = ц - iam /(соцо)— комплексная магнитная проницаемость, су™— удельная
магнитная проводимость.
40
ГЛАВА 1
Рис. 1.4. Граница раздела двух сред
В заключении раздела запишем граничные условия для векторов Е и Н при
наличии на границе раздела поверхностных токов и зарядов (рис. 1.4):
[ п„,Ёт - Ё'2' ] п'",[ п0,Н|1’-Й‘2)] = т|е, (1.1.9)
е /’cWp’W - £е /'iiWfrf1) /1 -I ini
~£кЬ )П0 “ 5 , Ц0 (И И В )П0 - $ , (1.1.10)
где rje, fjm — комплексные амплитуды поверхностных плотностей электрического
и магнитного токов; — комплексные амплитуды поверхностных плотностей
электрического и магнитного зарядов. Заметим, что под поверхностными токами
и зарядами в (1.1.9) и (1.1.10) понимаются как сторонние токи и заряды, так
и заряды, возбуждённые электромагнитным полем.
На поверхности идеального электрического проводника граничные условия при-
нимают более простую форму (Е^ = Й<2' = 0 ):
8„(по,41|е(1,) = ^)[й„,ё(')] = о,
= О, [n0,H<1’] = fje,
(1.1.11)
то есть на идеальном металле магнитные токи и заряды не существуют.
Соответственно, на идеальном магнитном проводнике отсутствуют электричес-
кие токи и заряды:
(по,£^(1)) = О, [п0Л(1)] = ЧГ,
цо(по,р(1)Н(1)) = ^,[по,Н(1)] = О.
(1.1.12)
1.2. Средний баланс энергии и эквивалентные схемы
приемной и передающей антенн
Для понимания действия антенны нужно иметь представление об ее энергетичес-
ких характеристиках как некоторой электродинамической системы. Окружив антенну
замкнутой поверхностью S, можно говорить о потоке энергии через эту границу
и о запасе энергии в ограниченном объеме V. Как будет показано, анализ этих
понятий позволит ввести в рассмотрение эквивалентную схему антенны, элементы
которой отражают баланс энергии установившегося электромагнитного процесса.
Итак, рассмотрим применительно к поставленной задаче уравнение среднего
баланса энергии гармонического во времени электромагнитного поля, (зависимость
Электтоо^нами^ские основы теории антенн
41
от времени полей будем учитывать в виде exp(zo)t)) внутри объема V [1]:
<jiSKds = -P-i2<a(Nm-N‘), (1.2.1)
где SKds— полный поток через поверхность SK комплексного вектора Умова-
Пойнтинга:
(1.2.2)
вещественная часть которого
Re SK
=(5«)=
(1.2.2а)
есть средний вектор Умова-Пойнтинга — среднее во времени за период колебание
Т = 2л / со значение плотности потока энергии. Величина
(1.2.3)
- средняя за период комплексная мощность. Выделяя под интегралом плотность
стороннего тока jcm в соответствии с соотношением
вместо формулы (1.2.3) запишем
—► —► —»
• г । ; ст
j = оЕ + ; ,
(1-2.4)
= 1 Jf m'EdV.
(1.2.4а)
> — средняя за период мощность потерь; ^Рсту — средняя за период сторон-
няя мощность.
Далее, средняя за период Т магнитная (Nm\ и средняя за период электричес-
кая \Ne} энергия в области V равны:
(ЛГ") = 1 JjiH2dV, = 1 feE2dV. (1.2.5)
1 V V
Наша задача состоит в том, чтобы получить общие энергетические характери-
стики антенны. Итак, пусть антенна — приемная или передающая — находится
внутри области V (рис. 1.5). Передающая антенна соединена с генератором, как это
схематически показано на рис. 1.6, а. Если же антенна — приемная, то она нагру-
жена входным сопротивлением приемника ZM (рис. 1.6, б).
Остановимся на антенне передающей. Расширяя область V так, чтобы ее гра-
ничная поверхность S оказалась в дальней зоне излучения (г —> ос), где векторы
Е и Н находятся в фазе, запишем:
42
ГЛАВА 1
Рис. 1.5
а) б)
Рис. 1.6. Эквивалентные схемы передающей (а)
и приемной (б) антенн
ds.
(1.2.6)
Поток вектора SK через полную границу S равен среднему значению за пе-
риод Т излучаемой мощности [1]:
(1-2.7)
которую удобно представлять в виде
(1.2.8)
вводя специальный параметр Rz - сопротивление излучения. Из формул (1.2.7)
и (1.2.8) вытекает следующее общее выражение сопротивления излучения
антенны:
(1.2.9)
Полученный результат нуждается в пояснении, так как ток I в (1.2.8) и (1.2.9),
вообще говоря, не определен однозначно. Если антенна не мала в сравнении
с длиной волны, то ток в разных ее частях может существенно различаться
по амплитуде. Например, рассматривая проволочные антенны, употребляют вы-
ражения «ток на клеммах» (там, где передающая антенна присоединяется к питаю-
щему устройству) и «ток в пучности» (в том месте, где его амплитуда максималь-
на). Это — две разные величины, каждая из которых может быть использована
в формуле (1.2.9). Исходя из этого, говорят о сопротивлении излучения, отнесенном
к клеммам или к пучности. Подобный вопрос в случае элементарных излучателей
не возникает.
Формулы (1.2.4а) можно записать в новом виде:
(Рп} = - [aE2dV = -I2Rn
\ / 2 J 2
(1.2.10)
Электродинамические основы теории антенн
43
Рст} = i \jcmEdV = -I*e
(1.2.11)
где Rn — эквивалентное сопротивление потерь антенны; е — комплексная амп-
литуда эквивалентной ЭДС питающего антенну генератора.
Разумеется, формулы (1.2.10) и (1.2.11) имеют ясное физическое содержание
лишь в том случае, когда в качестве 1 в них участвует тот же ток, что и в (1.2.8)
и (1.2.9). В дальнейшем это всегда будет предполагаться. Величины Rn и е, таким
образом, как и R2, отнесены к току I в определенном месте антенны.
Взяв теперь исходное уравнение баланса энергии (1.2.1), внесем в него рассмот-
ренные выше выражения величин (1.2.9) — (1.2.11):
-IZRZ = -—I2Rn
2 2 2
(1.2.11а)
О Ф
Разделив все слагаемые на I (при этом учитывается, что 1=1-1 ), получим
уравнение
(1.2.12)
которое можно истолковать как обобщенную формулу закона Ома, примененного
к эквивалентной схеме передающей антенны в виде последовательной цепи
(рис. 1.6,а и рис. 1.7,а). Тогда уравнение (1.2.12) выступает как основание для пред-
ставления антенны в виде последовательной эквивалентной цепи с комплексными
амплитудами тока I и ЭДС е (1.2.11), в которой фигурируют активные сопротив-
ления R1 и Rn, определяемые формулами (1.2.9), (1.2.10), и реактивное сопротив-
ление в точке «А» антенны:
(1.2.13)
Отметим, что (Nm\ и \Ne} — неотрицательные величины. Поэтому в тех
случаях, когда преобладает магнитная энергия (Nm\ реактивное сопротивление
ХА оказывается положительным (индуктивным). Если же преобладает электри-
ческая энергия, ХА отрицательно, т.е. имеет емкостной характер.
Итак, из анализа среднего баланса энергии установившегося электромагнитного
а) б)
Рис. 1.7. Эквивалентные схемы антенн: а) — передающей; б) — приемной
44
ГЛАВА 1
процесса передающей антенны возникает ее представление в виде последователь-
ной цепи, элементы которой имеют энергетическое выражение. Зная эти элемен-
ты, фактически располагают сопротивлением антенны
ZA = Rz+Rn+iXA> (1.2.14)
которое прямо или косвенно характеризует ее как «нагрузку» генератора. Эта
величина может представлять интерес при расчете питающего антенну устрой-
ства — радиопередатчика. В связи с этим еще раз подчеркнем, что комплексная
амплитуда тока I в (1.2.12), к которой отнесено сопротивление (1.2.14), может
выбираться различным образом, причем не всегда оказывается полезным пред-
ставление о входном токе проводимости антенны.
Вернемся к понятию реактивного сопротивления антенны и отметим одно
существенное обстоятельство. При нахождении в (1.2.13) разности (Nm \ - (Ne^ ин-
тегрирование в (1.2.5) производится по области V, граничащей в дальней зоне,
и этого достаточно, чтобы сопротивление ХА было вполне определенным (не зави-
сящим от размеров V). Желая убедиться в этом построим за границей S еще
одну замкнутую поверхность S'. Заключенная между ними область V может
быть, например, сферическим слоем (рис. 1.8). Разность (Nm^-\Ne^ внутри V
пренебрежимо мала. Действительно, применим к области V уравнение баланса
энергии (1.2.1). Поскольку V целиком лежит в дальней зоне, поток энергии через
ее границы S и S' можно считать чисто вещественным и мнимость г'2соцЛГто^ — (Nej\
в правой части исчезает. Все рассуждения сохраняют силу при неограниченном
расширении S', а это значит, что поле во внешнем по отношению к S бесконеч-
ном пространстве практически не влияет на величину реактивного сопротивления
антенны ХА.
Далее возникает вопрос о том, какое значение можно придавать каждому
из слагаемых выражения (1.2.13) в отдельности. Ведь если сравнить эту запись
с общим выражением реактивного сопротивления X = coL -1 / соС и принять во
внимание положительность величин (Nm \ и (Ne }, то формально можно полу-
чить:
Хс =----— = -4 fsE2dV, XL = coL = 4 Ltf2dV, (1.2.15)
I2 J I2 Г
откуда вытекают выражения для величин СА и ЬЛ :
Рис. 1.8. К вопросу определения реактивного сопротивления антенны
Электроднррмр^рс2си^ основы теории антенн
45
(1.2.16)
т.е. «эквивалентной емкости» и «эквивалентной индуктивности» антенны.
Однако интегралы (1.2.15) неограниченно возрастают с ростом V и это отражает
тот факт, что все рассуждения относятся к идеализированному установившемуся
процессу (который существует уже бесконечно долго), в результате чего запасы
энергии и \Ne} неограниченно велики. Тем не менее, формулы (1.2.15)
и (1.2.16) небесполезны, поскольку электрическая и магнитная энергии в бесконеч-
ном пространстве дальней зоны взаимно компенсируются. Написанные выражения
приобретают определенное содержание, если из Е и Н исключить компоненты,
создающие активный поток энергии. Итак, при пользовании формулами (1.2.15)
и (1.2.16) под Е и Н следует понимать компоненты поля, которым соответствует
реактивный поток энергии, т.е. ближнее поле.
Рассматривая приемную антенну на основании анализа ее баланса энергии,
также можно прийти к ряду принципиальных выводов. Эквивалентная схема при-
емной антенны может быть составлена в виде, показаном на рис. 1.7,6. Для цепи,
подключаемой к приемной антенне, антенна является генератором с комплексной
э.д.с. е и внутренним комплексным сопротивлением ZA = Rz + Rn + iXA . Приемник
на рис. 1.7,6 представлен комплексным сопротивлением Znp = Rnp + гХпр . В слу-
чае приемной антенны действуют способом, опираясь на то обстоятельство, что
на основании теоремы взаимности приемную антенну можно сопоставить с пере-
дающей и судить о ее параметрах, исходя из режима передачи. Это и будет
сделано в главе 3.
1.3. Расчёт электромагнитных полей, создаваемых
заданными электрическими и магнитными токами
в однородной изотропной среде
Ниже рассматривается внешняя задача анализа излучающей системы (антен-
ны), которая сводится к определению электромагнитного поля излучения в любой
точке пространства по известному распределению токов (электрических и магнит-
ных). Будем исходить из уравнений Максвелла (1.1.8).
1.3.1. Уравнения Гельмгольца и электродинамические потенциалы. В уравне-
ния (1.1.8) одновременно входят векторы Е и Н. Целесообразно перейти к уравне-
ниям, в которые входят либо только вектор Е, либо только Н.
Производя в (1.1.8) взаимную подстановку, в случае однородной среды получа-
ем:
rot rot Е = к2Ё - i (ОЦоНк J е’СТ “ ro^ 3 т,СТ >
rot rot Н = к2Н - г <D£g£K j та,ст + rot j е,ст ,
(1.3.1)
46
ГЛАВА 1
где к = к0 v £kHk — волновое число среды. С учётом векторного тождества
rot rot F = grad div F - V2F
систему (1.3.1) можно представить в виде:
V2E + k2E = -Ме,
V2H + k2H = -Мт,
где
Ме = -wopJe CTn +-^J—grad div - rot
гЮ£°£к (1.3.3)
Mm = -iGK0£K jm’m + —grad div jm’cm + rot je’cm.
Уравнения (1.3.1) — неоднородные уравнения Гельмгольца. Они являются линейны-
ми дифференциальными уравнениями второго порядка с постоянными коэффици-
ентами.
Для тех точек пространства, в которых источники отсутствуют, неоднородные
уравнения (1.3.1) переходят в однородные:
АЁ + к2Ё = 0,
ЛН + к2Н = 0,
(1.3.4)
где д = у2.
Неудобство уравнений (1.3.1) заключается в сложности выражений в их правых
частях. Поэтому в теории антенн с помощью соотношений:
Ё = -гсоцощАе +-------grad div Ае - rot Ат,
г®е0ЕК
Н = -га)Е„£КАт ч-----—grad div +rotAe.
(1.3.5)
обычно вводят два новых вектора (электродинамические векторные потенциалы)
Ае, Ат. После подстановки (1.3.5) в уравнения (1.3.1) имеем
е,сш
ДА” + кгАт
• т,ст
(1.3.6)
Запись (1.3.6) проще, чем (1.3.2). Поэтому в дальнейшем будем иметь дело с этими
уравнениями. Найдя из них векторные потенциалы, затем по формулам (1.3.5)
определим поля Е и Н.
1.3.2. Решение векторного уравнения Гельмгольца. Функции Грина. Пусть в неко-
тором объёме V заданы распределения объёмных плотностей сторонних электричес-
ких je,CT и магнитных jm,CT токов. Определим векторные потенциалы Ае, Ат. Будем
исходить из уравнений (1.3.6). Поскольку оба уравнения с формальной точки зрения
одинаковые, будем рассматривать уравнение
&A + k2A = -jcm,
(1.3.7)
Электродина^м^ основы теории антенн
47
где под А будем понимать либо Ае , либо Ат.
Запишем (1.3.7) в декартовой системе координат, в которой
7 Эх^о + ЗуУо 7z^0 ’
где у$, z^ — единичные векторы. Для любой компоненты Aj вектора
А (г = х, у, z) имеем:
(1.3.8)
Для решения (1.3.8) воспользуемся методом разделения переменных. Предста-
вим рассматриваемую компоненту векторного потенциала в виде:
Ai(x,y,z) = X(x)Y(y)Z(z). (1.3.9)
Функции, входящие в (1.3.9), заданы на бесконечном интервале, поэтому их можно
представить в виде интегралов Фурье. Например, для Х(х) имеем:
00
= jgi(X1)e-!^d%1, (1.3.10)
— 00
где <7i(Xj) — спектральная плотность. Выражение (1.3.10) можно трактовать как
бесконечный набор плоских однородных волн, распространяющихся вдоль и про-
тив оси ОХ с фазовыми скоростями va = co/Xi , гЛе величина играет роль
волнового числа. Аналогично
Y(y) =
00
/92(Х2)е-^
— 00
<1X2
00
= 1дз(Хз)е~гХзг dZ3*
—ОО
Подставив эти разложения в (1.3.9), получим:
Ai(x,y,z)
(^2л)3
00 ОО 00
J J jg(xi,%2,%3)
d%1 d%3 ,
(1.3.11)
—00 —00 —00
где g(Xi> X2> Хз) = 91(Х1)92(Х2)9з(Хз) — неизвестная спектральная плотность.
С учётом (1.3.11) уравнение Гельмгольца (1.3.8) будет иметь вид:
2 2 2 1
“Xi -Х2 -Хз х
(1.3.12)
х 9(Х1»Х2’Хз)е г12У n32dXi^X2dX3-
Для определения д(Х1>Х2>Хз) умножим (1.3.12) на ехр(г/^ + ix'2y + гхз^)/(2л:)3 ,
где X1> Х2’ Хз — фиксированные пока значения %i, Хз , и проинтегрируем (1.3.12)
по всему бесконечному пространству:
1
(2тг)3
00
f J рГ(х,г/,г) e!^+i^+i^dxdydz =
—00
48
ГЛАВА 1
= J J J(fc2 _Xi -%2 -Хз) 9(Х1,Х2,Хз)х
—00
1
X_(2Tt)3
x<£c dy dz ] d-/| dx2 d%3 •
oo
—00
Заметим, что
00
J_ р(Х1-ь)х dx = 6(xl -Xi),
2л J
—00
где 5(xi ~Xi) — дельта-функция Дирака, для которой
00
Js(xl -xiMxi =i •
—00
С учётом этого имеем
(k2-Xi2-Х22 “Хз2) 9(ХьХ2,Хз) =
(1.3.13)
(1.3.14)
e^i^^^^d^di/dz.
Полагая волновое число х(Х1>Х2»Хз) произвольным и обозначая точки источников
как х', у', z', а точки наблюдения (точки, в которых вычисляется поле) как х, у, z,
последнее уравнение переписываем в виде:
(k2 -Xi -Х2 "Хз) 0(ХьХ2,Хз) =
1
(л/2л)3
fjf№ y',z') е^х'+^у'+^г' dx'dy'dz' .
V
(1.3.15)
Здесь интегрирование производится только по тем точкам пространства, где име-
ются токи (объём V). Подставив (1.3.15) в (1.3.11) и меняя порядок интегрирования,
имеем
y',z') G(x,y,z\ x',y',z') dx'dy'dz'
(1.3.16)
J
где
G(x,y,z; x',y',z') =
e-i xdx-x')-i x2(y-y'}-i %3(z~z')
------Г 2,2,2----------d%2 ЙХз
Xi + X2 + Хз
(1.3.17)
— функция Грина для свободного пространства.
Выражение (1.3.16) справедливо для всех составляющих Аг-
Поэтому в векторном виде оно имеет вид:
(г = x,y,z).
Электродинамические основы теории антенн
49
А(р) = pCm(q) G(p,q)dV.
(1.3.18)
Через p(x,y,z) обозначена точка наблюдения поля, а через q(x',y',z')
источников поля.
По аналогии могут быть решены и уравнения (1.3.2):
точка
Ё(р)= jMe(q) G(p,q) dV
(1.3.19)
Н(р)= ]мт(<г) G(p,q)dV,
(1.3.20)
где G(p,q) также имеет вид (1.3.17).
Формулы (1.3.18)-(1.3.20) с соответствующей записью функций Грина справедли-
вы для любой системы координат. Функция Грина (1.3.17) может быть представлена
в различных формах. Наиболее часто используется выражение
4л
(1.3.21)
где R — расстояние между точками р и q; k0 = со/с.
В декартовой системе координат
Известны два представления функции Грина в цилиндрической системе коор-
динат [1]:
hl
OD -VX2“k2 \Z~Z
' j„ (хр) Л. (хр'^.
(1.3.22)
-ш(ф-ф')
e Л(2 ^gjhjpjp')^
(1.3.23)
Х~0
gn(h; p,p') = <
K‘2>(vp')Jn(vp),
(vp) Jn(vp')
n
% и h имеют смысл поперечного и продольного волновых чисел.
50
ГЛАВА 1
1.4. Электрические и магнитные волны
в безграничной среде
В предыдущем разделе была решена внешняя задача излучения: по известным
распределениям сторонних электрического je,cm и магнитного ^то>ст токов были
получены соотношения для Е и Н в любой точке. В частности, для векторных
потенциалов справедливы следующие интегральные соотношения:
Ае(р)= pe’cm(q)G(p,q)dV, Am(p) (q)G(p,q)dV, (1.4.1)
V V
где р (х, у, z) — точка наблюдения поля, q (х , у1, z') — точка источников поля.
Цель настоящего раздела — получить в явном виде выражения в различных
системах координат для электромагнитного поля в свободном пространстве (облас-
ти без источников), возбуждаемого источниками je,cm , jm’cm , расположенными
в некоторой области V. Будем полагать, что нам известны электродинамические
потенциалы Ае и Ат. Необходимо записать в компактной форме выражения для
Ё и Н.
1.4.1. Электрические и магнитные волны в декартовой системе координат.
Запишем уравнения Максвелла для комплексных амплитуд в области без источни-
ков в декартовой системе координат:
= -гсоц0цНж
= i(d£Q£ Е ,
(1.4.2)
= 2,
= Ш£.,Ь'Е.
V к z
В дальнейшем будем рассматривать электромагнитное поле, распространяющееся
вдоль оси OZ: Е ~ ехр (-г yz), Н ~ ехр(-гуг), где у — постоянная распростране-
ния.
Разрешая уравнения (1.4.2) относительно поперечных компонент, получаем:
(1.4.3)
где х2 =/с2£кЦ-у2.
Таким образом, соотношения (1.4.3) говорят о том, что электромагнитное поле
задаётся только двумя независимыми составляющими (EZ,HZ). Остальные состав-
ляющие можно выразить через них по формулам (1.4.3).
Электродинамические основы теории антенн 51
Во многих случаях для свободного пространства удобным оказывается пред-
ставление электромагнитного поля в виде так называемых электрических и маг-
нитных волн.
Для волны Е-типа (ТМ) Hz = 0. Их обычно называют поперечно-магнитными
(ТМ) или электрическими волнами. Для них соотношения (1.4.3) существенно упро-
щаются:
га>£0£к dEz
X2
(1.4.4)
Для волны Н-типа (ТЕ) Ez = 0. Это поперечно-электрические (ТЕ) или магнитные
волны. Для них из (1.4.3) вытекают следующие соотношения:
гсоц0ц dHz = гсоц0Ц дНг
X2 ду ' v %2 дх
iy дНг
/2 дх
(1.4.5)
Если поле не меняется вдоль оси OZ , то из формул (1.4.4) и (1.4.5) следует, что
оно распадается на два независимых поля с компонентами {Нх, Ну, Ez} и {Ех ,Ey,Hz}.
В общем случае при гармонической зависимости общее поле можно искать как
суперпозицию полей волн Е и Н-типов.
1.4.2. Электрические и магнитные волны в цилиндрической системе коор-
динат. Дано Aj в декартовой системе координат. Надо перейти к выражениям для
электродинамических потенциалов в цилиндрической (р, ср, z ) системе координат.
Можно просто воспользоваться выражением (1.3.16) и подставить в него выраже-
ние для функции Грина, записанное в цилиндрической системе координат. Однако
такая процедура является достаточно громоздкой.
Ниже будем считать известными выражения для электродинамических потен-
циалов в декартовой системе координат. Опишем процедуру перехода от Ах, Ау, Az
к Ар, , Az. В целях максимальной общности рассмотрим переход от декартовой
системы координат к произвольной криволинейной ортогональной системе для
произвольного вектора F. Запишем F в двух системах координат:
F = Fxx0 +Fyy0+ Fzz0, F = + F2e2 + F3e3 , (1.4.6)
где ej, ё2, e3 — единичные векторы криволинейной ортогональной системы коор-
динат. Из (1.4.6) следует, что
1*1 1*а? (*0 > ^1) + ?у (Уо, Cj ) + Fz (Zq , Cj ),
1*2 - lx(^0»®2) + l*2/(^0’^2) + l*z(^0’^2)> (1.4-7)
1*3 — l*o? (*0 ’ e3 ) + l*y (?/0 ’ e3 ) l*z (*0 > e3 )
В (1.4.7) скалярные произведения (ё7,ё7) есть направляющие косинусы. Для
52
ГЛАВА 1
их определения может быть использована связь
г
7~ ~—z0 >
hi I си, ди.- си,
vjsp Ui,U2,U2 — криволинейные ортогональные координаты,
Ламе.
Из (1.4.8) следует, что
(1.4.8)
коэффициенты
h; ди.
(1.4.9)
г
Рассмотрим конкретный случай — цилиндрическую систему координат. Для
неё: Ui = р , и2 = ср, = z , hi = 1, h2 = р, ^3 = 1 • Связь между прямоугольны-
ми и цилиндрическими координатами следующая:
х = рcosср, у - рsinср, z — z.
Определим направляющие косинусы. Очевидно, что
(х0, ер) = cos <р, (х0, еф) = - sin ср, (£о,ёг) = О,
(г/0, ёр) = sin ср, (^0,ёф) = coscp, (5оЛ) = °, (1.4.10)
(^о,Ср) 0, (Zq , еф) 0, (Zq,(?z) 1.
Запишем выражения для составляющих А в цилиндрической системе коорди-
нат через AX,AV,AZ :
Ар = Ах coscp + Ay sin ср, А,
Аналогично можно записать для jcm :
= -Ах sincp + Ay cos ср, Az = Az.
(1.4.11)
•cm -cm , -cm
3P = 3X coscp + л, sincp,
Лр =-L sincp + ^ coscp, (1.4.11a)
•cm -cm
3Z = 3Z •
Если ток jcm записан в декартовой системе координат, то проще найти сначала
Ax,Ay,Az, а затем по формулам (1.4.11) перейти в цилиндрическую систему ко-
ординат.
Если ток jcm проще записать в цилиндрической системе координат, то лучше
исходить из jp, Уф5 3z- Из (1.4.11), (1.4.11а) и (1.3.16) следует, что
Аер’т(р) = J[ jep'mcm cos (<р - <р') + ст sin (ф - ф ’)] G(p,q) dV',
^’m(p)= J[ Уф mcm COS (ф-ф1)-jp'™cmsin(<p-<p')]G(p,q)dV', (1.4.12)
V
^’™(P)= (jpmcm G(p,q)dV.
V
В выражениях (1.4.12) поле определяется в точке наблюдения p(p,cp,z), а интегри-
рование производится по точкам источников q(p’,cp',z')•
Электродинам^ основы теории антенн
53
Из (1.3.5) следуют выражения:
1А
рдр
(1.4.13)
Остальные составляющие электромагнитного поля можно определить с помо-
щью уравнений Максвелла.
1.4.3. Электрические и магнитные волны в сферической системе коорди-
нат. В сферической системе координат щ = г, = ф; hr = 1, h,Q = г ,
= г sin 0. Формулы перехода от декартовой системы координат к сферической
следующие:
х - г cos ф sin 0,
у = г sin ф sin 0,
Z = г cos
0.
(1.4.14)
С использованием общих формул (1.4.7) нетрудно записать соотношения между
Ar = А~ cos фsin 0 + A.. sin фsin 0 + A? cos 0,
/ Li I /С '
Aq = Ах cos ф cos 0 + Av 5Шфсоз0- Az sin0,
(1.4.15)
Afn = -A~ simp + A,, cosq.
MJ <Л> I I
Аналогичные соотношения можно записать и для jcm. Если известна запись
тока jcm в сферической системе координат, то при расчёте электромагнитного
поля проще исходить из других формул:
Aer’m(p)= Jpe,m(p,q) G(p,q)dV',
V
^’m(p) = [5Ге?дР,<?) G(p,q) dV’,
• О и
V
= ;-----g(p> w dV >
J sin 0 о ф
V
(1.4.16)
Fe’m(p,q) = CQSp + -ст,е,т
d (cos P)
60'
1 d (cos P)
sin 0' д ф'
cm,e,m
cos p = cos 0 cos 0' + sin 0 sin 0' cos (ф - ф')
Интегрирование в (1.4.16) производится по точкам д(г',0',ф'); р(г,0,ф) — точка на-
блюдения. Выражения для Е и Н в сферической системе координат также запи-
сываются с помощью (1.3.5).
54
ГЛАВА 1
1.5. Расчёт электромагнитных полей излучающих систем в
дальней, промежуточной и ближней областях
Как было показано выше, векторные потенциалы электромагнитного поля,
создаваемые известными электрическим и магнитным токами je,jm в объёме V,
в произвольной точке наблюдения р (х, у, z), определяются выражениями
Ae,m(x,y,z) =
(1.5.1)
где R = у(х - х')2 + (у - у')2 + (z - z')2 — расстояние между точками наблюдения
p(x,y,z) и интегрирования q (аУ, у', z'). Векторы Е и Н для любой точки простран-
ства определяются через векторные электродинамические потенциалы формула-
ми (1.3.5). Соотношения (1.3.5) и (1.5.1) являются строгими и применимы при любых
взаимных расположениях точек источников и точек наблюдения. Однако с помо-
щью их, как правило, не удаётся получить простые замкнутые (аналитические)
выражения даже для сравнительно простых излучающих систем. Поэтому прихо-
дится прибегать к упрощающим предположениям, связанным с разбиением про-
странства на дальнюю, промежуточную и ближнюю области.
Введём сферическую систему координат {г, 0, <р}, центр которой помещён внутри
излучающей системы (объём V на рис. 1.9, а). Пусть точки q(x ,у' ,z') и p(x,y,z)
изображают соответственно текущую точку интегрирования внутри излучающей
системы и точку наблюдения в окружающей однородной среде. Расстояние R,
входящее в формулу (1.5.1), в сферической системе координат записывается как
R = (г2 + г'2 -2r г' cos а)1 ! 2 ,
где г — расстояние от начала координат до точки р; г1
координат до точки q, а — угол между векторами г и г'
(1.5.2)
— расстояние от начала
(рис. 1.9, а).
Рис. 1.9. К вопросу деления пространства на дальнюю,
промежуточную и ближнюю области излучения
Электродинамические основы теории антенн
55
Если г > D, где D — максимальный линейный размер излучающей зоны, то
г > г' (точка наблюдения находится вне объёма с излучающими токами) и рассто-
яние R между точками р(г,0,ф) и д(г’,0',ф') можно приближённо представить
в виде ряда по степеням г' / г :
(/)
cos а (1 - cos а) +... .
1.5.1. Дальняя зона. Её часто называют зоной Фраунгофера. Для неё полагают
г » D , а следовательно и г
вать в следующем асимптотическим виде:
— ikr .
г’. В этом случае формулу (1.5.1) принято записы-
е.т
4itr J
;С,т
dV'
г и множитель
где нижнии индекс « оо » показывает, что это выражение справедливо при г —> <х>.
При выводе формулы (1.5.4) делаются два упрощения. Во первых, в знаменателе
подынтегрального выражения (1.5.1) приближённо полагается R
1 / г выводится из-под знака интеграла. Во вторых, в показателе экспоненты под
интегралом в (1.5.1) полагается R«r-r'cosa, то есть в разложении (1.5.3) учи-
тываются только два первых слагаемых. Учёт второго слагаемого в (1.5.3) при замене
R на приближённое выражение в показателе экспоненты объясняется тем, что от-
брасываемые члены должны быть малы по сравнению с величиной 2п (периодом
экспоненты с мнимым показателем). Таким образом, второе упрощение означает,
что лучи, проведённые в точку наблюдения р дальней зоны из начала координат,
и из текущей точки интегрирования q, считаются параллельными (рис. 1.9 ,б). Допол-
нительное слагаемое г'cos а в записи R носит название разности хода лучей. Оно
учитывает запаздывание сферических волн, приходящих в точку наблюдения
от двух точечных источников, расположенных в начале координат и в точке q (г1,0', ф').
В явном виде разность хода лучей можно записать следующим образом:
г’cos а ~ х' sin 0 cos ф + г/'зтОзтф + z'cos0. (1.5.5)
Уточним границу применимости формулы (1.5.4), то есть найдём внутреннюю
границу дальней зоны. Основное упрощение, которое было сделано, заключается
в отбрасывании третьего слагаемого в (1.5.3) при записи показателя экспоненты
под интегралом. Возникающая при этом фазовая ошибка оказывается приближённо
равной к (г’)2 sin2 а /(2г). Так как максимальное значение r^ax ~ D/2, то наиболь-
шая фазовая ошибка может быть Лфтах = к D2 /(8г). Обычно полагают Афтах
и тогда нижняя (внутренняя) граница дальней зоны определяется как
2D
(1.5.6)
При увеличении размера излучающей системы D граница дальней зоны быстро
отодвигается. Например, при D/A. = 10 дальняя зона начинается с расстояния
56
ГЛАВА 1
г > 200X, а при D/X = 100 началу дальней зоны соответствует г>20000Х. При
частоте / = 10 ГГц (X = Зсм) эти расстояния соответственно равны 6 м и 600 м.
Для перехода от векторных потенциалов А^т , определяемых формулами (1.5.4),
к векторам полей Е и Н в дальней зоне, можно воспользоваться соотношениями
(1.3.5). Однако проще исходить из уравнений Гельмгольца для Е и Н (1.3.2).
С точностью до слагаемых, имеющих радиальную зависимость 1 / г , соотноше-
ния (1.3.5) для дальней зоны принимают вид:
М‘ = -гк [+ 4” ] е0 - гк [Wj; - ] <р0,
м" = [ikw;1 % + X ] §0 + [ikw;4; + ц ] ф0,
где Wc = д/цор. / £оек - характеристическое сопротивление среды.
Так как решениями уравнений
у2 де,т _|_ 1с2Де’т
е/т
(1.5.7)
в дальней зоне являются выражения (1.5.4), нетрудно записать следующие расчёт-
ные соотношения для полей Е и Н:
Eq = -ik[WcA^ + А™ ], H^ = Ee/Wc,
Е. = -ik[WcА^ - А™ ], HQ = -Е^ / Wc,
Ег = Нг - 0.
(1.5.8)
На практике вычисление электродинамических потенциалов удобно произво-
дить в декартовой системе координат (i = х, у, z):
(1.5.9)
х exp [ ik (х1 sin 0 cos <p + у' sin 0 sin <p + z' cos 0)] da?' dy'dz' ,
а затем переходить к сферическим координатам с помощью соотношений (1.4.15).
Поскольку на практике наибольший интерес представляет поле в дальней зоне,
перечислим его основные свойства в этой области:
1. Электромагнитное поле от любой антенны в дальней зоне имеет поперечный
характер: составляющие векторов Е и Н в направлении распространения отсут-
ствуют (Ег = Нг = 0 ).
2. Поле в окрестности любой точки наблюдения в дальней зоне носит характер
плоской электромагнитной волны, то есть компоненты Eq и , а также Е^
и Hq находятся в фазе и их отношение как следует из (1.5.8) равно характеристичес-
кому сопротивлению среды:
Ее/Нф=ТУс,Еф/Не=-ТУс.
(1.5.10)
3. Зависимость поля от расстояния г имеет вид расходящейся сферической вол-
ны exp (-ikr) / г. Однако поверхности равных фаз для каждой компоненты поля
в общем случае не являются сферами, так как Eq и Е^ — комплексные функции,
зависящие от углов (р, 0 , а начало координат выбрано произвольно.
4. Пространственные распределения составляющих Е в дальней зоне не зависят
Эштт^ основы теории антенн
57
от расстояния г и описываются функциями угловых координат:
Ш<р) =
£е(в.<Р)
^0тах(®1’Ф1)
гф(0,Ф) =
£ф(0,ф)
Яф max (®2 > Ф2)
(1.5.11)
где 01, Ф1 и 02, Ф2 — углы максимального излучения для соответствующих
компонент. Функции Fq и Гф называют нормированными амплитудными ха-
рактеристиками направленности по полю для соответствующих составляю-
щих, а их графические изображения — нормированными амплитудными диаг-
раммами направленности по напряжённости.
5. Среднее по периоду значение плотности потока мощности < S > в дальней
зоне связано с комплексным вектором Умова-Пойнтинга £к известным соотно-
шением
S>=ReSK ^-Re[ExH] = rQRe[(EQH^-Ei?HQ)/2] .
В силу (1.5.8)
S
Ee(e,<p)|2 +|Е<р(е,<р)|2
2W,
Ё(0, Ф)|2
2W.
(1.5.12)
Из (1.5.12) следует, что вектор < S >
в дальней зоне направлен радиально. Мнимая
часть среднего значения плотности потока мощности равна нулю.
Угловая зависимость
№<е, ч>) = -------г----
< £(0о>Фо) шах
(1.5.13)
называется нормированной характеристикой направленности по мощности,
а её график — нормированной диаграммой направленности по мощности.
< $ >rmax — r-составляющая модуля вектора < S >г в направлении максималь-
ного излучения, задаваемого углами 0g, Фо-
1. 5.2. Промежуточная область (зона Френеля). При расчёте полей антенн
в промежуточной области используются следующие приближения:
1. Как и в случае дальней зоны R в знаменателе подынтегрального выражения (1.5.1)
принимается приближённо равным г (R » г) и выносится из-под знака интеграла.
2. В показателе экспоненты подынтегральной функции в (1.5.1) принимается
R к г - г' cos а + (г')2 sin2 а /(2г) ,
что соответствует отбрасыванию в степенном ряду членов выше второй степени.
Таким образом, в промежуточной области векторные потенциалы вычисляются
по формуле
_7/^7*
Al’m(r,e,4>) = -------- fj«.™(a;'iJ/')z-)ei4’"cosa-r'2sin2a/(2r)]dv,
ф 4лг J (1.5.14)
3. При выполнении операций пространственного дифференцирования в форму-
2
лах (1.3.5) отбрасываются все члены, имеющие радиальные зависимости 1/т
58
ГЛАВА 1
3
и 1 / г , аналогично тому, как это делалось при вычислении полей дальней зоны.
Следовательно, компоненты векторов полей Е и Н в промежуточной области
могут быть найдены по формулам (1.5.8) с помощью замены
де,т
^00
(1.5.15)
Анализ использованных приближений зоны Френеля приводит к тому, что
расстояние г, на котором они выполняются, должно находиться в пределах:
2D
(1.5.16)
Величина D/4 в левой части неравенства (1.5.16) учитывает амплитудную ошиб-
ку, возникающую в связи с заменой 1 / R на 1 / г .
При D = 10X промежуточная зона определяется как 13.5 X < г < 200 X , а при
D = 100X: 250 X < г < 20000 X. Более строгое рассмотрение допущений, сделанных
при расчёте полей в дальней и промежуточной зонах показывает, что границы этих
областей зависят не только от расстояния г, но и от углов наблюдения 0, ср, а также
от геометрии излучающей системы и характера распределения сторонних токов.
1.5.3. Ближняя зона. В ближней зоне электромагнитное поле имеет как попереч-
ные, так и продольные составляющие; зависимость от расстояния г носит нерегу-
лярный характер. При этом необходимо исходить из строгой формулы для электро-
динамического потенциала (1.5.1).
Поле в ближней зоне имеет квазистатический характер. В силу выполнения
условия: г « X можно пренебрегать запаздыванием. В результате пространствен-
ные распределения электрического и магнитного полей, создаваемых, например,
каким-то источником с электрическим моментом р, совпадают, соответственно
с полем статического электрического диполя и с полем постоянного линейного
тока.
Необходимость знания поля в ближней зоне связана с расчётом входного сопро-
тивления антенн, эффектов взаимной связи между близко расположенными антен-
нами (проблема электромагнитной совместимости), влияние поля на обслуживаю-
щий персонал.
1.6. Излучение электромагнитных волн
элементарными излучателями
1.6.1. Роль теории элементарных излучателей при определении поля излуче-
ния антенн. Элементарные излучатели — малые в сравнении с длиной волны
элементы тока проводимости или фиктивного (эквивалентного) тока — подробно
рассматривались в курсе электродинамики и распространения радиоволн. Присту-
пая к изучению антенн, нужно вспомнить свойства этих простейших излучателей.
Среди применяемых на практике антенн есть такие, которые во многом на них
похожи. Но наиболее важным является то, что более сложные антенны, соизмери-
мые с длиной волны, удобно анализировать, представляя их в виде совокупности
элементарных излучателей. Это обстоятельство, главным образом, и определяет
Элртспиродиррлигмррк]^ основы теории алрпенн 59
роль последних в теории антенн.
В теории антенн выделяют следующие элементарные излучатели: элементар-
ный электрический диполь (диполь Герца), элементарный магнитный диполь, эле-
ментарная электрическая рамка, элементарный щелевой вибратор, элементар-
ный излучатель Гюйгенса.
Существуют различные методы определения напряженности поля антенн, опи-
сываемые в литературе. Нами излагаются наиболее простые и наглядные. В част-
ности, для упрощения задачи раздельно рассматриваются решения для проволоч-
ных и апертурных антенн. Для расчёта излучения проволочных антенн использу-
ется известная теория элементарного электрического диполя. Необходимые сведе-
ния по теории такого диполя кратко излагаются ниже в данном разделе. Кроме
того, должно быть известно распределение тока вдоль проводов антенны. В антен-
нах из тонких проводов предполагается, что ток вдоль проводов изменяется толь-
ко по некоторому известному закону.
Проволочные антенны мысленно разбиваются на элементарные участки. Каж-
дый участок рассматривается как элементарный электрический диполь. Поле
антенны определяется как сумма полей, создаваемых отдельными элементами,
с учетом их поляризаций, амплитуд и фаз. Суммирование полей сводится
к интегрированию по источникам.
Таким образом, поле излучения проволочной антенны определяется как суперпо-
зиция полей, создаваемых элементарными излучателями с известными токами.
Для расчета поля излучения апертурных антенн наиболее простым является
так называемый апертурный метод. Сущность его состоит в том, что каждый
элемент площади раскрыва антенны рассматривается как гюйгенсовский источник
(элементарная площадка) и поле всей антенны в дальней зоне определяется сум-
мированием (интегрированием) всех элементарных полей с учетом их поляриза-
ций, амплитуд и фаз.
Для расчета поля излучения апертурным методом очевидно необходимо знать:
- значение поля в любой точке раскрыва антенны (т. е. закон распределения
поля по раскрыву);
- напряженность поля излучения, создаваемого гюйгенсовским источником. Рас-
пределение поля по раскрыву определяется приближенно, для разных антенн по-
разному. Этот вопрос более подробно рассматривается в главах об апертурных
антеннах.
Из вышеизложенного следует, что в принятом методе изучения проволочных
антенн и антенн СВЧ роль теории элементарных излучателей очень велика. Изу-
чение таких излучателей представляет большой практический интерес еще и по-
тому, что некоторые простейшие типы реальных антенн характеризуются пара-
метрами, весьма похожими на параметры элементарных излучателей.
Таким образом, любую излучающую систему можно рассматривать как сово-
купность множества элементарных излучателей. Это позволяет воспользоваться
принципом суперпозиции и определить поле антенны как геометрическую сумму
полей элементарных излучателей. Поля самих элементарных излучателей нахо-
дятся по заданному распределению тока с помощью решения уравнений Максвел-
60
ГЛАВА 1
ла. При их решении обычно полагают, что ток не меняется вдоль длины элемен-
тарного излучателя. К элементарным излучателям относятся: элементарный элек-
трический вибратор (диполь Герца), элементарная рамка с током (магнитный ди-
поль), элементарная щель в металлическом экране и излучатель Гюйгенса.
1.6.2. Элементарный электрический вибратор (диполь Герца). Диполь Герца
представляет собой тонкий проводник длиной I с шарами на концах. Шары создают
ёмкость, которая позволяет получить постоянную амплитуду тока вдоль проводника.
Вычислим поле электрического диполя в неограниченном пространстве. Помес-
тим диполь в начало сферической системы координат и ориентируем его вдоль оси
OZ (рис. 1.10). Объёмное распределение плотности тока в диполе представим в виде
fz(x',y',z') = Iz I jex =^=0,
(1.6.1)
где — момент тока диполя, 5(a) — дельта-функция Дирака.
Подставив (1.6.1) в первую формулу (1.5.1), найдём составляющие векторного элек-
трического потенциала в декартовой системе координат:
-ikr
z
У
(1.6.2)
Воспользовавшись формулами связи между выражениями для электродинами-
ческого потенциала в декартовой и сферической системах координат (1.4.15):
те т -ikr те т -ikr
z
= 0 .
COS 6
sin 0
4л
(1.6.3)
Далее, используя выражения (1.3.5) в сферической системе координат, после
подстановки в них (1.6.3) найдем составляющие электрического и магнитного полей:
X
Рис. 1.10. Диполь Герца
Электродум^ основы теории антенн
61
27riG)S0£K
(1.6.4)
4тгг(0£0£к
sin0
= 0 .
Рассмотрим электромагнитное поле диполя в различных зонах пространства.
1. Ближняя зона. Для ближней зоны kr « 1, то есть расстояние от диполя
до точек наблюдения в длинах волн (для среды без потерь) много меньше единицы
г / X « 1. При этом можно положить е~ikr ® 1, то есть пренебречь запаздыванием
поля. Тогда выражения (1.6.4) примут вид:
Iе I Iе I
Н(р = —^-ysinG, Ег =-----------cos0 ,
4ТСГ 2л1(О£пЕкГ'5
Р (1.6.5)
т. Ф . Л
Eq =----------- sm 0 .
4лг(О£0£кг'5
Из (1.6.5) следует, что электрическое и магнитное поля сдвинуты по фазе
на 90°, причём электрическое поле отстаёт по фазе от магнитного поля.
Комплексный вектор Умова-Пойнтинга, представляющий собой векторной про-
изведение Е на Н , носит реактивный (мнимый) характер. Это означает, что
в одну четверть периода энергия отдаётся источником окружающему простран-
ству, в другую четверть периода эта энергия возвращается к источнику, то есть
энергия ближнего поля находится в колебательном состоянии. Таким образом, вы-
ражения (1.6.5) определяют квазистационарные поля. Выражение для Н„ факти-
чески является формулой Био-Савара для элементарного линейного тока. Форму-
лы для напряжённости электрического поля совпадают с законом Кулона для двух
разноимённых электрических зарядов одинаковой величины. Ближняя зона называ-
ется областью реактивного ближнего поля.
2. Дальняя зона. Для дальней зоны kr » 1. Из (1.6.4) следует
Z I у Z /с „ у
Ео =-----2------sin0e гКг ,
4ЛГ С0£0£к
_ _ ЪI у Z /с „ _у
Нт = ——sin0e гКг .
ф 4тгт
(1.6.6)
Из (1.6.6) видно, что в дальней зоне электрическое и магнитное поля находятся
в фазе. Электромагнитное поле в дальней зоне является поперечным.
Среднее значение вектора плотности потока мощности в дальней зоне записы-
вается как
S > — Re SK — — Re [ Е х Н ] = Гд
sin 0, (1.6.7)
32^(0£0£к г*
и он (поток) ориентирован в направлении возрастания г, то есть энергия вибрато-
ром излучается в окружающее пространство.
62
ГЛАВА 1
Рис. 1.11. Амплитудные диаграммы направленности диполя Герца: а) — в
меридианальной плоскости; б) — в азимутальной плоскости; в) —
пространственная диаграмма направленности
Fq А 0 = const
у
Мощность излучения Р диполя находится интегрированием составляющей век-
тора
по поверхности сферы радиуса г:
п q л 2л
е
2 I
32л (О£0£к •
О
где Rs =2nWcl2 /(ЗХ2)
сопротивление излучения диполя. Формула (1.6.8) опреде-
ляет полную мощность излучения диполя в среднем за период.
Угловые распределения составляющих поля Е при г = const в дальней зоне
не зависят от г и могут быть описаны с помощью функций (Е = 0 ):
F<; <е,ф) = | Ee^’V) , F (6,<р) = О, (1.6.9)
I Ее max (61, Ф1)
где ©1, (pi — углы максимального излучения компоненты.
Из (1.6.6) следует, что
Fq(0, ср) = sin 6.
Это объёмная функция двух переменных {0, ср}.
Для анализа диаграммы направленности обычно вводят две плоскости: мериди-
ональную (ср = 0) и азимутальную (0 = л / 2). В меридиональной плоскости функ-
ция
Fq(0,<P = const) = sin©
(1.6.9а)
представляет собой две касательные окружности, центры которых лежат на пря-
мой, перпендикулярной оси вибратора и проходят через его середину (рис. 1.11, а).
В азимутальной плоскости напряжённость электрического поля не зависит от угла ср :
Fg(0 = тг/2,<р) = 1,
то есть диаграмма направленности представляет собой окружность с центром
на середине вибратора (рис. 1.11, б). Пространственное изображение диаграммы
направленности элементарного электрического вибратора дано на рис. 1.11, в.
Электродинамические основы теории антенн
1.6.3. Элементарный магнитный излучатель. Физическую модель элементар-
ного магнитного вибратора (рис. 1.12, а) можно получить, если взять стержень
из материала с магнитной проницаемостью значительно больше магнитной прони-
цаемости окружающей среды, например, из феррита. В качестве возбуждающего
устройства можно использовать петлю, обтекаемую током проводимости. Постоян-
ство вектора магнитной индукции вдоль стержня обеспечивается с помощью шаров
на его концах, выполненных из магнитного материала (ц Ф 1).
Определим поле элементарного магнитного диполя в неограниченном простран-
стве, поместив его в начало сферической системы координат и ориентируя его
вдоль оси OZ, как на рис. 1.10. Объёмное распределение плотности магнитного тока
представим в виде
7“(х,у,г) = 1Г г ад ад 8(2), j™ = j™ = о, (1.6.10)
где I — длина магнитного излучателя, I™ — амплитуда магнитного тока, пред-
ставляющая собой произведение модуля тангенциальной составляющей напряжён-
ности электрического поля на поверхности вибратора | ЕТ | на периметр его попе-
речного сечения.
Поле излучения, создаваемое элементарным магнитным излучателем, можно
найти с помощью формул (1.5.1) и (1.4.15). Но поскольку задача об элементарном
электрическом излучателе уже решена, поле аналогичного магнитного излучателя
проще всего найти, воспользовавшись принципом двойственности. Если в реше-
нии задачи (1.6.4) для электрического вибратора сделать следующую замену:
-ц„ц,Е -> Н,н -> Е,1‘ -Ц\ (1.6.11)
то получим выражения для составляющих электромагнитного поля элементарного
магнитного излучателя
Т. • А
Ет = - —— sin 0
ф 4л
тт 1 -ikr -ikr
f--coso e—+ike—
2л 1(£>Ц0Ц г г
(1.6.12)
Jmi -ikr --ikr -ikr
z t . Л e ... e , 2 e
-----------sin 0 —7— + гк —-— к -----------------
4лгсо|а0ц |_ г г г
Поле элементарного магнитного излучателя в дальней зоне (зоне излучения)
определяется формулами:
-Ит1к
Ео =-----z—sin Qe~ikr,
ф 4лг
iTmlk2
Г-Г _ 1/1Z cin
П q — ---------S1D. О С ,
4лтюц0ц
Er = Е, = Hr = Н, = 0.
(1.6.13)
64
ГЛАВА 1
Рис. 1.12. Магнитный диполь (а) и круговая рамка с током (б)
Соответственно, нормированные характеристики направленности в дальней зоне
описываются с помощью соотношений вида:
Гф(0, <p = O) = sin0,
Гф(0 = л/2, <р) = 1,
(1.6.14)
что говорит о том, что формы диаграмм направленности элементарных электри-
ческого и магнитного вибраторов одинаковы. Мощность излучения, в соответ-
ствии с формулами (1.6.7) и (1.6.8), определяется выражением
(kl)2
тт 12
12TIW;
(1.6.15)
Поскольку магнитный ток I™ имеет размерность напряжения, то излучаемую
мощность удобно определять через проводимость излучения Ст :
pz=1gs/“2, (1.6.16)
67lW
(1.6.17)
1.6.4. Элементарная рамка. Свойства элементарного магнитного вибратора ре-
ализуются в элементарной электрической рамке (петле тока). Элементарная рамка
(рис. 1.12, б) создаёт электромагнитное поле, линии магнитной составляющей кото-
рого расположены перпендикулярно плоскости рамки, а линии электрического
поля лежат в указанной плоскости или параллельны ей. Замкнутому контуру
(рис. 1.13, а), по которому протекает высокочастотный электрический ток с амп-
литудой Iq , можно сопоставить эквивалентный магнитный диполь (рис. 1.13, б)
с магнитным моментом
(1.6.18)
2*
Электродинамические основы теории антенн
65
а) б)
Рис. 1.13. Эквивалентность элементарного кольца с током (а)
магнитному диполю (б)
где S — площадь рамки. С другой стороны, магнитный момент для эквивалентного
магнитного диполя (рис. 1.13, б) определяется следующим образом:
т = qmlzQ,
(1.6.19)
где qm — магнитный заряд на концах вибратора.
Формулу (1.6.18) можно использовать на больших расстояниях г для малых
рамок:
d0«X, г » d0 , (1.6.20)
где cZq — максимальный размер рамки.
Установим связь между магнитным зарядом qm и комплексной амплитудой
фиктивного стороннего магнитного тока I™. Под элементом фиктивного магнитного
тока будем понимать тонкий цилиндр с поперечным сечением S и длиной I
(рис. 1.13, б), по которому протекает ток с комплексной амплитудой ЦТ. Таким
образом, I™ = j™S и J7 = z0 jm .
Из закона сохранения магнитного заряда имеем
dz
т
= -гсор
(1.6.21)
Умножив левую и правую части (1.6.21) на 5Az, получим
А Г™ • Л
Д12 = —гео Ад ,
где Al™ = (di™ / dz) Az ; Agm = pmS Az = pm AV — магнитный заряд в объёме
AV - Az, С учетом определения магнитного тока видно, что как на отрезке I,
так и вне его А1™ = 0. Изменение тока от нуля до максимального значения и
наоборот происходит только на концах отрезка I, то есть можно считать, что на
этих концах сосредоточены колеблющиеся магнитные заряды с комплексными ам-
плитудами:
_1_ л Тт / х .
q = ±iiz /со .
(1.6.22)
Следовательно, комплексная амплитуда магнитного момента элементарного маг-
нитного диполя определяется следующим образом:
3 - Неганов
66
ГЛАВА 1
— . л 2 —► ту! 7—►
m = -i —— zq = q lz0 ,
co
где
(1.6.23)
= гсоц0ц!0е5.
(1.6.24)
Таким образом, свойства элементарной рамки с током можно описать соотношения-
ми (1.6.12)—(1.6.14), в которых необходимо сделать замену (1.6.11). В частности, вместо
формул (1.6.13) для электромагнитного поля элементарной рамки в дальней зоне имеем
Е = W^sin
inr (1.6.25)
Те к2
_ 10 О ГУ С\о-гкг
Г10 — S1И vC у
4лт
где Iq — амплитуда высокочастотного тока в рамке.
Если рамка состоит из небольшого числа п витков, плоскости которых располо-
жены достаточно близко друг другу, напряженность поля возрастает в п раз и
„ 30k2SnH . Л _ikr
Е(? =--------smбе гкг. (1.6.26)
Действующая длина hd рамочной антенны может быть определена из сравне-
ния амплитудного множителя выражения (1.6.26) с выражением
£ф = ^^Ц(Ф,е),
откуда следует, что действующая длина рамки
2л
hd = kSn = —Sn. (1.6.27)
Как видно из последнего выражения, действующая длина рамки пропорциональ-
на числу витков и отношению площади рамки к длине волны.
При использовании рамок на длинных и средних волнах, когда отношение S / к
обычно мало, действующая длина также получается малой.
Диаграмма направленности рамки на основании выражения (1.6.26) равна:
= (ф, е) = Fj е) = sin е,
(1.6.28)
где 0 - угол, отсчитываемый относительно оси рамки (ось z на рис. 1.13, а).
Последнее выражение определяет диаграмму в плоскости, проходящей через
ось рамки (т.е. в плоскости, перпендикулярной плоскости самой рамки). Соответ-
ствующая диаграмма направленности имеет вид восьмерки, как для диаграммы
направленности элементарного диполя (рис. 1.11, а). В плоскости расположения
рамки излучение получается ненаправленным.
Пространственная диаграмма направленности имеет форму тороида, ось ко-
торого совпадает с осью рамки.
Поляризация электромагнитного поля, создаваемого небольшой рамкой, определя-
ется так же, как для любой кольцевой синфазной равноамплитудной антенны
Электродинамические основы теории антенн
67
(раздел 2.3).
Сопротивление излучения n-витковой рамки можно определить в результате
подстановки в выражение (1.2.7) значения напряженности поля из (1.6.26):
120л
2ти 7С
f f
Ф“0 0=0
3Ok2SnIeo
sinO
г2 sin 9 d(pd0 =
= 15/c4£2n2I0e2 jsin3 OdO = 20(/c2£n)210e2.
0
Сопротивление излучения, отнесенное к току Ц
рамки,
= 20(k2Sn)2 -31200Г^| Ом.
'о к 7
(1.6.29)
Коэффициент направленного действия можно легко определить, если учесть,
что диаграмма направленности опрделяется выражением F(p (0) = sin 0, т. е. имеет
такой же вид, как диаграмма элементарного диполя. Следовательно, коэффициент
направленного действия рамки, как и диполя Герца, будет равен
D = 1,5. (1.6.30)
Как видно из выражений (1.6.5) и (1.6.26), фаза напряженности поля рамоч-
ной антенны отличается на 90 градусов от фазы напряженности поля излуче-
ния вибратора, расположенного вдоль оси рамки, если считать, что их токи изме-
няются синфазно.
1.6.5. Элементарный щелевой вибратор (ЭЩВ). Свойства элементарной излу-
чающей щели (рис. 1.14) также достаточно просто описываются с помощью соотно-
шений, полученных для элементарного магнитного вибратора. Элементарный ще-
левой вибратор можно представить как бесконечно тонкую металлическую плас-
тину неограничных размеров, в которой прорезана щель длиной I и шириной А,
причём
A«Z«X. (1.6.31)
Электромагнитное поле ЭЩВ по своей структуре напоминает поле элементарного
магнитного вибратора, с тем отличием, что линии электрического поля Е в первом
полупространстве направлены навстречу линиям Е во втором полупространстве (рис.
1.14, б), но это различие несущественно так как оба полупространства независимы.
В соответствии с определением поверхностной плотности фиктивного магнитного тока
if = ^xj/0] = Exz0. (1.6.32)
Следовательно, магнитный ток в щели равен
I™ = 2ЕХ Л = 2U, (1.6.33)
где U -— напряжение между краями щели; множитель 2 учитывает специфику
поля на рис. 1.14, б.
Таким образом, для элементарного щелевого вибратора справедливы соотно-
68
ГЛАВА 1
Рис. 1.14. Элементарный щелевой вибратор
шения (1.6.12)-(1.6.17), в которых под магнитным током I™ необходимо понимать
выражение (1.6.33). В частности, для мощности излучения ЭЩВ справедлива фор-
мула (1.6.15). Если выразить эту же мощность через проводимость излучения Gx:
Pz = 0.5GxU2,
(1.6.34)
ТО
Gx =-------
3tcWc
8л
3w ш
«г*
(1.6.35)
Для свободного пространства Wc = 120л. Тогда проводимость излучения, входящая
в (1.6.34), (1.6.35) запишется как
(1.6.36)
1.6.6. Элементарный излучатель Гюйгенса. Ранее было показано, что поле в
объёме можно рассматривать как результат излучения источников, распределен-
ных на некоторой поверхности, причём для определения источников достаточно
знать поле на поверхности, т.е. полное поле в некотором объёме можно восстано-
вить на основании информации о его состоянии на поверхности, ограничивающей
этот объём. С таким утверждением связан принцип Гюйгенса.
Принцип Гюйгенса*, каждую точку фронта некоторой скалярной волны можно
принять за источник локальной сферической волны; новое положение фронта
может быть найдено в результате учёта действия всех локальных волн, то есть
при помощи условных поверхностных источников. В широком смысле под принци-
пом Гюйгенса можно понимать введение вторичных (эквивалентных) источников на
фронте распространяющейся волны. Таким образом, малые элементы поверхности
5 с заданным распределением поля могут фигурировать как элементарные излуча-
Элетстродиналсические основы теории антенн
69
Да?
Рис. 1.15. Элементарная площадка излучателя Гюйгенса
тели. Это так называемые элементы Гюйгенса, которые можно выделять в принци-
пе на самых различных поверхностях при расчёте различных полей.
Рассмотрим простейший элемент Гюйгенса в виде элементарной площадки
А*? = АхАг/ на плоскости z = 0 , параллельной фронту плоской однородной волны
(рис. 1.15). Распространение волны вдоль оси OZ можно трактовать как результат
излучения всей совокупности таких элементов, распределённых в плоскости z = 0. При
заданной поляризации плоской волны (см. рис. 1.15) плотности эквивалентных сторонних
поверхностных токов (элементы Гюйгенса) выражаются следующим образом:
= [zq, Hs] = -i0Hj , = [Es, z0] = -j/o Es •
(1.6.37)
Элементарный излучатель Гюйгенса представим как элемент фронта плоской
волны, магнитное поле которого Н® = HQ exp(icot) ( Hq — значение поля при
х = у = z = 0) можно заменить эквивалентным электрическим током = -Hq Ay ,
а электрическое поле Е® = Ео exp(icot) (Eq — значение поля при x = y = z = 0) —
эквивалентным магнитным током /Л1 = —Е0Ах. Поле, создаваемое таким элемен-
том, равно сумме полей, создаваемых расположенными перпендикулярно друг
другу элементарными электрическим и магнитным диполями с объёмными плот-
ностями:
г >ст = - XQ 1ех ад д(у) ад,
-т,ст ададад.
(1.6.38)
Подставив (1.6.38) в формулы (1.5.1) для векторных электродинамических потенци-
алов, находим
-ikr
-ikr
т
В сферической системе координат в соответствии с формулами (1.4.15) имеем
70
ГЛАВА 1
А?. = A?, cos (p sin 0, A™ = A™ sin ф sin 0,
J T ' / T *
Aq = Aj cos <p cos 0, Aq1 = A ™ sin ф cos 0, (1.6.40)
A® = -A* sincp, A™ = A™ coscp.
Подставляя (1.5.8) в сферической системе координат и подставляя туда выражения
(1.6.40), найдём составляющие электрического и магнитного полей в дальней зоне,
возбуждаемые электрическим диполем ( Ат = 0):
е iliW HAS / гх X • — \ — ikr
=------2— (cos 0 cos cp0o - sin (р<р0 )е
ikHQ&S
4лг
(sin cp0o + cos 0 cos (рср0 )е гкг
(1.6.41)
Аналогично определяем электромагнитное поле в дальней зоне, создаваемое эле-
ментарным магнитным током (Ае = 0):
---5---(cos ф0о - cos 0 sin фф0 )е гкг,
4л г
ikHfAS, _ . х . _ikr
----— (cos 0 sm ф0о + cos фф0 )е
4лг
(1.6.42)
Чтобы получить полное поле излучения элемента Гюйгенса в дальней зоне необ-
ходимо векторно сложить (1.6.41) и (1.6.42). С учётом того, что Ео = WCHO:
т =-----5---(1 + cos 0)(cos ф0о - sin фф0 )е гкг
4лт
(1 + cos 0)( sin ф0о + cos фф0 )е
4лШ.г
—ikr
(1.6.43)
Вычислим среднее значение значение вектора Умова—Пойнтинга:
(1.6.44)
--- с -
Следовательно, нормированная диаграмма направленности по мощности есть
т.2/л ч <S>r (1 + COS0)
(1.6.45)
< 5(0о,фо) max
Нормированные характеристики направленности по напряжённости выражают-
ся следующими формулами:
Ге(0,Ф) =
д9(е,<р)
тах(^1’Ф1) I
(1.6.46)
т
т
т
0
(ртах (02>Ф2)
Диаграммы направленности (1.6.46) в произвольной меридиональной плоскости
Электродинамические основы теории антенн
0°Л2
180°
а)
Рис. 1.16. Амплитудная диаграмма направленности излучателя Гюйгенса:
а) — в меридианальной плоскости; б) — объемная диаграмма направленности
ср = const есть кардиоиды (рис. 1.16, а); объёмная диаграмма направленности —
тело вращения кардиоиды (рис. 1.16, б). Таким образом, элемент Гюйгенса макси-
мально излучает в направлении оси OZ; в обратном направлении (0 = л) излуче-
ние отсутствует.
1.7. Некоторые теоремы электродинамики,
применяемые в теории антенн
Рассмотрим некоторые теоремы электродинамики, имеющих важное значение
в теории антенн.
1.7.1. Теорема взаимности. Из уравнений Максвелла можно получить различ-
ные соотношения, характеризующие взаимодействие двух источников. Если среда,
в которой происходит электромагнитный процесс, линейна и изотропна, то такого
рода соотношения взаимности оказываются симметричными. Этот факт и составля-
ет содержание теоремы взаимности.
Соотношение
|J(1)E(2)dV = J?2)E(1)dV (1.7.1)
будем считать основной формулировкой теоремы взаимности [1].
В (1.7.1) j(1)— объемная плотность тока, распределенного в области Vr; Ё(1) —
напряженность электрического поля от источника j(1); /2) — объемная плотность
тока в V2; Ё(2) — напряженность электрического поля от источника j(2).
Нелинейность и некоторые виды анизотропии среды, в которой расположены
источники, делают несправедливой формулировку (1.7.1).
Положим, что V, и V2 — две антенны, ранее изученные в режиме передачи,
когда j(1) характеризует распределение тока в одной из них, а j(2) — в другой.
Согласно предыдущему параграфу, это означает, что для каждой из рассматрива-
емых антенн построена эквивалентная схема и установлены токи эквивалентных
72
ГЛАВА 1
схем 1г и 12, соответствующие данным распределениям j(1) и /2). Подобно тому,
как это было сделано в (1.2.11), выразим левую и правую части выражения (1.7.1)
в виде:
p(1)£(2)dV =
fj(2)E(1)dV = I2U[2).
'2
(1.7.2)
В эту формулу входят комплексные амплитуды токов эквивалентных схем и 12
и напряжений на их клеммах U2} и , причем U2} учитывает влияние второй
антенны на первую, a U{2) — первой на вторую.
Подставляя выражения (1.7.1) в (1.7.2), получаем следующую формулировку
теоремы взаимности в терминах эквивалентных схем:
и
(1.7.3)
Эту же формулировку можно переписать в виде равенства
(1.7.3а)
где
21 —
12 —
взаимные сопротивления антенн. Теорема взаимности утверждает равенство вза-
имных сопротивлений.
1.7.2. Принцип двойственности. Сущность принципа перестановочной двой-
ственности уравнений Максвелла, установленного А.А. Пистолькорсом, заключа-
ется в следующем [1]. Уравнения Максвелла:
—"ф1
rot Е = -iopH,
—► —*•
rotH = i(deE
меняются ролями, если сделать замену
£ -Ц. (1.7.4)
При этом, очевидно, решение Е переходит в Н и обратно, т.е. как следствие
(1.7.4) имеем
(1.7.4а)
Однако необходима оговорка. Решение Ё до замены (1.7.4а) будет совпадать с ре-
шением Н после замены только в том случае, если Ё и Н подчинены идентич-
ным граничным условиям на идентичных границах. Поэтому принцип двойственно-
сти можно применять лишь к таким двум системам, относительно которых можно
сказать, что вектор Ё в первой из них ведет себя на границах так же, как и
вектор Н на таких же границах второй системы. Тогда операция (1.7.4) в готовом
решении для первой системы дает решение для второй системы, причем Ё пере-
ходит в Н и обратно (1.7.4а).
Электродинамические основы теории антенн
Иногда для придания уравнениям Маквелла полной симметрии вводят новые
величины Ё’ и Н' с одинаковой размерностью [17]:
Ёс = ррЁ, Нс = уррГа Н.
Тогда уравнения Максвелла принимают вид:
rotHc=kEc, rot Ec=kHc,
(1.7.5)
(1.7.6)
где к = 2л / X.
Если задано граничное условие для касательной составляющей Щ вектора Нс
на некоторой поверхности, и пусть при этом решением уравнений Максвелла
(1.7.6) является вектор Нс. Если теперь задано граничное условие для касательной
составляющей вектора Ес в виде
то из уравнений (1.7.7) вытекает, что
(1-7.7)
(1.7.8)
Таким образом, справедливость принципа двойственности в отношении векто-
ров Ёс и Нс очевидна. Докажем, что он справедлив и для векторов Е и Н.
Производя в равенствах (1.7.7) и (1.7.8) обратную замену переменных, получа-
ем, что если
то
-ррЕ =
Выражения Jico£a и J-kopa представляют собой масштабные множители. Так
как они одинаковы и у касательных составляющих векторов Ёт, Нх и соответ-
ственно у искомых векторов Ё, Н , то, следовательно, вектор Ес выражается
через касательную состаляющую Ёс точно так же, как вектор Нс через касатель-
ную составляющую Нс. В этом и состоит принцип двойственности.
Принцип двойственности можно также применять в формулировке, учитываю-
щей источники [1]. Тогда при оговоренных выше условиях решение уравнений
Максвелла Ё(1),Н(1) (1.1.6), полученное при стороннем электрическом токе je,
перейдет в решение Н(2), Ё(2), соответствующее таким же образом распределенно-
му магнитному току -jm, если, кроме (1.7.4) сделать замену je на ~jm
При расчете апертурных антенн для вычисления полей в дальней зоне удобно
пользоваться простым способом. Дело в том, что выражения дальних полей эле-
ментарных излучателей заранее известны. В то же время каждый элемент повер-
хности, на которой распределены электрический или магнитный ток, может рас-
сматриваться как элементарный электрический и соответственно магнитный излу-
чатель. Поэтому для вычисления поля Ё’,НГ достаточно выразить аналитически
поле излучения, создаваемое его произвольным элементом, несущим поверхност-
ный ток плотности fje и затем проинтегрировать это выражение по всей поверх-
ности. Совершенно аналогично находится и поле Е",Н" ; от поверхностной плотно-
сти магнитного тока .
74
ГЛАВА 1
Рис. 1.17. Рупорная антенна
Рис. 1.18. К выводу теоремы направленности
системы дискретных излучателей
В качестве примера рассмотрим в общих чертах применение понятия эквива-
лентных токов для определения поля рупорной антенны. Как видно из рис. 1.17,
вместо того, чтобы находить внешнее поле как поле излучения антенны А, нахо-
дящейся внутри рупора, можно воспользоваться данными о поле на поверхности
рупора 5, состоящей из внешней металлической поверхности £0 и плоской повер-
хности раскрыва №. Практически берут лишь поле в раскрыве (которое просто
определить), полагая действие металлической поверхности незначительным.
Таким образом, принцип двойственности можно сформулировать следующим
образом: решение уравнений Максвелла для магнитного вектора поля, найденное
при заданных в отношении этого вектора граничных условиях, имеет такой же
вид и для электрического вектора поля, при тех же граничных условиях, но задан-
ных в отношении электрического вектора.
1.7.3. Теорема перемножения при анализе диаграммы направленности систе-
мы из дискретных излучателей, одинаково ориентированных в пространстве.
Ниже рассмотрим систему из дискретных элементарных излучателей, одинаково
ориентированных в пространстве, то есть любой излучающий элемент может быть
совмещён в пространстве с другим путём только параллельного перемещения без
вращения. Введём общую декартову систему координат {x,y,z}, центр которой
расположен внутри излучающей системы. Выделим произвольный элемент с номе-
ром п (рис. 1.18), находящийся на расстоянии рп от начала общей системы коорди-
нат. Координаты xn,yn,zn, ориентируем параллельно соответствующим осям си-
стемы координат {x,y,z}. Введём также общую сферическую систему координат
{г, 0, ф}. В локальной сферической системе координат гп, 0П, фп электрическое поле
в дальней зоне каждого п - элемента имеет в общем случае компоненты Е^ , :
Е1”>=§Х)+ФоС (1.7.9)
В этой локальной системе координат каждая компонента поля излучения имеет вид:
Е(п) = а1пЕ(0)(0,ф) exp (-ikrn)/ гп , (1.7.10)
Электродинамические основы теории антенн
75
где 1п — ток на n-излучателе; нижние индексы « 0 » и «ср » опустим. Выразим коорди-
наты т„,
f V 7
через г, 0, ср. Так как расстояние гп до точки наблюдения Р есть
'п
(1.7.11)
Рп 2 г cos ct.^
где ап
угол между ортом т0 (г0 ТТ г ) и вектором
Рп + УоУп + ^0^71
то для дальней зоны
& г - р„ cos а~,. (1.7.12)
Соотношение (1.7.12) упрощается:
^(п) т F^\e, ср) ехр(-гкг) ехр(г/срп cosan) . (1.7.13)
г
В (1.7.10) мы положим 0 = 0П, ф = фп , так как для дальней зоны лучи, проведённые
из начала общей системы координат и из точки расположения излучаемого элемен-
та, считаются параллельными:
0П=0, ФП=Ф- (1.7.14)
Разность хода Arn = рп cos ап может быть вычислена как проекция вектора
Рп = %охп + УоУп + ^02п на °РТ г0, для которого справедливо представление
Гр = sin 0 COS ф + Уд sin 0 sin ф + Zg cos 0 . (1.7.15)
Следовательно,
Дгп =pncosan = хп sin 0 cos ф + уп sin 0 sin ф + zn cos 0 , (1.7.16)
при этом каждую компоненту результирующего поля с учётом (1.7.10)-(1.7.15) мож-
но вычислить как
Е = — F<® (0, ф) exp (- ikr) х
х In exp\ik (xn sin 0 cos ф + yn sin 0 sin ф + zn cos 0)].
n=l
Из (1.7.17) следует, что характеристика направленности всей системы может быть
представлена как
N
F (0, ф) = F(0) (0, ф) £ In exp [ i k рп cos ап ] =
П=1
(1.7.18)
= F(o’(0,<p) FW(0,q>) ,
где — комплексная характеристика направленности излучающего элемента,
N
F^(0,ф) = ехР(xn s^ncosФ + Уп sin® sinФ + zn cos®)}
п=1
(1.7.19)
— комплексный множитель направленности системы изотропных излучателей,
расположенных в точках размещения центров элементов.
В качестве примера применения (1.7.17) рассмотрим проволочную антенну дли-
76
ГЛАВА 1
ной L, ориентированную вдоль оси OZ с известным законом распределения тока
I(z). Антенну разобъём на элементарные электрические вибраторы длиной dz каж-
дый. Электрическое поле каждого элементарного электрического вибратора опре-
деляется формулой (1.7.10), а суммирование в (1.7.18) нужно заменить интегриро-
ванием по координате z. Для такой антенны
Ar = z cos 0,
и в результате имеем (начало координат помещено в середину антенны)
. wc
г—-
2гк
L/2
sin 6 exp (-г kr) J 7(z)exp(ifcz cos Q)dz.
- L/2
(1.7.20)
Результирующая характеристика направленности определяется, как и (1.7.20),
в виде произведения F<® , причём диаграмма направленности излучающего
элемента F^ = sin0, а множитель системы имеет вид:
Г(с,(9,ч>)
L/2
JI(z) exp(гkzcos0)dz.
-L/2
(1.7.21)
1.7 А. Множитель направленности для непрерывного распределения электро-
магнитных источников плоского излучающего раскрыва. При расчете апертур-
ных антенн обычно используют плоские излучающие раскрывы (см., например,
№ в 1.7.2) с непрерывным распределением электромагнитных источников в преде-
лах раскрыва. Если излучатели заполняют раскрыв непрерывно, то суммирование
в (1.7.17) заменяется интегрированием по площади. Если плоскость раскрыва со-
вместить с плоскостью z = 0, то формула для множителя направленности систе-
мы принимает вид:
F(c)(e,<p) = JJl (х,у) exp [ik sin0(xcos(p + ysin(p)} dxdy
(1.7.22)
где S - площадь раскрыва;
l(x,y)= 1(х,у) ехрГгФ(х,?/) - функция амплитудно-
фазового распределения возбуждения.
Вводя новые угловые переменные (пространственные частоты) = к sin 0 cos ср,
%2 = к sin 0 sin ср формулу (1.7.19) приводим к виду двумерного преобразования Фу-
рье от функции возбуждения:
F(c)(Xi,X2) =
00 ОО
f J J(x,t/)exp{i(xi^ + X2?/)}da:dl/,
(1.7.23)
—00 —oo
причем распределение возбуждения 1(х,у) отлично от нуля только в пределах
раскрыва . Поэтому множитель направленности F'c' (xi, Х2) является двумер-
ной функцией с ограниченным спектром. Преобразование Фурье для функций с
ограниченным спектром широко применяется в радиотехнических приложениях.
Вычисления по формуле (1.7.23) проводятся на ЭВМ по алгоритмам быстрого пре-
Элетстродиррм основы теории антенн
77
образования Фурье. Именно поэтому излучающие системы многих типов остронап-
равленных антенн оказывается удобным представлять в виде плоских раскрывов
той или иной формы.
1.8 . Самосогласованная постановка задач расчета полей
излучающих систем. Диполь Герца [13]
Ранее был описан общепринятый в научной и учебной литературе алгоритм
расчёта электромагнитных полей по заданным источникам, основанный на форму-
лах (1.3.18) - (1.3.21). Этот алгоритм неприменим для расчёта электромагнитного
поля в ближних зонах излучающих систем, так как отсутствует предельный
переход формул (1.3.19) — (1.3.20) при стремлении точки наблюдения p(x,y,z)
к точкам источника q(x',y',z'). Более того, на поверхности S , ограничивающей
объём V , в котором содержатся источники, по формулам (1.1.2) и (1.1.3) можно
ввести поверхностные плотности электрического и магнитного тока, определён-
ные через тангенциальные составляющие Е и Н. Поэтому при предельном пере-
ходе р —> q$, где q$ —точки источников на поверхности £ , соотношения (1.3.19)
и (1.3.20) должны переходить в тангенциальные составляющие Е, Н. Очевидно,
что с помощью функций Грина типа (1.3.21) такой предельный переход осуще-
ствить нельзя. Поэтому описанный выше алгоритм расчёта электромагнитных
полей по заданным источникам будем называть несамосогласованным (в том смысле,
что поля Е и Н не согласованны с источниками). Поэтому существует разрыв
между тангенциальным магнитным полем (поверхностной плотностью тока)
на поверхности излучающей структуры и электромагнитным полем вблизи этой
поверхности.
Поясним сказанное на простейшем примере электрического вибратора.
1.8.1. Тонкопроволочное приближение электрического вибратора. Обычно в элек-
тродинамике используют так называемую тонкопроволочную физическую модель элек-
трического вибратора: два бесконечно тонких идеально проводящих провода длиной I
каждый. Провода расположены как показано на рис. 1.19, образуя зазор шириной 2Ь,
к которому подключён генератор высокой частоты. Принципиальным моментом такой
физической модели является пренебрежение толщиной металлических проводов.
На первом этапе так называемой внутренней задачи анализа ищется распреде-
ление тока по вибратору [2, 3]. Продольный ток lz на электрическом вибраторе
(рис. 1.19) вводят на воображаемом металлическом цилиндре радиуса а (в дей-
ствительности толщиной проводов пренебрегают) как Iz = 2тшг|2, где Iz = —
Рис. 1.19. Тонкопроволочная физическая модель электрического вибратора
78
ГЛАВА 1
продольная поверхностная плотность тока на вибраторе, причём ток в зазоре
считается непрерывным.
Распределение тока находится либо из интегрального уравнения Поклингто-
на, либо из интегрального уравнения Халлена [2-4]. С математической точки
зрения интегральные уравнения Поклингтона и Халлена являются интеграль-
ными уравнениями Фредгольма первого рода, нахождение решений которых
является некорректно поставленной математической задачей [6, 7]. Математи-
ческая некорректность связана и с несамосоласованной физической моделью
электрического вибратора: металл и ток проводимости Iz разнесены в про-
странстве (на бесконечно тонком проводнике нельзя задать тангенциальное маг-
нитное поле Нф).
Общепринятый подход к расчету ЭМП электрического вибратора (рис. 1.19)
основан на определении z - составляющей векторного электродинамического
потенциала для электрического тока Az, определяемой через z -составляющую
тока на вибраторе Iz (z) = 2лат|2 (z) (r\z — составляющая поверхностной плотности
тока на вибраторе, а — радиус вибратора) [1]:
(1.8.1)
G(p,z - z')
1 -ikR
4/kR
(1.8.2)
R = yp + (z - z')2; — расстояние между точкой наблюдения p(p,z) и точкой источ-
ника q(0,z'), расположенной на вибраторе; к = соуец / с; е, р — относительные диэ-
лектрическая и магнитная проницаемости среды, окружающей вибратор; с —
скорость света; 21 — длина вибратора. Функция Грина (1.8.2) соответствует физи-
ческой модели электрического вибратора в виде бесконечно тонкой идеально про-
водящей нити конечной длины.
Физически G(p, z - z') — функция Грина свободного пространства от точечного
источника, помещенного в точку (р = 0, z = z'), т.е. на линию р = 0. Неизвестное
распределение тока Iz(z) по вибратору обычно определяется либо из интеграль-
ного уравнения Поклингтона, либо из интегрального уравнения Халлена. Зная фун-
кцию Iz(z), путем обычного дифференцирования выражения (1.8.1) по координа-
там pnz [1] несложно получить выражения для составляющих ЭМП излучения
вибратора в любой точке пространства. Полученные таким образом численные
значения полей Е и Н в ближней зоне электрического вибратора, по крайней
мере, по двум причинам должны проверяться на достоверность. Во-первых, опре-
деление неизвестного тока Iz(z) по вибратору из интегральных уравнений По-
клингтона и Халлена (интегральных уравнений Фредгольма 1-го рода) приводит
к некорректно поставленной задаче [7]. Во-вторых, использование при расчетах
поля функции Грина (1.8.2) приводит к несамосогласованной постановке задачи,
Электродинамические основы теории аюпенн
79
так как электрический ток и поверхность, на которой тангенциальное электричес-
кое поле обращается в нуль, разнесены в пространстве и в этом случае отсутству-
ет предельный переход от поля в ближней зоне к полю (току) на поверхности
вибратора.
В [8, 9] разработан метод сингулярных интегральных уравнений (СИУ), кото-
рый сводит задачу расчета тока по электрическому вибратору к решению СИУ,
что дает возможность математически корректно подойти к определению распре-
деления поверхностной плотности тока на вибраторе. Расчет ЭМП в ближней зоне
электрического вибратора основан на сингулярном интегральном представлении
(СИП) ЭМП через поверхностную плотность тока г|2 на вибраторе [10, 11]. При
этом используется другая физическая модель электрического вибратора - в виде
двух бесконечно тонких идеально проводящих полых трубок общей длиной 21
и радиуса а, между которыми включен генератор СВЧ [8, 12]. Полученное СИП
ЭМП позволяет вычислять его в любой точке пространства посредством интегри-
рования продольной составляющей поверхностной плотности тока по вибратору.
Одно из важных достоинств полученных соотношений состоит в том, что на повер-
хности вибратора СИП переходит в СИУ [13] для определения на ней неизвестного
распределения поверхностного тока. Этим распределением затем можно восполь-
зоваться для нахождения ЭМП излучения вибратора в любой точке пространства.
Впервые, по-видимому, метод СИП электромагнитного поля был предложен для
решения внутренних задач о собственных волнах экранированных полосково-ще-
левых структур СВЧ [20].
1.8.2. Самосогласованная физическая модель электрического вибратора[13,
14]. Будем использовать трубчатую модель электрического вибратора в виде двух
бесконечно тонких идеально проводящих цилиндрических трубок общей длиной 21
и радиуса а. Трубки расположены как показано на рис. 1.20, образуя зазор,
к которому подключен генератор высокой частоты. Будем использовать следую-
щие предположения:
1. Считается, что стороннее поле Ес™ в зазоре (г е [-Ь, Ь]) не зависит от коорди-
наты (р. Поэтому в цилиндрической системе координат система уравнений Макс-
велла, описывающая электромагнитное поле излучения электрического вибрато-
ра, распадается на две независимые системы относительно составляющих Ep,Ez,H^
и Hp,Hz,E(p [1]. Очевидно, что при рассмотрении поля излучения электрического
вибратора необходимо исходить из системы, описывающей поведение составляю-
Рис. 1.20. Трубчатая физическая модель электрического вибратора
ГЛАВА 1
80
< I), кроме области зазора длиной
щих Ер,Ег,Нф.
2. Трубки предполагаются бесконечно тонкими и идеально проводящими, так
что на их внешней поверхности существует только продольная составляющая по-
верхностной плотности электрического тока vfz =
3. Поверхностная плотность электрического тока г|| на внешних поверхностях
трубки и поверхностная плотность магнитного тока ц™ в зазоре вибратора при
р = а заменяется некоторой поверхностной плотностью электрического тока Т|г,
непрерывной в области зазора (вследствие подключения к нему генератора)
и обращающейся в нуль на концах вибратора.
4. Касательная составляющая комплексной амплитуды электрического поля Ez (а)
на вибраторе обращается в нуль всюду (р = a, z
2b (рис. 1.20), где она приравнивается некоторой возбуждающей функции Ест.
Здесь важно пометить, что модель трубчатого вибратора справедлива для лю-
бых размеров радиуса а трубок. Единственное ограничение: стороннее поле воз-
буждения в зазоре не должно зависеть от координаты ср. Общепринятая модель
тонкопроволочного вибратора в виде бесконечно тонкой идеально проводящей нити
конечной длины может использоваться только при условии а « . Кроме того,
модель тонкопроволчного вибратора не является самосогласованной. Для опреде-
ления ЭМП в ближней зоне необходимо принципиально учитывать толщину виб-
ратора: на идеально проводящей бесконечно тонкой нити нельзя ввести поле Н®,
связанное с поверхностной плотностью тока в соответствии с граничными электро-
динамическими условиями. Поэтому в такой модели происходит «отрыв» ЭМП от
тока проводимости на вибраторе. В литературе существуют работы [15], ставящие
под сомнение существование напряженностей электрического и магнитного полей,
непосредственно связанных с существованием тока проводимости на вибраторе.
1.8.3. Сингулярное интегральное представление электромагнитного поля.
В [10, 11] впервые получены СИП для составляющих ЭМП электрического вибра-
тора, определяющие поле в любой точке пространства через функции
Iz(z) = 2nax\z(z), Jz(z) = , (1.8.3)
az
определенные на внешней поверхности вибратора при р = а. В работе будем ис-
пользовать СИП для составляющих ЭМП в более удобном виде — записанные
относительно безразмерных переменных [16]:
-(p-l)sign(p-l) h
8л iaka
J0(-ipv)H^2)(-w)
sign (/г)
Электродинамические основы теории антенн
81
Яр(р, О =
-(p-l)sign(p-l)h
vJq (- iv )H^ (-i pv)
vJi (-ipv)H^ (-iv)
h
(1.8.4)
-(p-l)sign(p-l)
e
vJq (-iv)H^ (-ipv)
vJ j (-ipv)H^ (-iv)
sign(x) = { 0
при x < 0
при x = О
при х > О.
В СИП (1.8.4) Jn(x) — функция Бесселя первого рода порядка п (п = 0,1). В этих
соотношениях введены следующие безразмерные переменные: р - р/a, t = z/l,
t' == z'/I, h = ha, v = yjh2 - ka2; Wc — характеристическое сопротивление среды.
1.8.4. Сингулярное интегральное уравнение. В выражениях (1.8.4) под интегра-
лом стоят Iz(t) и Jz(t), которые представляют собой функции тока и производной
тока (по нормированной координате t) на вибраторе соответственно. Изначально
они неизвестны. Для того, чтобы их найти, необходимо получить СИУ относитель-
но производной тока, которое находится из представлений (1.8.5) посредством под-
становки в них граничных условий.
Возьмем выражение для Ez из (1.8.4) и подставим в него граничное условие
на поверхности вибратора р = а :
при Z G [-?, Iq - b] и Ро + Ъ, Q,
при Z G Iq - b,lft + ь],
(1.8.5)
где EZT — z -составляющая стороннего электрического поля в зазоре вибратора.
Ее можно представить в виде [8]:
(t) =
Uc(t),
82
ГЛАВА 1
где a(t) — профиль напряжения в зазоре, U — величина питающего напряжения.
В результате получаем СИУ относительно J2(t)(t е [—1,1]):
4т1ка
E?(t)
(1.8.6)
isign(h) - тс-L- Jq(-w)Hq2\-w) dhdt’.
h
Будем использовать профиль напряжения в зазоре в виде:
В этом случае интеграл
Int(t) =
do~b)/l
s(t')dt ’,
возникающий при обращении интеграла типа Коши (1.8.6) можно найти в аналити-
ческом виде [8]:
Int(t) =------
(b/j)
arcth
arcsin(b /1) (2t3 - 2t (b / Z)2 - t
tb/l-1
+ arcth
Таким образом, алгоритм вычисления ЭМП электрического вибратора следующий:
1. Из СИУ (1.8.6), которое получается из СИП (1.8.4) и граничного условия (1.8.5),
находится функция J2(t) (а, следовательно и Iz(t)), определенная на внешней
поверхности трубчатого вибратора.
2. Зная функции Jz(t) и Iz(t), по формулам (1.8.4) определяется ЭМП в любой
точке пространства, окружающей электрический вибратор.
Еще раз подчеркнем, что СИП (1.8.4) справедливы для любой точки простран-
ства, в том числе и для дальней зоны.
Электродинамические основы теории антенн 83
В главе 4 проведён анализ ЭМП полуволнового электрического вибратора в ближ-
ней и промежуточной зонах, поскольку в научной литературе отсутствует анализ
трансформации ЭМП непосредственно с электрического вибратора в пространство.
Такой анализ возможен только в рамках самосогласованных физической и матема-
тической моделей электрического вибратора. Что касается ЭМП в дальней зоне,
то оно хорошо описано в научной литературе (см., например, [2, 3-6, 17, 18]).
1.8.5. Диполь Герца. В общепринятой теории антенн под диполем Герца пони-
мают бесконечно тонкий идеально проводящий проводник конечной длины 21,
с шарами на концах, содержащими разные по знаку заряды. Шары создают ем-
кость, которая позволяет получить постоянную амплитуду тока вдоль проводника.
Такая физическая модель диполя Герца неприменима для расчетов ЭМП в его
ближней зоне. Во-первых, при расчетах ЭМП поперечным размером диполя Герца
пренебрегают, что можно делать только для дальней зоны. Поэтому ЭМП в точке
расположения диполя обращается в бесконечность. Для описания характеристик
диполя вводят момент тока диполя как произведение тока по бесконечно тонкому
проводнику на длину (в силу обращения ЭМП в бесконечность в месте расположе-
ния диполя). Момент тока диполя изначально не связан с напряженностями Е и Н
ЭМП. Однако он входит в конечные формулы для Е и Н. Для такой физической
модели диполя Герца напряженности Е и Н оказываются не связанными с током
проводимости (зарядами) на диполе. Поэтому в [15] делается вывод, о том, что
напряженности Е и Н, реально не связанные с зарядами на проводнике, являют-
ся лишь удобным математическим аппаратом для описания физики наблюдаемого
дистанционного взаимодействия тел (объектов) в дальней зоне. Подобные утверж-
дения были у академиков И.Е. Тамма и Р.Ф. Авраменко.
По мнению Харченко КП, «электромагнитная волна» - это поток реальных фотонов
заряда. Основной причиной, из-за которой возникает сомнение в справедливости теории
Максвелла, является отсутствие предельного перехода от тока на металле к полю
в ближней зоне.
Ниже рассмотрим самосогласованную физическую модель диполя Герца (эле-
ментарного вибратора) в виде бесконечно тонкой идеально проводящей цилиндри-
ческой трубки длиной 21 и радиусом а. Будем считать, что по сравнению с длиной
волны X, его размеры пренебрежимо малы:
а, I <§: X.
(1.8.7)
Таким образом, под самосогласованной физической моделью диполя Герца (эле-
ментарным электрическим вибратором) будем понимать трубчатую модель элект-
рического вибратора без зазора с дополнительными условиями (1.8.7).
Распределение тока на элементарном вибраторе возьмем в виде:
Iz(z) = I0[H(z + l)-H(z-l)],
(1.8.8)
Н(х) = <
1 при х > О,
О при х < 0.
84
ГЛАВА 1
— функция Хевисайда, 10 — амплитуда тока на диполе Герца. Тогда производная
тока Jz(z) = dlz(z)/dz будет иметь вид:
J2(z) = Io [8(2 4-1) - 8(2 -1)], (1.8.9)
где 8(х) — дельта функция.
Электромагнитное поле диполя Герца определялось из формул (1.8.4) с учетом
(1.8.8) и (1.8.9). Численные расчеты произведены при следующих геометрических
размерах: Z/A, = 0.25 х 10 , а/А = 0.25 х 10 , т.е. условия (1.8.7) выполнены. Ампли-
туда тока: Iq = 5.68 х 10~3 А.
На рис. 1.21 приведены в сферической системе координат распределения комп-
лексных величин Фд = (т/А,)а£д, Фг = (т/А.)аЕг, Фф = (?'/А)аН(р от координаты 0 при
Фг(0) 7.96 -103е 2.756-Ю^е 1.6 10’3е
90 90 90
Фф(0) 2.336-10’9е 8.692 • 10-10 е 4-1012 е
Y 4 7 90 90 90
270 270 270
Рис. 1.21. Распределение величин Ф0,Фг,Фф для диполя Герца в сфери-
ческой системе координат от координаты 0 на различных нормированных
расстояниях г /А от центра диполя: а) r/Х - 0.3 х 10”3,
б) т/А = 0.4 х 10“3, в) т/А = 300 х 10"3 (сплошные линии — Ке{Ф(0)} ; точками
— Im {Ф(0)}; штриховые линии — |Ф(0)|)
ЭлектпродинО;^^ основы теории аитенн
85
различных нормированных расстояниях r/Х от центра диполя. Очевидно, что вер-
хняя граница промежуточной зоны диполя при таких размерах антенны определя-
ется как г/Х = 0.5х10 . На графиках приведены распределения Фе, Фг, Фф
на максимальном расстоянии от диполя т/Х = 0.3 , что соответствует дальней зоне.
Как показали расчеты, при дальнейшем увеличении г происходит незначитель-
ное увеличение амплитуды поля (качественный характер поля не изменяется) ко-
торое заканчивается при г = 1.5Х -?-2.0Х .
В отличие от полуволнового вибратора (см. раздел 14.13), у диполя Герца име-
ется несколько интересных особенностей. Во-первых, у диполя вплоть
до г - 5 0 х 10-3 X наблюдаются только мнимые составляющие электрического поля
(Eq и Ег ) и реальная составляющая магнитного поля (Н®), т.е. поля Eq и
сдвинуты на 90°. Далее начинают проявляться реальные части электрических по-
лей и мнимая часть магнитного поля; фазы полей начинают изменяться. Поля
становятся синфазными примерно при г = 0.6Х. Дальняя зона для электрического
диполя (условие (Eq
max
max
) > 10) наступает на расстоянии г/Х > 3.2.
Ближняя зона элементарного диполя (и по видимому любой антенны) представ-
ляет собой открытый резонатор, который концентрирует электромагнитную энер-
гию. Установлено, что в промежуточной зоне электромагнитное поле не является
чисто поперечной волной: существует составляющая Ez (сравните с разделом 7.4.2).
Таким образом, предложенная самосогласованная физическая модель диполя Герца
позволила построить новую математическую модель, устраняющую разрыв между
током на поверхности излучателя и ЭМП в ближней зоне. При этом деление про-
странства излучения антенны на ближнюю, промежуточную и дальнюю зону явля-
ется нецелесообразным.
На основе самосогласованного метода, включающего в себя СИП (1.8.4) ЭМП и СИУ
(1.8.6), проведен электродинамический анализ ЭМП диполя Герца непосредственно
с поверхности вибратора до дальней зоны. При этом в работе была использована само-
согласованная физическая модель диполя Герца в виде идеально проводящей бесконеч-
но тонкой трубки конечной длины, по которой протекает постоянный ток (1.8.8).
Выявлены особенности поведения ЭМП в ближней и промежуточной зонах.
В частности установлено, что в промежуточной зоне, в отличие от общепринятого
мнения, электромагнитное поле не является чисто поперечным. Сделан вывод о
нецелесообразности деления пространства на ближнюю и промежуточные зоны.
Чисто поперечным ЭМП становиться только на расстояниях г > 2Х.
Основным достоинством самосогласованного метода является то, что в отличии
от традиционного алгоритма на основе функции Грина (1.8.2), имеется возможность
установить непрерывную трансформацию структуры ЭМП непосредственно с по-
верхности диполя Герца до дальней зоны. Поэтому, введенная самосогласованная
физическая модель диполя Герца совместно с самосогласованным методом позво-
лила построить новую теорию, согласно которой ЭМП в любой точке простран-
ства подчиняется уравнениям Максвелла и не имеет особенностей.
86
ГЛАВА 2
Глава 2. Электрические параметры передающих антенн
Параметры каждой антенны можно разделить на две группы. К первой отно-
сятся параметры, которые определяют или характеризуют электродинамический
режим антенны; они называются электрическими параметрами антенны. Вто-
рую группу составляют параметры, характеризующие крепежную и установоч-
ную арматуру, механизмы вращения, приспособления для транспортировки, вес,
стоимость и т. п.
Электрические параметры, в свою очередь, можно разделить на две группы:
группу А, которая определяет электродинамический режим антенны, и группу Б
характеризующую этот режим [17, 18]. К группе А относятся геометрические раз-
меры и форма поверхностей и проводов, по которым текут электрические токи,
частота колебания и распределение токов на проводах и поверхностях, электроди-
намические параметры материалов антенны и окружающей среды (о , £, ц). Груп-
па Б включает: диаграммы направленности, коэффициент направленного дейс-
твия, сопротивление излучения, электрическую прочность, действующую длину
и эффективную площадь, коэффициент полезного действия, входное сопротивле-
ние, диапазонность (полосу рабочих частот), поляризационные характеристики.
Прямая задача (задача анализа) в антенной технике заключается в определе-
нии параметров группы Б по известным параметрам группы А.
Обратная задача (задача синтеза) заключается в определении параметров груп-
пы А, которые обеспечивают получение заданных параметров и характеристик
группы Б.
2.1. Векторная комплексная диаграмма направленности (ДН)
антенны [2, 17]
Используя аналогию с полем элементарного электрического диполя, напря-
женность электрического поля произвольной антенны в дальней зоне можно пред-
ставить в виде [17,18]
Е = ® (е’ ф)“
(2.1.1)
Здесь 1д — комплексная амплитуда электрического тока в выбранной точке
А излучающей системы; Wc = д/ц/е — характеристическое сопротивление среды;
X — длина волны в среде; 1а — коэффициент пропорциональности (действующая
длина антенны; см. п. 2.7).
В выражении (2.1.1) комплексная векторная нормированная диаграмма на-
правленности F(0,cp) характеризует угловое распределение поля, а также его
поляризационные и фазовые свойства. При задании этой характеристики антенны
обычно оговаривается положение начала координат, относительно которого ве-
дется отсчет разности фаз.
Обычно электромагнитное поле в дальней зоне анализируют в сферической сис-
теме координат. Так как электромагнитное поле в дальней зоне является попереч-
ным [1], то оно, распространяясь вдоль оси г , имеет две составляющие: и Ед.
Элрзстриместсие параметры передаюи^их антенн
87
Напряженность магнитного поля в дальней зоне определяется следующим об-
разом [1]:
= E0/Wc , Не = -Ev/Wc . (2.1.1а)
Очевидно, что в дальней зоне
F (е, <р) = Ее (е, ч>) + fjp (6, <₽)
(2.1.2)
2.1.1. Амплитудная диаграмма направленности. В общем случае функции
Fq включают по два сомножителя:
Fe (е,ф) = Fe (0,<|>)е’Фв(е’ф)ёо, Ёф(0,ф) = Е(,,(О,<р)Р"1’>(О’'?)<ро, (2.1.3)
где вещественные положительные сомножители Fq и в (2.1.2) представляют собой
характеристики направленности — зависимости нормированных составляющих
комплексных амплитуд Еф и Eq поля излучения Ё от направления в пространстве
при неизменных расстояниях г и подводимой мощности:
Fe (9, q>) =
Ев (6, ф)
^0тах Ch ’ Ф1)
Е<;) (9, ф) =
ММ
(ртах (02’Ф2)
(2.1.4)
нормированные таким образом, что max F0 (0, ф) = 1, max Ftp (0, ф) = 1.. Здесь 0],Ф1
и 02’Ф2 — направления максимального излучения.
Величины Fq (0, ср) и (0, <р) называются нормированными амплитудными ДН.
Графические изображения характеристики направленности называются диа-
граммами направленности (ДН).
Выражения (2.1.4) относятся к ДН по полю. В некоторых случаях используется
понятие нормированных ДН по мощности:
Fe (е, ф) =
Sr max Ch ’ Ф1)
Гф (е, ф) =
s? (е,ф)
^Фтах (62,Ф2)
(2.1.5)
определяемых зависимостями составляющих потока мощности от
(0, ср) в пространстве. В (2.1.5) Sf = —Re Eq,H,
направления
Sr max (®1 > Ф1)
— модуль составляющей вектора Умова-Пойнтинга с вектором Eq в направлении
максимального излучения 0^, ср^; max (02, Ф2 ) ~ модуль составляющей вектора
Умова-Пойнтинга с вектором Е„ в направлении максимального излучения 02,Ф2-
Если измерять напряженность электрического поля в дальней зоне по повер-
хности среды радиуса г с центром в точке 0 , где находится антенна, то из трех
сферических координат будут изменяться только две - 0 и ф. В результате полу-
чим зависимости вида Eq (0, <р) = Е0/0 (0,ф),
электрического
поля ( Ё (9,ф)= S' fs (9,ф)
Еф (9, ф) = е;.,/ф (0, ф) - для амплитуды
— для модуля вектора Умова-Пойн-
тинга) П (0, ф) = П'/р (0, ф) = r2S
для угловой плотности мощности. Здесь штри-
хами обозначены амплитудные множители, независящие от угловых координат,
а функция f (0, ф) определяет ненормированную ДН по полю, fs (0, ф) — ненорми-
рованную ДН по мощности.
Так как плотность мощности ( П или *9 ) в дальней зоне пропорциональна квад-
рату напряженности электрического поля, поэтому применительно к одной и той
88
ГЛАВА 2
же антенне будем использовать обозначения: f (6, ф) — для ненормированной ДН
по полю и j (0, <р) — для ненормированной ДН по мощности. Тогда соотношения
(2.1.3) и (2.1.4) можно записать в другом виде
(0, ф) =
/Ф (0, ф)
Лр шах (®2 > Ф2 )
ПО ПОЛЮ,
(2.1.4а)
JQ max ’ Ф1)
(0, Ф) =
/ф (0, ф)
/<р max (®2 ’ Ф2 )
ПО МОЩНОСТИ.
(2.1.5а)
Для получения пространственной ДН следует в разных точках среды измерить
напряженность поля Е и изобразить на графике ее зависимость от направления
Угловая плотность мощности определяется выражением П = lim (ДР/ДО), где
AQ->0
ДР — поток мощности (поток электромагнитной энергии в единицу времени) через
телесный угол ДГ2.
2.1.2. Изображение ДН в пространстве выполняется в виде замкнутых по-
верхностей, являющихся геометрическим местом точек — концов отрезков, про-
веденных из начала координат в направлениях 0, ср; длины отрезков пропорци-
ональны значениям F (9. Ч>) или f2 (е, <р) в этих направлениях, где под функцией
F(0,cp) в дальнейшем понимаем одну из функций Fq (0,ф)или F® (0,ф).
На практике в целях упрощения обычно ограничиваются рассмотрением ДН
в двух главных взаимоперпендикулярных плоскостях, линия пересечения кото-
рых совпадает с направлением максимума ДН. Одну из этих плоскостей обыч-
но совмещают с вектором электрического поля антенны Е ( Е -плоскость), тогда
другая плоскость совпадает с вектором Н антенны ( Н -плоскость). В этом случае
ДН изображается плоскими кривыми в полярной или прямоугольной системах ко-
ординат. ДН по мощности есть ДН по полю, каждое значение которой возведено
в квадрат. Для построения ДН используется также логарифмический масштаб:
КДБ (0, <р) = 201g F (0, <р) = 101g F2 (0, ф), в котором хорошо передаются особенности
амплитудных ДН в широком динамическом диапазоне.
Часто для получения необходимой полноты представлений ДН достаточно вы-
полнить сечения двумя взаимоперпендикулярными плоскостями, проходящими
через направление максимального излучения.
На рис. 2.1 изображен вид в пространстве некоторой ДН Р(0,ф). Если отрезок
0М2 принять равным единице, то расстояние от начала координат 0 до произ-
вольной точки М1 на поверхности ДН определяется как = F (0, ф) .
Наиболее часто встречаются тороидальные, игольчатые, веерные и косе-
кансные диаграммы направленности
Особенностью тороидальной ДН (рис 2.2а) является почти равномерное излу-
чение в плоскости, перпендикулярной оси тороида. Область применения антенн
с тороидальными ДН - радиосвязь, радионавигация и радиовещание. Игольчатая
ДН имеет много боковых лепестков и ярко выраженный главный лепесток почти
симметричной формы (рис. 2.26). В веерных ДН (рис. 2.2в) ширина главного лепес-
Электрические параметры передающих антенн
89
Рис. 2.1. Пространственное изображение диаграммы направленности антенны [17]
Рис. 2.2. Виды диаграмм направленности
90
ГЛАВА 2
0, град
О
60
20
•о *| 1
~| ^•413 Г\1
С Qu
60
Рис. 2.3. Картографическое изображение диаграммы направленности антенны [3]
80 100 120 140 160 (р,град
тка в двух взаимно перпендикулярных плоскостях сильно отличается. Антенны
с игольчатыми и веерными ДН применяются в радиолокации и связных радио-
системах. В косекансной ДН веерный главный лепесток имеет несимметричную
форму (рис. 2.2,г), причем в одной из плоскостей (обычно вертикальной) он опре-
деляется уравнением F(0) = cosec 0, а в другой плоскости лепесток симметричен
и имеет малую ширину Антенны с такими ДН предпочтительны для самолетных
РЛС обзора земной поверхности и для наземных РЛС наблюдения за воздушной
обстановкой.
Пространственное изображение функции F(0, ср), как правило, является слож-
ным для построения и малоинформативным. Поэтому о форме пространственной
ДН обычно судят по ее сечениям в выбранных плоскостях. Для слабонаправленных
антенн используют главные сечения сферических антенн координат, экваториаль-
ную плоскость и пару меридиональных плоскостей. Для игольчатых и веерных ДН
чаще выбирают пары перпендикулярных сечений, проходящих через направление
максимального излучения. Одно из сечений, как правило, берется в плоскости,
где главный лепесток ДН имеет наименьшую ширину.
В тех случаях, когда требуется полностью охарактеризовать поле излучения
антенны по всем направлениям, применяют картографическое изображение ДН
[2,3], сущность которого состоит в следующем.
Если пространственную ДН антенны окружить сферой, то каждой точке ее
поверхности будет соответствовать определенное значение углов 0, ср. При проек-
тировании на поверхность сферы кривых, соответствующих равным значениям
интенсивности поля в ДН, их проекции образуют замкнутые кривые равной интен-
сивности. Участок поверхности сферы вместе с полученными кривыми равной ин-
тенсивности можно изобразить затем на плоскости с использованием какой-либо
картографической проекции: прямоугольной (рис. 2.3), полярной и др. Числа у кри-
вых на таких проекциях (рис. 2.3) указывают уровень поля по отношению к полю
в направлении главного максимума, а точки внутри отдельных групп замкнутых
кривых соответствуют направлениям главного и бокового максимумов.
Такой метод изображения пространственной ДН весьма нагляден и позволяет
в случае необходимости, легко построить плоские ДН в любой интересующей
плоскости.
Электрч^^ххкре параметры передающих антенн
91
0°
а) б)
Рис. 2.4. Изображение диаграмм направленности: а) - ненаправленной по полю в по-
лярной системе координат; б) — остронаправленной по мощности в декартовой системе
координат [17]
Ширина ДН в зависимости от назначения антенны лежит в очень широких
пределах — от десятков градусов до долей минуты. Поэтому различают два типа
ДН антенн: ненаправленные и остронаправленные ДН. Для ненаправленных антенн
важной характеристикой является степень приближения ДН к окружности, ко-
торая оценивается коэффициентом равномерности диаграммы направленности
и определяется как N = Емин
макс
—► —►
где Емин и Емакс
напряженности поля в на-
правлении минимального и максимального излучений на одинаковых расстояниях
от антенны. Если амплитудная ДН задана в нормированном виде, то N = Емин.
Коэффициент равномерности иногда определяют как вероятность — того, что
значения ДН будут не ниже заданного относительного уровня при случайном рав-
новероятном положении точки наблюдения. Эта вероятность для ДН в отдельных
секущих плоскостях определяется как отношение суммы угловых секторов, в ко-
торых значения ДН выше заданного уровня, к 360°.
Амплитудные диаграммы направленности остронаправленных антенн обычно
имеют несколько максимумов и минимумов (рис. 2.4,а). Наибольший по величине
лепесток называется главным, а другие, меньшие, — боковыми. Узкие ДН удобно
изображать в прямоугольных координатах, как это показано на рис. 2.4,6.
Степень концентрации электромагнитной энергии в пространстве в некоторой
степени характеризуется шириной главного лепестка диаграммы направленнос-
ти, которую часто сокращенно называют шириной диаграммы направленности.
Условились определять ширину ДН на некотором уровне s плотности мощности
от максимальной и обозначать эту ширину 20s (или 2<ps). Таким образом, ширина
ДН есть угол между двумя направлениями в пределах главного лепестка,в кото-
рых угловая плотность мощности составляет s от максимальной.
Наиболее употребительными уровнями отсчета являются: s=0,5; s=0,l и s=0.
Величину 20о,5 называют шириной ДН «по половинной мощности», 20о — шири-
ной ДН «по нулям» и 20о 1 — шириной ДН «на уровне 0,1» или «на уровне 10 дБ».
Отсчет на уровне 0,1 часто используется в тех случаях, когда нельзя четко за-
фиксировать направление нуля излучения или когда оно вообще отсутствует.
92
ГЛАВА 2
Способы определения ширины ДН пояснены на рис. 2.4,6. Следует отметить,
что уровню половинной плотности мощности соответствует уровень 0,707 по полю
или —3 дБ в логарифмическом масштабе. Уровню 0,1 по мощности соответствует
уровень 0,316 по полю или —10 дБ в логарифмическом масштабе.
Боковые лепестки обычно характеризуются данными по первому из них, име-
ющему, как правило, наибольшую величину. Такими данными являются величина
(уровень) максимума Fg0K1 и ег0 направление 0док1 обычно используется логариф-
мический масштаб при необходимости определения данных по боковым лепест-
кам, когда их уровень очень мал по сравнению с главным.
2.1.3. Поляризационные свойства; поляризационный базис [2]. Соотноше-
ние (2.1.2) можно записать в другом виде
F(0, ф) = F(6, ф)р(0, <p)e
(2.1.2а)
где векторный сомножитель р(0,ф) в (2.1.2а) представляет собой единичный вектор
поляризации с компонентами, ориентированными по направлениям базисных ор-
тов сферической системы координат 0О и фд :
Р (0, ф) = 0оре (0, ф) + ф0рф (0, ф)
(2.1.6)
2
причем модуль данного вектора Pq + р™
= 1 независимо от направления 0, ф
F(e, Ф) = (в,ф)+^(е,ф).
Компоненты р$ и р® характеризуют соотношение между вертикальной и гори-
зонтальной составляющими поля в дальней зоне антенны в выбранном направле-
нии, а также фазовый сдвиг между ними.
В общем случае оба компонента вектора поляризации р(0,ф) являются комп-
лексными, однако один из компонентов обычно полагают вещественным и рав-
ным а (фаза данного компонента включается в мнимый показатель экспоненты
гФ (0, ф) в третьем сомножителе (2.1.2а). Это главная (или основная) составляющая
поляризации. Второй компонент вектора поляризации, ортогональный главному,
называют паразитной (или кроссполяризационной) составляющей поляризации.
С учетом обозначений главной и паразитной составляющих поляризаций вектор
поляризации представляется в виде
р(0,ф)=г2Ла
(е, ф)+?пз
(2.1.7)
где ггд — базисный единичный вектор главной поляризации; а(0,ф) — вещест-
венная положительная функция; in3 — базисный единичный вектор паразитной
поляризации; ф(0,ф) — фазовый сдвиг между составляющими. Величина а2 < 1
представляет собой поляризационную эффективность антенны и показывает долю
плотности потока мощности в данном направлении на главной поляризации. Ана-
о
логично величина (1 — а ) равна доле плотности потока мощности паразитной по-
ляризации.
Рассмотрим поведение мгновенного значения вектора поляризации в поле из-
лучения антенны. На рис. 2.6 показана касательная плоскость к сферическому
фронту излучаемой волны в окрестности точки наблюдения М (волна уходит от
наблюдателя за плоскость рисунка). Координатные оси х и у на касательной плос-
кости ориентированы параллельно базисным векторам фд и 0g сферической сис-
Электрические параметры передаюи£их аюпенн
93
Рис. 2.5. Плоскость поляризации л
и картинная плоскость К [17]
Рис. 2.6. Поляризационный эллипс
на картинной плоскости[17]
темы координат антенны. Полагаем, что составляющая 6 соответствует главной
поляризации.
Поляризация передающей антенны определяется по поляризации ее поля
излучения, как правило, по электрическому вектору. В общем случае вектор Е
в каждой точке пространства с течением времени изменяет как свою величину,
так и направление. Эти изменения описываются поляризационными характеристи-
ками антенны. Так как вектор Е в дальней зоне коллинеарен вектору поляризации
р, поэтому описание поляризационных свойств антенны с помощью вектора Е или
вектора р тождественны.
При изучении поляризационных характеристик удобно ввести две вспомо-
гательные плоскости — плоскость поляризации к и картинную плоскость К
(рис. 2.5) [17].
Плоскость поляризации содержит в себе вектор Е и направление распро-
странения в точку наблюдения М. Если вектор Е вращается вокруг направления
распространения, то вместе с ним вращается и плоскость поляризации.
Поляризация называется линейной, если плоскость поляризации с течением
времени не меняет своего положения в пространстве. При этом различают гори-
зонтальную поляризацию (вектор Е параллелен поверхности земли), вертикаль-
ную поляризацию (плоскость поляризации перпендикулярна поверхности земли)
и наклонную поляризацию.
Поляризация поля называется вращающейся,если плоскость поляризации вра-
щается, делая один оборот за период высокочастотных колебаний поля.
Картинная плоскость перпендикулярна направлению распространения
и проходит через точку наблюдения. Так как вектор Е также перпендикулярен
направлению распространения, то он находится в картинной плоскости (рис. 2.6).
На картинной плоскости будем пользоваться прямоугольной системой коорди-
нат с началом в точке наблюдения М. Оси этой системы совместим с направля-
ющими ортами сферической системы координат в точке М и условно обозначим
94
ГЛАВА 2
через ре и р9 .
Эллиптическая поляризация является наиболее общим случаем поляризации,
когда конец электрического вектора описывает в картинной плоскости эллипс,
вращаясь со средней угловой скоростью со.
Поляризационные характеристики поля и, следовательно, антенны, полностью
определяются следующими параметрами эллипса (рис. 2.6):
— углом у наклона большой оси эллипса к оси 0 выбранной системы координат;
этот угол называется углом наклона поляризационного эллипса;
— коэффициентом равномерности эллиптической поляризации (коэффи-
циент эллиптичности), который определяет отношение малой полуоси эллипса
к большой
гэ = Ъ/а; (2.1.8)
— направлением вращения электрического вектора,которое определяется сле-
дующим образом: если смотреть вслед уходящей волне и видеть при этом вектор
Е вращающимся по часовой стрелке, то поле будет иметь эллиптическую поля-
ризацию правого вращения; при вращении вектора Е против часовой стрелки поле
имеет эллиптическую поляризацию левого вращения.
На рис. 2.6 ось г уходит за плоскость чертежа, следовательно, изображенное
направление вращения соответствует поляризации правого вращения. При поля-
ризации правого вращения коэффициенту гэ приписывать знак плюс, а при по-
ляризации левого вращения — минус. При тэ = 0 эллипс вырождается в прямую
линию и поле имеет линейную поляризацию. При гэ = ±1 эллипс становится окруж-
ностью; в этом случае говорят, что поле имеет круговую поляризацию.
Поляризационная характеристика — это зависимость э. д. с. в прием-
ной антенне линейной поляризации, принимающей электромагнитные волны
от рассматриваемой передающей антенны, от угла поворота А этой антенны
в картинной плоскости (рис. 2.7). Для каждого положения приемной антенны (на
рисунке изображен диполь Герца) амплитуда наведенной э. д. с. пропорциональ-
на наибольшей величине проекции вращающегося электрического вектора на ось
диполя. Если для всех углов А найти эту наибольшую проекцию и изобразить ее
в виде радиус-вектора в полярной системе координат на картинной плоскости,
то концы векторов дадут кривую, которая является поляризационной характе-
Рис. 2.7. Поляризационный эллипс и поляризационные характеристики
Эл^стрич^ские параметры передающих антенн
95
ристикой. Эта характеристика изображена на рис. 2.7,а пунктирной кривой, при-
чем масштаб ее выбран так, что при совпадении оси диполя с осями эллипса
амплитуды наведенных э. д. с. равны полуосям эллипса. Зная поляризационную
характеристику, легко определить параметры у и гэ поляризационного эллипса.
Для определения направления вращения знать поляризационную характеристику
недостаточно — нужны дополнительные измерения фазовых соотношений компо-
нент поля.
Отметим, что в общем случае для каждого направления в пространстве 0, (р
будет своя поляризационная характеристика.
На рис. 2.7,6 изображены вырожденный эллипс поляризации и поляризацион-
ная характеристика для случая линейной наклонной поляризации, а на рис. 2.7,в
— для круговой поляризации.
Расчет параметров поляризационного эллипса может быть выполнен
на основе представления поля вращающейся поляризации в виде суммы двух по-
лей линейной поляризации.
Вектор Е в дальней зоне представим как сумму взаимно перпендикулярных
поперечных компонент поля в сферической системе координат Е = Eq + Е^ . Пред-
ставляя мгновенные значения вектора £ в тригонометрической форме и принимая
в качестве опорной фазу компоненты Eq получаем
§ = 0qEq cos cot + фдЕф cos(tt)£ + \|/) ,
где Eq и Еф — амплитуды компонент; \|/ — разность фаз между компонентами Еф
и Eq . Положительное значение \|/ означает, что компонента Е^ опережает по фазе
компоненту Eq .
Здесь важно напомнить, что результирующий вектор двух полей, направле-
ния векторов которых не совпадают в пространстве и времени, с течением вре-
мени поворачивается по кратчайшему пути в сторону вектора поля, отстающего
по фазе.
Уравнение эллипса определим через мгновенные значения и линейно-по-
ляризованных составляющих:
£д = Eq COS (Ot, £ф = Еф cos(cdt + ф) . (2.1.9)
Этими выражениями определяется уравнение эллипса в параметрической фор-
ме с параметром cot. Положение конца результирующего вектора определяется,
таким образом, координатами $q и .
Если в формулах (2.1.9) исключить параметр cot, то получится уравнение
эллипса в канонической форме:
$1/Eq - 2£е£Ф cos + £2/Е2 = sin2 ф. (2.1.10)
Рассмотрим характерные частные случаи.
1. Составляющие Eq и Еф синфазны или противофазны, т. е. = 0, л, 2л,...
Из уравнения (2.1.10) для этого случая получим ^о/^ф =Ед/Еф, т. е. уравнение
прямой, наклоненной к оси 0 под углом у = arctg(^Q / ^). Следовательно, сумма
двух линейно-поляризованных синфазных (противофазных) полей также является
линейно-поляризованным полем.
2. Составляющие Eq и Еф имеют сдвиг по фазе \|/= (2n +1) л/2 (п = 0,1,2,...).
Из выражения (2.1.10) получим, $q/Eq + ё’2 /Е2 =1, что определяет эллипс, оси
которого совпадают с координатными осями 0 и ср ( у - 0 или у = 90° в зависимости
96
ГЛАВА 2
от соотношения модулей <pq и
3. Составляющие Eq и Еф имеют одинаковую амплитуду и сдвиг по фазе на л/2
или Зл/2. В этом случае выражение (2.1.10) дает уравнение окружности $q +$2 = Е2,
т. е. поляризация суммарного поля будет круговой. Отсюда вывод: для получения
поля чисто круговой поляризации (тэ I = 1) достаточно обеспечить излучение двух
линейно-поляризованных полей равной амплитуды и взаимно перпендикулярной
поляризации, фазы которых отличаются на л или Зл/2. При этом амплитуда ре-
зультирующего вектора будет равна амплитуде одной из линейно-поляризован-
ных компонент.
Параметры поляризационного эллипса при известных компонентах определя-
ются по формулам [17]:
tg2y = 2т cos у/(т2 -1),
(2.1.11)
т sin2 у - sin 2у cos у + (l/m)cos2 у
— о . / / \ • 2 ’
V т cos у + sm 2у cos у + (l/m)sin у
где т = Ед/Еф — отношение амплитуд компонент (при отсчете угла у от оси 0 ), а
V = arg £ф - arg Ё0
— разность фаз комплексных амплитуд этих полей.
Знак во второй формуле (2.1.11) выбирается в соответствии с приведенными
выше соображениями о направлении вращения результирующего вектора.
При известных параметрах поляризационного эллипса отношение амплитуд вза-
имно перпендикулярных компонент определится из формул (2.1.9) и (2.1.11):
m = ^tg^y + l)/(r2 + tg2y). (2.1.12)
2.1.4. Направленные свойства антенн вращающейся поляризации харак-
теризуют обычно парциальными ДН для взаимно перпендикулярных компонент.
Эти парциальные ДН в нормированном виде записываются как Fq (0, ф) для со-
ставляющей Eq и Еф (0, ф) для составляющей Еф.
Кроме того, может быть определена так называемая ДН по полной мощности
F2 (0, ф) = 5 (0, фУ^шах , где — величина, аналогичная модулю вектора Умова-
Пойнтинга для поля линейной поляризации и определяющая плотность потока
мощности через единичную площадку для поля вращающейся поляризации.
Для удобства описания характеристик вращающегося поля вводится понятие
полной амплитуды волны Е (0, ф) = Jeq (0, ф) + Е2 (0, ф), которая связывается с ве-
личиной S обычным соотношением [17]:
ё (е, <pf _ (е, Ф)+(е, Ф)
240л 240л
(2.1.13)
Для линейной поляризации полная амплитуда волны является модулем элект-
рического вектора суммарного поля. В остальных случаях эта величина не имеет
прямого физического смысла.
Нормированная ДН по полной мощности может быть определена из выражений
Электрические параметры передающих антенн
(2.1.13):
P2zfl л_|Ё(е.<р)|_ *е2(б,<р)+^(е,<р)
Г (ру Г 9 z х 9 z х
Emax Е| (0, ф) + Е2 (9, ф)
L х Jmax
(2.1.14)
Отсюда находится связь между ДН по полной мощности и парциальными ДН:
е2(0,ф) =
Ее2 (0, ф)
f2 (е, ф)
Eg (0, ф) + Е2 (9, ф)/mf
max
F2 (9, ф) + (0, ф)
Jmax
(2.1.15)
где m-i = EamitvEmTnav; и ЕттТ1ЯУ — значения амплитуд компонент поля
Г 1 ± V IlldA / ip II Id Л 7 V 11 Id Л. Ш ШаЛ </
в максимумах парциальных ДН.
Если направления максимумов парциальных ДН совпадают, то в формуле
(2.1.15) максимум знаменателей получается в направлении 0, ф, в котором мак-
симальны парциальные ДН: Fq (0, ср) = К, (0, ср) = 1. Для этого случая выражение ДН
по полной мощности упрощается [17]:
F2 (0, ф) = Fg (6, ф)/(1 +1/то?) + F2 (0, ф)/(1 + m2).
(2.1.16)
Таким образом, в этом случае для определения ДН по полной мощности через
известные парциальные ДН необходимо дополнительно найти отношение ампли-
туд компонент в максимуме ДН по полной мощности.
2.1.5. Поляризационный базис [2]. Разложение вектора поляризации по двум
линейным перпендикулярным составляющим, совпадающим с базисными век-
торами ©о и фо, накладывает ограничение на выбор главной поляризации: она
должна быть обязательно линейной, причем только вертикальной или горизон-
тальной. Однако возможны и иные случаи, когда в качестве главной должна быть
поляризация иного вида, например, наклонная линейная или круговая. Здесь уже
необходим иной поляризационный базис ггл, in3 . Остановимся кратко на его пос-
троении с использованием аппарата унитарных матриц:
где Ё
и11
Uoi
единичная матрица; ,
и12
и22
или [U] 17*
(2.1.17)
знаки комплексного сопряжения и транспо-
О
нирования соответственно.
Любая унитарная матрица второго порядка с точностью до произвольного фа-
зового множителя е^, полагаемого в дальнейшем равным единице, может быть
представлена в виде
[и] =
“12 й cos'/-
= е 5
w22j sin^e1^1
sin хе^2
i(\i>i +у?)
-cosхе v 1 27
(2.1.18)
Введенный выше соотношением (2.1.6) поляризационный вектор р(0,ф) в лю-
бой точке наблюдения может быть записан в виде произведения матрицы-строки
на матрицу-столбец:
(2.1.19)
4 - Неганов
98
ГЛАВА 2
Полный поляризационный вектор не изменится, если между двумя матричны-
ми сомножителями в правой части (2.1.19) поместить еще два сомножителя:
или
где
Ф0]М >
Рпз
(2.1.20)
(2.1.21)
(2.1.22)
Соотношение (2.1.20) дает разложение вектора поляризации в новом поляриза-
ционном базисе, составляющие которого согласно (2.1.21):
*гл = §0wll + Ф0^21 = §0 COSX + ф0 sinxeW1,
Чз = %W12 + Фои22 = Оо Sin хе*'1'2
(2.1.23)
- ФО cos хе*^1 +V2\
Здесь параметр х — угол поворота векторов , in3 , относительно ортов 90 , Фо •
Каждая из составляющих поляризационного базиса в (2.1.23) имеет единичный
модуль и описывает волну эллиптической поляризации общего вида. Характерным
свойством этих волн является ортогональность, т.е. векторы и гпз не интерфе-
рируют между собой и переносят мощность излучения антенны независимо один
от другого.
Наиболее простым примером пары ортогональных векторов ггл и in3 являет-
ся случай двух наклонных взаимно-перпендикулярных линейных поляризаций
(рис. 2.8,а), когда Ф1 = Фг = 0 , ах — произвольно (0 < Х^ я/2):
4л = % C0SX + Фо sinX > *пз =0OsinX-^Oc°SX-
Рис. 2.8. Примеры ортогональных поляризационных базисов
Электрические параметры передающих антенн
99
Другим, часто используемым на практике примером пары ортогональных век-
торов 1гл и in3 является случай двух круговых поляризаций противоположно-
го направления вращения (рис. 2.8,6), имеющий место при % = л/4 и =-л/2,
V2 = тс/2:
4л =О,7О7(ёо -гф0),
4з =О,7О7(гёо - фо).
(2.1.24)
В выражениях (2.1.24) главной поляризации соответствует правое вращение, па-
разитной
левое.
В общем случае произвольных параметров %, ф! и ф2 векторы , in3 характе-
ризуются одинаковым модулем коэффициента эллиптичности гэ
рно. 2.8,в) боль-
шие оси эллипсов в каждой точке пространства перпендикулярны между собой,
а направления вращения противоположны.
Комплексные компоненты вектора поляризации в новом поляризационном бази-
се (2.1.23) на основании (2.1.22) принимают значения
Ргл = Рб cos X + РФ sin Хе = аегф ,
Рпз = Ре sin%e"ZV2 - рф cosxe-^1^2
Vl-a2e^'+v>.
Таким образом, для полного описания поляризационных свойств дальнего поля
антенны достаточно указать необходимый поляризационный базис (2.1.23) и иметь
функциональные зависимости поляризационной эффективности а2 (9, ф) и фазо-
вого сдвига ф(0,ф) между основной и паразитной составляющими поляризации
от углов наблюдения 0, ф. Знания этих первичных параметров достаточно для
определения вторичных параметров: коэффициента эллиптичности гэ и угла ори-
ентации большой оси эллипса поляризации как функций углов 0 , ф.
Следует указать, что как поляризационная характеристика антенны (2.1.7),
так и амплитудная F (0, ф) не зависят от положения начала координат.
Диаграммы направленности на заданной поляризации поля при учете ампли-
тудных и поляризационных свойств антенн могут быть представлены в виде
(е> ч>) =
f (е, <р)а (е, <р)
[F(e,<p)a(e,<p)]max ’
Г(0,ф)д/1-а2(О,ф)
max
2.1.6. Фазовая характеристика антенны. Мнимый показатель степени
Ф (0, ф) третьего сомножителя в выражении (2.1.3) есть фазовая характеристика
направленности антенны по главной поляризации излучения. Она характеризует
изменение фазового сдвига компонента главной поляризации при перемещении
точки наблюдения по поверхности большой сферы радиуса г с центром в начале
выбранной системы координат и, следовательно, зависит от этого выбора.
Помимо фазовой характеристики Ф(0,ф) вводятся эквифазные поверхности в
дальней зоне, т.е. поверхности, на которых фаза компонента главной поляриза-
ции сохраняет одинаковое значение для всех углов наблюдения. Уравнение такой
поверхности может быть представлено в виде [2, 17]
100
ГЛАВА 2
г(о,ф) = го+^Ф(е,ф).
2л
(2.1.25)
Если эквифазная поверхность представляет собой сферу (без учета возможных
скачков на Х/2 при переходе через нуль амплитудной ДН), то центр такой сфе-
ры называют фазовым центром антенны. Для удаленного наблюдателя фазовый
центр является той точкой антенны, откуда исходят сферические волны поля
излучения. Простейшей фазовой характеристикой антенны является постоянная
функция
Ф(е,ф) = ф0 ±л,
где Фо — константа.
В этом случае, как следует из (2.1.25), эквифазные поверхности имеют вид
сфер (г = const^ и фазовый центр совпадает с началом координат. Если же функ-
ция Ф (0, ф) непостоянна, то возможны следующие случаи:
— антенна имеет фазовый центр, не совпадающий с началом координат;
— антенна не имеет фазового центра.
В каждом из этих случаев возможно упрощение вида фазовой характеристики
за счет соответствующего переноса начала системы координат. На рис. 2.9 с ис-
ходной системой координат г, 0, ф с центром в точке О показано положение начала
новой системы — точка О' с координатами в старой системе. В новой
системе координат г', 0, ф исходная фазовая характеристика видоизменяется из-за
наличия разности хода лучей r0cosa :
(2.1.26)
Ф' (0, ф) = Ф (0, ф) - кгц cos a =
= Ф (0, ф) - к (а?0 sin 0 cos ф + т/0 sin 0 sin ф + z0 cos 0).
х
Рис. 2.9. Определение фазовой характеристики антенны
Элрктпрические параметры передающих антенн
101
Если антенна имеет фазовый центр (первый случай), то координаты х^,у^,г^
могут быть подобраны так, что Ф'(0,ф) = const. Это возможно лишь при условии
приведения исходной фазовой характеристики к виду
Фо = к (л:0 sin 6 cos ф + у0 sin 0 sin ср + z0 cos 0 + v),
(2.1.27)
где v — некоторая константа.
Отсюда можно утверждать, что антенна имеет фазовый центр только в том
случае, если ее фазовая характеристика может быть представлена в форме (2.1.27).
Многие реальные антенны такие, как рупорные, спиральные, турникетные и дру-
гие имеют фазовые характеристики, в той или иной степени отличные от (2.1.27) и,
таким образом, не имеют фазового центра в строгом понимании (второй случай).
Однако и для таких антенн можно указать точку .Xq, у$, Zq (так называемый центр
излучения), относительно которой поверхность равных фаз наименее уклоняется
от сферической, а фазовая характеристика наиболее близка к постоянной функ-
ции.
Рассмотренные понятия фазового центра антенны и центра излучения относят-
ся к компоненту на главной поляризации излучения. Для поля паразитной поля-
ризации фазовая характеристика направленности может быть найдена с помощью
соотношения
фпз (е> ф) = Ф (6, ф) + V (0, ф),
где Ф (0, (р) — фазовая характеристика на главной поляризации; \|/ (0, ср) — фазовый
сдвиг компонента вектора паразитной поляризации по отношению к компоненту
главной поляризации. Здесь также могут быть введены понятия фазового центра
и центра излучения.
2.2. Коэффициенты направленного действия
и усиления антенны [17]
2.2.1 Коэффициент направленного действия (КНД) Э(0,ф) передающей ан-
тенны определяется сравнением данной антенны с некоторой эталонной антенной,
направленные свойства которой хорошо известны. В качестве эталонных наиболее
широко используются: совершенно ненаправленный (изотропный) излучатель,
диполь Герца и полуволновый вибратор (см. гл. 4). В отношении эталонных антенн
предполагается, что их к. п. д. равен 100%. Кроме того, говоря о поле или плот-
ности мощности, создаваемой эталонной антенной, имеют в виду эти величины,
определенные в максимуме ее ДН.
КНД антенны в направлении 0, ф называется отношение значения вектора
Умова-Пойнтинга S (0, ф), создаваемой в этом направлении данной антенной,
к значению вектора Умова-Пойнтинга Sg создаваемой в этом же направлении
эталонной антенной,при условии равенства полных мощностей излучения рас-
у у
сматриваемой Р и эталонной антенн Рд :
d (е, <р) = s (е, <Р)Д, при р1 = (2.2.1)
где индекс э относится к эталонной антенне.
Существует другое, эквивалентное первому, определение КНД, которое впер-
102
ГЛАВА 2
вые было введено А.А. Пистолькорсом в 1929 г.: КНД антенны называется чис-
ло, показывающее, во сколько раз нужно увеличить мощность излучения эта-
лонной антенны по сравнению с мощностью излучения данной антенны для
того, чтобы в заданном направлении получить одинаковые значения векторов
Умова-Пойнтинга, а следовательно, при одинаковых расстояниях — одинаковые
напряженности поля
при S (0, ср) = Sd или Е (9, ф) = Еэ и г = const.
Из определения ДН по мощности следует, что
5(0,<p)=5maxF2(O,<p),
где £тах — значение вектора Умова-Пойнтинга в направлении максимального из-
лучения, a F2 (0, ф) —нормированная ДН по мощности. Имея это в виду, по опре-
делению (2.2.1) получаем
D (0, <р) = ,SmaxF2 (0, ф)Д, = D0F2 (0, <р), (2.2.3)
где Dq — КНД в направлении максимального излучения данной антенны. Таким
образом, КНД зависит от угловых координат и эта зависимость определяется ДН
антенны по мощности.
Когда, сравнивая антенны, называют их КНД, то обычно имеют в виду Do
— максимальные значения КНД. Чем больше Do, тем большую пространственную
концентрацию электромагнитной энергии обеспечивает антенна и тем больше на-
пряженность поля в направлении максимума ДН при заданной мощности излуче-
ния.
2.2.2. Коэффициент направленного действия антенн вращающейся поля-
ризации определяется так же, как и для антенн линейной поляризации.
Если для приема поля вращающейся поляризации используется поляризацион-
но полностью согласованная приемная антенна (см. § 3.5), мощность излучения
допустимо рассчитывать через полную амплитуду волны.
Воспользуемся, например, определением (2.2.1) и будем считать, что мощность
излучения эталонной изотропной антенны линейной поляризации равна полной
мощности излучения исследуемой антенны, а угловая плотность мощности иссле-
дуемой антенны определяется выражением (2.1.13). Тогда полный КНД определит-
ся выражением (2.2.6) в котором под F2 (6, ф) следует понимать нормированную ДН
по полной амплитуде волны вращающейся поляризации (2.1.15).
После преобразования получим
D (0,<p)= Do (0, <р) + D,., (0,<р), (2.2.4)
где
De (6. ф) =
4лГ(2 (0, <р)
Fe2(0,<p)+F2(0,<p)/m2
sin 0 dQdty
0=0 <р=0
парциальный КНД для составляющей поля Eq , а
Электрические параметры передающих антенн
103
D4>(ei<p) п 2п
J J
0=0 <р=0
471^(0, <р)
m2Fe (0, ср) + F2 (6, ф) sin 0 dQdtp
— парциальный КНД для составляющей .
В квадратных скобках выражений для Dq и записаны ДН по полной мощ-
ности, нормированные к максимуму ДН соответствующей компоненты.
Если направления максимумов парциальных ДН совпадают, то
A) = Dq0 + D9o , (2.2.5)
где Dqo и Оф — значения парциальных КНД в максимумах соответствующих ДН.
Парциальные КНД определяют иногда несколько по-другому: за основу берут
равенство мощности излучения изотропной антенны мощности, связанной с со-
ответствующей компонентой [17]. При этом слагаемые в правой части (2.2.5) будут
содержать весовые множители.
Зависимость поляризационных характеристик антенн от угловых ко-
ординат определяется зависимостью от угловых координат Коэффициента эл-
липтичности гэ (0, ф) и угла наклона большой оси эллипса у (0, ф). Функция гэ (0, ф)
называется поляризационной диаграммой.
Изменение поляризационных характеристик во времени. Выше были рас-
смотрены поляризационные характеристики антенны с неизменными во време-
ни параметрами при излучении ею монохроматических волн. Поле такой антен-
ны называется полностью поляризованным. Если преднамеренно или случайно
изменяются во времени величины гэ и у, но вектор $ совершает вращательное
движение с некоторой средней частотой о то поле называется частично поляри-
зованным. Если же положение самого вектора £ для каждого момента времени
является случайным, то поле является неполяризованным (деполяризованным).
Характерным примером неполяризованного электромагнитного поля является
поле, излучаемое нагретыми телами.
2.2.3. Коэффициент усиления (КУ) О(0,ф)антенны определяется так же,
как и КНД, только сравниваются не мощности излучения, а мощности, подводи-
мые к антеннам. Для эталонной антенны мощность излучения и подводимая мощ-
ность равны, так как ее к. п. д. принят, равным 100%. Реальные антенны имеют по-
тери и их мощность излучения меньше подводимой мощности на величину потерь.
Выражение (2.2.1) применительно к определению КУ имеет вид
g (е, <₽) = р* /рА
при 5 (0, ф) = S3.
(2.2.6)
Так как РА = PS/r|, то
Для направления максимума ДН
Go _ А)П •
(2.2.7)
(2.2.7а)
2.2.4. Пересчет КНД при переходе от одной эталонной антенны к дру-
гой часто требуется на практике и производится с помощью простых соотношений.
104
ГЛАВА 2
Пусть Dj (0, (р) — КНД антенны по отношению к первому эталону, D2 (6, ф) —
ко второму эталону, a D21 — КНД второго эталона по отношению к первому.
Пользуясь определением (2.2.1), можно показать, что
D2(e,4>)=D1(e,4>)/D21.
Так как для эталонных антенн используется отсчет КНД только в максимуме их
ДН, то величина D21 не зависит от угловых координат.
2.2.5. Расчет КНД часто выполняется по известному полю антенны в дальней
зоне, хотя могут быть использованы и другие методы.
Будем считать, что антенна помещена в начале сферической системы ко-
ординат и находится в свободном пространстве. Далее предположим, что ан-
тенна излучает поле линейной поляризации и амплитуда этого поля известна
во всех точках поверхности сферы радиуса г , т. е. известна ДН антенны по полю
Е(0,ф) = ЕтахГ(0,ф). Воспользуемся определением КНД (2.2.1), а в качестве эта-
лона возьмем изотропную антенну.
Учитывая, что для изотропной антенны
J о / '
у у
то из условия Рэ = Р , получим
т2Е2
1 ^тах
4л240л
f F2 (9, ф)зт 0 dQdy.
о о
Так как £(0,ф) = Е2 (0,ф)/24Ол, то по определению (2.2.1) получим
D (0, ф) = 4kF2 (0, ф)/ f [ F2 (0, ф)зт 0 cZ0ckp .
/ 0=0 ф=0
В направлении максимального излучения F2 (0, ф) = 1, поэтому
Dq = Ак Г Г F2 (0,ф)эт0 d0ckp.
/ 0=0 <р=0
(2.2.8)
(2.2.9)
Из выражений (2.2.8) (2.2.9) следует, что КНД однозначно определяется нормиро-
ванной ДН. Это существенно упрощает многие расчеты.
Как будет показано выше КНД апертурных антенн может быть рассчитан и
непосредственно по известному полю в раскрыве.
2.2.6. Расчет КУ при известной ДН сводится к расчету КНД и к. п. д. Расчет
последнего обычно затруднен. Поэтому КУ определяют, как правило, экспери-
ментально, сравнением измеренных мощностей на входе данной антенны и эта-
лонной, при которых индикатор в дальней зоне регистрирует одинаковые напря-
женности поля.
2.2.1. КНД диполя Герца и излучателя Гюйгенса по отношению к изотроп-
ному излучателю. Нормированная ДН диполя Герца имеет вид F (0, ф) = sin 0.
Подставив это выражение в формулу (2.2.9), получим величину О0=1,5.
Электрические параметры передающих антенн
105
Для излучателя Гюйгенса ДН по модулю электрического вектора записывается
в виде F (0, ср) = 0,5(1 + cos 0). Подставив это выражение в формулу (2.2.9), после
интегрирования получим D0=3.
2.3. Сопротивление излучения
2.3.1. Закон сохранения энергии электромагнитного поля в применении
к передающим антеннам записывается в виде
ген
— -L Р -1_ 7Р
1 — П 'г irim ,
(2.3.1)
у
где Р — мощность излучения; Рц — мощность потерь в антенне; Р^т — мощность
реактивных полей, связанных с антенной, и Рген — мощность, отдаваемая гене-
ратором в антенну. Этот закон может быть сформулирован следующим образом:
активная мощность на выходе генератора, подключенного к антенне, равна сумме
мощностей излучения и тепловых потерь в антенне и окружающей среде, а ре-
активная мощность генератора равна мощности реактивных полей в пространстве
вокруг антенны и в самой антенне.
2.3.2. Мощность излучения антенн рассчитывается одним из следующих
четырех способов:
— если известны комплексные амплитуды напряжения и тока на входе антен-
ны, то суммарная активная мощность может быть определена из соотношения
Ръ + Рп = 0,5 Ре(иГ). (2.3.2)
Если мощность потерь мала по сравнению с мощностью излучения или может
быть определена отдельно, то, используя (2.3.2) можно найти, мощность излуче-
ния;
— если известно распределение токов на токонесущих поверхностях антенны,
то мощность излучения (а также реактивная мощность) может быть определе-
на по методу наведенных электродвижущих сил. Этот способ будет рассмотрен
выше;
— если излучение полностью определяется полями на некоторой ограниченной
поверхности (апертуре) антенны, то мощность излучения может быть определена
интегрированием вещественной части вектора Умова-Пойнтинга по этой поверх-
ности; этот метод рассматривается в гл. 4;
— если известны поля в дальней зоне, то рассчитывается вектор Умова-Пойн-
тинга (в дальней зоне он веществен) и интегрированием этого вектора по замкну-
той поверхности определяется мощность излучения.
Рассмотрим последний способ.
2.3.3. Метод интегрирования вектора Умова-Пойнтинга. Пусть Е и Н
— известные комплексные амплитуды полей в дальней зоне. Тогда комплексный
вектор Умова-Пойнтинга
5 = 0,5 ЁхН
= О,5ЁН*то
(2.3.3)
веществен а его направление совпадает с единичным радиус-вектором сферичес-
г у
кой системы координат Tq . Мощность Р определим интегрированием выражения
106
ГЛАВА 2
(2.3.3) по поверхности сферы радиуса г
окружающей антенну:
(2.3.4)
—►
Считая, что dS параллельно т0, из (2.3.3) и (2.3.4) получаем
Р = 0,5 EHds.
(2.3.5)
Площадь элемента сферической поверхности равна
9
ds = г sin 0d0d(p.
С учетом известного для
по формуле (2.3.5) получим
свободного пространства соотношения Е/Н = 120л
240л J
е=Оф=о
sin 6 dOdtp.
Записав модуль электрического вектора в виде Е = Е
max
F(O,(p), гдеЕтах — мак-
симальное значение амплитуды поля при данном г , получим
max
240л
л 2л
J J F2 (0, (p)sin 6 d0d<p.
0=0 ф=0
(2.3.6)
Таким образом, для расчетов по методу интегрирования вектора Умова-Пойнтин-
га достаточно знать нормированную ДН и напряженность поля в максимуме ДН
на заданном расстоянии.
Мощность излучения диполя Герца можно, например, рассчитать только что
рассмотренным способом, если в формулу (2.3.6) подставить выражение для элек-
трического поля диполя в свободном пространстве:
6 sin 9 d0d<p.
После интегрирования получим
=407t2lg(!1Af,
(2.3.7)
где!0
амплитуда тока в диполе.
2.3.4. Сопротивление излучения как параметр передающей антенны приме-
няется главным образом для линейных антенн, в которых понятие полного тока
имеет смысл.
Пусть I — модуль тока в каком-либо сечении антенны. Тогда равенство
Ps =0,5J2Rs
(2.3.8)
у
определяет сопротивление излучения R . Фактически в антенне этого сопротив-
ления как детали (резистора) нет; это просто коэффициент при квадрате тока
у
в формуле мощности. Величина R характеризует эффективность антенны: при
малой величине сопротивления излучения трудно обеспечить высокий к. п. д.
антенны.
dj^icmpuuecT^e параметры пщуедающих антенн
107
у V
Как следует из определения (2.3.8), при данной мощности Р величина R за-
висит от тока, который выбран в качестве отсчетного,
R1 = 2Pz/l2 . (2.3.9)
у
Обычно в антеннах распределение тока неравномерно. Поэтому, вводя R как па-
раметр антенны, нужно условиться об отсчете тока. Наиболее естественно за се-
чение отсчета взять входные клеммы. Если — модуль тока на входе антенны, то
сопротивление излучения, отнесенное ко входу антенны, равно
Rq =2PZ/. (2.3.10)
При распределении тока в вибраторной антенне, близком к синусоидальному,
часто используется определение сопротивления излучения, отнесенного к току в
пучности,
R% =2P^/ln. (2.3.11)
Сопротивление излучения диполя Герца определим по формуле (2.3.9), учи-
тывая, что у этого излучателя ток 10 постоянен по длине провода и поэтому за
отсчетное можно взять любое сечение. Воспользовавшись выражением (2.3.7), по-
лучим
Rq = 807t2(Z1/X)2.
(2.3.12)
2.4. Входное сопротивление
Входное сопротивление передающей антенны определяется отношением на-
пряжения к току на ее входных клеммах и характеризует антенну как нагрузку
для генератора. Этот параметр используется главным образом для линейных ан-
тенн, у которых входное напряжение и ток физически определены и могут быть
непосредственно измерены. В диапазоне СВЧ, когда понятия напряжения и тока
становятся неопределенными, пользуются эквивалентными схемами, параметры
которых определяются относительно эквивалентных параметров питающего вол-
новода.
Рис. 2.10. Эквивалентные схемы передающей антенны: Zo - входное сопротивление;
Go - входная действительная проводимость; Во - входная мнимая проводимость
108
ГЛАВА 2
Обозначим входное сопротивление антенны Zq ; которое в общем случае являет-
ся комплексным: Zq = Rq + гХд и может быть представлено эквивалентной схемой
рис. 2.10,а. Сопротивление Кд называется активным входным сопротивлением,
а Хд — реактивным входным сопротивлением. В некоторых случаях удобно
пользоваться входной проводимостью антенны Уд = Gg + гВд. Соответствующая
эквивалентная схема показана на рис. 2.10,6.
2.4.1. Эквивалентная схема антенны по входному сопротивлению стро-
ится обычно на основе равенства мощностей, поступающих в антенну и в эквива-
лентный ей двухполюсник (рис. 2.10,а). Учитывая, что модуль тока на входе антен-
ны равен Iq , а также равенство (2.3.1), условие эквивалентности можно записать
в виде
о, 5I02Z0
ген
— Р + Гц + iPim
Отсюда получаем
Zq = ZP^/ll + 2РП/11 + i2Pim/ll ,
где каждый член справа является сопротивлением, отнесенным к току на входе
антенны. Первый член определяет сопротивление излучения, второй — сопротив-
ление потерь, а третий — реактивное сопротивление. Итак,
ио - Ro2 + Rq + iXq .
(2-4.1)
Активное входное сопротивление является суммой сопротивлений излучения и по-
терь:
реактивное сопротивление Хо характеризует ту часть электромагнитного поля,
которая сосредоточена вблизи антенны и не излучается.
Расчет полного входного сопротивления Zq при современном состоянии теории
антенн возможен с помощью СИУ, особенно сложно определение сопротивления
потерь и реактивного сопротивления.
Наиболее общий способ расчета Хо — строгое решение электродинамической
задачи — может быть использован только в редких случаях. Поэтому обычно для
определения Хо применяют различные приближенные методы расчета.
Если напряжение и ток на входе антенны могут быть измерены, то входное
сопротивление может быть определено как отношение этих величин.
Входное сопротивление зависит от частоты, причем активная и реактивная
составляющие по-разному изменяются с частотой. Графически эта зависимость
изображается или в координатах частота — сопротивление или на комплексной
плоскости R, X с указанием частот, на которых измерено или рассчитано вход-
ное сопротивление.
2.4.2. Коэффициент согласования передающей антенны с фидерной ли-
нией введем из следующих соображений. Пусть генератор нагружен на согласо-
ванную с ним линию передачи без потерь. Тогда при включении на конце линии
нагрузки с сопротивлением, равным волновому, вся мощность от генератора будет
поглощена этим сопротивлением. На практике часто ни генератор, ни антенна
не согласованы полностью с соединяющей их линией передачи. При этом в антенну
поступает только часть мощности генератора, а другая часть отражается от входа
Электрические параметры передающих антенн
109
линии и антенны. Коэффициентом согласования Lnpg назовем отношение активной
мощности Ракт, поступающей в антенну, к мощности Ро, которая поступит в со-
гласованную нагрузку, включенную вместо рассматриваемой антенны, при одном
и том же генераторе:
^прд = Ракт/Ро • (2.4.3)
Коэффициент Ьпрд определяется через коэффициент отражения в линии передачи
от входа антенны или через известное входное сопротивление антенны.
2.5. Коэффициент полезного действия антенны
Потери электромагнитной энергии в передающей антенне в процессе излуче-
ния определяются ее превращением в тепло в металлических конструкциях ан-
тенны, в диэлектрике антенны, в том числе в изоляторах, в земле, в окружающих
предметах и строениях. В антеннах с большим высокочастотным напряжением
специфичными являются потери на ионизацию воздуха в коронном и факельном
разрядах.
К.п. д. определяет эффективность антенны как преобразователя направляемых
у у
волн в радиоволны и выражается отношением т| = Р / (Р + РП), где Рц — мощ-
2
ность потерь. Разделив в этом выражении числитель и знаменатель на I / 2, по-
лучим
у
С понижением частоты к. п. д. обычно понижается за счет уменьшения R ; у ан-
тенн длинноволнового диапазона он падает иногда до 10%.
К. п. д. антенно-фидерного устройства зависит как от потерь в антенне, так
и от потерь в линии передачи, соединяющей генератор с антенной. Этот к. п. д.
определяется как отношение излученной (полезной) мощности ко всей мощности,
поступившей от генератора на вход линии передачи,
Pz
Лафу = —ё-----------> (2.5.2)
где Pm — мощность потерь в линии передачи. К. п. д. линии передачи г|Л опреде-
у
ляется отношением мощности на выходе линии РА = Р + Рп к мощности на входе
линии
у
Умножив числитель и знаменатель выражения (2.5.2) на Р + Рц получим
Лдфу -
т.е. к. п. д. антенно-фидерного устройства равен произведению к. п. д. линии пере-
дачи на к. п. д. антенны.
110
ГЛАВА 2
2.6. Электрическая прочность и высотность антенн [17]
2.6.1. Электрическая прочность антенны характеризуется наибольшей мощ-
ностью или наибольшим напряжением в антенне, при которых еще не происходит
электрический пробой диэлектриков конструкции антенны (изоляторов, гермети-
зирующих вставок, обтекателей) или окружающего антенну воздуха. Правильным
выбором конструкции и тщательным изготовлением антенны почти всегда можно
добиться того, что пробой в воздухе начнется раньше пробоя диэлектриков антенн.
Напряженность электрического поля, при которой начинается пробой, называет-
ся критической напряженностью поля,а соответствующая ей мощность на входе
антенны — предельно допустимой мощностью. Рабочую мощность антенны,
разрешенную для эксплуатации, выбирают в 2—3 раза меньшей предельно до-
пустимой. При определении предельно допустимой и рабочей мощности ориенти-
руются на те высоты полета и режимы работы антенны, при которых электричес-
кая прочность антенны минимальна.
Электрический пробой воздуха заключается в том, что под действием высоко-
частотного электрического поля воздух в некотором объеме сильно ионизируется
и из диэлектрика превращается в проводник или полупроводник с заметной про-
водимостью. Энергия ионизации и нагревания воздуха при протекании тока через
ионизированную область является энергией потерь. Высокочастотный разряд че-
рез ионизированную область образует добавочные проводники, замыкающие раз-
личные участки антенны. Эти добавочные проводники расстраивают антенну, что
может привести к резкому снижению мощности излучения и нарушениям в работе
радиолинии. При возникновении дугового разряда и значительной мощности пере-
датчика (порядка сотен ватт) в небольшом объеме выделяется большое количество
тепла. Это опасно в пожарном отношении, особенно на летательных аппаратах.
2.6.2. Высотность антенно-фидерного устройства определяется высота-
ми в атмосфере, при которых это устройство может работать без пробоя при
заданной мощности передатчика. С увеличением высоты электрическая прочность
воздуха сначала падает, достигая минимума на высотах 40—100 км, затем сно-
ва возрастает. Для аппаратуры самолетов, высота полета которых не превышает
30 км, под высотностью понимают максимально допустимую высоту по усло-
виям электрического пробоя. Для аппаратуры летательных аппаратов ракетного
типа, в том числе космических, которые проходят зону минимальной электричес-
кой прочности, иногда приходится устанавливать зону высот запрещения рабо-
ты на передачу или же резкого снижения мощности излучения.
2.7. Действующая длина передающей антенны
Определение действующей длины основано на том, что выражение для напря-
женности электрического поля в дальней зоне антенны с любым распределением
тока вдоль- ее оси может быть записано в таком же виде, как и для диполя Герца,
имеющего равномерное распределение тока:
Ё = i36kldI ^~гкг^р (0, <р), (2.7.1)
где I — комплексная амплитуда тока в некотором сечении антенны; 1д — действу-
Элртапрические параметры передситл^их амтенн
111
ющая длина антенны. Таким образом, действующая длина любой антенны есть
длина прямолинейной антенны с равномерным распределением тока, которая
при одинаковых токах в отсчетных сечениях создает в свободном пространс-
тве такую же напряженность поля в направлении максимального излучения,что
и рассматриваемая антенна. Отсюда находим выражения для максимального
значения амплитуды напряженности электрического поля (при F (0, ср) = 1) и для
действующей длины
^Тпах — ЗО/cZ^l/r , 1$ rEmax/30kI.
(2.7.2)
Как видно, действующая длина антенны с неравномерным распределени-
ем тока зависит от того, в каком сечении отсчитывается расчетный ток в (2.7.2).
В частности, для действующей длины, отнесенной ко входу антенны, имеем
1м = rEmax /ЗОИо . (2.7.3)
Расчет действующей длины при известной напряженности электрического
поля производится непосредственно с помощью формулы (2.7.2).
Для прямолинейных антенн с синфазным распределением тока действующую
длину можно определить с помощью понятия «площади тока». Действительно,
как для диполя Герца (В.4), так и для любой антенны (2.7.2) напряженность поля
пропорциональна произведению некоторой длины на ток, которое может быть ис-
толковано как площадь под графиком равномерного распределения тока с ампли-
тудой J на длине 1g. Так как при синфазном распределении тока поля от всех учас-
тков провода в точке наблюдения, находящейся в дальней зоне, сложатся в фазе
в направлении, перпендикулярном оси провода, то, считая каждый элементар-
ный участок провода диполем Герца длиной dz с амплитудой тока l(z) (рис. 2.11),
для этого направления получаем
Рис. 2.11. К определению действующей длины антенны
112
ГЛАВА 2
Интеграл в этом выражении также представляет собой «площадь тока»:
При условии равенства полей в направлении максимального излучения данной
антенны и антенны с равномерным распределением тока на длине 1$ их «площади
тока» должны быть равны, т. е. Sj = IqI Отсюда находим
2=0
На рис. 2.11 для примера показано определение действующей длины, отнесен-
ной к току на входе антенны.
2.8. Диапазонные свойства передающих антенн
Диапазон рабочих частот антенны есть интервал частот от /тах до /min, в ко-
тором все параметры антенны не выходят из заданных пределов. Очевидно, этот
диапазон будет определяться тем параметром, который быстрее других выходит
из заданных пределов при изменении частоты, чаще всего это входное сопротив-
ление (коэффициент согласования). Для некоторых типов хорошо согласованных
антенн, например рупорных, определяющим может быть КНД.
При /тах //min < 1,7 -j- 2,0 обычно говорят о полосе рабочих частот антенны
Af ~ /max _ /min • Ширину полосы рабочих частот определяют в единицах частоты
или в процентах к средней частоте диапазона
А/ _ 9 /max ~ /min
Jср /max + /min
При Д///ср < 10% антенну называют узкополосной, или резонансной, а при
А///ср > 10% — широкополосной. Если Д///ср > 100%, антенну называют широко-
диапазонной и ее диапазонные свойства характеризуют коэффициентом перекры-
тия диапазона Кд = /max//min • Часто полосу рабочих частот или коэффициент
перекрытия диапазона определяют отдельно для каждого параметра.
Выше были определены диапазонные свойства антенны для такого случая, ког-
да при изменении частоты антенна не перестраивается. Некоторые антенны конс-
труируются так, что имеется возможность изменения ее параметров в процес-
се работы. В этом случае диапазоном рабочих частот будет интервал /тах - /min,
в котором параметры антенны могут поддерживаться в заданных пределах за счет
перестройки. При этом нужно иметь в виду, что для каждого положения органов
настройки полоса пропускания антенны должна быть шире спектра частот колеба-
ний, излучаемых антенной.
Электрические параметры передающих антенн
113
2.9. Некоторые дополнительные связи между
параметрами передающей антенны
Существует простая связь между значением вектора Умова-Пойнтинга и мощ-
ностью излучения:
S (0, <р) = PZD (0, ф)/4лт2 .
(2.9.1)
у
Так как Р = РдТ], то
5(0,ф) = РЛО(0,ф)/4лг2. (2.9.2)
Выражая величину S через амплитуду электрического вектора в дальней зоне,
получаем
Е(9,ф) = Л/бОР4С(е,ф)/г. (2.9.3)
2.9.1. Связь между КНД, действующей длиной и сопротивлением излу-
чения находится следующим образом. Считая к. п. д. антенны равным единице
у 2 у
и учитывая, что Р =0,51 R , из выражения (2.9.3) получаем
Е (0, ф) = I д/з0Р2О(е,ф)/т.
(2.9.4)
Напряженность электрического поля выражается через действующую длину фор-
мулой (2.7.2). Из этой формулы и (2.9.4) получим
1д = ^А)/30^ >
(2.9.5)
Dq =30k2Z|/Kz .
Отсюда для сопротивления излучения получим формулу
R1 =3Qk2ll/DQ .
(2.9.6)
(2.9.7)
у
Величины Iq и R , естественно, должны быть отнесены к одному и тому же току.
2.9.2. Теорема подобия [17] является следствием линейности уравнений Мак-
свелла и в своем простейшем виде формулируется следующим образом: антен-
на, работающая при частоте колебаний Д , не изменит свои параметры, если при
новой частоте колебаний /2 = k/i ее геометрические размеры будут уменьшены
в к раз (Z2 = li/к), электрическая проводимость будет увеличена в к раз (о2 - коу),
а электрическая и магнитная проницаемости материалов и среды останутся без
изменения. Величина к называется коэффициентом масштабного пересчета,или
коэффициентом подобия антенн.
На основании теоремы подобия производится моделирование при разработке
и исследовании антенн. Если натурные размеры антенн слишком велики для ис-
следования ее в лабораторных условиях (например, составляют десятки и сотни
метров), то строится модель этой антенны, уменьшенная в к раз по сравнению
с натурой, и на модели проводится измерение ДН, КНД, входного сопротивления
и т. п. Эти параметры модели будут точно такими, как у натурного образца, если
они измерялись на частоте, в к раз большей рабочей частоты натуры при выпол-
нении всех остальных условий, указанных выше.
114
ГЛАВА 2
На практике необходимое изменение проводимости в модели оказывается за-
труднительным или вообще невозможным. Если потери в антенне играют большую
роль, то невыполнение условия о2 - приведет к неверным значениям входного
сопротивления и к. п. д.
Электрические параметры приемных антенн
115
Глава 3. Электрические параметры
приемных антенн [3, 17]
Способ отбора энергии от антенны в приемник зависит от диапазона волн, на-
значения антенны и ряда других обстоятельств. Он может быть электрическим
(включение фидера в разрыв проводов антенны), магнитным (применение рамок),
электромагнитным (применение волноводов), комбинированным.
На рис. 3.1 показан электрический способ возбуждения фидера короткой
по сравнению с длиной волны приемной антенны.
3.1. Эквивалентная схема приемной антенны [17]
Эквивалентная схема приемной антенны может быть составлена в виде, как
показано на рис. 3.1. Для цепи, подключаемой к приемной антенне, антенна яв-
ляется генератором, имеющим э. д. с. с комплексной амплитудой е и внутренним
(собственным) комплексным сопротивлением
ZA=RA+iXA. (3.1.1)
Это сопротивление не зависит от подключаемой нагрузки и характеризует
собственно антенну. Его реактивная часть ХА характеризует реактивные поля
стоячих волн, а активная часть RA характеризует переизлученную мощность
и мощность потерь в короткозамкнутой антенне. В соответствии с этим можно
_ _у _
записать RA — R + Иц.
Комплексная амплитуда э. д. с. е в эквивалентной схеме определяется напря-
женностью поля и конструкцией приемной антенны, а внутреннее сопротивление
— только конструкцией антенны.
Приемник на эквивалентной схеме представлен комплексным сопротивлением
Комплексная амплитуда тока в цепи антенны определяется очевидным соотно-
шением
1 — е / (ZA + Znp).
(3.1.3)
Рис. 3.1. Эквивалентная схема приемной антенны
116
ГЛАВА 3
3.2. Основные электрические параметры приемной антенны [17]
Напряжение и мощность сигнала на входе приемника при заданной напряжен-
ности приходящего поля зависят от параметров антенны и входной цепи приемни-
ка, так как ток, определяющий эти величины, зависит от ZA и Znp в соответствии
с формулой (3.1.3).
3.2.1. Внутреннее сопротивление приемной антенны было рассмотрено
в предыдущем параграфе.
3.2.2. Диаграмма направленности приемной антенны по напряжению
есть зависимость комплексной амплитуды э. д. с. (тока) на клеммах антенны
от направления прихода плоской электромагнитной волны при прочих равных
условиях. Определенная таким образом ДН зависит только от свойств самой ан-
тенны. Она записывается в видее(0,ф) или 1(0, ср). Как следует из выражения (3.1.3),
нормированные ДН по э. д. с. и току одинаковы и определяются обычным спосо-
бом:
F (0, ф) — е (0, ф)/етах — I (0, ф)/^тах •
Здесь мы предполагаем, что напряженность электрического поля антенны в даль-
ней зоне зависит только от одной составляющей ( Eq или Е®). Такое предположе-
ние справедливо, например, для электрического вибратора или рамочной антен-
ны. Таким образом, под F(0, ф) понимаем либо составляющую Fq , либо .
ДН приемной антенны по мощности называется зависимость мощности, вы-
деляющейся на активной части входного сопротивления приемника Кпр от направ-
ления прихода электромагнитной волны. Так как эта мощность пропорциональна
квадрату тока, то, очевидно, нормированная ДН по мощности является квадра-
том ДН по току (напряжению): Р2(0,ф).
Способы графического изображения ДН приемной антенны такие же, как и для
передающей (см. раздел 2).
3.2.3. Коэффициент направленного действия приемной антенны, так же
как и передающей, характеризует направленные свойства антенны и определя-
ется сравнением с эталонной антенной, которую будем считать изотропной. Одно
из распространенных определений КНД формулируется следующим образом:
КНД приемной антенны D(0, ф) показывает, во сколько раз нужно увеличить
мощность передатчика, чтобы при приеме на ненаправленную антенну полу-
чить то же отношение мощности сигнала к мощности помехи,что и при при-
еме с направления 0, ф на направленную антенну, причем предполагается, что
плотность мощности помехи равномерна во всех направлениях.
Учитывая некоторую специфичность и малую наглядность КНД приемной ан-
тенны, дадим определение, эквивалентное данному выше и освещающее работу
приемной антенны еще с одной стороны: КНД приемной антенны в направлении
0, ф называется отношение мощности в нагрузке этой же антенны при приеме
поочередно со всех направлений волн одинаковой интенсивности.
3.2.4. Коэффициент полезного действия приемной антенны есть отноше-
ние мощности, отдаваемой антенной в нагрузку, к мощности, которую она отдава-
ла бы в ту же нагрузку, если бы не имела потерь. Можно показать (см. раздел 2),
Элезстричес]^^ параметры приемных аытенн
117
что к. п. д. приемной антенны определяется так же, как и к. п. д. передающей ан-
тенны соотношением
Величина Rn зависит от потерь электромагнитной энергии в металле и диэлектри-
ках антенны, а также в окружающих антенну предметах, в том числе и в земле,
если антенна к ним близко расположена.
3.2.5. Коэффициент усиления (КУ) приемной антенны определяется так
же как и КНД, с той лишь разницей, что учитываются потери энергии в антенне.
Если приемник подключается к клеммам антенны без промежуточного фидера,
то КУ равен
Go = П А • (3-2.2)
Если же приемник подключается к антенне через фидер с потерями, то КУ,
отнесенный ко входу приемника, равен
Gq - Плфу А,
(3.2.3)
где Плфу “ к- п- Д- антенно-фидерного устройства в целом.
3.2.6. Действующая длина приемной антенны 1д(0,ф) определяется как
коэффициент, имеющий размерность длины и связывающий между собой ком-
плексную амплитуду электрического поля Е приходящей волны и комплексную
амплитуду э. д. с. е (0, ср) на клеммах антенны:
е(0,ф)= 1д (0,ф)Е.
Введя нормированную ДН по напряжению, получим
(3.2.4)
етах-^ (^> ф) = Апах^д^ (А ф), (3.2.5)
где L — значение действующей длины для направления максимального приема.
Когда говорят о действующей длине, то обычно имеют в виду именно это ее зна-
чение. Из (3.2.5) следует, что
етах Апах^д и (ц етах/Апах •
(3.2.6)
3.2.7. Э
ективная площадь приемной антенны Аэ(0,ф) — это коэффи-
циент, имеющий размерность площади и связывающий между собой величину
вектора Умова-Пойтинга приходящей волны и мощность, выделяющуюся в согла-
сованной нагрузке,
Рпро (°. <р) = SA3 (е, <р), (3.2.7)
где Рпро (0, ф) — мощность в согласованной нагрузке при приеме с направления 0, ф;
5 = Е2/240л - величина комплексной амплитуды вектора Умова-Пойтинга; Е -
напряженность электрического поля в дальней зоне (составляющая Eq или Е^);
Аэ (0, ф) — эффективная площадь для направления 0, ф. Вводя нормированную
ДН по мощности, записываем Рпр0 (0,ф) = Р^Р2 (0,ф) и Аэ (0,ф)= A™F2 (0,ф). При
этом из соотношения (3.2.7) получаем
Р^О=^А^. (3.2.8)
118
ГЛАВА 3
Таким образом, величина
4” = P™po/S = 240лР™о/£2 (3.2.9)
есть эффективная площадь, определенная для направления максимального при-
ема. Говоря об эффективной площади антенны, обычно имеют в виду именно эту
величину.
Для апертурных антенн вводят коэффициент использования площади антенны,
равный отношению эффективной площади к геометрической площади раскрыва:
q = A3/S.
(3.2.10)
3.2.8. Шумовая температура антенны ТА или антенно-фидерного уст-
ройства Тдфу является параметром, специфичным для приемных антенн, и будет
изучаться в разделе 3.4.6.
3.2.9. Рабочий диапазон волн (частот) определяется как полоса частот,
в которой все параметры антенны не выходят из заданных пределов.
Все перечисленные параметры могут быть рассчитаны для режима приема при
известной конструкции антенны и заданной рабочей длине волны. В этом, одна-
ко, нет необходимости. Принцип взаимности, рассматриваемый ниже, позволяет
установить, что основные параметры антенны в режиме приема и передачи оди-
наковы.
3.3. Применение принципа взаимности для расчета
параметров антенн [17]
ленности F (0
3.3.1. Принцип взаимности для антенн изложим, следуя А. А. Пистолькорсу
[17]. Рассмотрим две произвольные и произвольно ориентированные в пространс-
тве антенны 1 и 2 (рис. 3.2,а). Будем считать известными параметры этих антенн
в режиме передачи: входные сопротивления ZA = RA + гХА , диаграммы направ-
, ф), действующие длины 1д , отнесенные ко входным клеммам, коэф-
фициенты полезного действия ц, коэффициенты направленного действия D(0, ф).
Включим антенну 1 на передачу, для чего подключим к ее клеммам генератор
с комплексной амплитудой э. д. с. частоты со и с внутренним сопротивлением Z^
(рис. 3.2,6). Антенна 1 создает при этом поле излучения, напряженность которого
у антенны 2, работающей в режиме приема, равна • В цепи антенны 2, нагру-
женной на входное сопротивление приемника Z2, под действием поля антенны 1
возникает ток 121 •
Включим теперь антенну 2 на передачу при комплексной амплитуде э. д. с.
генератора е2 той же частоты со и с внутренним сопротивлением генератора Z2,
равным входному сопротивлению приемника, когда антенна 2 работала в режиме
приема (рис. 3.2,в). Поле излучения антенны 2 у антенны 1, работающей в режиме
приема, будет иметь напряженность Е12.
В цепи антенны 1 возникает ток 2. Входное сопротивление приемника в цепи
антенны 1 Zx выберем равным внутреннему сопротивлению генератора, который
подключается к антенне 1, когда она работала в режиме передачи.
На основе теоремы взаимности можно сравнить действие одной и той же антен-
ны в режимах приема и передачи и таким путем выяснить, какое значение имеют
Электрические параметры приемных ммтенн
119
б)
в)
Рис. 3.2. К применению принципа взаимности для антенн [17]
параметры передающих антенн для оценки свойств приемных. Такая задача была
выполнена в 1935 г. М. С. Нейманом.
Рассмотрим еще раз формулировку теоремы взаимности:
Для этих двух антенн теорему взаимности можно переписать в виде:
Найдем токи /21й ^12 в антеннах, работающих в режиме приема. Для этого рас-
смотрим случай работы антенны 1 на передачу (рис. 3.2, б). Ток в этой антенне
С учетом ДН рассмотрим две антенны. Комплексную амплитуду напряженности
электрического поля, создаваемого первой антенной в некоторой точке второй,
обозначим Е21- Эта величина пропорциональна характеристике направленности
первой антенны (6, ф) и ее току (в силу линейности уравнений поля). Для дальней
зоны величину Е21 можно записать в виде [17]:
. ЗО/с/д!^
F1 (0, ф) ехр(-гкг)
где г — расстояние между антеннами; 0 и ф - утлы, определяющие направление
от оси антенны 1 к антенне 2. Напомним, что предполагается, что напряженность
электрического поля в дальней зоне антенны имеет только одну составляющую
(Eq или Еф).
Подставив ток (3.3.2) в формулу (3.3.3), после преобразований получим
е = ^21(^1+^А1) г
1 30klfliFi (0, ф) ехр(-гкг)
(3.3.4)
В этой формуле все величины относятся к режиму передачи. Включив антенну
2 на передачу, аналогично получим
30/с?д2Е2 (0, ф) exp(-ikr)
(3.3.5)
120
ГЛАВА 3
Подставив полученные значения комплексных амплитуд э. д. с. в равенство
(3.3.1) и собрав слева все величины, относящиеся к антенне 1, а справа - к антен-
не 2, получим
*12(^1 + Z^i) _ 121(^2 + ^А2) (3 3 6)
адд1^(9,ф) E21la2F2M '
Выражение в левой части этого равенства не зависит ни от одной из величин
в правой части. Действительно, параметры /д1, Z1? ZAi, F1(0,q>) антенны 1 никак
не зависят от параметров антенны 2. От параметров антенны 2, конечно, зависит
величина Е2±, но ее отношение к вызванному ею же току в первой антенне 112 за“
висит только от параметров антенны 1. Таким образом, в равенстве (3.3.6) слева
и справа стоят две независимые равные величины. Это дает основание заключить,
что каждая из этих величин порознь равна одной и той же постоянной, которую
обозначаем буквой N.
Таким образом, для любой антенны
Inp(Z + ZA)/E^F(0,<p) = W, (3.3.7)
где Е — комплексная амплитуда напряженности электрического поля, действу-
ющего на антенну, работающую в режиме приема; 1пр — ток в цепи антенны
в режиме приема при воздействии поля Е; Z - сопротивление, подключаемое
к клеммам антенны; ZA - входное сопротивление антенны, определенное в режиме
передачи; 1Д и F(0, ср) — действующая длина и ДН, так же определены в режиме
передачи.
Теперь из формулы (3.3.7) определим ток в цепи антенны при работе ее на при-
ем
/пр = NElaFM/(Z + ZA). (3.3.8)
Обращаясь к эквивалентной схеме приемной антенны (см. рис. 3.1), заключаем,
что числитель выражения (3.3.8) представляет комплексную амплитуду э. д. с. ге-
нератора в этой схеме:
«max =™maxV(&<P). (3-3-9)
сопротивление ZA — внутреннее сопротивление приемной антенны, а сопротивле-
ние Z является сопротивлением приемника Znp , подключенного к клеммам ан-
тенны. Так как ZA определялось в режиме передачи как входное сопротивление
антенны, то из эквивалентной схемы в режиме приема следует, что для одной
и той же антенны входное сопротивление в режиме передачи и внутреннее со-
противление в режиме приема одинаковы. В выражении (3.3.9) F(0, ср) — ДН опре-
деленная в режиме передачи, а зависимость е от углов есть ДН в режиме приема.
Отсюда заключаем, что нормированные ДН одной антенны в режимах передачи
и приема одинаковы.
Пользуясь тем, что выражение (3.3.9) справедливо для любой антенны, пос-
тоянную N определим для простейшей антенны - диполя Герца. Пусть линейно-
поляризованная электромагнитная волна с амплитудой электрического вектора Е
падает под углом 0 на диполь Герца, лежащий в плоскости поляризации волны
(рис. 3.3). Э д. с., наведенная на элементарном участке, пропорциональна проекции
вектора Е на ось диполя и длине участка de = Е sin 0dl. Полная э. д. с. на клеммах
равна сумме элементарных э. д. с.
ern4V = Emaxli sin0. (3.3.10)
11 id Л. шал х z
Элетстрические ттрамртры прием/ных ашпенн
121
Рис. 3.3. Диполь Герца в режиме приема
Для диполя Герца в режиме передачи, как было отмечено ранее 2Д = Zj
и F(0,cp) = sin 6. Подставив эти величины в формулу (3.3.9) и сопоставив значение
э. д. с., полученное на основе принципа взаимности (3.3.9), э. д. с., полученной не-
посредственным расчетом (3.3.10), определим, что N = 1. При этом формула (3.3.9)
будет иметь вид
етах = ф) • (3.3.11)
Вспомнив определение действующей длины для приемной антенны (3.2.6),
на основании формулы (3.3.11) заключаем, что действующая длина антен-
ны в режиме приема равна действующей длине той же антенны в режиме
передачи.
Величины к. п. д., КНД и КУ для передающей антенны однозначно опреде-
ляются через F(0,tp), 1Д и ZA, поэтому они одинаковы для режимов передачи
и приема данной антенны.
3.4. Энергетические соотношения в цепи приемной антенны и вли-
яние приемной антенны на помехозащищенность радиолинии [17]
Следует различать собственно приемник и приемное устройство, включающее,
кроме приемника, приемную антенну и фидер. Соответственно нужно различать
чувствительность приемника и чувствительность приемного устройства.
Целесообразно различать два режима работы приёмного устройства. Первый
режим условно назовем режимом сильного сигнала. В этом режиме сигнал на-
столько больше внешних помех и внутренни^Илумов приемного устройства, что
помехами и шумами можно пренебречь. Такой режим характерен для приемников
средней и малой чувствительности. Второй режим условно назовем режимом сла-
бого сигнала. В этом режиме интенсивность внешних помех или внутренних шумов
соизмерима с интенсивностью принимаемого сигнала. Второй режим характерен
для приемников большой чувствительности, вплоть до предельной. Благодаря
широкому динамическому диапазону приемников оба режима часто реализуются
в одном и том же устройстве.
3.4.1. Режим сильного сигнала в радиолиниях ДВ, СВ и КВ. В этих диапазо-
нах входные цепи приемника обычно имеют высокое входное сопротивление; пот-
ребление мощности во входной цепи незначительно. Поэтому чувствительность
122
ГЛАВА 3
приемника определяется минимально необходимым напряжением Пмин на входе
приемника. Чувствительность приемного устройства определяется минимально
необходимым значением, амплитуды напряженности электрического поля Емин
в пункте приема.
Напряжение на входе приемника при непосредственном подключении его к ан-
тенне может быть определено из эквивалентной схемы рис. 3.1:
- е^пр / Фа + ^ир) • (3.4.1)
Так как обычно Znp » ZA, то U ~ е. Учитывая соотношение (3.3.11) получаем
* EmaxMW), (3-4.2)
из которого следует, что в режиме сильного сигнала для увеличения напряжения
на входе приемника необходимо увеличивать действующую длину антенны и ори-
ентировать максимум ДН в направлении приходящего сигнала. К. п. д. приемной
антенны в этом случае существенной роли не играет.
Чувствительность приемного устройства при известной чувствительности при-
емника может быть определена из выражения
^мин ~ Циин / ^д-Г(0,ф). (3.4.3)
При заданной чувствительности приемника чувствительность приемного уст-
ройства тем выше (величина Емин тем меньше), чем больше L и чем ближе направ-
ление приема к направлению максимума ДН.
В режиме сильного сигнала помехи работе радиолинии могут быть созданы
специальными станциями помех или мощными радиостанциями, работающими
на частотах, близких к рабочим частотам радиолинии.
При этом, если направление от антенны 1 на источник помех 2 совпадает
с направлением на передатчик радиолинии 3 (рис. 3.4,а), антенна никак не влияет
на помехозащищенность радиолинии. Если же указанные направления различают-
ся на заметный угол Д (рис. 3.4,6), то направленные свойства антенны дают воз-
можность существенно улучшить отношение сигнал/помеха. В этом случае вли-
яние антенны на отношение сигнал/помеха на входе приемника характеризуют
коэффициентом помехозащищенности Кпз, который определяется следующим
образом:
Рис. 3.4. Различные ситуации падения полезного сигнала 3 и помех 2 на антенну 1: а) - ис-
точники помех сигнала расположены на одной линии; б) - направления падения полезного
сигнала и помех не совпадают [17]
Электрические параметры приемных дмтенн
123
где F2(0',(p') — значение ДН в направлении на источник сигнала; F2(0", <р") — зна-
чение ДН в направлении на источник помех. Отсюда видно, что помехозащищен-
ность в режиме сильного сигнала определяется только формой ДН.
Существенного увеличения КПЗ можно добиться, повернув антенну на угол
Р так, чтобы минимум ДН был направлен на источник помех (направление 2’).
Наибольшее значение Кпз получится, очевидно, в том случае, когда максимум ДН
совпадает с направлением на источник сигнала, а направление на источник помех
совпадает с минимумом ДН.
Поэтому при одном источнике помех целесообразно применять антенны с ДН
типа «кардиоида» или «восьмерка», которые имеют четко выраженный минимум
и малое изменение уровня в широком секторе углов вблизи максимума. При не-
скольких точечных источниках помех желательно иметь приемную антенну с не-
широким главным лепестком, с малым количеством и малым уровнем боковых
лепестков.
3.4.2. Режим сильного сигнала в радиолиниях СВЧ. В диапазоне СВЧ, как
известно, интересуются мощностью на входе приемника, а не напряжением. Соот-
ветственно в режиме сильного сигнала, когда помехи и шумы малы по сравнению
с полезным сигналом, чувствительностью приемника называют минимально необ-
ходимую мощность сигнала на входе приемника Рпр мин. Чувствительность прием-
ного устройства можно по-прежнему оценивать величиной FMIiH. Для нормальной
работы радиолинии необходимо обеспечить Рпр > Рпр мин и Е > Емин.
Сначала рассмотрим случай, когда приемник подключается к антенне не-
посредственно, без фидерной линии — в соответствии с эквивалентной схемой
рис. 3.1.
Мощность, рассеиваемая на активной составляющей входного сопротивления
приемника, может быть определена выражением
(3.4.5)
амплитуда тока в цепи приемной антенны.
2
пр
полу-
чаем
пр ’
В режиме сильного сигнала необходимо стремиться к получению на входе
возможно большой мощности. Как следует из формулы (3.4.6) это имеет место
при полном согласовании, т.е. когда RA = RIip и Хпр = -ХА. Для режима полного
согласования из формулы (3.4.6) получаем
Рпр — е / 8-R^.
(3.4.7)
у
Если при этом антенна не имеет потерь, т.е. Кд = R , и прием производится
с направления максимума ДН, то на вход приемника будет поступать наибольшая
из всех возможных мощность при данной напряженности приходящего поля:
124
ГЛАВА 3
= emax / 8RS = / 8rZ •
(3.4.8)
Эта величина называется оптимальной мощностью. При этом считается, что
приемная антенна полностью поляризационно согласована с приходящим полем.
О поляризационном рассогласовании см. в разделе 3.5.
При наличии потерь в антенне мощность уменьшается
(3.4.9)
Из формулы (3.2.9) оптимальная мощность определяется как
PnDO = Е2Аэ / 240л. (3.4.10)
lip V '
Из выражений (3.4.8) и (3.4.10) находятся полезные соотношения между Аэ, 1Д,
Вг в режиме приема такие же, как и для режима передачи
А. = 30л£2 /КЕ;
<7 А '
1Л = JaIr^ / 30л.
А V '
(3.4.11)
Связь между КНД и другими параметрами антенны в режиме передачи опре-
деляется формулой (2.9.6):
Do = 30k2l2 /Rs.
' г "t
На основании принципа взаимности формула (2.9.6) справедлива и для прием-
ной антенны. С помощью выражений (2.9.6) и (3.4.11) получаем важную формулу
для расчета КНД через эффективную площадь Аэ
Do = ^кАэ/к2. (3.4.12)
Эта формула особенно часто используется в диапазоне СВЧ, где понятия действу-
ющей длины и сопротивления излучения мало наглядны.
Цепочка расчетных формул для оптимальной мощности теперь имеет вид
Е2 1д = Е2 Аэ = Е2 D°^2
8Я1 240л 960л2 ’
(3.4.13)
При рассогласовании приемника с антенной, учитывая выражения (3.4.6) и (3.4.8),
получаем для направления максимального приема
4RZR
, "XX V ± vnp
пр ° (KZ / ц + Кпр )2 + (ХА + Хпр )2‘
(3.4.14)
Отношение мощности на входе приемника к оптимальной упр - Рпр / Риро называ-
ется коэффициентом передачи мощности антенной цепи.
В рассматриваемом случае — при непосредственном подключении приемника
к антенне — коэффициент передачи мощности будет равен
Рассмотрим теперь случай, когда приемник подсоединяется к антенне с помо-
щью фидера (рис. 3.5). Если линия на обоих концах согласована (Znp = W и W = ZA),
то мощность на входе приемника будет отличаться от оптимальной лишь на вели-
чину потерь в антенне и в фидере:
Элетутрические параметры гуоиемных алутпенн
Рис. 3.5. Схема соединения приемника 2 с антенной с помощью фидера 1 (W — волновое
сопротивление фидера) [ 17 ]
^пр ~ ^проЛПл “-^проЛлФУ* (3.4.16)
При рассогласовании на одном из концов или на обоих одновременно мощность
на входе приемника будет меньше этой величины, так как мощность, отраженная
от мест рассогласования, будет частично переизлучаться, а частично переходить
в тепло в антенне и фидере.
Пусть приемник согласован с фидером, а антенна нет. Такое положение часто
встречается в антенно-фидерных устройствах метрового и дециметрового диапа-
зонов, работающих в сравнительно широкой полосе частот.
В этом случае Znp = W и ZA W и входное сопротивление фидера Znp а = W.
Мощность на входе приемника будет равна мощности на входе фидера, за исклю-
чением потерь в фидере
Л,р=РааПл- (3-4.17)
Мощность на входе фидера Раа можно определить из выражения (3.4.14) при
Рпр = W и Хпр = 0 . При этом
4RZW
Рпр = Рпро —-------2----- (ЗА18)
(R1 / Г| + Wy + ХА2
После несложных преобразований окончательно получим
_______^'Чафу________
RA[(1 + W/RA)2+(XA/RA)2]'
(3.4.19)
В диапазоне СВЧ антенна обычно хорошо согласована с фидером, т. е. ZA = W,
в то время как приемник часто рассогласован с фидером. В этих условиях
от приемника часть электромагнитной энергии отражается к антенне и полно-
стью переизлучается, так как фидер согласован с антенной. Доля отраженной
от приемника энергии определяется квадратом модуля коэффициента отражения
о
на входе приемника Г . Таким образом, при отсутствии потерь в антенне и в фи-
дере на вход приемника попадает мощность Рпр о (1 - Г2). С учетом потерь эта мощ-
ность определяется выражением
Р,;р=РпРо(1-Г2)П4ФУ (3.4.20)
Так как Г = (1 - К^в )/(1 + Кбв ),
то
126
ГЛАВА 3
4КЛ
^пр = ^про 2 Г1лфу • (3.4.21)
(1 + Кбв)2
Коэффициент передачи мощности при этом равен
4К/г
Ynp =------^гЛлфу- (3.4.22)
(1 + Кбе)2
Из формул (3.4.19) и (3.4.22) следует, что в режиме сильного сигнала на приемном
конце радиолинии СВЧ необходимо стремиться к повышению к. п. д. антенно-фи-
дерного устройства и улучшению согласования.
Влияние мощных точечных источников помех на работу радиолинии в этом
случае такое же, как и в режиме сильного сигнала в диапазонах ДВ, СВ и КВ.
Основным средством борьбы с этими помехами является выбор формы ДН и ее
ориентации относительно источников сигнала и помех.
3.4.3. Коэффициент различимости в режиме слабого сигнала. В режи-
ме слабого сигнала мощность полезного сигнала на входе приемника соизмерима
с мощностью внешних помех и собственных шумов приемника. При этом нор-
мальное функционирование линии обеспечивается при отношении dnp = Рс / Рп,
не меньшем коэффициента различимости
Дпр=(^с/^п)тт- (3-4.23)
Коэффициент различимости зависит от конструкции приемника, спектраль-
ных характеристик помех и шумов и способа обработки сигнала. У современных
приемников /7Пр приближается к единице, а в некоторых случаях может быть
и меньше.
3.4.4. Режим слабого сигнала в радиолиниях ДВ, СВ и КВ. Для данного
режима характерно то, что собственные шумы приемника можно не принимать
во внимание, так как интенсивность внешних помех в этих диапазонах обычно
гораздо больше интенсивности собственных шумов.
Как полезный сигнал, так и внешние помехи, попадающие по частоте в полосу
пропускания приемника, совместно проходят через антенну и фидерный тракт,
поэтому к. п. д., действующая длина и степень согласования антенно-фидерного
устройства на величину dnp почти не влияют. Покажем, что эта величина в ряде
случаев существенно зависит от направленности антенны.
Для простоты предположим, что помехи приходят к антенне равномерно
со всех сторон (рис. 3.6), т. е. источник помех в отличие от источника сигнала
непрерывно распределен в пространстве. При этом эффективное значение напря-
женности поля помех у антенны Еп целесообразно определить так, чтобы вели-
о \
чина Еп / 120л равнялась потоку мощности помех через единичную площадку,
приходящему к антенне из единичного телесного угла. (Здесь в рассмотрение при-
нимается только та часть поля помех, поляризация которой соответствует поля-
ризации антенны, а частоты находятся в полосе приемника.) При таком определе-
нии Еп поток мощности, приходящий из элементарного телесного угла, очевидно,
равен E2dQ / 120л. Если эффективная площадь антенны в направлении 0 , (р равна
Аэ(0,ф), то элементарная мощность, принимаемая антенной с этого направления,
равна EndfL43(0,<p) / 120л, а элементарная мощность на входе приемника равна
Электрические парамергры приемных ангпенн
127
Рис. 3.6. Воздействие помех, приходящих к антенне А равномерно со всех сторон ( F(0, <р)
- ДН приемной антенны) [17]
dPn
120л
Аэ(9, ф) sin ОсЮсйр
(3.4.24)
В силу случайного характера полей помех их мощности при приходе с разных
направлений суммируются на входе приемника:
0=0 <р=0
120л
л 2л
f F2 (0, ф) sin 0й6с1ф
0=0 ф=0
(3.4.25)
Воспользовавшись выражением (2.2.7) для КНД и (3.4.12) для Аэ , получим
Рп = УпрЕ^2/120л. (3.4.26)
Мощность сигнала на входе приемника определится так же, как и в режиме силь-
ного сигнала, т. е. выражениями (3.4.13) и (3.4.14)
Pc = Ynp^np О = Ynp£2D(A2 / 960тг2 , (3.4.27)
где Е — комплексная амплитуда поля сигнала. Так как эффективное значение на-
пряженности поля сигнала
то
р _ Упр^сАА
480л2
(3.4.28)
Разделив выражение (3.4.28) на (3.4.26), для отношения сигнал/помеха в направле-
нии максимума ДН получим
4л
(3.4.29)
Таким образом, при равномерно распределенных помехах в пространстве при-
менение направленных антенн дает увеличение отношения Рс / Рп в Do / 4л раз.
При неравномерном распределении помех в пространстве выигрыш в dnp за счет
направленности антенны будет зависеть от этого распределения и, в общем, бу-
дет меньше указанной выше величины. При сосредоточенных источниках помех
влияние антенны на помехозащищенность также оценивается выражением (3.4.4).
3.4.5. Режим слабого сигнала в диапазоне СВЧ. Для этого режима характер-
но то, что помехи в этом диапазоне создается сосредоточенными и распределен-
128
ГЛАВА 3
Рис. 3.7. К определению шумовой температуры антенны: 1 — область космического излу-
чения; 2 — сосредоточенный источник космического излучения; 3 — источник сигнала; 4
- поверхность земли [17]
ными источниками радиоизлучения (рис. 3.7), а также тепловым радиоизлучением
Земли, окружающих предметов и атмосферы. Абсолютный уровень этих помех,
как правило, очень мал, поэтому имеет смысл снижать собственные шумы при-
емника, увеличивая его чувствительность. В случае применения параметрических
и квантово-механических устройств чувствительность приемника может быть до-
ведена до величин порядка 10-16 -10-18 Вт. При столь высоких чувствительностях
заметную роль начинают играть помехи, вызванные тепловым движением элект-
ронов в антенне, фидере, устройствах согласования и коммутации, т.е. так назы-
ваемый собственный шум антенно-фидерного устройства.
3.4.6. Эффективная шумовая температура антенны ТА или антенно-фи-
дерного устройства ТАфу вводится как параметр приемной антенны при приеме
слабых сигналов диапазона СВЧ по аналогии с источниками теплового шума.
При исследовании радиоприемных устройств СВЧ эффективная шумовая тем-
пература источников шумов Тэ (в градусах Кельвина) вводится как коэффициент,
связывающий мощность шумов и полосу пропускания;
Рш = kT3\f, (3.4.30)
где к = 1,38 ♦ 10-23 Вт • с/К - постоянная Больцмана.
Исходя из определения (3.4.30) говорят о «собственной шумовой температуре
антенны», о «шумовой температуре источника помех» и т.д. Если шумовая темпе-
ратура Тэ некоторого источника известна, то создаваемая им на входе приемника
мощность шумов определяется по формуле (3.4.30).
Рассмотрим сначала случай, когда антенна и фидер не имеют потерь и полно-
стью согласованы. При этом помехи на входе приемника будут только внешнего
по отношению к антенне происхождения.
Эффективную шумовую температуру, характеризующую суммарную мощ-
ность всех внешних помех, называют условно шумовой температурой излучения
и обозначают . Ее обычно рассчитывают, вводя понятие яркостной темпера-
туры источников помех Тя . Участок поверхности источника помех имеет темпе-
Электрические параметры приемных антенн 129
ратуру Тя , если создаваемая им интенсивность помех равна интенсивности
радиоизлучения соответствующего участка абсолютно черного тела, имеющего
температуру Тя ; при этом предполагается, что абсолютно черное тело имеет та-
кую же пространственную конфигурацию, что и источник помех. Интенсивность
есть спектральная плотность мощности, выходящей через единичную площад-
ку поверхности излучающего тела в единичный телесный угол. Из теории абсо-
лютно черного тела известно, что в радиодиапазоне зависимость интенсивности
его излучения от яркостной температуры подчиняется закону Ре лея-Джинса:
1ю=2/с7я/Х, (3.4.31)
где к — постоянная Больцмана.
Будем считать, что на месте источника помех находится абсолютно черное
тело с таким же распределением интенсивности излучения по поверхности, что
и у источника помех. Определим мощность шумов на входе приемника. Пусть dS
есть проекция элементарной площадки dS' на излучающей поверхности на плос-
кость, перпендикулярную направлению от площадки dS' к антенне, имеющей
в этом направлении эффективную площадь ^(0,ср).Интенсивность излучения рас-
сматриваемой площадки на одной поляризации, соответствующей поляризации
приемной антенны, равна I^dS / 2. Коэффициент 1/2 появился вследствие того,
что для каждого момента времени поляризация поля помех с равной вероятнос-
тью может быть любой. На приемную антенну попадает только та часть мощности,
которая излучается площадкой dS' в телесный угол, опирающийся на площадку,
равную эффективной площади антенны d£l' = Аэ (0, ф) / г2. Здесь г — расстояние
от dS' до антенны.
Таким образом, спектральная плотность мощности излучения от площадки dS'
на входе приемника, согласованного с антенной, равна
dPt0 = 0,5I^dSdQ’ = 0,51&АЭ (0, <p)dS / г2 . (3.4.32)
Величина dQ = dS / г2 есть телесный угол, под которым видна от антенны излуча-
ющая площадка dS', причем, как известно, dfl = sin 0d0d<p.
Так как поля помех, приходящих с разных участков излучающей поверхности,
статистически независимы, то полная спектральная плотность мощности помех
на входе приемника определится суммированием величин (3.4.32) по всем направ-
лениям от антенны на участки излучающей поверхности
Р, = |к(Ш(Мда.
где Q - телесный угол, под которым излучающая поверхность наблюдается от
антенны. Учитывая, что полная мощность шумов на входе приемника Рш = ,
а также выражения (3.4.33) и (3.4.12), получаем
л 2л
Рш=/сА/— f [ тя(0,(p)F2(0,<p)sin0d0d(p. (3.4.33)
4л J J
0=0 <р=0
На основании выражения (3.4.30) шумовую температуру излучения введем
с помощью формулы
Рш = k^fTz. (3.4.34)
Сравнивая выражения (3.4.33) и (3.4.34), находим, что
5 - Неганов
130
ГЛАВА 3
а) б)
Рис.3.8. Эквивалентные шумовые схемы антенны: а) - источники помех разделены;
б) - результирующий источник помех [17]
л 2л
7’Е=-^-[ f T,(e,<p)F2(e,<p)smeded<p.
4 л J J
0=0 (р=0
(3.4.35)
Обратим внимание на то, что величина зависит не только от параметров антен-
ны, но и от интенсивности и распределения внешних источников помех. Данные
по пространственному распределению Тя(0,ср) можно найти в литературе [17].
Собственные шумы антенны определяются сопротивлением потерь антенны Rn,
температуру которого нужно считать равной температуре окружающей среды
ТфА (физическая температура антенны). С учетом потерь эквивалентная схема
антенны как генератора шумовой э. д. с. имеет вид, изображенный на рис. 3.8,а.
у
На этой схеме сопротивлению R приписана определяемая формулой (3.4.35) шу-
мовая температура , отличная от температуры окружающей среды, а сопро-
тивлению потерь Кд приписана температура окружающей среды 7\A, равная фи-
зической температуре антенны.
Внешние шумы и шумы за счет потерь в антенне статистически независимы,
поэтому нужно складывать их среднеквадратичные значения:
или в обозначениях рис. 3.8,6:
4k7’A(RZ + ЙП)Л/ = 4/c7'sA/RZ + 4/сТфлй„Д/ ,
где 7д - эффективная шумовая температура антенны. Отсюда после несложных
преобразований для шумовой температуры антенны получим выражение
В
, ( -----+ ?фА f- П • (3-4.36)
ВТ + Rn RX + Rn
Коэффициент при равен к. п. д. антенны ц, а при ТфА равен 1 - т|. Таким об-
разом
ТА=ТЕт1 + ТфА(1-п). (3-4.37)
По аналогичной методике учитываются шумы за счет потерь в фидере вместе
с включенными в него различными устройствами. Приведем формулу для шумо-
вой температуры антенно-фидерного устройства
^АФУ = 1ДфА0- — Л) + ^ЕЛ]ЛлТпр + (1— Лл )7фл , (3.4.38)
Электрические параметпры приемных антенн
131
где т]л - к.п.д. линии передачи вместе с включенными в него устройствами; 7фл -
физическая температура линии передачи (фидера); у' - коэффициент передачи
мощности антенной цепи без учета потерь в антенне и линии передачи. Формула
(3.4.38) получена в предположении, что антенна с фидером согласована, а прием-
ник не согласован. При этом у' нужно рассчитывать по формуле (3.4.22), положив
у л ФУ = 1 • Рассогласование приемника с фидером часто используется для умень-
шения шумов входной цепи приемника при реализации предельной чувствитель-
ности в диапазоне СВЧ.
3.5. Поляризационные характеристики приемных антенн [17]
Поляризацию приемной антенны будем определять поляризацией поля, созда-
ваемого этой антенной в режиме передачи. При этом, естественно, поляризацион-
ные характеристики данной антенны в режиме передачи и приема одинаковы.
Поляризационная согласованность приемной антенны по отношению к набегаю-
щей волне характеризуется коэффициентом поляризационной согласованности
Упол — ^про / ^про ’ (3.5.1)
где Рпро - оптимальная мощность в приемной антенне при полном поляризацион-
ном согласовании; Р™0 - оптимальная мощность при поляризационном рассогла-
совании.
Коэффициент поляризационной согласованности может изменяться в пределах
О < упол < 1. Антенны, имеющие упол = 1, называются поляризационно полностью
согласованными,а при упол = 0 - поляризационно полностью развязанными.
Общий случай поляризационных соотношений иллюстрируется рис. 3.9,а.
На рис. 3.9,6 показан вид на эллипсы поляризации со стороны антенны 1. Коэф-
фициент упол зависит от коэффициентов эллиптичности Кэ1 и Кэ2 антенн 1 и 2 и от
угла Ду между осями их поляризационных эллипсов (рис. 3.9,6). Эта зависимость
выражается формулой
(1 + К2ЛК^) cos2 Ду + (К2} + К2э2 ) sin2 Ду + 2КЭ1КЭ2
(1 + К2! )(1 + К22)
Рис. 3.9. Взаимные пространственные положения поляризационных эллипсов передающей
и приемной антенны: а) - общий вид поляризационных соотношений; б) — вид на эллипсы
поляризации со стороны антенны 1 [17]
(3.5.2)
б)
5 *
132
ГЛАВА 3
Упол
Рис. 3.10. Зависимости коэффициента поляризационной согласованности упол от парамет-
ров поляризационных эллипсов передающей 1 и приемной 2 антенн: а) — при угле между
большими осями эллипсов Ду = 0 ; б) - при Ду = 45°; в) - при Ду = 90°; г) - при различных
Ду и фиксированных значениях Кэ1 и Кэ2 [17]
О 22,5 45 67,5 Ду°
г)
Здесь нужно учитывать, что коэффициент Кэ должен быть со знаком плюс при
правом вращении и минус — при левом. При ситуации, изображенной на рис. 3.9,
Кэ1 имеет знак плюс, а Кэ2 - минус (но в пространстве векторы вращаются в одну
сторону!). Изменение угла Ду имеет смысл в пределах 0 < Ду < 90°.
Из выражения (3.5.2) видно, что полная поляризационная развязка (упол = 0)
обеспечивается только при чисто круговых поляризациях противоположного
направления вращения (Кэ1 = — КЭ2 = ±1) или же при одинаковых эллипсах поля-
ризации с противоположными направлениями вращения и перпендикулярными
большими осями (Кэ1 = -Кэ2, Ду = 90°), в том числе при линейных взаимно пер-
пендикулярных поляризациях.
Получение поляризационных развязок величиной 35-40 дБ является достаточ-
но сложной и в то же время важной технической задачей, ибо поляризацион-
ная развязка часто является единственным средством избавиться от мешающего
действия посторонних излучений.
Полное поляризационное согласование (упол = 1) достигается только в следую-
щих случаях:
а) чисто круговой поляризации падающего поля и приемной антенны при оди-
наковых направлениях вращения (Кэ1 = Кэ2 = 1);
б) линейной поляризации при параллельных плоскостях поляризации
(Кэ1 = Кз2 = О, Ду = 0);
Электрические параметры приемных антенн
133
Рис. 3.11. Коэффициенты поляризационной согласованности для различных поляризаций
передающей (1) и приемной (2) антенн: а) Кэ1 = Кэ2 = 0, Ду = 0 , упол = 1;
6) КЭ1 = Кэ2 = 0 , Ду = 90°, упол = 0 ; в) КЭ1 = 0 , |Кэ2| = 1, упол = 0,5 ;
г) = ^э2 ~ ’ Упол — 1 ’ Д) ~ ~ — 1 ’ Упол ~ ’ е) — Кд2 , Ду — 0 , Упол — >
ж)Кэ1=-Кэ2, Ду = 0 , уП0Л=(1-К2)2/(1 + К2)2; з)Кэ1=-Кэ2, Ду = 90°, упол =0 [17]
в) эллиптической поляризации при Кэ1 = Кэ2 и параллельных больших осях
эллипсов (Ду = 0).
Некоторые характерные графики, иллюстрирующие зависимость коэффициен-
та поляризационной согласованности от параметров поляризационных эллипсов
и их взаимного расположения, показаны на рис. 3.10. В частности, из графиков
рис. 3.10,г видно, что при любых соотношениях между Кэ1 и Кэ2 наилучшее по-
ляризационное согласование получается при Ду = 0 , а наихудшее — при Ду = 90°.
На рис. 3.11. показаны эллипсы поляризации для характерных поляризационных
ситуаций, встречающихся в различных радиолиниях.
3.6. Антенна как пассивный рассеиватель [3]
В режиме приема антенна, наряду с мощностью, передаваемой в нагрузку,
рассеивает часть падающей мощности обратно в окружающее антенну пространс-
тво и с этих позиций является некоторым пассивным рассеивателем, имеющим
вполне определенную радиолокационную заметность (активным рассеивателем
134
ГЛАВА 3
И
W+1
Рис. 3.12. Эквивалентный многополюсник антенны [3]
можно считать передающую антенну в момент работы передающего устройства).
Полную мощность, рассеиваемую приемной антенной, и ее распределение
в пространстве нельзя определить только через характеристики и параметры ан-
тенн в режиме передачи. Формально это связано с тем, что распределение тока
в антенне в режиме приема отличается от распределения тока в режиме передачи
и не выражается друг через друга. Это обусловлено различием в системе возбуж-
дения антенны в обоих режимах. Если в режиме передачи возбуждение сторон-
ними источниками осуществляется в некоторой ограниченной области антенны,
то в режиме приема сторонние источники (внешнее падающее поле) распределены
по всей поверхности антенны.
Различие характеристик антенны в режиме приема и передачи будет еще бо-
лее наглядно, если представить антенну в виде некоторого эквивалентного мно-
гополюсника. Размерность многополюсника определим из следующих рассужде-
ний. Произвольное распределение тока на поверхности антенны с любой степенью
точности можно представить в виде конечного разложения по некоторой системе
линейно независимых базисных функций. Количество членов в этом разложении
зависит от электрического радиуса антенны kl ( 21 - максимальный размер антен-
ны, называемый диаметром; к = 2л/Х - волновое число), и точности представле-
ния. Обычно достаточно взять порядка kl членов разложения.
Пусть базисные функции на поверхности антенны и нормировка базисных фун-
кций выстроены таким образом, что каждое распределение тока, соответствующее
-ikr
j-й базисной функции, дает поле излучения, представленное виде Fj (0, <р)-,
где Г (0, (р) - нормированная векторная диаграмма направленности j-ro распреде-
ления тока, причем
т.е. можно считать, что диаграммы Fj (0, ср) являются ортонормированными фун-
кциями, описывающими закон распределения электрического поля в типах волн
(модах), могущих существовать в окружающем антенну пространстве. Поставим
в соответствие каждой такой моде один из входов 2, 3, ..., АНТ многополюсника
и пусть общее число таких входов будет N. Добавим еще один вход 1, соответс-
твующий реальному входу антенны (при этом для определенности полагаем, что
в фидерной линии, подходящей к антенне, существует только один тип волны).
Образованный таким образом 2(М+1)-полюсник и является эквивалентным много-
полюсником антенны (рис. 3.12). Теперь заметим, что в режиме передачи стороннее
возбуждение подводится только к одному входу 1 антенны. Обозначая нормиро-
ванную амплитуду падающей на вход 1 волны через U^d = Jei(Pnad , где Р^д,
^пад ~ соответственно мощность и фаза падающей на вход 1 волны, можно найти
Электрические параметры приемных антенн
135
поле излучения антенны в режиме передачи:
JV 4-1 /СТ*
4ер (Л0,ф) = £ S^Fj (0,ф)----------
7=2 Г
где
N+1
к(е,ф) = — У §д^(е,ф)
С1 3=2
Fq (О, ф)-
(3.6.2)
(3.6.3)
- нормированная диаграмма направленности антенны; q - нормирующий коэф-
фициент; Зд - коэффициенты матрицы рассеяния эквивалентного многополюс-
ника [s].
Матрица рассеяния [s]b общем случае может быть определена в процессе ре-
шения соответсвующей дифракционной задачи на антенне при последовательном
возбуждении каждого из входов эквивалентного многополюсника и имеет следу-
ющий наиболее общий вид:
S11 S12
S21
SN+1 SN+12
S1N+1
S2N+1
SW+UV+1
Соответственно в режиме приема при согласованном входе 1 рассеянное антен-
ной поле
N+1
Ё' (г, е, <р) = Vw u^pFt (е, Ф)
1=2
N+1N+1 . .
=Vw J £ (0)е
1=2 j=2
(3.6.4)
гДе ипад (з
= 2,...,N + 1)- комплексные амплитуды падающих на входы 2,...,N + 1
волн, определяемые из разложения той части Евз падающего поля Епад, которая
-ikr
взаимодействует с антенной по системе базисных функций К- (0, ф)-:
W+l z.x -ikr
Ёвз (г А ф) = Vw U^F? (0, ф)-------. (3.6.5)
>2 Г
При этом оставшаяся часть падающего поля Епад - Евз проходит за антенну, как
бы не замечая ее. Таким образом, в области за антенной (эту область называют
теневой областью относительно направления падения) первичное падающее поле
изменяется на величину - Евз, которую называют теневой составляющей Ётен
рассеянного поля:
Етек =-Е^(л0'.Ф')- <3-66)
где 0', ф' - углы, определяющие направление падающего поля в теневой области
(рис. 3.13); с углами 0,ф в освещенной относительно антенны области они свя-
заны соотношениями 0' = л - 0, ф' = л + ф . Кроме того, фактическая поляризация
первичного падающего поля в освещенной Епа^ и теневой областях Егпад остается
неизменной, но меняется форма записи при переходе через начало координат
(рис. 3.13). Поэтому, представляя в освещенной области
136
ГЛАВА 3
Z Епад
—*.
Рис. 3.13. Пояснение к изменению формы записи поля Е'пад по сравнению
——►
с записью поля [3]
-ikr
^пад (?’ ф) — ^пад ф)
—т!ст
= (e.«p)§o + Са (°-Ч>)фо У~
(3.6.7)
получаем в соответствии с рис. 3.13 в теневой области
р-гкг
Enaa(r,e',<?')=Fnaa(&,<S>')------
= (Са (0'> ф')ёо - Са (6’> ф')фо У~~ =
= (Fnad О - 0,71 + ф)б0 - F^q (тс - 0, 71 + ф)ф0
(3.6.8)
Аналогичное изменение формы записи имеет место для Е'вз (г,6',ф')по сравнению
С ^вз (у ’ ф) ’
Если антенна в режиме приема (вход 1) нагружена на несогласованную на-
грузку, имеющую коэффициент отражения Г1? то к рассеянному полю (3.6.4) до-
бавляется составляющая поля рассеяния Е33(г,0,ф), возникающая в результате
отражения от нагрузки и последующего излучения (рассеивания) в окружающее
антенну пространство. Величина этой составляющей
W+1W+1
Ё’ (г, е, ф) = Vw £ Y unadsij
1=2 j=2
SnFi (0, ф)
—tier
u^ij^ (e> ф)^—
(3.6.9)
Сравнение выражений (3.6.2), (3.6.4) и (3.6.9) показывает, что в режиме передачи
известны коэффициенты матрицы рассеяния (j = l,2,...,n +1), что в силу при-
нципа взаимности эквивалентного многополюсника антенны позволяет определить
коэффициенты а — Sji. Однако этого недостаточно для определения остальных
коэффициентов матрицы рассеяния [s], которые используются при определении
рассеянного поля в режиме приема.
Заметим, что та часть мощности Рвз падающего поля, которая взаимодейству-
ет с антенной в режиме приема, конечна и в соответствии с (3.6.1), (3.6.5)
Электрические параметры приемных антенн
137
(3.6.10)
где Sr - сферическая поверхность радиуса г в дальней зоне антенны.
Полагая Рвз = const, выясним, какой должна быть структура падающего
на антенну поля, чтобы мощность рассеянного поля Р", обязанного отражению
от нагрузки, была максимальной.
В соответствии с (3.6.9)
Sr
□Л тс 7V+1JV+1
| ||f (о, <р)| sin OdQdcp
о о i=2
пади пад81г>11 ~
(3.6.11)
fw+lW+1
Х^ ТгО) Т 7*0)О .О*
/ 4 / j Uпад^nads13sll
U=2 1=2
При преобразованиях в (3.6.11) использованы соотношения (3.6.1), (3.6.3).
Максимальное значение (3.6.11) достигается при выборе комплексных амплитуд
падающего поля из условия
, (3.6.12)
где А - произвольный коэффициент пропорциональности.
При этом
Подставляя (3.6.12) в (3.6.5) получаем, что при заданном коэффициенте от-
ражения , наибольшая часть мощности, рассеиваемой антенной в результате
переотражения от нагрузки, достигается при условии, что форма падающего
на антенну поля пропорциональна комплексно-сопряженному полю антенны в ре-
жиме передачи:
Ёпад (лМ = (0,q>)----= ВЁ."ср (г.о.ф), (3.6.14)
3=2 г
где В - произвольная константа.
Если в антенне отсутствуют потери, то матрица [s] эквивалентного многопо-
люсника является унитарной и выполняется соотношение
С учетом этого выражение (3.6.13) принимает вид
1 ”sllFi
(3.6.15)
138
ГЛАВА 3
При Fj = 0 отражение от нагрузки отсутствует, и поле рассеяния Е" исчезает. Поле
рассеяния Е" называют антенной составляющей рассеяния, так как диаграмма
направленности этой составляющей совпадает с диаграммой направленности ан-
тенны, а ее амплитуда зависит от коэффициента отражения от нагрузки.
Заметим, что условие (3.6.12) по сути является условием, при котором из па-
дающего на антенну поля автоматически выделяется та его часть, которая прини-
мается антенной. Поэтому с учетом (3.6.12) и унитарности матрицы [$]выражение
(3.6.9) для антенной составляющей рассеяния приобретает вид
Ё" (г, 9, ф) =
y/WАГ! (1 “ SJ !
-гкг
ciF(e,(p)—
(3.6.16)
Составляющую поля рассеяния Ё (соотношение (3.6.4)) называют структурной
составляющей (или конструктивной составляющей), так как причина ее сущест-
вования связана с рассеянием на конструктивных «теневых» элементах поверхнос-
ти, а также на значительно рассогласованных участках, образующих физическую
структуру антенны (под «теневыми» участками поверхности антенны понимают
такие участки, на которых в режиме передачи возбужденный ток отсутствует или
очень мал; например, внешняя поверхность стенок рупорной антенны, теневая
относительно облучателя поверхность зеркальной антенны и т.д.). Сильно рассо-
гласованными участками антенны может быть, например, излучающая апертура
антенной решетки с плохо согласованными отдельными излучателями. Диаграмма
направленности структурной составляющей рассеяния может существенно отли-
чаться от диаграммы направленности антенной составляющей даже при падающем
поле, удовлетворяющем условию (3.6.12). Лишь для очень ограниченного класса
антенн диаграммы направленности структурной и антенной составляющих сов-
падают и возможно взаимное гашение поля рассеяния антенной и структурной
составляющих. Подобная ситуация имеет место, например, для плоских синфаз-
ных антенных решеток с плохо согласованным раскрывом при падении плоской
волны по нормали к плоскости решетки, а также для тех антенн, матрица рассе-
яния которых может быть представлена в виде четырехполюсника (как правило,
это антенны электрически малого размера, например, полуволновый или более
короткий вибратор). В последнем случае сумму антенной и структурной составля-
ющих с учетом соотношений (3.6.4), (3.6.9) и (3.6.12) можно записать в виде
Ё (г, 9, ф) = Ё’ (г, 0, ф) + Ё’ (г, 0, ф) = VWAs*2
s22 + s12s21
Из свойств унитарности матрицы [s] имеем
* *
s12s22 “ “s21sll,
sllsll - 1 “ s12s12-
Используя эти соотношения окончательно получаем
Ё (г, 0, ф) = yJWA (,Г1 ~ 1} s21F2 (0, ф)
-ikr
= Vwaq —^12 f (e, <p)
-ikr
(3.6.17)
Электрические параметры паяных антенн
139
Как следует из (3.6.17), при Г\ = $п сумма антенной и структурной составляю-
щих рассеянного поля оказывается равна нулю.
Коэффициент А в соотношениях (3.6.12), (3.6.15)-(3.6.17) выбирают из условия
наилучшего выделения в падающем на антенну поле плоской волны составляющей
(3.6.14):
А = -^Ьт^Б’(еО’Ч>оН(0О’(₽о)’ (3.6.18)
C^W 4л
где Eq - комплексная амплитуда падающей с направления (Оо, Фо) плоской волны.
Полное рассеянное поле складывается из структурной, антенной и теневой со-
ставляющих:
Ёрас (г, 9, <р) = Ё' (г, 9, ф) + Ё" (г, е, ф) + Ё^ (г, 9, ф) . (3.6.19)
В силу различного пространственного распределения этих составляющих осущес-
твить в общем случае их взаимное гашение во всем угловом секторе пространства
невозможно. Однако, подбирая комплексные амплитуды рассеянного поля струк-
турной, антенной и теневой составляющих, можно понизить уровень рассеянного
поля в заданном направлении. Существует также весьма ограниченный класс ан-
тенн, называемых антеннами с минимальным рассеянием (например, электри-
ческие и магнитные диполи). В антеннах этого класса пространственное распреде-
ление антенной, структурной и теневой составляющих рассеянного поля одинаково.
Поэтому, подбирая комплексные амплитуды поля рассеяния этих составляю-
щих, можно уменьшить до нуля рассеянное поле антенны во всем пространстве,
т.е. сделать антенну с нулевой радиолокационной заметностью. В остронаправлен-
ных антеннах диаграммы рассеяния теневой составляющей слабо пересекаются
в пространстве с диаграммами рассеяния остальных составляющих. Поэтому час-
тичное гашение рассеянного поля в заданном направлении возможно лишь в пе-
реднем относительно раскрыва антенны полупространстве путем подбора величин
структурной и антенной составляющих рассеянного поля в этом направлении.
Приемная антенна является диссипативным рассеивателем, так как часть
мощности падающего на антенну поля поглощается в нагрузке приемной антенны.
Поэтому для приемной антенны как диссипативного рассеивателя имеет место
фундаментальное соотношение между полной мощностью поглощения (в нагрузке)
Рн и мощностью рассеяния Ррас :
Ррас Рн (3.6.20)
Знак равенства в соотношении (3.6.20) справедлив лишь при условии, что повер-
хность антенны является поверхностью абсолютно «черного» типа, т.е. вся мощ-
ность, заключенная в части поверхности фронта падающей волны, совпадающей
с геометрической поверхностью апертуры антенны, поглощается ее нагрузкой.
Другими словами, сумма структурной и антенной составляющих рассеянного поля
должна быть равна нулю. Из соотношения (3.6.20) также следует, что приемная
антенна может обладать нулевым рассеянием только при условии чисто реак-
тивной нагрузки, когда Рн = 0 . При наличии активной составляющей нагрузки на
входе приемной антенны последняя не может быть полностью радиолокационно
невидимой.
140
ГЛАВА 3
3.7. Параметры электромагнитной совместимости антенн [3]
Любая приемная антенна наряду с полезным сигналом принимает мешающие
сигналы соседних радиотехнических систем. Прием мешающих сигналов может
привести к нарушению работы той или иной радиосистемы, находящейся в поле
излучения соседних радиосистем. При этом говорят, что электромагнитная сов-
местимость (ЭМС) таких радиосистем не обеспечена. Одним из основных каналов
передачи и приема мешающих сигналов соседних радиосистем является канал
передающая антенна одной радиосистемы - окружающее пространство - приемная
антенна другой радиосистемы. Поэтому для оценки электромагнитной совмести-
мости соседних радиотехнических систем (РТС) необходимо уметь рассчитывать
мощность сигнала, приходящего со входа передающей антенны одной радиосис-
темы на вход приемной антенны другой радиосистемы на некоторой произвольной
частоте f, лежащей в интервале 0,2/0 - 5/0 , где /0 _ рабочая частота радиосис-
темы, для которой анализируется электромагнитная совместимость с соседними
радиосистемами. Полагая, что каждая, из рассматриваемых антенн по частоте f
имеет один вход, а сами антенны и окружающее их пространство линейны, нахо-
дим очевидную линейную зависимость между мощностью на входе передающей
антенны и мощностью Р% на входе приемной антенны:
р2 (/)=<;(/)?!(/) (3-7.1)
Коэффициент <;(/) называют коэффициентом связи двух антенн на частоте/.
Этот параметр является одним из основных при анализе электромагнитной сов-
местимости двух РТС. Если антенны соседних РТС расположены в дальней зоне
на расстоянии г друг от друга, то плотность потока мощности передающей днтен-
ны в месте расположения приемной антенны
Р(М2) =
(3.7.2)
где Gi - коэффициент усиления передающей антенны в направлении максимума
диаграммы направленности; F\ (М2 ) ~ значение нормированной диаграммы направ-
ленности передающей антенны в направлении на приемную антенну.
Используя соотношения (3.7.1), (3.7.2) получаем выражение для коэффициента
связи антенн:
4 яг
где
Gi (М2 ) = Gi |Fj (М2 /; G2 (Mj ) = G2 |f2 (Mj f,
(3.7.3)
(3.7.4)
- соответственно коэффициенты усиления передающей и приемной антенн в на-
правлении друг на друга.
Если коэффициент связи антенн определяется относительно некоторых одно-
модовых сечений фидерных трактов, то в выражение (3.7.3) добавляются сомно-
жители Цдб1 (/), T|d52 (/) , характеризующие коэффициент полезного действия от-
резков фидерного тракта первой и второй РЭС:
А О
Ч = — 4)51 (/)Сч (М2 )Г|^2 (/)G2 (Mj )|i;|2.
i i L1 у
(3.7.5)
Элентриместсие параметры приемных антенн
141
Таким образом, коэффициент связи антенн рассчитывают через их характе-
ристики направленности. Особенность заключается в том, что эти характеристики
должны быть известны в широкой, в том числе и нерабочей, полосе частот. Кроме
того, на частотах выше рабочей частоты тракт питания антенны становится мно-
гомодовым и, таким образом, у антенны появляется несколько входов. Поэтому
приходится рассчитывать матрицу Г?(/)1 коэффициентов связи между входами
обеих антенн.
Выражение (3.7.5) показывает возможные пути обеспечения ЭМС РТС за счет
уменьшения коэффициента связи их антенн, а именно: увеличение расстояния
между антеннами (способ очевидный, но далеко не всегда приемлемый); умень-
шение коэффициента усиления каждой из антенн в заданной полосе частот в на-
правлении на другую антенну, в частности, с помощью формирования провалов
в диаграммах направленности антенн в указанных направлениях или установ-
ки экранов между антеннами; применение поляризационно-развязанных антенн;
использование резонансного согласования антенн с фидерной линией на рабочей
частоте, что приводит к резкому рассогласованию, а следовательно, и падению
коэффициента усиления антенн на нерабочих частотах; применение фидерных
линий с большой постоянной затухания на нерабочих частотах.
Вообще с позиции обеспечения ЭМС при разработке антенно-фидерных уст-
ройств важно обеспечить не только «хорошие» характеристики в требуемой рабо-
чей полосе частот РТС, но и «плохие» характеристики за пределами этой полосы.
Если антенны расположены на произвольном расстоянии друг от друга, в час-
тности, в промежуточной или ближней зоне, то коэффициент связи антенн опре-
деляется через их поле излучения в режиме передачи:
1 ^^пад1^пад2
(3.7.6)
Здесь через Ё^, Ё2, Н2 обозначены электрическое и магнитное поля первой и
второй антенн в произвольной точке на поверхности 5 при подаче на вход каждой
из антенн в режиме передачи мощностей PnaQi и Рпад2 '> П, Г2 - коэффициенты от-
ражения от входов этих антенн. При этом поле одной из антенн, например
и коэффициент отражения от ее входа находятся в присутствии второй ан-
тенны, т.е. учитывается реакция второй антенны, как пассивного рассеивателя
на поле излучения первой антенны. Поле Ё2, Н2 второй антенны может существо-
вать как в присутствии, так и в отсутствие первой антенны. Поверхность 5 - про-
извольная замкнутая, охватывающая либо только первую, либо только вторую
антенну.
При расчете полей Н±, Ё2, Н2, входящих в соотношение (3.7.6), требуется
решение соответствующей задачи возбуждения антенн в режиме передачи. Эта
задача, как правило, хорошо разрешима для антенн, работающих на основной
(рабочей) частоте. Для нерабочих частот поля излучения известны лишь для про-
стейших типов антенн (вибраторных, щелевых, в виде открытых концов волно-
водов и др.). Поэтому, несмотря на относительную простоту соотношения (3.7.6),
пользование им требует существенного развития методов и алгоритмов расчета
полей излучения антенн на нерабочих частотах.
142
ГЛАВА 3
Для слабонаправленных и других типов антенн, для которых известно взаим-
ное сопротивление Z^ между первой и второй антеннами, коэффициент связи
4Z122ReZKW1
(3.7.7)
(Zh+WjXZ^+ZJ-Zj2,
где Z11? Z22 - входные сопротивления первой и второй уединенных антенн; -
волновое сопротивление фидерной линии первой антенны; Zw - сопротивление на-
грузки, включенное непосредственно на вход второй антенны.
Более подробные сведения о методах расчета коэффициента связи между ан-
теннами в широкой полосе частот можно найти в [3].
Электрические симметричные вибраторы
143
Глава 4. Электрические симметричные вибраторы
На рис. 4.1 приведены наиболее применяемые, в практических конструкциях,
различные виды симметричных вибраторов, т.е. двух одинаковых проводников I.
Для изготовления вибраторов используются хорошо проводящие металлы.
В диапазонах КВ и СВ в антеннах обычно применяются многожильные гибкие
провода (антенные канатики). В диапазоне СВЧ вибраторы выполняются из стерж-
ней или полых трубок.
Вибраторы большого поперечного сечения часто выполняют из нескольких па-
раллельных проводов малого сечения; эти провода соединяются перемычками
на концах и в нескольких сечениях по длине. Пример такой антенны показан
на рис. 4.1, ж.
В диапазоне СВЧ вибраторы часто выполняются в виде стержней или трубок
некруглого сечения. Выбраторы таких сечений при изучении их характеристик
заменяются эквивалентным вибратором круглого сечения той же длины с некото-
рым эквивалентным радиусом аэ
Электрические вибраторы получили самое широкое распространение как в виде
самостоятельных антенн, так и в сложных системах — антенных решетках. При
Рис 4.1. Симметричные вибраторы[17]:
а) — цилиндрический вибратор; б) - петлевой вибратор Пистоль-
корса; в) - вибратор с емкостной нагрузкой на концах;
г) - широкополосный цилиндрический вибратор; д) - биконичес-
кий вибратор; е) — широкополосный плоскостной Ж-образный
вибратор; ж) - вибратор Надененко
144 ГЛАВА 4
расчете любой антенны, в том числе и электрического вибратора, предполагает-
ся, что задана ее геометрия и известны электрические параметры образующих ее
проводников и диэлектриков. Задача расчета (анализа) заключается в нахождении
электрических характеристик антенны. Эта задача сводится к определению элект-
ромагнитного поля во всех точках пространства, окружающего электрический виб-
ратор. Знание поля позволяет определить диаграмму направленности, КНД, вход-
ное сопротивление и т.д. Задача решается на основе уравнений Максвелла, гранич-
ных условий на поверхностях раздела и условия излучения: в поглощающей среде
поля должны стремится к нулю на бесконечности. Это сложная внешняя электро-
динамическая задача. Поэтому анализ поля антенны разделяют на две части: внут-
реннюю и внешнюю задачи [2,3].
Внутренняя задача заключается в определении некоторого эквивалентного тока
в тонком электрическом вибраторе (предполагается наличие тока и в зазоре ан-
тенны). При этом определяется и входное сопротивление вибратора, определяе-
мое, как правило, отношением напряжения, приложенного к зазору, к току
в центре зазора вибратора. Внешняя задача состоит в определении поля излучения
в любой точке окружающего пространства по известному распределению тока
по электрическому вибратору.
В настоящей главе описаны самосогласованные и приближенные алгоритмы
расчета распределения тока вдоль вибратора, входного сопротивления и алгоритм
нахождения ЭМП в ближней зоне вибратора. /х
4.1. Классическая постановка задачи о
распределении тока по тонкому вибратору.
Уравнение Поклингтона [5]
Ниже в этом разделе рассмотрим электрический виб-
ратор простейшей геометрии - излучатель ЭМВ в виде
двух тонких проводников длиной и ?2 радиуса а, воз-
буждаемый в области разрыва генератором ВЧ (рис. 4.2).
Под воздействием ЭДС генератора на проводниках воз-
никают продольные электрические токи, которые рас-
пределяються в соответствии с граничными условиями.
Если проводники имеют одинаковые длины (Ц = 1% = Z),
то электрический вибратор называеться симметричным.
При теоретическом исследовании вибратора, прежде
всего, следует установить закон распределения излуча-
ющих токов по его поверхности, т.е. решить внутреннюю
задачу анализа [2,3]. После этого можно приступить
к внешней задаче анализа — определению характерис-
тики направленности вибратора и других вторичных па-
раметров.
Для тонких вибраторов (а « I X)
Рис. 4.2 Геометрия электри-
электродинамичес- ческого вибратора
Электрические симметричные вибраторы 145
кая модель для внутренней задачи анализа строится на основании тонкопроволоч-
ного приближения электрического вибратора [2,5,27].
1. Поверхностный продольный электрический ток Г|| заменяется расположен-
ной на оси вибратора бесконечно тонкой нитью продольного электрического тока
Iz(z) = 2iiariz(z). Этот ток считается непрерывным в области зазора и обращается
в нуль на концах вибратора: Iz(l) = = 0 • Торцевые токи игнорируются.
2. Касательная составляющая вектора электрического поля Ez(z), создаваемая
нитью тока на боковой поверхности воображаемого цилиндра, охватывающего нить
тока при р = а, обращается в нуль всюду, кроме области зазора длиной 2Ь,
где она приравнивается некоторой возбуждающей функции Ecm(z). Для узких за-
зоров (b -> 0) функцию Ест (z) можно считать постоянной.
3. Возбужденное электрическим вибратором электрическое поле в пространстве
не зависит от азимутальной коородинаты ср.
В областях, содержащих сторонние электрические токи, уравнения Максвелла
в терминах комплексных амплитуд имеют вид [1]:
rot Е = -г<оцаН,
rot Я = + je’cm.
Ct
Векторы электромагнитного поля Е и Н выражаются через электродинамический
потенциал Ае для электрического тока следующим образом [1]:
Ё = -1шпАе н—-—grad div Ае,
(41 р
H = rotAe,
~-е,ст -ikR
1-----Z.----dV'
R— расстояние между точкой наблюдения (x,y,z) и точкой (x',y',z'), где распо-
ложен источник : R = J(x - х')2 + (у - у')2 + (2 - z')2 .
Если электрические токи параллельны оси z, то векторный потенциал Ае
также имеет лишь z-составляющую. Тогда соотношение (4.1.1) при рассмотрении
поля, не зависящего от координаты ср, принимает вид:
Создаваемое элементом тока jz’cmdV
электрическое поле равно:
146
ГЛАВА 4
-ikR
G(z - z') = --
AnR
— функция Грина свободного пространства.
Следовательно, напряженность электрического поля, возбуждаемое током
с объёмной плотностью jz’cm, параллельным оси z равно:
1
гсоап
(4.1.2)
Если ток распределён по поверхности кругового цилиндра, ось которого совпа-
дает с осью z, это выражение сводится к поверхностному интегралу. Более того,
для цилиндра радиуса а « Л можно считать, что ток по азимутальной координа-
те (р распределен по поверхности цилиндра равномерно. Если точка наблюдения
находится на поверхности цилиндра, то выражение для R принимает вид:
и, следовательно, распределению поверхностного тока можно сопоставить эквива-
лентный нитевидный источник, расположенный на оси z на расстоянии а от точки
наблюдения. Таким образом, считая, что выражение (4.1.2) для Ez даёт рассеянное
поле, нетрудно записать уравнение Поклингтона [2,5]:
d2G(z - z')
dz2
+ k2G(z - z')
dz' = -io)£aEzm (z)
(4.1.3)
относительно неизвестного тока Iz(z) = 2лат^(г) ( t}z — линейная плотность продоль-
ного поверхностного электрического тока), где Ezm(z) — z-составляющая падаю-
щего (или наведённого) поля, причем на поверхности вибратора Ez(z) + Ezm(z) = 0.
Пределы интегрирования в (4.1.3) определяются продольными размерами виб-
ратора. Впервые уравнение типа (4.1.3) было использовано Поклингтоном для дока-
зательства того, что распределение тока в тонком проводнике близко к синусои-
дальному, а скорость волны тока равна скорости света.
Если рассмотреть (4.1.3) как дифференциальное уравнение второго порядка
2 1 1
— flz(z')G(z-z')dz' + fc2 flz(z'JG(z-z')dz' =-йжаЕс™ (z),
dz2 J,
(4.1.4)
относительно неизвестной функции
fl2(zfp(z-zW,
то при разрыве при z = 0 в виде дельта функции [A(z) = 5(z)] нетрудно получить
Электрические симметричные вибраторы
интегральное уравнение Халлена [2]:
147
(4.1.5)
где U — напряжение в зазоре; k, Wc — волновое число и характеристическое
сопротивление среды, в которой находится вибратор, С — неизвестная постоян-
ная.
4.1.1. Интегральное уравнение Халлена-Неганова [28]. Перепишем интеграль-
ное уравнение Поклингтона (4.1.3) в несколько другом виде:
dz' = -г4гаоел Е~т (z)
Vv XZ* ' '
(4.1.6)
Будем понимать соотношение (4.1.6) как дифференциальное уравнение второго по-
рядка относително неизвестной функции, представленной определённым интегра-
лом
Предполагая, что вибратор возбуждается постоянным сторонним полем Eq , опре-
делённым в области зазора, т.е.
ст
z
при
при
рассмотрим соотношение (4.1.6) в трех областях:
z € Н До -Ь],
= -г471С0£0£Е0;
ze[Iq -Ъ,1о +Ь],
(4-1.7)
z е [ Zq + Ъ,1].
Верхний индекс j (j = 1,2,3) указывает на принадлежность к соответствующей об-
ласти. Уравнения (4.1.7) необходимо решать совместно с граничными условиями для
тангенциальных составляющих электрического и магнитного полей на поверхнос-
тях раздела областей (z = Iq - b, z = Iq + b). Относительно z-составляющей вектор-
148
ГЛАВА 4
ного потенциала Az граничные условия выглядят так:
л (D - л (2)
^Z **Z
л (2) _ Л (3)
^z ’
а А^ д А™
dz dz
д А&} _ d А<3)
dz dz
z = lQ-b,
z = lQ + b.
Для случая симметричного вибратора (l0 = 0) выражение для Az можно запи-
сать следующим образом (z g [-1,1]): '
lf _ e~ikR i 2riU
J г(г ’ rdz =c cos kz ~ kbw ч'(г) - (4.1.8)
-I c
где
V(z) =
1 - cos kb cos kz,
sin kb sin к z ,
< 7
Z G [-b, b],
z e [-b ,b],
U = 2bE0 — напряжение в зазоре вибратора, С — неизвестная постоянная опреде-
ляемая из дополнительных условий. Интегральное уравнение (4.1.8) будем назы-
вать интегральным уравнением Халлена-Неганова [28]. В предельном переходе
при Ь —> 0 оно переходит в известное обычное интегральное уравнение Халлена
(4.1.5).
Правая часть интегрального уравнения Халлена-Неганова (4.1.8) обладает не-
прерывной первой производной в отличии от известного уравнения (4.1.5), первая
производная правой части которого при 2 = 0 имеет разрыв первого рода. Это
обстоятельство является следствием того, что уравнение Халлена (4.1.5) описыва-
ет случай возбуждения вибратора генератором расположенным в точке 2 = 0 (раз-
рыв вибратора имеет нулевую длину).
4.2. Сингулярные интегральные уравнения в теории трубчатых
электрических вибраторов [8]
4.2.1. Самосогласованная физическом модель трубчатого электрического виб-
ратора. Будем использовать трубчатую модель электрического вибратора в виде
двух бесконечно тонких полых идеально проводящих цилиндрических трубок об-
щей длиной 21 и радиуса а. Трубки расположены как показано на рис 4.2, образуя
зазор к которому подключен генератор высокой частоты. Будем использовать сле-
дующие предположения.
Считается, что стороннее поле Ezm (z g [Zq — b, Zq + b], Zq — центр зазора)
в зазоре не зависит от координаты Ф. Поэтому в цилиндрической системе коорди-
нат система уравнений Максвелла, описывающая электромагнитное поле излуче-
ния электрического вибратора, распадается на две независимые системы относи-
тельно составляющих Ер, Ez, Н„ и Н Hz, Е„ [1]. Очевидно, что при рассмотре-
Элртстричестсие силип&трич/ные вибра/торы
149
нии поля излучения электрического вибратора необходимо исходить из системы,
описывающей поведение составляющих Ер, Ег, Н®.
Трубки предполагаются бесконечно тонкими и идеально проводящими, так что
на их внешней поверхности существует только продольная составляющая поверх-
ностной плотности электрического тока т|2 = Н®.
Поверхностная плотность электрического тока т|2 на внешних поверхностях
трубки и поверхностная плотность магнитного тока г]™ в зазоре вибратора
при р = а заменяется некоторой поверхностной плотностью электрического тока
r[z, непрерывной в области зазора (вследствие подключения к нему генератора)
и обращающейся в нуль на концах вибратора.
Касательная составляющая вектора электрического поля Ez(z) на вибраторе
обращается в ноль всюду (р = а, z < I), кроме области зазора длиной 2Ъ (рис. 4.2),
где она приравнивается некоторой возбуждающей функции Ezm (z).
Здесь важно отметить, что модель трубчатого вибратора справедлива для лю-
бых размеров радиуса а трубок. Единственное ограничение: стороннее поле воз-
буждения в зазоре не должно зависеть от координаты ср. Общепринятая модель
тонкопроволочного вибратора в виде бесконечно тонкой идеально проводящей нити
конечной длины может использоваться только при условии а « X. Кроме того,
модель тонкопроволочного вибратора не является самосогласованной. Для опреде-
ления ЭМП в ближней зоне необходимо принципиально учитывать толщину виб-
ратора: на идеально проводящей бесконечно тонкой нити нельзя ввести поле Н^,
связанное с поверхностной плотностью тока в соответствии с граничными элект-
родинамическими условиями. Поэтому в такой модели происходит “отрыв” ЭМП
от тока проводимости на вибраторе.
4.2.2. Сингулярное интегральное уравнение для трубчатого
вибратора. Будем рассматривать излучение трубчатого электрического вибрато-
ра (рис. 4.2), не зависящее от угла Ф. Исходной для получения СИУ является
однородная система уравнений Максвелла, записанная в цилиндрической системе
координат. В предположении отсутствия вариации поля вдоль оси Ф, система
уравнений распадается на две независимые системы относительно составляющих
Ер, Ez, Ну и Нр, Hz, Еф. Очевидно, что при рассмотрении поля излучения тонкого
вибратора необходимо исходить из системы, описывающей поведение составляю-
щих Ер, Е2 и Яф:
Из (4.2.1) следует уравнение Гельмгольца для составляющей 77 :
(4.2.2)
При рассмотрении поля излучения трубчатого вибратора, не зависящего
от угла ср, справедливо следующее интегральное уравнение:
150
ГЛАВА 4
-гсобо Е.
dz
fl(z')G2(z>z,)dz
(4.2.3)
ш
z
относительно тока I(z) = 27iar[f(z) (ц| = Нф(р - а)).
Ядро G2(z,z') в интегральном уравнении (4.2.3) в цилиндрической системе коор-
динат имеет вид [21]:
G2(z,z') =
СО
Интегральное уравнение (4.2.3) описывает распределение тока l(z) на трубча-
том вибраторе радиуса а. В отличие от уравнения Поклингтона (4.1.3), справедли-
вого для конечной нити с током, функция Грина G2(z,z') в (4.2.3) имеет особен-
ность.
Производя дифференцирование в (4.2.3), получим:
• TTfCm
I(zf)M1(z,z')dzf,
(4.2.4)
Mi(z,z')
00
- h2 )е ih(-z z }JQ (- га^Лг2 - k2 (- ia'lh? -k2 .
Воспользуемся методом, описанным в [8]. Для устранения расходимости в M^(z,z')
при z = z' перейдём от тока I(z) к его производной Г = —. С этой целью проин-
тегрируем правую часть (4.2.4) по частям: “Z
fl(z')e^2' dzr = ~—eihzI(z)
J h
ihz'
l\z')dz'.
h
Учитывая отсутствие тока на торцах вибратора (l2(z = I) = Iz(z = -I) = 0) , перей-
дём к производной тока I’(z). Для удобства будем использовать безразмерные
переменные t = z/l, t' = z'/l, а/Х, b/l, l/X :
I'(z')dz'
где J(t) = dl(lt)/dt.
Перепишем интегральное уравнение (4.2.4) следующим образом:
Электрические симметричные вибраторы
151
где
трСТП
Vv
(t)= p(tw2(t,m
(4.2.5)
M2(t,t') =
оо 9 9
1 ’ -ia?(Z/a)(t-t') (ka) — X
8тш2 J *
—00
(4.2.6)
x Jo I~i\ v? ~ (ka)2 ] I -i\lx2 - (ka)2 I dx,
а новая переменная x = ah .
Вводя новую функцию
gCr) = к
(ka)2 - x2
x
-iy/x2 -(ka)2 jl-i^jx2 ^-(kaf j,
перепишем (4.2.6) в более компактном виде:
00
M2(t,f) = f e-^^-^g^dx.
SnV J
—00
(4.2.7)
Используя свойства функций Бесселя [26]:
I0(x) = J0(-ix),
ni
к0(х) = - -
£
Н(02)(-гх),
найдём выражение для д(х) при х —> оо :
lim {р(х)} —> - 7ia?J0(-21 х |)Hq2\-i | х |) = -2ixIG (| х |)К0 (| х |).
Подставляя вместо произведения Iq(x)Kq(x) их асимптотику при
10(х)К0(х) -»
X—>00
получим:
Вводя новую функцию
lim д(х) = -isgn(x) = дт(х).
X—>00
Лд(х) = д(х)-до0(х)
и подставляя ее в (4.2.7), получим:
х -> оо [26]:
152
ГЛАВА 4
00
M2(t,tr) =----. (Дд(ж) + gjjc))dx =
8тГСГ J
00 00
8rc2a2 J 8л2а2 J
— 00 —00
Согласно [29]
00 . I z Л •
f ) sgn(a?)
J i
—00
I1
I
Таким образом, в ядре
М2выделили особенность Коши:
м2(м') =
/ 00
—J—- [e_^(Z/a)(*-t)Ag(x)da? -
8л2а2 J
2а/Г
t-t'}
Подставляя полученное выражение для M2(t,t') в уравнение (4.2.5), имеем
-iasaE^m=—п f
4я2а2 J t - «
(4.2.8)
где
max
e ix(z/a)(t t^Ap(x)dx,
max
Ag(a?) = i sgn(a?) - л
-(fca)2
Jo
X
(- X2 - (ka)2 (- гл/x2 - (ka)2).
После несложных преобразований сингулярное интегральное уравнение (4.2.8) за-
пишем в более компактном виде:
dt' = ae(t) +
(j(t')M(MW = F(t),
(4.2.9)
где o-£(t) = 4maZft)SaE0 -£(t), E™ = Eo -£(t) — известная функция, играющая роль
источника и определённая в области зазора:
(4.2.10)
Электрические симметричные вибраторы
где E^m(z) — заданная функция источника в зазоре вибратора.
153
4.2,3. Метод решения сингулярных интегральных уравнений. Рассмотрим
СИУ (4.2.9):
- p^dt'= F(t), (4.2.11)
71 J t -t
где
F(t) = о £(t) +
M(t, t') = -
00
l/a Г e-^/a)(t-t')Ag(a;)cte
2tc
—oc
(4.2.12)
Ag(x) = i sgn(x) - л
x - (ka)
xJ0 -iyjx2 - (ka)2 H^2) -iyjx2 - (ka)2
i2n а/X TT
—--------sUq .
Wc b/l
Здесь e(t) — отличный от нуля, нормированный к единице, профиль напряжения
в зазоре вибратора, Uq = 2Е0Ь.
Для регуляризации уравнения (4.2.11) воспользуемся формулой обращения ин-
теграла типа Коши для решения, не ограниченного на концах интервала [—1,1] [30].
В соответствии с этой формулой имеем:
J(t) =
где ад — произвольная константа, требующая определения. Исходя из тождества:
1 1
J(t)dt = J
dl(t)
dt
dt = fdl(t) = 1(1) - Д-1) = О
найдём значение постоянной а0:
154
ГЛАВА 4
а0
dt dt' = 0.
(4.2.13)
Первый интеграл в левой части легко вычисляется при использовании подстанов-
ки t = sin р; его значение равно л. Вычислим внутренний интеграл в двойном
интеграле. Для этого рассмотрим известные интегралы для ортогональных полино-
мов Чебышева [26]:
dy = nU^x).
(4.2.14)
Преобразовав левую часть (4.2.14) при п-1, получим
Из последнего выражения видно, что интересующий нас интеграл равен нулю
(/'е[-1,1]):
1
I* . ---------------dt - 0.
.iVi-t2 (t-t')
Окончательно получаем, что в (4.2.13) ад =0.
После подстановки в (4.2.13) выражения для F(t), получим интегральное урав-
нение Фредгольма второго рода относительно производной тока:
J(t) =
J(tff)M(t',t")dt'dt4.
(Zo-b)/Z
Введя обозначение
Int(t) =
(10-Ъ)/1
£(t’)dtr,
упростим выражение для J(t):
J(t) = — -----\ (4.2.15)
Элетстричест^е симметричрме вибраторы
155
Таким образом, внутренняя электродинамическая задача для тонкого электри-
ческого вибратора сведена к интегральному уравнению Фредгольма второго рода,
методы решения которого хорошо известны [31,32].
В выражении (4.2.15) производную тока можно выразить через новую неизвест-
ную функцию <p(t):
-a + <p(t)
Для неизвестной функции (p(t) получаем другое интегральное уравнение Фред-
гольма второго рода:
.. 1 V rVi -1'2 „..
cp(t) =—---------------------\ L 7M(f,t")dtffdf.
Л j j t' - t _ t"2
(4.2.16)
Уравнение (4.2.16) можно решать разными способами. Рассмотрим два из них:
с помощью разложения экспоненты в ядре в ряды по функциям Бесселя и полино-
мам Чебышева, а так же при непосредственном применении к (4.2.16) квадратур-
ных формул типа Гаусса.
В подынтегральном выражении для в (4.2.12) показательные функции
разложим в ряды по функциям Бесселя и полиномам Чебышева 1-го и 2-го
рода [26]:
а к=1
00
eiax = J0(a) + 2^?4(a)4(x); х е [-1,1].
к=1
Тогда ядро M(t',tn)
можно записать в виде разложения по полиномам Чебышева
I-го и П-го рода:
—4 • 00 т-И-к
п=0
(4.2.17)
^п,к
00
= 1 &glx)dXy
— 00
2, п = 0;
5П =
[1, п ф 0.
(4.2.18)
После подстановки (4.2.18) в (4.2.15) получим следующее соотношение:
156
ГЛАВА 4
1
J(t) = -
ст Int(t)
n—Q
(4.2.19)
J
которое позволяет искать неизвестную функцию J(t) в виде разложения по поли-
номам Чебышева 1-го рода:
(4.2.20)
где Afc — неизвестные постоянные.
Предполагая, что функция J(f) с хорошей степенью точности описывается по-
линомом степени не выше N, бесконечный ряд в (4.2.20) можно оборвать на этом
числе N. Подтверждением данного предположения может служить быстрое умень-
шение коэффициентов . Подставив выражение для J(t) в (4.2.19), получим сис-
тему линейных алгебраических уравнений (СЛАУ) относительно неизвестных ко-
эффициентов Afc :
4 N
A-к = ki + = 1» 2,3,..., TV, (4.2.21)
7Г £
n=l
Intn
f V
V Tn(y)Int(y)
Чтобы найти ток на вибраторе после решения СЛАУ (4.2.21), возьмём интеграл
от производной тока:
t
I(t)= h(t)dt = -~
J 71
N
t ' A-k^k)
dt' =
(4.2.22)
Actyc-lW
к
Здесь было проведено вычисление интегралов от полиномов Чебышева с исполь-
зованием их представлений через тригонометрические функции:
Элекрурумеские силиуупурууные вибраторы
157
Tfc(cosp) = cos(kp),
Ufc(cos Р) = sin((fc + 1)Р)
sinp
и замены переменной интегрирования х = cos Р :
arccos t
sin(fcP)
arccos t
sin(k arccos t)
sin(arccos t)
sin(arccost) Г o’ Z4._
-----------= U^k.
k
Рассмотрим коэффициенты ak n , определяемые формулами (4.2.18). При (k + n)
— чётном, подынтегральная функция в (4.2.19) тоже является чётной, поэтому
интегрирование можно проводить от 0 до оо (при численных расчетах — хтах),
с одновременным умножением интеграла на 2. При (к + п) — нечётном, подынтег-
ральная функция является нечётной и интеграл равен 0. Тем самым количество
вычисляемых коэффициентов (интегралов) уменьшается примерно в четыре раза
(ак,п = ап,к) и> как следствие, значительно сокращается время вычислений.
Другой способ решения уравнения (4.2.16) — использование квадратурных фор-
мул для вычисления интегралов [33]:
dx
~П?)Ж)
(4.2.23)
где = cos((2fc - 1)л/2ЛГ) — нули полинома Чебышева TN(x), тц = cos(ln/N) —
нули полинома Чебышева (к = 1,N, I = 1,N -1), <р(х) — полином степени
не больше (2N — 2 ).
Заменяя интегралы в (4.2.16) квадратурными суммами (4.2.23), получим систему
линейных уравнений относительно значений функции Ф в нулях полинома Чебы-
шева TN(x):
N
Ф/с — ~<Рк,р(^р + Фр),
р=1
где
158
ГЛАВА 4
К-1,р Ip Ф/с ф(^эк)*
Разлагая неизвестную функцию ф(х) в ряд по полиномам Чебышева (TN(^) = О,
поэтому верхний предел IV-1):
W-1
ф(^) = ^АкТк(х)
к=1
(4.2.24)
и подставляя значения (рк в (4.2.21), получим систему линейных уравнений отно-
сительно коэффициентов Ак. Данная система является переопределенной, т.к. чис-
ло уравнений на одно больше числа неизвестных, поэтому положим формально
нижний предел суммирования в (4.2.24) равным нулю. Нетрудно показать, что
коэффициент должен равняться нулю, что может явиться вспомогательным
критерием правильности численных расчетов.
4.3. Сингулярное интегральное представление (СИП)
электромагнитного поля электрического вибратора
[Ю, 11]
Ниже описан вывод СИП ЭМП и проведен электродинамический анализ ЭМП
вблизи электрического вибратора. Дано сравнение численных результатов распре-
деления ЭМП в ближней зоне, полученных с помощью метода СИП, с результата-
ми общепринятого подхода. Показана некорректность общепринятого подхода
в ближней зоне антенны.
4.3.1 Сингулярное интегральное представление электромагнитного поля. Будем
рассматривать ЭМП идеально проводящего электрического вибратора в виде по-
лой трубки длиной 21 и радиуса а, возбуждаемого в области разрыва
(z е [Zo — b, 10 + Ъ]) генератором высокой частоты (рис. 4.2). В предположении отсут-
ствия вариации поля вдоль координаты ср, будем исходить из системы уравнений
Максвелла, описывающей поведение составляющих Ep,Ez,H^. В этом случае про-
дольная составляющая поверхностной плотности тока т|2 на поверхности вибрато-
ра связана с составляющей объемной плотности тока jz следующим образом:
= Н (p,<p,z)8(p - а) = 8(р - а),
2ка
где Iz (z) = 2кат]2 (z) — ток на вибраторе, 5(р - а) — дельта функция Дирака.
Будем также исходить из выражения для электродинамического потенциала
i
A‘(p,z)= ^Iz(z')G(p,z - z')dz',
-I
симме^^ ви&раторы
159
которое является исходным для получения СИП электромагнитного поля вибрато-
ра. Но в качестве функции Грина в цилиндрической системе координат будем
использовать следующее представление [19,21]:
1 00
G(p,z - z’) = — J e~ih(z~z]g(h,p)dh,
8кг •
(4.3.1)
где
g(h, p) = i
Jo (~ipv)H(02) (-iav)
Jo (~iav)H{2) (-ipv)
при p s a
при p> a,
J0(x)— функция Бесселя 1-го рода нулевого порядка; Hj2)(x)— функция Ханкеля
2-го рода нулевого порядка, v = y/h2 - к2 .
Выражение (4.3.1) есть функция Грина свободного пространства, записанная
в цилиндрической системе координат с учетом отсутствия зависимости поля
от координаты <р , от точечного источника, расположенного в точке (р = a,z = z'),
т.е. на поверхности электрического вибратора. Выбор функции Грина G(p,z-z')
под знаком интеграла в выражении для электродинамического потенциала в виде
(4.3.1) соответствует физической модели трубчатого вибратора.
Составляющие электромагнитного поля вибратора при этом определяются
по формулам [1]:
1 з2Ае
гсо80£ dpdz ’
В2 = -гсоцощ42
1
йо£()£ dz2
лде
Н.=~- (4.3.2)
dp
Переходя от электродинамического потенциала к напряженностям электри-
ческого и магнитного полей, приходим к следующим интегральным представлени-
ям для составляющих электромагнитного поля вибратора в любой точке простран-
ства через ток 12(г)на его поверхности:
Ер(р,г) = . 1 ku'JG'Vz-zW,
га)£0£ д
1 1
Ez (Р, *) = -J Iz (z ’)G^ (р, z - z ')dz(4 3 3)
2СО£0£ д v ’
I
H„(p,z) = -ps(z')G™(p,z-z')dz',
-г
где
8кг
00
J e-‘h^gp(h,p)dh,
—00
G»’(p,z-z') =
00
— {ea^gz(h,p)dh,
8кг J
(4.3.4)
160
ГЛАВА 4
1 ОО
e-ih(z-z )g^h, pjdh.
sv(h,p)=-^>
vJ0 (~iav)H{2} (-ipv)
vJ1 (~ipv)H(02) (-iav)
p
9P (h, p) =
d2g(h, p) _ fhvJ0 (~iav)H[2) (-ipv)
dpdz hvJx (-ipv)H(02) (-iav)
p < a,
p > a
gz(h,p) = -i(op0pg(h,p) +
1 d2g(h,p)
2CO80£ dz2
= (k2 -h2)g(h,p) =
v2 Jo (-iav)H^ (-ipv) p > a
y2J0(-ipv)H{2)(-iav) p < a.
Функции G™, G^, Gz1} при p = а содержат особенности. Ниже выделим их
в явном виде.
Учитывая что, при z
> Z0(iz),
il^iz), lim In (z)Km (z) -> —
l2H°° 2z
получаем
lim g (h,a) - - h
2a h n
h
lim g (h, a) = -—
_m P Tta
(4.3.5)
h
ih
lim g (h, a) - -sign(h)—
nn 2 na
Поскольку асимптотические значения подынтегральных функции в (4.3.4) не равны
нулю, то несобственные интегралы в интегральных представлениях (4.3.3) не схо-
дятся, и простое усечение в них бесконечных пределов может привести к невер-
ным физическим результатам. Поэтому непосредственный переход выражений (4.3.2)
при р —> а в известные граничные условия невозможен.
Выделим особенности в (4.3.3) в явном виде. С этой целью из подынтегральных
функций д , д (h,p), gz(h,p) в (4.3.4) вычтем их асимптотические выражения (4.3.5)
и перейдем от функции Iz(z) к ее производной dlzjdz в соотношениях для Ер
и Ez:
Электрические симметричные вибраторы
161
W =
dz
В результате получим следующие СИП [10]:
Е (p,z) = —JJJ.z ")[G(p,z - z') + G£(p,z - z ’)]dz',
ZCO£n£ J,
Ez (p, z) = ------- Jz (z ’)[G2 (P, z - z') + G” (p, z - z ')]dz (4 3
ICO£0£ j
I
Hv (p, z) = - Ji,(z')[Gp (p, z - z') + g; (p, z - z')]dz
-I
определяющие поле электрического вибратора в любой точке пространства через
функции Jz(z') и Iz(z'), определенные на его поверхности.
Функции Сф и G2 представляют собой сходящиеся интегралы:
1 оо
G„(p,z-z') = —
8л •
^g4,(h,p)dh,
оо
Gz(p,z-z') = — j
8л J
e~M^^(h,p)dh,
где
p) =
-(p-a)sign(p-a) h
vJ0(-iav)H{2}(-ipv) p > a
yJx (-ipv)H{Q} (-iav) p < a,
(4.3.7)
Ags(h,p) = sign(h) -
л-у/ар
— Jo (-ipv) p > a
h
^2
— Jo (~ipv)H(02) (-iav) p < a.
Функции G“(p,z-z') и Gz(p,z-z') определяют следующим образом:
G?(p, z - z') =---^-=------,
4л2 ^/ap (p — аУ +(z — z')
(4.3.8)
G:(p,z-z') = -
4л2Tap (P-a)2 + (z-z')2
6 - Неганов
162
ГЛАВА 4
Представляет интерес предельный переход СИП (4.3.6) при р
(поле на поверхности вибратора). В этом случае:
4 ла
(4.3.9)
Рассмотрим G(p,z-z') при условии р —> а. При больших h , Gy(a,z-z) обра-
щается в ноль. При малых
Je ih^z z^ vJQ(-iav)H^\-iav) +
—00
Учитывая соотношения для функций Jo (z) и Н[2}
получаем:
dh.
(z) при малых аргументах:
I0(iz), lim Jo (z)Kx (z)
1 00 1
f e-^-^dh =-----5(z - z').
8л а 4ла
(4.3.10)
h :
Ф
С учетом (4.3.10) из (4.3.6) следует что:
-—5(z-z')]dz' = n*(z).
4ла
Аналогично для Е :
1О£0£
Таким образом, СИП для составляющих электромагнитного поля (4.3.6) при р -> а,
z е [-Щ строго переходят в их значения на поверхности вибратора.
Подставляя (4.3.7), (4.3.8) в (4.3.6) получаем следующие выражения для E2(p,z),
Ep(p,z) и Нф(р,2) [16]:
w
8л гака
со
Г ihl (t—t ’)
sign(h)
-(p-l)sigm(p—1)/г
(4.3.11а)
dh- —
dt'
Электрические симметричные вибраторы
Ep(p,t) =
Wc
8тс2гака
-(p-l)stgn(p-l)|h|
(4.3.116)
+71Л
vJQ(-iv)H^}(-ipv) p > 1
vJl (-ipv)H<2)(-iv) p < 1
(4.3.11b)
где t = z/l, t' = z' /I, h = ha, v =
I = l/a, p = p/а, Wc
характерис-
тическое сопротивление среды.
4.3.2. Сингулярное интегральное уравнение. В выражениях (4.3.11) под интег-
ралом стоят Iz(t) и Jz(t), которые представляют собой функции тока и производ-
ной тока (по нормированной координате t) на вибраторе соответственно. Изна-
чально они не известны. Для того чтобы их найти, необходимо получить СИУ
относительно производной тока, которое находится из представлений (4.3.11) по-
средством подстановки в них граничных условий.
Возьмем выражение для Ег из (4.3.11) и подставим в него граничные условия
на поверхности вибратора р = а :
при z е [-Цо - b] U [i0 + Ь,1],
при z g [Zo - Ъ, 10 + Ь]
(4.3.12)
где Ezm— z-составляющая стороннего электрического поля в зазоре вибратора.
Ее можно представить в виде:
Ezm(t) = aUs(t)/2Ь,
где g(t) — профиль напряжения в зазоре, U — величина питающего напряже-
ния.
В результате получаем СИУ относительно Jz (t):
6*
164
ГЛАВА 4
dt' = (t) -
2л
е а
isign(h) -
JQ(-i^h2 ~(ka)2)H(2}(-i-yjh2 -(ka)2)
dhdt'.
(4.3.13)
Проще использовать профиль напряжения в зазоре в виде [16]:
В этом случае интеграл
(l0+b)/l А. .12
Int(t) = [ - £(t ')dt'
* f '— f
(/o-b)/l b L
I
f
возникающий при обращении интеграла типа Коши можно найти в аналитическом
виде (что ускоряет численные расчеты):
Int(t) = (ArcSin(b / Z) ( 2t3 - 2t (Ъ /1)
tb/l-1
ArcTh
+ ArcTh
- гъ/z^/i - (ь/z)2
4.3.3. Выражения для составляющих ЭМП, полученные традиционным ме-
тодом. Получим выражения для ЭМП в ближней зоне, используя традиционное
представление функции Грина:
G(p,z-z') =
1 e-ikR
4 л R
(4.3.14)
которая отвечает физической модели вибратора в виде бесконечно тонкой нити
расположенной на оси z , которая приводит к несамосогласованной постановке
задачи. При этом функция Грина (4.3.14) используется в подавляющем большинстве
научных работ и рассматривается как основной момент алгоритма расчета ЭМП в
Электрические симметричные вибраторы
165
ближних зонах антенн в учебной и научной литературе.
Используя (4.3.14), получаем:
i
Ae(p>z)= Jw)
-I
dz'.
(4.3.15)
С помощью (4.3.2), получаем выражения для составляющих поля:
ттт 1 _ — ikalR
Ер(р, t) = . с fI(t ')7Р(р, t) dt
4makal R
ттт 1 _ —ikalR
Ez(p,t) = -2 fl(t’)Z(p,t)—=-dt’,
4niaka I К
-i 1 -ikalR
4nar * R
(4.3.16)
- - 1 +ikalR _ - (3 + 3ikalR-ka2l2R2}(t-t')
= —&—p> /Р(р. 0 = -------------gj------------p,
Л ’ R
. у 2T*2 z >\2 3ika i ka Z 1 / t’ \
fz(p>t) — ka I + (t — t) — =7(1 + ikalRJ,
.a it it tt
и t = z /1, t' = z' /1, I =1 / a, p = p / a, R = J(p / I j + (t-t')2, Wc
ческое сопротивление среды.
характеристи-
4.3.4. Сравнение самосогласованного метода с традиционным подходом. На
рис. 4.3 приведены графики сравнения для составляющей Ez рассчитанные мето-
дом СИП (а) и традиционным методом (б) на поверхности вибратора: р = 1. При
расчете ЭМП с помощью самосогласованного метода в качестве тока использовался
ток полученный из СИУ (4.3.13). Расчеты производились для параметров: I /1 = 1 / 4,
а / X = 1 / 400 , Ъ /1 = 1 /100, 10 = 0, We = 120л , U = 1В . При традиционном подходе
использовались соотношения (4.3.16). Из рисунка видно, что при расчете поля Ег
методом СИП выполняется граничное условие на металле — тангенциальная со-
ставляющая обращается в ноль (рис. 4.3,а). При расчете поля традиционным подхо-
оо, при t
дом выполнение граничного условия на металле не наблюдается (рис. 4.3,6).
Было установленно, что самосогласованный метод находится в согласии с усло-
вием на ребре Ер а
ребре не выполняется (рис. 4.3,6).
При р > 1.5 численные результаты полученные с помощью самосогласованного
1. В случае классического подхода условие на
и традиционного методов совпадают.
166
ГЛАВА 4
Рис. 4.3. Функция Ez(p,t) а, рассчитанная методом СИП (а) и традиционным
методом (б) при р = 1
4.4. Распределение тока по электрическому вибратору
(анализ при самосогласованном подходе) [8]
4.4.1. Распределения поверхностной плотности тока для симметричного
вибратора. При решении уравнения (4.3.13) методом обращения, необходимо за-
дать профиль напряжения в зазоре. Если взять его в виде константы, то интеграл
Int(t) в точках - Go ± Ь)/1 будет расходящимся. Это происходит потому, что
в этих точках подынтегральная функция имеет разрыв второго рода, который
компенсируется только для < t < t2 одинаковым стремлением к бесконечности
слева и справа. Данный разрыв имеет место при моделировании напряжения
в зазоре обобщенной ступенчатой функцией. При описании напряжения в зазоре
функцией, не имеющей разрывов (что и должно быть в реальности), мы получим
интеграл, не имеющий особенностей.
Возьмем профиль напряжения в зазоре в виде
fO,
e(t) = 1 /------------9
(4.4.1)
В этом случае интеграл Int(f) будет ограничен для всех значений переменной t.
Вместо профиля (4.4.1) можно взять любой другой непрерывный профиль, об-
ращающийся в нуль на краях зазора вибратора. Ограничений на выбор функции,
моделирующей форму профиля, нет. Однако выбор функции, отличной от (4.4.1),
может усложнить вычисления. Но при численных расчетах значения Int(t) доста-
точно вычислить один раз в конечном числе точек и впоследствии пользоваться
сохраненными результатами.
При вычислении значений Int(f) в двойном интеграле можно одно интегрирова-
ние провести аналитически:
Электрические симм^ггу^ичт^ье вибраторы
167
Intn J
s(x)dxdy =
£(Ж) j
тп(у)
1-х e(3c)Un_1(x)dx.
Здесь был использован известный интеграл для полиномов Чебышева:
dx = uUn_1(y),
При вычислении Int(t) (область интегрирования соответствует области зазо-
ра вибратора) для значений t лежащих за пределами области зазора, интегриро-
вание проводится обычными численными методами. Для значений t, соответству-
ющих области зазора, интеграл разбивается на два (стандартный метод вычисле-
ния несобственных интегралов). Под интегралом в выражении для перейдем
к новой переменной z = t l/b :
= b/02 dz „
J x — t J z — tl/b
-b/l -1 7
= f-1 ~ 2 f 71 - (г ь/02 - 71 ~ t2 ) dz + 71-t2 f -1 - - Z 2 dz.
iz-tl/bV ) iz-tl/b
(4.4.2)
Последний интеграл в (4.4.2) берется аналитически:
Г°> __________
|лsgn(t)-J(tl/b)2 -1,
|t l/b\ < 1;
\tl/b\>l.
Для случая b/l « 1 (малый зазор):
yl — (zb/Z)2 ® 1
и | tl/b
Int(t) = -Titl/b - лsgn(t)7(tl/b)2 -1.
В результате получили простую формулу для Int(t).
168
ГЛАВА 4
На рисунках 4.4 — 4.11 представлены результаты расчета тока по вибратору
при различных геометрических параметрах вибратора. На этих рисунках приведе-
ны и значения для параметров N и a?max : N — число функций Чебышева перво-
го рода в сумме выражения (4.2.20) или второго рода в (4.2.22), хтах — верхний
и нижний пределы интегрирования в ядре СИУ (4.3.13). Следует отметить, что для
симметричного электрического вибратора число слагаемых в суммах в (4.2.20)
и (4.2.22) в два раза меньше, так как распределение тока должно быть четным,
а следовательно, слагаемые в этих суммах, содержащие функции Чебышева чет-
ного (нечетного) порядка, должны быть равны нулю.
Приведённые расчеты хорошо согласуются с данными, приведёнными в работе
[34].
Z _ 1 а _ 1 b _ 1 . _ п
X 4 X 400 I 100
N — 20, хтах —10
Рис. 4.4
Электрические симметричные вибраторы
169
I 1 а 1 b 1 л
X 2 X 400 I 100
N = 20, Хтах =Ю
’ Ш4Л
Рис. 4.5
Рис. 4.6
170
ГЛАВА 4
/ а 1 Z? 1
~ = 1, —— —--, — =---, Iq = 0, N = 20, xmax =10
X X 400 / 100 ’max
Рис. 4.7
I, A
Zo=O, N = 20, xmax =10
I _ 1 a 1 b 1
X " 4* X “ 40’ I ~ 100’
Рис. 4.8
Электрические симметричные вибраторы
171
L-L £__L
X ~2’ X " 40’
- = —, /0 =0, ^ = 20, Хтах =10
Z 100
Рис. 4.9
i__J_ £__L A=_L
X ' 10 ’ X " 40 ’ I ~ 100
Zq — 0, N — 20, xmax 10
Рис. 4.10
172
ГЛАВА 4
I, А
L-i а -_L b ~ 1
X - ’ X ’ 40’ 7~Too’
/q — 0, N — 20, xmax —10
Рис. 4.11
4.4.2. Распределения тока для несимметричного вибратора. Для несиммет-
ричного электрического вибратора (10 * 0) профиль напряжения в зазоре выби-
рался в виде
£(t) = <------------------
-10)/Ь)2,
I t-lo/I |> b/Z;
\t~l0/l\<b/l.
Вычисление Int(t) проводится аналогично случаю симметричного вибратора,
но при этом используется замена переменной интегрирования z = (t I -10) / b.
Физически важным случаем является пример полуволнового вибратора:
2Z / X = 1 / 2. В этом случае распределение тока не должно зависеть от положения
зазора (точки приложения напряжения) [2]. Как видно из рис. 4.4 — 4.8 для симмет-
ричного вибратора и рис. 4.12 — 4.17 для несимметричного вибратора, это утверж-
дение действительно имеет место для действительной части тока I, что является
подтверждением правильности проделанных расчетов и говорит о “физической
сходимости”. При этом заметим, что математическая сходимость не всегда гаран-
тирует сходимость к правильному решению.
На рисунках 4.12 — 4.20 представлены графики зависимости распределения
тока по несимметричному вибратору при различных параметрах его геометрии.
Смысл остальных параметров на рис. 4.4 — 4.11 такой же, как и для симметрично-
го вибратора.
Проводились исследования внутренней сходимости алгоритма, разработанного
Электрические симметричные вибраторы
173
на основе СИУ (4.2.11). Общий вывод следующий: для достижения относительной
погрешности порядка одного процента достаточно ограничиться N = 10, хтах =1.2;
для достижения относительной погрешности порядка 0.1 процента требования дол-
жны быть более жёсткими: N = 50 , хтях = 10.
' ПИЛ
L-l а _ 1 A_JL ~L
X “ 4’ X ” 400’ I ~ 100’ ° ~ 4
7V = 20, xmax=10
Рис. 4.12
L-L д _ 1 A__L -L
X “ 4’ X " 400’ l ~ 100’ 0 “ 2
Рис. 4.13
174
ГЛАВА 4
l__]_ 1 b__S_
X “ 4’ X " 400’ I ~ 100’ Z° “ 4 ’
N = 20,
•^max
= 10
Рис. 4.14
/ _ 1 а _ \ Ъ _ 1 I
X ” 4’ X “ 40’ I ~ 100’ 0 " 4
Рис. 4.15
Электрические симметричные вибраторы
175
L-L £_J_ *=_L i =L
X ~ 4 ’ X ” 40 ’ I ~ 100 ’ 0 2 ’
N = 20, хтах = 10
7 111С1Л
Рис. 4.16
L-L £-J_ ь = 1
X ” 4’ X " 40’ I ~ 100’
N = 20, хтах = 10
Рис. 4.17
Z__j_ a__ 1 b _ 1 I
X 2’ X~40’ I “100’ Z°“?’ jV“20’ xmax-10
Рис. 4.18
1-— A= 1 i -L
X 10’ X 40’ Z 100’ Z° “ 2’
N — 20, xmax —10
Рис. 4.19
Электрические симметричные вибраторы
177
I _ а _ 1
X -1’ X ” 40’
А 1 1
— =----, /0 = —, N - 20, хтах -10
/ 100 ° 2
Рис. 4.20
4.4.3. Расчет входного сопротивления. Входное сопротивление электрического
вибратора является важнейшим параметром, определяющим согласование входа
антенны в нужной полосе частот. Обычно входное сопротивление вибратора опре-
деляется с помощью метода эквивалентной цепи, согласно которому симметрично-
му вибратору ставится в соответствие разомкнутая на конце двухпроводная линия
с потерями [2,17,18]. Ниже для расчета входного сопротивления симметричного
электрического вибратора используется метод сингулярного интегрального урав-
нения (СИУ). Входное сопротивление вибратора определяется как отношение на-
пряжения, приложенного к зазору, к току в точке питания
Z„=U/J(z = 0) = 1772^(2 = 0),
где т|2 — поверхностная плотность электрического тока на вибраторе (рис. 4.2).
Алгоритм следующий: задавалось напряжение в зазоре вибратора U = 1 В и оп-
ределялось Т|2 в точке z = 0 методом СИУ.
На рис. 4.21 приведены результаты сравнения зависимостей комплексного вход-
ного сопротивления от нормированной длины волны. На этих рисунках сплошные
кривые — результаты, полученные по методу СИУ, штриховые кривые — расче-
ты по методу эквивалентной цепи [2,17,18]. Наблюдается хорошее качественное
совпадение поведения этих кривых.
Существенное расхождение в значениях Re{ZeaJ в окрестностях последова-
тельного резонанса вибратора при I / X « 0.25 и в окрестностях параллельного
резонанса вибратора при I / X « 0.5 Более того, последовательный резонанс
(lm{Zex} = О) наступает при меньших значениях длины электрического вибрато-
ра, при этом значения активного входного сопротивления Re{Zex} при 1/Х « 0.25
178
ГЛАВА 4
(последовательный резонанс по методу СИУ) порядка 120 Ом вместо 75 Ом
по методу эквивалентной цепи. Аналогичная картина наблюдается и в случае па-
раллельного резонанса вибратора: последовательный резонанс по методу СИУ
также наступает при меньших значениях длины электрического вибратора и зна-
чение активного входного сопротивления на резонансной частоте меньше значения
Re |Zor}, полученного по методу эквивалентной схемы.
На рис. 4.22 приведены зависимости комплексного входного сопротивления
от I /1 для толстых вибраторов.
В заключение сформулируем основные ограничения метода эквивалентной цепи
при расчете входного сопротивления.
а)
Рис. 4.21. Зависимости сравнения результатов расчета комплексного входного
сопротивления Zex электрического вибратора от нормированной длины
I / X : а) I / а = 60; б) I / а = 20 (сплошные кривые — метод СИУ, штриховые
кривые — метод эквивалентной цепи [2,17,18])
Re , Ом
800
600
0.1 0.2 0.3 0.4 0.5 //х
б)
Рис. 4.22. Зависимости комплексного входного сопротивления Z)ix электри-
ческого вибратора от нормированной длины I / X : 1 — I / а = 15; 2 — I / а = 10;
3 — I / а = 5 (сплошные кривые — Re{ZeT}, штриховые кривые — )
Эшттричрские симм^1ири2^21^!£. вибраторы
179
Во-первых, метод эквивалентной цепи «плохо» работает для длинных вибрато-
ров. Поэтому в [2] приведены значения входного сопротивления только для норми-
рованных длин I / X < 0.6.
Во-вторых, с увеличением радиуса а вибратора наблюдаются большие расхож-
дения между методами СИУ и методом эквивалентной цепи. Этот вывод является
следствием того, что метод СИУ справедлив для любых значений а при един-
ственном условии, что поле возбуждения в зазоре не зависит от азимутальной
координаты. Метод эквивалентной цепи основан на тонкопроволочном приближе-
нии [2].
4.4.4. Электромагнитное поле излучения полуволнового электрического виб-
ратора [1]. Проведем электродинамический анализ ЭМП симметричного электри-
ческого вибратора при следующих его размерах: I/X = 1 /4, а/Х = 1/400,
b/l = 1/100 и при напряжении U = 1В. При таких параметрах численное решение
СИУ (4.3.13) было получено в [8]. На рис. 4.4 приведено комплексное распределение
тока 1г от координаты t = z/l: сплошная кривая соответствует Re{l2}, пунктир-
ная кривая — .
На рис. 4.23 приведены, в сферической системе координат, распределения ве-
личин Фе = аЕег /X , Фг = аЕгг /X , Фф = / X от координаты 0 при различных
нормированных расстояниях г / X от центра вибратора. Отметим, что в дальней
зоне величины Фе, Фг, Фф перестают зависеть от нормированного параметра
г / X . На этих рисунках сплошными кривыми обозначены реальные части величин,
точками — мнимые части величин, штрихами — модули величин. На рис. 4.23,в
показаны распределения величин Ф0, Фг, Фф на расстоянии от вибратора г = 1.83Х,
что соответствует дальней зоне [2]. Как показали расчеты, дальнейшее увеличе-
ние г приводит лишь к незначительным изменениям амплитуды ЭМП (полная
стабилизация наступает на г = 10Х), не изменяя качественный характер излуче-
ния. Поэтому распределения ЭМП электрического вибратора на больших расстоя-
ниях не показано.
Напомним, что верхняя граница промежуточной зоны определяется соотноше-
нием: г < 2D2 /X , где D — максимальный размер антенны [2]. Для электрического
полуволнового вибратора D = 21 = X / 2. Поэтому верхняя граница промежуточной
зоны для полуволнового вибратора определяется как г / X = 0.5.
Из анализа этих графиков можно сделать следующие основные выводы:
1. В промежуточной зоне ЭМП не является чисто поперечным: продольное элек-
трическое поле ЕТ по модулю даже несколько больше составляющей Ее. Этот
вывод находится в противоречии с общепринятым положением теории антенн:
ЭМП в промежуточной зоне является чисто поперечным (см. например, [2]).
2. Максимальное излучение соответствует азимутальной плоскости 0 = л / 2
сферической системы координат. Вдоль этого же направления происходит и макси-
мальное излучение Н — магнитного поля. Максимум составляющей Ег соответ-
ствует оси вибратора при 0 = 0 и 0 = я, причем на этой оси Н = 0. Поэтому
вектор Умова-Пойтинга 5 = [Е,Н]/2 на оси вибратора равен нулю и перенос
энергии вдоль оси вибратора не происходит. Максимальный перенос энергии соот-
180
ГЛАВА 4
0 6 0
а) б) в)
Рис. 4.23. Распределение величин Fq , Fr , для полуволнового вибратора
в сферической системе координат от координаты 0 на различных нормиро-
ванных расстояниях г / X от центра вибратора: а) — г / X = 0.3 ,
б)
г / X = 0.4 , в)
г /Х = 1.83
(сплошные линии
Re {F(0)} ;
точками — Im{F(0)}; штриховые линии —
F(0))
ветствует 0 = л / 2; Зл / 2, причем в этом направлении участвует только Ее (Ег = 0
при 0 = л / 2; Зл / 2). Составляющая Ег обеспечивает колебательный процесс ЭМП
около вибратора вдоль координаты 0 попеременно во времени от одного конца
вибратора к другому, тем самым вибратор как бы образует открытый колеба-
тельный контур. В таком контуре вблизи ребер вибратора наблюдается макси-
мальная концентрация электрического поля; максимальная концентрация магнит-
ного поля находиться в азимутальной плоскости 0 = л / 2.
3. Были приведены расчеты по установлению границы пространства, в котором
можно считать, что поле излучения является чисто поперечным. За такую границу
было принято значение г / X , при котором Е
означает максимальное значение модуля соответствующей составляющей
10, где индекс шах
9 max
r max
Эле^тричестсие симм^три^тые вибраторы
181
поля. Оказалось, что при г/Х = 0.4
« 0.822,
max
max
при
г/1 = 1.83 -
max
max
max
max
при
r/k = 5 -
« 20.4 ,
при г/X = 10
= 41. Таким образом за нижнюю границу зоны излучения полуволно-
вого электрического вибратора, в которой ЭМП можно считать чисто поперечным,
принято соотношение г / X > 2.
Таким образом, предложенная самосогласованная физическая модель электри-
ческого вибратора позволила построить новую математическую модель, устраня-
ющую разрыв между током на металле и ЭМП в ближней зоне. При этом деление
пространства излучения антенны на ближнюю, промежуточную и дальнюю зону
является нецелесообразным.
На основе самосогласованного метода, включающего в себя СИП (4.3.11) ЭМП
и СИУ (4.3.13), проведен электродинамический анализ ЭМП полуволнового элект-
рического вибратора непосредственно с поверхности вибратора до дальней зоны.
При этом в работе была использована самосогласованная физическая модель элек-
трического вибратора в виде двух идеально проводящих бесконечно тонких трубок
конечной длины между которыми включен генератор СВЧ.
Выявлены особенности поведения ЭМП в ближней и промежуточной зонах
электрического вибратора. В частности установлено, что в промежуточной зоне,
в отличие от общепринятого мнения, электромагнитное поле не является чисто
поперечным. Сделан вывод о нецелесообразности деления пространства на ближ-
нюю и промежуточные зоны. Чисто поперечным ЭМП становиться только на рас-
стояниях г > 2Х.
Основным достоинством самосогласованного метода является то, что в отличии
от традиционного алгоритма на основе традиционной функции Грина, имеется
возможность установить непрерывную трансформацию структуры ЭМП непосред-
ственно с поверхности антенны до дальней зоны. Поэтому, введенная самосогласо-
ванная физическая модель электрического вибратора совместно с самосогласован-
ным методом позволила построить новую теорию, согласно которой ЭМП в любой
точке пространства подчиняется уравнениям Максвелла.
4.5. Криволинейный полосковый вибратор, расположенный на
цилиндрической поверхности [24]
Ниже на примере криволинейного полоскового вибратора (КПВ), расположен-
ного на цилиндрической поверхности р = а (рис. 4.24), показана возможность пост-
роения СИУ с экспоненциальной функцией Грина (4.3.14), а так же приведен эф-
фективный метод их решения.
4.5.1. Постановка задачи. Физическая модель вибратора.Криволинейным по-
лосковым вибратором (КПВ) будем называть металлическую полоску, располо-
женную на цилиндрической поверхности р = а (рис. 4.24). Ширина полоски 21,
182
ГЛАВА 4
Рис. 4.24 Криволинейный вибратор
угловая длина 2^. В зазоре шириной 2Ь действует стороннее электрическое поле
Е™, которое создает электрический ток, распределяющийся по поверхности ан-
тенны таким образом, что создаваемое им ЭМП удовлетворяет уравнениям Макс-
велла в свободном пространстве, граничным условиям на поверхности проводника
и условию излучения на бесконечности.
Для анализа вводятся следующие упрощения:
- проводник предполагается идеально проводящим, бесконечно тонким вдоль
координаты р и достаточно узким (21 « а, 21« X, где X — длина волны в сво-
бодном пространстве), поэтому будем учитывать только продольную составляю-
щую поверхностной плотности тока т]ф(ф,2);
- зазор в проводнике также считается узким (2Ъ « 2ла), и продольная состав-
ляющая Т|ф(ф, z) непрерывна в области зазора;
- на концах полоски поверхностная плотность тока обращается в нуль:
г|ф(^,г) = 0;
- распределение поверхностного тока по ширине в первом приближении мож-
но считать квазистатическим [25]:
(4.5.1)
где - неизвестная функция, описывающая азимутальное распределение поверх-
ностной плотности тока.
4.5.2. Вывод сингулярного интегрального уравнения. Для узкого КПВ объем-
ная плотность тока на полоске имеет вид:
(4.5.2)
В данной постановке имеем две компоненты векторного потенциала:
/р(рГ
Д(рГ
£.4(9)
sin((D - ф )
7 7 G(p,q)dV',
соэ(ф - ф )
(4.5.3)
где функцию Грина свободного пространства G(p,q) будем использовать в виде [1]:
Электрические симметричные вибраторы
183
-ikR
G(p, q) =
(4.5.4)
R — расстояние между точками р и q, которые в цилиндрической системе коорди-
нат определяются следующим образом:
R = ^/р2 +p,2-2pp'cos((p-(p’) + (z-z')2. (4.5.5)
Подставляя (4.5.2) в (4.5.3), получаем компоненты векторного потенциала:
Ар(Р)\
АДр).
£.пДф'-2')
sin(<p - ср')
cos(<p - ф')
G(p, a,tp',z ')с£ф ’ dz',
(4.5.6)
где S — поверхность криволинейного вибратора (рис. 4.24). Компонента Е элект-
рического поля и векторный потенциал А связаны дифференциальным соотноше-
нием [21]:
Е^Р) =
aW.
ik
/с2Аф(р)+ grad9 div А
(4.5.7)
где Wc - характеристическое сопротивление среды. Подставляя (4.5.6) в (4.5.7),
получаем поле Е от поверхностной плотности тока т|ф, распределенного по по-
верхности 5:
„ , , aW. г
E,(p) = -г- £
гк JS
K2(p,s) dS.
(4.5.8)
Здесь:
Kr(p,s) = к2 со8(ф — ф')G(p, s),
(ikR +1) .
K2(p,s) =----—-----sm(9 - ф )G(p,s),
(4.5.9)
где под символом s = s(a,9’,z') понимается точка, принадлежащая поверхности
S' вибратора. Учитывая, что д / д<р —> -д / dtp', получаем:
aWc
ik
aWc
ik
^(p^z'Jdz'ckp’.
Сф
(4.5.10)
д
Вводя нормированные переменные:
* = Ф/£, Г = ф7£, t,t' е [-1;!];
x = z/l, x' = z'/l, х,х' е [-1;1];
d = I / а, г — кр, Э = ка
(4.5.11)
и квазистатическое распределение поверхностной плотности тока по ширине по-
184
ГЛАВА 4
лоски от нормированных переменных:
перепишем (4.5.10) в виде:
Ev(r,t,x)
iWc
1
= jт|ф(t ')Dp (r, t, x, t ')dt ’+
-i
(4.5.12)
В выражении (4.5.12):
(r,t,x,t')
dx'\ p = 1,2,
2 cos(ffi-f)) e"i8R
4л SR^
K2(r,t,x,t',x') =
(i&RH +1) sin(4(t -1')) e~i&R*
R 2 4л SRH ’
RH = / 32 +1 - 2(r / 3)cos(£(t -1')) + d2(x -x')2.
Полагая, что тангенциальное электрическое поле в зазоре КПВ (т = а,
по модулю равно стороннему азимутальному электрическому полю
и переходя к производной поверхностной плотности тока по переменной t', при
г = $ , х = 0 получаем интегральное уравнение, записанное относительно функ-
ции Лф(^ ) и ее первой производной ri^t') = дт)ф(£’)/д£':
E$m(t)
iW^d
(4.5.13)
с ядрами:
cos(^(t-t’))
» ! I и VvtAz
(4.5.14)
Электрические симметричные вибраторы 185
Здесь L = 5/2(1 - cos(^(t - t'))) + d2x2 . Несложно показать, что ядра Kp(t,t') (р = 1,2)
интегрального уравнения (4.5.13) в неявном виде содержат особенности (это следует
из свойств полных эллиптических интегралов К(т) и Е(т) [26], к которым сво-
дится асимптотика ядер):
In t — t'
lim K2(t,t') =
1 1
27id3^ t -1'
(4.5.15)
Переписывая (4.5.13) с учетом (4.5.14), (4.5.15), получаем сингулярное интеграль-
ное уравнение следующего вида (t е [-1,1]):
1 1
-1 -1
-1 -1
(4.5.16)
где:
Rp(t,t') =
2jid£
lim Ko(t,t
(4.5.17)
a = 2лЗ^/(iWc) - константа.
4.5.3. Решение сингулярного интегрального уравнения. Решать СИУ (4.5.16)
будем методом моментов. Неизвестная функция т]<р(О и ее первая производная
г]' (t') представляются в виде полиномиальных рядов:
N
^kAkTk(f)
(4.5.18)
где Т^х) - полином Чебышева первого рода порядка k, U^(x) - полином Чебы-
шева второго рода порядка к, — неизвестные коэффициенты разложения.
Подставляя разложения (4.5.18) в СИУ (4.5.16), имеем:
186
ГЛАВА 4
N
-t Uk_1(t,)Rl(t,t,)dtt +
(4.5.19)
Сингулярные интегралы в (4.5.19) определяются аналитически:
dt' =
= c£4+i(t') + + c™uk_3(t"),
(4.5.20)
V Tk(t')
r(D = 71 r(3) _ 71
k 4(k + l)’ k 4(k-l)’
C<2,=-^ (fc2-l)
Представим разностные ядра (4.5.17) в виде рядов Фурье (р = 1,2):
im—w
^р(^) — t R"mpe ’
7П = -00
2 . л
| /• -гт —w
R-mp ~ ~7 I Rp(,a?)e dw,
4 J
-2
(4.5.21)
где w = t -1 ’.
Используя известные разложения экспоненты по полиномам Чебышева и фун-
кциям Бесселя [26]
Электрические симметричные вибраторы
-im—t'
S т"'2
im—t' , ,
2 = £ (2 - 80Л )(-l)fc ik Jk (тп/ 2)Тк (t).
к=0
187
(4.5.22)
Jn (тл / 2)
тл /2
(4.5.23)
получаем две двойные суммы:
е 2 = У y^(-l)fcifc+ fcnJcfc(7n7i:/2)x
п-1 к=1
xJcn (тл / 2)17^ (t (t),
N N
(4.5.24)
im—(t-t')
2
k=0 n=l
(4.5.25)
xCn (тл / 2)Jfe (тл / 2)Tk (t ')ип_г (t),
где:
Подставляя (4.5.24) в (4.5.21), получаем эффективное разложение разностного
ядра Ri(t,t') в двойной полиномиальный ряд с коэффициентами
п=1 /с=1
М
“™fc= Ё (~l)kik+nknRmlCk(mn / 2)Сп{тл / 2).
т=-М
(4.5.26)
Подставляя (4.5.25) в (4.5.21), получаем разложение второго ядра с аналогичны-
ми коэффициентами:
N N
n=lk=G
00
“nk = E <.-l)k(2-S0:k)in+k-1nRm2Cn(mn/2)Jk(m7z/2),
m=—oo
(4.5.27)
где
188
ГЛАВА 4
fl,n = к,
5п’к = [0,П^к
- символ Кронекера.
Подставляя (4.5.20), (4.5.26), (4.5.27) в (4.5.19) с учетом ортогональных свойств
полиномов Чебышева
J I „ п е ®п,к’ J’l Un(t)Uk(t)dt ®п,к’
-1 VI-t2 2“Чо -1 2
получаем систему линейных алгебраических уравнений (СЛАУ) для определения
неизвестных коэффициентов разложения Ак в (4.5.18):
N
Еп = + С - ~
k=l
Здесь:
М
Pn,fc=? Е ^)kik+n^RmlCk(mn/2)Jcn(mn/2),
2 m=-M
М
РпЛ=л X (.-V/cin+k~1nkRm2Cn(mn/2)Jk(mn/2),
m=—M
n(3) p(l)x -|_ p(2)s _|_ р(3)г
Pn,k °n-l,k+l + 4c °n-l,k-l+4c °n-l,fc-3>
- матричные коэффициенты,
1
Vl-t2E™(t)Un_i(t)dt
— коэффициенты разложения стороннего поля по полиномам Чебышева.
4.5.4. Расчет амплитудной диаграммы направленности криволинейного по-
лоскового вибратора в азимутальной плоскости. Амплитудную диаграмму на-
правленности в дальней зоне КПВ в азимутальной плоскости z = 0 можно опреде-
лить по простой формуле [2,3]:
Яф(ф)
Еф max (ФО )
(4.5.28)
где
при
^<р max (ФО )
- максимальное значение составляющей , которое имеет место
(р - (р0. Азимутальное электрическое поле проще определить из функцио-
нального интегрального соотношения (4.5.12), которое удобно переписать в виде:
Электрические симметричные вибраторы
189
Еф(т,ф,^ = |пФ(*’)к1(Л
')dt' +
(4.5.29)
|п'Ф(СК2(гЛф,г W,
где
К^гЛф,*')^
4лг
г e~i&R
d cos(cp -£,£') J . dp,
—1 V 1 _ P R
K2(r,t,(p,t') = -
We
4tu3
d sin(cp — £,£') f (i&R +1)
R = 7r2 / 32 + ! - 2(r / 9) соб(ф - ') + d2(t - P)2.
В (4.5.29) введены нормированные параметры (4.5.11). Поверхностная плотность
тока и ее первая производная по t в соответствии с (4.5.18) записываются в виде:
П (t) =
N
f(t)=YAkUk^’
k=0
N
f’(t} = -Y Ak(k + l)Tk+1(t).
k=0
(4.5.30)
Подставляя (4.5.30) в (4.5.29), получаем выражение для компоненты Еф электри-
ческого поля:
11/ f2
Elp(r)(p,t)= Г [ , „ /(f)Mi(r,<P,t,P,t')dpdt +
-i-Ji-p2
vi-t,27i-p2
(4.5.31)
где
М^ЛфЛР,*')
—£-^соз(ф-^’)-----
4та R
М2(т,фЛР,£') =
Wc
4лгЯ
-гЗК
d sin(9 - ')(iSR +1)——
R3
(4.5.32)
Для интегралов по переменной t' в (4.5.31) применим формулы квадратурного
интегрирования [26]:
190
ГЛАВА 4
Г л/1-Г2/(4 ’)dt'
Здесь:
- весовые коэффициенты,
— абсциссы соответствующих сумм. Аналогичные формулы также применимы
к внутренним интегралам по переменной Р :
М1(2)(Г>ФЛ0,*')
dp
0г
= cos
Окончательно получаем выражение для Е® :
Еф (г, ф, t) = У У w^)M1 (г, ф, t, р^, Sj )f(Sj) +
^2 j=1 i=1
(4.5.33)
Необходимо отметить, что выражение (4.5.33) справедливо как для дальней,
так и для ближней зоны антенны. Амплитудная диаграмма направленности Гф
определяется подстановкой (4.5.33) в (4.5.28) при условии г » G, t = 0.
4.5.5. Численное моделирование криволинейного полоскового вибратора. Вна-
чале приведем на рис. 4.25 численные результаты для полуволнового вибратора
(2^а/ X = 0.5) в воздухе (Wc =120л) с малой кривизной излучающей поверхности
(2^ = 10°).
Было установлено, что для относительной внутренней сходимости менее 0,1%
достаточно брать число полиномов Чебышева в разложениях (4.5.18) N = 50, число
Фурье — гармоник в разложениях (4.5.21) М = 50. При построении амплитудной
диаграммы направленности в дальней зоне число слагаемых в квадратурных сум-
мах можно ограничить Qj = Q2 = 5...10. Для ближней зоны эти значения существен-
но больше. В наших расчетах было положено в (4.5.33) Qi = Q2 = 40 При этих
параметрах расчет графиков рисунка 2 на ПЭВМ занял менее 15 секунд (AMD
Athlon(tm)-64 2.4 ГГц), что говорит об эффективности алгоритма.
Из рисунка 4.25,а видно, что распределение поверхностной плотности тока на
криволинейном вибраторе (2^ = 10°) практически не отличается от распределения
поверхностного тока на трубчатом полуволновом вибраторе [7], то же можно ска-
Электрические симметричные вибраторы
191
Рис 4.25. Распределение поверхностной плотности тока (а) и амплитудная
диаграмма направленности полуволнового КПВ с малой кривизной в азиму-
тальной плоскости (б); 1 — действительная часть П<р(^), 2 - мнимая часть
2^ = 10°, z = 0, г = 2000.
Рис 4.26. Амплитудные диаграммы направленности КПВ
в азимутальной плоскости с различной степенью кривизны:
а) ~ 2^ = 20°, б) ~ 2с = 40°, в) - 2^=60°
зать и о диаграмме направленности. Но в отличие от линейного полуволнового
вибратора, криволинейный не имеет нулей излучения, и чем больше степень
кривизны, тем сильнее это заметно. На рис. 4.26 представлены диаграммы направ-
ленности полуволновых криволинейных вибраторов с угловой шириной
2£, = 20°,40°,60°. Распределение поверхностной плотности тока здесь не приводят-
ся по причине малых отличий от рис. 4.25,а, что также говорит об устойчивости
решения.
На рис. 4.27 приведены результаты анализа амплитудной диаграммы направ-
ленности волнового КПВ (2Е>а / X = 1) с различной степенью кривизны.
Непосредственно на графиках показан сам вибратор (жирная линия на уровне
0.8). Здесь представлена последовательная картина изменения диаграммы в зави-
симости от угловой ширины полоски. Можно видеть, что при малом значении
£ —> 0 максимумы излучения приходятся на ср = 0 и ср = л. При S, —> л происходит
сдвиг максимумов на 90°.
192
ГЛАВА 4
100 80
100 80
100 80
260 280
Рис 4.27. Амплитудные диаграммы направленности волнового КПВ в азиму-
тальной плоскости с различной степенью кривизны, геометрия которых
показана на диаграммах
Таким образом, проведенные расчеты, позволяют сделать вывод о том, что
функция Грина (4.5.4) является удобным и универсальным преставлением, позво-
ляющим строить сингулярные и гиперсингулярные интегральные уравнения
для различных излучающих структур в различных системах координат. Интег-
ральные уравнения, полученные Поклингтоном и Халленом с помощью (4.5.4),
являются некорректными только вследствие некорректности физической модели
вибратора. Результаты, описанные в разделе 5 этого параграфа, хорошо согласу-
ются с результатами в [7], где было использованы другие представления функции
Грина G(p, q). По результатам расчета можно сделать следующие выводы:
- распределение поверхностной плотности тока на криволинейном вибраторе мало
зависит от кривизны излучателя. Это означает, что ток, рассчитанный
на линейном вибраторе, можно использовать для корректного расчета ЭМП
в ближней зоне криволинейных антенн вибраторного типа;
— криволинейный вибратор не имеет нулей в амплитудной диаграмме направлен-
6*
Электрические симметричные вибраторы
193
ности в азимутальной плоскости. То же можно сказать и об амплитудной диаграм-
ме направленности трубчатого вибратора в меридиональной плоскости;
— при увеличении угловой длины криволинейного вибратора (при неизменной
электрической длине 21 / X) происходит существенное изменение картины ампли-
тудной диаграммы направленности. В частности, происходит сдвиг максимума из-
лучения на 90 градусов (рис. 4.27).
4.6. Приближенное распределение тока по электрическому
вибратору, используемые при расчете его характеристик
в дальней зоне [2]
Обычно при расчете характеристик электрического вибратора в дальней зоне
используют приближенные распределения тока по электрическому вибратору за-
писанные выше. Эти распределения были получены при нестрогом решении урав-
нения Халлена (4.1.5) [2,17,18]. Они имеют следующий вид:
sin k(l} — z)
sin klY
sin k(l2 - z)
sin kL
(4.6.1)
4itiU sin kt sin kL
WAsin/cfL + L)
значение тока в точке питания
> ^1^2
длины по-
луплеч вибратора. Формула (4.6.1) является приближенной.
Для симметричного вибратора =l2 = Z) формула (4.6.1) упрощается:
Io sin k(l - z)
sin/d
(4.6.2)
Из уравнения непрерывности
Iz(z) + zcoQ(z) - 0,
(4.6.3)
получаем формулу для распределения погонного заряда на единицу длины вибра-
тора [Кл/м]:
coskft — z)
sin klj
- cos k(l2 + z)
npuz
sin kL
npuz
(4.6.4)
Для симметричного вибратора
7 - Неганов
ГЛАВА 4
194
/rfflllfc лЛйк
/ /21 = 1
Рис. 4.28. Приближенные распределения тока и заряда по электрическому
вибратору [2]
Q(z) =
±Л/НаБа [J0 COSk(? - |z|)
sin kl
(4.6.5)
верхний знак + относится к z < 0.
На рис. 4.28 приведены распределения тока и заряда по формулам (4.6.1) - (4.6.5)
по электрическому вибратору при различных геометрических его размерах. Сплош-
ные кривые - распределения тока, пунктирные кривые - распределение заряда.
Анализ графиков на рис. 4.28 позволяет сформулировать основные свойства
распределений тока и заряда на тонких вибраторах:
1. На концах вибратора имеют место узлы (нули) тока и пучности заряда.
На расстоянии 0.25 от концов образуются пучности тока и узлы (нули) заряда, еще
через 0.25Х — узлы тока и пучности заряда и т.д.;
Элркпгришхк^ симметпрг^сные вибраторы
195
2. Ток и заряд в каждой точке вибратора сдвинуты между собой по фазе (во
времени) на угол 90°;
3. Фаза тока и фаза заряда меняются скачком на 180° при переходе через ноль;
4. Ток в точках питания остается непрерывным, а заряд изменяется скачком;
5. В нессиметричном вибраторе пучности токов и зарядов на разных плечах
не одинаковы и их отношение зависит от их плеч и 12:
= Qm = sin pZ2
ln2 Qn2 sinpz/
В частности, при lY ж 0.5Х, 12 Ф 0.5Х ток и заряд в любой точке плеча 12 близко
нулю (?! +12 = 0.66л на рис. 4.28).
О распределении тока для вибраторов длиной 21 <§: 1 говорят, что оно синфаз-
ное, а для вибраторов длиной 21 > 1 — переменно-фазное.
Следует подчеркнуть, что распределения тока и заряда только стремятся
к синусоидальному закону при а / X —> 0 , никогда не становясь точно синусоидаль-
ными. Выражение (4.6.1) особенно несправедливо вблизи узлов тока, где векторный
потенциал определяется уже не локальным значением тока в данной точке вибра-
тора, а суммарным действием токов, текущих по достаточно удаленным участкам.
Действительное распределение тока в узлах не может обращаться в ноль и отли-
чается от синусоидального закона тем сильнее, чем толще вибратор.
Несмотря на приближенность распределений тока (4.6.1) в вибраторных антен-
нах, эти распределения успешно используются во внешней задаче при ДН, КНД
и сопротивления излучения вибратора. Это объясняется тем, что указанные пара-
метры являются интегральными характеристиками от функции распределения тока
и небольшие ошибки вблизи узлов распределения не дают заметного вклада
при интегрировании.
4.7. Электрические параметры прямолинейного симметричного
вибратора в дальней зоне [17]
4.7.1. Напряженность электрического поля, создаваемого симметричным виб-
ратором в некоторой точке М свободного пространства окружающего вибратор
может быть определена как векторная сумма полей, создаваемых в этой точке
всеми бесконечно малыми участками вибратора длиной dz (рис. 4.29). Так как
длина участка dz может быть сколь угодно малой, то распределение тока на этом
участке можно считать равномерным. Таким образом, симметричный вибратор
можно считать состоящим из непрерывно распределенных диполей Герца длиной
dz. Напряженность электрического поля в дальней зоне вибратора от каждого
такого участка в точке М рассчитывается по формуле (2.1.1).
Заменив в этой формуле 10 на 1(г), на dz, найдем комплексную амплитуду
напряженности электрического поля от каждого элементарного участка:
7*
196
ГЛАВА 4
Рис. 4.29. К расчету поля излучения в дальней зоне симметричного вибратора
dE0
= гЗОк
I(z)dz sin(0)
(4-7.1)
т.к. при ориентации вибратора вдоль оси z в пространстве существует только
меридиональная составляющая Ев, г' - расстояние от участка dz до точки М.
Если использовать сферическую систему координат, начало которой совпадает
с центром вибратора, а полярная ось z — с осью вибратора, то поле симметрич-
ного вибратора, как и диполя Герца, будет осесимметричным, т. е. не будет зави-
сеть от азимутального угла ф .Суммируя поля отдельных участков симметричного
вибратора, удобно найти элементарное поле двух симметричных участков (1) и (2)
на рис. 4.29:
dEfl = dE™
+ dE™,
(4.7.2)
а затем проинтегрировать полученное выражение по длине вибратора в пределах
О < z < I-
С учетом (4.7.1) и условия симметрии распределения тока (I(z) = I(-z)), получа-
ем
dEe = i3QkI(z)dz sin(0)
(4.7.3)
В дальней зоне разница между г/ и т2, наибольшее значение которой равно
длине вибратора, мало влияет на амплитуду поля, поэтому в знаменателе выра-
жения (4.7.3) можно считать г' « т2 ® г. В показателе степени этого делать нельзя,
так как разность расстояний может дать значительную разность фаз, тем боль-
шую, чем больше размер антенны по сравнению с длиной волны. Учитывая сказан-
ное, а также очевидные равенства т2 — г = z cos(0) и г/ — г = — z cos(0), из выраже-
ния (4.7.3) получаем
Электрические симметричные вибраторы
197
i4(}kp~ikr /
dEQ =1^----------------I(z)dz sin(0) (eitecos(e) + e-ifczcos(0)
/у* '
i6Gke~ikr
(4.7.4)
sin(0)I(z)dz cos(kz cos(0)).
Напряженность поля, создаваемую вибратором в точке М, можно найти ин-
тегрированием по всем элементам:
i
Е„ = J dE, =
2~ О
гбОк e~ikr
I
sin(0) f l(z)cos(kzcos(0))dz.
2=0
(4.7.5)
Как видно из выражения (4.7.5), величина поля и его зависимость от полярного
угла определяются распределением комплексных амплитуд тока по вибратору
и длиной вибратора. Соответственно магнитное поле вибратора имеет только
азимутальную составляющую = Ев /Wc.
Величина интеграла (4.7.5) слабо зависит от вида функции I(z). Поэтому для
вычисления поля действительное распределение тока во многих случаях можно
заменить синусоидальным (4.6.2):
I(z) = In sin(k(Z - z)), при 0 < z < I.
Тогда получим
i60kIne~ikr
sin(0) j sin(k(l - z))cos(kzcos(0))dz.
z=0
(4.7.6)
Отметим, что симметричный вибратор имеет фазовый центр, расположенный
в середине вибратора. Действительно, в выражении (4.7.6) фаза поля не зависит
от угловых координат, а множитель е~гкг / г описывает сферическую волну.
Вычисление интеграла в выражении (4.7.6) производиться заменой произведе-
ния тригонометрических функций их суммой. Выполнив вычисления, для ампли-
туды получим
601п cos(kZ cos(0)) - cos(kZ)
sin(0)
(4.7.7)
Формула для расчета напряженности поля через ток на входе антенны 10 имеет
вид
6OIo cos(kZ cos(0)) - cos(kZ)
r sin(kZ) sin(0)
(4.7.8)
В формулах (4.7.7) и (4.7.8) произведем переход от тока в пучности к току на входе
произведен на основании равенств, полученных из формулы (4.6.2) при z = 0:
Io = In sin(kl). (4.7.9)
4.7.2. Диаграмма направленности симметричного вибратора определяется
множителем в выражении (4.7.7), зависящим от угла,
198
ГЛАВА 4
Рис. 4.30. Диаграммы направленности симметричного вибратора для распре-
делений тока, изображенных на рис. 4.28 [17]
/е(0) =
cos(ZcZcos(0)) - cos(kZ)
sin(0)
(4.7.10)
Нормированная ДН получается умножением выражения (4.7.10) на нормирую-
щий множитель, равный величине, обратной fmax . При 21 < 5Х / 4 ДН имеет
один максимум, перпендикулярный оси. Для этого случая из формулы (4.7.10),
положив 0 = л/2, получим /етах = l-cos(/cZ). Таким образом, нормированная ДН
записывается в виде:
W =
cos(kl cos(O)) - cos(kZ)
(1 - cos(ZcZ)) sin(0)
при 21 <
51
(4.7.11)
4
При 21 > 5X / 4 необходимо определить направление максимального излучения
и затем вычислить нормирующий множитель.
Нормированные ДН представлены на рис. 4.30. Пространственные ДН получают-
ся вращением этих кривых вокруг оси z. При увеличении I / X ДН сужаются.
Однако уже при 21 > X в ДН появляются побочные лепестки, затем главный лепе-
сток расщепляется на несколько. Чем больше I / X , тем уже каждый лепесток
и тем больше их число. Из-за расщепления ДН вибраторы длиной 21 > 5л / 4
на практике применяются редко.
Для очень коротких вибраторов (kl 1) ДН имеет вид
(klY
Ш = Fe(6)=sin(0).
(4.7.12)
В этом легко можно убедиться, воспользовавшись разложением косинусов в сте-
пенной ряд. Таким образом, короткие вибраторы (2Z X / 2) имеют такую же ДН,
как и диполь Герца.
4.7.3. КНД симметричного вибратора может быть найден с помощью выра-
жения (2.2.9) по известной нормированной ДН. В частности, для ДН, определяемой
формулой (4.7.11), имеем
cos(kZ cos(0)) - cos(ZcZ)
(1 - cos(fcZ))
sin(0)
(4.7.13)
Элетсгпртгч^ск^ сцл^иетпричные вибраторы
199
Интеграл в (4.7.13) выражается через интегральный синус и косинус.
ДН и КНД полуволнового вибратора. Для этого вибратора kl = л/2
т.е. ненормированная и нормированная ДН совпадают:
0 max
(0) = F(0) = cos — cos(0) /sin(0).
Для полуволнового вибратора интеграл в формуле (4.7.13) равен 1.22, поэтому
D = 1.64.
4.7.4. Действующая длина симметричного вибратора рассчитывается с по-
мощью выражения (2.7.3), причем Етах определяется по формуле (4.7.7). Для виб-
раторов с одним максимумом ДН действующая длина, отнесенная ко входу антен-
ны, на основании определения (2.7.3) получаеться равной
гдо = ^-^-(l-cos^)).
(4.7.15)
Учитывая соотношение (4.7.9), получаем
2 1- cos(kZ)
л° k sin(kl)
(4.7.16)
лп = — (1 - cos(/cZ)) = — sin
Напряженность электрического поля в максимуме ДН рассчитывается через
действующую длину по известной формуле
Ев = 30к1
V
до
(4.7.17)
Действующая длина полуволнового вибратора одинакова при отсчете как
к току в пучности, так и к току на входе, так как у этого вибратора пучность тока
совпадает со входными клеммами. Подставив в выражения (4.7.16) и (4.7.17) I = X / 4,
получим
« 0.64(21).
(4.7.18)
Действующая длина коротких вибраторов (21 X) относится обычно ко вход-
ным клеммам. При kl <s: 1 tg(kZ/2) « kl/2, поэтому по формуле (4.7.16) получаем
Ьдо — If
(4.7.19)
т.е. действующая длина коротких симметричных вибраторов равна половине их
геометрической длины.
Действующая длина вибраторов с концевой нагрузкой также определяется
по отношению к току на входе. Порядок расчета такой же, как и при выводе
формулы (4.7.18), только для определения Е0тах нужно использовать соответству-
ющее распределение тока. За счет концевой нагрузки распределение тока на конце
200
ГЛАВА 4
вибратора становится более равномерным, поэтому в общем случае действующая
длина вибратора с концевой нагрузкой больше, чем без нее.
4.7.5. Сопротивления излучения симметричного вибратора может быть рас-
считано с помощью известного поля в дальней зоне. Так как поле определено
приближенно в предположении синусоидального распределения тока по вибрато-
ру, то и сопротивление излучения будет иметь приближенное значение тем
более точное, чем тоньше вибратор.
Учитывая в выражении (4.7.7) осевую симметрию поля вибратора и указанные
выше соотношения, для сопротивления излучения, отнесенного к току в пучности,
получаем выражение
, =(. j(eos(Hcos(e)-eos(W))) de.3o([Sj(4fci) - 2Si(2/d)] sin(2kl) +
+ [С + ln(fcl) + Ci(4kl) - 2Ci(2fcl)] cos(2kl) + 2[C + ln(2kl) - Ci(2kZ)]},
(4.7.20)
где Si(.r) и Ci(x) ~ интегральные синус и косинус аргумента х, а С«0.577 -
постоянная Эйлера. График зависимости от отношения величин I / X , постро-
енный по этой формуле, показан на рис. 4.31.
Отметим две характерные точки: для полуволнового вибратора R^ « 73.1 Ом,
а для волнового R^ & 200 Ом.
4.7.6. Входное сопротивление симметричного вибратора может быть опре-
делено через известные выражения для напряжения и тока на его входе. Таким
способом пользуются в случае тонких вибраторов, когда эти выражения достаточ-
но просты и точны. В случае не очень тонких вибраторов (1/2а < 1000) обычно
пользуются экспериментальными данными. На рис. 4.32 показаны эксперименталь-
ные кривые зависимости активной Ко и реактивной Хо, где нижний индекс “0”
у составляющих входного сопротивления означает, что ток берется в точке пита-
Рис. 4.31. Сопротивление излучения симметричного вибратора, отнесенное к
току в пучности [17]
Электрические симметричные вибраторы
201
ния, составляющих входного сопротивления цилиндрического симметричного виб-
ратора для разных относительных диаметров [17].
Отметим некоторые наиболее важные закономерности.
При I < X / 4 активное сопротивление мало зависит от толщины вибратора и с
увеличением длины монотонно растет. При I / X « 0.5 входное активное сопротив-
ление достигает максимума, затем уменьшается, затем снова возрастает при при-
ближении к I = X и т. д. Положение максимумов Ro сильно зависит от толщины
вибратора: для очень тонких вибраторов максимум достигается при длинах I,
близких к пк / 2, где п — целое число. Таким образом, большое значение Ro
будут иметь вибраторы длиной 21 & X, 2Х, ЗХ,... Чем толще вибратор, тем при мень-
ших I / к достигается максимум Ro и тем меньше его величина. Если зафиксиро-
вать длину вибратора и изменять рабочую частоту (длину волны), то окажется,
что более толстые вибраторы будут более диапазонными, так как их входное
сопротивление меняется более плавно, чем у тонких вибраторов.
Реактивная составляющая входного сопротивления Хо с изменением I / к так-
же изменяется в очень широких пределах между положительными и отрицатель-
ными значениями, проходя через нуль. Увеличение толщины вибратора уменьша-
ет максимальные значения, сглаживает кривую Хо(I/к), т. е. ведет к расширению
рабочего диапазона вибратора.
С увеличением длины вибратора бегущая составляющая волн тока становится
все больше. При этом максимумы реактивной составляющей входного сопротивле-
ния уменьшаются, а максимумы и минимумы активной составляющей сближают-
ся, стремясь в пределе к величине волнового сопротивления вибратора Ze. Когда
длина каждого плеча вибратора станет больше примерно десятка длин волн, вход-
ное сопротивление будет активным, близким к величине Zo.
Резонансная длина 21 вибратора — это такая длина, при которой реактивное
сопротивление на входе антенны Хо = 0. Для очень тонких вибраторов резонансная
длина 2Z близка к целому числу полуволн: к / 2, к, ЗХ / 2,... Однако даже у беско-
нечно тонких вибраторов резонанс наступает при нескольких меньших длинах волн,
чем указано. Чем больше толщина вибратора, тем больше так называемое укоро-
чение вибратора, т. е. отличие резонансной длины от величины, кратной целому
числу полуволн.
Резонанс при 21 ~ к/2 называется первым, при 21 » к — вторым и т. д. При
увеличении номера резонанса абсолютное значение укорочения растет. Эти укоро-
чения выражаются формулами
(2AZ)i - (ЧД’
(2Д!)2 = X - (2I„ )2,
(4.7.21)
где AZ ~ укорочение на одном плече вибратора.
Как видно из рис. 4.32, характер изменения реактивного сопротивления вблизи
нечетных и четных резонансов различен. Поэтому эквивалентные схемы антенны
по входному сопротивлению будут неодинаковыми при различных резонансах. Это
202
ГЛАВА 4
Х0(Ом
1200
800
400
0
-400
-800
-1200
-1600
О 0.2 0.4 0.6
а) б)
Рис. 4.32. Активные (а) и реактивные (б) составляющие входного сопротивле-
ния симметричных вибраторов различной длины I и толщины 2а [17]
иллюстрируется рис. 4.33, где показаны кривая реактивного входного сопротивле-
ния и соответствующие эквивалентные двухполюсники. Вибратор фиксированной
длины при изменении частоты вблизи нечетных резонансов эквивалентен последо-
вательному резонансному контуру, а вблизи четных — параллельному. При 21 < X / 2
вибратор имеет емкостное входное сопротивление, при X / 2 <21 < X — индуктив-
ное и т. д.
Собственная длина волны Хо (первая гармоника) симметричного вибратора
есть наибольшая из длин волн, при которой данный вибратор не имеет на входе
реактивного сопротивления, т. е. длина волны на первом резонансе. Выполнив
в формулах (4.7.21) замену л —> Хо и (21р) —> 21 получим
Хо =2[2Z + (2Al)J. (4.7.22)
Таким образом, собственная длина волны несколько больше удвоенной полной
геометрической длины вибратора.
Изложенная выше методика позволяет получить необходимые данные по вход-
ному сопротивлению вибраторов произвольной длины и толщины. Однако она тре-
бует или сложных расчетов или использование экспериментальных данных. Одна-
ко в ряде частных случаев существуют достаточно простые расчетные формулы.
Рассмотрим некоторые из них.
Входное сопротивление полуволнового вибратора. Для тонкого вибратора дли-
ной 21 - 1 / 2 различные методы дают одинаковое значение входного сопротивле-
ния
Электрические симметричные вибраторы
203
Рис. 4.33. Двухполюсники, эквивалентные симметричному вибратору [17]
Zo = (73.1 + г‘42.5) Ом (4.7.23)
Таким образом, вибратор, имеющий длину, равную точно А./2, не настроен
в резонанс: он имеет на входе реактивное сопротивление индуктивного характера.
Это хорошо видно и на рис. 4.33. С увеличением толщины обе составляющие вход-
ного сопротивления немного возрастают, причем реактивная составляющая возра-
стает больше, чем активная.
Укорочение полуволнового вибратора AZ, необходимое для настройки вибрато-
ра в резонанс, зависит как от толщины вибратора, так и от формы входного
зазора. Для достаточно тонких вибраторов паразитную емкость в зазоре можно не
учитывать. При этом укорочение можно определить из аналогии с разомкнутой
длинной линией.
Обозначим ХА реактивное сопротивление на входе вибратора при 21 = А, / 2
и найдем наименьшую длину эквивалентной линии, имеющей такое же входное
сопротивление. Так как ХА > 0, то длина эквивалентной линии должна лежать
в пределах 1 / 4 < 1Э < А / 2, при этом можно записать 1Э = 1/4 + Д1. Входное сопро-
тивление разомкнутой линии, как известно, равно
X = -Wctg(k?a) = -Wctg(fc(X / 4 + AZ)). (4.7.24)
Укоротив линию на отрезок AZ, получим первый резонанс. Эту величину AZ
и будем считать укорочением полуволнового резонансного вибратора (на одно пле-
чо). Волновое сопротивление линии должно быть равно волновому сопротивлению
вибратора We. Последнее изменяется по длине вибратора, поэтому под ним подра-
зумевают (для полуволнового вибратора) некоторое усредненное по длине значе-
ние. Для расчета We имеется несколько примерно равноценных приближенных
204
ГЛАВА 4
формул. Воспользуемся формулой, полученной для не очень толстых цилиндри-
ческих вибраторов [17],
W =120 In
(4.7.25)
\ \а 7 7
Из формулы (4.7.24), положив X = ХА , получим
cos к— cos (к Al) - sin к— sin(kAl)
г \
в /
sin к
(4.7.26)
cos(kAZ) + cos к
sin(kAl)
Укорочение AZ/Х составляет несколько процентов, поэтому cos(/cAZ)«l,
a sin(fcAZ) « kAL. Отсюда, учитывая, что /сХ/4 = л/2, и полагая Х/2 » 21, из вы-
ражения (4.7.26) получаем
AZ 2Ха
Т~ 7iW ‘
о
(4.7.27)
С учетом формулы (4.7.25) и положив ХА » 42.5 Ом, из равенства (4.7.27) получим
А1
(4.7.28)
здесь Al = Alj в обозначениях формулы (4.7.21) которые можно использовать
при X / 2а > 50 .
Существуют расчетные формулы и для более толстых вибраторов [17].
Входное сопротивление волнового вибратора У такого вибратора, если считать
распределение тока синусоидальным, 10 = 0. Фактически вибратор излучает, сле-
довательно, имеется бегущая волна тока, при этом 10 Ф 0. Для расчета входного
сопротивления такого вибратора при не очень большой его толщине (21/ а >100)
может быть применена аналогия с разомкнутой на конце двухпроводной линией
с потерями. Эта линия также имеет на входе составляющую тока, соответствую-
щую бегущей волне. Примем действительную часть волнового сопротивления ли-
нии W = We (4.7.25). Постоянная распространения является комплексной величиной
у = а - гр, (4.7.29)
где а - фазовый коэффициент, который в первом приближении можно принять
равным /с; Р — коэффициент затухания на единицу длины линии. Будем считать
сопротивление излучения равномерно распределенным по длине вибратора,
при этом сопротивление на единицу длины эквивалентной длинной линии будет
равно R^ /I, а коэффициент затухания [17]
Р = ^-. (4.7.30)
ZWe
Электрические С21мм^тр]£^^^ вибраторы
205
Активная составляющая входного сопротивления линии с потерями равна
О TIT J 20Z
Ro = Wish ---------------------
0 6 ^ch(2pZ) - cos(2/cZ)
(4.7.31)
При 21 / a > 100 величина £Z «: 1, поэтому можно ограничится первыми члена-
ми разложения в ряд гиперболических синуса и косинуса: sh(20Z)»2£Z,
ch(2pZ) « 1 + (2pZ)2 / 2. Учитывая также, что при 21 « Xcos(2/cZ) » 1, из формул (4.7.30)
и (4.7.31) получаем
W2
72
(4.7.32)
У тонких вибраторов это сопротивление может достигать очень больших значе-
ний, что затрудняет согласование.
Укорочение волнового вибратора, необходимое для его настройки в резонанс,
вычисляется примерно так же, как и для полуволнового вибратора. Однако ввиду
известных сложностей в определении Хо приводим график (рис. 4.34) зависимости
укорочения AZ /1 от относительной толщины вибратора.
Входное сопротивление вибратора вдали от резонансов. При 0 < 2Z < 0.4Х
и 0.6Х < 2Z < 0.9Х на входе нет ни пучности, ни узла тока. При таких длинах рас-
пределение тока можно считать близким к синусоидальному, а значение реактив-
ностей делекими от нуля. Поэтому можно вести расчет следующим способом.
Из очевидного равенства 0.51^-Rfn = имеем
sin2(/cZ)
(4.7.33)
Величина рассчитывается по формуле (4.7.20) или определяется по графи-
ку рис. 4.33. Реактивное входное сопротивление можно считать равным выходному
Рис. 4.34. Зависимость укорочения вибратора длиной 21 » X от его относи-
тельной толщины [17]
206
ГЛАВА 4
сопротивлению эквивалентной длинной линии без потерь. Таким образом,
= Ra - iWectg(W) =
sin (kl)
- zWectg(kl).
(4.7.34)
Входное сопротивление очень коротких вибраторов (21 X) может быть, ко-
нечно, определено по формуле (4.7.34). Однако активную часть этого сопротивле-
ния можно рассчитать гораздо проще - через действующую длину, которая
в случае 21 1 равна 1Д =1. Воспользовавшись формулой для сопротивления из-
лучения (оно же входное) диполя Герца заменив lY на 1Д =1, получим
= 80 л:2
(4.7.35)
Итак для короткого вибратора
(4.7.36)
4.7.7. Настройка и диапазонность симметричных вибраторов. Широкопо-
лосные вибраторы. Настройка в резонанс является обязательным условием эф-
фективной работы на передачу большинства линейных антенн. При заданном на-
пряжении на клеммах амплитуда тока на входе антенны
о
(4.7.37)
сильно зависит от величины Хвх. Максимальное значение амплитуды тока Io тах
получается при Хвх =0 т. е. при настройке в резонанс. Так как мощность излуче-
ния пропорциональна квадрату тока, то при неизменном напряжении на клеммах
мощность излучения резко возрастает при приближении режима работы к резо-
нансному. Настройка в резонанс имеет смысл только для узкополосных антенн.
Поэтому узкополосные антенны часто называют настроенными.
Реактивное входное сопротивление антенны в общем случае состоит из соб-
ственного реактивного сопротивления антенны ХА и сопротивления органов на-
стройки Хн : Хвх = ХА + Хн.
Рассмотрим основные методы изменения Хвх, т. е. настройки симметричных
вибраторов.
Подбор резонансной длины вибратора является лучшим способом его настрой-
ки, если вибратор предназначен для работы на одной фиксированной частоте.
Резонансная длина определяется формулами (4.7.21). При этом, если на частоте /х
длина вибратора соответствует первому резонансу (полуволновый вибратор), то
этот вибратор будет настроен в резонанс на частотах, кратных /х, т. е. при
f ж 2^,3/j, ... Здесь знак равенства приближенный, потому, что укорочение вибра-
тора только в первом приближении пропорционально номеру резонанса. Такой
способ настройки широко применяется в диапазоне коротких волн при работе
на фиксированных частотах.
Элетрпрические симметричные вибраторы
207
Рис. 4.35. Настройка вибраторов с помощью концевой нагрузки:
а) - в виде провода, перпендикулярного оси вибратора; б) - из двух
крестообразных проводов; в) - из широких металлических полос;
г) — из проволочных зонтов [17]
Изготовить вибратор, длина которого равна резонансной, не всегда возможно,
так как построить симметричный вибратор длиной, скажем, 100 м уже довольно
затруднительно. Эти трудности возрастают на подвижных объектах.
Настройка с помощью концевых нагрузок применяется для уменьшения про-
дольного размера вибратора. Этот способ также пригоден только для работы на
фиксированных частотах. Его возможности в уменьшении продольного размера не
очень велики, так как длина концевых нагрузок, как правило, не может быть
больше длины вибратора. Примеры выполнения вибраторов с концевыми нагруз-
ками показаны на рис. 4.35.
Концевые нагрузки применяются для настройки в основном вблизи первого
резонанса. Эквивалентная длина концевой нагрузки Г зависит от длины проводов
этой нагрузки ак и числа проводов. При числе радиальных проводов больше шес-
ти концевая нагрузка действует как сплошной диск. Подбором длины ак и числа
проводов добиваются выполнения условия первого резонанса
! + !’ = /=-- (А!). (4.7.38)
pl V /1
Применением концевых нагрузок достигается не только увеличение амплитуды
тока за счет резонанса: одновременно растет сопротивление излучения, так как
действующая длина увеличивается. Действительно, сравнивая распределения тока
для ненагруженного вибратора (пунктир на рис. 4.35,а) и нагруженного, можно
заметить, что у первого 1Д ® I, а у второго I < 1Д <21.
Настройка с помощью сосредоточенных реактивностей — катушек индуктив-
ности и конденсаторов — применяется в случае невозможности выполнить антен-
ну необходимых размеров, а также при необходимости перестраивать антенну
в широком диапазоне частот. Например, в самолетных КВ связных станциях тре-
буется настройка передатчика на любую частоту в диапазоне от 2,0 до 30 МГц.
208
ГЛАВА 4
Размеры самолетной антенны нельзя изменить существенно не только в полете,
но и на земле. Поэтому применяется набор переключаемых катушек и конденсато-
ров.
Общая схема последовательного включения реактивности настройки показана
на рис. 4.36,а. Условием резонанса является
Хн = -ХА. (4.7.39)
Если сама антенна далека от резонанса и не является очень толстой (21/ а > 100),
то для расчета ХА распределение тока приближенно можно принять синусоидаль-
ным. При этом
Хн = +Wectg(fcZ).
(4.7.40)
При использовании комбинированной настройки (с концевой нагрузкой) вместо
I нужно подставить 1 + 1'. Из формулы (4.7.40) видно, что при 2Z<X/2 Хн >0,
т.е. для настройки нужно включить катушку (рис. 4.32,6) с индуктивностью
(4.7.41)
Эта катушка как бы “удлиняет” вибратор до первого резонанса и поэтому называ-
ется удлинительной катушкой.
При X / 2 < 21 < X Хн < 0 , т.е. для настройки нужно включить конденсатор
(рис. 4.36,в) с емкостью
2nfWectg(kl)
(4.7.42)
Этот конденсатор как бы “укорачивает” вибратор до первого резонанса и поэто-
му называете» укорачивающим конденсатором.
Элементы настройки в виде сосредоточенных реактивностей не могут вли-
ять на распределение тока вдоль вибратора — они меняют лишь амплитуду тока
и его фазу по отношению к питающему напряжению. Поэтому ни ДН, ни действу-
ющая длина, ни сопротивление излучения не изменяются при подключении кату-
шек и конденсаторов ко входу антенны.
При работе на частотах, близких к первому резонансу, характер изменения
реактивного входного сопротивления такой же, как у последовательного контура
(см. рис. 4.33), поэтому для настройки применяется параллельный колебательный
контур (рис. 4.36,д), у которого кривая зависимости реактивного сопротивления
от частоты имеет обратный наклон по отношению к такой же кривой для последо-
вательного контура. Вблизи второго резонанса применяется последовательный ко-
лебательный контур (рис. 4.36,г). Такое включение согласующих контуров позволя-
ет расширить полосу частот, в которой реактивные сопротивления антенны
и контура взаимно компенсируются.
Диапазонность симметричного вибратора определяется изменением по частоте
входного сопротивления и ДН.
Для тонких вибраторов, полоса пропускания которых невелика, изменение ДН
в полосе пропускания можно не принимать во внимание и определять диапазон-
Электрические си^итиетричные вибратпоры
209
г)
0)
Рис. 4.36. Настройка симметричного вибратора с помощью соединительных
реактивностей [17]
ность по изменению входного сопротивления. Так как такие вибраторы вблизи
резонанса эквивалентны колебательному контуру, то и полоса пропускания мо-
жет определяться так же, как для колебательного контура.
Если окажется возможным непосредственно рассчитать логарифмический дек-
ремент затухания антенны 5, то полоса пропускания может быть рассчитана по
известной формуле [17]
А/ 6
Л 71'
(4.7.43)
Для расширения полосы пропускания нужно увеличить §. Делать это за счет
увеличения тепловых потерь невыгодно, так как при этом уменьшается к. п. д.,
поэтому такой способ иногда применяется лишь в приемных антеннах в тех случа-
ях, когда к. п. д. не играет роли. Включение органов настройки обязательно увели-
чивает добротность антенны и сужает полосу пропускания. Увеличение длины
вибратора или применение концевых нагрузок увеличивает Rz уменьшает Хн
и поэтому является эффективным средством расширения полосы пропускания. На-
конец, уменьшение запасов реактивной энергии в распределенных реактивностях
антенны также улучшает диапазонность. Запасы энергии в собственных реактивно-
стях вибратора характеризуются его волновым сопротивлением We = <jL0 / Со ,
где Lo и Со — некоторые усредненные по длине вибратора погонные индуктив-
ность и емкость. Запасы реактивной энергии тем меньше, чем меньше волновое
сопротивление.
Широкополосные вибраторы — это вибраторы с пониженным волновым сопро-
тивлением, т. е. вибраторы большой толщины. Эскизы таких вибраторов показаны
на рис. 4.1,г-ж и на рис. 4.37. За счет пониженного волнового сопротивления абсо-
лютные значения реактивных сопротивлений уменьшаются [см., например, фор-
210
ГЛАВА 4
Рис. 4.37. Широкополосные плоские вибраторы: а) — треугольный; б) —
трехстержневой плоский [17]
мулу (4.7.34)], кривые зависимости реактивного входного сопротивления от часто-
ты у толстых вибраторов вблизи резонансов сглаживаются (рис. 4.32,6). Вблизи
второго резонанса у толстых вибраторов резко понижается активное входное со-
противление (см. рис 4.32,а), что упрощает согласование с фидером.
Для того чтобы извлечь все выгоды из расширения полосы при утолщении
вибраторов, нужно принять меры для. уменьшения емкости между торцами виб-
раторов на входе антенны. Для уменьшения этой емкости входную часть толстых
вибраторов выполняют в виде конусов (см. рис. 4.1,г,ж).
Полоса пропускания толстых цилиндрических вибраторов может достигать 50%.
Большую полосу пропускания можно получить у биконических вибраторов
(см. рис. 4.1, д). Чем больше угол при вершине конуса у(), тем шире полоса про-
пускания. У толстых и биконических вибраторов полоса пропускания по входному
сопротивлению столь велика, что определяющим диапазонность может стать из-
менение ДН с частотой.
На практике находят применение также плоскостные широкополосные вибра-
торы, один из которых показан на рис. 4.1, е —так называемый Ж-образный
вибратор.
Другие примеры выполнения плоскостных широкополосных вибраторов пока-
заны на рис. 4.37. Их длина (горизонтальный размер) обычно составляет (0.3 - 0.4) Хо,
где Хо — длина волны в середине полосы пропускания. Распределение тока
у плоскостных вибраторов сильно отличается от синусоидального, поэтому ДН
и другие характеристики определяются в основном экспериментально.
Электрические симметричные вибраторы 211
4.8 Петлевой вибратор Пистолькорса [17]
Конструкция петлевого вибратора показана на рис. 4.1,6 и 4.38. Он состоит
из двух вибраторов — активного и пассивного, которые связаны сильной электро-
магнитной связью за счет ближних полей и кондуктивной связью с помощью
перемычек на концах вибратора. В общем случае диаметры вибраторов могут
быть различными. Впервые такой вибратор был предложен А. А. Пистолькорсом
в 1936 г.
Если длина вибратора 21 » X / 2, то в обоих плечах устанавливаются стоячие
волны тока одинаковой фазы с пучностью в середине вибраторов. В середине пас-
сивного вибратора (в точке О) заряд равен нулю, т. е. в этой точке нулевой потен-
циал по отношению к экрану (земле). Это является существенным конструктивным
достоинством петлевого вибратора — в точке О его можно заземлять, например,
закрепляя на металлической заземленной мачте или на стойке, соединенной
с корпусом летательного аппарата.
Диаграмма направленности петлевого вибратора очень близко совпадает с ДН
полуволнового вибратора (см. рис. 4.30), так как обязательным условием изготов-
ления вибратора является выполнение неравенства d X, где d — расстояние
между активным и пассивным вибратором. Таким образом, по нормированной ДН
петлевой вибратор эквивалентен обычному полуволновому вибратору. Однако вход-
ное сопротивление и сопротивление излучения будут существенно отличными при
одинаковых токах на входе 10: у петлевого вибратора имеется еще ток 12 в пас-
сивном вибраторе, который может быть как больше, так и меньше тока 1().
Входное сопротивление петлевого вибратора. Рассмотрим петлевой вибратор
длиной 21 (рис. 4.39,а) с радиусами активного 1 и пассивного 2 вибраторов
и с расстоянием между ними d . Токи в серединах этих вибраторов (они же — токи
в пучностях) имеют амплитуды 10 и 12 и одинаковые фазы. Направления этих
токов и приложенного напряжения показаны на рисунке 4.38 для некоторого мо-
мента времени.
Напряжения и токи могут быть представлены в виде суммы напряженней токов
для двух видов колебаний в вибраторах: синфазных колебаний (рис. 4.39,6) и про-
тивофазных колебаний (рис. 4.39,в). Токи и напряжения синфазных и противофаз-
ных колебаний будут точно описывать режим колебаний в петлевом вибраторе,
если выполняются условия
Рис. 4.38. Распределение тока и заряда на петлевом вибраторе
212
ГЛАВА 4
Ic m
f©©t
Uc Uc
б)
п!с
Рис. 4.39. Суперпозиция
п!с
ТО 01
nUr
токов и напряжении в петлевом
.да"
nU,
О)
вибраторе [17]
п
с
п
п
с
с
п
Uc+nUc=U0; Ic+In=I0, (4.8.1)
где индекс " С " относится к режиму синфазных, а индекс " П" — противофазных
колебаний. Величина п примерно равна отношению волновых сопротивлений
Wel / We2:
(4.8.2)
При одинаковых напряжениях на клеммах обоих вибраторов (рис. 4.39,6) ток
во втором вибраторе будет в п раз больше, так как волновое сопротивление
этого вибратора в п раз меньше. Если в обоих вибраторах нужно поддерживать
одинаковый ток (рис. 4.39,в), то на клеммы первого вибратора нужно приложить
в п раз большее напряжение, чем на клеммы второго вибратора.
Схему рис. 4.39,6 можно заменить схемой рис. 4.35,г. Как видно в режиме синфаз-
ных колебаний петлевой вибратор эквивалентен обычному полуволновому вибра-
тору, плечи которого составлены из параллельно соединенных вибраторов разной
толщины. Входное сопротивление этого вибратора равно (в предположении сину-
соидального распределения тока)
= Rc - iWcctg (kl) =
(4.8.3)
где Rc = RIn «73.1 Ом - входное сопротивление полуволнового вибратора;
Wc = WelWe21 (Wel + We2) — эквивалентное волновое сопротивление в синфазном ре-
жиме; Wel и We2 рассчитываются по формуле (4.7.25).
В режиме противофазных колебаний петлевой вибратор может быть представ-
лен двумя последовательно включенными закороченными на конце двухпроводны-
ми линиями без потерь длиной примерно в четверть волны (см. рис. 4.39,в,д). Вход-
ное сопротивление каждой линии равно
Zn = iWritg(7d) =
(l + n)Uc
27п
(4.8.4)
где Wn - волновое сопротивление двухпроводной линии, составленной из прово-
дов разного диаметра.
Электрические симметричные вибраторы
213
500
400
300
100
0.5
0
Рис. 4.40. Зависимость входного сопротивления петлевого вибратора от
соотношения диаметров проводов [17]
Входное сопротивление петлевого вибратора определяется отношением
(4.8.5)
Отсюда с учетом формул (4.8.2)~(4.8.4) получим
2(l + n)2ZnZc
2Zn+(l + n)2Zc
(4.8.6)
Как видно из выражения (4.8.6), в системе наблюдается три резонанса (Хл = 0),
т.е. петлевой вибратор имеет более широкую полосу пропускания, чем обычный
вибратор.
Вблизи резонанса (I » X / 4) Zn —> оо, поэтому величиной (1 + п) Zc в знамена-
теле (4.8.6) можно пренебречь. Кроме того, при I « X / 4 реактивная составляющая
Zc стремится к нулю. Учитывая это, из выражения (4.8.6) получаем.
ZA « RA я (1 + п)2 Rc = 73.1(1 + п)2 Ом
(4.8.7)
График зависимости R0(ri) показан па рис. 4.40. Для наиболее часто встречаю-
щегося случая одинаковых диаметров п = 1 и RA = 4 • 73.1 ® 292 Ом. Если нужно
иметь входное сопротивление меньше этой величины, то диаметр активного виб-
ратора должен быть больше диаметра пассивного, и наоборот.
4.9. Особенности применения симметричных вибраторов [17]
Симметричные вибраторы применяются в диапазонах от коротких волн до сан-
тиметровых. Симметричный вибратор используется и как элемент сложной антен-
ной системы: в качестве облучателей зеркальных антенн, элементов возбуждения
антенн директорного типа, излучателей антенных решеток и т. п.
Так как электрическая симметрия получается при симметричном расположе-
нии вибратора относительно окружающих предметов, то вблизи экранов вибрато-
214
ГЛАВА 4
ры должны располагаться (и располагаются) параллельно поверхности экрана.
С увеличением высоты подъема антенны над экраном его влияние на распределе-
ние тока по вибратору уменьшается и при высотах, больших (3-5)Х, становится
пренебрежимо малым. При этом вибратор можно располагать произвольно,
не нарушая симметрии.
На рис. 4.41 показан симметричный вибратор, используемый на дозвуковых
самолетах в радиовысотомерах УКВ диапазона [17]. Это толстый вибратор, разде-
ленный посередине изолятором 2. Каждое плечо вибратора 1 крепится к фюзеля-
жу 5 металлическими стойками 3 обтекаемой формы. Стойки имеют длину при-
мерно X / 4 и образуют двухпроводный четвертьволновый изолятор. Изолятор од-
новременно является согласующим устройством, так как его входное сопротивле-
ние с понижением частоты относительно центральной становится индуктивным,
а у вибратора емкостным. Изолятор, кроме того, является симметрирующим уст-
ройством для питания симметричного вибратора от несимметричного кабеля 4.
В силу ряда особенностей космических летательных аппаратов в них широко
используются симметричные вибраторы даже в диапазоне коротких волн [17].
Влияние экрана (земли) на диаграмму направленности и входное сопротивле-
ние вибратора так же, как и влияние других предметов, окружающих антенну,
сводится к тому, что часть электромагнитной энергии, излученной вибратором,
отражается от этих предметов. Поле в каждой точке пространства является ре-
зультатом интерференции непосредственно излученного и отраженного полей. При
этом распределение поля в пространстве, т. е. ДН вибратора, будет отличаться
от того, которое было бы в отсутствие отражающих предметов — ДН искажается.
Кроме того, отраженное поле, возвращаясь к вибратору, изменяет величину
и распределение тока в нем. Это приводит к изменению входного сопротивления
вибратора.
В общем случае точно оценить влияние окружающих предметов затруднитель-
но. Однако наибольшее значение для практики имеет вопрос о влиянии хорошо
проводящих плоских поверхностей (земля, металлический экран), параллельно
~Х/2
Рис. 4.41. Симметричный вибратор для самолетного высотомера [17]
Э^ртстричестулр силуирпу^ичр/ые вибраторы 215
которым обычно располагаются симметричные вибраторы.
Метод зеркальных изображений применяется для оценки влияния хорошо про-
водящих поверхностей. Из электростатики известно, что электрическое поле то-
чечного заряда, расположенного на высоте h над идеально проводящей плоской
поверхностью (рис. 4.42,а), в верхнем полупространстве не изменится, если заме-
нить проводящую поверхность зарядом противоположного знака, расположенным
на удалении 2h от действительного заряда на линии, перпендикулярной поверх-
ности.
Рассмотрим теперь диполь Герца — провод с зарядами противоположного зна-
ка на его концах. При изменении зарядов во времени по проводу течет ток I. Как
видно из рис 4.42,6 влияние плоского экрана на поле диполя Герца в верхнем
полупространстве можно учесть, заменив его зеркальным изображением диполя.
При горизонтальном расположении диполя ток в его зеркальном изображении
направлен в сторону, противоположную току в самом диполе, т. е. сдвинут по
фазе на л. Построением нетрудно убедиться, что ток в зеркальном изображении
вертикального диполя Герца будет синфазным.
Метод зеркальных изображений имеет и более строгое электродинамическое
обоснование — с помощью граничных условий на идеально проводящей плоскости.
Симметричный горизонтальный вибратор, изображенный на рис 4.42,в можно
считать состоящим из расположенных по оси вибратора диполей Герца. Поэтому
зеркальным изображением горизонтального симметричного вибратора будет такой
же вибратор с противофазным током. Таким образом, поле горизонтального виб-
ратора над идеально проводящей плоскостью можно рассчитать как сумму полей
самого вибратора и его зеркального изображения.
Здесь отметим, что при малой высоте (h < 0.1Л,) поле вибратора почти полнос-
Рис. 4.42. Зеркальные изображения: а) - точечного заряда; б) - диполя
Герца; в) — симметричного вибратора [17]
216
ГЛАВА 4
тью компенсируется полем зеркального изображения, т. е. антенна мало эффек-
тивна. При h = X / 4 поля вибратора и его зеркального изображения в направле-
нии, перпендикулярном отражающей поверхности, складываются. Поэтому гори-
зонтальные вибраторы диапазона УКВ обычно располагают над экраном и именно
на этой высоте.
Если земля не очень хороший проводник, то ее влияние также можно учесть
методом зеркальных изображений, приписывая току зеркального изображения
относительную амплитуду и фазу, соответствующие коэффициенту Френеля
для данных поляризации и свойств поверхности. Расчеты и измерения показыва-
ют, что потери в земле приводят к уменьшению амплитуды поля и к изменению
формы ДН.
Влияние земли на входное сопротивление вибратора после построения зер-
кального изображения может быть учтено с помощью метода наводимых э. д. с.
(см. § 8.3). На рис. 4.43 показан рассчитанный этим методом график зависимости
Rnth / X) Для горизонтального полуволнового вибратора над идеально проводящей
поверхностью. С удалением вибратора от поверхности сопротивление излучения
стремится к его значению для свободного пространства. На очень малых расстояни-
ях от земли сопротивление излучения очень мало, так как при этом поле излуче-
ния вибратора почти полностью компенсируется противофазным отраженным
полем.
Питание симметричных вибраторов в режиме передачи или подключение при-
емника к ним должно осуществляться с помощью симметричного фидера. Если
применяется коаксиальный кабель, то вблизи клемм вибратора ставится симмет-
рирующее устройство.
Симметричные фидеры имеют волновое сопротивление около 200— 600 Ом.
При непосредственном их подключении к вибратору с низким входным сопротив-
лением, например к полуволновому, получается недопустимо большое рассогла-
сование. Для устранения этого недостатка широко применяют шунтовое возбужде-
80
73.1
60
40
20
0.2 0.4 0.6 0.8 h/X
Рис. 4.43. Сопротивление излучения
горизонтального полуволнового вибра-
тора, расположенного над идеально
проводящей поверхностью [17]
21
2L
Рис. 4.44. Шунтовое питание
симметричного вибратора [17]
Электрич^стсие симмегтц^ вибраторы
217
ние симметричного вибратора от симметричного фидера, которое позволяет
в широких пределах изменять входное сопротивление, или же согласующий транс-
форматор.
Схема шунтового питания показана на рис. 4.44, шунт представляет собой две
последовательно соединенные двухпроводные линии, ширина которых d X.
В этих линиях текут противофазные фидерные токи 1Ш, поле излучения которых
очень мало за счет малого d . Однако ближнее магнитное поле шунта очень велико.
Оно охватывает основной вибратор и возбуждает в нем синфазный ток 1в, кото-
рый и создает поле излучения. Такое устройство напоминает автотрансформатор.
У полуволнового вибратора при изменении 1Ш от 0 до X / 4 входное сопротивле-
ние изменяется от 0 до 290 Ом (при одинаковых диаметрах проводов). Шунтовое
питание имеет и некоторые конструктивные преимущества: провод вибратора
можно заземлять в его середине.
218
ГЛАВА 5
Глава 5. Кольцевые (рамочные) антенны
5.1. Введение [17]
5.1.1. Типы кольцевых (рамочных) антенн. Рассмотренные выше антенны
представляют собой различные конструктивные варианты симметричного вибра-
тора. Они называются также разомкнутыми антеннами, или антеннами электри-
ческого типа. Наряду с ними применяются также замкнутые антенны, или антен-
ны магнитного типа. Примером антенны такого рода является так называемая
круглая антенна В.В. Татаринова в виде синфазного проволочного кольца или мно-
гоугольника с неизменной амплитудой на проводе. Часто замкнутые проволочные
антенны называют рамочными антеннами.
Рамочная антенна может состоять из одного витка провода (одновитковая рам-
ка) или нескольких последовательно включенных соосных витков провода (много-
витковая рамка). Различают рамочные антенны, размеры которых малы в сравне-
нии с длиной волны (электрически малые рамки), и рамочные антенны, размеры
которых сравнимы с длиной волны. Для увеличения действующей длины электри-
чески малых рамок они иногда снабжаются магнитным сердечником.
Применяются также экранированные рамки. Назначение экрана, в который по-
мещается рамка, состоит в том, чтобы предохранить ее от влияния окружающих
предметов, приводящего к нарушению электрической симметрии рамки.
5.1.2. Электрические параметры в дальней зоне электрически малой ра-
мочной антенны. Электрически малые рамки применяются на практике преиму-
щественно в качестве приемных антенн. Поэтому рассмотрим работу рамочной
антенны в режиме приема.
Пусть на плоскую одновитковую рамку произвольной формы (на рис. 5.1,а
для простоты изображена круглая рамка) падает плоская электромагнитная вол-
на, вектор Умова-Пойнтинга S которой образует угол 0 с нормалью к плоскости
рамки (рис. 5.1,6). Полагая, что размеры рамки малы в сравнении с длиной вол-
ны, можно определить комплексную амплитуду ЭДС е, индуцированную в рамке
в соответствии с законом индукции
е = -гсоФ,
где Ф = pHS sin 0 - комплексная амплитуда магнитного потока, пересекающего
рамку. Здесь s - площадь рамки; ц - магнитная проницаемость среды; Н - комп-
лексная амплитуда напряженности магнитного поля.
Учитывая, что для вакуума Н = Е
/120л, получаем
. цю -
е = -г---s Е
120л
sin 0.
(5.1.1)
Для свободного пространства ц = =4л-10 7 Гн/м. Кроме того, о = /сс, где
к = 2л / X и с = 3 • 108 м/с. Подставляя значения ц и со в формулу , будем иметь
е = -iks
sin 0.
(5.1.2)
Е
Кольцевые [рамоцные} амтенны
219
б)
Рис. 5.1. К определению электрических параметров электрически малой рамки [17]
Если рамка состоит из п витков, то ЭДС будет в п раз больше:
е = -ikns
Е sin 6.
(5.1.3)
Амплитудное значение ЭДС равно
Наибольшая величина амплитудного значения ЭДС соответствует условию
. ллО .
тлтг = кПЗЕ.
Il id А
(5.1.5)
Таким образом, ДН рамки имеет вид «восьмерки» F(0) = sin 6 в плоскости, перпен-
дикулярной рамке и содержащей ее ось (рис. 5.2), и вид окружности в плоскости,
содержащей рамку. ЭДС, индуцированная в рамке волной, приходящей с левого
(О < 0 < 180°) полупространства, отличается по фазе на л от ЭДС, индуцированной
в рамке волной, приходящей с правого (180° <0<36О°) полупространства. ЭДС
сдвинута по фазе на угол ±л / 2 по отношению к фазе электрического (и магнит-
ного) поля падающей волны в центре рамки.
Направленные свойства рамки позволяют использовать ее для определения на-
правления на радиостанцию. Например, если перпендикуляр к плоскости рамки
совпадает с направлением распространения радиоволны, то ЭДС в рамке равна
нулю (пеленгация по минимуму сигнала).
Действующая длина рамки по определению равна
значение етах из (5.1.5), получаем
max
Е . Подставляя
Iq = kns.
(5.1.6)
Обычно рамка вместе с конденсатором настройки С (см. рис. 5.1,а) образу-
ет входной контур приемника. Максимальное напряжение, снимаемое с контура
(в точках аа’), равно
max Qemax knsQ Е
где Q - добротность контура, образованного рамкой и конденсатором.
Эффективную действующую длину рамки определяют как
эф
(5.1.7)
Сравнивая (5.1.6) и (5.1.7), получаем
эф
Для увеличения 1дэф нужно, чтобы произведение SQ было максимальным. Это
значит, что рамка заданной площади должна иметь максимальную добротность,
т.е. минимальное омическое сопротивление. Этим свойством обладает круглая рамка,
- ^тпйу / е - knsQ.
11 id л '
220
ГЛАВА 5
Рис. 5.2. ДН электрически малой рамки
имеющая наименьший периметр при заданной площади.
Сопротивление излучения рамки можно определить по формуле (2.3.6), под-
ставляя вместо li значение 1д из (5.1.6):
R% = 3207i4(ns/X2)2. (5.1.8)
2
Так как у электрически малой рамки отношение s / А. <§: 1, то ее сопротивление
излучения ничтожно мало. Мал поэтому и КПД рамки, ввиду чего на длинных
и средних волнах рамки применяются преимущественно в качестве приемных ан-
тенн. Как известно, на указанных волнах качество приема зависит не от КПД
антенны, а от отношения сигнал/помеха. Направив ось рамки ( 0 = 0°и 0 = 180° )
на мешающую станцию, можно существенно улучшить качество приема. Следует
отметить, что увеличение числа витков рамки ограничено из-за роста ее индук-
тивности, которая для настройки контура рамки в резонанс не должна быть боль-
ше вполне определенной величины. Эта величина зависит от начальной емкости
контура (рис.5.1,а).
5.1.3. Рамки с магнитным сердечником. Значительного увеличения дейс-
твующей длины рамочной антенны можно достигнуть, применяя рамки с маг-
нитными сердечниками. Для изготовления сердечника используется материал,
имеющий свойства диэлектрика (ничтожно мала проводимость), но обладающий
большим значением относительной магнитной проницаемости ц. Широко применя-
ются для этой цели ферриты, у которых величина ц составляет несколько сотен
и даже тысяч. Если в рамку вставить магнитный сердечник ( рис. 5.3), то магнит-
ный поток сквозь нее возрастет.
Способность сердечника концентрировать магнитный поток характеризуют маг-
нитной проницаемостью сердечника, которую можно определить по формуле
цс=ц/[1 + (М-ОТ
(5.1.9)
где 7V - коэффициент размагничивания, учитывающий размагничивающее дейс-
твие концов сердечника и зависящий от его формы.
Аналитические выражения для коэффициентов размагничивания имеются
только для некоторых сердечников правильной геометрической формы. Наиболь-
ший интерес представляет выражение для вытянутого сфероида, так как широко
применяемые на практике сердечники в виде призмы и цилиндра в первом прибли-
жении могут быть аппроксимированы вытянутым сфероидом. Расчет коэффициен-
та размагничивания в этом случае можно вести по следующей формуле:
(5.1.10)
Кольцевые (рамочные) антенны
221
Рис. 5.3. Рамка с магнитным сердечни-
ком [17]
Нс
120
100
80
60
40
20
4 8 12 16 20 24 28 l/d
Рис. 5.4. Зависимость магнитной проницае-
мости сердечника от отношения I / d [17]
где £ = y/(l2 -d2) / Z2 - эксцентриситет сфероида; I и d - большая и малая оси сфе-
роида.
На рис. 5.4 приведены рассчитанные по формулам (5.1.9) и (5.1.10) графики за-
висимости магнитной проницаемости вытянутого сфероида от отношения его осей
при различной относительной магнитной проницаемости сердечника.
При применении магнитного сердечника ЭДС в рамке возрастает, следователь-
но, увеличивается и ее действующая длина, которую можно определить по фор-
муле
1д = кзп^рд, (5.1.11)
где Цд - магнитная проницаемость антенны; П]_ - число витков рамки с магнитным
сердечником.
Магнитная проницаемость антенны связана с магнитной проницаемостью сер-
дечника цс соотношением
На = тАцс, (5.1.12)
где тпд - коэффициент, который зависит от отношения длины рамки 1р к длине
сердечника 1С (см. рис. 5.3) и может быть определен по формуле
mA « 1 - 0,3Zp / 1С. (5.1.13)
Различие между величинами тд и цс объясняется тем, что величина магнит-
ного потока в сердечнике убывает от его середины к краям. Формула (5.1.13) спра-
ведлива, если рамка намотана с постоянным шагом и расположена симметрично
относительно сердечника. Смещение рамки к концу сердечника ведет к уменьше-
нию ТПд .
Применение магнитного сердечника приводит также к росту индуктивности
рамки L . Если витки намотаны вплотную, то можно считать, что индуктивность
пропорциональна квадрату числа витков
L = /с^рП2, (5.1.14)
где - коэффициент пропорциональности, - магнитная проницаемость рамки
как катушки индуктивности, определяемая соотношением
М-р тррс
(5.1.15)
222
ГЛАВА 5
Приемник
а)
Рис. 5.5. К пояснению антенного эффекта рамки [17]
Коэффициент тр зависит от отношения длины рамки к длине сердечника
и растет при увеличении этого соотношения [17]. Если 1р =1С, то тр = 1. Обычно
индуктивность рамки задана из условия согласования антенны со входом прием-
ника, тогда можно записать
L = крг2 = kippn2.
где п - число витков рамки без сердечника, обеспечивающее такую же индуктив-
ность, что и рамка с сердечником, при одинаковом размере обеих рамок. Тогда
имеем
(5.1.16)
Подставляя (5.1.16) в (5.1.17), получаем
1д = ksnpA / (5.1.17)
Таким образом, действующая длина рамочной антенны с магнитным сердеч-
ником возрастает в рА / Jpp раз в сравнении с действующей длиной рамочной
антенны без сердечника.
Во многих случаях можно считать, что » рА. Тогда
1д = ksn^pA. (5.1.18)
Следовательно, применение магнитного сердечника дает возможность при
неизменной площади витка рамки увеличить ее действующую длину в у/р^ раз
или при неизменной действующей длине уменьшить площадь витка в у]рА раз,
что в ряде практических случаев (например, на летательных аппаратах), явля-
ется важным.
5.1.4. Экранированные рамки. Выше было сказано, что диаграмма направ-
ленности рамки имеет вид симметричной восьмерки, а направление нулевого при-
ема перпендикулярно плоскости рамки. Однако ДН может быть искажена из-за
нарушения электрической симметрии рамки. Это явление называется антенным
эффектом рамки. Он может иметь место, например, тогда, когда рамка установ-
лена несимметрично, так что половины, симметричные по конструкции, имеют
Кольцевые [рамоу/ные} антенны 223
различную емкость по отношению к корпусу радиоприемника и другим окружаю-
щим предметам. Из-за этого токи и I2, протекающие по обеим половинам рамки
(рис.5.5,а), будут разными по величине и фазе.
Это можно интерпретировать как наличие в рамке синфазного 1С и противо-
фазного 1п токов (рис.5.5,б). Значения этих токов определяются из соотношений
~ + ^С’ ^2 ~ I-п ~ ^С’
откуда
In=(h+I2)/^IC = (lx -12)/ 2. (5.1.19)
Для простоты рассуждений влияние различия токов Ij и 12 поясним, пола-
гая, что рамка работает в режиме передачи и возбуждается тремя генераторами
(рис. 5.5,в). Генераторы с комплексной амплитудой ЭДС, равной е^, вызывают
в плечах рамки 1 и 2 противофазные токи 1п. ДН рамки, обтекаемой этими тока-
ми, имеет в горизонтальной плоскости вид восьмерки.
Генератор с комплексной амплитудой ЭДС, равной е2, вызывает в плечах рам-
ки синфазные токи 1С. Так как расстояние между плечами b <sz X, то оба плеча
излучают как один вертикальный несимметричный вибратор, и ДН рамки, обте-
каемой синфазными токами, имеет в горизонтальной плоскости вид окружности.
Результирующая ДН зависит от амплитудных и фазовых соотношений токов 1С
и 1п. Наличие токов 1С приводит к искажению ДН, которое может проявиться в из-
менении направления нулевого излучения (приема), или в том, что в ДН вообще
не будет провалов до нуля. При использовании такой рамочной антенны в режиме
приема для пеленгации радиостанций угловая точность измерений ухудшается.
Таким образом, различие токов в плечах рамки можно трактовать как результат
наличия синфазных токов. Чтобы устранить антенный эффект рамки, нужно ус-
транить эти токи.
Для этой цели рамку помещают в металлическую трубку-экран (рис.5.6), ко-
торый в верхней части имеет зазор. Электромагнитная волна наводит на внешней
поверхности экрана противофазные и синфазные токи. Однако на зазоре (в точках
аа') разность потенциалов возникает только за счет противофазных токов. Бла-
годаря этой разности потенциалов появляются противофазные токи на внутренней
поверхности экрана, а также и в самой рамке за счет электромагнитной связи.
Таким образом, рамка с экраном представляет собой высокочастотный трансфор-
матор.
Иногда экран изготовляют в виде незамкнутой заземленной обмотки, уменьша-
ющей емкостную связь между рамкой и окружающими ее предметами.
Рис. 5.6. Экранированная рамка [17]
224 ГЛАВА 5
5.1.5. Питание рамочных антенн. Рис. 5.7 иллюстрирует два способа пита-
ния рамочных антенн. Первый из них состоит в том, что несколько (на рис. 5.7,а
три) симметричных изогнутых трубчатых вибраторов располагаются по периметру
круглого кольца. Питание от общего коаксиального фидера 1 к каждому симмет-
ричному вибратору подается проводом, проложенным вначале внутри радиальной
трубки, а затем внутри одного плеча вибратора. Длина каждого симметричного
вибратора обычно равна или меньше половины длины волны. При этом направле-
ние тока по периметру кольца не меняется. Некоторое изменение величины тока
вдоль кольца на ДН рамочной антенны влияет незначительно.
При втором способе питания (рис. 5.7,6) применяют симметричный двухпровод-
ный фидер. Перекрещивая провода фидера в центре антенны и выбирая периметр
рамки равным или меньше 2Х, обеспечивают одинаковое направление тока по всем
вибраторам, образующим рамку. При этом максимум ДН лежит в плоскости рам-
ки.
5.1.6. Радиодевиация рамочных антенн летательных аппаратов. Элект-
рически малые рамки с магнитными сердечниками применяются на летательных
аппаратах для радиокомпасов. Рамочная антенна помещается заподлицо с обшив-
кой аппарата в специальном углублении - ванне, обычно цилиндрической формы
(рис.5.8). Напряженность электромагнитного поля убывает от раскрыва ванны к ее
Рис. 5.7. Способы питания рамочных антенн: а — коаксиальным фидером; б - двухпровод-
ным симметричным фидером [17]
Рис. 5.8. Вращающаяся рамочная антенна в цилиндрической ванне: 1 - рамка; 2 - меха-
низм вращения рамки; 3 - ванна [17]
Кольцевые (рамочные) антенны 225
дну и тем сильнее, чем глубже ванна. Поэтому обычно применяют неглубокие ван-
ны, а сердечнику придают форму параллелепипеда малой высоты. Раскрыв ванны
закрывают плоским диэлектрическим обтекателем.
Под влиянием приходящей волны на поверхности летательного аппарата воз-
буждаются токи, которые являются источником вторичных волн. Эти волны ин-
терферируют с приходящей волной, что приводит к изменению структуры поля
вблизи летательного аппарата. Вследствие этого ДН рамки несколько искажа-
ется. Это явление называется радиодевиацией. Величина радиодевиации зависит
от типа летательного аппарата и места размещения на нем рамки [17].
5.2. Электрические параметры кольцевых антенн, размеры
которых сравнимы с длиной волны, в дальней зоне [18]
Часто применяются горизонтальные рамочные антенны, размеры которых
не являются электрически малыми. Впервые такую ненаправленную в горизон-
тальной плоскости антенну, формирующую поле горизонтальной поляризации,
предложил В.В. Татаринов [18]. Обычно оценивается диаграмма круговой антенны,
вдоль которой амплитуда и фаза тока не изменяются [17,18].
5.2.1. Вывод общих выражений для поля излучения. Определим напряжен-
ность поля, создаваемого в дальней зоне кольцевой антенной, показанной на рис.
5.9, расположенной в плоскости хоу с центром в начале координат.
Пусть точка наблюдения р находится в плоскости xoz. Угловая координата 0
отсчитываются от оси oz , совпадающей с осью кольца, ср - угол от оси ох. Будем
считать, что кольцо проволочное с радиусом г' = а , а линейный электрический
ток I на нем задан в функции угловой координаты ср': I = 1(<р').
Для определения меридиональной и азимутальной составляющих напряжен-
ности электрического поля можно воспользоваться общими выражениями (1.5.8),
(1.5.10). При этом следует учесть, что магнитные токи отсутствуют: jm = 0.
Учитывая это, получим
ie~ikr
Eq = —-— p(Nx sin <p - N cos cp), (5.2.1)
2лг и
где
a)
Рис. 5.9. К расчету напряженности поля в дальней зоне кольцевой антенны [18]
6)
8 - Неганов
226
ГЛАВА 5
Nz = Jl(cp')eifcr cosa cos(Z,z)dl.
I
В нашем случае точка наблюдения располагается в плоскости xoz , следовательно,
(р = 0.
Учтем далее, что кольцо с током целиком расположено в плоскости хоу , сле-
довательно, cos(l,z) = cos 90° = 0. Как видно из рис. 5.9,6, угол (I, х) между направ-
ленным элементом dl и осью ох равен 90° +(р', следовательно, cos(Z,a?) = -sincp';
угол (Z, у) между dl и осью оу равен <р', следовательно, cos(Z, у) = cos ср'.
В нашем случае
cos a = sin 0 sin 0' cos(cp - (p') + cos 0 cos 0' = sin 0 cos cp
так как угол 0' между осью oz и направлением г' на любой элемент кольца
равен 90°.
В дальнейшем будем считать, что антенна располагается в свободном про-
странстве, для которого Wc = 120л.
Учитывая сказанное, получаем для меридиональной составляющей напряжен-
ности электрического поля следующее выражение:
ie ikr 120л cos 0
2V
j«<p')e'L-s,n',cos'p'sin<?'cH.
I
(5.2.2)
Здесь Le = 2ла / X - длина кольца, отнесенная к длине волны, или электрическая
длина кольца. Это важный параметр, который мы будем использовать в дальней-
шем.
Учитывая также, что dZ = Rdcp’, заменяя пределы интегрирования, получаем
окончательно
2л
Е0 = ie~ikr cos е [ Дф ’)сгЬе sin е cos ф sin ф, d(p, (5 2 3)
Г J
о
Аналогичным образом получаем для азимутальной составляющей напряжен-
ности электрического поля следующее выражение:
2л
Ev=-ie~ikr^- f 1(Ф >!'L‘sin е cos ’ ’ cos <р' Лр'
г о
(5.2.4)
Полученные выражения (5.2.3) и (5.2.4) являются общими для дальней зоны и
пригодны для любого распределения тока на кольце. Пока не задан закон измене-
ния тока J(cp'), они не могут быть упрощены.
5.2.2. Кольцевые синфазные равноамплитудные антенны. Пусть ток
на кольце не меняется ни по фазе, ни по амплитуде, т.е.
Дф’) = 1о,
тогда
Кольцевые (рамочные} дмтенны
227
2л
еЧ) Г
iLe sin 0 cos ср'
cos (р' dtp',
(5.2.5)
О
Ее - 0.
Преобразуем выражение (5.2.5) для Е®, учитывая, что функция Бесселя 1-го
порядка есть:
2т J
О
izcosq'
v COS ф dtp .
Поэтому
„ . -ikr 30LpIn cos 0 т , 4
Еф = -ге г/сг---—-------(z) =
r (5.2.6)
60тсЕеХп т /т * /а\ —ikr
=------— Jj (Le sin 0)e .
Таким образом, напряженность электрического поля проволочной кольцевой
синфазной равноамплитудной антенны содержит лишь одну азимутальную со-
ставляющую. Последнее выражение показывает, что при заданной длине волны
напряженность поля прямо пропорциональна току кольца и его радиусу.
5.2.3. Диаграмма направленности кольцевой синфазной равноамплитуд-
ной антенны. Диаграмма направленности антенны определяется выражением
/(<p,0) = J1(Lesin0).
(5.2.7)
Это выражение не зависит от угла <р, что вполне естественно ввиду полной
симметрии антенны в плоскости кольца. При 0 = 0, т.е. вдоль оси кольца, /(0) = О
независимо от радиуса кольца. При 0 = 90°, т.е. в плоскости кольца, sin 0 = 1
и /(0) = А (Ье); здесь значение функции зависит от электрической длины кольца
Le. Функция Бесселя 1-го порядка достигает максимума при Le =1,84. Поэтому
диаграмма направленности рассматриваемой кольцевой антенны также будет до-
стигать максимума в плоскости кольца (0 = 90°) при Le <1,84. При значении аргу-
мента, равном 3,83, функция Бесселя обращается в нуль. Поэтому при Le =3,83
в плоскости кольца получается нулевое значение диаграммы направленности
( 0 = 90° ; Le sin0 = 3,83 ; /(0) = 0). При Le > 3,83 диаграмма направленности в пре-
делах одного квадранта расщепляется на лепестки. Диаграммы направленности
кольцевой синфазной равноамплитудной антенны разных размеров в плоскости,
проходящей через ось кольца, изображены в полярных координатах на рис. 5.10.
Как видно из рисунков, при малых размерах кольца ДН имеет фор-
му восьмерки, так же, как и для элементарного диполя, расположенно-
го вдоль оси кольца. При значительных размерах кольца максимум излу-
чения приближается к осевому направлению. При дальнейшем увеличении
радиуса рамки ДН приобретает лепестковую форму. Число целых лепест-
ков ДН (в пределах одного квадранта) равно числу корней бесселевой фун-
кции. Обычно применяются рамочные антенны, у которых Le < 2. Все ДН пос-
троены приблизительно в таком масштабе, что максимальные значения у них
одинаковы.
8 *
228
ГЛАВА 5
Рис. 5.10. ДН круглой рамки в азимутальной плоскости с равномерным распределением
тока при разных значениях Le [17]
Поляризацию электромагнитного поля, создаваемого кольцевой синфазной
равноамплитудной антенной, нетрудно определить, если учесть, что вектор Е
напряженности поля антенны содержит лишь одну азимутальную составляющую.
Следовательно, линии электрического поля антенны лежат в плоскостях,парал-
лельных плоскости кольца. Соответственно, вектор напряженности магнитного
поля Н в любой точке в дальней зоне содержит лишь меридиональную состав-
ляющую. Он лежит в плоскости, проходящей через ось кольца и перпендику-
лярен вектору Е,а также вектору Умова-Пойнтинга, характеризующему на-
правление распространения (направление прямой, проведенной из центра кольца
в рассматриваемую точку).
Выражение (5.2.6) показывает, что фаза напряженности поля рассмотренных
кольцевых антенн отличается на 90° от фазы напряженности поля элементарного
электрического диполя или симметричного вибратора, расположенной вдоль оси
кольца. На это указывает наличие дополнительного множителя i в выражениях
для электрических полей этих антенн при отсутствии этого множителя в (5.2.6).
5.2.4. Сопротивление излучения. Мощность излучения всякой антенны в сво-
бодном пространстве может быть определена с помощью выражения:
= —— [p2ds
120л J
(5.2.8)
где Е - действующее значение напряженности поля, создаваемого антенной
в дальней зоне; ds = г2 sin OdtpdO - элемент площадки.
Подставляя вместо Е соответствующее значение из (5.2.6), получаем для син-
фазной равноамплитудной кольцевой антенны.
(5.2.9)
Обычно (5.2.9) записывают в виде [17]:
Кольцевые (рамочные} антенны
229
Р- = 607t22Le^[J3(2Le) + J5(2Le) + JY(2L._) +
(5.2.10)
Сопротивления излучения рассматриваемой антенны, отнесенное к току Jo
кольца,
К = — = 60л22ЬД73(2Ье) + J5(2Le) + J7(2Le) +...]. (5.2.11)
*0
5.2.5. Коэффициент направленного действия. Коэффициент направленного
действия кольцевой синфазной равноамплитудной антенны, диаграмма направ-
ленности которой не зависит от угла (р, может быть определен с помощью выра-
жения
D = -------------. (5.2.12)
F2 (0) sin OdO
о
Это выражение определяет КНД в направлении максимума диаграммы излу-
чения.
Выражение F(9) для нормированной диаграммы направленности кольцевой ан-
тенны можно получить, если разделить (5.2.7) на максимальное значение диаграм-
мы
F(6) =
/(6)
/max (®)
(Le sin 0)
*/. (-^e sin )
(5.2.13)
Здесь 0ш - угол, в направлении которого получается максимум диаграммы.
Следовательно,
sin OdO
2 J? (Lp sin )
X v r 9 v '
Я
J2(Le sin 0) sin OdO
0
(5.2.14)
5.3. Применение сингулярных интегральных уравнений
для электродинамического анализа кольцевой антенны
Под кольцевой антенной (КА) будем понимать идеальный проводник произ-
вольного поперечного сечения s, свернутый в кольцо радиуса а и имеющий за-
зор угловой шириной 2Д. Поперечное сечение s проводника может быть нерегу-
лярным, но длина контура сечения ls должна быть постоянной. Первым шагом
полного электродинамического анализа антенны является установление закона
распределения тока по длине проводника. Эквивалентом данной излучающей
структуры являются две наиболее простые кольцевые антенны: цилиндрическая
(ЦКА) и плоская (ПКА).
Цилиндрическая кольцевая антенна (ЦКА) представляет собой узкий идеаль-
но проводящий ленточный проводник шириной 21, свернутый в кольцо радиуса
а (рис.5.11,а). Под плоской кольцевой антенной (ПКА) будем понимать бесконечно
230
ГЛАВА 5
а) б)
Рис. 5.11. Кольцевые полосковые антенны: а) - цилиндрическая (ЦКА),
б) - плоская (ПКА)
тонкое кольцо шириной 21, лежащее в плоскости 2 = 0 (рис.5.11,6). Данные излуча-
ющие структуры эквивалентны КАпри условии 21 = ls. Это следует из того факта,
что токи высокой частоты протекают по поверхности металла (скин-эффект).
К зазорам угловой ширины 2А приложено стороннее электрическое поле Е^т,
имеющее гармоническую зависимость от времени ( exp{zo)t}). Под действием это-
го поля на антеннах возникает поверхностный ток. Следует отметить, что точек
приложения может быть сколько угодно. Например, в случае, показанном
на рис.5.7а, их три, что необходимо для обеспечения равномерного распределе-
ния тока по проводнику.
Теоретическому исследованию кольцевой антенны посвящено большое количес-
тво работ. Однако расчеты характеристик антенн основываются на равномерном
распределении тока [17,18]. Характерной особенностью большинства работ являет-
ся использование несамосогласованного подхода к расчету ЭМП: поле излучения
рамочной антенны определяется по заданному (не найденному) из каких-то физи-
ческих соображений распределения тока по проводнику. Такой подход может быть
оправданным лишь при выполнении ряда условий лишь для излучателей малых
размеров или при определенных условиях их возбуждения. В общем случае необ-
ходимо найти распределение тока по антенне при заданной сторонней ЭДС.
В данной главе проводится электродинамический анализ ЭМП в ближней зоне
ЦКА и ПКА. Приводятся распределения поверхностной плотности тока по про-
водникам при различных радиусах кольца. Анализируется зависимость входного
сопротивления антенны от нормированной длины окружности кольца.
5.3.1. Постановка задачи. Физические и математические модели антенн.
Для анализа антенн вводятся следующие упрощения. Идеально проводящие бес-
конечно тонкие проводники, образующие кольца, предполагаются достаточно
узкими ( 21А,), поэтому будем учитывать только продольную составляющую
поверхностной плотности тока ти. Зазоры также считаются узкими ( 2аД X)
и продольные составляющие т](р непрерывны в области зазора.
В рамках принятой физической модели напряженности электромагнитного
поля Е и Н выражаются через векторный электродинамический потенциал для
электрического тока А = р0 Ар + Фо Ар > ( Ро,Фо " °РТЬ1 цилиндрической системы ко-
ординат) следующим образом [1]:
Кольцевые (рамочные) антенны
231
W о-
Ё = —- (кг А + grad div А),
ik
Н - rot А,
(5.3.1)
где Wc - характеристическое сопротивление среды, к - волновое число среды,
в которой находится излучатель.
Переходя в цилиндрическую систему координат, в рамках принятой физичес-
кой модели, азимутальная составляющая электрического поля на поверхности
антенны (р = а) выражается через составляющие Др и Ар векторного электродина-
мического потенциала А
(рД>) -
(5.3.2)
Составляющие вектора А в цилиндрической системе координат определяются
через составляющие объемной плотности тока j^q) на антенне [21]
(5.3.3)
где р - точка наблюдения, q - точка источника, G(p, q) - функция Грина. Для оп-
ределения ЭМП в ЦКА удобно использовать следующее представление функции
Грина G(p,q) в свободном пространстве в виде [19]:
00 00
G4(p,<p,Z;p»') = ^ У Ге-Л(~)9n(/l>p,p')d/1;
8т J
П--СО -ап
(5.3.4)
где
!
-к
H^2)(-wp )Jn(-wp),p
Р,Р) = 1 ,2)
H^(-TVp)Jn(-2t>p’),p
НпЧх) ~ функция Ханке ля второго
(5.3.4а)
рода порядка п,
Jn(x) - функция Бесселя первого рода порядка п. Выражение (5.3.4) представля-
ет собой бесконечный спектр цилиндрических волн, распространяющихся в ра-
диальном направлении и модулированных по оси z. При р > р ’ спектр волн, для
которых h2 <к2, является распространяющимся, а спектр волн, для которых
hr > к2 - затухающим.
Для расчета ПКА будем использовать другое представление функции Грина
G(p,q) свободного пространства [21]:
Gn(p,(p,z;p',(p',z')
z-z'|
О
*Vn(xpVn(xp')
(5.3.5)
4 m
Выражение (5.3.5), в противоположность выражению (5.3.4), представляет собой
бесконечный спектр плоскоцилиндрических волн, распространяющихся вдоль оси
z в обе стороны от плоскости z = z'. Здесь при %2 < к2 волны являются распростра-
232
ГЛАВА 5
няющимися, при %2 > /с2 — экспоненциально затухающими.
В дальнейшем будем учитывать связь между векторами объемной j и поверх-
ностной fj плотностями тока:
J(p,cp,z) = fj(cp, z)5(p - а)
для ЦКА и
J(p,9,z) = f|(p,(p)5(z)
(5.3.6а)
(5.3.66)
для ПКА. В (5.3.6) &(х -х’) - дельта-функция.
При подстановке (5.3.66) в (5.3.3) компоненты электродинамического потенциала
Ар и А™ ( z = 0, р е [0;оо),ф е [-л; л]) для ПКА имеют вид:
л а+1
Ар(ф)(р,Ф)= J J Пф(р\фУ^р(ф)(р,р\ф,Ф>*риф',
-па-1
(5.3.7)
где
G"Up, р', ф, ф') =
I I
р'
4лг
8Ш(ф - ф')
соэ(ф - ф')
(5.3.7а)
00
00
4(ХРУп(Хр’)<*Х-
При подстановке (5.3.6а) в (5.3.3) для ЦКА имеем (ре [0;оо),ф е [-к; л]):
Ар(<р)(р’Ф)= е |пф(ф>’)С^((р)(ф,ф,,г,2,)с12,с1ф’,
-тс -I
(5.3.8)
а I ыщф-ф)
8т, ] сов(ф - ф')
/к ч Hjl2)(-wa)Jn(-wp),p
9п р) =
H}/(-wp)Jn(-wa),p
-ih(z-z')
gn(h,p)dh,
(5.3.8а)
В зазорах антенн выполняется граничное условие:
Еф + Ес™ = 0, (5.3.9)
ЕфШ - стороннее электрическое поле. Причем (5.3.9) для ЦК А выполняется в облас-
ти z е [-1; I], ф е [—Л; А], для ПКА - в области р g [а — I; а +1], ф g [-А; А].
Представим и т|ф рядами Фурье по переменной ф.
Для ЦКА:
00 00
Е7(Ф,2)= X ет (z)e“'m<₽- ПФ(<М) = X , (5.3.10)
т=— оо т=—оо
где
л л
4m(2) = i fE™(V,2)e!'mWn™ (z)U (5-З.Юа)
2л J 2л J
-л -л
Кольцевые (рамочные) антенны
233
Для ПКА:
00 00
£$m(P’‘P)= Z Пф(Р,Ф)= £ nm(p)e-im<₽,
т=-оо т—-<х>
где
я л
е™(р) = ± f E^m(p,<p)eim4>d<p, 1C(P) = ^ fn9(P,V)eimW
2n J 2тг J
-л -л
(5.3.11)
(5.3.11а)
Подставляя (5.3.10) в (5.3.2), с учетом (5.3.9) получаем для ЦКА бесконечную
систему интегральных уравнений (z е [-1; I]):
WP J
с -I
т - 0, ±1... ± оо,
(5.3.12)
где Wc - характеристическое сопротивление среды, относительно азимутальных
гармоник поверхностной плотности тока т]ф(ф,г). В (5.3.12)
00
ajj~(z,z') = — f H^\-ia\lh2 - к2 )Jn(-ia^lh2 -k2)e~lh^z~z ^dh.
flL v / z J IL x z IL * z
—00
Подставляем (5.3.11) в (5.3.2), с учетом (5.3.9) получаем для ПКА аналогичную
бесконечную систему интегральных уравнений (р е [a -1, а + Z]):
TJZ ет (Р) —
ИС.
а+1
J Пт(р')Рт(р>р'Мр';
т - 0,±1... ± оо
(5.3.13)
относительно
В (5.3.13)
азимутальных гармоник поверхностной плотности тока т|ф(Р,ф)‘
Рт (Р, Р') = к2 (a^_i (р, р') + а”+1 (р, р ’))-г а™ (р, р'),
РР
с4(р,р’)= Г J?.P-—- Jw(xpVm(XP')dx.
О 7х2 - к2
Вводя нормированные переменные, получаем интегральные уравнения для ЦКА
и ПКА(е е[-1;1]):
4Le
Wc^
4m(t) =
1
а
-1
m = 0,±l... ± oo.
(5.3.14)
Для ЦКА
Pm(t,t') = p4(tif) = L2(a4_i
(t,t'))-2m2<4 (t.f).
(t, t ) + a^+1
00
’><)(-Ф2 - - L2e )dx,
234
ГЛАВА 5
Для ПКА:
т-
гх
о
t = (р - а) /1, t ’ = (ра) /1.
Здесь Le = 2тга / А, - электрическая длина кольца, £ = I / а.
5.3.2. Бесконечная система сингулярных интегральных уравнений.
Ядра Pw(t,t') в интегральном уравнении (5.3.14) в неявном виде содержат
сингулярности.
Выделим сингулярности в am(t,t'). Воспользовавшись пределами
lim Jm(x(^ + l))Jm(x(^’+l)) =
1 cos(S,x(t -1'))
«^ + ОД,И)’
(5.3.15)
lim l&(-ix)Jm(-ix) =—,
lit' 'lit' ' 7
X—>00 TtX
вытекающими из свойств функций Бесселя при неограниченном возрастании ар-
гумента [50], получаем:
= Ит = -
г J^t +1 f cos(E>x(t -1 )).
=r-:-Lax —
2
e
(5.3.16)
(oo)a^(t,t’) = lim a^(t,t’) = -
X—>00 71 J
0
i f cos(£x(t -1 )).
=^—ax =
2
e
- —K0(iLe^ t -1'),
где Kq(x) - модифицированная функция Ханкеля нулевого порядка. В свою оче-
редь,
lim Kf/zLgS, t -t') = - In t -t'.
(5.3.17)
Учитывая соотношения (5.3.15) - (5.3.17), можно представить в виде:
(5.3.18)
т
п
т
0
где
(t, t •) = 4 (/^ (t, t ') + 4+1 (t, t •)) - 2m2/^ (t, t'),
F" (t, t') = L2 (/£(t, t •) + /£+1 (t, t ’)) - 2 " (t, t ’),
(fy + l)(£t +1)
Кольцевые (рамочные) антенны
235
In t -1'
Z” (t,f) = Ym(M')Ko - * 1)+ 4n ln|* “
- разностные ядра. Здесь
e ^dx,
„ If fr 2 2 ^f'+1 T2
n ^TTi l e Kt+w+i)
= 2—(L2 - m2).
Подставляя (5.3.18) в (5.3.14), получаем обобщенную бесконечную систему одно-
мерных относительно поперечной координаты t СИУ с логарифмическими особен-
ностями для ЦКА и ПКА(тп = 0,1... ± oo;t е [—1;1]):
T]m(t')ln t-t'dt', (5.3.19)
где
5.3.3. Метод решения системы сингулярных интегральных уравнений.
Решение СИУ (5.3.19) производится методом ортогонализирующей подстановки
(МОП), подробно описанном в [8]. Искомая функция представляется в виде поли-
номиального ряда (т = 0,1... ± оо):
ОО
к=0
l\ll -12
(5.3.20)
с неизвестными коэффициентами a!w\ В (5.3.20) Tk(t) - полином Чебышева перво-
го рода порядка к. Ядра и функции e^I(t) преобразуются к виду:
00 оо
n=0 к=0
4Le
О
оо
e™(t)=X4m4(t)
п=0
(5.3.21)
с помощью соотношений:
Rm(t,t’)Tn(t)Tfc(t’)
dtdt'
236
ГЛАВА 5
p(m) _
,-rr <
j Cv L*
При определении G^V
f V j fV
мулу:
J для ПКА целесообразно использовать квадратурную фор-
f(t)
, Л
что позволяет свести двойной интеграл к двойной сумме.
При определении G^l. для ЦКА эффективным является использование разло-
жения экспоненты по функциям Бесселя Jn(x)n полиномам Чебышева Tn(t) [26]:
ОО
etet = J0(x) + 2^ik Jk(x)Tk(t); t e [-1; 1].
k=l
Подставляя (5.3.20) и (5.3.21) в (5.3.19) и ограничивая суммирование по пи к
до N, а суммирование по т до М, получаем набор систем линейных алгебраи-
ческих уравнений (СЛАУ) для определения неизвестных коэффициентов а!ш' :
N
k=Q
п = 0,1...N, т = 0,1... ± М,
<^к &к,0’
к
где 5n i(. - символ Кронекера, 8^д- его инверсия:
1,п = к, — [0,п = к,
Ьпк=1
0,п*к, ’ [1,п^?с.
$п,к
Искомое распределение поверхностной плотности тока в силу (5.3.10), (5.3.11)
и (5.3.20) будет выглядеть следующим образом:
м Д A^Ti (t}
m=-Mk=0 l\l~t
Если использовать квазистатическое приближение поверхностной плотности
тока по ширине проводника
п<р(фД)= X —/ 2
т=-М Wl — t
и подставить его в систему (5.3.19), то коэффициенты можно получить не-
посредственно из СИУ:
4™) = 4iLe е^(0), (5.3.23)
W£ Р
vvcr> гт
Кольцевые (рамочные) ацтенны
237
Рт= ГК™(°’Чй'+ХтЛ1п(2).
Л Vi-t'2
Тогда полный ток, протекающий по кольцевой антенне с проводником произ-
вольного сечения s (при условии 21 = ls)
(5.3.24)
При вычислении Рт в (5.3.24) можно использовать как ядро так
и K^(t,t’)- На результаты вычисления это практически не влияет.
Таким образом, мы получили обобщенную систему СИУ (5.3.19), записанную
относительно Фурье-гармоник r|m(t') поверхностных плотностей токов тцДф, t) ЦКА
и КПА и простое выражение для распределения тока 1(ф) по кольцевой антенне.
5.3.4. Определение входного сопротивления антенн. В разделе 5.3.2 было
получено выражение (5.3.24) для тока 7(ф) кольцевых антенн. Зная распределение
тока 1(ф), можно определить входное сопротивление антенны Zex :
вх
ЩО)
1(0)’
(5.3.25)
Здесь:
А
ит = f
Ест (ф, t)d(p
- напряжение, создаваемое сторонним электрическим полем в зазоре. Целесооб-
разно положить
J Ест (ф, t)cty
Входное сопротивление с учетом (5.3.25) и (5.3.24) определяется в виде:
Wc^
вх
4tiZLp
m
(5.3.26)
m=-oo
Записывая нормированное стороннее электрическое поле в зазоре
Ecw (ф, t) =
лЛа
2 аД-Сф/Д)2,
получаем следующие коэффициенты Фурье - гармоник:
££(*)=
j Ест (ф, t) ехр(гтф)йф
-А
1 Ji(Am)
л Am
(5.3.27)
При электродинамическом анализе антенн была также использована аппрокси-
мация стороннего электрического поля в зазоре и постоянной функцией:
238
ГЛАВА 5
Ф
с Фурье - коэффициентами:
4J(t) =
2л
А
Ест (<р, t) exp(im<p)d(p
-A
1 sin(Am)
2л Am
(5.3.28)
Применение двух видов аппроксимации Ест при электродинамическом анализе
антенны показало, что решение системы СИУ практически не зависит от формы
Ест в зазоре. Для точного построения поверхностной плотности тока (с погреш-
ностью менее 1%) необходимо учесть 20-30 Фурье-гармоник.
Подставляя (5.3.28) в (5.3.26), получаем простую формулу для расчета входного
сопротивления ЦКА и КПА:
Zex = WC/ (2LeN),
N =
sin Am
Am
(5.3.29)
m
Для ЦКА и ПКА были проведены расчеты функций Z%x (Le) и Z™x (Le) соответс-
твенно. Расчеты показали, что графики Z^x (Le) и Z™x (Le) практически совпадают,
но модель ЦКА удобнее в использовании, так как при этом один из интегралов
в (5.3.21) определяется аналитически:
dt' = лЛо(£,а?),
что упрощает РД в (5.3.29)
dt ’+ Хтл1п(2).
(5.3.30)
Здесь
JQ(^x)dx.
Также можно учесть, что Р_т = Рт, что позволяет сократить время расчета
в два раза. Для вычисления интеграла в (5.3.30) удобно использовать квадратур-
ную формулу (5.3.22). Так как Z$x(Le) « Z^x(Le), то далее будем рассматривать
обобщенную зависимость Zex(Le).
На рис. 5.12 приведен график Zex(Le). Действительная часть Zex обозначена
сплошной кривой, мнимая часть Zex - штриховой кривой. Расчеты выполнены при
2А = 20° , £ = 0.2.
Из графика видно, что при Le < 0.4 сопротивление носит индуктивный харак-
тер, активная часть Zex мала. При Le » 0.45 наблюдается пик активного сопро-
Кольцевые (рамочные) антенны
239
Рис. 5.12. Зависимость входного сопротивления Zex от Le; кривая 1 - ReZex,
кривая 2 - ImZex
тивления, а реактивная его часть меняет знак. Подобные результаты получены
и в [35].
На рис. 5.13 представлена поведение функции Zex(Le) для Le = 1..4 при измене-
нии ширины полоски. Геометрические пропорции антенны показаны непосредс-
твенно на графиках.
Как видно из приведенных графиков, при увеличении ширины полоски и не-
изменном радиусе кольца кривые Zex (Le) становятся более пологими, реактивная
часть Zex носит емкостной характер, а также снижается активное сопротивление
антенны. Следует отметить, что подобные результаты можно получить только
при корректной постановке внутренней задачи, приводящей к сингулярным ин-
тегральным уравнениям.
5.3.5. Анализ распределений поверхностных плотностей токов. С помо-
щью методики, описанной в разделе (5.3.3), были проведены численные расчеты
системы СИУ (5.3.19) для ПКА при следующих параметрах: % = 0.01, Wc =120л,
2А = 10°. Параметр Le (отношение длины кольца к длине волны) был переменным.
На рис. 5.14 показано распределение поверхностной плотности тока при
Le = 0.5.
На рис. 5.15 приведены распределения Цф(ср,£) при Le =1.5. Зависимость фун-
кции T)(p((p,t) от координаты ф имеет более существенный характер. Характерным
для обоих случаев ( Le =0.5 и Le = 1.5) является выполнение условий на ребрах
антенны для Цф(ф,£) (t = ±1) [5]. Сходимость полиномиального ряда очень хорошая
(N<6).
Но ситуация коренным образом меняется, когда в длине полоски укладывается
целоечисло длин волн (т.е.Ье = т, т = 1,...оо), причем 2л( а - А) / X < Le < 2л(а + А) / X.
Таким образом, резонанс тока в ПКА наблюдается для некоторого диапазона час-
тот возбуждения вблизи Le = т, причем чем шире полоска, тем шире резонанс-
ная область. Этим ПКА отличается от ЦКА, у которой резонанс возникает строго
при Le = т. Рассмотрим возбуждение антенны при Le = 1. (Рис.5.16).
Здесь четко видно, что амплитуда поверхностной плотности тока намного
больше, чем в предыдущих случаях, а азимутальное распределение практически
240
ГЛАВА 5
а)
б)
1 1.5 2 2.5 3 3.5 4
г)
Рис. 5.13. Входное сопротивление кольцевой антенны: а) - 2, = 0.025 , б) - % = 0.05,
в) - = 0.1, г) - % = 0.2; кривая 1 - Re Zex , кривая 2 - Im Zex ; 2Д = 20°
Рис. 5.14. Поверхностная плотность тока ПКА при Le = 0.5 : а) — азимутальное распределе-
а)
ние, б) - распределение по ширине полоски; 1 - Re Zex , 2 - Im Zex
Кольцевые (1рамочные) антенны
241
Рис. 5.15. Поверхностная плотность тока ПКА при Le - 1.5 : а) - азимутальное распределе-
ние, б) - распределение по ширине полоски; 1 - Re Zex , 2 - Im Zex
0.06
-0.04
0.04
0.02
0
-0.02
П(0,0> A/\ ]
! /1
r~ ”
2 1
ijs ••• i-r 11 ti и 'j 'pr. p. ,_r p
1 1 1 1 t
О
0.5
Рис. 5.16. Первый резонанс тока (Le =1) для ПКА: а) - азимутальное распределение,
б) - распределение по ширине полоски; 1 — ReZex, 2-ImZex
я)
Рис. 5.17. Возбуждение антенны в области первого резонанса (Le - 0.99): а) - азимутальное
распределение, б) - распределение по ширине полоски; 1 - Re Zex , 2 - Im Zex
б)
242
ГЛАВА 5
синусоидально. Более того, полиномиальный ряд для гармоники с номером т = Le
становится расходящимся в точке t = 0, и пик поверхностной плотности тока на-
ходится на радиусе а (т.е. t = 0), потому что для него выполняется условие резо-
нанса: 2па / X = 1.
На рис. 5.17 показан случай возбуждения при Le = 0.99 (резонансная область).
Как видно из рисунка, максимум сместился в сторону большего радиуса
Ррез > а > Для которого выполняется условие 2тгррез / X = 1. Сходимость полиноми-
ального ряда (5.3.17) в данном случае плохая.
Продольное распределение поверхностной плотности тока при определенных
геометрических размерах антенны не является квазистатическим [36], поэтому
метод, использованный в [36], является менее «правильным», хотя и позволяет
определять ЭМП в любой точке пространства (включая излучающую поверхность)
и входное сопротивление антенны в рамках самосогласованного подхода [13].
Метод, описанный в данной работе, позволил выявить интересный эффект: при
резонансе максимум поверхностной плотности тока протекает по радиусу, удов-
летворяющему условию 2лррез / X = m, т = 0,1...оо. Возможно, что при 2ла / X = т
концентрация тока на ребрах полоски равна нулю, и он «фокусируется» на ра-
диусе а. Этим ПКА отличается от ЦКА, у которой при резонансе поверхностная
плотность тока концентрируется именно на ребрах. По формулам (5.3.1) несложно
определить электромагнитное поле антенны в любой точке пространства.
5.3.6. Диаграммы направленности кольцевых антенн с учетом распре-
делений тока по кольцу. В разделе 5.2.4 приведены ДН кольцевой синфазной
равноамплитудной антенны в меридиональной плоскости при различных значе-
ниях Le. В азимутальной плоскости ДН такой антенны имеет вид окружности,
т.е. от угла ср ДН не зависит. Ниже рассмотрим ДН кольцевой антенны при реаль-
ном распределении поверхностной плотности тока.
Для узких кольцевых антенн азимутальные распределения поверхностной
плотности тока т]^(ф, t) для ЦКА и поверхностной плотности тока T|JJ(<p, t) для ПКА
практически совпадают. Поэтому в дальнейшем в этом разделе ЦКА и ПКА будем
называть просто кольцевой антенной.
На рис. 5.18 приведены ненормированные азимутальные распределения повер-
хностного тока в центре кольца тцДср) = т$(<р,О) « T]”(a,(p) при разных параметрах
кольца при напряжении в зазоре (U = 1 В).
На рис. 5.19-5.25 приведены ДН (в дальней зоне) кольцевой антенны при разных
значениях Le. Анализ ДН показывает, что реальные распределения г|ф(<р) при-
водят к появлению интересных зависимостей ДН от ср. Например, при Le = 0.5
в азимутальной плоскости наблюдается однонаправленное излучение.
Кольцевые ( ралючные) антенны
243
а)
б)
д) е)
Рис. 5.18. Азимутальные распределения поверхностной плотности тока т]ф(ф) кольцевой
цилиндрической антенны при различных электрических длинах кольца Le :
a) -Le= 0.1; б) - Le = 0.3 ; в) - Le = 0.5 ; г) - Le = 1; д) - Le = 2 ;
е) - Lp - 3 ; ж) - L = 6 ; 1 - Re ZRT , 2 - Im
244
ГЛАВА 5
2
Кольцевые (рамочные) антенны
245
260 280 260 280
246
ГЛАВА 5
Рис. 5.19. Амплитудная диаграмма направленности кольцевой антенны в меридиональной
(1) и азимутальной (2) плоскостях при различных значениях нормированной электричес-
кой длины кольца Le : а) - Le = 0.1, б) - Le = 0.3, в) - Le = 0.5 ,
г) - Le - 1, д) - Le = 2, е) - Le = 3 , ж) - Le = 6
Классифи/кад^и^ тлллп/ы несимметр^аъых антенн
Глава 6. Несимметричные антенны [3,17]
247
6.1. Классификация, типы несимметричных антенн [17]
Под общим названием «несимметричные антенны» объединяют различные не-
симметричные вибраторы и собственно несимметричные антенны.
К несимметричным вибраторам относятся: вибраторы со смещенными клемма-
ми (рис. 6.1,а); разноплечие вибраторы (рис. 6.1,6, в); вертикальный вибратор над
экраном конечных размеров (рис. 6.1,з). Несимметричные вибраторы используются
в основном в диапазонах УКВ и КВ.
Несимметричные антенны — это провода, стержни, башни, мачты, располо-
женные у поверхности земли или вблизи экранов, размеры которых обычно мож-
но считать большими по сравнению с размерами антенны. Это в основном антенны
ДВ и СВ. на рис. 6.1,2 - ж последовательно показаны несимметричные антенны:
открытая вертикальная антенна, Г - образная антенна, Т — образная антенна
и антенна с многократным снижением [17].
а)
777777777777
д)
в)
Рис. 6.1. Несимметричные электрические вибраторы и антенны [17]
248 ГЛАВА 6
6.1 Л. Несимметричные вибраторы со смещенными клеммами (рис. 6.1,а)
используются главным образом в резонансном режиме, когда на их длине укла-
дывается целое число полуволн тока (рис 6.2). При изменении положения клемм
в резонансном режиме изменяются значение тока в пучности и входное сопро-
тивление, но кривая распределения тока изменяется мало. У вибраторов длиной
в нечетное число полуволн ДН такая же, как и у симметричных вибраторов
(рис. 6.2, графики справа).
Если длина вибратора составляет целое число длин волн, то имеет место не-
симметричное распределение тока I(z) = In sin k(l - z), где z — координата, отсчи-
тываемая от середины вибратора вдоль его оси, а I — половина геометрической
длины вибратора. При этом ДН рассчитывается по методу, изложенному в § 4.7,
и имеет вид
F(0) = A sin
( тл
(6.1.1)
где А — нормирующий множитель; т = 2,4,... - число полуволн тока на длине виб-
ратора; 6 - угол, отсчитываемый от оси вибратора. Значения т = 1,3,5,... соответс-
твуют симметричному распределению тока.
У толстых вибраторов и у тонких при (^ + ^) > X существенное значение имеют
бегущие волны, которые у вибратора со смещенными клеммами более ярко выра-
жены, чем у симметричного. При этом ДН становится несимметричной и в значи-
тельной степени зависит от положения клемм. На рис. 6.3,а показана эксперимен-
тальная ДН вибратора длиной 2Х при +12 = 8, За и /12 = 6. ДН в осевом сечении
имеет вид двух изрезанных лепестков, прижатых к оси. На рис. 6.3,6 показана ДН
того же вибратора при симметричном питании.
Входное сопротивление вибратора со смещенными клеммами было впервые
рассчитано Кингом[17]. Результаты расчетов входного сопротивления по методу
Кинга можно интерпретировать следующим образом. Предположим, что в сере-
дине между клеммами вибратора можно поместить бесконечный металлический
плоский экран, перпендикулярный оси вибратора, без нарушения режима работы
вибратора, Входное сопротивление может быть представлено последовательным
соединением входных сопротивлений вибраторов длиной и 12, расположенных
! !
Рис. 6.2. Резонансные распределения тока для оценки диаграммы направленности
несимметричного вибратора со смещенными клеммами [17]
Класси^ика^ия^ типы нусшклитуриуныж антенн
249
а)
б)
Рис. 6.3. Экспериментальные диаграммы направленности вибратора длиной 2Л.
при несимметричном (а) и симметричном (б) питании [17]
над металлической плоскостью. Расчет входного сопротивления таких вибраторов
будет проведен ниже.
6.1.2. Разноплечий вибратор с питанием в середине (см. рис. 6.1,6) об-
разован двумя проводами одинаковой длины и разных диаметров ( 2а1 и 2а2 )
На не очень толстых разноплечих вибраторах (I > 5QyJa1a2) при их длинах, близких
к резонансным или меньших Х/2 , распределение тока близко к синусоидальному.
Соответственно ДН будет такой же, как и у вибратора с плечами одинакового
диаметра.
Входное сопротивление может быть рассчитано по формулам для симметрич-
ного вибратора, при этом для расчета волнового сопротивления может быть ис-
пользована приближенная формула
120 In
(6.1.2)
Эта формула получена из выражения (4.7.25) на основании аналогии с двухпровод-
ной линией, составленной из проводов разного диаметра [17].
6.1.3. Вертикальный вибратор над экраном конечных размеров (см. рис.
6.1,з) используется главным образом в диапазоне УКВ и выполняется, как прави-
ло, в виде стержня, расположенного над металлическим диском. Если размеры
экрана не очень велики, то токи затекают на нижнюю сторону экрана и наружную
оболочку питающего коаксиального кабеля. Очевидно, чем меньше размеры экра-
на, тем больше эти токи и тем сильнее их влияние на ДН и входное сопротивление
антенны. В качестве примера на рис. 6.4 показана снятая экспериментально ДН
четвертьволнового несимметричного вибратора, расположенного над металличес-
ким диском диаметром 6Х (сплошная кривая). Пунктиром показана ДН того же
вибратора над бесконечной идеально проводящей плоскостью.
Входное сопротивление несимметричного вибратора над диском зависит от дли-
ны вибратора и диаметра диска. При диаметре диска, большем 1,5Х, поправка
на конечный диаметр диска не превышает ±10 Ом для активного и реактивного
сопротивлений и уменьшается с увеличением диаметра диска.
250
ГЛАВА 6
е
Рис. 6.4. Экспериментальная ДН четверьтьволного вибратора,
расположенного над диском диаметром 6А, [17]
6.2. Несимметричные антенны и метод зеркальных изображений
117]
Несимметричные антенны различных типов показаны на рис. 6.1,г - ж. Антен-
ны состоят из вертикальных и горизонтальных проводов и стержней. Иногда эти
провода могут быть слегка наклонными, Распределение амплитуд и направление
токов при высоте антенн, меньшей X/4, показаны на этих же рисунках.
Конструктивное выполнение несимметричных антенн зависит от геометричес-
ких размеров, т. е. от диапазона волн, в котором работает антенна.
г
6.2.1. Основные параметры несимметричных антенн при большой про-
водимости земли могут быть рассчитаны с помощью метода зеркальных изобра-
жений, так как землю в первом приближении можно считать бесконечной плос-
костью. На рис 6.5,а изображены открытая антенна и ее зеркальное изображение.
Известно, что токи в каждом элементе вертикального зеркального изображения
равны по амплитуде и фазе токам в симметричных элементах самой антенны. Та-
ким образом, несимметричная антенна высотой h, расположенная над идеально
проводящей плоскостью, создает в верхнем полупространстве ( 0 < 6 < 90° на рис.
6.1,г) такое же поле, как вибратор длиной 2h при одинаковых токах на входе.
Симметричный вибратор, образованный несимметричной антенной и ее зер-
кальным изображением, называется эквивалентным несимметричной антенне.
Из рис. 6.5,6 следует, что несимметричная антенна с горизонтальными провода-
ми, расположенная' над идеально проводящей плоскостью, по полю в верхнем
полупространстве имеет своим эквивалентом симметричный вибратор с емкостной
нагрузкой на конце.
Классификации типы нссиммст^дичмы^ длстенн
251
а)
Рис. 6.5. Несимметричные антенны и их зеркальные изображения [17]
6.2.2 Расчет поля и ДН несимметричной антенны производится по фор-
мулам для эквивалентного симметричного вибратора, находящегося в сводном
пространстве. Рассчитывая параметры несимметричных антенн по формулам, от-
носящимся к симметричным вибраторам, в последних необходимо сделать замену
обозначений: I -> h и ак —> I . Для углов 0 > 90° (нижнее полупространство) поле
излучения отсутствует. В горизонтальной плоскости излучение несимметричных
антенн так же, как и эквивалентных симметричных вибраторов, ненаправленное.
6.2.3. КНД несимметричной антенны высотой h в два раза больше, чем
КНД эквивалентного симметричного вибратора (длиной 2h). Например, КНД чет-
вертьволновой антенны (h = Х/4), рассчитанный по формуле (2.2.6), Do =3,28. Так
как в случае несимметричной антенны интегрирование по 0 нужно выполнять
в пределах от 0 до л/2 , то знаменатель в формуле (2.2.6) будет в два раза меньше,
а КНД в два раза больше, чем для соответствующей симметричной антенны.
6.2.4. Действующая длина несимметричной антенны может быть, конеч-
но, рассчитана с помощью формул (2.7.3) и (2.7.2), согласно которым действу-
ющая длина любой антенны определяется как длина прямолинейного вибрато-
ра с равномерным распределение тока, находящегося в свободном пространстве
и создающего при одинаковых токах такую же напряженность поля в максимуме
252
ГЛАВА 6
ДН, что и рассматриваемая антенна. Так как при одинаковых токах несиммет-
ричная антенна и эквивалентный ей симметричный вибратор создают одинаковую
напряженность поля, то их действующие длины также одинаковы. Напряженность
электрического поля в вернем полупространстве должна при этом рассчитываться
по формуле (2.7.1). Такое определение действующей длины для несимметричных
антенн неудобно и ненаглядно: оно дает значение, вдвое больше рассчитанного
по «площади тока» и по э.д.с., наведенной на клеммах несимметричной антенны
в режиме приема. По этим причинам действующую длину несимметричной ан-
тенны принято определять как длину вертикального диполя Герца (или антенны
с равномерным распределением тока), расположенного непосредственно над про-
водящей плоскостью и создающего при одинаковых токах такую же напряжен-
ность поля в максимуме ДН, что и рассматриваемая антенна.
Пусть 1Г- длина диполя Герца; 1д - действующая длина несимметричной ан-
тенны и 1д - действующая длина эквивалентного симметричного вибратора, оп-
ределенная по отношению к диполю Герца в свободном пространстве. Напряжен-
ность электрического поля вертикального диполя Герца над плоскостью за счет
зеркального изображения удвоится по сравнению со свободным пространством
и будет равна Ед = бОк^ 1/г. По новому определению нужно считать напряжен-
ность электрического поля несимметричной антенны = Ед = 60klg I/r. Эта же
напряженность поля выражается через параметры эквивалентного симметрично-
го вибратора формулой (2.7.1) =30kl^I/r. Из сравнения этих формул следу-
ет, что Iq = 0,51g , т. е. действующая длина несимметричной антенны в два раза
меньше действующей длины эквивалентного симметричного вибратора.
Применительно к несимметричным антеннам употребляют термин «действую-
щая высота» и обозначают ее hd. При этом напряженность поля несимметричной
антенны рассчитывается по формуле
Е = (ббккд I/r)F(Q,<p). (6.2.1)
6.2.5. Сопротивление излучения и входное сопротивление несимметрич-
ной антенны. Так как при одинаковых токах несимметричная антенна излучает
в два раза меньшую мощность, чем эквивалентный симметричный вибратор (не-
симметричная антенна не излучает в нижнее полупространство),то сопротивле-
ние излучения несимметричной антенны в два раза меньше, чем сопротивление
излучения эквивалентного симметричного вибратора. При этом для определения
Rn можно воспользоваться формулой (4.7.20), подставив в нее перед скобками
коэффициент 15 вместо 30 и заменив I на h. Для открытой антенны можно так-
же воспользоваться результатами для симметричного вибратора, заменив I на h
уменьшив вдвое значения сопротивлений по оси ординат.
При одинаковых токах 1А на входных клеммах напряжение на этих клеммах
у эквивалентного симметричного вибратора должно быть в два раза больше, чем
у несимметричной антенны (рис. 6.5,а). Из рис. 6.5,а видно, что в режиме приема
электромагнитные волны одинаковой интенсивности наведут на клеммах несим-
метричной антенны в два раза меньшую э. д. с., чем на клеммах эквивалентного
симметричного вибратора. Следовательно, действующая длина несимметричной
антенны в два раза меньше, чем эквивалентного вибратора: Uc = 2UH. Следова-
тельно, входное сопротивление несимметричной антенны в два раза меньше вход-
Классификация^ типы несилг^етричныа? антенн 253
ного сопротивления эквивалентного симметричного вибратора
Z^H) = 0,5Zj}. (6.2.2)
Таким образом, для расчета входного сопротивления несимметричных антенн
можно пользоваться имеющимися данными по входному сопротивлению эквива-
лентных симметричных вибраторов. При этом нужно произвести указанные выше
замены обозначений и полученные значения сопротивлений уменьшить вдвое.
Уменьшение активной составляющей вдвое было объяснено выше при обсужде-
у
нии величины Rfi. Реактивная составляющая входного сопротивления уменьшает-
ся вдвое за счет уменьшения вдвое волнового сопротивления антенны
Xм = 0,5Х(с). (6.2.3)
Все, что было сказано ранее в гл. 4 о настройке и диапазонности симметрич-
ных вибраторов, в полной мере относится и к несимметричным антеннам. Отметим
одну важную особенность: настройка с помощью концевой емкостной нагрузки
в несимметричных вертикальных антеннах используется гораздо чаще, чем в сим-
метричных вибраторах, так как в многих случаях, особенно на длинных волнах,
трудно построить антенну достаточно большой высоты, а создать разветвленную
концевую горизонтальную часть проще.
6.2.6. Эквивалентная высота горизонтальной части антенны h' (рис. 6.6)
зависит от числа, диаметра и длины составляющих ее проводов. При высоте ан-
тенны h < 0,2Х горизонтальные провода вместе с их зеркальными изображениями
можно рассматривать как разомкнутые на конце двухпроводные линии. На осно-
вании этого для расчета величины h’ антенны с N одинаковыми горизонтальными
лучами получено уравнение
ctg(fch') = ^-ctg(Wr), (6.2.4)
где Wr и 1Г - волновое сопротивление и длина горизонтальных проводов, a WB -
волновое сопротивление вертикальной части антенны.
Рис. 6.6. Распределение тока на несимметричной короткой антенне
с горизонтальной частью [17]
254 ГЛАВА 6
При расчете величины h' антенн с высотой h < 0,2А, требуется применение более
строгих методов.
6.2.7. Несимметричные короткие антенны — это антенны, высота которых
много меньше длины волны. Распределение тока в них описывается небольшим
отрезком синусоиды и может считаться линейным (рис. 6.6). Линейное приближе-
ние в распределении тока дает несущественные ошибки в расчете ДН и входного
сопротивления при h < Х/8.
Основные характеристики коротких антенн могут быть, конечно, рассчитаны
указанным выше общими для несимметричных антенн способами. Однако, имея
в виду широкое распространение коротких антенн (особенно в диапазонах ДВ
и СВ), а также возможность использовать линейное приближение в распределе-
нии тока, целесообразно некоторые характеристики коротких антенн рассмотреть
отдельно.
Диаграмма направленности всех коротких антенн в горизонтальной плоскости
имеет вид почти правильной окружности, а в вертикальной плоскости — половины
«восьмерки», т. е. F (0, ср) = sinG при 0 < 0 < тс/2.
Действующая высота коротких антенн проще всего определяется по методу
равенства площадей тока (см. § 2.10). Ясно, что при отсутствии горизонтальной
части (h ’ = 0)hd = h/2, а при ее большом разветвлении hd —> h ,так как при этом
распределение тока на вертикальной части приближается к равномерному.
Входное сопротивление коротких антенн состоит из сравнительно небольших
у
по величине сопротивлений излучения R и потерь Rn и большого емкостного
сопротивления ХА:
(6.2.5)
Сопротивление излучения равно половине сопротивления излучения дипо-
ля Герца, определяемого по формуле (2.3.12), в которую вместо длины диполя
нужно подставить действующую длину эквивалентного симметричного вибратора
= 2hd. Здесь действующая высота та же, что и в формуле (2.7.3). Реактивное
сопротивление можно определить как входное сопротивление разомкнутой линии
длиной h + h' с волновым сопротивлением WB, равным половине волнового сопро-
тивления эквивалентного симметричного вибратора. Таким образом,
ZA = 1600 (hd/k)2 +Rn- iWBctg(k(h + h')).
(6.2.6)
Настройка коротких антенн производится с помощью удлинительных катушек,
индуктивность которых определяется из условия Хн = —ХА :
Ь(и) = WBctgk (h + h ')/2л f.
(6.2.7)
Удлинительные катушки обычно имеют большую индуктивность. Активное со-
противление их проводов может достигать значительных величин — до единиц
Ом. Из-за больших величин реактивностей самой антенны и органов настройки
и малой величины активного сопротивления короткие антенны имеют большую
добротность, доходящую до сотен единиц. Поэтому полоса пропускания коротких
антенн получается узкой, а напряжения в антенне - большими.
6.2.8. Учет фазы тока в зеркальном изображении [3]. Согласно методу зер-
кальных изображений источник радиоизлучения, расположенный над бесконечно
протяженной и идеально проводящей плоскостью, создает в освещенном полу-
Кла^сификауия^ типы несилииетрг£чн.ы.д? антенн
255
а)
б)
Рис. 6.7. Зеркальное изображение симметричного вибратора: а) — общий вид;
б) - определение направления тока в зеркальное изображение вибратора [3]
пространстве такое же поле, какое создали бы два источника излучения, поме-
щенные в свободное пространство, один из которых представляет собой реальную
антенну, а второй — ее зеркальное изображение в экране. Зеркальный источник
располагается при этом на продолжении нормали к поверхности на расстоянии,
равном высоте h реальной антенны. Амплитуда тока в зеркальном источнике
(антенне) при полном отражении равна амплитуде тока в реальной антенне.
Что касается направления (т. е. фазы) тока в зеркальном изображении антен-
ны, то оно может быть указано только с учетом граничных условий на поверх-
ности экрана.
Зеркальные изображения симметричного вибратора при различных его ориен-
тациях относительно экрана, а также направлениях силовых линий поля Е антен-
ны и ее зеркального изображения показаны на рис. 6.7, а, б.
Как видим, на поверхности экрана тангенциальная составляющая Ет резуль-
тирующего поля обращается в ноль, если в горизонтальном вибраторе и его
изображении токи текут в противоположных направлениях (т. е. противофазны),
256
ГЛАВА 6
а в вертикальном вибраторе и его изображении — в одном направлении (токи син-
фазны).
Направление тока в изображении произвольно ориентированного вибратора
определяется как для суммарного тока 12, состоящего из горизонтальных и вер-
тикальных составляющих.
Более сложные антенны при построении их зеркальных изображений могут
быть разложены на более простые элементы, для которых правила зеркального
изображения известны.
В отличие от идеального отражающего экрана земная поверхность не дает
полного отражения; часть энергии падающей волны проникает в толщу земли
и там затухает, превращаясь в тепло. Поэтому строгий учет влияния реальных
параметров почвы на излучение антенн оказывается более сложным. Однако его
результаты показывают, что и в этом случае принцип зеркального изображения
также может быть использован для расчета поля, но только в дальней зоне (диа-
грамма направленности). При этом зеркальное изображение излучателя, как и для
металлического экрана, располагается под плоской земной поверхностью, а ток 12
в нем принимают равным току реальной антенны Ц , умноженному на коэф-
фициент отражения R от полупроводящей земной поверхности (коэффициент
Френеля):
(6.2.8)
где R = R егФ ( R
— модуль коэффициента отражения, Ф — его фаза).
В зависимости от ориентации вектора Е отражающей поверхности различают
коэффициенты Френеля для горизонтального и вертикального поляризованных
полей. Причем эти коэффициенты зависят от угла падения волны, электрических
параметров почвы (проводимости с, диэлектрической проницаемости е)
и длины волны X. Соответствующие расчетные формулы приводятся в курсе теории
электромагнитного поля.
Таким образом, применение метода зеркального изображения позволяет свести
задачу об антенне над экраном (или землей) к задаче о двух связанных антеннах
с известным соотношением токов:
I2/l ае^1 = R = |R| егф .
6.3. Широкополосные несимметричные вибраторы и антенны [17]
Расширение полосы пропускания несимметричных вибраторов и антенн дости-
гается такими же методами, как и симметричных вибраторов: утолщением прово-
дов цилиндрических вибраторов и применением конических и плоскостных конс-
трукций.
6.3.1 Диско — конусная антенна является типичной широкополосной не-
симметричной антенной. Ее конструкция показана на рис. 6.8,а. Она образована
из биконической антенны (см. рис. 4.1,6) при замене одного конуса диском. Питание
к диско - конусной антенне поводится с помощью коаксиального кабеля, причем
центральный провод присоединяется к диску, а наружная оболочка - к конусу
в его вершине. Этот способ возбуждения напоминает схему антенны верхнего пи-
тания.
Классификация, типы несимметричных антенн
257
2а2
2аг 200 600/, МГц
а) б)
Рис. 6.8. Диско — конусная антенна: а) - продольный разрез; б) — зависимость кбв
(кривая 1) и угла наклона максимума ДН (кривая 2) от частоты [17]
800МГц
300МГц
500МГц
Рис. 6.9. ДН диско - конусной антенны для трех частот [17]
Широкополосные свойства диско — конусной антенны так же, как и биконичес-
кого вибратора, объясняются хорошим согласованием с внешним пространством.
Наименьшая рабочая частота называется «частотой среза», так как в области низ-
ших частот с уменьшением частоты Кбв в питающем кабеле резко, почти скачком,
уменьшается. Длина волны, соответствующая частоте среза, называется наиболь-
шей рабочей длиной волны и равна ^макс « 3,6Z, т. е. длина образующей должна
быть несколько больше четверти наибольшей длины волны. Установлено, что с
уменьшением размеров d и t граница полосы рабочих длин волн расширяется в
сторону более коротких волн и что оптимальным углом конуса является 2\|/0 = 60°.
Между размерами устройства возбуждения должно соблюдаться соотношение:
9 - Неганов
258
ГЛАВА 6
t ® 0,3d. Радиус основания конуса равен = Zsin\|/() + d/2. Радиус диска обычно
выбирается равным а2 = 0,7^.
У хорошо сконструированных диско - конусных антенн коэффициент пере-
крытия диапазона '^макс1'^мин доходит до 5 при Кбв >0.5 в питающем фидере с
волновым сопротивлением 50 Ом. На рис. 6.8,6 показана зависимость КБВ в коак-
сиальном кабеле с волновым сопротивлением 50 Ом для антенны с частотой среза
200 МГц (кривая 1).
ДН диско — конусной антенны в горизонтальной плоскости круговая. ДН в вер-
тикальной плоскости зависит от угла при вершине конуса у0 , отношения а2/а1 и
от рабочей частоты. Она имеет вид двух лепестков, которые с увеличением часто-
ты сужаются, все более прижимаясь к образующим конуса. На рис. 6.9 показаны
экспериментальные ДН диско — конусной антенны для трех различных частот, а
на рис. 6.8, б показана зависимость утла отклонения максимума ДН в зависимости
от частоты для антенны с частотой среза 200 МГц с указанной выше геометрией,
обеспечивающей наибольшую полосу пропускания (кривая 2).
Поляризация диско — конусной антенны линейная, меридиональная, т. е. век-
тор Е лежит в плоскостях, содержащих ось антенны.
Диско - конусные антенны применяются в основном как слабонаправленные
антенны метрового и дециметрового диапазонов. В диапазоне ДЦВ диск и конус
выполняются сплошными, а в метровом дйапозоне — для облегчения конструкции —
из стержней, расположенных по радиусам у диска и по образующим у конуса.
6.4. Диаграммы направленности антенны с учетом влияния земли.
Несимметричный вибратор [3]
Несимметричным обычно называют такой вибратор, одно плечо которого
по размерам или форме отличается от другого. Примем вначале для простоты
рассмотрения землю идеально проводящей и плоской. Антенну и ее зеркальное
изображение заменим точечными излучателями, расположенными в их фазовых
(геометрических) центрах (рис. 6.10). Тогда получим систему из двух вибраторов,
разнесенных на расстоянии 2h и имеющих равные амплитуды токов.
Суммарное поле такой системы в плоскости расположения вибраторов может
быть найдено с использованием множителя решетки:
Е = АЬ (е) = EJ^ (0),
где Ej = (0) - напряженность поля симметричного вибратора без уче-
та влияния земли; А и (0) - соответственно напряженность поля вибрато-
Рис. 6.10. К расчету ДН вибратора с учетом влияния земли [3]
Классификация, типы несимметричных антенн
259
ра в направлении максимального излучения и его диаграмма направленности;
Zv (Ю~ sin(N\|//2)/sin(\|//2) - множитель системы, учитывающий в данном случае
влияние земли; \|/ = k2h sin 0 + Ф - сдвиг по фазе между полями антенны и ее зер-
кального изображения в точке наблюдения; 0 - угол между направлением в точку
наблюдения и горизонтальной плоскостью; N — число излучателей (в рассматри-
ваемом случае N = 2).
При горизонтальной поляризации электрические поля излучения и токи в ре-
альном вибраторе и его зеркальном изображении противофазны ( Фг = л) и
Ег = 2Afx (0)sin[ 2л—sin0 |. (6.4.1)
I л, )
В случае вертикальной поляризации, когда Фв = 0 ,
суммарное поле
Ев = 2Aj\ (0)cos
2 л—sin 0
(6.4.2)
Из выражений (6.4.1) и (6.4.2) следует, что основным параметром, определяю-
щим направленные свойства антенны в вертикальной плоскости, является относи-
тельная высота подвеса h/k. В горизонтальной плоскости ДН остается без измене-
ния, так как множитель системы fN (0) не зависит от азимутального угла ср.
9*
в)
Рис. 6.11. ДН горизонтального вибратора над экраном [3]
260
ГЛАВА 6
Если горизонтальный вибратор в свободном пространстве создает ненаправлен-
ное излучение в вертикальной плоскости (экваториальная плоскость вибратора),
то в присутствии земли ДН, как это следует из (6.4.1), приобретает лепестковый
характер. С увеличением высоты подвеса над землей число лепестков увеличи-
вается, нижние лепестки приближаются к земле, ДН становится уже. При этом
число боковых лепестков при углах 0 в пределах 0 - 90° равно числу полуволн,
укладывающихся на высоте подвеса антенны h. Кроме того, излучение вдоль зем-
ной поверхности ( 0 =0) отсутствует, а напряженность поля в направлении макси-
мального излучения удваивается по сравнению со случаем вибратора, находяще-
гося в свободном пространстве.
Если вибраторная антенна расположена вертикально над земной поверхнос-
тью, то она также меняет свои направленные свойства, приобретая многолепест-
ковый характер (рис. 6.10). Как следует из выражения (6.4.2), максимум излучения
при этом направлен вдоль земной поверхности.
Формулы (6.4.1) и (6.4.2) можно использовать при инженерных расчетах ДН
антенн коротких волн.
При учете конечной проводимости земли модуль коэффициента отражения
от ее поверхности R < 1. Следовательно, амплитуда тока в зеркальном изобра-
жении вибратора меньше, чем в реальном, и при расчете ДН системы нельзя ис-
пользовать множитель решетки (0). В этом случае необходимо геометрически
суммировать поля в дальней зоне от антенны и ее зеркального изображения.
Введем обозначения: ЕА = Е1 и Ези = Е2 (рис 6.10 (2)), тогда суммарное поле
Е = Е, + Е2 = Ег + RE1 = Ei Г1 + R ei(-k2h sin 6+Ф)
= E1/E2 - коэффициент отражения от земной поверхности.
Переходя к модулю выражения (6.4.3), получаем
Е - |Ej| yjl + |К|2 + 2 R cos (k2hsin 0 + Ф).
(6.4.3)
(6.4.4)
Расчет ДН антенны по формуле (6.4.4) показывает, что влияние конечной про-
водимости земли сводится к незначительному расширению диаграммы и к за-
мене направлений нулевого излучения направлениями минимального излучения
(рис. 6.11, пунктир; рис. 6.12,6).
Более строгий учет параметров земли показывает, что при горизонтальной
поляризации появляется составляющая поля антенны вдоль земной поверхности;
при вертикальной же поляризации максимум излучения приподнимается над зем-
лей.
В случае антенн иных типов учет влияния земли на их направленные свойства
производится с помощью формул, аналогичных полученным выше.
Входное сопротивление и сопротивление излучения симметричного вибратора,
расположенного вблизи земной поверхности или металлического экрана, рассчи-
тывают с учетом взаимного влияния между вибратором и его зеркальным изоб-
ражением. Расчет производится с помощью метода наведенных ЭДС и сводится
к отысканию вносимых сопротивлений в антенну со стороны зеркального источ-
ника.
Вносимое сопротивление убывает с увеличением расстояния между антеннами,
поэтому при достаточно высоко поднятых антеннах [h > (2...3)Х] взаимное влияние
можно не принимать во внимание. Следует также подчеркнуть, что сопротивле-
Классификация, типы несимметричных антенн
261
120° 90°
10
- = 0.25
h
20°
180
20
б)
Рис. 6.12. ДН вертикального вибратора над экраном [3]
ние вертикального вибратора в значительно меньшей степени зависит от своего
зеркального изображения, чем сопротивление горизонтального вибратора.
На практике широкое распространение получили несимметричные вертикаль-
ные заземленные вибраторы, представляющие собой вертикальный по отноше-
нию к земле или металлической поверхности провод, к нижнему концу которого
присоединена одна из клемм генератора (или приемника) (рис. 6.13,а). Вторая клем-
ма генератора соединяется с землей или металлическим экраном. Таким образом,
земля или металлическая поверхность играют роль второго плеча вибратора.
В случае бортовых антенн ЛА вертикальный вибратор может являться продол-
жением коаксиальной (рис. 6.13,6) или полосковой линии.
На длинных и средних волнах (диапазоны НЧ и СЧ) земля по своим свойствам
является хорошим проводником и ее действие на ДН и входное сопротивление
несимметричного вибратора можно учесть влиянием зеркального изображения
с тем же направлением тока равной величины.
Следовательно, замена земли зеркальным изображением вибратора сводится
к переходу от несимметричного вертикального вибратора длиной I к симметрич-
ному длиной 21 (рис. 6.13,в). Поэтому ДН такого вибратора в вертикальной плоскос-
ти выражается той же формулой, что и для симметричного вибратора:
z , cos(7clsin0)- cos kl
F(0) = —-P-----4-------при I < 0,7Z ,
(1 - cos/cZ)cos0
где угол 0 изменяется в пределах 0 < 0 < 180°.
Таким образом, ДН несимметричного вибратора в вертикальной плоскости за-
262
ГЛАВА 6
V////////,
б)
О 0.2 0.4 0.6 0.8 1
г)
Рис. 6.13. Вертикальный заземленный вибратор: а) упрощенная схема; б) питание вибрато-
ра коаксиальной линией; в) вибратор и его зеркальное изображение; г) ДН в вертикаль-
ной плоскости при различной длине [3]
висит только от отношения l/Х (рис. 6.13,г), а в горизонтальной плоскости является
ненаправленной. При этом максимум излучения направлен вдоль земной поверх-
ности. Если длина несимметричного вибратора превышает 0,71, то интенсивность
излучения вдоль земли падает, а боковые лепестки возрастают.
В случае антенн коротких и метровых волн (диапазоны ВЧ и ОВЧ), когда зем-
лю нельзя считать идеально проводящей, ток в зеркальном изображении может
быть определен с помощью коэффициентов отражения. Расчеты ДН при учете
конечной проводимости земли показывают, что максимум излучения направлен
под некоторым углом 00 к горизонтальной плоскости и этот угол тем меньше, чем
выше проводимость почвы и больше рабочая длина волны.
Так как излучение несимметричного вибратора происходит только в одно (вер-
хнее) полупространство (рис. 6.13,г), мощность излучения оказывается в два раза
меньшей, чем у соответствующего симметричного вибратора в свободном про-
странстве с тем же значением тока.
Как известно, мощность излучения пропорциональна сопротивлению излуче-
ния, поэтому сопротивление излучения несимметричного вертикального вибрато-
ра длинной I в два раза меньше, чем у симметричного длиной 21.
В случае четвертьволнового несимметричного вибратора I = Х/4
Классифитсаг^ия^ типы нрсимм^тричмых дмтенн
263
Действующая высота несимметричного вибратора также в два раза меньше
действующей высоты симметричного вибратора: = (l/2)h^g .
6.5. Особенности применения несимметричных антенн [17]
6.5.1. Схемы питания несимметричных антенн разделяются на схемы
последовательного и схемы параллельного питания.
По схеме последовательного питания построены: антенны нижнего питания
(рис. 6.14,а), антенны среднего питания (трубчатые антенны) (рис.6.14,г) и антен-
ны верхнего питания (рис. 6.14,0).
По схеме параллельного питания (с кондуктивным возбуждением) построены
шунтовые антенны (рис. 6.14,в).
Часто применяется трубчатая антенна (рис. 6.14,г), излучающими элементами
которой являются: верхняя часть, соединенная с центральным проводом коакси-
ального фидера, и нижняя часть - наружная оболочка коаксиального фидера. На-
пряжение питания подводится в сечении Б. На разомкнутом конце верхней части
всегда образуется узел тока. Так как нижний конец антенны соединен непосредс-
твенно с землей, то в этом сечении всегда будет пучность тока, соответствующая
короткому замыканию эквивалентной длинной волны.
Если диаметры проводов не очень велики, то распределение тока на нижней
части описывается косинусоидой 1Н (г) = Гц cos kz, а на верхней части — синусо-
идой IB (z) = 1ц sin k (h - z), где z отсчитывается от поверхности земли. Так как в
сечении Б токи IH (z) и IB (z) равны, то связь между величинами токов iff и Гц
определяется из соотношения
777777777777/
а)
7////7////77
в)
777777А V7777/
77777Т777777/
б)
д)
Рис. 6.14. Способы питания несимметричных антенн [17]
7////////////
е)
264
ГЛАВА 6
iff cos kh0 = 1$ sin к (h - h0 ).
В практических конструкциях трубчатые антенны часто имеют высоту при-
мерно Х/4. Если у такой антенны диаметр верхней и нижней частей одинаков, то
распределение тока не будет зависеть от отношения h0/h и будет иметь вид, по-
казанный на рис. 6.14,г. Входное сопротивление этой антенны (в сечении Б) можно
определить из условия независимости мощности излучения и реактивной мощнос-
ти от способа получения данного распределения тока в антенне
(6.5.1)
где ZA - входное сопротивление, отнесенное к току 1А в основании антенны. Сопро-
тивление ZA рассчитывается известным способом. Для настроенной четвертьвол-
новой антенны оно равно 36,5 Ом. Учитывая, что при синусоидальном распреде-
лении тока
~ *П’
1Б - In sin k(h-h0 ),
из равенства (6.5.1) получаем
ZE = 36,5/sin2 k(h - h0), Ом. (6.5.2)
Отсюда видно, что входное сопротивление антенны чисто активное и изменя-
ется от 36,5 Ом при hQ = 0 до оо при h0 = h. Коаксиальный кабель с волновым со-
противлением 75 Ом будет согласован с антенной, если он подключается на высоте
ho « 0,5/г .
В антенне верхнего питания (рис. 6.14,6), в отличие от трубчатой антенны, ем-
костное возбуждение осуществляется не вертикальным проводом, а горизонталь-
ными проводами или диском. Здесь излучающим элементом является наружная
поверхность внешнего провода вертикальной коаксиальной линии. Токи на этой
поверхности возбуждаются верхним элементом антенны, подключенным к цент-
ральному проводу коаксиальной линии. Такая антенна была предложена Г. 3. Ай-
зенбергом а 1940 г. для диапазона СВ. Она имеет ряд преимуществ перед антенна-
ми нижнего питания. Так как пучность тока находится у земли, то распределение
тока получается достаточно равномерным даже у сравнительно коротких антенн
У
(рис. 6.14, д). При этом увеличивается R и к. п. д.
Эквивалентная схема антенны верхнего питания показана на рис. 6.14,е,
на котором конденсатор С представляет емкость горизонтальной части антенны
по отношению к земле, a RA и ХА отсчитываются в сечении Б.
6.5.2. Влияние конечной проводимости земли на параметры несимметрич-
ных антенн сводится прежде всего к уменьшению к. п. д. и соответственно коэф-
фициента усиления за счет потерь в земле. Расчет потерь в земле и учет влияния
конечной проводимости земли на ДН пока остаются сложной и громоздкой проце-
дурой. Приближенная формула для расчета ДН [17] получается «модифицирован-
ным» методом зеркальных изображений, который заключается в том, что вели-
чина тока в зеркальном изображении для случая идеально проводящей плоскости
умножается на комплексный коэффициент отражения Френеля, соответствующий
параметрам поверхностного слоя земли.
Качественное представление о влиянии конечной проводимости земли не ДН
и амплитуду поля дает рис. 6.15, на котором показаны ДН по меридиональной
составляющей электрического вектора поля, создаваемого четвертьволновым
Класси^икал^ля^ типы несиммет^^ антенн
265
60 30 0 30 60
Рис. 6.15. Влияние конечной проводимости земли на ДН четвертьволнового вибратора [17]
90
вибратором над идеально проводящей плоскостью (пунктир) и над плоскостью
с потерями (сплошная линия).
Наиболее общее выражение для к. п. д. несимметричных антенн имеет вид
т| = Rz/(Kl + , (6.5.3)
где R$ - сопротивление потерь в экране или в земле, R^ - активное сопротивле-
ние органов настройки (чаще всего — удлинительной катушки). Вопрос о к. п. д.
особенно остро стоит для антенн длинных и сверхдлинных волн, которые вынуж-
денно оказываются электрически короткими, с малым сопротивлением излучения.
К. п. д. этих антенн иногда не превышает 10 — 15 %. При этом очень важно снизить
потери в органах настройки и в земле. Для уменьшения удлинительной катушки
применяют широко разветвленную горизонтальную часть.
Если этого окажется недостаточно, то применяют антенну с многократным
снижением (см. рис. 6.1, ж). В этой антенне с помощью катушек настройки добива-
Заземление
Противовес
Земля
б)
Рис. 6.16. Заземление и противовес [17]
266
ГЛАВА 6
ются синфазных токов во всех снижениях. Так как расстояние между снижениями
значительно меньше длины волны, то наряду с увеличением сопротивления из-
лучения за счет увеличения числа излучающих проводов происходит увеличение
этого сопротивления за счет наведенных э. д. с. К. п. д. при этом возрастает.
Антенные трешетки
267
Глава 7. Антенные решетки
7.1. Антенные решетки и их классификация
Направленность действия простейшей антенны — симметричного вибратора —
невысокая. Для увеличения направленности действия уже на первых этапах
развития антенной техники стали применять систему вибраторов — антенные
решетки (АР). Напомним, что АР называется система одинаковых излучающих
элементов, идентично ориентированных в пространстве и расположенных по оп-
ределенному закону. В зависимости от расположения элементов различают линей-
ные, поверхностные и объемные решетки, среди которых наиболее распростра-
нены прямолинейные и плоские АР. Иногда излучающие элементы располагаются
по дуге окружности или на криволинейных поверхностях, совпадающих с формой
объекта, на котором расположена АР (конформная АР).
В настоящее время в АР используются как слабонаправленные элементы (ме-
таллические и щелевые вибраторы, волноводы, диэлектрические стержни, спира-
ли и т. д.), так и остронаправленные элементы (зеркальные, рупорные и др.).
Применение антенных решеток обусловлено следующими причинами. Решетка
из N элементов позволяет увеличить приблизительно в N раз КНД (и соответс-
твенно усиление) антенны по сравнению с одиночным излучателем, а также су-
зить луч для повышения точности определения угловых координат источника из-
лучения в навигации, радиолокации и других радиосистемах. С помощью решетки
удается поднять электрическую прочность антенны и увеличить уровень излучае-
мой (принимаемой) мощности путем размещения в каналах решетки независимых
усилителей высокочастотной энергии. Одним из важных преимуществ решеток
является возможность быстрого (безынерционного) обзора пространства за счет
качания луча антенны электрическими методами (электрического сканирования).
Помехозащищенность радиосистемы зависит от уровня боковых лепестков (УБЛ)
антенны и возможности подстройки (адаптации) его по помеховой обстановке. Ан-
тенная решетка является необходимым звеном для создания такого динамическо-
го пространственно-временного фильтра или просто для уменьшения УБЛ. Одной
из важнейших задач современной бортовой радиоэлектроники является создание
комплексированной системы, совмещающей несколько функций, например ра-
дионавигации, РЛС, связи и т. д. Возникает необходимость создания антенной
решетки с электрическим сканированием с несколькими лучами (многолучевой,
моноимпульсной и т. д.), работающей на различных частотах (совмещенной) и име-
ющей различные характеристики.
Имеется ряд конструктивно-технологических преимуществ антенных решеток
для бортовых и наземных устройств по сравнению с другими классами антенн.
Так, например, улучшение массогабаритных характеристик бортовой аппаратуры
происходит за счет использования печатных антенных решеток. Снижение стои-
мости больших радиоастрономических телескопов достигается благодаря примене-
нию зеркальных антенных решеток.
Антенные решетки могут быть классифицированы по следующим основным
268 ГЛАВА 7
признакам: геометрии расположения излучателей в пространстве, способу их воз-
буждения, закономерности размещения излучающих элементов в самой решетке,
способу обработки сигнала в решетке, амплитудно-фазовому распределению токов
(поля) по решетке и типу излучателей. В зависимости от геометрии расположе-
ния излучателей АР подразделяются на линейные, дуговые, кольцевые, плоские,
выпуклые (цилиндрические, конические, сферические и др.) и пространственные
(трехмерные) (рис. 7.1). Пространственная решетка в простейшем случае представ-
ляет собой систему из двух плоских решеток, параллельно расположенных в про-
странстве.
Размещение излучателей в самой решетке может быть эквидистантное, у кото-
рого шаг (расстояние между излучателями) - величина постоянная (рис. 7.1, а-ж),
и неэквидистантное, у которого шаг меняется по определенному закону или слу-
чайным образом (рис. 7.1, з). В плоской АР излучатели могут быть расположены в
узлах прямоугольной или косоугольной координатной системы (рис. 7.2, а).
ж)
Рис. 7.1. Антенные решетки: а) - линейная; б) — дуговая; в) - кольцевая; г) - плоская;
д) - цилиндрическая; е) - коническая; ж) - сферическая; з) - неэквидистантная [3]
а)
Амтекные решетки
269
Вход
Рис. 7.2. Плоская прямоугольная (а) и гексагональная (б) решетки
Вход
приемные
элементы
передающие
элементы
облучатель / / /
фазовращатели г
в)
Рис. 7.3. Возбуждение излучателей в решетке: а) — последовательная схема;
б) ~ параллельная схема; в) - схема питания типа «елочка»;
г) - пространственное возбуждение [3]
270 ГЛАВА 7
Если косоугольная сетка состоит из равносторонних треугольников, то такая
структура образует правильные шестиугольники и называется гексагональной
(рис. 7.2, б).
По способу возбуждения (питания) излучателей различают решетки с пос-
ледовательным и параллельным питанием. Возможен также пространствен-
ный способ возбуждения, который называют иногда оптическим или «эфирным»
(рис. 7.3, г) [3].
Частным случаем параллельного питания является схема типа «елочка», об-
разующаяся за счет каскадного деления подводимой мощности на две части (рис.
7.3, в). В случае пространственного возбуждения элементы решетки возбуждаются
падающей волной от первичного облучателя (рис. 7.3, г).
В питающем антенную решетку тракте (фидере) возможна различная про-
странственно-временная обработка сигнала. Изменение фазового распределения в
решетке с помощью системы фазовращателей в питающем тракте (рис. 7.3, г) поз-
воляет управлять максимумом диаграммы направленности. Такие решетки называ-
ются фазированными антенными решетками (ФАР). Если к каждому излучателю
ФАР или к их группе подключается усилитель мощности, генератор или преоб-
разователь частоты, то такие решетки называются активными фазированными
антенными решетками (АФАР) (рис. 7.4, а,б). Приемные АР с саморегулируемым
амплитудно-фазовым распределением в зависимости от помеховой обстановки на-
зываются адаптивными. Приемные АР с обработкой сигнала методами когерентной
оптики называются радиооптическими. Приемные АР, в которых вся обработка
ведется цифровыми процессами, называются цифровыми АР.
Совмещенные антенные решетки имеют в своем излучающем раскрыве два (или
более) типа излучателей, каждый из которых работает в своем рабочем диапазо-
не.
Антенные решетки, формирующие с одного излучающего раскрыва несколько
независимых (ортогональных) лучей и имеющие соответствующее число выходов,
называются многолучевыми.
В зависимости от соотношения амплитуд токов возбуждения различают решет-
ки с равномерным, экспоненциальным и симметрично спадающим амплитудными
распределениями относительно центра решетки. Если фазы токов излучателей
изменяются вдоль линии их размещения по линейному закону, то такие решетки
называют решетками с линейным фазовым распределением. Частным случаем та-
ких решеток являются синфазные решетки, у которых фазы тока всех элементов
одинаковы.
7.1.1 Методы расчета характеристик антенных решеток. В начале рас-
смотрим расчет АР, образованных системой полуволновых вибраторов. В строгой
электродинамической постановке задача об излучении системы тонких полуволно-
вых вибраторов аналогична ранее рассмотренной задаче об излучении одиночно-
го вибратора. Различие состоит в замене одного вибратора системой вибраторов,
каждый из которых возбуждается своим сторонним источником. Поступая, как при
строгом решении задачи излучения симметричного вибратора, можно установить
связи между сторонними источниками и параметрами АР. Токи в излучателях АР
могут быть найдены из совместного решения системы интегральных уравнений.
Такое решение оказывается на порядок сложнее, чем для одиночного излучате-
ля, и весьма затрудняет выявление основных закономерностей антенных решеток.
Антенные решетки
271
Генераторы (умножители,
усилители)
а)
Решетки (секции возбуждения
и фазирования)
б)
Рис. 7.4. Активные фазированные решетки: а) — активный элемент в каждом излучателе;
б) - активный элемент в каждом излучателе (модульная конструкция) [3]
С этой целью в теории антенн используют приближенные методы, в которых об-
щую задачу расчета АР условно разделяют на две задачи: внешнюю и внутрен-
нюю. Решение внешней задачи состоит в нахождении характеристик направлен-
ности антенны при известном амплитудно-фазовом распределении токов (полей)
по элементам АР. Это распределение считается известным из решения внутрен-
ней задачи и достигается соответствующим подбором сторонних источников воз-
буждения. Решение внутренней задачи состоит в определении амплитудно-фазо-
вого распределения в АР при заданных сторонних источниках, что необходимо
для возбуждения (питания) АР. Решение внешней задачи можно провести в общем
виде для различных АР и установить характеристики направленности. Поэтому
ниже подробно остановимся на общем приближенном методе расчета внешней
задачи. Следует заметить, что методы решения внутренней задачи оказывают-
ся различными для разных типов излучателей АР и будут рассмотрены позднее.
Поле излучения антенной решетки представляет собой результат интерференции
полей отдельных излучателей. Поэтому надо найти отдельно поле от каждого из-
лучателя в данной точке пространства, а затем сумму полей всех излучателей при
учете амплитудных и фазовых соотношений, а также поляризации полей.
Расчет диаграммы направленности таких антенн целесообразно проводить в
следующем порядке [3]:
272 ГЛАВА 7
Определить амплитудную и фазовую диаграммы излучения отдельных элемен-
тов, составляющих антенную решетку.
Найти фазовый центр каждого излучателя и заменить их воображаемыми
точечными излучателями, расположив последние в фазовых центрах реальных
излучателей. Каждому точечному излучателю приписать равномерную фазовую
диаграмму и амплитудную диаграмму реального излучателя. Тогда точечный из-
лучатель по внешнему действию будет полностью эквивалентен реальному излу-
чателю.
Вычислить амплитуды и фазы полей, создаваемые эквивалентными излучате-
лями в произвольной точке пространства (каждым в отдельности). При этом рас-
сматривать поле на большом (по сравнению с размерами антенны и длиной волны)
расстоянии от точки наблюдения до всех излучателей (одинаковом и равном рас-
стоянию до какого-либо излучателя). Однако, расчет фаз следует вести с уче-
том разницы в расстояниях до каждого излучателя. При определении разницы в
расстояниях в целях упрощения следует считать направления на точку наблюде-
ния параллельными для всех излучателей. При вычислении фаз надо определять
фазы по отношению к фазе поля какого-либо одного излучателя, принимаемой
за начальную.
Определить амплитуду и фазу поля всей антенны путем геометрического сум-
мирования полей всех составляющих ее излучателей, учитывая амплитудные и
фазовые соотношения, а также поляризацию полей.
7.2. Излучение линейной синфазной решетки [3]
Простейшей АР является линейная, в которой излучающие элементы распола-
гаются вдоль прямой, называемой осью решетки, на равных расстояниях друг от
друга (эквидистантная АР). Расстояние d между фазовыми центрами излучателей
называют шагом решетки. Если все элементы АР имеют одинаковые фазы, то она
называется синфазной. Линейная АР помимо самостоятельного значения является
часто основой при анализе других типов АР.
При расчете поля излучения синфазной антенны с равномерным амплитудным
распределением приходится иметь дело со сложением некоторого числа одинако-
во поляризованных гармонических колебаний с равными амплитудами и фазами,
отличающимися друг от друга на одинаковый угол. Сумма таких колебаний опре-
деляется как сумма (ряд таких колебаний) членов геометрической прогрессии или
геометрическим путем. Пусть имеется:
A cos art + A cos (ot + 2\|/) +... + A cos (tot + (N - 1».
Представим каждое слагаемое вектором, имеющим модуль, равный амплиту-
де поля излучения А, и расположенным соответственно фазе колебания . При
суммировании векторов образуется правильный многоугольник (рис. 7.5). Опишем
вокруг него окружность радиусом р с центром в точке О, тогда ad = 2psin(Ah|//2),
так как ZaOd = М|/. Из ЛаОЬ А = 2psin\g/2 откуда р = A/2sin(\g/2). Таким образом,
амплитуда результирующего колебания
ad - А
sin(M|//2)
sin \jj/2
Аытенмые решетки
273
О
Рис. 7.5. Векторная диаграмма суммирования полей излучателей [3]
б)
Рис. 7.6. Линейная решетка излучателей: а) — решетка вертикальных вибраторов;
б) — решетка горизонтальных вибраторов; в) — к расчету ДН линейных АР [3]
Фаза результирующего колебания по отношению к фазе начального колебания
определяется величиной угла dab и равна (N-1)\|//2. Сумма всех колебаний
A cos (cot + (п -1) v) = А
71=1
sin(A/w/2) (
------——-COS COt+
sin\|//2
(7.2.1)
где v — разность фаз между соседними колебаниями.
Фаза результирующего колебания опережает фазу исходного на угол
(N -l)V/2.
Получили распространение антенные решетки, составленные из вертикальных
или горизонтальных полуволновых вибраторов (рис. 7.6, а,б).
Такие антенны обычно состоят из синфазно питаемых полуволновых вибрато-
ров, одинаково ориентированных и расположенных на одинаковом расстоянии d
друг от друга. Направление расположения образует прямую линию.
274
ГЛАВА 7
Для расчета диаграмм направленности заменим каждый вибратор эквивален-
тным точечным излучателем, расположив его в фазовом центре, т.е. в середине
вибратора. Тогда независимо от того, горизонтальные или вертикальные вибра-
торы в решетке, схема примет вид, показанный на рис. 7.6, в. Поле такой ан-
тенны — результат интерференции полей вибраторов. Будем считать, что все
излучатели в решетке имеют одинаковые ДН. Так как вибраторы параллельны, то
поля одинаково поляризованы, а следовательно, можно пользоваться полученной
выше формулой для суммарного поля. Рассматривая поле далеко от антенны, т.е.
на расстоянии г » X , можно считать, что Tj. || г2 || ||... || гп (см. рис 7.6, в).
Пусть мгновенное значение тока в пучности каждого вибратора описывается
уравнением i = I sin cot. Тогда суммарное электрическое поле в точке наблюдения
от всей антенны
п
е = <6’ ч>)cos(cot-krn), (7.2.2)
г=1
где fi (0,ф) — диаграмма направленности эквивалентного излучателя в решетке,
которую примем в рамках приближенной теории, одинаковой для всех излуча-
телей; А — постоянный (амплитудный) множитель, не зависящий от углов 0, ср;
гп — расстояние от п -го излучателя до точки наблюдения.
Примем фазу поля от наиболее удаленного излучателя (в рассматриваемом
случае — первого) за начальную. Тогда для определения фазы поля п -го излу-
чателя необходимо предварительно выразить расстояние от этого излучателя до
точки наблюдения через расстояние . Из рис. 7.6, в видно, что
т2 = - d sin 0,
r3 ~ r2 ~ sin 0 = 4 - 2d sin 0,
rn = l)d sin 0.
Подставляя значение rn в формулу (7.2.2), получаем
= Afi (0,cp)cos {шt -к Ti -(n -l)dsin0
n
= / Afi (0,(p)cos {cot -ki} +k(n- l)d sin 0} =
(7.2.3)
TV -1
2
kd sin 0
где \|/ = fed sin 0 — разность фаз между полями соседних излучателей; к = 2л/Л,.
Проведем анализ полученного выражения. Амплитудная диаграмма направлен-
ности, согласно формуле (7.2.3), определяется как
sin —Nd sin 0
f (e, <p) = a | л (e, <p)| —------т
sin — dsin0
(7.2.4)
Антенные решетки
275
и представляет собой произведение диаграммы
составляющего
излучателя
A\fl (0,ф)|
на множитель системы антенны:
71
sin —Nd sin 0
/(с)(е)=—7^-------у
sin — dsinO
)
(7.2.5)
Из формулы (7.2.3) следует, что фаза поля изменяется при изменении угла
0. Таким образом, при отсчете расстояния от наиболее удаленного излучателя
синфазная антенна не имеет равномерной фазовой диаграммы, а выбранная точка
начала отсчета расстояний не является фазовым центром.
Фазовой диаграммой будем называть в дальнейшем ту часть выражения, опре-
деляющего фазу поля, которая не зависит от времени (см. (7.2.3)):
т (е, ф)
= Г1 + — (N - l)dsin6.
Л Л
Выясним, имеет ли рассматриваемая антенна фазовый центр и где он находит-
ся. Предположим, что фазовый центр имеется и находится на линии расположе-
ния излучателей на расстоянии х от первого излучателя. Обозначим расстояние от
фазового центра до точки наблюдения через Tq и выразим расстояние через Tq :
rl = ro + х sin 6 , тогда
‘i'(e><P)=-Vro "
Л
2тг . _ 7С ч\ 1 . п
— х sm 0н— (N - l)d sm 0
Если Xq — координата фазового центра, то это выражение при х = не долж-
но зависеть от 0. Требуя выполнения этого условия, получаем
2л
х sin 0 + — (N - l)d sin 0 = 0
откуда х = d(N -1) / 2.
Таким образом, рассматриваемая антенна имеет фазовый центр, который сов-
падает с ее геометрическим центром. Этот вывод справедлив в общем случае для
любой синфазной антенны.
При отсчете расстояния от фазового центра с учетом того, что амплитуда поля
практически не меняется при перемене начала отсчета в пределах антенны, элек-
трическое поле равно:
cos (cot - kr^y.
(7.2.6)
Так как вибраторы, образующие решетку, обладают слабой направленностью,
ДН решетки в основном определяется множителем решетки (множитель системы)
/^(0,ф), который зависит от числа излучателей и расстояния между ними, вы-
раженного в длинах волн d/X (см. (7.2.5)). Этот множитель не зависит от угла ф,
а это значит, что в плоскости, перпендикулярной линии расположения излуча-
телей (при 0 = 0°), амплитудная ДН решетки совпадает с диаграммой одиночного
излучателя, а поле возрастает пропорционально числу излучателей:
276
ГЛАВА 7
/ = А|л(е,Ф)|лг,
что следует из выражения (7.2.4) при 0 = 0°.
В плоскости, проходящей через линию расположения излучателей ( ф = const),
амплитудная ДН решетки отличается от амплитудной ДН одиночного излучателя.
Пусть в этой плоскости ДН одиночного излучателя ненаправленная. Тогда ампли-
тудная ДН решетки будет определяться только множителем решетки, который в
нормированном виде записывают как
. Nw
sin—-
N sin
Множитель решетки F'c'(0) является периодической функцией с периодом 2л
и при изменении угла 6 проходит через свои максимальные и минимальные значе-
ния. Поэтому ДН решетки имеет многолепестковый характер (рис. 7.7).
В каждом из периодов этой функции имеется один главный лепесток и несколь-
ко боковых. График функции F^c'(9) симметричен относительно точек ф = 0 ± 2л,...,
а сама функция при этих значениях максимальна.
Между соседними главными лепестками имеется N — 1 направлений нулевого
излучения и N - 2 боковых лепестков, максимумы которых убывают при удалении
от каждого главного лепестка. Наименьшими при этом являются те лепестки амп-
литудной ДН, которые находятся в середине интервала между соседними главны-
ми максимумами. Относительная величина боковых лепестков
тбл
mmax
TV sin
где р = 1,2,3... . В решетках с большим числом излучателей уровень первых боко-
вых лепестков может быть найден по упрощенной формуле
^тбл 1
^mmax (2р + 1)л
и при N > 12 величина первого бокового лепестка равна 0,217 (или -13,2 дБ) отно-
сительно главного.
На практике обычно требуется получить амплитудные ДН решетки с одним глав-
-2л —л 0 л 2л V
Рис. 7.7. График функции sin(iV\|//2)/ (N sin(i|j/2H (заштрихованная часть
соответствует реальной амплитудной ДН ( —л/2 < 0 < л/2 )) [3]
Антенные решетки
277
ным максимумом излучения. Для этого необходимо, чтобы в интервал изменения
обобщенной координаты = kd sin 0 , определяемый неравенством -kd < у <kd и
соответствующий реальной ДН решетки (- л/2 < 0 < л/2), попадал лишь один глав-
ный максимум функции sin(Afy/2)/f/V sin(tp/2)) (рис. 7.7). Это будет в том случае,
если ширина интервала изменения , равная 2kd, меньше 4л, т.е. 2kd < 4 л. Та-
ким образом, расстояние между соседними излучателями в решетке должно быть
меньше длины волны генератора. Угловые границы главного лепестка по уровню
нулевого излучения могут быть найдены из формулы (7.2.6) путем приравнива-
ния
так
нулю числителя множителя решетки sin —Ndsin0
= 0 или — Nd sin 0 - ±л
как множитель решетки с изменением угла изменяется значительно быстрее,
чем первый множитель формулы (7.2.6), и определяет в основном ДН решетки. Из
последнего соотношения следует sin 0g = ±Х / (Nd). При большом числе излучате-
лей (N > 4) можно принять sin 0g « 0g . Отсюда угловая ширина главного лепестка
ДН 20о « 2Х / (Nd) или 20g « 115°Х / (Nd). Таким образом, для получения узких ДН
необходимо увеличивать длину антенны Nd . Однако, поскольку расстояние меж-
ду излучателями должно быть меньше длины волны генератора (для получения
одного главного максимума излучения), повышения направленности добиваются
увеличением числа излучателей решетки N. Ширину ДН по уровню 0,7 поля (по
половинной мощности) можно определить по приближенной формуле
A, X
20g 5 « 0,89-рад или 20g к « 51°---. (7.2.7)
и,5 Nd н м 0,5 Nd
Формула (7.2.7) тем точнее, чем больше число вибраторов в решетке при задан-
ной величине отношения d/X. Практически ею можно пользоваться, если Nd > ЗХ.
Если излучатели, образующие линейную синфазную антенну, обладают направ-
ленными свойствами в плоскости, проходящей через линию их расположения (рис.
7.8), то расстояние между излучателями можно взять большим длины волны ге-
нератора (d > X). В этом случае в интервале изменения обобщенной координаты у
соответствующей реальной ДН решетки, может оказаться несколько максимумов
функции sin(7V\p/2)/(N sin(\[f/2)).
В результирующей ДН они будут отсутствовать, если в этих направлениях
ДН одиночного элемента решетки имеет нулевое или почти нулевое значение. Та-
ким образом, выбором соответствующего расстояния между излучателями (d > X)
можно получить результирующее излучение с относительно низким уровнем бо-
ковых лепестков.
Если расстояние между излучателями выбрано таким, что можно пренебречь
влиянием их полей друг на друга, то КНД решетки можно подсчитать по при-
ближенной формуле Dg « ND01, где Dg^ — коэффициент направленного действия
одиночного излучателя в свободном пространстве. Рассмотренные линейные ре-
Рис. 7.8. Линейная решетка направленных излучателей
278
ГЛАВА 7
шетки обладают направленностью только в одной плоскости
положения излучателей.
в плоскости рас-
7.3. Линейные АР с равноамплитудным возбуждением и
линейным изменением фазы [27]
7.3.1. Множитель системы линейной АР. Рассмотрим линейную эквидистан-
тную АР, элементы которой расположены вдоль оси z (рис. 7.9). Предположим,
что решетка состоит из нечетного числа излучателей N = 2М +1, причем цен-
тральный элемент расположен в начале координат, -М и М — номера нижнего и
верхнего элементов соответственно. Тогда положение п -го элемента характеризу-
ется координатами хп = 0 , уп = 0 , zn = nd. Предположение, что число излуча-
телей нечетно, введенное для упрощения анализа, не является принципиальным.
Все полученные ниже соотношения остаются справедливыми при четном числе
излучателей N = 2М.
Полагаем, что комплексная амплитуда тока в п -м излучателе
In = I ехр(-гпф), (7.3.1)
т. е. токи во всех элементах равны по амплитуде, а фаза тока в каждом из эле-
ментов отстает от фазы в предыдущем на величину ф (линейный, или прогрес-
сивный, закон изменения фазы; рис. 7.10, б). Подобное распределение тока ши-
роко используется на практике. Заметим, что вопрос практической реализации
требуемого распределения токов достаточно сложен, в частности, из-за эффекта
взаимной связи, неодинаковой для центрального и крайних элементов. При на-
стоящем анализе полагается, что токи в элементах решетки известны с учетом
эффекта взаимной связи ДН одного элемента в решетке остается такой же, как в
случае уединенного излучателя**. В качестве элементов для простоты рассмотрим
ненаправленные излучатели, поэтому при расчете ДН достаточно ограничиться
анализом множителя системы.
Используя общие соотношения находим, что разность хода для п -го элемента
по сравнению с центральным, расположенным в начале координат, Дтп = nd cos 0,
а множитель системы
м
exp[in(kd cos 0 - vp)],
п=-М
(7.3.2)
причем выражение (7.3.2) (в котором опущен несущественный постоянный, мно-
житель I) справедливо для любой из компонент поля Eq или , создаваемой из-
лучателями в дальней зоне.
Выражение под знаком суммы в (7.3.2) представляет собой геометричес-
кую прогрессию из N членов, знаменатель которой р - exp[?(kdcos0 — ф)],
а первый член прогрессии, соответствующий п = —М, определяется как
- - (
Qi = exp[—iM(kd cos 0 — ф)] = р~ . Используя формулу для суммы геометрической
** Если заданы токи в элементах АР, ДН одного элемента соответствует режим, когда
данный элемент возбужден, а на входе остальных элементов токи равны нулю. Для вибра-
торных антенн это соответствует размыканию входных точек. Подобные разомкнутые эле-
менты (при длине плеча I X / 2 ) оказывают сравнительно малое влияние, которым можно
пренебречь.
Aitrn^HHbLe решетки
279
-M
Рис. 7.9. Линейная эквидистантная АР
Амплитуда I м . < 1 1 е - । 2 • • < 1 1 1 П = 0 • •——! 1 -1 • •—: -2 • • ! 1 1 1 -М • • ' а) Фаза • \ \ \ \ \ • • \ б)
Рис. 7.10. Законы изменения амплитуды (а) и фазы (б) линейной АР [27]
280
ГЛАВА 7
прогрессии S = (рД' -1) / (р -1), получаем
у(с) = p-M(pN _ 1) / (Р _ 1) = p-M{pN/2pN/2 _ pN/2p-N/2} / (р1/2р1/2 _ р^/2р-1/2}
Вынесем из числителя дроби pN^, а из знаменателя р1//2. В результате полу-
чим член = р(2М+1-1)/2 — рм. Введем обобщенную угловую переменную
и = N(kd cos 0 - \р) / 2
(7.3.3)
и преобразуем оставшуюся дробь с использованием формулы Эйлера:
ехр(ш) - ехр(-ш)
sin и
ехр(ш / N) - ехр(-ш / N) sin(u / N)
sin[N(kd cos 0 - kg) / 2]
sin[(kd cos 0 - kg) / 2]
(7.3.4)
Выражение (7.3.4) получилось чисто вещественным. Это значит, что фазовая
диаграмма направленности АР не зависит от угловых координат и лишь меняется
скачком на л при переходе через нуль выражения (7.3.4). Таким образом, линейная
АР с распределением токов (7.3.1) независимо от величины kg излучает волну со
сферическим фронтом и ее фазовый центр совпадает с серединой АР. Выражение
для нормированной амплитудной ДН (нормированный амплитудный множитель
системы) имеет вид
F<c)(0) =
1 sin[N(kd cos 0 - kg) / 2]
/(С)(6гл)
sin[(kd cos 0 - kg) / 2]
(7.3.5)
где f'С\^гл) — значение функции f'c' в направлении главного максимума 0 = 0^.
Знак модуля в дальнейшем для упрощения записи будем опускать. Обратим вни-
мание, что величина (kd cos 0 - kg) в аргументе числителя и знаменателя (7.3.5) ха-
рактеризует сдвиг фаз между полями двух соседних элементов в дальней зоне. В
зависимости от фазового сдвига kg изменяется положение максимума излучения.
Соответственно различают режимы нормального, наклонного и осевого излуче-
ний.
7.3.2. Режим нормального излучения (kg = 0). При kg = 0 все элементы ре-
шетки возбуждаются синфазно. Максимум излучения ориентирован по нормали
(0гЛ = 90°) к оси решетки, так как в этом направлении разность хода равна нулю
и поля складываются синфазно. Это — режим нормального излучения. Диаграмма
направленности описывается функцией
(с) _ sin[(Nkd cos 0) / 2]
sin[(kd cos 0) / 2]
(7.3.6)
В направлении 0^ = 90° выражение (7.3.6) представляет собой неопределенность
(с\
вида 0/0, при раскрытии которой по правилу Лопиталя получаем jv 7(0z,i) = N-
Соответственно нормированная ДН системы имеет вид
(с) _ sin[(Nkd cos 0) / 2] _ sin и
N sin[(kd cos 0) / 2] N sin(u / N)
(7.3.7)
где и = (Nkd cos 0) / 2.
Элементарное рассмотрение основных свойств линейной АР можно осущест-
Антенные решетки
281
Е(в=е02)
с(е=е01)
9
Рис. 7.11. Векторные ДН линейной АР в некоторых точках наблюдения [27]
вить, не прибегая к анализу выражения (7.3.2). Каждое слагаемое в (7.3.2), про-
порциональное полю излучения соответствующего элемента, будем изображать
как вектор на фазовой (комплексной) плоскости. На рис. 7.11 последовательно
представлены векторные диаграммы для нескольких точек наблюдения. Еще раз
подчеркнем, что рассматриваемые векторные диаграммы отражают фазовые соот-
ношения между полями отдельных элементов и никак не связаны с расположени-
ем векторов в пространстве.
В точке А (0 = 90°, разность хода Ат = 0) все векторы синфазны между собой,
в результате суммарное поле имеет максимальное значение. Таким образом, в на-
правлении нормали к оси АР формируется максимум ДН. В точке В синфазность
сложения уже нарушается, причем векторы, соответствующие элементам с по-
ложительными индексами, опережают, а с отрицательными — запаздывают по
отношению к вектору с индексом п = 0 на величину nkAr = nkd cos 0. Для сумми-
рования векторов в точке В можно совместить начало каждого вектора с кон-
цом предыдущего и полученную ломаную замкнуть результирующим вектором
(см. рис. 7.11), который, естественно, будет меньшим, чем в точке А. При даль-
нейшем уменьшении угла 0 «веер» векторов раскрывается все сильнее, соответс-
твенно результирующий вектор становится все меньше, пока в точке С, угловое
положение которой в этой точке обозначим как 0 = 0qi , не обратится в нуль. Как
видно, фазовый сдвиг между отдельными векторами, равный kd cos 0qi , составля-
ет в этой точке 2п / N. Отсюда
cos0ol = X / Nd.
(7.3.8)
Заметим, что условие (7.3.8) может быть выполнено, только если Nd > X. В
противном случае в ДН отсутствуют направления с нулевым излучением. Чем
больше произведение Nd (чем длиннее решетка), тем уже основной лепесток ДН.
282
ГЛАВА 7
При 0 < 0qi начинается область формирования боковых лепестков. Максимум пер-
вого бокового лепестка получается в точке D. Интересно отметить, что в области
бокового излучения векторы, соответствующие средним элементам, компенсиру-
ют друг друга (см. рис. 7.11), и суммарный вектор определяется только вкладом
элементов, расположенных вблизи краев АР. Поэтому интенсивность боковых ле-
пестков в принципе можно уменьшить, выбирая закон распределения токов, спа-
дающий к краям решетки.
В точке Е суммарный вектор опять обращается в нуль. При дальнейшем умень-
шении угла 0 продолжается процесс формирования дальних боковых лепестков.
Однако при сравнительно большом d возможен случай, когда фазовый сдвиг меж-
ду соседними векторами достигает величины 2л , т. е. все векторы опять оказыва-
ются расположенными параллельно друг другу и их сумма дает дополнительный
главный максимум. Это может иметь место при угле 0 = 0em тах, определяемом
соотношением
^штах arccos(X / d). (7.3.9)
Из (7.3.9) видно, что для исключения дополнительных главных максимумов в ДН
синфазной решетки из изотропных элементов необходимо выбирать
d<X. (7.3.10)
В точках B’,Cr,D',E' векторные диаграммы имеют аналогичный вид, изменяется
только знак фазового сдвига между нолями соседних элементов. Для построения
ДН необходимо в радиальных направлениях, соответствующих рассмотренным
точкам, отложить отрезки, пропорциональные результирующим векторам в каж-
дой точке. Характерный вид подобной диаграммы (в плоскости, проходящей через
ось решетки) приведен на рис. 7.12. При построении ДН учтена симметрия системы
относительно оси решетки и плоскости, перпендикулярной оси. Соответствую-
щая пространственная ДН получается путем вращения кривой, изображенной на
рис. 7.11 вокруг оси решетки.
Перейдем к более детальному анализу ДН, описываемой выражением (7.3.7).
Направления, в которых излучение отсутствует, определяются из условия
Nkd cos 0Qm / 2 = ±тл, где т = 1,2,..., причем знак плюс соответствует углам 0 < 0^г,
а знак минус — углам 0 > 0гл. Соответственно находим
cos0От = ±тХ / Nd. (7.3.11)
При т=1 выражение (7.3.11) совпадает с полученным ранее (7.3.8). Если Nd » X
(реально при Nd » ЗХ), то из (7.3.11), используя формулу
cos а = sin(7t / 2 - ос) « л / 2 - а
для углов а, близких к л / 2 , имеем 0О1 ® л / 2 - X / Nd. В силу симметрии диа-
граммы относительно нормали к оси решетки ширина основного лепестка ДН по
уровню нулевого излучения определится по формуле
Д0О = 2(0^ - 0О1) « 2Х / Nd « 115°Х / Nd. (7.3.12)
Ширину ДН по половинной мощности (по уровню 0,7 поля Е) можно найти по
приближенной формуле
Д0О>5 « 0,89Х / Nd « 51°Х / dN. (7.3.13)
Направления максимумов боковых лепестков приближенно можно определить
из условия максимума числителя (7.3.7), так как знаменатель, этого выражения,
Антенные решетки
283
Рис. 7.12. ДН линейной АР в ее плоскости при различном
числе элементов N и шагом d [27]
особенно при большом Nd , меняется значительно медленнее числителя. Отсюда,
приравнивая аргумент числителя к ±(2т + 1)л / 2, имеем
cos 6тЯХ m = ±(2т + 1)Х / 2Nd, т = 1,2,...
(7.3.14)
Подставляя значение 6 = 0max?n из (7.3.14) в (7.3.7), получаем относительный
уровень боковых лепестков (УБЛ):
1/^N
sin
(7.3.15)
Величина максимальна для т = 1, с ростом т интенсивность боковых ле-
пестков сначала убывает, затем возрастает. Минимальное значение <^т имеет при
аргументе синуса в (7.3.15), равном ±тг / 2 . Угловое положение этих лепестков мож-
но определить, приравняв аргумент синуса в знаменателе (7.3.7) к л / 2, откуда
получим cos 9 = ±1 / 2d. Ясно, что для исключения возрастания УБЛ необходимо
выполнение условия
d<X/2.
(7.3.16)
Условие (7.3.16) предъявляет более жесткие требования к шагу решетки, чем
требование (7.3.10), при котором отсутствуют дополнительные главные максимумы.
При большом значении N ( N > 10) для первых боковых лепестков можно полу-
чить приближенную формулу
£>т « 2/[л/(2т + 1)].
(7.3.17)
Из (7.3.17) имеем, что при т = 1 (первый боковой лепесток) ^=0,21 (или
= -13,3 Дб) и не зависит от N.
На рис. 7.12, а приведена серия расчетных ДН [27], демонстрирующих зависи-
284
ГЛАВА 7
мость ширины основного лепестка при различных N, на постоянном шаге решетки
d = 0,5Х. Серия ДН, приведенных на рис. 7.12, б для различных сочетаний N и d
(но таких, что (N - l)d = const = 4л), демонстрирует практическую неизменность
основного лепестка и возникновение вторичных главных максимумов при d > X.
7.3.3. Режим наклонного излучения ( 0 < у < kd ). В этом режиме максимум
излучения отклоняется от нормали к оси решетки, причем на такой угол, при
котором разность фаз за счет разности хода для отдельных элементов компенси-
руется сдвигом фаз из-за несинфазности возбуждения. Рассмотрим, например,
два соседних элемента сп = 0ип=1 (см. рис. 7.9). Разность фаз за счет разности
хода для элемента с п = 1 по отношению к полю центрального элемента состав-
ляет +kd cos 6 , а за счет возбуждения фаза его поля отстает на величину ( -\|/).
Компенсация наступает, когда kdcos9-у = 0 , откуда
cos 0аа = ц/ / kd . (7.3.18)
Из (7.3.18) видно, что при возрастании у от 0 до kd направление максимума
излучения отклоняется от нормали и приближается к оси решетки, т.е. отклоня-
ется в ту же сторону, в которую происходит отставание возбуждения элементов
решетки (рис. 7.13). Эффект перемещения направления максимального излучения
при изменении фазового сдвига \|/ находит широкое практическое применение в
сканирующих АР.
Выражение для ДН в плоскости, проходящей через ось решетки, имеет вид
(7.3.5), причем /^(9^) = N, как и в случае синфазного возбуждения. Направления
нулей излучения определяются из условия равенства нулю числителя (7.3.5), т.е.
N(kd cos 0Qm - у) / 2 = ±тл, откуда
cos0Qm = / kd ± mk / Nd. (7.3.19)
Ближайшим к главному максимуму направлениям нулевого излучения соот-
ветствуют углы 001 и 0q(—1) (см. рис. 7.13), причем
0О1 = arccos(cos 02Л + X / Nd), 60(—1) = arccosfcosG^ - k / Nd).
В отличие от режима нормального излучения нули расположены несиммет-
рично относительно 0гл . Ширина ДН по уровню нулевого излучения может быть
Рис. 7.13. ДН линейной АР в ее плоскости при различных фазах кр
между соседними элементами [27]
0< ip< kd
i/j^kd
Антенные решетки
285
определена как разность углов 6q(-1) и @01 т- е- Л@о ~ @0(-1) _@01-
При малых отклонениях максимума ДН от нормали и Nd :» 1 степень несиммет-
рии невелика и величина А0О может быть рассчитана по приближенной формуле
А0П ~2Х/ Ndsin0?/J == 115°Х/Ndsin0?J.. (7.3.20)
V/ • С, J L * J t v '
Величина A0q 5 при малых отклонениях определяется как
Аб0)5 « O^OX/NdsinO^ 51°Х / NdsinO^. (7.3.21)
Из (7.3.20) и (7.3.21) видно, что по мере увеличения отклонения ДН от нормали
основной лепесток расширяется в 1 / sin 0гл раз по сравнению со случаем синфаз-
ного возбуждения.
Направления максимумов боковых лепестков могут быть найдены из прибли-
женного соотношения:
cos 0max ш - vg / kd ± (2m + 1) / 2Nd. (7.3.22)
Относительный УБ Л определяется выражением (7.3.15) т.е. так же, как в режи-
ме нормального излучения.
Найдем условия, при которых отсутствуют дополнительные главные макси-
мумы в режиме наклонного излучения. Как отмечалось в разделе 7.3.2 указанные
максимумы возникают тогда, когда фазовый сдвиг между полями двух соседних
элементов достигает 2л. В рассматриваемом случае это возможно в таких направ-
лениях 0 = 0ew тах, когда kd cos 0еш тах - kg = ±2л , причем знак плюс соответству-
ет появлению вторичного главного максимума в области 0 < дгл, а минус — в
области 0 > 0гл . Обозначим kg / kd = у , тогда получим
cos0gmmax = у ± X / d. (7.3.23)
o/fLlllClA. / х z
Во избежание появления вторичных главных максимумов необходимо, что-
бы правая часть превышала (по модулю) единицу. Минимальное значение правой
части (7.3.23) соответствует знаку минус, поэтому должно выполняться условие
(у - X / d) < -1. Отсюда получаем требование к шагу решетки:
d<X/(l + y). (7.3.24)
F<c)(0)
iff — kd cos 60у 0 / a у/ = 0
\ 71 \ / 1 \/ । у V । *
0 20 40 60 80 100 120 140 0, град
Рис. 7.14. ДН линейной АР в ее плоскости при разных фазовых
сдвигах kg ( N = 7, d = 0,5Х ) [27]
286
ГЛАВА 7
Учитывая, что в режиме наклонного излучения у = \|/ / kd = cos 0^, формулу
(7.3.24) удобнее использовать в виде:
d <'k/(l + cosQZJl). (7.3.25)
Если помимо отсутствия дополнительных главных максимумов необходимо,
чтобы УБЛ убывал при удалении от главного лепестка, к шагу решетки предъяв-
ляется более жесткое требование
d < 1 / 2(1 + cos 0^). (7.3.26)
Результаты расчета ДН линейной АР из семи изотропных элементов с шагом
d = 0,51, возбужденных с фазовым сдвигом = 0 и у = kd cos 60°, приведены на
рис. 7.14, в прямоугольной системе координат.
Отметим, что при приближении у к kd главные лепестки слева и справа от оси
решетки сливаются и суммарный главный лепесток ДН приобретает двугорбый
характер (см. рис. 7.14). Это происходит тем быстрее, чем меньше Nd. т. е. чем
шире главные лепестки. В данном случае термин «наклонное излучение», теряет
свой смысл.
7.3.4. Режим осевого излучения. При у = kd синфазное положение полей от-
дельных элементов осуществляется, как следует из (7.3.18), в направлении оси
решетки, т. е. 0гл = 0. Это — режим осевого излучения. Диаграмма направленнос-
ти в плоскости, проходящей через ось решетки, приобретает вид, изображенный
на рис. 7.15. При \|/ > kd из (7.3.18) получаем cos 6^ > 1. Последнее означает, что
ни в каком направлении поля не складываются синфазно. Однако и в этом случае
максимум излучения направлен вдоль оси решетки ( 0^ = 0), поскольку здесь
фазовый сдвиг между полями элементов решетки минимален; во всех других на-
правлениях он больше. С увеличением ц/ по сравнению с kd угол между векторами
на фазовой плоскости в направлении 0 = 0°, равный ( kd - у), приближается к
(-2тг / N), при котором излучение вдоль оси исчезает (критический режим). Это
происходит при у = .
Покажем, что возрастание vp в интервале kd < \|/ < сопровождается (при
одинаковом Nd ) сужением основного лепестка ДН и возрастанием УБЛ. В режиме
Рис. 7.15. Множитель линейной АР при у = kd и \|/ = ( N = 14, d = 0,251) [27]
Антенные решетки
287
осевого излучения ДН может быть рассчитана по общей формуле (7.3.5), причем
в направлении главного максимума:
— (kd - у)
/ — (kd - \|/)
f ) = sin
(7.3.27)
Из (7.3.27) видно, что при у = kd величина /^(©гл) = N (как и ранее). Если
> kd, то ) < N. Форма ДН симметрична относительно направления 0?Л = О
(см. рис. 7.14). Положения нулей ДН определяются соотношением (7.3.19), в котором
следует использовать только знак минус, поскольку все нули расположены при
0 > 0гл. Для первого нуля имеем
cos0o(_i) = V / kd - X / Nd. (7.3.28)
Для длинных решеток в пределах главного лепестка можно считать
9
cos 0 — 1 — 0 / 2. Тогда с учетом симметрии ДН относительно направления макси-
мума излучения:
При у = kd
A0q — 20q(—1) — 2^27^ / Nd — \|/ / kd +1.
А0О = 2л/2-7?1 / Nd « 162°^/Nd.
(7.3.29)
(7.3.30)
При \|/ > kd основной лепесток ДН сужается (при одном и том же Nd ), причем тем
сильнее, чем больше . Это продолжается вплоть до = kd + 2л / N , когда,
как видно из (7.3.29), А0О = 0 , и излучение вперед пропадает.
Положение максимумов боковых лепестков определяется такой же формулой
(7.3.22), как и в режиме наклонного излучения. Однако относительный уровень
их:
f ) sin[(2m + 1)л / 2N]
возрастает, поскольку с увеличением у падает величина /^(©гд), определяемая
(7.3.27).
Указанные факторы — сужение главного лепестка и увеличение УБЛ — по-
разному влияют на величину КНД. Вначале, по мере роста \|/ преобладает фактор
сужения главного лепестка, вследствие чего КНД возрастает, достигая макси-
мума в оптимальном режиме( ц/ = Vopt Р- Затем КНД падает из-за возрастания
боковых лепестков. В оптимальном режиме при Nd » X :
А0О « 118°7^/ Nd, А0О)5 « 61°7^/Nd.
Максимум первого бокового лепестка в оптимальном режиме
= 0,33 (или -10 дБ).
(7.3.31)
(7.3.32)
Отсутствие дополнительного главного максимума в режиме осевого излучения
обеспечивается выполнением для шага решетки условия (7.3.24) при подстановке
соответствующего значения у . Убывающий закон изменения УБЛ обеспечивается
при шаге решетки в 2 раза меньше, т. е. при
Максимуму КНД согласно определению, соответствует максимальное значение поля в
точке на оси антенны при условия неизменности уровня излучаемой мощности. Если же не-
изменной сохраняется амплитуда токов в элементах решетки, то, естественно, максимум
поля в указанной точке имеет место при синфазном сложении полей, т. е. при у = kd
288
ГЛАВА 7
d < к / 2(1 + у).
(7.3.33)
На рис. 7.16 изображены ДН линейной АР из 14 изотропных элементов, распо-
ложенных с шагом d - 0,25Л., при = kd и у = \gopt
Если возбуждение отдельных элементов АР осуществляется бегущей волной
(например, с помощью линии питания), распространяющейся вдоль оси решетки
с фазовой скоростью v, то фазовый сдвиг между двумя соседними элементами
V = ]3d, где Р = кс / v, — скорость света. Величину с / v, численно совпадающую
с коэффициентом у = у / kd , называют коэффициентом замедления. Подобные АР
носят название антенн бегущей волны (АБВ). Все формулы для АР, полученные
выше, справедливы для АБВ, если в них осуществить подстановку у = kdc / v. В
частности, ДН описывается формулой
причем /'‘С'(62Л) = IV при 0 < с / v < 1. Если с / v > 1, то f *40^) определяется фор-
мулой (7.3.27). Режиму нормального излучения соответствует АБВ с бесконечной
фазовой скоростью ( у = с /v = 0), режиму наклонного излучения — АБВ с быст-
рой волной (y = c/ v<l). Главный лепесток антенны с быстрой волной наклонен в
сторону движения возбуждающей волны. В режиме осевого излучения АБВ долж-
на возбуждаться медленной волной ( у = с / v >1).
а) б) б)
Рис. 7.16. Варианты расположения вибратор- Рис. 7.17. Множитель решетки (а)
ных излучателей в линейной АР с нормальным из двух излучателей (б)
(а) и осевым (б) излучениями [27]
Антенные решетки 289
Все приведенные в этой главе соотношения справедливы для АР из абсолютно
ненаправленных элементов. При построении конкретных АР необходимо исполь-
зовать элементы, максимум излучения которых совпадает с 0гл. На рис. 7.16 по-
казаны варианты расположения вибраторных излучателей в АР с нормальным (а)
и осевым (б) излучениями. Направленные свойства элементов следует учитывать,
умножая их ДН на функцию Fv Л
На практике иногда используется система, состоящая всего из двух излучате-
лей, выполненных обычно в виде симметричных электрических вибраторов (СЭВ)
с ориентацией, соответствующей рис. 7.16, б. При d = 0,25Х, у = 90° и равных амп-
литудах токов подобная АР работает в режиме осевого излучения и обеспечивает
однонаправленное излучение с максимумом в направлении 0 = 0 (здесь поля обоих
излучателей складываются); в противоположном направлении излучение отсутс-
твует (поля вычитаются). Множитель системы для этого случая ( N = 2) имеет
вид:
= sin(fcd cos 0 - 90°) / 2 sin i (kd cos 0 - 90°) = cos -i (kd cos 0 - 90°) (7.3.35)
и описывает кардиоиду (рис. 7.17). Если считать, что рассматриваемая система
образована путем добавления излучателя 2 (с фазой, запаздывающей на 90°) к
исходному излучателю 1, то излучатель 2 называют директором (по отношению к
излучателю 1). В обратной ситуации, когда к исходному излучателю 2 добавляется
излучатель 1 (с фазой, опережающей на 90°), последний называют рефлектором.
7.4. Влияние неравномерности амплитудного
распределения на ДН линейной АР [27]
Выше рассматривались решетки с равноамплитудным возбуждением элемен-
тов, УБЛ которых в режиме нормального излучения (—13,2 дБ) довольно велик.
При этом было установлено (см. 7.3.2), что в направлении боковых лепестков
основной вклад в результирующее поле дают крайние элементы решетки. Следова-
тельно, интенсивность боковых лепестков в принципе можно уменьшить, выбирая
закон распределения токов, спадающий к краям АР. В то же время подобное рас-
пределение токов приводит к расширению основного лепестка ДН по сравнению
Рис. 7.18. Векторные диаграммы для линейной АР из семи элементов: а) — для синфазной
равноамплитудной решетки; б) — для АР при убывании амплитуды токов к краям АР [27]
10 - Неганов
290
ГЛАВА 7
с равноамплитудной решеткой такой же длины. Это легко показать с векторных
диаграмм на фазовой плоскости. Рассмотрим синфазный режим возбуждения, ког-
да поля всех элементов складываются синфазно в направлении нормали к оси ре-
шетки независимо от амплитудного распределения, т. е. 0^ = 90°. В направлении
первого нуля ( 0 = О01) векторная диаграмма для синфазной равноамплитудной
решетки имеет вид, изображенный на рис. 7.18, а. Поскольку длины векторов про-
порциональны токам в соответствующих элементах, то при убывании амплитуды
токов к краям АР векторная диаграмма для угла 0 — 6qi будет отличаться только
длиной векторов, причем угол между двумя соседними векторами по-прежнему
будет равен kd cos 0О1 (рис. 7.18, б). Легко видеть, что суммарное поле теперь уже
не будет равно нулю. Для достижения нуля векторы должны развернуться на
несколько больший угол kd cos 0qi > kd cos 0O1, что приводит к условию 0g i < 0gi-
Таким, образом, спадающее амплитудное распределение увеличивает ширину ос-
новного лепестка ДН Д0О = 2(0гл -0gi).
Рассмотрим подробнее свойства АР из изотропных элементов с амплитудным
распределением «косинусоидального»типа, широко применяемым на практике:
In = I cos — exp(-in\|/). (7.4.1)
Сначала проанализируем синфазный режим ( \|/ = 0). Используя формулу Эйле-
ра, представим (7.4.1) в виде:
I =— ехр [-inn / (N -1)] + — exp [inn / (N -1)].
(7.4.2)
Первое слагаемое в (7.4.2) соответствует равноамплитудному распределению с
линейным запаздыванием фазы от элемента к элементу на величину л / (N — 1).
Второе слагаемое отличается от первого только знаком фазы. Для расчета ДН
можно использовать формулу (7.3.4). В результате получим
N
sin
kd cos 0 -
sin
N
sin — kd cos 0 -
sin — kd cos 0 +
При большом числе элементов можно считать, что N — 1« N. Обозначая
и = Nkd cos0 / 2 и нормируя функцию (7.4.3) к ее значению при 0 = 0^ = 0, полу-
чаем
(7.4.4)
Направления нулей излучения, положения и величина боковых лепестков мо-
гут быть определены путем анализа функции (7.4.4) по методу, приведенному
в 7.3.2. При Nd » X ширина основного лепестка ДН определяется по формулам
Д0О « 172°Х / Nd, Д0О 5 « 68,8°Х / Nd. (7.4.5)
Относительный уровень первого бокового лепестка составляет = 0,066 или
23 дБ (вместо — 13,2 дБ в случае равноамплитудного распределения).
Для дальнейшего уменьшения боковых лепестков необходимо использовать
Антенные решетки 291
распределения токов, более резко спадающие к краям решетки, например по за-
кону «косинус в квадрате». Однако при этом сильнее расширяется основной лепес-
ток ДН. Отметим, что противоположный случай — возрастание амплитуды токов
к краям решетки — приводит к резкому росту боковых лепестков и на практике
обычно не используется. Характерные значения параметров ДН синфазных реше-
ток с неравномерным амплитудным распределением (при d < Л, / 2) можно полу-
чить, используя данные табл. 7.1 для линейных непрерывных излучателей длина
которых L « Nd.
Если элементы неравноамплитудных решеток из изотропных элементов возбуж-
даются с линейным фазовым сдвигом , то изменения, происходящие при этом
с ДН, подобны рассмотренным выше. В частности, если 0 < ц/ < kd , то максимум
излучения поворачивается в сторону запаздывания фазы, причем cos = у / kd .
При \|/ > kd наступает режим осевого излучения ( 9гл = 0). Для исключения допол-
нительных главных лепестков при любом амплитудном распределении необходи-
мо выполнение таких же условий (7.3.24), что и для равноамплитудных АР.
7.5. Влияние фазовых искажений на ДН линейной решетки [27]
Выше предполагалось, что токи, возбуждающие элементы АР, синфазны,
либо распределение фазы имеет линейный характер. Именно такие фазовые рас-
пределения обычно используются на практике. Однако из-за неточностей из-
готовления решетки или из-за других факторов фазовое распределение может
оказаться отличным от требуемого. Это отличие (фазовые ошибки) может носить
систематический или случайный характер. В данном разделе рассмотрим влия-
ние систематических ошибок. Влияние случайных фазовых ошибок на ДН антенн
приведено выше. Ограничимся случаем, когда фазовые ошибки пропорциональны
первой, второй или третьей степени номера излучателя в решетке:
ехр[г\|/^ах 2n / (N -1)] (линейные ошибки),
exp{z\|/max[2™ / (N -1)]2} (квадратичные ошибки)
ехр{й|/^ах[2п / (N -1)]3} (кубические ошибки).
Здесь Vmax > Vmax ’ Vmax — максимальные величины фазовых ошибок на краю ре-
шетки по сравнению с центральным элементом.
При линейном исходном, распределении фазы и линейных фазовых ошибках
результирующее фазовое распределение примет вид
ехр[-ш(у - Д\|/)]
(7.5.1)
где Ду = 2утах 1 / (N -1). Из (7.5.1) видно, что наличие фазовых ошибок не меняет
линейного характера фазового распределения, а лишь изменяет результирую-
щий сдвиг фаз между токами в соседних излучателях. При этом остаются спра-
ведливыми все формулы, полученные ранее для линейного фазового распреде-
ления, если в них вместо у подставить (у - Ац/). В частности, новое направление
максимума излучения 0'^, определяемое из соотношения cos0^ = (у - Ду) / kd ,
сместится на некоторый угол Д0, зависящий от знака фазовой ошибки. Величина
ДО не зависит от вида амплитудного распределения.
При квадратичных и кубических фазовых ошибках аналитические формулы
10*
292
ГЛАВА 7
для ДН становятся весьма громоздкими и здесь не приводятся. Элементарная трак-
товка происходящих при этом процессов может быть дана следующим образом.
Пусть исходные токи являются синфазными ( \|/ = 0). В первом приближении за-
меним квадратичное распределение фазы двумя линейными (рис. 7.19). Тогда каж-
дую половину антенны можно рассматривать как решетку с линейным фазовым
распределением, ДН которой отклоняется в сторону запаздывания фазы. С ростом
Vmax суммарная ДН будет соответственно расширяться, причем независимо от
знака Vmax • При больших Vmax появляется провал в середине основного лепест-
ка. Точный анализ показывает, что помимо расширения основного лепестка ДН
при квадратичных фазовых ошибках происходят увеличение УБЛ и исчезновение
(«заплывание») нулей ДН.
Кубические фазовые искажения в первом приближении можно аппроксимиро-
вать ломаной линией, каждый из отрезков которой соответствует линейному рас-
пределению фазы (рис. 7.20). На рис. 7.20 изображены также ДН каждой из частей
решетки с линейным фазовым распределением (с учетом размеров каждой из час-
тей). Суммарная ДН поворачивается, при этом увеличивается боковое излучение
со стороны, в которую поворачивается максимум излучения. Результаты точно-
го расчета ДН при квадратичных и кубических фазовых ошибках представлены
на рис. 7.21 и 7.22 соответственно для решетки из семи изотропных излучателей
d = 0,5Z с равноамлитудным распределением. Степень искажений ДН, вызывае-
мых фазовыми ошибками, снижается при амплитудном распределении, спадаю-
щем к краям решетки.
При произвольном законе амплитудно-фазового распределения (АФР) полу-
чение аналитических выражений, описывающих ДН, становится весьма сложной
задачей. В этом случае для расчета ДН оказывается более целесообразным непос-
редственное суммирование полей от каждого элемента с применением ЭВМ.
В заключение отметим наличие класса АФР, обеспечивающих существование
у излучателя фазового центра. К этому классу, как показано в [27], относятся
распределения, четные по амплитуде относительно середины антенны и нечетные
(с точностью до постоянной составляющей) по фазе. Фазовый центр при этом
совпадает с центром антенны.
7.6. Излучение двух связанных вибраторов [37]
Рассмотрим простейшую АР, состоящую из двух симметричных электрических
вибраторов.
7.6.1. Направленные свойства системы из двух связанных вибраторов.
Взаимодействие связанных вибраторов аналогично взаимодействию связанных ко-
лебательных контуров с сосредоточенными параметрами. Поле одного вибратора
наводит в другом вибраторе некоторую э. д. с., что эквивалентно изменению сопро-
тивления излучения или входного сопротивления вибратора.
Поле, создаваемое системой вибраторов, является результатом сложения по-
лей, создаваемых отдельными вибраторами, с учетом фаз этих полей, определя-
емых как разностью хода лучей, так и разностью фаз токов в излучателях.
В данном разделе рассматривается работа двух связанных симметричных виб-
раторов. Получаемые при этом результаты нетрудно распространить на случай
Амтеыные решетки
293
Рис. 7.19. ДН линейной АР (а) с квадратичным
изменением фазы (б) [27]
б)
а) б)
Рис. 7.20. ДН линейной АР (а) с куби-
ческим изменением фазы (б) [27]
Рис. 7.21. Множитель системы линейной АР из семи изотропных излучателей (d = 0,5л)
f(c)(g)
с квадратичными фазовыми ошибками [27]
/IX!' п' -№ / * м' X Р 3 тпадсЗ = 0 о
1 • 1 1 иг 1 Л 45° 1 у
I 1 1 ► И 1 1 । 1 1 1 1 С)Г\О А...
1 1 с < ' / ;;; L1; 1 IdQ ’. to 1
/ !• । ’! / '1 * 1 ' 1 / 1 1 \ to
4 >> «I ♦ * 1 f 1 1 ’ 1 ' ' 1 1 1 • 1 to 1 to** * *
• * ♦ _ to 1 1 || и : : V1 L' лХ п to \ 1 / ♦
- - —* “ X /х \ У /7\i // \ 1 V г I 1 1ц 11 Vi 11 ! 1—• П 1 1 1/ 1 1 1 । । ' 4 Ллг iX*
20 40 60 80 90 100 120 140 160 0, град
Рис. 7.22. Множитель системы линейной АР из семи изотропных излучателей (d = 0,5/.)
с кубическими фазовыми ошибками [27]
294
ГЛАВА 7
нескольких связанных вибраторов.
Выведем формулу для расчета характеристики направленности двух парал-
лельных связанных вибраторов 1 и 2, находящихся на расстоянии d друг от друга
(рис. 7.23), питаемых токами и 12 • Обозначим
i = (7.6.1)
h
где q — отношение модулей токов, — сдвиг фазы тока 12 по отношению
к току Ii.
Рассмотрим поле в меридиональной плоскости вибраторов xoz.
Проведем направления в произвольную точку наблюдения М, находящуюся в
дальней зоне, от центров 1 и 2-го вибраторов. Так как расстояние между вибра-
торами d несоизмеримо мало по сравнению с расстояниями до точки наблюдения
(?1 и т2), направления в точку М можно считать параллельными. Опустив из цент-
ра первого вибратора перпендикуляр на направление т2 , найдем разность рассто-
яний от вибраторов до точки наблюдения, равную Дг = d cos 0 , где — угол между
нормалью к оси вибратора и направлением в точку наблюдения.
Обозначим напряженность поля, создаваемого в точке наблюдения, первым
вибратором через Е|. Выразим напряженность поля второго вибратора в точке на-
блюдения М через напряженность поля первого вибратора, приняв ее фазу в точ-
ке наблюдения за нулевую. Так как напряженность создаваемого вибратором поля
пропорциональна току в вибраторе, и влиянием разности расстояний от вибратора
до точки наблюдения на амплитуду напряженности поля можно пренебречь, то
Ё2 = Eiqe~ikdcos^eixv, где kd cos 6 — сдвиг фаз полей из-за разности хода лучей
(пространственный сдвиг фаз).
Найдем суммарное поле, создаваемое обоими вибраторами в данной точке:
i{x\f~kd cos 0)
Ё = Ёх + Ё2
= Ei
(7.6.2)
На основании рисунка 7.23, а, угол 0 является дополнительным по отношению
к углу и, запишем
601} cos(kl sin 0) - cos kl
ri sin kl cos 0
Обычно интересуются величиной напряженности суммарного поля, а не ее фазой.
Поэтому, переходя к модулю выражения (7.6.2), получаем (как было, условлено
ранее, знак модуля опускается)
60L,i coslkl sin 0) - cos kl Г 2 “ ‘ “
=--------------------------Jl + q + 2q cos(y - kd cos 0).
r COS0
(7.6.3)
Или E = A fi(Q) f
Цб).
Как видно из (7.6.3), амплитудная характеристика направленности системы из
двух связанных вибраторов определяется двумя множителями. Первый множитель
fl(Q) представляет собой характеристику направленности симметричного вибра-
тора, находящегося в свободном пространстве. Второй множитель /^(0) учитыва-
ет наличие второго вибратора; он зависит от расстояния d между вибраторами,
от отношения амплитуд токов в вибраторах q и от сдвига фаз токов в вибраторах
у. Этот множитель называют множителем системы.
Антенные решетки
295
а) б)
Рис. 7.23. Геометрия двух связанных электрических вибраторов в меридиональной (а) и
азимутальной (б) плоскостях [37]
у/=90°
у/=180°
v = 0,5
180°
90°
180°
90
Рис. 7.24. Нормированные ДН двух связанных вибраторов при разных расстояниях ( d) и
фазах ( ср) между ними [37]
у/ = 90°
d/X= 0,25
Рис. 7.25. Влияние отношения модулей токов q на ДН двух связанных вибраторов в эква-
ториальной плоскости ( d/A = 0,25) [37]
296
ГЛАВА 7
В экваториальной плоскости (рис. 7.23, б) направленные свойства данной сис-
темы определяются только множителем системы, так как одиночный симмет-
ричный вибратор в этой плоскости ( 6 = 0) не обладает направленными свойства-
ми. Напряженность суммарного поля в экваториальной плоскости определяется
выражением:
E - A(1 - cos
+ q2 +2q cos(\|/ - kd cos (p)
(7.6.4)
где q> — угол между линией, соединяющей оси вибраторов, и направлением в точ-
ку наблюдения, лежащую в экваториальной плоскости.
В зависимости от величин d/к, q и ф, диаграммы направленности могут иметь
различную форму. На рис. 7.24 представлены нормированные диаграммы направ-
ленности двух связанных вибраторов при различных расстояниях между ними и
различных значениях ф (при q = 1). На рис. 7.25 показано влияние величины q на
диаграмму направленности связанных вибраторов.
При увеличении расстояния между вибраторами (начиная от d/X = 0,5) диа-
грамма направленности приобретает многолепестковый характер; чем больше d/X,
тем больше лепестков (рис. 7.26).
Особенно важен случай однонаправленного излучения. Пусть токи в вибрато-
рах одинаковы по величине (q = 1). Тогда формулу (7.6.4) воспользовавшись фор-
мулой для косинуса двойного угла, можно привести к виду
- Л (ф kd ]
Е = 2А(1 - cos kl) cos —-cos ф .
(7.6.5)
Положим теперь, что ф = ±90°, и расстояние между вибраторами d = А,/4. При
этом формула (7.6.5) принимает вид
Е = 2А(1 - cos kl) cos(±45° - 45° cos ф).
Множитель /(ф) = cos(±45° - 45° созф) описывает кардиоиду. При ф = +90° и ф = 0
этот множитель обращается в единицу; при ф = 180° он обращается в нуль. Таким
образом, в направлении ф = 0° напряженность поля удваивается (по сравнению с
90°
270°
Рис. 7.26. ДН двух связанных вибраторов в азимутальной плоскости при d = 2Х
(q = 1, Ф, = 0) [37]
Ау/тетунъье решетки
297
полем одиночного вибратора, возбуждаемого током, одинаковым с текущим по
одному из связанных вибраторов). Это увеличение в одном направлении происхо-
дит за счет уменьшения поля в других направлениях. При ф = -90° напряженность
поля удваивается в обратном направлении ( ф = 180°); поле равно нулю в направ-
лении ф = 0°. Поясним эти результаты. Если ток во втором вибраторе опережает по
фазе ток в первом вибраторе, то в точке наблюдения, находящейся в направлении
ф = 0, поля от обоих вибраторов складываются в фазе, так как сдвиг фаз за счет
несинфазности возбуждающих токов ( ф = 90°) компенсируется пространственным
сдвигом фаз: ( фр = kd = (2тт/2с)(Л/4) = 90°). Этот сдвиг фаз берется со знаком минус,
так как второй вибратор находится дальше от точки наблюдения, чем первый. В
обратном направлении ( ф = 180°) множитель /(ф) обращается в нуль, потому что
в этом направлении поля от первого и второго вибраторов складываются в проти-
вофазе и компенсируют друг друга, так как фП0ЛМ = ф + фр = 180°.
Если ток во втором вибраторе отстает по фазе на 90° от тока в первом вибрато-
ре ( ф = -90°), то получается обратная картина. В первом случае ( ф = 90°) второй
вибратор усиливает излучение в направлении на первый вибратор. Во втором
случае ( ф = -90°) он усиливает излучение в обратном направлении и ослабляет
излучение в направлении первого вибратора.
Вибратор, усиливающий излучение в направлении на другой вибратор и ос-
лабляющий излучение в обратном направлении, называется рефлектором (от-
ражателем). Чтобы рефлектирующее действие вибратора было полным (в одном
направлении поле увеличивается, а в противоположном — равно нулю), в рас-
сматриваемом случае ( d = Л/4) токи в обоих вибраторах должны быть равны по
величине ( q = 1), а ток в рефлекторе — опережать ток во втором связанном виб-
раторе на 90° (рис. 7.27, а).
Вибратор, ослабляющий излучение в направлении на другой вибратор и уси-
ливающий излучение в противоположном направлении, называется директо-
ром (направителем). В идеальном случае директор должен работать в режиме
(рис. 7.27, б): q - 1, фг- = - л/2 (при d = Х/4).
Отметим, что в обоих случаях напряженность поля увеличивается в направле-
нии отставания фазы возбуждающего тока.
Получить однонаправленное излучение можно и при расстояниях между виб-
раторами, отличных от Л/4. Как видно из формулы (7.6.5), условие отсутствия
излучения в направлении ф = 180° можно записать в виде ф + kd = 180°.
Для выполнения этого условия при d < Л/4 угол сдвига фаз ф должен быть боль-
ше 90° . Хотя диаграмма направленности при этом оказывается однонаправленной и
максимум излучения лежит в направлении ф = 0°, однако напряженность поля в
этом направлении не удваивается. Чем ближе друг к другу расположены вибрато-
ры, тем меньшая напряженность поля получается в направлении максимального
. излучения (считая, что при изменении d величина тока в вибраторах постоянна).
При d —> 0 сдвиг фаз ф, необходимый для получения однонаправленного из-
лучения, стремится к 180°. При этом мощность излучаемого системой вибраторов
поля стремится к нулю. Для того чтобы мощность, излучаемая системой из двух
связанных вибраторов, обладающей однонаправленными свойствами, при умень-
298
ГЛАВА 7
Рефлектор
Директор
Рис. 7.27. ДН двух связанных вибраторов в азимутальной плоскости ( q = 1, d = К/а ):
а) —= 0 , V2 = л/2 '> б) —vpi — 0 , \|/2 = -я/2; в) — в общем случае [37]
шении d/A не изменялась, токи в вибраторах должны возрастать.
При d/A —> О токи в вибраторах должны стремиться к бесконечности.
Возбуждение каждого из двух связанных вибраторов токами, сдвинутыми по
фазе, усложняет систему питания. Поэтому почти во всех случаях вибраторы,
выполняющие роль рефлекторов или директоров, не содержат источников питания
(генераторов), т. е. являются пассивными. Они возбуждаются электромагнитным
полем активного (питаемого) вибратора. Работа пассивных вибраторов подробно
будет рассмотрена дальше. Здесь только отметим, что в случае пассивных вибра-
торов не удается осуществить режим, обеспечивающий полное рефлекторное или
директорное действие, так как не удается получить совместно q = 1 и = ±90°.
Поэтому не получается полного удвоения поля в главном направлении и нуля поля
— в обратном. Диаграмма направленности в этом случае имеет вид рис. 7.27, в.
Действие рефлектора или директора оценивается коэффициентом защитного
действия ^>заи,, равного отношению напряженности поля, излучаемого в глав-
ном направлении, к напряженности поля, излучаемого в обратном направлении,
^>защ ~ ^Ф=о/-^'(р=18О° или
= 201g , дБ.
.Л/ - n
Антпетуные решетки 299
7.6.2. Метод наведенных ЭДС. Сопротивления излучения и входные со-
противления связанных вибраторов [27,37]. Полное сопротивление каждого
из связанных вибраторов состоит из двух частей: собственного сопротивления,
т.е. сопротивления, которым обладает данный вибратор в свободном пространстве,
и сопротивления, наведенного электромагнитным полем второго вибратора.
Таким образом, в общем виде можно записать Z^ = Z^ + meZ^2,
У У
где Z| — полное сопротивление излучения первого вибратора; Z^ — собственное
сопротивление излучения первого вибратора; HaeZi2 — сопротивление, наведенное
на первый вибратор вторым.
Точно так же
ZS I НЛв
2 - ^22 + ^21 >
где zf — полное сопротивление излучения второго вибратора; Z22 — собственное
сопротивление излучения второго вибратора, навZ21 — сопротивление, наведенное
на второй вибратор первым.
Сопротивление излучения связанного вибратора можно найти методом наведен-
ных э. д. с. Идея этого метода была предложена независимо друг от друга в 1922 г.
советским ученым Д. А. Рожанским и французом Бриллюэном. Непосредственно
к расчету антенн этот метод применен И. Г. Кляцкиным, А. А. Пистолькорсом
и В.В. Татариновым.
Метод наведенных э. д. с. позволяет находить наведенные и, как будет видно из
дальнейшего, собственные сопротивления вибраторов, а также амплитуды и фазы
токов в пассивных вибраторах.
Изложим сущность данного метода. Рассмотрим два связанных произвольно
ориентированных друг относительно друга симметричных идеально проводящих
вибратора. Поле второго вибратора может создать у поверхности каждого беско-
нечно малого элемента dx первого вибратора составляющую, параллельную оси
этого вибратора (тангенциальную составляющую), Exi2 > вследствие чего в эле-
менте dx возникает (наводится) ЭДС:
de
12
“ &Х12
Однако при этом нарушаются граничные условия, согласно которым на по-
верхности идеального проводника тангенциальная составляющая напряженности
электрического поля равна нулю. Для выполнения граничных условий в элементе
dx должна появиться ЭДС — de12, компенсирующая ЭДС de^ • Вблизи повер-
хности элемента dx появляется тангенциальная составляющая напряженности
электрического поля — Дг12, равная по величине и противоположная по фазе
тангенциальной составляющей наведенного поля Exl2. Вследствие этого тангенци-
альная составляющая напряженности суммарного электрического поля у повер-
хности элемента dx обращается в нуль, и граничное условие выполняется. Появ-
ление тангенциальной составляющей напряженности поля — Ех12 говорит о том,
что под влиянием поля второго вибратора происходит перераспределение поля
первого вибратора. ЭДС - ds12 создается генератором, включенным в первый виб-
ратор. Энергия, затрачиваемая генератором для создания этой ЭДС в элементе dx,
переходит в энергию электромагнитного поля.
Если известны ЭДС, возникающая на поверхности элемента dx, и ток в этом
элементе Ixi можно определить мощность dP^, затрачиваемую генератором пер-
300
ГЛАВА 7
вого вибратора (под действием поля второго вибратора) на создание поля, компен-
сирующего тангенциальную составляющую напряженности электрического поля
второго вибратора на поверхности данного элемента. При этом ток в элементе dx и
составляющая Еж12 на поверхности этого элемента могут иметь различные фазы.
Считают, что закон распределения тока по одному из связанных вибраторов в
результате действия поля другого вибратора не изменяется и приближенно может
полагаться синусоидальным.
Формула для расчета dPf^ аналогична формуле для мощности, выделяемой в
цепи переменного тока
dP12 п ^12^x1 п ^12^
где dsj2 — комплексная амплитуда наведенной ЭДС на поверхности элемента dx
первого вибратора; Ех12 — комплексная амплитуда тангенциальной составляю-
щей напряженности электрического поля, создаваемого током второго вибратора
вблизи элемента dx первого вибратора; — комплексная (сопряженная) ампли-
туда тока в элементе dx первого вибратора.
Полная мощность, расходуемая генератором первого вибратора на создание в
окружающем пространстве электромагнитного поля, тангенциальная составляю-
щая напряженности электрического поля которого компенсирует на всей поверх-
ности вибратора I тангенциальную составляющую напряженности электрического
поля, создаваемого током второго вибратора, равна
РХ2 = (7.6.6)
Z *
Итак, мощность, отдаваемая генератором первого вибратора под действием
поля второго вибратора, определяется током, текущим по первому вибратору,
и тангенциальной составляющей напряженности электрического поля, создава-
емого вторым вибратором вблизи первого. Ее активная часть представляет собой
излученную мощность. Реактивная часть характеризует электромагнитное поле,
колеблющееся вблизи вибратора. Выражение (7.6.6) — математически формулиру-
ет метод наведенных ЭДС.
Известно, что комплексную мощность можно определить по формуле
* 1 *
P = -UI =-II Z,
2 2
где I — комплексная амплитуда тока в данной цепи; U — комплексная амплитуда
напряжения на входе цепи; Z — полное сопротивление цепи.
Аналогично можно записать:
Р12=^п11п1’Ш^2, (7-6.7)
где Ini — комплексная амплитуда тока первого вибратора (в пучности); Ma6ZX2 -
сопротивление, наведенное вторым вибратором на первый, отнесенное к току в
пучности.
Приравнивая правые части выражений (7.6.6) и (7.6.7), решая полученное ра-
венство относительно waeZX2, получаем
Антенные решетки
301
навгх! навг>2
пае
(7.6.8)
Здесь 1х1 = 1*п± sin k(l - х) - L^i • f(x), где f(x) — функция распределения тока.
Следовательно, чтобы определить сопротивление, наведенное на первый вибра-
тор вторым, нужно знать закон распределения тока в первом вибраторе, его ком-
плексную амплитуду в пучности и тангенциальную составляющую напряженности
электрического поля, создаваемого вторым вибратором у поверхности первого.
Активная составляющая наведенного сопротивления™06/^ характеризует ак-
тивную мощность, излучаемую первым вибратором под действием поля второго.
Реактивная, составляющая наведенного сопротивления woeXf2 характеризует
мощность электромагнитного поля, связанного с вибратором, возникающего так-
же под действием поля второго вибратора.
Формула (7.6.8) пригодна для расчета наведенного сопротивления в самом об-
щем случае: при любом взаимном расположении вибраторов, при любой их длине,
при различных соотношениях токов в них. Однако расчет по этой формуле весьма
сложен.
Наведенное сопротивление рассчитать значительно проще в частном случае,
когда связанные вибраторы имеют одинаковую длину, оси их параллельны и токи
в них имеют одинаковую величину и фазу (рис. 7.28). Очевидно, что в этом случае
сопротивление, наведенное первым вибратором на второй, равно сопротивлению,
наведенному вторым вибратором на первый. В этом частном наведенное сопротив-
ление называется взаимным ( )• При известном взаимном сопротивлении двух
вибраторов весьма просто рассчитать наведенное сопротивление, если задано со-
отношение токов в вибраторах.
Напряженность электрического поля , создаваемого у поверхности перво-
го вибратора током второго вибратора, определяется выражением (1.3.5), в пред-
положении, что Ат = 0. Запаздывающий вектор-потенциал ( Ае) тока 1Х2 нахо-
дится по формуле (1.3.18).
Графики, изображающие зависимости R12 = fd / X и = fd / X при
h / X = const, представлены на рис. 7.29, из которых видно, что активная и реак-
Рис. 7.28. Геометрия двух связанных одинаковых и параллельных вибраторов
302
ГЛАВА 7
Рис. 7.29. Зависимости действительной (а) и мнимой (б) частей взаимного сопротивления
вибраторов от d/A [37]
тивная составляющие взаимного сопротивления в зависимости от относительного
расстояния между вибраторами d / А принимают как положительные, так и от-
рицательные значения и при некоторых значениях d/A проходят через нуль. Та-
кой ход кривых взаимных сопротивлений объясняется изменением фазы наведен-
ной э. д. с. при изменении расстояния между вибраторами. Если фаза наведенной
э. д. с. равна или противоположна фазе текущего по вибратору тока, то взаимное
сопротивление является чисто активным. Если фаза наведенной э. д. с. отличается
от фазы текущего по вибратору тока на л / 2 , то взаимное сопротивление явля-
ется чисто реактивным.
Активная составляющая взаимного сопротивления может быть положительной
или отрицательной; К12 отрицательно в тех случаях, когда под действием поля
второго вибратора мощность поля, излучаемого первым вибратором, уменьшает-
ся (при неизменном токе в первом вибраторе).
Для расчета взаимных сопротивлений связанных вибраторов одинаковой длины
I существует приближенная формула [37]:
Z12 = г 30(1 - cos kl)F
(7.6.9)
= (р(А0) + (р(А2) - cp(^li )2 cos kl.
Функции (р(Ап) определяются по формулам:
-ifc7(^-^-V2)2+d2
ф(-^п) — о .—
k\](h - ril +1 / 2)2 + d
-ikyj(h+nl-l/2)2+d2
О
k\](h + nl — l/2)2+d2
(7.6.9a)
Формула (7.6.9) применима для расчета взаимных сопротивлений параллель-
Амтемные решетки
303
ных вибраторов с электрической длиной плеча kl. Для расчета активной состав-
ляющей взаимного сопротивления формулой (7.6.9а) можно пользоваться при
любых расстояниях между вибраторами. Погрешность в этом случае не превы-
шает нескольких процентов и падает, при увеличении расстояния между виб-
раторами. Для расчета реактивной составляющей взаимного сопротивления
формулой (7.6.9а) можно пользоваться только при расстояниях между цент-
рами вибраторов Rq = лД2 + d2 > 1,51 -г 2Z. Погрешность при этом не превышает
2 4-5%. [37]
Метод наведенных эдс может быть применен также для определения собс-
твенного сопротивления излучения вибратора. При этом следует предположить,
что вблизи элемента провода dx действует тангенциальная составляющая напря-
женности электрического поля , создаваемого током, текущим абсолютно
по всем элементам этого вибратора. Очевидно, что для выполнения граничных
условий на поверхности элемента dx должна возникнуть составляющая напря-
женности электрического поля Ех , равная по величине, но противоположная
по фазе составляющей Ех11(Е^°б = -Ехц). Формула для определения собственного
сопротивления излучения вибратора совершенно аналогична случаю двух связан-
ных вибраторов:
(7.6.10)
В результате интегрирования выражения (7.6.10), задаваясь синусоидальным
распределением тока, получаются формулы для расчета активной и реактивной
составляющих собственного сопротивления излучения, отнесенных к пучности
тока.
у
Формула для расчета Кц совпадает с формулой для расчета сопротивления
у . у у
излучения Rn , полученной методом вектора Умова-Пойнтинга, т. е. = Rn . Это
понятно, так как при расчете сопротивления излучения методом вектора Умова-
Пойнтинга также, как и в данном случае, исходят из синусоидального распреде-
ления тока.
Активная составляющая сопротивления излучения, полученная обоими мето-
дами не зависит от радиуса провода, так как определяется полем в дальней зоне
вибратора,
у
Формула для расчета Хп имеет вид:
= Х% = 30(2Si2kl + sin2kl(T + lnkl + Ci2kl-21n-) + (76Ц)
+ cos 2kl(-Si4kl + 2Si2kl).
По методу вектора Умова-Пойнтинга такая формула не может быть получена,
так как этот метод учитывает только излученное электромагнитное поле, реактив-
ная же составляющая сопротивления излучения определяется связанным с полем,
находящимся вблизи вибратора. Формула (7.6.11) получается интегрированием
выражения Ex±Ixdx непосредственно по поверхности вибратора, и поэтому Х^
зависит от формы этой поверхности и от размеров его поперечного сече-
ния. Если а -> 0, то в случае полуволнового вибратора формула (7.6.10) дает
304
ГЛАВА 7
у у
Zn = Zn = 73,1 + г42,5 Ом. Такой же результат дает и строгий метод расчета при
использовании только нулевого приближения (синусоидальное распределение
тока). Для вибраторов всех других длин реактивная составляющая собственного
сопротивления излучения при а —> 0 стремится к бесконечности.
Результаты, полученные по методу наведенных ЭДС, тем более точны, чем
тоньше вибратор.
7.6.3 Расчет наведенного и полного сопротивлений излучения [37]. Пусть
имеются два активных связанных вибратора, токи в которых не равны ни по ам-
плитуде, ни по фазе. Требуется найти полное сопротивление излучения каждого
вибратора.
Заменим связанные вибраторы (рис. 7.30, а) эквивалентной схемой, состоящей
из двух связанных колебательных контуров с сосредоточенными параметрами
(рис. 7.30, б). Каждый контур содержит генератор высокой частоты, сопротивле-
ния Zu или Z22, равные собственным сопротивлениям вибраторов, и наведенные
нав нав
сопротивления Z12 и Z21, являющиеся неизвестными.
Напряжение генератора, включенного в связанный контур, компенсирует па-
дение напряжения на собственном сопротивлении контура и на сопротивлении
связи. Учитывая это, запишем уравнения Кирхгофа для данной эквивалентной
схемы, считая, что сопротивления связи (взаимные сопротивления) известны. Эти
уравнения имеют вид:
&п1 - ^nl^ll + ^п2^12 > ^п2 = ^n2Z22+^nlZ21 • (7.6.12)
Здесь Uni и Un2 — напряжения первого и второго генераторов, пересчитанные к
точкам пучности тока в вибраторах; 1п1 — комплексная амплитуда тока в пучности
тока первого вибратора; 1П2 — комплексная амплитуда тока в пучности тока вто-
у
рого вибратора; Z^ — собственное сопротивление излучения первого вибратора,
у
отнесенное к пучности тока; Z22 — собственное сопротивление излучения второго
вибратора; Z12,Z2j — взаимные сопротивления (сопротивления связи).
Данные уравнения позволяют при заданных напряжениях 17п1 и Un2 и извест-
ных собственных и взаимных сопротивлениях определить токи в вибраторах. По-
лагая, что токи в вибраторах найдены, определим наведенные сопротивления.
Пусть = • Перепишем уравнения, учитывая, что Z12 = Z2j :
Unl =Inl(Z1S1 + qe^Z12), Un2=In2(Z^+-e~^Z12). (7.6.13)
q
a) 6)
Рис. 7.30. Эквивалентная схема (б) двух связанных контуров (а).
(К методу наведенных ЭДС) [37]
Антенные решетки
305
Выражения для полных сопротивлений контуров (вибраторов) можно получить
из (7.6.13):
Е
(7.6.14)
X ryS . —zw <7
2 - ^22 +~е ^12'
q
7.6.4. Расчет тока в пассивных вибраторах [37]. Пассивные вибраторы
широко применяются для создания однонаправленного излучения в качестве реф-
лекторов и директоров.
Чтобы вибратор играл роль рефлектора или директора, ток в нем должен
иметь определенную величину и фазу по отношению к току в активном вибраторе
(в идеальном случае при расстоянии между вибраторами d = Х/4 должны выпол-
няться условия q = 1 и \|/ = ±90°).
Величины q и у для пассивного вибратора зависят от расстояния между пас-
сивным и активным вибраторами и от величин активного и реактивного сопротив-
лений пассивного вибратора. Эти величины можно регулировать, изменяя реак-
тивное сопротивление пассивного вибратора.
Рассчитаем величины q и \|/. Пусть имеется два связанных симметричных виб-
ратора (рис. 7.31, а), из которых один пассивный. Заменим эти вибраторы эквива-
лентной схемой рис. 7.31, б.
Уравнения Кирхгофа для этой системы имеют вид:
= Inlzll + In2z12
(7.6.15)
0 = In2Z22 + W12 + ^п2^н ,
где Z12 — взаимное сопротивление вибраторов; Хн — реактивное сопротивление
настройки, включенное в пассивный вибратор и отнесенное к пучности тока.
Можно считать известными ток в активном вибраторе Ini, а также собственные
Z11’Z22 и взаимное Z12 сопротивления, поскольку относительная длина вибраторов
Z / X и относительное расстояние между вибраторами d / X заданы. Задано также
сопротивление настройки ( Хн ). Таким образом, в уравнениях (7.6.15) неизвестен
только ток во втором вибраторе ( 12), который определяется через ток на первом
вибраторе:
а)
Рис. 7.31. Эквивалентная схема (б) связи активного вибратора с пассивным (а) [37]
306
ГЛАВА 7
Ранее было обозначено 12 Д1 ~ • Поэтому
де’4' = -(й12 + гХ12)/(й2£2 + И*22 + *«))
Так как полное сопротивление излучения вибратора равно сумме собственного
и наведенного сопротивлений излучения, то наведенные сопротивления вибрато-
ров равны:
Z12 = К12 + г Х12 = 9е НЧ2 + ^12) >
НСМЗ zy2z НЛвпЕ । • НОв xzS 1 —i\ll / т~> . „•'V \
Z21 = Л21+г Х21=-е у(К12 + гХ12).
9
(7.6.16)
Таким образом, если известно взаимное сопротивление вибраторов (оно зави-
сит только от относительных геометрических размеров системы I / X, d / X, h / X)
и известны отношения амплитуд токов q и сдвиг фаз токов у в вибраторах, то
наведенное сопротивление определяется весьма просто по формулам (7.6.16).
Полная мощность, излучаемая двумя связанными вибраторами, равна
рЕ _ pL , pS _ 1 т2 pS , 1 т2 pS
r - rl + 12 +“Jn2K2
Для определения входных сопротивлений связанных вибраторов существуют
приближенные формулы. В случае коротких вибраторов (расстояние от точек пи-
тания до узла тока не менее 0,15Х) входное сопротивление связанного вибратора
можно определить по формуле
*7^
zc£ = <7-6-17а)
sin kl sin kl sin kl
где zf — полное сопротивление излучения связанного вибратора.
В случае длинных вибраторов (расстояние от точек питания до минимума тока
меньше 0,15А,) входное сопротивление связанного вибратора рассчитывается по
другой формуле:
асв асв
sh2acel-------sin 2kl ----------sh2acel + sin 2kl
Zce = WjJ6----------------------iW^ —---------------------
ch2acel - cos 2kl ch2acel - cos 2kl
(7.6.176)
В (7.6.176) учтено влияние одного вибратора на волновое сопротивление другого
вибратора и на его коэффициент затухания.
Здесь
Хнав
! — реактивное наведенное сопротивление, приходящееся на единицу длины
вибратора, определяемое по формулам:
Х^ав
г) ттНЛв
za12
тэнав
К12
IW™
Отсюда находится модуль отношения токов
Антеынъм решетки
307
(7.6.18)
Относительная фаза тока в пассивном вибраторе
, ^12 а %22 +
\|/ = л + arctg —— - arctg —
^12 R22
(7.6.19)
у у
Входящие в формулы (7.6.18) и (7.6.19) сопротивления к22>^22’^12 и Х12 отнесе-
ны к пучности тока. Поэтому сопротивление настройки Хн, включаемое в сере-
дину вибратора, также необходимо относить к пучности тока. Сопротивление
Хн пересчитывается к пучности тока в случае короткого вибратора по формуле
о
Хн = Xhq sin kl. В случае длинного вибратора такой пересчет можно сделать по
формуле, учитывающей распределение тока по закону гиперболического синуса:
^нО
н
sn (а + гк)1,
где а — коэффициент затухания без учета влияния активного вибратора.
В случае пассивного вибратора q и ф взаимозависимы. При изменении Хн ме-
няются одновременно обе эти величины. Поэтому добиться одновременно нуж-
ных значений q и для пассивного вибратора невозможно. Пассивный вибратор
обычно настраивают так, чтобы получить максимальный коэффициент защитного
действия. Получаемые при этом величины q и 1|/ отличаются от соответствующих
величин в идеальном случае ( q = 1, ц/ = 90°), и поэтому максимальное защитное
действие обычно получается не больше 10—20.
Ток в пассивном рефлекторе должен опережать по фазе ток в активном вибра-
у
торе. Выясним, при каком характере реактивного сопротивления ( Х22 + Хн ) реф-
лектора это условие выполняется. Рассмотрим выражение (7.6.19). Если применя-
ются полуволновые вибраторы с расстоянием между ними примерно d « X/4, то
взаимные сопротивления R12 ~ +40 Ом, Х12 « —28 Ом. Поэтому
arctg —— = Vi = arctg
+40 )
Тогда
V = 180°
+ 325° - arctg
= 145° - v2 •
Или \|/ = 145° - ip2.
Чтобы сдвиг фаз у был положительным и близким к 90°, угол
VJ2 _ arctg (Х22 + Хн)/К22
должен быть положительным, а это будет только в том случае, когда Х22 + Хм
положительно. Если аналогично рассуждать для вибраторов другой длины и с рас-
стояниями, изменяющимися в пределах от 0, IX до 0,25Х, то придем к такому же
выводу (например: I / X = 0,5 и d / X = 0,25, при этом К12 = 105 Ом, Х12 = —80 Ом,
= 323°). Таким образом, анализ формулы (7.6.19) показывает, что пассивный
вибратор будет играть роль рефлектора в том случае, когда его полное реактив-
308
ГЛАВА 7
ное сопротивление (собственное плюс сопротивление настройки) имеет индуктив-
ный характер. Этот вывод справедлив, если 0,1Х < d < 0,2 5Х.
Если пассивный вибратор должен работать в режиме директора, то угол сдви-
га фаз \|/ должен быть отрицательным. Проанализировав формулу (7.6.19) для дан-
ного случая, как это было сделано для рефлектора, придем к выводу, что для
работы пассивного вибратора в режиме директора при 0,1А, < d < 0,25Х , его полное
реактивное сопротивление должно быть отрицательным, т. е. должно иметь ем-
костный характер.
Для получения оптимального рефлекторного действия расстояние между реф-
лектором и активным вибратором следует брать примерно (0,15 4-0,2 5)Х, а реак-
тивное положительное сопротивление — приблизительно 10—50 Ом.
В коротковолновом диапазоне пассивные вибраторы обычно настраивают,
включая в середине вибратора настроечное реактивное сопротивление в виде от-
резка короткозамкнутой двухпроводной линии, длину которой можно регулиро-
вать передвижным короткозамыкателем. В диапазонах метровых и дециметровых
волн настроечное сопротивление обычно не применяется. Пассивный вибратор на-
страивается изменением его длины.
Чтобы пассивный вибратор работал в качестве рефлектора, его полная длина
должна быть несколько больше Х/2 (входное сопротивление разомкнутой на конце
двухпроводной линии, длина которой больше X / 4, имеет индуктивный харак-
тер).
Чтобы пассивный'вибратор работал в качестве директора, его полная длина
должна быть несколько меньше X / 2. Величина необходимого удлинения или уко-
рочения определяется расстоянием между вибраторами и их толщиной.
7.7. Многовибраторные настроенные синфазные антенны [18]
Рассмотренные выше простейшие антенны являются ненаправленными или сла-
бонаправленными. В качестве остронаправленных настроенных антенн использу-
ются антенны, образованные системой синфазных вибраторов.
Многовибраторные синфазные антенны впервые появились в середине 20-х го-
дов и использовались для целей дальней связи на коротких волнах. В дальнейшем
такие антенны стали применяться и на метровых волнах в радиолокационной ап-
паратуре.
Подобная антенна состоит из большого числа вибраторов, горизонтальных или
вертикальных, возбуждаемых синфазно и подвешиваемых на высоких мачтах в
вертикальной плоскости.
На рис. 7.32 показана схема четырехэтажной антенны, имеющей по 8 полу-
волновых горизонтальных вибраторов в каждом этаже с рефлектором, располо-
женным на расстоянии четверти волны от антенны. Расстояния между центрами
вибраторов, а также между этажами берутся равными половине длины волны.
Каждая пара полуволновых вибраторов антенны питается от фидерной линии.
Напряжение в проводах фидера через каждую половину длины волны меняется
по фазе на 180°. Поэтому для обеспечения синфазности питания вибраторов прово-
да фидера перекрещиваются через каждую половину длины волны, как показано
на рис. 7.32 и 7.33. На рис. 7.33 пунктирными кривыми показано распределение тока
и заряда на вибраторах. Сплошная косинусоида по вертикали изображает распре-
Антенные решетки
309
К передатчику
Рис. 7.32. Схема многовибраторной антенны [18]
Рис. 7.33. Схема синфазного питания вертикальной секции антенны [18]
деление напряжения вдоль фидера. Как видно из рисунка, вибраторы питаются
в пучности напряжения. Это облегчает решение задачи согласования антенны с
фидером. При указанной схеме включения (см. рис. 7.33) сопротивление нагрузки
для фидера, создаваемое парой вибраторов, получается значительным (тысячи
ом). Вследствие того, что вибраторы подключаются к фидеру через промежутки,
равные половине длины волны, сопротивления нагрузки по фидеру складываются
как сопротивления, включенные параллельно. Результирующее сопротивление на-
грузки в основании секции получается соизмеримым с волновым сопротивлением
фидера, что облегчает задачу согласования нагрузки с фидером.
Многовибраторная синфазная антенна концентрирует излучение в направлении,
перпендикулярном плоскости расположения вибраторов. Для того чтобы излуче-
ние происходило лишь в одну сторону от указанной плоскости, устанавливается
рефлектор, обычно пассивный, представляющий собой такую же систему виб-
раторов, как и собственно в антенне, возбуждаемый полем антенны. Настройкой
рефлектора, например, с помощью короткозамыкающих мостиков, подключен-
310 ГЛАВА 7
ных к нижним зажимам секций, добиваются (см. рис. 7.32) того, чтобы получился
максимум отношения напряженности поля, излученного вперед, к напряженнос-
ти поля, излученного назад. Для этого токи вибраторов рефлектора должны опе-
режать по фазе токи вибраторов антенны примерно на 90°.
Рефлекторы из вибраторов используют в антеннах коротких волн. На метро-
вых волнах в качестве рефлектора обычно используется металлический лист или
сетка, располагаемая на расстоянии примерно в четверть длины волны от вибра-
торов антенны.
Многовибраторные синфазные антенны стационарных установок коротковолно-
вого диапазона подвешиваются на металлических опорах или на мачтах с оттяж-
ками высотой до 75 м и с пролетом между мачтами до 150 м. Нижний этаж ан-
тенны подвешивается на высоте (0.25 - 0.5) X. Вибраторы коротковолновых антенн
выполняются из медных или биметаллических проводов диаметром 4-6 мм, а на
метровых волнах - из жестких трубок диаметром около 10 мм. Резонансная длина
каждого вибратора на несколько процентов меньше, чем половина длины волны.
Требуемое укорочение тем больше, чем толще вибраторы. Вибраторы изолируются
друг от друга специальными палочными изоляторами.
Рассмотрим кратко, как определяются основные параметры многовибраторной
синфазной антенны.
Диаграмма направленности антенны в горизонтальной плоскости определя-
ется числом р вибраторов в одном ряду (этаже). Форма этой диаграммы не зависит
от числа этажей; влияние земли проявляется лишь в том, что направление мак-
симума излучения поднимается над горизонтом на небольшой угол, зависящий
от высоты подвеса антенны.
Выражение для расчета ненормированной диаграммы направленности в гори-
зонтальной плоскости имеет следующий вид:
(7.7.1)
Здесь ф — угол, отсчитываемый относительно линии расположения вибраторов
в горизонтальном ряду. Это выражение получается в результате перемножения
диаграммы направленности Д(ф) полуволнового вибратора и множителя системы
фр (ф) из р синфазных излучателей, находящихся на расстоянии d = X / 2 друг от
друга. В последнем выражении не учтено влияние рефлектора. Это влияние мож-
но приближенно учесть, если считать, что излучение во всех направлениях в
передней полуплоскости (для ф от 0 до 180°) удваивается, а излучение в задней
полуплоскости (для ф в пределах 180 — 360°) равно нулю.
Пример диаграммы направленности в горизонтальной плоскости синфазной ан-
тенны из восьми вибраторов в этаже показан на рис. 7.34.
Диаграмма направленности антенны в вертикальной плоскости определяется
числом q этажей и высотой подвеса антенны (рис. 7.35). Эта диаграмма не зависит
от числа вибраторов в этаже. Для расчета вертикальной диаграммы пользуются
следующим выражением:
Аытенные решетки
311
Рис. 7.34. Диаграмма направленности в полярных
координатах в горизонтальной плоскости синфазной
антенны, имеющей восемь вибраторов в этаже [18]
Рис. 7.35. К расчету диаграммы на-
правленности в вертикальной плос-
кости синфазной антенны [18]
/(ф) = fq (Ф)/з (ф) =
sin (khQ cos 0).
(7.7.2)
В приведенном выражении /д(0) ~ множитель, определяющий направленное дейс-
твие системы из q синфазных ненаправленных излучателей, расположенных на
расстоянии d = X / 2 друг от друга (так как горизонтальный вибратор каждого
этажа не обладает направленностью в вертикальной плоскости); /3(0) — множи-
тель, учитывающий влияние земли. Этот множитель представляет собой диаграм-
му направленности противофазной системы из двух идентичных излучателей,
разнесенных на расстояние 2/iq , где Kq — средняя высота подвеса антенны над
землей. В выражении (7.7.2) не учтено влияние рефлектора. Это влияние можно
учесть так же, как для диаграммы направленности в горизонтальной плоскости,
т. е. удвоить значения диаграммы в передней полуплоскости и считать, что из-
Рис. 7.36. Диаграмма направленности в декартовых координатах в вертикальной плоскости
синфазной шестиэтажной антенны [18]
312
ГЛАВА 7
лучение назад отсутствует. Пример диаграммы направленности в вертикальной
плоскости синфазной шестиэтажной антенны показан на рис. 7.36.
Для вычисления диаграмм направленности остронаправленных антенн реко-
мендуется сначала определить направления нулевого излучения, т. е. определить
углы, при которых все сомножители обращаются в нуль, затем рассчитать глав-
ный лепесток по точкам. Амплитуды боковых лепестков можно определить как
значения диаграммы направленности, вычисленные для направлений, средних
между соседними нулями.
Результаты вычисления диаграмм направленности показывают, что чем боль-
ше вибраторов в ряду (этаже), тем сильнее сжимается излучение в горизонтальной
плоскости, а чем больше этажей, тем больше сжимается излучение в вертикаль-
ной плоскости. Увеличение высоты подвеса антенны при неизменном числе этажей
прижимает максимум излучения к плоскости горизонта.
Коэффициент направленного действия рассматриваемой антенны с учетом вли-
яния рефлектора и земли может быть определен по приближенной формуле [18]
D = 8pq. (7.7.3)
7.8 Директорные антенны (антенны типа “волновой канал”) [18]
Директорная антенна иногда называется антенной типа “волновой канал” [18].
Такая антенна представляет собой ряд параллельных вибраторов длиной около
полуволны каждый, расположенных на общей рее на расстояниях около четверти
длины волны друг от друга (рис. 7.38) Один из вибраторов питается от генератора
и называется активным. Остальные вибраторы возбуждаются электромагнитным
полем питаемого вибратора и называются пассивными.
При правильной настройке антенны максимум излучения ее получается вдоль
оси расположения вибраторов.
7.8.1. Антенная система из двух вибраторов: питаемого и пассивного
[18]. Простейшая антенна типа “волновой канал” состоит из двух вибраторов (рис.
7.37). На рис. 7.37 вибратор 1 питается от источника, создающего на зажимах виб-
ратора напряжение U\; вибратор 2 — пассивный, возбуждаемый полем вибратора
1. В цепь вибратора 2 для настройки включено реактивное сопротивление в виде
отрезка линии с короткозамыкающей перемычкой (КЗ). Расстояние между вибра-
торами обозначено через dg.
Вибратор 2 можно рассматривать как приемный и тогда его эквивалентная
схема будет иметь вид, показанный на рис. 7.37, б. На этой схеме е2 — ЭДС, на-
веденная полем вибратора 1; R22 и Х22 — активная и реактивная составляющие
собственного сопротивления вибратора; Х2Н ~ реактивное сопротивление шлейфа
на зажимах вибратора.
При расстоянии между вибраторами, равном (0.1—0.25) X и индуктивном ха-
рактере сопротивления пассивного вибратора он действует как рефлектор, т.е.
создает преимущественное излучение в направлении от пассивного вибратора к
активному.
Индуктивный характер сопротивления пассивного вибратора может быть обес-
печен соответствующим подбором положения КЗ. На практике требуемая настрой-
ка (с короткозамкнутыми зажимами) по сравнению с резонансной кривой создает
Аитен/ные решетки
313
а) б)
Рис. 7.37. Антенная система из двух вибраторов (а); эквивалентная схема вибратора 2,
рассматриваемого как приемная антенна (б) [18]
Направление
максимального
излучения
Директоры
Рис. 7.38. Директорная антенна
индуктивный характер сопротивления Х22 и обеспечивает рефлекторное действие
пассивного вибратора.
При тех же расстояниях между вибраторами, но емкостном характере сопро-
тивления пассивного вибратора он действует как директор, т.е. создает преиму-
щественное излучение в направлении от активного вибратора к пассивному. Ем-
костный характер сопротивления пассивного вибратора может быть достигнут
путем его укорачивания.
Активное сопротивление питаемого вибратора под влиянием пассивного за-
метно уменьшается. Так например, пассивный директор при d = 0.25Л. уменьшает
активное сопротивление питаемого вибратора от 73 Ом примерно до 50 Ом. Еще
большее снижение активного сопротивления получается при наличии несколь-
ких пассивных директоров, устанавливаемых в директорной антенне. Это обсто-
ятельство затрудняет согласование антенны с фидером и делает целесообразным
применение в качестве питаемого элемента шлейф-вибратора Пистолькорса.
Значения КНД системы из активного и пассивного вибраторов колеблются в
зависимости от настройки пассивного вибратора в довольно широких пределах,
достигая максимальной величины Dmax =5-6 при оптимальной настройке и опти-
мальном расстоянии от активного вибратора до директора, равном (0.1 - 0.12)Х. Оп-
314
ГЛАВА 7
тимальное расстояние (с точки зрения максимума КНД) для системы, состоящей
из полуволнового вибратора и пассивного рефлектора, приблизительно равно
(0.16 - 0.18)Х.
Одновременное применение и рефлектора, и директора приводит к некоторому
увеличению КНД и уменьшению угла раствора диаграмммы направленности. Для
иллюстрации в [18] пример диаграммы направленности такой системы из трех
вибраторов. Коэффициент направленного действия такой системы при оптималь-
ной настройке имеет величину около 8.
Увеличение числа пассивных директоров, располагаемых один перед другим на
определенном расстоянии, образует многовибраторную антенну, обладающую еще
большим направленным действием.
7.8.2. Многовибраторные директорные антенны [18]. На рис. 7.38 пока-
зана директорная антенна, состоящая из питаемого вибратора (А), пассивного
рефлектора (Р) и ряда пассивных директоров. Все пассивные вибраторы настраи-
ваются так, чтобы максимальное излучение получалось в направлении общей оси
антенны в сторону директоров. Излучение в обратном направлении получается
минимальным при одном рефлекторе, и поэтому нет смысла применять большее
число рефлекторов, так как они возбуждались бы слабо и не оказывали заметно-
го влияния на диаграмму направленности.
Как следует из сказанного выше, для системы из двух вибраторов, (активного
и пассивного) необходимый сдвиг фаз тока в пассивном рефлекторе получается
при индуктивном характере его сопротивления что достигается соответствующим
удлинением рефлектора. По этой же причине сопротивление пассивных директо-
ров должно иметь емкостной характер, для чего длина директоров берется мень-
ше, чем резонансная.
Необходимое для правильной настройки изменение длины зависит от толщины
вибраторов. Чем толще вибратор, тем меньше его волновое сопротивление и тем
больше надо изменять длину вибратора для достижения нужной настройки.
Если перед активным вибратором находятся N -1 пассивных директоров, то,
обобщая полученные выше результаты, записываем следующую систему уравне-
ний для определения токов в элементах антенны:
2ц11 + Z12e3l2 + ^13вз^3 + - + ^пвз^п = е1’
^21^1 + %22взЧ + ^23вз^3 + - + %2пвз1п = 0,
^nl^l + ^п2вз^2 + ^пЗез^З + ••• + ^ппвз^п ~ 0*
Здесь сопротивления Z и токи I — комплексные величины, и решение системы
уравнений представляет значительные трудности.
При проектировании антенны с пассивными элементами обычно рассматривают
ряд вариантов волнового канала с различными расстояниями между вибраторами
и длиной вибраторов и выбирают наилучший вариант. Расстояние d между излу-
чателями, как правило, выбирают в пределах d = (0.1...0.3)Х, т. е. не обязательно
равными X / 4.
Расчетным путем можно получить только ориентировочные значения рассто-
яния d и длины вибраторов. Исследование антенны с пассивными элементами по-
казывает, что для получения наилучших результатов амплитуда и фаза тока в
Амтенные решетки
315
а) б)
Рис. 7.39. К расчету антенны типа “волновой канал”: а) упрощенная схема (1 - активный
вибратор; 2 - рефлектор; 3 - директоры); б) вспомогательный график для определения
КНД [3]
них должны подстраиваться. Это можно осуществить путем изменения сопротив-
ления Z2n. На коротких волнах в качестве такого подстроечного сопротивления
применяют шлейф, который подключают к входным клеммам вибратора. На СВЧ
подстройку пассивного вибратора производят изменением его длины в небольших
пределах.
Опыт показывает, что при одинаковых поперечных сечениях вибраторов пас-
сивный рефлектор должен быть на несколько процентов длиннее активного виб-
ратора, а пассивный директор короче. На коротких волнах чаще всего использу-
ется работа пассивного элемента в качестве рефлектора. На УКВ и СВЧ широкое
распространение получили антенны типа «волновой канал» (рис. 7.39, а), состоя-
щие из одного активного вибратора, одного рефлектора и нескольких директоров.
Увеличение числа директоров сужает ДН и увеличивает интенсивность излуче-
ния в направлении главного максимума. Применение рефлекторов свыше одного
лишено смысла, так как поле за рефлектором значительно ослаблено и второй
рефлектор малоэффективен. Иная картина с директорами, так как каждый пос-
ледующий директор попадает в интенсивное поле антенны и оказывает значитель-
ное влияние на диаграмму излучения. КНД такой антенны может быть определен
по формуле [18]
D « kjL / X,
где L — полная длина антенны, - коэффициент, зависящий от длины антенны
и определяемый по графику на рис. (7.39, б).
Для иллюстрации на рис 7.40 показана диаграмма направленности, полученная
экспериментально. Расстояние от активного вибратора до рефлектора 0.17Х, рас-
стояние от вибратора до 1-го директора и между директорами равно 0.25 А,. В этой
диаграмме довольно большие боковые лепестки. Изменением настройки можно не-
сколько уменьшить боковые лепестки за счет увеличения угла раствора главного
лепестка.
На рис. 7.41, а приведен график для ориентировочного определения шири-
ны главного лепестка диаграммы направленности в зависимости от относительной
длины антенны L / А. Сплошная кривая относится к плоскости, перпендикулярной
осям вибраторов; пунктирная — к плоскости расположения вибраторов. Как видно
316
ГЛАВА 7
Рис. 7.40. Экспериментальная диаграмма направленности антенны из питаемого вибра-
тора, рефлектора и шести директоров: в плоскости, перпендикулярной осям вибраторов
(сплошная); в плоскости вибраторов (пунктир) [3]
Рис. 7.41. Ширина (по половинной мощности) главного лепестка диаграммы направленнос-
ти директорной антенны в зависимости от ее относительной длины (а); кривая коэффи-
циента направленного действия директорной антенны в зависимости от ее относительной
длины (б) [18]
Рис. 7.42. Скрещенные вибраторы
Антенные решетки
317
из рисунка, с увеличением длины антенны ширина диаграммы направленности
уменьшается все медленнее и медленнее. Объясняется это тем, что чем длин-
нее антенна, тем сильнее приходится расстраивать директорные вибраторы и тем
меньше амплитуды токов в них, особенно в пассивных вибраторах, более удален-
ных от активного.
7.9. Скрещенные вибраторы с вращающейся поляризацией [18]
Если скрещенные излучатели (рис. 7.42) питать равноамплитудными токами,
сдвинутыми по фазе на л / 2 , то в направлении оси z будет возбуждаться поле с
круговой поляризацией, в плоскости расположения вибраторов (плоскость хОу)
— поле с линейной поляризацией, а во всех остальных направлениях возник-
нут поля с эллиптической поляризацией. В диапазоне метровых и дециметровых
волн широкое применение находят взаимно перпендикулярные (скрещенные) по-
луволновые вибраторы, а на сантиметровых волнах — взаимно перпендикулярные
(крестообразные) полуволновые щели на широкой стенке волновода.
Систему из двух перпендикулярных вибраторов с совмещенными центрами
принято называть турникетной антенной (рис. 7.42). В зависимости от соотно-
шения токов на входах вибраторов могут быть реализованы различные режимы
работы антенны.
Режим всенаправленного излучения. При питании вибраторов токами равных
амплитуд с фазовым сдвигом л / 2 пространственно-амплитудная ДН имеет вид,
показанный на рис. 7.43, б. Нули излучения отсутствуют, максимумы излучаются
в перпендикулярных обоим вибраторам направлениях, т.е. вдоль положительной
и отрицательной полуосей z. В плоскости расположения вибраторов поляризация
излучения линейная, в остальных направлениях — эллиптическая. В направлении
оси z поляризация излучения чисто круговая. Направления вращения вектора по-
ляризации в двух полупространствах, разделенных плоскостью хОу, противопо-
ложны. Таким образом, в поле излучения содержатся все возможные состояния
вектора поляризации. Интересен вид фазовых характеристик направленности в
плоскости хОу (рис. 7.43, в) — они аналогичны спирали Архимеда. Незамкнутость
линий равных фаз при обходе вокруг антенны в плоскости хОу в дальней зоне
свидетельствует об отсутствии фазового центра.
7.9.1. Скрещенные вибраторы. На рис 7.43 в начале координат расположены
два скрещенных полуволновых вибратора, вибратор 1 ориентирован вдоль оси
х, а вибратор 2 - вдоль оси у. Токи в вибраторах сдвинуты по фазе на л / 2
Диаграмма направленности вибратора 1 в любой плоскости, проходящей через
ось х, представляет собой восьмерку, максимум которой лежит в вертикальной
плоскости yOz. В частности, в плоскости xOz диаграмму направленности полувол-
нового вибратора 1 можно записать приближенно в виде
F(0)-cose, (7.9.1)
где 0 — угол, отсчитываемый от направления оси z.
Диаграмма направленности вибратора 2 также представляет собой восьмерку в
любой плоскости, проходящей через ось у. Максимум этой диаграммы расположен
318
ГЛАВА 7
Вход 1 Вход 2
Рис. 7.43. Турникетный вибратор: а) - конструкция; б) - амплитудная ДН;
в) - фазовая ДН [2]
Антенные решетки
319
в горизонтальной плоскости xOz, Диаграмма направленности вибратора 2 также
определяется выражением (7.9.1), но оно соответствует плоскости yOz.
Рассмотрим поляризационные характеристики поля, создаваемого скрещенны-
ми вибраторами.
В направлении оси z (точка на рис. 7.44) вибратор 1 возбуждает вертикаль-
но поляризованную составляющую поля Ев, а горизонтальный вибратор 2 - го-
ризонтально поляризованную составляющую поля Ег. Так как амплитуды этих
составляющих равны (оба вибратора в направлении оси z излучают одинаково), а
сдвиг по фазе между ними равен л/2 (он соответствует фазовому сдвигу между
токами в вибраторах), то поле оказывается поляризованным по кругу. При этом
если ток в вибраторе 1 опережает по фазе ток в вибраторе 2 = -И^), то на оси
z возбуждается поле левого вращения. В противном случае (Ц = U2) поле имеет
правое вращение.
В точке наблюдения, расположенной в горизонтальной плоскости xOz (точка
Р2 на рис. 7.44) и характеризуемой углом 0, поле оказывается поляризованным
эллиптически. Большая ось поляризационного эллипса определяется амплитудой
напряженности поля, излучаемого вибратором 2 в направлении его максимально-
го излучения, т. е. равна Етах и ориентирована вертикально. Малая ось этого эл-
липса определяется амплитудой напряженности поля, излучаемого вибратором 1
в направлении, составляющем угол 0 с его осью, т. е. Е = Етах cos 0. Коэффициент
эллиптичности т при этом
т = cos 0.
(7.9.2)
Чем больше угол 0, тем меньшим оказывается коэффициент эллиптичности.
При 0 = 0 т = 1, что соответствует круговой поляризации (точка на оси z ). Ког-
да 0 = 90° (ось х) т = 0 и поле имеет линейную поляризацию.
В любой точке, расположенной в плоскости yOz (точка Р3 на рис. 7.44) поляри-
зация результирующего поля также оказывается эллиптической. Коэффициент
эллиптичности определяется тем же выражением (7.9.2), но в отличие от преды-
дущего случая большая ось эллипса будет ориентирована горизонтально.
Примерно такими же поляризационными характеристиками, как в плоскостях
Рис. 7.44. Поляризационные диаграммы скрещенных вибраторов [18]
320
ГЛАВА 7
(7.9.3)
(7.9.4)
(7.9.5)
xOz и yOz, обладает и поле скрещенных вибраторов в любой промежуточной плос-
кости, проходящей через ось z. Различие будет состоять в ориентировке осей по-
ляризационного эллипса: если плоскость, в которой находится точка наблюдения,
расположена под углом <р к оси х, то большая ось эллипса будет ориентирована
под углом (р + 90° (точка Р4 на рис. 7.44).
В плоскости хОу поле обладает линейной поляризацией. При этом результи-
рующая напряженность поля не зависит от направления ср , и суммарный вектор
электрического поля лежит в плоскости хОу. Вибратор 1 возбуждает в точке Р5
комплексную амплитуду напряженности поля
(!) _ 30№д12 ikr
— J-L Dill v|Jo ,
а вибратор 2 -
(2) _ 30к/1д12 ikr
— CUo
Результирующая напряженность поля
Eq = + Е® = г
Из последней формулы видно, что амплитуда результирующей напряженнос-
ти поля не зависит от угла (р. Таким образом, в плоскости хОу напряженность
поля не зависит от направления — антенна обладает ненаправленной диаграммой.
Как уже было отмечено, в скрещенных вибраторах токи должны быть равны
по амплитуде и сдвинуты по фазе на ±л / 2 .
Один из вариантов схемы питания скрещенных вибраторов показан на рис. 7.45,а.
Каждый из вибраторов имеет входное сопротивление около 70 Ом и питается при
помощи фидера, согласованного с этим сопротивлением. Так как фидер, питаю-
щий вибратор 1, длиннее фидера, питающего вибратор 2, на А^ / 4, то ток в
вибраторе 1 отстанет по фазе на л / 2 от тока в вибраторе 2.
На рис. 7.46 приведена схема питания скрещенных вибраторов при помощи
коаксиального фидера. Так как фидер, питающий вибратор 2, длиннее фидера,
при помощи которого питается вибратор 1, на А^ / 4 , то ток в вибраторе 2 будет
отставать по фазе от тока в вибраторе 1.
В другом варианте фазовый сдвиг между токами обеспечивается подбором длин
вибраторов. Здесь питающее напряжение при помощи общего фидера подводится
к зажимам вибраторов (рис. 7.45,6). Длина вибратора 1 выбрана несколько мень-
шей чем А / 2. По этой причине реактивная составляющая входного сопротивле-
ния этого вибратора будет иметь емкостной характер (Z± = Ki - iX±). Длина вибра-
тора 2 взята большей, чем А / 2 , но меньшей чем А. Поэтому реактивная состав-
ляющая входного сопротивления вибратора 2 приобретает индуктивный харак-
тер (Z2 = В-2 +гХ2). Регулируя длины вибраторов 2^ и 212, можно так подобрать
их, чтобы токи были сдвинуты по фазе на л / 2. Под воздействием напряже-
ния UА в вибраторах протекают токи и 12. Ток, протекающий через зажимы
вибратора 1,
fi=4Ki+i4Xi’ (7Л6)
Z1
а ток, текущий через зажимы вибратора 2,
ю»
Актемные решетки
321
a) 6)
Рис. 7.45. Варианты схем питания, обеспечивающих сдвиг по фазе, близкий к л / 2 : изме-
нением длины фидера (а); изменением длин вибраторов (б) [18]
Рис. 7.46. Схема питания скрещенных вибраторов при помощи коаксиального кабеля [18]
Активные составляющие входного сопротивления вибраторов слабо зависят от
частоты (fij - R2 =70 Ом), поэтому изменение длин 2Zj и 2Zg влияет главным об-
разом на реактивные составляющие и Х2- Из векторной диаграммы видно, что
ток опережает напряжение UA, а ток 12 отстает от него. Варьируя размеры 2Zj
и 2^2, добиваются, чтобы фазовый сдвиг между токами в вибраторах получился
равным примерно л / 2.
Критерием правильности подбора этих размеров является поляризация, близ-
кая к круговой в направлении нормали к плоскости расположения вибраторов.
Антенны из скрещенных полуволновых вибраторов находят широкое приме-
нение на практике. На дециметровых и сантиметровых волнах такие системы ис-
пользуются в качестве облучателей зеркальных антенн с круговой поляризацией.
При этом для создания требуемой диаграммы направленности (в пределах одной
11 - Неганов
322
ГЛАВА 7
Рис. 7.47. Директорная антенна с вращающейся поляризацией [18]
Z/2
▼i i +k/4
&)
Рис. 7.48. Плоскостной шунтовой вибратор (а) для многоэтажной турникетной телевизион-
ной передающей антенны (б) со схемой питания на двухпроводных линиях (в) [2]
Аытенпые решетки 323
полусферы) скрещенные вибраторы используют совместно с дисковым контрреф-
лектором.
На метровых волнах широкое применение находят директорные антенны с вра-
щающейся поляризацией. В частности, такие антенны используются в радиотеле-
метрии. Конструктивно директорная антенна с вращающейся поляризацией объ-
единяет две одинаковые линейно поляризованные директорные антенны (рис. 7.47).
Необходимые фазовые и амплитудные соотношения обеспечиваются применением
специальных схем питания активных вибраторов.
7.9.2. Пример построения многоэтажной турникетной телевизионной
передающей антенны из решетки плоскостных шунтовых вибраторов [2].
Режим всенаправленного излучения используют при создании телевизионных
передающих антенн с горизонтальной поляризацией, располагаемых на высоких
мачтах. В качестве элементов решеток для таких антенн наряду с обычными ци-
линдрическими удобно использовать плоскостные шунтовые вибраторы, предло-
женные Б. В. Брауде (рис. 7.48). Плечи вибратора выполняются из ряда параллель-
ных металлических трубок, заполняющих окаймляющую прямоугольную рамку. В
точках ЪЪ плечи вибратора замыкаются на мачту (что обеспечивает молниезащи-
ту), а в точках аа прикладывается возбуждающее напряжение. Оптимальные раз-
меры плоского вибратора: а - 0,26Хср; I = 0,16А,ср. В этом случае в полосе частот
±7,5% входное сопротивление почти постоянно и равно 140 Ом.
Для сужения ДН телевизионной антенны в вертикальной плоскости может быть
использовано несколько синфазных этажей из турникетных вибраторов, распо-
лагаемых на примерно полуволновых расстояниях один от другого (рис. 7.48, б).
При четном числе этажей излучение вверх и вниз отсутствует и максимум излу-
чения создается в горизонтальной плоскости. Вибраторы разных этажей, находя-
щиеся в одной вертикальной плоскости, питаются одной двухпроводной линией,
а находящиеся в другой вертикальной плоскости — другой двухпроводной линией
(рис. 7.48, в). Линии настраиваются на бегущую волну и соединяются параллель-
но, причем одна из линий выполняется длиннее другой на Х/4, что обеспечивает
сдвиг фаз в вибраторах каждого турникета на л/2. Двухпроводные линии «пе-
рекрещиваются» между этажами, чем обеспечивается синфазность возбуждения
вибраторов в разных этажах.
Режим регулируемой поляризации поля. Очевидно, что подбором соотношения
амплитуд и фаз токов на входах скрещенных вибраторов в направлении оси z (т. е.
в направлении максимального излучения) может быть обеспечена любая желаемая
поляризация поля. Это открывает дополнительные возможности осуществления
поляризационной избирательности в радиосистеме. При передаче регулирование
токов на входах вибраторов можно осуществить с помощью электрически управ-
ляемых фазовращателей и делителей мощности. При радиоприеме вибраторы тур-
никетной антенны могут быть присоединены к отдельным приемникам и сложение
сигналов от каждого радиоканала может производиться на промежуточной или
даже на низкой частоте (т. е. после детектирования). В последнем случае приемная
антенна вместе с приемниками может принимать волны любой поляризации.
н *
324
ГЛАВА 7
7.10. Взаимодействие излучателей в решетке и диаграмма
направленности излучателя [3,27]
В антенных решетках, состоящих из близко расположенных излучателей, на-
блюдается эффект взаимного влияния излучателей друг на друга за счет излуча-
емых электромагнитных полей. Взаимодействие между антеннами, размещаемыми
в пространстве, имеет место всегда, но проявляется по-разному.
Расположение одной антенны относительно другой в дальней зоне не вызывает
изменения характеристик этих антенн. В антенной решетке слабонаправленных
излучателей с шагом порядка длины волны имеется сильное взаимодействие. В
результате этого у одиночного элемента меняются ДН, сопротивление излучения,
входное сопротивление, резонансная частота, рабочая полоса и электрическая
прочность. Это взаимодействие будет различным в зависимости от шага решетки,
взаимной ориентации и направленности излучателя, места излучателя в решетке
(в центре и на краю). В электрически сканирующих антеннах при движении луча
взаимодействие излучателей изменяется.
Физика происходящего процесса взаимодействия может быть пояснена следу-
ющим образом. Возбуждение одного излучателя в решетке наводит токи (поля) в
соседних излучателях, которые начинают переизлучать. Поэтому ДН одиночного
излучателя формирует фрагмент решетки. При управлении фазовым распреде-
лением в ФАР меняются наводимые токи и, соответственно, взаимодействие. В
зависимости от типа излучателя в решетке наводимые токи (поля) проявляются
по разному. В резонансных излучателях (вибраторных, щелевых) распределение
тока по элементу сохраняется и в первом приближении остается гармоническим,
а изменяется лишь амплитуда тока. В излучателях бегущей волны и апертурных
излучателях меняется распределение тока или поля по элементу. Для удобства
расчетов решеток с различными типами излучателей вводится определение ДН
элемента в решетке. В соответствии с ГОСТ 23282-78 под ДН излучателя в ре-
шетке Fn(0,9) понимается ДН возбуждаемого элемента, при этом все остальные
излучатели нагружены на согласованные нагрузки. Эта ДН может существенно
отличаться от ДН одиночного слабонаправленного элемента наличием глубоких
провалов для некоторых направлений. Эти провалы вызваны интерференцией
прямой и переизлученных волн. В ФАР, при формировании луча в направлении
«провала» ДН элемента резко падает КНД решетки и, следовательно, излучаемая
антенной мощность. При этом резко возрастает коэффициент отражения от входа
излучателя вследствие изменения входного сопротивления. Под входным сопро-
тивлением излучателя в решетке понимают входное сопротивление элемента при
возбуждении всей решетки плоской волной с линейным фазовым распределением,
соответствующим направлению луча 0^, (ргл . Входное сопротивление излучате-
ля зависит от фазового распределения, т.е. от направления формирования луча
zex (еал, Фад ) ♦ Существует связь между Fn (0^, ф^ ) и величиной Zex (0гл, (ргл ), из
которой можно найти одну величину по другой. Экспериментально удобнее нахо-
дить Fn (0гл, фгл ), а расчетно
Zex (егл > Фал)-
Остановимся на методах расчета взаимодействия излучателей в решетке. Стро-
гое решение этой задачи связано со значительными математическими трудностя-
ми. Так, для простейшей решетки резонансных металлических вибраторов в сво-
бодном пространстве (отсутствуют элементы крепления и экран) взаимодействие
Антенные решетки
325
может быть найдено из совместного решения системы интегральных уравнений,
каждое из которых аналогично интегральному уравнению для одиночного симмет-
ричного вибратора [2].
Для оценки взаимного влияния вибраторных и щелевых излучателей использу-
ется метод наведенных ЭДС, или метод наведенных сопротивлений.
Из (7.6.10) активное погонное сопротивление
coscp,
где <р — сдвиг фаз между напряженностью поля и током в элементе вибратора.
Мощность, излучаемая антенной длиной L — это средняя во времени мощ-
ность, расходуемая на сопротивлении и определяемая как:
IxExdtdx.
Излучаемую мощность можно также выразить через сопротивление излучения
= (1дР^)/2 и ток в пучности вибратора 1П. Из сравнения двух последних урав-
нений следует:
Т
RY =----V f [lxExdtdx. (7.10.1)
J J
ПП 0L
Полученное выражение позволяет рассчитать сопротивление излучения решет-
ки, активные составляющие входных сопротивлений и собственное сопротивление
излучения одиночного вибратора. Если под Ех понимать поле, создаваемое j -м
вибратором на поверхности г-го вибратора, то вычисляемое по формуле (7.10.1)
у
сопротивление называется наведенным сопротивлением излучения Rf- в i -ый
вибратор со стороны j -го. Полное сопротивление излучения г -го вибратора в
решетке из N элементов:
У
где — собственное сопротивление излучения г -го вибратора, определяемое из
(7.10.1), где Е® — поле самого вибратора. Излучаемая антенной мощность
При равенстве токов в вибраторах находим сопротивление излучения антенны
Проведены многочисленные расчеты наведенных сопротивлений, и наиболее
значительные для практики результаты сведены в графики и таблицы, из кото-
у
рых Rd двух параллельных полуволновых вибраторов определяется как функция
расстояний d между ними и смещения h вдоль их осей. Расчеты (рис. 7.49) при-
ведены для случая синфазной работы вибраторов при равных амплитудах токов в
326
ГЛАВА 7
них (кривая R^2) и для случая работы со сдвигом фазы в п/2 (кривая qR^)» когДа
h/1 = 0.
Наведенные сопротивления в вибраторах при равных токах в них называются
у
взаимными. Ход кривых Rfi, объясняется уменьшением амплитуды наведенного
поля с увеличением расстояния и изменением его фазы. При расстоянии d = 0,43Z
активная составляющая наведенного сопротивления равна нулю. Это значит, что
средний сдвиг фазы поля второго вибратора по отношению к полю первого достиг
значения л/2 . С дальнейшим увеличением d наведенное сопротивление становится
отрицательным, а следовательно, снижается сопротивление протекающего тока.
у
Найденные сопротивления излучения решетки R^ позволяют определить КНД
с учетом взаимодействия излучателей решетки и влияния взаимодействия на на-
правленность из соотношения
1 А2(9,ф)
30 R?
Здесь А (0, ср) ненормированная амплитудная ДН антенны, связывающая электри-
ческое поле с током I и расстоянием г :
Зависимость КНД синфазной антенной решетки из параллельных полуволно-
вых вибраторов с равными токами от шага приведена на рис. 7.50.
у
Найденное выше R^ для полуволнового вибратора, как известно, совпадает с
активной частью входного сопротивления. Реактивную составляющую входного
сопротивления вибратора в решетке с учетом взаимодействия получим, проведя
аналогичные расчеты для величины I (Еу/ТуЛ.
7.10.1. Связь комплексных наведенных сопротивлений через активные
взаимные наведенные сопротивления для синфазной АР и активные взаим-
ные наведенные сопротивления АР со сдвигом фаз л/2. Известно, что комп-
лексные наведенные сопротивления могут быть найдены через активные взаимные
наведенные сопротивления для синфазной работы вибраторов и через наведенные
сопротивления АР со сдвигом фаз л/2. Покажем это сначала для двух полуволно-
вых вибраторов (рис. 7.51) [3].
Рассмотрим диаграмму направленности антенны с активным директором (реф-
лектором). Если в системе из двух одинаковых вибраторов принять один из элемен-
тов за антенну, то второй окажется директором или рефлектором в зависимости
от положения его относительно антенны (перед или позади). Диаграмма направ-
ленности такой антенны У(9,ф) равна произведению ДН единичного излучателя
/1 (®> ф) на множитель решетки (рис. 7.52).
f (е, Ф) = ад (е, ф)
sm——
2
• Ф
sm —
2
Здесь ф = kd sin 6 + уi — сдвиг по фазе между полями антенны и директора за
счет разности хода лучей и сдвига по фазе тока между элементами .
Так как в данном случае число излучателей N = 2,
Антенные решетки
327
Рис. 7.49. Зависимости активной составля-
ющей наведенного (взаимного) сопротивле-
ния от расстояния между вибраторами d/X
при синфазном возбуждении
у
(кривая Rfa) и при питании
в квадратуре (кривая ) [27]
Рис. 7.50. Зависимости КНД решетки
от шага между излучателями d/X для
различного числа излучателей N [3]
Рис. 7.51. К расчету пол-
ных входных сопротив-
лений вибраторов [3]
Рис. 7.52. Диаграммы направленности антенны с активным
директором (рефлектором): а) — в вертикальной плоскости; б)
— в горизонтальной плоскости [3]
328
ГЛАВА 7
Vi
f (0, ср) = Aft (0, (р)2 cos — = 2Afy (0, <p)cos — d sin 0 +
2 \ A
Для однонаправленности антенны с директором необходимо, чтобы d = Х/4 и
1|/ = -л/2, тогда f (0, (р) = 2Aj[ (0, (p)cos — (sin 0-1)
ставать от тока антенны.
т.е. ток в директоре должен от-
В случае антенны с рефлектором условием работы будет d = Х/4 и щ = л/2,
т.е. ток в рефлекторе должен опережать ток в антенне. На рис. 7.52, а,б показаны
ДН вибраторной антенны с «активным директором» (рефлектором) в двух главных
плоскостях.
Расчет антенны с пассивными направляющими элементами следует начать с
определения тока в элементах, зависящего от положения и настройки элементов.
Метод наведенных ЭДС позволяет найти токи в антенне.
Пусть имеется два полуволновых вибратора, расположенных параллельно, к
входным клеммам которых подключены источники с ЭДС е± и в2 (рис. 7.53, а).
Рассматривая вибраторы как электрические цепи, можно записать
е1 - h%l ’ е2 ~ ^2^2 ’
где Z± и Z2 — полные входные сопротивления вибраторов, найденные с учетом их
взаимного влияния.
Рассмотрим случай, когда второй вибратор пассивный (е2 = 0) и клеммы его
замкнуты на некоторое сопротивление Z2H (рис. 7.53, б).
е2 П^2п
в)
б)
Рис.7.53. К расчету антенны с пассивным направляющим элементом
Антенные решетки
329
Ток в этом элементе не может быть равен нулю из-за взаимодействия вибрато-
ров. Следовательно,
е2 - 0 - I2 (Z2 + Z2h),
откуда
^2 + z2m
или
^22 + %2н + Z21 = ° ,
где Z2± — наведенное сопротивление; Z22 — собственное сопротивление вибратора.
Заменив наведенное сопротивление взаимным, получим
Z2h + Z22 + iz21Me-^i = 0 , (7.10.2)
а
где а — отношение амплитуд токов в вибраторах; — сдвиг по фазе между то-
ками.
Учитывая связь между токами первого и второго вибраторов
I2 = , (7.10.3)
и решая совместно уравнения (7.10.2) и (7.10.3), находим ток во втором вибраторе
через ток в первом:
Входным сопротивлением антенны в данном случае является входное сопротив-
ление активного вибратора
Zex = ^1 = ^11 + а-^12взе •
Подставив в последнее выражение значение отношения токов из предыдущего
уравнения, получим
Действительная часть этого выражения определяет сопротивление излучения
антенны.
Для этого обозначим сопротивления первого и второго вибраторов соответс-
твенно: Zu , Z22 — собственные; Z12 , Z2^ — наведенные; Z1? Z2 — полные:
В общем случае токи в вибраторах могут иметь произвольный фазовый сдвиг на
величину и отношение амплитуд и токов а , тогда
Очевидно, что Z12 пропорционально току 12 и Z21 — току . Если комплексное
наведенное сопротивление при а = 1 и = 0 обозначить через взаимное Ze3, то
Z12 = Ze3ae^.
Взаимное сопротивление определяется через наведенные сопротивления излу-
у
чения при синфазной работе R^2 и при сдвиге фазы токов л/2 (работа в квадратуре)
qR^2, т.е. Ze3
— ^12 В результате получаем
330
ГЛАВА 7
ZT = (73 + г’42,5) + (Rfc + 9K§)ae*|,i, Z2 = (73 +142,5) + -(Kf2 + qR^2)ae^ .
При наличии N излучателей в решетке входное сопротивление i -го вибратора
определяется выражением
N
Zt- =(73+ 142,5)+ £z0-,
г=1
Найденные соотношения справедливы для бесконечно тонких полуволновых
вибраторов. С увеличением толщины вибратора в случае метода наведенных ЭДС
растут ошибки при определении реактивной части входного сопротивления. Пол-
ное взаимное сопротивление Ze3, стремится к собственному сопротивлению при
d - 0 (см. рис. 7.49).
Метод наведенных ЭДС позволяет приближенно решать и ряд других задач в
антенной технике.
7.11. Входное сопротивление излучающего элемента АР.
Мощность, излучаемая АР [27]
Знание входного сопротивления излучающего элемента в АР необходимо при
проектировании системы питания, обеспечивающей требуемое АФР. Входное со-
противление каждого излучающего элемента ( Zexn) определяется не только его
собственной конструкцией, но и взаимным влиянием соседних элементов, кото-
рое, в свою очередь, зависит от АФР возбуждающих токов и положения элемента
в АР.
Поясним методику расчета Zexn на примере простейшей АР, состоящей из двух
одинаковых излучателей. Поскольку рассматриваемая система линейна, для токов
и напряжений на входах каждого излучателя ( Igi’^02 и ^01’^02 соответственно)
можно записать систему линейных уравнений типа уравнений Кирхгофа:
U01=Z11I01+Z12I02, (7111)
^02 - ^21-Toi +^22-^02»
где нижний индекс «0» означает, что ток и напряжение ( i = 1,2) берутся в
точках питания, причем Ini = / sin kl, = П(^ / sin kl ( i = 1,2). Коэффициенты
Zn,Z22 носят название собственных сопротивлений, a Z12,Z21 — взаимных сопро-
тивлений и имеют следующий смысл. Пусть второй вибратор разомкнут в точках
входа, т. е. Iq2 =0. Тогда из первого уравнения (7.11.1) имеем Z^ = l/gj /101. При
разомкнутом первом вибраторе Z22 = У02 /102. Таким образом, каждое из собс-
твенных сопротивлений равно входному сопротивлению соответствующего вибра-
тора в режиме, когда другой вибратор разомкнут. В первом приближении обычно
считают, что влияние разомкнутых вибраторов невелико (это справедливо, если
длина плеч вибратора отлична от резонансной длины), и отождествляют собс-
твенное сопротивление с входным сопротивлением каждого вибратора в свободном
пространстве.
В рабочем режиме, когда оба вибратора возбуждаются соответствующими на-
пряжениями, из (7.11.1), поделив первое уравнение на 101, а второе на 102 , полу-
чим значения входных сопротивлений вибраторов в составе решетки:
Антенные решетки
331
(7.11.2)
Zex2 ~ U02 / А)2 “ Z22 + -~Z21
-*02
нав
21 »
(7.11.3)
где добавочные сопротивления, входящие в состав входных сопротивлений, носят
название наведенных сопротивлений, причем
г?нав _ ^02 г? гунав _ 4)1 г?
z12 ~~—z12 ’ Z21 - ~—"21*
201 -*02
(7.11.4)
Как видно из (7.11.4), при равных токах, т. е. Jgj = Iq2 , взаимные сопротивления
равны наведенным. Отметим, что с помощью принципа взаимности можно пока-
зать, что Z12 ~ ^21 ’ причем это равенство сохраняется при разных длинах виб-
раторов и произвольном взаимном расположении в пространстве. Для наведенных
сопротивлений подобное равенство, как следует из (7.11.4) справедливо, однако
наведенные сопротивления могут быть найдены через взаимные, если известны
токи на входах излучателей.
Для нахождения взаимного сопротивления вибраторов может быть использован
метод наведенных ЭДС, описанный выше. Рассмотрим ситуацию, когда токи на
входах вибраторов равны, т. е. Iqi = Iq2 = -^о > причем считаем, что распределение
тока в вибраторе, работающем в составе АР, остается таким же, как в свободном
пространстве, и описывается выражением:
J0
sin kl
sink(l — x).
(7.11.5)
Объем V соответствует объему, занятому током, т. е. объему вибратора. Напря-
женность электрического поля Е в точках, соответствующих объему, занятому
первым вибратором, представим в виде суммы двух полей: Ец — поля, создан-
ного током, текущим в первом вибраторе, и Е12 — поля, созданного током, те-
кущим во втором вибраторе. Плотность тока в первом вибраторе j = Zqi(I1/*S'), где
S — поперечное сечение вибратора, Zq± — единичный вектор вдоль оси первого
вибратора. При этом (7.11.2) приобретает вид
Zexl
+ ^12 ^01^1 dSdzi
(7.11.6)
*4* *
где/у = (Iq / sin kl) sin k(I - x^). Сравнивая (7.11.6) c (7.11.2) при условии Z01 = l02, ви-
дим, что первое слагаемое в (7.11.5) может быть использовано для расчета собс-
твенного сопротивления , а второе — для расчета взаимного сопротивления
Z12 = Z21. При различных конфигурациях вибраторов собственное сопротивление
Z22 можно найти, определив входное сопротивление, как
Zexl
и применив это определение ко второму вибратору. Следует иметь ввиду, что
в большинстве таблиц и графиков взаимные сопротивления отнесены к пучности
332
ГЛАВА 7
вхп
вхп ' ““вхп '-'пп
тока; в предположении синусоидального распределения, тока пересчет взаимных
сопротивлений ко входным точкам осуществляется путем деления на sin kl. Рас-
чет входных сопротивлений излучателей других типов встречает значительные
сложности, поэтому часто используют экспериментальные данные.
Для решетки из N излучателей входное сопротивление каждого из излучателей
рассчитывается по формуле, аналогичной (7.11.2) и (7.11.3):
м
Еунав
^тп •>
т=-М
т^п
где Znn — собственное входное сопротивление п -го излучателя; Zmn
ное сопротивление, отнесенное к току на входе п -го излучателя. В качестве Z
обычно используются значения наведенных сопротивлений, обусловленные вза-
имодействием излучателей только с номерами пит, без учета остальных эле-
ментов.
Полная мощность излучения АР может быть в отсутствие потерь найдена как
сумма мощностей, излучаемых каждым излучателем, по формуле
м м
наведен-
ное
тп
вхп
V
п=—М
п=-М
7.12. Коэффициент направленного действия линейных АР [27]
Коэффициент направленного действия линейных АР, как и любой антенны,
может быть вычислен по формуле (2.2.6). Для точного расчета необходимо знать
ДН с учетом направленных свойств одного элемента. Однако в случае достаточно
длинных антенн ДН решетки в основном определяется множителем системы. Рас-
смотрим решетку с произвольным амплитудным распределением токов по зако-
0 ). Для расчета КНД в направлении 6 = 6?Л справедлива
п
формула
м
п--М
sin nkd
> cos nw---------
— nkd
71=1
М-п
т±т+п
\т=—М
где в отличие от принятых обозначений,
м
у
п--М
М
при ф
п=—М
Рассмотрим синфазный равноамплитудный режим (ф = 0, In = I, '(0^) = NI).
Результаты расчета по формуле (7.12.1) показывают, что практически при любом
фиксированном числе излучающих элементов N максимум КНД наблюдается при
d « 0,9Х. При дальнейшем увеличении расстояния между элементами КНД умень-
Антенные решетки
333
шается в связи с появлением (при d / X = 1) дополнительных главных максимумов.
Однако если задана длина решетки L = (IV-l)d (для длинных антенн L « Nd), то
для получения максимума КНД более целесообразно выбирать d / X = 0,5. При та-
ком значении шага УБЛ убывает при удалении от направления максимума из-
лучения (См. 7.3.22). Кроме того, при дальнейшем уменьшении d КНД остается
практически неизменным. При d / X = 0,5 , учитывая, что kd = л , sin nkd = 0 , из
(7.12.1) получаем
D = D0=N.
(7.12.2)
Этот же результат можно объяснить тем, что для изотропных элементов при
d , кратных X / 2, активная часть взаимных сопротивлений обращается в нуль и
у
яри фиксированном значении Р мощность делится поровну между всеми элемен-
тами. При этом ток в каждом элементе будет в 1 / \/N раз меньше, чем ток в одном
у
элементе, излучающем ту же мощность Р . Суммарное поле в направлении макси-
мума будет превышать поле одного элемента в N(1 / y/N) = y/~N раз, соответствен-
но КНД решетки возрастет в N раз.
Для длинных решеток N « L / d, поэтому
= 2L / X.
О0
Перейдем к режиму осевого излучения, когда \\i = kd. При d/X = 0,25
(sin2nkd = О), что соответствует согласно (7.3.33) убывающему закону изменения
УБЛ, величина КНД, как и в предыдущем случае, равна N. Однако теперь шаг
решетки в 2 раза меньше, так что
D = N
*L/d = ±L/ X.
(7.12.3)
Таким образом, при одной и той же длине антенны L в режиме осевого излу-
чения при = kd значение КНД можно получить в 2 раза больше, чем в режиме
нормального излучения.
Анализ формулы (7.12.1) показывает, что при ц/ > kd наблюдается сначала
дальнейший рост КНД, а затем его резкое снижение. Сказанное справедливо при
шаге решетки, удовлетворяющем условию (7.3.33), практически при d / X = 0,25. В
оптимальном режиме, соответствующем максимуму КНД, при Nd » X
(у / kd)opt = 1 + 2,94 / Nkd , (7.12.4)
D = 1,82N « 1,82L / d = 7,2L / X. (7.12.5)
Физические причины подобной зависимости КНД от величины у обсуждались
в 7.3.4. Здесь только отметим, что формулу (7.12.4) часто упрощают, полагая
2,94 » л. Тогда для длинных антенн
(V / kd)opt « 1 + X / 2^d « 1 + X / 2L. (7.12.6)
При этом фазовый сдвиг между полями двух соседних элементов в направлении
^гл ~ 0 составляет величину -п / N; соответственно поля крайних элементов отли-
чаются друг от друга по фазе на л. Для антенны бегущей волны (АБВ) оптималь-
ный коэффициент замедления определяется соотношением аналогичным (7.12.6)
(с / v)Opt = Yopt ~ 1 + X / 2L. (7.12.7)
Общий вид поведения КНД равноамплитудной АР в зависимости от у = \|/ / kd
при d = 0,25Х представлен графиком на рис. 7.54 (сплошная линия). Обратим вни-
мание на практически постоянное значение КНД на начальном участке графика,
334
ГЛАВА 7
Рис. 7.54. Зависимости КНД равноамплитудной антенной АР от у: сплошная линия
d = 0,25Х, штриховая линия — ограничение на d по формуле (7.3.23) [27]
т. е. в режиме наклонного излучения. Это объясняется тем, что расширение глав-
ного лепестка при его отклонении от нормали компенсируется уменьшением те-
лесного угла, занимаемого данным лепестком, поскольку он приобретает в про-
странстве воронкообразную форму (см. рис. 7.13).
Перейдем теперь к амплитудным распределениям, спадающим к краям решет-
ки. В синфазном режиме ( у = 0) при d = 0,5Х из (7.12.1) получим
(7.12.8)
Из сравнения с (7.12.1) имеем
м
(7.12.9)
Отношение (7.12.9) называют коэффициентом использования линейной АР ( v),
который учитывает снижение КНД при спадающем амплитудном распределении
по сравнению с синфазным равноамплитудным возбуждением. При известном ко-
эффициенте v
D = vD0 =v-2L/k. (7.12.10)
В частном случае при косинусоидальном амплитудном распределении в синфаз-
ном режиме ( v = 0) для длинных антенн коэффициент v = 0,81. Для этого ампли-
тудного распределения зависимость КНД от величины у = / kd , справедливая
при шаге d , определяемом (7.3.33), приведена на рис. 7.54 (штриховая линия). Как
видно, при косинусоидальном амплитудном распределении также существует оп-
тимальный режим, причем величина оптимального замедления больше, чем при
равноамплитудном возбуждении. Больше оказывается и значение КНД в опти-
мальном режиме при косинусоидальном распределении. Это объясняется тем, что,
как и в равноамплитудных решетках, по мере роста у при ц/ > kd одновременно
происходят два процесса — сужение главного лепестка и возрастание относитель-
Антенные решетки
335
ного уровня боковых лепестков. Однако из-за спадания амплитуды токов к краям
решетки фактор сужения главного лепестка при возрастании у дольше оказывает
преобладающее действие. Для других амплитудных распределений, более резко
спадающих к краям, например по закону In = I cos2 [ли / (N -1)], эффект возрас-
тания КНД в оптимальном режиме проявляется еще сильнее.
Таким образом, можно сделать следующие выводы. Линейные решетки с рав-
ноамплитудным возбуждением имеют максимальное значение КНД по сравнению
с другими типами рассмотренных выше распределений в режиме нормального из-
лучения. В режиме осевого излучения больший КНД имеют решетки с неравно-
мерным амплитудным распределением, спадающим к краям.
Все сказанное справедливо, если поля отдельных элементов в равном направле-
нии складываются синфазно или с малым фазовым сдвигом. В противном случае,
когда формирование диаграммы во всех направлениях, в том числе в направлении
главного максимума, осуществляется на разностном эффекте, теоретически воз-
можно достижение существенно большей направленности, однако использование
подобных решений (так называемых «сверхнаправленных» или «реактивных» ан-
тенн) встречает практически непреодолимые трудности из-за резкого возрастания
амплитуд токов. Отметим, что увеличение амплитуд токов (приемлемое, однако,
с практической точки зрения) начинает проявляться уже в АР с осевым излуче-
нием в оптимальном режиме с равномерным распределением токов, тем более при
спадании их к краям решетки.
Фазовые ошибки, как квадратичные, так и кубические, приводят к снижению
КНД. Степень снижения КНД зависит помимо величины ошибки также от типа
амплитудного распределения. Если амплитудное распределение спадает к краям
решетки, то при прочих равных условиях влияние фазовых ошибок уменьшается,
так как снижается вклад в результирующее поле от наиболее расфазированных
крайних элементов.
7.13. Понятие о непрерывном линейном излучателе [27]
Теория непрерывных линейных излучателей широко используется как для
расчета конкретных антенн (например, провода с током), так и для анализа более
сложных систем, например излучающих поверхностей.
Расчет множителя системы непрерывного линейного излучателя длиной L с
АФР, описываемым функцией I(z) = I(z)exp[t\|/(z)], может быть осуществлен по
общей формуле. Однако проще использовать полученные ранее выражения для
7 линейных АР, рассматривая непрерывный излучатель как предельный слу-
чай АР (см. рис. 7.9), если число излучателей стремится к бесконечности (N —> оо),
шаг решетки — к нулю ( d —> 0), но так, что Nd = const = L. Для синфазного
равноамплитудного распределения ( I(z) = I, \y(z) = 0 ) формула (7.3.7) примет для
непрерывного линейного излучателя следующий вид:
F^ = sinu/u, (7.13.1)
где и = /cLcosO / 2. При получении (7.13.1) учтено, что в знаменателе (7.3.7) в силу
малости аргумента ( d —» 0) можно положить sinx « х. Выражение (7.13.1) спра-
ведливо при любой физической природе источников, образующих непрерывное
ГЛАВА 7
336
распределение, при этом функция I(z) может соответствовать реальному элект-
рическому току, магнитному току или некоторым эквивалентным излучателям;
влияние их на результирующую ДН учитывается множителем Fq .
Для синфазного косинусоидального амплитудного распределения
гс\
(I(z) = I cos(ttz / L), \|/(z) = 0) выражение для Fv 7 получим из (7.4.4), используя со-
отношение sin(a: ± л / 2) = ± cos х :
F® = (л2 / 4)cosu / ((л / 2)2 / и2). (7.13.2)
Принципиальной особенностью непрерывных линейных излучателей при любом
распределении возбуждающего тока по сравнению с дискретными решетками яв-
ляется отсутствие вторичных главных максимумов поскольку здесь d 0. Графи-
ки функций (7.13.1) и (7.13.2) показаны на рис. 7.55 (кривые 1 и 2 соответственно) в
зависимости от обобщенной переменной и.
В табл. 7.1 приведены выражения, описывающие множитель системы непре-
рывных линейных излучателей при различных амплитудных распределениях (в
том числе при разных значениях А — относительного уровня возбуждения края
антенны), а также характерные значения параметров ДН (без учета направленных
свойств элемента), справедливые для синфазного режима возбуждения. Данные
могут быть использованы для анализа АР, шаг которых достаточно мал, в об-
ласти основного и первых боковых лепестков (дальние боковые лепестки для АР
несколько больше).
В синфазном режиме для равномерного распределения ( I(z) = 1) согласно
(7.12.2) имеем D = Dq =2L / X. При неравномерном распределении КНД снижается;
величина его рассчитывается как D = vDq , причем коэффициент использования
L/2
-L/2
I(z)dz
-L/2
(7.13.3)
Выражение (7.13.3) сходно с (7.12.9) и справедливо для «ненаправленных» ан-
тенн. Значения v при различных амплитудных распределениях в синфазном ре-
жиме приведены в табл. 7.1.
Рис. 7.55. Множитель системы непрерывных линейных излучателей при различных амп-
литудных распределениях: 1 — синфазное равноамплитудное распределение; 2 — синфаз-
ное косинусоидальное амплитудное распределение [27]
Таблица 7.1 [27]
Амплитудное распределение I(z) Формула множителя системы __ . kL Л Fc(u) и = cosO 2 А0О д%,5 Уровень первого бокового лепестка, дБ Коэффициент использования v = D / Dq
I(z) = 1 sin и / и 1154 51°Х -13,2 1
cos(tlz / L) л2 cos и 4 (л / 2)2 - и2 1724 68.8° X -23 0,81
о cos (лз / L) 2 sinw /2 2\ ЩТ1 —и ) 229,24 83, Г X -32 0,667
1 - 4(1 - A)(z / L)2 3 ж sinw Ач cost/, А 2(1 А) + 2 + А [ и uz iXsinw +2(1 - А) —— и6 J
A = 0,8 121,54 52,74 -15,8 0,994
A = 0,5 130,6°Х 55,64 -17,1 0,970
A = 0 163,8°Х 664 -20,6 0,833
Антенные решетки
СлЭ
338
Таблица 7.1 [27] (Продолжение)
Амплитудное распределение I(z) Формула множителя системы kL „ Fc (и) и = —— cos 0 Д0О ^0,5 Уровень первого бокового лепестка, дБ Коэффициент использования v = D / Dq
А + (1-А)х xcos(ttz / L) 1 Г А sin и Л
to | Й 7* > * 1 > ЬО 3 ‘с № СЛ 1 £ £ 1 1
А = 0,5 132,4° X 55,6° X -17,6 0,966
А = 0,316 143,8°Х L 58,4° X -20,0 0,935
А = 0,1 162,1°Х 63,0°Х -22,4 0,874
1 - (2z / L) z \2 . и ,и\ sm — / — 1 2 2) 229,2°Х L 73,4° X -26,4 0,750
71 - (2г / L)2 А 00 139,6°Х 58,9° X L -17,6 0,925
Антенные решетки
339
Линейное распределение фазы в непрерывных линейных излучателях дости-
гается за счет возбуждения бегущей волной, распространяющейся вдоль оси
z с фазовой скоростью и (антенны бегущей волны — АБВ). При этом функция
v|/(z) = -(с / v)kz = -ykz , где у = с / v — коэффициент замедления волны; с — ско-
рость света. Изменения, происходящие с ДН линейного излучателя при изменении
фазовой скорости, подробно описаны в 7.3.4. Для расчета множителя системы при
линейном фазовом распределении в приведенных в табл. 7.1 формулах для Fv 7 до-
статочно вместо и подставить (fcL / 2)(cos 0 - с / v) и произвести соответствующую
нормировку. В частности, в режиме осевого излучения ( с / v > 1) при равноамп-
литудном распределении множитель
(7.13.4)
При равноамплитудном распределении и v = с ( у = 1) может быть рассчитан
по аналогии с АР длиной L с помощью формулы (7.12.3). В оптимальном режиме
(yopt = 1 + А, / 2L) значение КНД определяется формулой, аналогичной (7.12.5). При
спадающем к краям амплитудном распределении, как и в случае АР оптимальное
значение у возрастает, при этом увеличивается и КНД. Влияние квадратичных и
кубических фазовых ошибок аналогично изменениям, происходящим с ДН антен-
ных решеток.
В качестве примера непрерывного линейного излучателя рассмотрим провод
с током (рис. 7.56), изменяющимся по закону I(z) = I exp(-ikz). Пример интересен
(с\
тем, что результирующая ДН сильно отличается от вида функции Fv 7. Действи-
тельно, поскольку и = с(у = 1), то максимум множителя системы соответствует
0^ = 0. Однако элемент провода с током (фактически ЭЭВ) в этом направлении
вообще не излучает (множитель элемента Fo = sin 6); максимум его излучения ори-
ентирован под углом 0 = 90° к оси провода. В результате максимум ДН получается
dz
F(d)
Рис. 7.57. ДН непрерывного линейного
провода с током в сечении, параллельным
оси провода [27]
Рис. 7.56. К вопросу определения амплитуд-
ной ДН провода с током [27]
340
ГЛАВА 7
в некотором направлении 6тах < 90°, которое при большом значении L / X можно
приближенно найти из условия максимума числителя (7.13.4), т. е. из равенства
ZcL(cos0max -1) / 2 = — п / 2 (взят знак минус, поскольку искомый угол 0тах > 0^.
Окончательно получим
cos0„,av = 1 — Л, / 2L.
ШАЛ '
(7.13.5)
Вид ДН в сечении, параллельном оси провода, приведен на рис. 7.57. Про-
странственная ДН имеет форму конической воронки. В качестве самостоятельного
излучателя провод с бегущей волной тока обычно не применяется. Однако в ан-
тенной технике с успехом используются различные комбинации из таких проводов
(например, ромбическая антенна).
7.14. Плоские антенные решетки [27]
Рассмотренные ранее линейные АР в режимах нормального и наклонного из-
лучений позволяют сформировать направленное излучение только в одной плос-
кости, проходящей через ось решетки. Плоские АР дают возможность сконцент-
рировать излучение в узкий пучок в двух плоскостях. Форма плоской АР (форма
раскрыва решетки) может быть прямоугольной, круглой, шестиугольной и т. д. и
определяется как требованиями, предъявляемыми к форме ДН, так и конструк-
тивными особенностями системы. Излучатели в плоских АР располагаются в узлах
прямоугольной или треугольной (гексагональной) сетки (рис. 7.58).
Рассмотрим подробнее излучение плоской АР прямоугольной формы с располо-
жением изотропных излучателей в плоскости z = 0 в узлах прямоугольной сетки.
Пусть решетка состоит из Ny = %Му +1 рядов излучателей, параллельных оси у,
причем расстояние между рядами равно dy. Каждый ряд состоит из Nx = 2МХ +1
излучателей с шагом dx. Координаты излучателей в плоскости решетки опреде-
ляются как = n^.d.r.(—M^ <п~< Мг) и уп - n-.d.d—M.. < . Тогда множи-
ft JU JU v JU JU ju ' J it у у 4 у у у7 г л
тель системы (рис. 7.59) примет вид
(7.14.1)
-Мт -М.
«Ли-
АТ/ Ау
а) б)
Рис. 7.58. Прямоугольная (а) и гексогональная (б) сетки плоской АР
Антенные решетки
341
Z д Р{Г,6,(р)
Рис. 7.59. Геометрия плоской АР пря-
моугольной формы [27]
Рис. 7.60. ДН плоской синфазной решетки: а) — с
двухсторонним излучением, б) — с экраном [27]
Наиболее простым является случай, когда распределение тока может быть
представлено в виде произведения двух функций, зависящих только от х и толь-
ко от у:
I(n)= Wx)7(nv). (7.14.2)
Пусть решетка возбуждается равноамплитудно, причем
/(пх) = ехр(-шхфх),
f(ny) = ехр(-гпуфу).
(7.14.3)
(7.14.4)
Тогда амплитудный множитель системы имеет вид, справедливый для произволь-
ной плоскости (ф = const), проходящей через нормаль к плоскости решетки:
sin
(kdx sin G cos ф - ф т)
sin
Ж
—— (kdy sin G sin ф - ф^)
N
(7.14.5)
sin — (kdx sin G cos ф - фх)
sin
— (kdy sin 6 sin ф - \yy)
Можно показать, что каждый из сомножителей в (7.14.5) соответствует множи-
телю системы линейной АР, ориентированной вдоль осей х или у с АФР (7.14.3) и
(7.14.4) соответственно. Такие же выводы справедливы для любых распределений
возбуждающего тока, представленных в виде функций, разделяющихся по коор-
динатам X и у.
При фх = ф^ = 0 (синфазная решетка) максимум излучения ориентирован по
нормали к плоскости решетки (рис. 7.60,а). Излучение в нижнее полупространство
устраняется обычно либо выбором однонаправленных излучающих элементов,
либо с помощью экранов (рис 7.60,6). Форма ДН в каждой из главных плоскостей
(xOz и г/Oz) определяется только геометрией решетки в этой плоскости и ампли-
тудно-фазовым распределением в этой же плоскости. При этом справедливы все
342
ГЛАВА 7
приведенные в разделах 7.2-7.3 оценки для параметров ДН линейной АР.
При линейном фазовом распределении, когда фх < kdx и < kdy (что харак-
терно для плоских АР), направление максимума основного лепестка (6гл, Фгл) оп~
ределяется из условий равенства нулю числителей обоих сомножителей в (7.14.5):
sin ©гл coscp^ = yx/kdx , sinG^ sincp^ = yy/kdy , (7.14.6)
откуда получаем соотношения, справедливые при любом амплитудном распреде-
лении:
У '
(7.14.7)
Для расчета ДН в произвольной плоскости помимо выражений типа (7.14.5) мо-
гут быть также использованы результаты теории линейных АР. Достигается это
введением понятия эквивалентной линейной решетки. Рассмотрим для примера
ДН квадратной решетки с шагом dx = dy = d в плоскости, след которой, состав-
ляющий угол ср = фр = 45° с осью а?,на рис. 7.61 обозначен как s — s (диагональная
плоскость). Пусть элементы решетки возбуждаются синфазно и равноамплитудно
(I(n) = I). Проведем через точки расположения излучателей штриховые линии,
перпендикулярные следу s — s. Для любой точки наблюдения в интересующей нас
плоскости в дальней зоне излучатели, лежащие на одной из этих линий (обозна-
чим число таких излучателей через т), равноудалены, соответственно поля их
складываются синфазно. Поэтому при вычислении ДН плоской решетки в плоскос-
ти s — s действие всех излучателей можно заменить излучением одного эквива-
лентного элемента с током ml, расположенного в любой точке штриховой линии.
На рис. 7.61 для удобства эквивалентные излучатели изображены на прямой
вне плоскости решетки. Совокупность таких эквивалентных элементов и образует
Рис. 7.61. Плоская квадратная АР: s - s — диагональ решетки, А - А — линейная АР с
эквивалентным излучателем [27]
Антенные решетки
343
эквивалентную линейную решетку с шагом с1экв = d/yj2 . Длина эквивалентной ре-
шетки в рассматриваемом случае равна диагонали квадрата, а распределение то-
ков остается синфазным и близко к треугольному, что соответствует весьма низ-
кому уровню первого бокового лепестка ( —26,4 дБ). Это существенно ниже, чем в
главных плоскостях, наименее благоприятных с точки зрения бокового излучения.
Если сравнить ширину ДН в главных и диагональной плоскостях квадратной АР,
то они оказываются почти равными, так как спадание амплитуды к краям экви-
валентной АР компенсируется увеличением ее длины по сравнению с размером
стороны квадрата, определяющим ширину ДН в главных плоскостях.
При произвольном значении угла ф = Фо эквивалентная АР получается неэкви-
дистантной. Для такой решетки ДН можно рассчитать как сумму ДН нескольких
эквидистантных АР. Отметим, что при использовании реальных излучающих эле-
ментов множитель системы, соответствующий эквивалентной решетке, необходи-
мо умножить на функцию, описывающую ДН одного элемента в плоскости ф = фо
Соответственно поляризационная характеристика поля излучения определяется
поляризационными свойствами излучающего элемента в этой плоскости.
При несинфазном возбуждении элементов плоской АР для нахождения токов
в элементах эквивалентной АР необходимо складывать токи соответствующих
элементов плоской решетки с учетом фаз, т. е. складывать комплексные значе-
ния токов. Обратим внимание, что при отклоненном главном максимуме обычно
рассматриваются сечения пространственной ДН в двух плоскостях: проходящей
через ось z и направление ф = ф^ (условно-вертикальная плоскость) и перпенди-
кулярной ей, проходящей через направление максимума излучения. На основании
метода эквивалентной линейной решетки можно утверждать, что для изотроп-
ных элементов по мере отклонения максимума излучения от нормали изменяется
(расширяется) форма ДН только в вертикальной плоскости; во взаимно перпен-
дикулярной ей плоскости форма ДН при отклонении не меняется.
Отметим, что главные плоскости наиболее опасны с точки зрения возникнове-
ния вторичных максимумов, поскольку шаг эквивалентных решеток максимален
именно в этих плоскостях. При размещении излучателей в узлах прямоугольной
сетки он составляет dx и cL (см. рис. 7.58), во всех остальных сечениях шаг экви-
валентной решетки меньше. Поэтому, если удовлетворяется условие, аналогичное
(7.3.26):
_Л/(1 + sin вгл )] , dy < [А/(1 + sin 0гл
(7.14.8)
где 02Л — угол отклонения максимума ДН в соответствующей плоскости отно-
сительно нормали к плоскости АР, то вторичные главные максимумы отсутс-
твуют при отклонении ДН в любой плоскости. Для гексагональной сетки макси-
мальный шаг эквивалентной решетки имеет место в сечении ф = тг/2 и составляет
ddKe = dJ3/2. Следовательно, при гексагональной сетке для устранения вторичных
главных максимумов необходимо шаг d выбирать из условия
d < 2Х Гл/3 (1 ч- si
sin
(7.14.9)
Указанное обстоятельство является преимуществом гексогональной сетки по срав-
нению с прямоугольной с точки зрения возможностей размещения излучающих
элементов, поскольку условие (7.14.9) менее жесткое, чем (7.14.8).
В общем случае КНД плоских АР может быть рассчитан по формуле (7.14.5).
Для прямоугольных синфазных решеток из однонаправленных излучателей из
344
ГЛАВА 7
(7.14.5) следует, что
TtD~D.
«Л/
(7.14.10)
где Dx и Dy — КНД эквивалентных линейных АР, параллельных осям х и у соот-
ветственно. Формула (7.14.10) справедлива для достаточно больших решеток при
dx = dy = Х/2 и амплитудном распределении, разделяющемся по координатам
х и у, что обычно выполняется на практике. Если обозначить размеры решетки
по осям х и у соответственно через Lx и Ly, то, используя формулы (7.14.10) и
(7.12.10), получим
(Ttvx2Lx/X)(vy2Ly/k) = 4jcvaS/x2
(7.14.11)
где vx и Vy — коэффициенты использования эквивалентных линейных решеток,
параллельных осям х и у; S = LxLy — площадь поверхности решетки, называ-
емой по аналогии с поверхностными антеннами апертурой решетки; va = vxVy
— коэффициент использования поверхности (КИП) решетки. Если амплитуды
возбуждающих токов равны, то va = 1 независимо от формы раскрыва. Таким
образом, для синфазно возбужденных плоских АР, как и для линейных, КНД
максимален при равноамплитудном возбуждении; если амплитуда спадает к кра-
ям, КНД уменьшается (va < 1). Для круглых решеток значения va могут быть ис-
пользованы из табл. 7.1.
При несинфазном возбуждении элементов, когда фаза изменяется по линей-
ному закону и максимум ДН отклоняется от нормали на угол 0^, определяемый
(7.14.7), основной лепесток, как уже отмечалось, расширяется по закону 1/cos 0?л
только в вертикальной плоскости ср = сргл. Ширина лепестка в другой, перпендику-
лярной плоскости не меняется, поэтому КНД может быть рассчитан по формуле
D = 47tva5cos0MA2 , (7.14.12)
справедливой, если направление максимума ДН не слишком приближается к плос-
кости решетки. Уменьшение КНД при отклонении ДН можно объяснить умень-
шением эквивалентной поверхности, перпендикулярной направлению максимума
(рис. 7.62).
7.15. Излучение плоской и пространственной
синфазных решеток [3]
Для сужения ДН в двух ортогональных плоскостях, т.е. для получения излу-
чения в узком телесном угле, применяют плоские решетки (рис. 7.63), состоящие
из Ni рядов излучателей по оси х Каждый ряд состоит из TV2 излучателей по оси
у. Таким образом, общее количество излучателей в решетке составляет N =
Р — точка наблюдения в дальней зоне, Р'— проекция точки Р на плоскость, в
которой находится решетка.
При расчете ДН плоской решетки сначала рассчитывают ДН линейной решетки
(одного ряда), а затем каждый ряд излучателей заменяют эквивалентным то-
чечным излучателем, помещенным в фазовом центре линейной решетки. Следова-
тельно, расчет плоской синфазной решетки сводится к расчету линейной решет-
ки, расположенной вертикально (рис. 7.63,6), каждый эквивалентный излучатель
которой имеет амплитудную диаграмму
Антенные решетки
345
Рис. 7.62. Уменьшение КНД плоской АР за счет уменьшения эквивалентной
поверхности [27]
а)
Рис. 7.63. Плоская решетка излучателей: а)
б)
общий вид; б) — к расчету ДН решетки
346
ГЛАВА 7
^3
а) б)
Рис. 7.64. Пространственная решетка: а) — общий вид;
б) — к расчету ДН пространственной решетки [3]
sin
N2Vi
ад (е, Ф)
sin
V2
где = kd2 sin 0 .
Суммируя поля таких излучателей в дальней зоне с учетом равенства ампли-
туд токов в вибраторах и принимая ДН элементов решетки Д (0, ср) одинаковыми,
получаем
sin ^1 sin N2V2
Ет (е> ф) = Afi (е> ф)
Ф1 • ¥2
sm sin —
(7.15.1)
где = kd^ sin 0 и = kd^ sin ср - обобщенные координаты; 0 и (р — углы, отсчи-
тываемые от нормали к антенне в соответствующих плоскостях.
Для получения одного главного максимума диаграммы направленности в об-
ласти углов -л/2 < 0 < л/2 и -л/2 < (р < л/2 расстояние между излучателями в ре-
шетке должно быть меньше длины волны di 2 < •
Плоская решетка, выполненная из симметричных вибраторов, имеет два глав-
ных максимума излучения, соответствующих углам 0 = 0°(ф = 0°) и 0 = 180° (ф = 0°).
При этом амплитуда поля в максимуме ДН
Em(0°,0°)=A/1(0'1,0'’)W1N2.
Для увеличения пространственной направленности, т.е. уменьшения ширины
основного лепестка в обеих главных плоскостях, применяются трехмерные (про-
странственные) решетки, состоящие из нескольких одинаковых плоских ре-
шеток, расположенных параллельно и следующих друг за другом (рис. 7.63, а).
При расчете ДН каждая плоская решетка заменяется эквивалентным точечным
излучателем (рис. 7.63, б) и рассчитывается множитель антенны с использованием
формулы (7.2.1) суммирования полей:
Антенные решетки
347
Ет (е,ч>) = Afi (е,ф)/п1 (е)/„2 (ф)Л>з (“) =
sin sin N24/2
sin
= Afi (е, <р)----2---------2---------2_
v 7 . V1 • V2 • Уз
sm —L sin —— sin —-
(7.15.2)
где \|>з = kd% sin(90 - а), причем угол a = 6 при расчете ДН в горизонтальной плос-
кости (пл. zOx на рис. 7. 64, а и б) и угол a = ср при расчете ДН в вертикальной
плоскости (пл. zOy).
Если плоские решетки запитываются в фазе, то для обеспечения максималь-
ного излучения в том же направлении, что и максимальное излучение каждой
решетки, расстояние между ними должно равняться X. Для уменьшения га-
баритов антенны расстояние берется равным Х/2, а питание осуществляется со
сдвигом фазы п. В обоих случаях антенна имеет максимум излучения в направле-
нии линии расположения решеток в обе стороны a = 0° и a = 180° (рис. 7.64).
Для создания направленного излучения в одну сторону фазы питания двух плос-
ких решеток должны быть сдвинуты на тг/2 , а расстояние между ними dg = Х/4.
7.16. Решетка с линейным набегом фазы. Антенны с электричес-
ким сканированием [3]
Рассмотрим систему идентичных излучателей, параллельных друг другу и
расположенных на одной прямой (рис. 7.65). Пусть амплитуды токов в излучателях
одинаковы, а фаза тока в любом излучателе отличается от фазы тока предыдуще-
го излучателя на одну и ту же величину ц/у, т.е. фазовое распределение по антенне
линейное. Примем фазу тока в первом излучателе за нулевую, тогда фаза в п -м
излучателе будет (п — l)vi, и поле, созданное этим излучателем в дальней зоне,
найдем как
Ёп = Afi (0,<p)cos(cot - krn + (п - l)vi). (7.16.1)
Учитывая, что rn = -(п -l)dsin0 (рис. 7.65, а), выражение (7.16.1) запишем
в виде
Ёп = Afi (0, cp)cos (pt - ki\ + (п - l)(kd sin 0 +)).
Поле всей линейной АР определяется, как и ранее, суммированием полей от-
дельных излучателей:
о -у, -(л-1>1 -(TV-l/Ki
б)
а)
Рис. 7.65. Линейная решетка с линейным набегом фазы: а)
б) — схема возбуждения [3]
к расчету ДН;
348
ГЛАВА 7
(7.16.2)
где \|/ = kd sin 6 + — сдвиг по фазе между полями соседних излучателей в точке
наблюдения; Tq — расстояние от фазового (геометрического) центра решетки до
точки наблюдения.
Рассмотрим множитель антенны
(7.16.3)
В отличие от синфазной антенны этот множитель зависит от сдвига фаз пита-
ния излучателей .
Максимум излучения в такой антенне имеет место для тех направлений в про-
странстве, для которых удовлетворяется условие у = 2лр , где р = 0,±1,±2,..., т.е.
разность фаз полей излучателей, вызванная разностью хода лучей, полностью
компенсируется разностью фаз токов излучателей:
kd sin 0?/1 + w-i =kd sin0?/1
Сч/v I -L Gvv
+ Vl?
kd )
= 2irp,
(7.16.4)
откуда
sinO,,,
Это уравнение называют уравнением качания луча, ар — номером луча мак-
симального излучения.
Требуемое линейное фазовое распределение в решетке можно получить путем
питания излучателей линией с бегущей волной (рис. 7.65, б). При таком питании
фазовый сдвиг между токами соседних излучателей = (—2л/Х)уй; у — замедле-
ние фазовой скорости в питающей линии: у = c/vф ='к/'кл .
Подставим в выражение (7.16.4) значение = -kyd . Тогда уравнение качания
луча примет вид
sin 0?л
(7.16.5)
Из (7.16.4) следует, что диаграмма направленности имеет несколько главных
максимумов. Найдем условие существования одного главного максимума в преде-
лах углов 0 от - л/2 до л/2 .
В множителе антенны
/ • (V
jV7(0)=sin —— / sm —
\ У/ \
Антенные решетки
349
-2л
О
а)
б)
Рис. 7.66. Множитель решетки с линейным набегом фазы из пяти элементов (заштрихова-
ны участки, соответствующие реальной ДН - л/2 < 0 < л/2) при различных значениях xpi:
а) — = 0 , б) — - kd [3]
этому изменению угла 0 соответствует интервал изменения обобщенной коор-
динаты -kd + < у < kd + . Так как периодичность функции fn (0) составля-
ет 2л, аргумент у должен удовлетворять условию —2л < у < 2л . Следовательно,
-2л < -kd + Vi, 2л > kd + . Отсюда условие существования одного луча с номе-
ром р = 0 в синфазной решетке (у]. = 0) следующее: kd < 2л и d < X (рис. 7.66, а).
В этом случае бгл = 0° , т.е. главный максимум излучения перпендикулярен оси
антенны.
Если, в частности, = kd , то условие существования одного луча (нулевого)
имеет вид 2kd < 2л и d < Х/2 . Единственный главный максимум решетки в этом
случае направлен вдоль ее оси (рис. 7.66, б), т.е. 0гл = 90°. При промежуточных
значениях < kd направление максимального излучения луча с номером р = 0
составляет некоторый угол, отличный от 0 и 90° , а шаг X/2 < d < X.
Допустимую величину шага в решетке при 0 < 0гл <90° можно найти из соотно-
шений —2л < —kd + Vi, 2л > kd + . Подставляя в первое неравенство значение
из уравнения качания (7.16.4) при условии р = 0 , получаем —2л < — kd - kd sin &гл,
откуда
d<X/(l + sin0a/1). (7.16.6)
Направления нулевых значений поля в ДН антенны можно найти из выраже-
ния (7.16.3), приравняв числитель к нулю:
sin —Nd sin0g +
Vi
= 0
откуда
— Nd sin 0q + —
X I и kd)
где р = 0, ±1, ±2,... и sin 0О = рХ / (Nd) -/ kd .
350
ГЛАВА 7
Направления максимумов боковых лепестков приближенно можно найти по
максимальным значениям числителя (7.16.3), т.е. принимая
kd
= ln-Nd
sin0?n
откуда
sin 0^ = (2p -1)——
v z/Vd
Vi
kd
Из уравнения (7.16.4) следует, что перемещение луча в антенной решетке в
пространстве может быть осуществлено: 1) изменением частоты колебаний под-
ключенного генератора или приемника; 2) изменением фазового сдвига меж-
ду излучателями с помощью системы фазовращателей, включаемых в питающий
тракт; 3) коммутацией (переключением) излучающих элементов решетки, шага
излучателей или отрезков питающих трактов. Если эти управления положением
луча осуществляются электрически, то такие антенны называются электрически
сканирующими. Остронаправленные электрически сканирующие антенны позво-
ляют осуществлять быстрый (безынерционный) обзор пространства, установку
луча в заданную точку пространства, сопровождение цели и т.д. В антеннах с ме-
ханическим сканированием управление лучом достигается поворотом, вращением,
качанием и т.д. всей антенной системы, что ограничивает скорость сканирования.
Если в решетке изменение фазового распределения осуществляется механически-
ми фазовращателями или коммутаторами, то такие антенны называются элект-
ромеханическими сканирующими. В остронаправленной антенне с электромеха-
ническим сканированием при неподвижности всей антенной системы вращаются
или перемещаются (механически) малоинерционные элементы, что позволяет
увеличить скорости движения луча.
Частотно-сканирующая антенна конструктивно наиболее проста, но элек-
трическое управление положением ДН осуществляется, как правило, только по
одной угловой координате. При фазовом способе сканирования в плоских решетках
(изменением фазового сдвига между излучателями по столбцам и строкам) луч
перемещается по двум угловым координатам. Под воздействием управляющего
тока (напряжения) фаза в фазовращателе изменяется или дискретно дискретным
фазовращателем, или плавно. При управлении фазовым распределением в ан-
тенне при сканировании — фазировании антенны — дискретный фазовращатель
дает ошибки в установке фазы. Фазовращатель с плавной характеристикой уп-
равления таких ошибок не имеет, однако сопряжение плавного фазовращателя с
системой управления лучом (ЭВМ) приводит, как правило, к дискретности изме-
нения фазы. Дискретность фазирования антенны, происходящая при дискретно-
коммутационном способе сканирования и фазовом сканировании с дискретным фа-
зовращателем, имеет определенные преимущества, как например, возможность
уменьшения влияния различных дестабилизирующих факторов на характеристи-
ки направленности. Антенные решетки с фазовым или дискретно-коммутационным
способом управления лучом называют фазированными антенными решетками.
Такие антенны находят широкое практическое применение.
При квадратичных и кубических фазовых искажениях изменения в ДН плос-
ких решеток аналогичны описанным в разделе 7.5. Оба вида искажений приводят
к снижению КНД.
Антенные решетки
351
7.17. Антенные решетки с неравноамплитудным
распределением [3,17]
В зависимости от назначения системы и требований к направленным свойс-
твам используемые антенны могут существенно отличаться от простейших моде-
лей. Амплитудное распределение по решетке бывает спадающим к краям решетки
(рис. 7.67) для уменьшения уровня боковых лепестков, затухающим по экспоненте
при последовательном возбуждении линией передачи или другой сложной формы.
Излучатели могут располагаться на выпуклых поверхностях, иметь различную
ориентацию в пространстве и размещаться неэквидистантно. В этих случаях для
определения поля излучения в дальней зоне необходимо суммировать поля отде-
льных излучателей с учетом поляризации, амплитуды и фазы, т.е.
N
Обозначив для 0 и (р - составляющих поля п -го излучателя диаграммы направ-
ленности через Fq (0,ф), Fq, (0,фп); комплексные амплитуды через Аф , А^ ;
фазы возбуждения через фп получим по аналогии с (7.16.2)
N
Е6 = У ^0nF0, (9,<p)exp(-ifcrn +
п=1
N
= X А₽ЛП (0, ф)ехр (-г/стп +уп);
п=1
Ё = 0дЕф + ФоЕф
Здесь 0q , фд — единичные орты сферической системы координат.
В этих выражениях не удается вынести за знак суммы амплитуду и ДН эле-
мента, а фазовое распределение в решетке получается сложным. Поэтому не пред-
ставляется возможным свернуть эти суммы в замкнутые выражения, удобные для
анализа.
Решить задачу синтеза антенной решетки, т.е. определения параметров решет-
ки по заданной диаграмме направленности из анализа сумм не удается. Редким
исключением из этого является синтез линейных оптимальных эквидистантных
решеток с дольф-чебышевским амплитудным распределением. Такие решетки с
линейным фазовым распределением позволяют получить минимально возможный
уровень боковых лепестков (УБЛ) при заданной ширине луча или при заданном
Рис. 7.67. Спадающее амплитудное распределение по элементам решетки [3]
352
ГЛАВА 7
уровне боковых лепестков минимальную ширину луча [3]. В инженерной практике
для построения антенных решеток радиосистем используют следующий подход.
На стадии предварительных расчетов для нахождения формы, размеров решет-
ки, амплитудного распределения переходят от дискретной системы к непрерывно
излучающей, т.е. решетки заменяют излучающими раскрывами. В этом случае
суммы переходят в определенные интегралы, которые могут быть вычислены в
удобном для анализа виде.
Характеристики излучающих раскрывов хорошо известны в теории антенн
СВЧ [3] и позволяют выбрать различные варианты построения антенной решетки
по заданным ширине луча, УБЛ, КНД, сектору сканирования, рабочей поло-
се частот и т.д. Далее проводят дискретизацию, заменяют излучающий раскрыв
решеткой излучателей с эквивалентными параметрами и численными методами
(путем прямого суммирования полей) определяют основные характеристики. Ис-
пользуя современные вычислительные средства и варьируя параметры выбранных
вариантов антенных решеток, по результатам численных расчетов устанавлива-
ют оптимальный вариант антенны для принятых критериев качества [3].
Равноамплитудные системы находят широкое применение на практике. Однако
эти системы имеют сравнительно большой уровень боковых лепестков. Как было
показано выше, уровень первого бокового лепестка равноамплитудной синфазной
системы составляет 0,212. У системы осевого излучения (при > 1) он еще выше.
Между тем желательно уменьшить уровень боковых лепестков, особенно в слу-
чае приема, когда с направлений боковых лепестков могут поступать интенсивные
мешающие сигналы (помехи). С этой целью применяют системы с неравноампли-
тудным распределением токов (полей).
Если по системе излучателей изменять амплитудное распределение, то это
будет приводить к изменению ширины главного лепестка и уровня боковых ле-
пестков. Так, например, расчеты показывают, что чем сильнее спадает к краям
системы амплитудное распределение, тем главный лепесток шире, а уровень бо-
ковых лепестков меньше. Можно подобрать такое амплитудное распределение,
которое в каком-то смысле будет оптимальным.
Под оптимальным в смысле Дольфа — Чебышева [38] амплитудным распреде-
лением вдоль антенны с заданной величиной L/Х понимают такое распределение,
при котором уровень боковых лепестков является минимальным для заданной ши-
рины главного лепестка или ширина главного лепестка является минимальной
для заданного уровня боковых лепестков.
Рассмотрим, как определить оптимальное амплитудное распределение для эк-
видистантной синфазной решетки. Пусть решетка состоит из нечетного числа
(2N +1) ненаправленных излучателей. Нумерацию излучателей будем вести от
середины решетки (рис. 7.68). Тогда множитель решетки имеет вид
о----О------О О"
-N -п -2 -1
<2 п N
Рис. 7.68. К определению оптимального амплитудного распределения
по антенной решетке [17]
Антенные решетки
353
N
Пусть амплитудное распределение симметрично а_п = ап. Кроме того, учтем,
что
rn = г — nd sin S, п = 0, ±1, ±2,...
Тогда, опуская не зависящий от 9 множитель е~™г будем иметь
N
= ад + 2^ ап cos пи ,
п=1
(7.17.1)
где и = kd sin Я.
Обозначим cos и = х. Из тригонометрии известно, что косинус кратного угла
(cos пи) может быть представлен в виде полинома степени п от cos и. Следова-
тельно, множитель системы можно записать в виде
N
(7.17.2)
Коэффициенты Во, , ..., BN определяются через коэффициенты а0, , ..., aN
путем решения системы (N +1) алгебраических уравнений.
Можно показать [17], что оптимальное амплитудное распределение соответс-
твует такому выбору коэффициентов ag, ctj, ..., aN , а следовательно, и коэффи-
циентов Во, В[, ..., Вдг, при котором множитель системы выражается полиномом
Чебышева TN (ах), где а — постоянная величина, определяемая ниже. Таким об-
разом,
/с)(&)= ^BNxn =TN(ax).
71=0
Напомним, что полиномы Чебышева записываются в виде
TN (0 = cos (N arccos Q при -1 < £ < 1;
TN(0 = ch (NAr ch£) при С, < -1 и £ > 1.
Подставляя значения N, можно получить
(7.17.3)
(7.17.4)
Т± (0 = 8?4 - 8С2 + 1, Т5 (£) = Ж5 - 20CS + 5Q .
В интервале -1 < £ < 1 наибольшие (по абсолютной величине) значения функции
МО равны единице,
за пределами этого интервала с
ростом £ функция TN (0
монотонно возрастает.
Если выбрать а > 1, то монотонно возрастающая часть графика TN (ах) будет
соответствовать главному лепестку ДН. Направление главного лепестка опреде-
ляется значениями 9 = 0; и = 0 ; х = 1; С = а. Следовательно, величина главного
максимума равна
Ус (3) = Ус (0) = TN (а) = ch (Narcha).
(7.17.5)
Так как максимумы боковых лепестков равны единице, то их относительный уро-
12 - Неганов
354 ГЛАВА 7
вень составляет
F6oK = ch 1 (Narcha).
(7.17.6)
Первые нули ДН (ближайшие к главному лепестку) определяются наибольшим
корнем уравнения TN (ах) = 0.
Учитывая (7.17.4), получаем
N arc cos ах0 = л/2
откуда
х'О = — cos
а
2N
Так как х - cos (kd sin 0)
sin0o =
—arc cos —cos
kd \a
2N
(7.17.7)
Если задан уровень боковых лепестков, то из (7.17.6) определяется параметр
а , а по (7.17.7) — ширина главного лепестка по нулям. Возможен и обратный по-
рядок расчета. ДН при ах > 1 рассчитывается по второй формуле из (7.17.4), а при
ах < 1 — по первой формуле из (7.17.4).
Оптимальность рассчитанной таким образом ДН является следствием того, что
из всех полиномов степени N с одинаковым старшим коэффициентом полином Че-
бышева Tjy (С) наименее уклоняется от нуля на отрезке — 1 < < 1. Следовательно,
ДН, описываемая полиномом, имеет наименьший уровень боковых лепестков.
Для нахождения оптимального амплитудного распределения необходимо в
(7.17.3) приравнять коэффициенты при одинаковых степенях и таким образом оп-
ределить коэффициенты BN. Затем, используя указанную ранее связь между ко-
эффициентами clq , , ... и Во , В1, ... можно рассчитать амплитудное распреде-
ление.
Если зафиксировать длину антенной решетки L и бесконечно увеличивать
число излучателей, то можно сделать предельный переход к непрерывной систе-
ме с оптимальным распределением.
Амплитудная ДН при этом описывается функцией
f(v)= cos
(7.17.8)
где
и = 0,5/cL sin 0; у = Arch (L/Fqok )
Расчеты показывают, что этой амплитудной ДН соответствует амплитудное
распределение, которое на краях системы стремится к бесконечности. Для ре-
ализации этого распределения необходима бесконечная энергия. Так как такое
распределение практически нельзя осуществить, то ограничиваются квазиоп-
тимальным распределением, которое имеет конечный подъем на краях системы
(рис. 7.69). При этом ширина главного лепестка несколько увеличивается.
Квазиоптимальным является, например, распределение вида
Jo Ч\1-
(7.17.9)
где Jq (t) — функция Бесселя от мнимого аргумента; z — координата точки, из-
Аытенные решетки
355
О
Рис. 7.69. Пример квазиоптимального амплитудного распределения [17]
меняющаяся по системе в пределах -L/2 < z < L/2; у
уровню наибольшего бокового лепестка
число, определяемое по
(7.17.10)
2
ДН при указанном распределении описывается функцией
F(d) = sin- у2/лД»2 - у2 •
Существуют и другие квазиоптимальные распределения [17].
(7.17.11)
7.18. Неэквидистантные антенные решетки [17, 27]
Отказ от эквидистантного расположения излучающих элементов позволя-
ет придать решеткам ряд новых свойств, таких как устранение дополнительных
главных максимумов при увеличении расстояния между элементами и уменьше-
ние уровня бокового излучения в решетках с равноамплитудным возбуждением
[41]. Это позволяет, в частности, решить проблему исключения большого числа
элементов из исходной эквидистантной решетки (что существенно упрощает ан-
тенну) без заметного ухудшения ДН последней.
Рассмотрим для примера синфазную решетку с шагом, удовлетворяющим
условию d < X. Регулярное «изъятие» элементов, например через один, при-
менять нельзя, так как при этом в направлениях 6вт тах, определяемых как
0бШ тах = ас cos (x/d), возникнут дополнительные главные максимумы. Если же
осуществить нерегулярное разрежение, например, по случайному закону, то в
указанных направлениях условия синфазного сложения полей отдельных элемен-
тов, приводящие к образованию вторичных главных максимумов, нарушаются. В
направлении же нормали к решетке поля по-прежнему будут складываться син-
фазно, следовательно направление максимума ДН не изменится. Ширина основ-
ного лепестка A6q 5’b разреженных решетках примерно сохраняется такой же,
как в исходной решетке, однако увеличивается средний УБЛ. Величину КНД
разреженных решеток можно рассчитать просто как D « N , где N — число ос-
тавшихся элементов, поскольку эффект взаимной связи здесь уменьшается из-за
увеличения расстояния между излучателями. Таким образом, исключение элемен-
тов приводит к уменьшению КНД. Решетки с большим разрежением используются
12 *
356
ГЛАВА 7
б)
Ni
в)
Рис. 7.70. К пояснению эквивалентности между эквидистантной решеткой (а), непрерыв-
ной системой (б) и неэквидистантной решеткой (в) [17]
обычно там, где важна большая разрешающая способность, например в радиоас-
трономии.
Ослабление боковых лепестков при заданной ширине главного лепестка может
быть осуществлено не только оптимальным амплитудным распределением в экви-
дистантной антенной решетке, но и оптимальным расположением излучателей в
неэквидистантной равноамплитудной решетке. Эти две системы в некотором смыс-
ле эквивалентны друг другу. Рассмотрим этот вопрос подробнее.
Пусть имеется эквидистантная решетка с неравноамплитудным, например
квазиоптимальным, распределением a(zn), где zn — координата n-го излучате-
ля, n = l,2,...,N (рис. 7.70,а). Для простоты рассуждений положим, что 2V —ве-
лико, а расстояния d между соседними излучателями малы в сравнении с длиной
решетки. Тогда дискретную решетку можно заменить непрерывной системой с
линейной плотностью тока по системе (амплитудным распределением), равной
(z = zn + d, п = 1,2,...N)
a' (z) - a (zn )/d. (7.18.1)
Функция a'(z) является ступенчатой, однако, полагая, что токи в соседних
излучателях отличаются нерезко, и учитывая малость расстояния d, эта функ-
ция на рис. 7.70,6 изображена плавной кривой.
Площадь, ограниченная кривой a'(z) и осью абсцисс, определяет полный ток
системы. Разобьем эту площадь на площадок одинаковой величины А, тогда
Антенные решетки
357
где L — длина системы излучателей.
Рассмотрим одну из площадок, соответствующую отрезку Az = z" - z' (рис.
7.70,6). Для нее
af (z)dz.
(7.18.2)
z=z
Заменим теперь непрерывную систему решеткой N± дискретных излучателей, аб-
сциссы которых равны абсциссам центров тяжести указанных выше площадок, а
амплитуды равны величине А (рис. 7.70,в). Так как линейные плотности токов этих
двух систем равны, то
А/Az = a1 (z)
или
Az = А/ a' (z).
Подставляя значение a' (z) из (7.18.1), получаем
Az = Ad/a(zn). (7.18.3)
Расстояния между соседними излучателями неэквидистантной решетки при
больших практически равны величинам Az и, следовательно, эти расстояния
обратно пропорциональны величинам токов в соответствующих излучателях эк-
видистантной решетки.
При реализации неэквидистантной решетки не возникает трудности обеспече-
ния сложного неравноамплитудного распределения.
Ранее было показано, что у эквидистантной решетки в направлении любого
главного лепестка поля всех излучателей синфазны. При неэквидистантном рас-
положении разности хода лучей от соседних излучателей различны для любого
направления, кроме нормального к оси решетки. Поэтому у неэквидистантной ре-
шетки подавлены главные лепестки высших порядков, что является другим ее
достоинством.
При заданной ширине ДН число излучателей неэквидистантной решетки мо-
жет быть меньше, чем у эквидистантной решетки. Это объясняется тем, что ши-
рина ДН решетки зависит в основном от ее длины, выраженной в длинах волн, и
в меньшей мере от закона расположения излучателей.
Расчет ДН неэквидистантных решеток при большом числе излучателей произ-
водится ввиду его громоздкости с применением ЭВМ.
К неэквидистантным решеткам относятся также решетки, у которых излуча-
тели расположены по случайному закону. Расчет ДН таких решеток производится
статистическими методами.
7.19. Понятие о синтезе антенны по заданной
диаграмме направленности [17]
7.19.1. Задача синтеза антенны. В предыдущих параграфах данной гла-
вы показано, как решается задача определения (анализа) ДН заданной системы
излучателей при заданном амплитудно-фазовом распределении токов (полей) по
системе. Это так называемая прямая задача теории антенн. Большое внимание
358
ГЛАВА 7
Рис. 7.71. Непрерывная прямолинейная система излучателей
уделяется решению обратной задачи теории антенн — задаче синтеза антенны
по заданной ДН. В более узком смысле задача синтеза состоит в определении ам-
плитудно-фазового распределения токов по выбранной системе излучателей при
заданной амплитудной ДН. Фазовой ДН при этом не интересуются.
Задача синтеза более сложна, чем задача анализа и требует применения более
сложного математического аппарата. Кроме того, эта задача не имеет однознач-
ного решения, т. е. одну и ту же амплитудную ДН можно получить с помощью
различных амплитудно-фазовых распределений. Для того чтобы сделать задачу
однозначной, необходимо задать еще и фазовую ДН.
Поясним особенности решения задачи синтеза на примере непрерывной пря-
молинейной системы длиной L (рис. 7.71). Элементарный участок dz этой системы
можно рассматривать как излучатель антенной решетки, изображенной на рис.
7.9, причем следует считать, что излучатели расположены непрерывно. Поэтому,
переходя от суммы к интегралу, можно множитель непрерывной системы пред-
ставить в виде [17]:
L/2
/с)(ф)= f a(z)e^<2Vfacos‘1’dz. (7.19.1)
-L/2
Сделаем в этой формуле замену
и = 0,5fcL cos Ф ; w = Zz/L ;
a (w) = a (w)exp i\\f (w).
Тогда
1
/(c)(v)= [a(w)eiuwdw. (7.19.2)
-1
Задача синтеза состоит в решении интегрального уравнения (7.19.2) относи-
тельно функции a (w). Это решение можно получить следующим образом. Учтем,
что при w < -1 и w > 1 (т. е. за пределами системы излучателей) d (w) = 0. Тогда
(7.19.2) можно представить в виде
ОО
/ (и) = J a (w ) ег uw dw .
—ОО
(7.19.3)
Применяя к (7.19.3) преобразование Фурье, получаем
(7.19.4)
Антенные решетки
359
Отметим, что не для всякой функции функция a(w) является решени-
ем интегрального уравнения (7.19.3). Решение существует только для определенно-
го класса функций так называемых целых функций конечной степени [17].
Следовательно, если ДН описывается такой функцией, то может быть найдено
точное решение для амплитудно-фазового распределения вдоль системы. Для того
чтобы это решение было равно нулю при w > 1, нужно удовлетворить условию
которое означает, что полная (активная и реактивная) энергия системы должна
быть конечной величиной.
7.19.2. Приближенный синтез антенны. В инженерной практике требуе-
мая ДН может быть задана в виде графика или в виде функции, не относящейся
к классу целых функций конечной степени. Такая ДН может быть реализована
лишь приближенно. Для этого требуемая ДН /с (и) аппроксимируется другой ДН
Ус'(и), и задача состоит в том, чтобы найти такое распределение, a(w), при ко-
тором функция у.' (и) наименее уклоняется от функции fc (и) в каком-либо смысле
(например, по абсолютной величине их разности).
При практическом выполнении расчетов можно /с (и) разложить в сходящийся
ряд (например, в ряд Фурье) по некоторым функциям fn (и), называемым пар-
циальными ДН. Для каждой функции fn (и) находят парциальное распределение
an (w). Полное амплитудно-фазовое распределение имеет вид
N
a (w) = У ап (w). (7.19.5)
п=1
Чем больше членов ряда учитывается при расчете, тем точнее аппроксимируется
заданная ДН. Разработаны и другие методы нахождения функции a(w) как для
непрерывных систем, так и для антенных решеток [17].
7.19.3. «Сверхнаправленностъ». Из изложенного выше следует, что с помо-
щью прямолинейной системы конечных размеров можно сформировать ДН любой
формы, с любой наперед заданной точностью. Например, можно получить КНД
сколь угодно большой величины у антенны малых размеров. Такая антенна на-
зывается сверхнаправленной. Анализ показывает [17], что у сверхнаправленной
системы амплитуда тока должна быть очень большой и, кроме того, амплитуда и
фаза тока должны резко меняться вдоль системы.
При практической реализации такого распределения встречаются большие
трудности. Кроме того, быстрое изменение фазы тока вдоль системы при больших
его амплитудах означает, что с антенной связана большая реактивная мощность.
Следовательно, добротность системы велика, а ее полоса пропускания мала. Из-за
больших токов потери в системе будут значительны, а к. п. д. мал.
По указанным причинам следует избегать сверхнаправленности. О ее величине
судят по коэффициенту сверхнаправленности
360
ГЛАВА 7
(7.19.6)
Интеграл в знаменателе пропорционален излученной мощности, так как он берет-
ся в области действительных углов (0 < Ф < л , т. е. —лЬ/Х < и < лЪ/Л,), а интеграл
___ _ __________ _ _ _ _ __ _ д-л dX _ Я-* rtim
в числителе пропорционален всей мощности, излученной Р и реактивной Р ,
которая связана с ближним полем антенны.
Следовательно,
v = (Р1 + pim)/p^
(7.19.7)
Отношение Pim/= Q есть добротность антенны, поэтому
v = 1 + Q.
(7.19.8)
Так как при наличии сверхнаправленности реактивная мощность много больше
излученной мощности, то такие антенны называются реактивными.
Антенна может быть реактивной из-за чрезмерно высоких требований не толь-
ко к ее КНД, но и к крутизне ДН, а также из-за ее чрезмерно малых размеров
в сравнении с длиной волны (даже при умеренных значениях КНД и крутизны
ДН).
7.20. Антенны бегущей волны и ДН линейной антенны [3]
Ранее рассмотрены линейные вибраторы, вдоль которых ток распределен по
закону стоячей волны.
Наряду с указанными широко применяются линейные излучающие системы
из одинаковых источников электромагнитного поля, расположенных непрерывно
или дискретно вдоль заданного направления в пространстве, ток (поле) по кото-
рым распределен по закону бегущей волны.
Примерами таких систем являются прямолинейный провод с электрическим
током, протяженная щель вдоль узкой стенки прямоугольного волновода, система
одинаковых излучателей, центры которых расположены на прямой линии (антен-
ная решетка), а также антенны, выполненные на основе замедляющих систем,
способных поддерживать поверхностные волны: диэлектрические стержневые,
спиральные, импедансные.
Возбуждение подобных антенн бегущей волны, реализующих осевое излучение
(или близкое к нему), осуществляется с одного конца, а режим бегущей волны
обеспечивается применением согласующих нагрузок на противоположном конце
или надлежащим выбором параметров замедляющей системы.
Характерной особенностью антенн бегущей волны является малость размеров
поперечного сечения излучающей системы. Рабочая полоса частот таких антенн
составляет обычно единицы процентов (значительно реже десятки процентов).
Диаграмма направленности линейного излучателя. В силу линейности
уравнений электродинамики поле системы излучателей представляет собой сумму
полей отдельных элементов. Если излучатели при этом одинаковы, ДН линейной
излучающей системы может быть записана в виде:
f(e,<p) = A(e,<p)/(c)(e), (7.20.1)
Антенные решетки
361
б)
Рис. 7.72. К расчету множителя направленности дискретной (а) и непрерывной (б) линей-
ной излучающей системы [3]
где /1(0, ф) — векторная комплексная ДН элемента излучающей системы; /^с'(0)
— скалярный комплексный множитель направленности (множитель решетки) сис-
темы изотропных излучателей, располагаемых в точках размещения центров ре-
альных излучателей.
Для дискретной линейной антенной решетки множитель направленности
N
f (0) = IneikZncosG , (7.20.2)
п=1
где 1п = — комплексная амплитуда возбуждения п -го излучателя; к = 2л/Х
— фазовая постоянная свободного пространства; zn — координата излучателя п;
0 — угол, отсчитываемый от оси антенны (рис. 7.72, а)
В случае возбуждения линейной решетки с числом излучателей N токами
равной амплитуды с линейно нарастающим вдоль решетки фазовым сдвигом*)
In = суммирование согласно формуле (7.20.2) приводит к
следующему выражению нормированного множителя направленности (множителя
решетки):
f(c\q) =
(7.20.3)
где ф = kd (cos 0 - у) — сдвиг по фазе между полями соседних излучателей в точке
наблюдения; d — шаг решетки; у = civф = y^/kd — замедление фазовой скорости
*> Фаза отсчитывается вдоль линии расположения излучателей от первого (п = 1) kN -му
излучателю
362
ГЛАВА 7
волны возбуждения.
Непрерывную линейную излучающую систему — линейный излучатель можно
рассматривать как предельный случай линейной антенной решетки длиной L с
числом элементов, стремящимся к бесконечности (рис. 7.72,6).
Тогда суммирование в (7.20.2) необходимо заменить интегрированием:
L/2
/(с)(6) = f l(z)e<tecosedz. (7.20.4)
-L/2
Здесь I (z) = Iqc^^ — распределение тока в излучателе по амплитуде и фазе.
Множители направленности (7.20.2), (7.20.4) дискретной и непрерывной излуча-
ющих систем не зависят от азимутальной координаты ср и обладают симметрией
относительно оси z.
Пусть непрерывный линейный излучатель возбуждается током постоянной ам-
плитуды Iq с фазовым распределением, соответствующим бегущей волне с замед-
лением фазовой скорости Ч = с/и$
I (г) = 1ае~^кг
(7.20.5)
Подставляя (7.20.5) в (7.20.4) и производя интегрирование и нормировку, для
нормированного множителя направленности получим
F(U) =
(7.20.6)
где U — kL (cos 6 — у)/2 — обобщенная координата, имеющая смысл половины раз-
ности фаз колебаний в точке наблюдения от крайних точек излучателя с учетом
как пространственной разности хода лучей kL cos 9, так и полной разности фаз
возбуждения крайних точек излучателя.
Множитель направленности (7.20.6) — вещественная функция. Поверхности
равных фаз поля излучения имеют вид сфер с центром в середине излучателя.
Фазовый центр такого излучателя находится в его середине независимо от зна-
чения замедления фазовой скорости у .
График функции sinU/U показан на рис. 7.73,а. Эта функция непериодическая
и имеет одно наибольшее значение, равное единице при U = 0. Из формулы (7.20.6)
следует, что уровень первого бокового лепестка относительно главного состав-
ляет 0,21 (-13,2 дБ). Проанализируем множитель F(lT) непрерывной системы,
который определяет ее направленные свойства, так как направленность элемен-
на которых выделены
тарных источников, образующих непрерывную систему, выражена весьма слабо.
На рис. 7.73, б-е изображены графики функции sin U/U
штриховкой части, находящиеся в интервале -kL(l + у)/2 < U <kL(l-y)/2 обоб-
щенной координаты U. Этот интервал изменения U соответствует реальной ДН,
т.е. значениям угла 180°
> 9 > 0 (область реальных углов).
В случае у = 0 (синфазная система) интервалу углов 180° > 9 > 0 соответствует
интервал -kL/2 <U < kL/2 (рис. 7.73,6) Диаграмма направленности, изображенная
на этом рисунке, довольно хорошо совпадает с ДН дискретной решетки, если
число излучателей в ней N > 6 (при расстоянии между соседними излучателями
d = 1/2).
Для определения ширины ДН по уровню напряженности 0,7 поля необходимо
положить F(U07) = 0,707, т.е. решить трансцендентное уравнение
5л
3
г
I
я
1
Антеннш решетки
5л -Зл -л
Рис. 7.73. К анализу множителя непрерывной системы излучателей: а)
sin U/U \ б)-е) — графики функции sin 17/17 при у = 0 ; 0 < у < 1; у = 1
вид функции
I
а
sin 17/17 = 0,707.
Из решения этого уравнения следует =1,39, откуда
170>7 = kLsinОо>7/2 и 2005 « 0,89Z/L = 51°X/L.
1 (фазовая скорость волны возбуждения превышает скорость света)
Если О
что соответствует линейному изменению фазы вдоль провода, то интервал изме-
нений U сдвигается влево по оси U (рис. 7.73,в,г). Главный максимум ДН наклоня-
ется при этом к оси решетки по направлению распространения волны (cos 9гл = у)
и при у = 1 (фазовая скорость волны равна скорости света) он ориентирован вдоль
оси системы (режим осевого излучения).
При у > 1 (антенна возбуждается замедленной волной) весь интервал измене-
364
ГЛАВА 7
ния обобщенной координаты U , для которого 180° > 0 > 0 , расположен в преде-
лах отрицательных значений оси U. Если у незначительно превышает единицу,
то главный максимум ориентирован в направлении оси провода, но его величина
уменьшается (рис. 7.7 3,д). С увеличением замедления у величина главного мак-
симума может сравняться с величиной первого бокового лепестка и ДН провода
будет состоять из нескольких примерно одинаковых лепестков (рис. 7.73,е).
Ширина ДН отклоненного луча при у < 1 может быть определена по формуле
20q,5 ~ 0,89А/Ьэф ,
где Ьэф
« L sin 0^ — эффективная длина раскрыва системы.
Эта формула справедлива во всем секторе углов, кроме сектора, примыкающе-
го к оси решетки и равного одной ширине главного лепестка ДН. В этом секторе
не существует точки, соответствующей уровню 0,7 поля с одной стороны главного
лепестка ДН.
При излучении точно в направлении оси провода, имеющего большую длину
(L > 5Х), ширина ДН при у = 1
20о>5 ~ 2(0,89 X/L)1/2 = 108°(Л./Ь)1/2.
Таким образом, при осевом излучении зависимость ширины ДН от относитель-
ной длины антенны L/Х более слабая, чем в случае синфазной антенны или ан-
тенны с линейным изменением фазового сдвига, т.е. предполагается, что элемен-
тарные источники, образующие непрерывную антенную систему, направленными
свойствами не обладают.
Следовательно, при отклонении ДН, т.е. при сканировании, ширина ДН из-
меняется; изменяется также ширина и форма боковых лепестков. Если при у = 0
главный лепесток ДН имеет форму диска (рис. 7.74,а), при у = 1 — вытянутого эл-
липсоида вращения (рис. 7.74,в), то при 0 < у < 1 направления главного излучения
образуют поверхность конуса вращения относительно оси системы (рис. 7.74,6)
Таким образом, линейные антенны осевого излучения обеспечивают направ-
ленность в двух взаимноперпендикулярных плоскостях, в то время как синфаз-
ные линейные антенны поперечного излучения концентрируют мощность в узкий
пучок только в экваториальной плоскости.
1. Тогда центральная часть главного
Ширину главного лепестка ДН при осевом излучении можно сузить, если пе-
рейти к режиму небольшого замедления у
лепестка множителя направленности sinU/U уходит в область мнимых углов (рис.
7.73,д), и главный лепесток существенно обостряется. Однако уровень боковых
а) б) в)
Рис. 7.74. Режимы излучения антенны бегущей волны: а) — поперечное излучение;
б) — наклонное; в) — продольное излучение [3]
Антенные решетки
лепестков, определяемый по отношению к значению функции sinU/U на грани-
це области реальных углов, повышается. Компромисс между сужением главного
лепестка и ростом уровня боковых лепестков может быть достигнут при выборе
границы реальных углов, удовлетворяющих условию U & -л/2. Это условие од-
новременно обеспечивает максимальный КНД линейной антенны с замедленной
фазовой скоростью и называется условием оптимальности линейной антенны с
замедленной фазовой скоростью возбуждения:
kL . л
—(у -1) --или
Отсюда следуют соотношения
У опт
опт
(7.20.7)
(7.20.8)
позволяющие найти оптимальное замедление при заданной длине антенны или вы-
числить оптимальную длину при заданном значении замедления. Соответственно
выражение для ширины ДН принимает вид
(7.20.9)
Таким образом, переход от значения у = 1 к оптимальному замедлению приво-
дит к сужению главного лепестка ДН при осевом излучении примерно в 1,8 раза.
Если у = 1, а элементарные источники, образующие линейную антенну (про-
вод с бегущей волной), обладают направленными свойствами [/i(9)=sin0, см.
(7.20.1)], то в направлении оси провода (6 = 0°), где множитель системы sinU/U
максимален, результирующее поле обращается в нуль, так как в выражении
(7.20.1) sin 6 = sin0° = 0 . В связи с этим результирующее поле оказывается мак-
симальным в некотором промежуточном направлении, составляющем угол 91гл с
осью провода. При большой относительной длине провода (kL » 1) это направление
максимального излучения может быть приближенно определено с использовани-
ем (7.20.6) путем приравнивания числителя значению ±1:
sin [kL/2(cos 02Л - у)] = ±1,
откуда
^(cos012>/l
и
cos 2л
(7.20.10)
При большой длине провода угол 01гл мал и соб012Л можно разложить в ряд:
откуда 01 гд « yjk/L = 57°5/A/L .
Так, если X/L = 1,25, то 01
cosOi
A. Ov v
= 50°, если же X/L = 3,5 ,
то 01 = 30° (рис. 7.75).
366
ГЛАВА 7
270° 270°
Рис. 7.75. Зависимость направления максимального излучения антенны бегущей волны от
ее длины [3]
Изменение длины волны генератора слабо сказывается на направлении макси-
мального излучения 01 , а также на входном сопротивлении. Поэтому провод в
режиме бегущей волны является диапазонной антенной.
Следует учитывать тот факт, что реальные антенны бегущей волны имеют
не постоянное, а спадающее от начала к концу амплитудное распределение поля
(тока) вследствие наличия затухания, обусловленного излучением энергии. Это
вызывает изменение формы ДН провода. Однако если поле в конце провода умень-
шается не более чем в три раза по сравнению с полем в начале, то искажения ДН
незначительны и при расчете ДН можно пользоваться множителем направленнос-
ти F (U) = sin U/U.
7.21. Коэффициент направленного действия
антенны бегущей волны [3]
При известной полной нормированной ДН антенны с учетом амплитудной ДН
одиночного элемента, КНД линейного излучателя может быть найден по общей
формуле для КНД. Вычисления КНД упрощаются, если принять элементы, обра-
зующие непрерывную излучающую систему, ненаправленными (изотропными).
После подстановки множителя направленности F (U) = sin U/U в выражение
(2.2.6), интегрирования и ряда преобразований для КНД линейного излучателя в
области значений замедления 0 < у < 1, соответствующих поперечному (0 - 90° ,
рис. 7.74,а,б) и наклонному излучению, имеем [3]
D « 2L/X при L » X.
В режиме осевого излучения (у = 1) КНД линейной антенны вдвое превышает
КНД в режиме наклонного излучения:
D » 4L/X.
Если замедление волны у в линейном излучателе больше единицы, то КНД
возрастает по сравнению со значением 4£/Л, из-за сужения главного лепестка
ДН. Однако с ростом у увеличивается уровень боковых лепестков, что приводит
Антенные решетки
367
к падению КНД. Оптимум по КНД достигается при значении обобщенной коорди-
наты U-n-n ~ -л/2:
Uz I b 9 I V /
Donm~7,2L/X, L » X. (7.21.1)
Сравнение условия оптимальности линейной антенны с замедленной фазовой
скоростью (у > 1)
и опт « -- = ЛЬ(1 ~ * или -п = kL(l - Уопт)
с наблюдаемой в направлении максимума главного лепестка (0 = 0°) полной разно-
стью фаз полей излучения начального и конечного элементов линейной излуча-
ющей системы
17 — /cL(cos9 у) — /сБ(1 Уопт)
показывает, что у оптимальной системы эта разность фаз составляет около 180°.
7.22. Полосковые антенны типа «волновой канал» Уда-Яги
и антенные решетки [57]
В последнее время распространение получила дипольная полосковая антенна
типа «волновой канал», или МПИ Уда-Яги (рис. 7.76). Она используется для созда-
ния различных АР и ФАР.
МПИ Уда-Яги выполнен на подложке с высоким значением относительной диэ-
лектрической проницаемости и вполне совместим с НПЛ и монолитными устройс-
твами. В полосе частот шириной 48 % антенна имеет КСВ не более 2, коэффициент
обратного излучения не хуже 12 дБ, уровень кроссполяризации не более —15 дБ
и абсолютный коэффициент усиления в интервале 3...5 дБ. МПИ должен найти
широкое применение в системах беспроводной связи, суммирования мощности,
ФАР и АФАР, а также в решетках отражающего типа для ММ диапазона волн.
На рис. 7.77 показана схема плоскостной АР с излучателями Уда-Яги.
Рис. 7.76. Полосковый вариант антенны типа «волновой канал» (МПИ Уда-Яги)
368
ГЛАВА 7
Рис. 7.77. Полосковая антенная решетка с излучателями Уда-Яги
Щелевые антенны
369
Глава 8. Щелевые антенны
8.1. Классификация щелевых антенн и их расчет с помощью
принципа двойственности [17]
8.1.1. Типы щелевых антенн. Щелевая антенна представляет собой отверс-
тие, прорезанное в металлической поверхности и возбуждаемое источником элек-
тромагнитных колебаний. Преимущественное применение находят антенны в виде
прямоугольных узких щелей шириной (0.03 - 0.05)Х и длиной около половины дли-
ны волны. Если по металлической поверхности течет ток, а щель расположена
так, что пересекает линии тока (рис. 8.1, а), то на кромках щели появляются
переменные заряды разного знака, а внутри щели — электрическое поле. Следо-
вательно, напряжение между краями полуволновой щели распределены вдоль ее
длины примерно по синусоидальному закону. На концах щели напряжение равно
нулю.
Если щель расположена вдоль линий поверхностного тока, то на краях щели
заряды не появляются, так как щель практически не искажает распределения
поверхностных токов (рис. 8.1, б). Чем больше острый угол между продольной осью
щели и направлением поверхностных токов, тем интенсивнее возбуждается щель.
Электрическое поле в щели, наряду с поверхностными токами, является ис-
точником излучения электромагнитных волн. Щель, излучающую в обе стороны от
металлической поверхности, называют двусторонней. На практике чаще применя-
ют односторонние щелевые антенны. Чтобы устранить излучение в одно полупрос-
транство, щель с соответствующей стороны закрывают резонатором (рис. 8.2, а).
Обычно в нем расположено возбуждающее антенну устройство.
Помимо прямолинейных щелей находят применение фигурные щели, напри-
мер уголковые, П-образные, крестообразные, гантельные (рис. 8.2, б-д). Во всех
этих случаях длина щели (между точками 1 и 2) имеет величину около половины
длины волны. Кроме того, применяются различные варианты кольцевых щелей,
например круговые (рис. 8.2, б). Широкое применение нашли волноводно-щелевые
антенны. Они будут рассмотрены далее.
Металлическая
поверхность
а) б)
Рис. 8.1. Прямолинейная щель в бесконечном экране: а) — щель пересекает линии тока,
б) — щель вдоль линии тока [17]
370
ГЛАВА 8
Рис. 8.2. Варианты щелевых антенн [17]
в)
е)
Предположим, что щель прорезана в плоском тонком, идеально проводящем
экране, и что первоначально (до прорезания щели) ток возбуждался внешним
источником лишь на одной стороне металлической поверхности. Так как щель из-
лучает в оба полупространства, разделенные металлической поверхностью, то
токи появятся и на другой ее стороне.
8.1.2. Принцип двойственности. Принцип двойственности описан в разделе
1.8.2. Покажем его применимость на примере щели в идеально проводящей плос-
кости. Рассмотрим полуволновый симметричный металлический вибратор, име-
ющий форму бесконечно тонкой пластинки шириной d, и прямоугольную щель
таких же размеров, прорезанную в бесконечном металлическом листе (рис. 8.3).
Пусть по вибратору протекает ток I. Принимая, что d X, можно считать, ток
вдоль вибратора распределен по синусоидальному закону (см. § 4.6). Структура
магнитного поля вблизи вибратора изображена на рис. 8.3, а. Так как по закону
полного тока
то для касательной составляющей магнитного поля в непосредственной близости
к поверхности вибратора нетрудно получить выражение
Нте = I / 2d. (8.1.1)
Следовательно, величина Нгв, как и ток I, будет вдоль вибратора изменяться
по синусоидальному закону. На остальной воображаемой бесконечной плоскости
(на рис. 8.3, а она изображена пунктиром), являющийся продолжением плоскости
вибратора, касательная составляющая магнитного поля вибратора равна нулю,
так как по соображениям симметрии магнитные силовые линии перпендикулярны
указанной плоскости.
Обратимся теперь к щелевому излучателю (рис. 8.3, б). Пусть напряжение меж-
ду краями щели равно U. Касательная составляющая электрического поля в щели
ЕТв, как и напряжение, изменяется вдоль щели по синусоидальному закону и
определяется по формуле
ЕТЩ = U/d.
(8.1.2)
Щелевые антенны
371
а) б)
Рис. 8.3. Магнитное поле вблизи вибратора (а); электрическое поле вблизи щели (б) [17]
Предполагая, что проводимость металлического экрана, в котором прореза-
на щель, равна бесконечности, найдем, что всюду вблизи экрана касательная
составляющая электрического поля равна нулю. Структура электрического поля
вблизи щели изображена на рис. 8.3, б и, как видно из рисунка, не отличается от
структуры магнитного поля вблизи вибратора.
Следовательно, можно выбрать амплитуды I и U так, чтобы граничные усло-
вия для магнитного вектора в случае вибратора и для электрического вектора в
случае щели были одинаковы. Отсюда вытекает, что к этим излучателям приме-
ним принцип двойственности. Металлический вибратор принято называть вибра-
торным аналогом щелевого излучателя, имеющего те же размеры и форму, а
щель — щелевым аналогом вибратора.
Принцип двойственности позволяет по известным электрическим параметрам
металлического вибратора определять электрические параметры его щелевого
аналога, и наоборот.
8.1.3. Поле излучения прямолинейной щелевой антенны. Применим прин-
цип двойственности для определения поля излучения прямолинейной щелевой ан-
тенны длиной 21. Напряженность электрического поля симметричного электричес-
кого вибратора в дальней зоне в соответствии с (2.1.1) можно представить в виде
. 601д cos(/cZcos0) - coskZ
Едв = г----------~ 7 7 . п---е , (8.1.3)
г sm kl sin 6
где Iд — ток в точках питания.
Напряженность магнитного и электрического полей в свободном пространстве
связаны соотношением
НЧ>в = Евв /120л.
Следовательно,
372
ГЛАВА 8
_ • IA cos(kl cos 0) - cos kl -ikr
*** 2лт sin kl sin 0
(8.1.4)
Подставляя в эту формулу значение 1А из (8.1.1), получаем
_ . Нтв cos(kl cos 0) - cos kl -ikr
фв nr sin kl sin 0
Для того, чтобы найти поле излучения щелевого аналога, заменим в соответствии
с принципом двойственности Нфв и Нхв соответственно на Е^щ и Ети, :
„ _ . Етщй cos(kl cos 0) - cos kl
w nr sin kl sin 0
Учитывая (8.1.2), получаем
(ргц
. Uщ cos(kl cos 0) - cos kl
nr sin kl sin 0
(8.1.5)
Здесь Uxu, — напряжение в точках питания щели (рис. 8.3). Для магнитного поля
щели в дальней зоне легко получить выражение
sin kl sin 0
_ . ищ cos(kl cos 0) - cos kl _^г
0ш - ~l----
120 кг
(8.1.6)
Ориентация векторов поля излучения относительно щели показана на рис 8.4.
Из формул (8.1.3)-(8.1.6) следует, что ДН щелевого излучателя и его вибра-
торного аналога одинаковы, однако ориентация векторов поля различна: при
совпадающих осях щели и вибратора поляризация этих излучателей отличается
на 90°.
В плоскостях, проходящих через продольную ось щели (например, в плос-
костях xOz и yOz), ДН полуволновой щели имеет вид восьмерки (рис. 8.5, а), а в
плоскости, перпендикулярной этой оси (в плоскости хОу) — вид окружности (рис.
8.5, б). Если щель является односторонней, то имеет смысл рассматривать ее ДН
только для «освещенного» полупространства. В этом случае ДН представляет собой
половину диаграммы (в соответствующей плоскости), изображенной на рис. 8.5.
Рис. 8.4. Ориентация векторов поля излучения
щели [17]
Рис. 8.5. ДН двусторонней щели [17]
Щелевые антенны
373
8.1.4. Проводимость прямолинейной щелевой антенны. Предположим, что
симметричный вибратор и его щелевой аналог — двусторонняя прямолинейная
щель — создают в дальней зоне поля одинаковой интенсивности. Приравнивая
друг к другу правые части формул (8.1.3) и (8.1.5), находим условие равенства ам-
плитуд полей излучения
- бОлЬ.
(8.1.7)
Здесь Пщ и 1д относятся к одинаково расположенным точкам на щели и соответс-
твенно на вибраторе, например к точкам питания.
Условие (8.1.7) можно сформулировать так: один ампер тока в вибраторе вызы-
вает такое же по величине поле излучения, как и 60л вольт на щели.
Поскольку ДН обоих излучателей одинаковы и, кроме того, равны интенсив-
ности полей, то можно утверждать, что при выполнении условия (8.1.7) будут
одинаковыми и излученные мощности:
Эти мощности можно представить в виде
у у
где Ra — сопротивление излучения вибратора; — проводимость излучения
щели. Приравнивая правые части выражений и используя соотношение (8.1.7),
получаем формулу, устанавливающую связь между проводимостью излучения,
отнесенной к определенным точкам щелевого излучателя, и сопротивлением из-
лучения, отнесенным к аналогичным точкам вибраторного аналога,
Сщ = R%/(60n)2. (8.1.8)
Принципом двойственности можно пользоваться для определения не только мощ-
ности излучения, а следовательно, и активной проводимости (сопротивления ан-
тенны), но также реактивной мощности, связанной с антенной, и ее реактивной
проводимости (сопротивления). Поэтому, распространяя формулу (8.1.8) на комп-
лексную проводимость щелевой антенны и комплексное сопротивление вибра-
торной антенны ZA получаем
Ущ=гА/(60п)2. (8.1.9)
Подставим в (8.1.9) значение ZA из (4.7.34). Тогда
Ущ = (Ra - iWectgkiy(60к)2. (8.1.10)
Формула (8.1.10) является приближенной. В ней не учтено, что полуволновая щель
(как и полуволновый вибратор) не настроена в резонанс и что для такой настрой-
ки необходимо щель укоротить. Величина укорочения может быть определена по
формуле (4.7.28), в которую вместо радиуса а вибратора нужно подставить чет-
верть ширины щели, т.е. 0.25d.
Из формулы (8.1.10) вытекает, что реактивные составляющие входного сопро-
тивления вибратора и входной проводимости его щелевого аналога имеют одина-
ковый знак. Следовательно, одинаковые по длине щель и вибратор будут иметь
входные сопротивления разного знака. Например, щель длиной менее 0.5Х имеет
входное реактивное сопротивление индуктивного характера, в то время как виб-
374
ГЛАВА 8
ратор такой же длины имеет входное сопротивление емкостного характера.
В случае односторонней щели поле излучения по-прежнему определяется по
формуле (8.1.5), однако, так как излучение происходит только в одно полупрос-
транство, то мощность излучения, а следовательно, и проводимость излучения
будут вдвое меньше, чем в случае двусторонней щели, и для определения прово-
димости излучения щелевой антенны нужно пользоваться формулой
Сщ =rJ/2(60k)2. (8.1.11)
8.1.5. Способы возбуждения прямолинейной щелевой антенны. На рис. 8.6
изображены применяемые на практике способы возбуждения полуволновой пря-
молинейной щелевой антенны. На метровых волнах питание антенны может осу-
ществляться симметричным двухпроводным фидером (рис. 8.6, а). На дециметро-
вых волнах обычно применяют коаксиальный фидер, внутренняя жила которого
присоединяется к одной кромке щелевой антенны, а оплетка — к другой.
Считая, что напряжение вдоль полуволновой щели распределено по синусои-
дальному закону, из формулы (8.1.6) можно получить следующее выражение для
сопротивления излучения односторонней щелевой антенны:
RE=2(6Wsin2fc
73.1
где х — расстояние между точками питания щели и ее концом (рис. 8.6, б).
Если питать щель в середине (х = X / 4), то п » 1000 Ом, что значительно
больше волнового сопротивления обычно применяемых коаксиальных фидеров.
Поэтому с целью согласования фидера с антенной точки питания смещают к одно-
му концу щелевой антенны.
Другой способ согласования состоит в применении щелевого аналога петлевой
антенны (рис. 8.6, в). Как известно, петлевой вибратор обладает свойством ав-
тотрансформации сопротивлений: его сопротивление излучения зависит от соот-
ношения диаметров вибраторов. Аналогично, сопротивление излучения петлевой
щелевой антенны зависит от соотношения ширины щелей ф и d2: чем больше от-
ношение d2 / di, тем сопротивление излучения меньше. Выбирая должным образом
отношение d2 / di, можно осуществлять согласование щелевой антенны с фидером
питания.
На рис. 8.6, г изображен резонаторно-зондовый метод возбуждения щели. Пита-
емые коаксиальным фидером зонд возбуждает колебания внутри прямоугольного
резонатора. Токи, текущие по внутренней поверхности стенок резонатора, в свою
очередь, возбуждают щель. Такой способ возбуждения обычно применяется в ко-
ротковолновой части дециметрового диапазона и на более коротких волнах, так
как длина зонда для настройки его в резонанс должна быть около четверти длины
волны. Можно уменьшить длину зонда, применяя схему возбуждения, изобра-
женную на рис. 8.6, д. Здесь длина зонда равна ширине резонатора, причем обыч-
но «0.1-0.15Х. Для настройки зонда в резонанс применяют короткозамкнутый
отрезок длинной линии (шлейф), расположенный вне резонатора.
Антенны, изображенные на рис. 8.6, а-д, являются узкополосными, причем по-
лоса пропускания антенны определяется двумя факторами: резонансными свойс-
твами самого щелевого излучателя и резонансными свойствами возбуждающего
устройства (зонда, резонатора, элементов настройки).
Щелевые антенны
375
Рис. 8.6. Способы возбуждения прямолинейной щелевой антенны: а) — двухпроводной
линией; б) — коаксиальной линией; в) — щелевым аналогом петлевой антенны; г), д)
— зондом через коаксиальную линию; е) — резонатором [17]
Для расширения полосы пропускания щели нужно увеличить ее ширину. Нахо-
дят, например, применение щели шириной 0.1-0.15Х. Полосу пропускания зонда
можно расширить, увеличивая его толщину. Применяют, например, толстые зон-
ды конической и каплевидной формы. Для того, чтобы резонатор не был узкопо-
лосным, его поперечные размеры и ?2 (рис. 8.6, г) не должны быть меньше X / 4.
Пример широкополосной щелевой антенны изображен на рис. 8.6, е. Широкая
щель возбуждается резонатором, внутри которого расположен Т -образный воз-
будитель. Каждая половина возбудителя вместе с резонатором образует коротко-
замкнутый на конце отрезок длинной линии. Длина и поперечные размеры возбу-
дителя выбираются так, чтобы его входная реактивная проводимость в некоторой
полосе частот компенсировала реактивную проводимость щели. При указанных на
рис. 8.6, е размерах антенны ее полоса пропускания характеризуется графиком,
из которого видно, что при Kge > 0.5 антенна перекрывает почти двукратный диа-
пазон волн [17]. Более подробная геометрия возбуждений щелевой антенны с резо-
натором приведены на рис. 8.7.
Простейшая полуволновая щелевая антенна на металлической площадке ко-
нечных размеров может быть возбуждена резонатором в виде короткозамкнутого
четвертьволнового отрезка прямоугольного волновода с волной Н10 (рис. 8.7, а).
Питание подводится коаксиальным кабелем, внешний проводник которого при-
соединяется к одной стороне щели, а внутренний — к другой. Резонатор играет
роль металлического изолятора, и его реактивная проводимость компенсирует
собственную реактивную проводимость щели.
Входное сопротивление полуволновой щелевой антенны с настроенным резо-
натором на экране больших электрических размеров в пучности напряжения (в
центре щели) равно Нщ = Z?/(2К&, ^= 970 Ом [17]. Чтобы согласовать это сопро-
тивление с волновым сопротивлением коаксиальной линии Ze, следует подключить
линию ближе к краю щели, на расстоянии I от края, определяемом из уравнения
376
ГЛАВА 8
Рис. 8.7. Возбуждения щелевой антенны с резонатором [2]
2L
sin pZ = %в1Кщ. Конструктивно удобно расположить резонатор так, чтобы одной
широкой стороной он примыкал к экрану и ввести коаксиальную линию внутрь
резонатора через другую широкую сторону (рис. 8.7, б).
8.2. Излучение щелей, прорезанных в металлических телах
конечных размеров
Реальные излучатели в отличие от рассмотренного выше идеального щелевого
излучателя располагаются не на бесконечном плоском экране, а на телах конечных
размеров. В этом случае принцип двойственности, строго говоря, не применим, и
для определения поля излучения разработаны другие приближенные методы, два
из которых рассматриваются ниже.
8.2.1. Метод поверхностных токов поясним на следующем примере. Пусть
в плоском прямоугольном экране S прорезана односторонняя полуволновая щель,
к которой от внешнего источника приложено возбуждающее напряжение (рис. 8.8).
Экран разделяет все пространство на два полупространства. То из них, в которое
обращена щель, назовем освещенным, а другое — затененным. Предположим вна-
чале, что экран является бесконечным. Тогда щель излучает только в освещен-
ное полупространство. Поле в этом полупространстве, а следовательно, и токи,
бегущие от щели по освещенной поверхности экрана, можно найти, применяя,
М,
W
Ег
Затененное
полупрост-
ранство
.М.
Освещенное
полупрост-
ранство
Рис. 8.8. К пояснению метода поверхностных токов [17]
Щелевые антенны
377
например, принцип двойственности. Поле в освещенном полупространстве форми-
руется как излучением щели, так и излучением всех поверхностных токов экрана.
Обозначим электрический вектор этого поля Е[.
Поле щели и конечного экрана в освещенном полупространстве Е1 можно при-
ближенно рассматривать как разность поля Е{ и поля Еэ1 токов, текущих по все-
му бесконечному экрану за вычетом конечного экрана S
Аналогично в затененном полупространстве
Так как при бесконечных размерах экрана поле в затененном полупространстве
Ё2 = 0, то
Е2 = -Еэ2. (8.2.2)
Зная распределение поверхностных токов и рассматривая каждый элемент повер-
хности в качестве излучателя Герца, можно определить поля Еэ1 и Еэ2 , а следо-
вательно, и искомые поля Е1 и Ё2-
Можно эту же задачу решить и несколько иначе, определяя поле излучения
как сумму поля излучения собственно щели (магнитного вибратора) и поля излу-
чения токов, обтекающих экран S. На рис. 8.9 приведены ДН полуволновой щели
в плоскости, перпендикулярной продольной оси щели.
Обсудим особенности ДН щелевых антенн на экранах конечных размеров (раз-
мер экрана 2L х 2Н на рис. 8.9). В плоскости вектора Н (т.е. в плоскости, проходя-
щей через щель) излучение вдоль щели равно нулю, явление дифракции волн
на краю экрана сказывается слабо и ДН почти не зависит от размеров экрана. В
переднем полупространстве она примерно совпадает с ДН щели в бесконечном
экране, в заднем полупространстве имеется небольшой лепесток.
В плоскости вектора Е (т.е. в плоскости, перпендикулярной щели) ДН сильно
зависит от размера экрана 2L, и незначительно зависит от размера 2Н. В этой
плоскости ярко выражена дифракция волн на краю экрана. На собственное излу-
чение щели накладывается добавочное излучение, появляющееся из-за возбужде-
ния краев экрана, что приводит, с одной стороны, к появлению поля за теневой
стороной экрана, с другой — к искажению формы ДН в переднем полупространс-
тве. Вследствие интерференции волн, излучаемых непосредственно щелью и из-
лучаемых при дифракции у краев экрана, появляются максимумы и минимумы
излучения, число которых тем больше, чем больше отношение 2L / X.
На рис. 8.9 штриховыми линиями показаны экспериментальные ДН щелевой
антенны в плоскости вектора Е (штриховые кривые) в зависимости от размеров
экрана. На том же рисунке приведены теоретические ДН (сплошные кривые),
рассчитанные по приближенной методике, когда распределение поверхностного
электрического тока на передней стороне экрана предполагается совпадающим с
распределением поверхностного электрического тока в бесконечном экране (так
называемое приближение физической оптики). На рис. 8.10 приведены теоретичес-
кие ДН в плоскости вектора Н, вычисленные в предположении, что размер 2Н
является конечным, а размер 2L бесконечно велик. Экран в этом случае пред-
ставляет собой бесконечную полосу, являющуюся вырожденным эллиптическим
цилиндром. Теоретические расчеты здесь проведены строгим методом собственных
378
ГЛАВА 8
L/X=0.5 Ь/Х=1
270“
Рис. 8.9. а) — ДН щелевой антенны на конечном экране в плоскости вектора Ё ; б) — ДН
на бесконечном экране (пунктирные линии — эксперимент, сплошные — расчет) [18]
180 180"
Рис. 8.10. ДН щелевой антенны на конечном экране в плоскости вектора Н [2]
Щелевые awneHjibi
379
0,40 0,45 0,50 L/X
0,40 0,45 0,50 L/1
а) б)
Рис. 8.11. Экспериментальные графики входного сопротивления двусторонней щелевой
антенны [2]
Рис. 8.12. Кольцевая щелевая антенна на цилиндре [2]
функций.
На практике применяются не только односторонние, но и двусторонние щели,
расположенные на площадках ограниченных размеров. Если в антенне на рис. 8.6,
е, удалить резонатор, то получится двусторонняя щелевая антенна. ДН в каждом
полупространстве примерно такие же, как ДН на рис. 8.9 для освещенной области
пространства. Однако в плоскости вектора Е излучение вдоль поверхности экрана
оказывается строго равным нулю. Входное сопротивление двусторонней щелевой
антенны на большом по сравнению с длиной волны экране может быть определе-
но по формулам из [2]. Для резонансной полуволновой щели оно равно примерно
485 Ом. На рис. 8.11 приведены экспериментальные графики активной (а) и реак-
тивной (б) составляющих входного сопротивления вблизи резонанса двусторонней
щелевой антенны в большом экране. Из графиков следует, что резонансная длина
щели L оказывается несколько меньше полуволны и уменьшается с увеличением
ширины щели d.
В качестве всенаправленных антенн СВЧ получили распространение кольцевые
380
ГЛАВА 8
щелевые антенны, располагаемые на телах вращения, в частности на круговом ме-
таллическом цилиндре 1 (рис. 8.12, а). Кольцевая щель 4 выполняется с помощью
коаксиального резонатора 2 в виде закороченного сверху на цилиндр четверть-
волнового металлического стакана. Питание к резонатору подводится коаксиаль-
ной линией 3 в точке а. Если средняя длина периметра резонатора л (д + г2 ) < К
в нем существует и наиболее интенсивно возбуждается только Т-волна. Напря-
жение в щели при настройке стакана в резонанс распределяется равномерно по
азимуту, на поверхности цилиндра возникают продольные электрические токи,
и получается антенна, подобная цилиндрическому электрическому вибратору. В
азимутальной плоскости излучение равномерно, а в меридиональной плоскости
ДН существенно зависит от длины возбуждаемого цилиндра.
Если же л (д + т2 ) > А, то в резонаторе кроме Т -волны возбуждается еще волна
типа Иц коаксиальной линии, критическая длина волны которой Хкр ® л(д + т2).
Пусть длина резонатора I = А / 2. Тогда Т-волна оказывается подавленной, в то
время как существует . Напряжение в щели оказывается распределенным в
азимутальном направлении помимо продольных поперечные составляющие по-
верхностных электрических токов и излучение антенны существенно изменяется.
Наличие поперечных составляющих токов приводит к появлению излучения вдоль
оси цилиндра. Антенна излучает по всем направлениям, причем ДН очень слабо
зависит от длины цилиндра.
На рис. 8.12, б показано распределение напряжения в щели при питании ан-
тенны в двух диаметрально противоположных точках резонатора. Напряжение в
щели в точке а отличается по фазе на л от напряжения в точке b, поэтому при
любой длине резонатора I Т-волна оказывается подавленной и напряжение в щели
распределяется по азимуту по закону синуса.
Особый интерес представляет кольцевая щелевая антенна с бегущей по ази-
муту волной напряжения в щели. В этом случае питание к резонатору (рис. 8.12)
подводится в четырех равностоящих точках щели с относительным фазовым сдви-
гом последовательно на -л/2. Если длину резонатора выбрать равной Ав /4 для
волны Нц, то напряжение в щели (без учета высших типов волн) изменяется
по закону бегущей волны 17(ф) = Uq ехр(-гф). Кольцевая щелевая антенна с бегу-
щей волной напряжения излучает вдоль оси z электромагнитное поле круговой
поляризации, подобное полю турникетной антенны (см. рис. 7.43). Как показывают
расчеты и эксперименты, ДН такой антенны слабо зависит от размеров и формы
металлического корпуса.
8.3. Волноводно-щелевые антенны
8.3.1. Возбуждение щелей в волноводе. Широкое распространение получили
волноводно-щелевые антенны, применяемые преимущественно на сантиметровых
волнах. Щели могут прорезаться в волноводах любого сечения, однако чаще всего
используются прямоугольные волноводы с волной типа Н10. Картина поверхностных
токов, текущих на внутренней стороне стенок волновода, изображена на рис. 8.13, а.
Как уже отмечалось выше, для того чтобы щель излучала, она должна пересе-
кать линии поверхностного тока. Варианты излучающих щелей показаны на рис.
8.13, б, а неизлучающих — на рис. 8.13, в.
Если в волноводе устанавливается режим стоячих волн, то для наиболее ин-
Щелевые антенны
381
АУ
Рис. 8.13. Прямоугольный волновод: а) — распределение поверхностного тока; б) — излу-
чающие щели; в) — неизлучающие щели; г) — возбуждение щели с помощью штыря [17]
тенсивного возбуждения щели она должна располагаться вдоль оси волновода в
местах, где существует пучность той составляющей тока, которая ее возбуждает.
Если же в волноводе устанавливается режим бегущих волн, то щель будет воз-
буждаться одинаково при любом значении ее координаты z .
Продольная щель 4 в широкой стенке волновода возбуждается поперечной со-
ставляющей тока. Так как поверхностная плотность этой составляющей изменяет-
ся по закону
Jx ~ ЛтО sin(juc/a),
то интенсивность возбуждения щели тем больше, чем сильнее удалена щель от
средней линии широкой стенки волновода. Продольная щель, расположенная на
средней линии стенки, не возбуждается.
Интенсивность возбуждения продольной щели 6 в узкой стенке волновода не
зависит от ее смещения поперек этой стенки, так как плотность тока Jy по ширине
стенки не меняется.
Поперечная щель в широкой стенке волновода возбуждается продольной со-
ставляющей тока. Так как плотность этой составляющей изменяется по закону
J2 = Jzq cos(ra?/a), то интенсивность возбуждения щели тем больше, чем ближе
она к средней линии.
Интенсивность возбуждения наклонной щели 7 в узкой стенке волновода зави-
сит от угла наклона, а интенсивность возбуждения наклонно смещенной щели 5
— как от угла наклона, так и от величины смещения щели от средней линии. Ре-
зонансная длина щели близка к половине длины волны в воздухе и слабо зависит
от расположения щели на стенке волновода.
Все рассмотренные выше щели излучают поле линейной поляризации. Приме-
ром щели, излучающей поле вращающейся поляризации, является крестообраз-
ная щель 3. Она состоит из двух взаимно перпендикулярных щелей. Одна из них
возбуждается продольным током, другая — поперечным.
Так как плотность тока Jz меняется по косиносуидальному закону, а плотность
тока Jx — по синусоидальному, то можно расположить щели на таком удалении
от средней линии, чтобы амплитуды этих плотностей токов были равны. Если
учесть, что продольный и поперечный токи сдвинуты по фазе на п / 2 относитель-
382
ГЛАВА 8
но друг друга, то ясно, что крестообразная щель будет излучать поле круговой
поляризации.
Щель, расположенную вдоль линий поверхностного тока, также можно воз-
будить, располагая вблизи нее металлический штырь таким образом, чтобы поле
волновода наводило в нем ЭДС, а следовательно, и ток. Растекающиеся от штыря
радиальные поверхностные токи пересекают щель и возбуждают ее. Варианты рас-
положения штырей приведены на рис. 8.13, г.
8.3.2. Диаграммы направленности одиночной полуволновой щели, проре-
занной в стенке волновода, можно приближенно определить, заменяя волновод
прямоугольной пластиной или эллиптическим цилиндром и пользуясь для расчета
методами, изложенными в предыдущем параграфе. Обычно в Н-плоскости ДН
имеет вид половины восьмерки, а в Е-плоскости в зависимости от ориентации
щели подобна одной из ДН изображенных на рис. 8.9.
8.3.3. Эквивалентные параметры щелей в волноводе. Проводимость излуче-
ния во внешнее пространство щели, прорезанной в стенке волновода, может быть
приближенно определена по формуле (8.1.11). Щель представляет собой нагрузку
для волновода в общем случае комплексную. Если щель резонансная, т.е. ее длина
близка к X / 2 , то нагрузка является активной. Предположим, что длина волново-
да бесконечна или он нагружен на согласованную нагрузку. Тогда мощность пада-
ющей со стороны генератора волны частично отражается от щели и возвращается
в сторону генератора (отраженная волна), частично проходит по волноводу мимо
щели (прошедшая волна) и частично излучается в свободное пространство.
Если воспользоваться аналогией между волноводом и двухпроводной длинной
линией [17], то следует отметить, что такое же распределение мощностей полу-
Рис. 8.14. Щели, возбуждаемые продольным (а) и поперечным (г, д) током, и их эквива-
лентные схемы (б, в, е) [17]
Щелевые дмтенны
383
чается, когда в некотором сечении линии подсоединены сосредоточенные сопро-
тивления, причем мощность потерь в этих сопротивлениях равна мощности излу-
чения щели. Анализ показывает [17], что в общем случае щель следует заменить
четырехполюсником, однако в некоторых случаях допустима замена в виде сосре-
доточенного сопротивления (проводимости). Рассмотрим, например, поперечную
щель в широкой стенке волновода (рис. 8.14, а). Нетрудно видеть, что поперечная
щель возбуждается продольной составляющей тока. В длинной линии продольный
ток проходит через последовательно включенное сопротивление. Поэтому попе-
речная щель эквивалентна сопротивлению, включенному в линию последователь-
но (рис. 8.14, б).
Продолжая эту аналогию, можно сказать, что щели, возбуждаемые попе-
речной составляющей поверхностного тока волновода (рис. 8.14, гид), можно
заменить сосредоточенной проводимостью, включенной в эквивалентную линию
параллельно (рис. 8.14, е). Такой способ возбуждения характерен для продольной
щели в широкой стенке волновода (рис. 8.13, г), а также наклонной (в частности, и
продольной) щели в узкой стенке волновода (рис. 8.13, д).
Если щель возбуждается и продольным и поперечным токами, то ее эквивален-
тная схема есть сочетание последовательно и параллельно включенных сопротив-
лений, т.е. представляется в виде четырехполюсника.
Предположим, что поперечная щель в широкой стенке волновода имеет резо-
нансную длину и потому на эквивалентной схеме может быть представлена после-
довательным сопротивлением R?z,. Обозначим подводимую по волноводу мощность
у
Рподв, излученную щелью мощность Р и проходящую мимо щели по согласо-
ванному с нагрузкой волноводу мощность РПрОх. Заменяя часть волновода, рас-
положенную справа от щели (рис. 8.14, а), сопротивлением, равным волновому
сопротивлению волновода, получим эквивалентную схему, изображенную на рис.
8.14, в.
Очевидно, что
Pz = 0.512R* ,
прозе
= 0.5I2We.
Нормированное сопротивление щели равно
Так как Р-п-пп^
р — р
гподв 1
ТО
прох •
(8.3.1)
(8.3.2)
Можно показать, что формула (8.3.2) пригодна также для определения нормиро-
ванной проводимости продольной щели.
Определяя мощность излучения и подводимую мощность через напряженность
магнитного поля в волноводе, можно получить следующие формулы для расчета
нормированных величин проводимостей сопротивлений щелей [17]:
для продольной щели в широкой стенке волновода
= 2.09-----cos
sin
(8.3.3)
для поперечной щели в широкой стенке волновода
384
ГЛАВА 8
= 0.523
— cos
ab
cos
(8.3.4)
для наклонной щели в узкой стенке волновода
30 X
sin a cos (лХ / (2Xe ))sin а
(8.3.5)
Здесь Лб = к / yjl-(к / 2а)2; а — угол наклона щели (рис. 8.14, д); х — смещение
щели относительно средней линии широкой стенки волновода.
Если щели не настроены в резонанс, то эквивалентные им сопротивления (про-
водимости) являются комплексными.
8.3.4. Многощелевые антенны. Одиночная щель, прорезанная в стенке вол-
новода, имеет слабо выраженные направленные свойства. Для получения узких
ДН применяют многоэлементные волноводно-щелевые антенны. Варианты таких
антенн изображены на рис. 8.15. Если щели возбуждать синфазно, то максимум
главного лепестка будут ориентирован перпендикулярно плоскости расположения
щелей, причем в плоскости, перпендикулярной продольной оси волновода, ДН
будет широкой, а в плоскости, содержащей ось волновода, — узкой и тем уже,
чем больше длина антенны.
Синфазное возбуждение щелей можно осуществить двумя способами: либо
а) г)
в) е)
Рис. 8.15. Варианты волноводно-щелевых антенн: а), б), в) — прямофазные; г), д), е)
— переменно-фазные; а), б), д), е) — резонансные; в), г) — нерезонансные [17]
12*
Щелевые антенны 385
выбрать расстояние d между соседними щелями, равное Лв, и расположить их
идентично вдоль стенки волновода (рис. 8.15, a-в), либо выбрать расстояние, рав-
ное Хв / 2, а дополнительный сдвиг фаз на п реализовать за счет неидентичного
расположения щелей (рис. 8.15, г-е). Антенны с идентичным расположением ще-
лей называются прямофазными, а антенны, у которых соседние щели имеют до-
полнительный сдвиг фазы на тс — переменно-фазными.
В случае «шахматного»расположения продольных щелей в широкой стенке вол-
новода (рис. 8.15, г) дополнительный сдвиг фаз, равный тс, достигается за счет
того, что поперечная составляющая поверхностного тока меняет свое направление
на обратное при переходе средней линии (см. рис. 8.13, а), При встречно наклонном
расположении щелей через Хв / 2 на узкой стенке волновода (рис. 8.15, д) также
достигается их синфазное возбуждение. Можно расположить продольные щели на
средней линии широкой стенки волновода, а синфазное возбуждение обеспечить,
размещая возбуждающие штыри по разные стороны щелей (рис. 8.15, е).
Достоинством антенн, изображенных на рис. 8.15, г-е, является малое расстоя-
ние между соседними щелями, что позволяет устранить главные лепестки высших
порядков.
Синфазные антенны обычно работают в режиме стоячей волны, для обеспече-
ния которого в конце антенны устанавливается короткозамыкающий поршень (см.
рис. 8.15, а, б, д, е). В режиме стоячей волны могут работать антенны при всех
вариантах расположения щелей, приведенных на рис. 8.15, если в конце каждого
волновода установить короткозамыкающий поршень. Расстояние между поршнем
и последней щелью должно быть таким, чтобы щель находилась в пучности той
составляющей поля (пли тока), которой она возбуждается. Поэтому, например, от
продольной щели поршень должен находиться на расстоянии, кратном нечетному
числу четвертей волны (в волноводе), а от поперечной щели — на расстоянии,
кратном целому числу полуволн.
Синфазные многощелевые антенны являются резонансными (узкополосными)
антеннами. Это объясняется тем, что отражения от щелей, расположенных на
удалении или Хв / 2 , складываются в фазе и поэтому при небольшом изменении
частоты нарушается согласование антенны с питающим ее волноводом.
Лучшими диапазонными свойствами обладают нерезонансные антенны. У них
щели располагаются на расстоянии d, несколько большем или меньшем Хв / 2.
Поэтому отражения от отдельных щелей складываются не в фазе, и в некоторой
полосе частот происходит взаимная компенсация отражений.
Чтобы устранить влияние волны, отраженной от конца антенны, применяют
согласованную с антенной поглощающую нагрузку (8.15, в, г). В режиме бегущей
волны могут работать антенны при всех вариантах расположения щелей, приве-
денных на рис. 8.15, если в конце каждого волновода установить поглощающую
нагрузку. Обычно в ней теряется 5—7% мощности антенны.
8.3.5. Диаграммы направленности многощелевой антенны в плоскости,
перпендикулярной раскрыву и содержащей продольную ось волновода (продоль-
ной плоскости), могут рассчитываться по формулам, выведенным в гл. 7 для ан-
тенных решеток. Для расчета множителя решетки в случае равноамплитудной
волноводно-щелевой антенны можно применить формулы (7.3.4) или (7.3.5). Влия-
ние на ДН многощелевой антенны направленных свойств одиночной щели невели-
ко. В первом приближении можно считать, что в продольной плоскости одиночная
13 - Неганов
386
ГЛАВА 8
щель имеет такие же направленные свойства, как и при ее расположении в беско-
нечном экране.
Для того чтобы уменьшить уровень боковых лепестков волноводно-щелевой
антенны, применяют спадающее к ее концам амплитудное распределение, которое
достигается тем, что различные щели неодинаково сильно связаны с полем вол-
новода. Например, в случае продольных щелей в широкой стенке волновода (рис.
8.15, г) спадающее распределение получается, если расстояние между щелями и
средней линией стенки убывает к концам антенны.
8.3.6. Эквивалентные схемы многощелевых антенн. Используя аналогию
между волноводом и длинной линией, можно представить многощелевую антенну
в виде линии, вдоль которой включен ряд сосредоточенных нагрузок, соответс-
твующих щелям. Так, например, резонансным антеннам, изображенным на рис.
8.15, а, б, соответствуют эквивалентные схемы, представленные на рис. 8.16, а, б.
Последовательные сопротивления (и параллельные проводимости), включенные в
линии на удалении Ле или Хв / 2 друг от друга, при пересчете к точкам включения
первой нагрузки складываются. Таким образом, нормированное входное сопротив-
ление антенны с поперечными настроенными щелями равно
г = пгщ, (8.3.7)
где п —число щелей, а нормированная входная проводимость антенны с продоль-
ными настроенными щелями на широкой стенке или наклонными щелями на узкой
стенке равна
9 = 719^. (8.3.8)
Для того чтобы антенна была согласована с питающим волноводом, необходимо
выполнить условия
пгщ = 1, пдщ = 1. (8.3.9)
Из этих соотношений можно определить гщ и ди,, а затем по формулам (8.3.3)-
(8.3.5) найти величины х и а, определяющие расположение щелей на стенке волно-
вода. В случае, когда связь отдельных щелей с волноводом различна (например,
Хв/4
б)
Рис. 8.16. Эквивалентные схемы многощелевой антенны с поперечными (а) и продольными
(б) щелями [17]
Щелевые дмтен/ны
387
при неравноамплитудном распределении ноля по раскрыву антенны) расчет со-
гласования антенны с питающим волноводом несколько усложняется [17].
8.3.7. Щелевые антенны и антенные решетки. Антенна Вивальди [57].
Широкополосные антенны нашли самое широкое применение в ФАР и АФАР диа-
пазонов СВЧ и КВЧ. Базовой конструкцией является антенна с расширяющимися
щелями в симметричной щелевой линии (СЩЛ), или антенна Вивальди, показа-
на на рис. 8.17. Питающий фидер 2 представляет собою НПЛ, размещенную на
обратной стороне подложки. Эта НПЛ связана с двухсторонней щелевой лини-
ей 1, располагающейся (относительно полосковой линии) в экранных плоскостях.
Двухсторонняя щелевая линия 1 (общей длиной I) заканчивается на одном конце
круглой щелевой полостью 3. Ширина линии на другом ее конце увеличивается по
экспоненте до размера w. Питающий фидер 2 заканчивается шлейфом 4 на основе
радиальной линии.
Антенна Вивальди обладает большой широкополосностью (отношение крайних
частот рабочего диапазона составляет 5:1) и достаточно большим диапазоном уг-
лов перемещения луча. Это позволяет использовать ее для создания ФАР высоко-
го качества. Одна из ФАР на антеннах Вивальди показана на рис 8.18.
Для создания этих антенн требуются большие затраты времени и средств, пос-
кольку их проектирование остается сложной задачей. В особенности это относится
Рис. 8.17. Плоскостная антенна на основе нерегулярной щелевой линии — антенна Виваль-
ди: 1 — щелевая линия; 2 — питающий фидер; 3 — щелевая полость; 4 — шлейф [57]
Рис. 8.18. Фазированная антенная решетка на антеннах Вивальди [57]
13 *
388 ГЛАВА 8
к конструированию ФАР и АФАР, в которых имеет место большое взаимодейс-
твие между элементами.
Обычно расстояние между ЭИ делают меньше половины длины волны в сво-
бодном пространстве для самой высокой частоты рабочего диапазона в целях ус-
транения боковых лепестков ДН. При выборе полосы частот с перекрытием 5:1
расстояние между элементами АР может быть меньше одной десятой длины волны.
Взаимная связь между ЭИ может при этом стать столь большой, что вызовет
провалы в ДН и (или) аномалии в полосе частот либо секторе сканирования. Тем не
менее, ФАР этого класса используется очень широко и весьма перспективны для
АФУ различного назначения.
8.4. Применение метода сингулярных интегральных уравнений для
расчета плоской электромагнитной волны на прямоугольном от-
верстии в идеально проводящей плоскости [13]
Ранее была рассмотрена узкая щель, для расчета которой был применен при-
нцип двойственности. Для широких щелей нет возможности применять этот при-
нцип, так как нет решения для широкого симметричного металлического вибра-
тора. Ниже рассмотрено отверстие прямоугольной формы, для решения задачи
дифракции плоской электромагнитной волны на котором применен метод СИУ.
В [43] рассмотрена задача дифракции плоской электромагнитной волны на пря-
моугольном отверстии в идеально проводящей плоскости в промежуточной об-
ласти (дифракция Френеля) [1]. Задача решена в приближении Кирхгофа [44],
которое означает, что на теневых сторонах непрозрачных тел напряженности
электрического и магнитного полей обращаются в нуль, и вне тел падающая вол-
на не деформируется. Вторая особенность решения задачи заключается в том, что
использовалась функция Грина свободного пространства в виде:
G(p, q) =
-ikR
(8.4.1)
где R — расстояние между точкой наблюдения р = р(х, у, z) и точкой источника
q - q(x', у', z'), находящегося в отверстии экрана; к = о / с— волновое число; с
— скорость света.
Применение функции Грина (8.4.1) не допускает предельного перехода от дифра-
гируемого поля к полю на отверстии в экране [13]. Ниже получено самосогласо-
ванное решение задачи дифракции плоской электромагнитной волны Е-поляриза-
ции на прямоугольном отверстии в идеально проводящей плоскости, устраняющее
приближение Кирхгофа. Причем под самосогласованным решением (физической
регуляризацией задачи) [13], понимается получение сингулярных интегральных
представлений электромагнитного поля (ЭМП) относительно тангенциального
электрического поля в отверстии и решение сингулярного интегрального уравне-
ния (СИУ), которое получается из СИП при его рассмотрении на отверстии. Пред-
ложенный метод является обобщением подхода, предложенного в [45], на случай
дифракции волны на одномерной щели.
Щелевые антенны 389
8.4.1. Постановка задачи. Сингулярное интегральное представление
(СИП) электромагнитного поля. Рассмотрим дифракцию плоской ЭМВ на пря-
моугольном отверстии в идеально проводящей плоскости XOZ (рис. 8.19). На плос-
кость падает вдоль оси у плоская гармоническая электромагнитная волна, линей-
но поляризованная вдоль оси OZ (рис. 8.19) с составляющими:
• г\с*(0)
= AeiM-iky , й(0) = , (8.4.2)
к2 ду
где е — относительная диэлектрическая проницаемость среды, в которой находит-
ся металлический экран; А — комплексная амплитуда волны.
Для решения задачи будем использовать метод частичных областей. Разложим
комплексные амплитуды дифрагируемого ЖЭМП в первой и второй областях за-
дачи (полупространствах перед экраном и за ним (рис. 8.19)) Ё, ( 8 = 1,2) в
интегралы Фурье:
Ё^(х,у,г) = Г Г ^(h^yy-^e-^dhdfi,
J—ОО J—00
Hls>(x,y,z) = Г Г° fl^s\h,(i,y)e~ihxe~i^zdhdp.
J—00 J—00
(8.4.3)
Из уравнений Гельмгольца для z-составляющих комплексных амплитуд дифра-
гируемого ЭМП для первой и второй областей (рис. 8.19) следует, что ( s = 1 при
У < 0, s = 2 при у >0) [1]:
^(Ь,р,у) = А«(/г,р)е5®^>а\
^s)(h,P,2/) = B(s) (h,p)esgn<!/)a!'.
(8.4.4)
где а = \jh2 + р2 - fc2; A(s\h, Р), B(s)(h,P)
неизвестные постоянные;
-1 при у < О,
sgn(i/) = < 0 при у = О,
1 при у > 0.
Обратные преобразования для интегралов Фурье (8.4.3) от z-составляющих ком-
плексных амплитуд ЭМП при у = 0 есть ( s = 1,2):
Рис. 8.19. Геометрия задачи
390
ГЛАВА 8
^>(h,p,t/ = o) =
l a
Г feW(x>')eitee'₽2’dx'dz',
I a
?4s)(h,P,y = 0) = —Ц- f f^s)(x',z’)eite'ei₽2’da:'dz',
(2") ]i 4
(8.4.5)
где e^z\x,z) - E^z\x,y = 0,2), h^z\x,z) = H^z\x,y = 0,2). При записи (8.4.5) было
тено, что ez = 0 при х > a, z >1.
Справедливы следующие граничные условия ( х
a
E(z0) (х, у = 0, z) + (х, у = 0, z) = Е^2) (х,у = 0,z) = ez(x,z), •
H{z}(x,y = 0,2) = H{z\x,y = 0,2) = hz(x,z),
где Ez — комплексная амплитуда мгновенного значения составляющей пада-
ющей волны, из которых следуют следующие равенства:
I а
A(1)(/i,₽) = A(2)(h,P) = —!—. f fe (x',z')eihx'+ifiz'dx'dz',
(2*)2 -I
I а
B(ll(h,p) = B,2,(h.p)Ц- f [hz(х',z’)eihx'+ipz'dx'dz'.
(2"f J
(8.4.7)
Подставляя (8.4.5) в (8.4.3) с учетом (8.4.4), (8.4.6), (8.4.7) можно получить следу-
ющие СИП для 2-составляющих комплексных амплитуд ЭМП:
r,t';p,t)dp'dt'
У 9
ez(p',t')dp'dt'
[r2+(f-t)2][r2Z2+(p'-p)2]’
(8.4.8)
Hz(x,y,z) = J J/i2,(p',t')T2(p',t';p,t)dp'dt
hz(p',t')dp'dt'
где
OO QO
Tz(p’,t';p,t) = ^— f |
(2л)2 J J
Sgn(r)r7iae2+y2-x2
Sgn(r)r(?a£+y) e-is(p-p')e-i’Y(t-t,)c/yJet
При записи (8.4.8) ввели нормированные переменные:
r = y/l,la =l/a,x = kl,y = ^l,e = ah,
р = х / а, р' = х' / a, t = 2 /1, t' - z' /1
и воспользовались интегралом:
Щелевые антенны
391
(ат)2 + (а - а')2
sgn(r)r
lim
При 1/ —> 0 ( г -> 0) Т2(р', t;р, t;г) -> О, a
= sgn(r)7i6(a - а')
и из (8.4.8) следует, что
т.е. СИП (8.4.8) при у —> О описывает переход дифрагированного поля в поле в
области отверстия.
Используя уравнения Максвелла для Фурье-составляющих , 91^ в первой и
второй областях ( s = 1,2), можно получить следующие соотношения:
(8.4.9)
Далее воспользуемся граничными условиями при у = 0 :
ЁТ(х, 0, z) + ZqE^(х, 0, z) = Ё^(х, 0, z); х, z е (-оо; оо);
Ё^(х,0,г) = ёг(х,?);х g [-a;a], z е [-Щ
(8.4.10)
H^(x,0,z) + XqH^\x,0,z) = XqH^(x,0,z); х g [-a;a], z g [-l;l]
где E2 , — комплексные амплитуды падающей волны (8.4.2); Xq, z0 — единич-
ные вектора декартовой системы координат.
Подставляя (8.4.2), (8.4.3) в (8.4.10), с учетом (8.4.4), (8.4.5), (8.4.7) можно полу-
чить интегральное уравнение (ИУ) относительно неизвестной интегральной функ-
ции ez(x,z) ( р g [-1; 1], t g [-1;1]):
f Je2(p',t')K(p,t;p',f)dp'df = iE0
-1-1
(8.4.11)
где
K(p,t;p',f) =
(8.4.12)
ОО 00
—ОО —ОО
8.4.2. Метод решения двумерного сингулярного интегрального уравне-
ния. С учетом вида ядра (8.4.12) ИУ (8.4.11) несобственные интегралы по е и у
содержат особенности, поэтому ИУ (8.4.11) является сингулярным. Непосредствен-
392
ГЛАВА 8
ное выделение особенностей в двухмерном интегральном уравнении представляет
собой сложную задачу. Поэтому сначала сведем ИУ (8.4.11) к бесконечной системе
одномерных СИУ.
Из условий поведения ЭМП вблизи ребер [46] следует, что при .г —> а
оо. Поэтому в нормированных координатах
О, а при z
е2(х,?/)
р, t будем искать ez (р, t) в виде следующего ряда по полиномам Чебышева второго
рода Пп(р) порядка п :
z
(8.4.13)
где A^(t) — неизвестные функции, зависящие от координаты t, подлежат опре-
делению.
Очевидно, что несобственный интеграл по £ в (8.4.12) является расходящим-
ся: при £
для улучшения сходимости интеграла по этой переменной разложим экспоненту
ехр(га(р' - р)) по полиномам Чебышева второго рода:
оо подынтегральная функция ведет себя как £ exp(-i£(p - р')). Поэтому
00
(8.4.14)
где Jwn(e) — функция Бесселя первого рода порядка fc(Z). Подстановка (8.4.13),
(8.4.14), в ИУ (8.4.11) с одновременным умножением (8.4.11) на функции
Um(p)yl - р2 (т = 0,оо)и интегрированием по р по отрезку [—1; 1], приводит к бес-
конечной системе ИУ ( t е [—1; 1]):
/V 1 оо оо
Тц/т fe» У )d£dy
(т = 0, со),
(8.4.15)
^О^тО ’
Tnm(E;Y) = 2rin~m(n + D(m + 1)^±Й^ф±1^д(Е,у),
5шо — символ Кронекера.
Несобственные интегралы по £ в (8.4.15) теперь сходятся: подынтегральные
функции при £
оо сходятся как 1 / £2 .
Выделим особенности по переменной t в системе ИУ(8.4.15); с этой целью рас-
смотрим интегралы:
00
пт
—00
пт
(8.4.16)
при у
оо
(8.4.16) J
означает несобственный интеграл от -со до +оо по пере-
—00
менной у за исключением отрезка [-%; %]. Найдем асимптотику функций Тпт (е, у)
Щелевые антенны
393
при у
(8.4.17)
’'пт
= 2тп~т (п + l)(m +1) 'У'ООУ+А-)
Прибавляя и вычитая асимптотику (8.4.17) в (8.4.16) и используя известные со-
отношения для интегрального косинуса Ci(x) [28] получим бесконечную систему
СИУ с логарифмическими особенностями ( t е [-1;1]):
1
2tn,„ J A, (t') (О.5772 + 1п% + In 11 - t'
-1
О
cos <^(t' -1) -1
I
dt dt' - iE0dm0; (m = 0, N)
(8.4.18)
Коэффициенты A^t), являющиеся функциями от переменной te[-l;l] будем
искать в виде следующего представления через полиномы Чебышева первого рода
T^n\t) порядка d :
И/
1
Ad(t) = -== У (8.4.19)
где В^1' — неизвестные постоянные коэффициенты, подлежащие определению.
Метод решения СИУ типа (8.4.18) хорошо описан в [8].
8.4.3. Численный анализ. Сравнение полученных результатов с дифрак-
цией Френеля [1]. Разработанный алгоритм решения двухмерных СИУ прежде
всего исследовался на внутреннюю сходимость, которая показана в таблице 1, где
показаны значения ez (р, 0) в некоторых точках отверстия с размерами а = Л, I = X
для Е-плоскости. Установлено, что для получения относительной погрешности вы-
числения ЭМП менее 0,5 % достаточно взять D = N -12 членов разложения рядов
(8.4.13) и (8.4.19).
В качестве примера на рис. 8.20 приведены распределения модуля электричес-
кого поля в отверстии e2(p,t) в плоскости Н (t = 0) (а) и в плоскости Е (р = 0) (б) при
дифракции плоской ЭМВ Е-поляризации на прямоугольном отверстии с размера-
ми а/Х = 1/2, Z/X = l/2. На рис. 8.21 приведены нормированные распределения
s-составляющей электрического поля в плоскости Н:
394
ГЛАВА 8
Ez (р, t = 0, г)
zmax
(p,t = O,r)
на разных расстояниях г от прямоугольного отверстия (а/Х = 1/2, 1/Х = 1/ 2).
На рис. 8.22 приведены на этих же расстояниях г нормированные распределения
z-составляющей электрического поля в плоскости Е\
Ez(p = O,t,r)
zmax
(р = O,t,r)
Штриховыми кривыми обозначены нормированные распределения, полученные в
приближении Кирхгофа [1]. Показано, что при расстояниях от экрана г > ЗХ са-
мосогласованный метод и приближение Кирхгофа дают практически одинаковые
результаты.
Комплексные значения функции ez (р, 0)
для фиксированных значений координаты
р = х / а при различных значениях N (при D = N ).
Таблица 8.1
N/ /Р р = -0.5 р = 0 р = 0.2 р = 0.8
8 -0.001631+ +0.0915011 -0.001819+ +0.0994101 -0.001908+ +0.0919281 -0.001242+ +0.0737361
10 -0.001570+ +0.0845831 -0.001949+ +0.0911241 -0.001832+ +0.0899171 -0.001113+ +0.0738111
12 -0.001577+ +0.0854501 -0.001953+ +0.0921331 -0.001799+ +0.0888761 -0.001139+ +0.0734531
Таким образом, самосогласованный метод решения некорректных задач элек-
тродинамики [13] устранил две типичные некорректности. Во-первых, предложен-
ный метод позволяет при решениях задач дифракции на телах обойтись без при-
ближения Кирхгофа. Во-вторых, устранен разрыв между ЭМП вблизи отверстия
и тангенциальными составляющими поля в отверстии. Кроме того, разработан ме-
тод решения двухмерных сингулярных интегральных уравнений путем сведения к
бесконечной системе одномерных сингулярных уравнений. Предложенный подход
может быть обобщен на более сложные задачи дифракции.
Щелевые антенны
395
а) б)
Рис. 8.20. Распределение модуля электрического поля в отверстии e2(p,t) в плоскости Н
(t = 0) (а) и в плоскости Е ( р = 0)
Рис. 8.21. Нормированные распределения функции z-составляющей электрического поля в
плоскости Нна разных расстояниях г от экрана ( а / X = 1 / 2; I / X = 1 / 2 ): а) — г / X = 0.5,
Рис. 8.22. Нормированные распределения функции z-составляющей электрического поля в
плоскости Е на разных расстояниях г от экрана (а/Х = 1/2;?/Х = 1/ 2):а) — г / X = 0.5,
б) — г / X = 1
б)
396
ГЛАВА 9
Глава 9. Антенны бегущей волны
Ранее были рассмотрены антенны, представляющие собой линейные
электрические вибраторы, щелевые вибраторы и рамочные антенны, ток или поле
вдоль которых распределены по закону стоячей волны.
Наряду с указанными широко применяются линейные излучающие системы из
одинаковых источников ЭМП, расположенных непрерывно или дискретно вдоль
заданного направления в пространстве, ток (поле) по которым распределен по
закону бегущей волны.
Примерами таких систем являются прямолинейный провод с электрическим
током, протяженная щель вдоль узкой стенки прямоугольного волновода, система
одинаковых излучателей, центры которых расположены по прямой линии (антен-
ная решетка), а также антенны, выполненные на основе замедляющих систем,
способных поддерживать поверхностные волны: диэлектрические стержневые,
спиральные,импедансные.
Возбуждение подобных антенн бегущей волны, реализующих осевое излучение
(или близкое к нему), осуществляется с одного конца, а режим бегущей волны
обеспечивается применением согласующих нагрузок на противоположном конце
или надлежащим выбором параметров замедляющей системы. Этим объясняется
общий недостаток таких антенн — значительные потери мощности в согласующей
нагрузке, а, следовательно, низкий КПД. В тех случаях, когда режим бегущей
волны удается реализовать без согласующей нагрузки, КПД антенны оказывается
высоким. При распространении по антенне бегущая волна в поперечном
направлении затухает по экспоненциальному закону. Это затухание, вызванное
излучением и отчасти потерями в проводе, необходимо учитывать при расчете
КПД антенны. Однако при расчете ДН и КНД затуханием часто пренебрегают и
считают распределение тока равномерным.
Характерной особенностью антенн бегущей волны является малость размеров
поперечного сечения излучающей системы. Рабочая полоса таких антенн составляет
обычно единицы процентов (значительно реже десятки процентов).
9.1. Излучение прямолинейного провода с бегущей волной тока [3]
Закономерности прямолинейного провода длиной L с бегущей волной тока (рис.
9.1,6) рассмотрим путем предельного перехода от линейной АР длиной L с числом
элементов, стремящимся к бесконечности (рис. 9.1,а).
9.1.1. Диаграмма направленности линейного непрерывного излучателя
[3]. Итак, рассмотрим вначале эквидистантную решетку из N одинаковых из-
лучателей, расположенную вдоль оси z, d — шаг решетки. В силу линейности
уравнений электродинамики поле системы излучателей представляет собой сумму
полей отдельных элементов. Если излучатели при этом одинаковы, ДН линейной
излучающей системы может быть записана в виде
7(e,q>) = 71(e,<p)/(c’(e), (9.1.1)
где /х(0, <р) — векторная комплексная ДН элемента излучающей системы; / с (0)
Антенны бегущей волны
397
М(г, О, ф)
а)
м(г, е, ф)
б)
Рис. 9.1. К расчету множителя направленности дискретной (а) и непрерывной (б) линейной
излучающей систем
- скалярный комплексный множитель направленности (множитель решетки)
системы изотропных излучателей, располагаемых в точках размещения центров
реальных излучателей.
Для дискретной линейной антенной решетки множитель направленности
N
/c>(9) = ^Ineifa”cose, (9.1.2)
71=1
где 1п = — комплексная амплитуда возбуждения п -го излучателя, к = 2л / X
— фазовая постоянная свободного пространства, zn - координата излучателя п;
6 - угол, отсчитываемый от оси антенны (рис. 9.1,а).
В случае возбуждения линейной решетки с числом излучателей N токами
равной амплитуды с линейно нарастающим вдоль решетки фазовым сдвигом
In = Ione , суммирование согласно формуле (9.1.2), приводит к
следующему выражению нормированного множителя направленности (множителя
решетки):
F(c)(0) =
sin(Ar\|/ / 2)
N зш(ф / 2) ’
(9.1.3)
где ф = /cd(cos 0 - у) - сдвиг по фазе между полями соседних излучателей в
точке наблюдения; у = с / = ф} / (kd) — замедление фазовой скорости волны
возбуждения.
398
ГЛАВА 9
Непрерывную линейную излучающую систему - линейный излучатель — можно
рассматривать как предельный случай линейной антенной решетки длиной L с
числом элементов, стремящихся к бесконечности (рис. 9.1,6). Тогда суммирование в
(9.1.2) необходимо заменить интегрированием:
L/2
/(©)= f I(z)eikzcosf>dz.
-L/2
(9.1.4)
Здесь I(z) = 10егф(2' - распределение тока в излучателе по амплитуде и фазе.
Множители направленности (9.1.2)
излучающих систем не зависят от азимутальной координаты (р и обладают
симметрией относительно оси z.
Пусть непрерывный линейный излучатель возбуждается током постоянной
амплитуды 10 с фазовым распределением, соответствующим
замедлением фазовой скорости у = с / Уф :
iyfcz т /су
(9.1.4) дискретной и непрерывной
бегущей волне с
l(z) = 10е
Подставляя (9.1.5) в (9.1.4) и производя интегрирование и нормировку, для
нормированного множителя направленности получим
F(u) =
sin(U)
(9.1.6)
где U = kL / 2(cos(0) - у) — обобщенная координата, имеющая смысл половины
разности фаз колебаний в точке наблюдения от крайних точек излучателя с учетом
как пространственной разности хода лучей kL cos(O), так и полной разности фаз
возбуждения крайних точек излучателя.
Множитель направленности (9.1.6) — вещественная функция. Поверхности
равных фаз поля излучения имеют вид сфер с центром в середине излучателя.
Фазовый центр такого излучателя находится в его середине независимо от
значения замедления фазовой скорости у .
График функции sin(U) / U показан на рис. 9.2,а. Эта функция непериодическая
и имеет одно наибольшее значение, равное единице при U = 0. Из формулы (9.1.6)
следует, что уровень первого бокового лепестка относительно главного составляет
0,21 (-13,2 дБ).
Проанализируем множитель F(U) непрерывной системы, который определяет
ее направленные свойства, так как направленность элементарных источников,
образующих непрерывную систему, выражена весьма слабо. На рис. 9.2,б-е
изображены графики функции | sin(U) / U |, на которых выделены штриховкой
части, находящиеся в интервале -kL(l + у) / 2 < U < кЦ1 - у) / 2 обобщенной
координаты U. Этот интервал изменения U соответствует реальной ДН, т.е.
значениям угла 180° > 0 > 0 (область реальных углов).
В случае у = 0 (синфазная система) интервалу углов 180° > 0 > 0 соответствует
интервал —kL / 2<U < kL / 2 (рис. 9.2,6). Диаграмма направленности, изображенная
на этом рисунке, довольно хорошо совпадает с ДН дискретной решетки, если
число излучателей в ней N >6 (при расстояниях между соседними излучателями
d = к / 2 ).
Для определения ширины ДН по уровню 0,7 поля необходимо положить
F(Uq 7) = 0.707, т.е. решить трансцендентное уравнение
Антенны бегущей волны
Рис. 9.2. К анализу множителя непрерывной системы излучателей: а) - вид функции
sin([J) / U; б)-е) - графики функции sin(l7) / U при у - 0; 0 < у < 1; у = 1; у » 1
400
ГЛАВА 9
-in(U) = 0.707.
Из решения этого уравнения следует = 1.39, откуда
7 т л л
Uq 7 - —sin(0O5), и 20О5 ® 0.89— = 51° —.
2 L L
Если 0 < у < 1 (фазовая скорость волны возбуждения превышает скорость
света), что соответствует линейному изменению фазы вдоль провода, то
интервал изменений U сдвигается влево по оси U (рис. 9.2,в,г). Главный максимум
ДН наклоняется при этом к оси решетки по направлению распространения
волны ( cos9гл = у) и при у = 1 (фазовая скорость волны равна скорости света) он
ориентирован вдоль оси системы (режим осевого излучения).
При у > 1 (антенна возбуждается замедленной волной) весь интервал изменения
обобщенной координаты U , для которого 180° > 0 > 0 , расположен в пределах
отрицательных значений оси U. Если у незначительно превышает единицу, то
главный максимум ориентирован в направлении оси провода, но его величина
уменьшается (рис. 9.2,д). С увеличением замедления у величина главного максимума
может сравняться с величиной первого бокового лепестка и ДН провода будет
состоять из нескольких примерно одинаковых лепестков (рис. 9.2,е).
Ширина ДН отклоненного луча при у < 1 может быть определена по формуле
где Ьэф ~ L sin 0О 5 — эффективная длина раскрыва системы.
Эта формула справедлива во всем секторе углов, кроме сектора, примыкающего
к оси решетки и равного одной ширине главного лепестка ДН. В этом секторе не
существует точки, соответствующей уровню 0,7 поля с одной стороны главного
лепестка ДН.
При излучении точно в направлении оси провода, имеющего большую длину
L > 5Х, ширина ДН при у = 1
Таким образом, при осевом излучении зависимость ширины ДН от относительной
длины антенны L / А более слабая, чем в случае синфазной антенны или антенны
с линейным изменением фазового сдвига; в предположении, что элементарные
источники, образующие непрерывную антенную систему, направленными
свойствами не обладают. Следовательно, при отклонении ДН, т.е. при сканировании,
ширина ДН изменяется; изменяется также ширина и форма боковых лепестков.
Если при у = 0 главный лепесток ДН имеет форму диска (рис. 9.3,а), при у = 1 -
вытянутого эллипсоида вращения (рис. 9.3,в), то приО < у < 1 направления главного
излучения образуют поверхность конуса вращения относительно оси системы (рис.
9.3,6).
Таким образом, линейные антенны осевого излучения обеспечивают
направленность в двух взаимно перпендикулярных плоскостях, в то время как
синфазные линейные антенны поперечного излучения концентрируют мощность в
узкий пучок только в экваториальной плоскости.
Ширину главного лепестка ДН при осевом излучении можно сузить, если
Амтенны бегущей волны
401
а)
б)
Рис. 9.3. Режимы излучения антенны: а) — поперечное излучение, б) — наклонное излуче-
ние, в) - продольное излучение [3]
1. Тогда центральная часть главного
перейти к режиму небольшого замедления у
лепестка множителя направленности | sin(l7) / U | уходит в область мнимых углов
(рис. 9.2,д), и главный лепесток существенно обостряется. Однако уровень боковых
лепестков, определяемый по отношению к значению функции | sin(U) / U | на
границе области реальных углов, повышается. Компромисс между сужением
главного лепестка и ростом уровня боковых лепестков может быть достигнут при
выборе границы реальных углов, удовлетворяющих условию U
одновременно обеспечивает максимальный КПД линейной антенны с замедленной
фазовой скоростью и называется условием оптимальности линейной антенны с
замедленной фазовой скоростью возбуждения:
kL , ч. л 7iL(l - у) 71
----(у — 1) =-или-------=----.
—тс / 2. Это условие
Отсюда следуют соотношения
i опт
опт
-1)
(9.1.8)
позволяющие найти оптимальное замедление при заданной длине антенны и
вычислить оптимальную длину при заданном значении замедления. Соответственно,
выражение для ширины ДН принимает вид
20™т = 2 121^. = 60,6° Д.
(9.1.9)
Таким образом, переход от значения у = 1 к оптимальному замедлению приводит
к сужению главного лепестка ДН при осевом излучении примерно в 1,8 раза.
Если у = 1, а элементарные источники, образующие линейную антенну
(провод с бегущей волной), обладают направленными свойствами ( /1(6) = sin 9, см.
(9.1.1)), то в направлении оси провода 6 = 0°, где множитель системы sin(U) / U
максимален, результирующее поле обращается в нуль, так как в выражении (9.1.1)
sin 9 = sin 9° = 6. В связи с этим, результирующее поле оказывается максимальным
в некотором промежуточном направлении, составляющем угол 01гл с осью провода.
402
ГЛАВА 9
При большой относительной длине провода (kL » 1) это направление максимального
излучения может быть приближенно определено с использованием (9.1.6) путем
приравнивания числителя к значению ±1:
sin[fcL(cos вгл - у)] = ±1,
откуда
(cos 01гл -1) = ± -
cos 01г,г
(9.1.10)
При большой длине провода угол 0^ мал и cos0la/l можно разложить в ряд:
cos 01гл ~ 1_ ®1гл / 2 = 1 - X / (2L),
откуда 01гл « у/к/ L = 57° /Ь.
Так, если X / L = 1.25 , то 01гл = 50°, если же л / L = 3,5 , то 0^г/г = 30° (рис. 9.4).
Изменение длины волны генератора слабо сказывается на направлении
максимального излучения 01гл, а также на входном сопротивлении. Поэтому
провод в режиме бегущей волны является диапазонной антенной.
Следует учитывать тот факт, что реальные антенны бегущей волны имеют
не постоянное, а спадающее от начала к концу амплитудное распределение поля
(тока) вследствие наличия затухания, обусловленного излучением энергии. Это
вызывает изменение формы ДН провода. Однако если поле в конце провода
уменьшается не более чем в три раза по сравнению с полем в начале, то
искажения ДН незначительны и при расчете ДН можно пользоваться множителем
направленности F(U) = sin(U) / U.
90° L = Л
270°
90° L = ЗХ
270°
Рис. 9.4. Направления максимального излучения антенны бегущей волны при разных ее
длинах [3]
Аытенны бегуидей волны
403
9.1.2. Коэффициент направленного действия антенны бегущей волны [3].
При известной полной нормированной ДН антенны с учетом амплитудной ДН оди-
ночного элемента, КНД линейного излучателя может быть найден по формуле
для КНД (2.2.6). Вычисления КНД упрощаются, если принять элементы, образую-
щие непрерывную излучающую систему ненаправленными (изотропными).
После подстановки множителя направленности F(U) - sin([7) / U в выражение
(9.1.4), интегрирования и ряда преобразований для КНД линейного излучателя в
области значений замедления 0 < у < 1, соответствующих поперечному ( 0 = 90° ,
рис. 9.3,а,б) и наклонному излучению, имеем [3]
D « 2L / X при L » Л.
В режиме осевого излучения (у = 1) КНД линейной антенны вдвое превышает
КНД в режиме наклонного излучения:
D « 4L / X.
Если замедление волны у в линейном излучателе больше единицы, то КНД
возрастает по сравнению со значением 4L / X из-за сужения главного лепестка
ДН. Однако с ростом у увеличивается уровень боковых лепестков, что приводит к
падению КНД. Оптимум по КНД достигается при значении обобщенной координаты
опт
Uonm «7.2L/X,L»X. (9.1.11)
С/1Ь I /b • 7 х '
Сравнение условия оптимальности линейной антенны с замедленной фазовой
скоростью (у > 1)
Т Т Tt.L(l У Q'n'fn ) 7 Т /1 \
Uопт ~ ~ Л или —я = kL(l — уопт).
Z Л
с наблюдаемой в направлении максимума главного лепестка 0 = 0° полной разностью
фаз полей излучения начального и конечного элементов линейной излучающей
системы
U = Щсоб 0 -1) = кЦ1 - уопт)
показывает, что у оптимальной системы эта разность фаз составляет около 180°.
9.2. Ромбическая антенна [17]
9.2.1. Принцип действия. Антенна имеет форму ромба и располагается обычно
горизонтально (рис. 9.5). У одного острого угла подается питание от фидера 1,
у другого антенна присоединена к нагрузочному сопротивлению 2, равному ее
волновому сопротивлению. В результате этого вдоль сторон ромба распространяется
бегущая волна тока.
Ромбическая антенна применяется на коротких волнах для дальних радиосвязей
ионосферной волной как в качестве приемной, так и в качестве передающей
антенны. При работе на передачу в нагрузочном сопротивлении обычно должна
рассеиваться значительная мощность, поэтому в качестве нагрузки используют
длинную поглощающую линию, изготовленную из стального провода. У приемной
ромбической антенны нагрузкой может служить резистор.
По длине ромба расстояние между его сторонами изменяется. Поэтому меняется
и волновое сопротивление антенны. Чтобы выравнять волновое сопротивление.
404
ГЛАВА 9
Рис. 9.5. Ромбическая антенна [17]
Рис. 9.6. К пояснению принципа действия ром-
бической антенны [17]
стороны ромба изготавливают из двух расходящихся проводов. Обычно такие
ромбические антенны имеют волновое сопротивление около 700 Ом.
Принцип действия ромбической антенны поясним с помощью рис. 9.6. На нем
изображены главные лепестки диаграмм направленности всех четырех сторон
ромба. Острый угол ромба выбран равным 2Вгл, где 9гд - угол отклонения каждого
главного лепестка от оси провода. Из рис. 9.6 ясно, что при этом лепестки 1,2,3
и 4 ориентированы вдоль большой диагонали ромба. Можно показать [17], что
поля излучения всех сторон антенны складываются в направлении большой
диагонали ромба синфазно. Поэтому главный лепесток ДН ориентирован в этом же
направлении.
Выше было показано, что угол отклонения лепестка от оси прямолинейного
провода мало меняется с изменением X, если отношение!, / X велико.Следовательно,
при изменении длины волны будут в известных пределах сохраняться и условия
формирования главного лепестка ДН ромбической антенны. Поэтому ромбическая
антенна является диапазонной по направленным свойствам. Так как антенна
нагружена на активное сопротивление, равное ее волновому сопротивлению, то
она является диапазонной также и по согласованию с фидером питания.
9.2.2. Диаграммы направленности. Диаграммы направленности ромбической
антенны определяются путем сложения полей излучения ее четырех проводов и
имеют следующий вид [17]:
в горизонтальной плоскости
/(ф) =
соз(Ф0 + ф) соз(Ф0 - ф)
1 - 5ш(Ф0 + ср) 1 - sin(O0 - ф)
xsin
[1 - sin(<D0 + ф)]
[l-sin(<D0 -ф)Ь,
(9.2.1)
в вертикальной плоскости, содержащей большую диагональ ромба,
f(3) =----------------sin2
1 - sin Фо cos &
[1 - 5ш(Ф0) cos(3)]
sin(/cH sin 3),
(9.2.2)
где Фо - половина тупого угла ромба (рис. 9.6); Н — высота подвеса ромба над
землей; 3 - угол возвышения, отсчитываемый от горизонтального направления;
Антенны бегущей волны 405
(р - азимутальный угол, отсчитываемый от большой диагонали. Последний
множитель формулы (9.2.2) учитывает влияние земли, которая принята идеально
проводящей.
На рис. 9.7 приведены типичные ДН ромбической антенны. Из рисунка
видно, что ромбическая антенна имеет сравнительно большой уровень боковых
лепестков. Значительное ослабление боковых лепестков достигается в двойной
ромбической антенне, предложенной Г.З. Айзенбергом [17]. Она состоит из двух
питаемых синфазно ромбических антенн, расположенных рядом и удаленных в
горизонтальном направлении вдоль малой диагонали на расстояние d друг от друга
(рис. 9.8). ДН антенны в горизонтальной плоскости имеет вид
У (ср) = /о (ср) cos(0.5kd sin ср). (9.2.3)
Здесь/о((р)- ДН одиночной ромбической антенны, определяемая по формуле(9.2.1),
a cos(0.5kd sin ср) есть множитель двухэлементной синфазной решетки. Расстояние
d выбирается так, чтобы направление первого нуля множителя совпадало с
направлением наибольшего бокового лепестка ДН одиночной ромбической антенны,
благодаря чему эффективно уменьшается уровень боковых лепестков.
9.2.3. Коэффициент полезного действия ромбической антенны в пределах
диапазона рабочих частот изменяется: с увеличением длины волны он падает.
Обычно КПД имеет величину 50-60 %. Сравнительно низкий КПД является недо-
статком ромбической антенны.
9.3 Спиральные антенны
9.3.1. Классификация и типы спиральных антенн [3]. На частотах 300
МГц и выше широкое применение находят цилиндрические спиральные антенны
(рис. 9.9,а), излучающие поле с круговой поляризацией в направлении оси.
Антенна состоит из проволочной спирали 1 длиной несколько X при диаметре
витка, примерно равном X / л. Один конец спирали остается свободным, а другой
соединен с внутренним проводником коаксиальной линии 3. Внешний проводник
коаксиальной линии присоединяется к металлическому экрану 2 для ослабления
обратного излучения антенны. В спирали возникает бегущая волна электрического
тока и максимум излучения оказывается ориентированным вдоль оси в сторону
движения волны тока.
Различают регулярные (рис. 9.9,а), геометрические параметры которых (шаг
S , радиус намотки а, длина витка спирали L , угол подъема витка а, диаметр
провода) постоянны по длине антенны I, и нерегулярные (рис. 9.10,б,в) спиральные
антенны. В общем случае спиральные антенны излучают волны эллиптической
поляризации.
По числу заходов М (ветвей) и способу их намотки спиральные антенны могут
быть одно- и многозаходными с односторонней (рис. 9.10,а) или двусторонней
(встречной) намоткой (рис. 9.10,6).
В ряде случаев для увеличения жесткости конструкции намотка спирали
осуществляется на диэлектрическом каркасе (рис. 9.11), что одновременно
приводит к дополнительному замедлению фазовой скорости волны в антенне.
406
ГЛАВА 9
30° 60° 90° 30° 60° 90°
а) б)
Рис. 9.7. Типичные ДН ромбической антенны: а) — в горизонтальной плоскости; б) — в вер-
тикальной плоскости [17]
Рис. 9.8. Двойная ромбическая антенна: 1 - линия питания; 2 - линия к нагрузке [17]
а) б) в)
Рис. 9.9. Спиральные антенны: а) - цилиндрическая регулярная; б) — нерегулярная кони-
ческая с постоянным шагом намотки; в) - цилиндрическая с переменным шагом [17]
а)
б)
Рис. 9.10. Цилиндрические регулярные спиральные антенны: а) - многозаходная (четырех-
заходная) с односторонней намоткой; б) - многозаходная (четырехзаходная) с двусторон-
ней (встречной) намоткой [17]
Антенны бегущей волны
407
ЕЖ
Рис. 9.11. Спиральная антенна с дополнительным замедлением
I
I
I
I
D « (0.25...0.40)Х i
а) б)
Рис. 9.12. Режимы излучения спиральной антенны: а) - поперечное излучение, б) — осевое
излучение, в) - излучение с ДН воронкообразной формы [3]
Рис. 9.13. Зависимость фазовой скорости различных типов собственных волн от величины
ка в цилиндрической спиральной антенне [3]
408
ГЛАВА 9
9.3.2. Теория регулярной цилиндрической спиральной антенны [3]. Стро-
гое решение электродинамической задачи для спирали как излучающей системы
показывает, что в ней может распространяться система волн Тп, называемых
собственными. В зависимости от отношения диаметра спирали к длине волны в
собственной волне Тп может резонировать та или иная азимутальная пространс-
твенная гармоника. Индекс " п" резонирующей пространственной гармоники и оп-
ределяет характер излучения спиральной антенны (диаграмму направленности,
поляризационные и фазовые характеристики).
Характерны три вида форм ДН цилиндрической спиральной антенны. Если
диаметр спирали D < 0,2Х , то в ней преобладает волна типа То , характеризующаяся
изменением фазы тока в пределах 360° на протяжении нескольких витков;
амплитуда волны вдоль спирали постоянна, а фазовая скорость = с. За счет
отражения волны То от конца спирали в ней устанавливается режим стоячей
волны, излучение вдоль оси спирали отсутствует и максимум излучения антенны
получается в поперечной плоскости спирали (рис. 9.12,а). Ближайший тип волны
Ту при этом имеет весьма малую амплитуду и вклад этой волны в общее поле
излучения незначителен.
Когда диаметр витка D спирали лежит в пределах (0.25 - 0.40)Х, в антенне
преобладает волна Ту, и максимум излучения направлен вдоль оси спирали (рис.
9.12,6). Возникающая при этом в спирали волна низшего типа То , а также волны
высших типов Тп при п > 1 быстро затухают по длине спирали, а их вклад в ДН
невелик.
При дальнейшем увеличении диаметра спирали ( D > 0.4 5Х) в собственной волне
Тп определяющей является вторая азимутальная пространственная гармоника
(волна Т2), и ДН приобретает коническую (воронкообразную) форму (рис. 9.12,в).
Угол раскрыва «воронки» зависит от относительного диаметра спирали.
Режим осевого излучения ( D ~ (0.25 - 0.40)Х ), когда длина провода витка
спирали примерно равна рабочей длине волны ( L «X), является основным
режимом работы спиральных антенн.
В режиме осевого излучения витки спирали излучают весьма интенсивно,
благодаря чему к концу спирали практически излучается вся подводимая к антенне
мощность; отражение от конца спирали отсутствует и в ней устанавливается
режим бегущей волны. Фазовая скорость волны Ту при этом меньше скорости света
с: “0.8с (рис. 9.13) Для обеспечения круговой и близкой к ней поляризации
поля, а также интенсивного излучения каждого витка в осевом направлении (ось
z , рис. 9.14,6) необходимо, чтобы выполнялось то же условие L « X.
Рассмотрим излучение одного витка спирали длиной L = X с волной Ту. Будем
считать виток плоским. Распределение тока в витке подчиняется закону ,
где Iq — ток в начале витка; LT - текущая координата, отсчитываемая вдоль витка.
При длине витка Ly = L = X распределение тока по нему можно представить в
виде 1ое-гср. Здесь <р — азимутальный угол в плоскости витка (рис. 9.14,а,б).
Пусть распределение тока по витку (в момент времени t — 0) соответствует
сплошной линии на рис. 9.14,в (виток изображен в развернутом виде). Так как
токи вблизи точек а, с, е малы, приближенно можно заменить виток двумя
изогнутыми горизонтальными полуволновыми синфазными излучателями (рис.
9.14,а) с током 1Х. Поле излучения витка Е поляризовано горизонтально, и
максимум ДН ориентирован вдоль оси z витка. Через четверть периода (t = Т / 4)
Антенны бегуньей волны
409
а) б)
в)
Рис. 9.14. К излучению витка спирали с волной Тг: а,) б) - замена витка спирали эквива-
лентным горизонтальным и вертикальным излучателями;
в) - развертка витка спирали [17]
картина распределения тока сместится на X / 4 в направлении движения бегущей
волны (пунктир на рис. 9.14,в). Теперь виток можно приближенно заменить двумя
вертикальными полуволновыми излучателями с током 1у, и поле излучения будет
вертикально поляризовано (рис. 9.14,6). Видим, что за один период колебаний
вектор электрического поля повернется в пространстве на 360°. Следовательно,
в режиме волны Т\ спиральная антенна излучает поле вращающейся (круговой)
поляризации с максимумом вдоль оси z антенны. Направление вращения поля
соответствует направлению намотки спирали.
В реальной спиральной антенне виток лежит не в одной плоскости, а имеет
некоторый шаг намотки S (рис. 9.15). Если шаг намотки и диаметр витка выбраны
так, что сдвиг фаз между напряженностями полей, создаваемых первым (№1) и
последним (№2) элементами витка спирали равен 2л. то в направлении оси спирали
сохраняется круговая поляризация и максимум излучения:
2тг _ 2л ~ Л ,
----L-----S = 2л. 9.3.1)
11
'^зам
Здесь 2лЯ / % - сдвиг фаз между полями начального и конечного элементов витка,
определяемый разностью хода лучей; 2лХзам / L - сдвиг фаз полей указанных
элементов, определяемый сдвигом фаз токов этих элементов.
Из (9.3.1) следует соотношение между параметрами спирали L и S,
410
ГЛАВА 9
Рис. 9.15. К расчету витка спирали, обеспечивающей круговую поляризацию
соответствующие Крутовой поляризации,
L = (S + k)/y,
(9.3.2)
где у = с / = X / Хзаж -
замедление волны в спирали.
Удовлетворение условию (9.3.1) при конструировании антенны не обеспечивает
максимального значения КНД. Спиральная антенна - антенна осевого излучения
с замедленной фазовой скоростью волны тока вдоль оси антенны. В таких антеннах
[3] максимальный КНД получается при сдвиге фаз между полями излучения
первого и последнего витков, равном л, т.е. вместо (9.3.1) должно выполняться
условие
где N ~ число витков спирали.
Отсюда
£ + X + X / (2N)
(9.3.3)
Таким образом, при соблюдении условия (9.3.2) в направлении оси антенны
получается круговая поляризация, а при соблюдении условия (9.3.3) — максимальный
КНД при некоторой эллиптичности поля излучения. Поскольку замедление волны у
с увеличением длины волны увеличивается (рис. 9.13), соотношения (9.3.2) и (9.3.3)
нарушаются незначительно, и спиральная антенна сохраняет удовлетворительные
значения параметров в диапазоне длин волн (О.7-1.2)Хо, где Хо - длина волны,
для которой подобраны оптимальные размеры антенны. При этом значение утла
подъема витка спирали а = arcsine / L) может лежать в пределах 12 -18°.
Если цилиндрическая спиральная антенна обеспечивает режим осевого
излучения при коэффициенте перекрытия по частоте Кп — Xmax / Amin » 1.7,
то конические спиральные антенны более широкополосны (Кп « 2...3). Так как в
конической спирали витки имеют различную длину, на любой частоте рабочего
диапазона в спирали имеется группа витков (рабочая область), на каждом из
которых укладывается примерно одна длина волны типа Ту. При изменении частоты
рабочая область перемещается вдоль оси спирали. Следовательно характеристики
направленности таких антенн определяются не общим числом витков (или полной
длиной спирали), а лишь числом витков в группе с волной Ту (длиной этого участка
спирали). Излучение остальных витков слабо влияет на общее поле антенны.
В многозаходных цилиндрических спиральных антеннах с односторонней
намоткой (рис. 9.10,а) при осевом излучении (волна Ту) рабочий диапазон
411
Антенны бегущей волны
3
(р = 2лМ
Рис. 9.16. Точки возбуждения многозаходной спиральной антенны [3]
дополнительно расширяется вследствие подавления в них ближайших низших и
высших типов волн.
Многозаходная спиральная антенна с двусторонней намоткой (рис. 9.10,6)
позволяет управлять поляризацией поля излучения, если число заходов (ветвей)
М > 2 . Так, для волн Tr±1i, обеспечивающих в спиральной антенне режим прямого
осевого излучения с правой и левой круговой поляризацией, комплексная
амплитуда токов возбуждения меняется от захода к заходу по закону
-i2n(Z-l)M
(9.3.4)
при волне
и по закону
k - W
(9.3.5)
при волне Т_у.
Здесь Iq ~ амплитуды токов; I - номер симметричной точки (номер захода),
отсчитываемый от произвольного захода по направлению возрастания угла ф
(I = 1,2,...,М) (рис. 9.16). Если заходы возбуждаются одновременно токами if и If,
то поляризация в направлении оси — эллиптическая с осевым коэффициентом
поляризационного эллипса
При Iq > 10 поляризация поля излучения — правая, при Iq < Iq — левая, при
Iq = Iq линейная. Случай Iq = 0 ( If = 0) соответствует полю с круговой правой
(левой) поляризацией.
9.3.3. Цилиндрическая спиральная антенна как линейная решетка [3].
Направленные свойства спиральной антенны осевого излучения можно опреде-
лить, рассматривая спираль как линейную решетку, состоящую из ряда излуча-
телей ~ витков (рис. 9.17,а,б). При этом
Fe(0) = F10(e)F(c)(6), Рф(6) = Fllp(9)F(c)(e).
(9.3.6)
412
ГЛАВА 9
Рис. 9.17. К определению поля излучения спиральной антенны (а,б) и кольца с бегущей
волной тока [3]
Множители 1*10(0) и ^„(б) представляют собой ДН одного витка соответственно
для меридиональной и азимутальной составляющих поля. Эти множители для
витка (кольца) радиуса а (рис. 9.17,в), по длине которого укладывается п длин
волн, имеют вид
Fie(0) ~ pn-iCfcasinO) + Jn+i(kasin0)]cos0,
^i<p (0) = Jn-1 (ka sin 0) - Jn+1 (ka sin 0),
(9.3.7)
где к = 2n / % ; J<n+i) ~ функция Бесселя действительного аргумента, причем п = 1
относится к противофазному возбуждению, п = 2 — к синфазному [2]. Формулы
(9.3.7) позволяют также рассчитывать излучение круглых рамочных антенн с
радиусом а = (X / 2л)п и распределением стороннего тока = exp(-m(p);n = 1,оо.
Рассчитанные по формулам (9.3.7) ДН витка для различных азимутальных
гармоник при ка = п приведены на рис. 9.18.
Антенны бегущей волны
413
F10(6)
0.0 20 40 60 6,град
Гкр(0)
б)
Рис. 9.18. Диаграммы направленности (0-я и <р-я компоненты) азимутальных про-
странственных гармоник [3]
а)
Функция F^C\G) в (9.3.6) есть множитель решетки и имеет вид
(9.3.8)
где N - число витков; £ - шаг спирали (рис. 9.17,6); = 2л/ Хзам - сдвиг по фазе
токов двух соседних витков; у = X / h3aM .
Из выражений (9.3.7), (9.3.8) и рис. 9.18 следует, что режим прямого (или
обратного) осевого излучения обусловлен излучением первой азимутальной
пространственной гармоники (п = ±1). Причем при п = 1 поляризация в направлении
оси z - правая круговая, прип = -1 - левая круговая. Все другие пространственные
гармоники не обеспечивают режима осевого излучения.
Ширина ДН спиральной антенны с постоянным диаметром витка, ее КНД и
входное сопротивление могут быть определены по формулам [18]:
(9.3.9)
Обычно число витков антенны не превышает 7-8. Ширина ДН при этом
составляет около 40°. Для получения более узких ДН применяются решетки
спиральных излучателей.
Формулы (9.3.9) справедливы, если число витков п > 3 , углы подъема спиралей
а лежат в пределах от 12 до 16°, а L/Х меняется от 0.75до 1.3[18].
При приближенных расчетах длину витка L принимают равной расчетной
длине волны Х0 , шаг спирали £ = (0.15 - О.З)Х0 , а коэффициент укорочения волны
2, = X / Хсп = 1.25. Рабочий диапазон определяется из условия 0.7L < X < 1.3L .
414
ГЛАВА 9
Диаметр экрана выбирается в пределах (1.0 -1.6)L , где L — длина спирали.
Заметим, что длина витка может быть выбрана так, что поля излучения
будут складываться в фазе в направлении, противоположном направлению
движения волны тока. При этом спиральная антенна работает в режиме обратного
излучения.
Нетрудно показать, что в этом случае вместо условий (9.3.3) и (9.3.2)
соответственно справедливы условия [17]:
L = (X-S)/y,
L = (X - X / 2N - 5)
(9.3.10)
Активное входное сопротивление [17] спиральной антенны осевого излучения
имеет величину 60-90 Ом и несколько растет с увеличением параметра ка. Оно
мало зависит от числа витков. Это объясняется тем, что при изменении числа
витков сохраняется режим бегущих волн вдоль спирали.
Поляризация поля [17] излучения спиральной антенны наиболее близка к
круговой в направлении оси спирали. При увеличении угла 0 (рис. 9.17) коэффициент
эллиптичности плавно уменьшается и близок к нулю при 9 = 90°. Направление
вращения вектора поля излучения соответствует направлению намотки провода
спирали.
Фазовый центр [17] спиральной антенны, строго говоря, отсутствует, так как
фазовая диаграмма антенны отличается от сферы. Приближенно можно считать,
что фазовый центр расположен вблизи геометрического центра спирали. На
практике положение фазового центра определяется опытным путем.
К достоинствам цилиндрических спиральных антенн следует отнести простоту
конструкции и широкую диапазонность ( Xmax / Amjn ® 1.7 ).
Недостатком является невозможность формирования при помощи одной спирали
диаграмм направленности шириной менее 25° (число витков нельзя брать больше
П) [18]
9.3.4. Решетки из нескольких идентичных спиралей [18]. Для получения
более узких диаграмм направленности применяются решетки из нескольких иден-
тичных спиралей. На рис. 9.19 показана решетка из четырех спиралей, предна-
значенная для обострения диаграммы направленности в двух главных плоскостях.
Рис. 9.19. Решетка из четырех спиралей [18]
Ампь^н/ны бегуньей волны
415
Диаграмма направленности ее как в горизонтальной,
кости определяется выражением
f kd А
/(0) = Л (0)2 cos —-sin0
\ 7
так и в вертикальной плос-
(9.3.11)
где Л(0) - диаграмма направленности одиночной спирали; d — расстояние между
центрами спиралей; 0 — угол, отсчитываемый от оси антенны (рис. 9.19).
9.3.5. Плоские спиральные антенны [17]. Плоская спиральная антенна может
быть образована путем вырезания спиральной ленты из металлического листа. В
зависимости от формы кромок спирали различают архимедову (арифметическую)
(рис. 9.20,а) и равноугольную (логарифмическую) (рис. 9.20,6) спиральные антенны.
Последнюю называют также логоспиральной антенной. Антенны могут быть одно-
заходные, двухзаходные и многозаходные.
Архимедовой спирали соответствует в полярных координатах уравнение вида
p = aq> + b, (9.3.12)
где р - радиус — вектор; <р - полярный угол; а и Ъ — константы (рис. 9.21,а).
Ленточный проводник образован двумя такими кривыми, отличающимися
значениями параметра Ъ (см. рис. 9.20,а). Ширина ленты равна, таким образом,
w = Ь2 - .
Двухзаходная спираль выполняется из двух идентичных лент, причем одна из них
повернута относительно другой на 180°. Обычно ширину лент и зазора выбирают
равной, тогда для двухзаходной спирали
а = 2ю/л. (9.3.13)
Уравнение логарифмической спирали имеет вид (9.21,6)
р = Ьехр(щр). (9.3.14)
Спираль называется также равноугольной потому, что касательная, проведенная
к ней в любой точке, образует с радиус — вектором угол, постоянный для данной
спирали.
а)
Рис. 9.20. Плоские двухзаходные спиральные антенны: а) - архимедова (арифметическая);
б) - равноугольная (логарифмическая) [17]
416
ГЛАВА 9
ср = О Ф = О
а) б)
Рис. 9.21. Архимедова (а) и логарифмическая (б) спирали
У двухзаходной логарифмической спиральной антенны первая ветвь образована
двумя одинаковыми спиралями, одна из которых р2 повернута относительно
другой Pi на угол 5 :
Pi = Ьехр(скр), р2 = Ьехр(а(ср - 5) = Врт
(9.3.15)
где
(9.3.16)
Вторая ветвь по отношению к первой повернута на 180°
образована спиралями
Рз - Ъ ехр(а(ср - л)), р4 = Ъ ехр(а(ср - л - 5) = Вр3.
относительно центра и
(9.3.17)
Спиральная антенна в свободном пространстве излучает в обе стороны. Для
получения однонаправленного излучения размещают ленточную спираль на одной
стороне диэлектрической пластины, металлизированной с другой стороны или
расположенной в раскрыве металлического резонатора.
Принцип действия двухзаходной архимедовой спиральной антенны можно
пояснить, рассматривая ее приближенно как двухпроводную линию, по которой
распространяется бегущая волна, причем ток в одном из проводников запаздывает
относительно тока в другом проводнике. Последнее обстоятельство и приводит к
излучению.
Пусть проводники возбуждаются в центре антенны в противофазе (рис. 9.22),
причем на этом рисунке один из проводников для большей ясности изображен
пунктиром. Если намотка равномерна, то для смежных элементов двух проводников
разность хода по проводу спирали от центра равна
А = лр0,
где pg - средний радиус витка спирали.
Поскольку оба провода возбуждаются в противофазе, то разность фаз токов в
смежных элементах равна
(9.3.18)
2л
(9.3.19)
Условие синфазности, когда у = 2лт (где т — целое число), имеет вид
13*
Антенны бегущей волны 417
Рис. 9.22. К пояснению принципа действия двухзаходной спиральной антенны [17]
Ро
= 2т -1.
(9.3.20)
При этом оба провода образуют «резонансные» кольца с бегущей волной тока.
Именно эти кольца и создают основную долю излучения, так как излучение
остальных витков будет в значительной мере взаимно компенсироваться.
Наибольший практический интерес представляет первый резонанс ( т = 1), так
как он обеспечивает осевое излучение поля вращающейся поляризации. Ввиду
интенсивного излучения первого резонансного кольца амплитуда тока вне его
(при р > pg) резко убывает.
При изменении длины волны меняется пропорционально и радиус резонансного
кольца, а электрические параметры антенны остаются неизменными. Таким
образом, спираль будет представлять собой весьма широкополосную антенну.
Наибольшая рабочая длина волны антенны Хтах определяется максимальным
радиусом спирали ртах:
^тах ^Кртах •
Для пояснения действия логарифмической спиральной антенны
безразмерный радиус - вектор
• Р ь ( ч
р = — = — ехр(аф)
(9.3.21)
введем
(9.3.22)
и представим его в виде
р' = ехр[а((р - ф0)], (9.3.23)
где
ф0 = а-11п(Х / Ь). (9.3.24)
Из формул (9.3.23) и (9.3.24) видно, что изменение длины волны эквивалентно
изменению фд , т.е. простому повороту всей спирали на угол фд относительно
ее оси. Характеристики антенны должны при этом оставаться неизменными.
Следовательно, антенна является широкополосной. Диаметр спирали должен быть
приближенно равен Хтах. Минимальная длина волны диапазона определяется
размером начального витка спирали, так как величина Xmin соответствует
резонансу на первом витке. Поскольку Атах и Xmjn не связаны между собой, можно
14 -Неганов
418
ГЛАВА 9
а)
Рис. 9.23. Экспериментальные ДН двухзаходной архимедовой спиральной антенны [17]
обеспечить рабочие диапазоны весьма значительной ширины. Удовлетворительные
ДН были получены в диапазоне с двадцатикратным перекрытием [17].
Диаграмма направленности плоской спиральной антенны, расположенной в
раскрыве резонатора, состоит из одного щирокого лепестка. Для иллюстрации
на рис. 9.23 приведены ДН двухзаходной архимедовой спирали, состоящей из
3.5 витков в плоскости, перпендикулярной спирали, причем направление 0 = 0
совпадает с нормалью к плоскости спирали.
Ширина ДН для составляющей Eq несколько меньше, чем для составляющей
Е(р. Резонатор (обычно цилиндрической формы) может несколько исказить форму
ДН спирали.
Поляризация поля плоской спиральной антенны — вращающаяся благодаря
тому, что по спирали распространяется бегущая волна тока. По мере отклонения
от осевого направления коэффициент эллиптичности убывает и в плоскости
спирали близок к нулю.
Согласование антенны с фидером питания, как и форма ДН, сохраняется в
широком диапазоне частот.
Логарифмические спиральные антенны относятся к классу частотно —
независимых антенн. Изменение поляризации поля является удобным критетием
для определения границ диапазона. Принято под «рабочим диапазоном» понимать
полосу частот, в которой коэффициент эллиптичности поляризационного эллипса
в направлении оси антенны не менее 0.5.
На частотах, при которых длина плеч больше длины волны, входное
сопротивление остается постоянным и активным. Его величина зависит от значения
коэффициента, определяющего ширину плеч. На рис. 9.24 показано изменение
входного активного сопротивления R в зависимости от величины к.
Логарифмическая спиральная антенна имеет высокий КПД. Измерения
показали, что для антенн, длина плеч которых больше или равна одной длине
волны, КПД примерно равен 98%. Для антенн, плечи которых короче, КПД
быстро уменьшается.
9.3.6. Коническая спиральная антенна [17]. Коническая спиральная антенна
(рис. 9.25) отличается от цилиндрической спиральной антенны (рис. 9.9, а) большим
коэффициентом перекрытия диапазона. У такой антенны условие круговой поля-
Антенны бегущей волны
419
Рис. 9.24. Входное сопротивление плоской лога- Рис. 9.25. Коническая спиральная антенна
рифмической спиральной антенны [18]
ризации будет выполняться в диапазоне от наибольшей длины волны Хтах , вели-
чина которой определяется наибольшим радиусом спирали атах, до наименьшей
длины волны Xmin, величина которой определяется наименьшим радиусом спи-
рали amin. Коэффициент перекрытия диапазона конической спиральной антенны
имеет величину более двух. Следует отметить, что режим волны Т[ имеет место
лишь на той части витков спирали, размеры которых удовлетворяют условию
(9.3.2) Именно эта «активная» часть витков создает осевое излучение вращающей-
ся поляризации. Поэтому при одинаковом числе витков коническая спиральная
антенна формирует более широкую ДН, чем цилиндрическая спиральная антенна.
С укорочением длины волны «активная» область спирали перемещается в сторону
витков с меньшим диаметром. Вместе с ней перемещается и фазовый центр ан-
тенны [17].
9.3.7. Коническая логарифмическая спиральная антенна может быть
представлена как проекция плоской логарифмической спиральной антенны на по-
верхности конуса. Эскиз однозаходной спирали, а также используемая система
координат изображены на рис. 9.26. Большое применение на практике получили
двухзаходные спиральные антенны. Кривые, ограничивающие одну ветвь коничес-
кой спиральной антенны, определяются уравнениями
где
Pi = Ъ ехр
<sin(0o)
< tg(ct)
В = ехр
Р2 = ВР1,
sin(0o)
tg(a)
(9.3.25)
(9.3.26)
Ф
6 — угол поворота одной кромки спирали относительно другой. Смысл обозначений
Pj, р2 , b , 0д , а, ср ясен из рис. 9.26.
Вторая ветвь спиральной антенны по отношению к первой повернута по углу ф
на 180° . Питание антенны осуществляется со стороны вершины конуса. В отличие
от плоской логоспиральной антенны, которая является двунаправленной (без
резонатора), коническая логоспиральная антенна является однонаправленной:
максимум излучения ориентирован в сторону вершины конуса. Следовательно,
антенна работает в режиме обратного излучения. Прямое излучение (в сторону
основания конуса) при угле 0О < 15 практически отсутствует. Ширина ДН сильно
зависит от угла а между радиус — вектором и касательной к логарифмической
спирали. Чем угол а меньше, тем ширина ДН больше. При достаточно малом угле
14*
420
ГЛАВА 9
Рис. 9.26. Коническая логарифмическая спиральная антенна [17]
е = о° 0 90° 270° 90° 180° = о° е = о° 270° 90° С 270° 180° 180°
Рис. 9.27. Типичные ДН конической логоспиральной антенны при различных углах а : а)
- а = 73°; б) - а = 60°,
сплошная линия - Е ; пунктир - Ее; 0О = 10° [17]
о .
параметрами, определяющими конфигурацию спирали,
ширина ветви, определяемая 6 или ;
определяющий скорость раскручивания спирали; диаметр основания атах
а можно получить ДН, близкую к полусфере с поляризацией излучения, близкой
к круговой (рис. 9.27).
Таким образом
являются: угол при вершине конуса 20о
угол а
и диаметр вершины amjn.
Металлические ветви антенны монтируются на диэлектрическом опорное
конусе. Быстрое спадание тока вдоль проводника спирали, наблюдаемое в плоской
спиральной антенне, имеет место и в конической спирали. Это позволяет
использовать аналогичный способ возбуждения, т. е. прокладывать кабель по
одной из ветвей, замыкая его внутренний проводник на вторую ветвь в вершине
конуса. Холостой кабель на второй ветви улучшает симметрию возбуждения.
Антенны бегугцен волны
421
Диаграмма направленности конической логоспиральной антенны зависит от
угла конусности 0О и в меньшей степени от угла а.
Границы диапазона со стороны высоких частот, как и у плоской антенны,
определяются диаметром спирали amjn у вершины конуса, а со стороны низких
частот — диаметром основания атах
В качестве примера приведем такие данные [18]. Спираль с параметрами 0О =10;
= 0.85 - 0.9 ; а = 73° ; dmjn = Xmin / 4атах = З^-max / 8 имеет уровень обратного
излучения не более 15 дБ, а коэффициент эллиптичности в направлении оси
не меньше 0.5. Поле сохраняет поляризацию, близкую к круговой, в пределах
широкого углового сектора по обе стороны от оси антенны (до 0О =70°).
Входное сопротивление конических логоспиральных антенн практически не
меняется в рабочем диапазоне частот. Его величина зависит от угла при вершине
конуса. Это зависимость показана в табл. 9.1 [18].
На величину входного сопротивления существенное влияние оказывает размер
amin > угол при вершине конуса и диаметр кабеля.
Таблица 9.1. [18]
д0 У0 10 15 30 90
Средняя величина входного сопротивления, Ом 129 147 153 164
В заключение отметим, что спираль может располагаться не только на
конической поверхности, но и на поверхностях другой формы. Например, нашли
применение логарифмические спирали, расположенные на поверхности сферы.
Применяются также различные модификации рассмотренных антенн. Например,
в качестве облучателя зеркальной антенны с коническим вращением луча
используются две конические логарифмические спирали, переключаемые для
приема излучения с круговой поляризацией левого и правого вращения. Две соосные
конические логоспиральные антенны позволяют сформировать квазиизотропную
ДН. Коническая логоспиральная антенна по форме ДН, согласованию с
линией питания и поляризации поля весьма широкополосна. Максимальная и
минимальная длины волн рабочего диапазона ориентировочно определяются
соотношениями [17]
^max — 8^тах’ ^min — ^min’
где атах и amjn — наибольший и наименьший радиусы спирали.
Конический логосприральный излучатель пременяется в качестве слабо-
направленной антенны, а также в качестве облучателя зеркальных антенн.
9.4. Применение сингулярных интегральных уравнений к электро-
динамическому анализу цилиндрической спиральной антенны
Цилиндрическая спиральная антенна с линейным шагом намотки (далее
ЦСА) является одной из разновидностей спиральных антенн, относящихся к
классу антенн бегущей волны. Исследование антенн подобного типа велось на
протяжении длительного времени различными приближенными методами [18],
422
ГЛАВА 9
суть которых заключается в замене реальной антенны сильно упрощенным
физическим эквивалентом — решеткой или анизотропно-проводящей моделью. Это
обусловлено, прежде всего, довольно сложной геометрией структур и сложностью
их математического описания. Расчеты приближенными методами можно считать
справедливыми и оправданными только для дальней зоны излучения. Между тем,
в настоящее время возрос интерес именно к ближней зоне излучающих структур,
что связано с вопросами электромагнитной экологии и электромагнитной
безопасности.
В данном разделе проведен строгий электродинамический анализ ЦСА
с применением теории сингулярных интегральных уравнений (в рамках
самосогласованного подхода [13]). Такой подход к решению задачи (называемый
В.А. Негановым [13] также методом физической регуляризации (МФР)) ранее
был применен для электродинамического анализа линейных и криволинейных
вибраторов, кольцевых рамочных антенн и колец с разрывом.
9.4Л. Самосогласованный подход к решению задачи. Как было отмечено
выше, основой приближенных расчетов ЦСА служит физический эквивалент,
представляющий собой совокупность элементов, обладающих простой геометрией.
В рамках самосогласованного подхода структура рассматривается в целом, интег-
ральном виде (впрочем, разбиение на отельные элементы вполне допустимо и не
вызывает никаких противоречий). Основой анализа является базовая поверхность
(БП), на которой строится сингулярное интегральное уравнение (СИУ) [13].
Выбор базовой поверхности диктуется двумя соображениями: удобством ее
математического описания и удобством записи на ней граничных условий для
ЭМП.
ЭМП на базовой поверхности S возникает под действием возбуждающей
функции. Для ЦСА она представляет собой напряженность электрического
поля, локализованную на электрически малой части S ( As X2). Особенность
возбуждающей функции в том, что она может быть задана с гораздо большей
степенью достоверности, чем распределение поверхностной плотности тока на 5 с
' размерами, соизмеримыми с длиной волны. С учетом перечисленных соображений,
для расчетов была выбрана корректная физическая модель, показанная на рис.
9.28.
Будем считать, что ЦСАпредставляет собой идеально проводящий бесконечно
тонкий проводник шириной 21 X, свернутый в спираль радиуса а, имеющую
угловую ширину 22, и расположенную симметрично относительно начала
координат. Расстояние между витками 1в = 2nh. Параметр h будем называть
коэффициентом подъема. Он является постоянным и не зависит от координат р
и z , что соответствует винтовой спирали с линейным шагом. Зная коэффициент
подъема h, радиус а и угловую ширину 2S, спирали несложно определить линейную
длину спирали Lcn и угол намотки а(р):
Lcn = 2^а2 + /г2, а(р) = arctg(/i / р).
С одного конца в точке ср0, называемой точкой питания, имеется зазор
угловой шириной 2<р3 <§: X (| <рд I + I Фз £) > в котором действует сторонняя ЭДС
(возбуждающая сила), создающая в зазоре ( р е[а - l,a + Z],cp е [<р0 - <р3,Фо + <р3],
z = /нр) напряженность стороннего электрического поля Е^.т (р, ср, z). Под действием
Антенны бегущей волны
423
Рис. 9.28. Геометрия цилиндрической спиральной антенны
стороннего электрического поля на поверхности S (р е [а - l,a +1], ср е = fap)
антенны возникает поверхностный электрический ток, непрерывный в области
зазора. Полагая, что полоска узкая, можно считать, что вектор поверхностной
плотности тока содержит две компоненты (рис. 9.29):
П(Р, <Р) = Фог1ф(Р,ф) + VUpM
где
ПФ(Р,<Р) = Пт(Р,<Р)
П2(Р><Р) = Пт(Р><Р)
г|т(Р,ф) - неизвестная пока функция, описывающая распределение плотности
поверхностного тока по спирали. Подобное соотношение применимо и для
составляющих электрического поля на металле (рис. 9.29):
_ _ о _ _ h
<Р
(9.4.1)
здесь = Е(р, <р) - функция, описывающая тангенциальную напряженность
электрического поля на спирали.
На поверхности £ антенны, представляющей собой идеально проводящий
металл, для тангенциальных компонент напряженностей электрического поля
выполняется граничное условие:
ст _ q
(9.4.2)
где - напряженность электрического поля, создаваемое поверхностной
плотностью тока fj, Е?т - напряженность электрического поля, возникающая под
действием сторонней ЭДС.
424
ГЛАВА 9
kz
Рис. 9.29. Проекция витка спирали на ось (pOz; р е [а - Z;a + Z]
9.4.2. Сингулярное интегральное уравнение. Не давая подробных выкладок,
приведем лишь основные моменты вывода сингулярного интегрального уравнения.
В данной постановке задачи имеем три компоненты векторного потенциала [21]:
4р(Р)
< Ар(р)
Аг(Р)
4л
р' sin(tp - <р')
p'cos((p — <р') >
h
(9.4.3)
Ms)
Здесь s - {р(р'} - точка поверхности S : (р' е [а -1, а +1], (р' е [-^, ^]), ds = р' dp' dtp'
- бесконечно малый ее элемент, р = {р, ср, z} - точка наблюдения векторного
потенциала поля А,
+ р'2- 2pp'cos((p - ф') + (z - fap')2.
- расстояние между точкой излучения и точкой источника.
Учитывая связь между векторным потенциалом А. и вектором напряженности
электрического поля Е [1], для составляющих и Ez можно записать следующие
дифференциальные соотношения:
-^-Е,п = к2 А(Г) + gracL div А, ——Ez = k2Az + grad2 div A (9.4.4)
jy Y Y Y yy * *
Из физических соображений удобнее пользоваться первым уравнением в
(9.4.4). С учетом (9.4.3) и первого выражения связи в (9.4.1), можно записать
следующее интегральное соотношение, связывающее касательную составляющую
напряженности электрического поля на металле с поверхностной плотностью тока
на спирали:
ЕТ(Р)=
4nik
j r|T(s)K(p,s)ds,
s
(9.4.5)
где
Антенны бегущей волны
425
Р1(р,$) = р’соз(ф-ф’), 02(P>S) = -Р
рзт(ф-ф') +
sin((p - (р')
Приравнивая z = /кр и используя граничное условие (9.4.2) на поверхности 5 , из
(9.4.5) получаем двумерное интегральное уравнение вида (р е [а - 1,а + 1],ф е [-£»£,]):
(р,ф) = J Гт|т(р \фЭ^1(Р, Р \ <Р, <P’)<*s
(9.4.6)
где
!
р
-ikR
К(р,р',ф,ф') = соз(ф-ф')
-И(р,р’,ф,ф’) -
-ikR
Sinc(2\|/)
а8тс(ф-ф') + —;
. ф-ф
h
к
e~ikL
2(р,р',ф,ф') = ik—— + —5-
+ р' -2рр'соз(ф-ф') + h (ф-ф')
. sinx
Smc(x) =-----
4nik
~wT
поэтому распределение поверхностной плотности
поведения на краях полоски (р = а -1, р = а + 1)
а распределение поля - равномерным [25]
Полоска является узкой (21 X)
тока по ширине с учетом его
можно считать квазистатическим
Пт(Р,ф) =
Лф)
ст
(р, ф) « Етст (а, ф) = Ест (ф).
- (р - аГ
Вводя в (9.4.6) нормированные переменные
и соотношения (9.4.7), получаем одномерное интегральное уравнение, записанное
относительно неизвестной функции /(t'), описывающей распределение по р
поверхностной плотности тока вдоль полоски (t е [-1,1]):
о ’ Ест (t) =
(9.4.9)
f(t')K(t,t')dt\
Р(х, т) = 0! (х, т) 3
Z(x, т) =
К(г) = J
-iSR
Р(а?, т)
dx
q(x) = (1 + (х / d))
-Z(x,t) +Р2(^Т)
426
ГЛАВА 9
Р1(^,т) =
q(x) cos(^t), р2(х,т) = -$2(х + d)2q(x)Sinc(^u)
Sinc(^c) +
+ — Sine2 — т + Sine2 — т
d <2 ) V2 )
4лгШ
w
Ядро К(т) в неявном виде содержит сингулярность при т = 0. Без доказательства
укажем, что
lim К(т) = (1 - ) In
। 2 с2j2zи 2 . I \
"l” о о t Р S ® \Q "Ь !)•
Таким образом, выражение (9.4.9) преобразуется в СИУ (t е [—1,1]) :
1
-аЕст (t) = [ f(t ')D(t, t ')dt' +
(9.4.10)
с регулярным ядром
D(t) = К(т) - lim K(t).
Отметим, что СИУ с ядрами, содержащими особенность вида (t-t')-2 [42],
называют гиперсингулярными.
Решать СИУ (9.4.10) можно различными методами. Авторы пользовались
методом ортогонализирующей подстановки, подробно описанном в [8]. Здесь
мы только укажем, что суть его сводится к поиску решения в виде конечного
полиномиального ряда, учитывающего граничные условия для поверхностной
плотности тока на концах полоски (т|2 (| 11= 1) = 0):
N
(9.4.11)
к=0
где Uк (£) - полиномы Чебышева второго рода порядка к, ортогональные на отрезке
[-1,1] с весовой функцией w(t) = л/1 -t2 , А^ - неизвестные коэффициенты, которые
находятся из соответствующей системы линейных алгебраических уравнений.
Отметим, что ток I вдоль полоски связан с неизвестной функцией f следующим
соотношением:
В
Дф)= T|T(p,(p)dp = 7Cf(<p).
a-l
При численном моделировании следует обратить внимание на аппроксимацию
стороннего электрического поля E^m(t) в зазоре. Напряжение U в разрыве
спиральной антенны между точками 1 и 2 (рис. 9.30) определяется следующим
образом.
Антенны бегущей волны
427
AZ
Рис. 9.30. Проекция области зазора ЦСА на плоскость <рОг (р = а). Точками 1 и 2 обозначе-
ны кромки зазора
fEcTm(l)dl.
(9.4.12)
В дальнейшем будем полагать напряжение равным 1 Вольт: U12 = 1 Из рис. 9.30
видно, что линейная длина зазора 13 = 2ср3 л/а2 + Ь2 . Условию (9.4.12) удовлетворяет
функция вида:
Ест (t) = 1 fl, t е [Ьо - Ь, Ьо + Ь],
Т 2£b\'a2 + h2 I0, 4 й 1ьо ~ ь,bo + b]-
где 2b = 2ф3 / S, нормированная ширина зазора (b <s: 1), b0 - <p0 / £, - нормированная
координата точки питания.
9.4.3. Численный анализ цилиндрической спиральной антенны. ЦСАс точ-
ки зрения распределения тока может работать в режиме стоячих, бегущих или
смешанных волн. Первые два случая являются идеализацией и на практике пред-
ставляют собой режим смешанных волн с явным преобладанием той или иной вол-
ны. При распространении по антенне бегущая волна тока затухает. Это затухание,
вызванное излучением и отчасти потерями в проводе необходимо учитывать, од-
нако при расчетах диаграмм направленности (ДН) и коэффициента направленного
действия (КНД) затуханием часто пренебрегают и считают распределение тока
равномерным [18].
Для расчетов излучения спиральных антенн в дальней зоне существует
приближенная теория [18]. Строгое решение электродинамической задачи
для спирали как для излучающей системы показывает, что в ней может
распространяться система волн Тп, называемых собственными. В зависимости
от отношения диаметра спирали к длине волны в собственной волне Тп может
преобладать та или иная азимутальная пространственная гармоника. Индекс
" п" пространственной гармоники и определяет характер излучения антенны
(диаграмму направленности, поляризационные и фазовые характеристики). Нужно
оговориться, что эти соображения в силу абстрактности спирали справедливы
только для дальней зоны излучения, так как электромагнитное поле в ближней
зоне жестко привязано к конкретной геометрии и конкретному распределению
428
ГЛАВА 9
тока. Тем не менее, с точки зрения упомянутой теории характерны три режима
излучения ЦСА, определяющиеся соотношением а / Л — поперечное, осевое и
воронкообразное [18].
Ниже произведен строгий электродинамический анализ ЦСА. Геометрические
параметры % = {a,£„h,Z} СИУ (9.4.10) дают четыре степени свободы и позволяют
производить расчет множества структур: линейных полосок, криволинейных
полосок, конформно расположенных на цилиндрической поверхности, замкнутых
колец, разомкнутых колец и цилиндрических спиралей с линейным шагом,
поэтому для проверки достоверности получаемых результатов был рассмотрен ряд
тестовых задач.
Суть тестирования заключалась в анализе с помощью СИУ (9.4.10) распределений
тока для более простых и уже рассчитанных излучающих структур. Затем
осуществлялось последовательное усложнение геометрии антенн, вплоть до
геометрии, соответствующей ЦСА. Наиболее важными практическими случаями
можно считать расчет распределений тока на полосковых вибраторах и кольцах с
длиной полоски, составляющей одну или половину длины волны. Следует отметить
хорошее совпадение с результатами для трубчатого электрического вибратора в
[8,10], где для расчетов использовалось СИУ, записанное относительно производной
тока, полученное на основе спектрального представления функции Грина в
цилиндрической системе координат. Следующим шагом был расчет полукольца
как частного случая криволинейного вибратора, конформно расположенного
на воображаемой цилиндрической поверхности. Был сделан вывод о том, что
распределение тока по полоске при ее относительно сильном, но гладком изгибе,
меняется незначительно. С точки зрения физики такие результаты считаются
физически адекватными, а с точки зрения решения СИУ — устойчивыми к
изменению параметров моделирования. Из распределений тока по волновым
кольцам с разрывом шириной, много меньше длины волны, было показано,
что ток на концах полоски стремится сохранить свою непрерывность за счет
возникающего в разрыве тока смещения, а из сравнения колец и полуколец с
L / X = 1 / 2 было видно, что при сближении концов полоски действительная часть
тока уменьшается и входное сопротивление антенны становится индуктивным.
Далее производился расчет незамкнутого кольца с емкостным переходом,
строгий электродинамический анализ которого возможен только с помощью СИУ
(9.4.10). При этом полученные результаты имеют простую физическую трактовку.
Емкостный переход образован концами полоски, идущими параллельно друг другу.
Расстояние между концами полоски много меньше длины волны. Получается, что
на комплексных распределениях тока в области перехода t е [0.75,1] о [-0.75,-1]
наблюдается почти линейное уменьшение амплитуды тока, что соответствует
равномерному распределению заряда, пропорционального, как известно [21]
производной с11(ф) / d(p.Причем заряды на разных концах полоски противоположны
по знаку. Сама же структура представляет собой открытый колебательный контур
с распределенными в пространстве параметрами.
Таким образом, тестовые задачи подтвердили работоспособность модели, а также
показали хорошую сходимость (при N < 25 в (9.4.11) относительная погрешность
расчета 5 < 0.1% ), устойчивость и физическую адекватность результатов. Следует
отметить, что для случая замкнутого кольца СИУ (9.4.10) с помощью несложных
подстановок можно преобразовать в СИУ с сингулярностью другого вида (вторая
степень особенности Гильберта), и искать его решение в виде тригонометрических
Амтенны бегущей волны
429
рядов. Но замкнутые кольца мы здесь рассматривать не будем.
На рис. 9.31-9.33 приведены основные результаты численного моделирования
ЦСА. Для всех случаев источник возбуждения находился в точке b0 = срд / % = -0.95.
Рис. 9.31 соответствует спирали диаметра 2а / X = 0.1, спираль показана на
диаграммах, соответствующих меридианной плоскости излучения (рис. 9.31,в-
9.33,в). Соотношение между максимумами излучения в меридианной и азимутальной
плоскостях | Е^макс | / | Eqmcikc | указаны в подрисуночных надписях. При таком
размере спирали и амплитудном распределении тока (рис. 9.31,а) в антенне
доминирует режим стоячей волны, в комплексном распределении наиболее сильно
выражена мнимая часть тока (рисунок 9.31,6). Антенна излучает преимущественно
в поперечном направлении.
Рис. 9.32 соответствует спирали диаметра 2а / X = 0.3. В данном случае мнимая
часть тока соизмерима с действительной, но при распространении по спирали
она испытывает большее ослабление. Такое поведение тока соответствует режиму
смешанных волн, причем можно видеть своего рода краевой эффект — усиление
коэффициента стоячей волны при приближении к свободному концу спирали. Здесь
можно говорить об осевом излучении (рис. 9.32,в), максимумы ДН в азимутальной
плоскости наблюдаются при углах 30 и 170° (рис. 9.32,г), но на самом деле они
приблизительно в 4 раза меньше максимумов ДН в меридианной плоскости, так
как определяются при 0 = 90° (вертикальная ось рис. 9.32,в).
На рис. 9.33 показана характеристика излучения спирали при 2а / л = 0.6.
Амплитуды мнимой и действительной части волн тока (рис. 9.33,6) практически
равны, и при распространении по спирали испытывают почти одинаковое
ослабление (по закону, близкому к экспоненциальному), поэтому усиление
коэффициента стоячей волны на свободном конце незначительно (рис. 9.33,а). Как
видно из сравнения рисунка 9.32,г и рисунка 9.33,г, максимумы в ДН сместились
на примерно на 90°, а в меридианной плоскости наблюдается уход от осевого
излучения. Если бы ДН азимутальной плоскости не зависела от угла ср , то в целом
излучение антенны можно было бы считать воронкообразным.
На основании результатов, представленных в данном разделе, можно сделать
следующие выводы:
- результаты расчетов ДН в дальней зоне ЦСА соответствуют представлениям,
данным в рамках приближенной теории [18], но имеют нетривиальный
характер;
- в режимах смешанных или бегущих волн затухание при распространении
тока по спирали может быть значительным, поэтому вопрос о пренебрежении
затуханием является спорным;
- результаты расчетов распределений тока физически адекватны и имеют простое
объяснение;
- в режиме смешанных волн на свободном конце спирали можно наблюдать
краевой эффект - усиление коэффициента стоячей волны тока.
Из СИУ (9.4.10) несложно определить входное сопротивление антенны.
Таким образом, на примере ЦСА описан алгоритм самосогласованного метода.
Построена простая и вместе с тем корректная физическая модель структуры.
Приведены основные моменты вывода сингулярного интегрального уравнения —
математической модели, имеющей строгое соответствие корректной физической
модели. Показано, что наряду с регулярными спиральными структурами,
430
ГЛАВА 9
Рис. 9.31. ЦСА в режиме стоячей волны тока. Геометрические параметры моделирования:
Lcn / Л. = 2, 2а / X = 0.1, 21 / X = 0.01, h / А. = 0.0217; а) - амплитудное распределение тока,
б) - комплексное распределение тока (сплошные кривые Re(IT), штрихованные - Im(IT));
в) - нормированная амплитудная диаграмма направленности в меридианной плоскости
180
антенны (расположение спирали показанно на рисунке), г) - нормированная амплитудная
диаграмма направленности в азимутальной плоскости антенны,
(рмакс
вмакс
-0.5
Антенны бегущей волны
431
|М<Р/Ч) 1Л
0.5
0.5
1.0
180
180
МфАМ
а)
б)
Рис. 9.32. ЦСА в режиме смешанных волн. Геометрические параметры моделирования:
Lcn / А. = 4 , 2а / А = 0.3, 21 / X - 0.015, h / А = 0.0939; а) — амплитудное распределение тока,
б) — комплексное распределение тока (сплошные кривые - Re(IT), штрихованные - Im(lT));
в) — нормированная амплитудная диаграмма направленности в меридианной плоскости
антенны (расположение спирали показано на рисунке), г) - нормированная амплитудная
диаграмма направленности в азимутальной плоскости антенны,
(ржаке
г»
^Ожакс
« 0.25
432
ГЛАВА 9
а)
180
Рис. 9.33. ЦСА в режиме бегущей волны тока. Геометрические параметры моделирования:
Lcn / X = 8, 2а / X = 0.6, 21 / X = 0.03, h / X = 0.0825; а) - амплитудное распределение тока,
б)~ комплексное распределение тока (сплошные кривые Re(IT), штрихованные — Im(JT));
в)
180
в) ~ нормированная амплитудная диаграмма направленности в меридианной плоскости
антенны (расположение спирали показанно на рисунке), г) - нормированная амплитудная
диаграмма направленности в азимутальной плоскости антенны,
сржакс
Омаке
Антенны бегущей волны
433
полученная математическая модель позволяет производить электродинамический
анализ структур с более простой геометрией — полосковых вибраторов,
криволинейных вибраторов, конформно расположенных на воображаемой
цилиндрической поверхности, замкнутых колец и колец с разрывом, что
говорит о ее универсальности. Используя соответствующие граничные условия,
модель можно использовать как для задач на собственное излучение, так и для
дифракционных задач.
Тестовое моделирование и сравнение результатов с известными, полученными
с помощью других представлений функции Грина, является хорошей проверкой
на достоверность. Дополнительным критерием достоверности является хорошая
внутренняя сходимость решения.
Результаты расчетов распределений тока по спиральной антенне соответствует
физике процесса, имеют простое объяснение и хорошо согласуются с приближенной
теорией. Наблюдаются характерные диаграммы направленности (боковое, наклонное
и осевое излучение) и режимы работы антенны (стоячей, бегущей и смешанной
волны). Строгий электродинамический анализ позволил выявить краевой эффект
— усиление коэффициента стоячей волны в режиме смешанных и бегущих волн
тока при распространении к свободному концу спирали.
По-видимому, самосогласованный подход на сегодняшний день является
наиболее общим при строгом электродинамическом анализе любых классов антенн.
Еще одним его несомненным преимуществом является отсутствие разделения
пространства на зоны излучения (ближнюю, промежуточную и дальнюю) и
возможность расчета ЭМП в любой точке пространства, включая точки базовой
поверхности.
9.5. Антенны поверхностных волн [17,3]
Данные, приведенные в этом разделе, по ДН и КНД линейного излучателя с
бегущей волной относятся к антенне из ненаправленных элементов. Собственная
направленность элемента может изменить как общую ДН, так и КНД антенны.
Например, в случае линейной антенны с продольными токами нуль элементов
излучения ориентирован по оси антенны, и режим осевого излучения
невозможен.
Антенны бегущей волны, реализующие режим осевого излучения, являются
антеннами поверхностных волн. Поверхностные волны возникают на границах
раздела сред с различными электрическими параметрами, фазовая скорость в одной
из которых меньше, чем в другой. Одной из таких сред в антенной технике обычно
является воздух, а другой - среда, в которой распространяются замедленные
электромагнитные волны ( V& < с ). При этом амплитуда волны медленно затухает
в продольном направлении и быстро убывает (по экспоненциальному закону) при
удалении от границы раздела сред по направлению нормали.
9.5.1. Основные типы антенн поверхностных волн [17]. Антенна повер-
хностных волн состоит из возбудителя и направителя (рис. 9.34). Возбудитель
конструируют так, чтобы он передавал как можно большую часть энергии от
генератора в направитель, причем волна, распространяющаяся вдоль направите-
ля, является поверхностной волной. Излучающим элементом антенны является в
434
ГЛАВА 9
б)
1
д)
Рис. 9.34. Типы антенн поверхностных волн: 1 - возбудитель; 2 — направитель [17]
г)
основном направитель. Непосредственное излучение возбудителя обычно бывает
слабонаправленным и поэтому образуются боковые лепестки ДН. Кроме того, оно
интерферирует с излучением направителя и искажает главный лепесток.
Направитель представляет собой отрезок линии передачи поверхностной
волны. Как известно, фазовая скорость такой волны меньше скорости света.
Для формирования поверхностной волны в качестве направителя используют
замедляющие структуры.
Обычно направитель бывает либо диэлектрическим (рис. 9.34,а), либо
металлическим ребристым (рис. 9.34,б,г,е).
По форме направителя антенны поверхностных волн подразделяют на плоские
линейные (рис. 9.34,а,б), стержневые (рис. 9.34,в,г) и дисковые (рис. 9.34,д,е).
У линейных и дисковых антенн замедляющую структуру обычно располагают
на экране — металлической подложке. Наибольшее распространение получили
антенны, изображенные на рис. 9.34,в,г. Первая называется диэлектрической
стержневой антенной, а вторая — ребристо-стержневой антенной.
Для согласования антенны со свободным пространством толщину направителя
к его концу уменьшают, благодаря чему фазовая скорость поверхностной волны
в конце направителя приближается к скорости света и устраняется отраженная
Антенны бегущей волны 435
волна. Таким образом, вдоль направителя распространяется бегущая волна.
Это позволяет рассматривать антенну поверхностных волн как разновидность
антенн осевого (продольного) излучения. У таких антенн, как известно, главный
лепесток ДН ориентирован вдоль направления движения волны (в данном случае
от возбудителя к концу направителя).
С другой стороны, антенну поверхностных волн можно отнести к апертурным
антеннам, рассматривая в качестве апертуры поверхность направителя.
Следовательно, если определить касательные составляющие электрического и
магнитного полей на поверхности направителя и рассматривать каждый элемент
поверхности как элементарный излучатель, то, пользуясь апертурным методом,
изложенным в гл. 12 можно определить поле излучения антенны поверхностных
волн.
В качестве возбудителей плоских линейных и стержневых антенн используют
односторонне направленные излучатели: рупор, вибратор с рефлектором, решетку
из щелей, открытый конец волновода. Возбудитель дисковой антенны должен
быть не направленным в плоскости диска. Обычно для этой цели используют
несимметричный вибратор.
9.5.2. Импедансные антенны [3]. Особенностью антенн данного типа явля-
ется использование импедансных структур, способных поддерживать плоские или
цилиндрические поверхностные волны.
При этом антенна конструируется так, что отражение волны от конца структуры
мало, и в антенне устанавливается режим, близкий к режиму бегущей волны.
Плоские линейные импедансные антенны поверхностных волн. На рис.
9.35. показаны импедансные антенны в виде плоских металлических пластин с
диэлектрическим слоем. При возбуждении полем вертикальной поляризации в
антенне (в плоском диэлектрическом слое) возникает волна основного типа EOq
плоская или цилиндрическая (рис. 9.35,в,г).
Поверхностное сопротивление поверхностной Е-волны есть отношение касатель-
ных составляющих электрического и магнитного полей на границе раздела в
воздухе:
(9.5.1)
Для поддержания замедленной волны это сопротивление должно быть
чисто реактивным и носить индуктивный характер. Практически толщину
слоя диэлектрика выбирают малой h / Ад « 1. В этом случае для замедления у
справедлива приближенная формула [18]:
у « 1 + к2/г2(1 - е)
(9.5.2)
где к = 2тг / А,; е = 2а / Eq - относительная диэлектрическая проницаемость
диэлектрического слоя.
Рассмотрим антенну, изображенную на рис. 9.35,а. Будем считать, что длина
выступающей за пределами направителя части экрана Ьэ = оо. Пусть относительная
диэлектрическая проницаемость направителя равна е.
Волны типа Е, как известно из теории электромагнитного поля [1], могут
распространяться вдоль направителя, если в раскрыве возбуждающего рупора
электрический вектор параллелен оси у . Если толщина направителя
436
ГЛАВА 9
б)
Рис. 9.35. Импедансные антенны: а) плоская линейная; б) дисковая;
в),г) картина поля соответственно плоской и цилиндрической волны основного типа в за-
медляющей структуре [3]
h < к / 2a/s - 1,
то будет распространяться только волна типа Ео (рис. 9.35,а), не имеющая
критической длины волны. Амплитуда поля будет убывать по экспоненциальному
закону в направлении оси Оу (рис. 9.35,в). Волна типа Ео имеет две составляющие:
Еу и Ez. Поверхностная волна будет распространяться вдоль оси Oz с фазовой
скоростью , которая может быть определена из трансцендентного уравнения
tg(/ch-J£“Y2) = Wy2 /7е“V2’ (9.5.3)
где коэффициент замедления у = с / т>ф. Если kh —> 0 , то у —> 1 и Иф —> с. Если kh
растет, то у -> уё и Vф = с / л/ё. Таким образом, фазовая скорость поверхностной
волны находится в пределах
Пренебрегая излучением с боковых и торцевой стенок направителя, можно в пер-
Антенны бегущей волны
437
вом приближении считать, что антенна имеет излучающий раскрыв с размерами
L и а. Амплитудно-фазовое распределение в этом раскрыве можно приближенно
считать разделяющимся. Вдоль оси Oz фаза изменяется по закону бегущей вол-
ны, а амплитуду в первом приближении можно считать неизменной (если потери
в диэлектрике и в подложке малы). Вдоль оси Ох распределение поля такое же,
как в возбудителе.
Из сказанного следует, что ДН антенны в плоскости yOz ( Е - плоскости)
зависит только от продольного размера L и по теореме умножения диаграмм
может быть представлена в виде
/(6) = /о (0)7(с)<е).
(9.5.4)
Здесь /о(0) - ДН элементарного излучателя, в качестве которого можно принять
полоску длиной dz (см. рис. 9.35). Так как у поверхности направителя касательная
составляющая электрического поля ориентирована вдоль оси Oz (перпендикуляр-
но краям полоски), то такую полоску можно рассматривать как прямолинейную
щель, для которой в Е - плоскости /о(0) = 1 (см. главу 8); / с (0) - ДН непрерывной
прямолинейной равноамплитудной системы осевого излучения. Как было показа-
но ранее [17]
(с) Q = sin[0,5/cL(E, - cos 0)]
1 J 0,57cL(^ - cos 0)
(9.5.5)
Так как у > 1, то главный лепесток ДН ориентирован вдоль оси Oz. ДН имеет
вид, типичный для антенн осевого излучения. Для оценки формы ДН нужно
учесть, что из-за бесконечной длины металлического экрана имеет смысл только
верхняя половина ДН.
Формула (9.5.5) получена в предположении, что толщина направителя не
меняется по длине антенны, т.е. у - const. В действительности для согласования
антенны со свободным пространством ее толщину уменьшают к концу (пунктирные
линии на рис. 9.35). В этом случае и формулу (9.5.5) нужно подставлять среднее
значение у по длине антенны.
Оптимальная длина антенны (при которой КНД максимален) определяется по
формуле
Lonm = X / 2(у -1). (9.5.6)
Диаграмма направленности антенны в плоскости xOz ( Н - плоскости)
определяется также по формуле (9.5.4), в которой под /о(0) следует понимать ДН
полоски шириной а и длиной dz, но теперь уже в плоскости Н, т. е. /0 (0) есть ДН
возбудителя в плоскости Н, так как размер и амплитудно-фазовое распределение
вдоль оси Ох у полоски и возбудителя одинаковы.
У реальных антенн длина экрана не бесконечна. У края экрана происходит
дифракция волн, что влияет на форму ДН. Если Ьэ = 0 , то для расчета ДН в
освещенном полупространстве формула (9.5.4) применима, но хорошее совпадение
расчетных и экспериментальных ДН получается в том случае, если в формуле
(9.5.4) под /о(0) понимать ДН излучателя Гюйгенса, расположенного в раскрыве
антенны. Можно показать [17], что
/о(0) = 7y2-cos20. (9.5.7)
Так как максимумы функций /о(0) и /^с (0) имеют место соответственно при
438
ГЛАВА 9
Рис. 9.36. ДН антенны поверхностных волн в плоскости, перпендикулярной экрану [17]
углах 0 = 90° и 0 = 0°, то главный лепесток ДН отклонен от экрана на некоторый
угол, который тем меньше, чем больше длина антенны и чем больше замедление
а. Типичная ДН приведена на рис. 9.36. Некоторое излучение наблюдается и в
затененное полупространство (ниже экрана). Если длина выступающей за пределы
направителя части экрана Ьэ Ф 0 , то для определения поля излучения нужно
учитывать еще излучение токов, обтекающих выступающую часть экрана, что
значительно усложняет расчет.
Волны типа Н будут распространяться вдоль направителя в том случае, если
электрический вектор поля в раскрыве возбудителя (см. рис 9.35) параллелен оси
Ох. Для того чтобы распространялась только основная магнитная волна типа Hq ,
необходимо выполнить условие
h < 0,75Х/Vs-l.
В отличие от волны типа Ео волна типа Но имеет критическую длину волны,
поэтому для того чтобы волна Но могла существовать, необходимо выполнить
условие
h > 0,25Х / Vs -1.
Расчет поля излучения антенны в случае волны типа Hq производится так же,
как и в случае волны типа Ео. Различие между двумя антеннами состоит в том, что
в случае волны типа Но не только при конечной длине экрана, но и при бесконечной
его длине главный лепесток отклонен от плоскости экрана. Это объясняется тем,
что касательная составляющая электрического вектора в раскрыве антенны парал-
лельна оси Ох (см. рис. 9.34), а следовательно, ДН элементарного излучателя в
плоскости yOz должна рассчитываться как для элементарной щели в Н - плоскости
по формуле
/0 (0) = sin 0.
Таким образом, излучения вдоль экрана (при 0 = 0) нет в случае волны типа Hq .
9.5.3. Импедансные антенны с гофрированными металлическими струк-
турами [3]. Помимо обычного диэлектрика для построения импедансных антенн
используются гофрированные металлические структуры плоской или цилиндри-
ческой формы (рис. 9.37).
Антепны бегуньей волны
439
в) г)
Рис. 9.37. Импедансные антенны на основе металлических плоских (а), цилиндрических (б)
гофрированных замедляющих структур и размеры ячеек замедляющих структур (в, г) [3]
Замедляющее действие гофров (рис. 9.37,в,г) объясняется тем, что ниже поверх-
ности S волна движется только в поперечном направлении (вдоль оси у), отражаясь
от дна канавки гофра, и имеет нулевую поступательную скорость вдоль оси z.
Степень замедления всей волны пропорциональна той доле ее энергии, которая
попадает в гофры.
Граница 5 ( у = 0) между гофрами и свободным пространством обладает
анизотропной проводимостью: токи могут течь только вдоль продольной оси z.
Каждая канавка гофра представляет собой короткозамкнутую на конце
ленточную линию длиной (высотой) h с волной типа Т и входным сопротивлением
гХ
вх
- iW^tg
при идеальной проводимости металла.
Условие существования поверхностной волны: h < X / 4 (или 2л/г / Х< л / 2). В
этом случае поверхностное сопротивление (9.5.1) - индуктивное. Учет дискретности
гофрированной структуры (скачкообразное изменение фазы в соседних канавках)
накладывает дополнительное ограничение d < X / 2у на период структуры (рис.
9.37,в).
При известных параметрах замедляющей структуры фазовая скорость основной
волны типа Еоо, распространяющейся в направлении оси z, перпендикулярной
гофрам, определяется формулой
2л т
— h
(9.5.8)
440
ГЛАВА 9
Рис. 9.38. Зависимость обратной величины замедления волны от параметров ребристой
структуры [3]
Здесь I - ширина канавок гофра.
Из (9.5.8) следует, что с увеличением глубины канавки фазовая скорость
убывает и при h = X / 4 равна нулю, что соответствует срыву распространения
поверхностной волны. Отношение h / 1, при котором происходит срыв, зависит от
«густоты» структуры, т.е. от отношения h / d (рис. 9.38).
Стержень с периодически расположенными металлическими дисками
(составная часть ребристо-стержневой антенны (рис. 9.37,6)) образует
замедляющую структуру, вдоль которой могут распространяться волны типов Еоо
и НЕj , близкие по структуре к волнам в линии поверхностной волны. Как и в
плоских гофрированных структурах, поверхность цилиндра S ( г = ) обладает
анизотропной проводимостью. Применительно к антеннам осевого излучения
большее практическое значение имеет волна НЕ± . В отличие от диэлектрического
волновода (стержня), анизотропно-проводящие гофры подавляют продольную
магнитную составляющую Hz этой волны, так что Hz « Ez / Wq . Поэтому при
расчете поля излучения рассматривается лишь основная электрическая волна j,
по существу единственно возбуждающаяся при устройстве питания в виде ко-
нического рупора с волной типа Нп в круглом волноводе (см. рис. 9.37,6).
Для Е — волн с касательными к S составляющими Ez и Н„ поверхностное
сопротивление (9.5.1) определяется структурой электромагнитного поля в кольцевых
канавках.
Индуктивный характер поверхностного сопротивления, как и в случае
плоской гофрированной структуры, имеет место при /г = г2-г1 < X / 4. Замедление
поверхностной волны у = 1 при h = 0 ; если же h / Л, = 0,15 , то у « 2. При дальнейшем
увеличении h / л приблизительно до 0,25 замедление у неограниченно растет.
Замедление волны лишь незначительно зависит от отношения I / d ; на практике
принимают I / d > 0,5.
Излучение импедансных антенн (см. рис. 9.35,а и 9.37,а,6) в основном вертикально
поляризовано. Возбуждение может осуществляться рупорным облучателем (рис.
9.35,а), широким открытым волноводом (рис. 9.37,а), соответствующей щелевой
системой, круглым волноводом с волной типа Иц или коническим рупором (рис,
9.37,6). При этом ДН импедансной антенны находят как ДН линейного излучателя
Ащтетн/ны бегущей волны
441
замедленной бегущей волной.
Разобьем мысленно замедляющий слой диэлектрика (рис. 9.35,а) на узкие
полоски плоскостями уОх. Тогда ДН антенны
Р(0,Ф) = Fi(e,(p)F(c)(0),
(9.5.9)
гдеР1(0,ф) - ДН прямоугольного раскрыва одной из прямоугольных полосок; F^C\Q)
- множитель направленности.
Таким образом, выражения для ДН соответственно в плоскостях Е и Н
представляются формулами [3]
Fe (0) = cos 0 —
L N
FH(0) =
(9.5.10)
(9.5.11)
где L - длина замедляющей (направляющей) поверхности.
Выражение (9.5.11) для ДН в плоскости Н показывает, что при значительной
ширине замедляющей структуры а ДН в большой степени определяется одиночной
характеристикой направленности (0), т.е. законом распределения поля
возбудителя вдоль оси х.
В случае гофрированной плоской металлической поверхности каждую канавку
можно рассматривать как щелевой излучатель. Это приводит к тем же формулам
(9.5.10), (9.5.11) с заменой в первой из них cos(0) на единицу, что несущественно,
так как ДН в основном определяются вторыми сомножителями.
При расчете по формулам (9.5.10), (9.5.11) предполагается, что толщина слоя
диэлектрика или глубина канавок не меняется по длине антенны, т.е. у = const.
В действительности для согласования антенны со свободным пространством ее
«толщину» уменьшают к концу (пунктирные линии на рис. 9.37,а). В этом случае
в формулы (9.5.10), (9.5.11) следует подставлять среднее значение у по длине
антенны L.
Диаграмма направленности цилиндрической гофрированной антенны также опре-
деляется главным образом множителем направленности (множителем решетки).
Диаграмма направленности одиночного элемента антенны - кольцевой канавки
(рис. 9.37,6) в главных плоскостях при возбуждении волной типа Ец имеет вид
F1E (0) = Jq (ka sin 0) cos 0 +
F1H (0) = Jq (ka sin 0) cos 0 -
Jx(ka sin 0)
—----------(1 - cos 0),
ka sin 0
Jj(ka sin 0)
—----------(1 - cos 0).
ka sin 0
Здесь Jn(x) - функция Бесселя n-го порядка.
Излучение обладает в первом приближении симметрией вращения. Если
возбуждение ребристо-стержневой антенны осуществляется коаксиальной линией
с волной типа Т, то для ДН одиночного элемента справедливо выражение
1*1(0) = Ji(ka sin 0).
442
ГЛАВА 9
В этом случае в направлении оси z антенны поле имеет нулевое значение.
Диаграмма направленности принимает конусообразную форму, причем вектор
электрического поля всегда направлен радиально.
Оптимальная длина импедансных антенн, при которой КНД максимален,
определяется по формуле [17]:
опт
2(7 -1)'
(9.5.12)
При конструировании плоских антенн с поверхностной волной металлический
экран за слоем диэлектрика (рис. 9.35,а) или ребристой структурой (рис. 9.37,а)
имеет не бесконечную, а конечную длину L9. В результате главный максимум
излучения вследствие дифракции волны на краю экрана оказывается «отжатым»
от плоскости экрана (и тем меньше, чем больше длина антенны L и замедление у ).
Характерный вид ДН в плоскости yOz для этих случаев показан на рис. 9.39.
В случае ребристо-стержневой антенны, которая проста в изготовлении,
соответствующим выбором размеров могут быть реализованы значения замедления
у большие, чем для диэлектрических поверхностных излучателей, что позволяет
получить значения ширины ДН в пределах 6 - 8°. Однако уровень бокового
излучения антенн такого типа довольно значителен. Преимуществом ребристо-
стержневых антенн является не только возможность выбора фазовой скорости
в широких пределах, но и ее варьирование вдоль излучателя, что позволяет
реализовать ДН с заданными параметрами.
Рабочая полоса частот импедансных антенн определяется в основном характе-
ристиками согласования возбуждающего устройства с замедляющей структурой и
обычно составляет 15-20 %.
9.5.4. Антенны вытекающей волны [3]. Поверхностные волны, возбуждае-
мые вдоль граничной поверхности, могут быть условно разделены на направляе-
мые и излучаемые. У направляемых волн фазовая скорость вдоль границы раздела
сред с различными электрическими параметрами меньше скорости света, у излу-
чаемых - больше. Механизм излучения линейного излучателя в последнем случае
принципиально отличается от механизма излучения собственно антенн поверх-
ностных волн (импедансных антенн).
Рис. 9.39. ДН импедансной антенны на экране конечных размеров [3]
Антенны бегущей волны
443
Рис. 9.40. Принцип построения открытого продольного излучателя [3]
Излучаемую (вытекающую) волну можно рассматривать как поверхностную
с фазовой постоянной kz = 2л / X
если пренебречь потерями в самой антенне
т.е. излученной энергией.
Направление главного максимума ДН,
волны, определяется соотношением
к?
к и постоянной затухания а > 0. Затухание
определяется потерями на излучение
формируемой антенной вытекающей
COS0
(9.5.13)
.V .^z
Простейшим видом антенны подобного рода является, например, прямоугольный
волновод, в середине узкой стенки которого прорезана продольная щель (рис. 9.40).
В этом случае длина волны в линии равна длине волны в волноводе ( = X в), а
затухание зависит от ширины щели и толщины стенки волновода.
Действие антенн вытекающей волны в первую очередь обусловлено излучением,
возникающим при «невозмущенном» распространении излучаемой волны вдоль
граничной поверхности. Множитель направленности подобного линейного
излучателя определяется выражением
ikz cos 0
(9.5.14)
/(0) = Jl(z)e
о
Здесь длина антенны L отсчитывается от сечения соответствующего ее входу.
В (9.5.14) функция распределения поля (тока) в излучателе имеет такую же
зависимость фазового сдвига вдоль структуры, как и излучаемая волна, т.е.
I(z) = 10(2)е-^.
Функция Iq(z) является вещественной и положительной. Таким образом,
/(0) = [/0(z)e-'fc*y-cos®)zdz.
т.е. в соответствии с формулой (9.5.13) при 0 = 0
гд. Форма ДН антенны
Синфазное сложение отдельных составляющих излучения (от элементарных
источников, образующих антенну, вытекающей волны) происходит при условии
cos0 =
вытекающей волны (без учета направленных свойств единичных элементарных
источников) зависит от функции распределения J(z) и тем самым от характера
затухания излучаемой волны. При постоянном затухании излучаемой волны
(например, при неизменной ширине продольной щели в волноводе) Iq(z) с
увеличением координаты z убывает по экспоненциальному закону. Однако /0(2г),
а тем самым и распределение излучения, можно менять в широких пределах,
если соответствующим образом выбрать закон изменения затухания. Определение
444
ГЛАВА 9
у
характера затухания или функции связи a(z) = Р (z) / P(z), где P(z) - мощность,
у
подводимая вдоль поверхности к точке z ; Р (г) - мощность, излучаемая отрезком
единичной длины в точке z при заданном распределении I0(z) осуществляется
так же, как и в случае излучателей с поперечным излучением, возбуждаемых
бегущими волнами. Различие состоит лишь в том, что здесь происходит непрерывное
излучение, и обычно направление главного максимума ДН относительно нормали
к антенне значительное (составляет приблизительно 40-50°).
Экспериментальные исследования поля длинной продольной щели в ближней
зоне позволяют заключить, что волна в волноводе накладывается в щели на
«щелевую волну», которая распространяется вдоль щели со скоростью света и на
конце антенны частично отражается. Чем шире щель, тем большая часть энергии
приходится на эту волну.
В антенне вытекающей волны помимо продольной щели излучение может созда-
ваться с помощью близко расположенных друг к другу щелей или отверстий другой
формы в узкой стенке волновода. Механизм излучения остается неизменным до тех
пор, пока расстояния между отверстиями малы по сравнению с длиной волны.
9.5.5. Диэлектрические стержневые антенны поверхностных волн.
Стержневая диэлектрическая антенна [17]. Стержневая диэлектрическая
антенна (см. рис. 9.34,в) состоит из сплошного диэлектрического стержня, воз-
буждаемого отрезком волновода. Материалом для изготовления стержня служат
—3 —4
диэлектрики с весьма малым значением тангенса угла потерь (порядка 10 -10 )
и значением относительной диэлектрической проницаемости порядка нескольких
единиц (полистирол, тефлон, стеатит).
Поперечное сечение стержня может быть прямоугольным, квадратным, однако,
наибольшее распространение получили диэлектрические антенны круглого
сечения.
При длине волны 10 см и более питание диэлектрической антенны осуществляется
обычно с помощью коаксиального фидера (рис. 9.41,а). Первичным возбудителем при
этом служит несимметричный вибратор, располагаемый внутри короткозамкнутого
с одной стороны отрезка круглого волновода. Длина вибратора и его удаление от
торца волновода выбираются по соображениям согласования антенны с фидером
питания.
В диапазоне сантиметровых волн для питания диэлектрической антенны обычно
используется волновод. В этом случае для согласования стержня с волноводом на
а)
б)
Рис. 9.41. Способы питания диэлектрических стержневых антенн: а) — коаксиальным фи-
дером; б) — волноводом [17]
Антенны бегущей волны
445
конце волновода располагают согласующую камеру и срезают на конус начальный
участок диэлектрического стержня (рис. 9.41,6).
Приближенный расчет параметров диэлектрической антенны основан на
предположении, что вдоль диэлектрического стержня распространяются такие
же волны, как и вдоль бесконечно длинного диэлектрического волновода. При
указанных выше способах возбуждения вдоль стержня может распространяться
основная несимметричная волна типа НЕ±}, структура которой показана на рис.
9.42. Волна типа НЕц является поверхностной [56]. Часть энергии волны переносится
стержнем, а часть — пространством, окружающим стержень. Интенсивность
поверхностной волны убывает в радиальном направлении.
Фазовая скорость, с которой электромагнитная волна распространяется вдоль
диэлектрического стержня, зависит от диэлектрической проницаемости материала
стержня, а также от отношения диаметра стержня d к длине волны (рис. 9.43). Из
рис. 9.43 видно, что с уменьшением диаметра стержня (в сравнении с длиной
волны) фазовая скорость приближается к скорости света. Для каждого значения
диэлектрической проницаемости существует такая величина отношения D / Л,,
при которой эти скорости уже практически равны.
Максимальный диаметр стержня Dmax выбирают из условия существования
в круглом запитывающем волноводе, заполненном диэлектриком, только волны
основного типа х, а минимальный диаметр Dmin - из условия уменьшения от-
ражений от конца стержня.
Для определения оптимальных значений максимального и минимального
диаметров конических стержней могут быть использованы следующие формулы,
полученные на основании опытных данных [3]:
^шах
Расчет ДН антенны с коническим стержнем проводится так же, как и для ан-
тенны с цилиндрическим стержнем, при условии замены конического стержня
цилиндрическим среднего радиуса а = (-Dmax + Dmin) / 4 . Между длиной стержня
(9.5.15)
mm ^2, 5я(е -1)'
Л(Е - 1)
Линии электрического поля
Линии магнитноого поля
Рис. 9.42. Структура поля волны
типа НЕп
Рис. 9.43. Зависимость обратной величины ко-
эффициента замедления (1/у = и^/с) волны
типа НЕп от отношения D /1 и от £ [17]
446
ГЛАВА 9
L и замедлением у существует оптимальное соотношение.
Обычно длина стержня L лежит в пределах (3 - 7)Х, а диаметр составляет
(0,5-0,3)Х при относительной диэлектрической проницаемости стержня е = 2...5.
Если длина стержня незначительно превышает оптимальную, то основной ле-
песток ДН сужается, но быстро растет уровень боковых лепестков. Дальнейшее
увеличение длины антенны может привести к раздвоению основного лепестка ан-
тенны.
Одиночные стержневые антенны в зависимости от размеров имеют ширину ДН
20о R > 15...25°. Для получения более узких ДН и повышения КНД применяют антен-
ные решетки стержневых антенн. Диаграмма направленности в этом случае при
равномерном возбуждении решетки определяется перемножением ДН одиночного
стержня и множителя решетки.
Под излучающим раскрывом антенны понимают боковую поверхность стержня.
Так как касательные к поверхности стержня составляющие электрического и
магнитного полей известны из решения уравнений Максвелла для бесконечного
диэлектрического волновода, то можно определить поле излучения стержня
конечной длины [17]. ДН антенны выражается формулой (9.5.4), где рсц0) -
множитель системы, определяемый по формуле (9.5.5). Что касается множителя
одиночных излучателей, из которых состоит непрерывная система, то он в Е - и
Н— плоскостях соответственно имеет вид [17]
/оя(0) = Ji (ka sin Q) / ka sin0, (9 5 16)
foH (6) = cos 6^1 (ka sin 0) / ka sin 0,
где a = d / 2, а угол 0 отсчитывается от оси стержня. Здесь под одиночным
излучателем следует понимать участок поверхности стержня длиной dz (см. рис.
9.41,а). Так как обычно L » а, то форма ДН определяется в основном множителем
системы.
Оптимальная длина диэлектрического стержня Lonm определяется по форму-
ле (9.5.6), а КНД — по формуле (2.2.4). При увеличении длины стержня ширина
главного лепестка уменьшается, если L < Lonm. Однако при L > Lonm — резко
возрастает уровень боковых лепестков и может наблюдаться раздвоение главного
лепестка.
С помощью одностержневой антенны можно получить ширину главного лепестка
обычно не уже 15 — 20°. Если требуются более узкие ДН, то применяют синфазную
решетку стержневых излучателей. Заметим, что иногда диэлектрическая антенна
применяется для получения воронкообразной ДН. В этих случаях используется
осесимметричная волна типа Ещ.
9.5.6. Ребристо-стержневая антенна [17]. На конце диэлектрической ан-
тенны из цилиндрического стержня (рис. 9.34,в) возникают отраженные волны,
увеличивающие уровень боковых лепестков. Для уменьшения отражений от конца
и соответственно снижения уровня бокового излучения и реализации режима,
близкого к бегущей волне, применяются диэлектрические стержни конической
формы (рис. 9.34,в)
Ребристо-стержневая антенна (см. рис. 9.34,г) состоит из ряда параллельных
металлических дисков, расположенных вдоль оси антенны. Для крепления дисков
служит металлический стержень. Для формирования волны типа НЕц может
быть применен возбудитель в виде рупора либо симметричного вибратора,
Антенны бегущей волны 447
перпендикулярного оси антенны, причем заднее излучение антенны в последнем
случае устраняется диском - рефлектором.
Расчет электрических параметров ребристо-стержневой антенны производится
аналогично расчету параметров диэлектрической стержневой антенны.
Необходимые для расчета значения фазовой скорости поверхностной волны,
распространяющейся вдоль ребристого стержня, приведены в литературе [17].
Следует отметить, что ребристо-стержневую антенну можно рассматривать
как директорную антенну, у которой круглые диски играют роль пассивных
вибраторов. Так как эти диски являются «толстыми», то ребристо-стержневая
антенна более диапазонна по направленным свойствам, чем обычная директорная
антенна. Диапазонность ребристо-стержневой антенны по согласованию с линией
питания зависит от типа возбудителя.
Ребристо-стержневые антенны находят применение на сантиметровых,
дециметровых и метровых волнах. В последнем случае для уменьшения веса и
парусности диски можно изготовлять из сетки или перфорированного листового
материала.
9.5.7. Дисковые антенны поверхностных волн [17]. Плоские линейные и
стержневые антенны поверхностных волн являются односторонне направленны-
ми антеннами. В отличие от них дисковые антенны поверхностных волн (см. рис.
9.34,д,е) являются ненаправленными в плоскости диска и обладают направленнос-
тью в плоскости, содержащей ось симметрии диска.
Цилиндрическая поверхностная волна распространяется от расположенного в
центре антенны возбудителя к периферии диска. Если мысленно разбить диск на
ряд секторов, то каждый из них можно рассматривать как продольно-излучающую
антенну поверхностных волн, главный лепесток которой направлен в сторону
движения поверхностной волны и несколько отклонен от металлической подложки
(из-за конечных размеров диска). ДН всей антенны имеет вид сплюснутого тора.
Направитель антенны изготовляют в виде либо диэлектрического, либо
ребристого металлического диска, толщина которого убывает к периферии для
согласования антенны со свободным пространством.
Для расчета ДН дисковой антенны определяют предварительно фазовую
скорость поверхностной волны, а затем вычисляют поле излучения круглого
раскрыва антенны [17].
9.5.8. Применение антенн поверхностных волн [17]. Отличительной осо-
бенностью антенн поверхностных волн является малая толщина направителя, что
позволяет применять их в качестве мало выступающих (низкосилуэтных) или не-
выступающих антенн. Известно, например, применение линейной плоской антен-
ны в качестве глиссадной антенны, встроенной заподлицо в посадочную полосу на
аэродроме.
Широко применяются антенны поверхностных волн на летательных аппаратах. В
этом случае роль металлической подложки играет обшивка летательного аппарата.
Место установки антенны может существенно влиять на ее направленные свойства.
Стержневые антенны для уменьшения лобового сопротивления устанавливаются
по продольной оси летательного аппарата, обычно в его носовой или хвостовой
части. Стержневые антенны применяются также в качестве облучателей зеркальных
антенн.
448
ГЛАВА 9
Вопросы, связанные с теорией комплексных волн [58], в частности волн с
полем, убывающим в поперечном направлении - невытекающих комплексных
волн, освещены в [59-60].
В заключение отметим, что недостатком антенн поверхностных волн является
относительно большой уровень боковых лепестков. Антенны с диэлектрическим
направителем имеют заметные потери, а при увеличении длины волны
резко возрастает их вес. Для уменьшения веса иногда применяют стержневые
диэлектрические антенны полой (трубчатой) конструкции.
14*
Антенны СВЧ в интегральном исполнении
449
Глава 10. Антенны СВЧ в интегральном исполнении
К современным антенным устройствам предъявляются весьма жесткие тре-
бования по электродинамическим характеристикам, а также габаритам, массе,
стоимости, технологичности и т.д. В связи с необходимостью создания невысту-
пающих антенн для летательных аппаратов, а также простых и технологических
антенн более широкого назначения возник большой интерес к микрополосковым и
печатным антеннам СВЧ. Использование планарной технологии обеспечивает вы-
сокую производительность размеров антенн, технологичность, низкую стоимость,
малые габариты и массу. Методами планарной технологии могут быть выполнены
не только излучатели, но и линии передачи, согласующие элементы, фазовраща-
тели, переключатели и пр.
Под плоскостными (планарными) антеннами СВЧ будем понимать как одиноч-
ные микрополосковые и печатные излучатели, так и образованные на них линей-
ные антенные решетки. Антенны СВЧ могут излучать волны линейной, круговой и
эллиптической поляризации, обеспечивать работу в многочастотных режимах.
Элементы излучающих структур могут иметь самую разнообразную геометри-
ческую форму: прямоугольную, круглую, треугольную, эллиптическую, кольце-
вую и др. Эти структуры могут работать как в резонансном, так и в нерезонансном
режимах и могут возбуждаться полосковой линией, коаксиальным кабелем, за
счет электромагнитной связи и т.д.
Недостатками планарных антенн являются: узкополостность, малые предельно
допустимые мощности, трудность конструирования перестраиваемых устройств и
изменения параметров печатных элементов.
Одной из первых была разработана печатная полосковая антенна, показанная
на рис. 10.1 [47]. Излучатель представляет собой длинную металлизированную по-
лосу, возбуждаемую в нескольких точках с помощью ветвящейся схемы из полос-
ковых линий. Расстояние между точками возбуждения меньше длины волны в диэ-
лектрике подложки. При разбиении полосы на несколько частей образуется как бы
антенная решетка из прямоугольных или квадратных элементов. Такие элементы
получили самое широкое распространение в качестве микрополоскоых и печатных
излучателей резонансного типа (рис.10.2).
Конструктивно излучатель состоит из прямоугольного ленточного проводника 1,
Рис. 10.1. Полосковая печатная антенна [47]
Рис. 10.2. Печатный микрополосковый излу-
чатель резонаторного типа [47]
15 - Нсганов
450
ГЛАВА 10
расположенного на тонком диэлектрическом основании 2 с проводящем экраном 3.
Толщина диэлектрика выбирается обычно меньше 0.1 X ( X - длина волны в свобод-
ном пространстве). Излучатель чаще всего возбуждается полосковой линией пере-
дачи 4, для которой эта система является плоским, заполненным диэлектриком
резонатором с потерями, обусловленными излучением. Края резонатора образуют
две излучающие щели I и II, расстояние между которыми 1 приблизельно равно
Хв/2 , где Хв - длина волны в диэлектрике.
Линейно поляризованное излучение, направленное в основном по нормали к
плоскости антенны, создается составляющими электрического поля, параллель-
ными проводящей плоскости. Размер Ъ , вообще говоря, может быть различным,
но он определяет входное сопротивление антенны, которое для Ъ « Хв/2 составляет
несколько сотен Ом. Излучатель прямоугольной формы при резонансе обладает
коэффициентом усиления более 6 дБ при относительной диэлектрической прони-
—3
цаемости подложки а2 = 2.35 и tg о < 10 . Однако ширина рабочей полосы частот
резонансных антенн не превышает, как правило, нескольких процентов по уровню
Кст и = 2. Применяя разнообразные схемы питания излучателей, можно создать
антенну, работающую на нескольких достаточно близких частотах. Однако это
приводит к снижению коэффициента использования эффективной поверхности
эквивалентного раскрыва. Некоторого расширения рабочей полосы частот можно
достичь в конструкции, показанной на рис.10.3 [47].
Особый интерес представляют плоскостные антенны треугольной, ромбической
и эллиптической формы. Показано, что наилучшими диапазонными свойствами
обладает эллиптический излучатель, причем оптимальным оказался эллипс с эк-
сцентриситетом, равным 0.8.
10.1. Классификация печатных полосковых антенн [48]
В настоящее время разработано и исследовано теоретически и эксперимен-
тально большое количество вариантов печатных полосковых антенн (ППА). Диа-
пазон длин волн, в котором используются антенны этого класса, простирается от
метров до миллиметров. Для изготовления полосковых излучателей используются
разнообразные материалы, сами антенны в силу своей конформности размещаются
на объектах различной формы. Вследствие этих факторов весьма затруднительно
дать общую классификацию ППА. Нами предлагается следующая классификация
по нескольким характерным признакам.
10.1.1. Классификация ППА по форме излучающего элемента. На рис. 10.4
приведены наиболее распространенные конфигурации излучающих элементов:
а) — прямоугольный, б) — дисковый, в) — кольцевой, г) — эллиптический,д) — треу-
гольный.
10.1.2. Классификация ППА по виду подстилающей диэлектрической
структуры. Типичные конфигурации подстилающей диэлектрической структу-
ры представлены на рис. 10.5: а) - диэлектрическая пластина, б) - диэлектрическая
экранированная подложка, в) - экранированная подвешенная подложка, г) - мно-
гослойная структура. Частным случаем однослойной структуры является антенна
с возбуждающим зазором.
Антенны СВЧ в интегральном исполнении 451
в) г) д)
Рис. 10.3. Печатный резонаторный эле-
мент с расширенной рабочей полосой
частот [47]
Рис. 10.4. Формы излучающих элементов [48]
б)
а)
Рис. 10.5. Разновидности подстилающей диэлектрической структуры [48]
10.1.3. Классификация ППА по форме геометрического тела, на котором
располагается ППА. На рис. 10.6 приведены типичные конфигурации поверхнос-
тей для размещения ПА: а) - на плоской поверхности, б) - на цилиндрической
поверхности, в) - на сфере.
10.1.4. Классификация ППА по способу возбуждения излучающего элемен-
та. На рис.10.7 представлены наиболее распространенные варианты возбуждения:
а) - от коаксиальной линии (КЛ), б) - от КЛ через элемент связи в виде узкой
полоски 3, в) - от микрополосковой линии (МПЛ), г) - от щелевой линии (ЩЛ),
д) - электромагнитным способом (без гальванического контакта).
Еще раз отметим, что любая классификация является условной. Кроме того, воз-
можно неоднозначное выделение того или иного варианта. Например, на рис. 10.7
возбуждение от щелевой линии или копланарного волновода можно отнести к
случаю электромагнитного возбуждения.
452
ГЛАВА 10
Рис. 10.6. Размещение полосковых излучателей
Х/2
3
б)
щл
в) г)
Рис. 10.7. Способы возбуждения ППА [47]
10.2. Полосковые печатные антенны прямоугольной и круглой
формы
Наиболее подробно исследованы прямоугольные излучатели. Предложены раз-
личные способы их возбуждения, согласования и режимы работы.
Наиболее простой вариант возбуждения печатного излучателя 1 с помощью КЛ
2, подсоединенного перпендикулярно проводящей плоскости (рис. 10.7, а). В этом
случае экран коаксиального кабеля присоединяется к экрану, а центральный про-
водник пропускается через подложку и соединяется с металлической пластиной в
специально подбираемой точке.
Ажпенны СВЧ в щутегралъном у^полненгш
453
Представляет интерес питание излучателя через элемент связи 3 вида узкой
полоски, параллельной излучателю 1 (рис. 10.7, б). Питание к полоске подводится
при помощи коаксиального кабеля со стороны экрана. Согласование определяется
длиной элемента связи и зазором между излучателем и полоской. Возбуждение
печатных излучателей с помощью коаксиальных линий представляет интерес в
низкочастотной части диапазона СВЧ. Возбуждать излучатель микрополосковой
линией 4 желательно в точке, где его входное сопротивление близко волновому
сопротивлению МПЛ. Это достигается с помощью узкого выреза (отрезка компла-
нарной линии), параллельного оси излучателя (рис.10.7, в).
В качестве диэлектрического основания обычно используются диэлектрики с
—4 —3
параметрами £ « 2.5 4-10 и tg о ~ 10 4-10 . Толщина основания h может состав-
лять ( 0.1 4- 0.01) X.
Для получения поля вращающей поляризации необходимо создать две пары
излучающих щелей, расположенных перпендикулярно друг к другу и возбужда-
емых сигналами с фазовым сдвигом л/2. Для этого выбирают квадратный излуча-
тель, возбуждаемый в двух точках соседних сторон квадрата [47].
Таким образом, составными частями ППА, например с излучателем прямо-
угольной формы (рис. 10.5,6), являются металлическая пластина 1, экран 3 и диэ-
лектрическое основание 2 (подложка).
Микрополосковые излучатели относятся к резонансным антеннам. Упрощенно
можно считать, что объемный резонатор микрополоскового излучателя огра-
ничен вертикальными стенками из идеального магнитопроводящего материала,
расположенными по периметру пластины. В прямоугольных микрополосковых ан-
теннах обычно используется низший тип резонанса, при котором L»Xe/2, где
к “ Длина волны в полосковой линии передачи с шириной проводни-
ка w < X/2 , - относительная диэлектрическая проницаемость диэлектрической
подложки. Составляющая электрического поля Е~ в поперечном сечении полоско-
вой линии (вдоль координаты у) между пластиной и экраном распределена почти
равномерно, а в продольном (вдоль координаты а?)-по синусоидальному закону с
пучностями на краях пластины. Заметные отклонения от такого идеализированно-
го распределения наблюдаются только вблизи углов пластины и в окрестностях
точки питания.
Модель излучающей системы микрополосковой антенны можно строить раз-
личными способами. Например, можно учесть поверхностные электрические токи,
текущие по пластине и по экрану, а также вертикальные токи электрической
поляризации в диэлектрике подложки. Однако нахождение распределения излуча-
ющих электрических токов представляет сложную электродинамическую задачу
и область растекания этих токов заметно превышает размеры пластины. Поэтому
такая модель излучающей системы используется сравнительно редко, в основном
при стремлении учесть конечные размеры экрана по методу физической оптики.
Чаще применяют более простую модель излучающей системы, согласно которой
микрополосковая антенна трактуется как эквивалентная щелевая антенна в плос-
ком бесконечном экране без диэлектрика. Специальные исследования подтвердили,
что точность этой модели вполне достаточна для понимания принципа действия
антенны и ориентировочных расчетов поля излучения. Форма эквивалентной щели
полагается совпадающей с формой краев металлической пластины.
На рис. 10.10 показано распределение магнитных токов j™ и j™ в эквивалентной
454
ГЛАВА 10
а)
б)
в)
ч Ь/2*
г)
е)
Рис. 10.8. Некоторые способы возбуждения вибраторных МПА: а) - двухпроводной НПЛ
в центре; б) - двухпроводной НПЛ в центре с согласующим трансформатором;
в) - с питанием с торца МПИ; г) - НПЛ с излучателями с одной стороны линии;
д) - НПЛ с излучателями с обеих сторон линии; е) - линией питания под
некоторым углом а по отношению к МПИ [47]
а) б)
Рис. 10.9. Прямоугольные микрополосковые антенны с питанием коаксиальной (а)
и полосковой линией (б) [2]
Антпенны СВЧ в интегральном исполнении
455
Рис. 10.10. Распределение магнитных токов в щелевом излучателе, эквивалентном микро-
полосковой антенне [2]
а) б)
Рис. 10.11. ДН микрополосковой антенны с прямоугольной пластиной в плоскости Е (а) и в
плоскости Н (б) [2]
Х/2
ЕЗ
Z/////////////Z
Рис. 10.12. Вибраторные печатные излучатели [47]
456
ГЛАВА 10
поля играют равномерно распределенные синфазные токи
щели, построенное исходя из картины распределения поля Ег в резонаторе прямо-
угольной микрополосковой антенны. Главную роль в формировании излучаемого
•т
и , создающие
линейно поляризованное излучение с вектром Ё, параллельным оси х. Токи
и 7x4 содержат на каждой боковой стороне пластины по два протифазных участ-
ка, излучение которых в значительной степени взаимно компенсируются (точная
компенсация имеет место в плоскостях zOx и zOy ). Пользуясь методикой расчета
полей излучения антенн, сформулированной выше, можно получить следующие
выражения для ДН прямоугольной микрополосковой антенны:
W) = cos о sin ср
sin и
sin и
/Ф(0,ф) = cos и cos <р cos 0
v и
(poLsin0)2
7t2 - (P0L cos 0)2
(10.2.1)
и
где и - O.50ow sin 0 cos ср ; и = O.5PoLcos0; p0 = 2л/Хо • В выражении для
L первый член в скобках соответствует излучению двух торцевых ще-
лей с равномерным распределением магнитного тока, второй член - из-
лучению боковых щелей. Напомним, что размер L должен определять-
ся из условия резонанса, т.е. из соотношения L « 0.5Хд /е, . Характерный вид
ДН прямоугольной микрополосковой антенны изображен на рис.10.11. Из-за
совместного участия в излучении двух торцевых щелей КНД прямоугольной мик-
рополосковой антенны получается несколько выше, чем КНД односторонней по-
луволновой щелевой антенны, и составляет 3,5-7,0 (меньшим значениям КНД со-
ответствует более высокие значения диэлектрической проницаемости подложки,
уменьшающие размеры пластины и снижающие направленность).
При оценке КПД полосковых антенн следует учитывать три вида потерь мощ-
ности: 1) омические потери в пластине и экране; 2) потери в неидеальном диэлек-
трике подложки; 3) ответвление части подводимой к антенне мощности в возника-
ющую поверхностную волну (диэлектрическая подложка на экране представляет
собой замедляющую структуру, способную поддерживать такую волну). Совмест-
ное действие трех факторов снижает КПД до 50-80%, причем меньшие значения
соответствуют более тонким подложкам.
Существенным недостатком одиночного микрополоскового излучателя явля-
ется узкополостность, связанная с резонансным механизмом действия антенны.
Установлено соотношение « £1D[X0/16h], гдеП - КНД; h - толщина подложки.
Характерные значения добротности излучения для одиночных излучателей легко
регулируются подбором положения точки питания. Входное сопротивление антен-
ны прямоугольной формы максимально при питании на краю (несколько сотен ом)
и изменяется пропорционально множителю sin2 (тш/L) при расположении точки
питания на расстоянии а от центра антенны. Выбор правильного положения точки
питания при сохранении настройки на резонанс избавляет от необходимости при-
менять отдельные согласующие устройства.
Широкое применение нашли узкие линейные резонасные излучатели. Дли-
на такого излучателя равна половине длины волны в диэлектрике. Питание его
осуществляется либо непосредственным подсоединением МПЛ, либо за счет
электромагнитной связи (рис.10.12). Наибольшая степень электромагнитной связи
Антенны СВЧ в интегральном исполнении
457
Рис. 10.13. Щелевой излучатель [47]
Рис. 10.14. Частично экранирован-
ный резонаторный излучатель [47]
Рис. 10.15. Дисковый резонаторный излучатель [47]
достигается, когда излучатель расположен на границе диэлектрика и свободного
пространства, а линия питания погружена в диэлектрическое основание. При этом
вибратор оказывается на большем удалении от экрана, чем линия питания. Из-
меняя расстояние между вибратором и экраном, можно достигнуть максимальной
ширины полосы пропускания и наибольшего КПД при заданном углублении ли-
нии питания в подложку. Расположение вибратора влияет также на его резонан-
сную частоту. Диаграмма направленности вибратора с электромагнитной связью
мало зависит от степени связи. Микрополосковые и печатные антенны могут также
выполняться на основе щелевого излучателя, возбуждаемого компланарным вол-
новодом (рис. 10.13). Они оказались удобными для построения антенных решеток.
По принципу действия щелевые излучатели, возбуждаемые МПЛ, аналогичны
волноводно-щелевым антеннам.
К недостаткам микрополосковых и печатных излучателей можно отнести вы-
сокий уровень кроссполяризованного излучения. Он может возникать по самым
разным причинам: из-за паразитного резонанса на неоднородностях полосковых
линий, излучения поверхностных волн, микрополосковых линий питания и т.д.
Используя закрытые или частично экранированные линии передачи, можно не-
сколько снизить уровень кроссполяризационного излучения, например, распола-
гая излучатель 1 в плоскости одной из заземленных пластин 2 (рис. 10.14). Вдоль
кромки экранного окна установлены короткозамыкающие штыри 3, соединяющие
оба экрана.
Особый интерес при конструировании и расчете планарных антенн представляет
выбор материала диэлектрической подложки. При этом существенными являются
458
ГЛАВА 10
следующие параметры: диэлектрическая проницаемость, диэлектрические поте-
ри, теплопроводность, способность сохранять форму и размеры в различных кли-
матических условиях и в процессе эксплуатации, чистота обработки поверхности,
допуски на размеры по толщине, неоднородность, электропроводность. Процесс
выбора материала является многофакторным, многие факторы имеют противоре-
чивое влияние на параметры антенн, что вынуждает прибегать к компромиссным
решениям. Значение 8^ определяет предельные возможности миниатюризации реа-
лизуемого устройства СВЧ. При этом необходимо произвести оценки максимально
возможного отклонения значения , при котором выходные параметры устройс-
тва изменяются в допустимых пределах. Стабильность тангенса угла диэлектри-
ческих потерь также способствует воспроизводимости выходных характеристик
устройства. Для уменьшения тепловых потерь и потерь на отражение необходимо
выбирать диэлектрик, обработанный так, чтобы шероховатость не превышала по-
ловины глубины проникновения поля в металл.
При использовании в качестве излучателя круглых дисковых элементов центр
излучателя соединен перемычкой с экраном, а возбуждающий зонд находится на
некотором удалении от центра и питается коаксиальной линией через отверстие в
экране. Диаметр диска выбирается из условия возбуждения волны низшего типа,
например для диэлектрика с =2,47 на частоте f = 2,9 ГГц диаметр составляет
3,78 см. Точка питания определяется из условия согласования с питающим трак-
том, но следует отметить, что сопротивление антенны уменьшается при смеще-
нии этой точки к центру. На рис. 10.15 показан излучатель, возбуждаемый проти-
вофазно в двух точках.
Полоса рабочих частот такого излучателя зависит от полосы пропускания про-
тивофазного делителя мощности. Возбуждая элемент с одного входа и нагружая
на второй, можно осуществить его согласование и изменять диаграмму направ-
ленности (ДН).
10.3. Печатные резонаторные излучатели для формирования
излучения круговой поляризации
Микрополосковые антенны могут быть легко приспособлены для излучения
волн с круговой поляризацией. В квадратных излучателях для этого необходимо
возбудить в резонаторе колебания двух ортогональных линейных поляризаций с
равной амплитудой и взаимным фазовым сдвигом ±л/2. В конструкции рис.10.16,
а для этого используется 3-дБ квадратурный направленный ответвитель, отде-
льные и развязанные входы которого соответствуют излучению волн с правым или
левым вращением вектора поляризации. В конструкции рис. 10.16, б точка питания
располагается в угле пластины, а размеры сторон пластины несколько отличают-
ся. Вследствие этого резонансные частоты антенны для двух ортогональных ли-
нейных поляризаций оказываются выше и ниже рабочей частоты, причем разницу
между частотами выбирают исходя из необходимости получения фазового сдвига
90° между колебаниями двух линейных поляризаций. В конструкции рис. 10.16,
в питающая линия возбуждает в микрополосковом колебания, соответствующие
излучению линейной поляризации. Колебания с ортогональной линейной поляри-
зацией возбуждаются с помощью щели, прорезанной наклонно в металлической
Антенны СВЧ в интегральном исполнении
459
д)
Рис. 10.16. Способы получения круговой поляризации в полосковых
печатных антеннах [2, 47]
460
ГЛАВА 10
пластине антенны. Щель связи вызывает «расщепление» резонансных частот для
двух линейных поляризаций, и при правильном подборе этого «расщепления»уда-
ется выполнить условия излучения круговой поляризации на средней частоте.
При использовании излучателей круглой формы применяют четыре точки воз-
буждения с определенными фазами (рис.10.16, г). Круговую поляризацию можно
получить используя пятиугольный излучатель (рис.10.16, д). Используя эллип-
тический излучатель (рис.10.16, е) можно также получить излучение круговой
поляризации.
10.4. Печатные антенные решетки
Наряду с одиночными излучателями широкое применение получили печатные
антенные решетки. Обладая сходством конструкции, печатные антенные решетки
отличаются друг от друга в основном типом применяемых излучателей, а также
способом их возбуждения. Рассмотрим лишь некоторые виды печатных решеток.
На рис. 10.17. показана простейшая печатная антенная решетка из излучателей 1
резонаторного типа. Четырехэлементная антенная решетка имеет коэффициент
усиления около 13,5 дБ. Ширина полосы пропускания составляет 1,79% на уровне
менее двух. Уровень боковых лепестков 11 дБ. Ширина ДН равна 20 и 68° в
Е- и Н-плоскостях соответственно.
Особое внимание привлекают печатные вибраторные антенные решетки (рис.
10.18). Решетка, состоящая из полуволновых печатных вибраторов (рис.10.18, а),
питается через фазирующие полуволновые линии задержки. Изменение формы,
взаимного расположения и способа питания вибраторов от несимметричной полос-
ковой линии позволяет менять характеристики антенн. При всех преимуществах
печатных антенных решеток они весьма узкополосны.
Так, решетка, показанная на рис.10.18,б, содержащая 5x8 элементов и пи-
таемая в центре, сохраняет форму ДН в полосе частот 7% при уровне боковых
лепестков 11... 19 дБ. Согласование, однако, обеспечивается лишь в узкой полосе
частот. В решетке, показанной на рис.10.18,е, в зависимости от нагрузки на конце
несимметричной МПЛ может быть реализован режим стоячей или бегущей волны.
Решетка, содержащая 9x9 элементов, выполненная на подложке с h = 0,794 мм и
е2 = 2,32, на частоте 17,4 ГГЦ работает в полосе 0,4% в режиме стоячей волны и
в полосе 3% в режиме бегущей волны. При этом уровень боковых лепестков нахо-
дится в пределах 12... 19 дБ. Анализ антенных решеток обычно проводят обобщен-
ным методом наводимых ЭДС [47].
Рис. 10.17. Линейная антенная решетка из полосковых излучателей резонаторного типа
[47]
Антенны СВЧ в интегральном исполнении
461
Рис. 10.18. Различные варианты топологии печатных вибраторных решеток [47]
На рис. 10.19 в качестве примера приведена расчитанная ДН 20-элементной
эквидистантной решетки для е - 2,35; h = 0,343Х ; 2Ь = 0,05Х. Взаимное расположе-
ние полосковых излучателей е решетке показано на рис.10.20, причем расстояние
между соседними элементами d равно длине поверхностной волны. Такая решетка
возбуждается набегающей поверхностной волной. Возбуждение распространяю-
щихся вдоль координаты у (см.рис. 10.20) поверхностных Н- волн, вообще говоря,
не вызывает трудностей [47]. Для этого требуется возбудитель с явно выражен-
ной составляющей поля Ех, причем эффективность возбуждения тем выше, чем
больше толщина слоя диэлектрика. Хорошим возбудителем, например, является
Е-секториальный рупор с поляризацией вектора Е, параллельной оси х.
В настоящее время происходит интенсивное становление теории и совершенс-
твование технологии полосковых печатных антенн, отличающихся большим раз-
нообразием конструкций и пригодных для применений в качестве как самостоя-
тельных антенн, так и элементов антенных решеток. Освоенный диапазон частот
микрополосковых антенн простирается от 300 МГц до 20 ГГц. Основными направ-
лениями исследований являются создание надежных методов автоматизированного
проектирования микрополосковых антенн, объединенных с питающими трактами,
совершенствование конструкции излучателей и антенных решеток, расширение
рабочей полосы частот, повышение КПД и продвижение в диапазон миллиметро-
вых волн.
462
ГЛАВА 10
IF
-75-60-45-30-15 0 15 30 45 60 75 е°
Рис. 10.19. Расчетные ДН 20-элементной решетки из полосковых излучателей [47]
Рис. 10.20. Взаимное расположение полосковых излучате-
лей впечатной решетке
Рис.10.21. Поперечное сечение
микрополоскового вибратора
10.5. Применение метода СИУ к расчету
микрополосковых антенн [62]
Основной недостаток присущий практически всем публикациям по микрополос-
ковым антеннам - это отсутствие самосогласованного решения для распределения
поверхностной плотности тока по микрополосковому вибратору. Это означает, что
данное решение не позволяет непосредственно переходить от тока на излучающей
поверхности к полю вне ее и обратно, т.е. не выполняются граничные условия.
Так, в [48] на основе тензорных функций Грина рассмотрены граничные задачи
для полосковых антенн, расположенных на подложках плоской, цилиндрической
и сферической форм. Но поверхностный ток на полосках задавался из некоторых
физических соображений.
Ниже описан самосогласованный подход, позволивший построить электроди-
намическую теорию микрополоскового вибратора. В некотором смысле она явля-
Амтенны СВЧ в ил/тегралъном исполнении 463
ется обобщением теории полосковых вибраторов, конформно расположенных в
свободном пространстве на цилиндрической поверхности [49]. Причем под самосо-
гласованной теорией излучающей структуры понимается сингулярное интеграль-
ное представление (СИП) электромагнитного поля и сингулярные интегральные
уравнения (СИУ), получаемые из СИП при его рассмотрении на поверхности,
где расположен вибратор. Самосогласованный подход, по сути, является методом
фичической регуляризации некорректных электродинамических задач, связан-
ных с применением интегральных уравнений Фредгольма первого рода [13]. Ниже
представлены основы самосогласованной электродинамической теории микропо-
лоскового вибратора.
10.5.1. Постановка задачи. Физическая модель излучателя. Микрополос-
ковый электрический вибратор представляет собой тонкий идеально проводящий
проводник длиной 21 и шириной 2а , расположенный на диэлектрический подложке
с односторонней металлизацией и возбуждаемый в области разрыва шириной 2Ь
генератором высокой частоты (10.21). Под воздействием ЭДС генератора на повер-
хности вибратора возникают электрические токи, которые распределяются на его
поверхности таким образом, что создаваемое ими электромагнитное поле (ЭМП)
удовлетворяет уравнениям Максвелла, граничным условиям на идеально прово-
дящей бесконечной металлической плоскости, на поверхности вибратора и усло-
вию излучения на бесконечности.
Задачу расчета параметров любой антенны обычно решают в два этапа. На
первом этапе (внутренняя задача анализа антенны) определяют поверхностные
электрические или магнитные токи на некоторой вертикальной поверхности, кото-
рую называют поверхностью излучения. На втором этапе (внешняя задача анализа
антенны) по найденным токам на поверхности излучения определяют ЭМП в лю-
бой точке пространства.
Будем использовать физическую модель микрополоскового электрического
вибратора (рис.10.21), аналогичную тонкому [2,5] и трубчатому [8,9] электрическим
вибраторам:
1. Микрополосковый вибратор предполагается бесконечно тонким и идеально
проводящим.
2. Полосковый проводник предполагается достаточно узким ( 2а <§: I, X), так
что поперечной составляющей поверхностной плотности электрического тока Г)^
пренебрегаем по сравнению с продольной Т|2 .
3. Микрополосковый вибратор возбуждается сторонней гармонической ЭДС,
включенной в зазор, так что функция r|2(a?,z) предполагается непрерывной в об-
ласти у = d , хе [-a, a], z е [-Ц], т.е. и в области зазора.
4. В области у = d , х е [-а, а], z е [-Z, Z] справедливы следующие граничные ус-
ловия:
ц2(т,-/) = ц2(а?,Н) = 0,
(10.5.1а)
Ёх (х, z) = 0 при х е [-а, а]
[4-b]u[b,Z],
(10.5.16)
Ex(x,z) = -Ё^Т при х е [-а,а], z е [-b,Ь], (10.5.1 в)
где Е2т - напряженность стороннего электрического в зазоре вибратора.
5. Напряженность стороннего тангенциального электрического поля Ё^т имеет
464
ГЛАВА 10
лишь составляющую Efт.
Разложим векторы напряженностей электрического поля Е, магнитного поля
Н и поверхностной плотности тока rj на вибраторе по координатам х, z в интег-
ралы Фурье:
00 ОС
—ОС' —ОС
ОО ОС
(10.5.2)
f [H(J/,p,h)e_i₽x“itedpdh,
—30 —ОС'
00 00
fF(p,h)e"i₽x'fcdpdh,
—00 —оо
4л2
ОО 00
—00 —00
00 00
.<(т/,0Л) = —f [н(х',з/,г')ег₽ж +lhzdx'dz',
4л J J
—00 —00
(10.5.3)
а I
F(p,h) = -^ J
п0 — единичный вектор нормали к границе раздела первой и второй сред, на-
правленный из первой среды во вторую.
В (10.5.3) учтено, что поверхностная плотность электрического тока ц отлична
от нуля только на поверхности вибратора: у = d , х е [-a,a], z е [-Ц].
На плоскости у = d Фурье-образ } тангенциальной составляющей на-
пряженности электрического поля Ет и Фурье-образ F = {F^F-,} поверхностной
плотности тока rj на вибраторе связаны через матрицу поверхностных импедансов
[Z] плоскости у = d следующим образом [25]:
(10.5.4)
где Zifj (i, j = 1,2) — элементы матрицы поверхностных импедансов [Z] есть функ-
ции переменных р , h Фурье-пространства: Zi j = Z^ (p,h). Для определения мат-
рицы поверхностных импедансов [Z] проще сначала найти матрицу поверхностных
адмитансов [Y]:
(10.5.5)
где i (г, j = 1,
элементы матрицы поверхностных адмитансов Y , которые
Антенны СВЧ в интегральном исполнении
465
также являются функциями переменных р и h.
Так как из матричных соотношений (10.5.4) и (10.5.5) следует, что матрица [Y]
есть обратная матрице [Z], поэтому просто установить связь между элементами
этих матриц:
Zn (₽Л)= У22(РЛ)/д(₽Л), Z12(РЛ) = -У12(РЛ)/д(РЛ),
Z21 (РЛ) = - У21 (РЛ)/д(РЛ), z22 (РЛ)= Уц (РЛ)/д (РЛ),
(10.5.6)
где А (РЛ) - Уц (РЛ)У22 (₽Л)-У12 (РЛ)У21 (РЛ).
Элементы матрицы поверхностных адмитансов плоскости у = d легко опреде-
ляются через матрицу входных адмитансов
области у > d
и матрицу
области у < d (рис. 10.21) [25]:
(10.5.7)
Матрицы входных адмитансов вводятся следующим образом [25].
(1,2)1 Г (1,2)
12 cz
Д2) (1,2)
22 JL^vC
(10.5.8)
^(1)
где ё£ 7
Фурье-образы
тангенциальных составляющих напря-
женностей электрического и магнитного полей в плоскости у = d области у < d, а
»(2) %(2) у/’С2) у/(2)
'х ’ lz ’ х > ’/(z
Фурье-образы тангенциальных составляющих напряжен-
ностей электрического и магнитного полей в плоскости у - d области у > d (рис.
10.21).
Поперечные составляющие ё^1’2' и JQ1’2) всегда можно
дольные составляющие и .7^1,2) [1]:
определить, зная про-
<,(1,2) = ih (+ 03Wo g^1’2^ 1
fc2e|i - h2 dx h dy j
^(1,2) = [ Ю££0 <(1>2) ! ay41>2) ’
?С2£Ц - h2h dy dx
(10.5.9)
Определив ё^1,2) и .7/Р’2)
условий, подставив их в выражения (10.5.9) и затем, выразив
J1,2)
из решения уравнений Гельмогльца с учетом граничных
Jifj1’2) через
, получаем значения элементов матриц входных адмитансов плоскости
у = d областей у
и у
^(Р(₽Л)=
^/с2^! -p2)ctgr1d
НоМ1®г1
у<р (₽л) =-У« (₽л)=
ih^ctg^d
ц0Ц1®П
ГЛАВА 10
у(1) /р h\ =
y(p(p,h)=
МоН2<°г2
42) (М) = -у21} (₽-&) = hP
НоИ2°>г2
y^?(fi,h)=--2£2ll2~-2 ,
Ц0Ц2°>г2
(10.5.10)
где Гу = Jk2£j[i,j - р2 - h2 , (j = 1,2); к — волновое число, со — циклическая частота,
Ед — электрическая постоянная, р.д — магнитная постоянная, е^ , Pj — относи-
тельные диэлектрическая и магнитная проницаемости подложки соответственно;
е2 , Р-2 — относительные диэлектрическая и магнитная проницаемости окружаю-
щей среды соответственно.
10.5.2. Сингулярное интегральное представление электромагнитного
поля. Для узкого вибратора (а I) учитывается только продольная составляю-
щая поверхностной плотности тока х]г , поэтому матричное соотношение (10.5.4)
переходит в скалярное:
где
(10.5.11)
ОО 00
Z^1(x,,z'fxfz) = -^v f (z11(^,h)e~i^x~x%~ih^~z'^dh, (10.5.11а)
4л2 J J
—ОО —оо
Для узких полосок, ширина которых много меньше длины волны, поперечное
относительно полоски (т.е. по координате х) распределение поверхностной плотнос-
ти тока rjz (х, z) с учетом поведения поля вдоль ребер х = ±а [46] можно описать с
помощью функции 1/^1 - (х/а)2 [25]. Поэтому функцию двух переменных т|г (x,z),
описывающую распределение поверхностной плотности тока, можно представить
в виде произведения двух функций одной переменной, одна из которых описывает
ее поперечное распределение (по координате х), а вторая — продольное распреде-
ление (по координате z).
(10.5.12)
где f(z) — неизвестная функция, характеризующая продольное распределение
поверхностной плотности тока на полоске (по координате z).
Нетрудно показать, что в (8.5.11а) при h —> оо
lim Zn (p,h) = 2ft (P,h) = ihSrgn(h)
(10.5.13)
где
Антенны СВЧ в интегральном исполнении
467
-1, при h < О,
sgn (h) = i О,
при h = О,
при h > О,
поэтому интеграл по h в (10.5.11а) является расходящимся. Устраним эту расхо-
димость следующим образом. Во-первых, подставляя (10.5.12) в (10.5.11), перейдем
к новой неизвестной функции f (z') = df (zydz’ с помощью интегрирования по z'
в (8.5.11) по частям с учетом граничных условий /(-/) = /(?)= 0. Во-вторых, в по-
дынтегральном выражении в (10.5.11) прибавим и вычтем слагаемые с асимптоти-
ческим сомножителем Z^ (0,h). В результате можно записать следующее СИП для
Ez на плоскости у = d через неизвестную функцию f = df(z'^ldz':
-Z£ (р, h)"| e~ih(z~^dpdh dz' -
(10.5.14)
где
27CCO£q [&2 + £1 ]
Jq (P«) — функция Бесселя первого рода нулевого порядка.
При выводе (8.5.14) было учтено, что [29,50,51]
грх'
00
Jsgn(/i)e ih^z z^dx-
10.5.3. Сингулярное интегральное уравнение. Подставив (10.5.14) в гранич-
ное условие (10.5.1в), несложно получить следующее СИУ с ядром Коши относи-
тельно неизвестной функции /'(z'):
4тс
(10.5.15)
-l
Иг
~ih(z~z')d$dh dz
468
ГЛАВА 10
где Е?т (z) — напряженность стороннего возбуждающего электрического поля в
зазоре.
Отметим главную особенность СИУ (10.5.15): оно справедливо для любого спо-
соба возбуждения микрополоскового вибратора при учете только одной составля-
ющей поверхностной плотности тока ц~ меняется в зависимости от способа
возбуждения только видЕ|т в правой части этого уравнения, т.к. поверхностная
плотность тока T[z(x,y^ в соответствие с физической моделью задачи в области
зазора остается непрерывной функцией.
Применяя формулу обращения интеграла Коши [30] для решения не ограничен-
ного на концах интервала [-1,1] с учетом условия / (-1) = /(?) = 0, можно получить
интегральное уравнение Фредгольма второго рода, численное решение которого
является математически корректной задачей:
агсо£0 [е2 + £i ]
4л
(10.5.16)
е ih^z z ^dfidh dz"dz' .
При выводе (10.5.15) и (10.5.16) в выражении для электрического поля в зазоре
было положено х = 0 , так как граничные условия (10.5.1) справедливы для любой
точки области у = d , хе [-a, a], z е [-1,Z],
Напряженность электрического поля в зазоре вибратора в случае симметрич-
ного запитывания обоих его плеч удобно представить в виде:
(10.5.17)
Подобным выражением была представлена напряженность стороннего электри-
ческого поля в зазоре трубчатого электрического вибратора в работе [8]. Непос-
редственно способы подключения фидера к микрополосковому вибратору для
симметричного запитывания его плеч подробно описаны в [48,52,53].
При численном анализе распределений поверхностной плотности тока по элек-
трическому вибратору было установлено, что оно практически не зависит от вида
стороннего электрического поля в зазоре, а только от амплитуды электрического
поля. Например, при анализе использовалось электрическое поле в зазоре в виде
постоянной ступеньки, применяемое для аппроксимации возбуждающего электри-
ческого поля в зазоре рамочной антенны [54].
Методы решения интегральных уравнений Фредгольма второго рода подроб-
но изложены, например, в [23]. Решение конкретно этого уравнения искалось в
виде:
ОО
Л (г/0
J
Антенны СВЧ в интегральном исполнении
469
где Тп (z/Г) — полиномы Чебышева первого рода.
Оригинальный метод решения подобного уравнения предложен в [8].
10.5.4. Численные результаты. Ток на поверхности вибратора можно опре-
делить по формуле:
а
-а
Входное сопротивление вибратора определяется следующим выражением:
где V — напряжение в зазоре вибратора.
На рис. 10.22 представлены графики распределения действительной (сплош-
ная линия) и мнимой (штриховая линия) составляющей тока на поверхнос-
ти полоскового вибратора. Данные распределения рассчитаны при 2ЪЕ$ = 1 В.
На рис. 10.22,а диэлектрическая проницаемость подложки равна Ej = 1, а на
рис. 10.22,6 — £1=3. Все расчеты выполнены для вибраторов со следующими па-
раметрами: длина плеча вибратора — I = 0.25k ; толщина вибратора — 2а = 0.025k,
ширина зазора — 2Ь = 0.0 IX , толщина подложки — d = 0.1k.
На рис. 10.23 представлены зависимости действительной (а) и мнимой (б) частей
входного сопротивления микрополоскового вибратора от длины плеча вибратора,
нормированной на длину волны (сплошной линией показаны графики для вибра-
тора, расположенного на подложке с £i = 1, а штриховой линией — £i = 3). Все
расчеты выполнены для вибраторов со следующими параметрами: толщина виб-
ратора — 2а = 0.025k , ширина зазора — 2b = 0.01k , толщина подложки — d = 0.1k.
Из графиков видно, что для вибратора с £i = 3 наступает значительно больше
резонансов на рассматриваемом отрезке Z/k, чем для вибратора с £i =1.
Таким образом, предложен самосогласованный метод расчета микрополосково-
го электрического вибратора при симметричном возбуждении его плеч, позволив-
ший построить эффективный алгоритм определения его входного сопротивления.
Рис. 10.22. Зависимости распределения тока на поверхности микрополоскового вибратора:
a) Ej = 1 ; б) £} = 3 (сплошная линия-действительная часть, штриховая-мнимая часть) [62]
б)
470
ГЛАВА 10
Метод достаточно просто может быть обобщен и на другие способы возбуждения:
с помощью щелевой линии, электромагнитным способом (без гальванического кон-
такта) [48] и т.д. В этих случаях отсутствует зазор в полосковом проводнике (рис.
10.20), а стороннее электрическое поле распределено по всей области микрополос -
кового проводника ( у = d , [-a,a], z е [-1,1]), причем на полоске = 0 ,
где Е£т — стороннее тангенциальное электрическое поле возбуждения; Ех — тан-
генциальное электрическое поле, создаваемое непрерывной поверхностной плот-
ностью тока на полоске. Напомним, что с точки зрения разработанного алгоритма
в статье физическая модель микрополоскового вибратора с наличием зазора также
не приводит к разрыву тока по вибратору. Поэтому способ возбуждения микро-
полоскового вибратора определяется областью существования Ехг в физической
модели задачи.
а)
б)
Рис. 10.23. Зависимости действительной (а) и мнимой (б) частей входного сопротивления
полоскового вибратора: а) £х = 1; б) £Т = 3 [62]
Частотно-независимые антенны
471
Глава 11. Частотно-независимые антенны [2, 74, 101]
11.1. Принципы построения частотно-независимых антенн [2, 74]
К частотно-независимым антеннам относят слабонаправленные излучатели,
способные работать, в диапазоне с отношением верхней и нижней граничных час-
тот 5:1 и более, при сохранении хорошего качества согласования входа и при не
слишком сильном изменении формы ДН. Потребность в таких антеннах возни-
кает при создании широкополосных систем связи, систем радиоразведки и ра-
диопротиводействия. В понимании механизма действия частотно-независимых ан-
тенн основным является принцип электродинамического подобия. Этот принцип
устанавливает идентичность ДН и входных сопротивлений двух различных ан-
тенн без потерь на частотах и со2, если форма этих антенн одинакова (рис.
11.1), а соответствующие размеры обратно пропорциональны отношению частот
/ L2 = ft)2 / coj. Такие антенны с одинаковыми размерами в длинах волн называ-
ют электродинамически подобными.
Выполнить единственную антенну так, чтобы она оставалась в строгом смысле
электродинамически подобной самой себе на различных частотах, можно лишь
в том случае, если ее форма определяется только угловыми размерами. Про-
стейший пример — бесконечно длинный вибратор с плечами конической формы.
Другие формы структур, задаваемых в сферических координатах параметричес-
ким уравнением R = р(0, ф) и определяемых только угловыми размерами, можно
найти, решая уравнение Kg(Q, ф) = g(Q', ф'). Это уравнение предполагает, что пер-
воначальная форма антенны д(0,ф) после увеличения масштаба по радиусу в К
раз совпадает с исходной формой, повернутой в пространстве. К числу решений
принадлежат, например, пространственные эквиугловые спирали, задаваемые
параметрическим уравнением К(0,ф) = еа^+<Ро^Т(0), где Т(0) — произвольная фун-
кция, в частном случае — константа. Пример плоской бесконечной эквиугловой
структуры, образуемой парой металлических плеч, показан на рис. 11.2, а. Края
I
Вход Вход
Рис. 11.1. Электродинамически подобные вибраторные антенны [74]
472
ГЛАВА 11
Рис. 11.2. Бесконечные структуры, определяемые угловыми размерами:
а) - плоская; б) - на конической поверхности [2]
плеч определяются уравнениями эквиугловых спиралей р(ф) = А ехр а(ср + Фо), где
А и (р0 — постоянные величины, определяющие масштаб по координате р и пер-
воначальный угол поворота плеча, параметр а равен котангенсу угла т между
радиусом и касательной к спирали. Вблизи центра плечи структуры обрезают и в
образовавшийся зазор подводят возбуждающее напряжение. Заметим, что про-
странственные структуры из эквиугловых спиралей можно создавать, располагая
металлические плечи по поверхности конуса (рис. 11.2, б).
Замечательной особенностью как плоских, так и пространственных эквиугло-
вых спиральных структур является своеобразная автоматическая отсечка излу-
чающих токов. Это явление состоит в том, что амплитуды токов, возникающих
в спиральных плечах под действием генератора, резко уменьшаются (в 100 раз
и более) после прохождения витка спирали, периметр которого примерно равен
длине волны. Остающаяся невозбужденной внешняя часть структуры может быть
отброшена, и это почти не сказывается на ДН антенны и входном сопротивлении.
Явление отсечки токов впервые было обнаружено экспериментально и впоследс-
твии подтверждено с помощью электродинамических расчетов.
Вследствие отсечки токов в излучении эквиугловой спиральной структуры ко-
нечных размеров участвует только центральная часть с диаметром, примерно
равным X / 3 (так называемая активная область). При изменении частоты элек-
трические размеры активной области остаются постоянными и в результате воз-
можно создание антенн с почти постоянным входным сопротивлением и мало ме-
няющейся ДН в 10-кратном и даже большем диапазоне частот. Нижняя граница
рабочего диапазона определяется из условия равенства длины волны периметру
последнего витка структуры. Верхняя граница рабочего диапазона определяется
соизмеримостью с длиной волны размеров области возбуждения антенны, где гео-
метрия спиральных линий оказывается нарушенной из-за наличия соединения с
линией питания антенны.
При создании плоских спиральных эквиугловых антенн, а также в ряде дру-
гих случаев положительное значение имеет еще одно обстоятельство, связанное
с принципом перестановочной двойственности. Дело в том, что плоская структу-
ра, определяемая угловыми размерами, может одновременно трактоваться и как
электрическая (вибраторная), и как магнитная (щелевая) излучающая система.
Обозначим ее входное сопротивление через Zj и заметим, что согласно принципу
двойственности при взаимной замене металлической и щелевой частей структуры
Частотно-независимые антенны
473
Рис. 11.3. К пояснению принципа дополнительности [74]
ее сопротивление изменяется и принимает значение Z2, определяемое формулой
2 2
Z2 = Zc / (4Zi) = (60д) / Zj. При совпадении формы электрической и дополнитель-
ной магнитной частей структуры имеет место равенство Z± = Z2 и входное со-
противление оказывается равным Zj = Z2 = 60л Ом на любой частоте. Простейший
пример выполнения этого условия показан на рис. 11.3.
Итак, можно сформулировать следующие принципы создания частотно-неза-
висимых антенн:
1. В антенне должно выполняться условие автоматической отсечки излучающих
токов, гарантирующее постоянство электрического размера излучающей части
антенны,— принцип отсечки токов:
2. Форма антенны должна определяться в основном угловыми размерами;
3. Форма щелевой части плоской антенны должна совпадать с формой вибра-
торной части (принцип дополнительности).
Первостепенное значение принадлежит принципу отсечки токов. Нарушение
второго и третьего принципов в реальных антеннах не обязательно приводит к
заметному ухудшению частотных свойств.
11.2. Частотно-независимые спиральные антенны [2, 74]
На рис. 11.4 изображена простейшая плоская диапазонная антенна, плечи ко-
торой ограничены четырьмя логарифмическими спиралями:
Р1 = А ехр(аср), р2 = Mpi, р3 = А ехр[а(<р - л)], р4 = Мр3 .
Питание такой антенны, прорезанной в металлическом листе больших разме-
ров, осуществляется с помощью гибкого коаксиального кабеля, проложенного
вдоль одного из плеч. При числе витков 1,5—2,5 ДН антенны состоит из двух
широких лепестков, максимумы которых перпендикулярны плоскости антенны.
Излученное поле в главных направлениях имеет в рабочем диапазоне частот 20:1
эллиптическую поляризацию с коэффициентом эллиптичности не менее 0,5. Так
как изменение частоты для такой антенны эквивалентно ее повороту в пространс-
тве вокруг оси, перпендикулярной плоскости листа, то ширина лепестков не оста-
ется постоянной, а периодически изменяется в пределах 40-50° во всем рабочем
диапазоне частот.
Коэффициент стоячей волны в 50 Ом коаксиальней линии на любых частотах
рабочего диапазона не превышает 2,0. Изменение параметров а и М не оказывает
значительного влияния на диапазонные свойства антенны и приводит лишь к из-
менению среднего значения входного сопротивления. Экспериментально установ-
474
ГЛАВА 11
Рис. 11.4. Эквиугольная спиральная
антенна [74]
Рис. 11.5. Плоская двухзаходная спираль
Архимеда [74]
лено, что хорошие результаты получаются при а = 0,30 и М = 0,62.
Определенными недостатками эквиугловых спиральных антенн являются
сложность формы и заметное «плавание» параметров при изменении частоты. Эти
недостатки преодолены в плоских архимедовских спиральных антеннах, постро-
енных на основании принципа автоматической отсечки тока. Такие антенны проще
по форме, а главное — их параметры являются более стабильными в диапазоне
частот. Здесь рассмотрим простейшие антенны на основе двухзаходных спиралей
Архимеда, хотя на практике число заходов может быть увеличено до четырех и
более.
Плечи плоской двухзаходной спирали Архимеда описываются уравнениями
Pi (ср) = аср + Ъ , р2 (tp) = а(ф - л) + Ъ, где р , <р — полярные координаты; а и b — пос-
тоянные величины.
Антенна выполняется из двух проводников, которые, в частности, могут иметь
плоскую форму и выполняться печатным способом на тонком листе высокочастот-
ного диэлектрика (рис. 11.5). Расстояние между проводниками Др и ширина про-
водников Д постоянны по углу ср , причем обычно расстояние между проводника-
ми берется равным ширине проводников (принцип дополнительности). Возможны
два режима возбуждения антенны: противофазный и синфазный. В противофаз-
ном режиме начальные точки спиралей А и В присоединяются к двухпроводной
линии или же возбуждаются коаксиальные кабелем, проложенным вдоль одного
из плеч. Направления токов в начальных точках спирали показаны на рис. 11.6,
а. В синфазном режиме начальные точки спиралей 1 замыкаются между собой и
присоединяются к внутреннему проводнику коаксиального кабеля 2 (рис. 11.6, б).
Наружный проводник кабеля присоединяется к противовесу в виде плоской метал-
лической шайбы. Противовес может выполняться печатным способом на обратной
стороне диэлектрического листа 3, несущего спиральные проводники. Централь-
ная часть синфазной антенны вместе с противовесом представляет собой распре-
делитель в виде несимметричной полосковой линии и в излучении не участвует.
Направления токов в начальных точках спиралей при синфазном возбуждении
показаны на рис. 11.6, б.
Рассмотрим с физических позиций механизм образования излучения архиме-
довских спиральных антенн. В первом приближении антенну можно рассматривать
Частотно-независимые антенны
475
На вход
Рис. 11.6. Противофазное (а) и синфазное (б) возбуждение архимедовских
спиральных антенн: 1 - начальные точки спиралей; 2 - внутренний проводник
коаксиального кабеля; 3 - диэлектрический лист [74]
как двухпроводную линию, свернутую в спираль. Предположим, что на каждом
проводнике спирали имеется бегущая волна тока, причем расстояние между про-
водниками Ар <§: X. Выясним фазовые соотношения токов в проводниках {спирали
при двух режимах возбуждения.
Противофазное возбуждение. Пусть в начальных точках спирали (см. рис. 11.5)
фазы токов равны: Фд = л и Фв = 0. Выделим две точки спирали, расположенные
на разных ветвях, на одинаковых расстояниях I от точек Аи В. Запаздывание фазы
в этих точках по отношению к А и В одинаково и равно р/, и, следовательно,
фазы токов в точках Р и Q: Фр = —J3Z + л , Фг> = -fil. Пусть точки Р и Q лежат на
окружности радиуса р. Рассмотрим точку Р’, соседнюю с точкой Р, но лежащую
на другом проводнике спирали. Дополнительное запаздывание фазы в точке Р’ по
отношению к точке Q при Ар X приближенно составит -лРр, и, следовательно, в
точке Р’ фаза тока Фр' = -pZ - лРр. Разность фаз токов АФ в соседних проводниках
спирали в точках Р’ и Р составит АФ = Фр - Фр' = лРр + л . Найдем значения ради-
уса рп, при которых ДФ = 2лп , п = 1,2,..., и токи в соседних проводниках в точках
Р и Р’ синфазны. Соответствующее условие имеет вид 2лрп = (2п - 1)Х , п = 1,2,... Из
него следует, что на окружностях с периметром, равным нечетному числу длин
волн, токи в соседних проводниках спирали находятся в фазе и могут интенсивно
излучать электромагнитные волны. Наибольшую интенсивность имеет излучение
токов в районе окружности с радиусом X / (2л), причем после прохождения вит-
ков с таким радиусом токи в проводниках спиральной линии резко уменьшают-
ся. Последующие витки спирали, для которых условие синфазности выполняется
при п = 1,2,..., практически оказываются невозбужденными и не влияют на работу
антенны. Таким образом, активная область плоской архимедовской спиральной
антенны в режиме противофазного возбуждения условно может быть заменена
одним витком радиуса X / (2л) с распределением эквивалентного электрического
тока по закону бегущей волны (одноволновая рамка):
^пф(ф) = (11-2.1)
Периметр этого эквивалентного витка равен длине волны. Так как приведенные
рассуждения справедливы для любой длины волны, то противофазная спираль-
ная антенна является частотно-независимой как по входному сопротивлению, так
476
ГЛАВА 11
и по ДН, если только рабочая частота превышает некоторое граничное значение,
зависящее от наружного диаметра антенны.
Синфазное возбуждение. Рассматривая аналогично фазовые соотно-
шения токов в проводниках спирали при синфазном возбуждении, мож-
но легко установить, что токи в соседних витках синфазны на окружностях
с радиусами рт , удовлетворяющими условию 2лрт = 2тк , т = 1,2,... Из-за
интенсивного излучения токов в районе окружности с радиусом X / л проис-
ходит автоматическая отсечка токов и витки с радиусами р > X / л оказывают-
ся невозбужденными. Таким образом, активная область плоской архимедовской
спиральной антенны в режиме синфазного возбуждения условно может быть за-
менена одним витком радиуса X / п с распределением эквивалентного электричес-
кого тока по закону бегущей волны (двухволновая рамка):
^ф(ф) = (11-2.2)
Границы рабочего диапазона антенны определяются из условия Кпф < X / л < _RBH,
где Квн — внешний радиус антенны; Кпр — радиус металлического противовеса в
возбуждающем устройстве.
Характеристики направленности архимедовских спиральных антенн. При рас-
чете ДН удобно расположить архимедовскую спиральную антенну в экватори-
альной плоскости сферической системы координат (начало координат совпада-
ет с центром спирали). Тогда, предполагая, что излучение антенны обусловлено
распределением сторонних токов (11.2.1) или (11.2.2), и основываясь на методике
расчета полей, изложенной в § 7.3, можно получить следующие формулы для
расчета ДН:
/д (0, <р) = i[Jn-i (п sin 0) + Jn+1 (n sin 0)] cos 0e
/ф (0, ср) = i[ Jn_t (n sin 0) + Jn+1 (n sin 0)]e"w,
(11.2.3)
где Jn±1(j?) — функции Бесселя, причем n—1 относится к противофазному возбуж-
дению спирали, п=2 — к синфазному. Формулы (11.2.3) позволяют также рассчи-
тывать излучение круглых рамочных антенн с радиусом а = (X / 2л)тг и распреде-
Рис. 11.7. ДН архимедовских спиральных антенн: а) - противофазное; б) - синфазное воз-
буждение [74]
п = 2
Частотно-независимые антенны
477
лением стороннего тока И = exp(-mcp), п - 1,2,...
На рис. 11.7 показаны рассчитанные по формулам (11.2.3) ДН в меридиональ-
ной плоскости ср — 0. Ввиду симметрии антенны ДН построены лишь для одного
квадранта. Полные пространственные ДН имеют вид тел вращения вокруг оси z
антенны. Как следует из формул (11.2.3), составляющие /е и всюду находятся в
фазовой квадратуре. Поэтому полное поле излучения антенны имеет преимущес-
твенно эллиптическую поляризацию. Однако в плоскости спирали составляющая
/з всегда обращается в нуль и получается линейно поляризованное поле. Чисто
круговая поляризация возникает в осевом направлении 0 = 0 (или л) при противо-
фазном возбуждении спирали. При синфазном возбуждении излучение вдоль оси
отсутствует.
В архимедовских спиральных антеннах можно реализовать одностороннее из-
лучение, если с нижней стороны спирали расположить экран или замкнутый ко-
роб. Однако, это приводит к дополнительной частотной зависимости параметров
антенны и снижает ее диапазонность.
11.3. Логопериодические антенны [2, 74]
Принцип автоматической отсечки излучающих токов воплощен также в антен-
нах с логарифмической периодичностью параметров в зависимости от частоты,
для краткости называемых просто логопериодическими антеннами. Одна из пер-
вых антенн такого типа показана на рис. 11.8. Плечами антенны являются своеоб-
разные структуры из взаимно чередующихся вибраторов в форме выступов и впа-
дин. Геометрия структур характеризуется безразмерным периодом т = Rn / Кп+1,
коэффициентом формы ст = rn / Rn и углами аир. Обычно используются струк-
туры с параметром су = Vt . Плечи антенны в начале координат разделены зазором.
Возбуждающий коаксиальный кабель припаивается оплеткой к одному плечу ан-
тенны на всем его протяжении, внутренний проводник кабеля присоединяется к
началу другого плеча антенны.
Экспериментально было установлено, что электрический ток в выступах
Рис. 11.8. Плоская логопериодическая антенна [74]
478
ГЛАВА И
структуры при удалении от центра возрастает, достигая максимума в месте рас-
положения резонансных выступов примерно четвертьволновой длины. Направ-
ления наиболее интенсивных токов, определяющих излучение антенны, показа-
ны стрелками на рис 11.8. После прохождения резонансных выступов токи резко
уменьшаются, т. е. происходит их отсечка. С уменьшением частоты излучаемых
колебаний последовательно возникают резонансы выступов, более удаленных от
центра. Отношение двух частот, на которых резонируют соседние выступы, со-
ставляет в точности величину т = / со2. Поэтому входное сопротивление и ДН
антенны оказываются периодическими функциями логарифма частоты колеба-
ний. При правильном подборе параметров структуры изменение характеристик
антенны в пределах одного периода оказывается небольшим. Точное повторение
этих изменений от периода к периоду обеспечивает удовлетворительное поведе-
ние характеристик антенны в очень широком диапазоне частот. Границы рабочего
диапазона в первом приближении определяются частотами резонанса крайних вы-
ступов, наиболее близких к центру антенны и наиболее удаленных от него. Легко
может быть достигнут рабочий диапазон частот 10:1 и более.
Среднее входное сопротивление плоской логопериодической антенны обычно
превышает 100 Ом и зависит от значения углов а и 0. При а = 0 = 45° форма ме-
таллической части антенны совпадает с формой ее щелевой дополнительной части
о
и в соответствии с формулой = (60л) входное сопротивление должно состав-
лять около 188 Ом. Измерения дают несколько меньшее значение, равное при-
мерно 150 Ом. Уменьшение среднего входного сопротивления, желательное для
облегчения согласования входа антенны с 75-ом коаксиальным кабелем, может
быть достигнуто уменьшением угла 0. ДН плоской логопериодической антенны со-
стоит из двух широких лепестков, ориентированных перпендикулярно плоскости
плеч. Излучение в плоскости антенны невелико для всех направлений. Вектор Е в
Рис. 11.9. Формы логопериодических структур [74]
Частотно-независимые антенны
479
Рис. 11.10. Однонаправленные логопериодические вибраторные антенны: а) - пространс-
твенная; б) - плоская [74]
направлении максимального излучения поляризован параллельно оси х, а излу-
чение с поляризацией, параллельной оси у, мало. Ширина лепестков ДН зависит
от безразмерного периода структуры т. При изменении т от 0,80 до 0,25 при уг-
лах а = Р = 45° происходит плавное уменьшение ширины лепестков по половинной
мощности от 73 до 38°.
При совершенствовании логопериодических антенн были найдены значительно
более простые формы плеч (на рис. 11.9, а-г показана только половина антенны).
Было также обнаружено, что разворот плеч антенны относительно оси эс на угол
\|/ < 90° может обеспечить однонаправленное излучение в сторону вершины струк-
туры (рис. 10.10, а). Направление максимума излучения совпадает с биссектрисой
угла у.
В предельном случае у = 0 оба плеча антенны совмещаются, и образуется плос-
кая логопериодическая антенна (рис. 11.10, б). Такую антенну удобно трактовать
как линейную решетку симметричных вибраторов монотонно изменяющейся дли-
ны, возбуждаемых двухпроводной линией с перекрещивающимися проводниками.
Линия возбуждается от генератора со стороны вибраторов меньшей длины. Конс-
труктивное выполнение плоской антенны, не требующее специального симметри-
рующего устройства, показано на рис. 11.11, а. Для объяснения действия вибра-
торной логопериодической антенны следует вначале выделить активную область с
наибольшими излучающими токами. В первом приближении эта область включает
в себя вибратор резонансной длины (размер плеча около X / 4) и пару вибрато-
ров, примыкающих к нему с двух сторон. Другие вибраторы из-за значительной
расстройки возбуждаются слабее, и их влияние на излучаемое поле невелико.
Условия возбуждения и взаимное влияние вибраторов активной области соче-
таются таким образом, что более длинный вибратор ведет себя как рефлектор и
ток в нем опережает по фазе ток резонансного вибратора. Напротив, ток в более
коротком вибраторе отстает по фазе от тока резонансного вибратора, и короткий
вибратор играет роль директора. Совместное излучение нескольких вибраторов
активной области усиливается в направлении вершины антенны и компенсируется
в обратном направлении, т. е. в сторону расположения более длинных вибраторов.
Форма измеренной ДН в плоскостях Е и Н для одного из образцов плоской антен-
ны показана на рис. 11.11, б. В плоскости Е ДН получается уже из-за направлен-
ных свойств одного вибратора в этой плоскости.
480
ГЛАВА 11
30°
На вход антенны
излучения
60°
90°
60°
90°
30°
б)
Рис. 11.11. Вибраторная логопериодическая антенна:
а) - конструкция; б) - ДН в Н- и Е-плоскостях [74]
Рабочая полоса частот вибраторной логопериодической антенны снизу ограни-
чивается допустимыми габаритами самых больших вибраторов ( Zmax ~ Хтах / 4) и
сверху — размерами самого малого вибратора ( Zmjn » -^min / 4). Однако для со-
хранения удовлетворительного направленного действия на крайних частотах ра-
бочего диапазона следует позаботиться, чтобы вибратор, резонирующий на самой
длинной волне, имел после себя еще один-два более длинных вибратора-рефлек-
тора, а вибратор, резонирующий на самой короткой волне, имел впереди себя,
т. е. ближе к точкам возбуждения, два-три более коротких вибратора-директора.
Практически удается в 10-кратном диапазоне длин волн с помощью вибраторных
логопериодических антенн получать почти неизменные характеристики направ-
ленности при коэффициенте отражения на входе Г < (0,20 - 0,25).
Участок двухпроводной линии между точкой возбуждения и началом активной
области антенны используется для канализации мощности. Короткие вибраторы,
расположенные на этом участке, обладают большим реактивным сопротивлением
и почти не нагружают линию, лишь несколько уменьшая ее эквивалентное волно-
вое сопротивление. Мощность, проходящая по распределительной двухпроводной
линии, интенсивно излучается активной областью, и поэтому участок линии от
вершины антенны до начала активной области работает в режиме бегущей вол-
ны.
Излучающие плоские раскрывы апертурных антенн
481
Глава 12. Излучающие плоские раскрывы
апертурных антенн [2, 3, 18]
12.1. Внутренняя и внешняя задачи теории
апертурных антенн СВЧ [3]
Апертурные антенны — это антенны, излучение у которых происходит через
раскрыв, называемый апертурой (от латинского apertura — отверстие).
К апертурным антеннам относятся в первую очередь такие антенны, как ру-
порные, линзовые и зеркальные. Из самого названия этих антенн следует, что их
конструкция и принцип действия аналогичны соответствующим акустическим и
оптическим системам, которые в действительности и явились их прототипами. У
апертурных антенн, как правило, можно выделить плоский излучающий раскрыв
№ (рис. 12.1).
Характерной особенностью антенн такого типа является то, что в излучении
участвуют сравнительно большие проводящие поверхности, по которым протека-
ют токи высокой частоты (внутренняя поверхность рупора, металлопластинчатой
линзы, облучаемая поверхность зеркала). Эти токи на поверхности могут иметь
различное направление, меняющееся от точки к точке. Следовательно, апертур-
ные антенны — это антенны с поверхностными токами. По принципу действия,
конструкции и методам изучения они существенно отличаются от проволочных
антенн. Последние являются антеннами с линейными токами, так как в них токи
протекают только в осевом направлении проводов, образующих антенну (хотя и
текут по поверхности проводов).
Апертурные антенны применяются, главным образом, в диапазоне СВЧ, т. е.
в) г)
Рис. 12.1. Примеры апертурных антенн: а) — открытый конец волновода;
б) — рупорная антенна; в) — зеркальная антенна; г) — линзовая антенна [3]
16 - Неганов
482
ГЛАВА 12
на волнах короче 1 м вплоть до субмиллиметровых. Малая длина волны позволяет
сконструировать антенны, размеры которых много больше длины волны. Следова-
тельно, возможно создание остронаправленных антенн, имеющих сравнительно
небольшие размеры. Кроме того, возможно создание антенн,имеющих диаграмму
направленности особой формы, определяемой специальным назначением антенны
(например, антенна обзора земной поверхности с борта летательного аппарата,
антенна радиовысотомера и т. п.).
Небольшие размеры антенн позволяют делать их быстроподвижными. Мож-
но осуществлять механическое перемещение одних частей антенны относительно
других или даже вращать всю антенну с целью качания (или вращения) диаграм-
мы направленности, производя тем самым обзор пространства.
Апертурные антенны являются основным типом радиолокационных антенн. Они
также находят широкое применение в радионавигации, радиоастрономии, в радио-
технических системах управления искусственными спутниками Земли и косми-
ческими кораблями, в тропосферных и радиорелейных линиях и т. п.
Уравнения Максвелла устанавливают связь между первичными источниками
(зарядами и токами) и электрическим и магнитными полями, излучаемыми этими
источниками. Уравнения Максвелла формально можно использовать для расче-
та поля излучения произвольной антенны. Однако при этом возникают трудно
преодолимые проблемы математического характера, связанные с отысканием ре-
шений уравнений Максвелла, удовлетворяющих граничным условиям на поверх-
ности сложной формы. Поэтому при изучении антенн СВЧ задача по определению
поля излучения этих антенн, как правило, разбивается на две части: внутреннюю
и внешнюю. При решении внутренней задачи находятся касательные составляю-
— с — с
щие напряженностей электрических Ех и магнитного Нх полей на некоторой за-
мкнутой поверхности S, охватывающей антенну (рис. 12.2). При решении внешней
задачи по найденному полю и НТ на поверхности 5 находятся напряженности
электрического Е и магнитного Н полей излучения антенны.
При таком подходе решение внутренней задачи существенно зависит от типа
антенны и будет рассмотрена в дальнейшем при изучении конкретных типов апер-
турных антенн СВЧ. Решение внешней задачи не зависит от конкретного вида
антенны и рассматривается в этом разделе.
Поле излучения апертурных антенн может быть также определено через токи,
протекающие по поверхности антенны. Однако в этих антеннах характер рас-
пределения токов обычно является достаточно сложным и должен быть пред-
варительно найден. Распределение тока на проводящей поверхности антенны в
большинстве случаев определяется приближенно, например с помощью законов
геометрической оптики. Затем обтекаемая током проводящая поверхность антенны
Рис. 12.2. К пояснению определения поля излучения рупорных антенн СВЧ [3]
Излучающие плоские раскрывы апертурных антенн 483
разбивается на элементарные площадки dS с поверхностной плотностью тока ц(б').
Поле излучения апертурной антенны определяется как суперпозиция элементар-
ных полей, создаваемых элементарными площадками.
Таким образом, если в проволочных антеннах элементарным излучателем был
элемент длины провода с током (диполь Герца), то в апертурных антеннах в ка-
честве элементарного излучателя удобнее использовать элемент поверхности с
током.
Решение задачи об излучении апертурной антенны может проводиться не толь-
ко через токи на проводящей поверхности, но и через поле в ее раскрыве. Вмес-
то того чтобы находить распределение тока на поверхности антенны каким-либо
методом (например, методом геометрической оптики), определяют распределение
поля в ее раскрыве. Каждый элемент площади раскрыва можно рассматривать как
источник Гюйгенса, который создает некоторую напряженность поля в точке на-
блюдения. Полная напряженность поля определится путем суммирования полей,
создаваемых в точке наблюдения всеми элементами поверхности раскрыва.
Определение поля излучения через поле в раскрыве производится путем ис-
пользования принципа эквивалентных токов. Такой путь решения антенной задачи
является характерной особенностью приближенных методов анализа апертурных
антенн СВЧ, отличающих их от методов анализа проволочных антенн, и широко
применяется.
Описанные схемы решения задачи об излучении через токи на поверхности
антенны или через поле в ее раскрыве являются типичными для многих поверхнос-
тных антенн. Например, для зеркальных антенн применяют оба метода; поле из-
лучения рупорных и линзовых антенн определяют только через поле в раскрыве.
Неточность указанных методов заключается в том, что токи на поверхности
антенны или поле в ее раскрыве определяются приближенно. Для упрощения ре-
шения условия задачи идеализируются. Например, в случае рупорной антенны
поле в раскрыве находится в предположении бесконечной длины рупора и идеаль-
ной проводимости его стенок. Делая такое допущение, мы не учитываем высшие
типы волн, неизбежно возникающие на конце рупора. Кроме того, считая рупор
бесконечным, мы принципиально не можем ожидать наличия какого-либо поля,
связанного с полем в рупоре, на внешней поверхности рупорной антенны. В дейс-
твительности же поле на внешней поверхности не равно нулю вследствие затека-
ния токов на эту поверхность с конца рупора. В случае зеркальных антенн поле в
раскрыве обычно находится также приближенно с помощью методов геометричес-
кой оптики, а поле на «тыльной» поверхности принимается равным нулю.
Аналогичные допущения принимаются и для других типов антенн. Более стро-
гий анализ и экспериментальная проверка показывают, что указанные допущения
не приводят к заметным ошибкам в области главного лепестка диаграммы направ-
ленности. В области же боковых и задних лепестков ошибки могут быть значитель-
ными. Однако для инженерных расчетов указанный приближенный метод вполне
приемлем, тем более, что получаемые при его применении ошибки оказываются
одного порядка с ошибками, возникающими вследствие неточностей в изготовле-
нии антенн.
Часто применяется простой метод геометрической оптики. Однако пользовать-
ся им можно далеко не всегда. В одних случаях он дает достаточно точные ре-
зультаты, в других может дать большие ошибки. Можно показать, что законы
16*
484
ГЛАВА 12
геометрической оптики нельзя применять в точках резкого изменения векторов Е
и Н (например, вблизи границы геометрической тени или вблизи геометрической
точки фокуса).
Законы геометрической оптики в большинстве случаев нельзя использовать не-
посредственно для расчета поля излучения. Однако они дают возможность просто
и с достаточной точностью найти распределение поля в раскрывах некоторых ан-
тенн, в частности зеркальных и линзовых. В этом случае методы геометрической
оптики дают хорошее приближение к точной теории, если выполняются неравенс-
тва:
X I; X « RM
ИН ’
где I — линейные размеры тела, на которое падает электромагнитная волна; Кмин
— минимальный радиус кривизны отражающей поверхности в каждой точке от-
ражения.
Ниже метод геометрической оптики используется для нахождения поля в рас-
крывах линзовых и зеркальных антенн.
Итак, рассмотрим некоторую замкнутую поверхность S, на внешней повер-
хности которой в каждой точке Р заданы комплексные амплитуды касательных
— с -* с
составляющих напряженностей электрического и магнитного полей Ех (Р), Нх (Р)
(рис. 12.2). Предполагается, что сами поля изменяются во времени по гармоничес-
кому закону: exp{icot}.
В электродинамике известен принцип (теорема) эквивалентности, в соответс-
твии с которым заданные на произвольной поверхности S касательные составляю-
— С -* с
щие напряженностей полей Ех и Нт , можно заменить эквивалентными электри-
ческими це и магнитными токами:
Пе= п0,Н
-т
Т|
(12.1.1)
где п$ — единичный вектор внешней нормали к поверхности S.
Поверхность 5 в общем случае может совпадать с частью поверхности S’ ан-
тенны (рис. 12.2). Если антенна выполнена из хорошего проводника, то на каса-
— С
тельная составляющая напряженности электрического поля Ех (а следовательно
и поверхностная плотность магнитного тока ) равна нулю. При этом эквивален-
тный поверхностный ток переходит в реально существующий на S’ электрический
ток. Поэтому для такого случая интегрирования при определении векторных элек-
тродинамических потенциалов проводится уже не по замкнутой поверхности S, а
по той части поверхности, на которой эквивалентный и реальные токи (или каса-
тельные составляющие полей) отличны от нуля. Более точно, обычно поверхность
5 стараются выбирать таким образом, чтобы на значительной ее части S’ можно
было пренебречь эквивалентными или реальными токами, а на оставшейся части
№ = S — S' интегрирования выполнялось в замкнутом виде с целью упрощения
вычислений:
Ае’т(М)
dV',
(12.1.2)
где R — расстояние между точкой наблюдения М и точкой источника q.
Для апертурных антенн в качестве № обычно выбирают плоский раскрыв ан-
Излучающие плоские раскрывы апертурных антенн
485
тенны, полагая, что на остальной части поверхности 5 эквивалентные и реальные
токи равны нулю.
Для определенности будем считать, что раскрыв расположен в плоскости
z - 0, тогда
Je’7n(x,2/,z) = fje’m(x,!/)5(z)
и соотношение (12.1.2) упрощается:
(12.1.3)
(12.1.4)
где R = л](х - х')2 + (у - у')2 + z2 .
у
Интегрирование в (12.1.4) производится по плоскому раскрыву S в прямо-
угольной системе координат OXYZ, причем ось OZ направлена в сторону, проти-
у
воположную внешней нормали п0 к поверхности о (рис. 12.3).
К апертурным относят антенны, у которых в соответствии с принципом эк-
вивалентности может быть выделена плоская поверхность раскрыва 5s, форми-
рующая остронаправленное излучение. Наиболее распространены зеркальные (в
частности, параболические), а также рупорные и линзовые апертурные антенны.
КНД апертурных антенн связан с площадью раскрыва S и длиной волны X общей
формулой
П = (4л5/Х2)к^, (12.1.5)
у
где kn < 1 — общий (результирующий) коэффициент использования поверхности,
зависящий от вида амплитудно-фазового распределения возбуждения и других
факторов.
Ширина луча по уровню —3 дБ апертурной антенны в какой-либо плоскости,
перпендикулярной поверхности раскрыва, обратно пропорциональна линейному
размеру раскрыва L в этой плоскости:
Д0О,5 =(51°X/L)^, (12.1.6)
где кд > 1 — коэффициент расширения луча, зависящий от формы раскрыва и
вида амплитудно-фазового распределения возбуждения.
Конструкции распределителей апертурных антенн обычно строят таким обра-
зом, что мощность возбуждения к каждому элементу раскрыва в приближении
геометрической оптики доставляется независимыми лучами, проходящими одина-
ковую электрическую длину от общего входа антенны. Поэтому в соответствии с
М(т,0,ф)
п0
у
Рис. 12.3. Расположение плоского раскрыва S относительно системы координат [3]
486 ГЛАВА 12
принципом построения распределителя апертурные антенны могут быть условно
отнесены к антеннам с параллельной схемой питания элементов излучающей
системы (в отличие от антенн бегущей волны, характеризуемых последовательной
схемой питания). Положительной особенностью параллельной схемы возбуждения
является сохранение синфазности элементов раскрыва и вида амплитудного рас-
пределения независимо от длины волны. Поэтому многие конструкции апертурных
антенн, в частности зеркальных, являются частотно-независимыми и допускают
одновременную работу антенны в диапазонах от метровых до миллиметровых. Ра-
зумеется, при этом сохраняется зависимость КНД и ширины луча от длины волны
согласно формулам (12.1.5) и (12.1.6).
Из этих формул также следует, что КНД апертурных антенн может неограни-
ченно возрастать, а ширина луча стремится к нулю при увеличении отношения
S / к . Однако в реальных конструкция апертурных антенн максимально дости-
жимый КНД оказывается ограниченным из-за влияния случайных погрешностей
при выполнении антенны. Достигнутый уровень технологии производства позво-
ляет создавать апертурные антенны с КНД 108 и более. Апертурные антенны пер-
венствуют по направленности среди других типов антенных устройств.
12.2. Внешняя задача излучения плоского раскрыва (апертуры)
антенн СВЧ [3]
Между напряженностями электрического и магнитного полей и векторными
потенциалами А^т для дальней зоны в сферической системе координат справед-
ливы следующие соотношения [1]:
-ik WCA^
(12.2.1)
ГПА Де’т Де’т
ГДе , ^(рсо
дальней зоне:
компоненты электродинамических векторных потенциалов в
----- {je'm(x’,y',zYkr'cosadV',
4лг J
V
(12.2.2)
где je,m — объемные плотности электрического и магнитного токов,
г' cos а = х' sin 0 cos <р + у' sin 0 sin ср + z' cos ср
(12.2.3)
— разность хода лучей от двух точечных источников расположенных в начале
координат ( г = 0) и в точке источника Р(т\ 0', ср'), Wq = соцд /к — характеристи-
ческое сопротивление среды.
Пусть на некоторой плоской поверхности S при z = 0, ограничивающей объем
V, где расположены je и jm , определены напряженности полей Es, Hs, через
которые определяются эквивалентные поверхностные токи:
(12.2.4)
где п0 = -Zq
внешняя единичная нормаль к поверхности S.
/^m{x,y,z) =
Излучающие плоские раскрывы апертурных антенн
487
Так как при z = О
je’m(x',yf,z') = r\e’m(x',y')d(z'),
и (12.2.2) в декартовой системе координат переписывается в виде:
p-ikr f
A^’m(x,i/,z) = —----- J fje’m(x',?/')exp{i/csin0(x,cos<p + у' sinq>)}dx'dy', (12.2.5)
т,™ „ „2 х я,2 , ~2
где г = \]х + у + z .
Из (12.2.4) и (12.2.5) следует, что поверхностные токи и векторные электродина-
мические потенциалы имеют только х- и у-компоненты.
Перейдем от декартовых к сферическим координатам с помощью соотношений
для произвольного вектора В (с учетом, что Bz - 0):
Ве = (Вж cos ф + Bv sin ф) cos 0,
В(п = -By. sin ф + B1t cos ф.
Тогда соотношения (12.2.1) принимают вид:
Eg = -ik Wc (До x COS ф + До v sin ф) COS 0 + (-До x sin ф + До у cos ф)
sin ф + До у cos ф) - (До х cos ф + До у sin ф) cos 0
(12.2.6)
Предположим, что вектор напряженности электрического поля Ё$ на па-
—► с
раллелен оси OY, а вектор напряженности магнитного поля Нт параллелен оси
ОХ:
Е? = еуу0 , fif = hxx0 , (12.2.7)
где Xq , pg — единичные орты прямоугольной системы координат; ev , hx — комп-
лексные амплитуды полей на при z = 0.
Свяжем с прямоугольной системой координат OXYZ сферическую систему ко-
ординат {г, 0, ф}, причем начало обеих систем координат совпадают, угол 0 отсчи-
тывается от оси OZ, угол ф от оси ОХ (рис. 12.3).
Подставляя значения (12.2.7) в (12.2.4)-(12.2.6) с учетом того, что ng =2д, полу-
чаем векторное интегральное соотношение, определяющее напряженности элект-
ромагнитного поля в точке наблюдения Р(т, 0, ф) в дальней зоне через касательное
с с у
электромагнитное поле Ev , Нх на плоском раскрыве 5 :
ike-ikr
4лг
sin ф + фд cos 0 sin ф) х
х exp (ikr' cos a)dxfdy' +
„-ikr
г-^~ hM)-
4лг J
(12.2.8)
x(0o cos 0 sin ф + фд cos ф) exp (ikr' cos a^dx'dy',
н<Р(лб,‘р) = ^-, (r,e,<p) =
где 0O , Фо — единичные орты сферической системы координат, для разности хода
лучей г'cos а справедлива формула (12.2.3).
488
ГЛАВА 12
у
Введем локальное волновое сопротивление Zs на поверхности S :
7 [™оё] еу
Zj с = — —-------.
h hx
(12.2.9)
Подставляя (12.2.9) в (12.2.8), получаем
ik e,lcr
4л r
W
—-cos0 0
s
О “
W,
-СОБф COS0 +
Фо exp (ikr' cos a)dx'dyf
(12.2.10)
H = Wc[tqE~
т. e. поле в дальней зоне имеет поперечный характер к направлению распростра-
нения т0 волны.
12.3. Излучение прямоугольной и круглой площадок при разных
амплитудных распределениях поля [18]
Раскрывы многих апертурных антенн имеют прямоугольную или круглую фор-
му. В связи с этим представляет интерес рассмотреть поле излучения этих площа-
док при различных распределениях поля в пределах самих площадок.
Как было показано, напряженность в дальней зоне может быть рассчитана по
известному полю на поверхности плоского раскрыва с помощью формул (12.2.10).
Рассмотрим вначале прямоугольную площадку с известным амплитудным рас-
пределением электромагнитного поля. Введем прямоугольную систему координат
с началом в центре площадки (рис. 12.4). Ось z направим по нормали к площадке,
а оси х и у — параллельно ее сторонам.
Электромагнитное поле в пределах площадки будем считать линейно поляри-
зованным с электрическим вектором Ev, параллельным оси у, и магнитным век-
тором Нх, параллельным оси х. Тогда выражения, определяющие комплексные
амплитуды вектора электрического поля и его составляющих в дальней зоне,
принимают вид:
= Л + cosee lfer г tfcr'sinecos(<p-<p')d5
2Х г J у
S
= Л + cosSe lfcrcos(() Г£ ikr’sineCos(<p-q>')djS
4 2л г J у
S
Кроме того, по-прежнему
(12.3.1)
Ё = Ее0о + Ефф0. (12.3.2)
В выражениях (12.3.1) учтено, что вектор Ёу параллелен оси у.
Далее для сокращения мы будем определять только комплексную амплитуду
полного вектора Е. Комплексные амплитуды составляющих этого вектора Eq и Е®
легко могут быть определены путем умножения полученных для Е выражений на
sin ф и cos ф.
Излучающие плоские раскрывы апертурных антенн
489
Рис. 12.4. Ориентация прямоугольной площадки в декартовой и сферической системах
координат [18]
Расчет поля излучения будем вести по формуле (12.2.10), которую несколько
преобразуем к виду, удобному для анализа прямоугольных площадок. Из рис. 12.4
видно, что
г' cos <р' = х',
r'sintp' = у'.
Учитывая также, что в прямоугольной системе координат dS = dx’dy', получаем
следующую форму записи выражения (12.2.10):
а/2 Ъ/2
Е = А J J E!/(.T',?/'X>!'fSir‘Wj-''mf,p+y'slrl'0)dx'dy’,
-а/2-Ъ/2
где для сокращения введено обозначение
. 1 + cos 0 ехр(-гкт)
2Х
(12.3.3)
(12.3.3а)
Формула (12.3.3) позволяет найти поле в любом направлении, определяемом уг-
лами 0 и ф. Однако наибольший интерес представляет поле в двух главных плос-
костях xOz,yOz,B которых лежат векторы Н и Е соответственно. Вследствие этого
принято называть поле в плоскости xOz полем в плоскости Н (обозначая его Efj),
а поле в плоскости yOz — полем в плоскости Е (обозначая его Ее ).
Все точки плоскости xOz имеют сферическую координату ф = 0. Следовательно,
формула (12.3.3) для указанной плоскости примет вид:
а/2 Ь/2
Eu(x',y')eikx'sinf>dx’dy'.
-а/2-Ь/2
(12.3.4)
Точки плоскости yOz имеют координату ф = л / 2, следовательно,
а/2 Ь/2
ЁЕ = A [ [ Ey(x,,y,)eiky,sinedxfdy'. (12.3.5)
-а/2-Ь/2
Рассмотрим теперь круглую площадку с радиусом d. Пусть вектор Ёу по-пре-
жнему параллелен оси у,а Нх — оси х. Тогда исходными выражениями для рас-
чета поля излучения будут являться те же формулы (12.3.1) и (12.3.2), как и для
случая прямоугольной площадки. Для круглых площадок более удобно использо-
490
ГЛАВА 12
M(r, 0, <р)
Рис. 12.5. Полярная система координат для анализа поля излучения
круглых площадок [18]
вать полярную систему координат р, ф' (рис. 12.5), в которой
г' - р, dS = pdtp'dp.
Тогда формулу (12.2.10) запишем в виде
2п а
Ё = А Г |Х,(р,<p')eifc₽sinpdq’dp.
о о
Вводя безразмерные переменные
R = —; u = kasin0 = —sinO,
а 2
где d = 2а — диаметр площадки, перепишем выражение (12.3.6):
2л 1
Ё = Аа2 Г (Ey(R,(p,)eiuRcos^~<p^Rd^,dR.
0 0
(12.3.6)
(12.3.7)
Для поля в главных плоскостях (xOz и yOz) получаем следующие расчетные
формулы:
2л 1
Ён = Аа2 Г
0 0
2л 1
ЁЕ = Аа2 [ [Еу(р,фУмК81п<₽'Мф7Ш.
0 о
(12.3.8)
(12.3.9)
Формулы (12.3.4) и (12.3.5) для прямоугольной площадки, а также (12.3.8) и
(12.3.9) для круглой площадки позволяют найти поле излучения при различных
распределениях поля на площадках. Так как во многих практических случаях
поле в раскрыве антенны стремятся сделать синфазным, вначале рассмотрим из-
лучение площадок с синфазным полем, а влияние фазовых искажений рассмотрим
отдельно.
Вначале выведем формулы для поля излучения с учетом конкретного ампли-
тудного распределения Ev , а затем проанализируем полученные результаты.
Излучающие плоские раскрывы апертурных антенн
491
12.3.1. Прямоугольная площадка.
1. Амплитуда поля на площадке постоянна: Еу = Eq = const. Такое равноамп-
литудное распределение поля в раскрыве антенн практически не встречается. Этот
случай здесь рассматривается как идеальный. В реальных антеннах поле в рас-
крыве чаще всего к краям площадок убывает, иногда до нуля. Однако рассмот-
рение такого идеализированного случая совместно с реальными позволяет лучше
оценить влияние распределения амплитуд на характеристики излучения.
Напряженность поля в плоскости Н будет:
Ь/2 а/2
-Ь/2 -а/2
ikx'sin&dx' = ASE9
sin 9
(12.3.10)
где а и Ь — стороны площадки; S = ab — площадь излучающей площадки.
Напряженность поля в плоскости Е определяется формулой
f Jet)
а/2 Ъ/2 sin ---Sin
Ee=AEq f dx' f e^'s^dy' = ASEq—------------------
-a/2 -b/2 — sin0
(12.3.11)
2. Амплитуда поля вдоль оси х меняется по косинусоидальному закону:
—» —►
Ej. = Еа cos(rcx' / а).
у V
(12.3.12)
Заметим, что приблизительно такое поле существует в открытом конце прямо-
угольного волновода с волной типа Н10.
Поле в плоскости Н будет
Ь/2 а/2
= АЁ0 Г
-Ъ/2
Г кх
I cos----е
J а
-а/2
ite'sin9dx'=-A5E0
(12.3.13)
Как видно из этого выражения, изменение поля на площадке вдоль оси х при-
вело к другому характеру зависимости напряженности поля в дальней зоне от
угла 0.
Вдоль направления оси у поле на площадке не меняется, поэтому в плоскости Е
поле в дальней зоне носит другой характер:
а/2 , Ь/2
= АЁ0 [ cos—dx’ f егку‘sin9dy' = - ASE0
J a J л
-а/2 -b/2
(12.3.14)
— sin
2
Таким образом, для плоскости Е получили выражение, отличающееся от
(12.3.11) только постоянным множителем 2 / п .
12.3.2. Круглая площадка.
1. Амплитуда поля на площадке постоянна. Вследствие осевой симметрии
Ен = Ev = Eq и поле излучения согласно (12.3.7) будет описываться формулой:
492
ГЛАВА 12
Ё = Аа2Ё0
1 2 тс
KdK jeiwRcos((p-(p')d(P =
1
= Аа2Ё02л [RJ0(uR)dR = ASEq 2J1 .
J и
О
(12.3.15)
Здесь использованы известные соотношения
2л
Jo(2) = j_ feizc°sФ^ф , 2Ji(z)= [zJ0(z)dz, (12.3.16)
2л J J
o
где Jn (z) — функция Бесселя n-го порядка от аргумента z.
2. Амплитуда поля спадает к краям площадки. Закон убывания поля к краям
круглого отверстия может быть различным. В качестве примера рассмотрим слу-
чай, когда поле меняется по закону
Ёу = Ёо (1 - R2)".
(12.3.17)
Здесь, как и прежде, R = р/ а; п = 0,1,2,3,... Кривые изменения амплитуды поля
вдоль радиуса площадки для различных п показаны на рис. 12.6. Такая зависимость
встречается в зеркальных антеннах с рефлектором в виде параболоида вращения.
Вследствие осевой симметрии получаем:
АЁ02па2 [(1 - R2 )n Jo (uR)RdR =
о
(12.3.18)
где
= АЁ05Ап+1(и) / (п +1),
и!
(и / 2)п
табулированная лямбда-функция.
Еу
0,8
0,6
0,4
0,2
Jn (^)
0 0,2 0,4 0,6 0,8 R
Рис. 12.6. Кривые распределения амплитуды напряженности поля по радиусу круглой
площадки для случая, когда поле меняется по закону Ё$ = Ёо(1 - R2)n [18]
Излучающие плоские раскрывы апертурных антенн
493
12.3.3. Диаграммы направленности прямоугольной и круглой площадок.
Полученные выражения для поля излучения позволяют легко проанализировать
направленные свойства площадок. Учитывая значение множителя А (12.3.3а) и
обозначая для сокращения
ka
sin 9
для прямоугольной площадки,
fcb .
—sm0
для прямоугольной площадки,
(12.3.19)
kd
sin0
для круглой площадки,
2
получаем следующие выражения для нормированных диаграмм направленности:
а) прямоугольная площадка с Ev = Ео = const:
&
F(0) = . (12.3.20)
2 и
б) прямоугольная площадка с Ev = Eq cos(mr' / а):
F(0) = 1 + COS0—; (12.3.21)
2 (9 г
1-----и
\7C )
в) круглая площадка с Ёу = Eq = const:
F = l+cos0 2Jx(u) (12.3.22)
2 w
г) круглая площадка с Ev = Eq (1 - R2 )n :
1 + cosO „ , .
F(0) =-------An+1(u).
(12.3.23)
Как видно, все приведенные выражения состоят из двух сомножителей. Пер-
вый сомножитель представляет собой диаграмму направленности элементарной
площадки (источника Гюйгенса), второй есть «множитель решетки», определяю-
щий направленные свойства системы излучателей (в данном случае совокупности
элементарных площадок), рассматриваемых как ненаправленные. Таким образом,
указанные формулы еще раз иллюстрируют теорему о перемножении диаграмм,
рассмотренную ранее.
Изменением первого сомножителя обычно можно пренебречь, приравняв его
единице (особенно в пределах небольших изменений угла 0 ), так как он изменяет-
ся очень медленно по сравнению с изменением второго сомножителя (рис. 12.7).
Диаграммы направленности для прямоугольной площадки с неизменным и коси-
нусоидальным распределением поля показаны на рис. 12.8. На рис. 12.9 приведены
графики лямбда-функций первого и второго порядков, определяющих диаграммы
направленности круглой площадки для указанных распределений поля на ней.
Из приведенных рисунков и формул следует, что максимум излучения воз-
бужденных синфазно площадок получается в направлении нормали к ним (т. е.
при и = 0 , при этом получается неопределенность, которая просто удаляется по
правилу Лопиталя). Физически это вполне очевидно. В направлении нормали дли-
494
ГЛАВА 12
и
Рис. 12.7. Геометрическое перемножение диаграмм направленности: результирующая диа-
грамма F(0) = р(0) получается путем перемножения радиус-векторов и р2 для каждого
значения 0 [18]
F(0)
0,8
0,707
0,6
0,2
2 л 4 3 6 2л 8 Зл
— л
2
Рис. 12.8. Диаграмма направленности прямоугольной площадки с постоянными (1) и коси-
нусоидальным распределением (2) амплитуд поля на ней (синфазное возбуждение) [18]
Рис. 12.9. Диаграммы направленности круглой площадки с постоянными (1) и спадающим к
краям распределением (2) амплитуд поля (синфазное возбуждение) [18]
495
Излучающие плоские раскрывы апертурных антенн
на пути от всех элементов поверхности площадки до точки наблюдения одинакова
(предполагается, что точка наблюдения М достаточно удалена). Следовательно,
при синфазном возбуждении площадки все элементы ее поверхности будут созда-
вать в точке наблюдения элементарные поля, совпадающие по фазе. Результи-
рующая напряженность будет равна арифметической сумме всех составляющих
и достигнет максимального значения. При отклонении от нормали появится раз-
ность хода лучей от отдельных элементов поверхности площадки, вследствие чего
создаваемые ими поля не будут синфазными и результирующая напряженность
поля уменьшится.
Из рис. 12.8 и 12.9 также видно, что уменьшение амплитуды поля к краям
площадок приводит к уменьшению уровня боковых лепестков и к расширению
основного лепестка.
Определим ширину диаграммы направленности по половинной мощности. Для
этого по кривым, изображенным на рис. 12.8 и 12.9, определим значения и, при
которых F(0) = 0,707 :
1. Для прямоугольной площадки с Е
отсюда
v = Eq = const, F(0O 5) = 0,707 при и = 1,39,
t/ J
sin 6
где I = а или I = Ъ.
При а » X или Ъ » X можно принять, что sin0o 5 « 0О>5 . Тогда получаем следу-
ющие значения для ширины диаграммы направленности:
в плоскости Н
20о5 - 0,89Х / а рад или (20о>5)° = 5IX / а ,
аналогично в плоскости Е
(20О5)° = 51Х/Ь. (12.3.24)
2. Для прямоугольной площадки с Ev = Eq cos(tue' / а) из графика находим
и = (ka / 2) sin 0 = 1,86, откуда для плоскости Н при а » X , имеем
20Q 5 = 1,18Х / а рад или (20О 5)° = 68Х / а, (12.3.25)
для плоскости Ё ширина диаграммы направленности по-прежнему будет равна
(20о>5)° = 51Х / Ь.
3. Для круглой площадки с Е,, - Еп = const из графика определяем
У V
и = —sin 0 = 1,62, откуда ширина диаграммы в градусах для обеих плоскостей
2
Ё и Н будет равна
(20О 5)° = 60Х / d. (12.3.26)
— — 2 п
4. Для круглой площадки с Еу = Ео(1- R ) ширина диаграммы направленности
зависит от показателя степени п:
при п = 1 (20О 5)° = 73Х / d,
при п = 2 (20g 5)° = 84Х / d.
В заключение сведем в табл. 12.1 основные параметры, характеризующие на-
496
ГЛАВА 12
правленные свойства прямоугольной и круглой площадок при различном распре-
делении поля на них, в предположении, что а » 1 и d » к. Приведенный в табл.
12.1 коэффициент использования площадки раскрыва антенны к определяется как
отношение эффективной поверхности антенны Sd к ее геометрической площади
раскрыва S:
k = Sd/S.
(12.3.27)
Таблица 12.1 [18]
Тип площадки Распределение поля на площадке Ширина диаграммы по половинной мощности Амплитуда 1- го бокового лепестка Коэффициент использования площади раскрыва к
% ДБ
Прямоугольная Ev = Eq = const 51 — а 21 -13,5 1,00
Прямоугольная - й Ev = Eq cos y a 68— а 7 -23,1 0,81
Круглая Ё.. = Eq = const У v 60 — а 13 -17,6 1,00
Круглая tqi II o11 1 73— а 6 -24,6 0,75
Круглая Ey = E0(l-R2)2 84— а 3 -30,6 0,56
Проведенный анализ направленных свойств площадок позволяет сделать сле-
дующие выводы.
1. При синфазном возбуждении площадок максимум излучения получается в
направлении нормали к ним.
2. Диаграмма направленности зависит от отношения ширины площадки к
длине волны. Для рассмотренных форм площадок на диаграмму направленности
влияет только тот размер площадки, который лежит в плоскости определения
диаграммы направленности.
3. Для больших (по сравнению с длиной волны) площадок ширина диаграммы
направленности прямо пропорциональна отношению длины волны к соответству-
ющему размеру площадки.
4. Уменьшение амплитуды поля к краям площадки приводит к уменьшению
амплитуды боковых лепестков и к расширению главного лепестка. Это наглядно
видно из табл. 12.1. Если изменение амплитуды поля происходит только вдоль
одного направления, то и вызванное этим изменение диаграммы направленнос-
ти произойдет только в плоскости, соответствующей ему [см., например, случай
прямоугольной площадки при Еу = Ёо cos(twc' / а) ]. Уменьшение амплитуды поля
к краям площадки приводит также к уменьшению коэффициента использования
площади раскрыва.
плоские раскрывы аррртурных антенн 497
12.4. Влияния фазовых искажений на излучение площадки [18]
До сих пор мы предполагали, что поле на площадке синфазное. Для получе-
ния остронаправленной диаграммы игольчатого типа стремятся создать синфазное
поле в раскрыве антенны. Однако всякого рода технические погрешности при вы-
полнении антенн приводят к нарушению синфазности поля в ее раскрыве, т. е. к
фазовым искажениям. Кроме того, в отдельных случаях для получения диаграммы
направленности особого вида (например, косекансной), а также для электричес-
кого качания луча приходится формировать поле в раскрыве антенны не синфаз-
ным, а с некоторым заданным законом распределения фаз (который во времени
может периодически меняться).
Будем считать, что поле на площадке определяется функцией с разделяющи-
мися переменными
Ё^^^Е^Е^у1)^, (12.4.1)
где уц — единичный вектор определяющий направление вектора Еу.
В этом случае можно ограничиться рассмотрением распределения только вдоль
одного направления, например вдоль оси х. Обозначим закон изменения фазы в
направлении х функцией
у(2х7 а) = v(^) • (12.4.2)
Практически любое распределение фазы поля на площадке может быть пред-
ставлено в виде степенного ряда
V(S) = + V2^2 + • • • + Vn V1 + • • • (12.4.3)
Из структуры формулы (12.4.3) видно, что коэффициенты разложения
Vi, V2> •••> 'Ии — суть максимальные фазовые искажения от соответствующих со-
ставляющих, получающиеся на краю площадки, когда £ = 1, т. е. х' = ±а / 2.
В большинстве случаев при анализе практически встречающихся фазовых ис-
кажений можно ограничиться первыми тремя членами ряда. Рассмотрим влияние
каждого из этих членов раздельно. Для упрощения задачи будем считать, что
амплитуда поля в пределах площадки неизменна.
12.4.1. Линейное изменение фазы: \|/(^) = В этом случае поле на площадке
описывается выражением
Еи(х',у') = уоЕое-^.
Поле в дальней зоне в плоскости Н будет
Ён = АЁ0Ь^ f ei(u~^d^ = у0АЕ0 Sm(“ V1).
2 J и - \|/i
(12.4.4)
Сравнивая полученное выражение с формулой (12.3.14), выведенной для син-
фазного распределения поля на площадке, замечаем, что различие между ними
лишь в том, что и заменено на и - . Следовательно, диаграмма направленнос-
ти будет такой же, как и при синфазном поле, но будет смещена относительно
нормали к площадке. Направление максимума определится из равенства и = vpi,
откуда угол отклонения главного максимума от нормали к площадке
0 = arcsin^y! / ka).
(12.4.5)
498
ГЛАВА 12
Для больших площадок ( а » X ) и не очень больших значений Vi ( - 71) фор-
мула (12.4.5) принимает вид
0 2У1 _ V1
ка па
Легко показать, что этот угол равен углу поворота фронта волны в пределах
площадки. В [18] показано, что
ур! =1к & — ак,
откуда угол поворота фронта волны на площадке а = 2\|/-£ / ка , следовательно,
а = 0'.
Таким образом, линейное изменение фазы в раскрыве антенны приводит к от-
клонению диаграммы направленности почти без изменения ее формы. Это свойс-
тво может быть использовано для электрического качания луча и в некоторых
антеннах находит практическое применение. Более строгий анализ показывает,
что основной лепесток диаграммы направленности расширяется пропорционально
1 / cos 0'. При небольших 0' этим расширением можно пренебречь
4д?
12.4.2. Квадратичное изменение фазы: \р(а?) = \|/2 —:
площадке равно: а
. В этом случае поле на
Еу = УвЕО ехР *И2 “
Поле, создаваемое площадкой, определится интегралом
(12.4.6)
который выражается через так называемые интегралы Френеля С(и) и S(u) с по-
мощью равенства:
и. i-t2
е 2 dt = C(u) + iS(u),
о
(12.4.7)
где
Таким образом (12.4.6) может быть представлено в виде
4\|/2^2
sin2 0 [С(и)-С(г?) + г5(и)-гЭД].
(12.4.8)
Здесь
sin0 +
sin0 -
(12.4.9)
На рис. 12.10 изображены диаграммы направленности, рассчитанные по (12.4.8),
Излучающие плоские раскрывы апертурных антенн
499
AF(0)
AF(0)
Рис. 12.10. Диаграммы направленности прямоугольной площадки с равноамплитудным
полем, фаза которого меняется по квадратичному закону [18]
A F(0) A F(0)
-8 0 8 и -8 0 8 и
Рис. 12.11. Диаграммы направленности прямоугольной площадки с равноамплитудным
полем, фаза которого меняется по кубическому закону [18]
AF(0)
-8 0 8 и
Рис. 12.12. Диаграммы направленности прямоугольной площадки с косинусоидальным из-
менением амплитуды и квадратичным изменением фазы поля [18]
500 ГЛАВА 12
для различных значений \g2 •
Из приведенных кривых видно, что изменение фазы поля на площадке по
квадратичному закону приводит к исчезновению нулей между лепестками диа-
граммы направленности. Основной лепесток расширяется, причем это расширение
особенно сильно проявляется на малых уровнях (порядка 0,2—0,3) нормированной
диаграммы направленности вследствие слияния основного лепестка с боковыми.
При больших значениях \|/2 в главном лепестке образуется провал, ширина лепес-
тка резко увеличивается.
Таким образом, квадратичное изменение фазы в отличие от линейного может
привести к существенному искажению диаграммы направленности. Величина этих
искажений определяется значением \|/2 • При \|/2 < п / 2 искажения незначительны,
при больших значениях \|/2 искажения становятся существенными. Направление
главного максимума при квадратичном изменении фазы остается таким же, как
и при синфазном поле, так как диаграмма симметрична относительно нормали к
площадке.
12.4.3. Изменение фазы поля по кубическому закону: \|/(х) = у3
женность поля на площадке
8аг'3
——-. Напря-
сг
= ^0Е0 ехР
Формула для расчета диаграммы направленности при указанном виде фазовых
искажений получается чрезвычайно сложной. В книге [18] приводится, например,
следующее выражение для диаграммы направленности, представляющее собой
ряд из производных высшего порядка:
°О п
F(9) = (-if 2Е1_ро(3тг)(0)
(12.4.10)
где 1*о (0) — диаграмма направленности при синфазном возбуждении.
Вследствие сложности формулы (12.4.10) практически она может быть исполь-
зована только при малых значениях \|/з , когДа можно ограничиться несколькими
членами ряда.
Получающиеся диаграммы направленности при кубическом законе изменения
фазы на площадке приведены на рис. 12.11, из которых видно, что направление
главного максимума диаграммы направленности смещается. Кроме того, диаграм-
ма искажается и становится асимметричной. Боковые лепестки с одной стороны от
главного лепестка сильно возрастают, а с другой уменьшаются.
Диаграммы направленности, показанные на рис. 12.10 и 12.11, относятся к слу-
чаям равноамплитудного возбуждения площадок.
Если амплитуда поля к краям площадок будет убывать (например, по косину-
соидальному закону), то фазовые искажения будут значительно меньше влиять на
форму диаграмм направленности. Это естественно, так как наибольшее изменение
фазы будет на краях площадок, но влияние краев будет незначительным вследс-
твие малой амплитуды поля на них. Рис. 12.12 иллюстрирует это положение.
В заключение заметим, что характер изменения поля и соответствующие
диаграммы направленности, показанные на рис. 12.10, имеют место в рупорах,
расширяющихся в плоскости Е. Случай, показанный на рис. 12.12, соответствует
Излучающие плоские раскрывы апертурных антенн 501
рупору, расширяющемуся в плоскости Н. Предполагается, что в обоих случаях
прямоугольный рупор возбуждается волной типа Н10. Более подробно это будет
показано в следующей главе.
12.4.4. Случайные фазовые ошибки [3]. Остановимся кратко на влиянии слу-
чайных фазовых ошибок на характеристики плоского раскрыва. Случайные ошиб-
ки имеют вероятностное распределение и учет их влияния в простейшем случае
сводится к анализу средних характеристик антенны (средней диаграммы направ-
ленности F(0,(p) и среднего КНД D), причем усреднение должно проводиться по
ансамблю однотипных антенн. В ряде случаев, когда ошибки являются эргодичес-
кими, усреднение можно проводить во времени для одной и той же антенны.
Итак, пусть фазовые ошибки ф(р) являются случайной стационарной величи-
ной с нулевым средним значением и известным значением дисперсии о2 = vj/2 (р).
Известен также радиус корреляции фазовых ошибок рр , определяющий расстоя-
ние между ближайшими точками на раскрыве,, в которых случайные ошибки ока-
зываются почти независимыми друг от друга. Средняя диаграмма направленности
при этих предположениях имеет вид [3]
К(0,Ф) =е
Fq (6, <р) + о
а 2 2
2 Ро
2 2 • 2 а
it р0 sin 9
DX2
(12.4.11)
где F(0, ф) — диаграмма направленности; D — КНД антенны в отсутствие фазовых
ошибок.
Максимальное уменьшение КНД плоского раскрыва можно оценить по фор-
муле
Ds = De~°2
(12.4.12)
где через обозначим КНД в присутствии случайных ошибок.
Анализ соотношений (12.4.11),(12.4.12) показывает, что наличие случайных фа-
зовых ошибок приводит к уменьшению КНД плоского раскрыва и появлению в
средней диаграмме направленности добавочного бокового фона (второе слагаемое
в выражении (12.4.11)), уровень которого уменьшается с ростом размеров раскры-
ва.
12.5. Коэффициент направленного действия и эффективная
поверхность площадок [18]
2
Пусть излучающая система представляет собой отверстие площадью S » X в
бесконечном плоском экране, совпадающем с плоскостью z = 0 (рис. 12.3). Возбуж-
дение отверстия осуществляется из нижнего полупространства плоской электро-
магнитной волной, распространяющейся в направлении оси z и характеризуемой
составляющими электромагнитного поля Ех и Hy = Ех / Wc , где Wc = / £а .
Коэффициент направленного действия поверхностных антенн удобно опреде-
лять через их эффективную поверхность [18]:
502
ГЛАВА 12
Рис. 12.13. Модель синфазного раскрыва в виде отверстия в плоском экране [2]
Эффективная поверхность плоских раскрывов (площадок) целиком определяет-
ся их геометрическими размерами, формой, длиной волны и законами распреде-
ления поля в пределах этих площадок.
В предположении, что излучающая площадка возбуждается электрическим
полем, ориентированным вдоль оси у (рис. 12.13) эффективная поверхность опре-
деляется следующим образом [2]:
(12.5.1)
Для площадок, возбуждаемых синфазным полем,
(12.5.2)
Рассмотрим, каково соотношение между эффективной поверхностью S& и гео-
метрической площадью S площадок при некоторых законах распределения поля.
12.5.1. Площадка произвольной формы с равноамплитудным синфазным
распределением поля имеет эффективную поверхность
Излучающие плоские раскрывы апертурных антенн
503
(12.5.3)
Таким образом, при синфазном и равноамплитудном поле эффективная по-
верхность площадки равна ее геометрической площади.
12.5.2. Прямоугольная площадка с косинусоидальным изменением ампли-
туды синфазного поля: Еу = PqEq cos(tle' / а) имеет эффективную поверхность
b/2 a/2 f
Ео f dyf J cos^-dx
9 r L -ь/2 -g/2_________
b/2 a/2
„2 f j , f 2
E0 I dy I COS ---
-b/2 -a/2
(12.5.4)
что составляет около 81% от геометрической площади.
То, что при неравноамплитудном возбуждении площадки ее эффективная по-
верхность оказывается меньше геометрической, является естественным. Действи-
тельно, в рассматриваемом случае амплитуда поля к краям площадки убывает
и, следовательно, элементы площадки, более близкие к краям, будут создавать
меньшую напряженность поля, чем элементы площадки, расположенные в сере-
дине. Ослабление поля к краям площадки эквивалентно уменьшению ее размеров,
если площадку рассматривать как возбуждаемую равномерно.
Уменьшение эффективной поверхности площадки, обусловленное ослаблением
поля к ее краям, наглядно иллюстрируется табл. 12.1. В этой таблице приведены
значения коэффициента использования площади раскрыва R для неравномерно
возбуждаемой круглой площадки. При быстром спадании амплитуды поля к
краям площадки коэффициент к резко падает.
В соответствии с принципом эквивалентности электромагнитное поле в верхнем
полупространстве можно трактовать как создаваемое излучением вторичных ис-
точников, распределенных по какой-либо поверхности, полностью охватывающей
истинные источники поля. Удобно выбрать в качестве такой поверхности плоскость
z = 0. Строгий расчет распределения эквивалентных электрических и магнитных
токов в плоскости z - 0 достаточно сложен, однако физическая интуиция и знание
известных положений геометрической оптики подсказывают, что полное элек-
тромагнитное поле в отверстии больших электрических размеров близко полю
невозмущенной падающей плоской волны, а токи на верхней теневой поверхности
экрана пренебрежимо малы по сравнению с эквивалентными токами в отверстии.
Поэтому отверстие можно заменить излучающим раскрывом £ и пренебречь из-
лучением остальных участков плоскости z = 0.
Элементарная площадка раскрыва dS = dxdy представляет источник Гюй-
генса, создающий при z > 0 и г —> оо электромагнитное поле dE, описываемое
формулой [2]:
504
ГЛАВА 12
(0О cos (р - Фо sin ф)
г(1 + cos 6)е гкг
2Хт
Гех (х, y)eik sin cos<P+« sin 4»da.d?/; (12 5 5)
в которой возбуждение раскрыва Ех(х,у) для общности предполагается неравно-
мерным и несинфазным.
При синфазном возбуждении раскрыва максимальное излучение оказывается
ориентированным вдоль оси z, где разность хода лучей для всех элементов рас-
крыва равна нулю. Модуль вектора Е в дальней зоне в этом направлении
max
(12.5.6)
Для определения КНД раскрыва необходимо знать также полную мощность из-
лучения. Проще всего найти ее, вычисляя поток вектора Умова-Пойнтинга через
поверхность раскрыва:
(12.5.7)
Вычисление является приближенным, так как полное поле в раскрыве не является
строго равным полю плоской электромагнитной волны.
Используя определение КНД в виде (2.2.1), приходим к выражению для КНД
раскрыва [2]
^тах
Ё'тах
WCPZ
При равномерном и синфазном распределении Ех = const интегралы легко вы-
числяются и приводят к результату
D() = 4л5 / X2.
(12.5.8)
Таким образом, плоский синфазный раскрыв с равномерным распределением
возбуждения имеет эффективную поверхность,точно равную площади раскры-
о
ва. Увеличивая отношение S / к , КНД синфазного раскрыва можно увеличить
до очень больших значений. Например, квадратный раскрыв со стороной 10Х мо-
жет иметь КНД, равный 1250.
При неравномерном и несинфазном распределении возбуждения КНД раскрыва
оказывается меньше максимального значения, определяемого формулой (12.5.8).
Это следует из неравенства Шварца:
2
\Ey(x,y)dS
j|£y (х, у)
Уменьшение КНД при неидеальном АФР принято оценивать так называемым
апертурным коэффициентом использования поверхности
Излучающие плоские раскрывы апертурных антенн
505
7 sd D
k = - —
S Do
(12.5.9)
5 Ey(x,y) dS
Значение k не зависит от формы ДН элемента раскрыва, и поэтому в (12.5.9)
вместо Ev можно использовать любую функцию возбуждения 1(х, у).
12.6. Сравнение множителя направленности плоского раскрыва
различной формы [2]
Так как ДН одного элемента раскрыва в полупространстве z > 0 является почти
постоянной функцией [см. множитель перед интегралом в (12.5.5)], то ширина луча
и уровень боковых лепестков в ДМ раскрыва определяются множителем направ-
ленности системы.
12.6.1. Множитель направленности раскрыва прямоугольной формы.
Рассмотрим сначала раскрыв прямоугольной формы размером а х Ъ (рис. 12.14).
Наиболее простым является случай, когда распределение возбуждения может
быть представлено произведением двух множителей, зависящих только от а? и
только от у: I(x,y) = 1(х)1(у) — так называемое разделяющееся амплитудно-фа-
зовое распределение. Тогда множитель направленности также имеет вид произве-
дения
а/2 Ъ/2
/Е(е,ф)= f I(x)e*fcsin®cos<pdx f , (12.6.1)
-а/2 -Ъ/2
причем каждый сомножитель совпадает с множителем направленности линейной
антенны, ориентированной в одном случае по оси х, а в другом — по оси у.
При равномерном и синфазном распределении I(x) = I(y) = const интегралы в
(12.6.1) легко вычисляются и множитель направленности представляется в виде
Рис. 12.14. Плоский прямоугольный раскрыв
506
ГЛАВА 12
Рис. 12.15. Рельеф множителя направленности идеального прямоугольного раскрыва [2]
У
sinT
sinT
= 0.5fca sin 0 cos <р ; Т
= 0.5kb sin 0 sin (р.
У показан па рис. 12.15, где ввиду симметрии изображен только
можно выделить
2. Поле в нижнем полупространстве 0 > л / 2 не
и это полупространство исключа-
'Р1/ являют-
У
= sin^ 0, а граница области видимости
хг = O.Ska cos ср;
где Ч7
Рельеф двумерной функции (12.6.2) на плоскости обобщенных угловых пере-
менных Т
один квадрант плоскости. Точками обозначены максимумы главного и боковых
лепестков. Уровни вершин лепестков отмечены цифрами. Вокруг каждого бокового
максимума показаны сечения лепестков линиями уровня половинной мощности.
Линии нулевого уровня излучения, являющиеся границами отдельных лепест-
ков, показаны тонкими линиями. Рис. 12.15 инвариантен к размерам раскрыва,
поскольку они учтены в угловых переменных. Так же как и при анализе линейных
антенн, па плоскости обобщенных угловых переменных Т
область видимости, границы которой соответствуют направлениям излучения в
плоскости раскрыва при 0 = л
может быть вычислено по формуле (12.6.2)
ется из рассмотрения. Линии постоянного угла 0 на плоскости Т
ся эллипсами: [Тх / (0.5/са)]2 + / (0.5fcb)
при sin 0 = 1 в параметрической форме задается соотношениями Ч7
х¥уг = 0.5/сЬзп1ф.
Для примера на рис. 12.15 показана граница области видимости при а = 41 и
Ъ = 5.5Х. С увеличением размеров раскрыва область видимости расширяется и в
нее попадает все большее число боковых лепестков. Наибольшие боковые лепестки
получаются в главных плоскостях xOz и yOz. Этот вывод остается справедливым
и для неравномерных амплитудно-фазовых распределений возбуждения, и поэ-
тому анализ пространственного множителя направленности прямоугольного рас-
Излучающие плоские раскрывы апертурных антенн
507
крыва обычно ограничивают изучением его сечений главными плоскостями xOz
и yOz. Полученные там оценки ширины луча, уровня боковых лепестков, влия-
ние вида функции возбуждения па форму множителя направленности сохраняют
свое значение для главных плоскостей прямоугольного раскрыва. В частности, при
равномерном и синфазном возбуждении ширина луча по половинной мощности
Д0.5= 5ГХ/а (в плоскости xOz) и Ао50^ = 51°Х / b (в плоскости yOz). Выражая
отсюда а и Ъ и подставляя их значения в формулу для КНД (12.5.8), получаем
Do = 4лаЬ / X2 = 32700 / (АО 50^АО 50°).
Максимальный КНД прямоугольного раскрыва представить в виде произведе-
ния трех множителей Do = 4лаЬ /X2 = л(2а/Х)/(2Ь/Х) = nDxDy, где Dx = 2а / X
и Dy = 2b / X — КНД идеальных линейных антенн с размерами: а » X и b » X;
множитель л можно трактовать как эквивалентный КНД одного элемента рас-
крыва.
При неравномерном, но разделяющемся по координатам х и у распределении
возбуждения КНД прямоугольного раскрыва снижается и результирующий КИП
можно оценить по формуле к = кхку , где кх и ку — значения КИП эквивалент-
ных линейных антенн, параллельных осям х и у.
Можно показать [2], что доля полной мощности, излучаемой через главный
лепесток, т. е. эффективность главного лепестка, при а, b » X примерно равно
произведению эффективностей главных лепестков эквивалентных линейных ан-
тенн, параллельных осям х и у: (1 - Pg) « (1 - Рд.)(1 - 0„), где Pg — коэффициент
рассеяния прямоугольного раскрыва; рх и — коэффициенты рассеяния эк-
вивалентных линейных антенн. Таким образом, полный коэффициент рассеяния
прямоугольного раскрыва Pg = рх + р„ - РЖР^ . При синфазном равномерном воз-
буждении Рх = Рп = 0,097 и pg ® 0,185 .
12.6.2. Множитель направленности круглого раскрыва. Для него удоб-
но использовать сферические координаты и выражение для элемента поверхнос-
ти dxdy = rdrd(p. Разность хода лучей в показателе подынтегральной экспоненты
sin 0(д? cos ср + у sin ф) = г sin 0 соб(ф - ф') и формула для множителя направленности
круглого раскрыва радиуса а принимает вид
Г(0,ф) = f р(т\ф')ег7сг'sin0cos((₽-<p')r'dr'йф\ (12.6.3)
о о
Предположим, что функция возбуждения не зависит от азимутального угла:
1(г') = (1 - А) + Д[1 - (г' / а)2 Г , п = 1,2..., (12.6.4)
где 1 - А — уровень поля на краю раскрыва, т. е. пьедестал. Тогда интеграл (12.6.3)
выражается через так называемые лямбда-функции ЛП(Т):
F(6) = 2па2 [(1 - А)Л, (Т) + ДЛ„+1 (Т) / (п +1)],
(12.6.5)
где Т = ka sin 0
угловая переменная, аналогичная угловым переменным и ?
используемым при анализе прямоугольного раскрыва.
Лямбда-функции просто связаны с функциями Бесселя Jn(T): ЛП(Т) =
n!Jn(T)
с? / 2)п ’
Функции jA^T) и Л2(Т)
являющиеся множителями направленности круглого
508
ГЛАВА 12
F(0)
0,8
0,6
0,4
0,2
0 л 2п
Рис. 12.16. Множители направленности круглого синфазного раскрыва при равномерном
Aj и спадающем Л2 амплитудных распределениях [2]
а) б)
Рис. 12.17. Рельефы множителей направленности прямоугольного (а) и круглого (б) рас-
крывов [2]
2
раскрыва при амплитудных распределениях 1(г) = const и I(r) = 1 - (г / а) , пока-
заны на рис. 12.16. Отметим, что множитель направленности круглого раскрыва
при амплитудных распределениях вида (12.12) обладает осевой симметрией и не
зависит от угла <р. Таким образом, пространственные рельефы бокового излуче-
ния в прямоугольном и круглом раскрывах принципиально различны (рис. 12.17):
Ширина луча по уровню 0,707 круглого раскрыва с равномерным синфазным
возбуждением выражается формулой ДО = 59°X / (2а) при уровне боковых лепест-
ков около 0,132 (по полю), или —17,6 дБ. При спадающем к краям раскрыва амп-
Излт/'чаюгцие плоские раскрывы апертт/рных антенн
509
wmin wmax
Рис. 12.18. К определению понятия эквивалентной линейной антенны [2]
о
литу дном распределении 1 - (г / а) ширина луча возрастает в 1,23 раза, а уровень
боковых лепестков снижается до —24,7 дБ. Одновременно происходит снижение
КИП до 0,75 и уменьшение коэффициента рассеяния до значения pg « 0.002 про-
тив первоначального значения Pg «0.162 при равномерном амплитудном распре-
делении.
12.7. Метод эквивалентного линейного излучателя в анализе плос-
кого раскрыва [2]
Рассмотрим произвольный по форме плоский раскрыв с заданным амплитуд-
но-фазовым распределением 1(х,у). Если раскрыв возбужден синфазно, то на-
правление главного максимума перпендикулярно его плоскости. Множитель на-
правленности раскрыва выражается интегралом (12.2.10). Входящую в показатель
подынтегральной экспоненты величину xq cos (р0 + yq sin фд = н(фо) можно тракто-
вать как расстояние в плоскости раскрыва от начала координат до проекции точки
интегрирования Q на направление и, задаваемое углом фр (рис. 12.18). Принимая
это во внимание и переходя к повернутым на угол фо декартовым координатам и,
v, z, легко привести формулу (12.6.1) к виду множителя направленности эквивален-
тной линейной антенны длиной L™. = um,Y - :
F 1 lllclA. 111111
'Ll
“max
f (0, Фо) =
f I3K(u)eifc“sin0
du
(12.7.1)
IL •
“mm
где эквивалентное амплитудно-фазовое распределение возбуждения выражается
интегралом
v2(u)
j I(u,v)dv.
v^u)
Здесь Vi(u) и Vz(u) — уравнения кривых, определяющих нижнюю и верхнюю гра-
ницы раскрыва. При синфазном и равномерном амплитудном распределении зна-
чение 1эк(и) фактически равно длине хорды, проходящей через точку Q парал-
лельно оси V.
510
ГЛАВА 12
12.7.1. Круглый раскрыв. В круглом раскрыве радиуса а с равномерным син-
фазным возбуждением эквивалентное амплитудное распределение в линейной ан-
тенне длиной Ьэк = 2а имеет вид
при и
Такое распределение является спадающим к краям, и это объясняет расшире-
ние главного лепестка на 16% и снижение уровня боковых лепестков на 4,3 дБ в
круглом раскрыве по сравнению с квадратным раскрывом со стороной 2а.
Снижение уровня боковых лепестков и расширение луча в круглом раскрыве
не сопровождается падением к, который при равномерном возбуждении равен
единице.
12.7.2. Квадратный раскрыв. Для диагональной плоскости равномерно воз-
бужденного синфазного квадратного раскрыва со стороной а эквивалентное ам-
плитудно-фазовое распределение в линейной антенне длиной Ьэк = ау/2 линейно
спадающей к краям функцией
1ж(й) = 10а-Л(1 - |и|) при |it| < ау/2 .
Подстановка этого распределения в формулу (2.7.1) и интегрирование приво-
дят к множителю направленности F(G, л / 4) = sin2 \|/ / \|/2 , где \|/ = 0,7070а sin 9, ха-
рактеризующемуся шириной луча по уровню 0,707 АО ~ 52°Z / а и весьма низким
уровнем боковых лепестков: —26,5 дБ. Ширина луча в диагональной плоскости
квадратного раскрыва лишь на 2% превышает ширину луча в главных плоскос-
тях. Это объясняется тем, что спадание амплитуды возбуждения к краям экви-
валентной линейной антенны компенсируется увеличением ее длины в л/2 раз по
сравнению с размером раскрыва в главной плоскости.
Волноводные излучатели и рупорные антенны
511
Глава 13. Волноводные излучатели
и рупорные антенны [18]
13.1. Излучение из открытого конца волновода [18]
На дециметровых и более коротких волнах широкое применение находят ру-
порные антенны и, в частности, антенны в виде открытого конца прямоугольного
или круглого волновода. Излучатели этого типа используются самостоятельно, а
также как облучатели линзовых и зеркальных антенн.
В технике СВЧ в качестве канализирующих устройств широкое применение
находят различные типы волноводов. Наиболее распространенными среди них яв-
ляются волноводы прямоугольного и круглого сечений. Однако волноводы могут
быть использованы не только для канализации электромагнитной энергии, но и
для ее излучения.
Излучение может происходить прежде всего из открытого конца волновода.
Кроме того, излучение может быть из щелей, специально для этой цели проре-
занных в определенных местах волновода. Здесь мы рассмотрим только излучение
из открытого конца волновода.
Открытый конец волновода можно рассматривать как простейшую антен-
ну СВЧ. Действительно, открытый конец представляет собой площадку с электро-
магнитным полем, во многом подобную тем площадкам, излучение которых было
рассмотрено в главе 12.
Однако между открытым концом волновода и рассмотренными в главе 12 пло-
щадками имеются различия. Во-первых, волна на конце волновода не является по-
перечно электромагнитной типа ТЕМ, как в случае указанных площадок, а име-
ет более сложную структуру. Во-вторых, кроме падающей, имеется отраженная
волна. В-третьих, наряду с основным типом волны на конце волновода возникают
высшие типы волн. Кроме того, поле источника существует не только в раскрыве
волновода, но и в какой-то мере и на его внешней поверхности вследствие зате-
кания на эту поверхность токов с конца волновода.
Для приближенного решения задачу разбивают на две: внутреннюю и вне-
шнюю. Внутренней задачей является нахождение поля в раскрыве волновода. При
этом считают, что поле в раскрыве представляет собой сумму полей падающей и
отраженной волн основного типа колебаний. Высшие типы волн, возникающие на
конце волновода, и токи, неизбежно появляющиеся на внешней поверхности вол-
новода, не учитываются. Внешней задачей является нахождение поля излучения
по известному полю в раскрыве.
13.1.1. Прямоугольный волновод. Основным типом волны в прямоугольном
волноводе является волна типа Н10, структура которой показана на рис. 13.1. Рас-
пространяющаяся в волноводе основная волна Н10, дойдя до его открытого кон-
ца, частично излучается и частично отражается обратно к генератору. В месте
перехода от волновода к пространству, т. е. в раскрыве, возникают волны высших
типов, а также появляются поверхностные токи на наружных поверхностях стенок
512
ГЛАВА 13
Рис. 13.1. Прямоугольный волновод (а) и структура поля в нем при волне типа Н10 : в плос-
кости хОу (б); в плоскости xOz (в); в плоскости yOz (г) [18]
волновода. Для полубесконечного круглого волновода существует точное решение
электродинамической задачи об излучении в свободное пространство, получен-
ное Л.А. Вайнштейном. Для поля излучения прямоугольного волновода строгого
решения не найдено. В инженерных расчетах предполагают, что касательные со-
ставляющие поля в раскрыве волновода (а, следовательно, и эквивалентные элек-
трические и магнитные токи) представляют сумму падающей и отраженной волн
основного типа колебаний:
= (1 + Г)Е0 sin
1 Ео . пх'
-(1 - Г)-----— sm-----
Хп 120л а
(13.1.1)
К Ел пх'
-----— cos-----
2а 120 л а
где Eq — напряженность электрического поля падающей волны в середине рас-
крыва волновода; — длина волны в волноводе; X — длина волны в свобод-
ном пространстве; Г — комплексный коэффициент отражения. По данным экс-
периментальных исследований, в прямоугольном волноводе с отношением сторон
b / а = 0,45 коэффициент отражения составляет 0,3 - 0,2 и имеет фазу л / 3 - л / 2.
причем первые цифры относятся к нижней рабочей частоте волновода, вторые — к
верхней.
Выражения для поля излучения, создаваемого в дальней зоне таким открытым
концом волновода, найдем с помощью формул, полученных в разделе 12.3:
Zn _
1 + —— cosO _ikr
—----------е—-- JX, (х', у’)^'sin ‘‘dx'dy',
s
Ед
+ cos 0
(13.1.2
-ikr
[Ev(x',y')eikx'sin(,dx'dy'.
s
Волново&ные излт^чатели и рупр/рные д/н/трпны
513
Определим вначале отношениеZB / 2ф.Из (13.1.1) следует, что волновое сопро-
тивление фронта волны на открытом конце волновода
120л.
Заметим также, что для воздуха ZB = 120л. Следовательно,
ZB _1-Г л
1 + Г хв '
С учетом последней формулы комплексная амплитуда напряженности электри-
ческого поля в главных плоскостях определится выражениями
2Л
лХ
cos 0
-ikr a/2 t b/?
----- f cos —dx' f
-а/2
-Ъ/2
sinO
-ikr
cosO
kb . „
smO
'sin6dy' =
\ sm
(13.1.3)
—ikr
ЕН = гУо
2л
cos^V^’sine
a
Ъ/2
-а/2
-Ъ/2
- seq
= ^yQ —
лЛ
COS
(ka .
— smO
\2
sinO
-ikr
где S = ab — площадь раскрыва волновода; 6 — угол, отсчитываемый от оси z (рис.
12.3).
Из (13.1.3) видно, что при Г - 0 и Хв = А, эти формулы переходят в формулы,
полученные в главе 12 для синфазной прямоугольной площадки с косинусоидаль-
ным и равномерным распределением поля соответственно.
На рис. 13.2 показаны экспериментально снятые кривые модуля и аргумента
коэффициента отражения от открытого конца стандартного волновода 3-см диа-
пазона в зависимости от частоты [18].
Построенные по (13.1.3) расчетные (сплошные кривые), а также эксперимен-
тальные (пунктир) диаграммы излучения из открытого конца прямоугольного вол-
новода показаны на рис. 13.3.
13.1.2. Круглый волновод. Основными типами волн в круглом волноводе яв-
ляются волны типа Нц и Е01. Структуры полей для этих типов волн показана на
рис. 13.4.
Принимая указанные выше допущения относительно стуктуры поля в раскрыве
круглого волновода и решая аналогично внешнюю задачу, получаем выражения
для поля излучения. Так, например, для волны типа имеем
17 - Неганов
514
ГЛАВА 13
120 _____________________________
8500 9000 9500 /МГц
Рис. 13.2. Зависимости модуля Г| и аргумента <р коэффициента отражения открытого кон-
ца стандартного волновода от частоты [18]
F(0)
0.8
0.4
0
40 80 120 160
77-пло( жость
0 40 80 120 160 0°
Рис. 13.3. Диаграммы направленности излучения из открытого конца прямоугольного
волновода при а / А, = 0,71; Ъ / 1 = 0,32 ; X = 3,2 см; Г =0,28 (слошные кривые - расчет,
пунктирные кривые - эксперимент) [18]
Рис. 13.4. Структура поля в круглом волноводе при волнах типа (а) и Е01 (б) [18]
б)
Волноводные излучатели и рупорные антенны
515
Рис. 13.5. Диаграммы излучения из открытого конца круглого волновода, возбуждаемого
волной типа Нп (слошные кривые - расчет, пунктирные кривые - эксперимент) [18]
F(0)
= -6 0 л к а
- COS0
х cos ср
O,58J/(kasin0) е ikr
3,41а . п
-----sin0
(13.1.4)
-60пк2а
COS0
т /7 ч JitkasinQ) е гкг
х sin cpJi (ka) —-----------
ka sin 0 r
Здесь a — радиус волновода; угол ср отсчитывается в плоскости хОу от оси х;
0 — полярный угол, отсчитываемый от оси z (рис. 12.3).
На рис. 13.5 показаны диаграммы излучения раскрыва круглого волновода с
волной типа Ну j.
13.1.3. Оценка открытых волноводов как антенн [18]. Таким образом, ан-
тенны в виде открытого конца волновода являются принципиально слабона-
правленными. Действительно, для получения остронаправленных характеристик
необходимо, чтобы размеры излучающей поверхности были много больше длины
волны. Размеры же раскрыва волновода не могут быть больше определенных, так
как в противном случае в волноводе могут возникнуть волны высших порядков,
которые нарушают нормальную работу волноводного тракта. Для прямоугольно-
го волновода с волной типа Н10 размеры сечения определяются неравенствами
X / 2 < a < X; b < X / 2. Обычно берут
а « (0,62 — 0,95)Х , b~0,5a.
При таких размерах ширина диаграммы направленности как в плоскости Н,
так и в плоскости Е получается большая (см. рис. 13.3). Аналогичная картина будет
и для круглого волновода (рис. 13.5).
Другой особенностью волноводных излучателей является их относительно
плохое согласование со свободным пространством. Вследствие резкого изменения
условий распространения электромагнитной волны при переходе от волновода к
свободному пространству, коэффициент отражения для стандартных волноводов
достигает по модулю величины Г| = 0,25 — 0,30.
17*
516
ГЛАВА 13
В силу указанных недостатков антенна в виде открытого конца волновода нахо-
дит ограниченное применение. Обычно она используется там, где требуется широ-
кая диаграмма направленности и где сравнительно сильное отражение от конца не
играет существенной роли (например, в случае приемных антенн). Открытый ко-
нец волновода может быть использован также в качестве облучателя более слож-
ных антенн или как элемент решетки излучателей.
Волноводы круглого сечения для этих целей применяются значительно реже,
чем прямоугольного. Одной из причин этого является неустойчивость поляризации
поля. Даже при незначительных деформациях волновода возможен поворот струк-
туры поля вокруг оси волновода. По этим причинам применение круглого волно-
вода как облучателя в основном ограничивается антеннами с коническим качанием
луча. При этом для повышения стабильности поля в волноводе возбуждение его
ведется от прямоугольного волновода через плавный переход.
13.2. Электромагнитные рупоры [18]
13.2.1. Типы электромагнитных рупоров и методы их анализа [18]. Для
получения более острой диаграммы направленности сечение стандартного волно-
вода можно плавно увеличивать, превращая волновод в рупор. В этом случае
структура поля в волноводе в основном сохранится.
В горле рупора, т. е. в месте его соединения с волноводом, все же возникают вы-
сшие типы волн. Однако если угол раскрыва рупора не слишком велик, то волны
всех типов, кроме основного, быстро затухнут в окрестностях горловины рупора,
а по рупору будет распространяться только колебание основного типа.
Плавное увеличение сечения волновода улучшает также согласование его со
свободным пространством. Модуль коэффициента отражения от конца прямо-
угольного волновода (рупора) с волной типа приближенно может быть выра-
жен следующей формулой:
|Г| = (1-Л. / Л.в)/(1 + Х / Хв).
Увеличение раскрыва рупора в плоскости вектора Н приводит к приближению
длины волны в рупоре Л в к длине волны в свободном пространстве X. При этом
коэффициент отражения Г стремится к нулю.
Основные типы рупоров образуются в результате расширения прямоугольного
или круглого волновода. Если расширение прямоугольного волновода происходит
только в одной плоскости, то получается секториальный рупор. В зависимости от
того, в какой плоскости происходит расширение, различают Н-плоскостные (рис.
13.6, а) и Е-плоскостные (рис. 13.6, б) секториальные рупоры.
Если прямоугольный волновод расширяется сразу в двух плоскостях, получа-
ется пирамидальный рупор. Последний может быть остроконечным (рис. 13.6, в) и
клинообразным (рис. 13.6, г). Кроме указанных типов, применяется еще комбини-
рованный прямоугольный рупор, показанный на рис. 13.6, д.
Расширяющийся круглый волновод образует конический рупор (рис. 13.6, е).
Из перечисленных типов наибольшее распространение получили секториальные
и пирамидальные рупоры. Конические рупоры в силу недостатков, присущих из-
лучателям в виде открытого конца круглого волновода, применяются значительно
реже. Комбинированный рупор (рис. 13.6, б) имеет несколько меньший коэффици-
Волноводные излучалп^ли и рутюркые
517
Рис. 13.6. Основные типы электромагнитных рупоров [18]
L'
Рис. 13.7. Продольное сечение прямоугольного рупора [18]
ент отражения, чем пирамидальный, но вследствие более сложной конструкции
применяется реже последнего.
Рассмотрим продольное сечение прямоугольного рупора плоскостью Е или Н
(рис. 13.7). Величина R называется длиной рупора, точка О — вершиной рупора,
угол при вершине 2(рр — углом раскрыва, размер ар — шириной раскрыва рупора.
Очевидно, что в пирамидальном рупоре все эти величины, полученные при сече-
нии рупора плоскостью Е, в общем случае будут отличаться от соответствующих
величин, полученных при сечении рупора плоскостью Н.
Исследование рупорных антенн вследствие больших математических трудно-
стей обычно ведется приближенным методом. Первоначально определяется поле
в раскрыве рупора. При решении этой задачи рупор предполагается бесконечно
длинным, а его стенки — идеально проводящими. Поле в рупоре находится путем
решения уравнений Максвелла. При этом учитывается способ возбуждения рупо-
ра: те составляющие поля, которых не должно быть в структуре возбужденной
волны, считаются равными нулю.
Полученное таким образом решение для бесконечного рупора считается при-
ближенно верным и для рупора конечной длины.
После решения внутренней задачи обычным методом решается внешняя зада-
ча, т. е. находится поле излучения.
518
ГЛАВА 13
13.2.2. Способы уменьшения длины рупора [18]. Существенным недостатком
рупорных антенн является сравнительно большая длина рупоров. Длина рупора
пропорциональна квадрату одного из размеров раскрыва. Это накладывает серь-
езные ограничения на использование электромагнитных рупоров в качестве остро-
направленных антенн.
Существует два пути решения задачи уменьшения длины рупора. Первый за-
ключается в применении многорупорной антенны. Идея метода состоит в том, что
требующийся большой размер раскрыва однорупорной антенны разбивают на п
частей, где п — число рупоров, образующих многорупорную антенну. Тогда дли-
на R каждого рупора может быть уменьшена в п2 раз по сравнению с длиной R’
однорупорной антенны.
Схема многорупорной антенны для п = 4 показана на рис. 13.8. Рупоры распо-
лагаются вдоль прямой линии и соединяются между собой так, чтобы длина пути
волны от общего волновода до любого из рупоров была одинаковой. Этим достига-
ется синфазность возбуждения рупоров.
Недостатком многорупорной антенны является трудность обеспечения точной
синфазности возбуждения всех рупоров и усложнение конструкции. По этой при-
чине пространственные решетки из рупоров применяются редко.
Другой путь уменьшения длины рупорной антенны состоит в применении спе-
циальных устройств, корректирующих фазовые искажения в раскрыве рупора.
Существует много методов коррекции. Одни из них основаны на том, что ис-
кусственно выравнивается длина пути, проходимого электромагнитной волной от
вершины рупора до всех точек раскрыва. В других используются различные типы
линз, помещаемых в раскрыве и выравнивающих фазовый фронт волны.
На рис. 13.9 показан один из методов выравнивания длины пути. Секториальный
рупор изогнут таким образом, что длина пути луча 1, идущего по средней линии
рупора от его вершины до раскрыва, равна длине пути любого другого луча (на-
пример, 2), идущего от вершины рупора к любой точке раскрыва. Легко показать,
что кривая АВС, по которой растянуты стенки согнутого рупора, должна иметь
форму параболы. Действительно, для того чтобы поле в раскрыве было синфаз-
ным, должно выполняться равенство
2л
— (2т0) =
кх
откуда
Рис. 13.8. Схема многорупорной антенны [18]
Волноводные излл^чатели и рупорные антенны
519
Рис. 13.9. Один из методов выравнивания фаз поля в раскрыве рупора [18]
Ускоряющая
линза
АВ,ЭБ
+1
-1
-3
Замедляющая
линза
0.4 0.8 1.2 1.6 2.0 ///о
Рис. 13.11. Изменение КНД пирамидальных
и конических рупоров с частотой [18]
Рис. 13.10. Рупорная антенна с линзой,
помешенной в ее раскрыве [18]
z = т0 - гх = х2 / 4R . (13.2.1)
Уравнение (13.2.1) есть уравнение параболы. Следовательно, форма сгиба долж-
на быть параболической.
На рис. 13.10 показаны рупорные антенны с помещенными в их раскрыве лин-
зами.
13.2.3. Применение рупорных антенн [18]. В качестве самостоятельных ан-
тенн рупоры применяются главным образом в тех случаях, когда не требуется
очень острая диаграмма направленности и когда антенна должна быть достаточно
диапазонной. Рупорные антенны могут работать в широком диапазоне частот.
На рис. 13.11 показано изменение AD — КНД пирамидальных и конических рупо-
ров с частотой. По оси абсцисс отложена рабочая частота, нормированная к часто-
те fo , на которой рупор «оптимален». Как видно из рисунка, уменьшение КНД на
3 дБ происходит либо при уменьшении частоты на 40%, либо при ее увеличении
на 160%. Очевидно, что выгоднее использовать рупор на более высоких частотах
по сравнению с частотой, на которой он является оптимальным.
Практически с помощью рупорной антенны можно перекрыть приблизительно
двойной диапазон волн. Собственно говоря, диапазонность рупорной антенны ог-
раничивается не рупором, а питающим его волноводом.
Большая диапазонность рупорных антенн и простота конструкции являются
существенными достоинствами этого типа антенн СВЧ, благодаря которым они
находят широкое применение в технике антенных измерений и измерений харак-
теристик электромагнитного поля.
520
ГЛАВА 13
Электромагнитные рупоры также широко применяются в качестве облучателей
более сложных антенных устройств, например для облучения линз и зеркальных
антенн. Эта область применения будет рассмотрена в последующих главах.
13.3. Рупорные антенны [18]
13.3.1. Н-плоскостной секториалъный рупор [18]. Для нахождения струк-
туры поля в рупоре используем цилиндрическую систему координат у , р, (р. При
возбуждении волновода волной Н1() поле будет иметь только следующие компонен-
ты Нр, и Еу. Остальные составляющие будут равны нулю. Решая с учетом этого
систему уравнений Максвелла и используя асимптотические выражения функций
Ханкеля для больших значений аргумента /ср , получаем следующие значения для
составляющих поля:
— cos
-i(kp-Vo)
У
(13.3.1)
240<р0/ср у р
— sin
2 ср0
-г'(кр-\|/0)
Ну — Еу — Ер — 0.
Здесь Ео — напряженность электрического поля в точке рупора с координатами
у = 0, ср = 0, р = pg, причем р0 » л .
Формулы (13.3.1) показывают, что при больших /ср составляющая Нр —> 0 и
поле в рупоре представляет собой поперечную электромагнитную цилиндрическую
волну. Вследствие того, что у большинства применяемых рупоров раскрыв плос-
кий, а волна в рупоре цилиндрическая, поле в раскрыве не будет синфазным.
Для определения фазовых искажений в раскрыве рассмотрим продольное сече-
ние рупора, показанное на рис. 13.13. Дуга окружности с центром в вершине рупора
О проходит по фронту волны и, следовательно, является линией равных фаз. В
произвольной точке М', имеющей координату х, фаза поля отстает от фазы в
середине раскрыва (в точке О') на угол
= ^(ОМ' - R) = ^(a/r2 + x2 - R) =
Л Л
(13.3.2)
Так как обычно в рупорах х R, то можно ограничиться первым членом пра-
вой части разложения, т. е. принять
Дфд. = Tlx2 / XR. (13.3.3)
Таким образом, фаза поля в раскрыве рупора меняется приблизительно по
квадратичному закону. Если фазовые искажения будут велики, то, как было по-
казано выше, это приведет к сильным искажениям диаграммы направленности.
Максимальный сдвиг фазы поля в раскрыве относительно его середины (точки
О') очевидно будет на краях рупора и составит величину
Волново&ные излучатели и рупорные антенны
521
Рис. 13.12. Цилиндрическая система коорди- Рис. 13.13. К определению фазовых иска-
нат для анализа секториальных рупоров [18] жений в раскрыве рупора [18]
Дфмякг - / 4ХК . (13.3.4)
т MdKV Р ' v 7
Формулы (13.3.3) и (13.3.4) являются приближенными. Ими можно пользовать-
ся, когда R > ар / 2 или <р0 < 45°. В применяемых рупорах эти условия обычно
выполняются.
Иногда удобно максимальные фазовые искажения в раскрыве рупора опреде-
лять через его длину и половину угла раскрыва фд [18]:
_ 2лК(1 - cos ф0)
Д'Имакс ’ (13.3.5)
cos фд
которая верна при любых R и ф0.
Из (13.3.5) следует, что при заданной величине раскрыва поле в раскрыве будет
тем меньше отличаться от синфазного, чем больше длина рупора R. Однако рупо-
ры очень большой длины конструктивно не удобны. Габаритные ограничения тре-
буют нахождения компромиссного решения, т.е. определения такой длины рупо-
ра, при которой максимальный фазовый сдвиг в его раскрыве не будет превышать
некоторой допустимой величины. Эта величина обычно определяется наибольшим
значением коэффициента направленного действия, которое можно получить от
рупора заданной длины. Как будет показано ниже, для Н-секториального рупо-
ра максимально допустимый фазовый сдвиг составляет 3тс / 4, что соответствует
следующему соотношению между оптимальной длиной рупора, размером раскры-
ва ап и длиной волны X:
Ь7
опт
= / ЗХ.
Ъ7
(13.3.6)
Что касается распределения амплитуд поля в раскрыве рупора, то для вели-
чин, определяющих амплитуды, принимаем
ф х'
2фо cip
-Н
(13.3.7)
Н<р ~
Таким образом, поле в раскрыве Н-секториального рупора окончательно пред-
ставим выражениями
(13.3.8)
522
ГЛАВА 13
где Eo — напряженность поля в середине раскрыва.
Поле излучения найдем по формулам (12.3.4) и (12.3.5). Подставляя в них значе-
ния Eg = Еу из (13.3.8), получаем
ар/2
Ен = AEQbp |
~ар/2
их'
cos
(13.3.9)
bp/2
e£=ae0 j
-bp/2
'sinG
ар/2
Ttx'
-г
(13.3.10)
J cos
-dp/2
Интегралы в (13.3.9) и (13.3.10) после некоторых преобразований могут быть вы-
ражены через интегралы Френеля, определяемые формулами (12.4.7). В результа-
те получим следующие значения для поля излучения:
„ л п 1 a/AR
Ej{ — AEgbp х
exp
. TtkR
2 sin 0
[C(uj) + C(u2) - iS(ux) - iS(u2)] +
(13.3.11)
. ttXR
2 sinO
[C(u3) + C(u4)-iR(u3)-i5(u4)]
p
где
щ =
^-a/XR
S=t + a/XR
P
2 sinO
2sin0
u2 ~
u4 =
P
a
2 sinO
2 sinO
Формула (13.3.11) определяет напряженность поля в комплексной форме. Для на-
хождения амплитуды поля необходимо вычислить модуль этой величины. Выра-
жение для диаграммы направленности получим, взяв модуль комплексной вели-
чины, стоящей в фигурных скобках формулы (13.3.11).
Аналогично находится напряженность поля в плоскости вектора Е:
AR
_ . tiAR
bn ехр г----
р 4си
-iS(vi) - iS(v2)] sin
где
=
А определяется (12.3.3а).
[C( ) + C(v2) -
sinO
kbD
—— sin 0,
(13.3.12)
р a/AR
a/AR
Волноводные излучатели и рупорные антенны
523
Из (13.3.12) видно, что диаграмма направленности в плоскости Е:
Г£(0) =
1 + cos 0 . ( kb
--------sm —
sin0,
получается такой же, как у площадки с равноамплитудным и синфазным полем,
что естественно, так как поле в раскрыве рупора вдоль оси у не меняется.
Характерной особенностью поля излучения в плоскости Н является зависимость
его фазы от направления при неизменном расстоянии. Эта зависимость выражена
в формуле (13.3.11) множителем sin0 в показателе степени фазового множителя.
Зависимость фазы поля от направления приводит к тому, что в рупорной антенне
нет такой точки, которая могла бы быть принята за фазовый центр излучения.
Коэффициент направленного действия рупорной антенны может быть рассчи-
тан по формуле
4лЬпК 9 9
D = —{[C(u) + С(г>)]2 + [^(u) + S(v) ]2},
Лао
(13.3.13)
где
На рис. 13.14 показаны построенные по (13.3.13) графики зависимости коэффи-
циента направленного действия D от относительного размера раскрыва рупора
ар / X. Графики построены для рупоров различной длины. Для того чтобы исклю-
чить зависимость КНД от размера рупора Ьр, по оси ординат отложено произ-
ведение XD / Ьр. Значение КНД находится путем умножения ординаты кривой на
Ьр / X.
Из рисунка видно, что для каждой длины рупора существует определен-
ная ширина раскрыва ар, при которой КНД достигает максимального значения.
Уменьшение КНД при дальнейшем увеличении раскрыва рупора ар (длина рупора
2 3 4 5 6 8910 15 л /Л,
Рис. 13.14. Зависимость коэффициента направленного действия Н-секториального рупора
от относительной ширины раскрыва при различной длине рупора [18]
ГЛАВА 13
524
Рис. 13.15. Зависимость коэффициента направленного действия Е-секториального рупора
от относительной ширины раскрыва при различной длине рупора [18]
R = const) объясняется резким возрастанием фазовых искажений в раскрыве.
Рупор, который при заданной длине имеет максимальный КНД, называется
оптимальным. Из кривых, изображенных на рис. 13.15, видно, что точки макси-
мума на кривых R / X = const соответствуют равенству
откуда Копт = % / ЗХ. При такой длине рупора максимальные фазовые искажения
в его раскрыве согласно (13.3.5) будут Аймаке = Зя / 4.
Если длину рупора взять больше оптимальной, определяемой равенством
(13.3.6), то при той же площади раскрыва КНД рупора возрастает. Однако это
возрастание будет незначительным и в большинстве случаев не оправдает увели-
чения габаритов. Действительно, точкам максимума КНД на кривых рис. 13.15 со-
ответствует, как легко убедиться при непосредственном подсчете, коэффициент
использования площади раскрыва v = 0,64.
Если длину рупора непрерывно увеличивать, то в пределе при R —> со мы по-
лучим синфазное поле в раскрыве рупора. Как было показано выше, коэффициент
использования синфазной площадки с косинусоидальным распределением ампли-
туды поля равен v = 0,81. Таким образом увеличение длины рупора по сравнению
с его оптимальной длиной не может повысить КНД более чем на 20 %.
Коэффициент полезного действия рупорных антенн вследствие малых потерь
практически может быть принят за единицу. Поэтому коэффициент направленно-
го действия и коэффициент усиления рупорных антенн практически совпадают.
13.3.2. Е-плоскостной секториальный рупор [18]. При возбуждении волны
типа Н10 можно положить, что
Ер = ЕХ =Н(р =0. (13.3.14)
Опуская промежуточные выкладки, напишем окончательные формулы для
поля в раскрыве Е-плоскостного секториального рупора
Волноводные излучатели и рупорные антенны
525
cos
(13.3.15)
120л 2а
Здесь р = 2л / ; р — расстояние от горловины рупора.
Из формул (13.3.15) видно, что основным отличием поля в Е-плоскостном рупо-
ре от поля в волноводе является цилиндрическая форма волны. Вследствие этого в
раскрыве рупора будут фазовые искажения, аналогичные искажениям в Н-плос-
костном рупоре.
Если угол раскрыва рупора 2<р0 невелик, то можно положить = Еу .В этом
случае напряженность электрического поля в раскрыве может быть представлена
следующей формулой:
(13.3.16)
Поле излучения Е-плоскостного рупора в плоскости Н
cos
(13.3.17)
sin 6
Из (13.3.17) следует, что диаграмма направленности в Н-плоскости Е-плоскос-
тного рупора такая же, как у открытого конца волновода.
Поле в плоскости Е:
(13.3.18)
Здесь
(13.3.19)
Здесь так же, как и в случае Н-плоскостного рупора, для нахождения ампли-
туды поля необходимо вычислить модуль комплексных величин, определяемых
выражениями (13.3.17) и (13.3.18). Диаграмма направленности Е-плоскостного рупо-
ра в плоскости вектора Е определится модулем выражения, стоящего в квадрат-
ных скобках формулы (13.3.18), умноженным на (1 + cosG) / 2.
Коэффициент усиления Е-плоскостного рупора определяется выражением
526
ГЛАВА 13
(13.3.20)
Кривые зависимости КНД от размеров рупора представлены на рис. 13.15.
Здесь, как и в случае Н-секториального рупора, кривые имеют экстремум. Точки
экстремума приблизительно определяются равенством
откуда
опт
/2Х.
(13.3.21)
При таких соотношениях размеров рупора максимальные фазовые искажения на
краях раскрыва достигают значений
А V макс
= п / 2.
Коэффициент использования площади раскрыва v оптимального Е-плоскостно-
го секториального рупора такой же, как оптимального Н-плоскостного рупора,
т. е. v = 0,64.
При выборе размеров Е-плоскостного рупора можно руководствоваться такими
же соображениями, которые были изложены выше применительно к Н-плоскост-
ному рупору.
13.3.3. Пирамидальный рупор [18]. Приближенно можно считать, что фронт
волны в пирамидальном рупоре имеет сферический характер. Фазовые искажения
в раскрыве рупора определяются выражением
(13.3.22)
где Rh — длина рупора в плоскости Н, RE — длина рупора в плоскости Е.
Для остроконечного рупора R^ = RE , для клиновидного рупора RE.
Структура поля в плоскостях Е и И подобна структуре поля в этих же плоскос-
тях в Е- и Н-плоскостных секториальных рупорах соответственно. Вследствие это-
го диаграмма направленности пирамидального рупора в плоскости Е определится
формулой (13.3.18), а в плоскости Н — аналогичной формулой для Н-плоскостного
секториального рупора (13.3.2).
Определим КНД пирамидального рупора. Напряженность электрического поля
в раскрыве может быть выражена следующим образом:
cos
(13.3.23)
Тогда КНД
[е5с15 |2
D = х {[С(«) + ОД]2 + [ОД) + ОД)]2} х
X2 I EgdS “pbp
S (13.3.24)
Волноводные излл^чдлп&ш и рт^пощные антенны
527
Сравнивая формулы для КНД Н- и Е-плоскостного и пирамидального рупоров
нетрудно заметить, что они связаны между собой следующим соотношением:
л2
DnHn =--------DeDh . (13.3.25
ПИР 90- К Л И V
Используя формулу (13.3.25), можно рассчитать КНД пирамидального рупора
с помощью графиков для Е- и Н-плоскостного секториальных рупоров. В этом слу-
чае формулу (13.3.25) удобно представить в виде
(13.3.26)
так как величины, стоящие в круглых скобках (13.5.5), непосредственно отложены
по осям ординат на указанных графиках.
13.3.4. Упрощенный расчет поля излучения рупоров с прямоугольным
раскрывом [18]. Полученные выше формулы для расчета поля излучения рупо-
ров сравнительно сложны и расчет по ним получается трудоемким. Это объясня-
ется тем, что приведенные выше выражения (12.3.11), (12.3.12), (13.3.17) и (13.3.18)
учитывают изменения фазы поля в раскрывах рупоров. Вследствие этого форму-
лы для поля излучения содержат величины, определяемые через комплексные
интегралы Френеля. Для нахождения амплитуд поля и диаграмм направленности
рупорных антенн необходимо, как уже указывалось, вычислять модули комплек-
сных выражений, входящих в эти формулы, что несколько усложняет расчет.
В ряде случаев, когда не требуется большая точность в вычислениях (напри-
мер, когда производится предварительный прикид очный расчет), можно ограни-
читься более грубыми расчетами, при которых изменение фазы поля в раскрыве
рупора не учитывается.
В этом случае неизбежно приходим к выражениям (13.1.3), которые описывают
поле излучения из открытого конца волновода. При этом выражения для поля из-
лучения как секториальных, так и пирамидального рупоров будут одинаковыми.
Таким образом, поле в дальней зоне в главных плоскостях может быть выра-
жено формулами (13.1.3), учитывая, что в плоскости Е вектор напряженности
электрического поля будет иметь только одну составляющую Eq , т. е. Ее = Eq , а в
плоскости Н Ен = Еф. Под Хв будем понимать длину волны в раскрыве рупора. Для
Е-секториального рупора она будет такая же, как в питающем рупор волноводе;
для Н-секториального и пирамидального рупоров можно принять А,в = X и Г = 0 .
Расчет по формулам (13.1.3) не приводит к существенным погрешностям лишь
в случае, когда фазовые искажения невелики и, по крайней мере, не превышают
максимально допустимых ( л / 2 в плоскости вектора Е и Зя / 4 в плоскости векто-
ра Н).
528
ГЛАВА 13
Следует, однако, заметить, что неучет фазовых искажений поля в раскрывах
рупоров влечет за собой потерю большого количества ценной информации, такой,
например, как влияние этих искажений на диаграмму направленности, наличие
экстремума в функциональной зависимости КНД от площади раскрыва рупора
при неизменной его длине, отсутствие в рупоре фазового центра и т. п.
13.3.5. Конический рупор [18]. Основным типом колебаний, возбуждаемых
в коническом рупоре, является волна типа Нц. Анализ конических рупоров при-
нципиально не отличается от анализа прямоугольных. Вследствие этого, а также
из-за громоздкости математических выкладок мы его здесь приводить не будем.
Конические рупоры, как и прямоугольные, имеют оптимальные размеры. Связь
этих размеров с КНД показана на рис. 13.16.
На рис. 13.17 показаны типичные диаграммы направленности конического ру-
пора L = 3,5Х, dp = 3,4Х .
Ширина диаграммы направленности оптимального конического рупора на
уровне половинной мощности приближенно определяется формулами.
(260>5 )е - 60
(200,5 )н
(13.3.27)
В электрической плоскости диаграмма несколько уже, чем в магнитной. Если
требуется одинаковая направленность в обеих плоскостях, то круговой коничес-
кий рупор следует деформировать в эллиптический. Отношение осей эллипса бе-
рется приблизительно равным 1,25. Вектор электрического поля должен быть
параллелен малой оси.
Оптимальные конические рупоры имеют коэффициент использования площади
раскрыва v = 0,5. Следовательно, коэффициент усиления таких рупоров может
быть приближенно рассчитан по следующей простой формуле:
G = D = 4m$v / X2 = 5(d / X)2. (13.3.28)
Длина оптимального рупора связана с диаметром его раскрыва и длиной волны
соотношением
Рис. 13.16. Зависимость оптимальных размеров
конических рупоров от коэффициента направ-
ленного действия [18]
Рис. 13.17. Типичные диаграммы на-
правленности оптимального коническо
го рупора, имеющего D = 17,7 дБ [18]
Врлмово^ые излл^чптели и рупорные антенны
529
R = dl /2,4А-0,15Х. (13.3.29)
Нетрудно заметить, что размеры оптимального конического рупора представ-
ляют собой нечто среднее между размерами Н- и Е-плоскостных секториальных
рупоров. Для заданного КНД размеры конического и пирамидального оптималь-
ных рупоров отличаются незначительно. Вследствие этого выбор типа рупора оп-
ределяется главным образом конструктивными соображениями. Кроме того, сле-
дует учитывать, что в коническом рупоре так же, как и в круглом волноводе,
возможен неконтролируемый поворот структуры поля вокруг оси волновода. Если
такой поворот недопустим, то следует предпочесть пирамидальный рупор.
13.3.6. Расчет рупорных антенн [18]. Основной задачей расчета рупорных
антенн является определение главных размеров рупора: % и Ьр и R. Исходными
данными обычно являются длина рабочей волны 1 и ширина диаграммы направ-
ленности в плоскостях Е и Н — (20g 5 )Е и (20g 5 соответственно.
Для однозначного решения задачи этих данных недостаточно. Может быть мно-
жество рупорных антенн, в которых на заданной волне обеспечивается требуемая
ширина диаграммы направленности, но имеются отличия в других электрических
характеристиках (в полной форме диаграммы направленности и, следовательно,
в КНД, в коэффициенте отражения, в положении фазового центра излучения).
Вследствие этого излагаемый здесь приближенный метод расчета относится к рас-
чету оптимальных рупоров, т. е. рупоров, соотношение размеров которых опре-
деляется формулой (13.1.3).
Порядок расчета следующий. По заданной ширине диаграммы направленности
определяют размеры раскрыва рупора ар и Ьр. Если эти углы заданы в градусах
на уровне половинной мощности, то размеры ар и Ьр могут быть определены по
следующим формулам:
а) для Е-плоскостного секториального рупора
ар — 68Х / 20о ,
б) для Н-плоскостного секториального
ар — 80А / 20о,5,
в) для пирамидального рупора
ар = 80А / 20g,5 ,
Ьр — 5 ЗА / 20о5 ;
рупора
(13.3.30)
(13.3.31)
(13.3.32)
Ьр = 53А / 20
0,5 j
а) б)
Рис. 13.18. Зависимость размеров раскрыва оптимального рупора от требуемой
ширины диаграммы направленности на различных относительных уровнях
(по напряженности поля) [18]
530 ГЛАВА 13
В общем случае, когда ширина диаграммы задана на любом уровне, удобно
пользоваться графиками, изображенными на рис. 13.18. Эти графики могут быть
использованы для построения ориентировочной формы основного лепестка диа-
граммы направленности, когда размеры ар и Ьр уже выбраны.
Определив ар и Ьр, по формулам (13.3.7) и (13.3.21) находим оптимальные раз-
меры рупора и Rh . Для пирамидального рупора эти размеры могут быть раз-
личными и несовместимыми. В этом случае берется наибольшее значение с тем,
чтобы фазовые искажения в раскрыве не превысили допустимых.
Для весьма слабонаправленных рупоров формулы (13.3.30) — (13.3.32) неверны.
В этом случае обычно пользуются экспериментальными данными.
Зеркальные антенны
531
Глава 14. Зеркальные антенны [17]
14.1. Принцип действия зеркальных антенн
и элементы их конструкции [17]
14.1.1. Принцип действия зеркальных антенн в режиме передачи
заключается в преобразовании с помощью хорошо отражающей поверхности
специальной формы (зеркала) поля слабонаправленного первичного источника
(облучателя) во вторичное поле, реализующее заданные направленные свойства
антенны в целом. Обычно в зеркальных антеннах осуществляется преобразование
широкой ДН облучателя в узкую ДН антенны.
На рис. 14.1, а показаны основные элементы зеркальной антенны — зеркало 1
и облучатель 2. Первичная и вторичная ДН показаны на рис. 14.1,6 и в
соответственно.
Для получения достаточно выраженного эффекта отражения размеры зеркала
должны быть много больше длины волны. В зеркальной антенне осуществляется
преобразование сферического или цилиндрического фронта волны от первичного
облучателя в плоский фазовый фронт на выходе антенны (для узких ДН) или
фазовый фронт специальной формы (для ДН специального вида - косекансных
И.Т.П.).
Основные типы зеркальных антенн показаны на рис. 14.3, 14.5, 14.11, 14.13,
16.24. В параболах вращения облучатель должен быть точечным, в цилиндрическом
параболоиде — линейным.
14.1.2. Зеркало в соответствии со своим назначением должно полностью отра-
жать падающие на него электромагнитные волны. Поэтому его поверхность выпол-
няется из хорошо проводящих металлов. Наилучшими отражающими свойствами
обладают сплошные металлические поверхности, толщина которых должна быть
в 2-3 раза больше толщины скин-слоя. Сплошные отражатели выполняются в виде
металлических листов или же пленок (фольги), наносимых на легкую диэлектри-
ческую основу типа пенопласта или же на стеклоткань.
б)
Рис. 14.1. Принцип действия зеркальной антенны [17]
в)
532
ГЛАВА 14
Рис. 14.2. Несплошные отражающие поверхности [17]
С целью уменьшения веса и ветровых нагрузок отражающую поверхность
иногда выполняют в виде перфорированных листов (рис. 14.2,а), однолинейной
сетки из проводов круглого (рис. 14.2,в) или прямоугольного (рис. 14.2,г) сечения и
двухлинейной сетки (рис. 14.2,6).
При несплошном отражателе часть электромагнитной энергии просачивается
сквозь него, образуя нежелательное заднее излучение и уменьшая коэффициент
усиления антенны.
Качество несплошного отражателя характеризуют коэффициентом
прохождения Т = PnplPnaQ , где Рпр - мощность, просочившаяся через некоторый
участок поверхности отражателя, a PnaQ ~ мощность, падающая на этот участок.
Отражатель считается хорошим, если Т <0,01-0,02.
Перфорированный отражатель и отражатель из двухлинейной сетки
нечувствительны к поляризации падающих волн. Для перфорированного отражателя
удовлетворительные значения коэффициента прохождения получаются при
диаметре отверстий, меньше 0,2 X, и при суммарной площади отверстий не более
0,5-0,6 всей площади листа. Двухлинейная сетка работает удовлетворительно при
размерах ячейки, меньших 0,1 X, и диаметре проводов 0,01 X и больше.
Отражатели из однолинейной сетки обладают поляризационной селективностью:
они эффективно отражают электромагнитные волны, вектор Е которых
параллелен проводам и практически полностью пропускают электромагнитные
волны перпендикулярной поляризации. Для получения достаточно малых
коэффициентов прохождения расстояние между проводами должно быть меньше
0,1 X при поперечных размерах проводов 0,01 X и больше.
14.1.3. Облучатель является слабонаправленной антенной. Специфическими
требованиями к такой антенне являются:
а) формирование поля со сферическим или цилиндрическим фронтом волны;
б) формирование амплитудной ДН, обеспечивающей требуемое облучение
зеркала и малый уровень излучения вне угла раскрыва зеркала (угол 2Ф0 на рис.
14.1,6).
Исходя из принципа действия зеркальной антенны, можно сформулировать
следующие достаточно очевидные требования к облучателям этих антенн [3]:
1. Облучатель должен иметь фазовый центр, который располагается в фокусе
Зеркальные алипенны 533
параболоида вращения; для параболического цилиндра облучатель должен
формировать цилиндрическую волну с линией фазовых центров, расположенных
на фокальной линии параболического цилиндра.
2. Амплитудная диаграмма направленности облучателя должна быть такова,
чтобы почти вся мощность от облучателя попадала на зеркало. В излучателе
должно отсутствовать излучение в направлении, противоположном направлению
на зеркало. Кроме того, поскольку амплитудное распределение в раскрыве зеркала
создается в основном диаграммой облучателя, форма амплитудной диаграммы
облучателя должна соответствовать требуемой форме амплитудного распределения
поля в раскрыве зеркала.
3. Облучатель находится в поле, отраженном от зеркала, поэтому его габариты
должны быть как можно меньше, чтобы он создавал минимальное затенение для
поля зеркальной антенны.
4. Поскольку электрическая прочность и частотные свойства зеркальной антенны
в основном ограничиваются облучателем, эти параметры облучателя должны
соответствовать аналогичным параметрам всей зеркальной антенны.
Наиболее распространенными типами облучателя являются вибраторные,
щелевые и волноводно-рупорные облучатели. Рассмотрим их конструктивные
особенности.
14.1.4. Анализ и синтез зеркальных антенн [17].
1. Прямая задача (задача анализа) в теории зеркальных антенн заключается в
расчете поля излучения антенны по известному полю облучателя при заданной
геометрии антенны. Как указывалось выше, наиболее распространенным является
апертурный метод, с помощью которого поле в дальней зоне рассчитывается
по известному полю в раскрыве. При этом не учитывается излучение токов,
затекающих на обратную сторону зеркала, излучение контурных токов на обрезе
зеркала, рассеяние электромагнитных волн, отраженных от зеркала, облучателем
и конструктивными элементами крепления облучателя. Тем не менее обычно
получаются вполне удовлетворительные результаты в определении поля в основном
лепестке ДН и в нескольких ближайших боковых лепестках.
2. Обратная задача (задача синтеза) заключается в определении геометрических
параметров антенны и ДН облучателя по заданной амплитудно-фазовой ДН антенны
в дальней зоне. Несмотря на значительные трудности, в решении этой задачи
имеются заметные успехи. Здесь синтез зеркальных антенн не рассматривается.
14.1.5. Области применения зеркальных антенн [17]. Зеркальные антенны
широко применяются практически во всех отраслях радиотехники из-за простоты
конструкции, больших коэффициентов усиления и узких ДН, простоты получе-
ния заданного отношения ширины ДН в главных плоскостях, широкой полосы
пропускания, высокого к. п. д. и т.п. они применяются в очень широком диапазоне
волн - от оптического диапазона до коротких волн.
При установке зеркальных антенн на летательные аппараты в корпусе последних
делаются специальные вырезы, закрываемые радиопрозрачным обтекателем. При
расчете ДН зеркальных антенн, установленных на летательных аппаратах, обычно
нет необходимости учитывать влияние корпуса последнего, по крайней мере, это
относится к главному и ближайшим к нему боковым лепесткам.
Зеркальные антенны, работающие на прием, имеют такую же точно
534
ГЛАВА 14
конструкцию, как и передающие, за исключением того, что фидер может иметь
меньшее сечение. При конструировании приемных зеркальных антенн обращают
особое внимание на уменьшение уровня бокового излучения в целях увеличения
помехоустойчивости приема и уменьшения шумовой температуры.
14.2. Геометрические характеристики параболических антенн [17]
14.2.1. Профиль зеркала. Как показано выше, апертурные антенны имеют
наибольший КНД при плоском фазовом фронте в их раскрыве (поверхность 5 на
рис. 14.1). Для расчета профиля зеркала, обеспечивающего плоский фронт волны
в раскрыве, используется закон равенства оптических длин путей между фронта-
ми. Условия применимости законов геометрической оптики в зеркальных антеннах
выполняются, так как их размеры обычно много больше длины волны.
Пусть на фокусе антенны F (рис. 14.3,а) находится источник сферических
волн. Плоский фронт волны в раскрыве будет в том случае, если для луча,
отражающегося от произвольной точки на поверхности зеркала, выполняется
условие равенства расстояний FPC = FOZ' или
FP + PC = FO + OZ’. (14.2.1)
Если выразить отрезки, входящие в это равенство, через фокусное расстояние
f (расстояние от фокуса до вершины зеркала О) и полярные координаты р и Ф
точки отражения Р , то из равенства (14.2.1) получим
р + [рсозФ - (/ - Ь)] =/ + [/-(/ - П)],
где h - глубина зеркала. Отсюда
р = 2// (1 + cos Ф). (14.2.2)
Уравнение (14.2.2) есть уравнение параболы в полярных координатах с началом
в ее фокусе и с параметром р = 2f. Используемая часть параболы ограничивается
раскрывом АВ. Ось Oz является осью параболы и называется оптической осью
зеркала.
Если глубина зеркала h > /(Фо > л / 2), то оно называется короткофокусным,
а если h < /(Фо < л / 2), то длиннофокусным.
В прямоугольной системе координат уравнение параболического профиля имеет
вид
х2 = 2pz - 4fz.
(14.2.3)
14.2.2. Геометрические характеристики зеркала определяются из полу-
ченных уравнений профиля. При z = h, х = L / 2, где L — размер раскрыва. От-
сюда, используя уравнение (14.2.3), получаем
L2 = 16fh.
Из уравнения (14.2.2) при Ф = Фо получим
L = 4/tg (Фо / 2).
(14.2.4)
(14.2.5)
Формулы (14.2.4) и (14.2.5) указывают на то, что геометрия зеркала полностью
определяется заданием пары из четырех параметров.
Наиболее употребительными являются пары L , / и L , Фо. Профиль зеркала
Зеркальные антенны
535
Рис. 14.3. К определению геометрических характеристик параболических антенн [17]
определяется только фокусным расстоянием f.
При заданном размере раскрыва L изменение положения облучателя на оси
зеркала должно сопровождаться изменением профиля зеркала так, чтобы новое
фокусное расстояние было равно расстоянию от облучателя до вершины зеркала,
иначе не будет обеспечена синфазность поля в раскрыве. Увеличение фокусного
расстояния при заданном L ведет к уменьшению глубины зеркала — зеркало
становится более мелким. Уменьшение фокусного расстояния при тех же условиях
делает зеркало более глубоким.
При заданном фокусном расстоянии можно построить зеркала с одинаковым
профилем, но с разными размерами раскрыва. Эти зеркала будут отличаться и по
глубине h , и по углу раскрыва Фо.
14.2.3. Отражающие поверхности параболических зеркальных антенн стро-
ятся на основе рассмотренного параболического профиля. При вращении пара-
болы вокруг оптической оси получается поверхность параболоида вращения (рис.
14.3,6), для облучения которой должен использоваться точечный облучатель.
При параллельном перемещении профиля вдоль некоторой прямой получается
поверхность параболического цилиндра (рис. 14.3,в), для облучения которой должен
использоваться линейный облучатель. Антенна с таким зеркалом называется
цилиндропараболической. У нее синфазность отраженной волны в раскрыве в
направлениях, параллельных О'х$, обеспечивается за счет параболического
профиля, а в направлениях О'у$ — за счет одинаковой фазы поля линейного
облучателя, расположенного вдоль фокальной оси.
14.3. Цилиндропараболические антенны [17]
14.3.1. Конструктивная схема цилиндропараболической зеркальной антенны
изображена на рис. 14.3,в. Длина линейного облучателя, фазовая ось которого
должна совпадать с прямой FF, обычно выбирается равной размеру раскрыва а.
Крепление облучателя можно осуществить на левом и правом обрезах зеркала,
536
ГЛАВА 14
не затеняя дополнительно раскрыв антенны элементами крепления. Соотношение
размеров а и Ъ может быть самым разнообразным, однако, как правило, размер
а в 2-5 раз больше размера Ъ . Чем больше а, тем меньше влияние краев антенны.
Предельные соотношения между размерами определяются следующим образом.
Для сохранения возле зеркала цилиндрического фронта волны должно быть f < а.
Из (14.2.4) имеем
f = о /167г < а, отсюда ЬЛгакс < Ajah.
14.3.2. Основные типы облучателей цилиндропараболических антенн
изображены на рис. 14.4. В диапазонах метровых, дециметровых и сантиметровых
волн применяется облучатель в идее линейной решетки полуволновых синфазных
вибраторов (рис. 14.4,а). В диапазонах метровых и дециметровых волн возбуждение
вибраторов осуществляется коаксиальным кабелем, а в диапазоне СВЧ — волно-
водом, как показано на рис. 14.4,6. Вибраторы волноводно-вибраторной антенны
располагаются по средней линии широкой стенки волновода на расстоянии по-
ловины длины волны в волноводе, при этом синфазность возбуждения достигается
попеременным разворотом вибраторов на 180°.
Облучатель в виде волноводно-щелевой антенны показан на рис. 14.4,в;
характеристики такой антенны описаны выше.
У облучателей, показанных на рис. 14.4,6 и в, положение максимума ДН в
горизонтальной плоскости (плоскость y$O'z на рис. 14.3 будем условно называть
горизонтальной) в некоторых случаях может оказаться чувствительным к
изменению частоты. Линейным облучателем сантиметрового и миллиметрового
диапазонов, свободным от этого недостатка, является сегментно-параболический
облучатель (рис. 14.4,г). Он представляет собой две параллельные металлические
пластины, расположенные на расстоянии, равном размеру широкой стенки
волновода, и замкнутые металлической пластинкой параболического профиля.
Фокус этой параболы находится в раскрыве; в фокусе помещается открытый конец
прямоугольного волновода. Между пластинами возбуждается волна типа Н01. В
узком и длинном раскрыве пластин получается синфазное поле горизонтальной
поляризации. Для получения вертикальной поляризации нужно использовать волну
Т. Поле, излучаемое сегментно-параболическим облучателем, в непосредственной
близости от раскрыва имеет цилиндрический фронт волны, ось которого показана
пунктиром F - F на рис. 14.4,г.
Важной характеристикой линейных облучателей является их ДН в вертикальной
плоскости К(Ф). Эти ДН показаны на рис. 14.4 кривыми 5.
ДН многовибраторного облучателя представляет собой окружность(рис. 14.4,а);
она энергетически невыгодна, так как большая часть электромагнитной энергии
проходит мимо зеркала и не участвует в формировании главного лепестка
ДН. Для уменьшения заднего излучения применяются контррефлекторы:
полуцилиндрический с осью, совпадающей с осью вибраторов (рис. 14.4,6), и
плоский (рис. 14.4,е). Диаграммы направленности волноводно-вибраторного,
волноводно-щелевого и сегментно-параболического излучателей имеют вид,
изображенный на рис. 14.4,е. При необходимости для сужения ДН облучателей (рис.
14.4,б-г) применяются симметрические наклонные пластины, образующие рупор
(рис. 14.4, ж и з).
Зеркальные антенны
537
>-„/2
Рис. 14.4 Линейные облучатели: 1 — вибратор; 2 — контррефлектор; 3 — волновод;
4 - рупор; 5 — диаграмма направленности [17]
538
ГЛАВА 14
14.3.3. Распределение амплитуд поля в раскрыве цилиндропараболической
антенны удобно описывать в прямоугольной системы координат х$О'у$ (см. рис.
14.3,в). При этом функцию, описывающую распределение амплитуд, обычно мож-
но считать распределяющейся по переменным^ , у$:
Es (xS’ys)~ Eoe(xs)e(ys)y (14.3.1)
где Eq - максимальная амплитуда поля в раскрыве; е )— нормированная функция
распределения амплитуд в вертикальной; e(y^^— в горизонтальной плоскости.
Если пренебречь концевыми эффектами на линейном облучателе, то
распределение амплитуд в горизонтальной плоскости, т.е. функция е(у$^ не
отличается от распределения амплитуд по линейному облучателю. Таким образом,
цилиндропараболическая антенна в горизонтальной плоскости имеет такую же
ДН, как и линейный облучатель в этой плоскости.
Распределение амплитуд поля в раскрыве в вертикальной плоскости, т.е. функция
определяется, главным образом, формой диаграммы направленности
облучателя в этой плоскости Е(Ф). Однако на распределение поля влияет и форма
зеркала так же, как это имеет место в линзовых антеннах.
При расчете амплитудного распределения дифференциальное уравнение,
связывающее угловые и линейные координаты в раскрыве (рис. 14.5), находится из
уравнения профиля зеркала (14.2.1) с учетом равенства х$ = р sin(O) :
dxs / dO = f I co£i<S> 12). (14.3.2)
Из этого уравнения и условия сохранения энергии в трубке лучей получим, как
и для линзовых антенн, нормированное распределение амплитуд поля в раскрыве
для случая, когда максимум ДН облучателя перпендикулярен раскрыву
e(xs) = Г(Ф)со$2(Ф / 2). (14.3.3)
В правую часть этого равенства переменная х$ явно не входит. При расчетах
нужно пользоваться соотношением xs = 2f tg(O/2), которое получается из
Рис. 14.5. К расчету распределения ампли-
туд поля в раскрыве цилиндропараболичес-
кой антенны [17]
Рис. 14.6. Антенна с несимметричным
зеркалом [17]
Зеркальные антенны 539
уравнения (14.2.2).
При несимметричной схеме антенны (рис. 14.6) из-за влияния профиля
зеркала распределение амплитуд поля в вертикальной плоскости получается
несимметричным, даже если максимум симметричной ДН облучателя направлен
в середину зеркала.
14.3.4. Диаграммы направленности цилиндропараболической антенны рас-
считываются по формулам, полученным ранее для прямоугольного раскрыва,
по известному распределению амплитуд поля е = e(xs)- е(у$). При этом исполь-
зуется сферическая система координат т,0,ср с началом О' в центре раскрыва и с
полярной осью z, перпендикулярной раскрыву. В качестве главных выбираются
плоскости x$O'z и ysO z (см. рис. 14.3,в).
Ширина ДН определяется по формулам 20о 5 / Ь и 20д;5 = тЛ. / а
причем коэффициент тх зависит от распределения амплитуд только по оси х$ ,
а коэффициент Шу - по оси уg (поле в раскрыве считается синфазным).
14.3.5. Коэффициент направленного действия может быть рассчитан как
по известной ДН, так и по распределению поля в раскрыве. КНД в направлении
максимума ДН рассчитывается по формуле:
Do = 4nqS / X2.
Для цилиндропараболических антенн S = аЪ, а коэффициент использования
площади q находится по формулам для прямоугольного раскрыва. КИП этих антенн
дольно высок — примерно 0,7-0,8 из-за того, что в горизонтальной плоскости
облучение и распределение поля в раскрыве обычно близко к равномерному.
14.3.6. Коэффициент усиления рассчитывается по формуле Go = цОд. Одна-
ко необходимо разобраться, что понимать под КПД зеркальной антенны в этом
выражении. Если Dq определяется по ДН антенны с учетом всех боковых и задних
лепестков, то в формуле Gg = Л А) величина г] учитывает только потери в металле
и диэлектриках зеркала, облучателя и элементов крепления. Такой расчет КУ
возможен лишь в том случае, если известна экспериментальная ДН, измерить
которую не всегда удается.
Другой метод заключается в том, что ДН рассчитывают приближенно - только
по полю в раскрыве. При этом потери мощности за счет неполного ее перехвата
зеркалом (см. рис. 14.5) учитываются коэффициентом перехвата т|д; если зеркало
не сплошное, то сюда же относятся и потери за счет просочившейся мощности.
Теперь КУ может быть вычислен по формуле
С0=О0цЛл, (14.3.4)
где ц по-прежнему характеризует потери в металле и диэлектриках. Потери на
облучение, характеризуемые t|jj , являются «потерями» лишь в том смысле, что
определяемая ими электромагнитная энергия не участвует в формировании поля
излучения в нужном направлении.
Если не учитывать потери за счет мощности, просочившейся через несплошной
отражатель, то для цилиндрической антенны мощность потерь на облучение
пропорциональна заштрихованной на рис. 14.5 части ДН облучателя, которую
следует изобразить в масштабе мощности [F2 (Ф)]. Отсюда найдем
540
ГЛАВА 14
Фо 2л
Пп = f F2 (Ф)^Ф / [F2 (Ф)йФ. (14.3.5)
-Фо О
Выражение для КУ можно привести к виду
Go = дгг]4л£ / X2, (14.3.6)
где
9 = (14.3.7)
- коэффициент, который называется эффективностью или выигрышем антенны.
14.3.7. Оптимальный облучатель и оптимальный угол раскрыва - такой
облучатель и такой угол раскрыва, которые обеспечивают максимальное значение
выигрыша при заданных геометрических размерах раскрыва.
Рассмотрим случай, когда задан облучатель со своей ДН Е(Ф). При неизменном
размере раскрыва будем изменять фокусное расстояние, т.е. угол раскрыва Фо (при
этом, естественно, профиль зеркала также должен изменяться). С увеличением
Фр потери на облучение уменьшаются и т]д растет. С другой стороны, увеличение
Фр ведет к большему спаду амплитуды поля на краю -раскрыва, т.е. к более
неравномерному амплитудному распределению, что выражается в уменьшении q.
Примерный ход этих зависимостей показан на рис. 14.7,а. Как видно из рисунка,
при некотором угле раскрыва ФрОпт достигается максимум выигрыша. Оптимальный
угол раскрыва зависит только от формы ДН облучателя и для типовых облучателей
составляет 70° - 90°.
Теперь зафиксируем некоторый угол раскрыва Фр и фокусное расстояние f и
будем изменять ширину ДН облучателя. При этом относительное значение угловой
плотности мощности s в направлении на край зеркала будет изменяться (рис. 14.7,6).
По мере расширения ДН уровень s возрастает, распределение поля в раскрыве
становится все более равномерным, величина q растет, а т|уу падает. Максимум
выигрыша достигается при некотором оптимальном уровне Sonm плотности
Рис. 14.7. К определению оптимального облучателя и оптимального угла раскрыва [17]
Зеркалыные антенны
541
мощности на краю зеркала. Облучатель, у которого ширина ДН (2®sonm)
на уровне Sonm равна углу раскрыва зеркала 2Ф0. называется оптимальным
облучателем.
У наиболее распространенных цилиндропараболических антенн Sonm лежит в
пределах 0,1-0,2 и зависит как от формы ДН облучателя, так и от выбранного угла
раскрыва зеркала.
14.4. Антенна с зеркалом в виде параболоида вращения
(параболическая антенна) [17]
14.4.1. Конструктивная схема этой антенны показана на рис. 14.3,6. Ввиду
осевой симметрии антенны (относительно оптической оси Oz) для получения син-
фазного поля в раскрыве применяются точечные облучатели.
Параболические антенны предназначены в основном для формирования
осесимметричных ДН игольчатого типа. При несимметричном облучении можно
получить ДН различной ширины в главных плоскостях.
14.4.2. Основные типы точечных облучателей для параболических антенн
показаны на рис. 14.8. Там же показаны примерные ДН (сплошной линией - в плос-
кости Е, пунктирной - в плоскости Н).
Двухвибраторный облучатель (рис. 14.8,а, б) представляет собой систему
активный полуволновый вибратор — пассивный рефлектор. Активный вибратор
питается от коаксиального кабеля с помощью симметрирующего устройства (на
рисунке - устройство типа полуволновых щелей). Максимум ДН ориентирован в
сторону активного вибратора. Для облучателей такой конструкции креплением
может служить сам жесткий коаксиальный кабель (рис. 14.8,г). Малые размеры
облучателя, отсутствие тяг и стоек крепления обеспечивают небольшое затенение
раскрыва, поэтому двухвибраторный облучатель широко применяется в антеннах
с малым относительным размером раскрыва. ДН такого облучателя в плоскостях
Е и Н заметно различаются (рис. 14.8,в), распределение амплитуд поля в раскрыве
получается не осесимметричным, поэтому зеркальная антенна имеет в Н -
плоскости более узкую ДН, чем в Е - плоскости. Двухвибраторный облучатель
имеет фазовый центр, расположенный между вибраторами на оси системы.
Облучатель в виде полуволнового вибратора, питаемого от коаксиального
кабеля, с дисковым рефлектором (рис. 14.8,6) также имеет фазовый центр,
расположенный между вибратором и диском. Этот облучатель имеет почти
осесимметрическую диаграмму направленности, которая хорошо аппроксимируется
выражением F(Ф) = соз2(Ф) (рис. 14.8,е). Рефлектор имеет диаметр примерно 1,5 X
и при небольших размерах раскрыва может создать заметное затенение.
В сантиметровом диапазоне волн при необходимости иметь малогабаритный
облучатель широко применяются двухвибраторный (рис. 14.8,ж) и
четырехвибраторный (рис. 14.8,з) облучатели, возбуждаемые открытым концом
волновода, и двухщелевой облучатель (рис. 14.8,и). В облучателях (рис. 14.8,ж, з)
вибраторы, близкие к концу волновода, являются настроенными полуволновыми
вибраторами, а удаленные от них примерно на четверть волны удлиненные
вибраторы являются рефлекторами. Максимум ДН ориентирован в сторону
542
ГЛАВА 14
и) к) л)
Рис. 14.8. Типовые конструкции точечных излучателей [17]
Зеркальные антенны 543
волновода, вследствие чего оказывается возможным крепить облучатель так,
как показано на рис. 14.8,г. Сужением волновода и выбором расстояния между
открытым концом волновода и вибратором обеспечивается согласование облучателя
с волноводом и уменьшение заднего лепестка. ДН облучателя типа рис. 14.8,ж
имеет примерно такую, как на рис. 14.8,е.
Двухщелевой облучатель представляет собой прямоугольный резонатор,
возбуждаемый волноводом и настраиваемый винтом в торце (рис. 14.8,к). В
резонаторе прорезаны две параллельные полуволновые щели, расстояние между
которыми равно примерно X при этом ДН близка к осесимметричной (рис. 14.8,е).
Все рассмотренные облучатели имеют малые габариты, но их полоса пропускания
не превышает 10%. Кроме того, щели в кабеле и резонаторе, а также сужение
волноводов ограничивают передаваемую мощность.
От указанных недостатков свободны широко применяемые рупорные облучатели:
пирамидальные (рис. 14.8,л) и конические (рис. 14.8,н). Пирамидальный рупор
позволяет за счет изменения размеров раскрыва ар и Ьр изменять в широких
пределах ДН — от осесимметричной до резко несимметричной. ДН конического
рупора в Е -плоскости уже, чем в Н -плоскости. Пирамидальный рупор в общем
случае не имеет фазового центра: положения фазовых центров для плоскостей Е и
Н различны (рис. 14.8,ж). Разница в положении фазовых центров тем больше, чем
больше разница в ширине ДН в главных плоскостях. Положение фазовых центров
необходимо каждый раз проверять и, если разница в их положении превышает
X / 8, корректировать профиль зеркала.
Общим недостатком рупорных облучателей является сравнительно большая
площадь раскрыва и связанное с этим затенение раскрыва антенны, а также
необходимость в специальных стойках крепления.
14.4.3. Распределение амплитуд поля в раскрыве параболоида вращения
естественно описывать в полярной системе координат , ф^ с центром в центре
раскрыва О' (см. рис. 14.3,6). Задавшись ДН облучателя по мощности Г2(Ф,фз-),
найдем распределение амплитуд поля в раскрыве. При этом должно быть учтено,
что параболоид вращения является поверхностью двойной кривизны и что облу-
чатель излучает сферические волны.
Выделенная элементарная трубка лучей изображена на рис. 14.9 в двух
проекциях. Используя уравнение (14.3.3), условие сохранения энергии в трубке
лучей, а также уравнение (14.2.2) с заменой эс$ на т$-, для нормированного
распределения амплитуд электрического поля в раскрыве получим выражение
е OS, ) = F (Ф-4>S >os2 (Ф / 2). (14.4.1)
Сравнивая формулы (14.3.3) и (14.5.1), можно отметить, что у параболоида
Рис. 14.9. К расчету распределения амплитуд поля в раскрыве параболоида вращения [17]
544 ГЛАВА 14
вращения получается более быстрое спадание амплитуд поля к краю раскрыва,
чем у параболического цилиндра.
В общем случае распределение амплитуд поля в круглом раскрыве получается
сложным, с неразделяющимися переменными. Для его аналитического или
графического описания требуется несколько сечений r$ - const и (р^ = const.
При осесимметричной ДН облучателя распределение амплитуд не зависит от
координаты . Если ДН получателя имеет разную ширину в главных плоскостях,
то распределение амплитуд поля в раскрыве будет неравномерным как по радиусу,
так и по азимуту.
14.4.4. Диаграмма направленности параболической антенны рассчитыва-
ется по методике, изложенной в §4.5 для круглого раскрыва. Необходимое для
расчета амплитудное распределение находится изложенным выше способом
Ширина ДН в главных плоскостях определяется, как и для
цилиндропараболических антенн выражением 20о 5 = пГк /2а (а - радиус
раскрыва), однако при подобных амплитудных распределениях коэффициент
т для круглого раскрыва больше, чем для прямоугольного, и в реальных
конструкциях составляет примерно 65° - 80°.
14.4.5. КИП и коэффициент перехвата для параболической антенны имеют
тот же смысл, что и для цилиндропараболической антенны. КИП рассчитывается
по методике, изложенной в гл. 4 для случая круглого раскрыва, а коэффициент
перехвата находится по формуле
Фо 2л
j F2 (Ф,ф5-)8т(Ф)с1Фс1ф5
1)П = . (14.4.2)
J J F2 (Ф,<р5 )sin(O)d®d<piy
Ф=0 ф5=0
14.4.6. Выигрыш д = qr|n для параболических антенн, так же как и для цилин-
ропараболических, имеет оптимум в зависимости от угла раскрыва зеркала Фд
и формы ДН облучателя. При осесимметрическом облучении Ф0опш ~ 65° - 80°, а
оптимальный уровень облучения краев зеркала Sonm «0,1 или —10 дБ.
14.5. Антенны с зеркалом в виде вырезки из параболоида
вращения
14.5.1. Зеркала в виде вырезок из параболоида вращения используются
главным образом в антеннах с веерной ДН, т.е. ДН, имеющей существенно разную
ширину в главных плоскостях. Облучатели таких зеркал, естественно, должны
быть точечными.
Антенны с зеркалом в виде вырезки из параболоида вращения при
формировании веерной ДН имеют ряд конструктивных преимуществ перед
цилиндропарабоическими антеннами из-за малых габаритов облучателя.
г •
Зеркальные антенны 545
Однако цилиндропараболические антенны имеют обычно более высокие
значения эффективности и меньший уровень боковых лепестков.
14.5.2. Симметрично-усеченный параболоид показан на рис. 14.10,а. У этой
антенны углы раскрыва в главных плоскостях разные, ширина ДН облучателя в
этих плоскостях также должна быть разной. Для усеченного параболоида враще-
ния отношение большого размера раскрыва к малому обычно не может превышать
5_6, так как при больших отношениях облучатель в плоскости малого размера
раскрыва антенны будет иметь слишком большой размер.
С целью уменьшения уровня боковых лепестков, а такжевеса антенны и габаритов
обтекателя (на летательных аппаратах) симметричная вырезка из параболоида
вращения может быть выполнена по контуру равноинтенсивного облучения (рис.
14.10,6). Если уровень облучения краев зеркала выбран оптимальным, то такая
антенна при заданной площади раскрыва будет иметь наибольший КУ.
14.5.3. Несимметричные вырезки из параболоида вращения (рис. 14.10,в)
используется для уменьшения или устранения влияния отраженных электромаг-
нитных волн на облучатель и влияния рассеяния отраженных волн на облучателе
на ДН антенны, особенно на уровень боковых лепестков.
14.5.4. Облучатели антенн с зеркалом в виде вырезки из параболоида
вращения должны иметь существенно разную ширину ДН в главных плоскостях.
Этому требованию лучше всего удовлетворяет пирамидальный рупор. Так как у
него положение фазовых центров для главных плоскостей различно, то иногда
профиль зеркала корректируется (обычно в плоскости малого размера раскрыва).
При очень больших углах раскрыва в плоскости большого размера применяются
специальные широкоугольные облучатели.
14.5.5. Распределение амплитуд поля в раскрыве рассчитывается по извес-
тной ДН облучателя с помощью формул для параболоида вращения (14.4.1) при
ограничении углов Ф в соответствии с геометрией вырезок.
14.5.6. Диаграммы направленности, КНД и КУ для раскрыва, показанно-
го на рис. 14.10,а, приближенно можно рассчитывать по формулам для прямо-
угольного или эллиптического раскрыва. Раскрыв, изображенный на рис. 14.10,6
почти всегда является эллиптическим; соответственно используются формулы,
приведенные в [17]. Для расчета указанных параметров антенн в другими формами
вырезок применяется численное интегрирование.
а) б) в)
Рис. 14.10. Вырезки из параболоида вращения [17]
18- Неганов
546
ГЛАВА 14
14.6. Двухзеркальные и многозеркальные антенны
14.6.1. Конструктивная схема простейшей двухзеркальной антенны
поясняется рис. 14.11, на котором изображено осевое сечение системы, состоящей
из поверхностей вращения вокруг оси F2O'.
В двухзеркальной антенне плоский фазовый фронт в раскрыве формируется с
помощью двух отражающих поверхностей: малого зеркала 2 и большого зеркала
1. При заданном фронте волны облучателя 3, сферическом или близком к нему,
можно подобрать бесчисленное множество пар отражающих поверхностей,
обеспечивающих плоский фронт в раскрыве. В этом состоит одно их основных
преимуществ двух- и многозеркальных систем перед однозеркальными. Имеющиеся
две (или более) степени свободы в выборе отражающих поверхностей можно
использовать не только для фазировки. Но и для регулирования амплитудного
распределения в раскрыве, уменьшения фазовых ошибок при широкоугольном
качании луча и т.п.
Другое преимущество заключается в том, что облучатель может быть
размещен вблизи вершины большого зеркала, за которым находятся передатчик
и элементы фидерного тракта. При этом уменьшается осевой размер антенны, а
длина волновода, идущего к облучателю, заметно сокращается. Это упрощает
конструкцию фидерного тракта, улучшает согласование, уменьшает потери и
шумовую температуру антенно-фидерного устройства.
Главным недостатком двухзеркальной антенны является затенение раскрыва,
создаваемое малым зеркалом. Поперечные размеры этого зеркала должны быть
заметно больше, чем поперечные размеры облучателя однозеркальной антенны
при одинаковых требованиях к антеннам. Этот недостаток в значительной мере
устраняется применением для большого зеркала отражающей поверхности с
поворотом плоскости поляризации на 90° (см. ниже п. 5), а для малого зеркала
- отражателя (рис. 14.11) излучает волны вертикальной поляризации. Тогда
малое зеркало, выполненное из вертикальных проводов, отражает волны этой
поляризации. После отражения от большого зеркала после становится горизонтально
поляризованным, для него малое зеркало «прозрачно».
14.6.2. Основные схемы двухзеркальных антенн изображены на рис. 14.12.
В большинстве случаев в качестве большого зеркала 1 используется параболоид,
фокус которого обозначен . Если малое зеркало 2 находится перед фокусом па-
раболоида (рис. 14.12,а), как в телескопе Кассегрена, то двухзеркальная система
называется системой Кассегрена, в которой малое зеркало имеет гиперболический
профиль с дальним фокусом в точке F2 или является плоским (рис. 14.12,в). Если
Рис. 14.11. Двухзеркальная антенна [17]
Зеркальные антенны
547
а) б) в)
Рис. 14.12. Основные схемы двухзеркальных антенн [17]
малое зеркало находится за фокусом параболоида (рис. 14.12,6), как в телескопе
Грегори, то двухзеркальная система называется системой Грегори, в которой ма-
лое зеркало имеет эллиптический профиль с дальним фокусом в точке Г2 .
При выборе для большого зеркала профиля, отличного от параболического,
изменяется и профиль малых зеркал. В частности, в антеннах с качанием луча в
широком секторе находит применение сферическое большое зеркало.
14.6.3. Диаграмма направленности осесимметричной зеркальной антен-
ны может быть рассчитана по форумам для круглого синфазного раскрыва. Если
большое зеркало — параболоид вращения, то распределение амплитуд поля в
его раскрыве, без учета затенения малым зеркалом, будет таким же, как в рас-
крыве эквивалентного параболоида, построение которого поясняется рис. 14.11,
кривая 4.
С помощью осесимметричных двухзеркальных антенн формируется ДН
игольчатого типа.
Если приняты описанные выше специальные меры по устранению эффекта
затенения, фактическое распределение амплитуд поля в раскрыве будет иметь
провал в центре, что снижает КНД антенны. Это снижение тем больше, чем
больше относительная площадь малого зеркала:
D'q «D0[l-2(d/2a)2],
(14.6.1)
где Dq — КНД раскрыва без учета затенения; d - диаметр малого зеркала; а -
радиус большого зеркала.
14.6.4. Двух зеркальная антенна с большим плоским зеркалом разработана
специально для широкоугольного качания узкого при неподвижном фидерном
тракте. Схема антенны показана на рис. 14.13. антенна является осесимметрич-
ной. Она состоит из неподвижного параболоида вращения 1, подвижного плоского
зеркала 2 с поворотом плоскости поляризации на 90° и неподвижного точечного
облучателя 3 вертикальной поляризации. При этом зеркало 1 выполнено из про-
волок круглого или прямоугольного сечения, лежащих в вертикальных плоскос-
тях. В раскрыве параболоида обычным способом формируется плоский фазовый
фронт (лучи 4), перпендикулярный оси антенны (при вертикальной поляризации).
Если бы не было плоского зеркала, то такая антенна сформировала бы ДН с мак-
симумом, направленным в правую сторону. При отражении от плоского зеркала
фронт волны остается плоским, но максимум излучения ориентируется влево. Так
18*
548
ГЛАВА 14
Рис. 14.13. Двухзеркальная антенна с большим плоским зеркалом [17]
как при отражении от плоского зеркала плоскость поляризации поворачивается
на 90°, то зеркало 1 из вертикальных проволок не мешает излучению влево элек-
тромагнитных волн горизонтальной поляризации (лучи 5). Если плоское зеркало
повернуть от нормали к оси на некоторый угол а, то отраженные от него лучи
отклоняются на угол 2а , на этот же угол отклонится максимум ДН.
Компактность антенны с большим плоским зеркалом, малая длина и
простота конструкции фидерного тракта объясняют ее широкое использование в
радиолокационных станциях летательных аппаратов.
14.6.5. Отражатель с поворотом плоскости поляризации на 90° (рис.
14.14) состоит из сплошного металлического листа 1 и прикрепленных к нему
параллельных металлических пластин 2 шириной X/4, расположенных на рас-
стоянии t = (0,12 — 0,25)Х друг друга. Волны, поляризации которых параллельна
пластинам (волны параллельной поляризации), не могут распространяться между
пластинами, так как две соседние пластины образуют для этих волн запредельный
волновод. Поэтому они отражаются от входной поверхности, почти совпадающей
с передним кромками пластин, испытывая при отражении изменение фазы элек-
трического вектора на л. Волны перпендикулярной поляризации свободно про-
ходят между пластинами и отражаются от задней поверхности также с потерей
фазы на л.
Пусть, как показано в нижней части рис. 14.14, падающее поле в некоторый
момент времени имеет вертикальную поляризацию с электрическим вектором
Еп • Отражающую поверхность поставим перпендикулярно направлению
распространения, причем так, чтобы плоскости ребер составляли с плоскостью
поляризации поля угол 45°. Падающее поле может быть разложено на два
синфазных поля с векторами Е^ и Еп •
Отраженное поле с вектором Egmp в момент t0 сдвинуто по фазе на входной
поверхности на л относительно Е^.
Вектор Еотр в момент t0 совпадает по фазе с Еп ; он соответствует падающему
полю, пришедшему на переднюю поверхность полпериода назад, и поэтому отстает
по фазе на л за счет двойного прохождения расстояния Х/4 между передней и
Зеркальные антенны
549
Рис. 14.14. Отражатель с поворотом плоскости поляризации на 90° [17]
задней поверхностью и еще на л за счет отражения от задней стенки. Векторы
отраженного поля в момент показаны на рис. 14.14 пунктиром. Составляющие
отраженного поля синфазны на передней поверхности. При этом отраженное поле
будет линейно поляризовано и повернуто на 90° в пространстве относительно
падающего. Отражатель с указанными свойствами может быть построен также на
основе взаимно перпендикулярных однолинейных сеток, расположенных друг от
друга на расстоянии Х/4.
Характеристики отражателей с поворотом плоскости поляризации на 90°
чувствительны к изменению частоты, так как для нормальной работы расстояние
между передней и задней отражающими поверхностями должно быть равно X/4.
14.7. Зеркальные антенны с диаграммой направленности
специальной формы [17]
14.7.1. Диаграмма направленности специальной формы — это такая ДН,
форма которой отличается от формы ДН, сформированной плоским синфазным
раскрывом. К ДН специальной формы относится, например, косеканская ножевая
ДН (рис. 14.15). Антенны с косеканской ДН конструируются главным образом для
наземных РЛС обнаружения и целеуказания (рис. 14.15,а) и для самолетных радио-
локационных бомбоприцелов (рис. 14.15,6). В вертикальной плоскости ДН имеет вид
прижатого к горизонту узкого лепестка (рис. 14.15,в) с вытянутым «хвостом» ма-
лых уровней под большими углами к горизонту. Если изменение угловой плоскости
9 9
мощности в вытянутой части ДН примерно следует закону cosec 6 / cosec 0^, то
интенсивность принятого сигнала при постоянной высоте полета самолета будет
мало зависеть от дальности до цели. Это существенно улучшает наблюдаемость
целей и упрощает конструкцию РЛС. ДН указанных РЛС в горизонтальных плос-
костях (в плоскостях 0 = const) должна быть узкой для повышения разрешающей
способности по азимуту (рис. 14.15,г).
Существует несколько способов получения косекансных ДН. Рассмотрим два
наиболее распространенных.
550
ГЛАВА 14
а) б)
0 10 20 30 40 50 60 0° 1,5 1,0 Q5 О Q5 1,0 (р
в) г)
Рис. 14.15. Косекансные диаграммы направленности [17]
14.7.2. Антенны самолетных радиолокационных бомбоприцелов обычно
выполняются в виде цилиндрического зеркала со специальным профилем (рис.
14.16,а). Нижняя часть зеркала 1 близка по форме к параболическому цилиндру
с фокальной осью F; она формирует главную часть ДН и шириной 20о 5 (см. рис.
14.15, в).
Верхняя часть зеркала 2 имеет специальный профиль, с помощью которого
получается необходимое распределение плотности мощности которого получается
необходимое распределение плотности мощности в косеканском «хвосте» ДН.
Для трубки лучей (рис. 14.16, а) закон сохранения энергии записывается в виде
p(<D)d<D = p(0)d0, где р(0) ~ угловая плотность мощности. Изменение кривизны
зеркала, выражаемой через дФ / d0, ведет к изменению р (0) по сравнению с
р(ф). Это позволяет подобрать профиль зеркала так, чтобы получить заданную
косеканскую ДН.
Узкая ДН в горизонтальной плоскости формируется линейным облучателем,
горизонтальный размер которого определяет ширину ДН. В качестве линейного
облучателя может быть использована сегментнопараболическая антенна (см. рис.
14.4, г) или металловоздушная линза.
14.7.3. Антенны наземных РЛС обнаружения и целеуказания с косекансной
ДН строятся обычно на основе зеркал в виде симметрично усеченного параболо-
ида вращения (см. рис. 14.10,а). Для получения специальной ДН используется не-
сколько точечных облучателей, один из которых находится в фокусе зеркала и
обеспечивает формирование основной части ДН (облучатель 1 на рис. 14.16,6), а
остальные смещены из фокуса перпендикулярно оптической оси зеркала. Каждый
облучатель формирует свою «парциальную»ДН. Подбором фаз питания, распреде-
ления мощности и расстояния между облучателями получают необходимую сум-
марную ДН в вертикальной плоскости. Этот способ формирования специальной ДН
Зеркальные антенны
551
а) б) в)
Рис. 14.16. Способы формирования косекансной диаграммы направленности [17]
называется способом парциальных диаграмм. По сравнению с рассмотренным в
п. 14.8.2 он имеет преимущество в конструктивной простоте (используются точеч-
ные облучателем вместо линейных), однако ДН в вертикальной плоскости получа-
ется хуже: изрезанная, с существенными провалами за счет интерференционных
явлений (рис. 14.16,в). Другим недостатком является разная ширина парциальных
лучей в горизонтальной плоскости, так как смещение облучателя из фокуса по
вертикали ведет не только к отклонению и расширению парциальной ДН в верти-
кальной плоскости, но и к ухудшению фазового распределения в горизонтальной
плоскости.
Расчет распределения мощностей по облучателям и расстояния между ними
производится путем подбора на основе метода векторных диаграмм сложения
полей в дальней зоне (с учетом разности хода за счет разноса облучателей).
14.8. Технические допуски на размеры зеркальных антенн
при изготовлении и в процессе эксплуатации [17]
14.8.1. Точность изготовления зеркальных антенн, т.е.степень приближения
их истинных размеров к расчетным, влияет на амплитудноеи фазовое распределение
в раскрыве и, следовательно, на ДН и КУ. Изменением амплитудного распределения
обычно можно пренебречь. Определяющей является разфазировка в раскрыве.
Основными причинами расфазировки являются отклонение поверхности зеркала
от расчетной и смещение облучателя из фокуса зеркала.
14.8.2. Отклонение поверхности зеркала от расчетной 1, как показано
на рис. 14.17, может произойти в обе стороны. Оно является случайным и заранее
нельзя сказать, в какую именно сторону произойдет отклонение на разных учас-
тках поверхности.
Рассмотрим отражение в том месте зеркала, где имеется отклонение его
поверхности на величину Др (рис. 14.17). На этом рисунке луч после отражения от
измененной поверхности 2 показан параллельным оптической оси. Фактически это
не так, однако ошибка в определении расфазировки при таком предположении
будет незначительной.
Отличие оптической длины пути от расчетной определяется как
AL = А'А + АС = Др(1 + собФ) и при данном Ар больше у вершины зеркала.
552
ГЛАВА 14
Рис. 14.17. Отклонение поверхности зеркала от расчетной [17]
Расфазировка Ду' при отклонении профиля в одну сторону равна
Ду' = kAL =
2л
Др(1 + cos<D).
(14.8.1)
Отклонение профиля зеркала на разных участках поверхности может произойти
в разные стороны. При этом расфазировка в раскрыве будет иметь разные знаки на
разных участках. Если считать, что при данном Др отклонении профиля в разные
стороны дает одинаковую величину расфазировки, то ожидаемая разность фаз
между полями на различных участках в раскрыве может оказаться равной
Ду = 2Ду' = — Др(1 + cosO). (14.8.2)
X
Расфазировка в раскрыве должна быть меньше некоторой допустимой величины
Дуаоп • Ориентируясь на наибольшую возможную расфазировку, примем Ф = 0 и
получим, что допустимое отклонение поверхности зеркала
АРдоп — ^Vdon^ /
(14.8.3)
Ранее было показано, что при Ду < л / 4 изменения в ДН и КНД можно не
принимать во внимание. Положив Дуаоп = л / 4, получим
Дрдоп <Х/32. (14.8.4)
При менее жестких требованиях к ДН и КНД иногда можно допустить
расфазировку Дуаоп < л / 2. При этом
Дрдоп <Х/16. (14.8.5)
Статистический анализ влияния неточностей в изготовлении профиля зеркала
на КНД показывает, что если Др < О, IX, то КНД снижается по сравнению с
расчетным не более чем на 20%.
При изготовлении и в процессе эксплуатации возможность выдерживать
абсолютный допуск Д Рдоп тем меньше, чем больше размеры зеркала. Поэтому
нельзя построить зеркальную антенну со сколь угодно высоким КНД. Из работы
[17] следует, что при современной технологии максимальный размер антенн
подвижных объектов не превышает 1000 X, а для наземных антенн - 2000 X.
14.8.3. Смещение облучателя из фокуса вдоль оптической оси вызывает
симметричные фазовые ошибки в раскрыве. ДН при этом расширяется и может
Зеркальные антенны
553
Рис. 14.18. Вынос облучателя из фокуса вдоль фокальной оси [17]
даже раздвоиться; растут боковые лепестки. Однако ДН остается симметричной.
Рассмотрим смещение облучателя из фокуса в сторону зеркала и обозначим его
Д/ (рис. 14.18). Расфазировка определится разностью длин оптических путей FAC
по лучу 1 и F'AD по лучу 1 от смещенного облучателя. Пренебрегая величинами
второго порядка малости, будем считать одинаковыми длины отрезков АС и AD,
а также длину катета АВ и гипотенузы AF' в прямоугольном треугольнике F'BA.
Тогда AL = FB = Af соб(Ф). Вычитая эту абсолютную разность оптических путей
из наибольшей (для Ф = 0), для расфазировки относительно центра раскрыва
получаем
Д\|/ = k(Af - Af cos Ф) = kAf (1 - cos Ф). (14.8.6)
Как видно, наибольшая относительная расфазировка получается на краю
зеркала при Ф = Фо. Приняв Д<Идоп = 71 / 4 , получаем
Д/0ОП <Х /8(1- сойФ„ ). (14.8.7)
При больших смещениях, чем Afdon , ДН расширяется, КНД и КУ уменьшаются
более, чем это допустимо по условиям нормальной работы.
Смещение облучателя из фокуса в направлении от зеркала вызывает несколько
меньшую разность длин оптических путей, чем в первом случае, и Afdon получается
больше. Однако и в этом случае пользуются обычно формулой (14.8.7).
14.8.4. Вынос облучателя из фокуса перпендикулярно оптической оси
может быть случайным из-за неточности изготовления, но может быть и пред-
намеренным — для отклонения направления максимума ДН от оптической оси
антенны.
На рис. 14.19, а показан ход лучей в параболической антенне с облучателем,
фазовый центр которого находится в точке F' на расстоянии от фокуса антенны
F. На рисунке длина всех отрезков лучей, исходящих из фазового центра F',
одинакова и равна длине крайнего луча F ’ А. При этом концы отрезков лучей
будут находиться на линии сечения фронта волны плоскостью рисунка (пунктирная
линия).
Наклон фронта определяется разностью длин оптических путей AL от точки F ’
до плоскости раскрыва АВС по отношению к длине пути по лучу F' ОВ , идущему
к вершине зеркала. При малом отклонении фронт близок к плоскому (кривая 1 на
554
ГЛАВА 14
а)
б)
D / ^макс > %
0,8
0,6
0,4
0 2 40 / (20о 5)
2)
Рис. 14.19. Смещение облучателя перпендикулярно оптической оси (а, б) и графики изме-
нения фазового фронта (в) и КНД (г) при этом [17]
рис. 14.19,6), при большом - он заметно искривляется (кривая 2).
Наклон фазового фронта вызывает отклонение максимума ДН от оси антенны
(кривая 3), а отличие фронта от плоскости ведёт к расширению и искажению
ДН. Так как искажения фронта несимметричные, то и искажения ДН также
получаются несимметричными, особенно в боковых лепестках.
Теоретические и экспериментальные исследования [17] показывают, что угол
наклона фазового фронта 0 (рис. 14.19,6) и степень его искажения зависят от угла
выноса облучателя а0 и относительно фокусного расстояния f'/ а (рис. 14.19,в).
Чем больше относительное фокусное расстояние, тем ближе угол отклонения
максимума ДН к углу выноса облучателя и тем меньше искажения фронта волны.
Оптимальным углам раскрыва зеркала по КУ соответствуют значения f / 2а,
равные 0,3-0,4. При этом 0 « 0.85ад . Если допустить снижение КНД по отношению
к КНД синфазного разрыва DMaKC на 10%, то, как следует из рисунка 14.19,г, угол
отклонения максимума ДН может составлять примерно 2(29 0>б)- Таким образом,
для антенн, оптимальных по КУ, угол отклонения или качания луча не превышает
±2(20о>5) при снижении КНД на 10%.
Зеркальные антенны
555
14.9. Диапазонные свойства зеркальных антенн [17]
14.9.1. Ширина полосы частот зеркальной антенны определяется, как и
для других антенн: допустимым снижением КБВ в фидере; допустимым снижением
КУ, допустимым изменением ширины ДН,а в антеннах специальной формы —
допустимым отклонением формы ДН от заданной; заданными требованиями к
изменению в полосе частот уровня и распределения бокового излучения.
14.9.2. Диапазонность по согласованию зависит от полосы пропускания са-
мого фидерного тракта, от величины и изменения с частотой входного сопротив-
ления облучателя и от влияния отражений от зеркала на согласование. Попадание
электромагнитной энергии в облучатель и фидерный тракт после отражения от
зеркала называется реакцией зеркала. Она наиболее сильно выражена в антеннах
обычной схемы (рис.14.20), у которых облучатель находится в наиболее интенсив-
ной части потока отраженных волн.
В расчетах по согласованию реакцию зеркала можно учесть коэффициентом
отражения Гд, приведённым к выходному сечению фидера. Его модуль
определяется отношением мощности, попавшей в фидер после отражения от
зеркала, к полной мощности излучения облучателя, а фаза, как следует из рис.
14.20, — расстоянием I от места отражения до выходного сечения облучателя и
электрической длиной пути в облучателе. Если имеет большое значение, то
антенну трудно согласовать в сколько-нибудь широкой полосе частот, так как
фаза Гд быстро изменяется с частотой из-за большой величины отношения 21 / X.
Для уменьшения реакции зеркала в настоящее время разработан ряд
эффективных способов. Схема одного из них показана на рис. 14.20. металлический
компенсирующий отражатель 2, выполняемый обычно в виде диска, по размерам
подбирается так, что отраженные от него волны имеют в фидере такую же
амплитуду, как и волны от зеркала 1. Поместив этот диск на расстоянии X / 4
от места основного отражения, получим компенсацию отраженных волн у
облучателя 3. Этот способ хорош своей простой и диапазонностью, однако он имеет
и существенный недостаток - появление добавочного бокового излучения за счёт
рассеяния волн на диске.
К другим способам относится применение несимметричных зеркал (см. рис.
14.6) и отражающих поверхностей с поворотом плоскости поляризации на 90° (см.
Рис. 14.20. Реакция зеркала на облучатель и способ ее уменьшения [17]
556
ГЛАВА 14
рис. 14.14). Последний способ хотя и значительно уменьшает реакцию зеркала,
не относится к числу широкополосных, так как сама поверхность является
узкополосной.
14.9.3. Диапазонностъ зеркальных антенн по направлению излучателя
(КНД и ширине ДН) велика, их направленные свойства мало зависят от частоты.
Ширина ДН, определяется соотношением 20о 5 = тХ / L, увеличивается пропор-
ционально длине волны. Однако за счет расширения ДН облучателя при увеличе-
нии X облучение зеркала становится более равномерным, коэффициент т умень-
шается и ДН расширяется в меньшей степени, чем увеличивается длина волны.
Эта своеобразная «автокомпенсация» имеет место и в отношении КНД.
В заключение отметим, что наибольшей диапазонностью по всем параметрам
обладают зеркальные антенны с несимметричным зеркалом и облучателем в виде
пирамидального рупора.
Линзовые антенны
557
Глава 15. Линзовые антенны [17]
15.1. Основные типы линзовых антенн [17]
Линзовые антенны являются апертурными антеннами оптического типа. В ре-
жиме передачи линза обычно преобразует расходящийся пучок лучей в парал-
лельный (рис. 15.1); в режиме приема — наоборот. В дальнейшем будем рассмат-
ривать работу линзовых антенн в режиме передачи. В терминах волновой оптики
это означает, что линза преобразует волну с неплоским фазовым фронтом (или
наоборот). Такая линза, предназначенная для формирования острой ДН, называ-
ется фокусирующей.
Применяются так же линзы со сложной формой поверхности, предназначен-
ной для формирования ДН специального вида. Ниже будут рассмотрены только
фокусирующие линзы.
Различают линзы осесимметричные и цилиндрические. Первые образуются
вращением профиля линзы вокруг ее оптической оси (рис. 15.2,а), вторые - пере-
мещением профиля линзы вдоль прямой линии (рис. 15.2,6,2,0).
Линзовая антенна состоит из облучателя и линзы. Облучатель должен напра-
вить на линзу по возможности большую часть излученной им энергии, так как
энергия, не перехватываемая линзой, бесполезно тратится на образование боко-
вых лепестков. Отношение мощности падающей на линзу волны Рл к мощности
облучателя Ро^л называют коэффициентом перехвата линзовой антенны:
Лпх — ^лМобл •
Если линза осесимметрична, то облучатель должен формировать сферическую
волну, т. е. иметь фазовый центр, который совмещается с фокусом линзы. Такой
облучатель называется точечным. В качестве точечных облучателей обычно при-
меняют: пирамидальный рупор, открытый конец волновода, систему вибратор
— рефлектор и другие слабонаправленные излучатели. Облучение цилиндрической
линзы осуществляется линейным облучателем, создающим цилиндрическую вол-
ну, а его линия фазовых центров (фазовая ось) совмещается с фокальной линией
линзы. В качестве линейных облучателей обычно применяют прямолинейные ре-
шетки вибраторов или щелевые излучатели, показанные на рис. 15.2.
Поверхность линзы, обращенную к облучателю, называют освещенной, а дру-
гую, являющуюся раскрывом — теневой. Точку пересечения оси линзы с освещен-
ной поверхностью называют вершиной линзы (точка О на рис. 15.3), а расстояние
от фокуса линзы до вершины — фокусным расстоянием. Угол между лучами,
проходящими через вершину и край линзы, называют углом раскрыва линзы
(угол Фо на рис. 15.3)
Формирование параллельного пучка лучей может может производиться пре-
ломлением лучей на одной из поверхностей линзы или на обеих. В первом случае
линза называется одноповерхностной, во втором — двухповерхностной.
С точки зрения геометрической оптики условию фокусировки (равенству опти-
ческих путей всех лучей от облучателя до плоского раскрыва) можно удовлет-
ворить, либо увеличивая оптическую длину пути центральных лучей в большей
558
ГЛАВА 15
Рис. 15.1. К пояснению фокусирующего действия линзы: а) замедляющая линза; б) уско-
ряющая линза (сплошные линии — лучи; пунктирные линии — фазовые фронты) [17]
б)
а)
б)
Рис. 15.2. Типы линзовых антенн: а) диэлектрическая осесимметричная; б) диэлектричес-
кая цилиндрическая; в) металлодиэлектрическая осесимметричная; г) металлопластинча-
тая цилиндрическая с фокусировкой в Н-плоскости; д) металлопластинчатая цилиндри-
ческая с фокусировкой в Е-плоскости; е) металлопластинчатая осесимметричная [17]
Линзовые антенны
559
t
t’ t”
E--- ---------
a) 6)
Рис. 15.3. К выводу уравнения профиля линзы: а) замедляющей; б) ускоряющей [17]
мере, чем периферийных, либо уменьшая оптическую длину периферийных лу-
чей в большей мере, чем центральных. Первый способ реализуется в замедляю-
щих линзах, в которых фазовая скорость меньше скорости света, а коэффициент
преломления материала линзы п > 1. Второй способ реализуется в ускоряющих
линзах, в которых фазовая скорость больше скорости света, а коэффициент пре-
ломления материала линзы п < 1. Ясно, что наибольший продольный размер
(толщина) замедляющей линзы - в центре (рис. 15.3,а), а ускоряющей линзы
— на краях (рис. 15.3,6).
Кроме ускоряющих и замедляющих линз, применяются геодезические линзы, в
которых формирование плоского фазового фронта в раскрыве достигается увели-
чением геометрической длины пути от облучателя до раскрыва без изменения фа-
зовой скорости. Это можно трактовать как «геометрическое замедление» лучей.
Если коэффициент преломления по объему линзы не меняется, то такая линза
называется однородной. В противном случае линза называется неоднородной.
Из замедляющих линз находят применение диэлектрические и металлодиэ-
лектрические линзы, из ускоряющих - металлопластинчатые (см. рис. 15.2).
Лучи, падающие от облучателя на линзу, частично проходят сквозь нее, а
частично отражаются в разных направлениях. Это вредное явление пытаются ос-
лабить.
15.2. Уравнение профиля и толщина линзы [17]
Определим профиль одноповерхностной линзы с плоским раскрывом из усло-
вия фокусировки.
15.2.1. Замедляющие линзы. Выберем профиль освещенной поверхности лин-
зы таким образом, чтобы в точках А и О’ (рис. 15.3,а) фазы полей были одинаковы.
Так как АА’=О’О”, то одинаковыми будут фазы полей и в точках А’ и О”. Ввиду
произвольного выбора точки А поле в раскрыве линзы будет синфазным. Условие
равенства оптических длин путей запишется в виде
560
ГЛАВА 15
р = f + пОО'.
Так как ОО' = FOf и FO' = р cos Ф , то
р = 7(п-1)/(псозФ-1). (15.2.1)
При п > 1 — это уравнение гиперболы в полярной системе координат, центр кото-
рой совпадает с дальним фокусом гиперболы, а величина п - это эксцентриситет
гиперболы.
Толщину линзы t = ОО” определим из соотношения
t = p0 cos Фо - f.
Определяя f из (15.2.1) и учитывая, что р0 = L / 28тФ0, где L — размер раскрыва
линзы, получаем
Для уменьшения веса и стоимости линзы, а также потерь в ней, желательно,
чтобы толщина линзы была минимальной. Так как размер раскрыва линзы опре-
деляется требуемой шириной ДН, то, как это видно из формулы (15.2.2), толщи-
ну линзы можно уменьшить, либо увеличивая коэффициент преломления, либо
уменьшая угол раскрыва линзы.
При увеличении п растет отражение от поверхностей линзы, поэтому выбира-
ют п < 2. Если же уменьшать угол Фд , то растет фокусное расстояние, а следо-
вательно, и продольный размер антенны. Обычно считается приемлемым соотно-
шение f ~ L.
По указанным причинам диэлектрические линзовые антенны с большим разме-
ром раскрыва применяются редко.
15.2.2. Ускоряющие линзы. Расчет профиля и толщины линзы ведется в этом
случае по той же методике, что и для замедляющей линзы. Выполняя соответс-
твующие выводы, получаем формулу профиля линзы
р = /(1 - n) / (1 - п cos Ф). (15.2.3)
Формула (15.2.3) имеет такой же вид, как и формула (15.2.1), однако при п<1
она представляет собой уравнение эллипса в полярной системе координат, центр
которой совпадает с дальним (по отношению к линзе) фокусом, а п есть эксцент-
риситет эллипса.
Толщина линзы определяется по формуле
(15.2.4)
Рис. 15.4. Отклонение лучей при выносе облучателя из фокуса линзы [17]
Линзовые антенны
561
Здесь под толщиной линзы f понимается наибольший продольный размер (на
краю линзы) при условии, что толщина в центре линзы равна нулю. Величина
t” выбирается из соображения механической прочности. Полная толщина линзы
равна
t = t’ + t”.
При заданном размере раскрыва линзы ее толщину можно сократить, умень-
шая коэффициент преломления п или угол раскрыва Фо . Однако при уменьшении
п растет отражение от поверхностей линзы.
15.2.3. Смещение облучателя из фокуса перпендикулярно оптической оси
(рис. 15.4) нарушает синфазность поля в раскрыве линзы. Можно показать [17],
что если угол отклонения а мал, то распределение фаз в раскрыве линзы являет-
ся почти линейным, и это приводит к повороту ДН также на угол а , но в направ-
лении, обратном смещению облучателя, благодаря этому можно осуществлять
качание ДН линзовой антенны.
При увеличении угла а фазовое распределение становится нелинейным: боль-
шое значение приобретают кубические фазовые искажения. Они приводят к иска-
жениям ДН и ограничивают угол качания луча в пределах нескольких ширин ДН.
Некоторого расширения угла качания можно достичь с помощью двухповерх-
ностных линз, профиль которых выбирается таким образом, что при смещении
облучателя в некоторых пределах от оптической оси фронт волны наклоняется,
но остается почти плоским. При этом фазовое распределение является почти ли-
нейным. Расчет таких линз, называемых апланатическими, приведен в литера-
туре [88].
15.3. Распределение амплитуд поля в раскрыве [17]
Диаграмма направленности синфазного раскрыва зависит от распределения на
нем амплитуд поля. Найдем это распределение.
15.3.1. Замедляющие линзы. Пусть облучатель цилиндрической линзы имеет
ДН по мощности р(Ф), где величина р(Ф) - угловая плотность мощности на участ-
ке единичной длины, измеряемой вдоль фокальной оси. Обозначим через S(X^)
плотность потока мощности (величину вектора Умова-Пойтинга) в раскрыве линзы.
Ее можно рассматривать как амплитудное распределение по мощности вдоль оси
(амплитудное распределение вдоль фокальной оси считаем равномерным).
Пренебрегая потерями в материале линзы и потерями на отражение от ее повер-
хности и исходя из условия энергетического баланса в трубке лучей, приравняем
друг к другу потоки мощности в пределах угла АФ и отрезка ДХ$- (рис. 15.5,а)
р(Ф)АФ = S(Xs)AXs (15.3.1)
или, переходя к дифференциалам, получаем
S(Xs) = р(Ф)йФ/йХ5 . (15.3.2)
Из уравнения профиля линзы с учетом соотношения Х$ = р sin Ф имеем
Х5 = f(n - 1)зтФ / (псозФ -1). (15.3.3)
Продифференцировав левую и правую части этого равенства по Ф, получим
562
ГЛАВА 15
Рис. 15.5. К определению амплитудного распределения в раскрыве линзы: а) замедляю-
щей; б) ускоряющей [17]
(1Ф / dXs = (п cos Ф -1)* 2 / /(п - l)(n - cos Ф). (15.3.4)
Подставляя (15.3.4) в (15.3.2), получаем
S(X5) = р(Ф)(псоз Ф -1)2 / f(n - l)(n - cos Ф). (15.3.5)
Введем нормированную ДН облучателя по мощности соотношением
2
F (Ф) = р(Ф) / рМакс ’ гДе Рмакс ~ угловая плотность мощности в направлении мак-
симума излучения облучателя. Кроме того, учтем, что S(X^) = Е2(Х<?) / 240л.
Подставляя эти соотношения в (15.3.5) и извлекая квадратный корень из обеих
частей равенства, получаем формулу для расчета амплитудного распределения
поля в раскрыве линзы
E(XS) = М^Ф^Ф). (15.3.6)
Здесь постоянный множитель N = у/^А^Рмакс / / , а функция
Ai (Ф) = (п cos Ф -1) / у/(п - l)(n - cos Ф) (15.3.7)
характеризует влияние линзы на амплитудное распределение поля в раскрыве. На
рис. 15.6,а приведен график А^Ф) при п=1,5. Из графика видно, что влияние линзы
приводит к спаданию поля к краям раскрыва. Это можно объяснить тем, что оди-
наковым элементарным углам ДФ соответствуют участки AXS , увеличивающиеся
к краям раскрыва (рис. 15.5,а).
Формула (15.3.6) справедлива также для осесимметричной линзы, если под Xs
понимать расстояние от центра раскрыва. В этом случае множитель А|(Ф) следует
заменить на множитель А2(Ф), имеющий вид
А2(Ф) = у(п cos Ф -1)3 / (n - cos Ф) / (п -1). (15.3.8)
График множителя А2(Ф) приведен на рис. 15.6,а для случая п=1,6.
Аппроксимируя амплитудное распределение (15.3.6) приемлемой функцией,
можно рассчитать ДН, КНД, КИП и другие параметры линзовой антенны.
Вызванное линзой спадание поля к краям раскрыва приводит к уменьшению
уровня боковых лепестков, расширению главного лепестка и падению КНД. Чтобы
Линзовые антенны
563
Рис. 15.6. Графики множетелей А^Ф), Д2(Ф), В^Ф), В2(Ф) для цилиндрических и осесим-
метричных линз: а) замедляющих; б) ускоряющих [17]
сделать амплитудное распределение более равномерным, необходимо применять
облучатели с более широкой ДН. Однако при этом падает коэффициент перехвата,
так как растет доля мощности, не попадающей на линзу.
15.3.2. Ускоряющие линзы. В этом случае формула амплитудного распре-
деления в раскрыве выводится тем же способом, что и для замедляющей линзы.
Получаем
E(XS) = ЫЕ(Ф)В(Ф). (15.3.9)
В случае цилиндрической линзы
В(Ф) = В^Ф) = (1 -псобФ) / 7(1 - n)(cos Ф - п). (15.3.10)
В случае осесимметричной линзы
В(Ф) = В2(Ф) = 7(1-п cos Ф)3 /(совФ-п) / (1 - и). (15.3.11)
Графики функций В^Ф) и В2(Ф) приведены на рис.15.6,б для п=0,6. Из них видно,
что влияние ускоряющей линзы приводит к подъему амплитуды поля по краям
раскрыва. Это можно объяснить тем, что одинаковым элементарным углам ДФ
соответствуют участки ДХ$-, уменьшающиеся к краям раскрыва (см. рис. 15.5,6).
Вызываемый ускоряющей линзой подъем амплитудного распределения к кра-
ям раскрыва позволяет использовать облучатели с относительно узкой ДН, бла-
годаря чему удается получить большую величину коэффициента перехвата, чем
в случае замедляющей линзы.
15.4. Зонирование линз [17]
Толщина линзы прямо пропорциональна размеру раскрыва (см. формулы (15.2.2)
и (15.2.4)) и при больших раскрывах может составлять много длин волн, что уве-
личивает вес линзы и потери в ней. Этот недостаток можно уменьшить зонирова-
564
ГЛАВА 15
Рис. 15.7. Зонированные линзы: а) замедляющая; б) ускоряющая [17]
нием линзы. При зонировании часть материала, из которого изготовлена линза,
удаляется так, что линза принимает ступенчатую форму. На рис. 15.7 показаны
профили линз, имеющих по две зоны. Число зон может быть и большим.
Синфазность поля в раскрыве зонированной линзы обеспечивается благодаря
тому, что разность оптических длин путей лучей, проходящих через разные зоны,
отличается на целое число длин волн, следовательно, разность фаз составляет при
этом целое число раз по 2л. Пусть в соседних зонах разность оптических длин
путей составляет одну длину волны. Определим при этом форму профиля линзы.
15.4.1. Замедляющие линзы. Оптическая длина пути на отрезке FC\ (рис.
15.7,а) до зонирования составляла FO2 + п • О2О±, а после зонирования она равна
FO}. По условию разность оптических путей равна X. Тогда
(ТО2 + 'пд'З) — F Oj — X,
где d% = О2С\ - толщина зоны на оптической оси. Так как FO2 = FC\ - d3 , то легко
получить
d3 = Х/(п-1). (15.4.1)
Фокусное расстояние второй зоны f2 = FO2 связано с фокусным расстоянием
первой зоны Д = FOi соотношением
Л = /1 - d3 = /1 - ~ !)•
Эту формулу нетрудно обобщить на любое число зон. Ясно, что фокусное рассто-
яние m-й зоны меньше фокусного расстояния на величину (m - l)d3. Тогда
fm =/i-(m-l)X/(n-l). (15.4.2)
Таким образом, профиль зонириванной замедляющей линзы представляет собой
семейство гипербол с фокусом в одной точке, с эксцентриситетом п и с фокусны-
ми расстояниями, определяемыми формулой (15.4.2).
Из рис. 15.7 видно, что толщина зонированной линзы не может быть меньше
толщины одной зоны. Дополнительная толщина t" выбирается из соображений ме-
ханической прочности линзы, так что полная толщина определяется из соотно-
шения
t = t'+t"
X/(n-l) + t".
(15.4.3
Линзовые антенны 565
Недостатком зонированных линз является наличие вредных зон (рис. 15.7,а). Лучи
в пределах вредной зоны не образуют у раскрыва параллельного пучка лучей, а
рассеиваются, что приводит к росту боковых лепестков и падению КНД антенны.
15.4.2. Ускоряющие линзы. Исходя из соображений, аналогичных приведен-
ным выше, можно получить формулы для толщины зоны и фокусного расстояния
зонированной ускоряющей линзы (рис. 15.7,6):
d3 = Х/(1-п); (15.4.4)
fm =/i+(m-l)X/(l-n). (15.4.5)
Таким образом, профиль зонированной ускоряющей линзы представляет собой
семейство эллипсов с фокусом в одной точке, эксцентриситетом п и с фокусными
расстояниями, определяемыми формулой (15.4.5).
Толщина ускоряющей зонированной линзы равна
t = t ’+ t « А. / (1 - n) +1". (15.4.6)
Здесь t" определяется из соображений механической прочности линзы.
Зонированные ускоряющие линзы имеют вредные зоны (рис. 15.7,6), однако в
отличае от замедляющих линз поле в пределах вредных зон отсутствует. Следова-
тельно, амплитудное распределение поля в раскрыве имеет провалы, что приво-
дит к появлению дополнительных боковых лепестков и падению КНД антенны.
Заметим, что влияние вредных зон как в замедляющих, так и в ускоряющих
линзах можно в значительной мере ослабить, если зонирование осуществлять на
непреломляющей (эквифазной) поверхности линзы. Однако такие линзы отлича-
ются более сложной конструкцией.
15.5. Отражение электромагнитных волн от поверхностей линз
и меры по его уменьшению [17]
Как уже отмечалось ранее, часть энергии облучателя отражается от линзы.
Это приводит к образованию задних лепестков, искажает амплитудно-фазовое
распределение в раскрыве и, кроме того, нарушает режим бегущих волн в линии
передач за счет попадания отраженной энергии в облучатель. Отражение проис-
ходит от обеих поверхностей линзы. Та волна, которая отражается от эквифазной
поверхности (на рис. 15.8,а это поверхность раскрыва), фокусируется в облуча-
теле; волна, отражающаяся от неэквифазной поверхности, большей частью рас-
сеивается. При нормальном падении плоской волны на плоскую границу раздела
величина коэффициента отражения равна
г = |(п-1)/(п + 1)|. (15.5.1)
Освещенная поверхность линзы не является плоской, однако приближенно фор-
мулу (15.5.1) можно применить для расчета отражения лучей, ориентированных
вдоль оси линзы. Из формулы видно, что отражение тем больше, чем сильнее
коэффициент преломления отличается от единицы (в любую сторону).
Отражения можно устранить, если на освещенную поверхность линзы нанес-
ти слой диэлектрика, выбирая его толщину dc и коэффициент преломления пс
такими, чтобы волны, отраженные от обеих поверхностей согласующего слоя,
были равны по амплитуде и сдвинуты по фазе на 180°. Анализ показывает, что
566
ГЛАВА 15
а)
б)
Рис. 15.8. Отражение энергии от линзы: а) облучатель в фокусе; б) облучатель вынесен из
фокуса; А - падающий луч; В - луч, отраженный от раскрыва; С - луч, отраженный от
освещенной поверхности [17]
при нормальном падении лучей толщина слоя должна составлять 0,25 Ас, где Ас
— длина волны в слое, равная Ас = А, / пс, а коэффициент преломления слоя дол-
жен быть равен пс = Vn. Согласующий слой является аналогом четвертьволнового
трансформатора, применяемого в фидерных устройствах.
Существует ряд способов, при которых отражение от линзы не устраняется,
но его влияние на режим питания ослабляется. Эти способы можно разбить на две
группы. Первая характеризуется таким изменением формы или положения лин-
зы, при котором ни одна из ее поверхностей не является эквифазной, благодаря
чему отраженные лучи не фокусируются в облучателе. Примером может служить
вынос облучателя из фокуса перпендикулярно оптической оси (рис. 15.8,6).
Для второй группы характерна компенсация отражений от эквифазной поверх-
ности. Так, например, если осесимметричную линзу разрезать на две части вдоль
плоскости, содержащей оптическую ось, и одну часть сместить относительно дру-
гой вдоль этой оси на А / 4, то отраженнные от двух частей линзы волны придут
к облучателю в противофазе и компенсируются.
15.6. Диэлектрические линзы [17]
Коэффициент преломления материала линзы определяется через его относи-
тельную диэлектрическую проницаемость с помощью соотношения
п = л/е.
При прохождении энергии через линзу часть ее поглощается диэлектриком.
Считая, что в линзе движется плоская волна, можно приближенно определить
полное затухание в линзе как затухание на пути, равном толщине линзы t. Тогда
Pt = 27,3 —ntg6, дБ, (15.6.1)
Л
где 5 — угол потерь диэлектрика; р — коэффициент затухания. К. п. д. линзы, учи-
тывающей потери в диэлектрике, определится по формуле
Л = exp(-2pt). (15.6.2)
Наличие потерь в диэлектрике является недостатком диэлектрических линз.
Линзовые антенны 567
С целью уменьшения потерь для изготовления линз обычно применяют диэлек-
трик с малым значением произведения ntg5, например, полистирол (п = 2,3 - 2,6;
tg 6 = 0,0001). Зонирование линз также существенно уменьшает потери, поскольку
толщина линзы при этом лишь немного превышает толщину одной зоны [формула
(15.4.1)].
Достоинством диэлектрических линз является широкополосность и независи-
мость фокусирующих свойств от поляризации поля. Однако зонирование диэлек-
трической линзы лишает ее широкополосности, так как толщина зоны зависит от
длины волны [см. формулу (15.4.1)].
Если линза содержит т зон, а допустимая несинфазность в раскрыве состав-
ляет Удоп > то относительная полоса рабочих длин волн, в пределах которой не-
синфазность меньше допустимой, определяемой по формуле
2ДА, / Xq = у доп / 2л(т — 1). (15.6.3)
Здесь ДА, - допустимое отклонение длины волны в любую сторону от средней дли-
ны волны А,о.
Пусть линза изготовлена с такой точностью, что наибольшее отклонение ее
толщины от номинального значения равно At. Это вызывает несинфазность в рас-
крыве, равную
\|/ = (2л / А,)(п - 1)Д£.
Считая, что допустимая несинфазность равна 1|/доп > получаем формулу, опреде-
ляющую требования к точности изготовления линзы в виде
At = А.\|/доп / я(п -1). (15.6.4)
Из формулы видно, что при больших значениях п нужна высокая точность изго-
товления линзы.
15.7. Металлопластинчатые линзы [17]
Как известно, коэффициент преломления естественных диэлектриков всегда
больше единицы. Среда с коэффициентом преломления, меньшим единицы, может
быть сформирована с помощью параллельных металлических пластин.
Пусть вектор Е набегающей волны параллелен пластинам (рис. 15.9). Можно
считать, что соседние пластины образуют прямоугольный волновод, у которого
размер в Н-плоскости равен расстоянию между пластинами а, а размер в Е-плос-
Рис. 15.9. К пояснению принципа действия металлопластинчатой линзы [17]
568
ГЛАВА 15
кости не ограничен. Фазовая скорость в пространстве между пластинами опреде-
ляется по формуле
= с / а/1 - (Л. / 2а)2.
Следовательно, коэффициент преломления среды равен
п = с / пф = 71 - (X / 2а)2. (15.7.1)
Изменяя расстояние между пластинами, можно менять величину п, а выбирая
соответствующим образом размеры и форму пластин — создать линзу: цилиндри-
ческую, осесимметричную или специального типа.
В зависимости от того, в какой плоскости линза осуществляет фокусировку,
различают Н-плоскоспгпг/ю (см. рис. 15.2,г) и Е-плоскостную (см. рис. 15.2,д) цилин-
дрические линзы. Эллиптический профиль Н-плоскостной линзы формируется за
счет того, ширины прямоугольных пластин увеличиваются к краям линзы. Плас-
тины В-плоскостной линзы одинаковы по размерам, но их кромки, «освещенные»
облучателем, имеют эллиптическую форму. У осесимметричной линзы размеры и
формы пластин такие, что ее освещенная поверхность образует часть эллипсоида
вращения (см. рис. 15.2,е).
Металлопластинчатые линзы просты по конструкции и имеют высокий к. п. д.
Однако им присущи определенные недостатки. Их фокусирующие свойства зависят
от поляризации падающей волны. Линзы не фокусируют волны, у которых вектор
Е перпендикулярен пластинам.
В металлопластинчатой среде наблюдается дисперсия, так как п зависит от
длины волны. Следовательно, в отличие от диэлектрической линзы металлоплас-
тичная незонированная линза не является диапазонной, так как при отклонении
длины рабочей волны от номинальной, поле в раскрыве линзы становится несин-
фазным.
Дифференцируя (15.7.1) по X, получаем изменение коэффициента преломления
в виде
д 1 - п2 Ак
Ап «----------.
п X
(15.7.2)
Если максимальная толщина линзы (см. рис. 15.3,6) равна t', то наибольшее из-
менение оптической длины пути равно Ant', а несинфазность в раскрыве, причем
величина t" на несинфазность в раскрыве не влияет
\|/ = Ant' 2тс / X.
Подставляя в это выражение значение Ап из (15.7.2), можно получить следу-
ющую формулу относительной полосы рабочих волн, в пределах которой несин-
фазность меньше \|/доп :
2АХ _ пЦдоп X
к (1 - п)2Л t'
(15.7.3)
Из этой формулы видно, что полоса пропускания линзы обратно пропорци-
ональна ее толщине. Это объясняется тем, что чем больше толщина линзы, тем
больший путь проходит луч в диспергирующей среде и тем сильнее влияет изме-
нение длины волны на несинфазность в раскрыве.
По этой причине зонирование металлопластинчатой линзы расширяет ее поло-
су пропускания, так как, хотя зонирование само по себе придает линзе частотно-
Линзовые антенны
569
зависимые свойства, заметное уменьшение толщины линзы, которым оно сопро-
вождается, приводит в итоге к расширению полосы пропускания.
Можно показать, что относительная полоса пропускания зонированной линзы
равна [89]:
2ДХ _ V доп п
X л 1 + пт
(15.7.4)
15.8. Метал л о диэлектрические линзы [17]
Металлодиэлектрик представляет собой пространсвенную решетку металли-
ческих частиц, размеры которых в направлении, параллельном вектору Ё, малы
в сравнении с длиной волны. Для механического крепления частиц применяют
диэлектрический материал с коэффициентом преломления, близким к единице
(обычно пенистый материал с п « 1,03). На параметры линзы этот материал прак-
тически не влияет.
Как известно, в обычном диэлектрике под действием внешнего поля происходит
поляризация молекул, причем от степени их поляризации зависит электрическая
проницаемость диэлектрика. Сходное явление имеет место и в металлодиэлектри-
ке, в котором роль отдельных молекул играют металлические частицы. Частицы
могут иметь форму шариков, дисков, лент и т. п. (рис. 15.10)
Электрическая проницаемость металлодиэлектрика (как и обычного диэлект-
рика) может быть определена по формуле
£ = е0(1 + Na / е0) , (15.8.1)
где N — число частиц в единице объема; а - коэффициент поляризуемости одной
частицы; е0 - диэлектрическая проницаемость свободного пространства.
Коэффициент поляризуемости зависит от формы и размеров частицы. Так, на-
ример, для тонкого круглого диска радиуса R
а = (16 / 3)К3е0.
Коэффициент преломления металлодиэлектрика определяется из соотношения
п = / £0 = yjl + Na I Eq . (15.8.2)
В этой формуле не учитывается отличие магнитной проницаемости металлодиэ-
лектрика от магнитной проницаемости свободного пространства. Это справедливо
для плоских частиц, размер которых в направлении распространения волны нич-
Рис. 15.10. Металлодиэлектрические линзы с применением шариков (а),
дисков (б), лент (в) [17]
570 ГЛАВА 15
тожно мал. В случае неплоских частиц структура магнитного поля искажается,
что приводит к уменьшению магнитной проницаемости и падению величины п.
Если при уменьшении длины волны размер частиц в направлении вектора Е
перестает быть малым в сравнении с X, то формула (15.8.1) теряет силу, а метал-
лодиэлектрик становится диспергирующей средой.
Линза, изготовленная из шариков или дисков (рис.15.10,а и б), ввиду их осевой
симметрии пригодна для фокусировки волн любой поляризации. В случае линзы,
изготовленной из лент (рис. 15.10,в), электрический вектор волны должен быть
параллелен узкой стороне ленты.
Металлодиэлектрические линзы имеют преимущества перед диэлектрическими
(большой к. п. д. и меньший вес) и металлопластинчатыми линзами (широкополос-
ность).
15.9. Металловоздушные (геодезические) линзы [17]
В рассмотренных ране линзах выравнивание фронтового фронта, а следова-
тельно и оптических длин путей производилось применением ускоряющих или за-
медляющих сред. Однако можно отказаться от таких сред и выровнять волновой
фронт, если сделать одинаковыми геометрические длины путей от облучателя
до всех точек раскрыва. Для этого необходимо применять направляющие устройс-
тва, которые придают траектории луча заданную форму.
15.9.1. Направляющие устройства в металловоздушных линзах - металли-
ческие листы (рис. 15.11). Они образуют ряд волноводных каналов, вдоль которых
направляются волны.
Если в любой точке поверхностей радиусы кривизны много больше длины вол-
ны, то анализ распространения волн в волноводных каналах может производить-
ся методами геометрической оптики. В частности, для такой среды справедлив
принцип Ферма. Следовательно, лучи вдоль поверхностей будут ориентированы
по геодезическим линиям, так как расстояние вдоль геодезической линии между
двумя точками поверхности является кратчайшим. При расчете линз считают, что
поверхность, вдоль которой ориентированы лучи, расположена посередине между
двумя соседними металлическими листами. Одна такая поверхность изображена
на рис. 15.11 пунктиром.
15.9.2. Структура электромагнитного поля в линзе может быть различ-
ной. Если вектор Е перпендикулярен металлическим листам, то расстояние меж-
ду ними выбирают меньше X / 2. При этом в линзе может распространяться лишь
Рис. 15.11. К пояснению принципа действия металловоздушной линзы [17]
Линзовые антенны
571
Рис. 15.12. Вариант металловоздушной линзы
(пунктирные линии показывают ход лучей) [17]
волна типа ТЕМ. Ввиду отсутствия в этом случае критической длины волны линза
является широкополосной.
Если вектор Е параллелен металлическим листам, то расстояния а между
ними выбирают из условия
X / 2 < а < X, т.е. а < X < 2а.
При этом в линзе может распространяться лишь основная волна типа Нг Приве-
денное условие ограничивает диапазон рабочих волн линзы.
15.9.3. Вариант металловоздушной линзы, применяемой в качестве линей-
ного облучателя цилиндрических зеркальных антенн, изображен на рис. 15.12.
Цилиндрическая волна от первичного облучателя (открытого конца волновода) 6
распространяется между параллельными пластинами 1 и 2. Профиль 3 линзы вы-
бран таким, что длины путей всех лучей выравниваются и в пространстве между
пластинами 4 и 5 фронт волны параллелен раскрыву. Расчет профиля линзы про-
изводится исходя из условия фокусировки [17].
15.10. Линзы с переменным коэффициентом преломления
(неоднородные линзы) [17]
15.10.1. Неоднородная линза — это такая линза, в разных точках которой
коэффициент преломления неодинаков. С помощью неоднородных линз можно ре-
шить все те задачи, которые решаются однородными линзами, в частности задачу
фокусировки расходящегося пучка лучей облучателя. Преимущество неоднород-
ных (фокусирующих) линз состоит в том, что они могут иметь профиль простой
геометрической формы (прямая линия, окружность), в то время как однородные
фокусирующие линзы имеют профиль более сложной формы (гипербола, эллипс).
Рассмотрим в качестве примера неоднородную металлопластинчатую линзу с
продольным сечением прямоугольной формы (рис. 15.13). Пусть п(х) — зависимость
коэффициента преломления от координаты х, Пд — значение п(х) при х - 0, f -
фокусное расстояние линзы, a t — ее толщина. Точечный источник волн находится
в фокусе (точка F). Для того, чтобы на выходе линзы получить плоский волновой
фронт, нужно, чтобы оптическая длина пути произвольного луча FAA’ была рав-
572
ГЛАВА 15
Рис. 15.13. Неоднородная линза с продольным сечением прямоугольной формы [17]
на оптической длине пути центрального луча FOO’. Приравнивая эти величины,
можно получить следующую формулу для расчета п(х):
п(х) = п0 - (\//2 + а;2 - /) / t. (15.10.1)
Следовательно, коэффициент преломления должен убывать от середины линзы к
краям. В случае металлопластинчатой линзы это легко достигается тем, что рас-
стояния между соседними пластинами к краям линзы уменьшаются.
15.10.2. Линза Люнеберга представляет собой вариант неоднородной линзы,
позволяющий осуществить неискаженное качание луча на любой угол. Если тре-
буется качать луч в некоторой плоскости на 360°, то ясно, что линза должна
обладать симметрией относительно оси вращения облучателя, сохраняя при этом
фокусирующие свойства.
Сечение цилиндрической линзы Люнеберга приведено на рис. 15.14,а. Коэффи-
циент преломления линзы изменяется по закону
n(p) = ^2а2 - р2 / а, (15.10.2)
где а — радиус цилиндра; р - расстояние от оси цилиндра.
Пусть в точке F находится облучатель. Так как линза является неоднородной,
то лучи (за исключением центрального) будут криволинейными. Можно показать,
что лучи, выходящие из линзы, образуют параллельный пучок лучей. У поверх-
ности линзы п = 1, и поэтому отражения лучей не будет. Вращая облучатель вок-
руг линзы, можно отклонять ДН на любой заданный угол. Двумерное качание
луча можно осуществлять с помощью сферической линзы Люнеберга, имеющей
аналогичное устройство. При большом размере линзы Люнеберга проявляется ее
недостаток — большой радиус вращения облучателя.
15.10.3. Модифицированная линза Люнеберга лишена этого недостатка. Это
достигается размещением облучателя внутри линзы, так что радиус вращения
облучателя значительно меньше радиуса линзы. Ход лучей в модифицированной
линзе показан на рис. 15.14,6.
Простой способ реализации цилиндрической линзы Люнеберга изображен на
рис. 15.15. Однородный диэлектрик 1 с относительной электрической проницаемос-
тью £г помещается между пластинами 2. Если электрический вектор параллелен
Линзовые антенны
573
б)
Рис. 15.14. Ход лучей в линзе Люнеберга (а) и в модифицированной линзе Люнеберга (б) (F
— облучатель; пунктирная линия - траектория движения облучателя) [17]
4 3 ,2 1
J____/ I_____________ /______/
Рис. 15.15. Вариант цилиндрической модифицированной линзовой антенны Люнеберга [17]
пластинам, то фазовая скорость для волны основного типа равна
= с / - (^ / 2а')2 ,
а коэффициент преломления
п = - (А, / 2а')2 ,
(15.10.3)
где а’ - расстояние между пластинами.
Выбирая должным образом закон изменения величины а’ вдоль радиуса лин-
зы, можно удовлетворить соотношению (15.10.2). Центральная часть 3 модифици-
рованной линзы Люнеберга вращается. Питание рупора 4 осуществляется через
вращающееся сочленение 5.
574
ГЛАВА 16
Глава 16. Фазированные антенные решетки [3,17]
16.1. Общие сведения о фазированных антенных решетках.
Схемы построения. Элементная база
Фазированные антенные решетки (ФАР) отличаются от АР, рассмотренных в
гл.7, включением в антенный тракт системы фазовращателей или коммутаторов,
осуществляющих управление фазовым или амплитудно-фазовым распределением
для электрического сканирования.
Большой практический интерес представляют антенны с управляемым поло-
жением главного лепестка ДН. Управление (сканирование) можно осуществить,
например, смещая облучатель линзы или зеркала из фокуса перпендикулярно
оптической оси (см. гл. 14, п.8.4). При этом происходит наклон фазового фронта и
лепесток отклоняется в сторону отставания фазы поля в раскрыве антенны.
Хотя такой способ сканирования, называемый электромеханическим, широ-
ко применяется, его возможности ограничены относительно небольшой угловой
скоростью перемещения лепестка из-за инерционности подвижной части антенны
(сканера).
Значительно большую скорость перемещения можно получить с помощью ан-
тенн с электрическим сканированием. У таких антенн нет подвижных частей,
а изменение фазового распределения в раскрыве антенны осуществляется чис-
то электрически: путем изменения токов или напряжений на управляющих уст-
ройствах. Опыт показал, что электрическое сканирование удобно осуществлять с
помощью многоэлементных антенн (решеток). Антенные решетки с управляемым
фазовым распределением полей (токов) по раскрыву получили наименование фа-
зированных антенных решеток (ФАР).
ФАР, у которых фазовое распределение регулируется с помощью фазовра-
щателей, включенных в линии питания излучателей, называются решетками с
фазовым сканированием. ФАР, у которых фаза поля (тока) каждого излучателя
может принимать лишь несколько дискретных значений, называются решетками
с коммутационным сканированием. ФАР, у которых фазовое распределение ре-
гулируется путем изменения рабочей частоты, называются решетками с часто-
тным сканированием.
16.1.1. Схемы построения ФАР [3]. Нашли применение различные схемы
построения ФАР в зависимости от требований к системе. Пространственный способ
возбуждения (называемый еще распределителем оптического типа) [3] допускает
два варианта антенн: отражательную ФАР (рис. 16.1,6) и проходную ФАР (рис.
16.1,а). Фидерный способ возбуждения (распределитель закрытого типа) допускает
последовательное, параллельное, двоично-этажное (елочки) питание излучателей
и фазовращателей, а также их комбинации (рис. 16.3). Находят применение гиб-
ридные антенны - совместное использование ФАР и антенн оптического типа. На
рис. 16.2 приведена схема гибридной зеркальной антенны (малоэлементная ФАР и
фокусирующее зеркало), допускающая электрическое сканирование в ограничен-
Фазировар/иые антенные решетки
575
б)
(ЛГ-1)Ф
г) д)
Рис. 16.1. Пространственный способ возбуждения: а) - проходная решетка; б) - отража-
тельная решетка; фидерный способ возбуждения: в) - последовательная схема; г) - парал-
лельная схема; д) - параллельная схема типа «елочка» [3]
Рис. 16.2. Гибридная зеркальная
антенна[3]
Рис. 16.3. Комбинированная схема воз-
буждения [3]
576
ГЛАВА 16
Рис. 16.4. «Купольная» гибридная
антенна, образованная плоской
ФАР и линзой, расширяющей сек-
тор сканирования [3]
Коммутатор / Ф// ^Jy-L Q/v'L "Ф]у» у-
у- у у-
\/ф7_ [ф]_ [ф]_ [ф]_ [ф]_
йп
Л4
От генератора) у$Д \~фД \~фД
Рис. 16.5. ФАР с системой коммутаторов и фазовра-
щателей [3]
31
Рис. 16.6. ФАР с одним излучающим раскрывом и тремя независимыми лучами [3]
ном секторе углов при высокой направленности действия. Сочетание радиолинзы с
ФАР или применение направленных излучающих элементов ФАР (зеркал, подре-
шеток и т.д.) позволяет получить те же результаты: уменьшение числа управляе-
мых фазовращателей при ограниченном секторе сканирования.
Сочетание линзы с ФАР позволяет расширить сектор сканирования плоской
ФАР. Одновременно с этим происходит ухудшение других характеристик антен-
ной системы (рис. 16.4).
Цилиндрическая решетка излучателей, подключаемая коммутаторами (с фа-
зовращателями или без них) к возбуждающей системе полосковых линий, вол-
новодов, радиальных волноводов и других элементов, позволяет сканировать в
широком секторе углов (рис.16.5).
Возможно применение многолучевых антенн, формирующих с одного излу-
чающего раскрыва несколько ДН [3], каждой из которых соответствует входной
18 *
Фазированные антенные решетки 577
тракт антенны.
Многоканальный коммутатор, подключенный к входам многолучевой антенны,
позволяет дискретно перемещать луч в пространстве в соответствии с характе-
ристиками многолучевой антенны.
Необходимость использования многолучевого режима в радиотехнических сис-
темах приводит к созданию ФАР с несколькими независимыми сканирующими
лучами. Возможный путь решения таких задач состоит в совмещении многолу-
чевых антенн с системой управляемых фазовращателей и возбуждаемых через
направленные ответвители магистральных волноводов [3] (рис. 16.6).
Каждая из приведенных схем построения ФАР имеет свои преимущества и
недостатки, а выбор той или иной схемы определяется требованиями, предъяв-
ляемыми к радиотехнической системе, последующей обработкой СВЧ-сигнала, а
также элементной базой.
Элементная база ФАР включает: излучатели, фазовращатели, коммутаторы,
сумматоры (делители) мощности и линии передач СВЧ.
16.1.2. Фазовращатели для ФАР. Центральным элементом, «кирпичиком»,
из которого строится ФАР, служит фазовращатель. Его важнейшими характе-
ристиками являются мощности потерь, управления и предельно допустимая рабо-
чая полоса частот, быстродействие, зависимость фазового сдвига от управляюще-
го воздействия, габариты и стоимость. Волноводное, коаксиальное, полосковое,
микрополосковое исполнение фазовращателя определяет выбор не только тракта
СВЧ, но и типа излучателя. В диапазоне СВЧ широкое применение нашли по-
лупроводниковые (pm-диодные) и ферритовые фазовращатели, которые принято
разделять на проходные и отражательные, взаимные и невзаимные, дискретные
и плавные, с памятью фазового сдвига и без запоминания. Проходной фазовра-
щатель - это четырехполюсное согласованное устройство СВЧ, вносящее допол-
нительный фазовый сдвиг от 0 до 360 в зависимости от управляющего сигнала.
Отражательный фазовращатель - это двухполюсное устройство (короткозамкну-
тый отрезок линии СВЧ), у которого фаза отраженной волны также управляется.
Короткое замыкание выходных клемм в проходном фазовращателе преобразует
его в отражательный, а отражательный фазовращатель может быть преобразован
в проходной за счет применения мостового устройства.
Взаимный фазовращатель обладает одинаковым вносимым фазовым сдвигом
при прямом и обратном направлении распространения волны, невзаимный же
фазовращатель этим свойством не обладает. Как правило, невзаимный фазовра-
щатель использует в электрически управляемой среде невзаимный эффект, на-
пример эффект Фарадея в феррите. Взаимный отражательный фазовращатель с
У-циркулятором образует проходной невзаимный фазовращатель.
Дискретный фазовращатель изменяет фазу выходного сигнала дискретно
(скачками) на А = 360 /М. Величину М для удобства управления ЭВМ выбирают
равной двум в целой степени, т.е. М = 2Р , где р = 1,2,3 - разряд фазовращателя.
Дискретный фазовращатель вносит максимальную фазовую ошибку А/2. Нашли
применение фазовращатели с А = 90° - двухразрядные, А = 45° - трехразрядные,
А = 22,5° - четырехразрядные и с меньшими дискретами. Серийно выпускают-
ся (как готовые изделия) полупроводниковые и ферритовые дискретные фазовра-
щатети с использованием прямоугольной петли гистерезиса (ППГ). Они обладают
19 - Неганов
Таблица 16.1. Фазовращатели в ФАР [3]
Тип фазовращателя Часто- та, ГГц % Число разрядов Мощность, Вт Потери, Дб Быстро- действие, мкс Мощность управле- ния, Вт Энергия управле- ния, мкДж Коли- чество диодов
Полупроводниковые отражательные (взаимные)
Волноводный 15 ±4,2 2 2 1,0 0,5 мм 3
Коаксиальный 10 ±4,0 2 10 1,1 1 0,5 — 3
Полосковый 1,55 ±5,2 2 10 0,9 1,5 — 3
« Проходной полупроводниковый (взаимный)
Волноводный 5 ±5 4 15 1,7 1,0 16
Полосковый 8,5 ±2,5 4 30 2 1 1,0 — 24
Ферритовый взаимный проходной для произвольной поляризации
Волноводный 15,3 ±5 — 3 0,8 50 0,33 — —
Ферритовый невзаимный проходной
Волноводный дискретный 5,65 ±4,5 5 600 0,95 3 800 —
Волноводный аналоговый 5,6 ±4,0 — 100 0,7 10 800 —
578 ГЛАВА 16
Фазированные антенные решетки;579
элементом памяти, т.е. сохраняют внесенный фазовый сдвиг после снятия управ-
ляющего воздействия. Аналоговые фазовращатели - фазовращатели с плавным
изменением фазы от управляющего тока (напряжения), могут иметь дискретность
фазирования при сопряжении с системой управления лучом антенны ЭВМ.
Широко применяются ферритовые взаимные и невзаимные фазовращатели,
проходные и отражательного типа для различных поляризаций волны. Характе-
ристики различных типов фазовращателей приведены в таблице 16.1.
Разработаны фазовращатели на различные уровни мощности, рабочие диапазо-
ны и разрядности. Ферритовые фазовращатели на длинах волн короче 5 см могут
обладать меньшими потерями, чем полупроводниковые. Полупроводниковые фа-
зовращатели имеют большее быстродействие и меньшие массу и габариты, но сто-
имость их выше. Увеличение разрядности приводит к дополнительным потерям,
большей стоимости и увеличению мощности управления.
Размещение в плоской решетке с шагом (0,5-0,7) X излучателей с фазовраща-
телями, элементами крепления и управляющими цепями накладывает жесткие
ограничения на их размеры. Эти трудности растут с уменьшением рабочей длины
волны и в миллиметровом диапазоне волн (особенно в коротковолновом части)
приводят к новым конструктивным решениям электрически сканирующих антенн:
электрически управляемым транспарантам др. Одним из важнейших критериев
выбора фазовращателя является его стоимость, в значительной степени опреде-
ляющая стоимость всей ФАР.
В диапазонах КВ и УКВ в качестве устройств фазирования нашли применение
управляемые линии задержки - коммутируемые отрезки линии с волной Т длиной
порядка половины раскрыва ФАР. Такие фазовращатели, называемые тромбон-
ными, обеспечивают работу в широком диапазоне частот.
Известны СВЧ-фазовращатели, использующие сегнетоэлектрики и газораз-
рядную плазму, но не нашедшие практического использования из-за низкой тем-
пературной стабильности и других неудовлетворительных характеристик.
16.1.3. Излучатели для ФАР. Вторым важнейшим элементом ФАР СВЧ-диа-
пазона является излучатель, в качестве которого используют вибраторы, откры-
тые концы волноводов, диэлектрические стрежневые, спиральные, щелевые и
печатные излучатели и другие слабонаправленные антенны. Выбор типа излуча-
теля определяется рабочим диапазоном и полосой частот, излучаемой мощнос-
тью, требуемой поляризацией, сектором сканирования луча и конструктивным
исполнением фазовращателя и тракта СВЧ. В рабочей полосе частот и секторе
сканирования излучатель должен иметь ДН без провалов и должен быть согла-
сован. Оптимальная ДН излучателя плоской решетки, при которой излучатель
будет во время сканирования согласован, а КНД максимальным, представляется
как VcosO , где 0 -угол, отсчитываемый от нормали к раскрыву для произвольной
плоскости. Это легко показать следующим образом. Допустим, что излучатели в
секторе сканирования согласованы, т.е. входные сопротивления неизменны. Следо-
вательно, излучаемая мощность при отклонении луча неизменна. Из теории
решеток и излучающих апертур известно, что при отклонении луча КНД падает
по закону cos0
т.е. Do(0) = Dq cos0. Так как Do
4лт2^
где С - —и поле ан-
240л
тенны Ет есть сумма полей элементов, то Ет (0) = Emi (0)л/cos 0 . Это справедливо
19 *
580
ГЛАВА 16
Рис. 16.7. ДН элемента решетки с учетом взаимодействия для идеального (пунктирная
линия) и реального излучателей [3]
для эквидистантных больших решеток, в которых можно не учитывать краевые
эффекты. Отличие ДН излучателя от идеальной приводит к падению КНД и соот-
ветствующему рассогласованию тракта (рис. 16.7).
Диаграмма направленности элемента в решетке зависит от параметров излуча-
теля, шага и конфигурации решетки, наличия конструктивных элементов креп-
ления, укрытия и т.д. Улучшения ДН элемента и, следовательно, согласования
можно достичь применением дополнительных элементов: многослойных диэлект-
рических покрытий, направляющих элементов (директоров, рефлекторов), диэ-
лектрических заполнений, импедансных поверхностей и т.д.
В последние годы были проведены обширные теоретические и эксперименталь-
ные исследования перечисленных излучателей ФАР с целью поиска наилучших
результатов. В теории были разработаны физические и математические модели
для численных методов решения соответствующих краевых электродинамических
задач. Созданы программы расчета характеристик и их оптимизации, которые
позволяют по заданным требованиям к ФАР выбрать излучатели различных ти-
пов [3].
К элементной базе ФАР относятся системы распределения мощности СВЧ на
различных линиях передачи: мостовые устройства, направленные ответвители,
двухканальные и многоканальные системы распределения мощности, поляризато-
ры и другие элементы трактов СВЧ-антенн.
Потребность в этой элементной базе зависит от выбранной схемы построения
поляризационных характеристик. При пространственном способе возбуждения
моноимпульсной ФАР используется несколько мостов СВЧ, с помощью которых
формируются суммарно-разностные ДН. Фидерный способ возбуждения или со-
здание ФАР с управляемой поляризацией резко усложняет систему распределе-
ния мощности СВЧ.
Широкоугольное сканирование в выпускных ФАР или управление поляризаци-
ей поля дополняет элементную базу коммутаторами СВЧ.
16.1.4. Многолучевые и совмещенные ФАР. Многолучевой ФАР называют
такую решетку, которая имеет несколько входов, причем фазовое распределе-
ние изменяется при переключении передатчика (или приемника) с одного входа
на другой. Поэтому фазированные многолучевые (матричные или многоканальные)
антенны (МА) - это антенны, имеющие несколько независимых входов (в режиме
приема выходов), каждому из которых соответствуют диаграммы направленност;:
(лучи), разнесенные в пространстве.
Фазированные антенные решетки 581
16.2. Пространственно-временная обработка сигнала
в антенных системах [3]
В процессе развития радиотехники и электроники антенны претерпели сущест-
венное изменение: из простых устройств (один вибратор или несколько) преобразо-
вались в сложные управляемые многоэлементные системы с активными приборами.
Если на первых этапах развития антенна должна была обеспечить эффективное
излучение и прием, то потом от антенны потребовалось значительное усиление,
получаемое за счет направленности действия. С появлением радиосистем локации,
навигации и управления приемные антенны стали осуществлять пеленгацию, т.е.
определять угловые координаты излученных или отраженных волн с возможно
большей точностью. Резкий рост оснащенности радиоэлектронными средствами,
произошедший в последний период, создал проблему электромагнитной совмес-
тимости (ЭМС). Для осуществления ЭМС в приемных антеннах возникла необхо-
димость формирования глубоких провалов в ДН для направления прихода помех.
Поскольку помеховая обстановка меняется, потребовались самоприспосабливаю-
щиеся антенны, называемые адаптивными. Появление новых видов боевых дейс-
твий (радиоэлектронная борьба) привело к необходимости решения в антенной
технике проблем, аналогичных перечисленным, но при более сложных услови-
ях. В настоящее время радиосистемы должны работать при действии нескольких
мощных широкополосных помех в условиях независимого перемещения помехоно-
сителей. Таким образом, в этих случаях антенна ведет пространственную обработ-
ку сигнала, т.е. становится динамическим пространственным фильтром. Антенны
с электрическим сканированием также являются антеннами с пространственной
обработкой сигнала.
В современных передающих и приемных антенных системах возникла необхо-
димость временной обработки сигнала (в частотной области). В антенный тракт ре-
шетки может включиться система параллельно работающих активных элементов
(приборов): генераторов, усилителей, смесителей, преобразователей частот, ана-
лого-цифровых преобразователей и т.д. Замена одного активного элемента (в пе-
редатчике или приемнике) на систему параллельно работающих в антенном тракте
элементов позволяет решить ряд задач антенной технике. Остановимся только на
некоторых моментах.
Включение активного элемента в антенный тракт делает антенну, как правило,
невзаимным и нелинейным устройством, что существенно изменяет облик антен-
ны в режиме передачи и приема. Независимая пространственная обработка сиг-
налов в антенне, а затем временная обработка в приемнике затрудняет, а иногда
исключает получение полной информации о пространственно-частотном распре-
делении источников в окружающем пространстве (радиосцене). Параллельная про-
странственно-временная обработка ряда выборок из падающих волн в приемной
антенне позволяет увеличить объем одновременно поступающей информации.
Дальнейшее совершенствование различных радиосистем стимулирует решение
новых задач антенной техники, одним из направлений развития которой явля-
ется создание антенн с пространственно-временной обработкой. Применяя в та-
ких системах новые конструкторско-технологические решения решения (сверхши-
рокополосные, печатные, микрополосковые, совмещенные и др.), достижения в
микроэлектронике, когерентной радиооптике, голографии и т.д., можно достичь
желаемых результатов. Поэтому рассмотрим возможные методы пространственно-
582
ГЛАВА 16
временной обработки сигнала в антенне.
Многообразие используемых и создаваемых антенн принято классифицировать
по рабочим диапазонам волн, их электрическим характеристикам, конструктор-
ско-технологическому исполнению, областям применения и т.д. Такие классифи-
кации не учитывают функциональных возможностей современных антенн. Пре-
вращение антенны из устройства в систему изменяет подход к их классификации.
Целесообразно подойти к развитию антенн как к совершенствованию некоторой
радиосистемы и рассматривать различные существующие, разрабатываемые и
вновь предлагаемые антенны и процессы, происходящие в них, с единых пози-
ций. Критерием классификации и развития антенн можно принять обработку ин-
формации (сигнала), происходящую в антенне и ее СВЧ-тракте. Такая обработка
может осуществляться на частотах принимаемого (или излучаемого) сигнала, на
более высоких или более низких (промежуточных) частотах, быть линейной или
нелинейной, аналоговой или цифровой, адаптивной и т.д. Так как поле, падающее
на отдельный элемент решетки, характеризуется поляризацией, амплитудой и
фазой, в антенной решетке обработка сигналов по амплитуде и фазе может быть
дополнена поляризационной обработкой.
На рис.16.8 приведена классификация антенн по способу обработки сигналов. На
начальном этапе развития радиотехники применялись вибраторные антенные ре-
шетки, в фидерном тракте которых арифметически суммировались напряжения,
наводимые отдельными вибраторами при падении волны по нормали к полотну
АР. Появился простейший, используемый и сейчас, вид АР- синфазные острона-
правленные антенны. Вторым видом простейших АР являются антенны бегущей
волны (АБВ), в которых суммирование напряженности от отдельных вибраторов
для заданного направления прихода волны происходит с учетом фазовых сдвигов
в питающей линии. Третьим видом АР можно считать ненаправленные бортовые
антенны, в которых для излучения в окружающее пространство и устранения
явлений дифракции и затенения носителем применяется система разнесенных
слабонаправленных излучателей. Четвертый вид- совмещенные антенны- возник
в последнее время и применяется в случае необходимости использования одной
апертуры для работы нескольких антенн на различных частотах. Это достигается
встраиванием одной антенны (решетки, облучателя) в другую. Система излучате-
лей, настроенных на ряд частот и возбуждаемых одной линией передачи, обра-
зует, как известно, один из видов широкополостных антенн. Все эти виды можно
объединить в один класс многоэлементных антенн (поз. 1 на рис. 16.8).
В РЛС широкое применение нашли моноимпульсные антенны, в которых с одно-
го раскрыва одновременно формируются три луча, т.е. три диаграммы направлен-
ности, называемые суммарно-разностными. В таких антеннах три канала обра-
ботки сигнала (суммарный и разностные- угломестный и азимутальный) позволяют
увеличить по сравнению с одноканальной системой точность определения угловых
координат при прочих равных условиях. Антенная решетка или эквивалентная ей
апертурная антенна позволяет сформировать несколько ортогональных ДН, осу-
ществить одновременный обзор пространства и произвести обработку сигнала в
нескольких независимых каналах. В соответствии с предлагаемой классификацией
такие антенны образуют класс многолучевых антенн (поз. 2 на рис.16.8), в излуча-
ющей части которых одновременно создается набор амплитудно-фазовых распре-
делений (АФР). Каждому из них соответствует определенный вход.
Переизлучающие антенны (поз.З на рис. 16.8) представляют собой класс прие-
Антенны с обработкой сигналов
584
ГЛАВА 16
мопередающих устройств, в которых фокусируется проходящая волна обратно в
направлении источника падающей волны. Простейшая переизлучающая антенна
представляет собой угловой отражатель. Его дискретным аналагом является ре-
шетка Ван-Этта. В зависимости от назначения переизлучающие антенны могут
быть активными и пассивными элементами радиосистемы. В активных переизлу-
чающих антеннах осуществляется усиление принятых сигналов, изменение (сме-
щение) частоты принимаемого сигнала, модуляций колебаний (с целью передачи
информации в требуемом направлении). Все эти функции могут выполняться и
одновременно. Переизлучающие решетки на основе диаграммообразующих много-
лучевых антенн обладают лучшими параметрами.
Рост скоростей летательных аппаратов потребовал от антенн РЛС быстрого
безынерционного сканирования луча в пространстве при сохранении направлен-
ных свойств, достигнутых в зеркальных антеннах с механическим сканировани-
ем. Это привело к интенсивному развитию фазированных антенных решеток с
электрическим сканированием: частотным, фазовым и коммутационным (поз.4 на
рис.16.8).
Появление активных антенн (поз.5 на рис.16.8) вызвано стремлением увели-
чить излучаемую мощность, уменьшить тепловые потери, увеличить надежность
ФАР, а в слабонаправленных антеннах уменьшить габариты и расширить рабо-
чую полосу. До тех пор, пока в антенне (ФАР) используются линейные взаимные
устройства для создания управляемых АФР, не делается различия между ха-
рактеристиками антенны при приеме и передаче, и рассматривается обработка
сигнала в режиме, наиболее удобном для анализа. Переход к активным антеннам
приводит к появлению независимых приемных и передающих антенн, хотя и не
исключает наличия приемопередающих.
Динамическими (или антеннами с временной модуляцией параметров) (поз.6
на рис. 16.8) называются антенны, которые имеют характеристики, изменяющиеся
во времени. Изменяемыми параметрами могут быть: амплитудное и фазовое рас-
пределения поля (токов) в раскрыве, линейные размеры антенны, время исклю-
чения отдельного элемента решетки и т.д. Периодическое изменение параметров,
в принципе, позволяет осуществить быстрое сканирование луча в пространстве,
сформировать заданные характеристики направленности. Так, с помощью пере-
ключения элементов решетки в динамических антеннах могут быть получены ДН
с малым уровнем боковых лепестков.
Адаптивными, или самонастраивающимися, называют антенны, характерис-
тики которых приспосабливаются (оптимизируются) в процессе работы к меняю-
щимся внешним условиям. Процесс адаптации происходит автоматически в соот-
ветствии с алгоритмом, заложенным в антенной системе, в которую может входить
не только система обработки сигнала, но и система управления лучом. В процессе
адаптации изменяется характеристика направленности на основе обработки при-
нятых ею сигналов. Например, в зависимости от помеховой обстановки в ДН адап-
тивной антенны может формироваться один или несколько глубоких провалов в
направлении прихода мешающих сигналов. В зависимости от критерия адаптации
в этом классе антенн можно выделить несколько видов (поз.7 на рис. 16.8).
Антеннами с нелинейной обработкой сигнала (поз. 8 на рис.16.8) называют ан-
тенные решетки, сигнал на выходе которых является произведением или корре-
ляционной функцией (перемножение и усреднение во времени) сигналов от от-
дельных элементов. Используя различные методы нелинейной обработки сигнала
Фазированные алтейные решетки
585
(умножение, возведение в степень, деление, усреднение и т.д.), можно постро-
ить антенны, свойства которых будут существенно отличаться от свойств антенн
обычного типа. Так, перемножая сигналы от элементов решетки (мультиплика-
тивная антенна), можно существенно сузить ее ДН. В антеннах с логическим син-
тезом - разновидности антенн с нелинейной обработкой сигнала - удается полу-
чить очень низкий уровень боковых лепестков ДН. Это достигается применением
логических устройств типа «да-нет», «или», «и», «больше-меньше» при срезании
боковых лепестков для всех сигналов, превышающих определенный уровень. Сле-
дует отметить, что в таких антеннах формирование ДН существенно изменится
при воздействии не одного, а сразу двух или более сигналов.
Широкое распространение в системах апертурного синтеза получил принцип
нелинейной обработки сигнала (поз.9 на рис.16.8), под которым понимают созда-
ние сплошной апертуры с помощью небольшого числа подвижных антенн. Метод
основан на априорной информации о траектории движения носителя подвижной
антенны. Его сущность заключается в приеме сигналов при движении, их запо-
минании и соответствующем сложении, как это делается в большой ФАР. Антен-
ны с синтезированной апертурой являются перспективными для бортовых РЛС с
повышенной разрешающей способностью (наблюдение земной поверхности) и ра-
диотелескопов. Бортовые РЛС с синтезированной апертурой позволяют получить
высокую линейную разрешающую способность по угловым координатам, соот-
ветствующую линейной разрешающей способности обычной антенны с раскрывом
в сотни и тысячи длин волн.
Следует отметить, что в антеннах с нелинейной обработкой сигнала, включая
антенны с синтезированной апертурой, сужение ДН не приводит к увеличению
усиления антенны. Более того, происходит снижение за счет дополнительных по-
терь при обработке.
Новый класс приемных антенн с цифровой обработкой сигнала - цифровые ан-
тенные решетки (поз.10 на рис.16.8)-включает в себя системы усилителей, смеси-
телей, фазовых детекторов и аналого-цифровых преобразователей, а также ЭВМ,
с помощью которых осуществляется цифровое формирование ДН.
Радиооптические антенные решетки (поз.11 на рис.16.8) представляют собой
приемные антенны с оптической обработкой сигнала. Принятое каждым излуча-
телем АР колебание СВЧ переносится на промежуточную частоту и после усиле-
ния с помощью многоканального модулятора света (динамического транспаранта)
преобразуется в колебания оптического диапазона. Дальнейшая обработка осу-
ществляется в оптическом диапазоне с помощью системы, содержащей лазер,
коллиматор, линзы, диафрагмы, оптические фильтры, транспаранты и т.д. В этой
системе происходит аналоговая обработка пространственно-временной информа-
ции. В результате на выходе в реальном масштабе времени формируется оптичес-
кое изображение радиолокационной обстановки в пространстве перед приемной АР.
С помощью оптико-электронных устройств это изображение может быть преобра-
зовано в сигналы для последующей обработки в ЭВМ.
Освоение все более коротких волн вплоть до оптического диапазона, отсутствие
необходимой элементной базы для работы в этих диапазонах, трудность построе-
ния электрически сканирующих антенн этого диапазона на принципах построения
антенн предшествующих диапазонов привели к идее использования голографичес-
ких методов для формирования и управления ДН антенн, получивших название
голографических.
586
ГЛАВА 16
Голографические антенны (поз.12 на рис.16.8)- это новый класс планарных ан-
тенн в виде амплитудных (полосковых) либо фазовых структур, обладающих фо-
кусирующими свойствами зонных пластин и секционных линз. Они могут быть
фокусированы как в дальнюю, так и в ближнюю зоны.
Приведенная классификация допускает одновременное применение двух или
более способов обработки сигналов в одной антенн. Так, существуют моноимпуль-
сные ФАР с фазовым сканированием и адаптацией или приемные цифровые мно-
голучевые антенны. Подобное разделение антенн оказывается удобным и в теоре-
тическом плане.
Общую конструкторскую задачу построения антенн по заданным требовани-
ям, т.е. синтез антенн, в теоретическом плане принято разделять на внешнюю и
внутреннюю задачи. Решение внешней задачи для антенн с обработкой сигнала
практически сводится к построению антенной решетки, обеспечивающей задан-
ную направленность в секторе обзора (сканирования). Решение внутренней задачи
должно обеспечивать необходимое возбуждение антенны, найденное из решения
внешней задачи, и требуемую обработку сигнала. В зависимости от способа об-
работки центр тяжести решения внутренней задачи перемещается с одних уст-
ройств на другие.
Решение внешней задачи-построение антенной решетки - может быть выпол-
нено без учета последующей обработки сигнала и оказывается весьма общим для
различного класса антенн. Поэтому далее рассмотрены возможные типы решеток
и общие характеристики.
16.3. Основные особенности сканирования [17]
При качании лепестка наблюдаются общие для всех типов способов сканирова-
ния особенности, которые рассматриваются ниже.
16.3.1. Одномерное сканирование можно осуществить с помощью как повер-
хностных, так и линейных антенных решеток. Если для сканирования использу-
ется прямолинейная эквидистантная решетка (рис.16.9), то ориентация главного
лепестка ДН определяется в виде [17]:
sin = mk/d + %, т - 0 ; ±1; ±2; ... (16.3.1)
Коэффициент замедления
= y/kd , (16.3.2)
а следовательно, и ориентацию главного лепестка при неизменной рабочей длине
волны генератора X можно регулировать, изменяя, например с помощью фазов-
ращателей сдвиг фаз \|/ между соседними излучателями. Это соответствует слу-
чаю фазового сканирования.
Из формулы (16.3.1 )видно, что ориентацию главного лепестка можно регу-
лировать, изменяя длину волны (частоту) генератора. Это соответствует случаю
частотного качания. Следует заметить, что при т - 0 (луч нулевого порядка) час-
тотное качание можно осуществлять только если £ зависит от частоты, т.е. если
для питания антенной решетки применить линию с дисперсией.
Для того чтобы главный лепесток некоторого порядка т сканировал в преде-
лах всей области действительных углов ( -90° < &гл < 90°), необходимо изменять
Фазированные антенные решетки
587
Рис. 16.9. К определению геометрических
параметров антенной решетки при скани-
ровании [17]
Рис. 16.10. К пояснению искажения
главного лепестка ДН при сканирова-
нии [17]
частоту или замедление в определенных пределах. Если изменять частоту или
замедление в более широких пределах, то лепесток порядка т уходит в область
«мнимых» углов, но при этом в области действительных углов может появиться
соседний главный лепесток (порядка т +1 или т -1).
Сектором сканирования называют часть области действительных углов, в
пределах которой сканирует главный лепесток. Обозначая через Эс границу сим-
метричного сектора сканирования (рис. 16.10), условие единственности главного
лепестка можно записать в виде [17]:
d/l <(l + |sin3c|)_1 (16.3.3)
Если сектор сканирования несимметричен относительно нормали к антенне,
то под Зс следует понимать большую по абсолютному значению величину.
16.3.2. Двумерное сканирование можно осуществить с помощью поверхнос-
тных (двумерных) антенных решеток. Если для сканирования используется плос-
костная эквидистантная решетка (см.рис.7.59), то ориентация главного лепестка
определяется формулами (17.13.6), которые запишем в виде
cos Ф~?Л = m^X/d-+ , т~ = 0,± 1,± 2,..., (16.3.4.)
VW V / «Л# ** •Ау ' сА/ 7 7 7 7 X Z
где
созФ
(16.3.5.)
/ dy + ^у ,
ту =
(16.3.6)
Переход от угловых координат Фхгл , Фугл к сферическим координатам 0^ , (р^
можно выполнить с помощью соотношений
(16.3.7)
Каждой ориентации главного лепестка, т.е. каждой паре значений углов 0гл,
фгл соответствует пара значений коэффициентов £,а., . Следовательно, двумер-
ное сканирование главного лепестка по заданному закону можно осуществить,
изменяя по соответствующему закону коэффициенты замедления.
16.3.3. Искажения главного лепестка. При синфазном возбуждении прямо-
линейной решетки главный лепесток ориентирован нормально к раскрыву, а ши-
рина главного лепестка определяется по формулам (7.19.6а). При отклонении глав-
ного лепестка от нормали он расширяется, что можно объяснить уменьшением
588
ГЛАВА 16
эффективной длины раскрыва. Анализ показывает, что если лепесток отклонен от
нормали на угол 0?Л
то эффективная длина раскрыва Ь^ф связана с его
действительной длиной L соотношением
Ьэф «LcosO^ « Nd cos 0^. (16.3.8)
Таким образом, эффективная длина раскрыва приобраетает простое геомет-
рическое толкование: это проекция длины волны раскрыва на направление линии
равных фаз излученной волны (рис. 16.9). Следовательно, ЬЭф-это длина раскрыва
синфазной решетки, имеющей такую же ширину лепестка, что и данная решетка
при ориентации главного лепестка в направлении 0?~,г. Расширение главного лепес-
тка при его отклонении от нормали ограничивает величину сектора сканирования
лепестка прямолинейной решетки. В тех случаях, когда требуется осуществлять
неискаженное сканирование в широком секторе углов ( ±60° и более), применяют
непрямолинейные, например, дуговые или кольцевые решетки, либо несколько
прямолинейных решеток, каждая их которых работает в своем секторе сканиро-
вания.
При отклонении лепестка от нормали нарушается также его симметрия отно-
сительно направления 0^ , причем 0g 5 > 0р 5 (рис.16.10).
Ранее было показано, что множитель прямолинейной решетки изотропных
излучателей имеет вид воронки (см.рис. 7.13). Обычно излучатели являются на-
правленными. Из-за направленности каждого излучателя в плоскости, перпенди-
кулярной оси решетки, пространственная ДН решетки имеет вид луча, сечение
которого (при 0 = дгл ) расположено по части поверхности конуса. Такое искаже-
ние называется конусностью лепестка.
Так как на ДН антенной решетки влияют направление свойства одиночного из-
лучателя, входящего в решетку, то в зависимости от формы ДН излучателя при
сканировании могут наблюдаться дополнительные искажения главного лепестка,
например смещение 0гл.
16.3.4. Сектор сканирования и число управляющих элементов ФАР [3].
Расчет характеристик ФАР по сравнению с расчетом ранее рассмотренных антенн
значительно усложняется, так как требуется определять эти характеристики в
секторе сканирования, т.е. ряде положений луча в пространстве, рабочей полосе
частот, а также учитывать возможные различия в фазовом распределении и раз-
мещении излучателей. Прямые численные методы суммирования полей элементов
ФАР малопригодны для выявления основных закономерностей. Поэтому в теории
ФАР развиты приближенные, но достаточно точные методы анализа и расчета,
позволяющие установить последовательно влияние дискретности размещения и
управления, полосы частот и сектора сканирования на основные характеристики.
Пространственный сектор сканирования ФАР может быть задан предельным
отклонением луча по азимуту +(рск и углу места ±0СК или телесным углом обзо-
ра Пск в стерадианах. Зная требуемую рабочую длину волны X, направленность
действия (ширину луча 20о 5 и 2ф05 или КНД Dq ), можно установить минимальное
число управляющих элементов N. Размер антенны L связан с шириной луча со-
отношением 20о в = Ширина ДН элемента ФАР по нулевому уровню должна
быть больше 20ск по крайней мере на 20о 5 , т.е. размер элемента Ъэл определяется
как
Фазированные антенные решетки
589
Приближенное число управляемых элементов
N
(16.3.9)
Известны и другие подходы к определению N, например, на основе КНД:
A = ^D0. (16.3.10)
4л
Практически число управляемых элементов в ФАР превышает найденное по
формулам (16.3.9) и (16.3.10) и связано с допустимым уровнем боковых лепестков
(УБЛ) и изменением направленности в секторе сканирования. В плоской АР при
движении луча изменяется его ширина, УБЛ и соответственно КНД, что огра-
ничивает используемый на практике сектор сканирования до ±45... ±60 . Для по-
лучения больших секторов сканирования возможно применение системы плоских
решеток [3] или выпуклой ФАР.
Необходимое число управляющих фазовращателей в плоской ФАР будет най-
дено из условия дискретизации излучающего раскрыва.
16.3.5. Полоса пропускания ФАР. Рассмотрим частотные свойства, связанные
с построением ФАР, в предположении, что элементная база (фазовращатель,
излучатель, линия передачи и т.д.) не ограничивает полосу пропускания.
В ФАР с параллельным питанием линиями равной электрической длины на-
чальное фазовое распределение не зависит от частоты и может быть равномерным.
Широкополосные (диапазонные) фазовращатели создают фазовые сдвиги, также
независимые от частоты. При отклонении луча от нормали с плоской решеткой на
угол 0гл необходим фазовый сдвиг у между двумя произвольными излучателями,
отстоящими друг от друга на расстоянии d в плоскости сканирования, определяе-
, 2ndsin6ZJl
мни по формуле у =---------—. Изменение длины волны А на величину ДА приве-
те
дет к отклонению луча на А0гл, определяемому из условия
2nd sin 0гл _ 2nd sin (0^ ± Д0гл )
V X А + ДА
Отсюда находим частотный ход луча:
А /Ч
А® = ~’
(16.3.11)
который не зависит от размера антенны и растет с отклонением луча 0?л. В ре-
зультате изменяется направленность действия: растет УБЛ и падает КНД. За-
давшись допустимым изменением характеристик, можно найти рабочую частоту.
Если принять, что смещение луча не должно превышать половины его ширины,
то
ДА л 1 А ДА А
---^907.77 ~--------> ---- ~ --------- •
A 2LCOS0 A 2Lsin0?J,
(г
Если задаться допустимым падением КНД на 1 дБ в секторе ±60°
(16.3.12)
, то расчеты
590
ГЛАВА 16
Рис. 16.11. Ширина луча в зависимости от относительной длины решетки и угла сканиро-
вания при равномерном возбуждении [3]
позволят установить простую связь между рабочей полосой частот (%) и шириной
диаграммы направленности антенны (град):
(Д///)% « 20о>5. (16.3.13)
В качестве критерия рабочей полосы может быть принято изменение уровня
боковых лепестков. При определении полосы необходимо также учитывать харак-
теристики сигналов (очень короткие импульсы, длинные импульсы с меняющейся
частотой и т.д.) [3]. Переход к пространственному или последовательному возбуж-
дению элементов АР мало изменяет полосу пропускания. Незначительная рабочая
полоса и ее уменьшение с ростом направленности являются существенными недо-
статками ФАР.
Известны два способа построения широкополостных ФАР. При первом способе
фазовращатели в ФАР заменяют управляемыми линиями задержки: отрезками
линий с волной типа Т, плавно (дискретно) изменяющимися длину в пределах
половины длины раскрыва антенны («тромбонными» фазовращателями). В такой
антенне разность хода лучей компенсируется длиной питающих линий. Такие уст-
ройства реализуются в KB-диапазоне и мало пригодны на СВЧ.
Второй способ основан на использовании выпуклых ФАР. Как следует из соотно-
шений (16.3.11) и (16.3.12), расширение полосы пропускания достигается уменьше-
нием 6гл . В этих ФАР широкоугольное сканирование обеспечивается коммутацией
излучающей части антенны, а формирование луча происходит в условиях, близ-
ких к излучению по нормали в плоских АР. В осесимметричных выпуклых ФАР
удается не только ослабить или устранить частотный ход луча в широкой полосе
частот, но и уменьшить частотное изменение ширины ДН [3]. Однако конструкция
таких антенн значительно сложнее по сравнению с конструкцией плоских антенн,
так как кроме фазовращателей необходима система коммутаторов, управляющая
излучающим сектором, и растет число управляемых элементов ФАР.
Фазированные амтенлкые решетки
591
16.3.6. Наибольшая допустимая частота сканирования [17]. Электри-
ческое сканирование может производиться с большой угловой скоростью. Анализ
показывает [17], что при этом могут происходить искажения ДН из-за нестацио-
нарных процессов в раскрыве антенны. Действительно, если период сканирования
сравним с временем распространения волны от одного конца раскрыва к другому,
то при сканировании распределение фаз в раскрыве не будет «успевать» устанав-
ливаться по линейному закону. Отклонение фазового распределения от линейного
закона приводит к искажению ДН. Следовательно, мгновенная ДН (зависимость
напряженности поля в равноудаленных от антенны точках в данный момент вре-
мени при сканировании) будет отличаться от статической ДН (при отсутствии
сканирования).
Если фазовые искажения становятся настолько велики, что фаза по раскрыву
меняет знак, то ДН содержит более одного главного лепестка. Частота сканиро-
вания, при которой ДН распадается на несколько главных лепестков, называется
критической. Для того чтобы ДН не искажалась существенно, частота сканиро-
вания должна быть много меньше критической. При этом отклонение фазового
распределения от линейного будет меньше максимально допустимого значения
АУлшкс •
Допустимую частоту сканирования в секторе 26с, симметричном относительно
нормали к антенн, можно определить по формуле
^доп _ А V макс _ ____
(о 2л2 L2 sin2 0с ’
где о - рабочая частота генератора, X -рабочая длина волны.
(16.3.14)
16.4. Антенные решетки с фазовым сканированием [17]
Различают ФАР с фидерным питанием и с пространственным (оптическим)
питанием, а также с плавным изменением фазы и с дискретным (коммутацион-
ным) изменением фазы.
16.4.1. Фидерное питание может осуществляться по последовательной
(рис.16.12, а) или параллельной (рис.16.12, б) схеме. Применяются также комбини-
рованные схемы.
Наименьший сдвиг фаз между токами в соседних излучателях соответствует
главному лепестку нулевого порядка и может быть записан в виде
\|/ = kd sin 0гл. (16.4.1)
Пусть сканирование происходит в пределах всей области действительных уг-
лов -л/2 < 0гл < л/2. Тогда 0С = ± л/2, а условие единственности главного лепестка
(16.4.1) принимает вид d < Х/2. Для обеспечения сканирования величина \|/ должна
изменяться в пределах
-л < \|/ < л. (16.4.2)
При последовательной схеме питания нарастающее вдоль антенной решетки
запаздывание фаз токов излучателей обеспечивается благодаря тому, что сигнал
к каждому излучателю поступает после прохождения через все предыдущие фа-
зовращатели. При этом фазовый сдвиг в каждом фазовращателе согласно (16.4.1)
592
ГЛАВА 16
а)
Рис. 16.12. Последовательная (а) и параллельная (б) схемы фидерного питания антенной
решетки с фазовым сканированием [17]
Вход
б)
должен быть одинаковым и изменяться в пределах ±л, т.е. интервал изменения фаз
должен составлять 2л.
При параллельной схеме питания нарастающее вдоль антенной решетки запаз-
дывание фаз токов излучателей обеспечивается благодаря тому, что в каждом
последующем (считая от середины) фазовращателе фазовый сдвиг изменяется в
больших (на ±л) пределах, чем в предыдущем фазовращателе. Следовательно, в
крайних фазовращателях фаза должна изменяться в пределах ±0,5(N - 1)тг, т.е. в
±0,5(ЛГ - 1)раз больше, чем при последовательной схеме.
Диаграмма направленности антенны не изменится, если в любом излучателе
фазу тока изменить на целое число раз по 2л. Поэтому и при параллельной схеме
питания пределы изменения фаз в каждом фазовращателе могут составлять ±л,
если применить фазовращатели со сбросом фазы на целое число раз по 2л.
Недостаток параллельной схемы- влияние неидентичности фазовращателей.
Недостатки последовательной схемы- пониженная электрическая прочность, так
как вся мощность должна проходить через первый фазовращатель, и малая на-
дежность. Так как выход из строя одного фазовращателя может нарушить работу
всей антенны.
При большом числе излучателей фидерные схемы питания отличаются слож-
ностью и громоздкостью и в основном находят применение на дециметровых и
более длинных волнах. В сантиметровом диапазоне волн отдают предпочтение про-
странственной схеме питания.
16.4.2. Пространственное питание состоит в том, что энергия на антенную
решетку поступает от облучателя, например рупора. Различают ФАР линзово-
го (рефракционного) и отражательного (рефлекторного) типа. В первом случае
(рис.16.13,а) применяются две антенные решетки: собирающая и излучающая (рас-
сматривается режим передачи). Излучатели обеих решеток попарно соединены
линиями передачи через проходной фазовращатель. Две решетки и фазовращатели
образуют аналог линзы. Для того, чтобы преобразовать сферическую (или цилин-
дрическую) волну в плоскую, нужно предусмотреть соответствующие запаздыва-
ния по фазе в фазовращателях, либо применить специальные линии задержки.
Величина задержки по фазе для любого излучателя определяется по формуле
(16.4.3)
Фазированные антенные решетки
593
„а Линза
* *
решетка Фазовращатели Излучающая
решетка
Облучатель
б)
Рис. 16.13. Схемы пространственного питания антенных решеток с фазовым сканировани-
ем линзового (а) и отражательного (б) типа [17]
где х и у -прямоугольные координаты излучателя (начало координат в точке О;
ось Оу направлена на читателя); /-фокусное расстояние линзы; к = 2л/А,.
В линзе отражательного типа (16.13, б) сигнал через фазовращатели проходит
дважды благодаря отражению от короткозамкнутых концов, а функции приема и
излучения волн выполняются одной и той же решеткой.
16.4.3. Плавное изменение сдвига фаз между соседними излучателями можно
осуществить с помощью плавных механических или электрических фазовращате-
лей. Первые применяются при небольшой скорости сканирования. Часть волновод-
но-щелевой переменнофазной антенны с механическим изменением фазы изоб-
ражена на рис. 16.14. Антенна состоит из двух металлических частей (уголкового
профиля), из которых одна является неподвижной, а другая перемещается с по-
мощью специального провода, который на рисунке не показан.
Антенна представляет собой решетку с последовательным питанием (см.
рис. 16.12,а). Роль фазовращателя играет отрезок волновода между двумя сосед-
ними щелями. При изменении размера а меняется фазовая скорость (а следова-
тельно
соседних щелях, равный
и длина волны Хв) в волноводе и изменяется сдвиг фаз между полями в
V =
(16.4.4)
594
ГЛАВА 16
Рис. 16.14. Вариант антенны с механическим фазовращателем [17]
Учитывая формулы (16.3.1), (16.3.2) и (16.4.4) и полагая, что d<X, можно пока-
зать, что в области действительных углов существует только главный лепесток
порядка т = -1, причем
sinS^ = X/Xe -X/2d (16.4.5)
или
sin Эгл = /1 - (Х/2а)2 - A,/2d . (16.4.6)
Пределы изменения размера а определяются закономерностями, известными
из теории волноводов: при уменьшении ширины волновода возрастает его зату-
хание, а при увеличении ширины могут возникнуть высшие типы волн. Поэтому
практически размер а должен находиться в пределах 0,6Х < а < 0,95Х. Эти нера-
венства ограничивают возможные пределы качания лепестка.
Четвертьволновые дроссельные пазы служат для уменьшения излучения энер-
гии через зазоры между двумя частями волновода. При большой скорости скани-
рования применяют плавные электрические фазовращатели, например ферри-
товые [17]. Недостатками ФАР с плавным изменением фазы являются большие
потери в фазовращателях, сложность управляющих схем, высокие требования к
идентичности и стабильности работы фазовращателей.
Указанные недостатки в значительной степени устраняются применением диск-
ретно-коммутационного способа сканирования, предложенного профессором МАИ
Л.Н. Дерюгиным в 1960г. При этом способе фазирование осуществляется с помощью
коммутаторов или дискретных фазовращателей, имеющих фиксированные значе-
ния фазы, устойчивых к различным дестабилизирующим факторам, что дости-
гается применением в полупроводниках, ферритах и других управляемых средах
соответствующих режимом работы, при которых используются устойчивые (край-
ние) участки их характеристик (насыщения, гистерезиса и т.д.). Управление лучом
в случае сводится к простейшим операциям включения или выключения отдельных
коммутаторов. Этот способ сканирования приводит к появлению коммутационных
фазовых ошибок, равных половине дискрета изменения фазы в фазовращателе,
т.е. А/2 . Коммутационные фазовые ошибки вызывают снижение КНД, увеличение
УБЛ и дискретность движения луча при сканировании. Аналогичное ухудшение
направленности имеет место в ФАР с непрерывными фазовращателями в резуль-
тате дискретности фазирования от сопряжения с системой управления луча ЭВМ
тоже дискретной.
Фазированные антенные решетки 595
16.4.4. Дискретное изменение сдвига фаз между соседними излучателями
можно осуществить с помощью коммутационных фазовращателей. Простейший
коммутационный фазовращатель на п позиций состоит из п нерегулируемых фа-
зовращателей и п коммутаторов, при поочередном включении которых фаза на-
пряжения на выходе фазовращателя изменяется скачками через дискреты. Рав-
ные
А\|/и = 2л/п.
Например, при п=4 фаза может принимать значения 0, л/2, л, Зл/2 .
Предложен ряд вариантов коммутационных антенн [91]. Для пояснения принци-
па коммутационного сканирования обратимся к рис. 16.15, на котором изображена
схема одного варианта коммутационной антенны с фидерным питанием.
По линии питания (волноводу) распространяется бегущая волна с замедлением
Излучатели
Коммутационный
фазовращатель
Вход
Нагрузка
Рис. 16.15. Вариант коммутационной антенны [17]
б)
Рис. 16.16. Распределение фазы (а) и фазовых ошибок (б) по коммутационной антенне [17]
596
ГЛАВА 16
£ = Х,/Хв , где Ле -длина волны в волноводе. На каждый излучатель прямолинейной
решетки сигнал поступает через одну из четырех ветвей коммутационного фазов-
ращателя. Распределение фаз по антенне зависит от того, какие из коммутаторов
находятся во включенном состоянии.
На рис. 16.16,а на оси абсцисс изображена решетка из N излучателй, а на оси
ординат-фазовое распределение. Линейный набег фазы питания равен ц/л (а?) = tkx,
а возможные значения фаз излучателей располагаются на прямых, параллельных
\|/Л (х) и образующих сетку допустимых фазовых уровней (Д\уи, 2Д\уи, ЗД\|/М,...).
Расстояние между соседними уровнями равно дискрету фазы Д\|/м.
Согласно формуле (16.4.1) прямая \|/0 (а?) = tyx соответствует требуемому фазо-
вому распределению, обеспечивающему отклонение лепестка от нормали на угол
. Для наилучшего приближения к требуемому распределению фаз каждый фа-
зовращатель должен быть включен так, чтобы фазовая ошибка Д\|/ не превышала
0,5Д\|/и . Распределение фаз по антенне при идеализированном (с ошибкой 0,5Д\|/и )
непрерывном расположении излучателей описывается при этом ступенчатой кри-
вой (рис.16.16, а), а распределение фазовых ошибок представляет собой пилооб-
разную функцию (рис. 16.6,6). Наличие фазовых ошибок приводит к искажению ДН
антенны, уменьшению ее КНД и росту уровня боковых лепестков. Следует от-
метить, что при коммутационном сканировании главный лепесток перемещается
скачками.
Влияние коммутационных ошибок на характеристики антенны зависит от на-
чального фазового распределения в ФАР, положения точки начала отсчета фаз
и числа излучателей. При начальном фазовом распределении Ф (а?) = const для
направления луча 0^ , при котором требуемый фазовый сдвиг между соседними
излучателями кратен дискрету фазирования, т.е. = kd sin 0^г = Ду (где v -целое
число), фазовые ошибки в ФАР и ухудшение характеристик отсутствуют. Для на-
правлений луча, при которых имеет место \|/ = kd sin 6'гл = Ду + , возникают мак-
симальные фазовые ошибки, периодически повторяющиеся по раскрыву. В этом
случае резко (зачастую недопустимо) возрастает один из боковых лепестков и зна-
чительно падает КНД. В теории коммутационных антенн показана возможность
уменьшения УБЛ путем размывания их в широком секторе углов при различных
положениях луча. Это достигается в плоских АР квадратичным начальным фазо-
вым распределением [3]:
(16.4.7)
Здесь п, т- номера излучателей с прямоугольным размещением излучателей в
решетке из N столбцов и Q строк и с п = т = 0 в центре АР.
Из-за наличия коммутационных фазовых ошибок КНД антенны уменьшается
[3]:
D = D0
(16.4.8
Здесь Do -КНД эквивалентной антенны без коммутационных фазовых ошибок.
Уровень бокового излучения (по полю) обусловлен коммутационными фазовы-
597
Фазироваплуые амтенные решетки
ми ошибками плоской АР с равномерным распределением поля [3]:
(16.4.9)
Дискретность изменения фазы приводит к скачкообразному перемещению луча
в пространстве и определяет точность установки луча. На точность влияет поло-
жение начала отсчета фазы (в центре или крайний излучатель). Среднее значение
дискретного перемещения луча при расположении начала отсчета фазы в центре
[3]:
(16.4.10)
но
т.д. могут использоваться фазовращатели с раз-
™ 2nN
Разрядность фазовращателя, т.е. дискретность фазирования А, может быть
установлена из условия максимума коэффициента усиления антенны G = Dr|, где
Г| -КПД антенны, включающий потери в фазовращателе. Увеличение разрядности
дискретного фазовращателя приводит к увеличению потерь, т.е. падению т|
возрастанию КНД. В зависимости от рабочего диапазона частот, уровня техно-
логии, требований к УБЛ, А0
рядностью от 2 до 5. Значение разрядности определяется в каждом конкретном
случае.
Квантование амплитудного распределения в раскрыве связано с размещени-
ем излучателей в апертуре антенны. Квантование по амплитуде, как и по фазе,
обуславливает нарушение непрерывности распределения поля, которое может но-
сить периодический характер и вызывать возникновение дополнительного уров-
ня боковых лепестков, аналогичных по структуре дифракционным лепесткам ДН.
Исходным фактором дискретизации излучающего раскрыва является практичес-
ки реализуемый шаг в решетке. Размеры поперечного сечения фазовращателя с
элементами крепления и управляющими цепями в СВЧ- диапазоне оказываются
такого же порядка, как допустимый шаг, определяемый из режима однолучевого
сканирования в КВЧ и на более высоких частотах [3]. Возможно увеличение в 2/ л/з
раза шага в решетке с треугольной сеткой размещения излучателей, при которой
условие имеет вид [3]:
(16.4.11)
гл. max
Второй возможный путь увеличения шага излучателей- применение неэкви-
дистантного размещения излучателей. В остронаправленной антенне допустимый
шаг может быть также увеличен путем ограничения сектора сканирования 9гг тах.
В этом случае применяется направленный элемент АР с шириной ДН 2 0гл тах, в
качестве которого может быть использована направленная антенна (апертурный
излучатель) или группа синфазно возбужденных слабонаправленных элементов,
называемая подрешеткой и управляемая одним фазовращателем.
Размеры Lx,y подрешеток выбирают в соответствии с заданным сектором ска-
нирования и допустимым уровнем дифракционных максимумов высших порядков.
Последнее можно пояснить следующим образом.
При отклонении луча ФАР к краю сектора сканирования начинается возрас-
тание уровня дальнего бокового лепестка, вызванное наличием в множителе ре-
шетки с большим шагом побочных главных лепестков и излучением за пределы
598
ГЛАВА 16
Лк
Рис. 16.17. Диаграмма направленности идеального (1) и
реального (2) излучателей решетки и главные лепестки
множителя решетки (3) [3]
Рис. 16.18. Зависимость измене-
ния амплитудного распределе-
ния в раскрыве ФАР от разме-
щения и формы излучателя [3]
сектора сканирования элемента АР (рис. 16.17).
Размеры подрешеток Lxy вдоль осей х, у соответственно можно определить из
соотношения
%
(1 + 0 s*n ®гл max
(16.4.12)
где £ - допустимый УБЛ дальнего бокового лепестка (дифракционного максимума
высшего порядка).
Зная Lx у или соответственно шаг излучателей и размеры раскрыва, можно
найти число управляемых элементов плоской ФАР.
Для получения малых УБЛ необходимы, как известно, плавные, спадающие
к краю раскрыва амплитудные распределения. Изменение амплитудного распре-
деления в АР производится дискретно и зависит от шага размещения и формы
апертуры излучателя (рис. 16.18).
Дискретность обуславливает появление дополнительных боковых лепестков
квантования, которые могут быть уменьшены треугольной сеткой расположения и
частичным перекрытием апертур элементов.
Достоинством коммутационной антенны по сравнению с ФАР, в которых при-
меняются фазовращатели с плавным изменением фазы, является более простое
управляющее устройство. Которое при необходимости относительно легко сопря-
гается с ЭВМ. Кроме того, коммутационная антенна отличается большой стабиль-
ностью электрических параметров.
Фазшррванмые дмтенмые решетки
599
16.4.5. Изменение характеристик направленности в секторе сканиро-
вания [3]. В рабочем диапазоне частот и секторе сканирования происходят изме-
нения ширины ДН (см. рис.16.11), КНД и уровня боковых лепестков. В антеннах с
круговой или управляемой поляризацией изменяется поляризационная характе-
ристика. Наиболее важным для радиотехнической системы является коэффици-
ент усиления (КУ) ФАР в секторе сканирования. Коэффициент усиления является
интегральным параметром, учитывающим все изменения направленности и все
тепловые потери в фазовращателях, излучателях и системе возбуждения.
На стадии проектирования ФАР произвести точный расчет ожидаемого КУ в
секторе сканирования и диапазоне частот затруднительно. Это связано с трудно-
стями нахождения в фидерной системе возбуждения тепловых потерь и рассогла-
сования, а при пространственном способе возбуждения - дополнительных потерь
на рассеивание облучателем и коллекторной решеткой. Можно приближенно оце-
нить изменение КУ в секторе сканирования из соотношения
^) = («« >п . <“=>
Здесь S - площадь излучающего раскрыва; Кип - апертурный коэффициент ис-
пользования, учитывающий амплитудное распределение; F (0гл ) - ДН излучателя
в решетке с учетом взаимодействия элементов; ц - КПД ФАР, учитывающий все
потери в излучателях, фазовращателях и системе возбуждения.
Диаграмма направленности излучателя в решетке Р(0гл) существенно отли-
чается от идеальной ДН F (0) = a/cos0 наличием провалов в ДН для некоторых
направлений и меньшим КНД для углов 0 > 45°. Эти обстоятельства приводят к
значительному падению КУ при отклонении луча. Провалы в ДН элемента (пар-
циальной ДН) вызывают так называемое «ослепление» ФАР для определенных на-
правлений луча. Это сопровождается резким возрастанием УБЛ. Ослепление ФАР
недопустимо, поэтому для исключения этого явления проводится оптимизация
парциальной ДН с помощью выбора типа излучателя, его размещения, диэлект-
рического заполнения или укрытия и т.д.
Коэффициент полезного действия ФАР существенно зависит от рабочего диа-
пазона волн (УКВ, СВЧ, КВЧ и т.д.) и элементной базы. На СВЧ потери могут
составлять в фазовращателях приблизительно 1-1,5 дБ; потери в системе воз-
буждения, включая формирователи суммарно-разностных ДН антенны, того же
порядка. В результате КПД может составить 50-60%.
Для определения уровня достигнутых результатов при проектировании и из-
готовлении ФАР их характеристики направленности сравнивают с эквивалентной
зеркальной антенной, которая является эталоном.
16.4.6. Характеристики управления и общетехнические характеристи-
ки [3]. Темп обзора пространства, время установки луча в произвольную точку
сектора сканирования, точность установки луча (или нуля разностной ДН моно-
импульсной антенны) и потребляемая мощность управления лучом относятся к ха-
рактеристикам управления ФАР. Эти характеристики, в свою очередь, зависят от
параметров фазовращателей, выбранной схемы построения, принятых конструк-
тивных решений и системы управления лучом. Между этими характеристиками
имеется взаимосвязь. Так, быстродействие фазовращателя может быть увеличено
600
ГЛАВА 16
за счет большей мощности управления. При движении луча требуемая скорость
переключения фазовращателей зависит от начальной точки фазирования. При
выборе ее в центре раскрыва скорость уменьшается в два раза по сравнению с
начальной точкой фазирования по краю, точность установки луча тоже может
быть изменена выбором начальной точки фазирования или алгоритмом управле-
ния. Алгоритмы фазирования системы управления лучом зависят от размещения
излучателей в решетке, схемы построения, конструктивных решений и т. д. Так,
размещение излучателей в узлах прямоугольной сетки координат (рис.16.18,а) до-
пускает строчно-столбцовый способ управления лучом по двум угловым коорди-
натам. Неэквидистантное размещение излучателей приводит к поэлементному уп-
равлению фазовращателями, что может уменьшить быстродействие.
Удаление от фазовращателей системы управления лучом влияет на ее харак-
теристики. В полотне ФАР с плотным размещением элементов, не допускающим
расположения между фазовращателями элементов системы управления, послед-
няя удалена от ФАР и связана с ней системой линий передач управляющих ко-
манд. Это обстоятельство ухудшает рассматриваемые характеристики и услож-
няет ФАР. Отражательная решетка лишена этих недостатков, так как позволяет
разместить систему управления на обратной стороне отражающего полотна.
Отмеченные взаимосвязи хотя и влияют на характеристики управления, но за-
висят от быстродействия фазовращателя, мощности управления и дискрета фази-
рования. Так, на стадии предварительного проектирования время установки луча
находят как время переключения фазовращателей с учетом системы управления.
Основная часть мощности управления потребляется фазовращателями. Хотя
мощность управления одним фазовращателем может составлять от долей до еди-
ниц ватт, мощность, поступающая к полотну ФАР от системы управления, до-
стигает киловатт. Эта мощность плюс мощность потерь СВЧ в ФАР определяют
температурный режим. В передающих ФАР возникает необходимость системы
теплоотвода. Изменение температуры полотна при работе влияет на характерис-
тики ФАР.
Точность установки луча (нуля разностной ДН) может быть достаточно высо-
кой при большом числе излучателей N, как это следует из (16.4.10). Точность оп-
ределения угловых координат целей радиотехнической системой зависит от даль-
нейшей обработки сигнала.
Как и любая другая радиосистема, ФАР имеет следующие общетехнические
характеристики: стоимость, габариты, массу, надежность, боевую живучесть,
ремонтопригодность, условия эксплуатации, электромагнитную совместимость и
т.д. Эти системные характеристики зависят как от антенны, так и от всей систе-
мы, технологии, производства, развития элементной базы и т.п. Однако можно
выделить ряд параметров ФАР, в первую очередь, определяющихся стоимостью
фазовращателя с управляющим элементом и их числом в решетке. Массогаба-
ритные характеристики зависят от используемой элементной базы, которая мо-
жет состоять из волноводов, полосковых и микрополосковых линий, интеграль-
ных схем СВЧ и т.д. Схема построения (проходная, отражательная, с фидерным
возбуждением и т.д.) и конструктивное исполнение отдельных элементов и всей
системы определяют надежность, ремонтопригодность, живучесть и т.д. Излуча-
тели с фазовращателями или их группа могут быть выполнены в виде отдельных
устройств-модулей (или печатных плат). Такое модульной исполнение имеет ряд
преимуществ, например, простоту замены вышедшего из строя элемента.
601
Фазированные антенные решетки
16.5. Антенны с частотным сканированием [3,17]
Из всех электрически сканирующих антенн частотно-сканирующие являются
наиболее простыми, экономичными и надежными. Они могут работать в любом
диапазоне частот. В них отсутствует система управляемых фазовращателей, и из-
менение фазового распределения достигается изменением частоты передающего
(приемного устройства). Метод частотного сканирования принципиально позво-
ляет электрически сканировать в двух плоскостях, но практическое применение
нашло частотное сканирование в одной плоскости, а в другой плоскости- фазовое,
комутационное или механическое сканирование. Антенна с частотным сканирова-
нием применяется в системах обзора воздушного пространства и управления воз-
душным движением. Были созданы современные РЛС с частотным сканированием
по углу места и другими методами сканирования по азимуту. Такие антенны могут
быть использованы для решения широкого круга задач: воздушной разведки, об-
зора земной поверхности, слепой посадки и военной техники.
Антенны с частотным сканированием имеют определенные преимущества пе-
ред ФАР. Они просто осуществляют многолучевое сканирование: для получения
многолучевой ДН необходимо излучать и принимать одновременно сигналы на
нескольких частотах. Другим преимуществом является возможность мгновенного
обзора пространства путем излучения широкополосного сигнала с линейным из-
менением несущей. Специальная обработка в приемной системе (метод частотного
детектирования, фильтра сжатия и т.д.) позволяет провести селекцию целей и оп-
ределить их угловое положение. Недостатком антенн с частотным сканированием
является слабая помехозащищенность: отсутствует возможность адаптации ДН к
помеховой обстановке, нет возможности уйти от помехи сменой рабочей частоты.
В антеннах СВЧ с частотным сканированием излучатели, как правило, рас-
положены на возбуждающей системе. Линейная решетка излучателей может
иметь параллельную или последовательную схему возбуждения коаксиалом, вол-
новодом, змейкой (зигзагообразной линией) или другой замедляющей системой
(рис. 16.19). Для получения управляемой карандашной ДН необходима двухмерная
б)
Рис. 16.19. Возбуждение линейной решетки излучателей с частотным сканированием:
а) - по параллельной схеме; б) - по последовательной схеме; в) - на основе волноводной
периодической замедляющей системы [3]
602 ГЛАВА 16
решетка, образуемая системой линейных решеток на плоскости, цилиндре или
другой поверхности. Один из методов формирования узкого луча заключается в
использовании цилиндрического зеркала, облучаемого линейной решеткой (гиб-
ридная антенна).
Различают два типа антенных решеток с частотным сканированием: с последо-
вательным и параллельным питанием. На практике преимущественно применяет-
ся первый тип. Поясним принцип действия такой антенны с помощью рис. 16.19,б,
на котором изображен змейковый волновод, питающий решетку излучателей.
Ориентация главного лепестка определяется формулой (16.3.1. Следовательно,
[17],
X I X
sin9? =m- +------, т = 0,±1,±2,... (16.5.1)
7 7 А 7 7 7 7 \ Z
а а Хд
О
Важным параметром антенны с частотным сканированием является углочас-
тотная чувствительность, равная величине поворота лепестка (в градусах),
приходящейся на один процент изменения частоты (длины) волны. Дифференци-
руя (16.3.1), можно получить
df/f
(16.5.2)
Величина f dtjdf характеризует дисперсию в волноводе. Следовательно, угло-
частотная чувствительность растет с увеличением замедления и дисперсии и,
кроме того, зависит от направления главного лепестка.
Расчеты показывают [17] , что при использовании прямолинейного отрезка
прямоугольного волновода максимальный сектор сканирования лепестка при от-
сутствии лепестков высших порядков находится в пределах углов от -90° до +14°.
При этом средняя углочастотная чувствительность составляет лишь 1,61° на 1%
изменения частоты.
В [3] рассматривают углочастотную чувствительность в градусах на процент
изменения частоты:
7гр
(16.5.3)
,3n sin 9 -
А = —= 0,573---------
ах/х 2
где 0,573-переводной коэффициент размерности входящих величин; угр = c/vgp -
замедление групповой скорости.
о Xdy
Замедление групповой и фазовой скоростей связаны выражением уг„ = у--------.
1 dX
Если известна дисперсионная характеристика, то угр можно легко найти [3]. Из
выражения (16.5.3) следует, что углочастотная чувствительность зависит от на-
правления луча (величины отклонения и знака 6), дисперсионных свойств систе-
мы и отношения /d. Для повышения углочастотной чувствительности антенны
необходимо использовать канализирующие системы с большим замедлением угр,
что сопровождается ростом потерь в тракте. Наличие потерь в тракте накладывает
ограничения на длину решетки, так как с ростом длины уменьшается КПД, что, в
свою очередь, ограничивает получение узких ДН отдельной решетки. На рис. 16.20
приведена зависимость КПД от отношения затухания на длину волны к ширине
ДН: аХ / (2Оо 5). Сплошные линии соответствует равномерному амплитудному рас-
Фазированные антенные решетки
603
Рис. 16.20. Зависимость КПД антенны от отношения затухания на длину волны к ширине
ДН [3]
пределению, пунктирная - экспоненциальному распределению, которое допускает
увеличение сектора сканирования вдвое путем коммутации направления возбуж-
дения при тех же АХ/Х и КПД.
Проведенный анализ различных канализирующих систем антенн с частотным
сканированием [3] позволяет выбрать оптимальный вариант, исходя из заданных
требований.
Для того чтобы можно было осуществить сканирование в пределах большого
сектора и при этом мало менять частоту генератора, нужно использовать антен-
ны с большим замедлением. Этого достигают, увеличивая отношение l/d (напри-
мер, применяя змейковые волноводы или спиральные волноводы), либо уменьшая
Хв (помещая внутрь волновода замедляющую, например, ребристую структуру).
Анализ показывает, что при увеличении 6, падает КПД антенны из-за роста
потерь в линии питания антенной решетки. Это ограничивает длину антенны, а
следовательно, и минимальную достижимую ширину главного лепестка.
16.6. Линейная решетка СВЧ-излучателей [3]
В различных антеннах СВЧ с обработкой сигнала, включая ФАР, использу-
ют линейные решетки излучателей как составные части или как самостоятельные
антенны. Из линейных решеток образуют частотно-сканирующую антенну, ци-
линдрическую ФАР или самолетную четырехлучевую антенну доплеровской на-
вигационной системы. Излучателями такой антенны могут быть щели, полосковые
вибраторы или печатные излучатели. Излучатели последовательно возбуждаются
волноводом, полосковой или микрополосковой линией. Получили распространение
волноводные многощелевые антенны, полосковые многощелевые антенны, полос-
ковые вибраторные, печатные линейные решетки излучателей и т.д. (рис. 16.21-
16.24).
Использование той или иной линии передачи и излучателя зависит от рабочей
волны, полосы частот, уровня излучаемой мощности, допустимых потерь и тре-
буемой поляризации поля. Печатные дисковые излучатели относительно просто
604
ГЛАВА 16
Поглощающая
нагрузка
От генератора
Рис. 16.21 Волноводно-щелевая антенна [3]
Вход I Нагрузка
проводник линии
Рис. 16.22. Линейная решетка бегущей волны с
печатными резонансными вибраторами [3]
Рис. 16.23. Щелевая решетка, возбуж-
даемая трехпластинчатой симметричной
полосковой линией с различными волно-
выми сопротивлениями [3]
Рис. 16.24. Печатный излучатель [3]
Фазированные антенные решетки 605
создают любую поляризацию в отличие от щелевых и полосковых вибраторов, ко-
торые более удобны для линейной поляризации. Печатные излучатели и возбужда-
ющие их полосковые линии имеют конструкторско-технологические преимущества
перед волноводными линейными решетками, но расчет их более сложен, трудое-
мок и проводится численными методами решения электродинамических задач.
Расчет линейной решетки последовательного питания рассмотрим на приме-
ре широко распространенной волноводно-щелевой решетки (ВЩР), для которой
разработаны методы расчета различного уровня точности и сложности. Наиболее
точный и строгий электродинамический анализ ВЩР учитывает взаимодействие
щелей во внешнем пространстве, внутри волновода по основной волне и волнам
высшего типа, а также ширину щели и толщину стенок волновода. Однако этот
метод довольно сложен, трудоемок и основан на использовании специально раз-
работанных программ численного решения этой задачи.
Возможны различные упрощения строгого анализа ВЩР. Так, для учета вне-
шнего взаимодействия при тонких щелях можно использовать метод наведен-
ных ЭДС. Для щелевых излучателей в этом методе рассматривают наведенные
магнитодвижущие силы. Внутреннее взаимодействие щелей можно приближенно
учитывать только по основной волне с помощью так называемого метода рекур-
рентных соотношений. Это наиболее простой и наименее точный энергетический
метод расчета, при котором не учитываются внешне и внутреннее взаимодействия.
Предполагается, что фазовый сдвиг между соседними излучателями по питаю-
щему волноводу равен электрическому расстоянию между ними 2кд/Хв , а фазовое
распределение в раскрыве антенны линейное.
Для определения амплитудного распределения в антенне и согласования вол-
новода используется следующая эквивалентная схема ВЩР. Волновод с излуча-
ющими щелями представляется отрезком эквивалентной линии с включенными
эквивалентными проводимостями g или сопротивлениями г в зависимости от рас-
положения щели на волноводе. Значения эквивалентных параметров р и г счита-
ются такими же, как у одиночной щели в волноводе. Они известны из решения
задачи об излучении щели и приведены в [3]. Эквивалентные схемы различных
видов щелей в прямоугольном волноводе показаны на рис. 16.25.
Наклонные щели в узкой стенке волновода с волной Н10 возбуждаются попереч-
ными токами, и эквивалентная схема представляется эквивалентностью проводи-
мостью, включенной параллельно в линию. Изменением знака угла наклона ±5
щели вносится дополнительный фазовый сдвиг л за счет переменно-фазной связи
излучателя с полем питающего волновода. Это дополнительный сдвиг к сдвигу
по питающему волноводу 2Tid/'ke позволяет вдвое уменьшить шаг d в решетке и
обеспечить формирование одного луча. Так, для синфазного возбуждения щелей
в волноводе при одинаковом наклоне щели необходимо, чтобы d = Хв. Однако это
недопустимо, так как d > X. Изменение знака наклона щели (см. рис. 16.21, а) поз-
воляет синфазно возбудить щели при d = Хв/2. Наклонные щели в волноводе со-
здают поле излучения с горизонтальной поляризацией Ег (основной) и паразитной
поляризацией Ев (кроссополяризованной составляющей). При небольших углах на-
клона 5 потери мощности на паразитную поляризацию незначительны, например,
при 8 < 15° они составляют менее 1%. Изменение угла 5 регулирует излучаемую
щелью мощность по отношению к подводимой. При постоянной величине 8 и со-
гласовании волновода с конечной согласованной нагрузкой в ВЩР получаем экспо-
606
ГЛАВА 16
Расположение
щели
Эквивалентная
схема
Эквивалентная проводимость
или сопротивление
Рис. 16.25. Размещение щели в волноводе и его эквивалентные схемы [3]
ненциальное амплитудное распределение. Равномерное амплитудное распределение
в решетке для максимального КНД или спадающее амплитудное распределение в
решетке для максимального КНД или спадающее амплитудное распределение к
краям решетки для уменьшения УБЛ достигается поэлементным изменением угла
наклона щели 6. Зная амплитудное распределение по ВЩР и принимая потери в
согласованной нагрузке, равными 5-10%, легко определить величину связи пос-
ледней (ближайшей к нагрузке) щели с волноводом и последовательно связи всех
остальных щелей [3].
Волноводные многощелевые антенны разделяют на два типа: резонансные, у
которых луч направлен по нормали к решетке, и нерезонансные, у которых луч
отклонен от нормали. Резонансные антенны имеют шаг d = А,в/2 , что приводит
к арифметическому суммированию модулей коэффициентов отражения от всех
щелей на входе антенны. В волноводе устанавливается режим, близкий к стоячей
волне, согласованная нагрузка может быть заменена короткозамкнутым волновод-
ным шлейфом. С помощью известных методов вход такой антенны можно согласо-
вать с источником (генератором).
При отклонении луча ВЩР от нормали указанных явлений не происходит, так
как d Ф Х,б/2 , и обычно устанавливается режим смешанных волн с КБВ порядка
0,4-0,8. Волновод в этом случае должен заканчиваться согласованной нагрузкой.
Кроме использования при частотном сканировании, ВЩР применяют при элек-
Фазированные антенные решетки
607
тромеханическом сканировании, когда антенна неподвижна, а механически пе-
ремещается малоинерционный элемент, приводящий к перемещению луча в про-
странстве. Таким элементом является тонкая диэлектрическая или металлическая
пластина, расположенная внутри волновода по всей его длине. Перемещение этой
пластины вызывает изменение величины у и, следовательно, направления луча.
При сканировании в ВЩР возникает так называемый «эффект нормали», прояв-
ляющийся в резком падении КУ при проходе луча через нормаль. Это происходит
из-за рассогласования волновода. Для устранения «эффекта нормали» необходимо
поэлементное согласование каждой щели с волноводом.
В заключение остановимся на последовательности расчета ВЩР по заданным
20О5, 02Л и УБЛ. Из соотношения (16.5.3) для волновода с выбранным направле-
нием возбуждения (т.е. с учетом знака 0гл ) определяем необходимый шаг d. Далее
—, где коэффициент берем
гл
находим длину ВЩР из соотношения 20о 5 -
в зависимости от требуемого УБЛ. Приближенно величина может быть взята та
же, как и для апертурных антенн. Далее в зависимости от поляризации выбираем
продольные, поперечные, наклонно-смещенные и другие типы щелей. Рассчиты-
ваем связь щели с полем волновода для обеспечения выбранного амплитудного
распределения.
Изложенный метод, называемый энергетическим расчетом, дает расхождение
с экспериментом. Ошибки расчета возрастают с уменьшением числа щелей и могут
составлять до 30% при N < 15. Учет взаимодействия щелей для выбранной схемы
построения антенны позволяет увеличить точность расчета.
16.7. Многолучевые и совмещенные антенные решетки [3, 17]
Принцип действия многолучевой антенны поясним с помощью рис. 16.26. На нем
изображена антенная решетка, состоящая из N излучателей. Сигнал от генерато-
ра подается на любой из М входов и распределяется между между излучателем
с помощью пассивного многополюсника. Он представляет собой волноводную схе-
му, обеспечивающую линейное изменение фазы вдоль антенной решетки, причем
величина сдвига фаз \|/ между соседними излучателями, а следовательно, и ори-
ентация главного лепестка определяется номером входа, на который поступает
сигнал. В [17] под многополюсником понимается диаграммообразующее устройство
(ДОУ). В [3] предполагается, что каждому входу антенны соответствует своя ДН.
Таким образом, диаграмма направленности антенны зависит от типа волновод-
Рис. 16.26. К пояснению принципа действия многолучевой антенны [17]
608
ГЛАВА 16
5 4 3 2 1
Входы
а)
Линии передачи
Рис. 16.27. Многолучевая антенная решетка последовательного питания (матрица Бласса)
(а) и формируемые ею главные лепестки (б) [17]
ной схемы, получившей поэтому наименование диаграммообразующей или мат-
ричной схемы. Предложено много разновидностей таких схем [17]. Рассмотрим
некоторые из них.
На рис. 16.27,а изображена антенна последовательного питания, в которой ли-
нии передачи, подсоединенные к излучателям, связаны в местах пересечения с
помощью направленных ответвителей. Направления ответвления энергии показа-
ны стрелками.
К каждому излучателю по сравнению с предыдущим излучателем сигнал про-
ходит дополнительный путь, равный
I - d(sec р + tgP),
(16.7.1)
гдеР - угол между линией передачи и осью антенной решетки (рис.16.27).
Тогда согласно формуле (16.5.1) ориентация главного лепестка может быть оп-
ределена с помощью выражения
sin 0гл = wtkjd + (sec р + tgP) X/A , т - 0, ± 1, ± 2, ... (16.7.2)
Следовательно, каждому значению Р (каждому входу антенны) соответствует
свой главный лепесток (рис. 16.27,б). Переключая (механически или электрически)
входы антенны, можно осуществить скачкообразное сканирование луча. При пода-
че питания одновременно на несколько входов можно сформировать веер лучей.
На рис. 16.28,а изображен вариант антенны параллельного питания. Диаграммо-
образующая схема содержит отрезки волновода, длина которых от входа к выходу
одинакова, два постоянных фазовращателя и четыре делителя мощности, на двух
выходах которых сигналы одинаковы по величине, но сдвинуты по фазе на л/2.
19*
Фазированные антенные решетки
609
Делители
а)
Рис. 16.28. Многолучевая антенна параллельного питания (матрица Батлера) (а) и форми-
руемые ею главные лепестки (б) [17]
Лучи
В качестве таких делителей мощности могут быть использованы щелевые мосты.
ДОС, показанная на рис. 16.27, а называется матрицей Бласса.
Можно считать, что при прохождении сигнала через делитель в прямом на-
правлении фаза не меняется, а в диагональном направлении фаза отстает на л/2.
При подаче сигнала на вход 1 антенны распределение фаз на антенной решетке
соответствует рис. 16.28,а. Если d = 1/2 , то лепесток (нулевого порядка) согласно
формулам (16.3.1) и (16.3.2) отклонен от нормали к антенне на угол 0гл = arcsin0,25
(рис. 16.28,6). При подаче сигнала на вход 4, симметричный входу 1, луч на угол
0?;7 =-а г с sin 0,25.
Нетрудно показать, что при подаче сигнала на входы 2 и 3 сдвиг фаз между
соседними излучателями составляет соответственно ±Зл/4, а лепесток отклонен
от нормали на угол 0гл = ±arcsin 0,75.
При возрастании числа излучателей резко растет необходимое число делите-
лей и фазовращателей, что является недостатком многолучевых антенн такого
типа. ДОС, показанная на рис. 16.28,а называется матрицей Батлера.
Матрица Батлера собирается на основе трехдецибельных направленных ответ-
вителей (мостов) и статических (фиксированных) фазовращателей и используется
для решеток с бинарным числом излучателей: N = 2п (п=1, 2, 3,...). Решетка фор-
мирует семейство N лучей, симметричных относительно нормали. Развязка меж-
ду входами обеспечивается свойствами мостовых соединений при согласовании
излучателей и остальных частей тракта. В матрице Батлера имеется (log2 N^N/2
мостов и 0og2 (N —1)4/2 фазовращателей.
В матрице Бласса используется большее число направленных ответвителей,
согласованные нагрузки, вносящие дополнительные потери, и питающие линии
разной длины. Различные фазовые распределения для парциальных лучей в ДОС
Бласса (последовательного типа) реализуются за счет разных углов наклона го-
ризонтальных линий передач. Матрица Бласса позволяет использовать различное
число излучателей и спадающие к краям амплитудные распределения, а также
уменьшать по сравнению с матрицей Батлера число входов. Существуют раз-
личные модификации ДОС последовательного и параллельного типов. Так, моди-
фицированная ДОС Бласса устраняет согласованные нагрузки, уменьшает длину
линий передач путем включения фазовращателей. На рис. 16.29 показана МА, пос-
троенная по схеме с последовательной разводкой, называемой матрицей Бласса.
Теоретически для МА важно установить возможное количество лучей, что
20 - Неганов
610
ГЛАВА 16
Рис. 16.29. Диаграммообразующая схема
многолучевой антенны: модифицирован-
ная ДОС Бласса [3]
Fn(0)|
ZJk
Рис. 16.31. Двухчастотная совмещенная ФАР, образованная решеткой вибраторов, разме-
щенных над второй вибраторной или волноводной решеткой [3]
Рис. 16.30. Пересечение лучей в секторе
обзора [3]
соответствует допустимому уровню пересечения парциальных ДН, и условия не-
зависимости входов, т.е. развязки между отдельными входами. Если известен из-
лучающий раскрыв антенны и сектор формирования лучей 0, то можно создать
N амплитудно-фазовых распределений для формирования лучей, каждому из ко-
торых соответствует парциальная комплексная ДН Fn(0,cp), где n=l,2,3,...N. Из
математики известно, что система функций Fn (0, <р) образует систему ортогональ-
ных функций, если выполняются условия
при mtn,
(16.7.3)
при mtn.
0
j Fn (Q,(p)Fm (0,<p)sin0d(pdO = < 4л
Здесь Dn - КНД для n-го луча.
Условие ортогональности (16.7.3) позволяет установить максимальное число не-
зависимых лучей в МА. Так, если рассматривать остронаправленные антенны с
равномерным амплитудным и линейным фазовым распределениями, то из (16.7.3)
можно найти допустимый уровень пересечения ортогональных парциальных ДН.
Этот уровень для линейной и плоской антенн в главных плоскостях составляет
2/л (-4дБ). В диагональных плоскостях уровень пересечения падает до 0,4 (-9дБ).
Этот уровень пересечения определяет число N лучей в секторе 0 (рис.16.30). Уро-
Фазированные антенные решетки
611
М(г,9,ф)
Рис. 16.32. Двухчастотная совмещенная ФАР, образованная «вкладыванием» одной решет-
ки в другую в одном раскрыве (плоскости) [3]
вень пересечения определяет падение КНД для одного входа антенны в рабочем
секторе углов.
Входы МА будут развязаны, если выполнены условия (16.7.3), ДОС обеспечи-
вает необходимые амплитудно-фазовые распределения и согласование, а дискре-
тизация раскрыва проведена в соответствии с теорией ФАР.
В приемных антенных решетках с различной обработкой сигнала (активных,
цифровых, радиооптических и др.) условия формирования независимых лучей су-
щественно изменяются [3].
Остановимся на возможных принципах построения совмещенных ФАР диапа-
зона СВЧ. Совмещаемые решетки можно расположить одна над другой на неко-
тором расстоянии (рис. 16.31). Причем верхняя решетка является вибраторной, а
излучателями нижней решетки могут быть волноводы, щели, вибраторы и др.
Буквами Д, /2 на рисунке отмечены соответствующие рабочие частоты ФАР.
Совмещение решеток можно выполнить в одном излучающем раскрыве, разме-
щая излучатель одного диапазона между излучателями другого диапазона. Такое
совмещение удобно проводить для щелевых, волноводных и вибраторных излуча-
телей (рис.16.32). Имеется принципиальная возможность построения совмещенных
ФАР на одной излучающей решетке, обладающей широкополостными свойства-
ми, достаточными для работы на частотах и /2. Однако здесь возникает про-
блема размещения в решетке системы направленных частотно-разделительных
фильтров, помимо фазовращателей для каждого диапазона. Известны и другие
построения этих антенн с различными гибридными антеннами [3]. Совмещение двух
решеток одна над другой или одна в другой приводит к ухудшению их электроди-
намических характеристик. Проведенные исследования таких антенн показывают,
что совмещение приводит к падению усиления, увеличению УБЛ и ограничению
сектора сканирования. При соотношении частот Д//2 ~ 2...4 особенно ухудшаются
характеристики высокочастотной решетки. Разработаны различные методы ослаб-
ления взаимного влияния при совмещении и расчете совмещенных ФАР [3].
20*
612
ГЛАВА 16
16.8. Активные ФАР [3]
Фазированные антенные решетки и построенные на их основе антенные систе-
мы с пространственно-временной обработкой сигнала обладают большими фун-
кциональными возможностями и широко применяются. Одним из существенных
недостатков ФАР являются значительные потери. В бортовых ФАР применение
полосковой техники позволяет снизить стоимость, повысить надежность и умень-
шить массу и габариты.
Полосковые и микрополосковые устройства применяются для канализирующих
систем, делителей мощности, направленных ответвителей, излучателей, фазов-
ращателей и т.д. Существенным недостатком полосковой техники являются зна-
чительные потери в сантиметровом диапазоне и особенно в коротковолновой ее
части, которые еще более увеличивают общие потери в ФАР. Включение активного
элемента (генератора, усилителя, преобразователя частот) в тракт СВЧ-излуча-
телей ФАР позволяет не только устранить потери, но и существенно изменить
систему возбуждения, формирование луча и его управления. Активный элемент
(или прибор) в тракте возбуждения превращает антенную решетку из пассивного
взаимного устройства в активную фазированную решетку, в которой при приеме
и передаче используют различные активные элементы. Последнее объясняется не-
взаимностью активностью элементов. Практическое применение нашли приемные,
передающие и приемопередающие АФАР, имеющие одну антенную решетку с
антенными переключателями или циркуляторами для каждого излучателя.
Наличие активного элемента в передающих АФАР позволяет поднять КПД и
достичь очень больших мощностей излучения, упростить требования к фазовра-
щателям, поднять надежность и получить ряд других преимуществ.
Активный элемент в приемных АФАР позволяет не только понизить шумовую
температуру антенны (поднять чувствительность), но и провести обработку сиг-
нала на частотах принимаемого сигнала или на более низкой промежуточной либо
более высокой частоте при голографических методах обработки. При этом в при-
емной АФАР можно проводить пространственно-временную обработку сигнала,
используя аналоговые, цифровые, корреляционные, радиооптические и другие
известные методы обработки сигнала. Становится также возможным существенное
улучшение некоторых антенных характеристик. Однако это неизбежно будет свя-
зано с ухудшением других характеристик.
16.9. Антенные решетки с обработкой сигнала [17]
Находят применение также антенные решетки с обработкой сигнала. Заданные
электрические параметры у таких антенн (ширина ДН, отношение сигнал/помеха,
уровень боковых лепестков) достигаются путем соответствующей (например, ло-
гической, корреляционной) обработкой сигналов, поступающих от элементов ан-
тенной решетки.
16.9.1. Методы обработки сигнала. Во всех рассмотренных выше типах ан-
тенных решеток сигналы, принятые отдельными излучателями, складывались на
выходе антенны (рассматривается режим приема). Это простейший вид обработки,
сигналов. Антенные решетки с такой обработкой сигналов называются адаптивны-
Фазг^рова/нмые дмтепные решетки
613
ми. Предложен ряд других методов обработки сигналов, в результате чего удается
создать антенны, имеющие известные преимущества в сравнении с аддитивными.
Из этих новых антенн рассмотрим два типа: корреляционные (мультипликатив-
ные) антенны и антенны с логическим синтезом.
16.9.2. Корреляционные (мультипликативные) антенны. Рассмотрим
простейшую антенную решетку, состоящую из двух направленных излучателей
(рис.16.33). Пусть на решетку под углом 0 падает плоская волна. Напряжения на
выходе излучателей можно записать в виде
U1=Ucos(nt, (16.9.1)
U2 = U cos(cot + kd sin 0) = U cos o)(t + t) , (16.9.2)
где
т = de 1 sin 0.
(16.9.3)
Произведем над сигналами последовательно операции умножения и усредне-
ния, тогда результирующий сигнал будет иметь вид
___________________ т
U = UiU2 = U2 cos cot cos co(t + т) = lim — f U1U2dt =
T->°°
(16.9.4)
cos(fcd sin 0) =
U sin(2/cd sin 0)
4 sin(/cd sin 0)
Операции умножения и усреднения двух функций определяют корреляцион-
ную функцию, откуда следует название антенны.
Функция
1 sin(2kd sin 0) . мдпкч
Fc(0) =-------------= cos(/cd sm 0) (16.9.5)
2 sin(/cdsin0)
есть ДН двухэлементной корреляционной антенны. Из (16.9.5) и [17] заключаем,
что корреляционная двухэлементная антенна имеет такую же ДН, как и обычная
(аддитивная) двухэлементная синфазная антенна с вдвое большим расстоянием
между элементами. Таким образом, корреляционная обработка сигнала привела к
сужению ДН.
Аналогичные результаты можно получить с многоэлементными антенными ре-
У множите ль
Интегратор
I
Рис. 16.33. К пояснению принципа действия корреляционной антенны [17]
614
ГЛАВА 16
-90 -60-30 0 30 60 0°
а)
Рис. 16.34. К пояснению подавления боковых лепестков методом логического синтеза [17]
-90 -60-30 0 30 60 0°
тетками. Предложен ряд методов разбиения антенной решетки на секции с после-
дующим перемножением и усреднением сигналов.
Заметим, что выражение (16.9.4) определяет величину постоянного напряже-
ния. Для того чтобы получить на выходе антенны переменное напряжение частоты
Q , можно в канал одного излучателя включить переменный фазовращатель и
осуществлять фазовую модуляцию сигнала с частотой Q .
Если излучатели 1 и 2 являются направленными, то результирующий сигнал
будет пропорционален произведению ДН излучателей. Это открывает дополни-
тельные возможности для формирования остронаправленной диаграммы.
16.9.3. Антенная система с логическим синтезом. ДН состоит из несколь-
ких, чаще всего двух, антенн. Логическое синтезирование состоит в сравнении
амплитуд сигналов от отдельных антенн и использовании логических устройств
типа «да-нет» для отпирания или запирания приемника, либо подсоединения его
к одной из антенн.
В качестве примера на рис.16.34,а изображены ДН двух антенн: остронаправ-
ленной fi (0) и ненаправленной /2 (0) • Боковые лепестки остронаправленной антен-
ны будут полностью подавлены (рис. 16.34,6), если вход приемника открыт при
fl (0)| > |/г (е)| и закрыт при |/2 (0)1 > |/1 (0)1 -
Другим примером может служить многоэлементная антенная система, приме-
няемая на летательных аппаратах. Для борьбы с экранирующим действием кор-
пуса аппарата каждый элемент имеет направленную диаграмму и принимает сиг-
налы, проходящие в пределах только определенного телесного угла. Логическое
устройство подсоединяет к приемнику ту антенну, бна выходе которой амплитуда
сигнала наибольшая. Таким образом, синтезированная ДН является квазиизотроп-
ной.
16.10. Основные применения многолучевых антенн [3]
Одна из задач современной антенной техники - построение многофункциональ-
ных пассивных и активных антенных систем, обеспечивающих высокоэффектив-
ную работу различных радиотехнических комплексов. Возможный путь реализа-
ции таких антенных систем состоит в использовании многолучевых антенн (МА).
Интерес к МА определяется их способностью формировать в пространстве веер
Фазированные антенные решетки
615
ДН, каждой из которых соответствует определенный входной канал. Наиболее
простой путь построения многофункциональных антенных систем заключается в
рациональном использовании основных достоинств многолучевых и однолучевых
устройств. Примером является использование МАР в радиолокационных станциях
(РЛС) бокового обзора. В сочетании с ФАР многолучевая антенная решетка поз-
воляет существенно расширить их возможности и улучшить характеристики на-
правленности. В частности, использование МАР в качестве излучающих элементов
ФАР приводит к возможности сканирования несколькими независимыми лучами
или к существенному расширению сектора однолучевого сканирования [3]. При-
менение ДОС пассивных МА позволяет также решать задачи создания активных
МАР, сложение мощности в общей нагрузке и синхронизацию большого числа ге-
нераторных элементов. Объединение решетки излучателей и активных элементов
с помощью ДОС позволяет придать им свойство переизлучения электромагнитных
волн в направлении их прихода и обеспечит увеличение коэффициента усиления
антенны при работе на прием. Такие антенны называются переизлучающими. Они
находят применение в системах связи.
Рассмотрим применение МАР и их ДОС в ФАР. Одним из основных требова-
ний, предъявляемых к современным ФАР, является достижение максимально
высокого усиления от антенны в максимально широком секторе углов сканирова-
ния. Обеспечение широкоугольного сканирования приводит к необходимости при-
менения расположенных близко друг от друга слабонаправленных излучателей.
При этом значительными становятся трудности конкретных конструкторских ре-
шений, связанных с размещением большого числа различных устройств СВЧ в
малом объеме. Одним из возможных путей преодоления этих трудностей является
увеличение направленности излучающих элементов с одновременным обеспечени-
ем управления положением максимума их ДН. Эффективность сканирования при
этом достигается синхронным смещением ДН одиночного излучателя и множителя
решетки. Функцию излучателя ФАР с управляемой ДН может выполнять МА в
совокупности с переключателем каналов. На рис.16.35 представлена схема такой
линейной антенной решетки, состоящая из решетки излучателей 1, объединен-
Рис. 16.35. Схема ФАР с применением МА для увеличения сектора однолучевого сканиро-
вания: 1-излучателя; 2-ДОС, 3-переключатели каналов; 4-управляемый фазовращатель;
5-направленный ответвитель; 6-согласованная нагрузка; 7-магистральный волновод [3]
616
ГЛАВА 16
них группами ДОС 2. Коммутация входов ДОС осуществляется переключателями
каналов 3, которые соединяются с проходными фазовращателями 4. Разделение
мощности СВЧ производится направленными ответвителями 5, в одно из плеч
которых включены согласованные нагрузки 6. Мощность возбуждения подается на
вход магистрального волновода 7.
Диаграмма направленности такой ФАР определяется выражением
(е)=fn (е)—
(16.10.1)
где Fn (0) - ДН многолучевой антенны, соответствующая ее n-му входу (для слу-
чая, представленного на рис.16.35 индекс п может принимать значения 1, 2, 3);
Q-количество ДОС, входящих в состав антенны; d0 -расстояние между одноимен-
ными излучателями соседних ДОС (рис.16.35); у -сдвиг по фазе между соседними
управляемыми излучателями.
Такая антенна работает следующим образом. При подключении генератора к
ее входу колебания СВЧ, пройдя через магистральный волновод 7, направленные
ответвители 5 и фазовращатели 4, поступают на входы переключателей каналов
3. Положение максимума формируемой антенной ДН определяется не только зна-
чением сдвигов фаз фазовращателей, но и номером входа ДОС, возбуждаемого
переключателями каналов. Таким образом, диаграмма направленности МА, состо-
ящей из группы излучателей ФАР, объединенных ДОС, может скачком изменять
свое положение в зависимости от состояния переключателя каналов. Изменение
величины \/ сдвига по фазе между соседними управляемыми фазовращателями
антенны позволяет изменять положение максимума ДН ФАР в пределах каждой
из парциальных ДН МА, являющейся сложным комбинированным излучателем
рассматриваемой ФАР. При этом максимумы входящего в (16.10.1) множителя ре-
шетки высших порядков могут располагаться в области действительных углов. В
ДН ФАР они проявляются как боковые лепестки, уровень которых равен значе-
нию соответствующей парциальной ДН МА в направлении конкретного максимума
множителя решетки высшего порядка. Для иллюстрации на рис.16.36 показаны
парциальные ДН трехлучевой МА, график множителя решетки и ДН ФАР в це-
лом. Из сказанного следует, что сектор однолучевого сканирования рассматри-
ваемой ФАР определяется и ограничивается сектором формирования лучей МА,
входящих в состав ФАР.
Рис. 16.36. Диаграмма направленности ФАР и ее элементов [3]
Фазированные антенные решетки
617
dQ
Н-----------И
3|
Рис. 16.37. Схема ФАР с несколькими независимо сканирующими лучами: 1-излучатели;
2-ДОС; 3-управляемые фазовращатели; 4-направленные ответвители; 5-магистральный
волновод [3]
Необходимость использования многолучевого режима радиотехнических ком-
плексов приводит к задаче создания ФАР с несколькими независимо сканирую-
щими лучами. Возможный путь решения этой задачи также состоит в совмещении
достоинств МА и ФАР.
На рис. 16.37 представлена схема ФАР с несколькими управляемыми лучами.
Она состоит из решетки излучателей 1, объединенных ДОС 2. Одноименные входы
ДОС через фазовращатели 3 и направленные ответвители 4 подключены к магис-
тральным волноводам 5; количество независимых лучей ФАР должно быть равно
количеству магистральных волноводов и количеству входов ДОС.
В такой ФАР могут быть использованы компактные МА, например, на основе
многоволновых волноводов, а также другие МА. Диаграмма направленности ФАР
для n-го входа определяется соотношением
^пФАР СО = Fn СО
sin Q ykdQ sin 0 - Vn )/2
Рис. 16.38. Диаграммы направленности многолучевой ФАР
с независимо сканирующими лучами [3]
618
ГЛАВА 16
где \|/п “ сдвиг по фазе между соседними управляемыми фазовращателями п-го
канала ФАР.
В описанной ФАР достигается возможность сканирования несколькими незави-
симыми остронаправленными лучами, причем сектор сканирования каждого луча
ФАР ограничивается парциальной ДН, отвечающей соответствующему входу ДОС
(рис. 16.38). Это является недостатком рассмотренных ФАР, так как с их помощью
нельзя обеспечить сколь угодно малое угловое расстояние между соседними неза-
висимыми остронаправленными лучами.
Обтекатели антенн и покрытия объектов, снижающие ...619
Глава 17. Обтекатели антенн и покрытия объектов,
снижающие их радиолокационную видимость
17.1. Обтекатели антенн [3, 17]
Обтекатели антенн — это радиопрозрачные оболочки, предназначенные для
защиты антенн от воздействия внешней среды. Они защищают антенну от механи-
ческих (ветровых) нагрузок, опасности электрического пробоя в условиях низких
давлений, перегрева и т.д.
Большинство СВЧ-антенн летательных аппаратов (ЛА) имеют обтекатели, в
первую очередь, для уменьшения вносимого ими аэродинамического сопротив-
ления. Антенны ЛА в ряде случаев нуждаются в обтекателях для защиты их от
электрического пробоя при низких давлениях и особых условиях работы.
Наземные антенные системы требуют наличия радиопрозрачных укрытий для
защиты их от атмосферных воздействий и взрывной волны. Исходя из назначения
антенных обтекателей и укрытий, к ним предъявляют ряд различных сложных
и противоречивых требований по механической прочности, термостойкости, аэ-
родинамическому сопротивлению, радиопрозрачности и уменьшению искажений
характеристик излучения антенн.
Обтекатели приводят к амплитудным искажениям поля антенны за счет
частичного поглощения электромагнитной энергии в материале обтекателя и отра-
жения от его стенок, а также к фазовым искажениям, связанным с прохождением
плоской волны через неплоскую поверхность обтекателя. Эти искажения приводят
к уменьшению дальности действия радиостанций и ухудшению их точностных ха-
рактеристик. Указанные выше требования учитываются при разработке конструк-
ции обтекателей, выборе материала и технологии изготовления.
Иногда обтекателями называют диэлектрические кожухи, закрывающие облу-
чатели антенн. Эти колпаки позволяют осуществить герметизацию волноводно-
го тракта и увеличение (благодаря наддуву) его электрической прочности. Кроме
того, они могут использоваться как устройства, согласующие облучатели со сво-
бодным пространством.
17.1.1. Классификация обтекателей [17] может осуществляться по их фор-
ме. На летательных аппаратах применяют плоские, конические, оживальные,
полусферические, сегментные, сфероцилиндрические, каплевидные обтекатели
(рис. 17.1). Применяются обтекатели и более сложной конфигурации.
Плоские (или слегка изогнутые) обтекатели обычно устанавливают заподлицо с
обшивкой летательного аппарата под крыльями или под фюзеляжем. Конические
обтекатели устанавливают в носовой или хвостовой части скоростного летатель-
ного аппарата, а при меньших скоростях применяют оживальные и полусфери-
ческие обтекатели. Остальные типы обтекателей устанавливают внизу или ввер-
ху фюзеляжа, причем на скоростных летательных аппаратах обычно применяют
каплевидные обтекатели, имеющие меньшее лобовое сопротивление.
Для наземных антенн применяют сегментные, сфероцилиндрические, полу-
620
ГЛАВА 17
Рис. 17.1. Типы обтекателей, применяемых на летательных аппаратах:
1 — каплевидный; 2 — полусферический; 3 — оживальный; 4 — сегментный;
5 — плоский; 6 — сфероцилиндрический; 7 — конический [17]
сферические и сферические обтекатели.
По количеству диэлектрических слоев, образующих обтекатели, последние
делятся на однослойные и многослойные. Обтекатель с встроенной внутри ди-
электрического слоя однолинейной металлической сеткой (из параллельных
проводов) называется армированным.
17.1.2. Требования, предъявляемые к обтекателям [3,17], делятся на
радиотехнические и нерадиотехнические. Первые определяются тем, что обтека-
тель влияет на радиотехнические параметры антенны. Энергия волны, падающей
от антенны на обтекатель, не вся проникает сквозь него: часть, энергии поглоща-
ется в стенке обтекателя из-за конечного значения тангенса угла потерь диэлект-
рика, а часть отражается от него. Поглощение и отражение энергии эквивалентно
уменьшению коэффициента усиления антенны. Кроме того, многократное отраже-
ние энергии от обтекателя, антенны и близлежащих частей корпуса летательного
аппарата приводит к искажениям главного лепестка и к росту уровня боковых
лепестков. Наконец, часть отраженной энергии может попасть в облучатель и при-
вести к падению К^в в волноводном тракте. Поэтому обтекатель должен обладать
максимальной радиопрозрачностью, т.е. минимальным поглощением и отражением
энергии.
Радиопрозрачность обтекателя зависит от поляризации падающей на
него волны: она различна для случаев параллельной и перпендикулярной
поляризации (электрический вектор соответственно лежит в плоскости па-
дения и перпендикулярен ей). Поэтому влияние обтекателя может проявлять-
ся в изменении поляризации волны.
Как будет показано ниже, влияние обтекателя может проявиться также
в изменении положения главного лепестка относительно антенны, что при-
ведет к ошибкам при определении направления на пеленгуемую цель. Все эти
изменения должны находиться в допустимых пределах. К нерадиотехническим
требованиям относятся требования к механической прочности, теплостойкос-
ти, влагостойкости, устойчивости против эрозии (вызванной влиянием песка,
пыли, гидрометеоров).
17.1.3. Материалы обтекателей [3] весьма разнообразны. На дозвуковых ле-
тательных аппаратах широко применяются пластмассы, в частности, полистирол,
обычно в виде пенистой структуры. Применяются также слоистые или сотовые
конструкции из стеклоткани, пропитанной различными смолами — эпоксидной,
фенольной, силиконовой. Теплостойкость этих материалов на больших скоростях
полета недостаточна. В этих случаях находят применение керамопластики (смесь
Обтетсатели антенн и поюрылпия объектов* снижаютл^ие ...
621
слюды со стеклянным связующим материалом), пирокерамика (термически об-
работанное стекло), керамика на основе кремнезема. Наземные обтекатели часто
собираются из отдельных плоских диэлектрических панелей или представляют
собой надувные эластичные оболочки.
В настоящее время в нашей стране и за рубежом большое внимание уделяется созданию
новых материалов и разработке новых технологических методов изготовления обтекателей.
Удовлетворить сложный комплекс требований, предъявляемых к антенным обтекателям, в
значительной степени можно улучшением характеристик (радиотехнических, термичес-
ких и механических) применяемых материалов. В различных диапазонах используют разные
радиопрозрачные материалы. Материалы антенных обтекателей включают пластики,
керамические и композиционные материалы, материалы с металлическими элемен-
тами, а также материалы покрытий для защиты от дождевой эрозии, обледене-
ния, грозовых разрядов и т.д.
Пластики являются наиболее широко применяемыми материалами. Они обеспе-
чивают высокий коэффициент прохождения электромагнитной энергии, имеют
сравнительно небольшую массу и удобны технологически. Стеклопластики на ос-
нове эпоксидной и некоторых других смол обладают хорошей теплостойкостью. По-
лиамидные пластики, армированные кварцевым волокном, обеспечивают хорошие
конструктивные и радиотехнические характеристики, стабильность свойств в ши-
рокой полосе частот и температур. Тангенс угла диэлектрических потерь tgft для
большинства из этих материалов не более 0.03, диэлектрическая постоянная ег
колеблется от 3.2 до 4.7-5.0.
В многослойных конструкциях обтекателей для слоев большой плотности широко
используются стеклотекстолиты (стеклоткань плюс смола); для слоев малой плотнос-
ти применяются сотовые структуры из стекла или хлопчатобумажных тканей, стек-
лосетчатые материалы и т.п. Однако такие композиционные материалы недостаточно
однородны, что приводит к дополнительным искажениям амплитудных и фазовых
характеристик.
В отличие от стеклотекстолитов керамика и стеклокристаллические материалы весь-
ма однородны и дают меньший разброс параметров. Керамические материалы (ситал-
лы) используются для малогабаритных обтекателей ЛА. Диэлектрическая постоянная
этих материалов выше ( &r = 5.5-9.3), а активные потери малы ( tg& < 0.001). Обте-
катели из ситалла и подобной керамики могут успешно применяться при сверхвысо-
ких скоростях и работать в условиях жесткого термоудара (с темпом нагрева до
250-300 °C). Из-за малой толщины стенок они практически не искажают характерис-
тик антенны.
Большие возможности для улучшения как механических, так и радиотехничес-
Рис. 17.2. Металлический перфорированный обтекатель [3]
622
ГЛАВА 17
ких характеристик антенных обтекателей открывает использование диэлектричес-
ких стенок с металлическими элементами, представляющими собой реактивные ре-
шетки. Еще большими возможностями в этом направлении обладают металлические
перфорированные поверхности на диэлектрической подложке. Пример опытной раз-
работки такого обтекателя, представляющего собой двумерную щелевую решетку,
показан на рис. 17.2, где 1 — слой диэлектрика; 2 — металлический слой; 3 — щели
с клиновидными кромками.
17.1.4. Особенности конструкций обтекателей [3]. Остановимся кратко на
особенностях конструкции и расчета обтекателей ЛА [3]. Большинство антенных
систем СВЧ закрывается обтекателями или располагается за радиопрозрачными
окнами.
При сверхзвуковых скоростях полета в условиях работы обтекателей возника-
ют следующие особенности.
1. Аэродинамический нагрев внешней поверхности и стенок обтекателя. Это
приводит к необходимости использования термостойких материалов и создания
гладких внешних поверхностей обтекателей. С увеличением скорости температура
растет. Так на вершине носового обтекателя современного самолета температу-
ра достигает 250-300 °C, а в некоторых случаях 1400-1500 °C и выше. При рез-
ком изменении температуры пограничного слоя большой температурный градиент
внутри стенки может привести к разрушению обтекателя. Кроме того, антенная
система в ряде случаев требует принудительного охлаждения из-за значительного
повышения температуры в антенном отсеке.
2. При больших скоростях полета сквозь полосу осадков за счет ударов ка-
пель дождя, снега, града происходит постепенное разрушение обтекателя - эро-
зия. Вершина обтекателя значительно больше подвержена эрозии, чем боковые
поверхности, и поэтому должна защищаться в первую очередь (специальным пок-
рытием, металлическим наконечником и т.п.). Эрозия может возникнуть также за
счет испарения нагретого материала при обтекании воздухом, например, при
быстром вхождении ЛА в верхние слои атмосферы. Для борьбы с этим явлением
необходимо применять жаростойкие материалы.
3. Поверхность обтекателя даже при сравнительно небольших скоростях по-
лета электризуется вследствие трения о частицы снега, дождя, крупинки льда.
Это может привести к импульсным разрядам и образованию короны. Для отвода
заряда от диэлектрика на металлический корпус могут использоваться полупро-
водниковые покрытия, которые при правильном выборе их проводимости не будут
заметно ухудшать радиопрозрачность обтекателей.
Остановимся на особенностях работы антенных систем РЛС, навигационных
и других радиостанций, закрытых обтекателями. Антенны большинства указан-
ных радиостанций имеют управляемые (сканирующие) ДН, поэтому угол падения
электромагнитной волны на стенку обтекателя в процессе работы антенны изменя-
ется. Кроме того, в ряде случаев антенны, закрытые обтекателями, должны рабо-
тать в широкой полосе частот или на нескольких разнесенных частотах.
Таким образом, обтекатели ЛА должны обеспечивать в рабочем диапазоне час-
тот хорошее согласование внутреннего и внешнего пространства обтекателя при
прохождении электромагнитной энергии через его стенку под различными углами
падения(для уменьшения искажений в амплитудном распределении). Далее, при
сканировании на разных участках волнового фронта падающей волны в стенках
Обтекатели антенн и покрытия объектов, снижающие ...623
обтекателя создаются различные набеги фазы, которые приводят к фазовым ис-
кажениям и, следовательно, к ошибкам пеленга и ухудшению точностных харак-
теристик.
Кроме указанных амплитудных и фазовых искажений падающей волны при про-
хождении ее через стенки обтекателя, возникают искажения диаграмм направ-
ленности за счет возбуждения вторичных волн на участках с резким нарушением
регулярности поверхности обтекателя и возбуждения поверхностных волн на об-
текателе.
Перейдем к рассмотрению основных вопросов проектирования антенных обтека-
телей ЛА. Главными из них являются выбор формы обтекателя, материала для
обтекателя и структуры его стенок.
Решение всей задачи в целом для системы антенна - обтекатель может быть
получено только при одновременном учете как аэродинамических и механических,
так и радиотехнических требований.
Остановимся коротко на решении каждой задачи в отдельности.
1. Форма обтекателя ЛА определяется почти исключительно требованиями ми-
нимального аэродинамического сопротивления и зависит от места расположения
антенны. Основные типы обтекателей представлены на рис. 17.3.
К первой группе относятся носовые обтекатели; размеры их могут колебаться от
небольших конусов с диаметром основания (4-5) X ( X —длина волны) до крупногаба-
ритных тел вращения с параболической или оживальной образующей с диаметром
основания (20-40) X (рис. 17.3, а).
Вторую группу составляют обтекатели, устанавливаемые в нижней части фю-
зеляжа и защищающие антенные устройства навигационных и сходных с ними
РЛС. Продольные размеры обтекателей этой группы, как правило, 2,5-3 м и более 1
(рис. 17.3, б).
В третью группу объединены обтекатели, имеющие конфигурацию плоских или
слабоизогнутых поверхностей (рис. 17.3, в), закрывающие вырезы в (фюзеляже.
К последней группе можно отнести все остальные типы обтекателей, напри-
мер, обтекатели в виде двугранного клина, расположенные в кромке крыла
(рис. 17.3, г).
Из обзора типов обтекателей следует, что их форма практически полностью
диктуется конфигурацией ЛА. Только в инфракрасном диапазоне волн форму об-
текателя выбирают, исходя из требований к качеству изображения объекта. В этом
случае могут использоваться только сферические или пирамидальные обтекатели.
Все другие формы (в том числе и конические) приводят к недопустимо большим
Рис. 17.3. Основные типы антенных обтекателей [3]
624
ГЛАВА 17
Рис. 17.4. Конструкции стенок обтекателей:
1 — однослойная монолитная стенка; 2 — трехслойная стенка с плотными внешними сло-
ями; 3 — пятислойная структура; 4 — семислойная структура;
5 — трехслойная с плотным внутренним слоем;
6 — структуры с реактивной решеткой (однослойные и многослойные) [3]
искажениям теплового пятна. Для скоростных объектов предпочтительными явля-
ются пирамидальные обтекатели с 8-10 гранями и углом при вершине, меньшим
или равным 40°.
17.1.5. Выбор структуры стенок обтекателей. В отличие от решения пер-
вых двух задач проектирования обтекателей (выбор формы и материала) струк-
туру стенок определяют, исходя, главным образом, из радиотехнических требо-
ваний.
Выбором соответствующей конструкции и материала стенок достигают необхо-
димой радиопрозрачности обтекателей в заданном диапазоне волн и секторе углов
сканирования. По конструкции стенок обтекатели делятся на однослойные, много-
слойные (трех-, пяти-, семислойные), с плавно изменяющимися свойствами и т.п.
В однослойные и многослойные стенки могут быть вмонтированы металлические
каркасы, представляющие собой для проходящих волн реактивное сопротивление.
На рис. 17.4 изображены варианты конструкций стенок обтекателя. Однослойные
стенки, для обеспечения хорошей радиопрозрачности и фазовых характеристик
прошедшей волны в заданном секторе углов падения могут быть по толщине полу-
волновыми или существенно меньшими длины волны. Многослойные стенки с той
же целью выполняются с различным законом изменения плотности слоев: чере-
дующейся или увеличивающейся от периферии к центру стенки. Решетки метал-
лических элементов в зависимости от формы и размеров элементов представляют
собой для проходящей волны индуктивное или емкостное сопротивление и также
улучшают амплитудные и фазовые характеристики поля излучения при прохож-
дении через стенки обтекателей.
Критерием пригодности выбранной структуры является выполнение требова-
ний по радиопрозрачности и фазовым искажениям в рабочем диапазоне частот
при всех возможных углах падения электромагнитной волны на стенки обтекате-
Обтекатели антенн и покрытия объектов, снижающие ...
625
ля, изменяющихся при сканировании лучом антенны.
Расчет диаграммы направленности антенны с учетом обтекателя разбивается
на два этапа: 1) нахождение искаженных обтекателем амплитудных и фазовых
характеристик прошедшей волны; 2) расчет по этим характеристикам ДН всей
системы «антенна — обтекатель» в дальней зоне,
Влияние обтекателя на ДН антенны можно охарактеризовать коэффициентом
прохождения Тф) электромагнитной волны через стенки обтекателя. Коэффици-
ент прохождения является функцией угла падения волны на обтекатель и может
быть выражен через коэффициент отражения Г(0) (в пренебрежении потерями в
стенках):
|Т(Р)|2 = 1 - |Г(Р)|2 .
В общем случае при наличии в обтекателях участков с малыми радиусами кри-
визны (соизмеримыми с длиной волны) определение комплексных коэффициентов
Т(р) и Г(р) оказывается весьма сложным. Один из наиболее распространенных ме-
тодов заключается в представлении стенки обтекателя в виде эквивалентной сту-
пенчатой линии, состоящей из отрезков с разными волновыми сопротивлениями и
геометрическими длинами. Геометрическая длина каждой ступени равна толщине
одного слоя, а волновое сопротивление эквивалентного отрезка линии равно вол-
новому сопротивлению соответствующей среды и, как известно, зависит от поля-
ризации падающей волны и угла ее падения.
Волновое сопротивление Wj и электрическая «толщина» у г- каждого слоя много-
слойной стенки определяются из следующих соотношений:
а) при перпендикулярной поляризации поля падающей волны
Wi = -..-......—
J% - sin2 р
(17.1.1)
б) при параллельной поляризации волны
л/8,- - sin2
Wi=^--------
где — определяется по той же формуле (17.1.1); — толщина слоя; 8г- — от-
носительная диэлектрическая постоянная; Р — угол падения электромагнитной
волны на стенку обтекателя (рис. 17.5, а).
Если в слоях диэлектрической стенки заключены двумерные решетки из
металлических элементов, образующие пространственные реактивности для про-
ходящей волны, то в эквивалентных линиях они учитываются сосредоточенными
реактивностями. Место их включения в линии соответствует месту установки ре-
шетки в слое.
Для определения коэффициента отражения при заданной конструкции стенки
обтекателя можно, используя аналогию с длинными линиями, применить круговые
диаграммы полных сопротивлений. На практике допустимое значение коэффициен-
та прохождения должно приблизительно удовлетворять условию Т(р) > 0.75.
Необходимо иметь в виду, что круговые диаграммы дают невысокую точность
расчетов фазовых характеристик при хорошем согласовании стенок, так как при
этом соответствующие характеристики входного сопротивления лежат вблизи цен-
тра диаграммы, и небольшое линейное смещение их приводит к большим ошибкам
626
ГЛАВА 17
а)
Рис. 17.5. К выбору отсчета углов при расположении антенны под обтекателем (а) и ДН
антенны с обтекателем (б) [3]
в отсчете электрической длины линий (фазы).
Зная коэффициент прохождения Т электромагнитной волны через стенки об-
текателя, сечение ДН антенны в плоскости, близкой к максимуму излучения, с
учетом влияния обтекателя можно определить по формуле
1
/(6) = f Es |Т(е, х)| eika sin eeiv(e-x)dx,
-1
где Е$ — амплитудное распределение поля по раскрыву антенны без обтекателя;
Т(0,х) — коэффициент прохождения, зависящий от угла 0 и текущей координаты
х раскрыва антенны, отсчитываемой от его середины (см. рис, 17.5) \g(0,a?)— на-
бег фазы волны, прошедшей через обтекатель, зависящий от тех же переменных.
На рис. 17.5, б для примера показана ДН (в пределах главного лепестка) зер-
кальной антенны с раскрывом 2а = 15А, и пятислойным обтекателем при отклоне-
нии антенны относительно продольной оси на угол 0гЛ = 50°. Видим, что влия-
ние обтекателя привело к смещению максимума ДН на величину порядка 12’ при
почти неизменной форме главного лепестка.
В отсутствие отклонения луча антенны ( 0гл = 50°) смещения максимума ДН не
наблюдается.
Большой практический интерес представляет расчет конструкции стенок и вы-
бор материала по заданным амплитудно-фазовым характеристикам обтекателей,
т.е. решение задачи синтеза. Следует различать параметрический и структурный
синтез.
Параметрический синтез предполагает определение параметров каждого слоя,
если предварительно выбрана структура стенки; структурный синтез решает бо-
лее общую задачу — построение оптимального обтекателя с расчетом конструкции
Обтекатели антенн и покрытия объектов^ снижаюзцие ...627
стенок и их параметров. Благодаря электродинамической эквивалентности диэлект-
рических слоистых стенок со ступенчатыми линиями передачи, при решении задач
их синтеза пригодны хорошо разработанные методы синтеза СВЧ ступенчатых
переходов и фильтров.
По аналогии с фильтрами можно рассчитывать стенки с функциями рабочего
затухания чебышевского или максимально плоского типа в рабочей полосе частот,
Функция рабочего затухания, введенная по аналогии с фильтрами, равна обрат-
ной величине квадрата модуля коэффициента прохождения
В методе син-
теза обтекателей, заимствованном из теории фильтров, в качестве критерия опти-
мизации используется минимизация модуля коэффициента отражения в рабочей
полосе частот с учетом различных углов падения волны на стенки обтекателя.
Дальнейшее развитие метода синтеза должно идти по пути создания оптималь-
ных обтекателей. Критериями оптимизации могут служить минимальные искажения
амплитудно-фазового распределения проходящей волны в рабочей полосе час-
тот и требуемом секторе сканирования, минимальные отклонения равносигнальной
зоны и др. Подобная оптимизация по одному или нескольким критериям может быть
получена из решения соответствующей минимаксной задачи с использованием сов-
ременных методов и средств вычислительной математики.
17.1.6. Армированные обтекатели [17]. По принципу действия армирован-
ные обтекатели напоминают многослойные. Действительно, диэлектрический лист
и армирующая однолинейная сетка образуют слоистую структуру (рис. 17.6). Выби-
рая должным образом диаметр проводов и расстояние между ними (от отношения
этих величин к длине волны зависит коэффициент отражения сетки), можно до-
биться взаимной компенсации отражений от сетки и диэлектрического листа [17].
Рис. 17.6. Армированный обтекатель: 1 — диэлектрик; 2 — провод
Рис. 17.7. К пояснению влияния обтекателя на ДН антенны:
1 — антенна; 2 — обтекатель [17]
628
ГЛАВА 17
17.1.7. Влияние обтекателя на диаграмму направленности антенны.
На ДН слабонаправленной антенны (например, облучателя) обтекатель оказыва-
ет влияние, однако некоторое изменение формы ДН в этом случае обычно не
имеет существенного значения. Иначе обстоит дело в случае остронаправлен-
ных антенн. Даже небольшое угловое смещение ДН может оказаться сравнимым с
шириной главного лепестка и недопустимым. Поясним влияние обтекателя с по-
мощью рис. 17.7. Предположим что по раскрыву антенны L распределение поля
является симметричным по амплитуде и синфазным. ДН антенны определяется
по формуле
7i(6) = (l + cos
i/sinG exp[iO1(t/)]di/,
где е^у) - амплитудное распределение поля по раскрыву антенны без обтекателя,
Ф^г/) - набег фазы волны по антенне, зависящей от тех же переменных.
Максимум ДН будет ориентирован перпендикулярно раскрыву антенны.
Волна падает на обтекатель под различными углами. Чем больше угол паде-
ния, тем длиннее путь, проходимый волной в диэлектрическом слое, тем,
следовательно, сильнее затухание в нем и больше вносимое слоем запаздывание
по фазе.
Рассматривая воображаемый раскрыв антенны за пределами обтекателя, мож-
но считать, что из-за влияния обтекателя распределение поля становится несим-
метричным по амплитуде и несинфазным. ДН при этом определяется по формуле
• ( 2тг
/2(0) = (l + cose) е2 (у)Т(у) ехр г —
г/sin О ехр[гФ2(г/)]йу,
гдее2(а?) - амплитудное распределение поля по раскрыву антенны без обтекателя,
Ф2(х) - набег фазы волны по антенне, зависящий от тех же переменных.
Главный лепесток ДН отклонится на некоторый угол а от оси антенны в сто-
рону отставания фазы (на рис. 17.7) и, так как функция Ф(х) является, вообще
говоря, нелинейной, то возрастет уровень боковых лепестков и исказится форма
главного лепестка. Величина и знак угла а изменяются, когда при сканировании
ДН она отклоняется от оси обтекателя. Расчет обтекателя должен производиться с
учетом допустимого значения угловой ошибки а.
ДН остронаправленной антенны может исказиться при неточном выдерживании
толщины стенки обтекателя. Действительно, обтекатель переменной толщины, по
существу, является диэлектрической линзой, которая превращает падающий на
нее параллельный пучок лучей в пучок расходящихся лучей. Поэтому предъявля-
ются жесткие требования к постоянству толщины стенки обтекателя. В необходи-
мых случаях производится доводка обтекателя по толщине стенки. Если на повер-
хность или внутрь обтекателя попадают гидрометеоры или другие частицы (пыль,
капли масла и т. д.), то они вызывают искажение ДН и, кроме того, уменьшают
радиопрозрачность обтекателя в процессе его эксплуатации, что может повлиять
на форму ДН и радиопрозрачность.
Обтекатели антенн и покрытия объектов, снижающие ...629
17.2. Покрытия объектов, снижающие
их радиолокационную видимость
К одним из покрытий объектов, снижающих их радиолокационную видимость,
относятся малоотражающие конформные покрытия. В настоящее время сущест-
вуют различные способы их создания. Ниже рассмотрим конформные покрытия,
формируемые на основе киральных слоев [133]. Одним из свойств киральной среды
является деполяризация электромагнитных волн (ЭМВ), которая может привести
к уменьшению коэффициента отражения от покрытия или к изменению угла отра-
жения ЭМВ от объекта, т.е. к снижению его радиолокационной видимости.
Обычно киральные среды в СВЧ — диапазоне изготавливают путем внедрения в
диэлектрик киральных металлических элементов: спиралей, плоских проводящих
элементов S - формы и т.д. [133]. Напомним, что понятие киральности в широком
смысле связано с проявлением зеркальной асимметрии объекта. Простейшим при-
мером кирального элемента может служить кольцо с разрывом (рис. 17.8). С помо-
щью таких колец и создается малоотражающее конформное покрытие объектов,
снижающее их радиолокационную видимость. Для объяснения принципа работы
такого покрытия ниже решается задача дифракции плоской электромагнитной
волны на идеально проводящем разомкнутом кольце.
Очевидно, что киральная среда будет проявлять свои свойства в том случае,
если на металлическом кольце будет возникать ток проводимости, т.е. напряжен-
ность магнитного поля падающей волны должна иметь перпендикулярную состав-
ляющую на плоскости кольца.
17.2.1. Дифракция плоской электромагнитной волны на идеально про-
водящем разомкнутом кольце [135]. В научной литературе [21, 43] давно ре-
шена двухмерная задача дифракции плоской электромагнитной волны (ПЭМВ) на
бесконечном идеально проводящем цилиндре. Аналогичная задача решена и для
диэлектрического цилиндра [1]. В [134] решена задача дифракции ПЭМВ Е-и
Н-поляризацией на круглом диэлектрическом цилиндре с идеально проводящей уз-
кой металлической полоской конечной длины на боковой поверхности. Было пока-
зано [134], что диаграмма направленности дифрагированного поля существенно
зависит от угла падения волны по отношению к металлической полоске на диэ-
лектрическом цилиндре. Ниже решена задача дифракции ПЭМВ Н -поляризации
на идеально проводящем разомкнутом кольце. Показано, что при определенном
размере зазора разомкнутого кольца дифрагированное поле концентрируется в
области зазора [135].
Постановка и физическая модель задачи
Геометрия задачи поясняется на рис.17.8. На идеально проводящее бесконеч-
но тонкое разомкнутое кольцо, расположенное на воображаемой цилиндричес-
кой поверхности р = а, под углом <р0 падает ПЭМВ. Ширина полоски 2h, угловая
длина 22,, линейная длина 2Zn = 2£а , угловая ширина зазора 2А = 2л - 2£,,
ная ширина зазора 213 = 2(л - Q sin(S,) / S, . На поверхности металлического
линей-
кольца
(р - а, ср < %, z < h) выполняется граничное условие:
+Ё{®} =0, (17.2.1)
где Ё^ - вектор тангенциального электрического поля, возбуждаемый вектором
630
ГЛАВА 17
пэмв
Рис. 17.8 Геометрия задачи
ц, Е^р - вектор тангенциального электрического
поверхностнои плотности тока ц
поля ПЭМВ, падающей на кольцо.
При решении задачи вводятся следующие упрощения:
— проводник предполагается идеально проводящим, бесконечно тонким и до-
статочно узким ( 2h
тве), поэтому можно учитывать только продольную
ной плотности тока т|ф(ф, z);
— на концах полоски поверхностная плотность
Пф(ф = |^|^) = о;
— распределение поверхностной плотности тока по
нии считается квазистатическим [25]:
где X - длина волны в свободном пространс-
составляющую поверхност-
тока обращается в нуль:
ширине в первом приближе-
ПФ(Ф,г) =
/(ф)
(17.2.2)
где /(ср) ~ неизвестная функция, описывающая азимутальное распределение по-
верхностной плотности тока.
Сингулярное интегральное уравнение
Пусть на структуру под углом ф0 падает ПЭМВ с Н -поляризацией,
три составляющие: H^\Ep ,Еф\ Объемная плотность тока на полоске в
денных упрощений имеет вид:
;ф(р,Ф,2) = г|ф(ф,2)5(р - a); |z| < Ь,|ф| <
В данной постановке имеем две компоненты векторного потенциала:
эт(ф - ф'Г
7 7 G(p,q)dV',
соэ(ф - ф )
имеющая
силу вве-
(17.2.3)
" Ар(р)
где функция Грина G(p,q) определяется следующим образом:
(17.2.4)
(17.2.5)
G(p,q) = —
4л
а для расстояния R между точкой источника Q = {р<р', г’} и точкой наблюдения
р = {р,ср,z} в цилиндрической системе координат справедлива формула:
Обтргсатели антенн и покрытия объектов ышжаюицие ...
631
Подставляя (17.2.3) в (17.2.4), получаем компоненты векторного потенциала:
^р(р)! f . , Гsin(q> - <р')'
1 4 = а Пф(<Р >г Л (
/4ф(Р)] J |cos((p- <p)J
*S*
G(p, a, ipz ')d<p' dz',
(17.2.6)
где 5 - поверхность полоски (рис. 17.8). Компонента Е„ электрического поля и век-
торный потенциал связаны дифференциальным соотношением [21]:
Я<р(р) =
aWc
ik
к2Ау(р) + gradqj div А(р)
(17.2.7)
где Wc — характеристическое сопротивление среды. Подставляя (17.2.6) в (17.2.7),
получаем Еф как функцию от поверхностной плотности тока т|ф, распределенного
по поверхности S полоски:
ч aW(
Е<р(р) = —
гк
]п<р(«) Ki(p,s) —
Здесь:
Кх (р, s) = к соб(ф - ф ')G(p, s),
К2(р, s) = + 8ш(ф - ф ')G(p, s)
где под символом s = {a,<p',z'} понимается точка, принадлежащая поверхности S
вибратора. Учитывая, что д / 6<р —> -д / Эф', получаем:
Е^Р) =
J JncpCtp'^Wp^
aW(
ik
£ h д
] т|ф(ф',z') — К2(р,ф',z')dz’dip'.
(17.2.8)
Вводя нормированные переменные:
(17.2.9)
d = h / a, г = kp, & - ka
с учетом (17.2.2), перепишем (17.2.8) в виде:
Effi(r,t,x) V V Q
—= J/(t,)Dp(r,t,x,t')dt’+d J/(t') —Dp(r,t,a?,t')dt',
c -1 -1
где:
(17.2.10)
dx', p = 1,2.
4TC
K2(r,t,a?,t',x') =
(i$RH +1) sin(^(t -1')) e49Rw
R 2 4л &RH
632
ГЛАВА 17
RH = 7г2 / О2 +1-2(r/0)cos(^(t-t')) + d2(T-a:')2.
Используя граничное условие (17.2.1) и переходя к производной поверхност-
ной плотности тока по переменной t', при г = 3 , х = 0 получаем интегральное
уравнение, записанное относительно функции f(t') и ее первой производной f \t')
= W)/a’:
iW„d
= 5 Jf(t')Kj(t,t')dt' - J/'(t')K2(t,t')dt
(17.2.11)
К1(м.) = Ар°^^-))£^
(17.2.12)
K2(t,f) = — [(i&L +1) ~»^—^—dx.
VT^2 l3
В (17.2.12) L = 5^2(1 - cos(^(t -1'))) + d2a?2 . Несложно показать, что ядра Kp(t,t’)
(р = 1,2) интегрального уравнения (17.2.11) в неявном виде содержат особенности
(это следует из свойств полных эллиптических интегралов К(т) и Е(т) [26], к ко-
торым сводится асимптотика ядер):
UmK1(t,t') = —— lnt-f , limK2(t,f) =— -—♦ (17.2.13)
1 2nd t-+t' 2nd^t-t'
Переписывая (17.2.11) с учетом (17.2.12), (17.2.13), получаем сингулярное интег-
ральное уравнение следующего вида (t,t' е [—1; 1]):
4'1)(0= - j/'(f)R2(t,t')dt'-
t -t' dt' +
dt',
(17.2.14)
где:
(17.2.15)
с = 2лЭ'£, / (iWc) — константа.
Решение сингулярного интегрального уравнения. Численные результаты
Решать СИУ (17.2.14) будем методом моментов. Неизвестная функция f(t') и ее
первая производная /’(f) представляются в виде полиномиальных рядов:
/(t') = ^Vl-t'2Afc!7)c_1(t'); = \ (17.2.16)
fc=i fc=i Vl-t'2
где Тд. (х) — полином Чебышева первого рода порядка k, (х) - полином Чебыше-
ва второго рода порядка к, А^ - неизвестные коэффициенты разложения.
633
Обтекатели антенн и покрытия объектов, снижающие ...
Подставляя разложения (17.2.16) в СИУ (17.2.14), имеем:
=
= y,Ak [71 -1 '2 Uk^(t '^(t, t ')dt' + У Akk [ Tk
dt'- (17.2.17)
N
Tk(t')
- — dt .
Сингулярные интегралы в (17.2.17) определяются аналитически:
Tk(t')
к
С(3) = 71
к 4(к -1)
-1)
Представим разностные ядра (17.2.15) в виде рядов Фурье (р = 1,2):
im—w
т=-со
(17.2.19)
тр
-im—w
2 dw,
Используя известные разложения экспоненты по полиномам Чебышева и фун-
кциям Бесселя [26]
гт t b_i .zc_i7 «7ь(штс /2)
2 =2У(-1Г ---2-2lZ/c_1(t),
г—7 тл / 2
к=1
• л . N
—2771 — t .
2 = 2,(2-60)fc)(-l)fc?Jfc(m7i/2)Tfc(t).
к=0
(17.2.20)
. 71
im—t
е 2
= 2Yin-lnJn{m7l/2)Un_l(t).
“ тп / 2
П=1
(17.2.21)
получаем две двойные суммы:
N N
е 2 =Y y(-l)fc?+nJcnJcfc(m7t/2)Jcn(m7t/2)Ufc_1(t,)Un_1(t), (17.2.22)
634
ГЛАВА 17
im-(t-t')
е *
N N
где:
хСп(тл / 2)Jk(mn / 2)Tfc(t ,)Un_1(t)],
(17.2.23)
Jv (ас)
Cp(x) - 2—^—
* x
Подставляя (17.2.22) и (17.2.23) в (17.2.19), получаем разложения разностных
ядер R^tft1) и R2(t,t') в двойные полиномиальные ряды:
N N
п=1 к=1
R2(t,t')
N N
= YYankTk(tVn-lW,
п=1 к=0
где:
м
ип,к= Е ik+n^RmlCk(mn / 2)Сп(тл / 2),
т=-М
М
anl= Е ^k^-S0,k)in+k~1nRm2Cn(mn/2)Jk(mn/2),
т=-М
(17.2.24)
(17.2.25)
— матричные коэффициенты,
|1,п = к,
&пк =
’ 0,п?к
V 7
— символ Кронекера.
Подставляя (17.2.24) в (17.2.17) с учетом ортогональных свойств полиномов Че-
бышева :
^7=^t = 7-4— Уь f7iy?u„(t)Ufc(t)dt = £б„Л,
VI - Г 2 “ йк,0 _* 2
получаем систему линейных алгебраических уравнений (СЛАУ) для определения
неизвестных коэффициентов разложения Ак в (17.2.16):
N
у = Е +₽«л - э2^2С -
к=1
где
м
P'r'Vo S ik+nnkRmlCk(mn / 2)Jcn(mn / 2),
2 т=-М
М
₽п,к=л Е (^kin+k^kRm2Cn(mn/2)Jk(rnn/2),
т=-М
= Cfc ^n-l,k+l + Ск ^п-1,к-1 + Ск ^п-1,к-3>
Обтекатели антенн и покрытия объектов, снижающие ...
635
Е„ = | о JVl-t2E$m (t)Un^ (t)dt.
-1
В дальнейшем мы будем рассматривать четыре случая падения ПЭМВ:
1. Падение со стороны металлической полоски (угол фд = 0, волна распростра-
няется против оси х). В этом случае E^m ПЭМВ и электрическое поле Е^1, созда-
ваемое поверхностной плотностью тока т|(р, описываются выражениями
E™(r,t,x) = e^^-E^lt) =
(17.2.26)
г = /ср, t = ф / ^,Х = Z / I.
2. Боковое падение (угол фд = 90° , волна распространяется против оси у ). При
этом выражение для компоненты электрического поля E£w ПЭМВ и электрическо-
го поля Е^1', создаваемого поверхностной плотностью тока т](р, имеют вид
Е:'т (г, t, х) = eIrsin^,E^)(t) = -e,9sin^. (17.2.27)
3. Падение со стороны зазора (угол <Pq = 180° , волна распространяется вдоль
оси х), при этом:
Ecm(r,t,x) = e~ir cos , Е™ (t) = -е-*Эс0£У (17.2.28)
в)
Рис 17.9. Распределение поверхностной плотности тока по полукольцу;
1 — действительная часть ru(£), 2 - мнимая часть ^„(t) '> а) ~ Фо = 9 > 6) - ф0 = 90° ,
в) - ф0 = 180, г) - ф0 = 270 [135]
636
ГЛАВА 17
F^ 100 80
260 280
б)
F^ 100 80
260 280
г)
Рис 17.10. Распределение величины F„((p) в дальней зоне ( /ср = 2000 ) при различных углах
падения (р0 ПЭМВ на полукольцо (геометрия структуры и ПЭМВ приведены непосредс-
твенно на графиках), имеющее электрическую длину L3 = 1
4. Боковое падение (угол фо = 270° ,
этом:
волна распространяется вдоль оси у). При
Ec™(r,t,x) = е"sin = -e-i9sin^ . (17.2.29)
Рассмотрим решение СИУ (17.2.14) в перечисленных случаях для полукольца
( 2S, = 180°), имеющего электрическую длину L3 = 2ln / X -1, где 21п = 2^а - ли-
нейная длина металлической полоски; ln / h = Юл, волновое сопротивление среды
Wc - 120л. При этом & = 2па / Z = Ьэп / £, = 2, d = £,/г / ln = 1 / 20. Результаты расче-
та приведены на рис.17.9. На рис. 17.10 приведены распределения нормированной
амплитудной диаграммы направленности дифрагированного поля:
Д(р(р,ф)
max (Р> Фо )
(17.2.30)
где Е([) (р, <р, z = 0) - напряженность дифрагированного электрического поля в даль-
ней зоне (/ср » 1), создаваемая поверхностными токами, приведенными на рис.17.9.
Обтекатели антенн и покрытия объектов, снижающие ...637
Рис 17.11. Падение ПЭМВ на разомкнутые кольца с различными электрическими длинами
Ьэ и соответствующие распределения величины F„(<p) в дальней зоне ( кр = 2000 ) [135]
На рис. 17.10 б,г представлены распределения амплитуды дифрагированного поля
для случая бокового падения ПЭМВ. В этом случае образуется четыре лепест-
ка, причем азимут максимума излучения образует с направлением падения угол,
приблизительно равный 270 градусам. На рис. 17.10, в показано распределение
в случае падения ПЭМВ со стороны разрыва. Максимум дифрагированного поля
находится на стороне падения ПЭМВ.
На рис.17.11 показано падение ПЭМВ на разомкнутые кольца, имеющие раз-
личную электрическую длину L3. Видно, что при L3 «1.15 обратное отражение
ПЭМВ отсутствует (17.11, б).
Расчеты показали, что разработанный алгоритм обладает хорошей внутренней
сходимостью — для достижения точности порядка 1% в разложениях (17.2.16)
достаточно удержать около 10 коэффициентов. Метод определения разностных
ядер, подтвердил свою эффективность. Даже при небольших значениях М (М < 10)
в разложениях (17.2.25) получается приемлемый результат (чего не наблюдается
в случае использования квадратурных сумм [26]). При моделировании использова-
лись значения N = 50 , М = 50.
17.2.2. Малоотражающее конформное покрытие. Малоотражающее покры-
тие состоит из трех слоев. Первый слой, лежащий непосредственно на защищаемом
объекте, - поглотитель, выполненный из радиопоглощающего материала, второй
и третий слои представляют собой взаимно ортогональные трехмерные решетки
из резонансных элементов в виде одинаково ориентированных разомкнутых ме-
таллических колец, внедренных в диэлектрик с относительной диэлектрической
проницаемостью е , зазоры разомкнутых колец ориентированы со стороны погло-
тителя (Рис. 17.12). Средний радиус а металлических разомкнутых плоских колец
с угловой длиной разрывов менее 90° и расстояние между соседними центрами
разомкнутых колец d определяются из соотношений:
где — центральная длина волны диапазона ЭМВ, падающих на защищаемый
объект, £ — относительная диэлектрическая проницаемость диэлектрика во вто-
ром и третьем слоях.
638
ГЛАВА 17
Высоты прямых
диэлектрических
параллелепипедов
А б)
длина прямых
диэлектрических
параллелепипедов
Рис. 17.12. Структура малоотражающего покрытия (а) и прямой диэлектрический парал-
лелепипед с решеткой в виде одинаково ориентированных разомкнутых плоских колец
на одной из его поверхностей (б) для создания 3 и 2 слоев поглощающего покрытия со
взаимно ортогональными трехмерными решетками: 3 — слой, составленный из горизон-
тально склеенных диэлектрических параллелепипедов (б); 2 — слой, составленный из
вертикально склеенных диэлектрических параллелепипедов; 1 - поглотитель;
А,Б,В,Г — обозначение граней прамого параллелепипеда
В качестве поглощающего слоя может быть использовано, например, покры-
тие, включающее в себя в качестве полимерного связующего синтетический клей
“Элатон” на основе латекса и в качестве магнитного наполнителя - порошкооб-
разный феррит или карбонильное железо при соотношении компонентов, мас.%:
синтетический клей “Элатон” на основе латекса 80-20, порошкообразный феррит
или карбонильное железо 20-80 [136].
Известен способ изготовления малоотражающего покрытия для электромагнит-
ных волн, включающий несколько слоев из различных пластмасс и формирование
на одной из их поверхности двухмерных решеток резонансных элементов [139].
Однако этот способ дает технологию изготовления только двухмерных решеток.
Целью изобретения является возможность создания форм малоотражающих пок-
рытий конформных поверхностям защищаемых объектов и технологию изготовле-
ния трехмерных решеток из резонансных разомкнутых плоских колец.
Способ реализуется следующим образом. На первом этапе на поверхность за-
щищаемого объекта наносится слой поглощающего материала (первый слой в
покрытии). На втором этапе создаются двухмерные решетки в виде разомкнутых
плоских колец, расположенных на линии, соединяющей их центры на одной из
поверхностей (грань А на рис. 17.12,6) одинаковых гибких прямых диэлектрических
параллелепипедов с перпендикулярной ориентацией зазоров колец по отношению
к ребру параллелепипеда, определяющих толщины второго и третьего слоев, и с
ширинами, равными длине между соседними центрами разомкнутых колец. Длины
прямых параллелепипедов определяются размерами защищаемого объекта. Для
Обтетсатели аптенн и покрытия объектов^ снижающие ...639
создания второго слоя покрытия прямые диэлектрические параллелепипеды скле-
ивают в горизонтальных плоскостях, причем поверхность (грань А на рис. 17.12,6)
с двухмерной решеткой из разомкнутых колец приклеивается к противоположной
поверхности (грани В на рис. 17.12,6) свободной от разомкнутых колец другого
параллелепипеда. Для создания формы покрытия конформной поверхности за-
щищаемого объекта необходимо сначала приклеить один гибкий прямой диэлек-
трический параллелепипед к слою из радиопоглощающего материала, так чтобы
плоскости разомкнутых колец были перпендикулярны поверхности из радиопогло-
щающего материала, и зазоры ориентированы к этой поверхности. Далее одновре-
менно приклеиваются две поверхности (грани) следующего гибкого прямого диэ-
лектрического параллелепипеда с поверхностями приклеенного параллелепипеда
и радиопоглощающего материала. Противоположную поверхность (грань) прикле-
иваемого параллелепипеда по отношению к двухмерной решетке (грань В на рис.
17.12,6) склеивают с поверхностью (гранью) с двухмерной решеткой приклеенного
прямого параллелепипеда, а перпендикулярную поверхность (грань) по отноше-
нию к поверхности (грани) с решеткой (Грань Г на рис. 17.12,6) к поверхности из
радиопоглощающего материала (слой 1). Операция повторяется пока полностью
не покрывается поверхность поглотителя. На третьем этапе аналогично создают
третий слой поглощающего покрытия, т.е. гибкие прямые диэлектрические парал-
лелепипеды последовательно склеиваются в вертикальных плоскостях и одновре-
менно приклеиваются ко второму слою. В результате в третьем и втором слоях
малоотражающего покрытия формируются взаимно перпендикулярные трехмер-
ные решетки из разомкнутых колец с ориентацией зазоров к поглотителю.
По отношению к поглотителю [137], в котором применяется система замкнутых
колец, образующих двухмерные решетки, используются решетки из разомкнутых
колец, поэтому предлагаемое малоотражающее покрытие является более широко-
полосным. Другим важным преимуществом предлагаемого покрытия по отноше-
нию к известному поглотителю является то обстоятельство, что используются
разомкнутые кольца, которые в отличие от замкнутых изотропных переизлучате-
лей, являются неизотропными переизлучателями электромагнитной мощности.
Ориентация зазоров разомкнутых колец с обратной стороны падения волны по
отношению к поглотителю выбрана из тех соображений, что происходит пере-
распределение максимума электромагнитной мощности в сторону поглощающего
слоя.
Рассчитанная амплитудная диаграмма направленности в азимутальной плос-
кости дифрагированного поля плоской ЭМВ Н-поляризации (вектор Н перпен-
дикулярен плоскости разомкнутого кольца) на металлическом разомкнутом коль-
це, расположенном в азимутальной плоскости в воздухе, показана на рис. 17.11,
сплошной линией на рисунке показана геометрия плоского кольца, стрелкой ука-
зано направление падения плоской ЭМВ. При такой ориентации разрыва дифра-
гированное поле направляется в область поглотителя и за счет этого уменьшается
коэффициент отражения ЭМВ от покрытия.
Для устранения зависимости коэффициента отражения от поляризации вол-
ны в третьем слое поглощающего покрытия (рис.17.12,а) вводится трехмерная ре-
шетка из разомкнутых колец, повернутых на 90° в меридиональной плоскости к
разомкнутым кольцам первой решетки во втором слое поглощающего покрытия,
при этом ориентация разрывов в кольцах остается по отношению к поглотителю.
640
ГЛАВА 17
Коэффициент отражения покрытия с двумя такими взаимно перпендикулярными
решетками практически не зависит от угла поляризации падающей на него вол-
ны.
Способ формирования трехмерных решеток заключается в предварительном
создании двухмерных решеток из одинаковых резонансных разомкнутых метал-
лических плоских колец, расположенных на линии, соединяющей их центры на
одной из поверхностей, определяющей высоту гибких диэлектрических паралле-
лепипедов с ширинами, равными расстоянию между соседними центрами разо-
мкнутых колец и длинами, определяемыми размерами защищаемого объекта.
Зазоры в разомкнутых кольцах ориентированы перпендикулярно к одному из
ребер поверхности прямого диэлектрического параллелепипеда, на которой сфор-
мирована двухмерная решетка. Разомкнутые кольца могут выполняться из метал-
ла, печатанием их рисунков электропроводящей краской, пастой, клеем, либо
используются методы напыления. Способ создания конформного малоотражаю-
щего покрытия следующий. На первом этапе на защищаемый объект наносится
слой поглотителя. При создании второго слоя поверхности (грани) с двухмерными
решетками гибких прямых диэлектрических параллелепипедов последовательно
одновременно приклеиваются в горизонтальных плоскостях к противоположным
поверхностям по отношению к двухмерным решеткам следующих прямых гиб-
ких диэлектрических параллелепипедов и перпендикулярной поверхности (грани)
прямого гибкого диэлектрического параллелепипеда к слою поглотителя так, что-
бы ориентации разрывов были направлены к поглотителю. Для создания третьего
слоя с двухмерной решеткой из резонансных колец прямые гибкие диэлектричес-
кие параллелепипеды последовательно склеиваются между собой в вертикальных
плоскостях и одновременно приклеиваются к поверхности второго слоя.
Возможные области применения: защитные малоотражающие покрытия для
поверхностей самолетов, космических аппаратов и других объектов и устройств
специального и бытового назначения.
20*
Парал^р^тгчрс^сий синтез при nppeicmuppea/нии антенн
641
Глава 18. Параметрический синтез при
проектировании антенн
18.1. Особенности расчета и проектирования антенн [3]
В последние годы расчет и конструирование современных антенн значительно
усложнились из-за увеличения числа характеристик, подлежащих определению,
а также из-за стремления оптимизировать и более точно рассчитывать характе-
ристики антенн, избегая экспериментальных проверок. Нахождение оптимального
варианта антенной системы по заданным требованиям значительно увеличивает
объем расчетов.
Известны различные методы расчета антенн, отличающиеся сложностью и
соответственно точностью результатов. На стадии предварительного проектиро-
вания необходимы приближенные методы, позволяющие специалистам, знакомым
лишь с общей теорией антенн и практикой их использования, определять основ-
ные характеристики новых типов антенн. Это привело к созданию инженерных
методик расчета с введением ряда приближений и упрощений, что повлияло на
точность расчета характеристик и ограничение пределов их применимости. Наряду
с этим интенсивно развиваются строгие методы расчета, позволяющие оптимизи-
ровать проектируемое устройство по тому или иному критерию с использованием
ЭВМ. Характеристики антенн, найденные с помощью приближенных инженерных
методик, могут быть уточнены строгими методами.
При расчете и проектировании антенных систем решение общей задачи прихо-
дится искусственно разделять на ряд отдельных частных задач. Решение этих
задач с учетом их взаимосвязи дает возможность рассчитывать характеристики
сложных антенных систем и искать вариант антенны, наиболее соответствующий
предъявляемым требованиям. Такой подход позволил создать независимые методы
инженерного расчета АР с электрическим сканированием, АФАР и их элемен-
тов.
За последнее время в конструировании и производстве антенн произошли
существенные изменения. Разнообразие используемых на практике типов антенн,
существенные их различия в зависимости от назначения, привели к возникнове-
нию ряда самостоятельных отраслей современного антенностроения с присущими
им конструкторскими решениями, используемыми материалами, технологией, ви-
дом производства и т. д. Такими уже сложившимися можно считать отрасли круп-
ного антенностроения, ФАР, АФАР, антенн летательных аппаратов и судовых
антенн, а также космических антенных систем. Намечается возникновение других
отраслей. В каждой из них свои специфика и особенности конструирования.
Остановимся на особенностях проектирования ФАР и АФАР. Сложность антен-
ных систем приводит к их высокой стоимости. Поэтому процесс проектирования в
значительной мере сводится к изысканию таких решений, которые с учетом клас-
са РЛС, требований размещения, мобильности, серийности производства, изме-
нения внешних воздействий и т.п. позволят найти приемлемый компромисс между
стоимостью антенной системы и ее характеристиками.
*/2 21 - Неганов
642
ГЛАВА 18
При проектировании ФАР на первый план выдвигается вопрос создания еще
в процессе разработки опытного образца РЛС крупной серии элементов антенн с
требуемыми параметрами и невысокой стоимостью. Поэтому уже в начале проек-
тирования ФАР должны быть рассмотрены технологические возможности отрас-
левой промышленности, создающей массовую элементную базу ФАР или АФАР,
определены варианты элементной базы для данного типа РЛС, и выработаны тех-
нические и экономические требования к каждому элементу с учетом его серийного
производства. Особенно важно на этом этапе определить возможность получения
в процессе промышленного выпуска элементов ФАР повторяемости значений их
параметров от экземпляра к экземпляру и сохранения этой повторяемости во всем
диапазоне изменений внешних воздействий.
Следующий этап проектирования - разработка вариантов функциональных
схем ФАР или АФАР, отвечающих заданным техническим требованиям, а также
учитывающих конструкторско-технологические особенности построения антенны.
На этом этапе целесообразно рассмотреть варианты построения, имеющие сущес-
твенные различия, например, пассивная ФАР и АФАР (на передачу или прием),
приемная ФАР с обработкой сигнала и управлением лучом - на несущей или про-
межуточной частотах и т. п. Это позволит более тщательно и детально оценить
возможности существующей технологии и выбрать в дальнейшем наиболее оп-
тимальный для данного типа РЛС вариант такой сложной системы. Существен-
ным моментом проектирования на этом этапе является расчет потерь потенциала,
вызванных применением в РЛС той или иной схемы АР. Должны быть учтены
как прямые потери энергии, например, в системе распределения мощности или
управления лучом, так и потери коэффициента усиления антенны, вызванные
дискретностью фазирования, ступенчатой аппроксимацией линейного фазового
фронта, отклонением луча от нормали или ошибками амплитудно-фазового рас-
пределения. Эти потери влияют на тактические характеристики системы. Прямые
потери можно пересчитать в потери коэффициента усиления ФАР и потенциала
РЛС. На потери потенциала в РЛС с ФАР сильно влияют ошибки фазового рас-
пределения, возникающие в раскрыве решетки и достигающие (особенно в АФАР)
значительных величин.
Статистическая теория антенн позволяет оценить падение коэффициента усиле-
ния и других характеристик ФАР в зависимости от статистики фазового распре-
деления в ее раскрыве. Для получения оценки необходимо знать эту статистику. В
многоканальных и многокаскадных системах, какими являются ФАР и АФАР. Эта
задача решается достаточно сложно.
Результаты расчета характеристик нескольких схем ФАР, каждая из которых
отвечает заданным техническим требованиям, позволяют на завершающем эта-
пе проектирования сопоставить их и выбрать наилучшую. Опыт проектирования
ФАР показывает, что такое сопоставление целесообразнее делать по энергопот-
реблению (КПД, если речь идет о передающей ФАР, или суммарным потерям,
если рассматривается приемная ФАР), надежности, стоимости и массогабаритным
характеристикам. В зависимости от класса РЛС каждой из этих характеристик
должен быть придан соответствующий вес. Интегральное оценивание позволяет
принять окончательное решение о выборе наиболее оптимального варианта ФАР.
18.1.1. Задачи синтеза антенн. Ранее были рассмотрены задачи расчета
поля излучения различных типов антенн. На практике в ряде случаев требуется
Парамртпрический синтез при прректрроврмии амтенн
643
создание антенн с характеристиками направленности, отличными от рассмотрен-
ных выше. Другими словами, возникает довольно общая задача построения антенн
по заданным диаграммам направленности (например, типа косеканс, секторной
и др.).
Кратко эту задачу называют синтезом антенн. В свою очередь, задача построе-
ния антенн по заданным характеристикам разделяется на математическую тео-
рию синтеза антенн и конструкторскую разработку антенн.
Математическая теория синтеза позволяет выяснить принципиальные возможно-
сти построения той или иной желаемой диаграммы направленности и найти требуе-
мые для реализации заданных диаграмм амплитудно-фазовые распределения поля
или токов на заданной антенне, излучающем раскрыве или выпуклой поверхности.
В задачу конструкторской разработки антенны входит практическая реализация
найденных распределений с необходимой точностью. Последняя обеспечивается
как имеющейся технологией изготовления и материалами, так и соответствующей
конструкцией антенны.
В настоящее время методы решения задачи синтеза антенн по требуемой фор-
ме ДН развиты для большинства известных типов антенн. Поэтому для упрощения
изложения остановимся на рассмотрении решения задачи синтеза на примере ли-
нейной излучающей системы [41]. Необходимо помнить, что в основе задач синте-
за антенн лежат некорректно поставленные задачи [13].
18.2. Распределительные и излучающие системы антенн [66]
В любой антенне всегда можно выделить следующие базовые элементы: входное
устройство (ВУ), согласующее устройство (СУ), распределительная система (PC)
и излучающая система (ИС).
Входное устройство предназначено для передачи мощности от генератора к
антенне. Оно может иметь несколько, а иногда сотни и тысячи каналов, которые
обеспечивают одновременную работу антенны на разных частотах или независи-
мое формирование различных диаграмм направленности (ДН).
Согласующее устройство обеспечивает в питающем тракте заданный коэффи-
циент отражения электромагнитного поля во всей рабочей полосе частот. Наряду
с традиционными схемами согласования, используемыми в технике СВЧ, в ан-
теннах появляются дополнительные возможности согласования при рациональном
построении распределительной и излучающей систем. Поэтому в реальных конс-
трукциях антенн согласующее устройство может оказаться совмещенным с ними.
Распределительная система создает необходимое распределение тока (поля) в
излучающей системе, обеспечивающее формирование ДН с заданными парамет-
рами. В реальных конструкциях антенн иногда эти системы оказываются совме-
щенными.
Реальная излучающая система представляет собой некоторую поверхность, по
которой текут электрические токи, возбуждающие электромагнитные волны. При
моделировании в качестве ИС может рассматриваться не только эта поверхность,
но и любая охватывающая ее замкнутая поверхность, по которой «текут» фиктив-
ные электрические и магнитные токи, создающие такую же ДН, что и реальные
электрические токи.
Рассмотрим несколько примеров выделения базовых элементов в конкретных
‘/2 21 *
644
ГЛАВА 18
ИС
PC
СУ
Рис. 18.1. Различные антенны и их базовые элементы:
а) - рупорная антенна, б) - волноводная решетка, в) - двухзеркальная антенна;
ВУ - входное устройство, СУ - согласующее устройство,
ИС - излучающая система, PC - распределительная система [66]
антеннах. В простейшей, рупорной антенне (рис. 18.1,а) в качестве ИС можно рас-
сматривать отверстие прямоугольной формы, называемое обычно раскрывом или
апертурой, с распределенными на ней эквивалентными электрическими и магнит-
ными токами.
Распределительная система образована отрезком прямоугольного волновода,
обеспечивающего распространение только основного типа волны Н10,и пирами-
дальной горловиной рупора, осуществляющей трансформацию поля из выходно-
го сечения волновода в апертуру. При этом СУ совмещено с PC. Согласование
осуществляется выбором размеров пирамидального рупора; ВУ служит отрезок
прямоугольного волновода.
В нерезонансной волноводно-щелевой решетке (рис. 18.1, б) в качестве ИС мож-
но рассматривать совокупность всех щелей с эквивалентными магнитными токами
в них; PC представляет волновод с этими щелями, расположенными на его широ-
кой стенке по определенному закону, гарантирующему создание требуемого рас-
пределения поля в ИС. Согласование антенны обеспечивается выбором размеров
щелей и поглощающей нагрузкой в волноводе. Поэтому в данном случае роль СУ
играет PC, а ВУ является отрезком волноводного тракта.
В многоканальной двухзеркальной параболической антенне (рис. 18.1, в) излуча-
ющей системой удобно считать кольцевой раскрыв с эквивалентными электричес-
кими и магнитными токами. Рупорные облучатели, малое и большое зеркала образу-
Параметрический синтез при проектировании антенн
645
ют конструкцию PC; СУ выполнено отдельным блоком и обеспечивает согласование
облучателей различного диапазона волн с многоканальным ВУ, которое осущест-
вляет передачу подводимой мощности в соответствующий рупорный облучатель.
Таким образом, основными базовыми элементами любой антенны являются ИС
и PC.
18.3. Классификация основных задач параметрического синтеза
распределительных и излучающих систем [41]
При автоматизированном проектировании любой антенной системы приходится
решать следующие две прикладные задачи, получившие в литературе соответс-
твенно названия внешней и внутренней [41]:
- по известным требованиям к характеристикам антенны определить геомет-
рию раскрыва ИС и оптимальное амплитудно-фазовое распределение (АФР) поля
(тока) в нем, обеспечивающих реализацию этих требований;
- по найденному АФР поля в раскрыве ИС спроектировать реализующую его
PC.
На практике к параметрам антенн предъявляются самые различные требова-
ния, например, к форме главного лепестка (луча) и уровню боковых лепестков ДН
в различных угловых секторах, в том числе и в процессе сканирования, поляри-
зационной структуре излучаемого электромагнитного поля, КНД, конфигурации
и размерам раскрыва, реализуемости АФР поля и нем и т. и. К параметрам PC
предъявляется ряд требований: прежде всего возможность реализации найденно-
го в результате решения внешней задачи АФР поля, минимальность потерь мощ-
ности, оптимальность геометрических и весовых характеристик и т.п.
Практика и теория последних лет показали, что наиболее актуальными явля-
ются следующие четыре класса внешних задач:
1. Проектирование криволинейных ИС произвольной геометрии по известным
требованиям к амплитудно-фазовой (комплексной) ДН и АФР поля в раскрыве
антенны (типичным примером задачи этого класса является проектирование кри-
волинейных щелевых излучателей).
2. Проектирование ИС по заданным требованиям к амплитудной ДН и ограни-
чениям на АФР поля в раскрыве антенны. Задачи этого класса наиболее широко
встречаются па практике, так как часто интересуются лишь амплитудной ДН; от-
сутствие, требований к фазовой ДН дает лишнюю степень свободы в выборе более
простого, чем в задачах первого класса, АФР поля в раскрыве антенны.
3. Проектирование ИС по заданным требованиям только к амплитудной или
фазовой ДН и амплитудному или фазовому распределению поля в раскрыве. Ес-
тественно, что в этих задачам следует найти соответственно фазовое или ампли-
тудное распределение поля. К подобным задачам приводит необходимость создания
в ряде случаев фазовых ДН специального вида, обеспечения электрической проч-
ности антенных решеток, ряд вопросов оптического моделирования и обработки
сигналов и т. п.
4. Проектирование ИС с оптимальными интегральными параметрами - КНД,
коэффициентом рассеяния и т. п. Им в последнее время уделяется много внима-
ния при проектировании антенн с обработкой сигналов, больших малошумящих
антенн для радиоастрономии и космической связи.
646
ГЛАВА 18
Целесообразно отметить, что при рассмотрении этих задач, в той или иной
мере ставится также вопрос оптимизации геометрии ИС, особенно для антенных
решеток, так как его решение позволяет сократить число излучателей в них, что
для практики имеет большое значение.
В результате решения внешней задачи любого из перечисленных выше классов
всегда определяется один и тот же параметр — АФР поля в раскрыве антенны,
который является основным для проектирования PC. Поэтому внутренние задачи,
в отличие от внешних, не имеют такой широкой классификации, а их отличи-
тельные особенности связаны лишь с реализацией тех или иных физических про-
цессов в PC с учетом электродинамических свойств конкретных ИС. В настоящее
время большое внимание уделяется следующим направлениям в разработке PC:
- проектирование фазированных и многолучевых антенных решеток;
- проектирование антенных решеток с учетом внешних и внутренних электро-
динамических эффектов взаимовлияния;
- проектирование PC, максимально использующих конструкцию ИС (таковы,
например, PC криволинейных щелевых излучателей, двухзеркальных антенн со
специальными профилями зеркал и т.п.).
18.4. Исходные соотношения для прикладных задач
параметрического синтеза излучающих систем [66]
Диаграммы направленности антенн. Для разработки математических моделей
ИС необходимо прежде всего знать соотношения, связывающие ДН антенны с
АФР возбуждения (тока, напряжения, поля) в ее раскрыве. Для этого введем, как
Рис. 18.2. К выводу формулы для ДН излучающей системы
Параметрический синтез при проектировании антенн
647
показано на рис. 18.2, прямоугольную (с ортами xo,^o,zo) и сферическую (с ортами
т0, Оо, ф0 ) системы координат, имеющие общее начало в точке 0.
Пусть в некоторой области S (объем, поверхность, линия), расположенной в
бесконечной однородной среде, распределены сторонние источники электромаг-
нитного поля, например, в виде электрических и магнитных токов. Векторная
ДН (по полю) излучающей системы S, характеризующая закон изменения напря-
женности электрического поля в дальней зоне, может быть рассчитана по фор-
муле
W) = ге(е,ф)ё0 + гф(0,ф)фо. (18.4.1)
Азимутальная Кф(0,ф) и меридианальная Fg(0, ф) составляющие ДН (проекции
Г(0,ф) соответственно на орты 0О и ф0 описываются соотношениями:
*е(0,Ф)
= Fx (0, ф) cos ф + Fv (0, ф) sin ф cos 0 -
—(0, ф) sin 0 — W 1 [Fma. (0, ф) sin ф + Гтзс(0,ф) cos ф],
(18.4.2)
К (0, ф) = Fv (0, ф) cos ф - Fx (0, ф) sin ф -
-W""1 Г F
(0, ф) sin ф + Fmy (0, ф) cos ф - Fmz (0, ф) sin ф
(18.4.3)
где W ~ характеристическое сопротивление среды.
га(е.ч>) = J Ja (х, у, z) exp[ik(x cos ф sin 0 + у sin ф cos 0 + z cos 0)]d5
та (x> У ’2) ехр[г/с(х cos ф sin 0 + у sin ф cos 0 + z cos 0)]d5
(18.4.4)
(18.4.5)
J
индекс а принимает значения x,y,z; k = 2л/X — волновое число; Jx, Jy, Jz, Jmx,
Jmy, Jmz - проекции на орты , yQ, z0 соответственно векторов плотности электри-
ческого J(x,y,z) и магнитного Jm(x,y,z) токов, которые меняются во времени по
гармоническому закону.
В дальнейшем показано, что анализ многих ИС можно заменить моделирова-
нием некоторого эквивалентного криволинейного излучателя, конфигурация ко-
торого полностью определяется геометрией раскрыва антенны. Поэтому распишем
соотношения (18.4.1) - (18.4.5) более подробно для криволинейного излучателя.
Пусть криволинейный излучатель L описывается системой дифференцируемых
параметрических функций:
х = x(t),y = y(t),z = z(t),-l < t < 1.
Обычно такой излучатель возбуждается только электрическим J(t) или маг-
нитным Jm(t) током, причем, как правило, он или направлен вдоль одной из осей
координат ОХ, ОУ, OZ, или в каждой точке кривой направлен по касательной, к
ней.
Рассмотрим эти два случая подробнее. Пусть, например, электрический
ток J(t) направлен вдоль оси ОХ, тогда Jx(t) = J(t), a Jy (t) = Jz(t) = 0. Под-
ставляя эти значения в (18.4.2) —(18.4.5) и учитывая, что в данном случае
dS = dl = sjx'(t)2 + y'(t)2 + z'(t)2dt - длина элементарного участка кривой L, полу-
чаем
648
ГЛАВА 18
Fg(O, ф) = cos OcoscpFJO, ср),
Fy (0, ф) = - sin <pFx (0, ф),
где
(18.4.6)
F x (0, (p) = J exp{z/<[x(t) sin 0 cos <p + y(t) sin 0 sin cp + z(t) cos 0]}dt
Z(t) = 7^'(t)2 + ?/'(t)2 + z'(t)2dt,
(18.4.7)
(18.4.8)
J (t) — комплексная амплитуда вектора тока J(t). Аналогичные по структуре вы-
ражения для ДН получаются в том случае, когда ток направлен вдоль оси OY или
OZ.
Пусть вектор тока J(t) тангенциален контуру излучателя в каждой его точке,
тогда его проекции таковы:
Jx(t) = J(t)cos(L,x) = / Z(t),
Jy(t) = J(t)cos(L,t/) = J(t)y'(t) / l(t),
Jz(t) = J(t)cos(L,z) = / Z(t).
(18.4.9)
Здесь — углы между касательной к кривой L в произвольной точ-
ке t и осями системы координат OXYZ. Подставляя выражения (18.4.9) в (18.4.2)
— (18.4.4) и учитывая, что составляющие вектора плотности магнитного тока, а
следовательно, и доставляющие Fma(Q,ф) равны нулю, получаем
*е(0,Ч>)= p№'(t)
cos 0 cos (р + уr(t) cos 0 sin ср -
(18.4.10)
-z'(t) sin 0] exp{ifc[x(t)] sin 0 cos (p + y(t) sin 0 sin cp + z(t) cos 0]}dt,
ф(е,<₽) = p(t)[-x'(t)
sintp + y'(t) cos cp] x
(18.4.11)
x exp{ik[x(t)] sin 0 cos cp + y(t) sin 0 sin cp + z(t) cos 0]}dt.
Аналогичные по форме выражения для ДН получаются и в случае возбуждения
криволинейною излучателя магнитным током Jm (t).
Рассматривая формулы (18.4.10), (18.4.11), видим, что азимутальная Fq(0,(р) и
меридианальнаяГф(О,ф) составляющие ДН (для простоты обозначим их в дальней-
шем через F(0,cp)) излучателя с тангенциальным к L или коллинеарным одной из
осей координат электрическим или магнитным вектором тока, могут быть описаны
следующим выражением:
F(0, ф) = j J(t)ц(0, ф, t)dt,
(18.4.12)
ц(0,Ф,О = /(0,cp,t)exp{i/c[a?(t)sin0cos(p + y(t) sin 0 sin+ z(t)cos0]}, (18.4.13
где/(0,ф,£)— ДН элементарного участка кривой L.
Например, для рассмотренных выше частных случаев, когда вектор электри-
Парамхтпрнч^стсий синтез при проекршдюваныи антенн 649
ческого тока направлен вдоль оси ОХ или тангенциален контуру L излучателя,
диаграмма направленности
l(t) cos 0 cos ср -
для составляющей Е(0,ф), когда ток направлен вдоль оси ОХ,
-Z(t)sin9 -
для составляющей Ек(0,ф), когда ток направлен вдоль оси ОХ,
х (t) cos 0 cos ф + у (t) cos 0 sin ф - z (t) sin 0 -
для составляющей Fg(0, ф), когда ток тангенциален контуру L,
-x'(t)sin<p + т/(£)созф -
для составляющей 1*^(0, ф), когда ток тангенциален контуру L.
Эти выражения получаются при простом сопоставлении формул (18.4.12) (18.4.13)
соответственно с формулами (18.4.7) и (18.4.8), а затем с (18.4.9) - (18.4.11).
Теперь видно, что каждая из диаграмм Ее(0,ф) и Fa (0, ф) определяется только
скалярной, а не векторной функцией АФР тока. Это обстоятельство существенно
облегчает процесс моделирования, поскольку необходимо искать только функцию
J(t),a не три ее проекции.
Па практике широко применяются антенные решетки (дискретные ИС) раз-
личных типов. Азимутальная и меридианальная составляющие ДН таких систем
описываются дискретным аналогом формулы (18.4.12)
N
Е(0,ф,1) = /пИт(0,ф), (18.4.14)
п=1
где
цп(0,ф) = /(0, ф) ехр{г7фгп sin 0 cos ф + уп sin 0 sin ф + zn cos0]}, (18.4.15)
N - число излучателей в решетке: Jn,f(0,(p),(xn,yn,zn)— соответственно комп-
лексная амплитуда возбуждения, ДН без учета взаимовлияния и координаты п-го
изолированного элемента (излучателя).
Чаще всего интересуются характерными сечениями (их иногда называют глав-
ными) ДН, которые, как правило, дают необходимую информацию о всей про-
странственной диаграмме. В качестве таких сечений обычно используют поверх-
ности 0 = 0О, ф = фо или другие поверхности, пространственное положение которых
определяется спецификой конкретной радиосистемы.
18.4.1. Основные уравнения. Соотношения (18.4.12) — (18.4.15) позволяют со-
ставить общие исходные уравнения для разработки математических моделей вне-
шних задач каждого из четырех классов. Рассмотрим для определенности криволи-
нейный излучатель и произвольное сечение пространственной ДН, определяемое,
например, углом 0 = 0О. В соответствии с (18.4.12) это сечение комплексной ДП
описывается при известных конфигурациях L излучателя и АФР тока J(t) интег-
ралом
1
j дад0о,Ф, t)dt.
-1
В задачах первого класса заданы требования к амплитудно-фазовой ДН (пусть
650
ГЛАВА 18
они описываются некоторой известной из требований к ДН комплекснозначной
функцией F0(90,<p)), поэтому общее уравнение задач этого класса должно быть
таким:
1
Jj(t)p(0o,<p,t)dt = F0(60,<p). (18.4.16)
Соотношение (18.4.16) является линейным интегральным уравнением Фред-
гольма относительно тока J(t),a функции Fo(0o,(p) и pi(0Q,<p,t) заданы; последняя,
как видно из (18.4.13), полностью определяется параметрическими функциями
кривой L и ДН ее элементарного участка. Напомним, что решение
уравнения (18.4.16) представляет собой некорректно поставленную задачу.
В задачах второго класса заданы требования только к амплитудной ДН [поэто-
му они описываются функцией Fo(0o,(p)]; отсюда ясно, что общее уравнение таких
внешних задач необходимо записать так:
jJ(t)p(0o,<p,t)dt =|Fo(0o,(p) .
(18.4.17)
Это нелинейное интегральное уравнение относительно J(t).
В задачах третьего класса заданы требования к амплитудной фазовой ДН (их
можно описать соответственно функциями Ко(0о,ф) и arg(Fo(0o,(p))) и амплитуд-
ное J(t) или фазовое ^(t) = arg J(t) распределение тока в раскрыве антенны. Пред-
ставляя распределение тока J(t) в виде J(t) ехр[гТ(£)] комбинируя попарно амп-
литудную и фазовую диаграммы с амплитудным и фазовым, распределениями
тока, получаем четыре типа подобных задач. Две из них, в которых фигурируют
требования к амплитудной ДН, описываются уравнением
J(t)|exp[2vP(t)]p(0o,(p,t)dt = Fo(0, (р)
(18.4.18)
а там, где предъявляются требования к фазовой диаграмме, уравнением
J(t) exp[i4/(t)]p,(0o^,t)dt
= arg(Fo(0,9)).
(18.4.19)
Эти уравнения, так же как и в задачах второго класса, являются нелинейными
интегральными уравнениями относительно амплитудного J(t) или фазового 'P(t)
распределения тока.
В задачах четвертого класса речь идет об оптимизации интегральных парамет-
ров антенн — коэффициентах направленного действия, концентрации и рассея-
ния, извлечения мощности и т. п. Напомним определения КПД D в направлении
максимума ДН:
F(0, ф) sin 0d0dф
(18.4.20)
где F(0, ф) - нормированная к максимуму ДН.
Коэффициент концентрации характеризует ту долю мощности по сравнению
Параметрический синтез при проектировании антенн
651
со всей излученной антенной мощностью, которая содержится в заданном теле-
сном угле О :
Kfc(Q) =
(18.4.21)
Коэффициент рассеяния характеризует ту долю от всей излученной антенной
мощности, которая содержится в боковых лепестках ДН. Если главный луч ДН
занимает в пространстве телесный угол , то коэффициент рассеяния
Кр (Qr) = 1 - Кк (Ог). (18.4.22)
Коэффициент извлечения мощности ц характеризует предельные возможности
антенны по извлечению мощности из падающей на нее неплоской электромагнит-
ной волны:
dS |ЕТ (х, у, z)|2 dS j|E2 У, z)
dS
(18.4.23)
S
где E-\(x,y,z) и E2(x,?/,z) — соответственно электрические векторы АФР поля в
раскрыве антенны и падающего па него поля.
Используя выражение (18.4.14), легко записать соотношения, аналогичные
(18.4.16)—(18.4.23), и для антенных решеток. Оптимизацию их геометрии в боль-
шинстве случаев можно свести к перечисленным выше задачам. Для этого до-
статочно из физических или конструктивных соображений выбрать начальное
приближение геометрии антенны (например, схему расположения и число излу-
чателей решетки) и затем, оптимизируя ее, т. е. целенаправленно уменьшая об-
щее число излучателей, решать каждый раз одну ту же внешнюю задачу, пока
не перестанут выполняться заданные требования к параметрам ДН и к АФР воз-
буждения в раскрыве решетки.
Любое из соотношений (18.4.16) — (18.4.19) можно рассматривать как оператор-
ное уравнение
Р(х) = у , (18.4.24)
где х - искомая характеристика (АФР возбуждения в задачах первого и второго
классов и амплитудное или фазовое распределение возбуждения в смешанных за-
дачах); у - ДН (комплексная в задачах первого класса, амплитудная или фазовая
— в задачах второго и третьего классов); Р - оператор, который математически
описывает реально существующий физический процесс трансформации АФР воз-
буждения из раскрыва антенны в поле излучения дальней зоны.
18.4.2. Экстремальные и ограничительные требования. Уравнение перво-
го рода (18.4.24) для устранения некорректности следует решать с учетом требо-
ваний к искомому распределению возбуждения (тока) J(t), обеспечивающих его
практическую реализацию в раскрыве ИС. Они могут быть двух видов: экстре-
мальные и ограничительные. Первые содержат требования общего характера к
распределению тока, например, в случае криволинейного излучателя — мини-
мального значения интеграла
652
ГЛАВА 18
1
’|j(t)|2 dt, (18.4.25)
-1
который пропорционален мощности омических потерь в антенне. Это связано с
тем, что операторы Р, описывающие электродинамическую модель непрерывной
ИС, обладают «сглаживающим» действием -они слабо «реагируют» на высокочас-
тотные составляющие спектра АФР возбуждения в раскрыве антенны. Физически
это означает, что такие составляющие не вносят заметного вклада в ДН т е. в
активную мощность излучения, и их мощность переходит в реактивную мощность
ближнего электромагнитного поля, поэтому для практики естественна постанов-
ка экстремальных требований общего характера к АФР возбуждения, таких как
минимальность мощности омических потерь, реактивной мощности и т. п. Можно
сформулировать экстремальные требования к другим свойствам АФР возбужде-
ния, например его «гладкости» и т.п.
Ограничительные требования описывают конкретные свойства АФР тока с
помощью параметров, имеющих определенный физический или практический
смысл. Например, при моделировании ИС из N дискретных излучателей часто из
соображений электрической прочности предъявляется требование: максимальная
мощность max Рп , подводимая к излучателю при неравномерном возбуждении, не
п г>
должна превышать мощность Ро, подводимую к отдельному излучателю при рав-
номерном возбуждении, более чем в определенное число раз q, т. е. max[Pn / Ро] < q.
п
Это требование имеет конкретный практический смысл. Действительно, если к ВУ
системы подводится некоторая мощность Pq , то при равномерном возбуждении
ИС в излучатель попадает мощность Ро = Ро / N , а при неравномерном
Подставляя эти выражения в приведенное выше неравенство, получаем сле-
дующее требование по реализации амплитудного распределения в системе из N
дискретных излучателей:
L-^max
(18.4.26)
Аналогично строятся ограничительные требования и в других задачах. Напри-
мер, в случае незамкнутого щелевого криволинейного излучателя из физических
соображении необходимо потребовать, чтобы распределение тока на его концах
обращалось в нуль, и т. п.
18.5. Решение задач параметрического синтеза на основе
вариационного похода [66]
Теоретически необходимые для нормального функционирования реальных ра-
диосистем ДН описываются, как правило, так называемыми «нереализуемыми»
функциями. Физически это означает, что такие диаграммы не могут быть точно
Па^аметримест^й синтез при проектпировании антенн 653
воспроизведены при таком АФР поля в апертуре антенны, а математически, что
уравнение не имеет точного решения. На практике не требуется точного воспроиз-
ведения ДН, так как обычно достаточно реализовать ее параметры с определен-
ными допусками. Поэтому появляется возможность найти так называемое квази-
решение (приближенное решение) уравнения (18.4.24) и попытаться удовлетворить
при этом предъявляемым требованиям как к ДН, так и к АФР возбуждения,
обеспечивающим его реализацию. Уравнение (18.4.24) при известном операторе Р
описывает связь между ДН и АФР возбуждения в апертуре антенны и, следова-
тельно, является математической моделью ИС. Для построения прикладной ма-
тематической модели ИС используются различные методы нелинейного програм-
мирования. Ряд этих методов (или их модификаций) применен ниже при решении
конкретных задач. Однако основное внимание уделено методологии построении
прикладных математических моделей на основе вариационного подхода с исполь-
зованием множителей Лагранжа. Это вызвано следующими обстоятельствами:
- во-первых, вариационный подход — наиболее разработанное в методическом
отношении направление решения задач нелинейного программирования и, кроме
того, оно тесно связано с вопросами определения экстремума функций многих
переменных при наличии ограничений, рассматриваемыми в известных курсах
теории оптимизации;
- во-вторых, вариационный подход позволяет сравнительно просто решать за-
дачи нелинейного программирования небольшой размерности, какими во многих
случаях и являются задачи моделирования ИС;
- в-третьих, методология вариационного подхода может быть использована и
при рассмотрении других методов решения задач нелинейного программирова-
ния, например градиентных, различных способов построения штрафных функ-
ций и т. п.
Применим вариационный подход сначала к простейшей задаче первого класса
— моделированию криволинейного излучателя по известным требованиям к ком-
плексной слабонаправленной ДН, заданной на произвольной конической поверх-
ности 0 = 0О. Пусть известны: геометрия излучателя L и направление вектора тока
в нем; желаемая форма нормированной диаграммы Fq(0, ср); допустимая ошибка 5
F<e, <₽)
<Ро 2 п, <р0
Рис. 18.3. К моделированию криволинейного излучателя со слабонаправленной ДН [66]
654
ГЛАВА 18
(18.5.1)
отклонения синтезируемой диаграммы F(0,(p) от заданной Fo(0,<р) (рис. 18.3):
2л
J|F(0o,<p) — Fg(0o,<p)[2 dtp <8,
о
а требования к реализуемости АФР возбуждения в излучателе описываются усло-
вием минимальности мощности омических потерь (18.4.25).
В этой задаче в качестве целевой функции естественно принять функционал
(18.4.25) (обозначим его пропорциональный мощности омических потерь
MxUCt)} =
J(t) dt.
Тогда рассматриваемая задача моделирования сводится к задаче нелинейного
программирования, а именно, минимизации целевой функции (функционала)
при ограничении (18.5.1) (в виде неравенства) на допустимую ошибку от-
клонения синтезируемой ДН F(0, (р) от заданной Fq (0, ср). Можно показать, что ана-
логично тому, как задача минимизации целевой функции многих переменных при
наличии ограничений сводится, как известно, к минимизации специально постро-
енной с помощью множителей Лагранжа функции, так и рассматриваемая задача
минимизации функционала при ограничении (18.5.1) эквивалентна задаче
определения экстремума следующего функционала:
1 2л
j|F(0o,<p)- Fo(0o,<p)|2d<p
О
где a — пока неизвестный множитель Лагранжа.
Действительно, в соответствии с методологией использования множителей
Лагранжа задача минимизации целевого функционала при ограничениях
(18.5.1) сводится к определению экстремума функционала:
2л
a j|F(0o,q>)-Fo(0o,<p)|2 dcp
о
M{J(t)} = a f IJ(t)|2 dt
(18.5.2)
M{J(t)} = f|J(t)|2dt
(18.5.3)
где а - множитель Лагранжа. Разделив обе части выражения (18.5.3) на a, и обоз-
начив a-1M{J(t)} через , a-1 через a , получим приведенное выше выраже-
ние (18.5.2). Этот функционал, как будет ясно из дальнейшего, более удобен, чем
функционал M{J(t)} для реализации на ЭВМ численных методов расчета опти-
мального АФР тока возбуждения J(t).
Чтобы найти распределение тока J(t) достигающие при заданных Fo(0,cp) и 5
экстремум , прообразуем сначала функционал (18.5.3), подставив в него
в место ДН F(0,q>) ее выражения из (18.4.12) при 0 = 0О. Тогда используя опера-
цию комплексного сопряжения (обозначена звездочкой *), запишем функционал
в виде
= a
1 2л 1
J(t)/(t)dt+ j j JW(0o, Ф, t)dt -FO(0O, cp)
(18.5.4)
Ларальетрцческцц синтез при проектировдмии антенн
655
j J* (t)p* (0О, <р, t)dt - Fq (Qq , ф) с!ф.
Рассмотрим произвольно малое изменение (вариацию) 5J(£) АФР тока J(t) и от-
вечающую ему вариацию dM{J(t)} функционала
6M{J(t)} = M{J(t) + 6J(t)} - M{J(t)}. (18.5.5)
Подставляя в функционал (18.5.3) последовательно J(t) + 5J(t) и J(t), найдем по
формуле (18.5.4) вариацию 6M{J(t)}; оставляя в ней члены, содержащие вариацию
тока 8J(t) в первой степени (главную часть вариации 5M{J(t)}), получаем
r 1 2 л Г 1
8M{J(t)} = < JaJ(t)8j’(t)dt+ J j
-1 0 -1
J(t)p.(Oo, ср, t)cit х
ц (0О, ф, t)8J (t)dt - Fq (0о , ср) J |л (0q , ф, t)8J (t)dt с1ф
(18.5.6)
faJ (t)5J(t)dt + J J J (t)p (0о,ф, t)dt
-1 о -1
| ц(0о, ф, t)6J(t)dt - Fo* (0О, ф) | ц(0о, ф, t)5J(t)dt dtp >.
Изменяя в двойных и тройных интегралах выражения (18.5.6) порядок интегри-
рования, вводя новую переменную £, и используя операцию комплексного сопря-
жения, вариацию SM{J(t)} можно переписать следующим образом:
1 2л
j J(£)d£ j ц(0о, ф, ^)ц* (0О, ф, £ )йф -
aJ(t) +
*
2л
Го(0о,ф)ц (0о,ф,^ф 8J (t)dt!> +
0
1 1 2тс
/* /* 5j- * sj*
j aJ (t) + J J (^)d£> j ji (0O, Ф, S,)p(0o, Ф, t)d(?
-1 -1 0
(18.5.7)
- J Fq (0q , ф)ц(0о, ф, *)Й> (t)dt >.
Если некоторое АФР тока J(t) доставляет экстремум функционалу M{J(t)}, то
при любой вариации 5J(t) (или 8J (t)) вариация 8M{J(t)} = 0, а это может быть
только в том случае, когда подынтегральные выражения, стоящие в квадратных
скобках (18.5.7) равны нулю:
656
ГЛАВА 18
1 2л 2л
aJ(t) + f J(£)d£ J p(Oo, <p, £)/ (0O, <p, t)d(p - Fq (Oo , ф)ц* (0O, ф, t)dq =
-io о
Введем обозначение
2л
K(^, t) = j ц(Оо, Ф, (0О, Ф, t)d<p
0
и перепишем (18.5.8) в виде
1 2л
«J(t) + jJ&K^, J Fo (0O, <р)ц* (60, <p, t)d(p = 0.
-1 0
0. (18.5.8)
(18.5.9)
(18.5.10)
Уравнение (18.5.10), получившее в литературе название уравнение Эйлера, яв-
ляется исходным соотношением для расчета оптимального АФР тока при модели-
ровании криволинейного излучателя со слабонаправленной ДН, когда предпола-
гается, что требования к точности ее воспроизведения во всех угловых секторах
практически одинаковы.
При синтезе остронаправленной диаграммы задаются требования к форме ее
главного луча Гд(6о,ф) и уровню боковых лепестков £(0о,ф). Эти разные требова-
ния можно учесть, например, введением в функционал (18.5.2) неотрицательной
весовой функции р(ф) следующим образом:
= а
1 2л
J|Лt)|2 dt + J |F(00, <р) - Fo (60, <p)|2 p(<p)dq>.
-1 0
(18.5.11)
Простейшая из функций р(ф) берется такой (рис. 18.4):
F(0, ф)
0 фх ф2 2 л, ф
0 Ф1 ф2 2л, ф
Рис. 18.4. К построению весовой функции [66]
72 21 *
Параметрический синтез при проектировании антенн
657
<1,(ре[(р1,(р2]
Р(ф) -
[Y,<pe [(0,90,(92,271)],
(18.5.12)
где [cpi, ф2 ] — область задания главного луча ДН. Константа у позволяет регулиро-
вать уровень боковых лепестков и добиваться выполнения условия F(Og, 9) < ^(Oq , 9).
Более сложные весовые функции позволяют учитывать и боле сложные требования
к главному лучу ДН и уровню ее боковых лепестков.
К сожалению, по заданным требованиям к диаграмме указать оптимальную
функцию р(9) не представляется возможным. Однако даже такой простой прием,
как целенаправленное изменение параметра у по результатам сравнения синтези-
руемом диаграммы с заданной, позволяет достаточно быстро провести на ЭВМ
моделирование и добиться выполнения заданных требовании. Функционал (18.5.11)
получается из (18.5.2) лишь введением в нее весовой функции р(9). Поэтому урав-
нение Эйлера для определения распределения тока при моделировании криволи-
нейного излучателя, формирующего остронаправленную диаграмму, выводится
аналогично уравнению (18.5.10):
1 2л
aJ(t)+ jлгуж- jfb(6o.<p)p(<p)H*(eo
-1 о
9, t)d9 = 0 ,
(18.5.13)
но здесь
К(^, t) = j ц(Оо, 9, ^)/ (0О,9, t)p(9)d9.
о
(18.5.14)
Оптимальное распределение комплексных амплитуд возбуждения излучателей
антенной решетки описывается дискретным аналогом уравнения (18.5.13)
Ш=1
-Fn= 0,и = 1,2,..., N,
(18.5.15)
где
тп
2л
= (%, ф)Рп (0О, Ф)Р(Ф)^Ф
0
(18.5.16)
2л
Fo (00, Ф)Рп (00 > ф)р(ф)^ф •
(18.5.17)
Уравнение (18.5.15) получается так же, как и уравнение (18.5.13), функционала
(18.5.11), в котором
[ | J(t)|2 dt
-1
следует заменить на сумму
о
N
п=1
а ДН F(0q,9) в соответствии с формулой (18.4.14) — суммой
22 - Неганов
658
ГЛАВА 18
N
, •^пМ'пХ^О ’ ф)
П~1
Чтобы в антенных решетках учесть требование (18.4.26), достаточно ввести в
первые члены уравнений этой системы весовые множители рп > 0, которые управ-
ляют амплитудами возбуждения Jn излучателей. Целенаправленно изменяя рп,
можно получить требуемые результаты.
Моделируя ИС вариационными методами, можно учесть и ряд важных для
практики дополнительных требовании к диаграмме, например нормировку к мак-
симуму излучению антенны, ширину главного луча по нулям на уровне половин-
ной мощности.
18.6. Множитель Лагранжа [66]
При рассмотрении численных методов решения уравнения Эйлера множитель
Лагранжа а считался известным. Его действительно можно определить из усло-
вия связи типа (18.5.11) в котором, как следует из теории оптимизации [41], необ-
ходимо оставить только знак равенства:
fJ(t)p(e0,(p,t)dt-F0(e0,(p) p((p)dcp
(18.6.1)
где Ео(0о,ф),р(ф) и 5 - известные величины; J(t) - решение уравнения Эйлера
(18.5.12). При фиксированном а. Следовательно, множитель Лагранжа а неявно
входит в левую часть соотношения (18.6.1). Составим функцию
Р(а) =
2л 1
J j /(адео,ф,г)й*-го(Оо,ф) р(ф)йф
О -1
(18.6.2)
В [15] показано, что а>0, а функция Р(а) является монотонно возрастающей.
При а = 0 первое слагаемое в правой части (18.6.2) также стремится к нулю. Дейс-
Рис. 18.5. К расчету оптимального значения множителя Лагранжа [66]
сантез прц проектировании антенн 659
твительно, при а = 0 не учитываются требования к АФР тока излучателе и поэто-
му, как следует из теории синтеза ИС [15, 16], можно создать ДН, сколь угодно
мало отличающуюся от заданной функции Fg(0g,cp).
Поэтому при известной величине 6 > 0 функция Р(а) имеет единственный корень
ад, который является оптимальным значением множителя Лагранжа (рис. 18.5).
Можно указать два метода его расчета: последовательных приближений и вари-
аций.
Метод последовательных приближений. Общий подход к определению опти-
мального значения а0 заключается в отыскании тем или иным способом корня
трансцендентного уравнения (3(a) — 0. Поэтому, для вычисления ад можно пред-
ложить, например, следующий итерационный процесс [41]:
1. Определить интервал (а', а"), содержащий перемену знака функции р(а). Так
как функция Р(а) монотонна, его легко найти, приняв, например, а' = О придав
а" достаточно большое значение.
2. Рассчитать вспомогательные параметры
hi = 0,5(а" - а'),^ = а' + h. (18.6.3)
3. Построить на первом, втором, ..., n-м шаге (п = 1,2,3...) полином второй сте-
пени
где
5Po,n + 2р1,п
тп
10
,п
Р(а
(18.6.4)
(18.6.5)
(18.6.6)
(18.6.7)
(18.6.8)
(18.6.9)
h„ = 1ъ -2
?
а
и определить наименьший корень этого полинома.
4. Оценить отличие этого корня от оптимального по формуле
«о
т.е. с точностью hn+1 за ад можно принять vn.
Из выражения для h ясно, что итерационный процесс (18.6.3) - (18.6.9) прак-
тически через несколько шагов сходится к а0. Например, при hi = 1, п = 2,3 соот-
ветствующие приближения к ад отличаются от точного не более, чем на 2,5 - IO-4
—12
и 2-10 . При расчете а0, как следует из (18.6.8) и (18.6.9), следует знать значе-
ния функции Р(а) в точках an + mhn , т.е. при этих значениях необходимо решить
уравнение (18.5.13). Приведенный алгоритм реализуется на ЭВМ.
Метод вариаций. Придавая а какое-нибудь значение aj > 0 решаем уравне-
ние (18.5.13) и находим соответствующее распределение возбуждения J(t). Зная
660
ГЛАВА 18
его, вычисляем по (18.6.2) значение функции 0(a) в точке cq и определяем на-
правление для последующего изменения параметра a. Например, если 0(cq) < 0,
увеличиваем а с каким-нибудь выбранным дискретным шагом (чаше всего пере-
менным) до тех пор, пока не придем к такому значению an, что 0(an) > 0. Оче-
видно, оптимальное значение лежит на отрезке [ai,an]. Часто при практических
расчетах целесообразно выбрать cq достаточно малым, а ап изменять по закону
а110те-1,(п = 2,3,...).
18.7. Криволинейный широкополосный излучатель [66]
Как отмечалось выше, в этой главе проводится по одной и той же схеме (фор-
мализованное задание, разработка физической и математической моделей, пост-
роение прикладной математической модели, параметрический синтез) детальное
рассмотрение автоматизированного проектирования излучающих и распредели-
тельных систем различных антенн. Поэтому с методической точки зрения эту схе-
му целесообразно сначала проиллюстрировать на примере сравнительно простой
антенны, например слабонаправленной антенны системы амплитудно-фазо-мет-
рической пеленгации объекта (АФПО), позволяющей определить его азимут. Та-
кие радиостанции широко используются в системах ближней и дальней навигации
для определения местоположения летательных аппаратов.
Эта антенна должна осуществлять сканирование по азимуту (углу ср ) и форми-
ровать ДН кардиоидной формы
F0(0,<p) = (l + cos(p)/2 (18.7.1)
Перейдем к поэтапному описанию процесса проектирования антенны с такой
ДН, и рассмотрим сначала внешнюю задачу.
18.7.1. Блок формализованного задания. Напомним, что при описании про-
цесса проектирования в БФЗ осуществляется анализ исходных данных, а ФЗ
составляется для проектирования на ЭВМ конкретных антенн при наличии уже
разработанной схемы АП для данного класса. Поэтому в этом и всех следующих
пунктах в БФЗ основное внимание уделяется анализу исходных данных, на осно-
вании которого составляется проектное задание. Системы АФПО проектируются,
как правило, для работы в дециметровом и метровом диапазонах волн с коэффи-
циентом перекрытия Кд = 2... 4 ( Кд = %тах / , где Хтах и Xmjn — соответс-
твенно максимальная и минимальная длина волны). Поэтому к антеннам АФПО
предъявляются следующие требования: широкополосностъ (Кп = 2... 4); малога-
баритность и сопряжение с формой объекта для улучшения аэродинамических
свойств; электрическое сканирование в секторе углов 0 < ф < 2тг ДП кардиоидной
формы; реализуемость АФР возбуждения в раскрыве антенны.
В настоящее время известны два типа широкополосных антенн: частотно-не-
зависимые и криволинейные щелевые излучатели с резонаторным возбуждением.
Хотя теория первых (логопериодических, взаимодополняющих структур) раз-
работана достаточно хорошо, их использование для систем АФПО становится
проблематичным из-за значительных размеров апертуры для дециметрового и
метрового диапазонов волн к принципиальной невозможности обеспечить элект-
рическое сканирование ДН. Сформулированным выше требованиям удовлетворяют
Параметрический синтез при проектировании антенн 661
криволинейные щелевые излучатели с резонаторным возбуждением. Перейдем к
их анализу.
18.7.2. Блок физической модели. Рассмотрим расположенную в неограниченной
идеально проводящей и бесконечно тонкой металлической поверхности S кри-
волинейную щель, возбуждаемую резонатором произвольной формы (рис. 18.6)
Строга говоря, ИС такой, антенны является вся поверхность 5 (с прорезанной в
ней щелью), по которой при возбуждений резонатора текут электрические (вне
щели) и магнитные (в щели) токи.
На практике обычно используют узкие щели, ширина которых h много меньше
локального радиуса г ее кривизны и длины волны A, (h « г, X). Тангенциальная со-
ставляющая напряженности электрического поля в щели в общем случае является
функцией E(t,v) двух координат, где t отсчитывается вдоль контура; v — вдоль
радиуса кривизны в каждом сечении t (рис. 18.6). Известно, что интеграл от этой
функции вдоль оси Ov в каждом сечении апертуры является напряжением U(t)
между внешним и внутренним контурами щели в этом сечении:
h
U(t)= [E(t,v)dv.
о
Поэтому, пренебрегая в первом приближении электрическими токами, теку-
щими вне апертуры (ширины h), криволинейной щели.
Эту щель можно заменить бесконечно тонким криволинейным излучателем той
же формы, что и щель, с АФР напряжения U(t).
18.7.3. Блок математической модели. Пусть геометрия этого излучателя
описывается параметрическими функциями х - x(t), у = y(t), z = z(t), (-1 < t < 1).
В соответствии с (18.4.12) азимутальная и меридианальная Fq „,(0,ф) составляющие
ДН такой антенны определяются соотношением
1
fo,<p(e>4>)= ср, t)dt, (18.7.2)
-1
где U(t) — АФР напряжения в щели.
В случае вертикальной поляризации излучаемого электромагнитного поля ДН
кардиоидной формы должна формироваться только меридианальной составляю-
щей Fe(9,q>).
Рис 18.6. К моделированию криволинейного щелевого излучателя [22]
662
ГЛАВА 18
Рис. 18.7. К построению математической модели
18.7.4. Блок прикладной математической модели. На практике в большинс-
тве, случаев расстояние L между объектами, например летательным аппаратом
и базовой радиостанцией (БРС), составляет десятки или сотни километров при
относительной высоте Н расположения друг относительно друга менее несколь-
ких километров. Поэтому, как видно из рис. 18.7, угол А0 « Н / L не превышает
нескольких градусов и, следовательно, ДН кардиоидной формы достаточно сфор-
мировать только в горизонтальной плоскости 0 = л / 2. Следовательно, математи-
ческую модель рассматриваемой внешней задачи надо записать так:
I7(t)p — , ф, t dt
(18.7.3)
где
и Г2L, Ф; = f Г2Е; <р; t 'I t) COS <₽+!/(() sin <p] (18 7 4)
v 2 J у 2 J
Формула (18.7.3) следует из (18.7.2) при подстановке в нее значения 0 = л / 2.
Уравнение (18.7.3) характеризует внешнюю задачу первого класса. Для нее раз-
работана прикладная математическая модель, которая сводится к минимизации
(18.4.25) при ограничении (18.5.7), описывающим допустимую квадратичную ошиб-
ку 5 отклонения проектируемой ДН от заданной Гд(0о,ф).
Обычно для слабонаправленных антенн задается допустимая относительная
ошибка z - z(t), отклонения синтезируемой ДН от заданной:
|F(e0,<p)-F0(90,<p)
|Fo(9o.<P)|
< А, 0 < (р < 2 л.
Подставляя эту оценку в формулу (18.5.1) для расчета 5 , получаем
Таким образом, внешняя задача проектирования антенны с ДН кардиоидной
формы свелась к необходимости решения уравнения Эйлера типа (18.5.3):
(18.7.6)
при оптимальном значении параметра а, которое однозначно определяется вы-
численным выше значением. Все эти операции осуществляются в блоке синтеза.
18.7.5. Блок синтеза. В данной задаче можно реализовать процесс АП и оп-
ределить оптимальное АФР напряжения в щели. Для этого необходимо знать
Параметрический синтез при проектировании антенн
663
конкретные значения ряда параметров антенны и ее ДН, которые становятся из-
вестными после проработки технических и конструктивных требований. Пусть,
например, известно, что:
- криволинейный излучатель расположен в плоскости Z = 0 и является эллип-
тическим с большой и малой полуосями, равными соответственно Хтах и Xmin
- коэффициент перекрытия рабочих частот Кп = 3, a Xmin = 1 м;
- допустимое относительное отклонение диаграмм А = 0,1.
Для определения оптимального АФР распределения в щели необходимо ре-
шить уравнение (18.7.6) одним из методов, изложенных [3,4] при оптимальном а,
определяемом, как следует из (18.7.51 - значением 5 = 0,1[0,75л]°’5 «0,16. Приме-
няя, например, метод сеточных функций, переведем (18.7.6) в систему линейных
уравнений типа
N
т,п
т-1
(18.7.7)
п
п = 1,...,N,
в которой в формулы для коэффициентов Fn и Кт п на то подставить вместо
Fo(0o,(p) и Ц(во»Ф>^) соответственно функции (18.7.1) и (18.7.1).
Система (18.7.7) решается на ЭВМ по стандартным программам, например ме-
тодом Жордана с выбором главного элемента, а параметр а рассчитывается по
; 2 - Х^ [66]
Рис 18.8. Диаграмма направленности эллиптического излучателя: 1 - X
Рис. 18.9. Амплитудно-фазовое распределение напряжения
в эллиптическом излучателе: 1 - Хтах; 2 - Xmin [66]
max ’
664
ГЛАВА 18
схеме (18.6.3) - (18.6.9). При N = 40 и начальных значениях а' = 0 и а’ = 1 оптималь-
ное значение а определяется уже на третьем шаге с точностью до 10-4. Численные
результаты АП представлены на рис. 18.8 и 18.9. Таким образом внешняя задача
АП криволинейного излучателя решена.
18.8. Решение задач синтеза антенн методом
физической регуляризации [13]
Ранее были описаны методы решения задач синтеза антенн, основанные на
математических моделях, в основе которых лежат интегральные уравнения Фред-
гольма первого рода, решения которых представляют собой некорректно постав-
ленные задачи. Обычно они решаются путем их сведения к функционалам [7].
Ниже рассмотрим другой метод решения обратных задач электродинамики: по
заданной амплитудной диаграмме направленности определить амплитудно-фазо-
вое распределение поля на излучающей поверхности или поверхностную плот-
ность тока на металлической части антенн.
Будем считать заданными сингулярные интегральные представления ЭМП че-
(5)д-
рез тангенциальную напряженность магнитного поля v Нт на металлической час-
ти б'о поверхности антенн:
(18.8.1)
Используя на поверхности S антенны граничное условие Ёт(г е *9) = 0 , получа-
ем из первого соотношения (18.8.1) векторные СЙУ для определения неизвестной
векторной функции 'S'HT:
(S«)H(?,)b1®(r(),?')ds = 0, (18.8.2)
So
где Tg — вектор, описывающий поверхность «Sq . Заметим, что тензорная функция
6^(то,т') содержит сингулярности и поэтому интегральное уравнение (18.8.2) не яв-
ляется векторным интегральным уравнением Фредгольма первого рода, т.е. оно не
относится к некорректно поставленным задачам.
Далее будем предполагать, что на некоторой поверхности (для определен-
ности цилиндрической поверхности, описываемой поверхностью Т]. — {pi, ф, 0}) в
дальней зоне, задана амплитудная диаграмма направленности
F(q>,0) = Гф(ф,е)ф0 + ^е(ф,0)0о, (18.8.3)
^*ф(Р1 ’ Ф»
max (Pl > Ф1 > )
Кф(Ф,0)=
W0) =
£е(р1,ф)0)
^0 max (Pl ’ Ф2 ’ )
Е<р max, Eq тах — максимальные составляющие направленности электрического
поля на поверхности .
Параметрический синтез при проектировании антенн
665
Разложим составляющие нормированной амплитудой диаграммы направлен-
ности на малые участки:
^Ф Nq
= XA"(pFv’I,(<i’’e)+(18-8'4)
п=1 п-1
Здесь на малых участках Апф , Аш0 ( п = 1,...,ДОф; т — 1,...,Nq ) диаграммы направ-
ленности Рф((р,0), Fq(cp,0) аппроксимированы постоянными значениями функций
Рф цф,0), Fq (ф,0) в серединах участков Ancp , Am0 ( п = т = 1,...,М).
Представляя каждый малый участок Апф, Am0 = т = 1,...,М) со-
гласно гипотезы Гюйгенса-Френеля элементарным излучателем [1], излучающим
сферические волны в сторону антенны, решим ( N + М) задач дифракции на ан-
тенне ( г = г0):
. ikpG
= Д,-------; n = l,...,N + M.
s p
(18.8.5)
Здесь
4 = A„<pF,;,’li(<P,0)<Po I
Напомним, что (18.8.5) является сингулярным интегральным уравнением. На-
пример, если антенна представляет собой электрический вибратор, то (18.8.5) со-
держит гиперсингулярность 1 / (z - г')2.
Общее решение задачи (поверхностная плотность тока на антенне) определяет-
ся как:
<s>HT(r0,<p,e) = Е (5)н<"’(г0,<р, 0).
72=1
(18.8.6)
Таким образом, математический аппарат СИУ позволил устранить некоррект-
ную постановку задачи и решить в корректной форме обратную задачу.
В качестве примера описанного выше алгоритма реализованы задачи синтеза
для антенн в виде электрического вибратора и кольцевой цилиндрической ан-
тенны. Задачи решались в два этапа. На первом этапе решалась задача анализа:
определялись амплитудные диаграммы направленности по заданной геометрии
антенны. На втором этапе определялось распределение комплексной поверхност-
ной плотности тока на антенне (тангенциальная напряженность магнитного поля).
Наблюдалось полное соответствие задач анализа на уровне рассматриваемых 0.05%
относительных погрешностей.
Таким образом, зная электромагнитное поле антенны в дальней зоне может
быть просто определенно электромагнитное поле в ближней зоне этой антенны.
666
ГЛАВА 19
Глава 19. Измерение параметров и характеристик
излучения антенн [3, 121]
19.1. Измерение диаграммы направленности
Основными измеряемыми параметрами антенн обычно являются входное со-
противление (или коэффициент отражения от входа антенн) в рабочей полосе час-
тот, а также такие характеристики излучения, как диаграмма направленности и
коэффициент усиления. Причем в подавляющем большинстве случаев эксперимен-
тально измеряется лишь амплитудная диаграмма направленности, гораздо реже
фазовая и поляризационные диаграммы. При измерении характеристик излуче-
ния антенн, кроме традиционных требований к точности измерения, существенное
значение приобретают экономические показатели, связанные со строительством
значительных по размерам измерительных антенных полигонов, безэховых изме-
рительных камер, затратами на измерительную аппаратуру, а также экологические
проблемы, связанные с воздействием электромагнитного поля на окружающую сре-
ду и соседние РЭС. В силу принципа взаимности изменение диаграммы направлен-
ности и коэффициента усиления может проводиться при работе антенны как в ре-
жиме передачи, так и в режиме приема. Поэтому выбор режима работы измеряемой
антенны определяется удобствами измерений. Исключение представляют антенны с
невзаимными элементами.
Входное сопротивление антенны в лабораторных условиях иногда определяют
с помощью измерительной линии, включаемой между генератором и антенной. Из-
меряя КБВ и положение ближайшей к антенне пучности в распределении эпюры
напряженности электрического поля вдоль линии с помощью диаграммы круговых
сопротивлений или формул Татаринова, можно определить входное сопротивление
антенны. На практике часто интересуются лишь уровнем согласования антенны
с фидерной линией в требуемой полосе частот. Эти измерения выполняются с по-
мощью автоматических измерителей КСВ. Ниже более подробно рассматриваются
методы измерения характеристик направленности антенн.
Существуют следующие основные методы измерения амплитудной диаграммы
направленности:
- полигонные (лабораторные) измерения в дальней зоне антенны;
- метод облета, исследуемой антенны по заданной траектории;
- радиоастрономический метод измерения по внеземным источникам излучения;
- коллиматорный метод;
- голографический (апертурно-зондовый) метод измерения в ближней зоне ан-
тенны;
- измерение диаграммы направленности на модели антенн.
Рассмотрим особенности перечисленных.методов измерений диаграммы направ-
ленности.
19.1.1. Метод полигонных (лабораторных) измерений в дальней зоне.
Простейшая структурная схема этого метода представлена на рис. 19.1. Исследу-
Измерение параметров и характеристик излучения антенн
667
Рис. 19.1. Схема метода полигонных измерений [3]
емая антенна 3 (для определенности работающая в режиме приема) располагается
на опорно-поворотном устройстве 4. На некотором расстоянии г в дальней зоне
этой антенны расположена вспомогательная передающая антенна 2, возбужда-
емая генератором 1. Приемное устройство 5 имеет стрелочный или цифровой
регистратор (индикатор) 6,поступающей на вход приемного устройства мощнос-
ти. Зависимость показаний этого индикатора р от угла поворота 0 антенны 4 при
некотором фиксированном угле поворота <pj является сечением диаграммы на-
правленности антенны по мощности р(0, фу) в плоскости ср = (р/ = const. Выбирая
различные значения угла <ру = (pj, <р2, •••> можно измерить диаграмму направленности
в различных сечениях. В качестве простейшего приемного устройства может быть
детекторная секция с последующим усилением мощности. Нормированная ампли-
тудная диаграмма направленности по полю определяется следующим образом:
F(O,<Pi) =
Р(9. ф j)
Pmax(^’ Pj )
(19.1.1)
Минимальное расстояние между исследуемой и вспомогательной антеннами вы-
бирают из условия обеспечения требуемой точности измерения диаграммы направ-
ленности [15]. В идеальном случае поле, падающее от вспомогательной антенны 2
на исследуемую антенну 4, в пределах апертуры этой антенны должно представ-
лять собой плоскую волну. Обратимся к рис. 19.2, на котором показаны слабона-
правленная вспомогательная антенна с фазовым центром в точке О} и исследуемая
антенна с размером L2. При конечном расстоянии г между антеннами фронт вол-
ны, падающей от антенны на антенну А2, является не плоским, а цилиндричес-
ким. Максимальная фазовая ошибка на краях антенны
AVmax = (19'L2)
л Л, V ) 4т
Как известно, при \|/тах - л/8 искажения в диаграмме направленности уже не-
значительны (менее 1%). Подставляя это значение в левую часть (19.1.2), по-
Рис. 19.2. Исследуемая и вспомогательная антенны [3]
668
ГЛАВА 19
лучаем оценку для выбора минимального расстояния между антеннами:
(19.1.3)
Выражение (19.1.2) справедливо для остронаправленной исследуемой антенны
и при условии, что вспомогательная антенна слабонаправленная относительно ис-
следуемой, т.е. Li < Ь2, где — максимальный размер апертуры вспомогательной
антенны. Если Li сравним с , то расстояние г следует выбирать с учетом того,
что амплитуда поля, падающего от антенны Aj на антенну А2, была постоянна
в пределах апертуры антенны А2. Это требование приводит к следующей оценке
при выборе расстояния г :
(19.1.4)
Если исследуемая и вспомогательная антенны являются слабонаправленными, т.е.
L2 < X, то минимальное расстояние между антеннами выбирают из условия
г > 2Ъ2. (19.1.5)
I
При проведении измерения важно обеспечить отсутствие отражений от земли
(пунктир на рис. 19.1) и других окружающих предметов. Для ослабления влия-
ния земли при полигонных измерениях антенны Aj, А2 размещают на специальных
вышках, а на земную поверхность укладывают щиты с поглощающим электромаг-
нитное поле покрытием. Это позволяет обеспечить высокую точность измерения не
только формы основного лепестка, но и боковых лепестков до уровня -30...-40 дБ.
Для исключения влияния окружающих предметов и обеспечения экологической
чистоты измерения проводят в специальных помещениях, покрытых изнутри пог-
лощающим материалом и называемых безэховыми камерами. Для ускорения и ав-
томатизации измерений в качестве регистрирующих устройств используются само-
писцы или ЭВМ и автоматизированные поворотные устройства.
19.1.2. Метод облета антенны по заданной траектории и астрономи-
ческий метод измерения. Одним из главных недостатков полигонных измерений
в дальней зоне является необходимость обеспечения значительных расстояний меж-
ду исследуемой и вспомогательной антеннами при измерении диаграмм острона-
правленных антенн. Так, при X = 1 м и 20о 7 = 1° требуемое минимальное расстояние
равно 5-7 км. При этом существенно возрастают затраты на строительство поли-
гонов, увеличиваются погрешности измерений из-за влияния земли и возрастает
потребляемая мощность используемых при измерении СВЧ-генераторов.
Частично устранить эти недостатки позволяют метод облета исследуемой
антенны по заданной траектории и радиоастрономический метод измерения.
В первом из них вспомогательная антенна располагается на самолете или вертоле-
те, который совершает облет исследуемой остронаправленной антенны по задан-
ной (часто круговой) траектории в дальней зоне антенны. Однако этот метод имеет
ограниченное применение из-за сложности, высокой стоимости, малой производи-
тельности измерений и относительно малой точности из-за невозможности посто-
янно выдерживать точную траекторию полета. При радиоастрономическом методе
измерений в качестве источника излучений используется естественное, излучение
внеземных источников (Солнце, Лебедь а,Кассиопея а ,Дева а, Центавр а и др.)
в диапазоне прозрачности атмосферы и ионосферы Земли 1.25 см <Х< 20 м. Роль
Измерение параметров и характеристик излучения антенн 669
поворотного устройства выполняет вращение Земли вокруг своей оси. Учитывая
малые угловые размеры указанных внеземных источников, в первом приближении
можно считать, что их яркостная температура является дельта-функцией углово-
го положения источника:
Тя (0, Ф) = с5(0 - 0М, Ф - Фм), (19.1.6)
где с — константа, определяющая полную мощность излучения.
Подставляя (19.1.6) в (19.1.7), получаем
I’aE(6u><Pu) = :^7a£Jr2(9u.4>u). (19.1.7)
4л
Следовательно мощность шумов, принимаемая остронаправленной антен-
ной от одиночного источника внеземного излучения пропорциональна диаграмме
направленности антенны по мощности. Недостатком радиоастрономического метода
измерений является малая скорость измерений, ограниченность измерений сече-
ний диаграммы только в плоскостях вращения Земли. Кроме того, так как внезем-
ные источники являются широкополосными, измеренная диаграмма является ре-
зультатом усреднения в полосе частот приемного устройства, поэтому метод имеет
ограниченное применение при измерении узкополосных антенн.
19.1.3. Коллиматорный и голографический методы измерений. При этих
методах отпадает необходимость в выборе больших расстояний между антеннами и
измерения проводятся в ближней зоне антенн. В коллиматорном методе измерений
(рис. 19.3) поле плоской волны от вспомогательной антенны 5, возбуждаемой гене-
ратором 4, создается с помощью коллиматора 1. В качестве коллиматора исполь-
зуются зеркальные, линзовые и некоторые другие типы антенн, причем раскрыв
коллиматора должен быть больше раскрыва исследуемой антенны 2. Диаграмма на-
правленности антенны измеряется как зависимость амплитуды, регистрируемой
приемным устройством 3, от направления между нормалью к раскрыву антенны и
нормалью к фронту плоской волны.
В голографическом (апертурно-зондовом) методе измерений с помощью слабо-
направленного перемещающегося зонда и амплифазометра измеряется ампли-
тудно-фазовое распределение координатных составляющих поля на некоторой по-
верхности 5 в ближней зоне. Поверхность £ может быть произвольной, но для
удобства измерений чаще всего ее выбирают в виде плоскости, расположенной не-
посредственно перед излучающей апертурной антенны, реже - в виде сферы или
цилиндрической поверхности, охватывающей антенну. По измеренному на S полю
вычисляют диаграмму направленности антенны. В силу теоремы единственности
Фронт волны
до коллиматора
Фронт волны
после коллиматора
Рис. 19.3. Коллиматорный метод измерений [3]
670
ГЛАВА 19
для однозначного определения диаграммы направленности поверхность S должна
быть замкнутой. В частности, если S является плоскостью, то ненормированная
диаграмма направленности антенны f (0, tp) с. линейной поляризацией выражает-
ся через амплитудно-фазовое распределение Es (х, у) на плоскости S следующим
образом:
ОО
7(0,(р) = A j jE5(^y)eftsin0(3:'cos<(,+ssin<(’)dxdy, (19.1.8)
- ОО
где А — некоторый постоянный коэффициент.
При реальных измерениях Е$ на плоскости ограничиваются областью, совпа-
дающей или немного превышающей размеры апертуры антенны. Поэтому интегриро-
вание в (19.1.8) выполняют по конечным пределам. Для ускорения вычисления
интеграла (19.1.8) используются ЭВМ и специальные алгоритмы быстрого преоб-
разования Фурье [3].
Динамический диапазон измерения диаграммы направленности при коллима-
торном и голографическом методах измерений составляет 40-45 дБ.
19.1.4. Измерение диаграммы направленности антенны на моделях.
Если изготовить модель антенны, все размеры которой уменьшены в п раз по
сравнению с реальной антенной, причем параметры магнитных и диэлектрических
материалов у модели, и реальной антенны совпадают (ем = &а,рм = ца), а удель-
ная проводимость проводников модели в п раз больше чем у реальной антенны,
то в соответствии с принципом электродинамического подобия поля излучения
модели на частоте fM = nf, где f — частота реальной антенны, и реальной антен-
ны совпадают. Подставляя параметры модели LM = La/n, Хм = X / п в соотношение
(19.1.3), получаем, что при полигонных измерениях минимальное расстояние до
дальней зоны модели rMrnin уменьшится в п раз по сравнению с расстоянием rmin
до дальней зоны реальной антенны
'м min Л , Л
Л, / П ЛИ П
(19.1.9)
Основная трудность при изготовлении модели антенны заключается в выполне-
нии соотношения оЛ= . Однако невыполнение этого соотношения в антеннах с
малыми потерями практически не сказываются на точности измерения диаграммы
направленности.
19.2. Измерение коэффициента усиления антенны
Коэффициент усиления антенны чаще всего измеряется в полигонных (лабо-
раторных) условиях методом сравнения с коэффициентом усиления эталонной ан-
тенны. Структурная схема измерения показана на рис. 19.4. При этом расстояние г
между исследуемой и вспомогательной Ав антеннами выбирают в соответствии
с (19.1.3), (19.1.4). В первом измерении к выходу генератора 1 через аттенюатор 2
и измеритель коэффициента отражения 3 подключается измеряемая антенна Аи,
вращением которой на опорно-поворотном устройстве 6 добиваются максимально-
го уровня мощности Ра в измеряемом (регистрируемом) устройстве 5. Мощность на
выходе регистрирующего устройства поступает с выхода приемного устройства 4.
Измерение параметров и характеристик излучения антенн
671
Рис. 19.4. Схема измерения коэффициента усиления антенны
Для повышения точности измерений с помощью аттенюатора эти показания пере-
водятся в середину шкалы регистрирующего устройства. Используя соотношения
из [3], нетрудно связать уровень регистрируемой мощности Ри с мощностью ге-
нератора Рген, ослаблением аттенюатора N, коэффициентами отражения от входа
антенны измеряемой Ги и вспомогательной Гес антенн, коэффициентами усиления
этих антенн Си, Св и коэффициентом передачи (по мощности) приемного устройства
пр
(19.2.1)
Во втором опыте вместо измеряемой антенны подключают эталонную с извест-
ным коэффициентом усиления Сэ и поляризацией, совпадающей с измеряемой
антенной, и повторяют измерения. Получаем выражение для мощности в регистри-
рующем устройстве, аналогичное (19.2.1):
(19.2.2)
Сравнивая выражения (19.2.1) и (19.2.2), находим
= G,
Ры (1 - |ГЦ |2)
рэ Na (1- Гэ2)
(19.2.3)
Если измеряемые и эталонные антенны хорошо согласованы, а аттенюаторы
одинаковы, то
G =G3—. (19.2.4)
vv Cf '
Для обеспечения достаточной точности измерений коэффициенты усиления изме-
ряемой и эталонной антенн должны быть одного порядка.
672
Совре./иенна.я теория и практические применения антенн
Заключение
Книга содержит необходимый минимум сведений, который, надеемся, позволит
читателям ориентироваться в теории антенн. Авторы хотели представить не толь-
ко стандартный набор сведений о современных антеннах, но и обратить внимание
читателей на ряд новых антенных структур, характерных для современных, а
также перспективных систем сверхбыстрой обработки информации (СБОИ).
Ниже в заключение скажем несколько слов о новых, перспективных с нашей
точки зрения, фрактальных антенных структурах.
Основные свойства фрактальных антенных решеток (многодиапазонность, КНД,
уровень боковых лепестков) зависят, в первую очередь, от базовой геометричес-
кой структуры: квадратной, треугольной, гексагональной. Некоторые из геомет-
рических структур при определенном сочетании параметров являются эффектив-
ными в том смысле, что многие элементы решетки перекрываются. Фрактальные
решетки, в частности кольцевые, могут быть реализованы как в виде волноводов,
так и в виде микрополосковых антенн.
Введение фракталов при решении задач синтеза антенных решеток позволило
получать следующие типы антенных решеток [65]:
а) с относительно низким уровнем боковых лепестков, высоким КНД, но тре-
бовательным к точности изготовления и расположению излучателей. Свойства та-
ких решеток близки к классическим, однако в ряде случаев можно упростить
алгоритмы синтеза таких фрактальных решеток по сравнению с обычными [140];
б) менее требовательного к точности расположения излучателей (особенно при
большом их числе), но имеющего низкий КНД и достаточно высокий уровень
высоких боковых лепестков. По своим свойствам фрактальные антенные решетки
похожи на решетки со случайным расположением элементов. Они синтезируются
введением эквидистантных антенных подрешеток (генераторных функций). Введе-
ние широкого класса генераторных функций приводит к возможности построения
фрактальных антенных решеток с различным уровнем боковых лепестков и раз-
личной формой диаграмм направленности [142].
Одной из интереснейших сфер применения антенных структур, в том числе
микрополосковых антенн, является их использование для изучения влияния ЭМП
на биологические объекты, восприятия живыми системами электромагнитного из-
лучения.
Можно привести множество примеров природных антенных систем. Это, пре-
жде всего, естественные приемные антенны растений, воспринимающие солнечное
и иные виды излучения. Для растений процессы восприятия ЭМВ носят не менее
сложный характер, чем для животных (достаточно вспомнить их роль в процессе
фотосинтеза). В то же время есть существенная разница в восприятии внешних
ЭМП животными и растениями. В частности, «приемные антенны» растений име-
ют несомненное сходство с антеннами радиотехнических систем. Чтобы убедиться
в этом, достаточно сравнить логарифмическо-периодическую телевизионную ан-
тенну (рис. 3.1, а) с остовами игл и прожилками листьев растений (рис. 3.1, б).
Конечно, внешнее сходство не означает полную аналогию природных и тех-
нических систем. Так, показанная на рис. 3.1, а антенна представляет собой
разомкнутую двухпроводную систему, со своими вибраторами и строгим под-
Заключение
673
б)
Рис. 3.1. Логарифмическо-периодическая телевизионная антенна (а)
и различные остовы игл и листьев (б)
держанием поляризации. В растении же, например в прожилках листьев (см.
рис. 3.1, б), двухпроводность и поддержание поляризации отсутствуют, хотя име-
ется проводимость. Однако можно говорить о достаточно явной аналогии меж-
ду диэлектрическими антеннами, используемыми вплоть до УФ диапазона, и
листьями и иглами растений, поскольку в диэлектрических открытых антеннах
используется режим поверхностной волны. Более того, лист (иглу) можно рас-
сматривать как плоскую диэлектрическую антенну с эквивалентом направляющей
(усиливающей сигнал) радиотехнической структуры — прожилками листа.
В зависимости от преобладающего диапазона частот, принимаемых конкрет-
ным видом растений, эволюционно строилась и приемная антенна растений. «На-
стройка» на диапазон сводилась к варьированию резонансной структуры, системы
вибраторов, т.е. к изменению числа, формы и взаимного расположения прожилок,
а также других электрофизических, геометротопологических и фрактальных ха-
рактеристик.
Для биофизических опытов можно оценить диапазон «настройки» природных
антенн растений на технические ЭМП. В частности, рассчитаны антенные пара-
метры иглы хвойного дерева (сосны): длина иглы 14 мм, диаметр иглы 1 мм, ко-
эффициент замедления 14, коэффициент укорочения (длины волны) 0.88.
Не только листья и иглы можно ассоциировать с природными антеннами. Не
только штыревые (иглы) и плоские (листья) формы растений могут быть прием-
никами ЭМВ, но и трехмерные формы, которых в растительном мире множество.
Большинство из них ассоциируется со спиралью, цилиндром, эллиптическим ци-
линдром, которые дополняются осевыми «стержнями». Это напоминает техничес-
кую коаксиальную линию и резонатор, в общем случае — открытую коаксиальную
резонансную структуру. Эти структуры обладают рядом уникальных свойств. На-
пример, спектр колебаний такой структуры является равномерным (эквидистант-
ным), что делает ее весьма перспективной для использования в электронике СВЧ,
квантовой радиофизике и т.д.
В настоящее время разработчики технических средств, следуя опыту природы,
конструируют антенные системы, используя фрактальный принцип самоподобия.
674
Соврем^ная теория и праюррчрысие у^имен^ия дмтенн
88.9 мм
44.5 мм
мм
мм
мм
800 мм
Рис. 3.2. Фрактальная антенна Серпинского, синтезированная пятью итерациями с коэф-
фициентом масштаба 5 - 2 [57]
Примером может служить фрактальная антенна Серпинского (рис. 3.2). Она вы-
полняется на диэлектрической подложке, имеющей толщину 1.588 мм и диэлект-
рическую проницаемость s = 2.5. Антенна синтезирована посредством пяти итера-
ций, обозначенных окружностями на рис. 3.2. По своим характеристикам антенна
Серпинского является логарифмической в пяти диапазонах.
Более сложная фрактальная антенна, конфигурация которой уже мало отличи-
ма от рисунка (в плоскости) дерева или кустарника, приведена на рис. 3.3. Такая
антенна имеет «сгущенные» частотные диапазоны и очень мощную спектральную
структуру с большим числом резонансных частот.
В [144] предложены кольцевые фрактальные решетки.
Все более широкое применение в радиотехнических и иных системах обработки
информации находят коротковолновая часть диапазона КВЧ и оптический диапа-
зон. Последний используется не столько в антенных трактах современных ССОИ,
сколько в устройствах обработки информации в антенном тракте на несущей час-
тоте радиосигнала. Это ведет к огромным выигрышам в массогабаритных пара-
метрах АФУ и радиотехнического комплекса в целом, а также к существенному
увеличению скорости обработки информации.
Заслуживают внимания проблемы использования передовых интегральных
технологий при построении как элементарных излучателей, например микро-
полосковых, щелевых и им подобных, так и антенных решеток разного клас-
са, создаваемых на основе этих излучателей, а также плоскостных и особенно
объемных интегральных схем для выполнения важнейших элементов управления
диаграммой направленности антенны и антенной решетки. Наибольшие успехи в
создании диаграммообразующих устройств (матриц) были достигнуты именно при
использовании объемных интегральных схем.
В последние годы при создании антенных комплексов большое внимание уде-
ляется обработке информации в аналоговом виде с использованием фотонных
(оптических) цепей. Уже осуществлены фазированные антенные решетки, в ко-
торых применяются оптические методы формирования, обработки, передачи и
распределения сверхширокополосных сигналов. Аппаратура, обеспечивающая та-
кой подход, отличается безынерционностью, сверхвысокой широкополосностью.
помехоустойчивостью и высокой стабильностью, а также имеет малые габаритны-
размеры и массу. В итоге скорость при аналоговой обработке сигналов оказываетс -
на три порядка выше, чем при цифровой.
Заключение
675
80 см
а) б)
Рис. 3.3. Фрактальная древовидная антенна (а) и увеличенные фрагменты антенны около
точки запитывания (б) [57]
Авторы желают читателям успехов в освоении курса антенн и разработке но-
вых устройств.
676
Современная теория и практические применения антенн
Приложение 1
КРАТКИЙ ТОЛКОВЫЙ СЛОВАРЬ
ПО АНТЕННО-ФИДЕРНЫМ УСТРОЙСТВАМ [57]
Антенна — устройство для излучения и приема радиоволн. Передающая антен-
на преобразует энергию электромагнитных колебаний высокой частоты, сосредо-
точенную в выходных колебательных цепях радиопередатчика, в энергию излу-
чаемых радиоволн. Приемная антенна выполняет обратную функцию: преобразует
энергию распространяющихся радиоволн в энергию, сосредоточенную во входных
колебательных цепях приемника.
Антенна типа «волновой канал» — директорная антенна, антенна бегущей
волны в виде ряда параллельных линейных электрических вибраторов длиной,
близкой к половине длины волны, которые расположены в одной плоскости вдоль
линии, совпадающей с направлением максимального излучения (приема). Иногда
такую антенну называют антенной Уда-Яги. Один из ее вибраторов (активный)
служит для подвода энергии высокочастотных колебаний. В остальных вибраторах
(пассивных) наводятся (возбуждаются) электрические токи вследствие пространс-
твенной электромагнитной связи между ними и активным вибратором. Фаза токов
в рефлекторе и директорах, регулируемая изменением их длины, устанавливает-
ся таким образом, что вдоль антенны в направлении от рефлектора к директорам
образуется бегущая волна. При регулировке антенны директоры укорачивают на
4... 10 %, а рефлектор удлиняют на 5... 10 % по сравнению с активным X / 2, вибра-
тором, длина которого немного меньше, где X — длина рабочей волны. Расстояние
между вибраторами обычно составляет (0.1...0.3) А,. Коэффициент направленного
действия (КНД) такой антенны растет с увеличением числа пассивных вибрато-
ров и доходит до 20...30. Антенну типа «волновой канал» применяют для передачи
и приема преимущественно в диапазоне метровых волн, в частности для приема
телевизионных программ.
Антенна рупорная — антенна в виде металлического волновода с плавно уве-
личивающимся сечением. У выхода рупора при достаточно малом угле раствора
плоская поверхность, проходящая через его кромки, получается почти синфаз-
но возбужденной. Коэффициент использования поверхности такой антенны равен
0.5...0.8, а коэффициент направленного действия обычно находится в пределах
10... 100. Рупорная антенна широко применяется в качестве облучателя зеркальных
и линзовых антенн.
Антенный эффект (АЭ) — нежелательное излучение или прием электромагнит-
ных волн проводниками электрического тока, не предназначенными для этих це-
лей. Наиболее часто АЭ проявляется в линиях передачи энергии высокочастотных
колебаний, соединяющих радиопередатчик или радиоприемник с антенной, в фи-
дерах. В радиоустройствах АЭ приводит к искажению диаграммы направленности
(ДН) антенн, уменьшению КПД линии передачи. В двухпроводной линии передачи
АЭ появляется из-за нарушения симметрии расположения проводов относительно
окружающих предметов или присоединяемых к линии устройств, в коаксиальном
кабеле — из-за нарушения контакта между внешней оболочкой и заземлением шиI
корпусом прибора, в волноводе — из-за появления щелей в местах стыка отде-
Приложение 1 677
льных отрезков волновода. В рамочной антенне АЭ называется искажение ее ДН,
возникающее при нарушении симметрии самой рамки или соединительных прово-
дов и присоединяемых устройствах, что приводит к появлению нежелательного
приема в направлении нормали к плоскости рамки.
Антиподы оптические — пространственные изомеры с одинаковыми химичес-
кими и физическими свойствами, но разными направлениями (знаками) вращения
плоскости поляризации света. По структуре молекулы оптических антиподов от-
носятся друг к другу, как предмет к своему зеркальному изображению. Антипод,
вращающий плоскость поляризации света вправо, называется правовращающим,
или (+) -антиподом, а вращающий влево — левовращающим, или (-) -антиподом.
Оптические антиподы часто встречаются в природных веществах.
Атмосфера Земли (от гр. atmos — пар и sphaira — шар) — газовая оболочка,
окружающая Землю. Атмосферой принято считать ту область вокруг Земли, в
которой газовая среда вращается вместе с Землей как единое целое. Атмосфера
обеспечивает возможность жизни на Земле и оказывает большое влияние на раз-
ные стороны жизни человечества. Она защищает поверхность Земли от разруши-
тельного действия падающих метеоритов, большая часть которых сгорает при
вхождении в плотные слои атмосферы.
Атмосфера имеет четко выраженное слоистое строение. Основные черты сло-
истой структуры атмосферы определяются в первую очередь особенностями вер-
тикального распределения температуры. В самой нижней ее части — тропосфере,
где наблюдается интенсивное турбулентное перемешивание, температура убыва-
ет с увеличением высоты. Уменьшение температуры по вертикали составляет в
среднем 6 К на 1 км. Высота тропосферы изменяется от 8...10 км в полярных
широтах до 16... 18 км у экватора. В связи с тем что плотность воздуха быстро
убывает с высотой, в тропосфере сосредоточено около 80 % всей массы атмосфе-
ры. Над тропосферой расположен переходный слой — тропопауза (температура
190...220 К), выше которой начинается стратосфера. В нижней части стратосферы
(так называемой изотермической области, или нижней стратосфере) уменьшение
температуры с высотой прекращается и температура остается приблизительно
постоянной до высоты 25 км. В лежащей выше области (так называемой области
инверсии, или верхней стратосфере) температура начинает возрастать и достига-
ет максимума ( «270 К) на уровне стратопаузы, расположенной на высоте около
55 км. Слой атмосферы, находящийся на высотах от 55 до 80 км, в котором вновь
происходит понижение температуры с высотой, называется мезосферой. Над ней
находится переходный слой — мезопауза, выше которой располагается термосфе-
ра, где температура, увеличиваясь с высотой, достигает очень больших значений
(свыше 1 000 К). Еще выше (на высотах 1000 км и более) находится экзосфера, из
которой атмосферные газы рассеиваются в мировое пространство за счет диссипа-
ции. Здесь происходит постепенный переход от атмосферы к межпланетному про-
странству. Обычно все слои атмосферы, находящиеся выше тропосферы, называ-
ются верхними, хотя иногда к нижним слоям атмосферы относят и стратосферу
или только ее нижнюю часть.
Вентиль электрический — электротехническое устройство, проводимость ко-
торого в значительной мере зависит от направления электрического тока. В од-
ном (прямом) направлении проводимость вентиля на один или несколько порядков
выше, чем в противоположном (обратном). Существуют управляемые и неуправля-
емые вентили. В управляемых вентилях проводимость меняется в момент подачи
управляющего сигнала.
В неуправляемых вентилях управляющий электрод отсутствует и перевод их
678
Современная теория и и/рактические п/рименения антенн
из состояния с низкой проводимостью в состояние с высокой проводимостью обус-
лавливается подачей на вентиль напряжения, превышающего напряжение вклю-
чения.
Волна бегущая — волна, которая при распространении переносит энергию в
отличие от волны стоячей. Бегущие волны могут распространяться как в свобод-
ном пространстве, так и вдоль каких-либо линий, например кабелей, волноводов
и т.п. Обычно бегущая волна в линии передачи возникает в том случае, когда со-
противление нагрузки равно волновому сопротивлению линии.
Волна стоячая — волна, возникающая вследствие интерференции волн, рас-
пространяющихся в противоположных направлениях. Стоячие волны образуются
при отражениях волн от преград и неоднородностей (в линии передачи, на трассе
распространения радиоволн и т.п.) результате наложения отраженной волны на
прямую. Различные участки стоячих волн колеблются в одной и той же фазе, но с
различной амплитудой. В стоячей волне в отличие от волны бегущей не происходит
перенос энергии.
Всякий волновой процесс, связанный с распространением возмущений, может
сопровождаться образованием стоячих волн. Такие волны могут возникать не толь-
ко в газообразных, жидких и твердых средах, но и в вакууме при распростра-
нении и отражении электромагнитных возмущений, например в электрических
длинных линиях. Антенны радиопередатчиков часто выполняют в виде прямоли-
нейного вибратора или системы вибраторов, по длине которых устанавливаются
стоячие волны. В отрезках волноводов и замкнутых объемах различной формы,
используемых в качестве резонаторов устройств СВЧ и КВЧ, устанавливаются
стоячие волны определенных типов. В электромагнитных стоячих волнах электри-
ческие и магнитные поля разделяются. «Чистые»стоячие волны могут установиться
только при отсутствии затухания в среде и полном отражении волн от границы
раздела сред или некоторого препятствия. Обычно одновременно со стоячими
волнами в линии передачи присутствуют и бегущие волны, подводящие энергию к
местам ее поглощения или излучения.
Волновод — имеющий резкие границы канал, по которому распространяются
волны. Для электромагнитных волн СВЧ волноводами служат металлические тру-
бы различных сечений или диэлектрические стержни, для света —цилиндричес-
кие и конические трубки.
Волновое число — величина, связанная с длиной волны X соотношением
к = 2л/Х (число волн, укладывающихся на длине 2л).
Волновой вектор — вектор к направление которого совпадает с направлением
распространения волны бегу щей,численно равный волновому числу к.
Волновой пакет — распространяющееся волновое поле, занимающее в каж-
дый момент времени ограниченную область пространства. Волновой пакет может
возникнуть у волн любой природы (звуковых, электромагнитных и т. п.). Такой
волновой «всплеск» в некоторой области пространства может быть представлен
в виде суммы монохроматических волн, частоты которых лежат в определенных
пределах.
Диаграмма направленности — графическая зависимость напряженности элек-
трического поля излученной волны (измеренной на больших и одинаковых рассто-
яниях от антенны) от направления излучения. Направленность излучения антенны
приводит к повышению напряженности поля волны в направлении максимального
излучения и таким образом создает эффект, эквивалентный эффекту, вызывае-
мому увеличением излучаемой мощности.
Дифракция радиоволн — явления, возникающие при встрече радиоволн с пре-
Приложегсие 1
679
пятствиями. Радиоволна, встречая при распространении в однородной среде пре-
пятствие, изменяется по амплитуде и фазе и проникает в область тени, отклоня-
ясь от прямолинейного пути.
Длина волны X — расстояние между двумя максимумами или минимумами
возмущения; X = сТ, где с — скорость распространения волны, Т — период волны,
т.е. время, за которое частица среды совершает одно полное колебание. Указанное
соотношение справедливо для гармонической волны любой природы.
Зенит (фр. zenith, от араб, земт, буквально — путь, направление) — точка не-
бесной сферы, расположенная над головой наблюдателя. В зените небесную сферу
пересекает линия, направленная из места наблюдений вертикально вверх. Точка
небесной сферы, противоположная зениту, называется надиром.
Излучатель изотропный — воображаемая антенна, излучающая во все направ-
ления электромагнитную энергию одинаковой интенсивности. Обладает круговой
диаграммой направленности в любой плоскости. В антенной технике изотропный
излучатель принимается в качестве эталона при сравнительной оценке направ-
ленных свойств различных антенн, в частности при определении их коэффициен-
та направленного действия. Созданию антенн, близких по своим направленным
свойствам к изотропному излучателю, уделяется большое внимание. В частности,
они необходимы для использования на искусственных спутниках Земли, не стаби-
лизированных в пространстве. Такие антенны позволяют обеспечить устойчивую
связь со спутником при изменении его положения в пространстве.
Импеданс (англ, impedance, от лат. impedio — препятствую) в электротехнике
— устаревшее название полного сопротивления электрической цепи при синусои-
дальных напряжении и токе.
Интерференция волн — сложение в пространстве двух или нескольких волн,
при котором в разных точках получается усиление или ослабление амплитуды
результирующей волны. Интерференция характерна для всяких волн независимо
от их природы — на поверхности жидкости, упругих (например, звуковых), элек-
тромагнитных (например, радиоволн или световых).
Ионосфера (от ионы и гр. sphaira — шар) — ионизированная часть верхней
атмосферы; расположена на высоте более 50 км. Верхней границей ионосферы
является внешняя часть магнитосферы Земли. Ионосфера представляет собой
природное образование разреженной слабоионизированной плазмы, находящейся
в магнитном поле Земли и обладающей благодаря своей высокой электропровод-
ности специфическими свойствами, определяющими характер распространения в
ней радиоволн и различных возмущений. Только благодаря ионосфере возможен
такой простой и удобный вид связи на дальние расстояния, как радиосвязь.
Канал связи — канал передачи (технические устройства и тракт связи), в кото-
ром радиосигналы, содержащие информацию, распространяются от передатчика к
приемнику. Технические устройства (усилители электрических сигналов, устройс-
тва кодирования и декодирования сигналов и др.) размещают в промежуточных
(усилительных или переприемных) и оконечных пунктах связи. В качестве тракта
связи используются разнообразные линии — проводные (воздушные и кабельные),
радио- и радиорелейные, волноводные, световодные и т.д. Передатчик преобра-
зует сообщения в сигналы, подаваемые на вход канала. По принятому сигналу на
выходе канала приемник воспроизводит переданное сообщение. Передатчик, канал
связи и приемник образуют систему связи, или систему передачи информации.
Когерентность (от лат. cohaerens — находящийся в связи) — согласованное
протекание во времени и пространстве нескольких колебательных или волновых
процессов, проявляющееся при их сложении. Колебания называются когерентны-
680 Современная теория и практические применения антенн
ми, если разность их фаз остается постоянной во времени и при сложении коле-
баний определяет амплитуду суммарного колебания. Два гармонических (синусо-
идальных) колебания одной частоты всегда когерентны. Гармоническое колебание
описывается выражением a(t) = A cos(2n/t + ср), где a(t) — колеблющаяся величина
(например, напряженность электрического и магнитного полей). Частота гармони-
ческого колебания /, его амплитуда А и фаза ф постоянны во времени.
При сложении двух гармонических колебаний с одинаковой частотой f, но раз-
ными амплитудами и А2 и фазами ф^ и ф2 образуется гармоническое колебание
той же частоты. Амплитуда результирующего колебания, квадрат которой опре-
деляется выражением А% = А? + А| +2AjA2 соз(ф1 -ф2), может изменяться в пре-
делах от Al + А2 до Ai - А2 в зависимости от разности фаз фх + ф2. Интенсивность
результирующего колебания также зависит от разности фаз ф^ + ф2.
Коэффициент использования поверхности антенны — коэффициент к, учи-
тывающий неравномерность и несинфазность возбуждения основной излучающей
поверхности, прохождение мимо нес части энергии и т.п. Для идеально плоской,
синфазно и равномерно возбужденной поверхности к = 1, на практике к = 0А..0.8.
Для создания синфазно возбужденной поверхности широко используются техни-
ческие приемы из оптики и электроакустики.
Коэффициент направленного действия — коэффициент показывающий, во
сколько раз нужно увеличить мощность излучения при замене данной реальной
антенны гипотетической ненаправленной антенной (изотропным излучателем),
чтобы напряженность электромагнитного поля осталась неизменной. КНД вводит-
ся для количественной оценки эквивалентного выигрыша в излучаемой мощности.
Приближенно он равен отношению AknS/7?, где к — коэффициент использова-
ния поверхности антенны; S — излучающая площадь антенны, м2; X— длина
волны,м. Поскольку КНД обратно пропорционален квадрату длины волны, у ан-
тенн, работающих в диапазоне СВЧ, он достигает значений порядка 105...10 .
Коэффициент полезного действия антенны — отношение излучаемой ан-
тенной мощности ко всей подводимой к ней мощности. Не вся подводимая к ан-
тенне мощность излучается. Часть ее теряется в проводах и изоляторах антен-
ны, а также в окружающей антенну среде (земле, поддерживающих антенну
конструкциях и т.д.).
Коэффициент усиления антенны — произведение коэффициента направлен-
ного действия (КНД) на коэффициент полезного действия (КПД) антенны.
Мираж (фр. mirage) — оптическое явление в атмосфере, состоящее в том, что
вместе с отдаленным предметом (или участком неба) видно его мнимое изобра-
жение, смещенное относительно предмета. Если предмет находится за линией го-
ризонта, видно только мнимое изображение. Мираж может располагаться под
предметом (нижний мираж), над предметом (верхний мираж) и сбоку от него
(боковой мираж). Мираж возникает из-за искривления лучей света, идущих от
предмета, вследствие аномального распределения показателя преломления света
в атмосфере, которое связано с распределением температуры (и следовательно,
плотности) воздуха.
Озон — соединение из трех атомов кислорода (О3), резко пахнущий взрывчатый
газ синего цвета. Обычно образуется в атмосфере при электрических разрядах во
время грозы или под действием ультрафиолетовых лучей Солнца, определяет ха-
рактер поглощения солнечной радиации в земной атмосфере. Содержится в нич-
тожном количестве: толщина слоя озона, приведенного к нормальным условиям
давления и температуры (760 мм. рт. ст. и 0°С), в среднем для всей Земли составля-
ет 2.5...3 мм, в экваториальных областях — около 2 мм, а в высоких широтах — до
Приложение 1 681
4 мм. Основная масса озона в атмосфере расположена в виде слоя (озоносферы) на
высоте 10...50 км с максимумом концентрации на высоте 20...25 км. В тропосфере
содержание озона очень мало, изменчиво во времени и по высоте.
Поляризация волн — нарушение осевой симметрии распределения возмуще-
ний напряженностей электрических и магнитных полей электромагнитных волн
(например, в поперечной волне относительно направления се распространения).
Наибольшая поляризация волн имеет место в случае электромагнитных волн оп-
тического диапазона.
Радиоастрономия — раздел астрономии, в котором небесные объекты (Солн-
це, звезды, галактики и др.) изучаются на основе исследования излучаемых ими
радиоволн в диапазоне от долей миллиметра до нескольких километров. Иногда
к этому разделу относят и радиолокационную астрономию, которую называют в
этом случае активной радиоастрономией, в отличие от пассивной радиоастроно-
мии, занимающейся наблюдениями собственного радиоизлучения небесных объ-
ектов.
Разрешающая способность (разрешающая сила) антенны — свойство антенны
разделять «изображения» двух близких друг к другу точек объекта. Наименьшее
линейное или угловое расстояние между двумя точками, при котором их изобра-
жения не сливаются, называется линейным или угловым пределом разрешения.
Обратная ему величина обычно служит количественной мерой разрешающей спо-
собности.
Рассеяние радиоволн (света) — изменение характеристик потока радиоволн
(света) при его взаимодействии с веществом. Такими характеристиками могут
быть пространственное распределение интенсивности, частотный спектр, поляри-
зация. Часто рассеянием называют только обусловленное пространственной не-
однородностью среды изменение направления распространения волны. В световом
диапазоне рассеяние воспринимается как несобственное свечение среды.
Рефракция радиоволн (света) — то же, что и преломление света, т.е. измене-
ние направления световых лучей при изменении показателя преломления среды,
через которую эти лучи проходят.
Рэлея закон — закон, гласящий, что интенсивность I рассеиваемого средой
света обратно пропорциональна четвертой степени длины волны X падающего
света (I ~ 1/Х2) в случае, когда среда состоит из частиц-диэлектриков, размеры
которых намного меньше X. Установлен Дж. У. Рэлеем в 1871 г. Если энергия испу-
щенного фотона равна энергии поглощенного, рассеяние называется рэлеевским.
Сопротивление излучения антенны к — параметр, характеризующий из-
лучающие свойства антенны. При длине вибратора I < X / 4 под сопротивлением
излучения обычно подразумевают отношение излученной мощности к квадрату
эффективного значения силы тока, измеренного у нижнего конца вибратора. Чем
больше R, тем больше излучаемая мощность (при заданном токе в вибраторе),
выше КПД антенны, шире полоса пропускаемых частот и ниже максимальная
напряженность электрического поля, возникающая у поверхности провода ан-
тенны при заданной подводимой мощности. Так как максимальная напряженность
поля во избежание ионизации окружающего воздуха и пробоя изоляторов, под-
держивающих антенну, не должна превосходить определенного значения, то чем
больше R, тем больше максимальная мощность, которую можно подвести к ан-
тенне. Сопротивление излучения увеличивается с ростом отношения Z/Х, а также
с повышением равномерности распределения тока подлине вибратора. Расширение
полосы пропускаемых частот и снижение максимальной напряженности поля до-
стигаются также увеличением диаметра провода антенны или применением не-
682
Совремеюиая теория и пракяпимесюля применения антенн
скольких параллельно соединенных проводов, что снижает волновое сопротивле-
ние антенны).
Стратосфера (от лат. stratum — слой и гр. sphaira — шар) — слой атмосферы
между тропосферой и мезосферой (от 8... 16 км до 45...55 км), в котором темпера-
тура растет с высотой. Газовый состав стратосферного воздуха сходен с тропос-
ферным, но в стратосфере меньше водяного пара и больше озона. Наибольшая
концентрация озона в слое на высоте от 20 до 30 км. Тепловой режим стратосферы
в основном определяется лучистым теплообменом, в меньшей степени — верти-
кальным движением и горизонтальным переносом воздуха. В целом стратосфера
близка к лучистому равновесию, т.е. температура в ней определяется равенством
энергии, поглощаемой и излучаемой молекулами воды, углекислого газа и озона.
Телесный угол — часть пространства, ограниченная некоторой конической по-
верхностью. Частными случаями телесного утла являются трехгранные и много-
гранные углы. Значение телесного угла равно отношению площади вырезаемой
этим углом части сферы с центром в вершине телесного угла к квадрату радиуса
сферы. Единицей измерения телесного угла является стерадиан, равный теле-
сному углу, с вершиной в центре сферы, вырезающему на поверхности сферы
площадь, равную площади квадрата со стороной, равной радиусу сферы. Полная
сфера образует телесный угол, равный 4л стерадиан.
Трансформатор СВЧ, КВЧ — трансформатор полного сопротивления, устройс-
тво для преобразования полного электрического сопротивления СВЧ или КВЧ
линии передачи (полого или диэлектрического волновода, коаксиальной длинной
линии, полосковой и (или) щелевой линии) в целях согласования ее с нагрузкой
либо, наоборот, для получения требуемого их рассогласования. Применяется в
СВЧ и КВЧ технике, АФУ. К трансформаторам относятся также устройства для
преобразования типов волн в волноводах.
Согласующее (рассогласующее) действие большинства трансформаторов осно-
вано на использовании трансформирующих свойств отрезков линии передачи, в
которых имеются неоднородности. Последние вызывают отражения (возмущения)
волн, что приводит к изменению эквивалентных активного и (или) реактивного
сопротивлений соответствующего участка линии передачи. Для создания неодно-
родностей применяют штыри, диафрагмы, короткозамкнутые шлейфы, диэлект-
рические втулки, стыки волноводов, имеющих различные размеры поперечного
сечения, и т.д.
Тройник СВЧ, КВЧ — Т-образный соединитель, отрезок волновода, имеющий
ответвления в одном либо нескольких направлениях, В простейшем тройнике к
основному прямоугольному волноводу под некоторым углом (например, 90°) подсо-
единяется дополнительный прямоугольный волновод, примыкающий к его узкой
(так называемый Н-трой-ппк) или широкой (так называемый Е-тройник) сторо-
не. Такие тройники используются, главным образом, в делителях и сумматорах
мощности, антенных переключателях РЛС, трансформаторах СВЧ (в качестве
реактивных шлейфов).
Двойные тройники (объединенные Н- и Е-тройники), обладающие свойства-
ми мостовой цепи, находят применение в балансных антенных переключателях,
измерительных мостах (для измерения сопротивлений в диапазоне СВЧ-КВЧ),
балансных смесителях частоты (построенных по балансной схеме), трансформа-
торах СВЧ и других устройствах СВЧ и КВЧ. Используются также смешанные
тройники — волноводно-коаксиальные (от прямоугольного волновода ответвляется
коаксиальная линия).
Тропопауза (от гр. tropos — поворот, изменение и pausis — остановка, прекра-
Приложение 1
683
щение) — переходный слой между тропосферой и стратосферой. Толщина от
нескольких сотен метров до 2...3 км. В тропопаузе градиент температуры уменьша-
ется, нередко наблюдается инверсия температуры. За высоту тропопаузы обычно
принимают высоту верхней границы тропосферы, которая зависит от географи-
ческой широты, циклонической деятельности и времени года (летом она больше,
чем зимой).
Тропосфера (от гр. tropos и sphaira) — нижняя, преобладающая по массе часть
земной атмосферы,в которой температура понижается с высотой. Область тропос-
феры простирается в среднем до высот 8... 10 км в полярных широтах, 10... 12 км
— в умеренных, 16... 18 км — в тропических.
Фазовращатель СВЧ, КВЧ (фазосдвигатель) — устройство, предназначенное
для изменения фазы электромагнитных колебаний на выходе линии передачи СВЧ
или КВЧ (полого или диэлектрического радиоволновода, коаксиальной длинной
линии, полосковой линии) относительно фазы колебаний на ее входе, осуществля-
емого посредством изменения электрической длины этой линии.
Фазоинвертор — электрическое устройство, преобразующее входное напряже-
ние в два напряжения, сдвинутые по фазе на 180°. Простейшим фазоинвертором
является электрический трансформатор с симметричной вторичной обмоткой,
имеющей отвод от средней точки. Часто в качестве фазоинвертора используют
колебательный контур, у которого имеется отвод от средних точек в индуктив-
ной или емкостной ветвях (от средней точки катушки индуктивности или общей
точки двух последовательно включенных конденсаторов). В радиотехнических ус-
тройствах получили распространение сначала ламповые, а позднее — транзис-
торные фазоинверторы с разделенной нагрузкой. В таких фазоинверторах выход-
ные сигналы на аноде (коллекторе) и катоде (эмиттере) имеют разную полярность
(сдвинуты по фазе на 180°)- Существуют и другие фазоинверторы, например на
составных транзисторах. Фазоинверторы используют также в измерительной ап-
паратуре, устройствах вычислительной техники и др.
Циркулятор — многоплечевое (многополюсное) устройство для направленной
передачи энергии ВЧ, СВЧ, КВЧ электромагнитных колебаний. Энергия, под-
веденная к одному из плеч, передается в другое (строго определенное) плечо в
соответствии с порядком их чередования. Различают электронные и ферритовые
циркуляторы. В электронных циркуляторах используется способность некоторых
активных фазовращателей создавать необратимый фазовый сдвиг в рад (см. так-
же фазоинвертор). Такие циркуляторы выполняют на основе дискретных элемен-
тов — транзисторов, диодов, резисторов. Существуют электронные трехплечие
циркуляторы (У-циркуляторы) с сосредоточенными параметрами, применяемые в
диапазоне частот от единиц до нескольких десятков мегагерц. Действие феррито-
вых циркуляторов основано на способности ферритов, намагниченных во внешнем
постоянном магнитном поле, создавать при взаимодействии с электромагнитным
полем (волной) невзаимный фазовый сдвиг, невзаимный поворот плоскости по-
ляризации либо такую комбинацию волн, которая обеспечивает их распростра-
нение только в одном из плеч. Различают V-, X- и Т-ферритовые циркуляторы.
Ферритовые X- и У-циркуляторы используются в антенно-фидерных трактах для
переключения антенны или модуля сложной ФАР из режима передачи в режим
приема.
684
Современная теория и практические применения антенн
Приложение 2
УЧЕНЫЕ, ВНЕСШИЕ СУЩЕСТВЕННЫЙ ВКЛАД
В РАЗВИТИЕ ЭЛЕКТРОДИНАМИКИ, ТЕОРИИ
И ПРАКТИКИ АНТЕНН И РАСПРОСТРАНЕНИЯ
РАДИОВОЛН
Ампер Андре Мари (Ampere; 1775-1836) — великий французский физик, ма-
тематик и химик.
Открыл магнитное взаимодействие токов, установил закон этого взаимодейс-
твия (закон Ампера) и сделал вывод, что все магнитные явления сводятся к чис-
то электрическим эффектам. Согласно гипотезе Ампера, внутри любого магнита
циркулирует множество круговых электрических токов, действие которых и обус-
ловливает магнитные силы. Открыл магнитный эффект катушки с током — соле-
ноида.
Брюстер Дейвид (Brewster; 1781-1868) — известный английский физик. Описал
явление хроматической поляризации в одноосных и двухосных кристаллах, от-
крыл круговую поляризацию света, явление двойного лучепреломления в средах
с искусственной анизотропией.
Введенский Борис Алексеевич (1893-1969) — видный советский физик, про-
фессор Всесоюзного электротехнического института и МГУ, академик АН СССР.
Работал в лабораториях Н.Н.Андреева, В.К. Аркадьева, М.В. Шулейкина. Основные
труды в области радиофизики и радиотехники. Фундаментальные исследования ме-
тодов генерации и приема радиоволн, в особенности диапазона УКВ. Показал, что
характер распространения УКВ в области прямой видимости обусловлен интер-
ференцией прямых и отраженных от земной поверхности лучей, впервые решил
задачи дифракционного распространения УКВ для случая сферической Земли и
распространения УКВ вокруг земного шара с учетом не только дифракции, но и
рефракции в тропосфере. Главный редактор Большой советской энциклопедии.
Вольта Аллесандро (Volta; 1745-1827) — известный итальянский физик и фи-
зиолог, один из основоположников учения об электричестве. Создал первый хи-
мический источник тока — вольтов столб (1800 г.), открыл контактную разность
потенциалов.
Гаусс Карл Фридрих (Gauss; 1777-1855) — знаменитый немецкий математик,
астроном, геофизик, профессор Геттингентского университета. Внес фундамен-
тальный вклад в теоретическую и прикладную математику, астрономию, геоде-
зию. Общеизвестен его труд «Общая теория земного магнетизма» (1838 г.). Вывел
более простую и менее общую, чем у М. Б. Остроградского, формулу преобразова-
ния объемных интегралов в поверхностные, не содержащую операции диверген-
ции (1841 г.).
Гельмгольц Герман Людвиг Фердинанд (Helmholtz; 1821-1894) — выдающийся
немецкий физик, математик, физиолог и психолог. Профессор физиологии уни-
верситетов в Кенигсберге, Бонне, Гейдельберге, Берлине. Дал математическое
Приложение 2
685
обоснование закона сохранения энергии и, проанализировав большинство извест-
ных в его время физических явлений, показал всеобщность этого закона, в час-
тности то, что происходящие в живых организмах процессы также подчиняются
закону сохранения энергии. Этот вывод стал наиболее сильным аргументом против
концепции особой «живой силы», якобы управляющей организмами. Впервые до-
казал применимость принципа наименьшего действия к тепловым, электромаг-
нитным и оптическим явлениям, вскрыл связь этого принципа со вторым началом
термодинамики. Работы Гельмгольца по электромагнетизму, оптике и акустике
большей частью связаны с его физиологическими исследованиями. Он обнаружил
явление колебательного разряда лейденской банки, что сыграло существенную
роль в развитии теории электромагнетизма, попытался измерить скорость распро-
странения электромагнитных возмущений, однако ему это не удалось, развил
теорию аномальной дисперсии. В 1881 г. выдвинул идею об атомарном строении
электричества. По предложению Гельмгольца Г. Герц произвел опыты, доказав-
шие существование электромагнитных волн.
Генри Джозеф (Henry; 1797-1878) — известный американский физик. Постро-
ил мощные электромагниты и электродвигатель, в 1832 г. открыл независимо от
М. Фарадея самоиндукцию, в 1842 г. установил колебательный характер разряда
конденсатора.
Герц Генрих Рудольф (Hertz; 1857-1894) — великий немецкий физик, один из
основателей электродинамики, ассистент Г.Гельмгольца профессор Высшей тех-
нической школы в Карлсруэ, профессор Боннского университета. Исходя из урав-
нений Максвелла, в 1886-1889 гг. на опытах доказал существование электромаг-
нитных волн (ЭМВ) и исследовал их свойства (отражение от зеркал, преломление
в призмах и т.д.). Эти волны Герц получал с помощью изобретенного им вибратора
(вибратор Герца). Подтвердил выводы максвелловской теории о том, что скорость
распространения ЭМВ в воздухе равна скорости света, установил тождественность
основных свойств ЭМВ и световых волн, изучал распространение ЭМВ в провод-
нике и указал способ измерения скорости их распространения. Развивая теорию
Максвелла, Герц придал уравнениям электродинамики симметричную форму, ко-
торая наглядно демонстрирует полную взаимосвязь между электрическими и маг-
нитными явлениями. Создал электродинамику движения тел, исходя из гипотезы
о том, что эфир увлекается движущимися телами, однако данная теория ока-
залась в противоречии с опытом и позднее уступила место электронной теории X.
Лоренца. Впервые наблюдал и дал описание внешнего фотоэффекта, разрабатывал
теорию резонаторного контура, изучал свойства на катодных лучей, исследовал
влияние ультрафиолетовых лучей на электрический разряд. В ряде работ по меха-
нике дал теорию удара упругих шаров, рассчитал время соударения и т.д. Работы
Герца по электродинамике сыграли огромную роль в развитии науки и техники и
обусловили возникновение беспроволочной телеграфии, радиосвязи, телевидения,
радиолокации и т.д. Именем Герца названа единица частоты колебаний.
Капица Петр Леонидович (1894-1984) — великий советский физик, профес-
сор МФТИ, академик, лауреат Нобелевской премии по физике. Предложил
(совместно с Н.Н. Семеновым) метод определения магнитных моментов атомов
в атомном пучке, предложил и обосновал импульсный метод получения сверх-
сильных магнитных полей, обнаружил в сильных магнитных полях линейную
зависимость электрического сопротивления ряда металлов от напряженности
поля (закон Капицы). Разработал метод и построил установки для сжижения гелия
686 Современная теория и практические применения антенн
и воздуха (1934-1939 гг.). Открыл сверхтекучесть жидкого гелия (1938 г.). Разрабо-
тал СВЧ генераторы сверхбольшой мощности. Обнаружил устойчивый плазмен-
ный шнур при СВЧ разряде в плотных газах.
Гуляев Юрий Васильевич (родился в 1935 году) — академик РАН, директор
института радиотехники и электроники. Выдвинул и разработал идею использова-
ния поверхностно-акустических волн (ПАВ) в электронике, предсказал и исследо-
вал новый тип ПАВ, известных как волны Гуляева-Блюстейна.
Котельников Владимир Александрович (1908-2003) — видный советский уче-
ный в области радиотехники, профессор Московского энергетического института,
академик, директор Института радиотехники и электроники АН СССР. Основные
труды посвящены проблемам совершенствования методов радиоприема, изучению
помех радиоприему и разработке методов борьбы с ними. Внес большой вклад в
развитие теории потенциальной помехоустойчивости. Под руководством В. А. Ко-
тельникова были проведены работы по радиолокации Марса, Венеры, Меркурия.
Кулон Шарль-Огюстен (Coulumb; 1736-1806) — знаменитый французский фи-
зик и военный инженер. В 1784 г. изобрел электрические весы, действие которых
было основано на свойстве металлических нитей иметь при кручении силу ре-
акции, пропорциональную углу кручения, и применил их для измерения силы
отталкивания одноименно заряженных шариков. В 1785 г. открыл фундаменталь-
ный закон электричества, названный его именем. Одновременно с исследовани-
ем электрических сил изучал взаимодействие магнитных стрелок и установил,
что сила магнитного притяжения обратно пропорциональна квадрату расстояния
между молекулами.
Ломоносов Михаил Васильевич (1711-1765) — величайший русский ученый-
естествоиспытатель мирового значения, поэт, языковед и литературовед, худож-
ник, историк, поборник развития отечественного просвещения, науки и эконо-
мики, академик Петербургской академии наук. В 1748 г. создал при ней первую в
России химическую лабораторию. По его инициативе основан Московский универ-
ситет (1755 г.). Развивал атомно-молекулярное представления о строении вещес-
тва. В период господства теории теплорода утверждал, что теплота обусловлена
движением корпускул (молекул). Сформировал принцип сохранения материи и
движения, исключил флогистон из числа химических агентов, заложил основы
физической химии, исследовал атмосферное электричество и силу тяжести, со-
здал учение о цвете, изготовил ряд оптических приборов, открыл атмосферу на
Венере, описал строение Земли, объяснил происхождение многих полезных ис-
копаемых и минералов, опубликовал руководство по металлургии. Подчеркивал
важность исследования Северного морского пути, освоения Сибири.
Максвелл Джеймс Клерк (Maxwell; 1831-1879) — великий английский физик,
создатель классической электродинамики, один из основателей статистической
физики. Профессор Маришал-колледжа в Абердине, а также Лондонского и Кем-
бриджского университетов, основатель первой в Великобритании специально
оборудованной физической лаборатории — Кавендишской. Научная деятельность
Максвелла охватывает проблемы электромагнетизма, кинетической теории газов,
оптики, теории упругости и др. Свою первую работу он выполнил, когда ему еще
не исполнилось 15 лет. Одни из первых его исследований были посвящены физио-
логии и физике цветного зрения и колориметрии. Он провел теоретическое иссле-
дование устойчивости колец Сатурна и показал, что эта устойчивость может быть
лишь в том случае, если кольца состоят из не связанных между собой твердых
Приложение 2 687
частиц.
В своих исследованиях Максвелл математически развил воззрения М. Фарадея
на роль промежуточной среды в электрических и магнитных взаимодействиях.
Он пытался (вслед за Фарадеем) истолковать данную среду как всепроникающий
мировой эфир, однако эти попытки не были успешны. Дальнейшее развитие фи-
зики показало, что носителем электромагнитных взаимодействий является элек-
тромагнитное поле (ЭМП), теорию которого Максвелл и создал. В этой теории он
обобщил все известные к тому времени факты макроскопической электродинамики
и впервые ввел представление о токе смещения, порождающем магнитное поле
подобно обычному току (току проводимости, т. е. перемещающимся электрическим
зарядам). Максвелл выразил законы ЭМП в виде системы четырех дифференци-
альных уравнений в частных производных. Общий и исчерпывающий характер
этих уравнений проявился в том, что их анализ позволил предсказать многие
неизвестные до того явления и закономерности. Так, их них следовало существо-
вание электромагнитных волн (ЭМВ), впоследствии открытых Г. Герцем. Исследуя
эти уравнения, Максвелл пришел к выводу об электромагнитной природе света
и показал, что скорость любых других ЭВМ в вакууме равна скорости света. Из
теории Максвелла вытекало, что ЭВМ производят давление. Это опытным путем
подтвердил русский ученый П.Н.Лебедев.
Мандельштам Леонид Исаакович (1879-1944), — известный советский физик,
один из основателей отечественной научной школы по радиофизике, академик
АН СССР. В 1928 г. открыл (совместно с Г.С. Ландсбергом) комбинационное рассея-
ние света. Совместно с Н.Д. Папалекси выполнил основополагающие исследования
по нелинейным колебаниям, разработал метод параметрического возбуждения
электрических колебаний, предложил радиоинтерференционный метод. Труды по
рассеянию света.
Ньютон Исаак (Newton; 1643-1727) — великий английский физик и математик.
Заложил теоретические основы механики и астрономии, открыл закон всемирного
тяготения, разработал (наряду с Г. Лейбницем) дифференциальное и интегральное
исчисления. Изобретатель зеркального телескопа, автор важнейших опытов по
оптике.
Ом Георг Симон (Ohm; 1787-1854) — известный немецкий физик, профессор
Мюнхенского университета. Труды по электричеству, оптике, кристаллооптике,
акустике. В 1826 г. открыл основной закон электрической цепи, названный его
именем.
Остроградский Михаил Васильевич (1801-1861) — великий русский ученый,
математик, профессор офицерских классов Морского кадетского корпуса, главно-
го педагогического института, главного артиллерийского училища в Петербурге.
Основные работы посвящены математическому анализу, теоретической механике,
математической физике и др. Вывел и обосновал основную формулу преобразова-
ния объемных интегралов в поверхностные, содержащую выражение диверген-
ции (1835 г.), решил задачу о распространении волн на поверхности жидкости,
заключенной в бассейне, имеющем форму кругового цилиндра. Труды по теории
упругости, небесной механике, теории магнетизма, теории дифференциальных
уравнений, вариационных принципов и др.
Папалекси Николай Дмитриевич (1880-1947) — известный советский физик,
профессор Одесского политехнического института, академик АН СССР. В 1923-
1935 гг. вместе с Л. И. Мандельштамом руководил научным отделом Центральной
688 Современная теория и практические применения антенн
радиолаборатории в Ленинграде. С 1935 г. работал в Москве в физическом и энер-
гетическом институтах АН СССР. Председатель Всесоюзного научного совета по
радиофизике и радиотехнике при АН СССР. В 1914—1916 гг. проводил работы по
направленной радиотелеграфии, опыты по радиосвязи с подводными лодками и
телеуправлению, руководил разработкой первых образцов отечественных радио-
ламп. Совместно с Л. И. Мандельштамом выполнил основополагающие работы по
нелинейным и параметрическим колебаниям. Ими открыты и изучены резонанс
и-го рода, комбинационные и параметрические резонансы, разработан метод па-
раметрического возбуждения электрических колебаний. С помощью предложен-
ного ими интерференционного метода они детально исследовали распространение
радиоволн над земной поверхностью и осуществили точное измерение их скоро-
сти.
Попов Александр Степанович (1859-1906) — великий русский физик и элек-
тротехник, изобретатель электрической связи без проводов (радиосвязи, радио).
Преподаватель физики и электротехники Минного офицерского класса и Техни-
ческого училища Морского ведомства в Кронштадте, профессор физики Петер-
бургского электротехнического института.
Первые научные исследования А.С. Попова были посвящены анализу наивы-
годнейшего действия динамоэлектрических машин и индукционным весам Юза.
Ознакомившись с опубликованными работами Г. Герца по электродинамике,
А.С. Попов стал изучать электромагнитные явления. Пытаясь найти способ эф-
фективной демонстрации опытов Герца перед большой аудиторией, занялся конс-
труированием более наглядного индикатора электромагнитных волн, изучаемых
вибратором Герца. Хорошо понимая потребность России в средствах беспроводной
сигнализации, В.С. Попов в начале 1890-х гг. поставил перед собой также задачу
использовать электромагнитные волны для сигнализации. Поиски решения этих
задач проходили в два этапа: отыскание достаточно чувствительного индикатора
электромагнитных волн; разработка прибора, способного надежно регистриро-
вать электромагнитные волны, излучаемые вибратором Герца. В качестве индика-
тора А.С. Попов выбрал радиокондуктор (когерер). К весне 1895 г. был изготовлен
чувствительный и надежно работавший приемник, пригодный для беспроводной
сигнализации (радиосвязи). Он обнаруживал посылаемые передатчиком радиосиг-
налы на расстоянии до 60 м. При проведении опытов А.С. Попов заметил, что
подсоединение к когереру вертикального металлического провода (антенны) при-
водило к увеличению расстояния уверенного приема.
На состоявшемся 25 апреля (7 мая) 1895 г. заседании физического отделения
Русского физико-химического общества А.С. Попов сделал научный доклад об
изобретении им системы связи без проводов и продемонстрировал ее действие.
Весной 1897 г. во время опытов, проводившихся в Кронштадтской гавани, была
достигнута дальность радиосвязи 600 м, а летом 1897 г. при испытании радио-
связи на кораблях — 5 км. А.С. Попов обнаружил, что металлические корабли
влияют на распространение электромагнитных волн, и предложил способ опре-
деления направления на работающий передатчик, заложив тем самым основы ра-
диолокации.
Снеллиус (Снелль) Виллеброрд (Snell; 1580-1626) — известный нидерландский
астроном и математик, профессор Лейденского университета. Установил закон
преломления света, названный его именем. Труды по плоской и сферической три-
гонометрии.
22 *
Приложение 2 689
Тесла Никола (Tesla; 1856-1934) — известный сербский изобретатель в области
электро- и радиотехники. С 1884 г. проживал в США. В 1888 г. описал (независимо
от итальянского физика Г. Феррариса) явление вращающегося магнитного поля.
Разработал многофазные электрические машины и схемы распределения много-
фазных токов. Пионер в области создания ВЧ техники — генераторов, трансфор-
маторов и др. (1889-1891 гг.). Исследовал (позже А.С.Попова) возможность передачи
электрических сигналов и электроэнергии без проводов.
Умов Николай Алексеевич (1846-1915) — выдающийся русский ученый, инже-
нер, профессор Московского университета. Его первые работы были посвящены
колебательным процессам в упругих средах. Теорию этих процессов он распро-
странил на термомеханические явления в данных средах (1870 г.).
В 1870 г. ввел понятие плотности потока энергии (на 10 лет раньше английского
физика Д. Пойнтинга), предложил общее решение задачи о распределении элект-
рических токов на проводящих поверхностях произвольного вида (1875 г.). Открыл
эффект хроматической деполяризации лучей света, падающих на матовую повер-
хность, выполнил ряд блестящих исследований по теории земного магнетизма.
Фарадей Майкл (Faraday; 1791-1867) — великий английский физик, химик,
основоположник учения об электромагнитном поле. Обнаружил вращение магнита
вокруг проводника с током и вращение проводника с током вокруг магнита (1821).
Открыл явление электромагнитной индукции, лежащее в основе электротехники.
Доказал тождество различных видов электричества: полученного от трения, «жи-
вотного», «магнитного» и др. Открыл законы электролиза, ставшие аргументом в
пользу дискретности вещества и электричества. Ввел понятие о силовых линиях.
Открыл явление пара- и диамагнетизма (1845 г.), установил вращение плоскости
поляризации света в магнитном поле (эффект Фарадея), что явилось первым сви-
детельством связи между магнитными и оптическими явлениями, ставшей позд-
нее подтверждением электромагнитной теории света Максвелла.
Фок Владимир Александрович (1898-1974) — видный советский физик-тео-
ретик, академик АН СССР. Известен фундаментальными трудами по квантовой
механике и электродинамике, общей теории относительности. Разработал методы
самосогласованного поля для многоэлектронных систем (метод Хартри - Фока),
вторичного квантования. Исследования по распространению радиоволн, матема-
тической физике, философским вопросам физики, теории тяготения, квантовой
теории поля, теории многоэлектронных систем, функциональным методам теории
поля и статистической физики, теории дифракции и т.д.
Фраунгофер Иозеф (Fraunhofer; 1787-1826) — известный немецкий физик,
профессор Мюнхенского университета. Основные труды посвящены физической
оптике. Усовершенствовал технологию изготовления больших ахроматических
объективов, изобрел окулярный микроскоп и гелиометр. Наблюдал и первым объ-
яснил наличие линий поглощения в солнечном спектре (линии Фраунгофера; 1814
г.). Впервые применил дифракционные решетки для изучения спектров (1821 г.).
Предложил метод наблюдения дифракции света в параллельных лучах.
Френель Огюст Жан (Fresnel; 1788-1824) — знаменитый французский физик,
член Лондонского королевского общества, создатель волновой теории света. Важ-
нейшими результатами его научной деятельности являются: создание законченной
теории дифракции, основанной на использовании принципа Гюйгенса; опытное ис-
следования влияния поляризации на интерференцию и обоснование поперечного
характера световых волн (1821 г.); разъяснение вопроса о цвете кристаллических
23 - Неганов
690_____________Современная теория и пракрпрческ^ прим^етгия арргенн
пластинок; открытие круговой и эллиптической поляризаций и разъяснение этих
явлений с волновой точки зрения (1822 г.); объяснение явления вращения плос-
кости поляризации как двойного лучепреломления циркулярно поляризованного
света (1822 г.); установление законов отражения и преломления (формулы Фре-
неля); открытие эллиптической поляризации при полном внутреннем отражении;
создании теории двойного лучепреломления и обоснование кристаллооптики’.
Шиллер Николай Николаевич (1848-1910) — известный русский физик, про-
фессор Харьковского университета. Работая в лаборатории у Г. Гельмгольца, за-
нимался измерениями диэлектрической проницаемости веществ предложенным им
же методом. На опытах доказал принцип замкнутости токов (1900 г.). Сформули-
ровал принцип невозможности непрерывного понижения или повышения темпе-
ратуры путем замкнутых адиабатических процессов (аналогичную формулировку
дал немецкий ученый К. Каратеодори в 1909 г.). В 1874 г. впервые применил метод
электрических колебаний для определения диэлектрической проницаемости.
Шулейкин Михаил Васильевич (1884-1939) — один из крупнейших советских
радиофизиков в области радиотехники, профессор Института народного хозяйс-
тва и МВТУ, академик АН СССР. Развил теорию дисперсии коротких волн в од-
нородной ионизированной среде, вывел формулу для определения эквивалентной
диэлектрической проницаемости ионосферы, коэффициента распространения и
поглощения волн как функции частоты. Показал, каким образом следует опреде-
лять величину фазовой скорости. Ввел понятие критической частоты, на которой
коэффициент преломления ионосферы превращается в нуль, и доказал, что рас-
пространение волн, более длинных, чем критические, происходит без отражения
от ионосферы и волна уходит в заатмосферное пространство. Разработал теорию
длинноволновых антенн, провел исследование рамочных антенн.
Щукин Александр Николаевич (1900-1990) — известный советский ученый,
академик, специалист в области радиотехники, радиофизики, распространения
радиоволн. Основные работы посвящены распространению электромагнитных
колебаний в различных средах, процессам ионизации земной атмосферы и их
влиянию на распространение радиоволн. В ряде работ рассматриваются вопросы
радиосвязи, автоматического управления и применения теории вероятностей к
прикладным задачам. Ввел импедансные граничные условия, названные его име-
нем (первая публикация в 1940 г.; в своих лекциях использовал эти условия го-
раздо раньше).
Литепату pa
691
Литература
1. Неганов В.А., Осипов О.В., Раевский С.Б., Яровой Г.П. Электродинамика и рас-
пространение радиоволн: учебник для радиотехнич. специальностей вузов / под
ред. В.А. Неганова и С.Б. Раевского. Изд 3-е, доп. и перераб. — М.: Радиотехника,
2007. - 744 с.
2. Сазонов Д.М. Антенны и устройства СВЧ: учеб, для радиотехнич. спец, вузов.
— М.: Высш. шк. 1980. — 432 с.
3. Воскресенский Д.И.,Гостюхин В.Л.,Максимов В.М.,Пономарев Л.И. Устройс-
тва СВЧ и антенны / под ред. Д.И. Воскресенского. — Изд. 2-е, доп. и перераб. - М.:
Радиотехника, 2006. — 376 с.
4. Воскресенский Д.И.,Гостюхин В.Л.,Максимов В.М.,Пономарев Л.И. Устройс-
тва СВЧ и антенны / под ред. Д.И. Воскресенского. — М.: Изд — во МАИ, 1999.
- 528 с.
5. Вычислительные методы в электродинамике / Под ред. Р. Митры. - М. -
Мир, 1977. - 486 с.
6. Тихонов А.Н. О некорректно — поставленных задачах // Вычислительные
методы и программирование, 1967. — Вып.8. — с.3-33.
7. Тихонов А.Н., Арсенин В.Я. Методы решения некорректных задач. — М.: На-
ука, 1974. — 223 с.
8. Неганов В.А., Нефедов Е.И., Яровой Г.П. Электродинамические методы проек-
тирования устройств СВЧ и антенн -М. «Радио и связь» 2002. — 415 с.
9. Неганов В.А., Матвеев И.В. Новый метод расчета тонкого электрического
вибратора // Изв. вуз. Радиофизика, 2000. — Т.43 - №3. — С. 412 — 420.
10. Неганов В.А. Сингулярные интегральные представления электромагнитно-
го поля электрического вибратора в его ближней зоне // ДАН, 2004. - №5. _
С.617 - 619.
11. Неганов В.А. Самосогласованный метод расчета электромагнитных полей в
ближних зонах излучающих структур, описываемых координатными поверхнос-
тями // ДАН, 2006. - Т.408. - №5. - С.234-237.
12. Неганов В.А., Павловская Э.А., Яровой Г.П. Излучение и дифракция электро-
магнитных волн / под ред. В.А. Неганова. — М.: Радио и связь, 2004. — 264 с.
13. Неганов В.А. Физическая регуляризация некорректных задач электродина-
мики. —М.: Сайнс-Пресс, 2008 -450 с
14. Неганов В.А. Сингулярные интегральные уравнения как метод физической
регуляризации некорректных электродинамических задач радиотехники и связи
// Успехи современной радиоэлектроники, 2005. — 12 — с.16-24.
15. Харченко К.П., Сухарев В.Н. «Электромагнитная волна», лучистая энергия
- поток реальных фотонов. - М.: КомКнига, 2005. - 128 с.
16. Неганов В. А., Лемжин М.И. Электродинамический анализ электромагнитно-
го поля в промежуточной и ближней зонах полуволнового электрического вибра-
тора и диполя Герца // Физика волновых процессов и радиотехнические системы,
2007. - Т10. - №2. - С.4-10.
17. Лавров А.С., Резников Г.Б. Антенно-фидерные устройства. Учебное пособие
для вузов. — М.: «Сов. радио», 1974. - 368 с.
18. Драбкин А.Л., Зузенко В.Л., Кислов А.Г. Антенно-фидерные устройства. Изд.
2J *
692
Современная теория и прапстлгческие прим&н^шя антенн
2-ое, доп. и перераб. - М.: «Сов. радио», 1974. - 536 с.
19. Неганов В.А., Нефедов Е.И., Порубов В.В. Гофрированно — щелевые ли-
нии передачи СВЧ — диапазона // Изв. вузов. Радиофизика, 1989. Т.32. - №4 -
С.487 - 491.
20. Неганов В.А. Метод сингулярных интегральных представлений полей в за-
дачах о собственных волнах экранированных полосково — щелевых структур. //
РЭ, 1989. - С.2251-2260.
21. Марков Г.Т., Чаплин А.Ф. Возбуждение электромагнитных волн. — М. - Л.:
Энергия, 1976. — 376 с.
22. Неганов В.А., Матвеев И.В. Применение сингулярного интегрального урав-
нения для расчета тонкого электрического вибратора // ДАН, 2000. - Т.373. -
№1. - С. 36-38.
23. Неганов В.А., Табаков Д.П. Применение сингулярных интегральных уравне-
ний для электродинамического анализа плоской кольцевой антенны // Антенны,
2008. - №10(137). - С. 25 - 33.
24. Неганов В.А., Табаков Д.П., Чванова Т.Ю., Шарипова А.А. Электродинами-
ческий анализ криволинейного полоскового вибратора, расположенного на ци-
линдрической поверхности // Физика волновых процессов и радиотехнические
системы, 2008. - Т. 11. - №1 -С.14-21
25. Неганов В.А., Нефедов Е.И., Яровой Т.П. Полосково-щелевые структуры сверх
и крайневысоких частот. — М.: Наука. Физматлит, 1996. — 304 с.
26. Справочник по специальным функциям / Под ред. М. Абрамовича и И. Сти-
гана. - М.: Наука. Физматлит, 1979. — 832 с.
27. Антенно — фидерные устройства и распространение радиоволн: учебник для
вузов / Г.А. Ерохин, О.В. Чернышев, Н.Д. Козырев, В.Г. Кочержевский; под ред.
Г.А. Ерохина. - М.: Радио и связь, 1996. — 352 с.
28. Неганов В.А. Сингулярное обобщенное уравнение Халлена для электрическо-
го вибратора // Физика волновых процессов и радиотехнические системы, 2001.
- Т.4. - №1. - С.40-43.
29. Гахов Ф.Д.,Черский Ю.И. Уравнения типа свертки. — М.: Наука, 1978. -
296 с.
30. Гахов Ф.Д. Краевые задачи. - М.: Наука, 1977. - 640 с.
31. Канторович Л.В., Крылов В.И. Приближенные методы высшего анализа. —
М.-Л.: ГИФНЛ, 1962. - 708 с.
32. Верлань А.Ф.,Сизиков В.С. Методы решения интегральных уравнений с про-
граммами для ЭВМ. - Киев: Наук, думка, 1978. - 292 с.
33. Панасюк В.В.,Саврук М.П.,Назарук З.Т. Метод сингулярных интегральных
уравнений в двумерных задачах дифракции. — Киев, Наук, думка, 1984. — 344 с.
34. Эминов С.И. Теория интегрального уравнения тонкого вибратора // Радио-
техника и электроника, 1993. - Т.38. — Вып.12 — С. 2160-2168.
35. Неганов В. А.,Святкин Н. М. Метод сингулярного интегрального уравнения
в задаче о распределении тока в кольцевой полосковой антенне, 2005. — Т. 8. - №2.
- С. 61 - 67.
36. Неганов В. А.,Корнев М. Г. Применение метода сингулярного интегрального
уравнения к анализу рамочной антенны // Физика волновых процессов и радио-
технические системы, 2003. - Т. 6. - №1 — С.41 — 45.
37. Кочержевский Т.Н. Антенно-фидерные устройства. — М.: Связь, 1968. —
484 с.
Литература
693
38. Антенные решетки. Методы расчета и проектирования (Обзор зарубежных
работ) / Под общей ред. Л.С. Бененсона. — М.: Советское радио, 1966. — 368 с.
39. Хургин Я.И.,Яковлев ВЛ. Методы теории целых функций в радиофизике,
теории связи и оптике. — М.: Гос. издательство физике — математической лите-
ратуры, 1962. - 220 с.
40. Зелкин Е.Г. Построение излучающей системы по заданной диаграмме на-
правленности. — М.: Госэнергоиздат, 1963.
41. Бахрах Л.Д.,Кременецкий С.Д. Синтез излучающих систем. — М.: Сов. Ра-
дио, 1974. — 232 с.
42. Лифанов И.К. Метод сингулярных интегральных уравнений и численный
эксперимент. — М.: ТОО «Янус», 1995. — 520 с.
43. Никольский В.В. Электродинамика и распространение радиоволн / В.В. Ни-
кольский. — М.: Гл. ред. Физ.-мат. литературы, 1973. - 607 с.
44. Виноградова М.Б. Теория волн / М.Б. Виноградова,О.В. Руденко,А.П. Сухо-
руков. — М.: Наука, 1979. — 383 с.
45. Неганов В.А. Самосогласованный метод расчета задачи дифракции плос-
кой электромагнитной волны на одномерной щели // Антенны, 2007. — №11(126).
- С.48-53.
46. Митра Р. Аналитические методы теории волноводов / Р. Митра, С. Ли; пер.
с англ.; под ред. Г.В. Воскресенского. М.: Мир, 1974. - 323 с.
47. Микроэлектронные устройства СВЧ: учебное пособие для радиотехнических
специальностей вузов / Г.И. Веселов,Е.Н. Егоров,Ю.Н. Алехин и др.; Под ред. Г.И.
Веселова. - М.: Высш, шк., 1988 — 280 с
48. Электродинамический расчет характеристик полосковых антенн / Б.А. Пан-
ченко,С.Т. Князев,Ю.Б. Нечаев и др. — М.: Радио и связь, 2002 - 256 с.
49. Неганов В.А., Клюев Д.С. Сингулярные интегральные уравнения в теории
конформных цилиндрических полосковых излучающих структур // Физика вол-
новых процессов и радиотехнические системы. - 2006. - Т.9. - №4, С. 13-26.
50. Прудников А.П.,Брычков Ю.А.,Маричев О.И. Интегралы и ряды. Специаль-
ные функции. — М.: Наука, гл. ред. физ-мат. лит., 1983. - 752 с.
51. Прудников А.П.,Брычков Ю.А.,Маричев О.И. Интегралы и ряды. Элементар-
ные функции. — М.: Наука. Гл. ред. физ —мат. лит., 1981. - 798 с.
52. Панченко Б.А.,Нефедов Е.И. Микрополосковые антенны. - М.: Радио и связь,
1986. - 144 с.
53. Бубнов Г.Г. Антенны радиоустройств. — М.: Знание, 1978. — 64 с.
54. Заборонкова Т.М.,Кудрин А.В., Петров Е.Ю. К теории рамочной антенны в
анизотропной плазме // Известия вузов. Радиофизика. - 1988. - Т.41. - №3. - С.
358-373.
55. Манжиров А.В., Полянин А.Д. Справочник по интегральным уравнениям.
Методы решения. - М.: Факториал Пресс, 2000. - 385 с.
56. Взятышев В.Ф. Диэлектрические волноводы. - М.: Сов. радио, 1970. -
216 с.
57. Нефедов Е.И. Антенно-фидерные устройства и распространение радиоволн.
- М.: издательский центр «Академия», 2006. — 320 с.
58. Веселов Г.И., Раевский С.Б. Слоистые металло-диэлектрические волноводы.
- М.: Радио и связь, 1988. - с. 247.
59. Гетманцева Т.Н.,Раевский С.Б. О комплексных волнах в круглом диэлект-
рическом волноводе. - Изв. вузов СССР. Сер. Радиофизика, 1978. — т.21. - №9. —
694
Современная теория и пражпшческие прилирмния д/нтенн
с. 1332-1337.
60. Веселов Г.И., Раевский С.Б. Комплексные волны круглого диэлектрического
волновода. — Радиотехника и электроника, 1983. — т.28. - №2. - с.230-236.
61. Веселов Г.И.,Раевский С.Б. О спектре комплексных волн круглого диэлектри-
ческого волновода. - Радиотехника, 1988. - т.38. - №2. — с.230-236.
62. Неганов В.А. Клюев Д.С.,Соколова Ю.В. Метод расчета входного сопротивле-
ния микрополоскового электрического вибратора / / Известия вузов. Радиофизи-
ка, 2008. — Том LI, №12.
63. Зелкин Е.Г.,Кравченко В.Ф. Задачи синтеза антенн и новые методы их ре-
шения. Кн.1. - М.: ИПРЖСР, 2002. - 72с.
64. Зелкин Е.Г., Кравченко В.Ф. Синтез антенн на основе атомарных функций.
Кн.2. /Под ред. В.Ф. Кравченко. — М.: Радиотехника, 2003. — 72с.
65. Кравченко В.Ф., Масюк В.М. Новый класс фрактальных функций в задачах
синтеза антенн. Кн.З. - М.: ИПРЖСР, 2002. - 72с.
66. Автоматизированное проектирование антенн и устройств СВЧ / Д.И. Вос-
кресенский,С. Д. Кременецкий,А.Ю. Гринев, Ю.Ю. Котов: учеб, пособие для вузов.
- М.: Радио и связь, 1988 - 240 с.
67. Зелкин Е.Г.,Соколов В.Г. Методы синтеза антенн. - М.: «Сов. радио», 1980
- 294 с.
68. Бахрах Л.Д.,Галимов Г.К. Сканирующие зеркальные антенны. — М.: Наука,
1981. - 302 с.
69. Химмелъблау Д. Прикладное нелинейное программирование. — М.: Мир, 1975.
- 234 с.
70. Жук М.С.,Молочков Ю.Б. Проектирование линзовых, сканирующих, широ-
кодиапазонных антенн и фидерных устройств. - М.: Энергия, 1973. — 493с.
71. Кочержевский Г.Н. Антенно-фидерные устройства. — М.: Радио и связь,
1981. - 280 с.
72. Кочержевский Г.Н.,Ерохин Г.А.,Козырев Н.Д. Антенно-фидерные устройства.
- М.: Радио и связь, 1989. ~352 с.
73. Лавров Г.А. Взаимное влияние линейных вибраторных антенн. — М.: Связь,
1975. - 128 с.
74. Марков Г.Т.,Сазонов Д.М. Антенны. — М.: Энергия, 1975. — 528 с.
75. Минкович Б.М.,Яковлев В.П. Теория синтеза антенн. — М.: Сов. Радио, 1969
- 269 с.
76. Монзинго Р.А., Миллер Т.И. Адаптивные антенные решетки: пер. с англ. /
Под ред. В.А. Лексаченко. — М.: Радио и связь, 1986. — 446 с.
77. Справочник по спутниковой связи и вещанию / Под ред. Л.Я. Кантора.
— М.: Радио и связь, 1983. — 288 с.
78. Связь с подвижными объектами в диапазоне СВЧ: Пер. с англ. / Под ред.
М.С. Ярлыкова и М.В. Чернякова. — М.: Связь, 1979. - 520 с.
79. Фрадин А.З. Антенно-фидерные устройства. — М.: Связь, 1977. - 440 с.
80. Фок В.А. Проблемы дифракции и распространения электромагнитных волн.
— М.: Сов радио, 1970. — 440 с.
81. Хмельницкий Е.А. Оценка реальной помехозащищенности приема в КВ —
диапазоне. — М.: Связь, 1975. — 232 с.
82. Черенкова Е.Л., Чернышов О.В. Распространение радиоволн. — М.: Радио и
связь, 1984. — 272 с.
83. Чернышов О .В., Васильева Т.Н. Прогноз максимальных применимых частот.
Лт^тература
695
- М.: Наука, 1973. - 386 с.
84. Ямпольский В.Г., Фролов О.П. Оптимизация антенных систем линий связи.
— М.: Радио и связь, 1991. - 272 с.
85. Шифрин Я.С. Вопросы статистической теории связи. - М.: Сов. радио, 1970.
- 384 с.
86. Кюн Р. Микроволновые антенны (антенны сверхвысоких частот). — Л.: Судо-
строение — 1967. — 518 с.
87. Ямпольский ВТ., Фролов О.П. Антенны и ЭМС. — М.: Радио и связь, 1983.
- 272 с.
88. Фельд Я.Н.,Бененсон Л.С. Антенно-фидерные устройства. ч.2. Изд. ВВИА им.
Н.Е. Жуковского, 1959.
89. Зелкин Е.Г., Петрова Р.А. Линзовые антенны. — М., Сов. радио, 1974. —
277 с.
90. Щелевая экранированная линия / В.А. Неганов, В.В. Порубов (СССР). —
4383893/24-09. Заяв. 25.02.088 Опубл. 07.06.90 Бюл. №21. Авт. Св-во 15 699 23 СССР,
МКИ4 Н 01 РЗ/08
91. Дерюгин Л.Н., Зимин Д.Б. Коммутационные сканирующие антенны. — В сб.
«Сканирующие антенны сверхвысоких частот». М.: «Машиностроение», 1964. —
С. 124-158.
92. Проблемы антенной техники /Под ред. Л.Д. Бахраха и Д.И. Воскресенского.
— М.: Радио и связь, 1989. - 368 с.
93. Пистолькорс А.А. Антенны. — М.: Связьиздат, 1974. - 480 с.
94. Щелкунов С.,Фринс. Г. Антенны. Теория и практика. - М.: Сов. радио, 1955.
- 603 с.
95. Татаринов В.В. Коротковолновые направленные антенны. — М.: Связьиздат,
1936. - 178 с.
96. Вендик О.Г. Антенна с немеханическим качанием луча. — М.: Сов. радио,
1961. - 36 с.
97. Амитей Н.,Галиндо В.,By Ч. Теория и анализ фазированных антенных ре-
шеток. Перевод с англ, под ред. А.Ф. Чаплина. — М.: Мир, 1974. — 455 с.
98. Сканирующие системы СВЧ. — М.: Сов. радио - Т.1, 1966.— 565 с.; Т.2, 1969.
- 496 с.; Т.З, 1971. - 436 с.
99. Уолтер К. Антенны бегущей волны / Перевод с англ, под ред. А.Ф. Чаплина.
— М.: Энергия, 1970. - 446 с.
100. Антенны и устройства СВЧ / Под ред. Д.И. Воскресенского. — М.: Сов. ра-
дио, 1972. - 318 с.
101. Сверхширокополосные антенны / Пер. с англ, под ред. Л.С. Бененсона. — М.:
Мир, 1964. - 416 с.
102. Рамсей В. Частотно — независимые антенны. — М.: Мир, 1964. — 176 с.
103. Юрцев О.А.,Рунов А.В.,Казарин А.Н. Спиральные антенны — М.: Сов радио,
1974. - 223 с.
104. Шубарин Ю.В. Антенны сверхвысоких частот. — учебное пособие для ра-
диофакультетов вузов УССР.: Изд-во Харьковского гос. Университета. - Харьков,
1960. - 284 с.
105. Антенны / Пер. с англ, под ред. А.И. Шпунтова. — М.: Сов. радио, 1951.
- 292 с.
106. Сильвер С. Антенны сантиметровых волн. T.I и II / Пер. с англ, под ред. Я.Н.
Фельда. — М.: Сов. радио, 1950. ~ Т.2 - 319 с;
696
Современная теория и практические применения антенн
107. Антенны (современное состояние и проблемы) / Под ред. Л. Д. Бахраха и
Д.И. Воскресенского. - М.: Сов. радио, 1979. - 208 с.
108. Надененко С.И. Антенны. Учебное пособие для электротехнических инсти-
тутов связи и радиотехнических факультетов вузов. — М.: Государственное изда-
тельство литературы по вопросам связи и радио, 1959 — 560 с.
109. Марков Г.Т. Антенны. — М.: Госэнергоиздат, 1960. — 536 с.
110. Драбкин А.Л.,Зузенко В.А. Антенно-фидерные устройства. - М.: Сов. ра-
дио, 1961. — 816 с.
111. Белоцерковский Г.Б. Основы радиотехники и антенны. Часть. II. Антенны.
— М.: Сов. радио, 1969. — 328 с.
112. Ратхаммель К. Антенны / Пер. с нем. — С.-Пб.: Издательство «Бояныч»,
1998. - 656 с.
113. Захарьев Л.Н.,Леманский А.А.,Щеглов К.С. Теория излучения поверхност-
ных антенн. — М.: Сов. радио, 1969. - 232 с.
114. Корбанский И.Н. Антенны. Учебное пособие для вузов. — М.: Энергия, 1973.
- 336 с.
115. Шипков Г.А. Задачник по антенно-фидерным устройствам. Учебное пособие
для радиотехнических вузов и факультетов. — М.: Высшая школа, 1966. — 179 с.
116. Белоцерковский Г.Б. Задачи и расчеты по курсу «Основа радиотехники и
антенны». — М.: Машиностроение, 1966. — 199 с.
117. Воскресенский Д.И.,Пономарев Л.И.,Филиппов В.С. Выпуклые сканирующие
антенны. — М.: Сов. радио, 1978. — 301 с.
118. Покрас А.М., Сомов А.М.,Цуриков Г.Г. Антенны земных станций спутнико-
вой связи. — М.: Радио и связь, 1985. — 288 с.
119. Белоусов С.П.,Клигер Г.А. Электромагнитная совместимость средневолно-
вых антенн // Труды НИИР, - 1983. - №3. — С.25-29.
120. Антенны и устройства СВЧ: Проектирование фазированных антенных ре-
шеток / Д.И. Воскресенский,В.Л. Гостюхин,Р.А. Грановская и др.; Под ред. Д.И.
Воскресенского. — М.: Радио и связь, 1981. — 112 с.
121. Методы измерения характеристик СВЧ / Л.Н. Захарьев, А.А. Леманский,
В.И. Турчин и др.; Под ред. Н.М. Цейтлина. - М.: Радио и связь, 1985. — 368 с.
122. Каплун В.А. Обтекатели антенн СВЧ. — М.: Сов. радио., 1974.
123. Обтекатели антенн / Под ред. А.И. Шпунтова - М.: Сов. радио, 1950.
124. Айзенберг Г.З. Коротковолновые антенны. — М.: Гос. издательство литера-
туры по вопросам связи и радио, 1962. — 815 с.
125. Айзенберг Г.3.,Ямпольский В.Г.,Терешин О.Н. Антенны УКВ / под ред. Г.З.
Айзенберга. В 2-х ч. — М.: «Связь», 1977. 4.1 — 382 с., 4.2 — 288 с.
126. Пистолькорс А.А. Антенны. - М.: Связьиздат, 1947. — 480 с.
127. Белоцерковский Г.Б. Антенны. — М.: Оборониз, 1962 г.
128. Никольский В.В. Антенны: учебное пособие для электротехнических инсти-
тутов связи. — М.: «Связь», 1966. — 368 с.
129. Фрадин А.З. Антенны сверхвысоких частот. — М.: «Советское радио», 1957.
- 635 с.
130. Фрадин А.З. Антенно - фидерные устройства: учебн. пособие для вузов
связи. М.: «Связь», 1977 — 440 с.
131. Айзенберг Г.З. Антенны ультракоротких волн. — М.: - «Связьиздат», 1957.
- 700 с.
132. Кравченко В.Ф.,Потапов А.А.,Масюк В.М. Атомарно — фрактальные фун-
Лшт^рагпл[ра
697
кции в задачах синтеза антенн // Зарубежная электроника. Успехи современной
радиоэлектроники, 2001. - №6. — с.4-40.
133. Неганов В.А., Осипов О.В. Отражающие, волноведущие и излучающие
структуры с киральными элементами. — М.: Радио и связь, 2006. — 280 с.
134. Неганов В.А., Сарычев А.А. Расчет поля электромагнитной волны, отражен-
ной от идеально проводящей металлической полоски конечной длины, располо-
женной на диэлектрическом цилиндре // Физика волновых процессов и радиотех-
нические системы, 2007. — Т.10 - №2. — с.95 — 103.
135. Неганов В.А., Пряников Е.И., Табаков Д.П. Дифракция плоской электромаг-
нитной волны Н — поляризации на идеально проводящем разомкнутом кольце / /
Физика волновых процессов и радиотехнические системы, 2008. — Т.Н. - №1 - с.
22 - 29.
136. Борзенко Г.П., Ткачев Н.А. Поглотитель электромагнитных волн и способ
его изготовления. — 9611654/09. Заяв. 1996.08.13. (РФ). Опубл. 1998.09.20. (статус: по
данным на 17.09.2007 — прекратил действие). Патент RU2119216 С1.
137. Шабанов С.Г. Радиопоглощающее покрытие, способ получения и управ-
ления его свойствами и устройство для дистанционного измерения отражатель-
ных свойств покрытий на объектах в СВЧ - диапазоне радиоволн. 2155420 С1.
- 2000.08.27.
138. Радиотехнические системы: учеб, для вузов по специальности «Радиотех-
ника» / Ю.П. Гришин, В.П. Ипатов, Ю.М. Казаринов и др.; под ред. Ю.М. Каза-
ринова. — М.: Высшая школа, 1990. — 496 с.
139. Gianvittorio J.P., Rahmat — Samii Y. Fractal antennas: a novel antenna min-
iaturization technique, and applications. IEE Antennas and Propagation Magazine,
2002, vol.44, no.l pp. 20-36.
140. Werner D.H., Werner P.L., Frequency - independent features of self - simi-
lar fractal antennas, Radio - Science, 1996 - V.31- №6 — p.1331 — 1343.
141. Werner D.H., Werner P.L., Haupt R.L. Fractal antenna engineering: Theory
and design of fractal antenna arrays. IEE Antennas and Propagation Magazine,
1999, V.41 - №5 - p. 37-59.
142. Werner D.H., Werner D.P., On the synthesis of fractal radiations pattens,
Radio Science, 1995, vol.30. no.l pp.29-45.
143. Кравченко В.Ф., Масюк B.M. Новый класс фрактальных функций в зада-
чах анализа и синтеза антенн. Книга 3. _ М.: Издательское предприятие редакции
журнала «Радиотехника», 2002. — 73 с.
144. Кравченко В.Ф., Масюк В.М. Кольцевые фрактальные антенные решетки //
Электромагнитные волны и электронные системы, 2004. - №5. — Т.9. — с.3-12.
145. Неганов В.А., Табаков Д.П. Применение теории сингулярных интегральных
уравнений к электродинамическому анализу цилиндрической спиральной антен-
ны // Физика волновых процессов и радиотехнические системы, 2009. - Т.12. —
№2 - с. 20 - 29.
698
Современная теория и практические применения антенн
Предметный указатель
Антенна
- апертурная 481
- бегущей волны 396
— коэффициент направленного действия 403
- Вивальди 387
- волноводно-щелевая 380
— диаграмма направленности 382
- двухзеркальная 546
- зеркальная 531
- импедансная 435
- кольцевая (рамочная) 218
— диаграмма направленности 227
— коэффициент направленного действия 229, 242
— сопротивление излучения 228
— электрические параметры 218
- линзовая 557
- логопериодическая 477
- многозеркальная 546
- многолучевая 26
- многощелевая 384
— диаграмма направленности 385
- несимметричная 247
— входное сопротивление 252
— действующая длина 251
— диаграмма направленности 251
- о дно лучевая 24
- параболическая 534, 541
- передающая 35, 86
— действующая длина 110
— диапазонные свойства 112
— коэффициент согласования 108- печатная полосковая 450
— прямоугольной и круглой формы 452
- поверхностных волн 433
— дисковая 447
- приемная 35, 115
— внутреннее сопротивление 116
- - действующая длина 117
— диаграмма направленности 116
— коэффициент направленного действия 116
— коэффициент полезного действия
— коэффициент усиления 117
— поляризационные характеристики 131
— эффективная площадь 117
- ребристо-стержневая 446
Предметный указатель
699
- ромбическая 403
- рупорная 511, 520
- спиральная 405
- частотно-независимая 471
— спиральная 473
- цилиндропараболическая 535
- щелевая 369
Антенная решетка 267
— , множитель системы 278
— неэквидистантная 355
— плоская 340
— фазированная 574
— , полоса пропускания 589
— , активная 612
Вибратор криволинейный полосковый 181
- элементарный щелевой 67
Волновод круглый 513
- прямоугольный 511
Входное сопротивление 107
Высотность ПО
Диаграмма направленности 86
— амплитудная 87
— , измерение 666
Диполь Герца 60
Зона
- ближняя 58
- дальняя 55
- Френеля 57
Излучатель криволинейный широкополосный 660
- элементарный 58
— магнитный 63
— Гюйгенса 68
Коэффициент направленного действия 101
- усиления 103
— антенны, измерение 670
- полезного действия 109
Линза геодезическая 570
- диэлектрическая 566
- замедляющая 559
- Люнеберга 572
- металловоздушная 570
700
Современная теория и практические применения антенн
- металлодиэлектрическая 569
- металлопластинчатая 567
- неоднородная 571
- ускоряющая 560
Малоотражающее конформное покрытие 637
Метод поверхностных токов 376
Множитель Лагранжа 658
Мощность излучения антенн 105
Обтекатели антенн 619
Параметрический синтез 641
Печатные антенные решетки 460
Поляризационный базис 92, 97
Рамка элементарная 64
Раскрыв квадратный 510
- круглый 510
Рупор конический 528
- электромагнитный 516
Сингулярное интегральное уравнение 81
Сопротивление излучения 105
Теорема взаимности 71
Теорема подобия 113
Уравнения Гельмгольца 45
Уравнение Поклингтона 144
Уравнение Халлена-Неганова 147
Фазовая характеристика антенны 99
Функция Грина 46
Электрическая прочность 110
Электрический вибратор 143
— сингулярные интегральные уравнения 148, 163
— сингулярное интегральное представление 153
— распределение тока 166
— расчет входного сопротивления 177
Электродинамический потенциал 45
Электромагнитные волны 50
— в декартовой системе координат 50
— в цилиндрической системе координат 51
— в сферической системе координат 53
Сведения об авторах
701
Сведения об авторах
Неганов Вячеслав Александрович, 1952 года рождения.
В 1977 году окончил Куйбышевский государственный универ-
ситет, в 1983 году - аспирантуру при ИРЭ РАН. Доктор фи-
зико-математических наук, профессор, заведующий кафедрой
основ конструирования и технологий радиотехнических систем
Поволжской государственного университета телекоммуника-
ций и информатики (ПГУТИ). Награжден значком “Почетный
радист”, лауреат губернской премии в области науки и техни-
ки в 2002 году. В.А. Неганов является специалистом в области
радиофизики. В списке научных работ В.А. Неганова более 500
наименований, в том числе 15 монографий (издательства “На-
ука”, “Педагогика-ПРЕСС”, “Радио и связь”), 27 авторских
свидетельств и патентов. Его работы опубликованы в цент-
ральных изданиях (“ДАН”, “Радиотехника и электроника”,
“Известия вузов. Радиофизика” и др.). В.А. Неганов является
членом редколлегий журналов “Электродинамика и техника
СВЧ и КВЧ” (г. Москва), “Вестник новых медицинских техно-
логий” (г. Тула). За разработку ферритовых развязывающих
приборов КВЧ-диапазона награжден двумя серебряными ме-
далями ВДНХ. В.А. Неганов - председатель докторского сове-
та Д219.003.01 в ПГУТИ, член докторского совета Д212.218.01
в Самарском государственном университете. Им подготовлены
3 доктора и 20 кандидатов наук. В настоящее время под его
началом шесть аспирантов и два докторанта.
Основные направления научной деятельности: некорректные
задачи, воздействие КВЧ- излучения с биологическими объек-
тами и разработка соответствующей медицинской аппаратуры,
биофизика.
Табаков Дмитрий Петрович, 1984 года рождения. В 2006
году с отличием окончил Поволжскую государственную ака-
демию телекоммуникаций и информатики (ПГАТИ, г. Самара).
В настоящее время является аспирантом третьего года обу-
чения в ПГУТИ, специальность 01.04.03 — Радиофизика, на-
учный руководитель — В.А. Неганов. В списке научных работ
более 20 наименований, в том числе 10 статей, опубликованных
в журналах, находящихся в списке ВАК.
Область научных интересов: техника СВЧ и КВЧ — диапа-
зонов, некорректные задачи электродинамики, ближняя зона
излучающих структур.
702
Современная теория и практические применения антенн
Яровой Геннадий Петрович, 1943 года рождения, доктор
физико-математических наук, профессор, действительный
член академии космонавтики им. К.Э. Циолковского, академии
проблем качества и Российской академии естественных наук.
Президент Самарского государственного университета, за-
ведующий кафедрой радиофизики и компьютерного моделиро-
вания радиосистем. Тематика научных исследований связана
с разработкой методов анализа распространения электромаг-
нитных волн в широком частотном диапазоне и в различных
волноведущих системах и конструированием на их основе при-
боров и систем целевого назначения.
В списке опубликованных работ 140 наименований, в том
числе 12 книг, 4 авторских свидетельства на изобретение. Яв-
ляется главным редактором трех периодических научных
журналов, в том числе журнала «Физика волновых процессов
и радиотехнические системы» из списка ВАК.
Заслуженный работник высшей школы РФ, лауреат ордена
Почета РФ, лауреат пяти медалей Федерации космонавтики
России: академика В.И. Челомея, академика М.В. Келдыша,
академика С.П. Королева, академика В.П. Глушко, Ю.А. Гага-
рина.
Он обладатель почетного знака РАЕН «За заслуги в раз-
витии науки и экономики», почетного знака III степени «За
заслуги в области космонавтики», дважды лауреат Самарской
губернской премии в области науки и техники.
Содержание 703
Содержание
Предисловие.......................................................3
Предисловие авторов...............................................4
Список основных сокращений........................................6
Список основных обозначений.......................................7
Введение 9
В.1. Назначение и классификация антенн............................9
В.2. Структурная схема однолучевой антенны [2]...................24
В.З. Многолучевые антенны [3]....................................26
В.3.1. Классификация и схемы построения.......................26
В.3.2. Исторический обзор [2].................................31
Глава 1. Электродинамические
основы теории антенн____________...______.....-----........-.....-- 35
1.1. Передающая и приемная антенны...............................35
1.2. Средний баланс энергии и эквивалентные схемы приемной и передающей
антенн...........................................................40
1.3. Расчёт электромагнитных полей, создаваемых заданными электрическими
и магнитными токами в однородной изотропной среде................45
1.3.1. Уравнения Гельмгольца и электродинамические потенциалы.45
1.3.2. Решение векторного уравнения Гельмгольца. Функции Грина...46
1.4. Электрические и магнитные волны в безграничной среде........50
1.4.1. Электрические и магнитные волны в декартовой
системе координат................................................50
1.4.2. Электрические и магнитные волны в цилиндрической системе
координат........................................................51
1.4.3. Электрические и магнитные волны в сферической
системе координат................................................53
1.5. Расчёт электромагнитных полей излучающих систем в дальней,
промежуточной и ближней областях....................................54
1.5.1. Дальняя зона...........................................55
1.5.2. Промежуточная область (зона Френеля)...........57
1.5.3. Ближняя зона...........................................58
1.6. Излучение электромагнитных волн элементарными излучателями..58
1.6.1. Роль теории элементарных излучателей при определении поля
излучения антенн..............................................58
1.6.2. Элементарный электрический вибратор (диполь Герца).....60
1.6.3. Элементарный магнитный излучатель......................63
1.6.4. Элементарная рамка.....................................64
1.6.5. Элементарный щелевой вибратор (ЭЩВ)....................67
1.6.6. Элементарный излучатель Гюйгенса..................... 68
1.7. Некоторые теоремы электродинамики, применяемые в теории антенн.71
704 Современная теория и практпичес1сие пр]1менения дмтенн
1.7.1. Теорема взаимности............................................71
1.7.2. Принцип двойственности........................................72
1.7.3. Теорема перемножения при анализе диаграммы направленности
системы из дискретных излучателей, одинаково ориентированных в
пространстве.....................................................74
1.7.4. Множитель направленности для непрерывного распределения
электромагнитных источников плоского излучающего раскрыва........76
1.8. Самосогласованная постановка задач расчета полей
излучающих систем. Диполь Герца [13]...............................77
1.8.1. Тонкопроволочное приближение электрического вибратора.....77
1.8.2. Самосогласованная физическая модель электрического
вибратора [13, 14]...............................................79
1.8.3. Сингулярное интегральное представление электромагнитного поля.80
1.8.4. Сингулярное интегральное уравнение........................81
1.8.5. Диполь Герца..............................................83
Глава 2. Электрические параметры
передающих антенн [2, ___...._________........._..._____86
2.1. Векторная комплексная диаграмма направленности (ДН)
антенны [2, 17]....................................................86
2.1.1. Амплитудная диаграмма направленности......................87
2.1.2. Изображение ДН в пространстве.............................88
2.1.3. Поляризационные свойства; поляризационный базис [2].......92
2.1.4. Направленные свойства антенн вращающейся поляризации......96
2.1.5. Поляризационный базис [2].................................97
2.1.6. Фазовая характеристика антенны............................99
2.2. Коэффициенты направленного действия и усиления антенны [17]..101
2.2.1 Коэффициент направленного действия (КНД).................101
2.2.2. Коэффициент направленного действия антенн
вращающейся поляризации.........................................102
2.2.3. Коэффициент усиления (КУ)................................103
2.2.4. Пересчет КНД при переходе от одной эталонной антенны
к другой........................................................103
2.2.5. Расчет КНД...............................................104
2.2.6. Расчет КУ................................................104
2.2.7. КНД диполя Герца и излучателя Гюйгенса по отношению
к изотропному излучателю........................................104
2.3. Сопротивление излучения......................................105
2.3.1. Закон сохранения энергии электромагнитного поля
в применении к передающим антеннам..............................105
2.3.2. Мощность излучения антенн................................105
2.3.3. Метод интегрирования вектора Умова-Пойнтинга.............105
2.3.4. Сопротивление излучения..................................106
2.4. Входное сопротивление........................................107
2.4.1. Эквивалентная схема антенны по входному
сопротивлению...................................................108
Содержание
705
2.4.2. Коэффициент согласования передающей антенны...........108
2.5. Коэффициент полезного действия антенны.....................109
2.6. Электрическая прочность и высотность антенн [17]...........110
2.6.1. Электрическая прочность...............................110
2.6.2. Высотность антенно-фидерного устройства...............110
2.7. Действующая длина передающей антенны.......................110
2.8. Диапазонные свойства передающих антенн.....................112
2.9. Некоторые дополнительные связи между параметрами передающей
антенны.........................................................113
2.9.1. Связь между КНД, действующей длиной и сопротивлением
излучения....................................................113
2.9.2. Теорема подобия [17]..................................113
Глава 3. Электрические параметры
приемных антенн [3, 17]-----------------.........---...-----------115
3.1. Эквивалентная схема приемной антенны [17]..................115
3.2. Основные электрические параметры приемной антенны [17].....116
3.2.1. Внутреннее сопротивление приемной антенны.............116
3.2.2. Диаграмма направленности приемной антенны
по напряжению................................................116
3.2.3. Коэффициент направленного действия приемной
антенны......................................................116
3.2.4. Коэффициент полезного действия приемной антенны.......116
3.2.5. Коэффициент усиления (КУ) приемной антенны............117
3.2.6. Действующая длина приемной антенны....................117
3.2.7. Эффективная площадь приемной антенны..................117
3.2.8. Шумовая температура антенны...........................118
3.2.9. Рабочий диапазон волн (частот)........................118
3.3. Применение принципа взаимности для расчета
параметров антенн [17]..........................................118
3.3.1. Принцип взаимности для антенн.........................118
3.4. Энергетические соотношения в цепи приемной антенны и влияние
приемной антенны на помехозащищенность радиолинии [17]..........121
3.4.1. Режим сильного сигнала в радиолиниях ДВ, СВ и КВ......121
3.4.2. Режим сильного сигнала в радиолиниях СВЧ..............123
3.4.3. Коэффициент различимости в режиме слабого сигнала.....126
3.4.4. Режим слабого сигнала в радиолиниях ДВ, СВ и КВ.......126
3.4.5. Режим слабого сигнала в диапазоне СВЧ.................127
3.4.6. Эффективная шумовая температура антенны...............128
3.5. Поляризационные характеристики приемных антенн [17]........131
3.6. Антенна как пассивный рассеиватель [3].....................133
3.7. Параметры электромагнитной совместимости антенн [3]........140
706 Современная теория и практические применения антенн
Глава 4. Электрические симметричные
вибраторы______________.................._............___...____________143
4.1. Классическая постановка задачи о распределении тока по тонкому
вибратору. Уравнение Поклингтона [5].................................144
4.1.1. Интегральное уравнение Халлена-Неганова [28]................147
4.2. Сингулярные интегральные уравнения в теории трубчатых
электрических вибраторов [8].........................................148
4.2.1. Самосогласованная физическая модель трубчатого
электрического вибратора...........................................148
4.2.2. Сингулярное интегральное уравнение для трубчатого
вибратора..........................................................149
4.2.3. Метод решения сингулярных интегральных уравнений............153
4.3. Сингулярное интегральное представление (СИП) электромагнитного
поля электрического вибратора [10, 11]...............................158
4.3.1 Сингулярное интегральное представление электромагнитного
поля...............................................................158
4.3.2. Сингулярное интегральное уравнение..........................163
4.3.3. Выражения для составляющих ЭМП, полученные традиционным
методом............................................................164
4.3.4. Сравнение самосогласованного метода с традиционным
подходом...........................................................165
4.4. Распределение тока по электрическому вибратору (анализ при
самосогласованном подходе) [8].......................................166
4.4.1. Распределения поверхностной плотности тока для симметричного
вибратора..........................................................166
4.4.2. Распределения тока для несимметричного вибратора............172
4.4.3. Расчет входного сопротивления...............................177
4.4.4. Электромагнитное поле излучения полуволнового
электрического вибратора...........................................179
4.5. Криволинейный полосковый вибратор, расположенный
на цилиндрической поверхности [24]...................................181
4.5.1. Постановка задачи. Физическая модель вибратора..............181
4.5.2. Вывод сингулярного интегрального уравнения..................182
4.5.3. Решение сингулярного интегрального уравнения................185
4.5.4. Расчет амплитудной диаграммы направленности криволинейного
полоскового вибратора в азимутальной плоскости.....................188
4.5.5. Численное моделирование криволинейного полоскового
вибратора..........................................................190
4.6. Приближенное распределение тока по электрическому вибратору,
используемое при расчете его характеристик в дальней зоне [2]........193
4.7. Электрические параметры прямолинейного симметричного вибратора в
дальней зоне [17]....................................................195
4.7.1. Напряженность электрического поля, создаваемого симметричным
вибратором.........................................................195
4.7.2. Диаграмма направленности симметричного вибратора............197
4.7.3. КНД симметричного вибратора.................................198
4.7.4. Действующая длина симметричного вибратора...................199
Содержание 707
4.7.5. Сопротивления излучения симметричного вибратора.......200
4.7.6. Входное сопротивление симметричного вибратора.........200
4.7.7. Настройка и диапазонность симметричных вибраторов.
Широкополосные вибраторы. Настройка в резонанс...............206
4.8 Петлевой вибратор Пистолькорса [17].......-.................211
4.9. Особенности применения симметричных вибраторов [17].........213
Глава 5. Кольцевые (рамочные) антенны.................................— 218
5.1. Введение [17]..............................................218
5.1.1. Типы кольцевых (рамочных) антенн..................... 218
5.1.2. Электрические параметры в дальней зоне электрически
малой рамочной антенны.......................................218
5.1.3. Рамки с магнитным сердечником....................... 220
5.1.4. Экранированные рамки..................................222
5.1.5. Питание рамочных антенн...............................224
5.1.6. Радио девиация рамочных антенн летательных
аппаратов....................................................224
5.2. Электрические параметры кольцевых антенн, размеры которых
сравнимы с длиной волны, в дальней зоне [18]....................225
5.2.1. Вывод общих выражений для поля излучения..............225
5.2.2. Кольцевые синфазные равноамплитудные антенны..........226
5.2.3. Диаграмма направленности кольцевой синфазной
равноамплитудной антенны.....................................227
5.2.4. Сопротивление излучения...............................228
5.2.5. Коэффициент направленного действия....................229
5.3. Применение сингулярных интегральных уравнений для
электродинамического анализа кольцевой антенны..................229
5.3.1. Постановка задачи. Физические и математические
модели антенн................................................230
5.3.2. Бесконечная система сингулярных интегральных
уравнений....................................................234
5.3.3. Метод решения системы сингулярных интегральных
уравнений....................................................235
5.3.4. Определение входного сопротивления антенн.............237
5.3.5. Анализ распределений поверхностных плотностей
токов........................................................239
5.3.6. Диаграммы направленности кольцевых антенн с учетом
распределений тока по кольцу.................................242
Глава 6. Несимметричные антенны [3,17]____________________....__.....247
6.1. Классификация, типы несимметричных антенн [17].............247
6.1.1. Несимметричные вибраторы со смещенными клеммами.......248
6.1.2. Разноплечий вибратор с питанием в середине............249
6.1.3. Вертикальный вибратор над экраном конечных размеров...249
6.2. Несимметричные антенны и метод зеркальных изображений [17].250
6.2.1. Основные параметры несимметричных антенн..............250
708
Совремегуная теория и практические применение антенн
6.2.2 Расчет поля и ДН несимметричной антенны.....................251
6.2.3. КНД несимметричной антенны...................................251
6.2.4. Действующая длина несимметричной антенны.....................251
6.2.5. Сопротивление излучения и входное сопротивление
несимметричной антенны.............................................252
6.2.6. Эквивалентная высота горизонтальной части антенны...........253
6.2.7. Несимметричные короткие антенны.............................254
6.2.8. Учет фазы тока в зеркальном изображении [3].................254
6.3. Широкополосные несимметричные вибраторы и антенны [17]..........256
6.3.1 Диско — конусная антенна.....................................256
6.4. Диаграммы направленности антенны с учетом влияния земли.
Несимметричный вибратор [3]..........................................258
6.5. Особенности применения несимметричных антенн [17]............. 263
6.5.1. Схемы питания несимметричных антенн.........................263
6.5.2. Влияние конечной проводимости земли.........................264
Глава 7. Антенные решетки...................................................................... 267
7.1. Антенные решетки и их классификация.............................267
7.1.1 Методы расчета характеристик антенных решеток................270
7.2. Излучение линейной синфазной решетки [3].........................272
7.3. Линейные АР с равноамплитудным возбуждением и линейным
изменением фазы [27]..................................................278
7.3.1. Множитель системы линейной АР...............................278
7.3.2. Режим нормального излучения ( щ = 0).....................280
7.3.3. Режим наклонного излучения ( 0 < у < kd )...................284
7.3.4. Режим осевого излучения.....................................286
7.4. Влияние неравномерности амплитудного распределения на ДН
линейной АР [27]......................................................289
7.5. Влияние фазовых искажений на ДН линейной решетки [27]...........291
7.6. Излучение двух связанных вибраторов [37].........................292
7.6.1. Направленные свойства системы из двух связанных
вибраторов.........................................................292
7.6.2. Метод наведенных ЭДС. Сопротивления излучения
и входные сопротивления связанных вибраторов [27,37]...............299
7.6.3 Расчет наведенного и полного сопротивлений
излучения [37].....................................................304
7.6.4. Расчет тока в пассивных вибраторах [37].....................305
7.7. Многовибраторные настроенные синфазные антенны [18].............308
7.8 Директорные антенны (антенны типа “волновой канал”) [18]........312
7.8.1. Антенная система из двух вибраторов: питаемого
и пассивного [18]..................................................312
7.8.2. Многовибраторные директорные антенны [18]...................314
7.9. Скрещенные вибраторы с вращающейся поляризацией [18]............317
7.9.1. Скрещенные вибраторы........................................317
7.9.2. Пример построения многоэтажной турникетной
телевизионной передающей антенны из решетки плоскостных
шунтовых вибраторов [2]............................................323
Содержание 709
7.10. Взаимодействие излучателей в решетке и диаграмма направленности из-
лучателя [3,27]....................................................324
7.10.1. Связь комплексных наведенных сопротивлений через
активные взаимные наведенные сопротивления для синфазной
АР и активные взаимные наведенные сопротивления АР
со сдвигом фаз л/2.............................................326
7.11. Входное сопротивление излучающего элемента АР. Мощность,
излучаемая АР [27]................................................330
7.12. Коэффициент направленного действия линейных АР [27]..........332
7.13. Понятие о непрерывном линейном излучателе [27]...............335
7.14. Плоские антенные решетки [27]................................340
7.15. Излучение плоской и пространственной синфазных решеток [3]...344
7.16. Решетка с линейным набегом фазы. Антенны с электрическим
сканированием [3]..................................................347
7.17. Антенные решетки с неравноамплитудным распределением [3,17]..351
7.18. Неэквидистантные антенные решетки [17, 27]...................355
7.19. Понятие о синтезе антенны по заданной диаграмме
направленности [17]................................................357
7.19.1. Задача синтеза антенны..................................357
7.19.2. Приближенный синтез антенны.............................359
7.19.3. «Сверхнаправленность»...................................359
7.20. Антенны бегущей волны и ДН линейной антенны [3]..............360
7.21. Коэффициент направленного действия антенны бегущей волны [3].366
7.22. Полосковые антенны типа «волновой канал» Уда-Яги и антенные
решетки [57]..................................................... 367
Глава 8. Щелевые антенны...._________________________..........._........... 369
8.1. Классификация щелевых антенн и их расчет с помощью принципа
двойственности [17]................................................369
8.1.1. Типы щелевых антенн......................................369
8.1.2. Принцип двойственности...................................370
8.1.3. Поле излучения прямолинейной щелевой антенны.............371
8.1.4. Проводимость прямолинейной щелевой антенны...............373
8.1.5. Способы возбуждения прямолинейной щелевой антенны........374
8.2. Излучение щелей, прорезанных в металлических телах конечных
размеров...........................................................376
8.2.1. Метод поверхностных токов................................376
8.3. Волноводно-щелевые антенны....................................380
8.3.1. Возбуждение щелей в волноводе............................380
8.3.2. Диаграммы направленности одиночной полуволновой
щели............................................................382
8.3.3. Эквивалентные параметры щелей в волноводе................382
8.3.4. Многощелевые антенны.....................................384
8.3.5. Диаграммы направленности многощелевой антенны............385
8.3.6. Эквивалентные схемы многощелевых антенн..................386
8.3.7. Щелевые антенны и антенные решетки. Антенна
Вивальди [57]...................................................387
710
Современная теория и прагстичестсие применения дмпьенн
8.4. Применение метода сингулярных интегральных уравнений для расчета
плоской электромагнитной волны на прямоугольном отверстии в идеально
проводящей плоскости [13].............................................388
8.4.1. Постановка задачи. Сингулярное интегральное
представление (СИП) электромагнитного поля.........................389
8.4.2. Метод решения двумерного сингулярного интегрального
уравнения..........................................................391
8.4.3. Численный анализ. Сравнение полученных результатов
с дифракцией Френеля [1]..........................................393
Глава 9. Антенны бегущей волны....м.................................................. 396
9.1. Излучение прямолинейного провода с бегущей волной тока [3]......396
9.1.1. Диаграмма направленности линейного непрерывного
излучателя [3]....................................................396
9.1.2. Коэффициент направленного действия антенны
бегущей волны [3].................................................403
9.2. Ромбическая антенна [17]........................................403
9.2.1. Принцип действия...........................................403
9.2.2. Диаграммы направленности...................................404
9.2.3. Коэффициент полезного действия.............................405
9.3 Спиральные антенны..............................................405
9.3.1. Классификация и типы спиральных антенн [3].................405
9.3.2. Теория регулярной цилиндрической спиральной
антенны [3].......................................................408
9.3.3. Цилиндрическая спиральная антенна как линейная
решетка [3].......................................................411
9.3.4. Решетки из нескольких идентичных спиралей [18].............414
9.3.5. Плоские спиральные антенны [17]............................415
9.3.6. Коническая спиральная антенна [17].........................418
9.3.7. Коническая логарифмическая спиральная антенна..............419
9.4. Применение сингулярных интегральных уравнений
к электродинамическому анализу цилиндрической спиральной антенны......421
9.4.1. Самосогласованный подход к решению задачи..................422
9.4.2. Сингулярное интегральное уравнение.........................424
9.4.3. Численный анализ цилиндрической спиральной антенны.........427
9.5. Антенны поверхностных волн [17,3]............................. 433
9.5.1. Основные типы антенн поверхностных волн [17]...............433
9.5.2. Импедансные антенны [3]....................................435
9.5.3. Импедансные антенны с гофрированными металлическими структура-
ми [3]............................................................438
9.5.4. Антенны вытекающей волны [3]...............................442
9.5.5. Диэлектрические стержневые антенны поверхностных
волн. Стержневая диэлектрическая антенна [17].....................444
9.5.6. Ребристо-стержневая антенна [17]...........................446
9.5.7. Дисковые антенны поверхностных волн [17]...................447
9.5.8. Применение антенн поверхностных волн [17]..................447
Содержание 711
Глава 10. Антенны СВЧ в интегральном
исполнении...............______.....____...._________......___________449
10.1. Классификация печатных полосковых антенн [48]................450
10.1.1. Классификация ППАпо форме излучающего элемента...........450
10.1.2. Классификация ППАпо виду подстилающей
диэлектрической структуры........................................450
10.1.3. Классификация ППАпо форме геометрического тела,
на котором располагается ППА.................................... 451
10.1.4. Классификация ППАпо способу возбуждения
излучающего элемента...........................................451
10.2. Полосковые печатные антенны прямоугольной и круглой формы..452
10.3. Печатные резонаторные излучатели для формирования излучения
круговой поляризации.............................................458
10.4. Печатные антенные решетки..................................460
10.5. Применение метода СИУ к расчету микрополосковых антенн [62]..462
10.5.1. Постановка задачи. Физическая модель излучателя..........463
10.5.2. Сингулярное интегральное представление
электромагнитного поля...........................................466
10.5.3. Сингулярное интегральное уравнение.......................467
10.5.4. Численные результаты.....................................469
Глава 11. Частотно-независимые
антенны [2, 74, 101]___________....________.........__........________471
11.1. Принципы построения частотно-независимых антенн [2, 74]......471
11.2. Частотно-независимые спиральные антенны [2, 74]..............473
11.3. Логопериодические антенны [2, 74]............................477
Глава 12. Излучающие плоские раскрывы
апертурных антенн [2, 3, 18]..____________________.......______........481
12.1. Внутренняя и внешняя задачи теории апертурных антенн СВЧ [3].481
12.2. Внешняя задача излучения плоского раскрыва (апертуры)
антенн СВЧ [3].....................................................486
12.3. Излучение прямоугольной и круглой площадок при разных
амплитудных распределениях поля [18]...............................488
12.3.1. Прямоугольная площадка...................................491
12.3.2. Круглая площадка.........................................491
12.3.3. Диаграммы направленности прямоугольной и круглой
площадок.........................................................493
12.4. Влияния фазовых искажений на излучение площадки [18].........497
12.4.1. Линейное изменение фазы..................................497
12.4.2. Квадратичное изменение фазы..............................498
12.4.3. Изменение фазы поля по кубическому закону................500
12.4.4. Случайные фазовые ошибки [3]........................... 501
712 Современная теория и пралспримеские применения аррпенн
12.5. Коэффициент направленного действия и эффективная поверхность
площадок [18]....................................................501
12.5.1. Площадка произвольной формы с равноамплитудным
синфазным распределением поля.................................502
12.5.2. Прямоугольная площадка с косинусоидальным
изменением амплитуды синфазного поля...........................503
12.6. Сравнение множителя направленности плоского раскрыва различной
формы [2].........................................................505
12.6.1. Множитель направленности раскрыва прямоугольной
формы..........................................................505
12.6.2. Множитель направленности круглого раскрыва.............507
12.7. Метод эквивалентного линейного излучателя в анализе плоского
раскрыва [2]......................................................509
12.7.1. Круглый раскрыв........................................510
12.7.2. Квадратный раскрыв.....................................510
Глава 13. Волноводные излучатели
и рупорные антенны [18].....__________________________________...___511
13.1. Излучение из открытого конца волновода [18].................511
13.1.1. Прямоугольный волновод.................................511
13.1.2. Круглый волновод.......................................513
13.1.3. Оценка открытых волноводов как антенн [18].............515
13.2. Электромагнитные рупоры [18]................................516
13.2.1. Типы электромагнитных рупоров и методы их анализа [18].516
13.2.2. Способы уменьшения длины рупора [18]...................518
13.2.3. Применение рупорных антенн [18]........................519
13.3. Рупорные антенны [18].......................................520
13.3.1. Н-плоскостной секториальный рупор [18].................520
13.3.2. Е-плоскостной секториальный рупор [18].................524
13.3.3. Пирамидальный рупор [18]...............................526
13.3.4. Упрощенный расчет поля излучения рупоров
с прямоугольным раскрывом [18].................................527
13.3.5. Конический рупор [18]..................................528
13.3.6. Расчет рупорных антенн [18]............................529
Глава 14. Зеркальные антенны [17]__________________......_____..._531
14.1. Принцип действия зеркальных антенн и элементы
их конструкции [17]..............................................531
14.1.1. Принцип действия зеркальных антенн.....................531
14.1.2. Зеркало................................................531
14.1.3. Облучатель.............................................532
14.1.4. Анализ и синтез зеркальных антенн [17].................533
14.1.5. Области применения зеркальных антенн [17]..............533
14.2. Геометрические характеристики параболических антенн [17]...534
14.2.1. Профиль зеркала........................................534
14.2.2. Геометрические характеристики зеркала..................534
Содержание 71-3
14.2.3. Отражающие поверхности.................................535
14.3. Цилиндропараболические антенны [17].........................535
14.3.1. Конструктивная схема...................................535
14.3.2. Основные типы облучателей цилиндропараболических
антенн.........................................................536
14.3.3. Распределение амплитуд поля в раскрыве.................538
14.3.4. Диаграммы направленности...............................539
14.3.5. Коэффициент направленного действия.....................539
14.3.6. Коэффициент усиления...................................539
14.3.7. Оптимальный облучатель и оптимальный
угол раскрыва..................................................540
14.4. Антенна с зеркалом в виде параболоида вращения
(параболическая антенна) [17].....................................541
14.4.1. Конструктивная схема...................................541
14.4.2. Основные типы точечных облучателей.....................541
14.4.3. Распределение амплитуд поля в раскрыве
параболоида вращения...........................................543
14.4.4. Диаграмма направленности параболической антенны........544
14.4.5. КИП и коэффициент перехвата............................544
14.4.6. Выигрыш................................................544
14.5. Антенны с зеркалом в виде вырезки из параболоида вращения....544
14.5.1. Зеркала в виде вырезок из параболоида вращения.........544
14.5.2. Симметрично-усеченный параболоид.......................545
14.5.3. Несимметричные вырезки из параболоида вращения.........545
14.5.4. Облучатели антенн с зеркалом в виде вырезки
из параболоида вращения........................................545
14.5.5. Распределение амплитуд поля в раскрыве.................545
14.5.6. Диаграммы направленности, КНД и КУ.....................545
14.6. Двухзеркальные и многозеркальные антенны....................546
14.6.1. Конструктивная схема простейшей двухзеркальной антенны.546
14.6.2. Основные схемы двухзеркальных антенн...................546
14.6.3. Диаграмма направленности осесимметричной
зеркальной антенны.............................................547
14.6.4. Двухзеркальная антенна с большим плоским зеркалом......547
14.6.5. Отражатель с поворотом плоскости поляризации на 90°....548
14.7. Зеркальные антенны с диаграммой направленности специальной
формы [17]........................................................549
14.7.1. Диаграмма направленности специальной формы.............549
14.7.2. Антенны самолетных радиолокационных бомбоприцелов......550
14.7.3. Антенны наземных РЛС обнаружения и целеуказания........550
14.8. Технические допуски на размеры зеркальных антенн
при изготовлении и в процессе эксплуатации [17]...................551
14.8.1. Точность изготовления зеркальных антенн................551
14.8.2. Отклонение поверхности зеркала от расчетной.............551
14.8.3. Смещение облучателя из фокуса вдоль оптической оси......552
14.8.4. Вынос облучателя из фокуса перпендикулярно
оптической оси.................................................553
714
Современная теория и практические пршшпрршя алрпенн
14.9. Диапазонные свойства зеркальных антенн [17]..............555
14.9.1. Ширина полосы частот зеркальной антенны.............555
14.9.2. Диапазонность по согласованию.......................555
14.9.3. Диапазонность зеркальных антенн по направлению
излучателя..................................................556
Глава 15. Линзовые антенны [17]_________________________________...557
15.1. Основные типы линзовых антенн [17].......................557
15.2. Уравнение профиля и толщина линзы [17]...................559
15.2.1. Замедляющие линзы...................................559
15.2.2. Ускоряющие линзы....................................560
15.2.3. Смещение облучателя.................................561
15.3. Распределение амплитуд поля в раскрыве [17]..............561
15.3.1. Замедляющие линзы...................................561
15.3.2. Ускоряющие линзы....................................563
15.4. Зонирование линз [17]....................................563
15.4.1. Замедляющие линзы...................................564
15.4.2. Ускоряющие линзы....................................565
15.5. Отражение электромагнитных волн от поверхностей линз и меры
по его уменьшению [17].........................................565
15.6. Диэлектрические линзы [17]...............................566
15.7. Металлопластинчатые линзы [17]...........................567
15.8. Металле диэлектрические линзы [17].......................569
15.9. Металловоздушные (геодезические) линзы [17]..............570
15.9.1. Направляющие устройства.............................570
15.9.2. Структура электромагнитного поля....................570
15.9.3. Вариант металловоздушной линзы......................571
15.10. Линзы с переменным коэффициентом преломления
(неоднородные линзы) [17]......................................571
15.10.1. Неоднородная линза.................................571
15.10.2. Линза Люнеберга....................................572
15.10.3. Модифицированная линза Люнеберга...................572
Глава 16. Фазированные антенные решетки [3,17]....™.. 574
16.1. Общие сведения о фазированных антенных решетках.
Схемы построения. Элементная база..............................574
16.1.1. Схемы построения ФАР [3]............................574
16.1.2. Фазовращатели для ФАР...............................577
16.1.3. Излучатели для ФАР..................................579
16.1.4. Многолучевые и совмещенные ФАР......................580
16.2. Пространственно-временная обработка сигнала
в антенных системах [3]........................................581
16.3. Основные особенности сканирования [17]...................586
16.3.1. Одномерное сканирование.............................586
16.3.2. Двумерное сканирование..............................587
16.3.3. Искажения главного лепестка.........................587
Содержание
715
16.3.4. Сектор сканирования и число управляющих
элементов ФАР [3].............................................588
16.3.5. Полоса пропускания ФАР................................589
16.3.6. Наибольшая допустимая частота сканирования [17].......591
16.4. Антенные решетки с фазовым сканированием [17]..............591
16.4.1. Фидерное питание......................................591
16.4.2. Пространственное питание..............................592
16.4.3. Плавное изменение сдвига фаз..........................593
16.4.4. Дискретное изменение сдвига фаз.......................595
16.4.5. Изменение характеристик направленности
в секторе сканирования [3]....................................599
16.4.6. Характеристики управления и общетехнические
характеристики [3]............................................599
16.5. Антенны с частотным сканированием [3,17]...................601
16.6. Линейная решетка СВЧ-излучателей [3].......................603
16.7. Многолучевые и совмещенные антенные решетки [3,17].........607
16.8. Активные ФАР [3]...........................................612
16.9. Антенные решетки с обработкой сигнала [17].................612
16.9.1. Методы обработки сигнала..............................612
16.9.2. Корреляционные (мультипликативные) антенны............613
16.9.3. Антенная система с логическим синтезом................614
16.10. Основные применения многолучевых антенн [3]...............614
Глава 17. Обтекатели антенн и покрытия объектов,
снижающие их радиолокационную видимость...................... 619
17.1. Обтекатели антенн [3, 17]..................................619
17.1.1. Классификация обтекателей [17]........................619
17.1.2. Требования, предъявляемые к обтекателям [3,17]........620
17.1.3. Материалы обтекателей [3].............................620
17.1.4. Особенности конструкций обтекателей [3]...............622
17.1.5. Выбор структуры стенок обтекателей....................624
17.1.6. Армированные обтекатели [17]..........................627
17.1.7. Влияние обтекателя на диаграмму направленности
антенны.......................................................628
17.2. Покрытия объектов, снижающие их радиолокационную видимость..629
17.2.1. Дифракция плоской электромагнитной волны
на идеально проводящем разомкнутом кольце [135]...............629
17.2.2. Малоотражающее конформное покрытие....................637
Глава 18. Параметрический синтез
при проектировании антенн..641
18.1. Особенности расчета и проектирования антенн [3]............641
18.1.1. Задачи синтеза антенн.................................642
18.2. Распределительные и излучающие системы антенн [66].........643
716 Современная теория и практические применения антенн
18.3. Классификация основных задач параметрического синтеза
распределительных и излучающих систем [41]........................645
18.4. Исходные соотношения для прикладных задач параметрического
синтеза излучающих систем [66]....................................646
18.4.1. Основные уравнения......................................649
18.4.2. Экстремальные и ограничительные требования..............651
18.5. Решение задач параметрического синтеза на основе вариационного
похода [66].......................................................652
18.6. Множитель Лагранжа [66].....................................658
18.7. Криволинейный широкополосный излучатель [66]................660
18.7.1. Блок формализованного задания...........................660
18.7.2. Блок физической модели..................................661
18.7.3. Блок математической модели..............................661
18.7.4. Блок прикладной математической модели...................662
18.7.5. Блок синтеза............................................662
18.8. Решение задач синтеза антенн методом
физической регуляризации [13]................................... 664
Глава 19. Измерение параметров и характеристик
излучения антенн [3, 116].......________________.___________...__....666
19.1. Измерение диаграммы направленности..........................666
19.1.1. Метод полигонных (лабораторных) измерений в дальней зоне.666
19.1.2. Метод облета антенны по заданной траектории
и астрономический метод измерения...............................668
19.1.3. Коллиматорный и голографический методы измерений........669
19.1.4. Измерение диаграммы направленности антенны
на моделях......................................................670
19.2. Измерение коэффициента усиления антенны.....................670
Заключение_______...._........__________......................_.............._..... 672
Приложение 1. Краткий толковый словарь по антенно-фидерным
устройствам.......................................................676
Приложение 2. Ученые, внесшие существенный вклад
в развитие электродинамики, теории и практики антенн
и распространения радиоволн.......................................684
Литература........................................................691
Предметный указатель..............................................698
Сведения об авторах...............................................701
Монография
Неганов Вячеслав Александрович
Табаков Дмитрий Петрович
Яровой Геннадий Петрович
Современная теория и практические
применения антенн
Под редакцией
Неганова В.А.
В авторской редакции.
Компьютерный дизайн и верстка - И.М. Градинарь
Формат 70x100/16. Бумага офсетная.
Гарнитура Journal. Печать офсетная. Печ. л. 45,0.
Тираж 1000 экз. Зак. № 277
Издательство «Радиотехника».
107031, Москва, К-31, Кузнецкий мост, д. 20/6.
Телефакс: (495) 621-48-37; 625-78-72, 625-92-41.
E-mail: info@radiotec.ru
www.radiotec.ru
Отпечатано с оригинал-макета
в типографии ООО «Самарский дом печати»
443052, г. Самара, пр. Кирова, 24.
Неганов BA.
Физическая регуляризация некорректных задач электродинамики: линии
передачи, антенны, дифракция электромагнитных волн. — М.: «САИНС-
ПРЕСС», 2008. - 432 с., 122 ил.
ФИЗИЧЕСКАЯ
РЕГУЛЯРИЗАЦИЯ
НЕКОРРЕКТНЫХ ЗАДАЧ
ЭЛЕКТРОДИНАМИКИ
матических моделей задач (физические допу-
ISBN 978-5-88070-161-2
УДК 537.87
ББК 32.84
Н 41
Изложены основы физической регуляри-
зации некорректных задач электродинамики,
связанной с особенностями физических и мате-
щения, некорректные математические выклад-
ки, отсутствие предельного перехода). Подход,
по мнению автора, обладает большими воз-
можностями, чем метод регуляризации Тихо-
нова А.Н. интегральных уравнений Фредгольма
первого рода, названный в книге методом ма-
тематической регуляризации. Метод физичес-
кой регуляризации (МФР) применен к анализу волноведущих и излучающих
структур, а также задачам дифракции электромагнитных волн на некоторых
телах. МФР позволил впервые корректно осуществить анализ полей в ближ-
них зонах некоторых антенн, устранить несамосогласованное приближение
Кирхгофа в задачах дифракции, установить связь поверхностной плотности
тока про-водимости с напряженностями электрического и магнитного полей
для диполя Герца и т. п.
Для специалистов в области радиотехники и радиофизики СВЧ, элект-
ромагнитной совместимости РТС, математической теории дифракции и
математического моделирования электродинамических структур самого
широкого назначения. Может быть полезна преподавателям вузов, докто-
рантам, аспирантам и студентам старших курсов соответствующих
специальностей.
Рецензенты:
Л.И. Пономарев
Московский авиационный институт (технический университет),
С.Л. Просвирнин
Радиоастрономический институт НАН Украины (г. Харьков),
С.Б. Раевский
Нижегородский государственный технический университет
MuAU
Неганов В.А., Осипов О.В., Раевский С.Б., Яровой Г.П.
Электродинамика и распространение радиоволн. Учебник / Под ред. В.А. Не-
ганова и С.Б. Раевского. Изд. 4-е, доп. и перераб. — М.: Радиотехника, 2009.
— 744 с, ил.
ISBN 978-5-88070-154-4
УДК 537.87(075.3)
ББК 22.3
Н 41
Книга написана активно работающими в об-
ласти электродинамики учеными. Излагаются
теория электромагнитного поля с акцентом на
радиотехническую электродинамику и анализ
волновых процессов; рассматриваются отра-
жение и преломление волн, излучение и диф-
ракция; описываются основные закономернос-
ти распространения электромагнитных волн в
различных безграничных средах (изотропных,
анизотропных, диспергирующих, неоднород-
ных), в направляющих и резонансных струк-
турах, в природных условиях. Обсуждаются методы математического моде-
лирования в электродинамике, опирающегося на применение ЭВМ.
Отличительной особенностью книги является обсуждение современных
проблем электродинамики: расчет электромагнитных волн в ближних зонах
излучающих структур (самосогласованный метод расчета), комплексных волн
в волноведущих структурах и др.
Предназначается для студентов радиотехнических и радиофизических
специальностей вузов,а также инженеров-радиотехников и радиофизиков.
Табл. 5. ил. 280. Библиогр. 378 назв.
Рецензенты:
В.Ф. Кравченко - докт. физ.-мат. наук, проф. ИРЭ РАН;
В.Н. Митрохин - докт. техн, наук, проф. МГТУ им. Баумана;
кафедра радиопередающих и антенно-фидерных устройств
Московского авиационного института
(зав. кафедрой проф., докт. техн, наук Д.И. Воскресенский)',
кафедра электроники физического факультета
Воронежского государственного университета
(зав. кафедрой проф., докт. физ.-мат. наук А.М. Бобрешов)
Дмтшюо Негшюд Лотппоа А ...А.
Детерминированный хаос и фракталы
в дискретно- нелинейных системах
Антипов О.И., Неганов В.А., Потапов А.А.
Детерминированный хаос и фракталы в дискретно-нелинейных системах.
- М.: Радиотехника, 2009. - 235 с., ил.
ISBN 978-5-88070-237-4
УДК 530.1:621.372+621.396
ББК 32.96
А 72
В монографии рассмотрены явления де-
терминированного хаоса. и фрактальности в
дискретно-нелинейных системах на примере
устройств импульсной силовой электроники,
приведены некоторые основные определения
современной нелинейной динамики и некото-
рые математические методы целочисленных и
дробных мер.
Представленные явления стохастической
работы могут наблюдаться в широком классе
систем с переменной структурой, действие ко-
торых может быть описано системами дифференциальных уравнений с пе-
ременными коэффициентами, скачкообразно меняющими свои значения с
течением времени в зависимости от состояния системы. Объектами исследо-
вания явились импульсные стабилизаторы напряжения различных типов и
структур. Научной новизной является применение как фрактальных, так и
мультифрактальных мер детерминированного хаоса к анализу стохастичес-
кой работы импульсных стабилизаторов
Для специалистов,интересующихся проблемами детерминированного ха-
оса,численным моделированием дискретно-нелинейных систем.
Рецензенты:
докт. техн, наук, проф. Дмитриков В.Ф. (г. Санкт-Петербург)
докт. физ.-мат. наук, проф. Бобрешов А.М. (г. Воронеж) -