Автор: Дезоер Ч. Видьясагар М.
Теги: регулирование и управление машинами, процессами математика
Год: 1983
Текст
Ч. ДЕЗОЕР, М. ВИДЬЯСАГАР
СИСТЕМЫ
С ОБРАТНОЙ СВЯЗЬЮ:
ВХОД-ВЫХОДНЫЕ
СООТНОШЕНИЯ
Перевод с английского А. С. БЕРНШТЕЙНА
Под редакцией Ю. С. ПОПКОВА
МОСКВА «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
1983
32.81
Д26
УДК 62-50
FEEDBACK SYSTEMS:
INPUT —OUTPUT
PROPERTIES
G. A. DESOER
Department of electrical engineering
and computer sciences
Univercity of California
Berkeley, California
M. VIDYASAGAR
Department of electrical engineering
and computer sciences
Montreal, Canada
Academic Press
New York San Francisco London 197S
A subsidiary of Harcourt Brace
Jovanovich, Publishers /
Системы с обратной связью: вход-выходные соотношения. Дезоер Ч„ В и д ь я-
сагар М. — М.: Наука. Главная редакция физико-математической литературы, 1983. —
280 с.
Авторы продолжают направление, разрабатывающее общий теоретико-функциональ-
ный взгляд на проблемы теории управления и выясняющее аспекты, общие для систем,
описанных самыми разнообразными операторами и еще недавно изучавшихся порознь.
Ядро книги составляют теоремы о существовании, единственности, ограниченности, ре-
шений замкнутых систем, используемые затем при исследовании устойчивости. Основы
математического аппарата (теория функций) изложены в первых главах. Многочислен-
ные примеры и упражнения разъясняют излагаемый материал.
Илл. 22, библ. 116 назв.
„ 1502000000— 070
Д 053(02)-83 180'83
Copyright © 1975, by Academic Ргем Tnc. -
All Right Reserved.
© Издательство «Наука>.
Главная редакция физико-математической
литературы, 1983
ОГЛАВЛЕНИЕ
От редактора перевода ......................................... .
Предисловие..................................................• • •
Обозначения.......................................................
Г лае а 1. Статические нелинейности...............................
1. Секторные условия...........................................
2. Статическая нелинейность с линейной обратной связью.........
3. Нелинейность со многими входами и выходами............ • • •
Библиографический комментарий..................................
Г лава 2. Нормы...................................................
1. Норма: определение и примеры................................
2. Эквивалентные нормы.........................................
3. Соотношения между нормированными пространствами.............
4, Геометрическая интерпретация нормы..........................
5. Норма линейного отображения ...........................
6, Два примера.................................................
7. Норма и спектральный радиус................
8. Мера матрицы................................................
Библиографический комментарий..................................
Г лава 3, Общие теоремы......................./••••••.............
1, Постановка задачи...........................................
2. Теорема о малом коэффициенте роста................
3. Теорема о малом коэффициенте роста по приращениям...........
4, Ограниченность..............................................
5. Теорема существования и единственности......................
6. Теорема о преобразовании контура............................
7, «^-устойчивость...........................................
8. Общий вид уравнения замкнутой системы................. . • •
Библиографический комментарий............................ • • •
Глава 4. Линейные системы ........................................
0. Введение....................................................
1, Линейные системы с обратной связью с дробно-рациональными пе-
редаточными функциями .........................................
2. Необходимые и достаточные условия устойчивости: метод факто-
ризации .......................................................
3. Линейные системы с динамической обратной связью (случай дроб-
но-рациональной передаточной функции)..........................
4. Системы с обратной связью, описываемые операторами свертки • •
5. Графический критерий устойчивости.................
6, Дискретные системы..........................................
7. Линейные нестационарные системы.............................
8. Системы с медленно изменяющимися параметрами................
9. Линеаризация................................................
Библиографический комментарий..................................
5
7
10
11
11
14
17
18
19
19
22
24
27
29
33
37
39
45
46
47
50
54
56
57
61
63
64
65
67
67
68
73
85
94
122
141
144
152
4
ОГЛАВЛЕНИЕ
Г лава 3, Применение теоремы о малом коэффициенте роста........... 153
1. Непрерывные системы—LP-устойчивость ........................ 153
2. Да-устойчивость — круговой критерий ....................... 155
3. Метод экспоненциального взвешивания — L00-устойчивость .... 159
4. Дискретные системы —/^-устойчивость.................... 163
5. Линейные системы с медленно изменяющимися параметрами.... 164
6. Пример нелинейной системы.............................. 165
7. Существование периодических решений.................... 168
8. Критерий Попова........................................ 172
9. Неустойчивость......................................... 174
Библиографический комментарий.................................. 184
Г лава 6. Пассивность............................................ 185
0. Введение................................................... 185
1. Обоснование из теории цепей................................ 186
2. Скалярное произведение.................................. 187
3. Общие положения............................................ 189
4. Пассивные системы: определение и примеры................... 190
5. Теорема о пассивности..................................... 197
6. Критерий Попова........• • .............................. 202
7. Дискретный случай.......................................... 207
8. Критерий средней логарифмической вариации................ 210
9. Теория усилителей........................................ 215
10. Связь теорем о пассивности и о малом коэффициенте роста . . . 232
11. Обратимость отображения 1-\-Н ............................ 237
12. Теоремы о неустойчивости.................................. 241
Библиографический комментарий................................. 244
Приложение А. Интегралы и ряды................................... 246
А.1. Регулярные функции....................................... 246
А.2. Интегралы................................................ 248
А.З. Ряды..................................................... 250
Приложение В. Преобразование Фурье............................. 251
В.1, £1-теория.............................................. 251
В.2. Да-теория.............................................. 252
В.З. Преобразование Лапласа................................. 253
П ри ложение С. Свертки....................................... 254
С.1. Введение............................................... 254
С.2. Свертка функций........................................ 255
С.З. Свертка меры и функции................................. 257
С.4. Свертка последовательностей............................ 259
Приложение D. Алгебры.......................................... 260
D.L Алгебры................................................. 260
D.2. Идеалы............................................... 263
D.3. Обращения в алгебре ................................... 264
Прил о же ние Е, Лемма Веллмана—Гронуолла...................... 266
Литература..................................................... 270
Предметный указатель • . . • .................................. 276
ОТ РЕДАКТОРА ПЕРЕВОДА
В современной теории управляемых систем довольно контрастно
начали проявляться два, в некотором смысле альтернативных,
подхода, один из которых базируется на концепции пространства
состояний, другой —на концепции «вход —выход».
Описание поведения управляемой системы в пространстве со-
стояний предполагает возможность ее декомпозиции до элемен-
тарного уровня, описания поведения каждого ее элемента и свя-
зей между ними. Тем самым для построения математической мо-
дели системы в пространстве состояний необходима довольно
детальная информация о ее внутренней структуре и образующих
ее элементах.
К настоящему времени развиты довольно эффективные методы
исследования поведения управляемых систем в пространстве со-
стояний. К ним прежде всего относятся методы анализа устойчи-
вости, основы которых были заложены А. И. Ляпуновым и затем
развиты в многочисленных работах советских и зарубежных уче-
ных. Существенный прогресс был достигнут в статистическом
анализе управляемых систем.
Большинство результатов теории оптимального управления,
аналитического конструирования регуляторов, теории фильтрации
и стохастического управления связано с использованием математи-
ческих моделей систем в пространстве состояний.
Однако, если обратиться к истории теории управляемых систем,
а затем «заглянуть» в ее будущее, то можно обнаружить довольно
явную тенденцию роста сложности объектов этой теории и как
ее следствие — уменьшение достоверной информации о внутрен-
нем устройстве этих объектов. Так, например, определение коор-
динат состояния для описания пространственного движения лета-
тельного аппарата не представляет сейчас больших затруднений,
тогда как «назначение» координат состояния, характеризующих
рост растения, является совсем нетривиальной проблемой.
Сложность современных объектов теории управляемых систем
не только в том, что «трудно» построить модель в пространстве
состояний. Возможно, это сделать «легко», но размерность этой
модели столь велика, что изучение ее поведения становится без-
надежным.
О ОТ, РЕДАКТОРА ПЕРЕВОДА
В этой ситуации концепция «вход — выхода приобретает явную
конкурентоспособность. Она предполагает, что внутреннее устрой-
ство системы неизвестно, что доступной является информация
о входе и выходе, и нацеливает на исследование преобразования
вход —выход, которое описывается в общих терминах функцио-
нального анализа.
Такой подход с теоретической точки зрения открывает воз-
можности создания теории систем, опирающейся на достаточно
общие и универсальные ее понятия. Он оказывается полезным и
для инженера, так как в определенном смысле возрождает при-
вычные для него понятия передаточных функций и импульсных
характеристик линейных систем, развивает их на системы других >
классов, открывает возможность практического использования
более общей характеризации систем, чем это делается в методах
пространства состояний.
Предлагаемая вниманию советского читателя книга посвящена
изложению методов анализа устойчивости и смежных вопросов
в управляемых системах, описываемых в терминах «вход —вы-
хода. Она написана известными специалистами в этой области
проф. Дезоером и проф. Видьясагаром. В данной книге рассмат-
ривается широкий круг проблем, связанных с анализом устойчи-
вости линейных систем с сосредоточенными и распределенными па-
раметрами, дискретных и нелинейных систем. Большинство резуль-
татов формулируется в виде частотных критериев, и в этом смысле
представляет собой обобщение метода В. М. Попова.
Следует отметить, что способ изложения материала, принятый
авторами, весьма своеобразен и потребует у читателя некоторой
адаптации. Однако затраченные усилия с избытком компенси-
руются той информацией, которая может быть извлечена из этой
книги.
Ю. Попков
ПРЕДИСЛОВИЕ
За последние 15 лет теория нелинейных систем с обратной
связью совершила большой скачок в своем развитии. С одной
стороны, этот успех обусловлен новыми достижениями в теории
функций Ляпунова, основными среди которых являются фунда-
ментальные работы Зубова, Иошидзавы и Хана. Поэтому в нашей
книге мы отказались от изложения теории функций Ляпунова.
С другой стороны, методы функционального анализа, впервые при-
внесенные в теорию нелинейных систем с обратной связью Санд-
бергом и Цеймсом, развивались не менее быстро, что привело
к получению многочисленных результатов, связанных с опреде-
лением вход-выходных свойств нелинейных систем с обратной
связью. Главное достоинство этих методов состоит в том, что с их
помощью можно исследовать системы с распределенными парамет-
рами почти с той же легкостью, как и системы с сосредоточен-
ными параметрами, причем изучение систем с одним входом и
с многими входами и выходами ведется по одной и той же схеме.
Все это в равной мере относится как к непрерывным, так и
к дискретным системам.
По этим причинам в нашей книге основное внимание уделяется
исследованию свойств систем с обратной связью с многими вхо-
дами и выходами, содержащими подсистемы с распределенными
параметрами, и особенно подробно изучаются непрерывные си-
стемы. Наша цель состоит в развитии важнейших методов, при-
водящих к выявлению основных вход-выходны.х свойств систем
с обратной связью. Однако мы не пытались дать энциклопеди-
чески исчерпывающее решение задач, решаемых этими методами.
При изложении материала мы скорее считали необходимым найти
золотую середину между иллюстрацией различных методов на
простых примерах и дальнейшим развитием наиболее сильных и
менее известных результатов.
Читателями нашей книги могут быть инженеры-разработчики
с хорошей математической подготовкой, интересующиеся пробле-
мами теории нелинейных систем с обратной связью. Основная
часть материала составила курс лекций, прочитанных в Беркли
для студентов инженерного факультета в период их подготовки
к экзаменам на звание магистра. Опыт показал, что те студенты, *
которым на младших курсах читался серьезный курс математичес-
8
ПРЕДИСЛОВИЕ
кого анализа, а на старших —курс теории управления, усваивали
материал без особых затруднений. Рассчитывая на такого рода
читательскую аудиторию, мы все же сочли необходимым изло-
жить в первых двух главах математический аппарат, постоянно
используемый в следующих главах. Полезные математические
факты, доказательство которых могло бы слишком сильно увести
нас в сторону от основного пути, собраны в 5 приложениях.
Кроме того, предполагаемый уровень знаний нашей аудитории по-
зволяет нам при обосновании различных подходов обращаться
к аналогиям из законов сохранения энергии и рассуждениям, при-
нятым в теории управления и в теории цепей. Мы также пола-
гаем, что читатели легко поймут такие термины, как «положитель-
ная обратная связь», «прямая ветвь замкнутой системы», «пере-
даточная функция» и «импульсная характеристика».
В главе 1 приводится несколько простых свойств систем с об-
ратной связью, приведенные здесь же примеры простейших не-
линейных систем призваны проиллюстрировать связь и независи-
мость задач существования, единственности, непрерывной зависи-
мости и ограниченности решений уравнений этих систем.
В главе 2 рассматриваются многочисленные свойства норм,
норм операторов и нормированных пространств, необходимые
для понимания последующего материала.
Теоремы, представленные в главе 3, носят очень общий и
абстрактный характер; помочь читателю разобраться в них должны
разнообразные практические примеры, приведенные здесь же.
Глава 4 посвящена исследованию линейных систем.
В главе 5 показано, каким образом можно использовать тео-
рему о малом коэффициенте роста *): в каждом из девяти разделов
указанная теорема привлекается для изучения свойств отдель-
ного класса систем с обратной связью.
Наконец, в главе 6 намечен общий структурный подход
к понятию «пассивности» и обсуждаются вопросы применения
теоремы о пассивности.
Короче говоря, мы сочли необходимым изложить здесь основ-
ные результаты и важнейшие методы таким образом, чтобы
читателю в дальнейшем было нетрудно разобраться в современ-
ных работах по тематике книги.
Несколько слов о нашей совместной работе. Дезоер разрабо-
тал план книги и к зиме 1973 года почти полностью написал
первые три главы и приложения. В то же время новейшие
исследования оттеснили черновые наброски остальных трех глав
в разряд устаревших. Видьясагар, который и ранее интересовался
возможностью написания такого рода книги, совместно с Дезое-
г) В переводе говорится о «коэффициенте усиления» везде, где речь идет
•о технических реализациях. По отношению же к операторам представляется
более удобным говорить о «коэффициенте роста». Автор в обоих случаях упо-
требляет термин «gain», (Прим, перев.)
ОБОЗНАЧЕНИЯ
9
ром пересмотрел материал первых трех глав; последние главы
были написаны заново. Эта работа была проделана в Беркли
летом 1973 года. Ответственность за все ошибки несут оба автора.
При работе над книгой, в которой с единой точки зрения
рассмотрены многочисленные результаты, полученные различ-
ными исследованиями более чем за десятилетний период, авторы
столкнулись с трудной задачей: как отметить научный вклад
отдельных исследователей? Одно время Дезоер пытался собрать
достаточно полную библиографию, однако очень скоро был вынуж-
ден оставить свои попытки из-за чрезмерно большого ее объема.
Поэтому было решено ссылаться на те работы, в которых мы
почерпнули либо новые для нас оригинальные методы, либо
решение отдельных проблем. Таким образом, ссылаясь на работы
отдельных авторов, мы вовсе не утверждаем этим их приоритета.
Решение всех вопросов, касающихся приоритетов и различий
работ разных авторов, мы предоставляем историкам науки. Тем не
менее мы приносим извинения всем тем, в отношении которых
в этом вопросе могли быть допущены ошибки-, и заверяем этих
авторов в непреднамеренности наших ошибок.
Подготовка книги включала в себя большую долю предвари-
тельных исследований, которые были бы невозможны без под-
держки и поощрения со стороны ряда организаций и учрежде-
ний. Дезоер считает себя обязанным Национальному научному
фонду, Национальному бюро по аэронавтике и космическим
исследованиям (НАСА), Программе объединенных служб по элек-
тронике и Калифорнийскому университету. Нам также приятно
поблагодарить тех, кто внес свой вклад в многочисленные дис-
куссии и уточнения, а также коллег и бывших студентов, при-
нимавших активное участие в напряженной работе семинара по
нелинейным системам с обратной связью. Как говорил Э. А. Гил-
лемин, «мы не можем назвать кого-либо без упоминания всех
остальных, а назвать имена всех нельзя из-за опасений забыть
того или другого». Видьясагар признателен руководству универ-
ситета сэра Джорджа Вильямса (университет Конкордия), кото-
рое сделало возможным его пребывание в Беркли, а также
Национальному научно-исследовательскому центру Канады за
научную поддержку.
ОБОЗНАЧЕНИЯ
алгебра со сверткой в качестве операции умножения элементов
<2^2 алгебра с двусторонней сверткой в качестве операции умножения
элементов
[а, &] замкнутый интервал: {xe|R|a^x^d}
(а, /?] интервал: {х е R | а < х 6}
В (х; г) открытый шар радиуса г с центром в точке х
Б (х, г) замкнутый шар радиуса г с центром в точке х
10
ОБОЗНАЧЕНИЯ
С поле комплексных чисел
С+ замкнутая правая комплексная полуплоскость: {zeC’Rez^O}
Сл линейное пространство упорядоченных л-ок из С
Qmxn кольцо матриц, содержащих т строк и п столбцов, элементы кото-
рых принадлежат С
пространство функций со скалярным произведением {f: #->
е расширенное пространство функций со скалярным произведением
X нормированное пространство функций {f: ST ->27 11/1| <оо}
Хе расширенное нормированное пространство функций
LP (R) [LP (R+)] пространство функций {/: R->R} таких, что функция
11—► | f (t) интегрируема над полем R [или R*, соответственно]; обычно р =
= 1, 2, со
IP пространство последовательностей г=(г0, zlt z2, •••) таких, что ряд
оо
У] I Zk 1Р СХОДИТСЯ
0
R поле действительных чисел
R+ множество неотрицательных действительных чисел {х е R | х >= 0}
Rn линейное пространство упорядоченных n-ок из R
Rnxm кольцо матриц, содержащих п строк и т столбцов, элементы кото-
рых принадлежат R
R [s] коммутативное кольцо многочленов от s
R (s) коммутативное поле рациональных функций от s
sgnx функция, равная 1, 0 и —1, при х<0, х = 0 их>0 соответ-
ственно
Z кольцо целых чисел: {..., —1, 0, 1, ...}
Z+ множество неотрицательных целых чисел: {0, 1, 2, ...}
| • | обозначает модуль действительного или комплексного числа, норму
вектора из Rn или Сл
|| • У обозначает норму (в общем случае), норму функции, например |f |,
или норму линейного оператора | А |
Шл е^-норма функции g
|/|р норма функции f, как элемента пространства LP
=> знак импликации («следует», «влечет»)
€=> знак эквивалентности.
Жирным шрифтом выделены операторы, обычно отображения Хе в Хе.
Определения, уравнения, утверждения, теоремы, замечания и т. д. про-
нумерованы по разделам. Хотя в нумерации могут быть пропуски, недоразу-
мений возникнуть не должно.
При ссылках на пункты внутри одного раздела используются только но-
мера пунктов, например: «определение (3)», «следствие (11)». При упоминании
пунктов из других разделов той же главы указывается номер раздела и номер
пункта: «определение (2.3)», «теорема (7.1)». Ссылки из других глав допол-
няются номером главы: «уравнение (2.3.2)», «теорема (3.2.1)».
Рисунки пронумерованы по главам.
Каждый термин выделен курсивом в его определении.
Глава 1
СТАТИЧЕСКИЕ НЕЛИНЕЙНОСТИ
В этой главе мы хотим привлечь внимание читателя к некото-
рым важным особенностям теории нелинейных систем. Большин-
ство линейных задач, встречающихся в технических приложениях,
имеет ту особенность, что для любого разумного входного воз-
действия решение существует, причем является единственным и
непрерывно зависит от входного воздействия. В некоторых слу-
чаях (особенно важных на практике) ограниченное входное воз-
действие вызывает появление на выходе системы ограниченного
сигнала. Ниже мы покажем, что в нелинейных системах перечис-
ленные четыре свойства: существование, единственность, непре-
рывная зависимость решения и конечность коэффициента усиле-
ния — вовсе не всегда сохраняются даже в очень простых примерах,
а именно, в статических нелинейных системах с линейной обрат-
ной связью.
Кроме того, в этой главе мы определим некоторые наиболее
полезные классы нелинейностей. Здесь рассматриваются только
статические системы. В разделе 1 определяются нелинейности,
удовлетворяющие секторным условиям, и приводятся отдельные
их математические модели. В разделе 2 вводится понятие линей-
ной обратной связи и устанавливаются соотношения между харак-
теристиками разомкнутой и замкнутой систем. В последнем раз-
деле рассматриваются нелинейности с несколькими входами и
выходами.
1. СЕКТОРНЫЕ УСЛОВИЯ
1.1. Нелинейность с одним входом
Простейший статический нелинейный элемент имеет один вход
и один выход, связь между которыми описывается характери-
стикой <р. Выходной сигнал у (/) в момент t определяется соотноше-
нием у (/) = <р[и (/)] для всех t. В общем случае <р является отно-
шением между действительными числами и вовсе не обязательно
функцией. Если бы мы в наших дальнейших рассуждениях до-
пустили, что характеристика <р зависит от времени, т. е. y(t) =
= <p[u(Z), f], то потребовалось бы внести единственное изменение:
все неравенства должны выполняться для любых t.
1. Определение. Пусть <p: R->₽, причем <р(0) — 0. Будем гово-
рить, что <р принадлежит сектору (ki, тогда и только тогда,
когда kie2<еф(е)<ktf? для любых eeR таких, что е =/*(). Ана-
логичным образом, будем говорить, что ф принадлежит сектору
IS
ГЛ. 1. СТАТИЧЕСКИЕ НЕЛИНЕЙНОСТИ
[Ль Л2) тогда и только тогда, когда Лхе2 е<р (е) < Л2ег для любых
е е R таких, что е=#0,
Секторные условия можно задать несколькими способами. Мы
перечислим их в теореме эквивалентности.
2. Теорема эквивалентности. Пусть Л1( = причем kr^k2.
Пусть, кроме того, <p: R->R, причем <р(0) = 0. Тогда следующие
четыре условия эквивалентны:
(D Лх^ф(е)/е ==£Л2, Ve¥=0,
(ii) Лхе* < еф (е) sg Л2е2, Ve s R,
(iii) [ф (е) - Лхе] [ф (е) - Л2е]<0, Ve e R,
(iv) | ф (е) — се21 «С г21 е |2, Ve e R,
где с = |(Лх + Л2), г = |(Лх-Л2), kik2 = c2 — r2.
3. Следствие. Если в дополнение к условиям теоремы (2) ki > О,
то из условия (i) следует, что
(V)
i Ф2 (е) < еср (е) < ф2 (е) Ve е R.
Доказательство.
(!)<=> (ii). Поскольку (ii) выполняется при е = 0, необходимо
рассмотреть только те случаи, когда е=/=0. Умножая (i) на е2, полу-
чим (ii). Умножая (ii) на е~2, приходим к (i).
(iii ) <=> (iv). Учитывая, что Л1Л2 = с2 —г2, выполним ряд преоб-
разований:
(ф — Лхе) (ф — Л2е) = ф2 — 2 <ре k^e2 = (ф — се)2 — г2е2,
откуда следует, что (iii) <=> (iv).
(ii)=>(iii).
О 2s (еф — Лхе2) (еф — Л2е2) = е2 (ф — k±e) (ф — Л2е),
следовательно, (iii) справедливо, так как e22s0.
(iii)=>(ii). Заметим, что (прие=#0) й2е22= Лхе2. Тогда из нера-
венства, полученного умножением (iii) на е2, следует, что еф(е)
заключено между Ке2 и Л2е2.
(i)=i>(v). При Лх>0 из (i) вытекает, что ф (е)/е> 0 для любых
е Ф 0. Обращая (i) и умножая результат на ф2 (е), приходим к (v).
(v)^>(i). Возможен случай, когда ф(е) = 0 для любых е.
1.2. Нелинейность с многими входами
В этом случае качественно ничего не изменится, если предпо-
ложить, что число входов конечно. Поскольку ниже во все нера-
венства входят только скалярные произведения, мы будем рас-
1. СЕКТОРНЫЕ УСЛОВИЯ
сматривать гильбертово пространство Ж. В большинстве прило-
жений 0%" = ₽"•
4. Эквивалентные условия. Обозначим через гильбертово
пространство с действительным скалярным произведением <-|-> и
нормой || -|. Пусть <р: и ф (9) = 9, где 9 —нулевой вектор
пространства Ж. Пусть kx и ^ — действительные числа, причем
Тогда условия (iii') и (iv') эквивалентны:
(iii') (<р (ё) — kxe | <р (е) — k^e) < 0
(iv') |ф(е) — се |2 sg г21 е |2 Veee%^,
где
fei + ^а ^г — ^1
С~ 2 ’ 2
ИЛИ
ki + kt — 2с, kiki = c2 — г2.
Доказательство. Эквивалентность становится очевидной
после раскрытия скалярного произведения из левой части (НИ)
и выделения полных квадратов:
О 2s <Ф (с) — kxe | ф (е) — А2е) =
= <Ф (е) |ф (е)> - 2 <ф (е) | е> + (с2 - г2) (е | е) =
= |ф(е) — сер — г2|е|2.
Упражнение 1. Привести геометрическую интерпретацию определения (1)
с помощью графика (р.
Упражнение 2. Привести геометрическую интерпретацию условий (iii') и
(iv') в пространстве R* для 6=1, 2 и и. (Для случая 6 = 2 график ф (е) дод-
жей лежать в диске радиуса г || е || с центром в точке се.)
Упражнение 3. Предполагая, что 0 < 62, привести интерпретацию
следующих неравенств в пространстве IR2:
hi Х<2 <ф (*) *> 62е р Уе a R1,
£ 'Iф («) № «S <<Р (е) I «> " <₽(e)ll* VeaR».
Упражнение 4. Пусть ф: еЗ? ф(0)=‘0 и 0<<ki<,k2. Показать,
что (все неравенства выполняются для любых е е ):
(а) <е|ф(е)>Э»*15е||*=>:,еПф(в)|^^-:,<р(е)|»)
(Ъ) <е|Ф(е)>^ !ф(е)?=>kJ!ФЮЗ«*»! еР.
14
ГЛ. 1. СТАТИЧЕСКИЕ НЕЛИНЕЙНОСТИ
2. СТАТИЧЕСКАЯ НЕЛИНЕЙНОСТЬ
С ЛИНЕЙНОЙ ОБРАТНОЙ СВЯЗЬЮ
Простейшим примером нелинейной системы с обратной связью
является статическая нелинейность, охваченная линейной обрат-
ной связью. Сначала мы рассмотрим систему с одним входом и
одним выходом.
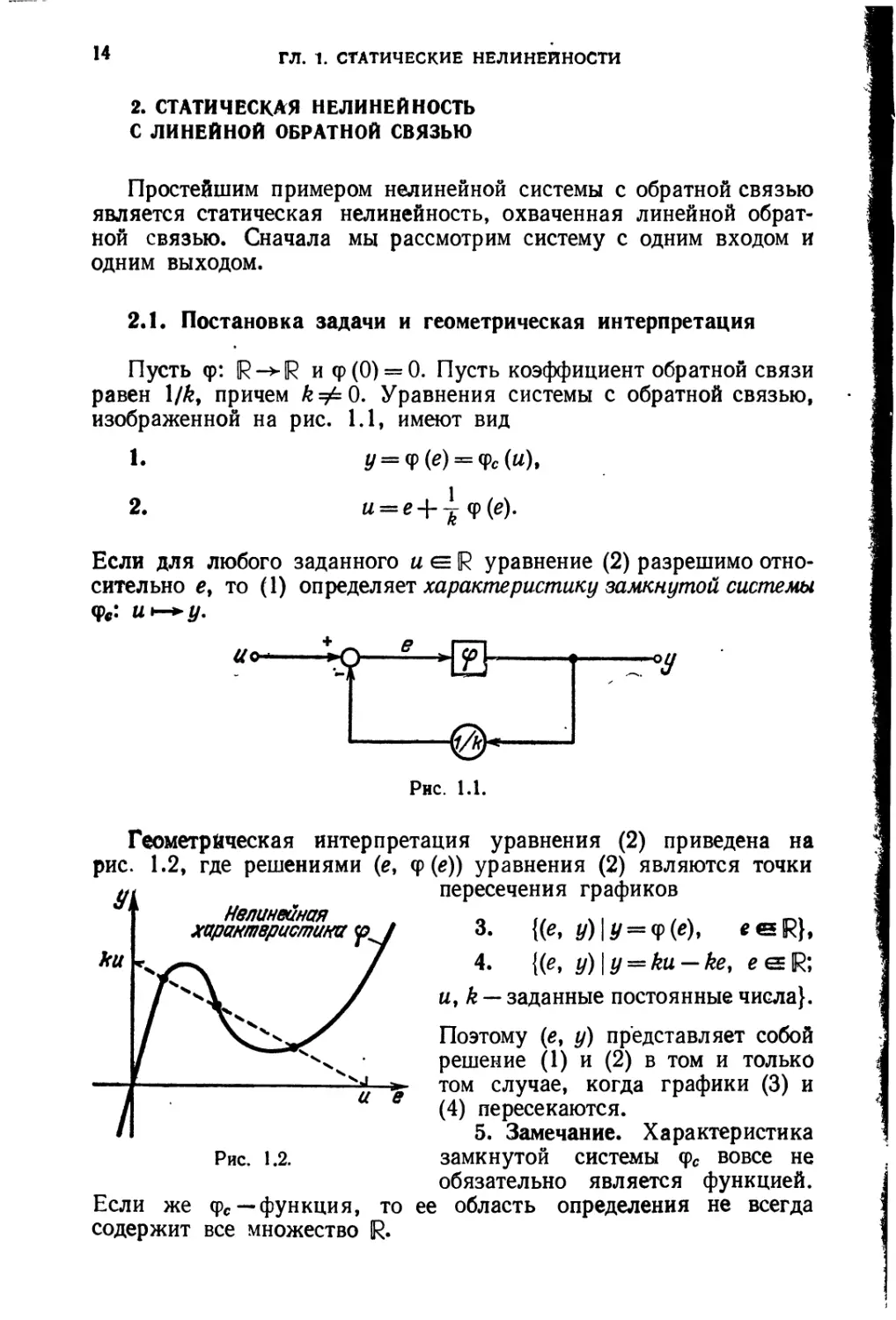
2.1. Постановка задачи и геометрическая интерпретация
Пусть (р: и ср (0) = 0. Пусть коэффициент обратной связи
равен 1/&, причем ^=/=0. Уравнения системы с обратной связью,
изображенной на рис. 1.1, имеют вид
1. */ = ф(е) = фс(н),
2. u = e + |<p(e).
Если для любого заданного и <= R уравнение (2) разрешимо отно-
сительно е, то (1) определяет характеристику замкнутой системы
ф«: и.*-*-у.
ио-
Рис. 1.1.
Геометрическая интерпретация уравнения (2) приведена на
рис. 1.2, где решениями (е, <р (е)) уравнения (2) являются точки
пересечения графиков
3. {(е, 0)|У = ф(е), «®R}.
4- {(е, у) | у — ku — ke, es R;
и, k — заданные постоянные числа}.
Поэтому (е, у) представляет собой
решение (1) и (2) в том и только
том случае, когда графики (3) и
(4) пересекаются.
5. Замечание. Характеристика
замкнутой системы фс вовсе не
обязательно является функцией.
Если же фе —функция, то ее область определения не всегда
содержит все множество R.
2. НЕЛИНЕЙНОСТЬ С ЛИНЕЙНОЙ ОБРАТНОЙ СВЯЗЬЮ
15
б. Замечание. На этом простом примере видно, что при изу-
чении нелинейных систем следует различать вопросы существова-
ния, единственности, непрерывной зависимости (от входного воз-
действия) решений, конечности коэффициента усиления системы.
Упражнение 1. В каждом случае (а)-—(е) выбрать <р( •) и k так, чтобы
(а) для некоторого и уравнение (2) не имело бы решений;
(Ь) для некоторого и уравнение (2) имело бы несколько решений;
(с) для некоторого и уравнение (2) имело бы бесконечно много решений;
(d) для некоторого и решение е не являлось бы непрерывно зависящим от и\
(е) при и —и0, где г/0 —конечное число, е->оо.
Упражнение 2. Привести пример характеристики ср: такой, что
(а) для любого и е R уравнение (2) имело бы единственное решение е,
и
(Ь) не существовало бы конечного числа b такого, что если —1, 1],
то е е [— Ь, 5], т. е привести пример системы, в которой «ограниченному
входному воздействию» не всегда соо!ветствует «ограниченный выходной сигнал».
2. 2. Секторные условия
В дальнейшем мы будем считать, что характеристика фс может
представлять собой либо функцию, отображающую подмножество
множества R в R, либо отношение на множестве R2, т. е. мно-
жество упорядоченных пар (и, фс(и)) из RxR. В обоих случаях
выражение «характеристика фс принадлежит сектору [а, &]» озна-
чает, что график фс принадлежит сектору [а, 6], т. е. множеству
{(а, у)\аи^у^Ьи}%
7. Теорема. Для системы, заданной уравнениями (1) и (2):
8. ф принадлежит сектору [0, оо) тогда и только тогда, когда фс
принадлежит сектору [0, k)\
9. ф принадлежит сектору (—k, оо) тогда и только тогда,
когда фс принадлежит сектору (—оо, k).
Доказательство. Заметим, что при е=/=0
Ф(е)
фс (ц) = Ф(е) = g
“ <+Ьи ч-тт2’
/V «V О
9(g)
<Рс(“) _ g
“ 1 1 9<g)‘
к е
Зависимость <pc(u)/u от <р(е)/е изображена на рис. 1.3. Эквива-
лентность утверждений (8) и (9) вытекает непосредственно из
этого графика.
11. Замечание. В теореме (7) не утверждается ни то, что для
каждого и ер решение <ре(и) существует, ни то, что оно един-
или
10.
16
ГЛ. 1. СТАТИЧЕСКИЕ НЕЛИНЕЙНОСТИ
ственно, ни то, что оно непрерывно зависит от и. Этой теоремой
устанавливается лишь связь графиков функции ф и отношения
Фс(и). Например, согласно теореме (7), если а#=0 и определено
одно или несколько отношений фДи), то из того, что характе-
ристика ф принадлежит сектору
[О, оо), вытекает, что 0^фс(и)/и<
<^k. Иначе говоря, если ф принадле-
жит сектору [0, оо), то «коэффициент
усиления прямой ветви» нелинейной
системы с обратной связью принад-
лежит сектору [0, k). Таким образом,
ограниченное входное воздействие и
вызывает появление ограниченного
выходного сигнала фс(и) независимо
от того, единственно ли решение
Фе (и). Это первый из многочислен-
ных примеров, с которыми мы стол-
кнемся позднее, где вопрос конечности коэффициента усиления
может быть разрешен без решения проблем существования, един-
ственности и непрерывной зависимости решения.
. 2.3. Соотношения между производными
Как и раньше, ф: R-причем ф(0) = 0. Предположим, что
функция ф дифференцируема на R и — 6<^ф'(г) <°о для всех
eeR. Тогда отображение е»—►«, определенное соотношением (2),
а именно
12. «=е + |ф(е).
является дифференцируемым и имеет положительную производ-
ную на R. Следовательно, соответствующее обратное отображение
ц>—дифференцируемо и имеет положительную производную.
Композиция и н-* фс (и) дифференцируемых отображений и е и
е I—► Ф (е) = фс (ы) также дифференцируема. Согласно (1)
d(pc (и)_dtp (е) _ dtp (е) de
du du de du
и в соответствии с (2)
d<p (е)
d(pc (и)_ de
du ~ , 1 dq>(e) ’
k de
ИЛИ
13. Vc = —и—.
1+|ф'
3. НЕЛИНЕЙНОСТЬ СО МНОГИМИ ВХОДАМИ
17
где подразумевается, что ф' вычисляется в точке е, а — в соот-
ветствующей точке и, т. е. при и = е + (1/^)(р(е).
Учитывая сказанное, мы можем сформулировать следующую
теорему.
14. Теорема. Пусть функция <р: дифференцируема на IR,
причем ф(0) = 0. Пусть, кроме того, k>0 и фс, как функция
от ф, определяется соотношениями (1) и (2). Тогда
(а) если ф': R->(—k. оо), то
(i) отображение фс: ш—+ у дифференцируемо и — оо<
<фс(н)<&;
(ii) отображение и е дифференцируемо, взаимно однозначно
и является строго возрастающим;
(iii) из u = 0 следует, что фс(и) = 0;
(Ь) ф': IR->[0, оо) тогда и только тогда, когда ф£: IR->[0, k)
Доказательство.
(ai) следует из приведенных выше рассуждений и равенства (10);
(aii) становится очевидно после рассмотрения производной
соотношения (2) по е;
(aiii) выполняется, поскольку, согласно (1) и (2), фс(0) = 0;
(Ь) следует непосредственно из (13).
Упражнение 3. Что можно сказать об области определения отображения
и\—если выполняется условие (а) теоремы (14)? Показать, что с увеличе-
нием и возрастает и е, однако у = фс(и) может уменьшаться на некоторых
интервалах.
Упражнение 4. На примере уравнения г/ = ф(х), где ф: R->R и ф' (х) > 0
при любых х е R, показать, что вопросы существования и единственности
могут решаться независимо друг от друга, (а) Показать, что в случае, когда
для некоторого заданного у существует решение х0, это решение является
единственным. (Ь) Привести пример, когда при некоторых ф и у уравнение
(/=ф(%) не имеет решения.
3. НЕЛИНЕЙНОСТЬ СО МНОГИМИ ВХОДАМИ И ВЫХОДАМИ
Здесь мы только перечислим результаты для случая, когда и, е
и у являются элементами пространства 1РЛ. Сначала вниманию
читателя предлагается подготовительное упражнение.
Упражнение 1. Обозначим через (• | • ) действительное скалярное произве-
дение в линейном пространстве 35. Пусть х, у s X и
Тогда 1
2. <х|$/>=Ш2ЧШ2.
Следующее утверждение обобщает теорему (2.7).
3. Утверждение. Пусть ф: (Rn-причем ф(6) = 9. Пусть
(п X л)-матрица К является матричным коэффициентом усиления
ветви обратной связи (см. рис. 1.4) системы с обратной связью,
18
ГЛ. 1. СТАТИЧЕСКИЕ НЕЛИНЕЙНОСТИ
заданной уравнениями
4. u = e4-Kq>(e),
5. У = ф(е) = фс(«).
Пусть А1г А2 е Рпхя и
Тогда
(а) <ф (е) — Л1в | ф (е) - Л2е> =| ф (е) - Ле|» — | Лер;
(Ь) следующие неравенства эквивалентны:
(i) (ф (е) — Лхе | ф (е) — Л2е> ==s 0 Ve <=
(ii) |ф(е) —ЛеР^| Лер VeeR";
(iii) ((ЛхК + /) фс (u) — AiU | (АгК +1) фс (и) — Л2и) О
Vu е ₽я;
(iv) | (/ + ЛК) фс (и) - Au Р < | ЛКфс (и) - Au Р
Vu sp".
Доказательство. Утверждение (а), эквивалентность не-
равенств (i) и (ii), (iii) и (iv) следуют непосредственно из упраж
нения 1. Эквивалентность (i) и (iii) следует из (4) и (5), если
подставить и —Кфс(и) вместо е и фс(ы) вместо ф(е).
Рис. 1.4.
Совершенно очевидно, что прежде чем изучать динамику си-
стем, необходимо развить методы описания входных воздействий.
Для этого в следующей главе мы рассмотрим понятие нормы.
БИБЛИОГРАФИЧЕСКИЙ КОММЕНТАРИЙ
Материал этой главы хорошо известен специалистам. Анало-
гичные результаты можно найти, например, у Джонсона [57],
Тетачара и др. [91].
Глава 2
НОРМЫ
В этой главе мы введем ряд понятий и фактов, которые не-
однократно понадобятся нам впоследствии. Необходимо все время
помнить, что норма является своего рода мерной линейкой для
измерения векторов пространства а также действительных и
векторных функций, как элементов соответствующих пространств.
Кроме того, мы будем применять норму для измерения «коэффи-
циента роста» линейных операторов.
В разделе 1 приводятся определение нормы и многочисленные
примеры, часто используемые в следующих главах. В разделе 2
определяется понятие эквивалентности норм и доказывается, что
все нормы в конечномерных пространствах эквивалентны. В раз-
деле 3 устанавливаются отношения включения между некоторыми
нормированными пространствами, необходимые для дальнейших
исследований. Геометрическая интерпретация нормы приводится
в разделе 4; эта интерпретация дает наглядное представление
о понятии нормы и способе определения различия между нор-
мами. В разделе 5 вводится понятие нормы линейного отображе-
ния. Два примера отображений типа свертки приводятся в раз-
деле 6. В разделе 7 подробно рассматривается связь между нор-
мой и спектральным радиусом. И, наконец, в разделе 8 вводится
и обсуждается понятие меры матрицы, тесно связанное с поня-
тием нормы. Мера матрицы используется для нахождения верх-
них и нижних оценок решений дифференциальных уравнений и
разрешения вопросов существования и единственности этих реше-
ний в точках равновесия.
1. НОРМА: ОПРЕДЕЛЕНИЕ И ПРИМЕРЫ
1. Определение. Пусть Е — линейное пространство над полем К.
(Обычно в качестве К рассматриваются R или ©.) Нулевой вектор
пространства Е обозначается через 6. Будем говорить, что функ-
ция р: £-»-|R+ является нормой в пространстве Е тогда и только
тогда, когда
(i) х е Е и х 6 => р (х) > 0;
(И) р(ах) = |а|р(х) VaeK, VxeE;
(iii) p(x + «/)=cp(x)4-p(i/) Vx, ijeE (неравенство тре-
угольника).
Замечание. В заданном линейном пространстве Е норму можно
определить различными способами. Однако, задавая некоторую
20
гл. i. нормы
норму р в линейном пространстве Е, мы определяем нормиро-
ванное пространство (Е, р).
Пример 1. Рассмотрим в качестве линейного пространства Е
пространство С". Условие xsQ’ означает, что x — (xlt х2,..., хп),
где Xi е (D для любых i. Мы часто будем пользоваться следую-
щими нормами в С":
п
2. |x|i=2k/l;
£ = 1
/ « \ 1/Р
з. |х|р = (S . где l=ssp<co;
ч = 1 !
4. Jx||oo = max | х,-1.
i
Норма I х ]2 называется евклидовой нормой элемента х.
Упражнение 1. В пространстве R" определить нормы, аналогичные приве-
денным выше. Изобразить множество {х 11| х!!р = 1} при р = 1, 2, 4, со в про-
странстве R*.
Пример 2. Пусть Е — пространство бесконечных последователь-
ностей комплексных чисел: x = (|i, |2, ...), где 5,-eiC при i =
= 1, 2, ... На подходящих собственных подмножествах простран-
ства Е часто используются следующие нормы:
5. |х|1= I&I;
£ = 1
/ оо \1/Р
в. И₽= S 1Р)
4 = 1 /
7. ||x||oo = sup |&|.
/>1
Соответствующие нормированные пространства обозначаются
через Z1, 1р, Iе0.
Мы употребили выше выражение «на подходящих собственных
подмножествах пространства £», поскольку нормы, определенные
соотношениями (5) —(7), обладают тем свойством, что множество
М = {х е Е | р (х) < оо} является линейным подпространством про-
странства Е (через р (х) обозначена любая из норм (5) — (7)). Этот
факт вытекает непосредственно из неравенства Минковского: дей-
ствительно, если Xi, х2 е М, то Xi + x2e М, так как р(хх) +
+ р(х2)^р(Х1 + х2).
Пример 3. Пусть E = {f: R -> R | f — локально интегрируемая
(по Лебегу) функция}. На подходящих собственных подмноже-
ствах пространства Е часто используются следующие нормы:
8. |хЬ = $|х(0|Л;
9. ИР = ($|х(01рЛ)1/₽. 1^Р<оо;
10. | х I» = ess sup | х (01 = inf {а е R | р, Ш11 х (01 > а}] = 0},
1. НОРМА. ОПРЕДЕЛЕНИЕ И ПРИМЕРЫ
21
где через р [Л] обозначена лебегова мера множества е^1). Соот-
ветствующие нормированные пространства обозначаются через
В более общем случае, задав положительную, непрерывную и
ограниченную на R функцию w. R->R, норму |х|р можно опре-
делить выражением
И- Кр<оо.
Норма |х|оо определяется соответствующим образом.
Пример 4. Пусть Е = {/: R-*R", f = fz, .... f„| все функ-
ции ft локально интегрируемы (по Лебегу)}. Обозначая символом
| • | произвольную норму в R", определим
12. mp==6lf(0M)I/₽, 1<Р<оо;
13. 1/1100 = ess sup \f (0|.
/sR
Упражнение 2. В линейном пространстве Е, определенном в примере 2,
найти элемент для которого ||xji=oo, но Привести пример
элемента для которого ||х 11^ = 00. (Эти примеры подтверждают необхо-
димость оговорки о «подходящих собственных подмножествах пространства £».)
Замечание. Обычным, хотя и не слишком глубокомысленным
упражнением в функциональном анализе, является проверка того
факта, что выражения (2)—(13) удовлетворяют аксиомам нормы.
Пример 5. Пусть Е = ©"Х" — множество всех (пхп)-матриц
с элементами из ©. Множество Е является линейным простран-
ством. В пространстве ©яХл можно определить следующие нормы:
14. || Л ||o = max | |; <. / n
15. 14- 2 IM lt /-1 / n X 1/2
16. Mlls= s Ы» 1 \и«1 / n
17. |Л li = max 2 i
18. i
где Xi(A4) —f-е собственное значение матрицы М.\
19.
п
| Л loo = max у, I av |.
1 /=1
г) В дальнейшем для упрощения записи мы будем писать sup | х (/) | вместо
ess sup | х (t) |,
22
ГЛ. 2. НОРМЫ
В этом примере мы рассматривали матрицы как элементы линей-
ного пространства. В следующих разделах мы будем считать,
что матрицы определяют линейные отображения, и норму матрицы
будем выбирать согласованно с нормами пространств образов и
прообразов соответствующего отображения.
Упражнение 3. Обозначим через | • | некоторую норму в пространстве Рл
Пусть функция Ф (•) непрерывна и отображает отрезок [О, Г] в Рл. Вычисляя
интегральные суммы, показать что
IIТ [| т
20. И Ф(О^| !Ф(ФоЛ.
В действительности, как мы увидим позднее, неравенство (20) выполняется
для любой нормы в пространстве Рл Более того, оно также справедливо для
любой интегрируемой по Лебегу функции ф, отображающей отрезок |0, Г] в Рл-
2. ЭКВИВАЛЕНТНЫЕ НОРМЫ
1. Определение. Пусть Е — линейное пространство. Обозначим
через | • |а и |-|& Две различные нормы в пространстве Е. Нормы
I • L и |'|* называются эквивалентными в том и только том случае,
когда существуют два положительных числа ггц и ти таких, что
2. mi || х ''а < |х Цд ^та | Vxe£.
Следует отметить, что для всех х е Е в неравенстве (2) должны
фигурировать одни и те же числа mt и ти. Отношение между
двумя нормами, выражаемое неравенством (2), является отноше-
нием эквивалентности. (Читателю предоставляется возможность
проверить, что это отношение обладает свойствами рефлексивности,
симметрии и транзитивности.)
Если две нормы эквивалентны, то последовательности, сходя-
щиеся по одной из норм, сходятся также и по другой. Аналогич-
ные утверждения справедливы и для свойств непрерывности и
ограниченности по норме. Короче говоря, эквивалентные нормы
определяют одинаковые топологии. В приложениях некоторые
нормы предпочтительнее, поскольку их исследование, как мы
увидим ниже, дает возможность получить более интересные
результаты.
Упражнение 1. Пусть
Г°,9 НЯ]
L0 0.9J-
Вычислить норму матрицы А, используя формулы (14)—(19) из примера 5
(раздел 1). Доказать, что при k-+co. Прокомментировать полученные
результаты.
3. Теорема. Все нормы в пространстве Сл эквивалентны.
2. ЭКВИВАЛЕНТНЫ^ НОРМЫ
23
Доказательство.
(а) Сначала покажем, что любая норма |>| в пространстве ©я
является непрерывной функцией в том смысле, что каким бы
способом хеС’ни стремился к действительное число |х|
стремится к || X |. Обозначим через Xi и Xi i-e компоненты векторов
х и X в некотором базисе {ех, е2, .... еп}. Известно, что из х->Х
следует, что Xi Xt для i — 1, 2, ..., п. Используя аксиомы
нормы для любых х, Хе 0я, получаем
II п || п
0<1И-1Л1<1*-*1= S (Xi-X^ei |Xi-*i|-H|.
h=i || ;=i
Следовательно, из х-*-Х вытекает, что |х|-*-|Х|.
(Ь) Пусть
Soo =={*<= С" ||х||оо=1}.
Очевидно, что множество S«> ограничено. Кроме того, оно зам-
кнуто, поскольку является прообразом множества {1} относительно
непрерывного отображения |• !«>. Пусть через |-| обозначена про-
извольная норма в пространстве 0я. Тогда непрерывная функция
z->-|z|, ограниченная на замкнутом и ограниченном множестве S«>,
достигает своих максимума и минимума в точках гт и гм соответ-
ственно. Таким образом,
О <|zm К 1И<112А11 VzeSoo.
Пусть х — произвольная точка из 0я, причем х#=6, тогда
X /1X loo е Soo. Поэтому
12т|<1йЬН8гл11 х^е.
Отсюда
1) | X |ео IX | I Zjj [ IX |оо VxffiC".
Таким образом, нормы |-| и Ц - Цоо эквивалентны. Эквивалент-
ность любой другой пары норм, например, |>| и |-|' устанавли-
вается в силу свойства транзитивности.
4. Обозначения. Начиная с этого момента, мы будем вычислять
нормы в пространствах R” и ©я, нормы в пространствах функций
и нормы линейных операторов. Некоторые авторы используют
символ |-| для обозначения первой из этих норм и ||-||| —для
двух последних. Мы же будем обозначать через | • | нормы в R" и
<D", а через |-| — нормы в пространствах функций и нормы линей-
ных операторов. Кроме того, через |«| мы будем обозначать
абсолютное значение чисел из R и С.
5. Замечание. В бесконечномерных пространствах свойство
эквивалентности всех норм выполняется вовсе не всегда. Например,
в пространстве бесконечных последовательностей (пример 2, раз-
24
ГЛ. 2. НОРМЫ
дел 1), если
Xi = (l, 0, 0, ...), х2 = (1, 2-1, О, ...), х3 = (1, 2-1, 3-\ О, ...), ...»
то
|x*|co=l VieZ+,
и последовательность {х*} сходится. Однако
I ** Hi 00 ПРИ k-^-ca.
6. Пример. Пусть Е — пространство последовательностей, члены
которых принадлежат Ся, т. е. х е Е в том и только том случае,
когда х = (|1, |2, ...) и при i=l, 2, ... Обозначим через
|-| произвольную норму в Тогда ||<| представляет собой
неотрицательное число, равное норме вектора & в пространстве С".
Теперь на некоторых подходящих подмножествах пространства Е
можно определить нормы
7. 1*111=5 I&I;
i=l
/ 00 11/р
8. |*1р = ( 5 I Si 1^1 >
v=i /
9. lx||oo=sup
Соответствующие нормированные пространства обозначаются сим-
волами In и Проверить, что при определении пространства 1„
с использованием различных норм в пространстве С” мы приходим
к одним и тем же собственным подмножествам пространства Е.
8. СООТНОШЕНИЯ МЕЖДУ НОРМИРОВАННЫМИ ПРОСТРАНСТВАМИ
В дискретных системах входное воздействие полностью задается
соответствующей последовательностью чисел. Поэтому мы будем
рассматривать пространство последовательностей, члены которых
принадлежат R (или ©). Определяя в этом пространстве нормы
соотношениями (1.5)—(1.7), мы получаем нормированные прост-
ранства I1, 1р и
1. Теорема. Для любого целого числа ре(1, оо) выполняется
цепочка строгих включений I1 az 1р с /°°.
Доказательство. Пусть x = (£i, |2, • ••), где ПРИ
любых i е Z+- Выберем произвольное целое число ps[l, оо).
00
Если хе/₽, то У, |р<°°. Тогда для любого целого k
i«=l
<•1
3. СООТНОШЕНИЯ МЕЖДУ ПРОСТРАНСТВАМИ
и, следовательно, х е /°°. Таким образом, 1р с /°° при р е
е [1, оо).
Кроме того, для любых целых N 0 и р^ 1
N i N \р
(=1 \<=1 /
Отсюда, переходя к пределу при Af->oo, получаем, что, как только
хе Z1, |х|р =С||х||1 <оо. Следовательно, I1 с 1р.
2. Упражнение 1. Используя пример 2.6, проверить что
3. /д сczдля целых чисел р <= (1, оо),
и показать, что (3) представляет собой цепочку строгих включений.
В непрерывных системах входные воздействия и выходные
сигналы являются функциями времени /, причем обычно /^0.
Для упрощения изложения мы будем использовать теорию инте-
грала Лебега1). Будем говорить, что функция f: (R+-локально
интегрируема в том и только том случае, когда f интегрируема
на любом ограниченном интервале, т. е. на любом интервале
[a, ft], где O^a^ft<оо.
Будем говорить, что функция f: R+->IR принадлежит прост-
ранству Lp для любого заданного ре[1, оо) в том и только том
случае, когда f локально интегрируема и
[|/(ПМ<оо.
о
Норму в Lp определим соотношением
1СО \1/р
4. И1Р= J 1/(0 м .
\о /
Назовем функцию f: R+-»-|R принадлежащей пространству L*
в том и только том случае, когда ess sup | f (t) | < оо. Будем
считать, что
5. |Л«>= esssup \f (01.
'>0
Говоря о ess sup |/(/) |, мы имеем в виду следующее определение:
ess sup | f (t) I = inf {a 11 f (t) | а почти везде},
т. e. неравенство | f (/) | sg а выполняется везде, за исключением
множества меры нуль, и esssup является наименьшим числом,
удовлетворяющим этому неравенству. В дальнейшем мы будем
писать sup вместо esssup.
1) Читатель, слабо знакомый с теорией интеграла Лебега, может считать,
что все функции являются кусочно-непрерывными (см. Приложение А).
26
ГЛ. 2. НОРМЫ
Необходимо раз и навсегда понять, что элементами простран-
ства Lp являются классы эквивалентности в том смысле, что
если f и g^Lp, но
lf-g|p=O,
то функции f и g (которые могут быть различными функциями)
рассматриваются, как один и тот же элемент пространства Lp.
Эти соображения позволяют нам употреблять sup|x(/)| вместо
ess sup | х (Z) |, поскольку всегда найдется функция y(t) из того же
класса эквивалентности, что и х(0, такая, что ess sup | х (/) | =
- sup | у (/)
6. Упражнение 2. Пусть /(/)== sin / при /^Ои g(/)=l при t >0, g(0)=2
Показать что
supi/(/)|=l, sup |g(/); = 2, U’00=UI'0o ‘
Пусть задано некоторое число р, причем р е [1, оо]. Хорошо
известно, что линейное пространство Lp с нормой | - |p полно,
т. е. каждая последовательность Коши сходится в Lp к некото-
рому элементу из Lp. Полные нормированные пространства назы-
ваются банаховыми пространствами.
1. Утверждение. Если функция f: принадлежит L1 f| L°°,
то f Lp при р е [1, оо).
Доказательство. Поскольку feL1, мера Лебега мно-
жества /, где / = 11 f(t) 1}, конечна. Поэтому, учитывая, что
feL00, получаем: $ | f (t) |₽di <оо. Обозначим через Iе дополнение
/
множества /, тогда
оо>$ \f для всех ре[1, оо).
Iе 1е
Из выведенных неравенств следует справедливость утверждения.
Связь пространств L1, L* и L00 легко показать на диаграмме
Венна (рис. 2.1). Диаграмма иллюстрирует тот факт, что из
f е L1 П L°° следует f е L?.
8. Упражнение 3. Рассмотрим функции, отображающие R+ в Р и заданные
следующими выражениями*
j_
. , 1. f., 1 t.f 1 >+<4
. . t , . i i+/4 . < 1 >+<2
ht it—z,_t-• —r-•
<4 /2'
Показать, что эти функции удовлетворяют отношениям включения, изобра-
женным на диаграмме Венна (рис. 2.1).
4. ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ НОРМЫ
27
9. Упражнение 4. Пусть [а, 6] —ограниченный интервал, т. е. а и b конечны.
Показать, что L1 [а, 6] о LP [а, Ь] о L°° [а, 6], где
U>[at b] = U: [a,b |R
ь
\Pdt<OD
a
10. Упражнение 5. Пусть l^p<oo и функция fp: R+->R имеет вид
1 12/P
/1/2[l+10g/]J
Показать, что при p' e [1, оо) и fp ф p', но fp s Lp-
11. Замечание. В дальнейшем мы будем рассматривать функ-
ции, отображающие R+ в R. При этом все введенные выше опре-
деления останутся применимыми, за одним исключением: |/(01
будет интерпретироваться, как выбран-
ная нами норма вектора f (/) е R", причем
для решения каждой конкретной задачи
мы будем выбирать норму, исходя из со-
ображений удобства вычислений и полу-
чения наилучших оценок. Такой подход
допустим, поскольку все нормы в R" эк-
вивалентны.
12. Обозначения. Иногда мы будем
рассматривать функции, отображающие R
или R+ в R или R". Для обозначения мно-
жеств таких функций мы введем символы L% (R+) и Ln (R), причем
LS(R+)= Л R+
множество Ln(R) определяется соответствующим образом. При
n= 1 индекс п будем опускать. Если из контекста понятно, какова
область определения рассматриваемой функции (R или R+), будет
применяться сокращение L%.
4. ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ НОРМЫ
Чтобы дать читателю более наглядное представление о норме,
мы покажем ниже, что с каждой нормой связано выпуклое мно-
жество определенного типа. И наоборот, любому такому выпук-
лому множеству можно сопоставить некоторую норму. Сначала
мы введем ряд определений.
1. Определения. Пусть Е — линейное пространство над полем R
или ©. Множество К из Е называется выпуклым в том и только
том случае, когда х, у <= К. => Ах + (1 — X) у е К при любых
Xs(0, 1]. Множество К из Е называется уравновешенным в том
fp- <»—►
28
ГЛ. S. НОРМЫ
и только том случае, когда х е К => ах е К при любых | а | 1.
Множество К из Е называется поглощающим в том и только том
случае, когда существует число Х(х)^0 такое, что
хеЦх)/(. Множество [у|у — Хх, >.еR+| называется лучом Ох
2. Теорема. Пусть Е —линейное пространство.
(А) Если N: E->R+ —норма в пространстве Е, то единичный
шар, связанный с W (•), а именно, множество
В = {хеЕ^(х)<1|,
является выпуклым, уравновешенным и поглощающим множеством,
причем В пересекается с каждым лучом Ох на конечном интер-
вале, т. е. для любого хеЕ существует kN<oo такое, что
Oxf|B = {y[«/ = Xx, O^XsgXyy}.
(В) Если множество К.С.Е является выпуклым, уравновешен-
ным и поглощающим и, кроме того, К. пересекается с каждым
лучом Ох на конечном интервале, то функция рк: E->R+, опре-
деленная и виде
3. pK(x) = inf {Х|Х>0 и х®ХЛ},
является нормой в пространстве Е.
4. Замечание. Необходимость условия пересечения множества К
с лучом очевидна. В самом деле, пусть ACcR2 и/С = {(х, i/)|xe
eR, Легко заметить, что К —выпуклое, уравновешен-
ное и поглощающее множество, однако р* не является нормой:
р»(хо) = О при х0 = (1, 0).
Доказательство. (А) По условию N — норма.
(i) Множество В выпукло, поскольку из условия х, у&В
вытекает, что W (х) «g 1, Af 1. Рассмотрим произвольное число
Хе[0, 1]. Тогда
N[Хх + (1 - X)у} N (Хх) + У [(1 -1) у} =
»ХЛЦх) + (1-Х) АГ («/)<!.
Следовательно, Хх + (1 — к) у принадлежит В для всех >.е[0, 1].
(В) Множество В уравновешено, так как, если хеВ, то
N (x)s^ 1. Поэтому при любых |а 1 Af (ах)==|а | N (х) |а 1,
т. е. ах е В для всех | а | 1.
(iii) Множество В является поглощающим, поскольку для
любого х ® Е N (х) < оо и x/Af (х) еВ, т. е. xe<V (х) В.
(iv) Oxf]B = {Xx|X^O и /V(Xx)s^l}. Тогда А'(Хх)^! в том
и только том случае, когда | X | «с 1/N (х), т. е. Хх е Ох П В тогда
и только тогда, когда 0^X«C l/Af (х).
(В) По условию множество К обладает четырьмя свойствами.
Нам нужно показать, что функция рк удовлетворяет аксиомам
нормы.
(i) Из (3) следует, чторх(в) = 0. Теперь покажем, что рК(х)>
> 0 при х 8. Доказательство проведем методом «от противного».
б. НОРМА линейного отображения
29
Допустим, х0=£9, но Рк (х0) = 0 = inf {Х| 1>0, хоеХК}. Тогда
при любых 1>0 xoslK, т. е. (1/1)х0 е К. Отсюда следует,
что весь луч Ох0 содержится в К, что противоречит условию.
(ii) Поскольку множество К поглощающее, Рк(х)<оо для
любых х s В.
(iii) рк (ах) = | а | рк (х), так как множество К уравновешено.
Действительно, если ах е КК для некоторого X, то | а | х е ХК,
или х е (1/1) К. Следовательно,
Рх(*) = -|^ТРх(ах).
(iv) Неравенство рк(х+у)^Рк(х) + рк(У) следует из свой-
ства выпуклости множества К и определения функции рк- Из
определения рк для любого в>0
х „ у , if
PkW+* И Рк(У)+е
Поскольку К выпукло (ниже для упрощения мы опустим индекс /С),
Р(х)+е______х Р(у) + е___У jz
Р(*)+Р(У)+2е р(х)+е ‘r p(x) + p(y)-f-e р(у) + е
Поэтому для любых е>0 х+у е [р (х) + р (у) + 2е] К., т. е.
Р(х + у)^р(х) + р(у).
5. НОРМА ЛИНЕЙНОГО ОТОБРАЖЕНИЯ
5.1. Пространство линейных отображений
Пусть Е — линейное пространство над полем К, где К есть R
или С. Обозначим через £ (Е, Е) класс всех линейных отобра-
жений Е в Е. £ (Е, Е) представляет собой линейное простран-
ство, если определить сложение отображений А и В как
1. (А + В)х = Ах+В(х) Va<=K, VA, B<=Z(E, Е)
и умножение отображения А на число а как
2. (аА)х = а(Ах) VaeK. Vxe=£, VA(=Z(E, Е).
Кроме того, можно определить операцию умножения отображе-
ний А и В как композицию отображений А и В;
3. (АВ)х=А(Вх) Vx(=E, VA, ВеХ(Е, Е).
Отметим, что операция умножения некоммутативна. Легко про-
верить, что
(i) операция умножения, определенная сооиюшешим ю,, м.со-
цнативна;
30
ГЛ. 2. НОРМЫ
(ii) операции сложения и умножения дистрибутивны;
(iii) операции умножения и умножения на число коммутативны;
(iv) I, тождественное отображение Е в Е, является единицей
относительно операции умножения.
Таким образом, множество X (Е, Е) с тремя операциями,
определенными соотношениями (1) —(3), представляет собой (не-
коммутативную) алгебру с единицей1).
4. Замечание. Приведенные в этой главе определения и резуль-
таты легко распространить на линейные отображения линейного
пространства Е в линейное пространство F. Однако в разделе 5.2,
где вводится понятие нормы отображения, необходимо строго
различать понятия нормы в области определения и нормы в обла-
сти значений. Для того чтобы избежать усложнения обозначений,
мы ограничимся лишь изучением пространства £ (Е, Е), т. е.
случаем, когда область определения и множество значений являются
одним и тем же пространством.
5.2. Норма отображения
Пусть | • | обозначает норму в пространстве Е и А е £ (Е, Е).
Определим функцию |-|, отображающую подмножество множества
X (Е, Е) в |R+, соотношением
5-
6. Утверждение. Определение (5) эквивалентно следующему
определению:
7. | А | = sup | Az |.
l»l-1
8. Определение. Функция | А | называется нормой линейного
отображения А, порожденной нормой | |.
Чтобы показать, что (5) и (7) эквивалентны, положим z =
= х/|х|. Тогда
1Л21=| л17т| = |т7ГЛх1 = Л^Г’
Соотношение (7) имеет геометрическую интерпретацию. Пусть
К —выпуклое, уравновешенное, поглощающее множество, соот-
ветствующее норме |.|, т. е. единичный шар /С«={х®£||х|< 1}..
Пусть через АК обозначен образ множества К при отображении А.
Тогда (7) эквивалентно соотношению
9. |A|-inf{X| АКаЛК}.
!) Общие определения и свойства алгебр кратко освещены в Приложе-
нии D.
б. НОРМА ЛИНЕЙНОГО ОТОБРАЖЕНИЯ
31
Короче говоря, | А || представляет собой наименьший коэффициент X,
при котором множество КК включает в себя множество АК.
10. Теорема. Пусть Л — невырожденное линейное отображе-
ние Сл в Сл, |• | — произвольная норма в пространстве ©Л, а —
порожденная ею норма на множестве (пхп)-матриц, элементы
которых принадлежат С- Тогда
(а) существует постоянное число 0, зависящее только от п
и | • |, такое, что
"• ' I < ₽ ТИТ:
(Ь) в евклидовом пространстве 0=^1.
Доказательство.
(а) Согласно определению эквивалентности норм и в силу
Теоремы (2.3), существуют постоянные числа а/ и ат такие, что
at max | aif |< | А | ^ат max | аи |.
<. I i,i
Тогда (11) следует из формулы Крамера.
(Ь) Матрица А допускает полярное разложение в виде A=^UH,
где U — унитарная матрица, т. е. U*U=I, а /7 —эрмитова мат-
рица. Заметим, что
| det А | = | det U11 det Н | = | det Н |.
Поскольку матрица А невырождена и Я2 = Л*Л, то Я —поло-
жительно определенная матрица. Обозначим через Л>, ftg, ..., Л„
характеристические числа матрицы Я, причем будем полагать для
определенности, что hL^h2^... ^hn. Из свойств нормы отобра-
жения, порожденной евклидовой нормой (см. (1.18)), следует
12 . 8Л|=|Я|=йя и цл-м=|Я-Ч=-^-.
Поэтому
13 ял-ij_______1 (М"-1 ми
U. |Л 5-^hlhi ... hn - det Я ~ | det 4 | *
Отметим, что неравенство (13) превращается в равенство при
= /г3 = ... = йл. Действительно, правая часть (13) больше левой
части (13) И (йя/й*) раз.
fe = 2
5. 3. Непрерывные линейные отображения
Пусть (£, | • |) — нормированное пространство над полем К,
а символом |-| обозначена норма отображения в некотором под-
пространстве пространства X (Е, Е). Определим множество
32
ГЛ. 2. НОРМЫ
Х(Е, Е):
14. Х(Е, Е} = {А е=Х(Е, Е)||Л|<оо}.
Теорема. С учетом введенных выше предположений для любых
А, В^Х(Е, Е), любых аеК и любых хеЕ
15. |Лх|<|Л ||х|;
16. |аЛ| = |а||Л|;
»7. 1Л + В||<Я Л || + ||В|;
18. |i ЛЕЦ^Ц Л ||||В|.
Доказательство. Неравенства (15) —(18) вытекают непо-
средственно из определения (7). Например,
|ЛВ||= sup | ЛВг|<| Л || sup |5г| = |Л||В|.
lz| = l lz| = l
Из этой теоремы следует, что множество X (Е, Е) является
алгеброй. Можно показать, что если (Е, |-|) —полное простран-
ство, т. е. Е —банахово пространство, то X (Е, Е) является бана-
ховой алгеброй с нормой (7), точнее говоря, X (Е, Е) представ-
ляет собой некоммутативную банахову алгебру с единицей.
Упражнение 1. Пусть А е X (Е, Е). Показать, что следующие утвержде-
ния эквивалентны:
(i) линейная функция А непрерывна в точке 0 е Е;
(ii) линейная функция А непрерывна на Е;
(iii) | А норма отображения А, конечна.
Упражнение 1 подтверждает, что X (Е, Е) — класс всех непре-
рывных линейных отображений нормированного пространства Е
в самое себя. Некоторые авторы называют элементы X (Е, Е)
«ограниченными» линейными отображениями, имея в виду, что
А е X (Е, Е) в том и только том случае, когда Л s X (Е, Е) и
сужение Л на шар единичного радиуса является ограниченным
отображением. Однако такая терминология противоречит общему
определению ограниченного отображения одного нормированного
пространства в другое.
Замечание. Предположим, что мы определили в X (Е, Е)
норму N (•) так, что в дополнение к аксиомам нормы выполняется
неравенство
19. N(AB)^N(A)N(B),
и норма |-| в пространстве Е такова, что
20. I Лх;=сМ(Л)|х1 Vx<=E, УЛ<=#(Е, Е).
В этом случае будем говорить, что N (•), норма (отображения)
в ^(Е, Е), согласована с нормой в Е.
6. ДВА ПРИМЕРА
38
Упражнение 2.
(i) Пусть || • || —норма» порожденная нормой |«|, а У (•) —некоторая норма,
согласованная с | • |. Показать, что
21. | А К N (Л) УЛ е= % (Е, Е);
(ii) показать, что функция A i—► max | ац ( удовлетворяет аксиомам нормы
в пространстве матриц, но не подчиняется неравенетву (19);
(iii) показать, что норма Ai—f I 0// |аУ/2 согласована с евклидовой
\i.i /
нормой;
(iv) используя примеры раздела 1, показать, что для 2, оо норма
[ А |р, определенная соотношениями (1.17) —(1.19), порождается нормой | х |р.
6. ДВА ПРИМЕРА
Приводимые ниже примеры иллюстрируют факт зависимости
нормы отображения от нормы в пространстве. Результаты этого
раздела будут использованы в дальнейшем.
Пример 1. Пусть (Е, |.|00) = L°°(R+) = {f: R+ ->-R11f[«><оо}.
Пусть Я —линейное отображение, определенное на Е с помощью
интегрируемой функции h: R+->R:
1. Н: u>->- Hu — h*u
т. е.
t
2. (Ни] = и (т)dx Xft е= R+.
о
Предполагается, что
= Г |Л(0|Л<оо.
о
3. Теорема. Для (£, | - |оо) н Н, определенных в примере 1,
(а) Я: L00-*!00;
(b) | Я |, норма линейного отображения Я, удовлетворяет
равенству | Я L = | ft [ь т. е. |h*u Ц» [fth |u|a> Vu sL" и
[ft*u|oo может быть сколь угодно точно приближена к ||ft|i|ula>
за счет соответствующего выбора и.
Доказательство. Вычислим сначала норму отображения Я.
Ниже для упрощения выкладок мы опустим индекс оо: например,
|и| будет обозначать £°°-норму функции и: R+->R. В доказатель-
стве мы рассмотрим три нормы: абсолютную величину действи-
тельного числа | и (t) |, норму |и| в пространстве L00 и |Я [ — норму
отображения в <5? (£, Е).
2 Ч. Дезоер, М. Видьясагар
34
ГЛ. 2. НОРМЫ '
4. | Н | — sup | h * и || = sup sup | (ft * и) (/) | =
l|u«=l H| = W>0
= sup sup
||U||=1 />0
t
'\jh(t — x)u (т)dx
о
t
sup sup (I ft (t — т) 11 и (т) I dx .
ii«u=iL<>og
Поскольку || м||=1,
I/7 j^sup | ft (t — т) I dx^\ \h(t')'ldt'.
<>og g
Следовательно,
5. |Я|^Г|Л(П|Л'-=М1.
о
Из неравенства (5) следует, что // — непрерывное линейное ото-
бражение L“ в L°°. Отсюда же вытекает, что |Л|х представляет
собой верхнюю оценку для нормы отображения Н-. L^-^-L00.
Покажем, что ||Л||г равна норме отображения |Я|. Рассмотрим
последовательность входных воздействий и}, us, ... таких, что
|U;|— 1, и положим для /=1, 2, 3, ...:
и(: Т Н-* «/ (т) = sgn [Л (/ — т)], TS R+, / Е Z+
и ft(/) = 0 при /<0. Вычислим значение реакции на воздействие
«,(•) в момент времени t:
t
(h * ut) (t) = J | ft (/ — т) I dr «J || ft * ut loo, t = 1, 2,3,...,
о
где M« обозначает норму в пространстве Е. Отсюда с учетом (5)
при /=1, 2, 3, ... получаем
t со
51 h (т) | dx =С | ft * ut Joo || Н || < $ | ft (т) | dx = || ft ||i.
о о
Полагая /->оо, приходим к равенству ||/7|| = ||ft||i.
Пример 2. Пусть Е = L2 (IR) = {f: (R—*-R 11|/Ь <оо}. Пусть Н —
линейное отображение, определенное в пространстве L? в виде
Н: и>—^ Ни, где
6. (Я«)(0= f ft(/-r)«(T)dT V/e|R.
— ОО
7. Теорема. Если линейное отображение Н определено соотно-
шением (6), где Л е L1, то
(а) Н: L2-+L2;
6. ДВА ПРИМЕРА
35
(b) ||А/||‘2, норма линейного отображения L2), удов-
летворяет равенству
8. ' IН ||2 = max | И (/со) |.
(oeR
Доказательство. Поскольку функция h принадлежит L1,
ее преобразование Фурье (h) = h (/со) является равномерно непре-
рывной функцией, причем зГ(й)->-0 при со->оо (см. Приложе-
ние В. 1.1). Рассматривая все приведенные ниже интегралы над
полем R и используя равенство Парсеваля и теорему о свертке,
получим
1| Ни || = || h * и HI = $ (й * и) (0 (й * и) (0 dt —
= J (Л*и) (/®)(й*«)* (/со)da = § |h(/со) |21 й (/со)|2 da.
Согласно теореме Парсеваля,
II и Ila = 1 <=> II и |2 = -^<=> f I и (/со) I2 da = 1.
У 2л 2л J
Следовательно, для любых и таких, что |ы|2=1,
| //w III <max [| h (/co) |2].
(oeR
Таким образом, норма отображения Н удовлетворяет неравенству
9. || Н ||2 sg max | h (ja) |.
(oeR
Отметим, что функция со •—► | h (ja) | имеет максимум, так как
она непрерывна на R и стремится к нулю при |со|-*оо. Пока-
жем, что норма |//|2 действительно равна выражению в правой
части (9). Ясно, что при Х>0
=/w- я
и
«Г [exp (— X/2) cos со©/] —
При Х->0 последнее выражение стремится к л [6 (со — со©)+
+ 6 (со 4- со©)], где S( ) —дельта-функция Дирака. Выберем в каче-
стве со© точку, в которой функция со •—► | А (/со) | достигает макси-
мума, и для каждого X выберем нормирующий множитель п(Х)
так, чтобы норма функции
их (0 — п (X) |ехр (— X/2)] cos <*>о4
2*
36
ГЛ. 2. НОРМЫ
равнялась единице. Так как I й (/<о) | непрерывна, то
г^о-max ,й(»|.
(О
Таким образом,
| Н |2 = шах | й (/со) |.
(О
10. Замечание. Полученные результаты могут быть распро-
странены на случай, когда и и Л* и являются вектор-функциями,
т. е. отображениями R+ в Кл. Это обобщение предлагается в каче-
стве упражнения.
Упражнение 1. Пусть функция и: R+ -> Rn локально интегрируема, И пред-
ставляет собой матричную импульсную функцию, т. е. Н: R+->RnXrt. Пред-
положим, что элементы (i, /•!, 2, , п) матрицы Н принадлежат/,1.
Обозначим через ff линейный оператор вида
Н: и»—► Йи—Н ♦«,
где
00
(Н ♦ и) (0 Я (/—т)« (т) du.
Показать, что (11), (12) и (14) удовлетворяют определению нормы отображения
(а) и е=1%
Сражения Й
11. l^loo—maxJ 2'Л//(Т) dx''
' б /=1
00 п
J] | (0 р di; показать, что для нормы отобра*
о i=-\
жения Й
12- |Я!а~(\пах),/2»
где
13. =max max X, [fl* (/©)• У (/co)]
G) i
и Х/(Л1) является i-м собственным значением1) эрмитовой матрицы М:
00 п
(С) Sell—J (t) | di\ показать, что для нормы отобра-
0 i = l 1
жения R
14. I^Jx-maxf 5 |Лг/(/)|Л.
f 0
(R+)‘ l«looemax SUP |м<(0|? показать, что для нормы ото*
') Напомним, что собственные значения эрмитовой матрицы являются дей-
ствительными числами.
7. НОРМА И СПЕКТРАЛЬНЫЙ РАДИУС
87
7. НОРМА И СПЕКТРАЛЬНЫЙ РАДИУС
Пусть Л е Сл х л и
1. г (Л) = max 1^(4)!.
Величина г (4) называется спектральным радиусом 4.
2. Упражнение 1. Показать, что для любой нормы отображения
2а. г(Л)^||Л||.
Для заданной матрицы А мы попытаемся найти норму в про-
странстве ©л, порождающую «минимальную» норму А. Докажем
для этого следующую теорему.
3. Теорема. Пусть через N обозначено множество всех норм
в пространстве ©Л. Тогда для любой матрицы
4. inf I sup -^^] = r(4). .
i-igmLec» |JCi J
В силу определения точной нижней грани (4) эквивалентно
неравенству (2а) и утверждению о том, что для любого е>0 и
любой матрицы 4еСлхя существует норма в С" такая, что
порожденная ею норма удовлетворяет неравенству
5. ||4||^г (4)4-8.
Доказательство. Обозначим через J жорданову форму
матрицы 4; тогда существует неособенная матрица Р такая, что
J = PAP~i = A + U,
где Л — диагональная матрица, а элементами матрицы U являются
нули и единицы, причем все ненулевые элементы расположены
на диагонали, проходящей над главной диагональю. Для некото-
рого малого числа б>0 определим неособенную матрицу Di
D = diag[l, 6-1, б-2, .... б^»-1»].
Тогда DJD~l = Л4-б1/. Определим следующую норму |-| в С"’
Xi—►|DPx|2, где |• |» — евклидова норма в пространстве <С*. Порож-
денная ею норма имеет вид:
| А max I Ах: = max |DP4x|2.
lx | = 1 lDPx|t=l
Полагая z-=DPx, 'получаем DPAx = DPAP~1D~1z>^(A.-{-bU)z;
поэтому
|4|2=max ((A 4-61/) z | (Л 4-6[/) z>
< max {| Az I? 4-261 <l/z | i/z> 14-S’I (4)+26r (4)+6\
или |4|^r(4)4-6. Выбирая б«^е, приходим к неравенству (5).
38
ГЛ. 2. НОРМЫ
Использование полученного результата затруднено тем, что
выбор нормы в соотношении (4) зависит от вида матрицы А.
Однако наша теорема весьма эффективна в тех приложениях, где
речь идет лишь об одной матрице, поскольку подбор нормы в этих
случаях не вызывает затруднений.
Упражнение 2. Пусть (V — некоторая норма в пространстве СЛ. Показать,
что функция Xi—► N (Рх) является нормой в Сл тогда и только тогда, когда
Р —неособенная матрица, принадлежащая Слхл- Показать, что в случае, когда
Р — особенная матрица, функция р: Xi—N (Рх) удовлетворяет аксиомам (ii)
и (iii) нормы (см. определение (2.1.1)) и аксиоме (Г):
I') р (х) 0 Ух е Сл,
заменяющей аксиому (i). Функция р называется полунормой.
Упражнение 3 (теорема о сжимающем отображении). Мы приведем форму-
лировку теоремы о сжимающем отображении в форме, удобной для приложе-
ний. Доказательство теоремы от этого практически не меняется, и его можно
найти в обычном учебнике.
Теорема. Пусть (Р, ^ — метрическое пространство и (<$?, ||»||) — банахов©
пространство Пусть р0 е Р и х0 е а®. Рассмотрим два замкнутых шара:
Bp={peP|d(p, Р0)<гр},
{* е। КМ-
Если
(i) функция f: Вр х В^ -> <£$ непрерывна в Вр х В^
(ii) существует некоторое число k < 1 такое, что
I/ (Р, x)—f (р, х')k ] х—х' I Ур е= Вр, Vx, х' е В#9
(iii) ||/(Р. *o)-xol=s(1-ft)r« VpeSp,
ТО
(а) для любых р (= Вр итеративный процесс
*п+1 (Р) = / [Р. хп (р)], Хо (р) = Х0
сходится к единственной непрерывной функции х: Вр-+В^ такой, что
*(Р)=/[Р. х(р)1 VpeSp;
(b) сходимость является равномерной по р в Вр, т. е. для заданных k
и Вр
I«(Р)—х„ (р) |Vp е Вр, Уп<=2+.
(Указание: для решения задачи проверить, что хд (р) е В& при всех п 1
й всех р е Вр,)
В общем случае любая функция типа / (р, • ), отображающая множество В&
в банахово пространство о® и удовлетворяющая неравенству вида (ii), назы-
вается сжатием множества В^.
Упражнение 4. Пусть А — непрерывное отображение банахового простран-
ства Е в самое себя. Число X е С будем называть спектральным числом ото*
брожения А тогда и только тогда когда отображение А — X/ необратимо
в пространстве Е. Спектром Sp (Д) отображения А назовем множество всех
8. МЕРА МАТРИЦЫ
39
спектральных чисел 4, а спектральным радиусом — положительное число
r(4) = sup |1|.
X е= Sp (Л)
(а) Показать, что
(4-1/)-! = — 2 b"'*+1,4ft,
*=о
причем ряд сходится абсолютно в X (£, Е) при | 1 | > [ А
(Ь) Показать, что (4 — V)"1 е Х(Е, Е) при |1|>||4||.
Упражнение 5. Пусть 4, В е X (£, Е) и Е — банахово пространство.
Показать, что в общем случае неравенства
г {АВ) || 4 || г (В), г (АВ) г (4) г (В)
могут не выполняться. (Указание: рассмотреть две (2x2)-матрицы, одна из
которых нильпотентна.)
8. МЕРА МАТРИЦЫ
Обозначим через | • | некоторую норму в пространстве и
через || • || — порожденную ею норму в пространстве (СлХл. Функция
|| • ||: СЛХЛ->1Р+ является выпуклой и поэтому в каждой точке
ХеС"хл имеет одностороннюю производную по направлению
в любом направлении т. е. предел
существует для всех X и всех А. Односторонняя производная по на-
правлениюфункции || • || в точке / е (Сл х л в направлении А называется
мерой матрицы А и обозначается р(Л). Таким образом,
1. И(Л) = Ит!/+е^1-1.
е\о °
Факт существования этого предела мы докажем ниже в лемме (4).
Понятие меры матрицы возникло в теории дифференциальных уравнений.
Рассмотрим уравнение х(/) = 4 (/)х(0, где 4 (/) —непрерывная функция. Будем
считать, что односторонняя производная в положительном направлении функ-
ции- ti—>|ф(/) [, где ф(/) — решение дифференциального уравнения, ограни-
чена, т. е.
2. D+ । <р (0 | = lim ,l<P«+6)l-l<P(Qi =
е\о в
_ ,,т |ф(0+94(0ф(0|-|<р(0| п+94 (ОН I ф(0 I— I <Р(0 1
л 11111 Л ф
0\0 0 9\0 °
Отсюда с учетом (1)
3. D+ I Ф (01 (4 (0) I Ф(0|.
Неравенство (3) сильнее обычного неравенства
р+1ч>(О1«М(опф(О1-
40
ГЛ. 2. НОРМЫ
Действительно, мера ц (Л (/)) может быть отрицательной в то время, как
норма || A (t) у всегда неотрицательна.
4. Лемма. Мера р (Л) корректно определена для любой мат-
рицы А е Сяхя.
Доказательство. Обозначим через f (9) отношение в правой
части (1). Покажем, что /(9) уменьшается при 9\0, причем
f(9) ограничена снизу. Отсюда последует, что предел функции
f(9) при 9\0 существует.
Пусть £е(0, 1). Тогда
Л9/(^9) = I 7 ч-ле Л |-1=|Л(7 + 9Л) + (1-Л)/|-1<
<Л||/4-9Л j + 1 -k- 1 = £(|| 14-9Л I- 1) = £9/(9).
Таким образом, /(£9) ^/(9) при is(0, 1), т. е. функция f
уменьшается с уменьшением 9. Кроме того, f(9)5s —| Л |, по-
скольку при 9>0
9/(9) = |7 + 9Л|-1>1-6|Л|-1=—9|Л|,
что доказывает лемму.
Свойства меры р. Для удобства мы перечислим ряд свойств
меры р в следующей теореме.
5. Теорема. Пусть Л, В е Сяхя и мера р определена соотно-
шением (1). Тогда
6. (а) р(/) = 1, р (—/) = —!, р(0) = 0.
(Замечание: из того, что ц (Д) = 0, вовсе не следует, что А=0);
7. (b) -1Л |<-р(- Л)^р(Л)<| Л
8. (с) р(сЛ) = ср(Л) ус^О;
9. (d) р(Л+ <?/) = р (Л)-f-с yceR;
10. (е) тах[р(Л) —р(—В), —р(—Л) + р(В)]^
<р(Л + В)<р(Л) + р(В);
(f) функция р: Cnxn->R выпукла на ©яхя;
11. р[ХЛ + (1 -Х)В]=сХр(Л) + (1 -%)р(В) у%<=[0, 1],
12. (g) |р(Л)-р(В)| <|р(Л-В)|<|Л-В|,
|р(Л) — р(В) |<Р(В-Л)|<8 Л —В|;
13. (h) — р(— Л)<ЯеМЛ)<р(Л), 1 = 1, 2, .... п;
14. (i) -р(-Л)|х|< Лх | и — р (Л) | х | sg | Ах | ух е ©я.
(Замечание: значение |Лх| не всегда ограничено сверху
числом р (Л) | х |);
(j) Пусть | • | — норма в пространстве Ся и Р е Сяхя — неособен-
ная матрица. Обозначим через рР меру матрицы, определенную
q помощью нормы, порожденной нормой | • |Р, т. е. функцией
8. МЕРА МАТРИЦЫ
41
[х|р = |Рх|. Тогда
15. рР(Л)=р(РЛР-1);
(к) Если матрица А' неособенная, то
16. _(г(_Л)^(|Л-Ч)-1<8Л|.
Доказательство, (а) немедленно вытекает из Определе-
ния (1);
(Ь) Поскольку 0 > 0, то из неравенства треугольника следует,
что
_|Л|_ м 1-1. U+M|-L_| д |
и
_1 л |_ 1—в|Л| —1 _ 1—8| —Л|—1 Ц+8(-Л)|-1
— IЛ |--§-------------j----<---------g-----.
Наконец, соотношение между р(Л) и —р(—Л) следует из
О -11 + 2В (Л - А) |- 1 1'+2.Л|-1+|1-2М|-1
&
(с) При с = 0 равенство (8) вытекает из (6). При с>0
li /+ем 1-1 _ „ п+с0Л||-1
е — а
Так как О 0, то с0\О при 6\0.
... П+в(Л+с/)1-1_ (,+ев)|/+т+а л|~’
w е ~ о
_ |/+нЬ"Л|-1 ,
--------.-----+ с.
1 +св
Отсюда получаем равенство (9), поскольку для любых с ® R при
0\0 6/(1 +с0)\О.
(е) |/ + О(Л + В)|-1=|(|/-|-2еЛ + / + 20В|-2)<
< | (|/+ 20 Л | - 1) +1 (П + 29В | - 1).
Отсюда при 6\0 следует, что р (Л + В) (Л) + р (В). Из этого
неравенства вытекает, что
18. р(Л) = р(Л + В-В)^р(—В) + р(Л + В)
и
19. р(В) = р(Л4-В-Л)^р(— Л) + р(Л + В),
т. е. выполняется и первое неравенство (10).
42
ГЛ. 2. НОРМЫ
(f) Выпуклость функции р вытекает из (8) и второго нера-
венства (10).
(g) Второе неравенст о (12) следует из (7). Чтобы убедиться
в справедливости первого неравенства (i2), заменим В на —В
в (18):
р(А)-р(В)^р(А-В).
Заменяя А на —А в (19), получим
р (В) — ц (А) р (В — Д),
откуда и следует утверждаемое.
(h) Обозначим через ее С" нормированный собственный век-
тор матрицы А, принадлежащий собственному значению 1г; поэтому
Ae — kie и Ц/Ц-9 (—А)|^\е — 01ге|. Тогда
|/+в(-Л)5-1 |е-вМ|-1 _ I1-9XH-1
9 9 9
При 0\О правая часть этого неравенства стремится к ReA./, а
левая —к —р(—А). Из неравенства
1/4-9ЛЦ-1 _ |е+9М|-1 |1+бХг|-1
9 9 — 9
при О\0 получаем второе неравенство (13).
(i) При 0>О
I дх I = |х—(х —9Лх) | | х—(/ —9Л) х I > |Х|—|/—6Л||х| _
• ' 0 0 * ' в
где, переходя к пределу, мы отмечаем, что левая часть не зависит
от 0. Второе неравенство (14) получается аналогичным образом,
если заменить А на — А и учесть, что | Ах | = | — Ах |;
(j) |/ + 0А|1р= sup |х + 0Ах|р =
|к|р =1
= sup |Px + 0RAP~1Px| = |l Z + 0PAP-1||.
I Px Ip = 1
(k) Согласно (14),
— p(—Л)|х|^|Лх| и inf | Лх | = (|| Л”1 Ц)”1,
lx| = l
откуда следует первое неравенство (16). Чтобы получить второе
неравенство, вычислим норму обеих частей равенства ЛЛ”Х = /.
8. МЕРА МАТРИЦЫ
43
24. Теорема. Пусть х = (хг, х2...хп) е и А = (ау) s (D"*".
Тогда
г=1
|Л1(Д) = тах
i
/ п V/f
X Is = ( У, I Xi I2 j ;
\i=l /
|| Л||1 = тах 5 I Il
i i
Re (azz) + 2 | ay 11;
t
L i# J
М112==[тахМЛ*Л)у'2:
jx2 (Д) = max (Д + Д*)/2];
i
I x |oo = max | xi |; | A ]|oo = max У | aif |;
Ноо(Л) = тах [Re (0^ + 2 \<fy\ .
Доказательство. Вычисление меры рДД) (£ = 1, 2, оо)
является простым упражнением на использование определения.
(Л* обозначает, как обычно, матрицу, комплексно сопряженную
матрице Д.)
Упражнение 1. Показать, что р,2(Л)==0, если А 0 и матрица А является
кососимметрической или косоэрмитовой матрицей.
Упражнение 2. Пусть A s Рлхл — особенная, положительно полуопреде-
ленная, симметрическая матрица. Показать, что р,2 (—Д) = 0.
26. Комментарии. Согласно Теореме (24) р (Л) легко вычислить
при р=1, оо или оценить при р = 2. р(Л) может быть меньше
соответствующей нормы | Л |. И, наконец, мера р (Л) может быть
отрицательной.
В качестве приложения понятия меры матрицы приведем два
утверждения. В первом из них мы установим верхнюю и нижнюю
границы для решений линейного дифференциального уравнения,
а во втором — достаточное условие существования и единствен-
ности рабочей точки в теории цепей.
27. Теорема. Пусть Л (/) —регулярная функция, отобра-
жающая |R+ в ©пхл. Тогда решение уравнения
28. И (0 = Л (t)x (О
удовлетворяет неравенствам
t. '
< IX (О I < I х (fe) I exp ц (Л (Г)] di'\.
V» )
44
ГЛ. 2. НОРМЫ
Доказательство. Обозначим через x(t) произвольное нену-
левое решение уравнения (28), n(/) = |x(Z)| и через D+n(t) — пра-
востороннюю производную п (•) в момент Л Тогда, по определению,
для всех t ф D, где D — не более чем счетное множество точек
разрыва А (•), справедливо равенство
30. ом «) - iin. -^g+g—_ |im I МО+«3 (,), и I -1«ИI.
е\о 9 е\о 8
Однако
|х(/) + еД(Пх(П1<|7 + бЛ(П1|х(О1.
Подставляя это неравенство в (30) и используя определение меры
матрицы р, получаем
31. D+n (/) р [Л (0] п (t).
Поскольку п(0>0 для всех t, из (31) вытекает неравенство
интегрируя которое, приходим к второму неравенству в (29).
Первое неравенство в (29) доказывается сходным образом.
Во многих приложениях часто бывает необходимо определить
рабочую точку (или точку устойчивости) систем, описываемых
уравнением
32. X = f(x) + u,
где и, xgR" и f, Задача состоит в нахождении такого
xeR", что f (х) = — и. При этом важно знать, разрешимо ли
уравнение при любом и е R", и если разрешимо, то является ли
решение единственным. Приводимая ниже теорема устанавливает
достаточное условие существования и единственности решений.
Обозначим через Df(x) производную функции f в точке х, т. е.
якобиан функции f в точке х.
33. Теорема. Пусть/: Rn-»-Rn —непрерывно дифференцируемая
функция. Тогда, если существует функция т: R+-»-R такая, что
34. (х)]< — m(|x|)<0
где т(а)>0 для всех а>0 и
СО
35. J т (a) da = оо,
о
то x>—*~f(x) является (^-диффеоморфизмом пространства R" на
самое себя, т. е. функция f представляет собой непрерывно диф-
ференцируемую биекцию R" на R", имеющую непрерывно диффе-
ренцируемое обращение. Таким образом, для любого и е R" урав-
нение (32) имеет решение х, зависящее от х в (^-образе.
БИБЛИОГРАФИЧЕСКИЙ КОММЕНТАРИИ
45
Доказательство. Справедливость теоремы может быть уста-
новлена с помощью теоремы Пале, если мы покажем, что, во-первых,
det[Df(х)]Ф0 для любых xeR", и, во-вторых, из |х|-*-оо
вытекает \f(x) |->оо. Первое из этих условий выполняется, так
как для любых z/eR”, отличных от нуля,
|Of(x)z/| = |-D/:(x)z/|>-p.[Df(x)]| #:s&m(|x|)|0|>O
(здесь мы использовали (14) и предположение (34)).
Для доказательства второго условия разложим функцию f по
теореме Тейлора в окрестности нуля ©я:
f(x)=f(0)4-Rof(Xx)d%
Io
X.
Отсюда, последовательно используя неравенства (14), (11) и (34),
получаем
|f(x)> KDf(Xx)dXx -|/(0)>-pKDf(Xx)dX}|x| - |/(0)|>
L0 J 10 '
>-jlx[P/(Xx)]dX|xl-|f(O)>$m(X|x|)dX|x|-|f(O)H
о о
J т (a) da -1 f (0) |,
убеждаясь в справедливости второго условия, как следствия
предположения (35).
36. Замечание. Теорема останется справедлива, если неравен-
ство (34) заменить неравенством
37. р[—Df(x)]< —m(|x|)<0 yxelR".
БИБЛИОГРАФИЧЕСКИЙ КОММЕНТАРИЙ
Определения и факты, касающиеся понятий нормы и эквива-
лентности норм, изложены обычным образом [108, 41, 44, 55].
Примеры читатель может опустить. Понятие нормы оператора
введено в техническую литературу Сандбергом в его многочислен-
ных статьях, опубликованных с 1963 года, а также Цеймсом
примерно в то же время (см. библиографию в конце книги).
Понятие меры матрицы введено Дальквистом [23]. Неравенство
(8.29) можно найти в книге Коппеля [21]. Теорема (8.33) дока-
зана Дезоером и Ханедой в статье [36].
Глава 3
ОБЩИЕ ТЕОРЕМЫ
Эта глава содержит общие результаты, поскольку абстрактные
рассуждения позволяют сэкономить время. Действительно, пред-
положим, что мы решили дюжину частных задач и обнаружили,
что в их решениях существует некая общая схема. Естественно,
было бы полезным извлечь из нее суть того подхода, который
привел нас к решениям задач; тогда, столкнувшись с новой про-
блемой, мы бы знали, как приступить к ее решению. Такой под-
ход, конечно, очень заманчив, но какова его цена? Построение
общего подхода к различным задачам требует от исследователя
особой тщательности. В самом деле, при решении. какой-либо
конкретной задачи отдельные ее особенности хорошо известйы и
понятны, что, в сущности, и используется в решении без особых
оговорок. Иными словами, знакомство с предметом исследования
порождает убеждение в том, что задача легче, чем она есть на
самом деле. При общем подходе все необходимые свойства должны
быть точно сформулированы, а каждый шаг рассуждений тща-
тельно исследован. С другой стороны, часто случается, что неко-
торые довольно простые абстрактные рассуждения приводят к весьма
общим и полезным теоремам. Ряд теорем такого рода здесь и
приводится.
В первом разделе мы опишем общую схему исследований,
которая будет использована в дальнейшем.
В следующих разделах мы сформулируем, докажем и обсудим
теорему о малом коэффициенте роста в общей форме и в форме
для приращений.
В разделе 4 доказывается теорема об ограниченности решения,
имеющая интересное обращение.
В разделе 5 доказывается весьма общая теорема существова-
ния и единственности, с помощью которой удается доказать, что
большинство систем с обратной связью, часто применяемых
в практике, в ответ на заданные входные воздействия воспроиз-,
водят выходной сигнал однозначным образом.
Раздел 6 посвящен доказательству теОремй преобразования
контура, которую можно трактовать как теорему устойчивости
эквивалентных систем.
В заключительном разделе вводится понятие ^-устойчивости
и рассматриваются основные свойства систем с обратной связью.
1. ПОСТАНОВКА ЗАДАЧИ
47
1. ПОСТАНОВКА ЗАДАЧИ
Большинство систем с обратной связью можно представить
в виде, приведенном на рис. 3.1. Символами их и и2 обозначены
входные воздействия, символами yi и у2 — выходные сигналы,
а символами et и е2 —сигналы ошибки; и,, у( и et (i = l, 2) яв-
ляются функциями времени, обычно определенными для0 или
Рис. 3.1.
для t е Z+ и принимающими значения из R, R" (иногда С"), из
некоторого нормированного или гильбертова пространства. В наи-
более общем виде наша задача состоит в следующем: при неко-
торых заданных заранее предположениях об операторах Hi и Я2
показать, что если функции Ui и и2 принадлежат некоторому
классу, то функции е2, yi и у2 также принадлежат этому же
классу.
Система с обратной связью описывается уравнениями
1. Ui = @1 Я2б2,
2. и2 = е2— Н1&1»
Здесь Hi(H2) — оператор подсистемы прямой ветви (ветви обрат-
ной связи), вырабатывающей реакцию yi (соответственно у2) под
действием сигнала ех (соответственно е2). Уравнения (1) и (2) имеют
очевидную «управленческую» интерпретацию (рис. 3.1).
Рис 3.2.
Заслуживает внимания и 2п-полюсная' интерпретация этих
уравнений (на рис. 3.2 изображена четырехполюсная система).
Пусть вектор-функция ui с компонентами (иг)1 и (ы,)2 принимает
значения из R2. Оператор Hi представляет собой оператор «сопро-
тивлений», преобразующий входные токи в выходные напряже-
4»
ГЛ. 3. ОБЩИЕ ТЕОРЕМЫ
ния. Оператор является оператором «проводимостей», преобра-
зующим входные напряжения в выходные токи. Уравнение (1)
выражает закон Кирхгофа для токов, а уравнение (2) —закон
Кирхгофа для напряжений.
Общие положения. Поскольку мы собираемся изучать самые
разнообразные объекты, а именно непрерывные и дискретные
системы, а также системы, в которых функции uit et и у, являются
действительными функциями, либо принимают значения из R" или
даже из нормированных пространств (распределенные системы),
установим следующие общие положения. Пусть
: подмножество множества R+ (обычно, sF = R+ или Z+);
V: нормированное пространство с нормой | • I (обычно V = R,
R", С, Сл);
aF: {f: ->еГ}-множество всех функций, отображающих sF b«F.
Функциональное пространство ®F является обычным линейным
пространством над полем С (или R) с определенными в нем пото-
чечными операциями сложения и умножения на число:
(/+*)(O = f(O+g(O Vf, g<=«F, WeF,
(af)(0 = af(0 V/SeF, V/eeF, Vae£ (или R).
Для каждого T e sF через Рт обозначено линейное отображение
пространства «F в самое себя такое, что
( t>T
9^ —нулевой вектор пространства V. Линейность Рт следует
из определения. Отображение Рт представляет собой проектор
в пространстве «F, так как Рт — Рт. Функцию }т мы будем назы-
вать срезкой функции f в точке Т.
Введем в пространстве «F некоторую норму |-| и определим
нормированное линейное подпространство X линейного простран-
ства «F.
5. X = {f-. «Г->Г||/1<оо}.
^Обычно
|Л = Г|/(О1<# или
О О'
Определим также расширенное нормированное пространство Хе,
соответствующее нормированному пространству Х-.
6. Xe = {f- VTe^"|M<oo}.
Мы будем полагать в дальнейшем, что норма | • |, используе-
мая в определениях пространств X и Хе (см. (5) и (6)), удовле-
творяет следующим условиям:
1. ПОСТАНОВКА ЗАДАЧИ
49
7. (i) для любых f&Xe отображение Т«—*|/>| монотонно
возрастает;
8. (ii) для любых f^X | fT | -> J f || при Т ->оо.
Полезно ввести обозначение:
Принимая во внимание условия (7) и (8), мы можем перефор-
мулировать определения (5) и (6) пространств X и Хе: функция f
принадлежит X в том и только том случае, когда действительная
функция Т н—► ||fr || ограничена на множестве ; функция f при-
надлежит Хе в том и только том случае, когда функция 7V>|/г|
отображает в R (здесь ограничение на рост функции отсутст-
вует!). Если в качестве V* выбираются R или Кя, а в качестве
I • || — Лр-норма, то вместо символа X мы будем использовать обо-
значения Lp или Ln, а вместо Xe — Lpe или Lne- В дискретном
случае будут использоваться символы 1р, 1р, 1р и 1рв.
Упражнение 1.
(а) Выберем в качестве X пространство L00, Пусть f: t ь—► exp (f2). Опре-
делить, является ли функция / элементом L00 или
(b) Привести примеры последовательностей, принадлежащих ZJ, но не при-
надлежащих Z1, и последовательностей, принадлежащих /^°, но не являющихся
элементами /°°.
Упражнение 2. Рассмотрим сужение Рт на множестве X (но обозначе-
ние Рт сохраним для дальнейшего). Показать, что Ь Таким
образом, Рт представляет собой непрерывный линейный оператор, заданный
на X, причем его норма не превосходит 1.
Большинство моделей, применяемых в теории систем, является
неантисипативными. Поэтому мы должны ввести понятие неанти-
сипативного отображения. Отображение Н: Хе-+Хе называется
неаншисипативным тогда и только тогда, когда
9. РТНРТ = РН
Упражнение 3. Считая, что отображения Ях, Hf. Хе~*Хе неантисипа-
тивны, показать, что отображение НГН2 также неантисипативно.
(Указание: учесть, что суперпозиция двух функций ассоциативна.)
Упражнение 4. Пусть h е L1 (R) и и s L2 (R). Показать, что отображение
Я: L2(R)->L2(R) вида
Н: и\—► Hu=h * и,
т. е.
(Ни) (/) = J Л (/—т) (т) Jt, t s R,
— 00
неантисипативно тогда и только тогда, когда h(t)^Q почти везде на интервале
(— оо, 0).
Упражнение 5. Показать, что условие (7) выполняется вовсе не для любых
норм || • || в пространстве
50
ГЛ. 3. ОБЩИЕ ТЕОРЕМЫ
(У к а з а н и е: рассмотреть пространство мер р,, заданных на R+; опреде-
лить норму, как в Приложении (с.3.3); показать, что [ || > !; р !| при некото-
ром р,.)
Упражнение 6. Выполнение введенного в рамках общих положений усло-
вия (7) не всегда является необходимым. Рассмотрим в качестве X класс функ-
ций, преобразуемых по Фурье (согласно изложенному в Приложении В, PczcSf,
L2 cz Jo, б (t) е X, ...). Пусть f s Хе и fT=PTf^<X. Определим норму
функции fT\
|М = sup lfr(/«o)| Vfetf, VTeR.
где fT — преобразование Фурье функции fr.
(а) Показать, что для f е L2 (R) приведенное выше соотношение является
нормой.
(Ь) Пусть f (/) = ? 1 (— /) — 0,26 (Z— 10-3), где через 1 (/) обозначена функ-
ция «единичный скачок». Показать, что |l Pof || = || f0 || > || f ||.
Упражнение 7. Некоторые типы соединений неантисипативных подсистем
не являются неантисипативными. Привести пример.
(У к а з а н и е: рассмотреть дискретную систему с обратной связью, где
еъ У1- Z+->IR, «2 = 0, Н2 — тождественное отображение, (Я1е1)(п) =— (п) +
+ ^i (л — 1) для всех п е Z+-)
Обсудить, что произойдет, если слегка изменить так, чтобы (Н^) (п) =
= —(l+e)«i («)+ei(n—1), где е< 1.
Упражнение 8. Пусть Hlt Н2. Хе -> Хе. Показать, что
(/ + Н2Н^ = (I + НгН^ Н19
если — линейное отображение, а отображения (/ + Я2Я1)-1 и (/ + Я1Я8)-1
определены в пространстве Хе и переводят Хе в самое себя. Привести струк-
турную схему, соответствующую этому равенству. Показать, что равенство
может нарушиться, если отображение Нъ не будет линейным.
Упражнение 9. В рамках приведенных выше общих положений допустим,
что функция и2 тождественно равна нулю. Полагая, что отображение (/4-Я2^1)-1
определено в пространстве Хе и переводит Хе в Хе, показать, что для системы
с обратной связью, изображенной на рис. 3.1 и заданной уравнениями (1) и (2),
У1 = +W' U1 yU1 е с.
Упражнение 10. Приведем второе определение неантисипативного отобра-
жения. Пусть, как и раньше, Н: Хе-+Хе. Отображение Н называется неан-
тисипативным тогда и только тогда, когда для любых Т & ЯГ и любых х,
10. Рт%=Рту РтНх = РтНу.
Показать, что определения (9) и (10) эквивалентны.
2. ТЕОРЕМА О МАЛОМ КОЭФФИЦИЕНТЕ РОСТА
Теорема о малом коэффициенте роста является весьма общей
теоремой, устанавливающей достаточные условия того, что «огра-
ниченное входное воздействие»’вызывает «ограниченную реакцию».
Теорема сформулирована так, чтобы совершенно отделить вопросы
ограниченности от вопросов существования, единственности и т. д.
1. Теорема. Рассмотрим систему, изображенную на рис. 3.1.
Пусть Ни Н2: Хе->Хе, е19 e2&Xg. Определим иг и и2 соотно-
2. ТЕОРЕМА О МАЛОМ КОЭФФИЦИЕНТЕ РОСТА
51
шениями
2. Ui = е± +
3. и2 = е2 — Н&.
Предположим, что существуют постоянные числа Pi, р2, Yi^O,
у2^0 такие, что
4* | (Н 1в1)г || ух || е1Т II + Pi> | у у.
5. || (Н2е2)т || ?2 Игт 11 + Р2 /
Тогда, если уху2 < 1 > то
6. (i) || е1Т || <; т—- (I и1Т || + у21| и2т || + Р2 + Y2P1),
iW2 V7e=^T.
7. I e2r I (II иътII + Ti II Wir II + Pi + Y1P2)
1 Г1Г2
(ii) Если, кроме того, ||иг ||, || u2||<oo, то нормы функций еъ
е2, Уъ Уъ конечны и ||ei|| и ||е2|| ограничены сверху выражениями
из правых частей (6) и (7) с отброшенными индексами Т.
8. Определение. Допустим, что для заданного оператора
Hi*. Хе-+Хе существуют такие действительные числа Pi и ух, что
8а. ||(Я1Х)г||^ У1||хг|| + Р1 Vx е VTeeT".
Очевидно, что число ух неодназначно определяется неравенст-
вом (8а). Интуитивно ясно, что нас интересует то наименьшее ух,
при котором (8а) еще выполняется. Назовем коэффициентом роста
оператора число у(7/х) вида
8b. Yi(//i) = inf {yi *= |R+1 BPf (8а) выполняется}.
Эта точная нижняя грань часто обозначается через у(Нг) или уь
Используя введенный термин, переформулируем теорему (1):
если у (/71) у (//2), произведение коэффициентов роста операторов
Т/i и Н2, меньше 1, то в предположении, что решение существует,
любая пара ограниченных входных воздействий (ult и2) определяет
пару ограниченных реакций (ylt у2), а отображение («х, и2)>—*
Уъ) имеет конечный коэффициент роста.
Упражнение. Предполагая, что отображение Нг неантисипативно, показать,
что неравенство (8а) может быть заменено неравенством
,8с. |Я1Х|^у1||х|| + Р1 VxScS? (но не Хе1).
Отметим, что в неравенстве (8с) индекс Т опущен, поскольку функция'х опре-.
делена только в пространстве X.
9. Комментарии.
(а) Общность. Теоремн (1) справедлива как для непрерывных-,
так и для дискретных систем. Кроме того, система может иметь
как один вход и один выход (т. е. ?^«R), так и несколько' вхо-
52
ГЛ. 3. ОБЩИЕ ТЕОРЕМЫ
дов и выходов (т. е. 2^ = КЛ), и даже может быть определена
в любом нормированном пространстве (распределенная система).
(Ь) Формулировка. При формулировке теоремы выдвинуто мини-
мальное число допущений; предполагается, что и соот-
ветствующим образом определены иг и и2. На практике функции
и и, задаются заранее, а функции и ег вычисляются. Поэтому
при формулировке теоремы не затрагивается вопрос существова-
ния решений уравнений (2) и (3). Кроме того, на практике
числа Р/ и у/ вычисляются, исходя из условия мажорируемое™
функции функцией уг || eiT I + Р,- для всех и всех
Т е dT. Для вычислений полезно использовать неравенство (2.8.29)
и лемму Веллмана — Гронуолла (см. Приложение Е).
(с) Форма предположений усовершенствована по сравнению
с различными версиями той же теоремы, доказанной Сандбергом
[77—82], Цеймсом [112], Ли и Дезоером [59]. В обычной форму-
лировке Рх = 0, так что теорема неприменима к системам со ста-
тическим нелинейным элементом <р: R->R, где
а также к некоторым системам, содержащим нелинейный элемент
с характеристикой гистерезисного типа или с насыщением, в то
время как теорема (1) справедлива и в перечисленных случаях.
(d) Результаты распространимы и на случай, когда Hi и Нъ
являются отношениями (т. е. многозначными функциями). В ука-
занном случае неравенства (4) и (5) должны выполняться для
всех «образов» каждой функции (i=l, 2). Этот факт
чрезвычайно полезен при изучении систем с обратной связью,
содержащих нелинейный элемент с характеристикой гистерезисного
типа.
(е) Теоремы (2.6.3), (2.6.7) и упражнение 1 (раздел 2.6) очень
удобны для вычисления коэффициентов роста отображений типа
свертки.
Упражнение 1. Используя теорему (1), построить пример системы (напри-
мер, типа рассмотренных в главе 1), для которой существование решения и/или
его единственность и/или непрерывная зависимость от входного воздействия
нарушаются даже в том случае, когда произведение коэффициентов роста
?("i)V(#a) меньше 1.
Доказательство теоремы (1). Согласно (2) для любых
ТеаГ
10. би = Uir — (Н 1в2)т.
Поскольку здесь все векторы принадлежат пространству
11* l4?Klairl+l(#«0k)rl<l*irl + frtarl + ₽« VTe«T'<
2. теорема о малом коэффициенте роста
53
Аналогичным образом из (3) получаем:
12. ^2г|| + Т1|^1г1 + Р1 VT .
Следовательно, учитывая, что у2^0, для любых ТезГ*
13. J е\т J У1у21 eir 14“ (I J 4- ?2 II ^2714- Р2 + ?2pi)*
Так как уху2 < 1, то
14. | е1Т Л < Т—уГу8 U1T1 + V« i 14- Р» 4- Y2P1) •
Доказательство остальных положений теоремы очевидно.
Упражнение 2. Рассмотрим систему с обратной связью, где иъ еи уъ е2,
у2. R+->R, Нг и Н2 отображают L°°(R+) в самое себя, и2^0. Кроме того,
Я1*1в£*еь где g—заданная функция, принадлежащая P(R+), и (Н2е2) (/) =»
= ф[е2(/), /J, где ф: RxR+-*R — непрерывная функция, принадлежащая сек-
тору [0, k). Предположим, что для всех иг е L°° (R+) существует единственное
решение еъ уг е L00^). Построить ограничения на число k и функцию g( •)
так, чтобы из € L°° (R+) следовало, что r/x s L00 (|R+> Показать, что при
найденных условиях существует число m такое, что
II Flloo « «II «1 loo
Упражнение 3. Повторить упражнение 2 для дискретной системы, т. е.
для случая, когда ult еъ уг: Z+->R, Нх и Н2 отображают /°° в самое себя
и т. д.
Упражнение 4. Рассмотрим систему с обратной связью» для которой «8 = 0
и Я2=₽/, т. е. (I + H1)e1^tii. Предположим, что Ях: и (I + H^1: Х~*
+£. Показать, что в этом случае у [(/+/Л)"1] < оо тогда и только тогда,
когда существуют постоянные числа а и причем е>0, такие, что
|l(/+tfl)«|S=eH + ₽; VesX.
Если м2 s 0, нет смысла рассматривать коэффициенты роста Я,
и Н2 отдельно друг от друга: в таких случаях удобнее ввести
«коэффициент усиления замкнутого контура» H^Hi. Следующее
следствие иллюстрирует эту идею.
15. Следствие. Рассмотрим систему, изображенную на рис. 3.1,
где и2 = 0. Пусть Hi, Н2: Хе-+Хе, ех^Хе. Определим
16. Ui = ei-\-H^Bii,
17. e2 = H\6i.
Предположим, что существуют постоянные числа y2i^0, у2^0,
₽2i и Рх такие, что
l|(^iei)r|^Yi]eir||4-Pi J
Тогда, если yai < 1, то
R1TI < i_j„ (I «1ТI + Р«1)»
1 nil
ll/ir 8 12.* (8 «it I + Р»х)+Рх-
1 гВ1
54
ГЛ. 3. ОБЩИЕ ТЕОРЕМЫ
Отметим, что комментарии (9) применимы к следствию (15).
Согласно этому следствию, если «коэффициент усиления замкну-
того контура» не превосходит 1, то система с обратной связью
имеет конечный коэффициент усиления. Сравнить следствие с тео-
ремой (1.2.7).
Доказательство следствия (15) предоставляется читателю в ка-
честве упражнения.
3. ТЕОРЕМА О МАЛОМ КОЭФФИЦИЕНТЕ РОСТА ПО ПРИРАЩЕНИЯМ
Здесь мы докажем теорему, устанавливающую условия сущест-
вования, единственности, ограниченности и непрерывности решения.
1. Теорема. Рассмотрим систему с обратной связью, изобра-
женную на рис. 3.1 и заданную уравнениями (1.1) и (1.2). Пред-
положим, что для каждого Т множество Рт^е является полным
нормированным, т. е. банаховым пространством. Пусть Hi, Н%: Хе-+-
-+Хе. Пусть, кроме того, существуют постоянные числа yi и Та
такие, что для любого 7 и любых е Хе
2. 1(Д1В)г-(Д1Г)Н<Шт-ГН.
3. КТОт- (ДаГН^Шг- Гг|.
Тогда, если Т1У2< 1, то
(i) для любых их, и% е Хе существует единственное решение
ех,- yi, у% е Хе, которое можно построить методом последова-
тельных приближений;
(ii) отображение (ых, и%)*—е%) является равномерно непре-
рывным на множествах РтХехРтХ. и ХхХ\
(iii) если, кроме того, решение, соответствующее м1==иа = 0,
принадлежит X, то
Ui, и%&Х=$ ег, е% е X.
4. Комментарии.
(а) Если отображение Hi линейно, то предположение (2) пре-
вращается в следствие предположения (2.4). Действительно, если
для некоторого ух
IKHxDrl^TlUrll VT<=aT,
то
|[Я1(£-Ог1<Т11£г-Гг| vg,
(b) Теорема о малом коэффициенте роста по приращениям
позволяет ответить на вопросы о существовании, единственности,
ограниченности и непрерывной зависимости решения.
(с) Простым упражнением является доказательство того, что
из неравенств (2). и (3) вытекает неантисипативность отображе-
ний Ht и Я,.
3 ТЕОРЕМА О МАЛОМ КОЭФФИЦИЕНТЕ
55
5. Определение. Для заданного неантисипативного оператора
Ях: удовлетворяющего неравенству (2), точная нижняя
грань множества всех действительных чисел при которых (2)
все еще выполняется, называется коэффициентом роста по при-
ращениям оператора Обычно это число обозначают через у(Ях)
или просто через
Доказательство, (i) Из уравнений (1.1) и (1.2)
^2 = ^2 + [Hi (^i — Н2^2)],
откуда, выполняя операцию срезки, получаем
^2Т= ^2t + [^i (^i — Н2е2)]Т V7* е .
Учитывая, что операторы Нх и Я2 неантисипативны, выводим
уравнение вида ^2г = /(^2т) относительно е2Т\
е2Т — и%т + \Н 1 [щт — (Н2е2т)т]}т'
Функция f является сжатием пространства Рт%е- Действи-
тельно, для любых ТеоГ и любых е2т» е'ът из РтХеь учетом (2)
и (3) находим:
I {Hi[wir~ (^2e2r)r]}r~ {Н1[игт~ (Н2е'2т)т]}т\\
Y1II (^2^2Г)Г“~ (^2^2т)т || Т1?2 || ^2Г““ ^2Т |«
По условию Y1V2 < 1, следовательно, f является сжатием. Поэтому
при любых Т е и любых Ui, и2 е решение е2Т однозначно
определяется как элемент пространства Рт^е- То же самое можно
утверждать и о решении е1Г, поскольку из (1.1) и неантисипатив-
ности оператора Н2 следует, что
£ir == Uit — (Н 2е2Т)т-
(и) Для любого ТеоГ и любых (иь ц2), (и{, и2) ^ХехХе
существует единственное решение (е19 е2), (е'19 е2) е ХехХе. Кроме
того,
^iT — uit~ (Н2е2т)т> eir^Uvr — (Н2е2т)т-
Вычтем второе равенство из первого и вычислим нормы обецх
частей получившегося равенства. Тогда, используя неравенство
треугольника, получим:
IIeir — eir II II Wir — и'\т II + у2 II ^2Г — ^2т !•
Аналогичным образом:
II ^2Г—^2т || II и2т — ^2т I + Yi || е1Т — е{т !•
Из этих неравенств следует, что
в* l^ir“"^irl^]~i^(l|wir—Wirll + ^l ^2Г"“«27’|) УТеоГ*,
откуда вытекает справедливость утверждения (И).
56
ГЛ. 3. ОБЩИЕ ТЕОРЕМЫ
(iii) следует из (6) и соответствующего неравенства для es,
если в них подставить uj — и2 = 0.
Упражнение 1. Сформулировать и доказать следствие теоремы (1), анало-
гичное следствию (2.15) теоремы (2.1).
Упражнение 2. Рассмотрим систему, удовлетворяющую всем условиям тео-
ремы (1). Предположим, что иъ йь ui, й2<=Хе, однако щ—йх и иг — й2 при-
надлежат X. Показать, что е2 — е, е <5? и
—L^-CI «1 —Й11+У2|1«а-Й«!).
4. ОГРАНИЧЕННОСТЬ
Теоремы о малом коэффициенте роста и малом коэффициенте
роста по приращениям можно рассматривать, как две крайних
формы проявления факта ограниченности решения. В первой из
них предполагается лишь конечность коэффициентов роста опе-
раторов Ях н (см- (2-4) и (2.5)), а во второй теореме, наобо-
рот, вводятся чрезвычайно жесткие условия: коэффициенты роста
во приращениям тех же операторов должны быть конечны
(см. (3.2) и (3.3)). В этом разделе мы сформулируем и докажем
теорему, использующую предположения промежуточной степени
жесткости: мы наложим ограничения на композицию Я2Я2, кото-
рую можно, хотя и нестрого, считать «коэффициентом усиления
замкнутого контура».
1. Теорема. Рассмотрим систему, изображенную на рис. 3.1 и
заданную уравнениями (1.1) и (1.2). Предположим, что опера-
торы Я1 и Я2 неантисипативны, коэффициент роста у (Я2) и коэф-
фициент роста по приращениям у(Я2) ограничены, т. е. у(Ях)<
<оо и №)< оо. Тогда
(а) если существует е>0 такое, что1)
2. |(/ + Я2Ях)е|г^8|е|г Vee#„ VTedT,
то из («1, вытекает, что любое решение (е2, е2),
принадлежащее Х,хХе, также принадлежит ХхХ и для неко-
торого А<оо
3. Rd(I«11+1 «2|), t = l, 2, V«i, u2e<5f.
(b) Если («1, ы2) и (ех, е2) связаны неантисипативным отобра-
жением, переводящим ХхХ в ХхХ, с конечным коэффициентом
роста, то из (3) следует (2).
Доказател ьство.
(а) Рассмотрим некоторую пару воздействий (их, и^ХхХ
и соответствующее ей решение (е2, е2) уравнений (1.1) и (1.2)
такое, что elt ег е Хе. Тогда
вх+Я2Я1С1 = Ui — [Я2 (Я1Сх+и2) — Я 2Я х^х].
*) Для упрощения обозначений мы будем писать | и2 |г вместо | uiT |.
5. ТЕОРЕМА СУЩЕСТВОВАНИЯ И ЕДИНСТВЕННОСТИ
57
Применяя операцию срезки к обеим частям этого равенств^ и
учитывая, что оператор Рт линеен, получаем
Рт (/ + Я2Ях) ег = РгЫ1 - Рт [Н2 (Н& + и2) - НйН1е1].
Отсюда, поскольку у(//2)<°°, вытекает:
! (J + ei ||г «С | ui Jr + у (Нг) I и2 |г.
Учитывая предположение (2) и устремляя Т к бесконечности
в правой части этого неравенства, с помощью (1.8) приходим
к неравенству
8 1т I «11 + Т (Hi) || «2
Поэтому
5. klKyll«lll + yV(^2)S«2l,
т. е. ехе<5?. Так как e2 = u2 + ^i^i> то
6. IIM^WI + T^l^llwd + v Т(//2)||ив|].
L с о j
Таким образом, мы убеждаемся в справедливости (3), выбирая
в качестве k число, равное
тахЦ-1у(Я2), ly^), 1+|у(Я1)?(#.)]•
(Ь) Пусть и2 = 0, тогда для и, е X существует единственное
решение е,^Х такое, что (/ + Н2Н,)е, == их. Из (3) следует, что
у[(1 + Я2//х)-1] < оо. Поэтому для любых ТезГ
II Рте, || = | Рт U + Н2Н,Г' (/ + Н2Н,) е, || <
< Y [(/ + Н2Н,)-'] | Рт (/ + Н2Н,) е, |,
откуда вытекает неравенство (2).
Упражнение 1. Чтобы показать, что условие (2) тесно связано с Крите*
рием Найквиста, рассмотрим следующий частный случай. Пусть ux, е19 yt: R+->
->R, и2=0 и Н2 — тождественное отображение. Пусть Hie^g *elt где g &
е L1(R+), причем ее изображение по Лапласу g(s) является дробно-рациональ-
ной функцией, аналитичной при Res^O и стремящейся к нулю при |$|-►аэ.
Показать, что если диаграмма Найквиста функции g (т. е. отображение
(0 1—► g(/<o), со е Р) окружает критическую точку (—1,0) не менее одного раза,
то (2) не выполняется. (Указание: использовать представление Ях в про-
странстве состояний; выбрать подходящие начальные условия й экспонен-
циальное представление для ех (•).)
5. ТЕОРЕМА СУЩЕСТВОВАНИЯ И ЕДИНСТВЕННОСТИ
В этом разделе мы будем полагать, что of = R+. В самом
деле, вопросы существования и единственности для дискретного
случая в отличие от непрерывного случая никак не связаны друг
58
ГЛ. 3. ОБЩИЕ ТЕОРЕМЫ
с другом. Вместо решения в виде функции, отображающей !Р+ в V,
мы должны в каждый момент времени находить одну точку в V.
Пример такого решения для дискретного случая, когда
x(n) = f [х (n)] + u(n),
где х(п), и(п)ЕКл, f: КЛ->1РЛ, определяется теоремой (2.8.33).
Нам хотелось бы показать, что существование и единственность
решения (ех, е2) уравнений (1.1) и (1.2) в пространстве ХехХе
могут быть гарантированы при весьма умеренных предположениях,
которые обычно, намного слабее предположений, обеспечивающих
конечность коэффициента роста.
Для упрощения обозначений удобно считать пары (ux, и2)
и (ех, е2) элементами ХехХе и обозначать их через и и е соответ-
ственно. Аналогичным образом вместо отображений Hi и Н2 мы
будем рассматривать отображение
Н: ХехХе->ХехХе
вида
//: (ех, е2)*-*(Я2е2, -Н^).
Тогда уравнения (1.1) и (1.2) превращаются в
1. и = е-\-Не.
Кроме того, не должно возникнуть никаких недоразумений, если
мы заменим обозначение ХехХе символом X*.
В следующей теореме для оператора Н определяется условие
типа условия Липшица, выполнение которого обеспечивает сущест-
вование одного и только одного решения е^Х2е уравнения (1)
При любом и €= Х2е.
2. Теорема. Пусть отображение Н\ Xj-^X2e неантисипативно
и = R+. Обозначим через Pt проектор, определенный на X2
соотношением (1.4). Определим другой проектор:
3. Pf, д==Р/ + д — Ph А, / А ее R+.
Тогда, если для всех компактных интервалов 1 cz R+ существуют
числа y(Z)< 1 и А(/)>0 такие, что для любого t^ I и любых
е, удовлетворяющих равенству P(e = Pte\
4. нА. д(Яе-Яе')1К?1|Л. л(е-е')11
(здесь ради простоты записи мы не указываем на зависимость
чисел А и у от I) и если при любых t и А пространство Pt, ьХ\
является полным, то для любого и^Х'} уравнение и = е-\-Не
имеет одно и только одно решение.
Доказательство. Предположим, что мы вычислили неко-
торое решение для всех x^t (/^0), и покажем, что это реше-
ние может быть продолжено и притом единственным образом на
5 ТЕОРЕМА СУЩЕСТВОВАНИЯ И ЕДИНСТВЕННОСТИ
.69
все множество R+. Пусть / — компактный интервал, включающий
в себя t, причем множество / П (/, °о) непусто. Для чисел Д и у,
соответствующих выбранному /, введем обозначения:
5а. ёд = Р(, де = Pt, — Pte
и
5b. йд = Pt, &и.— Pt, &u — P tu.
Принимая во внимание свойство неантисипативности отображе-
ния Н, применим оператор Pt д к обеим частям уравнения и =
= е-}-Не:
6. ёд = йд — Pt, Ji (Р$ + ёд).
Уравнение (6) имеет вид ёд = /(ёд), поскольку йд задано зара-
нее, а Р& известно. Поэтому/: А, -> А. д^е-
Покажем, что / является сжатием пространства Pt, Дей-
ствительно, для всех ёд, ёд е Pt,
7. 5 f (ёд) - / (ёд) || = || Pt, д [Н (Pte +ёд) - Я (Pte’ + ёк)] 1
< Y (/) II А. д (ёд — ёк) || < V (/) || ёд — ёд ||.
(Здесь мы использовали свойство линейности Pt, д, соотношения
(5), (6) и неравенство (4).) Из (7) следует, что / представляет
собой сжатие (полного) нормированного пространства Pt, &<£*, так
как по условию у (/) < 1. Таким образом, итеративный процесс
ё<с + 1> = /(ё(дл’), n = 0, 1, 2...............
начатый из произвольного начального приближения ёд', сходится
к единственному решению на интервале (t, /-|-Д]. Начиная этот
процесс при / = 0 и повторяя его шаг за шагом, изменяя t, мы
построим единственное решение уравнения (1) на интервале (0, оо).
8. Следствие. Предположим, что в дополнение к условиям
теоремы (2) отображение Н линейно. Тогда с учетом (5) — (7) усло-
вие (4) приобретает следующий вид: для любого компактного
интервала существуют числа у(/)<1 и Д(/)>0 такие, что
8а. | Pt, ьНёь | у Ц ёд ||
для всех t е / и для всех ёд е Pt,
Доказательство вытекает непосредственно гз неравенства (7).
9. Комментарии, (а) Наиболее важным примером технической
системы, в которой это условие не выполняется, является вибра-
ционная еледящая система [46]. В простейшем случае Я1 —инте-
гратор (т. е. подсистема с передаточной функцией 1/s), Нг — стати-
ческая нелинейность с характеристикой <р(е2)=1 при е2^0
и ф(еа) = —1 при е2<0.
60 ГЛ. S. ОБЩИЕ ТЕОРЕМЫ
(Ь) Одним из основных моментов приведенной выше теоремы
является правильное определение величин интервалов квантования
по времени. Для любого выбранного компактного интервала /
неравенству (4) при всех t е I должны удовлетворять одни и те же
числа у (I) и Д(/). Решение строится на последовательности
интервалов длиной Д(/)>0; поэтому в конечном счете процесс
распространится вне компактного интервала I. Тогда выбирается
новый компактный интервал, например для которого существуют
свои числа у(/')иДи )и т- Д. Ясно, что такой процесс никогда
не завершится, так как, согласно условиям теоремы, для любого
компактного интервала / существует число Д(/)>0, «работаю-
щее» при всех t е /.
(с) Если отображение Н стационарно, то можно выбрать после-
довательность компактных интервалов, каждый из которых
получается сдвигом предыдущего, и использовать везде одни
и те же числа f и Д. В некоторых случаях, связанных с неста-
ционарными системами, при продолжении решения вправо по оси
времени величина Д (/) должна выбираться все меньше и меньше,
чтобы в (4) выполнялось условие у(/)<1. В этих случаях не
существует единственного числа Д, «работающего» при всех
t eR+.
Упражнение 1. Рассмотрим следующий частный случай, когда
(а) контур обратной связи разомкнут, т. е. Я2 отображает в нулевой
вектор;
(Ь) «1 (0 — ^1 (0, i/i (/) е Рл, и ( ) —регулярная функция (см. Приложе
ние А. 1.2);
(с) определено дифференциальным уравнением t),
где функция f непрерывна на множестве РлхРлХР+.
Наложить ограничения на функцию f так, чтобы вход-выходное отобра-
жение Ui ।—► Ух удовлетворяло неравенству (4).
Упражнение 2. Пусть функции иъ еъ отображают Р+ в R. Примем, что
Допустим, что (Н^) (/) = ф (еъ /), где функция ф непрерывна, и для
некоторого у <, оо выполняется условие
|ф(о, /) —Ф(о', 01 i я —°' Vo, o'eR, t •—► ф (0, t) e
Пусть, кроме того, (H2e2) (0 = (g ♦ е2) (0, где g е= L* (R+). Показать, что для
любого е L* существует одно и только одно решение ех и е2 е LJ0.
(Указание: рассмотреть уравнение (0 — ut (t) — (g ♦ еа) (0, где е8 (0 =
иФк1(0» 0- Принять во внимание, что функция /: t н-► j | g(x) | dx непре-
рывна, причем f (0)«ж0.)
Упражнение 3. Рассмотрим уравнение
10. а (0 — и (0 + j 6 (t—т) е (т) dx,
где и: R+^R*, для некоторого ре[1, оо] и G: R+->Rnxn, причем
все элементы О принадлежат LJ. Показать, что уравнение (10) имеет одно
и только одно решение е(«)еЬ^для каждого ue-LpM. (Указание:
6. ТЕОРЕМА О ПРЕОБРАЗОВАНИИ КОНТУРА
61
t
функция 11—► ! G (0 | принадлежит пространству L*; функция 1»—► | Q (т) | dr
непрерывна, монотонно возрастает и равна 0 при /«=0.)
Упражнение 4. Рассмотрим уравнение
t
11. е (0 = и (/) + j f (т, е (т), и (т)] dr, t 0,
где и: R+ —Rn, и eL“, функция f: R+х Рл X Рл-> 1РЛ непрерывна и удовлет-
воряет условию Липшица, т. е. существует число k е R+ такое, что
IW 5, П)—f 5', П)! ^k\g-Г ; y/eR+, у£, Г, ПеРл-
Показать, что уравнение (11) имеет одно и только одно решение для
каждого и е
6. ТЕОРЕМА О ПРЕОБРАЗОВАНИИ КОНТУРА
Сначала приведем два поучительных упражнения.
Упражнение 1. Пусть Нг и /( — отображения пространства в
(Отметим, что мы не предполагаем, что отображения Нх и К линейны.) Тогда
(/Ч-К/Л)*1: в том и только том случае, когда (I
Хе -> Хе. (Необходимое условие очевидно. Для доказательства достаточного
условия рассмотреть равенство /— КНХ (J + KН^1 = (J+KHJ'1.)
Упражнение 2. Пусть Et F и G—линейные пространства. Пусть g: G-+E,
a fi и отображают Е в F. Показать, что
(А +Аг) °g^fi g+fi*g-
(Указание: согласно определению (Д +/а) (х) -»А (x)+f2 (*)•) Показать, что
если £«»F«=G, то для того, чтобы
g• (fi“g ° /1+g °
функция g должна быть, за исключением тривиальных случаев, линейным
отображением пространства Е в самое себя.
Рассмотрим систему S с обратной связью, изображенную на
рис. 3.1 и заданную уравнениями
1. Ui ® 4“ //2g2,
2. w2 = e2 — Нхеъ
Попытаемся преобразовать заданную систему S с обратной связью
в другую систему SK с обратной связью так, чтобы система 5
была «устойчивой» тогда и только тогда, когда «устойчива» систе-
ма S#. Мы покажем, что применение к системе S# некоторых
теорем таких, как теоремы (2.1) и (3.1), позволяет получить
интересные условия устойчивости для системы S. Структура
системы S# приведена на рис. 3.3 и определяется ходом доказа-
тельства следующей теоремы.
3. Теорема. Пусть ff19 Н2, К и (/ + Kffi)-1 отображают
в Тогда, если отображение К линейно, то
62
ГЛ. 3. ОБЩИЕ ТЕОРЕМЫ
(а) если функции мх, u2, е±, е2 принадлежат Xt и являются
решениями S, т. е. уравнений (1) и (2), то функции их — Ки2,
= + КНi)elt е2 также принадлежат пространству <5?, и
представляют собой решения Sk, т. е. уравнений (5) и (7)
(см. ниже);
(Ь) и наоборот, если функции «х — Ки2, и2, т)Х, е2 принадле-
жат и являются решениями Sk, то функции «х, и2, ех =
= (7 + КН^хц, е2 также принадлежат Хе и представляют собой
решения S;
Рис. 3.3.
(с) утверждения (а) и (Ь) останутся справедливы и в том
случае, если Хе везде заменить на
(d) если и2 = 0, то утверждения (а), (Ь) и (с) будут выпол-
няться и в тех случаях, когда отображение К нелинейно.
Доказательство. Поскольку отображение К линейно, то
из (2) следует, что
4. Ke2 = tf(u2 + tfxex) = Kw2-]-/<tfxex.
Подставляя (4) в (1), находим, что
ех = «1 — (Н2 — К) е2— Ки2 — КН^
и
5. т]х = (/ 4- КН^ вх = (w2 — Ки2) — (Н2 — К) в2.
Выражая ех через т]Х:
6. e^U + KHi)-1^,
из (2) получаем:
7. е2 — и2-]-Н1(1 + КН1)-1‘Г]1.
Уравнения (5) и (7) задают систему SK, изображенную на рис.
3.3; действительно, ег связано с цх соотношением т]х = (J + KHi) ех
(см. (5)). Утверждение (а) вытекает из способа вывода соотноше-
ний (5) и (7) из (1) и (2). Утверждение (Ь) доказывается просле-
живанием тех же построений в обратном направлении с исполь-
зованием упражнения 1. Утверждение (с) очевидно. И, наконец,
7. ^-УСТОЙЧИВОСТЬ
63
в справедливости (d) легко убедиться, если принять во внимание,
что свойство линейности отображения К используется лишь
однажды, а именно, при получении равенства (4).
8. Комментарий. Внимательное изучение приведенного доказа-
тельства позволяет убедиться, что предположение о том, что
отображение (/ + Л7Л)-1 определено в Хе, вовсе не является
необходимым. Действительно, мы пользовались лишь тем фактом,
что для системы с обратной связью, изображенной на рис. 3.3,
функции г]1, е2 и уг принадлежат Хе для любой пары входных
воздействий (ub и2) из XI, или, иначе говоря, что система уравнений
Ц1 = (wi — Ли2) — (Н2 — К) е2,
е2 = и2 + уъ У1 = (гц - Куд
имеет единственное решение (rib е2, ух), принадлежащее
ХехХехХе.
Упражнение 3. Применить теорему о преобразовании контура системы
рис. 3.3 к 2п-полюсной системе, изображенной на рис. 3.2.
7. «^-УСТОЙЧИВОСТЬ
В дальнейшем мы будем рассматривать лишь системы, заданные
уравнениями (1.1) и (1.2) и имеющие вид, приведенный на рис.
3.1. Отметим, что теоремы об устойчивости, такие как теорема (2.1),
теорема (3.1), упражнение 1 из раздела 3 и теорема (4.1), гаран-
тируют не только принадлежность функций е2, г/х, у2 к про-
странству X при условии, что «1, u2 е X, но также существование
постоянного числа k такого, что
1. ki II <И “ill+ 11 «2II). i = 1.2, |
2. Ш^(||«1Н11«2||). i = l, 2 J VU1’ U2^X-
При этом важно иметь в виду, что число k не зависит от их
и и2. Поэтому можно ввести следующее определение.
3. Определение. Систему, заданную уравнениями (1.1) и (1.2),
назовем X-устойчивой, если существует постоянное число &<оо
такое, что выполняются неравенства (1) и (2).
В этом смысле теорема о преобразовании контура (6.3) содержит
условия, выполнение которых позволяет утверждать, что система S
«^-устойчива тогда и только тогда, когда ^-устойчивой является
система SK. Таким образом, теорему (6.3) можно назвать теоре-
мой «^-устойчивости.
Связь между устойчивостью и неустойчивостью. Полагая, что
термин «неустойчивость» определен естественным образом, приведем
следующее утверждение, содержащее условия, при нарушении
которых система становится «неустойчивой».
4. Утверждение. Пусть отображение Н: Х2е->Х*е и (/-[-Я)’1:
X9-+XI неантисипатцвны. Тогда система с обратной связью
64
ГЛ, 3. ОБЩИЕ ТЕОРЕМЫ
(I -\-Н)е = и «устойчива» в том смысле, что обладает следующими
свойствами:
(а) функция е определяется через функцию и с помощью
неантисипативного отображения, переводящего в <8?2;
(Ь) существует такое число у<оо, что для всех нера-
венство выполняется в том и только том случае, когда
отображение (/4-Я) обратимо, причем обратное отображение
(/4-Я)-1 переводит X2 в X2, обладает свойством неантисипатив-
ности и имеет конечный коэффициент роста.
Доказательство. Достаточность. Очевидно.
Необходимость. Отображение по условию неантисипа-
тивно и переводит и е X2 в некоторое е е X2.
Связь между устойчивостью и неустойчивостью можно пояснить
с помощью дихотомического дерева; для выделения шагов дихо-
томии мы пометим их последовательностями нулей и единиц.
0: Отображение (/ 4- Я)"1 не может быть определено во всем
пространстве X2. Тогда задача определения устойчивости
системы не может быть поставлена, поскольку для некото-
рого и е X2 нельзя вычислить е, т. е. уравнения не имеют
решения при некотором и е X2.
1: Отображение (/4-Я)-1 определено во всем пространстве J?2.
'1.0: ^ — строгое подмножество (/4-Я)-1[<5?г]. Тогда для неко-
торого и е X2 решение е — (/ 4-Я)-1 и не принадлежит X2.
1.1: (l + Hj-^X^czX2.
1.1.0: у[(/4-Я)~1] = оо. Тогда существует последовательность
{wj а X2, которой соответствует последовательность
{е,}с:Х2 для всех I, однако || ег |/| щ | -* оо.
1.1.1: у[(/4-Я)"1]<оо.
1.1.1.0: Отображение (/4-Я)-1 антисипативно.
1.1.1.1: Отображение (/4-Я)-1 неантисипативно.
^-устойчивость имеет место лишь в случае 1.1.1.1. В главе 5
мы рассмотрим некоторые классы неустойчивых систем с обратной
связью, соответствующих случаям 1.0 и 1.1.1.О.
8. ОБЩИЙ ВИД УРАВНЕНИЯ ЗАМКНУТОЙ СИСТЕМЫ
Если отображение Ях линейно, а отображение Я2, быть может,
нелинейно, то возможно два способа установления связи между мх
и yi. Такая гибкость очень удобна для различных вычислений.
1. Теорема. Рассмотрим систему, изображенную на рис. 3.1.
Пусть Я1, Я2, (/4-ЯхЯз)-1, (/4-Я2Я1)"1 являются отображениями
Хе в Хе. Тогда, если к2 = 0 и отображение Ях линейно, то
2. yi = HX(I + Н.Н^ иг = (1 + HtH^ H1Ui.
библиографический комментарии 88
Доказательство.
3. Ях + = /Ях + (ЯХЯ2) Ях = (/ + ЯХЯ2) Ни
где мы сначала использовали свойство ассоциативности произве-
дения двух функций, а затем определение суммы двух функций.
Кроме того, если отображение Ях линейно, то
4. Ях + ЯхЯ2Ях = Я1(/ + Я2Ях).
Объединяя (3) и (4) в одно равенство, умножая обе его части
слева на (/ + ЯхЯ2)-1 и справа на (/-j-Я^х)"1, получаем (2).
Упражнение. Рассмотрим систему с обратной связью, изображенную на
рис. 3.1, где «х, «х. Vi- R+ —R", u2(t)=0 для любых t. Предположим, что
подсистема Hi состоит из последовательного соединения заданного «объекта» Р
и «компенсатора» G, т. е. H^PG. Допустим, что Р и G линейны. Поскольку
5. Vi^PGfJ + HtPGY-iui,
рассмотрим «сравнивающую» систему, состоящую из «объекта» Р и последова-
тельно включенного с ним «компенсатора» Go. Обозначим через у0 выходной
сигнал разомкнутой системы:
6. yo^PGoii.
Выберем Go следующим образом:
7. Go=G(/ + /72P„G)-4
Тогда при Р = Рп Уо = У1 Для всех и. Допустим теперь, что Р изменяется от
Рп до Р = Ря-|-ДР. В этом случае, согласно (6),
Ду0 = ДРО0и.
(а) Показать, что
8. Д4Гх = (/+Р6Я2)-1Д4г0.
(Ь) Доказать справедливость (8) при малых ДР, вычисляя производные
в функциональных пространствах. (Указание: принять во внимание, что
PG (/ + Я2РО)-! = (/ + РОЯ»)’1 PG.)
9. Комментарий. Формула (8) очень важна, поскольку из нее
следует, что если коэффициент усиления контура PGH2 велик, то
изменение Р в заданных пределах ДР вызывает в замкнутой
системе (5) значительно меньшие изменения выходного сигнала,
чем в разомкнутой системе (6). Это свойство является одним из
основных в технических приложениях систем с обратной связью.
БИБЛИОГРАФИЧЕСКИЙ КОММЕНТАРИЙ
Общая постановка задачи заимствована у Сандберга [75—77, 80]
и Цеймса [110—112]. Подробное исследование свойства неансипа-
тивности можно найти у Сакса [70, 71]. Теорема о малом коэф-
фициенте роста рассматривалась многими авторами для различных
целей и с различной степенью общности. Наиболее общие форму-
лировки можно найти в работах Сандберга [80] и Цеймса [112].
3 Ч. Дезоер, М. Видьясагар
66 ГЛ. 3. ОБЩИЕ ТЕОРЕМЫ
Теорема существования и единственности представляет собой
формализацию обычного доказательства, применяемого к инте-
гральным уравнениям Вольтерра второго рода (см., например,
работу Цеймса [ПО]). Теорема о преобразовании контура имеет
длинную историю. Она была известна и использовалась Сандбер-
гом [74, 80] и Цеймсом [112]; установление избыточности условия
линейности оператора К при и2 = 0 принадлежит Сандбергу [81].
Уравнение (8.8) хорошо известно в теории чувствительности [65].
Результат из раздела 2, связанный с доказательством ограничен-
ности решения, принадлежит Уиллемсу [103].
Глава
ЛИНЕЙНЫЕ СИСТЕМЫ
0. ВВЕДЕНИЕ
Большая часть результатов теории нелинейных систем осно-
вана в той или иной степени на свойствах линейных систем с
обратной связью. Поэтому важно развить результаты теории
линейных систем с обратной связью и представить их в такой
форме, чтобы они стали легко применимыми и в нелинейном слу-
чае. В этом и заключается основная цель настоящей главы.
В дальнейшем мы будем предполагать, что входные воздействия
и (•) и реакции у (•) рассматриваемых линейных систем являют-
ся элементами пространства Кл. При п = 1 мы будем называть
эти системы одноконтурными или системами с одним входом и
одним выходом. В случае п> 1 системы будут называться мно*
гоконтурными или системами с п входами и п выходами. Везде,
где только возможно, теоремы формулируются для многоконтурных
систем; результаты, специфичные для одноконтурных систем, при-
водятся главным образом для того, чтобы продемонстрировать
отличия, свойственные многоконтурным системам.
В первых трех разделах рассматриваются исключительно ста-
ционарные системы с сосредоточенными параметрами, т. е. сис-
темы с дробно-рациональными передаточными функциями. В раз-
деле 1 основное влияние уделяется выявлению различий в свойствах
одно- и многоконтурных систем (см. теорему (1.12)). В разделе 2
для того же класса систем развивается метод разложения для
получения необходимых и достаточных условий устойчивости
многоконтурных систем и приводятся основные понятия, которые
понадобятся в дальнейшем при изучении многоконтурных систем
с распределенными параметрами. Раздел 3 посвящен системам •
динамической обратной связью и исследованию вопроса о сокра-
щении нулей и полюсов.
В разделе 4 мы обращаемся к системам с распределенными
параметрами и определяем для них необходимые и достаточные
условия устойчивости, которые будут использованы в следующих
главах книги. Здесь же описаны некоторые важные идеи — такие,
как метод разложения на взаимно псевдопростые справа множи-
тели, и, кроме того, приведены исчерпывающие результаты для
особо распространенного на практике класса многоконтурных
систем, являющихся устойчивыми, хотя их передаточные функции
имеют конечное число полюсов в замкнутой правой полуплоскости.
Графический критерий устойчивости систем о распределенными
3*
68 ГЛ. 4. ЛИНЕЙНЫЕ СИСТЕМЫ
параметрами изложен в разделе 5. Здесь один за другим рассмат-
риваются все более общие случаи; наиболее общий результат
приводится без доказательства, поскольку доказательство потре-
бовало бы слишком сильного углубления в теорию ’ почти-перио-
дических функций. В разделе 6 развиваются основные результаты
применительно к дискретным системам; особое внимание уделяется
их сравнению с аналогичными результатами, полученными
для непрерывных систем. В разделе 7 представлены важнейшие
результаты, относящиеся к линейным нестационарным системам,
в том числе необходимые и достаточные условия устойчивости
«разомкнутой» системы и теоремы о процессах как в непрерывных,
так и в дискретных системах.
В разделе 8 с помощью методов Ляпунова вычисляются оценки
для скорости изменения параметров нелинейной системы, при
которой вся система сохраняет экспоненциальную устойчивость,
если система с «замороженными» параметрами экспоненциально
устойчива. Решение задачи в такой постановке удобнее, чем
сведение ее к хорошо известным условиям для линейного случая.
И, наконец, в разделе 9 решается задача линеаризации: при
каких условиях линеаризированная модель нелинейной системы
дает правильные результаты на всем множестве R+? Среди других
вопросов, рассматриваемых здесь, приводятся результаты, доказы-
вающие справедливость использования эквивалентных схем для
анализа и синтеза систегл и применения вариационных уравнений
в задачах управления и оптимизации.
1. ЛИНЕЙНЫЕ СИСТЕМЫ С ОБРАТНОЙ СВЯЗЬЮ
С ДРОБНО-РАЦИОНАЛЬНЫМИ ПЕРЕДАТОЧНЫМИ ФУНКЦИЯМИ
Обозначения:
R [s] — коммутативное кольцо многочленов (комплексной) пере-
менной s с коэффициентами из поля R. Можно показать, что R [s]
является кольцом главных идеалов.
R (s) — (коммутативное) поле дробно-рациональных функций
переменной s о коэффициентами из поля R.
R"14? [s] (Rwx? ($))—класс всех (т X ^-матриц в элементами из
кольца R[s] (из поля R(s) соответственно). Если W (s) е Rmx? [s],
то матрица N ($) называется многочленной.
С —расширенная комплексная плоскость, т. е. комплексная
плоскость с бесконечно удаленной точкой.
Мы рассмотрим два случая: в первом из них будем изучать
линейную стационарную систему с обратной связью с одним вхо-
дом и одним выходом с коэффициентом обратной связи f, при-
чем прямой ветви системы соответствует передаточная функция
g (s) е R (s); во втором случае будет исследоваться линейная
стационарная система с обратной связью с п входами и п
1. ДРОВНО-РАЦИОНАЛЬНЫЕ ПЕРЕДАТОЧНЫЕ ФУНКЦИИ
69
выходами, где ветвь обратной связи определяется матрицей
/?еК',хл, а прямой ветви соответствует передаточная функция
G(s) e|R"x"(s). Структурная схема системы изображена на рис. 4.1,
где через и обозначено входное воздействие, через у — выходной
сигнал, а через е — сигнал ошибки. Уравнения системы имеют
вид:
1. y = G*e,
2. е = и — Fy,
3. у (s) = G (s)[I + F d(s)]->« (s), у (s) = -М- й (з),
1+/£($)
4. A(s)=6(s)[Z + Fd(s)]-\ Й(8) = -^-.
l+fe(s)
Мы будем говорить, что передаточная функция & ($) е Клхл (s)
[g (s) е R (s)] является правильной (строго правильной) в том
и только том случае, когда элементы
G(s) [функция g ($)] ограничены при
s = оо (стремятся к нулю при $->оо,
соответственно).
5. Определение. Дробно-рацио-
нальная передаточная функция Н ($)
называется экспоненциально устойчи-
вой в том и только том случае,
—©-
Рис. 4.1.
когда она правильна и все ее полюсы имеют отрицательные дей-
ствительные части.
6. Утверждение. Если передаточная функция Н (s) е Клхп (s)
экспоненциально устойчива и строго правильна, то соответствующая
ей импульсная характеристика Н (t) со своей производной Й (f)
обладает следующими свойствами:
(а) существуют постоянные числа hm>Q и а>0, зависящие
от функции Н, такие, что
7.
(b) существуют постоянные числа /^>0 иа>0 такие, что
+ V^O,
где через | Н (/) | обозначена норма матрицы Н (t) е Кяхп, порож-
денная некоторой выбранной нормой в пространстве Rn.
Доказательство. Утверждение легко доказать, разложив
элементы Й (s) на простые дроби.
Основные вход-выходные свойства систем е экспоненциально
устойчивыми передаточными функциями мы сформулируем с помо-
щью следующей теоремы.
70
ГЛ. 4. ЛИНЕЙНЫЕ СИСТЕМЫ
9. Теорема. Пусть передаточная функция замкнутой системы
Н (s) е (Рлхя (s) экспоненциально устойчива и строго правильна.
Тогда
(а) для любого минимального представления функции Й (s)
(т. е. любого минимального представления системы в простран-
стве состояний х = Ax-i-Ви, у = Сх) точка равновесия х = 0
является экспоненциально и равномерно (по t) устойчивой в целом;
(Ь) если ueLJ, то у = Н * и е Lln у Lh, функция у
абсолютно непрерывна и y(t)-*-0 при /->оо;
(с) если ue Ln, то у = Н * и е Ln П У L„, функция у
непрерывна и у(/)-*-0 при /-»-оо;
(d) если u^L^, то у = Н *u<=L™, y^L^ и функция у
равномерно непрерывна;
(е) если ueL” и u(t)-+-um при /->оо, где ит — постоянный
вектор из R”, то у (t)Й (0) ит при /->оо, причем сходимость
является экспоненциальной;
(f) если u^Ln и 1<р<оо, то y = H*u^Lpn и i/eZ-S.
Доказательство вытекает из результатов, изложенных в При-
ложении С. Асимптотика (пункт е) следует из свойств преобра-
зования Лапласа.
Упражнение 1. При использовании z-преобразования вместо преобразова-
ния Лапласа мы будем называть дробно-рациональную передаточную функцию
Й (г) экспоненциально устойчивой в том и только том случае, когда она яв-
ляется правильной (ограниченной на бесконечности) и модули всех ее полюсов
меньше 1 (т. е. полюсы принадлежат открытому единичному кругу). Сформу-
лировать и доказать неравенство, соответствующее неравенству (7), и теорему,
аналогичную теореме (9).
Рассмотрим теперь, как связаны свойства передаточной функ-
ции G(s) разомкнутой системы с расположением полюсов переда-
точной функции замкнутой системы. Эта связь очень важна для
решения вопросов устойчивости.
10. Утверждение. Пусть функции Й (s), G(s) принадлежат
(s) и связаны соотношением (4). Тогда
11. Z-F^(s) = [/ + FG'(s)]-1.
Если, кроме того, detF=#O, то рс е © является полюсом Н (s)
тогда и только тогда, когда рс есть полюс [/ -f-FG(s)]-1.
Доказательство. Соотношение (11) легко получаете я в ре-
зультате соответствующих преобразований равенства (4). Вторая
часть утверждения вытекает из (11), поскольку detF#=O.
12. Теорема. Пусть g (s) е R (s) и (j (s) e R"*'’ (s). Обозначим
через © расширенную комплексную плоскость. Кроме того, будем
полагать, что h (s) и Й (s) определены соотношениями (4). Тогда
1. ДРОБНО-РАЦИОНАЛЬНЫЕ ПЕРЕДАТОЧНЫЕ ФУНКЦИИ
71
(i) рс е © является полюсом й (з) тогда и только тогда, когда
рс <= © — нуль функции 1 + fg (s);
(ii) если рсе© — нуль функции det [/ 4- FG (s)], то рсеС —
также полюс Й (з) (обратное утверждение неверно);
(iii) если рсе© —полюс Й (з), то рс является нулем функции
det [/ + FG (s)], либо полюсом G (з);
(iv) если функция G(s) экспоненциально устойчива, то функ-
ция Н (s) также экспоненциально устойчива тогда и только тогда,
когда det [/ 4- FG (з)] не имеет нулей на бесконечности и, кроме
того, все нули этой функции имеют отрицательные действитель-
ные части.
13. Замечания.
1. Отметим, что мы нигде не предполагали, что функции g (s)
и G(s) правильны.
2. В теореме (12) впервые в книге использовалось понятие
расширенной комплексной плоскости. Сохранить корректность
наших рассуждений без этого понятия невозможно по следующей
причине: если функция Й (s) имеет полюс в точке з = оо (что
эквивалентно неправильности Н (з) или неограниченности Й (з) на
бесконечности), то система будет вырабатывать неограниченные
выходные сигналы под действием некоторых ограниченных воз-
действий. Например, если f=l ug(s) = — s/(s-f-1), то fi(s) = — s.
При этом ограниченное воздействиеsin (/а) вызове? появление
неограниченно возрастающего сигнала реакции t 2t cos (Р).
Таким образом, согласно (i) и (ii) при 14- fg (со) = 0 (или
det [/ 4- FG (оо)] = 0) замкнутая система не является ^-устой-
чивой.
3. Очень важно иметь в виду, что множество полюсов функ-
ции Н (з) в © может быть «шире» множества нулей функции
det[/4*(s)] в ©• Например, пусть F=/ и
74-FG(s) = diag[s, 1/s, (з-1)/(з4-1), (з-)-l)/(s- 1)].
Тогда det[/-]-G(s)] = 1 при любых и
[/4-G(s)]-1 = diag[l/з, з, (s4-l)/(s- 1), (s —l)/(s4-1)].
Поэтому согласно (10) функция Й (з) имеет полюсы в точках
8 = 0, —1, 1, оо, хотя det[/4~G(s)J ообще не имеет нулей.
14. Пример. Рассмотрим простой пример, когда функция G(s)
правильна и стремится к 0 при з->оо. Пусть F = I и
Г 2s 1 1
<7(0- .
72
ГЛ. 4. ЛИНЕЙНЫЕ СИСТЕМЫ
Тогда
[Z + FG(s)]-i =
S— 1
Г=н
2
з+1
1 “I
s+l
Sa+ 1
S2—1 .
/7(s) =
~ 2
s+l
2
Ls+i
i
s+l
1_____1
s+l S— 1 -
И
det[Z + d(s)]=|±l.
Поэтому det [7 -|- G (s)] не имеет нулей ни в замкнутой правой
комплексной полуплоскости, ни на бесконечности; <j(s) имеет
полюс второго порядка $ = 1; det [7 + 6 (s)] имеет полюс первого
порядка s=l; Н ($) имеет полюс первого порядка s=l. Следо-
вательно, замкнутая система неустойчива, несмотря на то, что
функция det [7 4-G(s)] не имеет нулей в замкнутой правой полу-
плоскости и равна 1 на бесконечности.
Доказательство теоремы (12).
(i) Заметим, что если р0 — полюс функции f (s), то |g(s)|->oo
при s->p0. но тогда, согласно (4), й(з)->1 при s-»-po. Поэтому
дробно-рациональная функция 4(s) может иметь полюс в точке
рс еС только в одном-единственном случае, а именно, при 1 +
+ fj?(pc) = O. И наоборот, если 1 4- fg (рс) = 0, то числитель пра-
вой части соотношения (4) £>(s)->—1 при s->pc; следовательно,
дробь (4) в точке рс несократима, и рс является полюсом функ-
ции ft(s).
(ii) Согласно условию теоремы
det[/ + F&(pc)] = O.
Для доказательства методом «от противного» допустим, что
15. функция [7 + FG (s)]-1 ограничена в некоторой окрестности
точки рс.
Тогда функция
s det {[7 4- F6 (s)]"1} = {det [7 + FG (s)]}-1
также ограничена в окрестности точки рс, что противоречит исход-
ному предположению! det [7 + FG (рс)] = 0. Поэтому, в силу соот-
ношения (11), функция I — Ftf(s) имеет полюс в точке рс по-
следовательно, Й (s) также имеет полюс в точке рс.
(iii) вытекает из (10) и правила Крамера.
(iv) Необходимость. По условию функция Н (s) экспоненци-
ально устойчива, т. е. правильна и не имеет полюсов в замкну-
той правой полуплоскости. Тогда, согласно (iii), функция
det [7 + FG (s)] не может иметь нулей ни на бесконечности, ни
в замкнутой правой полуплоскости.
2. УСЛОВИЯ УСТОЙЧИВОСТИ: МЕТОД ФАКТОРИЗАЦИИ
73
Достаточность, Принимая во внимание условия, наложенные
на функции G(s) и det [/-[-FG(s)], из (iii) выводим, что все по-
люсы функции Й ($) конечны и имеют отрицательные действи-
тельные части.
Упражнение 2. Сформулировать теорему, аналогичную теореме (12), для
случая применения г-преобразования.
Упражнение 3. Привести пример, когда матрица F вырождена и утвер-
ждение, обратное пункту (ii) теоремы (12). неверно. (Например, F = diag(l,0);
G(s) = diag[(s+l)-i, (s— l)-i] )
2. НЕОБХОДИМЫЕ И ДОСТАТОЧНЫЕ УСЛОВИЯ УСТОЙЧИВОСТИ:
МЕТОД ФАКТОРИЗАЦИИ
В этом разделе мы выведем необходимые и достаточные усло-
вия устойчивости системы с обратной связью, которой соответ-
ствует передаточная функция1)
1. //(s) = G(s)[/4-FG(s)]-1,
где G ($) е Клхл (s) и F еРлхл. Система изображена на рис. 4.1.
Для системы с одним входом и одним выходом проблема устой-
чивости решается тривиально, поскольку, если /=/= 0, то функция
la. h (s) = . f <
l+fe(s)
является экспоненциально устойчивой тогда и только тогда, когда
l+/g(s) не имеет нулей при Res^O, включая точку s = oo.
Пример (1.14) показывает, что очевидное распространение этого
результата на систему с п входами и п выходами приводит к оши-
бочному выводу. С другой стороны, если представить дробно-ра-
циональную функцию g(s) в виде отношения n(s)/d(s) взаимно
простых многочленов п($) и d(s), то, как мы знаем, функция
h(s) вида (1а) экспоненциально устойчива тогда и только тогда,
когда многочлен d(s)+fn(s) не имеет нулей в замкнутой правой
полуплоскости.
Здесь мы попытаемся вывести аналогичный критерий для си-
стемы с и входами и и выходами. Для этого необходимо на-
учиться раскладывать дробно-рациональную функцию G(s) в про-
изведение N (s) D’1 (s) многочленных матриц N (s) и D ($), взаимно
простых в некотором смысле. Тогда функция Н (s) будет экспо-
ненциально устойчивой в том и только том случае, когда много-
член det [D (s) + FN ($)] не будет иметь нулей в замкнутой правой
полуплоскости.
х) Поскольку в этом разделе мы будем иметь дело только с передаточ-
ными функциями, мы опустим значок <А> везде, где он используется для обо-
значения преобразования Лапласа. (Даже самая правильная система обозна-
чений время от времени с необходимостью оказывается громоздкой!)
74
ГЛ. 4. ЛИНЕЙНЫЕ СИСТЕМЫ
2. 1. Факторизация
Пусть матрицы N (s) и D (з) принадлежат 1РЛХЛ [з]. Назовем
многочленную матрицу Д общим правым делителем матриц N
и D в том и только том случае, когда существуют многочленные
матрицы и Dr такие, что
2. М = АГХД и D = DXA.
Отметим, что все матрицы из равенств (2) принадлежат Клхл[з];
поэтому, в силу (2), многочленные матрицы N и #ХД равны при
всех з е 0. То же можно утверждать и относительно матриц D
и РХД.
Если Р, Q, R е Rnx" [з] и P = QR, то говорят, что матрица R
является правым делителем матрицы Р, а матрица Р кратна
слева матрице R.
Матрица Д е Рлхл [з] называется наибольшим общим правым
делителем матриц N и D, принадлежащих Клхл[з], в том и только
том случае, когда
(а) матрица Д —общий правый делитель матриц N и D;
(Ь) матрица Д кратна слева каждому общему правому дели-
телю матриц N и D.
Квадратная матрица с элементами из |R[s] называется унимо-
дулярной тогда и только тогда, когда ее определитель равен не-
нулевому действительному числу. В силу правила Крамера, мат-
рица, обратная унимодулярной, принадлежит Клхл[з], т. е. является
многочленной матрицей. В общем случае матрица, обратная мат-
рице из 1РЛХЛ [s], принадлежит 1РЛХЯ [з], но вовсе не всегда Клхл (з).
Если многочленная матрица Д, наибольший общий правый
делитель многочленных матриц N н D, унимодулярна, то говорят,
что матрицы N и D взаимно просты справа. Взаимно простые
слева матрицы и наибольший общий левый делитель определяются
аналогичным образом.
3. Теорема факторизации. Пусть элементы (дхт)-матрицы
Н (з) принадлежат IR (з). Тогда существуют две многочленные
матрицы N(s) и D(s) такие, что
4. /7 (з) = АГ (s) D-1 (s) Vs е С,
причем N (з) и D(s) взаимно просты справа, т. е. каждый наи-
больший общий правый делитель матриц N(s) и О(з) является
унимодулярной матрицей.
4а. Замечания.
(а) Аналогии между (4) и скалярным случаем очевидны. В ска-
лярном случае многочлены n(s) и d(s) определены по модулю,
которым является их общий делитель, а именно отличное от нуля
число. Здесь же многочисленные матрицы N и D определены по
модулю, которым является их правый делитель —унимодулярная
многочленная матрица.
г. условия устойчивости: метод факторизации
П
(Ь) Если матрицы N и D взаимно просты справа, то много-
члены det N (s) и det D (s) вовсе не обязательно будут взаимно
простыми. Этот факт легко установить, рассматривая, например,
матрицы W = diag(s — 1, s —2) и D = diag(s —2, s—1).
(с) Очевидно, что матрицу Н ($) можно представить в другом
виде: Н (s) = Z)-1 (s) R (s), где матрицы N (s) и D (s) взаимно про-
сты слева. Такое представление пригодится нам в дальнейшем.
(d) Можно показать, что в случае, когда матрица Н ($) огра-
ничена на бесконечности, det D (s) = k det (si — A), где A — матрица
любой минимальной реализации [Л, В, С, D] матрицы Н (s) и
6 —ненулевое число.
(е) Все операции, которым мы будем подвергать матрицы
в дальнейшем, законны, поскольку IR является полем. При пере-
ходе от поля R к полю С никаких изменений не потребуется. На
практике такой переход совершается при разложении в кольце
R[s] многочленов на множители; при этом часто случается, что
множители (s — Zi) принадлежат кольцу <D[s].
Итак, аналогии между скалярным и матричным случаями уста-
новлены. Теперь мы покажем, как привести матрицу Н (s) к ка-
нонической форме (4) с помощью следующей процедуры вычис-
ления матриц N и D.
Процедура. Пусть матрица Н (s) представлена в виде;
~ "11 (S)
di(s)
«<?1 (s)
L dj (s)
"im GO ~
(s)
nqm (s)
(s)
где tiij(s) и dj (s) — многочлены, причем многочлены df(s) (j = 1,
2, ..., m) — наименьшие общие кратные числителей элементов
/-го столбца матрицы Н (s). Из (5) вытекает, что
6.
’nu(s) ... nlm(sy
(s) ... Пдт (s)-
0 I-1
dm (s)
Я(з) =
0
Обозначим последние многочленные матрицы через N (s) и D(s)
и заметим, что detZJ(s) =^0. Вычисляя наибольший общий дели-
тель R(s) матриц N и D, получаем
tf(s) = JV(s)£(s), D(s) = D(s)^(s) Vs®(D,
причем элементы всех матриц принадлежат |R[s]. Поскольку
"det D(s)^ 0, матрица R(s) обязательно неособенная, откуда и
следует корректность канонической формы (4).
Способ вычисления наибольшего общего правого делителя пред-
ставляет собой решение следующей задачи.
76
ГЛ. 4. ЛИНЕЙНЫЕ системы
8. Задача. Пусть заданы две многочленные матрицы N (s) и
D(s), причем N (s) е R?xm [s], D (s) e Rmxm [s] и detD(s)=£O.
Найти
(а) две многочленные матрицы Un(s) и Un(s), удовлетворяю-
щие соотношению (9);
(b) наибольший общий правый делитель R(s) матриц JV (s)
и D(s);
(с) две взаимно простые справа многочленные матрицы Vu(s)
и Vji(s) такие, что
9. l/u(s)D(s)4-l/12(s)tf(s) = 7?(s) Vs«=(D
и
10. N (s) D-1 (s) = V21 (s) VFi (s) Vs е (D за исключением по-
люсов.
11. Процедура. Мы будем использовать элементарные опе-
рации над строками матриц, элементы которых принадлежат
кольцу R[s]. Существует три типа элементарных операций над
строками:
(i) умножение любой строки на ненулевое число; •
(ii) перестановка любых двух строк;
(iii) для i^=j умножение строки / на произвольный многочлен
р (s) е R [s] и сложение результата со строкой i.
Действие любой такой элементарной операции над строками
матрицы М (s) е Rmxm [s] эквивалентно умножению М слева на
матрицу, отличающуюся от единичной (гихт)-матрицы тем, что
к последней применена требуемая элементарная операция над
строками. Заметим, что определитель любой матрицы, соответст-
вующей элементарной операции, равен ненулевому числу; следо-
вательно, такие матрицы являются унимодулярными, а их обрат-
ные матрицы представляют собой многочленные матрицы.
Пусть
12. F(s) = [£$][ 7» F(s)sRW[s]
(/) т M(s)-F(s).
(2) Если все элементы первого столбца матрицы М (s), за
исключением (1,1)-элемента, равны нулю, перейти к (б); иначе —
перейти к (5).
(3) Среди элементов первого столбца матрицы М (s) выбрать
какой-либо ненулевой элемент наинизшей степени. Если необхо-
димо, переставить местами две строки так, чтобы выбранный эле-
мент оказался (1,1) элементом. Обозначить полученную матрицу
через M =
(4) Разделить тл на ти (1 = 2, 3, ..., /, где / — число строк
матрицы (s)). Тогда
18. Шц®(“2, 3, ..., /,
УСЛОВИЯ УСТОЙЧИВОСТИ: МЕТОД ФАКТОРИЗАЦИИ
77
где степень многочлена гд меньше степени многочлена fnu. Вы-
честь из i-й строки (1 = 2, 3, ...,/) первую строку матрицы (s),
умноженную на qtl. В результате получится новая матрица Л? (s),
первым столбцом которой будет (/йи, г21, г31, гуг).
(5) М (s) = М (s); перейти к (2).
(6) Если матрица М ($) содержит только одну строку или
столбец, перейти к (9). Иначе перейти к (7).
(7) Удалить первую строку и первый столбец матрицы М (s) @
е [si, получая таким образом новую матрицу М (s) ffi
6= R(/-l)x(A-l) [s] *
(8) A4(s) = A4(s}; перейти к (2).
(9) Конец.
Применение процедуры (11) к матрице F(s) приводит к по-
строению верхней треугольной матрицы, принадлежащей множе-
ству |R('n+?)xm [sj таким образом, доказано существование матрицы
U(s) еf>(m+?)x(m+?)[s] такой, что' для всех ssC
14 m{|Ai (s) | ^ia (s)l Г® (s)l_R (s)"|}m
UV(S)J “ Го"J}4 ’
m q m m
Поскольку U (s) принадлежит |R('"+?)x('"+7)[s] и равна произведе-
нию матриц, соответствующих элементарным операциям над стро-
ками, то det U (s) = с Ф 0, где с — постоянное число, и V (s)=U~1 (s) s
s p(m+?)x(m+j) |-sj Отметим, что det /? (s) =£ О, так как det D (s) 0.
Умножая (14) слева на матрицу V (s), получаем:
15. D(s) = V11(s)7?(s), N(s) = Vn(s)R(s)
Кроме того,
16. Un(s)D(s) + U12(s)N(s) = R(s) Vse=©
и, следовательно, в силу соотношения (15)
17. Un (s) Кц (s)+U(s) V2i (s) = I Vsefl).
Из (15) следует, что матрица R(s) является общим правым
делителем матриц N (s) и D(s). Из (16), (17) и леммы (20), дока-
занной ниже, вытекает, что R (s) — наибольший общий правый
делитель матриц 2V(s) и D(s). Из (15) также следует, что
18. y(s)D-1(s) = V21 (s)Vu(s),
где матрицы Ун и У21 взаимно просты справа (как показано
в лемме (20)).
19. Упражнение 1.
(а) Выписать матрицы, соответствующие всем элементарным операциям
над строками;
(Ь) Выписать матрицы, соответствующие операциям, обратным элементар-
ным операциям над строками;
78
ГЛ. 4. ЛИНЕЙНЫЕ СИСТЕМЫ
(с) Показать, что вычисление обратной матрицы сводится к пе-
ремножению матриц, соответствующих элементарным операциям над
строками.
20. Лемма. Пусть W (s) е [s] и D(s) eRmxm[s]. Тогда су-
ществуют две многочленные матрицы Р (s) е [s] и Q (s) е
sRmxm[s] такие, что
21. P(s)N(s) + Q(s)D(s) — 1щхт Vs<=(D
в том и только том случае, когда матрицы N (s) и D(s) взаимно
просты справа.
Доказательство.
Необходимость. Предположим обратное; тогда существует
общий правый делитель матриц N и D (обозначим его через R (s)),
не являющийся унимодулярной матрицей, т. е.
22. • N = NR, D = DR,
где Д7 и D — многочленные матрицы, а степень многочлена
det R (s) не меньше 1. В таком случае из (21) следует, что
23. [P(s)tf(s) + Q(s)D(s)]R(s) = / VsseC.
Мы пришли к противоречию. Действительно, сомножитель в скоб-
ках — многочленная матрица; поэтому det [Р (s) N (s) 4- Q (s) D (s)] —
многочлен, но det R (s) — также многочлен, причем его степень
не меньше 1; следовательно, равенство (23) не выполняется.
Достаточность. В результате применения процедуры (11)
к матрицам M(s) и D(s) вычисляются наибольший общий пра-
вый делитель R (s) и две многочленные матрицы P(s) и Q (s) такие,
что (см. (16))
24. Р (s) N(s) + Q (s) D (s) = R (s).
Поскольку матрицы N и D взаимно просты справа по условию,
матрица R (s) унимодулярна; следовательно, R-1 (s) е Rmxm [sj.
Умножая (24) слева на R-1(s), приходим к соотношению
25. R-1 (s) Р (s) АГ (s) + R-1 (s) Q (s) D (s) = 1,
из которого немедленно вытекает (21).
Упражнение 2. Показать, что матрицы N (s) & [s] и D (s) ® Rmxm [s]
взаимно просты справа тогда и только тогда, когда матрица
имеет полный ранг (в коммутативном кольце R [s]); рассматривая эту матрицу
как элемент пространства (уя+лихт, заключаем, что ее ранг должен быть ра-
вен tn при любых s а С-
\\УСЛОВИЯ УСТОЙЧИВОСТИ: МЕТОД ФАКТОРИЗАЦИИ 79
\
2. 2. Необходимые и достаточные условия
Мы вновь переходим к изучению системы с обратной связью
с п входами и п выходами, полагая, что G (s) е R'1X'1 (s) — переда-
точная функция разомкнутой системы, a F е R'lxn — матрица коэф-
фициентов усиления ветви обратной связи. Структурная схема
этой системы приведена на рис. 4.1. Мы также предполагаем,
что G (s) — правильная функция, т. е. ограничена на бесконечности.
30. Теорема. Пусть функция G(s)eRnx,1(s) правильна, /7еКяхп и
31. det[/+FG(oo)]#=0.
Пусть, кроме того, G(s) = N (s)D-1(s), где N (s) и D(s) —взаимно
простые справа многочленные матрицы. Тогда передаточная функ-
ция замкнутой системы И (s) — G (s) [/ + FG (s)]-1 экспоненциально
устойчива в том и только том случае, когда все нули многочлена
det [D (s) + FN (s)] имеют отрицательные действительные части.
(В действительности мы должны показать, что функция Н (s)
правильна и рс является полюсом Н (s) тогда и только тогда,
когда рс представляет собой нуль многочлена det [D (s) -\-FN (s)].)
Упражнение 3. Сформулировать и доказать аналогичную теорему для слу-
чая использования г-преобразования.
Доказательство теоремы (30). Покажем, что функция
Н (з) — правильная. В самом деле
32. /7(s) = G(s)[/ + FG(s)]-1 =
= G (s) Adj [/ 4- FG (s)] {det [Z 4- FG (s)]}-1.
Поскольку функция G(s) —правильная, обе матрицы в правой
части (32) ограничены на бесконечности. Согласно (31) последний
сомножитель также ограничен на бесконечности; следовательно,
функция //($) —правильная. Отсюда вытекает, что все полюсы
функции Н (s) расположены в замкнутой комплексной плоскости.
Теорема будет доказана, если нам удастся показать, что
33. рс е © — полюс функции И (s) тогд! и только тогда, когда
рс е (D — нуль многочлена det [О (s) 4- FN ($)].
Необходимость. Пусть функция Н ($) имеет полюс рс е ©.
Принимая во внимание формулу разложения для G(s), получаем
34. Н (s) = N (s)[D(s) + FN (s)]-1 —
= N (s) Adj [D (s) 4- FN (s)] {det [D (s) 4- FN (s)]}-1.
Поскольку N (s) и D (s) — многочленные матрицы и F — постоянная
матрица, из (34) следует, что если рс является полюсом функ-
ции Н (s), то рс — также и нуль многочлена s <—► det [£> (s) 4-^Аф)].
Достаточность. Пусть многочлен det [D (s) 4- FN (s)] имеет
нуль Покажем, что рс — полюс Н ($). В силу того, что
матрицы N (s) и D (s) взаимно просты справа, согласно лемме (20)
80
ГЛ. 4. ЛИНЕЙНЫЕ СИСТЕМЫ
существуют многочленные матрицы Р (s), Q (s) е R^[s] такие, что
35. P(s)M(s)-|-Q(s)D(s) = Z Vse(g.
Прибавляя и вычитая из левой части (35) многочленную матрицу
Q(s)FN(s), приходим к равенству
36. [Р (s) - Q (s) F] N(s) + Q (s) [D (s) + FN (s)l = I Vs G= (D-
Матрицы W (s) и D(s)4-FAf(s) взаимнр просты справа. Подстав-
ляем (34) в (36):
37. {[Р (s) - Q (s) F] Н (s)+Q (s)} [D (s) + FN (s)J = I Vs е ©.
Следовательно,
38. det {[Р (s) - Q (s) F] H (s) + Q (s)J X
X det [D (s) + FN (s)] =1 Vs «= ©.
Согласно условию, pc s © — нуль второго сомножителя в (38); по-
этому для справедливости (38) в точке рс необходимо, чтобы
точка рс была полюсом первого сомножителя в (38). Так как
P(s), Q(s) и F — многочлены, они не имеют полюсов в ©. Отсюда
вытекает, что функция Н (s) должна иметь полюс в точке рс.
Таким образом, справедливость (33) установлена и теорема доказана.
40. Замечание. Из (35) следует, что
det [Р (s) G (s) 4- Q (s)] det D (s) = 1 Vs <= ©.
Поэтому
41. po^C-полюс функции G(s) тогда и только тогда, когда
posC —нуль многочлена detD(s).
43. Следствие. Если выполняются условия теоремы (30), то
П (5~Рсд
44. det [/ + FG (s)] = = det [Z + FG (oo)]^-----,
П (s-Pod
«= i
где {po/} и {pci} (i = 1, 2, ..., m) — соответственно множества по-
люсов функций G (s) и H (s) (кратные полюса входят в множества
в соответствии со своим порядком).
Доказательство. Вычислим определители обеих частей
равенства (32):
т
ТТ (S —рс/)
45. det [/ + FG (s)] = = det- +(s)1 = k--------------.
L ' v 'J det n (s) det D (s)
П (S-Pod
i= i
Последнее равенство в (45) получено с учетом (33), (34) и (41);
£ = det[/4-FG(oo)]=/=0 согласно предположению (31). Кроме
\2. УСЛОВИЯ УСТОЙЧИВОСТИ; МЕТОД ФАКТОРИЗАЦИИ 81
того, число Ьолюсов функций G (s) и Н (s) одинаково, поскольку
в противном случае правая часть (45) на бесконечности либо рав-
нялась бы нулю, что противоречит условию (31), либо неограни-
ченно возрастала, вопреки предположению о правильности функ-
ции G(s).
46. Замечание. Из (44) следует, что множество нулей функ-
ции det [Z -|- FG (s)] может быть собственным подмножеством мно-
жества {рС(} полюсов передаточной функции замкнутой системы
(см. пример 1.14). Отсюда же вытекает, что при соблюдении усло-
вий теоремы (30), если функция G(s) экспоненциально устойчива,
то функция Н ($) экспоненциально устойчива в том и только том
случае, когда все нули определителя det [Z-|-FG (s)] имеют отри-
цательные действительные части.
50. Другой вывод следствия (43). Обозначим через Z?o =
= [Л, В, С, D] — минимальное представление передаточной функ-
ции разомкнутой системы G(s). Очевидно, что
51. G (s) = C (si — А)-1 В-]-D.
Из рис. 4.1 ясно, что функция е, входное воздействие подсистемы G,
удовлетворяет равенству e — u — Fy. Несложные вычисления при-
водят к уравнениям состояния замкнутой системы:
52. х = [А - В (Z + FD)-1 FC]x + B(I + FD)-1 и,
53. y = [C-D(I + FD)~lFC]x + D(I A-FD)-lu =
= (Z + DF)-1 Сх + (I + DF)-1 Du.
Мы построили представление замкнутой системы. Оно является
минимальным, поскольку, и это легко показать методом от про-
тивного, наличие ветви обратной связи не может нарушить пол-
ной управляемости и полной наблюдаемости прямой ветви системы.
Поэтому собственные частоты замкнутой системы численно равны
собственным значениям матрицы А —В (I A-FD)-1 FC. Далее, учи-
тывая, что det (PQ) = det Р det Q и det (/MAZ) = det (Z A-NM),
получаем:
54. det [sZ — Л -[- В (Z -|- FD)-1 FC] =
= det (si - Л) det [Z + (si - Л)-1 В (I + FD)-1 FC] =
= det (si - Л) det [Z + (I + FD)-1 FC (si - A)-1 B] =
55. = det (si - A) det [(Z + FD)-1] det [Z + FC (si Л)-1 В + FD].
Как легко видеть, из (51) следует, что последние два определителя
в (55) равны соответственно det [Z + Z?G (сю)]*1 и det [Z+FGfs)].
Тогда из (54):
56. det [Z + FG(s)] = det [Z + FG(co)]det tS/~’
Соотношение (44) следует из (56), так как представления разом-
82
ГЛ. 4. линейные системы
кнутой системы = В, С, D] и замкнутой системы (52) —(53)
минимальны.
58. Замечание об обращении матриц в Кяхп (s). Пусть матрица
Н (s) представлена в виде
59. H(s) = N (s) D~l (s),
где N, ОеК"хл[$] — взаимно простые справа матрицы. Мы знаем, что
60. ре С—полюс функции Н (s) тогда и только тогда, когда
р е С - нуль многочлена det D (s), и
61. ге©-полюс функции Я-1(з) тогда и только тогда, когда
z еС - нуль многочлена det N (s).
Следует иметь в виду, что мы нигде не рассматривали свойств
бесконечно удаленных полюсов. Кроме того, поскольку функции
detD(s) и detM(s) могут иметь общие нули, может случиться,
что функции Н (s) и будут одновременно иметь полюс
в некоторой точке sеф. В качестве примера приведем функцию
tf(s) = diag[(s+l)/(s-l), (s-l)/(s+l)]. л
62. Замечание о нулях функции /-)-Fd(s). Предположим, что
условия теоремы (30) выполняются. Назовем матрицу I-\-FG(s),
по аналогии со скалярным случаем, матричной возвратной раз-
ностью. Эта матрица может быть представлена в еиде произведе-
ния (D-\-FN)D~l, где многочленные матрицы взаимно просты
справа и det F =/= 0. Мы знаем, что р является полюсом матрич-
ной возвратной разности тогда и только тогда, когда det D(p) — 0.
Для упрощения предположим, что det (£> + FN) 0. Тогда по
аналогии со скалярным случаем назовем точку z нулем матрич-
ной возвратной разности / + FG (•) в том и только том случае,
когда det [D (z) 4- FN (z)] = 0. Отметим, что, как указывалось выше,
некоторая точка реф может быть одновременно и нулем и по-
люсом матрицы /4-Fd( ).
Упражнение 4. Предположим, что матричная возвратная разность пред-
ставлена в виде произведения двумя способами:
I + FG (s) = Nr (s) D;1 (s) = (s) (s),
где многочленные матрицы Nr и Dr (Ni и D/ соответственно) взаимно просты
справа (слева). Показать, что для zeC detN/(z) = 0 тогда и только тогда,
когда det Wr(z) = 0.
В скалярном случае нули и полюсы передаточных функций,
как известно, хорошо отражают динамические свойства системы.
Этот факт обобщается на матричный случай с помощью следую-
щей теоремы. Для простоты мы будем рассматривать системы,
которым соответствуют квадратные матрицы.
63. Теорема. Пусть выполняются условия теоремы (30). Тогда
(i) р е С является полюсом функции I -\-FG (s) в том и только
том случае, когда существует входное воздействие и системы
2. УСЛОВИЯ УСТОЙЧИВОСТИ- МЕТОД ФАКТОРИЗАЦИИ
83
с матричной передаточной функцией I + FG (s)t представимое в виде
и (0 = У иа 6“ (0, где иа <= ©я,
а
такое, что соответствующая реакция системы при нулевом началь-
ном состоянии удовлетворяет равенству
64. e(t) = rept для всех />0,
причем 0„=#=ге©я;
(ii) если г е С - нуль функции / + FG (•), то
(а) существуют ненулевой вектор g е С" и многочлен У, masa
a
такой, что при входном воздействии
65. u(0 = l(0^+yma6“(0
a
соответствующая реакция системы с передаточной функцией
/4-FG(-) при нулевом начальном состоянии удовлетворяет соот-
ношению
66. е [0 0—, 0„; «(•)] = 0Я при t > 0;
(b) если, кроме того, точка z не является полюсом функции
/-|-FG(), то существует ненулевой вектор y's©" такой, что
67. ф (0 = у' у [0 0—, 0Я; и (•)] = 0 при всех t > 0,
где «(•) определено соотношением (65), причемg — произвольный
вектор из ©", а та — векторы из 0я, зависящие от вектора g;
(iii) если v е © не является ни нулем, ни полюсом функции
I + FG(), то для всех ненулевых векторов fee©" существует
многочлен такой, что воздействие
68. и (0 = 1 (0 e*‘k + 2 та б“ (0
a
вызывает реакцию системы в нулевом состоянии вида
69. е[0 0—, 0Я; и (•)] =» [Z + FG (v)] kevt Ф 0я для всех />0.
Доказательство. Мы только наметим путь доказатель-
ства утверждений (!) и (11). Используем упражнение 4 и пред-
ставим функцию Z4-Fd(s) в виде произведения Z4-FG(s) =
= D]1 (s) Nt (s); точка p является полюсом тогда и только тогда,
когда det Di (р) — 0; точка г является нулем тогда и только тогда,
когда detAfz(z) = O. Поскольку матрицы Ni(-) и Di(-) взаимно
просты слева, то Ni(s)P (s) = I — Di(s)Q(s) для любых seC.
(1) Если р — полюс функции Z + FG(s), то существует вектор
г е©" такой, что Dz(p)r = 0„. Поэтому Dz(s)r = (s —p)fe(s), где
84 гл. 4. линейные системы
&(-)е©л[з], т. е. вектор, элементами которого являются много-
члены. Выберем входное воздействие й (s) = Р (s) k (s), тогда
6(s)^Djl(s)Nt(s)P (s)k(s) =
= D?* (s) [7 - Dz (s) Q (s)] k (8) = -4 - Q (s) k (s).
Формула (64) становится очевидной, поскольку последний член
выражения для ё (з) представляет собой многочлен от s. Обратное
утверждение легко доказывается методом от противного.
(ii) (а) Если г —нуль функции I-\-FG(s), то существует нену-
левой вектор^такой, что Ni(s)g=ftn- Следовательно, A7(z)g/(s — г)—
вектор (обозначим его через р (s)), элементами которого являются
многочлены. Выберем т (s) в выражении (65) равным — P(s)p (з),
тогда
ё (S) = Dr* (s) {tf, (s) s4-2 + Nt (s) [- P (s) p (s)]} = Q (s) p (s).
Так как ё (s) — многочлен от s, то е(/) = 6„ при всех />0.
(Ь) Доказательство этого утверждения проводится аналогич-
ным образом, если выбрать y' = c'Dz(z), где c'Afz(z) = 6„.
Мы завершим проведение аналогий между скалярным и матрич-
ным случаями следующей теоремой.
70. Теорема, (а) Точка р£ е Q является полюсом функции
A=g(l 4-f^)-1 тогда и только тогда, когда рс — нуль возвратной
разности l+/g, т. е. когда 1 -[- fg (рс) = 0.
(Ь) Допустим, что det F =/= О, функция 6 (s) е КяХя (з) правильна
и det [7 + F6 (оо)] #= 0. Тогда точка рс является полюсом функции
ТУ = 6(7 +EG)-1 в том и только том случае, когда рс — нуль мат-
ричной возвратной разности 7 + FG.
(с) Если функция 6 (или g) правильна, т. в. ограничена на
бесконечности, и det [7 + Гб (оо)] =£= 0 (или 1 + (оо) 0), то
функция Й (или А) правильна.
Доказательство. Утверждения (а) и (с) очевидны. При
доказательстве утверждения (Ь) воспользуемся для разнообразия
разложением G на взаимно простые слева множители: 6 = D+V.
В таком случае
Й - (7 + 677)-1 б - (D + NF)-1 Я.
Замечая, что матрицы D+NF и /7 взаимно просты слева (дейст-
вительно, NP + DQ = 7 тогда и только тогда, когда N(P — FQ) +
+ (D + NF)Q= I), получаем, что рс является полюсом функции Й
в том и только том случае, когда рс — нуль det [D +777].
Поскольку матрица F неособенна, матрицы D+flF и D взаимно
3 СИСТЕМЫ С ДИНАМИЧЕСКОЙ ОБРАТНОЙ СВЯЗЬЮ
85
просты слева (в самом деле, NP -\-DQ = l тогда и только тогда,
когда (D+ ^F)(F~1P) + D(Q — F~1P) = I), а так как I-\-GF =
— D~l(D-\-NF), то рс — нуль функции I-\-GF (а также функции
/4-FG = F(/4-dF)F-1) тогда и только тогда, когда рс является
также нулем функции det[D + 2VF]. Следовательно, точка рс —
полюс Н тогда и только тогда, когда эта точка —нуль I-\-FG.
71. Замечание. Если матрица F — особенная, то утверждение
(Ь) выполняется не всегда. Чтобы убедиться в этом, рассмотрим
случай, когда G = diag[(s —I)-1, (s-f-1)-1], F = diag(0, 1). Функ-
ция И имеет полюсы s=l и s = — 2, а функция I-^-Fb равна
нулю только при 8 = — 2.
3. ЛИНЕЙНЫЕ СИСТЕМЫ С ДИНАМИЧЕСКОЙ ОБРАТНОЙ СВЯЗЬЮ
(СЛУЧАЙ ДРОБНО-РАЦИОНАЛЬНОЙ ПЕРЕДАТОЧНОЙ ФУНКЦИИ)
Рассмотрим непрерывную линейную стационарную замкнутую
систему с п входами и п выходами. Обозначим входное воздей-
ствие, реакцию и сигнал ошибки системы символами и, у и е
соответственно, а передаточные функции прямой ветви и ветви
обратной связи —через Go и Gf. Предположим, что обе передаточ-
ные функции дробно-рациональны и правильны:
1. y = Gye; Go eRnx/,(s), функция Go —правильная;
2. e = u — Gfy:, G/eRnx/,(s), функция G/ —правильная.
Кроме того, мы везде будем считать, что
3. det [7 + 60 (со) Gf (со)] = det [7 + Gf (со) Go (оо)] =# 0.
Таким образом, функция (7 +O/Go)-1 корректно определена на
множестве Rnx" (s), поскольку det [7 + Gf (s) Go (s)] =£ 0.
Наша цель состоит в том, чтобы определить необходимые и
достаточные условия экспоненциальной устойчивости системы,
описываемой передаточными функциями
4. Не: и~е, 77e(s) = [7 + Gf (s)Go(s)]-1, ,
5. Ни'. f79(s) = Go(s)[7 4-G/(s)Go(s)]_1.
Упражнение. Предполагая, что функции Go, Gf е Рпхп (а) правильны
(ограничены на бесконечности), показать, что det [/+G/(oo) Go (со)| #= 0 тогда
и только тогда, когда функции Не и На правильны.
Один из возможных подходов к решению поставленной задачи
состоит в следующем: выбрать некоторые минимальные реализации
функций Go и Gf, затем с их помощью получить минимальные
реализации Не и Ну и потребовать, чтобы характеристические
многочлены полученных матриц Ае и Ау были устойчивыми. Вместо
этого мы используем метод факторизации, изложенный в разделе
2.1. Сначала мы рассмотрим систему в одним входом и одним
86
ГЛ. 4. ЛИНЕЙНЫЕ системы
выходом. Прежде всего представим дробно-рациональные переда-
точные функции g0 и gf в виде отношения взаимно простых
многочленов:
Ал- ^0
6- go=rfT’
u0
Тогда
8.
9.
где п0 и d0 —взаимно простые многочлены;
где nf и df — взаимно простые многочлены.
he = (1 + gfg.)-1 =-Цг-г-,
е \ is/so/
nodf
hy-go(l+gfg^ = nfno + d^‘
Многочлены числителя и знаменателя выражений (8) и (9) вовсе
не обязательно взаимно просты. В самом деле, в (8) общие дели-
тели могут иметь пары многочленов dQ и df и п0. В (9)
аналогичная ситуация может наблюдаться для пары многочленов
df и п0. По этой причине было бы ошибочным утверждать, что
нули многочлена n;n0 + dzd0 являются полюсами функций he и hy.
Интуитивно ясно, что сходное явление имеет место и для систем
с п входами и п выходами; кроме того, при изучении таких систем
необходимо учитывать, что произведение матриц, вообще говоря,
не обладает свойством коммутативности.
Рассмотрим систему с п входами и п выходами, описываемую
уравнениями (1) и (2), предполагая, что соотношение (3) выпол-
няется. Выведем необходимые и достаточные условия экспонен-
циальной устойчивости функций Не и Ну, заданных соотношениями
(4) и (5). В действительности мы получим более сильный результат,
а именно: найдем многочлены, корни которых являются полюсами
функций Ну и Не. Представим функции Go и Gf в следующем виде:
Ю. Go = NqDo\ где No. Do — взаимно простые справа
матрицы;
11. Gf = Df'Nf, где Nf. Df& 1РЛХЛ [s] — взаимно простые
г слева матрицы.
Мы, естественно, считаем, что detDo^0 и detD/^O1). Введем
обозначение
12. Q=DfDo + NfNo
1) В большинстве формул, представленных в разделе 3, явная зависимость
функций от s не указывается, поскольку в этом нет необходимости. Например,
соотношение (12) выражает равенство двух многочленных матриц, т. е. факт
равенства величин в правой и левой частях (12) при всех ssC; соотношение (10)
выражает равенство двух матриц дробно-рациональных функций или равенство
величин, представленных в левой и правой частях (10), при всех se С, за
исключением полюсов функций. Аналогичным образом неравенство det £>0 =# 0
означает, что многочлен det Do не является нулевым элементом кольца R [s]
или что функция s ।—► det Do (s) не равна нулю при всех s е С.
3. СИСТЕМЫ С ДИНАМИЧЕСКОЙ обратной связью
«7
и преобразуем равенства (4) и (5):
13. H^DoQ-'Df, Hy = N^~lDf.
Отметим, что detQ^O, поскольку, согласно (3), при s->oo
функция Не стремится к невырожденной матрице, элементами
которой являются постоянные числа. Пусть матрица L — наиболь-
ший общий левый делитель матриц Q и Df, тогда
14. Й = ЛЙ, Df = LDf,
где L, Q, Df £^*"[5], причем матрицы D, и Q взаимно просты
слева, т. е. существуют многочленные матрицы Р и Q такие, что
15. D/P + QQ^l.
Поэтому
16. H^Dy^Df.
Пусть матрица Re — наибольший общий правый делитель матриц
Do и Q. Тогда
17. Q=QeRe,
18. Do — DoRe,
где Re, Qe, Do s Кяхя [«], причем матрицы Qe и Do взаимно
просты справа, т. е. существуют многочленные матрицы Ре и Qe
такие, что
19. PeD0 + QeQe = l.
Подставляя (17) в (15), получаем DfP + QeReQ = I, откуда сле-
дует, что матрицы Df и йе взаимно просты слева. Таким образом,
20. He = D0DflDf, где
йе, Df взаимно просты слева>
Do, взаимно просты справа.
Действуя аналогичным образом с функцией Ну, получаем
21. H^NoQ-'Df.
Если матрица Ry является наибольшим общим правым делителем
матриц No и Q, то
22. Й = QyRy,
23. No = NoRy,
где Qy, Ry, No e Rnxn [s], причем матрицы йу и No взаимно
просты справа, т. е. существуют многочленные матрицы Ру и Qy
такие, что
24. PyNo-\-QvQy = I.
88
ГЛ. 4. ЛИНЕЙНЫЕ СИСТЕМЫ
Можно показать, что Df и взаимно просты слева. Таким
образом,
г, , a f Df взаимно просты слева,
25. Hy = N0QylDh где { / ' F
( Ny, йу взаимно просты справа.
26. Теорема. Для системы, заданной уравнениями (1) и (2) и
подчиняющейся соотношению (3), при введенных обозначениях
имеют место следующие эквивалентные утверждения:
27. ре е (D — цолюс Не ре — нуль det йг;
28. Ру е (D — полюс Ну<=5>ру — нуль det й9.
Теорема (26) немедленно приводит к необходимым и достаточ-
ным условиям экспоненциальной устойчивости функций Не и Ну,
а именно: все нули определителей det йе и det й9 должны распо-
лагаться в открытой левой комплексной полуплоскости.
Доказательство. Заметим, что из (3) и предположения о
правильности функций Со и Gf вытекает правильность функций
Не и Ну. Поэтому мы будем рассматривать полюсы только в
замкнутой комплексной плоскости ©. Мы докажем только эквива-
лентность условий (27); эквивалентность (28) доказывается
аналогичным образом.
Достаточность. Умножая (19) справа на ЙГ1^, получаем
29. Р Дйе lDf + QeDf = РеНе + QeDf = Qe'bf.
По условию det йе (ре) = 0. Поскольку матрицы йе и Df взаимно
просты слева, точка ре является полюсом правой части равенства
(29) (см. доказательство теоремы (2.30)). Присутствующие в левой
части (29) матрицы Ре, Qe и Dt принадлежат Кяхя [s] и поэтому
ограничены в любой окрестности точки ре. Таким образом, ре
представляет собой полюс функции Не.
Необходимость. Используя правило Крамера, представим (20)
в следующем виде:
По условию точка ре — полюс функции Не. Однако матрицы Ьо,
Adj Йе и bf принадлежат кольцу |Rnx"[s] и, следовательно, не
имеют полюсов в замкнутой комплексной плоскости; поэтому
из (30) вытекает, что det йе (ре) = 0.
31. Интерпретация теоремы (26). Пусть р—1, 2 или оо. Если
все нули определителей det й„ и det й9 расположены в левой
комплексной полуплоскости, то
(а) функции Ht и Ну экспоненциально устойчивы;
(Ь) при любом и е Ln функции е и у принадлежат LS;
3. СИСТЕМЫ С ДИНАМИЧЕСКОЙ ОБРАТНОЙ СВЯЗЬЮ
89
(с) при любом и е Ln и для любой минимальной реализации
функций Go и Gf соответствующие траектории х0( •) и xf (•), начи-
нающиеся из нулевого состояния, принадлежат Ln-
Упражнение. Доказать перечисленные выше предложения. [Указание:
использовать теорему (1.9) и заметить, что любая минимальная реализация
обладает свойством полной наблюдаемости.]
35. Замечание. При введенных обозначениях
36. {нули det [/4-G^Go]} с: {полюса Не\\
37. {нули det [7 + G/Go]} с {полюса Ну\ (J {нули det
Эти отношения включения показывают, насколько опасно пытаться
определять устойчивость передаточных функций Не и Ну замкнутой
системы, рассматривая только нули дробно-рациональной функции
11—► det [/ Gf (s) О® (s)].
Доказательство. Включения (36) и (37) вытекают из (27),
(20), (4) и (28), (25), (5) соответственно. В самом деле,
38.
39.
det (7 + GA)
det(/+GfGo)
det Qe
det Do det Df ’
det Qy det Ry
det £>e det Df
Приводимые ниже примеры преднамеренно просты. Их назна-
чение — проиллюстрировать связь полюсов функций Go, Gf, Не, На
и нулей функций Q и det (/ -[- G/Go).
42. Пример 1. Функции Go и Gy не являются экспоненциально
устойчивыми; функция Не неустойчива, а функция Ни экспонен-
циально устойчива:
г s + 2
S— 1
I «
о0=вд--[’0|
Gj-DfAV-i';1
O'irqs + 2) 0 1-1 #
s—2J [ 0 s-f-1 J ’
0 ]-хГ —(з4-2) 0
s(s-2)J [ ° -2(s+D
det (/ 4- GzGo) = det +G/ (oo) Go (oo)] = j}
0
$4-1
90
ГЛ. 4. ЛИНЕЙНЫЕ СИСТЕМЫ
43. Пример 2. Функции Gf и G# не являются экспоненциально
устойчивыми; функция Не экспоненциально устойчива, функция
Ну неустойчива:
о
s+l
s-2
det (/ + G/Go) = (5+У+2>-; det [/ + Gf (oo) Go (oo)] = 1;
° 1-
s+d’
50. Интерпретация нулей det Q (s). Для системы, заданной
уравнениями (1) и (2), утверждения (27) и (28) означают, что
устойчивость передаточных функций Не и Ну полностью характе-
ризуется расположением нулей определителей detQe(s) и det £ly(s)—
соответственно. Передаточные функции Не и Ну, однако, опреде-
ляют реакцию системы с обратной связью лишь при нулевом
начальном состоянии. Для изучения реакции системы при нену-
левом начальном состоянии мы должны рассмотреть другое пред-
ставление системы в пространстве состояний. Пусть [Лг, Bit Cit £>,] =
= Rt, где i — 0, f, является некоторым минимальным представле-
нием функций 60 и Gf. Обозначим соответствующие состояния
через х0 и xf. Тогда (xj, xJ)T —вектор состояния системы с обрат-
ной связью. Естественно, его размерность, вообще говоря, не
минимальна. Заметим, что det Di (s) = kf det (si — At), где i = 0, f.
Мы утверждаем, что
51. det Q (s) = 0 — характеристическое уравнение системы
с обратной связью, заданной уравнениями (1) и (2).
Это, в частности, означает, что если detQ(X) = O при неко-
тором X, то при некотором начальном состоянии с и входном
воздействии и а 0 процесс в системе имеет вид се^.
Для доказательства утверждения (51) мы используем разложе-
ния (10) и (11) и перепишем уравнения системы:
„ ( Dov = e, „ ( w = Nfy,
y^Goe, или { и — e = Gfy, или {
= [Dfu — Dfe = w,
3. СИСТЕМЫ С ДИНАМИЧЕСКОЙ ОБРАТНОЙ СВЯЗЬЮ
91
где мы ввели новые переменные v и w. Новые четыре уравнения
соответствуют дифференциальным уравнениям, поскольку Л/о, Д»
Nf и Df — многочленные матрицы. Последовательными подстанов-
ками исключим из этих уравнений переменные е, w и у и полу-
чим следующую эквивалентную систему уравнений:
(NfN0 + DfDo) v = Dfu, у =
е = DqV, w = Nfy = NfNoV.
При заданном и и допустимых начальных условиях из первого
уравнения этой системы определяется решение /»—>у(/), /^0,
функции у, е и w вычисляются подстановками. Поскольку эти
подстановки содержат только произведения многочленных матриц,
посторонних решений не возникает. Таким образом, мы приходим
к выводу, что характеристическое уравнение системы с обратной
связью имеет вид det (^Л^о + ^/^о) = det Q = 0.
59. Представление в пространстве состояний. Система с обрат-
ной связью, заданная уравнениями (1) и (2), состоит из подси-
стем, описываемых своими передаточными функциями. Это позво-
ляет нам рассматривать реакции подсистем и всей замкнутой
системы только при нулевом начальном состоянии. Для опреде-
ления выходных сигналов при произвольных начальных состояниях
предположим, что обе подсистемы описываются их представлени-
ями /?0 и Rf в пространстве состояний:
60. Rq = (Ло, Во, Со, Dq), откуда Go (s) — Cq (si — Ло)“1 Bq 4- Во,
61. Rf = (Afi Bh Cf, Df)t откуда Gf(s) = Cf(sI — Af)-1 Bf-\-Dfl
причем эти представления могут быть неминимальны. Нам хотелось
бы научиться изучать поведение фазовой траектории системы
с обратной связью при выбранных произвольным образом вход-
ном воздействии и начальном состоянии.
Мы будем полагать, что
62. det [/ + Gf (оо) Go (op)] = det (I + DfD0) 0.
Обозначим через x0 и xf состояния подсистем, заданных представ-
лениями /?0 и Rf; тогда x = (xj, х/)т —вектор состояний замкну-
той системы. Покажем, что при выполнении условия (62) пред-
ставление Rc замкнутой системы имеет стандартную форму Rc =
= (Л, В, С, D). Знания Rc достаточно для описания связи вход-
ного воздействия, начального состояния и реакции системы. Дей-
ствительно, реакция у замкнутой системы при нулевом состоянии
имеет вид:
64. у (s) = Ну ($) й ($) = [С (si - А)-г В + D] й (s),
а фазовая траектория, начинающаяся при /=»0 из х(0), опреде-
ляется равенством
65. х (s) = (si - А)-1 х (0) + (si - Л)-1 Вй (s).
92
ГЛ. 4. ЛИНЕЙНЫЕ СИСТЕМЫ
• Для решения вопросов ограниченности траектории состояния
вспомним определение (1.5) экспоненциально устойчивой
системы и свойства ее передаточной функции (теорема (1.9)), из
которых выясняется, что необходимо связать собственные числа Kci
замкнутой системы (определенные как собственные числа мат-
рицы А) с собственными числами представлений /?0 и Rf (т. е.
с собственными числами матриц До и At соответственно). Такова
причина, вынуждающая нас вычислять матрицу А.
Матрицы А, В. С и D, определяющие представление Rct легко
получить из уравнений, описывающих подсистемы и их взаимо-
связь. Как и в уравнениях (1) и (2), символами и и у обозна-
чены входное воздействие и реакция замкнутой системы, а сим-
волом е — сигнал ошибки. Тогда
(а) для подсистем
gg ( Д = Аохо -|- Вое, ( Xf = AfXf -|- В/t/,
( У — CqXq Dffi, ( Уг = СfXf -\-D/у.
Здесь использован тот факт, что сигнал ошибки е и реакция у
являются соответственно входным и выходным сигналами подси-
стемы прямой ветви, и, кроме того, «/ — входной сигнал подсистемы
ветви обратной связи.
(Ь) Связь подсистем
67. е = и — y2 = u — CfXf — Dfy.
Построим представление Rc, исключая е из первых трех урав-
нений (66) и уравнения (67). Из (67) и второго уравнения (66):
68. е = (I + DfDo)~l (и — DfCoXg — C/Xf).
Подставив (68) в первые три уравнения (66), после некото-
рых преобразований получим:
aq AfAv-BoU+DfD^-iDfCo - Ва (I + DfD^Cf 1
05,‘ Н-[ S^(/+D0Dr)-iC0 Af-B^Z + DoDf^DoCf]’
71. C = [(Z + DoD/)-1Co -(l + D0Df)-'D0Cf],
Соотношения (69) — (71) определяют представление Rc замкну-
той системы. Отметим симметрию, элементов матрицы А: меняя
местами индексы 0 и /, из одной строки матрицы получаем дру-
гую. Это свойство пропадает в матрицах В, С и D из-за отсут-
ствия симметрии в точках приложения воздействия и, что легко
увидеть на блок-схеме системы с обратной связью.
Идея построения соотношения между собственными числами
матриц Д, До и Д/ весьма проста. Все преобразования мы опу-
скаем; они включают в себя элементарные операции над стро-
ками и столбцами блоков матрицы si —А, использование равен-
3. СИСТЕМЫ G ДИНАМИЧЕСКОЙ ОБРАТНОЙ СВЯЗЬЮ
93
ства Da(I + DfDa)~1 — (I + D0Df)~1Do и учет следующего факта:
если М и N представляют собой (pxq)- и (q х р)-матрицы, то
det (1Р + MN) = det (Ig + NM).
Детали читатель может почерпнуть в работе Сю и Ченя [56].
Результат можно выразить следующим образом: если через Ха»
Хо* и "kft обозначены собственные значения замкнутой системы
(т. е. матрицы А), матриц Ао и Af, то
det[/+G/(s)G0(s)]
72. det (si — А) = det (si — Ло) det (si — Л,) det [/_|-G/(oo)G0(co)] ’
или
73. det [I + Gf(s) Go (s)] =
= det [/ + Gf (00) Go (00)] .
1 I (s —Ao<) [1 (s — Afi)
Нетрудно заметить, что соотношения (72) и (73) являются обоб-
щением (2.56) и (2.44).
Еще раз отметим, что множество нулей det [/ + Gf (s) Go (s)]
может быть собственным подмножеством множества собственных
чисел {Хс,} замкнутой системы; действительно, дробь в правой
части (73) может быть сократима. С другой стороны, согласно (73)
в случае, когда ReX0,<;0 и ReXz,-<0 для всех i, все Ха могут
иметь отрицательные действительные части тогда и только тогда,
когда все нули det[/ + G/(s)Go(s)] имеют отрицательные действи-
тельные части.
Для фазовой траектории справедливо следующее утверждение.
74. Утверждение. Если все собственные значения Ха замкну-
той системы имеют отрицательные действительные части, то при
всех начальных состояниях х(0) = [х£(0), xj (0)]* и при всех огра-
ниченных входных воздействиях м sL® фазовая траектория
замкнутой системы t»—»• х (t) ограничена; это же утверждение спра-
ведливо для функций е(') и у(-).
Упражнение 5. Получить формулы (69) —(71) для случая, когда матрицы
Do и Df—нулевые.
Упражнение 6. Показать, что из минимальности представлений 7?0 и Rf
не следует минимальность Rc.
Упражнение 7. Пусть передаточная функция Ну замкнутой системы задана
соотношением (5). Показать, что
75. (а) (/ - Qf (s) Йу (s)J [/ + <jf (s) d0 (s)J = 1 Vs <= С;
(b) если
det (/ + D/Do) = det (/ + D0Df) = 0,
то, во-первых, ^(s)->0 при s->oo и, во-вторых, замкнутая система не
может иметь представления в пространстве состояний стандартного вида
(А. В. С. D).
94
ГЛ. 4. ЛИНЕЙНЫЕ СИСТЕМЫ
4. СИСТЕМЫ С ОБРАТНОЙ СВЯЗЬЮ ОПИСЫВАЕМЫЕ
ОПЕРАТОРАМИ СВЕРТКИ
В предыдущих разделах мы рассматривали только дробно-ра-
циональные передаточные функции и, следовательно, ограничива-
лись изучением моделей систем с сосредоточенными параметрами.
Теперь мы переходим к системам с обратной связью, состоящим
из подсистем, вход-выходные свойства которых описываются
с помощью операторов свертки. Таким образом, наши исследова-
ния охватят модели систем с распределенными параметрами.
Результаты, приведенные в Приложениях С и D, будут использо-
ваться без каких-либо комментариев.
t Чтобы ощутить общность такого
описания, напомним, что Л. Шварц
показал, что любой линейный стаци-
е------------------- онарный оператор, удовлетворяющий
весьма слабым условиям по непре-
4.2. рывности, представим в виде свертки,
т. е. в форме и * Т * и, где Т —
обобщенная функция. Если оператор, кроме того, неантисипати-
вен, то носитель обобщенной функции Т принадлежит R+, и
наоборот, если носитель (R+ принадлежит Т, то оператор обладает
свойством неантисипативностих).
Рассматриваемая система изображена на рис. 4.2. Входное
воздействие и, сигнал ошибки е и реакция у представляют собой
функции, отображающие R+ в 1РЛ. Мы будем также полагать, что
эти функции могут быть обобщенными: 6-функции будут появ-
ляться в наших рассуждениях довольно часто. Линейные ста-
ционарные подсистемы G и F характеризуются своими импульс-
ными характеристиками G(-) и F (-). Уравнения системы имеют
Рис.
вид:
1. y = G*e, или y=Ge,
2. u = e + F*G*e, или u=e + FGS.
Поэтому
За. Н (s) = G(s)[Z + F(s)G(s)]-1
и
3b. I — F (S)^(S) = [/ + / (s)G(s)]-1
в той части комплексной полуплоскости, где одновременно опре-
делены изображения по Лапласу функций F(-) и G(-).
В этом разделе для обеспечения устойчивости замкнутой системы
мы потребуем, чтобы ее импульсная характеристика Н (•) при-
х) Читатель может пополнить свои знания в этой области, познакомившись
с книгой: Шварц Л. Анализ. —М.: Мир, 1978. {Прим, ред.)
4. СИСТЕМЫ, ЗАДАННЫЕ ОПЕРАТОРАМИ СВЕРТКИ
95
надлежала &#пХп(0). В таком случае
4. IUIи\\р при l^p^oo,
т. е. замкнутая система £р-устойчива при всех ре[1, оо]. Обрат-
ное утверждение неверно, поскольку класс импульсных характе-
ристик может быть расширен функциями с сингулярной мерой [92].
Мы будем пользоваться сокращением оЛ вместо orf (0), а через
IН U обозначим норму Н (•) е о^пХп, полагая, что это не слиш-
ком усложнит наши исследования.
По причинам в основном технического характера на протяже-
нии всего раздела мы будем считать, что матричная передаточная
функция F(s) ветви обратной связи принадлежит алгебре е^/лХл.
К сожалению, такое допущение исключает из рассмотрения все
«неустойчивые» подсистемы в ветви обратной связи, в том числе
часто встречающийся случай обратной связи по скорости. Такова
плата за возможность иметь в прямой ветви элементы с распре-
деленными параметрами, которые могут быть и неустойчивыми.
В первой теореме при очень общих условиях доказывается,
что если импульсная характеристика //(•) замкнутой системы
принадлежит orfnXn(c) при некотором о^О, то функция G(-)
должна удовлетворять определенным условиям.
5. Теорема. Рассмотрим систему, заданную уравнениями (1)
и (2), матричная передаточная функция Р (•) ветви обратной связи
которой принадлежит <а^лХл. Пусть G( •) — матричная обобщенная
функция с носителем в |R+, и предположим, что в некоторой окре-
стности начала координат в выражение для G (•) входят, быть
может, 6-функции, но без своих производных. Пусть импульсная
характеристика Н (•) замкнутой системы однозначно определяется
уравнением
6. Н + Н *F*G = G, или H — G — H*F*G.
Тогда, если Н (•) е &£пхп (а) при некотором а^О, то
(i) функция G(-) преобразуема по Лапласу; для некоторого
а>0 ее изображение G (•) аналитично при Res>a, принадлежит
алгебре е^/лхл(а) и может быть продолжено мероморфной функ-
цией в область Res><r,
(ii) функция G(-) представима в виде
7. 6(s) = &r(s)[^(s)]'\ где ^(s) еет/яХя (ст);
(iii)
8. inf | det [/Ц-Р (s)G(s)]|>0.
Re s>a
Замечания.
1. Нигде не делалось предположений ни о том, что матрица
/’(•) постоянна, ни о ее невырожденности, если она все-таки
96
ГЛ. 4. ЛИНЕЙНЫЕ СИСТЕМЫ
постоянна. Это позволяет нам рассматривать системы, в которых
число входов может не совпадать с числом выходов. Если мат-
ричная функция F(-) прямоугольна, то ее можно превратить
в квадратную, дополнив нулевыми строками или столбцами.
2. Из теоремы (5) следует, что при весьма слабых ограниче-
ниях, наложенных на G(), и в предположении, что уравнения
замкнутой системы разрешимы, а функция Н (•) имеет экспонен-
циальный порядок роста, можно вывести разнообразные свойства
функции G(-).
Доказательств теоремы (5). (i) При t = 0 уравнение (6)
принимает вид:
9. Но —Go— HoFoGo или Ho(I + F0Go) = Go,
где через Fo, Go и Но обозначены интенсивности импульсов, отно-
сящихся к моменту f = 0, в разложениях импульсных характе-
ристик F(-), G(-) и Я(-). Для того чтобы Но являлось единст-
венным решением уравнения (9), необходима неособенность матрицы
/ + F0G0. Введем обозначение:
10. Ё(s) = [/ + Р(s)б (s)]-1 = I — Р (S) Й(s).
Так как Ё (s) = I — Р (s)H (s) (см. упражнение 2) и Р, Н <=
ее^/"х"(а), то Ё е @^пхп (а). Поэтому функция E(s) ограничена
при Res^a, аналитична при Res>o и стремится к I-\-F0G0
при Res-*oo. Таким образом, функция s<—* 1/det Ё (s) мероморфна
при Res>o, аналитична и ограничена вдали от нуля в некото-
рой области Res>a, если а достаточно велико. Отсюда следует
(см. Приложение D.3.3), что Ё-1 (s) е &РпХп (а). Однако, согласно
(10), это означает, что /6(-)4-F(-)*G(-)eо^пхп(а). Следова-
тельно, функция F*G преобразуема по Лапласу, а функция Рб
аналитична при Res>a. Кроме того, Рб можно аналитически
продолжить мероморфной функцией в область Re s > о, поскольку
det Ё (s) может иметь только изолированные нули при Res>o.
Так как G(.) = ^(s)[/-b#(s)G(s)], то такой же вывод можно
сделать и по отношению к G(-). Таким образом, б—НЁ'1^
(И) Так как функция G(*) преобразуема по Лапласу, то
Й (s) = 6(j-}-Рб)~1. Используя методы теории матриц, можно по-
казать, что
11. d(s) = ^(s)[E(S)]-1,
где функция P(s) определена соотношением (10).
(iii) Как мы уже видели, из Н (•) е е^'ЛХп СЛедует Е (•) е
Еа/лХ"(<т), если только detE(-)^aP (о). Поэтому существует
конечное число k такое, что | det Ё (s) | k, если Res^a. Отсюда
4. СИСТЕМЫ, ЗАДАННЫЕ ОПЕРАТОРАМИ СВЕРТКИ
&
в свою очередь вытекает, что
,2- । я Л л г=Idet I7+(s)l । 55 i "Р” Res^CT’
I det E (s) | k
что достаточно для доказательства (8).
Разложение (7) впервые указывает на сходство теории систем
с дробно-рациональными передаточными функциями и теории систем
с обратной связью, задаваемых операторами свертки.
Упражнение 1. Предположим, что n=l, g (0=go6 (О+ga (О, причем
ga (•) е L1 и f (s) = fo=£O. Показать, что неравенство (8) эквивалентно утвер-
ждению о том, что функция si—> 1 +fog (s) не имеет нулей при Res^o. Это
свойство имеет место тогда и только тогда, когда диаграмма Найквиста функ-
ции g (т. е. график функции со ।—>g(o + /<o), где ogR) не пересекает или
не обходит по замкнутому контуру точку (—1//0, 0) в (Q. Интерпретации этого
свойства при других графических критериях приведены в разделе 5.
Упражнение 1 важно по следующей причине. Условие (8)
может нарушиться в двух случаях: (i) если det [/ + F(sQ) G (s0)] = 0
при некотором s0, для которого Res0^a, или (ii) если ука-
занное So хотя и не существует, но существует последователь-
ность {sx}, где Re Si о, такая, что det [/ + F (sz)G (s,)]0 при
>оо. Второй случай при сформулированных в упражнении
1 условиях невозможен. Кроме того, упражнение указывает спо-
соб проверки, имеет ли место первый случай, путем изучения
только поведения функции (oi—* &(<т4-/со).
Упражнение 2. Показать, что для системы, о которой идет речь в тео-»
реме (5), справедливы соотношения:
13а. Н = G (/ + FG)'1 = (/ + GF)'1 G,
13b. G = Н (/ - FH)'1 = (/ - HF)'1 H,
13c. (/ — FJY) (/ + FG) = /,
13d. (I — HF)(I + GF) = I.
Связь между соотношениями (13a) и (13b) становится очевидной, если заметить,
чю Н получается из G введением обратной связи F вокруг (?, a G получается
из Н введением обратной связи — /7 вокруг Н.
Упражнение 3. Показать, что Ё &оДпХп, если Н и F Хп.
Показать, что если, кроме того, F'1 ^о^пХп, то Н (=о/^пХп тогда и только
тогда, когда Ё & отЁпХп-
Итак, для того чтобы импульсная характеристика замкнутой
системы имела экспоненциальный порядок роста, функция G(-)
должна быть представима в виде (7). Теперь мы можем сформу-
лировать очень общую теорему, которая применима в различных
важных практических случаях.
4 Ч. Дезоер, М. Видьясагар
98
ГЛ. 4. ЛИНЕЙНЫЕ системы
14. Теорема. Рассмотрим систему с обратной связью, задан-
ную уравнениями (1) и (2). Предположим, что F(JSe^"x"
импульсная характеристика Н (•) замкнутой системы определяется
единственным образом, функция G() преобразуема по Лапласу
и, следовательно, Н (s) = G(s)[Z + F (s)d(s)]-1 в общей области
сходимости. Тогда Н е в том и только том случае, когда
(i) существуют функции (•) и & (•), принадлежащие е>/пХп,
такие, что
15. G(s) = ®/’(s)^r-1(s);
кроме того, выполняется условие несократимости: какова бы
ни была последовательность {sj, где Resj^O, такая, что
lim | det & (s,) | = 0, тем не менее всегда
<-»<»
lim inf | det (sj + F (зг) (s;)] | > 0.
i-*oo
Это условие в дальнейшем мы будем использовать в краткой
форме: упорядоченная пара функций [detJ?, det^ + fW")]
удовлетворяет условию (Я).
(»)
16. inf | det [/ + / (s) G (s)] | > 0.
Res >0
Доказательство.
Необходимость. Представим соотношение, связывающее 6 и Й,
в следующем виде: G = H (I — РЙ)-1. Полагая = Я, &—I — FH,
мы получим (15). Условие несократимости (N) также выполняется,
поскольку
det + /©/) = det 1 — 1 Vs при Res^O.
Таким образом, (i) доказано.
Рассмотрим соотношение (13с) и вычислим определители обеих
его частей; тогда
17. det[Z + /G] = [det(/-M)]-4
Так как I — РЙ то функция I — РЙ, а также ее опреде-
литель ограничены при Res^O. Поэтому (16) следует из (17).
Достаточность. Прежде всего покажем, что из (15) и (16)
следует неравенство
18. inf | det (s) + / (s) (s)] | > 0.
Re s 0
Докажем справедливость (18) методом от противного, т. е. пред-
положим, что (18) не выполняется. Рассмотрим последовательность
4. СИСТЕМЫ, ЗАДАННЫЕ ОПЕРАТОРАМИ СВЕРТКИ
99
{s/} (Re $3=0) такую, что det [.^ ($04-A (s,)®//" ($)]-> О при
। -> оо. Так как det 4* А©^"] = det $ • det (/ 4- Аб), то если
det (J?+ £W'')->0 при i-^-oo, то либо det^-»-O, либо
det(/ + FG)-> 0 (возможно, после выделения подпоследовательности
из {$,})• Последнее невозможно в силу (16). Допустим тогда,
что det ^($) -► 0. Однако, поскольку пара функций (det
det(^-|-Ав/*) удовлетворяет условию (2V),
lim inf | det (sO 4-A (s{) &^(Si)] | > О,
(—*oo Res 0
что противоречит нашему предположению. Таким образом, нера-
венство (18) доказано. Методами теории матриц находим, что
= G (/4-AG)'1 = <&/* (^ 4-А®^")-1. Учитывая (18) и результаты,
приведенные в Приложении D3.3, получаем: (^Г4-А®/’)-1 е
£а/’Хл, если Н ^етёпХп.
Упражнение 4. Доказать теорему (14) в другой формулировке. Пусть
Р е Тогда Й = д (/Ц-Лб)-1 е @^п^п в том и только том случае, когда .
существуют функции и такие, что Ь — и
inf | def [£) (s) 4- ? (s) «чГ (s)] | > 0.
Res >0
19. Следствие. Предположим, что fi и d=
где и пара функций (det det (^ 4-А®-/*))
удовлетворяет условию (N). Тогда Н = д(1 + FGY1 <= о^пХп в том
и только том случае, когда выполняется неравенство (16).
Теорема (14), нетрудная для формулирования и доказательства,
имеет много интересных следствий. Предположим, что заданы
функции А е <з^лХл и G, и необходимо определить, принадлежит ли
алгебре е^лХл функция /7 = G(/4*AG)-1. Как нам следует посту-
пить? Прежде всего необходимо проверить, выполняется ли усло-
вие (16). Если оно не выполняется, то функция Н наверняка
не принадлежит &^пХп, так как справедливость (16) является
необходимым условием принадлежности функции Н алгебре &^пХп
(см. теорему (5)). Если же (16) не нарушено, то еще нет гаран-
тий того, что Н е @^пХп.
Чтобы убедиться в этом, рассмотрим следующий пример. Пусть
Тогда
100
ГЛ 4 линейные системы
и условие (16) выполняется. Однако
L (s-1) (s+2)
и, очевидно, что И ф о^п^п. Таким образом, для того чтобы
заключить, что Н е кроме установления справедливости
(16), следует убедиться, что G представима в виде (15), причем
соответствующие функции удовлетворяют условию (W)
Теперь перед нами встает следующая задача Предположим,
что функция G может быть представлена в виде (15), где
& е ет/'г><л, однако условие (М) не выполняется. Что можно
вывести из такого предположения? Вообще говоря, ничего, хотя
надо попытаться построить другое разложение G. Однако, если
функции и являются так называемыми «вззимно псевдо-
простыми справа» матрицами, то появляется возможность сделать
определенные выводы. Изучим это свойство подробнее.
20. Определение. Два элемента и & алгебры &#пХп назы-
ваются взаимно псевдопростыми справа, если существуют элементы
й, W' ^о^п><п такие, что
(i) det W* (s) =/= 0 для всех s таких, что Res^O, | s | < оо;
(ii) +
21. Определение. Пара (©^, ^) называется взаимно псевдо
простым справа разложением функции G, представляющей собой
изображение по Лапласу функции G(-), если
(i) G = ^rJr-1;
(ii) и & взаимно псевдопросты справа;
(iii) для любой последовательности {sj такой, что Res^O
и s,i->oo при Z->oo,
lim inf det (sx)|>0.
I —*-co
22. Утверждение. Если функция G (s) e IR"*" (s) правильна,
го она имеет взаимно псевдопростое справа разложение.
Доказательство. Если функция G (s) е IR"*" (s) — правиль-
ная, то существуют взаимно простые справа многочленные матрицы
N и D такие, что ND~1 = G. Кроме того, мы можем считать, что
столбцы матрицы О, рассматриваемые как функции, правильны.
/?
Пусть det D(s) = — 8, обозначает наибольшую степень s
i = i
в i-м столбце D(s). Так как все столбцы D — правильные функции,
4. СИСТЕМЫ, ЗАДАННЫЕ ОПЕРАТОРАМИ СВЕРТКИ
101
ТО
п. k
У, &>=
i=l i=l
Пусть
М (s) = diag[(s+ 1)61, (s+l)4
И
23. = NM-\ & = DM-1.
Тогда и & являются правильными дробно-рациональными
матрицами с полюсами s = —1, и поэтому & ^<?Лпхп. Кроме
того, G = ^S^-1. Таким образом, выполняется условие (i) опре-
деления (21). Поскольку N и D взаимно просты справа, то
существуют многочленные матрицы Р и Q такие, что
24. PN + QD = I для всех s.
Обозначим через а целое число, не меньшее степени произ-
вольного элемента матриц Р и Q. В этом случае обе дробно-рацио-
нальные матрицы
25. 2Z = P(s + l)~a, ^ = Q(s+ l)“a
принадлежат алгебре о^пХп. Используя (24), введем матрицу
26. ^^^^-(PyV+QD) М-1 ($+1 )-«=М-1 ($+1 ($)
Очевидно, что W" (s) е о^пхп и det Ж (s) = ($+ l)~z, где/ = ап +
/? А
+ У, mt — целое число. Поэтому det W' (s) #= 0, если Re s 0 и
£=1
»s|<oo. Таким образом, выполняется условие (ii) определения (21).
И, наконец,
det Ь (s) = det D (s) [det М (s)]-1 = J [ (s- pi)'"i П (s -1 )-6/-
1=1 i=l
Отсюда следует, что det£)(s)->l, если |s|->oo. Следовательно,
пара (©/", ^), заданная соотношениями (23), в силу определе-
ния (21) является взаимно псевдопростым правым разложением G •
Упражнение 5. Показать, что функция из (23) правильна
Упражнение 6. Пусть пара (@^, j^) —взаимно псевдопростое справа раз-
ложение функции G. Показать, что G мероморфна в С+ и точка р, для кото-
рой Rep >0, —полюс функции G тогда и только тогда, когда detj^(p) = O.
Упражнение 7. Пусть функция (j имеет взаимно псевдопростое справа
разложение (@^, ^) Показать, что какова бы ни была последовательность
{sj, для которой Resz-^0 и lim ! s£| = oo, lim sup G (sz-) I < оо Иначе
£—*•00 i—*oo
говоря, если G имеет взаимно псевдопростое справа разложение, то G ($) дол-
жна оставаться ограниченной при | s | -> оо, если Res^O.
102
ГЛ. 4. ЛИНЕЙНЫЕ СИСТЕМЫ
Важность взаимно псевдопростого разложения легко усмотреть
из следующей теоремы.
27. Теорема. Пусть Fse/”x", G = ©^^-1, где (@У*, пред-
ставляет собой взаимно псевдопростое справа разложение G.
Тогда 77 = G(/-|-FG)-1 е®'/яхп в том и только том случае, когда
28. (i) inf | det[/+^(s)G(s)]| >0
Res >0
И
29. (ii) det [<F (s) + F (s) (s)] =#= 0,
если det & (s) = 0 и Re s 2= 0.
Доказательство.
Необходимость. Предположим, что Н^.&^пхп. Тогда нера-
венство (28) вытекает из теоремы (14). Для доказательства (29)
покажем, что если (29) не выполняется, то Wes/"*". Пусть s0
таково, что det [ J? (s0) + F (se) ©/* (s0)] = 0 и Re s0 3s 0. Так как ©-/*
и взаимно псевдопросты справа, то существуют #, и W1
из о^пхп такие, что
30. 2?®? + ^^ = ^
и det W" (s) =/= 0 при Re s 2s 0. Из (30) получаем:
йЙ -J- tyb + fyFN = Й7 + VFN,
(U - N+ + FN) = Й?,
31. (U-tyfyH + ^ffiCD + FH)-1.
При s->s0 правая часть (31) неограниченно возрастает, потому
что det (^ + fis^) -*• 0, a det V? (s0) =# 0. Тогда левая часть (31)
также должна неограниченно возрастать. Однако функции й —
и ограничены в области Res^O. Следовательно, при s->s0
функция Н должна быть неограниченной, т. е. Й Таким
образом, из Й е @Лпхп следует (29).
Достаточность. Пусть неравенства (28) и (29) выполняются.
Нам необходимо показать, что Й е е^пхп. Для этого сначала по-
кажем, что пара (det det (^ + /'©/")) удовлетворяет условию
(N). Пусть последовательность {s,} (Re s,-3=0) такова, что
det^(sf)-»-0 при i->oo. Так как lim inf | det & (s{) | > 0 при
|sz|-»-oo, то последовательность {s;} ограничена. Поэтому из нее
можно выделить сходящуюся подпоследовательность, предел кото-
рой обозначим через $0. Тогда Reso^O и det^(so) = 0. Соглас-
но (29) отсюда вытекает, что det ($#) + f (s0) (s0)] ф 0. Таким
образом, пара (det det (^ +г®/5)) удовлетворяет условию (Af).
4. СИСТЕМЫ, ЗАДАННЫЕ ОПЕРАТОРАМИ СВЕРТКИ
103
Этот факт вместе с неравенством (28) позволяет на основании
теоремы (14) заключить, что Н^о^пхп.
Упражнение 8. Доказать теорему (27) в иной формулировке. Если пара
(©^» представляет собой взаимно псевдопростое справа разложение
функции й и F е <2т/лхл, то H = G (I +FG)”1 е о^пхп тогда и только тогда,
когда
inf | det (s) + F (s) (s)] _| > 0.
Res>0
32. Замечание. Как уже упоминалось выше (непосредственно
после следствия (19)), неравенство (28) (или условие (16)) яв-
ляется необходимым, но не достаточным условием того, что функ-
ция Й принадлежит алгебре &^пхп. Теорема (27) позволяет точно
определить, когда (28) становится достаточным условием устой-
чивости. Пусть (®/\ ^ — взаимно псевдопростое справа разло-
жение функции G, функция F принадлежит &4пхп и неравенство
(28) выполняется. Тогда Й е <&йпхп в том и только том случае,
когда еправедливо неравенство (29). Это условие интерпретируется
следующим образом. Ясно, что det -\-F@^) = det det (I + FG).
Допустим, det J?(s) = 0 при Res^O. Если значение det (I + ЙО)
конечно, то det (^4-/©/^) = 0 и.Н<£&#"хп. Этот случай рас-
смотрен в примере сразу же после следствия (19). Если же
det (J + FG) имеет полюс в точке s, то значение произведения
det & det (/ + йй) не определено, и величину det(/-(-FG) следует
вычислять непосредственно.
Теореме (27) показывает, насколько важно уметь находить
взаимно пасвдопростое справа разложение заданной передаточной
функции G. Указанная задача упрощается, если принять во вни-
мание утверждение (33), из которого следует, что необходимо
определять взаимно псевдопростое справа разложение только для
«неустойчивой части» функции G(-).
33. Утверждение. Предположим, что (©^, .^j —взаимно псев.
допростое справа разложение G (•) и Gx (•) е <&#пхп. Тогда
(©/*4-01^, ^) является взаимно псевдопростым разложением
G4"Gi.
Доказательство. По условию G = ©^z'^_1, поэтому
б 4- Gi = (©/* 4- Gi^) Из условия также следует, что
liminf | det (s) |>0 при |s|->oo, если Res^O. Таким обра-
зом, необходимо показать, что и & взаимно псевдо-
просты справа. Так как, по условию, и & взаимно псевдо-
просты справа, то существуют функции Ut и W из <rfnxn
104
ГЛ. 4. ЛИНЕЙНЫЕ СИСТЕМЫ
такие, что det Ж(з)! =/= С при Res^O и |s,<oo и
34. + = Ж
Отсюда
U (&К + Gi^) + (°Т - ^Gi) & = Ж
т. е. + и & взаимно псевдопросты справа.
Применяя теорему (27), получим совершенно iочные необхо-
димые и достаточные условия устойчивости одного класса мно-
гоконтурных систем с обратной связью.
36. Теорема. Пусть функция G(-) имеет вид:
k mi
37. G(s)= У У —- + <jft(s) = Ga(s)4-G6(s),
". <s-^
где Rep,-5=0 при всех i и Gb е Пусть
38. G„ (s) = (s) О-1 (з),
где N и О —взаимно простые справа многочленные матрицы,
а столбцы матрицы D — правильные функции. Пусть F е о^п*п.
Тогда Н = G(I H-FG)-1 е ^п'п в том и только том случае, когда
39. (i) inf , det [/4-F(s)G (s)] |> 0
Res 0
И
40. (ii) det [D (p,-) + F (pA N (pt) + F (pt) Gt (pt) D (p,)] #= 0
при i = 1, 2, ..., k.
Доказательство. По известным функциям N и D с по-
мощью соотношений (23) построим функции ©/* и Пара
(®У\ ^) является взаимно псевдопростым справа разложением
функции GM, а потому, согласно утверждению (33), пара
(@^Г 4-Gd<^, ^) —взаимно псевдопростое справа разложение функ-
ции G. Таким образом, в силу теоремы (27), Н тогда и
только тогда, когда выполняется (39) и, кроме того,
41. det (s) + F (s) &Г (s) + F (s) Gb (s) & (s)J =# 0,
как только det^(s) = O и Res^O. Однако из способа построе-
ния и ясно, что det (s) = 0 при Res^O в том и только
том случае, когда s = pf (f = l, 2, ..., fe). Далее, @^(s) =
= ^(s) УИ-1 (s), (s) = D (s) (s) и det Л4 (pt) =# при i = 1,
2, ..., k. Таким образом, (41) превращается в (40).
4. СИСТЕМЫ, ЗАДАННЫЕ ОПЕРАТОРАМИ СВЕРТКИ
105
42. Следствие. Пусть п=1 (скалярный случай) и предполо-
жим, что
k
43. g (s)= У У —(s) = ?«($)4-
zT, /=i (s~p^
причем gb^.&£. Тогда h =g/(l + lg) e в том и только том
случае, когда
44. inf | l+f(s)^(s)|>0,
Res>0
45. /(р,)=#0, 1 = 1,2..................k.
Доказательство. Пусть ga(s) = n(s)/d(s), причем много-
члены п (s) и d(s) не имеют общих нулей. Тогда (39) превращается
в (44), а (40) приобретает вид:
46. d + f (pi) n (pi) + f(pi) gb (pi) d (pi) #=0, i = 1, 2.k.
Однако, поскольку d (pi) = 0 и n (pi) =£ 0, (46) превращается
в (45).
48. Замечание. Если функция G имеет несколько полюсов
в правой полуплоскости, пользоваться разложением (38) затруд-
нительно. Поскольку условие (40) носит локальный характер,
можно отдельно рассматривать каждый полюс. Обозначим через
Ri(s) главную часть разложения Лорана матрицы G в окрестно-
сти точки Pi (i = 1, 2, ..., k), а через Л4/ —разность G — Ri-
Функция Mi аналитична внутри диска малого радиуса с центром
в Pi'
G (s) = [Ri (s) + Mi (p^] + (s) - Mi (Pi)l
Слагаемое в первых скобках является правильной дробно-рацио-
нальной матрицей, имеющей взаимно простое справа разложение
(например, М/Д-1); второе слагаемое (обозначим его через Ф/)
локально аналитично и Ф/(р1) = 0. Поэтому
G(s) = Ni(s)Dr(s) + ^i(s).
Читателю в качестве упражнения предлагается показать, что (40)
можно заменить на
50. det[Di(pi) + F(pi)Ni(pi)]^Oi f = l, 2, ..., k.
Упражнение 9. При обозначениях и предположениях замечания (48) по-
казать, что функция Н имеет полюс pi тогда и только тогда, когда (50) не
выполняется.
106
ГЛ. 4. ЛИНЕЙНЫЕ СИСТЕМЫ
5. ГРАФИЧЕСКИЙ КРИТЕРИЙ УСТОЙЧИВОСТИ
Хорошо известно, что графический критерий Найквиста очень
важен по трем причинам:
(i) он основан на непосредственно измеряемых эксперименталь-
ных данных, которые могут быть получены с высокой точностью.
Критерий Найквиста не похож на критерии Рауса— Гурвица и
Льенара — Шипара, использующие данные интерполяции изме-
рений;
(ii) критерий Найквиста применим к системам с распределен-
ными параметрами;
(iii) если система неустойчива согласно критерию Найквиста,
то легко понять, как именно надо изменить конструкцию системы,
чтобы она стала устойчивой.
В этом разделе мы приведем графический критерий для систем
с распределенными параметрами с и входами и и выходами и для
скалярного случая.
Рассмотрим частный случай системы, удовлетворяющей теореме
(4.36), когда передаточная функция подсистемы в ветви обратной
связи является постоянной матрицей F. Как и раньше,
k mi
' <^22Лй+й^
Графический критерий используется для проверки неравенства
(4.39). Введем обозначения
2. det[Z + FG(s)]=l+g(s) =
оо I
-i+^w+2^''+2 2<j=?>
t = 6 fe = la=l
где ga&L1, У, |g(|<oo, Rep* 2s О при 6=1, 2, .... / и p.* —
i=0
кратность полюса pk определителя det[/-RFG(s)] —может быть
не равна m*. В действительности 0^p*sgnm*. Мы будем пола-
гать, что 0 = /о> ^>0 для всех i>0. В скалярном случае, как
и в следствии (4.42), проверяемое выражение имеет вид (2), при-
чем для простоты мы примем f=\.
Графический критерий основан на исследовании образа оси /о
при отображении s>—*l+g(s). Сначала определим фазу функции
1 +g (/®) Для всех
4. 9 (/w) = arg[ 1 -j-g (/©)] = Im {log [1 -Rg (»]}.
В использовании выражения (4) есть две трудности. Во-первых,
функция l-f-g(/co) может быть равна нулю при некоторых <о.
в. графический критерий устойчивости
107
В этом случае (4.39) нарушается, т. е. передаточная функция
замкнутой системы не принадлежит е^яхя, и никаких дальней-
ших действий предпринять нельзя Во-вторых, один или более
полюсов ph могут лежать на оси /со. В таких случаях мы будем
«прокалывать» ось /и в каждом из полюсов. Иначе говоря, если
Ik обозначает отрезок оси /со длиной 2р с центром в полюсе рк
(р>0 и достаточно мало), то во всех полюсах, расположенных
на оси /©, мы заменим отрезки Ik полуокружностями радиуса р
с центром в точке pk, лежащими в правой полуплоскости. Вдоль
проколотой оси /и функция s»—* 1 -|-g (s) равномерно непрерывна
и фаза 9 везде определена. С каждой точкой проколотой оси /со
связана ее ордината со, т. е. определена биекция точек действи-
тельной оси — оо<со<;оо и проколотой оси /со По этой при-
чине мы, нарушая определение 9 (/со), будем тем не менее поль-
зоваться символом 9 (/со) для обозначения фазы функции 1-(-£($)
в точке s с ординатой со, лежащей на оси /со. Таким образом,
с увеличением со при прохождении вокруг полюса рк = /со* по-
рядка mk справедливо равенство 9 [/ (со* + р)] — 9 [/ (со* — р)] =
= —/п*л + О(р), т. е. 9(-) уменьшается на величину т*л.
Итак, мы определили непрерывную функцию 9 (/со) и нам оста-
лось только выбрать ветвь логарифмической функции, входящей
в (4). Будем считать, что
если 0<| 1 + £ (/0) I < оо, то 9(/0) равно 0 или л в зависи-
мости от того, положительно или отрицательно значение 1 -f-g (/0);
если l+g(-) имеет полюс в точке со = 0, то 9(/0) равно 0
или п в зависимости от того, положительна или отрицательна
функция 1 4-g (а) при ое(0, р), где р достаточно мало.
Теперь мы окончательно определили непрерывную функцию
со и-» 9 (/со), являющуюся фазой функции 1 + g (s) вдоль проколо-
той оси /со. Обозначим через V# ось /со, проколотую описанным
выше способом. Графический критерий основан на исследовании
образа Уо при отображении 1 4-g(-), который мы будем обозна-
чать символом (для диаграммы Найквиста).
Теперь мы последовательно рассмотрим три все более слож-
ных случая.
Случай I. Все функции g{ в (2) равны нулю.
Тогда функция l+g(s) аналитична при Res>0, за исклю-
чением полюсов рк, и согласно лемме Римана — Лебега 1 +g (s) -> 1
при |s|->oo, если ResSaO. Этот предел достигается равномерно
по args, если | args | «С л/2. Поэтому для любого е>0 сущест-
вует такое достаточно большое г>0, что
(а) все полюсы р* попадают в множество В(0; г)П©+, т. е.
в правую половину диска с центром в начале координат и с ра-
диусом г;
(Ь) для всех | а | л/2 справедливо неравенство 11 + g (fe/a) | <
< 1 +••
108
ГЛ. 4. ЛИНЕЙНЫЕ СИСТЕМЫ
Обозначим через правую полуокружность, ограничивающую
упомянутый выше полудиск. Функция 1 4-g (•) мероморфна внутри
множества В (0; г)ПС+ и равномерно непрерывна на его границе
/oU^r. Следовательно, можно воспользоваться принципом аргу-
мента: l+g(-) не имеет нулей внутри V0U^/- тогда и только
гогда, когда полное приращение аргумента 6 при обходе V0U^
по часовой стрелке равно Д6= р*. Так как, согласно (Ь), функ
k
ция 1 4-£ ограничена вдали от нулей, не принадлежащих В(0; г),
справедлива следующая теорема.
5. Теорема. При определениях (1), (2), (4) и в предположе-
нии, что gi = Q при всех /1>0, неравенство
6. inf ! det [I 4- FG(s)]|> 0
Res 0
выполняется тогда и только тогда, когда
7. 1 +g(ja) =#0 при всех <oe|R
и
8. А9 = lira [б (/Q) - 0 (— /й)] = £ = пр,
й->00 k
где суммирование ведется по всем полюсам pk, лежащим в откры-
той правой полуплоскости.
Предел (8) имеет следующую интерпретацию. По мере увели-
чения со от —оо до 4-оо вдоль оси /со, на которой «выколотых
полюсы функции 14-g(-), соответствующая точка вычерчивает
кривую ©ТЛ обходя начало координат £ р* = пр раз против часо-
вой стрелки. Здесь пр равно числу полюсов в открытой правой
полуплоскости, причем кратные полюса входят в пр столько раз,
каков их порядок. Отметим также, что, согласно неравенству (7),
кривая не проходит через начало координат.
Случай II. Требование равенства нулю всех функций gt сни-
мается, однако мы предполагаем, что существует бесконечная по-
следовательность неотрицательных чисел {п,} и положительное
число т>0 такое, что по = 0 и
10. ^ = П/т для любых
Этот важный частный случай имеет место
(а) в системах, содержащих в своем составе одну однородную
линию передачи без потерь или несколько таких линий, длины
которых относятся друг к другу как рациональные числа;
(Ь) в системах управления и моделях биосистем, содержащих
либо одну линию задержки либо несколько линий задержки,
величины запаздывания которых относятся друг к другу как
рациональные числа.
Из условия (10) можно вывести два следствия:
5. ГРАФИЧЕСКИЙ КРИТЕРИЙ УСТОЙЧИВОСТИ
109
(а) числа относятся друг к другу как рациональные числа:
= для любых i, AeZ+;
(b) функция со»—*Sf*exp(—периодична .с перио-
дом 2л/т.
Пусть
11. /(s) = i + S = 1 +
1=0 i = 0
По лемме Римана — Лебега при |s|->оо и Res^O
12а. l+g(s)-+f(s) равномерно по args на [—л/2, л/2]
и
12b. 1 + g (s) -> 1 + gQ при s—>oo вдоль действительной оси.
Пусть
13. <Р (со) = arg/(/со).
Поскольку функция со»—*/(/со) периодична с периодом 2л/т,
14. ф^со + ^j —ф (со) = т2л VgjeR,
где /и —целое число. Если т = 0, то функция со »—*ф(ю) перио-
дична. Если ту=0, то полное приращение фазы за один период
равно /п2л и
15. ф (со) = Хсофр (со),
где Х = тт, а функция фр(-) периодична.
Из (12а) следует, что образ Vo при отображении si—>l+g(s)
приближается при i со | -> оо к замкнутой кривой W^oo вида
16. Ф-Гоо =ф(/<о) | о (0 < y} •
Если в (15) X не равно нулю, т. е. т=#0 в (14), то при w->oo
кривая приближается к замкнутой кривой ©zFoo и фаза 6 (/ •)
неограниченно возрастает на множестве [R, поскольку при доста-
точно больших значениях со кривая ©Ж9 бесконечно близко стя-
гивается к ©zT’oo и в пределе 0 увеличивается на т2л за один
период.
Графический критерий устойчивости для случая II, представ-
ленный ниже в виде теоремы (18), является частным случаем
критерия устойчивости общего вида (см. теорему (30)). Этот кри-
терий можно установить также методом конформных отображений,
используя преобразование z = exp(—st) (cm. [103]).
18. Теорема. При определениях (1), (2) и (4) и в предполо-
жении, что числа ti относятся друг к другу как рациональные
110
ГЛ. 4. ЛИНЕЙНЫЕ системы
числа, т. е. связаны соотношением (10), неравенство
19. inf | det [/ + FG (s)] | > 0
Re s 0
выполняется тогда и только тогда, когда
20. l+go¥=0,
21. 1 +§(/<•>) =/= 0 для всех weR,
22. Д6 = 5 Ръ
к
суммирование ведется по всем полюсам открытой правой
полуплоскости, причем кратные полюса считаются в соответствии
с их порядком.
Из условия (22) следует, что % = 0 или /п = 0; графический
смысл (22) заключается в том, что замкнутая кривая ©^*оо не
окружает начало координат. Кроме того, согласно (21) и (12а)
ни одна из кривых и ®^*оо не окружает начало координат.
Случай III. Общий случай: никаких дополнительных ограни-
чений.
Мы не будем доказывать соответствующую теорему, а лишь
сформулируем графический критерий и объясним, в чем его отли-
чие от предыдущих случаев. Как и раньше, функция / задается
соотношением (11):
25. f(s) = 1+5 gte-^,
i=0
являясь почти-периодической функциейг) в правой полуплоскости.
Условия (12а) и (12b) продолжают выполняться. Так как функ-
ция ►/(/(>)) почти-периодична, то для любого заданного е>0
существует е-сдвиг т8, удовлетворяющий условию
26. I/(/©)-/О+ /те)|<е для всех io е R.
Кроме того, последовательность 8-сдвигов / (е)-относительно плотна
на множестве R, т. е. любой интервал длины I (е) содержит по
меньшей мере одно число те2). Отсюда получаем очень важное
следствие. Рассмотрим образ компактного интервала [0, I (е)] при
отображении
27. = {z <= (D | г = / (/co), 0=gco«£/ (e)}.
Пусть aeZ и
28. = {* S 01*« f (/©), a/(e) © «5 (a + 1) Z (e)}.
*) Определение почти-периодической функции см. в [22].
•j Этет факт недробно описан в [22]
6. ГРАФИЧЕСКИЙ КРИТЕРИЙ УСТОЙЧИВОСТИ
111
Из определения I (в) следует, что для всех aeZ кривая
находится в е-окрестности кривой ®^*z. Поэтому образ оси /со
при отображении f(-) находится в е-близости от @^z. Для е из
(26) и (28) на основании леммы Римана —Лебега существует
число С28>0 такое, что для всех | со | > Q8 образ множества V#
при отображении 1 + £ (•) находится в 2в-близости от W*z. При
достаточно больших |<о| кривая попадает и остается в 2е-окрест-
НОСТИ Кривой ®//'z.
Можно показать, что фаза ф почти-периодической функции
/(/со) представима в виде
29. ф(со) = 1со + Л(со), ®e|R,
где XeR и функция й(-) почти-периодична и, следовательно,
ограничена на множестве R. Отметим, что Х^=0 тогда и только
тогда, когда для достаточно малого е соответствующая кривая ®/"z
окружает начало координат.
Для формулирования графического критерия удобно обозна-
чить через N (®/*z; 2е) 2е-окрестность кривой1 определенной
соотношением (27). Принимая во внимание сказанное, сформули-
руем графический критерий устойчивости.
30. Теорема. При определениях (1), (2) и (4) неравенство
81. inf | det [7 + F(! (s)] | > О
Re s 0
выполняется тогда и только тогда, когда
(i) 1+& =А0;
(ii) положение кривых {zе©\z = f(ja>), со<= R} и {ze©|z =
“ 1+g (/®)> по отношению к началу координат О ком-
плексной плоскости таково, что
(а) для достаточно малого в > 0 точка О не принадлежит мно-
жествам N 2в) и {г <= © | z = 1 +g (/©), 0 sg со < й8};
(Ь) для того же е и соответствующего ему сдвига т8 необхо-
димо, чтобы
|Ф(т8)-ср(0)|<у;
(с) lim [6 (/со) - ф (/©)] = б (/0) - ф (/0) + прп,
Ш-ФСО
где в —фаза функции 1+g, ф —фаза функции /, пр — число по-
люсов функции g в открытой правой полуплоскости, причем
кратные полюса считаются в соответствии со своим порядком.
32. Замечания.
1. При определении устойчивости системы графический кри-
терий (30) требует знания последовательностей {gz} и {/,} (i =
в0, 1, ...) для построения кривой ®^*z и функции ф(-).
112
ГЛ. 4. ЛИНЕЙНЫЕ СИСТЕМЫ
2. Условие (Ь) фактически означает, что кривая @7^ не окру-
жает начало координат. Действительно, согласно (13), функция ср
представляет собой фазу /; в силу (26), 1/(/те) —/(0) | из
условия (а) следует, что I / (/т8) | и | / (0) | превосходят 2е. Поэтому,
согласно условию (Ь), при увеличении | со I от 0 до т8 точка / (/со)
вычерчивает кривую, не окружающую начало координат.
3. В простых случаях при выбранном 0 нетрудно оценить
числа й8 и I (е), после чего достаточно изобразить только образы
компактных интервалов. В более сложных случаях построить
нижнюю оценку для I (е) не так легко. В отдельных случаях
число к в соотношении (29), будучи, например, положительным,
настолько мало, что величина Хсо на интервале [0, I (е)] незна-
чительна по сравнению с /г (со). Pehiaя систему диофантовых урав-
нений, в которую входят члены известных нам последовательно-
стей {£/} и {/J (Z = 0, I, ...), можно вычислить нижнюю оценку
для числа X, если оно положительно, а затем определить ниж-
нюю оценку для I (е) так, чтобы условие (Ь) обеспечивало выпол-
нение равенства Х = 0.
Упражнение. Используя графический критерий, определить, устойчива ли
следующая система: ult еъ уг: R+ -> R; и2 = 0, коэффициент усиления прямой
ветви равен действительному постоянному числу k, передаточная функция ветви
обратной связи равна e~s; число k принимает значения из интервала (0, оо).
Проверить ответ, непосредственно вычислив импульсную характеристику
системы.
6. ДИСКРЕТНЫЕ СИСТЕМЫ
С дискретными системами исследователи сталкиваются довольно
часто, например,
(а) при моделировании систем, являющихся дискретными по
своей природе, например, цифровых фильтров или систем, управ-
ляемых вычислительными машинами, где входные воздействия и
реакции измеряются не непрерывно, а в определенные моменты
времени.
(Ь) при аппроксимации моделей непрерывных систем, когда
входные и выходные сигналы приближенно представляются сту-
пенчатыми функциями; например, и (I) = ak при kT<zt<.(k-\-1) Т,
где ak (& = 0, 1, ...) — постоянные величины.
(с) при решении на вычислительных машинах задач теории
непрерывных систем.
Во всех перечисленных случаях входные и выходные сигналы
можно рассматривать как последовательности, заданные на мно-
жестве неотрицательных целых чисел Z+ и принимающие значе-
ния из банахова пространства (т. е. полного нормированного
пространства). Обычно таким пространством бывает R, С, О'7,
Клхл и т. д.
6 ДИСКРЕТНЫЕ СИСТЕМЫ
113
6.1. Существование и единственность
Рассмотрим еще раз систему, структурная схема которой
изображена на рис. 4.1. Поскольку мы будем исследовать диск-
ретный случай, то и, е и у представляют собой последовательно-
сти из 1РЛ. Определим условия, при которых существует единст-
венная последовательность е, соответствующая каждой последо-
вательности и. В дальнейшем мы будем полагать, что F и
G —нестационарные динамические операторы, обладающие свой-
ствами линейности и неантисипативности. Введем обозначения:
1. S'* —множество всех линейных отображений х, действующих
из Z+ в 1РЛ;
2. и, е, у е S'*, или и, е, у: Z+-например,
u = (u0, Ui, и2, ...);
i
3. F: Sn->Sn и (Fx)i=2
i
4. G: Sn->Sn и (Gx)i= J] GijXf.
/=0
Отметим, что мы не накладываем никаких ограничений на раз-
мерность векторов входных, выходных сигналов и сигнала ошибки;
если эти размерности различны, то матрицы F и G всегда можно
дополнить строками или столбцами, состоящими из нулей.
5. Теорема. Последовательность е е S'*, удовлетворяющая
уравнению
6. е = и — FGe
и соответствующая каждой последовательности и е S'*, сущест-
вует и притом определяется единственным образом тогда и только
тогда, когда
7. det (/ + Fm> mGm> m) #= 0 для любых т е Z+-
Доказательство. Так как система, изображенная на
рис. 4.1, характеризуется уравнениями
8а. е = и — Fy,
8b. у = Ge,
ясно, что пара (е, у) е S'*х Sn, удовлетворяющая уравнениям (8а)
и (8Ь) и соответствующая каждому и е S'*, существует и един-
ственна тогда и только тогда, когда (6) имеет единственное реше-
ние е е S'*, соответствующее каждому и е S'*. Поэтому мы скон-
центрируем наши усилия на доказательстве существования и
единственности решения уравнения (6).
114
ГЛ. 4. ЛИНЕЙНЫЕ СИСТЕМЫ
Достаточность. Представим матричное уравнение (6) в виде
системы уравнений, а затем перейдем к системе уравнений отно-
сительно бесконечного множества неизвестных е0, ех, ...» ет, ...»
характеризующих состояние системы в отдельные моменты вре-
мени. Матрица коэффициентов, умножаемая на вектор (е0, ех, ...),
в полученной системе уравнений является нижней треугольной
матрицей, а ее диагональные элементы равны Z4-Fo,oGo,o> ...
...» I + Fm,mGm,m> ... Таким образом, если (7) выполняется, то
для любого и е 8п можно найти единственное решение е е 8п
уравнения (6).
Необходимость. Доказательство проведем методом от против-
його. Допустим, что (7) не выполняется, и обозначим через k
наименьшее целое число, при котором det {I + Pk,kGk,k) — ^- Тогда
для любого заданного и е Sn значения е0, е19..., е*_х вычисляются
единственным образом. Для ek уравнение имеет вид
k k
или после группирования всех известных величин в правой части,
а всех неизвестных — в левой:
fe —lfe—1 fe—1
10. (14- Fkt kGk, k) ek = uk — 2 Fb.iGi.jej— У*, F^kGkjej*
t=0 / = 0 /«0
В зависимости от конкретного вида последовательности и ранг
правой части (10) может либо отличаться от ранга I + Fk,kGk,k>
и тогда (10) вообще не будет иметь решений, либо совпадать
с рангом I + FktkGk,k, и в этом случае (10) будет иметь беско-
нечно много решений. Однако в обоих случаях уравнение (10),
а следовательно, и уравнение (6) не может иметь единственного
решения.
Теорема (5) при довольно слабых ограничениях, наложенных
на F и G, определяет очень простые необходимые и достаточные
условия разрешимости замкнутой системы, заданной уравнениями
(8а) и (8Ь). Важными предположениями о функциях F и G
являются лишь их линейность и неантисипативность. В осталь-
ном же эти функции могут быть как стационарными, так и не-
стационарными, статическими или динамическими.
Упражнение 1. Используя теорему (5), легко вывести большое число кри-
териев разрешимости различных классов дискретных систем с обратной связью.
В качестве упражнения мы приведем один из наиболее важных случаев.
Пусть функция G: Sn-+Sn стационарна, т. е. (Z —7) = ^_/ (из пред-
положения о неантисипативности G вытекает, что ^«=0 при i <0), a F:
->Sn — нестационарная статическая функция, т. е. F^i — Fi, Fit/ = 0 при
i > /. Тогда уравнение (6) имеет единственное решение е е Sn, соответствую-
щее каждому u е S'1, в том и только том случае, когда
П. det (У+У'от^о) ¥= 0 для любых meZt.
6. ДИСКРЕТНЫЕ СИСТЕМЫ
115
6.2. Z-n реобразование
Основные свойства г-преобразования являются прямым след-
ствием свойств степенных рядов, г-преобразование заданной по-
следовательности а = (а0, «1, а2» •••)» ГДе ai (* =0, 1» 2, ...) при-
надлежит банахову пространству Е, определяется формулой
12. 2(а) = й(г) = 2 ak2rk.
At =0
Этот степенной ряд от гг1 имеет, радиус сходимости га и сходится
вне замкнутого диска В(0; га) радиуса га с центром в начале
координат. Хорошо известно, что
13. ra= lim sup ИМ1/*.
k -* 00
Кроме того,
(а) правая часть (12) абсолютно сходится при любом |z|>-ra;
(b) для любого 6>0 тот же ряд сходится равномерно в до-
полнении множества В(0; ra + 6);
(с) правая часть (12) представляет собой аналитическую функ-
цию в открытом множестве | г | > га.
В дальнейшем для обозначения г-преобразования мы будем
использовать значок например, a = 2(a), G = B(G).
Покажем, как связаны преобразование Лапласа и г-преобра-
зование. Сопоставим а — (а0, alt а^, ...) и временною «функцию»
00 оо
У! akd (t — k). Ее преобразование Лапласа равно о^е-*4. Сра-
о - о
внивая полученное выражение е (12), замечаем, что г соот-
ветствует е4. Таким образом, открытая левая полуплоскость
Res<0 соответствует В(0; 1) —открытому единичному диску
{г|<1; замкнутая правая полуплоскость С+, Res 5s О, соот-
ветствует дополнению В (О, 1), т. е. множеству |г|^1. Это
наблюдение очень полезно при использовании доказательств,
полученных для непрерывного случая, в дискретном случае.
14. Теорема. Обозначим через а = (а0, аъ а2, •••) последова-
тельность из банахова пространства Е, через а и га — ее г-пре-
СО
образование и радиус сходимости ряда 2 а>ёг~к- Тогда для любой
о
простой замкнутой спрямляемой кривой у в области |г|>го,
обходящей начало координат один раз против часовой стрелки,
15. а* = 2^^>5(г)г*-1(1г, £ = 0, 1, 2, ...
v
Приведенные результаты можно найти в монографиях Дьедонне
[41, гл. 9] и Хилла и Филлипса [51, гл. 5.4].
116
ГЛ. 4. ЛИНЕЙНЫЕ СИСТЕМЫ
6.3. Устойчивость дискретных систем с обратной связью
Здесь мы предоставим читателям в качестве упражнений до-
казательство различных теорем. Эти упражнения не вызовут осо-
бых затруднений, поскольку читателям известно, как доказыва-
лись соответствующие теоремы для непрерывного случая Кроме
того, теоремы для дискретного случая часто проще и понятнее,
чем их непрерывные аналоги. На эту особенность мы будем всегда
обращать внимание читателя.
Рассмотрим дискретную линейную систему с обратной связью,
изображенную на рис. 4.2. Подсистемы G и F стационарны и
описываются сгоими импульсными характеристиками и F соот-
ветственно. Будем полагать, что
18а. Snxn — множество всех отображений, действующих из Z+
в Клхл;
18b. G, F<==Snxn, например, G = (G0, Gb G2, ...), где G, e Rnxn
при любых i е Z+.
Уравнения системы с обратной связью имеют вид:
т
19а. е=и— F*y, или ет = ит — У Рт-М,
< =о
19b. у = G * е, или ут = У, бт_^.
( = 0
Если функции и, е, у, G и F г-преобразуемы, то (19а) и (19b)
можно представить в иной форме:
20а. ё(г) =й (г) — F(z)e(z),
20b. у (г) = G (г) ё (г).
Заметим, что если функции G и F z-преобразуемы, то переда-
точная функция замкнутой системы удовлетворяет следующим
соотношениям:
21а. tf = G (/4-Й?)-1,
21b. (/ - FH) (I + FG) = (I +FG) (/ - FH) = /.
Однако в любом случае функция Н удовлетворяет временному
соотношению
22. Н = G — H*F*G.
Если функция 0(г) дробно-рациональна, a F (г) — постоянная
функция, то можно сформулировать теорему, аналогичную тео-
реме (2.30) и следствию (2.43).
23. Теорема. Пусть G (г) — дробно-рациональная правильная
функция, a F (z) = F — постоянная функция. Предположим, что
24. det [/ 4- FG (оо)] = det (/ 4- FG0) =£ 0
6. ДИСКРЕТНЫЕ СИСТЕМЫ
117
И
С(г) = ^(г)/5“1(г),
где многочленные матрицы Л/ (?) и D (z) взаимно просты спра-
ва. Тогда
(а) передаточная функция замкнутой системы Н (г) экспонен-
циально устойчива (т. е. все ее полюса содержатся в В(0; р)
для некоторого р< 1) в том и только том случае, когда все нули
многочлена det [D (z) + FN (г)] принадлежат открытому диску
В (0; 1) единичного радиуса;
25. (b) det(/ + FG(z)| = ^|iz; =
det Н (z)
_ det [D (z) + FN (г)]
det D (z)
П ^-Ра}
= det(/ 4-FGo)^-------
П (2 —Ро,-)
1 = 1
где {po<} и {pcJ (Z = 1, 2, n) —множества полюсов функций G(z)
(или нулей detZ)(z)) и H (г)) или (нулей det [D(z) + FN(z)] соот-
ветственно. В обоих случаях полюсы входят в эти множества
•столько раз, каков их порядок.
Отметим, что замечания (2.46), (2.58), (2.62) и теорема (2.70)
также справедливы в рассматриваемом случае. Кроме того, допу-
щение (24) совершенно целесообразно, поскольку, согласно тео-
реме (5), оно является необходимым и достаточным условием
существования единственного решения уравнений замкнутой
системы.
26. Следствие. Если функция Н (•) е 1Рлхл (г) экспоненциально
устойчива, то
(а) для любого минимального представления (в виде =
= Axk + Buk, yk = Cxk + Duk) функции Н (z) точка равновесия
х = 0 устойчива в целом экспоненциально и равномерно по fe;
(b) если и е 1рп для любого ре[1, оо], то у = Н*и^.1р и,
кроме того, и ^->0 при &->оо и р<оо;
(с) если ме/“и где «оо —постоянный вектор из Rn,
то yk->H при Ze->oo, причем сходимость экспоненциальна.
В тех случаях, когда G(z) не является дробно-рациональной
функцией, мы будем использовать прямое обобщение теоремы
Винера (см. Приложение D. 3.6). Обозначим символом |-| любую
подходящую норму в пространстве Кл, а также порожденную ею
норму в пространстве Клхл. Последовательность (а0> Дь ^2> •••)
векторов из (матриц из Клхл) принадлежит, по определению,
118
ГЛ. 4. ЛИНЕЙНЫЕ СИСТЕМЫ
оо
ZA (ZiXn), если S lat <оо, а ее г-преобразование, по определению,
£=0~
принадлежит Zi (ZAXzz).
Следующая лемма послужит важным инструментом в дальней-
ших исследованиях.
27. Лемма. Пусть М = (Af0, Afx, М2, ...) —последовательность
00
из Кпхл. Допустим, что М е Дх„, т. е. | М |i = I I < °°* Тогда
*=о
(а) z-преобразование г •—* М (г) последовательности М является
аналитической функцией при |г|>1, равномерно непрерывной
функцией на единичной окружности (Osg 0^2л), | M(z)|sg||Af
при всех | г | 1 и М (г) -> Мо, если | г | -> оо;
(Ь) последовательность М обратима в /ЯХЯ, т. е. существует
последовательность Р = (Р0, Plt Р2, ...), где |Р||i<оо, такая, что
М*Р — Р*М = (1, О, 0, ...), тогда и только тогда, когда
28а. . inf | det М (z) | > 0;
i*i
(с) для любой последовательности и^1„ (т. е. последователь-
ности и = (и0, «1, «2, ...) такой, что
S ы₽=(Мр)р«*>)
k=0
28b. J М * и |р || М ||х I1 и ||р, 1 «2 р < оо.
Теперь сформулируем полное множество необходимых условий.
29. Теорема. Рассмотрим систему, заданную уравнениями (19а)
и (19b). Предположим, что ГеДХя, а замкнутая система имеет
единственное решение (е, </) s S" х S", соответствующее каждой
входной последовательности и е Sn (или в эквивалентной форме Н
единственным образом определяется из (22)). Тогда, если Н е /АХя,
то
30. (i) функция G является г-преобразуемой;
31. (ii) функция G аналитична вне некоторого шара В(0; г)
конечного радиуса г<оо;
32. (iii) функция G представима в виде У (z) Z?-1 (г), причем
ЛЦ-), Р(-)еДХя;
33. (iv) все особые точки функции G, лежащие в области
{г 11 < | г | <г}, представляют собой изолированные полюсы;
34. (v) inf | det [/ + F (г) G (г)] | > 0.
i*l=i
35. Замечания.
(i) Теорема (29) — значительно более общая, нежели тео-
рема (4.5) —ее аналог для непрерывного случая, поскольку здесь
6. ДИСКРЕТНЫЕ СИСТЕМЫ
119
нет предположения, соответствующего допущению из теоремы (4.5):
«G —обобщенная функция, представление которой в некоторой
окрестности начала координат содержит б-функции, но без их
производных». В дискретном случае функция G должна быть
только линейной и стационарной.
(ii) Согласно теореме (4.5), все особые точки G должны лежать
в некоторой полуплоскости, в то время как в настоящем случае
все особые точки G должны быть заключены в некотором диске
из С. Как будет показано ниже, в результате того, что все особые
точки G принадлежат компактному множеству, метод разложения
на взаимно псевдопростые справа множители применим к дискрет-
ным системам с гораздо большим успехом, чем к непрерывным.
Сформулируем аналог теоремы (4.14) для дискретного случая.
36. Теорема. Рассмотрим систему с обратной связью, заданную
уравнениями (19а) и (19b). Допустим, что функция G г-преобра-
зуема и F е /ix«- Тогда Н е 1п\п в том и только том случае,
когда
37. (i) существуют матрицы N, D из ?пх« такие, что
(a) det Do ¥= 0;
(b) det [D(z)-J-F (z) W (?)]=/= 0, если | z | 5= 1 и detD(z) = 0;
(c) G(z) = 2V(z)[D(z)]-1;
38. (ii) inf | det [/ + F (г) G (z)] | > 0.
l»l > i
39. Замечание. Нетрудно проверить, что условия (ia) и (ib)
гарантируют только существование пары (detD, det (D-|-/W)),
удовлетворяющей условию несократимости (AZ) в области {z| |z| 1}.
В нашек? случае мы используем тот факт, что все функции D(z),
N (г) и F(z) имеют конечные пределы при |z|->oo, а именно,
Do, No и Fo.
Теперь мы переходим к взаимно псевдопростым справа разло-
жениям и теоремам об устойчивости, основанным на этом понятии.
40. Определение. Два элемента и из /Ах« называются
взаимно псевдопростыми справа, если существуют элементы
U, V', W1 е /АХп такие, что
(i) det (z) =# 0~ при |z|Ssl, |z|<oo;
41. (ii) для всех |z|^= 1.
42. Определение. Пара (®/Л, SF) называется взаимно псевдо-
простым справа разложением функции G, представляющей собой
г-изображение функций G, если
(i) G = ®T>-4;
(ii) и S взаимно псевдопросты справа;
(iii) det >о^0.
120
ГЛ. 4. ЛИНЕЙНЫЕ СИСТЕМЫ
43. Замечание. Как и в непрерывном случае при использова-
нии преобразования Лапласа, для того чтобы функция G имела
взаимно псевдопростое справа разложение, необходимо, чтобы
все полюсы G, лежащие вне единичного диска, принадлежали
некоторому компактному множеству. Однако в отличие от непре-
рывного случая здесь не появляется новых ограничений на функ-
цию G, так как если G имеет полюса, расположенные сколь
угодно далеко от начала координат, то согласно (29) Н ф 1'пхп,
и дальнейший анализ не обязателен.
44. Теорема. Пусть F 1пХп и = причем (@гГ, G)
является взаимно псевдопростым разложением функции G. Тогда
Н е 1пХп в том и только том случае, когда
45. (i) inf |det[/4-F(z)G(z)]|>0;
lz I > 1
46а. (ii) det (г) + F (г) (z)]#=0,
если detJ?(z) = O и |z|^l.
46b. Теорема. Пусть F ^Ihxn и G = причем (@^, Sf)
является взаимно псевдопростым разложением функции G- Тогда
Н е 1\хп в том и только том случае, когда
47а. inf I det [J? (z) + F (z) (z)] | > 0.
Izl^l
Для случая, когда функция G(z) имеет конечное число полюсов
в области {z^C||z|^l}, справедлива следующая теорема.
47b. Теорема. Пусть F е ZAx« и предположим, что G (z) пред-
ставима в виде:
48. ви= 2 2 ^+йи=о.и+<ш
где Gb е= /Ах«. причем
49. Gu(z) = N(z)D-'(z),
где многочленные матрицы N и Ь взаимно просты справа,
а столбцы D — правильные функции. Тогда Н е 11п\п в том и
только том случае, когда
50. (i) inf | det [/ + F (z)G (г)] | >0;
I z|> 1
(ii) det [D (p,) + F (Pi)N (Pi) + F (Pi) Gb (Pi) D (p,)] =#= 0
при i= 1, 2, ..., k.
6. ДИСКРЕТНЫЕ СИСТЕМЫ
121
51. Следствие. Пусть и=1,
/? т-
52.
i = l/=1
и f, gb^ Z1. Тогда h (= I1 в том и только том случае, когда
53. (i) inf H+f(z)g(z)|>0;
iz | > 1
54. (ii) f(p.)=^O при Z= 1, 2, ...» k.
1Ль\ завершим изучение дискретных систем рассмотрением
графического критерия устойчивости. Пусть функция G (г) задана
в виде (48) и F е Наша цель состоит в следующем: зная
поведение функции С(г/6), где 6е[0, 2л], проверить, выпол-
няется ли условие (50). Определим функцию
55. 1 + g (z) = det [/ + F(z)G(z)].
Очевидно, что g (г) представима в виде (52). Графический кри-
терий устойчивости применяется к образу множества D= {г = е/е,
О е [0, 2л]} при отображении 1 +g (z). Если g (г) имеет
полюс в некоторой точке е/0°, то «проколем» £), удаляя из мно-
жества D множество {г = е/0, 9^[9О —6, 90 + б]} и добавляя к D
множество {г = [1 4-т] (6 —6о)]е/0, 9е[90 —6, 90-f-6]}, где функция
представляет собой треугольный импульс:
56.
Л(х) =
0, если
х + б, если
6 — х, если
| х |> 6,
X €= [— б, 0),
х е [0, б].
Выберем б>0 достаточно малым так, чтобы
inf |l+g(?)|>0,
2eS0o
где
Sf)0= = 1^г^1-|-т](9— 90), 9 [9о“ б, 90 + б]},
причем So0 не содержит полюсов функции g, отличных от е'0°.
Простую замкнутую кривую, полученную после «прокалывания» £),
будем обозначать все тем же символом D. Каждой точке 9 е [0, 2л]
можно сопоставить единственным образом элемент Z), который
будет обозначаться через г (9).
Определим функцию
57. £i(e) = g[z(0)L
Определим теперь аргумент функции 1 +gi(9). Очевидно, что
при изменении 9 от 0 до 2л функция gi(9) равномерно непре-
рывна по 6. Кроме того, без потери общности можно предполо-
122
ГЛ. 4. ЛИНЕЙНЫЕ СИСТЕМЫ
жить, что 1 4-gi(0) ¥= 0, поскольку в противном случае условие (50)
нарушается и система неустойчива. Поэтому введем функцию
58. q>(6) = Im log[l 4-g1(6)],
выбирая ветви логарифмической функции так, чтобы <р(0) = 0
(или л), если l+gi(0)>0 (или 1 + gi (0) < 0).
Учитывая введенные определения и предположения, сформу-
лируем графический критерий устойчивости дискретных систем.
59. Теорема. При введенных выше условиях
60. inf | l+g(z)|>0
|Z| >1
тогда и только тогда, когда
61. (i) 14-£о¥=0;
62. (ii) inf |l+£i(0)l>O;
9е[0, 2л]
63. (iii) ф (2л) — ф (0) = 2л •/ир,
где тр — число полюсов g (г), лежащих вне замкнутого единич-
ного диска.
Упражнение 2.
(а) Показать, что условие (60) выполняется тогда и только тогда, когда,
во-первых и, во-вторых, l+g(z)=£0 при \г 1.
(Ь) Определим функции £ = зп1 для любых z s С и h(£)~g (S'1)- Показать,
что условие (60) выполняется тогда и только тогда, когда 1 (g) 0 при
(с) Доказать теорему (59), применяя принцип аргумента к функции
5-*1+й(5).
Упражнение 3.
(а) Пусть z—es. Показать, что условие (60) выполняется тогда и только
тогда, когда
64. inf | 1 +g (es) | > 0;
Res >0
(b) Пусть
g (*)- S «ли i(es)= 2 g^-
k=0 k=0
Доказать теорему (59), применяя теорему (5.18) к условию (64).
7. ЛИНЕЙНЫЕ НЕСТАЦИОНАРНЫЕ СИСТЕМЫ
Линейные нестационарные системы обладают некоторыми осо-
бенностями по сравнению с линейными стационарными системами.
Мы укажем лишь две из них:
1. Линейные стационарные системы описываются интегралом
свертки в то время, как линейные нестационарные системы харак-
теризуются интегральным оператором. В результате линейные
стационарные системы удобно изучать и во временной области
7. ЛИНЕЙНЫЕ НЕСТАЦИОНАРНЫЕ СИСТЕМЫ
123
и в частотной (с помощью преобразования Лапласа), а линейные
нестационарные системы можно исследовать лишь во временной
области.
2. Нестационарные системы в отличие от стационарных могут
быть //"-устойчивыми, но в то же время не быть L1-устойчивы ми,
и наоборот. Линейные стационарные системы //"-устойчивы тогда
и только тогда, когда они /Л-устойчивы.
В этом разделе при выводе многих результатов, касающихся
устойчивости, мы не будем предполагать, что рассматриваемые
системы являются неантисипативными, поскольку такое предполо-
жение обычно не влияет на ход наших рассуждений.
7.1. //"-устойчивость
Рассмотрим систему, реакция которой при нулевом начальном
состоянии задается соотношением
1- у(0 = У! (О U (! — h) 4- J №(/, T)«(T)dT=(Fw)(0,
i =— oo —00
где u, y: |R->|R. Допустим, что
(i) все функции a»,(-) и w(-, •) измеримы1);
(ii) для всех t е R
2. 2
i =— oo
3. J | w (t, т) I dr<oo.
— OO
Везде на протяжении этого раздела мы будем обозначать сим-
волом | • | норму в пространстве /.“. Пусть И — пространство вход-
ных воздействий — представляет собой £“(|R), а У — пространство
выходных сигналов — является множеством всех измеримых функ-
ций, отображающих R в R. Тогда из условий (2) и (3) следует,
что отображение W переводит U в Y и обладает свойством линей-
ности. Кроме того, область определения W полностью совпадает
с 21\ для любого заданного «(•) такого, что |ы||<оо, значение
у (0 однозначно определяется соотношением (1), причем | у (t) | <
< оо для любых t е IR. Наша цель состоит в получении условий
//"-устойчивости системы, реакция которой при нулевом началь-
ном состоянии описывается соотношением (1).
Выражение «система //"-устойчива» можно понимать двумя
способами:
х) Отсюда, в частности следуем что функция w •) измерима почти при
всех t R.
124
ГЛ. 4. ЛИНЕЙНЫЕ СИСТЕМЫ
(I) входное воздействие вызывает реакцию у = Wu, е L°°;
(II) существует постоянное число £<оо такое, что ||у|| =
= || №и|| ^с|| и\\, если только
Согласно первой формулировке, ограниченное входное воздей-
ствие вызывает ограниченную реакцию. Вторая формулировка
более конкретна, чем первая: она включает в себя (I) и дополни-
тельное утверждение: отношение норм входного и выходного сиг-
налов и и y = Wu не превосходит некоторого конечного числа
Определим число
4. Соо = sup У t)|Jt
Joo' /
и сформулируем теорему.
5. Теорема. Формулировки (I), (II) и
6. (III) Соо<00
эквивалентны.
Доказательство проведем в следующей последовательности:
(III) ZZ> (II) ZZ> (I) ZZ> (III).
(Ill) zz> (II). Для заданного и е L30 получаем
7.
Так как || и || не зависит от /, то у <= LXJ и ||г/||^Соо|| и\\. Таким
образом, (II) выполняется п*ри с = с^.
(II) zz> (I). Очевидно.
(I) zz> (III). Доказательство основано на использовании прин-
ципа равномерной ограниченности. Пусть А — произвольное мно-
жество индексов и (гр, / Л)— семейство непрерывных линейных
функционалов, отображающих банахово пространство X в линей-
ное нормированное пространство У. Если для каждого хе X множе-
ство (гр (*), е ^) есть ограниченное подмножество множества У,
то {|| г]/ |i, t е А} — ограниченное подмножество множества R. При-
меняя этот принцип к нашему случаю, положим X = = L°°, У = |R,
а семейство линейных функционалов (t]z, t е |R) определим сле-
дующим образом: для каждого /eR отображение ty:
задается соотношением:
8. т]Ди) = У — ti)+ т)^(т)йт.
i= — 00 —оо
Очевидно, что функционал г], линеен и непрерывен на основании
предположений (2) и (3). Определим норму ||т]/||. Очевидно, что
| w (t, т) | dr || uj,
7. ЛИНЕЙНЫЕ НЕСТАЦИОНАРНЫЕ СИСТЕМЫ
125
поэтому
9. ,1Н= sup 'r]/(w)'^z2 1ш(/, T)|dT = 6/.
и ' 1 i= —со - оо
Теперь мы покажем, что неравенство (9) в действительности
является равенством. Для этого покажем, чго для любого е>0
можно найти функцию и е L(x такую, что || и || = 1 и — 8,
где bf взято из правой части (9) Задавая е, выберем открытый
интервал /ь содержащий t~ th такой, что
10. J w(t, т) eft | 2“’Ч
Пусть функция и принадлежит пространству L°° и определена
в виде
, ( sgnwi(t), * если
11. и(Т'={
( sgn w (t, т), если I
Тогда || и |! = 1 и
qz(u)= У Wi(t) + w(t. t) (ft+ &’(C т) I \u(x)\dx^
1 U U
t, i
5? У w, (/) ; + w (t, r) t/т — w(t, r)|dr^
I---- R J /.
00
i =—oo
Следовательно, || t]^1| = b<.
Предположим, что формулировка (I) справедлива, т. е. для
всех wgA00 множество {т]Ди), t е R} ограничено. Тогда, согласно
принципу равномерной непрерывности, множество {||т)/||, t е IR}
также ограничено. Отсюда, в силу (П),
(оо оо \
У, | (/) 4” | (/, Т) | (ft i — Cqq оо,
i= —оо —оо '
что в точности совпадает с (III).
13. Замечания.
(а) Отметим, что нигде не предполагалось, что W обладает
свойством неантисипативности.
(Ь) Если и: и z/: R->Rm, то все функции Wi(-) и
ау(«, •) представляют собой (тхп)-матрицы и (12) остается спра-
ведливым, если символ |-| рассматривать, как некоторую норму
в
126
ГЛ. 4. ЛИНЕЙНЫЕ СИСТЕМЫ
(с) Число ст, на самом деле, — норма линейного отображения IF,
переводящего L°° в Lm.
Упражнение 1. Рассмотрим систему с обратной связью, 1Дг ункции up
ei Уг- R+ -> R, Нг Н2 отображают L°° в самое себя, и2 = 0. Предположим,
что
(Hzei) (/)= J w{t, i)et (t) dx,
— ОО
где •) удовлетворяет неравенству (3), и
(Я2е2)(0 = ф[М0, Л,
где <р: R X R4.-> R —непрерывная функция, принадлежащая сектору [0, k),
(а) Вывести условия, содержащие постоянные и k пр* выполнении
которых из щ е L00 следует ух е L°°
(b) Пусть функция о>(«, •) удовлетворяет неравенству (3), а ф—функция
с насыщением, т е. для каждого произвольно выбранного малого числа у>0
существует некоторое f<oo такое, что 1ф(о, t) ; у1 о1 + р для любых
о е R и любых t е R+ Показать что независимо от величины из ut е L00
вытекает е L00.
В дискретном случае имеет место теорема, похожая на тео-
рему (5).
14. Теорема. Рассмотрим систему, входной и выходной сиг-
налы и и у которой являются функциями, отображающими Z+
в Пусть
15. у (k) = У, w (k, i) и (i) = (Wu) (k),
i = 0
где w(k, i)^RnXn удовлетворяет неравенству
ос
16. У (kt ()|<оо для любых
4 = 0
Тогда следующие условия эквивалентны:
(i) u^r^y^l00;
' 17. (ii) существует с<оо такое, что [г/5^ с||и|
для любого и е Z";
©О
(iii) для любого ieZ+.
< = 0
Доказательство этой теоремы аналогично доказательству тео-
ремы (5) и потому опущено
Упражнение 2. Показать, что (16) выполняется1 если отображение W не-
антисипативно, т. е. w(k, i)«=0 при
7. ЛИНЕЙНЫЕ НЕСТАЦИОНАРНЫЕ СИСТЕМЫ
127
7. 2. ^-устойчивость
Рассмотрим систему, заданную вход-выходным соотношением
ОО
18. #(/)= S w(i, т)и(т)с!т для любых t е R,
— 00
где «(•), «/(•): R->-IR. Предположим, что ueL1, а функция
w(t, •) ограничена при всех fe|R. Тогда //(/) однозначно опре-
деляется соотношением (18) для каждого /eR. Выведем условия
^-устойчивости системы, описываемой (18).
19. Теорема. Пусть функции у(-) и ы(-) связаны соотноше-
нием (18). Тогда
(I) и, кроме того, существует постоянное
число с<оо такое, что | у Ц с | и V, в том и только в том
случае, когда
20. (II) sup $ | w (t, T)|dt = Ci<oo.
— оо
Доказательство.
Достаточность. Пусть ,«(•) е L1 и (20) выполняется. Тогда
для функции «/(•) из (18)
J |у(0|<#=^ $ J | w(t, т) || и(т) \<frdt =
— 00 —ОО—00
= $ Н |ш(/, т) | <# ? | и (т) | dr sS Ci 1
— оо V—оо J
(здесь для установления возможности изменения порядка интег-
рирования использовалась теорема Фубини). Отсюда следует (I),
если считать, что с = сх.
Необходимость. Пусть и (т) = б (т — К). Функции «(•) соответ-
ствует в силу (18) функция «/(•): y(i) = w(t, К). Если (I) выпол-
няется, то функция £/(•) должна принадлежать пространству L1.
(Заметим, что хотя функция 6(т — X) не принадлежит L1, она
может быть сколь угодно точно аппроксимирована в (*)-слабом
смысле элементами пространства L1.) Другими словами,
§ | w (t, X)|d/<oo.
— 00
Пусть % изменяется на множестве IR и, по-прежнему,- и (т)«
==6(т — X). Тогда из (I) следует, что соответствующие функции
w(t, X) должны принадлежать L1 при каждом X *= а семейство
функций (/, X), Z должно быть равномерно ограниченным»
128
ГЛ. 4. ЛИНЕЙНЫЕ СИСТЕМЫ
Следовательно,
со
sup f | w (t, X)|d/<oo,
bsR-io
что эквивалентно условию (20).
21. Замечание. Отметим, что сх —норма оператора W, рас-
сматриваемого как отображение L1 в самое себя.
Для изучения //-устойчивости при р е (1, оо) снова рассмот-
рим систему, заданную соотношением (18), предполагая, что
функции w(t, •) и «(•) локально интегрируемы.
22. Теорема. При введенных только что предположениях, если
(а) для некоторого постоянного числа
оо
23. $ | w(t, т)| dr^em<2co при любых t е R,
— оо
(Ь) для некоторого постоянного числа сх
оо
24. jj |йу(/, т) | dt сх < оо при любых teR,
— 00
то для любого заданного ре [1, оо]
u^Lp(—оо, оо)=>ре//(—оо, оо).
В действительности,
-L-L 11
25. hllp^c/сД ||w|р> где
26. Замечания.
(i) Условие (23) является необходимым и достаточным усло-
вием //^-устойчивости, а условие (24) необходимо и достаточно
для ^-устойчивости.
(ii) Условия (23) и (24) можно представить в иной форме:
существуют постоянные числа и сх такие, что
II w(t, ) |!х ^Соо<00 при любых /eR,
|| w (•, т) |х сг < оо при любых т е R.
Для стационарного случая w (/, x) = f(t — т), а условия (23) и (24)
эквивалентны и сводятся к предположению о том, что функция f( • )
принадлежит пространству L1.
(iii) Из (23) не следует (24) и наоборот. В самом деле,
положим
w(t,
Тогда (23) выполняется, а (24) —нет.
(iv) Результаты останутся справедливыми, если функции и и у
принимают значения из R" и Rm соответственно, а функция
7. ЛИНЕЙНЫЕ НЕСТАЦИОНАРНЫЕ СИСТЕМЫ
129
w(t, т) является (тхп)-матрицей. В этом случае | w(t, т) | сле-
дует считать нормой отображения w(t, т).
Доказательство. Учитывая, что теорема (19) доказана,
мы должны рассмотреть только случай 1 <оо. Для всех t eR
lf<(01 < Г МО т) 11 и (т): dx
— оо
«£ J [Iw (О 11/₽ ।и <т> ИIIw (О т) l1/?ldx
— ОО
| w (t, т) 11 и (т) |р dx
up
ОО IV?
J | w (t, х) I ст
— со I
(здесь мы использовали неравенство Гельдера). Согласно (23)
11/(0 К
w(t, т) || и (т) |р dx
00
J | w (t, x) 11 и (т) |p dx dt
Используя (24), получаем
— 00
f|u(T)|₽dT f МО xjjdi^c^cjufp.
— 00 —00
Следовательно, | у ^с\1рс'т | и |p.
Упражнение 3. Привести пример функции w (•, •), удовлетворяющей нера-
венству (24), но не удовлетворяющей неравенству (23).
Упражнение 4. Доказать более сильное утверждение, чем теорема (22):
система, заданная соотношением (18), L^-устойчива при всех ре[1, оо] тогда
и только тогда, когда она одновременно Р-устойчива и Ь°°-устойчива.
27. Применение теоремы (22). Рассмотрим линейную нестацио-
нарную систему, для которой ult elt е2> Уъ Уъ- R+-+R и
28. yi=g*elt
29. ydt) = k(t)e2(t),
где функция k (•) непрерывна на R. Допустим для простоты, что
«а == 0. Тогда уравнения системы могут быть представлены в сле-
дующем виде:
30. M0 = «i(0-*(0te*ei)(0,
31. МО = (2* «1) (0-(2*^2) (О-
Так как уравнения (28) и (29) линейны, выполняются условия
теоремы о малом коэффициенте роста по приращениям. Таким
образом, решение этой системы не только ограничено, но и су-
ществует, единственно, непрерывно зависит от входного воздействия.
б Ч. Дезоер, М. Видьясагар
130
ГЛ. 4. ЛИНЕЙНЫЕ системы
(a) L™-устойчивость. Очевидно, что
Ui е L°° => «1, е2 е L00,
если либо
33а.
либо
33b.
sup |Л(0 I $ g (т) I di < 1,
<>о $
ОО
sup ( |g(t — т) k (т) |dr = c»< 1.
<>Оо
(b) [^-устойчивость. Очевидно, что
если либо
34а.
либо
34b.
ejeL1,
sup J \k(t)g(t — r)\dt = ci
sup | k (t) Ij |g(0\dt < 1.
T 0 Q
(с) ^-увпюйчивость. Если одновременно выполняются усло-
вия (33а) и (34а) или условия (33b) и (34b), то для любого р е
е (1, оо) из Ut е Lp вытекает, что еъ е2 е Lp.
Упражнение 5. Рассмотрим линейную нестационарную систему, заданную
уравнениями (30) и (31). Предположим, что g е L1 и
k (/) kQ+2kt cos <nQt при любых t e= |R+,
где и действительные постоянные числа. Применим к нашей системе
теорему о преобразовании контура (3.6.3), полагая линейное отображение К
равным Тогда ветвь обратной связи определяется функцией г/^созсоо/,
а выходной сигнал контура в прямой ветви преобразованной системы равен
y^—gt + ei. Предположим, что gi(J(&) носит низкочастотный характер, т. е.
l£z (/®) I < I Si (i^c) I (<ос/ю)2 ПРИ <® > Определить, является ли система
^-устойчивой, и показать, что при (d0>*(dc число Может стать очень
большим.
7.3. Устойчивость процессов
Рассмотрим систему, изображенную на рис. 4.1. В конечном
счете нам хотелось бы показать, что если коэффициент обратной
связи нестационарной системы k(-) принадлежит Lx[0, со), то
разомкнутая система //-устойчива в том и только том случае,
когда замкнутая система //-устойчива и выполняются очень общие
условия.
7. ЛИНЕЙНЫЕ НЕСТАЦИОНАРНЫЕ СИСТЕМЫ
131
Сначала мы получим несколько вспомогательных результатов.
Поскольку важнейшие теоремы основаны на интегральном урав-
нении, связывающем импульсные характеристики разомкнутой и
замкнутой систем, мы прежде всего покажем, что уравнения
замкнутой системы разрешимы и притом единственным образом,
и вход-выходное соотношение этой системы имеет вид (18). Две
леммы, приведенные ниже, можно расценивать как черновую
работу, подготавливающую вывод основных результатов; при
желании читатель может перейти непосредственно к теореме (50)
без всякого для себя ущерба.
37. Лемма. Рассмотрим систему с обратной связью, изобра-
женную на рис. 4.1, и предположим, что и, е, у: R+-Пусть
функция G(/, т) ограничена на любом компактном подмножестве
из R2 и /((•) е LlnXne (R+). Тогда для каждого и е Llne (R+) сущест-
вует и притом единственная функция е е Lie(IR+), удовлетворяю-
щая уравнению
t
38. = r)e(T)dv.
о
Кроме того, для любого Т <оо существует число Сг<оо такое,
ЧТО I ет Ii Sg ст | ит 11.
Замечание. Лемма (37) сформулирована для функции и, принадлежащей L*t
поскольку L* является наибольшим из расширенных пространств в том смысле,
что Li cz и L°° cz L\ и вообще Lf cz L\ при р е [1, оо].
Доказательство. Представим (38) в виде
39. e(t)==u(t) — (KGe)(t),
где KG: Ь'пе (R+)->£Ae (R+). Вычисляя срезку функции e(t) из (38)
на отрезке [0, Г], получаем
40. eT(t) = uT(t)-(FeT}(t),
где функция Fi £Д0, Т]->££[0, Т] определена интегралом
t
41. (Fx) (t) = \K (0 G (t, т) x (т) dr
о
при любых t е [0, Т]. Отметим, что F можно рассматривать как
сужение оператора РтКОРт на пространство £„[0, Т], где Рт —
проектор, заданный посредством (3.1.4).
Уравнение (40) имеет единственное решение ers£i[0, Т],
соответствующее каждому ure£«[0, Т], если спектральный ра-
диус оператора Ft меньше 1. Определим семейство операторов
(Rt, TeR+), где RT-. £40» Л-’-ЩО, 7] и
(Rtx) (0 = j | К (01gTx (т) dr,
б*
132
ГЛ. 4. ЛИНЕЙНЫЕ СИСТЕМЫ
причем
42.
gr = sup |G(/, т)|.
о<6 т т
Покажем, что спектральный радиус р(7?г) оператора 7?г, рас-
сматриваемого как отображение А1 [0, 71] в самое себя, равен
нулю. ЧитателючВ качестве упражнения предлагается проверить,
что при m е Z+ и оператор Л1 [О, Tj-^L1 [О, Г] имеет
вид
43.
(₽тх)(0 = |К’(0| ( \\K(s)\gTds
О и
т-1
ёТх(^ 1
7-1--НГ“Т.
(т—1)1
Незначительно изменив теорему (19) и замечание (21), получаем
44.
7 Г t
|ЛгЦ = sup f |ZC(OI f |K(s)|grds
0<T<7*> J
т-1
gr
(т—1)1
' tn
(m—1)1
(W
(tn—1)1 ’
T
где
45.
T
bT = \\K(t)\di<<x>.
0
Отсюда немедленно вытекает, что |7?г при m->oo; по-
этому р(/?г)= lim || A?? ||1/m = 0. Сейчас можно также показать, что
т->оо
р (FT) «g р (7?г) = 0. Таким образом, оператор (/4-Гг)-1 корректно
определен на LA[O, Т] и ||(/ + Fr)-1||sS ^ЦГтЦвСг. Следова-
о
тельно, решение е( •) е Llne (IR+), удовлетворяющее (38) и соответ-
ствующее каждому и (•) е Lhe (|R+), существует и единственно,
Причем I ег ст( «Г 111-
Упражнение 6. Показать, что R™ имеет вид (43). (Указание: см. ра.
боту Видьясагара [96].)
Упражнение 7. Применяя методы, аналогичные использованным при дока-
зательстве леммы (37), показать, что если функция G(t, т) ограничена на
каждом компактном подмножестве из R2 и К (•) е Llne [0, оо), то для каждого
и (•) е [0, оо) существует и притом единственная функция у е L™e [0, оо),
удовлетворяющая уравнению
t t
46. у (t) — j G x) и (т) —J G (t, т) К (t) у (t) dx.
Кроме того, для любого Т <оо существует dr<oo гакое£ что [Уг||00<
< dT | иТ Цсо-
7. ЛИНЕЙНЫЕ НЕСТАЦИОНАРНЫЕ СИСТЕМЫ
133
Упражнение 8. Доказать лемму (37) и выполнить упражнение 7, исполь-
зуя следствие (3.5.8).
47. Лемма. Пусть функция G(Z, т) ограничена на каждом
компактном подмножестве из R2 и /< (•) е Lhxne (R+). Тогда сущест-
вует и притом единственная функция Н (•, •), удовлетворяющая
уравнению
t
48. H(t, n) = G(t, t)-$G(/, v)K(»)H(v,i)dv, 0<т^/<оо.
т
Кроме того, функция H(t, т) ограничена на любом компактном
подмножестве из R2.
Доказательство. Зафиксируем т е R+ и рассмотрим урав-
нение (48) относительно неизвестной функции Н (•, т). Тогда,
согласно упражнению 7, функция //(•, т) единственным образом
определяется из (48), и для каждого Т < оо существует конечное
число dr такое, что
49. \H(t, T)||<dr sup |G(/, т)|
z
при любых t e [т, Г]. Из (49) вытекает, что H (t, т) ограничена
на каждом компактном подмножестве из R2, поскольку таким
свойством обладает функция G(t, т).
Теперь мы в состоянии сформулировать основную теорему,
выявляющую характер вход-выходного соотношения замкнутой
системы, изображенной на рис. 4.1.
50. Теорема. Рассмотрим систему, приведенную на рис. 4.1,
где и, е, у: R+->R". Предположим, что функция G(t, т) ограни-
чена на каждом компактном множестве из R2 и функция К (•)
принадлежит Mxne(R+). Тогда для каждого usL„e(R+) система
уравнений
t
51. y(t)=^G(t, T)e(r)dT, е (t) = и (0 - К (0 у (0
имеет единственное решение z/eL„e(R+) вида
У(0-{н(1,т)и(т)Л=(/?в)(О,
о
где Н(‘, ^ — единственное решение уравнения (48).
Доказательство. Предположим, что ueL’e(R+) при
некотором ре[1, сю]; тогда ueUe(R+). Следовательно, система
уравнений (51) имеет единственное решение е (и, значит, у), при-
надлежащее L„«(R+). Рассмотрим функцию г = Ни. Очевидно, что
zf=Lne(R+), а, стало быть, zeU«(R+), и, кроме того, г/=z удов-
134
ГЛ. 4. ЛИНЕЙНЫЕ СИСТЕМЫ
летворяет (51). Но поскольку (51) имеет единственное решение,
то у —Ни.
52. Замечание. Итак, согласно теореме (50):
(i) система с обратной связью, изображенная на рис. 4.1,
имеет решение;
(ii) вход-выходное соотношение этой системы имеет вид (18);
(iii) импульсные характеристики замкнутой и разомкнутой
систем связаны уравнением (48).
Приводимые ниже три теоремы позволяют связать некоторые
свойства импульсных характеристик разомкнутой и замкнутой
систем.
53. Определение. Пусть функция F-. R+->Rnxn измерима и
локально интегрируема. Здесь и далее мы будем предполагать,
что F(t, т) = 0 при /<т. Определим нормы
54а. = sup \F(t, т)|; k теК+ GO
54b. fi = |Fh= sup J |F(/, x)|df; t6=r+;
54с. foo=|F|oo= sup J|F(/, т) 1 dr. t Gi R-f- Q
С учетом этих определений обозначим через Sb линейное норми-
рованное пространство
55. S» = {F: |^Ь<оо}.
Аналогичным образом введем линейные нормированные простран-
ства Si и
56. Замечание. Пусть вход-выходное соотношение системы
имеет вид:
57. у (t) = J F (t, т) и (т) dr = J F (t, t) и (т) dr.
о о
Тогда
(i) F е Sb в том и только том случае, когда и е L1 у е L“;
кроме того, существует конечное число сь такое, что |j/|oo<
(ii) F <= Si в том и только том случае, когда система с вход-
выходным соотношением (57) /Л-уСтойчива;
(iii) F е SOT в том и только том случае, когда система с вход-
выходным соотношением (57) /.“-устойчива.
58. Теорема. Предположим, что функция /<: R+->R',xn при-
надлежит пространству L1 (R+), и функции G: R+-*Rnxn и Я: R^_->
7. ЛИНЕЙНЫЕ НЕСТАЦИОНАРНЫЕ СИСТЕМЫ
135
->РПХЛ связаны соотношением (48). Тогда Н <= Sb в том и только
том случае, когда Ge Ss.
Доказательство.
Достаточность. По условию функции G и Н связаны урав-
нением (48) и С е S4. Пусть функция gb = | G |» определена по-
средством (54а). Тогда из (48)
59. | Н (t, т) | ^gb+gb $| К (v) 11Н (v, т) | dv.
%
Зафиксируем произвольным образом т из |R+. Применяя лемму
Веллмана —Гронуолла к неравенству (59), получаем
60. \H(t, T)|^gftexp g^|K(v)|dv ^gfrexp[gd||K (xj,
% J
где
61.
|К|1 = Г |K(v)|dv.
0
Так как оценка в (60) не зависит ни от t, ни от т, то We Sb.
Необходимость. Уравнение (48) можно представить в ином
виде, а именно:
t
62. G(t, — т) + $Я(/, v)K(v)G(v, t)dv.
Эквивалентность (48) и (62) легче всего вывести, заметив, что
если Н — импульсная характеристика системы, состоящей из под-
системы G, охваченной обратной связью К, то G представляет
собой импульсную характеристику системы, «©стоящей из под-
системы Н с обратной связью — К. Уравнения (62) и (48) одно-
типны и формально отличаются друг от друга лишь тем, что
функции G и Н поменялись местами, а функция К. заменена
на—К. Очевидно, что —/СеL1 (R+), если KeLx(R+). Таким
образом, принимая во внимание соображения, использованные
при доказательстве достаточного условия этой теоремы, выводим,
что G е Sb, если Н е Sb.
63. Теорема. Если выполняются условия теоремы (58), то
Н е Sb П Soo тогда и только тогда, когда G е Sb f) S«>.
Доказательство.
Достаточность. Предположим, что Gb е Sb f) Sro. Тогда, в силу
теоремы (58), Н е St) и остается показать, что Н е S«. Из (48)
136
ГЛ. 4. ЛИНЕЙНЫЕ СИСТЕМЫ
получаем
64. T):dT^J|G(/, т)|4т4-
О о
+ $$\G(t, v)\\K(v)\\H (v, T)|dvdr<
О т
«££<» + gb 5 51 (v) 11н (v> T)|dvdr =
О т
= goo + g* $ I к (v) I JI н (V, т) |dxdv.
О о
Определим функцию
t
m(t) = \\H(t, т) I dx.
О
Тогда (64) примет вид:
65. m(t)<sga>-}-gb\\K(y)\m(v)dv.
о
Применяя лемму Веллмана —Гронуолла к (65), получаем
68. т (О ==S gx exp L, j | К (v) | dv I < gm exp (gb || К |!i).
L о J
Следовательно, функция /и(«) ограничена, и H^S^.
Необходимость. При доказательстве этого условия, как и в тео-
реме (58), используется свойство симметрии функций G и Н.
69а. Теорема. Если выполняются условия теоремы (58), то
Н е Sb Г) Si тогда и только тогда, когда G е S6Q Sx.
Доказательство теоремы (69а) предоставляется читателю в ка-
честве упражнения.
Упражнение 9. Разъяснить смысл теорем (58), (63) и (69а), связывая
свойство устойчивости разомкнутой и замкнутой систем.
Сформулируем основную теорему этого раздела.
69b. Теорема. Рассмотрим систему, изображенную на рис. 4.1,
где и, е, у: К+->КЛ, прямая ветвь которой содержит линейную
стационарную подсистему с передаточной функцией
k mi
70. G(s) = 6ft(s)+ У У -^7 = ^(s) + 6B(s).
, («“Л)7
где (s) eLix„ f] L^xn, Rep{Ss0 при i = 1, 2, ..., k-, mt=l, если
Repj = O, а ветвь обратной связи содержит статический усилитель
7. ЛИНЕЙНЫЕ НЕСТАЦИОНАРНЫЕ СИСТЕМЫ
137
с нестационарным коэффициентом усиления
71. F (0 = Fo + Fv(t),
где ЕоеКяхп, Fv(-)^Lhxn. Тогда следующие утверждения
эквивалентны:
(I) замкнутая система /.“-устойчива и ее импульсная характе-
ристика W (•, •) ограничена на IR2;
(II) замкнутая система D’-устойчива при всех ₽s[l, оо] и
1F(-, •) ограничена на R2;
72. (Ill) (I) inf | det [7 + F0G(s)] |>О
Res ^sO
И
73. (ii) det [I? (a) + F0N (Pi) + F0Gb (Pi) 6 (Pi)] ф 0, i=1, 2.k,
где Ga(s) = N (s)D-1 (s), матрицы N и б взаимно просты справа,
а столбцы D являются правильными функциями.
Доказательство проведем в следующей последовательности:
(II) => (1)=>(Ш)=5(П).
(II) (I). Очевидно.
(1)=>(Ш). Предположим, что (I) выполняется. Тогда импульс-
ная характеристика замкнутой системы W (•, •) принадлежит
множеству Sofl-Soo. Поэтому, согласно теореме (63), функция
Т/р (/, т) I—► Н (7 — т), где Й — обращение по Лапласу функции
G(7 + FoG)_1 — также принадлежит Sftn«Soo. С учетом замечания
(26ii) выводим, что Н (•) е Ll (R+). Отсюда по теореме (4.36)
следует справедливость утверждения (III), т. е. неравенств (72)
и (73).
(III) =5 (II). Пусть Й = G (7 + F0G)-1. По теореме (4.36) из (III)
вытекает, что Й е о^пхп. В самом деле, функция Н не содержит
в своем представлении 6-функций и поэтому принадлежит LlnXn-
Следовательно, функция Hit (7, т) •—* Н (t — т) принадлежит
•Soo П Si. Если Н <= L°°, то Т/i е П Soof) Sx; отсюда на основании
теорем (63) и (69а) следует утверждение (II).
Покажем теперь, что функция 77 действительно принадлежит
L00. Так как Й удовлетворяет соотношению Й-\-fiF0G = G, то
из (70) получаем, что
Й + HF06b + HFOGU — Gb + G„,
или
74. Й+ЙР^ь=6ь + (1-ЙРо)Оа.
Поскольку H<=L'nXn и Gh&UxnQLTxn, функции Й, ЙР06ьидь
из (74) аналитичны при Res>0, ограничены и равномерно
138
ГЛ. 4. ЛИНЕЙНЫЕ СИСТЕМЫ
непрерывны при Re s = 0. Поэтому такими же свойствами обладает
и функция (/ — HF^bu из (74).
Чтобы показать, что обращение по Лапласу функции
(/ — HF^Ga принадлежит L^Xrt, рассмотрим произвольный элемент
матрицы (/ — HFQ)Ga, представив его в виде г (s)<p(s), где г— раз-
ложение на элементарные дроби по pi (i = l, 2, k), а фе<^.
Таким образом, мы можем изучать все полюсы? (•) независимо
друг от друга. Мы утверждаем, что если ср е а/ и функция
[m!/(s —a)m+1]<p(s) аналитична в точке a, и Rea>0, то
г У-1Г 1^ гоо
l(s-a)^+4 ’
и, кроме того, если Rea = 0 и ф(а) = 0, то /еЛ°°при условии,
что т = 0.
Заметим, что
t
75. f (0 = J (t - r)m ('-T) <p (t) dx =
o.
= J (t — x)m ea(Z-T) <p (t) dx — J (t — x)m d1 <p (r) dx.
о t
Используя разложение бинома, представим первый интеграл
в виде:
2 (Г) § (— тУе-ат ф (т) = 2 (7)^т-,еа/ф(1> №=0’
<=о' о «=о'
где последнее равенство является следствием того, что функция
<p(s)/(s — a)m+1 аналитична в точке а тогда и только тогда, когда
<р(О(а) —о для i = 0, 1, т. Кроме того, если либо Rea>0
и meZ+, либо Rea = 0 и т = 0, то функция
ограничена при числом у. Тогда для всех
IKOKvlTk
Следовательно, f s L00 и поэтому Н е L“x»«
76. Следствие. Пусть выполняются условия теоремы (69b) и
неравенства (72) и (73). Пусть г] и у являются решениями
уравнений
77а. y = Gu-GFoy-GFvy,
77b. т) = Gu — GFox].
Тогда, если и е L00, то г] (/) — у (t) -> 0 при t -> оо.
Доказательство. Пусть Й = (I -}- GF0)~l (5. В таком случае
Н еиХпДЬ”хл« Кроме того, по теореме (69b) Перепи-
7. ЛИНЕЙНЫЕ НЕСТАЦИОНАРНЫЕ СИСТЕМЫ
139
шем (77а) и (77b) в иной форме:
78а. у = Н*и — Н* Fvy,
78b. i} = H *и.
Вычитая (78а) из (78b), получаем
т\ — у = Н *Fvy.
Поскольку yeZ," и то FvyeL„. И так как tfs
<=/Дх„ПЛ”х„, то (т) — y)(t) = (H * Fvy) (0->0 при /~>оо.
Упражнение 10. Предположим, что Fv (•) е. L%Xn, но вовсе необязательно,
что Fv (.) е L}lXrt. Применяя теорему о малом коэффициенте роста, вычислить
оценку для IF (•) Ь, при которой замкнутая система £°°-устойчива.
79. Замечания. 1. Принимая во внимание теорему (69b), мы
можем сказать, что неравенства (72) и (73) являются достаточ-
ными, но не необходимыми условиями £°°-устойчивости замкнутой
системы. Если (72) и (73) не выполняются, как в случае, когда
Я = О(/ + ГоО)-1^в7/«хп>
можно утверждать, что либо замкнутая
система не является //"-устойчивой, либо ее импульсная характе-
ристика Н (•) не ограничена.
2. Из теоремы (69b) и упражнения 10 следует, что в ветвь
обратной связи может быть введен усилитель с произвольно боль-
шим коэффициентом усиления из Lhxn без нарушения свойства
устойчивости всей системы, однако существует предельный коэф-
фициент усиления из £пхя, при превышении которого система
перестает быть устойчивой.
Теперь мы приведем аналогичные результаты для дискретного
случая. Теоремы для дискретного случая значительно проще своих
непрерывных аналогов, поскольку любая последовательность из
пространства /А обязательно принадлежит пространству Мы
только сформулируем теоремы, оставляя их доказательство чита-
телям в качестве упражнений.
80. Теорема. Рассмотрим систему с обратной связью, изобра-
женную на рис. 4.1, где и, е, у: Z+-*-R"; элементы матриц G
и F определяются уравнениями
*—1
81. (Ge)(k)^ ^G(k,
i—0
82. (Fy)(k) = F{k)y(k).
Тогда система уравнений
83а. e = u — Fy,
83b. y = Ge
140
ГЛ. 4. ЛИНЕЙНЫЕ СИСТЕМЫ
имеет единственное решение в виде
л—1
85. f/(^)=2 H(k, i)u(i),
I =о
где H(-t ^ — единственное решение уравнения
л—1
86. H(k, i) = G(k, 0—2 G(k> i),
l = i
87. Замечания.
1. Как обычно, сумма по пустому множеству индексов пола-
гается равной нулю.
2. Элементы матрицы G не только неантисипативны, т. е.
G(&, 0 = 0 при k<zit но обладают дополнительным свойством:
G(£, k) = 0 при всех k е Z+. Это означает, что действие входного
сигнала проявляется на выходе с задержкой на один такт. Такое
явление имеет место, например, если подсистема G представима
в виде:
%k+i = Ak%k + yk — CkXk,
где x: Z+ ->IRm и Л, В, С отображают пространство Z+ в соответ-
ствующие пространства.
По аналогии с множествами Sbt Sx и Soo определим множества
88а. «ft = JG: г+^₽яхя| sup |G(t, /)|<оо1, 1 i. /eZ+ J ( oo 'I
88b. «i = {G: Z+-*Rnx" | sup У |G(i, /)|<oo}, t /<=z+ ,=0 J ( oo 1
88с. «00= 0: Z+->R"xn|sup 5 |G(t, /)|<cc. 1 <ez+/==o '
Упражнение И. Показать, что множества и являются подмножест-
вами Привести физическое истолкование каждого из множеств
89. Теорема. Предположим, что G, Я: Z+->IRnx/I, G(&, 0 =
— Н 0 = 0 при причем GnH связаны уравнением (86).
Пусть, кроме того, функция F: Z+->IR'lx'1 принадлежит простран-
ству 1пхп- Тогда Н (соответственно §х или Soo) в том и только
том случае, когда G е $ь (<§х или Soo).
90. Теорема. Рассмотрим систему, изображенную на рис. 4.1,
где и, е, у. Z+“>Rn, прямая ветвь которой содержит линейную
стационарную подсистему с передаточной функцией
91.
= ^G, (z) + Ga (z),
8. СИСТЕМЫ С ИЗМЕНЯЮЩИМИСЯ ПАРАМЕТРАМИ 141
где Gt> Inxn, | Pi |>= 1 при i = 1, 2, ..., k, а подсистема обратной
связи представляет собой статический усилитель с нестационарным
коэффициентом усиления F: Z+вида
F(k) = F0 + Fv(k),
где Fo е IR'1*'1 и Fv^.l\ Уп. Тогда следующие утверждения
эквивалентны:
(I) замкнутая система /°°-устойчива;
(II) замкнутая система /^-устойчива для всех ре[1, оо];
92. (Ill) (i) inf | det [/4-F0'G (2г) |> О
I* | > 1
И
93. (ii) det[b(pi) + FQN(pi) + FoprGb{pi)D(pi)]^()t
Z=l, 2, kt
где Ga (z) = N (z) D'1 (z), матрицы N и Ь взаимно просты справа,
а столбцы матрицы D — правильные функции.
94. Замечание. В отличие от непрерывного случая неравенства
(92) и (93) являются необходимыми и достаточными условиями
/^-устойчивости замкнутой дискретной системы.
8. СИСТЕМЫ С МЕДЛЕННО ИЗМЕНЯЮЩИМИСЯ ПАРАМЕТРАМИ
На практике часто , встречаются системы, некоторые параметры
которых с течением времени изменяются довольно медленно. Для
таких систем естественной является следующая задача. Пусть
заданная система устойчива (в некотором смысле), когда все ее
параметры неизменны; сохранит ли система устойчивость, если
параметры будут медленно изменяться? В этом разделе мы рас-
смотрим дифференциальные системы, причем, учитывая, что при
переходе от линейных систем к нелинейным задача усложняется
незначительно, мы представим результаты для нелинейного случая.
Применяемый подход предложен Барменом [4].
Пусть система задана уравнением
1. x = f(x, st),
где 8 —положительное число. Обозначим через |х| /2-норму
х е Кл. В дальнейшем мы будем предполагать, что
(А1) функция f: КЛХ|Р+->КЛ принадлежит С1 и f(0, р) = 0
для всех р^О;
(А2) функция f удовлетворяет условию Липшица, т. е. суще-
ствует постоянная />0 такая, что
\f(x, p) — f(x', р)|^/|х — х'\ Vх» х'еКл;
(АЗ) существует положительное число т) такое, что
IW(X> p)l<nlxl V(x> Р) ® II^XlR-p
142
ГЛ. 4. ЛИНЕЙНЫЕ СИСТЕМЫ
Поскольку D2f (х, р) обозначает производную функции f по ее
второму аргументу, при малом т) векторное поле х>—>f(x, t)
медленно изменяется с течением времени. При фиксированном т]
за счет выбора малого е мы всегда можем добиться, чтобы систе-
ма (1) стала настолько медленно изменяющейся, насколько нас
это устраивает.
Если параметры в (1) постоянны, то (1) приобретает вид
2. * = р),
где р & R+— постоянное число. Мы будем называть (2) уравнением
«замороженной» системы, или, более точно, уравнением системы,
параметры которой зафиксированы при t = p/z.
Для описания устойчивости введем два определения.
3. Определение. Нулевое решение уравнения (1) называется
равномерно экспоненциально устойчивым в целом тогда и только
тогда, когда существуют положительные числа с и а такие, что
4. |<р(/; /0, х) |аСс|х\е-а<‘—для гсех t^to^O, yxe|R\
где <р(/; to, х) —решение (1) в момент t при начальном состоя-
нии х в момент t0.
5. Определение. Нулевое решение уравнения (2) называется
равномерно экспоненциально устойчивым в целом равномерно по р
тогда и только тогда, когда существуют положительные числа k
и о такие, что
6. | ф/ (t, х; р) | «Сk | х | е-°* у/5s О, у (х, р)®Рлх|Р+,
где Ф/(^, х; р) — решение «замороженной» системы (2) в момент t
при начальном состоянии х в момент / = 0.
7. Теорема. Рассмотрим системы (1) и (2), полагая, что функ-
ция /(-, •) удовлетворяет условиям (А1) —(АЗ). В таком случае,
если нулевое решение (2) равномерно экспоненциально устойчиво
в целом равномерно по р, то при достаточно малом е нулевое
решение уравнения (1) равномерно экспоненциально устойчиво
в целом.
В линейном случае уравнение (1) превращается в ^ — А(/)х,
а уравнение (2) приобретает вид х = А (р) х. Условие (6) эквива-
лентно требованию, чтобы все собственные значения А (р) принад-
лежали области Res< —а для всех р^О. Условие (А1) выпол-
няется, если t н-► А (/) принадлежит С1; условие (А2) эквивалентно
ограниченности функции t * А (/) на R+; условие (АЗ) превра-
щается в | DA (О I «С И Для любых t 0.
Доказательство. Решение системы (2) с фиксированными
параметрами удовлетворяет интегральному уравнению
8. <р/(т, xj р)=х+$/[ф/(Г, х; р), p}dt'.
О
8. СИСТЕМЫ С ИЗМЕНЯЮЩИМИСЯ ПАРАМЕТРАМИ
143
Дифференцируя (8) по действительной переменной р, для любых
р s R+- и любых х е Р" получаем
9. £>зф/(т, х\ = х; р), p]Dtq>f(t', х; р) +
О
+ D8f[<p/(/', х; р), p]}di'.
Используя (6) и (А2), из (8) находим, что
10. <р/(т, хг, p)Ss-!y!- при 0<т=с-2^- = Т у(х, p)eR"xR+.
Учитывая (6), (А2) и (АЗ), из (9) с помощью леммы Веллмана
получаем, что для некоторых положительных чисел тит'
11. |£>3ф/(т, х; р)|aSm'Iх|е"” при любых
(т, х, p)sR+xRnxR+.
Выберем число Р^(/п + о)/2о и функцию
12. V (х, р) = J | ф; (т, х; р) |2₽ dx
о
в качестве функции Ляпунова для системы (2) с фиксированными
параметрами. Очевидно, что VeC1, V (0, р) = 0 для любых р^О.
Из (6) и (10) вытекает, что существуют постоянные и k2 такие,
что
13. &x|x|2P^V (х, p)^k2\x\2^ у (х, р) е RnxR+.
И, наконец, из (12)
14. V(2) (х, р) = lim И<Р(й.х;Р) P]-V(x, р)-
л-»о п
Таким образом, функция V действительно является функцией
Ляпунова для системы (2) с фиксированными параметрами.
Покажем, что эта функция является функцией Ляпунова и
для системы (1), если е достаточно мало. Рассмотрим производ-
ную функции
V (х, е/) = JI ф/ (т, х; et) |2₽ dx
о
по времени вдоль решения уравнения (1):
16. V(1) (х, еГ) = DtV (х, at) f (х, ot) + D2V (x, ei) e, =
= —|x|a₽4-D2V(x, e/)*8.
144
ГЛ. 4. ЛИНЕЙНЫЕ системы
Но
D2V (х, e()=20j | ф/ (т, х; е/)|2<₽-1)ф£ (т, х; е/)Е>3ф(т, х; ei)dx.
о
Поэтому
I D2v (X, st) I < I X 2₽ 20 f dx = M | x |2₽,
0
где M — конечное число, зависящее от выбора 0. Тогда (16) при-
обретает вид
V(d(x, е/)<-(1-вМ)|х|2₽-
Если 8 <1/44, то V(i)<0; учитывая (13) и оценивая отношение
V(i)/V, мы видим, что решения уравнения (1) ограничены:
18. |ф(/; t0, х0)|<с|х0|е~
где с— (&2/&1)1/2₽ и а = (1 — е/И)/(20&1).
Упражнение. Сформулировать теорему (7) для линейного случая, введя
во все условия характеристики, свойственные именно линейному случаю.
9. ЛИНЕАРИЗАЦИЯ
Одним из важнейших и часто используемых в задачах анализа
И1 синтеза методов является линеаризация; этот метод заключается
в замене нелинейной системы аппроксимирующей линейной систе-
мой, «близкой» к заданной нелинейной системе. Такое приближе-
ние, естественно, является только локальным, в том же смысле,
как в пространстве (R2 касательная только локально аппроксими-
рует кривую.
9.1. Постановка задачи
Мы ограничимся изучением дифференциальных систем и по-
пытаемся вывести условия, при которых уравнения, линеаризо-
ванные вдоль заданной траектории, приводят к правильным ре-
зультатам на всем множестве R+. Используя терминологию теории
цепей или теории управления, мы собираемся построить условия,
при которых эквивалентная схема точно прогнозирует траекторию
заданной системы в пространстве состояний при всех /^0.
Рассмотрим систему дифференциальных уравнений
1. х = /(х, й, 0>
где f:
2. /(0, 0, /) = 0 для любых /^0,
3. х(0) = 0.
Уравнение (1) связывает фазовую траекторию х(-) с входным воз-
действием й (•). Условия (2) и (3) указывают, что скорость системы
9 ЛИНЕАРИЗАЦИЯ
145
при нулевом входном воздействии всегда равна нулю и что си-
стема начинает движение из нулевого состояния при t — Q. При-
веденная выше форма условий (2) и (3) выбрана нами для удоб-
ства их использования. Перейти к такой форме можно всегда
путем замены системы координат.
Теперь мы введем предположения, обеспечивающие существо-
вание и единственность решения уравнения (1) при условиях (2)
и (3).
4. Предположение. При любых фиксированных х е R" и й е
eR" функция f(x, й, •): R+->Rn регулярна; при любых фикси-
рованных ueR” и t е R+ функция f(-, й, t) удовлетворяет ло
кальному условию Липшица по х; при любых фиксированных
х eR" и t е R+ функция f (х, -, t) непрерывна.
Мы будем полагать, что входной сигнал й состоит из «опор-
ного» сигнала и0 и небольшого сигнала возмущения и, т. е.
5. й == ц0 + и.
В дальнейшем предполагается, что и0 и и являются регулярными
функциями от t, определенными на множестве J?+; отсюда следует,
что при фиксированном xeR" функция «(/), /] регу-
лярна. Поэтому фазовая траектория может также рассматриваться
как сумма
6. x = x0 + L
причем предполагается, что х0 определено при всех урав-
нением
7. х0 = /(х0, «о> 0. хо(0) = 0.
Функция | определяется соотношением (6).
Рассмотрим функцию <•—*[хо(0> «о (0] и в R" xRmX[R+ —мно-
жество
8. ^ = {[xo(O + S, u0(t) + u, /]\и\^ит,
где и ит — положительные числа. Множество можно пред-
ставить себе как трубку, окружающую «опорную траекторию»
>[хо(0, мо(0]. Для построения аппроксимирующей системы
мы введем дополнительные предположения.
9. Предположение. При некоторых £т>0 и ит>0 на мно-
жестве функция f имеет ограниченные непрерывные вторые
частные производные по х и по й и
sup I I, sup | I, sup I I
у' I дх/ I у*71 dxk ди,-1 I ди/ ди/, |
146
ГЛ. 4. ЛИНЕЙНЫЕ системы
конечны при всех допустимых значениях i, k, I, j и h. Разложим
функцию f около опорной траектории:
ю. f [Хо (0+5(0, «о(0 + «(0, 0 =
=/[хо(0, МО, П+ВДМО, МО, 05(0+
+ОДМ0, «о(О, 0«(0 + ?[5(0, и (0, о,
где через Dtf обозначена производная f по i-му аргументу. За-
метим, что Dif[x0(t), u0(t), 0 представляет собой якобиан функ-
ции f, вычисленный вдоль опорной траектории; поэтому это
известная функция времени, отображающая IR+ в К'1ХЛ. Анало-
гично DJ[x0(t), u0(t), 0 является (п х т)-матрицей частных про-
изводных по й{ и, кроме того, известной функцией времени,
отображающей |R+ в Клхл.
Представив остаточный член разложения Тейлора в стандарт-
ном виде [41, стр. 190]
g(l, и, 0 = $(1-ЬИ<2)
о
[««tn. «ио+мно.
из предположения (9) получим, что существует S<oo такое, что
И. |g(£, и, t) | < S (| 11 + (и |)2 при любых
[МО+ 5, Wo(O + «,
Другими словами, функция g является малой второго порядка
равномерно по I, так как S не зависит от t. Обозначим через
A (t) и B(t) производные в разложении (10) и перепишем (1):
12. t = A(O5+B(O« + g(5, и, t), £(0) = 0.
Если отбросить член второго порядка малости g(|, и, t), получим
13. |о=Л(05о+В(П«, 5о(0)=0.
Уравнение (12) эквивалентно уравнению (1) и точно описывает
исходную нелинейную систему. Уравнение (13) представляет собой
линейное приближение (12) вдоль опорной траектории [М+ «о(•)].
Интуитивно ясно, что если линеаризированное уравнение (13)
«устойчиво», то при «малых» и решение уравнения (13) удовлет-
воряет нашим требованиям. Это предположение обретает строгую
форму в виде теоремы (20), приводимой в следующем подразделе.
Из (13) обычным образом получаем
14. |0(/) = $Ф(/, т)В(т)м(т)+,
о
где через Ф(/, т) обозначена переходная матрица состояний для
уравнения (13).
9. ЛИНЕАРИЗАЦИЯ
147
Упражнение 1. Привести пример, доказывающий, что если для некоторого
конечного числа /С и любого t из Р+ справедливо | Ф (/, 0) | < /С, то малый
входной сигнал и (•) не обязательно вызывает малый сигнал х (•) (имеется
в виду малость в смысле L°°-нормы).
Упражнение 2. Привести пример, из которого следует, что | Ф (/, т) | -> 0
при (/ —т)~>оо (/^0, т^О).
Упражнение 3. Показать, что из (9) следует, что для любого 8>0 су-
ществует 6(8) такое, что при любых /^0
15- (|5l + |u|)<26=>|g(g, и, /)1<е(151 + 1« I)-
9.2. Основной результат
Учитывая введенные выше предположения и обозначения, сфор-
мулируем основную теорему.
20. Теорема. Рассмотрим систему (1), подчиняющуюся предпо-
ложениям (4) и (9). Пусть функция и0: IR+->Rm регулярна,
а функция х(-) определена на |R+ соотношением (7). Пусть | (•) и
Со (•) определены уравнениями (12) и (13). Кроме того, предпо-
ложим, что
(А1) существует А4<оо такое, что для любого t^O
t
21. $|Ф(/, T)|dx^M;
о
(А2) существует N <оо такое, что для любого t^Q
i
22. $|Ф(/, T)B(T)'dT<W;
о
(АЗ) для любого 8>0 существует 6(e) такое, что при любом
23. (|g| + |u|)<25=> № и, /)|<8(| 5| + |и|).
Тогда, если при некотором ее(0, 1/Л4) и соответствующем ему
(согласно (23)) 6 выполняется неравенство
24«
то (везде имеется в виду /.“-норма)
25. |5о|^^|«К(1 - еЛ4)6<6,
26. R|<6,
97
|ыЦ 1-еМ ‘
28. Комментарий. Здесь мы обсудим значение теоремы (20).
Предположения (21) и (22) являются необходимыми и достаточ-
ными условиями устойчивости аппроксимирующего линейного
уравнения (13) при ограниченном входном сигнале и ограничен-
ном состоянии [39]. Согласно предположению (23) остаточный
148
ГЛ. 4. ЛИНЕЙНЫЕ СИСТЕМЫ
член g должен быть второго порядка малости (по |£| и |и I)
равномерно по /.
Теперь рассмотрим выводы. В силу (25) и (26), если возму-
щенное входное воздействие и ограничено в соответствии с (24),
то и £о и | —состояния линеаризованной и исходной нелинейной
систем —не отклоняются более чем на 6 от опорной траектории.
Из (27) следует, что отношение максимума разности %(t) и |о(О
к максимуму входного воздействия | и || может быть сделано сколь
угодно малым, т. е. при малых входных сигналах реакция ►
•—► (0 исходной нелинейной системы может быть сколь угодно
точно приближена реакцией /н->|0(/) аппроксимирующей линей-
ной системы на всей полупрямой R+. Если правая часть уравне-
ния (1) линейно зависит от и, то оценка (27) может быть опре-
делена еще точнее (см. неравенство (34)).
30. Следствие. Рассмотрим частный случай, когда правая часть
уравнения (1) линейна по й, т. е.
31. х = /(х, + й.
Уравнение (12) приобретает вид
32. l = A(t)l + B(t)u + g(l, t),
и предположение (23) упрощается:
(АЗ') для любого е>0 существует 6>0 такое, что при лю-
бых /$s0
33. |£|<6=}|£(|, 0l<8|U
В этом случае, если (24) выполняется, то выполняются и нера-
венства (25) и (26), и, кроме того,
34.
П»| ^1-еЛГ
35. Комментарий. В только что описанном случае оценка го-
раздо более жесткая, так как при малых (т. е. малых S)
е может быть выбрано сколь угодно малым; следовательно, со-
гласно (34), отношение |£ —|011/11 loll максимального отклонения
| (I) от to (0 к максимальному значению |0 (0 можно сделать сколь
угодно малым. Иными словами, относительная ошибка между не-
линейной и линеаризированной системами (т. е. £ (/) — £о (0) может
быть сведена к сколь угодно малой величине. Этот факт был про-
верен с помощью вычислений [30].
Доказательство теоремы (20). Если необходимо, уве-
личим число N из (22) так, чтобы 1 — еМ <;Л/-|-еЛ4. Для дока-
зательства временно предположим, что
36. |g(£, и, 0|<e(|g| + |u|) для любых
(5, и, 0sR"xRmXR+.
9 ЛИНЕАРИЗАЦИЯ
149
Решение уравнения (12) имеет вид
37. ^(0 = $Ф(/, + и,
о
или, в силу (13),
38. |(О = Во(О + $Ф(Л и,
о
Переходя к /.“-нормам в (14), получаем | 1| N | и 1, откуда сле-
дует (25). Учитывая временное предположение (36) в (38), на-
ходим
40. |В(0|<;|Ы01+е$|Ф(/, ni(|g| + |u|)dr.
о
Выберем момент времени Т из интервала (0, оо) и рассмотрим
(40) при t е [0, Т]. Поскольку функция А (•) регулярна (и по-
этому ограничена на отрезке [0, Т]), функция Ф(/, I') ограни-
чена на множестве [0, TJxfO, Т]; таким образом, применение
леммы Веллмана — Гронуола к (40) позволяет заключить, что
|1г||<оо для любого конечного Т. Следовательно, для любого
Ге(0, оо) из (40) получаем |£г ||«5У |и|Ц-вМ | + е,М I «|,
откуда, полагая гМ<1, определяем
1ц I ПРИ любом Т е(0, оо).
Так как правая часть (41) не зависит от Т, при Т->оо функция
►НИ является монотонно неубывающей, но ограниченной;
следовательно,
42.
41.
т. е. неравенство (26) справедливо при временном допущении (36).
Просматривая наше доказательство в обратной последовательно-
сти, мы видим, что Ц(0|^6 и |и(/)|<6 на интервале [0, оо);
поэтому. необходимо потребовать только, чтобы (36) выполнялось
при всех (|, «, /), принадлежащих множеству
^ = {[хо(О + В, ио(0 + «. |ы|^6, fSsO}.
Следовательно, при условиях теоремы неравенства (25) и (26)
выполняются. Из (38)
дно-|ф(*. п1[|«(пжт1И'<
о
<8Mag|4-|u|)<eMa6-6ol+ISol+l«D,
150
ГЛ. 4. ЛИНЕЙНЫЕ СИСТЕМЫ
откуда
Н-?о1<т=^вЛ1(Ио11+8«!)<л^г11«1.
что доказывает справедливость (27).
Доказательство следствия (30). Справедливость (25)
и (26) устанавливается так же, как в теореме (20). Рассматри-
вая (38), где функция g зависит лишь от £ и t, с помощью (33)
заключаем, что
16(0-боК)|ФК, OIIW|Л'<
о
<еЛ1 (|6-6о| + |6о|),
откуда немедленно следует (34).
9. 3. Дискретный случай
Линеаризация дискретных систем выполняется по той же схеме,
как и в непрерывном случае. Исходная система задается разност-
ным уравнением:
50. x(k+V) = f[x(k), u(k), £] при любых &sZ+,
где f: R'Ix|R.mxZ+->|R'1. В дальнейшем предполагается, что
51. х(0) = 0.
Как и раньше, входной сигнал й и реакция х представляются
в виде сумм:
52. й (k) = м, (k) + и (Л), х (k) = х0 (k) 6 (k),
где %,(•) удовлетворяет уравнению
53. x0(k+ 1) = /[х0(&), u0(k), fc], х,(0) = 0.
Пусть, как и раньше, 6m>0 и ит>0. Определим множество
54. ^ = {[*>(*) +6 (*). uo(k) + u(k), fc]||6(*)|<U
|н (k) | ит при любых k <= Z+}.
Предположим, что
55. (а) при некоторых 6m>0 и ит>0 функция f имеет не-
прерывные вторые частные производные по х и й на множестве %7;
56. (Ь) при всех допустимых значениях i, k, I, j uh величины
SUpl_^4-|. supl^l, supl
<g I ^xk &xi I у I &xk &uj I / I |
конечны. (Здесь точные верхние грани берутся по всем (х, й, k)
из й7.)
9. ЛИНЕАРИЗАЦИЯ
151
Раскладывая (50) по формуле Тейлора около (x0(ft), Uo(k),k],
получаем точное нелинейное разностное уравнение
57. I (k + 1) = A (k) I (k) + B(k)u (k) +g [g (k), и (k), ft], g (0) = 0.
Аппроксимирующее линейное уравнение имеет вид
58. l0(k+l)=^A(k)^(k) + B(k)u(k), М0) = 0.
Отметим, что из (55) и (56) следует, что остаточный член g в (57)
удовлетворяет следующему условию:
59. для любого 8 > 0 существует б (е) >• 0 (не зависящее от k)
такое, что
60. |g(£, М, k) I <8 (I I I 4- | и |) при любых fteZ+,
если | | +1 и | < 26.
61. Теорема. Рассмотрим систему уравнений (50) и (51). Пред-
положим, что выполняются условия (55) и (56) и, кроме того,
(А1) существует число М. <оо такое, что
к — 1
62. 2 |Ф(^> /+1)1<М ПРИ любых k е Z+;
/=о
(А2) существует число /С<оо такое, что
к— 1
63. У, | Ф (k, j 4-1) В (/) | ^ К при любых k е Z+.
/ = о
Пусть 8е(0, l/Af) и б(е) выбрано так, чтобы удовлетворялось
(59). Тогда, если
то (символ I-] обозначает /“-норму)
65. -8М)б<б,
66.
й7 15-6,1 вМ(14-Ю
о/’ |«| ^ 1-еМ *
Следствие. Если функция f в уравнении (50) линейно зависит
от й, т. е.
68. х (k4-1) = f [х (k), ft] 4- В (ft) й (ft),
то оценка (67) может быть усилена:
ДЕ-6,1^ *м
Igol ^1-еМ-
152
БИБЛИОГРАФИЧЕСКИЙ КОММЕНТАРИЙ
БИБЛИОГРАФИЧЕСКИЙ КОММЕНТАРИЙ
Трудности, связанные с сокращением нулей и полюсов в мно-
гомерном случае, могут быть разрешены переходом к описанию
систем в терминах пространства состояний с использованием
понятий управляемости и наблюдаемости. Чисто алгебраический
подход, изложенный в разделах 1 — 3, предложен в нескольких
работах [66, 68, 97, 104, 37]. Материал раздела 4 последовательно
развивался различными исследователями. Дезоер [27] предложил
обобщенную формулировку критерия Найквиста, которая в даль-
нейшем применялась Дезоером и By [31] и Дезоером и Калье
[37, 17] для определения устойчивости замкнутых систем все более
общего вида. Метод разложения на псевдопростые справа мно-
жители предложен Видьясагаром. Графический критерий устой-
чивости, рассмотренный в разделе 5, для случая периодически
следующих импульсов исследован Виллемсом [99, 103], а в общем
случае — Калье и Дезоером [16]. Девис [24, 25] независимо от них
получил аналогичные результаты. Подробное исследование дискрет-
ных систем, содержащее отдельные элементы рассуждений раздела 6,
можно найти в работах [34, 106]. Исчисление норм (раздел 7),
по-видимому, имеет давнюю историю в математической литера-
туре [44], прикладные аспекты изложены, например, в работах
[83, 100, 105]. Идея использования принципа равномерной огра-
ниченности для доказательства двух типов /^-устойчивости при-
надлежит Дезоеру и Томазяну [26]. Способ применения спект-
рального радиуса (раздел 7) заимствован из работы [96], а ранние
исследования по устойчивости процессов можно найти в [18, 95].
Метод, изложенный в разделе 8, предложен Барменом [4]. И,
наконец, раздел 9 содержит современную версию исследований,
начатых Дезоером в работе [29].
Глава 5
ПРИМЕНЕНИЕ ТЕОРЕМЫ
О МАЛОМ КОЭФФИЦИЕНТЕ РОСТА
Здесь мы покажем, насколько просто получить различные тео-
ремы об устойчивости систем в терминах «вход — выход» с исполь-
зованием известной теоремы о малом коэффициенте роста (3.2.1)
и (3.3.1) и методов, представленных в главах 2 и 4 и Прило-
жении. Наша цель заключается скорее в выявлении гибкости
этих методов, а не в полном перечислении известных результатов.
В разделе 1 с помощью теоремы о малом коэффициенте роста
и результатов главы 4 выводятся условия //-устойчивости. Раз-
дел 2 содержит достаточные условия ^-устойчивости, отлича-
ющиеся от приведенных в разделе 1, в двух основных аспектах:
во-первых, эти условия могут быть проверены в частотной обла-
сти, а, во-вторых, они менее жестки. В разделе 3 обсуждается
чрезвычайно важный метод экспоненциального взвешивания и при-
водится критерий /.“-устойчивости, который может быть проверен
в частотной области. Некоторые результаты, аналогичные полу-
ченным в двух первых разделах, но применимые к дискретным
системам, приводятся в разделе 4. В разделе 5 исследуются
линейные системы с медленно изменяющимися ’параметрами и
выводится условие //-устойчивости таких систем, если «заморожен-
ная» система устойчива. В разделе 6 на примере несложной
нелинейной системы иллюстрируется способ использования тео-
ремы о малом коэффициенте роста. В разделе 7 показано, как
эту же теорему можно применить для доказательства факта суще-
ствования периодических решений неавтономных нелинейных
дифференциальных уравнений. Раздел 8 содержит доказательство
хорошо известного критерия Попова с помощью теоремы о малом
коэффициенте роста. И, наконец, в разделе 9 исследуются два
метода получения условий неустойчивости нелинейных систем
с обратной связью.
1. НЕПРЕРЫВНЫЕ СИСТЕМЫ — //-УСТОЙЧИВОСТЬ
Мы рассмотрим системы с обратной связью, вид которых
показан на рис. 3.1, где представляет собой линейный оператор
свертки, а Нг — статическая нестационарная нелинейность. Наша
общая идея: предполагая, что нелинейность Н2 можно аппрокси-
мировать стационарным линейным отображением у2 (/) = /Се2 (/),
применить теорему о малом коэффициенте роста, чтобы показать,
что исходная нелинейная система устойчива, если устойчива
154
ГЛ. 6. ПРИМЕНЕНИЕ ТЕОРЕМЫ О КОЭФФИЦИЕНТЕ РОСТА
линейная стационарная система, содержащая Hi в прямой ветви
и К в ветви обратной связи, при условии, что Я2 не слишком
сильно отличается от К.. Сначала мы докажем теорему о LP-устой-
чивости при ре[1, оо].
1. Теорема. Рассмотрим многоконтурную систему с обратной
связью в форме, представленной на рис. 3.1, где иь и2, еъ ег,
У1, Уг‘ R+->R". Подсистема Hi линейна, стационарна и опреде-
ляется соотношением
t
2. (Hiei) (0 = $ 6 (I - т) ei (т) dx,
о
где функция G (•) преобразуема по Лапласу и, кроме того,
3. d(s) = ©/’(s)^-r’(s),
где е <2^'лхп и пара (©^, представляет собой взаимно
псевдопростое справа разложение G. Подсистема Д2 статична
и описывается соотношением
4. (ад(0 = Ф[е2(0, *],
где функция <p: R"X|R+->[R'’ непрерывна по своему первому аргу-
менту и регулярна по второму. Предположим, что
6. «1, и2 <= Lpn => yi, у2 е Lpne.
При этих условиях, если существуют постоянная матрица /CeR"*"
и действительные числа у и 0 (0 = 0, если р<оо) такие, что
7. |<р (ст, 0 — 7<ст| | <г | + 0 V/e|R+, V<re|Rn,
и если
8. (a) inf | det [/ф-Кб (s)] | > 0,
Res>0
9. (b) det \&> (s) + Ke#" (s)]0 при Res^O и detJ?(s) = O,
10. (с) 8Як(.)|л-Т<1,
где
11. Йк (s) = & (s) [/ + КЪ (s)]-1 = [7+6 (s) X?16 (s),
тогда при каждом pe[l, co]
12. ui, u2^L^=>ei, eit yu y2^L„.
и система LP-устойчива.
Доказательство. Подробное доказательство предоставлено
читателю в качестве упражнения. Общий алгоритм доказательства
состоит в следующем. Сначала применить теорему о преобразо-
вании контура (3.6.3). Зат.ем показать, что из условий (8), (9)
и теоремы (4.4.27) следует, что функция Hr(-) принадлежит е^яхп.
И, наконец, показать, что предположение (10) и теорема о малом
коэффициенте роста приводят непосредственно к выводу (12).
2. КРУГОВОЙ КРИТЕРИИ
165
Упражнение 1. Объяснить, почему в (7) предполагается, что 0 = 0, если
р<оо, хотя это предположение отсутствует при р = оо.
Если функция (р удовлетворяет условию Липшица, то исполь-
зуя теорему о малом коэффициенте роста по приращениям (3.3.1),
можно сформулировать следующее следствие.
13. Следствие. Если в условиях теоремы (1) условие (6)
заменить на
14. |[ф(о, /)-/(а]_[ф(а',
—(у'| V/<= |R+, Va, а'е
то выводы теоремы (1) могут быть усилены:
(а) для каждой пары ux, и2 е Lpn существует единственное
решение ех, е2, у2 е L* (которое вычисляется методом после-
довательных приближений);
(Ь) решение непрерывно зависит от и19 и2.
Замечание. Важно заметить, что при получении этих резуль-
татов мы нигде не накладывали ограничений на вид зависимости
функции ф от t.
Упражнение 2. Пусть р = оо, т. е. uv u2&L^. Показать, что теорема (1)
и следствие (13) останутся справедливыми, если условия (7) и (14) будут
выполняться лишь для а, принадлежащих некоторому шару, радиус которого
зависит от ji иг 1^ и 1 и2
Упражнение 3. Предположим, что функция ф удовлетворяет условию (14)
для некоторого у е Р, а разложение функции G (•) в некоторой окрестности
начала координат содержит 6-функции (но без своих производных). Пусть
через Go обозначена «амплитуда» импульса при / = 0. Показать, что, если
det (/ + КОо) * 0, то uv и2 е= L?e => ev е2, yv у2 е L£,.
2. £2-УСТОЙЧИВОСТЬ — КРУГОВОЙ КРИТЕРИЙ
Результаты предыдущего раздела основаны на использовании
неравенства
1. | Нк * е jp | Нк UIе I/»
справедливого для всех р е [1, оо]. Теорема (1.1) и следствие (1.13)
весьма полезны, поскольку предоставляют в наше распоряжение
достаточное условие //-устойчивости для всех значений р. Однако
практическое применение теоремы (1) иногда усложняется из-за
необходимости вычисления нормы | Нк (•) U, входящей в условие
(10). В настоящее время неизвестно, как только на основании
знания1) функции Н где со е R+, вычислить |#k(-)U или
определить верхнюю оценку для | Нк (•) U- Поэтому для опреде-
х) Мы можем указать лишь нижнюю оценку для |
W eels
156
ГЛ. 5. ПРИМЕНЕНИЕ ТЕОРЕМЫ О КОЭФФИЦИЕНТЕ РОСТА
ления точного значения ||Я/с(-)||^ мы вынуждены сначала найти
обратное преобразование Лапласа функции заданной
соотношением (1.11), а затем, пользуясь определением нормы Ц-Ц,
вычислить I Нк(-) ||л. При исследовании, например, распределенных
/?С-схем этот процесс слишком трудоемок и требует обычно при-
менения методов интерполяции.
В настоящем разделе мы воспользуемся теоремой о малом
коэффициенте роста для построения достаточного условия /Аустой-
чивости и выведем так называемый «круговой критерий». Приво-
димые здесь результаты выгодно отличаются от приведенных
в предыдущем разделе. Во-первых, в условие (8) теоремы (4),
приводимой ниже, входит £2-норма оператора Н#, в результате
чего это условие слабее условия (1.10). Во-вторых, справедливость
условия (8) может быть легко установлена на основании знания
функции
Для дальнейших рассуждений нам понадобится следующий
факт.
2. Утверждение. Пусть Н е о^пхп и е еЦ. Тогда
3. IIН * е |2 {sup Xmax [Я* (/«) И (/©)]J1/2.1 е |„
Доказательство основано на применении равенства Парсеваля
и предоставляется читателю в качестве упражнения.
Сначала мы сформулируем теорему о ^-устойчивости, содер-
жащую основную идею, а затем перейдем к круговому критерию.
Для удобства обозначим через D[a, b] замкнутый диск в R2,
диаметром которого является отрезок с концами в точках (а, 0)
и (&, 0).
4. Теорема. Рассмотрим многоконтурную систему с обратной
связью, представленную на рис. 3.1, где мх, и2, elt е2, уъ у2:
R+~>IR'1, подсистема Hi определена посредством (1.2) и (1.3), а
подсистема Н2 задается соотношением (1.4). Допустим, что из иъ
и2 е Ln вытекает, что у2, у2 е L„e- Тогда, если существуют мат-
рица К е Rnxn и постоянное число у е R такие, что
5. |ф(о, t) — Лст | sg у | о | V/е |R+, Vo е R",
и если
6. (a) inf | det[Z + Kd(s)]|>0,
Res^O
7. (b) det \S> (s) + (s)] Ф 0 при Res 3=0 и det^(s) = O,
8. (с) у sup Xmax [H*K (/©) fiK (»] < 1,
<osR
причем Нк(-) определено соотношением (1.11), то
9. «1, м2е Lan=^>ei, e2, yit y2^L3n.
Доказательство оставлено читателю в качестве упражнения.
2. круговой критерии
157
В сложившейся ситуации теорема (4) не может быть применена
лишь к функции G (/со), поскольку для проверки условия (6)
необходимо знание G(s). Однако, если справедливость (6) уста-
новлена, можно перейти к проверке условия (8) в частотной
области, и необходимость исследования функции Нк( •) во времен-
ной области отпадает. Напомним (см. раздел 4.5), что при неко-
торых дополнительных условиях неравенство (6) можно проверить
графическим исследованием функции С(/со).
Теперь мы сформулируем круговой критерий в более общей,
чем обычно, форме. Учитывая значимость этого критерия, мы
приведем его доказательство полностью. Удобство критерия состоит
в том, что его условия легко проверяются на основе доступных
экспериментальных данных, а именно, диаграммы Найквиста.
10. Теорема (круговой критерий). Рассмотрим одноконтурную
систему, представленную на рис. 3.1, где «lt u2, ei, е2, yi, у2.
R+-*R. Подсистема Hi определяется уравнением
11. =
причем
k
Re pi 0 при i = 1, 2, ..., k, gb е L1. Подсистема Н2 определяется
уравнением
13. й(0 = ф[е2(0. П.
где функция <р: RxR+->R непрерывна по первому аргументу
и регулярна по второму. Кроме того, предполагается, что <р
принадлежит сектору [а, Р], т. е.
14. аст2 ==g сир (ст, /) р<т2 V/<=R+, VoeR.
Для удобства введем следующие обозначения!
15. t = Р = -Ц^
и предположим, что £=/=(). При этих условиях u2&L*=5
=Фе1( е2, yi, у2<=1? тогда и только тогда, когда расположение
полюсов и диаграмма Найквиста функции g (т. е. отображение
с проколами в соответствующих точках) удовлетво-
ряют одному из условий!
(а) если 0<а<р, то нет никаких ограничений на располо-
жение полюсов g, но диаграмма Найквиста g ограничена вне
диска D[—1/а, —1/Р] и охватывает его пр раз, обходя его против
часовой стрелки, причем пр равно числу полюсов функции g
с положительными действительными частями;
158
ГЛ. б. ПРИМЕНЕНИЕ ТЕОРЕМЫ О КОЭФФИЦИЕНТЕ РОСТА
(Ь) если 0 = а<р, то функция g не должна иметь полюсов
в открытой правой полуплоскости, а диаграмма Найквиста g
должна оставаться справа от вертикальной прямой с абсциссой
—1/Р» т. е.
Reg(/w)>-j VcoeR;
(с) если а<0<р, то функция g не должна иметь полюсов
в замкнутой правой полуплоскости, а диаграмма Найквиста g
должна полностью содержаться внутри диска D[—1/а, —1/Р].
Доказательство. Теорема является прямым следствием
теоремы о преобразовании контура и теоремы о малом коэффи-
циенте роста и может также рассматриваться как следствие
теоремы (4). Прежде всего отметим очевидность следующего факта:
независимо от того, какой из случаев (а) —(с) исследуется, диа-
грамма Найквиста функции g не должна проходить через точку
(—1/1, 0), но должна обходить вокруг нее против часовой стрелки
точно пр раз, где пр — число полюсов gB открытой правой полу-
плоскости. Поэтому, согласно графическому критерию (4.5.5),
отсюда следует, что ункция ^(s) = g(s)/[l +££($)] принадлежит
Применим теорему (4), полагая /< = £/. Условие (8) приоб-
ретает вид
16.
psup
<0
g(/tt>)
l+gg(/®)
<1.
Теперь легко показать (предоставляем читателю возможность про-
делать это в качестве упражнения), что для z е ©
17а. если О<а<0, то условие р|г|<| 1+£г| эквивалентно
ограниченности функции z вне диска D[—1/а, —1/0];
17b. если О = а<0, то условие р \z | <| 1 + |г| эквивалентно
неравенству Rez>—1/0;
17с. если а<О<0, то условие р|z|<11 4-|г| эквивалентно
тому, что функция г содержится внутри диска £>[—1/а, —1/0].
Таким образом, условия теоремы (4) удовлетворены, и наша
теорема доказана.
18. Замечание. При 0->а>О, согласно секторному усло-
вию (14), характеристика <р превращается в прямую с наклоном а;
диск D[—1/а, —1/0] стягивается в критическую точку (—1/а, 0);
и, наконец, круговой критерий сводится к графическому крите-
рию [теорема (4.5.5)].
Упражнение 1. Пусть оригинал функции gj из условия (12) теоремы (10)
принадлежит но не принадлежит L1. Привести измененную версию тео-
ремы (10) и доказать ее.
Упражнение 2. Рассмотрим систему с обратной связью с п входами и п вы-
ходами. Пусть Hi определяет реакцию при нулевом начальном состоянии под-
системы с входом ej и выходом уи заданной уравнениями
Л^Ах+Ве^ x(Q)^Ot у^Сх,
3. МЕТОД ЭКСПОНЕНЦИАЛЬНОГО ВЗВЕШИВАНИЯ
159
Матрицы А е В е и — постоянные, все собственные зна-
чения матрицы А имеют отрицательные действительные части.
Обозначим через G (ja))—С (jwl — Л)"1 В передаточную функцию под-
системы Пусть подсистема Н2 задана уравнением у2 (/) = <р [е2 (/), /], при
чем характеристика ф: РлхР+->Рл непрерывна. Показать, что если н2 = 0,
матрица / — d*(/®) d(/<D) положительно полуопределена для всех ® е Р,
а для некоторого ее(0, 1)
Фтр (о, t) ф (о, /) (1 — 8) отро Va е Rrt, V/^0,
то для любого их s L* функции ev yv у2 принадлежат L2 f] L°° и стремятся
к нулю при t -> оо. (Указание: использовать определение /2-нормы в Рл
и то, что
со п
О £ = 1
при х е L2; учесть, что импульсная характеристика G (t) подсистемы Нг имеет
вид О(/)«яСехр(Л/)В, принадлежит и d (/) ==СВ6 (/)4-СЛ exp (At)B^
^aJnxn-')
Упражнение 3. Рассмотрим одноконтурную систему с единичной обратной
связью* заданную уравнением
t
У (!)e j S (* — т) k (т) е (т) == (Ge) (/),
причем g е L1 (0, оо),
со
*(Т)= 2] ехр (/ашт),
— 00
00
где У] | ka < оо. Показать, что
— со
(а) для всех Т > 0 импульсная характеристика G является непрерывным
линейным отображением, действующим из PTL^ в PTL2e\
(b) Y(G)sSl!glli 2
— 00
(с) если у(0)<1, то замкнутая система /Аустойчива.
8. МЕТОД ЭКСПОНЕНЦИАЛЬНОГО ВЗВЕШИВАНИЯ —
^-УСТОЙЧИВОСТЬ
Результаты, полученные в разделе 1, являются весьма общими,
поскольку определяют условия //-устойчивости для любых р,
однако возможность их практического применения затруднена
тем, что одно из основных условий (1.10) нельзя непосредственно
проверить в частотной области. В сформулированной в разделе 2
теореме аналогичное условие можно проверить в частотной обла-
сти, однако теорема теряет общность, будучи справедливой только
при В этом разделе, используя метод экспоненциального
взвешивания, мы выведем условие /-“-устойчивости в форме,
160
ГЛ. 5. ПРИМЕНЕНИЕ ТЕОРЕМЫ О КОЭФФИЦИЕНТЕ РОСТА
похожей на критерий Найквиста, что, как нетрудно заметить, тре-
бует введения дополнительных предположений.
Метод экспоненциального взвешивания основан на двух фактах:
(1) Если
1.
то для всех а е R
2. у (t) e.ai — g (t) sat * е (t)
(2) Пусть символом X (•) обозначено преобразование Лапласа;
тогда, если f(s) — X [/ (/)], то
Здесь через / (/) обозначена функция 1*—► f (/) exp (а/); исполь-
зование символа e вместо общепринятого е позволит нам избе-
жать путаницы в изображении экспоненты и сигнала ошибки.
3. Теорема. Рассмотрим одноконтурную систему с обратной
связью, приведенную на рис. 3.1. Подсистема Hi описывается
уравнением
4. yi(t) = (g*ei)(t),
подсистема Н2 задается, как
5. «/2(0 = ф[е2(0. Л»
предполагается, что и2 = 0 и
6. e^g (/) е L1 fl L? для некоторого а > 0,
7. ф принадлежит сектору [а, 0], где р>0.
При этих условиях, если a-сдвиг диаграммы Найквиста
функции g, т. е. образ отображения <о*—(—a-{-/w), удовлет-
воряет теореме (2.10), то из Ui^LX следует, что ех, yi&LX,
и, кроме того, существуют числа mi и т2 такие, что
8а. killoo’sSmilUxIco,
8Ь. | в2 |оо ^2 0 «2 loo.
Доказательство. Система с обратной связью определяется
уравнением
9- ytf) =\g(t — t)u(i;)dr-$£(/-т)ф[#(т), т]йт =
о о
ю. =о(0-Хг(^~'г)ф[г/(т),
о
где для простоты индекс «1» опущен и свертка g*u обозначена
через v. Из (6) следует, что Представим (10) в эквива-
3. МЕТОД ЭКСПОНЕНЦИАЛЬНОГО ВЗВЕШИВАНИЯ»
161
лентном виде:
11. га‘у (t) — e.atv (0 — $ еа (t~x}g (t — т) епТ<р [у (т), т] dr.
о
Определим функции
12а. yw(t) = &aty(t),
12b. vw(0 = 8^'(0.
12c. gw (/) = tftgtt),
тогда уравнение (11) превращается в
13. yw (0 = vw (t) - \gw (t - t) 8a/<p [8-aTyw (t) , t] dr.
0
Поскольку отображение
14. о i—► 8a/<p [e~aTo, /]
принадлежит сектору [а, 0], а диаграмма Найквиста отображе-
ния со ►—<-gw (/со) —g (—а +/со) удовлетворяет теореме (2.10), то,
согласно той же теореме, yw(-) е Ц, если vw(- ) Ц, и кроме
того, для некоторого числа р
15. 11М)]Л<р|[М)Н.
где через | [yw (• )]^ j2 обозначена £2-норма срезки [yw (•)], функ-
ции yw('). Легко показать, что
16. 1[»юИИ<^Моо<8*^11м|1оо.
Из секторного условия для отображения (14) получаем:
17. | {еоТф [8-^ (т), T]}z h < 01 [yw ()]/12
еа/I И ||оо = «"Pl || И joo,
У 2а
где
Возвращаясь к (9), находим:
|g(0l^|f(0l + $|g(*-T)| |ф[У(т), т] | dr |gh Л и IL +
О
+ е-0* j еа | g (t — т); е"х | ср [у (г), т] | dr,
о
откуда, применяя неравенство Шварца, получаем:
I У (!) I 1 g 11II “ 1!оо + е-а' II g (Т) 8ОТ |g II |8атф [&-aXyw (т), т]}, ||2 -С
lg i.Xll и too 4- li g (T) 8ut ||2 Pl || U Joo,
0 Ч. Дезоер, M. Видьясагар
162
ГЛ. 5. ПРИМЕНЕНИЕ ТЕОРЕМЫ О КОЭФФИЦИЕНТЕ РОСТА
т. е. неравенство (8Ь) доказано. Доказательство неравенства (8а)
оставлено в качестве упражнения.
19. Следствие. Если функция «(•) в теореме (3) ограничена
на R+ убывающей экспонентой, то такому же ограничению удов-
летворяют функции е(-) и у(-).
Доказательство. По условию существуют числа г, ае
е IR+ такие, что
20. V/^0.
Без потери общности предположим, что 0<а<а. Тогда из (9)
получаем:
&а‘у (/) = eaZu (/) — J 8а V-^g (t — т) 8атф [у (т), т] dx.
о
Заметим, что
(i) функция /ь—>еа/ц(/) ограничена;
(ii) отображение о н-* е^ф [е^о, т] принадлежит сектору [а, Р];
(iii) функция /»—>ea'g(/) удовлетворяет условию (6), в кото-
ром а заменено на (a —а)/2.
Следовательно, согласно теореме (3), функция е^у (/) ограничена.
Теперь мы приведем простое обобщение теоремы (3). Это
обобщение основано на следующей лемме.
’21. Лемма. Пусть
k mi
22. G (s) = 2 (T=fe/ + ® (s) + & (s)’
1=1 z = i
где Re p; 5=0; /и, = 1, если Repj = O и Gb e L„xn f) L'hxn. Предпо-
ложим, что F ^a^nxn. Тогда, если H— G(lf6)~1 то
H Lnxn f) Lnxn-
Доказательство. По условию H = G{1-f-FG)-1 eе^яхл,
кроме того, H удовлетворяет равенству
23. Н + НЙОЬ +HFGa — (jb + (ju,
откуда
24. Н 4- HFGb — Gb — (I — HF) Ga.
Поскольку функция (1 — НЙ)(зи аналитична при Res>0, огра-
ничена и равномерно непрерывна при Res = 0, можно показать
так же, как сделано при доказательстве теоремы (4.7.69b), что
— HF)GU] eLnxnfl и в частном случае —
Так как
25. Й---------ЙМь + <Зь + (1-ЙР)6а>
где все слагаемые из правой части принадлежат LAx/гП^пхл» то
очевидно, что Н e£AXnQL^xn.
4. ДИСКРЕТНЫЕ СИСТЕМЫ —/Р-УСТОЙЧИВОСТЬ
163
26. Теорема. Рассмотрим систему с обратно} связью, изобра-
женную на рис. 3.1, полагая, что подсистемы и Н2 заданы
уравнениями (4) и (5) соответственно. Предположим, что и2 (/) = О
и для некоторого а>0
k mi
27. гй-ПЙ5/+«*'!>'
i=l/=l
28. Re pi ^ — a\ mt — 1, если Re pi = — a,
29. ^(ОеЬ’ПР,
30. <p принадлежит сектору [a, 0].
Тогда, если a-сдвиг диаграммы Найквиста функции g удовле-
творяет теореме (2.10), где в качестве правой полуплоскости при-
нято множество {s: Res^s — а}, то из axeL“ следует, что ег,
i/i и выполняются неравенства (8а) и (8Ь).
Несложное доказательство этой теоремы предоставлено чита-
телю в качестве упражнения.
4. ДИСКРЕТНЫЕ СИСТЕМЫ — /^-УСТОЙЧИВОСТЬ
В этом небольшом разделе мы сформулируем наиболее важ-
ные дискретные аналоги результатов, полученных в разделе 1.
Точные формулировки теорем, аналогичных приведенным в раз-
делах 2 и 3, здесь не представлены, поскольку являются совер-
шенно очевидными.
1. Теорема. Рассмотрим многоконтурную систему с обратной
связью, изображенную на рис. 3.1, где иг, и2, ег, е2, уг, уг: Z+-*
->Rn. Подсистема Hi линейна, стационарна и описывается
уравнением
2. У1 = 6*еъ
где
3. G (г) = ©/* (г) (z),
<s/", & е /Ахл и пара (®^*, составляет взаимно псевдопростое
справа разложение G. Подсистема Н2 является статической и
задана уравнением
4. Л VieZ+.
При этих условиях, если существуют постоянная матрица К s
г 1РЛХЛ и действительные постоянные у и v (причем v = 0 при
р<оо) такие, что
5. |ф(ст, 0 —+
6. , iirf Jdet[Z + W(z)]|>0,
7. det[.S’r(z)4^®^:(z)]#=0 при |z|Ssl и det ^(z)=JX
8.
6*
164
ГЛ. 5. ПРИМЕНЕНИЕ ТЕОРЕМЫ О КОЭФФИЦИЕНТЕ РОСТА
где
9. Я = 2-1{б(г)[/ + К0(г)]-1},
тогда для каждого р е [1. оо]
Ю. иъ и2<= lpn=>elt е2, уи у2(=1р.
Упражнение 1. Доказать теорему (1).
Упражнение 2. Сформулировать и доказать аналоги теорем (2.3) и (3.26)
для дискретного случая.
5. ЛИНЕЙНЫЕ СИСТЕМЫ С МЕДЛЕННО ИЗМЕНЯЮЩИМИСЯ
ПАРАМЕТРАМИ
Рассмотрим многоконтурную линейную систему, заданную урав-
нениями
1. I/i(0 = (<3*^i)(0.
2. 1/2 (0 = К (0 (0-
Если К (0 принимает значения из некоторого подмножества 8
кольца Rnx'2 и функция (/4-GAf)-1G принадлежит &/пХп при
всех А! то можно предположить, что нестационарная система,
заданная уравнениями (1) и (2), устойчива при условии, что/((-)
изменяется достаточно медленно. Ниже мы точно определим зна-
чение выражения «достаточно медленно». Заметим, если функцию
/<(•) «заморозить», придав ей значение К(т), передаточная функ-
ция получившейся линейной стационарной замкнутой системы
станет равной
3. /?т (s) = [7 + G (s) Д’(т)]'1 G(s).
4. Теорема. Рассмотрим многоконтурную систему с обратной
связью, изображенную на рис. 3.1, где ult и2, elt е2, yit у2. IR+^R".
Предположим, что подсистемы /7Х и Н2 заданы уравнениями (1)
и (2) соответственно, причем функция /С(-) принимает значения
из некоторого ограниченного подмножества $ кольца R"x". Пусть
для каждого функция [/-|-G (s) Af]-16(s) принадлежит
&/яхл. При этих условиях, если
5. sup J | Нх (т — т') [К (т) — К (т')] | du' < 1,
Т<=1?+0
где
6. /7T(s) = [/4-G(s)/((T)]_1d(s),
то «1, «геГ => сх, е2, уъ у2 е L00. Если
со
7. J |//г(т-т')[К(т)-К(т')]|4т<1,
6 ПРИМЕР НЕЛИНЕЙНОЙ СИСТЕМЫ
165
то «1, Ui^Ll=5ei, е2, th, z/2 е L1. Если условия (5) и (7) выпол-
няются одновременно, то для каждого р е [ 1, оо]
«1, u2 eLp=) е2, е2, уъ у2 е Lp.
Доказательство. Уравнение замкнутой системы имеет вид
8. (0 = — (G * Куг) (/) — (G * Ки2) (0 + (G * их) (f) =
--------------------------------------(G */<«/!) (0 + (G*u)(0,
где
9. Ы(0 = Ы1(0_0(0Ы2(0.
Пусть т е IR+- Тогда (8) можно представить как
Ю. yr (0 + [G * К (т) уД (0 = (G * и) (0 4- {G*IK (т) - К (0] z/i} (0.
Проведем операцию свертки обеих частей (10) с оригиналом
функции [/4-G ($)0 (т)]-1, принадлежащей, по условию теоремы,
алгебре &^пХп, тогда (10) примет вид
t
И. (0 = (Нг * м) (0 + $/Ут (т — (D—K (т')| У (О dr'.
о
В частном случае при t = x уравнение (11) превращается в
12. у! (т) = (70 * и) (т) + Нх (т — т') [/< (т) — К (т')] у (т') dt'.
о
Рассмотрим отображение
13. (Fy) (т) = $ 70 (т — т') [0 (т) — К (т')] у <т') dx'.
о
Используя результаты раздела 4.7, выводим, что левая часть (5)
является £°°-нормой отображения F, в то время как левая часть (7)
представляет собой Р-норму того же отображения. Справедливость
доказываемой теоремы следует из теоремы о малом коэффициенте
роста.
14. Замечание. Согласно предположению, Йх( при
каждом теК+. Поэтому условия (5) и (7) выполняются одновре-
менно, если функция К(-) изменяется достаточно медленно. Идея
теоремы основана на том, что функция К (•), в сущности, остается
постоянной на интервалах времени, равных «памяти» функции
#т(), т. е. интервалах времени, в течение которых функция
Нх (•) значительно отличается от нуля.
6. ПРИМЕР НЕЛИНЕЙНОЙ СИСТЕМЫ
На рис. 5.1 изображена схема, состоящая из параллельного
соединения линейного стационарного двухполюсника и нели-
нейного нестационарного конденсатора; ехема питается от источ-
166
ГЛ 5 ПРИМЕНЕНИЕ ТЕОРЕМЫ О КОЭФФИЦИЕНТЕ РОСТА
ника тока и(-). Обозначим через g(-) импульсную характери-
стику т. е. реакцию на единичный импульс напряжения;
тогда двухполюсник описывается соотношением
t
1. i (t) — J g (t — т) v (t) dr, I 0.
о
Характеристика нелинейного нестационарного конденсатора имеет
вид
2. 0с = ф(<7, 0,
где q и vc — заряд и напряжение на обкладках конденсатора
(рис. 5.1). По закону Кирхгофа
V = Vc и
3. 4 (0 =
t
T]dT,
о
Рис. 5.1. где и(-) равно току, создава-
емому источником.
4. Утверждение. Рассмотрим схему, изображенную на рис. 5.1
и заданную уравнением (3). Пусть
(а) характеристика <р: RxR+->IR регулярна по I для каждого
фиксированного q\
(b) на всех компактных интервалах I cz R+ характеристика <р
удовлетворяет условию Липшица с постоянной у(/)<оо;
(с) характеристика <р принадлежит сектору [а, Р], причем
р.
Введем обозначения:
Пусть g^orf. Тогда, если
6. $4-ag(s)=/=0 при Res^O,
7. sup | £ (» [/О 4- Zg (/о)]-11 < 1,
со > 0
то для любого « eL'UL2 функции g, (), v принадлежат Z,2, функ-
ции q, v принадлежат £°° и q(t), v(t)->0 при t->oo.
8. Комментарии.
(а) Если usL1, то от источника на схему поступает заряд
конечной величины.
(Ь) Время зарядки нелинейного конденсатора ограничено сек-
торным условием и регулярност ю характеристики <р (q, ). Отме-
тим, что нестационарный конденсатор является активным элемен-
том, т. е. он может выступать в роли источника энергии.
6. ПРИМЕР НЕЛИНЕЙНОЙ СИСТЕМЫ
167
(с) Поскольку g (s) — входная проводимость двухполюсника ©^,
неравенство (6) означает, что параллельное соединение и
линейного конденсатора емкостью 1/аФ представляет собой устой-
чивую разомкнутую систему.
Доказательство утверждения 4. Так как <р удовле-
творяет условию Липшица, то для доказательства факта сущест-
вования единственного решения q\ R+ -> R уравнения (3) можно
применить теорему (3.5.2). Рассмотрим функцию
9- Ф(<7,/) = <р(<7,
Заметим, что коэффициент роста ф не превосходит а как в L*,
так и в Ц. Перепишем уравнение (3):
t
10- <? (0 + ® (g* q) (0 = « (0 -\g(t-т) Ф1<7 (т), т]с(т.
о
Введем обозначения:
11. ®(s) = [s + ag (s)]-1,
Й (s) = g (s) w (s) = g (s) [s + Kg (s)]-1.
Поскольку gea< а с учетом условия (6) функция s+ag(s)
ограничена вдали от нуля в С+» то функция w принадлежит е^.
В самом деле, представим w(s) из (11) в виде
12> “’W-7+rl s+1' J *
Так как ш(з) равно произведению элементов &/, то
По той же причине h е Вспомним, что g е ; тогда функ-
ции со(/со) и col—*А(/«) принадлежат L2, поскольку при
]со|—>-оо обе функции имеют порядок роста О(1/со). Таким обра-
зом, w, h е orf f) L2, т. е. не содержат в своем разложении 6-функ-
ций. Следовательно, w, h <= L1 Q L2. Производя свертку обеих час-
тей (10) с функцией w, получаем
t
13. q(t) — \h(t — т)<р[<7(т), x]dx.
о
Будем рассматривать (12) как уравнение системы с обратной
связью. Здесь для любого и е L1 QL3 функция ш*и принад-
лежит L2, а неравенство (7) представляет собой условие малости
коэффициента роста, использующее Р-нормы. Поэтому если и е
eLHJT.2, то q<=L2. Согласно секторному условию, функции
v (.) = <р [?(•), •] и ф [<?(•), •] принадлежат L2; таким образом,
в силу (10) q^L2. Следовательно, q^Lm и д(/)->0 при /->оо
(см. упражнение 1, Приложение В.2). Из этих рассуждений
с учетом секторного условия , ытекает, что v^L°° и и(/)->0
при
168
ГЛ. 5. ПРИМЕНЕНИЕ ТЕОРЕМЫ О КОЭФФИЦИЕНТЕ РОСТА
Упражнение 1. Сформулировать и доказать утверждение, аналогичное
утверждению (4), для схемы, состоящей из n-полюсника, соединенною с п не-
линейными нестационарными конденсаторами.
Упражнение 2. Доказать, что функции w и /г, определенные соотноше-
нием (11), являются элементами пространства L°°, (У к а з а н и е: X (до) =
= (s).)
7. СУЩЕСТВОВАНИЕ ПЕРИОДИЧЕСКИХ РЕШЕНИЙ
В этом разделе мы покажем, как локальная форма теоремы
о малом коэффициенте роста может быть иногда использована для
установления факта существования периодического решения неав-
тономного дифференциального уравнения и определения оценок
для амплитуды решения.
Сначала сформулируем теорему существования и единствен-
ности в форме, удобной для дальнейшего применения.
1. Лемма. Пусть ^ — банахово пространство (т. е. полное
нормированное линейное пространство) и функция f:
непрерывно дифференцируема в смысле Фреше при всех /Еэ®.
Предположим, что существуют некоторый элемент х0 е & и неко-
торое число [0, 1) ^акие, что
2. II/' (х)|k< 1 при хеВ[х0; Р/(1 — £)]»
где
3. В[х0; Р/(1-£)] = {хе=<^! |х —х0||^₽/(1 -k)}
и
4. PSs|/(*o) —*о|.
Тогда существует единственный элемент JfeB[x0; 0/(1—&)]
такой, что
5. X = f(X).
6. Замечание. В лемме ничего не утверждается относительно
возможности существования соответствующих точек вне шара
В[х0; р/(1—£)].
Доказательство. Если точки х и у принадлежат шару
В\х0\ 0/(1-£)Ъ то
sup IfИ+(1-а)4г]|-|х-0КА|х-0|.
ае[0, 1]
Поскольку &<1, функция f является сжатием полного метриче-
ского пространства В [х0, Р/(1 — &)]• Следовательно, существует
единственная точка X, принадлежащая шару В[х0, Р/(1 — &)],
такая, что Х = /(Х).
Упражнение 1. Провести подробное доказательство леммы (1). (Указа-»
н и е: рассмотреть последовательность {хх}, где xx-==f (х^), (i»l, 2, ...)
Лучший способ объяснить какой-либо метод —привести пример
И описать все шаги так, чтобы общность метода стала очевидной.
7. СУЩЕСТВОВАНИЕ ПЕРИОДИЧЕСКИХ РЕШЕНИЙ
169
7. Пример. Рассмотрим уравнение Дюффинга:
8. у a2f/+ Zn/3 = a cos со/, Т =
где а, Ь и а —постоянные числа. Мы будем полагать, что со ^=а,
в противном случае даже при b = 0 уравнение (8) вообще не будет
иметь периодических решений. Мы исследуем вопросы существо-
вания и локальной единственности периодических решений
уравнения (8) при малом Ъ («слабая» нелинейность) и при малом
а («слабое» воздействие).
Поскольку 0=7^ а, при fe = 0 уравнение (8) должно иметь
периодическое решение вида yQ(t) = a0cos со/. Рассматривая его
как приближенное решение (8) и пренебрегая третьим гармони-
ческим членом
з 1
COS3 X = COS X + -J- cos Зх,
4 4
получаем уравнение для aQ:
9. а? 4- (а2 — <о2) а0 = а.
Представляя (8) в виде системы уравнений в форме Коши, пола-
гая, что х(/) = [Х1(0» х2 (О Г. находим
10 х = [ ° Чх + Г ° 1
Л [—a2 0]A^[acos(o( — bxU"
Полагая, что [xi(0]3 известно, представим уравнение (10) в виде
х = Ах + §[х(0]. откуда
х (0 = Ф (0 х (0) + $ Ф (/ - т)£[х (т)] dx,
о
где Ф (t — т) = exp A (t — т). Потребуем, чтобы это решение было
периодическим с периодом Т (и не содержало никаких субгармо-
ник!); тогда х(7') = х(0) и
х (0 = Ф (0 [I - Ф (Г)]-1 $ Ф (Т - T)g[х (т)] dx 4- Ф (/ - т) g [х (т)] dx,
6 о
причем на отрезке
т
И. = T)£[x(T)]dr.
о
Упражнение 2. Привести точное выражение для матрицы W (/, т) при
(/, т) е [0, Г]х[0, Г] в примере 7.
170
ГЛ 5 ПРИМЕНЕНИЕ ТЕОРЕМЫ О КОЭФФИЦИЕНТЕ РОСТА
Пусть xQ— приближенное решение уравнения (10) —соответст-
вует yQ\ тогда
12.
Х.И = [Х„(О,
Применяя лемму (1), покажем что уравнение (11) имеет решение,
близкое к х0 (/). Заметим, что (11) имеет вид х = /(х). Введем
норму
13. || х ||== max sup |хД/)|.
i = 1, 2 0 t Т
Известно, что пространство о® непрерывных функций <р: [0, Т]->
->R2 с нормой (13) является банаховым пространством. Вычислим
число р из (4) и оценим (х).
14. ||/(хо) —Хо|| =
т
= max sup
« = 1, 2/е[0, Г]
о
| Ь | о
l4-a®m=₽,
где wM — постоянное число, зависящее от Т и резонансной
частоты а,
т
I f (х) || max sup | wi2 (/, т) 36x1 (т) | dx <
4=1,2 /е[о. г]о
31 b | max | хх (/) |2.
0^/^ т
Однако
max | Xi (0 ’ max | хХ0 (0 I + max | хх (/) — xi0 (/) | = а0 +1| х — х01|.
Таким образом,
15. \\f'(x)\\^3\b\wM[aQ + \\x-xQ\\\\
т. е. оценка имеет вид (2). Используя (14) и (15), выпишем усло-
вие (2) полностью, откуда следует, что число k <= [0, 1) таково, что
Г I & I а№>м I2
16. 3|Ь|^[ао + -(Г^у.^ <Л<1.
Тогда, если k, удовлетворяющее (16), существует, то существует
и периодическое решение х такое, что
I b I a*w лл
17.
где kQ — наибольшее из чисел, удовлетворяющих (16).
Очевидно, что нужное k существует в следующих предельных
случаях:
(I) Если числа а, а, со заданы (и, следовательно, aQ опреде-
ляется уравнением (9)) и число b достаточно мало, то неравенство
7. СУЩЕСТВОВАНИЕ ПЕРИОДИЧЕСКИХ РЕШЕНИЙ
171
(16) всегда выполняется почти Для всех k < 1. Другими словами,
если нелинейность слабая, то вблизи х0 обязательно существует
периодическое решение с периодом Т, удовлетворяющее оценке (17).
(II) При заданных й, а и со и достаточно малых а неравен-
ство (16) справедливо для некоторого &<1 Действительно, при
а—решение а0 уравнения (9) также стремится к нулю, а при
малых а0 число #<1, удовлетворяющее неравенству (16), всегда
существует. Поэтому и в данном случае при достаточно малой
амплитуде входного воздействия вблизи х0 обязательно существует
периодическое решение с периодом Т.
18. Комментарии.
(I) К сожалению, описанный метод неприменим к автономным
системам. Первая трудность заключается в отсутствии функции
возмущения, из-за чего невозможно сказать что-либо о периоде
периодического решения. Вторая трудность состоит в том, что даже
в тех случаях, когда период известен, в окрестности решения
уравнение, аналогичное (10), не является уравнением сжатия.
В самом деле, предположим, что уравнение
x = Ax+g(x),
где А е 1РЛХП, имеет периодическое решение х с периодом Т.
Тогда, как и раньше,
т
19. W(t, r)g[*(?)]dr.
о
Производная х также представляет собой периодическую функцию
с периодом Т и удовлетворяет уравнению
что легко установить дифференцированием уравнения относитель-
но X. Поэтому
г
20. х (/) = $ W (/, т) g' [х (т)] i (т) dx.
о
Следовательно, норма отображения
т
T)g' [x(r)]z(T)dT
о
не меньше 1. Таким образом, хотя (19) имеет вид х = /(х), но,
согласно (20), ||/'(*)11^1» т- е- функция f не является сжатием.
Для установления факта существования периодических решений
автономных систем применяются топологические методы.
(II) По сравнению с нашими предыдущими результатами усло-
вие сжатия является локальным, поэтому утверждение о сущест-
вовании и единственности периодических решений справедливо
только в шаре В[хв, 0/(1—£)].
172
ГЛ. 5. ПРИМЕНЕНИЕ ТЕОРЕМЫ О КОЭФФИЦИЕНТЕ РОСТА
8. КРИТЕРИЙ ПОПОВА
В этом разделе, используя теорему о малом коэффициенте
роста, мы докажем критерий Попова в упрощенной форме. В раз-
деле 6 главы 6 мы представим критерий Попова в более общем
виде. Здесь же мы лишь проиллюстрируем еще один случай
применения теоремы о малом коэффициенте роста.
1. Теорема. Рассмотрим стационарную систему с одним входом
и одним выходом, заданную уравнениями
2.
3.
— g %
е2 = <р (ej),
где функция ф: R-»-[R непрерывна и принадлежит сектору [О, Л],
geL1 и gEa/. Предполагается, что для любого Ui^L2 функ-
ции 6, и е-г принадлежат Ц. Если для некоторого q^O сущест-
вует 6>0 такое, что
1^6>0
4.
Re[(I + .’/со'g (/со)] 4-
Vco^O,
то еи 61, е2 е L2, если только их, е L2.
Доказательство. Изменим структуру системы, сохранив
величины сигналов ej и е2: в прямую ветвь перед нелинейностью ф
вставим элемент с передаточной функцией 1/(1 +qs), а в ветви
обратной связи изменим передаточную функцию на (1 4-<7s)g(s);
при этом входной сигнал Ui необходимо заменить на Ui + qiii.
Затем применим теорему о преобразовании контура, добавим
усилитель с коэффициентом усиления — (k/2) параллельно прямой
ветви и охватим ветвь обратной связи дополнительной обратной
связью с таким же усилителем.
Для того чтобы 61 и е2 не изменились, следует ввести компен-
сирующее воздействие (k/2)(ui + qili), как показано на рис. 5.2.
Применяя теорему о малом коэффициенте роста, мы будем поль-
зоваться /Анормами (Z <= L2).
8. КРИТЕРИЙ ПОПОВА
173
Докажем, что коэффициент усиления у (Hi) подсистемы Hi
не превосходит величины k/2. Выходной сигнал Hi равен уг =
= ф(е1)~-ky\i!2, а входное воздействие —= + Из рис. 5.2
видно, что для любого Т>0
IIУ1 Гт = | {ф Ох (/)] - 4 lei (О + Че\ (О]}2 di =
= f Ф[МО]{Ф 0i(0 —dt-
ъ'
- kq J ф [ех (/)] ё1 (/) 4- (4)21| ГЦ Гт-
О
Первый интеграл неположителен согласно секторному условию.
Обозначив через Ф первообразную функцию <р и полагая Ф (0) = 0,
получаем
IУ1 Гт < - 01 (Г)] + кдф [ех (0)] + )’ hi Гг^
<(4)2Ь1Гт + ^Ф[ех(0)],
где использовано свойство <р, вытекающее из секторного условия:
Ф (о) О для любых о е R. Таким образом,
8. У(ЯХ)^4-
Теперь докажем, что коэффициент усиления у(Я2) подсистемы Н2
меньше, чем 2/k. Пусть для простоты
h (/<о) = hr (/о) 4- jht (/о) = (14- qja) g (ja), ® <= R,
и
9. ₽(7®) = Лг(/®) + 4*
Тогда предположение (4) приобретает вид
10. 0(/w)2&6>O.
Коэффициент усиления у(Я2) определяется выражением
11. у(Я2) = sup
h (/ю)
14-4а(/®)
2 h (/со)
— , oup 2 ю 2 k -4-й(/ш) ₽(/«)- 4 +iht (io>)
b SUP - ®eR P0®)4-j 4-ihiU®)
174
ГЛ 5 ПРИМЕНЕНИЕ ТЕОРЕМЫ О КОЭФФИЦИЕНТЕ РОСТА
Учитывая (10), получаем (зависимость от со для простоты не ука-
зывается):
поэтому
13.
где
14.
»-т
+ А'
+ ihi
46
k
46
8= inf -j=----------------------------->0.
+ +[A, (/®)12
Возвращаясь к (11), находим
15. V(/72)= .
Из (8) и (15) ясно, что у (//J у (Я2) К1 — < 1, следова-
тельно, т]! = еj + qex е А2; /^-коэффициент усиления элемента с
передаточной функцией (1 4- qs)'1 равен 1, откуда || ех ||2 || rji I2 <00.
Следовательно, е19 ёг е L2. Согласно секторному условию, е2 =
= Ф (ех) е= Л2.
9. НЕУСТОЙЧИВОСТЬ
Практически все предыдущие разделы были посвящены полу-
чению условий устойчивости систем с обратной связью. В этом раз-
деле мы выведем условия, при которых заданная система явля-
ется неустойчивой. С математической точки зрения определить
достаточные условия неустойчивости гораздо сложнее, чем доста-
точные условия устойчивости. В последнем случае необходимо
показать, что под действием любых входных сигналов из некото-
рого класса система воспроизводит выходные сигналы, принад-
лежащие тому же классу. Поэтому для решения такой задачи
можно применять различные общие методы. При определении
условий неустойчивости нужно показать, что реакция системы
на некоторые входные воздействия из определенного класса не
принадлежит тому же классу. Это означает, что исследователь
имеет дело не с общими теоремами и их доказательством, а с
частными ситуациями. Последнее обстоятельство и является
основной трудностью при доказательстве теорем о неустойчивости
систем.
Здесь мы приведем два возможных толкования понятия не-
устойчивости и получим условия, обеспечивающие неустойчивость
9 НЕУСТОЙЧИВОСТЬ
175
каждого типа. В разделе 9.1 мы покажем, что при определенных
условиях входное воздействие системы, принадлежащее L2, вызы-
вает реакцию, не принадлежащую L2, и, кроме того, опишем
множество тех входных сигналов из L2, под действием которых
система не воспроизводит выходные сигналы из L2. В разделе 9.2
изучается случай, когда входной сигнал из L2 хотя и вызывает
появление на выходе сигнала, также принадлежащего L2, но опе-
ратор системы не является неантисипативным.
Рассмотрим систему с обратной связью, заданную уравнениями
!• #1 = U1 — /У2^2»
2. ^2 “^2 4“ ^1^1»
где и и2 —входные сигналы, а ег и е2 —сигналы ошибки. Выход-
ными сигналами системы являются уг — и £/2 = Кроме
того, здесь, как и в главе 3, предполагается, что функции ux, и2,
£Х, ^2» Уъ Уч принадлежат расширенному банахову простран-
ству Хе.
Предполагая для простоты, что ц2 55 0, объединим уравнения
(1) и (2) в одно:
3. ex = их — 77277хвх.
Определить понятие «неустойчивости» системы, заданной уравне-
нием (3), можно несколькими способами:
(i) При некотором их^.Х уравнение (3) не имеет решений,
принадлежащих Хе.
(ii) При некотором е X уравнение (3) имеет решение в Хе,
но не имеет решений в X.
(iii) При каждом Ui е X уравнение (3) имеет решение е X,
однако отношение между и ei не является неантисипативным.
Отметим, что мы не задавались целью перечислить все возмож-
ные способы определения неустойчивости и упомянули лишь
некоторые из них. Из приведенных видов неустойчивости случай
(i) имеет место при довольно слабых условиях (см. раздел 3.5).
Поэтому здесь рассматриваются условия, при которых система
неустойчива в смысле определения (ii) (раздел 9.1) и в смысле
определения (iii) (раздел 9.2).
9.1. Метод ортогонального разложения
В этом разделе изучается ситуация, в которой «ограниченное»
входное воздействие вызывает появление «неограниченного» сиг-
нала на выходе системы. Применение излагаемого ниже метода
вовсе не ограничено случаем /Лнеустойчивости, однако именно
в этом случае можно получить условия, которые легко прове-
ряются.
176
ГЛ. В. ПРИМЕНЕНИЕ ТЕОРЕМЫ О КОЭФФИЦИЕНТЕ РОСТА
Предлагаемый метод в общих чертах состоит в следующем.
Пусть задан неантисипативный оператор .G: Ц-+Ц- Предполо-
жим, что оператор G неустойчив в том смысле, что образ про-
странства L2 при отображении G не полностью содержится в L2.
Обозначим через М прообраз L2 при отображении G. Тогда М
является подпространством пространства L2, а при определенных
ограничениях, наложенных на G, даже замкнутым подпространст-
вом пространства ZA Рассматривая систему с обратной связью,
изображенную на рис. 3.1, где подсистема Н± определяется опе-
ратором G, мы покажем, что при выполнении условия малости
коэффициента роста реакция уг не принадлежит L2, если = О
и Ui s где через М1 обозначено ортогональное дополне-
ние М.
Начнем наши исследования с леммы о замкнутости М. В этом
разделе символ ||-|| используется для обозначения Л2-нормы.
4. Лемма. Пусть оператор G: линеен и неантипаси-
вен и М — подпространство пространства L2 — определено следую-
щим образом:
5. M-{xsL2: Gxg=L2}.
Тогда, если оператор G удовлетворяет условиям
6. V71 < оо , Зрг <оо: || (Gx)r|^ рт II * Иг Vx е= L2
и
7. 3^(G)<oo: \\Gx\\^yM(G)\\x\\ Vxs=M,
то М — замкнутое подпространство пространства L2.
8. Замечания.
(1) Согласно условию (6) отображение GT' А2 [О, T]->L2[0, Т]
вида
9. Grf = (Gx)r VfeL2[0, Т],
где х —произвольный элемент Ц такой, что xT = f, непрерывно.
Отметим, однако, что не предполагается ограниченности множе-
ства {рг}.
(2) Условие (7) означает, что на множестве М оператор G
имеет конечный коэффициент рогга.
Доказательство. Рассмотрим последовательность {хг} из
М, сходящуюся к хое£2. Покажем, что хоеА4. По условию,
Gxi е L2 для любых 1 £ Z+ и, согласно (7), {Gxz} — последователь-
ность Коши в L2. Поскольку пространство А2 полно, то {Gxz}
сходится к некоторому элементу из L2, который обозначим через
у. Принимая во внимание (6), заключаем, что для каждого Т <оо
последовательность {[Gxjr} сходится к [Gxo]r. Но тогда [Gx0]r =
= ут при любых Т <оо , т. е. Gx0 = f/, и, следовательно, Gx0 е L2.
Из определения множества М вытекает, что х0 е М.
9. НЕУСТОЙЧИВОСТЬ Р7
Следующая теорема о неустойчивости по форме близка к тео-
реме (3.2.1).
10. Теорема. Рассмотрим систему с обратной связью, изобра-
женную на рис. 3.1, где и Н2 отображают Ц в самое себя.
Допустим, что для каждой пары и2 из ЦхЦ существует
соответствующая пара е2 из Цх1Л, удовлетворяющая системе
уравнений:
Па. е1=и1 — Н2е2,
11b. e2 = u2 —
Предположим, что существуют конечные числа у(Я2) и 0 такие,
что
12. f (Н2х)т !| ^ у (Д2) |Ы + ₽ VxeZA
Пусть, кроме того, оператор Hx — G\L*-+L*e линеен, неантисипа-
тивен, удовлетворяет условиям (6) и (7), а подпространство Л1,
заданное условием (5), является собственным подмножеством ТА
Тогда
(i) если Yjj(G) у(Н2) 1 и 0 = 0, то ух ф L2, когда u2ss0,
и иг =/=0 (Л41 — ортогональное дополнение Л4);
(ii) если ул! (G) у (Н2) < 1, то для каждого u2sL2 существу-
ет соответствующее постоянное число m (||и2||) такое, что ухфЪ\
когда е М1 и |ui|| > m (||и2||).
Доказательство. Согласно ограничениям, наложенным
на оператор Нъ множество М представляет собой замкнутое
подпространство пространства ТА Поскольку М — собственное
подмножество Л2, его ортогональное дополнение М1 — непустое
подпространство L2.
Сначала рассмотрим случай, когда ум (G)y (Т/2) 1, 0 = 0 и
и2 = 0. Доказательство проведем методом от противного, предпо-
лагая, что «1 =# О’, «1 е М1 и ух = Gex е L2. Тогда е М и
13. y^Ux-ex.
Так как ux=#0, ux е М1 и то (их |ех) =0 и, следовательно,
в. b2M«il2+IM2>hP.
С другой стороны, Уч = Н2Нхех. откуда
15. 11^|1^УШУл1(С)||е1||^|е11
что противоречит (14). Поэтому ух ТА
Пусть теперь у{H2)yM(G) — k<. 1. И в этом случае доказа-
тельство ведется от противного в предположении, что Ui=/=0,
и е L2. С учетом (12) из (14) получаем:
16. \\у2\? = ^их? + 1ех^^{у(Н2)Цух\\ + \\и21] +0}2^
W (tf2)[WG)kill+M + P}2 =
=^к1112+2й[Т(//2)|«2||+3]к111+Ь(^)11«2Л+РГ =
= ^|<М*4-2Лс II «-xl+Л
178
ГЛ. 5. ПРИМЕНЕНИЕ ТЕОРЕМЫ О КОЭФФИЦИЕНТЕ РОСТА
где
П. с = y(772) ||и2|| + р.
Представим неравенство (16) в ином виде:
18. ||и1||2^-(1-^)||е1||2 + 2^Ь1|| + ^
При фиксированном u2^L2 и постоянных k и с можно показать,
что наибольшее значение правой части (18) равно f2/(l —&2).
Поэтому, если || ux || >с2/ (1 — k2) = т (|| и21|), то неравенство (18)
никогда не выполняется. Полученное противоречие свидетельству-
ет о том, что уг L2.
Мы завершим этот раздел критерием неустойчивости, сход-
ным по форме с круговым критерием (2.10).
19. Теорема. Рассмотрим систему с обратной связью, изобра-
женную на рис. 3.1, где ux, u2, ех, e2i Уъ Уъ' R+~>R. Подсистема
Нг задается уравнением
20. (Я1е1)(0 = (^*е1)(0,
где функция g-(-) преобразуема по Лапласу и g(s) имеет вид
k mt
причем gb^L1, Reр,->0 при i=l, 2, k, fyEC при всех
i, /. Подсистема Я2 задается уравнением
22. (ад(0 = <р[е2(0, Л,
где функция <p: Rx|R+->|R непрерывна по первому аргументу и
регулярна по второму и
23. ф принадлежит сектору [а, Р], 0>О.
Предположим, что на всех компактных интервалах I cz IR+
функция ст •—*ф(о, t), где t постоянно на каждом интервале I,
имеет конечный коэффициент роста по приращениям (т. е. ф (ст, t)
удовлетворяет условию Липшица на R). Пусть g-=(a-j-P)/2,
p = (a —Р)/2, причем |=#=0. Предположим также, что для каж-
дой пары («!, м2) из ЦхЦ существует единственная пара (elt е2)
из ЦхЦ, удовлетворяющая системе уравнений (11). Тогда систе-
ма с обратной связью /Анеустойчива, если диаграмма Найквиста
функции g (/со) удовлетворяет одному из следующих условий:
(а) если 0<а<р, то диаграмма Найквиста функции g не
должна пересекать диск D[—1/a, —1/0], но окружает его в на-
правлении против часовой стрелки меньше, чем пр раз, где пр—•
число полюсов g (•), лежащих в правой полуплоскости;
(Ь) если 0 = а<р, то пр>0 и диаграмма функции g должна
лежать в замкнутой части комплексной плоскости (ze®: Rez^
9. НЕУСТОЙЧИВОСТЬ
179
(с) если а<0<р, то пр>0 и диаграмма Найквиста функции
g должна лежать внутри диска D[—1/а, — 1/0].
Доказательство. Теорема доказывается с помощью тео-
ремы о преобразовании контура. Определим отображения
L'e—^LJe'
24. (Я15е1)(/) = (^*е1)(0,
26. (Я25е2) (0 = <р [е2 (/), /] - 1ег (/) = [е2 (0, 0.
Покажем, что условия теоремы (10) выполняются, если Н± и //2
заменить в них на и Н^- Поскольку отображение <р^ принад-
лежит сектору [—р, р], отображение удовлетворяет неравен-
ству (12), где у(//2|) = р и р = 0. Из условий, наложенных на
диаграмму Найквиста функции g (/со), следует, что g^(/co) ограни-
чена при о) е R, но имеет в открытой правой полуплоскости по
меньшей мере один полюс. Легко проверить, что отображение Яц
удовлетворяет условию (6), так как g^(-)^Ue.
Нам остается проверить справедливость (7). Очевидно, что
в исследуемом случае подпространство М состоит из функций,
принадлежащих Л2, нулями изображений по Лапласу которых
являются полюса g^(s\ Допустим, /'(•)е/И; тогда функция g^(s)
аналитична при Res>0 и g^(](n)f (/со) е L2(R). Кроме того,
используя равенство Парсеваля, получаем, что для всех f^M
27. ||&*Л = 2^Ш-)Й-)11^
< sup | ^ (/со)| ~ ||/ (•) || = sup |gz (/©) 11| f (•) ||.
Таким образом, удовлетвор ет условию (7), где
28. Ym(G) = sup |gU/®)l-
Справедливость теоремы следует из теоремы (10), поскольку, со-
гласно круговому критерию, для диаграммы Найквиста функции
д(/со) (см. теорему (2.10))
(G0 У (^20 = SUP I Si (/®) IР < 1 •
©G= R
Другой подход к вопросу о L2-неустойчивости, основанный на
применении метода ортогонального разложения, излагается в главе 6
(раздел 6.12).
9.2. Антисипативные операторы
В этом разделе исследуется неустойчивость особого вида,
а именно, случай, когда «ограниченное» входное воздействие хотя
и вызывает появление «ограниченного» выходного сигнала, однако
180
ГЛ. 5. ПРИМЕНЕНИЕ ТЕОРЕМЫ О КОЭФФИЦИЕНТЕ РОСТА
отображение, определяющее связь входного и выходного сигна-
лов, не является неантисипативным.
Мы сначала докажем теорему общего вида, а затем исполь-
зуем ее для получения условий неустойчивости.
29. Теорема. Пусть SS — банахова алгебра с единицей I, a ай?+ —
подалгебра алгебры «$?, содержащая /, т. е. если хеа®+ и г/е
то xy^ffi и ух^'^. Пусть х, у^&+ и $ —ограни-
ченное связное подмножество поля С (или R). Предположим, что
для каждого ае$ элемент х + ау обратим, т. е. (х + ау)-1 е
и множество всех таких обратных элементов ограничено, т. е.
существует конечное число т такое, что
30. | (х Ц- он/)-11| т <Z оо Vа е 8.
Тогда (x-f-ay)-1 епри любых aeS в том и только том слу-
чае, когда (х + ay)-1 е <^+ для некоторого а *= 8.
Док аз ате л ьство.
Необходимость. Очевидно.
Достаточность. Утверждение справедливо при у = 0; поэтому
предположим, что у=#=0 и (х + аоу)-1 е <^Э+, где аое$. Прежде
всего заметим, что если (х + ау)-1 еи |а — а'|<
< (| УI •/и)-1, то элемент (х + а'у)-1 существует и принадлежит <^+
независимо от того, принадлежит ли $ число а'. Этот факт сле-
дует из того, что
х + а'у = хay + (а'- а) у = [7 + (а'- а) у (х + ay)-1] (х+ay)
и из принципа сжимающих отображений для банаховых алгебр.
Пусть (х + aoy)-1 —элемент, принадлежащий <^+ по условию;
выберем число а из $ произвольным образом. Поскольку мно-
жество 8 связно, существует конечная последовательность alt
Оз, ..., адг+1 = а такая, что |az — az+11 <(||у [• т)'1 при i = 0, 1, ...
..., N. Из | ax — а01 <Z (| у | • т)-1 и (х 4* «of/)-1 В+ следует, что
(x-j-Oiy)-1е<^+; так как |оз — ах|<(||у|• т)-1 и (x-j-aiy)-1 е<^+,
то (х + осзу)-1 е е®+. Повторив это рассуждение N раз, мы полу-
чим, что (х-|-аЛг+1у)-1 = (х+ау)-1 е<^+. Теорема доказана, если
учесть, что а выбрано произвольным образом.
31. Замечание. Основная идея доказательства состоит в сле-
дующем: задавшись элементом (x-j-aoy)-1, принадлежащим <з5?+,
мы можем показать, что элемент (хЧ-аху)-1 также принадлежит
<30* при достаточном малом |ах — а01. Предположение (30) об огра-
ниченности множества обратных элементов (хЧ-ay)-1 фактически
означает, что верхняя оценка для |ax —а0| не зависит от а0.
Поэтому при условии (х + аоу)"1 е для того, чтобы показать,
что (х + «У)-1 е ^+, если величина | a — a01 превосходит указан-
ную верхнюю оценку, мы строим «цепочку» чисел ах, аз,..., аЛЧх,
принадлежащих f, такую, что |at—сч+il достаточно мало.
9. НЕУСТОЙЧИВОСТЬ
181
Упражнение 1. Пусть в дополнение к условиям теоремы (29) (хЧ-аог/)-1 е
€= о®+. Показать, что (х-[-ау)-1 е о®+, если
32. inf ' а-а'i
Упражнение 2. Доказать следующее усиление теоремы (29). Пусть о® —
банахова алгебра с единицей /; о®4" — подалгебра, содержащая /; х, у s о®1-.
Обозначим через {«/}, где / GE J, конечную или счетную совокупность точек
из С (или R) такую, что
(i) (x + a/f/)-1 е о®+
00 + V/eJ;
(iii) sup inf ar —a/|^6;
/eJ#/
(iv)
Тогда, если (x + a/t/)"1 e о®4' при некотором j(=J, то (x + ay)”1 e <^Э+, как
только
33. inf 1 a — a,- j < (| у !| • /и)"1.
/е J
Теперь мы проиллюстрируем, насколько важны полученные
выше результаты для решения вопросов устойчивости.
34. Утверждение. Пусть l^p^oo; обозначим через & (Lp)
множество непрерывных линейных операторов, отображающих Lp
в самое себя, и через <^+ (Lp) — подмножество множества ^3(Lp).
состоящее из всех неантисипативных операторов, принадлежащих
<£8(Ьр). Тогда o%(Lp) является банаховой алгеброй с единицей,
а (Lp) — подалгеброй алгебры <^(ЛР), причем q%+(Lp) содер-
жит единицу.
Применим теорему о малом коэффициенте роста для полу-
чения условий неустойчивости в смысле определения (iii).
35. Теорема. Рассмотрим систему, заданную уравнениями (1)
и (2). Предположим, что Z7X и Н2 являются продолжением на Хе
непрерывных линейных отображений, заданных на X (сужение
/71 и /72 на X мы будем также обозначать через /7Х и ZZ2). Пусть
существует непрерывное линейное отображение К, заданное на
X. которое может быть продолжено на Хе, такое, что оператор
(Z4-K/71)-1 определен на Хе и непрерывен на X. Тогда, если
36. ||#X(Z4-KZ7X)“1M#2 —К|| = р< 1,
то
(i) оператор (7 + /72/71)-1 определен на Хе и непрерывен на Х\
(ii) оператор (I неантисипативен тогда и только
тогда, когда неантисипативен оператор (Z + KHx)-1',
(iii) система уравнений (1) и (2) имеет единственное решение
(ех, е2), где
37а. ex = (Z -j- (их — ZZ2u2),
37b. e2 = (Z Z7х/72)—1 (u2 4“ HxUi).
182
ГЛ. 5 ПРИМЕНЕНИЕ ТЕОРЕМЫ О КОЭФФИЦИЕНТЕ РОСТА
Комментарий. Поскольку Нг и Н2 линейны, е2 можно предста-
вить в следующем виде:
38. ^2= и2 Н1 (Z 4“ Н2Н1)-1 (Ui — Н2и2).
Доказательство. Утверждения (i) и (iii) доказываются
почти так же, как теорема о малом коэффициенте роста. Для до-
казательства (ii) рассмотрим совокупность элементов <г®(х),
заданных соотношением
39. Fа = I КН\ 4- «(#2 — ^С)» & [0> 1 ]•
Поскольку оператор (I + KHiT1 определен, то согласно условию
(36) при всех осе[0, 1] оператор Fa' корректно определен на (х).
Кроме того, множество таких обратных элементов ограничено,
так как
4о.
Поэтому в силу теоремы (29) оператор F^ неантисипативен при
всех ае[0, 1] тогда и только тогда, когда F^ неантисипативен
при некотором зе[0, 1]. В частности, оператор Fa{ = (I 4-#2#i)"1
является неантисипативным в том и только том случае, когда
Го1 = (/ 4- КНг)-1 — неантисипативный оператор.
Вернемся к системам с обратной связью, описываемым операто-
рами свертки, и приведем некоторые результаты, не претендуя
на общность, чтобы не усложнять изложения.
41. Определение. Множество , по определению, состоит из
всех обобщенных функций f(-) вила
42. f(t) = £ /16 (/-/<) +/а(< ,
I = — оо
где tit fi^R, fa. IR->IR и
43. jp Л'<оо, f |fo(/)|d/<oo.
i =—co —oo
Множество <27^2 превращается в линейное пространство очевидным
образом. Если определить норму
44.
Ик= S М+ Г \fa(f)\di,
I = — ОО —00
а в качестве произведения элементов / и g изв^8 рассматривать
их свертку, то превратится в банахову алгебру. можно
также рассматривать как двустороннюю банахову алгебру orf,
определенную в Приложении D. Дейвтвительно, если определить
9. НЕУСТОЙЧИВОСТЬ
183
orf в виде
45. ©^ = {f(.)e=©^2: f(0 = 0 V/<0}
то ©^ — подалгебра алгебры ©^2.
Обозначим через ©/2 множество изображений по Лапласу
всех элементов из ©^2. Условия, при которых элемент из ©т/2 обра-
тим, устанавливаются следующей теоремой.
46. Теорема. Пусть /е©^2. Тогда 1//е©^2 в том и только
том случае, когда
47. inf |/($)|>0.
Res = 0
Пусть Тогда 1/^е©^2 в том и только том случае, когда
выполняется условие (47), и тогда и только тогда, когда
48. inf |/(s)j>0.
Re s 0
Рассмотрим еще одну теорему об устойчивости систем с обрат-
ной связью.
49. Теорема. Пусть G, F^e^2xn. Тогда Н = G (I -\-FGy1 <=
е Хл в том и только том случае, когда
50. inf |det[/ + F(s)G(s)]|>0.
Re s = 0
Теперь мы можем перейти к получению условий неустойчи-
вости.
51. Теорема. Рассмотрим многоконтурную систему с обратной
связью, изображенную на рис. 3.1. Пусть подсистема Нг опреде-
ляется уравнением
52. f/i(O = (G*ei)(O»
где G е <г^пхп, а подсистема задана в виде
53. М0=ф[М0» Л»
где функция <р: R^xR-^R" непрерывна по первому аргументу и
регулярна по второму. Предположим, что е2, yi, y2^Lne(R),
при условии, что иг, u2^Ln(!R). Тогда если существуют матрица
К s Клхя и действительные постоянные числа у и ₽ (₽ = 0 при
р<оо) такие, что
54. |<р(о, I) — /Са|^у|ст| + Р VoeR", V/eR+,
55. inf | det [/ + KG (s)] | > 0,
Re s == 0
56.
где
57. ^ = G(/ + W1.
184
ГЛ 5 ПРИМЕНЕНИЕ ТЕОРЕМЫ О КОЭФФИЦИЕНТЕ РОСТА
ТО
58. U1, и2 е Ln (IR) => еъ е2, ylt i/2e^(R),
и, кроме того, отображение (иъ е2) неантисипативно
тогда и только тогда, когда
59. inf | det [I + KG ($)] | > 0.
Re s 0
Справедливость теоремы следует из теоремы (35).
60. Следствие. Если среди условий теоремы (51) условие (56)
заменить на
61. sup |Як(/(0)| у<1,
то теорема (51) останется верна для р = 2.
62. Теорема. Рассмотрим одноконтурную систему с обратной
связью, изображенную на рис. 3.1, где подсистема определена
уравнением (t) = (g* е}) (t), где а подсистема H2
имеет вид #г(0 = <р[М0» Л» причем ф принадлежит сектору
[a. PL где 0<а<р. Обозначим через D[—1/а, —1/Р] диск в С,
диаметром которого является отрезок, соединяющий точки —1/а+/0
и —1/Р+/0. Тогда если диаграмма Найквиста функции g (/со)
не пересекает диск D[—1/а, —1/Р] и окружает его в направле-
нии против часовой стрелки хотя бы один раз, то
иъ и2 g= L2 (R) еъ е2, у19 у2 g= L2 (R)
и отображение (ub и2)(ех, е2) не является неантисипативным.
БИБЛИОГРАФИЧЕСКИЙ КОММЕНТАРИЙ
Первые формулировки теоремы о малом коэффициенте роста
и кругового критерия принадлежат Сандбергу [75] и Цеймсу [112],
использовавшим метод экспоненциального взвешивания [79] и [111].
Этот же метод применялся и в работе [5]. Теоремы об устойчи-
вости, и в том числе круговой критерий, основанные на методах
Ляпунова, доказаны Броккеттом [10, 11] и Нарендрой и Голдуи-
ном [62]. Теорема о линейных системах с медленно изменяющимися
параметрами является обобщением идеи Сандберга [83], а теорема
о существовании периодических решений заимствована из работ
Хольцмана [52, 54]. Пример нелинейной системы взят из [79].
Такеда и Берген [90] впервые предложили метод ортогонального
разложения для исследования ^-неустойчивости; системы, не
являющиеся неантисипативными, рассмотрены Виллемсом [99].
Неустойчивость систем также изучалась Броккеттом [14], приме-
нявшим методы Ляпунова, и Девисом [24, 25], использовавшим
теорию операторов Фредгольма. И, наконец, применение теорем
о малом коэффициенте роста к системам с широтно-импульсной
модуляцией можно найти в работе [86].
Глава 6
ПАССИВНОСТЬ
0. ВВЕДЕНИЕ
В этой главе рассматривается понятие пассивности, играющее
существенную роль в теории цепей и вообще в физике. В раз-
деле 1 для пояснения формализма приводится пример простейшей
цепи. Математические свойства скалярного произведения пред-
ставлены в разделе 2. Затем, как и в главе 3, следует раздел,
посвященный описанию основных положений. Этот абстрактный
раздел позволяет выявить различные задачи, являющиеся частными
случаями общей постановки. Главная особенность наших исследо-
ваний состоит в том, что они будут вестись в гильбертовом про-
странстве. В разделе 4 вводится определение пассивного оператора
и представлены многочисленные примеры таких операторов, часто
используемые в дальнейшем. Читателю нет необходимости подробно
изучать примеры и выполнять каждое упражнение, поскольку
при последующем их использовании мы будем давать соответст-
вующие разъяснения. Теоремы о пассивности, изложенные в раз-
деле 5, соответствуют теореме о малом коэффициенте роста, рас-
смотренной в главе 3. Именно эти теоремы и составляют основные
результаты настоящей главы. В разделах 6 и 7 приводится кри-
терий Попова для одно- и многоконтурных систем, для непрерыв-
ного и дискретного случаев. Предметом исследований раздела 8
является критерий логарифмической вариации, интересная особен-
ность которого заключается в том, что при достаточно малой
средней скорости изменения коэффициента усиления ветви обратной
связи нестационарная система устойчива, если устойчива соответ-
ствующая система с «замороженными» параметрами. Этот результат
завершает исследования, начатые в разделе 5 главы 5. Метод
антисипативных усилителей и его применение описаны в разделе 9:
здесь изложена общая схема метода и два основных способа
факторизации. В следующем разделе при довольно общих усло-
виях показано, что теоремы о пассивности и о малом коэффици-
енте роста эквивалентны; иначе говоря, здесь доказывается, что
если факт устойчивости системы с обратной связью можно уста-
новить с помощью теоремы о пассивности, то при весьма общих
условиях эту систему можно преобразовать к эквивалентной ей
системе, устойчивость которой устанавливается теоремой о малом
коэффициенте роста, и наоборот. Задача обратимости оператора
вида 1-\-Н является одной из фундаментальных при изучении
186
ГЛ. 6. ПАССИВНОСТЬ
систем с обратной связью. В разделе 11 понятие пассивности
применяется для получения достаточных условий того, что I -\-Н—
биекция. Последний раздел содержит общую теорему неустойчи-
вости, основанную на понятии пассивности. Эта теорема затем
используется для построения критерия неустойчивости, анало-
гичного по форме критерию Попова.
1. ОБОСНОВАНИЕ ИЗ ТЕОРИИ ЦЕПЕЙ
Рассмотрим двухполюсник, на входе которого действует напря-
жение и(-) и протекает ток /(•). Мощность, подводимая к двух-
полюснику в момент /, равна v (t)i(t) (рис. 6.1). Если через
S (10) обозначить энергию, запасенную в двухполюснике к мо-
менту /0, то естественно называть двухпо-
люсник пассивным в том и только том
случае, когда
t
1. ^(tQ) + \v(t)i(t)dt^Q Vy(-), /(•),
to
Такое определение выглядит естественным,
так как значение интеграла равно величине
энергии, подведенной к двухполюснику на интервале времени [/0, /].
В более общем случае n-полюсник ©Ж* можно рассматривать
как отношение, заданное на множестве /х/, где & = {f: [R
т. е. на множестве всех пар (v(-), j(‘))G2^x/, являющихся
парами допустимых входных напряжений и токов. Полагая, что
к началу функционирования n-полюсника при / = — оо в нем
нет запаса энергии, будем называть ©/" пассивным в том и только
том случае, когда
t
2. Re V(v, 0е/х7( V/eR
— 00
(здесь звездочкой * обозначен комплексно сопряженный транспо-
нированный вектор). Конечно, в данном случае комплексно сопря-
женный вектор у* совпадает с вектором у, но если напряжения
и токи представлены в комплексной форме, справедлива только
такая запись.
Одним из первых связь пассивности и устойчивости исследовал
Юла, изучавший линейный случай. Его метод, однако, может
быть распространен и на нелинейные системы. Мы сформулируем
его в виде теоремы.
3. Теорема. Пусть (возможно, нелинейный) n-полюсник @/Г
обладает следующим свойством: о, i е L2ne (R) для любых пар
(и, Г) . Предположим, что система имеет вид, приведенный
на рис. 6.1, и для любого входного воздействия e^L2ne(R) реак-
9
2. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ
187
ция и, i принадлежит L2ne. Тогда если п-полюсник @7^ пассивен,
то из ее Ln вытекает, что || v ||2 || е ||2 и ||/||2^ к Иг-
Доказательств о. Пусть, по определению,
<v|i>r= S v(t)*i(t)dt.
— оо
Тогда предположение о пассивности эквивалентно неравенству
4. (у |/>г^0 V(v, OeaFxoF, V7\
Согласно закону Кирхгофа для напряжений e = p-}-i, и так как
ее£2, то
5. оо > (е | е) (е I е}т = {v + i | v + i)T =
= I и)т + (v I 0r + 0* I 0r + 0’ I ОгЭ5 (у I ^)r + (i I Or»
где на последнем этапе использовано свойство пассивности. Тео-
рема доказана, поскольку неравенство (5), будучи справедливым
для всех Т, выполняется и при Т ->оо.
6. Комментарий. Мы обязаны ввести предположение, что для лю-
бого е е L2 существует по меньшей мере один выходной сигнал.
Только после этого можно использовать пассивность для доказа-
тельства устойчивости системы. Однако никаких предположений
и выводов о единственности и/или непрерывной зависимости ре-
шений сделать нельзя.
2. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ
Любая функция, ниже обозначаемая символом отобра-
жающая в ©, где — линейное пространство над по-
лем ©, называется скалярным произведением в том и только том
случае, когда она удовлетворяет следующим аксиомам (здесь
знак * обозначает операцию комплексного сопряжения):
si. = + <%:/>,
SI1.
SIII.
SIV.
<Х| У> = <£!*>*»
<х| Ку) = К(х\у),
(X I х) > 0 <zz> X =^= 0
Vx, у. у' Vie©,
где 0 —нулевой вектор в пространстве
Упражнение 1. Доказать следующие следствия аксиом скалярного произ-
ведения:
(а) Функция х ।—► {х | х)1/2 является нормой в пространстве <а%^. Ниже
она будет обозначаться через !i х ||, так что, по определению,
1. l!x'2=(x x}
Норма и скалярное произведение связаны неравенством (Вварца:
2. |<х( У) Vx,
188
ГЛ. 6 ПАССИВНОСТЬ
причем равенство имеет место в том и только том случае, когда х и у линейно
зависимы, либо равны нулю в отдельности или одновременно.
3. (Ь) {х+х' у) = {х \у) + {х’\у\,
4. (с) (Хх , = (х 1у)
5. Комментарии.
(а) При заданном х е отображение у * (х | у) является
линейным функционалом над е%^;
(Ь) В большинстве приложений мы будем полагать, что —
линейное пространство над. полем R и скалярное произведение
(• | •) представляет собой действительную функцию. Тогда, в силу
аксиомы SII, (х | у) = (у | х) для всех х, у^&С. Кроме того,
функция, отображающая упорядоченную пару (х, у)
в (х| у) е R, является билинейной, т. е. для любых х е ©2Г функ-
ция у*—*-(х\у) линейна, а для любых линейна функция
*-*<*!«/>•
6. Примеры.
(I) Пусть х, 1/еР или (С, тогда (х|у) = х*у, т. е. (х\у) равно
произведению комплексно сопряженного числа х* и числа у.
(II) Пусть х, уеС", т. е. х = (5ь ..... g„) и у =
п
= Oh. П2.....Пл), тогда (х I у} = 2] W
г = 1
(III) Пусть х, у (R+->-[P, причем х, у^1У, тогда
<x|i/) = f x(/)t/(O^>
о
(Если х и у — комплексные функции, то подынтегральное выра-
жение заменяется на х* (/) у (/).)
(IV) Пусть х, у. К+->-([Л причем х, у^Ы, тогда
о
где х* — комплексно сопряженная транспонированная к х вектор-
функция.
(V) В приведенных примерах мы можем ввести весовой коэф-
фициент и заменить подынтегральные выражения на w (t) х* (t) у (t),
где w (•) — ограниченная и непрерывная функция, причем w(t)>
>0 для всех t. Обычно, w (t) = е-20“' (а>0).
(VI) Пусть х, уеГп, причем x(i) = [xi(i), xa(i), .... хп(i)],
У(О = [Л(О. МО. •••. М все хДО. МО (&= 1, 2, .... n)
принадлежат R; тогда
со п
<х | У) = S S Xk (i) yk (i).
4=0/2=1
3. ОБЩИЕ ПОЛОЖЕНИЯ
189
3. ОБЩИЕ ПОЛОЖЕНИЯ
Пусть — множество моментов времени. (Обычно — R+,
R, Z или Z+ = {0, 1, 2, ...}.) Пусть ^ — линейное пространство
со скалярным произведением (-|-). Пусть aF —класс функций х:
eF -> V, скалярное произведение (• | •) определено на подмноже-
стве множества sF. Если <£Г = R+, и = R" и через (•» •) обозна-
чено обычное скалярное произведение в R", то
1.
И при eF" = Z+
2.
= $ (х(/), y(t))dt,
О
<х\у) = ^ (x(i), «/(О)-
1=0
Как и раньше, для любого TesF через Рт будем обозначать
линейный оператор, определенный на множестве aF так, что для
любых хе/, TeeF"
3.
( x(t)
(Рг*)(0=| 0
при
при
t^T, t,
t>T,
где 0 —нулевой вектор пространства V. Очевидно, что Р) = РТ,
т. е. Рт — проектор при каждом Т. Мы часто будем использовать
обозначение хт = Ртх- Проектор Рт определяет линейное подпро-
странство пространства «F, а именно,
PraF = {g е | g = PTf для некоторой функции f е sF} =
= {g<=aF|g(0 = 9 при t>T}.
Определим множество е%~е:
5. = {х е eF | VT е sF", ||хгр = <хг|хт) <оо},
представляющее собой пространство всех функций х, для которых
при всех Т ecF норма хт конечна. Из неравенства Шварца сле-
дует, что | (хр | ут) | < оо для любых Т е sF", если х, у е е%?е. Опре-
делим множество аЙГ:
6. &Г = {хе/ ||х||2 = (х|х)<оо}.
Потребуем, чтобы скалярное произведение удовлетворяло следую-
щим условиям:
8. HI. Для всех хе<=5Ге функция Т->-|хг| монотонно возра-
стает.
9. НИ. Для всех xGaT lim |хг| = |х|.
Г—оо
10. НШ. Для всех х, в любых Те/"
<ХТ I Ут) = <хг I у) = <х I Ут) — <Х I у)т-
Отметим, что скалярное произведение, определенное в каждом из
примеров раздела 2, удовлетворяет всем перечисленным*условиям.
190
ГЛ. 6. ПАССИВНОСТЬ
4. ПАССИВНЫЕ СИСТЕМЫ: ОПРЕДЕЛЕНИЕ И ПРИМЕРЫ
В этом разделе мы используем рассмотренные выше положе-
ния для определения понятия пассивной системы. Здесь же будут
приведены некоторые примеры важнейших пассивных систем.
Пусть Н: Назовем оператор Н пассивным в том
и только том случае, когда существует постоянное число 0 такое,
что
1. <Ях|х>г^0 Vxe=^Te,
Назовем оператор Н: -> оЗГе строго пассивным в том и только
том случае, когда существуют 6>0 и 0 такие, что
2. (tfx|x)r^S||xr||2 + 0 Vxge^,
Назовем оператор Н: пассивным по приращениям
в том и только том случае, когда
3. (Ях — Нх' |х — х')г^0 Vx, х'е <2%^, VTeeT.
Назовем оператор Н: строго пассивным по прираще-
ниям в том и только том случае, когда существует 6>0 такое,
что
4. {Нх — Нх' |х-“х')г^6||х — х'||т Vx, х'е^, VT ееГ'.
5. Комментарии.
(а) Если оператор Н линеен, то 0 в (1) и (2) можно выбрать
равным нулю. Гораздо важнее, что если Н — линейный опера-
тор, то
(i) Н пассивен тогда и только тогда, когда он пассивен по
приращениям;
(ii) Н строго пассивен тогда и только тогда, когда он строго
пассивен по приращениям.
(Ь) Очень важно различать понятия пассивности, строгой пас-
сивности и т. д., определенные на расширенном пространстве
и более общее понятие положительной определенности. В раз-
деле 9 мы введем понятие положительно определенного опера-
тора с помощью условия
<#x|x)^0 Vxe=^T,
где Н\ -xSF. Если Н — неантисипативный оператор, то эти
два понятия не отличаются друг от друга (см. лемму (9.2)),
в противном случае различие поступает со всей ясностью (упраж-
нение 2, раздел 9).
В оставшейся части раздела мы рассмотрим в примерах и
упражнениях различные классы пассивных систем.
6. Пример 1. Пусть оператор Н-. Ц-+Ц определен соотно-
шением
7. Ни = h*u9 где /i е и и е Ц.
4. ПАССИВНЫЕ СИСТЕМЫ: ОПРЕДЕЛЕНИЕ И ПРИМЕРЫ
191
Поскольку h е <2^, оператор Н неантисипативен. Мы утверждаем,
что
8. // — пассивный оператор тогда и только тогда, когда
Re [h (/со)] 0 при любых со е [R;
9. Я —строго пассивный оператор тогда и только тогда, когда
при некотором 6>0
Re [h (/со)] S для любых со s R.
Доказательство основано на следующей цепочке равенств*
оо
(и\Н*и)т = (ит\11*и)= {uT\h*uT') = £ Re[4(/co)] |йг(/со) |2d(o,
—оо
где последовательно использованы аксиома (3.10), свойство не-
антисипативности оператора Я и теорема Парсеваля. Утвержде-
ния (8) и (9) выводятся из полученного равенства с учетом того,
что
00
— ОО
Пример 2. Пусть Н — (пхп)-матрица с элементами из orf и
// — оператор, определенный соотношением Hu = h*u при всех
u^Lne- Поэтому //: Lne-^Uie. Утверждается, что
10. //—пассивный оператор тогда и только тогда, когда эрми-
това матрица Й (]<») +Н* (/со) положительно полуопределена при
любых со е IR;
11. //—строго пассивный оператор тогда и только тогда,
когда при некотором 6>0
A/min [Н (j(&) + Н* (/©)] 6 > О Vco О,
т. е. для любых со е R наименьшее характеристическое число
эрмитовой матрицы Й + (/со) не меньше 6.
Упражнение 1. Подробно доказать утверждения (10) и (11).
Упражнение 2 (дискретный случай). Пусть оператор Н: определен
соотношением Hu=h*u> где /i=(/i0( hlt h2, .JeZ1 Пусть u e Z*. Показать,
что H—пассивный (строго пассивный) оператор тогда и только тогда когда
Re [h (е/0)] 0 (для некоторого 6 > 0 Re [h (еу0)] 6) при всех 0 е [0, 2л].
Упражнение 3 'дискретный случай). Пусть оператор И: ^пе-^^пе определен
соотношением Hu=H*u, где Hv Н2, ...}(= п. Пусть и е 11пе
Показать, что А/—пассивный (строго пассивный) оператор тогда и только
тогда, когда при всех 0 е [0, 2л] эрмитова матрица Н (еуи) + Я* (ejQ) положи-
тельно полуопределена (Zmin [Н (е/0)4-Я* (еу0)] ^6 при некотором 6>0, со-
ответственно)
Пример 3. Рассмотрим систему, евязь входного и выходного
сигналов которой задается соотношением у —Ни, где и, у: R+->
192
ГЛ. 6. ПАССИВНОСТЬ
->КЛ. Уравнениями системы являются
12. = g(O) = go, /^0;
13. =
где IR+ -> IR" и /? е Клхя. Систему можно представить в виде
совокупности п интеграторов с входом и,- (/) и выходом (/)
(уравнение (12)) и выходных усилителей, на входах которых дей-
ствуют линейные комбинации (/), g2 (0> • ••»!» (0> а на выходах
вырабатываются реакции yz(t), .... </л(0> согласно урав-
нению (13). При любом и(-) из Ци реакция системы Н опреде-
лена. Мы утверждаем, что оператор Н пассивен, если R — сим-
метрическая положительно полуопределенная матрица.
Доказательство. Для любых ugL«(R+) и Te|R+
(и | Ни)? = <« I У)т = <У I и)т = f I1 (0 RTl (0 di.
о
£т (/) /?т£ (t)dt — криволинейный интеграл в Rn вдоль кривой
для t е [0, Т]. Так как матрица R симметрична, то
значение интеграла не зависит от пути интегрирования, поэтому
интеграл можно вычислять вдоль отрезка прямой X»—> (1 — X) £0 +
+-Ц(Т), где £о = £(0)< Тогда
<« Ни}т = j {g0 + X [g (Л - Во]Г /?т [I (Л - g0{ dk =
= [В (Т’) - М 4-1 [I (Т) - goF R' LI (Л - Во] =
= |г(Л/?кл-||;₽10,
откуда следует, что оператор И пассивен в силу положительной
полуопределенности матрицы R.
Упражнение 4.
(а) Показать, что даже в том случае, когда Ео = 0 я R — положительно
определенная матрица, вовсе не обязательно, чтобы система Н, заданная урав-
нениями (12) и (13), являлась строго пассивной.
(Ь) Используя свойство симметричности матрицы R, показать, что путь
интегрирования приведенного выше интеграла зависит только от расположе-
ния начальной и конечной точек интегрирования. Показать, что отсюда выте-
кает соотношение
2gT(0«t(0-^llTW Ы]-
Упражнение 5. Пусть Н: е и через К обозначен нестационар-
ный коэффициент усиления, причем К'. оле-+е%е и
(К«) (0»^(0«(0,
где функция k\ ограничена на Показать, что
(а) если оператор Н пассивен, то также пассивен и оператор КНК\
(Ь) если оператор И строго пассивен и функция k ограничена вдали от
нуля на множестве «Г, то опера юр КН К также строго пассивен.
4. ПАССИВНЫЕ СИСТЕМЫ: ОПРЕДЕЛЕНИЕ И ПРИМЕРЫ 193
Пример 4. Рассмотрим систему Н, изображенную на рис. 6.2,
и обозначим ее входной и выходной сигналы через и и у соот-
ветственно. Уравнения системы имеют вид:
14. (£) + <* (0 = «(0> <*(0) = <Уо»
15. у(0=ф[°(0].
где «, а, у. |R+->-|R, а функция <р: R->-R непрерывна. Мы
утверждаем, что система Н пассивна, если q^O и <р принадле-
жит сектору [0, оо).
Доказательство. Для всех и всех
<Ди!«>г = (ф (а);«>т = <Ф (о)|до + ст>г =
т т
= 7$ Ф [° (0] 6 (0 di + $ а (0ф [ст (/)]<#•
. о о
Поскольку ф принадлежит сектору [0, оо), второй интеграл не-
отрицателен. Определим Ф: R-*-R
равенством ।— ------------,
к! J <г, ль ! У
16. Ф(<0 = $ф(5)<£; LJrdbz1___________J/z
о
Рис. 6.2.
очевидно, что Ф(о)^0 для любых
о е R. Используя Ф для вычисления первого интеграла и за-
мечая, что 7^0, находим:
{Ни | и)т - дФ [а (0)] Х/и е= Ц, Х/Т 0,
откуда следует, что система Н пассивна.
Упражнение 6. Показать на примере, что если в рассмотренной выше
системе функция ср зависит от времени, но по-прежнему принадлежит сектору
[0, оо) при любых / е {R+, то система Н может и не быть пассивной.
Упражнение 7. Изменим порядок соединения подсистем на рис. 6.2. По-
казать, что полученная система не будет пассивной при любых ф, принадле-
жащих сектору [0, k). (Указание: рассмотреть функцию ф(сг) = о при
о>0 и ф(о) = 0 при о<0.)
Упражнение 8. Рассмотрим систему, аналогичную изображенной на рис. 6.2Д
но имеющую п входов и п выходов. Пусть Р, Q е Рлхл, o(t), и (/), y(t) е R* и
17. QdW + P(j(i)^u(t)9
18. У(П = <Р[а(ОЬ
где ф: РЛ->РЛ— непрерывная функция, причем
19. отРф (о) 0 Vo е Рл.
Предположим, что
фт (о) Q = [grad V (o)JT Vo g= Рл,
где функция V: принадлежит С1 и У(о)^0 при любых оеРл. По-
казать, что оператор Н: и\—пассивен. Показать, что если Ф/(сг)=//(а/)
при z==l, 2, ..., п, т. е. i-я компонента вектора ф(о) зависит только от о/, и
если каждая функция fa принадлежит сектору [0, оо), то соотношения (19) и
(20) выполняются при P = Q=I Построить функцию V (о) для такого случая.
7 Ч. Дезоер, М. Вндьясагар
194
ГЛ. в. ПАССИВНОСТЬ
где мы учли,
и
N
Рис.
Пример 5. Рассмотрим систему, изображенную на рис. 6.2 при
введенных выше условиях и обозначениях: система задана урав-
нениями (14) и (15), имеет место (16), q>0 и <р принадлежит
сектору [0, оо). Мы утверждаем, что если ^>0 и для некото-
рого aSsO
21. <p0=inf^g^2a9,
то при о (0) = 0
т
22. J е>"и(/)<р(о(0]Л^0 VTssO, V«e/?.
о
Доказательство.
г т
J еми (/) <р [а (/)] di = J ё** (qd + а) ф (a) dt =
о о
т
= [а (Т’)] _ J е»а/ (2са?Ф [о (0] - а (/) <p [a (t)]} At,
i
что Ф[а(0)] = 0, так как о(0) = 0. Первое слагае-
мое неотрицательно, поскольку ф
л принадлежит сектору [0, оо), а ин-
Д У теграл неотрицателен в силу (21).
Упражнение 9 (пассивная система с бло-
ком умножения). Пусть в системе, изобра-
6*3 женной на рис. 6.3, и у е L*, а через ф
обозначена статическая нестационарная не-
линейность, характеристика ф (•, t) которой принадлежит сектору (0, k) для
некоторого Ле(0, со]. Пусть АГ: удовлетворяет условию: при
некотором 6^0
(Afa)(0$*6^0 VhgLJ, V/^0.
Выходной сигнал у равен произведению сигналов реакции подсистемы N и
нелинейности ф. Показать, что система пассивна. Ввести дополнительные усло-
вия, при которых система становится строго пассивной
Пример 6. Пусть Р: Ц->Ц и Л—нестационарный коэффи-
циент усиления, т. е. К* Ц-+1Л, причем
26. (Лх) (/) = k(t)x (i) Vt g= R+,
где k (•) — абсолютно интегрируемая на R+ функция и
0 <1 kx = inf k (/) < k (t) sup k (t) = k2 < co.
Класс всех таких операторов обозначим через <2%%; если #i>0,
то тот же класс будем обозначать ЯГ. /Мы утверждаем, что
27. если Р —пассивный (строго пассивный) оператор и Z? (•) е
(&(*) еЯГ) — монотонно невозрастающая функция, то опе-
ратор ЛР пассивен (строго пассивен);
4. ПАССИВНЫЕ СИСТЕМЫ: ОПРЕДЕЛЕНИЕ И ПРИМЕРЫ
195
28. если Р —пассивный (строго пассивный) оператор и k(•) @
s 9С — монотонно неубывающая функция, то оператор РАС пасси-
вен (строго пассивен).
29. Комментарий. Условия абсолютной непрерывности функ-
ции &(•) необходимо и достаточно, чтобы
(a) k (•) являлась почти везде определенной функцией, и
(Ь) существовал неопределенный интеграл от k () (см. [60]).
Доказательство утверждения (27). Для всех
и всех 7'^0
г
30. (и | КРи)т = $ и (t)k (0 (Ри) (0 Л =»
о
г
= k (Т) (и | Ри)т- \ k (t) (и I Рд\/ di Ss 0,
о
так как первое слагаемое неотрицательно, а интеграл неположи-
телен, поскольку Р — пассивный оператор, fe (Т) 3s 0 при всех Т
и &(1)<0 при всех t
Доказательство утвер ждения (28). При любых и а
eL’, любых Гэ=0
т
(и | РКи>т = <К-Ч(и I РКи)т = J (Ku) (t) [P(Ku)(t)]dt.
Отметим, что и «= LI тогда и только тогда, когда Ku е LI, по-
скольку Поэтому полученный интеграл отличается от
интеграла (30) лишь тем, что функция k(t) заменена на
Следовательно, рассуждая, как при доказательстве утвержде-
ния (27), приходим к выводу, что оператор РК пассивен.
Упражнение 10. Доказать утверждения (27) и (28) о строгой пассивности
и аналогичные утверждения для дискретного случая
В следующем примере в отличие от примера 6 вместо функ-
ции k рассматривается монотонная функция >#(/)ехр (otf)> и
методом экспоненциального взвешивания доказываются условия
пассивности.
Пример 7. Пусть существуют числа kt и k2 такие, что 0^
^ki^k(t)^k2<oo цля всех /. Пусть оператор k: LI-+LI
задан соотношением (26), оператор g: L*-+Li определен соотно-
шением gx = g*x, где g^&#. Предположим, что 0>О и функ-
ция g может быть аналитично продолжена в область — Р Res «<
<0. Пусть, кроме того, существует число 6>0 такое, что
31. Reg(/to)^6>0 VtoeR
и
32. Reg (/to —0)^=0 VogR.
7*
196
ГЛ. 6. ПАССИВНОСТЬ
Тогда
(i) если для некоторого о е (0, 20) функция t»—> k (/) exp (erf)
монотонно неубывает, то оператор gk строго пассивен и имеет
конечный коэффициент усиления; при 6 = 0, 0 = о> 0 оператор gk
пассивен;
(ii) если для некоторого а е (0, 20) функция t >—► k (/) exp (—at)
монотонно невозрастает, то оператор kg строго пассивен и имеет
конечный коэффициент роста.
33. Комментарий. Если k е 5JT, то в утверждении (i) условие
можно представить в следующем виде:
84. dlogfeffl, g
at k (t)
Доказательство.
(i) Введем функцию p(t)—l/k(i). Тогда для некоторых pt и рг
С <Zpi^p(t)^p2,
причем функция t»—► р (/) exp (— at) монотонно невозрастает. По-
этому при некотором достаточно малом 6i>0, поскольку 20 >
> о > 0, [р (/) — 61] ехр (—20/) — также монотонно невозрастающая
функция. (Чтобы удостовериться в этом, вычислите производную
логарифма рассматриваемой функции!) Тогда для любых
и любых полагая v — ku, получаем
(и | gku)T = \ P0)v (0 (gv) (t) di = 6X J v (t) (gv) (i) di +
0 0
36. + J {[p (/) - 6X] <r2₽'} v (t) & (gv) (/) & di.
0
Первый интеграл превосходит величину
38. 616*1 IKr,
а второй интеграл неотрицателен. Сомножитель в скобках поло-
жителен и монотонно невозрастает, поэтому, применяя ко второму
интегралу вторую теорему о среднем, находим, что он равен
[p(0)-6j] $ v(t)№‘(gv)(t)di,
о
где Т' — некоторое число из [0, Т]. Срезка функции t^v(t)ехр 0/
в точке Т' принадлежит L2. Поэтому, обозначая ее изображение
по Лапласу через vт и замечая, что
(gv)(t) = e?*(g * v)(t) = (ge& * ve^)f
В. ТЕОРЕМА О ПАССИВНОСТИ
197
с помощью теоремы Парсеваля получаем, что второй интеграл
равен
со
40. 2^ $ S (I® - ₽) I (/©) I® Ss 0
— ОО
(последнее неравенство следует из условия (32)). Из (36), (38) и
(40) получаем, что оператор gk строго пассивен и, кроме того,
Доказательство (ii) ведется аналогичным образом, по-
скольку
41. {и | kgu}T = (ku | gu)T = (v | gk~lv)T
и свойство монотонного неубывания функции exp экви-
валентно монотонному невозрастанию функции k(t)exp(—о/).
42. Комментарий. Выкладки в (41) справедливы при очень
общих условиях, а именно: оператор k должен быть самосопря-
женным, у(Л)<оо и у(Л-1)<;оо.
б. ТЕОРЕМА О ПАССИВНОСТИ
В этом разделе теорема о пассивности формулируется в упро-
щенной и общей формах. Мы будем руководствоваться знанием
теории цепей и соображениями, высказанными в разделе 1, и
используем общие положения разделов 3 и 4.
Сначала сформулируем упрощенный вариант теоремы о пассив-
ности.
1. Теорема. Рассмотрим систему с обратной связью, изобра-
женную на рис. 3.1, где «2 = 0, так что
2. = Ui — Z/2£2,
3. в2 = Н 1^1,
причем Нъ Н2: Предположим, что при любом
существуют решения е± и е2 соответственно уравнений (2) и (3)
из Не. Тогда, если оператор Нг пассивен, оператор Н2 строго
пассивен и и± е <2%^, то е еЖ.
Доказательство. Последовательно используя уравнения (2)
и (3), получаем
4. (и 11Н= <ei \ Н 1^1)7' 4- (Н2еа | е2)т 0 -f- 621 е2 ||г 4- р2,
где 62 и р2 — постоянные числа, причем 62>0, поскольку опера-
тор Я2 строго пассивен. Применяя к (4) неравенство Шварца и
учитывая, что иг е отГ, находим
5. I! Wi |lr |l Hfa ||г 621| /71^1 ||т 4- Р2 VTeeT",
откуда следует, что функция Т»—► | |т ограничена, т. е. еа =
198
ГЛ. в. ПАССИВНОСТЬ
Упражнение 1. Пусть в условии строгой пассивности для Я2 число не*
отрицательно. Вычислить из (5) постоянную k такую, что
УТяГ.
6. Комментарий.
(а) Приведенная форма теоремы о пассивности легка для дока-
зательства, применения и запоминания. Построить пример из тео-
рии цепей для иллюстрации теоремы элементарно просто (см.
рис. 3.2): источники тока подключены к параллельному соеди-
нению пассивного и строго пассивного 2п-полюсников.
(Ь) В теореме не утверждается, что и H^t принадлежат «5Г.
В скалярном случае нетрудно построить контрпример, если пред-
положить, что «1 (•) —треугольный импульс тока, Hi — индуктив-
ность 1 Гн, Hi — параллельное соединение индуктивности 2 Гн и
сопротивления I Ом. После воздействия на схему треугольного
импульса входной ток становится равным нулю, но через индук-
тивности продолжает протекать постоянный ток. Таким образом,
«1 и Н&ъ не принадлежат ZA
(с) Чтобы утверждать, что функции ег и ei = HiCi принадле-
жат е2Г, необходимо ввести дополнительное предположение о ко-
нечности коэффициента роста оператора Hi или Ht, как это
делается ниже в теореме (10).
(d) Интуиция подсказывает, что вовсе не обязательно требо-
вать, чтобы оба оператора Hi и Ht были пассивными; достаточно,
чтобы «активность» одного из них так компенсировалась «пассив-
ностью» другого, чтобы параллельное соединение подсистем Hi
и Ht являлось строго пассивной системой. Именно об этом гово-
рится в теореме (10).
(е) Очевидно, что, комбинируя в различных сочетаниях пас-
сивные системы, примеры которых приведены в главе 4, можно
сформулировать не один десяток теорем о L’-пассивности.
Теперь мы переходим к более общей версии теоремы о пас-
сивности.
10. Теорема. Рассмотрим систему с обратной связью, изобра-
женную на рис. 3.1 и заданную уравнениями
12. gi = ui — H??i,
13. е2 = u2 -|- Htfi,
где Hi и Hi отображают Предположим, что для любых
Ui и ut из существуют решения ei и е2 из Пусть, кроме
того, существуют постоянные числа ух, Pi, 6Х, PJ, е2 и р2 такие,
что
14. i HiX 1г ух | х |г+ Pi,
15. <х|Я1х>г^б1|х|Я-₽;,
16. <ЯаХ|Х>г>82|Ягх|}- + р;
Vx s VT <
5. ТЕОРЕМА О ПАССИВНОСТИ
199
Тогда, если
17. 6i“b®i2>0,
то
Ui, и2 е => еъ е2, е «ЯГ.
18. Комментарии.
(а) Общность. Теорема (10) применима как к непрерывным
(е^~ = R+), так и к дискретным (еГ' = ZJ системам, причем системы
могут быть одноконтурными (?^«[R), многоконтурными (?^ = |R«)
и даже распределенными ($7 — пространство со скалярным про-
изведением).
(Ь) Из условия (14) следует, что оператор имеет конечный
коэффициент роста.
(с) Если е2 = 0, то, согласно (17), 6i>0; поэтому теорема
справедлива и в тех случаях, когда /Л —строго пассивный опе-
ратор с конечным коэффициентом роста, а Н2 — пассивный опера-
тор. Если же е2=#0, то при рассмотрении схемы соединения двух
двухполюсников, аналогичной изображенной на рис. 3.2, можно
заметить, что оператор «сопротивлений» Нг рассеивает больше
энергии, чем сопротивление величиной 610м, а оператор «прово-
димостей» Н2 рассеивает больше энергии, чем сопротивление вели-
чиной е2 Ом; таким образом, согласно условию (17), рассматри-
ваемая система не запасает, а рассеивает энергию.
(d) Если Н2 — биекция «ЯГе на «ЯГе, условие (16) превращается в
<у\НГу>т^Му^г + ^ Уу&Ж„
т. е. при е2>0 условие (16) означает, что оператор Н2* строго
пассивен.
Доказательство. Для любых и19 и2&&~ и любого Т
используя (12) и (13), получаем:
20. (ег | Н+ \#2^21 =
= (ui — И2е2 | Нт + {Н2е21 и2 4- Н= {th IН+ {Н2^21
Применяя к последнему равенству условия (14), (15), (16) и нера-
венство Шварца, находим, что
21. бхкхГт + егВ^Гг^
I wi h Vi !т+ Pi I wi (т +1! и2 Нт I Н2е2 flr — Pi — PJ.
Чтобы исключить Н2е2 из (21), заметим, что H2e2^=u1 — elt откуда
22. -2Ытк1НМ.
Подставляя (22) в (21) и заменяя в правой части в2 на | е2|, находим:
23. (614~ е2) Ц ei If J ei Jr [(2 | е2 + ух) | щ |г +1 и2 [г] +
+1 ui |т I |г + Pi I ui |г +1 е2 | II (г — Р1 —
200
ГЛ. 6. ПАССИВНОСТЬ
Учитывая предположение (17): 614-82>0, представим полу-
ченное неравенство в виде:
24. ЫКВДМгНП
где b (Т) и с (Т) —монотонно возрастающие функции, стремящиеся
при Т->оо к конечному пределу, поскольку и19 Обо-
значим эти пределы через b и с соответственно. Тогда из (24)
25. || ег ||r < b (Г) + [b* (Т) + с (71)]1'2 < b + (&2 + с)1/а VT е
Таким образом, Отсюда, согласно (14), у^Н^. Из (12)
и (13) ытекает, что е2 и Н2е2 также принадлежит
26. Следствие. Если условия теоремы (10) выполняются, то
(а) при отображение а2*—+Н2е2 пассивно;
(Ь) при и3эО отображение пассивно.
Упражнение 2. Разъяснить смысл следствия (26) в терминах теории цепей.
Доказательство следствия (26).
(а) Из (20) при Ur = 0 для любых и2 е о%~в и любых Т о оГ
получаем
(и21 Н2е2)т = (в11Нуе\)т + {Н\е*)тSi II eiIfr + Pi + 8г1|Н2е2Ц-=
— (®i + ®а) II ^i + Pi + Pi PI + р2.
Следовательно, отображение и2»—+ Н2е2 пассивно. Мы не можем
доказать, что это отображение строго пассивно, поскольку наши
предположения не исключают случая, когда подсистема Н2 воспро-
изводит нулевые реакции на всевозможные входные воздействия.
(Ь) Доказательство очевидно.
27. Следствие. Если в дополнение к условиям теоремы (10)
Р1 = Р1 = Рз = 0, то отображения (ц1э а2}*—*еь е2, являются
ZA устойчивыми.
Доказательство. Очевидно, что b и с в (25) являются
однородными многочленами от |«i| и ||и2|| первой и второй сте-
пени соответственно. Поэтому, согласно (25), существует число
&<оо такое, что
ki 11^ k max (|| Ui ||, || ||).
Остальные отображения /Аустойчивы в силу (12), (13) и (14).
При обсуждении теоремы о малом коэффициенте роста (3.2.1)
мы отмечали, что при наложении ограничений на коэффициенты
ро:та по приращениям получаются более сильные результаты, чем
при введении ограничений на коэффициенты роста. Действительно,
в теореме (3.2.1) утверждается, что нормы выходных сигналов
ограничены, в то время как теорема (3.3.1) содержит еще и усло-
вия существования, единственности и непрерывной зависимости
решений. Похожая ситуация складывается при рассмотрении
теорем о пассивности и строгой пассивности.
30. Теорема. Рассмотрим систему с обратной связью, заданную
уравнениями (12) и (13), где и Н2 отображают в самое
б. ТЕОРЕМА О ПАССИВНОСТИ
201
себя. Предположим, что при любых их, и2^^ЯС система воспро-
изводит решение еъ е2^^е. Пусть Ях0 = 0 и Н20 = 0. Тогда,
если
(а) отображение Нг имеет конечный коэффициент роста по
приращениям и строго пассивно по приращениям, т. е. сущест-
вуют постоянные числа 0<ух<оо и ^>0 такие, что
31. Нхх' Цг^ТхЦх — х'||г, ) Vx, х'
32. (Нхх-Нхх' ix —х'>т5=6111 х-х'Цг J VT ЕвГ;
(Ь) отображение Н2 пассивно по приращениям, т. е.
33. (Н2х — Н^х' |х — х')г^0 Vx, х'е^Ге, VTeeT',
то
(i) при любых иъ и2 е 0%^ функции ех, е2, уи Уъ е5Г и опре-
деляются единственным образом;
(ii) отображения (их, u2)i—>ex и (иъ и2)*—+е2 равномерно не-
прерывны на х<2%Г;
(iii) отображения (их, и2)ь-*ех, (ux, w2)>—>е2, (ux, и2)»—> /7хех,
(ux, u2)»—*Я2е2 являются /Аустойчивыми.
Доказательство.
(i) По условию /Ух0 = 0 и /720 = О, полагая поэтому х'=0
в (31), (32) и (33), приходим к (14), (15) и (16), где ух = 7х,
61=61>0, 82 = 0 и рх, PJ и р2 равны нулю. Тогда, согласно тео-
реме (10), ех, е2, Ух, Уъ^о%\ Чтобы убедиться в единственности
решения, рассмотрим пары входных воздействий (wx, u2), (wj, w2)
и соответствующие им пары решений (ех, е2) и (е{, е^). Как и при
доказательстве теоремы (10), находим, что для любых Т
34. (ех — е[ | //x£i — (^2 — е2\Н2е2 — Н2е^т —
= (ui — и[ \ Н^х — Н+ (и2 ~и2\Н2е2 —- Н2е'^)т.
Используя условия (31), (32), (33) и неравенство Шварца, полу-
чаем:
35. 6ХI ех — ei [г | их — [г ух || ех —• Jr +
+1 — и'21|г [I ех — е{ Цг +1 их — и\ ||г].
Таким образом, если их = «1 и u2 = u2> то из (35) следует, что
ex = ej, а затем из (13) находим, что е2==^-
(ii) Для установления факта равномерной непрерывности ото-
бражений представим правую часть (35) в виде
36. |’ Cj — е\ ||г [|| и2 — ||г + Yi || Ui — ||r] + [|| их — |г • || и2 — и2 ||г].
Сомножители, заключенные в квадратные скобки, представляют
собой возрастающие функции от Т, сходящиеся при Т->оо
к конечным пределам, равным, например, 2Ь6Х и с6х. Следователь-
202
ГЛ. в. ПАССИВНОСТЬ
но, из (35) и (36) при 61 > 0 выводим, что
ki-eJ|J-<26Se1-e;|r4-c УТеГ,
где b и с — однородные многочлены от | Ui — u't | и | ut — uj | первой
и второй степени соответственно. Тогда
38. ki-e't 1т^Ь + (Ьг + сУ'2
Поскольку b и с постоянны и функция | • |г монотонно возрастает
с ростом Т, в неравенстве (38) можно отбросить индекс Т.
И, наконец, если «[->«1 и ва2Г (т. е. |и,- — где
1=1, 2, и, следовательно, I и,- — и’( Jr-*• 0 для любых Г), тогда
в силу (38) |ei —Аналогичным свойством обладает et,
так как из (14) и (31) следует, что
39.
Таким образом, единственность и равномерная непрерывность
решений на Xajf установлены.
(Ш) ^-устойчивость следует из неравенств (38), (39), (31) и
уравнения = Ui —cr.
8. КРИТЕРИЙ ПОПОВА
Теорема о пассивности очень важна для вывода критерия
Попова и его обобщений.
Случай I. Характеристика ф принадлежит сектору [0, оо),
' . т. е. ф(0) = 0 и <тф(о)^0 для любых
* fa * г(?) Л aeR-
। 1. Теорема. Рассмотрим систему, изо-
I г-s—I браженную на рис. 6.4. Пусть функция
I *»—। п ф: R-*-R непрерывна и принадлежит
сектору [0, оо). Пусть g: IR+-+-R, get
Рис. 6.4. е L1 (|R+) и gs Предположим, что
для любого воздействия иг такого, что
«1, «1 е L*. функции принадлежат Ц. Тогда, если ut. tit s
® L2 и существует q 0 такое, что
2.
inf Re [(1+ qj<a) g (»] - 6 > О,
® >0
TO
(i) eu eu е%, уъ y9, yt&L*;
(11) функции yif yt непрерывны, принадлежат L°° и стре-
мятся к нулю при <-»-оо.
3. Упражнение 1. Показать, что если иъ е то функция их принад-
леяшт L°°, непрерывна и uY (t) ->0 при / оо. (Указание: t«—► (t) ut (/)e
ei L1, поэтому ее интеграл непрерывен и имеет конечный предел при t оо.)
6. КРИТЕРИЙ ПОПОВА
208
Упражнение 2. Показать, что при введении в систему, изображенную на
рис. 6.4, входного воздействия w2> теорема (1) останется справедлива, если
g L2. (Указами е: использовать свойство линейности для замены и9
эквивалентным воздействием заметить, что если z2=^»«e, то
W производная g, как обобщенной функции.)
Доказательство. Преобразуем исходную систему к виду,
представленному на рис. 6.5, и определим подсистемы Hi и Ht
уравнениями Hii\i^yi, Н^г2^ у2-\- qy2. Как показано в примерах 4
и 1 (раздел 4), оператор Hi пассивен, а оператор Ht строго
пассивен. Поэтому согласно следствию (5.26) из иг, iii е L* выте-
кает, что z/i = e2eZA Поскольку g&L1 и оператор Я,
имеет конечный коэффициент роста; следовательно, yt, у2, гце/А
Тогда для исходной системы ei, ei^L2, и поэтому функция я
е L°° непрерывна и (/)->•
->0 при Такими
же свойствами обладает и
функция У1 (0 = <р [ех (/)]; в
самом деле, функция ф
непрерывна и отображает
компактные множества из
R в компактные множества
Рис. 6.5.
из R. Указанными свой-
ствами обладает также функция у2, так как y2 = g*e2 и g^L1.
Случай II. Характеристика ф принадлежит сектору [0, Л].
5. Теорема. Рассмотрим систему, изображенную на рис. 6.4,
где ф принадлежит сектору [0, Л]. Предположим, что выполняются
все приведенные ранее условия, кроме (2). Тогда, если существуют
g>0 и 6>0 такие, что
6. - Re[(l + <7/<o)g(»] + -^Ss6>0 VcoSaO,
то выполняются положения (i) и (ii) теоремы (1).
7. Графическая интерпретация. Если представить
$(/со) в виде g (/<») = £•(/«>)+/& (/<•>), то (6) будет выполняться
в том и только том случае, когда
gfi>gi (/®) «С & (» + [ - б] Vco <= |R+.
Это неравенство необходимо проверять лишь при со 0, поскольку
gr (ja>) и cog, (/со) — четные функции. Неравенство эквивалентно
следующему утверждению: кривая со •—* [gr (/со), cog; (/со)] лежит
в комплексной плоскости ниже прямой с угловым коэффициентом
\/q, проходящей через точку (6— \/k, 0). Так как 6>0 можно
выбрать сколь угодно малым, то кривая со ► [gr (ja), agi (/со)]
лежит ниже прямой с угловым коэффициентом 1/g, проходящей
через точку (—1/k, 0), и ограничена вдали от этой прямой.
204
ГЛ. в. ПАССИВНОСТЬ
Доказательство. Для подвистемы Hi (рис. 6.5) при всех
Ts&O
<тц1Н 1Т]1)г=<в1 4- <7<?х I Ф (<?!»т = <611Ф (61)>Г+<7 <ё1; ф (61)>т
> у <Ф (61) I <Р («1)>т - <?ф [61 (0)]
(здесь использовано обозначение, принятое в примере 4 раздела 4).
Обозначая последний член через 0Х, получаем
(iii I Н 1Л1)г у II #1Л11г — ₽!•
Оператор /7г линеен, имеет конечный коэффициент роста, так как
f EL1 И И
<еа I Н^т inf Re [(1 + qja>) g (/©)] J е» |Ь
(1)G₽
Поэтому Hi и H2 удовлетворяют условиям теоремы пассивности
(5.10) и отображение «х 4-<7«i •—* (Ль ег) является /Аустойчивым.
Остальные выводы доказываются так же, как и в теореме 1.
8. Комментарий. Теорему (5) можно доказать с помощью
следующих вычислений. Уравнение системы имеет вид (индекс 1
для упрощения записи опущен):
9а. u = e + g*<p(e).
Поскольку йеР и ®^, то после дифференцирования (9а)
получаем:
9b. й=е+^*ф(б).
Все функции, входящие в уравнения (9), принадлежат простран-
ству L*, поэтому мы можем рассматривать скалярные произведения
срезок этих функций:
<й4-<7«|ф(е)>т =
= (е~-^|ф(е)^г + (7<ё|<Р(б)>г + ^ + №)*ф(е) +-пг-|<Р(е^г-
С учетом неравенства Шварца, секторного условия и предполо:
жения (6) находим, что для
(II и |4- q || й ||) | ф (е) |г Ss бф (е) |4Г - <?Ф [е (0)].
Следовательно, ф (е) е L2. Тогда, согласно (9а) и (9Ь), е *= L*
и е е Р.
10. Замечание. В теоремах (1), (5) и (11) предполагается, что
статическая нелинейность стационарна. Если же нелинейность
удовлетворяет секторному условию, но зависит от времени произ-
вольным образом (как, например, в круговом критерии), то можно
6. КРИТЕРИЙ ПОПОВА
205
построить пример системы, являющейся неустойчивой при неко-
торых входных сигналах.
Случай III. Подсистема g содержит интегратор, характеристика
Ф принадлежит сектору [е» Zs-J-e], где е — некоторое достаточно
малое положительное число.
11. Теорема. Пусть функция ф: R->|R непрерывна и принад-
лежит сектору [в, fe + s], где е — некоторое достаточно малое
положительное число. Пусть
g(t) = r+g1(t),
причем г>0, и Предположим, что для
системы, изображенной на рис. 6.4, если wx, йх е Ц, то elt е2 е
е L*e. Тогда, если существует число <?>0 такое, что для неко-
торого 6>0
12. Re [(1 4- ge (»] 6 VcoSsO,
где
13. ge (/w) = g (/co)[1 4- eg (/и)]-1,
и если иъ йг е L2, то еъ elr е2 <=L2, еъ е2^Ь°° и ех (0 -> 0, е2 (/) 0
при /->оо.
Доказательство. Так как г>0, то при достаточно малом
в > 0 функция [14-8gr(s)]“1 принадлежит оЛ. Поэтому g8(s),
sge (s) е <2т/ [см. теорему (4.4.10)]. Следовательно, со »—► (1 + 7Л°) X
X(/со) —непрерывный линейный оператор с конечным коэффи-
циентом роста. Преобразуем систему, приведенную на рис. 6.4,
следующим образом: охватим g положительной обратной связью
с коэффициентом е, заменяя, таким образом, g на ge из (13),
а параллельно с нелинейностью ф соединим усилитель с коэффи-
циентом — е, получая нелинейность с характеристикой Ф8(е1) =
=Ф(е1) —821, принадлежащую сектору [0, &]. Совершив указанные
преобразования, мы приходим к системе, удовлетворяющей
теореме (5).
14. Замечание. При доказательстве теорем (1), (5) и (11) свой-
ство линейности подсистемы g нигде не использовалось; однако
мы постоянно учитывали, что передаточная функция (1 + ?s)£(s)
соответствует системе с конечным коэффициентом усиления, обла-
дающей свойством пассивности [(2), (6) или (12)].
Распространить критерий Попова на многомерные системы до-
вольно просто. Основная идея иллюстрируется следующей теоремой.
15. Теорема. Рассмотрим систему, заданную уравнениями
16. = — Не2,
17. е2 = ф(*1),
где Ui, е2: Пусть характеристика ф: непре-
рывна, причем ф (0) = 0. Пусть матрицы Р и Q принадлежат КЛХЛ
206
ГЛ. в. ПАССИВНОСТЬ
и таковы, что нули функции s»—*det(/’4-sQ) лежат в открытой
левой полуплоскости. Пусть для некоторой симметрической поло-
жительно определенной матрицы К е Рлхл
18. V£e|R"
и существует скалярная функция V: Кл->₽+, принадлежащая
С1, такая, что
19. Ф (e)TQ » W (е) Ve е 1РЛ.
Пусть Н, DH: L^-^Lm, через DH обозначено отображение
х ►—* И (t). Предположим, что из их, di е LJ вытекает, что е1г
ег^им. Тогда, если существует б>0 такое, что
21. <(P+QD)tfx+to|x>r^6|xfr VxeL^, VT<=R+,
то e2«=<p(ei) s£J, если ult di^Ln. Если, кроме того, Н и DH
отображают ££ в £„, то ex, Qei е Ln и, если матрица Q невырож-
дена, то ех, е2е£“ и ei(/)->0, е2(/)->0 при /->-оо.
Доказательство (основная идея). Преобразуем исходную
систему к виду, представленному на рис. 6.6. Покажем, что опе-
ратор Hi пассивен:
22. <Т|! | Я1тц>т = {Pei 4- Qei - Дф (*) | ф (ej)> т =
т т
= $ [Pei - Kq> (ех)]тФ (ei) dt + J ф(ех)т0е1 di.
о о
Первый интеграл неотрицателен в силу секторного условия (18).
Вычислим второй интеграл:
т еНЛ
\4(etfQ<iidi~ $ ф = V Ь(Т)] - V ^(0)].
0 е, (0)
Поскольку V (1)3^0 при любых |е|Кл, из (22) следует, что
оператор Hi пассивен. Согласно условию (21) оператор Н2 (см.
рис. 6.6) строго пассивен. Тогда из теоремы (5.1) следует, что
е2 — ф (ei) е Ln, как только ult iii^Lsn.
При дополнительном предположении о том, что Н, DH: Ln-*-Ln,
мы получаем, что Не2, DHe2 е £«. Следовательно,
T|i = (Р + QD) Ui - Н2е2 е L-n.
Так как (Р + sQ)-1 — экспоненциально устойчивая матричная пере-
даточная функция, то
ei = (P + QD)-i(ni + Ket)^L*n.
И, наконец,
Pei + Qei = т]х+Ке2 е £«,
т. дискретный случаи
907
откуда следует, что QeieLJ. Таким образом, если матрица Q
невырождена, то еь т. е. eieL" и 0 при /->оо.
Аналогичными свойствами обладает функция et, поскольку
из (18) следует, что
I <?1 (01R11Ф [*1 <01I > I ф к (01 Is lmIn (К) VI 0,
где через 1т<п(Ю обозначено наименьшее собственное значение
Рис. 6.6
матрицы К, причем lmin(K)>0, так как К — положительно
определенная матрица.
Упражнение 3. Провести формальное доказательство теоремы (15) подобно
тому, как доказана теорема (5) в комментарии (8).
7. дискретный СЛУЧАЙ
Методы исследования дискретных систем несколько отличаются
от методов, применяемых в непрерывном случае. Для простоты
мы будем рассматривать лишь системы с одним входом и одним
выходом. Поэтому еь уг, у*. Z+->R и
У
1.
п =0
V
<б|ф(б)>№ 2 е(п)<р[е(п)].
п = 0
Вместо оператора дифференцирования будут использоваться опе-
ратор обратной разности
2. (7е)(л) = е(л) —е(л — 1)
и оператор прямой разности
3. (Де) (л) = е (п 4-1) — е (п)
Аналогично,
(VGx) (л) = (Gx) (л) — (Gx) (л — 1).
4. Замечание. Некоторые особенности, свойственные только
дискретным системам, приводят к тому, что дискретные задачи
208
ГЛ 6. ПАССИВНОСТЬ
решаются легче непрерывных. Например, если х = [х(0), г(1),
х(2), ...]е/2, то обязательно хе/* и х(я)->0 при п->оо.
5. Теорема. Рассмотрим систему, в которой и19 е19 е2, Уъ
Z+->R и
6* #1 =* — G#2»
7. е2 = ф(е1).
Пусть характеристика <р: |R->R принадлежит сектору [а, Р],
где О^а^р, оператор G неантисипативен и действует из 1*е в
Предположим, что для некоторого существует 6>0 такое, что
8. /(G+?VG+ib|x\ ^6<x|x>jv Ухе=Ц, VNf=Z+.
V P / / N
Тогда
(а) если a>0 и
9. S-A>°>
4a* *
то из и e P следует, что eu e2 e P\
(b) если характеристика <p принадлежит сектору [0, ₽] и
монотонно возрастает, оператор G имеет конечный коэффициент
роста, т. е. существует у (G) е R такое, что
10. |Gxk<T(G)№ Vxe/J, V^eZ+)
то из «1 е Р следует, что еъ е2 е Р.
Доказательство.
(а) Поскольку
u1=ei+Gq>(e1),
то
Vux = 4- VGq> (Сх),
и для всех N Е Z+
15. + (e1)>JV = /ei-5^|ф(е1) 4-
\ Р I / Л'
+ ^G + ^VG +-р) ф(^1) + <7 ’ Ф (^1)^-
Согласно первому секторному условию, первое слагаемое неотри-
цательно. Далее,
16. <Vex Ф(г1)>Лг= У ф[^х(п)][ex(n) —ei(n— 1)] =
^/ = 0
N N
- 2 w-vn-1)]! -; 2
л—О п=0
7. ДИСКРЕТНЫЙ СЛУЧАЙ
209
Так как из (15) получаем, что
17. (ih + q^Ui. | <р (e^N >
> ((G + <?VG +1) ф(ej I ф(е^ - ^ |ejRr.
Замечая, что | V«1|^2ju1), и используя неравенство Шварца,
находим:
18. (1+2<7)|Ы1Нф(е1)к^(б-<)|Ф(е1)|^ VJV.
Следовательно,
19. |ф(е1)Ж(1+2<7)[и11(б-£2)~’,
т. е. (р(^)е/2. Кроме того, ^е/2; поскольку ki I2 t Ф (^i) Р/а*«
(Ь) В этом случае характеристика <р не только принадлежит
сектору [0, Р], но и является монотонно неубывающей функцией,
т. е. (ох — а2) [ф (ох) — ф (а2)] 0 при любых ах, a3eR. Как и
раньше, имеет место равенство (15). Однако оценка (16) здесь
несколько отличается:
N
22. <?а q>(eiy)N= У ф[а(п)]1а(п)-А(л- 1)]>
0
N ег (л) е, (АГ)
S j ф(о)<!о= $ ф(о)с1о = Ф[а(Л,)]^:0 VAI,
п == 0 ег (п — 1) 0
где использовано свойство ех(—1) = 0. Поэтому в рассматриваемом
случае в (17) последнее слагаемое отсутствует, и (18) приобре-
тает вид
23. (1 + 2^) [ Ui || || ф (а) к б IIФ (A) In VAI,
откуда при находим, что | ф (а) | II «t I (1 + 2?)/6. Так как
оператор G имеет конечный коэффициент роста,
24. |А| = |0ф(А)Кт(0)|ф(А)1<оо-
26. Замечания.
(I) В теореме не требуется, чтобы подсистема G была линейной
или стационарной.
(II) Теорема доказывается так же успешно, если вместо опе-
ратора обратной разности (3) использовать оператор прямой
разности (2). Изменения в доказательстве незначительны.
27. Следствие. Если оператор G линеен, стационарен и, в част-
ности, является оператором свертки, а импульсная характеристика
соответствующей системы (g0, gu g2, ...) принадлежит I* и ее
z-преобразование g (г) ограничено на окружности единичного
радиуса | z | = 1, то условие (8) может быть проверено на графике
функции бн-* g (е/в) в комплексной плоскости (здесь 0 изменяется
2t0
ГЛ. в. ПАССИВНОСТЬ
от 0 до я). В самом деле, это условие при г=е/в, О^в^л,
приобретает вид
Re[l+<7(1 +
Напомним, что если ё (г) — % [е (•)] — г-преобразование последова-
тельности {е(0), е(1), г (2), то z~l'e(z) представляет собой
г-преобразование последовательности {0, е(0), е(1), е(2),
8. КРИТЕРИЙ СРЕДНЕЙ ЛОГАРИФМИЧЕСКОЙ ВАРИАЦИИ
Критерий средней логарифмической вариации является общим
результатом о ^-устойчивости линейной нестационарной системы,
изображенной на рис 6.7, а. Интересная особенность этого крите-
рия состоит в том, что он определяет ограничения на среднюю
скорость увеличения логарифма коэффициента обратной связи k (t)
и сдвинутую диаграмму Найквиста функции w. Для доказательства
критерия необходимо точно описать свойства усилителей, однако
не нужно предполагать, что подсистемы ТЛустойчивы.
Рис. 6.7
Описание системы и предположения. Система описывается
уравнениями
I. yi = w*eu = ei = u — yt,
где функции и, ех, ух и у» отображают R+ в IR, и
2. w(O = wo6(O4-wa(O,
где ®9 е R и для некоторого ст0 е R t •—* wa (0 exp (о00 е L1 (R+);
8. £()<=<РГ,
где |R+-I функция f абсолютно непрерывна и 0<inff(/)«^
<supf(0<oo|.
t
4. Функция w{ • ) = X [w] может быть аналитически продолжена
s область Res> —<тс при некотором <jc2>0.
5. При всех и sL! функции ех и ух принадлежат Li.
». КРИТЕРИИ СРЕДНЕЙ ЛОГАРИФМИЧЕСКОЙ ВАРИАЦИИ
fill
в. Пусть o,h 6 (0, ос), тогда лежащая в комплексной плоскости
кривая со►—*-— uSh), asp, вместе с точкой (w0, 0) назы-
вается с^-сдвинутой диаграммой Найквиста функции ш. Пред-
полагается, что ©•—►»> (/e>—<TSh)-»-u»o при ®->оо.
Обозначение. Оператор ei—*w*ег обозначается симво-
лом w, таким образом, w — ядро (или импульсная характеристика)
оператора w. Через w обозначена соответствующая передаточная
функция.
Упражнение 1. Предположение (5) является очень слабым.
(а) Пусть l+tt>ee(/z)=0 при некотором t' е R+. Что можно сказать
о существовании решения?
(Ь) Построить ограничения на и k (•), при которых система имеет
н притом-единственное решение.
8. Теорема. Пусть система, изображенная на рис. 6.7, а,
удовлетворяет предположениям (1) —(5). Тогда, если (^-сдвинутая
диаграмма Найквиста функции w не пересекает отрицательную
действительную полуось (т. е. множество {г е С | Re z^O, Im z=0})
и если при некоторых Т>0 и г^О
10. sugy $ logA(x)j+ciT<2r<2ff,h,
где через [/ (т)]+ обозначена функция шах[/(т), 0], то система
£а-устойчива.
Доказательство теоремы состоит из двух частей: сначала
проводится разложение Л(-) и вводится «усилитель» т; затем
применяется теорема о пассивности (5.10) и используется пример 7
(раздел 4). Усилитель задается неантисипативным оператором
свертки т, определенным на Ц, имеет передаточную функцию т (•)
и обладает следующим свойством: операторы т и пг1, сужен-
ные до имеют конечные коэффициенты роста.
Прежде всего мы докажем лемму о разложении функции &(•).
12. Лемма. Если функция k(-) принадлежит &С и удовлетво-
ряет условию (10), то существуют функции &+(•) и &-(•) такие,
что
13. (i) &(/)=М0*-(0;
14. (ii) функции &+(/) и k_(t) ограничены вдали от нуля и
ограничены на множестве R+;
15. (iii) функция &+(Z) exp (2г<) монотонно не убывает;
16. функция А_(/)ехр(—2rt) монотонно не возрастает.
Усилитель т строится в соответствии со следующей леммой.
18. Лемма. Если функция w удовлетворяет предположениям
(2) и (4), причем w0>Q, а ее сдвинутая диаграмма Найквиста,
как в теореме (8), не пересекает отрицательную действительную
полуось, то существует неантисипативный оператор свертки т
такой, что функция т аналитична при Res> — oSh, причем
212
ГЛ. 6. ПАССИВНОСТЬ
t »—► tn (t) exp (<rShO e orf и tn (s) -> 1 при | s | oo; кроме того, при
некоторых 6i, 62>0
19. Re [th (J® — 6sh)] 6i > 0,
20. Re [th (ju — osh) w(ja — osh)] 62 > 0
при всех (oEx; и, наконец, функция tn~l(s) аналитична при
Res> — oSh и ограничена в области Res^ —aSh-
21. Комментарий. Из леммы (18) следует, что операторы т и
лг1, суженные до L2, имеют конечные коэффициенты роста; дей-
ствительно, поскольку oSh>0, функции со»—►т(/со) и (Он—►[/п(/о))]_1
ограничены на R.
Упражнение. Показать, что при к/0 —0, применяя теорему о преобразова-
нии контура, исходную систему можно преобразовать к такой системе, где
число Wq, хотя, возможно, и весьма мало, но больше нуля
Леммы (12) и (18) мы докажем несколько позже. Сейчас,
используя эти леммы, перейдем к доказательству теоремы (8).
Доказательство теоремы (8). Обратимся к рис. 6.7, а
я б. Так как функции k+, и операторы т. т-1 обладают соот-
ветствующими свойствами, система, изображенная на рис. 6.7, а,
/Аустойчива тогда и только тогда, когда ZA устойчива система,
приведенная на рис. 6.7,6. Оператор прямой ветви mwk+= gk+
строго пассивен и имеет конечный коэффициент роста. Можно
показать, что условия, введенные в примере 7 (раздел 4), выпол-
няются (см. (10), (15) и (20)). Кроме того, функция tn(s)w(s)
аналитична при Res> — osh<0 и стремится к t^o>0 при |s|->
оо; следовательно, Re [tn (/со) w (/со)] 62 > 0 при любых о е R,
поскольку действительная часть аналитической функции достигает
своего минимума на границе области аналитичности.
Оператор ветви обратной связи k-ttr1 строго пассивен, по-
скольку условия примера 7 (раздел 4) соблюдены (см. (16) и
учесть свойства аналитичности и (19) функции ггг1 (s)). Таким
‘Образом, L2-устойчивость системы (рис. 6.7, б) вытекает из тео-
ремы о пассивности (5.10).
Доказательство леммы (12). Пусть Z(0 = log&(0. Так
как функция /: R+->R ограничена. Рассмотрим весовую
функцию треугольного вида
m fa—ПРИ
Н(0«=) Т
I 0 при t^>T.
Отметим, что Д (0 — 6(0 — [1 (0 — 1 (/ —Т)]/Т, где 1(0 —единич-
ный скачок. Определим функции
t
24. М0 - J[/ (T)]+p(/~T)dT
«. КРИТЕРИИ СРЕДНЕЙ ЛОГАРИФМИЧЕСКОЙ ВАРИАЦИИ
213
И
25. L (0 = l(t)-l+ (t).
Согласно условию (10), функция /+ ограничена на R: в самом деле,
26. 0</+(/)<2гТ V/=s0.
Так как функция / ограничена по условию, то ограничена и
функция L. Следовательно, функции k+ = exp 1+ и k_ = exp /_ огра-
ничены вдали от нуля и ограничены на |R+. И, наконец, из соот-
ношения (25) следует, что k (/) = k+ (t) k_ (t) при любых t^zO.
Таким образом, (i) и (ii) установлены.
Дифференцируя (24), получаем
t
i+ (0 = [/ (0]+ -1 [/ (т)]+ L [1 (Z - Т) - 1 (Z - т - Т)] dr.
Так как первый член неотрицателен, а второй член ограничен,
согласно (10), числом 2г, то Z+ (/) — 2г V/ 0, т. е. k+ (/) exp 2rt—
монотонно неубывающая функция. Аналогичным образом из (25)
выводим, что /_(0^2г V/^О, т. е. й_(/)ехр(—2г/) — монотонно
невозрастающая функция.
Нам осталось построить неантисипативный оператор свертки т.
Сначала мы установим метод построения неантисипативного опе-
ратора свертки с заданной фазовой характеристикой.
30. Лемма. Пусть задана фазовая характеристика со
со е IR, являющаяся нечетной, т. е. дифференцируемой функцией,
причем фо и ее производная ф0 принадлежат L4(|R). Тогда
(i) существует функция X е L1 (IR) такая, что X (/) = 0 при /<0 и
31. Im X (/со) = ф0 (/со);
(ii) существует функция zsL1^) такая, что г(/)=»0 при
/<0 и
32. 1 + z (/со) = exp [1 (/со)];
(iii) если для всех со е R выполняется неравенство
— п<Фо(/со)<л,
то
33. arg[l 4-f (/©)]== фо (/со), l+z(s)=#0 при Res^O.
Упражнение. Показать, что при <р0, ф0 е Р функция фв принадлежит L°°,
является равномерно непрерывной и ф0 -> 0 при | со ; оо. (Указание:
использовать лемму Римана—Лебега.)
214
ГЛ. в. ПАССИВНОСТЬ
Доказательство леммы (30).
(i) Так как ф0 s обратное преобразование Фурье этой
функции также принадлежит L? и
ф0</)=я2НоПт
О->ОО
1 /фо (/©) ехр (/со/) da>.
Поскольку фо и фо S L*, то фоеР (IR) (Приложение В.2.5). Вместо
нечетной функции / >—♦ <р0 (0 рассмотрим четную функцию ф, (/) —
=фо (0 Sgn t. Ясно, что фе (/) a L1 (R) и ф, (/©) при всех со принимает
действительные значения. Пусть X (() == ф, (/) -f- фо (0- Тогда X в L1 (R),
Х(0 = 0 при /<0 и функция X удовлетворяет соотношению (31).
Кроме того, X (s) — аналитическая функция, ограниченная при
Res^O.
(ii) Заметим, что
Зв. exp [X (/©)]. ехр [фе (/со)] exp [/фо (/«)]
И
оо
37. exp[X(s)]-2
л—О
Во временнбй области
38. г(О-Х(О + (Х*Х)(/) + ...+д-(Х*Х*...#Х)(О + ...
Так как XePflR) и |X*XJi^|X|v|Xh, очевидно, что ряд (38)
сходится по /.‘-норме и | z^ag exp (| X t)— 1. Поскольку простран-
ство L1 (R) полно, zePflR). И, наконец, согласно (38), г(/) = 0
при (<0.
(iii) Если — л <ф0(/®)< л, то мы вправе прологарифмиро-
вать равенство (38) (при этом выбранная ветвь логарифмической
функции пересекает отрицательную действительную полуось) и
arg[l 4-?(»] = фо(» VwsR.
Так как функция X аналитична и ограничена при Res 3s О, то,
согласно (37), функция l+z(s) мажорируется вдали от начала
координат в полуплоскости Res 3s О функцией ехр (—|X|li).
Доказав лемму (30), мы фактически установили, каким обра-
зом по заданной фазовой характеристике ф0 построить функцию
1 + z, которая вместе со своим обращением аналитична при Res>
>0 и ограничена при Res 3=0. Теперь с помощью этого резуль-
тата мы покажем, как построить усилитель т.
Доказательство леммы (18). Согласно условию (2),
функция w аналитична при Res5г — oSh> — По предположе-
нию, й> (/со — о,ь) 0 при любых со s R; следовательно,
ft ТЕОРИЯ УСИЛИТЕЛЕН
215
log [да (/<в — aSh)] — аналитическая функция при всех wsR. Поэ-
тому функция arg w (ja — oSh) корректно определена (с точки зрения
свойств диаграммы Найквиста) и является С°°-функцией от ® на
множестве R. Кроме того, arg да(/о — oSh)-^0 при |<oi->-oo, по-
скольку, согласно (6), да(/<й —о,ь)->да0>-0 при
Чтобы определить ф0, выберем частоту Q достаточно большой,
чтобы значение | arg да (/со — а,ь) I было малым при всех | со | > Q,
меньшим, например, величины л/12; тогда
41. фв(/со) =
— у arg [да (/® - osh)] при <о 1 < Q.
~ при | со i > Q,
где число се R выбрано таким образом, чтобы обеспечить непре-
рывность функции ф0. С учетом свойств диаграммы Найквиста и
способа построения (41) получаем
I Фе (» , < y . Ф» (/®) + arg [да (/со — osh)] | < у
для всех (osR.
Из (41) следует, что ф0, фве£Л (Производная фв определена
на R везде, за исключением точки | со | = Q, где она может иметь
скачок.) Согласно лемме (30), существует функция z (s), обладаю-
щая свойством (33). Пусть
44. т (s) = J [б (О -Ь z (/) ехр (— <W)] ехР (— s/) <ft =
о
= 1+z(s+ff5h).
Из (41), (44) и свойств z следует, что
(I) функции m(s) и m-1(s) аналитичны и ограничены при
Res^sO;
(II) функции со► m (/со — oSh) и со •—* т (jot — osh) w (/со — oSh)
равномерно непрерывны на R, при | со | -> оо стремятся к 1 и
дав>0 соответственно, а их фазовые характеристики принадлежат
интервалу (—л/2, л/2). Следовательно, существование чисел 61
и 6«, удовлетворяющих (19) и (20), доказано.
На этом мы закончим доказательство критерия логарифмиче-
ской вариации.
9. ТЕОРИЯ УСИЛИТЕЛЕЙ
Основная причина, вызывающая необходимость введения уси-
лителей, состоит в следующем: после умножения некоторых опе-
раторов на соответствующим образом выбранный «усилитель»
можно проверить, что полученное произведение удовлетворяет
условиям теоремы о пассивности. Например, функция
ГЛ. 6. ПАССИВНОСТЬ
2К
пассивна тогда и только тогда, когда Re[gr(/(o)]^ О, т. е. диа-
грамма Найквиста функции g лежит в правой полуплоскости.
При доказательстве критерия Попова вводится усилитель т (s) »
= l+?s, в результате чего упомянутое условие приобретает вид
Re [(1 о,
т. е. кривая <о •—* [gr (/®), <t>gt (/<о)] должна лежать ниже прямой
с коэффициентом наклона l/q, проходящей через начало коор-
динат. Таким образом, при изучении операторов свертки мы рас-
сматриваем усилитель, как средство для придания функции g (s)
свойства пассивности за счет того, что фаза функции/и (До) g (/<о)
изменяется в интервале (—л/2, л/2). Если /и (s) — дробно-рацио-
нальная и неантисипативная функция и и»—>tn*u отображает
L2 (R) в L2 (R), то т (s) может не иметь полюсов в замкнутой пра-
вой полуплоскости.
Необходимость выполнения последнего условия несколько
ограничивает выбор фазы. Если по такой причине мы допускаем,
чтобы функция rn(s) имела полюсы в правой полуплоскости, и
требуем, чтобы функция и*—+т*и отображала L2 (R) в L2(R), то
для нахождения ядра t m(t) по пг (•) мы должны выбрать
мнимую ось /со в качестве пути интегрирования при вычислении
обратного преобразования Лапласа. Отсюда следует, что функ-
ция /н-^/и(/) не равна тождественно нулю при /<0, т. е. уси-
литель не описывается неантисипативным оператором.
Поскольку в дальнейшем мы будем полагать, что усилители
вовсе не обязательно должны быть неантисипативными, наши
исследования начнутся изучением свойства антисипативности.
9.1. Неантисипативные и чисто антисипативные операторы
В этом разделе мы будем полагать, что — гильбертово
пространство над полем R со скалярным произведением
Поэтому (х, у) (х | у) — билинейное отображение. Обычно в ка-
честве 0%^ будут рассматриваться пространства L2(R), Ln(R), I2
или Рп. Пусть отображение Н переводит либо в самое себя,
либо е в самое себя. Напомним, что отображение Н называется
неантисипативным тогда и только тогда, когда из РТх = РтУ сле-
дует, что РтНх = РтНу при любых х, у^о& (или gJ%S) и любых
Т Это условие можно представить в ином виде: РТН =
= РТНРТ для любых Т е еГ'. Таким образом, «прошлая реакция»
неантисипативного оператора определяется только «прошлыми»
воздействиями. Напомним также, что если оператор Н неантиси-
пативен и Н: то его можно продолжить до отображе-
ния, также обозначаемого через Н, переводящего в
продолженное отображение Н определяется соотношением РтНх =
= РтНРтх для любых хЕеХг и любых Т Заметим, что
9. ТЕОРИЯ УСИЛИТЕЛЕЙ
217
если х е оЯГ,, то Ртх s т. е. элемент НРтх всегда корректно
определен. И, наконец, будем говорить, что отображение антиси-
пативно, если оно не является неантисипативным.
1. Определение. Отображение Н: называется чисто
антисипативным тогда и только тогда, когда из (I — РТ)х^
^(1 — Рт)У следует, что (Z — Рт)Нх = (1 — РТ)Н (/ — Рт) У для
любых х, и любых Т или, в эквивалентной форме,
когда (I — Рт) Н = — Рт) Н (I — Рт) Для любых Т Таким
образом, «будущая» реакция чисто антисипативного оператора
зависит только от «будущих» воздействий.
Упражнение 1. Пусть Н: и i—► h ♦ и, где h е Ll (R), и s L2 (R). Наложить
условия на h, при которых отображение Н: (а) неантисипативно; (Ь) чисто
антисипативно; (с) не является ни неантисипативным, ни чисто антисипативным.
Существование антисипативных операторов (как результат вве-
дения понятия антисипативного усилителя) приводит к некоторым
трудностям в применении преобразования Фурье для установле-
ния пассивности. Лемма (2) и упражнение 2 устанавливают по-
лезные факты.
2. Лемма. Пусть отображение /7: неантисипативно.
Тогда
3. {Эб>0: <х|Ях>^6||х||а V/GoT}
в том и только том случае, когда
4. {36^0: {и\Ни)т^&1хт12 Vxe^},
причем в (3) и (4) участвует одно и то же число 6.
Доказательство. Необходимость, Для любых и
Ut <2%
и
(и | Ни)т = (UTI (Ни)т) = (ит I (Ниг)т) = (ит I Ниг) S || иг||2,
где последовательно применялись условие (3.10), свойство неан-
тисипативности и условие (3). Следовательно, (4) выполняется
при S, использованном в (3).
Достаточность. Пусть в (4) и е переходя к пределу при
7->ээи применяя условие (3.9), приходим к (3).
Важность предположения о неантисипативности Н в лемме (2)
подчеркивает следующее упражнение.
Упражнение 2. Пусть Н: L2 (R)-> L2 (R), причем Hu — h^u. Пусть h(t)~
= 6 (0 + 1 (0 exp (— 0 + 1 (—0 ехР 0 f s R. Показать, что
(a) Re $ (/со)] 1 при любых о е R;
(Ь) (х | h * х) || xl|2 при любых х s L2 (R).
Найти и s L2 и Т е R такие, что {и | h * и}т < 0.
Отсюда следует, что в случае, когда отображение Н антиси-
пативно, условия (3) и (4) не эквивалентны. Напомним, что
218
ГЛ. (. ПАССИВНОСТЬ
согласно определению (4.2) отображение Н: называется
пассивным (строго пассивным, если 6>0), если Н удовлетворяет (4).
Пусть Н: -ь-aft'. Тогда, если условие (3) выполняется при
6 = 0 (8>0, соответственно), мы будем называть отображение
е%"'положительно определенным (строго t^-положительно опреде-
ленным). Понятие «^-положительной определенности вводится
для того, чтобы подчеркнуть специфику свойств операторов, опре-
деленных на множествах и в%^,.
Теперь лемму (2) можно переформулировать: если оператор
Н: неантисипативен, то он -положительно определен
(строго -положительно определен) тогда и только тогда, когда
он пассивен (строго пассивен).
5. Замечание. Если Я —оператор свертки, то условие (3) легко
проверить, используя теорию преобразования Фурье. Чтобы опре-
делить, выполняется ли условие (4), следует применить лишь
теорему о пассивности. Поэтому в дальнейшем нам иногда необ-
ходимо убедиться лишь в неантисипативности исследуемого опе-
ратора.
Введем понятие сопряженного отображения.
6. Определение. Пусть отображение И: <$%' линейно.
Отображение Н*, определенное соотношением
7. (х\Ну) = (Н*х\у) ^х,уе^,
называется сопряженным к Н. Если Н — Н*, то Н называется
самосопряженным отображением.
Упражнение 3. Учитывая, что (х, и) i——билинейное отображение,
показать, что отображения Н, Н*: йЛ линейны, если они являются
сопряженными друг другу.
Упражнение 4.
Показать, что (а) / и РТ—самосопряженные отображения;
(Ь) Н**=Н.
8. Лемма. Пусть отображение Н: линейно. Тогда Я
чисто антисипативно в том и только том случае, когда отображе-
ние Я*, сопряженное Я, неантисипативно.
Доказательство. Необходимость. Поскольку Я чисто
антисипативно для всех х, и всех ТбР, то
<х | (7 - РТ) Ну) = <х | (I - РТ} Н (7 - Рт) у),
откуда, используя определение (6), находим
<Я* (7 - Рт) х у) = <(/ - Рт) Н* (7 - Рт) х | у).
Так как у выбрано произвольным образом и еЗГ — гильбертово
пространство, то
РГН*(1 -Рт)х = 0 Чх<=<ЗГ.
Учитывая, что отображение Я* линейно, получаем РТН* =РтН*Рт-
Достаточность доказывается прослеживанием приведенных
рассуждений в обратном порядке.
9. ТЕОРИЯ УСИЛИТЕЛЕЙ
219
9.2. Схема метода антисипативных усилителей
Принимая во внимание трудности, вызываемые введением анти-
сипативных операторов, представим общую схему метода в сле-
дующем виде.
9. Утверждение. Пусть — гильбертово пространство над
полем R. Предположим, что существует усилитель А1, заданный
антисипативным отображением Af: представимым в виде
произведения:
10. Af = ALAf+, где AL, ©ЯГ причем отображения
Л41, Afz!, Aflj!: Ofопределены корректно.
Пусть, кроме того,
11. Отображение AL линейно, следовательно, ML и (All)-1
определены корректно;
Рис. 6.8.
12. Коэффициенты роста’ отображений Al, Af+, ML М *, Л171,
(All) 1 конечны.
Тогда, если одна из систем 5, SM и (рис. 6.8) является
£8-устойчивой, то £Аустойчивы и остальные две системы.
Упражнение 5. Доказать утверждение (9).
В большинстве приложений операторы Нг и Н2 неантисипа-
тивны. Поскольку оператор М антисипативен, этим же свойством
обладают МНг и Н2М. Если Л4+ —неантисипативный оператор,
то операторы подсистем системы Sm+, а именно М+Нг (All)"1 и
MLHiM+> также неантисипативны. Следовательно, для установ-
ления пассивности системы может быть применена лемма (2).
Следующая лемма устанавливает связь свойств операторов МН
и M+H(ML)~\
15. Лемма. Пусть Н-. и оператор М удовлетворяет
условиям (10) —(12). Тогда утверждения
220
ГЛ. в. ПАССИВНОСТЬ
1в. (i) существует 6^0 такое, что (и | МНи)^ б |и |2 при
любых и е и
17. (ii) существует 6' 5s 0 такое, что (х | М*Н (ML^x) 6' ||х|2
при любых х е <Эг
эквивалентны, причем числа б и б' одновременно либо поло-
жительны, либо равны нулю.
Доказательство. Пусть х, u&<ST и x — Atlu; тогда, со-
гласно (12), |х|^у(А11) |1и| и |«||«Sy [(AfL)_1]|x|. Поэтому
(и I А1Яи> = <и IМ_М+Ни) = (MLu | М+Ни) - <х | М+Н (ML)-1 х),
откуда немедленно следует эквивалентность (16) и (17).
Теперь мы можем сформулировать теорему.
20. Теорема. Рассмотрим систему S, изображенную на рис. 6.8,
где операторы Hi и Я2 неантисипативны и переводят «ЯГ в Ж.
Предположим, что при всех их, u2 е &/Г решения ех и е2 принад-
лежат е?Гв. Пусть, кроме того, существует антисипативный уси-
литель М: удовлетворяющий условиям (10) —(12) и (21):
21. операторы А1+, (A4+)-1, ML, (ML)-1 неантисипативны.
Тогда, если
22. (ij у (МН1)<ос;
23. (ii) при некотором б>0 (х | MHix)^ б ||х|а для любых
х е
24. (iii) (х | Я2Л4-1х) 0 для любых xseTT,
то система S является ГАустойчивой.
Доказательство. Система Sm+ удовлетворяет условиям
теоремы о пассивности. В самом деле, используя (22) и (12),
находим, что
25. y[M+Hi(ML)~']^
-С у [M_M^Hi (ML)-1 All] у [(AL)-1] у [(All)-1] <
< у [(Л!.)-1] у (MHJ у [(All)-1] < оо.
Применяя лемму (15) к (23) и (24) и учитывая неантисипа-
тивность операторов, получаем, что
26.
Поэтому согласно (5.27) система 8м+ £2-устойчива; следовательно,
в соответствии с утверждением (9) /Аустойчива и система S.
27. Замечание. Для доказательства теоремы достаточно пред-
положить, что операторы MHi и Н^М-1 являются -положи-
тельно определенными.
Главным этапом метода является факторизация оператора М.
Прежде чем излагать различные способы факторизаций, мы рас-
смотрим несколько примеров. Заметим, что в приложениях доста-
точно знать, что конкретный оператор М может быть факторизо-
ван, т. е. удовлетворяет условиям (10) —(12), но вовсе не обяза-
9. ТЕОРИЯ УСИЛИТЕЛЕН
221
тельно вычислять операторы М+ и М_. Теорема о факторизации (62),
приводимая в конце этого раздела, определяет достаточные усло-
вия существования операторов М+ и А1_ с требуемыми свойствами.
9.3. Примеры
Пример 1. Рассмотрим систему с обратной связью, представ-
ленную на рис. 3.1, где
28. H1ei = g*e1, g<=o4\
29. (Я2е2)(0 = ф[М)]»
причем функция <р: |R -> R монотонно неубывает, т. е.
30. |<р(а)-<р(р)](а-₽)^0 Va, pe=|R,
и существует такое £<оо, что <р принадлежит сектору [0, ft].
Отметим, что операторы Hi и //2, заданные соотношениями (28)
и (29), неантисипативны и переводят L? (R) в Ц (IR).
31. Теорема. Рассмотрим систему с обратной связью, опера-
торы Hi и Н2 которой определены соотношениями (28) и (29).
Предположим, что существует антисипативный оператор свертки М,
импульсная характеристика которого имеет вид
32. т (0 = 1 - z{t) = 1 - J (I - ft) - za (/),
— ОО
где
зз. Sl^|<oo, и ti(=R.
Допустим, что
34. |Z|= S |z.-l + kJi<l
и существует S>0 такое, что
35. Re [/ft (j(a)g (/to)] ^6> 0 VoieR.
Тогда, если либо
36. za (•) 0 и Zi Ss 0 при любых i,
либо
37. <p (•) —нечетная функция,
то система /Аустойчива.
38. Замечание. Из условий (32) —(34) вытекает, что
(а) М — линейное отображение;
(Ь) коэффициент роста по приращениям отображения М удов-
летворяют неравенству у(М)<_2',
(с) отображение М обратимо, причем М-1: L2 (R) -> L2 (R) и
Y(M-i)^(l -|Z|->).
222
ГЛ. «. ПАССИВНОСТЬ
Доказательство теоремы (31). Согласно теореме факто-
ризации (62), оператор М представим в виде произведения. Тогда
теорему можно считать доказанной, если будет показано, что
(a) y(Mffi)<Zoo;
(b) антисипативный оператор MHi является строго еХ”-поло-
жительно определенным (условие (23));
(с) оператор HtM~l является яЯГ-положительно определенным
(условие (24)).
Но
у(МЯ1)<2|^|л<о°.
условие (23) выполняется, так как по теореме Парсеваля
<х| МНгх} = ~ Re [/п (/®) g (/©)] | х (jot) |а d®
>6|х|« Vx(=L*(R)
оператор Н^М-1 является -положительно определенным, согласно
леммам (40) и (46). Следовательно, если факторизация М воз-
можна, то теорема справедлива.
40. Лемма. Если функция <р: монотонно неубывает и
принадлежит некоторому сектору [0, Л], где Л<оо, то для всех
х (•) е L? (R) и всех т е R
41. J x(t+x)(p[x(i)]dt^ f х(0ф[х(0]Л.
— СО —со
Если, кроме того, ф —нечетная функция, то
42.
СО 00
J x(t + x)q>[x(t)]dt «s J х(Оф[г(0]Л.
— ОО
Доказательство. Заметим, что из xeL4(R) следует, что
ф[х(-)] eP(R) и Ф[х( •)] sL1 (IR), где по определению d<b/di=
=<р (х), Ф (0) = 0. Так как ф монотонно неубывает, то для любых
MsR
р
43. Ф (а) — Ф (р) = J ф (g) (а — Р) <р (а) = аир (а) — Рф (а).
Полагая а = х(/), Р=х(/4-т) и рассматривая интегралы над
полем R, находим
44. $ х (0 ф [х (/)] dt — $ х (t 4- т) ф [х (/)] di 5s
— со —оо
{ф[х(0]Л- fФ[х(/4-т)]<//=0,
— ОО — ОО
откуда следует (41).
•. ТЕОРИЯ УСИЛИТЕЛЕН
223
Если функция ф нечетна, то Ф — четная функция, и, кроме
(41), имеем
f {х(0ф[х(0] + х(/ + т)ф[х(/)]}Л =
— 00
- $ \х (/) Ф [х (0] - [— х (t + т) ф [х (/)]]} di
—со
{ф1*(0И- fф[— х(/ + т)]Л = 0
— оо —оо
(здесь мы использовали (43) и свойство четности Ф), откуда выте-
кает (42).
46. Лемма. Пусть функция ф: R-»-R монотонно неубывает,
принадлежит сектору [О, Л], где Л<оо. Пусть оператор М удов-
летворяет условиям (32) и (33). Тогда, если либо
47. zo(/)^0 VleR и г,-2s0 Vi
либо
48. Ф —нечетная функция,
то справедливо неравенство (24).
Доказательство. Введем обозначение Z: х<—*г*х, хе
eZ?(R), где г(/)х=2гг6(/-/,) + го(0. Тогда M = I-Z, у(Л1)<2
и у (Л4-1) < схэ. Пусть v = Мх, тогда и е L2 (R) в том и только
том случае, когда xeP(R). Кроме того,
49. (v\HtM~1v) = {Mx]Hix) VveL2(R),
= <(7-Z)х| ф[%(.)]> VxeP(R),
откуда после раскрытия скалярного произведения правая часть
(49) приобретает следующий вид (все интегралы рассматриваются
над полем R):
J х (О ф I* (01 dt-[(z*x) (0 ф [х (/)] dt =
= $х(0ф[х(/))Л-2г4*а-6)Фк(0]<«-
— J г (т) (J х (/ — т) Ф |х (/)] dt} dx.
Используя лемму (40) и одно из условий (47) и (48), находим, что
50. <»|ЯаЛ1-1о>Х1-|г|)5х(0ф[х(0]^^0 Vt>e=L8(R),
где последнее неравенство следует из (34) и секторного условия.
Пример 2. Расвмотрим систему, аналогичную описанной в тео-
реме (31). Пусть оператор /71 задан соотношением (28), функ-
ция ф: R->R имеет ограниченную производную, т. е. для
224
ГЛ. 6. ПАССИВНОСТЬ
некоторых Р>0, 8>0 и a eR
51. а < а + Р — Д Vx, «/eR, х=#у.
х У
Если диаграмма Найквиста функции g (ja) не охватывает точку
(—1/а, 0), то рассматриваемую систему с помощью теоремы о пре-
образовании контура можно привести к системе, для которой
выполняется теорема (31).
Шаг 1. Введем усилитель с коэффициентом усиления —al
параллельно подсистеме Н2 и охватим обратной связью с коэф-
фициентом — а/ подсистему Новая нелинейность имеет вид
Н2 — а1 и описывается характеристикой о»—* <р (о) — ао, принад-
лежащей сектору [0, р — е]. Оператор линейной подсистемы равен
Hi(I -{-аН^-1 и представляет собой оператор свертки с импульс-
ной характеристикой, принадлежащей алгебре orf, поскольку g е
е оЛ и диаграмма Найквиста g (ja) не охватывает точку
(—1/а, 0).
Шаг 2. Охватим нелинейность положительной обратной связью
с коэффициентом (1/Р) I и введем усилитель с коэффициентом
(1/Р) Z параллельно линейной подсистеме; тогда результирующая
нелинейность имеет вид
52. (ZZ* —aZ)[Z —р-х(Л7а —aZ)]~x =
= (//2-а/)[(а + Р)/-Я2)]-1р/.
Отметим, что функция, обратная (52), существует, так как нели-
нейная характеристика Р~х (//2 — ос/) строго возрастает, а ее про-
изводная меньше (Р —е)/Р < 1. Линейная подсистема описывается
оператором
$-4 + Н. (/ 4-аАЛ)-1 = р-i [Z + (а+ Р) Ht] (/ +аН1)~\
И, наконец, замечая, что постоянные множители р и Р-1 могут
быть сокращены, что никак не повлияет на /^-устойчивость си-
стемы, получаем
53. Н2 = (f/2 - al) [(а + р) I - Н2]~1
и
54. Н. = [/ + (а + Р) Нг] (/ + аН^К
Характеристика нелинейности Н2 строго роз астает и принадле-
жит сектору [0, Р/е]. Импульсная характеристика подсистемы Нг
принадлежит алгебре оЛ. Таким образом, мы свели исходную
систему к системе, удовлетворяющей теореме (31).
9.4. Факторизация с помощью логарифмов
55. Лемма. Пусть eJF — гильбертово пространство, М — линей-
ное непрерывное отображение && в самое себя. Тогда, если
Л1—-положительно определенное отображение, отображение М"11
9. ТЕОРИЯ УСИЛИТЕЛЕЙ
определено, является линейным, непрерывным и переводит сЯГ
в то отображение logAl обладает теми же свойствами, что
и М1.
Рассуждения удобно проводить, используя понятие банаховой
алгебры. Класс [е%^] всех линейных непрерывных отображений,
переводящих гильбертово пространство в самое себя, пред-
ставляет собой алгебру. Сложение и умножение на число таких
отображений определены обычным образом. В качестве операции
умножения выбрана композиция отображений. Если, кроме того,
выбрать норму отображений как норму, порожденную нормой
в гильбертовом пространстве е%^, то
|/Ц=1 и |AMM^|AM|Af2j,
где /—тождественное отображение и Afb Af2 —произвольная
пара линейных непрерывных отображений, переводящих oft* в еЯГ.
Поскольку — полное прострагсгво, нормированная алгебра
[е>^] также полна, т. е. является банаховой алгеброй.
Доказательство. Пусть / —тождественное отображение,
определенное на и se(C. По определению, резольвента М
представляет собой отображение ь>—► (si — Af)-1, переводящее не-
которое подмножество множества С в е%^; область определения
резольвенты р(А1) является открытым множеством. Так как ото-
бражение Af-1 определено, является непрерывным, линейным и
переводит оХ" в то отображение (si — Al)-1 корректно опре-
делено в некотором открытом диске 5(0; г) с центром в начале
координат.
С другой стороны, так как отображение М непрерывно, его
спектр о(А1), т. е. множество С — P(Af), принадлежит диску
5(0; |А1|). Поскольку Af —линейно, является сЗГ-положительно
определенным и непрерывно, отображение (si — Af)-1 корректно
определено при всех Res<0. Следовательно, можно найти про-
стую замкнутую спрямляемую кривую Г, которая не касается
отрицательной действительной полуоси (в том числе и в начале
координат) и окружает спектр отображения М.
Пусть D — область, заключенная внутри Г. В области D и на
кривой Г функция $»—>logs аналитична, поэтому log М: I? (R)
->L2(R) задается интегралом Данфорда — Тейлора [43]:
log Al « log s (si — Af J-1 ds.
f
Упражнение. Показать, что отображение (s/—Af)"1 корректно определено
на при | s | > М [, является непрерывным и линейным. ^Указание;
ОО \
1 / MW I I
рассмотреть равенство (s/ — Af)"1= I Z — 1 == - / •1
»/,8 ч. Дезоер, М. Видьясагар
228
ГЛ. 6. ПАССИВНОСТЬ
Обозначим через класс операторов свертки М таких, что
М: и*-+т*иу где
56. т (/) = У /П/6 (/ — tt) + та (t),
—оо
причем {/п,} е I1, та (•) е Ll (R) и i(e|R при любых I. Отметим,
что М, вообще говоря, не является антисипативным оператором.
Af переводит L2 (R) в L* (R) и при всех и е L2 (R)
57. |Л1и1а<
< | и h sup
(д
lwt‘ + rha(l&)
— ОО
00
S
— оо
mt i + ;| mal'i
<1 и |2
Если обозначить сомножитель в скобках через | М |, то легко по-
казать, что функция | -|, определенная таким образом, представ-
ляет собой норму в а®. Поэтому Л1 е «г®— линейное непрерывное
отображение. Если М, N то отображения аМ (при
любых а е С), MN и NM также принадлежат <з%). По теореме
Фубини MN = NM и |AfA|^|Af||JV|. Так как единица / при-
надлежит «$?, получаем, что
58. —коммутативная банахова алгебра с единицей.
Определим Р+ —проектор на (следовательно, Р+Р+ = Р+).
Поскольку Ми = т*и,
59. = m(t — i)u (r)dx = j т (£) и (t — £) dg.
О —oo
Положим
00 t-j-
60. (P+Mu)(/) = J — £)d|= J tn (t — т) u (t) dx,
0— —oo
P+M — антисипативный оператор свертки, переводящий L2 (R)
в £2(R). Пусть
62.
P- = /-P+,
P-M — чисто антисипативный оператор свертки, переводящий
£2(R) в L2(R). Пусть а®с (э®а) — класс всех неантисипативны»
(чисто антисипативных) непрерывных операторов, определенных
на L2(R). Множества и замкнуты относительно операций
сложения, умножения (т. е. суперпозиции функций) и умножения
на число. Следовательно, <^с и — подалгебры Если нормы
Р+М и Р-М конечны, то Р+Л4 и Р-М принадлежат а®с и
соответственно.
9. ТЕОРИЯ УСИЛИТЕЛЕЙ
227
Упражнение 1. Показать, что ЛВ-5/еД, АтВп е при любых
т, п е Z+, если Л, В е о®с.
Упражнение 2. Пусть Л, В е Рлхл. Показать, что если матрицы А и В
коммутативны, т е. АВ = ВА, то ехр Л ехр В = ехр В ехр Л = ехр (Л -4-В). По-
казать на примере, что эти равенства, вообще говоря, не выполняются, если
АВ=£ВА.
62. Теорема факторизации. Пусть о®—банахова алгебра не-
прерывных операторов свертки вида (56). Пусть М g А Если
оператор М является -положительно определенным и М'1 е о®,
то в случае, когда || Р+ log М || и | Р_ log М | конечны,
(а) оператор М факторизуется:
63. М == Af_Af+, где А4_ е о®а, А1+ е <2®с;
(Ь) Alzp е Д и М2 е
Доказательство. Поскольку L2 (R) — гильбертово про-
странство, оператор М является -положительно определенным,
Al"1 е о®, то, согласно лемме (55), log М корректно определен
в поэтому Р+ log М и Р_ log М также корректно определены
в е®. Пусть
М+ = ехр (Р+ log А.'), А4_ = ехр (Р_ log А4).
Так как экспоненциальная функция аналитична в (D, то М+ и
М. — непрерывные операторы свертки, принадлежащие <а®с и о®а
соответственно. Тем же свойством обладают и их обращения, так
как
64. А4+1 = ехр (— Р+ log Al), All! = ехр (— Р- log М),
Поскольку А4+, Go® и е® — коммутативная алгебра,
65. М.М+ «= ехр (Р+ log М) ехр (Р_ log А1) =
«= ехр [(Р+ + Р-) log А4] х» ехр (log Af) — М.
Аналогичным образом можно показать, что Af+A1_»A1. И,
наконец, А!^1 е о®с, так как Р+ log М е в®с и
= ехр (- Р+ log М) - 2 •
««*0
67. Замечание. В приведенном доказательстве необходимо,
чтобы алгебра &J3 являлась коммутативной. Поэтому теорема не
выполняется, за исключением частных случаев, для операторов
свертки, переводящих Ln (IR) в L»(|R), из-за того, что их ядра
представляют собой матрицы, а произведение двух матриц, вообще
говоря, некоммутативно. По этой причине теорема (62) не приме-
нима к многоконтурным системам.
*/» 8*
ГЛ. в. ПАССИВНОСТЬ
2»
9. 5. Факторизация с помощью проекторов
В приводимой здесь теореме факторизации отсутствует условие
коммутативности банаховой алгебры.
68. Теорема факторизации. Пусть ^ — банахова алгебра с еди-
ницей 7. Пусть П+ —проектор на о%\ т. е. П+: Л?-> Л? — линейный
оператор такой, что П+П+ = П+ Определим проектор П_ соотно-
шением
69. П_ = /-П+,
где / — тождественное отображение на S3. Предполагается, что
70. |П+|< 1 и |П_|^1.
Пусть S3* и ДЕ —множества значений операторов П+ и П_ соот-
ветственно. Предполагается, что S3* и S3. — подалгебры, т. е. оба
множества замкнуты относительно умножения. Пусть Af е S3.
Тогда, если существует оператор такой, что
71. |Z|<1
и
72. Af = 7-Z,
то
(i) оператор М может быть представлен в виде
73. М = 7 — Z = Af.Af+, ’где Af_, Af+ е а®, причем Af_ и Af+
обратимы в Д?;
(ii)
74. Af_, (АЕ)-1 е 7
75. Af+, (Af+)-le/e^+,
где 7 ® <а®+ (7 ® S3.) — подпространство всех элементов из S3 вида
а/4-Af, где aeR, Af еД. (S3-, соответственно).
76. Комментарии. (I)
(I) Здесь отсутствует предположение о коммутативности бана-
ховой алгебры Д?, что очень важно для применения теоремы
к многоконтурным системам.
(II) Из (71) и (72) следует, что |А11 4-jZ|<2. Если неко-
торый заданный элемент N должен быть факторизован, но его
норма не меньше 2, то может быть введен числовой множитель
и элемент N представлен в виде —
(Ill) Чрезвычайно важными условиями являются (70) (посколь-
ку проекторы в нормированных пространствах не обязательно
удовлетворяют неравенствам (70)) и то, что S3, и S3± — подалгебры.
Доказательство теоремы (68) основано на следующей лемме.
79. Лемма. Пусть {Q*}» {№*} (6=1» 2, ..^ — последова-
тельности в Д?+ и S3. соответственно. Предположим, что при
9 ТЕОРИЯ УСИЛИТЕЛЕЙ
229
Jr|<гс, где re®, rceR и гс>0, степенные ряды
80. I 4- 2 Qkr" = Q (г),
1
81. Z + 5/V* = P(r),
1
82. I + 2^ = А^(г)
1
сходятся. Отсюда вытекает, что Q, Р и N — аналитические функ-
ции от г в В(0; гс), принимающие значения из Ж /фД?+,
соответственно. Тогда, если эти функции связаны соотношением
Q = P/V, то последовательность {Qfr}cz<^ однозначно определяет
последовательности {Pk} cz и _
Доказательство. Подставим в соотношение Q — PN выра-
жения функций в виде степенных рядов; затем, используя хорошо
известную теорему об аналитических функциях, приравняем
коэффициенты и получим:
Qi = Pi + Nit
откуда
Р^П+Qi, A/^rLQx,
и
fe—1
Qk = Pk + Uk+ *=1.2......
i = 1
откуда
Р* = пД&- £Р*_лА fe=l, 2,...,
' i = i /
и аналогичное соотношение для Nk (£=1, 2, ...). Таким образом,
все Рк и Nk однозначно выражаются через Qk последовательными
подстановками.
Доказательство теоремы (68).
Шаг 1. Рассмотрим следующие уравнения при |r | 1:
84. P = f+(P) = Z4-rn+(ZP),
85. N = f- (N) = I + гП- (Л/Z),
где для упрощения обозначений мы используем символы Р и
N вместо Р (г) и N (г). Функции /+ и /L представляют собой
сжатие в самом деле, для любых Рх, Р2
86. n+(Pl)-f+(P2)ll = kn+[Z(P1-P2)]||<|r|BZ|||Pi-P2|,
где сначала мы использовали свойство линейности оператора П+
и дистрибутивный закон в Д?, а затем применили (70). Так как
3 Ч. Дезоер, М. Видьясагзр
230
ГЛ. 6. ПАССИВНОСТЬ
|r||Z|< 1, f+ —сжатие «ЗЭ. Аналогично доказывается, что f- —
сжатие
Таким образом, Р и N вычисляются методом последовательных
приближений при P0 = N9 = I: снова используя линейность и
дистрибутивный закон, получаем:
87. Р-/ + £Р*г\ # = / +
1
где Pft+i = II+(ZP*), NM = П_(NkZ), k = 0, 1, 2, ... Кроме того,
при всех k Pk е <^+, JV* е <$?_, Р <= I ф «®+, N е I ф е®_. Реше-
ния Р и N — аналитические функции в с®(0; |Z|-1), причем
88. |Р|<(1 - |r ||Z|)-\
и аналогичное неравенство справедливо для
Шаг 2. Вспоминая, что П+4-П_ = /, из уравнений (84) и (85)
находим:
89. (/— rZ) Р = / — гП_ (ZP),
90. JV(/-rZ) = /-rn+(AZ).
По условию, | Z | < 1, поэтому при | г | < | ZI-1 (7 —rZ)’1eo50
ОО
и равен сумме степенного ряда У ZM, сходящегося в <а® (0; | Z Ц-1).
о
Используя (70) и (88), получаем
|rIL(ZP)|<|r||Z||P|<
Аналогичная оценка имеет место для |гП+ (NZ) Поэтому эле-
менты 7 — г\ 1_ (ZP) и 1 — гГ1 + (NZ) алгебры • обратимы при
| г | < || Z Ц-1/2. Обратные элементы определяются степенными рядами,
сходящимися в с-lZ? (0; || Z и принимают значения из /ф<^_
и 7фЖ- Тогда из (89) и (90)
91. (7 - rZ)-1 = Р [1 - гП_ (ZP)]-1 = [/ — гП+ (7VZ)]1 N.
Так как в (91) пять степенных рядов имеют общую область схо-
димости, а именно диск (0; |)Z||-1/2), единственность решения
устанавливается с помощью леммы (79), причем
Р = [I - гП+ (WZ)]-1, 2V = [7 гП_ (ZP)]1
и
92. (I — rZ^ — PN.
В (92) операторы (7—rZ)"1, Р и N представляются степенными
рядами, сходящимися при \г (< | Z Ц”1. Подставляя г=1, находим
93. 7 — Z = Л/-1?-1 = М^М±9
ТЕОРИЯ УСИЛИТЕЛЕЙ
231
где Л14. = Р1, ЛЕ = АЕ1. Все свойства ЛЕ и М+ установлены
в процессе доказательства.
94. Применение. Применим теорему факторизации в следующем
частном случае. Пусть — банахова алгебра, определенная в
разделе 5.9.2, а именно — множество обобщенных функций /(•)
вида
95. НО» 5 М(/-6) + /И0.
£ = —ОО
где /,ер, причем /,<0 (=0, >0) при i<0 (t = 0, >0 соот-
ветственно);
S lAKoo,
£ = —оо
М-)= R-*R И fa(-)eL4R).
Обозначим через e^x'1 множество (пхп)-матриц, элементы которых
принадлежат . Пусть матричная функция F (•) вида
96. F(0= £ ^(/-^ + ^(0
£ = —-00
является элементом выберем норму:
97. |FU= Е 1Л1 + Г\Fa(t)\di,
1 =— ОО —оо
где | • | — произвольная норма отображения в Клхл. Произведение
двух элементов в определено как их свертка. При этих
условиях легко проверить, что *п — банахова алгебра, 1 • S (/) —
единица и алгебра <s^7Xrt некоммутативна, за исключением
случая п=1.
Пусть — подмножество о^хп, состоящее из элементов
F(), удовлетворяющих условиям
98. Fi = (^Vi<(K Fa(t) = O V/<0.
Тогда — подалгебра ^лхл, содержащая единицу. Опреде-
лим <?rfnxn — подмножество о4пх\ состоящее из элементов F { ),
удовлетворяющих условиям
99. F,= 0 Vi>0, Fa(t) = O V/>0.
Множество также является подалгеброй с^лХп, содержа-
щей единицу. Если рассматривать как множество всех
импульсных характеристик устойчивых систем с п входами и п
выходами, то множество е/^_хг/ составляют все неантисипативные
8*
232
ГЛ. 6 ПАССИВНОСТЬ
импульсные характеристики из a^,xn, a s^lXn состоит из всех
чисто антисипативных импульсных характеристик, принадлежащих
алгебре е^хп.
Определим операторы П+: и П_; хл
в следующем виде:
(П+Л (/) = J Л6 (t - h) + ?а+ (О,
<=о
(П_Г)(/)= £ W-tt + F^t),
i =— ОО
где
Fa. (0 =
Fa(t),
О,
/<0;
Fa(t), /<0,
о,
Можно показать, что П+ отображает о^Хп в е^+Хп, П*=П+
(т. е. П+— проектор) и область изменения П+ в точности совпа-
дает с <2т^ХХП- Аналогичным образом показывается, что П_ отобра-
жает о^*Хп в <2т^1хл, 1Г = П_ и <2^1хп представляет собой пря-
мую сумму тождественного оператора / и области изменения П_.
Кроме того, из определения (97) нормы в алгебре вытекает:
VFe^Xn>
т. е. |П+||^1, ЯП_|< 1.
Поскольку выдвинутые предположения составляют условия
теоремы факторизации (68), мы получаем следующую теорему.
101. Теорема. Пусть М причем M = /—Z, где
|ZU< 1. Тогда оператор М представим в виде
102. M = MJW+,
где операторы Л1_ и Л4+ обратимы в
103. Mzl^<^nXn и М+,
104. Замечание. При разложении в произведение логарифмов
(см. теорему (62)) нормы проекторов Р+ и Р_ могут быть боль-
ше 1, однако банахова алгебра, элементами которой являются эти
проекторы, должна быть коммутативной. В теореме (101) нормы
проекторов П+ и П_ не должны превосходить 1, однако банахова
алгебра может не обладать свойством коммутативности.
10. СВЯЗЬ ТЕОРЕМ О ПАССИВНОСТИ
И О МАЛОМ КОЭФФИЦИЕНТЕ РОСТА
В разделе 5.8 мы построили одну из форм критерия Попова,
используя теорему о малом коэффициенте роста, а в разделе 6.6.1
для построения того же критерия применили теорему о пассив-
10. ПАССИВНОСТЬ И КОЭФФИЦИЕНТ РОСТА
233
ности. Судя по этим результатам, можно заключить, что указанные
теоремы связаны друг с другом. Однако важно понимать, что они
вовсе неэквивалентны. Действительно, обращаясь к формулировкам
теоремы о малом коэффициенте роста (разделы 3.1 и 3.2), мы видим,
что эти теоремы справедливы в нормированных пространствах
(Д, Ln, L™ и т. д.), в то время как теорема о пассивности
выполняется в пространствах со скалярным произведением (обычно
в гильбертовом пространстве, прототипом которого является
пространство L2). Ниже мы выясним, какие дополнительные усло-
вия необходимы для обеспечения «эквивалентности» названных
теорем.
На связь свойства пассивности с коэффициентом роста ука-
зывает и следующий пример, заимствованный из теории линей-
ных цепей Рассмотрим линейный стационарный п-полюсник,
заданный матрицей полных сопротивлений Z. Если v и i —
изображения по Лапласу напряжения и тока, действующих на
полюсах схемы, то
1. £> = Zi.
Такой п-полюсник можно также задать матрицей рассеяния S,
связывающей падающую волну а с отраженной (рассеянной) вол-
ной Ь:
2. b = Sd.
Вводя, как это обычно делается, нормализующую линию
передачи с сопротивлением 1 Ом, будем считать, что
3. v = b + d, t=d — b-
Следовательно,
4. S = (Z-I)(1 + Z)-L
Из физических соображений ясно, что если линейный стационар-
ный п-полюсник пассивен (т. е. Z — пассивный оператор, или,
как принято говорить в теории цепей, Z — положительно полу-
определенная матрица), то энергия отраженной волны b не больше
энергии падающей волны d. Таким образом,
5. оператор Z пассивен тогда и только тогда, когда
Y(S)^1.
Это предположение, взятое из теории линейных стационарных
n-полюсников, дополняет общие положения, введенные в раз-
деле 3, и уточняется в следующей лемме.
7. Лемма. Пусть Н. —> <2%^е. Предположим, что отобра-
жение
8. (/+//)’1:
234
ГЛ. в. ПАССИВНОСТЬ
существует. Определим отображение S: соотношением
9. S = (//-/)(/ + Н)-1.
Тогда
(а) отображение Н пассивно с постоянной ₽ = 0, т. е.
10. <flxlx)rs&0 VTeaT,
в том и только том случае, когда коэффициент роста S не пре-
восходит 1, т. е.
11. | Sy |» | у VTeaT;
(b) отображение Н имеет конечный коэффициент роста у
с аддитивной постоянной 0, равной нулю, т. е.
12. 8Ях|г^у|х|т Vxe^, VTe=r,
и строго пассивно, т. е. существует 8>0 такое, что
13. <//х|х>г^8|х|2т Vxe?Tf. VTeeF
в том и только том случае, когда коэффициент роста S меньше 1,
т. е. при некотором у'е (0, 1)
14. VTeeF.
Упражнение 1. Учитывая, что оператор Z в (4) линеен, показать, что
S = (/ 4-Z)“l (Z— /). (Указание: вычислить разность между этим выраже-
нием и (4), указать, когда используется свойство линейности Z.) Показать
примере, что в нелинейном случае (// — I) (I+ Я)-1 ¥= (/4-И)"1 (Н — I)
15. Комментарий. Согласно лемме (7), если выполняется усло-
вие (8), ;О во всех тех случаях, когда оператор «полных сопро-
тивлений» Н пассивен, коэффициент роста соответствующего опе-
ратора «рассеяния» S не превосходит 1, и наоборот; кроме того,
если только оператор «полных сопротивлений» Н строго пассивен
и имеет конечный коэффициент роста, то коэффициент роста опе-
ратора «рассеяния» S меньше 1. В отличие от обычных для тео-
рии цепей построений, в лемме (7) не предполагается, что опе-
раторы Н и S линейны или стационарны.
Прежде чем приступить к доказательству леммы (7), устано-
вим несколько тождеств. Каждому у из поставим в соответ-
ствие х из
16. г = +
Тогда
17. Sf/ = (7/-/)x, // = (/ + Юх.
Отсюда
18. =||//х!2г+!хГг-2<х Нк)т
и
1». IУ |2Г = \Нх Гг + к Гт + 2 <Х I Н х) г.
10 ПАССИВНОСТЬ И КОЭФФИЦИЕНТ РОСТА 235
Таким образом, для всех и ГеаГ
20. |$уГг = |Яг-4<х|Ях>г.
Доказательство леммы (7).
(а) Эквивалентность (10) и (11) следует непосредственно из (20).
(Ь) Необходимость. Учитывая (12) и (17), из (13) получаем,
что
4 (х | Нх)т46 J х|’г Ss \у 2s у'1у рг,
где у' удовлетворяет неравенству 0<у'<тах[1, 4в(1+у)-1].
Подставляя последнее неравенство в (20), выводим (14).
Достаточность. Подставим (20) в неравенство (14):
4{x\Hx)r^y'iyfT = у' [|Ях|г+ ||хЦг 4-2 <х| /7х>г].
Поскольку у's (0, 1),
(х\Нх)Т^^1хГт.
где у* = у7(4 — 2у') > 0. Следовательно, отображение Н строго
пассивно, причем р = 0, т. е. выполняется неравенство (13).
Исключая у из (14) с помощью тождеств (18) и (19), получаем,
что
у'|Ях|8г^(4^2у')|Ях|г|х|г-у'|1х|’г.
Отсюда следует справедливость условия конечности коэффициента
роста, если положить у = (4 — 2у')/у'.
Упражнение 2. Построить блок-схему системы S, полагая, что под-
система Н задана. (Указание: 5 = 2Я(/4-//)4-/; S = — (//2)х
Хр + (^~ /) ( 2~ ’ иметь в виду, что в нелинейном случае Н • 2/ у= 21Н.)
Упражнение 3. Объяснить, в чем важность предположения (8), рассмат-
ривая систему, в которой оператор Н: строго пассивен, имеет
конечный козк{х|)ициент роста, но отображение / + Н необратимо. (Указа-
ние- принять <^={0}, =|R и вспомнить результаты, приведенные
в главе 1.)
Упражнение 4. Предполагая, что условие (8) выполняется и оператор Н
пассивен по приращениям показать что коэффициент роста по приращениям S
не превосходит 1.
Чтобы выявить связь теоремы о малом коэффициенте роста и
теоремы о пассивности, рассмотрим систему S, заданную уравне-
ниями
24. =et 4-/7ге2, u2 = es —
где £1, е2 <= „ Яь Я2 отображают в самое себя.
Применим теорему о преобразовании контура (3.6.3) к системе S,
выделяя отдельные шаги.
236
ГЛ б ПАССИВНОСТЬ
Подсистема Ну прямой ветрд
Введем обратную связь с коэффици-
ентом — 1:
Нх(!+Н^
Умножим на 2 выходной сигнал:
2Я, (/ + //!)->
Введем параллельную ветвь с коэф-
фициентом — 1: ,
2Я. (/ + Н,)-1-/-
= (Нх-1) (J+HJ-1-St.
Подсистема Нъ ветви обратной связи
Введем параллельную ветвь с коэф-
фициентом — 1:
Н2 — 1
Умножим на 1/2 входной сигнал:
(«2-0 (р)
Введем обратную связь с коэффици-
ентом — 1:
(W2- /) (4 /)[/+(//2-/)(Р)]'1 =
= (Я,-+ = Sa
Можно показать, что при описанном преобразовании системы S
входные воздействия и и2 следует заменить на — и2 и +
4- и2 соответственно. Полученная система S изображена на
рис. 6.9. Теорема о преобра-
зовании контура (3.6.3) позво-
ляет заключить, что система 3,
заданная уравнениями (24), -
устойчива тогда и только тогда,
когда -устойчива система S,
Рис 6.9.
при условии, что отображения
(Z-J-Z/i)-1, (Z + /72)-1: е существуют.
Теперь мы сделаем два замечания:
(а) Если НА удовлетворяет условию пассивности (10), Н2
удовлетворяет условиям конечности коэффициента роста (12) и
строгой пассивности (13), то, согласно лемме (7), у (Sx) 1 и
у(32) =С(1 — ?')< 1. Тогда по теореме о малом коэффициенте
роста (3.2.1) система S является ^'-устойчивой, следовательно,
в силу теоремы о преобразовании контура система S также -
устойчива;
(Ь) Если у (Si) 1 и y(S2)^(l — у'Х 1, то Нг удовлетво-
ряет (10), Н2 удовлетворяет (12) и (13); поэтому, согласно тео-
реме о пассивности (6.5.10), система S является ^Г-устойчивой;
тогда по теореме о преобразовании контура оЗГ-устойчива и
система 3.
Мы нигде не говорили, что теоремы о пассивности и малом
коэффициенте роста эквивалентны в том смысле, что, если
-устойчивость системы можно установить, используя одну
из этих теорем, то такой же вывод можно сделать и с помощью
другой теоремы. С одной стороны, теорема о пассивности сфор-
мулирована для пространств со скалярным произведением, в то
время как теорема о малом коэффициенте роста справедлива для
11. ОБРАТИМОСТЬ ОТОБРАЖЕНИЯ / + Н
237
нормированных пространств. С другой стороны, могло бы пока-
заться, что необходимо выполнение условия о существовании
обратных отображений (I + Hi)-1, (/ + //2)"1’ e^e-*Q%Fe- Однако
ничего не изменится, если (/-{-/Л)”1 и (/ + //2)_1 рассматривать
как отношения, обратные I + Hi и
В следующем разделе мы установим условия, при которых
отображение I + H обратимо.
И. ОБРАТИМОСТЬ ОТОБРАЖЕНИЯ 1+Н
При исследовании систем с обратной связью мы постоянно
сталкиваемся с уравнением вида и = (1 +Н)е. Если известно, что
отображение I + H обратимо в некотором пространстве (обозначим
его через е%^), то при любом и е Ж уравнение имеет единст-
венное решение в Заметим также, что для корректного
использования теоремы о преобразовании контура мы должны
быть уверены, что отображение I -\-KHi обратимо. Ниже мы при-
ведем две теоремы, определяющие условия обратимости этих
отображений. В обеих теоремах рассматриваются пространства
со скалярным произведением.
1. Теорема. Пусть — гильбертово пространство и F:
-><2?Ге. Предположим, что отображение F строго пассивно по
приращениям и имеет конечный коэффициент роста по прираще-
ниям, т. е. существуют 6>0 и у<оо такие, что
2. (Fx — Fx' |х —х')г^6.|х —x'|r
Vx, х' g= VT (= dT,
3. [Fx-Fx'Jr^ySx-^ Sr-
Тогда
(i) отображение F является биекцией из на <э%^, т. е.
корректно определено отображение F-1, переводящее Ж е в
(ii) отображение F~l имеет конечный коэффициент роста по
приращениям: у (F-1) 1 /6;
(iii) отображение F1 удовлетворяет условию
4. {F-Ч - F-4 \2-z'}T^ F-1* - F-1?' ||2г
Vz,
Упражнение 1. Показать, что из (2) и (3) следует, что у >5 6.
Упражнение 2. Показать, что из (3) следует неантисипативность отобра-
жения F, а из (4) — неантисипативность отображения F-1
Условие (3) имеет следующий смысл: для всех Т е еГ' неанти-
сипативное отображение F* равномерно (по Т) .непре-
рывно по Липшицу в целом в пространстве Рт^е с постоянной
Липшица у. Аналогично, согласно (ii), при любых ТеоГ
неантисипативное отображение F-1: равномерно непре-
рывно по Липшицу в целом в Рт^е с постоянной Липшица 1/6.
238
ГЛ. 6. ПАССИВНОСТЬ
Доказательство теоремы (1).
(i) Согласно упражнению 1, у ^>6. Выберем произвольным
образом г из и отличное от нуля число а. Тогда уравнение
z = Fx эквивалентно уравнению
5. x = az + x — aFx = f(x, г).
Если а = 00 = 6/7*, то функция Д определенная уравнением (5),
представляет собой сжатие PT^fe. Действительно, используя (2)
и (3), при любых Т е <£Г и любых х, х' е получаем
в. lf(x, z)—f(x'9 z)lr = [x — xf — a(Fx — Fx')lT =
= | x — x' (J- — 2a (x — xf | Fx — Fx’}T + a21 Fx — Fx’ |r
^|x-x' |Hl-2aS + a272].
Минимизируя правую часть (6) по а, находим, что ее минимум
&J== 1 — (62/у2) достигается приа = 6/у2. Поэтому постоянная сжа-
тия меньше 1 и не зависит от Т. Следовательно, при произ-
вольно заданном г е <2%^ существует одно и только одно реше-
ние х е удовлетворяющее уравнению (5). Этот вывод экви-
валентен тому, что отображение F-1, переводящее в самое
себя, корректно определено.
(ii) Из (2) следует, что
I Fx — Fx' |г 61 х — х' |г Vx, х' е УТ е
откуда, полагая г = Гх и х = Г-1г, находим:
7. Vz, z'<=£Ге,
О
(iii) вытекает из (2), если заменить х' и х на F^z' и FAz
соответственно.
8. Следствие. Пусть F — неантисипативное линейное отобра-
жение, переводящее off, в и обладающее конечным коэф-
фициентом роста. Тогда, если F строго пассивно, то отображе-
ние Г-1 является неантисипативным линейным строго пассивным
отображением в самое себя, причем
{F^z\z}T>^\F-4\T Vz^^Tei УТе=^Г.
Доказательство очевидно: требуемые свойства вытекают из
условий (2) и (3) для линейного отображения F.
В следующей теореме показано, что условие конечности коэф-
фициента роста по приращениям теоремы (1) можно заменить
условием непрерывности.
10. Теорема. Пусть — гильбертово пространство, простран-
ство Рг^ е полно при всех Те зГ и F: Предположим,
что для каждого Т е зГ отображение PtF, переводящее Ртъ%\
в „ непрерывно. Тогда, если отображение F строго пассивно
11 ОБРАТИМОСТЬ ОТОБРАЖЕНИЯ 1 + Н
239
по приращениям, т. е. существует 6>0 такое, что
И. (Fx — Fx' |х — х')г^6|х — х'|г Vx, х'ео5Гг, УГезГ,
то
(а) отображение F является биекцией на
(Ь) коэффициент роста по приращениям отображения F"1 не
больше в’1.
12. Комментарии. В теории систем с обратной связью теорема
(10) применяется следующим образом. Предположим, что Н: оЖ\->
и при всех Т отображение РТН- Рт<^?-+ Рт^Т* непре-
рывно. Тогда
(а) если отображение Н пассивно по приращениям, то (/ ф-Я) —-
биекция на и коэффициент роста по приращениям отоб-
ражения (/ф-//)-1 не превосходит 1;
(Ь) если отображение Н строго пассивно по приращениям
(с постоянной бн), то (/ф-Я) — биекция на и коэффици-
ент роста по приращениям отображения (/ф-W)-1 не превосхо-
дит (1 4-бн)-1.
Упражнение 3. Привести пример отображения Н оХ обладаю-
щего конечным коэффициентом роста по приращениям, являющегося строго
пассивным (но не пассивным по приращениям), для которого отображение
PrH' Рт£%\ непрерывно, однако отображение (/ф-Z/)"1 необра-
тимо (Указание: принять = <£7"={0}, г е. Н задано своим гра-
фиком в R2. Выбрать Н так, чтобы при некотором у е R уравнение (/ф-Я)г/ =
= 0 имело бы несколько решений; отсюда последует, что (/ф- является
отношением, а не функцией. Использовать результаты, полученные в главе Г.)
Доказательство теоремы (10). Из (11) и неравенства
Шварца получаем:
| Fx — Fx' Ы х — х' |т (Fx — Fx'! х — х'> т 6 J х — х' |г.
Поэтому
12. J Fx — Fx'|'r^6l|x — xz||r Vx, xz e
откуда следует, что F —взаимно однозначная инъекция на
Таким образом, функция F'1 определена на множестве значений
e^(F) отображения F и, согласно (12),
13. У И —/Ь Vt/, t/'ee^(F), VTeaT.
Слелозательпо, коэффициент роста по приращениям F-1 конечен
на (F). Легко показать, что из непрерывности F и неравенст-
ва (13) вытекает замкнутость off (PTF) (см. упражнение 4, приве-
денное ниже).
Остается показать, что (F) = <2%^. Для упрощения выкла-
док положим 6=1 и (11) и определим Н\ е уравне-
нием
14. Fx = (/-b/f)x или F = I-{-H.
240
ГЛ 6 ПАССИВНОСТЬ
Тогда, поскольку Н непрерывно на Рто%Се, из (11) при 8 = 1 вы-
текает, что
15. (Нх-Нх'\х-х')г^ Vx,x'e=£fe,
т. е. отображение Н пассивно по приращениям. Пусть S: е^? (В)->
задано соотношением
16. S = (Н -/)(/ + Я)'1,
поэтому, если у и х связаны соотношением y = Fx, то
17. y = Fx<=3> у = х + Нх<=э Sy = Hx — x.
Поскольку Н пассивно по приращениям, то S: (F)е
имеет коэффициент роста по приращениям, не превосходящий 1
(см. упражнение 4, раздел 10). Следовательно,
20. WSy-Sy’^Wy-у'Ъ Vy,y'E=^(F), VTf=dT.
Хорошо известно (см. [61]), что отображение PfS, переводящее
замкнутое множество (PTF)czPT^e в Рт^е и удовлетворяющее
условию Липшица, подобному (20), может быть продолжено отоб-
ражением 5: Рт^е-> Рт^е> Для которого условие (20) выпол-
няется.
Определим отображение В: в виде В: //>—>
G/ —5у). Тогда на множестве е^(В)
2i. в= t(/-s)=4R-(^-/)a+^)-1i =
» | [(/ + Я) - (Н - /)] (I + Я)*1 = (/ + Я)-1 - F-\
Другими словами, FB=I на множестве <=% (F). Покажем, что
отображение В является обратным отображению F на всем про-
странстве т. е. (F) — о%Се. Выберем произвольным обра-
зом у е off е и определим
22. х = Ву.
Докажем, что Fx = y или FBy=y при любом у е т. е. что
В —обращение F на всем Доказательство проведем методом
от противного, предполагая, что при выбранном у е сущест-
вует некоторое Т ^оГ такое, что
23. \\y-Fx\\T>Q.
Поскольку отображение И непрерывно на Рто%Се, существует
> 0 такое, что
24. ||х —*||г>г)=>||Ях-Я.Пг^4\3-Fx |г.
Выберем х0 = * + X (у — Вх), где X> 0 — достаточно мало, чтобы
12. ТЕОРЕМЫ О НЕУСТОЙЧИВОСТИ
241
||хп — Х|г<т). Для выбранного х9 определим у0 соотношением
yo = Fxo = Xo + Hxo.
Таким образом, yoEe^(F) и Ву0 = х0. Используя (21) и раскры-
вая скалярные произведения, находим
25. (уь-д- (Ву0 — Вд) | (Ву0 — Ву))т =
= (Уо - у) +• у ($уо - sg) | -J (у» - 0) - у (Sy0 - Зд)}г-
= ||1й-^3т-Ч |$0о- Ws*0,
где последнее неравенство получено в соответствии с (20). Так
как Вуь — хь и Х = Ву, то (25) принимает следующий вид:
27. <Уо-д — (хо-Х)\хо-Х')1^Ъ.
Вспомним, что ya = Fx0 = (l -\-Н)х« и
х0 - х = X (д - Fx) = X (д — х - Нх),
и перепишем (27) с учетом того, что Х>0:
(Нхо-д + х\д-х-Нх}г^О.
Добавляя и вычитая НХ и замечая, что Fx = Х-\-НХ, находим
</7х0 — Нх — (д — Fx)\g — Fx)T^0,
или
30. (Hx-Hx\g-Fx)T;^g-Fx\fr.
Отсюда с учетом неравенства Шварца и (24) выводим:
2-10- FXlt ^lg- FXfr,
что противоречит предположению (23). Следовательно, отобра-
жение B — — является обратным отображе-
нию F = I-{-H на и off(F)==Q%Ce. Таким образом, F =
= (7 4-/7) —биекция на Часть (Ь) теоремы (10) следует
из только что доказанного и неравенства (13).
Упражнение 4. Показать, что отображение PTF непрерывно и из (13) сле-
дует. что (Р^/7)— замкнутое подмножество множества PT^fCg (Указа-
ние: рассмотреть сходящуюся последовательность использовать
условие (13) и свойство непрерывности PTF.)
12. ТЕОРЕМЫ О НЕУСТОЙЧИВОСТИ
В этом разделе мы выведем критерий неустойчивости, по
своей форме похожий на критерий Попова, излагавшийся
в разделе 6. Как и в разделе 5.9.1, наши теоремы основаны на
методе ортогональной декомпозиции L2, и при их доказательстве
мы будем применять некоторые теоремы из раздела 5.9 I.
242
ГЛ. 6. ПАССИВНОСТЬ
Мы начнем с общей теоремы, иллюстрирующей наш подход.
1. Теорема. Рассмотрим систему с обратной связью, заданную
уравнениями
2. ₽! = «! — Не2,
3. 82 = п2 08ъ
где elt е2, ut, и2: ₽+->Кл; G, Н: Це (IR+)-> L„e (IR+)- Предполо-
жим, что каждой паре (иь и2) из (IR+) X L„ (|R+) соответствует
единственное решение уравнений (2) и (3) (8Ъ е2) из ZJU(R+)x
xLne(|R+). Пусть, кроме того,
4. оператор G неантисипативен, линеен и удовлетворяет усло-
виям (5.9.6) и (5.9.7);
5. Если Не —О, то 8 = 0.
Пусть существует 6eR такое, что
6. <е|бе)г^6|ег|» VeeAl,
где множество М определено в (5.9.5), и eeR такое, что
7. (е\Не}г^ъ1(Не)тР Уее=Ц.
Тогда, если М — собственное подмножество L2 и
8. б4-в>0,
то yi = GeiqL L*, как только Ui = 0, и4=/=0 и
Доказательство. Как и в теореме 5.9.10, поскольку М —
собственное подмножество L2, М — непустое подпространство про-
странства ZA Пусть Ui==0, u2=/=0 и UjeAf1. Доказательство
проведем от противного, предполагая, что Ge2 е L2. Отсюда сле-
дует, что Так как ui = 0 и игеМ1, то
9. (ег Gei'>r 4- (е21 Не2}т —
= (81 е2 — и4)т'-|- <82 I Ui — 81)т = — (811 (82 I Ui)r = 0.
С другой стороны, из (6) и (7) получаем
10. (8j | Ge^r + (е2 | Не2)т^Ь ||е1Г|2 + е || (Не2)гS2 = (« + «)Iе1ГГ
Так как б + е>0, (9) и (10) могут выполняться одновременно
только в том случае, когда е! = 0. Это означает, что, во-первых,
G8i = 0, а, во-вторых, согласно (5), Не2 = 0 при 82 = 0. И, нако-
нец, поскольку e1 — Ge2 + u2, легко видеть, что условия е, = 0,
е2 = 0, и2#=0 противоречивы. Следовательно, Ge^L2.
Теперь мы докажем теорему, дополняющую теорему (6.5).
11. Теорема. Рассмотрим систему, заданную уравнениями (2)
и (3), где «1, и2, ci, е2: F+->R. Пусть подсистема О линейна,
неантисипативна и описывается уравнением
12. (08) (Г) = (£*е)
12. ТЕОРЕМЫ О НЕУСТОЙЧИВОСТИ
243
где в
13. функция g(-) абсолютно непрерывна.
(Отсюда следует, что g(-)&L'ei т. е. g измерима везде, за
исключением, возможно, точки / = 0, где она может иметь в своем
разложении 6-импульс; gT(-)^o^ при всех Тсоо.) Пусть,
кроме того, g(-) преобразуема по Лапласу; ее изображение g (•)
может быть аналитически продолжено в область {s: Res^O} и
является мероморфной функцией в этой области. Предположим
также, что
14. отображения и со *—► (/<о) ограничены на
множестве R.
Подсистема Н описывается уравнением
15. (Я₽)Ю=Фк(0Ь
где <p: R —непрерывная функция, принадлежащая сектору
[О, Л]. И, наконец, предположим, что для каждой пары («ъ и2) е
eL2xL* существует решение (е1( е2) уравнений (2) и (3), при-
надлежащее ЦхЦ. Тогда, если функция g (•) имеет хотя бы один
полюс в области {s: Res>0} и существуют действительные числа
q'^0 и г>0 такие, что
16. Re[(l 4- jqa>)g (/<о)] +0 VoieK,
и если
17. <р(х) = 0=5>х = 0,
то система /.’-неустойчива.
Доказательство. Если Ui~ 0, то рассматриваемую си-
стему с обратной связью можно преобразовать к виду, приведен-
Рис. 6.10.
ному на рис. 6.10. Полученная система описывается следующими
уравнениями:
18. z (0 = [(Я+ЧЙ) * *1] (0 + «2 (0 = v (0 + «а (0.
19. e^t)------------------<р[М0],
20. г(0 = М0 + ?М0-
Пусть отображения Hi и //2 имеют вид: Н\- *и, Я2: ►
»—♦ — ei. Тогда, как показано в примере 6 (раздел 4), оператор
244
ГЛ. 6. ПАССИВНОСТЬ
Н2 удовлетворяет неравенству (7), где е = 1 /k. Оператор Hi яв-
ляется оператором свертки с ядром h1 = g-\-qg. Ограничения,
наложенные на функции g и g, позволяют заключить, что опера-
тор Hi удовлетворяет условиям (5.9.6) и (5.9.7). Поэтому про-
образ Мх пространства L2 при отображении Hi является замкну-
тым подпространством L2. Поскольку функция g имеет особые
точки в области {s: Res>0}, — собственное подмножество Л2.
Теперь с помощью равенства Парсеваля легко убедиться в том,
что
21. (x\hi*x)^5 inf {Re(/со)}• ||х||2,
если х(-) и [hi *%(•)] принадлежат ZA Принимая во внимание свой-
ство неантисипативности оператора Hi и используя лемму (9.2),
из (21) получаем
<x| inf {Reht (/co)} • ||xr||2 =
(i)GR
= inf {Re[(1 + jqa)g (/co)]} VxeLJ.
©eP
Тогда, если выполняется неравенство (16), то Hi удовлетворяет
условию (6), где 6 = г — l/k. Поэтому 6-|-е = г>0. Следовательно,
согласно теореме (1), существует входное воздействие u2 е L2
такое, что соответствующая реакция у не принадлежит L2. Пусть
= {[1/(1 +<7$)]й2($)}- Тогда w2gL2, однако y<£L2, т. е.
система Р-неустойчива.
БИБЛИОГРАФИЧЕСКИЙ КОММЕНТАРИЙ
Теорема (1.3) для линейного случая доказана Юлой и др.
[109]. Общие положения (раздел 3) введены Сандбергом [79],
Цеймсом [112] и Виллемсом [103]. Примеры 1—3 (раздел 4) хо-
рошо известны в литературе, посвященной теории цепей При-
мер 5 описан Хо и Нарендрой [19]. Примеры 6 и 7 можно найти
в работе Сандарешана и Тэтачара [87]. Теоремы.о пассивности до-
казаны Сандбергом [79], Цеймсом [112], Хо й Нарендрой [19].
Критерий Попова для систем с распределенными параметрами
впервые сформулирован Дезоером [28], а его обобщение на мно-
гоконтурные системы принадлежит Ли и Дезоеру [59]. Дискрет-
ные системы исследовались в работе [58]. Теорема (8.8) представ-
ляет собой усиленный вариант теоремы, доказанной в хорошо
известной работе Цеймса и Фридмана [47], и принадлежит Рама-
райяне и Тэтачару [67]. Идея использования антисипативных
усилителей впервые высказана О’Ши [63]. Метод факторизации
с использованием логарифмов предложен Цеймсом и Фалбом [114]
и развит Сандарешаном и Тэтачаром [89]. Пример системы, содер-
БИБЛИОГРАФИЧЕСКИЙ КОММЕНТАРИИ 245
жащей монотонную нелинейность, рассмотрен Цеймсом и Фалбом
[114]. Другой метод факторизации можно найти в работе Виллемса
103]. На возможность применения этого метода к многоконтур-
ным системам с использованием /Анорм указал Видьясагар. Связь
теорем о пассивности и малом коэффициенте роста для линейного
случая хорошо известна из литературы по теории цепей. Связь
тех же теорем в нелинейном случае (см. раздел 10) рассматрива-
лась Андерсоном [1]. Теорема (11.1) заимствована из работы
Сандберга [82], а теорема (11.10) — из работы Броудера [15]. Тео-
рема о продолжении отображения PTS, использованная при дока-
зательстве теоремы (11.10), доказана Минти [61]. Результаты по
неустойчивости, изложенные в разделе 12, принадлежит Такеде и
Бергену [90].
Приложение А
ИНТЕГРАЛЫ И РЯДЫ
АЛ. РЕГУЛЯРНЫЕ ФУНКЦИИ
В теории систем одним из наиболее часто используемых клас-
сов кусочно-непрерывных функций является класс регулярных
функций. Ниже мы определим функции такого рода и приведем
их основные свойства.
1. Определение. Пусть (Е, || • ||) — полное линейное нормирован-
ное, т. е. банахово, пространство. Пусть I — интервал в R. Отобра-
жение f: I-+E называется ступенчатой функцией тогда и только
тогда, когда существует конечное разбиение интервала Z:
k
Z «= U [х/, х/+1], где XjCX/4-i при любых i,
/ж=0
такое, что функция f постоянна на каждом открытом интервале
(хь x/+i). (Замечание: если Z = |R, то х0 = — оо, х* = оо.)
2. Определение. Пусть Z — интервал и Е — банахово простран-
ство. Функция f: I-+E называется регулярной тогда и только
тогда, когда для всех хе Z функция f имеет односторонние пре-
делы. Более строго, пусть [а, Р] — замыкание интервала Z, тогда
для всех хе/, отличных от Р, при Л->0
3. lim f (х + й) = / (х +) существует
л>о
(следовательно, норма ||/(х+) [ конечна), и для всех х'е Z, отлич-
ных от а, при Zz->0
4. lim/(x'— h) = f(x—) существует
h < О
(следовательно, норма ||/ (х—)|| конечна).
5. Теорема. Функция f: 1 -> Е регулярна в том и только том
случае, когда на всех компактных х) подынтервалах интервала I
существует предел равномерно сходящейся последовательности
ступенчатых функций.
Доказательство немедленно следует из того, что если
функция /*: /->Е непрерывна, то она регулярна; кроме того,
если функция ft Z->|R монотонна, то она регулярна.
*) Напомним, что интервал называется компактным тогда и только тогда,
когда он замкнут и ограничен
АЛ. РЕГУЛЯРНЫЕ ФУНКЦИИ
247
6. Следствие. Если функция f регулярна, то множество точек
ее разрывов может быть несчетным. Пример: f: (О, 1)->IR, где
f: />—*-sgn[sin (exp 1/0].
7. Следствие. Если функция f: 1->Е регулярна, то она огра-
ничена на каждом компактном подынтервале интервала Z.
8. Следствие. Пусть функции I-+Eh где Ei (i = 1, 2,..п) —
п
банаховы пространства, регулярны. Пусть функция g:
t = i
где F — банахово пространство, непрерывна. Тогда сложная функция
...» I-E
регулярна.
Из следствия (8) вытекает, что если /, g\ I — регулярные
функции, то также регулярны функции /»—(0 + g(0, /»—(0g(0
и t f (t)/g(t), причем в последнем случае необходимо, чтобы
g(0#=O при любых t&I.
Упражнение 1. Пусть Л /->Р и g: /(/)-> R. Привести примеры функ-
ций fag, подтверждающие следующие утверждения:
(а) если функции / и g регулярны, то g*f может не быть регулярной;
(Ь) если функция f непрерывна, а функция g регулярна, то g°f может
не быть регулярной.
9. Легко определить неопределенный интеграл от регулярной
функции /. Пусть f: [а, Ь]~+Е, тогда, по определению,
t t
10. ф(0« (x)dx = lim \fv(x)dx,
a v^qoa
где fv (0 — последовательность ступенчатых функций, равномерно
сходящаяся к функции f на (а, 0.
11. Очевидно, что <р(0 имеет производную везде, кроме точек
разрыва функции /, однако в этих точках ср имеет правую и ле-
вую производные, т. е.
12. ф' (Г 4-) = f (Г +) и ф' (Г -) = f (Г —),
если Г—точка разрыва.
13. Определение. Функция f: [а, £>]->₽ называется абсолютно
непрерывной на [а, Ь] тогда и только тогда, когда для любого
е>0 существует 6>0 такое, что для любой конечной системы
подынтервалов (cq, £<), определенной на [а, 6], со свойством
£ |а/-М<S
f-i
выполняется неравенство
S ।/(«а—/(₽о! <»•
С-1
248
ПРИЛОЖЕНИЕ А. ИНТЕГРАЛЫ И РЯДЫ
14. Специальные случаи.
(1) Если указанная в определении (13) система состоит из
одного подынтервала, то легко видеть, что если f абсолютно не-
прерывна на [а, Ь], то она равномерно непрерывна на [а, Ь].
(2) Если f удовлетворяет условию Липшица на [а, Ь], то она
абсолютно непрерывна на [о, Ь].
(3) Если f абсолютно непрерывна на [а, Ь], то она является
функцией с ограниченным изменением на [д, Ь].
(4) Если /: (a, b]->R — интеграл регулярной функции, то /
абсолютно непрерывна.
(5) Существуют классические примеры монотонно возрастаю-
щих функций, которые являются непрерывными, но не абсолютно
непрерывными.
Важность введения понятия абсолютно непрерывной функции
подтверждается следующей теоремой (см. [60]).
15. Теорема. Если функция /: [a, b]->-lk абсолютно непре-
рывна, то
(а) ее производная f' (х) существует и конечна почти везде;
(Ь) если положить /(х) = /'(х), где функция /' определена и
равна нулю почти везде, то
/<х) = $/(£)<£+/(«) Vxe[u, 4
а
И наоборот, если f представима в виде
= + Vxeja, />],
а
где функция g интегрируема на [о, fr], то / абсолютно непре-
рывна на [а, Ь].
А.2. ИНТЕГРАЛЫ
Ниже мы сформулируем некоторые свойства интеграла Лебега,
которые используются в основном тексте книги. Читатели, зна-
комые с интегрированием по Лебегу, могут рассматривать этот
параграф как краткий обзор основных положений. Остальные
читатели должны лишь знать, что
(1) понятие интеграла Лебега является расширением известного
понятия интеграла Римана; класс функций, интегрируемых по
Лебегу, включает в себя класс функций, интегрируемых по Риману
(который в свою очередь состоит из непрерывных, кусочно-непре-
рывных и регулярных функций);
(2) аналитические свойства функций, интегрируемых по Лебегу,
проще свойств функций, интегрируемых по Риману.
Логика основной части книги не нарушится, если эти чита-
тели будут считать приведенные ниже свойства аксиомами.
А.2. ИНТЕГРАЛЫ
249
Одно из наиболее важных свойств интеграла Лебега устанав-
ливается следующей теоремой.
1. Основная теорема сходимости [69, стр. 76]. Пусть функ-
ция g интегрируема на интервале I (конечном или бесконечном).
Пусть {fn} (n = 0, 1, 2, ...) —последовательность функций, опре-
деленных на /, таких, что для любого п I f'n (х) | ^g (х) при любом
хе/. Тогда, если почти для всех хе/ последовательность {fn}
сходится при м—>оо к пределу, обозначаемому через f(x), то
\f(x)tix = lim \fn(x)dx и lim $ | f — fn | dx = 0.
I n -><x> / n —*•00 !
2. Неравенство Гельдера [69, стр. 75]. Пусть f, g: R-*-R.
Пусть, кроме того, числа р, q е [ 1, оо] удовлетворяют соотноше-
нию \/р-+-!/(?= 1. Тогда, если f^Lp и g^L4,
(a) fg е= £,»;
(b) Ugh^UUgU.
При р — 2 неравенство Гельдера превращается в неравенство
Шварца.
3. Неравенство Минковского [69, стр. 5]. Если ре[1, оо] и
f, g<^ Lp, то
8/+^<1ЛР+ШР.
4. Утверждение. Пусть f: и 1=ср<оо. Тогда, если
функция f е Lp равномерно непрерывна на R, то ->0 при
j/|—>оо. (Заметим, что функция f равномерно непрерывна, если
М”)
5. Утверждение. Если f: R -> R и f s Р f| L°°, то f e Lp при
p e [1, оо].
6. Утверждение. Пусть f: [a, b]->-R, где —co<a<&<oo.
Если f^Lp[a, ft] при некотором p e [1, оо], to feLx[a, &].
Упражнение. Привести пример, показывающий, что утверждение, обратное
утверждению (6), неверно.
7. Утверждение [60, стр. 227]. Если /: |R-и fsL1, то
lim F \f(t + h)-f(t)\dt = Q.
'•-oj00
8. Теорема Тонелли [60, стр. 145]. Пусть т и п — положитель-
ные целые числа. Пусть функция f- Rm х R" -► R локально инте-
грируема. Тогда если
(а) для всех х е Rm, за исключением принадлежащих множе-
ству Е меры нуль, функция у>—- | f (х, у) | интегрируема над R" и
(Ь) повторный интеграл конечен, то
(1) функция (х, </)•—*f(x, у) интегрируема на RmxRn;
(ii) J [ J f(x, y)dyldx = J f(x,y)dxdy.
9 Ч. Дезоер. M. Видьясагар
250
ПРИЛОЖЕНИЕ А. ИНТЕГРАЛЫ И РЯДЫ
9. Замечания.
(1) Знак абсолютной величины в условии (Ь) существен: см.
контрпример в [60, стр. 144].
(2) Согласно теореме Тонелли, в случае, когда существует
один из повторных интегралов от функции |/|, повторный и двой-
ной интегралы от функции f равны. В силу симметрии двойной
интеграл равен каждому из повторных интегралов.
(3) В приложениях с помощью теоремы Тонелли можно уста-
новить существование двойного интеграла, изучая лишь один из
повторных интегралов, т. е. проверяя, выполняется ли условие (Ь).
Неопределенный интеграл
10. Теорема. Пусть / — интервал (конечный или бесконечный)
из R. Функция F: Z->|R является неопределенным интегралом
некоторой интегрируемой функции f в том и только том случае,
когда F абсолютно непрерывна. f = f почти везде на интервале/.
Упражнение 1. Если / el1 2 3, то lim /(/) существует (и конечен)-
/ —* оо
А.З. РЯДЫ
В нашей книге рассматриваются последовательности *хл,
где хп е R, Клхл и т. д. Поэтому здесь мы приведем свойства
последовательностей, члены которых принимают значения из нор-
мированного пространства Е. Норма в Е обозначается через ||-||.
В большинстве случаев пространство Е является полным, т. е.
банаховым, пространством.
Для/ заданной последовательности {хя}, где п = 0, 1, 2, ...
(т. е. функции и»—отображающей Z+ в Е), можно опреде-
лить n-ю частичную сумму sn:
1. sn =Хо4”*14“ *2+ ••• +Ям-
СО
2. Определение. Назовем ряд ^хп сходящимся к s тогда и
о
только тогда, когда limsn = s. (Это определение сходимости по
п —> оо
норме в пространстве Е.)
3. В случае, когда нормированное пространство £ полно,
00
говорят, что ряд У, хп сходится абсолютно тогда и только тогда,
о
оо
когда сходится ряд У \хп I, составлеииый из положительных дей-
0
ствительных чисел.
При изучении свертки последовательностей нам понадобится
аналог теоремы Тонелли. Вместо функций двух переменных будем
рассматривать двойные последовательности.
ВЛ. L'-ТВОРИЯ
251
4. Теорема. Пусть (т, n)t—^а„п — двойная последовательность
в пространстве Е (т. е. функция, отображающая Z+XZ+ в Е).
00
Если ряд 2 I °mn I сходится при п = 0, 1, 2, ... и
т=0
Выражения в правой части равенства называются повторными
рядами.
5. Теорема (неравенство Гель дер а для последовательностей).
Пусть х = (ха, х», xs, ...), у=“(у^ У1, у%, ...) —последовательно-
сти в Е, т. е. х, у: Z+-+E. Пусть р, ?е(1, оо], причем 1/рЧ-
4-1/<7=1. Если хеР и у е I4, то
У I хкук | < оо
k = о
(оо
т. е. скалярное произведение хТу= £хкуц сходится абсо-
о
лютно в и
в. у, \хкук' ^1х|рИ
»S=0
Свертки последовательностей рассматриваются в Приложении С.4.
Приложение В
ПРЕОБРАЗОВАНИЕ ФУРЬЕ
Здесь перечислены основные результаты, часто используемые
в нашей книге.
8.1. Д' ТЬОРИЯ
1. Теорема. Если f‘. |R-»-R, feL1 и /(/<о)= J f(t)е~,мdi, то
-ОО
оо
(а) функция он—*/(/<«))= $ / (t)е~'ш di равномерно непрерывна
— ОО
на R;
(b) f е
9*
252
ПРИЛОЖЕНИЕ В. ПРЕОБРАЗОВАНИЕ ФУРЬЕ
(С) |/ (/<о)|->0 при | о | -> со (лемма Римана — Лебега);
(d) max|/(/®)K|f|i;
00
1 с *
(е) f (t) = I f (/co' da почти везде на R;
— oo
(f) если, кроме того, в окрестности точки t функция f является
функцией с ограниченным изменением, то
2. |[/0 + 0)-/а-0)] = ^а1йп J j(ja)e^da.
В. 2. /«-ТЕОРИЯ
1. Теорема. Пусть /: R->R и fe£2. Если
2.
/лг(/®)= $ f(t)r™dl, (V = l, 2, ...
-АГ
ТО
(а) при N-+oo где /е£2;
. (Ь) (ИЮ2-^(8/Ю2;
(е) при (V->oo
1 V
й J f(ja)e^da
— TV
3. Замечания.
(а) В пунктах (а) и (с) теоремы (1) имеется в виду сходимость
по норме в пространстве L2. Сходимость по норме не следует
путать в сходимостью в точке (в качестве примера рассмотреть
явление Гиббса);
(Ь) Фурье-преобразование отображает L2 на L2, причем /Анормы
функций f и f равны с точностью до коэффициента К1 /2 л:
(с) (в качестве примера можно привести функ-
цию /(/), равную 1 при и 0 при |/|>1);
(d)
(е)
4. Теорема Парсеваля. Если f, g& L2, то
(a) f*g='fg',
со со
(b) J / (О g (0 j /♦ (ja) g (/®) da',
—со —00
В.З. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
253
. 5. Теорема (Сандберг).
(а) Если f и / <= L2, то / е L1.
(Ь) Если / и / е L2, то f е L1.
Доказательство. Если /, / е L®, то / е L’ и /<о/ (/ш) е L1.
Таким образом,
j I / (/“) I d<o = j .Д»)»/, К1 + ®гУ1а । ? (» i]d(0
ТтЬ)*А[1 (1 + ®8)|/(/®)12<Ч*'‘-
= Кл (I / K +1 ®/ (/®)й),/* < ©О.
Упражнение 1. Пусть / и / е L*. Показать, что / е L00 и |/(/)|->0 при
/-►оо (Указание: рассмотреть интеграл от //, ...)
Упражнение 2. Если / е L2 и if е L2, то / е L1.
В.З. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
Преобразование Лапласа обладает более простыми свойствами
по сравнению с преобразованием Фурье, поскольку преобразуе-
мыми являются лишь функции, тождественно равные нулю при
t < 0. Кроме свойств, вытекающих из теории преобразования
Фурье, наиболее интересные факты устанавливаются теоремами
(4) и (5).
1. Определение. Если функция f: R+->-|R локально интегри-
руема, ее преобразование Лапласа определяется соотношением
(la) f(s) = $ f(t)e~stdt, где s = o4-/©,
о
причем область определения функции f зависит от сходимости
интеграла.
Преобразование Лапласа функции / мы будем обозначать
через X (/).
2. Утверждение. Если интеграл (1а) сходится абсолютно при
s = $o, то функция $—*/(s) аналитична при Res>Reso.
3. Утверждение. Если f е L1 (R+) (или L? (|R+) или L" (₽+))> т0
функция si—»f (s) аналитична при Res>0.
Для обобщенных функций и функций из пространства La
устанавливаются следующие необходимые и достаточные условия.
4. Теорема [85]. Пусть /—аналитическая функция, определен-
ная в правой полуплоскости Res>a0- Тогда / является преобра-
зованием Лапласа обобщенной функции с носителем в |R+ тогда
и только тогда, когда функция |/(s)| мажорируется многочленом
от |«| при достаточно больших o = Res.
254
ПРИЛОЖЕНИЕ С. СВЕРТКИ
Степень этого многочлена зависит от обобщенной функции,
например, X [6(n)]«s".
5. Теорема. Функция / является преобразованием Лапласа
функции f: R+-»-R, принадлежащей L*, тогда и только тогда, когда
(а) функция f аналитична при о>0;
(Ь) для некоторого M<z<x> (зависящего от /)
ОО
$ |/ (o + /w)|2dw «== /И при всех о > 0.
— 00
Приложение О4
СВЕРТКИ
С.1. ВВЕДЕНИЕ
Для двух заданных функций и и h, отображающих R+ в IR,
можно вычислить (при некоторых условиях) их свертку u* ft,
определяемую интегральным соотношением
t
1. (u*h)(t) = ^h(t—x)u(x)dx = y(t) для 1^0.
о
Основные причины использования свертки для математического
описания линейных систем состоят в следующем:
(а) При очень слабых условиях Л. Шварц доказал, что любая
стационарная линейная система может быть задана сверткой,
ядром которой является обобщенная функция;
(Ь) Это обстоятельство позволяет по одной и той же схеме
изучать системы с медленно меняющимися параметрами, распре-
деленные системы и системы с запаздыванием [85, втр. 162].
2. Замечание. В простейшем случае ft( ) представляет собой
импульсную характеристику линейной стационарной неантисипа-
тивной системы, передаточная функция h(s) которой является
дробно-рациональной функцией от s, причем | ft (s) | -> 0 при $->оо.
При таком предположении
(А) все полюсы функции ft(s) принадлежат открытой левой
полуплоскости тогда и только тогда, когда ft е L1.
Если (А) выполняется, то
(i) функция h убывает не медленнее экспоненты, т. е. для
некоторого ftm<oo и некоторого а>0
\h(t)\^hme~^ V/g=R+;
(ii) h{t) = h(0+) 6(0 +МО» гДе Функция ftx(0 убывает не
медленнее экспоненты, причем значение ft(0+), возможно, равно
нулю. Естественно, что Л(0+)= lim sfo(s).
«-*00
С. 2. СВЕРТКА ФУНКЦИЙ
255
(iii) Если ugL1, то y^L1 и, кроме того, функ-
ция у непрерывна и y(f)-*-Q при /->оо. Если usP, то
у s L21~| L°°, ysL2 и, кроме того, у непрерывна и y(t)-+O при
/—»-оо.
(iv) При Isgpsgoo, если u&Lp, то у, у е Lp и функция у
непрерывна.
Положения (i) и (ii) очевидны, a (iii) и (iv) вытекают из тео-
ремы (С.2.14).
Упражнение 1. Пусть выполняется условие (А) и при некотором целом
m>l lim sm+1A(s)=c, где с—постоянное число. Сформулировать дополни-
|з|—*со
тельные положения. (Указание: рассмотреть функции h, h, ...,
С.2. СВЕРТКА ФУНКЦИЙ
£г-теория
1. Теорема. Пусть и, v, w: R+->R. Если и, v, w^L1, то
2. и » w е L1 и | и * w Ji «С | и [i • | w |х;
3. u*w — w*u и (u*v)*w = u*(v*w).
4. Комментарий. Линейное пространство L1, в котором свертка
выбрана в качестве операции умножения, представляет собой
алгебру, поскольку операции сложения, умножения на число и
умножения удовлетворяют всем необходимым аксиомам (см. При-
ложение D). Более того, эта алгебра является банаховой, так как
II и # w Si | и h • | w Ji и пространство L1 полно. В соответствии с (3)
алгебра является коммутативной банаховой алгеброй, не обладаю-
щей, однако, единичным элементом.
Упражнение 1. Обсудить возможность применения теоремы (1) в теории
систем. Рассмотреть реакцию различных типов взаимного соединения линейных
стационарных подсистем с импульсными характеристиками из L1.
Доказательство теоремы (1) основано на применении
теоремы Тонелли. Так как все интегралы рассматриваются над R+,
мы будем опускать пределы интегрирования. Оценим | w * и ]:
5. | (w * и) (/) | = | $ w (/ — т) и (т) dr | «g J | w (t — т) | и (х) | dx,
причем интеграл в правой части (5) может принимать бесконечные
значения для некоторых t. Кроме того, вычислим 11 и * w Ц:
6. J | (w * и) (/) | di $ | $ | w (t — т) 11 и (т) | dx] (U.
Рассмотрим другой повторный интеграл:
7. jj | $ | w (t — т) 11 и (т) | di dx =
8. = J | и (т) | J|w(Z —т)|сй]с!т =
9. =1 и h J w |i < oo.
256
ПРИЛОЖЕНИЕ С. СВЕРТКИ
Неравенство (6) очевидно, однако интеграл в правой части (6)
может быть расходящимся. Повторный интеграл (7) с обратным
порядком интегрирования, равный интегралу (8), ограничен в силу
неравенства (9). По теореме Тонелли интеграл (6) сходится,
поскольку сходится повторный интеграл (7). Таким образом,
установлена справедливость (2). Формула (3) вытекает из (2) и
теоремы Тонелли.
10. Следствие. Пусть W: R+->R'Ixn и и: R+->Rrt. Если все
элементы W и и принадлежат L1, то
п.
где
12. |«|1 = р«(/)|Л, =
и | и (t) | — некоторая норма функции u(t) в пространстве R",
а | W (t) | — порожденная ею норма матрицы в R'IX'1.
13. Замечание. Если и, w^L1, то
(а) функция w*u может быть не ограничена (на R+) и раз-
рывна;
(Ь) предел функции w*u при t-+oo может быть отличен
от нуля;
(с) функция w*u^wu ограничена, равномерно непрерывна и
стремится к нулю при <o->oo;
(d) функция w*u может не принадлежать L1.
Упражнение 2. Пусть f: и f: ti—► (1 +0-1 Пустьg: ->IR,
причем g(0е/(1—0 ПРИ *6(0, О и g (/)=»() при всех других значениях t
Показать, что f ♦ g £°° (|R+). Пусть
<Р(0= 5 2~nf(t—n)
п=2
Показать, что предел функции £*Ф при /~>оэ отличен от нуля и что для
любого Т > 0 существует f такое, что | (g * ф) (/') | Г.
ZZ-теория
14. Теорема. Пусть u, w: R+->R и ре[1, оо]. Если u^Lp
и w е= L1, то
15. ||ку*Ы||р<||даМ|и|р.
Доказательство. Предположим, что 1<р<оо, тогда
| (пу * и) (t) | $ | w (t — т) |1/р | и (т) | • | w (t — т) |1/<z dx.
Первый сомножитель, согласно теореме (1), принадлежит прост-
ранству Lpt а второй — пространству Lq. Следовательно, согласно
неравенству Гельдера,
* и) | | W (/ — т) 11 u (х) drj1/p [J I w (/ — т) dx^,q-
С 3. СВЕРТКА МЕРЫ И ФУНКЦИИ
267
(Заметим, что последний сомножитель мажорируется | w |J}/<Z.) Взяв
ZAнормы от обеих частей и используя теорему (1), находим:
I' w * | w (t — т) | \ и (т)| pdx]
При р=1 неравенство (15) превращается в хорошо известное
неравенство (2). При р = оо неравенство (15) очевидно, поскольку
мы можем взять существенную точную верхнюю границу (ess sup)
по и от интеграла свертки.
16. Замечания.
(I) Неравенство (15) теоремы (14) распространимо на вектор-
ный и матричный случай аналогично тому, как это сделано
в следствии (10).
(II) В теореме (14) функция ш*и может быть не ограничена,
разрывна и ее предел при /->оо может быть отличен от нуля.
(III) Если w& L1 и ueL2, то существует более точная оценка
(см. (3.6.7))
| w * и max | w (/ш) 11| и |2.
(О
Кроме того, можно показать [93, 6], что
w*u = wil.
(IV) Неравенство (15) становится строгим неравенством только
при р—1, оо, так как | w |г является нормой отображения и»—*
► w * и, переводящего L00 в Lm (см. (2.6.3)).
Упражнение 3. Если w е L1 и и е L°°, то
(а) функция w ♦ и равномерно непрерывна (Указание: использовать
утверждение (А.2.4));
(Ь) предел vd ♦ и при /->со не обязательно равен нулю. (Указание:
вспомните о реакции некоторых систем на ступенчатое воздействие!)
Упражнение 4. Если L2 и и е L2, то
(a) vd * и — vlu е L1;
(Ь) функция принадлежит L°°, равномерно непрерывна и (vd*u)
при f -> со.
Упражнение 5. Наложим более строгие ограничения на функцию vd. Пусть
w е U П £°°, тогда w е LP при 1 р оо. Если, кроме того, и е L1, то функ-
ция ш*иеЬ2ПЛ°° является равномерно непрерывной и стремится к нулю
при / -> со. (Указание, учесть, что w * и е L1.)
Упражнение 6. Проверить подробно теорему (14) для случая, когда и (/) е 1РЛ
и W (/) Убедиться в справедливости каждого шага доказательства,
используя свойства нормы, нормы отображения и т. д.
С.З. СВЕРТКА МЕРЫ И ФУНКЦИИ
Моделями физических систем часто являются их импульсные
характеристики, которые в своем представлении могут содержать
6-импульсы. Это обстоятельство вынуждает нас изучать не импульс-
258
ПРИЛОЖЕНИЕ С. СВЕРТКИ
ную характеристику системы ш, а ее переходную функцию р.
Например, если w представляет собой сумму локально интегри-
руемой функции Wi и 6-импульсов:
1. ®(0 = a»i(0 + Saft8(< — tk), 0
О
то соответствующая функция р, имеет вид:
2. р (0 = J w (f) df
Н-
и состоит из суммы J и «ступенек» высотой а*, появ-
ляющихся при tk (£ = 0, 1, 2, ...). Верхним Пределом интеграла
выбрана величина /+, поскольку мы требуем, чтобы функция р
была непрерывна справа. Функция р,, заданная соотношением (2),
является частным случаем меры на множестве R+. В частности,
мера интервала (а, &] равна р,(&) —р,(а). Обычно [69] интеграл
измеримой функции f: R+-существует и обозначается через
ц(/): 5Мц = н(/)-
Пусть
3. lHl = sup | р (/) |,
где точная верхняя грань берется по всем непрерывным функ-
циям f: с компактным носителем, обладающим свойством:
sup I/(/)]< 1.
f >0
4. Определение. Мера р, называется ограниченной тогда и только
тогда, когда |р, Ц<оо.
Упражнение 1. Для случая, когда р определена соотношением (2), а функ-
ция w имеет вид (1), показать, что
|рЦ=Т I®!(01 I a* I-
о 0
Свертка функции g: R+->|R с мерой p, обозначается (g*g) и
определяется следующим образом:
5. (P*g)(0 = J g(t-r)d^(r).
Например, для меры р, заданной соотношениями (1) и (2),
t k
(ц * g) (/) = 5 ((- Т) g (т) dr + У, afg (t - tf),
о о
где Л —наибольшее целое число такое, что tf^t.
С. 4. СВЕРТКА ПОСЛЕДОВАТЕЛЬНОСТЕЙ
259
Можно установить следующий факт [42].
6. Теорема. Пусть р — ограниченная мера на R+.
(а) Если р е [ 1, оо] и geLp(p+), то свертка р *g определена
почти везде в
7- IH
(Ь) Если функция g непрерывна, то свертка p*g определена
почти везде и непрерывна.
(с) Если функция g непрерывна и стремится к нулю при /->оо,
то p*g->-0 при t-+oo.
С.4. СВЕРТКА ПОСЛЕДОВАТЕЛЬНОСТЕЙ
Пусть а = (а0, ait аг, ...) и b — (b0, Ь1г bt, ...) —последователь-
ности действительных чисел, т. е. функции, отображающие Z+ в R.
Свертка а и Ь определяется как последовательность у:
1- й*Ь = (у0, уь у2, ...),
где
п
2. У*, вл-А, n = 0, 1, 2, ...
Л =•= О
Заметим, что свертка двух последовательностей из Р является
последовательностью, также принадлежащей Р. Точнее говоря,
справедлива следующая теорема.
3. Теорема (Апостол [2]). Если а и b — последовательности
из Р и
4. = a и 5Ь* = Р,
О о
то
5.
а ♦ b е I1
и с учетом обозначения (2)
6. = la*|V5
О 0 \ О ' \ о z
Поскольку неравенство Гельдера выполняется для последова-
тельностей, справедлива следующая теорема.
7. Теорема. Пусть р е [1, оо]. Тогда, если последовательность а
принадлежит /р, а последовательность Ь принадлежит Z1, то
8.
9. Замечание. Соотношения (5) и (8) выполняются и в тех
случаях, когда члены последовательностей а и b принадлежат Кяхя
или любому нормированному пространству при условии, что
260
ПРИЛОЖЕНИЕ D. АЛГЕБРЫ
в последнем случае определена операция умножения двух элемен-
тов и |а6К|а|| Ь\\ для всех а и Ь. Действительно, внимательно
рассматривая определ-ения и соответствующие доказательства и
учитывая общее определение сходимости в нормированных прост-
ранствах (А.2.2) и свойства нормы, можно убедиться, что спра-
ведливость каждого шага доказательства не нарушается.
При ложе нив D
АЛГЕБРЫ
Здесь вводятся некоторые общие определения и устанавли-
ваются факты, связанные с алгебрами, подробно обсуждаются
свойства .алгебр orf и о^п*п и, наконец, формулируются отдель-
ные полезные теоремы обращения.
D.I. АЛГЕБРЫ
1. Определение. Линейным пространством называется множе-
ство V элементов в совокупности с полем К и двумя операциями:
сложением (т. е. отображением V*xV'определенным на V,
й‘умножением на число (т. е. отображением T^xlK-причем
сложение обладает свойствами ' ссоциативности и коммутативности,
относительно сложения существует нулевой вектор 0 и для каждого
элементаveV"существует ему противоположный элемент -с/еУ;
операция умножения на число является ассоциативной, дистри-
бутивной относительно сложения и, кроме того, = и для любых
2. Определение. Если на множестве кроме умножения на
число, определить умножение элементов, то и превратится в ал-
гебру. Строго говоря, множество orf называется алгеброй над
полем К в том и только том случае, когда
(1) линейное пространство над К (следовательно, на мно-
жестве определены операции сложения и умножения на число);
(2) определено умножение элементов, т. е. отображение (х, у)*—*
♦—*ху, переводящее orfxod в оЛ и обладающее свойством ассо-
цш тивности:
(ху) z = x (yz) = xyz Vx, i/, г e
(3) умножение дистрибутивно относительно сложения:
х (^-|-г) = ху + хг, (у+ z)x = yx + zx Vx, у, гЕэ/;
(4) умножение и умножение на число коммутативны:
(ах) (Ру) = (ар)(ху) Va, ре К, Vx, уе©^.
D. 1. АЛГЕБРЫ
261
3. Замечания.
(а) Аксиомы (3) и (4) можно выразить иначе, а именно: умно-
жение является билинейным отображением изе/ха/в&/ (над
полем К).
(Ь) Если умножение элементов коммутативно, то алгебра назы-
вается коммутативной.
(с) Алгебра orf вовсе не обязательно должна обладать единич-
ным элементом, т. е. элементом е таким, что ех == хе = х для любых
х е orf.
(d) Если множество А, удовлетворяющее аксиомам (1) —(4),
является, кроме того, банаховым пространством над полем К (т. е.
полным нормированным пространством) и если |||^||Ку| для
любых х, у е то А называется банаховой алгеброй. Если
имеет единичный элемент е, то норма обычно выбирается так,
чтобы J е || = 1.
4. Примеры.
1. Множество всех (п х п)-матриц с элементами из поля К вместе
с обычными операциями сложения, умножения и умножения на
число представляет собой некоммутативную алгебру с единичным
элементом (в качестве единицы выступает единичная матрица).
2. Класс всех линейных непрерывных отображений из % в S,
где £ — п[ оизвольное нормированное линейное пространство,
является некоммутативной алгеброй с единичным элементом.
(В качестве умножения здесь принята композиция линейных ото-
бражений.)
3. Пусть sz^ = L1(|R) с операцией свертки, выбранной в каче-
стве произведения элементов, orf представляет, собой коммутатив-
ную алгебру без единицы. (Единицей является функция 6(/), не
(финадлежащая //(К).)
4. Пусть элементы множества orf представимы в следующем
виде:
1 = 0
о, ко,
где g0 е L1 (R+); gt е R при любых I и
оо
У lg»'<°°; 1 =t0", o<zti
i =0
при любых i. Сложение элементов в определено как поточеч-
ное сложение функций, а умножение на действительное число
определено обычным образом. Произведение двух элементов f,
определено как их свертка. Строго говоря, если g задано
262
ПРИЛОЖЕНИЕ D. АЛГЕБРЫ
соотношением (5), а / имеет вид
в. £ Z*« (/“«).
И — О
то свертка f*g определяется как функция
7. (f»g)(t)^(f^go)(i) + £^(/-4)+
+ £/#.(<-«) + s (/-(* + «)]
Упражнение 1. Используя свойство полноты U и свойства , показать,
что второе и третье слагаемые в (7) принадлежат L1. Доказать, что /*£==£*/^
е если /, g е
Согласно упражнению 1, множество©^ замкнуто относительно
умножения, поэтому является коммутативной алгеброй (над
полем R) с единицей 6 (Z). Определим норму в
со
8. = + S 1£.1-
/=о
Тогда легко видеть, что
9.
и
10. |6|л=1.
Таким образом, множество с нормой (8) представляет собой
нормированную алгебру, которая вдобавок полна [51]. Иными
словами, arf является коммутативной банаховой алгеброй с еди-
ницей.
Упражнение 2. Пусть /е£Р(Р4), где 1^к<х>, и weed Показать,
что для любого р е |1, оо] f taeLf и
Упражнение 3. Пусть / е L* (Р+) и и> е Показать, что / » w е L3 и
f » w ' f sup
<0
Обобщите результат на случай, когда / е L* (|R+) и w е &/£плп (Указание
использовать теорему (2.6.7).)
Расширения
И. Определение. Пусть oeR. Определим алгебру (о) как
множество, состоящее из элементов вида (5), где, кроме того, мы
требуем, чтобы
12. t^*ge(/)e-°'eL1(R+)
D. 2. ИДЕАЛЫ
263
\
И
oo
13. у | gk I e-ka < oo.
fe=O
Норму в orf (а) зададим в виде
И. lih<a) = Ua(0e-"lt+kK"<rf4.
Упражнение 4. Показать, что orf (а) замкнута относительно операции
свертки, определяемой соотношением (7).
Упражнение 5. Показать, что при преобразование Лапласа
g(s) обладает следующими свойствами:
(а) функция g голоморфна в открытой правой полуплоскости Re s > a;
(b) функция g ограничена при Re s и; в действительности
sup !g(s)
Res^ri
(с) функция co ।—(a4-/(0) непрерывна и ограничена на |R
15. Определение. Пусть ae!R и (а) — множество всех
упорядоченных n-ок g = (gi, ёг, gn) таких, что gt^&£(a)
при i = 1, 2,..., п. Аналогичным образом, пусть е^яхя(а)—
множество всех (пхга)-матриц G — (gtj) (i, j =1, 2, ..., п) таких,
ЧТО gij (= orf (о).
Упражнение 6. Показать, что о^пХп (о) является некоммутативно » бана-
ховой алгеброй с единицей.
Упражнение 7. Пусть Н е &£пхп. Будем полагать, что Н определяет
отображение в самое себя, причем Н: и\—► Я * ц. Определим в простран-
стве Rrt /°°-норму соотношением
|х(0| = тах'Х,(0|.
Показать, что норма отображения Н имеет вид
|Я|=тах £ 1A4/-)U
1 /«1
где — 0-элемент матрицы Я.
D.2. ИДЕАЛЫ
1. Определение. Множество^ называется идеалом коммутатив-
ной алгебры тогда и только тогда, когда
(а) о/ —линейное пространство и s7cz©^;
(b) i е => ix е для любых х е ©^.
2. Определение. Алгебра ©^ и пустое множество ф являются
идеалами алгебры ©^ и называются тривиальными идеалами оЛ.
Идеал алгебры ©^ называется собственным идеалом оЛ тогда
и только тогда, когда и е7=/=©^, т. е. —непустое
собственное подмножество ©^.
264
ПРИЛОЖЕНИЕ D. АЛГЕБРЫ
Упражнение 1. Рассмотрим коммутативную алгебру всех диагональных
(пхи)-матриц с элементами из R. Показать, что множество U всех диагональ-
ных матриц X, для которых хп==0, является идеалом.
Упражнение 2. L1 (Р+) является идеалом алгебры , определенной выше.
Упражнение 3. Рассмотрим алгебру — {/ е L1 (IP); свертка в качестве
умножения}. Показать, что множество
Л/(Оо) = 0 для некоторого фиксированного <о0}
является идеалом алгебры
Упражнение 4. Рассмотреть алгебру из примера D1 4.4. Показать, что
множество 2Z={/e(3^’: f (so)=0 для некоторого фиксированного s0 где
Re s0 0} — идеал алгебры
3. Теорема. Пусть ©^ — коммутативная алгебра с единицей е
и U — собственный идеал алгебры od. Если х s то х не имеет
обратного элемента в , т. е. ху^е
Доказательство. Доказательство проведем методом от
противного, полагая, что некоторый элемент х е <?7 имеет обрат-
ный себе элемент х-1, поэтому хх-1 = е. Тогда для любого у е оЛ
хгху е ©^, и поскольку — идеал, то х (х-1#) е е7. С другой сто-
роны, используя свойство ассоциативности, получаем, что
х (х'ху} = (хх-1) у = еу = у.
Таким образом, произведение х с каждым элементом алгебры
покрывает ©/, что противоречит предположению о том, что идеал
о? — собственное подмножество алгебры оЛ.
D.3. ОБРАЩЕНИЯ В АЛГЕБРЕ оЛ
Основной результат принадлежит Хиллу и Филлипсу.
1. Теорема. Пусть g е ©^, тогда g имеет обратный элемент
в в том и только том случае, когда
2. inf |g(s)|>0.
Re s О
Упражнение 1. Предположим, что ge Рс orf. Показать, что неравенство
(2) никогда не выполняется. (Указание: использовать лемму Римана —
Лебега.)
Доказательство теоремы (1).
Необходимость. Пусть х — обратный элемент для g, т. е.
= Поскольку g, х^о.4, для любых s таких, что Res^O,
g (s) х (s) = 1. Кроме того, так как х е ©^, то
sup ! x(s) I ||x|U <оо.
Res^ 0
Следовательно, для любых s таких, s что Res^O,
|g (s) | = I x(s) r1 I! xJZ
Достаточность. Доказательство этой части теоремы см. у
Хилла и Филлипса [51].
D.3. ОБРАЩЕНИЯ В АЛГЕБРЕ
265
Все окончательно проясняется, если отметить следующее. Если
бы существовало s0 е © такое, что Re s0 0 и g (s0) = 0, то функ-
ция g принадлежала бы собственному идеалу алгебры и не
имела бы обратного элемента из оЛ. Поэтому для того, чтобы
в оЛ существовал элемент, обратный g, для любых seC таких,
что Res^O, должно выполняться неравенство |g(s) |> 0. С другой
стороны, если в области Res^O существовала бы последователь-
ность {$*}, для которой | g (sk) I -> оо при |s*l->oo, изображение
по Лапласу функции g~l не обладало бы свойством ограниченности
при Res^O.
3. Следствие. Пусть G е тогда G имеет обратный эле-
мент в оЛпхп в том и только том случае, когда
4. inf det G {s)1 > 0.
Res ^0
Доказательство очевидно, если принять во внимание
правило Крамера и то, что из /, g е оЛ следует
Упражнение 2. Сформулировать теорему (1) и следствие (3) для алгебр
оЛ (о) и (о).
Дискретный случай
Здесь мы сформулируем аналог приведенной выше теоремы (1)
для дискретного времени.
Рассмотрим все односторонние последовательности,
и, в частности, последовательности из пространства
= gi, g2, у, lgil = Jgf<oo>. Линейное про-
v О '
странство Z1 превращается в коммутативную алгебру с единицей,
если в качестве операции умножения использовать свертку после-
довательностей. Согласно теореме (С.4.3), пространство I1 замкнуто
относительно этой операции умножения.
Упражнение 3. Проверить, что пространство Z1 со сверткой, введенной
в качестве умножения, является алгеброй над полем IR в соответствии с опре-
делением (D.1.2).
Пусть g е Р; определим функцию
оо
g (Z) = 2 gkZ-*'
fe=0
Нетрудно доказать следующую теорему.
5. Теорема. Если g е Р, то
(а) (г) — аналитическая функция от z при I г !> 1;
268
ПРИЛОЖЕНИЕ D. АЛГЕБРЫ
(Ь) функция 9»—*-g(eiQ) равномерно непрерывна на интервале
(О, 2л];
(С) |#(*) |<|g| для любых I г Issl;
(d) g(z)-*-g0 при |z|->oo.
Сформулируем теорему Винера [98] —аналог теоремы 1.
6. Теорема. Пусть (односторонняя) последовательность g =
= (go, gi, gi, •), где go=£0, принадлежит пространству /*.
Тогда g имеет обратную последовательность из Z1 в том и только
том случае, когда кривая
7. 9 —£(^),
представляющая собой образ интервала [0, 2л] в ©, не проходит
через начало координат и не окружает его.
8. Теорему (6) можно переформулировать следующим образом.
Пусть g е Z1, тогда g имеет обратный элемент, принадлежащий Z1,
в том и только том случае, когда inf | g (г) | > 0.
|2|>1
Эквивалентность (6) и (8) вытекает из утверждения (d) теоре-
мы (5) и принципа аргумента.
Упражнение 4. Вместо алгебры I1 рассмотрим алгебру I1 (р). Пусть
Тогда
0<peR.
{оо '
g = (go, gl, go. •••) I gi S R, 2 I gk I < oo
0
Проверить, что Z1 (p) — коммутативная алгебра с единицей, и сформулиро-
вать теорему обращения, соответствующую теореме (6).
Приложение Е
ЛЕММА ВЕЛЛМАНА —ГРОНУОЛЛА
1. Лемма. Пусть
(i) функции f, g, k: R+-+-R локально интегрируемы;
(ii) g^= 0 и
(iii) ge=L?',
(iv) функция gk локально интегрируема на R.
Тогда, если функция и: R+-»-IR удовлетворяет условию
2. (t) + g(t)^ k(x)u(x)dx V/(=R+,
о
то для любых t е R+
3.
«(0<f(0+s(0$*(T) f(x)
Q
t 1
exp\k(xl)g(x1)dx1 dx.
X J
ЛЕММА ВЕЛЛМАНА - ГРОНУОЛЛА
26'
4. Частный случай. Пусть функция kt R+-><R локально интег
рируема на R+ и k^O. Если
б. u(/)^ с+ J k(x)u(x)dx Vt^O,
то
6. и (Z)«gcexp k k (T)dx I V/^0.
Io I
Доказательвтво. Общепринятое доказательство основано
на последовательности операций дифференцирования и требует
применения интегрирующего множителя
fe(/)exp —$Л(т)£(тМт|.
о I
Мы же проведем прямое доказательство леммы. Рассмотрим ин-
тегральное уравнение
7. y(/) = /(/)+£(0j*(T)y(T)dT, у(0) = /(0).
Решение (7) имеет вид
8- y(0 = /(0+g(0j*C0f(O fexp dx.
0 [ т
Используя (2) и (7), определим функцию £(/):
9. 5(0 — У (0 — «(О S* g (0 5 * СО [у (Т' — U (т) I dx.
о
Соотношение (9) представимо в форме (/). Поэтому
(в силу монотонности оператора Т)
Vn€=Z*.
Кроме того,
t II
(T"£)(0=g(0 \k Т2)#(Т2)Х
О Г
1п-1
X \ k (т3) g (хя)... J k(x„)^(x„)dxldxi...dxa =
о о
I fl ln-1
.10. ^g(t) J| (П— l)!]-1 К*(Т1)£(Т1)«Ы й (T) £ (t) dr.
ok J
26fc
ПРИЛОЖЕНИЕ E
Пусть'
11.
t
m(t) = \k(r)g(r) dx.
' 0
Заметим, что функция /и(-) непрерывна и m(t)^0 при /^0,
так что зыражение в скобках из (10) не превосходит [т (0Г*"1»
поскольку Цт)^(т)^0 при любых т, согласно условию (ii).
Следовательно, из (10) вытекает, что
С(03=-g(t)У k(x) | Ur) I dr.
о
Учитывая (iii), получаем, что для любого фиксированного t при
п оо
12.
UO^o.
И, наконец, неравенство (3) вытекает из (12), (9) и (8).
В дискретном случае имеем следующую лемму.
13. Лемма. Пусть {и*}, {/*}, {й*} (й = 0, 1, ...) —последова-
тельности действительных чисел из Z+- Пусть, кроме того,
14. ft* 0 при любых k е Z+- |
Тогда, если
15. u*^f* + * = °> ’• 2- ••••
то I
16. «*<;*+ 5 [ П О+Ш]. ft = 0, 1.2......................... &
где произведение (l-f-й/) при t.= ft—1 полагается равным I
<</<* 1
единице. I
Доказательство. Выпишем неравенство (15) для 6 = 0,
1, 2, ...» последовательно подставляя уже полученные неравен-
ства в очередное с использованием условия (14):
< А»
А 4" Мо> ;
^2 А + П + hi) hofe + hifi,
А 4- (1 4" hi) (1 h2) hofQ 4*
4” (1 4“ lh) hifi 4-
ЛЕММА ВЕЛЛМАНА - ГРОНУОЛЛА 269
Неравенство (16) нетрудно получить по индукции. Отметим,
что
(а) если hi^hM для некоторого hM и любых f, то
uk^fk+hM (i+W-'-1/*;
(Ь) если Для некоторого fM и любых i, то
Uk^fM П
0<1<л
ЛИТЕРАТУРА
I. Anderson В. D. О. The small gain theorem, the passivity theorem
and their equivalence. — J. Franklin Inst., v. 293, № 2, pp. 105—115,
Feb. 1972.
2. Apostol T. M. Mathematical Analysis.— Reading, Massachusetts
Addison — Wesley, 1957.
3. Baker R. A., Vakha ria D. J. Input-output stability of linear
time-invariant systems. — IEEE Trans. Automat. Control, v. AC-15, № 3,
pp. 316—319, June 1970.
4. Barman J. F. Well posedness of feedback systems and singular per-
turbations. — Ph. D. thesis, Univ. California, Berkeley, 1973.
5 Bergen A. R., I wens R. P., Rault A. J. On input-output sta-
bility of nonlinear feedback systems. — 1 EEE Trans. Automat. Control,
v. AC-11, № 4, pp. 742—745, Oct. 1966.
6. Bochner S., Chandrasekhar R. S. Fourier Transforms. —Prin-
ceton Studies 17, Princeton Univ. Press, Princeton, New Jersey, 1949.
7 Bourbaki N. Fonctions d’une variable rfcelle. Livre IV, Chaps. 1—3,
2nd ed. — Hermann: Paris, 1958. [Русский перевод: Бурбаки H.
Элементы математики, кн. 4. Функции действительного переменного,
части 1—3. — М.: Наука, 1965.]
8. Bourbaki N. Fonctions d’une variable reelle. Livre IV, Chaps. 4—7,
2nd ed. — Hermann. Paris, 1961. [Русский перевод: Бурбаки H.
Элементы математики, кн. 4. Функции действительного переменного,
части 4—7. —М.: Наука, 1965.]
9. Brauer F. Nonlinear differential equations with forcing terms.— Proc.
Amer. Math. Soc., v. 15, pp. 758—765, 1964.
10. Brockett R. W., Forys L. J. On the stability of systems contai-
ning a time-varying gain.— In: Proc. 2nd Allerton Conf., Univ of Illi-
nois, Urbana, Illinois, pp. 413—430, 1964.
11. Brockett R. W., Willems J. L. Frequency domain stability
criteria parts I and II. —IEEE Trans. Automat. Control, v. AGIO. № 3.
pp. 225-261; № 4, pp. 407—113, 1965
12 Brockett R. W. The status of stability theory for deterministic sy-
stems.—IEEE Trans. Automat. Control, v. AC-11, № 3, pp. 586—607,
July 1966.
13. Brockett R. W. Path integrals, Liapunov functions, and quadratic
minimization. —In: Proc. 4th Allerton Conf, on Circuits and System
Thoory, pp. 685—697, 1966.
14. Brockett R. W., Lee H. B. Frequency domain instability criteria
for time-varying a d nonlinear systems. — Proc. IEEE, v. 55, № 5,
pp. 604—618, May 1967.
15. Browder F. E. The solvability of nonlinear functional equations. -
Duke Math. J., v. 30, pp. 557—560, 1963.
16. Call i er F. M. De so er C. A. A graphical test for checkin; the sta-
bility of a linear time-invariant feedback system. —IEEE Trans. Automat.
Control, v. AC-17, № 6., pp. 773—780, Dec. 1972.
17. Callier F. M., Desoer C. A. Necessary and sufficient conditions
for the stability of л-input—л-output convolution feedback systems with
ЛИТЕРАТУРА
271
finite number of unstable poles.— IEEE Trans. Automat. Control, v. AC-18,
№ 3, pp. 295—298, June 1973.
18. Chen С. T. L^-stability of linear time-varying feedback systems —
J. SIAM Control, v. 6, № 2, pp. 186—193, May 1968.
19. Ch о Y. S., Narendra K. S. Stability of nonlinear time-varying
feedback systems. —In: Proc. 5th Allerton Conf., pp. 249—258, 1967.
20. Chu S. C., Metcalf F. T. On GronwalTs inequality. —Proc. Amer.
Math. Soc., v. 18. № 3, pp. 439, 440, June 1967.
21. Cop pel W. A. Stability and Asymptotic Behavior of Differential
Equations. —Boston, Massachusetts: Heath, 1965.
22. Corduneanu C. Problems globaux dans la theorie des equations inte-
grates de Volterra.—Annali di Matematica Рига et Applicata (IV), v. 67,
pp. 349—364.
23. Dahlquist G. Stability and error bounds in the numerical integrations
of ordinary differential equations.—Trans. Roy. Inst. Tech. (Sweden),
№ 130, 1959.
24. Davis J. H. Encirclement conditions for stability and instability of
feedback systems with delays.— Int. J. Control, v. 15, pp. 793—799,
April 1972.
25. Davis J. H Fredholm operators, encirclements and stability crite-
ria.—J SIAM Control, v 10, pp 608—622, Nov 1972.
26. [fesoer C. A., Thom a si an A. J. A note on zero-state stability
of linear systems. — In: Proc. 1st Allerton Conf., pp. 50—52, 1963.
27. De so er C. A. A general formulation of the Nyquist criterion. — IEEE
Trans., Circuit Theory, v. CT-12, № 2, pp. 230—234, June 1965.
28. De so er C. A. A generalization of the Popov criterion.— IEEE Trans
Automat. Control, v. AC-10, № 2, pp. 182—184, April 1965.
29. Desoer C. A., Wong К. K. Small signal behavior of nonlinear
lumped networks. —Proc. IEEE, v. 56, № 1, pp. 14—23, Jan 1968.
30. Desoer С. А.» Wu M. Y. Stability of multiple-loop feedback linear
time-invariant systems. —J. Math Anal. Appl., v 23, № 1, pp. 121 — 130,
July 1968.
31. Desoer C. A., Wu M. Y. Stability of linear time-invariant sys-
tems.—IEEE Trans. Circuit Theory, v. CT-15, № 3, pp. 245—250,
Sept 1968.
32. Desoer C. A. SI >wly varying system x—A(t)x.— IEEE Trans. Auto-
mat. Control, v. AC-14, № 6, pp. 780—781, Dec. 1969.
33. Desoer C. A. Slowly varying system x;+1 = A;X/. — Electron Lett.,
v. 6, № 11, pp. 339—340, 1970.
34. Desoer C. A., W и M. Y. Input —output properties of multiple-in-
putmultiple-output discrete systems, Part I. —J. Franklin Inst., v. 290. .
№ 1, pp. 11—24, July 1970.
35. Desoer C. A., Vi dy a sagar M. General necessary conditions for
input-output stability.—Proc. IEEE, v. 59, № 8, pp. 1255—1256
Aug. 1971.
36. Desoer C. A., Haneda H. The measure of a matrix as a tool to
analyse algorithms for circuit analysis. —IEEE Trans. Circuit Theory
v. CT-19, № 5, pp. 480—486, Sept. 1972.
37. Desoer C. A., Cal lie г F. M. Convolution feedback systems.—
J. SIAM Control, v. 10, pp. 737—746. Nov. 1972.
38. Desoer C. A., Schulman J. D. Cancellations in multivariable
continuous-time and discrete-time feedback systems treated by greatest
common divisor extraction. — IEEE Trans. Automat. Control, v. AC-18,
№ 4, pp. 401—402, Aug. 1973.
39. Desoer C. A. Notes for a second course on linear systems. —New
York: Van Nostrand Reinhold, 1970.
40. Dewey A. G., Jury E. I. A stability inequality for a class of non-
linear feedback systems. — IEEE Trans. Automat. Control, v. AC-11, № 1,
pp. 54—62, Jan. 1966.
272
ЛИТЕРАТУРА
41. Dieudonne J Foundations of Modern Analysis. — New York: Aca-
demic P”(ss, 1960. [Русский перевод: Дьедонне Ж. Основы
современного анализа. —М.: Мир, 1964.]
42. Dieudonne J. Treatise on Analysis, vol. II. —New York: Academic
Press, 1970.
43. Dunford N., Schwarz J. T. Linear Operators, part I: General
Theory —New York: Interscience Publishers, Inc., 1958. [Русский пе-
ревод: Данфорд H., Шварц Дж. Линейные операторы, т I,
Общая теория. —М.: ИЛ, 1962.]
44. Edwards R. Е. Functional Analysis. — New York: Holt, Rinehart &
Winston, 1965. [Русский перевод: Эдвардс P. Функциональ-
ный анализ. —M.: Мир, 1969.]
45 Estrada R. F., Desoer С. A. Passivity and stability of systems
with a state representation. — Int. J. Contr., v. 13, № 1, pp. 1—26, Jan.
1971.
46 Fliigge-Lotz I Discontinuous and Optimal Control. —New York:
McGraw-Hill Book Co., 1968.
47. Freedman M., Zames G. Logarithmic variation criteria for the sta-
bility of systems with time-varying gains.— J. SIAM Control, v 6, № 3,
pp. 487—507, Aug. 1968.
48. Goff man C., Ped rick G. First Course on Functional Analysis.—
Englewood Cliffs, N. J.: Prentice-Hall, 1964.
49. Goldberg R. R Fourier Transform.— London and New York: Cam-
bridge Univ. Press, 1961.
50. Hahn W. Stability of motion. —New York: Springer-Verlag, 1967.
51. Hille E., Phillips R. S. Functional analysis and semi-groups.—
Amer. Math. Soc. Coll. Publ., v. XXXI, New Providence, 1957.
52 Holtzman J. M. Contraction maps and equivalent linearization.—
Bell Sys. Tech. J., v. 46, № 10, pp 2405—2435, Dec. 1967.
53. Holtzman J. M The use of the contraction mapping theorem with
derivatives in a Banach space.—Q. Appl. Math., v. 26, № 3, pp. 462—465,.
Oct. 1968.
54. Holtzman J. M. Nonlinear Systems Theory. —Englewood Cliffs,,
N. J.: Prentice-Hall, 1970.
55. Householder A. S. The Theory of Matrices in Numerical Analy-
sis.—New York: Blairdell, 1964.
56. Hsu С. H., Chen С. T. A proof of the stability of multivariable sy-
stems.—Proc. IEEE, v. 56, № 11, pp. 2061-2062, Jan. 1966.
57. Johnson C. D. A note on control systems with one nonlinear ele-
ment.—IEEE Trans. Automat. Control, v. AC-11, № 1, pp 122—124,
Jan. 1966.
58. Krikorian J. S., Jr. A ^-stability criterion with frequency domain
interpretation for a class of nonlinear discrete systems. — IEEE Trans.
Automat Control, v. AC-17, № 3, pp. 365—368, June 1972.
59. Lee С. T., Desoer C. A. Stability of single-loop nonlinear feedback
systems.— In: Proc. 3rd Allerton Conf., pp. 259—269, 1965.
60. McShane S. Integration. — Princeton, N. J.: Princeton Univ Press,
1944
61. Minty G. J. Monotone (nonlinear) operators in Hilbert space. —Duke
Math J., v. 29, pp. 341—346, 1962
62. Narendra K. S., Goldwyn R. M. A geometrical criterion for the
stability of certain nonlinear nonautonomous systems. — IEEE Trans. Cir-
cuit Theory, v. CT-11, № 3, pp. 406—408, Sept. 1964.
63. O’Shea R. P. A combined frequency-time domain criterion for autono-
mous linear systems. — IEEE Trans. Automat Control, v AC-11, № 3, 1966
64. Paley R. E A C., Wiener N. Fourier transforms. — Amer Math.
Soc Coll Publ., v XIX, New Providence, 1934.
65. Perkins W. R. Sensitivity analysis. — In.: Cruz J. B. (ed.), Feedback
Systems, New York, McGraw-Hill, 1972.
ЛИТЕРАТУРА
273
66. Popov V. М. Some Properties of the Control Systems with Irreducible
Matrix-Transfer Functions.—Seminar on Differential Equations and Dyna-
mical Systems, Lecture Notes in Mathematics 144. —New York: Sprjnger-
Verlag, 1970.
67. Ra-narajan S., T hatha ch ar M. A. L. P-stabtl ity of time-va-
rying systems with global conditions on the time-varying gain. — Int. J.
Syst. Sci., v. 3, № 4, pp. 385—394, Dec. 1972.
68. Rosenbrock H. H. State Space and Multivariable Theory. — New
York: Wiley-Interscience, 1970.
69. Roy den H. L. Real Analysis. — New York: The Macmillan Co., 1963.
70. Saeks R. Causality In Hilbert space.— SIAM Rev., v. 12, № 3,
pp. 357—383, July 1970.
71. Saeks R. Resolution Space, Operators Systems.— New York: Sprin-
ger-Verlag, 1973.
72. Sandberg I. W. On the properties of systems that distort signals
(I and II). —Bell Sys. Tech. J., v. 42, pp. 2033—2047, Sept. 1963; v. 43,
pp. 91—112, Jan. 1964.
73. Sandberg I. W. On truncation techneques in the approximate ana-
lysis of periodically time-varying networks. — IEEE Trans. Circuit Theory,
v. CT-11, № 2, pp. 195—201, June 1964.
74. Sandberg I. W. On the J?2-boundness of solutions of nonlinear fun-
ctional equations.— Bell Sys. Tech. J., v. 43, pp. 1581— 1599, July
1964.
75. Sandberg I. W. A frequency domain condition for stability of feed-
back systems containing a single time-varying nonlinear element. —Bell
Sys Tech. J., v. 43, pp. 1601—1608, pt. II, July, 1964.
76. Sandberg I. W. Feedback-domain criteria for the stability of nonli-
near feedback systems.— Proc. NEC, v. 20, pp. 737—740, 1964.
77. Sandberg I. W. On the boundedness of solutions of nonlinear inte-
ral equations.— Bell Sys. Tech. J., v. 44, pp. 439—453, Mar. 1965.
andberg I. W. A stability criterion for linear networks containing
time-varying capacitors. — IEEE Trans. Circiut Theory, v. CT-12, № 1,
pp. 2—12, Mar. 1965.
79. Sandberg I. W. Some results on the theory of physical systems go-
verned bynonlinear functional equations.— Bell Sys Tech J., v. 44,
pp 871—898, May —June 1965.
80. Sandberg I. W. An observation concerning the application of the
contraction mapping fixed-point theorem and a result concerning the norm-
boundedness of solutions of nonlinear functional equations. — Bell Sys.
Tech J., v. 44, pp. 1809—1812, 1965
81. Sandberg I. W. Some stability results related to those of V. M. Po-
pov.—Bell Sys. Tech. J., v. 44, pp 2133—2148, Nov. 1965.
82. Sandberg I. W. Conditions for the causality of nonlinear operators
defined on a function space. —Q. of Appl. Math., v. XXIII, № 1,
pp. 87-91, Apr. 1965.
83. Sandberg I. W. On the stability of linear systems containing
a time-varying element with restricted rate of variation.— IEEE Int.
Conv. Rec (USA), v. 14, pt. 7, pp. 173-182, 196G.
84. Sandberg I. W. On generalizations and extensions of the Popov
criterion. — IEEA Trans Circuit Theory, v CT-13, № 1, pp. 117—118,
Mar. 1966.
85. Schwartz L. Theorie des Distributions. — Paris. Hermann, 1966.
86. Skoog R. A., Blankenship G. L. Generalized pulse-modulated
feedback systems: norms, gains, Lipschitz constants, and stability. — IEEE
Trans. Automat. Control, v. AC-15, № 3, pp. 300—315, June 1970.
87. Sundareshan M. K., Thathachar M. A. L. Testability of
nonlinear time-varying systems —conditions involving noncausal multi-
pliers.—IEEE Trans. Automat. Control, v. AC-17, №4, pp. 504—510,
Aug. 1972.
274
ЛИТЕРАТУРА
88. Sundareshan М. К., Thathachar М. A. L. Time domain cri-
teria for the Instability of nonstationary feedback systems. — IEEE Trans.
Automat. Control, v. AC-18, № 1, pp. 80—81, Feb. 1973.
89. Sundareshan M. K., Thathachar M. A. L. Generalized factoriza-
bility conditions for stability multipliers. —IEEE Trans. Automat. Con-
trol, v. AC-18, Ke 2, Apr. 1973.
90. Takeda S., Bergen A. R. Instability of feedback systems by
orthogonal decomposition of L2.— IEEE Trans. Automat. Control, v. AC-18,
№ 6, pp. 631—636, Dec. 1973.
91. Thathachar M. A. L., Srinath M. D., Krishna G. Stabi-
lity with nonlinearity in a sector.—IEEE Trans. Automat. Control,
v. AC-11, № 2, pp. 311—312, Apr 1966.
92. Thom a si an A. J. The Structure of Probability Theory with Appli-
cations.—New York: McGraw-Hill, 1969.
93. Titmarsh E. C. Theory of Fourier Integrals. — New York: Oxford
Univ. Press, 1938. (Русский перевод: Титчмарш E. Введение
в теорию интегралов Фурье.— М.— Л.: Гостехиздат, 1948.]
94. Vidyasagar М. Input-output stability of a broad class of linear
time-invariant multivariable feedback systems.—J. SIAM Control, v. 10,
pp. 203-209, Feb. 1972.
95. Vidyasagar M. L«-stability of time-varying linear feedback sy-
stems.—IEEE Trans. Automat Control, v. AC-17, № 3, pp. 412—414,
June 1972.
96. Vidyasagar M. Some applications of the spectral radius concept to
nonlinear feedback stability. — IEEE Trans, Circuit Theory, v. CT-19,
№ 6, pp. 608—615, Nov. 1972.
97. Wang S. H. Design of Linear Multivariable Systems. —Ph. D. Thesis,
Univ, of California, 1971.
98. Wiener N. The Fourier Integral and Certain of Its Applications.—
Cambridge Univ. Press, London and New York, 1933. [Русский пе-
ревод: Винер H. Интеграл Фурье и некоторые его приложения.' —
М.: Физматгиз, 1963.]
99. Willems J. С. Stability, instability, invertibility and causality.—
J. SIAM Control, v. 7, pp. 645—671, Nov. 1969.
100. Willems J. C. Some results on the L^-stability of linear time-varying
systems. —IEEE Trans. Automat. Control, v AC-14, Ke 6, pp. 660—665,
Dec. 1969.
101. Willems J. C., Brockett R. W. Some new rearrangement ine-
qualities having application in stability analysis. —IEEE Trans. Automat.
Control, v. AC-13, № 5, pp. 539—549, Oct. 1968.
102. Willems J. C. A survey of stability of distributed parameter sy-
stems.—In: Control of Distributed Parameter Systems. Publ by the ASME
for the J A AC, Aug. 1969.
103. Willems J. C. The Analysis of Feedback Systems.—Cambridge, Mas-
sachusetts: MIT Press, 1971.
104. W о 1 о v i c h W. A. The determination of state-space representation for
linear multivariable systems. —In: Second IFAC Symp. Muitivariable
Tech. Contr. Syst., Dusseldorf, Germany, October 1971.
105. Wu M. Y., Desoer C. A. Testability (l^p^oo) of nonlinear
time-varying feedback systems. —J. SIAM Control, v. 7, № 2, pp. 356—364,
May 1969.
106. Wu M. Y., Desoer C. A. Input-output properties of multiple-input-
multiple-output discrete systems, pt. IL —J. Frankli i Inst., v 290, № 2,
pp. 85—101, Aug. 1960.
107. Yoshizawa T. Stability Theory by Liapunov’s Second Method.—To-
kyo: Maruzen, 1966.
108. Yosida K. Functional Analysis. — New York: Academic Press, 1965.
[Русский перевод: Иосида К. Функциональный анализ. —М.;
Мир, 1967.]
ЛИТЕРАТУРА
275
109. You la D. C., Ca striota L. J., Carlin H. J. Bounded real
scattering matrices and the foundations of linear passive network
theory —IRE Trans Circuit Theory, v. CT-4, № 1, pp. 102—124, Mar.
1959.
110. Zames G. On the stability of nonlinear time-varying feedback sy-
stems.—Proc. NEC, v. 20, pp. 725—730, 1964.
111. Zames G Nonlinear time-varying feedback systems—conditions for
L^-boundedness derived using conic operators on exponentially weighted
spaced. —In: Proc. 3rd Allerton Conf., Oct. 1965.
112. Zames G On the input-output stability of nonlineai time-varying
feedback systems, pts. I and II. —IEEE Trans. Automat. Control,
v. AC-11, № 2, pp. 228—238, Apr. 1966; № 3, pp. 465-477, July 1966.
113. Zames G., Fa lb P. L. On stability of systems with monotone and
odd monotone nonlinearities. —IEEE Trans. Automat. Control, v. AC-12.
№ 2, pp. 221-222, Apr. 1967.
114. Zames G, Fa lb P. L. Stability conditions for systems with mono-
tone and slope restricted nonlinearities.— J. SIAM Control, v. 6, Afe 1,
pp. 89—108. Feb. 1968.
115. Zames G., К a liman R. R. On spectral mapping, higher order
circle criteria, and periodically varying systems. — IEEE Trans. Automat.
Control, v. AC-15, № 6, pp. 649—652, Dec. 1970.
116 Зубов В И. Методы А М. Ляпунова и их применение.—Л.: Изд-во
ЛГУ, 1957.
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Алгебра банахова 261
— коммутативная 261
—, обращение элементов 264
— с^(о) 262
— о^пхп (о) 263
— 226
228
228
Антисипативность, см. Оператор анти-
сипативный
Банахова алгебра 261
Банахово пространство 26
Веллмана—Гронуолла лемма 266
— неравенство (дискретный случай)
268
----непрерывный случай) 266
Возвратная разность 82
---- матричная 82
Делитель общий левый 75
-------наибольший 75
---- правый 75
-------наибольший 75
—, процедура выделения 76
Идеал, определение 263
— собственный 263
— тривиальный 263
Интеграл двойной 249
— Лебега 248—250
— повторный 249
Коэффициент роста 51
---- по приращениям 55
— усиления 8, 53
Критерий круговой 155
— неустойчивости 242
Критерий неустойчивости графи-
ческий 108
----Попова, дискретный случай 209
--------, многоконтурная система 205
•-------, одноконтурная система 202-
Лемма Веллмана—Гронуолла 266
— Римана—Лебега 252
Линеаризация дискретной системы 150
— , основной результат 147
— , постановка задачи 144
Липшица условие 61, 166
Матрица, мера 39
— многочленная 68
— правильная 69
— строго правильная 69
— унимодулярная 74
—, факторизация 74
Матрицы взаимно простые слева 74
-------- справа 74
----псевдо простые 99
Мера 258
— матрицы 39
----, примеры 43
----, свойства 40
— ограниченная 258
Метод ортогонального разложения 175
— факторизации 73
— экспоненциального взвешивания
159
Минковского неравенство 249
Множество выпуклое 27
— поглощающее 28
— уравновешенное 27
Неантисипативность, см. Оператор не-
антисипативный
Неравенство Гельдера 249
— Минковского 249
— Шварца 187
Неустойчивость, определение 175
—, теорема 177, 181 241
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
277
Норма, графическая интерпретация 27
— евклидова 20
— матрицы 21
— отображения 30
— последовательности 20
— согласованная 32
— эквивалентная 22
Нормированное пространство X 48
-----расширенное Хе 48
Нули передаточной функции 90
Пространство Xt Xe 48
- eJT, 1«9
Радиус спектральный 37, 39
Разность возвратная 82
----- матричная 82
Римана—Лебега лемма 252
Ряды 253
—, сходимость 253
Обратимость в алгебре 264
— оператора / + Н 237
Ограниченность 56
Оператор антисипативный 217
— неантисипативный 49, 50> 216
— положительно определенный 218
— пассивный 190
------по приращениям 190
— строго пассивный 190
--------по приращениям 190
—, факторизация, см. Факторизация
операторов
— чисто антисипативный 217
— Щ, П_, 228
— 226
- Рг, 49
Пассивность, см. Оператор пассивный
— по приращениям, см. Оператор пас-
сивный по приращениям
Поле С Ю
— С 68, 71
- Р 9
— R (s) 9
Полюсы передаточной функции 80
Попова критерий, см. Критерий По-
пова
Преобразование контура, см. Теорема
о преобразовании контура
— Лапласа 253
— Фурье 251, 252
z-преобразование 113
Проектор П+, П. 228
— Р_ 226
— Рт 49
Пространство банахово 26
__ /1 /р 24
*П» */!’ 1п
— Р, IP, °0 20
— L\ L\ Lw 21, 25, 26
— LP 25
- LP |a, d] 27
“ ±P (R+), Lpn (R 27
—<5? (£, E) 29
— X (Et E) 32
Свертка, определение 254
— последовательностей 259
—, свойства 255, 256
— функций 255
Сектор 11•
Секторное условие, определение 11, 15
-----, эквивалентность 12, 13, 17
Система автономная 171
— линейная 67
—, линеаризация 144
— многоконтурная 67
— нелинейная 144
— нестационарная 120
— одноконтурная 67
— с медленно меняющимися параме-
трами 164, 181
Спектр стображения 38
Спектральное число 38
Спектральный радиус 37, 39
Срезка функции 49
Существование решений 57
----- периодических 168
Теорема об ограниченности 56
— о коэффициенте роста 50
-----------по приращениям 54
— о неустойчивости 177 181, 242
— о пассивности 197
— о преобразовании контура 61
— о сжимающем отображении 38, 50,
54, 58, 168
— Парсеваля 252
— Попова, см. Критерий Попова
— существования и единственности 58
— Тонелли 249
Траектория опорная 145
— фазовая 144
Уравнение замкнутой системы 64
Усилители 215
Условие Липшица 61, 140
Устойчивость в целом 142
— равномерная 142
— экспоненциальная 69. 79
— X 63
278
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Устойчивость L00 121, 127, 139, 159
- LP 121, 127, 139, 153
- L* 155
- L1 127 139
- IP 141
Функция абсолютно непрерывная 247
— выпуклая 39
---. производная по направлению 39
— локально интегрируемая 20, 21, 25
— обобщенная 261
— передаточная замкнутой системы 96
— — правильная 96
---строго правильная 96
— • — экспоненциально устойчивая 96
— почти периодическая 117
Функция регулярная 246
— ступенчатая 246
Факторизация матриц, теорема 74
-----, процедура 76
— операторов с помощью логарифмов
224
— --------- проекторов 228
— передаточных функций 98, 100, 119
Характеристика 12, 13, 17
Характеристическое уравнение 90
Эквивалентность норм 22
— секторных условий 12, 13, 17
Ч. Дезоер, М. Видьясагар
Системы с обратной связью: вход-выходные
соотношения
Редактор Д. С. Фурманов
Техн, редактор И. Ш. Аквельрод
Корректоры О. А. Бутусова, Е. Я. Строева
ИБ № 11711
C,vho в набор 27.10.82. Подписано к печати 21.03 83.
Формат 6ОХ9О‘Л«- Бумага тип. № 1. Литературная
гарнитура. Высокая печать. Условн. печ. л. 17,5. Уч.-
изд. л. 18,4. Тираж 3600 экз. Заказ № 647. Цена 3 р.
Издательство «Наука»
Главная редакция
физико-математической литературы
117071, Москва, В-71, Ленинский проспект, 15
Ордена Октябрьской Революции, ордена Трудового
Красного Знамени Ленинградское производственно-
техническое объединение «Печатный Двор» имени
А. М. Горького Союзполиграфпрома при Государст-
венном комитете СССР по делам издательств, по-
лиграфии и книжной торговли. 197136, Ленинград,
П-136, Чкаловский ар., 15.
Отпечатано в типогр',*нч № 2 изд-ва «Наука»,
121099, Москва, Г-99, Шубинский пер. W. Зак. 2841