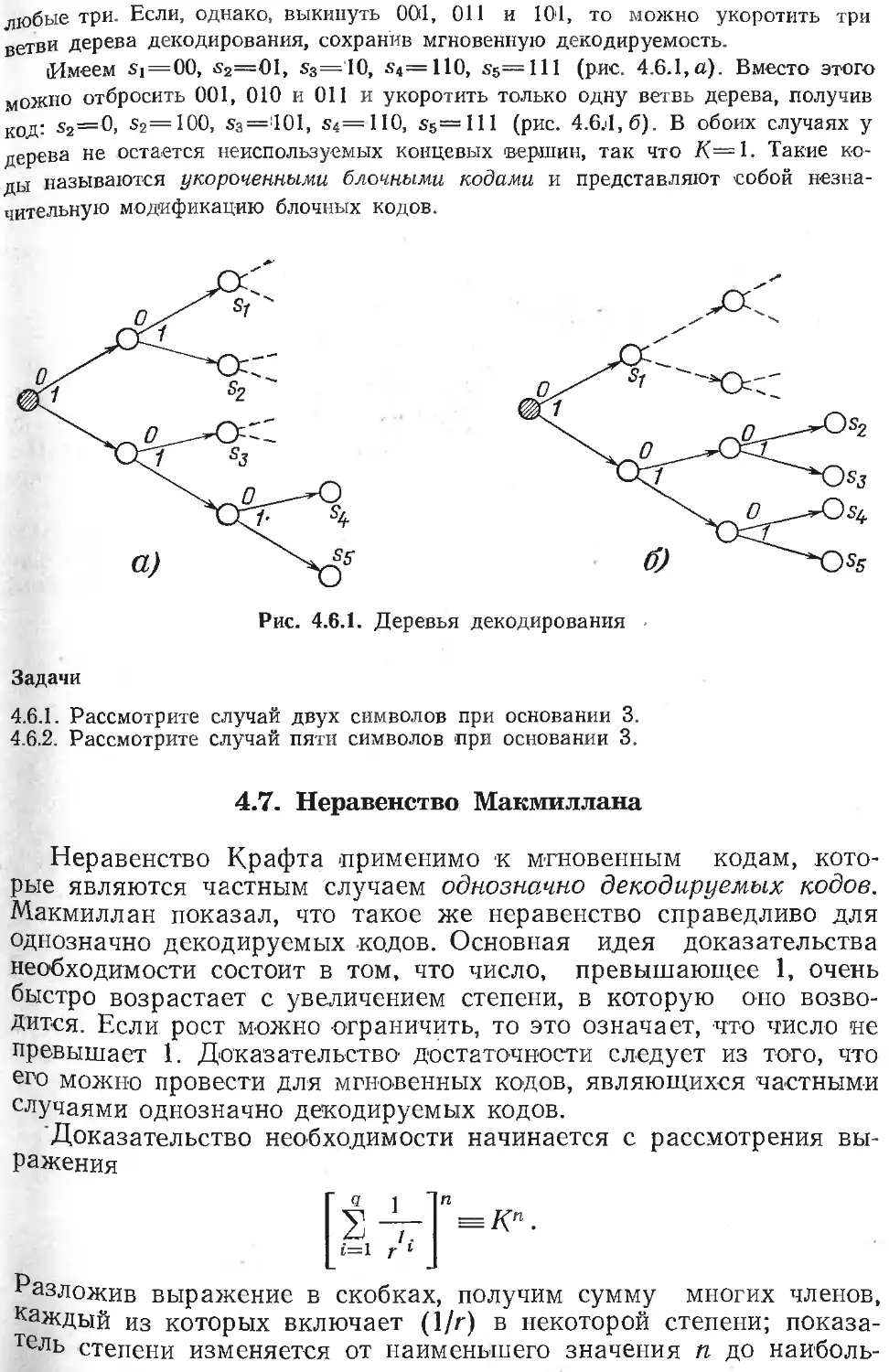
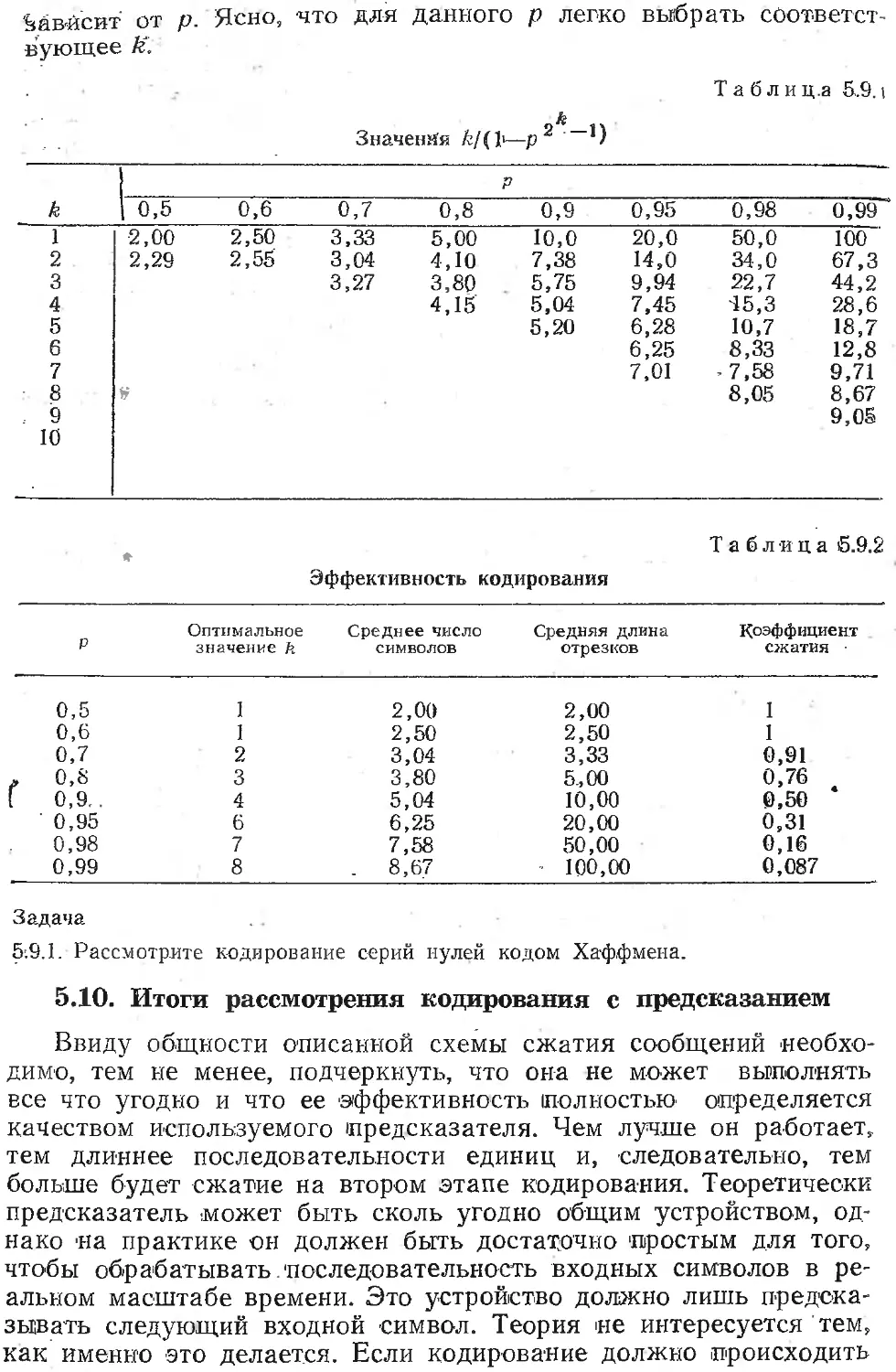
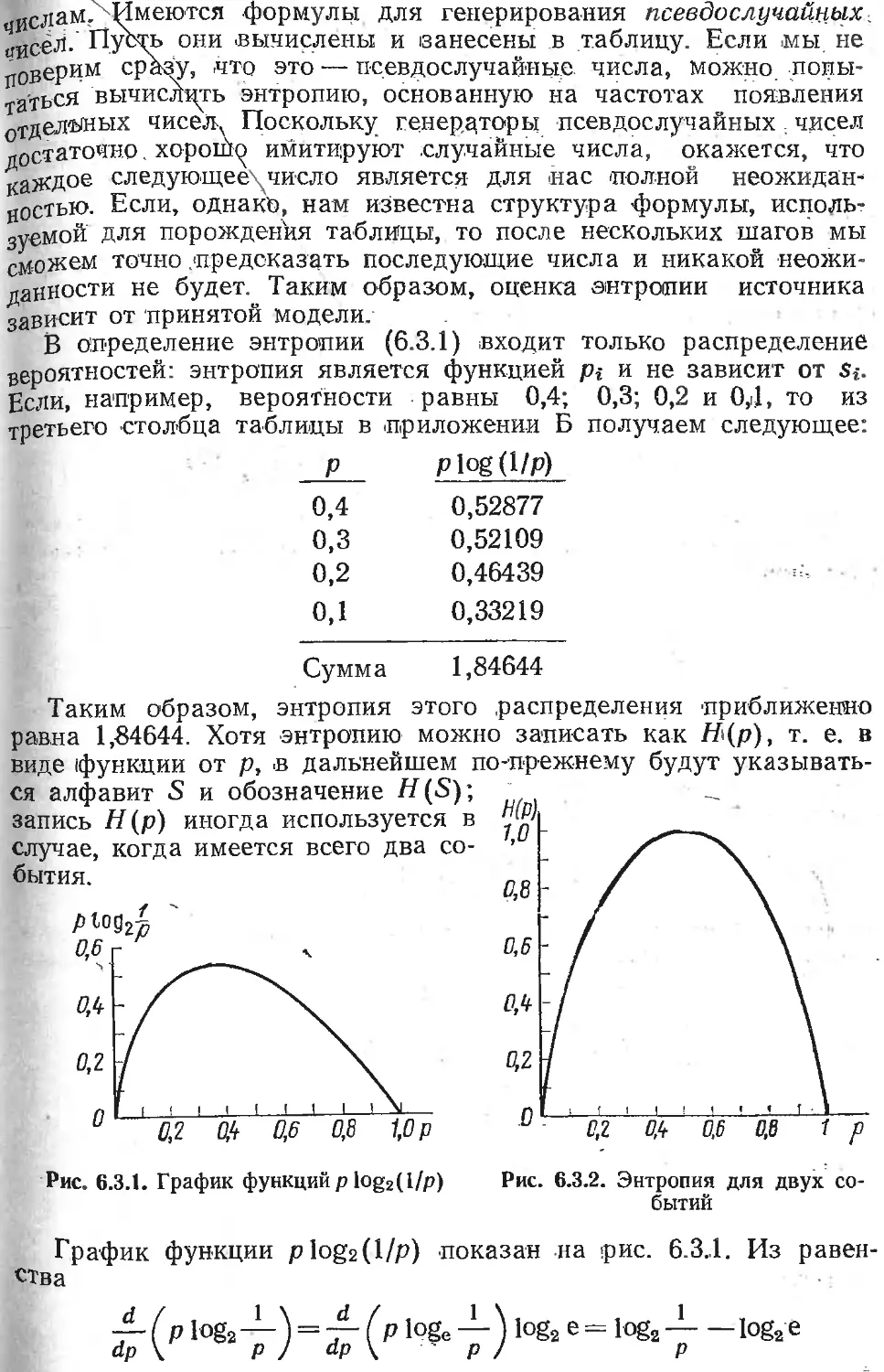
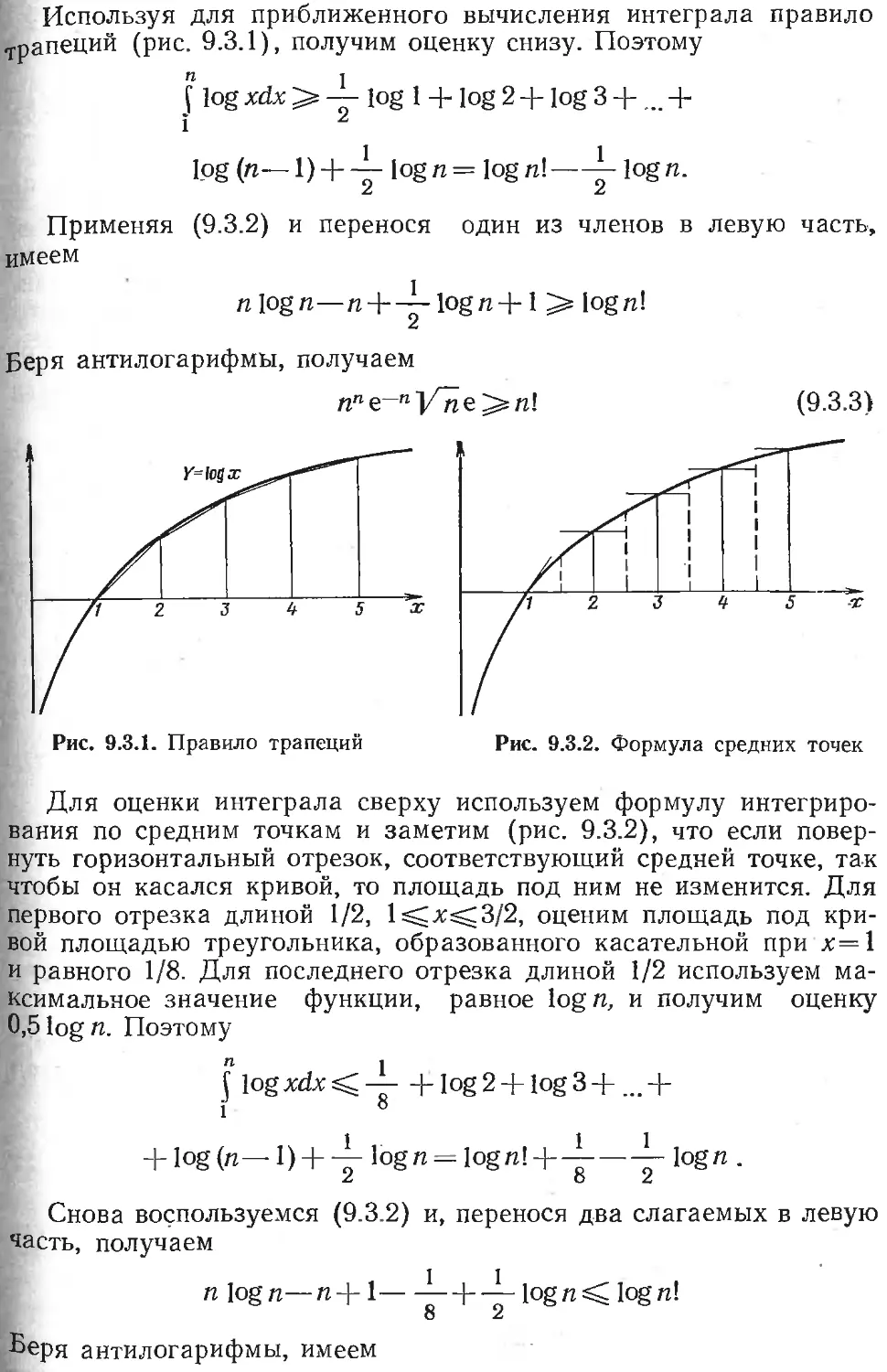
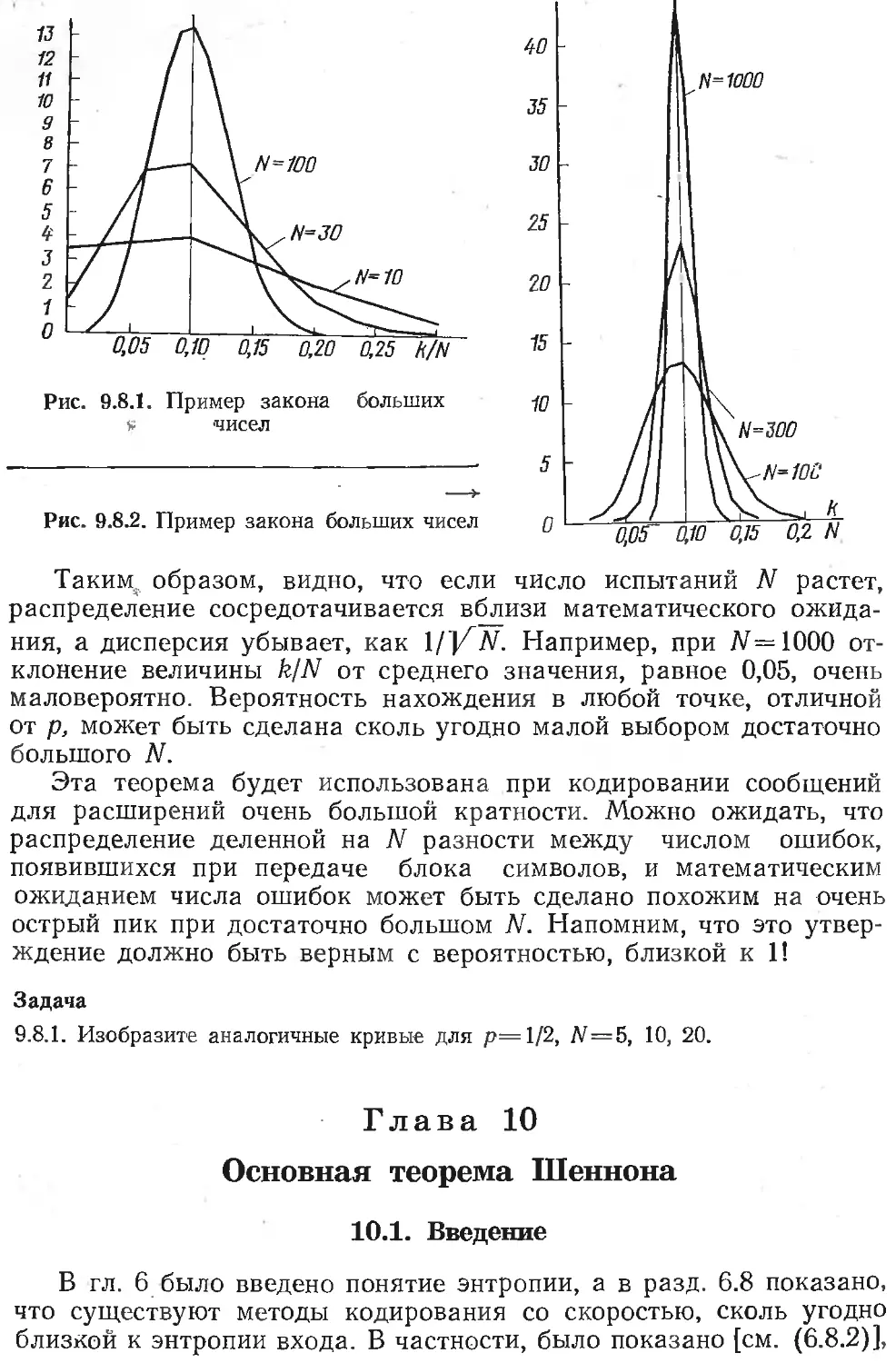
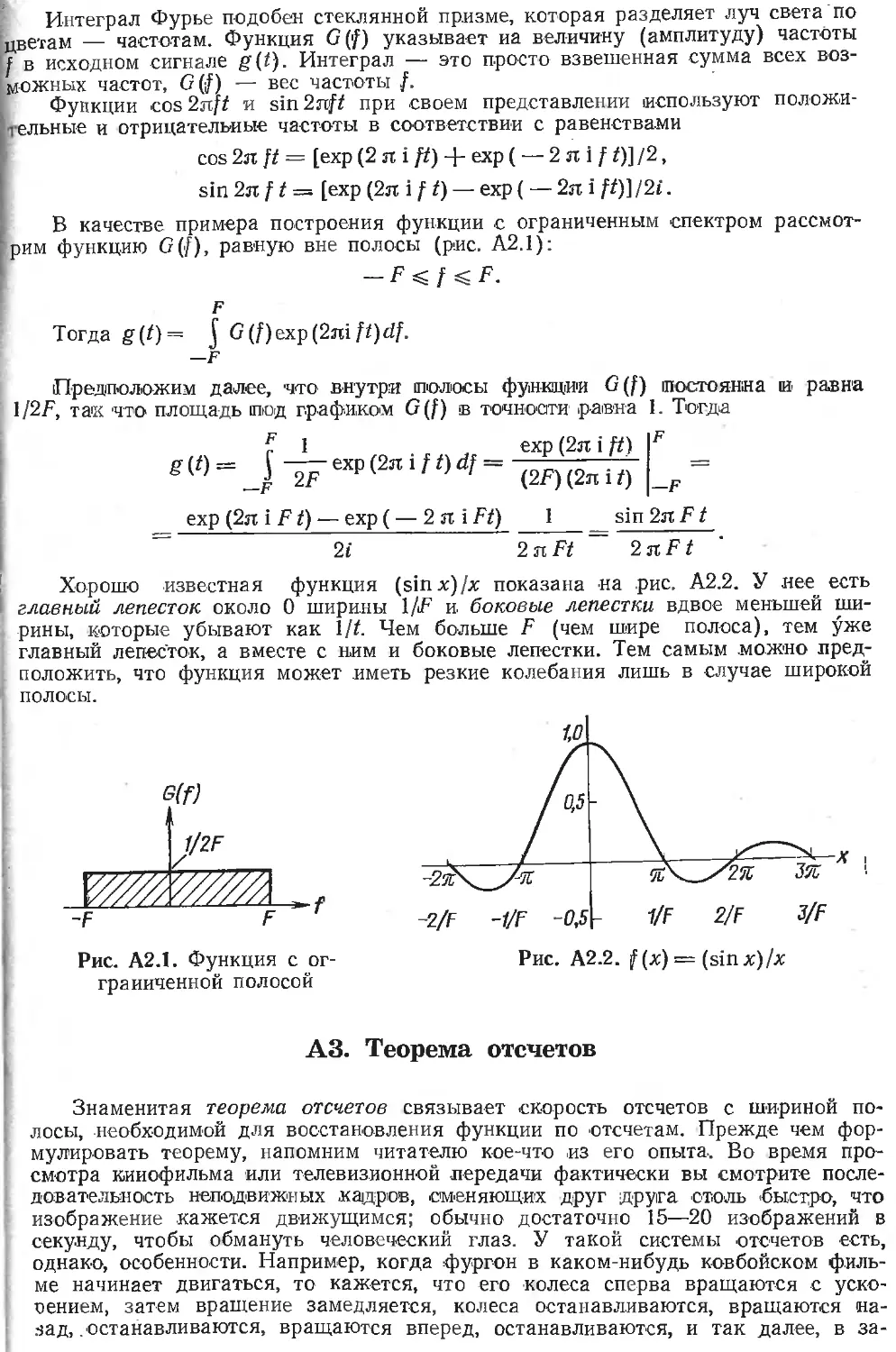
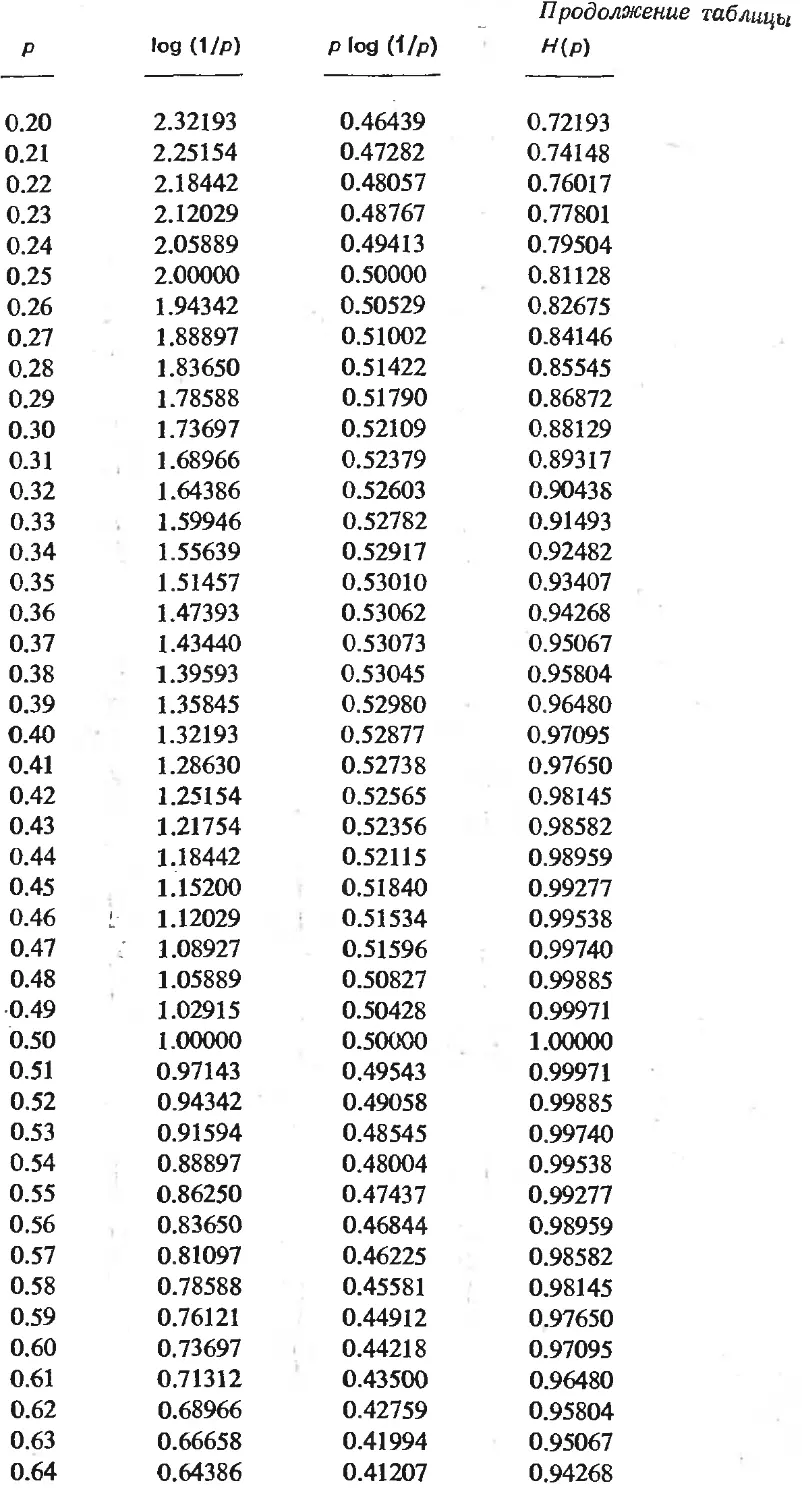
Текст
Р. В. Хэмминг
Теория кодирования
и теория информации
Перевод с английского
С. И. Гельфанда
под редакцией
Б. С. Цыбакова
МОСНВА,
„РАДИО И СВЯЗЬ”
1983
ББК 15.2
Х99
УДК 621.391.251 + 621.391.2
Хэмминг Р. В.
Х99 Теория кодирования и теория информации: Пер. с
англ. — М.: Радио и связь, 1983. — 176 с., ил.
75 к.
Рассматриваются основы теории кодирования и передачи информации.
Описываются свойства источника сообщения и каналов, дается классифи-
кация различных кодов. Особое внимание уделяется помехоустойчивым
-кодам с исправлением и с обнаружением ошибок. Приводятся примеры
использования теории кодирования и теории информации.
Для инженерно-технических работников, специализирующихся в об-
ласти передачи, хранения и обработки информации.
1502000000—094 ББК 15.2
X----------------103—83
046(01)—83 6Ф0.1
Редакция переводной литературы
Richard W. Hamming
Coding and Information Theory
Ричард В. Хэмминг
Теория кодирования и теория информации
Редактор Е. А, Засядько. Обложка художника С. Н. Голубева.
Художественный редактор Р. А. Клочков. Технический редактор Т. Н. Зыкина.
Корректор Я. Г. Зыкова
ИБ № 360
Сдано в набор 28.01.83 г. Подписано в печать 4.04.83 г.
Формат 60X90716 Бумага кн.-журн. Гарнитура литературная Печать высокая
Усл. печ. л. 11,0 Усл. кр.-отт. 11,25 Уч.-изд. л. 11,37 Тираж 7000 экз. Изд. № 20092
Зак. № 19 Цеиа 75 к.
Издательство «Радио и связь». 101000 Москва, Главпочтамт, а/я 693
Типография издательства «Радио н связь» Госкомиздата СССР
101000 Москва, ул. Кирова, д. 40
© 1980 by Prentice-Hall, Inc.
© Перевод на русский язык. Издательство «Радио и связь», 1983
Предисловие редактора перевода ,
Код Хэмминга является самым известным результатом теории
кодирования, а его автор — самым удивительным из ученых, ра-
ботавших в этой области. Дело в том, что Ричард Весли Хэмминг
имеет лишь две .публикации в области теории информации. Одна
из них [1*] содержит конструкцию кода Хэмминга, придуманную
еще до 1948 г., т. е. до появления работы К. Шеннона (i[2*],
с. 289), и, таким образом, представляет собой первую работу по
теории кодирования. Другая — это настоящая книга, вышедшая
30 лет спустя, когда теория кодирования прочно утвердила себя
как сложившееся научное направление. Поэтому появление этой
второй публикации Р. В. Хэмминга является в теории информации
событием незаурядным.
Наши специалисты хорошо знакомы с многими книгами по
теории информации и теории кодирования. Подавляющее боль-
шинство из них написано на высоком математическом уровне. Они
требуют от читателя глубокого знания алгебры и теории случай-
ных процессов, а также определенного уровня математической
культуры. В то же время теория информации — наука приклад-
ная, она служит теоретическим фундаментом техники связи, ра-
диолокации, техники обработки информации. Ее результаты долж-
ны находить практическое применение. Для этого нужно, чтобы
инженеры-проектировщики систем могли понять и оценить резуль-
таты теории. Как этого достичь? Долгое время господствовала
точка зрения, что нужно существенно повысить математическую
подготовку инженеров. Практика, однако, показывает, что выве-
сти математическую подготовку инженеров на требуемый для по-
нимания теоретических трудов уровень пока не удается. Причина
здесь состоит не столько в качестве преподавания или уровне ис-
ходной математической подготовки студентов, сколько в простой
истине: «нельзя объять необъятное» — невозможно совместить в
одном учебном процессе детальную инженерную и глубокую ма-
тематическую подготовку.
Где же искать выход? Нельзя ли пойти в противоположном
направлении и адаптировать теорию информации для инженеров?
Можно ли выделить из теории простые качественные и количест-
венные результаты и методы, существенно не обеднив ее?
Книга Р. В. Хэмминга .представляет собой шаг вперед в этом
(направлении. Она использует самый примитивный и наглядный
математический аппарат и с его помощью, а также с привлечени-
ем качественных рассуждений и интерпретаций пытается дать
представление об основных идеях и достижениях теории.
Чтобы усилить доступность, автор широко использует графиче-
ский материал, численные примеры, гибкую терминологию и под-
робные пояснения выкладок. Однако доступности нигде не прино-
сится в жертву верность результатов или точность интерпрета-
ций. В этом проявляется большое научное и педагогическое даро-
вание автора.
Мы надеемся, что книга Р. В. Хэмминга понравится читателям
и принесет пользу.
Б. С. Цыбаков
Предисловие
Материал книги естественно объединяет теорию кодирования
и теорию информации, которые изучают представления абстракт-
ных символов. В настоящее время эти теории разрослись столь
широко, что в короткой книге можно изложить лишь небольшую
их часть.
Обычно считается, что теория информации рассматривает «пе-
ресылку информации из одного места в другое» (передачу инфор-
мации). Однако эта задача абсолютно аналогична задаче «пере-
сылки информации от одного момента времени до другого» (хра-
нения информации). Обе задачи часто возникают при обработке
информации. Ясно, что кодирование информации для эффективно-
го хранения, а также надежное ее восстановление при наличии
шума очень важны при конструировании ЭВМ.
Поскольку задачи представления, передачи и преобразования
информации весьма существенны во многих областях науки и вы-
числительной техники, важно иметь доступное изложение теории
информации и теории кодирования. Каждый раз, когда появля-
ется необходимость в порождении, хранении или обработке ин-
формации, оказывается нужным знать, как сжать имеющийся
текст и как защитить его от возможных искажений. В книге бу-
дут изложены лишь наиболее существенные из многих известных
методов кодирования, однако можно надеяться, что имеющиеся
в книге многочисленные примеры подготовят читателя к исполь-
зованию других возможных методов.
Цель написания книги — изложить основы двух теорий и при-
вести примеры применения соответствующих идей на практике.
Необходимые предварительные знания математики и радиотехни-
ки сведены к минимуму. Используются лишь основы анализа и
теории вероятностей, а все выходящее за эти рамки приводится
с подробными объяснениями по мере необходимости. Для упроще-
ния изложения и доказательств многих результатов используются
методы, недавно развитые в вычислительной технике. Эти методы
объясняются по мере их использования, так что не предполагается
наличия у читателя предварительных знаний вычислительной тех-
ники. Многие другие доказательства были существенно упроще-
ны и иногда, следуя за развитием технологии, был добавлен но-
вый материал. Предприняты значительные усилия изложить ма-
териал (в особенности доказательство основной теоремы Шенно-
на) таким образом, чтобы было понятно, почему теоремы справед-
ливы, а не только чтобы привести математически строгое доказа-
тельство.
В гл. 1'1, посвященной алгебраическим кодам, приведены не-
обходимые математические результаты, относящиеся к конечным
полям. Ввиду сложности этих результатов глава помещена в ко-
нец книги и несколько выпадает из логически естественного по-
рядка изложения материала. При желании ее можно читать пос-
ле г.л. 3. В тексте часто допускаются повторения; важные идеи
рассматриваются по меньшей мере дважды с тем, чтобы читатель
лучше их усвоил.
В книге не затрагиваются многие важные вопросы; при этом
автор исходил из того, что лучше как следует изучить часть ма-
териала, чем сказать понемногу о многом. Таким образом, лектор
может по своему усмотрению многое добавить к изложенным воп-
росам, если он считает, что это будет полезно слушателям.
В книге используются обычные названия «коды Хэмминга» и
«расстояние Хэмминга»; использование здесь других терминов
было бы проявлением ложной скромности и лишь запутало чи-
тателя.
Автору трудно вспомнить все, чем он обязан другим, поскольку большинство
изложенных в книге фактов он узнал за годы работы в научно-исследователь-
ском отделе фирмы Bell. Чтение лекций в Высшем Военно-морском училище,
основанных на небольшой элегантной книге Н. Абрамсона «Теория информации
и кодирование» [1], снова пробудила интерес автора к этим вопросам. Во вре-
мя чтения различных коротких курсов по этим вопросам возникли многие упро-
щения, уточнения и примеры; автор благодарен многим своим слушателям за
помощь. Особенно существенной была помощь Альберта Вонга.
В процессе написания книги были составлены ее различные варианты на
ЭВМ фирмы Bostrom Management Corp., при этом весьма существенной была
помощь Ральфа Джонса. Однако, как обычно, ответственность за все ошибки
несет автор.
Р. В. Хэммииг
Глава1
Введение
1.1. Краткая аннотация
Хотя в книге используются такие красивые слова как инфор-
мация, передача и кодирование, при более близком рассмотрении
оказывается, что они в действительности представляют лишь ис-
точник сообщений с символами sb sq. Вначале ни о самих сим-
волах, ни о смысле, который в них может содержаться, ничего не
говорится. Предполагается только, что они однозначно разли-
чимы.
Далее вводятся вероятности рь ..., pq появления символов.
Вопрос о том, как найти Pi, в абстрактную теорию не входит. Для
каждого дискретного распределения вероятностей определено зна-
ет
чение энтропии Д—X p,log(l/pi). Функция Н, зависящая от рас-
i=i
пределения вероятностей pi, измеряет количество неопределенно-
сти, неожиданности или информации, содержащееся в распреде-
лении. Эта функция играет основную роль в теории и дает ниж-
нюю границу для средней длины кода. В дальнейшем также рас-
сматриваются более сложные вероятностные структуры, связан-
ные с символами s,.
Проблема представления символов алфавита источника st с
помощью другой системы символов (обычно двоичной, состоящей
из символов 0 и 1) составляет основную тему книги. Она сводит-
ся к следующим двум главным задачам.
1. Требуется представить символы источника так, чтобы их
представления были в некотором смысле далеки друг от друга.
В результате, несмотря на небольшие изменения (шум) этих пред-
ставлений, изменившиеся символы могут быть опознаны как не-
правильные и, возможно, даже исправлены.
2. Для повышения эффективности требуется представить сим-
волы источника в некоторой минимальной форме. Тогда миними-
Q
зируется средняя длина кода L= X рЛ, где — длина представ-
i=i
ления i-ro символа Sj. Энтропия дает нижнюю границу для L.
Таким образом, по существу, это — аострактнаяматематиче-
ская теория представления символов произвольного источника с
помощью заданного алфавита (обычно двоичного). В этой теории
нет передачи, хранения информации, шума, добавляемого к сиг-
налу. Все это лишь красивые слова, используемые для мотивиров-
ки теории. Будем продолжать использовать их, но читатель не
должен обманывать себя — предлагаемая теория является лишь
теорией представления символов.
1.2. История
Теория кодирования и теория информации возникли очень дав-
но. Многие главные идеи были понятны задолго до 1948 г., когда
возникла прочная основа для этих двух теорий. В 4948 г. Клод Е.,
Шеннон опубликовал в Bell System Technical Journal две статьи,
озаглавленные «Математическая теория связи» (перепечатаны в
[14]). Они почти сразу же сделали теорию информации широко
известной, и скоро в журналах появились статьи по теории ин-
формации, а на электротехнических и других факультетах различ-
ных университетов началось чтение лекции по этой дисциплине.
Для теории информации, что типично для внезапно возникающих
научных направлений, большинство первых приложений оказа-
лось неудачным, однако по-другому, видимо, невозможно устано-
вить границы применяемости новой теории. В результате того,
что от теории информации ожидалось больше, чем она могла
дать, наступило разочарование и сокращение числа читаемых кур-
сов. Сейчас можно, вероятно, дать более справедливую оценку
теории, находящуюся где-то между сильным энтузиазмом первых
дней и последующим разочарованием.
Теория информации устанавливает границы того, что можно
сделать, однако мало помогает при проектировании конкретных
систем. Делающийся отсюда вывод о бесполезности теории инфор-
мации является, как показывает следующая аналогия, неверным.
Рассмотрим теорию эволюции, которую предлагают студентам-
биологам. Хотя лишь очень немногим из студентов удастся при-
менять ее в течение жизни, эта теория может служить источником
ценных идей. Несмотря на отсутствие непосредственных примене-
ний, идеи теории эволюции могут быть плодотворно использова-
ны в других часто весьма далеких от биологии ситуациях, в кото-
рых имеются 1) небольшие изменения составных частей (откло-
нения); 2) выживание наиболее приспособленных (отбор).
При рассмотрении какого-либо учреждения, например, факуль-
тета вычислительной математики, университета, военной организа-
ции, банка, правительства или даже семьи, • возникают вопросы:
«Как возникла данная ситуация?» и «Какие силы обеспечили вы-
живание данной конкретной структуры?»
При более глубоком понимании силы теории возникают вопро-
сы: «Какие изменения в учреждении возможны при данной расста-
новке сил?» и «Как оно будет эволюционировать (что именно вы-
живет)?» Таким образом, идеи теории эволюции могут быть ис-
пользованы в ситуациях, весьма далеких от биологии.
Точно так же ряд идей теории информации можно применить
в ситуациях, весьма далеких от тех, которые в ней рассматрива-
ются. Применимость идей не всегда удается точно проследить •—
часто они лишь наводят на некоторую мысль — однако сами идеи
весьма полезны.
Примерно в то же время и в том же месте, что и теория ин-
формации, возникла теория кодирования. Однако публикация ос-
новной работы была задержана по патентным соображениям до
апреля 1950 г., статья появилась опять в Bell System Technical
Journal (перепечатана в [3, 4]). В теории кодирования математи-
ческие основы не столь сложны, как в теории информации, и по-
этому в течение долгого времени она не была столь же привлека-
тельной для теоретиков. Однако по прошествии времени в теории
кодирования начали применяться различные разделы математики,
такие как теория групп, теория конечных полей (теория Галуа) и
даже линейное программирование. В результате, к настоящему
времени теория кодирования стала активно развивающейся об-
ластыф математики [2, 8, 11, 12, 16].
В большинстве областей знания ошибки играют второстепен-
ную роль; они проявляются лишь на более поздних этапах иссле-
дования. Однако в теории кодирования и теории информации
ошибкам (шумам) отводят центральную роль. Поэтому эти тео-
рии особенно интересны, поскольку в реальной жизни шум при-
сутствует всюду.
С точки зрения логики теория .кодирования приводит к теории
информации, и теория информации определяет границы того, что
можно достичь подходящим методом кодирования информации.
Таким образом, обе теории тесно связаны между собой, хотя в
прошлом их развитие шло в значительной мере независимо. Одна
из основных целей написания данной книги — показать взаимо-
связь этих теорий. Более подробно история развития теории коди-
рования изложена в [3].
1.3. Модель системы передачи сигналов
Модель системы передачи сигналов содержит: 1) источник со-
общений; 2) кодирование для этого источника; 3) канал, по кото-
рому передается информация; 4) источник шума (ошибок), добав-
Рис. 1.3.1. Стандартная система передачи сигналов
ляющегося к сигналу в канале; 5) декодирование, и по возможно-
сти восстановление первоначальной информации по принятому
искаженному сигналу; 6) получатель информации.
Эта модель показана на рис. 1.3.1 и будет использоваться в
дальнейшем в качестве модели системы передачи сигналов. Мо-
дель отражает многие характерные черты применяемых в настоя-
щее время систем. Блок кодирования часто состоит из двух каска-
дов; в первом происходит кодирование для источника, а во вто-
D0M’__ дальнейшее кодирование для согласования с каналом. В
этом случае блок декодирования также состоит из двух каскадов.
Йачнем с концов системы и будем продвигаться к ее середине.
1.4. Источник сообщений
Рассмотрим источник сообщений. Теория кодирования и'тео-
рия информации во многом обязаны своей силой тому, что они
не определяют, что такое информация, а просто предполагают,
что задан источник сообщений как последовательность символов
Si, s2, ..., sq алфавита источника. В гл. 6 показано, что теория ин-
формации использует энтропию Н как меру информации, и ©то
позволяет определить, что значит количество информации. Одна-
ко такое определение является абстрактным, оно лишь частично
согласуется с общепринятыми представлениями об информации.
Возможно, именно представление о том, что здесь удалось форма-
лизовать и трактовать общие понятия информации, привело к та-
кой популярности теории информации на ее ранних этапах; раз-
личия в несходных ситуациях не были замечены, и считалось, что
теория применима во всех случаях. Данное определение приводит
к правильной мере информации во многих случаях (например,
при хранении и передаче данных) и поэтому люди стали думать,
что у них имеется одна из таких ситуаций, но они часто ошиба-
лись. Теория информации имеет дело не со смыслом информации,
а лишь с ее количеством.
Источник сообщений может быть самым различным: например,
книга, .печатное формальное уведомление и финансовый отчет
компании в равной мере являются источниками сообщений в обыч-
ном алфавите. Танец, музыка и другие формы человеческой дея-
тельности приводят к различным формам (символам) выражения
содержащейся в них информации и поэтому также могут считать-
ся источниками сообщений. Математические равенства — это еще
один источник сообщений. Рассматриваемые ниже коды являются
различными способами представления информационных символов
источника.
^Информация может существовать также в непрерывной форме;
Действительно, природа обычно приводит к информации именно в
такой форме. Однако на практике задача состоит в том, чтобы
брать отсчеты непрерывного сигнала через равные промежутки
®Рсмени и затем переводить их в цифровую форму (квантовать;
lyJ). Затем информация посылается как последовательность
цифр. Одна из причин использования цифровых отсчетов аналого-
вого сигнала заключается в том, что они могут передаваться на-
дежнее, чем аналоговый сигнал. Когда неизбежный шум в системе
передачи начинает искажать сигнал, цифровые импульсы могут
быть приняты (детектированы), .преобразованы и переведены в
стандартную форму до того, как их отправят далее к получателю.
В пункте назначения цифровые импульсы могут, при желании,
быть переведены снова в аналоговую форму. Аналоговые сигналы
не могут быть преобразованы в стандартную форму таким же спо-
собом, и поэтому чем дольше сигнал передается и чем больше он
обрабатывается, тем сильнее он искажается за счет малых оши-
бок.
Другая причина использования цифровых методов в современ-
ных системах состоит в том, что в настоящее время интегральные
схемы очень дешевы, и служат мощным аппаратом для гибкой и
надежной обработки и преобразования цифровых сигналов.
Хотя в теории информации есть раздел, посвященный анало-
говым сигналам, ограничимся цифровыми сигналами вследствие
большей простоты теории, а также потому, что, как отмечалось
выше, -значение аналоговых сигналов в технике постепенно умень-
шается. Почти все мощные большие ЭВМ являются цифровыми, и
в системах обработки информации они почти полностью замени-
ли прежние аналоговые машины. На 1979 г. осталось лишь не-
сколько больших гибридных систем общего назначения. Большин-
ство наших систем передачи информации, включая обычный теле-
фон, -быстро переводятся в цифровые.
1.5. Кодирование алфавита источника
Обычно информация (цифровые сигналы или попросту симво-
лы) представляется одним из двух возможных состояний; пере-
ключатель в верхнем или нижнем 'положении, включен или выклю-
чен, дырка на перфоленте выбита или нет, реле замкнуто или
разомкнуто, транзистор проводит или нет, магнитный домен име-
ет поле в одном или другом направлении и т. д. В настоящее вре-
мя устройства с двумя состояниями, названные двоичными, суще-
ственно надежнее устройств с несколькими состояниями. В резуль-
тате двоичные системы распространены гораздо шире, чем все
другие. Даже десятичные системы обработки информации, на-
пример, карманные калькуляторы, обычно конструируются на ос-
нове двоичных компонентов.
В качестве названий этих двух состояний принято использо-
вать символы 0 и 1, однако годятся любые два различных симво-
ла (знака), например, крестик и нолик. Иногда полезно рассмат-
ривать 0 и 1 не как числа, а как пару произвольных символов.
Рассмотрим сначала задачу представления различных симво-
лов алфавита источника. Если дана пара двоичных (с двумя со-
стояниями) устройств (цифр), их можно представить четырьмя
различными состояниями: 00, 01, 10, 11. Для трех двоичных цифр
получаем 23 = 8 различных состояний: ООО, 001, 010, 011, 100, 101,
НО, 111. Для системы, имеющей k двоичных цифр, обычно назы-
ваемых битами, общее число различных состояний равно 2к; это
легко получить, применив элементарные комбинаторные рассуж-
дения. Вообще, если есть k различных устройств, первое из кото-
рых имеет П1 состояний, второе — и2 состояний, Аое — nk со-
стояний, то общее число состояний, очевидно, равно произведению
П1П2 — nk- Если, например, ni=4, и2 = 2 и и3=5, то можно пред-
ставить 4X2X5=40 различных объектов (состояний). Это число
равно числу различных символов источника, которые можно пред-
ставить, если интересоваться только числом различных состояний.
В гл. 4 указывается, как принимать во внимание вероятности
появления различных символов. Сейчас рассматривается только
число различных состояний — это эквивалентно тому, что вероят-
ности появления всех символов считаются равными.
Выше рассматривались двоичные устройства с двумя символа-
ми; существуют, конечно, устройства с большим числом состоя-
ний, типа переключателя с нейтральным положением, имеющего
три состояния. Некоторые системы передачи сигналов также ис-
пользуют больше двух состояний, однако теория проще всего
строится в терминах двух состояний. Поэтому в книге обычно
речь идет о двоичной системе, а системы с г состояниями лишь
иногда упоминаются.
Люди часто приписывают последовательностям из нулей и
единиц некоторый смысл, например в коде ASCII (см. табл.
1.7.1). Однако ЭВМ (или система передачи сигналов) рассматри-
вает их лишь как последовательности из нулей и единиц. Цифро-
вая вычислительная машина обрабатывает двоичные последова-
тельности символов; смысл этим последовательностям придает
пользователь (или, быть может, устройства ввода и вывода).
ЭВМ просто комбинирует нули и единицы в соответствии со своей
конструкцией и введенной в нее программой. Логические схемы
ЭВМ не чувствительны к смыслу, который приписывается симво-
лам; это же справедливо для системы передачи сигналов.
Именно поэтому теория информации не рассматривает смысла
сообщений, и это дает ей возможность понять, как аппаратура
преобразует сообщения; теория дает метод исследования обра-
ботки информации.
В типичных случаях, как показано в гл. 2 и 3, кодирование
сообщений для передачи по каналу увеличивает избыточность
(точные определения даются в дальнейшем). Кодирование для ис-
точника (оно упоминалось в конце разд. 1.3) обычно уменьшает
избыточность, что показано в гл. 4 и 5.
Нужно представить себе источник как случайный или стоха-
стический и задаться вопросом, как можно закодировать, пере-
дать и восстановить переданную информацию. Переданы были,
конечно, некоторые конкретные сообщения, однако у проектиров-
щика системы нет никакого способа узнать, какие сообщения из
множества (ансамбля) возможных сообщений будут выбраны для
передачи. Проектировщик должен рассматривать посылаемое со-
общение как случайную выборку из множества всех возможных
сообщений и спроектировать систему таким образом, чтобы обес-
печить передачу всех возможных сообщений. Таким образом, по
существу, теория является вероятностной, однако в этой книге ис-
пользуются лишь элементы теории вероятностей.
Задачи
1.5.1. Найдите число различных автомобильных номеров вида «цифра, цифра,
цифра, буква, буква, буква».
1.5.2. Сколько команд может быть у ЭВМ, если каждая команда состоит из 8
двоичных символов.
1.6. Некоторые коды
Людям трудно обращаться с двоичным кодом. Обычно для че-
ловека более предпочтительным является выбор из множества
объектов. Подтверждением этому служит объем обычных алфави-
тов, содержащих от 16 до 36 различных букв (прописных и строч-
ных), а также десятичная система, содержащая 10 различных
символов. Таким образом, человеку часто удобно группировать
двоичные символы, называемые битами, в группы по три символа,
образуя таким образом восьмеричный код (с основанием 8). Этот
код приведен в табл. 1.6.1.
Таблица 1.6.1
Код
Двоичный Восьмерич- ный Двоичный Восьмерич- ный
ООО 0 100 4
001 1 101 5
010 2 110 6
011 3 111 7
При использовании восьмеричного представления числа часто
заключаются в скобки и снабжаются индексом 8. Например, де-
сятичное число 25 записывается в восьмеричной форме как
(31) 8. Так, в США рождество, которое отмечается 25 декабря,
совпадает с другим праздником, который называется Холовин и
отмечается 3'1 октября: Dec 25=Oct 31, (25)ю= (31)8.
В табл. 1.7.1 в качестве примера кода ASCII в левом столбце
приведены восьмеричные числа вместо двоичных. Перевод вось-
меричных чисел в двоичные и обратно настолько прост, что это
всегда можно легко проделать.
Иногда двоичные цифры объединяются в группы по 4, задавая
таким образом шестнадцатиричный код (табл. 1.6.2).
Поскольку ЭВМ обычно работают с байтами, каждый из кото-
рых состоит из 8 бит (в некоторых современных ЭВМ использу-
ются 9-битовые байты), шестнадцатиричный код лучше согласует-
ся с архитектурой ЭВМ; с другой стороны, восьмеричный код, по-
видимому, лучше согласуется с человеческой психологией. Поэто-
му на практике ни один код не может одержать уверенной по-
беды.
Код
Таблица 11.6.2
Двоичный Шестнад- цатирич- ный Двоичный Шестнад- цатирич- ный
0000 0 1000 8
0001 1 1001 9
0010 2 1010 А
ООП 3 1011 В
0100 4 1100 С
0101 5 1101 D
оно 6 1110 Е
0111 7 1111 F
1.6.1. Используя приближенное равенство 2S~3S, сравните вычислительные ма-
шины с двоичным и троичным основаниями.
1.6.2. Составьте восьмеричную таблицу умножения.
1.6.3. Используя таблицу 1.6.2, найдите двоичное представление для D6. Ответ:
110 10 110.
Задачи
1.7. Код ASCII
Пусть задан источник сообщений; рассмотрим сначала кодиро-
вание для этого источника. Стандартный код ASCII (табл. 1.7.1),
который представляет буквенные цифровые и некоторые другие
символы, является одним из примеров кода.
Этот код использует семь двоичных символов. Поскольку, как
уже отмечалось, ЭВМ работает с байтами, которые обычно явля-
ются блоками из 8 бит, один символ кода ASCII часто занимает
8 бит. Восьмой бит можно выбирать несколькими способами,
иногда равным 1, так что его можно использовать как тактовый
бит для синхронизации. Чаще ©тот бит выбирается так, чтобы об-
щее число единиц во всех восьми битах было четным (или нечет-
ным, см. пл. 2). Наконец, он может выбираться произвольно и ни-
как не использоваться. Для перевода в модифицированный код
ASCII, применяемый в 8-битовом телетайпном коде системы
LT 33, нужно взять 7-1битовый .код ASCII + (200) 8.
Цель, достигаемая установлением четного числа 1 в восьми
позициях, состоит в обнаружении любой одиночной ошибки, при
которой 0 заменяется на 1 или 1 на 0; при такой ошибке общее
число 1 во всех восьми позициях станет нечетным. Таким обра-
Семибитовый код AS II
Таблица 1.7.1
В-ришый иод в-ричный зримый 8-ричный /1 Символ
СомВо/г код CumBo/i , код CumBo.
ООО NUL 040 SP 100 140
001 SOH 041 I 101 A 141 a
002 STX 042 102 В 142 b
003 ЕТХ 043 # 103 c 143 c
004 EOT 044 $ 104 D 144 d
005 ENQ 045 О/ /о 105 E .145 e
006 АСК 046 & 106 F 146 f
007 BEL 047 107 G 147 g
010 BS 050 ( 110 H 150 h
011 НТ 051 ) 111 I 151 i
012 LF 052 * 112 J 152 j
013 УТ 053 + 113 К 153 k
014 FF 054 114 L 154 1
015 CR 055 - 115 M 155 m
016 SO 056 116 N 156 n
017 SI 057 / 117 О 157 о
020 DLE 060 0 120 P 160 p
021 DC1 061 1 121 Q 161 q
022 DC2 062 2 122 R 162 r
023 DC3 063 . 3 123 S 163 s
024 DC4 064 4 124 T 164 t
025 NAK 065 5 125 и 165 u
026 SYN 066 6 126 V 166 V
027 ETB 067 7 127 w 167 w
030 CAN 070 8 130 X 170 X
031 EM 071 9 131 Y 171 У
032 SUB 072 • 132 1 172 z
033 ESC 073 J 133 [ 173 {
034 FS 074 < 134 \ 174 1
035 GS 075 __ 135 ] 175 }
036 RS 076 136 176
037 US 077 * ? 137 — 177 DEL
зом, получается код с обнаружением ошибок, дающий некоторую
защиту от них. Возможно, еще более важно, что этот код позво-
ляет построить более простые и надежные устройства, поскольку
сама машина определяет присутствие ошибок и до некоторой сте-
пени ограничивает их отрицательные последствия.
Мы будем часто использовать проверку четности (или нечет-
ности) числа единиц. Она называется проверкой на четность, по-
скольку проверяется лишь четность (или нечетность) числа еди-
ниц в сообщении. У многих ЭВМ имеются очень полезные коман-
ды для определения четности содержимого накопителя.
Теперь можно лучше понять код ASCII (см. табл. 1.7.1). Ал-
фавит источника, д.пя которого применяется код ASCII, состоит
из 27 = 128 возможных знаков (символов). Эти знаки представля-
ются (кодируются) внутри ЭВМ двоичным кодом. Восьмую пози-
цию 8-битовых байтов кода ASCII можно использовать для про-
верки на четность. Три символа, напечатанные в табл. 1.7.1, пред-
ставляют восьмеричный код. Например, 127=4 010 111 (здесь опу-
щены первые 2 бита первого восьмеричного символа). Для про-
верки на четность имеем 127=1'1 010 111.
Задачи
1.7.1. Запишите буквы Р и р в двоичной форме.
1.7.2. Чему соответствует 01 010 011?
1.7.3. Используя код с основанием 4, запишите строчные буквы алфавита нз
кода ASCII.
1.7.4. Запишите прописные буквы алфавита из кода ASCII, используя код с
основанием 16.
1.8. Некоторые другие коды
Другим хорошо известным кодом является код Морзе, кото-
рый ранее широко использовался. Часть кода приведена в табл.
1.8.1. Считается, что тире в три раза длиннее точки. Может по-
казаться, что код Морзе двоичный, однако, в действительности,
он троичный (основание г=3), имеющий в качестве символов
точку, тире и пробел. Длительность пробела между точками и
тире в одной букве равна одной единице времени, между буква-
ми — трем, между словами — шести единицам времени.
Таблица 1.8.1
Код Морзе
Теперь на короткое время отвлечемся и введем некоторые обо-
значения. Далее постоянно будут нужны биномиальные коэффи-
циенты С(п, k) —nl/kl(n—k)l, с помощью которых подсчитывают,
сколькими способами можно выбрать k предметов из множества,
Содержащего п предметов. Здесь используется старое обозначение
C(n, k), 'поскольку его легче печатать на пишущей машинке и на-
бирать в типографии и оно легко обрабатывается большинством
ЭВМ. Применяемое в настоящее время обозначение I ”
встре-
чает затруднения при обработке на различных типах оборудова-
ния и плохо выглядит в тексте.
Код Морзе является неравномерным-, он использует выгоды
частого появления некоторых букв, например, Е, делая их корот-
кими, и весьма редкого появления других букв, например J, де-
лая их более длинными. Однако трудности, возникающие при по-
пытках различения слов в неравномерном коде, оказались весьма
существенными и привели к почти повсеместной замене кода Мор-
зе кодом ван Дюрена, в котором три позиции из семи содержат
единицы, а остальные четыре — нули. Этот код содерит С (7,3) =
-=35 возможных слов и, аналогично коду ASCII, дает возмож-
ность пользователю обнаружить много типов ошибок, поскольку
он точно знает, сколько единиц должно содержаться в каждом
отрезке принятого сообщения, состоящего из семи символов.
Другим часто используемым простым кодом является код
2-U3-5. Как видно из названия, два символа из пяти равны 1.
Удобно/что в коде имеется С (5, 2) = 10 слов. Один из способов
сопоставления десятичных цифр словам кода называется
01247-кодом. При этом способе последовательным символам ко-
дового слова сопоставляются веса 0, 1, 2, 4 и 7, и соответствую-
щая десятичная цифра равна сумме весов тех символов слова,
которые равны 1; единственное исключение составляет комбина-
ция 4, 7, соответствующая цифре 0. Код приведен в табл. >1.8.2.
Как и раньше, любая одиночная ошибка в сообщении будет
обнаружена, поскольку она приведет к нечетному числу единиц
в нем.
Таблица 1.8.2
Код 2-из-5
Десяти- Соответст- « , Л » Десяти- Соответст-
ричный вует числу ричный вует числу
110 0 0 1 2 0-|-1 0+2 0 0 1 0 1 1 0 6 7 2+4 0+7
1 0 1 0 0 0 0 1
0 Ц1 0 0 3 1+2 0 1 0 0 1 8 1+7
1 о;о 1 0 4 0+4 0 0 1 0 1 9 2+7
0 ЦО 1 0 5 1+4 0 0 0 1 1 0 4+7
Задачи
1.8.1. В табл. 1.8.2. приведен один из способов сопоставления числовых значе-
ний десяти возможным символам кода 2-из-5. Сколько существует кодов
2-из-5?
1.8.2. Запишите 125 кодом 2-из-5.
1.8.3. Сколько слов, удовлетворяющих проверке на четность, не используется
в коде ван Дюрена? Ответ: 129.
\ 1.9. Коды с основанием г
Как отмечалось выше, большинство систем представления ин-
формации в ЭВМ (и в других устройствах) используют два со-
стояния, хотя код Морзе служит примером системы передачи
сигналов с алфавитом из трех символов. Причина столь широкого
распространения двухсимвольных систем состоит в том, что уст-
ройства с двумя состояниями оказываются значительно надежнее,
чем устройства с большим числом состояний. Вместе с тем, чело-
век, очевидно, предпочитает работать с системами, имеющими до-
статочно много состояний; свидетельством тому является набор
букв алфавита вместе с различными знаками препинания и деся-
тичными цифрами. Поэтому иногда приходится рассматривать ко-
ды с алфавитом из г символов. Для кода Морзе г=3.
В алфавите английского языка содержится 26 букв, каждая из
которых может быть прописной или строчной, а также различные
знаки препинания. Часто применяется система, в которую входят
2'6 букв, 10 цифр и пробел — всего 37 символов. Этот важный
код будет обсуждаться в разд. 2.7.
При формальном подходе рассматривается алфавит источника
S, состоящий из q символов sb ..., sg. Они, в свою очередь, пред-
ставляются некоторыми другими символами, например, двоичным
кодом. Таким образом, можно рассматривать либо код ASCII
как состоящий из r=q=27 =128 символов sb ..., s12s, либо каждый
символ как блок из 8 двоичных цифр с битом, добавленным к
7 основным 'битам.
1.10. Служебные знаки
В процессе передачи информации обычно оказывается необ-
ходимым управлять со стороны источника работой удаленных
устройств. Например, нужно указать устройству, что делать с по-
сылаемой информацией. Поэтому оказывается необходимым
иметь несколько резервных символов, предназначенных для уда-
ленного устройства. Одним из таких символов может быть «Конец
передачи», другим — «Возврат каретки». Еще один символ может
означать «Изменить регистр» с верхнего на нижний или обратно.
Наконец, может существовать символ, означающий «Повторить
последнее сообщение». Весь первый столбец таблицы кода ASCII
содержит такие специальные знаки.
Как можно осуществлять это управление без ограничения ин-
формации, передаваемой по системе? Если, например, двоичные
Цифры используются как числа в передаваемом сообщении, то
можно избежать комбинаций битов, которые совпадают с управ-
ляющими символами для удаленного устройства. Если окажется,
что поток двоичных цифр содержит такой резервный символ, то
устройство отреагирует на него тогда, когда оно не должно этого
Делать. Ясно, что на передаваемое сообщение нужно налагать
некоторые ограничения, однако при этом возникает вопрос: «Как
это сделать наиболее безболезненно для пользователя системы.»
Один из возможных способов состоит в добавлении к каждому
блоку двоичных цифр еще одной цифры, например.О, если блок
представляет сообщение, и 1, если блок представляет управляю-
щую команду. Можно заметить, что если управляющие слова
встречаются редко, то применение этого способа приводит к су-
щественным потерям пропускной способности канала. Кроме то-
го, он не позволяет решить задачу ретрансляции управляющих
слов через одни устройства к другим.
Имеются другие способы решения задач передачи сообщения
через оконечное устройство, чтобы последнее на него не реагиро-
вало. Один часто используемый способ состоит в том, чтобы за-
ключить любой резервный символ в кавычки и организовать ра?
боту оконечного устройства так, чтобы оно не реагировало на то,
что заключено в кавычки, а лишь снимало их. Для того чтобы со-
хранить кавычки при прохождении по системе, их, в свою оче-
редь, следует также заключить в кавычки. Такой подход часто ис-
пользуется в ЭВМ, однако иногда он приводит к некоторой пута-
нице. Этот метод расстановки кавычек применяется, например, в
языке ФОРТРАН.
В языке ФОРТРАН появление кавычек приводит к тому, что
они удаляются из потока символов, и происходит копирование
следующего символа, независимо от того, является он кавычками
или нет. Если следующий символ не является кавычками, текст
копируется до очередного появления кавычек, которые удаляются,
после чего система выходит из состояния «Копировать следующий
символ». Если следующий символ — это кавычки, машина (про-
грамма), скопировав его, возвращается в нормальное состояние.
Таким образом, для получения одного символа кавычек нужно
повторить его дважды. Для того чтобы передать по системе сооб-
щения вида «Сообщение», следует написать «««Сообщение»»».
«Сообщение» может содержать любые резервные символы, отлич-
ные от (») (рис. 1.10.1).
Другой метод передачи резервных символов по системе, в
чем-то эквивалентный предыдущему, состоит в том, что удаленное
устройство переходит в соответствующее состояние при каждом
появлении' специального символа, однако перед совершением дей-
ствия система смотрит, совпадает ли следующий символ с теку-
щим специальным символом. Если совпадение имеется, то устрой-
ство лишь передает этот символ и переходит в нормальное со-
стояние. В противном случае устройство совершает действие, со-
ответствующее этой комайде. Таким образом, при появлении двух
одинаковых резервных символов система сбрасывает первый и
пропускает второй. Если исходное сообщение содержит некоторый
резервный символ два раза подряд, то в посылаемое сообщение
следует вставить еще два символа, и устройство выкинет первый и
третий из них.
Хотя этот метод кажется довольно сложным для программной
реализации на ЭВМ, теория конечных автоматов указывает путь
к быстрому решению (рис. 1.10.2). В начальном состоянии проис-
ходит считывание следующего символа, и если он является спе-
циальным, программа запоминает его в регистре и передает уп-
равление программе особого состояния. Программа особого со-
стояния считывает следующий символ и сравнивает его с симво-
лом в регистре. Если два символа совпадают, то специальный
символ копируется и удаляется из входного потока; в противном
случае программа выполняет команду особого состояния. После
этого автомат возвращается в начальное состояние.
Увалить Убштть
И И И " И ••
^Сообщение к
Копировать Копиг-Лап<ь
На выходе оолуче,х
„ Сообщение"
Рис. 1.10.1. Удаление кавычек
Рис. 1.10.2. Автомат со специаль-
ными символами
В математической логике эта задача называется задачей о
метаязыке и состоит в следующем: как описывать сам язык, в осо-
бенности, когда описание проводится на этом же языке? Обычно
используются интонации (кавычки) для указания, что речь идет
о самом языке, и эти интонации не употребляются в обычном раз-
говоре. Для решения этой общей задачи, возникающей в киберне-
тике и других областях обработки информации, имеются и другие
формальные методы; их также можно приспособить для преодо-
ления подобных возникающих трудностей.
При управлении цифровой ЭВМ ошибки различения уровней
метаязыка служат постоянным источником путаницы. Программа
на языке ФОРТРАН и следующая за ней команда COMPILE при-
надлежит разным языкам. В конце программы следует ставить
Два знака end, из которых один предназначен для метаязыкового
уровня, которому принадлежит COMPILE, и он указывает на
окончание исходной программы, а второй предназначен для фак-
тической программы на языке ФОРТРАН и используется во вре-
мя ее выполнения.
Задачи
1-10.1. Используя схему состояний, подробно опишите, как последовательность
«««Сообщение»»» обрабатывается описанной в тексте системой типа
1102 Ф0РТРАН-
Как послать знак DLE (удалить) через систему с «дублированием спе-
циальных символов»? Поместите его в поток и подробно проследите
за ним.
1.11. Краткое содержание книги
После представления основных задач, а также нескольких ко-
дов с различными свойствами, обсудим материал, содержащийся
в книге.
В гл. 2, 3 и 11 рассмотрены методы кодирования информации
(сообщений), при которых любые ошибки, если их число не пре-
вышает заданного уровня, обнаруживаются и (или) исправляют-
ся на приемном конце без дополнительного обращения к источни-
ку. При обнаружении неисправленной ошибки можно было бы за-
просить повторную передачу сообщения в надежде принять его в
следующий раз правильно. В общем случае возможность обнару-
живать и исправлять ошибки достигается добавлением к сообще-
нию некоторых символов, что приводит к некоторому удлинению
сообщения. Основная задача состоит в том, чтобы обеспечить не-
обходимую защиту от неизбежных ошибок (шума), используя не
слишком много дополнительных символов. Типичным примером
такого кодирования является кодирование для канала.
Сжатие сообщений важно с точки зрения эффективности. При
передаче сжатых сообщений время загрузки аппаратуры соответ-
ственно сокращается; с точки зрения хранения информации сжа-
тые собщения требуют меньшего объема памяти. Сжатие — это
кодирование источника. В гл. 4 и 5 представлены различные мето-
ды сокращения объема передаваемой информации. Для этого ис-
следуется структура посылаемых сообщений. Если информация
обладает явно выраженной структурой, то можно осуществить зна-
чительное сжатие сообщения и достичь значительного эффекта.
Из большого числа свойств сообщений, на основании которых
можно произвести сжатие, рассмотрены лишь некоторые наиболее
распространенные. Исследованы общие методы сжатия и опущены
многочисленные специальные приемы, которые, как правило, до-
статочно легко применимы.
В гл. 6 вводится основное понятие энтропии источника инфор-
мации и показывается, как энтропия связана с максимальным ко-
личеством информации, которое можно передать по каналу. Это
поможет до некоторой степени приобщиться к пониманию того,
что собой представляет информация. Первая теорема кодирования
Шеннона относится к каналу без шума, и ее сравнительно легко
доказать. Вторая теорема, приведенная в гл. 40, рассматривает
передачу информации по каналу с шумом; ее доказательство на-
много сложнее. К счастью, простой двоичный симметричный канал
является достаточно реальным частным случаем и для него легко
понять это доказательство. Доказательство теоремы в более об-
щем случае сложнее, и в книге дан лишь его набросок.
Две теоремы Шеннона устанавливают границы того, что мож-
но получить с помощью кодирования. К сожалению, вторая теоре-
ма не является конструктивной, и не объясняет нам, как на прак-
тике приблизиться к указанным в ней границам. Результат, одна-
ко, не является бесполезным, поскольку он указывает, когда мож-
но значительно улучшить системы передачи сигналов и когда мож-
но достичь лишь небольших улучшений.
В теории информации определение канала часто бывает доста-
точно абстрактным, что приводит к необходимости других спосо-
бов определения центрального понятия пропускной способности.
В приложении А кратко показано, как на практике измеряется
пропускная способность канала в -системе передачи сигналов.
Напомним читателю, что хотя часто используется терминоло-
гия, относящаяся к «передаче сигналов из одного места в другое»,
все сказанное можно применить к «передаче сигналов от одного
момента времени до другого» в некоторой системе памяти. В этом
случае первая теорема Шеннона (без шума) часто становится 'бо-
лее существенной.
Традиция в изложении теории кодирования и теории информа-
ции состоит в том, чтобы придерживаться, по возможности, наи-
более общего и элегантного пути, часто весьма абстрактного, ис-
пользующего много математики и далекого от практических аспек-
тов. Такой подход не является необходимым, поэтому будем ре-
гулярно останавливаться и показывать, как обсуждаемые вопро-
сы связаны со здравым смыслом с нуждами практики, и чем они
могут быть полезны при проектировании будущих систем. Попы-
таемся также приводить доказательства, которые, по возможности,
интуитивно очевидны, а не просто элегантны с математической
точки зрения. В процессе изложения подчеркиваются многочислен-
ные небольшие практические детали, важные при проектировании
системы в целом.
Уточним, наконец, принятый в книге подход. В настоящее вре-
мя используется много разных систем передачи сигналов и еще
больше их будет использоваться в ближайшем будущем. Поэтому
нецелесообразно рассматривать их одну за другой. Следует при-
нять более широкий, общий подход и сконцентрировать внимание
на таких основных понятиях, которые представляются наиболее
существенными для понимания уже имеющихся и -будущих систем
передачи сигналов. Действительно, такой подход является един-
ственно разумным в любой быстро развивающейся научной обла-
сти. Подход, основанный на изучении отдельных примеров, приво-
дит к тому, что новая система ставит студента в тупик. Таким
образом, наше изложение, по необходимости, часто является аб-
страктным и не содержит описания многих деталей существующих
систем.
Глава 2
Коды с обнаружением ошибок
2.1. Для чего нужны коды с обнаружением ошибок?
Из опыта известно, что высоконадежное оборудование нелегко
построить. Для определения того, что значит высоконадежное,
рассмотрим, сколько вычислений современная ЭВМ производит в
течение 1 ч. При скорости 1 оп/мкс ЭВМ производит 3,6-109 оп/ч,
а каждая операция состоит из многих действий. Для сравнения
укажем, что в 100 годах (что с большой вероятностью превышает
срок вашей жизни) содержится менее 3,16-109 с. Аналогично, на-
дежные системы передачи должны состоять из очень надежных
отдельных компонентов. Надежность при передаче слов живого
языка существенно отличается от надежности при передаче про-
грамм ЭВМ. Отсюда вытекает важность обнаружения ошибок.
Кроме того, как уже отмечалось, обнаружение ошибок 'весьма по-
лезно для обеспечения высококачественного обслуживания.
В случаях, когда возможно повторение, часто бывает доста-
точно лйшь обнаружить ощибку. После обнаружения ошибки со-
общение, операция или другое действие повторяются еще раз и
при некоторой удаче второе (или, возможно, третье) повторение
будет верным (см. разд. 2.5).
Нельзя обнаружить ошибку, если любой принятый символ
(или их множество) может служить сообщением. Ошибки можно
обнаружить только в том случае, если на возможные сообщения
наложены некоторые ограничения. Задача состоит в том, чтобы
свести ограничения на возможные сообщения к достаточно про-
стым. На практике «простой» обычно означает «легко вычисли-
мый». В этой главе рассмотрена задача построения кодов, позво-
ляющих на приемном конце обнаружить любую одиночную ошиб-
ку. В гл. 3 рассмотрена задача исправления на приемном конце
ошибок, возникающих при передаче сообщения.
2.2. Простые проверки на четность
Простейший способ кодирования двоичного сообщения для
обнаружения ошибок состоит в подсчете числа 1 в сообщении и
добавлении еще одного двоичного символа с тем, чтобы во всем
сообщении содержалось четное число 1. Таким образом, к (п—1)
символам сообщения добавляется n-я позиция для проверки на
четность. На приемном конце производится подсчет числа 1, и не-1
четное число 1 во всех п позициях указывает на появление по
крайней мере одной ошибки.
Ясно, что такой код не может обнаруживать двойные ошибки.
Однако нечетное число ошибок обнаружить можно. Если предпо-
ложить, что, во-первых, вероятность ошибки в каждой двоичной
позиции равна некоторому числу р и, во-вторых, ошибки в различ-
ных позициях независимы, то при п, много меньших 1/р, вероят-
ное число одиночных ошибок равно пр. Вероятность двойной
ошибки примерно равна п(п—1)р2/2, т. е. примерно половине
квадрата одиночной ошибки. Поэтому оптимальная длина прове-
ряемого сообщения зависит как от требуемого уровня надежности
(вероятности того, что двойная ошибка останется необнаружен-
ной), так и от вероятности р единичной ошибки на любой пози-
ции. Дальнейшие подробности излагаются в разд. 2.4.
Подсчет числа 1 и выбор четного их числа эквивалентен ис-
пользованию арифметики по модулю 2. Модуль 2 означает, что
каждое число делится на 2 (основание) и заменяется остатком.
В этой арифметике (в которой последовательный счет идет так:
О, .1, 0, 1, ...) производится подсчет по модулю 2 числа единиц в
первых (п—1) позициях сообщения, и затем результат помещает-
ся в п-ю позицию. Таким образом, среди п посылаемых символов
содержится четное число единиц. Такая проверка на четность ча-
сто рассматривается в теории. На практике обычно оказывается
удобным принять проверку на нечетность с тем, чтобы сообщение,
состоящее из всех нулей, не было верным. Легко провести необ-
ходимые изменения в теории кодирова-
ния, поэтому в дальнейшем будем про-
должать применять проверку на четность.
Для того чтобы вычислить четность
последовательности, состоящей’ из нулей
и единиц, можно использовать конечный
автомат с двумя состояниями (рис. 2.2.1).
Автомат начинает работу в состоянии О
и меняет его при появлении в сообщении
Рис. 2.2.1. Диаграмма для
вычисления четности
каждой 1. Состояние автомата в конце сообщения дает окончатель-
ную четность.
Во многих ЭВМ есть специальная команда для подсчета чис-
ла '1 в накапливающем регистре. Самая правая цифра получен-
ной суммы дает нужную четность. Если в ЭВМ нет этой или ка-
кой-нибудь эквивалентной команды, то следует заметить, что при
логическом сложении (исключающее ИЛИ, см. разд. 2.8) одной
половины сообщения с другой четность суммы остается такой же,
как у первоначального сообщения. Повторяя эту процедуру, мы
каждый раз уменьшаем длину сообщения вдвое, и в конце концов
получаем требуемую сумму всех 1 по модулю 2. Таким образом,
необходимое число логических сложений равно первому целому
числу, большему или равному log2n.
2.3. Коды с обнаружением ошибок
Обычно длинные сообщения, состоящие из двоичных символов,
Разбиваются на отрезки (блоки) по (п—1) символов в каждом, и
к каждому отрезку добавляется по одному символу; таким обра-
зом, получается передаваемый блок длиной п. При необходимости
последний блок дополняется нулями. Этот метод приводит к из-
быточности, равной п/(п—1) = 1 + 1/(п—1). Избыточность опреде-
ляется как отношение числа используемых двоичных символов к
минимально необходимому числу символов. Чистая избыточность
равна 1/(п—1).
Ясно, что для получения низкой избыточности следует приме-
нять длинные сообщения. Однако для получения высокой надеж-
ности 1предпочтительнее короткие сообщения. Таким образом, вы-
бор длины п посылаемых блоков сообщения является результатом
компромисса между двумя противоположными силами.
Код 2-из-5, упомянутый в разд. 1.8, является примером кода с
п=15, использующего проверку на четность. Код ван Дюрена
З-из-7 — 'пример кода, использующего проверку на нечетность.
Ни в одном из кодов не применяются все возможные блоки. Дру-
гим примером такого кода служит подсчет числа слов, иногда ис-
пользуемого при передаче телеграмм.
На практике для обнаружения ошибок применяется много
других простых кодов такого типа. Например, при записи содер-
жимого памяти на диск, барабан или ленту к множеству переда-
ваемых слов в качестве контрольного слова часто добавляется
логическая сумма всех слов. Аппаратная реализация этого метода
описана в [115].
2.4. Независимые ошибки — белый шум
Как указывалось выше, в обычной модели ошибок предпола-
гается, что, во-первых, вероятность ошибки в каждой позиции со-
общения равна одному и тому же числу р и, во-вторых, ошибки в
различных позициях независимы. Такая ситуация называется бе-
лым шумом по аналогии с белым светом, в котором по неточно-
му предположению с одинаковой .интенсивностью содержатся все
частоты, различаемые глазом человека. В этом случае теория
достаточно проста для понимания. Отметим, что часто на практи-
ке ошибки являются более вероятными в одних позициях, кроме
того, часто ошибки группируются в пакеты и не являются незави-
симыми. Например, корреляция между ошибками возникает при
общем электропитании, а также при близких вспышках молнии
(см. разд. 2.6).
Следует отметить, что вследствие быстрого развития техники
в процессе проектирования обычно невозможно точно знать, ка-
кие комбинации ошибок встретятся при работе устройства. По-
этому белый шум часто является разумным предположением.
В случае белого шума вероятность отсутствия ошибок в п по-
зициях равна (1— р)п. Вероятность ровно одной ошибки в п пози-
циях равна пр(1—р)п~{- Вероятность ровно k ошибок задается
/?-м членом разложения бинома
1 = [(1— р) + р]п =(1— РУ1 +пр(1—руг~1 +
+ п(п— 1)р2(1— р)п~2 /2 + ...+рп.
Например, вероятность ровно двух ошибок равна
п (п— 1) р2 (1 — р)п~2 /2.
(Вероятность четного числа ошибок (0, 2, 4, ...) можно полу-
чить, сложив два приведенных ниже разложения бинома и разде-
лив результат на 2:
1 = [(1 -р) + рр = 2 С (п, k) pk (1 —,
fe=0
Ki— p)—pp =2 (—ipc(n, &)pft(i—pp-fe,
k=0
i j_(i_9 nl" [n/2l
—— = 2 C(n, 2 m) p2m (1 — p)«-2m. ^2.4.1)
2--------------------------------------------------m=0
Квадратные скобки в (2.4.1) означают целую часть заключенного
в них числа. Вероятность нечетного числа ошибок (которые всег-
да обнаруживаются) получается вычитанием этого выражения
из 1.
Вероятности отсутствия ошибок соответствует первый член в
сумме (i2.4.1). Поэтому для нахождения вероятности необнаружи-
ваемых ошибок нужно отбросить в (2.4.1) первый член и полу-
чить
[п/2]
2 С(п, 2т)р2т(1 —-р)п~2т. (2.4.2)
т=1
Обычно заметный вклад вносит лишь несколько ‘первых членов
этой суммы.
Задачи
2.4.1. Найдите вероятность отсутствия ошибок при р=0,001 и п=100. Ответ:
ехр (-1/Ю).
2.4.2. Найдите вероятность необнаруживаемых ошибок при р=0,001 и п=100.
2.4.3. Пусть р=0,01, и вероятность необнаруживаемых ошибок должна быть
равной 0,005. Найдите наибольшую длину п, которую можно использовать.
Ответ: п=10 и почти п=11.
2.4.4. Решите задачу 2.4.1 при малом р и произвольном п. Ответ: ехр (—пр).
2.5. Повторная передача сообщения
После обнаружения ошибки часто можно повторить передачу
сообщения, вычисление или какой-либо другой из выполненных
процессов. Например, в ЭВМ фирмы Bell (отделение Bell Relay
Computers) для представления десятичных цифр используется
код 2-из-5 и при обнаружении ошибки 'предпринимается вторая и
Даже третья попытка вычислений. В случае, когда даже после
третьей попытки сообщение остается неприемлемым, выполнение
текущей задачи прерывается, и ЭВМ переходит к следующей за-
даче в надежде, что ее неисправная часть не будет применяться
при выполнении новой задачи.
При считывании с магнитной ленты принято использовать, по
крайней мере, код с обнаружением ошибок и в случае, когда про-
верки на четность не выполнены, производится повторное считыва-
ние. Число повторных попыток зависит от принятой модели оши-
бок. Если предположить, что произошла малая потеря намагни-
ченности, то можно надеяться, что при повторной попытке счи-
тывание будет произведено правильно. Если, однако, допустить,
что ошибка явилась результатом более стойкой неисправности, то
скорее всего, повторные попытки будут неудачными до тех пор,
пока не появится еще одна ошибка, так что проверка на четность
окажется выполненной. Следовательно, вместо правильного сооб-
щения будет получено сообщение с двумя ошибками! Таким об-
разом, стратегия «при обнаружении ошибки выполнять одну или
несколько повторных попыток» оказывается разумной только если
ожидаемые ошибки являются временными.
Проверки на четность уже давно используются в ЭВМ как на
аппаратурном, так и на программном уровнях [15]. Например, на
первых порах в случае ненадежного накопителя на магнитном ба-
рабане каждая операция записи сопровождалась логическим сло-
жением содержимого всех регистров, записываемого на барабан.
Сумма запоминалась в последнем регистре блока’ на барабане.
Затем производилось считывание с барабана для проверки пра-
вильности записи. Только после этого записанная информация
сбрасывалась из регистров памяти ЭВМ. Затем выполнялось счи-
тывание с барабана, и снова проводилась проверка на четность
(путем вычисления логической суммы всех регистров), которая
должна была давать тождественный нуль. В случае невыполнения
проверки на четность осуществлялось повторное считывание. Ме-
тод основывался на том, что для логического сложения х+х=0.
2.6. Простые коды для обнаружения пакетов ошибок
Ошибки (шум) в принятом сообщении чаще группируются в
пакеты, а не в отдельные изолированные позиции. Вспышки мол-
нии, флуктуации питающего напряжения, дефекты магнитной по-
верхности являются типичными причинами, приводящими к воз-
никновению пакетов ошибок.
Предположим, экспериментально получена максимальная дли-
на L пакета ошибок, который должен быть обнаружен. Для про-
стоты примем, что длина пакета L совпадает с длиной слова в
ЭВМ (легко внести изменения, необходимые для рассмотрения
других случаев). В этих условиях нужно выбрать подходящий код
с обнаружением ошибок 5(или .код с исправлением ошибок, как в
гл. 3), и вместо вычисления проверок на четность по битам сле-
дует вычислить проверку на четность по словам. В самом дёле,
работа со словами, а не с битами приводит к L независимым (пе-
ремежающимся) кодам, по одному для каждого двоичного симво-
ла в слове.
Если пакет перекрывает конец одного слова и начало другого,
то по-прежнему ни в каком коде не встретятся две ошибки, по-
скольку, по предположению, длина k пакета удовлетворяет усло-
вию
Таким образом, можно передавать сообщения по каналу с па-
кетами ошибок, если есть возможность определить конфигурацию
шумов и соответственно организовать проверки. Надежное аппа-
ратурное обеспечение описано в [15].
Пример. Сообщение Fall 1980 можно закодировать кодом ASCII для ис-
правления пакетов следующим образом (здесь проверки иа четность не исполь-
зуются) :
F = 106 = 01 000 НО 1 = 061 = 00 110 001
а= 141 =01 100 001 9 = 071 = 00 111 001
1 = 154 = 01 101 100 8 = 070 = 00 111 000
1 = 154 = 01 101 sp = 040 = 00 100 Контрольная 100 000 сумма = 0 = 060 = 00 ПО 00 000 111 = BEL. 000
•Контрольная сумма =00 000 111=iBEL
Таким образом, закодированное сообщение имеет вид Fall 1980 BEL, где
BEL —• символ кода ASCII для 00 000 111.
Задача
2.6.1. Пусть дано сообщение
101 01010
011 00110
000 11110
ПО 00110
111 10101
Добавить проверки для образования кода с обнаружением пакетов ошибок из
слов длиной 1 байт.
2.7. Буквенно-цифровые коды — взвешенные коды
Рассматривавшиеся до сих пор коды предполагали наличие
простого белого шума. Такое предположение хорошо описывает
канал в 'машинах многих типов, однако в некоторых системах вы-
падения (или вставки) символов при последовательной передаче
не обнаруживаются этими кодами, что приводит к нарушению
синхронизации.
Человеку свойственно делать ошибки другого рода. Типичным
примером ошибок человека является перестановка соседних цифр
при записи чисел: например, 67 превращается в 76. Другой стан-
дартной ошибкой может быть дублирование неправильной цифры
в трехзначном числе, в котором две соседние цифры совпадают:
например, 667 превращается в 677. Здесь происходит простая за-
мена одной цифры. Таковы две наиболее распространенные ошиб-
ки человека при записи чисел. В система^ содержащих как бук-
вы, так и цифры, очень часто путаются цифра «нуль» и буква
Достаточно часто встречаются ситуации, в которых полный
набор используемых символов состоит из букв, пробела и <10 де-
сятичных цифр. Таким образом, исходный алфавит содержит 26+
+ 1 + 10 = 37 символов. К счастью, 37 — 'простое число, что позво-
ляет применять следующий метод проверки. Символы сообщения
снабжаются весами 1, 2, 3, ..., начиная с проверочного символа
сообщения. Затем производится редукция суммы по модулю 37
(т. е. берется остаток от деления суммы на 37) так, что провероч-
ный символ может быть выбран таким образом, чтобы вся сумма
была сравнима с 0 по модулю 37. Заметим, что пробел, стоящий
в конце в качестве проверочного символа — это не то же самое,
что отсутствие символа.
Легко проверить, что любая перестановка двух соседних цифр
обнаруживается так же, как и дублирование неверной цифры
(что эквивалентно замене одного символа). Можно обнаружить
также много других изменений. Перестановка нуля и буквы О
также является заменой одного символа. Рассматриваемый код
очень полезен в процессах, предусматривающих участие человека.
Заметим, что длина сообщения не фиксирована и при необходи-
мости может превышать 37 символов (хотя при этом нужны спе-
циальные предосторожности). Такое кодирование можно исполь-
зовать в кредитных карточках, в списках для записи некоторых
названий и т. д. Вероятность того, что случайная последователь-
ность удовлетворяет такой проверке, равна 1/37. Таким образом,
используя эту простую проверку на четность, можно выявить око-
ло 97% случаев подлога.
Для того чтобы найти взвешенную сумму наиболее простым
способом, заметим, что при вычислении частичных сумм множест-
ва п чисел и окончательном их суммировании получаем, что пер-
вое число входит в окончательную сумму п раз, второе —
п—1 раз, следующее п—2 раза и т. д. Последнее число войдет в
сумму один раз. Таким образом, имеем требуемую взвешенную
сумму чисел, соответствующую используемым в сообщении симво-
лам алфавита.
Для пояснения процесса «суммирования сумм» рассмотрим
сообщение wxyz.
Из таблицы видно, как возникает взвешенная сумма. Этот
процесс иногда называется возрастающим цифрованием.
Сообщение Сумма Сумма сумм
W W W
X w + x 2w+x
У w+x-Yy 3w+2x+y
Z W+x+y+Z 4w+3x+2y+z
Пример. Пусть 0=0, 1 = 1, 2=2, ..., 9=9, А=10, В = 11, ... Z = 35, Ы=36.
Закодируем сообщение А6 7.
Следует поступить так:
Сумма Сумма сумм
А= 10 10 10
6 = 6 16 26
Ы = 36 52 78
7 = 7 59 137
X = X 59 + х 196+ х
196+ х | 37
185 5
11 +х
Поскольку 11+лг должно делиться на 37, получаем x=26=Q. Закодиро-
ванное сообщение имеет вид А6 7Q. Для того чтобы на приемном конце про-
верить правильность полученного сообщения, следует поступить так: <
А 6 Ы 7 Q 10X5=50 6X4=24 36X6=108 7X2=14 26X1=26 Сумма =1222=37X6 = 0 по модулю 37
Задачи
2.7.1. Пусть 0=0, 1 = 1, ..., 9=9, А=10, В=11, ..., Z=35, Ы=36. Закоди-
руйте B23F mod 37. Ответ: B23F9.
2.7.2. Является ли К9К9 правильным сообщением в коде из задачи 2.7.1?
2.8. Обзор модулярной арифметики
Поскольку проверки на четность используются в дальнейшем
довольно часто, следует иметь ясное представление об арифмети-
ке, лежащей в основе соответствующих преобразований. Как было
показано, сложение по модулю 2 является той арифметической
операцией, которая применяется в простых проверках на четность,
и оно совпадает с логическим сложением (исключающее ИЛИ).
Правила сложения таковы:
0 + 0 = 0
0+1 = 1
1+0=1
1 + 1 = 1
поСистеме нет других чисел, отличных от 0 и 1. Если действовать
на оРавилам обычной арифметики, то нужно разделить результат
и взять остаток. Когда позже будет рассматриваться алгеб-
ра линейных уравнений и многочленов с коэ фициентами, являю,
щимися числами в системе счисления ио модулю 2, то для сложе.
ния 'будет использоваться та же таблица. При умножении приме-
няются следующие правила:
0x0 = 0
0x1=0
1X0=0
1X1 = 1
Таким образом, умножение совпадает с логическим И.
Иногда 'будут применяться вычеты по модулю, отличному от 2.
Например, в предыдущем разделе использовались вычеты по мо-
дулю 37. В общих чертах теория для любого простого основания
р (например, 37) очень похожа на теорию для основания 2, так
что подробности здесь можно опустить. Для понимания соответ-
ствующей арифметики и алгебры следует лишь внимательно про-
честь начало этого раздела и внести небольшие изменения. При
сложении и вычитании по модулю р следует разделить каждое
число на р и взять положительный остаток.
При умножении по модулю т (когда т не простое число) сле-
дует быть более осторожным. Предположим, что числа а и Ь
сравнимы с числами’^' и Ь' по модулю т. Это означает, что а=
= а'тоАт, b=b'modm или a = a'+klm, b = b'+k2m для некоторых
целых чисел k и k'. Для 'произведения ab имеем ab=a'b'+
+ a'k2m +-b'kvm + kyk2m2, ab == a'b' mod m.
Рассмотрим теперь частный случай: tz=15, 6=12, m=10. Име-
ем a'=5, b' = 2 и fi^a'fc'sOmod 10. Но ни а, ни b не равны 0!
Важное свойство умножения, состоящее в том, что если произве-
дение равно 0, то по крайней мере один из сомножителей ра-
вен 0, выполнение только для простых оснований. Именно это оп-
ределяет важность простых оснований. Теперь видно, почему чис-
ло 37 было столь удобным в разд. 2.7. Читатель должен хорошо
разобраться в модулярной арифметике, особенно для простого
основания, поскольку в гл. 11 появится более сложная задача по-
строения соответствующей модулярной алгебры. Поэтому в сле-
дующем разделе дается еще один пример кодирования такого
типа.
2.9. Номера книг в системе ISBN
В большинстве научных книг и учебников в настоящее время ставится но-
мер ISBN (International Standart Book Number — номер книги ио междуна-
родному стандарту). Этот номер обычно состоит из 10 цифр и является кодо-
вым словом, которое издательство присваивает своим книгам. Типичным явля-
ется номер 0—1321—2571—4, хотя черточки могут стоять в разных местах (он"
вообще несущественны). Цифра 0 означает Соединенные Штаты и некоторые
другие англоязычные страны. Число 13 обозначает издательство Prentice-Hall-
Следующие 6 цифр составляют иом-ер книг®, присваиваемый ей издательство^
последняя цифра является взвешенной суммой, как в разд. 2.6. Арифметика
по модулю 10 непригодна, поскольку 10 — составное число. Поэтому использует-
ся проверочная сумма по модулю И, и если проверочная цифра равна 10, вы-
бирается символ X.
Среди своих книг автор нашел номер 0—1315—2447—X. Для проверки
правильности этого номера в системе ISBN поступаем следующим образом:
0
1 1 1
3 4 5
1 5 10
5 10 20
2 12 32
4 16 48
4 20 68
7 27 95
Х= 10 37 132 = (11)Х(12)=0 mod П
Все в порядке!
Здесь мы снова встречаемся с простым кодом с обнаруживанием ошибок,
предназначенным скорее для людей, а не ЭВМ. Ясно, что такие коды широко
распространены.
Задачи
2.9.1. Проверьте ISBN 0—13165332—6.
2.9.2. Проверьте ISBN 0—1391—4101—4.
2.9.3. Имеет ли смысл ISBN 07-—028761—-4?
2.9.4. Проверьте ISBN ваших книг.
Глава 3
Коды с исправлением ошибок
3.1. Необходимость в исправлении ошибок
Часто простой метод обнаружения ошибок с последующим по-
вторением передачи является недостаточным. Немедленно возни-
кает следующий вопрос: «Если ЭВМ может обнаружить ошибку,
почему бы ей не найти, где она произошла?» И, действительно,
при подходящем кодировании это можно сделать. Можно, напри-
мер, повторять каждый символ или каждое вычисление три раза,
и затем производить голосование. Однако, как будет показано, су-
ществуют -лучшие методы. В качестве примера, когда необходимо
использовать код с исправлением ошибок, можно указать переда-
чу информации с Марса на Землю. При этом время передачи на-
столько велико, что- к моменту обнаружения ошибки исходное со-
о Щение уже может быть стертым. В настоящее время (1979 г.)
этой системе передачи используется код, который может исправ-
ЯТв Д° Восьми ошибок в одном блоке цифр.
спРавление ошибок очень полезно также в типичных запоми-
Щих устройствах. Например, американское Бюро переписи на-
селения хранит большую часть имеющейся у него информации
на магнитных лентах. С течением времени качество записей су.
шественно ухудшается и наступает момент, когда некоторые из
них не могут 'быть надежно считаны. При этом первоначальный
источник информации часто оказывается уже недоступным, и по-
этому записанная на ленте информация теряется навсегда. Если
при кодировании информации предусмотрена возможность исправ-
лять ошибки, то соответствующие типы ошибок могут быть ис-
правлены.
Исправление ошибок можно производить на аппаратурном
уровне. Например, в ЭВМ NORC имелось устройство для просто-
го исправления изолированных ошибок, возникающих в запоми-
нающих устройствах на электронно-лучевых трубках. Часто ис-
правление ошибок производится только в запоминающих устрой-
ствах. ЭВМ STRETCH, построенная фирмой IBM для «более де-
тального изучения состояния дел», предусматривает исправление
одиночных ошибок и обнаружение двойных ошибок (см. разд. 3.7)
в большинстве своих устройств. На приемных испытаниях ЭВМ
STRETCH утверждалось, что в одной из .цепей в первые минуты
работы возникла ошибка, но схемы исправления ошибок ликвиди-
ровали ее и обеспечили правильную работу ЭВМ в течение часа.
Среди'имеющихся в настоящее время (1979 г.) ЭВМ система «Эк-
липс» обеспечивает аппаратурное исправление некоторых ошибок.
ЭВМ CRAY 1 предусматривает исправление ошибок в качестве до-
полнительной возможности запоминающих устройств. Проверка
на аппаратурном уровне описана в [15].
Исправление ошибок может осуществляться также на програм-
мном уровне, как это делает, например, американское Бюро пере-
писи населения при записи информации на магнитную ленту. Ра-
нее уже упоминалось о методах обнаружения ошибок при записи
на магнитный барабан на программном уровне. При этом также
можно использовать иоправление ошибок. Во многих случаях ко?
ды с исправлением ошибок предусмотрены в программном обеспе-
чении. Программный подход удобнее тем, что он позволяет ис-
правлять ошибки в более ответственных массивах информации и
пропускать менее ответственные. Более того, недостатки вычисли-
тельных систем выявляются только в процессе накопления опыта,
и только тогда становится ясным, где и какая нужна защита от
ошибок. Только после того, как моделирование защиты от ошибок
на программном уровне докажет свою способность справиться с
недостатками, защиту можно добавлять к системе на аппаратур-
ном уровне.
3.2. Прямоугольные коды
Первыми и наиболее простыми кодами с исправлением оши-
бок являются коды с утроением, в которых каждое передаваемое
сообщение повторяется три раза, а на приемном конце произво-
дится голосование по большинству. Ясно, что такая система ис-
правляет любые одиночные ошибки. Однако не менее ясно, что
такая система кодирования очень неэффективна. Три параллель-
ных ЭВМ вместе с устройством сравнения и прерывания при TJ“-
обходимости оказываются слишком дорогими. .Поэтому нужно
кать лучшие методы кодирования информации, позволяющие ис-
правлять одну ошибку.
Следующими по простоте кодами с исправлением ошибок
ляются прямоугольные коды, в которых сообщение представляет-
ся в прямоугольниках размером (т—il)X(n—1) (рис. 3.2.1), хотя
фактически сообщение не обязано иметь такой вид. Затем к каж-
дой строке, состоящей из т—1 символов, добавляется проверка
'на четность, так что длина строки становится
равной т символам. Аналогично, к каждому
|столбпу добавляется по одному проверочному
[символу. При этом несущественно, заполняет-
ся или нет правый нижний угол. Проверочный
символ выбирается так, чтобы общая сумма
|была четной, тогда четность последней строки
(равна четности крайнего правого столбца. Та-
ким образом, первоначальный прямоугольник
из (т—1)(и—1.) двоичных символов превра-
щается в массив из тп двоичных символов.
Поэтому избыточность равна 1 + 1/(т—1)+.
+ 11 (п—1) + 1/(т—1) (п—1). При заданном
не-
ис-
яв-
п-
Рис.
о
о
о
о
т-1
о о • •
о • •
о • •
о
о
о
о X
о х
о х
о
X
X X
Прямо-
коды:
о
X X
3.2.1.
угольные
О — позиции сообщений;
X — проверочные пози-
ции
тп избыточность тем меньше, чем ближе прямоугольник к квадра-
ту. Для квадратных кодов размера п имеется (п—I)2 информаци-
онных символов и (2п—1) проверочных символов вдоль сторон.
Прямоугольный код использовался, например, в запоминаю-
щих устройствах на электронно-лучевых трубках в ЭВМ NORC.
Прямоугольные коды часто применяются в ЗУ на магнитных лен-
тах [3, 15]. Продольные проверки на четность проводятся -вдоль
строк и в конце блока добавляется еще одна строка для формиро-
вания вертикальной проверки на четность. К сожалению, проек-
тировщики редко разрешают пользователю извлекать информацию
о проведенных проверках на четность и исправлять отдельные
ошибки с помощью подходящих программ.
Задачи
3.2.1. Рассмотрите все возможные прямоугольные коды с 24 информационными
символами.
3.2.2. Обсудите использование углового проверочного символа. Докажите, что
при проверках на четность он является проверочным символом как для
строки, так и для столбца. Рассмотрите применение в этой связи проверок
на нечетность.
3.3. Треугольные, кубические и п-мерные коды
При рассмотрении прямоугольных кодов можно -быстро прий-
и 'К треугольным, в которых каждый символ на диагонали (их
исло равно п, если сторона треугольника давна и) определяется
2—1о
проверкой на четность, в которую входят как соответствующая
строка, так и соответствующий столбец (рис. 3.3.1). Таким обра-
зом, при данном объеме мы уменьшаем избыточность. Треуголь-
ный массив информационных символов содержит п(п—1)/2 сим-
волов, и для проверок добавляется п символов. Следовательно,
избыточность равна 1+2/(п—1). Вспомним, однако, что при за-
данном объеме сообщения треугольник имеет более подходящий
размер п, чем соответствующий прямоугольник.
о к
х V
Рис. 3.3.1.
Треугольные коды
Рис. 3.3.2. Кубический код; показана
только одна плоскость с соответ-
ствующей ей проверочной позицией
Сразу же после того, как найден некоторый код, который луч-
ше простых прямоугольных кодов, возникает вопрос: «Насколько
вообще можно снизить избыточность?». В случае куба нужно про-
верить каждую плоскость в трехмерном пространстве (рис. 3.3.2).
Три пересекающихся проверочных ребра содержат (Зп—2) из п3
возможных символов. Таким образом, чистая избыточность равна
примерно 3/п2.
Если трехмерные коды лучше двумерных, то не будет ли .пе-
реход к большим размерностям еще более выгодным? Конечно,
это не значит, что требуется располагать символы в трехмерном
пространстве или пространстве более высокой размерности. Сле-
дует лишь представлять их расположенными таким образом для
того, чтобы правильно вычислять проверки на четность. После не-
которых размышлений о проверках по трехмерным плоскостям в
четырехмерном пространстве видно, что чистая избыточность рав-
на приблизительно 4/п3. Это позволяет сделать вывод, что наилуч-
шей является наивысшая возможная размерность пространства,
т. е. ситуация, когда (п+1) из 2П символов являются провероч-
ными. Таким образом, число проверок на четность должно быть
равно п+1. Расположенные в правильном порядке они дают чис-
ло, называемое синдромом, которое получается, если написать
символ 1 для каждой невыполненной проверки на четность и сим-
вол 0 для каждой выполненной проверки. Эти (п+1) символов
образуют (п+1)-значное число, и это число (синдром) может
различать 2n+I возможных событий, что вполне достаточно для
определения возможного положения единственной ошибки, а так-
же отсутствия ошибки. Заметим, что так же, как в простых кодах,
с обнаружением ошибок проверочные символы защищаются на-
равне с символами сообщения. Все посылаемые символы рассмат-
риваются на равных правах. Однако синдром имеет больше со-
стояний, чем необходимо для указания, что в сообщении нет
сшибки, а также для указания положения ошибки в случае, если
она произошла. Таким образом, произошла потеря эффективности.
Тем не менее, этот метод приводит к новому подходу к задаче по-
строения кодов с исправлением ошибок, который рассматривается
в следующем разделе.
Задачи
3.3.1. Постройте треугольный код с 10 информационными символами.
3.3.2. Подробно исследуйте четырехмерный 2X2X2 X 2-код.
3.4. Коды Хэмминга для исправления ошибок
В этом разделе используется алгебраический подход к задаче,
рассмотрение которой началось в предыдущем разделе, т. е. к за-
даче построения наилучшей схемы кодирования для исправления
одиночных ошибок при белом шуме. Предположим, что имеется
т независимых проверок, на четность. Слово «независимые» озна-
чает, конечно, что никакая сумма одних проверок не совпадает
ни с какой другой проверкой (напомним, что складывать нужно в
системе счисления по модулю 2). Так, три проверки на четность
в позициях
1 : 1, 2, 5, 7
2: 5, 7, 8, 9
3: 1, 2, 8, 9
являются зависимыми, поскольку сумма любых двух Строк совпа-
дают с третьей строкой. Таким образом, третья проверка на чет-
ность не доставляет никакой новой информации по сравнению с
двумя первыми и является лишней.
Синдром, который получается, если написать символ 0 для
каждой из выполненных проверок на четность и символ 1 для
каждой из невыполненных проверок, можно рассматривать как
число, состоящее из т цифр. Это число может различать не более
2™ событийХНеобходимо иметь синдром, соответствующий тому,
что все символы сообщения правильны, а также местоположение
ошибки в любой из п позиций сообщения. Это приводит к нера-
венству
2т>п4-1. (3.4.1)
Можно ли найти такой код? Ниже показано, как построить ко-
ды. для которых в условии (3.4.1) стоит равенство. Они дают ча-
стичное решение задачи построения подходящего кода и известны
как коды Хэмминга.
Простая идея, лежащая в основе кодов Хэмминга, состоит в
требовании того, чтобы синдром давал фактическое положение
а равный 0 синдром означал, что ошибка отсутствует,
должны быть проверки на четность? Посмотрим на двоич-
°шибки.
Какими
ное представление номеров позиций (табл. 3.4.1). Ясно, что если
синдром указывает позицию ошибки (когда она произошла), то
каждая позиция, для которой последняя цифра ее номера, за-
писанного в двоичном представлении, равна 1, должна входить в
первую проверку на четность (см. крайний правый столбец). Ак-
куратно продумайте, почему это так. Аналогично, во вторую про-
верку на четность должны входить те позиции, для которых рав-
на 1 вторая справа цифра их номера, записанного в двоичном
представлении и т. д.
Таблица 3.4.1
Проверочные позиции
Номер позиции Двоичное представление номера Номер позиции Двоичное пре дставл ение номера
1 0001 7 0111
2 0010 8 1000
3 ООП 9 1001
4 0100 10 1010
5 0101 - - -
6 оно
Таким образом, в первую проверку на четность входят пози-
ции 1, 3, 5, 7, 9, 11, 13, 15, ..., во вторую —- 2, 3, 6, 7, 10, 11, 14,
15, ..., в третью — 5, 6, 7, 12, 13, ,14, 15, ..., в следующую — 8, 9,
10, И, 12, 13, 14, 15 и т. д.
Для иллюстрации сказанного (табл. 3.4.2) построим простой
код с исправлением ошибки для четырех двоичных символов.
Таблица 3.4.2
Кодирование 4-битового сообщения и определение ошибки
Кодирование 1 2 3 4 5 6 7 . Позиции
1—011 0 11 0 0 Г 1 Сообщение Закодированное сообщение
'X 0 1 0 0 0 1 1 Ошибка Принятое слово
Определение ошибки Проверка 1: 13 5 7 0 0 0 1 Проверка 2: 2 3 6 7 10 11 Проверка 3: 4 5 6 7 0 0 11 Синдром = 0 11 = Поправление 1 0110011 не выполнена.-»-1 не выполнена -> 1 выполнена 0 3 -+• номер позиции ошибки Исправление ошибки Правильное сообщение
Должно выполняться неравенство 2т^п+1, при этом легко ви-
деть, что 23^ (4 + 3)+ 1 =8. Таким образом, нужно иметь т = 3
проверок на четность и тогда п=7= общее число символов (ин-
формационных и проверочных). Для удобства пусть позиции 1, 2
и 4 используются для проверок на четность. Тогда информацион-
ными являются позиции с номерами 3, 5, 6 и 7. Для того чтобы
закодировать информационное сообщение, запишем его в этих по-
зициях и вычислим проверки на четность. Пусть, скажем, сообще-
ние имеет вид_____1___0 1 1; пробелы указывают места, в кото-
рых должны находиться проверочные символы. Первая проверка
на четность, дающая значение первого символа, включает симво-
лы, стоящие на позициях -1, 3, 5 и 7; рассматривая сообщение, по-
лучаем, что первый символ равен 0. Теперь сообщение имеет вид
0__1__0 1 1. Вторая проверка на четность, включающая симво-
лы на позициях 2, 3, 6 и 7, приводит к тому, что второй символ
равен 1. Таким образом, частично закодированное сообщение по-
лучает вид 0 1 1__0 1 1. Третья проверка на четность символов
на позициях 4, 5, 6 и 7 дает четвертый символ, равный 0. Тогда
полностью закодированное сообщение имеет вид 0 1 10 0 1 1.
Для того чтобы увидеть, как код исправляет изолированную
ошибку, предположим, что послано сообщение 0 110 0 11, и
канал добавляет 1 к третьему слева символу. В результате иска-
женное сообщение имеет вид 0 1 0 0 0 1 1. На приемном конце
по очереди производятся проверки на четность. Первая проверка,
включающая символы на позициях 1, 3, 5 и 7, очевидно, не вы-
полнена, так что последняя цифра синдрома равна 1. Вторая про-
верка на четность, включающая символы на позициях 2, 3, 6, 7,
также не выполнена, так что вторая цифра синдрома также рав-
на 1. Третья проверка на четность, включающая символы на пози-
циях 4, 5, 6, 7, выполнена, так что старшая цифра равна 0. Рас-
смотрение синдрома как двоичного числа показывает, что он соот-
ветствует десятичному числу 3. Поэтому следует изменить (логи-
чески добавляя 1) символ на третьей позиции принятого сообще-
ния с С на 1. Полученная последовательность нулей и единиц яв-
ляется верной, и, выкидывая проверочные позиции 1, 2 и 4, по-
лучаем исходное информационное сообщение 1 0'1 1, стоящее на
позициях 3, 5, 6, 7.
Заметим, что вместе с информационными символами в одина-
ковой мере исправляются проверочные. Таким образом, код явля-
ется равномерно защищенным: после кодирования информацион-
ные и проверочные символы принимают равное участие в кодовом
слове. Привлекательная черта кода Хэмминга состоит в легкости
кодирования и исправления ошибок. Заметим также, что синдром
указывает положение ошибки независимо от того, какое сообще-
ние было послано; логическое прибавление 1 к символу, номер
позиции которого определяется синдромом, исправляет получен-
ное сообщение. Равенство нулю всех символов синдрома означа-
ет> конечно, что в сообщении нет ошибок.
Избыточность в примере с четырьмя информационными и тре-
мя проверочными символами оказывается довольно олыпой. Нели,
однако, число проверочных символов равно 10, то из неравенства
(3.4.1)'имеем 2105s 10+1+число информационных символов. Это
значит, что число информационных символов не превышает
1'024—11 = 1013. Поэтому чистая избыточность растет как двоич-
ный логарифм числа информационных символов.
Задачи
3.4.1. Рассмотрите код Хэмминга с четырьмя проверками.
3.4.2. Рассмотрите код Хэмминга с двумя проверками. Ответ: Код с утрое-
нием.
3.4.3. Покажите, что 1111111 — правильное сообщение.
3.4.4. Исправьте и декодируйте последовательность 1001111.
3.4.5. Найдите позицию ошибки в сообщении 011100010111110, закодированном,
как в задаче 3.4.1, с четырьмя проверками. Укажите правильное сообщение.
3.4.6. Найдите вероятность того, что случайная последовательность из 2™—-1
нулей и единиц является кодовым словом.
3.5. Эквивалентные коды
Приведенный выше пример дает один из способов кодирования
сообщения. Имеется много других эквивалентных кодов. Ясно,
что любая перестановка позиций кода приводит к коду, тривиаль-
но отличающемуся от первоначального. Аналогично, инверсия
(замена 0 на 1 и 1 на 0) символов, появляющихся на некоторой
фиксированной позиции во всех кодовых словах, приводит к коду,
тривиально отличающемуся от первоначального.
При желании замечание о перестановке позиций можно ис-
пользовать, чтобы переставить все проверочные позиции в конец
сообщения. .Может показаться, что при этом проверки на четность
и проведение исправлений становятся 'более сложными, однако
для ЭВМ число вычислений не увеличивается, поскольку при каж-
дой проверке по-прежнему нужно выбрать некоторые символы
принятого сообщения и установить четность суммы. Аналогично
изменяется синдром, хотя его сущность не меняется, и он по-преж-
нему однозначно соответствует позиции. Таким образом, номер
позиции символа, к которому следует логически добавить коррек-
тирующий бит, изменяется, однако ее можно найти либо по фор-
муле, либо из таблицы, устанавливающей соответствие между
синдромом и словом, содержащим 1 в позиции, которую нужно
исправить. Конечно, для длинного кода сообщение может состоять
из двух или более слов. Размер таблицы пропорционален п. Пер-
воначальный код Хэмминга использовал вычислительные методы,
а не табличный поиск, и, вообще говоря, для длинных кодов та-
кие методы необходимы.
Задача
3.5.1. Подробно рассмотрите кодирование и декодирование для кода с п=7,
если три проверочных символа передвигаются на позициях с номерами 5,
6 и 7.
3.6. Геометрический подход
Выше был представлен алгебраический подход к кодам с ис-
правлением ошибок. Другой, эквивалентный подход использует
я-мерную геометрию. В этой модели последовательность из нулей
и единиц рассматривается как точка n-мерного пространства.
Каждый символ задает значение соответствующей координаты в
о-мерном пространстве, (предполагается, что длина закодирован-
ного сообщения в точности равна п битам). Таким образом, име-
ется куб в n-мерном пространстве, каждая вершина которого
представлена последовательностью из п нулей и единиц. Прост-
ранство состоит только из 2П вершин и, кроме них, в пространстве
всех возможных сообщений ничего нет. Это пространство иногда
называют векторным.
Каждая вершина является возможным принятым сообщением;
однако лишь некоторые выбранные вершины — это посылаемые
сообщения. Одиночная ошибка в сообщении передвигает точку,
соответствующую сообщению, вдоль ребра воображаемого куба в
соседнюю вершину. Если .потребовать, чтобы любое посылаемое
сообщение находилось на расстоянии, по крайней мере, двух ре-
бер от любого другого возможного сообщения, то ясно, что любая
одиночная ошибка сдвинет сообщение вдоль ребра и принятое
сообщение выйдет из множества посылаемых сообщений. Если
минимальное расстояние между посылаемыми сообщениями равно
трем ребрам куба, то любая одиночная ошибка оставит принятое
сообщение ближе к посланному, чем к любому другому посылае-
мому сообщению, так что код будет исправлять одиночные
ошибки.
Фактически введено расстояние, равное минимальному числу
ребер куба, по которым нужно пройти, чтобы дойти от одной точ-
ки до другой. Это расстояние равно также числу бит, которыми
отличают последовательности, соответствующие двум вершинам.
Таким образом, расстояние можно рассматривать как логическую
сумму двоичных символов двух точек. Эта величина действитель-
но является расстоянием, поскольку она обладает следующими
тремя свойствами.
1. Расстояние от любой точки до самой себя равно 0.
2. Расстояние от точки х до отличной от нее точки у совпа-
дает с расстоянием от точки у до точки х и является положи-
тельным числом.
3. Выполнено неравенство треугольника, т. е. сумма длин двух
сторон треугольника (расстояние от а до с плюс расстояние от
с до Ь) не меньше длины третьей стороны (расстояние от а до Ь).
Это расстояние обычно называется расстоянием Хэмминга. Оно
Приспособлено для двоичного белого шума. Используя это рас-
стояние, можно определить различные объекты в пространстве.
“ частности, поверхность сферы с центром в некоторой точке
представляет собой множество точек, находящихся на заданном
расстоянии от центра. Поверхность сферы радиуса 1 с центром
/л п 0) _______ это множество всех вершин пространства, находя-
щихся’на расстоянии 1, т. е. множество всех вершин, имеющих
только один символ 1 в координатной записи (рис. 3.6.1). Число
таких точек равно С(п, 1).
Минимальное расстояние между вершинами множества посы-
лаемых сообщений можно выразить в терминах корректирующих
свойств. Для однозначности кода минимальное расстояние долж-
но быть по меньшей мере равно 1 (табл. 3.6.1). Минимальное рас-
Табл и ц а 3.6.1
Смысл минимального расстояния
Минимальное
расстояние
1 Однозначность
2 Обнаружение одиночных ошибок
3 Исправление одиночных ошибок (или обнаружение двойных
ошибок)
4 Исправление одиночных ошибок дополнительно к этому, об-
наружение двойных ошибок (или вместо всего этого обнару-.
жевие тройных ошибок)
5 Исправление двойных ошибок
стояние 2 дает обнаружение одиночных ошибок. Минимальное
расстояние 3 дает исправление одиночных ошибок; каждая оди-
ночная ошибка оставляет точку, расположенную ближе к первона-
(1,1,0) (1,1,1)
Рис. 3.6.1. Трехмерные сферы
с центрами (0, 0, 0) и (1, 1,1)
чгльному положению, чем к любому
другому посылаемому сообщению. Яс-
но, что код с этим минимальным
расстоянием может использоваться
также для обнаружения двойных
ошибок. Минимальное расстояние 4
дает исправление одиночных ошибок,
а также обнаружение двойных оши-
бок. Минимальное расстояние 5 дает
исправление двойных ошибок. Обрат-
но, для того чтобы обнаруживать или
исправлять ошибки соответствующей
кратности, код должен иметь соответ-
ствующее минимальное расстояние.
При исправлении одиночной ошибки (минимальное расстояние
3) каждое сообщение можно окружить единичной сферой, и эти
сферы' не перекрываются. Шар радиуса 1 состоит из центра и п
точек, по одной для каждой измененной координаты; таким обра-
зом, объем шара равен 1+«. Объем всего «-мерного пространст-
ва, т. е. число всех точек в нем, равен, очевидно, 2п. Поскольку
шары не пересекаются, максимальное число посылаемых соооще-
ний должно удовлетворять условию
объем сферы _ .
-------------минимальное число сфер
объем всего пространства
или
2«/(n+l)>2ft. (3.6.1)
Поскольку n = m + k, то 2m+h^2!l(n+1) или 2т^п+1. Именно
это неравенство было получено при использовании алгебраиче-
ского подхода [см. (3.4.1)].
Получим теперь ограничения для кодов с исправлением оши-
бок более высокой кратности. Так, при исправлении двойных оши-
бок минимальное расстояние должно равняться пяти, и нужно
расположить непересекающиеся шары радиуса 2 вокруг всех пере-
даваемых сообщений. Этот шар состоит из центра п точек, нахо-
дящихся на расстоянии 1 от центра, а также тех точек, у которых
изменены две координаты. Число таких точек равно биномиаль-
ному коэффициенту С(п, 2)=п(п—4)/2. Деля объем всего про-
странства 2п на объем такого шара, получаем верхнюю границу
для числа 2k возможных передаваемых сообщений в коде
2"/[l+n+n(n— l)/2]>2fe. (3.6.2)
Это неравенство не означает, что можно получить такое число
сообщений в коде; оно дает лишь верхнюю границу этого числа.
Аналогичные неравенства можно написать для больших шаров.
.В случае, если шары с центрами во .всех передаваемых сооб-
щениях полностью исчерпывают все 2п точек пространства, так
что каждая точка пространства находится в некотором шаре, код
называется совершенным. Совершенные коды обладают многими
симметриями (в геометрической модели каждая кодовая точка
эквивалентна любой другой кодовой точке), и теория этих кодов
является особенно простой. Совершенные коды существуют лишь
в сравнительно немногих случаях. Для них приведенные неравен-
ства обращаются в равенства.
Задачи
3.6.1. Обобщите границы (3.6.1) и (3.6.2) на коды с исправлением большего
числа ошибок.
3.6.2. Используя (3.6.2), вычислите и занесите в таблицу значения границы для
кодов с исправлением двойных ошибок (п=3, 4, 5, ..., 11).
3.7. Коды с исправлением одиночных ошибок
и обнаружением двойных ошибок
Часто неразумно ограничиваться лишь исправлением одиноч-
ных ошибок, поскольку двойная ошибка может ввести систему в
За'блуждение; в результате система по синдрому будет исправлять
°Шибку не в том месте, и в декодированном сообщении возникнут
тпи ошибки Вместо этого во многих (но не во всех) случаях до-
статочно разумно использовать коды с исправлением одиночных
ошибок :И дополнительно с обнаружением двойных ошибок. При
этом условие, необходимое для обнаружения двойных ошибок, со-
стоит в том, что минимальное расстояние должно увеличиться на
1 и равняться 4.
Для получения кода с дополнительным обнаружением двойных
ошибок из кода с исправлением одиночных ошибок, добавим еще
одну проверку на четность (и еще одну позицию), охватив этой
проверкой все сообщение. Тогда каждая одиночная ошибка по-
прежнему будет давать правильный синдром, а дополнительная
проверка на четность — 1. Двойная ошибка приведет к некоторо-
му ненулевому синдрому, но дополнительная проверка на четность
будет выполнена. Эта ситуация (а именно, появление любого
синдрома и выполнение дополнительной проверки на четность)
позволяет распознать двойную ошибку (табл. 3.7.1). Легко ви-
Таб лица 3.7.1
Обнаружение двойных ошибок
Первоначаль- ный синдром Новая провер- ка на четность Смысл
0 0 Правильно
0 ш Ошибка на дополнитель- ной позиции
Любой Такой же, как в коде для одиночной ошибки
Любой 0 Двойная ошибка
деть, что если две точки первоначального кода находятся на рас-
стоянии 3, то число единиц в этих точках имеет разную четность.
Таким образом, при выполнении дополнительной проверки на чет-
ность для двух таких точек получаются разные значения, так что
расстояние между ними увеличивается .до 4.
Приведенные рассуждения применимы как при алгебраическом,
так и при геометрическом подходе; они показывают, как оба под-
хода дополняют друг друга. До сих пор не приводились какие-
либо конструктивные методы построения кодов с исправлением
ошибок высокой кратности, а приводились только оценки для них.
В гл. 11 дается некоторое представление об этих методах. Пол-
ная теория кодов с исправлением ошибок разрабатывалась в тече-
ние многих лет и является довольно сложной. Поэтому здесь ука-
зывается лишь общий подход.
Заметим, что теория предполагает надежную работу устройств,
исправляющих ошибки; исправлению подвергаются только ошиб-
ки в принятом (вычисленном) сообщении.
Задача
3 7.1. Покажите, что рассуждения, использованные для дополнительного обна-
ружения ошибки, можно применить к любому коду с нечетным минималь-
ным расстоянием, получая код, имеющий на 1 большее (четное) минималь-
ное расстояние.
3.8. Применение идей
Как было сказано в разд. 1.2, рассматриваемые в книге идеи
имеют не только непосредственное, но и более широкое примене-
ние, в качестве примера упоминалась эволюция.
Основная идея обнаружения и исправления ошибок состоит в
том, что для успешной 'борьбы с ошибками передаваемые сообще-
ния располагают далеко друг ют друга (в 'пространстве возмож-
ных ошибок). Если два передаваемых сообщения недостаточно
далеки друг от друга, то одно из них может быть переведено
ошибкой (или ошибками) в другое или, по крайней мере, станет
настолько близко к нему, что на приемном конце при попытке
распознать сообщение произойдет ошибка.
'Присваивая имена переменным меткам в языках высшего
уровня ФОТРАН, КОБОЛ, АЛГОЛ, ПАСКАЛ и других, нужно
добиваться того, чтобы имена были далеки друг от друга; в про-
тивном случае описка или типичная ошибка при вводе может пе-
ревести одно используемое имя в другое. Если имена различают-
ся по крайней мере в двух позициях, то ассемблер обнаружит
одиночную ошибку. Таким образом, применение коротких мнемо-
нических имен должно быть ограничено для предотвращения пе-
реходов, обусловленных небольшими ошибками.
Рассмотрение расстояния Хэмминга оправдано только в слу-
чае белого шума. В разд. 2.7 и 2.9 показано, что расстояния, ко-
торые нужно использовать в различных случаях, зависят как от
психологического расстояния между именами, так и от распреде-
ления ошибок.
3.9. Итоги
В главе рассмотрены основы обнаружения и исправления оши-
бок, возникающих при наличии белого шума, а именно — указа-
но, каким должно быть минимальное расстояние между сообще-
ниями. Приведены методы построения кодов:
с обнаружением одиночных ошибок — минимальное расстоя-
ние=2;
с исправлением одиночных ошибок — минимальное расстоя-
ние=3;
с исправлением одиночных ошибок+с обнаружением двойных
ошибок—минимальное расстояние = 4.
Такие коды легко построить и реализовать как на програм-
мном, так и на аппаратном уровнях. Они могут использоваться
Аля компенсации слабых мест системы или для достижения на-
дежной работы систем, состоящих из ненадежных частей, не сле-
дует мириться с плохой работой аппаратуры, однако следует
иметь в виду, что за кодирование и возможность исправления
ошибок следует .платить увеличением объема памяти (или време-
нем передачи) и увеличением объема аппаратуры (или быстро-
действием). Нельзя получить что-либо полезное без каких-либо
затрат! Коды также заметно облегчают обслуживание, поскольку
они указывают на местоположение ошибки, и при ремонте не бу-
дет исправляться то, что не нужно, т. е. будет исправляться то,
что работает правильно, и не исправляться то, что служит причи-
ной ошибки.
В разд. 3.8 отмечается возможность более широкого использо-
вания понятия расстояния между сообщениями.
9
Глава 4
Неравномерные коды — коды Хаффмена
4.1. Введение
Все рассматривавшиеся до сих пор коды были равномерными.
Они называются блочными, поскольку все сообщения, на которые
разбивается поток посылаемых символов, имеют заданную длину
блока. Код Морзе, о котором говорилось в гл. 1, является приме-
ром неравномерного кода. Рассмотрим теперь такие коды более
подробно. Преимущество кодов, в которых сообщения кодируются
словами не обязательно равной длины, состоит в большей эффек-
тивности-, при их применении для представления информации мож-
но в среднем использовать меньше символов. Для этого нужно
иметь какие-то сведения о статистике посылаемых сообщений.
Если все символы источника равновероятны, то блочные коды
практически столь же хороши, как любые другие возможные ко-
ды (см. разд. 4.6). Если, однако, некоторые символы более веро-
ятны по сравнению с другими, то это можно использовать, коди-
руя чаще встречающиеся — более длинными словами. Именно
это делается в коде Морзе. Буква Е алфавита английского языка
встречается чаще других и кодируется точкой.
Однако в случае неравномерных кодов возникает фундамен-
тальная проблема: как на приемном конце различить отдельные
кодовые слова? Например, как в двоичной системе различить,
где кончается одно кодовое слово и начинается следующее?
Если вероятности появления различных символов источника
сильно отличаются друг от друга, то неравномерные коды могут
быть существенно более эффективными, чем блочные.
В этой главе учитываются лишь частоты появления различных
символов источника и не .принимается во внимание более тонкая
структура, которую возможно имеют сообщения. Примером такой
более тонкой структуры в английском языке является то, что за
буквой Q, как правило, следует буква U. Подобная корреляция в
посылаемом сообщении учитывается в гл. 5.
Задачи
4.1.1. Перечислите достоинства и недостатки неравномерных кодов.
4.2. Однозначное декодирование
Следует уточнить, когда имеются в виду символы, которые не-
обходимо передать, а когда — символы, с помощью которых про-
исходит передача сигналов в системе. Требующие передачи сим-
волы (например, буквы английского алфавита) называются сим-
волами источника, а символы, используемые при передаче (напри-
мер, 0 и 1 в двоичной системе), называются символами кодового
алфавита. В общем случае предполагается, что алфавит источника
состоит из q символов Si, ..., sq, а кодовый алфавит — из г симво-
лов (г — основание системы).
Первым необходимым свойством кода является однозначность
декодирования-, принятое сообщение должно иметь единственно
возможное толкование. Рассмотрим код, в котором алфавит ис-
точника S состоит из четырех символов, и они следующим обра-
зом кодируются в двоичном алфавите: Si = 0, s2 = 01, s3= 11,
s4=00.
Принятое сообщение ООП может означать одно из двух:
ООП = [ ®4’ 8з
1 $11 $з-
Таким образом, код не является однозначно декодируемым.
Хотя однозначность декодирования не всегда абсолютно необхо-
дима, она обычно весьма желательна.
Для того чтобы выразить сказанное яснее, дадим формальное
определение.
Определение. Назовем n-кратным расширением кода все воз-
можные последовательности, составленные из п символов перво-
начального кода для источника.
Такое расширение называется также «-кратным прямым про-
изведением кода. В «-кратном расширении содержится qn симво-
лов (слов). Это определение является необходимым, поскольку
на приемном конце посылаемые сообщения выглядят как последо-
вательности закодированных символов источника, и приемник дол-
жен решить, какая именно последовательность символов источни-
ка была передана. Для возможности однозначного декодирования
никакие две различные последовательности не должны совпадать,
Даже для различных расширений. Ясно, что система передачи сиг-
налов обладает однозначным декодированием, только если одно-
значна каждая последовательность. Это условие необходимо и до-
статочно, однако в такой форме его вряд ли можно использовать.
Задачи
4 2 1. Является ли код 0, 01, 001, 0010, ООП однозначно декодируемым?
4^2.2^ Является ли код 0, 01, 011, 111 однозначно декодируемым?
4.3. Мгновенные коды
Изучим следующий код: «! = 0, s2=10, s3 = 110, s4=ll'l. Посмот-
рим, как приемник декодирует сообщения, посылаемые в этом ко-
де. Приемник использует конечный автомат или, что эквивалент-
но, дерево решений. Автомат начинает действовать из начального
состояния (рис. 4.3.1); первая принятая двоичная цифра вызовет
переход автомата либо в концевое состояние Si, если цифра рав-
на 0, либо во вторую точку ветвления, если цифра равна 1. Сле-
дующая принятая двоичная цифра вызовет либо переход в конце-
вое состояние s2, если цифра равна
0, либо в третью точку ветвления,
если цифра равна 1. Далее, если
третья цифра равна 0, то произой-
дет переход в концевое состояние s3,
а если третья цифра равна 1, то в
концевое состояние s4. В каждом
концевом состоянии выдается, ко-
нечно, соответствующий символ и
Рис. 4.3.1. Дерево декодированияПРоисходит возврат в начальное со-
стояние. Заметим, что каждый бит
принятой последовательности просматривается только один раз, и
концевые состояния дерева — это четыре символа источника: Si, S2,
S3 и s4.
В этом примере декодирование является мгновенным, посколь-
ку при получении всего кодового слова приемник сразу же об
этом узнает и ему не нужно исследовать последующие биты, что-
бы решить, какой символ источника принят. Никакое кодовое
слово этого кода не является префиксом никакого кодового слова.
Код такого типа называется кодом с запятой, поскольку на конец
кодового слова указывает двоичная цифра 0, а также то, что дли-
на каждого кодового слова не превышает трех двоичных симво-
лов.
Следующий код обладает однозначным декодированием, но не
является мгновенным, поскольку нельзя решить, когда кончается
кодовое слово, не иследуя последующие биты: Sj = O, s2=01, s3 =
= 011, s4=lll. Это предыдущий код с перевернутыми кодовыми
словами. Причина неприятностей состоит в том, что некоторые
кодовые слова являются префиксами (иначе говоря, совпадают с
начальными частями) других кодовых слов.
Рассмотрим последовательность 0111... 1111. Ее можно де-
Si Si
кодировать только начиная с конца и сопоставлять каждым трем
единицам символ s4 до тех пор, пока не будет достигнуто первое
кодовое слово. Только после этого ему можно сопоставить один
из символов: sb s2 или s3.акйм о разом, приемник не может ре-
шить, получил ли он уже кодовое слово или ему нужно ждать до-
полнительных битов для завершения кодового слова. В приведен-
ном частном случае простейший способ декодирования сообщения
состоит в том, чтобы начинать с конца принятой последовательно-
сти. Этот способ требует значительной памяти, а также обуслов-
ливает задержку при декодировании.
Для получения мгновенного кода необходимо и достаточно,
чтобы никакое кодовое слово, соответствующее «,, не было пре-
фиксом никакого другого кодового слова, соответствующего «,.
Дерево решений, соответствующее немгновенному коду, имеет та-
кую структуру, при которой в момент принятия окончательного
решения о том, что полное кодовое слово уже пришло некоторое
время тому назад, происходит выдача соответствующего символа
источника и переход в некоторое не обязательно начальное, как
для мгновенных кодов, состояние. Как показывает приведенный
пример, принятие решения иногда требует, вообще говоря, не-
ограниченного объема памяти.
4.4. Построение мгновенных кодов
Ясно, что среди всех однозначно декодируемых кодов мгновен-
ные коды предпочтительнее немгновенных, поскольку, как будет
показано ниже (см. разд. 4.7), мгновенные коды не требуют до-
полнительных затрат. Поэтому рассмотрим задачу построения
мгновенных кодов.
Предположим, что требуется построить код для источника с
алфавитом S, состоящим из пяти символов «г-, а кодовый алфавит
должен быть двоичным. Для получения мгновенного кода (с запя-
той) можно символам источника сопоставить следующие слова:
s’i = 0, s2=10, «3=110, «4=11'10, «5=11'11 (рис. 4.4.1).
Рис. 4.4.2. Дерево декодирования
X)s5=mr
Рис. 4.4.1. Дерево декодирования
В этом коде использование 0 для первого символа уменьшает
Число дальнейших возможностей. Используем вместо этого для
Первых двух символов источника слова длины 2, полагая «1 = 00 и
s2=01. Тогда можно взять s3=10. Поскольку осталось закодиро-
вать еще два символа источника, то в качестве кода для s4 нель-
зя взять 11; вместо этого следует испробовать возможность s4 =
= 110 и тогда «5=111. Получим код: s1 = 00, «2=01, «з=10, s4=!l 10,
«5=111. Этот код, очевидно, является мгновенным, поскольку ни-
какое кодовое слово не служит префиксом никакого другого ко-
дового слова. Для него легко построить дерево декодирования
(рис.. 4.4.2).
Какой из этих кодов лучше (эффективнее)? Это зависит от ча-
стот, с которыми появляются символы Si. При этом, конечно, счи-
таем лучшим или более эффективным код, для которого средняя
длина посылаемого сообщения меньше. Этот вопрос подробно
исследуется в разд. 4.8. Ясно, что эффективность зависит от веро-
ятностей появления различных символов в посылаемом сообщении.
Задача ¥
4.4.1. Постройте аналогичный пример для шести слов.
4.4.2. Укажите вероятности, которые определяют, является ли более эффектив-
ным тот или другой код из этого раздела. Ответ: pi и Рз+Р4+Р5-
4.5. Неравенство Крафта
Рассматриваемое ниже неравенство Крафта дает условие суще-
ствования мгновенных кодов; оно показывает, для каких длин ко-
довых слов существует мгновенный код, но не показывает, как
его строить.
Теорема. Необходимое и достаточное условие существования
мгновенного кода для источника с алфавитом S из q символов
Si (i=l, ..., q), кодовые слова которого имеют длины
состоит в выполнении неравенства
k ,
(4.5.1)
£=1
где г — основание (число символов) в кодовом алфавите.
Неравенство Крафта легко доказать с помощью дерева деко-
дирования, существование которого следует из возможности мгно-
венного декодирования. Будем рассуждать по индукции. Для про-
стоты рассмотрим сначала случай двоичного алфавита (рис.
4.5.1). Если максимальная длина пути на дереве равна 1, то на
нем есть одно или два ребра длины 1. Таким образом, либо 1/2^
^1 — для одного символа источника, либо 1/2+1/2^1 — для
двух символов источника. Предположим далее, что неравенство
Крафта справедливо для всех деревьев длины меньше п. Для
данного дерева максимальной длины п ребра из первой вершины
ведут к двум поддеревьям, длины которых не превышают (п—1);
для этих поддеревьев имеем неравенства К,^1 и К"^1, где К.',
К" — значения соответствующих им сумм. Каждая длина /< в под-
дереве увеличивается на 1, когда поддерево присоединяется к ос-
цовному дереву, поэтому возникает дополнительный множитель
1/2. Таким образом, имеем 1/2/С+1/2К"<:2.
В случае произвольного недвоичного основания г имеется не
более г ребер, исходящих из каждой вершины, т. е. не более г под-
деревьев; каждое из них присоединяется к основному дереву, да-
вая дополнительный множитель 1/г. Отсюда снова следует утверж-
Рис. 4.5.1. Доказательство неравен-
ства Крафта:
а — верно для дерева длины 1; предполо-
жим, что верно для длины п—1; б — верно
для дерева длины п, K'fc+K72= К
дение теоремы.
Когда имеет место строгое неравенство? Легко заметить, что
если любая концевая вершина дерева является кодовым словом,
то К= 1. Строгое неравенство име-
ет место лишь в случае, когда
некоторые из концевых вершин
не используются. Если, однако,
в случае двоичного кодового ал-
фавита какя-нибудь концевая
вершина не используется, то пре-
дыдущее решение оказывается
лишним, и соответствующая циф-
ра может быть удалена из каж-
дого кодового слова, декодирова-
ние которого проходит через эту
вершину. Таким образом, если
имеет место строгое неравенство,
то код неэффективен, но для двоичных деревьев очевидно, как
можно его улучшить.
Заметим еще раз, что теорема утверждает существование та-
кого кода и ничего не говорит о конкретных кодах. Может суще-
ствовать код, который удовлетворяет неравенству Крафта и тем
не менее не является мгновенным, однако в этом случае сущест-
вуют коды с теми же /j, являющимися мгновенными.
Посмотрим, как неравенство Крафта применяется к двоичным
блочным кодам,' в которых все 2’” кодовых слов имеют одну и ту
же длину т. Непосредственная подстановка в левую часть нера-
венства показывает (как следовало ожидать), что сумма в точно-
сти равна 1.
Покажем теперь, почему коды с запятой удовлетворяют нера-
венству Крафта. Код с запятой, алфавит которого состоит из г
символов (г — основание), имеет один фиксированный символ, на-
зываемый запятой; он используется для обозначения конца всех
кодовых слов, за исключением самых длинных; конец слов мак-
симальной длины декодер узнает непосредственно по их длине.
Имеется одно слово — сама запятая — длины 1. Число слов
Длины 2 равно (г—1), длины 3 — (г—I)2, длины (k—1) — (г—
наконец, число слов длины k равно г (г—l)fe. Объединяя
слагаемые всех слов одинаковой длины, можно записать сумму
Крафта в виде
1 /Г + (г— I)//-2 + (г — 1 )2/Г3 + ... +
+ (г— l)fe-2 /rk~x + г (г— l)fe-1 /rk .
Сумма последних двух членов равна
(Г— (1 + Г— l)/rft-! = Г (Г— l)ft-2 /гк~Х .
Производя г раз аналогичное преобразование, получаем, что
ряд сводится к выражению — {/} = 1, так что для кодов с запя-
г
той неравенство Крафта переходит в равенство.
В следующих двух примерах предполагается, что заданы толь-
ко длины кодовых слов, поскольку в теорему входят только они,
а не сами слова. Если длины двоичных кодовых слов равны 1, 3,
3 и 3, то сумма Крафта равна 1/2+3/8=7/8, и мгновенный код с
такими длинами существует. Одно из слов длины 3 может быть
сокращено до слова длины 2. Если, однако, длины равны 1, 2, 2
и 3, то сумма равна 1/2+2(1/4),+1/8=9/8, и мгновенный код с та-
кими длинами не существует.
Применим теорему еще к одному примеру. Предположим, что
г=3 и требуется получить слова с длинами 1, 2, 2, 2, 2, 2, 3, 3, 3
и 3. Левая часть неравенства Крафта равна 1/3+ 5 (1/9) + 4(1/27) —
= 28/27, так что найти мгновенный код с такими параметрами не-
возможно. Если удалить последнее
кодовое слово длины 3, то сумма бу-,
/ q Дет в точности равна 1, и такой код
О/f можно найти. Для нахождения мгно-
____——>4 fc- г,
^42венного кода с такими длинами по-
ложим Si = 0, s2 = 10, s3 = ll, s4 = 12,
ry ss = 20, «6 = 21, s7 = 220, s8 = 221. При
таком построении непосредственно
просматривалось дерево декодиро-
вания (рис. 4.5.2) и троичные (осно-
Рис. 4.5.2. Дерево декодирования вание 3) численные эквиваленты ко-
дов систематически увеличивались с
тем, чтобы легко было следить за рассуждениями. Читатель дол-
жен. иметь в виду, что 0, 1 и 2 — это произвольные символы, а не
числа. Поэтому произвольная перестановка трех символов перево-
дит код в практически ему эквивалентный.
Задачи
4.5.1. Удовлетворяет ли неравенству Крафта код с запятой с Zi=l, /2=2,
..., lh=k, ... (имеющей бесконечную длину)? Используйте г—2.
4.5.2. Обобщите задачу 4.5.1 на произвольное основание г.
4.6. Укороченные блочные коды
Вернемся на время к рассмотренным ранее блочным кодам. Если имеется
2™ двоичных кодовых слов (гт в системе с основанием г), то для представ-
ления каждого символа источника можно использовать т двоичных цифр. Пред-
положим, однако, что число символов источника не равно точной степени ос-
нования. Чтобы увидеть, что произойдет, разберем случай пяти символов. Из
восьми двоичных слов: ООО, 001, 010, 011, 100, 101, 110, 111 нужно отбросить
любые три. Если, однако, выкинуть 001, ОН и 101, то можно укоротить три
ветви дерева декодирования, сохранив мгновенную декодируемость.
Имеем Si=00, s2=01, s3=10, s4=110, s6= 111 (рис. 4.6.1,fl). Вместо этого
можно отбросить 001, 010 и 011 и укоротить только одну ветвь дерева, получив
кОД. s2=0, s2=100, s3=;101, s4= 110, s5= 111 (рис. 4.6j1,6). В обоих случаях у
дерева не остается неиспользуемых концевых вершин, так что К=1. Такие ко-
ды называются укороченными блочными кодами и представляют собой незна-
чительную модификацию блочных кодов.
Задачи
Рис. 4.6.1. Деревья декодирования
4.6.1. Рассмотрите случай двух символов при основании 3.
4.6.2. Рассмотрите случай пяти символов при основании 3.
4.7. Неравенство Макмиллана
Неравенство Крафта применимо к мгновенным кодам, кото-
рые являются частным случаем однозначно декодируемых кодов.
Макмиллан показал, что такое же неравенство справедливо для
однозначно декодируемых кодов. Основная идея доказательства
необходимости состоит в том, что число, превышающее 1, очень
быстро возрастает с увеличением степени, в которую оно возво-
дится. Если рост можно ограничить, то это означает, что число не
превышает 1. Доказательство’ достаточности следует из того, что
его можно провести для мгновенных кодов, являющихся частными
случаями однозначно декодируемых кодов.
'Доказательство необходимости начинается с рассмотрения вы-
ражения
Разложив выражение в скобках, получим сумму многих членов,
каждый из которых включает (1/г) в некоторой степени; показа-
тель степени изменяется от наименьшего значения п до наиболь-
2
k=n
шего nl, где I — наибольшая длина кодового слова. Таким обра-
зом, получаем выражение
Уь
гк '
где Nk — число кодовых слов (с основанием г) длины k. Посколь-
ку код обладает однозначным декодированием, Nh не может быть
больше, чем rh, где rh — число различных последовательностей
длины k, составленных из букв кодового алфавита с основанием
г. Поэтому получаем неравенство
nl k
—~п^—n+l<Znl
k=n rk
(+1 появляется потому, что нужно учесть как первый, так и пос-
ледний член в сумме). Это — искомое неравенство, поскольку
для любого х>1 при достаточно большом п имеем xn>nl. По-
скольку п можно выбрать достаточно большим, получаем, что
число К (сумма Крафта) не превышает 1.
Отсюда видно, что переход от мгновенно декодируемых кодов
к более общим однозначно декодируемым дает очень небольшой
выигрыш: для обоих классов кодов длины кодовых слов должны
удовлетворять одному и тому же неравенству.
4.8. Коды Хаффмена
Сначала (предположим, что заданы вероятности различных пе-
редаваемых символов. Как и в коде Морзе, желательно сопостав-
лять наиболее частым символам наиболее короткие последова-
тельности. Если вероятность Его символа равна а длина соот-
ветствующего кодового слова — Z<, то средняя длина кодового-
8
слова LCp= 2 Pili.
i—1
Без ограничения общности можно считать, что pt занумерова-
ны в убывающем порядке. Если длины Z{ при этом занумерованы
не в обратном порядке, т. е. если одновременно не выполнены це-
почки неравенства pi^pz^ps^ — ^Pq, Z1^Z2^Z3^...^/g, то
код не является эффективным в том смысле, что можно получить
меньшую среднюю длину, меняя сопоставление кодовых слов сим-
волам Si, s2, ..., sq. Для доказательства этого утверждения пред-
положим, что при некоторых тип, m<Zn выполнены неравенст-
ва рт>рп и 1т>1п- При вычислении средней длины для первона-
чального кода, среди других имеем
старые члены: рт1т + рп1п.
Переставляя кодовые слова, соответствующие символам sm и
sn, получаем
новые члены: pmln + pnlm-
Вычитая старые члены из новых, получаем изменение средней
длины, обусловленное перестановкой
новые — старые: рт (ln—lm) + pn = (рт~Рп) Gn~ <°-
Из сделанных выше предположений следует, что это число отри-
цательно; переставляя кодовые слова, соответствующие символам
sm и sn, уменьшаем среднюю длину кода. Таким образом, прихо-
дим к заключению, что выполнены указанные две цепочки нера-
венства.
Рассмотрение кодов Хаффмена начнем с кодирования в двоич-
ном алфавите. Случай r-ичного алфавита рассмотрен в разд. 4.11.
Термин символ источника применяется здесь для обозначения
входов Sj, а кодовый алфавит — для обозначения алфавита, в ко-
торый происходит кодирование.
Первое доказываемое утверждение состоит в том, что два наи-
менее часто встречающихся символа источника должны кодиро-
ваться словами одинаковой длины. Для мгновенного кода никакое
кодовое слово не является префиксом другого, поэтому (q—1)-е
кодовое слово не совпадает с началом q-то кодового слова. По-
этому все символы q-ro слова, лежащие дальше этого начала,
можно отбросить, и в дереве декодирования не возникнет недора-
зумения. Таким образом, два самых длинных кодовых слова име-
ют одинаковую длину, и из дерева декодирования вытекает, что
они отличаются последней цифрой.
Доказательство свойств кодирования, а также метод кодиро-
вания основаны на том, что на каждом шаге происходит сведение
кода к более укороченному. Объединим два наименее вероятных
символа алфавита источника в один символ, вероятность которо-
го равна сумме соответствующих вероятностей. Таким образом,
нужно построить код для источника, у которого число символов
уменьшилось на 1. Повторяя этот процесс несколько раз, прихо-
дим к более простой задаче кодирования источника, алфавит ко-
торого состоит из символов 0 и 1. Возвращаясь на один шаг на-
зад, имеем, что один из символов нужно разбить на два символа;
это можно сделать, добавив к соответствующему кодовому слову
символ 0 для одного из символов и символ 1 — для другого. Воз-
вращаясь еще на один шаг назад, нужно таким же образом раз-
бить один из трех имеющихся символов на два символа, и так
далее. На рис. 4.8.1 показан процесс редукции для одного частно-
го случая, а на рис. 4.8.2 — соответствующий процесс разбиения
(расширения). На основании этого рассмотрения общий случай
становится очевидным.
Почему этот процесс порождает эффективный код? Предполо-
жим, что существует более короткий код, т. е. такой, у которого
сРедняя длина L' удовлетворяет условию L'<ZL. Сравним два де-
рева декодирования. В эффективном двоичном коде все концевые
вершины должны быть заняты и не должно быть мертвых ребер.
(Наличие мертвого ребра позволяет уменьшить длину кода, уда-
ляя соответствующий двоичный символ из всех концевых вершин,
путь к которым проходит через эту бесполезную точку.)
Если в дереве есть только два слова максимальной длины, то
они должны иметь общую последнюю вершину ветвления и соот-
ветствовать двум наименее вероятным символам. До редукции де-
рева эти два символа дают вклад /g(pg+pQ-i), а после редукции
(lq—4) (pq+pq-i), так что средняя длина кода уменьшается на
Pq + Pq-l-
Si Pi
S1 S2 s3 Sq S5 L 0,У 0,2 0,2 0,71 0,1) Первона- чальный ктоаник ОЛ. 0,2 0,2 z ^0,2 Первая ревущая 0,^ ^sWt ^0,2 Вторая ревущая .0,6 ^Ofi Третья ревущая
Рис. 4*8.1. Процесс редукции
Si Pi
Si 1 ^D/t 1 0,4 1 Ofi 1 0,6
Sz 01 ^0,2 01 0,1, Pl M 00' Oft
S3 000 ^0,2 ООО 0,21 £00^0,2] 01
S4 0010+0,1 ta-o,2j 001
S5 0011+0,1 W011
О
1
Рис. 4.8.2. Процесс разделения
Если 'число слов максимальной длины больше двух, то можно
использовать следующее предположение: кодовые слова одинако-
вой длины можно переставлять, не уменьшая средней длины кода.
На основе этого предположения можно считать, что два наименее
вероятных символа имеют одну и ту же вершину последнего ветв-
ления. Таким образом, после редукции средняя длина кода умень-
шилась на pq + pq-l.
Итак, в любом случае можно укоротить код и уменьшить сред-
нюю длину кода на одну и ту же величину.
Применим эту процедуру к двум сравниваемым деревьям де-
кодирования. Поскольку обе средние длины уменьшились на одну
и ту же величину, неравенство между средними длинами сохра-
нится. Повторное применение этой процедуры сводит оба дерева
к двум символам. Для кода Хаффмена средняя длина равна 1;
для другого кода она должна быть меньше 1, что невозможно.
Таким образом, код Хаффмена является самым коротким из воз-
можных кодов.
Процесс кодирования неоднозначен в нескольких отношениях.
Во-первых, сопоставление символов 0 и 1 двум символам источни-
ка на каждом этапе разбиения является произвольным, что, одна-
ко, приводит лишь к тривиальным различиям. Во-вторых, в слу-
чае, когда вероятности двух символов равны, неважно, какой из
символов поставить в таблице выше другого. Полученные коды
могут иметь различные длины кодовых слов, однако средние дли-
ны кодовых слов для двух кодов совпадают.
Для двух различных кодов Хаффмена рассмотрим вероятности pi = 0,4;
Рг=0,2; р3=0,2; р4=0,1; р5 = 0,1.
Si
Si
s2
Sj
S5
______Pi_
00^0,4
Ю ^0,2
11 ^0,2
010^-0,1]
Dll^OJ]
00 Ofi
10 0,2
Q21
011
00 0&
7,2
1 О,В
01
О
1
Рис. 4.8.3. Другой метод кодирования
Если помещать склеенные состояния 1 как можно ниже, то, в соответствии
с рис. 4.8.2, получаем длины (1, 2, 3, 4, 4) и средняя длина равна
L = 0,4(1)+ 0,2 (2)+0,2(3)+ 0,1 (4) + 0,1 (4) = 2,2.
Если, с другой стороны, ставить склеенные состояния как можно выше
(рис. 4.8.3), то получим длины (2, 2, 2, 3, 3) и средняя длина равна
/. = 0,4 (2) + 0,2 (2) + 0,2 (2) + 0,1 (3)+
+ 0,1(3) = 2,2.
Оба кода имеют одинаковую эффектив-
ность (среднюю длину), но разные на-
боры длин кодовых слов.
Какой из этих двух кодов следует
выбрать? Более разумным выбором явля-
ется тот, при котором длина меньше ме-
няется по ансамблю сообщений. Поэто-
му следует вычислить дисперсию длины
для каждого из этих двух случаев:
Var (I) = 0,4 (1 — 2,2)2 + 0,2 (2 — 2,2)2 + 0,2 (3 — 2,2)2 + 0,1 (4 — 2,2)2 +
+ 0,1 (4 —2,2)2= 1,36;
Var (II) = 0,4 (2 — 2,2)2 + 0,2 (2 — 2,2)2 + 0,2 (2 — 2,2)2 +
+ 0,1 (3 — 2,2)2 + 0,1 (3 — 2,2)2 = 0,16.
Таким образом, при использовании для кодировании сообщений конечной
длины второй код имеет существенно меньшую дисперсию длины и поэтому, воз-
можно, является более предпочтительным. Весьма вероятно, что, помещая скле-
енное состояние возможно выше, получим код с наименьшей дисперсией.
Задачи
4.8.1. Построить код Хаффмена для pi ==1/2, р2=1/3 и рз=1/6.
4.8.2. Постройте код Хаффмена для pi=.l/3, р2=1/4, рз=1/5, р4='1/6 и рз =
= 1/20.
4.8.3. Построить код Хаффмена для pi=l/2, р2=4/4, рз= 1/8, р^= 1/16 и ръ—
= 1/16.
4.8.4. Построить код Хаффмена для pii=27/40, р2=9/40, рз = 3/40 и р4=1/40.
4.9. Частные случаи кодов Хаффмена
Интересно рассмотреть несколько частных случаев кода Хаф-
фмена. Первый случай, если все символы источника равновероят-
ны и если их число точно равно q=2m, то (двоичный) код Хаф-
фмена является блочным, все кодовые слова которого имеют одну
и ту же длину т (рис. 4.9.1). Если число символов источника не
равно точно 2т, то получаем укороченный блочный код (см.
Разд. 4.6).
Более интересным является второй случай. Предположим, что
сумма вероятностей двух наименее вероятных символов источника
1 Состояния, полученные при сведении кода к более короткому. — Прим.
Перев.
больше, чем вероятность наиболее вероятного символа, т. е.
pq-i+pq>pi. В процессе построения кода Хаффмена (см. рис.
4.9.1) соответствующий склеенный символ перейдет в 'первую
строку списка кодовых слов. Далее два следующих символа с
наименьшими вероятностями склеиваются и переходят в первую
строку следующего списка и т. д. Если первоначальное число
—i/w —J
—J Либо Pi = 1/2m-^ блочный
код, либо Pq-i+Pq > Ду — уко-
роченный блочный код.
Рис. 4.9.1
Рис. 4.9.2. Два возможных случая
символов q является точной степенью двойки, то в процессе пере-
хода к коду для двух символов каждый символ пройдет через
одинаковое число этапов разделения, так что каждое кодовое сло-
во получит при этом одинаковое число двоичных символов. Та-
ким образом, снова получается блочный код. Если q не является
точной степенью 2, то незначительное изменение этого процесса
приводит к укороченному блочному коду (см. разд. 4.6).
Процесс кодирования Хаффмена приводит к существенной эко-
номии только в том случае, если вероятности появления различ-
ных символов источника сильно отличаются друг от друга. Имен-
но этого можно было бы ожидать после простых размышлений:
только при весьма отличных друг от друга вероятностях окупает-
ся переменная длина кодовых слов.
Если, например, вероятности весьма различны, так что
2 9
Pj>~ 3 Рь (4-9.1)
d fe=H-i
для всех j, то возникает код с запятой. Другими словами, нера-
венство (4.9.1) утверждает, что каждая вероятность не меньше,
чем две трети суммы всех следующих вероятностей.
Для доказательства начнем с рассмотрения нижней части рис.
4.9.2. Сумма pq + pq-\ может быть либо меньше, либо больше
рд-2, но не может превосходить рд_3. Таким образом, на следую-
щем шаге получаем сумму pq + pq-i + pq-2 и pq-2 объединяется с
другими р только один раз. Повторяя это рассуждение на каж-
дом шаге, видим, что получается код с запятой. Код с вероятно-
стями pi=l/2, pk= l/2k(k<iq), pg = l/29-1 является таким кодом и
допускает реализацию в виде кода с запятой.
Задача
4 (Трудная). Обсудите, что происходит в случаях, промежуточных между
двумя основными случаями.
4.10. Расширения кода
В разд. 4.2 было определено расширение кода. Теперь пока-
жем, что это понятие является полезным. Для определенности,
рассмотрим пример, в котором имеется два символа источника
si и «2 с вероятностями pi = 2/3 и р2=1/3. Средняя длина кода
равна 1.
Кодирование
sx; Pi = 2/3, S!->0
$2; р2~ 1/з, s2 —> 1
Для 2-кратного расширения берутся сразу два символа
Кодирование
SiSi; Pi, 1 = 4/9 SlSj- >1
si > pi ,2 = 2/9 S1S2~ >01
s2si; p2,i = 2/9 S2S1~ >000
S2 S2 > p2,2 = 1/9 ^2 ^2 ~~ >001.
Здесь Ди в четыре раза больше, чем р2,2- Для сравнения при-
ведем среднюю длину, нормированную делением на 2; она равна
17/18=0,94444... Следующее расширение, при котором берутся
три символа, дает 76/81 = 0,93827. Беря по четыре символа Si за
один раз, получаем среднюю длину кода, равную 0,93827.
Таким образом, расширения увеличивают разброс вероятно-
стей и позволяют добиться некоторого сжатия с помощью кодов
Хаффмена. В разд. 6.9 будет показано, что нижняя граница для
того, что можно достичь в этом примере, равна 0,91830....
Задача
4.10.1. Вычислите среднюю длину расширений, рассмотренных в этом разделе.
4.11. Коды Хаффмена с основанием г
Легко провести модификацию кода на случай кодового алфа-
вита из г символов. На каждом шаге можно, вообще говоря, со-
поставить не два, а г различных символов. Однако, если об этом
заранее не позаботиться, на последнем шаге может оказаться не-
возможным найти в точности г слов для кодирования. Наимень-
шее увеличение средней длины кода произойдет, если неполная
группа состоит из наименее вероятных символов. Поэтому при
первом разбиении нужно сопоставить г символов (верхнюю груп-
пу из г символов), затем следующие г символов и так далее до
тех пор, пока это возможно; последний (нижний) шаг разделения
С0Держит все, что осталось. На каждом шаге редукции г симво-
лов заменяются на один символ, так что число символов умень-
шается на (г—1)- Таким образом, нужно 'разделить число симво-
лов на (г—1) и взять остаток. Если остаток 'больше 1, то следует
сгруппировать равное остатку число символов в один новый сим-
вол; если остаток равен 1, то при первой редукции нужно взять г
символов, а если он равен 0, то (г—1) символов. На всех следую-
щих шагах г символов с наименьшими вероятностями группиру-
ются в один символ. Таким образом, окончательно получаем точ-
но г символов, которые нужно закодировать. Этим г символам
сопоставим кодовые слова 0, 1, ...
Sj Pi
81 1 0,22 1 0,22 1 OfiO 0 1JJD
s2 2 0,20 2 0,20 2 fo,22 1
s3 3 0,18 3 0,18 3 1 / 0,20 2
00 ~ 0,15 00 0,15 otr 0,18 3
S5 DI 0,10 01 0,10 th
s6 02 0,08 02 0,08 02
Sy «8 030 031 0,05 0,02 1030^0,07 JDJ7 03
Рис. 4.11.1. Код Хаффмена с основа-
нием 4
... (г—1). Па рис. 4.11.1 показано
такое кодирование с основанием
4 в применении к частному слу-
чаю, взятому из оригинальной
статьи Хаффмена.
Для доказательства эффек-
тивности сначала следует, если
необходимо, добавить несколько
символов, имеющих нулевую ве-
роятность. Это даст возможность
получить такой алфавит из сим-
волов Si, для которого на каждом
шаге объединяются точно по г
символов. Тогда все концевые
вершины дерева будут заполнены и, рассуждая так же, как для
двоичного дерева, получаем, что никакое другое кодирование не
может быть более эффективным.
Задача
4.11.1. Рассмотрите добавление символов с нулевой вероятностью для получения
точно k(r—1)4-1 символов.
4.12. Шум в вероятностях кода Хаффмена
Предположим, что оценки вероятностей pi неточны. Как при
этом ухудшается средняя длина кода? Короче говоря, будут ли
малые ошибки в оценках сильно ухудшать (или улучшать) си-
стему?
Для ответа на этот вопрос обозначим через pi вероятности,
которые должны использоваться при построении кодов Хаффме-
на, и пусть
р'г = А+ег (4.12.1)
являются фактически используемыми вероятностями. Ясно, что
1 5
— 3^ = 0, (4.12.2)
4 i=i
(поскольку как pi, так и p'i — распределения вероятностей, и .их
суммы равны 1.
В качестве одной из мер величины ошибок е; рассмотрим
1 q
— Уе% = о2. (4.12.3)
Я z=i
Умножив (4.12.1) на Ц и разделив на q, получим новую среднюю
длину кода
£' = —2 lip't = — 2 ltPt+— 2^ег = £ + — 2
q Я Я Я
Последний член дает изменение средней длины кодового слова.
Налагая на условия (4.12.2) и (4.12.3), применим метод
множителей Лагранжа для нахождения крайних случаев. Выра-
жение Лагранжа имеет вид
Частные производные по ег должны быть равны 0: таким обра-
зом:
— = — (If—К—2рег) = 0 (z= 1,2, ... ,q). (4.12.4)
де{ q
Сложив эти выражения, получим
— 2 I.—Z = 0 (4.12.5)
Я i
и из этого равенства определим А. Умножая (4Л2.4) на и сум-
мируя, получим
— 2 /гег-2р — 2 ^г = 0 (4.12.6)
я i я i
и из этого равенства определим р. Наконец, умножая (4.12.4) на
Ц и суммируя, получим
-1-2 2 2 e^z = °-
Я i Я i Ч
Используя X (4.Г2.5) и р из (4.,12.6) имеем
Используя'(4.12.3), этому выражению можно придать вид
= [дисперсия (/г)] [дисперсия (е$)]. (4.12.7)
°™ значения являются экстремально возможными (чебышевски-
ми) при данном о2. Последнее равенство показывает, что чем
больше дисперсия длин Ц, тем сильнее ошибки в оценке pi могут
Увеличить (или уменьшить) среднюю длину кодового слова.
Следующий пример показывает, что ошибки e-t могут оставить
среднюю длину без изменения. Пусть <7^3 и для некоторого е{
имеем
Ci = (Z2 Z3) е,
G3 ^1)
е3=(^-г2)е, (4-12-8)
е. = 0 (t>3).
Я'СНО, ЧТО — 2 6г = 0.
я
Для нахождения соответствующего о2 из выражения (4.12.3)
имеем
[ (^—У2~+ У2 + (h~4)2] е2 = о2.
Рассмотрим теперь изменение средней длины кода:
h ei + h ег + h ез + 0 = (li 1%—
li ls 1% I3 1% ^i I3 ^i ^з ^2) = О-
Поэтому вг из (4.12.8) не изменяют среднюю длину кода.
На основании этого можно заключить, что коды Хаффмена яв-
ляются сравнительно грубыми; небольшие изменения вероятно-
стей не могут серьезно ухудшить систему. Однако мы не рассмат-
риваем вопрос о возможном улучшении системы в целом от ис-
пользования новых вероятностей при ее проектировании.
4.13. Использование кодов Хаффмена
Построение кодов Хаффмена является в значительной мере
рекурсивным и их легко реализовать программными средствами
на ЭВМ. Схема декодирования конечным автоматом (деревом), о
которой говорилось в разд. 4.2, дает метод декодирования кодов
Хаффмена с применением одного r-ичного ветвления на каждый
принятый г-ичный символ. Метод является быстрым и простым, и
каждый принятый символ просматривается только один раз.
Для источников с разумным объемом алфавита кодирование
кодов Хаффмена проводится посредством табличного поиска.
Если имеется большой объем информации, которую нужно поме-
стить в долговременную память ЭВМ, и если вероятности симво-
лов источника значительно отличаются друг от друга, то может
оказаться выгодным закодировать информацию подходящим ко-
дом Хаффмена для того, чтобы сэкономить долговременную па-
мять ЭВМ. Как было показано, степень экономии зависит от того,
насколько сильно вероятности отличаются друг от друга.
Написаны программы, которые автоматически просматривают
текст, строят код, сжимают текст, запоминают его и алгоритм де-
кодирования. Программа подсчитывает частоты символов источ-
ника и добавляет один специальный символ, называемый конец
текста, который встречается один раз. Этот специальный символ
используется для окончания декодирования. Известно, что такие
ПГ)ограммы снижают объем памяти, необходимой для хранения
данных, более чем вдвое.
Задача
4 13.1. Рассмотреть составление программы для Э.ВМ, которая строит код Хаф-
фмена по р,.
4.14. Коды Хэмминга — Хаффмена
Можно ли объединить процессы сжатия источников кодами
Хаффмена и защиты от шумов кодами Хэмминга? Известный до
сих пор процесс состоит в том, что сперва производится кодиро-
вание 'Кодом Хаффмена, затем выходная «последовательность раз-
бивается на 'блоки, которые кодируются подходящим кодом Хэм-
минга, защищающим от шума. Для декодирования используется
обратный процесс: сперва декодируется код Хэмминга, а затем —
код Хаффмена.
'Возникает естественный вопрос: нельзя ли добиться лучшего
результата с «помощью единого процесса кодирования? Возмож-
ность сделать это представляется читателю. Заметим, «что при де-
кодировании вершины дерева, близкие к концевым, не должны
использоваться другими .ветвями дерева. Один из таких обнару-
живающих ошибки неравномерных кодов приведен ниже:
Кодирования Ошибки
s1 = ООО 001
s2 = 0110 010
100
s3=1010 0111
s4 = 1100 1011
s5=llll 1101
1110
Задачи
4.14.1. Для последнего кода изобразите дерево декодирования и убедитесь, что
дерево «работает».
4.14.2. Рассмотрите использование для кодов Хэмминга дерева декодирования,
а не вычислительных методов, приведенных в гл. 3.
4-14.3. Покажите, что ошибка в одном символе для кода с запятой s1 = 0, s2=
= 10, s3=ll может распространяться как угодно далеко. Указание:
Рассмотрите sj [s3] ns2.
Глава 5
Другие полезные коды
5.1. Введение
Существует много кодов, используемых в различных практи-
ческих ситуациях. Обсудим лишь некоторые, наиболее важные из
них.
Сначала рассмотрим марковские процессы, которые позволя-
ют анализировать некоторые громоздкие вероятностные 'структу-
ры, типичные, скажем, для мгновенных задач; эти структуры со-
держат больше параметров, чем набор частот появления симво-
лов и кодах Хаффмена.
Далее рассмотрим весьма общий метод кодирования с пред-
сказанием, позволяющий использовать любую структуру, которая
может помочь точно .предсказать следующий символ. Чем лучше
предсказывается следующий символ, тем короче сообщение, ко-
торое нужно использовать. При этом о методе предсказания ни-
чего не говорится; предполагается лишь, что написана програм-
ма, включающая в себя все используемые сведения о структуре
сообщения. Этот метод является весьма общим для сжатия дан-
ных. Таким образом, как было обещано ранее, переходим к весь-
ма общим методам и пропускаем много, частных кодов, приме-
няемых в определенных случаях. Можно надеяться, что, встре-
тившись с конкретной ситуацией и зная приведенные здесь ко-
ды, читатель сможет предложить свой собственный метод под-
ходящего кодирования сообщений.
Далее обсуждается замечательная идея случайного кодиро-
вания, которая, с одной стороны, имеет практическое примене-
ние, а с другой — используется при доказательстве основных ре-
зультатов теории информации. Приводимый здесь частный слу-
чай, называемый кодированием с перемешиванием, широко ис:
пользуется при составлении программ для ЭВМ, а также в дру-
гих ситуациях.
Наконец, рассматриваются коды Грея, используемые для на-
дежного перехода от аналогового представления данных к ци-
фровому и обратно. Такой переход настолько часто встречается
на практике (поскольку природа, в основном, снабжает нас ана-
логовыми сигналами), что эти коды входят в обязательную про-
грамму обучения инженеров по вычислительной технике и всех
тех, кто имеет дело с реальными сигналами.
Подробности, относящиеся к этому .материалу, можно найти
в работе /[9].
5.2. Что такое марковский процесс?
До сих пор в книге использовались лишь вероятности .появ-
ления различных символов s(, s%,.. . ,sq алфавита источника-
Знакомство с естественными языками показывает, что структу-
в английском
какая буква стоит пе-
языка гораздо богаче. Как отмечалось выше,
языке за буквой Q почти всегда следует буква U; вероятность
встретить букву U сильно зависит от того, какая буква стоит пе-
пел ней. В теории вероятностей p(U|Q) означает вероятность
встретить U при условии (обозначается |), что только что была
буква Q. В общем случае для марковского процесса /-го порядка
величина p(Sj|Si Si ,...,siq ) является условной вероятностью
встретить Si при условии, что 'Предшествующими были буквы Si,,
Si »• • • > в указанном порядке. Подчеркнем, что последова-
тельность символов имеет вид Sit, sis,..., s;Q, Sf.
Именно такая ситуация возникает на практике; предыдущая
часть сообщения часто может сильно влиять на вероятность по-
явления следующего символа источника.
,На языке вычислительной техники источник с нулевой па-
мятью использует каждый символ источника независимо от того,
что ему предшествовало. Источник с памятью j-го порядка ис-
пользует в точности / символов, и именно это соответствует мар-
ковскому процессу /-го порядка.
•Считается, что система всегда находится в каком-то состоя-
нии. Для источника с памятью первого порядка имеется q состоя-
ний, по одному для каждого из символов S{ алфавита источника.
Примером предсказания с памятью первого порядка является
предсказание погоды типа: «Погода завтра будет такой же, как
сегодня». Для источника с памятью второго порядка имеется q2
состояний, по одному для каждой пары символов источника. Ли-
нейное предсказание z/n+1=2//n—уп-\ является источником с па-
мятью второго порядка; следующее значение уп+} оценивается по
двум предыдущим — уп и yn-i- В общем случае для источника с
памятью /-го порядка у марковского процесса имеется qi состоя-
ний..
Рассматривая простой пример источника с памятью первого порядка, пред-
положим, что имеется алфавит из трех символов — а, b и с. Пусть вероятность
того, что за буквой а следует любая из трех букв, равна 1/3. Пусть вероятность
того, что за буквой b снова следует буква Ь, равна 1/2, а вероятность того, что
за буквой b следует буква а пли с, равна 1/4. Наконец, пусть вероятность того,
что за буквой с следует другая буква с, равна 1/2, а вероятность того, что за с
следует а и Ь, равна 1/4. Тогда имеем
р(Ь[а) = 1/3, р(с|а)=1/3,
p(b\b) = l/2,
p(b\c) = l/4, р(с|с) = 1/2.
такого же типа полезно, рассматривать граф
Р (с|Ь) = 1/4,
Р(а\а)= 1/3,
р (п|й) = 1/4,
р(а|с) = 1/4,
Для марковского процесса
перехоаов. В этом случае, -конечно, имеется три состояния (.рис. 5.2.1), помечен-
НЬ1Х буквами а, Ь, с и обозначенных кружками. Каждая стрелка соответствует
пеРеходу из одного состояния в другое; вероятность перехода равна числу, стоя-
щему у этой стрелки. Например, р(а\Ь) соответствует стрелке, идущей из b в
• и равна 1/4. В нашем примере у каждого состояния имеется три входящих
три выходящих стрелки.
Этой диаграмме можно придать конкретны смысл, пусть а ооозначает
хорошую погоду, ft— дождь и с — снег. Если сегодня хорошая погода, то назавт-
ра с равными, вероятностями может быть хорошая погода, снег или дождь.
Если, однако, сегодня идет снег или дождь, то в половине случаев завтрашняя
погода будет совпадать с сегодняшней, и на каждый из оставшихся прогнозов
приходится лишь по' одному шансу из четырех.
Граф -можно представить в виде матрицы
а f ft С
а /1/3 1/3 1/3\
-+Ь 1 1/4 1/2 1/4
с \1/4 1/4 1/2/
(5.2.1)
причем текущее состояние обозначается буквой слева от матрицы, а следующее
состояние — буквой над матрицей. Элементы матрицы называются переходны-
Рис. 5.2.1. Граф переходов
ми вероятностями. Сумма всех элементов лю-
бой матрицы переходных вероятностей должна
равняться 1, поскольку текущее состояние дол-
жно обязательно перейти в какое-то состояние.
Предположим теперь, что вместо текущего
состояния имеется лишь распределение вероят-
ностей (ра, ръ, Рс) для текущего состояния,
где ра+рь+Рс=1. Может случиться, что одна
из вероятностей р, равна 1, а остальные две р< равны 0; это означает, что теку-
щее состояние точно определено. Если умножить этот вектор-строку справа на
матрицу переходных вероятностей (5.2.1), получим распределение вероятностей
завтрашней погоды:
(Ра, РЬ, Рс)
/1/3 1/3
1/4 1/2
\1/4 1/4
1/3\
1 /4 I = [Ра/3 + Pb№ + Рс/4, Ра/3 + Рб/2 + Рс/4,
1/2/
Ра /3 + рь/4 + Рс/2].
Для нахождения вероятностей на 2 дня вперед нужно еще раз умножить
этот вектор на матрицу переходных вероятностей (5.2.1). Поскольку умножение
матриц (и векторов) ассоциативно, вместо этого можно сначала умножить мат-
рицу на себя, получив квадрат матрицы, а затем умножить распределение спра-
ва на этот квадрат. Квадрат матрицы переходных вероятностей равен
1/3 1/3 1/3\ /1/3 1/3
1/4 1/2 1/4 1/4 1/2
1/4 1/4 1/2/ \1/4 1/4
1/3\ /10/36 13/36 13/36’
1./4 = 13/48 19/48 16/48
1/2/ \13/48 16/48 19/48.
Записывая матрицу в виде
j /40 52 52\
— I 39 57 48 ,
144 \39 48 57/
(5.2.2)
сразу видим, что элементы квадрата матрицы переходных вероятностей меня-
ются не так сильно, как элементы первоначальной матрицы (5.2.1). Если воз-
вести в квадрат матрицу (5.2.2), получим матрицу для предсказания погоды
на 4 дня вперед. В этом частном случае несложно доказать, что последователь-
Hbie1 степени матрицы переходных вероятностей сходятся к никоторой предель-
ной матрице.
. Сохраняется ли для последовательных матриц . -переходных вероятностей
павенство 1 суммы элементов любой строки? Для доказательства- того, - что это-
свойство сохраняется, образуем .из двух общих матриц Р и Р' элементы третьей
матрицы Р"
Pl.i X Pi,kPk,P
k
Предположение о суммах элементов в строках имеют вид Xp4,h—1, Sp'i,.fc=l.
-Поэтому
XPt,i~ S (S Pi,kPkj) 3 S Pi.kPk.i= S Pi,h =1 •
у j k k j k
что; и требовалось.
Какой вид имеет распределение вероятностей состояний а, b и с для предель-
ной матрицы? Ясно, что это распределение не должно меняться при переходе
к следующему дню; иначе говоря, для частного случая матрицы (5.2.1) должно.
выполняться следующее равенство:
(Ра, РЪ, Ре)
1/3
1/4
1/4
1/3 1/3\ -
1/2 1/4 = (ра, рь, Рс)-
1/4 1/2/
Это эквивалентно системе из трех уравнений:
Ра/3 + рь/4 + рс/4 = ра> ..
PalS + pb/2 + pel4 = РЬ, или
—2Ра№ Pbl4 -V Рс!4 = ®,
Pal^ ~ Pbl^ ~i~ Ре/4 ~ , .
Ра/3 + рб/4 + рс/2 = рс,
Ра/3 -j- pfe/4 — рс/2 = 0.
Лишь 'два из этих трех уравнений являются независимыми, .так что буде i -ре-
шать два первых уравнения с дополнительным условием ра+рь+рс=1. После
некоторых алгебраических преобразований получаем стационарное распределение
Ра = 3/11, рь = ре — 4/И. (5.2.3)
Таким образом, независимо от первоначального распределения вероятностей
для матрицы переходных вероятностей (5.2.1) получаем одно и то же распре-
ление вероятностей (3/11, 4/11, 4/11).
Задачи
5.2.1. Вычислите еще четвертую и восьмую степени матрицы переходных вероят-
ностей (5.2.1) и сравните, насколько отличаются друг от друга элементы
в каждой из четырех матриц.
5.2.2. Вычислите стационарное распределение вероятностей состояний, используя
матрицу переходных вероятностей (5.2.2).
5.3. Эргодические марковские процессы
Описанный выше марковский процесс называется эргодическим:
из любого состояния можно перейти в любое другое состояние и
с течением времени система приходит к предельному распределе-
нию, не зависящему от начального состояния. Это не значит, что
Для приведенной .выше матрицы с течением времени погода ста-
новится смесью хорошей 'погоды, дождя и снега; это только озна-
чает, что наши ожидания со временем превращаются в вероят-
ностную смесь состояний. Долговременный прогноз не зависит от
сегодняшней погоды.
Существует много других типов марковских процессов. На-
пример, на рис. 5.3.1 показан граф, соответствующий неэргодиче-
Рис. 5.3.1. Неэргодический граф
скому источнику. Сразу видно
что, выйдя из состояния а, мы ни-
когда не попадем снова в это со-
стояние. В зависимости от пути,
по которому пойдем в первый раз,
можно либо попасть в единствен-
ное заключительное состояние d,
либо ходить по трем состояниям
g, h и i. Графы такого типа не
могут, по нашему мнению, служить хорошей моделью для источ-
ника информации, так что они в дальнейшем не обсуждаются.
Даже если имеется такое множество состояний, что из любо-
го одного можно попасть в любое другое, вероятности не обяза-
тельно стабилизируются. Рассмотрим, например, шахматную дос-
ку, в которой разрешены переходы на одну клетку влево, впра-
во, вверх или вниз, но не по диагонали. Начиная с белой клетки,
после четного числа переходов мы оказываемся на белой клетке,
а после нечетного — на черной клетке. Следовательно, вероятно-
сти зависят от цвета клетки, на которой мы находимся .в данный
момент. Таким образом, теория всех возможных марковских про-
цессов, в принципе, является достаточно запутанной. Однако мар-
ковские процессы, которыми интересуются в теории информаци-
онных систем, являются эргодическими и не обладают такими
странными свойствами. В конце концов в длинной последователь-
ности вероятности символов сообщения устанавливаются равны-
ми некоторым фиксированным числам. Как уже отмечалось, на-
личие предельного распределения вероятностей не означает фак-
тического смешивания символов. Легко, например, понять, что
значат слова предельное состояние или множество предельных
состояний. Столь же легко увидеть, что если множество предель-
ных состояний не совпадает с множеством всех состояний систе-
мы, то система неэргодична, так как имеются состояния, из ко-
торых нельзя попасть в другие состояния. Кроме того, следует
избегать любого периодического чередования состояний. Предпо-
лагается, что любой источник, который в дальнейшем придется
кодировать, является эргодическим. Однако появление неэргоди-
ческих источников не является абсолютно невозможным. Возни-
кающие сложности нетрудно преодолеть. В дальнейшем предпо-
лагается, что все наши системы эргодичны.
Задача
5.3.1. Изобразите графы для марковских процессов с символами 0 и 1 и памятью
первого, второго и третьего порядков.
5.4. Эффективное кодирование
эргодического марковского процесса
Ясно, что .марковскую структуру источника можно использо-
вать для улучшения кодирования. Для каждого состояния мар-
ковской системы, можно применить соответствующий код Хаффме-
на построенный по вероятностям выхода из этого состояния. В
зависимости от того, насколько сильно меняются вероятности в
каждом состоянии, выигрыш в кодировании может быть большим
или меньшим. Однако при увеличении памяти марковского про-
цесса выигрыш уменьшается, а число состояний быстро растет.
Построим такие коды Хаффмена для матрицы, описывающей погоду (см.
разд. 5.2). Для состояния а (сегодня) имеем (завтра) двоичное кодирование:
ас=1’> 5 = 00, с = 01, Ра= 1/3, рь = 1/3, рс=1/3, Ла = 5/3= 1,6667...
Для состояния Ь: а=10, 5 = 0, с=11, ра=1/4, рь = 1/2, рс=1/4, Lb = 3l% =
= 1,5.
Для состояния с: а=10, 5 = 11, 5с=0, ра='1/4, рь = 1/4, рс=1/2, Lc=3/2 =
= 1,5.
Для стационарного распределения получим [используя стационарные не-’
роятности (5.2.3)] среднюю длину кода: £м=3£о/11+4£ь/11+4£с/11 = 17/1-1.:=
= 1,5454 ...
Одновременно выполним- кодирование в соответствии со средними частотами
букв а, 5 и с. Эти частоты совпадают, очевидно, со стационарными вероятностя-
ми (5.2.3) ро=3/11, рь=4/11, рс=4/11. Код имеет вид: а=01, 5 = 00, с=1.
Таким обоазом,
3 4 4 18
Ь = ТГ(2) + ТГ(2) + ТГ(1)==ТГ‘
Следовательно, средняя длина кода LM для кодирования в отдельных со-
стояниях меньше,, чем для кодирования, основанного на средних частотах
Lm= (17/11) < (18/11) = L.
Как и следовало ожидать, в системах марковского типа средняя длина кода
уменьшается.
Задача
5.4.1. Пусть вероятности для хорошей погоды а равны р(а|а)=3/4, р(5|а) =
= р(с|а) = 1/8, а остальные вероятности такие же, как в этом разделе.
Покажите, что Lm~ 11/8< 12/8=L.
5.5. Расширения марковского процесса - "
(см. разд. 4.2) было определено расширение источника.
, восьмеричный код является трехкратным расширени-
ем двоичного кода. В некотором смысле расширение — это прос-
то объединение нескольких символов источника. Нам нужно ис-
следовать расширение марковского процесса.
'Определение. Пусть S — марковский информационный источ-
ник m-го порядка с алфавитом sb s2, ..., sg и переходными веро-
ятностями
Ранее
Например
(5.5.1)
Тогда n-кратное расширение этого источника обозначается Sn=
— Т- око имеет qn символов t\, tz,.. ., tqn. Каждый символ t — это
последовательность п символов алфавита S. Система Sn является
марковским процессом k-ro порядка, где k — наименьшее целое
число, большее или равное m/п. Поскольку каждый 'символ tt со-
ответствует некоторой последовательности из п символов Sj, пере-
ходные вероятности источника Т
(5.5.2)
можно получить из первоначальных переходных вероятностей ис-
точника S, предсказывая по очереди каждый символ s,, исходя
из m предыдущих символов. Переписывая (5.5.2) и несколько
раз применяя (5.5.1), получаем (при kn^m)'
... ,sin | SiltSi2-SJm) =
= P fa. Is/,, Sit, ... , Sim) p (st, |Sj2, s/3, . ..
...»sJm, Sil) ...p (sin\sin_m, Si^.
Здесь предполагается, что в противном случае последний
член должен иметь .вид
Полученный результат еще потребуется в этой главе.
5.6. Кодирование с предсказанием
Только что было показано, что использовать структуру пере-
ходных вероятностей в исходных сообщениях для уменьшения
длины закодированных сообщений; код Хаффмена учитывает час-
тоты отдельных входных символов, а марковский процесс позво-
ляет учесть также зависимости между символами. В исходных
сообщениях существует много других структур, позволяющих
уменьшить длину закодированных сообщений, однако их слишком
много для того, чтобы провести подробное исследование в этой
книге. Поэтому рассмотрим общий случай, когда предполагает-
ся, что имеется либо программа, либо какое-либо устройство,
посредством которых можно выявить структуру сообщения и ис-
пользовать ее для предсказания следующего символа. Предполо-
жим для простоты, что источник является двоичным. С помощью
программы произведем кодирование входной последовательности
двоичных сообщений в последовательность двоичных символов, со-
держащую сравнительно длинные отрезки символов 0, разделен-
ные относительно более редкими символами 1. На втором этапе
кодирования, на котором возникает сжатие, посылается последо-
вательность чисел, в которой каждое число указывает длину со-
ответствующей серии нулей. Приемник может восстановить пер-
воначальное сообщение, используя практически такое же обору-
дование, как при кодировании.
5.7. Кодер для кодирования с предсказанием
Допустим, что исходное сообщение обладает некоторой струк-
турой, которую можно выявить и использовать для предсказания
следующего символа. Независимо' от типа структуры, предположим,
ЧТо существует программа, предсказывающая следующий сим-
вол. Метод предсказания может быть либо 'фиксированным, ли-
бо адаптивным в том смысле, что он может изменяться в зави-
симости от 'Качества предыдущих предсказаний. Он может быть'
линейным или нелинейным; о существе метода предсказания ни-'
чего не говорится.
Следует отметить, что в конкретных случаях программа может
быть достаточно произвольной. Рассматриваемый метод основан
на единственном предположении, что в большинстве случаев про-
грамма правильно предсказывает следующий символ. Чем луч-
ше предсказание, тем сильнее в конце концов сжимается исход-
ное сообщение.
Имеется источник S с входными символами Si (рис. 5.7.,1).
буквой Р на рис. 5.7.1,о обозначена предсказывающая програм-
ма, которая по последовательности символов Si.(i<n) вычисляет
ожидаемое значение рп следующего символа. В предположении,
Рис. 5.7.1. Кодирование с предсказанием
что входной и выходной алфавиты являются двоичными с симво-
лами 0 и 1, производится логическое сложение фактического сим-
вола sn и предсказанного значения рп. Результатом является
ошибка еп п-го предсказания. Выходной символ еп равен 0, если
предсказанное значение рп совпадает с символом sn, и равен 1,
если предсказание было неверным. Предсказатель Р также знает
еп, так что он может исправлять свои предсказания и к моменту
следующего предсказания точно знать всю предыдущую последо-
вательность сообщений.
Как сказано выше, если предсказатель достаточно хороший,
последовательность еп состоит, в основном, из нулей с редкими
единицами между ними. Случайное предсказание давало бы при-
мерно равное число нулей и единиц. Даже при плохом предска-
зании число нулей существенно больше числа единиц.
5.8. Декодер
На приемном конце (см. рис: 5.7.1,в) имеет декодер, который,
по существу, совпадает с предсказателем. Предположим, что уст-
ройство Р в декодере в точности совпадает с соответствующим
устройством в кодере. Тогда, начиная с одного и того же состоя-
ния, оба устройства делают одинаковые предсказания. Когда на
декодер поступает символ 1, он логически прибавляет эту ошибку
к своему предсказанию и выдает правильное значение. Как и
раньше, сообщение об ошибке еп поступает на предсказатель.
Незначительные различия в форме поступающей информации на
передающем и приемном концах требуют лишь незначительного
изменения устройств; поэтому обе стороны системы передачи сиг-
налов, по существу, одинаковы.
Для оценки этой системы нужно иметь ее математическую мо-
дель. Пусть р — вероятность того, что устройство Р правильно
предсказывает каждый символ. (Заметим изменение роли р: те-
перь р — вероятность правильного предсказания.) В дальнейшем
предполагается, что эта вероятность постоянна, поскольку в про-
тивном случае возникает некоторая известная структура, которую
можно учесть в предсказателе. По той же причине можно пред-
положить, что каждая ошибка предсказания независима от дру-
гих ошибок. Сама формула для предсказания может, конечно,
быть рекуррентной, предполагается лишь независимость ошибок.
Пусть q=l—р — вероятность ошибки предсказания. Естественно
считать, что р^1/2, поскольку иначе можно просто поменять мес-
тами р п q, заменяя предсказанные нули на единицы, й наоборот.
Эти вероятности не следует путать с ошибками, возникающи-
ми в работе аппаратуры; они связаны с предсказателем Р. 'Вслед-
ствие сделанных выше предположений относительно Р в выход-
ной последовательности из нулей и единиц имеется фиксирован-
ная вероятность ошибки и соседние символы независимы. Ошиб-
ки поставляют белый шум (см. разд. 2.4). Большое значение р со-
ответствует хорошему кодеру; р, близкое к 1/2, означает, что
предсказания практически совпадают с простым угадыванием.
5.9. Длины серий
Вероятность р(п) серий из п нулей равна p(n)=pnq (п=0,
1,...) (поскольку после каждой такой серии появляется едини-
ца). Суммируя по всем возможным длинам п, имеем
2 = Р" =т^-= —= Ъ
п=о 1~Р 9
как и следовало ожидать.
Предположим, что для представления длины серии решено по-
слать двоичное число, состоящее из k цифр. По причинам, кото-
рые скоро станут ясны, что можно сделать только в случае, ес-
ли длина серии находится между 0 и 2й—2. Приемник генерирует
указанное число нулей и затем одну 1. Если дослано число 0, то
приемник просто генерирует одну 1. Если .послано число 2ft—1,
приемник генерирует 2k—1 нулей, за которыми не следует 1. Если
после этого послано число 0, то, конечно, генерируется 1; для лю-
бого другого числа генерируется указанное число нулей и затем
единица. Таким образом, передав достаточное число fe-значных
двоичных чисел, можно указать любую длину серии, состоящей из
нулей.
,Мы не будем пытаться 'использовать код Хаффмена. Перво-
начально входной алфавит был, вообще говоря, бесконечным, по-
скольку могли встретиться серии любой длины; после разбиения
на серии, состоящие не более чем из k цифр при желании исполь-
зовать код Хаффмена.
Возвращаясь .к предложенному методу, найдем среднее число
посылаемых символов. Для этого нужно сложить произведения
вероятностей появления на число цифр, посылаемых в каждом
случае. Таким образом, имеем
Длина серии Число посылаемых цифр
0^n<(2fe —1)—1 k
2ft—l<n^2(2fe —1)—1 2k
2(2ft—l)^n^3(2fe—1)—1 3k
И Т.Д.
Поэтому .средняя длина равна (через m обозначено число
2ft—1, а через р(п) —вероятность появления серии нулей длины
п):
[р (0) + р (1) + ... + р (m— 1)] k + [р (т) + р (т +1) + ... + р (2 т—
—,1)] 2 k + [р (2 т) + р (2 т + 1)+ ... + р (Зт— 1)] 3k-\-...
Поскольку p(n)=pri'q, получаем
?[1+р + ...+pm“1Jfe + <7Pm[l +р+ 2fe +
+ qp2m\l + p+ ...+ pm~1]3fe+ ...
Суммируя члены в скобках, приводим это выражение к виду
q {^~Pm)lq} H+2pm + 3p2'n+...]k.
Эта сумма, в свою, очередь, равна j.
q[(i—pm)/q] (l—pm)~2k = kj(\—pm).
Нужна небольшая таблица (табл. 5.9.1) функции k(l—pzk i),
которая позволяет для данного р^1/2 выбрать наилучшее k
(табл. 5.9.2).
Средняя длина серий равна
S kp*q=q—4г=Г1“-
k=i (1—Р)а 1 — Р
Из обеих таблиц видно, что эффективность .кодирования серий
зависит от выбора k и для оптимального кодирования выбор k
Зависит от р. Ясно, что для данного р легко выбрать соответст-
вующее К.
Т а б л и ц.а 5.9. ।
Значение Л/(1>—р 2 В
k р
0,5 0,6 0,7 0,8 0,9 0,95 0,98 0,99
1 2,00 2,50 3,33 5,00 10,0 20,0 50,0 100
2 2,29 2,55 3,04 4,10 7,38 14,0 34,0 67,3
3 3,27 3,80 5,75 9,94 22,7 44,2
4 4,15 5,04 7,45 15,3 28,6
5 5,20 6,28 10,7 18,7
6 6,25 8,33 12,8
7 7,01 - 7,58 9,71
8 8,05 8,67
, 9 9,05
10
Таблица 5.9.2
Эффективность кодирования
р Оптимальное значение k Среднее число символов Средняя длина отрезков Коэффициент сжатия -
0,5 1 2,00 2,00 1
0,6 1 2,50 2,50 1
0,7 2 3,04 3,33 0,91
, 0,8 3 3,80 5,00 0,76
Г 0,9.. 4 5,04 10,00 0,50 ‘
' 0,95 6 6,25 20,00 0,31
0,98 7 7,58 50,00 0,16
0,99 8 . 8,67 100,00 0,087
Задача
5.9.1. Рассмотрите кодирование серий нулей кодом Хаффмена.
5.10. Итоги рассмотрения кодирования с предсказанием
Ввиду общности описанной схемы сжатия сообщений необхо-
димо, тем не менее, подчеркнуть, что она не может выполнять
все что угодно и что ее 'Эффективность полностью определяется
качеством используемого предсказателя. Чем лучше он работает,
тем длиннее последовательности единиц и, следовательно, тем
больше будет сжатие на втором этапе кодирования. Теоретически
предсказатель может быть сколь угодно общим устройством, од-
нако на практике он должен быть достаточно простым для того,
чтобы обрабатывать.последовательность входных символов в ре-
альном масштабе времени. Это устройство должно лишь предска-
зывать следующий входной символ. Теория не интересуется тем,
как именно это делается. Если кодирование должно происходить
g реальном мгс та е времени, то возникают: трудности, связан-
ные- с объемом буфера, но в задачах вычислительной техники
это не очень существенно.
5.11. Что такое перемешивание?
Перемешивание.— это метод .сокращения избыточности. ан-
самбля из т сообщений, которые, были выбра-ны из существенно
большего, ансамбля iM возможных сообщений. .Этот метод дает,
однако, сокращение лишь в некотором специальном смысле. .
Для конкретности рассмотрим множество всех возможных фамилий, имен
переменных в программе на языке ФОРТРАН или любое другое большое мно-
жество названий. В каждом частном случае, например в одной, платежной ве.-.
домости, в конкретной программе и в другом процессе обработки- имен, нсполь-.
зуется лишь очень небольшая часть всех возможных имед. Предположим для,
определенности, что ожидаются 500 имен. Можно выделить..10 бит (210— 1024 —.
это число более чем вдвое превосходит 500). Для каждого имени сначала берут-
ся -его первые 10 бит, затем к ним логически прибавляются следующие 10 бит,
затем следующие 10 бит и так далее, до окончания имени (дополняя, если нуж-
но; последние биты до 10 бит необходимым числом нулей). Такой процесс одно-
значно порождает по данному .имени перемешанную сумму, при этом, .конечно,,
два разных имени могут дать одинаковые перемешанные суммы.
Для данного исходного имени поместим указатель на исходное имя. в таб-
лицу перемешивания в том месте, где находится вычисленный 10-битовый .пе-
ремешанный номер (или в место, смещенное <на постоянную величину)-. В ре-
зультате получается таблица указателей, направленных обратно к исходным
именам; эта таблица позволяет прямо найти требуемое имя .путем -перехода
от таблицы перемешивания к .вычисленному месту, я не путем поиска требуе-
мого в таблице имен.
Дак найти вероятность того, что два разных имени дадут одну и ту же пе-
ремешанную сумму? Если после перемешивания имена становятся случайными
(а логическим сложением каждых 10 бит мы пытаемся достичь именно этого),
то имеется примерно 5002 возможных вариантов столкновений. Как в известной
задаче о днях рождения, в которой вероятность того, что дни рождения хотя
бы у./двух из 23. возможных , людей совпадают,. существенно больше, половины,
так и здесь вероятность по крайней мере одного столкновения очень велика.
Вместе с тем, вероятность того, что. некоторое фиксированное имя вступцу в
столкновение с каким-либо другим именем, меньше 1/2, поскольку число мест
6 таблице- имен более чем вдвое превышает, число имен. Таким образом,, при
‘перемешивании (кодировании) типичного имени в 10-битовое слово, вероятность
•его столкновения с каким-либо другим именем меньше половины. Однако,, ве-
роятность столкновения между какими-либо из 500 имен весьма велика, и сле-
дует допустить возможность его появления.
5.12. Обработка столкновений
Что делать со столкновением? Простой метод состоит в том, чтобы' взгля-
®Уть на вычисленное (путем перемешивания) место в таблице. Если оно пусто,
то в него вносится соответствующая запись; если оно занято, то нужно про-
таблицу м внести -новую запись в -первое следующее -пустое место.
Это^овначает, что когда позднее производится поиск некоторой записи, следует
смотреть не только на вычисленное место; если находящийся на. этом месте
указатель дает неправильное имя, то следует продолжать просматривать по-
следующие непустые места- и проверять, дают ли их указатели нужное имя.
Этот поиск следует продолжать до тех пор, пока либо будет найдено нужное
имя,' либо после полного -просмотра оно не встретится. В последнем случае в
таблице нет записи, соответствующей нужному имени. Если требуется сделать
новую запись, как, например, при трансляции программы на языке ФОРТРАН,
то ее нужно поместить в эту пустую ячейку. Таким образом, строится таблица
перемешанных имен.
Конечно, если бы -все имена были -известны заранее, то .можно было бы-
найти метод кодирования, позволяющий избежать столкновений. Если, однако,
приходится иметь дело с растущими таблицами имен или не хочется терять
времени на поиск подходящего кодирования, тогда .рассматриваемый подход,
который можно назвать случайным кодированием, оказывается полезным.
5.13. Удаление из таблицы
В некоторых задачах иногда может оказаться необходимым удалить имя
из списка имен. -Этого не происходит при трансляции с языка ФОРТРАН, однако
может встретиться в некоторых других приложениях. Как это сделать? Ясно,
что следует вычислить адрес указателя имени, и если имя находится там (или
в' одной из следующих ячеек), то его необходимо оттуда удалить. Если вслед
за удаленной записью имеется занятая ячейка, то нужно посмотреть, не была
ли соответствующая запись сдвинута вниз, н в этом случае ее нужно подвинуть
обратно вверх. В действительности, необходимо рассмотреть все последующие
записи до первой пустой ячейки для того, чтобы знать, куда их следует поме-
стить. Проще всего сделать это, создавая псевдофайл имен из следующих со-
седних указателей и заново вводя эти имена. Таким образом, производится об-
новление файла вычисленных имен.
5.14. Итоги рассмотрения перемешивания
Если имеется набор имен, которые представляются очень длин-
ными последовательностями символов (по крайней'мере некото-
рые из них), то описанный метод сжимает их до последователь-
ностей, длина которых лишь слегка превосходит минимальную.
Некоторое превышение минимальной избыточности уменьшает
частоту столкновений и сопутствующие нм затраты машинного
времени. iBonpoc о том, насколько превысить минимально воз-
можную длину (в битах), должен решаться инженерами. В на-
шем примере использовался один лишний двоичный символ, и
ппимерно половина ячеек таблицы оставалась пустой. Примене-
ние двух лишних символов резко уменьшит -число столкновений,
однако увеличит вдвое объем требуемой памяти.
Таким образом, случайное кодирование основано на исполь-
зовании числа, а не структуры ожидаемых записей. Оно позво-
ляет употреблять сильно сжатую таблицу в режиме прямого об-
ращения, а не поиска. Вместо 'поиска 'Применяются вычислитель-
ные 'Методы (аглоритм перемешивания), поскольку происходит
непосредственный переход к вычисленному адресу, и для нахож-
дения нужной записи, если .только она существует, требуются в
худшем случае простые логические операции.
Случайное кодирование" основано на том, что алгоритм пере-
мешивания дает случайные кодовые слова. Ясно, что два имени,
отличающиеся одной буквой, дают разные слова. Столкновение
двух сильно различающихся друг от друга слов может произой-
ти лишь случайно. Используемый здесь алгоритм перемешива-
ния очень прост, и существует развитая теория построения алго-
ритма перемешивания для различного типа данных [ilO]. Ясно,
что этот алгоритм весьма эффективен, но, возможно, его можно
еще улучшать. Здесь этот вопрос не рассматривается.
Случайное кодирование приводит к некоторой равномерности
данных от источника, обладающего неизвестной, но сложной струк-
турой; оно стремится сгладить неоднородности.
Мы хотим подчеркнуть два основных результата. Во-первых,
метод случайного кодирования в некоторых случаях является по-
лезным методом кодирования данных; он уменьшает избыточ-
ность, не используя фактически называющую эту избыточность
структуру сообщений (имен). Во-вторых, рассмотренный метод яв-
ляется примером общего метода случайного кодирования (см.
гл. 10).
5.15. Цель кода Грея
Другой важный код — код Грея. Он построен для того, чтобы
удовлетворить некоторые общие требования, которые наилучшим
образом можно описать на частном примере, хотя код Грея нахо-
дит 'более широкое применение. Предположим, что имеется коди-
рующий аналоговый диск (рис. 5.15.1); щетки просматривают этот
Рис. 5.15.1. Восьмисек-
торный аналоговый диск
Диск, причем каждая свою дорожку. Для того чтобы зарегистри-
ровать, насколько повернулся диск, дорожки разделены на сек-
торы. Для типичной двоичной системы число секторов . должно
быть степенью двойки, что 'приводит к п-значному двоичному
числу. Число дорожек равно, конечно, п, по одной дорожке для
каждой цифры :(на рисунке число дорожек равно трем).
Если используется двоичное кодирование секторов, то, ска-
жем, при повороте диска от двоичного числа 011 к следующему
двоичному числу 100 значение на каждой щетке изменится. Пред-
положим, что происходит попытка считывания в момент смены
секторов. Можно ожидать, что эта попытка приведет к считыва-
нию любого из восьми возможных чисел.
Код Грея—это такой метод кодирования, при котором номера
соседних секторов диска отличаются друг от друга только одной
цифрой. ,В этом случае результатом попытки считывания в мо-
мент, когда щетки находятся между двумя секторами, может
явиться только номер одного из двух секторов.
5.16. Подробное представление кода Грея
Только что было дано определение кода Грея, однако оно не
дает единственного кода. На практике используется один простой
код, который обычно и называется кодом Грея.
Этот код Грея определяется индуктивно. Для кода с одной
цифрой имеется два состояния, обозначаемые 0 и 1 (рис. 5.16.1).
Запишем их в виде столбца. Заметим, что при движении по кру-
гу происходит также переход от 1 к 0 (при переходе снизу
вверх по столбцу). Под этим столбцом запишем столбец из тех
же символов в противоположном порядке и поставим перед пер-
выми двумя строками символ 0, а перед последними двумя —
символ 1. Сразу ясно, что при переходе от первоначального мно-
жества символов к добавленному изменяется лишь первый сим-
вол с 0 на 1, а остальные символы не меняются. При переходе
между строками добавленного множества также происходит из-
менение лишь одного символа, поскольку добавленные строки
расположены аналогично первоначальным, но в противополож-
ном порядке. Переход от последней строки к первой отвечает из-
менению лишь первого (добавленного) символа. На рис. 5.16.1 по-
казан переход кодов с одной цифрой к кодам с двумя цифрами,
переход к’кодам с тремя цифрами и часть перехода к коду с че-
тырьмя цифрами:
Задача' / .
5.16.1., Покажите, что для четырех двоичных символов можно Построить не-
сколько различных кодов, в которых переход к следующему сектору
изменяет лишь один символ.
5.17. Декодирование кода Грея
= Числа, поступающие с диска аналогового устройства, в ти-
пичных ситуациях представлены кодом Грея. Однако обычно для
дальнейшей обработки их на ЭВМ нужно перейти к двоичному
п-редс^влению. При чтении слева 'Направо видно, что lice встре-
чающие^ нули являются правильными, и это же верно для пер-
вой единицы. Однако символ, следующий за первой появившейся
единицей, доджей быть инвертирован1.
Если следующий символ является 0, то инверсию, следует
продолжить. Ёсли символ 1, то его нужно инвертировать и пре-
кратить инверсию до тех пор, пока снова не встретится 1. Таким
образом, число встретившихся единиц определяет, нужно ли ин-
вертировать следующий символ. Его нужно инвертировать, если
ранее встретилось нечетное число единиц, и не нужно, если —
четное. Это простое правило вместе с общей простотой метода де-
лает данный код наиболее приемлемым в случае, когда при пере-
ходе между двумя последовательными числами должно проис-
ходить изменение только одного символа. Легко построить соот-
ветствующую диаграмму состояний.
Задача
5.17.1. Постройте диаграмму состояний для декодирования кода Грея.
5.18. Другие коды
Некоторый интерес представляет вопрос о потере синхронизации в системе
декодирования, когда в потоке символов, поступающих н а приемник, выпадает
одни нз символов или вставляется лишний. В случае кода Хаффмена это при-
водит к некоторым затруднениям, однако обычно приемник достаточно быстро
восстанавливает синхронизацию. Вопрос о среднем времени в течение которого
синхронизация восстанавливается, достаточно сложен, хотя он неоднократно
рассматривался. Ясно, что в любом конкретном случае можно провести модели-
рование кода с ошибками методом Монте-Карло и на основе результатов .такого
моделирования сделать соответствующие выводы. Ошибки синхронизации в
ЭВМ обычно не возникают — возможна только замена символов.
Один из способов, позволяющих избежать сложностей, связанных с восста-
новлением синхронизации, состоит в использовании параллельного канала. Дру-
гой-способ, применяемый при последовательной передаче, состоит во вложении
сообщения в блок большей длины, на обоих концах которого имеются синхро-
низирующие импульсы.
В настоящее время, когда стоимость надежных .кварцевых часов невелика,
обычно используется тактовая синхронизация либо от одних часов, либо от не-
скольких, показания которых постоянно синхронизируются. Такой метод обес-
печивает одинаковый отсчет времени как у передатчика, так и у приемника.
Этот вопрос не настолько интересен с общей точки зрения, чтобы идти дальше
постановки задачи и указания очевидных решений. Другие методы кодового
сжатия можно найти в работе [5].
5 Т. е. О должен быть заменен на 1, а 1 на 0. — Прим, перев.
Глава6
Энтропия и первая теорема Шеннона
6.1. Введение
.До сих пор рассматривалась теория кодирования; теперь при-
ступим к рассмотрению теории информации. Теория кодирования
отвечает на следующие вопросы: 1) как построить коды для бе-
лого шума (основной вопрос)? 2) как сжать сообщение, когда
известна его вероятностная структура?
Займемся общим методом описания структуры источника. Для
этого понадобится понятие энтропии. Хотя энтропия давно• . ис-
пользовалась, во. многих физических задачах, и .ее понятие в -тео-
рии информации сильно .напоминает классическое определение,
тем не менее в теории информации энтропия изучается сама по
себе без обращения к многочисленным аналогиям. Для нас энт-
ропия будет просто функцией распределения вероятностей pi. Не-
которые аналогии приведены в .[7, 8].
Теория информации объединяет защиту от шума и эффектив-
ное использование канала. Однако простая модель шума в кана-
ле (белый шум) иногда оказывается нереальной и в таких слу-
чаях приходится рассматривать более общие конфигурации оши-
бок. Это приводит к важному понятию пропускной способности
канала, которое вводится в гл. 8.
Результат, который является .целью изучения, — это основная
теорема Шеннона из гл. 10, связывающая пропускную способ-
ность канала С (более точно будет определена далее) и макси-
мально возможную скорость передачи сигналов. Доказывается
замечательная теорема, утверждающая, что .можно сколь угодно
близко подойти к максимальной скорости передачи сигналов,
достигая при этом сколь угодно низкого уровня ошибок. К сожа-
лению, доказательство не является конструктивным, так что тео-
рия информации дает границы того, что можно достичь, и не го-
ворит, как. этого достичь. Тем не менее, как уже упоминалось в
разд. 1.2, эта теория весьма полезна.
В настоящей главе доказывается очень частный случай основ-
ной теоремы: теорема -кодирования без шума, когда проблемы,
связанные с шумом, игнорируются. .После того, как эта теорема
и ее доказательство станут понятными, более ясным станет и до-
казательство основной теоремы; в этих щелях нужно лишь исполь-
зовать ряд предварительных результатов из гл. 9.
6.2. Информация
Пусть задан алфавит источника, состоящий из q символов 8Ь
82, . . . , Sq И соответствующие вероятности p(Si) =P1, p(s2) =Р2, ...,
..., p(Sq)=pg. Сколько информации поступает при приеме одного
из этих символов? Если, например, Pi = l (а остальные р^ равны,
очевидно, 0), то никакой неожиданности, никакой информации
нет, поскольку заранее известно, каким должно быть сообщение.
Если вероятности сильно отличаются друг от друга, то появление
маловероятного символа является более неожиданным и при этом
получается большее количество информации, чем при появлении
высоковероятного символа. Таким образом, в некотором смысле
информация обраТра вероятности появления.
Представляется'1-естественным, что удивление аддитивно-, ин-
формация от двух различных независимых символов равна сум-
ме информаций от каждого из них в отдельности. Поскольку для
получения .вероятности' составного события нужно перемножить
вероятности двух независимых событий, количество информации
естественно определить как /(«;) =log2(l/pi)- Поэтому в результа-
те имеем
/ (Sj) + 7 (s2) = log2 (1/р± Рг) = 7 (s±, s2).
Эта формула показывает, что произведение вероятностей соот-
ветствует сумме информаций. Таким образом, определение согла-
совано с .многими нашими представлениями о том, чем должна
быть информация.
Понятия неопределенность, неожиданность и информация свя-
заны между собой. Прежде чем событие (эксперимент, прием
символа сообщения и т. д.) произойдет, имеется количество не-
определенности; когда событие происходит, возникает количество
неожиданности; после того как оно произошло, имеется выигрыш
в количестве информации. Все эти величины равны между собой.
Такое определение является техническим, основанным на ве-
роятностях, а не на смысле, который .могут нести символы для
человека, принимающего сообщение. Этот факт сильно смущает
тех, кто смотрит на теорию информации со стороны; они не пони-
мают, что это в высшей мере техническое определение включает
в себя лишь часть того разнообразия, которое содержится в
обычном понятии информации.
Для того чтобы увидеть, в чем это определение противоречит
здравому смыслу, зададим следующий вопрос: «Какая книга со-
держит больше .всего информации? Вопрос, конечно, нужно стан-
дартизировать, указав размер книги, страницы и тип шрифта,,
а также множество используемых знаков (алфавит). После этого-
ответ, очевидно, будет таким: «Больше всего информации содер-
жит книга, текст которой является полностью случайным!» Каж-
дый новый символ должен быть абсолютно неожиданным (обос-
нование этого утверждения содержится в разд. 6.4).
Какое основание логарифма следует использовать? Ответ на
этот вопрос определяется лишь из соображений удобства; по-
скольку все логарифмы пропорциональны друг другу. Это непо-
средственно вытекает из основного соотношения
loga х = logb x/logb а = (loga b) logb x.
Удобно--использовать логари мы это основанию1 2; 'получающа-
яся единица информации называется битом (двоичной единицей);
В. случае, основания е (его приходится использовать при некото-
рых. аналитических рассмотрениях) единица информации называ-
ется натом. Наконец, иногда применяется основание 10, И"ёббт-
ветствующая единица называется Хартли в честь'Р. В. Л. Харт-
ли, который первым предложил логарифмическую меру информа-
ции.
- Слово бит имеет .в книге два различных смысла: обозначает
цифры в двоичной'системе представления ч:псел и единицы ин-
формации; Эти понятия не. ’.совпадают, и в случаях, когда- рас-
сматривается информационная задача- и .возможна путаница, сле-
дует говорить о бите информации. ’ i ;'' "
Одно основание логарифма легко перевести в другое, посколь-
ку
¥ log10 2 = 0,30103...; log210 = 3,32193...,
logw е = 0,43429 ..., loge 10 = 2,30259 ...»
loge 2 = 0,69315 , log2 e = 1,44270 ....
6.3. Энтропия
-Если при приеме символа st получаем I(Si) единиц информа-
ции, то сколько информации принимается .в среднем? -Ответ со-
стоит в.том, что, поскольку вероятность получить I(Si) единиц
информации равна pi ,то в среднем для каждого символа sj имен-
ем
/(«z)=pf iog2(i/pf). . .
Следовательно, усредняя по всему алфавиту символов Siti по-
лучаем .
2 рг № (^рЭ-
f==l
Следуя традиции, эту важную величину (по основанию г) обо-
значим следующим -образом:
q / 1 \
Hr (S) = 2 Pi l°gr I— I • (6’2 3 * *-1)
i=l \ /
Она называется энтропией системы S с символами s< и вероят-
ностями pi. Ясно, что
7/r(S) = 772(S)logr2.
Эта величина является энтропией источника в случае, когда при-
нимаются во внимание только вероятности pi символов st. В разд.
6.10 .рассмотрена энтропия марковского, процесса.
Следует отметить, что выражение типа: «рассмотрим энтро-
пию источника» имеет смысл только тогда, когда указана модель
источника. Снова обратимся в качестве примера к случайным
исламЛИмеются формулы для генерирования псевдослучайных.
пцсе^- ПуЬп> они .вычислены и занесены в таблицу. Если .мы не
п0Верим сразу, .что это — псевдослучайные, числа, можно, попы-
та'ться вычислить энтропию, основанную на частотах появления
Фтдел'ьных чиселл Поскольку генераторы псевдослучайных. чисел
достаточно. хоротщ) имитируют .случайные числа, окажется, что
каждое следующее\число является для .нас полной неожидан-
ностью. Если, однако, нам известна структура формулы, исполь-
зуемой для порождения таблицы, то после нескольких шагов мы
сможем точно .предсказать последующие числа и никакой неожи-
данности не будет. Таким образом, оценка энтропии источника
зависит от принятой модели.
В определение энтропии (6.3.1) входит только распределение
вероятностей: энтропия является функцией pi и не зависит от Si.
Если, например, вероятности равны 0,4; 0,3; 0,2 и ОД, то из
третьего столбца таблицы в приложении Б получаем следующее:
Р plog(l/p)
0,4 0,52877
0,3 0,52109
0,2 0,46439
0,1 0,33219
Сумма 1,84644
Таким образом, энтропия этого
равна 1,84644. Хотя энтропию можь
виде функции от р, в дальнейшем г
ся алфавит 5 и обозначение 77(5);
запись Н(р) иногда используется в
случае, когда имеется всего два со-
бытия.
распределения приближенно
э записать как 77i(p), т. е. в
э-прежнему будут указывать-
Рис. 6.3.2. Энтропия для двух со-
бытий
Рис. 6.3.1. График функций р log2(l/p)
График функции р log2(l/p) показан на рис. 6.3.1. Из равен
ства
-?~(р Iog2—= ~~ (Р l°ge — ) log2 е = log2 -log2 е
dp \ р J dp \ - р ) р
видно, что в точке р=0 кривая имеет вертикальную касательную,
а максимальное значение функции достигается три р=1/е.
В дальнейшем потребуется также равенство lim(xlogex) =0
Для его доказательства запишем левую часть в виде lim (1^1? \
jr-*O \ 1 lx J
и 'Применим правило Лопиталя, дифференцируя отдельно числи-
/ 1/х \
тель и знаменатель. Получаем —------------) = lim (—х) = 0.
Jt-*O \ — 1/X2 / л-»0
В качестве еще одного примера вычисления энтропии распре-
деления рассмотрим йсточник с алфавитом S={si, S2, -$з, s4, у
которого Р1 = 1/2, /?2= 1/4, р3=р4=1/8. При г=2 имеем энтро-
пию
(S)=4- 1о&2+-г 1о&4+4- 1о&8+4- 1о& 8=
Z 4 о о
= —-1 + —-2 + —-3 + — -3=1— бит.
2 4^8 8 4
В качестве примера применения понятия энтропии рассмотрим бросание
симметричной монеты, у которой выпадение герба и решетки считаются равно-
вероятными: ।
/ 1
I (Si) = log2 ( — ) = log2 2=1,
^2(S)=4'/<Sl) + 4"/(S2)=1-
Распределения, относящиеся всего к двум событиям, встречаются очень
часто. Если обозначить через р вероятность первого символа (события), то по-
лучаем, что функция энтропии
/ 1 \ 1
н2 (р) = Р log2 ( — ) + 0 — Р) 10g2 "-
\ р J ‘ —р
Значения этой функции приведены в последнем столбце таблицы, помещенной
в приложении Б. График ее показан на рис. 6.3.2. Заметим, что в точках р=0
и р= 1 функция имеет вертикальную касательную, поскольку
Аналогично при бросании правильной кости
а энтропия равна
4"'(4
6
Н (S) = 6
log2 6 — 2,5849... бит.
0з этого, примера видно, что в случае, когда все вероятности'рав-
ны, среднее значение по алфавиту совпадает с информацией, по-
лученной от одного события.
Энтропия распределения отражает одно из свойств распреде-
ления, так же как в статистике среднее значение отражает одно
из свойств распределения. Энтропия обладает свойствами как
арифметического, так и геометрического среднего.
Задачи
6.3.1- Сколько 'информации мы получим, выбрав одну карту из колоды, содер-
жащей 52 карты?
63 2. Вычислите энтропию распределения /4=1/3, рг=1/4, р3= 1/6, />4=1/9,
ps=l/12, р6=1/18. Ответ: 8/9+(11/12) log 3^2,34177.
6.4. Математические свойства энтропии
.Энтропия измеряет количество .неопределенности, неожиданно-
сти или информации, содержащееся в некоторой ситуации, ска-
жем, в приеме сообщения или в -результате эксперимента. Таким
образом, она является .важной функцией .вероятностей отдельных
возможных событий. При планировании эксперимента желатель-
но обычно максимизировать ожидаемое количество полученной
информации, т. е. максимизи-
ровать энтропию. Для этого
нужно, по крайней мере частич-
но, управлять вероятностями
различных исходов экспери-
мента; нужно подходящим об-
разом спланировать экспери-
мент. Критерий максимума эн-
тропии все чаще используется
в различных задачах. Поэтому
имеет смысл исследовать эн-
тропию саму по себе, независи-
мо от тех приложений, кото-
рые рассматриваются.
Энтропия обладает рядом
очень полезных математиче-
ских свойств, которые необхо-
димо исследовать прежде, чем
углубляться в теорию. Первое
СВОЙСТВО функции logeX МОЖНО
заметить с помощью рис. 6.4.1.
Проводя касательную в точке
(1, 0), находим, что ее наклон равен d(logex)/dx|a;=i = 1, так что
Уравнение касательной есть у—0=1 (х—1) или у — х—1.
Таким образом, при х>0 получаем полезное неравенство
lOgeX^X—1. = (6.4.1)
Равенство имеет место только в точке х=1.
Втооое важное свойство выражает фундаментальное wothqJ
шение между энтропиями двух вероятностных распределений.
Пусть первое .распределение есть х{, где (конечно) 2х<=1, а
второе — и 2г/г=1- Рассмотрим теперь выражение, .в которое
входят оба распределения вероятностей.
S Xi loge рИ =—L— 2 Xt loge f.
£1 \Xi ) loge 2 \x{ }
Используя предыдущее соотношение (6.4.1), получаем
-1— У xflogef-^<—— у Xi(—1 У (yt—Xi)^
loge2 f lOge2 -jJ l\Xi ) 10ge2
loge 2
Снова переходим к логарифмам <по основанию. 2 и получаем
фундаментальное неравенство
2 Xi log2 f 0. (6.4.2)
£=1 \ xi J
Заметим, что равенство имеет место только тогда, когда Хг=&-
для всех i.
Естественно, опросить, какие условия на распределение веро-
ятностей обеспечивают максимальное значение энтропии (мини-
мум, очевидно, достигается в случае, когда одно из ₽»=!, а‘ос-
тальные равны 0).
Имеем
Я2 (•$) = У] Pi log2 — при V Pi = 1.
i Pt t
Начнем с рассмотрения
q / i \ q q 1
//2(S) — log2<7=£ PilogJ— — log2?2 SPil°g2 — =
i=l \ \ Pi J i=l fel Wi
q 1
= lOg2e2 Pi lOge---- .
.. fel PPi
Применяя первое неравенство (6.4.1), получаем
q ( i \
//2(S) — log29^1og2e2 Pi-------1 <
\ Mi ]
log2 ( S —--S Pi ) 1O§2e 0 — !) = °-
\i=l ? i=l /
Таким образом,
^(SXlogaQ. (6.4.3)
равенство в (6.4.3) справедливо лишь в случае, когда все Pi=\!q~
Другое доказательство этого важного результата состоит в
йопользовании множителей Лагранжа и рассмотрении функции
f(Pl, Рг, ... >Pg) = S Pi loge +Х Pi—^ .
^L=^Sloge(-LVll + x=0’<i=l’2’
др, loge 2( \ pj J J
Поскольку последнее уравнение не зависит от /, то все р,.
должны быть равны между собой, и .каждое из них равно 1/q, где
q — число элементов распределения. Поэтому максимальное зна-
чение энтропии равно Д2(Х) =log2(g). Для каждого распределе-
ния, отличного от равномерного, энтропия меньше, чем log2 q.
Простое часто встречающееся применение этого принципа дает стандартная
система экзаменационных оценок А, В, С, D, F. Оставляя в стороне оценку F,
обладающую особыми свойствами (она указывает, что студент должен сдавать
экзамен еще раз), можно сделать вывод, что для получения из системы оценок
максимального количества информации нужно стремиться к тому, чтобы все-
остальиые оценки встречались одинаково часто. Можно, конечно, повысить зна-
чимость самых высоких знаний, ставя сравнительно мало оценок А. При этом,
однако, информации придается другой смысл, отличный от определенного вы-
ше. Обы'чная практика американской аспирантуры заключается в том, что ста-
вятся только оценки А и В. Это приводит к напрасной потере пропускной спо-
собности системы. Экстремальное распределение, при котором одно, из pt рав-
но 1, а все остальные равны 0, соответствует случаю постоянного сигнала. При
этом не передается никакой информации.
6.5. Энтропия и кодирование
Докажем теперь фундаментальное соотношение между сред-
ней длиной кода и энтропией H(S). Пусть задан некоторый мгно-
венный код. Пусть li — длины кодовых слов по некоторому ос-
нованию г. Из неравенства Крафта (4.5.1) имеем
• ‘ К=2 (l/rz4^1. (6.5.1$
i—1
Определим теперь числа Q<:
(Ъ = г~1ЧК. (6.5.2)
q
Тогда, конечно, £ Qi=l- Можно считать, что Q, задают распре-
1=1
Деление вероятностей. Поэтому можно использовать фундамен-
тальное неравенство (6.4.2).
S Р<1об2р^<0.
\ Pi /
Представляя логарифм частного в виде разности логарифм^!
заметим, что один член равен энтропии, так что
Q / 1 \ ч / 1 \
H2(S) = 3 Pi log2 — < У, Pi log2( — .
i=i \ Pi ) \ Qi )
Применив к правой части неравенства соотношение (6.5.2), По
лучаеМ'
Ч , в
Pi(log2/C— log2r £)<Jog2/(+2 Pili^r.
i=l i-l
Иопользуя неравенство Крафта, имеем К^Л, так что log2/(^
Отбрасывание ©того члена только усиливает неравенство. По-
этому
„ Ч
Н2 (SX У] (Pi li) logo г = L log2 г
i=l
ИЛИ
HT{S)^L, (6.5.3)
где L — средняя длина кодового слова
• <?
£=2>Л- (6.5.4)
1=1
Таким образом, получен искомый фундаментальный резуль-
тат: энтропия является нижней границей средней длины L. для
любой мгновенно декодируемой системы. В силу неравенства
Макмиллана из разд. 4.7, это утверждение остается справедли-
вым для любой однозначно декодируемой системы.
Для хороших ДВОИЧНЫХ. КОДОВ Л=1 и Iog2/(=0. Поэтому
строгое неравенство в двоичном случае имеет место, только если
Pi^Ri^^ i.
6.6. Кодирование Шеннона — Фано
В разд. 6.5 предполагалось, что длины кодовых слов Ц зада-
ны. Однако более реальным является случай, когда заданы ве-
роятности Pi. Кодирование Хаффмена дает длины кодовых слов,
причем каждая длина зависит от всего набора вероятностей.
Кодирование Шеннона — Фано не так эффективно, как1 коди-
рование Хаффмена, однако его преимущество состоит в том, что
по одной вероятности pi можно непосредственно найти длину к
соответствующего кодового слова. Пусть. даны символы. источни-
ка $i, S2,... ,sg и соответствующие вероятности. рь р2,. . ., Pq- ДлЯ
каждого pi найдется такое целое число £, что ..
logJl/p^Z^logjf/pJ + l. (6«.1)
Поэтому — ^rZi< —.
Pi Pi
Перейдем к обратным величинам и ‘Получим р-С^ (1/гг0 >
(jPi/r). Поскольку 5 Pi~l, то, суммируя эти неравенства, по-
дучаем'
l>V(l/r*)>—, (6.6.2)
i=l r
что дает неравенство Крафта. Поэтому существуют мгновенно
декодируемые коды, имеющие кодовые слова указанных длин.
Для определения энтропии распределения pi умножим (6.6.1)
на Рг и проведем суммирование по i:
#r(S)=2 PilogJ-L (3)4-1.
i=l \ Pi / 4=1
В терминах средней длины L кода (6.5.4) имеем
/7Г(3)<£</7Г (3)4-1. (6.6.3)
Таким образом, для кодирования Шеннона — Фано энтропия
снова дает нижнюю границу средней длины кода. Энтропия вхо-
дит также в верхнюю границу. Верхнюю границу для кодов
Хаффмена (см. гл. 4) получить нелегко, однако вследствие своей
оптимальности коды Хаффмена не могут быть хуже кодов Шен-
нона — Фано.
Как фактически найти кодовые слова? Следует просто сопо-
ставить их одно за другим. Например, из вероятностей pi=p?~
= 1/4, 03 = 04 = 05=06 = 1/8 получаем длины Шеннона — Фано
/1=/2 = 2, /з = /4 = /5 = /б=3.
После этого строим кодовые слова: S!=00, S2—OI, эз=100, $4=
=401, «5=110, «6= 111.
Неравенство Крафта, выполненное для кодирования Шенно-
на — Фано, гарантирует, что кодовых слов хватит для построе-
ния мгновенного кода. Такое упорядоченное сопоставление сразу
дает дерево декодирования.
Это показывает, что кодирование Шеннона — Фано является
достаточно хорошим. Интересно посмотреть, как возникает левое
из'неравенств в выражении (6.6.3). Прежде всего, если каждая
из вероятностей рг является некоторой отрицательной целой сте-
пенью основания г, то при указанном распределении длин кодо-
вых слов неравенство переходит в равенство, т. е. средняя длина
кодовых слов совпадает с энтропией. Для получения кодовых-слов
следует просто сопоставить символам возрастающие r-ичные чис-
ла нужных длин.
6.7. Насколько плохим является кодирование i
Шеннона — Фано?
Поскольку кодирование Хаффмена оптимально и мы времен-
но перешли к неоптимальному (в смысле затрат времени) коди-
рованию Шеннона — Фано, естественно задать вопрос: «Насколь-
ко плохим является кодирование Шеннона — Фано?».
.Рассмотрим следующие примеры. Для источника с алфавитов
s2 и вероятностями pi=l—l/2fe, p2=’l/2fe (/г^2) получаец
3og2(l/pi) ^log22= 1. Поэтому 1^=1. Однако для 12 имеем •
log2 f — ^ = Iog2 2й = /г = 1.2.
\’Р2 /
Итак, в этом случае код Хаффмена, состоит из двух двоичных
слов длины 1, а код Шеннона — Фано — из слова длины ; 1 дда
Si и.слова длины k для.s2. ; ' . . i
Прежде чем огорчаться из-за. малой эффективности, найдем
среднюю длину кодового слова. Ясно, что для кода Хаффмена
£х=1. Для кода Шеннона — Фано имеем
£ШФ = 1(1 - l/2ft) + k/2k = 1 + (k-^ 1)/2й .
В качестве другого примера потери эффективности рассмот-
рим случай, в котором все кодовые символы имеют одинаковую
вероятность 1/q. Код Шеннона — Фано дает log2?^l<log2?+l.
Если а не есть степень 2, то некоторые слова будут укорочены в
Имеем таблицу
k 1+(й-l)/2fe
2 1 + 1/4=4,25
3 1+,1/4=4,25
4 1+3/16=1,1875
5 1 + 1/8=4,125
6 1+5/64=4,078125
коде Хаффмена и не будут в ко-
де Шеннона — Фано.
Увеличение средней длины .ко-
дового слова при использовании,
кода Шеннона — Фано невелйко;
позже будет показано, что для
теории это несущественно; код
Хаффмена лучше кода Шенно-
на — Фано только в практических
приложениях.
6.8. Расширения кода
Понятие энтропии было введено для .простой ситуации, а
именно, в случае независимых символов с фиксированными ве-
роятностями появления Далее следует обобщить понятие (Энт-
ропии для расширений ,(см. разд. 4.2) и для марковских процес-
сов (см. разд. 5.2—5.5). Это приводится в разд. 6.8 и 6.10.
Потери при использовании кода Шеннона — Фано вместо кода
Хаффмена, которые измеряются в терминах энтропии, возника-
ют тогда, когда величины, обратные вероятностям появления
символов, не являются точными степенями основания г. Еслй про-
водить кодирование не по одному символу за один раз, а стро-
ить код для блоков из п символов, то можно рассчитывать бли-
же подойти к нижней границе Hr(s).
Еще важнее, что (см. разд. 4.10) вероятности в расширении
источника более разнообразны, чем вероятности исходного ис-
точника; поэтому можно ожидать, что чем выше кратность рас-
ширения, тем более эффективными окажутся как -коды Хаффме-
так и 'коды Шеннона — Фано. Рассмотрим сначала понятие
Расширения кода.
" Определение. Положим, что «.-кратное расширение алфавита
источника состоит из символов вида s^, Stz,..., Sin с вероятно-
стями' Qc"P<J>i s • • - Pin. Каждый блок из п первоначальных
символов становится одним .символом ti с вероятностью Обо-
значим этот алфавит Sn=T.
Такое определение уже встречалось в разд. 4.2 и 5.5.
Энтропия новой системы легко вычисляется:
в” / 1 \
яг(Х") = яг(Л=2 & 1^(4-)==
i=i \ Qi/
Представляя логарифм .произведения в виде суммы логариф-
мов, получаем
ЯГ(5«)=£(О logr
i=i й=1
п qn
= 2 2 PpPi*...Pini°8r
k=li—1
Для каждого члена внешней суммы по k имеем
чп
2 PQ /’ч - Pin 1о&
£-1
= 22 ... 2 Pi1Pi,...Pin^r
i=] i2=l in—i
Каждая сумма, в которую не входит ik, равна 1 (поскольку
сумма всех вероятностей равна 1). Поэтому остается только
сумма по ik. Но
1 ( 1 \
2 Pik^r — =#r(S).
lk=l \РЧ
Поскольку все члены в сумме по k равны, то
Нт (Т) =HT(Sn) = n Нт (5). (6.8.1)
Таким образом, энтропия и-кратного расширения источника
Б п раз больше энтропии первоначального источника. Заметим,
однако, что в нем имеется qn символов.
Теперь можно применить к расширению Т результат (6.6.3).
Имеем Hr(Sn) s^Ln<Hr(Sn) +!1, где Ln — средняя длина кодо-
Б°го слова для n-кратного расширения. Применяя (6.8.1) и про-
изводя деление на и, получаем
Hr (S) (Ln/n) < HT (S) + 1/n. (6.8.2)
Поскольку в расширении каждому символу ti соответствует J
символов Sik, шравильнее использовать меру L=Lnln. Таким об,
разом, для расширения достаточно высокой кратности средня^
длина кодового слова L может быть сколь угодно близкой
Hr(S). Это составляет содержание теоремы Шеннона о кодировсы
нии без шума: для п-кратного расширения справедливы границы
(6.8.2).
6.9. Примеры расширений
Предположим, что алфавит источника состоит из двух символов si, s2 с вд.
роятностями pi=2/3, Р2= 1/3. Энтропия равна
4? ^2 (S) = log2+-7-log2 3 = log23 — ~ =
О z о о
= 1,5849... —0,6666... =0,9182958...
Код Хаффмена дает «1=0, s2= 1, так что средняя длина кодового слова равна
1. Код Шеннона — Фано дает 4=1, 4=2, и средняя длина равна (2/3)1 +
+ (1/3)2=4/3=,1 + 1/3.
В разд. 4.10 приведена средняя длина кодов Хаффмена для некоторых рас-
ширений. Для кода Шеннона — Фано при расширении кратности 2, имеем
9
logs 4 4 — 2
«
9
loga 2^4 4 — з
9
loga ^4 4 — 3
9
log2—^4 4 = 4.
Средняя длина
Оказывается, что в данном случае можно вычислить коды Шеннона — Фано
для всех расширений. Для n-кратного расширения имеем:
Число членов Вероятность
С(п, 0) С(п, 1) 2п/Зп 2п-1/Зп
С (п, () 2n-i/3n
С(п, п) 1/зп '
Для нахождения Z» имеем
log2 (1/Pi) = log2 ( З'1 / 2n~9 = п log2 3 — (и — i) =
= n(log2 3— 1) + i lit (i = 1,2,..., n). (6.9.1)
Пусть
An — наименьшее целое число, большее n(logz3—1). (6.9.2}
Тогда средняя длина кода:
£Шф(п) = “3 с(«- /)2"-ЧЛге + 9 =
3 j=o
Лп 2 C(n, i) 2"-1’ + 2 [П — (П — i)l С (п, I) 2"-г .
i=0 i—0
-Известно, что разложение бинома (1+х)" можно записать в любом из двух
видов:
d + *)n =2 С(п, О*1’=2 С<-п’ (6.9.3)
i=e i=o
Дифференцируя второе разложение и умножая на х, получаем
п (1 + х)п~1 х = 2 С (п, Г)(п — i) х"-*.
i=0
Полагая в (6.9.3) и (6.9.4) х=2, имеем
" / 9п \ п
3" = 2:C(n. ( — )3n = 2c(n, i)(n—i)2n-f.
i=0 \ 3 / i=0
Поэтому Ьщф = (АпЗп-гпЗ‘п—2пЗг‘/3)/Зп=Ап+п/3, где из (6.9.2) -4n^n(log23—
- 1) =«(0,5849625...)
Приведем небольшую таблицу значений Ап, включив в последний столбец
параметры кодов Хаффмена:
п n (Iog2 3—1) Ап £ШФ Win Z-x Win
1 0,5849... 1 1,33333... 1,00000...
2 1,1699... 2 1,33333... 0,94444...
3 1,7549... 2 1,00000... 0,93827...
4 2,3398... 3 1,08333... 0,93827...
5 2,9248... 3 0,93333... 0,92263...
6 3,5098... 4 1,00000...
7 4,0947... 5 1,04762...
8 4,6797... 5 0,95833...
9 5,2646... 6 1,00000...
Ю 5,8496... 6 0,93333...
Из соотношения (6.5.3) нижняя граница равна Н(S) =0,91829. Параметры
к°Дов Шеннона — Фано приближаются к этой границе нерегулярно, однако, как
показывает предыдущий результат (см. разд. 6.8), в конце концов они достцГа
тот этой границы.
Подведем итоги рассмотрения.
1. Из неравенств (6.5.3) и Крафта следует, что для любого мгновенного Ко
да H2(S) s^L log2r.
2. Из неравенства (6.6.3) следует, что Я2(5)^ДШф log2r<//2(S) + log2r.
3. В разд. 4.10 показано, что вследствие оптимальности кода ХаффМе11а
ix log2r<Lm4) log2r.
4. Согласно (6.8.2) для n-кратного расширения справедливы неравенства
№ (S) « (L log2 r)/n fi2 (S) + log2 /-/(и).
На основании пп. 1—4 получаем, что для n-кратного расширения
Я2 ($):< Дх (") 10ёа г]/п « [/.Шф (и) log2 r]/n < Н2 (S) + (log2 r)/n,
где Lx (n) — средняя длина кода Хаффмена для n-кратного расширения и
£щф (Л) — средняя длина кода Шеннона — Фано для n-кратного расширения.
Таблица является экспериментальным подтверждением этого результата. По-
следние неравенства ясно показывают, почему в разд. 6.7 можно было утверж-
дать, что потери при переходе от оптимальных кодов Хаффмена к кодам Шен-
нона — Фано несущественны при больших и. Однако при небольших п эти по-
тери могут оказаться существенными.
6.10. Энтропия марковского процесса
В разд. 6.2 было введено понятие марковского (процесса,* ко-
торое позволяет учитывать некоторые структуры входного пото-
ка данных. В частности, марковские процессы учитывают зависи-
мости между последовательными символами. Теперь найдем энт-
ропию марковского процесса.
Какова вероятность того, что при заданных предыдущих сим-
волах s,, si2,...Sim следующим символом будет s{? В математи-.
ке эта условная вероятность обозначается следующим образом:
P(Si\silt Si2,...,Sim).
Отметим, еще раз, что последовательность символов будет
ТаКОИ. Sit , Sf2 , . . . , Sim 9
Для марковского процесса нулевого порядка вероятности за-
висят только от символа s, и для них можно использовать преж-
нее обозначение рг. Для марковского источника первого порядка
существенны частоты пар символов алфавита.
Используя определение количества информации через неожи-
данность, получаем, что информация при приеме символа s{ в
предположении, что мы уже наблюдали символы s^, s, 2,..., stm,
равна
7 (Si I Si I si,, Si., ...» Si/n)=log2[p(Si|Siv ..., SfJ"1].
Условная энтропия источника S с символами s, естественно
задается выражением
H(S^,St,,, Sfm) = 2 P (s£|s£l, Sis,..., siin) x
s
X tog2[p(s£|s£1,s£a,...
gTo' .выражение задает условную энтропию источника S при ус-
ловии, что наблюдалась последовательность символов s£1, s£
,. . > т ‘
рассмотрим теперь более общую систему, включающую вероят-
ности появления состояний марковского процесса. Пусть pts,,,
s- ,. • • > Sim ). — вероятность нахождения в состоянии sit, si2,...,
Тогда естественно определить энтропию марковской сис-
темы .как сумму произведений вероятностей состояний на условные
энтропии этих состояний, т. е. 'выражением
Н (S) = s р (s£1, Si2,..., sim) Н (S|s£1, s£l,..., sim).
sm
Используя приведенное выше определение условной энтропии,
получаем
н (S) = S 2 р J p (si is*i’ s«2> x
sm s
X lQg2[p(s£lS£1,S£l....sim)~4.
Так как
P (Sii> Si, , , S/m) p (S£ |S£1, Sil, ... , S.m)=p(S£1, Si2 , m, slm, S'),
то энтропия марковского процесса
H (5) = S Р (s£1, s£„ , sim, Si) log2 [p (s£ |s£1, s^ ,
s"»+l
6.11. Пример марковского процесса
Рассмотрим в качестве примера марковский процесс с двоичным алфавитом,
показанный на рис. 6.11.1. Аналитически этот марковский процесс второго по-
рядка задается следующим образом:
р (0|0,0) = 0,8 = р (111,1),
р (110,0) = 0,2 = р (0| 1,1),
р (0(0,1) = 0,5 = р (111,0),
р (1 (0,1) = 0,5 = р (0| 1,0).
Каковы вероятности состояний 0,0; 0,1; 1,0 и 1,1? Используя очевидную симмет-
рию, имеем р(0,0)) =р(1,1), р(0,1) =р(1,0). Поэтому справедливы уравнения
р(0,0) = 0,5р(0,1) + 0,8р(0,0),
р(0,1) = 0,2р(0,0)-|-0,5р(0,1).
Оба уравнения имеют одинаковый вид
0,2р(0,0) —0,5р(0,1) = 0. (6.11.1)
Рис. 6.11.1. Марковский процесс
Поскольку в каждый «момент систем
должна -находиться в -некотором состоя,
Н'ИИ, то
р (0,0)+ р (0,1)+р(1 ,0) + р(1 ,1) = I
или
2р (0,0) + 2р (0,1) = 1. . (6.Ц.2)
Решение уравнений (6.11.1) н
(6.11.2) имеет вид
р (0,0) = 5/14 = р (1,1),
р (0,1) = 2/14 ==р (1,0).
Это— стационарные вероятности эргоди-
ческого процесса.
В общем случае для стационарных вероятностей можно выписать уравне-
ния, однако их 'решение часто оказывается трудной задачей. Возвращаясь к
рассматриваемому примеру, составим таблицу для стационарных вероятностей:
Si, S12 si Р (*11 sb . Sli) Р <SO si2 > Р <si. • si2 SP
0 0 0 0,8 5/14 4/14
о 0 1 0,2 5/14 1/14
0 1 0 0,5 2/14 1/14
0 1 1 0,5 2/14 1/14
1 0 0 0,5 2/14 1/14
1 0 1 0,5 2/14 1/14
1 1 0 0,2 5/14 1/14
1 1 1 0,8 5/14 4/14
Исходя из этой таблицы, можно вычислить H(S):
H(S)=^.p (sh, Si) log2 [ 1 1 =
23 IT V 11 4> 12) J
= — (log2 10 — 3) + — (log2 10 — 1) + log2 2 = 0,801377 бит/символ.
6.12. Смежная система
Для нахождения энтропии .марковского источника нужно най-
ти стационарные вероятности состояний марковского процесса. Од-
нако, как отмечалось, вычислить их часто очень трудно. Поэтому
необходимо иметь какой-нибудь метод оценки энтропии. Приводи-
мый ниже метод основан на понятии смежной системы.
Как можно оценить энтропию марковского процесса? Рассмот-
рим для простоты марковский процесс первого порядка; при пере-
ходе к системе n-го порядка изменяется лишь обозначение.
Поскольку основным является фундаментальное неравенство
для двух распределений, попробуем использовать его для распре-
делений p(st), p(s,) и p(Sj, Si). Символ p(sj, Si) обозначает веро-
ятность пары символов; аналогично, p(sit Sj). Как отмечалось,
V р (Sj, St) = Р (S^ = Pi, Р (Sj, s^ = p (Sj) = pj.
U 1
Таким образом, используя (6.4.2), имеем
S Р tsi’ si) 10Й2
s2
P (Si) P (sj)
P(sj, Si)
с обращением в равенство в том и только в том случае, когда
p(Sj, Si)=p(Si)p(Sj) для всех i и /. Воспользуемся теперь выра-
жением для условной вероятности
P{S}, Si) = p(Si\Sj)p(sf),
получаем
2 Р (Sj, Si) 10ga
s2
P (sj)
P(Si\Sj)
Разлагая логарифм и перенося члены, имеем
Р (Sj, Si) log2
1
P(Si\Sj)
2 S P (si’ st) logs
Снова используем условную вероятность. Тогда
где Н(8) — энтропия распределения отдельных символов; соот-
ветствующий источник называется смежной системой. Поэтому
можно записать
2 p(s])H(S\Sj)^H(S),
и энтропия марковского процесса оценивается через энтропию
смежной системы, которая является источником с нулевой па-
мятью и вероятностью p(si)=pi.
Равенство имеет место только в случае, когда p(Sj, Si)=pjPi.
Поэтому доказано, что ограничения могут только уменьшить энт-
ропию.
Энтропию расширения марковского процесса легко найти, ис-
ходя из выполненных ранее вычислений энтропии марковского
источника и энтропии расширения. Для упрощения обозначений
Рассмотрим снова марковскую цепь первого порядка. Имеем
1
Н ) — i-j Z-J Р \lj, li) 1US2 sn sn
= 2 p (tj, tj) loga
s2n
1-
p
Однако процесс является процессом первого порядка, так что
Используя несколько раз исходное распределение вероятностей
получаем
P (tj, it) = p (s£s |sJn) p &г |s£1)... p (sin|sin_x
1 1 .
n(Sn)= 2 p(tj,ti)iog2
s2n L^l^n).
I
+ ...+ 2 p(tj, it) 10g2
s2n
P(sUs«n-l).
Каждый член можно упростить, суммируя по всем символам, не
входящим под знак логарифма:
2 Р (tj, tt) Iog2 Г----- - = 2 р (Sj, Iog2
S2« s2ra
1
P (Si|sy)
= H(S).
Поэтому H(Sn) = nH(S), как и следовало ожидать.
6.13. Итоги
Было введено понятие энтропии и показаны ее применения к
получению границ выигрыша при кодировании различных источ-
ников информации. Энтропия, измеряющая неопределенность, нео-
жиданность и информацию-, является естественным математиче-
ским понятием, применяемым в подобных ситуациях. На практи-
ке использование энтропии выходит далеко за эти рамки, однако
здесь >мы не можем рассматривать их.
Теорема Шеннона о кодировании без шума показывает, что
при использовании достаточно большого расширения источника
можно сколь угодно точно приблизить среднюю длину закодиро-
ванного сообщения к энтропии источника. Это доказано как для
простого источника, так и для более сложного марковского ис-
точника. Однако это не было доказано для всех возможных ти-
пов источников. Теорема кодирования без шума является пред-
вестником основной теоремы Шеннона о том, что даже при нали-
чии шума (ошибок) можно найти подходящую систему кодиро-
вания. Этот'результат доказывается в гл. 10.
Глава 7
Канал и взаимная информация
7.1. Введение
Напомним задачу, который мы занимаемся. Рассматривается
ссылка информации либо из одного места в другое (передача),
либо от °ДНОГО момента до другого (хранение). Процесс начина-
ется с источника информации (символов), показанного на рис.
71.1 слева; его символы кодируются таким образом, как обсуж-
далось в гл. 2—5. Затем закодированные символы передаются по
каналу. В реальных ситуациях в канале имеются шумы, т. е. со-
общение на выходе канала не всегда совпадает с входным. Да-
лее сообщение декодируется и посылается к месту назначения.
Рис. 7.1.1. Модель передачи сигналов
Сейчас наступило время более подробно исследовать канал.
В качестве основного' инструмента будем использовать понятие
энтропии, рассмотренное в гл. 6. Сколько информации в действи-
тельности передается по каналу? Как следует измерять взаимную
информацию между 'входом и выходом системы? Как определить
пропускную способность канала? Именно' эти вопросы обсужда-
ются в этой и следующей главах.
В дальнейшем нам нужно научиться исследовать систему со
стороны приемного конца, где вырабатываются решения, вместо
того чтобы начинать со стороны передающего конца и исследо-
вать прохождение сигнала по системе.
7.2. Информационный канал
Информационный канал — это статистическая модель среды,
через которую сигнал проходит или в которой он хранится. На
практике имеются физические ограничения на точность, с которой
может вестись передача. Для того чтобы вычислить, сколько ин-
формации можно передать по данному каналу, нужно формализо-
вать понятие канала и физических ограничений.
На рис. 7.2.1 показано, что понимается под каналом. Канал
описывается множеством условных вероятностей 7э(Ь,|аг) того,
пто входной символ йг из алфавита, содержащего q букв, перей-
дет в .выходной символ bj из алфавита, содержащего s букв. Для
Переходных вероятностей канала будет использоваться прописная
буква Р. Объемы q и s входного и выходного алфавитов не обя-
совпадать. Например, в случае кода с исправлением ощибО1£
возможных принимаемых символов много больше,
-----следовательно, s^q. Вместе с
тем канал может выдавать один и
тот же символ, когда на вхоч
подается один из некоторый
двух различных символов; в этощ
случае
В рассматриваемой модели ка-
нал полностью описывается мат-
рицей условных вероятностей
(Pi,i) = Заметим, что,
как обычно, индексы записаны в
обратном порядке. Строка мат-
рицы содержит вероятности того,
что данный входной символ
Ог перейдет в каждый из выходных символов bj. Эта матрица по-
казана на рис. 7.2.1.
Переходная матрица канала обладает следующими свойства-
ми: 1) ее i-я строка соответствует i-му входному символу а,;
2) ее /-й столбец соответствует /-му выходному
* s
3) сумма элементов строки равна 1, т. е.
Это означает, что каждый входной символ обязательно перей-
дет в некоторый выходной символ, и P(bj| at) —распределение
вероятностей переходов; 4) если р(а,)—вероятность появления
g s
входного символа аг-, то 2? Р(bj Iaf) р (at) -- 1.
i=i /=i
Это означает, что если в систему ввести какой-либо символ, то
какой-то символ из нее обязательно выйдет.
Вероятности Pt:j полностью характеризуют канал. При этом,
конечно, предполагается, что канал стационарен, т. е. вероятно-
сти не меняются со временем. В течение некоторого времени бу-
дем считать возникающие ошибки независимыми друг от друга.
заны <
алфавит -
алфавит .посылаемых символов
СЦ
а2
а3
b2
Ь3
л-
ач
¥
в
bs .
Рис. 7.2.1. Канал
символу bj\
S
2 Pi.i=% P(b}\aj) = \-
7.3. Соотношения в канале
В системе передачи информации входные символы выбирают-
ся с вероятностями р(а,). Поэтому принятые символы bj также
будут иметь некоторые вероятности появления p(bj). (Это обо-
значение является достаточно понятным, хотя оно и не удовлет-
воряет строгим математическим требованиям.) Два множества
вероятностей р(а4) и p(bj) связаны следующими соотношениями:
Р («1) Pi. 1 + Р (а2) Р2,1 + ... + р (ад) Pq, j = р (bj,
р (а2) Pi >2 + р (а2) Р2,2 +... + р (aq) Pq, 2 == Р(bj,
p(^.s +p(a2)P2.s+ ... + p(aq)Pq,s = p\bs), (7.3.1)
ИЛИ
в сокращенных обозначениях
Z: Р (Я) Р (bj\at) =р (bj) (j=l, 2,..., s).
i=l
Запишем вероятность появления пары символов аг и bj через
P(ai, bj). Тот же смысл будет иметь обозначение P(bj, at). Эту
вероятность можно выразить двумя способами:
Р (Я> bj) = р (at) Р (Ь}Я), Р (ait b}) = р (b})Р (at |bj).
Приравнивая эти две записи, получим
Р(Я\bj) = [Р(6,|аг) p(at)]/p (bj). (7.3.2)
Это равенство известно как формула Байеса для условных веро-
ятностей. Ясно, что оно симметрично .по обоим множествам сим-
волов. Вероятности P(bj\ai) называются прямыми условными ве-
роятностями, поскольку они исходят из входа канала, где задан
ait и определяют вероятности bj. В свою очередь вероятности
P(ai\bj) называются обратными условными вероятностями и от-
вечают на вопрос: «Задан символ на выходе; какой символ на
входе вызвал его?»..
Подставляя соотношения (7.3.1) в знаменатель формулы Байе-
са (7.3.2), можно .получить эквивалентное выражение
P(at\bj) = (P(bj\ai)p(ai))
S P(bj\ai)p(ai).
i=l
(7.3.3)
ч
Суммирование'по всем а;, очевидно, дает 2 P(ai|&j) = l. Эта
1=1
формула означает, что заданный выходной символ bj определен-
но является 'результатом того, что на вход канала был подан не-
который символ.
7.4. Двоичный симметричный канал
Двоичный канал является, вероятно, наиболее полезным при-
мером канала (рис. 7.4.1). Он имеет два входных — 0 и 1 и два
выходных символа — 0 и 1. Двоичный канал называется симмет-
ричным, если Ро,о=Р1л> Pi,o=Po,i-
Пусть вероятности входных символов равны р(а=0)=р,
р(а=1) = 1—р. Пусть, далее, переходные вероятности двоичного
симметричного канала равны Po,o=Pi,i=P, Po,i=Pi,o=Q-
Таким образом, матрицу канала можно представить
Р <Э\
О. Р/'
Соотношения (7.3.1 приобретают вид
pP+(l-p)Q = p(b=O),
pQ + (l—p)P= p(b=l). (7.4Л)
Отметим, что эти соотношения можно проверить непосредственны^,
вычислением их суммы: 51
p(6=0) + p(b=l) = p(P + Q) + (l-p)(P + Q) =
= (p+l_p)(P+Q) = (l)(l) = l.
Предположим теперь, что известен принятый символ; какова
заданный символ?
Вычислим сначала оба зиаме-
нателя в соотношении (7.3.3):
2 P(b1\ai)p(at)=Pp+
i=l
2
Рис. 7.4.1. Двоичный симметричный
канал
2 P(b.i\ai)p(ai) = Qp+P(i~р),
1=1
Затем
P(a = O|6 = O) = P>/[Pp + Q(l-p)],
P(a=l|6=0) = Q(l-p)/[Pp + Q(l-p)J,
P(fl = O|fe=l) = Qp/[Qp+P(l-p)],
P(a=l\b=l)==P(l-p)/[Qp+P(l-p)].
В эти соотношения входят вероятности символов источника.
В частном случае равновероятных входных символов (р=1/2)
имеем очень простые равенства
Р(а = 0|Ь=0) = Р = Р(а= 1|6=1),
P(a=l\b — 0) = Q = P(a=0\b=l).
Рассмотрим в качестве примера двоичный симметричный канал с Р=9/Ю и
<2=1/10. Предположим, кроме того, что вероятность посылки входного символа
я=0 равна 19/20=р, а вероятность посылки символа а—1 равна 1/20=1—Р-
Тогда
Р(а = 0|6 = 0) = 171/172,
Р(а = 116 = 0) = 1/172,
Р(а = 0|6 = 1)= 19/28,
Р(а = 1|6 = 1) = 9/28.
Таким образом, если принят символ 6=0, то почти наверняка был посла11
символ а=0. Вместе с тем, принят символ 6=1, то по-прежнему с вероятно'
стью 19/23>2/3 был послан символ а=0. Таким образом, независимо от того,
какой символ принят, следует считать, что был послан символ а=0!
Такое положение возникает каждый раз, когда выполняются оба неравен-
ства
Р(а = 0|6=0)>Р(а= 1|6 = 0),
Р (а = 0|6 = 1)> Р (а = 1 ]6 = 1).
Используя приведенные ранее равенства для двоичного симметричного ка-
нала, эти условия можно переписать в следующем виде:
Pp>Q(l — Р), Qp>P(1— Р)
или p>Q. Р>Р
Эти условия означают, что перекос в вероятностях при выборе входных
символов больше, чем перекос в канале. Рассмотренный пример показывает,
что каналы могут неправильно употребляться.
7.5. Энтропия системы
В гл. 6 было развито .понятие энтропии источника информа-
ции, который в дальнейшем будет отмечаться буквой А. Энтро-
пия измеряет среднее количество информации на символ источ-
ника или, другими словами, неопределенность, связанную с ис-
точником. Равенство 77(A) =0 означает, что источник неслучаен и
Н(А) максимальна, когда все аг- равновероятны. Энтропия опре-
деляется равенством
Нг(А)= 2 Р
i=l
(7.5.1)
Как уже отмечалось, энтропия обладает следующими свойст-
вами: 1) /7г(А)^0; 2) Hr(A)^.logrq, где q—число входных сим-
волов; 3) Hr(A) =Aogrq, когда все символы источника равноверо-
ятны.
Материал, представленный в оставшейся части этой главы,
дает систематическое применение понятия энтропии к модели си-
стемы передачи сигналов.
В точном соответствии с (7.5.1) энтропию принятых символов
следует определить равенством
яг(В) = 2 Р Ф>) log,
___1_
Р (bj)
(7.5.2)
Эта величина измеряет неопределенность выходных символов и
обладает теми же свойствами, что и энтропия источника, по-
скольку все свойства выводились, исходя из выражения энтро-
пии.
Аналогичные выражения для условной энтропии можно полу-
чить следующим образом. Имеем условную энтропию при задан-
ном bj\
ч
Hr(A\bj)=?. P(ai\bj)logr
1
P(Oi I bj)
(7.5.3)
Если усреднить (7.5.3) .по всем bj, используя, конечно, в каЧе.
стве весов соответствующие вероятности p(bj), получим
/7Г(Л|Б)= S p(bj)H(A\bj) =2 2 p(bj)P(at\bj) X
7=1 /=1 i=l
1 s q Г 1
x los' [п5й7>] “g S/ 'у i°&
Если проделать то же самое, начиная с передающего конца,
то в соответствии с (7.5.3) получим условную энтропию при ус-
ловии, что послан символ ас
Яг(В|аг) = 2 Р(Ь№) )ogr
i=i
1
f (6;| at)
Аналогично
(7.5.4), усредняя на этот раз по входному алфа-
виту, получаем соответствующую условную энтропию
Q S
НТ(В\А)=% Y P(ai,bj) logr
(7.5.5)
(7.5.6)
1
Р (bj\ai)
Рассмотрим теперь вместе оба конца канала. Для измерения
неопределенности совместного события для источника и прием-
ника определим аналогично совместную энтропию
<7 s
ЯГ(АВ)=2 ^ Р(аг, b}) log,
1
Р (at.bj)
(7.5.7)
Исследуем сначала совместную энтропию в частном случае,
когда А и В статистически независимы для всех i и / (это озна-
чает, что выход не зависит от входа).
Условие независимости выражается равенством P(ai, bj) =
=p(ai)p(bj). Поэтому совместная энтропия равна
<7 s , Г 1 1 Till
Wr(A,B)= 2 J р(аг)р(Ь7-) l°gr +logr — .
i=i i—i i- >
Поскольку
<Z s
S p(ai)=l и 3
f=i /=1
получаем (при независимых входе и выходе)
НГ(А,В) = НГ(А) + НГ(В). (7.5.8)
Обычно выход канала зависит, по крайней мере частично, от
входа (в противном случае зачем использовать канал?,). Тогда мож-
но записать
Р(йг,6;) = р(аг)Р(^.|аг),
и совместная энтропия равна
Q S
НТ(А,В) = % J] P(at, bj) \оёг
»=i /=1
1
p(«i)
Q s
+ 2 2 p (at b}) iogr
i=l /=1
1
p (Mat)
J]o s p(ai’ =p(ai)- Поэтому
HT(A,B)= 2 p(fl;)]ogr
i=l
1
P (Of)
Q S
+ 2 2p(«^)i°&-
i=l /—1
= Hr(A) + Hr(B\A).
(7.5.9)
Совместная энтропия равна сумме энтропии источника и услов-
ной энтропии при заданном Д.
Условная энтропия НГ(А\В) представляет собой потерю1 ин-
формации в канале при движении от входа к выходу. Она соот-
ветствует величине, которую нужно добавить к энтропии источ-
ника для того, чтобы получить совместную энтропию. Обычно
НГ(А\В) называется неопределенностью, а также энтропией шу-
ма в канале.
Поскольку А и В симметричны, то имеется, конечно, соотно-
шение, аналогичное (7.5.9):
НТ(А,В) = Нт(В)-\-Нт(А\В). (7.5.10)
Таким образом, в этом разделе были определены различные
энтропии: 77(B) равенством (7.5.2), Н (А, В) равенством (7.5.7),
Н(А\В) равенством (7.5.4), /7(В|А) равенством (7.5.6),
Н (A\bj) равенством (7.5.3) и Н (В |at) равенсвом (7.5.5). Каж-
дая из этих энтропий определяется соответствующим распределе-
нием вероятностей.
7.6. Взаимная информация
Рассмотрим снова систему передачи сигналов, показанную на
рис. 7.2.1. Входными символами являются а;, выходными — bj и
канал задается условными вероятностями Pt,j.
До приема выходного символа вероятность входного щ равна
Эта вероятность называется априорной вероятностью сим-
вола щ. После приема bj вероятность того, что был послан вход-
ной символ «г становится равной P(at\bj), т. ё. условной вероят-
ности аг при заданном bj. Эта вероятность называется апостери-
орной вероятностью символа bj. Изменение вероятности измеря-
ет, сколько получатель узнал, приняв bj. Идеальный канал, в ко-
тором отсутствует шум, характеризуется тем, что апостериорная
вероятность равна 1, поскольку, приняв bj, можно точно узнать,
что было послано. На практике ошибками пренебречь нельзя, по-
этому приемник не может абсолютно точно узнать, что было по-
слано. Разность между информационной неопределенностью до
(априорные вероятности) и после приема bj (апостериорные ве-
роятности) измеряет информационный выигрыш от приема bj.
Эта информация называется взаимной информацией и определи
ется естественным образом.
7(аг; —10gr|^7nT“J = 10gJ^rvl • (7-6-1)
Lp («r)J [в L p(«i) J ’
Если две вероятности p(Ci) и P(ai\bj) равны, то информа-
ционный .выигрыш отсутствует и взаимная информация равна ну-
лю. Передачи информации не происходит. Взаимная информация
может быть положительна только в том .случае, если после прие-
ма bi мы узнаем что-либо новое о вероятностях
Умножим числитель и знаменатель дроби под знаком логариф-
ма в (7.6.1) на p(bj). Поскольку
Р tfli I b^ р (b}) = P(at,bj) = P (bj | at) p (at),
имеем
7 (аг; Ь}) = logr [P (at, bj)/p (at) p (bj)] = I (bj; at).
Взаимная информация 7 (ar, bj) обладает следующими свойст-
вами.
1. Вследствие симметрии а; и bj имеем
I {«t; ^) = logr [Р (at\Ь})/р (аг)1,
/ (bj; at) = logr [P (bj| at)lp (b$\,
I(at - bj) = I(bj-, ai).
2. Имеем также
Нъ; bj)^I(ai). (7.6.3)
Это вытекает из определения 7(аг-) =logr[l/p(ai)] и равенст-
ва 7 (ar bj)=logrP(ai\bj)+I(а{).
Максимальное значение вероятности P(at\bj) равно 1, так что
максимальное значение логарифма этой вероятности равно 0, по-
этому 1(аг, bj)^.I(ai).
3. Если cti и bj независимы, т. е. если P(ai\bj)=p(ai) или,
эквивалентно, если P(ai, bj)—p(at)p(bj), то
7(аг; Ь}) = 0. (7.6.4)
Вследствие неизбежного шума поведение канала можно по-
нять лишь в среднем. Поэтому начнем усреднять взаимную ин-
формацию, используя соответствующие распределения вероятно-
стей на алфавитах. Имеем
Аналогично
7(A; b}) = % Р(at\bj) I (at\ bj) —
i
I (аС, B)=^P(bj\at) log/Ц^
j [ p\bj)
(7.6.5)
(7.6.6)
Окончательно получаем
/(Л; B)=S Р(аг)/(«г; В) =
= Х^Р(а„ Ь,} Ю& [М] _ I (В; Л) (7.6.7)
п0 симметрии. Первые две величины, определяемые равенствами
(7.6.5) и (7.6.6), называются условными взаимными информация-
ми. Величина I(Л; bj) измеряет прирост информации при прие-
ме bj. Величина I (ар, В) дает прирост информации об алфави-
те В, если был послан символ а<.
Третья величина I(Л; В), симметричная относительно Л и В,
дает прирост информации во всей системе и зависит не от кон-
кретных входных и выходных символов, а лишь от их частот. Эта
величина называется взаимной информацией системы и облада-
ет следующими свойствами.
1. /(Л; В) 2^0 (в силу фундаментального неравенства из разд.
6.4).
2. /(Л; В)=0 в том и только том случае, если Л и В неза-
висимы.
3. I(Л; В) =1 (В-, Л) (по симметрии).
Различные энтропии можно связать друг с другом при помо-
щи следующих алгебраических преобразований:
НЛ-. B) = s t p(°b^)iogR£bM-l =
t=l/=1 Lp(ai)p(Oj)J
= S 3 P(ai,bj)[logP(ai,bj)-~\ogp(ai)—\ogp(bj)] =
i=l /=1
= >4^] +
+^p(flf)log
i
1
P (bj)
= H(A) + H(B)— H (Л,В)>0.
+ ^p(bj)log
i
Используя (7.5.9) и (7.5.10) из предыдущего раздела, т. е. ра-
венства
И (Л; В) = Н(А) + Н(В\А)
= Н(В) + Н(А\В),
получаем два следующих результата:
Z (Л; В) = Я(Л)—Я(Л|В)>0
= #(В)—Я(В|Л)>0.
Поэтому
0<Я(Л|В)<7/ (Л),
0<#(В|Л)^Я(В);
Н(А,В)^Н (А)+ Н (В).
(7.6.8)
(7.6.9)
(7.6.10)
Неравенство (7.6.10) показывает, что совместная энтропия
ксимальна в случае, когда оба алфавита независимы.
В качестве примеров соотношений между введенными величщ
нами дадим следующие выражения для средней взаимной инфор,
мадии
И (А) + Н(В)—Н (А, В),
/(Д; В)= Н (А) —Н (Д|В),
И (В)—Н(В\А).
Неопределенность равна
Н(А\В) = Н(А)—I (А; В),
Н(В\А) = Н(В)—/(Д’; В).
Совместная энтропия равна
>Н(А) + Н(В)-ЦА; В),
Н(А; B) = i Н (А) + Н (В\А),
\Н(В) + Н(А\В).
7.7. Теорема Шеннона для семейств кодов
Выше указывалось, что в случае марковского процесса выгодно
использовать в различных состояниях различные алфавиты. Зада-
дим следующий вопрос: «Каков наиболее эффективный метод ко-
дирования источника?» При этом не будем обращать внимание
на практическую возможность реализации метода. Предположим,
что принят некоторый символ bj; каким образом можно было осу-
ществить оптимальное кодирование Ответ дается неравномер-
ным кодом Хаффмена, который зависит от P(a.i\bj). Этот код бу-
дет, конечно, меняться с изменением bj. Если использовать в каче-
стве /-го кода более удобный, но несколько менее эффективный
код Шеннона — Фано, то при получении bj для различных сле-
дует выбирать кодовые слова, длины k, j которых определяются при
обычных условиях (для всех i и фиксированного /)
logr [1/Р («г |&,)]< Ц. j < Iogr [ 1/Р (ог | &;)] + 1 (7.7.1)
или
Р(йг|^)>1/Л/>Р(яг1Ь7)/г.
Поскольку 2 Р(ailbi) = 1,
i=l для /-го кода выполнено неравенство Крафта, и Входной символ Код 1 КОД 2 Код s
для каждого j существует
мгновенный код. Пусть дли- ны li,j Для различных ко- С1 ‘1’1 ^2’1 4*2 ^2’2 4>s ^2»S
дов такие, как указаны в ^’1 /в>2
таблице:
Умножим соотношение (7.7.1) на P(ai|fej) и просуммируем по
есем i. По первой теореме Шеннона для /-го кода имеем
Q
Н(A\b}) P(at\b})bi./ = Lj<zH (Л|&у) + 1,
i=l
где Li — средняя длина /-го кода. Этот код должен использовать-
ся только в том случае, когда получен символ bj.
Поскольку вероятность получения bj равна p(bj), то, усредняя,
получим
8 q s
Н(А\В)^ p(bj)H(A\b})^ 2 p^P^^L,
7=1 i=l ;=1
где L — средняя длина кода, и снова
H(A\B)^L<H(A\B) + 1.
Переход к расширениям требует громоздких обозначений. Ясно,
однако, что при этом происходит: энтропии возрастают в п раз.
Поэтому, как и ранее, для и-го расширения имеем
Н (A IB) L (п)/п <Н (Л |В) + 1/п.
При достаточно большом п можно получить среднюю длину
кода, сколь угодно близкую к условной энтропии /7(Л|В). Таким
образом, теорема Шеннона о кодировании без шума обобщена на
семейство мгновенных (однозначно декодируемых) кодов.
Глава 8
Пропускная способность канала
8.1. Определение пропускной способности канала
Пусть заданы условные вероятности P(fej|aj) =Pi, j, опреде-
ляющие канал. Чему равно наибольшее количество информации,
которое можно передать по такому каналу? Этот вопрос является
основным в данной главе.
Взаимная информация связывает оба конца канала. Она опре-
деляется равенством (7.6.8).
/(А; В) = Н(А)—Н(А\В),
где Н(Л) — неопределенность источника до приема В, а Н(А\В) —
неопределенность источника после приема В. Таким образом,
I(Л; В) выражает изменение количества информации. Другое вы-
ражение для I(Л; В) задается соотношением (7.6.7)
I (Л; В)=2 р(а> Ь) logr
А.В
в котором опущены индексы и очевидным образом обозначены
Множества, по которым производится суммирование.
Р(а, Ь)
Р (а)Р (6)
В соотношение входят частоты входных символов р(а).
примере двоичного симметричного канала было показано (см
разд. 7.4), что неудачный выбор р(а) для данного канала может
сделать бессмысленной е.го работу. Ясно, например, что если ве-
роятность одного из символов равна 1, то вероятность всех других
равна 0, а постоянный сигнал не содержит информации. Как вы-
брать значения р(а), при которых по каналу передается наиболь-
шее количество информации, и чему оно равно?
Отложим задачу выбора р(а) и используем следующий стан-
дартный математический прием: определим пропускную способ-
ность канала как максимальное количество информации по всем
возможным выборам р(а):
C = max I (А ; В).
Р (С)
(8-1.1)
При таком определении пропускная способность зависит толь-
ко от Р(Ь|а), а нахождение соответствующего распределения р(а)
откладывается на более позднее время. Вероятности р(Ь) опре-
деляются по р(а) и Pitj с помощью соотношений (7.3.1). При этом
не возникает вопроса, как получить взаимную информацию, пре-
восходящую пропускную способность канала С, поскольку по
определению С является максимальным значением информации.
8.2. Канал, симметричный по входу
Из равенств (7.6.8) получаем следующее выражение для вза-
имной информации:
I (Л; В) = ЯГ(В)-ЯГ(В|Л).
Из соотношения (7.5.6) имеем
7(Л; В) = Яг(В)-2
*“7 Pin
1
Р(6|а)
= 77Г(В)-
А В
— S P(b\a)\ogT
P(b\a)
А В
В случае кодов, обладающих высокой степенью симметрии, на-
пример кода с проверкой на четность и с обнаружением ошибок,
совершенный код с исправлением ошибки, каждое кодовое слово
(здесь оно рассматривается как входной символ) в некотором
смысле эквивалентно любому другому кодовому слову; вероятно-
сти ошибок различных слов совпадают. Например, каждое кодо-
вое слово можно перевести в слово 0, 0, ..., О (в двоичной системе),
меняя .каждый единичный символ этого слова на нулевой. Если
в канале имеется белый шум (а большинство кодов предназначены
именно для таких каналов), то элементы каждой строки матрицы
канала получаются перестановкой элементов первой строки. Мно-
жества переходных вероятностей для каждого символа совпа-
дают.
Предполагая, что каждая строка является перестановкой пер-
вой
строки, получаем, что сумма
3 Р(Ь\а) logr
в
1
Р(6|а)
(8.2.1)
= №
е зависит от а. Независимо от того, какой символ а был выбран,
эта усредненная величина будет одна и та же. Поэтому можно
просуммировать по всем символам алфавита В и получить
I(A; B) = Hr(B)—W^p(a) = Hr(B)—W. (8.2.2)
А
Поэтому естественно ввести следующее определение.
Определение. Матрица канала, симметричного по входу, име-
ет вид
Рц Р12 ... P1S
Р-21 Р%2 ... Pis
Pill Р Q2 ... Р QS
где каждая строка является некоторой перестановкой первой
строки.
Предположим, что канал представляет собой расширение дво-
ичного симметричного канала. Каждый символ канала является
блоком из п двоичных символов, а каждый двоичный символ вы-
бирается независимо от других с вероятностью успеха Р (и ве-
роятностью неудачи Q). При таком определении коды с обнаруже-
нием ошибок и совершенные коды с исправлением ошибок соответ-
ствуют каналам, симметричным по входу.
I В качестве тривиального примера рассмотрим канал без шу-
ма, в котором каждый входной символ а переходит ровно в один
выходной символ Ь', другими словами, для каждого а ровно одна
вероятность Р(Ь\а) равна 1, а остальные P(fe|a) равны 0. Таким
образом, каждое слагаемое имеет вид
P(b\a) logr [1/Р (&|а)] = 0.
Поэтому 1^=0 и I (А; В) = НГ(В) = НГ(А), что и следовало ожидать.
8.3. Равномерный вход
Для канала, симметричного по входу, разумно использовать
равномерное распределение р(а) на алфавите входных символов.
Из соотношения (8.2.2) получаем, что для такого распределения
Z(A; В) = H%(B)—W. .(8.3.1)
Применим (8.3.1) к двоичному коду длины п, обнаруживающе-
му одну ошибку. Число входных символов q равно 2й”1, поскольку
(вследствие проверки на четность) допустимыми являются только
половина двоичных последовательностей длины п. Ввиду наличия
ошибок в канале на выходе можно получить любую двоичную
Число случаев Тип Вероятное ть последовательность. Имеем таблицу (в ко- товой Р обозначает вепоят
1 п п (п—I) Нет ошибок Одна ошибка Две ошибки *0 *0 3 3 1 <О ность отсутствия ошибки Но П7 — У Plh\a\ ЮР 1 ).
2 С (п, k) k ошибок pn-kQk в Lp№) Объединив слагаемые одинаковой вероятности с 0,
получим
(8.3.2)
w = У C(n,k) Pn~k Qk 10g2 Г-----J—
fe=o \_Pn~k Qk
Представим логарифм произведения в виде суммы двух лога-
рифмов: '
(n—k) log2(l/P) + 6 log2 (1/Q). (8.3.3)
Первое слагаемое вносит вклад в сумму (8.3.2):
10g2 (—У' -----—------- 4r±pn-kQk =
\Р ) kl(n — l — k)!n—k
= Р 10g2 ( — 'j У1 ---pn-l-k Qk =
&2\P ) KAn-\-k)\
= nP10g2^-^-^(P + Q)n~1 =nPlog2^y-).
Второе слагаемое в (8.3.3) дает аналогичный вклад в сумму
(8.3.2):
nQlog2(l/Q).
Объединив их, получаем
п [Р log2 (1/Р) + Q log2 (1/Q)] = п Н2 (Р),
где использовано естественное обозначение
Н2 (Р) = Р log2 (1/Р) + Q )og2 (1/Q). (8.3.4)
Поэтому взаимная информация (8.3.1) имеет вид
1(А; В)=Н2(В) — пН2(Р). (8.3.5)
8.4. Коды с исправлением ошибок
В разд. 1.3 указывалось, что иногда процесс кодирования раз-
бивается на два этапа, первый — для надлежащего согласования
источника информации, а второй — для согласования канала.
При желании можно дать определение канала так, чтобы второй
этап включался в канал. В действительности, иногда такое опре-
деление канала представляется более естественным с точки зре-
hI(1H пользователя. Посмотрим, что представляет собой такой
канал.
Пусть задан совершенный двоичный код с исправлением оши-
бок и длина кода равна п, а вероятность правильного приема сим-
вола в канале с белым шумом — Р. Тогда с точки зрения пользо-
вателя вероятности ошибок Pi,, равны следующим выражениям:
Фактическая вероятность
Нет ошибок P’l + nQPn-1
1 ошибка О
2 ошибки О
3 или более ошибок 1 — (вероятность отсут-
ствия ошибок)
Напомним, что в таком канале одиночная ошибка исправляет-
ся, а двойная ошибка превращается в тройную.
Таким образом, ошибки в этом канале, выраженные через
первоначальные ошибки, имеют весьма специфический вид. Одна-
ко к этому симметричному по входу каналу по-прежнему можно
применять методы, приведенные в предыдущем разделе.
Если исправление ошибок реализовано либо аппаратурно,
либо автоматически включается в программу обработки принятых
сигналов, то пользователь видит описанную выше картину. Кроме
того, как указывалось выше, в практических ситуациях, когда
имеется источник с неравными вероятностями появления различ-
ных символов, разумно использовать код Хаффмена, согласован-
ный с источником, а затем применить какой-нибудь код с исправ-
лением ошибок к блокам, составленным из сообщений кода Хаф-
фмена. При проектировании ЭВМ все чаще предусматривается ап-
паратурное обнаружение и (или) исправление ошибок. Вопрос о
том, рассматривать ли это как один процесс кодирования, как два
разных процесса или включать второй этап кодирования в канал,
зависит от вашего желания. На практике всегда ясно, как посту-
пать в конкретном случае.
Задачи
8.4.1. Примените изложенное в этом .разделе к коду длины 7, исправляющему
одну ошибку.
8.4.2. Обобщите материал этого раздела на коды с минимальным расстоянием 4.
8.5. Пропускная способность
двоичного симметричного канала
Если Р — вероятность правильной передачи, то переходная
матрица двоичного симметричного канала (рис. 8.5.1; см. разд. 7.4)
Р <2\
Q Р)'
Пусть р — вероятность выбора символа п = 0. Тогда 1—р есть
вероятность выбора символа а=1, и взаимная информация для
этого симметричного по входу канала задается равенством (8.2.2).
Используем логарифм по основанию 2 и временно пропустим иц.
деке 2 у энтропии Я, тогда I (Л; В) = Н— где с учетом (8.2.1)
r==S ^(b|a)l°g = log(v) +£log(^-J = /7<O.
Последнее равенство следует из (8.3.4), поэтому
7 (Л; В) = Н(В)—Н(Р).
(8.5.1)
Рис. 8.5.1
Для нахождения Н(В)
[ом. i(7.4.1]
р(Ь = 0)=рР+(1— p)Q,
+ (1—р)Р. Легко видеть,
+р(Ь=1)=1.
Для удобства положим
заметим, что
p(b=l)=pQ+
что р(Ь = О)-{-
P(b=O) = pP + (l-p)Q = x. (8.5.2)
Тогда р(Ь=1) = 1—х, и, используя обозначения в (8.3.4),
I (Л; В) = х log (1 lx) + (1 —х) log [1/(1 ~х)]—Н (Р) = Н(х)—Н (Р).
Для, того чтобы найти пропускную способность канала С, от-
ветим на следующий вопрос: «При каком выборе вероятности р
взаимная информация /(Л; В) будет наибольшей?» По отношению
к переменной х, тот же вопрос можно сформулировать следующим
образом: «При каком значении х максимальна функция Н(х) =
= х log (~) + (1— X) logf-T-)?»
\ х / \ 1 — х/
Из разд. 6.4 следует, что максимальное значение достигается
при х=1/2 и Н(1/2) = log 2/2 +log 2/2=log 2= 1.
Поэтому пропускная способность канала
С = шал/(Л; В) = 1— Н (Р). (8.5.3)
А
Из (8.5.2) можно найти значение р следующим образом:
х=1/2 = рР+(1— p)Q,
-|- = рР+(1—р)(1—Р) = рР+1—р—Р+рР.
Перенося некоторые слагаемые в другую часть равенства и груп-
пируя их, получаем (1—2Р)р=(1—2Р)/2.
Поскольку вероятность канала Р не равна 1/2 (в противном
случае информация не передается), можно разделить обе части
равенства на 1-—2Р и получить, что р=1/2. Соображения симмет-
рии приводят, конечно, именно к этому результату.
Таким образом, показано, что пропускная способность двоич-
ного симметричного канала задается выражением
С=1—Яа(Р) (8.5.4)
и достигается, когда два входных символа выбираются с одина-
ковыми .вероятностями.
8.6. Условная взаимная информация
Как в более общем случае можно найти вероятности символов
р(а), дающие пропускную способность канала? В этом разделе
приводится один полезный результат, который во многих случаях
помогает ответить на поставленный вопрос.
Возвращаясь к общему каналу, можно написать
ЦА; В)=2 Р (°) 2 log (ЦтЦ = 2 В),
А В \ Р("> / А
где введена условная взаимная информация
Ца; В)= 2 Р(Р\а) log
в
Р(Ь\а) \
Р(Ь) / ’
В общем случае / (с; В) зависит от а. Однако имеет место сле-
дующая теорема: если вероятности входных символов выбраны
так, что достигается пропускная способность канала С, то
Ца-, В) = С
для каждого а {для которого р(а)#=0).
Для доказательства этого предположим, напротив, что для
некоторого символа а\ эта величина превосходит С. Поскольку
среднее значение всех I {а; В) равно С, то для некоторого символа
а2 эта величина должна быть меньше С. Таким образом, Цар В)>
>С, Цсц- В)<С.
Рассмотрим бесконечно малое изменение, которое увеличивает
p(fii) и уменьшает р(й2) на одно и то же значение (сохраняя сум-
му вероятностей, равной 1). Скорость изменения /(Д; В) задается
разностью
[51(Д; В)/др{а1)] — [дЦА; В)/др(а2)].
Однако изменение вероятностей р{а) индуцирует изменение веро-
ятностей р{Ь). Скорость изменения каждой вероятности р{Ъ) рав-
на P(b|ai)—P(b|a2). Из выражения 1(Д; В) = 2 р{а) 2 Р(Ь|а) X
Xlog
Р (b\a) 1
. Р (а) J
для взаимной информации получаем, что общая ско-
рость изменения /(Д; В) равна.
2 Р(6|о1) log
В
-3 P(6|fl2) log
Р (b) J в
Р(Ь\а2)
РФ)
+ 2 р <а) I ~2 p(fcia)
А I В
[PtylaJ—P (Ь|а2)]| =
= /(ах; (В)—/(а2;В) —2 2 Р
В А
Р(Ь\а)
Р(Ь)
X
X [P^laJ—Р(Ь|О'2)] = /(а1; В) — Ца2; В) —V
в
-^|а2)] = /(а1^В)-/(а2; В)-(1-1) = /(а1; В)-/(а2; В) XX
Поскольку скорость передачи равна пропускной способности
канала, т. е. своему максимально возможному значению, и по-
скольку мгновенная скорость изменения при указанном прираще-
нии положительна, то при достаточно малом изменении p(fii) и
р(а2) можно получить скорость передачи, большую пропускной
способности. Поэтому предположение о том, что существует сим-
вол, для которого /(ai; В) больше пропускной способности, невер-
но. Если скорость передачи равна пропускной способности, то для
каждого входного символа условная взаимная информация равна
пропускной способности.
Этот результат в различных конкретных ситуациях часто может
помочь найти вероятности р(а), при которых достигается пропуск-
ная способность канала; эти вероятности можно искать одну за
Другой.
Глава 9
Предварительные математические сведения
9.1. Введение
Некоторые считают, что теорема доказана, когда приведено
логически правильное доказательство; другие считают, что теорема
доказана только в том случае, когда студент видит, почему она
обязана быть верной. Автор стремится придерживаться второй
точки зрения. Поэтому сейчас сделаем отступление и докажем,
а не просто сформулируем ряд результатов, необходимых для по-
нимания доказательства основной теоремы Шеннона. Изложение
будет достаточно подробным для того, чтобы читатель мог прочно
усвоить соответствующие результаты, а не просто ознакомиться
с ними. Поэтому в ряде случаев будут приведены сведения, не ис-
пользуемые в дальнейшем.
Две основные идеи — это идея n-мерного пространства и за-
кон больших чисел. Два математических результата — это при-
ближенные формулы для п! и для некоторых сумм биномиальных
коэффициентов. Выше уже было показано, что n-мерное простран-
ство оказывается полезным для представления кодовых слов. По-
скольку для достижения энтропии и, следовательно, пропускной
способности канала нужно использовать расширения кодов, раз-
мерность пространства при доказательстве действительно будет
очень большой.
Причина, по которой необходим закон больших чисел, состоит
в том, что вблизи оптимальных скоростей передачи информации
число ошибок в кодовом слове оказывается очень большим. Ис-
следование распределения вероятного числа ошибок является
центральным при доказательстве основного результата Шеннона.
Нам нужно будет также оценить хвост биномиального распре-
деления, чтобы показать, что его вклад не очень велик. Поэтому
потребуется знаменитая приближенная формула Стирлинга для
п\. Эта формула часто используется, но редко просто объясняется.
9.2. Гамма-функция Г(и)
Начнем с исследования некоторого определенного
как функции параметра п. Рассмотрим интеграл
Г (п) = J е~х 1 dx .
о
Показатель п—1 берется для удобства. При п> 1
полнить интегрирование по частям и получить
интеграла
(9.2.1)
можно вы-
Г(п) = х«-1
4~ (п— 1) J е—х хп~2 dx
о о
или
Г (п) = (п— 1) Г (п— 1).
При п= 1 имеем
Г (1) = J e~xdx= —е—х | = 1,
о о
Следовательно, для целых п
Г(2) = 1,
Г (3) = 21,
Г(4) = 31,
Г (и) = (и—1)1 (п=1,2,.„).
Гамма-функция дает естественное обобщение факториала, по-
скольку интеграл существует и для нецелых п.
Рассмотрим далее гамма-функцию в точке 1/2. Имеем
Г (1/2) = J е~х х~1/2 dx.
о
Подстановкой x—i2 можно избавиться от корня и привести инте-
грал к виду
ОО о / сю
Г (1/2) = J е-<2 — dt = 2 J e-i2 dt.
о * о
Поскольку подынтегральное выражение является четной функ
цией, тот же интеграл можно записать в виде
Г (1/2)= J e~t2dt.
-—сю
Этот интеграл часто называется интегралом ошибок.
Рассмотрим далее произведение
сю сю
Г (1/2) Г (1/2) = j e~x2dx j e~y2dy.
—СЮ ’—сю
Формально переходя к полярным координатам, получаем
2л <50 -—Г2 оо
[Г (1/2)]г= J J e~r2 rdrdG = 2л -—| = л.
0 0 2 о
Поэтому Г(1/2) = ]Лгс.
Для обоснования формального перехода к полярным координа-
там предположим, что рассматривается интеграл
I(L)= j е~хг dx j e~y2dy.
х
Из рис. 9.2.1 видно, что
2л L
j $e~r2rdrde^I(L
о о
2л LV2
sC J j е~'2 rdrd 6
о о
или
-t (1 _е-ь2) I (L) л (1 — e-2L2).
При L-^-oo получаем л^/(оо) =
= Г2(1/2)^л.
Рис. 9.2.1. Взаимосвязь прямоуголь-
ных и полярных координат
Таким образом, переход от прямоугольных координат к поляр-
ным обоснован, и равенство Г(1/2)= л доказано.
9.3. Приближение Стирлинга для п\
Приближенная формула Стирлинга имеет вид
и! ~ пп е~~п 2ли.
(9.3.1)
Несмотря на то, что она часто используется, ее полное доказатель-
ство приводится сравнительно редко. Приведем его, поскольку нам
нужна формула Стирлинга.
Величина и! является произведением, а искать приближенные
формулы для произведений довольно трудно. Поэтому будем
п
искать приближенное выражение для log и!: logn!=21og/j (все
/г=1
логарифмы в этом разделе берутся по основанию е). Вместо сум-
мы рассмотрим интеграл (берется интегрированием по частям):
п п
у logx<ir=(xlogx—х)| = п log п—n-f-1. (9.3.2)
1 1
Используя для приближенного вычисления интеграла правило
трапеций (рис. 9.3.1), получим оценку снизу. Поэтому
f log xdx > 2- log 1 + log 2 +log 3 + ...+
i 2
log (n— 1) + -j- log n = log n\-log n.
Применяя (9.3.2) и перенося один из членов в левую часть,
имеем
п logn—n + -^-logn+ 1 logn!
Беря антилогарифмы, получаем
пп&—"]/пе (9.3.3)
Для оценки интеграла сверху используем формулу интегриро-
вания по средним точкам и заметим (рис. 9.3.2), что если повер-
нуть горизонтальный отрезок, соответствующий средней точке, так
чтобы он касался кривой, то площадь под ним не изменится. Для
первого отрезка длиной 1/2, 1 ^х^З/2, оценим площадь под кри-
вой площадью треугольника, образованного касательной при х=1
и равного 1/8. Для последнего отрезка длиной 1/2 используем ма-
ксимальное значение функции, равное log/д и получим оценку
0,5 log п. Поэтому
f logxd№g:-J- +Iog2 + log3+...+
1 8
+ log(n— l) + 4- logn = logn! + 4--J- logn .
2 о 2
Снова воспользуемся (9.3.2) и, перенося два слагаемых в левую
часть, получаем
п log и—п-]- 1---—Ь — logп logп!
8 2
Беря антилогарифмы, имеем
ппе~пУпёг/8 (9.3.4)
Коэффициент С в приближении
nl = nne-nVn С (9.3.5)
с учетом (9.3.3) и (9.3.4) лежит в пределах е7/8^С^е или
2,39887. ..^С^ 2,71823... (9.3.6)
Поскольку ошибка при использовании формулы средних точек
примерно вдвое меньше ошибки при использовании правила тра-
пеций и эти две ошибки имеют разные знаки, то лучшим прибли-
жением для С будет взвешенное среднее
(2 е7/8 4- е)/3 = 2,50534 ... = С. (9.3.7)
Оказывается, что значением С (при бесконечном п) является
V~2ri= 2,50663...
Для точного вычисления коэффициента С (при бесконечном п)
применим следующий прием. Рассмотрим интеграл
Л/2
Ih= j cosfexdx(k^C).
о
При k^2 тригонометрическая подстановка приводит к равенству
я/2 Я/2
Ih = j cosft—2 х (1—sin2 х) dx = Д_2 + у cos*~2 х (—sin х) sin х dx.
о b
Интегрирование по частям дает
Разрешая это равенство относительно Д, получаем рекуррент-
ное соотношение для интеграла:
Д = (^-1)Д_2/й'(/г>2). (9.3.8)
Легко показать, что /1 = 1, 1о = л/2.
Заметим далее, что поскольку cos 1 для всех х из интер-
вала интегрирования, то Ды >Дь>Iik+\ Деля на Дь-i, имеем
1 >Дь/Дй-1>Д/4+1/Д/г-1-
Подставляя значения интегралов из (9.3.8), получаем
1 > 2 k
2ft—1 2fe —3
2ft 2ft —2’"
2
2
2 л 2fe
2 >2ft+ 1 ’
Числитель выражения в квадратных скобках можно сделать
равным (2/г)!, умножив числитель и знаменатель на знаменатель.
Используя равенство 2k(2k—2) (2k—4) ... 2 = 2Чг!, имеем
(2 ft)! 2fe
.2* (ft 1)2* (ft!) J 3>2ft+l
Извлечем квадратный корень из каждого члена (беря положи-
тельное значение корня):
1>г^Г (2Л)! >1Л 1—— -
. (ft!)222fe J |/ 2ft+1
Наконец, подставляя приближенное выражение (9.3.5) п! =
^n^e^l^nC в каждый факториал, получаем
1 > Vnk Г-----(2ft)2fee Jfel/2ftC— - Л-----------1.
22feftfe e-kVkCkk e-fe}/ftC J V + * 1
После сокращения получаем .соотношение
1 >]/2л/С>[1 —1/(2й+1)11/2.
Поэтому для больших k С—>- 2л.
Таким образом, получена приближенная формула Стирлинга.
Как показывает табл. 9.3.1, отношение приближенного значения,
вычисленного по формуле Стирлинга, к точному значению, удиви-
тельно близко к 1 даже для небольших значений п. Эта таблица
показывает, что приближение является относительно точным при
п->оо, однако разность точного и приближенного значений не стре-
мится к 0.
Таблица 9.3.1
Приближение Стирлинга
Значение по формуле
Стирлинга
Точное значение
Отношение прибли-
женного значения
к точному
1 0,92214
2 1,91900
3 5,83621
4 23,50618
5 118,01916
6 710,07818
7 4 980,3958
8 39 902,395
9 359 536,87
10 3 598 695,6
2
6
24
120
720
5 040
40 320
362 880
3 628 800
0,92214
0,95950
0,97270
0,97942
0,98349
0,98622
0,98817
0,98964
0,99079
0,99170
9.4. Биномиальная оценка
Другой необходимый математический результат состоит в вы-
числении числа вершин единичного куба из разд. 3.6, лежащих
на сфере радиуса кп. Другими словами, нужна оценка суммы бино-
миальных коэффициентов
1 + С(л,1) + С(п,2) + .„ + С(п,Ь), (9.4.1)
где 1/2. (Предполагается, что кп — целое число.)
Поскольку ХС1/2, члены монотонно возрастают, так что наи-
большим слагаемым является последнее.
С(п, Хп) = п!/[(Хп)! (п—А,и)!]. (9.4.2)
Применяя к каждому факториалу формулу Стирлинга, полу-
чаем
С (п, Ъп)~ ------------- пУ2яп_______________________
(X n)A/1 е~Лп V2лХп (n — X п)п~Лп е^(л1"Ап> У2л(п — Хп)
После перегруппировки членов имеем
С (п, Л. и)~
п
П^п пп~Лп
1
ХАп(1—Х)(1-А)п
е п У 2п "|/л
е-Япе-(п-Лп) [у Ух Уп Т|/2Й У(1 - X) п
Выражения в первой и третьей скобках в точности равны 1, а
выражения в остальных двух скобках дают
С(п, I . Г Г-------------11/2. (9.4.3)
* |УА0~ А J [2лХ(1—Х)п] ' '
Логарифм по основанию 2 знаменателя в первых скобках равен
log[XA(l — V-Al = Mog2i + (l— X) log(l— %) = - Я (%),
так что первый множитель в (9.4.3) есть
2пН<А>. (9.4.4)
Второй множитель — константа, умноженная на п~1/2.
Перепишем теперь исходную сумму (9.4.1) в обратном порядке
С(п,Кп)-\-С(п, Хи— 1) У „, + С(и, 1)4-1
и оценим ее суммой геометрической прогрессии. Для того чтобы
получить знаменатель этой геометрической прогрессии, заметим,
что, переходя. от одного слагаемого к другому при обычном по-
рядке записи (9.4.1), можно найти каждый биномиальный коэф-
фициент, умножая предыдущий последовательно на величины
п/1, (п—1)/2, (и—2)/3,..., (п—%n-|- 1)Ап.
Если начать с наибольшего члена С(п, Кп) и двигаться в об-
ратном порядке, нужно умножать на величины, обратные приве-
денным выше и расположенным в обратном порядке:
Кп/(п—Кп+ 1),..., 3/(п—2), 2/(n—1), 1/п.
Требуется оценить эти числа. Оценкой сверху этих чисел является
Z,/(l—X), так что оценка сверху суммы биномиальных коэффициен-
тов получается умножением наибольшего слагаемого на
- V (-Мт =______________!____=— (9.4.5)
£oV~V 1 — X/(l—X) 1—2Х' v
Подставляя все это в (9.4.1), используя (9.4.4) и (9.4.5),
лучаем
по-
C(n,k)^2nH<n
Л=0
1
2лХ(1 —X)
i-z / j_\1/2
1 — 2лД п )
Для всех п, таких что и^(1—Z,)/[2nZ,(l—2Z,)2] (напомним, что
С1/2), произведение последних трех сомножителей меньше 1. По-
этому для достаточно больших п
Яп
2 C(n,k)^2nHw>, (9.4.6)
k=0
где Н(&) — значение энтропийной функции в точке Z. Это нера-
венство потребуется нам позже.
9.5. Евклидово «-мерное пространство
Термин ««-мерное пространство» означает, что рассматрива-
ются п независимых переменных х}, х2, ..., хп. Термин «Евклидово»
означает, что используется Евклидово расстояние
Л + А+... + *2„ = г2 (9.5.1)
и можно определить сферу радиуса г с помощью этого выражения.
Так же как в классической Евклидовой геометрии, здесь легко
видеть, что объем «-мерного шара зависит от радиуса г как гп.
Для этого объема имеем
Vn(r) = C„r% (9.5.2)
где Сп — константа, зависящая от п. Например, С2=л и С3 = 4л/3
(заметим, что Ci = 2).
Для нахождения значений Сп используем тот же прием, что и
в разд. 9.2, где мы умножали интеграл, задающий гамма-функ-
цию, на себя, и переходили к полярным координатам (там этот
прием работал весьма успешно). Рассмотрим произведение п
таких интегралов. Имеем [с помощью (9.5.1)]
[Г (1/2)]” = л”/2 = J J ... j e-r‘dx1 dx2_ dxn=
•—OO -00 --ОС
= 7e--^dr.
о dr
Для того чтобы получить последнее равенство нужно провести
простое рассмотрение сферического слоя толщины Аг и сравнить
это равенство с результатом, полученным для двумерного про-
странства
r2d(nrz) , „7 . .
j е~г —----dr = 2л ( e~r rdr,
о dr о
Для которого в разд. 9.2 фактически использовался тот же прием
(хотя там он казался очень привычным).
Таким образом, с учетом (9.5.2) имеем
зт"/2 = Сп J е~r2 nr"—1 dr.
о
Положим r2—t. Тогда dr=Q,6t~1/2dt и
лп/2
„с °0 Дп—1)/2
f ег~* ---------dt=
2 oJ t1'2
=7e-tt(n/2-i) dt=^ г f—^=cnг f—+1 .
20 2 \ 2 / \ 2 /
Поэтому
Сп = л"/2/[Г(п/2+1)].
Легко показать, что C7l=2nCn_2/n, что позволяет составить табли-
цу (для объема единичного шара в n-мерном пространстве).
п Сп п сп
♦ 1 2=2,00000... 6 л3/6=5,16771...
2 л;=3,14159... 7 16 л3/105=4,72477...
3 4л/3=4,18879 ... 8 л4/24=4,0б871...
4 зг2/2= 4,93480... . . . - . .
5 8л2/15=5,26379... 2 k з1*/й!->0
Из таблицы видно, что объем единичного шара, или, другими
словами, коэффициент при гп, принимает наибольшее значение
при п=5 и затем сравнительно быстро убывает до 0, когда п-»-оо.
Для n=2k объем n-мерного шара радиуса г равен
(лЛ /А!) г2к = (л r2)k /k\
Отсюда сразу видно, что если Л>№, то увеличение k (или, что
эквивалентно, увеличение п) приводит к уменьшению объема. В
действительности, для заданного (сколь угодно большого) радиуса
г можно увеличить размерность п пространства настолько, что
объем шара радиуса г будет сколь угодно малым. Для пространств
нечетной размерности, исходя из первоначального определения
Г(п) по формуле (9.2.1), можно получить, что
Vn (г) = Спгп = л"/2 г" /[Г (n/2 + 1)].
Это выражение плавно меняется при увеличении п.
Найдем теперь долю объема n-мерного шара, лежащего на
расстоянии в от его поверхности (здесь в может быть сколь угодно
малым положительным числом). Имеем
объем слоя Сп г” — Сп (г — е)" । f ।____е
объем шара Cn г” \ г /
Это выражение стремится к 1 при увеличении п. Таким образом,
Б пространствах большой размерности почти весь объем шара
сосредоточен вблизи его поверхности. В действительности, если
требуется выполнить условия, чтобы слой был достаточно тон-
ким, а доля объема была достаточно близка к 1 (скажем, 99,44%),
можно найти такое По, что при всех п, больших п0, оба эти усло-
вия будут выполнены. Внутри шара большой размерности прак-
тически ничего нет; почти весь его объем сосредоточен на поверх-
ности.
Задача
9.5.1. Покажите, что для любого семейства подобных друг другу выпуклых фи-
гур «почти весь объем сосредоточен на поверхности».
9.6. Один парадокс
Результаты этого раздела в дальнейшем не используются; они включены для
того, чтобы показать, насколько ненадежны наши интуитивные представления
о сферах в Евклидовом «-мерном пространстве.
Предположим, что, как показано на рис. 9.6.1, задан квадрат размером 4X4
с центром в точке (0, 0) и в каждом из четырех углов квадрата расположен
круг единичного радиуса. Найдем радиус круга с центром в начале координат,
который касается изнутри этих четырех кругов. Он равен
г2 = 1/(1 — 0)2 — (1 — 0)а — 1 = Т/2- —1=0,414...
Рассмотрим далее аналогичную ситуа-
цию в трехмерном пространстве. Имеется
куб размером 4X4X4 с восьмью единичны-
ми шарами в углах. Радиус внутреннего ша-
ра равен Гз=]/3—4 = 0,732...
Рассмотрим, наконец, аналогичное по-
строение в «-мерном (пространстве. Имеется
куб размером 4X4X4... Х4 с единичными
шарами в углах, каждый из которых каса-
ется соседних шаров. Шары правильно упа-
кованы. Расстояние от начала коорди-
нат до центра произвольного шара равно
У\1—0)2+(1—0)2+-..+ (1—0)2=]/пГ Сно-
ва вычитая радиус углового единичного
него «-мерного шара
Рис. 9.6.1. Парадокс
шара, получаем радиус внутрен-
Гп = Т/«—1- (9.6.1)
При «=10 он равен Гю= ]/10—1=3, 16 ... —1=2,16 ... >2, и внутренний
шар вылезает за пределы куба! Возможно ли это? Шары, конечно, являются вы-
пуклыми фигурами, расстояние — правильным Евклидовым расстоянием, радиу-
сы угловых шаров равны, конечно, единице, так что сделанный вывод неизбежен.
При пГэИО внутренний шар вылезает за пределы куба, что противоречит всем
обычным представлениям.
Дальнейшие «чудеса» получаются, если рассмотреть отношение ооъема вну-
треннего шара к объему всего куба при разных п. В частном случае, когда ____
четное число, n — 2k, используем (9.6.1) и получаем
объем шара (Уп-1)" „ Cl/2fe—l)2ft
отношение = —-------------------— = Сп----------—------ = C2k--------—------
объем всего куба 4” 42й
_ nh (~|/2')2fe (~]/7 )2fe Г / _ 1 \ V2fe _
kl 42ft L\ ~V2k J J ~
nk 2k kk Г/ 1 W2fe~l/2fe
42feftl |\ 1
(9.6.2)
Используя формулу Стирлинга (9.3.1) для k\-. k\~kke_ft"|/2лй и известный
/ 1 V
результат™ анализа Пт ( 1—------- ) =е, из (9.6.2) получаем
х->сс\ х >
~ 2k kk
отношение —-----------
42kkk e-ky^k
e-^^f—Y e~
\ 8 / V231^
(9.6.3)
Но л e/8= 1,06747...
Взяв логарифм по основанию е от обеих частей равенства (9.6.3) при
, _ 1
k-^-oo получаем, что loge (отношение) = (0,065288 ...)k— у 2k——loge &—
1
— loge 2л->оо. Это значит, что множитель (ле/8)Л стремится к бесконечности
быстрее, чем убывают два других множителя и 1/jZ2nk в произведении
(9.6.3).
Следовательно, отношение объема внутреннего шара к объему куба, содер-
жащего все 22к=2п угловых единичных шаров, становится сколь угодно
большим.
Случай нечетной размерности n=2k—1 не меняет положения дел; лишь
детали становятся более запутанными.
Задача
9.6.1. Покажите, что при достаточно большом п прямая, соединяющая начало
координат с точкой (1, 1, ..., 1), становится «почти, перпендикулярной»
всем координатным осям. (Указание: cos 6= 1/1/ пЛ
9.7. Неравенство Чебышева и дисперсия
Если случайная величина X является дискретной, то среднее
значение ее квадрата задается математическим ожиданием
£{№}= § x2iP(Xi).
1=--СО
Если случайная величина непрерывна, то это значение задается
равенством
Е {X2} = j х2р (х) dx.
Поскольку подынтегральное выражение положительно, то для
любого е>0 имеем
J х2 р (х) dx^ J х2 р (х) dx,
—оо |х|»е
что можно записать ,в виде
Е {X2} J х2 р (х) dx J>e2 J р (х) dx.
|х|>е J х |
Следовательно,
E{X2}>e2Prob{|X|>e}
или
Prob{|X|>e}<E{X2}/e2. (9.7.1)
Это знаменитое неравенство Чебышева (справедливое как в непре-
рывном, так и в дискретном случаях).
Дисперсия случайной величины X, обозначаемая через V{X},—
это средний квадрат отклонения от среднего значения Е{Х}=а.
Таким образом, дисперсия случайной величины X равна
V {X} = Е {(X—а)2} = Е {X2}—2, а Е {X} + Е {а2} = Е {X2}—
—2а2 + а2 = Е{Х2}~ а2 = о2.
Ясно, что- поскольку, Е{1} = 1, то для любой константы с
У{с} =0. Кроме того, Е{сХ} =с2Е{Х).
Если Xi и Х2 — независимые случайные величины и
£{Хх}= аг, V{Х1} = о21,
Е {Х2} = а2, V {Х2} = о22,
то Е{(X,—(Х2-а2)} = Е{(Хх-а.)}Е{(Ха-аа)} = 0.
Дисперсия суммы двух независимых случайных величин Xi и Х2
равна
V + XJ = Е {(Хх + Х2- аг- aj2} = Е {(Хх- а,)2} + 2 Е
X (Ха—с2)} + Е {(Х2—а2)2} = V {XJ + V {Х2} = о2х + о22. " (97.2)
Следовательно, по индукции получаем, что дисперсия суммы
произвольного числа независимых случайных величин равна сум-
ме их дисперсий.
Задачи
9.7.1. Проведите доказательство неравенства Чебышева для дискретных случай-
ных величин.
9.7.2. Энтропия — это среднее значение log 1/рг. Найдите соответствующее вы-
ражение для дисперсии. .Ответ: Xp,log2 (1/р»)—Н2.
9.8. Закон больших чисел
Если проделать большое число испытаний Бернулли (это зна-
чит, что успех или неудача являются случайной величиной X при-
нимающей значения 0 или 1 соответственно, и каждое испытание
не зависит от всех других испытаний), то можно исследовать от-
ношение числа успехов к общему числу испытаний. При этом
можно надеяться, что отношение будет стремиться к вероятности
успеха при одном испытании. Для формальной постановки вопро-
са рассмотрим случайную величину Xi, принимающую значение 1,
если i-e испытание было успешным, и значение 0, если i-e испы-
тание было неудачным. Чему равно среднее арифметическое этих
случайных величин? Выпишем формулу для математического ожи-
дания этого среднего. Имеем
£j_L(X1 + X2+... + Xn)}=A2 £{хг} = а,
где а — математическое ожидание одного испытания.
Рассмотрим теперь дисперсию среднего арифметического.
Имеем v
поскольку с учетом (9.7.2) перекрестные члены равны нулю. Так
как все испытания одинаковы, получаем
W—у хЛ=4у, их,.}=-
Теперь можно применить неравенство Чебышева (9.7.1)
Prob ( — V
I п
Это неравенство можно переписать:
Probj —V (Xt — а)
I п
— Е
е2
о2
пе2 '
(9.8.1)
„ 1 \ 1 о2
е > > 1--------.
J по2
Теорема. Слабый закон больших чисел. Если Х2> •••> Хп —
независимые одинаково распределенные случайные величины со
средним значением а и дисперсией -о2, то для сколь угодно малых
е>0 и б>0 существует такое целое число п0, что при всех н>По
б?—в^— [Xj-pX2-T ... + е (9.8.2)
п
с вероятностью, большей 1—6.
Эта теорема утверждает, что среднее арифметическое может
быть сделано сколь угодно близким к математическому ожида-
нию а (по вероятности).
Для доказательства следует выбрать такое п0, что [см. (9.8.1)]
о2/н0в2<6, или «о>о2/бе2.
Поскольку эту теорему обычно понимают неправильно, прервем
изложение и дадим ее интерпретацию. Прежде всего, случайные
величины являются испытаниями Бернулли, т. е. отдельные испы-
«гания независимы — испытания не запоминают того, что случилось
в прошлом. Поэтому представление о законе больших чисел, как об
утверждении того, что любая последовательность неудач будет
позднее «скомпенсирована», является в корне неверным. В дей-
ствительности, любое отклонение от среднего будет после боль-
шого числа испытаний «сглажено» (с большой вероятностью), а
не скомпенсировано.
Далее, закон больших чисел не означает, что сумма становится
близкой к математическому ожиданию, которое, конечно, равно
пр. Например, при 10 бросаниях симметричной монеты можно
ожидать выпадения 5 гербов, однако даже столь большое значе-
ние, как 8, не является неожиданным. При миллионе бросаний
нельзя надеяться получить отклонение 3 (как это было при 8 гер-
бах в 10 бросаниях) от среднего значения; лишь в процентном
отношении с большой вероятностью происходит все более сильное
приближение к среднему значению. Недоразумение возникает в
«случае, если не обращать внимания на то, где стоит п. В действи-
тельности, п стоит в знаменателе, а в таком случае с большой
вероятностью разность между фактическим числом успехов и его
математическим ожиданием, деленная на п, убывает при возра-
стании п. Однако сама разность между фактическим числом успе-
хов и его математическим ожиданием может неограниченно расти
при возрастании п. В этом смысле закон больших чисел напоми-
нает рассмотренную ранее формулу Стирлинга (см. табл. 9.3.1).
Поскольку закон больших чисел играет основную роль в дока-
зательстве теоремы Шеннона, проиллюстрируем его эксперимен-
тально. Пусть вероятность некоторого события (успеха) равна
,р=1/Ю. Чему равна вероятность k успехов в N испытаниях Бер-
нулли? Эти k успехов могут произойти в любых k из N испытаний,
т. е. C(N, k) различными способами; таким образом, вероятность
k успехов (и, конечно, N—k неудач) равна
C(N,k)pk(l— p)N~k. (9.8.3)
Математическое ожидание числа успехов равно pN.
На рис. 9.8.1, по горизонтали отложена величина k/N, так что
распределение (9.8.3) сосредоточено вблизи значения р, равного
математическому ожиданию успеха при одном испытании.
Для того чтобы скомпенсировать сжатие по горизонтальной оси,
отложим величину, в N раз большую функции (9.8.3), т. е.
NC (N, k) pk (1 — p)N~k. (9.8.4)
Таким образом, площадь под кривой постоянна при разных N.
На рис. 9.8.1 показаны распределения для М=10, 30, 100. Видно,
что распределение сосредоточено вблизи р=1/10 и вероятность
уменьшается в точках, находящихся далеко от р=1/10. На рис.
9.8.2 вертикальная ось удлинена, что позволило привести резуль-
таты для М=Ю0, 300, 1000. На кривой, соответствующей М=1000,
нанесены не все точки; если нанести все точки, то кривая будет
довольно гладкой.
Рис. 9.8.1. Пример закона больших
s чисел
Рис. 9.8.2. Пример закона больших чисел
Таким* образом, видно, что если число испытаний N растет,
распределение сосредотачивается вблизи математического ожида-
ния, а дисперсия убывает, как Например, при М=1000 от-
клонение величины k/N от среднего значения, равное 0,05, очень
маловероятно. Вероятность нахождения в любой точке, отличной
от р, может быть сделана сколь угодно малой выбором достаточно
большого N.
Эта теорема будет использована при кодировании сообщений
для расширений очень большой кратности. Можно ожидать, что
распределение деленной на N разности между числом ошибок,
появившихся при передаче блока символов, и математическим
ожиданием числа ошибок может быть сделано похожим на очень
острый пик при достаточно большом N. Напомним, что это утвер-
ждение должно быть верным с вероятностью, близкой к 1!
Задача
9.8.1. Изобразите аналогичные кривые для р=1/2, N=5, 10, 20.
Глава 10
Основная теорема Шеннона
10.1. Введение
В гл. 6 было введено понятие энтропии, а в разд. 6.8 показано,
что существуют методы кодирования со скоростью, сколь угодно
близкой к энтропии входа. В частности, было показано [см. (6.8.2)],
что для n-го расширения при достаточно большом п при средней
длине кода Ln справедливы неравенства
Hr(S)^Ln/n<HT(S) + l/n.
Таким образом, энтропия Hr(S) дает границы того, что можно
достичь, и существует кодирование, которое позволяет сколь угод-
но близко подойти к теоретическому пределу.
Далее рассматривался канал, и пропускная способность С ка-
нала определялась равенством (8.1.1). В настоящей главе дока-
зывается фундаментальный результат того, что даже при наличии
шума можно сколь угодно близко подойти к пропускной способ-
ности канала. Точнее, можно передавать сообщения по каналу со
скоростью, сколь угодно близкой к пропускной способности, и с
надежностью, сколь угодно близкой к 1.
Теорема доказывается для двоичного симметричного канала,
поскольку в этом случае доказательство легче понять, и, кроме
того, такой канал часто встречается на практике. Укажем, как
обобщить идеи доказательства на более общие каналы. Строгое
.доказательство теоремы в общем случае достаточно сложно и не
помогает пониманию того, почему теорема верна.
10.2. Решающие правила
Пусть на приемном конце канала получен символ bj. Какое
следует сделать предположение о посланном символе щ? Это, ко-
нечно, зависит от канала, т. е. от переходных вероятностей
P(bj\a,i), а также от вероятностей символов источника p(ol)=pi.
Для того чтобы почувствовать, в чем здесь дело, в качестве
примера рассмотрим канал с матрицей переходных вероятностей
Pi, j = P(bj\a.i) следующего вида:
bj. Ь% Ь3
t
аг /0,5 0,3 0,2 \
а2->( 0,2 0,3 0,5 | - (10.2.1)
Оз \0,3 0,3 0,4 /
Пусть d(bj) — символ, выбираемый решающим правилом, кото-
рое используется при получении bj. Даже в том случае, когда
имеется равномерный вход, т. е. вероятность каждого символа
алфавита источника равна p(tZi) = l/3, для данного канала спра-
ведливо три правила:
d fo) = щ d (&J = a±
d(b2) = a1 d (b2) = «2 = (Ю.2.2)
d (b3) = Os d(Z>3) = O2 d (b3) = «2;
при этом у каждого правила имеются свои преимущества перед
другими. Отметим, что решение принимается по каждому символу
в отдельности, а не по последовательностям символов.
В общем случае имеется s правил по одному для каждОГо
полученного символа), каждое из которых может выбрать любой
из q входных символов. Таким образом, всего имеется qs возмог
ных решающих правил для выбора сц при получении bj.
Для выяснения вопроса о том, какое решающее правило ис-
пользовать, введем часто применяемый в статистике метод макси-
мального правдоподобия. Соответствующее правило говорит, ЧТо
нужно взять наиболее вероятный символ при имеющихся у вас
данных. Оно записывается следующим образом (в предположении
что все входные символы используются одинаково часто, что д0’
статочно разумно для двоичного симметричного канала):
d (bj) = а*,
где а* определяется условиями
Р (a*Ibj) ^P(at\bj) для всех i. (10.2.3)
Другими словами, если принят символ bj, то никакой символ
йг не может быть более вероятным, чем а*. Соответствующие ве-
роятности не являются переходными вероятностями канала. Для
|того чтобы ввести их, следует воспользоваться формулой Байеса и
получить
P(bj\a*)p(a*) > Р (bj\a{) р (ад
Р (bj) р (bj)
Дели все входные символы равновероятны, то р(а*)=р(а{) и
P(bj\a*)^P(bj\ai). (10.2.4)
Таким образом, условие максимального правдоподобия (10.2.3)
выражено через переходные вероятности канала.
В дальнейшем это правило используется даже в тех случаях,
когда символы входного алфавита не равновероятны. В общем
случае оно не является оптимальным, однако, как и при исполь-
зовании кода Шеннона — Фано (вместо оптимального кода Хаф-
фмена), для длинных последовательностей отход от оптималь-
ности будет незначительным. При этом правиле по-прежнему мож-
но получить требуемый результат. Это свидетельствует о некото-
рой устойчивости окончательного результата: на некоторых этапах
можно выбирать неоптимальный путь, и теорема тем не менее бу-
дет доказана.
Рассматриваемый пример (10.2.2) показывает, что правило
максимального правдоподобия не является однозначным. Ясно, что
применение правила максимального правдоподобия к каналу
(10.2.1) дает <7(Ь1)=Щ. Однако для Ь2 можно выбрать любое из
следующих трех правил: с?(Ь2)=й1> d(b2)=a2, d(b2)=a3.
Наконец, по правилу максимального правдоподобия, d(b3)=a2.
Таким образом, для данного канала существует три правила
(10.2.2) максимального правдоподобия.
Какова вероятность ошибки при использовании в данном ка-
нале этого решающего правила? Если записать вероятность ошиб-
ки в виде P(E\bj), то, поскольку вероятность выбранного символа
источника, а* при условии, что получен символ bj, равна P(a*\bj),
имеем вероятность ошибки при получении символа bj
Р(Е\Ь})=1- P[d(b})\b}]. (10.2.5)
Средняя ошибка РЕ задается равенством
РЕ = % Р (E\bj) p(bj).
В
Используя (10.2.5), ее можно записать в виде
Б В
Применяя формулу Байеса (см. разд. 7.3), можно выразить
условные вероятности через переходные вероятности канала (на-
помним, что все вероятности р(а) равны !/<?):
Ре = 1 — TJ Р (Ь\а*) р (а) =
в
= 1------ V Р(Ь\а*). (10.2.6)
9 в
Вычислим эту величину для нашего канала и решающего пра-
вила, записанного в последнем столбце выражения (10.2.2). Из
матрицы
0,5 0,3 0,2
0,2 0,3 0,5
.0,3 0,3 0,4.
и равенства (10.2.6) имеем
РЕ = 1 — (1/3) (0,5 + 0,3 + 0,5) = 1 — (1/3) (1,3) = 0,5666.
10.3. Двоичный симметричный канал
Докажем теперь основную теорему Шеннона для двоичного
симметричного канала. Для одного двоичного символа имеем стан-
дартную диаграмму переходов (рис. 10.3.1):
Сообщения Не использу- ются Приняты
000 001 000
010 001
011 010
ш 100 он
101 100
по 101
по
111
Рис. 10.3.1
Напомним, что Р — вероятность правильной передачи. Есте-
ственно предположить, что Q^l/2, поскольку, если Q>l/2, мож-
но просто поменять местами символы 0 и 1 в В.
Для п-го расширения канала (см. разд. 8.2) нужно выбрать
п двоичных символов. Например, для третьего расширения (вось-
меричный код) имеется код с исправлением одной ошибки (при
приеме по максимуму правдоподобия)
Ошибки отсутствуют: Р3
Одна ошибка: 3P2Q (исправляется)
Две ошибки: 3PQ2
Три ошибки: Q3
v P£~Q3 + 3PQ2 = Q2(Q + 3P).
Если Р = 0,99 (надежность 99%), получаем Р£~Зх10-4.
Таким образом, в этом случае приемник максимального прав-
доподобия работает по расстоянию Хэмминга. Это справедливо
также в случае белого шума для любого кода: минимальное рас-
стояние ^Хэмминга задает приемник максимального правдоподобия.
В случае, если на одинаковом минимальном расстоянии от приня-
того символа находятся сразу два сообщения, мы как бы отка-
зываемся и выбираем любое одно из них или бросаем монету и
случайно выбираем одно из двух сообщений (правильно поступая
в половине случаев). В случае, если на одинаковом расстоянии
находится более двух сообщений, по-прежнему можно выбирать
сообщение методом случайного выбора.
Ясно, что n-е расширение двоичного симметричного канала яв-
ляется каналом, симметричным по входу. Однако на практике та-
кой канал можно использовать разными способами.
10.4. Случайное кодирование
Предположим теперь, что п двоичных символов посылаются в
виде блока. Число всех возможных сообщений равно 2П, однако
для того чтобы обеспечить защиту от большого числа одновремен-
но появляющихся ошибок, допустимые сообщения следует выби-
рать возможно дальше друг от друга (относительно расстояния
Хэмминга). Поскольку пока читателю неизвестно, как сделать
это в общем случае, попробуем выбирать их случайно с возвраще-
ниями. Это эквивалентно тому, что для выбора каждого символа
каждого кодового слова производится бросание монеты. Можно
также представить себе урну, содержащую карточки со всеми 2”
возможными наборами из п нулей и единиц. Из урны выбираются
М карточек, причем после каждого выбора карточка возвращается
в урну. Так, производится выбор М кодовых слов, где
FM = 2" (е)/> 0). (10.4.1)
Записывая это выражение в виде Л4=2пС/2п£* , получаем, что
l/2n£1 можно сделать сколь угодно малым при достаточно боль-
шом п. Берем сколь угодно малую часть всех возможных сооб-
щений. (При этом какие-то сообщения могут встретиться несколь-
ко раз.)
Нарисуем эти последовательности в виде точек в подходящем
/i-мерном пространстве. Вероятность ошибки каждого символа
равна Q, так что среднее число ошибок равно nQ. Рассмотрим шар
радиуса nQ с центром в точке, соответствующей какому-нибудь
выбранному сообщению. Рассмотрим несколько больший шар,
увеличивая радиус на пег, так что радиус становится равным
(рис. 10.4.1) r= (Q + Ez)n (здесь г обозначает радиус, а не число
символов или основание системы счисления; ег настолько мало, что
Q + e2<l/2). Фактическое значение 62 зависит от ei и будет опре-
делено позже.
Рис. 10.4.1. Передающий
конец
Рис. 10.4.2. Приемный
конец
Закон больших чисел (см. разд. 9.8) показывает, что при доста-
точно больших п вероятность того, что принятое сообщение будет
лежать вне этого нового шара, может быть сделана сколь угодно
малой. (Поскольку почти весь объем п мерного шара сосредоточен
вблизи его поверхности, естественно интересоваться в основном
сферической оболочкой толщиной 2пег и радиуса nQ.) Таким об-
разом, если использовать прием по максимуму правдоподобия и
доказать, что с вероятностью, сколь угодно близкой к 1, никакие
два шара не пересекаются, то можно будет доказать, что прием-
ник почти наверное сможет определить, какое сообщение было по-
слано. Скорость передачи будет при этом сколь угодно близкой
к пропускной способности канала С, поскольку вероятность каж-
дого сообщения равна р=\1М и количество посылаемой информа-
ции почти наверное равно
Z(р) = log(1/р) = logЛ1 = п(С—"6^ бит/символ (10.4.2)
Таким образом, ei определяется, исходя из того, насколько ско-
рость передачи должна быть близкой к пропускной способности
канала.
Теперь рассмотрим ту же картину в n-мерном пространстве, но
только со стороны приемного конца (рис. 10.4.2). Центр шара на-
ходится б точке, соответствующей принятому слову bj. Начнем с
очевидного замечания о том, что ошибка возникает, если правиль-
ное сообщение не лежит в шаре или если в этом шаре имеется по
крайней мере еще одно возможное сообщение. Поэтому вероят-
ность ошибки РЕ задается равенством
P£«P{a|SS(r)} + P{«,eS(r)}P|B S(r) по меньшей j
I мере еще одно кодовое слово J
(10.4.3)
где символ е означает «содержится в», а £ «не содержится в».
Поскольку Р{й;е5(г)}<1, равенство (10.4.3) можно упростить,
отбрасывая этот сомножитель:
P£<SP{a,eS(r» + p[’ s<r) имеется по меньшей 1 (1044)
» I мере еще одно кодовое слово 1
Вероятность того, что по меньшей мере одно кодовое слово,
отличное от ait лежит в шаре, очевидно, не превосходит суммы ве-
роятностей того, что каждое кодовое слово, отличное от а,, лежит
в шаре. При этом по нескольку раз считаются те случаи, когда не-
сколько родовых слов попадают в выбранный шар с центром в а,.
Если, например, в этом шаре оказалось два кодовых слова, от-
личных от ai, то произошла одна ошибка, однако в нашу сумму
соответствующая вероятность входит дважды. Таким образом,
можно написать (суммирование по А—означает суммирование
по всему множеству А, кроме точки й<)
р f по меньшей мере одно кодовое слово,
I отличное от а<, лежит в S (г)
2 P{^s(r)},
> А-а.
где суммирование ведется по всем М—1 кодовым словам, которые
не были посланы. Из (10.4.4) имеем
РЕ^Р{а^З(г)} + S P{aeS(r)}.
Л—
(10.4.5)
Здесь первый член выражает вероятность того, что посланное
слово не лежит в шаре с центром в принятом слове (другими
словами, что принятое слово не лежит в шаре с центром в послан-
ном слове). Второй член является суммой по всем непосланным ко-
довым словам, каждое из которых может оказаться в шаре ра-
диуса г, который (по отношению к п) несколько больше расстоя-
ния Хэмминга, соответствующего среднему числу ошибок. Можно
надеяться, что после случайного выбора сообщений они так рас-
пределятся по всему пространству, что вероятность того, что в
шаре окажется другое сообщение, будет очень мала. Это про-
исходит вследствие того, что n-мерное пространство очень про-
сторно: вероятность того, что две случайные точки в пространстве
большой размерности окажутся близкими друг к другу, очень
мала.
Первый член в (10.4.5), зависящий только от сообщения аъ мо-
жет быть сделан меньшим, чем любое наперед заданное положи-
тельное число 6 = 6 (ег, п) (ввиду закона больших чисел), если вы-
брать длину блока п настолько большой, что расширенный шар
радиуса г=п(С2 + ег) будет содержать почти все наиболее вероят-
ные точки. Таким образом, из (10.4.5) имеем, что
+ 2 Р{аЕЕ S(r)}. (10.4.6)
д-й.
Один из способов интерпретации этого выражения состоит в
том, что первый член задает скорость ошибок и зависит только от
посланного кодового слова. Второй член зависит от всех осталь-
ных кодовых слов и связан со скоростью передачи сигналов, по-
скольку в него входит суммирование по всем \М—1 кодовым сло-
вам, отличным от посланного кодового слова.
10.5. Средний случайный код
Все, что было сделано до сих пор, представляется достаточно
разумным, за исключением, возможно, случайного выбора кода
(хотя можно надеяться, что перемешивание, описанное в разд.
5.11—5.14, подготовило читателя к идее случайного выбора). Та-
кой прием достаточно типичен при обычном исследовании задачи.
Однако следующая идея Шеннона, состоящая в том, что нужно
усреднить по всем возможным случайным кодам (а что еще оста-
ется делать?), не принадлежит к тем идеям, которые сразу при-
ходят в голову. Конечно, после того, как идея предложена, следует
ее испробовать.
Таким образом, необходимо провести усреднение по всем ко-
дам. Средние значения по всем кодам будут обозначаться волни-
стой чертой сверху. Кодовые слова выбираются из урны одно за
другим (или формируются символ за символом путем бросания
монеты), и общее число слов равно M = 2n<-C~ei > [см. равенство
(10.4.1)]. Всего имеется М слов длины п, так что общее число раз-
личных кодов равно 2пМ. При случайном выборе все эти коды рав-
новероятны, так что каждый из них появляется с вероятностью
1/2пМ. Усреднение, соответствующее этим вероятностям, дает сред-
нюю вероятность ошибки, равную РЕ. Константа б одинакова для
всех кодов и не зависит от всего кода. Поэтому после усреднения
До множеству всех кодов неравенство (10.4.6) имеет вид
К 6 + (М — 1) 6 + М P{ae^W(a =/= аг). (10.5.1)
Для вычисления P{aeS(r)} (a=^=aj) заметим, что каждое из
М слов выбирается случайно из множества всех 2П слов. Таким
образом, средняя вероятность того, что выбранное слово a(=£ai)
Лежит в шаре S(r), равно отношению числа последовательностей,
Лежащих в шаре, к 2П (общему числу двоичных последовательно-
стей длины п). Пусть N (г) — число последовательностей, лежащих
в шаре S(r). Тогда
= N (r)/2n (а=£ at). (10.5.2)
Поскольку канал является двоичным симметричным, то
N(r) = l + C(n, l) + C(n,2) + „. + C(n,r)=2 C(n,k).
fe=0
Напомним, что [из (10.4.2)] r=(Q + ez)n и С + ё2<1/2.
Используя биномиальное неравенство [см. (9.4.6)] с Q + ez=X,
получаем N (г) ^2nfr<X).
Поэтому из равенства (10.5.2) следует
2_п[1 _Я(А)] (10.5.3)
Таким образом, из (10.5.1) получаем
(10.5.4)
Учитывая равенство (8.5.3), для двоичного симметричного ка-
нала имеем 1—Н(Р) = С. Из определения Н (Р) ясно, что Н(Р) =
= H(Q). Поэтому показатель степени в (10.5.4) можно записать:
1-Я(Х)=1-Я((2+е2) =
= 1 -Я (Q) + Я(Q)—H (Q + е2) =
= С-[Я((2+в2)-Я(<2)].
Поскольку энтропия является выпуклой функцией Q, для лю-
бого Q можно использовать оценку
Н (Q + ва) Я (Q) + е2 (d Hid Q) |Q,
где (поскольку 0<Q<l/2)
dH , f 1 \ , /1 \ , /1 — Q V _
— = log ( — )— log ( ---- 1 = log (-— ) > 0.
d<2 k <2/ V-<?/ \ Q J
Поэтому 1—Я(Х) = С—ezlog[(l—Q)/Q]=C—es, и неравенство
(10.5.4) имеет вид
Р^&+М 2“"(С-Ез)
Из равенства (10.4.1) Л1 = 2'Л(С~Е|) и получаем
g _|_ 2'1(С-е1) 2-«(С-в3) — g 2~n<Ei—Ез) .
Следовательно, если выбрать ег достаточно малым, так чтобы
выполнялось неравенство
ei— е3 = ex— е2 log [(1 — Q)/Q] > 0,
то среднюю ошибку РЕ можно сделать сколь угодно малой, выбрав
достаточно большое п.
Таким образом, средний код удовлетворяет нашим требовани-
ям, поэтому должен существовать по крайней мере один код,
удовлетворяющий этим требованиям. Следовательно, доказан ре-
зультат Шеннона.
Теорема. Существуют коды, которые сколь угодно надежны и
передают информацию со скоростью, сколь угодно близкой к про-
пускной способности двоичного симметричного канала.
Почему же мы испытывали такие большие трудности при оты-
скании хороших кодов? Причина кроется в следующем: при до-
казательстве предполагалось, что длина блока п достаточно ве-
лика. На самом деле она не «достаточно велика», а очень и очень
велика!
При доказательстве теоремы Шеннона предполагается, что
посылаются только очень длинные сообщения. На практике обычно
нежелательно ждать появления таких длинных последовательно-
стей, прежде чем начать передачу. Кроме того, случайные коды
приводят к необходимости использования больших таблиц для
кодирования и декодирования, а это приводит к практическим
трудностям. Таким образом, теорема показывает, чего можно до-
стичь, но не говорит ничего о хороших кодах, за исключением того,
что они являются длинными и достаточно непрактичными.
10.6. Общий случай
Доказательство теоремы Шеннона в общем случае проводится
примерно тем же способом, что и для двоичного симметричного
канала. Различие в доказательствах проявляется при отыскании
метрики, заменяющей расстояние Хэмминга (пригодное только для
канала с белым шумом). Возникает Также задача подсчета числа
возможных сообщений, лежащих внутри шара, определяемого по
этому новому расстоянию. Наконец, вместо простой формулы для
пропускной способности канала следует использовать общее вы-
ражение.
Нужной метрикой является вероятность ошибки. Если шум
не является белым, то шары превращаются в эллипсоиды, длин-
ные оси которых направлены в сторону менее вероятных ошибок,
а короткие — в сторону более вероятных ошибок.
После того как подходящая метрика найдена, следует выбрать
шары равной вероятности с центрами в принятых словах, увели-
чить эти шары, как и ранее, так, чтобы согласно закону больших
чисел при достаточно большом п, переданное сообщение почти
наверняка лежало в этом шаре. Затем число сообщений М выби-
рается таким образом, чтобы при достаточно большом п вероят-
ность пересечения шаров была сколь угодно малой. В остальном
доказательство проводится так же, Как в случае двоичного сим-
метричного канала.
10.7. Оценка Фано
Для доказательства обращения теоремы Шеннона, утверждаю-
щего, что нельзя передавать сигналы со скоростью, превышающей
пропускную способность канала С, понадобится важная оценка,
полученная Фано. Для простоты используем обозначение
Ре =2 Р(а*,Ь)—\— РЕ,
в
где [см. равенство (10.2.5)]. Ре = 2 P(a,ty.
В, А—а»
Рассмотрим выражение
Н(Ре) + Ре logfa- 1) = Ре log +
+ Рв log ( J— ) =2 Р (а< У Х
\Ре В?А-а*
№
х log(—У+У P(G*,6) logf^V (10.7.1)
\ре ) в \Ре }
Неопределенность Н(А\В), задаваемая равенством (7.5.4), .вы-
ражается аналогичным образом
Н (Л) В) = 2 ^(а> 1°б
В,А—а«
1
/’(cld)
+ 2 Р ta*’ log
В
Вычитая из этого выражения равенство (10.7.1), получаем
Н(А\В)-Н(Ре )-Ре log(<7-l) =
= У Р (а, 6) log Г--—----- +
в,Т-а* L J
+ У P(a*,&)log[-^~ .
Т4! 4 S[p(a*|6)J
Для того чтобы применить неравенство logex^x—1, следует пе-
рейти к логарифмам по основанию 2: (logx/loge) <х— 1.
Применим это неравенство к каждому слагаемому в сумме.
Множитель 1/loge выносится из каждого слагаемого в правой ча-
сти. Оставшиеся члены в правой части дают
Н (А\В)-Н(Р£)log(9-1)^
,Л-а* L 14— !)Р(С|&) J
+ 2 />(а*,&)Г———1 =
4 2 р(Ь)-рЕ +Рв2р(Ь)-
1 В.А—а* В
-Ре =-^-(7-1)2 P(b)+PEV p(b)-(PE +PE) =
ч~ 1 В В
= Ре А~Ре —(Ре А-Ре ) = 0.
Отсюда следует важное неравенство Фано:
Н (А\В)^Н(Ре) + Ре log(<7— 1). (10.7.2)
Заметим сначала, что при выводе неравенства Фано не исполь-
зовалось никакое конкретное решающее правило, хотя вероятность
ошибки зависит от решающего правила. Зададимся далее вопро-
сом, когда (10.7.2) переходит в равенство? Равенство получает-
ся, когда logex=x—1, т. е. при х=1. Поскольку соответствующее
преобразование применялось в обеих суммах, это соответствует
тому, что Р(а\Ь) =Ре1‘(г— 1) для всех b ;и всех а^=а*, Р(а*|6) =
= 1—РЕ для всех Ь.
Второе равенство, конечно, следует из первого, потому что
2Р(п|Ь) = 1 для всех Ь.
А
10.8. Обратная теорема Шеннона
Для доказательства обратной теоремы Шеннона воспользуемся
неравенством Фано (10.7.2). Докажем, что если скорость передачи
превышает пропускную способность, то вероятность ошибки не
'может быть сделана сколь угодно малой. Другими словами, нель-
зя взять Л!=2П<С|Е) (е>0) равновероятных сообщений. Предполо-
жим, что такая попытка сделана. Тогда для п-го расширения ал-
фавита получаем, что изменение энтропии Н(Ап)—Н(Ап\Вп) не
превышает пС (пропускной способности, измеренной в блоках по п
[символам и определяемой как верхняя грань). Поскольку p=\fM,
'•имеем
Н (Ап) = 2 log Л1 = log Л1 = n (С + е).
[Далее Н (Ап)—Н(Ап\Вп) ^.пС. Перегруппировывая члены, полу-
чаем
п(С + е)—пС = пе,^Н(Ап \Вп).
^Применив неравенство Фано (10.7.2), запишем
nss^H(An \Вп) (РЕ ) + Ре log (q— 1).
'Поскольку Я(Ре)^1 (см. разд. 8.5), используем неравенство
q—l<Zq=M, тогда
п е 1 + РЕ (п С + п е), или (п е— l)/(n С + п е) РЕ.
: Поэтому
Ре (пе— 1)/(пС+пе) = (е— 1/и)/(С-|-е) ^е/С,
и правая часть не зависит от п. При и—>оо вероятность ошибки
РЕ отделена от 0. Таким образом, если скорость превышает про-
пускную способность, вероятность ошибки не может быть сделана
сколь угодно малой.
Для того чтобы проиллюстрировать эту теорему, предположим
что нужно передавать информацию со скоростью, превышающей
пропускную способность. Если передавать по каналу каждый вто-
рой символ, их можно достоверно передать по каналу. Что каса-
ется остальных символов, то для каждого из них приемник бросает
монету и угадывает этот символ примерно в половине случаев;
таким образом, примерно 3/4 сообщения передается верно, а
1/4 — ошибочно.
Глава 11
к
Алгебраическая теория кодирования
11.1. Введение
Основная теорема Шеннона показывает, что можно переда-
вать сигналы со скоростью, сколь угодно близкой к максимально
возможной, делая при этом сколь угодно малое число ошибок.
Доказательство основано на случайном кодировании, использую-
щем очень длинные коды; в очень длинном слове с большой ве-
роятностью произойдет много ошибок, которые должны быть ис-
правлены приемником. В гл. 3 показано, как построить коды с
исправлением одиночных и обнаружением двойных ошибок. Пока-
жем теперь, как построить и реализовать некоторые коды с исправ-
лением многократных ошибок.
Идея случайного кодирования кажется привлекательной до тех
пор, пока не начинаешь думать об аппаратуре, которую нужно
использовать на приемном и передающем концах. Если длина
кода очень велика, то кодовая таблица должна быть очень боль-
шой, так как по определению в случайном коде не может быть
никаких закономерностей, т. е. каждое кодовое слово нужно ис-
кать отдельно, поскольку не может быть никакой формулы, поз-
воляющей вычислять закодированное сообщение по информации
от источника. Хотя передавалось только одно из М возможных со-
общений, таблица для декодирования должна быть еще длиннее,
вследствие того, что принятым может оказаться любая из 2п по-
следовательностей длины п (в двоичном канале), и для каждой
такой последовательности должно быть отведено место в таблице.
В противном случае для нахождения правильного сообщения
нужно проделать очень много вычислений. Следовательно, прак-
тическое использование случайных кодов представляется безна-
дежным. Здесь уместно напомнить о кодах с перемешиванием
(разд. 5.11—5.14).
Таким образом, следует искать коды, обладающие некоторой
структурой. Для этого нужна алгебраическая теория конечных
[полей (полей Галуа). Алгебраическая теория кодирования являет-
ся очень обширной, и здесь она будет лишь слегка затронута, что
[позволит показать некоторые идеи, лежащие в основе построения
(кодов с исправлением многократных ошибок.
Настоящая книга не предназначена для специалистов, проек-
тирующих системы кодирования, хорошо приспособленные к слож-
ным ситуациям; она предназначена для тех, кто хочет познако-
миться с имеющимися достижениями. Если возникнет ситуация,
требующая более сложной теории, то, как мы надеемся, читатель
сможет по крайней мере уяснить себе имеющиеся у него возмож-
ности и обратиться к другим книгам для выяснения дальнейших
подробностей (например, [2, 6, 8, 11 —13, 15, 16]). Следует, однако,
предостеречь читателя, сказав, что на практике шум известен
недостаточно хорошо для того, чтобы использовать многие слож-
ные коды (обычно основанные на предположении о том, что шум
является белым). Иногда, однако, он известен достаточно хорошо.
Основное внимание уделим двоичным кодам потому, что они
чаще всего используются и потому, что коды с основанием г до
известной степени более сложны в обозначениях, хотя требуемые
для их рассмотрения идеи отличаются обычно несущественно.
11.2. Еще раз о кодах с проверкой на четность
и с обнаружением ошибок
Коды с проверкой на четность и с обнаружением одной ошибки
(см. разд. 2.2) имели одну проверку на четность по всем симво-
лам. Если записать 1 для каждого символа, который входит в
проверку, и 0 для каждого из оставшихся символов, то получим
матрицу (в данном случае она будет тривиальной матрицей раз-
мером mX 1) Л4 = (1, К 1.. 1).
Рассмотрим кодовое слово, которое обозначается теперь буквой
с; это вектор, состоящий из п двоичных цифр, например с= (0, 1,
О, ..., 1).
Пусть сг — соответствующий транспонированный вектор-стол-
бец. Имеем (используя, конечно, арифметические операции по
модулю 2)
Лкт=0 (11.2.1)
для каждого передаваемого кодового слова. Важно понять, по-
чему это равенство справедливо. При внимательном изучении
оказывается, что оно представляет собой другую форму записи
проверки на четность.
Предположим теперь, что при передаче кодового слова сделана
одна ошибка. Эта ошибка изменит один двоичный символ. Вспо-
миная, что рассматриваются арифметические операции по модулю
2, запишем принятое слово в виде с+е, где е вектор, все компо-
ненты которого равны 0, за исключением компоненты, соответ-
ствующей положению ошибки; эта компонента равна 1.
Рассмотрим, наконец, выражение
М (c-J-e)7" = Л4с7' -|-Л4 ет = Мет^0 (для одной ошибки).
Синдром принятого слова (результат применения проверки на
четность) в этом случае равен 1, если произошло нечетное число
ошибок, и 0, если четное число ошибок, включая случай отсутствия
ошибок.
11.3. Еще раз о кодах Хэмминга
В разд. 3.4 рассматривались коды с исправлением одной ошиб-
ки. В этих кодах использовались следующие проверки на четность:
1 •• 1, 3, 5, 7, 9, 11, 13, 15,...
2:2, 3, 6, 7, 10, 11, 14, 15,...
3:4, 5, 6, 7, 12, 13, 14, 15,..
4:8, 9, ю, И, 12, 13, 14, 15,...
и т. д.
Для част ого случая п=1 напишем матрицу
/0 0 0 1 1 1 Г\ 3-я проверка на четность,
Л4 = (° 1 1 0 0 1 1 2-я проверка на четность,
V 0 1 0 1- 0 1J 1-я проверка на четность,
в которой проверки перечислены в обратном порядке.
Пусть снова с — кодовое слово. Для каждого кодового слова
имеет место равенство
Л4с7'=0, (11.3.1)
поскольку оно фактически эквивалентно определению кодового
слова. Иначе говоря, матрица М переводит каждое кодовое слово
в нулевой вектор. Одиночная ошибка е приведет к тому, что будет
принято сообщение с+е и снова
М (с-)-е)т = М ст 4- М ет — М ет = синдром. (11.3.2)
Таким образом, синдром зависит только от ошибки и не зави-
сит от посланного кодового слова.
Произведение матрицы на вектор ошибок (у которого одна
компонента равна 1) дает соответствующий столбец матрицы.
Поэтому из формулы (11.3.2) вытекает, что столбцы проверочной
матрицы — это в точности те синдромы, которые могут возник-
нуть в случае одиночной ошибки.
Для любого кода с проверками на четность можно образовать
проверочную матрицу; в каждой строке этой матрицы равны 1 те
элементы, которые отвечают символам, входящим в соответствую-
щую проверку на четность, а 0 — элементы, отвечающие симво-
лам, не входящим -в соответствующую проверку на четность. Бу-
дем предполагать, что ранг этой проверочной матрицы М равен
числу строк в ней (используя, конечно, арифметику по модулю 2).
Например, ранг матрицы
/1111
М = / о о 1 1
\1 1 О О
(см. разд. 3.4) равен 2, поскольку справедливость первой провер-
ки вытекает из справедливости двух остальных проверок (сумма
всех трех строк есть 0 0 0 0). Если строки зависимы, то по край-
ней мере один символ синдрома определяется по остальным и
нельзя получить все возможные синдромы, т. е. происходит на-
прасная трата пропускной способности.
Процедура кодирования в случае произвольных проверок на
четность обеспечивает выполнение равенства Л4сг = 0 для всех
правильных кодовых слов. Таким образом, снова имеем, что
ошибка е приводит к приему сообщения с+е и
М (с-ф е)т = М ет — синдром
Синдром снова зависит только от ошибки.
В случае одиночной ошибки имеется следующий алгоритм де-
кодирования: синдром равен соответствующему столбцу провероч-
ной матрицы. Поэтому, сравнивая синдромы со столбцами прове-
рочной матрицы до получения полного совпадения, можно устано-
вить положение ошибки.
Таким образом, для каждого кода с исправлением одиночной
ошибки по синдрому можно найти соответствующий столбец про-
верочной матрицы М (число нулевой синдром означает отсутствие
ошибки).
Для кодов с исправлением кратных ошибок синдром равен сум-
ме (по модулю 2) столбцов проверочной матрицы, соответствую-
щих позициям прошедших ошибок. Если требуется найти соот-
ветствующие столбцы проверочной матрицы, т. е. положения оши-
бок, то это соответствие должно быть взаимно однозначным. Если
[появился синдром, который не является суммой разрешенного чи-
сла столбцов, то возникшие ошибки исправить нельзя. Можно
лишь сказать, что ошибки произошли.
Например, в случае кода с исправлением двойных ошибок
Каждый синдром, который может возникнуть в результате появ-
ления двух ошибок, должен ровно одним способом представляться
в виде суммы двух столбцов проверочной матрицы, т. е. не долж-
но существовать двух различных пар столбцов, приводящих к од-
ному и тому же синдрому, поскольку в противном случае оказа-
лось бы невозможным узнать, какая пара ошибок привела к на-
блюдаемому синдрому. Кроме того, никакая сумма двух столбцов
не должна быть равна никакому третьему столбцу. Другими сло-
вами,
М (e1-J-e2)y ==М ет1 + М ет 2 = синдром.
и каждый синдром должен однозначно появляться ровно из одной
пары ошибок ei и е2 или из одной одиночной ошибки.
Такие же рассуждения- можно применить к кодам с исправле-
нием кратных ошибок.
11.4. Еще раз о кодах
с обнаружением двойных ошибок
Матрицы для кодов с обнаружением двойных ошибок (см. разд. 3.7), мож-
но получить добавлением в качестве первой строки общей проверки иа четность;
например, для и=8.
11111111ч
000111101
0 110 0 110
,10 10 10 10/
Каждый <?индром, первый символ которого равен 1, должен образовывать из
остальных символов синдром одиночной ошибки, причем если этот последний
синдром равен 0, то это значит, что первый символ передан неверно (см. по-
следний столбец матрицы М). Если же первый символ полного синдрома ра-
вен 0, то имеется либо 0 ошибок, либо четное число ошибок, т. е. 2, 4, 6, 8....
В первом случае сообщение принято верно, а во втором неизвестно, что делать,
поскольку синдром не является столбцом матрицы М. Можно лишь утверж-
дать, что произошло четное число ошибок.
11.5. Многочлены или векторы?
Ранее (в гл. 2, 3 и 10) кодовые последовательности, состоящие
из нулей и единиц, рассматривались как векторы. Важный шаг
вперед состоит в том, что эта точка зрения заменяется на другую,
при которой они рассматриваются как многочлены: символы пред-
ставляют собой коэффициенты при степенях неизвестной (пере-
менной) х. Так, последовательность 1, 0, 1, 1, 0 рассматривается
теперь как многочлен Л (х) =х4+х2+х.
Можно считать, что такая точка зрения соответствует тому, что
кодовые последовательности нулей и единиц задаются теперь сво-
ими производящими функциями.
Другим примером является последовательность 0, 1, 1, 0, 1,
которой отвечает многочлен Рг(х) =х3+х2 + 1.
Во множестве всех многочленов данной степени с целочислен-
ными коэффициентами можно производить сложение и вычитание
(в арифметике по модулю 2 это одно и то же) любых двух много-
членов. Например, для указанных выше двух многочленов имеем
Pt(x) +Pz(x) =х4+х3+х+1.
Сложение ассоциативно, т. е. (Л+Лг) +/эз=-Ь (Р’з+Р’з)-
Нулевая последовательность (0, 0, 0, 0, 0) соответствует ну-
левому многочлену. Поскольку каждый ненулевой многочлен сов-
падает со своим обратным относительно сложения и сумма двух
многочленов снова является многочленом той же (точнее, не боль-
шей) степени, то множество всех многочленов данной степени п
образует группу. Напомним, что коэффициентами многочленов мо-
Ьут быть только 0 или 1.
> В разд. 2.7 рассматривались арифметические операции по задан-
ному модулю. Одна из целей, достигаемых при использовании
таких операций, состоит в том, что при этом употребляется лишь
конечное множество различных чисел. Для достижения этого в мо-
дулярной арифметике каждое число заменяется своим остатком
от деления на модуль т, так что используются лишь т остатков
О, 1, ..., tn—1, которые меньше т.
При рассмотрении множества многочленов видно, что степень
произведения двух многочленов равна сумме степеней сомножите-
лей. Для того чтобы ограничиться рассмотрением многочленов
t-тепени, не превышающей п (иначе многочлены нельзя будет ото-
ждествить с кодовыми последовательностями), следует ограни-
чить их степень. Для этого нужен многочлен, который будет слу-
жить в качестве модуля (основания). Как и в случае модулярной
Арифметики, где число делилось на основание и использовался
|статок, в случае многочленов все они делятся на многочлен-ос-
ование, степень которого равна п. Остатком от такого деления
гудет многочлен с п коэффициентами (степени п—1),
можно отождествить с кодовой последовательностью.
В разд. 2.8 показано, почему в качестве основания
который
следует
[рать простое число. Простое основание обладает тем свойством,
ито если произведение двух чисел равно 0, то по крайней мере
дно из них равно 0. Если основание не является простым, то мо-
жет случиться, что произведение двух чисел, каждое из которых
•тлично от нуля, оказывается нулевым. Аналогично, в качестве
ногочлена-основания следует брать простой многочлен. Простым
азывается такой многочлен, который нельзя представить в виде
роизведения двух нетривиальных многочленов меньшей степени
с коэффициентами в том же поле).
Коэффициент при старшей степени у многочлена степени п мо-
де ет случайно оказаться равным 0, так что фактически многочлен
будет иметь меньшую степень. Коэффициентами могут быть только
Клементы поля 0 или 1; многочлен, у которого коэффициент при
гтаршей степени х равен 1, будет называться унитарным.
У читателя может возникнуть вопрос: «Для чего нужно пере-
множать многочлены?» Ответ состоит в том, что в рассматривае-
мые в теории объекты желательно ввести как можно больше сим-
метрии и упорядоченности. В этом и только в этом случае полу-
венные коды будут достаточно симметричными и упорядоченными,
гак что можно надеяться, что аппаратура кодирования и декоди-
Ювания будет иметь простую структуру (т. е. ее будет легко скон-
струировать или реализовать в виде программы для ЭВМ). На
1рактике обычно нежелательно иметь случайные или недостаточно
[Труктурированные коды.
11.6. Простые многочлены
Простой многочлен — это такой унитарный многочлен, кото-
рый нельзя разложить на произведение двух многочленов более
низкой степени. Однако, поскольку для коэффициентов рассмат-
ривается поле с арифметикой по модулю 2, то нужно разобраться
какой вид приобретают обычные представления о многочленах’
Проведем экспериментальное исследование возникающих явлений.
При этом опустим доказательство свойств конечных полей, кото-
рые необходимы для изучения разложения на множители.
В случае многочленов степени 0 имеется один тривиальный
многочлен (если этот вырожденный элемент заслуживает назва-
ния многочлена), а именно Р=1. В обычной арифметике ему соот-
ветствует число 1.
Имеется ровно два унитарных многочлена степени 1, а именно
х, х+1, и оба они являются простыми (аналогично тому, что три-
виальный множитель 1 не учитывается при разложении чисел на
множители, при разложении многочленов не учитывается триви-
альный многочлен 1).
Имеется четыре различных унитарных многочлена степени 2
(каждый коэффициент при х и при 1 может быть 0 или 1):
х2 = х-х
х2+1 =(хф-1)(х+1)
х2 + х =х(х+1)
Х2 + х+1 простой.
Равенство х2+1 = (х+1)2-может показаться на первый взгляд
странным. Однако, раскрывая скобки в правой части, получаем
х2 + 2х+1. Поскольку 2=0 mod 2, имеем х2+2х+1 =х2+1.
Уверены ли мы в том, что многочлен х2+х+1 является про-
стым? Попробуем разделить его на каждый из двух многочленов
меньшей степени. Если бы многочлен х2+х+1 был приводим, то
соответствующими сомножителями могли бы быть только указан-
ные два многочлена первой степени. Ясно, что х не является дели-
телем. Попробуем провести деление на х+1:
х2 + х+1 |х+1
х2 + х х 0
0 1
0__0
1 = остаток.
Таким образом, х2+х+1 действительно является простым мно-
гочленом
В качестве примера рассмотрим еще восемь возможных кубических мног
членов:
Xs = Х-Х‘Х
Х3+ 1 =
х3 + х = х(х2 + 1)
X3 + X + 1 =
X3 + X2 = X2 (х + 1)
X3 4- X3 + 1 =
X3 4-Х2 + X =х(х2+х4~1)
X3 + X2 4" X + 1 =
Здесь приведены очевидные разложения на множители, а для остальных много-
членов оставлены пробелы.
Если кубический многочлен можно разложить на множители, то один из
сомножителей должен быть многочленом первой степени. Поскольку все много-
члены, делящиеся на х, указаны в таблице, осталось рассмотреть сомножитель
х+1. Для х3+1 имеем
1001 ]11_
п ТГГ
ю
п
и
и
0 = остаток.
Поэтому (х+1) (х2+х+1) =х3-Р 1.
Возьмем теперь многочлен х3 + х+1. Имеем
1011 | 11
и ИсГ
п
и
01
оо
1 = остаток.
Поэтому многочлен х3+х+1 является простым. Аналогично, простым является
многочлен х3+х2+1, поскольку х3+х2+1 =х2(х+1) + 1.
Наконец, рассмотрим многочлен х3+х2+х+1. Приведенные выше вычисле-
ния подсказывают, как разложить этот -многочлен на множители, т. е. можно
записать х2(х+1) + (х+1) = (х2+1) (х+1) и многочлен не является простым.
Таким образом, простыми унитарными многочленами степени 3 будут только
многочлены х3+х+1, х3+х2+1.
Мы не будем продолжать поиск многочленов все более высо-
кой степени. Ясно, что для каждого конкретного многочлена нуж-
но испробовать в качестве его делителей простые многочлены, сте-
пень которых не превосходит половины степени исходного много-
члена, и приведенные выше примеры показывают, как в некоторых
случаях можно производить разложение на множители в уме. (Мы
не пытаемся показать, как построить наилучшие коды; наша за-
дача состоит лишь в том, чтобы показать, как теория кодирова-
ния приводит к кодам с исправлением ошибок большой кратности,
обладающим хорошей структурой, которая делает реальной по-
пытку аппаратурной или программной реализации таких кодов.
Задачи
11.6.1. Докажите следующую теорему: сумма коэффициентов многочлена рав-
на 0 по модулю 2 в том и только том случае, когда многочлен делится
на х+1.
11.6.2. Зная число многочленов данной степени и число различных произведений
простых многочленов меньших степеней, получите число простых много-
членов данной степени.
11.7. Примитивные корни
Прежде чем вернуться к кодам с исправлением ошибок, сле-
дует сделать еще одно отступление. Корни п-й степени из едини-
цы — это корни уравнения хп—1 = 0, явный вид которых таков:
» e23Ii*/« (£ = 0, 1,2, ... ,п— 1).
Некоторые из этих корней (например, корень, соответствующий
£=1) обладают тем’ свойством, что их последовательные степени
порождают все остальные корни. В самом деле, если k взаимно
просто с п, то соответствующий корень обладает этим свойством.
Для того чтобы доказать это утверждение, рассмотрим последо-
вательные 'степени (т=1, 2, ..., п—1, п) корня exp (2nik/n). Эти
степени равны exp (2лУгт/п). Если бы какие-нибудь два из этих
степеней были равны между собой, то было бы выполнено равен-
ство
ехр (2л i kmjn) = exp (2 л i kmjri)
или
exp [2 л i k (nil—mz)/n] = 1.
Это означает, что fe(mi—m2)/n—целое число. Поскольку 'k вза-
имно просто с и, у них нет общих делителей, так что т.]—т2
должно делиться на п. Однако —т2 меньше п, так что тх — т2.
Таким образом, если k взаимно просто с п, последовательные сте-
пени соответствующего корня порождают все корни из единицы
(данной степени) и этот корень является примитивным.
Важность примитивных корней состоит в том, что каждый та-
кой корень может служить генератором всего множества исполь-
зуемых чисел.
11.8. Один частный случай
Совершенный код Хэмминга имеет и=2™—1 символов. При
п=7=2—1 существует матрица (см. разд. 11.3):
/0 0 о 1 1 1 1\
М = I о 1 100 1 11. (11.8.1)
Ч 0 1 0 1 0 1/
Известно, что любая перестановка столбцов матрицы М фактиче-
ски не меняет код, а влияет лишь на то, как и где ищется столбец,
соответствующий синдрому, возникающему при появлении одиноч-
ной ошибки.
Предположим, что простой многочлен х3+х+1 используется в
качестве многочлена-основания. Пусть а — корень этого много-
члена, так что а3+а+1 = 0 или а3 = а+1. Используя это равенство,
можно редуцировать третью и более высокие степени а к суммам
более низких степеней. Таким образом, каждый многочлен от а
можно представить в виде линейной комбинации элементов 1,
а и а2.
Рассмотрим теперь трехмерные векторы-столбцы с компонента-
ми 1, а, а2, расположенными снизу вверх. Будем сопоставлять та-
кие векторы последовательным степеням а, начиная с нулевой
степени. Заметим, что умножение на а сдвигает каждую компо-
ненту на одну позицию вверх и что каждый раз, когда возникает
третья степень а, используется соотношение а3 = а+1, так что в
качестве компонент вектора остаются только 1, а и а2. Различным
степеням а отвечают такие векторы:
0/1 \
a!l=a2 + a= I 1 |
\0 J
ГОХ /1 \
а= I 1 а5 = as-\-a2= а2-\-а-\-1 = ( 1 |
\0 / \1 J
/1 \ (1 \
а2 = I О а6 = а3 + а2 -J- а = а2 Ц- 1 = I о |
\0 / \1 /
/ОХ /°\
а3 = а+ 1 = I 1 j d = a3 + а = I о
V J U /
Таким образом, показано, что а является примитивным корнем
простого многочлена, поскольку последовательные степени а по-
рождают все семь различных ненулевых троек.
Если записать столбцы этой новой матрицы в виде
а6 а3 а4 а3 а2 а 1
1 1 1 0 1 0 0\
0 1 1 10 10 1
110 10 0 1/
(для удобства порядок столбцов изменен на обратный), то видно,
что получается перестроенная матрица М из (11.8.1). При таком
расположении столбцов нужно сравнивать вычисленный синдром
на приемном конце с последовательными степенями а (их можно
запомнить или порождать по мере необходимости). При совпаде-
нии синдрома с некоторым столбцом этот столбец представляется
в виде соответствующей степени а, отвечающей данному синдрому.
(Несколько другой, но эквивалентный код получается при исполь-
зовании многочлена x3-!-^2-!-!.)
Как осуществляется кодирование? Поскольку синдром 0, 0, ...
..., О должен означать отсутствие ошибок, нужно потребовать, что-
бы посылаемые многочлены без остатка делились на многочлен
а3+а+1. Таким образом, поместим сообщение в позиции, соответ-
ствующие а6, а5, а4, а3, и временно поместим нули в остальные три
позиции, соответствующие а2, а, 1. При делении полученного много-
члена на многочлен-основание получим некоторый остаток. Если
поместить этот остаток в последние три позиции нашего многочле-
на (или, если хотите, прибавить остаток к многочлену), то полу-
ченный многочлен будет делиться на основание без остатка. Имен-
но в этом и состоит процедура кодирования: нужно поместить в
последние три позиции остаток от деления на основание, после че-
го весь многочлен будет сравним с нулем по модулю простого мно-
гочлена.
Для того чтобы произвести декодирование на приемном конце,
нужно просто разделить принятый многочлен на многочлен-основа-
ние. Полученный синдром (остаток), будучи записан как некото-
рая степень а, указывает столбец, в котором произошла ошибка.
Следовательно, имеем новую точку зрения на рассмотренные ранее
коды Хэмминга, которая позволяет идти дальше.
Пример процедуры кодирования. Посмотрим, как кодировать сообщение
10 0 1-----— представленным выше кодом. Сообщение отвечает многочлену
а6+а3. Разделим этот многочлен на а34-а+1 и рассмотрим остаток
1001000 | 1011
1011 1010
0100
0000
1000
1011
ОНО
0000
110 = остаток.
Поэтому закодированное сообщение имеет вид (10 0 1110).
Предположим, что на подчеркнутом месте (т. е. в позиции, отвечающей а3)
произошла ошибка, так что принятое сообщение имеет вид (1 000 1 1 0).
Разделив полученное сообщение на тот же многочлен-основание, получим
1000110 | 1011
1011 1011
0111
0000
1111
1011
1000
1011
011= остаток.
• дг\
Этот 'Остаток представляет собой 1 I =а3, что соответствует четвертому сим-
\ 1 /
волу справа (где произошла ошибка). Для того чтобы иолучить 'Правильное
сообщение, нужно добавить к этому символу 1, после чего, отбрасывая послед-
ние три символа, можно получить первоначальное сообщение.
Задачи
11.8,1 . Найдите матрицу декодирования, соответствующую простому многочлену
х3+х2+1.
11.8.2 . Аналогично примеру из текста произведите кодирование и декодирование
сообщения 1010 при ошибке в позиции, отвечающей а2.
11.9. Регистры сдвига для кодирования
Теория алгебраических кодов приводилась в терминах много-
членов, поскольку при этом легко можно описать программную
или аппаратурную реализацию таких кодов. Кажущаяся сложность
описанного выше процесса деления для модулярного представле-
ния многочленов в действительности достаточно просто преодолима
с помощью регистров сдвига с обратной связью. Предположим,
•что рассматривается код длины 7, описанный в разд. 11.8, и тре-
буется закодировать сообщение 10 0 1. Закодированное сообще-
ние представляется многочленом вида
1 а6 + 0 а5 + 0 • а4 + 1 а3 + *а2 + *а + * 1
(звездочка означает, что соответствующий коэффициент подлежит
определению), который должен делиться на многочлен-основание
а3 + а+1 (см. разд. 11.8).
Сначала неизвестные коэффициенты полагаются равными нулю
и, как и ранее, производится деление на многочлен-основание для
получения остатка. После сложения остатка а2+а с первоначаль-
ным многочленом а6+а3 получается закодированное сообщение
а6+а3 + а2+а= (а3 + а+1) (а3 + а), которое точно делится на мно-
гочлен-основание а3 + а+1.
Как практически производится деление? Рассмотрим регистр
сдвига, показанный на рис. 11.9.1. Предполагается, что символы
сообщения поступают справа, начиная с символа, соответствую-
щего самой большой степени:, в конце вводятся три нулевых сим-
вола. Стрелки под регистром сдвига указывают направление об-
ратной связи. Если в старшем разряде содержится символ 1, то
он добавляется (или вычитается) к указанным стрелкам и симво-
лам. Детали процесса показаны на рис. 11.9.2, на котором опущены
первые несколько шагов, поскольку в течение первых четырех
шагов, пока первая цифра не дойдет до крайнего левого положе-
ния, не происходит ничего интересного. Таблицу на рис. 11.9.2 нуж-
но рассматривать, начиная с верхней строки. Во второй строке по-
казаны символы, возвращаемые обратной связью, а в третьей стро-
ке (непосредственно над двойной линией) содержится результат
сложения. (Для того чтобы процесс в точности соответствовал про-
цессу деления, показано прибавление 1 в крайней левой позиции;
на практике этот символ не возвращается.) Двойная линия указы-
вает на сдвиг, и под этой линией приводятся сдвинутые символы.
В трех строках между двойными линиями отображено происходя-
щее между двумя сдвигами. В этом примере имеется всего четыре
Кодировать
хЗ, 0,0,0
Цепи обратной связи
Рис. 11.9.1. Регистр сдвига с обрат-
ной связью
Сдвиг
Сдвиг
Рис. 11.9.2. Результаты работы ре-
гистра
Состояние
Обратная связь
Результат
СОвиг
множества по три строки. В последней строке записан остаток.
Непосредственное сравнение показывает, что регистр сдвига де-
лает то же самое, что и процесс деления углом.
На рис. 11.9.3 дана схема кодирующего устройства. Символы
сообщения по-прежнему поступают справа, однако теперь они вы-
ходят слева через переключатель (пунктирные линии). После вы-
Рис. 11.9.3. Кодер
числения остатка осуществляется выдача всех символов первона-
чального сообщения, а затем переключатель ставится в такое по-
ложение, при котором происходит выдача сдвинутого остатка, что
позволяет сформировать все закодированное сообщение (кроме
первого символа, равного 0). Процесс кодирования является очень
простым!
Практически построить регистр сдвига достаточно легко, даже
учитывая необходимость осуществлять сложение по модулю 2 в
каждой позиции. Столь же проста аппаратурная реализация
остальных частей кодера.
Нетрудно написать соответствующую программу для ЭВМ.
Для этого нужно проверить, равен ли единице крайний левый сим-
вол, и если это так, произвести логическое сложение с набором
символов, соответствующих линиям обратной связи (т. е. много-
члену-основанию). Затем произвести сдвиг, и всю процедуру по-
вторить. Нетрудно описать все это подробно.
Таким образом, процедура кодирования является достаточно
простой. Перейдем теперь к декодированию.
Задача
11.9.1. Напишите программу для кодирования сообщения по схеме, представ-
ленной в этом .разделе.
11.10. Декодирование кодов
с исправлением одиночных ошибок
На приемном конце нужно сделать то же самое, что и при ко-
дировании, с единственным исключением, состоящим в том, что
следует запомнить принятое сообщение, чтобы иметь возможность
сделать в нем необходимые исправления.
После осуществления процесса деления получается остаток:
синдром ошибки. Нулевой остаток означает: сообщение является
правильным и были посланы первые четыре символа этого сооб-
щения.
Если остаток не является нулем, то он равен некоторой сте-
пени а, например ah. Как найти эту степень? Для сравнительно
коротких кодов можно использовать табличный поиск, однако в
достаточно сложных случаях для такого поиска требуется слиш-
ком большой объем памяти (хотя в настоящее время, 1979 г., стои-
мость памяти быстро падает).
Возвращаясь к разд. 11.8, можно увидеть, что а7=1, так что
а6=1/а. По синдрому (остатку), который равен ah, можно полу-
чить цепочку равенств
(о6) ak =ak~l mod(a34-a-|- 1)
(cfl) ak~l = ak~2
которую нужно продолжать до тех пор, пока не будет получен
остаток 0 0 1=1. Отсюда находится k.
Предположим, например, что имеется сообщение 10 0 1110
из разд. 11.9 и произошла ошибка в символе, отвечающем а2, т. е.
принятое сообщение имеет вид 10 0 10 10. Процесс деления
происходит следующим образом (в упрощенной записи):
1001010
1011
1001
1011
100->остаток
Поэтому нужно начать с этого остатка, который равен некоторой
неизвестной степени а, скажем k-ой:
/1 \
ah = I о I
\о /
Будем последовательно проводить умножение на а6=1/а. Это
эквивалентно сдвигу всех символов на одну позицию вниз. Если
символ 1 сдвигается вниз из самой нижней позиции, то использует-
ся соотношение 1 = а + а3. Таким образом,
/О \
ав ah = ак—1 =11 I.
\0 /
до тех пор, пока не будет получена степень о°=1:
/О \
о6 ak-l — ak -2 / о |=1.
\1 /
В рассматриваемом случае k=2, так что нужно добавить 1 к
символу, соответствующему а2.
Если производить сдвиг в обратном направлении, то нужно ис-
пользовать степени а в качестве теста и при достижении согласо-
вания добавлять 1 к символу, который в результате сдвига выходит
на последнюю позицию.
Можно также начать со старшей степени а и идти вниз до тех
пор, пока не получится нужное совпадение. В этом случае можно
использовать сдвиг в прямом направлении.
Заметим, что при программной реализации все эти операции
нужно проводить только в случае, если произошла ошибка; в про-
тивном случае нужно лишь вычислить синдром и убедиться в том,
что он тождественно равен 0. В системах кодирования, работаю-
щих в реальном масштабе времени, нужно иметь возможность
производить вычисления, независимо от того, проделываются они
или нет.
11.11. Код с исправлением двойных ошибок
Для того чтобы продемонстрировать код с исправлением двой-
ных ошибок, понадобится более длинный, чем раньше, код Хэммин-
га, имеющий общую длину 15 и четыре проверки на четность. В
качестве возможного кандидата на роль многочлена-основания
рассмотрим многочлен х4+х+1. Ясно, что х не является делителем
этого многочлена. Если бы многочлен делился на х+1, то сумма
его коэффициентов была бы равна 0 (см. задачу 11.6.1). Поэтому,
чтобы убедиться, что рассматриваемый многочлен является про-
стым, достаточно проверить, что его делителем не является лишь
простой квадратичный многочлен х2 + х+1.
Далее нужно выяснить, удовлетворяет ли многочлен условию
примитивности. Начнем последовательно вычислять степени а
Получим, что а15=1, как и должно быть, и что ни одна меньшая
степень а не равна 1. Поэтому а является примитивным корнем,
и проверочная матрица имеет вид:
с14 а13 а12 е11 е10 а8 а'л cP cP cfi cP cfl а? а 1
11 1 10101100100 0\
01 11 101011001001
001 1 1 10101 1 0 0 1 0’
11101011001000 1/
Для того чтобы исправлять большее число ошибок, чем исправ-
ляет этот код (т. е. больше одной ошибки), к матрице нужно до-
бавить дополнительные строки. Добавим четыре дополнительных
строки. Как это можно сделать?
До добавления строк две различные двойные ошибки могут да-
вать одинаковые синдромы, т. е. ak+am=ah' +ат'. Например,
столбцы с и о2 дают тот же синдром, что и столбцы а12 и а14. Лю-
бая линейная операция над этими столбцами ни к чему не приве-
дет. Нужно что-то более сложное. Попробуем использовать в каче-
стве образующей элемент а. К сожалению, два синдрома
a1-}-a2 = s1= первый синдром,
a2x+a22 = s2= второй синдром,
где Qi и й2 — две различные степени а, связаны соотношением
S21 = (О1 + «г)2 = 4- 2 ах а2 + а\ = а\ + а\ = %.
Попробуем использовать в качестве второго синдрома куб пер-
вого синдрома, т. е. a3i + a32=s2. Имеем
s2 = а\ + а32 = (th + а2) (а\ + a1as + а\) = sx (а\ + а1а2 +
+ a22) = s1(a1n2 + s21),
так что ai + a2=s1; aia2=s2l + s2/sl (если Si^O).
Если заданы сумма и произведение двух чисел, то почти авто-
матически возникает мысль о квадратном уравнении и его корнях:
a2—(sx) а + (s2x + s2/Sj) = 0.
Эти два корня дают различные синдромы ошибок.
При наличии только одной ошибки синдромы равны: czi = Si,
a3i = s2 и s2i+s2/si=2s2i = 0. Таким образом, квадратное уравнение
приобретает вид
(a=s1
й2+51о!=0или 1а = 0.
В случае отсутствия ошибок Si = s2 = 0, и квадратное уравнение
приобретает вид
„ „ fa=O
а2 = 0, {
I а= 0.
Следовательно, для дополнительных нижних строк матрицы в
качестве образующей для порождения столбцов нужно использо-
вать элемент а3 вместо а. При этом столбцы будут соответствовать
1 а3 а6 а9 а12 а15 а18 ...
(в обратном порядке). Таким образом, полная матрица М имеет
вид
(1111010110010001
0111101011001001
0011110101100101
1110101 10010001
— — — — — — — — — — —
111101111 011110
101001010 010100.
110001100011000/
100011000110001/
Она являемся проверочной матрицей для исправления двойных оши-
бок. Синдром $i вычисляется по верхним строкам, а синдром s2 —
по нижним. С помощью квадратного уравнения из этих двух синд-
ромов получаются два корня, указывающие положение двух
ошибок.
11.12. Декодирование кодов с исправлением кратных ошибок
Существует простое правило декодирования кодов с исправле-
нием кратных ошибок. Задача состоит в том, чтобы аналогично
тому, как это сделано в разд. 11.11, отыскание ошибок представить
в виде алгоритма для ЭВМ. В случае кодов с исправлением двой-
ных ошибок задача сводится к нахождению корней квадратного
уравнения. Один из очень простых способов нахождения корней —
вычисление значений соответствующего многочлена второй степе-
ни, во всех позициях находящегося в памяти сообщения в процес-
се его сдвигов в регистре. Если некоторая степень а удовлетворяет
квадратному уравнению, она является корнем и указывает на
одну из ошибок, которую следует исправить.
Ясно, что это нужно делать только в случае, если ошибки про-
изошли. Однако в системах передачи, работающих в реальном
масштабе времени, одновременно нужно хранить в памяти не-
сколько сообщений. При работе такой системы происходит одно-
временный сдвиг и исправление ошибок в первом сообщении, вы-
числение поправок для второго сообщения и предварительная об-
работка третьего сообщения. Таким образом, минимальная задерж-
ка составляет два сообщения. Эта задержка может оказаться су-
щественной при работе цепей обратной связи управляющих си-
стем и может привести к неустойчивости.
11.13. Итоги
В этой главе показано, почему желательно применять хорошо
структурированные коды; при кодировании и декодирований таких
кодов можно использовать систематические (неслучайные) мето-
ды. Показано, как достаточно просто производить деление одного
многочлена на другой.
Показано, что синдром определяется ошибкой и не зависит
от сообщения. Далее обоснована необходимость' использования
множества многочленов по модулю данного простого многочлена.
Кроме того, рассмотрена необходимость дополнительного условия
существования у многочлена примитивного корня, при котором
обеспечивается возможность записи всех элементов в виде степе-
ней этого корня; в некотором смысле эта процедура эквивалентна
введению логарифмов.
Наконец, в качестве иллюстрации описанных методов был раз-
работан один код с исправлением двойных ошибок.
Мы не пытались изложить всю необходимую для обоснования
теорию конечных полей или построить общую теорию кодов. Мы
хотели показать лишь то, как построить код. Теория излагалась
таким образом, чтобы можно было легко выделить и исследовать
частные случаи; любой материал, выходящий за эти рамки, сде-
лал бы книгу слишком длинной и практически ничего не добавил
бы к имеющимся руководствам J2, 6, 8, 11, 13, 15, 16].
Приложение А.
Ширина полосы и теорема отсчетов
А1. Введение
Это приложение кажется слабо связанным с изложенным ранее материалом,
во всяком случае здесь используются другие математические средства. Одна, из
причин включения в книгу этого, приложения состоит в том, что матрица пере-
ходных вероятностей канала (см. разд. 7.2) (А,,) редко бывает известна на
практике. Более существенно то, что для передачи цифровой информации обыч-
но применяются аналоговые каналы, которые с большой'точностью можно счи-
тать линейными. Пропускная способность такого .канала обычно измеряется
шириной полосы, поэтому книга по теории информации -и теории кодирования
обязательно должна содержать, по крайней мере, первые понятия о ширине по-
лосы и связанных с ней вопросах.
Собственными функциями линейной, не меняющейся со временем системы
являются комплексные экспоненты, exp (2nifit).
Функция называется собственной, если система не меняет ее форму, а ме-
няет только ее амплитуду. Слова «не меняющаяся со временем» применительно
к системе означают, что поведение системы зависит лишь от ее входов, а не от
времени. Этим свойством обладает большинство систем связи. Линейность озна-
чает, что при вводе в канал суммы двух функций выход равен сумме отдель-
ных выходов. Этим свойством обладает большинство каналов, если только они
работают без перегрузки. Частота f измеряется как круговая (в аналитических
расчетах используется угловая частота <£> = 2nf). Независимой переменной обыч-
но является время I.
Функцией с ограниченным спектром называется такая функция, частоты ко-
торой лежат в некоторой ограниченной полосе. Хорошо известным примером
может служить высококачественная система звуковоспроизведения, для которой
типичными являются нижний предел, равный в лучших системах нескольким
герцам (обычно 15), а в других доходящий до несколько сотен герц и верхний
предел, приближенно равный 18000 Гц. Радио- и телевизионные станции имеют
ограниченные полосы частот, что позволяет избежать взаимных помех передач.
Во многих других системах имеются естественные границы ширины полосы ча-
стот, хотя почти во всех случаях полоса ограничена не так резко, как требует
теория.
А2. Интеграл Фурье
Интеграл Фурье является естественным математическим средством для ис-
следования функций с ограниченным спектром и представляет функцию g(t) в
виде суммы комплексных экспонент (собственных функций) следующим об-
разом:
СО
g(t)= jG(f) exp (2л ^Об-
стоящая под знаком интеграла функция G(f) называется преобразованием
Фурье функции g(t). Она связана с первоначальной функцией интересной
формулой
со
G(/) = jg(Oexp( —2я1/0<Й,
—оо
совпадающей с первой формулой, за исключением знака перед i; в одном из ин-
тегралов в показателе экспоненты стоит «Ч-i», а в другом — «—i».
Интеграл Фурье подобен стеклянной призме, которая разделяет луч света по
гам — частотам. Функция G(f) указывает иа величину (амплитуду) частоты
f в исходном сигнале g(t). Интеграл — это просто взвешенная сумма всех воз-
можных частот, G(/) — вес частоты
Функции cos 2jtfZ и sin 2nft при своем представлении используют положи-
тельные и отрицательные частоты в соответствии с равенствами
cos 2зт ft = [exp (2 зт i ft) ф- exp ( — 2 st i f /)] /2,
sin 2зт f t = [exp (2зт i f t) — exp ( — 2sr i ft)] /2i.
В качестве примера построения функции с ограниченным спектром рассмот-
рим функцию G(f), равную вне полосы (рис. А2.1):
F
Тогда g(t)= j G(f)exp(2ari ft)df.
—F
Предположим далее, что внутри полюсы функции G(f) постоянна и равна
1/2F, так что площадь под графиком G(f) в точности равна 1. Тогда
г 1 ехр (2зт i ft) F
_г-
ехр (2зт i F t) — exp (— 2 зт i Ft) 1 sin 2л Ft
2i 2 si Ft 2л F t
Хорошо известная функция (sinx)/x показана на рис. А2.2. У нее есть
главный лепесток около 0 ширины 1/F и. боковые лепестки вдвое меньшей ши-
рины, которые убывают как 1ft. Чем больше F (чем шире полоса), тем уже
главный лепесток, а вместе с ним и боковые лепестки. Тем самым можно пред-
положить, что функция может иметь резкие колебания лишь в случае широкой
полосы.
Рис. А2.1. Функция с ог- Рис. А2.2. f(x) — (sinx)/x
граииченной полосой
АЗ. Теорема отсчетов
Знаменитая теорема отсчетов связывает скорость отсчетов с шириной по-
лосы, необходимой для восстановления функции по отсчетам. Прежде чем фор-
мулировать теорему, напомним читателю кое-что из его опыта.. Во время про-
смотра кинофильма или телевизионной передачи фактически вы смотрите после-
довательность неподвижных кадров, сменяющих друг друга столь быстро, что
изображение кажется движущимся; обычно достаточно 15—20 изображений в
секунду, чтобы обмануть человеческий глаз. У такой системы отсчетов есть,
однако, особенности. Например, когда фургон в каком-нибудь ковбойском филь-
ме начинает двигаться, то кажется, что его колеса сперва вращаются с уско-
рением, затем вращение замедляется, колеса останавливаются, вращаются на-
зад, .останавливаются, вращаются вперед, останавливаются, и так далее, в за-
висимости от скорости. Причину этого легко понять. Когда колесо фургона
вращается .настолько быстро, что одна спица попадает на место другой, он.ц
кажутся неподвижными. В действительности, если одна спица за интервал
между двумя последовательными кадрами проходит ровно половину .расстояния
до следующей спицы, психологически кажется, что колесо, стоит неподвижно я
имеет вдвое большее число спиц. При скорости, незначительно превышающей
эту, спицы кажутся движущимися назад.
Это явление можно рассматривать как следствие простого тригонометриче-
ского тождества. Ясно, что в случае, когда интервал между двумя отсчетами
равен 1 (этого всегда можно, достичь путем выбора масштаба по оси времени),
любое число кратное 2я, можно удалить из-под знака синуса и косинуса. Эффек.
тивиую частоту можно еще уменьшить, выделяя из частоты полуцелые числа,
кратные периоду, поскольку это может лишь изменить знаки функций. Таким
образом, при отсчетах высокие частоты будут казаться низкими. Максимальная
частота, которую можно наблюдать без изменения, это та, для которой в каж-
дом полном периоде имеется два отсчета. Низкие частоты остаются неизменными,
тогда как высокие частоты превращаются в низкие, в том смысле, что в точках
отсчета обе частоты имеют одинаковые значения.
После того, как это стало понятным, можно сформулировать теорему от-
счетов. Пусть заданы отсчеты g(n) (для всех целых значений п) функции g(t)
с ограниченным спектром; можно образовать бесконечную в обе стороны сумму:
£(0 =
k==~CO
sin я (k — t)
Ь л (k — t)
Рассматривая слагаемые этой суммы в точках отсчета, например в точке
t=k, замечаем, что fe-oe слагаемое дает правильное значение g(k), а все осталь-
ные слагаемые равны 0. Таким образом, в этой точке сумма дает правильное
значение функции. Остается, конечно, следующий вопрос: «Имеет ли построен-
ная функция ограниченный спектр?» Результаты предыдущего раздела показы-
вают, что ответ положителен: после сдвига функция (sinx)/x по-прежнему име-
ет ограниченную полосу.
Поскольку книга ие является математическим курсом, в ней не делается
попытка доказать, что ряд сходится (он, очевидно, сходится в точках отсчета)
и что он сходится к правильной функции. И то, и другое верно.
А4. Ширина полосы и скорость изменения
В предыдущем разделе показано, что ширина полосы сигнала обратно про-
порциональна ширине основного лепестка функции (sin 2nFt)/(2nFt), т. е. для
получения узкого пика требуется широкая полоса. Ввиду отсутствия математи-
ческого аппарата здесь не удастся доказать, что никакая форма спектра G(f)
в заданной полосе дает более узкого пика по сравнению с тем, который полу-
чается для прямоугольной формы. .Поэтому придется привести лишь наводящие
соображения о том, почему это верно.
Для узкополосной функции невозможным является небыстрое изменение
само по себе; чтобы понять это, достаточно выбрать любую фиксированную
частоту, отличную от нулевой, и взять достаточно большую амплитуду, получая
таким образом сколь угодно большое изменение функции за сколь угодно ма-
лое время. Мы хотели бы получить быстрое изменение от одного крайнего зна-
чения до другого, от максимума до минимума, или наоборот. Это значит, что
на концах интервала мы хотели иметь горизонтальную касательную. Таким об-
разом, наша функция фактически похожа на cos 2nF<t(0^.2nFt^.n), и переход
от максимума к минимуму происходит за время 1/2 f. При этом снова появ-
ляется такое же обратно пропорциональное соотношение между частотой и
скоростью изменения сигнала.
Теорема отсчетов утверждает, конечно, то же самое; нужно иметь полосу
необходимой ширины; для правильного восстановления исходного сигнала нужно
иметь, по меньшей мере, два отсчета для наивысшей имеющейся частоты (пред-
полагая, что отсчеты берутся в течение всего времени от —оо до +°°).
А5. Амплитудная модуляция
Большинство людей, по крайней мере, краем уха слышали об AM — ампли-
тудной модуляции. Частота передачи, на которую вы настраиваете свой радио-
приемник, называется несущей; за постоянством этой частоты тщательно следит
передающая станция. Все, что делает радиостанция, — это меняет амплитуду
посылаемого сигнала, а вместе с тем, конечно, и принимаемого (рис. А5.1). Это
влечет небольшое изменение частоты, поскольку произведение двух косинусов
является суммой двух косинусов, сдви-
нутых относительно одной из первона-
чальных частот (см. ниже).
При настройке радиоприемник от-
фильтровывает все передаваемые часто-
ты, за исключением тех, которые близки
к несущей частоте. Затем принятый сиг-
нал тем или другим способом выпрямля-
ется: это значит, что отрицательные ча-
сти сигнала либо обрезаются, либо их
знак меняется, и они становятся положи-
тельными. После того, как выпрямленный
сигнал слегка сглаживается, он по форме примерно совпадает с модулирующей
кривой, которую станция накладывает на сигнал несущей частоты.
Какую роль при этом играет ширина полосы? Предположим, что музыкаль-
ная нота, которую нужно передать, является чистой .синусоидой cos 2nft, а не-
сущая волна cos 2и/о?, где fo много больше f. Посылаемый модулированный сиг-
нал является произведением двух косинусов
(cos 2эт ft) (cos 2л. f0 t) = cos 2л (f0 -j- f) t + cos 2л (f0 — f)t.
В каждом из двух слагаемых в правой части равенства достаточно информации
для восстановления исходного сигнала, если считать, что несущая частота fo
известна (несущая частота выбирается при настройке на дужную станцию). По-
этому существуют однополосные системы передачи сигналов, в которых пере-
дается только одно слагаемое, а другое подавляется.
Изучение этой формулы показывает, что для приема полосы частот исходно-
го сигнала нужно принять полосу такой же ширины, однако сдвинутую на не-
сущую частоту. Таким образом, для передачи информации нужна полоса неко-
торой .ширины, и чем она шире, тем больше различных сигналов можно пере-
давать. Г.рубо говоря, широкая полоса дает высокое качество, а при недоста-
точной ширине многие частоты подавляются, что приводит к низкому качеству.
То же самое верно для телефонных разговоров, хотя при этом в простей-
ших случаях несущей частоты нет. Телефонная аппаратура пропускает частоты
примерно до 3600 Гц и подавляет — выше 3600 Гц. При такой полосе обеспечи-
вается среднее качество передачи. Более высококачественные разговоры по теле-
фону («высококачественные» по воспроизведению тонов, а не по содержанию!)
потребовали бы более широкой полосы, а закон природы заключается в том, что
для увеличения ширины полосы нужно затрачивать средства и усиления. Пер-
воначально выбранная для телефона ширина полосы для того времени явилась
инженерным компромиссом между качеством и стоимостью, и теперь улучшить
ее нелегко, поскольку уже задействовано- очень много аппаратуры.
А6. Частотная модуляция
Вследствие, замираний и других свойств AM не столь хороша, как частотная
модуляция ЧМ. При AM модулируется амплитуда передаваемого сигнала, при
ЧМ— частота, т. е. информация передается путем непосредственного изменения
частоты. Используя при приеме автоматическую регулировку усиления, можно,
несмотря на замирания, поддерживать амплитуду на постоянном уровне.
Если в приемнике имеется фильтр, пропускающий все меньшую долю сиг-
нала по мере удаления от несущей частоты (она обычно много выше несущей
частоты при амплитудной модуляции), то соответствующим образом меняется
и энергия (или мощность, если измерять энергию в единицу времени). Таким
образом, грубо говоря, частотная модуляция использует сигнал A cos 2n[fo+/(Z)]?,
где f(t) мала по сравнению с несущей частотой /д. Снова для передачи инфор-
мации необходима некоторая полоса частот.
При частотной модуляции используется гораздо более широкая полоса, чем
при амплитудной; это позволяет значительно лучше подавлять шумы и точнее
воспроизводить передаваемый сигнал. При одинаковой ширине полосы ампли-
тудная и частотная модуляция одинаково эффективны.
А7. Импульсная модуляция
Обычно цифровые сигналы передаются с помощью двух состояний. Для
передачи можно использовать одну из двух .частот или одно из двух значений
напряжения (один из двух импульсов). В случае применения импульсов соот-
ветствующее представление через характеристические моды (собственные функ-
ции) не меняющейся со временем системы передачи сигналов, т. е. через функции
ехр (2n,ift), задается интегралом Фурье. Однако линейная система обеспечивает
каждой частоте свое усиление и фазовый сдвиг. Таким образом, «а приемном
конце импульс может приобрести форму, весьма отличную от первоначальной.
Дальнейшие искажения могут возникать из-за шума, неизбежного во всех ре-
альных системах.
Чем шире полоса, тем быстрее система может изменять свое состояние и
тем чаще импульсы могут посылаться по системе. Увеличивается не скорость
передачи импульсов, а их плотность по оси .времени. Неизбежное в системе пе-
редачи сигналов искажение не должно стать слишком большим до того, как
произойдет прием, коррекция, усиление и повторная передача сигнала. Распо-
лагая ретрансляторы достаточно близко друг к другу, искажения посылаемого
импульса можно поддерживать небольшим, так что надежность системы оказы-
вается высокой.
Иногда вместо того, чтобы символ 1 соответствовал наличию импульса, а
символ 0 — его отсутствию (или отрицательному импульсу), используется дру-
гая система, в которой символ 1 соответствует изменению состояния системы, а
О — отсутствию изменения состояния.
Разработано большое число систем импульсной модуляции. Необходимость
решения особенно трудного при построении таких систем вопроса о временной
синхронизации приводит к весьма сложным схемам. В импульсные системы ча-
сто вводятся устройства обнаружения и исправления ошибок.
А8. Ширина полосы с общей точки зрения
Цель настоящего приложения — познакомить читателя с различными сто-
ронами идеи о том, что пропускная способность канала эквивалентна ширине
полосы. Чтобы не использовать сложного математического аппарата, связанного
с интегралом Фурье, здесь приведены лишь наброски соответствующих резуль-
татов. 'В приложении указывается, что в некотором смысле пропускная способ-
ность, определяемая в теории информации, связана с шириной полосы. На прак-
тике пропускная способность часто понимается именно таким образом.
Теорема Шеннона позволяет надеяться, что утонченные методы кодирования
информации способствуют значительному улучшению подавления шума без пере-
хода к широкой полосе. Дальнейшему распространению такого подхода к ра-
дио- и телевизионной технике мешает сложность кодирования и декодирования.
Как мы видели, при хорошем кодировании используются очень длинные сооб-
щения, что ведет к необходимости большого объема памяти и к задержкам, не
говоря уже о сложностях обработки сигнала. Таким образом, практические
системы передачи сигналов редко достигают пределов, указанных теоремой
Шеннона. Однако в ближайшем будущем ситуация может измениться благо-
даря появлению дешевых микро-ЭВМ и дешевых цифровых запоминающих
устройств.
В телевидении нужно отразить все возможные изменения во всех точках
экрана за время от одного до другого кадра, а для этого необходима очень
широкая полоса. Однако психологические тесты показывают, что скорость вос-
приятия информации человеком не может превышать 40—50 бит/с. Даже учиты-
вая тот 'факт, что при рассмотрении одного и того же изображения разные
люди обращают внимание на разные его части, имеется превышение пример-
но в миллион раз того, что делается, над тем, что представляется минимально
необходимым. Именно в таких ситуациях теория Шеннона наиболее полезна:
она указывает инженеру, где можно получить большой выигрыш, а где в луч-
шем случае можно достичь лишь незначительных улучшений.
Спектр допустимых частот ограничен теми частотами, которые могут рас-
пространяться в земной атмосфере; большая часть этих частот уже занята для
различных целей. В некотором смысле полоса частот принадлежит «природным
ресурсам» и, -несомненно, ограничена, хотя не в том смысле, что ее использова-
ние уменьшает запасы, а в том, что невозможно одновременное ее использова-
ние для конкурирующих целей. Теория информации дает нам способ узнать,
когда полоса используется эффективно, а когда она расходуется напрасно.
Доступность дешевых -и надежных микро-ЭВМ увеличивает роль цифровых
методов передачи сигналов, которые допускают несложную защиту от шумов
(ошибок). Поэтому в этом кратком рассмотрении не затрагивались аналоговые
системы передачи сигналов.
Приложение Б.
Некоторые таблицы для вычисления энтропии
Пятизначные таблицы функций log2(l/p), plog2(l/p), Нг(р)
для р 0,00 (0,01) 1,00
р log (1/р) p.log (1/р) Н(р)
0.00 0 0
0.01 6.64386 0.06644 0.08079
0.02 5.64386 0.11288 0.14144
0.03 5.05889 0.15177 0.19439
0.04 4.64386 0.18575 0.24229
0.05 4.32193 0.21610 0.28640
0.06 4.05889 0.24353 0.32744
0.07 3.83650 0.26856 0.36592
0.08 3.64386 0.29151 0.40218
0.09 3.47393 0.31265 0.43647
0.10 3.32193 0.33219 0.46900
0.11 3.18442- 0.35029 0.49992
0.12 3.05889 0.36707 0.52936
0.13 2.94342 0.38264 0.55744
0.14 2.83650 0.39711 0.58424
0.15 2.73697 0.41054 0.60984
0.16 2.64386 0.42302 0.63431
0.17 2.55639 0.43459 0.65770
0.18 2.47393 0.44531 0.68008
0.19 2.39593 0.45523 0.70147
р log (1 Ip) P log (1/p) Продолжение таблицы W(P)
0.20 2.32193 0.46439 0.72193
0.21 2.25154 0.47282 0.74148
0.22 2.18442 0.48057 0.76017
0.23 2.12029 0.48767 0.77801
0.24 2.05889 0.49413 0.79504
0.25 2.00000 0.50000 0.81128
0.26 1.94342 0.50529 0.82675
0.27 1.88897 0.51002 0.84146
0.28 1.83650 0.51422 0.85545
0.29 1.78588 0.51790 0.86872
0.30 1.73697 0.52109 0.88129
0.31 1.68966 0.52379 0.89317
0.32 1.64386 0.52603 0.90438
0.33 1.59946 0.52782 0.91493
0.34 1.55639 0.52917 0.92482
0.35 1.51457 0.53010 0.93407
0.36 1.47393 0.53062 0.94268
0.37 1.43440 0.53073 0.95067
0.38 1.39593 0.53045 0.95804
0.39 1.35845 0.52980 0.96480
0.40 1.32193 0.52877 0.97095
0.41 1.28630 0.52738 0.97650
0.42 1.25154 0.52565 0.98145
0.43 1.21754 0.52356 0.98582
0.44 1.18442 0.52115 0.98959
0.45 1.15200 0.51840 0.99277
0.46 !. 1.12029 0.51534 0.99538
0.47 1.08927 0.51596 0.99740
0.48 1.05889 0.50827 0.99885
0.49 1.02915 0.50428 0.99971
0.50 1.00000 0.50000 1.00000
0.51 0.97143 0.49543 0.99971
0.52 0.94342 0.49058 0.99885
0.53 0.91594 0.48545 0.99740
0.54 0.88897 0.48004 0.99538
0.55 0.86250 0.47437 0.99277
0.56 0.83650 0.46844 0.98959
0.57 0.81097 0.46225 0.98582
0.58 0.78588 0.45581 0.98145
0.59 0.76121 0.44912 0.97650
0.60 0.73697 0.44218 0.97095
0.61 0.71312 0.43500 0.96480
0.62 0.68966 0.42759 0.95804
0.63 0.66658 0.41994 0.95067
0.64 0.64386 0.41207 0.94268
р log (1/р) Р log (1/р) Продолжение таблицы Н(р)
0.65 0.62149 0.40397 0.93407
0.66 0.59946 0.39564 0.92482
0.67 0.57777 0.38710 0.91493
0.68 0.55639 0.37835 0.90438
0.69 0.53533 0.36938 0.89317
0.70 0.51457 0.36020 0.88129
0.71 0.49411 0.35082 0.86872
0.72 0.47393 0.34123 0.85545
0.73 0.45403 0.33144 0.84146
0.74 0.43440 0.32146 0.82675
0.75 0.41504 0.31128 0.81128
0.76 0.39593 0.30091 0.79504
0.77 0.37707 0.29034 0.77801
0.78 0.35845 0.27959 0.76017
0.79 0.34008 0.26866 0.74148
0.80 0.32193 0.25754 0.72193
0.81 0.30401 0.24625 0.70147
0.82 0.28630 0.23477 0.68008
0.83 0.26882 0.22312 0.65770
0.84 0.25154 0.21129 0.63431
0.85 0.23447 0.19930 0.60984
0.86 0.21759 0.18713 0.58424
0.87 0.20091 0.17479 0.55744
0.88 0.18442 0.16229 0.52936
0.89 0.16812 0.14963 0.49992
0.90 0.15200 0.13680 0.46900
0.91 0.13606 0.12382 0.43647
0.92 0.12029 0.11067 0.40218
0.93 0.10470 0.09737 0.36592
0.94 0.08927 0.08391 0.32744
0.95 0.07400 О.О7ОЗО 0.28640
0.96 0.05889 0.05654 0.24229
0.97 0.04394 0.04263 0.19439
0.98 0-02915 0.02856 0.14144
0.99 0.01450 0.01435 0.08079
1.00 0.00000 0.00000 0.00000
список литературы
1. Abramson, N. Information Theory and Coding. New York: Mc-
Graw-Hill, 1963.
2. Berlekamp, E. R. Algebraic Coding Theory. New York:
McGraw-Hill, 1968.
3. Berlekamp, E. R., ed. Key Papers, in the Development of Coding
Theory. New York: IEEE Press, 1974.
4, .Blake, I., ed. Selected Papers on Algebraic Coding Theory.
Stroudsburg, Pa.: Dowden, Hutchinson and Ross, 1973.
5. Davisson, L. D., and Gray, R. M. Data Compression. Strouds-
burg, Pa.: Dowden, Hutchinson and Ross, 1976.
6. Gallager, R. G. Information Theory and Reliable Communica-
» tion. New York: John Wiley, 1968.
7. Gatlin, L. L. Information Theory and the Living System. New
York: Columbia University Press, 1972.
8. Guiasu, S. Information Theory with Applications. New York:
McGraw-Hill, 1977.
9. Jayant, N. S. Waveform Quantization and Coding. New York:
IEEE Press, 1976.
10. Knuth, D. E. The Art of Computer Programming, Vol. 3, Sorting
and Searching. Reading, Mass.: Addison-Wesley, 1973.
11. Mac Williams, J., and Sloane, N. J. A. The Theory of Error Cor-
recting Codes. (Elsevier, American ed.) Amsterdam: North-
Holland, 1977.
12. McEliece, R. J. The Theory of Information and Coding. Reading,
Mass.: Addison-Wesley, 1977.
13. Peterson, W. W., and Weldon, E. J., Jr. Error Correcting Codes,
2nd ed. Cambridge, Mass.: MIT Press, 1972.
14. Slepian, D., ed. Key Papers in the Development of Information
Theory. New York: IEEE Press, 1974.
15, Wakerly, J. Error Detecting Codes, Self-Checking Circuits and
Applications. Amsterdam: North-Holland, 1978.
16. Wozencraft, J. M., and Jacobs, I. M. Principles of Communica-
tion Engineering. New York: John Wiley, 1965.
Список литературы,
переведенной на русский язык
2. Берлекэмп Э. Р. Алгебраическая теория кодирования: Пер. с аигл. — М.:
Мир, 1971.
6. Галлагер Р. Теория информации и надежная связь: Пер. .с англ. — М.:
Сов. радио, 1974. ,
']0. Кнут Д. Е. Искусство программирования для ЭВМ. Т. 3. Сортировка и
поиск: Пер. с англ. — М.: Мир, 1978.
11. Мак-Вильямс Ф. Дж., Слоэн Н. Дж. А. Теория кодов, исправляющих ошиб-
ки: Пер. с англ. — М.: Связь, 1979.
13. Питерсон У., Уэлдон Э. Коды, исправляющие ошибки: Пер. с англ. — М.:
Мир, 1976.
16. Возенкрафт Дж. М., Джекобс И. М. Теоретические основы техники связи:
Пер. с англ. — М.: Мир, 1969.
Дополнительный список литературы
1*. R. W. Hamming. Error Detecting and Error Correcting Codes. — Bell Syst.
Tech. J., 1950, vol. 29, p. 147—160.
[Имеется перевод: P. В. Хэмминг. Коды с обнаружением и исправлением
ошибок. — В ки.: Коды с обнаружением и исправлением ошибок: Пер. с англ.
М.: ИЛ, 1956, с. 7—23.]
2*. С. Е. Shannon. A mathematical theory of communication. — Bell Syst. Tech.
J., 1948, vol. 27, p. 379—423, 623—656.
[Имеется перевод: К- Шеннон. Математическая теория связи. — В кн.:
К. Шеннон. Работы по теории информации и кибернетике. М.: ИЛ, 1963.]
Указатель
Абрамсон Н. 166
Абстрактная теория 6
Алфавит источника 6, 10
Алгебраическая теория кодирования
140
Амплитудная модуляция 166
Арифметика по модулю 2 22, 27
Байеса формула 9
Байт 13
Берлекэмп Э. Р. 166
Бит 11
— информации 80
Блэйк И. 166
Боковые лепестки 159
Бюро переписи населения США 31, 32
Вероятности переходов 64
— символов 6, 52
Взаимная информация 97, 103
— —, определение 104
---, свойства 104—106
Взвешенные коды 27
Возенкрафт Дж. М. 166
Га л лагер Р. 166
Гамма-фуикция 115
Гейтлин Л. Л. 166
Геометрический подход к построению
кодов 39
Граф переходов 63
Грей Р. М. 166
Дэвиссон Л. Д. 166
Двоичный симметричный канал 20,
99, 108, 131, 136
--- —, пропускная способность
111—113
Дерево решений 46
Джекобс И. М. 166
Дисперсия 124
— минимальная 59
— суммы 124
Жаян Н. С. 166
Закон больших чисел 125—128
И (команда) 29
Избыточность 23
Импульсная модуляция 162
Интеграл ошибок 116
— Фурье 58
Исключающее ИЛИ (команда) 22,29
Исправление ошибок 31
Испытания Бернулли 126—128
Источник информации 6, 9
---, определение 80
— с памятью 63
Канал 97
— двоичный симметричный 20, 99,
131, 136
— , определение 98
— , свойства 98
—, симметричный по входу 108
Кнут Д. Е. 166
Коды:
— ASCII 1.1, 12, 13, 27
— ван Дюрена 16
— взвешенные 27
— восьмеричные 12
— Грея 75
---, декодирование 76
— 2-из-б 16
— мгновенные 46, 47
— Морзе ,15
— неравномерные 16, 44
— «-мерные 34
— однозначные 45
— , потеря синхронизации 77
— прямоугольные 32
—, расширения 57
— с запятой 46, 49, 56
— с исправлением двойных ошибок
154
— с исправлением одиночных и обна-
ружением двойных ошибок 41, 144
— с исправлением ошибок 35
— с минимальной дисперсией 59
— с обнаружением ошибок 22
— 1 совершенные ПО
— треугольные 33
— Хаффмена 44, 52» 87, 91
---, использование 60
---, примеры 54, 55
--- с основанием г 57
L —, шум 58
L Хэмминга 35, 142, 148
--, пример 36
к —, проверки на четность 35, 142,
143
шестнадцатиричные 13
- эквивалентные 38
'одирование с перемешиванием 73
-------, столкновения 73
-------, удаление из таблицы 74
- с предсказанием 68
-------, декодирование 70
U------, длины серий 70
-------, кодер 69
- расширений марковского процес-
са 67
Хэмминга—Хаффмена 61
- Шениона—Фано 86
кодовое сжатие 21
конечные поля 140
конечный автомат 46, 60
1огическое сложение (исключающее
ИЛИ) 23, 24, 29
1ак-Вильямс Дж. 166
4ак-Элис Р. Дж. 166
Марковский процесс 62
-- эргодический 65
Матрица переходов 64
- •— предельная 65
Мгновенные коды 46
--, построение 47
Метаязык 19
Минимальное расстояние 40
Многочлены 144
простые 146
Множители Лагранжа 59, 85
Модель системы передачи сигналов 8
Модулярная арифметика 29, 146
Модуляция амплитудная 161
- импульсная 162
- частотная 162
1адежность 22
Мат (единица информации) 11
Мезависимые ошибки 24
^определенность 103
1еравеиство Крафта 48
- Макмиллана 51
- Чебышева 124
1еравномерные коды 16, 44
1есущая частота 162
1омера книг в системе ISBN 30
братные условные вероятности 99
днозначное кодирование 45, 51
ценка биномиальных коэффициен-
тов 119—121
Фано 137
шибки при считывании с барабана
26, 32
----------ленты 26, 33
Ошибочная перестановка символов 27
Парадокс 123
Питерсон В. В 166
Повторная передача 26
Поля Галуа 140
Потеря синхронизации 77
Правило максимального правдоподо-
бия 129, 133
Примитивный корень 148
Проверка на четность 14, 22, 36
-------, вычисление 23
------- нечетная 23
------- четная 22
Пропускная способность 97, 145
-----двоичного симметричного ка-
нала 111—113
-----, определение 146
Пространство п-мерное 114, 133
-----, расстояние 121
----- Евклидово 121
Прямое произведение 146
Прямые условные вероятности 99
Расстояние Хэмминга 39
-----, его смысл 40, 132
Расширение кодов 57, 88
-----, примеры 90, 132
Регистры сдвига 151
Решающее правило 129
Симметричный по входу канал 108,
109
----------, определение 108
Слепян Д. 166
Слоэн Н. Дж. А. 166
Служебные знаки 17
Случайный источник 11
— код 132
Смежная система 94
Собственные функции 158
Соотношения в канале 98
Средний случайный код 135
Средняя вероятность ошибки 135
— длина кода 6, 52
Стационарные вероятности 65
Сферы п-мерные 121
-----, коэффициенты 121
-----, таблица 122
-----, формула 122
Теорема кодирования без шума 78
-------------при нескольких алфа-
витах 106
— отсчетов 159
Теорема Шеннона основная 20, 78
128
-------, обращение 139
-------, общий случай 137
Укороченные блочные коды 50, 55
Унитарный многочлен 146
Условная вероятность 62
— взаимная информация 113
Уокерли Дж. 166
Устройства с двумя состояниями 10
Уэлдон Е. Дж. 166
Хартли (единица информации) 11
Цифровая модуляция 9, 158
Частотная модуляция 162
Чистая избыточность 23
Шеннон К. Е. 7
Ширина полосы 160
— — и скорость изменения 160
-----с общей точки зрения 162
Шум 24
—, его энтропия 103
— в кодах Хаффмена 58
Эволюция /
ЭВМ CRAY1 32
— NORC 32
— Эклипс 32
Энтропия 78, 80
— алфавита источника 101
— источника 80
— максимальная 84
— марковского процесса 92
— , основное неравенство 84
— принятого символа 101
— расширения 89
—, ее свойства 83—85
— совместная 102
— , ее таблицы 163
— условная 101
Эргодический марковский процесс 65
Эффективные коды 44, 48, 52
Оглавление
Предисловие редактора перевода . ....................... 3
Предисловие................. . .4
Глава 1. Введение..................................................... 6
1.1. Краткая аннотация 6
1.2. История.................... 7
1.3. Модель системы передачи сигналов................................. 8
1.4. Источник сообщений . . .... 9
1.5. Кодирование алфавита источника...................................10
1.6. Некоторые коды ..................................12
1.7. Код ASCII .................................. 13
1.8. Некоторые другие коды ...........................................15
1.9. Коды с основанием г . . . . .................17
1.10. Служебные знаки . . . 17
1.11. Краткое содержание книги .......................20
Глава 2. Коды с обнаружением ошибок.................................. 22
2.1. Для чего нужны коды с обнаружением ошибок?.......................22
2.2. Простые проверки на четность . 22
2.3. Коды с обнаружением ошибок . .......................23
2.4. Независимые ошибки — белый шум . ... 24
2.5. Повторная передача сообщения . .25
2.6. Простые коды для обнаружения пакетов ошибок ... 26
2.7. Буквенно-цифровые коды — взвешенные коды.........................27
2.8. Обзор модулярной арифметики......................................29
2.9. Номера книг в системе ISBN .... . 30
Глава 3. Коды с исправлением ошибок...................................31
3.1. Необходимость в исправлении ошибок...............................31
3.2. Прямоугольные коды...............................................32
3.3. Треугольные, кубические и n-мерные коды .........................33
3.4. Коды Хэмминга для исправления ошибок ............................35
3.5. Эквивалентные коды...............................................38
3.6. Геометрический подход............................................39
3.7. Коды с исправлением одиночных ошибок и обнаружением двойных
ошибок ...................................... . . 41
3.8. Применение идей . . ....... 43’
3.9. Итоги............................................................43
Глава 4. Неравномерные коды — коды Хаффмена . 7 ? 44
4.1. Введение........................................................44
4.2. Однозначное декодирование 45
4.3. Мгновенные коды............................................... 46
4.4. Построение мгновенных кодов.....................................47
4.5. Неравенство Крафта....................................... . . 48
4.6. Укороченные блочные коды ..................................50
4.7. Неравенство Макмиллана..........................................51
4.8. Коды Хаффмена...................................................52
4.9. Частные случаи кодов Хаффмена.................................. 55
4.10. Расширения кода................................................57
4.11. Коды Хаффмена с основанием г................................ 57
4.12. Шум в вероятностях кода Хаффмена . ... 58
4.13. Использование кодов Хаффмена . 60
4.14. Коды. Хэмминга—Хаффмена........................................61
Глава 5. Другие полезные коды........................................62
5.1. Введение .......................................................62
5.2. Что такое марковский процесс?...................................62
5.3. Эргодические марковские процессы ... . 65
5.4. Эффективное кодирование эргодического марковского процесса 67
5.5. Расширения марковского процесса ..... 67
5.6. Кодирование с предсказанием.....................................68
5.7. Кодер для кодирования с предсказанием.......................... 69
5.8. Декодер- .......................................................70
5.9. Длины серий.....................................................70
5.10. Итоги рассмотрения кодирования с предсказанием.................72
5.11. Что такое перемешивание?....................... 73
5.12. Обработка столкновений.........................................73
5.13. Удаление из таблицы.............................. ..........74
5.14. Итоги рассмотрения перемешивания ...........74
5.15. Цель кода Грея........................ . . 75
5.16. Подробное представление кода Грея............................. 76
5.17. Декодирование кода Грея................................... . 76
5.18. Другие коды.................................................. -77
Глава 6. Энтропия и первая теорема Шеннона......................... 78
6.1. Введение........................................................78
6.2. Информация . .... 78
6.3. Энтропия . . . . . ............80
6.4. Математические свойства энтропии.................... . . 83
6.5. Энтропия и кодирование..........................................85
6.6. Кодирование Шеннона—Фано......................-.................86
6.7. Насколько плохим является кодирование Шеннона—Фано? . . 87
6.8. Расширения кода......................................... .. 88
6.9. Примеры расширений ... ....... 90
6.10. Энтропия марковского процесса . . .. 92
6.11. Пример марковского процесса . . ’.....................93
6.12. Смежная система....................... . . . • 94
6.13. Итоги........................................................ 9®
Глава 7. Канал и взаимная информация.................................97
7.1. Введение . ......................97
7.2. Информационный канал 97
7.3. Соотношения в канале............................................98
7.4. Двоичный симметричный канал 99
7.5. Энтропия системы............................................. 101
7.6. Взаимная информация............................................103
7.7. Теорема Шеннона для семейств кодов ..... 106
Глава 8. Пропускная способность канала............................. 107
8.1. Определение пропускной способности канала . ... 107
8.2. Канал, симетричный по входу....................................108
8.3. Равномерный вход............................................. .109
8.4. Коды с исправлением ошибок......................................НО
8.5. Пропускная способность двоичного симметричного канала . . . 111
8.6. Условная взаимная информация...................................113
Глава 9. Предварительные математические сведения....................114
9.1. Введение ..................................................... 114
9.2. Гамма-функция Г(п)........................................... 115
9.3. Приближение Стирлинга для п! 116
9.4. Биномиальная оценка....................... . . 119
9.5. Евклидово п-мерное пространство 121
9.6. Один парадокс..................................................123
9.7. Неравенство Чебышева и дисперсия .124
9.8. Закон больших чисел.......................................... 125
Глава 10. Основная теорема Шеннона . . ... 128
10.1. Введение......................................................128
10.2. Решающие правила............... . . ................129
10.3. Двоичный симметричный канал 131
10.4. Случайное кодирование.........................................132
10.5. Средний случайный код . ................135
10.6. Общий случай ... . 137
10.7. Оценка Фано................................................. 137
10.8. Обратная теорема Шеннона......................................139
Глава 11. Алгебраическая теория кодирования ....................... 140
11.1. Введение . . ................................140
11.2. Еще раз о кодах с проверкой на четность и с обнаружением
ошибок..............................................................141
11.3. Еще раз о кодах Хэмминга..................................142
11.4. Еще раз о кодах с обнаружением двойных ошибок .... 144
11.5. Многочлены или векторы? . ................144
11.6. Простые многочлены 146
11.7. Примитивные корни 148
11.8. Один частный случай ..... ..................148
11.9. Регистры сдвига для кодирования...........................151
11.10. Декодирование кодов с исправлением одиночных ошибок . . . 153
11 11. Код с исправлением двойных ошибок ... . Г
11.12. Декодирование кодов с исправлением кратных ошибок .
11.13. Итоги................ ..................
Приложение А. Ширина полосы и теорема отсчетов
А1. Введение.............................................
А2. Интеграл Фурье
АЗ. Теорема отсчетов.....................................
А4. Ширина полосы и скорость изменения
А5. Амплитудная модуляция ....
Аб. Частотная модуляция ...................
А7. Импульсная модуляция ................................
А8. Ширина полосы с общей точки зрения ....
Приложение Б. Некоторые таблицы для вычисления энтропии
Список литературы..................................
Список литературы, переведенной на русский язык
Дополнительный список литературы
Указатель................................................
Уважаемый читатель!
В 1984 г. в издательстве «Радио и связь»
выйдут в свет книги:
Нуссбаумер Г. Быстрое преобразование Фурье
и алгоритмы вычисления сверток: Пер. с англ.—
16 л., ил.
Изложены вопросы, связанные с дискретны-
ми преобразованиями, которые применяются при
цифровой обработке сигналов. Особое внимание
уделено развитию теории и практическим алго-
ритмам выполнения циклической свертки и быст-
рого преобразования Фурье на основе линейных
полиномиальных преобразований. Изучены раз-
личные модификации предложенных алгоритмов
и их взаимосвязи.
Для инженерно-технических работников, за-
нимающихся решением прикладных задач циф-
ровой обработки сигналов.
Быстрые алгоритмы в цифровой обработке изо-
бражений: Пер. с англ./Под. ред. Т. Хуанга. —
15 л., ил.
Книга посвящена последним достижениям в
области цифровой обработки двумерных сигна-
лов: интегральным преобразованиям и медиан-
ной фильтрации. Среди эффективных в вычисли-
тельном отношении алгоритмов рассмотрены ал-
горитмы быстрого транспонирования двумерных
массивов во внешней памяти процессоров, поли-
номиальные алгоритмы быстрой двумерной сверт-
ки и вычисления дискретного преобразования
Фурье, алгоритмы Винограда вычисления диск-
ретного преобразования Фурье с уменьшенным
числом операций умножения.
Для научных работников, занимающихся во-
просами обработки двумерных сигналов.
И г л х а р т Д., Ш е д л е р Г. Регенеративное мо-
делирование сетей массового обслуживания: Пер.
с англ. — 7 л., ил.
Книга посвящена изучению динамики машин-
ных моделей как некоторого случайного процес-
са и созданию на этой основе статистических и
вероятностных методов их исследования. Ограни-
чение класса рассматриваемых моделей регене-
рирующими процессами позволило строить ста-
тистические процедуры с оцениваемой точностью.
Эффективность подхода иллюстрируется на при-
мере сетей массового обслуживания.
Для разработчиков и пользователей средств
моделирования.
Йенсен П., Барнес Д. Потоки в сетях. Про-
граммные методы: Пер. с англ. — 20 л., ил.
Книга посвящена задачам моделирования по-
токов в сетях. Материал представлен в форме,
удобной для инженеров-практиков: алгоритмы
решения различных задач по исследованию по-
токов в сетях четко изложены, хорошо иллюст-
рируются структурными схемами, сопровождают-
ся числовыми примерами. Содержит большое чи-
сло упражнений и задач.
Для инженерно-технических работников, за-
нимающихся проектированием сетей связи, ин-
формационных систем, сетей ЭВМ.
Приобрести эти книги Вы можете
во всех книжных магазинах, распространяющих
научно-техническую литературу