Теория
информации
Кодирование дискретных источников
Кодирование информации
для передачи по каналу с шумом
Кодирование с заданным
критерием качества
ДОПУЩЕНО
УЧЕБНО-МЕТОДИЧЕСКИМ ОБЪЕДИНЕНИЕМ
УЧЕБНИК
Б. Д. Кудряшов
Теория
информации
Допущено Учебно-методическим объединением вузов по университетскому
политехническому образованию в качестве учебного пособия для студентов
высших учебных заведений, обучающихся по направлению подготовки
230200 «Информационные системы».
С^ППТЕР'
Москва - Санкт-Петербург - Нижний Новгород - Воронеж
Ростов-на-Дону - Екатеринбург - Самара - Новосибирск
Киев - Харьков - Минск
2009
ББК 32.811Я7
УДК 621.391(075)
К88
Рецензент:
Коржик В. И., заслуженный работник высшей школы России,
доктор технических наук, профессор Санкт-Петербургского
государственного университета телекоммуникаций
им. М. А. Бонч-Бруевича
Кудряшов Б. Д.
К88 Теория информации: Учебник для вузов. — СПб.: Питер, 2009. — 320 с.:
ил. — (Серия «Учебник для вузов»).
ISBN 978-5-388-Q0178-8
В учебнике описаны алгоритмы работы современных методов сжатия данных, спосо-
бы эффективного представления аналоговой информации, методы анализа эффективности
систем помехоустойчивого кодирования. В последние годы появилась техническая ли-
тература, в которой описываются конкретные алгоритмы сжатия данных, применяемые
в современных стандартах и коммерческих программных продуктах. Отличие данного
учебника от аналогов состоит в том, что новые методы обработки информации излагают-
ся с позиций теории информации, как часть общей теории. Такой подход представляется
важным для подготовки потенциальных исследователей и разработчиков перспективных
информационных технологий.
I
ББК 32.811я7
УДК 621.391 (075)
Все права защищены. Никакая часть данной книги не может быть воспроизведена в какой бы то ни было форме
без письменного разрешения владельцев авторских прав.
Информация, содержащаяся в данной книге, получена из источников, рассматриваемых издательством как
надежные. Тем не менее, имея в виду возможные человеческие или технические ошибки, издательство не может
гарантировать абсолютную точность и полноту приводимых сведений и не несет ответственности за возможные
ошибки, связанные с использованием книги.
ISBN 978-5-388-00178-8
© Кудряшов Б. Д., 2009
© ООО «Лидер», 2009
Краткое содержание
Предисловие.................................................8
Введение...................................................10
Глава 1. Энтропия дискретных источников....................12
Глава 2. Неравномерное кодирование дискретных источников...57
Глава 3. Кодирование дискретных источников
при неизвестной статистике.........................92
Глава 4. Алгоритмы кодирования источников,
применяемые в архиваторах.........................128
Глава 5. Кодирование для дискретных каналов с шумом.......168
Глава 6. Измерение информации,
порождаемой непрерывным источником.......................204
Глава 7. Кодирование источника с заданным критерием качества.224
Глава 8. Квантование......................................253
Глава 9. Кодирование для непрерывных каналов с шумом......289
Список литературы........................................ 304
Предметный указатель......................................308
Содержание
Предисловие.....................................................8
Введение.......................................................  10
Глава 1. Энтропия дискретных источников.........................12
1.1.	Дискретные источники сообщений....................12
1.2.	Измерение информации. Собственная информация......16
1.3.	Энтропия..........................................18
1.4.	Выпуклые функции многих переменных ...............23
1.5.	Условная энтропия.................................27
1.6.	Дискретные случайные последовательности. Цепи Маркова.30
1.7.	Энтропия на сообщение дискретного
стационарного источника................................34
1.8.	Равномерное кодирование дискретного источника.
Постановка задачи......................................38
1.9.	Неравенство Чебышева. Закон больших чисел.........41
1.10.	Прямая теорема кодирования
для дискретного постоянного источника..................43
1.11.	Обратная теорема кодирования
для дискретного постоянного источника..................45
1.12.	Множество типичных последовательностей для дискретного
постоянного источника. Источники с памятью.............48
1.13.	Задачи...........................................51
1.14.	Библиографические замечания......................55
Глава 2. Неравномерное кодирование дискретных источников.......57
2.1.	Постановка задачи неравномерного
побуквенного кодирования...............................57
2.2.	Неравенство Крафта................................60
2.3.	Теоремы побуквенного неравномерного	кодирования...63
2.4.	Оптимальный побуквенный код — код Хаффмена........66
Содержание
5
2.5.	Избыточность кода Хаффмена..........................69
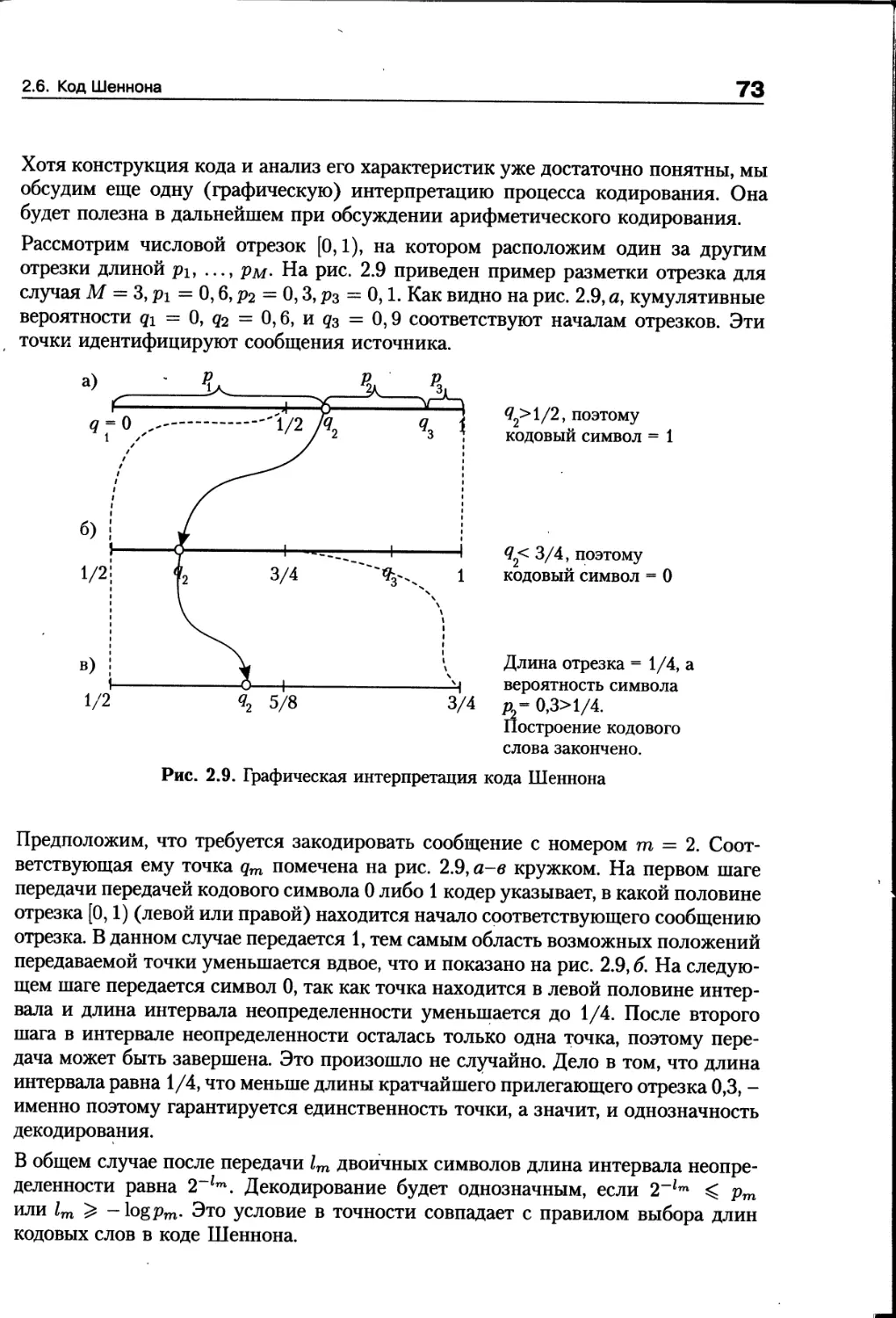
2.6.	Код Шеннона.........................................70
2.7.	Код Гилберта-Мура...................................74
2.8.	Неравномерное кодирование для стационарного источника...76
2.9.	Задачи..............................................89
2.10.	Библиографические замечания........................91
Глава 3. Кодирование дискретных источников
при неизвестной статистике.......................................92
3.1.	Постановка задачи универсального кодирования источников.92
3.2.	Несколько полезных комбинаторных формул.............95
3.3.	Двухпроходное побуквенное кодирование...............98
3.4.	Нумерационное кодирование..........................106
3.5.	Асимптотические границы избыточности
универсального кодирования...............................113
3.6.	Адаптивное кодирование.............................120
3.7.	Сравнение алгоритмов...............................125
3.8.	Задачи.............................................126
3.9.	Библиографические замечания .......................127
Глава 4. Алгоритмы кодирования источников,
применяемые в архиваторах.......................................128
4.1.	Монотонные коды....................................129
4.2.	Интервальное кодирование и метод	«стопка книг»...133
4.3.	Метод скользящего словаря (LZ-77)..................138
4.4.	Алгоритм LZW (LZ-78)...............................145
4.5.	Предсказание по частичному совпадению..............149
4.6.	Сжатие с использованием преобразования
Барроуза-Уилера...........................................155
4.7.	Сравнение способов кодирования.
Характеристики архиваторов................................164
4.8.	Задачи.............................................166
4.9.	Библиографические замечания........................167
Глава 5. Кодирование для дискретных каналов с шумом..................168
5.1.	Постановка задачи помехоустойчивого	кодирования....169
5.2.	Модели каналов.....................................172
5.3.	Взаимная информация. Средняя взаимная	информация ..175
6
Содержание
5.4.	Условная средняя взаимная информация.
Теорема о переработке информации........................178
5,5.	Выпуклость средней взаимной информации.............180
5.6.	Информационная емкость и пропускная способность....181
5.7.	Неравенство Фано...................................183
5.8.	Обратная теорема кодирования.......................187
5.9.	Вычисление информационной емкости
каналов без памяти......................................188
5.10.	Симметричные каналы ............................. 191
5.11.	Прямая теорема кодирования
для дискретных постоянных каналов...................196
5.12.	Типичные пары последовательностей.................200
5.13.	Задачи............................................202
5.14.	Библиографические замечания.......................203
Глава 6. Измерение информации,
порождаемой непрерывным источником..............................204
6.1.	Непрерывные вероятностные ансамбли.................205
6.2.	Дифференциальная энтропия. Взаимная информация
для непрерывных ансамблей............................206
6.3.	Дифференциальная энтропия случайных	векторов.......211
6.4.	Дифференциальная энтропия стационарных процессов
дискретного времени.....................................214
6.5.	Связь с энтропией дискретного ансамбля.
Множество типичных последовательностей
для непрерывного источника..............................219
6.6.	Задачи.............................................221
6.7.	Терминологические и библиографические замечания....223
Глава 7. Кодирование источника с заданным критерием качества....224
7.1.	Меры искажения. Постановка задачи кодирования......225
7.2.	Свойства функции скорость-искажение................228
7.3.	Простые примеры вычисления
функции скорость-искажение............................. 231
7.4.	Функция скорость-искажение для гауссовских
последовательностей.....................................236
7.5.	Обратная теорема кодирования для дискретного
постоянного источника при заданном критерии качества....240
7.6.	Множества типичных пар последовательностей.........241
Содержание
7
7.7.	Прямая теорема кодирования для дискретного
постоянного источника при заданном критерии качества......244
7.8.	Численный метод нахождения функции
скорость-искажение для источника без памяти...............247
7.9.	Задачи...............................................251
7.10.	Терминологические и библиографические замечания.....252
Глава 8. Квантование..............................................253
8.1.	Скалярное квантование................................254
8.2.	Векторное квантование................................262
8.3.	Квантователи на основе числовых решеток..............265
8.4.	Решетки на основе линейных кодов.
Сложность квантования.....................................278
8.5.	Квантование с помощью решеток
на основе сверточных кодов................................283
8.6.	Задачи...............................................288
8.7.	Библиографические замечания..........................288
Глава 9. Кодирование для непрерывных каналов с шумом..............289
9.1.	Каналы дискретного времени...........................289
9.2.	Канал непрерывного времени с аддитивным
белым гауссовским шумом...................................292
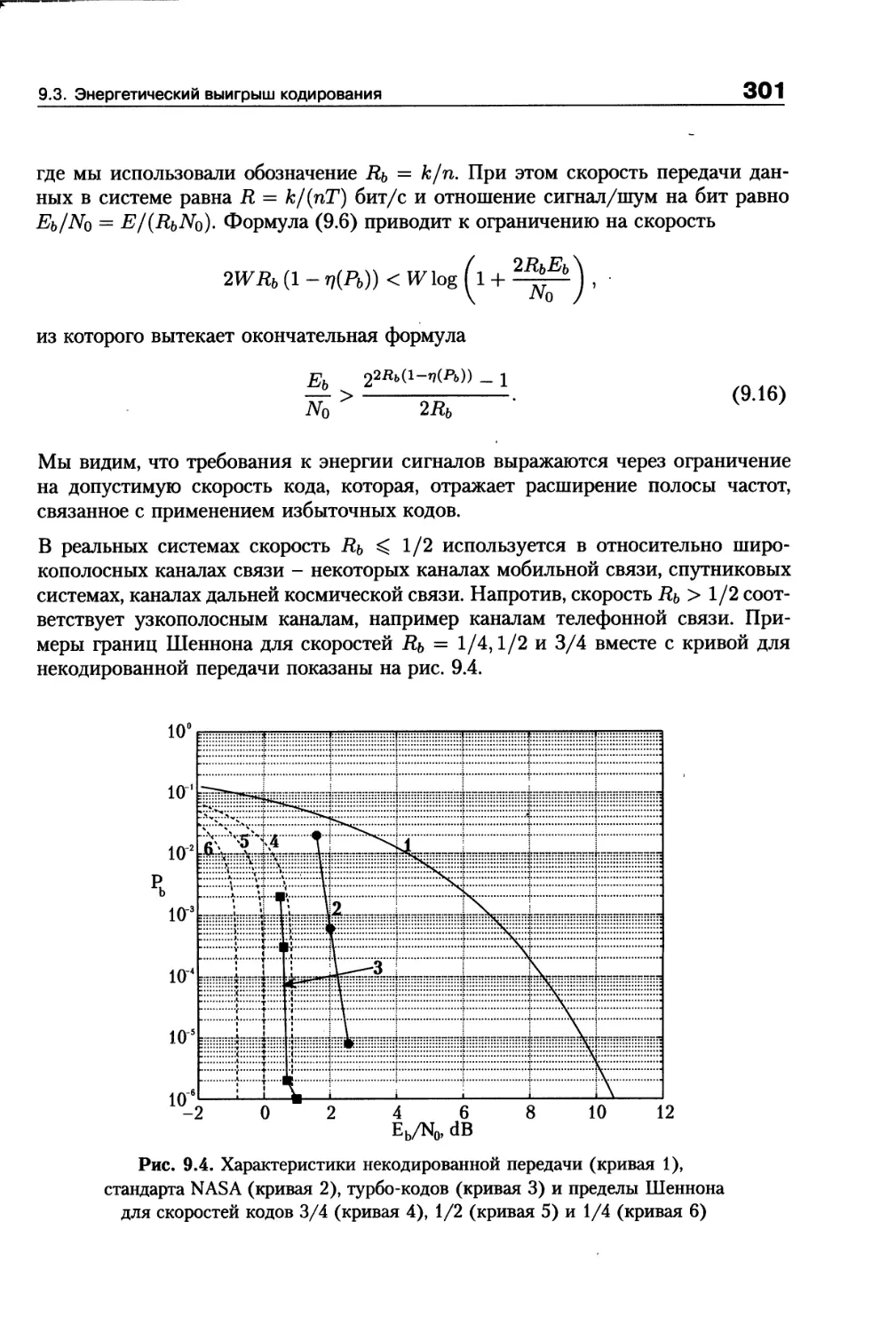
9.3.	Энергетический выигрыш кодирования...................296
9.4.	Задачи...............................................303
9.5.	Библиографические замечания .........................303
Список литературы.................................................304
Предметный указатель..............................................308
Предисловие
В наши дни уже нет необходимости объяснять, насколько важны информацион-
ные технологии вообще и теория информации в частности. Хотелось бы объяс-
нить, для чего написана эта конкретная книга и какие пробелы в существующей
литературе она заполняет.
Фундаментальный учебник В. Д. Колесника и Г. Ш. Полтырева [7], изданный
в 1982 году, покрывает все основные разделы Шенноновской теории информации
и почти совсем не утратил актуальности как вузовское пособие для студен-
тов. Действительно, набор основных сведений, представляющих собой основы
теории, остался прежним. Вот что существенно изменилось за четверть века, про-
шедшие с момента публикации учебника - это связь между теорией и практикой.
То, что в 80-е годы воспринималось как абстрактное математическое упражнение,
сегодня - решение конкретной практической задачи. Именно поэтому изме-
нилось и представление о подборе материала для краткого курса и о степени
важности различных понятий и разделов теории информации для подготовки
инженеров в области информационных технологий.
Представляемый вниманию читателя учебник ставит своей целью объяснить
с позиций теории информации, как работают те самые методы, которыми чита-
тель пользуется ежедневно, когда пользуется архиваторами файлов, слушает му-
зыку воспроизводимую МПЗ-проигрывателем, разговаривает по мобильному теле-
фону или смотрит фильм, записанный на DVD. Хотелось бы убедить студента
в том, что все это не так уж сложно, по крайней мере, для человека, воору-
женного знанием элементарных основ теории, фундамент которой был заложен
К. Шенноном еще в 1948 году.
Содержание книги формировалось, с одной стороны, в процессе многих лет пре-
подавания теории информации студентам технического вуза, с другой стороны -
в результате исследовательской работы в рамках проектов, связанных с разра-
боткой систем сжатия данных, сжатия речи, аудио- и видеоинформации, а также
систем модуляции и помехоустойчивого кодирования. Таким образом, данный
учебник - попытка смешать в правильной пропорции элементарные сведения
из комбинаторики и теории вероятностей, теоремы теории информации и кон-
кретные алгоритмы обработки информации с тем, чтобы получился легкий для
усвоения и полезный для читателя продукт.
Предисловие
9
Автор считает своим приятным долгом выразить свою признательность Г. Ш. Пол-
тыреву и В. Д. Колеснику, у которых автор учился теории информации (и мно-
гому другому) и продолжает учиться до сих пор. В. Д. Колесник читал рукопись
данного учебника и сделал много полезных замечаний, способствовавших его
улучшению. Практическая работа в разнообразных приложениях теории инфор-
мации стала возможной благодаря сотрудничеству с Г. Тененгольцем. Его под-
держка и полученный с его помощью помощью опыт неоценимы. Многие аспекты
сжатия информации автор обсуждал с Ю. М. Штарьковым. Эти дискуссии, а
также семинары Ю. М. Штарькова в большой степени повлияли на содержание
учебника.
В течение многих лет автор проводил совместные исследования с Р. Йоханнессо-
ном и его аспирантами в Университете г. Лунд (Швеция). Творческая обстановка
на кафедре Информационных технологий способствовала увлекательному и пло-
дотворному научному поиску, а личный пример Р. Йоханнессона помог лучше
понять, чему и как следует учить студентов.
Автор благодарен Лундскому университету, а также Университету г. Ульм (Гер-
мания) и компании Самсунг (Корея) за финансовую поддержку теоретических
и прикладных исследований в последние несколько лет.
Без сомнения, самыми важными были помощь и бескопромиссная критика жены
и соратника И. Е. Бочаровой. Содержание глав, посвященных кодированию ана-
логовых источников, интенсивно обсуждалось с ней и поэтому существенно пере-
секается с содержанием соответствующих разделов ее учебника [32}.
Введение
Теория информации наука с точно известной датой рождения. Ее появление на
свет связывают с публикацией работы Клода Шеннона «Математическая теория
связи» (1948) [20]. С тех пор теория информации прошла большой путь, обога-
тилась огромным числом интересных научных открытий и доказала свою прак-
тическую важность. Сегодня в повседневный обиход вошли высокоскоростные
модемы для телефонных каналов, лазерные компакт-диски для хранения инфор-
мации, жесткие диски большой емкости для персональных компьютеров, мобиль-
ные телефонные аппараты для сотовых систем связи и многие другие устрой-
ства, создание которых было бы невозможно без привлечения методологии и
математического аппарата, разработанных в рамках теории информации.
Хотя теории информации часто приписывают несколько более широкое значе-
ние, применяя ее методологию в естествознании и искусстве, с точки зрения
самого Шеннона, она может корректно рассматриваться только как раздел мате-
матической теории связи. Поэтому круг задач теории информации мы поясним
с помощью представленной на рис. В.1 структурной схемы типичной системы
передачи или хранения информации. В этой схеме под источником понима-
Рис. В.1. Блок-схема системы связи
ется любое устройство или объект живой природы, порождающие сообщения,
которые должны быть перемещены в пространстве или во времени. Это может
быть клавиатура компьютера, человек, аналоговый выход видеокамеры и т.п.
Поскольку, независимо от изначальной физической природы, все подлежащие
передаче сообщения обычно преобразуются в форму электрических сигналов,
именно такие сигналы мы и будем рассматривать как выход источника.
Цель кодера источника - представление информации в наиболее компактной
форме. Это нужно для того, чтобы максимально эффективно использовать ресур-
сы канала связи либо запоминающего устройства.
Введение
11
Далее следует кодер канала, задачей которого является обработка информации
с целью защиты сообщений от помех при передаче по каналу связи либо от воз-
можных искажений при хранении информации. Модулятор служит для преоб-
разования сообщений, формируемых кодером канала, в сигналы, согласованные
с физической природой канала связи или средой накопителя информации.
Остальные блоки, расположенные на приемной стороне, выполняют обратные
операции и предоставляют информацию ее получателю в удобном для исполь-
зования виде.
Итак, в теории информации можно выделить следующие разделы:
►	Кодирование дискретных источников. Иногда эту часть теории информации
называют кодированием без потерь, кодированием для канала без шума, сжа-
тием информации.
►	Кодирование информации для передачи по каналу с шумом. Речь идет о защите
информации от помех в каналах связи.
►	Кодирование с заданным критерием качества. В некоторых системах связи
искажения информации считаются допустимыми. Более того, информация
аналоговых источников вообще не может быть представлена в цифровой форме
без искажений. В данной главе речь идет о методах кодирования, обеспечиваю-
щих наилучший компромисс между качеством (оцениваемым некоторой объ-
ективной мерой искажения) и затратами на передачу информации. Сегодня
задачи такого типа стали особенно актуальны, поскольку они находят широкое
применение для цифровой передачи речи, видео- и аудиоинформации.
►	Кодирование информации для систем со многими пользователями. Здесь обсуж-
дается оптимальное взаимодействие абонентов, использующих какой-либо
общий ресурс, например канал связи. Примеры систем с множественным досту-
пом - системы мобильной связи, локальные сети ЭВМ.
►	Секретная связь, системы защиты информации от несанкционированного дос-
тупа. Здесь также можно указать широкий круг актуальных задач, лежащих
на стыке теории информации, теории вычислительной сложности алгоритмов,
исследования операций, теории чисел.
Из перечисленных разделов в данном пособии рассматриваются первые три.
Глава 1 Энтропия дискретных
источников
1.1. Дискретные источники сообщений
Цель этого параграфа - напомнить те понятия, определения и формулы теории
вероятностей, которыми мы будем пользоваться в дальнейшем.
Будем обозначать через X некоторое дискретное множество, то есть множество,
содержащее конечное или счетное количество элементов х G X. Элементы мно-
жества X назовем элементарными событиями, непустые подмножества А с X
мы называем событиями. Через | А| мы обозначаем мощность множества А (коли-
чество элементов в А), Если |А| > 1, такое событие называется сложным собы-
тием. В рамках теории информации подмножества X называются сообщениями,
а элементарные события х е X - элементарными сообщениями.
Напомним, что множество чисел {р(ж)}? х € X, задает распределение вероятно-
стей на дискретном множестве X = {ж}, если все числа р(х) неотрицательны и
удовлетворяют условию нормировки 52 р(я) = 1-
хЕХ
Вероятность сложного события А определяется как
Р(А) = ^р(х).
хЕА
Множество сообщений X в совокупности с распределением вероятностей {р(ж)},
х е X, образуют дискретный вероятностный ансамбль X = {ж,р(ж)|.
Рассмотрим множество П всевозможных подмножеств множества X. Заметим,
что если X - конечное множество, содержащее |Х| = N элементов, то количество
различных подмножеств будет |П| = 2N. Элементами П являются элементар-
ные и сложные события из X, пустое (невозможное) событие 0, достоверное
событие X, Для любого А е П определена операция взятия дополнения Ас, ддя
любой йары множеств А, В е Q определены операции объединения событий
АиВ и пересечения событий АГ)В. Иначе их называют суммой и произведением
событий соответственно. Для произведения событий мы будем пользоваться обо-
значением АВ = АПВ. Перечисленные операции над событиями определяют
множество Q как булеву алгебру событий. Справедливы формулы
1.1. Дискретные источники сообщений
13
Р(0) = 0;
Р(Х) = 1;
Р(АС) = 1 - Р(А);
Р(А U В) = Р(А) + Р(В) - Р(АВ).
События несовместны, если их пересечение - пустое множество. Для несов-
местных событий вероятность объединения равна сумме вероятностей событий.
Если условие несовместности не выполнено, вероятность объединения стано-
вится меньше суммы вероятностей. Это верно для любого числа событий. Оценка
м	м
п U	Е
т=1	тп=1
называется аддитивной оценкой вероятности суммы событий. Равенство в этой
оценке достигается только для несовместных событий.
Для произвольной пары событий А,В С X условной вероятностью события А
при условии В называется величина
при Р(В) =4 0 и величина Р(А\В) = 0 при Р(В) = 0.
Из этого определения следует
Р(АВ) = Р(А\В)Р(В).
Для совокупности произвольного числа событий из этой формулы выводится
соотношение
Р(Л ... Ап) = Р(А1)Р(А2\А1)Р(А3\А1А2)... P(An|A ... An-i).
События А,В С Xназывают независимыми, если
Р(АВ) = Р(А)Р(В).
Совместно независимыми называют события Аь ..., Ап С X такие, что
Р(АХ... An) = P(Ai)P(A2)... Р(АП).
Если А, В С X - независимые события, то
Р(А|В) - Р(А); Р(В|А) = Р(В).
м
Пусть несовместные события В1,...,Ям таковы, что Р( |J Нт) = 1. Такой
171=1
набор событий иногда удобно рассматривать как систему «гипотез» по отноше-
нию к заданному событию А. Имеет место формула полной вероятности
м
Р(А) = £ Р(А\Нт)Р(Нт)
т=1	*
14
Глава 1. Энтропия дискретных источников
и формула апостериорной вероятности, или формула Байеса,
Е Р(А\Нт)Р(Нт)
т—1
Произведением множеств X и Y называется множество
Z = XY = {(х,у) : х е Х,у G Y} -
множество упорядоченных пар, первый элемент которых принадлежит множе-
ству X, а второй - множеству У. Хотя обозначения для произведения множеств и
произведения (пересечения) событий совпадают, смысл этих понятий, очевидно,
различен. Какое из двух понятий имеется в виду, ясно из контекста.
Нетрудно подсчитать число элементов в множестве Z = XY:
|ХУ| = |Х|-|У|.
Перемножая произвольное число п множеств Х2, ..., Хп, получаем мно-
жество последовательностей длины п, составленных из элементов множеств-
сомножителей. В частном случае, когда все множества одинаковы, Xi = Х2 =
= ... = Хп = X, используется краткая запись
Х1%2 ...хп = хп = {Сп,..., хп) : Xi е X,i = 1,... ,п} .
Чтобы определить произведение вероятностных ансамблей X = {х,рх(х)} и
У = {?/,ру(?/)}, нужно на произведении множеств XY задать совместное рас-
пределение вероятностей {рху(х,у)}. В результате получим ансамбль XY =
= {(х>У))Рху(х,у)}‘ Нижний индекс при распределениях вероятностей указы-
вает, на каком множестве определено данное распределение. Этот индекс мы
указываем только в тех случаях, когда это важнр для однозначности понимания.
Определение произведения вероятностных ансамблей естественным образом рас-
пространяется на произвольное число ансамблей-сомножителей. Число сомно-
жителей п называют размерностью ансамбля-произведения, соответствующее
распределение вероятностей - многомерным (n-мерным). Если задано п-мерное
распределение, тем самым заданы и распределения для меньших размерностей.
В частности, для произведения двух ансамблей имеем
и®) = р(х’У)>
yeY
р(у) = 52 р(х> у)-
хех
Условным распределением вероятностей на элементах множества X при фикси-
рованном элементе у G У называется распределение
?(Ф) = <
Р(я?>у)
р(у) ’
если р(у) / О,
О в противном случае,
хеХ.
\
1.1. Дискретные источники сообщений
15
Ансамбли X и Y независимы, если имеют место тождества
р(ж, у) = р(х)р(у\ хеХ, у е У.
Используя эти понятия, легко обобщить формулу перемножения вероятностей,
формулу полной вероятности и формулу Байеса на произведение вероятностных
ансамблей. Например, справедлива формула
р(ж1,... ,хп) = р(ж1)р(ж2|ж1)р(жз|ж1ж2).. .р(жп|ж1,..., жп_1).
Большую роль в теории информации играют случайные ансамбли, элементы
которых - числа. Такие ансамбли являются случайными величинами. Матема-
тическим ожиданием случайной величины х е X называется
и = 52 хр(хУ
хех
Для произвольного множества X можно определить функцию р(х), х е X, при-
нимающую вещественные значения. Тем самым устанавливается отображение
X на множество вещественных чисел. Новый вероятностный ансамбль с мно-
жеством значений У = {у = ^(я)} является случайной величиной. Для вычис-
ления математического ожидания величины у не обязательно знать распреде-
ление вероятностей ру(у) для у. Имея распределение рх(ж) на X, величину
Му [у] можно получить, если воспользоваться следующим полезным свойством
математического ожидания:
Му[у] = Мх[ф)] = ^2 ф(х)Рх(х).	(1.1)
х^Х
Действительно,
мИу] = 52 ур^{у) = 52у 12 рх^=
y£Y	yeY х:<р(х)=у
= 52 52 урх (ж)= 52 52	= ^2
у€У х:<р(х)=у	y£Y х:<р(х)=у	хЕХ
Другими важными характеристиками случайных величин являются дисперсия
Dx [ж] = Мх Мх И)2]
и корреляционный момент
КХу{х, у) = Мху [(ж - М [ж]) (?/ - М [у])].
В определениях математического ожидания, дисперсии и корреляционного
момента нижние индексы указывают на ансамбли, по которым производится
усреднение. Мы будем писать этот индекс только в том случае, если из контекста
непонятно, о каком ансамбле идет речь.
Если для двух случайных величин корреляционный момент равен нулю, случай-
ные величины называют некоррелированными. Напомним следующие свойства
числовых характеристик:
16
Глава 1. Энтропия дискретных источников
1.	Для любых случайных величин х и у
М [ж + у] = М [ж] + М [?/].
2.	Если с - константа, а х - случайная величина, то
М [сж] = сМ [ж].
3.	Если х и у - независимые случайные величины, то
М [од] = М [ж] М [у].
4.	Для некоррелированных случайных величин х и у
D [ж + у] = D [ж] + D [?/].
5.	Если с - константа, а х - случайная величина, то
D [ся] = c2D [ж] .
6.	Если с - константа, а х - случайная величина, то
D [с + ж] = D [ж].
7.	Если х и у независимы, то К(х,у) = 0, то есть из независимости случайных
величин следует их некоррелированность. Обратное, вообще говоря, неверно.
Доказательство этих свойств - полезное упражнение на применение правила
(1.1).
1.2. Измерение информации.
Собственная информация
Задача количественного измерения информации возникла при решении кон-
кретных практических задач. Можно не сомневаться, что первоначальным моти-
вом было стремление уменьшить количество электрических сигналов, необхо-
димых для передачи сообщений по каналам связи. Поэтому разумной мерой
информации, содержащейся в сообщении, является мера, монотонно связанная
с затратами на передачу сообщения.
Условимся также о том, что сообщения представляют собой случайные события
(по крайней мере, с точки зрения получателя информации). Рассмотрим в каче-
стве источника произвольное дискретное множество X, и каждой букве х е X
припишем вероятность р(х).
Сформулируем интуитивные требования к мере ^(ж), определенной для всех
х е X, которую следует принять как меру информации, содержащейся в сооб-
щениях ансамбля X = {х,р(х)}.
► Поскольку предполагается, что эта мера будет определять затраты, связанные
с передачей или хранением сообщений, мера должна быть неотрицательной.
1.2. Измерение информации. Собственная информация
17
► Поскольку для нас несущественно, каким образом будут интерпретированы
и использованы передаваемые сообщения, мера должна однозначно опреде-
ляться вероятностью сообщения. Поэтому вместо будем писать ^(р(ж)).
► Установим характер зависимости меры от вероятности сообщений. Пусть име-
ется множество из двух равновероятных сообщений и стоит задача кодирова-
ния сообщений этого множества двоичными символами алфавита А = {0,1}.
Интуитивно ясно, что неплохой способ кодирования состоит в том, чтобы
сопоставить одному из сообщений символ 0, а другому - символ 1. Точно
также для кодирования четырех равновероятных сообщений можно исполь-
зовать последовательности длины 2, для восьми сообщений - длины 3 и т.д.
В этих примерах вероятностям 1/2, 1/4, 1/8, ...соответствовали затраты на
передачу, равные 1, 2, 3, ...единицам информационной меры соответственно.
Следовательно, разумно потребовать, чтобы мера информации удовлетворяла
соотношению м(Рт) = шм(р)-
► Рассмотрим последовательность сообщений xi, ..., хп, выбираемых незави-
симо из одного и того же множества X с одним и тем же распределением веро-
ятностей {р(ж)|. Из статистической независимости сообщений следует, что
знание предыдущих сообщений не помогает предугадать следующие. Поэтому
затраты на передачу последовательности складываются из затрат на пере-
дачу каждого отдельного сообщения. Получаем еще одно разумное требование
к информационной мере:
/1(^1,..., хп) = /4^1) +... + м(^п)
для независимых сообщений xi,..., хп.
Перечисленные требования к информационной мере приводят нас к следующему
определению.
Собственной информацией 1(х) сообщения ж, выбираемого из дискретного ан-
самбля X = {ж,р(ж)}, называется величина, вычисляемая по формуле
1{х) = -logp(:r).	(1.2)
В этой формуле не указано основание логарифма. Мы и дальше не будем его
указывать, всякий раз подразумевая, что логарифмы вычисляются по основа-
нию 2, если не оговорено другое. Это соответствует измерению информации
в битах. Если бы логарифм вычислялся по натуральному основанию, единицей
измерения информацией стал бы нат. Если основание десятичное - информация
измеряется в Хартли (в честь Хартли, который использовал формулу (1.2) еще
до Шеннона). Биты удобнее, поскольку они сразу показывают, сколько двоичных
символов надо потратить на передачу сообщения. В теоретико-информационных
исследованиях часто предпочитают наты, поскольку In х удобнее дифференци-
ровать, чем log х. Мы будем пользоваться битами.
Из определения собственной информации и свойств логарифма непосредственно
вытекают следующие свойства собственной информации:
18
Глава 1. Энтропия дискретных источников
► Неотрицательность: 1(х)	0, ж е X.
► Монотонность: если xi,x2 € X, p(zi) то I(a?i) /(я2).
► Аддитивность. Для независимых сообщений xi,..., хп имеет место равенство
п
Т(ж1, • • •, хп) =	I(xi).
г=1
Пример 1.2.1. Пусть X = {а, 5, c,d} и вероятности букв будут р(а) = 1/2,
р(Ь) = 1/4, р(с) = p(d) = 1/8. Тогда собственные информации букв равны
/(а) = 1, 1(b) = 2, 1(c) = 1(d) = 3 бит. Легко указать способ кодирования, при
котором на каждую букву будет затрачено по два бита. Наша мера информации
показывает, что на самом деле буквы несут различное количество информации,
и, может быть, разумнее тратить различное число битов на передачу различных
букв (как в азбуке Морзе). Позже мы вернемся к этому примеру и проверим
наше предположение.
Пример 1.2.2. Пусть X = {а, Ь} и вероятности букв будут р(а) = 0,05, р(Ь) =
= 0,95. Тогда 1(a) = 4,322,1(b) = 0,216. Мы получили дробные числа. Более того,
передача одного из двух символов может потребовать больше 4 битов информа-
ции! На второй символ предлагается тратить примерно 1/5 бита. Это на первый
взгляд кажется невозможным. Однако, как мы увидим позже, тратить целый бит
на передачу каждой буквы рассматриваемого источника - непозволительная
роскошь.
Нельзя ли было использовать для измерения информации другую функцию?
Этот вопрос поднимался много раз как на заре теории информации, так и
в последние годы. Доказано, что при предположениях, сформулированных выше
(и некоторых других предположениях, касающихся непрерывности и дифферен-
цируемости информационной меры), информационная мера единственна
с точностью до постоянного множителя, то есть с точностью до выбора основания
логарифма.
1.3. Энтропия
Определенная в предыдущем параграфе мера информации, содержащейся в сооб-
щении, представляет собой случайную величину. Собственная информация сооб-
щения х дискретного ансамбля X = {х,р(х)} характеризует «информативность»
или «степень неожиданности» конкретного сообщения. Среднее значение или
математическое ожидание этой величинь! по ансамблю X = {х,р(х)} будет харак-
теристикой информативности всего ансамбля.
Энтропией дискретного ансамбля X = {ж,р(х)} называется величина
Н(Х) = М [- logp(x)] = - 52 Нж) logp(x).
хех
1.3. Энтропия
19
Можно интерпретировать энтропию как количественную меру априорной неосве-
домленности о том, какое из сообщений будет порождено источником. Часто
говорят, что энтропия является мерой неопределенности. Приведем несколько
свойств энтропии, проясняющих смысл этого понятия и позволяющих оценивать
энтропию без точных вычислений.
Свойство 1.3.1. Н(Х) 0.
Свойство 1.3.2. Я(Х) log |Х|. Равенство имеет место в том и только в том
случае, когда элементы ансамбля X равновероятны.
Свойство 1.3.3. Если для двух ансамблей X и Y распределения вероятностей
представляют собой одинаковые наборы чисел (различающиеся только порядком
следования элементов), то Н(Х) = Н(У).
Свойство 1.3.4. Если ансамбли XuY независимы, то
H(XY)=H(X) + H(Y).
Свойство 1.3.5. Энтропия - выпуклая П функция распределения вероятностей
на элементах ансамбля X.
Свойство 1.3.6. Пусть X = {ж,р(х)} и А С X. Введем ансамбль X' = {х,р'(ж)},
задав распределение вероятностей р'(х) следующим образом:
( р(А)
// ч J ”Г7Г’жеЛ’
р (ж) = <	|Л|
( р(х),х ф А.
Тогда Н(Х')	Н(Х). Иными словами, «выравнивание» вероятностей элементов
ансамбля приводит к увеличению энтропии.
Свойство 1.3.7. Пусть задан ансамбль X ина множестве его элементов опре-
делена функция д(х). Введем ансамбль Y = {у = д(х)}. Тогда Я(У) Н(Х).
Равенство имеет место тогда и только тогда, когда функция д(х) обратима.
Смысл последнего утверждения состоит в том, что обработка информации не
приводит к увеличению энтропии.
Доказательства свойств 1.3.1, 1.3.3 и 1.3.4 мы оставляем читателю в качестве
очень простых упражнений. Доказательства свойств 1.3.5 и 1.3.6 будут даны
в следующем параграфе. Доказательство свойства 1.3.7 мы отложим до знаком-
ства с понятием условной энтропии (параграф 1.5).
Доказательство свойства 1,3.2. Рассмотрим разность левой и правой частей
доказываемого неравенства:
20
Глава 1. Энтропия дискретных источников
Я(Х) - log |Х|
= - $2 P(®) bg р(х) - р(ж) log | =
хЕХ	хЕХ
(с)	( 1 А
* lo8e
= ioge	=0-
\sGX । I xEX /
Поясним приведенные выкладки. Переход (а) основан на свойстве нормировки
вероятностей, (Ь) - на свойствах логарифма. Переход (с) использует хорошо
известное неравенство
In Ж X — 1,
эквивалентное неравенству
(1.3)
logrr (я — l)loge.
Нам придется еще не раз воспользоваться этим свойством логарифма, поэтому
остановимся на нем подробнее. Графики функций In х и (х — 1) приведены
на рис. 1.1. Из них видно, что неравенство превращается в равенство только
1.3. Энтропия
21
в одной точке х = 1. Поэтому в нашем случае необходимым и достаточным
условием равенства будет условие р(х) = 1/|Х|, х е X. Последующие переходы
снова используют условие нормировки вероятностей. Итак, разность оказалась
неотрицательной и, следовательно, свойство 1.3.2 доказано.	□
Сформулированные выше свойства имеют простую интерпретацию. Достаточно
вспомнить, что энтропия определяет информативность источника или средние
затраты на представление информации в двоичной форме. Рассмотрим, напри-
мер, источник с объемом алфавита 256. При любом распределении вероятностей
на буквах источника одного байта (8 бит) на букву достаточно для хранения
любого из сообщений источника. Свойство 1.3.2 говорит о том, что в предельном
случае, когда все буквы источника равновероятны, энтропия источника как раз
и равна 8 бит.
Предположим теперь, что речь идет о текстовом файле на русском языке. Если
использовать в качестве вероятностей букв их средние частоты появления
в тексте, то, подставив вероятности в формулу для энтропии, получим величину
близкую к 4,5. Это означает, что буква русского текста несет в среднем 4,5 бита, то
есть не следует тратить для ее хранения целый байт. Попробуем обработать файл
каким-либо стандартным архиватором. Окажется, что файл достаточно большого
объема сожмется примерно в 4 раза. Может показаться, что на самом деле энтро-
пия дает плохую оценку затрат на хранение букв источника. Это не совсем
верно. Обратимся к свойству 1.3.4. Из него следует, что затраты на хранение
последовательности букв можно подсчитать как сумму затрат на каждую букву
в том случае, когда буквы независимы. Это условие заведомо не выполняется для
осмысленного текста. Значит, нам необходимо научиться подсчитывать энтро-
пию источников зависимых сообщений. Этим мы займемся позже. Свойство 1.3.5
сыграет свою роль при анализе информационных характеристик источников.
Свойство 1.3.6 подсказывает, почему для одних ансамблей энтропия велика, для
других - мала. Все дело в том, насколько разнятся вероятности, с которыми появ-
ляются буквы. Знать, что некоторые буквы более вероятны, - это все равно что
иметь какую-то информацию еще до того, как буква будет порождена источни-
ком. Нужно только научиться использовать на практике эту априорную инфор-
мацию.
Перейдем к рассмотрению очень простого и очень важного примера - двоичного
ансамбля сообщений.
Пример 1.3.1. Рассмотрим двоичный ансамбль X = {0,1}. Положим р(1) = р,
р(0) = 1 — р = <?. Энтропия этого ансамбля
Я(Х) = -plogp- glogg = р(р).	(1.4)
Мы ввели специальное обозначение т?(р) для энтропии двоичного ансамбля,
в котором один из элементов имеет вероятность р. Эта функция будет часто
использоваться. Построим график зависимости т/(р) от р при р е [0,1]. Начнем
с крайних точек р = 0 и р = 1. В обоих случаях имеет место неопределен-
ность. Тем не менее, используя правило Лопиталя, легко вычислить предельные
22
Глава 1. Энтропия дискретных источников
значения т/(р) при р —> 0 и р 1. Получим т/(0) = ??(1) = 0. Далее, заметим,
что т/(р) = ??(1 — р), то есть функция симметрична относительно оси р = 1/2.
Это можно было бы также вывести, опираясь на свойство энтропии 1.3.3. Чтобы
найти экстремальные точки, следует вычислить производную функции ??(р):
7?'(р) = - logp + l°g(l - р)-
Точкой экстремума функции р(р) оказывается точка р = 1 /2. Вычисляя вторую
производную
т?"(р) = ~ loge/p - loge/(l - р) < 0,
убеждаемся в том, что это точка максимума. Этот результат можно было предска-
зать на основе свойства 1.3.2. Кроме того, нетрудно видеть, что вторая производ-
ная строго отрицательна. Отсюда следует, что энтропия двоичного ансамбля -
строго выпуклая вверх функция параметра р. График функции р(р) представлен
на рис. 1.2.
Программисты и инженеры, имеющие дело с двоичной информацией, привыкли
называть битом любой двоичный разряд в записи числа, содержимое двоичной
ячейки памяти или значение двоичного сигнала. Мы теперь знаем, что в терминах
теории информации один бит - максимальное среднее количество информа-
ции, переносимое двоичным сигналом. Если, например, вероятность единицы
равна 0,1, то энтропия двоичного ансамбля равна 0,469, то есть приблизительно
половине бита. Получается, что «инженерный бит» в данном случае в 2 раза
больше «теоретико-информационного бита».
1.4. Выпуклые функции многих переменных
23
1.4.	Выпуклые функции многих переменных
Нам предстоит исследовать поведение некоторых функций на множестве X
в зависимости от распределения вероятностей на X. Это означает, что мы будем
иметь дело с функциями нескольких переменных. Поведение функции одной
переменной мы привыкли изучать с помощью производных. По знаку первой
производной мы определяем, возрастает функция в данной точке или убывает.
Равенство нулю первой производной означает, что точка подозрительна на экс-
тремум. Знак второй производной (минус) говорит о выпуклости или (плюс) —
о вогнутости функции в точке и позволяет, в частности, классифицировать точки,
подозрительные на экстремум, как точки минимума, максимума или точки пере-
гиба.
Изучение выпуклости функции многих переменных помогает во многих случаях
судить о поведении функций, в частности, о существовании и единственности
их экстремумов, без выполнения громоздких вычислений.
В теории информации принято различать функции выпуклые вверх и функции
выпуклые вниз. В первом случае для краткости пишут, что функция выпукла П,
а во втором — что она выпукла U.
В следующих определениях мы опираемся в основном на геометрические пред-
ставления о выпуклости, а не на вычисление производных. Прежде всего, рас-
смотрим множество значений аргументов (область определения функции) и вве-
дем для него понятие выпуклости.
Множество аргументов функции запишем в виде вектора. Рассмотрим произ-
вольную функцию /(я?), определенную для всех векторов из некоторого мно-
жества R — {я?}. Само множество R мы считаем подмножеством т-мерного
евклидова пространства векторов с вещественными компонентами. На рис. 1.3
приведены примеры двумерных областей R.
Рис. 1.3. Примеры двумерных областей
Среди этих примеров множеств второе множество невыпуклое, остальные три -
выпуклые. Формальный критерий здесь такой: если для любых двух точек мно-
жества весь отрезок, соединяющий эти точки, принадлежит множеству, то мно-
жество является выпуклым.
Множество вещественных векторов R выпукло, если для любых я?, я?' е R и
любого а е [0,1] вектор у = ах + (1 — а)я/ принадлежит R.
24
Глава 1. Энтропия дискретных источников
В этом определении множество значений вектора у представляет собой одномер-
ную линейную функцию параметра а или, проще говоря, прямую. Эта прямая,
очевидно, проходит через точки х и ж'. Поскольку область изменения пара-
метра а ограничена отрезком [0,1], множество значений вектора у принадлежит
отрезку, соединяющему точки жиж'. Таким образом, формальное определение
в точности соответствует графической интерпретации.
Приведем важный для нас содержательный пример выпуклой области.
ТЕОРЕМА 1.1. Множество вероятностных векторов длины М выпукло.
Доказательство. Напомним, что компоненты вероятностных векторов неотрица-
тельны и сумма компонент равна 1. Будем записывать распределение вероятно-
стей на множестве X = {1,2,..., М} в виде вектора из М элементов. Для двух
распределений вероятностей, р = (pi,... ,рм) и р' = (р'15... ,р^), и параметра
а е [0,1] рассмотрим множество векторов вида
q = ар + (1 - а)р'.
Нужно доказать, что этот вектор тоже стохастический. Все элементы вектора
Q = (<7ь • • • неотрицательны, поскольку в правой части имеем сумму двух
неотрицательных векторов. Сумма компонент вектора q
мм	м
$2«< =	+ (1 - а) = а + 1 - а = 1.
1-—1	I— 1	®=1
Тем самым утверждение доказано.	□
Теперь мы готовы к тому, чтобы конкретизировать понятие выпуклой функции.
Функция /(ж) векторного аргумента х, определенная на выпуклой области Я,
называется выпуклой П на этой области, если для любых as, os' G R и любого
а е [0,1] имеет место неравенство
f(ax + (1 - а)®') > otf(x) + (1 - а)/(ж').	(1.5)
Отметим, что, если в (1.5) возможно равенство при некоторых значениях а е (0,1),
функцию называют нестрого выпуклой. В противном случае она называется строго
выпуклой. Выпуклость области определения функции нужна для того, чтобы
выражение в левой части (1.5) имело смысл.
Определение функции выпуклой U получается из (1.5) изменением знака нера-
венства на противоположный. Мы в дальнейшем рассматриваем только выпук-
лые П функции, считая, что перенос результатов на второй случай не составляет
труда.
Рисунок 1.4 поясняет понятие выпуклой функции многих переменных на при-
мере функции одной переменной. Из элементарных геометрических соображе-
ний следует, что правой части (1.5) при различных значениях а соответствуют
1.4. Выпуклые функции многих переменных
25
точки отрезка, соединяющего точки с координатами (a?i, и (ж2, /(ж2)). Левой
части соответствуют точки на кривой. Из рисунка видно, что
f(axi + (1 - а)^) > af(xi) + (1 - a)f(x2)
и определение выпуклости функции многих переменных хорошо согласуется
с привычным понятием выпуклости функции одной переменной.
Непосредственно из определения, используя метод математической индукции,
легко вывести следующее свойство выпуклых функций.
ТЕОРЕМА 1.2. Пусть f(x) - выпуклая А функция векторного аргумента х, опре-
деленная на выпуклой области R, и пусть константы 0ц,..., &м е [0,1] таковы,
м
что = 1. Тогда для любых х±,..., хм G R
т=1
(М
т=1
М
> 52 a^f(xт)*
т=1
(1.6)
Это свойство имеет следующую важную для дальнейшего применения интерпре-
тацию. Пусть константы ат, использованные в формулировке этого свойства,
означают вероятности соответствующих векторов жт. Тогда суммы в правой и
левой частях (1.6) будут математическими ожиданиями, если считать, что слу-
чайный вектор х принимает значение хт с вероятностью ат. Получаем полезное
неравенство
/(М[®]) >М(/(®)].	(1.7)
Именно это простое неравенство, часто называемое неравенством Йенсена, в даль-
нейшем сократит выкладки, связанные с анализом информационных характе-
ристик алгоритмов кодирования. Однако, чтобы пользоваться им, нужно быть
26
Глава 1. Энтропия дискретных источников
уверенным, что функция выпукла. Поэтому остаток параграфа будет посвящен
выводу признаков выпуклости функций многих переменных.
В формулировках следующих утверждений, вытекающих из определения выпук-
лых функций, предполагается, что все функции определены на одной и той же
выпуклой области.
Свойство 1.4.1. Сумма выпуклых функций выпукла.
Свойство 1.4.2. Произведение выпуклой функции и положительной константы
представляет собой выпуклую функцию.
Прямым следствием этих утверждений является еще одно свойство.
Свойство 1.4.3. Линейная комбинация выпуклых функций с неотрицательными
коэффициентами - выпуклая функция.
Теперь мы знаем, что доказать выпуклость функции многих переменных можно,
представив функцию в виде линейной комбинации других функций, выпуклость
которых доказать легко. Если, например, функция представлена в виде линейной
комбинации функций одной переменной, то анализ составляющих можно выпол-
нить, вычислив производные. Опираясь на эти результаты, докажем выпуклость
энтропии ансамбля как функции распределения вероятностей на множестве его
элементов.
ТЕОРЕМА 1.3. Энтропия Н(р) дискретного ансамбля с распределением вероят-
ностей р является выпуклой п функцией аргумента р.
Доказательство. Прежде всего, заметим, что постановка вопроса о выпуклости
энтропии корректна, поскольку ее область определения выпукла в соответствии
с доказанной выше теоремой 1.1. По определению энтропии
м	м
Н(р) = “ 52 PrnlogPm = 52 /”»(₽)•
т=1	7П=1
Рассмотрим слагаемые Каждое из них представляет собой функцию одной
переменной. Вторая производная этой функции равна — (loge)/pm и, следова-
тельно, отрицательна при всех рт е (0,1). Таким образом, энтропия выпукла
в силу свойства 1.4.3. Тем самым теорема доказана.	□
Заметим, что слагаемые fm(p) в (1.8) - строго выпуклые функции. Следова-
тельно, энтропия также строго выпукла.
В заключение параграфа мы приведем пример применения свойств выпуклых
функций как инструмента исследования свойств информационных мер. Докажем
свойство энтропии 1.3.6.
Доказательство свойства 1.3.6. Пусть имеется ансамбль X, |Х| = М. Запи-
шем вероятности букв в виде вектора р = (pi,... ,рм)« Для энтропии ансамбля
1.5. Условная энтропия
27
будем использовать обозначение Н(р). Докажем, частный случай утверждения,
а именно, что выравнивание вероятностей первого и второго элементов множе-
ства X приводит к увеличению энтропии. Обобщение на случай произвольного
подмножества А С X оставим читателю в качестве упражнения. Обозначим
Р = ((pi + Рг)/2, (pi +Р2)/2, рз, • • •, Рм). Нужно доказать неравенство
Н(р) > Щр).	(1.9)
Для этого введем обозначения
Р'=Р = (Р1,Р2,РЗ,---,Рм),
Р" = (Р2,Р1,РЗ,---,Рм)-
Заметим, что по свойству энтропии 1.3.3 два распределения имеют одинаковую
энтропию, то есть Н(р') = Н(р") = Н(р). Справедливо тождество р = (р' +р")/2.
Из выпуклости энтропии следует, что
Я(р) = н > |я(р')+ IW') = Н^-	°
1.5.	Условная энтропия
Как уже отмечалось, для эффективного кодирования информации необходимо
учитывать статистическую зависимость сообщений. Наша ближайшая цель -
научиться подсчитывать информационные характеристики последовательностей
зависимых сообщений. Начнем с последовательности, состоящей из двух сооб-
щений.
Рассмотрим ансамбли X = {ж} и Y = {у} и их произведение XY = {(ж, р),р(ж, р)}.
Для любого фиксированного у е Y можно построить условное распределение
вероятностей р(ж|р) на множестве X и для каждого х е X подсчитать собствен-
ную информацию
/(ф) = ~logp(rr|p),
которую называют условной собственной информацией сообщения х при фикси-
рованном у.
Ранее мы назвали энтропией ансамбля X среднюю информацию сообщений х е X.
Аналогично, усреднив условную информацию I(x\y) по х е X, получим величину
н(х\у) = - 52 1о&р(х\уУ	(1Л°)
хех
называемую условной энтропией X при фиксированном у е Y. Заметим, что
в определении (1.10) имеется неопределенность в случае, когда р(х\у) = 0. Выше,
в параграфе 1.3, отмечалось, что выражение вида z log z стремится к нулю при
z —> 0, и на этом основании мы считали равными 0 все слагаемые энтропии,
соответствующие буквам, вероятность которых равна 0. Точно так же в (1.10)
мы считаем равными нулю слагаемые, для которых р(ж|?/) = 0.
28
Глава 1. Энтропия дискретных источников
Вновь введенная энтропия Н(Х\у) - случайная величина, поскольку она зави-
сит от случайной переменной у. Чтобы получить неслучайную информационную
характеристику пары вероятностных ансамблей, нужно выполнить усреднение
в (1.10) по всем значениям у. Величина
H(X\Y) = - 22
xtXyEY
называется условной энтропией ансамбля X при фиксированном ансамбле Y. Отме-
тим ряд свойств условной энтропии.
Свойство 1.5.1. Я(Х|У) 0.
Свойство 1.5.2. Я(Х|У) < Н(Х), причем равенство имеет место в том и толь-
ко в том случае, когда ансамбли XuY независимы.
Свойство 1.5.3. Я(ХУ) = Я(Х) + H(Y\X) = H(Y) + Я(Х|У).
Свойство 1.5.4. Я(Хх...Хп) = Я(Хг) + Я(Х2|Х1) 4- Я(Х3р№) + • • • +
+ Я(Хп|Х1,...,Хп-1).
Свойство 1.5.5. H(XIYZ) < H(X\Y), причем равенство имеет место в том и
только в том случае, когда ансамбли X и Z условно независимы при всех у € У.
п
Свойство 1.5.6. H(Xi... Хп)	причем равенство возможно только
г=1
в случае совместной независимости ансамблей Xi,..., Хп.
Свойство 1.5.1 доказывается так же, как свойство энтропии 1.3.1. Мы приведем
два доказательства свойства 1.5.2. Первое основано на относительно простых
выкладках и использует неравенство (1.3). Другое доказательство приводится
в качестве примера использования выпуклости энтропии.
Доказательство свойства 1.5.2. По аналогии с доказательством свойства энтро-
пии 1.3.2
Я(Х|У)-Я(Х) = -^^p(x,y)logp(x\y) +
xeXyeY
+ 52 52 ^х' у"> log^x) = 52 52 у) log J©
xeXy^Y	xeXyeY
xeXy^Y	7
= 152 52 Hj/W)- 52 52 p(x>y))loge=°-
xeXyeY J
1.5. Условная энтропия
29
Это же свойство можно вывести из свойства выпуклости энтропии. Поскольку
энтропия ансамбля зависит только от распределения вероятностей, вместо выра-
жения Я(Х) будем писать Я(рх), где рх означает записанное в виде вектора
распределение вероятностей {р(ж)}. Тогда
Я(Х|У) (=> Му[я(рх|в)]<
? я(Му[рх|у]) =
= Н(рх) = Н(Х),
где Рх\у ~ условное распределение на X при фиксированном у, переход (а)
основан на определении условной энтропии, неравенство (Ь) - на выпуклости
энтропии, следующее затем равенство (с) основано на формуле полной вероят-
ности
Му [р(а:|у)] = ^р(х\у)р(у) = р(х).	g
Доказательство свойств 1.5.3 и 1.5.4УПо формуле перемножения вероятностей
р(ж,у) = р(х)р(у\х) = р(у)р(х\у),
р(ж1,..., хп) = р(х1)р(х2\х1)... p(a?nki,...,
Обе стороны этих тождеств нужно прологарифмировать, а затем усреднить по
всем случайным переменным.	□
Доказательство свойства 1.5.5. Рассмотрим ансамбль XYZ = {(ж, у, z),p(x, у, z)}.
При каждом у е Y определены условные распределения p(x,z\y) и р(х\у). Для
этих распределений запишем энтропии
Я(Х|у,2) = MXZ|J/[-logp(x|y2)],
Я(Х|у) = MX|s[-logp(x|y)].
По свойству 1.5.2
H(X\y,Z)<H(X\y).
После усреднения по всем у получим требуемое неравенство.	□
Из свойств 1.5.1-1.5.5 следует 1.5.6.
Обсудим «физический смысл» сформулированных свойств условной энтропии.
Свойство 1.5.2 устанавливает, что условная энтропия ансамбля не превышает его
безусловной энтропии. Свойство 1.5.5 усиливает это утверждение. Из него сле-
дует, что условная энтропия не увеличивается с увеличением числа условий. Оба
эти свойства неудивительны, они отражают тот факт, что дополнительная инфор-
мация об ансамбле X, содержащаяся в сообщениях других ансамблей, в сред-
нем уменьшает информативность (неопределенность) ансамбля X. Замечание
«в среднем» здесь очень важно, поскольку неравенство
Н(Х\у) Я(Х),
вообще говоря, неверно.
30
Глава 1. Энтропия дискретных источников
Применим выявленные свойства условной энтропии для доказательства свой-
ства энтропии 1.3.7, устанавливающего невозрастание энтропии при обработке
информации.
Доказательство свойства 1.3.7. Имеем ансамбль X = {х,р(х)}> определенную
на нем функцию д(х) и ансамбль Y = {у = р(ж), х е X}. Нужно доказать, что
Я(У) ^Я(Х).	(1.11)
По свойствам энтропии
Я(ХУ) = Я(Х|У) +Я(У) = Я(У|Х) +Я(Х).	(1.12)
>0	=о
Поскольку значения д(х) однозначно определены при заданном ж, имеем
H(Y\X) = 0. В то же время Я(Х|У) 0. С учетом этих обстоятельств из (1.12)
следует (1.11).	□
Напомним, что вычисление энтропии - это вычисление затрат на передачу или
хранение букв источника. Свойства условной энтропии подсказывают, что при
передаче буквы Xn+i следует использовать то обстоятельство, что предыдущие
буквы Xi, ..., Хп уже известны принимающей стороне. Это позволит вместо
Я(Хп+1) бит потратить меньшее количество Я(Хп+1|Х1,... ,Хп) бит. В то же
время свойство 1.5.6 указывает другой подход к экономному кодированию. Из
этого неравенства следует, что буквы перед кодированием имеет смысл объ-
единять в блоки и эти блоки рассматривать как буквы нового «расширенного»
источника. При этом затраты будут меньше, чем при независимом кодировании
букв. Какой из двух подходов эффективнее?
Ниже мы дадим более точную количественную характеристику этих двух подхо-
дов, но перед этим вспомним некоторые определения из теории вероятностей.
1.6.	Дискретные случайные
последовательности. Цепи Маркова
Вместо отдельных ансамблей и произведений конечного числа ансамблей мы
будем рассматривать теперь случайные последовательности из произвольного
числа событий. Если элементы случайной последовательности - вещественные
числа, то такие последовательности называются случайными процессами.
Номер элемента в последовательности трактуется как момент времени, в который
появилось данное значение. Множество значений времени может быть непре-
рывным либо дискретным, и множество значений случайной последовательно-
сти также может быть непрерывным либо дискретным. Сейчас нас интересуют
только дискретные процессы дискретного времени.
\
Случайный процесс xi, х2, ...со значениями Хг G X, i = 1,2,..., задан, если
для любых п указан способ вычисления совместных распределений вероятностей
1.6. Цепи Маркова
31
Проще всего задать случайный процесс, предположив, что его значения в раз-
личные моменты времени независимы и одинаково распределены. Тогда
п
'	1=1
где p(xi) - вероятность появления xi е X в момент времени г. Для описания
такого процесса достаточно указать вероятности р(х) для всех х е X (всего |Х|-1
вероятностей).
Описание более сложных моделей процессов будет громоздким, если не сделать
упрощающих предположений. Нам не обойтись без предположения о стационар-
ности.
Процесс называется стационарным, если для любых п и t имеет место равенство
p(Xi,.. . , Жп) = pfa+t, • • • , ^n+t),
в котором подразумевается, что Xi = х^и г = 1, ..., п. Иными словами, случай-
ный процесс стационарен, если вероятность любой последовательности не изме-
няется при ее сдвиге во времени (не зависит от положения последовательности
на оси времени).
Числовые характеристики (в частности, математическое ожидание) стационар-
ных процессов не зависят от времени. Рассматривая стационарные процессы,
мы можем вычислять независящие от времени информационные характеристики
случайных процессов.
Мы уже рассмотрели один пример стационарного процесса - процесс, значения
которого независимы и одинаково распределены. Источник, порождающий такой
процесс, называют дискретным постоянным источником (ДПИ).
Простейшей моделью источника, порождающего зависимые сообщения, является
марковский источник.
Случайный процесс х±, х2, ...называют цепью Маркова связности з, если для
любых п и для любых х = (®i,..., хп) е Хп справедливы соотношения
р(х) =р(ж1,...,жв)р(жв+1|ж1,...,а?в)р(жв+2|ж2...жв+1) X ••• х
Хр(жп |жп__в, . • • , Хп—1 )•
Иными словами, мы называем марковским процессом связности s такой процесс,
для которого при п > 8
р(хп |^1» • • • , Хп— 1) = р(жп|жп_з, . . . , Хп_ 1),	‘
то есть условная вероятность текущего значения при известных предшествую-
щих з не зависит от всех других предшествующих значений.
Значение марковского процесса xt в момент времени t принято называть состо-
янием в момент t Описание марковского процесса задается начальным распреде-
лением вероятностей на последовательностях из первых з значений (состояний)
32
Глава 1. Энтропия дискретных источников
и условными вероятностями вида р(хп\хп_8,..., жп_1) для всевозможных после-
довательностей (хп-з,... ,жп). Если указанные условные вероятности не изме-
няются при сдвиге последовательностей (жп_в,... ,жп) во времени, марковская
цепь называется однородной.
Однородная марковская цепь связности s = 1 называется простой цепью Мар-
кова. Для описания простой цепи Маркова с множеством состояний X =
= {0,1,...,М-1} достаточно указать начальное распределение вероятностей
{р(ж1), xi е X} и условные вероятности
TTij = P(xt = jfxt-i = i), i, j = 0,..., M - 1,
называемые переходными вероятностями цепи Маркова.
Переходные вероятности удобно записывать в виде квадратной матрицы размер-
ности М х М
п =	Я"00 7Г10	7Г01 7Гц	Я0,М-1
	. ТГМ-1,0	ТГМ-1,1 •	•*	7ГМ-1,М-1 _
называемой матрицей переходных вероятностей. Эта матрица - стохастическая
(неотрицательная, сумма элементов каждой строки равна 1).
Обозначим через pt стохастический вектор, компоненты которого - вероятности
состояний цепи Маркова в момент времени t, то есть pt —	. ,Pt(M - 1)),
где pt (г) есть вероятность состояния i в момент времени Л i = 0, ..., М — 1. Из
формулы полной вероятности следует, что
М-1
Pt+1G) = Р^№ц
3=0
или в матричной форме
Pt+i =	(1*13)
Отсюда для произвольного числа шагов п получаем
Pt+n = Ptnn-
Значит, вероятности перехода за п шагов могут быть вычислены как элементы
матрицы Пп.
Из (1.13) видим, что распределение вероятностей в момент времени t зависит от
величины t и от начального распределения рг. Отсюда следует, что в общем слу-
чае рассматриваемый случайный процесс нестационарен. Предположим, однако,
что существует стохастический вектор р, удовлетворяющий уравнению
р = рП.
(1.14)
1.6. Цепи Маркова
J33
Положим рг = р. Тогда, воспользовавшись (1.13), получим р2 = р и в конечном
итоге pt = р при всех t. Таким образом, однородная марковская цепь стацио-
нарна, если в качестве начального распределения выбрано решение уравнения
(1.14).
Стохастический вектор р, удовлетворяющий уравнению (1.14), называется ста-
ционарным распределением для цепи Маркова, задаваемой матрицей переходных
вероятностей П.
Финальным распределением вероятностей называют вектор
Poo = lira pt = lim р^*,	(1.15)
с—>оо	t—>оо
(если указанный предел существует).
Из этого определения следует, что финальное распределение - распределение
вероятностей в момент времени t. бесконечно далекий от начального момента
времени t = 1. Было бы естественно ожидать, что с течением времени зависи-
мость от начального распределения рх ослабевает и что р^ не зависит от рР
Оно не зависит также и от времени. Таким образом, распределение р^ тоже
(как и р), в некотором смысле, стационарное распределение. Как же соотносятся
между собой Роо и р?
Оказывается, для широкого класса простых цепей Маркова предел в (1.15) не
зависит от начального распределения рг и равен единственному решению урав-
нения (1.14), то есть р^ = р. Такие цепи называют эргодическими.
Как найти по матрице П, эргодична ли соответствующая цепь Маркова? Ответ
на этот вопрос заведомо положительный, если все элементы матрицы П поло-
жительны (не равны нулю). Более точное (но и сложнее проверяемое) усло-
вие состоит в том, что должна существовать некоторая положительная степень
по матрицы П такая, что все элементы матрицы Пп положительны при любых
п По.
Чтобы сформулировать необходимое и достаточное условие эргодичности, при-
дется ввести несколько определений.
Состояние цепи i достижимо из состояния J, если для некоторого п вероятность
перехода из состояния j в состояние г за п шагов положительна. Множество
состояний С называется замкнутым, если никакое состояние вне С не может
быть достигнуто из состояния, входящего в С.
Цепь называется неприводимой, если в ней содержится не больше одного замкну-
того множества. Цепь Маркова неприводима, в частности, тогда, когда все ее
состояния достижимы друг из друга.
Состояние i называется периодическим, если существует такое t > 1, что вероят-
ность перехода из г в г за п шагов равна нулю при всех п, не кратных t. Цепь, не
содержащая периодических состояний, называется непериодической.
34
Глава 1. Энтропия дискретных источников
В этих терминах мы наконец можем точно определить класс эргодических цепей
Маркова.
ТЕОРЕМА 1.4. Непериодическая неприводимая цепь Маркова эргодична.
С понятием эргодичности применительно к более широкому классу процессов,
чем цепи Маркова, мы познакомимся подробнее в связи с кодированием источ-
ников.
1.7.	Энтропия на сообщение дискретного
стационарного источника
Рассмотрим произвольный дискретный стационарный источник, порождающий
последовательность (xi, ж2,..., xt,...), xt е Xt = X, Из предположения о стаци-
онарности следует, что распределение вероятностей для буквы xt, порождаемой
в момент времени t, не зависит от t Следовательно, энтропия этого распре-
деления Я(Х*) = Я(Х) также не зависит от времени. Назовем ее одномерной
энтропией источника (или соответствующего случайного процесса). Обозначим
ее как Я1(Х).
Как уже было отмечено, величина Я1(Х) не определяет полностью информаци-
онные характеристики процесса, поскольку не учитывает зависимости букв.
Рассмотрим последовательность из п последовательных букв источника х =
= (®i,..., хп) е Xi%2 .• -Хп = Хп. Для стационарного процесса энтропия рас-
пределения вероятностей на таких блоках Н(Х±... Хп) = Я(ХП) не зависит от
расположения блока во времени, ее называют п-мерной энтропией источника.
Величина Я(ХП) определяет среднее количество информации в последователь-
ности из п букв. Нормированную величину
называют энтропией на букву последовательности длины п. Интуиция подсказы-
вает, что значения ЯП(Х) при больших п могли бы служить адекватной мерой
информативности источника.
Другой подход к измерению информации, порождаемой произвольным стацио-
нарным источником, состоит в том, что при передаче буквы хп все предыдущие
буквы ^1,..., xn-i можно считать известными декодеру. Среднее количество под-
лежащей передаче информации об хп определяется величиной условной энтро-
пии Я(ХП|Х1,... ,Xn-i). В силу стационарности конкретные значения индек-
сов не играют роли, важна лишь длина предыстории. Поэтому исцользуется
обозначение
н(хп\хъ..., хп^1) = ярсрр-1).
Следующая теорема устанавливает некоторые свойства двух информационных
мер ЯП(Х) и Я(Х|ХП“1) для стационарных источников.
1.7. Энтропия на сообщение
35
ТЕОРЕМА 1.5. Для дискретного стационарного источника
А.	Н(Х^Хп) не возрастает с увеличением п.
В.	Нп(Х) не возрастает с увеличением п.
с. нп(х) > яр^х”-1).
D. Пт ЯП(Х) = lira Н(Х\Хп).
п—*оо	п—>оо
Доказательство. Утверждение А следует из невозрастания энтропии с увеличе-
нием числа условий (свойство 1.5.5).
Из свойства 1.5.4 и стационарности источника имеем
Я(ХП) = Н(Х) + Я(Х|Хх) + • • • +
Заметим, что в правой части п слагаемых, из которых последнее - наименьшее
(в силу свойств 1.5.2 и 1.5.5). Поделив обе части на п, убеждаемся в справедли-
вости утверждения С. ,
Чтобы убедиться в справедливости утверждения В, выполним преобразования
Я(Х"+1) (=} Я(Хх...ХпХп+х) =
= Я(Хх... Хп) + Я(Х„+х |Хх,..., Хп) =
= Я(ХП) + Н(Х\Хп) <
(d)
< Н(Хп) + Я(Х|ХП-1) <
(е)
< Я(Х") + Я„(Х) =
= (п + 1)Яп(Х).
В этой цепочке переход (а) использует предположение о стационарности, (Ь) -
свойство условной энтропии, (с) вновь использует стационарность, a (d) и (е)
опираются на уже доказанные утверждения Л и С. Наконец, (f) следует из опре-
деления величины Нп(Х). Если теперь поделить правую и левую части на (п+1),
убеждаемся в справедливости утверждения В.
Перейдем к доказательству последнего утверждения. Прежде всего отметим, что
последовательности Нп(Х) и Н(Х\Хп) не возрастают и ограничены снизу
(поскольку неотрицательны). Значит, оба предела существуют. Из утверждения
С следует, что
lim ЯП(Х) > lim Н(Х\Хп).	(1.16)
п—>оо	п—>оо
36
Глава 1. Энтропия дискретных источников
В то же время, при любых натуральных т < п имеют место соотношения
Я(Х”) = Я(Хх...Хп) =
= Я(Х1... Хп) + Я(Хт+1 ...Хп\Х1,...,Хт) =
= тНп(X) + Н(Хт+1 |Хх,..., Хт) + ...
+Я(Хп|Х1,...,Х„_1)<
(с)
тВД + (п - т)Я(Х|Хт).
Здесь использованы: в (а) и (Ъ) - свойства условной энтропии, в (с) - стационар-
ность источника и невозрастание последовательности Н(Х\Хт) с увеличением
числа условий т. Поделив обе части полученного неравенства на п, перейдем
к пределу при п ос. Получим неравенство
lim ЯП(Х) Я(Х|Хт),
п—>оо
справедливое при любых т. Устремляя т к бесконечности, получаем
lim ЯП(Х) lim Я(Х|ХГО).	(1.17)
п—>оо	т—->оо
Из (1.16) и (1.17) вытекает доказываемое утверждение.	□
Введем обозначения
Яоо(Х) = lim ЯП(Х), Я(Х|Х°°) = lim ЩХ\Хп).
п—>оо	п—>оо
Основной результат теоремы состоит в том, что H^fX) = Н(Х\Х°°). В даль-
нейшем, изучая конструктивные методы кодирования, мы убедимся в том, что
именно эта величина определяет минимально возможные удельные затраты бит
на передачу одной буквы стационарного источника.
По сути, мы рассмотрели два подхода к анализу информативности стационарного
источника:
►	введение расширенного алфавита, буквами которого служат блоки из п сим-
волов источника;
►	учет зависимости текущей буквы от п предшествующих букв.
Несмотря на то что при каждом конкретном п второй подход дает более оптими-
стические оценки затрат на передачу или хранение информации (утверждение
0, в пределе (с увеличением параметра п) оба подхода становятся эквивалент-
ными.
Рассмотрим поведение последовательностей ЯП(Х) и Н(Х\Хп) для двух про-
стых моделей дискретных источников. Возможно, это сделает более понятными
и естественными сформулированные выше фундаментальные утверждения.
Пример 1.7.1. Энтропия на сообщение дискретного постоянного источника. Дис-
кретным постоянным источником мы назвали дискретный стационарный источ-
ник без памяти. По свойствам энтропии для источника без памяти имеем
1.7. Энтропия на сообщение
37
Я(Х1.. .Хп) = Я(Хх) +... + Я(ХП).
Н(Хп) = пН(Х).
Поделив обе стороны тождества на п, получим, что при всех п справедливо
равенство
ЯП(Х) = Я(Х)
и, следовательно,
Яоо(Х) = Я(Х).
Таким образом, энтропия на сообщение дискретного постоянного источника
в точности равна его одномерной энтропии. К тому же результату можно было
прийти с другой стороны. В силу стационарности и отсутствия зависимости
между сообщениями
Н(Х\Хп) = Я(Хп+1|Х!,..., Хп) = Я(Х),
следовательно,
Я(Х|Х°°) = Я(Х).
Таким образом, для рассматриваемой модели анализ информационных харак-
теристик сводится к подсчету энтропии одномерного распределения. Отсюда
совсем не следует, что при кодировании источников независимых сообщений
нужно кодировать каждую букву независимо от других.
Пример 1.7.2. Энтропия на сообщение марковского источника. Для стационар-
ного источника, описываемого моделью цепи Маркова связности з, можем запи-
Я(Х|Х") = Я(Х„+1|ХЪ... ,Хп) =
= Я(Хп+1|Хп_8+1,...,Хп) = Я(Х|Хв).
Правая часть не зависит от п, значит,
Я(Х|Х°°) = Я(Х|Х8).
Рассмотрим другой подход. Используя стационарность и свойства условной энтро-
пии, запишем
Я(ХП) = Я(Х,... XSXS+1 ...Хп) =
= Н(Хг... Х8) + Я(Х8+1... ХП|ХЪ..., Х8).	(1.18)
Из
Я(Х8+1 ...Xn\Xlt...,Xa) = Я(Х8+1|ХЪ..., Х8)+
+Я(Х8+2|Х1,..., Х8+1) + • • • + Я(ХП|Х1,... ,Х„_1),
учитывая марковость и стационарность, получаем
Я(Х8+1... Xn|Xi,...,Х8) = (п - з)Я(Х|Хв).
Теперь (1.18) принимает вид
Я(ХП) = зЯ8(Х) + (п - з)Я(Х|Хв).	(1.19)
Теперь можно поделить обе части на п и устремить п к бесконечности. Резуль-
татом будет ожидаемое равенство
Яоо(Х) = Я(Х|Х®).
38
Глава 1. Энтропия дискретных источников
Поучительно записать (1.19) в виде
о
ЯП(Х) = Н(Х\Х°) + -(ЯДХ) - яда8)) =
п
Q
= яда”) +-(я8(х) - яда8)).
Отсюда хорошо видно, какова разница между ЯП(Х) и Н(Х\Хп). При разбиении
последовательности букв на блоки длиной п мы получаем среднюю энтропию на
сообщение немного большую, чем минимальная достижимая величина Н(Х|Xs).
«Потери» или, точнее сказать, дополнительные затраты связаны с «забвением»
тех s букв, которые предшествовали рассматриваемому блоку.
1.8.	Равномерное кодирование дискретного
источника. Постановка задачи
Теперь, когда мы знаем теоретическую характеристику информационной про-
изводительности источника, можно было бы перейти к решению практической
задачи сжатия информации. Однако в данном параграфе мы рассмотрим метод
равномерного кодирования, который не имеет почти никакого практического зна-
чения. Более того, он, по сути, не является сжатием информации без потерь. Тем
не менее изучение равномерного кодирования представляется необходимым по
двум причинам. Во-первых, станет понятнее, почему энтропия совпадает с пре-
дельно достижимой скоростью передачи (хранения) информации (эта скорость
называется скоростью создания информации источником). Во-вторых, на этом
примере мы познакомимся с традиционным для теории информации способом
формулировки теоретических результатов - доказательством прямой и обратной
теорем кодирования.
При равномерном кодировании последовательность порождаемых источником
сообщений а?1,	**•» xi Е X, i = 1, 2, ...,. разбивается на блоки одинаковой
длины X. Каждый такой блок кодируется независимо от других.
Для кодирования используется некоторый алфавит А = {а}, называемым кодо-
вым, элементы алфавита называют кодовыми символами. Мы ограничимся рас-
смотрением двоичных кодов, то есть кодов над алфавитом А = {0,1}.
Равномерным кодом длины п называется любое подмножество С множества Ап,
то есть любое подмножество множества последовательностей длины п. Элементы
кода С называют кодовыми словами. Мощность кода |С| - это количество кодо-
вых слов в коде С.
Скоростью равномерного кода называется величина
Я =	(бит / букву источника),	(1.20)
где [а] обозначает округление числа а вверх до ближайшего целого.
1.8. Равномерное кодирование дискретного источника
39
Наиболее важным частным случаем равномерного кода является множество всех
последовательностей длины п, то есть С = Ап = {0,1}п. При этом скорость кода
R = (бит / букву источника).
Кодирование состоит в том, что каждый блок из N символов источника заме-
няется на п двоичных символов, записываемых в запоминающее устройство или
передаваемых по каналу связи. Таким образом, скорость кода - это удельные
затраты двоичных символов (битов) на передачу одной буквы источника.
В общем случае работа кодера (алгоритм кодирования) описывается отображе-
нием множества XN на множество слов кода С. Декодирование задается отоб-
ражением С на XN. Если оба отображения взаимно однозначные, то на выходе
декодера можно будет получить точную копию передаваемой последовательно-
сти. Взаимно однозначное кодирование возможно только тогда, когда
|X|N |С|	(1.21)
или
fl^log|X|>H(X).
Следовательно, если буквы источника не равновероятны (Н(Х) < log |Х|), то
скорость кода окажется заведомо больше энтропии источника.
Рассмотрим теперь ситуацию, когда условие (1.21) не выполнено. Тогда число
кодовых слов недостаточно для того, чтобы сопоставить каждой последователь-
ности источника свое кодовое слово. Для некоторых последовательностей сооб-
щений не найдется кодового слова, по которому декодер смог бы однозначно
восстановить переданную информацию. В общем виде процесс кодирования и
декодирования можно описать следующим образом.
Выделим в XN подмножество Т такое, что \Т\ = |С|, и каждой последова-
тельности из множества Т сопоставим индивидуальное кодовое слово. Множе-
ство Т мы будем называть множеством однозначно кодируемых последовательно-
стей. Остальным последовательностям из XN сопоставим произвольные кодо-
вые слова (например, всем последовательностям из Тс сопоставим одно и то
же кодовое слово). Декодер при получении некоторого кодового слова с е С
будет выдавать получателю соответствующую этому слову последовательность
из множества Т.
Из описания следует, что каждый раз, когда источник породит последователь-
ность из дополнения к множеству Г, выход декодера не будет совпадать со
входом кодера. Это событие называют ошибкой кодирования, и его вероятность
Ре = Р(х£Т)
называется вероятностью ошибки кодирования.
40
Глава 1. Энтропия дискретных источников
Пример 1.8.1. Рассмотрим троичный постоянный источник X = {а, 6, с} с рас-
пределением вероятностей р(а) = 1/2, р(Ь) = 1/3, р(с) = 1/6. Положим N = 2.
В этом случае множество XN состоит из 9 пар. Распределение вероятностей и
пример двоичного кода длиной п = 3 приведены в табл. 1.1.. Кодом служит
множество С = {О, I}3 (множество всех последовательностей длиной 3). Ско-
рость кода равна R = 3/2 бита на букву источника. Из таблицы видно, что
в качестве множества однозначно кодируемых последовательностей выбрано мно-
жество Т = {аа, аЬ, ас, ba, bb, be, са, cb}. Вероятность ошибки Ре = Р(ТС) = р(сс) =
= 1/36. При появлении на выходе источника последовательности сс декодер
будет выдавать получателю последовательность cb. Отметим, что в данном при-
мере кодирование могло быть и другим, но при любом другом выборе множества
Т вероятность ошибки была бы не меньше 1/36. В то же время выбор кодо-
вого слова для последовательности из дополнения к Т не влияет на вероятность
ошибки.
Таблица 1.1. Пример равномерного кода
Последовательность источника	Вероятность	Кодовое слово
аа	1/4	ООО
ab	1/6	001
ас	1/12	010
Ьа	1/6	011
bb	1/9	100
Ьс	1/18	101
са	1/12	110
cb	1/18	111
сс	1/36	111
Итак, задача построения равномерного кода со скоростью R для последователь-
ностей длины п эквивалентна задаче выбора |С| = 2nR однозначно кодируемых
сообщений. Хотелось бы построить такой код, который обеспечивал бы одно-
временно малую скорость и малую вероятность ошибки. Поскольку скорость
может быть уменьшена только за счет уменьшения размера множества Т, с умень-
шением скорости неизбежно увеличивается вероятность ошибки. Представляет
интерес ответ на вопрос, с какой скоростью возможно кодирование источника
при пренебрежимо малой вероятности ошибки?
Для заданного стационарного источника число Н называется скоростью создания
информации, если для любого R> Н существует равномерный код со скоростью
R, обеспечивающий сколь угодно малую вероятность ошибки, и в то же время
при любой скорости кода R < Н вероятность ошибки не может быть сделана
меньше некоторой положительной величины е.
Для того чтобы утверзрдать, что константа Н является скоростью создания инфор-
мации для данной модели источника, нужно доказать два утверждения. Пер-
вое устанавливает, что при R > Н достижима сколь угодно малая вероятность
1.9. Неравенство Чебышева. Закон больших чисел
41
ошибки. Это утверждение называют прямой теоремой кодирования. Второе утвер-
ждение состоит в том, что при R < Н вероятность ошибки не может быть
сделана произвольно малой. Это утверждение называется обратной теоремой
кодирования,
В определении понятия «скорость создания информации источником» неявно
участвует ограничение на множество способов кодирования, а именно, предпола-
гается, что блоки из фиксированного числа сообщений п преобразуются в кодо-
вые слова фиксированной длины N, Для обозначения кодов такого типа исполь-
зуют аббревиатуру FF (fixed-to-fixed). Помимо FF-кодов можно рассматривать
VF-коды (variable-to-fixed), преобразующие блоки переменной длины в кодовые
слова фиксированной длины, FV-коды (fixed-to-variable), когда для кодирования
блоков фиксированной длины используются коды с переменной длиной кодовых
слов, и, наконец, самый широкий класс кодов - VV-коды (variable-to-variable),
допускающие разбиение сообщений на блоки переменной длины и кодирование
блоков неравномерными кодами.
Строго говоря, чтобы утверждать, что число Н - скорость создания информации
источником, при доказательстве теорем кодирования нужно допустить выбор
способов кодирования из любого из четырех перечисленных множеств.
Логично предположить, что для стационарных источников скорость создания
информации совпадает с энтропией на сообщение источника, то есть имеют место
равенства
Н = Н(Х|Х°°) = Яоо(Х).
В настоящей главе мы приведем доказательства теорем кодирования для FF-
кодов для дискретных постоянных источников (стационарных источников без
памяти). В главе 2 будут изучены FV-коды и доказаны соответствующие тео-
ремы кодирования для произвольных стационарных источников. Анализ других
классов кодов (VF и VV) выходит за рамки нашего курса.
1.9.	Неравенство Чебышева.
Закон больших чисел
Доказательство теорем кодирования опирается на оценки вероятностей уклоне-
ния случайных величин от средних значений. В этом параграфе мы приведем
необходимые сведения об этих оценках из теории вероятностей.
Точный подсчет вероятностей больших уклонений бывает невозможен либо
в силу сложности задачи, либо по причине отсутствия точных сведений о веро-
ятностной модели. Поэтому часто пользуются оценками (верхними и нижними).
Наиболее важными с практической точки зрения являются верхние оценки, гаран-
тирующие, что вероятность неудачи не превосходит некоторого значения.
Рассмотрим дискретную случайную величину X = {х,р(х)}. Предположим что
все ее значения х е X неотрицательны, и при этом предположении оценим
вероятность события Р(х А) для некоторого числа А > 0.
42
Глава 1. Энтропия дискретных источников
Имеем	1
р{х > а) = 22 р(х) < 12	4 Sхр^ =
' л	л Л	Л “	/1
х^А	х^А
Первое из двух неравенств основано на том, что в области суммирования х/А 1.
Второе неравенство справедливо, поскольку, расширив область суммирования на
все множество X, мы добавили к сумме только неотрицательные слагаемые (все
значения х неотрицательны).
Введем обозначение тх = М [ж]. Полученный результат запишем в виде
Р(х > А)	(1.22)
2Т.
Ценность этой формулы состоит в том, что для оценки искомой вероятности
достаточно знать только одну числовую характеристику случайной величины -
ее математическое ожидание.
Пусть теперь X = {ж,р(ж)| - произвольная (необязательно неотрицательная)
случайная величина. Для произвольного е > 0 оценим вероятность Р (|ж — тж|
отклонения случайной величины х от ее среднего значения тх на величину,
не меньшую е. Положим у = |х — тх\. Для этой неотрицательной случайной
величины, используя (1.22), получаем
v»=м [(*	= м.
Е*	Е	Е
Результат запишем в виде
Р(\х~тх\>е)^,	(1.23)
где 0-2 = D[x]. Неравенство (1.23) называется неравенством Чебышева.
Рассмотрим теперь последовательность из п независимых случайных величин Хг,
i = 1, ..., п, имеющих одинаковое математическое ожидание тх и одинаковую
дисперсию о-2. Нас интересует вероятность
отклонения среднего арифметического п случайных величин от их математиче-
ского ожидания на величину, не меньшую е. Положим у = ~ хг- Из свойств
математического ожидания и дисперсии, принимая во внимание независимость
случайных величин xi, ..., хп, имеем
М[у] = тх, D[j/] = -ах.
п
Применив к случайным величинам у неравенство Чебышева (1.23), получим
новое важное неравенство
неравенство Чебышева для суммы независимых случайных величин.
1.10. Прямая теорема кодирования
43
Правая часть неравенства убывает с ростом числа слагаемых п. Следствием нера-
венства (1.24) является закон больших чисел:
Среднее арифметическое независимых случайных величин с одинаковыми матема-
тическими ожиданиями,равными т, и одинаковыми дисперсиями сходится по веро-
ятности к математическому ожиданию т.
Поясним термин «сходимость по вероятности». Говорят, что случайная после-
довательность ai, аг, * • • сходится по вероятности к пределу а, если для любого
е > 0 имеет место равенство
lim Р (|ап — а| е) = 0.
п—>оо
В действительности неравенство (1.24) - весьма слабая оценка вероятности,
записанной в левой части. На самом деле эта вероятность убывает с ростом п экс-
поненциально (пропорционально е~Сп, где С > 0), то есть гораздо быстрее, чем
С/п. Удобство формулы (1.24) состоит в простоте ее доказательства и использо-
вания. Чтобы воспользоваться неравенством Чебышева, достаточно знать только
математическое ожидание и дисперсию элементов последовательности независи-
мых случайных величин.
Еще одно замечание.
Закон больших чисел справедлив не только для независимых случайных вели-
чин. Для произвольного стационарного случайного процесса введем в рассмот-
рение некоторую функцию /, вычисляемую по п последовательным значениям
процесса. Последовательность значений функции f также образует случайный
процесс. Если для любого п и для любой функции / для последовательности
значений функции f справедлив закон больших чисел, такой процесс называют
эргодическим.
Среднее арифметическое идущих подряд значений процесса xi,..., хп представ-
ляет собой его среднее по времени. Математическое ожидание - это среднее по
множеству значений, вычисленное по заданному распределению вероятностей.
Его называют также средним по множеству реализаций. Поэтому часто эргоди-
ческий процесс определяют как стационарный процесс, для которого усреднение
по времени эквивалентно усреднению по множеству реализаций.
Таким образом, по определению, закон больших чисел справедлив для всех эрго-
дических процессов. Примеры эргодических процессов - последовательность неза-
висимых одинаково распределенных случайных величин, простая неразложимая
непериодическая цепь Маркова и т. п.
1.10.	Прямая теорема кодирования
для дискретного постоянного источника
Чтобы максимально упростить изложение, мы приведем доказательство теорем
кодирования только для самой простой модели - дискретного постоянного источ-
ника, то есть стационарного источника без памяти.
44
Глава 1. Энтропия дискретных источников
Более того, мы будем считать, что алфавит ограничен и что все вероятности букв
положительны. Последние предположения нужны для того, чтобы собственная
информация источника имела конечное математическое ожидание (энтропию) и
конечную дисперсию.
В конце главы мы вернемся к обсуждению равномерного кодирования для источ-
ников с памятью.“
ТЕОРЕМА 1.6. Пусть Н - энтропия дискретного постоянного источника. Для
любых е,5 > 0 существует по такое, что для любого п > по найдется равно-
мерный код, кодирующий источник блоками длиной п со скоростью R Н + 5
и вероятностью ошибки Ре в.
Другими словами, при скорости кода, хотя бы немного (на любую положитель-
ную величину 5) превосходящей энтропию, увеличением длины кодируемых бло-
ков (при правильном кодировании) можно добиться произвольно малой (меньше
любого наперед заданного положительного е) вероятности ошибки.
Доказательство. Сначала мы укажем правило кодирования, затем выберем пара-
метры кода так, чтобы скорость кода удовлетворяла условиям теоремы. После
этого оценим вероятность ошибки - убедимся в том, что она может быть сделана
сколь угодно малой.
Правило кодирования полностью описывается выбором множества Т С Хп одно-
значно кодируемых последовательностей сообщений источника. Выберем Т С Хп
следующим образом:
(1-25)
где через I(x) = -logp(o?) обозначена собственная информация последователь-
ности х € Хп, а через 5о обозначена положительная константа, значение которой
будет выбрано позже. Заметим, что множество Т состоит из таких последователь-
ностей, средняя собственная информация которых весьма близка к энтропии,
если величина 5о достаточно мала.
Из (1.25) и определения собственной информации следует, что вероятности после-
довательностей множества Т удовлетворяют неравенствам
2~п(Я+50) р/х\
(1.26)
Левая и правая части могут рассматриваться как оценки снизу и сверху для
вероятностей последовательностей из Т. Для оценки числа элементов в этом
множестве заметим, что
1 > Р(Г) = ]Гр(я:) |T|minp(®) > |т|2-п(я+4°).
хЕТ
Следовательно,
< 2п(Н+<5о)
(1.27)
1.11. Обратная теорема кодирования
45
По определению (1.20) скорость кода
д= rioglTH ^я + <?о + -.
п	п
(1.28)
С^шибка кодирования имеет место тогда,
тельность, не входящую в множество Т.
когда источник порождает последова-
Поэтому вероятность ошибки Ре удо-
влетворяет соотношениям
Ре = Р(х£Т) = Р
-Пх) - Н
п
> Jo
(1.29)
Последний переход учитывает, что по предположению теоремы буквы источ-
ника независимы и, в силу аддитивности собственной информации, информация
последовательности равна сумме информации отдельных букв. Заметим теперь,
что М[1(ж)] = Н. Это означает, что к последнему выражению в (1.29) можно
применить неравенство Чебышева. В результате имеем
, D [/(ж)]
е "	п502
(1.30)
Напомним, что по предположению о модели источника D[/(x)] - ограниченная
константа. Значит, для любой наперед заданной величины Jo можно теперь подо-
брать длину кодируемых блоков п так, чтобы вероятность ошибки была меньше
любого е.
Положим теперь Jo = J/2. При п п01 = D[Z(z)]/(J2s) из (1.30) имеем Ре е.
Из (1.28) следует, что при п по2 = 2/8 выполняется условие R < Н + 3. Сле-
довательно при n > no = max(noi,no2) скорость кода R и вероятность ошибки
Ре удовлетворяют требованиям теоремы.	□
В доказательстве теоремы участвовало множество Т, определенное соотноше-
нием (1.25). Его называют множеством типичных последовательностей. Это мно-
жество играет важную роль в теории информации. Мы уже установили некото-
рые его свойства, а некоторые другие свойства будут установлены при доказа-
тельстве обратной теоремы. Затем мы суммируем все эти свойства в специально
посвященном этому множеству параграфе 1.12.
1.11.	Обратная теорема кодирования
для дискретного постоянного источника
Мы приступаем к формулировке и доказательству обратной теоремы кодирова-
ния. Нам предстоит доказать, что невозможно обеспечить кодирование с малой
ошибкой при скорости меньшей, чем энтропия источника. Иными словами, сколь
угодно изобретательный инженер не сможет сжать информацию равномерными
кодами сильнее, чем это гарантируется приведенной выше прямой теоремой
кодирования.
46
Глава 1. Энтропия дискретных источников
Подобного рода «пессимистические» утверждения не только украшают теорию,
но и важны для практики, поскольку спасают инженеров от бесплодных усилий.
Как заметил известный российский ученый в области теории связи Л. М. Финк,
попытки преодолеть теоретико-информационные пределы аналогичны попыткам
получить от гидроэлектростанции больше энергии, чем энергия падающей воды.
ТЕОРЕМА 1.7. Для дискретного постоянного источника с энтропией Н сущест-
вует е> 0 такое, что для любого 6 > 0 для любого равномерного кода со скоростью
R^ Н - 8 вероятность ошибки удовлетворяет неравенству Ре е.
Иными словами, если скорость хотя бы ненамного (на любую положительную
величину 6) меньше энтропии, то вероятность ошибки уже не может быть сколь
угодно малой. На самом деле можно убедиться в том, что при больших длинах
блоков п вероятность ошибки будет довольно большой.
Доказательство. Представим себе оппонента, который не согласен с утвержде-
нием теоремы и считает, что сколь угодно точное кодирование возможно при
скорости меньшей, чем энтропия источника. Чтобы переубедить его, достаточно
указать для заданного источника некоторую строго положительную независя-
щую от длины кодируемых последовательностей величину е, которая была бы
оценкой снизу вероятности ошибки любого предложенного оппонентом кода со
скоростью Н — 8.
Код полностью описывается выбором множества Т\ однозначно кодируемых пос-
ледовательностей. По определению, скорость кода равна R = flog |Ti|]/n, следо-
вательно, код содержит
|Ti| 2nR 2п(я"б)	(1.31)
кодовых слов. Вместо вычисления нижней оценки для вероятности ошибки Ре
построим оценку сверху для вероятности правильного кодирования
Рс = 1 - Ре = 22 р(х).	(1.32)
®GT1
Введем вспомогательное множество
Т=<х
-I(x) - Н
п
(1.33)
где через I(x) = - logp(a) обозначена собственная информация последователь-
ности х е Хп, а через 6q - положительная константа, значение которой будет
выбрано позже. (Хотя это и не важно для доказательства, отметим, что (1.33)
совпадает с (1.25), то есть Т совпадает с множеством однозначно кодируемых
последовательностей, использованным для доказательства прямой теоремы коди-
рования.)
Разобьем теперь сумму в правой части (1.32) на две суммы:
Рс= 52 S
®6Т1ПТ	авбТ1ПТс
(1.34)
1.11. Обратная теорема кодирования
47
где через Тс обозначено дополнение к множеству Т. Оценим вторую сумму
следующим образом:
£ р(®) Е =р^=т)-
®еТ1ПТс	хетс
Эту вероятность мы уже оценивали при доказательстве прямой теоремы. Точно
так же, как при переходе от (1.29) к (1.30), с помощью неравенства Чебышева
получаем оценку
22 н®)
х€Т\птс
(1.35)
пб^
Для первой из двух сумм в (1.34) имеем
>, Р(®)
®ёТ1ПТ
(Ъ)
|Т1ПТ| max p(®) <
®Е11П1
lTil ?(®)<
®Е11П1
|Т1|имхр(®).
®tl
(1.36)
<
Здесь мы сначала в (а) оценили сумму сверху, умножив число слагаемых на мак-
симальное слагаемое. Затем в (Ь) использовали неравенство \Т\ П Т\ |Ti|. Пере-
ход (с) в (1.36) основан на том, что при расширении области поиска максимума
максимальное значение не уменьшается.
Подставим в (1.36) оценку мощности кода (1.31) и оценку максимальной веро-
ятности последовательностей из Т (1.26). Получим
^2 Р(®) < 2п(я-5)2~п(я-5о) = 2~n^s~So\	(1.37)
®еТ1ПТ
Подстановка (1.35) и (1.37) в (1.34) приводит к следующей оценке сверху для
вероятности правильного кодирования:
Рс < 2~та(г-До> + Р .	(1.38)
пдо
Пусть 5 - произвольное положительное число. Выберем теперь значение пара-
метра 5о равным Jo = 5/2. При таком выборе правая часть неравенства (1.38)
убывает с увеличением п.
Мы уже убедили оппонента в том, что с увеличением длины кодируемых блоков
вероятность ошибки не только не убывает, но и стремится к 1. Чтобы оконча-
тельно доказать теорему, нужно установить, что и при конечных длинах блоков
вероятность ошибки остается большой.
48
Глава 1. Энтропия дискретных источников
Сначала покажем, что вероятность ошибки положительна при любых длинах бло-
ков п. Поскольку мы договорились о том, что все буквы источника имеют поло-
жительные вероятности, для достижения нулевой вероятности ошибки нужно
назначить кодовое слово каждой последовательности сообщений, то есть объем
кода должен удовлетворять неравенству
|Тх| > |Х|”.
Для этого скорость кода должна быть
Л > logl^il/zz log|JC|.
(1.39)
Из свойства 1.3.2 следует, что Н(Х) log |Х| и, значит, (1.39) входит в противо-
речие с условиями теоремы, поскольку скорость должна быть меньше энтропии.
Итак, вероятность ошибки положительна при любых п.
Обозначим через по такое значение длины последовательностей п, что при п > по
справедливо неравенство Рс 1/2. При этом, конечно, вероятность ошибки
Ре 1/2. Теперь обозначим через £0 минимальную вероятность ошибочного
кодирования по всем п = 1, 2, ..., tiq - 1. Мы уже убедились в том, что > 0.
Примем е = min{so, 1/2}. Получаем неравенство Ре е, справедливее при всех
n = 1, 2, ....
Таким образом, мы нашли независящую от длины кода п нижнюю границу веро-
ятности ошибки е для всех кодов со скоростью R Н - 8. Тем самым теорема
доказана.	□
Как и в доказательстве прямой теоремы, мы воспользовались свойствами множе-
ства типичных последовательностей Т. Эвристическое обоснование теорем коди-
рования и более подробное обсуждение множества Т приведены в следующем
параграфе.
1.12.	Множество типичных
последовательностей для дискретного
постоянного источника.
Источники с памятью
Рассмотрим дискретный постоянный источник, порождающий последователь-
ность независимых сообщений из ансамбля X = {ж,р(ж)}. Множество типичных
последовательностей длиной п обозначим Tn(J). Оно определено выше как мно-
жество последовательностей, средняя собственная информация которых близка
к энтропии И(Х), то есть
Tn(S) = <x: —1(х) — Н(Х) о),
I п	I
(1.40)
где 6 - некоторая положительная константа. Подытожим некоторые свойства
множества Тп(8) в основном уже доказанные и использованные при доказатель-
стве теорем кодирования для дискретного постоянного источника.
1.12. Множество типичных последовательностей
49
ТЕОРЕМА 1.8. Для любого 6 > 0 имеют место следующие утверждения:
1.	lim Р(Тп(д)) = 1.
п—>оо
2.	Для любого натурального п справедливо неравенство
|ТП(<5)| 2п(я(х)+5).
3.	Для любого е > 0 существует по такое, что при всех п > п0
\Тп(6)\	(1-е)2п(я(х)"5).
4.	Для х е Тп(8)
2-п(Н(Х)+5)	2“п(я(х)”5).
Пункт 1 теоремы утверждает, что асимптотически почти все порожденные источ-
ником последовательности типичны, то есть принадлежат Тп(8). Второй и третий
пункты указывают на то, что при достаточно больших п в Tn(J) содержится при-
близительно 2пЯ(х) последовательностей. Тем самым установлена простая связь
между энтропией ансамбля и мощностью множества типичных последователь-
ностей сообщений ансамбля. Наконец, из четвертого пункта мы узнаем, что все
последовательности, входящие в Tn(J), асимптотически равновероятны, то есть
имеют вероятности, примерно равные 2“пЯ(х\
Доказательство. Первое утверждение следует из (1.29) и (1.30). Второе совпа-
дает с (1.27), четвертое - с (1.26). Остановимся на третьем утверждении.
Из первого утверждения следует, что для любого е > 0 найдется по такое, что
при п > по имеет место неравенство
Р(Тп(<5))>1-е.	(1.41)
Оценивая вероятность Тп(8) как произведение числа элементов в множестве на
величину максимального элемента и применяя утверждение 4, получаем
P(Tn(5)) |Tn(<J)| max р(х) < |ЗД|	(1.42)
®	(о )
Из (1.41) и (1.42) следует утверждение 3.	□
Теперь понятно, почему справедлива прямая теорема кодирования. Из утвер-
ждения 1 следует, что для получения малой вероятности оЩибки достаточно
кодировать последовательности из Тп(5). Поскольку таких последовательностей
примерно 2пН(х) (утверждения 2 и 3), для передачи номера последовательности
достаточно затратить пН(Х) бит на указание номера последовательности, то есть
Н(Х) бит на одно сообщение.
Столь же просто объясняется справедливость обратной теоремы. Если взаимно
однозначно кодируется М последовательностей, то суммарная вероятность одно-
значно кодируемых последовательностей из Тп(8) имеет порядок М2“пЯ(х\ Веро-
50
Глава 1. Энтропия дискретных источников
ятность ошибки примерно равна 1 - М2~пН^х\ Пока число М меньше 2nHW
(соответственно, скорость кода меньше Я(Х)), произведение М2~пН^ будет
маленьким, а вероятность ошибки будет заведомо большой.
Взглянем внимательнее, какие именно последовательности являются типичными.
Обозначим через тх(х) число появлений буквы х в последовательности х. Набор
чисел т(х) = {тДа:),^ е X} называют композицией последовательности х.
Цля дискретного постоянного источника вероятность последовательности х =
= (®i,..., хп) может быть записана в виде
р(®) =	= П р(хУх{х)-
i=i	хех
Это представление получено изменением порядка сомножителей в произведении.
Собственная информация последовательности в расчете на букву
= -J2^^1ogp(x).
п хех п
\
Эта величина близка к энтропии Я(Х), если
—- * „(х)
Мы пришли к естественному результату: множество типичных последовательно-
стей состоит из тех последовательностей, в которых доля элементов х прибли-
зительно равна вероятности символа ж.
Интересно ответить на вопрос, насколько важно предположение о независимости
букв источника. Из теоремы об энтропии на сообщение стационарного источника
интуитивно ясно, что скоростью создания информации произвольного стацио-
нарного источника является величина Яоо(Х) = Я(Х|Х°°). Хотелось бы думать,
что почти для всех векторов х достаточно большой длины п
р(х) « 2”пЯ°°(х)
и что число таких типичных векторов примерно равно 2""пЯо°(х>. Так ли это?
Посмотрим внимательнее на доказательство прямой и обратной теорем коди-
рования. Ключевым моментом в них было применение неравенства Чебышева
для суммы случайных величины. По сути, достаточно было бы более слабого
утверждения - аналога закона больших чисел.
Мы уже упоминали, что достаточное условие для сходимости среднего ариф-
метического (среднего по времени) к математическому ожиданию (среднему по
множеству реализаций процесса) - эргодичность. При любом фиксированном
параметре т мы можем определить множество однозначно кодируемых после-
довательностей как множество последовательностей ж, для которых
п
1.13. Задачи
51
» Н(Х\Хт).
или
п
1(х1,...,Хт)+ 52
г=тп+1
Понятно, что при больших п первый член в левой части не играет существенной
роли и условие эргодичности позволит доказать теоремы для любого конеч-
ного т. Выбирая т произвольно большим, можем утверждать, что достижима
скорость СКОЛЬ угодно близкая К Яоо(Х).
Остаются вопросы:
► какие процессы неэргодичны, как может случиться, что среднее по времени
не стремится с увеличением числа опытов к математическому ожиданию?
► как будут выглядеть теоремы кодирования для стационарного, но неэргоди-
ческого источника?
Ответы на эти вопросы, а также более точные определения и утверждения и
более строгие, чем приведенные выше, доказательства цытливый читатель найдет
в фундаментальных учебниках по теории информации [38], [3], [7].
1.13. Задачи
1.	Доказать, что мощность множества всех подмножеств множества из п элемен-
тов равна 2П.
2.	Вывести формулу полной вероятности.
3.	Вывести формулу Байеса.
4.	Доказать тождество |ХУ| = |Х||У|.
5.	Сколько различных последовательностей длиной п можно составить из эле-
ментов дискретного множества X = {0,..., q - 1}?
6.	Доказать сформулированные в параграфе 1.1 свойства числовых характери-
стик случайных величин.
7.	Для дискретного постоянного источника X = {а, Ь, с} для распределений веро-
ятностей
1)	р(а) =р(Ь) =р(с) = 1/3;
2)	р(а) = р(Ь) = 1/4, р(с) = 1/2;
определить собственную информацию каждой из букв, энтропию. Сколько
информации содержится в последовательности abaac ?
8.	Доказать, что линейная комбинация выпуклых функций с положительными
коэффициентами - выпуклая функция.
9.	Доказать, что
гг (Pl + Р2 + Рз\	#(Р1) , Я(Рг) , #(Рз)
_ + —_ + —_.
52
Глава 1. Энтропия дискретных источников
10.	Доказать теорему 1.2.
И. Алфавит источника X = {а, Ь, с} . Задана вероятность р(а) = а. Построить
зависимость энтропии Я(Х) от величины р(Ь) = /3.
12.	При каком соотношении между параметрами а и /3 простая марковская цепь
с матрицей переходных вероятностей
а 1 — а
П =
/3 1-/3
порождает последовательность независимых сообщений?
13.	Не выполняя вычислений, укажите стационарное распределение вероятностей
для цепи Маркова с матрицей переходных вероятностей
п =
1/2 1/2
0	1
14.	Неэргодическая цепь Маркова. Найдите стационарное распределение для цепи
Маркова с матрицей переходных вероятностей
1/2
0
3/4
0
0
2/3
0
1/2
1/2
0
1/4
0
0
1/3
о
1/2
15.	Двоичный источник задается простой цепью Маркова с матрицей переходных
вероятностей
П =
1/2 1/2
1/8 7/8
Найти собственную информации последовательности ОНО, найти Н(Х). По-
строить зависимости Я(Х|ХП) и Нп(Х) от п, найти Я(Л'|Х°°). Каково влия-
ние «зависимости букв» на скорость создания информации источником ?
16.	Представление реализации двоичного источника в виде последовательности длин
серий. При сохранении в память ЭВМ или на внешний носитель двоичные
последовательности, содержащие небольшое число единиц, можно записывать
в виде последовательности длин серий нулей. Будем писать О' вместо последо-
вательности из г нулей. Например, последовательность 0011000010100 может
быть записана в виде последовательности целых чисел (2,0,4,1,2). Таким обра-
зом, двоичная последовательность xlt... ,хп,..., ж, € X = {0,1} преобразу-
ется в последовательность неотрицательных целых чисел - t/i, у2,	, у% € Y =
= {0,1,...} длин серий нулей. Считая двоичный источник постоянным с веро-
ятностью единицы, равной р, найти распределение вероятностей на множестве
значений длин серий Y и энтропию Я(У).
1.13. Задачи
53
Подсказка. В процессе решения задачи появится геометрическое распределе-
ние, а при подсчете его энтропии потребуется формула для его математиче-
ского ожидания. См. задачу 17.
17.	Геометрическим распределением на множестве I = {0,1,2,...} называется рас-
пределение вероятностей вида р(г) = (1 — а)аг (почему?). Проверить выпол-
нение условия нормировки вероятностей. Найти математическое ожидание,
дисперсию и энтропию Н(Г).
Подсказка. При проверке условия нормировки нужно будет вычислить сумму
вида
оо
<t43)
i=0
Для этого достаточно вспомнить формулу суммы геометрической прогрессии.
Немного сложнее задача вычисления математического ожидания, поскольку
придется иметь дело с суммой
оо
^ia\	(1.44)
i=0
Однако заметим, что при дифференцировании (1.43) по а получится почти
(1.44). Значит, задача сводится к дифференцированию известного выражения
для суммы геометрической прогрессии. Вторая производная этого выражения
пригодится для подсчета дисперсии.
Еще один способ подсчета суммы (1.44) состоит в том, что сомножитель i под
знаком суммы можно представить в виде суммы i единиц, а затем поменять
порядок суммирования.
Ответы:
М[г] = D[i] =	Н(Г) =
u 1 — a lJ (1 — a)2	’	1 —a
18.	Относительной энтропией Кульбака-Лейблера распределения {р(х),х е X}
по отношению к распределению {q(x),x € X} называется функция
LQ>||<Z) = £p(x)log^.	(1.45)
Эту функцию можно рассматривать как меру различия двух распределений.
Очевидно, относительная энтропия равна нулю, если распределения совпа-
дают. Не столь очевидно, что она строго положительна, если два распределе-
ния различны. Докажите последнее утверждение.
Подсказка. Запишите относительную энтропию в виде
i(p|k) = -J2p(x)iog^
и воспользуйтесь неравенством log г < (z ~ l)loge.
54
Глава 1. Энтропия дискретных источников
19.	Равномерное распределение является экстремальным В том смысле, что оно
имеет наибольшую энтропию среди всех распределений вероятностей на мно-
жестве из заданного конечного числа элементов. Докажите следующее утвер-
ждение:
Геометрическое распределение является экстремальным (максимизирующим
энтропию) для дискретных случайных величин, принимающих счетное количе-
ство значений и имеющих заданное математическое ожидание.
Решение. Пусть р(г) = (1 — а)а\г = 0,1,... - геометрическое распределе-
ние, - произвольное распределение на том же множестве чисел с тем же
математическим ожиданием М[г] = а/(1 - а), Я(р) и H(q) - соответствующие
энтропии, причем Я(р) = т/(а)/(1 - а) (см. задачу 17). Тогда
оо	оо
= - £log q^ = _ 52q^log
i=0	i=0
!	оо	оо
= -Ь(р||«) - 52«(i)bgp(i)	(log(l - a) 4- г log се) =
г=0	i=0
= - log(l - a) - M[i] 16ga = - log(l - a) -	= H(p).
1 — a
20.	Имеется постоянный источник троичных сообщений. Алфавит источника
имеет вид X = {а, 6, с} . Для распределений вероятностей
1)	Р(а) = Р(Ь) = Р(с) = 1/3 ;
2)	р(а) = р(Ъ) = 1/4, р(с) = 1/2;
построить зависимости скорости равномерного кода от длины кодируемых
блоков при нулевой вероятности ошибки. Сопоставить скорость кодов с энтро-
пией источника.
21.	Рассмотреть троичные источники из предыдущей задачи. Исследовать зависи-
мость скорости равномерного кода от длины кодируемых последовательностей
при допустимой вероятности ошибки, равной 0.1.
22.	Весом Хэмминга последовательности х над алфавитом {0,... - 1} называ-
ется число ненулевых элементов в х. Сколько существует двоичных последо-
вательностей длиной п весом w?
Подсказка. Покажите, что число возможных выборов без возвращения w эле-
ментов из множества, содержащего п различных элементов, с учетом порядка
следования элементов,
А™ = п(п — 1) х • • • х (n — w + 1).
Далёе нужно показать, что число различных перестановок из w элементов
Pw = w(w — 1) х • • • х 1 = w\.
Наконец, число последовательностей длиной п весом ш равно числу выборок
без возвращения из п по w, если порядок следования элементов не учитыва-
ется:
1.14. Библиографические замечания
55
= (п\ = А"; = n(n-l)x-x(»-m + l) =
n W Pw	w!
—
wl(n — w)\‘
23.	Найти вероятность pn(w) того, что последовательность длины п на выходе
двоичного ДПИ с вероятностью единицы, равной р, будет иметь вес Хэмминга,
равный w.
Комментарий, Ответ этой задачи - формула биномиального распределения
Pn(w) =(”)PW(1- Р)^
24.	Двоичный постоянный источник X = {0,1} порождает единицы с вероят-
ностью р = 0.02. Исследовать зависимость вероятности ошибки от длины
кодируемых блоков при скорости двоичного кода 0.5 бита на букву источника.
25.	Найти вероятность того, что последовательность длины п = 10 на выходе
двоичного ДПИ с вероятностью единицы, равной р = 0.1, будет иметь вес Хэм-
минга, больший или равный w = 5. (Придется воспользоваться компьютером.)
Сравните этот результат с оценкой Чебышева вероятности этого события.
26.	Полиномиальное распределение. Сколько троичных последовательностей дли-
ной п содержат то нулей, ri единиц и т2 = п - т0 - и двоек? Найдите
вероятность такой последовательности при заданном распределении вероят-
ностей на элементах троичного алфавита. Обобщите результат на алфавиты
произвольного размера.
Подсказка, Ответ можно найти в главе 3, посвященной универсальному коди-
рованию источников.
1.14. Библиографические замечания
В этой главе почти нет ссылок на литературу, поскольку ее материал содержится
во всех монографиях и учебниках по теории информации. Из литературных
источников на русском языке заинтересованному читателю следует порекомен-
довать первоисточник [20]. Более основательное и подробное изложение фунда-
ментальных понятий теории информации содержится в учебнике В. Д. Колесника
и Г. Ш. Полтырева [7] - безусловно лучшем пособии на русском языке для сту-
дентов. Этот учебник, несмотря на почтенный возраст, незаменим для тех, кто
изучает теорию информации с серьезными намерениями.
Нельзя не упомянуть еще две книги: учебник Р. Галлагера [3] и монографию
И. Чисара и Я. Корнера [19]. Первую можно рекомендовать аспирантам, вторая
- виртуозно компактное изложение всех существенных фактов и идей, известных
на момент издания книги.
Глава 1. Энтропия дискретных источников
Наиболее цитируемой в настоящее время книгой по теории информации на
английском языке заслуженно является книга Т. Кавера и Дж. Томаса [38].
Представленный в этой главе традиционный вероятностный подход к определе-
нию информации и энтропии - не единственный возможный. Альтернативные
подходы можно найти, например, в классической статье А. Н. Колмогорова [8] и
книге В.Д. Гоппы [4].
Глава 2 Неравномерное
кодирование
дискретных
источников
В предыдущей главе мы убедились в том, что источники информации, вообще
говоря, избыточны: при эффективном кодировании можно уменьшить затраты
на передачу или хранение порождаемой ими информации. Для представления
данных потребуется тем меньше битов, чем меньше энтропия. Это значит, что
для эффективного кодирования удобны источники, в которых некоторые буквы
(последовательности букв) имеют существенно большую вероятность, чем дру-
гие буквы (последовательности). Не нужно долго изучать теорию информации,
чтобы догадаться, что для таких источников нужно использовать кодирование,
сопоставляющее часто встречающимся сообщениям короткие кодовые комбина-
ции, а редким сообщениям - длинные. Реализация этой простой идеи обсужда-
ется в данной главе.
Мы начнем с кодирования отдельных букв источника. Оптимальным побуквен-
ным кодом является код Хаффмена. Однако для того, чтобы понять, как пра-
вильно кодировать последовательности, нам придется изучить некоторые неопти-
мальные побуквенные коды — код Шеннона и код Гилберта-Мура. От них - один
шаг к пониманию арифметического кодирования, которое позволяет предельно
эффективно кодировать длинные последовательности и при этом обладает отно-
сительно небольшой сложностью.
2.1.	Постановка задачи неравномерного
побуквенного кодирования
Предположим, что для некоторого дискретного источника X с известным распре-
делением вероятностей {р(х),х е X} требуется построить эффективный нерав-
номерный двоичный код над алфавитом А = {а}. Как и в предыдущей главе,
мы сосредоточим внимание на двоичных кодах, то есть мы предполагаем, что
А = {0,1}. Дело в том, что, во-первых, все идеи в полной мере иллюстрируются
на этом примере. Во-вторых, обобщение на случай произвольного алфавита не
представляет никакой трудности. Помимо этого, на практике для кодирования
источников используются почти исключительно двоичные коды.
58
Глава 2. Неравномерное кодирование дискретных источников
В качестве примера источника рассмотрим алфавит русского языка. Сразу же
вспоминается азбука Морзе, которая сопоставляет каждой букве комбинацию
точек «•» и тире «-». Например, часто встречающейся букве «е» соответствует
комбинация «•», а более редкой букве «ч» соответствует комбинация «----•».
Однако более пристальный взгляд убеждает, что мы не получим хорошего кода,
просто заменив точки нулями, а тире - единицами. Нам будет не хватать пауз,
разделяющих символы внутри букв (пауза соответствует интервалу времени,
равному времени передачи точки), пауз, разделяющих буквы (3 точки), пауз,
разделяющих слова (7 точек). По сути, код Морзе - это недвоичный код.
Нам необходим такой двоичный код, который допускает однозначное разделение
кодированной последовательности на отдельные кодовые слова без использо-
вания каких-либо дополнительных символов. Это требование называется свой-
ством однозначной декодируемости.
Неравномерный побуквенный код С = {с} объемом |С| = М над алфавитом А
определяется как произвольное множество последовательностей одинаковой или
различной длины из букв алфавита А.
Код является однозначно декодируемым,если любая последовательность симво-
лов из А единственным способом разбивается на отдельные кодовые слова.
Пример 2.1.1. Для источника X = {0,1,2,3} среди четырех кодов:
1)	Ci = {00,01,10,11};
2)	С2 = {1,01,001,000};
3)	С3 = {1,10,100,000};
4)	С4 = {0,1,10,01};
первые три кода однозначно декодируемы, последний код - нет.
Первый код этого примера - равномерный код. Понятно, что любой равномер-
ный код может быть однозначно декодирован.
Для декодирования второго кода можно применить следующую стратегию. Деко-
дер считывает символ за символом, каждый раз проверяя, не совпадает ли полу-
ченная последовательность с одним из кодовых слов. В случае успеха получа-
телю выдается соответствующее сообщение, а декодер приступает к декодирова-
нию следующего сообщения. В случае кода С2 неоднозначности не может быть,
поскольку ни одно слово не является продолжением другого.
Если ни одно кодовое слово не является началом другого, код называется пре-
фиксным. Префиксные коды являются однозначно декодируемыми.
Код С3 заведомо не префиксный. Тем не менее мы утверждаем, что он однозначно
декодируемый. Каждое слово кода С3 получено переписыванием в обратном
порядке соответствующего слова кода С2. Для декодирования последователь-
ности кодовых слов кода С3 можно переписать принятую последовательность
в обратном порядке и для декодирования использовать декодер кода С2. Таким
образом, мы приходим к следующему выводу.
2.1. Неравномерное побуквенное кодирование
59
Префиксность - достаточное, но не необходимое условие однозначной декодируе-
мости.
Графически удобно представлять префиксные коды в виде кодовых деревьев,
в частности, кодовое дерево кода С2 примера 2.1.1 представлено на рис. 2.1.
Рис. 2.1. Пример двоичного кодового дерева
Узлы дерева размещаются на ярусах. На начальном (нулевом) ярусе располо-
жен один узел, называемый корнем дерева. Узлы следующих ярусов связаны
с узлами предыдущих ярусов ребрами. В случае двоичного кода из каждого узла
исходит не более двух ребер. Каждому ребру приписан один из кодовых сим-
волов. Принято соглашение о том, что ребру, ведущему вверх, приписывается
символ 0, а ребру, ведущему вниз, - символ 1. Таким образом, каждой вершине
дерева соответствует последовательность, считываемая вдоль пути, по которому
корень дерева связан с данным узлом.
Узел называется концевым, если из него не исходит ни одного ребра. Код назы-
вают древовидным, если в качестве кодовых слов он содержит только кодовые
слова, соответствующие концевым вершинам кодового дерева.
Древовидность и префиксность кода - синонимы. Всякий древовидный код явля-
ется префиксным, и всякий префиксный код может быть представлен с помощью
кодового дерева. Мы будем рассматривать только префиксные коды. В связи
с этим возникает вопрос: не потеряли ли мы оптимальное решение задачи, сузив
класс однозначно декодируемых кодов, среди которых мы ищем наилучшие?
Ниже мы убедимся в том, что ответ на этот вопрос отрицательный.
Обсудим теперь, какие именно префиксные коды считать хорошими. Поскольку
цель рассмотрения неравномерного кодирования состояла в уменьшении затрат
на передачу сообщений, то логично выбрать в качестве критерия качества сред-
нюю длину кодовых слов. Рассмотрим источник X = {1,..., М}, который порож-
дает буквы с вероятностями {pi,...	}• Пусть для кодирования букв источника
выбран код С = {с\,,см} с длинами кодовых слов li, ..., 1м соответственно.
60
Глава 2. Неравномерное кодирование дискретных источников
Средней длиной кодовых слов называется величина
м
Z = M[Zi] —
i—1
Еще один важный аспект, который должен быть учтен при сравнении способов
неравномерного кодирования, - сложность реализации кодирования и декодиро-
вания. В зависимости от области применения может изменяться и значение допу-
стимой сложности, и само понятие сложности. Например, при реализации алго-
ритма на универсальном компьютере практически отсутствует ограничение на
размер оперативной памяти, но имеет значение вычислительная сложность. При
реализации кодера и декодера в виде интегральной микросхемы или с помощью
специализированного сигнального процессора, напротив, используемая память
является ключевым параметром.
Как мы увидим далее, побуквенные коды часто используются как составная часть
более сложных алгоритмов. В этих случаях играет роль не только сложность
собственно кодирования и декодирования буквы, но и сложность построения
или модификации кода при изменении статистических данных об источнике.
Подведем итог. Мы формулируем задачу побуквенного неравномерного коди-
рования как задачу построения однозначно декодируемого кода с наименьшей
средней длиной кодовых слов при заданных ограничениях на сложность.
2.2.	Неравенство Крафта
Вернемся к примеру 2.1.1 и сравним коды Ci и Сг объемом 4. Код Ci равномер-
ный, все слова имеют длину 2. Нельзя ли выбрать слова короче? Действительно,
в коде Сг есть одно слово длиной 1, но чтобы сохранить объем кода и пре-
фиксность, пришлось на единицу увеличить длины двух других кодовых слов.
Этот пример показывает, что требование префиксности накладывает жесткие
ограничения на длины кодовых слов и не дает возможности' выбирать кодовые
слова слишком короткими. Формально эти ограничения записываются в виде
изящного неравенства, называемого неравенством Крафта.
ТЕОРЕМА 2.1. Необходимым и достаточным условием существования префикс-
ного кода объемом М с длинами кодовых слов h,.. • ,1м является выполнение нера-
венства Крафта
м
(2.1)
г=1
Доказательство. Начнем с необходимости. Мы должны убедиться в том, что
неравенство (2.1) верно для любого префиксного кода.
Рассмотрим двоичное кодовое дерево произвольного префиксного кода объемом
М с длинами кодовых слов Zi, ..., 1м- Выберем целое число L такое, что L
maxjZi. Продолжим все пути в дереве до яруса с номером L. На последнем
2.2. Неравенство Крафта
61
ярусе мы получим 2L вершин. Заметим, что концевая вершина исходного дерева,
расположенная на глубине 1г, имеет 2 потомка на глубине Ц + 1, 4 потомка
на глубине Ц + 2, и т.д. На глубине L будет 2L~li потомков этой вершины.
Множества потомков различных концевых вершин не пересекаются, поэтому
суммарное число потомков не превышает общего числа вершин на ярусе L.
Получаем неравенство
м
^22L~Zi < 2Л.
1=1
Поделив обе части на 2Ь, получим требуемый результат. Рисунок 2.2 иллюстри-
рует доказательство необходимости выполнения неравенства Крафта на примере
кода из четырех слов. В этом примере Zi = 2, 12 = /з = 3,	= 1, L = 3. Кодо-
вое дерево показано сплошными линиями, а ребра, появившиеся при продлении
дерева до яруса с номером L, показаны пунктиром.
Рис. 2.2. Пояснение к доказательству необходимости неравенства Крафта
для существования префиксного кода
Чтобы убедиться в достаточности, нужно показать, что из справедливости (2.1)
вытекает существование кода с заданным набором длин кодовых слов. Построим
такой код. Без потери общности можем считать числа Ц упорядоченными по
возрастанию.
Из общего числа 2Z1 вершин на ярусе Zi выберем одну любую вершину, сделаем
ее концевой и закрепим ее за первым кодовым словом. Продолжим оставши-
еся вершины до яруса Z2. Из общего числа возможных вершин нужно исклю-
чить 2/2“fl вершин, которые принадлежат поддереву, начинающемуся в узле,
соответствующем первому слову. На ярусе Z2 останется
2«2 _ 2^-h > 1
вершин. Последнее неравенство следует из (2.1), в чем нетрудно убедиться, поде-
лив обе его части на 2/2. Сделаем одну из них концевой и закрепим ее за вторым
словом. Аналогично, для третьего слова мы получим множество из
2^3 — 2*3-*2 — 2/з-/1	1
62
Глава 2. Неравномерное кодирование дискретных источников
вершин. В силу (2.1) всегда найдется одна для третьего слова. Продолжая постро-
ение, на последнем ярусе с номером 1м мы получаем
— 2^м~^м~2 — ... — 2^“^
вершин. Простые выкладки показывают, что это число не меньше 1, если нера-
венство (2.1) верно. Выбрав эту вершину для последнего слова, мы завершим
построение префиксного кода. Рисунок 2.3 иллюстрирует процесс построения
кодового дерева для набора длин кодовых слов Zi = 1, Z2 = 2,1з = I4 = 3.	□
4=1. Из 2А = 2 вершин выбираем одну
для слова длиной 4*1.
Zjb (	Имеем 22 -	= 2 вершины. Этого
уу \	достаточно для построения слова длиной 4-
я Имеем 23- 23 *2 - 23 ^ = 2. Этого достаточно
для завершения построения кода.
Рис. 2.3. Построение двоичного кодового дерева, удовлетворяющего неравенству Крафта
В примере, показанном на рис. 2.3, неравенство Крафта выполняется с равен-
ством. Внимательно просмотрев доказательство необходимости в теореме 2.1,
убедимся, что для достижения равенства в (2.1) кодовое дерево должно быть
полным, то есть каждая промежуточная вершина дерева должна иметь ровно 2
потомка и всем концевым вершинам должны быть сопоставлены кодовые слова.
Неравенство Крафта как бы ограничивает снизу длины кодовых слов префикс?
ного кода заданного объема М. На этом будет впоследствии построено доказа-
тельство обратной теоремы кодирования. В связи с этим важно быть уверенным,
что оно имеет место не только для древовидных (префиксных) кодов, но и
для любых других однозначно декодируемых кодов. Это утверждение является
содержанием следующей теоремы.
ТЕОРЕМА 2.2. Для любого однозначно декодируемого двоичного кода объемом М
с длинами кодовых слов li, ...,1м справедливо неравенство
м
(2.2)
г=1
Доказательство. Без потери общности можно считать 1м наибольшей из длин
кодовых слов. Выберем некоторое натуральное число N и запишем JV-ю степень
левой части неравенства в виде
2.3. Теоремы побуквенного неравномерного кодирования
63
n сомножителей
м м
= у . у	^liN\
ii=l i,N=l
В правой части имеем MN слагаемых. Их мы перегруппируем, упорядочив по
величине суммы длин кодовых слов lit +.. .+liN. Обозначим через Al количество
таких последовательностей кодовых слов, сумма длин которых равна lilL + ... +
+ liN = L. Тогда
(М	\ N NlM
i=l	/	L=1
Теперь заметим, что Al, то есть число таких последовательностей из N кодо-
вых слов, суммарная длина которых в точности равна L, не может быть больше
общего числа двоичных последовательностей длиной L. Таким образом, Al < 2L.
Поэтому
(М \ N NlM
i=l /	L=1
Извлечем из обеих частей корень TV-й степени. Получим
м
^2-^(W)1/JV=2i2S^.
1=1
Неравенство справедливо при любых 7V. Перейдя к пределу при 7V —> оо, в правой
части получим 1, что и доказывает теорему.	□
2.3.	Теоремы побуквенного неравномерного
кодирования
2.3.1.	Прямая теорема
Начнем непосредственно с формулировки теоремы кодирования.
ТЕОРЕМА 2.3. Для ансамбля X = {х,р(х)} с энтропией Н существует побуквен-
ный неравномерный префиксный код со средней длиной кодовых слов I < Н + 1.
Доказательство. У нас уже есть опыт доказательства прямой теоремы кодиро-
вания для случая равномерного кодирования источников. Доказательство той
теоремы было конструктивным в том смысле, что в явной форме был указан спо-
соб построения кода, удовлетворяющего условиям теоремы. Здесь мы могли бы
поступить так же. Однако мы воспользуемся случаем, чтобы продемонстрировать
пример неконструктивного доказательства. Опираясь на неравенство Крафта, мы
64
Глава 2. Неравномерное кодирование дискретных источников
установим существование кода, не указав, как можно его построить. Этот подход
достаточно типичен для теории информации. Больше того, для многих теорем
кодирования, доказанных несколько десятилетий назад, конструктивных методов
доказательства не известно до сих пор.
Итак, рассмотрим источник над алфавитом X = {1,..., М} с вероятностями букв
Pi,... ,рм- Сопоставим букве хт кодовое слово длиной lm = [- logpm"| при т =
(Запись [aj означают округление числа а вниз до ближайшего целого, а
запись [а] - округление числа а вверх до ближайшего целого.) Префиксный код
с таким набором длин кодовых слов в соответствии с теоремой 2.1 существует,
поскольку длины кодовых слов удовлетворяют неравенству Крафта
мм	мм
^2 2~1т = 52 2_|’_1о8р’"1	52 2iogpm = ^2	= 1.
m=l	m=l	m=l	m=l
Средняя длина кодовых слов кода
мм	м
I = 52Pmlm = ZZРт г~ lospmi < 52Рт +о =
т=1	т—1	т—1
М
= Н+^Рт=Н+1,
т—1
что и требовалось доказать.	□
Обсудим полученную оценку длины кодовых слов. Мы знаем (ниже это будет
установлено точно с помощью обратной теоремы кодирования), что достижи-
мая скорость кодирования примерно равна энтропии. Теорема гарантирует, что
средняя длина слов хорошего кода отличается от энтропии не больше, чем на 1.
Если энтропия велика, то проигрыш по сравнению с минимально достижимой
скоростью можно считать небольшим. Но предположим, что Н < 1. Например,
Н = 0,1. Теорема гарантирует, что существует код со средней длиной кодовых
слов не больше 1,1 бита. Но нам хотелось бы затрачивать на передачу одного
сообщение примерно в 10 раз меньше бит! Этот пример показывает, что либо
теорема дает неточную оценку, либо побуквенное кодирование в этом случае не
эффективно.
На примере двоичного источника мы убедимся теперь в том, что теорема доста-
точно точна и ее результат не может быть улучшен, если не использовать никакой
дополнительной информации об источнике. Действительно, предположим, что
дан двоичный источник X — {0,1} с вероятностями букв {б, 1-е}. Минимально
достижимая длина кодовых слов наилучшего кода, очевидно, равна 1. Теорема
говорит, что средняя длина кодовых слов не больше 1 + ?j(e), то есть стремится
к 1 при е —► 0. Таким образом, для данного примера двоичного источника теорема
точна.
Достижение скоростей (затрат на передачу одной буквы источника), меньших 1,
невозможно при побуквенном кодировании, поскольку длина кодового слова
2.3. Теоремы побуквенного неравномерного кодирования
65
не может быть меньше 1. Однако переход к кодированию блоков сообщений,
как мы увидим позже, решает эту проблему и позволяет сколь угодно близко
подойти к теоретическому пределу, равному энтропии Н. Конструктивным реше-
нием данной задачи является арифметическое кодирование, рассматриваемое
в конце данной главы.
2.3.2.	Обратная теорема
Обратная теорема неравномерного кодирования устанавливает нижнюю границу
средней длины кодовых слов любого однозначно декодируемого кода.
ТЕОРЕМА 2.4. Для любого однозначно декодируемого кода дискретного источ-
ника X = {ж, р(х)} с энтропией Н средняя длина кодовых слов [удовлетворяет
неравенству
I Н.	(2.3)
Другими словами, не существует кода со средней длиной кодовых слов меньше
Я, обладающего свойством однозначной декодируемости.
Доказательство. Пусть 1{х) обозначает длину кодового слова для сообщения х.
Имеем
_	__ _________________ _____________ 2~^(ж)
н -1 = - 52 1°gp(a;) - 52 №№ = 52 log тттг-
£х	, £х №
Применяя уже знакомое нам неравенство для логарифма
log х < (х — 1) loge,
получаем
= ioge 1522 /(ж) - 52I loge (1 - 52р^)= °-	(2-4)
хгеЕХ	х€.Х /	\ хЕ.Х /
Здесь мы использовали неравенство Крафта и условие нормировки вероятностей.
Из (2.4) следует утверждение теоремы.	□
Обсудим вопрос о том, при каких условиях возможно равенство в обратной
теореме. Для этого равенство должно иметь место в первом и втором неравен-
ствах в (2.4). В этом случае при каждом х должно выполняться соотношение
р(х) = В то же время для такого распределения вероятностей суще-
ствует префиксный код с длинами кодовых слов l(x) = |’-logp(rr)1 = “logp(z).
Для этого кода неравенство Крафта выполняется с равенством, и средняя длина
кодового слова равна I = Н.
Таким образом, мы установили справедливость следующего утверждения.
66
Глава 2. Неравномерное кодирование дискретных источников
СЛЕДСТВИЕ 2.5. Для существования кода со средней длиной кодовых слов I = Н
необходимо и достаточно, чтобы все вероятности сообщений х е X имели вид
р(х) = где {/(ж)} - целые положительные числа.
2.4.	Оптимальный побуквенный код
код Хаффмена
Предложенный Хаффменом алгоритм построения оптимальных неравномерных
кодов - одно из самых важных достижений теории информации как с теоре-
тической, так и с прикладной точек зрения. Трудно поверить, но этот алгоритм
был придуман в 1952 г. студентом Дэвидом Хаффменом в процессе выполне-
ния домашнего задания. Примечательно, что занятия вел Фано, на результаты
которого мы еще не раз сошлемся в следующих главах.
Рассмотрим ансамбль сообщений X =	с вероятностями сообщений
{pi,... ,рм}« Без потери общности мы считаем сообщения упорядоченными по
убыванию вероятностей, то есть Pi < Р2 < Рм* Наша задача состоит
в построении оптимального кода, то есть кода с наименьшей возможной средней
длиной кодовых слов. Понятно, что при заданных вероятностях такой код может
не быть единственным, возможно существование семейства оптимальных кодов.
Мы установим некоторые свойства всех кодов этого семейства. Эти свойства
подскажут нам простой путь к нахождению одного из оптимальных кодов.
Пусть двоичный код С = {с15...,см} с длинами кодовых слов {Zi,..., 1м}
оптимален для рассматриваемого ансамбля сообщений.
Свойство 2.4.1. Если pi < pj, то Ц lj.
Доказательство. Свойство легко доказывается методом «от противного». Пред-
положим, что Ц < lj. Рассмотрим другой код С", в котором сообщению Xi соответ-
ствует слово Cj, а сообщению Xj - слово сг. Нетрудно убедиться в том, что сред-
няя длина кодовых слов для кода С' меньше, чем для кода С, что противоречит
предположению об оптимальности кода С.	□
Свойство 2.4.2. Не менее двух кодовых слов имеют одинаковую длину 1м = шах™ 1т.
Доказательство. Если предположить, что имеется только одно слово максималь-
ной длины, то соответствующее кодовое дерево будет неполным. Очевидно, слово
максимальной длины можно будет сделать короче по меньшей мере на 1 символ.
При этом уменьшится средняя длина кодовых слов, что противоречит предполо-
жению об оптимальности кода.	□
Свойство 2.4.3. Среди кодовых слов длиной 1м = niaxm Zm найдутся два слова,
различающиеся только в одном последнем символе.
Доказательство. Согласно предыдущему свойству, два слова длиной 1м суще-
ствуют в любом оптимальном коде. Рассмотрим концевой узел, соответствующий
2.4. Оптимальный побуквенный код - код Хаффмена
67
одному из слов максимальной длины. Чтобы дерево было полным, должен суще-
ствовать узел, имеющий общий предшествующий узел с данным узлом. Соответ-
ствующие двум концевым вершинам кодовые слова имеют одинаковую длину 1м
и различаются в одном последнем символе.	□
Прежде чем сформулировать следующее свойство, введем дополнительные обо-
значения. Для рассматриваемого ансамбля X — {1,...,М} и некоторого кода
С, удовлетворяющего свойствам 2.4.1 - 2.4.3, введем вспомогательный ансамбль
Х' = {1,...,М-1}, сообщениям которого сопоставим вероятности {р^,... ,Рм-1}
следующим образом:
Р1=Р1,	•••, Рм-2=РМ-2, Р'м-1 = РМ-1 +РМ-
Из кода С построим код С" для ансамбля X', приписав сообщениям х^, ..., я/м_2
те же кодовые слова, что и в коде С, то есть с\ = cif i = 1, ..., М — 2, а сооб-
щению x'm-! - слово c'M_v представляющее собой общую часть слов см-i и
см (согласно свойству 2.4.3, эти два кодовых слова различаются только в одном
последнем символе).
Свойство 2.4.4, Если код (У для X1 оптимален, то код С оптимален для X.
Доказательство. Длины кодовых слов кодов С и С" по построению связаны
соотношениями
Отсюда
I
> _ J 1'т при т М - 2,
ьт — \
( чи-i + 1 ПРИ т = М — 1,М.
М	М-2
~ Рт^гп ~ PrrJm 4“ PM—l^M— 1 Ч” РМ^М ~
т=1	тп=1
М-2
= Рт^т Ч” (PM—1 Ч” Рм}{^М—1 Ч- 1) =
т=1
М-2
= У? Рт^т + р’м-11М-1 + РМ-1 +рм =
т=1
М-1
= Р'тУт + Рм-l +рм = 1' + РМ—1 + РМ>
т=1
М-1
где Г = Pmlm ~ средняя длина кодовых слов кода С". Последние два сла-
771=1	_
гаемых в правой части не зависят от кода, поэтому код, минимизирующий lf,
одновременно обеспечивает минимум для I.	□
Итак, сформулированные свойства оптимальных префиксных кодов сводят задачу
построения кода объемом М к задаче построения кодов объемом М' = М—1. Это
означает, что мы получили рекуррентное правило построения кодового дерева
68
Глава 2. Неравномерное кодирование дискретных источников
Input: Объем алфавита М, вероятности букв
Output: Двоичное дерево кода Хаффмена
Инициализация:
количество необработанных узлов Mq = М
while Mq > 1 do
в списке необработанных узлов найти два узла с наименьшими вероятностями.
Исключить эти узлы из списка необработанных.
Ввести новый узел, приписать ему суммарную вероятность двух исключенных
узлов.
Новый узел связать ребрами с исключенными узлами.
Mq «— Mq — 1.
end
Рис. 2.4. Алгоритм построения кодового дерева кода Хаффмена
оптимального неравномерного кода. Это правило в виде алгоритма представлено
на рис. 2.4.
После выполнения алгоритма будет получено кодовое дерево кода, который, как
доказано выше, имеет наименьшую возможную среднюю длину кодовых слов.
Пример 2.4.1. Рассмотрим ансамбль буквенных сообщений X — {а, 6, с, d, е, /}
с вероятностями букв {0,35, 0,2, 0,15,'0,1, 0,1, 0,1} соответственно. Кодовое
дерево и код Хаффмена показаны на рис. 2.5. Энтропия источника Н = 2,4016.
Средняя длина кодовых слов равна I = 2(0,35 + 0,2) + 3(0,15 + 3 х 0,1) = 2,45.
Согласно свойствам 2.4.1 - 2.4.4 не существует кода для X со средней длиной
кодовых слов меньшей, чем 2,45.
Рис. 2.5. Пример построения кода Хаффмена
Буква	Кодовое слово
а	00
b	10
с	010
d	011
е	110
f	111
2.5. Избыточность кода Хаффмена
69
2.5.	Избыточность кода Хаффмена
Из теоремы 2.3 следует, что для построенных по алгоритму Хаффмена кодов
средняя длина кодовых слов удовлетворяет неравенству
/<Я + 1,	(2.5)
где Н - энтропия ансамбля.
Разность
г = 1-Н
называется избыточностью неравномерного кода. Она показывает степень «несо-
вершенства» кода в том смысле, что при кодировании с избыточностью г на каж-
дое сообщение тратится на г бит больше, чем в принципе можно было бы потра-
тить, если использовать теоретически найлучший (возможно, нереализуемый)
способ кодирования.
Итак, из (2.5) следует, что для кода Хаффмена избыточность г < 1. Однако
при решении практических задач, как и в примере 2.4.1, избыточность оказыва-
ется существенно меньше 1. Поэтому хотелось бы получить более точную оценку
средней длины кодовых слов. Как уже говорилось, этого нельзя сделать, не огра-
ничив множество рассматриваемых источников. Р. Гал лагер в 1978 году в работе,
посвященной 25-летию кода Хаффмена, получил гораздо более точную оценку
избыточности, наложив ограничение на максимальную из вероятностей сообще-
ний. Сформулируем результат Галлагера в виде теоремы, которую мы приводим
здесь без доказательства.
ТЕОРЕМА 2.6. Пустьрх - наибольшая из вероятностей сообщений конечного дис-
кретного ансамбля. Тогда избыточность кода Хаффмена для этого ансамбля удо-
влетворяет неравенствам
г { Р1 + а	при Pl < 1/2,	(2 6)
( 2 - p(pi) - pi при рг 1/2,
где = -х log х - (1 - х) log(l - х) - энтропия двоичного ансамбля, и
а — 1 — log е — log log е « 0,08607.	(2.7)
Отметим, что оценка Галлагера довольно точна в широком диапазоне значений
pi. Для ансамбля с вероятностями сообщений {1/3, 1/3, 1/3, 0} имеем оценку
0,419. Истинная избыточность кода Хаффмена для этого источника 0,417. Для
троичного источника с распределением вероятностей {pi,l -pi,0} оценка тео-
ремы дает точный результат. Эти примеры говорят о том, что существенно улуч-
шить оценку, располагая только значением довольно трудно. В то же время
для примера 2.4.1 теорема 2.6 дает оценку г 0,35 + 0, 0861 = 0,4361 - при том,
что истинное значение избыточности г = 2, 45 - 2,4016 = 0,0484.
То, что оценка Галлагера недостаточно точна при pi < 0,5, стимулировало поиск
более точных оценок в рамках той же постановки задачи. Было опубликовано
довольно много работ на эту тему. Окончательный результат - точная граница
70
Глава 2. Неравномерное кодирование дискретных источников
для всех значений pi - приведен в работе Манстеттена [54]. Эта граница точна
в том смысле, что она не может быть улучшена, если известно только значе-
ние pi максимальной вероятности сообщений источника. Полная запись формул
Манстеттена заняла бы несколько страниц. Вместо этого на рис. 2.6 показаны
графики оценок избыточности из работ Галлагера и Манстеттена как функций
параметра pi.
2.6.	Код Шеннона
Построением оптимальных неравномерных кодов можно было бы закончить изу-
чение побуквенного кодирования. Тем не менее мы рассмотрим сначала код
Шеннона, который заметно хуже кода Хаффмена, а затем изучим еще более
плохие коды - коды Гилберта-Мура. В обоих случаях некоторое увеличение
избыточности по сравнению с оптимальным кодом оправдывается простотой
построения кодовых слов. При обсуждении прямой теоремы побуквенного коди-
рования уже говорилось о том, что избыточность 1 бит на букву не так уж
велика, если велико значение энтропии. В следующем параграфе мы перейдем
к кодированию последовательностей сообщений. Целая последовательность будет
рассматриваться как отдельное сообщение. Энтропия такого «расширенного»
источника будет очень большой, и главными проблемами будут уже не избыточ-
ность побуквенного кодирования, а сложность построения кодовых слов и слож-
ность их декодирования.
Рассмотрим источник, выбирающий буквы из множества X = {1,М} с веро-
ятностями {pi,... ,рм}« Считаем, что буквы упорядочены по убыванию вероят-
2.6. Код Шеннона
71
Input: Объем алфавита М, вероятности букв pi, i = 1, ..., М
Output: Список кодовых слов кода Шеннона
Сортировка:
for i = 1 to М do
j(i) 4— индекс г-й по убыванию вероятностей буквы алфавита
end
Кумулятивные вероятности:
«ли - °;
for i = 2 to M do
end
Кодовые слова:
for i = 1 to M do
d первые [ — logp/| разрядов после запятой в двоичной записи числа qi.
end
Рис. 2.7. Алгоритм построения кода Шеннона
ностей, то есть pi > Р2	Рм* Сопоставим, кроме того, каждой букве так
называемую кумулятивную вероятность по правилу
М-1
gi = o, q2=pi, •••, дм = 52Pi-
i=i
Кодовым словом кода Шеннона для сообщения с номером т является двоич-
ная последовательность, представляющая собой первые Zm = [- logpml разрядов
после запятой в двоичной записи числа
Алгоритм построения кода Шеннона приведен на рис. 2.7.
Пример 2.6.1. Рассмотрим тот же ансамбль, что и в примере 2.4.1. В табл. 2.1
приведены промежуточные вычисления и результат построения кода Шеннона.
Средняя длина кодовых слов I = 2,95. В данном случае избыточность кода Шен-
нона оказалась на 0,5 бита больше, чем избыточность кода Хаффмена. Кодовое
дерево кода показано на рис. 2.8. Из этого рисунка понятно, почему такой код
неэффективен. Кодовые слова для букв 6, d, е, f могут быть укорочены на 1 бит
без потери свойства однозначной декодируемое™.
Докажем для кода Шеннона однозначную декодируемость. Для этого выберем
сообщения с номерами г и J, г < j. Кодовое слово сг для г заведомо короче, чем
слово Cj для J, поэтому достаточно доказать, что эти слова различаются в одном
из первых Ц символов. Рассмотрим разность
J-1	г-1	j — 1
- Qi = 53?*: - ^,Pk=52?*: >
fc=l	fc=l	k=i
72
Глава 2. Неравномерное кодирование дискретных источников
Рис. 2.8. Кодовое дерево кода Шеннона для ансамбля из примера 2.6.1
Таблица 2.1. Построение кода Шеннона для примера 2.6.1
X	Рт	Qm	1>т	Двоичная запись qm	Кодовое слово ст
а	0,35	0,00	2	0,00...	00
b	0,20	0,35	3	0,0101...	010
с	0,15	0,55	3	0,10001...	100
d	0,10	0,70	4	0,10110...	1011
е	0,10	0,80	4	0,11001...	1100
f	0,10	0,90	4	0,11100...	1110
Вспомним, что длина слова и его вероятность связаны соотношением
li = [- logPil > -logft.
Поэтому
С учетом этого неравенства
В двоичной записи числа в правой части мы имеем после запятой Ц - 1 нулей и
единицу в позиции с номером Ц. Следовательно, по меньшей мере в одном из Ц
разрядов слова а и Cj различаются и, значит, Ci не является префиксом для Cj.
Поскольку это верно для любой пары слов, то код является префиксным.
Длины кодовых слов в коде Шеннона точно такие же, какие были выбраны при
доказательстве прямой теоремы кодирования. Повторив выкладки, получим уже
известную оценку для средней длины кодовых слов
1<Н+1.
Примечательно, что при построении кода Шеннона мы выбрали длины кодовых
слов приблизительно равными (чуть большими) собственной информации соот-
ветствующих сообщений. В результате средняя длина кодовых слов оказалась
приблизительно равной (чуть большей) энтропии ансамбля.
2.6. Код Шеннона
73
Хотя конструкция кода и анализ его характеристик уже достаточно понятны, мы
обсудим еще одну (графическую) интерпретацию процесса кодирования. Она
будет полезна в дальнейшем при обсуждении арифметического кодирования.
Рассмотрим числовой отрезок [0,1), на котором расположим один за другим
отрезки длиной pi, ..., рм- На рис. 2.9 приведен пример разметки отрезка для
случая М = 3, pi = 0,6, р2 = 0,3, р3 = 0,1. Как видно на рис. 2.9, а, кумулятивные
вероятности qi = 0,	= 0,6, и д3 = 0,9 соответствуют началам отрезков. Эти
точки идентифицируют сообщения источника.
<72>1/2, поэтому
кодовый символ = 1
Q< 3/4, поэтому
кодовый символ = 0
Длина отрезка = 1/4, а
вероятность символа
0,3>1/4.
Построение кодового
слова закончено.
Рис. 2.9. Графическая интерпретация кода Шеннона
Предположим, что требуется закодировать сообщение с номером т = 2. Соот-
ветствующая ему точка qm помечена на рис. 2.9, a-в кружком. На первом шаге
передачи передачей кодового символа 0 либо 1 кодер указывает, в какой половине
отрезка [0,1) (левой или правой) находится начало соответствующего сообщению
отрезка. В данном случае передается 1, тем самым область возможных положений
передаваемой точки уменьшается вдвое, что и показано на рис. 2.9, б. На следую-
щем шаге передается символ 0, так как точка находится в левой половине интер-
вала и длина интервала неопределенности уменьшается до 1/4. После второго
шага в интервале неопределенности осталась только одна точка, поэтому пере-
дача может быть завершена. Это произошло не случайно. Дело в том, что длина
интервала равна 1/4, что меньше длины кратчайшего прилегающего отрезка 0,3, -
именно поэтому гарантируется единственность точки, а значит, и однозначность
декодирования.
В общем случае после передачи 1т двоичных символов длина интервала неопре-
деленности равна 2~1т. Декодирование будет однозначным, если 2~1гп < рт
или lm - logpm. Это условие в точности совпадает с правилом выбора длин
кодовых слов в коде Шеннона.
74
Глава 2. Неравномерное кодирование дискретных источников
Заметим, что при выборе длины кодовых слов мы ориентировались только на
отрезок, лежащий справа от точки qm. Упорядоченность букв по убыванию веро-
ятностей гарантирует, что левый отрезок всегда будет длиннее правого.
2.7.	Код Гилберта-Мура
При построении кода Шеннона мы требовали упорядоченности сообщений по
убыванию вероятностей. В алгоритме построения кода Шеннона наиболее тру-
доемкой частью является сортировка букв входного алфавита. Мы можем сильно
упростить построение кода, если модифицируем кодирование таким образом,
чтобы упорядоченность не требовалась. Графическая интерпретация кода Шен-
нона, показанная на рис. 2.9, подсказывает почти очевидный путь к решению
этой задачи.
Предположим, что вероятности не упорядочены и при кодировании сообщения
с номером т нужно учитывать не только вероятность (длину отрезка) рт, но
и длину предшествующего отрезка pm_i, которая может быть очень маленькой,
почти нулевой (тогда длина слова будет большой, даже если вероятность рт
велика). Как избавиться от влияния pm-i?
Очень просто. Нужно соответствующую сообщению точку переместить из начала
отрезка (точка qm) в его середину (точка qm + рт/2), а длину кодового слова 1т
выбрать так, чтобы к концу передачи кодового слова интервал неопределенности
был не больше рт/2. Эти Zm бит и будут кодовым словом кода Гилберта-Мура!
Определим код Гилберта-Мура формально.
Рассмотрим источник, выбирающий буквы из алфавита X = {1,..., М} с веро-
ятностями {pi,... ,рм}« Сопоставим каждой букве т = 1,..., М кумулятивную
вероятность <?m = Рг и вычислим для каждой буквы величину ат по
формуле
____	. Рт
&т — Qm ।	2~*
Кодовым словом кода Гилберта-Мура для хт является двоичная последователь-
ность, представляющая собой первые = [- log(pm/2)] разрядов после запятой
в двоичной записи числа ат.
Алгоритм построения кода приведен на рис. 2.10.
Пример 2.7.1. Рассмотрим источник с распределением вероятностей pi =
0,1, Р2 = 0,6, рз = 0,3. Вычисления, связанные с построением кода Гилберта-
Мура для этого источника, приведены в табл. 2.2. Запись [а] обозначает пред-
ставление числа а в двоичной форме. В последнем столбце таблицы показано,
как выглядели бы кодовые слова ст соответствующего кода Шеннона, если бы
мы забыли упорядочить буквы по вероятностям. Видно, что код получился бы
непрефиксным (в отличие от кода Гилберта-Мура).
Докажем однозначную декодируемость кода Гилберта-Мура в общем случае. Для
этого выберем сообщения с номерами г и j, i < j. Понятно, что oj > ет*. Нужно
2.7. Код Гилберта-Мура
75
Input: Объем алфавита М, вероятности букв рг, i = 1,..., М
Output: Список кодовых слов кода Гилберта-Мура
Вспомогательные вероятности:
Qi = 0;
for г — 2 to М do
Qi = Qi-1 4- Рг-Г,
= qi 4- pi/2\
end
Кодовые слова:
for г = 1 to М do
а первые f- logp,] 4-1 разрядов после запятой в двоичной записи числа аг.
end
Рис. 2.10. Алгоритм построения кода Гилберта-Мура
Таблица 2.2. Пример кода Гилберта-Мура
	Рт	Qm		1т	Ст °	СтЬ
1	0,1	0,0=10,00000...]	0,05=[0,00001...]	5	00001	0000
2	0,6	0,1=[0,00011...]	0,40=[0,0 И 00...]	2	01	0
3	0,3	0,7=[0,10110...]	0,85=[0,11011...]	3	110	10
^Кодовые слова кода Гилберта-Мура
^Кодовые слова кода Шеннона без упорядочения вероятностей букв
доказать, что соответствующие слова Ci и Cj различаются хотя бы в одном из
первых min{/i,/j} кодовых символов. Рассмотрим разность
h=l	h=l
J-l
— ,Рэ ~~ Pi „ .Pj-Pi
~ 2^>h + “Г" >Pi + ~2~ ~
h=i
= Pj+Pi > ™x{pj,Pj}
2^2’
Вспомним, что длина слова и его вероятность связаны соотношением
Отсюда следует
ст. _ст. > maxWj} > 2-min^^}
3 г '	2
а это означает, что слова Ci и Cj различаются в одном из первых тт{/<,^}
двоичных символов, поэтому ни одно из двух слов не может быть началом
другого.
76
Глава 2. Неравномерное кодирование дискретных источников
Поскольку все слова кода Гилберта-Мура ровно на 1 длиннее слов кода Шен-
нона, получаем оценку средней длины кодовых слов
I < Н + 2.
°2< 1/2, поэтому
кодовый символ - О
°2> 1/4, поэтому
кодовый символ == 1
Рис. 2.11. Графическая интерпретация кода Гилберта-Мура
Длина отрезка = 1/4 < ц /2 = 0,3.
Построение кодового
слова закончено
Мы завершим рассмотрение кода Гилберта-Мура графической интерпретацией,
представленной на рис. 2.11 для источника из примера 2.7.1. Мы снова пред-
полагаем, что передается буква с номером 2. Ей соответствует точка а2. По
построению соседние точки а удалены от нее на расстояние по меньшей мере
Рг/2. Кодер передает бит за битом, при этом каждый раз интервал неопреде-
ленности сужается вдвое. Передачу можно завершить, когда длина интервала
неопределенности будет не больше ръ!^ В рассмотренном примере достаточно
передать 2 бита.
2.8.	Неравномерное кодирование
для стационарного источника
2.8.1.	Постановка задачи. Теоремы кодирования
В этом параграфе мы перейдем к решению задачи кодирования последователь-
ностей сообщений. Разумеется, если мы рассматриваем стационарный источник
(распределение вероятностей которого на буквах не меняется от буквы к букве),
то любой из описанных выше способов кодирования может быть использован
для кодирования отдельных сообщений источника. Во многих случаях именно
такой подход на практике оказывается самым простым и притом достаточно
эффективным.
2.8. Кодирование для стационарного источника
77
Вместе с тем можно выделить класс ситуаций, когда побуквенное кодирова-
ние заведомо неоптимально. Во-первых, из теоремы об энтропии на сообще-
ние стационарного источника следует, что учет памяти источника потенциально
может значительно повысить эффективность кодирования. Во-вторых, побуквен-
ные методы затрачивают как минимум 1 бит на сообщение, тогда как энтропия
на сообщения может быть значительно меньше единицы.
Итак, рассмотрим последовательность жх, ж2, ...,	€ X = {ж}, наблюдаемую
на выходе дискретного стационарного источника, для которого известно веро-
ятностное описание, то есть можно вычислить все многомерные распределения
вероятностей и по ним - энтропию на сообщение Н = Н^Х).
Пусть указан некоторый способ кодирования, строящий (для любых п для каж-
дой последовательности х е Хп) на выходе источника кодовое слово с (я?) дли-
ной 1(х). Тогда средняя скорость кодирования для блоков длиной п определяется
как
= —M[Z(®)]
п
бит/сообщение источника. Подбирая длину блоков, при которой средняя ско-
рость будет наименьшей, получаем следующее определение для средней скорости
кодирования:
R = inf Rn.
п
Мы пишем нижнюю грань (inf) вместо минимума, поскольку наименьшее значе-
ние скорости может достигаться в пределе при п —* ос.
Рассматриваемое кодирование в терминах, введенных в конце параграфа 1.8,
называется FV-кодированием (fixed-to-variable), поскольку блоки из фиксиро-
ванного числа сообщений п кодируются кодовыми словами переменной длины.
Наша задача - связать достижимые значения средней скорости FV-кодирования
с характеристиками источника, в частности его энтропией на сообщение Н. Нач-
нем с обратной теоремы кодирования.
ТЕОРЕМА 2.7. Для дискретного стационарного источника с энтропией на сооб-
щение Н для любого FV-кодирования имеет место неравенство
R^H.
Доказательство. Рассмотрим множество Хп. К его элементам применим теорему
побуквенного кодирования. Получим
М [/(ж)] > Н(Хп) = пНп(Х) пН^Х) = пН.
Второе неравенство здесь выполнено, так как Нп(Х) не возрастает с увеличением
п. Отсюда следует, что
Rn^H
при любых п. Таким образом,
R = inf Rn Н,
п
что и требовалось доказать.	□
78
Глава 2. Неравномерное кодирование дискретных источников
Почти столь же просто доказывается прямая теорема кодирования.
ТЕОРЕМА 2.8. Для дискретного стационарного источника с энтропией на сооб-
щение Н и для любого 6 > 0 существует способ неравномерного FV-кодирования
такой, для которого
R^H + 6.
Доказательство. Воспользовавшись прямой теоремой побуквенного кодирова-
ния для ансамбля Хп, мы можем утверждать, что для некоторого побуквенного
кода имеет место неравенство
М [Z(®)] < ЩХп) + 1 = пНп(Х) + 1.	(2.8)
По определению предела числовой последовательности существует достаточно
большое число ni такое, что при всех п пх имеет место неравенство
\Нп(Х)-Н\^6-,
из которого следует, что
ЯП(Х)^Я + ^, п>щ.	(2.9)
Найдем П2 такое, что при п > пг имеет место неравенство
С учетом (2.9) и (2.10) из (2.8) получаем при п > тах{пх,П2}
R = inf Rm Rn =
т
= М [/(а!)] < Яп(Х) + 1<Я+^ + 5 = Н + 8,
п	п 2	2
что и требовалось доказать.	□
Итак, выбрав достаточно большую длину блоков п и применив к блокам побук-
венное кодирование, мы получим кодирование со средней скоростью
Н ^R^H + o(n\
где о(п) -> 0 при п —► оо.
К сожалению, этот внешне оптимистический результат оказывается почти бес-
полезным на практике. Основное препятствие на пути его применения - экспо-
ненциальный рост сложности при росте длины блоков п. Поясним эту проблему
следующим простым примером.
Предположим, что кодированию подлежат файлы, хранящиеся в памяти ком-
пьютера. Символы источника - байты, и, значит, объем алфавита |Х| = 28 = 256.
При кодировании последовательностей длиной п = 2 объем алфавита вырас-
тает до |Х2| = 216 = 65 536. Далее при п = 3, 4, ...объемы алфавитов будут
224 = 16 777216, 232 = 4294967296,... . Работать с кодами таких размеров невоз-
ч можно.
2.8. Кодирование для стационарного источника
79
Описываемый в следующем параграфе метод арифметического кодирования поз-
воляет эффективно кодировать блоки длиной п с избыточностью порядка 2/п и
со сложностью, пропорциональной только квадрату длины блока п. За счет пре-
небрежимо малого проигрыша в скорости кода сложность может быть сделана
даже линейной по длине кода. Неудивительно, что арифметическое кодирование
все шире применяется в разнообразных системах обработки информации.
2.8.2.	Арифметическое кодирование
По отношению к алгоритму арифметического кодирования нетривиальным явля-
ется вопрос о том, кого считать его автором. Идею алгоритма приписывают
Элайесу, ссылаясь на книгу Абрамсона [25], опубликованную в 1963 году. До
конца 70-х годов эта идея не была востребована. Несколько статей, опубли-
кованных на рубеже 70-х и 80-х годов, носили скорее теоретический харак-
тер. Большую роль в понимании как идеи алгоритма, так и возможности его
использования для решения практических задач, сыграла статья Уиттена, Нила
и Клири [57]. Пожалуй, именно этих авторов нужно считать авторами алгоритма
в его нынешней форме. В то же время сам алгоритм является почти триви-
альным обобщением кода Шеннона на последовательности. Возможно, поэтому
в книге Кавера и Томаса [38] арифметическое кодирование называется алгорит-
мом Шеннона-Фано-Элайеса.
Рассмотрим для простоты дискретный постоянный источник, выбирающий сооб-
щения из множества X = {1,..., М}, с вероятностями {pi,... ,Рм}. Обозначим
через {qi, ... ,<?м} кумулятивные вероятности сообщений. Наша задача состоит
в кодировании последовательностей множества Хп = {я?}. При описании алго-
ритма мы будем использовать обозначение xj для краткой записи подпоследо-
вательности	в последовательности х = (xi,... ,жп).
Мы хотели бы применить к ансамблю Х-п = {я?} достаточно простой и эффек-
тивный побуквенный код. Упрощение состоит в том, что ни кодер, ни декодер
не хранят и не строят всего множества из |ХП| кодовых слов. Вместо этого при
передаче конкретной последовательности х кодером вычисляется кодовое слово
с(х) только для данной последовательности х. Правило кодирования, конечно,
известно декодеру, и он восстанавливает х по с(я?), не имея полного списка
кодовых слов.
Возможные кандидаты на использование в такой схеме - код Шеннона и код
Гилберта-Мура. Однако использование кода Шеннона предполагает упорядо-
ченность сообщений по убыванию вероятностей. При больших п сложность упо-
рядочения окажется недопустимо большой, поэтому единственным претендентом
остается код Гилберта-Мура.
В соответствии с правилом построения кода Гилберта-Мура кодовое слово фор-
мируется по вероятности р(х) и кумулятивной вероятности q(x) как первые
/(я?) = |’~logp(a?) +1] разрядов после точки в двоичной записи числа <т(я?) =
= д(®)+р(®)/2.
80
Глава 2. Неравномерное кодирование дискретных источников
Чтобы вычислить q(x), надо условиться о некоторой нумерации последователь-
ностей из Хп. Наиболее естественный способ нумерации - лексикографический
(алфавитный). Лексикографический порядок на последовательностях будет обо-
значаться знаком «^». Запись у -< х будет означать, что у лексикографически
предшествует х.
Понятие лексикографического порядка определяется следующим образом.
Для последовательностей длиной 1 (для отдельных сообщений из X) мы счи-
таем, что сообщение с меньшим номером предшествует сообщению с большим
номером. Если, например, элементы X - числа, то х -< ж', если х < х', х,х' е X.
Для двух последовательностей х = (xi,..., жп), у = (j/i,..., уп) обозначим через
i наименьший индекс такой, что Xi / yi. Тогда у -< х, если yi xit
Нетрудно видеть, что лексикографический порядок - это порядок, который обыч-
но используется при составлении словарей.
Итак, основная задача состоит в вычислении кумулятивной вероятности
«(®) =	(2.11)
У^Х
поскольку для источника без памяти вероятности последовательностей р(ж) вы-
числяются достаточно просто по формуле
п
р(х) =
г=1
Выведем рекуррентную формулу для q(x). Для этого выразим вероятность q(x™)
через q^x™-1). Следующая цепочка преобразований показывает, как это сделать:
9(®")= 52 p(pi)= 52	+ 52	52 p(pi-1pn) =
У1^1	Уп	у^-1=х^-1Уп^хп
= 52 р(«1-1)+ 52	52	=	+p(®i-1k(a;n)I
где q(xn) обозначает кумулятивную вероятность символа хп.
Подытожим наши выкладки в виде рекуррентных формул
<zW) = 9W1) +	(2.12)
р(ж?)=р(жГ1)р(жп).	(2.13)
Здесь каждая пара значений (д(ж|), р(ж|)) используется ровно на одном шаге
при вычислении следующей пары (д(ж|+1), р(ж|+1)). Поэтому при реализации
арифметического кодирования вновь вычисленные значения записываются в те
же ячейки памяти, в которых находились предыдущие значения. В приведен-
ном на рис. 2.12 алгоритме кумулятивные вероятности q(x\), i = 1,2,..., хра-
нятся в переменной F, а вероятности последовательностей р(ж|), i = 1,2,..., -
в переменной G.
2.8. Кодирование для стационарного источника
81
Input: Объем алфавита М
вероятности букв рг, i = 1,..., М
длина последовательности п
последовательность на выходе источника (т,..., жп),
Output: Кодовое слово арифметического кода
Кумулятивные вероятности:
Qi = 0;
for i = 2 to М do
Qi — Qi-1 + Pi-1
end
Кодирование:
for i = 1 to n do
F+-F + q(xi)G;
G <- p(xi)G;.
end
Формирование кодового слова:
с <— первые [- log G] + 1 разрядов после запятой в двоичной записи числа F + G/2.
Рис. 2.12. Алгоритм арифметического кодирования
Пример 2.8.1. Рассмотрим источник из примера 2.7.1: X = {а,Ь,с}, распре-
деление вероятностей ра = 0,1, ръ = 0,6, рс = 0,3. Вычисления, выполняемые
арифметическим кодером при кодировании последовательности х = (bcbab) дли-
ной п = 5, приведены в табл. 2.3. В этой таблице через F обозначено число
(F+G/2), округленное вниз с точностью до f- log G + 1] =9 двоичных разрядов.
Таблица 2.3. Кодирование последовательности арифметическим кодом
Шаг i	Xi	Р(®«)		F	G
0	-	-	-	0,0000	1,0000
1	b	0,6	од	0,1000	0,6000
2	с	0,3	0,7	0,5200	0,1800
3	b	0,6	0,1	0,5380	0,1080
4	а	0,1	0,0	0,5380	0,0108
5	b	0,6	0,1	0,5391	0,0065
6	Длина кодового слова [— log G + 1] =9 Кодовое слово F + G/2 = 0,5423	► F = 0,541 —► 100010101				
Графическая интерпретация процесса кодирования, аналогичная интерпретации
кодов Шеннона и Гилберта-Мура, показана на рис. 2.13.
Как показано на этом рисунке, на каждом шаге кодирования пересчитывается
начальная точка F и длина G отрезка, в котором будет расположено число,
соответствующее коду для заданной последовательности сообщений. Так, после
82
Глава 2. Неравномерное кодирование дискретных источников
б)
г)
A-0,1	^=0,6
а)
q = 0 J*
PaG
F = 0,1
paG
в)
F=0,52 |F
Д) 1
F= 0,538
F = 0,541
4G
Pc= 0,3
F=0;G- 1
xi = b
F=0,l; G-0,6
F F+G = 0,7
x
PCG.
F =
I F +G = 0,7
РА
F - 0,538; G-0,108
РА
F= 0,538
РА
F+G - 0,646
x r a
0,52; G=0,18
PbG	PCG F - 0,538; G - 0,0108;
—£-------a.—7~"p	,	2Z	x$ ~ b
0,539	T 0,542	F+G = 0,5488
0,5391+0,006
F = 0,541
PCG
С

Рис. 2.13. Графическая интерпретация арифметического кодирования
первого шага (х± = Ь) мы знаем, что точка будет расположена в отрезке [0,1,0,7).
Более детально этот отрезок показан на рис. 2.13, б. Поскольку вторая буква
Х2 = с, начальная точка перемещается в значение 0,52, а длина интервала умень-
шается до 0,18, и т.д. После пятого шага F = 0,5391. Добавив смещение G/2 и
округлив до 9 двоичных знаков, получим величину F = 0,541. Тем самым вся
последовательность сообщений отображается в одну точку интервала [0,1). Эта
точка помечена кружком на рис. 2.13, а-д. Как было показано выше, девяти раз-
рядов достаточно для того, чтобы Последовательность была восстановлена одно-
значно, то есть ближайшая возможная точка, соответствующая другой последо-
вательности сообщений, удалена от F на расстояние не менее 1/29 = 1/512.
Обсудим кратко вопрос о сложности кодирования.
Из описания алгоритма следует, что на каждом шаге кодирования выполняется
одно сложение и два умножения. Отсюда легко сделать неправильный вывод о
том, что сложность кодирования последовательности из п сообщений пропорци-
ональна п. Это неверно, поскольку на каждом шаге линейно растет сложность
выполнения самих операций сложения и умножения, так как нарастает число
двоичных разрядов, необходимых для записи операндов.
Предположим, что для представления вероятностей ..., рм использованы
числа разрядности d. После первого шага кодирования точное представление
F и G потребует 2d разрядов, ..., после п шагов кодирования кодер и декодер
2.8. Кодирование для стационарного источника
83
будут работать (в худшем случае) с числами разрядности nd, и, следовательно,
суммарная сложность имеет порядок
1 Л 1	1 п(п+1) _
d + 2d 4- • • • 4- nd —-—-d,
&
Таким образом, можно говорить о том, что сложность арифметического коди-
рования пропорциональна п2. На самом деле все же возможна практическая
реализация арифметического кодирования со сложностью п, но за счет некоторой
(очень небольшой) потери в точности вычислений и, следовательно, в эффек-
тивности кодирования. Практическая реализация арифметического кодирования
рассмотрена в следующем параграфе.
Отметим еще одну чрезвычайно важную особенность арифметического кодиро-
вания. Его легко адаптировать к случаю источников с памятью. Если, например,
в качестве модели источника рассматривается простая цепь Маркова, то алго-
ритм кодирования остается прежним - за тем исключением, что вместо одно-
мерных вероятностей pfa) и q(xi) нужно использовать условные вероятности
р(^|х<-1) и д(жг|а:г_1) = £ PG/ki-i).
y^Xi
2.8.3.	Декодирование арифметического кода
и некоторые аспекты практической реализации
арифметического кодирования
Как ясно из описания арифметического кодирования, при его практическом ис-
пользовании для кодирования последовательностей большой длины п возникают
следующие проблемы:
►	арифметическое кодирование требует большой (в пределе - бесконечной) точ-
ности вычислений, что ведет к недопустимо высокой сложности реализации;
►	для формирования кодового слова формально необходима вся последователь-
ность сообщений, что приводит к недопустимо большой задержке кодирова-
ния, равной длине кодируемой последовательности.
Оказывается, обе эти проблемы преодолимы. Решение состоит в том, что та часть
данных, которая не участвует в дальнейших вычислениях и уже не влияет на
окончательный результат, может быть исключена из вычислений и сразу выдана
на выход кодера. Тем самым уменьшается сложность вычислений и
задержка кодирования. Чтобы пояснить, как это делается, рассмотрим работу
декодера.
Начнем с анализа работы декодера кода Гилберта-Мура.
Пусть для источника X = {1,..., М} известны вероятности букв {pi,... ,рм}> по
которым подсчитаны соответствующие кумулятивные вероятности qm = 52™^ Pj,
величины От = qm +Рт/%, и длины слов lm = r-logtPm/2)] и кодовые слова
длины 1т, полученные округлением величин am* Округленные до 1т разрядов
после запятой числа ат мы обозначим через ат. Задача декодера состоит
84
Глава 2. Неравномерное кодирование дискретных источников
Input: Объем алфавита М
кумулятивные вероятности букв qi, i — 1,..., М
вход декодера а.
Output: Декодированная буква х
Инициализация: дм+i = 1; т = 1.
Поиск буквы:
while qm+i < <т do
т <— т 4-1.
end
Результат:
X —— Хт
Рис. 2.14. Алгоритм декодирования кода Гилберта-Мура
в восстановлении сообщения т по округленному значению а = ат. Эта задача
решается с помощью алгоритма, приведенного на рис. 2.14.
Убедимся, что алгоритм работает правильно. Для этого достаточно вспомнить,
что длина кодовых слов выбирается так, что в результате округления до 1т раз-
рядов величина ат =	+Pm/2 уменьшается не более чем на Рт/^ (погрешность
округления не больше Pm/ty- Поэтому имеют место неравенства
Qm &тп <
из которых ясно, что алгоритм правильно определяет индекс т закодированной
буквы.	\
В этом алгоритме при декодировании мы использовали только значения г т,
и не использовали значений аг. Это важно для применения к декодированию
арифметического кода. Точно так же при декодировании арифметического кода
для полученной из канала округленной величины F мы будем рекуррентно вычис-
лять ближайшее к F, но не превышающее F, значение кумулятивной вероятно-
сти q(x). Результатом декодирования будет соответствующая последовательность
сообщений х.
Итак, декодеру арифметического кода известны алфавит X — {1,..., М}, веро-
ятности {pi,... ,рм}> кумулятивные вероятности {qi, ..., длина последо-
вательности сообщений п и полученное из канала значение F. Задача состоит
в вычислении последовательности сообщений х. Эту задачу решает показанный
на рис. 2.15 алгоритм.
В этом алгоритме после выполнения i шагов переменная G равна вероятности
последовательности из первых i символов, а переменная S равна кумуля-
тивной вероятности q(x\).
Пример 2.8.2. Рассмотрим источник X = {а, 6, с} с распределением вероятно-
стей ра = 0,1, рь = 0,6, рс = 0,3. Пусть на вход декодера поступила двоичная
2.8. Кодирование для стационарйого источника
85
Input: Объем алфавита М
вероятности букв {pi,... ,рм}
кумулятивные вероятности букв qi, i = 1,..., М
длина декодируемой последовательности п
кодовое слово в виде числа F.
Output: Декодированная последовательность букв (т,..., хп)
Инициализация: дм+i — 1; S — 0; G — 1.
Декодирование:
for г — 1 to п do
31 = 1;
while S 4- qj+iG < F do
3	3 + 1-
end
G-PjG;
Xi = j.
end
Результат:последовательность (®i,..., xn)\
Рис. 2.15. Алгоритм декодирования арифметического кода
последовательность 0100010101. По этой последовательности нужно восстано-
вить последовательность закодированных сообщений. Простое (хотя и не совсем
честное) решение - заглянуть на несколько страниц назад, ведь в примере 2.8.1
мы получили именно эту последовательность на выходе кодера. Если же добро-
совестно следовать алгоритму, приведенному на рис. 2.15, то на промежуточных
шагах будут получаться числа, приведенные в табл. 2.4. Как видно из таблицы,
последовательность сообщений восстановлена правильно.
Вернемся к вычислительной сложности. Суть проблемы состоит в том, что во
всех вычислениях как в кодере, так и в декодере, мы выполняем вычисления над
переменными, разрядность которых равна длине закодированной последователь-
ности сообщений.
Рассмотрим подробнее работу кодера арифметического кода при кодировании
последовательности из примера 2.8.1. Обратимся к табл. 2.3. Видно, что после
третьего шага кодирования значение F уже не станет меньше 0,5 и больше 0,75
независимо от того, какими будут последующие сообщения источника. Значит,
первые два символа числа F уже не изменятся и могут быть переданы по каналу.
После этого можно выполнить нормировку (F *- 2(F - 0,5), G 2G) и про-
должить кодирование. Точно такую же нормировку выполнит и декодер. Тем
самым разрядность переменных сократится без потери в точности вычислений.
Нетрудно сформулировать общее правило выполнения такого рода нормировок.
Трудность возникает в том случае, когда двоичное представление F содержит
серию единиц после нуля (число F близко к 0,5, но меньше 0,5), то есть F =
= 0,01111.... Неопределенность завершится одним из двух способов. Либо
появится нулевой разряд (F = 0,01111... 10...), либо произойдет перенос
86
Глава 2. Неравномерное кодирование дискретных источников
в одном из младших разрядов (F = 0,10000... 0...). Если состояние неопре-
деленности продлится долго, то разрядности ячеек, используемых для хране-
ния F и G, может оказаться недостаточно. Выход состоит в том, что встре-
тившись с такой ситуацией, кодер изменяет форму хранения числа F. Число
разрядов уменьшается за счет того, что в памяти хранится не сама серия единиц,
а ее длина. В момент появления нуля на выход выдается последовательность
вида 0111... 1. Если же неопределенность завершилась переносом, то на выход
поступает 1000... 0.
Таблица 2.4. Декодирование последовательности из примера 2.8.2
Шаг	S	G	Гипотеза X	q(x)	S + qG	Решение Xi	р(я)
0	100010101-* F =0,541						
1	0,0000	1,0000	а	0,0	0,0000< F	ь	0,6
			b	0,1	0,1000< F		
			с	0,7	0,7000> F		
2	0,1000	0,6000	а	0,0	0,1000< F	с	0,3
			b	0,1	0,1600< F		
			с	0,7	0,5200< F		
3	0,5200	0,1800	а	0,0	0,5200< F	Ъ	0,6
			b	0,1	0,5380< F		
			с	0,7	0,6460> F		
4	0,5380	0,1080	а	0,0	0,5380< F	а	0,1
			b	0,1	0,5488> F		
5	0,5380	0,0108	а	0,0	0,5380< F	b	0,6
			Ь	0,1	0,5391 < F		
			с	0,7	0,5456> F		
Похожие приемы применяются при реализации декодера. Подробное описание
алгоритма и текст С-программы арифметического кодера и декодера можно найти
в статье [57].
На рис. 2.16 и 2.17 даны тексты программ арифметического кодирования на
языке MATLAB. Хотя в интерпретаторе MATLAB все переменные представля-
ются в формате с плавающей точкой с двойной точностью, приведенные про-
граммы имитируют работу с целыми числами в 32-разрядной арифметике.
Входом программы кодирования служит последовательность данных х и век-
тор кумулятивных вероятностей букв q. Элементами последовательности х =
= (®i,... ,жп) должны быть целые числа от 1 до некоторого М. Нули не допус-
каются, поскольку в языке MATLAB не разрешены нулевые индексы в массивах.
Вектор кумулятивных вероятностей q = (qi, ..., qm) имеет длину т = М+1. Его
элементы - целые числа из диапазона, определяемого числом двоичных разрядов,
2.8. Кодирование для стационарного источника
87
function y=int_arithm_encoder(x,q);
% х is input data sequence,
% q is cumulative distribution (model)
% у is binary output sequence
% Constants
k=16;
R4=2A(k-2); R2=R4*2; R34=R2+R4; % half,quarter,etc.
R=2*R2;	% Precision
% Initialization
Low=0;	% Low
High=R-1;	% High
btf=O;	% Bits to Follow
y=[ ];	%	code	sequence
% Encoding
for i=1 :length(x);
Range=High-Low+1;
High=Low+flx(Range*q(x(i)+1 )/q(m))-1;
Low=Low+fix(Range*q(x(i))/q(m));
% Normalization
while 1
If High<R2
y=[y 0 ones(1 ,btf)]; btf=O;
High=High*2+1; Low=Low*2;
else
If Low>=R2
y=[y 1 zeros(1 ,btf)]; btf=O;
High=High*2-R+1; Low=Low*2-R;
else
If Low>=R4 & High<R34
High=2*High-R2+1; Low=2*Low-R2;
btf=btf+1;
else
break;
end;
end;
end;
end; % while
end; % for
% Completing
If Low<R4
y=[y Oones(1,btf+1)];
else
y=[y 1 zeros(1,btf+1)];
end;
Рис. 2.16. MATLAB-программа арифметического
кодирования
используемых для представления вероятностей. В данной программе предпола-
гается, что исходные данные представляются не более чем b = 14 разрядами.
Вектор q получается как округленный вниз результат умножения компонент
«настоящего» вектора (с дописанной к нему справа единицей) на число В = 2Ь.
Например, если вероятности букв равны 0,1, 0,6 и 0,3, то соответствующие
кумулятивные вероятности равны (0,0,1,0,7), а входом программы будет вектор
88
Глава 2. Неравномерное кодирование дискретных источников
q= fix([0 0.1 0.7 1]*2Л14)= [0 1638 11468 16384]. (Оператор fix выполняет округ-
ление вниз до ближайшего целого.)
function x=int_arithm_decoder(y,q,n);
% у is binary encoded data sequence,
% q is cumulative distribution (model)
% x is output sequence
% n is number of messages to decode
% Constants
k=16; R4=2A(k-2); R2=R4*2; R34=R2+R4; R=2*R2;
m=length(q);
% Start decoding. Reading first к bits
Value=0; y=[y zeros(1 ,k)];
for ib=1 :k
Value=2*Value+y(ib);
end;
% Initialization
Low=0; High=R-1;
% Decoding
for j=1 :n
Range=High-Low+1;
aux=fix(( (Value-Low+1 )*q(m)-1 )/Range);
i=1; % message index
while q(i+1)<=aux, i=i+1; end;
x(j)=i;
High=Low+fix(Range*q(i+1 )/q(m))-1;
Low=Low+fix(Range*q(i)/q(m));
% Normalization
while 1
If High<R2
High=High*2+1; Low=Low*2;
ib=ib+1;
Value = 2*Value+y(ib);
else
if Low>=R2
High=High*2-R+1; Low=Low*2-R;
ib=ib+1;
Value = 2*Value-R+y(ib);
else
If Low>=R4 & High<R34
High=2*High-R2+1; Low=2*Low-R2;
ib=ib+1;
Value = 2*Value-R2+y(ib);
else
break;
end;
end;
end
end; % while
end; % for
Рис. 2.17. MATLAB-программа декодирования
арифметического кода
2.9. Задачи
89
Входом декодера помимо двоичной кодовой последовательности у и вектора q
является длина п последовательности я?, получаемой в результате декодирова-
ния у.
Кратко поясним работу кодера. Числу F в формальном описании алгоритма
в программе соответствует переменная Low. Числу G - переменная Range, при-
близительно равная разности High—Low. Если High меньше половины диапазона
или Low больше половины (это соответствует значениям F+G < 1/2и F > 1/2),
очередной кодовый бит может быть выдан на выход кодера и переменные High,
Low соответствующим образом модифицируются. Случай, когда Low>=R4 и
одновременно High<R34, соответствует описанной выше неопределенной ситу-
ации, возникающей при F, близких к 1/2, но меньших 1/2. В переменной btf
накапливается длина последовательности вида 0111... 1 либо 1000... 0, форми-
руемой кодером после разрешения неопределенности.
В программе декодирования числу S соответствует переменная Value, в осталь-
ном использованы те же обозначения переменных, что и в программе кодера.
Приведенные на рис. 2.16 и 2.17 тексты программ демонстрируют, что прак-
тическая реализация алгоритма арифметического кодирования не так проста и
изящна, как приведенные выше формальные описания. В то же время из этих
текстов видно, что кодирование и декодирование имеют линейную по длине
кодируемой последовательности сложность при фиксированном числе разрядов,
отведенных для представления исходных данных и промежуточных результатов
вычислений.
2.9.	Задачи
1.	Построить код Хаффмена для источника с вероятностями букв, равными
(0,3, 0,25, 0,15, 0,1, 0,1, 0,05, 0,05). Сравнить среднюю длину кодовых слов
с энтропией источника.
2.	Рассматривается троичный постоянный источник X с вероятностями букв
1)	р(а) = 1/2, р(Ь) = 1/4, р (с) = 1/4;
2)	р(а) =р(Ь) = р(с ) = 1/3.
Построить коды Хаффмена для отдельных букв алфавита X, для X2, для X3.
Сопоставить скорости кодов с энтропией источника.
3.	Для двоичного постоянного источника с вероятностью единицы, равной 0,1,
исследовать зависимость скорости кода Хаффмена от длины кодируемых бло-
ков.
4.	Оптимальное кодирование равновероятных букв. Построить код Хаффмена для
источника, выбирающего буквы из алфавита объемом М с равными вероятно-
стями. Подсчитать среднюю длину кодовых слов и избыточность как функцию
объема алфавита М, найти верхнюю и нижнюю границы избыточности.
90
Глава 2. Неравномерное кодирование дискретных источников
Промежуточные шаги. Код Хаффмена для этого источника содержит D =
= 2• 2^logм-1 -М слов длины [logМ\ нМ-D слов длины [logМ\ +1. Средняя
длина кодовых слов
о
I = [logMj + 2- —2tlogMJ,
и избыточность
г = Z-logM = 2-d-2-2"d,
где d = logM - [logMJ, d G [0,1). Дифференцированием no d находим, что
максимум избыточности достигается при d = 1 - logloge и равен 1 +logloge-
— loge « 0,0861.
5.	Троичный источник задан цепью Маркова с матрицей переходных вероятно-
стей
0	1/2
0	1/2	1/2
Р= 1/2 1/4 1/4
_ 1/4 1/2 1/4
Вычислить величины Н (X), Нп (X), п = 1, 2, ..., Н(Х/Хп\ п = 1, 2, ...,
считая начальное распределение на буквах совпадающим со стационарным
распределением. Определить скорость кодирования при кодировании кодом
Хаффмена ансамблей X, X2. Предложить способ кодирования, при котором
достигается скорость, равная скорости создания информации источником.
6.	Кодирование длин серий неравномерным кодом. Последовательность на выходе
двоичного источника разбивается единственным способом на последователь-
ности случайной длины вида 1,01,... ,0L“1l,0L. Для кодирования номеров
таких последовательностей используется код Хаффмена. Для двоичного посто-
янного источника с вероятностью единицы, равной р = 0,1, исследовать зави-
симость скорости кодирования от величины L . Под скоростью кодирова-
ния в данном случае понимается величина R = п/т, где т - средняя длина
, кодируемой последовательности источника; п - средняя длина кодовых слов.
7.	Неравномерное по входу и выходу (W) кодирование. Код Танстелла. Напомним,
что избыточность кода Хаффмена в большой степени определяется макси-
мальной из вероятностей букв. Следовательно, при кодировании источника
X = р(х) следует найти букву х0 € X, имеющую наибольшую вероятность, а
затем построить новый ансамбль Xi, элементами которого будут все буквы из
X \ жо и все пары (яо,я), х G X. Вероятности пар букв подсчитываются как
произведения вероятностей соответствующих букв.
Такое расширение алфавита можно продолжить, и с каждым шагом макси-
мальная вероятность букв расширенного алфавита становится меньше, и, соот-
ветственно, уменьшается избыточность кода, примененного к расширенному
алфавиту.
Для случая двоичного ансамбля сопоставьте данный способ кодирования
с кодированием длин серий, рассмотренным в предыдущей задаче.
2.10. Библиографические замечания
91
8.	Построить код Шеннона источника из задачи 1. Сопоставить среднюю длину
со средней длиной кодовых слов кода Хаффмена и с энтропией источника.
9.	Построить код Гилберта-Мура источника из задачи 1. Сопоставить среднюю
длину со средней длиной кодовых слов кода Хаффмена и с энтропией источ-
ника.
10.	Закодировать арифметическим кодом последовательность 01001 на выходе
двоичного источника с вероятностью единицы, равной 0,4. Сравнить длину
кодовой последовательности с собственной информацией последовательности
и с суммарной длиной кодовой последовательности при независимом кодиро-
вании символов кодом Шеннона.
И. Объяснить, почему завершение кодирования в программе на рис. 2.16 эквива-
лентно преобразованию кодового слова кода Шеннона в кодовое слово кода
Гилберта- Мура.
12.	Какие конкретно изменения нужно внести в алгоритмы и программы ариф-
метического кодирования и декодирования, чтобы применить их к источнику,
описываемому моделью простой цепи Маркова?
13.	Формально в программах на рис. 2.16 и 2.17 присутствуют операции деления,
которых не было в алгоритмах арифметического кодирования и декодирова-
ния. Почему это произошло? Можно ли избежать делений?
2.10.	Библиографические замечания
Часть главы, посвященная побуквенному неравномерному кодированию, почти
повторяет соответствующие главы учебников [3] и [7]. При ее написании исполь-
зовалась также монография [И]. Описание алгоритма арифметического коди-
рования и нюансов его реализации заимствовано из статьи [57]. Теоретическое
обоснование арифметического кодирования близко к приведенному в [38].
Глава 3 Кодирование
дискретных
источников
при неизвестной
статистике
Рассмотренные в предыдущей главе алгоритмы кодирования и эффективны, и
практичны. Однако их общим недостатком является то, что они эффективны
только в том случае, когда вероятностная модель источника совпадает или очень
близка к модели, для которой строился код. В данной главе мы рассмотрим
задачу кодирования источника без информации или при неполной информи-
рованности кодера и декодера о характеристиках источника. Методы кодирова-
ния для такой постановки задачи называют универсальными. Очевидная область
применения универсального кодирования - создание архиваторов для хранения
файлов в памяти ЭВМ. Эта задача служит полигоном для сопоставления эффек-
тивности различных подходов. В то же время имеются и другие важные при-
ложения. Универсальные методы кодирования источников без потери качества
являются важной составной частью современных кодеров аудио- и видеоинфор-
мации.
Мы начнем главу с логически простых схем кодирования, на примере которых
убедимся в том, что скорость кодирования при неизвестной статистике может
быть сделана сколь угодно близкой к скорости создания информации источни-
ком. Мы оценим потери, связанные с отсутствием априорной информации. Прак-
тическая значимость изучаемых методов проявится в следующем разделе, где
мы рассмотрим широко применяемые в архиваторах алгоритмы Зива-Лемпела,
а также алгоритмы, обеспечивающие рекордно высокое сжатие информации -
предсказание по частичному совпадению, и алгоритм Барроуза-Виллера.
3.1.	Постановка задачи универсального
кодирования источников
Универсальное кодирование предполагает, что входом кодера является после-
довательность сообщений х = (ж1,...,жп) некоторого источника X. Алфавит
кодера, длина последовательности п, алгоритм работы кодера известны декодеру
Статистические свойства источника заранее неизвестны. Задача, как и прежде,
3.1. Задача универсального кодирования
93
состоит в том, чтобы обеспечить эффективное кодирование, то есть найти пред-
ставление последовательности источника двоичной последовательностью наи-
меньшей длины. Однако решать задачу в такой постановке не имеет смысла.
Дело в том, что алгоритм кодирования, который «сжимал» бы любые последова-
тельности источника, не может существовать. Мы уже говорили, что при нерав-
номерном префиксном кодировании уменьшение длины одной кодовой после-
довательности на 1 символ достигается увеличением длины двух других после-
довательностей на 1 символ. Если считать все последовательности источника
одинаково вероятными, то любой алгоритм кодирования «в среднем» будет про-
игрывать равномерному кодированию, затрачивающему на каждое сообщение
log |Х| двоичных символов.
Мы существенно упростим ситуацию, если преположим, что источник сообще-
ний является стационарным. В этом случае мы можем подсчитать для него энтро-
пию на сообщение и тем самым определить минимально достижимую скорость
кодирования (обратная теорема кодирования остается справедливой при отсут-
ствии у кодера и декодера информации о характеристиках источника). Для ста-
ционарного источника естественно считать «хорошим» такой способ кодиро-
вания, который обеспечивает скорость, близкую к той скорости кодирования,
которая могла бы быть достигнута при известной статистике.
Заметим, что при решении многих практических задач есть возможность допол-
нительно сузить класс возможных моделей источника, то есть помимо пред-
положения о стационарности сделать и другие предположения. Любая апри-
орная информация может быть использована для повышения эффективности
кодирования.
Опираясь на эти соображения, приходим к такой постановке задачи.
Пусть Q = {си} представляет собой некоторый класс (множество) моделей источ-
ников (не обязательно дискретное). Например, в качестве Q может рассмат-
риваться множество дискретных постоянных источников. В этом случае кон-
кретный элемент множества определяется одномерным распределением веро-
ятностей на X. Обозначим через энтропию на сообщение источника для
заданной модели cu е Q. Пусть заданный алгоритм кодирования обеспечивает для
этой модели при кодировании последовательностей длины п среднюю скорость
Йп(си). Тем самым определена избыточность rn(cu) =	Избыточностью
кодирования для данного алгоритма для класса моделей Q называется величина
r„(Q) = sup [5n(w) - Нш] .	'	(3.1)
Задача состоит в построении алгоритма, минимизирующего избыточность rn(Q)
для заданного класса моделей Q.
Вполне естественно, что с увеличением длины п кодируемой последовательности
избыточность кодирования уменьшается. Если для заданного алгоритма имеет
место соотношение
lim rn(Q) = О,
п—>оо
94
Глава 3. Универсальное кодирование
такое кодирование называется универсальным для множества Q. Как мы увидим
ниже, построить универсальные алгоритмы кодирования совсем несложно, и мы
будем искать такие универсальные алгоритмы, для которых скорость убывания
избыточности максимальна.
Помимо ограничений на множество моделей источников, возможны ограничения
на множество допустимых алгоритмов. Мы отметим два наиболее важных таких
ограничения.
Во-первых, во многих практических задачах накладывается ограничение на допу-
стимую задержку кодирования. Примерами могут служить кодер для сжатия
файлов в реальном времени в процессе записи информации на жесткий диск или
кодер, входящий в состав модема и сжимающий информацию перед передачей
по линии связи. С другой стороны, можно указать широкий круг задач, в кото-
рых задержка кодирования не важна. Например, для производителя программ-
ного обеспечения при записи программ и данных на компакт-диск задержка
кодирования не имеет решающего значения.
По этому критерию различают две крайние ситуации. Один класс алгоритмов
рассчитан на применение в тех случаях, когда задержка недопустима. На англий-
ском языке такие алгоритмы называют on-line алгоритмами. Мы будем называть
их кодированием без задержки, или мгновенным кодированием. Общим свойством
таких алгоритмов является то, что при кодировании каждой поступающей буквы
источника разрешается использовать информацию о предшествующих буквах, но
не разрешается использовать информацию о последующих буквах.
Второй класс алгоритмов - алгоритмы для решения задач, в которых задержка не
имеет значения. Эти алгоритмы на английском языке называются off-line алго-
ритмами. Мы будем использовать термин «двухпроходное кодирование». Этот
термин правильно отражает суть кодирования при неограниченной задержке:
кодер сначала исследует статистические свойства последовательности и прини-
мает решение о стратегии кодирования. Затем, на втором проходе, производится
собственно кодирование.
Поскольку любой алгоритм мгновенного кодирования можно использовать
в системах с неограниченной задержкой, второй класс алгоритмов, конечно, пол-
ностью включает в себя первый класс. Вопрос, на который нам предстоит отве-
тить, - насколько велик выигрыш от «заглядывания вперед» при кодировании.
Еще одно ограничение, учитываемое при выборе алгоритма, - сложность коди-
рования и декодирования.
Итак, цель исследования алгоритмов универсального кодирования - построе-
ние кодеров, обеспечивающих минимальную избыточность для заданного класса
моделей при заданных ограничениях на задержку и сложность.
3.2. Несколько полезных комбинаторных формул
95
3.2.	Несколько полезных комбинаторных
формул
/
В этом параграфе нам постоянно придется подсчитывать количество последо-
вательностей, удовлетворяющих тем или иным свойствам. В связи с этим мы
посвятим отдельный параграф необходимым комбинаторным формулам.
Начнем с того, что рассмотрим множество последовательностей вида х =
= (ж1,...,жп), в которых элемент Xi может принимать одно из Mi значений,
i = 1,..., п. Очевидно, число различных х
|{я? = (ж1,...,жп) : е {0,- 1}, i = l,...,n}| = Л М;.	(3.2)
г=1
В частности, число различных М-ичных последовательностей длины п равно
Мп.
Предположим, что все компоненты х = (xi,..., хп) выбираются из одного и того
же множества объема М, но «без возвращения», то есть один и тот же элемент
не может повториться в х больше одного раза. Число таких последовательностей
представляет собой число размещений из М элементов по п
М'
Апм = М(М - 1) х • • • х (М - п + 1) = уу.	(3.3)
Эта формула следует из (3.2).
В частном случае, когда М = п, речь идет о всевозможных перестановках из М
элементов. Число различных перестановок из М элементов
Рм = М\.	(3.4)
Итак, существует А^ различных слов длиной п из неповторяющихся букв алфа-
вита объемом М. При этом подразумевается, что порядок следования букв в сло-
вах существенен, то есть слова, различающиеся порядком букв, различны. Под-
считаем теперь, сколько можно построить различных подмножеств объемом п
из алфавита объемом М в предположении, что порядок элементов в подмно-
жестве не играет роли. Среди упорядоченных последовательностей ровно
Рп = п! последовательностей каждого вида различаются только порядком следо-
вания элементов (то есть образуют теперь одно подмножество). Поэтому число
различных подмножеств
1П _ (М
м~\п
лп
Рп
М(М-1) х  х (м-n + l) _ М!
п!	п\{М — п)!’
(3.5)
96
Глава 3. Универсальное кодирование
Это количество называют числом сочетаний из М элементов по п. Здесь мы при-
вели два обозначения для числа сочетаний. Первое, распространено
в отечественной математической литературе. Второе, (^), используют в между-
народных математических и технических изданиях. Мы будем придерживаться
второго обозначения. Формула (3.2) не имеет смысла при М, п 0 и при М < п.
Формально число сочетаний из п элементов по к определяется формулой
п!
k\(n-k)l’
1,
О,
если n > fc > О,
если п 0 и к = 0 или к = п,
если к < 0 или к > п.
(3.6)
Числа (£) называют биномиальными коэффициентами в связи с использованием
в известной формуле бинома Ньютона
(а + Ь)п = ГМ?Г'г.
fc=O ' '
Подсчитаем количество двоичных последовательностей длиной п, содержащих
заданное число п единиц и т0 = п — п нулей. Заметим, что номера позиций
единиц образуют неупорядоченное подмножество множества чисел {1,..., п}. Из
(3.2) следует, что искомое число последовательностей
^т0,т1) = (") = -^7.	(3.7)
VO/ To’Ti!
Обобщим эту формулу на множество последовательностей над произвольным
алфавитом X = {О,...,М - 1}. Напомним, что композицией последователь-
ности х называется вектор т(я?) = (то(ш),... ,tm-i(®)), в котором тДж) обо-
значает число элементов xt = i в последовательности х = (жх,...,жп). Наша
ближайшая цель состоит в нахождении числа последовательностей х с заданной
композицией г = (т0,..., тм-i).
Начнем с того, что положим М = 3 и найдем число последовательностей длины
п с композицией т = (то, 71,72), п = т0 + и + Т2. Для этого зафиксируем неко-
торое расположение нулей (это можно сделать (^) способами) и подсчитаем
количество различных расположений п единиц на оставшихся п - т0 позициях.
Это число, как мы знаем, равно (п“То). Поскольку каждому расположению нулей
соответствует именно такое количество расположений единиц, общее число после-
довательностей
АТ/ \	/п\/п-т0\	п!	(п- То)!	п!
iv(t) =[ JI | =--------------------------------—---------.
\т0/\ Т1 /	т0!(п - То)! Т1!(п - То - Т1)!	t0!ti!t2!
Аналогично для алфавита произвольного объема М справедлива формула
до I
Мт) = т1т •	,	(3.8)
То!...Тм-1!
3.2. Несколько полезных комбинаторных формул
97
Эта формула является естественным обобщением формулы биномиальных коэф-
фициентов. Также естественно обобщается формула бинома Ньютона на случай
возведения в степень суммы нескольких слагаемых:
М-1
(й0 + ... + ам-1)п=	N(t) [J а?-
т: то+...+тм-1=п	г—О
Решим еще одну комбинаторную задачу: подсчитать количество различных ком-
позиций для последовательностей длиной п над алфавитом объемом М. Заметим,
что каждая композиция - это одно из представлений числа п в виде суммы
М слагаемых. Сколько всего таких представлений? Ответ получается довольно
просто.
ЛЕММА 3.1. Натуральное число п может быть представлено в виде суммы М
неотрицательных целых слагаемых (П^ГХ) способами.
Доказательство. Будем записывать последовательность из j нулей в виде (У.
Каждому разбиению числа п на целые слагаемые а± Ч--Нам = п соответствует
двоичная последовательность вида (0ai 1,0а21,..., 0ам). Длина последовательно-
сти равна п -I- М - 1, а вес равен М - 1. Понятно, что число разбиений равно
числу таких последовательностей, которое, в свою очередь, равно числу двоич-
ных последовательностей длиной п+М— 1, содержащих М—1 единиц. Это число
как раз равно	□
Из леммы 3.1 следует, что число различных композиций для последовательно-
стей длиной п над алфавитом объемом М
NT(n,M)= (П^7Х).	(3-9)
Полученные формулы достаточно просты для подсчетов на компьютере, но
неудобны для анализа. Ниже мы получим асимптотические формулы, достаточно
точные при больших п.
Все эти формулы основаны на формуле Стирлинга
у/2тгпппе~п ехр < ———г ? < п\ < л/2тгпппе“п ехр < —> .	(3.10)
( 12?2 -|- 1 J	( 12/п J
Ее подстановка в (3.8) дает
/ \ 1/2
хт/ ч /л Ч M~1 niogn-X, П logTj / j-p n \
N(t) < (2тгп) 2 2	<	I T1 — I	x
\ i TiJ
x exp < —----V ——-—- >.	(З.И)
12n ^12^ + 1	v ’
г	>
98
Глава 3. Универсальное кодирование
Отсюда получаем верхнюю оценку для логарифма числа последовательностей
с заданной композицией
log IV (т) < пН(р) - log(27rn) - I Vlog(pi), (3.12)
г
где в (3.10) - (3.12) индекс i пробегает те значения, для которых положи-
тельно. Через Pi обозначены вычисленные по х оценки вероятностей букв, то есть
Pi = ъ/п, а через Н(р) - энтропия ансамбля X, вычисленная по распределению
вероятностей р = (ро,... ,Рм-1)-
Помимо (3.12), можно также выписать менее точную, но более компактную оценку
loglV(r) < пЯ(р) - - 1 log(2Trn) + | log -—j-j—г-	(3.13)
Z	Z TL 1V1 “г* 1
В заключение сформулируем некоторые свойства биномиальных коэффициен-
тов. Напомним, что число (™) можно интерпретировать как число двоичных
последовательностей длиной п весом ш. Справедлива рекуррентная формула
Л.+ 1\ЛЛ/ „у
\ w J \w) \w — 1J
Действительно, любая последовательность длиной п -F 1 весом w может быть
получена либо из последовательности длиной п весом w дописыванием нуля,
либо из последовательности длиной п весом w—1 дописыванием единицы. Можно
теперь применить эту же формулу ко второму слагаемому в (3.14). Проделав это
многократно, получим тождество
Л. + Л _ ЛЛ Л. - 1\	+ /п - «, + Л
\ w J \wj \W — 1 /	\	1	/
3.3.	Двухпроходное побуквенное кодирование
Без потери общности будем считать, что источник выбирает сообщения из мно-
жества X = {0,... ,М — 1}. Пусть х = (®i,... ,жп) - последовательность на
выходе источника. Множество сообщений X и длину последовательности счи-
таем заранее известными кодеру и декодеру. На практике длина последователь-
ности либо передается отдельно в заголовке файла некоторым стандартным спо-
собом, либо в алфавите источника имеется специальный символ, указывающий
на завершение файла. В любом случае для всех методов универсального коди-
рования проблема конца файла решается одинаковым способом, и от способа ее
решения сравнительные характеристики алгоритмов не зависят.
Для простоты рассмотрим универсальное кодирование для класса источников
без памяти с неизвестным распределением вероятностей на буквах источника.
Очевидный способ решения задачи таков: кодер сначала просматривает последо-
вательность и определяет число появлений тп(а) каждой буквы а 6 X в последо-
вательности х длины п. Затем, используя полученную информацию, вычисляет
3.3. Двухпроходное побуквенное кодирование
99
оценки вероятностей сообщений и строит по ним некоторый код для множе-
ства X. На втором проходе этот код используется для кодирования последова-
тельности сообщений источника. Кодовое слово состоит из двух частей с (я?) =
= (с1(я?),С2(я?)). Первая часть, С1(ж), содержит информацию об использованном
коде, вторая, С2(я?), - собственно закодированную последовательность букв.
Декодер сначала по сДя?) строит код, затем по С2(«) восстанавливает одно за
другим закодированные сообщения.
В это описание укладывается целое семейство алгоритмов, отличающихся друг
от друга выбором кода и способом передачи служебной информации. Мы рас-
смотрим алгоритм, основанный на побуквенном кодировании кодом Хаффмена.
Поясним работу двухпроходного побуквенного кодера примером. Предположим,
что источником информации являются данные, хранящиеся в памяти ЭВМ
в виде байтов, то есть объем алфавита |Х| = 256. В качестве тестовой после-
довательности возьмем поучительную пословицу
IF_WE_CANNOT_DO_AS_WE_WOULD_WE_SHOULD_DO_AS_WE_CAN (3.16)
Мы заменили пробелы подчеркиваниями, чтобы сделать их видимыми и не забыть,
что пробел, как и любой другой символ, должен быть закодирован и передан.
Результаты статистического анализа кодируемого текста и соответствующий код
Хаффмена приведены в табл. 3.1. Обозначим через Zi и I2 длину первой и второй
частей кодового слова. Длина Z2 равна сумме длин кодовых слов информацион-
ной последовательности. Подсчитать ее легко:
I2 = 6 И- 6 4-12 х 2 + 5 х 3 + ... 4- 6 = 178.
Чтобы подсчитать Zi, нужно условиться о способе передачи информации о коде.
Первое, что приходит на ум, - перечислить буквы, длины кодовых слов, сами
кодовые слова. Этот подход заведомо неэффективен. Гораздо экономичнее пере-
дать структуру кодового дерева. Зная ее, декодер сам единственным образом
восстановит все кодовые последовательности.
Кодовое дерево для рассматриваемого кода показано на рис. 3.1. Все вершины
дерева размечены (нулями помечены промежуточные вершины, единицами -
концевые). Будем считывать символы, приписанные вершинам, ярус за ярусом,
начиная с корня дерева (сверху вниз). В данном случае мы получим двоичную
последовательность вида
00010000010100110111101101111.
Эта последовательность из 29 двоичных символов не только полностью описы-
вает дерево, но и несет информацию о количестве различных букв в последо-
вательности. Действительно, декодер по этой последовательности (также ярус
за ярусом) может восстановить дерево. Прочитав первый нулевой символ, он
узнает, что последовательность содержала по меньшей мере 2 различные буквы.
По следующим двум символам он определяет, что на первом ярусе концевых
узлов нет и, следовательно, на следующем (втором) ярусе имеется 4 вершины.
100
Глава 3. Универсальное кодирование
Прочитав 4 символа, получим концевую вершину на втором ярусе и 6 вершин на
3-м ярусе и т. д. На 6-м ярусе все вершины оказались концевыми, значит, постро-
ение дерева завершено. Чтобы завершить описание кода, нужно указать, какая
конкретно буква соответствует каждому кодовому слову. Для этого достаточно 8
бит на каждую букву. В результате затраты на информацию о коде составят
Zi = 29 + 8 х 15 = 149 бит.
Передача всего сообщения потребует
I = +12 = 149 4-178 = 327 бит.	(3.17)
Отметим, что без кодирования мы затратили бы 50 х 8=400 бит. При этом «вспо-
могательная» информация (информация о коде) составляет почти половину дли-
ны кодовой последовательности. С увеличением длины кодируемой последова-
тельности доля служебной информации уменьшается, и эффективность кодиро-
вания существенно возрастает.
Таблица 3.1. Код Хаффмена для текста (3.16)
Буква	Число появлений	Длина кодового слова	Кодовое слово
I	1	6	010000
F	1	6	010001
	12	2	00
W	5	3	100
Е	4	4	0101
С	2 ’	5	01001
А	4	4	1010
N	3	4	1011
О	5	3	110
т	1	6	011110
D	4	4	оно
S	3	4	1110
и	2	4	1111
L	2	5	OHIO
Н	1	6	011111
Затраты на служебную информацию можно уменьшить, если заметить, что для
одного и того же распределения вероятностей можно построить много кодов
Хаффмена, и все эти коды одинаково эффективны. Таким образом, нет необхо-
димости передавать точную структуру дерева, достаточно передать минимальные
сведения, достаточные для построения одного из кодов Хаффмена.
Назовем регулярным неравномерный код, в котором короткие кодовые слова
лексикографически предшествуют более длинным. Регулярный код для рассмат-
риваемого примера приведен в табл. 3.2, а его дерево - на рис. 3.2. Для описания
3.3. Двухпроходное побуквенное кодирование
101
регулярного кода достаточно указать число концевых вершин на каждом из яру-
сов с номерами 0..Zmax> где 1тах - максимальная длина кодового слова. Под-
счет количества битов, необходимых на передачу дерева для регулярного кода,
иллюстрирует табл. 3.3.
Рис. 3.1. Кодовое дерево кода Хаффмена для текста (3.16)
Таблица 3.2. Регулярный код Хаффмена
Буква	Номер яруса (длина кодового слова)	Кодовое слово
	2	00
0	3	010
W	3	011
А	4	1000
D	4	1001
Е	4	1010
N	4	1011
S	4	1100
и	4	1101
с	5	11100
L	5	11101
F	6	111100
Н	6	111101
I	6	111110
Т	6	111111
102
Глава 3. Универсальное кодирование
Таблица 3.3. Подсчет количества битов на передачу дерева регулярного кода
Ярус	Общее число вершин	Число концевых вершин щ	Диапазон значений Пг	Затраты в битах
0	1	0	0...1	1
1	2	0	0...2	2
2	4	1	0...4	3
3	6	2	0...6	3
4	8	6	0...8	4
5	4	2	0...4	3
6	4	4	0...4	3
Всего				19
Рис. 3.2. Кодовое дерево для регулярного кода Хаффмена
Для передачи описания регулярного кода оказалось достаточно 19 бит. Дополни-
тельный выигрыш можно получить, если учесть, что нет необходимости тратить 8
бит на указание соответствия букв словам регулярного кода. Достаточно указать
длину слова для каждой буквы алфавита. Кодер и декодер, зная состав множества
слов одинаковой длины, одинаково упорядочат их внутри множества, например,
в алфавитном порядке.
Именно так упорядочены буквы на рис. 3.2 и в табл. 3.2. После того как стала
известна структура дерева, декодер предает сначала 8 битами номер буквы, име-
ющей длину слова 2. Затем нужно указать, какие две буквы из 255 имеют длину
слова 3. Эти буквы можно выбрать (255) способами, передача номера комбинации
потребует [log (225)] бит. Продолжив, получим, что в общей сложности
3.3. Двухпроходное побуквенное кодирование
103
= 105 бит
Г, /247\]
+ log 9 )
У I
Г (ЧАЪХ
+ log ( 4 )
достаточно на передачу информации о буквах, сопоставленных вершинам регу-
лярного кодового дерева.
Итак, уточненный расчет количества битов дает для данного примера
I = 178 + 19 + 105 = 302 бит.	(3.18)
Этот способ кодирования информации о коде эффективнее, но и сложнее первого
рассмотренного метода. Основная проблема состоит в нумерации комбинаций
букв. Сравнительно простое решение этой задачи мы приведем ниже - при
изучении нумерационного кодирования.
Перейдем к нахождению оценки скорости универсального кода, работающего
по описанному выше алгоритму. Из рассмотрения примера вытекает следующее
утверждение.
ЛЕММА 3.2. Полное кодовое дерево, имеющее М концевых вершин, имеет М - 1
промежуточных вершин. Для полного описания дерева достаточно 2М — 1 бит.
Доказательство. Первое утверждение легко доказать методом математической
индукции. Мы предоставляем это сделать читателю в качестве упражнения. Для
доказательства второго утверждения достаточно указать алгоритм построения
описания дерева с помощью двоичной последовательности длиной 2М — 1. Такой
алгоритм был описан выше на примере кодирования текста (3.16).	□
Оценку асимптотической эффективности двухпроходного кодирования сформу-
лируем в виде следующей теоремы.
ТЕОРЕМА 3.3. При двухпроходном кодировании с использованием кода Хаффмена
дискретного постоянного источника с объемом алфавита М и энтропией Н сред-
няя скорость кодирования удовлетворяет неравенству
7?<# + l + -(MlogAf+ ЗМ-1).	’	(3.19)
п
Доказательство. Для заданной последовательности х через l-Дх) и по-
прежнему обозначаем длину первой и второй частей кодового слова. Инфор-
мация о коде может быть разбита на две части: информация о кодовом дереве
и информация о том, какая из букв соответствует каждой вершине кодового
дерева. Длина описания кодового дерева может быть оценена с использованием
леммы 3.2. Указание буквы для одной вершины потребует не более [logAf]
log М + 1 бит. В результате имеем оценку	'
Zi(a) ^2M-l-FMflogM] < MlogM + ЗМ - 1.	(3.20)
104
Глава 3. Универсальное кодирование
Длина второй половины кодового слова подсчитывается как
г=1
- 52	=
хех
= п 52 рп(хЖх) =
хЕХ
= пМ^Ж
(f)
< п(Н(рп) + 1).	(3.21)
Поясним эти выкладки. Через 1(х) мы обозначили длину кодового слова для
буквы х в построенном по х коде Хаффмена. Сначала (равенство (а)) мы запи-
сали длину всей последовательности как сумму длин отдельных кодовых слов.
Затем (равенство (Ь)) мы сгруппировали слагаемые, соответствующие одина-
ковым буквам алфавита. Затем в (c,d) мы использовали обозначение рп{х) =
= гп{х)/п для оценок вероятностей букв по последовательности ж. Далее (равен-
ство (е)) заменили сумму на математическое ожидание длины кодовых слов по
распределению вероятностей рп = {рп(ж)}- После этого введено обозначение
Н(рп) для энтропии ансамбля с распределением вероятностей, задаваемым век-
тором рп. Последнее неравенство (f) означает, что средняя длина кодовых слов
кода Хаффмена для источника с энтропией Н не превышает Н + 1.
С учетом (3.20) и (3.21) средняя скорость кодирования для заданной последова-
тельности х удовлетворяет неравенству
= ад = аджад s
п	п
Н(рп) + 1 + - (М log М + ЗМ - 1).	(3.23)
п
Следующий шаг доказательства - усреднение по всем последовательностям х.
В правой части от х зависит только энтропия. Поэтому рассмотрим ее отдельно:
М [Н(рп)] 2 Н (M [pJ)	Я(р) = Н.	(3.24)
Здесь неравенство (а) следует из выпуклости А энтропии как функции распре-
деления вероятностей. Для обоснования перехода (Ь) нужно убедиться в том,
что
м [рп] = Р,
(3.25)
3.3. Двухпроходное побуквенное кодирование
105
где через р обозначен вектор, компонентами которого являются вероятности
букв источника. Иными словами, нужно доказать, что в последнем векторном
тождестве равенство имеет место для каждой компоненты, то есть
М
гп(а)
п
= р(а), a 6 X.
Чтобы это доказать, введем индикаторную функцию
Ха (®) = *
1, при х = а,
О, при х / а.
Заметим, что
М [Ха(я)] = 1 X р(а) + 0 х (1 - р(а)) = р(а).
Теперь можно записать
М[^1 =^м[^Ха(х<) =
п п
L	1л=1
= ~ 52 М [Хаfa)] = р(а), а е X.
г=1
Отсюда следует (3.25) и из него - (3.24). В свою очередь, используя (3.24),
в результате усреднения в левой и правой частях (3.22) приходим к доказы-
ваемому результату (3.19).	□
Обсудим полученную оценку эффективности кодирования. Избыточность коди-
рования удовлетворяет неравенству вида
r = R-H ^1 + —,	(3.26)
п
где первое слагаемое в правой части обусловлено избыточностью использован-
ного побуквенного кода, второе - отсутствием информации о статистике источ-
ника. При п оо влияние второго слагаемого становится пренебрежимо малым,
и эффективность двухпроходного кодирования стремится к эффективности коди-
рования кодом Хаффмена при известном распределении вероятностей на буквах
источника.
Асимптотический результат (3.26) легко распространить на случай источников
с памятью. Для этого описанный способ кодирования нужно применить к бло-
кам достаточно большой длины. Практического значения такой подход не имеет,
поскольку с увеличением длины блоков экспоненциально растет объем алфавита
и, соответственно, длина первой (служебной) части кодового слова.
Еще одно замечание. В формуле (3.26) первое слагаемое избыточности (избыточ-
ность кода) не убывает с ростом длины кодируемой последовательности. Каза-
лось бы, прямой путь к повышению эффективности кодирования - применить
арифметическое кодирование вместо кода Хаффмена. При этом избыточность
кода будет ограничена сверху величиной 2/п, но за это уменьшение избыточ-
ности придется заплатить увеличением второго слагаемого, поскольку теперь
106
Глава 3. Универсальное кодирование
недостаточно описать структуру кода, а нужно передать вероятности всех букв.
Любопытно, что для ^рассматриваемого примера (3.16) передача самого текста
арифметическим кодом при известных оценках вероятностей букв потребует 178
бит, то есть в точности столько же, сколько требуется при использовании кода
Хаффмена, то есть замена кода Хаффмена арифметическим кодом не гарантирует
выигрыша в эффективности кодирования.
Метод, рассмотренный в данном параграфе, - наиболее очевидный способ пере-
дачи при неизвестной статистике источника. Мы показали, что для стационар-
ного источника избыточность кодирования асимптотически (с увеличением длины
кодируемой последовательности) стремится к избыточности кодирования при
известных вероятностях букв. В частности, при использовании арифметического
кодирования можно получить избыточность порядка
М-1	К
г(п) =------log п Ч--,	(3.27)
п	п
где М - объем алфавита, а К - константа, не зависящая от п.
В следующем параграфе мы опишем более сложный способ кодирования, оценка
избыточности которого примерно вдвое меньше, чем в правой части (3.27).
3.4.	Нумерационное кодирование
Сейчас мы рассмотрим один из исторически первых методов универсального
кодирования. Его автором является Б. М. Фитингоф [18].
Считаем, что алфавитом источника служит множество чисел X = {0,..., М -1}.
Пусть х = (®i,... ,жп) - последовательность на выходе источника. Рассмотрим
следующий способ двухпроходного кодирования.
Кодовое слово нумерационного кода состоит из двух частей. Первая часть содер-
жит закодированный равномерным кодом номер композиции тп(я?) = (то(я?),...
... , тм-1(«)) в списке всех возможных композиций последовательностей длины
п над алфавитом X. Вторая часть содержит закодированный равномерным кодом
номер данной последовательности х в лексикографически упорядоченном списке
последовательностей с одинаковой композицией тп(ш).
3.4.1.	Оценка избыточности
В параграфе 3.2 подсчитано количество различных композиций (формула (3.9))
=	(3.28)
и число последовательностей с фиксированной композицией АГ(т) (формула
(3.8))
3.4. Нумерационное кодирование
107
Для заданной последовательности х через Zi(o?) и Z2(as) обозначим длину первой
и второй частей кодового слова. Из формул (3.28) и (3.29) получаем формулу
для длины 1(х) кодового слова:
Ц®)
11(®) + Ы®) = P°g Nr (Af)] + riog-/V(r)] =
(3.30)
Обратимся к нашему текстовому примеру:
IF_WE_CANNOT_DO_AS_WE_WOULD_WE_SHOULD_DO_AS_WE_CAN
Непосредственный подсчет по формулам (3.28) - (3.30) приводит к результатам:
, Г, /50 + 255\1 '
h = log	I = 190 бит,
\ 2о& /
Г, (	50!
l2 = log ^12!5!24!зз!22!3 J = 150 ^ит<
Сравнивая с предыдущим примером, видим, что Zi неожиданно велико, a Z2 -
рекордно мало. Не может быть, чтобы не существовало более эффективного
правила передачи композиции.
С другой стороны, формула (3.28) точна, и, следовательно, уменьшение бито-
вых затрат может быть получено только в том случае, если мы откажемся от
равномерного кодирования номеров композиций. Для каких-то композиций мы
должны тратить еще больше битов, чем раньше, и тогда, возможно, для неко-
торых композиций кодирование станет значительно более эффективным. По-
видимому, в «привилегированное» положение должны быть поставлены те ком-
позиции, для которых «сжатие» в принципе осуществимо, то есть композиции,
содержащие сильно разнящиеся компоненты.
Мы будем отдельно передавать композицию, а затем указывать, какие буквы
соответствуют различным ее компонентам. Исходную композицию перед пере-
дачей отсортируем. В данном примере сортированная композиция имеет вид
т = (то,..., тм-1)=(12, 5, 5, 4, 4, 4, 3, 3, 2, 2, 2, 1, 1, 1, 1,0,..., 0). Для элементов
композиции имеют место неравенства
l^To^n, Ty+i^T;,
Приписав всем таким комбинациям одинаковые вероятности, с помощью ариф-
метического кодирования можно передать номер композиции, затратив не более
log
бит.
(3.31)
Осталось оценить затраты на передачу соответствия между буквами алфавита и
компонентами композиции. Для одинаковых значений композиции порядок сле-
дования букв несущественен. Введем композицию сортированной композиции и
обозначим ее т' = (tq, т(,...). В данном примере т'=(1,2,3,2,3,4,241). Достаточно
108
Глава 3. Универсальное кодирование
передать, в какую из этих 7 категорий попала каждая буква алфавита. Для под-
счета количества различных вариантов годится формула (3.8). Поэтому затраты
на передачу композиции можно подсчитать как
Zi = log I п £1 Tj
\ j'rj>0
'IE
\ J
= 25 + 108 = 133 бит. (332)
Окончательный результат для нумерационного кодирования составляет
I = li +12 = 283 бит.
Оценим теперь эффективность нумерационного кодирования для произвольного
дискретного постоянного источника с неизвестным распределением вероятно-
стей. Нас интересует случай, когда длина последовательности п достаточно велика
(выполняется неравенство п » М). Для оценки числа композиций вместо
формулы (3.28) мы воспользуемся оценкой
ЛГт(п,Л/) < (п + 1)м-1.
(3.33)
Она вытекает из того, что каждая из компонент принимает одно из (n +1) значе-
ний от 0 до п, а последняя компонента композиции однозначно вычисляется по
первым М — 1 компонентам. Для оценки числа последовательностей с заданной
композицией воспользуемся (3.12). Получим
Z(®) = Z1(®) + Ы®) = [log^(M)l + [logA^T)]
пЯ(р) - М 1 log(27rn) - i V logQjj) + (М - 1) log(n + 1) + 1.
А	"
г
Теперь поделим обе части на п и усредним по всем последовательностям х.
Результат сформулируем в виде теоремы.
ТЕОРЕМА 3.4. При нумерационном кодировании дискретного постоянного источ-
ника с объемом алфавита М и энтропией Н средняя скорость кодирования удовле-
творяет неравенству
й и 1о§(п + i) + к
(3.34)
где величина К не зависит от длины последовательности п.
Сравнивая этот результат с оценкой (3.27) средней скорости двухпроходного
арифметического кодирования, убеждаемся, что при больших п избыточность
нумерационного кодирования примерно вдвое меньше.
3.4. Нумерационное кодирование
109
3.4.2.	Реализация нумерационного кодирования
Рассмотрев методы двухпроходного кодирования, мы убедились в высокой эффек-
тивности нумерационного кодирования. Этот метод включает два этапа кодиро-
вания, каждый из которых требует передачи номера заданной последователь-
ности в некотором списке. При большой длине кодируемой последовательно-
сти списки могут быть большими, а вычисление номера последовательности -
слишком сложным.
Вернемся к примеру, рассмотренному в предыдущих параграфах. Длина после-
довательности букв источника была небольшой, п = 50. В то же время длины
кодовых последовательностей для первой и второй частей кодового слова полу-
чились равными 133 и 150 бит. Это значит, что списки содержали порядка 2133 и
2150 последовательностей. Понятно, что табличные или переборные методы для
кодирования и декодирования неприемлемы.
В этом параграфе мы покажем, что нумерационное кодирование может быть
выполнено с полиномиальной по п сложностью. Сначала мы опишем истори-
чески первый алгоритм, предложенный В. Ф. Бабкиным [1]. Затем рассмотрим
весьма практичный способ нумерации последовательностей, основанный на ариф-
метическом кодировании. Для знакомства с последними результатами в этой
области рекомендуем статью [16].
Начнем с нумерации двоичных последовательностей. Рассмотрим множество дво-
ичных последовательностей длиной п с весом Хэмминга w. Это множество обра-
зует сферу радиуса w в n-мерном хэмминговом пространстве, будем обозначать
Sn(w). Как мы знаем, общее число таких последовательностей |Sn(w)| = (£).
Задача кодирования состоит в том, чтобы для произвольной последовательности
х е Sn(w) вычислить ее номер J(x) в лексикографически упорядоченном мно-
жестве Sn(w). Для декодирования нужно уметь по номеру последовательности
J(x) вычислить саму последовательность я?.
Обозначим через рь ..., pw номера ненулевых позиций в я?, вычисленные от
последнего символа. Например, для х = (0100001010) номера позиций равны
pi = 2, р2 = 4, р3 = 9. Наряду с 7(ж) будем для номера той же последовательности
использовать обозначение J(pi,...,pw).
ТЕОРЕМА 3.5. Номер последовательности с номерами ненулевых позиций р^,... ,pw
т/	\ (Pw ~ 1\ ! (Pw-1 ~	| (pi ~	ZQ Qt-x
Дрь • • • >Pw) — I I + I 1 )+...+ [	).	(3.35)
\ w / \ w ~ 1 / \ 1 /
Доказательство. Подсчитаем, сколько последовательностей лексикографически
предшествует последовательности, содержащей старшую единицу на позиции pw.
Это прежде всего все те последовательности, которые имеют все w единиц на
позициях с номерами (вычисленными от конца) 1, 2,..., pw — 1. Число таких
последовательностей равно (Pww-1). Кроме того, нужно учесть все те последова-
тельности, которые содержат единицу на позиции с номером pw. Их остальные
110
Глава 3. Универсальное кодирование
w - 1 единиц расположены таким образом, что они предшествуют последова-
тельности с единицами на позициях pi,..., pw-i- Согласно нашим обозначениям,
число таких последовательностей равно J(pi,... ,pw-i). Итак,
= (Pw	(3.36)
\ W J
Поясним эту формулу на примере. Последовательности х = (0100001010) пред-
шествуют, во-первых, все последовательности весом 3, содержащие единицы только
на последних 8 позициях (их число (3)), во-вторых, последовательности вида
(01...) такие, что подпоследовательность из последующих 8 символов младше
рассматриваемой (таких последовательностей J(2,4)). Таким образом, в нашем
случае J(2,4,9) = (|) + J(2,4).
Формулу (3.36) можно применить ко второму слагаемому в (3.36). Проделав это
w — 1 раз, получим (3.35).	□
Например, для х = (0100001010) номер последовательности
Для передачи этого числа потребуется 7 бит, поскольку число различных после-
довательностей длиной 10 весом 3 равно (х3°) = 120 и flogl20"| = 7.
Рассмотрим задачу декодирования, то есть вычисления х по 7(ш). В решении
воспользуемся тождеством (3.15). Перепишем его в виде
\ w J \ w J \w —	\	1	/
Единица на позиции п вносит в сумму J(x) слагаемое, величина которого по
меньшей мере на 1 больше, чем могла бы внести любая комбинация из w единиц
на позициях с меньшими (считая от конца) номерами. Сравнив J(x) с (п“х),
мы можем вынести однозначное решение о том, имеется единица на позиции
с номером п или нет. Приходим к алгоритму, представленному на рис. 3.3.
В табл. 3.4 показаны вычисления, выполняемые декодером нумерационного кода
последовательности длиной п = 10 весом w = 3 при поступлении на его вход
числа J = 60.
В процессе кодирования и декодирования нумерационного кода многократно
используются значения биномиальных коэффициентов. При небольших длинах
последовательностей все эти значения можно вычислить заранее и хранить
в памяти кодера и декодера. Для вычисления коэффициентов при больших дли;
нах п можно воспользоваться рекуррентной формулой (3.14), не содержащей
умножений. В некоторых случаях удобнее бывает другая рекуррентная формула
a_n — w + 1/ п \
w \w — 1J'
3.4. Нумерационное кодирование
111
Input: Длина последовательности п
Вес последовательности w
Номер последовательности J(x)
Output: Декодированная последовательность букв х
Инициализация: S = J(®), W = w, N — п.
Декодирование:
while N > 0 do
if (N-1) < S &L W > 0 then
xN = 1, S S - (V)> W^w-l;
else xn = 0;
N+-N-1.
end
Результат последовательность (®i,..., xn);
Рис. 3.3. Алгоритм декодирования нумерационного кода
Таблица 3.4. Пример декодирования нумерацибнного кода
Номер позиции N	Число единиц в оставшихся позициях W	Текущее значение суммы S	Cw1)	Принятое реше- ние Хп
10	3	60	72	0
9	3	60	56	1
8	2	4	21	0
7	2	4	15	0
6	2	4	10	0
5	2	4	6	0
4	2	4	3	1
3	1	1	2	0
2	1	1	1	1
1	0	0	0	0
Нужно иметь при этом в виду, что все вычисления должны выполняться без
округлений, то есть разрядность чисел, над которыми выполняются арифмети-
ческие операции, должна быть равна длине кодовой последовательности.
Мы закончили рассмотрение нумерации двоичных последовательностей. Нуме-
рация последовательностей над произвольным алфавитом может быть выпол-
нена с помощью нумерации двоичных последовательностей следующим очевид-
ным способом. Сначала передаются номера позиций первого из символов алфа-
вита, затем для остальных позиций - номера позиций второго символа алфавита
ит.д.
112
Глава 3. Универсальное кодирование
Input: Композиция т — (то,.. ., тм-i);
Последовательность х = (т,... ,а?ь) с композицией т;
Output: Кодовое слово для х
Инициализация:
F = О, G = 1.
Начальные оценки вероятностей и кумулятивных вероятностей букв:
до = 0;
for i = 1 to М do
Pi-i — Ti-i/n; qi = qi-i -bpi-i ;
end
Кодирование:
for i — 1 to n do
F F 4- q(xi) x G;
G <- p(xi) x G;
Модифицируем композицию:
Txi * Txj lj
Уменьшаем длину:
n 4— n — 1;
Пересчитываем оценки вероятностей и кумулятивных вероятностей:
for i — 1 to М do
Pi—1 == Ti—1/nj
qi = Qi-i 4- pi-i ;
end
end
Формируем кодовое слово:
Кодовое слово х первые I = flog G"| разрядов после запятой в двоичном
представлении числа F.
Рис. 3.4. Алгоритм арифметического нумерационного кодирования
Другой подход к реализации нумерационного кодирования основан на использо-
вании арифметического кодирования. Этот метод мы рассмотрим применительно
к последовательностям над произвольным алфавитом X = {0,..., М - 1}.
Пусть т = (то,..., гм-i) обозначает композицию вектора. Задача состоит в том,
чтобы по последовательности х = (я?1,..., хп) вычислить ее номер в лексикогра-
фически упорядоченном списке всех последовательностей с заданной компози-
цией т. Длина записи номера должна быть равна
I = flogA/Xr)! = log
(3.38)
t0!...tm-i!
Приведенный на рис. 3.4 алгоритм решает эту задачу с помощью арифметиче-
ского кодирования с изменяющимися на каждом шаге вероятностями.
Поясним суть алгоритма примером.
3.5. Асимптотические границы избыточности
113
Пример 3.4.1. Пусть п = 10, т = (2,5,3), х = (2011021211). На первом шаге
кодирования распределение вероятностей на буквах принимается равным т/п =
— (2/10,5/10,3/10). Соответственно, вероятность первого символа последова-
тельности равна 0,3 и после первого шага кодирования G = 0,3. Поскольку
композиция известна кодеру и декодеру, на приемной и передающей сторонах
после передачи первого символа известна композиция оставшейся части после-
довательности я?, это значит, что распределение вероятностей на буквах после
первого шага (2,5,2)/9 = (2/9,5/9,2/9). Теперь передается 0, и, значит, после
второго шага кодирования G = 3/10 х 2/9. После 10 шагов
3	2	5	4	1
G
= -7х7хтХ-Х-Х
10	9	8	7	6
В алгоритме арифметического кодирования длина кодового слова равна f—log G] +
+ 1, что соответствовало применению кода Гилберта-Мура. Напомним, что необ-
ходимость увеличения длины кодового слова на единицу была обусловлена тем,
что мы не могли гарантировать, что лексикографически упорядоченные после-
довательности упорядочены по убыванию вероятностей. При нумерационном
кодировании последовательностям с одинаковой композицией приписываются
одинаковые вероятности, поэтому условие упорядоченности выполняется. Это
дает возможность отказаться от увеличения длины кодовой последовательности,
то есть можно применять код Шеннона, а не Гилберта-Мура. В данном примере
длина кодового слова
Z = [-logGl=
что в точности соответствует (3.38).
Декодером для данного кода будет арифметический декодер, который, заранее
зная композицию последовательности, обновляет вероятности и кумулятивные
вероятности букв точно так же, как это делалось при кодировании.
3.5.	Асимптотические границы избыточности
универсального кодирования
Вернемся к постановке задачи универсального кодирования. Напомним, что
в соответствии с (3.1) избыточностью кодирования последовательностей длины
п для класса источников Q называется величина
rn(fi) = sup [#n(w) - Я„] .	(3.39)
Избыточность rn(fi), разумеется, зависит от того, насколько широк класс источ-
ников. Предположим, что Q - множество дискретных постоянных источников
с алфавитом X = {0,1,..., М — 1}. Каждый источник полностью описывается
114
Глава 3. Универсальное кодирование
вероятностями букв. Запишем эти (неизвестные кодеру) вероятности в виде век-
тора в = (0о, • • •, 0м-1), и тогда Q совпадает с множеством 0 = {0} всех вероят-
ностных векторов длины М. При заданной модели в распределение вероятностей
на Хп имеет вид
М-1
Р(®1в) = п
i=0
где т(ж) = (то(сс),..., тм-1(®)) - композиция последовательности х.
В этих условиях теорема 3.4 представляет собой, по сути, прямую теорему коди-
рования, устанавливающую верхнюю границу избыточности. Из нее следует, что
при нумерационном кодировании
гп(Э) ^9~ llog(n + 1) + J;f,	(3.40)
2	п
где К не зависит от п.
Интересно знать, насколько нумерационное кодирование близко к оптималь-
ному. Для этого вычислим границу снизу для избыточности неравномерного
префиксного кода при неизвестных вероятностях букв дискретного постоянного
источника. Итак, наша задача состоит в вычислении величины
rn(0) = inf sup [Яп(в) - Н(Х|0)1,	(3.41)
где Н(Х\0) - энтропия ансамбля X при распределении вероятностей 0, а ниж-
няя грань вычисляется по всем возможным алгоритмам кодирования. Оставша-
яся часть параграфа содержит достаточно трудоемкое (но весьма поучительное)
доказательство обратной теоремы кодирования.
ТЕОРЕМА 3.6. Для дискретного постоянного источника с объемом алфавита М
избыточность универсального кода rn(Q) на сообщение последовательности дли-
ной п удовлетворяет неравенству
„ M-llogn + C
rn(0) > —z------~,	(3.42)
.	Tl
где постоянная С не зависит от п.
Сразу отметим, что нижняя граница (3.42) и верхняя граница избыточности
(3.40) при п -+ оо совпадают, что позволяет говорить об асимптотической опти-
мальности нумерационного кодирования.
Доказательство. Приведенное ниже доказательство принадлежит Кричевскому
[И]. Оно состоит из двух основных шагов. Сначала мы сведем поиск экстремума
по двум аргументам в (3.41) к поиску максимума некоторой функции (взаимной
информации между множеством параметров источника и последовательностями
на выходе источника) по распределению вероятностей на множестве парамет-
ров источника. Второй шаг состоит в том, что мы «угадаем» максимизирующее
распределение и подсчитаем величину максимума.
3.5. Асимптотические границы избыточности
115
Зададим на множестве 0 = {0} распределение вероятностей f(0). Искомую
избыточность (3.41) запишем теперь в виде
rn(9) = inf sup М/ [£.(0) - Я(Х|0)],	(3.43)
/(в)
где математическое ожидание вычисляется по всем случайным 0 с распределе-
нием вероятностей /(0). При выводе нижней границы избыточности мы можем
считать, что это распределение вероятностей известно кодеру источника. Поэтому
rn(0) > sup inf Mf [Яп(0) - H(X|0)] .	(3.44)
fW
Чтобы найти нижнюю грань по возможным способам кодирования, заметим, что
любой способ кодирования сопоставляет последовательности х = (®i,..., xn) е XN
кодовое слово некоторой длины Z(®). Множество длин кодовых слов любого
префиксного кода удовлетворяет неравенству Крафта
1.
хехп
Если имеет место строгое неравенство, то код заведомо неоптимален: по меньшей
мере одно из кодовых слов могло быть короче, а код остался бы префиксным.
Поэтому можно считать, что для оптимального кода сумма слагаемых в левой
части неравенства Крафта равна 1, следовательно, сами слагаемые представляют
собой распределение вероятностей на множестве Хп. Введем обозначение
q(x) = 2~1(х>
и назовем распределение вероятностей q(x) кодовым распределением. Примене-
ние кода Шеннона гарантирует существование кода со средней длиной кодовых
слов удовлетворяющего неравенствам
- $2 p(®l0)log«(®) < in(q,O) < - 52 М®|0) log ?(®) +1.
хехп	хехп
Поскольку нас интересует асимптотическая избыточность (n 1), для простоты
записи формул пренебрежем единицей в правой части и будем считать точным
равенство
1п(д,^) = - 52 H®|0)logQ(®)-	(3.45)
хехп
Усредняя по всем распределениям вероятностей 0, получаем
ЗД = - 52 . Р(®)1о8«(®)>	(3-46)
хехп
где
р(х) = М/ [р(®|0)] = 2 /(0)p(®|0)de.	(3.47)
116
Глава 3. Универсальное кодирование
Минимум правой части в (3.46) достигается при р(х) = q(x). Это доказывается
следующими выкладками:
- 52 p(®)fog?(®) + 52 p(®)iog?(®) = -ь(р||«) < о
хехп	хехп
(см. задачу 18 главы 1).
Теперь можно записать (3.44) в виде
Гп(0) >-supM/ p(®|0)log^^ .	(3.48)
n fW	?(®)
Тем самым завершен первый этап доказательства.
Выражение под знаком sup в правой части (3.48) представляет собой среднюю
взаимную информацию между двумя вероятностными ансамблями: ансамблем
сообщений X и ансамблем случайных векторов параметров модели источника
0. Свойства средней взаимной информации будут подробно изучаться в главе 5,
посвященной каналам связи. Из Этих свойств следует, что средняя взаимная
информация - строго выпуклая А функция распределения вероятностей /(0) и
имеет единственное максимальное значение. Всякое распределение вероятностей
/(0), при котором достигается максимальное значение, обладает тем свойством,
что при таких 0, что /(0) > 0, значения максимизируемой функции не зависят от
0 (подробнее о свойствах выпуклых функций и условиях на экстремум см. § 2.8
книги [7] и § 4.4 книги [3]).
В качестве семейства распределений на 0 выберем распределения Дирихле
(М-1	\ М-1 лАг-1
Ем П vfc’	<3-49>
г=0	/ г=0	' г'
где Л = (А0,...,Ам-1) - вектор параметров распределения Дирихле, Xi О,
i — 0,..., М — 1, Г(г) - гамма-функция, определяемая как
/•ОО
Г(з) = / tz~1e~tdt.
Jo
Отметим важные свойства гамма-функции:
Г(х) = (х-1)Г(х-1), Г (0=5^-
В частности, при целых значениях аргумента
Г(п) = (п —1)!.
Формула Стирлинга аналогично (3.10) дает асимптотическое приближение гамма-
функции в виде
Г(з) « y/27rzz~1^2e~zi z —> оо.
Точнее, для некоторой константы имеет место неравенство
|logГ(г) + zloge — (z — 1/2)logz| < Ki.	(3.50)
3.5. Асимптотические границы избыточности
117
Кроме того, в последующих выкладках нам потребуется интеграл Дирихле.
Для любых положительных аг, i = 1,...,п и непрерывной функции f имеет
место тождество
[ f \	) n^i-1dxi...da:n =
\i=1 / i=1
- П,упГЦ Г /(т)т(^-х “‘Hrfr.	(3.51)
Qv Jo
С помощью этого интеграла можно, в частности, проверить условие нормировки
распределения Дирихле.
Выберем в качестве распределения на множестве © распределение Дирихле
с параметрами А, = 1/2, г = 1,..., М,
(3.52)
г=0
Из (3.47) находим
JB г=0
Используя интеграл Дирихле, получаем
_ г(м/2) nSW.M + i/a)
PW ^„/2	Г(п + М/2)	'	*	'
Применение формулы (3.50) (после непростых выкладок, которые мы отложим
до конца параграфа) позволяет записать логарифм этой вероятности в виде
- logp(®) = пН	— logn + К(п),	(3.54)
где функция К(п) ограничена сверху константой.
После подстановки этого выражения в (3.48) нам предстоит усреднить его по
распределению р(®|0). Для этого используем следующую лемму.
ЛЕММА 3.7. При заданном векторе параметров в среднее значение ^эмпириче-
ской энтропии» источника Н при любых в связано с его энтропией Не(Х)
неравенствами
^р(х\е)Н - Не(Х) 0 ,	(3.55)
X	'	'
где - некоторая константа, Не(Х) = -	1 0; log 0* - энтропия источника.
Доказательство. Правое неравенство - прямое следствие выпуклости энтропии.
Остановимся на более важном для нас левом неравенстве в (3.55).
118
Глава 3. Универсальное кодирование
Из теории вероятностей известно, что математическое ожидание и второй момент
суммы п независимых случайных величин, принимающих значения 0 и 1 с веро-
ятностями 1 — р и р, равны пр и (п2р2+пр(1 —р)) соответственно. Отсюда следуют
тождества
= ndi,
X
(3.56)
(х) = п20? + п0Д1 - Oi).	(3.57)
X
Интересующую нас разность в (3.55) запишем следующим образом:
ЛГ—1	/ \	/ \
( izjx	1 W
п	п
х	г=0
М—1 ✓ \	/ \
и -£p(aW £
х	i=0
М-1
+ 0»log0i =
г=0
М-1	( .
+У2 У2	=
х г=0	П
(Ь)
(с)
М-1
= -!og]r
i=0
п20?+0,(1-0г)
n20i
loge.
Здесь переход (а) основан на (3.56), неравенство (Ъ), в котором усреднение пере-
несено под знак логарифма, основано на выпуклости U функции - log х. Далее
в (с) использованы (3.56) и (3.57), а затем - условие нормировки вероятностей,
и в (d) - неравенство для логарифма. Полученный результат доказывает левое
неравенство в утверждении леммы.	□
Вернемся к (3.48). Заметим, что
-	p(x|0)logp(®|0) = Я(Хп|0) = пЯв(Х).
х(ЕХп
Поэтому с учетом (3.54) и (3.55)
/ |Л\1	Р(®|®) М — 1 1	ТУ ( \	^1
Е log -г-г > —2— logn + Я(п) - —.
®GXn	7
3.5. Асимптотические границы избыточности
119
Это выражение не зависит от в, поэтому, как было пояснено выше, на выбранном
распределении вероятностей /(0) (3.52) достигается максимум в (3.48). Полу-
ченная оценка избыточности совпадает с утверждением теоремы, то есть дока-
зательство практически завершено. Осталось привести пропущенные выкладки,
сводящие (3.53) к (3.54).
Заметим, что в (3.53) можно игнорировать первую дробь, поскольку она не зави-
сит от п и т(я?) (мы учтем ее в виде слагаемого Кг)- Кроме того, слагаемые z log е
в (3.50) можно не учитывать, поскольку их вклад в числитель и знаменатель
второй дроби компенсируют друг друга. Поэтому из (3.53) имеем
М-1
-logp(a)
г=0	х	7
М-1\	( м\ „
п + —-— 1 log I п + — I + К2 =
Z у \ Z J
1
п
М-1
- 52 Ti(a5)1°g
г=0
/ M-1V
I ПН--— 1 logn +
\	" J
(	М-1\у Л м\ , „
п н--й— log 1 + — + К2,
\	2 J \	2п J
п +
Теперь, воспользовавшись хорошо знакомыми неравенствами
0 log(l + б) eloge,
нетрудно прийти к (3.54).	□
Обсудим полученные результаты. Во-первых, мы убедились, что асимптотиче-
ская избыточность универсального кодирования дискретного постоянного источ-
ника ограничена снизу величиной, пропорциональной объему алфавита и лога-
рифму длины последовательности. Больше того, нижняя граница избыточности
асимптотически совпадает с избыточностью нумерационного кодирования.
По ходу доказательства нам пришлось искать наилучшее кодирование, которое
задается «кодовым» распределением вероятностей на множестве последователь-
ностей, порождаемых источником. Согласно (3.53), оптимальные вероятности
однозначно определяются композицией последовательностей и, значит, должны
быть одинаковыми для последовательностей с одинаковой композицией. Как раз
такой выбор и обеспечивается нумерационным кодированием.
Ключевым моментом в доказательстве был удачный выбор распределения Дири-
хле в качестве распределения вероятностей на множестве источников. Почему
именно это распределение было выбрано и почему вектор параметров был именно
таким (Аг = 1/2, г = 0,..., М - 1)?
Выбор распределения Дирихле продиктован возможностью относительно про-
стого усреднения по множеству неизвестных параметров (благодаря применению
120
Глава 3. Универсальное кодирование
интеграла Дирихле). Более важный вопрос - выбор параметров распределения.
Одинаковые значения параметров отвечают симметрии задачи, но почему 1/2?
Одна из причин снова связана с простотой записи формул, поскольку в (3.50)
как раз вычитается 1/2. Вторая причина в том, что этот выбор, не будучи строго
оптимальным, тем не менее приводит к нужному результату. Удивительно то,
что такой выбор дает эффективное и практичное решение задачи адаптивного
универсального кодирования, рассматриваемой в следующем параграфе.
3.6.	Адаптивное кодирование
Мы переходим к изучению универсального кодирования без задержки. Кодеру
при поступлении на его вход очередного сообщения теперь недоступна информа-
ция о сообщениях, которые появятся в будущем. Поэтому способ кодирования
текущего сообщения будет зависеть только от того, какими были предыдущие
сообщения.
Естественным решением задачи является следующий подход. Кодер (и деко-
дер) по последовательности уже переданных сообщений оценивают вероятности
возможных значений следующего сообщения и строят для него код в соответ-
ствии с этими оценками вероятностей. Если источник стационарен, то с уве-
личением длины уже закодированной последовательности оценки вероятностей
будут все более точными. У декодера не возникнет проблем с восстановлением
данных, поскольку он располагает всей информацией, использованной кодером
для построения кода.
В рамках этой схемы есть несколько степеней свободы выбора конкретной моди-
фикации алгоритма. В частности, можно менять следующие характеристики:
►	длину последовательцости сообщений, по которой вычисляются оценки веро-
ятностей;
►	формулы для вычисления оценок вероятностей;
►	способ кодирования при известных оценках вероятностей.
Обсудим эти возможности. Начнем с вопроса о выборе длины «окна», то есть
длины последовательности, по которой оцениваются вероятности сообщений.
Интуитивно ясно, что увеличение длины окна должно приводить к росту точ-
ности оценок, то есть к повышению эффективности кодирования. Это сообра-
жение верно, если верна гипотеза о стационарности источника. В противном
случае выбор короткого окна может оказаться более удачным, поскольку поз-
волит кодеру и декодеру быстрее адаптироваться к изменениям статистических
свойств источника. Более детальный анализ показывает, что и для стационарного
источника достаточно выбирать окно, длина которого в несколько раз превышает
объем алфавита источника. Дальнейшее увеличение длины окна не приведет
заметному уменьшению избыточности. Исходя из этого кажется целесообразным
всегда выбирать окна конечной длины.
3.6. Адаптивное кодирование
121
Однако на пути реализации такого подхода имеется «подводный камень» - отно-
сительно высокая сложность кодирования. Дело в том, что при «бесконечном
окне» (когда окном служит вся предшествующая последовательность сообще-
ний) вся необходимая информация о предшествующих сообщениях хранится
в виде счетчиков числа появления различных букв (число счетчиков равно объ-
ему алфавита источника). При окне конечной длины при поступлении от источ-
ника новой буквы нужно не только нарастить на 1 значение соответствующего
счетчика, но и уменьшить на 1 значение счетчика для той буквы, которая в дан-
ный момент времени оказалась за пределами окна. Для этого придется пом-
нить всю последовательность букв, хранящихся в окне. С учетом этой трудности
вероятности обычно оцениваются по всей предшествующей последовательности.
(В действительности, в практических схемах сжатия применяют некоторые ухищ-
рения, позволяющие обеспечить быструю адаптацию оценок вероятностей без
хранения «окна». Описание этих схем выходит за рамки данного пособия.)
Выбор формул для оценивания вероятностей и выбор способа кодирования вза-
имосвязаны. На первый взгляд оценка вероятности того, что хп+± = а, должна
вычисляться по последовательности , хп по формуле
рп(а) =	(3.58)
где через тп(а) обозначено число появлений буквы а в последовательности длины
п. Однако при использовании этой формулы для некоторых букв оценка веро-
ятности окажется равной нулю. Это не вызовет серьезных проблем, если для
кодирования используется, например, код Хаффмена. Однако при использова-
нии кодов Шеннона, Гилберта-Мура или арифметического кодирования нуле-
вые.значения вероятностей недопустимы.
В литературе по кодированию источников можно найти много способов записи
оценок вероятностей букв (см., например, [И]). Например, можно воспользо-
ваться формулой
<3-59*
Смысл этого приближения состоит в том, что в числителе формулы добавлена
единица к счетчику числа появлений букв - тем самым мы исключили нулевые
вероятности. К знаменателю пришлось добавить объем алфавита, иначе нару-
шилось бы условие нормировки вероятностей. При увеличении длины п раз-
личие между формулами (3.58) и (3.59) становится несущественным, их можно
считать асимптотически эквивалентными. Однако при длине п, сопоставимой
с объемом алфавита М оценки, подсчитанные по формуле (3.59) будут зна-
чительно меньше несмещенных оценок (3.58), поэтому затраты на кодирова-
ние букв (минус логарифмы вероятностей букв) будут заметно больше. Отсюда
следует, что для коротких последовательностей формула (3.59) неэффективна.
122
Глава 3. Универсальное кодирование
Пример 3.6.1. Кодируем последовательность
IF_WE_CANNOT_DO_AS_WE_WOULD_WE_SHOULD_DO_AS_WE_CAN
Чтобы определить длину кодового слова, нужно вычислить число (7, представ-
ляющее собой оценку вероятности последовательности. До начала кодирования
(7 = 1. После кодирования буквы «I» в соответствии с (3.59) G = 1/256 и т.д.,
в результате шаг за шагом получим
G = 1 J_J_	=
256 257 258 259 260 261 ’' ’
12!(5!)2(4!)3(3!)2(2!)3
256-...-305 ' ’
Длина кодового слова
I = [- log G] + 1 = 342 бит.	(3.60)
Вывод нижней границы избыточности подсказывает, что, возможно, смещение
оценки в (3.59) выбрано не лучшим способом. Попробуем подставить смещение
1/2. Получим
й / ч _ т„(а) + 1/2 _ 2тп(а) + 1
Рп{ ’ п + М/2 2п + М '
(3.61)
Пример 3.6.2. Для той же последовательности входных данных, что и в преды-
дущем примере, с использованием оценки (3.61) получим
g = 1	=
256 258 260 262 264 266
23!!(9!!)2(7!!)3(5!!)2(3!!)3
256 •...•305
Здесь и дальше используются обозначения
(2n — 1)!! = 1 х 3 х ... х (2n — 1),
(2п)!! = 2 х 4 х ... х (2п).
Новая длина кодового слова
I = |-_ log (71 + 1 = 323 бит.	(3.62)
Отметим, что простое усовершенствование формулы дало заметный выигрыш
в эффективности кодирования. Еще более практичен подход, основанный на
введении в алфавит дополнительной буквы, которую мы назовем esc-символом.
Название буквы, как мы увидим позже, вполне соответствует способу ее приме-
нения.
Тем буквам алфавита, которые уже встречались в последовательности из п пред-
шествующих букв, приписываются вероятности
Рп(а) = 7^Г7> Тп(а)>0.
п +1
3.6. Адаптивное кодирование
123
Если же в момент времени n+1 появилась буква, которой ранее ни разу не было,
то передается esc-символ, которому приписывается вероятность
Pn(esc) = ——,
п + 1
а затем передается сама буква (при этом всем буквам, которые не встречались,
приписываются одинаковые вероятности).
Эту стратегию кодирования (называемую A-алгоритмом) можно подытожить
в виде следующей формулы:
Рп(а) = <
п + 1 ’
1 1
(3.63)
если тп(а) = О,
< п + 1 М — Мп ’
где Мп обозначает число различных букв, содержащихся в последовательности
длиной п. Подход, основанный на использовании esc-символа, мы исследуем
далее на примере, а затем оценим его эффективность применительно к произ-
вольному дискретному постоянному источнику.
Пример 3.6.3. (Алгоритм А.) Снова кодируем последовательность
IF WE CANNOT DO AS WE WOULD WE SHOULD DO AS WE CAN
После выполнения первых шагов кодирования в соответствии с (3.63) имеем
С=1
2 256 3 255 '
Следующему появлению пробела будет соответствовать сомножитель 1/6, тре-
тьему пробелу - сомножитель 2/13,..., последнему - 11/47. Получим
11!(4!)2(3!)3(2!)2	1
50!	256-255-...-242’
Следовательно, длина кодового слова
I = logG"! +1 = 291 бит.
(3.64)
Результат получился почти такой же, как при нумерационном кодировании, хотя
данный алгоритм является однопроходным. Таким образом, возможность «загля-
нуть в будущее» в данном примере не дает большого выигрыша в кодировании.
Эти вычисления легко обобщаются на случай произвольной последовательности
х = (ж1,..., хп) с композицией (л,..., тм). Получим
мп
м,

(М-Мп)! _
М\
Мп
А г‘(М-Мп)!
п! мп
М! П Тг
п!
М"м(п + 1)"м
124
Глава 3. Универсальное кодирование
Применим асимптотические оценки из параграфа 3.2. Повторив выкладки, исполь-
зованные при выводе (3.34), получим следующий результат.
ТЕОРЕМА 3.8. При адаптивном арифметическом кодировании дискретного посто-
янного источника с объемом алфавита М и энтропией Н средняя скорость коди-
рования удовлетворяет неравенству
Д^Н+^(п + 1) + К
2 п
где величина К не зависит от длины последовательности п.
(3.65)
Заметим, что асимптотические оценки эффективности адаптивного кодирова-
ния получаются примерно такими же, как и при нумерационном кодировании.
Это вполне согласуется с данными, полученными в примере 3.6.3 для короткой
последовательности на выходе источника.
Отметим, что алгоритм А (формула (3.63) ) - простой для понимания и анализа,
но не самый лучший. Действительно, после кодирования первой буквы источ-
ника на втором шаге мы имеем равные вероятности esc-символа и единствен-
ного известного кодеру и декодеру первого символа. Это не совсем справедливо,
поскольку с esc-символом ассоциируются все остальные буквы алфавита. Веро-
ятно, кодирование станет более эффективным, если на первых шагах esc-символ
будет иметь больший вес, но с течением времени приписываемая ему вероятность
будет уменьшаться.
Рассмотрим альтернативную оценку
Рп(а) = <
тп(а) - 1/2
п
Мп 1
2п М — Мп
если тп(а) > 0;
если тп(а) = 0.
(3.66)
Кодирование с использованием этой оценки назовем D-алгоритмом. Легко убе-
диться, что условие нормировки выполняется и что по сравнению с А-алгоритмом
заметно увеличена вероятность, приписываемая новым символам, по крайней
мере, на первых шагах кодирования. Проверим эффективность D-алгоритма на
том же примере.
Пример 3.6.4. (Алгоритм D.) После нескольких первых шагов имеем
11213141 15 1
” 1 ’ 2 256 4 255 6 254 8 253 10 12 252 “
Заметим, что в знаменателе - произведение двух арифметических прогрессий:
(2 х 4 х ... х 100) х (256 х 255 х ... х 242).
В числителе esc-символы породят произведение 1х2хЗх...х14, а каждая буква,
появившаяся т раз, вызовет появление произведения 1хЗх5х... х(2т - 3).
’ полом для всей последовательности получим
3.7. Сравнение алгоритмов
125
(2 х 12 - 3)!!((2 х 5 - 3)!!)2((2 х 4 - З)!!)3((2 х 3 - З)!!)2
G"	100!!	Х
14!
Х 256 • 255 •• 242’
Следовательно, длина кодового слова
I = Г- log G] + 1 = 283 бит.
Результат получился лучше, чем при кодировании по A-алгоритму, и в точности
такой же, как и при нумерационном кодировании. Таким образом, снова убеж-
даемся, что возможность «заглянуть в будущее» не всегда дает выигрыш при
кодировании.
Остановимся на практических аспектах адаптивного кодирования.
Для некоторых приложений использование арифметического кодирования может
оказаться нецелесообразным. В этом случае оно может быть заменено, например,
кодированием кодом Хаффмена. При этом, поскольку на каждом шаге коди-
рования распределение вероятностей букв меняется, возникает необходимость
построения нового кода Хаффмена после кодирования каждой буквы. На пер-
вый взгляд такой метод кажется неприемлемо сложным, но при ближайшем
рассмотрении оказывается, что он может быть реализован достаточно эффек-
тивно. Эта задача успешно решена в работе Р. Галлагера [44]. Поскольку за один
шаг распределение вероятностей и, соответственно, код Хаффмена сильно изме-
ниться не могут, фактическое число операций, требуемое для модификации кода,
оказывается весьма небольшим.
В завершение параграфа отметим, что формулы алгоритмов А и D совпадают
с оценками условных вероятностей символов при заданном контексте, приме-
няемыми в алгоритмах универсального кодирования РРМА [35] и PPMD [49]
соответственно. Алгоритмы PPM будут рассмотрены в главе 4.
3.7.	Сравнение алгоритмов
Для удобства сравнения алгоритмов их характеристики сведены в табл. 3.5.
В этой таблице в формулах для асимптотической избыточности через п обо-
значена длина последовательности, М- объем алфавита, а величины Кг, i = 1,
..., 5, представляют собой константы, не зависящие от п.
Полученные результаты показывают, что если не принимать во внимание слож-
ность алгоритмов, то предпочтительными являются нумерационное кодирование
и адаптивное арифметическое кодирование. Неожиданным кажется тот факт, что
возможность выполнения двух проходов при кодировании почти не сказывается
на достижимом сжатии. Причина в том, что адаптивное кодирование практиче-
ски оптимально (его избыточность близка к нижней границе), поэтому выигрыш
в принципе большим быть не может.
126
Глава 3. Универсальное кодирование
Таблица 3.5. Сравнение алгоритмов универсального кодирования
Алгоритм	Число проходов	Асимптотическая избыточность	Длина слова для текста (3.16)
Двухпроходное кодирование, код Хаффмена	2	1 + Ki/n	302
Нумерационное кодирование	2	М log п 4- Кз 2п	283
Адаптивное кодирование (алгоритм А)	1	М log п 4- К4 2п	291
Адаптивное кодирование (алгоритм D)	1	М log п 4- К$ 2п	283
3.8.	Задачи
1.	Выберите свою тестовую последовательность и для нее постройте таблицу,
аналогичную табл. 3.5.
Рекомендуем выбрать последовательности из следующего списка:
who chatters to you will chatter about you
шел козел с косой козой, шла коза с босым козлом
либо дождик, либо снег, либо будет, либо нет
на острую косу много и покосу! покоси-ка, коса!
два щенка щека к щеке грызли щетку в уголке
корабли лавировали, лавировали, да не вылавировали!
не узнавай друга в три дня, узнавай в три года
better late than never but better never late
men make houses but women make homes
кукушка хвалит петуха за то, что хвалит он кукушку
четыре чертенка чертили черными чернилами чертеж
can you can a can as a canner сап сап а сап?
early to bed and early to rise makes a man wise
от умного научишься, от глупого разучишься
do not trouble trouble until trouble troubles you!
не имей сто рублей, а имей сто друзей
2.	Для выбранного текста попробуйте вместо (3.61) использовать оценку вида
подбирая а так, чтобы минимизировать длину кодового слова (для выбора
придется воспользоваться компьютером!). Сравните результат с эффективно-
стью алгоритмов А и D.
3.9. Библиографические замечания
127
3.	Описанные в данной главе методы кодирования и их анализ ориентированы
на стационарный источник без памяти, хотя, как мы отмечали, они могут
быть модифицированы и для источников с памятью. Что конкретно нужно
изменять в алгоритмах А и D?
Подсказка, Решению этой задачи, по сути, посвящена следующая глава.
3.9.	Библиографические замечания
Часть материала данной главы приведена в книгах [И] и [4]. Своим представ-
лением об универсальном кодировании автор в большой степени обязан лич-
ным беседам с Ю. М. Штарьковым и его семинарам в Санкт-Петербургском
университете аэрокосмического приборостроения (ГУАП).
Сформулированная в этой главе постановка задачи универсального кодирования
лишь одна (самая простая) из многих, различающихся, в частности, критериями
эффективности и априорными знаниями об источнике. Прочитать об этом можно
в статьях [22], [24], [23].
Детальный анализ сложности методов нумерационного кодирования и метод
с наименьшей сложностью приведены в статье Б. Я. Рябко [16].
Глава 4 Алгоритмы
кодирования
источников,
применяемые
в архиваторах
В главе 2 мы познакомились с методами кодирования при известной статистике
источника. Было показано, что, применяя арифметическое кодирование, можно
получать скорость кодирования, сколь угодно близкую к нижнему пределу -
скорости создания информации источником. Затем в главе 3 мы получили такой
же оптимистический результат и для случая, когда статистические характери-
стики источника неизвестны. Понятно, что методы главы 3 можно применить
к буквенным последовательностям (вместо отдельных букв) и тем самым добить-
ся скорости кодирования, сколь угодно близкой к энтропии на сообщение. Дру-
гой очевидный способ развития этих методов - аппроксимация модели источ-
ника цепью Маркова достаточно высокого порядка. К сожалению, оба этих пути
оказываются непрактичными. Во-первых, их сложность быстро растет с увеличе-
нием длины блока или порядка аппроксимирующей цепи Маркова. Во-вторых,
при кодировании последовательностей конечной длины, в частности, при коди-
ровании типичных файлов пользователей персональных компьютеров, асимп-
тотически оптимальные методы не всегда дают наилучший результат. Точнее
говоря, различные способы кодирования, имея асимптотически эквивалентные
характеристики, существенно различаются по эффективности использования
в реальных условиях.
В данной главе мы опишем наиболее эффективные способы универсального
кодирования источников. Наиболее известные и широко применяемые - методы
Зива-Лемпела. Их описанию предшествует описание так называемых «моно-
тонных» кодов, метода интервального кодирования и метода «стопка книг». Эти
способы входят как составная часть в более сложные алгоритмы кодирования.
Помимо этого, они имеют самостоятельное значение, в частности, часто исполь-
зуются при кодировании видеоинформации.
Далее мы приводим описание алгоритмов-рекордсменов по сжатию - алгоритма
предсказания по частичному совпадению (PPM) и алгоритма Барроуза-Уилера.
4.1. Монотонные коды
129
В завершение главы мы обсудим критерии сравнения эффективности архивато-
ров и приведем характеристики лучших из них.
Точный анализ практических алгоритмов кодирования сложен и выходит за рамки
данного курса. Однако, как мы увидим из описания алгоритмов, они являются
естественным развитием асимптотически эффективных теоретико-информацион-
ных методов, описанных в предыдущих главах.
4.1.	Монотонные коды
Все рассмотренные в главе 3 универсальные кодеры, однопроходные и двух-
проходные, используют при кодировании полученные тем или иным способом
оценки вероятностей букв источника. Если объем алфавита очень велик (напри-
мер, если в качестве алфавита рассматриваются не отдельные буквы, а пары,
тройки букв), то хранение и модификация информации о каждой букве потре-
бует значительных затрат памяти и времени. В этих случаях достаточно эффек-
тивными оказываются простые методы универсального кодирования, которым
посвящен данный параграф.
Последовательность букв источника будет преобразовываться в последователь-
ность натуральных чисел, поэтому нам понадобятся префиксные коды беско-
нечного объема. Префиксный код множества натуральных чисел N={1,2,...} мы
будем называть монотонным, если для любых i,j G N, i < j, длины соответству-
ющих кодовых слов Ц и lj удовлетворяют неравенству Ц lj.
Приведем несколько примеров монотонных кодов.
Унарный код. Напомним, что запись вида 0т или 1т означает серию из т нулей
или единиц соответственно. Унарный код сопоставляет числу г двоичную комби-
нацию вида Г^О. Например, унарными кодами чисел 1, 2 и 3 являются после-
довательности unar(l)=0, unar(2)=10 и unar(3)=110 соответственно. Длина кодо-
вого слова для числа i равна Ц = i.
Нетрудно проверить, что унарный код оптимален (минимизирует среднюю длину
кодовых слов), если числа i распределены по геометрическому закону
Pi = (1 —	i = 1,2,...
с параметром а = 1/2, то есть при pi = 2”*, i = 1, 2, ... . Для значений а > 1/2
более эффективен код Голомба.
Код Голомба [47]. Введем параметр Т = 2т. Код Голомба для числа i состоит
из двух частей. Первая часть - унарный код числа [i/Tj + 1, вторая - двоичная
запись остатка от деления г на Г в виде последовательности длины т . Очевидно,
что длина кода Голомба для числа г равна Ц = \г/Т\ +1+т. Например, при т = 3
и i = 21 имеем [i/T\ + 1 = 3, остаток равен 5. Поэтому кодом Голомба числа 21
будет последовательность (И0)( 101)=110101.
В технической литературе код Голомба иногда называют кодом Райса.
Код Галлагера-Ван Вухриса [45] - естественное обобщение кода Голомба на слу-
чай, когда параметр Т не является степенью двойки. Как и в коде Голомба,
130
Глава 4. Архиваторы
префикс - это закодированное унарным кодом число [г/Т| +1. Далее следует дво-
ичный код остатка. Если log Т не целое число, то для представления некоторых
(меньших) значений остатка от деления г на Т используется m = [log Т\ бит, а
для остальных (больших) значений используется m +1 бит. Точнее говоря, оста-
ток кодируется кодом Хаффмена в предположении, что все значения остатка
равновероятны (см. задачу 4. в главе 2). Например, при Т = 5 кодовыми сло-
вами для значений остатков 0, 1, 2, 3 и 4 будут последовательности 00, 01, 10,
110 и 111 соответственно. В частности, при Т = 5 числу 21 соответствует кодовое
слово (1110)(01=111001), а числу 24 - слово (1110)(111)= 1110111.
Оптимальное значение параметра Т для кода Галлагера-Ван Вухриса связано
с параметром геометрического распределения а соотношением
ат -F aT+1 1 < ат~1 + ат.	(4.1)
Благодаря чрезвычайно простой схеме кодирования и достаточно высокой эффек-
тивности коды Голомба и Галлагера-Ван Вухриса часто применяют при кодиро-
вании аудио- и видеосигналов. А вот для применения в схемах универсального
кодирования они не очень хороши. Во-первых, нужно знать (или оценивать)
значение параметра Г, во-вторых, длина кодового слова Ц, как и для унарного
кодах линейно растет с увеличением числа г, и для некоторых распределений
вероятностей букв источника такое кодирование может быть неэффективным.
Код Левенштейна [13]. Этот код проще всего объяснить на конкретном при-
мере. Предположим, что нужно передать число i = 21. Двоичное представление
этого числа имеет вид 10101. Непосредственно использовать при кодировании
двоичные представления натуральных чисел нельзя, ибо такой код не будет
префиксным. Самый простой выход состоит в том, чтобы приписать в начале
слова префикс, указывающий длину двоичной записи числа (в данном случае
это число 5). Если это число закодировать префиксным (например, унарным)
кодом и приписать слева к двоичной записи числа, то код получится одно-
значно декодируемым. В данном примере для числа 21 получим кодовое слово
(11110)(10101)=1111010101. В общем случае длина двоичного представления
будет равна 2 [log г].
Теперь будем пошагово улучшать этот способ кодирования. Заметим, что первая
значащая цифра двоичной записи числа - всегда 1. Ее можно не передавать,
декодер сам допишет недостающую единицу, если будет знать длину двоич-
ной записи. Обозначим через bin (г) двоичную запись натурального числа i без
первой единицы, прямыми скобками обозначается длина двоичной последова-
тельности. Итак, простой монотонный код числа г имеет следующую структуру:
шоп(г) = (unar (|bin (г)| + 1) ,bin (г)) .	(4.2)
Например, mon(21)=(unar(5),0101)=ll 1100101.
Длины кодовых слов этого монотонного кода
li = 2 [log г J + 1.
(4.3)
4.1. Монотонные коды
131
Чтобы сделать запись еще короче, с длиной двоичной записи можно посту-
пить так же, как и с самим числом, то есть передать его значащие разряды
(кроме первой единицы), затем длину двоичной записи числа значащих разрядов
и т. д. Итерации продолжаются, пока не останется один значащий разряд. Чтобы
декодирование было однозначным, достаточно приписать префикс, содержащий
закодированное префиксным кодом число итераций. Заметим, что минимальное
число итераций равно 0 (при кодировании числа 1). Поэтому в качестве пре-
фиксного кода можно выбрать унарный код увеличенного на 1 числа итераций.
Полученное кодовое слово будет кодовым словом кода Левенштейна.
Например, для числа 21 вычисляется bin/(21)=0101, затем bin/(4)=00, bin/(2)=0.
Число итераций равно 3, поэтому кодовое слово кода Левенштейна имеет вид
lev(21) = (1110)(0)(00)(0101) = 11100000101.
Декодер кода Левенштейна сначала узнает, что итераций было 3. Прочитав один
значащий разряд (0) и дописав к нему в начало 1, получает последовательность
10. Это означает, что на предпоследней итерации длина числа была 2. Прочитав
2 разряда и дописав слева 1, получает 100. Теперь декодер считывает 4 разряда
и дописывает слева 1. Получается последовательность 10101, ей соответствует
число 21. Поскольку это уже последняя, 3-я, итерация, то число 21 является
результатом декодирования.
В табл. 4.1 приведены кодовые слова, полученные по правилу (4.2) и кодо-
вые слова кода Левенштейна для некоторых чисел натурального ряда и длины
кодовых слов.
Упрощенный код Левенштейна (код Элайеса).
Более простой код приведен в работе Элайеса [39]. Числу i = 1 припишем кодо-
вое слово elias(l)=0. Для чисел i > 1 кодовые слова вычисляются по следующем
правилу:
elias(z)=(unar(|bin'(|bin (г)|)|+2), bin'(|bin’(z)|), bin'(i))	(4.1.4)
То есть кодовое слово состоит из 3 частей. Справа (в третьей части) записано дво-
ичное представление числа без первой единицы. Ей предшествует вторая часть,
в которой пишется двоичное представление длины третьей части, тоже без пер-
вой единицы. Наконец, в первой части записан унарный код увеличенной на 2
длины второй части кодового слова.
Например, для числа 21 кодовое слово имеет вид
elias(21) = (1110)(00)(0101) = 1110000101.
Длина кодового слова кода Элайеса для произвольного числа i
li = ( lj 1 = 11	(4.4)
|_logzj 4- 2 |_log [logzjj + 2, г > 1,
и, следовательно, удовлетворяет неравенству
li	log г 4- 21og(l 4- log г) 4- 2, i = 1,2,... .	(4.5)
132
Глава 4. Архиваторы
Во втором слагаемом добавлена 1 под знаком логарифма, чтобы придать смысл
этому выражению при г = 1.
Таблица 4.1. Таблица монотонных кодов некоторых чисел
г	Монотонный код (4.2)		Код Левенштейна		Код Элайеса	
	шоп(г)	li	lev(i)	li	elias(i)	li
1	0	1	0	1	0	1
2	100	3	100	3	100	3
3	101	3	101	3	101	3
4	11000	5	110000	6	110000	6
		5		6		6
7	11011	5	110011	6	110011	6
8	1110000	7	1101000	7	1101000	7
		7		7		7
15	1110111	7	1101111	7	1101111	7
16	111100000	9	11100000000	И	1110000000	10
		9		И		10
31	111101111	9	11100001111	И	1110001111	10
32	15005	И	111000100000	12	11100100000	и
				12		и
63	1501®	и	111000111111	12	11100111111	и
215	1150015	31	140111111015	26	1501111015	25
21023	|1023qq1023	2047	14ОЮО119О1023	1041	11оО1эЮ1023	1043
Чтобы численно сравнить три монотонных кода, обратимся к табл. 4.1. Как ни
странно, простейший код (4.2) в большинстве случаев дает наилучший результат,
но для него длина кодовых слов растет с увеличением i быстрее, чем для двух
других кодов. Это видно, в частности, из сравнения формул (4.3) и (4.4). Коды
Левенштейна и Элайеса практически эквивалентны, и выигрыш кода Левен-
штейна проявляется только при астрономически больших значениях г.
Следующая теорема проясняет роль монотонных кодов в универсальном коди-
ровании источников.
ТЕОРЕМА 4.1. Пусть случайная величина i принимает значения из множества
чисел натурального ряда и распределение вероятностей случайной величины удо-
влетворяет условию: pi С pj, если i > j. Тогда при использовании кода Элайеса
средняя длина кодовых слов [удовлетворяет неравенству
1^Н(1 + о(Н)),
где через Н обозначена энтропия случайной величины I, и о(Н) —► 0 при Н —> оо.
4.2. Интервальное кодирование и метод «стопка книг»
133
Доказательство. Прежде всего, из упорядоченности вероятностей по убыванию
и условия нормировки вероятностей вытекают неравенства
Pi < - , г < —, i = 1,2,... .	(4.6)
г	Pi
Из (4.5) имеем
оо	оо
I = 52liPi 52р*(1о8 * + 2 log log г + 2)
г=1	г=1
ОС	1	ОО	Z	- \
VpUog— +2VpUog ( 1 + log —) +2 Я + 21og(l + Я) -I-2.	(4.7)
Здесь первое неравенство основано на (4.5), второе использует (4.6). Последнее
неравенство основано на выпуклости А функции log ж. Из (4.1) следует утвер-
ждение теоремы.	□
Теорема 4.1 утверждает, что монотонный код с длиной г-ro кодового слова порядка
log i + 2 log log i обеспечивает достаточно эффективное кодирование для любого
источника с монотонно убывающими вероятностями букв. Поскольку буквы все-
гда можно перенумеровать, то при кодировании можно не знать значения веро-
ятностей букв, а достаточно знать только, как эти вероятности упорядочены.
За отсутствие точной информации о вероятностях букв мы платим избыточно-
стью кодирования. При точно известных вероятностях побуквенное кодирование
имеет избыточность не больше 1. Избыточность универсального монотонного
кода имеет порядок 2 log Я -I- 2, что может быть приемлемым только при очень
больших значениях энтропии источника Я.
Отметим также простоту реализации кодирования. В отличие, например, от кода
Хаффмена, нет необходимости в хранении таблиц кодовых слов. Кодирование
и декодирование сводятся к вычислениям по приведенным выше достаточно
простым формулам.
4.2.	Интервальное кодирование
и метод «стопка книг»
В этом параграфе мы рассмотрим два способа взаимно однозначного преобра-
зования последовательности букв источника в последовательность чисел нату-
рального ряда. При определенных условиях (например, при сильной зависимости
букв) побуквенное кодирование преобразованной последовательности оказыва-
ется заметно более эффективным, чем кодирование исходной последовательно-
сти источника.
Начнем с интервального кодирования.
134
Глава 4. Архиваторы
Пусть X = {0,1,..., М—1} - алфавит источника и на выходе источника наблюда-
ется последовательность х-^ ж2,... . Алгоритм описывается рекуррентно. Предпо-
ложим, что начальная часть последовательности х^1 = (a?i,... уже зако-
дирована и передана и, следовательно, известна декодеру. Вместо буквы хп пере-
дается длина интервала (количество букв) между предыдущим и текущим появ-
лением данной буквы. Иными словами, кодер вычисляет и передает минимальное
число гп = г такое, что хп_г = хп. Тем самым исходная последовательность х^,
х2,... преобразуется в последовательность чисел п, г2, ... .
Для завершения описания алгоритма нужно определить правило вычисления
интервалов для тех букв, которые не встречались в последовательности а™"1.
Проще всего условиться о том, что первой передаваемой букве предшествовали
все буквы алфавита в заранее согласованном (для определенности, в алфавит-
ном) порядке.
Опишем метод «стопка книг».
Этот метод переоткрывался разными авторами и имеет несколько названий. По-
видимому, первым его описал и проанализировал его эффективность Б. Я. Рябко
[15]. Заметно позже в точности тот же алгоритм описан в [26] под названием
«move-to-front coding». Именно под таким названием он чаще всего упомина-
ется в технической литературе. Еще раз он открыт в [39] и назван «recency rank
coding». Это последнее название, которое можно перевести как «кодировайие
степени новизны», наиболее точно отражает суть дела.
Как и при кодировании длин интервалов, предположим, что начальная часть
последовательности я™-1 = (xi,... ,xn-i) уже закодирована и передана и, сле-
довательно, известна декодеру. Но теперь вместо буквы хп передается количе-
ство различных букв между предыдущим и текущим появлением данной буквы.
Иными словами, кодер вычисляет минимальное число гп = г такое, что хп_г = хп.
Затем вычисляется число dn различных букв в последовательности Тем
самым исходная последовательность xi, х2, ...преобразуется в последователь-
ность чисел di, d2, ... .
Для передачи букв, которые не встречались в х™можно использовать страте-
гию, описанную выше для интервального кодирования.
Пример 4.2.1. Пусть источник с алфавитом X = {а, Ь, с} породил последова-
тельность cabbbabbac. Рассмотрим работу двух методов кодирования в предполо-
жении, что по умолчанию кодеры (и декодеры) считают, что этой последователь-
ности предшествовала последовательность abc. Тогда при интервальном кодиро-
вании будет получена последовательность 0,3,3,0,0,3,1,0,2,9. При кодировании
с помощью стопки книг получим последовательность 0,2,2,0,0,1,1,0,1,2.
Поясним происхождение названия «стопка книг». Предположим, что студент,
готовясь к экзамену, сложил книги стопкой на столе. Всякий раз, выбирая из
стопки нужную книгу, после использования, он не возвращает книгу на свое
место, а кладет ее сверху. Верхняя книга теперь имеет наименьший номер, а
номера книг, которые раньше находились выше нее, увеличились на 1. Сколько
4.2. Интервальное кодирование и метод «стопка книг»
135
книг находятся выше данной? Ровно столько, сколько различных книг исполь-
зовалось между текущим и предыдущим использованием данной книги. Таким
образом, последовательность di, d2, ...и есть последовательность номеров книг,
извлекаемых из стопки.
Пример 4.2.2. Применим «стопку книг» к пословице
IF_WE_CANNOT_DO_AS_WE_WOULD_WE_SHOULD_DO_AS_WE_CAN
Для этого вместо букв нужно подставить их номера в таблице ASCII-кода.
В частности, пробелу соответствует число 32, а буквам A...Z - числа 65...90.
Результатом будет последовательность чисел
74, 72, 35, 88, 73, 3, 72, 71, 80, 1, 81, 86, 6, 76, 4, 3, 6, 86, 3, 10, 10, 3, 3, 6, 87, 83, 9,
6, 6, 7, 3, 8, 81, 9, 9, 9, 9, 7, 2, 5, 3, 10, 8, 3, 10, 10, 3, 13, 6, 13
Применим универсальный монотонный код, описываемый формулой (4.2). Зат-
раты на передачу последовательности составят 332 бита.
С одной стороны, мы получили заметное сжатие по сравнению с исходными
затратами, составляющими 50x8=400 бит. С другой стороны, сравнивая этот
результат с другими, приведенными в табл. 3.5, видим, что данный способ нес-
колько проигрывает тем, которые рассматривались в главе Д. Этот проигрыш -
адекватная плата за простоту реализации.
Нетрудно понять, почему описанные методы преобразования потоков данных
могут быть полезны при универсальном кодировании. Чем больше вероятность
буквы, тем короче интервалы между ее появлениями. После преобразования
последовательности источника в последовательность интервалов или последова-
тельность номеров в стопке книг наиболее вероятными будут малые числа. Тем
самым создаются предпосылки для успешного применения монотонных кодов,
описанных в предыдущем параграфе. Из описания двух алгоритмов следует, что
с точки зрения применения монотонных кодов метод стопки книг предпочти-
тельнее, поскольку порождает числа, меньшие или равные числам, порождаемым
интервальным кодером.
Ниже мы приводим верхнюю оценку средней скорости интервального кодиро-
вания, поскольку его анализ существенно проще. Понятно, что эта же граница
верна и для сжатия «стопкой книг».
ТЕОРЕМА 4.2. Пусть Н(Х) - энтропия одномерного распределения дискретного
стационарного источника. Средняя скорость интервального кодирования в соче-
тании с использованием кода Элайеса удовлетворяет неравенству
Я^Я(Х)(1 + о(Я(Х))),
где о(Н) —> 0 при Н оо.
Доказательство. Обозначим через п(а) длину интервала между г-м и (г - 1)-м
появлениями буквы х = а и через Ц(а) соответствующие затраты на передачу
буквы. В соответствии с оценкой (4.5)
136
Глава 4. Архиваторы
li(a) logn(a) + 21og(l + logn(a)) + 2.	(4.8)
Обозначим через 1(a) и г (а), соответственно, средние (по множеству последова-
тельностей источника) затраты на передачу буквы а и среднюю длину интер-
вала между появлениями буквы а. В силу выпуклости логарифма из (4.8) после
усреднения получаем
1(a) log f(a) + 2 log(l + log f(a)) + 2.	(4.9)
В соответствии с леммой Каца (Кас) (ее доказательство приведено ниже) имеет
место неравенство
,(«) 4 А,.	(4.10)
Подставим эту оценку в (4.8) и усредним по всем буквам алфавита. Далее снова
используем выпуклость логарифма. В результате получим
R = ^р(а)1(а) < Н(Х) + 2log(1 + Я(Х)) + 2.
а
Отсюда следует утверждение теоремы.	□
Итак, преобразование потока данных с помощью интервального кодирования или
кодирования по методу «стопки книг» с последующим применением кода Левен-
штейна (или кода Элайеса) гарантирует достаточно эффективное универсальное
кодирование при простой реализации кодера и декодера. Эти методы не требуют
накопления статистических данных об источнике и построения соответствую-
щего кода источника. Подобные идеи лежат в основе алгоритмов Зива-Лемпела,
изучаемых в следующих параграфах.
Сформулируем и докажем вспомогательное тождество, которое ниже нам потре-
буется в доказательстве леммы Каца.
ЛЕММА 4.3- Пусть случайная величина г принимает значения из множества нату-
ральных чисел {1,2,...} в соответствии с распределением вероятностей {pi,i =
= 1,2,...}. Тогда
оо
=	(4.11)
J=1
Доказательство. Напомним, что Р(г > j) = £^Pi. Нетрудно заметить, что
сумма в правой части содержит каждое слагаемое pi ровно i раз. Следовательно,
эта сумма равна математическому ожиданию г.	□
В теории вероятностей для дискретного случайного процесса хо, ...длины
интервалов между одинаковыми значениями процесса xt = а называют временем
возвращения процесса в состояние а. Более точно, время возвращения в состояние
а для стационарного процесса определяется как
г = min{& 1 : xq = Xk = а}.	(4.12)
Распределение вероятностей времени возвращения в а определяется формулой
Qa(r) = Р(ж1,... ,#r-i / а,хг = а|#о = а),	(4.13)
4.2. Интервальное кодирование и метод «стопка книг»
137
соответственно, среднее время возвращения в а
ОО
Га = ^rqa(r).	(4.14)
Г=1
ЛЕММА 4.4. {Лемма Каца.) Для дискретного стационарного источника такого,
что р(а) > 0 справедливо соотношение
гар(а) = Р(хп = а хотя бы для одного п, n = 0,1,...).	(4.15)
В частности, для эргодического источника
Доказательство. Рассмотрим произведение в левой части (4.15). Воспользовав-
шись леммой 4.3, получим
оо	оо
тар{а) = p(a)^\qa(r) =p(a')'^Qa(t),	(4.17)
t=l	t=l
где использовано обозначение
оо
QoW =	= Р(Г t).
j=t
Событие r t (время возвращения в а не меньше t) имеет место в том случае,
когда вслед за буквой а порождены t букв, ни одна из которых не совпадает с а,
то есть
Qa(fy = Р(я*1, • • • , Xt ф0 ~ •
Подстановка этого выражения в (4.17) дает
оо
гар(а) — Р(х0 = а)^2Р(а:1,...,ж4 а\х0 = а) =	,
t=i
оо
= У^Р(ж0 = a,x1,...,xt ^а).
t=i
Первое равенство основано на стационарности источника, второе - на опреде-
лении условной вероятности.
Введем в рассмотрение еще одно распределение вероятностей на множестве после-
довательностей источника. Это новое распределение соответствует инверсии во
времени последовательностей исходного источника, обозначим его как р(х),
х е Хп, п = 1, 2, .... Для произвольного п и любой последовательности х =
= (®i,... ,хп) обозначим через V последовательность, полученную из х инвер-
тированием порядка следования символов, то есть V = (жп,..., a?i). По определе-
нию, р^х) = р(х). Вероятности, вычисленные относительно этого распределения,
138
Глава 4. Архиваторы
будем обозначать как Р( ). Из последнего равенства с учетом стационарности
инверсного процесса имеем
оо
raPa(t) = 52 Р(ж0,..., Xt-1 / a,xt = а) =
t=l
= P(xt = а хотя бы для одного t = 1,2,...).
Вероятности появления хотя бы одной буквы а для исходного процесса и инверс-
ного одинаковы, тем самым доказано первое утверждение леммы. Для любого
эргодического процесса и любой буквы а такой, что р(а) > 0 эта вероятность
равна 1, из чего следует второе утверждение.	□
4.3.	Метод скользящего словаря (LZ-77)
Этот алгоритм после его опубликования Зивом и Лемпелом в статье [59] был
многократно модифицирован, некоторые модификации получили самостоятель-
ные названия с аббревиатурами вида LZX, где X - первая буква имени автора
модификации. В конце параграфа мы коротко обсудим практические аспекты
применения алгоритма, в частности, простые усовершенствования, повышающие
коэффициент сжатия. Начнем с формального описания алгоритма.
Параметром алгоритма является длина «окна наблюдения» W. Эту величину
можно также интерпретировать как «объем скользящего словаря».
Пусть Х = {0,1,...,М — 1} - алфавит источника и на выходе источника наблю-
дается последовательность xi, х2, ..., хп. Алгоритм работы кодера показан на
рис. 4.1. Кодер LZ-77 хранит в памяти скользящий словарь объемом W. Сло-
вами словаря служат всевозможные подпоследовательности следующих друг за
другом букв, содержащиеся в последних W буквах источника. При поступлении
на вход кодера очередных букв источника кодер находит как можно более длин-
ную последовательность, уже имеющуюся в словаре. В канал передается флаг
(1 или 0), указывающий на то, найдено или нет подходящее словарное слово.
В случае успеха (флаг равен 1) словарное слово передается указанием удале-
ния начала слова от текущей позиции и длины словарного слова. Расстояние до
слова d передается равномерным кодом, а длина слова (длина совпадения) I -
некоторым неравномерным кодом. Например, можно воспользоваться любым из
монотонных кодов. Если же словарного слова не нашлось, передается значение
флага, равное 0, и за ним следует очередная буква источника, передаваемая «без
кодирования».
Пример 4.3.1. Применим алгоритм LZ-77 к пословице
IF_WE_CANNOT_DO_AS_WE_WOULD_WE_SHOULD_DO_AS_WECAN
Условимся, что длины слов I кодируются монотонным кодом (4.2). Результаты
работы алгоритма шаг за шагом отображены в примере 4.3.1. В этой таблице Ьгп(-)
обозначает стандартный 8-битный код буквы, в графе «расстояние» в скобках
4.3. Метод скользящего словаря (LZ-77)
139
Заданы:
алфавит источника X = {0,1,..., М — 1};
длина «окна» W
Input: Длина последовательности п;
Последовательность источника ж = ж?;
Output: Кодовое слово с для х\
Инициализация:
N = 0, с - «пустое» слово;
while N < п do
Находим максимальное I такое, что ж$£| =
для некоторого de {1,..., РИ};
if I > 0 then (последовательность найдена)
►	к кодовому слову с дописываются:
флаг 1;
расстояние до образца d в виде двоичной
последовательности длины [log ТУ];
длина совпадения I в виде слова неравномер-
ного префиксного кода;
else (последовательность не найдена)
►	к кодовому слову с дописываются:
флаг 0;
новая буква xn+i в виде двоичной
последовательности длины [log М~\;
►	+
end

Рис. 4.1. Алгоритм LZ-77
указана текущая длина окна. От нее зависит число бит, отводимое на пере-
дачу расстояния между текущей позицией и найденным в таблице образцом.
Суммарные затраты на передачу последовательности составили 257 бит.
Пример показывает, что алгоритм LZ-77 существенно выигрывает по сжатию
по сравнению с логически более сложными методами главы 3. Больше того, из
табл. 4.2 видно, что эффективность алгоритма быстро растет по мере увеличения
объема скользящего словаря W.
Математический анализ алгоритма сложен и выходит за рамки данного пособия.
Однако следующие рассуждения позволяют понять характер поведения алго-
ритма с увеличением объема слораря. Действительно, длина кодовой последо-
вательности, сопоставляемой отрезку составляет
~ 1 + log(W9 + 2 log I бит.
140
Глава 4. Архиваторы
Таблица 4.2. Метод скользящего словаря (LZ-77)
Шаг	Флаг	Последовательность букв	d	I	Кодовая последовательность	Биты
0	0	I	—	0	0 bin(I)-0	9
1	0	F	-	0	0 bin(F)	9
2	0		—	0	0 bin(_)	9
3	0	W	—	0	0 bin(W)	9
4	0	Е	-	0	0 bin(E)	9
5	1		2(5)	1	1 010 0	5
6	0	С	—	0	0 bin(C)	9
7	0	А	-	0	0 bin(A)	9
8	0	N	—	0	0 bin(N)	9
9	1	N	0(9)	1	1 0000 0	6
10	0	О	-	0	0 bin(O)	9
11	0	Т	—	0	0 bin(T)	9
12	1		6(12)	1	1 0110 0	6
13	0	D	—	0	0 bin(D)	9
14	1	О	3(14)	1	1 0011 0	6
15	1		2((15)	1	1 0010 0	6
16	1	А	8(16)	1	1 01000 0	7
17	0	S	-	0	0 bin(S)	9
18	1	_WE_	15(18)	4	1 01111 11000	11
19	1	W	2(22)	1	1 00010 0	7
20	1	О	8(23)	1	1 01000 0	7
21	0	и	—	0	0 bin(U)	9
22	0	L	—	0	0 bin(L)	9
23	1	D	12(26)	1	1 01100 0	7
24	1	_WE_	8(27)	4	1 01000 11000	11
25	1	S	13(28)	1	1 011010	7
26	0	н	—	0	0 bin(H)	9
27	1	OULD_	9(33)	5	1 001001 11001	12
28	1	DO_AS_WE_	24(38)	9	1 011000 1110001	14
29	1	CAN	40(47)	3	1 101000 101	10
Итого						257
Эти биты потрачены на передачу I букв источника. Заметим, что с увеличением
объема словаря увеличиваются длины последовательностей, которые кодер нахо-
дит в словаре. Таким образом, при больших W (и, соответственно, Z) «мгновенная
скорость» кодирования
4.3. Метод скользящего словаря (LZ-77)
141
К(<Й>«	+	_ ЦИ2 + о(!).
где о(Г) —> 0 при увеличении W и Z. Теперь нужно установить связь между W и
I при больших W. Понятно, что сочетание букв, имеющее вероятность р, встре-
тится в словаре объемом W примерно pW раз. (Это, в частности, видно из леммы
Каца, которая устанавливает, что средние интервалы между такими событиями
имеют длину 1/р). Если pW » 1, то, вероятнее всего, сочетание букв имеет
продолжение, которое также имеется в словаре. Отсюда следует, что число появ-
лений типичных согласованных последовательностей в окне длиной W невелико
и что при больших W имеет место приближенное соотношение
где К - константа. Подставив это соотношение в выражение для скорости коди-
рования, получим
Усредняя по множеству последовательностей источника, приходим к приближен-
ному равенству
- Н^Х).
I—>ОО	I
Можно оценить скорость убывания избыточности с увеличением W. Основной
вклад в избыточность вносит слагаемое, связанное с необходимостью передачи
длины согласованного отрезка, то есть избыточность имеет порядок (logZ)/Z.
Поскольку асимптотически (для типичных последовательностей) W пропорцио-
нально log Z, то асимптотическое поведение избыточности кодирования с увели-
чением W определяется формулой
р _ TJ ( ул
R ДхДА)- logly •
Напомним, что скорость убывания избыточности универсального кодирования
последовательности длины п для методов главы 3 имеет порядок logn/n. Это
означает, что избыточность алгоритма LZ-77 убывает (асимптотически) намного
медленнее. Тем не менее соотношение между сложностью алгоритма и сжатием
именно для этого алгоритма оказалось едва ли не самым лучшим среди известных
на сегодняшний день алгоритмов.
Рассмотрим коротко некоторые аспекты практической реализации алгоритма и
его основные модификации.
Обсудим сложность алгоритма. Прежде всего, очевидно, сложности кодирова-
ния и декодирования не равны. Вычислительная сложность декодирования очень
низкая. Декодер непосредственно из битового потока получает информацию о
том, начиная с какой буквы и какой длины последовательность букв он должен
извлечь из памяти и выдать получателю.
142
Глава 4. Архиваторы
Напротив, кодер для каждого из значений I = 1, 2,.. .должен повторить попытку
поиска в окне длиной W (типичные размеры окна составляют от 2048 до 16384
символов) образцов, совпадающих с вновь поступившими буквами источника.
Такая «прямолинейная» реализация алгоритма неприемлемо сложна. Применя-
емые в архиваторах кодеры для быстрого поиска образцов в словаре кодера
используют хеширование.
Рассмотрим подробнее алгоритм работы быстрого кодера, использующего алго-
ритм LZ-77. Прежде всего, заметим, что с увеличением длины окна ссылки на
последовательности из 1 или 2 символов становятся неэффективными. Такие
последовательности проще передать по одной букве, затрачивая по 9 бит на
букву, как это делается для вновь встретившихся букв. Трехбуквенные после-
довательности рассматриваются как двоичные последовательности длиной 24, и
для них вычисляется хеш-функция, отображающая последовательность длиной
24 в двоичную последовательность длиной 12. Эта последовательность использу-
ется как адрес ячейки памяти, в которой хранится указание на место в окне, где
последний раз встречалось такое же сочетание букв. Эта информация использу-
ется далее при кодировании, а на ее место записывается указание на текущую
позицию.
Кодер, имея информацию о последнем появлении 3-буквенного сочетания, про-
веряет истинную длину совпадения. Далее кодер должен проверять другие места
в окне, где были такие же сочетания букв. Некоторые быстрые кодеры этого
не делают, теряя при этом в сжатии информации. Во многих задачах, особенно
при реализации кодеров на БИС, это вполне разумная плата за существенное
упрощение и ускорение работы кодера. Если же требуется более высокое сжа-
тие, необходимо для каждой позиции окна хранить и обновлять информацию о
том, в какой точке окна в последний раз встретилось такое же сочетание букв,
как и в текущей позиции.
С учетом этих упрощений алгоритм LZ-77 на сегодняшний день, пожалуй, самый
быстрый и на основе его модификаций построены практически все архиваторы.
Рассмотрим теперь подходы к повышению эффективности кодирования. Напом-
ним, что на каждом шаге кодирования формируются 3 случайные величины: дво-
ичный флаг, ссылка, принимающая значения из конечного диапазона {1,..., IV},
и длина совпадения, которая теоретически может быть любым натуральным чис-
лом, но на практике большие значения длин встречаются редко.
Один из путей к улучшению кодирования - использование более эффективных
кодов для этих величин, чем рассмотренные выше коды. В частности, можно
использовать адаптивное кодирование на основе арифметического кодирования
или кодов Хаффмена. Эта возможность используется во всех архиваторах.
Поучительной в этом смысле является модификация LZ-77, предложенная Фиала
и Гриине [41]. Ее называют алгоритмом LZFG. Рассмотрим сначала самый про-
стой вариант алгоритма LZFG, приведенный на рис. 4.2.
4.3. Метод скользящего словаря (LZ-77)
143
Заданы:
алфавит источника X = {0,1,..., М - 1}; длина «окна» W
Input: Длина последовательности п;
Последовательность источника х = х™;
Output: Кодовое слово с для ®;
Инициализация:
N = 0, с - «пустое» слово;
while N < п do
Находим максимальное I из диапазона {3,..., 17} такое, что
XN+1 = для некоторого d € {1,..., W};
if I > 2 then
►	к кодовому слову с дописываются:
число I в виде Ненулевой двоичной последователь-
ности длиной 4 (числам I = 3,..., 17 соответствуют
комбинации ООО 1, 1111);
расстояние до образца d в виде двоичной
последовательности длиной [log IV"|;
N+-N +I;
else (Z < 2)
►	к кодовому слову с дописываются:
последовательность 0000;
число букв L G {1,..., 16}, поступающих на выход
кодера непосредственно с выхода источника (без
кодирования), числам 1,..., 16 соответствуют
комбинации 0000,..., 1111
L букв источника, передаваемых без кодирования
в виде двоичных последовательностей длиной [log М~\;
end
Рис. 4.2. Алгоритм LZFG
Как и в LZ-77, на каждом шаге кодирования формируются кодовые комбинации
двух типов, один тип соответствует ссылке на уже содержащиеся в окне последо-
вательности букв, другой тип - непосредственной передаче последовательности
букв источника.
В этом алгоритме длины частей кодовых слов, равные 4, выбраны для того, чтобы
сделать удобной реализацию алгоритма на компьютере с байтовой организацией
памяти. Если выбрать W = 212 = 4096, то в любой из двух веток алгоритма длина
кодовой комбинации кратна 8, то есть составляет целое число байт.
Идея алгоритма понятна - уменьшить затраты битов на передачу тех отдель-
ных букв источника или пар букв, которые нецелесообразно передавать с помо-
щью ссылок на информацию, содержащуюся в скользящем словаре. Насколько
эффективно такое решение, показывает следующий пример.
144
Глава 4. Архиваторы
Пример 4.3.1. Применим алгоритм LZFG к пословице
IF_WE_CANNOT_DO_AS_WE_WOULD_WE_SHOULD_DO_AS_WE_CAN
Чтобы адекватно сравнивать с описанной выше версией алгоритма LZ-77, на
начальном этапе работы алгоритма будем учитывать, что при п < W фактиче-
ская длина окна равна п и для передачи числа d достаточно flogn] бит (вместо
[logW] бит). Результаты работы алгоритма по шагам приведены в табл. 4.3
Во втором столбце в скобках написана реальная длина окна, исходя из кото-
рой определялась необходимая длина записи расстояний до образца. Сопоставив
эту таблицу с табл. 4.2, нетрудно убедиться в том, что на этом коротком при-
мере алгоритм LZFG проиграл алгоритму LZ-77 в основном потому, что слабое
место LZ-77 - ссылки на короткие последовательности (длиной 1...3)- не про-
явило себя на короткой последовательности. Для длинных последовательностей
алгоритм LZFG в среднем эффективнее LZ-77.
Таблица 4.3. Пример использования алгоритма LZFG
Шаг	Длина совпадения	Расстояние до образца	Число «новых» букв	Кодовые символы	Переданные буквы	Затраты (бит)
1	0	—	16	0000 1111 bin(I... _)	IF_WE_ CANNOT _DO_	8+8x16 =136
2	1(<3)	-	2	0000 0001 bin(AS)	AS	8+8x2 =24
3	4	15(18)	—	0010 01111	_WE_	4+5=9
4	1(<3)	-	5	0000 0100 bin(WOULD)	WOULD	8+5x8 =48
5	4	8(27)	-	0010 01000	_WE_	4+5 =9
6	-		2	0000 0001 bin(SH)	SH	8+2x8 =24
7	5	9(33)	—	ООН 001001	OULD_	4+6 =10
8	9	24(38)		0111 011000	DO_AS _WE_	4+6=10
9	3	40(47)	-	0001 101000	CAN	4+6=10
Итого						280
Еще одна возможность увеличения сжатия - устранение избыточности коди-
рования, заведомо присущей описанному алгоритму. Поскольку в скользящем
словаре имеются одинаковые последовательности, одной и той же последова-
4.4. Алгоритм LZW (LZ-78)
145
тельности букв источника могут быть сопоставлены различные кодовые слова.
Поэтому некоторые кодовые слова просто никогда не используются.
В работе [41] описан способ хранения словаря в виде древовидной структуры.
Ребрам дерева соответствуют последовательности букв. Ссылки разрешены только
на узлы дерева. Поскольку число узлов меньше общего числа букв, уменьшаются
затраты на передачу адреса слова в словаре.
В различных статьях и патентах можно найти много других методов усовершен-
ствования алгоритма LZ-77. Задайте вашей любимой поисковой системе INTER-
NET ключевое слово «LZ-77», и вы найдете много интересной информации об
этом алгоритме.
4.4.	Алгоритм LZW (LZ-78)
Так сложилось, что из двух алгоритмов Зива-Лемпела второй алгоритм, описан-
ный в работе [60], поначалу казался более практичным и первым вошел в прак-
тику сжатия. В частности, он использован в стандарте V40bis для передачи дан-
ных по стандартным телефонным каналам общего пользования. С учетом моди-
фикации, предложенной Велчем в работе [56], ZL-78 действительно выглядит
элегантнее первого алгоритма. Ниже мы приводим описание этой модификации,
называемой алгоритмом LZW.
Алгоритм LZW показан на рис. 4.3.
Идея алгоритма состоит в том, что вместо последовательностей букв передаются
номера слов в некотором словаре. Кодер и декодер в процессе работы синхронно
формируют этот словарь. На каждом шаге словарь пополняется одним новым
словом, которое до этого в словаре отсутствовало, но является продолжением на
одну букву одного из слов словаря.
Пусть X = {0,1,..., М - 1} - алфавит источника и на выходе источника наблю-
дается последовательность xi, Х2, ... . Для простоты описания алгоритма будем
считать, что в начале работы кодера каждая из букв алфавита является словом
длиной 1 и входит в состав словаря. На каждом следующем шаге находим самое
длинное слово, совпадающее с началом подлежащей кодированию последова-
тельности. Пусть I - длина совпадения. Эти I букв передаются в виде ссылки
на соответствующее слово словаря. Если объем словаря равен с, то для передачи
этой ссылки достаточно flog(c - 1)] бит. Словарь пополняется новым словом,
которое получается дописыванием к использованному на данном шаге слову
следующей за ним в потоке кодируемых данных буквы.
Поскольку декодер не знает еще этой новой буквы, он сможет выполнить эту опе-
рацию только с задержкой на один шаг. Чтобы избежать неоднозначности коди-
рования, мы запрещаем кодеру пользоваться последним построенным словом
словаря, что отражено в алгоритме на рис. 4.3. Исключение составляет первый
шаг, когда словарь полностью известен кодеру и декодеру.
146
Глава 4. Архиваторы
Задан алфавит источника X — {0,1,..., М — 1};
Input: Длина последовательности п;
Последовательность источника х = х™;
Output: Кодовое слово с для х;
Инициализация:
АГ = 0;
с - «пустое» слово;
Словарь состоит из М слов длины 1, то есть из букв алфавита X
Число слов в словаре с = М.
while N < п do
►	Находим максимальное I такое, что совпадает
с j-м словом словаря при для некотором j < с
(на первом шаге допускается j = с).
►	к кодовому слову дописывается номер словарного
слова j в виде двоичной последовательности
длины flog (с — 1)1 (на первом шаге дописывается последовательность
длины [logci = [log All).
►	в словарь дописывается новое слово длиной I + 1
вида	= (a5^+zlia;N+i+i).
►	N^N + l;
►	с с 4-1;
end
Рис. 4.3. Алгоритм LZW
Описанный выше способ инициализации алгоритма - не единственный возмож-
ный. В частности, при кодировании коротких последовательностей нецелесооб-
разно инициализировать алгоритм, заполняя словарь всеми буквами алфавита
источника. Разумнее использовать принцип «esc-кода». В начале работы алго-
ритма словарь пуст и в нем, в ячейке с нулевым номером, хранится esc-код.
В дальнейшем, при получении от источника буквы, отсутствующей в словаре,
мы передаем esc-код, которому соответствует нулевая последовательность длины
[log(c - 1)1, а вслед за esc-кодом - стандартный код новой буквы. Работа кодера
LZW с такой инициализацией алгоритма поясняется следующим примером.
Пример 4.4.1. Применим алгоритм LZW к пословице
IF_WE_CANNOT_DO_AS_WE_WOULD_ WE_SHOULD_DO__AS_WE_CAN
Результаты работы алгоритма по шагам приведены в табл. 4.4.
Затраты на кодирование в данном примере оказались выше, чем для других
способов, но, внимательно посмотрев на таблицу, мы видим, что к моменту окон-
чания кодирования словарь уже содержит много очень полезных сочетаний букв,
которые пригодились бы при кодировании дальнейшего текста. Таким образом,
можно ожидать, что с увеличением длины кодируемой последовательности эффек-
тивность кодирования будет быстро нарастать.
4.4. Алгоритм LZW (LZ-78)
147
Таблица 4.4. Пример использования алгоритма LZW
Шаг	Словарь	Номер слова	Кодовые символы	Затраты (бит)
0	esc	-	-	-
1	I	0	bin(I)	0+8=8
2	F	0	bin(F)	log(l)+8=8
3		0	0bin(_)	Г1о8(2)] + 8 = 9
4	W	0	00bin(W)	riog(3)] + 8 = 10
5	Е	0	OObin(E)	Flog(4)] + 8 = 10
6	_с	3	Oil	3
7	с	0	000bin(C)	3+8=11
8	А	0	OOObin(A)	3+8=11
9	N	0	000bin(N)	3+8=11
10	NO	0	000bin(N)	4+8=12
и	О	0	OOOObin(O)	4+8=12
12	т	0	OOOObin(T)	4+8-12
13	D	3	0011	4
14	D	0	OOOObin(D)	4+8=12
15	0_	и	1011	4=4
16	_А	3	0011	4
17	AS	8	1000	4
18	S	0	OOOOObin(S)	5+8
19	_w	3	00011	5
20	WE	4	00100	5
21	Е_	5	00101	5
22	_WO	19	10011	5
23	OU	и	01011	5
24	и	0	OOOOObin(U)	5+8-13
25	L	0	OOOOObin(L)	5+8-13
26	D_	14	OHIO	5
27	_WE	19	10011	5
28	E_S	21	10101	5
29	SH	18	10010	5
30	H	0	00000bin(H)	5+8-13
31	OUL	23	10111	5
32	LD	25	11001	5
33	D_D	26	11010	5
34	DO	14	001110	6
148
Глава 4. Архиваторы
Таблица 4.4. Пример использования алгоритма LZW (продолжение)
Шаг	Словарь	Номер слова	Кодовые символы	Затраты (бит)
35	О_А	15	001111	6
36	AS_	17	010001	6
37	_WE_	27	011011	6
38	_СА	6	000110	6
39	AN	8	001000	6
40	N	9	001001	6
Итого				291
Анализ алгоритма LZ-78 заметно проще, чем алгоритма LZ-77. В частности,
в учебнике [38] приведено доказательство сходимости средней скорости кодиро-
вания к энтропии на сообщение. В данном пособии мы ограничимся нестрогим
эвристическим рассуждением, позволяющим понять асимптотическое поведение
алгоритма с ростом длины кодируемой последовательности.
Предположим, что для достаточно большого числа п последовательность х* =
=	уже закодирована и в процессе кодирования построен словарь
объемом с. По мере заполнения словаря в него включались последовательности
длиной I = 1, 2, ... . Разумно предположить, что в словарь попадали главным
образом все типичные последовательности длины Z. Как мы знаем из главы
1, количество типичных последовательностей длины I приблизительно равно
2ZHz(x), где Hi(X) = H(Xl)/l - энтропия на сообщение последовательности
длины I. Поэтому объем словаря связан с типичной длиной I очередной после-
довательности, включаемой в словарь, приближенным соотношением
3=1
с ростом I энтропии Hi убывают, но, начиная с некоторого значения, это убывание
замедляется и значение Hi приближается к пределу Н =	= Я(Х|Х°°).
Поэтому слагаемые в выражении для с можно рассматривать как возрастающую
геометрическую прогрессию со знаменателем 2я. Последнее слагаемое будет наи-
большим, поэтому имеет место приближенное равенство
с^121Н.
Средняя скорость кодирования на данном шаге
Поскольку величина I имеет порядок log с, скорость кодирования и объем словаря
(асимптотически при с —> оо) связаны соотношением
SwH+10510g£
log с
4.5. Предсказание по частичному совпадению
149
Это приблизительно такая же зависимость, какая имела место и для алгоритма
LZ-77. Кодирование в LZ-78 на первый взгляд кажется более эффективным,
поскольку, во-первых, формируемая кодовая последовательность не разбита на
части и, во-вторых, словарь состоит из несовпадающих словарных слов. Напро-
тив, важное преимущество LZ-77 состоит в том, что в LZ-77 словарь (за исклю-
чением начального этапа работы алгоритма) имеет постоянный объем. В LZ-78
объем словаря увеличивается с каждым шагом, и, в конце концов, его объем
превысит допустимый предел.
С точки зрения практического применения алгоритма LZW важно ответить на
два вопроса:
►	как организовать хранение в памяти кодера и декодера большого словаря,
составленного из слов различной длины, и
►	как поступать при заполнении этим словарем всего допустимого объема памяти.
Ответ на первый вопрос содержится в работе Велча [56]. Поскольку словарь
имеет древовидную структуру, то и хранить его нужно в виде дерева, сохра-
няя для каждого узла дерева адрес соседней вершины и адрес старшего потомка
вершины. При такой структуре словаря поиск в словаре также становится доста-
точно быстрым. Помимо этого, дополнительное ускорение поиска возможно
с помощью хеширования.
Второй вопрос сложнее. Тривиальные решения проблемы:
►	прекращение наращивания словаря после того, как исчерпана допустимая
память;
►	полный сброс памяти и возвращение алгоритма к начальному состоянию.
Оба варианта имеют свои достоинства и недостатки. Можно предложить различ-
ные альтернативные варианты алгоритма или найти их в INTERNET.
4.5. Предсказание по частичному совпадению
Сейчас мы рассмотрим наиболее «логичный» алгоритм кодирования при неиз-
вестной статистике источника. На первый взгляд он является почти тривиаль-
ным развитием адаптивного арифметического кодирования, которое обсужда-
лось в главе 3. Разница состоит в том, что в процессе кодирования вместо без-
условных вероятностей букв оцениваются их условные вероятности, при извест-
ном «контексте», то есть при известных предшествующих буквах. Клеари и Вит-
тену [35] принадлежит идея использовать контексты различной длины, зави-
сящей от предшествующей закодированной последовательности данных. Этот
метод кодирования получил название PPM (prediction by partial matching). Прак-
тическая реализация этой простой идеи порождает много вопросов, которые мы
кратко обсудим в данном параграфе.
150
Глава 4. Архиваторы
С момента опубликования исходной версии алгоритма было предложено очень
много его модификаций. Все же любой из РРМ-алгоритмов вкладывается в сле-
дующую схему.
Предположим, что последовательность = (xi,..., xt) первых t букв источника
уже передана и предстоит передать символ я*+1. При кодировании очередной
буквы выполняются следующие шаги.
1.	Находим контекст наибольшей длины d, не превышающей заданной
величины D. Под контекстом понимается последовательность з =
непосредственно предшествующая кодируемому символу и такая, что в точ-
ности такая же последовательность з уже встречалась в переданной последо-
вательности Я^"1.
2.	Для всех возможных значений символа x^i вычисляются оценки условных
вероятностей символа при известном контексте з,
3.	Значение символа xt^i кодируется арифметическим кодом в соответствии
с вычисленной на шаге 2 оценкой условной вероятности.
Варианты алгоритма РРМ отличаются друг от друга выбором максимальной
длины контекста D и, главное, способом выполнения шага 2, то есть вычисления
оценки условной вероятности символа.
Естественной оценкой условной вероятности буквы xt+\ = а после контекста
з = кажется оценка вида
rt(s,a)
В числителе этой формулы записано число появлений буквы а после контекста
з в предшествующей последовательности символов гс|, в знаменателе - общее
число появлений t в ж*"1. Однако арифметический кодер не сможет восполь-
зоваться этой формулой для тех букв а, которые не встречались с заданным
контекстом, то есть при тДз, а) = 0. Чтобы исправить ситуацию, следует восполь-
зоваться тем же подходом, что и при побуквенном адаптивном кодировании -
ввести esc-символы, указывающие на то, что при заданном контексте данная
буква не встречалась.
Стратегия РРМ-кодера (точнее его упрощенная версия, не учитывающая так
называемых «исключений», о которых речь пойдет ниже) иллюстрируется алго-
ритмом, представленным на рис. 4.4.
Итак, кодер старается передать букву арифметическим кодером в соответствии
с вероятностями, определяемыми контекстом наибольшей возможной длины.
Если это не удается сделать (буква еще не встречалась вслед за таким контек-
стом), передается esc-символ, контекст укорачивается на одну букву. В конечном
счете буква будет передана с учетом контекста меньшей (возможно, нулевой)
длины либо как «новая буква», если она не встречалась в уже закодированной
последовательности букв.
4.5. Предсказание по частичному совпадению
151
Заданы алфавит источника X = {0,1,..., М - 1}, максимальная длина контекста D
Input: Длина последовательности п;
Последовательность источника х = ж?;
Output: Кодовое слово с для х;
Инициализация:
t = 0;
с - «пустое» слово;
while t < п do
Находим наибольшее d такое, что d+i) > 0, d D.
Выбираем контекст s = ж*_^+1.
while pt(#t+i|s) — 0 do
Кодируем esc в соответствии с р*(езф).
Уменьшаем длину контекста:
d «- d — 1, s = ®Ud+i-
end
if d > 0 then
Кодируем #t+i в соответствии с р*(ф).
else
Кодирование без контекста:
if pt (х) > 0 then
Кодируем ж*+1 в соответствии с pt(x).
else
Вычисляем p(esc) и передаем esc.
Кодируем #t+i в соответствии с равномерным распределением на не
встречавшихся в х{ буквах
14- t + 1;
end
Рис. 4.4. Идея алгоритма PPM
Чтобы окончательно конкретизировать алгоритм, нужно выписать формулы для
вероятностей букв и esc-символов. Вопрос об адаптивном оценивании вероятно-
стей букв мы уже рассматривали в главе 3 в связи с адаптивным арифметическим
кодированием. Перепишем оценки (3.63) и (3.66) так, чтобы использовать их
в рамках алгоритма РРМ. Оценки условных вероятностей букв и esc-символов
для алгоритма А имеют вид
р*(ф) =
Pt(esc\s) =
rt\3,a)
rt(s) + 1’
1
n(s) + 1’
rt(s,a) > 0,
(4.18)
(4.19)
где 7t(s) и т*(а,а) обозначают число последовательностей, соответственно, з и
(s,a), содержащихся в последовательности длины t. Аналогично изменяются
оценки для алгоритма D:
152
Глава 4. Архиваторы
й(о|») =	r1(s,«)>o,	(4.20Х
А(“ф) = ад'	(4-21)
где Mt(s) - число различных букв, появившихся в последовательности длины
вслед за контекстом з.
Формулы (4.18)—(4.21) почти завершают описание двух версий алгоритма PPM:
РРМА, предложенного в работе [35], и его модификации PPMD, описанной
в [49]. Осталось еще одно небольшое, но важное усовершенствование, введенное
еще в самой первой работе [35]. Это усовершенствование называется техникой
«исключений» (exclusions). Поясним идею этого метода примером.
Предположим, что при кодировании текста на русском языке на некотором шаге
контекст имеет вид «кор», а следующая за ним буква - буква «т», причем соче-
тание букв «корт» ранее не встречалось. Предположим также, что предыдущие
появления последовательности «кор» имели продолжениями «а» и «с». В соот-
ветствии с алгоритмом, предается esc-символ и контекст укорачивается на еди-
ницу, то есть теперь контекстом будет «ор». Метод исключений рекомендует
принять во внимание то, что не все сочетания «ор» следует использовать для
подсчета условной вероятности буквы «т». Действительно, ведь и кодер и деко-
дер (благодаря передаче esc-символа) уже знают, что ни буква «а», ни буква «с»
не могут следовать за «ор». Формулы (4.18) - (4.21) в данном случае можно
уточнить, подставив в них вместо тД«ор») величину
<(ор) = Tt(op) - Tt (ора) - П (орс).
После такой корректировки знаменатели в оценках вероятностей букв умень-
шатся, а числители останутся прежними. Оценки вероятностей букв увеличатся,
а значит, затраты на передачу уменьшатся. (Заметим, что число различных букв
Мп(з) в числителе (4.21) тоже должно быть пересчитано с учетом исключений.)
Следующий пример поможет глубже понять работу алгоритма PPM.
Пример 4.5.1. Применим алгоритмы РРМ с параметром D=5 к пословице
IF_WE_CANNOT_DO_AS_WE_ WOULD_WE_SHOULD_DO_AS_WE_CAN
Результаты работы алгоритмов по шагам приведены в табл. 4.5 и 4.6. Знаки #
в графе «контекст» соответствуют контекстам нулевой длины. Штрихом поме-
чены те вероятности, которые подсчитаны с учетом исключений. В графе тДз)
представлено число появлений данного контекста и если он укорачивался в про-
цессе кодирования, то, через запятую, - число появлений укороченных контек-
стов. в графе Mt(s) также через запятую приведены значения числа различных
букв, следовавших за контекстом и его укорочениями.
Рассмотрим несколько характерных шагов кодирования на примере алгоритма
РРМА.
4.5. Предсказание по частичному совпадению
153
Таблица 4.5. Пример использования алгоритма РРМА
Шаг	Буква	Контекст 8	Tt(e)	PPMA	
				pt(esc\s)	Pt(a|s)
1	I	#	0	1	1/256
2	F	#	1	1/2	1/255
3		#	2	1/3	1/254
4	W	#	3	1/4	1/253
5	Е	#	4	1/5	1/252
6		#	5		1/6
7	С		1,6	1/2 x 1/6’	1/251
8	А		7	1/8	1/250
9	N	#	8	1/9	1/249
10	N	#	9		1/10
и	О	N	1,10	1/2 x 1/9’	1/248
12	т	#	11	1/12	1/247
13		#	12		2/13
14	D		2,13	1/3x1/12’	1/246
15	О	#	14		1/15
16		О	1,15	1/2	3/15’
17	А		3,16	1/4	1/14’'
18	S	А	1,17	1/2x1/16’	1/245
19		#	18		4/19
20	W		4		1/5
21	Е	_W	1		1/2
22		_WE	1		1/2
23	W	_WE_	1,1,1,5	1/2хГхГ	2/5’
24	О	_W	2,2,23	1/ЗхГ	2/22’
25	и	О	2,24	1/3x1/18’	1/244
26	L	#	25	1/26	1/243
27	D	#	26		1/27
28		D	1,27	1/2	6/25'
29	W		6		3/7
30	Е	_W	3		2/4
31		_WE	2		2/3
32	S	_WE_	2,2,2,7,31	1/ЗхГхГх1/3’	1/23’
33	н	S	1,32	1/2x1/25'	1/242	
34	о	#	33		3/34
154
Глава 4. Архиваторы
Таблица 4.5. Пример использования алгоритма РРМА (продолжение)
Шаг	Буква	Контекст 8	rt(s)	PPMA	
				pt(esc|s)	pt(a|s)
35	и	О	3		1/4
36	L	ои	1		1/2
37	D	OUL	1		1/2
38		OULD	1		1/2
39	D	OULD_	1,1,1,1,8	1/2хГхГхГ	1/4'
40 ,	О	_D	1		1/2
41		_DO	1		1/2
42	А	_DO_	1		1/2
43	S	_DO_A	1		1/2
44		DOAS	1		1/2
45	W	O_AS_	1		1/2
46	Е	_AS_W	1		1/2
47		AS_WE	1		1/2
48	С	S_WE_	1,3	1/2	1/3'
49	А	_WE_C	1		1/2
50	N	WE_CA	1		1/2
Итого |~62,44 + 185,621 4- 1 = 250 бит
Шаг 6. Пробел встретился второй раз. Поскольку предшествующая ему буква Е
встречалась только один раз, контекст имеет нулевую длину. Для такого контек-
ста пробел имеет вероятность 1/(5+1)= 1/6.
Шаг 7. Контекстом длины 1 по отношению к С является пробел. После про-
бела встречалась только буква W. Нужно передать esc (его вероятность равна
1/2) и перейти к контексту нулевой длины. Но и при контексте нулевой длины
буква С не встречалась. Снова надо передать esc, вероятность которого равна
1/7. Однако известно, что среди возможных букв не может быть буквы W. Это
повышает вероятность esc-символа до 1/6.
Шаг 22. Это наиболее типичный шаг, алгоритм работает на этом шаге весьма
эффективно. Контекстом по отношению к пробелу выступает _WE . Эта ком-
бинация уже встречалась, и за ней следовал пробел. Таким образом, следую-
щими буквами могут быть пробел и esc с равными вероятностями. Поэтому для
передачи пробела потребуется всего 1 бит.
Шаг 23. Букве W предшествует контекст _WE_. При предыдущем появлении
этого контекста за ним следовала другая буква (С). Поэтому передается esc
(вероятность 1/2). Контекст укорачивается и преобразовывается в WE_. За этим
4.6. Алгоритм Барроуза-Уилера
155
контекстом ранее следовала только С, и надо снова передавать esc. Его вероят-
ность без учета исключений была бы равна 1/2. Но при передаче предыдущего
esc мы уже информировали, что буква С исключена, поэтому вероятность esc-
символа равна 1. Контекст сократился до Е_. Снова вероятность esc равна 1, и
контекст сокращается до пробела. После пробела встречались W(2 раза), С, D и
А. Буква С невозможна, значит, вероятность W равна 2/5.
Шаг 32. Контекст к S - последовательность «_WE_>. Она встречалась дважды,
но ни разу после нее не было буквы S. Передаем esc, имеющий вероятность
1/3. Последовательно укорачивая контекст, приходим к контексту, состоящему
из одного пробела. Пробел уже встречался 7 раз, но ни разу перед S. Исключаем
буквы С и W, тогда возможны только D и А. Поэтому вероятность esc равна 1/3.
При подсчете вероятности буквы S при пустом контексте из 31 возможности
нужно исключить все буквы, которые следовали после пробела (все буквы W, С,
D, А, всего 9 букв). Окончательный результат 1/23.
Аналогичные (и еще более запутанные) подсчеты выполняет кодер для алго-
ритма PPMD. Как и должно было получиться, PPMD экономит биты на кон-
текстах, но добавляет их на передаче букв. Поскольку в нашем примере мы
кодируем короткую последовательность букв, алгоритм PPMD оказался заметно
эффективнее алгоритма РРМА.
4.6.	Сжатие с использованием преобразования
Барроуза-Уилера
Представленный в данном параграфе способ кодирования значительно отли-
чается от всех рассмотренных ранее. Авторы этого способа, Барроуз и Уилер,
описали его впервые в техническом отчете [33] в 1994 г. Предложенный алгоритм
показывали неожиданно хорошие результаты, но далеко не рекордные
в смысле соотношения между сложностью реализации и достижимым сжатием.
С тех пор значительные усилия специалистов в области сжатия данных были
направлены на то, чтобы повысить эффективность кодирования и найти теорети-
ческое обоснование алгоритма. В результате на основе преобразования Барроуза-
Уилера были построены архиваторы, которые наравне с РРМ-кодерами являются
рекордсменами по сжатию при сравнении на стандартных наборах файлов (см.
параграф 4.7).
Опишем сначала прямое преобразование Барроуза-Уилера. Будем иллюстриро-
вать его примером.
Пример 4.6.1. Прямое преобразование Барроуза-Уилера. Рассмотрим уже зна-
комую последовательность
IF_WE_CANNOT__DO_AS_WE_WOULD_WE_SHOULD_DO_AS_WE_CAN
Все циклические сдвиги последовательности должны быть лексикографически
упорядочены. Результат выполнения этого шага для данного примера представ-
лен в табл. 4.7.
156
Глава 4. Архиваторы
Таблица 4.6. Пример использования алгоритма PPMD
	Буква	Контекст 8	Tt(sj		PPMD	
					pt(esc\s)	
1	I	#	0	0	1	1/256
2	F	#	1	1	1/2	1/255
3		#	2	2	2/4	1/254
4	W	#	3	3	3/6	1/253
5	Е	#	4	4	4/8	1/252
6		#	5	5		1/10
7.	С		1,6	1,5	l/2x4/8'	1/251
8	А	#	7	6	6/14	1/250
9	N	#	8	7	7/16	1/249
10	N	#	9	8		1/18
и	О	N	1,10	1,8	1/2x8/18’	1/248
12	т	#	11	9	9/22	1/247
13		#	12	10		3/24
14	D		2,13	2,10	2/4x8/22’	1/246
15	О	#	14	11		1/28
16		О	1,15	1,11	1/2	5/28’
17	А		3,16	3,11	3/6	1/26'
18	S	А	1,17	1,11	1/2x10/30’	1/245
19		#	18	12		7/36
20	W		4	4		1/8
21	Е	_w	1	1		1/2
22		_WE	1	1		1/2
23	W	_WE_	1,1,1,5	1,1,1,4	1/2хГхГ	3/8’
24	О	_W	2,2,23	1,1,12	1/4x1’	3/42'
25	и	О	2,24	2,12	2/4x10/34'	1/244
26	L	#	25	13	13/50	1/243
27	D	#	26	14		1/52
28		D	1,27	1,14	1/2	11/52'
29	W		6	4		5/12
30	Е	_W	3	2		3/6
31		_WE	2	1		3/4
32	S	_WE_	2,2,2,7,31	2,2,2,4,14	2/4xl'xl'x2/4'	1/48’
33	н	S	1,32	1,14	1/2x13/50	1/242
34	о	#	33	15		5/66
4.6. Алгоритм Барроуза-Уилера
157
Шаг	Буква	Контекст 3	Tt(«)	Mt(s)	PPMD	
					pt(esc|s)	Pt(a|s)
35	и	О	3	3		1/6
36	L	ои	1	1		1/2
37	D	OUL	1	1		1/2
38		OULD	1	1		1/2
39	D	OULD_	1,1,1,1,8	1,1,1,1,5	1/2хГхГхГ	1/8
40		_D	1	1		1/2
41		_DO	1	1		1/2
42	А	_do_	1	1		1/2
43	S	_DO_A	1	1		1/2
44		DO_AS	1	1		1/2
45	W	O_AS_	1	1		1/2
46	Е	_AS_W	1	1		1/2
47		AS_WE	1	1		1/2
48	с	S_WE_	1,3	1,3	1/2	1/4
49	А	_WE_C	1	1		1/2
50	N	WE_CA	1	1		1/2
Итого [36,01 + 194,98] = 232 бит						
Результатом преобразования являются
►	последний столбец таблицы, строками которой служат лексикографически
упорядоченные циклические сдвиги исходной последовательности;
►	номер той строки, в которой записана исходная последовательность.
В нашем примере результатами преобразования являются последовательность
СС________LLWWWWISNUUAANNHWDD_AAOOO_______________OOEEDTESFDSE
и число 16.
Отметим примечательное свойство преобразованной последовательности: сим-
волы в ней «сгруппировались», она почти целиком состоит из серий одинаковых
символов. Это дает основание надеяться на то, что сжимать ее будет проще, чем
исходную последовательность. Платой за перегруппировку является необходи-
мость передавать номер строки (он же - номер позиции, на которой находится
первый символ исходной последовательности).
Покажем, как по результатам преобразования восстановить исходную последова-
тельность. Эта задача решается с помощью обратногб преобразования Барроуза-
Уилера. Поясним его на примере, представленном в табл. 4.7.
158
Глава 4. Архиваторы
Пример 4.6.2. Обратное преобразование Барроуза-Уилера.
В результате прямого преобразования известен последний столбец табл. 4.6 и
номер исходной строки. Требуется восстановить саму исходную строку. Мы легко
можем восстановить первый столбец таблицы циклических сдвигов. Для этого
достаточно просто произвести сортировку преобразованной последовательности.
Итак, в табл. 4.7 мы знаем первый, последний столбец и индекс исходной строки
(число 16).
Таблица 4.7. Лексикографическая сортировка циклических сдвигов
0	А	NIF_WE_CANNOT_DO_AS_WE_WOULD_WE_SHOULD_DO_AS_WE_	C
1	А	NNOT_DO__AS_WE_WOULD_WE_SHOULD_DO_AS__WE_CANIF_WE_	C
2	А	S_WE_CANIF_WE_CANNOT_DO_AS_WE_WOULD_WE_SHOULD_DO	
3	А	S_WE_WOULD_WE_SHOULD_DO_AS_WE_CANIF_WE_CANNOT_DO	
4	С	ANIF_WE_CANNOT_DO_AS_WE_WOULD_WE_SHOULD_DO_AS_WE	
5	С	ANNOT_DO_AS_WE_WOULD_WE_SHOULD_DO_AS_WE_CANIF_WE	
6	D	O_AS_WE_CANIF_WE_CANNOT_DO_AS_WE_WOULD_WE_SHOULD	
7	D	O_AS_WE_WOULD_WE_SHOULD_DO_AS_WE_CANIF_WE_CANNOT	
8	D	_DO_AS_WE_CANIF_WE_CANNOT_DO_AS_WE_WOULD_WE_SHOU	L
9	D	_WE_SHOULD_DO_AS_WE_CANIF_WE_CANNOT_DO_AS_WE_WOU	L
10	Е	_CANIF_WE_CANNOT_DO_AS_WE_WOULD_WE_SHOULD_DO_AS_	W
11	Е	_CANNOT_DO_AS_WE_WOULD_WE_SHOULD_DO_AS_WE_CANIF_	W
12	Е	_SHOULD_DO_AS_WE_CANIF_WE_CANNOT_DO_AS_WE_WOULD_	W
13	Е	_WOULD_WE_SHOULD_DO_AS_WE_CANIF_WE_CANNOT_DO_AS_	W
14	F	_WE_CANNOT_DO_AS_WE_WOULD_WE_SHOULD_DO_AS__WE_CAN	I*
15	Н	OULD_DO_AS_WE_CANIF_WE_CANNOT_DO_AS_WE_WOULD_WE__	S
16	I	F_WE_CANNOT_DO_AS_WE_WOULD_WE_SHOULD_DO_AS_WE_CA	N
17	L	D_DO_AS_WE_CANIF_WE_CANNOT_DO_AS_WE_WOULD_WE_SHO	\ U
18	L	D_WE_SHOULD_DO_AS_WE_CANIF_WE_CANNOT__DO_AS_WE_WO	U
19	N	IF_WE_CANNOT_DO_AS_WE_WOULD_WE_SHOULD_DO_AS_WE_C	A
20	N	NOT_DO_AS_WE_WOULD_WE_SHOULD_DO_AS_WE_CANIF_WE_C	A
21	N	OT_DO_AS_WE_WOULD_WE_SHOULD_DO_AS_WE_CANIF_WE_CA	N
22	О	rr__DO_AS_WE_WOULD_WE_SHOULD_DO_AS_WE_CANIF_WE_CAN	N
23	О	ULD_DO_AS_WE_CANIF_WE_CANNOT_DO_AS_WE_WOULD_WE_S	H
24	О	ULD_WE_SHOULD_DO_AS_WE_CANIF_WE_CANNOT_DO__AS_WE_	W
25	о	_AS_WE_CANIF_WE_CANNOT_DO_AS_WE_WOULD_WE_SHOULD_	D
26	о	_AS_WE_WOULD_WE_SHOULD_DO_AS_WE_CANIF_WE_CANNOT_	D
27	S	HOULD_DO_AS_WE_CANIF_WE_CANNOT_DO_AS_WE_WOULD_WE	
4.6. Алгоритм Барроуза-Уилера
159
28	S	_WE_CANIF_WE__CANNOT_DO_AS_WE_WOULD_WE_SHOULD_DO_	A
29	S	_WE_WOULD_WE_SHOULD_DO_AS_WE_CANIF_WE_CANNOT_DO_	A
30	т	_DO_AS_WE_WOULD_WE_SHOULD_DO_AS_WE_CANIF_WE_CANN	О
31	и	LD_DO_AS_WE_CANIF_WE_CANNOT_DO_AS_WE_WOULD_WE_SH	О
32	и	LD_WE_SHOULD_DO_AS_WE_CANIF_WE_CANNOT_DO_AS_WE_W	О
33	W	E_CANIF_WE_CANNOT_DO_AS_WE_WOULD_WE_SHOULD_DO_AS	
34	W	E_CANNOT_DO_AS_WE_WOULD_WE_SHOULD_DO_AS_WE_CANIF	
35	W	E_SHOULD_DO_AS_WE_CANIF_WE_CANNOT_DO_AS_WE_WOULD	
36	W	E_WOULD_WE_SHOULD_DO_AS_WE_CANIF_WE_CANNOT_DO_AS	
37	W	OULD_WE_SHOULD_DO_AS_WE_CANIF_WE_CANNOT_DO_AS_WE	
38		AS_WE_CANIF_WE_CANNOT_DO_AS_WE_WOULD_WE_SHOULD_D	О
39		AS_WE_WOULD_WE_SHOULD_DO_AS_WE CANIF WE CANNOT D	О
40		CANIF_WE_CANNOT_DO_AS_WE_WOULD_WE_SHOULD_DO_AS_W	Е
41		CANNOT_DO_AS_WE_WOULD_WE_SHOULD_DO_AS_WE_CANIF_W	Е
42		DO_AS_WE_CANIF_WE_CANNOT_DO_AS_WE_WOULD_WE_SHOUL	D
43		DO_AS_WE_WOULD_WE_SHOULD_DO_AS_WE_CANIF_WE_CANNO	Т
44		SHOULD_DO_AS_WE_CANIF_WE_CANNOT_DO_AS_WE_WOULD_W	Е
45		WE_CANIF_WECANNOT_DO_ASWE_WOULD_WE_SHOULDDO A	S
46		WE_CANNOT_DO_AS_WE_WOULD_WE_SHOULD_DO_AS_WE_CANI	F
47		WE_SHOULD_DO_AS_WE_CANIF_WE_CANNOT_DO__AS_WE_WOUL	D
48		WE_WOULD_WE_SHOULD_DO_AS_WE_CANIF_WE_CANNOT_DO_A	S
49		WOULDWE_SHOULDDOAS_WE_CANIF_WE_CANNOT_DO_AS_W	Е
Понятно, что в 16-й ячейке первого столбца мы найдем первую букву последо-
вательности, букву I. Заметим, что в силу цикличности в нашей таблице строка,
заканчивающаяся первой буквой, начинается со второй буквы. Буквой I закан-
чивается 14-я строка. Заглянув в ее первый столбец, заключаем, что вторым
символом был Е Каким был следующий символ?
Находим F в последнем столбце (строка 46) и считываем первый символ той же
строки. Оказывается, третьим символом был пробел. В этом месте мы сталки-
ваемся с небольшой проблемой. Пробелов в последнем столбце много. Какой из
них «правильный»?
Выручает то, что все строки таблицы лексикографически упорядочены. Одина-
ковые символы последнего столбца упорядочены по значениям соответствующих
символов первого столбца. Букве F последнего столбца соответствует 9-й по
счету пробел первого столбца. Значит, чтобы найти «наш» пробел, мы должны
пропустить 8 пробелов последнего столбца и остановиться на девятом. Так мы
попадаем на строку 34. В ее первом столбце находим следующий символ W.
Продолжив, мы правильно восстановим всю последовательность.
160
Глава 4. Архиваторы
Теперь нужно выбрать способ кодирования преобразованной последовательно-
сти. Для этого целесообразно использовать описанный выше в параграфе 4.2
метод «стопки книг».
Пример 4.6.3. Кодирование результата преобразования методом «стопки книг».
Перепишем результат прямого преобразования Барроуза-Уилера
СС________LLWWWWISNUUAANNHWDD_AAOOO___________________OOEEDTESFDSE
следующим образом. Будем писать символ esc всякий раз при появлении «новой»
буквы в тексте и «степень новизны» (число различных букв между предыдущим
и текущим появлением буквы), если буква встречалась. Получаем
esc 0 esc 0 0 0 0 0 esc 0 esc 0 0 0 esc esc esc esc 0 esc 0 2 0 esc 6 esc 0 9 5 0 esc 0 0 2
0 0 0 0 1 0 esc 0 4 esc 2 10 esc 4 2 3
Воспользуемся нумерационным кодированием для передачи этой последователь-
ности. Композиция последовательности и подсчет количества битов на ее пере-
дачу приведены в табл. 4.8.
Таблица 4.8. Кодирование композиции преобразованной последовательности
Буква	Количество	Биты
esc	15 .	log(50)
0	23	log(50-15+l)=log(36)
1	1	log(50-15-23+l)=log(13)
2	4	log(12)
3	1	log(8)
4	2	log(7)
5	1	log(5)
6	1	log(4)
7	0	log(3)
8	0	log(3)
9	1	log(3)
10	1	log(2)
Итого [33,98] 4-1=35 бит		
В первой строчке таблицы при определении числа битов мы приняли во вни-
мание то, что число различных букв в последовательности может принимать
значения от 1 до 50. Нули в преобразованной последовательности появляются
при повторении букв. Число нулей находится в интервале от 0 до 35. Исходя из
этого для передачи числа нулей достаточно log(36) бит, и так далее. Приведенный
в таблице подсчет подразумевает, что все значения в рассматриваемых диапазо-
нах равновероятны и применяется арифметическое кодирование. В этом случае
затраты на передачу композиции составят 35 бит. Можно использовать простое
4.6. Алгоритм Барроуза-Уилера
161
равномерное кодирование, отводя flog(z +1)] бит на передачу числа, значения
которого в диапазоне от 0 до i. Тогда затраты составили бы 38 бит.
Для передачи всех букв, соответствующих esc-символам последовательности, доста-
точно 8 х 15 = 120 бит.
Для передачи номера последовательности в списке всех последовательностей
с заданной композицией потребуется
50!	1	_ л
°g 23!15!4!2!1!... 1! “ 94 биТ ’
В итоге получаем оценку
I = 35 + 120 + 94 + 6 = 255 бит ,
где последние 6 бит учитывают затраты на передачу индекса исходной строки
в таблице циклических сдвигов. Затраты получились примерно такими же, как
и при использовании РРМА.
Заметим, что рассмотренный метод передачи преобразованной последовательно-
сти не очень эффективен. Он учитывает высокую вероятность нулей в преобразо-
ванной последовательности, но заведомо не учитывает их тенденции
к группированию.
С момента изобретения алгоритма Барроуза-Уилера в 1994 г. по настоящее время
было предложено много алгоритмов более эффективного кодирования результа-
тов преобразования. Один из самых удачных алгоритмов предложен Е. Биндером
(Binder Е.) в 2000 г. и называется методом кодирования расстояний.
Пример 4.6.4. Кодирование результата преобразования методом кодирования
расстояний.
Мы опишем этот алгоритм на нашем примере. Требуется передать последова-
тельность
СС_________LLWWWWISNUUAANNHWDD_AAOOO________________OOEEDTESFDSE
Подготовительный шаг состоит в том, что передаются позиции первого появ-
ления каждого из символов последовательности. В нашем случае достаточно
потратить flog 501 = 6 бит на передачу числа различных символов, 120 бит на
их значения и [(^)] = 42 бит на их позиции. В результате в памяти декодера
формируется строка наподобие той, которая записана в нулевой строке табл. 4.9.
В ней символом «?» помечены позиции, значения букв на которых декодеру пока
неизвестны.
Далее последовательно передаются повторные появления букв, но при этом не
принимаются во внимание буквы, непосредственно следующие за данной. Если
буква более не встречается, передается 0, в противном случае передается число
неизвестных позиций между текущим и следующим появлением такой же буквы
включительно без учета серии неизвестных букв, непосредственно следующих за
данной.
162
Глава 4. Архиваторы
В нашем примере буква С не встречается после первой серии из двух букв.
(В этой и остальных строчках анализируемая буква помечена значком «крышка».)
Поэтому передаем 0. Заметим, что на позиции 2 может быть только буква С. Дело
в том, что если бы на этой позиции стояла иная буква, то это было бы ее пер-
вым появлением и она была бы передана на подготовительном шаге. Именно
поэтому декодер восстанавливает вторую букву С без передачи дополнительной
информации.
Далее следует пробел. Следующее появление пробела произойдет на позиции
с номером 28. Эта позиция помечена крышкой. Декодер восстановит серию из
6 пробелов до буквы L без передачи дополнительной информации. Поэтому
достаточно передать число неизвестных символов от L до позиции, помеченной
крышкой включительно. Получив число И, декодер поместит пробел на нужную
позицию.
Аналогично обрабатываются все остальные символы, пока не будет восстанов-
лена вся последовательность. В нашем примере потребовалось 22 шага. Напом-
ним, что крышками во втором столбце таблицы отмечены обрабатываемая буква
и позиция, расстояние до которой нужно закодировать, в последнем столбце -
выход кодера расстояний уг, г = 0, 1, ... . В скобках указано максимально воз-
можное значение выхода кодера расстояний на данном шаге yirmax, г = 0,1,....
В данном примере кодер расстояний сформировал последовательность
у = (0,11,0,5,0,20,3,0,3,0,0,0,12,4,0,5,0,0,1,1,0,2,1).
Подумаем о способе ее передачи. Нули соответствуют случаям, когда соответ-
ствующий символ появляется в последний раз. Понятно, что число нулей не
больше числа различных букв Мп. Число позиций, на которых могут разме-
щаться нули примерно равно (неизвестному заранее) оставшемуся числу шагов,
которое в начале передачи не превышает п — Мп. Отношение этих чисел можно
было бы использовать как оценку вероятности нуля. В нашем примере для про-
стоты примем вероятность нуля равной 1/2 и будем тратить 1 бит на передачу
события «нулевой или ненулевой» символ.
Для каждого ненулевого числа нетрудно подсчитать его максимально возмож-
ное значение - это общее количество позиций, на которых может оказаться
следующее передаваемой повторное появление символа. В табл. 4.9 эта вели-
чина ?/г,тах для каждого шага приведена в скобках. Будем считать значения од
в интервале от 1 до од>тах равновероятными. Разумно для передачи последо-
вательности у использовать арифметическое кодирование, приписав буквам на
шаге i вероятности
В нашем примере такое кодирование потребует
22+ i°g Q9 24.2з . 22.19 • 16 • 15 • 11 • 4 • 3 • 2 • 1)	61 биТ'
4.6. АлгориУм Барроуза-Уилера
163
Таблица 4.9. Кодирование расстояний
г	Последовательность			Vit/yi, max)
0		? ? ? ? ? L ? W? ? ?IS NU ?A???H?D????O???	777777E77T77F77?	0
1	СС^	? ? ? ? ? L ?W? ? ?ISNU?А? 7 ?H?D? 7 7 70? ??????? ?E? ?T? 7 F 7 7 7		11(29)
2	сс	L ? W? ? ?IS NU ?A???H?D? 7 7 0? ??????? ?E? ? T ?7 F 7 7 7		0
3	сс	L LW? ? ?IS NU 7A777H7D? 77O777777777E77T77F77?		5(24)
4	сс_	LLWWWWt SNU? A? 7 ?HWD? ? 70? ? ?	777777E77T77F77?	0
5	сс_		LLWWWWI §NU?A? ? 7HWD7 ? 70? ? ?	??????E??T??F?7?	20(23)
6	сс_		LLWWWWI S&U7A?7 7HWD7 ? 70?? ?	??????E??T?SF???	3(22)
7	сс_		LLWWWWI SN0?A?N?HWD? ??o?????????e??t?sf???		0
8	сс«		LLWWWWI SNUUA?N?HWD?_? 70???????? ?E? ?T?SF? 7 7		3(19)
9	СС_	_ 	LLWWWWI SNUUAA&7HWD? A?O? ? ?	??????E??T?SF???	0
10	сс	L LWWWWI S NUUAANNftWD ? A ? О ? ? ?	??????E??T?SF???	0
11	сс_		LLWWWWI SNUUAANNH\to?_A?O? ??????? ?E??T?SF? ? ?		0
12	сс_		LLWWWWI SNUUAANNHWD? A7O777777777E77T7SF77?		12(16)
13	сс_		LLWWWWI SNUUAANNHWDD^A?O? ?t??????E?DT?SF??.7		4(15)
14	сс	LLWWWWI SNUUAANNHWDD A?O??	??????E? DT ? S F ? ? ?	0
15	сс__		LLWWWWI SNUUAANNHWDD AAO? ? _	? 7 7 7 ? ?E?DT? SF? ? ?	5(H)
16	СС_		LLWWWWI SNUUAANNHWDD_AAOOCb	????O?E? DT ? S F ? ? ?	0
17	сс _		LLWWWWI SNUUAANNHWDD AAOOO		oOe?dt?sf???	0
18	сс	LLWWWWI SNUUAANNHWDD AAOOO		OOE7DT? SF? 7 7	1(4)
19	сс_	__ 	LLWWWWI SNUUAANNHWDD AAOOO	OOEEf>TESF? 7 7	1(3)
20	сс	LLWWWWI SNUUAANNHWDD AAOOO	OOEEDtESFD? 7	0
21	сс	LLWWWWI SNUUAANNHWDD AAOOO		OOEEDTESFD? ?	2(2)
22	сс		LLWWWWI SNUUAANNHWDD AAOOO	OOEEDTE!§FD? e	1(1)
23	сс	LLWWWWI SNUUAANNHWDD AAOOO		OOEEDTESFDSE	
В общей сложности при использовании кодера расстояний будет затрачено
I = 6 + 120 + 42 4- 61 4- 6 = 235 бит,
где последние 6 бит учитывают затраты на передачу индекса исходной строки
в таблице сдвигов.
Мы получили примерно такой же результат, что и при использовании алгоритма
PPMD.
Описанные в данном параграфе алгоритмы имеют комбинаторную природу, внеш-
не весьма далекую от традиционных подходов, опирающихся на теорию инфор-
мации. Поэтому хотелось бы иметь теоретическое объяснение высокой эффек-
тивности рассмотренного алгоритма.
Оказывается, этот алгоритм очень близок к РРМ-алгоритмам, если их приме-
нять к последовательности, записанной в обратном порядке. При рассмотрении
РРМ-алгоритмов мы «предсказывали» следующую букву по контексту, состав-
ленному из некоторого числа предшествующих букв. Алгоритм Барроуза-Уилера
эффективно кодирует буквы, имеющие высокую вероятность при известных сле-
дующих буквах.
164
Глава 4. Архиваторы
Вернемся к нашему примеру В табл. 4.7 первые две строки начинаются с сочета-
ния «AN», которое в нашем тексте встретилось дважды. Ничего удивительного,
что алгоритм «угадал», что в обоих случаях предшествующей буквой была буква
«С». Она действительно имеет большую вероятность перед сочетанием «AN».
Далее в строках сгруппированы сочетания «AS». Им с большой вероятностью
предшествует пробел.
Рассмотрим стационарный источник. Предположим, что модель источника может
быть с достаточной точностью аппроксимирована цепью Маркова конечно связ-
ности т. При передаче длинной последовательности х = (»i,... ,®п) подпосле-
довательность з = (si,...,sm) встретится в тексте длиной п приблизительно
пр(з) раз. После циклического упорядочивания мы получим пр(з) строк, которые
будут начинаться с з = (si,..., sm), распределение вероятностей букв в послед-
нем столбце в этой части таблицы будет иметь вид р(ж|з). Использование одного
из универсальных кодов, например, метода «стопки книг», позволит потратить
на передачу этой части последовательности примерно пр(з)Н(Х\з) бит. Сумми-
руя по всем последовательностям s, приходим к скорости кодирования близкой
к Я(Х|Х™).
Это нестрогое объяснение позволяет указать класс источников, для которых
кодирование на основе преобразования Барроуза-Уилера будет особенно эффек-
тивным. Выход преобразователя - это, по сути, нестационарная последователь-
ность, которая состоит из стационарных подпоследовательностей, соответству-
ющих различным состояниям исходного источника. Рассмотренный в данном
параграфе алгоритм хорошо подходит для источников, которые могут быть аппрок-
симированы моделью с относительно небольшим числом состояний, причем при
известном состоянии условное распределение вероятностей должно быть близ-
ким к вырожденному (иметь небольшую энтропию). Этим условиям в большой
степени удовлетворяют некоторые тексты, листинги компьютерных программ
и т. п.
4.7.	Сравнение способов кодирования.
Характеристики архиваторов
Завершим главу сравнением изученных алгоритмов.
Сначала обратимся к тексту из 50 букв, на котором мы иллюстрировали прин-
ципы работы алгоритмов. Результаты вычислений сведены в табл. 4.10.
Хотя маленькая длина текста не позволяет делать надежных выводов о сравни-
тельных характеристиках алгоритмов, тем не менее приведенные в таблице дан-
ные довольно красноречивы. Предложенные относительно недавно алгоритмы
PPMD и кодирование с использованием преобразования Барроуза-Уилера суще-
ственно эффективнее других методов кодирования.
4.7. Сравнение способов кодирования. Характеристики архиваторов
165
Таблица 4.10. Сравнение алгоритмов на примере короткого текста
Алгоритм	Параграф	Затраты (бит)
Передача без кодирования		400
Двухпроходное кодирование, код Хаффмена	3.3	302
Нумерационное кодирование	3.4	283
Адаптивное арифметическое кодирование (алгоритм А)	3.6	293
Адаптивное арифметическое кодирование (алгоритм D)	3.6	283
Алгоритм LZ77	4.3	280
Алгоритм LZFG	4.3	299
Алгоритм LZW	4.4	291
Алгоритм РРМА	4.5	250
Алгоритм PPMD	4.5	232
Преобразование BW+ «стопка книг»	4.6	255
Преобразование BW+ кодирование расстояний	4.6	235
Интересно сравнить изученные алгоритмы в реальных условиях применения и
выбрать лучший из них. Эта задача не имеет однозначного решения. В част-
ности, при кодировании различных файлов данных предпочтительными будут
различные алгоритмы.
Многолетняя конкуренция разработчиков алгоритмов сжатия информации при-
вела к созданию наборов тестовых файлов, на которых принято производить
сравнение алгоритмов. Чаще всего используется набор, называемый Calgary Cor-
pus, состоящий из 19 файлов, общий объем которых составляет 3251493 байт.
В состав набора входят тексты на английском языке (художественные и тех-
нические), библиографический список, новости в виде сообщений электронной
почты, программы на языках С, Lisp и Паскаль, факсимильное изображение,
геофизические данные, исполняемые коды программ.
В табл. 4.11 приведены сведения об алгоритмах с наилучшим сжатием и (для
сравнения) результаты тестирования широко используемого архиватора PKZIP.
Представленные данные заимствованы с сайта http://compression.ca и отражают
достижения в области сжатия данных на конец 2002 года. На этом же сайте
можно получить более подробные данные об архиваторах.
166
Глава 4. Архиваторы
Таблица 4.11. Сравнение архиваторов на тестовом наборе Calgary Corpus
Архиватор (автор)	Принцип работы	Скорость (бит/байт)
RK 1.04.01 (М. Taylor)	LZ, PPMZ	1.8226
SBC 0.968 (S. J. Makinen)	Преобразование Барроуза-Уилера	1.8846
RAR(Win32)3.00b5 (Е.Рошаль)	LZ77 variant + Huffman	1.9244
ACB 2.00c (Г.Буяновский)	Associative Coding Algorithm	1.9546
PPMD vE (Д. Шкарин)	PPM	2.0153 2.0153
PKZIP 2.6.02 Win95 (PKWARE)	LZH, LZW	2.6062
Завершая главу, повторим, что сжатие компьютерных файлов лишь одно из мно-
гочисленных приложений теории кодирования дискретных источников. Каж-
дый из методов, перечисленных в табл. 4.10, 4.11,имеет свою область предпо-
чтительного применения в различных задачах хранения, обработки и передачи
информации.
4.8.	Задачи
1.	Дополните таблицу, построенную при решении задачи 1 главы 3 результа-
тами кодирования той же тестовой последовательности с помощью методов,
описанных в данной главе. Испытайте на вашей тестовой последовательности
один из популярных стандартных архиваторов (не забыв вычесть из размера
получаемых файлов размер заголовка).
2.	Рассмотрим источник, порождающий независимые одинаково распределенные
буквы (ДПИ). Будут ли методы данной главы эффективны в этой ситуации?
Проверьте вашу гипотезу на простом примере короткой последовательности
нулей и единиц с заданной вероятностью единицы.
3.	Предположим, что источником информации является звуковой сигнал в стан-
дартном формате импульсно-кодовой модуляции (16-битные отсчеты сигнала,
измеренные с частотой 44 100 Гц). Годятся ли для сжатия такой последователь-
ности данных описанные в данной главе алгоритмы?
4.9. Библиографические замечания
167
4.9.	Библиографические замечания
Основой данной главы являются оригинальные публикации, цитированные
в тексте главы, а также сведения из сети INTERNET.
Хорошими источниками информации о принципах работы, характеристиках и
способах практической реализации различных алгоритмов сжатия данных явля-
ются сайт http://www.compression.ru и книга [5].
Глава 5
Кодирование для
дискретных каналов
с шумом
В предыдущих главах мы решали задачу кодирования источников. Цель коди-
рования состояла в уменьшении затрат на передачу либо хранение информации.
Решение задачи может быть интерпретировано как «устранение» из потока пере-
даваемых данных избыточной информации, без которой возможно однозначное
восстановление сообщений источника.
В настоящей главе рассматривается кодирование с целью защиты передаваемой
информации от помех и искажений при передаче по каналам связи либо при
хранении информации. Решение задачи состоит в том, что при кодировании
в информацию искусственно вносится избыточность таким образом, чтобы при
искажении части передаваемых данных сообщения источника могли быть пра-
вильно декодированы. Таким образом, в некотором смысле задача кодирования
для каналов противоположна задаче кодирования источника.
В повседневной жизни мы используем примерно такой же способ защиты инфор-
мации от помех. Избыточность языка общения людей довольно высока (не слу-
чайно тексты сжимаются программами-архиваторами почти в 5 раз). Эта избы-
точность позволяет хорошо понимать собеседника, даже если разговор проис-
ходит в шумном помещении, или по телефонному каналу с большим уровнем
помех, или если дикция собеседника несовершенна.
Для построения эффективной системы связи теория информации рекомендует
сначала удалить избыточность из сообщений для уменьшения объема переда-
ваемой информации, а затем вводить избыточность для защиты информации
от ошибок. Приведенный выше пример показывает, что возможен другой путь:
можно использовать уже имеющуюся избыточность источника. Однако раздель-
ное решение задачи кодирования источников и задачи кодирования для каналов
на практике оказывается более продуктивным и позволяет добиться впечатляю-
щих результатов.
5.1. Постановка задачи кодирования
169
В процессе изучения кодирования источников мы описали конструктивные ме-
тоды кодирования, реально используемые сегодня в практике сжимающего коди-
рования. К сожалению, в задаче кодирования для каналов связи мы не сумеем
в рамках короткого курса пройти путь от постановки задачи до используемых
на практике способов защиты информации от ошибок. Более того, теория кодов,
исправляющих ошибки, - тема самостоятельного курса, опирающегося на мате-
матический аппарат линейной алгебры, комбинаторики и теории конечных полей
Галуа. Вопрос о том, насколько близки существующие сегодня методы кодиро-
вания к теоретически достижимым характеристикам, будет рассмотрен в главе 9.
Раздел, посвященный каналам связи, начинается с постановки задачи кодирова-
ния для каналов. Далее рассматриваются модели каналов. Затем вводится поня-
тие взаимной информации между случайными ансамблями, и для самых про-
стых моделей устанавливается предел достижимой скорости кодирования (про-
пускная способность каналов). Завершается глава доказательством прямой и
обратной теорем кодирования.
5.1.	Постановка задачи помехоустойчивого
кодирования
Начнем с примера. Рассмотрим систему связи, в которой входом канала являются
двоичные сигналы, соответствующие символам алфавита X = {0,1}. На выходе
канала каждый сигнал анализируется, и выносится решение в пользу одного из
двоичных символов выходного алфавита Y = X.
Будем считать, что подлежащая передаче информация представлена в двоичной
форме и поэтому элементарные сообщения представляют собой также двоич-
ные символы 0 либо 1. Таким образом, мы можем непосредственно использовать
входные символы канала для передачи сообщений источника. Предположим,
однако, что из-за шума в канале связи при передаче сигналов возможны ошибки.
Как можно усовершенствовать систему связи, с тем чтобы устранить ошибки или,
по меньшей мере, уменьшить их долю в принятой последовательности сообще-
ний?
Приведем примеры кодов, исправляющих ошибки.
Пример 5.1.1. Будем вместо сообщения 0 передавать последовательность ООО,
а вместо 1 - последовательность 111. Множество передаваемых по каналу после-
довательностей образует код, который в данном случае имеет длину 3 и содержит
2 кодовых слова (мощность кода равна 2). Считая, что правильная передача
символов более вероятна, чем неправильная, легко предложить разумную стра-
тегию принятия решений декодером. Если принятая из канала последователь-
ность «больше похожа» на ООО, чем на 111, декодер считает, что передавалось
сообщение 0, в противном случае принимает решение в пользу сообщения 1.
Иначе говоря, если число единиц меньше 2, решение принимается в пользу О,
в противном случае - в пользу 1.	□
170
Глава 5. Кодирование для каналов
Число несовпадающих позиций в двух последовательностях, х и у, называют рас-
стоянием Хэмминга между этими последовательностями. Описанный в примере
декодер является декодером, принимающим решения по принципу минимума
расстояния Хэмминга.
Назовем множество последовательностей у на выходе канала, декодируемых
в пользу некоторого кодового слова (точнее, в пользу сообщения, соответствую*
щего этому слову), решающей областью слова (сообщения). Решающие области
для данного примера приведены в табл. 5.1.
Таблица 5.1. Корректирующий код из примера 5.1.1
Сообщения	Кодовые слова	Решающие области
0	ООО	{ООО, 001, 010,100}
1	111	{011, 101, 110, 111}
Нетрудно видеть, что одиночная ошибка в канале связи при использовании такого
кода не опасна. Декодер примет правильное решение. Про такой код говорят, что
он исправляет все ошибки кратности 1. Заметим, что на передачу одного бита
информации данный код затрачивает 3 двоичных сигнала. Разумной характе-
ристикой кода служит его скорость, которая указывает количество бит инфор-
мации, переносимых одним сигналом. Скорость кода в данном примере равна
R = 1/3 = о, 33(бит/символ канала).
Рассмотрим еще один, немного более сложный, пример кода, исправляющего
одиночные ошибки.
Пример 5.1.2. Объединим биты передаваемого сообщения в пары. Множество
«расширенных сообщений» состоит теперь из 4 различных двоичных комбина-
ций. Приведенный в табл. 5.2 пример показывает одну из возможных конструк-
ций кода для этого множества сообщений.	□
Таблица 5.2. Код примера 5.1.2
Сообщения	Кодовые слова	Решающие области
00	00000	{00000,00001,00010,00100,01000,10000,11000,10001}
01	10110	{10110,10111,10100,10010,11110,00110,01110,00111}
10	01011	{01011,01010,01001,01111,00011,11011,10011,11010}
и	11101	{11101,11100,11111,11001,10101,01101,00101,01100}
Непосредственной проверкой можно убедиться в том, что этот код также не
боится однократных ошибок, но его скорость несколько больше, поскольку 5 сиг-
налов будет затрачено уже на передачу двух двоичных сообщений. Поэтому
2
R = - = 0,4 бит/символ канала.
5
5.1. Постановка задачи кодирования
171
Понятно, что рассмотренные коды не спасают полностью от ошибок при пере-
даче сообщений. Код примера 5.1.1 не защищает от двукратных ошибок. Код
примера 5.1.2 исправляет некоторые комбинации 2-кратных ошибок (например,
11000, 10001), но все остальные комбинации из 2 или большего числа оши-
бок неминуемо приводят к выдаче получателю неправильно декодированных
сообщений.
Приведенные выше примеры убеждают в том, что важными характеристиками
кода, защищающего информацию от ошибок, являются его скорость и помехо-
устойчивость. Последняя характеристика может быть численно измерена веро-
ятностью выдачи получателю ошибочного сообщения.
Перейдем теперь к формальной постановке задачи. Для этого рассмотрим схему,
представленную на рис. 5.1.
	► иеи	Кодер		► хехп	Канал		► УеУ"	Декодер		► Йе U
Рис. 5.1. Схема системы связи
В качестве множества сообщений без потери общности можно рассматривать
множество чисел U = {1,..., М}.
Кодом канала над алфавитом X называется любое множество последовательно-
стей А = {а?тп}, т = 1, ..., М, А е Хп. Сами последовательности называются
кодовыми словами, их длина п называется длиной кода, количество последователь-
ностей М называется мощностью кода, величина
fl=logM
п
называется скоростью кода. Скорость кода измеряется в битах на символ канала.
В частном случае, когда М = 2к, каждому из кодовых слов можно сопоста-
вить последовательность из к информационных символов (к бит). Для их пере-
дачи будет использовано кодовое слово длиной п. Скорость передачи в битах на
символ канала составит R = logM/n = к/п бит/символ.
На каждом такте работы системы связи кодер получает от источника некото-
рое сообщение и и преобразует в соответствующее кодовое слово х. В резуль-
тате передачи по каналу на выходе канала появляется последовательность у.
Декодер по последовательности у вычисляет оценку номера переданного сооб-
щения й. Событие й / и называется ошибкой декодирования, а его вероятность -
вероятностью ошибки.
Задача состоит в том, чтобы обеспечить наибольшую возможную скорость кода
при наименьшей вероятности ошибки. Эти два требования противоречат друг
другу. Приведенные выше примеры кодов показывают, что с увеличением числа
кодовых слов уменьшаются размеры решающих областей, уменьшается расстоя-
ние между кодовыми словами, увеличивается вероятность ошибки. Тем не менее
172
Глава 5. Кодирование для каналов
оказывается, что для каждого канала можно указать скорость кода, при которой
вероятность ошибки может быть сделана сколь угодно малой.
Число С называется пропускной способностью канала, если при любой скорости
кода R < С существуют коды, обеспечивающие сколь угодно малую вероятность
ошибки и, напротив, при R > С существует константа е > 0 такая, что вероят-
ность ошибки любого кода ограничена снизу величиной е (то есть вероятность
ошибки не может быть сделана сколь угодно малой).
Для того чтобы утверждать, что число С для заданной модели канала является
пропускной способностью, нужно доказать две теоремы кодирования: прямую
и обратную. Прямая теорема кодирования утверждает, что при любой скоро-
сти, меньшей С, достижима сколь угодно малая вероятность ошибки, обратная
теорема - напротив, что при скорости, большей С, вероятность ошибки будет
большой для любого кода.
При решении практических задач помехоустойчивого кодирования, помимо ско-
рости и вероятности ошибки, необходимо принимать во внимание еще один
параметр системы связи - сложность ее практической реализации. Как уже гово-
рилось, практические аспекты построения корректирующих кодов не рассмат-
риваются в данном курсе. В последующих параграфах мы научимся вычислять
пропускную способность для некоторых простых моделей каналов и докажем
соответствующие теоремы кодирования.
5.2.	Модели каналов
У нас есть опыт построения математической модели источника. Напомним, что
для описания источника мы требовали указания всех многомерных распределе-
ний вероятностей на буквах источника.
Как мы уже знаем, канал преобразует дискретную входную последовательность
над алфавитом X в выходную последовательность, элементы которой принадле-
жат, вообще говоря, другому алфавиту У. В реальных каналах искажения сигнала
в процессе передачи имеют разнообразную природу. Например, одним из источ-
ников помех является тепловой шум в среде распространения сигналов. Другие
источники - индустриальные шумы, взаимное влияние следующих друг за дру-
гом сигналов или сигналов соседних (в пространстве или по частоте) каналов
и т. п.
В любом случае нам удобно предположить, что искажения носят случайный
характер. Это предположение позволяет описывать канал, задавая условные рас-
пределения вероятностей выходных последовательностей при известных после-
довательностях на входе канала.
Входными воздействиями реального физического канала связи обычно служат
электрические сигналы, являющиеся непрерывными функциями времени, мно-
жество их значений также непрерывно. Множество значений сигналов на входе
модулятора, так же как и множество решений, принимаемых демодулятором,
дискретно. В зависимости от того, какую часть системы связи мы объединяем
5.2. Модели каналов
173
в понятии «канал», можно рассматривать каналы непрерывного времени и дис-
кретного времени, каналы с дискретным и непрерывным входом и выходом. Из
всего множества ситуаций в данной главе мы рассмотрим только дискретные (по
множеству входных и выходных символов) каналы дискретного времени.
Мы будем говорить, что модель канала задана, если для любых п и любых после-
довательностей х е Хп, у eYn указано правило вычисления условной вероят-
ности p(t/|jr).
Напомним обозначение х™ =	, хп). Канал называется стационарным, если
для любых j и п и любых € Хп, t/j+i € Yn условные вероятности	)
определяются однозначно значениями символов последовательностей и не зави-
сят от положения последовательностей во времени (от индекса j).
Канал называется каналом без памяти, если для любых j и п и любых х^™ е Хп,
€ уп
J+n
г=7 + 1
Согласно данному определению, в канале без памяти события, происходящие
при передаче последовательных символов, независимы.
Стационарный канал без памяти называют дискретным постоянным кана-
лом (ДПК).
Заметим, что классификация каналов аналогична классификации источников.
Однако задача кодирования для каналов значительно сложнее. Для произволь-
ного стационарного источника мы легко доказали прямую и обратную теоремы
кодирования и указали конструктивные асимптотически оптимальные методы
кодирования. Больше того, оптимальное кодирование оказалось возможным даже
при отсутствии априорной информации о модели источника. При изучении всех
каналов связи нам придется ограничиться в основном анализом ДПК с извест-
ными параметрами.
Для описания ДПК достаточно указать одномерные условные вероятности {р(1/|ж),
х € X, у е У}. Положим X = {0,..., К - 1}, Y = {0,	— 1}. Обозначим
Pij — Р^У = э\х = г), г G X, j G Y. Переходные вероятности канала pij удобно
записывать в виде матрицы
Роо	Р01	P0.L-1
Рю	Рп	P1,L-1
. Рк-1,О	РК-1,1	*	•• PK-1,L-1 .
Эта стохастическая матрица называется матрицей переходных вероятностей
канала. Она полностью описывает модель ДПК. Приведем два простых, но важ-
ных примера ДПК.
174
Глава 5. Кодирование для каналов
а) ДСК
б) ДСтК
Рис. 5.2. Примеры дискретных постоянных каналов
Пример 5.2.1. Двоичный симметричный канал (ДСК). Для данной модели X =
= Y = {0,1}, а переходные вероятности удовлетворяют условиям рю = Poi = Р,
Poo = Р11 = 1 - р. Матрица переходных вероятностей имеет вид
Р=	р
[ Р 1-Р.
Удобной графической иллюстрацией ДПК являются диаграммы, пример для слу-
чая ДСК показан на рис. 5.2, а. Узлы графа соответствуют входным и выходным
символам, ребра показывают возможные трансформации символов в канале, над
ребрами записаны соответствующие вероятности переходов.
В ДСК искажения последовательно передаваемых двоичных символов происхо-
дят независимо от результата передачи других символов, вероятность искажения
р (переходная вероятность ДСК) не изменяется во времени и не зависит от
значения передаваемого символа.
Пример 5.2.2. Двоичный симметричный канал со стираниями (ДСтК). Диаграмма
этой модели показана на рис. 5.2,6, а матрица переходных вероятностей имеет вид
р =	1—р — е е р
р si —р — е
Входной алфавит ДСтК содержит два символа, 0 и 1, а выходной алфавит помимо
этих двух символов содержит дополнительный символ г, который называют сим-
волом стирания. В ДСтК каждый из входных символов может с вероятностью
р превратиться в противоположный символ и с вероятностью е может при-
нять неопределенное значение, называемое стиранием. Вероятности ошибки р
и стирания е постоянны, они не зависят от результатов передачи предыдущих и
следующих символов и от значения передаваемого в данный момент символа.
Эти две модели имеют следующую практическую интерпретацию. Начнем с ДСК.
Рассмотрим работу достаточно типичной системы связи, в которой информация
передается двоичными сигналами $о и $1. Приемное устройство (демодулятор)
5.3. Взаимная информация
175
анализирует выход канала в течение промежутка времени, соответствующего
длительности элементарного сигнала, и вычисляет некоторую скалярную вели-
чину д. Решение принимается сравнением р с некоторым порогом Т. При р > Т
принимается решение в пользу одного из двух сигналов, для определенности,
si, в противном случае, при р Т решением будет з0. При правильном выборе
порога Т вероятности ошибок при передаче сигналов будут одинаковыми, и мы
приходим к модели ДСК. Недостаток такой простейшей схемы приема состоит
в том, что демодулятор теряет информацию о надежности принимаемых сигна-
лов. Очевидно, значениям р~Т соответствуют ненадежные решения, и инфор-
мация об этом могла бы быть полезной при последующей обработке принятой
последовательности.
Перейдем к рассмотрению модели ДСтК. Рассмотренную выше систему связи
можно усовершенствовать, введя «защитный интервал» или «зону стирания».
При /х > Т + Д и при р < Т - А принимаются решения в пользу 1 и 0 соответ-
ственно, а при Т - A р + А символ «стирается». Получаем модель ДСтК.
Это небольшое изменение заметно повышает эффективность системы, поскольку
задача исправления стираний проще задачи исправления ошибок. Один и тот же
корректирующий код позволяет исправить примерно в 2 раза больше стираний,
чем ошибок.
Добавим, что еще более эффективной (но и более сложной) будет система связи,
в которой демодулятор не принимает решение о каждом отдельном символе.
Выходом демодулятора является сама непрерывная случайная величина д. Канал
с дискретным входом и непрерывным выходом называют полунепрерывным кана-
лом, или каналом с мягкими решениями. Рассмотренные выше ДСК с ДСтК -
каналы с жесткими решениями.
5.3.	Взаимная информация.
Средняя взаимная информация
При изучении каналов связи нас будет интересовать возможность получения
информации о передаваемых сообщениях по символам, наблюдаемым на входе
канала. Говоря более формально, для заданного произведения ХУ={(ж, у)^р(х, у)}
дискретных ансамблей X и Y нужно количественно измерить информацию об
элементах х G X входного ансамбля, содержащуюся в выходных символах у Е Y.
Подходящей мерой такой информации является взаимная информация, опреде-
ляемая для любых пар (х,у) е XY соотношением
1(х;у) = 1(х) -1(х\у).
(5.2)
Отметим, что мы используем в выражении 1(х;у) в качестве разделителя точку
с запятой, чтобы не перепутать эту величину с собственной информацией 1(х, у)
пары сообщений (зс.'у).
Взаимная информация определена только для пар (х,у), имеющих ненулевую
вероятность.
176
Глава 5. Кодирование для каналов
Попробуем пояснить смысл введенного понятия. Уменьшаемое 1(х) представ-
ляет собой количество собственной информации, содержащейся в сообщении х.
Вычитаемое - условная собственная информация при известном у, иными сло-
вами, это количество информации, оставшейся в х после получения у. Таким
образом, разность 1(х\у) представляет собой изменение информации в х бла-
годаря получению у. Вполне разумно принять эту величину в качестве меры
информации, содержащейся в у об х.
Отметим свойства взаимной информации.
Свойство 5.3.1. Симметричность: 1(х\ у) = 1(у\ х).
Свойство 5.3.2. Если хиу независимы, то 1(х, у) = 0.
Доказательства этих свойств следуют из определения взаимной информации и
определений условной вероятности и независимости.
Взаимная информация характеризует пары сообщений и является случайной
величиной, определенной на произведении ансамблей XY.
Средней взаимной информацией между ансамблями X и Y называется величина
I(X-Y)=M[I(x;y)].
Формула, выражающая среднюю взаимную информацию через совместное рас-
пределение вероятностей, имеет вид
/(Х;Г)-££Р(г,9)1«8Й!И	(5.3)
xeXyeY
Заметим, что средняя взаимная информация определена для произвольных дис-
кретных ансамблей, включая ансамбли, содержащие элементы, имеющие нуле-
вую вероятность. (Вклад пар (х,у) таких, что р(х,у) = 0, в величину 7(Х;У)
равен нулю.)
Изучим свойства введенной информационной меры.
Свойство 5.3.3. Симметричность I(X\Y) = I(Y; X).
Свойство 5.3.4. Неотрицательность: 1(Х; У) > 0.
Свойство 5.3.5. Тождество I(X\Y) = 0 имеет место тогда и только тогда,
когда ансамбли XuY независимы.
Свойство 5.3.6.
/(X; У) = Я(Х) - Я(Х|У) = Я(У) - Я(У|Х) = Я(Х) + Я(У) - Я(ХУ).
Свойство 5.3.7. /(X; У) min {Я(Х), Я(У)} .
5.3. Взаимная информация
177
Свойство 5.3.8. /(X; У) min {log |Х|, log |У |} .
Свойство 5.3.9. Взаимная информация I(X\Y) - выпуклая А функция распре-
деления вероятностей р(х).
Свойство 5.3.10. Взаимная информация I(X;Y) - выпуклая U функция услов-
ных распределений р(у | х).
Доказательства. Свойство 5.3.3 следует из симметричности взаимной инфор-
мации. Усредняя правую и левую части (5.2) по всем парам (х,у) е ХУ, и
учитывая симметричность взаимной информации, получаем первые два тожде-
ства свойства 5.3.6. Последнее тождество следует из свойств условной энтропии.
Поскольку условная энтропия не превышает безусловной, из свойства 5.3.6 выте-
кает свойство 5.3.4. Условная энтропия равна безусловной только для независи-
мых ансамблей, поэтому справедливо и свойство 5.3.5. Свойство 5.3.7 также сле-
дует из 5.3.6 и свойства неотрицательности условной энтропии. Далее, свойство
5.3.8 является следствием 5.3.7 и свойства энтропии Я(Х) log |Х|. Доказатель-
ству свойств 5.3.9 и 5.3.10 о выпуклости взаимной информации мы посвятим
отдельный параграф 5.5.	□
Обсудим сформулированные и доказанные результаты. Интерпретируем сред-
нюю взаимную информацию /(X; У) как среднее количество информации об
элементах ансамбля X, содержащееся в элементах У. Свойство 5.3.3 устанавли-
вает, что 1(Х;У) - симметричная функция, характеризующая пару ансамблей
(Х,У).
Применительно к каналам связи можно говорить о том, что 7(Х; У) - количество
информации, переносимое одним символом канала. Свойство 5.3.4 говорит о том,
что эта величина всегда неотрицательна, что вполне логично. При этом эаметим,
что взаимная информация /(ж; у) между отдельными элементами принимает как
положительные, так и отрицательные значения.
Если выходные символы канала не зависят от входных, передача информации,
разумеется, невозможна. Это обстоятельство отражено в свойстве 5.3.5. Свойства
5.3.6 “5.3.8 полезны при вычислениях и для получения простых оценок взаимной
информации.
Выпуклость функций используется в задачах оптимизации при поиске экстре-
мальных значений. Переходные вероятности заданы изначально моделью канала,
но входное распределение - во власти кодера. Свойство 5.3.9, по сути, утвер-
ждает, что существует некоторое входное распределение, при котором взаимная
информация максимальна. Это распределение оптимально в том смысле, что оно
максимизирует количество информации, переносимое одним символом канала.
178
Глава 5. Кодирование для каналов
5.4.	Условная средняя взаимная информация.
Теорема о переработке информации
Введем еще одно понятие, используемое при анализе информационных харак-
теристик систем. Рассмотрим произведение трех ансамблей XYZ = {(ж, г/, z\
p(x^y,z)}. Зафиксируем элемент z е Z и рассмотрим условное распределение
Это распределение на ансамбле ХУ, равно как и любое другое, может быть
использовано для вычисления средней взаимной информации между X и У. Обо-
значим эту информацию как /(X; У|г). Формула для вычисления этой величины
имеет вид
Эта величина принимает случайные значения, вероятности которых определя-
ются распределением р(г).
Средней условной взаимной информацией между X и У при условии Z называется
величина
I(X; V|Z) = М [1(Х; У|г] = £ £ £ р(х, у, z) log	(5.4)
^eXyeYzez	P\y\z)
Разумеется, средняя условная информация обладает всеми свойствами средней
взаимной информации. Помимо этого, непосредственно из (5.4) получаем
1(Х; y|,Z) = Я(У|£) - H(Y|XZ).	(5.5)
С помощью этой формулы легко доказать тождества
7(Х;У^) = ДХ;У) + /(Х;2|У),	(5.6)
/(Х;УХ) = /(X;Z) + /(X;y|Z).	(5.7)
Первое из них доказывается следующей цепочкой преобразований:
7(Х;У£) = Я(Х) - H(X\YZ) =
= [Я(Х) - Я(Х|У)] + [Я(Х|У) - Я(Х|УИ)] =
= 1(Х;У) + 1(Х;£|У).
Второе тождество доказывается аналогично.
Частный случай системы обработки информации, в которой мы имеем дело
с тремя вероятностными ансамблями, показан на рис.5.3.
Входом системы являются элементы ансамбля X, выход первого устройства У
является входом второго, а выход второго устройства Z является выходом всей
системы. Специфической особенностью распределения вероятностей на множе-
стве XYZ является условная независимость X и Z при известном У. След-
ствием этой независимости является теорема, называемая теоремой о перера-
ботке информации.
5.4. Теорема о переработке информации
179
хеХ .
. ► 1
yeY
zeZ
♦ 2

Рис. 5.3. Система обработки информации
ТЕОРЕМА 5.1. Пусть X,Y uZ - вероятностные ансамбли, формируемые систе-
мой последовательной обработки информации, показанной на рис.53. Тогда имеют
место неравенства
1(У;7)	I(X;Z).
(5.8)
(5-9)
Доказательство. Воспользуемся (5.6) и (5.7):
I(X;YZ) = /(Х;У) + /(Х;7|У),	(5.10)
/(Х;У7) = 1(Х;2) + 1(Х;У|2).	(5.11)
В силу условной независимости X и Z при известном У имеем 7(Х;£|У) = 0.
Приравнивая правые части (5.10) и (5.11), получаем
7(Х; У) = /(X; Z) + /(X; Y\Z).
Поскольку второе слагаемое неотрицательно, получаем неравенство (5.8). Ана-
логично доказывается (5.9).	□
Неравенство (5.8) имеет следующее истолкование. Первое устройство можно
рассматривать как канал связи, второе - как устройство обработки информа-
ции на выходе канала. Теорема утверждает, что при такой обработке взаимная
информация между входом и выходом системы не увеличивается. Второе нера-
венство теоремы говорит о том, что обработка информации на входе системы
также не приводит к увеличению информации между входом и выходом. Иными
словами, никакая обработка информации (детерминированная или случайная)
не позволяет увеличить количество информации о входе системы, получаемой
на ее выходе.
Можно также рассматривать систему, показанную на рис.5.3, как последователь-
ное соединение двух каналов. В этом случае теорема устанавливает интуитивно
понятный факт: количество информации, проходящей через последовательное
соединение каналов, не может быть больше количества информации, проходящей
через каждый отдельный канал.
180
Глава 5. Кодирование для каналов
5.5.	Выпуклость средней взаимной
информации
В данном параграфе свойства средней условной взаимной информации будут
использованы для доказательства выпуклости средней взаимной информации
/(Х;У) как функции входного распределения и переходных вероятностей.
Будем использовать вектор р = (ро, • • • ,Рк-1) для обозначения распределения
вероятностей на входных символах X = {0,... , К - 1}. Для сокращения записи
и чтобы подчеркнуть, что нас интересует зависимость взаимной информации от
входного распределения, будем временно писать /(р) вместо /(Х;У).
В соответствии с определением выпуклой А функции, утверждение, которое нам
предстоит доказать, состоит в том, что для любых двух стохастических векторов,
Pi и р2, и любого вещественного числа а е [0,1] имеет место неравенство
I (api + (1 - а)р2) > al(Pi) + (1 - а)/(р2)-	(5.12)
Введем в рассмотрение вспомогательное множество Z = {1,2} и припишем его
элементам вероятности рД1) = а, pz(2) = 1 - а.
Рассмотрим теперь произведение трех ансамблей XYZ, в котором тройки
(х, у, z) е XYZ формируются по следующему правилу. Сначала в соответствии
с распределением p(z) выбирается один из двух элементов множества Z. Затем
в соответствии с выбранным z выбирается одно из двух распределений: рх(если
z = 1) или р2 (если Z-— 2) на множестве X. В соответствии с полученным
распределением порождается элемент х е X, и уже затем в соответствии с рас-
пределением р(у\х) генерируется элемент у G У. Заметим, что ансамбли Z и У
условно независимы при условии X.
Согласно введенным обозначениям имеем
1(Х;У|г = 1) = 7(р1);
/(Х;У|г = 2) = /(р2);
/(X;y|Z) = aI(p1) + (l-a)/(p2);
ДХ;У) = /(ар1 + (1-а)р2).
Поэтому доказательство неравенства (5.12) сводится к доказательству неравен-
ства
1(Х;У) >1(Х;У|И).	(5.13)
Чтобы доказать это, запишем двумя способами взаимную информацию 1 (У; XZ):
J(y;XZ) = 1(У;Х) + /(У;И|Х);	(5.14)
1(У;Х2) = I(Y;Z) + I(Y;X\Z).	(5.15)
В силу условной независимости Z и У имеем I(Y; Z]X) = 0. Взаимная инфор-
мация I(Y;Z) неотрицательна. Приравнивая ’правые части (5.14) и (5.15), полу-
чаем (5.13), что завершает доказательство выпуклости взаимной информации по
входным распределениям.
5.6. Информационная емкость и пропускная способность
181
Рассмотрим теперь взаимную информацию как функцию условных распределе-
ний р(у|ж). Временно обозначим через 1(Р) среднюю взаимную информацию,
вычисленную для заданной стохастической матрицы Р = {р(у|я),х е Х,у е У}.
Требуется доказать, что для любых двух стохастических матриц, А и Р2, и любого
а € [0,1] имеет место неравенство
I (aPi + (1 - а)Ра) < aJ(Pi) + (1 - a)J(P2).	(5.16)
Снова рассмотрим вспомогательное множество Z = {1,2} и припишем его эле-
ментам вероятности рг(1) = а, рг(2) = 1 - а. Построим новое произведение трех
ансамблей XYZ по следующему правилу. Сначала в соответствии с распреде-
лением р(х) выбирается один из элементов множества X и независимо от него
в соответствии с распределением p(z) выбирается один из двух элементов мно-
жества Z. Затем в соответствии с выбранным z выбирается одна из двух матриц
переходных вероятностей: Р = Pi (если z = 1) или Р = Р2 (если z = 2). В соот-
ветствии с выбранными элементом х и матрицей Р генерируется элемент у е У.
Заметим, что в данной модели ансамбли Z и X независимы.
В соответствии с введенными обозначениями имеем
/(X;y|z = l) = /(Pi);
I(X-,Y\z = 2) = 1(Р2);
I(X;Y\Z) = aI(Pi) + (1 - а)/(Р2);
ЛХ;У)=7(аР1 + (1-а)Р2).
Доказательство неравенства (5.16) теперь сводится к доказательству неравенства
7(Х;У) О(Х;У|2).	(5.17)
Запишем двумя способами взаимную информацию I(X-,YZ):
J(X;YZ) = I(X;Y) + I(X;Z]Y)’,	(5.18)
I(X;YZ) = I(X;Z) + I(X;Y\Z).	(5.19)
Из независимости X и Z имеем I(X; Z) = 0. Кроме того, 7(Х; Z^Y) 0. Поэтому,
приравнивая правые части (5.18) и (5.19), убеждаемся в справедливости (5.17) и,
в свою очередь, (5.16). Тем самым доказана выпуклость U взаимной информации
по условным распределениям.	□
5.6.	Информационная емкость
и пропускная способность
Задача, которую мы решаем в данном параграфе, состоит в том, чтобы выра-
зить достижимую скорость передачи информации по каналу через известные
нам информационные меры, такие как энтропия, взаимная информация и т. п.
Рассмотрим дискретный стационарный канал. Мы знаем, что количество инфор-
мации о входных символах X канала, содержащееся в выходных символах Y
определяется средней взаимной информацией	Это верно при передаче
182
Глава 5. Кодирование для каналов
одного символа канала. Из опыта изучения источников информации известно,
что кодирование последовательностей сообщений потенциально более эффек-
тивно, чем кодирование отдельных сообщений. Точно так же при кодировании
для каналов мы объединяем последовательные входные символы канала в блоки,
представляющие собой кодовые слова некоторого кода.
Таким образом, при использовании кодов длиной п количество информации,
получаемой декодером при передаче одного кодового слова, в среднем составит
/(ХП;УП) бит, что соответствует скорости передачи информации
-I(Xn; Yп) бит/символ канала.
п
Эта величина зависит от переходных вероятностей {р(у|ж), у е Yn, х е Хп} и
от распределения вероятностей на входе канала {р(ж), х е Хп}. Входное рас-
пределение следует выбрать таким, чтобы максимизировать скорость передачи
информации. Результирующую скорость запишем в виде
max ~1(ХП;УП) бит/символ канала.
{р(®)} п
Заметим, что длина кода п также является свободным параметром, она может
быть выбрана такой, чтобы скорость передачи была как можно больше. Эти
неформальные рассуждения приводят нас к следующему определению.
Величина
Со = sup max -/(Хп; Уп)	(5.20)
П {р(®)} п
называется информационной емкостью канала.
Напомним, что sup (supremum) обозначает наименьшую верхнюю грань множе-
ства, то есть наименьшее число, не меньшее, чем любой из элементов множества.
В отличие от максимального элемента, верхняя грань может не принадлежать
множеству. Пусть, например, А = {(п - 1)/п, п = 1,2,...}. Максимального
числа в этом множестве не существует, но sup А = 1, причем эта верхняя грань
совпадает с пределом последовательности при п —> оо. Аналогично в опреде-
лении информационной емкости канала наибольшее значение средней взаим-
ной информации на букву канала может достигаться при бесконечной длине
кода, поэтому в (5.20) нас интересует именно верхняя грань, а не максимальное
значение.
Итак, мы ввели в рассмотрение информационную емкость канала Со как некото-
рую функцию его переходных вероятностей. Мы предполагаем, что именно эта
величина характеризует потенциально достижимую скорость передачи по каналу.
Выше, в параграфе 5.1, мы определили пропускную способность канала С как
максимальную скорость, при которой возможна передача со сколь угодно малой
вероятностью ошибки. Естественно, возникает вопрос о том, как соотносятся
между собой эти две характеристики канала.
В главе 1, были введены два понятия: скорость создания информации источни-
ком Н и предел энтропии на сообщение источника Ноо(Х) = Н(Х\Х°°). Было
5.7. Неравенство Фано
183
доказано, что для произвольного стационарного источника эти две величины
равны.
Вопрос о соотношении между информационной емкостью канала и его про-
пускной способностью несколько сложней. Ниже мы докажем обратную тео-
рему кодирования, утверждающую, что информационная емкость Со ограни-
чивает сверху скорость, при которой достижима сколь угодно малая вероят-
ность ошибки. Для дискретного постоянного канала будет доказана прямая тео-
рема кодирования, согласно которой при скорости сколь угодно близкой к Со
достижима сколь угодно малая вероятность ошибки.
5.7.	Неравенство Фано
Для доказательства теорем кодирования нам нужно будет установить связь между
информационными характеристиками канала и источника, с одной стороны, и
практически важными параметрами — скоростью передачи информации и веро-
ятностью ошибки, с другой стороны. Неравенство Фано — ключ к решению этой
задачи.
На рис. 5.4 для иллюстрации вводимых ниже обозначений показана обобщенная
схема системы передачи сообщений,
-----► Система связи
и g и ______________
ve V=U
Рис. 5.4. Система передачи информации
Сообщениями являются элементы множества U = {и} = {0,..., М - 1}. Получа-
телю выдаются оценки сообщений. Множество оценок обозначено через V = {г>}.
Множества U и V совпадают. Всякий раз, когда и / v, имеет место ошибка
декодирования.
Если задана модель системы связи, то есть точно известны алгоритмы работы
кодера и декодера и математическая модель канала, тем самым определено про-
изведение ансамблей UV = {(u, v),p(u, v)}. С помощью распределения
вероятность ошибки Ре может быть вычислена по формуле
Ре =
и V^U
Вероятность правильного решения
Pc = 1 - Ре = ^2 12
и v=u
(5.21)
(5.22)
184
Глава 5. Кодирование для каналов
ТЕОРЕМА 5.2. (Неравенство Фано.)
H([7|V)^77(Pe)+Pelog(M-l),
(5.23)
где г)(-) обозначает энтропию двоичного ансамбля (см.( 1.4)).
Обсуждение. Прежде чем мы приступим к доказательству этого неравенства,
постараемся уяснить его смысл. В левой части неравенства имеем условную
энтропию источника сообщений при условии, что известно вынесенное декоде-
ром решение. Эта величина характеризует неопределенность о переданном сооб-
щении, оставшуюся на приемной стороне после вынесения решения. Каким обра-
зом можно было бы помочь декодеру устранить эту неопределенность? Предпо-
ложим, что в распоряжении декодера имеется добрый, но практичный джин. Он
знает истинное переданное сообщение, но требует плату за каждый бит получен-
ной от него информации. Какие вопросы нужно задать джину?
Одна из нетривиальных стратегий - такая. Сначала спросим джина, правильно
ли принятое решение. Поскольку множество возможных ответов состоит из двух
элементов, имеющих вероятности Ре и Рс = 1 - Ре, ответ джина обойдется нам
в среднем в г/(Ре) бит. Если решение было правильным (вероятность этого собы-
тия 1 - Ре), то дополнительной информации не требуется. Если же решение
ошибочно, то достаточно узнать, какое из остальных М - 1 возможных сооб-
щений было передано. Эта вторая ситуация имеет вероятность Ре и обойдется
нам в худшем случае в log(M — 1) бит. Итого для разрешения неопределенности
H(U\V) нам понадобится не более
Tj(Pe) + (1 - Ре) X 0 + Ре lOg(M - 1)
бит, что в точности совпадает с правой частью (5.23).
Эти эвристические рассуждения позволяют понять, почему неравенство Фано
имеет место, и облегчают запоминание формулы в его правой части. Конечно,
эти рассуждения нельзя считать доказательством неравенства Фано.
Обсудим коротко, какую полезную информацию мы можем извлечь из соотноше-
ния (5.23). Введем специальное обозначение 7(Ре) для правой части неравенства
Фано:
7(Ре) = п(Ре) + Ре log(M - 1)	(5.24)
и изучим поведение этой функции. В крайних точках 0 и 1 она равна, соответ-
ственно, 0 и log(M — 1). Беря последовательно первую и вторую производную,
убеждаемся в том, что функция 7(Ре) строго выпукла (7 и имеет максимум в точке
(М—1)/М. В этой точке 7(Ре) = log М. График функции 7(Ре) показан на рис. 5.5.
При доказательстве обратной теоремы кодирования нам понадобится следующее
свойство функции 7(Ре), которое поясняется представленным на рис. 5.5 графи-
ком: для любого 6 > 0 существует положительное е > О такое, что из неравенства
7(Ре) > 6 следует неравенство Ре > г.
5.7. Неравенство Фано
185
Рис. 5.5. Правая часть неравенства Фано
Доказательство. Используя (5.21) и (5.22), запишем выражения, участвующие
в неравенстве Фано (5.23), в следующем виде:
Я(17|У) = -^^p(u,v)\ogp(u\v) -	(5.25)
и v^u ‘	и v=u
' \
??(ре) = - 52 52 р(и' log Ре~ 5252	v>>log Pci <5-26>
и V^U	и v^u
pe iog(M -1) = 52 52p(u’v) log(M -<5-27>
и v^u
Рассмотрим разность
Д = H(U\V) - ri(Pe) - Pe log(M - 1).
Чтобы доказать (5.23), нужно доказать, что Д 0. Для этого вычтем из пра-
вой и левой части (5.25) соответствующие части тождеств (5.26) и (5.27). После
элементарных преобразований придем к равенству
и v^u
p(u\v)(M - 1)+	10g P(«|v)'
Следующий шаг основан на использовании неравенства
log х (х — 1) loge.
186
Глава 5. Кодирование для каналов
Применив его к обоим слагаемым, получим
Д с (loge)

~52 52^u’v)+
u v^u
U V=u	* '	' и v=u
Воспользуемся тем, что p(u,v) = p(v)p(u\v), и обозначениями (5.21) и (5.22).
Результат легко привести к виду
A log е х
д/ту 52 52	- Ре+Рс 52 52 р^ - Рс
и V0U	и v=u
Заметим теперь, что
52 52 р(”) = (^ -1) 52но = (м -1).
и v^u	V
(5.28)
(5.29)
Здесь мы использовали то, что сумма в левой части содержит всего М различных
слагаемых, и каждое из них встречается в этой сумме ровно (М — 1) раз. Кроме
того, справедливо равенство
52 52 р^ = 52 р(и)= 1 •	<5-30)
и v=u	и
Подстановка (5.29) и (5.30) в (5.28) приводит к неравенству А 0. Тем самым
неравенство Фано доказано.	□
Обобщим теорему 5.2 на случай передачи последовательностей сообщений. Для
этого рассмотрим систему связи, показанную на рис. 5.6. На этот раз входом
системы является последовательность сообщений и = (щ,..., un\ а выходом -
последовательность решений v = (yi,..., vn), е U = V = {0,..., М - 1},
г = 1,..., N. Вероятность ошибки при передаче г-го сообщения обозначается как
Pei =	Vi).
------> Система связи
u g UN _____________
VG V
Рис. 5.6. Система передачи информации
Введем в рассмотрение среднюю вероятность ошибки для последовательности
длины N
1 N
г=1
5.8. Обратная теорема кодирования
187
ТЕОРЕМА 5.3. Для последовательностей (u,v) е UNVN, составленных из эле-
ментов множества объема М, имеет место неравенство
LH(IJN\VN) < Г)(Ре) + Ре log(M - 1).	(5.31)
Доказательство. Напомним, что условная энтропия не возрастает с увеличением
числа условий. Поэтому
N	N
H(UN\VN) = ^/H(Ui\U1...Ui-1VN)^H(Ui\Vi).
г=1	г=1
Поделим обе части на N и к каждому слагаемому применим неравенство Фано.
Получим
1	1 N	1 N
-H(UN\VN) < - £ Tl(Pei)+^ X P* - !)•
t=l	i=l
Поскольку энтропия - выпуклая О функция, средняя по i энтропия не меньше
энтропии средней вероятности ошибки. Учитывая это, из последнего неравенства
получаем доказываемое неравенство (5.31).	□
5.8.	Обратная теорема кодирования
В этом параграфе для произвольного дискретного стационарного канала будет
доказано, что надежная передача информации со скоростью, превышающей инфор-
мационную емкость канала, невозможна.
Предполагается, что для передачи используется код С длины п, состоящий из
М = |С| кодовых слов. При этом скорость кода равна R = log |Af |/n, то есть
число кодовых слов равно М = 2nR. Мы считаем сообщениями источника номера
кодовых слов кода С. Чтобы упростить запись доказательства, сообщения считаем
равновероятными. Такое предположение не сужает общности, поскольку в про-
тивном случае, применив кодирование без потерь, можно было бы использовать
для передачи этих сообщений коды с меньшей скоростью.
ТЕОРЕМА 5.4. Обратная теорема кодирования. Для дискретного стационарного
канала с информационной емкостью Со для любого 8 > 0 существует число е > О
такое, что для любого кода со скоростью R> Со+ 8 средняя вероятность ошибки
удовлетворяет неравенству
Ре^ е.
Доказательство. Рассмотрим произвольный код С длиной п со скоростью R =
= log |С|/п. Обозначим через N длину последовательностей сообщений и е UN,
сопоставляемых словам кода С, через v е VN обозначим последовательности
решений, принимаемых декодером. Имеет место цепочка соотношений
188
Глава 5. Кодирование для каналов
nR = log |С| =
= Н(ХП) (< H(UN) =
= H(UN')-H(Un\VN) + H(UN\VN) =
(= I(UN; VN) + H(UN]VN)
(d)
I(Xn;Yn) + H(UN\VN)
(e)
пСо + п7(Ре).
Здесь мы сначала в (а) использовали предположение о равновероятности кодо-
вых слов, затем в (Ь) — свойство энтропии 1.3.7 (при преобразовании случайного
ансамбля UN в Хп энтропия либо сохранилась либо уменьшилась), далее (с) —
свойство взаимной информации, затем в (d) — теорему о переработке инфор-
мации 5.1, в (е) — неравенство Фано и определение информационной емкости
канала. Функция 7( ) определена соотношением (5.24).
Из последнего неравенства получаем
7(Ре)>Я-С'о><5.
Из свойств функции 7( ) (см. обсуждение перед доказательством теоремы 5.2)
следует, что из неравенства 7(Ре) > 6 следует существование положительного
£ > 0 такого, что Ре > е. Тем самым теорема доказана.	□
Итак, доказанная теорема утверждает, что, если скорость передачи информации
хотя бы ненамного (на любую положительную величину <5) превышает инфор-
мационную емкость канала, вероятность ошибки уже не может быть сколь угодно
малой. Она ограничена снизу положительной величиной е, независящей от длины
используемых кодов. Отметим особо, что результат получен для произвольного
стационарного канала.
Чтобы доказать прямую теорему кодирования, нам придется существенно сузить
множество рассматриваемых моделей. В следующих параграфах мы получим
относительно простые формулы для информационной емкости некоторых кана-
лов без памяти и уже затем докажем прямую теорему кодирования для дискрет-
ных постоянных каналов.
5.9.	Вычисление информационной емкости
каналов без памяти
Рассмотрим дискретный постоянный канал (стационарный канал без памяти),
заданный входным и выходным алфавитами X = {ж} и Y = {у} и матрицей
условных распределений Р = {р(?/|ж)}. Для данной модели канала для про-
извольных последовательностей х = (xf, . ..,жп) и у = (i/i,... ,уп) условные
вероятности р(?/|гс) вычисляются по формуле
Xi/i®) = Профд	<5-32)
г=1
5.9. Вычисление информационной емкости каналов без памяти
189
По определению, информационная емкость канала
Со = sup max -/(Хп; У”).	(5.33)
п {р(®)} П
Эта формула непригодна для вычисления информационной емкости по заданной
матрице Р, поскольку предполагает вычисление экстремума функции по счет-
ному числу параметров. Нам предстоит дать ответ на вопрос, нельзя ли упростить
(5.33), используя (5.32)? Положительный ответ на этот вопрос сформулируем
в виде следующей теоремы.
ТЕОРЕМА 5.5. Информационная емкость дискретного постоянного канала вычис-
ляется по формуле
Со= max 1(Х;У).	(5.34)
{р(х)}
Доказательство. Доказательство состоит из двух шагов. Сначала мы докажем,
что правая часть (5.34) является границей сверху на информационную емкость
канала. Затем мы докажем, что эта граница достигается при некотором распре-
делении р(ж).
При произвольном распределении {р(х),х Е Хп} запишем взаимную информа-
цию между входными и выходными последовательностями в виде
I (Хп; Уп) = Н (Yn) - Н (УП|ХП).	(5.35)
Воспользовавшись (5.32) и свойствами логарифма и математического ожидания,
выполним простые преобразования.
H(Yn\Xn)
М [- logp(?/|a?)] = М
п
г=1
п	п
= ^2Я(У4|Х4).
г=1	г=1
Из свойств энтропии мы помним, что
п
(5-36)
г=1
причем равенство имеет место только для независимых ансамблей. С учетом
выполненных выкладок вместо (5.35) получаем неравенство
п	п
I (Хп; У”) < £ 1Я (у) “ Н №<)) = Е1	У<)-	(5.37>
г=1	г=1
Тем самым мы, по сути, завершили первый шаг нашего доказательства. Предпо-
ложим теперь, что буквы на входе канала независимы, и докажем, что при этом
предположении в (5.37) имеет место равенство. Это будет означать, ч!о макси-
190
Глава 5. Кодирование для каналов
мум в (5.33) следует искать только среди таких распределений на Хп, которые
порождают последовательности независимых букв на выходе канала. Доказа-
тельство сводится к доказательству того, что при этом предположении имеет
место равенство в (5.36). Проще говоря, нужно доказать, что для дискретного
канала без памяти из независимости букв на входе канала следует независимость
символов на выходе канала.
Выходное распределение по формуле полной вероятности вычисляется как
р(у) = 52
®GXn
В предположении о независимости входных символов с учетом (5.32) получаем
Р(у) = 52 Пр(^)Пр(^кг) = 52	=
х^Хп г=1 i=l	®GXn г=1
= Е Е-Е Р(Я1)р(У1к1)  р(х2)р(у2\х2)  ...  р(хп)р(уп\хп).
Х1&Х х^ех хпех
Поочередно вынося сомножители за знаки сумм, приходим к равенству
п	п
р(у)=П 52 р(^)р(^1^) = Пр(у*)>
2=1 Xi^X	1=1
из которого и вытекает доказываемое утверждение о независимости выходных
символов канала.
Теперь мы знаем, что при независимых входных символах в (5.37) имеет место
равенство. Подстановка этого равенства в определение информационной емкости
(5.33) дает
Со = sup max - 52	у)-
n {p(®)} n
Заметим, что каждое слагаемое зависит только от распределения вероятностей
для соответствующего входного символа. Следовательно, поиск максимума может
быть выполнен для каждого отдельного слагаемого независимо от других. Полу-
чаем
1
Со = sup - max 1(Хг, Yi).
{?(*,)}
В силу стационарности канала все слагаемые суммы будут одинаковыми. Поэтому
Со = sup max 7(Х;У) = max /(Х;У).	□
п {р(ж)}	{р(ж)}
Мы пришли к вполне естественному результату: для стационарного канала без
памяти вычисление информационной емкости сводится к максимизации средней
взаимной информации между отдельными буквами по одномерным распределе-
ниям.
5.10. Симметричные каналы
191
Важен также доказанный попутно факт: пропускная способность канала без па-
мяти достигается при независимых буквах на входе канала. В этом смысле рас-
пределения, порождающие независимые буквы на входе канала, являются опти-
мальными.
Формула (5.34) много проще исходной формулы (5.33). При небольшом объ-
еме алфавита оптимизация по входным распределениям может быть выполнена
аналитически или численными методами с помощью стандартных компьютер-
ных программ. Известен алгоритм Блэйхута [31], решающий эту задачу весьма
эффективно.
Тем не менее хотелось бы иметь явное выражение, связывающее информацион-
ную емкость с параметрами канала. Для некоторых простых случаев такие выра-
жения получить несложно, и рассмотрению этих случаев посвящен следующий
параграф.
5.10.	Симметричные каналы
Нашей задачей является дальнейшее упрощение формулы для информационной
емкости канала. Сузив класс каналов до дискретных постоянных каналов (ДПК),
задаваемых матрицей условных вероятностей Р = {р(з/|я), х е X, у е У}, мы
получили формулу
Со = шах 7(Х;У).	(5.38)
{р(ж)}
Рассмотрим некоторые частные случаи вида матрицы Р.
ДПК называется симметричным по входу, если все строки его матрицы пере-
ходных вероятностей могут быть получены перестановками элементов первой
строки.
ДПК называется симметричным по выходу, если все столбцы его матрицы пере-
ходных вероятностей могут быть получены перестановками элементов первого
столбца.
ДПК называется полностью симметричным, если он симметричен одновременно
по входу и по выходу.
Пример 5.10.1. На рис. 5.7 показаны три диаграммы переходных вероятно-
стей каналов и соответствующие матрицы переходных вероятностей. Эти модели
описывают полностью симметричный, симметричный только по входу и симмет-
ричный только по выходу каналы.
Сформулируем те свойства симметричных каналов, которые упрощают вычис-
ление их информационной емкости.
192
Глава 5. Кодирование для каналов
Свойство 5.10.1. Для симметричного по входу канала без памяти
Со = max {Я(У)} - H(Y\x), х е X.
{р(ж)}
в) Симметричный по выходу канал
Рис. 5.7. Симметричные каналы
Свойство 5.10.2. Для симметричного по входу канала без памяти
C0^logL-H(Y\x\ хеХ.
Свойство 5.10.3. Для симметричного по выходу канала без памяти при равнове-
роятных входных символах выходные символы также равновероятны.
Свойство 5.10.4. Для полностью симметричного канала без памяти
Со = log|y| — Я(У|ж), хеХ.
5.10. Симметричные каналы
193
Доказательства. Начнем с первого свойства. Напомним, что
1(Х, У) = Я(У) - H(Y\X).	(5.39)
В свою очередь, вычитаемое можно записать как
H(Y\X) = ^p(x)H(Y\x).
X
Поскольку все строки матрицы переходных вероятностей одинаковы с точностью
до нумерации элементов, все условные энтропии Я(У|ж) одинаковы. Следова-
тельно, вычитаемое в (5.39) не зависит от входного распределения. Максими-
зация взаимной информации сводится к максимизации энтропии Я(У), что и
утверждается в свойстве 5.10.1.
Второе свойство следует из первого с учетом того, что энтропия ансамбля не пре-
вышает логарифма числа его элементов. Больше того, нам известно, что равен-
ство Я(У) = log |У| имеет место при равновероятных буквах ансамбля У. Свой-
ство 5.10.3 доказывается с помощью формулы полной вероятности
Р(у) = 52р(я:)р(у|х).
X
При равновероятных буквах на входе
р(у) = щ Ур(ук), у е у.
Сумма в правой части представляет собой сумму элементов столбца матрицы
переходных вероятностей. Поскольку в случае симметричного по выходу канала
столбцы одинаковы с точностью до перестановки их элементов, р(у) не зависит
от у и имеет место равенство р(у) = 1/ |У|. Из первых трех свойств немедленно
следует свойство 5.10.4.	□
Пример 5.10.2. Двоичный симметричный канал. Из свойства 5.10.4 получаем
формулу для информационной емкости двоичного симметричного канала
(рис. 5.7, а)
Со = 1 - г)(р).
График зависимости информационной емкости от переходной вероятности р пока-
зан на рис. 5.8.
Информационная емкость равна нулю при р = 1/2. В этом случае вход и выход
канала независимы. Естественно, с уменьшением р информационная емкость
растет до значения Со = 1 при р = 0. Информационная емкость симметрична
относительно точки р = 1/2. Это понятно, ведь при р > 1/2, переобозначив
выходные символы, мы получим канал с переходной вероятностью р < 1/2.
К сожалению, сформулированных свойств недостаточно для того, чтобы полу-
чить явные выражения для двоичного стирающего канала, показанного на
рис. 5.7, б. Для этого симметричного по входу канала имеет место только свойство
5.10.1, предполагающее оптимизацию по входному распределению при вычис-
194
Глава 5. Кодирование для каналов
Рис. 5.8. Пропускная способность ДСК
лении информационной емкости. Однако данная модель принадлежит к еще
одному широкому классу симметричных каналов, для которых задача вычис-
ления информационной емкости решается просто.
Канал называется симметричным в широком смысле, если перенумерацией выход-
ных символов его матрица может быть представлена в форме клеточной матрицы
Р=[Р1|Р2|...|РМ],	(5.40)
в которой каждая из подматриц X полностью симметрична (по входу и по
выходу).
Пример 5.10.3. Двоичный канал со стираниями. Матрица переходных вероят-
ностей ДСтК (рис. 5.7,6) перенумерацией выходных символов (перестановкой
столбцов) легко приводится к виду
p/=i-p-e р	б	:
р 1 - р - е е	?
Обе подматрицы этой матрицы симметричны по входу и по выходу, следова- \
тельно, ДСтК симметричен в широком смысле.
Свойство 5.10.5. Для симметричного в широком смысле канала максимум взаим- j
ной информации между входом и выходом (см. (538)) достигается при равноверо- \
ятных буквах входного алфавита.
5.10. Симметричные каналы
195
Доказательство. Поскольку симметричный в широком смысле канал заведомо
симметричен по входу, достаточно доказать, что равномерное распределение на
входе канала максимизирует энтропию выходного алфавита Y.
Рассмотрим представление матрицы переходных вероятностей в форме (5.40) и
обозначим через У,..., Ym подмножества символов выходного алфавита У, соот-
ветствующие подматрицам Pi,,Рм* Энтропию ансамбля У запишем в виде
м
я(у) = _ 52 52	log Иу) •	(5-41)
г=1 y^Yi
Введем обозначение
= 52 р(у)
veYi
для вероятности подмножества у. Набор чисел	образует распреде-
ление вероятностей на множестве индексов I = {1,...,М}. Заметим, что для
рассматриваемой модели канала вероятности	не зависят от распре-
деления {р(х)} на множестве X. Чтобы убедиться в этом, запишем условную
вероятность подмножества У при известном символе х:
Р(у»|®) = 52 р(у\х)
yeYt
Сумма в правой части по предположению не зависит от конкретного значения
ж, следовательно, при всех х имеет место равенство Р(У |ж) =
Преобразуем (5.41) к виду
я(у) = -52 log (vM =	<5-42>
г=1 yEYi	\ Чг /	.=1
М
где Я(/) = - £ Qi log Qi ~ энтропия множества индексов /, а
г=1
y€Yt qi qi
энтропия подмножества у. Поскольку первое слагаемое в (5.42) не зависит от
входного распределения, достаточно рассмотреть второе слагаемое. Заметим, что
если все элементы подматрицы Pi поделить на вероятность qi9 то результатом
будет стохастическая матрица, которая является матрицей переходных вероятно-
стей полностью симметричного канала. Согласно свойству 5.10.3 максимальная
энтропия выходного алфавита (равномерное распределение на выходе канала)
достигается при равновероятных входных символах. Таким образом, при равно-
вероятных символах на входе достигается максимум каждого слагаемого в правой
части (5.42) и, следовательно, максимум энтропии Я(У).	□
196
Глава 5. Кодирование для каналов
Пример 5.10.4. Вернемся к модели ДСтК, представленной на рис. 5.7, 6. Благо-
даря свойству 5.10.5 мы знаем, что информационная емкость этого канала равна
взаимной информации между входом и выходом при равновероятных входных
символах рж(0) = рж(1) = 1/2. Используя формулу полной вероятности, находим,
что
Р»(0) = Р»(1) =	PV(z) = Е.
Подставив эти значения в формулу для взаимной информации, после несложных
преобразований можно получить формулу для информационной емкости
= (1-Е) (1
Из этой формулы, в частности, следует очень простая формула для информаци-
онной емкости канала со стираниями и без ошибок. При р = 0 имеем
СЬ = 1 — s.
Результат кажется очевидным. Поскольку доля «стертых» символов равна е, то
доля успешно переданных и при этом (в данном случае) заведомо правильно
переданных символов как раз равна 1 — е. Проблема, однако, состоит в том,
что кодер не знает заранее, какие именно символы будут стерты. Тем не менее
полученная формула для информационной емкости говорит о том, что возможно
такое кодирование, при котором скорость кода будет такой же, как если бы пози-
ции стертых символов были известны заранее. При этом вероятность ошибки,
как следует из доказываемой ниже прямой теоремы кодирования, может быть
сделана сколь угодно малой.
5.11.	Прямая теорема кодирования для
дискретных постоянных каналов
Нам предстоит доказать прямую теорему кодирования, утверждающую, что при
скорости, меньшей информационной емкости, вероятность ошибки декодиро-
вания может быть сделана сколь угодно малой. Прямой путь к цели состоит
в построении последовательности кодов возрастающей длины п с убывающей
по мере роста длины кодов вероятностью ошибки. Парадокс состоит в том, что
таких конструкций кодов до сих пор не найдено, при том, что теорема кодиро-
вания, устанавливающая их существование, была успешно доказана Шенноном
более полувека назад.
Метод, использованный Шенноном, называется методом случайного кодирова-
ния. Идея его очень проста. При заданной длине и скорости кода множество
кодовых слов кода строится случайным выбором символов в соответствии с неко-
торым распределением вероятностей. При таком построении кода сам код может
рассматриваться как случайное событие, а его вероятность ошибки - как слу-
чайная величина. Предположим, что удалось найти математическое ожидание
5.11. Прямая теорема кодирования для ДПК
197
вероятности ошибки по множеству кодов и это значение оказалось равным неко-
торой величине в. Тогда, очевидно, мы сможем утверждать, что по меньшей мере
для одного из кодов вероятность ошибки не превышает е.
Итак, воспользуемся методом случайного кодирования для доказательства пря-
мой теоремы кодирования для дискретных постоянных каналов. Напомним, что
рассматриваемый канал задается матрицей условных вероятностей Р = {р(?/|ж),
xeX.yeY} получения выходных символов у е Y при передаче по каналу
символов х е X. Поскольку ДПК - канал без памяти, для любой пары последо-
вательностей х = (а?1,...,хп) е Хп, у = (угт-^Уп) £Yn условная вероятность
р(у\х) вычисляется как произведение побуквенных условных вероятностей:
п
p(l/|®) = Цр(у»|а:<).
г=1
Обозначим через т принятое декодером решение о номере переданного кодо-
вого слова при передаче кодового слова хт. Событие т / т представляет собой
ошибку декодирования при передаче сообщения т, вероятность этого события
обозначим как Рет. Считая все сообщения (номера кодовых слов) равновероят-
ными, среднюю вероятность ошибки определим соотношением
_ 1 Л _
Ре - м Y,Рет-
т=1
ТЕОРЕМА 5.6. Для дискретного постоянного канала с информационной емкостью
Со для любых е,8 > 0 существует достаточно большое число по такое, что для
любого натурального числа п п0 существует код длиной п со скоростью F& Со — 8,
средняя вероятность ошибки которого Ре е.
Иными словами, мы утверждаем, что при скорости кода сколь угодно близкой
к информационной емкости Со (но, конечно, меньшей Со хотя бы на малую
величину 8) увеличением длины кодовых слов можно добиться сколь угодно
малой вероятности ошибки (меньше любого е).
Доказательство. Нам предстоит проделать следующий путь:
1.	Построить ансамбль случайных кодов с заданной длиной и скоростью.
2.	Указать правило декодирования.
3.	Оценить среднюю по ансамблю кодов вероятность ошибки и доказать, что
вероятность ошибки убывает с увеличением длины кодов.
Шаг 1. Построим ансамбль кодов. Обозначим через р = {р(х),х е X} то распре-
деление вероятностей на X, при котором имеет место равенство Со = /(X, У), то
есть
р = arg max I(X;Y).
р={р(х)}
198
Глава 5. Кодирование для каналов
Каждый код из ансамбля мы будем получать случайным и независимым выбором
всех символов кодовых слов из множества X в соответствии с распределением
вероятностей р.
При заданной скорости кода R и его длине п число кодовых слов равно М = 2nR.
Исходя из условий теоремы, выбираем М таким, что
М - 1 < 2п(Со"г) М.
(5.43)
Шаг 2. Перейдем к описанию работы декодера. Формально правило принятия
решений декодером задается разбиением всего множества Yn на непересекающи-
еся решающие области Rm, т = 1,..., 7И, такие, что IJm=i = Yn, Rm A Rm' =
0 при m' / т. При получении на выходе канала последовательности у деко-
дер принимает решение в пользу сообщения с номером т (то есть считает, что
передавалось кодовое слово хт\ если у е Rm.
При равновероятных сообщениях оптимальным (с точки зрения минимума сред-
ней вероятности ошибки) является декодирование по принципу максимума прав-
доподобия (МП). При таком декодировании решение принимается принимается
в пользу того кодового слова хт, для вероятность р(у\хт) максимальна. Вероят-
ность р(у\хт) называют функцией правдоподобия кодового слова хт. Решающие
области декодера МП имеют вид
Rm = {у : р(1/|®т) > р(у\хт>), т! / т}.
Для доказательства прямой теоремы кодирования вместо оптимального деко-
дирования по МП мы для простоты рассмотрим описанное ниже неоптимальное
декодирование. На произведении множеств Хп х Yn определим вспомогательное
множество
Тп(0) = { (®, у) :
Ад®; w)-аду) о},
(5.44)
где 1(х,у) обозначает взаимную информацию между последовательностями х и
у, аО - положительная константа.
Множество Тп(0) называется множеством типичных пар последовательностей.
По принятой из канала последовательности у декодер принимает решение в
пользу хт в том случае, если (я?т, у) е Тп(0). Если таких кодовых слов несколько,
выбирается любое из них. Если же такого слова нет, декодер выдает получателю
произвольное решение. Конкретное значение 0 мы выберем позже в процессе
доказательства.
Заметим, что описанный декодер существенно отличается от МП декодера и,
конечно, проигрывает ему по вероятности ошибки.
Шаг 3. Приступим к выводу оценки вероятности ошибки декодирования.
Заметим, что ошибка возможна в случаях, когда имеет место по меньшей мере
одно из двух событий:
5.11. Прямая теорема кодирования для ДПК
199
► При передаче хт наблюдается последовательность у такая, что (®т, у) ф Тп(в).
► При передаче хт на выходе канала имеем некоторую последовательность у
такую, что для некоторого кодового слова хт>	имеет место (жт/, у) е
е Тп(0).
Вероятность первого из двух событий обозначим через Perni, второго - через
Рет2, соответствующие средние по множеству сообщений вероятности - через
Pei и Ре2. Для вероятности ошибки имеем оценку
Ре^Ре1+Ре2.	(5.45)
Знак неравенства использован потому, что два события, приводящие к ошибкам,
не являются несовместными. Черту над вероятностями ошибок будем использо-
вать для обозначения вероятностей, усредненных по множеству кодов. В частно-
сти, из (5.45) получаем
Ре^ Ре1+Ре2-	(5.46)
Дальнейший анализ опирается на свойства множества типичных пар. Эти свой-
ства будут востребованы и в других главах, сформулируем их в виде отдельной
теоремы.
ТЕОРЕМА 5.7. Пусть на произведении множеств Хп х Yn задано совместное рас-
пределение вероятностей {р(ш, у), х е Хп, у G Yn}, удовлетворяющее условиям
п	п
Р(®) = П^)- Р(»1®) =
1=1	1=1
и пусть при некотором в > 0 множество Тп(0) определено равенством (5.44). Тогда
имеют место утверждения
1. limn_ooP(Tn(0)) = l.
2. Если последовательности х и у выбраны независимо, соответственно, из Хп и
Yn с распределениями р(х) и р(у) =	, у), то
Р ((х,у) е Тп$У) < 2~п^х^~в\
Отложим доказательство этой теоремы до следующего параграфа и вернемся
к доказательству прямой теоремы кодирования.
Оценим вероятность Pei. Из определения множества Тп(0) следует, что средняя
по всем выборам кодового слова жт вероятность Pei совпадает с вероятностью
дополнения к Тп(0). Из первого утверждения теоремы 5.7 заключаем, что эта
вероятность стремится к нулю с увеличением п, более того, найдется noi такое,
что при п noi имеет место неравенство
Pei < |.	(5.47)
Перейдем к вычислению оценки для Ре2* Поскольку в рассматриваемом ансамбле
кодов кодовые слова выбирались независимо, для каждого из «неправильных»
кодовых слов вероятность образовать типичную пару с последовательностью на
200
Глава 5. Кодирование для каналов
выходе канала может быть оценена с помощью второго утверждения теоремы 5.7.
Вероятность Ре2 - это вероятность того, что хотя бы одно из М — 1 неправиль-
ных слов образует типичную пару с у. Воспользовавшись аддитивной границей
вероятности объединения событий, приходим к неравенству

Поскольку рассматриваемое распределение вероятностей на Хп максимизирует
взаимную информацию, имеем /(Х;У) = Со и с учетом (5.43) получаем
Ре2 2~п(г"*)
Выбрав в = J/2, можем утверждать, что для некоторого пог при п пог
(5.48)
Из (5.47) и (5.48) следует, что при п max {noi, П02} средняя по ансамблю кодов
вероятность ошибки не превышает е. Как уже говорилось, отсюда вытекает, что
хотя бы один из кодов ансамбля имеет вероятность ошибки не больше е. □
В результате доказательства прямой и обратной теорем кодирования установ-
лено, что скорость сколь угодно близкая к информационной емкости Со (но мень-
шая Со) достижима при сколь угодно малой вероятности ошибки, а при скорости
большей Со вероятность ошибки не может быть сделана произвольно малой.
Таким образом, Со совпадает с пропускной способностью канала С. В следую-
щем параграфе мы докажем свойства типичных пар и попытаемся использовать
эти свойства для понимания «физического смысла» пропускной способности как
точного значения потенциально достижимой скорости передачи информации.
5.12. Типичные пары последовательностей
В этом параграфе мы должны восполнить пробел в доказательстве прямой тео-
ремы кодирования - доказать теорему 5.7 о типичных парах последовательно-
стей.
Напомним, что речь идет о произведении множеств Хп х Уп, совместное рас-
пределение вероятностей на котором {р(х,у),х е Хп,у е Уп}, удовлетворяет
условиям
р(®) = П^), р(»1®) = Пр(з/41ж»)-
Чтобы сократить запись формул, будем использовать обозначение I = 7(Х;У).
Множество типичных пар последовательностей в этом случае определяется как
I	п	I
(5.49)
где 1(х;у) - взаимная информация между х и у, е - положительная константа.
5.12. Типичные пары последовательностей
201
Нас интересуют оценки вероятности множества Тп(е) в двух случаях: когда хну
выбраны в соответствии с распределением р(я?, у) = р(х)р(у\х) и когда последо-
вательности х и у выбраны независимо, то есть их совместная вероятность равна
произведению р(х)р(у). Чтобы избежать путаницы, первую из двух вероятностей
множества Тп(е) обозначим через P(Tn(s)), вторую через Р(Тп(е)).
Сформулируем теорему 5.7 в новых обозначениях
ТЕОРЕМА 5.8. При любых е > О
1.	limn__>00 Р (Тп(ё)) — 1.
2.	Р(Тп(е))^2-п^-£\
3.	Существует достаточно большое п£ такое, что при п£ Р (Тп(еУ)
(1-£)2-п(/+е\
Первое утверждение теоремы устанавливает, что с ростом длины п почти все
пары совместно выбранных последовательностей становятся типичными в том
смысле, что доля нетипичных последовательностей стремится к нулю.
Если же последовательности выбираются независимо, то, согласно второму утвер-
ждению, вероятность «случайно» получить типичную последовательность убы-
вает экспоненциально с увеличением длины п. Более того, показатель экспо-
ненты оказался равным взаимной информации I.
Третье утверждение устанавливает, что оценка, даваемая вторым утверждением,
экспоненциально точна.
Доказательство. Доказательство первого утверждения - простое упражнение на
применение неравенства Чебышева для сумм независимых случайных величин.
Предлагаем читателю выполнить его самостоятельно.
Сконцентрируем внимание на доказательстве других утверждений теоремы. Из
определения (5.49) следует, что для любых пар (х,у) из Тп(е)
1-е^
110g ^Х'у)
п р(х)р(у)
I + в
или
р(аг, у)2-п(/+£) ^р(х)р(у) р(х,у)2~п(‘1~е\
Вероятность Тп(е), вычисленная при независимом выборе х и у,
р(тп(£))=	р(х)Р(у).
(ш,у)бТ„(е)
(5.50)
(5.51)
Подстановка в это равенство верхней оценки из (5.50) приводит к искомой
верхней границе:
Р(ТП(£)) <	£	р(а!,!/)2-"(/-£) =
(®,у)етп(е)	. (
= 2-п(/-£>Р (Тп(£)) < 2-п(/-£).
202
Глава 5. Кодирование для каналов
Аналогично, левое неравенство из (5.50) дает оценку
Р(Гп(е)) >	р(х,у)2~п^ =2-”(/+£)p(Tn(e)).
(®,у)еТп(е)
Вероятность множества Тп(е) стремится к 1 при увеличении п, а значит, при
некотором п она станет больше 1-е. Тем самым завершаем вывод нижней
границы и доказательство теоремы в целом.	□
Теорема 5.7 позволяет понять, почему максимальная скорость кода для канала
без памяти определяется величиной С.
Предположим, что по каналу передано кодовое слово жт. Для того, чтобы деко-
дирование было правильным с вероятностью близкой к единице, все последо-
вательности совместно типичные с хт должны принадлежать решающей обла-
сти Rm. Это верно при всех т е {1,...,М}. Чтобы области не пересекались,
их число не должно быть слишком большим. Поскольку при больших длинах
кодов при любом типичном х совместно типичные с ним последовательности у
имеют суммарную вероятность порядка 2-пС, число кодовых слов не может быть
больше 2пС. Если же число слов 2nR меньше 2пС, то их суммарная вероятность
последовательностей у совместно типичных с «неправильными» кодовыми сло-
вами экспоненциально убывает с длиной кодовых слов примерно как 2~n(c-R\
и вероятность ошибки может быть сделана сколь угодно малой.
Еще раз напомним, что оптимистический результат, обещаемый теоремами коди-
рования, неконструктивен. Случайное кодирование — мощный метод анализа,
придуманный Шенноном, — не может быть использовано для построения хоро-
ших кодов. Дело в том, что для надежной передачи информации нужны довольно
длинные коды. С ростом длины кодов экспоненциально растет число кодовых
слов, а значит, и сложность описания кодов, сложность процедур кодирования
и декодирования. Поэтому используемые на практике коды имеют регулярную
структуру, что делает возможной реализацию кодирования и декодирования
с разумной сложностью.
5.13.	Задачи
1.	Для канала, представленного на рис. 5.9, а, при равновероятных буквах вход-
ного алфавита X, вычислить взаимные информации I (ж; у), х е X, у е У,
и среднюю взаимную информацию 1(Х;У). Дать качественное объяснение
полученным результатам.
2.	Для канала, представленного в виде диаграммы на рис. 5.9,6, не прибегая
к выкладкам, основываясь на свойствах взаимной информации, представить
график зависимости взаимной информации I (X; У) от величины вероятности
р(х = 1) = р.
3.	Для канала, представленного в виде диаграммы на рис. 5.9, в, не прибегая
к математическим выкладкам, основываясь на свойствах взаимной информа-
ции, представить график зависимости взаимной информации как функции
величины е при равновероятных символах входного алфавита.
5.14. Библиографические замечания
203
4.	Для каналов, представленных в виде диаграмм на рис. 5.9, г -и, вычислить
пропускные способности.
Рис. 5.9. Примеры каналов
5.14.	Библиографические замечания
Рассмотренные в данной главе вопросы не выходят за рамки соответствующих
глав учебников [7], [3]. Более того, нами опущены выводы асимптотических
экспоненциальных оценок вероятностей ошибок. Эти классические результаты
Галлагера являются украшением теории и весьма полезны при анализе асимп-
тотической эффективности кодовых конструкций. К сожалению, они выходят
за рамки семестрового курса теории информации и поэтому не вошли в данное
пособие.	'
Глава 6 Измерение
информации,
порождаемой
непрерывным
источником
Дискретными мы называем множества, число элементов в которых конечно или
счетно. Все остальные множества мы классифицируем как непрерывные. При-
мер - отрезок числовой оси. В вузовском курсе теории вероятностей переход от
дискретных множеств к непрерывным сводится в основном к формальной замене
распределений вероятностей плотностями и знаков сумм на знаки интегрирова-
ния. В теории информации все намного сложнее.
Поясним проблему простым примером. Любое число из дискретного множества
чисел мы можем записать конечным числом бит. При этом даже такое простое
число, как 1/3, содержит в своей записи бесконечное Число знаков. Конечно,
рациональные числа можно записывать в виде дроби и передавать числитель и
знаменатель отдельно. Но этот прием не подходит для таких чисел, как л/2, я, е
и т.д.
Отсюда понятно, что не стоит и пытаться точно передать информацию, порож-
денную непрерывным источником. Нужно каждый раз соглашаться на некоторый
допустимый уровень погрешности, зависящий от особенностей решаемой задачи.
Например, температура воздуха в помещении и температура тела больного изме-
ряется и записывается с точностью, отличающейся на порядок. Качество звука,
которое мы потребуем от мобильного телефона и от домашнего музыкального
центра, тоже несопоставимо. И так далее.
Прежде чем мы научимся вычислять информационные характеристики непре-
рывных источников, нам предстоит в параграфе 6.1 вспомнить основные тер-
мины, используемые при их описании, а также некоторые важные распределения
вероятностей. Далее в 6.2 следует понятие дифференциальной энтропии, которая
в данном случае уже не является характеристикой достижимой скорости кодиро-
вания, но позволяет объективно сравнивать «информативность» разных источни- ,
ков. В последующих главах мы будем изучать энтропию источников при наличии
ограничений на допустимые искажения. Эту величину в различных учебниках !
называют по-разному: функцией скорость-искажение или е-энтропией.

6.1. Непрерывные вероятностные ансамбли
205
6.1.	Непрерывные вероятностные ансамбли
Непрерывное множество, как и дискретное, может иметь произвольную природу,
но мы будем рассматривать наиболее естественную ситуацию, когда множеством
случайных событий являются действительные числа, то есть речь будет идти
о случайных величинах (с.в.). Более того, будем считать, что рассматриваемый
ансамбль X содержит все точки числовой оси, то есть X = (-оо, +оо). Это
предположение не сужает общности, поскольку всегда можно приписать нулевые
вероятности отрезкам, которые выходят за пределы возможных значений X.
Вероятностная мера на непрерывном множестве задается функцией распределе-
ния F(x), значение которой в точке я?о равно вероятности события х xq, то
есть
F{xq) = Р(ж < жо), —оо < xq < -Foo.
При известной функции распределения F(x) вероятность отрезка (а, 6] вычисля-
ется как
P(^(o,6]) = F(b)-F(o).
Таким образом, зная F(x), можно вычислить вероятность любого подмножества
значений X, тем самым функция распределения F(x) задает случайную величину
X.
Из неотрицательности вероятностной меры и условия нормировки следует, что
►	F(x) —> 0 при х —> -оо;
►	F(x) —> 1 при х —> -Foo;
►	F(rri) > F(x2) при Xi > ж2.
Итак, функция F(x) является неубывающей функцией, принимающей значе-
ния 0 и 1 при, соответственно, наименьшем и наибольшем возможном значении
аргумента.
Если функция F(x) дифференцируема, то ее производная
называется плотностью распределения вероятностей с.в. X.
Отметим следующие свойства плотности распределения:
►	f(x) > 0;
оо
►	J /(ж) = 1;
—оо
►	F(x) = f f(x)dx.
206
Глава 6. Непрерывные источники
По известной плотности распределения вероятность отрезка (а, 6] мы находим
по формуле
ь
Р(х е (а,Ь]) = У f(x)dx.
а
Примеры наиболее часто используемых распределений вероятностей приведены
в табл. 6.1.. При описании обобщенного гауссовского распределения использо-
вана гамма-функция Г(г), определяемая как
Г(«) = [ t^e^dt.
Jo
Ее свойства рассматривались в параграфе 3.5. Легко проверить (см. задачу 2.),
что при а = 1 обобщенное гауссовское распределение совпадает с экспоненци-
альным, при а = 2 из него получается нормальное распределение, а при а оо
оно стремится к равномерному.
Таблица 6.1. Примеры непрерывных случайных величин
Распределение вероятностей	Плотность f(x)	Характеристики		
		т	а2	h(X)
Равномерное	1	г п т	, хЕ а, 6 Ъ — а 0,	х < а,х > b	а 4- b 2	(Ь-«)2 12	log (6 - а)
Экспоненциальное	Хе~Хх, х > 0 0,	х < 0	1^ А	1 А2	logy А
Лапласа	р—А|®—т| 2	т	1 А2	1 2е tog у
Нормальное (гауссовское)	(х - т)2 -Л=е 2а2 сгу2тг	т	а2	log л/2тгесг2
Обобщенное гауссовское	67 ) - г) ( а, а) | х —т |а 2Г(1/а)6 . . 1 /г(3/а) a,fT = ff у Г(1/а)	т	а2	.	2Г(1/а)е1/а °g т/(а, а)
6.2.	Дифференциальная энтропия. Взаимная
информация для непрерывных ансамблей
Как уже говорилось, собственная информация для непрерывных источников не
определена, поскольку вероятность каждого отдельного значения стремится к ну-
лю. Не будет ошибкой сказать, что собственная информация значений (а значит,
и энтропия) непрерывного источника бесконечна. Возьмем, например, число тг.
Оно известно математикам с точностью до миллионов разрядов, но поиск про-
должается, и каждый следующий разряд несет новую информацию.
6.2. Дифференциальная энтропия
207
Итак, формула энтропии
ад = - 52 реверс*)
хЕХ
лишена смысла для непрерывных случайных величин. Возникает искушение
заменить сумму на интеграл, а вероятность на плотность и подумать над тем,
какой смысл несет вычисленная таким образом функция.
Дифференциальной энтропией непрерывного ансамбля X с заданной на нем плот-
ностью распределения /(ж) называется величина
h(X) = - [ f(x) log f(x)dx.	«	(6.1)
Jx
Примеры вычисления дифференциальной энтропии для наиболее часто встре-
чающихся распределений вероятностей даны в табл. 6.1.. В процессе изучения
свойств дифференциальной энтропии мы поймем, почему она, с одной стороны,
тоже «энтропия» (мера средней информации), хотя, с другой стороны, «диффе-
ренциальная».
Свойство 6-2.1. Дифференциальная энтропия может быть как положительной,
так и отрицательной.
Доказательство. Согласно формуле для дифференциальной энтропии равномер-
ного распределения (см. табл. 6.1.), для случайной величины, распределенной
равномерно на интервале длины а, имеем
h(X) = log а <
<0,
> о,
а 1,
а > 1.
□
Условимся под аХ понимать с.в., полученную из X умножением ее значений на
а. Аналогичйо а + X означает прибавление а к значениям из X.
Свойство 6.2.2.
Д(а + Х) = Л(Х);
h(aX) = ft(X) + log|a|.
Доказательство. Первое равенство легко получить из определения (6.1) с помо-
щью простой замены переменных при интегрировании.
Чтобы получить второе тождество, вспомним известное из теории вероятно-
стей правило вычисления плотности распределения для функций от случайных
величин.
Если Y = {у} получена из X = {ж} взаимно-однозначным преобразованием у(х),
то плотность fy(y) вычисляется по известной плотности /Ж(ж) по формуле
fy(y) = fx(x(y))
dx(y)
dy
(6.2)
208
Глава 6. Непрерывные источники
Поэтому если плотностью для X была /(ж), то аХ будет иметь плотность
Подстановка этой плотности в (6.1) приводит к требуемому результату. □
Мы доказали, что изменение математического ожидания (прибавление константы
к каждому значению с.в.) не изменяет дифференциальной энтропии, а умно-
жение на константу а увеличивает ее на log а. Первый из этих фактов поня-
тен, поскольку смещение с.в. напоминает изменение нумерации или переобо-
значение элементов дискретного множества. Второй факт объяснить сложнее,
поскольку мы привыкли к тому, что взаимно-однозначноё преобразование дис-
кретного ансамбля не изменяет его энтропии.
Рис. 6.1. Пример преобразования случайной величины
Рисунок 6.1 поясняет изменение энтропии при масштабировании. На нем пока-
зана плотность случайной величины X, равномерно распределенной на интер-
вале [0, а] и случайной величины Y = 2Х. Дифференциальные энтропии этих
с.в. связаны соотношением
h(Y) = h(X) + 1.
В чем смысл дополнительного бита?
Рассмотрим некоторое конкретное значение у G Y. Заметим, что 1 бита доста-
точно, чтобы указать, в каком из двух отрезков, [0, а) или [а, 2а], находится у.
После того как значение этого бита известно, информация, содержащаяся в у,
совпадает с информацией, содержащейся в любом значении х. Следовательно,
для передачи значений из Y нужно потратить на 1 бит больше, чем для значений
ансамбля X.
6.2. Дифференциальная энтропия
209
Этот пример подсказывает, что дифференциальная энтропия не указывает значе-
ние среднего количества информации в сообщениях непрерывного множества, но
зато дает возможность соизмерять количество информации в различных множе-
ствах, а также измерять изменение количества информации при преобразованиях
ансамблей. Отсюда и название: «дифференциальная» энтропия.
Если на XY = {(х,у)} задана двумерная плотность f(x,y) = f(x)f(y\x), то по
аналогии с дискретными ансамблями определяем условную дифференциальную
энтропию как
h(Y\X) = - [ [ f(x,y)logf(y\x)dxdy.
Jx Jy
В точности как и для дискретного случая, имеют место следующие утверждения.
Свойство 6.2.3.
h(XY) = h(X) + h(Y\X),
h(X\Y) < Л(Х),
равенство имеет место только для независимых ансамблей XuY.
В этой главе мы воспользуемся введенным в задаче 18 главы 1 понятием относи-
тельной энтропии дискретных распределений. По аналогии с (1.45) относитель-
ной энтропией Кульбака-Лейблера плотности А(ж) по отношению к плотности
/2 (х) называется функция
М/1ПЛ)= / A(*)iog£^<fc.	(6.3)
Jx J2W
Свойство 6.2.4. Для любых плотностей fi (ж) и /2 (#)
МАНЛт
с равенством в том и только в том случае, когда плотности совпадают.
Доказательство аналогично доказательству для дискретных распределений (см.
задачу 18 главы 1).
Опираясь на это свойство, мы установим верхние пределы для дифференциаль-
ной энтропии для некоторых важных классов распределений вероятностей.
Свойство 6.2.5. Если областью определения случайной величины служит отре-
зок длины а, то для любой плотности f(x)
fo(X)^loga,
с равенством в случае равномерного распределения.
Свойство 6.2.6. Для неотрицательных случайных величин с математическим
ожиданием т при любой плотности распределения f(x)
h(X) < log(em),
с равенством в случае экспоненциального распределения.
210
Глава 6. Непрерывные источники
Свойство 6.2.7. Для случайных величин с дисперсией а2 при любой плотности
распределения f(x)
h(X) <log\/2тге<т2,
с равенством в случае гауссовского распределения.
Последние три свойства устанавливают, что равномерное, экспоненциальное и га-
уссовское распределения являются экстремальными в том смысле, что они мак-
симизируют дифференциальную энтропию при различных ограничениях на рас-
пределения вероятностей.
Мы докажем свойство 6.2.5. Свойства 6.2.6 и 6.2.7 рекомендуем доказать само-
стоятельно.
Доказательство свойства 6.2.5. Согласно свойству 6.2.2 без потери общности
можно рассматривать интервал [0, а] в качестве области определения с.в. Пусть
f(x) и /о(^) обозначают, соответственно, произвольную плотность и равномер-
ную плотность на [0, а]. Рассмотрим разность
/•а	/»а
log а — h(X) =	/ f(x)\ogadx + / f(x) log f(x)dx =
Jo	Jo
= Г /(x)log^dx = L(/||/o).
Jo 1/a
Правая часть неотрицательна в силу свойства относительной энтропии 6.2.4. □
Продолжая аналогию с дискретными ансамблями, введем понятие средней вза-
имной информации между непрерывными ансамблями X и Y
I(X-,Y)= [ [ f(x,y)\og^^-dxdy.
Jx Jy	f \У)
Средняя взаимная информация для непрерывных величин имеет ту же интерпре-
тацию и те же свойства, что и для дискретных величин. Напомним те свойства,
которые будут востребованы в дальнейшем.
Свойство 6.2.8.
7(Х;У) = ДУ;Х) = h(Y) - h(Y\X) = h(X) - ВДУ);
Свойство 6.2.9.
7(Х;У) >0
с равенством только для независимых ансамблей XuY.
Свойство 6.2.10. I(X;Y) - выпукла вниз как функция условного распределения
вероятностей f(y\x)
6.3. Дифференциальная энтропия векторов
211
Еще одно замечательное свойство:
Свойство 6.2.11.
7(аХ;У) = 7(Х;У).
Оно легко доказывается с использованием свойства 6.2.2. Больше того, с помо-
щью формулы преобразования плотностей (6.2) легко установить, что средняя
взаимная информация (в отличие от дифференциальной энтропии) не изменя-
ется при обратимом преобразовании ансамблей.
Поучительные примеры вычисления взаимной информации для пары гауссов-
ских случайных величин приведены в задачах 7 и 8.
6.3.	Дифференциальная энтропия случайных
векторов
В данном параграфе мы будем решать задачу вычисления дифференциальной
энтропии для случайных последовательностей (векторов), элементы которых -
непрерывные с. в., а затем и для случайных процессов.
Рассмотрим последовательность х = (xi,..., хп) е Хп. Предположим, что известна
n-мерная плотность /(я?). Нас интересует
h(Xn) = - [ f(x)\ogf(x)dx.
Для независимых с.в. ответ прост: h(Xn) = h(Xi). Интересно найти нетри-
виальное решение задачи для содержательных моделей зависимых случайных
величин.
Нам пригодится следующее правило пересчета многомерных распределений веро-
ятностей при линейных преобразованиях случайных векторов.
Предположим, что вектор у = (j/i,	€ Yn получен из х е Хп обрати-
мым преобразованием с помощью дифференцируемых функций од = Тогда
распределением вероятностей д(у) для у будет
9(У) = РГ7(®),	(6.4)
где J - якобиан преобразования
Г dfa	dfi	dfi 1
		
dxi	дх2	дхп
df2	df2	d/2
		
dxi	дХ2	dxn
dfn	dfn	dfn
		
. dxi	9x2	dxn .
Из этого правила получаем обобщение свойства 6.2.2 на произвольные линейные
преобразования векторов.
212
Глава 6. Непрерывные источники
ТЕОРЕМА 6.1. Для любой невырожденной матрицы А размера п хп дифферен-
циальная энтропия ансамбля Yn = {у = хА, х е Хп} равна
h(Yn) = h(Xn) + log | det Л |.
Доказательство. На основании (6.4) имеем
Д(УП) = М (-logp(^)] = М [—log (/(;r)| det А|-1)] = ДрР)+ log|det А|. П
Поскольку, как мы уже выяснили, энтропия не зависит от математического ожи-
дания, временно ограничимся рассмотрением случайных векторов с нулевым
математическим ожиданием. Обозначим через Кх корреляционную матрицу тако-
го вектора я?,
Кх = М[ж'?].
Ее элементами являются корреляционные моменты = М[я;^], i,j = 1,... J.
При линейном преобразовании у = хА корреляционная матрица преобразован-
ного вектора примет вид
Ку = М [Л'я/жЛ] = А'Кх Л.	(6.5)
Например, если компоненты вектора х были независимы и имели единичные
дисперсии, то есть Кх = 1п, где 1п - единичная матрица размера п х п, то после
преобразования у = хА получим вектор у с корреляционной матрицей
Ку = Л'Л, det Ку = (det Л)2.	(6.6)
Из теории вероятностей мы знаем, что линейная комбинация гауссовских с.в. -
гауссовская с.в., а из линейной алгебры известно, что симметрическая матрица
К может быть представлена в виде произведения матриц
К = Т'ЛТ,	(6.7)
в котором матрица Т составлена из собственных векторов матрицы К, а Л - диа-
гональная матрица, на главной диагонали которой располагаются собственные
числа матрицы К.
Сопоставив (6.5), (6.6) и (6.7), приходим к заключению, что гауссовский век-
тор с любой заданной наперед корреляционной матрицей может быть получен
с помощью подходящего линейного преобразования из вектора независимых
гауссовских с.в. с единичными дисперсиями и, наоборот, найдется преобразо-
вание, приводящее произвольный гауссовский вектор к вектору из независимых
гауссовских с.в. с единичными дисперсиями.
Напомним общее выражение для n-мерной плотности гауссовского вектора с кор-
реляционной матрицей К и вектором математических ожиданий т
где Т - символ транспонирования. Теорема 6.1 указывает простой путь к получе-
нию дифференциальной энтропии гауссовского вектора. Результат вычислений
сформулируем в виде следующей теоремы.
6.3. Дифференциальная энтропия векторов
213
ТЕОРЕМА 6.2. Дифференциальная энтропия гауссовского вектора с корреляци-
онной матрицей К
h(Xn) = log ((2тге)п det К).	(6.9)
4b
Доказательство. Найдем разложение вида (6.7) для К. Обозначим через Ai,..., Ап
диагональные элементы матрицы Л, то есть собственные числа матрицы К. При-
меним преобразование х = у А к вектору у, компоненты которого - независимые
гауссовские с.в. с дисперсиями Ai,..., Ап. Применив теорему 6.1 после простых
выкладок получим (6.9).	□
СЛЕДСТВИЕ 6.3. Дифференциальная энтропия гауссовского вектора из п неза-
висимых компонент с дисперсиями ,...,
Ц*) = ^log(2?re) + V log <Ti.	(6.10)
г=1
Напомним, что согласно свойству 6.2.7 гауссовская с.в. имеет наибольшую энтро-
пию среди всех случайных величин с заданной дисперсией. Оказывается, что
аналогичным свойством обладает и многомерное гауссовское распределение.
ТЕОРЕМА 6.4. Дифференциальная энтропия произвольного вектора с корреля-
ционной матрицей К удовлетворяет неравенству
Л(ХП) | log ((2тге)п det К).	(6.11)
£
Доказательство. Без потери общности можно рассматривать векторы с нулевым
математическим ожиданием. Пусть /(я?) и д(х) - гауссовское и произвольное рас-
пределение вероятностей на Хп соответственно, причем обоим распределениям
соответствуют одинаковые корреляционные матрицы К = {kij},i,j = 1,...,п.
Дифференциальные энтропии этих распределений обозначим, соответственно,
через h(f) и Л(р). Прежде всего, заметим, что
- [ д(х) log f(x)dx = i log ((2тге)п det К).	(6.12)
JXn	2
Действительно, подставив в левую часть (6.12) n-мерную плотность (6.8), полу-
чим
-	/ g(x)\ogf(x)dx =
Jxn
=	-	^log((27r)ndet/f) -	f	g(x)xK~1xTdx =
2	2 JXn
=	-	^log((27r)ndet#) -	[	g(x)'^y^xikijxjdx	=
2	2	i=ij=i
214
Глава 6. Непрерывные источники
- ~ |log((27r)ndetAT) -	[ g(x)xiXjdx =
2	2 i=ij=i Jxn
=	- llog((27rrdet/<)-^f;^^fco =
г=1 j=l
=	- i log ((2тг)п det К) - log e =
= |log((27re)ndet/0.
В (а) мы приняли обозначение kij для элементов матрицы JC-1, в (Ь) поменяли
порядок интегрирования и суммирования. Под знаком интеграла получили кор-
реляционные моменты, это учтено в (с). Внутренняя сумма равна скалярному
произведению строки матрицы К на столбец К"1 с тем же номером. Поэтому
каждая внутренняя сумма равна 1. Поэтому имеет место переход (d).
Теперь из (6.12) вытекает, что разность левой и правой частей (6.11) есть
- f д(х) log = -L(g\|/) < О,
Jxn	J\x)
где неравенство основано на свойстве 6.2.4 относительной энтропии. Отсюда
следует утверждение теоремы. 1	□
6.4. Дифференциальная энтропия
стационарных процессов
дискретного времени
От энтропии векторов один шаг до энтропии стационарных случайных процессов
дискретного времени. Напомним, как этот шаг был сделан для дискретных про-
цессов. Мы ввели в рассмотрение энтропии Нп(Х) = Н(Хп)/п и Н(Х\Хп (см.
параграф 1.7) и рассматривали их пределы при п —► оо. Эти пределы совпадают
и были названы энтропией дискретного стационарного источника.
Точно так же мы определяем дифференциальную энтропию на сообщение для
стационарного процесса как
чч =
п
и дифференциальной энтропией случайного процесса дискретного времени назы-
ваем предел
м*) = Ит ЛП(Х).	(6.13)
п—>оо
Введя обозначения h(X|Xn) = h(Xn+11Хг... Хп) и Л(Х|Х°°) ’= Пт,^ h(X\Xn),
по аналогии с теоремой 1.5 можем установить, что для произвольного стацио-
нарного процесса
Лоо(Х) = h(X\X°°).
6.4. Дифференциальная энтропия стационарных процессов
215
Корреляционной функцией стационарного процесса мы называем функцию
К(п) = M[(xi - mx)(xi+n - тх)].
Из теории вероятностей мы знаем, что корреляционная функция - четная функ-
ция аргумента п и принимает максимальное значение, равное дисперсии процесса
при п = 0, то есть АГ(О) =
По известной корреляционной функции для каждого п можно построить симмет-
рическую корреляционную матрицу Кп =	1,... ,п, элементы которой
равны Kij = K(i- j) = K(j - г).
Теорема 6.2 дает возможность подсчитать hn(X) для гауссовского процесса. Под-
ставив (6.9) в 6.13 и перейдя к пределу, получим
। » / »г\ 1_	\ . log det	✓ г» j >\
I Доо(Х) =-log(2?re) + lim --------.	(6.14)
2	n—>oo	Tb
Итак, подсчет энтропии сводится к подсчету последовательности определите-
лей корреляционных матриц процесса. Если вспомнить о том, что определи-
тель равен произведению собственных чисел матрицы, то на самом деле нужно
построить последовательность собственных чисел и найти ее предел при п —► оо,
что тоже непросто.
Ниже мы приведем нетривиальный пример процесса, для которого вычисления
можно выполнить непосредственно по формуле (6.14), а затем рассмотрим более
общий подход, предложенный более полувека назад А. Н. Колмогоровым.
Напомним, что в случае дискретных ансамблей точный подсчет энтропии стаци-
онарного процесса мы смогли выполнить для источника независимых сообще-
ний и для цепей Маркова. Аппроксимация реальных процессов цепью Маркова
лежит в основе наиболее эффективных алгоритмов сжатия дискретных источни-
ков - алгоритмов PPM. Авторегрессионные процессы - естественное обобщение
понятие цепи Маркова на непрерывные источники дискретного времени.
Авторегрессионным (АР) процессом порядка р называется случайный процесс дис-
кретного времени, значения которого подсчитываются по формуле
р
Xi = - ajXi-j + z^ *	(6.15)
j=i
где aj, j = 1, ..., p, - некоторые постоянные коэффициенты, a i = 1,2,...
последовательность независимых одинаково распределенных случайных вели-
чин.
Из определения следует, что АР процесс - это последовательность на выходе
цифрового фильтра порядка р с бесконечным откликом, на вход которого пода-
ется последовательность независимых случайных величин. Если последователь-
ность Zi - гауссовская с нулевым Математическим ожиданием и дисперсией
то процесс жь Х2, ...называют процессом Гаусса-Маркова порядка р.
216
Глава 6. Непрерывные источники
Модель Гаусса-Маркова задается набором коэффициентов aj, j = 1,..., р, и дис-
персией ст2. Зная эти параметры, можно подсчитать корреляционную функцию
процесса, а затем и его энтропию. Начнем с процесса первого порядка.
Рассмотрим последовательность вида
Xi = pXi-i + Zi, г = 1,2,... .
Если xi - гауссовская с.в. с нулевым математическим ожиданием и дисперсией
ст2, a i = 1, 2,..., - независимые гауссовские с нулевым математическим ожи-
данием и дисперсией <т2 = (1 — р2)<т2, то последовательность xlf я2, ...образует
стационарный случайный процесс с корреляционной функцией К(п) = <т2рп.
При каждом п корреляционная матрица Кп последовательности длины п имеет
вид
1	р ••• рп-г "
рп-1 рп-2 ... т
К счастью, матрица имеет очень простую структуру и для нее несложно подсчи-
тать определитель (см. задачу 9.):
det/Cn = сг2(1 — р2)п-1.
Подстановка этой формулы в (6.14) приводит к следующему утверждению.
ТЕОРЕМА 6.5. Дифференциальная энтропия гауссовского АР процесса с диспер-
сией а2 и коэффициентом корреляции р
hK(X) = i log (2тгесг2(1 - р2)) .	(6.17)
Перейдем к рассмотрению АР процессов более высокого порядка р. Понятно, что
не следует рассчитывать на получение аналитических выражений типа (6.17) при
р > 1. Путь к ответу проходит через изучение спектральных свойств анализиру-
емых случайных процессов.
Спектральной плотностью мощности стационарного случайного процесса с функ-
цией корреляции К(п) называется функция
S(w)= K(ri)e~inu, а>€(-7г,тг].	(6.18)
п=—оо
В соответствии с этим определением спектральная плотность мощности - пре-
образование Фурье корреляционной функции. Функция S(cu) - неотрицательная
вещественная четная функция аргумента си.
Обсудим физический смысл понятия спектральной плотности мощности по отно-
шению к случайным процессам дискретного времени. Аргумент си привычно
6.4. Дифференциальная энтропия стационарных процессов
217
было бы интерпретировать как круговую частоту сигнала и тогда она измеря-
лась бы в радианах/с. Однако в (6.18) ш - безразмерная величина. Если счи-
тать, что рассматриваемый стационарный процесс получен измерениями значе-
ний процесса непрерывного времени (дискретизацией) через равные интервалы
времени (период дискретизации) Т секунд, то значения ш связаны со значениями
частот /, измеряемыми в герцах, соотношением ш = 2тг fT. Частота дискретиза-
ции fa = 1/Т. Следовательно, интервалу (-%, тг] для ш соответствует интервал
(~/а/2,/а/2] для «настоящей» частоты /. Согласно теореме отсчетов (теореме
Котельникова-Шеннона) этот интервал содержит весь спектр сигнала, который
может быть представлен своими отсчетами, измеренными с периодом Г. Итак,
си - круговая частота, нормированная по отношению к частоте дискретиза-
ции. Соответственно, интеграл от по малому интервалу можно трактовать
как дисперсию (энергию) случайного процесса в соответствующем частотном
диапазоне.
В соответствии с теоремой 6.1 обратимое линейное преобразование с определите-
лем равным единице не изменяет дифференциальной энтропии ансамбля. В каче-
стве такого преобразования можно выбрать преобразование Фурье, примененное
к последовательностям большой длины п. Известно, что с увеличением п коэф-
фициенты корреляции спектральных компонент преобразования Фурье стре-
мятся к нулю. Учитывая приведенные выше замечания о спектральной плотности
мощности и применяя к спектральным компонентам следствие 6.3, приходим
к фундаментальному результату, впервые полученному А.Н. Колмогоровым [51].
ТЕОРЕМА 6.6. Дифференциальная энтропия стационарного гауссовского процесса
со спектральной плотностью мощности S(v)
h^X) = ilog(27re) + 7- / logS(w)da>.	(6.19)
2	47Г J
Строгое доказательство теоремы 6.6 требует значительных усилий и опирается
на довольное сложный математический аппарат. С разными подходами к дока-
зательству можно познакомится в [17], [14] и [3].
Поясним применение теоремы 6.6 на примере АР процесса первого порядка. Для
этого нужно подсчитать его спектральную плотность мощности. В силу четности
корреляционной функции в тригонометрическом представлении комплексной
экспоненты синусную составляющую можно не учитывать. Получаем
S(cu) —	К(т) cos(mcu) = К(0) -I- 2	A7(m) cos(mcu) =
7П= —ОО	П=1
(°°	\	1 - п2
1 + 2 У рт cos(тш) I = а2-— --------г.
v ’]	l-2pcosw + р2
Чтобы выполнить последний переход, пришлось воспользоваться справочником
интегралов Двайта ([6], формула 417.2). Полученную спектральную плотность
подставляем в (6.19). Имеем
218
Глава 6. Непрерывные источники
1	1 Г*
h<x>(X) = - log (2тге) + —- / log (<т2(1 - р2)) dw -
2	4тг J
—	/ log (1 — 2pcosu> + р2) dw
J —TV
= I log (2тге) + | log (<T2(1 - p2)),	(6.20)
где использован табличный интеграл ([6], формула 865.71)
[ log (1 ± 2acosrr + a2) dx = 0, а2 1.
Jo
Как и должно быть, полученными двумя способами результаты (6.20) и (6.17)
совпали.
Для АР процесса произвольного порядка спектральная плотность мощности вычис-
ляется по формуле

(6.21)
которая вместе с теоремой 6.6 дает возможность подсчитать дифференциальную
энтропию произвольного гауссовского АР процесса.
Отметим, что корреляционная функция К(п) АР процесса связана с парамет-
рами модели (6.15), то есть с коэффициентами a>j, j = 1, ..., р и дисперсией сг|,
уравнениями Юла-Уокера:
р
tf(0) = -J>fetf(fc) + a2
к=1
Р
К(1) = -^2акК(1-к), 1 =
к=1
Для решения этих уравнений используется быстрый алгоритм Левинсона-Дар-
бина (см., например, [2]).
Отметим, что приведенное в этом параграфе решение задачи вычисления диф-
ференциальной энтропии для АР процесса можно рассматривать как аппрокси-
мацию дифференциальной энтропии для произвольного гауссовского процесса.
Выбираем некоторый порядок р аппроксимирующего АР процесса, и, решая соот-
ветствующие уравнения Юла-Уокера, подбираем его параметры. Затем вычис-
ляем спектральную плотность мощности и находим оценку дифференциальной
энтропии. Порядок аппроксимирующего процесса увеличиваем до тех пор, пока
его увеличение не перестанет существенно влиять на результаты вычислений.
В [34] (см. также [38]) доказано, что гауссовский АР процесс порядка р с задан-
ными значениями корреляционной функции К(0), ..., К(р) имеет наибольшую
дифференциальную энтропию среди всех стационарных процессов с теми же зна-
чениями корреляционных моментов К(0),..., К(р). Этот факт дает возможность
6.5. Множество типичных последовательностей
219
использовать приведенные выше формулы для получения оценок дифференци-
альной энтропии, а затем и функции скорость-искажение для широкого класса
практических задач.
6.5. Связь с энтропией дискретного ансамбля.
Множество типичных последовательностей
для непрерывного источника
Основное значение дифференциальной энтропии определяется ее применением
для подсчета функции скорость-искажение, которая будет введена в следующей
главе. Тем не менее представляется полезным пояснить смысл тех числовых
значений, которые мы получаем при подсчете дифференциальной энтропии по
приведенным выше формулам.
Рассмотрим с.в. с плотностью распределения вероятностей f{x). Разобьем область
ее определения X на непересекающиеся одинаковые достаточно маленькие интер-
валы Д и обозначим через А = {aj, i = • • • - 1,0,1,... множество значений
случайной величины в серединах интервалов. Этим значениям соответствуют
значения плотности а вероятности соответствующих интервалов прибли-
зительно равны /(аг)Д. Энтропия соответствующего дискретного ансамбля
Я(Л) = -^f(ai)Alog(/(ai)A) =
i	i
= ~ 52 /(°i)(i°8 Ж))Д - log A 52 Яаг)А «
i	i
« - [ f(x) log xdx - log Д = h(X) “ log A•	(6.22)
Jx
Из этих соотношений мы видим, что вклад в энтропию аппроксимирующего
дискретного ансамбля, определяемый плотностью f(x), совпадает с дифференци-
альной энтропией. При Д —> 0 равенство становится точнее, но и разность между
энтропиями Я(А) и h(X) растет. Важно то, что для двух разных распределений
разность энтропий дискретных ансамблей, получаемых квантованием соответ-
ствующих случайных величин, определяется разностью их дифференциальных
энтропий.
Заметим, что левая часть (6.5) представляет собой, по сути, затраты в битах
на кодирование дискретного (скалярно квантованного с шагом Д) источника, а
вычитаемое в правой части характеризует максимальную ошибку квантования.
Таким образом, (6.5) устанавливает связь скорости кодирования с ошибкой, и
эта связь определяется как раз дифференциальной энтропией.
Обратимся теперь к понятию множества типичных последовательностей, кото-
рое было введено для дискретных ансамблей, использовано при доказательстве
теорем кодирования и подробно рассмотрено в параграфе 1.12.
220
Глава 6. Непрерывные источники

Рассмотрим последовательность независимых одинаково распределенных с.в. х =
= (ж1,...,жп) с плотностью /(ж). По аналогии с (1.40) для некоторого 5 > О
определим множество
——\ogf(x) — h(X) сД,	(6.23)
п	J
Напомним, что множество типичных последовательностей источника с энтро-
пией Н имеет вероятность близкую к единице, все последовательности этого
множества имеют примерно одинаковую вероятность 2~пН и мощность мно-
жества примерно равна 2пЯ. Понятно, что в случае непрерывных источников
нет смысла говорить о вероятности отдельных элементов множества и о числе
его элементов. Вместо числа элементов для непрерывного множества А можно
вычислить его объем Vol(A) по формуле
Vol(A) = у dx.
Свойства Тп(8) для последовательности непрерывных с.в. устанавливает следу-
ющая теорема.
ТЕОРЕМА 6.7. Для источника независимых одинаково распределенных с.в. с диф-
ференциальной энтропией h = h(X) для любого^ > 0 справедливы утверждения:
А.
lim Р(ТП(<5)) = 1;	(6.24)
п—>оо
В. Для любого е > 0 при достаточнд большом п
(1 - £)2п(д"5) < Vol (ЗД)) < 2^+^.	(6.25)
Доказательство. Непосредственно из неравенства Чебышева (см. параграф 1.9)
можем записать
Отсюда, во-первых, вытекает первое утверждение теоремы, и, во-вторых, для
любого г > 0 при достаточно большом п получаем
1-е^Р(Тп(<5))<1.	(6.26)
Для доказательства утверждения В заметим, что для всех х е Тп(6) из опреде-
ления Тп(8) следуют неравенства
2-п(Л+5)	2-п(Л-<5)	(6.27)
Поскольку
Р(ЗД))= [ f(x)dx,
Jrn(6)
из (6.27) получаем
2-n(h+i)Vol (Tn(j)) р	2-п(Л-«)уо1(Т„^)).
С учетом (6.26) из этих неравенств вытекает утверждение В теоремы. □
6.6. Задачи
221
Итак, установлено, что дифференциальная энтропия характеризует объем мно-
жества типичных последовательностей. Как этим воспользоваться?
Во-первых, из теоремы следует, что при передаче последовательностей из Хп
достаточно учитывать только последовательности из Tn(J). Предположим теперь,
что, исходя из требований к точности аппроксимации последовательностей на
выходе непрерывного источника, нам удалось разбить Tn(J) на области некото-
рого маленького объема Vo такого, что замена любой точки х на некоторую дру-
гую (например, «центральную») точку соответствующей области, вполне допу-
стима. Тогда число областей окажется приблизительно равным Vol (Tn(J))/Vq.
Поскольку теперь вместо х достаточно передавать номер соответствующей обла-
сти, битовые затраты в расчете на одну компоненту х составят
_	1 Vol (Tn(<5))	.	1	_7
R ~ - log---«Л-----------log Vo.
п Vo	п
Полученное соотношение связывает скорость кода непрерывного источника
с достижимой ошибкой, на этот раз уже при векторном квантовании.
Более подробному изучению связи между информационными характеристиками
источника и достижимой ошибкой посвящена следующая глава, а вопросы ска-
лярного и векторного квантования рассматриваются в главе 8.
6.6.	Задачи
1.	Проверить формулы для математических ожиданий и дисперсий, приведен-
ные в табл. 6.1.
2.	Убедитесь в том, что обобщенное гауссовское распределение при а = 1, 2 и
при а -* оо совпадает, соответственно, с распределением Лапласа, гауссовским
и равномерным распределением.
3.	Проверьте приведенные в табл. 6.1 формулы для дифференциальных энтро-
пий.
4.	При каких параметрах распределений дифференциальная энтропия равна
нулю? Нарисуйте (не делая точных вычислений) на одном и том же гра-
фике плотности распределений с нулевой дифференциальной энтропией и
дифференциальной энтропией, равной 1.
5.	Докажите свойства 6.2.1-6.2.4.
6.	По аналогии с доказательством свойства 6.2.5 докажите свойства 6.2.6 и 6.2.7.
7.	Запишите в общем виде совместное распределение двух гауссовских случай-
ных величин: X, Y. Подсчитайте их дифференциальную энтропию и взаимную
информацию /(X; У). Нарисуйте график зависимости взаимной информации
от коэффициента корреляции X и У.
Подсказка, Согласно (6.8), достаточно указать корреляционную матрицу, кото-
рая однозначно определяется дисперсиями
<?2Х =М[(ж-тж)2]; ст2 = М[(?/- ту)2]
222
Глава 6. Непрерывные источники
и коэффициентом корреляции
_ М[(х - т^у - Шу)]
Ответ:
/(Х;У) = -|1оё(1-р2).
8.	Рассмотрим с.в. Y = {?/}, представляющую собой сумму независимых гаус-
совских с.в. X = {ж} и Z = {г}, то есть у = х + z, Например, у можно рас-
сматривать как выход канала при передаче сообщения х, на которое в канале
воздействует аддитивный шум z, Найдите взаимную информацию 7(Х;У).
Подсказка, Сумма гауссовских величин - гауссовская величина. Следовательно,
данная задача является частным случаем предыдущей. Достаточно определить
коэффициент корреляции X и Y.
Ответ:
____________________________
Р х/°х + az ’
1	/	2 \
J(X:y) = -log(l + ^ .
2 у /
Заметим, что с увеличением дисперсии шума взаимная информация умень-
шается и стремится к нулю.
9.	Подсчитайте определитель корреляционной матрицы п последовательных зна-
чений авторегрессионного процесса первого порядка.
Подсказка, Корреляционная матрица удовлетворяет (6.16). Приведите ее мето-
дом Гаусса к нижней треугольной форме, умножив каждую строку, начав со
второй, на р и вычитая ее из предыдущей. Получится матрица, на главной
диагонали которой все элементы, кроме одного (первого, который равен 1),
равны 1 - р2,
10.	Докажите следующие свойства корреляционной функции и спектральной плот-
ности мощности стационарного случайного процесса дискретного времени:
К(п) =	(6.28)
К(0)	|K(n)|; п > 0;	(6.29)
S(w) = S(-w);	(6.30)
S(u) - вещественная функция w;	(6.31)
[ S(u)du> = К(0) = а2. J —я	(6.32)
Подсказка, Чтобы доказать (6.29), рассмотрите заведомо неотрицательную
величину М[(ж4 - я*+п)2].
6.7. Терминологические и библиографические замечания
223
И. Выберите достаточно представительную реализацию (например, из 1000 отсче-
тов) реального сигнала. Это может быть строка изображения, фрагмент аудио-
сигнала, фрагмент речевого сигнала и т.п. Постройте зависимость дифферен-
циальной энтропии аппроксимирующего АР процесса от его порядка.
Подсказка. Задача не так сложна, как кажется на первый взгляд, если имеется
возможность воспользоваться библиотеками MATLAB. В частности, для чте-
ния аудиофайла можно использовать функцию wavread.m, для чтения изоб-
ражений - функцию imread.wav. После этого с помощью функции соггсо-
eff.m можно подсчитать корреляционные коэффициенты и с помощью levin-
son, m - параметры АР фильтра требуемого порядка. Иначе параметры АР
фильтра можно найти непосредственно по реализации с помощью функции
Ipc.m. Далее следуют подстановка параметров АР процесса в формулу (6.21)
и численное интегрирование, которое проще всего выполнить с помощью «ме-
тода прямоугольника», выбрав шаг интегрирования достаточно маленьким.
Интересно сравнить результаты расчетов с теми, которые можно получить
непосредственным применением формулы (6.14).
6.7.	Терминологические и библиографические
замечания
Так случилось, что понятие энтропии непрерывного источника, пережившее полу-
вековой юбилей, так и не получило общепринятого названия. В учебнике [7] она
называется относительной. В основопологающей работе К. Шеннона [20] нет
никакого специального названия для этой величины. Классическим руковод-
ством по кодированию непрерывных источников является книга Бергера [27].
Бергер называет энтропию непрерывного источника дифференциальной («differ-
ential»). Уже после того, как была написана книга [7], в литературе по теории
информации термин «относительная энтропия» укрепился за функцией Кульбака-
Лейблера (1.45). Поэтому, отступив от отечественной традиции, мы называем
в данном пособии энтропию непрерывного источника дифференциальной. Тер-
минология и содержание данной главы близки к [38].s
Мы ограничились рассмотрением источников дискретного времени. Об источ-
никах непрерывного времени можно прочитать в [7].
Глава 7 Кодирование
источника с заданным
критерием качества
Мы приступаем к рассмотрению одного из наиболее актуальных сегодня разде-
лов теории информации - к кодированию источников при заданных ограниче-
ниях на точность восстановления информации декодером.
Такие методы сжатия сегодня востребованы во многих областях обработки, хра-
нения и передачи мультимедиа данных. В зависимости от конкретной ситуации
применения для одних и те же данных могут быть предоставлены различные про-
пускные способности каналов связи или же ресурсы памяти. Отсюда - огромное
многообразие задач и большое число методов их решения.
Теория информации, как и в рассмотренных выше главах, дает лаконичный и точ-
ный ответ на вопрос о том, как оценить эффективность того или иного подхода
к кодированию источника при заданном уровне искажений. Следуя К. Шен-
нону, для заданной модели мы вычисляем так называемую функцию скорость-
искажение. Теоремы кодирования в данном случае утверждают, что характери-
стики, определяемые функцией скорость-искажение, достижимы (в отсутствие
ограничений на сложность реализации) и что кодов с лучшими характеристи-
ками, чем те, которые определены функцией скорость-искажение, не существует.
Таким образом, хорошими следует считать те методы кодирования, характери-
стики которых близки к теоретически достижимым. Цель данной главы -
научиться подсчету функции скорость-искажения по заданной модели источ-
ника. Знакомство с конструктивными методами кодирования непрерывных источ-
ников мы отложим до главы 8.
В начале главы мы уточним формальную постановку задачи, для чего нужно
будет условиться о том, что конкретно понимается под точностью восстанов-
ления закодированных данных. Далее мы введем понятие функции скорость-
искажение и изучим ее основные свойства. Затем следуют теоремы кодирования.
Как и для каналов связи, прямая теорема кодирования доказывается неконструк-
тивно, с помощью случайного выбора кодов.
7.1. Меры искажения
225
7.1. Меры искажения.
Постановка задачи кодирования
Для потребителя системы передачи или хранения информации критерием каче-
ства работы кодера и декодера является субъективное восприятие искажений.
С точки зрения потребителя искажения могут быть охарактеризованы как неза-
метные, допустимые, грубые и т.п. Разработчики систем кодирования также ста-
раются использовать субъективные критерии в своей работе, для чего к тести-
рованию аппаратуры привлекаются группы экспертов. Каждое такое измерение
качества требует значительных затрат времени и финансовых средств, поэтому
на этапе разработки кодеров необходимо использовать объективные критерии
качества.
Конечно, следует выбирать критерии так, чтобы уровень объективного качества
был монотонно связан с уровнем субъективного качества. Однако в большин-
стве случаев «повергнуть алгебре язык гармоний» не удается. Приходится, как
это часто бывает в теоретических исследованиях, накладывать на множестве мер
искажений такие ограничения, которые позволили бы с разумной сложностью
найти аналитические решения интересующих нас задач.
Итак, рассмотрим некоторое множество X = {ж}, элементы которого - сообще-
ния источника и второе множество, Y = {у}, которое будем называть аппрок-
симирующим. Мера искажения dn(x,y) определяется как функция на множестве
XnxYn = {(ж, у), х е Хп, у е Уп}, удовлетворяющая следующим ограничениям:
► Для любых х = (Ж1, ..., жп), у = (2/1,..., уп)
dn(.x,y) =-y2d(xi,yi),	(7.1)
г=1
где с?(ж, у) - так называемая побуквенная мера искажения.
►
с/(ж, у) 0 для всех х G X, у G Y.
Согласно этим условиям, при кодировании последовательностей сообщений ис-
точника мы рассматриваем только такие меры искажения, которые вычисляются
как среднее значение побуквенной меры по всем сообщениям последовательно-
стей, причем побуквенная мера обязательно неотрицательна. Оба ограничения
вполне естественны. Первое нормирует суммарную ошибку в последовательно-
сти сообщений по отношению к длине последовательности и позволяет объек-
тивно сравнивать кодеры, обрабатывающие последовательности разной длины.
Второе ограничение тоже понятно, оно означает, что аппроксимация приводит
к потере точности и d(x,y) указывает величину потери, связанной с заменой
точного значения х его аппроксимирующим значением у.
Приведем несколько примеров.
Пример 7.1.1. Вероятностная (Хэммингова) мера искажения.
Пусть X = {0,.... М - 1} - дискретное множество, и Y = X. Положим
226
Глава 7. Кодирование с потерей качества
d(x,y) = <
х = у;
х^у.
Соответствующая мера (7.1) представляет собой долю «ошибок» при выдаче
получателю у вместо истинной последовательности х. При большой длине после-
довательности dn(x,y) можно рассматривать как эмпирическую оценку вероят-
ности ошибочного символа, отсюда - название «вероятностная мера»
Пример 7.1.2. Абсолютная мера искажения. Пусть X - произвольное множе-
ство вещественных чисел и Y = X. Положим
d(x,y) = |ж-2/|.
Соответствующая мера (7.1) представляет собой нормированную сумму модулей
отклонения компонент у от компонент последовательности х.
Пример 7.1.3. Квадратическая мера искажения. Пусть X - произвольное мно-
жество вещественных чисел и Y = X. Положим
d(x,y) = (х-у)2.
Соответствующая мера (7.1) представляет собой среднеквадратическую ошибку
аппроксимации х последовательностью у. Последняя мера наиболее часто исполь-
зуется на практике. Ее можно рассматривать как мощность шума, наложенного
на исходную последовательность источника в результате кодирования. Отноше-
ние мощности кодируемого сигнала к мощности шума, порожденного кодером,
называют отношением сигнал/шум.
Отметим, что во всех примерах предполагалось, что сообщения и аппроксими-
рующие значения выбираются из одного и того же множества.
Рассмотрим теперь приведенную на рис. 7.1 модель системы, осуществляющей
кодирование при заданном критерии качества.
Рис. 7.1. Схема кодирования с заданным критерием качества
Последовательность сообщений источника разбивается на блоки длиной п. Каж-
дый из блоков должен быть аппроксимирован, по возможности с наименьшим
искажением, некоторой последовательностью у е Yn. Будем считать, что аппрок-
симирующие последовательности (кодовые слова) выбираются из дискретного
подмножества В = {&i,... ,Ьм} £ Yn, которое называют кодом, или (в тех-
нической литературе) кодовой книгой. Объем книги - некоторое конечное число
7.1. Меры искажения
227
М = \В\. Операция кодирования - это выбор наилучшего слова из кода. Ее
можно выполнить, поочередно перебирая кодовые слова и подсчитывая каждый
раз величину ошибки аппроксимации. Передаче по каналу или записи в память
подлежит номер т того слова, которое обеспечивает наименьшую ошибку.
Декодер хранит точную копию кода В и по полученному индексу т воспроиз-
водит аппроксимирующую последовательность у = Ьт.
Поскольку для передачи индекса т достаточно log М бит (для сокращения записи
мы считаем М степенью двойки), скоростью кода источника называется вели-
чина
Я =	— бит / сообщение источника.
п
При фиксированном коде В и заданной вероятностной модели источника можно
усреднением по всем х G Хп подсчитать среднюю ошибку
D = M[dn(x,y(x))],
где через у(х) обозначена последовательность у, которую кодер выбирает в каче-
стве аппроксимирующей последовательности для х.
Таким образом, основными характеристиками описанной системы кодирования
являются два числа: скорость R и средняя ошибка D. Наша задача - закодиро-
вать последовательность сообщений с наименьшей скоростью и с наименьшей
ошибкой.
Понятно, что уменьшение ошибки потребует увеличения числа кодовых слов.
Если же мы захотим уменьшить скорости кода, придется уменьшить число кодо-
вых слов, что приведет к увеличению средней ошибки. Таким образом, два тре-
бования противоречат друг другу. Придется зафиксировать один из параметров,
например, допустимое искажение D, и добиваться наименьшей скорости при
заданном искажении. Для некоторого алгоритма или класса алгоритмов постро-
ения кодов и заданных процедур кодирования, изменив требования к ошибке D,
можно получить функцию R(D), называемую функцией скорость-искажение.
Более формально, функцией скорость-искажение R(D) для заданной модели
источника называется функция вида
/?(£>) = inf min ЯП(В),	(7.2)
7 п B.D(BKD v 7
где нижняя грань берется по длинам кодируемых последовательностей, а мини-
мум - по таким кодам последовательностей длины п, которые удовлетворяют
ограничению на допустимую ошибку D.
Аналогично можно определить функцию искажение-скорость D(R).
Очевидно, определение (7.2) невозможно использовать для подсчета функции
скорость-искажение. Желательно (как это было сделано для кодирования источ-
ников без потерь и для каналов связи) научиться вычислять R(D) по модели
канала без перебора по всевозможным кодам источника, аналогично тому, как
228
Глава 7. Кодирование с потерей качества
для кодирования без потерь минимальная скорость кода определяется энтро-
пией источника, а максимальная достижимая скорость передачи информации по
каналу связи равна его пропускной способности.
Вернемся к схеме на рис. 7.1. Модель источника задана и тем самым задано рас-
пределение вероятностей на последовательностях из Хп. Для определенности,
будем считать источник непрерывным и описывать модель источника плотно-
стью распределения вероятностей /(ж), х е Хп. Заметим, что среднее количество
информации об Хп, доставляемой получателю декодером может быть подсчитано
как взаимная информация 7(Xn;Yn). Соответственно, затраты в битах в рас-
чете на одну букву источника составляют 7(Xn; Уп)/п бит. Все промежуточные
блоки от входа до выхода схемы на рис. 7.1 можно описать в виде условного рас-
пределения вероятностей	Многообразие таких плотностей полностью
включает в себя все мыслимые схемы кодирования, но нас интересуют только
такие плотности, при которых выполняется требование к допустимой ошибке,
которая в данном случае вычисляется как
^(^п) = /	/ f(x)tpn(y\x}dn(y,x)dxdy.
J ХпJYn
Теоретической функцией скорость-искажение называется величина
H(Z?) = inf min	-I(Xn-,Yn\	(7.3)
п	v„-.D^n)^D п
После ознакомления с предыдущими главами, не станет неожиданным то, что для
большинства моделей источников функции R(D) (7.2) и H(D) (7.3) совпадают.
Это означает, что при заданном D скорости сколь угодно близкие к H(JD) (но
большие H(D)) достижимы, а при скорости, меньшей H(D), средняя ошибка
неизбежно будет больше D.
Эти утверждения мы сформулируем, как всегда, в виде двух теорем кодирова-
ния - прямой и обратной. Но прежде, чем мы приступим к формулировке и
доказательству теорем кодирования, мы изучим свойства функции H(D) и рас-
смотрим несколько важных моделей источников и мер искажения, для которых
H(D) может быть вычислена в явной форме как функция параметров модели.
7.2. Свойства функции скорость-искажение
Прежде чем с помощью формулы (7.3) будут получены какие-нибудь полезные
результаты, ее нужно существенно упростить. В данном параграфе мы изучим
некоторые свойства которые позволят понять ее поведение и получить
простые выражения для этой функции для широкого класса моделей.
Первое свойство очень простое.
Свойство 7.2.1. H(D) 0.
Доказательство предоставляем читателю в качестве упражнения.
7.2. Свойства H(D)
229
Свойство 7.2.2. H(D) - невозрастающая функция аргумента D.
Доказательство. С увеличением D расширяется область поиска минимума в (7.3),
при этом результат поиска минимума, очевидно, не увеличивается.	□
Свойство 7.2.3. Для стационарного источника без памяти
H(D)= min 7(Х;У),	(7.4)
где = (р(у\х) - одномерное условное распределение на Y при известном х е X.
Доказательство. Имеем
1(ХП; Уп) = Д(ХП) - h(Xn\Yn) =
=	£ h(Xi) - £ h(Xi |Xi... Xi-iу... yn) >
г=1	г=1
(b)	JL	JL
> £ад)-£аду) =
i—1	i=l
=	(7.5)
г=1
где (а) использует независимость букв источника, а (Ь) - неубывание условной
энтропии с увеличением числа условий. Равенство в (7.5) достигается при
< п
<Pn(i/l®) =		<7-6)
г=1
где в обозначении учтено, что условная плотность может, вообще говоря,
зависеть от индекса г.
Поскольку нас интересует зависимость взаимной информации 7(ХП; Уп) от услов-
ного распределения вероятностей <рп, изменим на время обозначения: 7(Xn; Yn) =
= Так, (7.5) примет вид
'	1	1 п
г=1
В силу выпуклости U средней взаимной информации относительно условных
распределений (см. параграф 5.5)
1 n \	1 п
где^0 = -У>(<),	(7.7)
п I	п
г=1	/	г=1
причем равенство имеет место, если	ПРИ всех i = 1, • • ,п.
Из (7.5) - (7.7) следует, что наименьшее значение I(Xп; Yn) достигается в том
случае, когда условное распределений представляет собой произведение п
одинаковых одномерных плотностей, вычисленных как среднее одномерных плот-
> I
п
230
Глава 7. Кодирование с потерей качества
ностей, полученных из </?п. Чтобы завершить доказательство теоремы, осталось
доказать, что такое распределение удовлетворяет ограничению на ошибку Z), если
исходное распределение ему удовлетворяло.
Простые выкладки
D(tpn) = M[dn(a:,j/)] =
1	"	I ri
= м	[<*(*»> У*)] =
L г=1	J г=1
= “У / [ f(.x)^(y\x)d(x,y)dxdy =
n~iJxJY
= / f(x)<p0(y\x)d(x,y)dxdy = D(<p0)
Jx Jy
подтверждают, что при подстановке
n
i=l
ошибка не изменится. При этом
-/(%«; У”) = 1(<ро) = I(X;Y),
п
где /(X; У) вычислено при <р(х||/) = <Л)(ж|2/)« Теперь из определения (7.3) следует
требуемый результат.	□
Свойство 7.2.4. H(D) выпуклая U функция аргумента D.
Доказательство. Для сокращения записи доказательства рассмотрим случай источ-
ника без памяти, то есть считаем, что H(D) вычисляется по формуле (7.4). Нужно
доказать, что для любых D2 и a Е [0,1]
H(PQ) aH(Pi) +/1 - «)Я(Р2),
где использовано обозначение Da = aD± + (1 - a)P2. Обозначим через и ^2
те условные распределения, на которых достигаются, соответственно, H(Pi) и
Я(Р2), и положим <ра = a</?i + (1 - а)</?2. Доказываемое утверждение вытекает
из следующей цепочки преобразований:
ЯШ 2 1&а) =
= I(a^i + (1 - a)<p2)
(ь)
a/(^i) + (1 - a)I(^2) =
= аЯ(Р1) + (1-а)Я(Р2).
7.3. Примеры вычисления H(D)
231
Здесь (а) имеет место потому, что на распределении <ра не обязательно дости-
гается минимум взаимной информации 7(Х;У), равный (Ъ) следует из
выпуклости U средней взаимной информации.	□
Свойство 7.2.5. Для произвольного стационарного источника H(D) = 0 при
D £>о = min / f(x)d(y, x)dx,	(Д8)
у Jx
Доказательство. Пусть у$ обозначает тот элемент у, на котором достигается
минимум в (7.8). В качестве условной плотности выберем плотность,
с вероятностью 1 сопоставляющую последовательность у0 = (?/о, • * • ,2/о) любой
последовательности х е Хп. Поскольку последовательности х и у независимы,
7(ХП,УП) = 0 и, следовательно, H(D) = 0. Средняя ошибка при этом равна
величине DOi определенной формулой (7.8).	□
Итак, в данном параграфе мы узнали, что H(D) - выпуклая U монотонно убыва-
ющая неотрицательная функция, которая становится равной нулю при некоторой
ошибке. Конкретные примеры функций скорость-искажение будут приведены
в следующим параграфе на рис. 7.3 и 7.4.
Для источников без памяти мы получили формулу (7.4), которая очень похожа
на формулу для пропускной способности канала без памяти. Вместо макси-
мума - минимум и вместо поиска оптимального распределения на входе - поиск
среди условных распределений. В действительности поиск функции скорость-
искажение чуть сложнее, поскольку экстремум - условный, и ответ - функция,
а не число.
Заметим, что для источников с памятью свойство 7.2.5 дает не самую точную
оценку той минимальной ошибки, начиная с которой возможна аппроксимация
источника с нулевой скоростью (без передачи какой-либо информации о сооб-
щениях источника) (см. задачу 3).
7.3. Простые примеры вычисления функции
скорость-искажение
Все определения и утверждения в предыдущем параграфе приводились для непре-
рывного источника, но в равной степени могли быть записаны для дискретного
ансамбля и соответственно подобранного критерия качества.
Пример 7.3.1. Двоичный источник.
Начнем с примера двоичного ансамбля X = {0,1} и вероятностного крите-
рия качества. Вероятности символов положим равными р(0) = 1 — р,р(1) = р.
Источник порождает последовательности х е Хп независимых одинаково рас-
пределенных двоичных символов. Эти последовательности аппроксимируются
232
Глава 7. Кодирование с потерей качества
двоичными последовательностями у е {0,1}п так, чтобы при заданной скорости
аппроксимирующего кода минимизировать среднюю ошибку
D =	= ^М[йя(х,У)],
п
где dn(x,y) - расстояние Хэмминга (число несовпадающих позиций в х и у).
В соответствии со свойством 7.2.3 функцию скорость-искажение следует искать
по формуле
H(D)= min I(X;Y),
где условные вероятности задаются всего двумя числами, например,
<р(у = 0|ж = 0) и (р[у = 0|я = 1). Хотя поиск условного экстремума по этим
двум параметрам не кажется сверхсложной задачей, мы не пойдем по этому пря-
молинейному пути. Вместо этого мы сначала найдем нижнюю оценку взаимной
информации, а затем покажем, что эта оценка достижима при некотором <р.
Введем обозначение ф для операции сложения по модулю два и заметим, что
1, х^у.
Это означает, что ансамбль X ф Y = {х ф у} - ансамбль ошибок при аппрокси-
мации источника X символами из Y. При средней ошибке, равной D, взаимную
информацию 7(Х;У) можно оценить следующим образом:
7(Х;У) = Я(Х)-Я(Х|У) =
= Я(Х)-Я(ХфУ|У)
(Ъ)
Я(Х) - Н(Х ф У) =
= Ф)-’?(£>) 	,	(7.9)
Здесь в (а) замена X на X ф У при условии У представляет собой детерми-
нированное преобразование и поэтому не меняет энтропии. Неравенство (Ь)
имеет место потому, что условная энтропия не может быть больше безусловной,
и т/(а) = —a log а — (1 — a) log(l — а) - двоичная энтропия.
Предположив, что в (7.9) получено правильное выражение для функции скорость-
искажение, подберем к заданному ансамблю источника X такой ансамбль У, для
которого неравенства в (7.9) можно заменить на точные равенства. Такая пара
ансамблей показана на рис. 7.2.
7.3. Примеры вычисления H(D)
233
1-2D
1-p-D
1-2D
Рис. 7.2. Совместное распределение X и Y для двоичного источника
Положим вероятности аппроксимирующих символов равными р(у = 0) = 1 - А,
р(у = 1) = А. Вероятности символов х е X известны: р(х = 0) = 1 - р,
р(у = 1) = р. Условные вероятности выбраны исходя из требований к ошибке:
р(у = 0|ж = 1) = р(у = 1|х = 0) = D. Поэтому неизвестный параметр А находим
из уравнения
(1-А)(1-Г>) + АГ> = 1-р.
Решением является
\ - P~D
1 —2D’
что и показано на рис. 7.2.
Теперь заметим, что при D = min{p, 1 — р} правая часть (7.9) обращается в нуль.
Это легко объяснить. Среднюю ошибку, равную этой величине, можно получить,
всегда используя в качестве аппроксимирующего символа один и тот же символ,
0 либо 1, в зависимости от того, вероятность какого из них больше.
Итак, ансамбль, на котором достигается нижняя граница (7.9), найден и тем
самым найдена функция скорость-искажения. При этом мы так и не указали
в явном виде функцию <р, на которой достигается минимум взаимной инфор-
мации. При желании эту функцию можно легко получить, воспользовавшись
рис. 7.2.
Сформулируем полученный в этом примере результат в виде теоремы.
ТЕОРЕМА 7.1. Функция скорость-искажение двоичного источника независимых
символов с вероятностью единицы, равной р, при вероятностной мере искажения
равна
H(D) =
flip) ~
0,
0 < D min{p, 1 — р},
D > min{p, 1 — р}.
(7.10)
Типичный график H(D) для двоичного источника показан на рис. 7.3.
234
Глава 7. Кодирование с потерей качества
Рис. 7.3. Функция скорость-искажение для двоичного источника
Пример 7.3.2. 1ауссовский источник.
Рассмотрим последовательность независимых одинаково распределенных гаус-
совских с.в. с нулевым математическим ожиданием и дисперсией <т2, то есть
с плотностью
и вычислим функцию скорость-искажение при квадратическом критерии каче-
ства. Как и в предыдущем примере, начнем с вывода нижней границы на взаим-
ную информацию, а потом убедимся, что граница достижима. Итак, по аналогии
с двоичным источником
7(Х;У) = Л(Х)-Л(Х|У) =
= h(X) - h(X - У|У) h(X) - h(X - У) =
= log \/ 2тгеа2 — log х/2тгеР = log *	(7.11)
Здесь использована формула дифференциальной энтропии гауссовского ансамбля
из табл. 6.1. и то, что гауссовское распределение имеет наибольшую энтропию
среди всех распределений с заданной дисперсией (см. свойство 6.2.7).
Чтобы доказать достижимость границы (7.11), введем с.в. Z = X - У и будем
считать ее гауссовской с нулевым математическим ожиданием и дисперсией D.
В качестве распределения для У выберем гауссовское с нулевым математическим
ожиданием и дисперсией <т2 — a2-D. Поскольку сумма независимых гауссовских
с.в. есть гауссовская с.в. с суммарной дисперсией, дисперсия X = У + Z равна
7.3. Примеры вычисления Н(Р)
235
&у + D = ст2. Нетрудно видеть, что пара случайных величин X и Y удовлетворя-
ет (7.11) с равенством. (Мы опять обошлись без указания в явном виде условного
распределения ^(?/|ж), но его легко найти с помощью формулы Байеса).
Приведенные рассуждения имеют смысл только при D а2. Поскольку значение
у = 0 аппроксимирует значения с.в. X со средней ошибкой равной ст2, то при
D > а2 функция скорость-искажение тождественно равна нулю. Мы получили
следующий результат.
ТЕОРЕМА 7.2. Функция скорость-искажение источника независимых гауссовских
с.в. с дисперсией а2 при квадратическом критерии качества
(7.12)
Рис. 7.4. Функция скорость-искажение для гауссовского источника
Формулу (7.12) иногда удобнее записывать в виде
z 1	2 >
H(D) = max < -log^-,0>.
I £	U j
(7-13)
График функции скорость-искажение для гауссовского источника с единичной
дисперсией показан на рис. 7.4.
Попутно с доказательством теоремы 7.2 нами установлена оценка снизу функ-
ции скорость-искажение произвольного стационарного источника, порождаю-
щего независимые сообщения (см. (7.11)). Эту оценку часто называют границей
Шеннона.
236
Глава 7. Кодирование с потерей качества
СЛЕДСТВИЕ 7.3. (граница Шеннона), Функция скорость-искажение источника
независимых с.в. с дисперсией а2 и дифференциальной энтропией h(X) при квадра-
тическом критерии качества удовлетворяет неравенству
H(D) > h(X) - log JbwD.
(7.14).
7.4.	Функция скорость-искажение
для гауссовских последовательностей
В предыдущем параграфе по сути дела вычислялась функция скорость-искажение
для случайных величин, а теперь мы должны сначала рассмотреть случайные
векторы, а затем и случайные процессы. Здесь уместно вспомнить параграф 6.3.
При вычислении дифференциальной энтропии произвольного вектора мы вос-
пользовались тем, что: а) при линейном преобразовании гауссовского вектора
изменение его дифференциальной энтропии зависит от определителя матрицы
преобразования; б) из случайного вектора с заданной корреляционной матрицей
с помощью линейного преобразования можно получить вектор с независимыми
компонентами; в) гауссовский вектор имеет наибольшую дифференциальную
энтропию среди векторов с заданной корреляционной матрицей. Эти знания
будут использованы ниже при вычислении функции скорость-искажение.
В данном параграфе рассматривается только квадратическая мера качества, и
в качестве первого шага подсчитаем функцию скорость-искажение для последо-
вательности независимых (но не обязательно одинаково распределенных) гаус-
совских с.в. с совместной плотностью
п
/(®) = 1р^)>
г=1
где
Нам предстоит минимизировать взаимную информацию 7(ХП;УП) при усло-
вии, что среднеквадратическая ошибка на один символ не превышает заданной
величины D. В точности как в (7.5), получаем
7(ХП;УП) = Д(ХП) - h(Xn\Yn) =
= £ h(Xi) - £ h{Xi\Xx... Х^Уг... Уп) >
i=l	i=l
>	- Z>(W) =	(7.15)
i=l	i=l	i=l
7 А. Функция H(D) для гауссовского источника
237
Введем обозначение А = М[(ж^ - yi)2] для ошибки в i-й компоненте вектора х.
Из (7.15) с учетом (7.13) следует
n	п	z -	2 Л
/(X"; У") > $2 Я(Д) £ £ maJ - log 0 [.	(7.16)
i=l	г=1	г )
Понятно, что неравенства в (7.15) и (7.16) можно обратить в равенства соответ-
ствующим выбором условного распределения
Нужно теперь отыскать минимум правой части (7.16) по всем неотрицательным
Di,..., Dn таким, что
=	<7.17)
»» . -
1=1
Заметим теперь, что введение дополнительного ограничения
i = l,...,n,	(7.18)
не приводит к потере минимума. Действительно, предположим, что минимум
достигнут при таком наборе	что при некотором i имеем А > ст?
и при некотором j имеет место Dj < а? (такое j обязательно найдется, если
правая часть (7.16) положительна). Очевидно, замена Д на = ст? и Dj на
Dj = Dj + Di - сохраняет ошибку (7.17) неизменной, уменьшая слагаемое
с номером j в правой части (7.16). Следовательно, выбор А > ст? неоптимален.
Заметим теперь, что правая часть (7.16) выпукла U как функция аргументов
Di,...,£>n, поскольку она является суммой выпуклых и функций (см. пара-
граф 1.4). Поэтому любое выравнивание значений Di,...,Dn (не нарушающее
ограничений (7.18)) приводит к уменьшению суммы. Отсюда следует, что мини-
мум суммы (7.16) будет достигаться в том случае, когда все Di9 удовлетворя-
ющие (7.18) со строгим неравенством, одинаковы. При этом они должны быть
равны некоторому 0 такому, чтобы выполнялось (7.17). Окончательный результат
сформулируем в виде следующей теоремы.
ТЕОРЕМА 7.4. Для гауссовского вектора с независимыми компонентами, имею-
щими дисперсии a2,i = 1,..., п, при квадратической мере искажения функция
скорость-искажение вычисляется по формуле
t п	z	2
нщ = Е max 1 los Т’0 г ’	<719>
zn	I (7 J
г=1	4	'
где 0 выбирается таким, что
l£min{0,a?} = D.	(7.20)
1=1
238
Глава 7. Кодирование с потерей качества
Полученные соотношения заслуживают дополнительного обсуждения. Прежде
всего, заметим, что как средняя ошибка для вектора, так и средняя ошибка
для отдельных компонент будет не больше 0. Это означает, что при заданных
требованиях к средней ошибке D все компоненты, дисперсия которых меньше
D, игнорируются и при кодировании нужно принимать во внимание только
компоненты с большой дисперсией. Это правило подсчета затрат на кодиро-
вание получил название «обратного принципа заполнения водой». Объяснение
такого названия будет дано ниже после того, как полученные результаты будут
обобщены на гауссовские случайные процессы.
Рассмотрим теперь гауссовский вектор х =	. ,жп) с произвольной кор-
реляционной матрицей Кп. Напомним (см. параграф 6.4), что с помощью ортого-
нального преобразования (умножения на матрицу из собственных векторов) из х
можно получить вектор с независимыми компонентами с дисперсиями, равными
собственным числам матрицы Кп,
Напомним, что при взаимнооднозначном преобразовании ансамблей средняя вза-
имная информация не изменяется (см. свойство 6.2.11). Кроме того, ортонор-
мированное преобразование векторов сохраняет расстояние между векторами
(см. задачу 4.). С помощью этих аргументов легко приходим к следующему
утверждению.
ТЕОРЕМА 7.5. Для п-мерного гауссовского вектора с корреляционной матрицей
Кп, при квадратической мере искажения функция скорость-искажение вычисля-
ется по формуле
1	n	(	А	1
я(р) = ^£тах 1о«т>0 >	<7-21>
т—*	I	(7	J
г=1	4	'
где Xi, i = 1,..., n - собственные числа Кп,аО выбирается таким, что
1 п
-У min {в, ХА = D.	(7.22)
П - Л
г=1
Перейдем теперь к наиболее важному случаю, когда наблюдаемая на выходе
источника последовательность ^i, жг, ... - стационарная гауссовская с корре-
ляционной функцией /<(т). Напомним, что в параграфе 6.4 была введена спек-
тральная плотность мощности
S(w)= 52	Ш(= (-7Г,7Г]
п=—оо
и сформулирована теорема 6.6, связывающая дифференциальную энтропию про-
цесса с его спектральной плотностью мощности.
Повторим, что если разбить область значений ш на достаточно малые интер-
валы, то интегралы от S(u>) по этим интервалам характеризуют энергию процесса
7.4. Функция Н(Р) для гауссовского источника
239
в соответствующих спектральных диапазонах. При этом в силу свойств преоб-
разования Фурье случайные значения сигналов в э^их диапазонах асимптоти-
чески (с увеличением п) некоррелированы. Для гауссовских процессов некор-
релированность эквивалентна независимости. Поэтому к сигналам в частотных
поддиапазонах можно применить теорему 7.4. Эти рассуждения могут служить
эвристическим обоснованием следующей теоремы.
ТЕОРЕМА 7.6. Для стационарного гауссовского Процесса с ограниченной и инте-
грируемой спектральной плотностью мощности S (w) при квадратической мере иска-
жения функция скорость-искажение вычисляется по формуле
R(D) = ±- [ max(log^,oldw.	(7.23)
47Г	I V I
где 0 выбирается таким, что
[ min{0, S(w)}dw = D.
2^ J — 7Г
(7.24)
Подробнее о доказательстве этого результата можно прочитать в [7], [3].
Рис. 7.5. Функция скорость-искажение для гауссовского источника
Интерпретация вычислений по формуле (7.24) показана на рис. 7.5. Представьте
себе, что на гладкую поверхность воды опускается крышка неправильной формы.
Благодарю принципу сообщающихся сосудов уровень воды поддерживается посто-
янным, в нашем случае этот уровень определяется значением параметра 0. Эту
графическую интерпретацию называют «принципом заполнения водой».
Согласно (7.23) при вычислении R(D) интегрирование выполняется в тех интер-
валах частот си, где спектральная плотность превышает уровень 0.
240
Глава 7. Кодирование с потерей качества
7.5.	Обратная теорема кодирования
для дискретного постоянного источника
при заданном критерии качества
До сих пор в задачах кодирования с искажениями мы рассматривали в каче-
стве источника информации непрерывные случайные величины или случайные
последовательности. Напомним, что с точки зрения применения методов теории
информации принципиальное различие между дискретными и непрерывными
источниками состоит в том, что для непрерывных источников не определена
собственная информация для отдельных сообщений источника и поэтому вместо
обычной энтропии для них вычисляется дифференциальная энтропия.
В оставшейся части главы все доказательства приводятся для самого простого
случая - дискретных постоянных источников. Мы рассматриваем дискретные
источники, поскольку запись доказательств для них проще, чем для непрерыв-
ных. На самом деле в доказательстве обратной теоремы кодирования для пере-
хода к непрерывным источникам достаточно было бы поменять, там, где это надо,
обычную энтропию на дифференциальную. Обобщение же прямой теоремы коди-
рования или алгоритма подсчета функции скорость-искажение на непрерывные
источники потребовало бы значительно больших усилий.
Итак, имеется множество Хп последовательностей длины п на выходе источника
без памяти, выбираемых в соответствии с заданным на нем распределением веро-
ятностей р(х) =	, хп) = П?=1 Кодовая книга или код со скоростью
R для этого источника определен как множество из М = 2Rn последовательно-
стей из аппроксимирующего множества Yn. При построении кода мы стремимся
минимизировать величину средних искажений D = M[dn(®, у)], где мера искаже-
ния dn(x,y) удовлетворяет ограничениям, сформулированным в начале главы,
то есть неотрицательна, и dn(x,y) = £ d(xi,yi).
Приведенная ниже обратная теорема кодирования утверждает, что для достиже-
ния требуемого уровня средних искажений не выше D скорость R кода источника
должна быть не меньше значения функции скорость-искажение H(D).
ТЕОРЕМА 7.7. Пусть заданы дискретный алфавит постоянного источника X =
= {ж}, аппроксимирующий алфавит X = {ж} и мера искажения {d(x,y),x е X,
у € У}. Для любого кода со скоростью R и средней ошибкой D имеет место нера-
венство R H(D).
Доказательство. Следующая цепочка преобразований доказывает теорему
(а)
nR H(Yn)
(Ь)
> H(Yn) - H(Yn\Xn) =
п, уп
= Н(Хп) -H(Xn\Yn) =
7.6. Множества типичных пар последовательностей
241
>
(g)
(>
>
(±)
-Я(Х”|УП)>
\г=1	/
£(я(^)-я(ВД))>
г=1
г=1
г=1
Я(Я).
Переход (а) справедлив, поскольку энтропия кодовой книги не превышает лога-
рифма числа кодовых слов, (Ь) имеет место, поскольку вычитаемое неотрица-
тельно. Далее, (с) и (d) - хорошо известные свойства взаимной информации,
равенство (е) использует отсутствие зависимости букв источника. В (f) мы опу-
стили некоторые условия в вычитаемом, отчего вычитаемое могло только уве-
личиться. В (g) и (h) использованы определения взаимной информации и затем
функции скорость-искажение как минимума взаимной информации при огра-
ниченной ошибке, причем через Di обозначена средняя ошибка аппроксима-
ции Xi значениями из У;. Неравенство (i) основано на выпуклости функции
скорость-искажение, равенство (j) - на определении средней меры искажения
для последовательностей длины п.	□
7.6.	Множества типичных пар
последовательностей
Наша ближайшая цель - доказать прямую теорему для задачи кодирования
источников с заданной мерой искажения. Путь к этой цели лежит, как и в случае
кодирования для каналов, через анализ множества пар типичных последова-
тельностей. Однако той типичности, которой нам хватило для каналов связи,
будет недостаточно. В этом параграфе мы введем некоторые дополнительные
определения, в частности, новое, более «сильное» понятие типичных пар после-
довательностей.
Для произвольных (х,у) е Хп х Yn обозначим через рх,у(х,у) долю таких
позиций, на которых в х расположен символ ж, а в у на той же позиции рас-
положен у. Случайные величины рх,у(х,у) образуют двумерное распределение
вероятностей, которое можно интерпретировать как вычисленное по (х,у) мно-
жество «оценок» вероятностей пар букв. Понятно, что с увеличением длины
242
Глава 7. Кодирование с потерей качества
последовательностей случайные оценки вероятностей	у) сходятся по веро-
ятности к «истинным» вероятностям p®,y(a?, у) (о сходимости по вероятности см.
параграф 1.9).
Множество пар последовательностей длины п
(7.25)
будем называть множеством p-типичных пар последовательностей.
Как и прежде (см. параграфы 5.11, и 5.12), нам потребуется множество
Т«Че) =
(х,у) : -I(x-,y)-I(X-,Y)
п	I
(7.26)
которое мы теперь будем называть множеством I-типичных пар.
Аналогично,
Т^(£) = {(®, у) : |d(®; y)-D\^e},	(7.27)
где D = M[d(®; у)], называется множеством d-типичных пар.
Мера искажения называется ограниченной, если существует число Ртах такое,
что d(x,y) £>max для всех (ж,р) е X х Y.
ТЕОРЕМА 7.8. Для любого 8 > 0 и распределения вероятностей на множестве
пар Хп xYn = {(я?, у)}, удовлетворяющего условиям
п	п
р(®) = Пр(а:»)> р(1/|®) = Пр(зй|яч),	(7.28)
г=1	г=1
и ограниченной меры искажения d(x, у) для некоторого 0 < е 8 и достаточно
большого по множество p-типичных пар (е) содержит множества I-типичных
Т^Т\б) и d-типичных пар T^d\6) при всехп по .
Доказательство. Для p-типичной пары (х,у) е тЬр\е) имеем
7.6. Множества типичных пар последовательностей
243
(Ь)
(с)
ЕЕ Рх,у(х,у)1(х,у) - 52 52 р(^, у)
х£Х yGY	хеХ y£Y
52 Е у) ~ р(ж> у)] л®, у)
xexyeY
« ЕЕ \\Рх,у(х,у) ~р(ж,2/)]/(ж,2/)| =
xeXyeY
=- 52 52 \Р^у(х,у)-р(х,у)\ \1(х,у)\
xeXyeY
(f)
е|Х||У| max |1(ж, у)\ = cKq.
(я,у)
(7.29)
В этих выкладках мы сначала в (а) воспользовались условиями (7.28), затем
в (Ь) изменили порядок суммирования и заменили отношение числа одинако-
вых пар к длине п на оценку вероятности пары. Поясним этот переход подробнее.
Взаимная информация 7(«;у) является суммой частных информаций
причем пара 7(ж; у) встретится в этой сумме некоторое число п(ж, у) раз. Полу-
чим слагаемые вида п(х,у)1(х; ,у). Отношения п(хуу)/п обозначены как оценки
вероятностей пар рх,у(х,у).
После вынесения общего множителя в (с) мы учли (неравенство (d)), что модуль
суммы не больше суммы модулей и (е) что модуль произведения равен про-
изведению модулей. Далее в (f) мы усилили неравенство, заменив взаимные
информации на их максимальное значение, в итоге получили, что оцениваемая
величина не превышает произведения е на константу KQ. Выбрав е = 8/Kq,
убеждаемся в том, что рассматриваемая пара принадлежит Т^\б).
Аналогично доказывается d-типичность любой пары из ТпР\е).	□
Соберем воедино наши знания о типичных парах последовательностей. Вме-
сте с результатами параграфов 5.11, 5.12, теорема 7.8 дает возможность сфор-
мулировать в виде следствия те свойства множества p-типичных пар, которые
потребуются при доказательстве прямой теоремы кодирования.
СЛЕДСТВИЕ 7.9- Для дискретного источника без памяти и ограниченной меры
искажения для любого е > 0 при достаточно большой длине последовательностей
п множество p-типичных пар ТпР\е) обладает следующими свойствами:
1.	Если распределение напарах(х,у) удовлетворяет (728),то Р (т^р\е)^ > 1-е.
2.	Если векторы хиу выбраны независимо с распределениями соответственно р(х)
и р(у) = р(ш, у), то вероятности пар (ж, у) е (е) удовлетворяют нера-
венствам
(1 - s)2-n(J(x;Y)+£) Р ((ж, у) е Т^(е^	2"п(/(Х;У)-е).
244
Глава 7. Кодирование с потерей качества
3.	Если распределение на парах (х, у) удовлетворяет (7.28), то
М [d(®, у)К®, у) е т^>(£)] D + е.
Доказывать это следствие нет необходимости, поскольку оно является по сути
переформулировкой уже доказанных фактов (теоремы 7.8, 5.8).
Иными словами, во-первых, почти все пары длинных последовательностей р-
типичны, во-вторых, если последовательности выбираются независимо, то, напро-
тив, вероятность появления p-типичной пары экспоненциально убывает с уве-
личением длины последовательностей, а показатель экспоненты равен
Третье свойство говорит о том, что если пара последовательностей типична, то
мера искажения для нее близка к средней.
Для доказательства прямой теоремы кодирования нам понадобится решить еще
одну простую вероятностную задачу. Рассмотрим последовательность опытов,
имеющих два исхода: успех и неуспех. Вероятность успеха равна р. Сколько
нужно совершить опытов, чтобы вероятность отсутствия хотя бы одного успеха
была ничтожно мала (меньше заданной маленькой величины г)?
Отсутствие хотя бы одного успеха назовем ошибкой, и соответствующую веро-
ятность обозначим через Ре. В случае независимых испытаний число опытов М
нужно выбрать из условия
Ре = (1-р)м^е.	(7.30)
Нас интересует асимптотическая зависимость между р и М при малых р. Пере-
пишем последнее неравенство в виде
Ре = ем1п(1-р) е“Мр.
Выберем М = К/p, где К - некоторая положительная константа. Тогда
Ре^е~к.
Это означает, что при К = - 1ns вероятность ошибки будет не больше е. Полу-
ченный ответ интуитивно очевиден: если вероятность успеха при одной попытке
равна р, то для достижения хотя бы одного успеха нужно выполнить порядка
1/р попыток. Результат сформулируем в виде леммы.
ЛЕММА 7.10. При вероятности успеха в одном опыте равной р вероятность Ре
отсутствия успеха в серии из М К/р независимых опытов не превышает вели-
чины е~~к.
7.7.	Прямая теорема кодирования
для дискретного постоянного источника
при заданном критерии качества
Прямая теорема кодирования устанавливает существование кодов источника,
для которых скорость R при заданном допустимом среднем искажении D может
7.7. Прямая теорема кодирования
245
быть сделана сколь угодно близкой к соответствующему значению функции
скорость-искажение H(D). Один из способов доказательства этого утверждения
могло быть указание конкретного способа кодирования и декодирования, как это
было сделано в случае кодирования без потерь. Такое доказательство мы назвали
бы конструктивным. К сожалению, такое конструктивное решение задачи воз-
можно только для некоторых вырожденных ситуаций (например, при D = 0).
Чтобы доказать существование хороших кодов для произвольных источников
без памяти, придется воспользоваться уже знакомой нам техникой случайного
кодирования.
Итак, метод доказательства состоит в том, что среднее искажение оценивается
для кода, слова которого получены случайным независимым выбором кодовых
слов. При подсчете ошибки кодирования усреднение выполняется как по мно-
жеству последовательностей источника, так и по множеству кодов. Если среднее
значение искажений окажется равным D, то мы сможем утверждать, что найдется
хотя бы один код, для которого среднее искажение не больше D.
Как и в предыдущем параграфе, считаем меру искажения ограниченной, то есть
что существует число Z)max такое, что б/(ж, у) DmQX для всех (ж, у) е X х У.
ТЕОРЕМА 7.11. Для дискретного постоянного источника X = {ж, р(х)}, аппрок-
симирующего множества Y = {у} и заданной ограниченной меры искажений d(xy у),
для любых положительных е, 6 найдется достаточно большое число п0, такое, что
при п по при любом заданном D найдется код со скоростью R H(D) + 8,
и средним искажением не больше D + е, где
H(D) = min 7(Х;У) —
{pMz)}:M[d(^)]CP
функция скорость-искажение дискретного постоянного источника.
Иными словами, при любом D и любой скорости кода большей функции скорость-
искажение H(D) возможно кодирование со средними искажениями сколь угодно
близкими к D.
Доказательство. Доказательство, аналогично теореме кодирования для канала
с шумом, разбивается на три шага: построение ансамбля случайных кодов, выбор
процедуры кодирования, оценка величины средних (по ансамблю кодов и по
последовательностям источника) искажений.
Шаг 1. Ансамбль кодов. Предположим, что минимум взаимной информации
в формуле для функции скорость-искажение достигается на условном распреде-
лении {р(?/|ж)}. В совокупности с распределением на X = {ж,р(х)} это условное
распределение определяет совместное распределение на X х У и, в свою очередь,
распределение
р(у) = 52 НяОХук)
хех
на аппроксимирующем множестве. Выберем целое число М из условия
2™(Я(Г>)+20) дд < 2п(Я(£>)+3<9)^	(7.31)
246
Глава 7. Кодирование с потерей качества
где положительное число 0 будет выбрано позже. Код С = {ут, т = 1,..., М} С
С Yn длины п объема М для рассматриваемого источника строится случайным
независимым выбором символов кодовых слов из алфавита Y = {у} в соответ-
ствии с распределением р(у).
Заметим, что распределение р(я?) = ПГ=1 р(ж0 и независимый от х выбор аппрок-
симирующих последовательностей у с распределением р(у) = П?=1Р(?/г) порож-
дают еще одно («кодовое») совместное распределение на Хп х Уп, для которого
будем использовать обозначение
Рс(х,у) =р(ж)р(|/).	(7.32)
Шаг 2. Кодирование. Наиболее естественным (и, конечно, оптимальным по ошиб-
ке) было бы правило, которое сопоставляет последовательности х е Хп то слово
Ут ~	• • • ,Утп) € С, которое минимизирует искажение d(ym,x) =
= п SF=i	Это оптимальное правило трудно анализировать, вместо
него мы рассматриваем другое правило, которое заведомо хуже по ошибке, но
проще для анализа.
Для того чтобы описать правило кодирования, на произведении множеств Хп х Yn
введем множество p-типичных пар Т^р\0) в соответствии с (7.25)
=
< (®>v): Y, 52	< 0 г >
xeXyeY
(7.33)
где значение параметра 0 > 0 будет выбрано в ходе доказательства теоремы.
Последовательности источника х е Хп сопоставляется слово ут = (pmi,..., Утп)€
е С такое, что (х.у^) € Т^р\0). Если таких ут несколько, выбирается любое,
если же таких слов нет, сопоставляется слово уг.
Шаг 3. Вычисление средних искажений. Как следует из описания процедуры
кодирования, искажение для заданного х е Хп зависит от того, найдется ли
в кодовой книге последовательность у, образующая с х типичную пару. Для
рассматриваемого ансамбля случайных кодов и описанной процедуры кодиро-
вания на множестве Хп х Yn обозначим через Q событие, состоящее в том, что
случайная последовательность х и сопоставленная ей аппроксимирующая после-
довательность у образуют пару из 7^(0), противоположное событие обозначим
через В. Иными словами, Q или В имеют место, если случайно выбранный код
оказывается соответственно хорошим или плохим. Для средней меры искажения
тогда имеем
мс [d(x,y)] = мс [d(x,y)\g] рс(д) + мс [d(x,y)\B] рс(в)
Мс [d(x,y)\g] + PmaxPc(B).	(7.34)
Здесь мы воспользовались тем, что вероятность любого события не больше 1,
и тем, что средняя ошибка не больше максимальной. Индекс с при математи-
ческих ожиданиях и вероятностях указывает на то, что здесь подразумевается
«кодовое» распределение (7.32).
7.8. Алгоритм Блэйхута
247
Рассмотрим теперь отдельно два слагаемых в (7.34). Следствие 7.9, утверждение
3, позволяет записать
Mc[d(x,y)\g] ^D + 0.	(7.35)
Поскольку кодер совершает М независимых попыток выбора кодового слова и
достаточно одного «попадания» в ТпР\д) при том, что вероятность успеха в одной
попытке не меньше
п _ 9-n(H(D)-0)
Р — z
(Следствие 7.9, утверждение 2). Воспользуемся Леммой 7.10, согласно которой
РС(В) < e-Mp^exp{_2n(tf(D)+29)2n(H(D)-0)} =ехр{—2"9}	(7.36)
при скорости кода
R = logM	+ 30	(737)
п
Подставив (7.35) и (7.36) в (7.34), видим, что при 0 < е/2 при достаточно
большой длине кода ошибка станет меньше D+e. Одновременно из (7.37) заклю-
чаем, что при 0 < 6/3 скорость кода меньше H(D) + 8. Следовательно, выбор
в = min{e/2,5/3}, удовлетворяет всем требованиям теоремы.	□
Итак, мы доказали, что для дискретного источника без памяти с ограничен-
ной мерой искажения достижимая функция скорость-искажение R(D) (7.2) и ее
теоретический предел H(D) (7.3) совпадают.
Рассмотренная в данном параграфе модель может показаться далекой от практи-
ческих задач. Это не совсем верно. Подлежащие кодированию аналоговые данные
обычно поступают на вход кодера с выхода аналого-цифрового преобразователя,
поэтому фактически являются дискретными процессами дискретного времени.
Сложность применения теоретических оценок к реальным задачам связана с тем,
что мы умеем точно вычислять значения H(D) для весьма ограниченного набора
моделей, и эти модели связаны в основном со стационарными гауссовскими
источниками.
Существенным подспорьем в практическом применении теории кодирования для
источников с заданной мерой точности является рассматриваемый в следую-
щем параграфе численный алгоритм Блэйхута, позволяющий построить функ-
цию по дискретной модели или по ее оценке, полученной по реализации
последовательности данных на выходе источника.
7.8.	Численный метод нахождения функции
скорость-искажение для источника
без памяти
Задача состоит в вычислении теоретического предела функции скорость-иска-
жение
H(D)= min 7(Х;У),
248
Глава 7. Кодирование с потерей качества
где /(X; У) - средняя взаимная информация между входом квантователя X = {ж}
и аппроксимирующим множеством У = {у}. Алгоритм Блэйхутд [31] представ-
ляет собой численный алгоритм нахождения H(D). Предполагается, что алфа-
виты X и У дискретны. Прежде чем описывать алгоритм, введем необходимые
определения.
Энтропия Кульбака-Лейблера или относительная энтропия между двумя рас-
пределениями вероятностей р(х) и q(x) определяется как
Ь(р||0 = Z}p(z)log^.	:
хех	™	;
(Некоторые свойства L(p\\q) изучались в задаче 18 к главе 1.)	J
В терминах относительной энтропии средняя взаимная информация приобретает -!
вид
ЦХ-, Y) = У У р(х, s) log ~~х =
= L(p(x,y)\\p(x)p(y)).	(7.38) i
Задача нахождения функции скорость-искажение сводится к задаче нахожде- !
ния условного минимума средней взаимной информации (7.38) при условии, »
что средние искажения M[d(x, у)] < D. Это задача на условный экстремум, стан- ;
дартный способ ее решения - метод множителей Лагранжа, который сводит ее j
к решению задачи минимизация новой целевой функции но уже без ограничений.
А именно,	j
H(D) = min {/(Х;У) - A(M[d(®,j/)]-D)} =	J
{р(1/|я)}	,	j
= XD+ min F(p(x),p(y\x),d(x, у), А),	(7.39)	|
где А - решение уравнения	j
F(p(x),p(y\x\d(x,y)tX) = /(X; У) - XM[d(x,y)].	j
Основную идею алгоритма Блэйхута можно пояснить следующим образом. Пусть
имеются два выпуклых множества А и В и необходимо найти минимальное рас-
стояние Евклида между ними. Интуитивно понятный алгоритм выглядит так.
Берем точку х е А и находим ближайшую к ней точку у е В. Фиксируем най-
денную точку у и ищем ближайшую к ней точку в А и т.д. Ясно, что при использо-
вании такой итеративной процедуры найденное расстояние уменьшается на каж-
дом шаге. Известно, что если множества выпуклы и расстояние удовлетворяет	j
определенным условиям, то расстояние сходится к минимальному значению.	j
В частности, если множества представляют собой распределения вероятностей i
и расстояние понимается как энтропия Кульбака-Лейблера, то расстояние шаг |
за шагом сходится к минимальной энтропии Кульбака-Лейблера между двумя I
распределениями, то есть к искомому минимуму средней взаимной информации.
7.8. Алгоритм Блэйхута
249
В алгоритме Блэйхута эта же идея применяется для нахождения минимума функ-
ции F(-), а именно, задача минимизации функции F(-) разбивается на две задачи
минимизации, каждая из которых имеет аналитическое решение.
Перепишем функцию F( ) в виде
X
Р(у\х)
р(у)
А 52 52 р№р(у ЬИ®’ у) •
х у
(7.40)
Распределение вероятностей р(у) = Y^xp(x)p(y\x) зависит отр(?/|ж), по которому
мы ищем минимум. Временно забудем об этом и заменим р(у) на новую неза-
висимую переменную г(у). Тем самым задача сведена к двойной минимизации
функции вида
min min < Y^ Y^ p(x)p(y\x) log
{r(y)} {p(y\x)}
-a 52 52р(х)р(у\хМх> y)' 
x у	>
(7.41)
Такая замена допустима, поскольку (в этом нетрудно убедиться) минимум по
г(у) достигается как раз при г(у) = р(у).
Приходим к выражению
H(D) = AD 4- min min
{r(y)} {p(j/|a)}
< 52 52 log
< x у
-a5252h*w^) ’
x у
где D =	аР*(з/1ж) - условное распределение, на котором
X у
достигается минимум.
При фиксированном распределении р(з/|я) функция F( ) минимизируется рас-
пределением г(у) вида
г(у) = 52 рСФ(ук)>
X
совпадающим с р(у), а при фиксированном г(у) она минимизируется при услов-
ном распределении р(з/|я) вида
г(у)ехр(А</(ж,у))
МУ| Ег^ехрСЛ^х.у))-	(	7
У
Детали доказательства и вывод правила остановки можно найти в [31]. Итоговый
алгоритм представлен на рис. 7.6.
250
Глава 7. Кодирование с потерей качества
В этом алгоритме есть неопределенность, связанная с выбором набора значений
параметра Л. Этот выбор зависит от интересующего диапазона значений искаже-
ний, а также от конкретного распределения вероятностей изучаемой случайной
величины.
Input: Распределение вероятностей {р(х),х е X].
Мера искажений {d(x,y),x € Х,у е У}.
Порог точности в.
Максимальное число итераций N.
Output: Для множества значений искажения D
оптимальные условное распределение {р(з/|ж),х Х,у е У},
значение функции скорость-искажение H(D).
И нициал изация:
Выбираем множество значений параметров Л = {А < 0}
forall Л € Л do
Выбираем начальное распределение {г(г/)},
число итераций п = 0,
точность е,
пороги для вычисления правила остановки Те — 0, Ти — 2г,
while п < N или Ти — Те > е do
forall у € У do
сМ = ехрСММ)
У
Г(.У) = г(у)с(у)
end
Tl = - maxy log2 c(y), Tu = - £ r(?/) l°g2(c(?/))-
У
n n 4-1;
end
Формирование результатов вычислений:
forall (ж, у) € X х У do
/ I X = r(p)exp(Ad(a:,y))
v
end
D = Y^P&)p(y\x)d(x,y),
H(D) = AD-£p(®)log2£exp(Ad(a:,p))r(p)-
-Er(y)i°gc(?/)-
У
end
Рис. 7.6. Алгоритм Блэйхута для вычисления функции скорость-искажение
7.9. Задачи
251
В случае, когда исследуемый процесс задан реализацией данных, полученных
в ходе эксперимента, поступают следующим образом. Множество значений наблю-
даемого процесса разбивают на интервалы таким образом, чтобы в каждый интер-
вал попало хотя бы несколько значений. Середины интервалов (или средние зна-
чения величин, попавших в интервал) выбирают в качестве множества значений
дискретного источника.
7.9.	Задачи
1.	Докажите неравенство H(D) 0.
2.	Докажите свойство выпуклости функции скорость-искажение для стационар-
ного источника, не делая предположения об отсутствии памяти источника.
3.	Для стационарного источника с памятью укажите более точную оценку вели-
чины Dq в свойстве 7.2.5.
Подсказка. Ответ можно найти в [7], теорема 5.2.3.
4.	Покажите, что ортонормированное преобразование сохраняет расстояние между
векторами.
Подсказка. Достаточно показать, что ортонормированное преобразование сохра-
няет норму. Квадрат нормы вектора х можно записать как ||ж||2 = ххт. Под-
ставьте в это выражение вместо х вектор у = хА, где матрица А - матрица
ортонормированного преобразования.
5.	Найдите условное распределение </?(з/|я), при котором достигается функция
скорость-искажение двоичного источника.
6.	Найдите условное распределение </?(з/|я), при котором достигается функция
скорость-искажение гауссовского источника.
7.	в качестве множества кодов для двоичного источника можно использовать
двоичные коды с проверкой на четность. Аппроксимирующими кодовыми сло-
вами являются последовательности четного веса. В зависимости от длины
кода получаются разные скорости кодирования и, соответственно, разные иска-
жения. Для двоичного источника равновероятных символов постройте график
функции скорость-искажение R(D) для такого способа кодирования и срав-
ните с теоретической функцией H(D).
8.	В технике кодирования аналоговых источников качество квантования изме-
ряется отношением сигнал/шум, выражаемым в децибелах, вычисляемым как
2
101og10 ДБ>
где <т2 и D - дисперсия источника и среднеквадратическая ошибка.
Нарисуйте график зависимости предельно достижимого отношения сигнал/шум
от скорости для гауссовского источника. Каким будет ожидаемый выигрыш
в дБ от увеличения скорости на 1 бит на отсчет при различных скоростях
кодирования?
252
Глава 7. Кодирование с потерей качества
9.	Воспользуйтесь алгоритмом Блэйхута для нахождения функции скорость-иска-
жение для двоичного источника без памяти. Сравните полученный результат
с полученным аналитически.
10.	Воспользуйтесь алгоритмом Блэйхута для нахождения функции скорость-иска-
жение для гауссовского источника без памяти. Сравните полученный резуль-
тат с полученным аналитически.
7.10.	Терминологические и библиографические
замечания
На заре теории информации, в 50-е годы XX в., интенсивные исследования
в области кодирования источников с погрешностью шли параллельно в СССР
и США. Это был короткий период времени, когда обмен информацией между
учеными двух стран был возможен и результаты работы ученых школы Кол-
могорова были хорошо известны и заслуженно признавались американскими
учеными. Приоритет Колмогорова в доказательстве некоторых важных фактов
неоспорим, но термин «функция скорость-искажение» появился в работе Шен-
нона [21] раньше, чем аналогичное понятие «s-энтропия», которым пользовались
в СССР. Это различие в терминологии сохранялось долгое время и не создавало
никаких проблем. В частности, в учебнике [7] используется именно этот термин.
После издания переводов на русский язык книг Галлагера [3], Витерби и Омуры
[14] и некоторых других в большинстве книг читатель сталкивается уже с аме-
риканским (точнее сказать, международным) термином. Поэтому в данном посо-
бии использовано непривычное для самого автора название «функция скорость-
искажение».
При написании данной главы в большой степени использованы книги [7] и [38].
Наиболее полное изложение вопросов теории кодирования источников с погреш-
ностью содержится в книге Бергера [27]. Историю вопроса и состояние теории
на момент 50-летия теории информации можно изучить по юбилейной статье
[29].
Глава 8 Квантование
Из результатов предыдущей главы понятно, что теория информация устанав-
ливает теоретические пределы такой скорости передачи информации об источ-
нике, при которой возможно ее восстановление с заданным уровнем точности.
Методы, использованные для доказательств^ достижимости теоретического пре-
дела, непригодны для решения практических задач ввиду большой сложности.
В данной главе мы рассмотрим конструктивные алгоритмы кодирования источ-
ников при заданном критерии качества.
Любое устройство, обрабатывающее аналоговую информацию в цифровой форме,
имеет на входе аналого-цифровой преобразователь (АЦП), а для восстановления
аналоговой информации из цифровых данных используется цифроаналоговый
преобразователь (ЦАП). Пара АЦП и ЦАП образует простейший кодер и деко-
дер аналоговой информации и, как мы покажем ниже, этот кодер не так уж
плох. Он является частным случаем скалярного квантователя, то есть квантова-
теля, обрабатывающего отдельные (скалярные) значения на выходе источника.
Скалярным квантователям мы посвятим первый параграф данной главы.
Кодеры, рассматриваемые в предыдущей главе, объединяли сообщения источ-
ника в блоки. В инженерной литературе по кодированию источников такие кодеры
называют векторными квантователями. Понятно, что векторные квантователи
несоизмеримо сложнее скалярных. Нам предстоит ответить на два вопроса:
► Насколько велик выигрыш от применения векторных квантователей по срав-
нению со скалярными?
► Как правильно выбрать векторы аппроксимирующих значений для векторного
квантователя?
Ответы на эти вопросы будут даны во втором параграфе.
Векторные квантователи общего вида (так называемые неструктурированные
квантователи) сложны и могут быть использованы только для кодирования
очень коротких последовательностей. Однако существует специальный класс век-
торных квантователей - квантователи на основе числовых решеток, для которых
сложность кодирования много меньше, чем для неструктурированных квантова-
телей. Решетчатым квантователям посвящен третий параграф.
254
Глава 8. Квантование
Дальнейшее упрощение реализации квантования связано с применением кванто-
вателей, основанных на использовании сверточных кодов. Их краткое изучение
завершает главу.
8.1. Скалярное квантование
8.1.1. Основные определения и постановка задачи
Предполагаем, что на числовой оси определен непрерывный вероятностный ан-
самбль X = (—оо, оо), заданный плотностью распределения /(ж), х е X. Нам
нужно построить отображение множества X на дискретное аппроксимирующее
множество Y с X. Такое отображение можно задать, разбив X на прилегающие
друг к другу непересекающиеся отрезки Ij (Uj Л = X Л П Л' = 0 ПРИ 3 / /) и
выбрав по одной точке каждого отрезка в качестве одного из элементов у е Y.
Отрезки называют квантами, границы отрезков - границами квантов, элементы
множества Y - аппроксимирующими значениями.
Устройство квантования (квантователь) по значению х находит тот квант, кото-
рому принадлежит это значение, и сохраняет номер кванта для последующего
использования, например, кодирования и передачи по каналу. По номеру кванта
устройством восстановления (деквантователем) однозначно определяется соот-
ветствующее этому кванту аппроксимирующее значение у, которое выдается полу-
чателю вместо истинного значения х.
Для простоты предположим, что Y - конечное множество, число его элементов
|У| = Q представляет собой число квантов или объем аппроксимирующего алфа-
вита. Обозначим через у\,...,yq аппроксимирующие значения, а через 60, Ьь • • •,
bq - границы квантов. Подразумевается, что yi е Д = [bi-i,bi). Если плотность
f(x) определена на всей числовой оси, то Ьо = -оо, bq = оо.
Если все параметры квантователя (числа у г, г = 1,..., Q, bj, j = 0,..., Q) заданы,
то тем самым определена дискретная случайная величина Y = {у^ i = 1,..., Q},
вероятности значений которой вычисляются по формуле
Pi= J
bi-1
lx, i = 1,..., Q.
(8.1)
К последовательности аппроксимирующих значений на выходе квантователя
может быть применено неравномерное кодирование, в частности, арифметиче-
ское кодирование, скорость которого R будет сколь угодно близка к энтропии,
то есть
R = - logPj-
3
8.1. Скалярное квантование
255
В качестве меры искажения примем среднеквадратическую ошибку
D = М [(ж - з/О))2] = 52 / <ж “	(8.2)
Задача построения оптимального скалярного квантователя состоит в том, чтобы
обеспечить наименьшую скорость R при заданных ограничениях на ошибку D,
или, напротив, минимизировать ошибку квантования при заданной скорости.
Чаще всего на практике используют равномерное квантование. При таком кван-
товании длины интервалов одинаковы:
1ЛI = bj ~ fy-i ~ Д’ j = 1, • • • ? Q*
Величина Д называется шагом квантования. Аппроксимирующие значения (исклю-
чая крайние значения) размещают в середине квантов:
Важное свойство равномерного квантователя - простота его реализации. Про-
цедура квантования сводится к делению случайных величин х на выходе источ-
ника на шаг квантования Д. По каналу передают закодированный (например,
арифметическим кодом или кодом Хаффмена) номер кванта. При восстанов-
лении аппроксимирующее значение достаточно просто вычисляется по номеру
кванта и шагу квантования. В общем случае (при неравномерном квантовании)
вычислительные затраты на кодирование и декодирование намного больше.
Отметим еще одну особенность равномерного квантования. При равномерном
квантовании нет необходимости ограничивать объем алфавита Q. В параграфе 4.1
были описаны универсальные коды бесконечного объема, которые можно эффек-
тивно использовать в сочетании с равномерным квантованием, не ограничивая
допустимый интервал значений на входе квантователя.
При кодировании источников без потерь критерием оптимизации квантователя
была средняя длина кодовых слов или скорость кодирования при кодировании
последовательностей. При квантовании мы сталкиваемся с более сложной зада-
чей поиска условного минимума скорости (ошибки квантования) при заданном
ограничении на ошибку (или, соответственно, на скорость). Кажется почти оче-
видным, что те интервалы, на которых плотность распределения больше, должны
квантоваться точнее с тем, чтобы минимизировать среднюю ошибку. С другой
стороны, оказывается, что при таком неравномерном квантовании распределе-
ние вероятностей аппроксимирующих значений будет более равномерным, чем
при равномерном квантовании, следовательно, увеличится энтропия.
Ответить на вопрос, какое квантование лучше, проще всего в случае малых оши-
бок квантования (или большой скорости). Именно эта ситуация рассматривается
в следующем параграфе.
256
Глава 8. Квантование
8.1.2. Асимптотические характеристики равномерного
квантования
Характеристики равномерного квантователя можно достаточно легко вычислить
в предположении, что точность квантования велика, что соответствует малому
значению шага квантования Д. В этих условиях плотность распределения можно
принять постоянной в пределах одного кванта. Тогда равенства (8.1) и (8.2)
можно переписать в виде
Pi « Д/(%),	(8.3)
и
3 ij
Vj+^/2	2
~	/ {x-yj)2dx = ^.	(8.4)
J Vj-A/2
Скорость квантователя можно оценить следующим образом:
й = -52PjlogPj =
з
3
= -52^/(ж)1оё(д/(%))^»
3 h
«	№log(д№))dx =
3 ij
= - У f(x) log f(x)dx - log Д =
X
=} ft(X)-logA.
Здесь (а) использует (8.3), переход (b) основан на (8.1), приближенное равенство
(с) учитывает почти равномерность распределения на малом интервале инте-
грирования, (d) - определение дифференциальной энтропии h(X) случайной
величины с плотностью распределения f(x).
Итак, принимая во внимание (8.4), находим, что функция скорость-искажение
равномерного квантователя при малых Д задается соотношением
ВД«/г(Х)-^1оё(12£>).	(8.5)
Л
8.1. Скалярное квантование
257
Интересно сравнить с предельно достижимой скоростью при заданном искаже-
нии H(Z>). Воспользуемся нижней границей Шеннона (7.14), из которой следует,
что
Я(£>) > h(X) - | log(2TreZ>).	(8.6)
Из двух последних соотношений получаем, что при Д —> 0 избыточность равно-
мерного квантователя можно оценить неравенством
1	1ГР
R(D) - H(D) < - log — = 0.2546.	(8.7)
2	о
Этот факт был установлен В. Н. Кошелевым в 1963 г. [10], хотя чаще можно
встретить ссылки на более позднюю работу Гиша и Пирса [46].
Данная оценка указывает максимальную величину выигрыша, который может
быть получен за счет перехода от скалярного квантования к векторному. Потен-
циальный выигрыш относительно невелик, если на передачу каждого числа отво-
дится, скажем, 16 бит. Однако во многих задачах допустимые затраты не превы-
шают одного бита на отсчет. В таких условиях задача повышения эффективности
квантования по сравнению с равномерным скалярным квантованием остается
достаточно важной.
Завершая изучение равномерного квантования, отметим, что для большинства
источников без памяти характеристики равномерного квантования практически
совпадают с характеристиками изучаемого ниже оптимального скалярного кван-
тования при скорости выше 3-4 бит на отсчет. Это означает, что при больших
скоростях в неравномерном квантовании нет большого смысла, и единствен-
ной альтернативой равномерному квантованию является векторное квантование,
которое согласно формуле (8.7) потенциально позволяет сберечь приблизительно
0,25 бита на каждом отсчете.
8.1.3. Оптимальное скалярное квантование по критерию
минимума среднеквадратической ошибки
Существенные шаги в направлении повышения эффективности скалярного кван-
тования были сделаны Ллойдом (1957) [53] и Максом (1960) [55]. Независимо
друг от друга они решали задачу нахождения квантователя, минимизирующего
среднеквадратическую ошибку при заданном числе квантов, и предложили опи-
санный ниже способ построения оптимального квантователя по заданной плот-
ности распределения f(x).
При заданном числе квантов Q среднеквадратическая ошибка квантователя с гра-
ницами квантов Ьг, i = 0,...,Q, и аппроксимирующими значениями yif i =
= 1,..., Q, может быть вычислена по формуле
Q
D = М [(ж - у(ж))2]	[ (х ~ Уэ)2 f(.x)dx-	(8.8)
b/-!
258
Глава 8. Квантование
Приравняв производные правой части по bj и по у3 нулю, после простых вычис-
лений приходим к следующим уравнениям
Уз = —т-----------= —, 3 = 1, • • •, Q,
А
в которых использованы обозначения
bj	bj
Pj = f(x)dx, mj = У xf(x)dx.
bj-i	bj-i
(8.9)
(8.10)
Принимая во внимание (8.9) и (8.10), ошибка квантования (8.8) может быть
приведена к виду
где а2 представляет собой дисперсию одного значения случайной величины. Из
формул (8.9) и (8.10) следует, что границы квантов оптимального квантователя
делят пополам интервалы между аппроксимирующими значениями, а аппрокси-
мирующие значения являются «центрами тяжести» квантов. В общем виде найти
совместное решение (8.9) и (8.10) невозможно, однако показанный на рис. 8.1
алгоритм Ллойда-Макса (ЛМ), решает эту проблему.
При решении практических задач плотность f(x) бывает неизвестной. Вместо
нее имеется некоторая реализация случайной последовательности х\,... ,xn на
выходе источника. Оптимальный квантователь (в смысле минимума среднеквад-
ратической ошибки) в этом случае также может быть построен с помощью Алго-
ритма ЛМ с той разницей, что числа mj и pj в этом случае вычисляются по
формулам
mj — АГ"1 У2 хч
1 ,bj)
Pi =	|{ж : ж е	.
Заметим, что на первый взгляд ЛМ-квантователь должен быть заметно лучше
равномерного, поскольку принимает в расчет неравномерность распределения
квантуемых значений вдоль числовой оси. Он уделит «больше внимания» той
области, вероятность появления значений которой больше. Напротив, широкие
кванты и, соответственно, большая ошибка будет допущена для редких значений
случайной величины. Однако, как мы увидим ниже при сравнении характери-
стик квантователей, с учетом неравномерного кодирования на выходе квантова-
теля, выигрыш не так велик и зачастую не оправдывает увеличения сложности
квантования.
8.1. Скалярное квантование
259
Input: Плотность /(ж),
количество квантов Q,
точность приближения е,
и (или) максимальное число итераций ЛГ;
Output: Границы квантов 6о,...,
Аппроксимирующие значения yi,..., yq
Инициализация:
Выбираем произвольно начальное положение границ квантов 61,..., &q-i (границы
и Uq соответствуют нижней и верхней границе области значений величины х),
текущее и «новое» значения ошибки Dc = a2, D = оо,	>
текущее число итераций п = 0;
while Dc - D > е и (или) п < N do
► Dc — D\ п <— п 4-1;
► По формуле (8.9) обновляем аппроксимирующие
значения ?/i,... ,?/q.
► По формуле (8.11) вычисляем новое значение
ошибки D.
► По формуле (8.10) находим новые границы квантов 61,..., feq-i.
end
Рис. 8.1. Алгоритм Ллойда-Макса
Еще одно важное замечание: скорость кодирования данных на выходе ЛМ кван-
тователя не может быть меньше 1 бита на отсчет. Рассматриваемые ниже алго-
ритмы позволяют преодолеть этот порог.
8.1.4. Оптимальное квантование при заданной энтропии
аппроксимирующего множества
В этом параграфе мы возвращаемся к задаче поиска аппроксимирующих зна-
чений ?/1,..., yq и границ квантов Ьо> • • •, &Q, при которых достигается мини-
мальная ошибка. Однако теперь мы накладываем ограничение не на число кван-
тов Q, а на величину энтропии последовательности аппроксимирующих значе-
ний. Представленное ниже решение задачи впервые было опубликовано в уже
цитированной работе Т. Бергера [28].
Напомним, что при заданных у = (?/i,..., yq) и Ь = (Ьо,..., bq) ошибка и ско-
рость вычисляются по формулам
Р(Ь,у)
Q Ь1
= ^2 / ^-Vj)2f(x)dx,
Q
j=i
(8.12)
(8.13)
260
Глава 8. Квантование
где
bi
Pi= / i =	-
bi-i
Задача состоит в нахождении пары (Ь,у), минимизирующей ошибку при задан-
ной скорости Rq. Иными словами, требуется найти
D(Rq) = min D(b,y).
(Ь,|/):Я(Ь,|/КЯо
Данная задача является задачей нахождения условного экстремума функции,
и стандартный способ ее решения - метод множителей Лагранжа. Идея метода
состоит в том, что вводится вспомогательный параметр А, и вместо условного
минимума функции D(b,y) ищется обычный минимум функции
^(Ь, у. А) = Р(Ь, у) + А(Л(Ь, у) - До).	(8.14)
Попробуем объяснить, почему и как на этом пути достигается поставленная цель.
Случай А = 0 соответствует поиску оптимального квантователя без ограничения
на скорость и решением является ЛМ-квантователь. Выберем теперь некото-
рое значение А > 0. При Я(Ь, у) > Rq второе слагаемое вносит дополнительный
положительный вклад в минимизируемую функцию. Изменив А, можно добиться
того, что в качестве оптимальной пары (Ь, у) будет выбрана та, для которой
второе слагаемое в <р(Ь,у, А) равно нулю, то есть R(b,y) = Rq. Как же найти
такое А?
Предположим, что пара (Ьо,2/о) оптимальна для некоторой скорости R. Тогда
<£>(Ь0, Уо>л) = D(Pq, у0) + АЯ(Ьо, 2/о) “ лдо = D(R) + XR - AJ?o
представляет собой линейную функцию скорости Rq. Больше того, нетрудно убе-
диться в том, что эта функция - касательная к графику D(R) в точке R = Rq.
Это означает, что А нужно выбирать из условия
ЭОД
r=rq
Трудность состоит в том, что функция D(R) нам неизвестна, ее отыскание как
раз и является нашей задачей. Поэтому значения А находят перебором либо
задача решается в некотором диапазоне значений А и тем самым строится график
функции искажение-скорость в некотором диапазоне R.
При фиксированном А, дифференцируя (1.15) по каждой компоненте bj вектора
Ь, приходим к следующим условиям минимума функции <р(Ь, у, А):
(b._J/.)2_(6._2/.+i)2_Alog-^- = o, j =	—	(8.15)
Pj+i
При этом аппроксимирующие значения должны удовлетворять уравнениям (8.9)
8.1. Скалярное квантование
261
Уз =
(8.16)
К сожалению, найти совместное решение уравнений (8.15) и (8.16) непросто.
Один из путей к численному решению задачи - следующий. Значение до известно.
Выберем какое-либо значение Ь\. Тем самым мы определили величины pi и у г.
После этого можно выбрать &2 так, чтобы зависящие от этой величины р2 и у2
удовлетворяли уравнению (8.15). Продолжая рекурсию, находим все параметры
квантователя, но при этом может оказаться, что последняя граница кванта bq не
совпадает с верхней границей области значений ж. Чтобы исправить ситуацию,
нужно скорректировать начальный выбор параметра 61 и повторить вычисле-
ния. И так до тех пор, пока не будут найдены подходящие значения всех пара-
метров квантователя. Этот алгоритм - один из двух алгоритмов построения
оптимальных квантователей из работы [40].
На рис. 8.2 показаны функции скорость-искажение и зависимость R(D) скоро-
сти оптимального квантователя от ошибки гауссовского источника с единичной
дисперсией.
Рис. 8.2. Функция скорость-искажение H(D) и скорость R(D) для оптимального
скалярного квантователя со средней ошибкой D для гауссовского источника
с единичной дисперсией
Интересно, что если на этом графике привести зависимость скорость-ошибка для
оптимального равномерного квантователя, то эта кривая будет визуально неот-
личима от кривой для оптимального неравномерного квантователя. Более того,
262
Глава 8. Квантование
в работе [28] показано, что для лаплассовского (и для экспоненциального) источ-
ника оптимальным неравномерным квантователем как раз является равномер-
ный квантователь. Однако было бы неверно считать, что равномерный кванто-
ватель всегда близок к оптимальному. Например, для обобщенного гауссовского
источника с малыми значениях параметра а, а такая модель часто встречается
в задачах кодирования мультимедиа информации, выигрыш от неравномерности
шкалы квантования может быть значительным.
Заметим, что асимптотическая оценка избыточности скалярного квантования
(8.7) (граница Кошелева) довольно точно отражает характеристики скалярных
квантователей при скорости больше 1,5 бита на отсчет.
8.2.	Векторное квантование
8.2.1.	Основные определения и постановка задачи
Перейдем от числовой оси к множеству точек в n-мерном пространстве веще-
ственных чисел. Каждая точка - это вектор х = (xi,... ,хп). Множество таких
векторов обозначаем через Хп. Нам нужно построить отображение множества
Хп на дискретное аппроксимирующее множество С С Хп. Такое отображение
можно задать, разбив Хп на прилегающие друг к другу непересекающиеся обла-
сти Sj (Uj Sj = Хп, Sj P| Sjf = 0 при j / /) и выбрав по одной точке каждой
области в качестве одного из элементов Cj е С. Множество С называют кодом
или кодовой книгой, его элементы - кодовыми словами или аппроксимирующими
последовательностями, области Sj - решающими областями.
Для простоты предположим, что код С - конечное множество, число его эле-
ментов |С| = М представляет собой объем кода.
Считаем, что на множестве Хп задана n-мерная плотность распределения /(ж).
Если определены области Sj и элементы кодовой книги Cj, то можно вычислить
вероятности кодовых слов по формуле
Pj = Jf(x)dx, j =	(8.17)
Sj
к последовательности номеров аппроксимирующих векторов на выходе кванто-
вателя может быть применено неравномерное кодирование, в частности, арифме-
тическое кодирование, скорость которого будет сколь угодно близка к энтропии,
то есть получаем затраты на один отсчет (скорость квантования)
3
' В качестве меры искажения примем среднеквадратическую ошибку
' Р = 1м[||а!-С(а:)||2] =1^2 у ||®-Cj||2/(®)d®.	(8.18)
J St
8.2. Векторное квантование
263
Задача построения оптимального векторного квантователя состоит в том, чтобы
обеспечить наименьшую скорость R при заданных ограничениях на ошибку D
или, напротив, минимизировать ошибку квантования при заданной скорости.
8.2.2.	Оптимальное векторное квантование по критерию
минимума среднеквадратической ошибки
В работе [52] Линде, Бузо и Грэй предложили описанный ниже алгоритм (алго-
ритм LBG или ЛБГ) построения векторного квантователя. Этот алгоритм, по сути,
является обобщением алгоритма Ллойда-Макса на случай векторов произволь-
ной размерности.
Как и при скалярном квантовании, мы решаем задачу построения квантователя,
минимизирующего ошибку при заданном объеме кодовой книги. Предположим,
что задано разбиение пространства Хп на решающие области Sj и внутри каждой
области выбран аппроксимирующий вектор (кодовое слово) Cj, j =1,..., М.
Среднеквадратическая ошибка квантователя может быть вычислена по формуле
(8.18). Приравнивая производные ее правой части по Cj нулю, после простых
вычислений приходим к уравнениям
f xf(x)dx
J' = 1..Q <8',9)
Sj
Отсюда следует, что кодовые слова оптимальной кодовой книги являются «цен-
трами тяжести» соответствующих решающих областей. В отличие от скалярного
квантователя, мы не сможем в явном виде указать границы решающих областей.
Вместо этого мы укажем правило вычисления аппроксимирующего вектора Cj
для произвольной последовательности источника х. А именно, среднеквадра-
тическая ошибка будет наименьшей, если при заданном х предпочтение будет
отдано кодовому слову с$, минимизирующему ||я? - с$ ||2, то есть такому с<, что
при всех j / i выполняется неравенство
Ha.-c.il2 < ||®-Cj||2.	(8.20)
Границей области Si, отделяющей Si от Sj, является множество точек, для кото-
рых в (8.20) выполняется равенство. Уравнение общей границы имеет вид
(x,Ci-Cj} = i(c< + Cj,Cj -Cj).
Это плоскость перпендикулярная отрезку, соединяющему с* и cj. Теперь понятно,
что области Si - многогранники, заполненные точками, расстояние которых до Ci
меньше, чем до любой другой кодовой точки. Такие области называют областями
Вороного, или многогранниками Вороного,
Уравйение (8.19) и правило кодирования (8.20) подсказывают простую рекурсив-
ную процедуру оптимизации кодовой книги квантователя, приведенную в виде
алгоритма на рис. 8.3.
264
Глава 8. Квантование
Input: Набор n-мерных векторов (ел,..., ждг),
Объем кодовой книги М,
точность приближения е,
и (или) максимальное число итераций Г;
Output: Кодовая книга (ci,...,см)
Инициализация:
Выбираем произвольно начальную кодовую книгу из М векторов a, i — 1,..., М,
номер итерации t = О,
текущее и «новое» значения ошибки Dc = оо, D = 0.
Вспомогательные переменные:
счетчики Ni, векторы Si, i = 1,..., М;
while Dc - D > ей (или) t < Т do
Обнуляем переменные:
for j — 1 to M do
Nj = 0; Sj = 0;
end
Dc = D; D = 0
Цикл по векторам x:
for i = 1 to N do
►	Находим ближайшее к Xi кодовое слово Cj
►	Р <—£> + Цаз, — с7 ||2,
►	Sj i Sj 4“ Xi,
► Nj 4- Nj 4-1,
end
Модифицируем кодовую книгу
for j = 1 to M do
Cj=3j/Nj\
end
Новое значение ошибки:
D <- D/N-,
14-14-1;
end
Рис. 8.3. Алгоритм Линде-Бузо-Грэя
Предположим, что имеется последовательность n-мерных векторов (®i,... ,®w),
представляющая собой достаточно представительную базу данных, по которой
нужно построить наилучшую кодовую книгу объема М. Идея алгоритма состоит
в том, что, начиная с произвольной кодовой книги, на каждой итерации мы
перестраиваем решающие области в соответствии с (8.20), а затем корректируем
кодовую книгу в соответствии с (8.19).
Алгоритм LBG очень часто используют при решении разнообразных практиче-
ских задач. В то же время далеко не всегда кодовая книга, порожденная этим
алгоритмом, - лучшее решение. Один из недостатков - то, что алгоритм опти-
мизирует ошибку при заданном объеме кода, тогда как правильнее было бы
минимизировать ошибку при заданной энтропии номеров кодовых слов, то есть
8.3. Квантователи на основе числовых решеток
265
при заданной скорости кодирования. К сожалению, приемлемых по сложности
решении этой более сложной задачи неизвестно. Более существенный недоста-
ток - то, что структура получаемой кодовой книги нерегулярна и для такого рода
кодовых книг не удается предложить более простого алгоритма кодирования, чем
прямой перебор по всем кодовым словам.
В следующих параграфах мы будем рассматривать конструкции кодовых книг,
имеющие некоторые закономерности. Такие книги называют структурирован-
ными,
8.3.	Квантователи на основе числовых решеток
Самый простой пример числовой решетки - одномерная решетка - это мно-
жество точек числовой оси, следующих с фиксированным шагом Д, точнее, это
множество чисел---А, О, Д, 2Д,.... Этой решетке соответствует равномерный
скалярный квантователь. Многомерные решетки, конечно, имеют более сложное
описание. .
Мы знаем, что равномерное скалярное квантование проще реализуется, чем нерав-
номерное, и в то же время при использовании неравномерного кодирования
аппроксимирующих значений оно почти не проигрывает оптимальному неравно-
мерному квантованию. Точно так же решетчатые квантователи много проще про-
извольных (неструктурированных) векторных квантователей и, как будет пока-
зано ниже, почти оптимальны в смысле соотношения между скоростью и ошиб-
кой.
Применение числовых решеток в системах обработки информации не ограничи-
вается задачей квантования. На основе решеток, в частности, строятся сигнально-
кодовые конструкции для модуляции и кодирования сигналов в каналах с огра-
ничениями на полосу частот. Построению и анализу решеток для различных при-
ложений посвящено много работ. Настоящей энциклопедией по решеткам явля-
ется книга [9], из которой заимствованы многие из приведенных ниже сведений
о решетках.
8.3.1.	Определения и характеристики решеток
Основной способ построения структурированных квантователей, допускающих
относительно простое кодирование источника, - использование так называемых
числовых решеток. Начнем с определений.
В n-мерном пространстве вещественных векторов рассмотрим произвольный
набор из п линейно-независимых векторов {vi,..., vn}.
Множество точек вида
п
с =^kiVi,	(8.21)
1=1
где ki - произвольные целые числа, называется решеткой. Сами векторы t?i,..., vn
называются базисом решетки. Матрица, составленная из векторов
266
Глава 8. Квантование
называется порождающей матрицей решетки. Любая точка решетки может быть
представлена в виде
с = кМ,
где к - вектор с целочисленными компонентами.
Решетки, которые могут быть получены одна из другой поворотом или измене-
нием шкалы (умножением базисных векторов на скаляр), называют эквивалент-
ными.
Для каждой точки решетки определен ее многогранник Вороного - множество
точек решетки, расстояние которых до данной точки не больше, чем расстояние
до других точек.
Важные свойства решеток:
►	Любая решетка содержит последовательность из всех нулей в качестве одной
из точек.
►	Все области Вороного решетки конгруэнтны, они могут быть получены сдви-
гами одной области.
Базисные векторы	являются гранями параллелепипеда, содержащего
все точки вида
Q1V1 Ч----------hanVn, «г 6 [о,1),г = 1,2,...,п.
Этот параллелепипед называется фундаментальной областью решетки. Заметим,
что каждая фундаментальная область (как и многогранник Вороного) содержит
ровно одну точку решетки. В то же время, множество всех фундаментальных
областей покрывает все пространство векторов длины п. Отсюда следует, что
объем фундаментальной области совпадает с объемом многогранника Вороного.
Матрица
А = М • МТ
представляет собой матрицу Грамма решетки, а ее определитель равен квадрату
объема фундаментальной области (а значит, и многогранника Вороного).
Обозначим через S для определенности многогранник Вороного, содержащий
нулевую точку. Его объем можно подсчитать как
Vol(S) = [ dx =	(8.22)
s
8.3. Квантователи на основе числовых решеток
267
Пример 8.3.1. Буквой Z обозначают множество целых чисел. Очевидно, Z -
одномерная решетка. Множество Zn представляет собой множество целочислен-
ных последовательностей длины п или п-мерную кубическую решетку, В частно-
сти квадратная решетка И? задается порождающей матрицей
1
О
Фрагмент решетки, ее базисные векторы, фундаментальные области (пунктиром)
и области Вороного показаны на рис. 8.4.
Рис. 8.4. Квадратная решетка
Пример 8.3.2. Порождающей матрицей двумерной гексагональной решетки
можно выбрать
1 О
_ 1/2 V3/2 _
Фрагмент решетки, ее базисные векторы, фундаментальные области (пунктиром)
и области Вороного показаны на рис. 8.5.
Как мы увидим ниже в параграфе 8.3.3, с точки зрения квантования самым важ-
ным параметром решетки является нормализованный второй момент ее области
Вороного:
! J II II	1
п п /	\ l+2/n п Vol(S)1+2/n ’
и dx]
\s /
По известному второму моменту можно оценить избыточность квантования и вы-
игрыш по отношению к равномерному скалярному квантованию.
Избыточность (разность между скоростью и функцией скорость-искажение при
заданной ошибке D) при D —> 0 связана с нормализованным вторым моментом
неравенством (см. параграф 8.3.3, неравенство (8.27))
a(D)-tf(D)^|log(27reG„).
268
Глава 8. Квантование
В технике кодирования аналоговых источников для источника с дисперсией а2
эффективность кодирования измеряют отношением сигнал/шум , измеренным
в децибелах,
101°gio^ дБ >
где D - дисперсия источника и среднеквадратическая ошибка (см. задачу 8 8.
к главе 7). Для двух квантователей с функциями искажение-скорость D^R)
и D2(R) выигрыш первого по отношению к второму в децибелах вычисляется
как
mi	к
101og“ DAR) дБ 
В параграфе 8.3.3 мы покажем, что при малых ошибках квантования диспер-
сия ошибки пропорциональна нормализованному второму моменту квантова-
теля. Следовательно, при малых ошибках выигрыш решетчатого квантователя
с нормализованным моментом Gn по отношению к равномерному скалярному
(для него Gi = Gn = 1/12 при любых п) равен
—101og10(12Gn) дБ .
В табл. 8.1. приведены характеристики наилучших решеток малой размерно-
сти. В графе описания решеток приведены стандартные обозначения числовых
решеток из [9]. Пояснения к ним будут даны в следующем параграфе. Звез-
дочка в верхнем индексе используется для обозначения двойственных решеток.
Поясним этот термин.
8.3. Квантователи на основе числовых решеток
269
Пусть Ln - произвольная решетка. Двойственной к Ln называется решетка L*,
определяемая соотношением
L*n = {х : (я?, и) е Z для всех и G Ln},
Иными словами, двойственная решетка порождается векторами, скалярные про-
изведения которых с векторами исходной решетки - целые числа.
Если М - порождающая матрица для Lr{, то для двойственной решетки L*
порождающей будет матрица	где Т - символ транспонирования.
Примеры двойственных решеток будут даны ниже при описании конструкций
решеток малой размерности.
Таблица 8.1. Характеристики некоторых решеток
п	Название	Gn	Избыточность (бит)	Выигрыш (дБ)
1	Z	0.0833	0.2543	0
2	Аг	0.0802	0.2270	0.1664
3	Аз	0.0785	0.2115	0.2595
4	D4	0.0766	0.1938	0.3659
5	DI	0.0756	0.1844	0.4230
6	Е*6	0.0742	0.1709	0.5041
7	е;	0.0731	0.1601	0.5690
8	Ез	0.0717	0.1462	0.6530
12	К12	0.0701	0.1299	0.7510
16	Л16	0.0683	0.1111	0.8640
24	Лгд	0.0658	0.0839	1.0259
оо	-	0.0585	0	1.5329
Точки, соответствующие решеткам из табл. 8.1 и нижняя граница Задора на избы-
точность решеток, показаны на рис. 8.6. Из сравнения характеристик решеток
с нижней границей, соответствующей сферическому покрытию, вытекает опти-
мистический вывод о том, что существующие решетки относительно небольшой
размерности обеспечивают эффективность близкую к предельно достижимой.
Например, решетка Лича Л24, для которой сложность кодирования примерно
такая же как сложность декодирования кода Голея, уступает предельно дости-
жимой эффективности квантования по скорости кодирования меньше 0,1 бита
на отсчет и проигрывает по ошибке примерно 0,5 дБ.
Еще ближе к теоретическому пределу можно подойти с помощью решеток на
основе сверточных кодов. Такие решетки мы рассмотрим в параграфе 8.5.
8.3.2.	Важные примеры числовых решеток
Определение и просуые примеры числовых решеток мы рассмотрели в преды-
дущем параграфе. Здесь мы рассмотрим подробнее те решетки, которые могут
270
Глава 8. Квантование
Рис. 8.6. Избыточность и размерность некоторых решеток
и нижняя граница Задора на избыточность решеток
быть полезными при построении векторных квантователей небольшой размер-
ности (см. табл. 8.1.). Интересна связь конструкций этих решеток с конструкцией
коротких кодов, предназначенных для исправления ошибок в каналах связи. То,
что хорошие коды оказываются полезными для построения решеток, подсказы-
вает возможность поиска новых конструкций на основе более длинных блоко-
вых и сверточных корректирующих кодов. Известные вычислительно эффектив-
ные методы декодирования корректирующих кодов, как мы увидим, позволяют
упростить поиск ближайшей аппроксимирующей точки решетки.
Нижние индексы в обозначении решеток указывает на размерность, а верхний
индекс « * » обозначает двойственную решетку.
8.3.2.1.	Решетки АпиА^. Решетка Ап представляет собой обобщение двумерной
гексагональной решетки Аг, описанной в примере 8.3.2, на произвольную раз-
мерность. Прежде чем обобщить конструкцию Л2, приведем ее описание с помо-
щью другой порождающей матрицы
1 -1 О

О 1 -1
Заметим, что матрица не квадратная, базисные векторы на этот раз имеют боль-
шую длину, чем размерность пространства. Тем не менее все множество точек,
порождаемых решеткой, принадлежит двумерному пространству. Чтобы убедить-
ся в этом, заметим, что сумма элементов базисных векторов равна 0. Очевидно,
что это будет верно и для всех линейных комбинаций базисных векторов. Сле-
довательно, в трехмерном пространстве с координатами (ж,?/, г) множество точек
8.3. Квантователи на основе числовых решеток
271
числовой решетки Аг принадлежит плоскости, описываемой линейным уравне-
нием х + у + z = 0.
В общем случае решетка Ап совпадает с множеством (n-h 1)-мерных целочислен-
ных векторов, сумма элементов которых равна нулю. Порождающая матрица Ап
имеет вид
м =	’1-1	0 ••• 0	0 0	1-1-0	0 . 0	0	0-1-1
В частности, решетка Ai совпадает с решеткой целых чисел Z. Решетка Аз имеет
второй момент 0,078745. Оптимальной 3-мерной решеткой является решетка
A3 - решетка двойственная к А3.
Порождающая матрица решетки А* имеет вид
1	-1	0
1	0	-1
1	0	0
п	1	1
п+1	п+1	п+1
о о
о о
-1 о
1 1
п+1	п+1 .
8.3.2.2.	Объемноцентрическая кубическая решетка. Оптимальные трехмерные
решетки А£ и эквивалентны друг другу и эквивалентны объемноцентрической
кубической решетке (йсс-решетке) с порождающей матрицей
2
0 0
2 0
1 1
М= о
1
Координаты точек йсс-решетки одновременно все четны либо все нечетны. Заме-
тим, что последняя строчка матрицы М - порождающая матрица линейного
(3,1)-кода.
8.3.2.3.	Решетки Dn и D„. Решетка Dn образована целочисленными векторами,
сумма компонент которых четна. Такую решетку называют шахматной. Ее можно
получить, покрасив все точки решетки целых чисел Zn в шахматном порядке
и затем удалив точки одного цвета.
272
Глава 8. Квантование
В общем виде порождающая матрица Dn имеет форму
м =	2	Й	0	•••	0	0 1	1	0	•••	0	0 10 1-00 10 0-01
Ее последние (п-1) строк совпадают с порождающей матрице двоичного (n, п - 1)-
кода с проверкой на четность.
Двойственная к ней решетка задается матрицей
II 1 ь-	' 2	0	0	•••	0	0 0	2	0-0	0 0	0	2	•••	0	0 0	0	0	•••	2	0 . 1	1	1	•••	1	1
Ее последняя строка - порождающая матрица двоичного (п, 1)-кода с повторе-
ниями или проверочная матрица (п,п — 1)-кода с проверкой на четность.
Решетки и D% эквивалентны. Иными словами, - самодвойственная решетка.
8.3.2.4.	Решетки Eq, Ei и Решетки Е? и Е$ связаны с кодом Хэмминга. Порож-
дающими матрицами служат, соответственно,
м =	‘2000000' 0 2	0	0	0	0	0 0 0	2	0	0	0	0 0 0	0	2	0	0	0 1110 10 0 0 1110 10 .0011101.
и
	 2	0	0	0	0	0	0	0 '
	0	2	0	0	0	0	0	0
	0	0	2	0	0	0	0	0
м =	0	0	0	2	0	0	0	0
	1	1	1	0	1	0	0	0
	0	1	1	1	0	1	0	0
	0	0	1	1	1	0	1	0
	. 1	1	1	1	1	1	1	1.
8.3. Квантователи на основе числовых решеток
273
Последние три строки первой матрицы - проверочная матрица кода Хэмминга
(7,4), последние четыре строки второй матрицы - порождающая матрица расши-
ренного кода Хэмминга (8,4).
Решетку Eq можно получить из Eg, наложив на векторы (#i,..., xg) ограничения:
^1 + xg = 0, х2 + xg + х± + х5 + х6 + х? = 0.
В явном виде в пространстве размерности 6 решетка Eq задается матрицей
	0	0	0	2а/3	0	0
	0	0	0	0	2\/3	0
м =	2	2	2	0	0	0
	3	0	0	х/3	0	,0
	0	3	0	0	7з	0
	1	1	1	—>/з	—х/з	—х/з
Решетки Eq и Е7 имеют нормализованный второй момент 0.074347 и 0.073231,
то есть почти не уступают наилучшим решеткам в этих размерностях Е$ и Е7.
Решетка Eg - самодвойственная.
8.3.2.5.	Решеткиразмерности 12,16и24. Порождающая матрица решетки Коксте-
ра-Тодда К12.
4	0	0	0	0	0	0	0	0	0	0	0
0	4	0	0	0	0	0	0	0	0	0	0
0	0	4	0	0	0	0	0	0	0	0	0
2	-1	-1	2	0	0	0	а	а	0	0	0
1	0	0	0	2	0	а	0	а	0	0	0
1	0	0	0	0	2	а	а	0	0	0	0
2	0	0	0	0	0	—2а	0	0	0	0	0
0	2	0	0	0	0	0	—2а	0	0	0	0
0	0	2	0	0	0	0	0	—2а	0	0	0
1	1	1	1	0	0	а	а	а	—а	0	0
1	1	1	0	1	0	а	—а	а	0	—а	0
1	1	1	0	0	1	а	а	—а	0	0	—а
где а = \/3-
Порождающие матрицы решетки Барнса-Уолла Л1б и Лича Л24 приведены в виде
рис. 8.7 и 8.8 соответственно.
В решетках Л16 и Л24 в нижней части матрицы выделены строки, образую-
щие порождающие матрицы линейных двоичных кодов. В первом случае это
(16,5)-код Рида-Маллера, во втором (без последней строки) это (24,12)-код Голея.
274
Глава 8. Квантование
4
2 2
2	2
2	2
2	2
2	2
2	2
2	2
2	2
1111 11 1 1
1111 1 11 1
1111 1 11 1
1111 1 11 1
1111111111111111
Рис. 8.7. Порождающая матрица решетки Барнса-Уолла Aie.
Пустые позиции соответствуют нулям
4 2 2 2 2 2 2 2 2 2 2 2	2 2 2 2 2 2 2 2 2 2 2	
1 1 1 1 1 1 1 1 1 1 1	11 111 1 11 111 1 1 11 111 1 11 111 1 11 111 1 11 111 1 11111 11 1111 111 1 11 111 1 11 1111 11	1 1 1 1 1 1 1 1 1 1 1
3 2	11111111111 22222222222	11111 1 1 1 1 1 11 222222222222
Рис. 8.8. Порождающая матрица реГиетки Лича Л24.
Пустые позиции соответствуют нулям
8.3. Квантователи на основе числовых решеток
275
8.3.3. Асимптотические характеристики решетчатого
квантования
Тривиальным частным случаем векторного квантования является скалярное кван-
тование, рассмотренное в предыдущем параграфе. Мы установили что асимпто-
тически (при малых ошибках) скалярное квантование теряет приблизительно
0,255 бит на каждом отсчете в сравнении с теоретически достижимым преде-
лом скорости при заданной ошибке. Из теорем кодирования следует, что, уве-
личивая размерность квантователя, можно приблизиться сколь угодно близко
к s-энтропии источника. Поскольку с увеличением размерности быстро растет
сложность реализации кодирования, очень важно ответить на вопрос, насколько
быстро с ростом размерности повышается эффективность кодирования. В дан-
ном параграфе мы ответим на этот вопрос для случая, когда ошибки квантования
малы.
Будем в точности следовать тем рассуждениям, которые позволили получить
оценку эффективности равномерного скалярного квантователя.
Предположим, что ошибка квантования мала, а скорость квантования велика.
Кроме того, будем считать, что кодовая книга - многомерная решетка, а зна-
чит, все области Sj имеют одинаковую форму и размер. При малых ошибках
плотность распределения можно принять постоянной в пределах одной области.
Тогда вероятности аппроксимирующих векторов можно записать в виде
Pj = l f(x)dx « /(с,) J dx =/(cJVol(S7),	(8.23)
Sj	Sj
где
Vol(Sj) = У dx
Sj
представляет собой объем области Sj. Нам понадобится обозначение
ад-) = 11И12<^
Sj
для так называемого второго момента области S.
Из (8.18) получаем выражение для ошибки
D ™ ~с^2
j Si
f\\x-c^dx-
j	Si
Интеграл^ этом выражении зависит только от формы Sj и от выбора аппрокси-
мирующего вектора cj. По предположению, все области одинаковы и одинако-
выми будут значения интеграла. Обозначим через S ту область, которая содержит
276
Глава 8. Квантование
начало координат, и без потери общности поместим соответствующий вектор с3
в начало координат. Выражение для ошибки упростится:
/||®||2<te
О -
п^Рз Vol(S) nVol(S)’
(8-24)
Скорость квантователя при заданной ошибке D можно оценить следующим обра-
зом
3
« “&l°g(W)/(Cj))«
74
3
« “ Е / /(®) log (Vol(S)/(®)) dx =
j Si
=	/ (®) log/(®)d® + logVol(S) j =
Vn	/
= /i(X) — - logVol(S).	(8.25)
n
Через h(X) обозначена дифференциальная энтропия случайной величины с плот-
ностью распределения /(ж).
Интересно сравнить результат с предельно достижимой скоростью при заданном
искажении, то есть с функцией скорость искажение источника H(D). Восполь-
зуемся нижней границей Шеннона, из которой следует, что
H(D) > h(X) - 11оё(2тгеО).	(8.26)
Вычитая (8.26) из (8.25), получаем
Я(Р)-Я(Р) s? | log(27reD) - i log Vol(S) =
Zi	TL
1	2TreD
2	1Og Vol(S)2/n ’
Подставив теперь в это выражение ошибку (8.24), получим
B(D) - Я(Р) i log(27reGn),	(8.27)
где безразмерная величина
8.3. Квантователи на основе числовых решеток
277
Г Нж1|2 dx
~ ! J II II	t u(s)
п п/	\l+2/n	nVol(S)1+2/n
\fdx)
\s /
называется нормализованным вторым моментом области S.
Формула (8.27) получена Задором в 1966 г. (опубликована значительно позже
в [58]).
Заметим, что число Gn не изменяется при масштабировании области S. Действи-
тельно, при замене переменных ti = axt интеграл в числителе увеличится в ап+2
раз, а в знаменателе - в ап раз и после возведения интеграла в степень 1 + 2/п
множитель станет равным ап+2 и дробь останется без изменения. Таким образом,
Gn зависит только от формы S и от размерности п. Из (8.27) следует, что выбор
областей S должен по возможности минимизировать величину второго момента.
Для анализа конкретных квантователей полезен интеграл Дирихле
f f(xi + --- + хп)х“1 х*п —
J	Х1
dxn
Г(а1) • • -Г(ап)
Г(а1 + • • • + ап)
1dr1
где интеграл в левой части вычисляется по всем > 0, г = 1, ..., п, таким, что
xi Н---h хп 1, а Г(а) - гамма-функция
оо
Г(а) = I ya~1e~vdy.
О
С интегралом Дирихле и гамма-функцией мы уже встречались в параграфе 3.5,
где были приведены их определения и некоторые свойства.
С помощью интеграла Дирихле можно, например, подсчитать Gn для п-мерного
шара. Подстановка Xi = у? превращает область интегрирования в шар. Далее,
подставив ai = 1/2, г = 1,..., п, получим выражение для объема n-мерного шара
единичного радиуса
Для подсчета второго момента запишем U(S) в виде
17(5) = j xidx = п j xidx
i=1 s	s
и применим интеграл Дирихле при ai = 3/2 и = 1/2, i = 2r..,n. Второй
момент шара радиуса 1 равен
tfn =
п + 2
278
Глава 8. Квантование
В итоге нормализованный второй момент для шара равен
_ Г(п/2 +1)2/”
(п + 2)тг
(8.28)
С увеличением п величина Gn убывает и
lim Gn =	= 0.0585498...
п—>оо	2тге
Подстановка этой величины в (8.27) показывает, что именно при покрытии про-
странства сферическими областями избыточность кодирования становится рав-
ной нулю и тем самым Достигается минимальная возможная скорость кванто-
вания. Это и понятно, поскольку именно шар обладает наименьшей возможной
величиной второго момента. С другой стороны, ни при какой конечной размер-
ности шары не заполняют пространства и не могут быть решающими областями
реального квантователя.
Подстановка величины (8.28) в (8.27) дает нижнюю оценку достижимой скоро-
сти при конечной размерности квантователя. График, представленный на рис. 8.6,
дает ясное представление о скорости убывания избыточности с увеличением
размерности.
Напомнцм, что при выводе границ использовалось предположение о том, что
ошибка квантования мала. Благодаря этому предположению мы могли считать
плотность распределения постоянной в пределах одной области решений. Тем
не менее полученную выше границу считают ориентиром достижимой точности
даже при относительно низких скоростях кодирования (вплоть до скорости 1 бит
на отсчет).
8.4.	Решетки на основе линейных кодов.
Сложность квантования
Применение векторного квантования позволяет выиграть по ошибке по срав-
нению со скалярным квантованием ценой увеличения сложности квантования.
В общем случае при длине векторов п и при скорости R бит на отсчет потребу-
ется кодовая книга размера М = 2nR бит. Таким образом, при скорости, скажем,
5 бит на отсчет, и длине последовательности 10 векторное квантование уже не
может быть выполнено прямым перебором по множеству слов кодовой книги.
Использование решеток позволяет заметно упростить квантование. Больше того,
если в основе решетки - линейный блоковый код, то сложность квантования
близка к сложности «мягкого» декодирования блокового кода. Цель данного
параграфа - научиться квантованию с помощью декодирования блокового кода.
Для простоты описания ограничимся рассмотрением решеток над двоичными
кодами. Отметим, что для двоичных кодов декодирование (а значит и квантова-
ние) проще, чем для недвоичных* В то же время в [12] доказано, существование
8.4. Решетки на основе линейныхкодов
279
решеток над двоичными кодами с величиной второго момента 0.059831..., что
соответствует проигрышу менее чем 0,1 дБ по отношению к границе сферической
упаковки.
Если С - линейный двоичный (п, А:)-код, то числовая решетка, порожденная этим
кодом определяется как множество целочисленных последовательностей v е Zn
таких, что v = с mod 2 для некоторого се С.
Введенное таким образом множество точек с целочисленными координатами,
образует линейное пространство, следовательно, действительно образует число-
вую решетку.
Пример 8.4.1. Рассмотрим линейный код (3,2) с проверкой на четность. Его
порождающая матрица
1 0 1
Словами этого кода являются последовательности длины 3 четного веса. Постро-
им порождающую матрицу решетки, порожденной этим кодом. Заметим, что,
согласно определению решетки над двоичным кодом, любая последовательность
с четными компонентами заведомо принадлежит решетке. Любую такую после-
довательность линейно независимую со строками матрицы G можно добавить
к матрице G для получения порождающей матрицы решетки. В частности, можно
задать решетку над кодом (3,2) матрицей
2
0 0
1 0
0 1
М =	1
1
Эта матрица совпадает с порождающей матрицей решетки D3.
Рассмотрим теперь задачу квантования. От источника на вход квантователя посту-
пает вещественная последовательность х = (a?i, Х2,..., хп). Квантователь должен
найти в решетке точку, ближайшую к х. Номер этой точки должен быть передан
по каналу или сохранен в некотором запоминающем устройстве. При этом мы
никак не ограничиваем объем кодовой книги: компоненты вектора х могут при-
нимать любые значения и, соответственно, множество номеров точек решетки
бесконечно (счетно).
Для начала заметим, что квантование в прямоугольной решетке Zn (см. при-
мер 8.3.1) не составляет труда. Оно сводится к простому округлению компонент
вектора х. Прямоугольную решетку с шагом d будем обозначать как dZn. Кван-
тованйе в этой решетке сводится к делению всех компонент на шаг решетки и
округлению.
Если к каждому вектору произвольной решетки Л прибавить один и тот же век-
тор £ =	• ,£п получаем сдвиг решетки, его мы записываем в виде Л + £.
Очевидно, квантование в решетке Zn + £ легко сводится к квантованию в Zn.
280
Глава 8. Квантование
Основной шаг на пути к решению задачи квантования с использованием реше-
ток над кодами - представление решетки в виде объединения целочисленной
прямоугольной решетки и ее сдвигов.
Пример 8.4.2. Решетка D3 из предыдущего примера может быть представ-
лена как объединение прямоугольной решетки (см. пример 8.3.1), задаваемой
порождающей матрицей
2 О
О 2
О
О
2
М =
О О
с ее сдвигами на векторы (1, 1, 0), (1, 0, 1) и (0, 1, 1). Удобно обозначить рассмат-
риваемую прямоугольную решетку через 2Z3. Получаем представление решетки
Рз в виде
D3 = (2Z3) U (22з + (1,1,0» (J (2Z3 + (1,0,1)) J (2Z3 4- (0,1,1)).
В общем случае решетка Л(С) над двоичным кодом С представляется в виде
Л(С)= □ (2Zn + c).
с GC
Один из возможных «простых» способов квантования состоит в следующем.
Квантователь по очереди выполняет квантование в каждом из сдвигов прямо-
угольной решетки и запоминает результаты квантования и соответсвующую
ошибку. Из всех результатов выбирается наилучший. Результат квантования сос-
тоит из номера сдвига (номер кодового слова) и результатов квантования в соот-
ветствующем сдвиге прямоугольной решетки.
Пример 8.4.3. Выполним квантование вектора (1.2,8.9, -3.6) с помощью решет-
ки Z>3. Результаты вычислений приведены в табл. 8.2. Наилучшим оказалось
кодовое слово с номером 1. На приемную сторону передаем этот номер и индексы
(0,4,-—2). Декодер умножит эти индексы на 2 (шаг решетки) и прибавит сдвиг
(1,1,0). Аппроксимирующим вектором будет сумма двух последовательностей
равная (1,9,-4).
Таблица 8.2. Квантование в решетке D3 перебором по множеству кодовых слов
Номер	Сдвиг (кодовое слово)	Точка решетки	Индексы	Ошибка D
0	(0,0,0)	(2,8,-4)	(1-4,-2)	0.5367
1	(1,1,0)	(1,9-4)	(0,4,-2)	0.0700
2	(0,1,1)	(2,9,-3)	(1.4-2)	0.3367
3	(1,0,1)	(1.8,-3)	(0,4,-2)	0.4033
8.4. Решетки на основе линейных кодов
281
Описанный алгоритм квантования имеет сложность пропорциональную числу
кодовых слов линейного (п, Л)-кода, на котором основана решетка, то есть 2к,
Важно, что эта величина уже не зависит от скорости квантования в отличие от
квантования перебором по множеству слов кодовой книги.
Для дальнейшего упрощения квантования можно воспользоваться методами, раз-
витыми в рамках теории декодирования кодов, предназначенных для исправле-
ния ошибок в каналах связи. Чтобы воспользоваться этими методами, нужно
переформулировать задачу квантования последовательности х в задачу поиска
ближайшего к я? в смысле некоторой аддитивной метрики кодового слова се С.
Обозначим через ЛП(С) решетку над кодом С длины п. Задача квантования
последовательности х = (ж1,...,хп) состоит в нахождении последовательно-
сти у = (з/i, • • •, з/n) е ЛП(С), минимизирующей d(x,y) = п-1
Последовательность у однозначно определяется номером некоторого кодового
слова с 6 С, задающего сдвиг решетки 2Zn), и последовательностью индексов
i = (ii,... ,зп), описывающих положение точки в 2Zn. При известном х и задан-
ном кодовом слове с, индексы i вычисляются однозначно (с помощью поком-
понентного скалярного квантования в решетке 2Z), поэтому задача квантования
сводится нахождению слова с е С минимизирующего
п	п
= nd(x, у(с)) = ^2	!/t) = 52 ^с*)>	(8.29)
t=l	t=l
где через /з(с*) мы обозначили вклад кодового символа ct в ошибку, связанную
с принятием решения в пользу кодового слова с = (ci,..., сп).
Как мы видели на примере, в зависимости от значения кодового символа в дан-
ной позиции, аппроксимирующее значение может быть четным (принадлежать
множеству 2Z), либо нечетным (принадлежать множеству Z\2Z). В первом слу-
чае соответствующее значение кодового символа равно 0, во втором - 1.
Ближайшие к х четное и нечетное числа вычисляются по формулам
2зо
2ii + 1
2
2
х — 1
2
+ 1.
где квадратные скобки [ж], как и раньше, обозначают округление числа х до бли-
жайшего целого. Следовательно, кодовым символам 0 и 1 соответствуют индексы
го и и и метрики
.(0)	(г-2®)2,
/	Гт— 11 \2
м(1) = (®-2 —— -1) •
\	"	J
Обобщая последние тождества, получаем выражения для метрик двоичных кодо-
282
Глава 8. Квантование
Input: Последовательность источника х = (®i,..., хп)\
Output: Номер кодового слова с 6 С,
последовательность индексов г = (и,.,гп).
Шаг 1: Вычисление метрик и индексов
for t = 1 to п do
for с = 0 to 1 do
(с) = round((at - c)/2);
/zt(c) = (xt - 2it(c) - c)2 ;
end
end
Шаг 2: Вычисление кодового слова
Использовать любой алгоритм мягкого декодирования кода С для нахождения
кодового слова с — (ci,..., сп) минимизирующего метрику /z(c) = 22"=1 /й(с*) \
Формирование результата
Выход квантователя: номер кодового слова, последовательность индексов it(ct),
t — 1,..., п, соответствующих символам ct, t = 1,..., п, найденного кодового слова.
Рис. 8.9. Алгоритм квантования для решетки над кодом
вых символов и индексов соответствующих компонент в рещетке 2Z при задан-
ном входном символе xt, t = 1,..., п
i(ct) =	(8-30)
4b
/z(ct) = (xt - 2i(ct) - Ct)2.	(8.31)
В результате приходим к двухэтапному алгоритму квантования: сначала нахо-
дятся метрики и индексы позиций, затем - наилучшее кодовое слово. Формаль-
ное описание алгоритма приведено на рис. 8.9.
Пример 8.4.4. Выполним квантование вектора (1.2, 8.9, -3.6) в решетке Рз
с помощью алгоритма, приведенного на рис. 8.9. Результаты вычислений приве-
дены в табл. 8.3.
Мы привели два алгоритма квантования. Первый алгоритм концептуально проще,
вычислительная сложность второго намного меньше. Достаточно заметить, что
скалярное квантование каждой компоненты во втором алгоритме выполняется
один раз в начале работы алгоритма, а в первом алгоритме подразумевалось, что
оно выполняется для каждого кодового слова заново.
Выигрыш по сложности особенно велик, если для квантования (по сути, для
декодирования линейного кода с мягкими решениями на вводе) не требуется
полного перебора по множеству всех кодовых слов. Методы эффективного деко-
дирования линейных кодов выходят за рамки данного курса, однако ниже мы
рассмотрим один класс кодов, для которых оптимальное декодирование сводится
к задаче динамического программирования, - это сверточные коды.
8.5. Решетки на основе сверточных кодов.
283
Таблица 8.3. Квантование в решетке D3 с помощью мягкого декодирования
Шаг 1. Вычисление метрик и индексов				
Вход	Кодовый символ с = 0		Кодовый символ с = 1	
	Индекс	Метрика	Индекс	Метрика
1.2	1	0.64	0	0.04
8.9	4	0.81	4	0.01
-3.6	-2	0.16	-2	0.36
Шаг 2. Метрики кодовых слов				
Номер	Слово	Метрика слова		Индексы
0	(0,0,0)	0.64+0.81+0.16=1.61		(1,4-2)
1	(1,1,0)	0.04+0.01+0.16=0.21		(0,4-2)
2	(0,1,1)	0.64+0.01+0.36=1.01		(1,4,-2)
3	(1,0,1)	0.04+0.81+0.36=1.21		(0,4-2)
Результат квантования				
Номер кодового слова				1
последовательность индексов				(0,4,-2)
Восстановление				
	у = 2* (0,4,-2) + (1,1,0)		-(1,9,-4)	
Как мы увидим, на основе сверточных кодов можно построить квантователи
с хорошими характеристиками и вполне приемлемой сложностью практической
реализации.
8.5.	Квантование с помощью решеток
на основе сверточных кодов
Кодер двоичного сверточного кода можно представить в виде линейной схемы,
пример которой показан на рис. 8.10. На каждом такте ее работы на вход дво-
ичного регистра Поступает один информационный бит, при этом последователь-
ность, записанная в регистр, сдвигается. Комбинационная схема из сумматоров
по модулю 2 вычисляет кодовые символы (в данном случае 2 кодовых символа).
Рис. 8.10. Кодер сверточного кода
284
Глава 8. Квантование
Кодер на рис. 8.10 описывает сверточный код со скоростью R = 1/2 (один бит
на два кодовых символа). В общем случае, если по к входным битам вычис-
ляется п кодовых символов, скорость кода равна R = к/п. Мы ограничимся
рассмотрением кодов со скоростью R = 1/п.
Важный параметр кодера - длина регистра т, ее называют памятью или длиной
кодового ограничения кода (это разные понятия, но для скорости R = 1/п они
совпадают). В нашем примере т = 2.
Если регистр кодера содержит т двоичных элементов памяти, то в каждый
момент времени кодер находится в одном из 2т состояний, определяемых содер-
жимым ячеек регистра. При фиксированном состоянии кодера следующий кодо-
вый блок зависит только от значения информационного символа в Данный мо-
мент времени. Ни текущий блок, ни все последующие при известном состоя-
нии кодера не зависят от предыдущих информационных символов. Это важное
наблюдение позволяет описывать поведение кодера с помощью так называемой
решетчатой диаграммы, показанной на рис. 8.11.
Рис. 8.11. Решетчатая диаграмма сверточного кода
В литературе по помехоустойчивому кодированию эту диаграмму часто для крат-
кости называют решеткой. Мы здесь не используем этот термин, чтобы не возни-
кало путаницы между кодовой решеткой и числовой решеткой. (Дело в том, что
англоязычные термины trellis и lattice одинаково переводятся на русский язык,
как «решетка».)
На приведенной на рис. 8.11 полубесконечной диаграмме узлы соответствуют
состояниям кодера. Узлы размещены на ярусах, каждый ярус соответствует одно-
му моменту времени. Начальное состояние кодера обычно считают известным,
для определеннности, нулевым. Поэтому на нулевом ярусе размещается только
один (нулевой) узел. При поступлении очередного бита информации на вход
кодера, в зависимости от того, поступил 0 или 1, кодер переходит в одно из двух
состояний, что и показано на диаграмме. На следующем ярусе состояний стало 4,
но на последующих ярусах число состояний не растет, поскольку память нашего
кодера т — 2. На ребрах решетки надписаны кодовые символы, порождаемые
кодером при переходах из состояния в состояние.
8.5. Решетки на основе сверточных кодов.
285
Сверточный код можно определить как множество последовательностей, порож-
даемых сверточным кодером, или, что эквивалентно, как множество последова-
тельностей, считываемых вдоль различных путей решетчатой диаграммы.
Как мы видим, отличие сверточного кода от блокового в том, что длина его
бесконечна. Это не создает принципиальных трудностей при практическом при-
менении сверточных кодов в системах связи для защиты от ошибок или при
квантовании. Тем не менее, чтобы упростить изложение, мы перейдем к кодам
конечной длины - к усеченным сверточным кодам. Для этого мы будем полагать,
что на вход кодера с кодовым ограничением т после некоторого заранее огово-
ренного числа К информационных бит всякий раз подается последовательность
из т нулей. Эта последовательность нулей возвращает кодер в нулевое состоя-
ние. Кодирование следующего блока из К бит начинается из нулевого состояний
кодера. Нетрудно заметить, что теперь блоки из К бит передаются независимо, и
на каждый затрачивается {К + т)п двоичных кодовых символов. Мы получили
линейный блоковый код со скоростью
R'= у к s = т/с R-
(К + т)п К+<т
При больших К скорость нашего блокового кода В! пренебрежимо мало отли-
чается от скорости сверточного кода R = 1/п, и мы будем игнорировать это
различие.
Решетчатая диаграмма усеченного сверточного кода с К = 3 показана на рис. 8.12.
Рис. 8.12. Решетчатая диаграмма усеченного сверточного кода
Предположим теперь, что усеченный сверточный код используется как основа
для построения решетки. Задача квантования, то есть задача нахождения точки
решетки ближайшей к принятой последовательностей, в предыдущем параграфе
сведена к задаче нахождения кодового слова с минимальной метрикой. Кодо-
вые слова усеченного сверточного кода соответствуют путям в решетчатой диа-
грамме, начинающимся в нулевом узле на ярусе 0 и заканчивающихся в нулевом
286
Глава 8. Квантование
Input: Последовательность источника х = (яц,...,хп)\
Output: Информационная последовательность, определяющая кодовое слово
ближайшее к х
Инициализация:
Номер яруса t = 0.
Метрика нулевого узла приравнивается нулю, за этим узлом закрепляется "пустой"
путь.
Кодирование.
Цикл по ярусам:
for t = 1 to L do
Цикл по узлам яруса:
for j — 0 to 2m - 1 do
1.	Находим метрику каждого из двух путей, ведущих в данный узел, как сумм)
метрик предшествующих узлов и метрик ребер, связывающих
узлы-предшественники с данным узлом.
2.	Из двух кандидатов выбираем путь с минимальной метрикой, эту метрику
приписываем данному узлу.
3.	Путь, ведущий в узел, вычисляется дописыванием к пути, ведущему в
выбранный предшествующий узел, информационного символа,
соответствующего переходу из узла-предшественника в данный узел.
end
end
Формирование результата:
Путь, соответствующий единственному узлу на ярусе L, выдается получателю как
результат декодирования.
Рис. 8.13. Алгоритм Витерби для поиска пути с наименьшей метрикой
узле последнего яруса. Поскольку наша метрика аддитивна, метрика пути скла-
дывается из метрик отдельных ребер. Эту метрику можно рассматривать как
длину ребер и, таким образом, наша задача - задача нахождения кратчайшего
пути между двумя узлами графа. Это типичная задача динамического програм-
мирования.
Эффективный алгоритм декодирования сверточных кодов был предложен
А. Витерби в 1963 году. То, что алгоритм Витерби оптимален и является частным
случаем динамического программирования, было установлено Д. Форни в 1974
году в работе [42]. Помимо этого, Форни предложил описание сверточных кодов
с помощью решетчатой диаграммы и тем самым упростил описание алгоритма.
Алгоритм Витерби для решетчатой диаграммы длиной L = К -F m ярусов при-
веден на рис. 8.13. Алгоритм вычисляет информационную последовательность,
соответствующую кратчайшему пути, эта информационная последовательность
может быть использована как номер кодового слова. В совокупности с индексами,
вычисляемыми скалярным квантованием (см. предыдущий параграф), она одно-
значно идентифицирует точку многомерной числовой решетки над сверточным
кодом.
8.5. Решетки на основе сверточных кодов.
287
Таблица 8.4. Характеристики решеток над сверточными кодами
Кодовое ограничение	Gn	Избыточность (бит)	Выигрыш (ДБ)
1	0.0733	0.1621	0.5571
2	0.0665	0.0918	0.9800
3	0.0652	0.0776	1.0657
4	0.0643	0.0676	1.1261
5	0.0634	0.0574	1.1873
6	0.0628	0.0505	1.2286
7	0.0623	0.0448	1.2633
8	0.0620	0.0413	1.2843
9	0.0618	0.0390	1.2983
ОО	0.0585	0	1.5329
Л24	0.0658	0.0839	1.0259
Заметим, что сложность квантования, нормированная по отношению к числу
отсчетов на его входе, определяется теперь не полным числом кодовых слов
в коде, а кодовым ограничением кода т, точнее числом состояний 2т. Понятно,
что чем больше т, тем больший простор для выбора кодов, тем больше возмож-
ностей для кодирования с маленькой ошибкой. С другой стороны, увеличение
кодового ограничения приводит к увеличению сложности кодирования.
Зависимость нормализованного второго момента решеток над двоичными свер-
точными кодами от длины кодового ограничения приведены на рис. 8.14 и
в табл. 8.4.
Рис. 8.14. Избыточность решеток над сверточными кодами
как функция кодового ограничения
288
Глава 8. Квантование
Для сравнения приведены характеристики квантователя на основе решетки Лича,
для которой сложность кодирования примерно равна сложности декодирования
кода Голея (24,12). Мы видим, что по характеристикам решетка Лича близка
к решетке над сверточным кодом с кодовым ограничением 3, тогда как сложность
кодирования для решетки Лича примерно такая же как для сверточного кода
с ограничением 8. Из этого примера становится понятно, насколько эффективно
квантование с помощью решеток над сверточными кодами.
8.6.	Задачи
1.	Запишите формулы для выполнения равномерного скалярного квантования
с заданным шагом Д и вычисления аппроксимирующего значения по номеру
кванта.
2.	Подсчитайте нормализованный второй момент n-мерной кубической решетки.
3.	Покажите, что решетка Ai совпадает с решеткой целых чисел.
8.7.	Библиографические замечания
Большая часть главы посвящена числовым решеткам. Информация о них заим-
ствована, в частности, из статей Конвея и Слоэна и их монографии [9].
Приведенных выше сведений о сверточных кодах и их декодировании заведомо
недостаточно для глубокого понимания и практического использования. Подроб-
нее о сверточных кодах написано, например, в книге [14].
Обзор работ в области квантования на момент 50-летия теории информации
можно найти в [48].
Глава 9 Кодирование для
непрерывных каналов
с шумом
В главе 5 мы рассмотрели дискретные каналы и убедились в том, что инфор-
мационная емкость (максимум взаимной информации по входным распреде-
лениям) определяет максимальную достижимую скорость передачи информа-
ции, при которой может быть обеспечена сколь угодно высокая надежность.
Напомним, что скорость передачи измерялась в битах на один входной символ
канала.
Потребителю системы связи не очень интересна скорость в битах на символ.
Гораздо информативнее был бы ответ, выраженный в битах в секунду. Понятно,
что этот ответ зависел бы уже не только от способа кодирования и декодиро-
вания, но и от устройства модулятора и демодулятора. Такая постановка задачи
намного сложнее. Однако теперь, после изучения принципов измерения инфор-
мации непрерывных источников (раздел 6) и обретения опыта их анализа (раздел
7), мы готовы к тому, чтобы установить зависимость предельно достижимой ско-
рости передачи данных от наиболее важных характеристик канала: отношения
сигнал/шум и ширины полосы частот.
Как и для дискретных каналов, все результаты носят теоретический характер и
не конструктивны. Методам модуляции и кодирования посвящены специальные
разделы теории систем связи, эти вопросы выходят далеко за рамки курса теории
информации. Тем не менее в конце данной главы будет приведено сравнение
известных на момент написания учебника способов модуляции и кодирования
с предельными характеристиками, которые традиционно называют пределами
Шеннона.
9.1. Каналы дискретного времени
Обозначим через X и Y соответственно входной и выходной алфавиты канала
связи. Оба алфавита считаем непрерывными, без потери общности можно счи-
тать, что оба множества совпадают с множеством всех вещественных чисел.
290
Глава 9. Непрерывные каналы
В этом параграфе мы рассматриваем каналы дискретного времени. Это означает,
что входом канала является последовательность х = (ж1,ж2, • • • ,£п), ей соответ-
ствует выходная последовательность у = (2/1,2/2, • •, 2/п), а модель канала задается
условными плотностями распределения вида f(y\x) = f(yi,..., yn\xi,..., хп).
Как и в случае дискретных каналов, мы будем считать канал стационарным, то
есть условные плотности /(з/|®) независящими от положения последовательно-
стей х и у во времени. Помимо этого, мы изучаем только каналы без памяти, то
есть
/(1/1®) =П/(1ФД
Еще одно разумное упрощение модели состоит в том, что искажение сигнала
в канале не зависит от передаваемого сигнала. Мы рассматриваем модель, пока-
занную на рис. 9.1. Выход канала у связан с входом х соотношением
у = x + z,
в котором случайная величина z не зависит от х. Аналогичное соотношение имеет
место и для последовательностей, то есть у = х -F z. Из этого равенства следует,
что
/(1/1®) = /(I/ - ®|®) = /(«I®) = /(г).
Такая модель канала называется каналом с аддитивным шумом.
х------►( 4-

Рис. 9.1. Канал дискретного времени с аддитивным шумом
Для канала без памяти с аддитивным шумом имеет место соотношение
/(«)=П/(«<)• '
Действуя по аналогии с дискретными каналами, мы должны были бы определить
информационную емкость канала как максимум взаимной информации /(Х;У)
по всем распределениям на входе канала. Однако в случае канала с непрерывным
входом этот максимум будет бесконечным. Чтобы убедиться в этом, рассмотрим
сначала канал без шума. Взаимная информация в этом случае равна дифферен-
циальной энтропии входного распределения, и ее максимум может быть сколь
угодно большим. Например, в качестве входного алфавита можно выбрать все
множество целых чисел Z. Приписав числам этого множества одинаковые веро-
ятности, получим ансамбль с бесконечной энтропией, буквы которого передаются
абсолютно надежно.
9.1. Каналы дискретного времени
291
Если же шум присутствует, то в качестве входа канала можно выбрать решетку
dZ. С таким большим шагом решетки d, чтобы влиянием шума можно было бы
пренебречь. И в этом случае, как мы видим, энтропия входного алфавита тоже
может быть сделана сколь угодно большой.
Чтобы придать смысл решаемой задаче, нам следует наложить дополнительные
ограничения на множество входных сигналов. Наиболее естественным ограниче-
нием является ограничение на мощность входного сигнала.
Энергией входной последовательности х =	называется величи-
наЕ?=1х?.
Мощностью или средней энергией на отсчет называют величину
«.2
S(®) = i 
,	71
Информационной емкостью непрерывного стационарного канала дискретного вре-
мени с ограничением Е на мощность входных сигналов называется величина
Со = sup max -I(Xn-,YnY
П /(®):М[Е(®)]^Е 71
Как естественное обобщение результатов, полученных в главе 5 для дискрет-
ных каналов, приведем формулы для информационной емкости самых простых
и важных для теории и практики моделей каналов.
ТЕОРЕМА 9.1. Информационная емкость непрерывного стационарного канала
дискретного времени без памяти с ограничением Е на мощность входных сигналов
Со= max 1(Х;У).	(9.1)
/(®):М[Е(х)]^Е
Доказательство. По аналогии с дискретными каналами нужно сначала показать,
что правая часть (9.1) является оценкой сверху для информационной емкости.
Затем нужно показать, что эта оценка достигается в том случае, когда последова-
тельность на входе канала - последовательность независимых одинаково распре-
деленных величин. Доказательство опирается, в частности, на выпуклость вза-
имной информации как функции распределения вероятностей на входном алфа-
вите. Формальную запись доказательства предоставляем читателю в качестве
упражнения.	□
Мы называем канал гауссовским, если шум в канале имеет гауссовское распреде-
ление, вообще говоря, многомерное, описываемое (6.8). В данном параграфе мы
рассматриваем только гауссовские каналы без памяти, в которых одномерное
распределение шума имеет вид
1	г2
^ = -7Г^е~^-
292
Глава 9. Непрерывные каналы
ТЕОРЕМА 9.2. Информационная емкость гауссовского стационарного канала дис-
кретного времени без памяти с ограничением Е на мощность входных сигналов
1	/	F \
Со =-log 1 + — .	(9.2)
2	\	1*0 /
Доказать теорему читатель сможет самостоятельно, воспользовавшись формулой
для дифференциальной энтропии гауссовского распределения (таблица 6.1.) и
тем обстоятельством, что дифференциальная энтропия гауссовского распределе-
ния при заданной мощности (дисперсии) больше, чем дифференциальная энтро-
пия любого другого распределения с той же мощностью (свойство 6.2.7). Это
же свойство позволяет на основании теоремы 9.2 сформулировать следующее
утверждение.
СЛЕДСТВИЕ 9.3. Информационная емкость стационарного канала дискретного
времени без памяти с ограничением Е на мощность входных сигналов
1	( Е\
Отношение E/Nq называют отношением сигнал/шум. Как мы видим, эта вели-
чина определяет информационную емкость и в конечном счете достижимую
скорость надежной передачи информации по каналу.
Для того, чтобы утверждать, что информационная скорость действительно явля-
ется пропускной способностью канала, нужно доказать прямую и обратную тео-
ремы кодирования. Доказательство теорем кодирования для непрерывных кана-
лов выходит за рамки нашего курса. Тем не менее в дальнейшем вместо инфор-
мационной емкости будем использовать более часто используемое понятие «про-
пускная способность», принимая на веру справедливость теорем кодирования.
Ближайшая цель - вычисление пропускной способности каналов непрерывного
времени.
9.2.	Канал непрерывного времени
с аддитивным белым гауссовским шумом
В этом параграфе нам предстоит получить формулу пропускной способности
канала непрерывного времени. Строгое изложение этих вопросов потребовало
бы использования большого числа понятий, которые не использованы в данном
учебнике. Поэтому мы ограничимся эвристическими рассуждениями, обосновы-
вающими фундаментальный результат К. Шеннона, полученный им еще в 1948
году в работе [20].
Рассмотрим стационарный канал с аддитивным гауссовским шумом. Для опи-
сания модели гауссовского шума z(t) достаточно задать его корреляционную
функцию
Kz(t) = M[z(t)z(t -F г].
9.2. Канал непрерывного времени
293
Преобразование Фурье от корреляционной функции
/’ОО
5г(/)= / K(r)e~2,rifTdT
J—оо
представляет собой спектральную плотность мощности стационарного процесса
непрерывного времени. (Сравните с определением спектральной плотности мощ-
ности дискретного процесса (6.18).) Частота f измеряется в герцах и, вообще
говоря, принимает произвольные вещественные значения из интервала (-оо, оо).
Функция Sz(f) - вещественная неотрицательная и четная (см. задачу 10 главы 6).
Аналогично можно записать спектральную плотность мощности Sx(f) процесса
x(t) на входе канала. Тогда ограничение на мощность Е входного сигнала примет
вид
/оо
sx(f)df < Е.	(9.3)
-оо
Будем интерпретировать значения Sx(f) и Sz(f) как мощность соответственно
сигнала и шума на частоте f (правильнее было бы говорить о неперекрываю-
щихся малых интервалах частот, а не об отдельных частотах). При бесконечной
длине сигналов их проекции на гармонические функции становятся некорре-
лированными (см. [3], [7], [38]). Приходим к совокупности независимых парал-
лельных каналов, причем, согласно теореме 9.2, пропускная способность каждого
канала
11 Л
X bg 1 +
А	\
&(/)\
Интегрируя по частоте, приходим к формуле для пропускной способности ста-
ционарного канала с аддитивным гауссовским шумом
^(/)
(9.4)
где точная верхняя грань вычисляется по всем по всем спектральным плотностям
а9ж(/), удовлетворяющим ограничению (9.3) на мощность процессса.
Поиск экстремума методом множителей Лагранжа приводит к следующему резуль-
тату:
С =
тах{(0-5Д/)),О}
S*(f)
(9.5)
где 0 выбирается из условия
/>ОО
/ тах{(0 - £г(/)),0}(// = Е.
«/—ОО
294
Глава 9. Непрерывные каналы
Такое распределение энергии по частотам называют принципом разливания воды:
суммарная мощность сигнала и шума «растекается» таким образом, что уровень
везде одинаков, за исключением тех участков спектра, где мощность шума пре-
вышает этот уровень (в этих участках энергия сигнала равна нулю). Пример при-
веден на рис. 9.2. Параметр 0 подбирается так, чтобы площадь заштрихованной
области («объем воды») была равна разрешенной энергии сигнала. При вычис-
лении пропускной способности по формуле (9.5) интегрирование выполняется
по интервалам частот, в которых энергия сигнала положительна (0 > ЯД/)).
Рассмотрим теперь важные частные случаи. Прежде всего, предположим, что
спектральная плотность шума постоянна и равна Sz(f)=No/2 во всем диапазоне
частот. Такой процесс называют белым шумом. Физически белый шум существо-
вать не может, поскольку его мощность бесконечна.
С помощью обратного преобразования Фурье легко убедиться в том, что корре-
ляционная функция белого шума имеет вид
K3(t) =
где функция 5(f) - дельта-функция Дирака, определяемая соотношениями
5(f)
' 0 t/0,
оо t = О,
к	7
1.
Канал с аддитивным белым гауссовским шумом (АБГШ) - модель непрерыв-
ного по времени канала, аналогичная дискретной по времени модели канала без
9.2. Канал непрерывного времени
295
памяти. Соседние, сколь угодно близкие по времени отсчеты шума независимы,
поскольку корреляционная функция равна нулю во всех точках за исключением
нуля.
Из сопоставления (9.4) с (9.5) следует, что при равномерной плотности мощ-
ности шума Sz(f) оптимальное распределение мощности сигнала тоже будет
равномерным. Наложим теперь физически оправданное ограничение на ширину
полосы частот сигнала W Гц. Это означает, что спектральная плотность мощно-
сти сигнала равна Sx(f) = E/(2W).
Заметим, что любой сигнал конечной длительности имеет, строго говоря, бес-
конечный спектр. В этом смысле предположение об ограниченности спектра не
может выполняться в точности. Мы предполагаем, что доля энергии сигнала
в части его спектра за пределами полосы частот [— W, W] ничтожно мала. Под-
черкнем еще раз, что, говоря о полосе частот ширины W, мы подразумеваем
сигнал, спектр которого симметричен в интервале частот [~W,W].
С учетом сделанных замечаний получаем формулу для пропускной способности
канала с АБГШ с дисперсией шума ЛГо/2 и ограничениями Е и W, соответ-
ственно, на мощность и полосу сигнала
С = W log ( 1 + 777^-) бит/с.	(9.6)
\ W J\q )
Эта формула, пожалуй, один из главных результатов Шеннона. Он заслуживает
того, чтоб указать еще один путь к этой формуле.
Этот путь основан на теореме Котельникова-Шеннона, которая утверждает, что
сигнал, спектр которого равен 0 на частотах выше W, может быть точно восста-
новлен по значениям его отсчетов, взятых через интервалы времени
Т° = (секУнд)'
Этот удивительный факт можно физически обосновать тем, что самая высоко-
частотная гармоника спектра имеет период 1/ГИ, поэтому значение сигнала не
может сильно измениться за время, меньшее половины периода самой высокой
частоты спектра.
Следуя теореме Котельникова-Шеннона, вместо задачи передачи непрерывного
сигнала длительности Т можем решать задачу передачи его отсчетов через интер-
валы времени То. Тем самым задача сводится к вычислению пропускной способ-
ности канала дискретного времени.
Итак, за одну секунду предается 2W отсчетов, на каждый из которых затрачи-
вается энергия E/(2W), и к каждому отсчету прибавляется аддитивный шум
с дисперсией Nq/2. Таким образом, пропускная способность
\	/ \
i+W =ж1оч1+йАгЬ
/	\ W1V0 /
296
Глава 9. Непрерывные каналы
Если мы теперь откажемся от ограничения на полосу частот, то получим
(	' Е \ Е
С = lim W log (1 + —— | =	 бит/с.	(9.7)
ж-.оо	WNqJ	7Voln2	v 7
Чтобы получить этот результат, мы воспользовались правилом Лопиталя.
Полученные в данном параграфе формулы позволяют по заданным параметрам
канала подсчитать потенциально достижимую скорость передачи информации.
Пример 9.2.1. Телефонный канал. Хотя по паре телефонных проводов можно
передавать информацию в очень большом диапазоне частот, модем для телефон-
ного канала спроектирован так, чтобы весь сигнал помещался в полосе речевого
сигнала, то есть в полосе W = 3400 Гц. Это ограничение связано с исполь-
зованием на телефонных станциях аппаратуры уплотнения каналов, в которой
именно такая полоса отводится на каждый канал. При отношении сигнал/шум на
Гц, равном E/(WNq) = 100 из формулы (9.6) находим, что С & 22000 бит/с. Мы
знаем, что современные модемы надежно работают и при более высоких скоро-
стях. В этом нет противоречия. Дело в том, что реальные характеристики каналов
несколько лучше, чем те, что мы использовали при расчетах. Кроме того, совре-
менные модемы для телефонных линий используют очень непростые и очень
эффективные методы модуляции и корректирующие коды.
Как мы уже отмечали, пропускная способность лишь теоретический предел ско-
рости, при которой потенциально возможна надежная передача. Существующие
доказательства теорем кодирования не конструктивны, они не указывают спосо-
бов построения кода. Более того, известные сегодня разнообразные конструкции
кодов по своим характеристикам заметно уступают теоретически существующим
оптимальным кодам.
В следующем параграфе мы покажем, как теорема Шеннона используется на
практике для анализа эффективности кодирования, и сравним характеристики
существующих способов кодирования соотносятся с теоретическими пределами.
9.3.	Энергетический выигрыш кодирования
Пропускная способность, вычислению которой посвящены предыдущие пара-
графы, является характеристикой канала связи. Цель данного параграфа - ана-
лиз характеристик способов кодирования. Традиционной мерой эффективности
служат затраты энергии на передачу одного бита информации. Ниже мы сфор-
мулируем критерий эффективности более точно и посмотрим, насколько близки
характеристики применяемых на практике кодов к теоретическому пределу.
Рассмотрим канал с АБГШ без ограничения на полосу сигнала. Предположим,
что спектральная плотность мощности шума равна Nq/2, мощность передава-
емого сигнала равна Е ватт или джоулей/с, а скорость передачи составляет
R бит/с. Это означает, что затраты энергии на бит составляют
9.3. Энергетический выигрыш кодирования
297
Еь = — Дж/бит.
гС
Величину Еь/No называют отношением сигнал-шум на бит. Из (9.2) следует,
что при больших отношениях сигнал/шум пропускная способность пропорцио-
нальна логарифму отношения сигнал/шум, поэтому значения этой величи-
ны приводят в децибелах (дБ). Для числа А его значение в децибелах равно
101og10 А дБ.
Согласно (9.7) надежная передача возможно только при
R<C=Nq^2
или
Ек
> 1п2 = 0.693 = -1.59 дБ.	(9.8)
No
Итак, из теоремы кодирования для канала с АБГШ следует: надежная пере-
дача информации возможно только тогда, когда отношение сигнал/шум на бит не
меньше величины -1,59 дБ.
Насколько трудно достичь надежной передачи при таком отношении сигнал/шум?
Чтобы ответить на этот вопрос, рассмотрим передачу информации двоичными
сигналами без кодирования. Надежность передачи зависит от конкретной физи-
ческой среды распространения сигналов и выбранного соответствующего метода
модуляции и демодуляции. При использовании для передачи информации дво-
ичных противоположных сигналов при передаче символов 0 и 1 на выходе демо-
дулятора наблюдаются случайные величины с плотностями распределения
и
№|о) =
1 _
в
у/kNq
1
(у-у/Е)2
/(у|1) =
соответственно. Поскольку в отсутствие кодирования каждый сигнал несет один
бит информации, имеем Е = Еь. Если приемник выносит решение о том, что
передавался 0, если у < 0 и решение в пользу 1 в противном случае, то вероят-
ность ошибки в одном бите равна
Рь
f(y\O)dy =
/(y|l)dy =
4“)
(9-9)
(9.10)
(9.И)
где использовано обозначение
1	[°° И
<2(я) = -s= / е* 2 dy.
v2tt Jx
(9.12)
298
Глава 9. Непрерывные каналы
График зависимости вероятности ошибки при некодированной передаче от отно-
шения сигнал/шум приведен на рис. 9.3. На этом же рисунке показана асимптота
Шеннона Еь/No = -1,59 дБ. Из графиков, в частности, можно заметить, что для
достижения вероятности ошибки 10”6 требуется Еь/Nq = 10,53 дБ. Следова-
тельно, при такой вероятности ошибки потенциально достижимый энергетиче-
ский выигрыш кодирования составляет 1,59 -I- 10,53 = 12,06 дБ, или в 16 раз!
Цитируя Блэйхута, можно сказать, что улучшать каналы связи - выбрасывать
деньги на ветер. Лучше просто применить кодирование!
К сожалению, если принять во внимание некоторые практические ограничения,
то передача при Еь/Nq = -1,59 дБ окажется невозможной. Например, предполо-
жим, что информация передается двоичными сигналами и на приемной стороне
сначала выносится решение (0 или 1) о каждом сигнале, а уже затем выпол-
няется декодирование, то есть выбор кодового слова ближайшего к принятой из
канала двоичной последовательности. Такой метод обработки сигналов называют
декодированием с жесткими решениями.
Обозначим через р вероятность ошибочного решения о сигнале. Максимально
достижимая скорость кодирования в битах на символ канала Rc не превышает
пропускной способности ДСК с переходной вероятностью р, то есть
p = Q^I^,
где Е - энергия сигнала. При W оо длительность сигналов уменьшается,
Е —> 0, следовательно, р 1/2. Раскладывая двоичную энтропию р(р) по степе-
ням (р - 1/2) в окрестности точки р = 1/2, получаем
/1 \2
Rc < 2(loge) I - -р) .
Для функции Q(x) при малых значениях аргумента имеет место приближенное
равенство
Q(X) « 1 -
В итоге получаем
(9.13)
21oge Е
С< 7Г No
Для отношения сигнал/шум на бит Eb/N0 = E/(NqRc) имеем неравенство
> Jln2 = 1,09 = 0,37 дБ
/Vo 2
Эти подсчеты показывают, что потери, связанные с принятием жестких решений
на выходе демодулятора, составляют приблизительно 2 дБ. Асимптота, соответ-
ствующая декодированию с жесткими решениями, показана на рис. 9.3.
Вернемся к декодированию с мягкими решениями, то есть к такой системе связи,
в которой при выборе наилучшего кодового слова учитывается надежность полу-
ченных от демодулятора символов. Примем теперь во внимание ограничение
9.3. Энергетический выигрыш кодирования
299
Рис. 9.3. Характеристики некодированной передачи (1)
и пределы Шеннона для декодирования с жесткими (2) и мягкими (3) решениями
на полосу, точнее говоря, эффективность использования предоставленной для
передачи информации полосы частот.
Спектральной эффективностью кодирования называется величина
/3 = -^ бит/с/Гц .
Поясним смысл введенного параметра системы связи. Ограничение на полосу
W можно интерпретировать как ограничение на минимальную допустимую дли-
тельность сигнала Г, более того, величина Т обратно пропорциональна вели-
чине W. При использовании корректирующих кодов в передаваемую последова-
тельность вносится избыточность. Обозначим через Rc скорость кода или долю
информационных символов в передаваемой последовательности. Для того чтобы
сравнивать эффективность системы с кодированием и без кодирования, мы
должны приравнять их скорости передачи информации в битах в секунду. Мы
можем это сделать, пропорционально уменьшив длительность сигналов и, тем
самым, расширив полосу. В системе с кодированием длительность импульса
должна быть уменьшена до RCT, соответственно полоса частот пропорционально
увеличивается до W/Rc. Если спектральная эффективность без кодирования
была равной /3, она уменьшается до Яс/3. Таким образом, спектральная эффектив-
ность кодирования адекватно отражает плату за использование кодов - увеличе-
ние ширины полосы частот. Поэтому правильно сравнивать различные способы
кодирования при фиксированной спектральной эффективности.
300
Глава 9. Непрерывные каналы
Из формулы (9.6) для пропускной способности канала с АБГШ имеем
R < W log ( 1 + —— ) бит/с.
\	W IVо /
Отсюда находим границу снизу на отношение сигнал/шум при заданной спек-
тральной эффективности /3
Еь 2^-1
No > /3
(9.14)
Наиболее наглядными и практически интересными получаются результаты в слу-
чае, когда рассматривается передача сигналов со «скоростью Найквиста», то есть
Т = 1/(2И9 и используется корректирующий код со скоростью Rc. При этом
скорость передачи становится
R =	= 2ТГЯС
и спектральная эффективность равна /3 = 2RC.
Получаем еще одну границу границу снизу на отношение сигнал/шум при задан-
ной скорости используемого корректирующего кода
Еь
No
22R° - 1
2RC
(9.15)
Вернемся к рис. 9.3. На графике кривая вероятности ошибки без кодирования
пересекается с асимптотами Шеннона. Это означает, что при некоторой вероятно-
сти ошибки либо кодирование оказывается неэффективным, либо наши оценки
требуемого отношения сигнал/шум не верны.
Попробуем подправить оценки Шеннона с учетом того обстоятельства, что допу-
стима некоторая вероятность ошибки. Из результатов главы 7 следует, что, чем
больше допустимая ошибка, тем с меньшей скоростью может передаваться инфор-
мация, порождаемая источником. Из формулы (7.9) для функции скорость-иска-
жение двоичного источника с вероятностной мерой качества следует, что для
передачи равновероятных двоичных букв источника со средней вероятностью
ошибки Рь достаточно затратить 1 - ??(Рь) бит информации на одну букву источ-
ника.
Эффективная передача данных с заданной ошибкой может быть организована
следующим образом. Для передачи к бит информации сначала используется
сжимающий кодер, который отображает последовательность из к бит на более
короткую двоичную последовательность длины fc(l—??(Рь)) таким образом, чтобы
средняя ошибка не превышала Рь (такое отображение существует в силу пря-
мой теоремы кодирования с заданной мерой искажения). Полученные данные
защищаются от ошибок с помощью избыточного кода длины п со скоростью
Rc = fc(l - т/(Рь))/п = Рь(1 - г?(Рь)),
9.3. Энергетический выигрыш кодирования
301
где мы использовали обозначение Rb = к/п, При этом скорость передачи дан-
ных в системе равна R = к/(пТ) бит/с и отношение сигнал/шум на бит равно
Еь/Nq = E/(RbNo). Формула (9.6) приводит к ограничению на скорость
2ЖЯь(1-г?(Рь)) <W4og 1 +
2RbEb \
J
из которого вытекает окончательная формула
Еь 22Rb^~^Pb^ - 1
jVo > 2Rb
(9.16)
Мы видим, что требования к энергии сигналов выражаются через ограничение
на допустимую скорость кода, которая, отражает расширение полосы частот,
связанное с применением избыточных кодов.
В реальных системах скорость Rb 1/2 используется в относительно широ-
кополосных каналах связи - некоторых каналах мобильной связи, спутниковых
системах, каналах дальней космической связи. Напротив, скорость Rb > 1/2 соот-
ветствует узкополосным каналам, например каналам телефонной связи. При-
меры границ Шеннона для скоростей Rb = 1/4,1/2 и 3/4 вместе с кривой для
некодированной передачи показаны на рис. 9.4.
Рис. 9.4. Характеристики некодированной передачи (кривая 1),
стандарта NASA (кривая 2), турбо-кодов (кривая 3) и пределы Шеннона
для скоростей кодов 3/4 (кривая 4), 1/2 (кривая 5) и 1/4 (кривая 6)
302
Глава 9. Непрерывные каналы
Насколько далеки современные системы связи от границ Шеннона? Рассмот-
рим, скорость Яь = 1/2, которая по ряду причин считается наиболее «труд-
ной» и поэтому является объектом «состязаний» специалистов в области теории
помехоустойчивого кодирования.
В качестве первого примера приведем кодирование по стандарту NASA, исполь-
зованное в космических полетах Voyager-1 и Voyager-2 в 1977 к Юпитеру и
Сатурну. Для передачи изображений была использована каскадная схема на основе
кода Рида-Соломона со скоростью 223/255 и сверточного кода со скоростью
1/2. Таким образом, совокупная скорость 223/510=0,437 несколько ниже 1/2.
Вероятность ошибки Рь = 10-6 была достигнута при Еъ/Nq = 2,5 дБ. График
зависимости вероятности ошибки от отношения сигнал/шум для этой схемы
показан на рис. 9.4. Заметим, что задержка декодирования этого кода составляет
примерно 10000 двоичных символов.
Другой пример. В 1993 году Берру и Главье были предложены так называемые
«турбо-коды», которые позволили существенно приблизиться к теоретическому
пределу [30]. По сути, речь идет о последовательном соединении двух очень
простых кодеров, между которыми помещен перемежитель. Успех был достигнут
в большой степени за счет итеративного декодирования: декодируется первая
ступень, результаты передаются на вторую, затем декодируется вторая ступень
так, как будто первая была декодирована правильно, затем снова первая сту-
пень и т.д. Как оказалось, на каждой итерации доля ошибочных символов поне-
многу уменьшается и после нескольких (иногда нескольких десятков) итераций
достигается? рекордно низкая вероятность ошибки на бит.
График зависимости вероятности ошибки на бит от отношения сигнал/шум для
турбо-кода длины 216 приведен на рис. 9.4. Результаты впечатляющие, но нужно
иметь в виду, что они достигнуты при очень большой длине блока, и, следова-
тельно, большой задержке декодирования. Кроме того, для турбо-кодов, в отли-
чие от схемы на основе каскадирования кодов Рида-Соломона со сверточными
кодами, даже при маленькой вероятности ошибки декодирования символа веро-
ятность ошибки декодирования блока остается очень большой. Это накладывает
серьезные ограничения на области их практического применения. Тем не менее
в последние годы турбо-коды в различных конфигурациях начинают включаться
в международные стандарты на передачу данных.
Приведенные примеры показывают, что «зазор» между теорией и практикой
относительно невелик: он не превышает 1 дБ, что соответствует теоретически
возможному уменьшению мощности примерно в 1,26 раз. Тем не менее, как рас-
смотренные выше, так и другие близкие к оптимальным схемы кодирования
слишком сложны и требуют недопустимо большой задержки данных в кодере
и декодере. Разработка новых алгоритмов защиты информации от ошибок -
непростая, но очень увлекательная и весьма актуальная задача.
9.5. Библиографические замечания
303
9.4.	Задачи
1.	Связь гауссовского канала и ДСК. Предположим, что двоичными входными
сигналами канала дискретного времени без памяти с аддитивным гауссовским
шумом с нулевым математическим ожиданием и дисперсией No/2 являются
значения из двоичного множества {-у/Е, у/Е}. Эти сигналы соответствуют
передаче 0 и 1. На выходе канала принимаются жесткие решения: 0, если
выходной сигнал у > 0, и 1 в противном случае. Таким образом, имеем ДСК.
Постройте график зависимости пропускной способности этого канала как функ-
ции отношения сигнал/шум E/Nq. Сравните с графиком пропускной способ-
ности исходного канала (без квантования сигналов на входе и выходе).
2.	Связь гауссовского канала и ДСтК. Усложним приемник предыдущей задачи.
Предположим, что выбрано некоторое значение Г > 0, которое назовем поро-
гом стирания, и что решения принимаются по правилу
х = <
О,	У < -Г;
стирание, —Т ^у < Т;
1, У > т.
Получить выражение для значения Т, при котором достигается максимум про-
пускной способности соответствующего ДСтК. Построить график пропускной
способности ДСтК как функции отношения сигнал/шум, сравнить с пропуск-
ной способностью ДСК и гауссовского канала.
3.	Двоичный канал с непрерывным выходом.
Записать выражение для пропускной способности канала с двоичным вхо-
дом и непрерывным выходом. Используя численные методы интегрирова-
ния, построить график зависимости пропускной способности двоичного полу-
непрерывного канала от отношения сигнал/шум. Сопоставить полученные
результаты с результатами для ДСК, ДСтК, для канала с непрерывным входом.
9.5.	Библиографические замечания
Данная глава представляет собой краткий обзор основных теоретико-информа-
ционных результатов по кодированию для непрерывных каналов. Пропущенные
доказательства можно найти в учебниках [7], [3].
Анализ энергетического выигрыша кодирования в большой степени опирается
на вводную главу монографии Йоханессона и Зигангирова по сверточным кодам
[50]. Более подробный обзор состояния современной теории кодирования можно
найти в юбилейном выпуске журнала IEEE Information Theory, посвященном
50-летию теории информации, в статьях [43], [37], а также в недавнем обзоре [36].
Список литературы
1.	Бабкин В. Ф. Метод универсального кодирования независимых сообще-
ний неэкспоненциальной трудоемкости. Проблемы передачи информации,
7(4):13—21, 1971.
2.	Блейхут Р. Быстрые алгоритмы цифровой обработки сигналов. М.: Мир,
1989.
3.	Галлагер Р. Теория информации и надежная связь. М.: Советское радио, 1974.
4.	Гоппа В. Д. Введение в алгебраическую теорию информации. М.: Наука,
Физматлит, 1995.
5.	Ватолин Д., Ратушняк Л., Смирнов М., Юкин В, Методы сжатия данных.
Устройство архиваторов, сжатие изображений и видео. М.: Диалог-МИФИ,
2002.
6.	Двайт Г Б. Таблицы интегралов и другие математические формулы. М.:
Наука, М., 1977.
7.	Колесник В. Д., Полтырев Г. Ш. Курс теории информации. М.: Наука, 1982.
8.	Колмогоров А. Н. Три подхода к определению понятия «количество
информации». Проблемы передачи информации, 1:3-11, 1965.
9.	Конвей Дж., СлоэнН. Упаковки шаров, решетки и группы. Т. 1, 2. М.: Мир,
1990.
10.	Кошелев В. Н. Квантование с минимальной энтропией. Проблемы передачи
информации, 14:151-156, 1963.
11.	Кричевский РЕ. Сжатие и поиск информации. М.: Радио и связь, 1989.
12.	Кудряшов Б. Д., Юрков К. В. Границы случайного кодирования для второго
момента многомерных числовых решеток. Проблемы передачи информации,
43(1):53-64, 2007.
13.	Левенштейн В. И. Об избыточности и замедлении разделимого кодирования
натуральных чисел. Проблемы кибернетики, 14:173—179, 1965.
14.	Дж. К. Омура, Витерби А. Д. Принципы цифровой связи и кодирования. М.:
Радио и связь, 1982.
15.	РябкоБ.Я. Сжатие информации с помощью стопки книг. Проблемы передачи
информации, 16(4):16-21, 1980.
Список литературы
305
16.	Рябко Б. Я. Быстрая нумерация комбинаторных объектов. Дискретная
математика, 10(2):101-119, 1998.
17.	ФаноР. Передача информации. Статистическая теория связи. М.: Мир, 1965.
18.	ФитингофБ.М. Оптимальное кодирование при меняющейся и неизвестной
статистике сообщений. Проблемы передачи информации, 2(2):3—11, 1967.
19.	Чисар И., Кернер Я. Теория информации. Теоремы кодирования для
дискретных систем без памяти. М.: Мир, 1985.
20.	Шеннон К. Математическая теория связи. Работы по теории информации и
кибернетике, С. 243-332. М.: ИЛ, 1963.
21.	Шеннон К. Теоремы кодирования для дискретного источника при заданном
критерии качества. Работы по теории информации и кибернетике, С. 587-
621. ИЛ, 1963.
22.	Штарьков Ю. М. Универсальное последовательное кодирование отдельных
сообщений. Проблемы передачи информации, 23(3):3—17, 1987.
23.	Штарьков Ю. М., Чокенс Ч.Дж., Виллеме Ф. М.Дж. Оптимальное универсаль-
ное кодирование по критерию максимальной индивидуальной относительной
избыточности. Проблемы передачи информации, 33(1):21—34, 1997.
24.	Штарьков Ю. М., Чокенс Ч. Дж., Виллеме Ф.М.Дж. Мультиалфавитное взве-
шенное универсальное кодирование древовидно-контекстных источников.
Проблемы передачи информации, 40(1 ):98-110, 2004.
25.	Abramson N. Information theory and coding. McGraw-Hill, New York, 1963.
26.	Bentley J. L., Sleator D., Taijan R. E., Wei V. K. A locally adaptive data compres-
sion scheme. Proceedings of the 22nd Alterton Conference on Communication,
Control and Computing, pp. 233-242, Oct. 1984.
27.	Berger T. Rate distortion theory: A mathematical basis for data compression.
Prentice-Hall, Englewood Cliffs, NJ, 1971.
28.	Berger T. Optimum quantizers and permutation codes. IEEE Transactions on
Information Theory, 18(6):759-765, Nov. 1972.
29.	Berger T., Gibson J. D. Lossy source coding. IEEE Transactions on Information
Theory, IT-44(6):2693-2723, Oct. 1998.
30.	Berrow C., GlavieuxA. Near-optimum error-correcting coding and decoding: Turbo
codes. IEEE Transactions on Communications, COM-44(10):1261-1271, Oct.
1996.
31.	BlahutR.E. Computation of channel capacity and rate-distortion functions. IEEE
Transactions on Information Theory, 18(4):460-473, Jul. 1972.
32.	Bocharova I. Compression for multimedia. Lund University, 2007.
33.	Burrows M., Wheeler D. J. A block-sorting lossless data compression algorithm.
Report 124, Digital Systems Research Center Research, 1994.
34.	Choi B. S., Cover T. M. An information-theoretic proof of burgs maximum entropy
spectrum. Proceedings IEEE, 72:1094-1095, 1984.
306
Список литературы
35.	Cleary J. G., Witten I. H. Data compression using adaptive coding and partial string
matching. IEEE Transactions on Comminication, 32(4):396-402, Apr. 1984.
36.	Costello D.J., Forney G. t).,Jr. Channel coding: The road to channel capacity.
Proceedings of th IEEE, 95(6):1150-1177, Jun. 2007.
37.	Costello D. J., Hagenauer J. Applications of error-control coding. IEEE
Transactions on Information Theory, IT-44(6):2531-2560, Oct. 1998.
38.	Cover T. M., Thomas J. A. Elements of Information Theory. John Wiley & Sons,
New York, 1991.
39.	Elias P. Interval and recency rank source encoding: two on-line adaptive variable-
rate schemes. IEEE Transactions on Information Theory, IT-33(l):3-10, Jan.
1987.
40.	Farvardin N., Modesti.no J. W. Optimum quantizer performance for a class of
non-gaussian memoryless sources. IEEE Transactions on Information Theory,
30(3):485-497, May 1984;
41.	Fiala E. R., Greene D. H. Data compression with finite windows. Communication
of the ACM, 32, 1989.
42.	Forney G. D., Jr. Convolutional codes, II: Maximum likelihood decoding.
Information and control, 25(4):222-266, 1974.
43.	Forney G. D.,Jr., Ungerboeck G. Modulation and coding for linear gaussian chan-
nels. IEEE Transactions on Information Theory, IT-44(6):2384-2415, Oct.
1998.
44.	Gallager R. G. Variation on a theme by Huffman. IEEE Transactions on
Information Theory, IT-24(6):668-674, Nov. 1978.
45.	GallagerR. G., VanVoorhisD. C. Optimal source codes for geometrically distributed
integer alphabets. IEEE Transactions on Information Theory, IT-21(2):228-230,
Mar. 1975.
46.	Gish H., Pierce J. N. Asymptotically efficient quantizing. IEEE Transactions on
Information Theory, 14(5):676-683, Sep. 1968.
47.	Golomb S. W. Run-length encodings. IEEE Transactions on Information Theory,
IT-12(3):399-401, May 1966.
48.	Gray R. M., Neuhoff D. L. Quantization. IEEE Transactions on Information
Theory, IT-44(6):2325-2383, Oct. 1998.
49.	Howard P G. The design and analysis of efficient lossless data compression sys-
tems. Report CS-93-28, Dept, of Comp. Sci. Brown University, Providence, Rhode
Island, 1993.
50.	Johannessson R., Zigangirov. K. Sh. Fundamentals of Convolutional Coding. IEEE
Press, Piscataway, NJ, 1999.
51.	Kolmogorov A. N. On the shannon theory of information transmission in the case of
continious signals. IRE Transactions on Information Theory, IT-2:pp. 102-108,
1956.
Список литературы
307
52.	Linde Y., Buzo A., Gray R. М. An algorithm for vector quantizer design. IEEE
Transactions on Communications Trechnology, COM-28(l):84-95, Jan. 1980.
53.	Lloyd S.P. Least squares quantization in pcm. IEEE Transactions on Information
Theory, 28(2):129-137, Mar. 1982.
54.	Manstetten D. Tight bounds on the redundancy of Huffman codes. IEEE
Transactions on Information Theory, 38(1):144-151, Jan. 1992.
55.	Max J. Quantizing for minimum distortion. IRE Transactions on Information
Theory, 6(1):7—12, Mar. 1960.
56.	Welch T. A. A technique for high-performance data compression. IEEE Computer,
17(6):8-19, 1984.	,
57.	Witten I. C., Neal R. M., Cleary J. G. Arithmetic coding for data compression.
Communication of the ACM, 30(6):520-540, 1987.
58.	ZadorP. Asymptotic quantization error of continuous signals and their quantiza-
tion dimension. IEEE Transactions on Information Theory, 28(2):139-149, Mar.
1982.
59.	Ziv J., Lempel A. A universal algorithm for sequential data compression. IEEE
Transactions on Information Theory, IT-23(3):337-343, May 1977.
60.	Ziv J., Lempel A. Compression of individual sequences via variable-rate coding.
IEEE Transactions on Information Theory, IT-24(5):530-536, Nov. 1978.
Предметный указатель
А
Адаптивное арифметическое
кодирование, 164
Аддитивная оценка, 13
Алгоритм BW, 164
Алгоритм LZ-77, 138
Алгоритм LZ77, 164
Алгоритм LZ78, 145
Алгоритм LZFG, 142, 164
Алгоритм LZW, 145, 164
Алгоритм PPM, 149
Алгоритм РРМА, 150, 164
Алгоритм PPMD, 152, 164
Алгоритм Барроуза-Уилера, 155
Алгоритм Блэйхута, 247
Алгоритм Витерби, 286
Алгоритм двухпроходного
кодирования, 164
Алгоритм ЛБГ, 263
Алгоритм Лемпела-Зива, 138
Алгоритм Лемпела-Зива-Велча, 145
Алгоритм Ллойда-Макса, 258
Алгоритм предсказания по
частичному совпадению, 149
Алгоритм скользящего словаря, 138
Арифметическое кодирование, 79
Б
Базис решетки, 265
Белый шум, 294
Биномиальное распределение, 54, 55
Биномиальные коэффициенты, 96
Бит, 17
Булева алгебра событий, 12
В
Вероятность ошибки, 171
Вероятность ошибки декодирования,
171, 197
Вероятность ошибки кодирования, 39
Вес Хэмминга, 54
Взаимная информация, 175
Время возвращения, 136
Второй момент области, 275
Второй момент шара, 277
Выигрыш по отношению
к равномерному квантованию, 268
Выпуклая функция, 24, 51
Выпуклое множество, 23
Выпуклость средней взаимной
информации, 180
Г
Гамма-функция, 116, 277
Геометрическое распределение, 54
Граница Гиша-Пирса, 257
Граница Задора, 269, 276
Граница Кошелева, 257, 262
Граница Шеннона, 235, 256, 276
д
Декодирование с жесткими
решениями, 298
Декодирование с мягкими
решениями, 298
Дискретное множество, 12
Дискретный вероятностный ансамбль,
12
Предметный указатель
309
Дискретный постоянный источник,
31,37
Дисперсия, 15
Дифференциальная энтропия, 207
Длина кода канала, 171
И
Избыточность, 93, 105
Избыточность равномерного
квантователя, 257
Избыточность решетчатого
квантования, 267
Избыточность универсального
кодирования, 141, 149
Избыточность, нижняя граница, ИЗ
Интеграл Дирихле, 117, 277
Информационная емкость
гауссовского канала дискретного
времени с ограничением на
мощность, 291
Информационная емкость
дискретного постоянного канала, 189
Информационная емкость канала, 181
Информационная емкость
непрерывного канала без памяти
с ограничением на мощность, 291
Информационная емкость
непрерывного канала дискретного
времени с ограничением
на мощность, 291
Источник гауссовский, 234
Источник двоичный, 231
К
Канал без памяти, 173
Канал гауссовский, 291
Канал ДСтК, 174
Канал двоичный с непрерывным
выходом, 303
Канал двоичный симметричный, 174,
193, 303
Канал двоичный симметричный
со стираниями, 174, 194, 303
Канал дискретный постоянный, 173
Канал непрерывного времени, 292
Канал непрерывный дискретного
времени, 290
Канал непрерывный с аддитивным
шумом, 290
Канал полностью симметричный, 191
Канал с ограничением на полосу
частот, 295
Канал симметричный, 191
Канал симметричный в широком
смысле, 194
Канал симметричный по входу, 191
Канал симметричный по выходу, 191
Канал стационарный, 173
Канал телефонный, 296
Квант, 254
Квантование векторное оптимальное
по ошибке, 263
Квантователь, 253
Квантователь векторный, 253, 262
Квантователь Ллойда-Макса, 257
Квантователь неструктурированный,
253
Квантователь равномерный, 255
Квантователь скалярный, 253
Квантователь скалярный
оптимальный по ошибке, 257
Квантователь скалярный
оптимальный по энтропии, 259
Код «стопка книг», 133
Код арифметический, 79, 91
Код арифметический декодирование,
84
Код Галлагера-Ван Вухриса, 129
Код Гилберта-Мура, 74, 91
Код Гилберта-Мура, 70, 79, 83
Код Голомба, 129
Код для кодирования источников
с заданным критерием качества, 226
Код древовидный, 59
Код канала, 171
Код каскадный, 302
Код Левенштейна, 130
Код линейный, 278
Код монотонный, 129
Код неравномерный, 58
310
Предметный указатель
Код однозначно декодируемый, 58
Код оптимальный, 66
Код префиксный, 58
Код Райса, 129
Код Рида-Соломона, 302
Код регулярный, 100
Код сверточный, 283, 302
Код сверточный усеченный, 285
Код сверточный, длина кодового
ограничения, 283
Код сверточный, память кодера, 283
Код сверточный, скорость, 283
Код сверточный, состояние кодера,
283
Код Танстелла, 90
Код унарный, 129
Код Хаффмена, 66, 70, 89, 99, 100, 125
Код Шеннона, 70, 71, 74, 79, 91
Код Элайеса, 131
Кодирование FF, 41
Кодирование FV, 41, 77
Кодирование LZ-77, 138
Кодирование off-line, 94
Кодирование on-line, 94, 120
Кодирование VF, 41
Кодирование VV, 41, 90
Кодирование адаптивное, 120
Кодирование адаптивное, D-алгоритм,
124, 125
Кодирование адаптивное, А-алгоритм,
123, 125
Кодирование без задержки, 94
Кодирование двухпроходное, 94, 98
Кодирование длин серий, 90
Кодирование интервальное, 133
Кодирование мгновенное, 94
Кодирование нумерационное, 106, 125
Кодирование нумерационное,
декодирование, 110
Кодирование нумерационное,
избыточность, 106
Кодирование нумерационное,
реализация, 109
Кодирование расстояний, 161, 164
Кодирование универсальное, 94
Кодовая книга структурированная,
265
Кодовое дерево, 59
Коды для исправления ошибок, 169
Композиция, 97
Композиция последовательности, 50
Корректирующий код, 170
Корреляционная матрица, 212
Корреляционная функция, 214, 292
Корреляционный момент, 15
Критерий качества, 225
Критерий качества вероятностный,
231
Критерий качества квадратический,
234
Критерий качества объективный, 225
Критерий качества субъективный, 225
Кумулятивная вероятность, 71, 74, 80
Л
Лексикографический порядок, 80
Лемма Каца, 136
Линейное преобразование случайного
вектора, 211
М
Марковский источник, 31
Математическое ожидание, 15
Матрица Грамма, 266
Матрица переходных вероятностей,
173
Матрица переходных вероятностей
цепи Маркова, 32
Мера искажения, 225
Мера искажения абсолютная, 226
Мера искажения вероятностная, 225
Мера искажения квадратическая, 226
Мера искажения ограниченная, 242,
245
Мера искажения побуквенная, 225
Мера искажения
Метод «стопка книг», 160, 164
Метод LZ78, 145
Метод LZFG, 142
Метод LZW, 145
Предметный указатель
311
Метод PPM, 149
Метод РРМА, 150
Метод PPMD, 152
Метод Барроуза-Уилера, 155
Метод Лемпела-Зива, 138
Метод Лемпела-Зива-Велча, 145
Метод Лемпела-Зива-Фиала-Грине,
142
Метод предсказания по частичному
совпадению, 149
Метод скользящего словаря, 138
Метод случайного кодирования, 197,
245
Многогранник Вороного, 263, 266
Множество d-типичных пар, 242
Множество /-типичных пар, 242
Множество p-типичных пар, 242
Множество типичных пар, 198, 200,
242
Множество типичных
последовательностей, 45, 48
Множество типичных
последовательностей непрерывного
источника, 219
Модель канала, 172
Мощность кода, 171
Мощность множества, 12
Н
Независимые ансамбли, 15
Независимые события, 13
Некоррелированные величины, 15
Непрерывная случайная величина,
206
Неравенство Йенсена, 25
Неравенство Крафта, 60
Неравенство Фано, 183
Неравенство Фано для
последовательностей, 187
Неравенство Чебышева, 42
Неравенство Чебышева для суммы
независимых случайных величин, 42
Неравномерное кодирование, 58, 76
Несовместные события, 13
Нестрого выпуклая функция, 24
Нормализованный второй момент, 267
Нормализованный второй момент
области, 276
Нормализованный второй момент
решетки над сверточным кодом, 287
Нормализованный второй момент
шара, 277
Нумерационное
О
Область Вороного, 263
Обратная теорема кодирования для
неравномерного кодирования
стационарного источника, 77
Обратная теорема кодирования для
стационарного канала, 187
Обратная теорема Кодирования
неравномерными кодами, 65
Обратная теорема кодирования при
заданном критерии качества, 240
Обратная теорема кодирования
равномерными кодами, 46
Обратное преобразование
Барроуза-Уилера, 158
Ортонормированное преобразование,
251
Относительная энтропия, 248
Относительная энтропия
Кульбака-Лейблера, 53, 209
Отношение сигнал/шум, 226, 251, 268,
292
Отношение сигнал/шум на бит, 297
Ошибка кодирования, 39
П
Переходная вероятность ДСК, 174
Плотностью распределения
вероятностей, 205
Полиномиальное распределение, 55
Помехоустойчивость, 171
Порождающая матрица решетки, 266
Предел Шеннона, 298
Преобразование Барроуза-Уилера,
155
312
Предметный указатель
Преобразование ортонормированное,
238
Принцип заполнения водой, 239
Принцип максимума правдоподобия,
198
Принцип разливания воды, 294
Произведение вероятностных
ансамблей, 14
Произведение множеств, 14
Пропускная способность канала, 172,
181
Пропускная способность канала
с неограниченной полосой частот,
296
Пропускная способность канала
с ограниченной полосой частот, 295
Пропускная способность
непрерывного канала, 292
Процесс авторегрессионный, 215, 218,
222
Процесс Гаусса-Маркова, 215
Прямая теорема кодирования для
дискретного постоянного канала, 196
Прямая теорема кодирования для
неравномерного кодирования
стационарного источника, 78
Прямая теорема кодирования
неравномерными кодами, 63
Прямая теорема кодирования при
заданном критерии качества, 245
Прямая теорема кодирования при
равномерном кодировании , 44
Р
Равномерное кодирование, 38
Равномерное распределение, 54
Распределение вероятностей, 12
Распределение гауссовское, 206, 210,
221, 234
Распределение гауссовское п-мерное,
212
Распределение Дирихле, 116
Распределение Лапласа, 206
Распределение нормальное, 206
Распределение обобщенное
гауссовское, 206, 221
Распределение равномерное, 206, 209
Распределение экспоненциальное,
206, 209
Распределение экстремальное, 210
Расстояние Хэмминга, 170
Решающая область, 170
Решающие области, 262
Решетка Ai6, 273
Решетка Л24, 273
Решетка Л16, 269
Решетка Л24, 269
Решетка А2, 269
Решетка А3, 269
Решетка Ап, 270
Решетка А*, 270
Решетка Ьсс, 271
Решетка 269
Решетка Dg, 269
Решетка Dn, 271
Решетка JD*, 271
Решетка Е8, 269, 272
Решетка Е?, 269, 272
Решетка Е8, 269, 272
Решетка Ki2, 269, 273
Решетка Барнса-Уолла, 273
Решетка гексогональная, 267
Решетка двойственная, 268
Решетка Кокстера-Тодда, 273
Решетка кубическая, 267
Решетка Лича, 273
Решетка многомерная, 265
Решетка над кодом, алгоритм
квантования, 282
Решетка объемноцентрическая
кубическая, 271
Решетка числовая, 265
Решетка шахматная, 271
Решетка, порожденная кодом, 278
Решетки эквивалентные, 266
Решетчатая диаграмма, 284
Предметныйуказатель
313
с
Скорость кода источника, 227
Скорость кода канала, 170
Скорость кодирования, 77
Скорость Найквиста, 300
Скорость равномерного кода, 38
Скорость создания информации, 40
Сложное событие, 12
Сложность арифметического
кодирования, 83
Случайная величина, 15
Случайный процесс, 30
Случайный процесс эргодический, 51
Случайный процесс эргодический , 43
Собственная информация, 17, 51
Событие, 12
Спектральная плотность мощности,
216, 238, 293
Спектральная эффективность
кодирования, 299
Среднее искажение, 227
Среднее по времени, 43
Среднее по множеству реализаций, 43
Средняя взаимная информация, 176
Средняя взаимная информация
гауссовских случайных величин, 221
Средняя взаимная информация между
непрерывными ансамблями, 210
Средняя длина кодового слова, 59
Стационарное распределение, 33, 52
Стационарный случайный процесс, 31
Стохастическая матрица, 32
Стохастический вектор, 32
Строго выпуклая функция, 24
Сходимость по вероятнгости, 43
Т
Теорема Котельникова-Шеннона, 295
Теорема о переработке информации,
178
Теорема об энтропии на сообщение, 35
Тестовый набор Calgary Corpus, 165
Турбо-код, 302
У
Уравнения Юла-Уокера, 218
Условная вероятность события, 13
Условная средняя взаимная
информация, 178
Ф
Финальное распределение, 33
Формула Байеса, 14
Формула полной вероятности, 13
Формула Стирлинга, 97, 116
Фундаментальная область решетки,
266
Функция выпуклая, 230
Функция искажение-скорость, 227
Функция распределения, 205
Функция скорость-искажение, 227
Функция скорость-искажение
гауссовского источника, 234
Функция скорость-искажение
двоичного источника, 231
Функция скорость-искажение
последовательности гауссовского
вектора с заданной корреляционной
матрицей, 238
Функция скорость-искажение
последовательности независимых
гауссовских величин, 236
Функция скорость-искажение
стационарного гауссовского
процесса с заданной, 238
Функция скорость-искажение
теоретическая , 228
Функция скорость-искажение,
свойства, 228
Функция скорость-искажения для
равномерного скалярного
квантователя, 256
ц
Цепь Маркова, 31, 37, 52, 90
Цепь Маркова непериодическая, 33
Цепь Маркова неприводимая, 33
314
Предметный указатель
Цепь Маркова однородная, 32
Цепь Маркова простая, 32
Цепь Маркова связности з, 31
Цепь Маркова эргодическая, 33
Ч
Число перестановок, 95
Число размещений, 95
Число сочетаний, 96
Э
Экстремальное распределение, 210
Элементарное событие, 12
Энергетический выигрыш
кодирования, 296
Энтропия, 18, 34, 51, 63, 65, 78
Энтропия двоичного ансамбля, 21
Энтропия дифференциальная, 207,
221
Энтропия дифференциальная
авторегрессионного процесса, 216
Энтропия дифференциальная
авторегрессионного процесса
первого порядка, 216
Энтропия дифференциальная
гауссовского вектора, 212
Энтропия дифференциальная на
сообщение, 214
Энтропия дифференциальная
случайного вектора, 211
Энтропия дифференциальная
стационарного гауссовского
процесса с заданной спектральной
плотностью мощности, 217
Энтропия дифференциальная
стационарного процесса дискретного
времени, 214
Энтропия дифференциальная
условная, 209
Энтропия Кульбака-Лейблера, 248
Энтропия на сообщение, 34, 77, 90
Энтропия условная, 34
Я
Якобиан преобразования, 211
Борис Давидович Кудряшов
Теория информации: Учебник для вузов
Заведующий редакцией
Руководитель проекта
Ведущий редактор
Литературный редактор
Художественный редактор
Корректор
Верстка
А. Сандрыкин
П. Маннинен
Ю. Сергиенко
К. Кноп
Л. Аду веская
И. Тимофеева
А. Дмитриев
Подписано в печать 25.02.09. Формат 70x100/16. Усл. п. л. 25,8.
Тираж 3000. Заказ 14277.
ООО «Лидер», 194044, Санкт-Петербург, пр. Б. Сампсониевский, дом 29а.
Налоговая льгота — общероссийский классификатор продукции ОК 005-93,
том 2; 95 3005 — литература учебная.
Отпечатано по технологии CtP в ОАО «Печатный двор» им. А. М. Горького.
197110, Санкт-Петербург, Чкаловский пр., д. 15.
КЛУБ П P(O/XEC С И О КА Л
Основанный Издательским домом «Питер» в 1997 году, книжный клуб «Профессионал» собирает
в своих рядах знатоков своего дела, которых объединяет тяга к знаниям и любовь к книгам. Для
членов клуба проводятся различные мероприятия и, разумеется, предусмотрены привилегии.
Привилегии для членов клуба:
•	карта члена «Клуба Профессионал»;
*	бесплатное получение клубного издания - журнала «Клуб Профессионал»;
•	дисконтная скидка на всю приобретаемую литературу в размере 10% или 15%;
•	бесплатная курьерская доставка заказов по Москве и Санкт-Петербургу;
•	участие во всех акциях Издательского дома «Питер» в розничной сети на льготных условиях.
Как вступить в клуб?
Для вступления в «Клуб Профессионал» вам необходимо:
•	совершить покупку на сайте www.piter.com или в фирменном магазине Издательского дома
«Питер» на сумму от 800 рублей без учета почтовых расходов или стоимости курьерской до-
ставки;
•	ознакомиться с условиями получения карты и сохранения скидок;
•	выразить свое согласие вступить в дисконтный клуб, отправив письмо на адрес:
postbook@piter.com;
•	заполнить анкету члена клуба (зарегистрированным на нашем сайте этого делать не надо).
Правила для членов «Клуба Профессионал»:
*	для продления членства в клубе и получения скидки 10%, в течение каждых шести месяцев
нужно совершать покупки на общую сумму от 800 до 1500 рублей, без учета почтовых расходов
или стоимости курьерской доставки;
•	Если же за указанный период вы выкупите товара на сумму от 1501 рублей, скидка будет увели-
чена до 15% от розничной цены издательства.
Заказать наши книги вы можете любым удобным для вас способом:
	по телефону: (812) 703-73-74;
•	по электронной почте: postbook@piter.com;
•	на нашем сайте: www.piter.com;
•	по почте: 197198, Санкт-Петербург, а/я 619 ЗАО «Питер Пост».
При оформлении заказа укажите:
•	ваш регистрационный номер (если вы являетесь членом клуба), фамилию, имя, отчество, теле-
фон, факс, e-mail;
•	почтовый индекс, регион, район, населенный пункт, улицу, дом, корпус, квартиру;
•	название книги, автора, количество заказываемых экземпляров.
ИЗДАТЕЛЬСКИЙ ДОМ
КНИГА-ПОЧТОЙ
ЗАКАЗАТЬ КНИГИ ИЗДАТЕЛЬСКОГО ДОМА «ПИТЕР»
МОЖНО ЛЮБЫМ УДОБНЫМ ДЛЯ ВАС СПОСОБОМ:
•	по телефону: (812) 703-73-74;
•	по электронному адресу: postbook@piter.com;
•	на нашем сервере: www.pfter.com;
•	по почте: 197198, Санкт-Петербург, а/я 619,
ЗАО «Питер Пост».
ВЫ МОЖЕТЕ ВЫБРАТЬ ОДИН ИЗ ДВУХ СПОСОБОВ ДОСТАВКИ
И ОПЛАТЫ ИЗДАНИЙ:
Наложенным платежом с оплатой заказа при получении посылки на
ближайшем почтовом отделении. Цены на издания приведены ориентиро-
вочно и включают в себя стоимость пересылки по почте (но без учета
авиатарифа). Книги будут высланы нашей службой «Книга-почтой»
в течение двух недель после получения заказа или выхода книги из печати.
Оплата наличными при курьерской доставке (для жителей Москвы
и Санкт-Петербурга). Курьер доставит заказ по указанному адресу
в удобное для вас время в течение трех дней.
ПРИ ОФОРМЛЕНИИ ЗАКАЗА УКАЖИТЕ:
•	фамилию, имя, отчество, телефон, факс, e-mail;
•	почтовый индекс, регион, район, населенный пункт,
улицу, дом, корпус, квартиру;
•	название книги, автора, код, количество заказываемых
экземпляров.
Вы можете заказать бесплатный
журнал «Клуб Профессионал»
ИЗДАТЕЛЬСКИЙ ДОМ
^ППТЕР
WWW.PITER.COM
СЕЛИГЕР
ходить по магазинам?
наберите:
www.piter.com
Новые книги — в момент выхода из типографии
Информацию о книге — отзывы, рецензии, отрывки
Старые книги — в библиотеке и на CD
И наконец, вы нигде не купите
наши книги дешевле!
ИЗДАТЕЛЬСКИЙ ДОМ
СПЕЦИАЛИСТАМ
КНИЖНОГО БИЗНЕСА!
ПРЕДСТАВИТЕЛЬСТВА ИЗДАТЕЛЬСКОГО ДОМА «ПИТЕР»
предлагают эксклюзивный ассортимент компьютерной, медицинской,
психологической, экономической и популярной литературы
РОССИЯ
Москва м. «Электрозаводская», Семеновская наб., д. 2/1, корп. 1,6-й этаж;
тел./факс: (495) 234-3815,974-3450; e-mail: sales@piter.msk.ru
Санкт-Петербург м. «Выборгская», Б. Сампсониевский пр., д. 29а;
тел./факс (812) 703-73-73,703-73-72; e-mail: sales@piter.com
Воронеж Ленинский пр., д. 169; телефакс (4732) 39-43-62,39-61 -70;
e-mail: pitervm@comch.ru
Екатеринбург ул. Бебеля, д. 11а; тел./факс (343) 378-98-41,378-98-42;
e-mail: office@ekat.piter.com
Нижний Новгород ул. Совхозная, д. 13; тел. (8312) 41 -27-31;
e-mail: office@nnov.piter.com
Новосибирск ул. Станционная, д. 36;
тел./факс (383) 350-92-85; e-mail: office@nsk.piter.com
Ростов-на-Дону ул. Ульяновская, д. 26; тел. (8632) 69-91 -22,69-91 -30;
e-mail: piter-ug@rostov.piter.com
Самара ул. Молодогвардейская, д. 33, литер А2, офис 225; тел. (846) 277-89-79;
e-mail: pitvolga@samtel.ru
УКРАИНА
Харьков ул. Суздальские ряды, д. 12, офис 10-11; телефакс (1038067) 545-55-64,
(1038057) 751-10-02; e-mail: piter@kharkov.piter.com
Киев пр. Московский, д. 6, кор. 1, офис 33; тел./факс (1038044) 490-35-68,490-35-69;
e-mail: office@kiev.piter.com
БЕЛАРУСЬ
Минск ул. Притыцкого, д. 34, офис 2; тел./факс (1037517) 201 -48-79, 201 -48-81;
e-mail: office@minsk.piter.cdm
Ищем зарубежных партнеров или посредников, имеющих выход на зарубежный рынок.
Телефон для связи: (812) 703-73-73.
E-mail; fuganov@piter.com
bg Издательский дом «Питер» приглашает к сотрудничеству авторов.
Обращайтесь по телефонам: Санкт-Петербург — (812) 703-73-72,
Москва - (495) 974-34-50.
Заказ книг для вузов и библиотек: (812) 703-73-73.
Специальное предложение - e-mail: kozin@piter.com
ИЗДАТЕЛЬСКИЙ ДОМ
УВАЖАЕМЫЕ ГОСПОДА!
КНИГИ ИЗДАТЕЛЬСКОГО ДОМА «ПИТЕР»
ВЫ МОЖЕТЕ ПРИОБРЕСТИ
ОПТОМ И В РОЗНИЦУ
У НАШИХ РЕГИОНАЛЬНЫХ ПАРТНЕРОВ.
Дальний Восток
Владивосток, «Приморский торговый дом книги»,
тел./факс (4232) 23-82-12.
E-mail: bookbase@mail.primorye.ru
Хабаровск, «Деловая книга»,
ул. Путевая, д. 1а,
тел. (4212) 36-06-65, 33-95-31
E-mail: dkniga@mail.kht.ru
Хабаровск, «Книжный мир»,
тел. (4212) 32-85-51, факс 32-82-50.
E-mail: postmaster@worldbooks.kht.ru
Хабаровск, «Мирс»,
тел. (4212) 39-49-60.
E-mail: zakaz@booksmirs.ru
Европейские регионы России
Архангельск, «Дом книги»,
пл. Ленина, д. 3
тел. (8182) 65-41-34, 65-38-79.
E-mail: marketing@avfkniga.ru
Воронеж, «Амиталь»,
пл. Ленина, д. 4,
тел. (4732) 26-77-77.
http://www.amital.ru
Калининград, «Вестер»,
сеть магазинов «Книги и книжечки»,
тел./факс (4012) 21-56-28, 65-65-68.
E-mail: nshibkova@vester.ru
http://www.vester.ru
Самара, «Чакона», ТЦ «Фрегат»,
Московское шоссе, д.15,
тел. (846) 331-22-33.
E-mail: chaconne@chaccone.ru
Саратов, «Читающий Саратов»,
пр. Революции, д. 58,
тел. (4732) 51-28-93,47-00-81.
E-mail: manager@kmsvrn.ru
Северный Кавказ
Ессентуки, «Россы», ул. Октябрьская, 424,
тел./факс (87934) 6-93-09.
E-mail: rossy@kmw.ru
Сибирь
Иркутск, «ПродаЛитЪ»,
тел. (3952) 20-09-17, 24-17-77.
E-mail: prodalit@irk.ru
http://Vvww.prodalit.irk.ru
Иркутск, «Светлана»,
тел./факс (3952) 25-25-90.
E-mail: kkcbooks@bk.ru
http://Vvww.kkcbooks.ru
Красноярск, «Книжный мир», пр. Мира, д. 86,
тел./факс (3912) 27-39-71.
E-mail: book-world@public.krasnet.ru
Новосибирск, «Топ-книга»,
тел. (383) 336-10-26, факс 336-10-27.
E-mail: office@top-kniga.ru
http://Vvww.top-kniga.ru
Татарстан
Казань, «Таис»,
сеть магазинов «Дом книги»,
тел. (843) 272-34-55.
E-mail: tais@bancorp.ru
Урал
Екатеринбург, ООО «Дом книги»,
ул. Антона Валека, д. 12,
тел./факс (343) 358-18-98,358-14-84.
E-mail: domknigi@k66.ru
Челябинск, ТД «Эврика», ул.Барбюса, д. 61,
тел./факс (351) 256-93-60.
E-mail: evrika@bookmagazin.ru
http://www.bookmagazin.ru
Челябинск, ООО «ИнтерСервис ЛТД»,
ул. Артиллерийская, д. 124
тел. (351)247-74-03,247-74-09,247-74-16.
E-mail: zakup@intser.ru
http://Vvww.fkniga.ru,www.intser.ru
ЧЕБНИК
ДЛЯ ВУЗОВ
Теория информации
Кудряшов Борис Давидович — окончил Ленинградский
институт авиационного приборостроения (ныне Государственный
университет аэрокосмического приборостроения)
в 1974 году. В 2005 году Ученым советом Института
проблем передачи информации РАН ему была присуждена
ученая степень доктора технических наук.
В настоящее время — профессор кафедры
информационных систем Университета информационных
технологий, механики и оптики.
В учебнике описаны алгоритмы работы современных методов сжатия данных,
способы эффективного представления аналоговой информации,
методы анализа эффективности систем помехоустойчивого кодирования.
В последние годы появилась техническая литература, в которой описываются
конкретные алгоритмы сжатия данных, применяемые в современных стандартах
и коммерческих программных продуктах. Отличие данного издания состоит
в том, что новые методы обработки информации излагаются
с позиций теории информации как часть общей теории.
Такой подход представляется важным для подготовки потенциальных
исследователей и разработчиков перспективных информационных технологий.
Допущено Учебно-методическим объединением вузов по университетскому
политехническому образованию в качестве учебного пособия для студентов
высших учебных заведений, обучающихся по направлению подготовки
230200 «Информационные системы».
!^ППТЕР
Заказ книг:
197198, Санкт-Петербург, а/я 619
тел.: (812) 703-73-74, postbook@piter.com
61093, Харьков-93, а/я 9130
тел.: (057) 758-41-45, 751-10-02, piter@kharkov.piter.com
www.piter.com — вся информация о книгах и веб-магазин
ISBN: 978-5-388-00178-8