Автор: Коротков П.Ф.
Теги: термодинамика энергетика физика задачи по физике молекулярная физика
ISBN: 5-7417-0229-5
Год: 2004
Текст
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
Государственное образовательное учреждение
высшего профессионального образования
Московский физико-технический институт
(государственный университет)
П.Ф. Короткое
МОЛЕКУЛЯРНАЯ ФИЗИКА
И ТЕРМОДИНАМИКА
Основные положения
и решение задач
Рекомендовано Учебно-методическим объединением
Московского физико-технического института
(государственного университета)
в качестве учебного пособия
для студентов высших учебных заведений
по направлению "Прикладные математика и физика "
2-е издание
МОСКВА 2004
УДК 536.7
К66
Рецензенты:
Кафедра общей физики Московского инженерно-физического института
Доктор физико-математических наук, профессор А.В. Степанов
Короткое П.Ф.
К66 Молекулярная физика и термодинамика. Основные
положения и решения задач: Учебное пособие. — 2-е изд.
— М.: МФТИ, 2004.— 168 с.
ISBN 5-7417-0229-5
Приводятся основные положения молекулярной физики и термодина-
термодинамики, обсуждается их физический смысл и рассматриваются некоторые
приложения. Существенное внимание уделено решению задач, отражающих
содержание общего курса физики по рассматриваемому разделу. Пособие
содержит также большой методический материал, необходимый в учебном
процессе.
Для студентов и преподавателей физики высших учебных заведений.
УДК 536.7
Учебное издание
Короткое Павел Федорович
МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА
Основные положения и решение задач
Редактор О. П. Котова. Корректор К А. Волкова
Подписано в печать 30.04.04. Формат 60 х 84 V^. Бумага офсетная. Печать
офсетная. Усл. печ л. 10,5. Уч.- изд. л. 9,2. Тираж 1000 экз. Заказ № ф-140.
Государственное образовательное учреждение
высшего профессионального образования
Московский физико-технический институт (государственный университет)
Отдел автоматизированных издательских систем "физтех-полиграф*'
141700, Московская обл., г. Долгопрудный, Институтский пер., 9
Для заявок: тел. @95) 408-58-22 rio@mail.mipt.ru
ISBN 5-7417-0229-5 © Московский физико-технический институт
(государственный университет), 2004
© Короткое П.Ф., 2004
ОГЛАВЛЕНИЕ
Предисловие
Р а з д е л 1. Уравнение состояния 7
1.1. Идеальный газ G). 1.2. Смеси идеальных газов
(9). 1.3. Барометрическая формула A0). 1.4. Коэф-
Коэффициент теплового расширения и другие ко-
коэффициенты A2).
Р а з д е л 2. Статистические закономерности 16
2.1. Случайные события A6). 2.2. Соединения A8).
2.3. Биномиальное распределение B0). 2.4. Распре-
Распределение Пуассона B4). 2.5. Распределение Гаусса
B6). 2.6. Энтропия и информация B9). 2.7. Статис-
Статистическое и термодинамическое определение
энтропии C5).
Р а з д е л 3. Распределение Максвелла 41
3.1. Распределение вероятностей для компоненты
скорости D2). 3.2. Распределение вероятностей для
абсолютной величины скорости D6). 3.3. Средние
скорости D8). 3.4. Двумерное распределение Макс-
Максвелла E0). 3.5. Распределение вероятностей для
энергии молекул E1). 3.6. Перетекание газа через
очень малое отверстие E2). 3.7. Пределы примени-
применимости распределения Максвелла E3).
Р а з д е л 4. Распределения Больцмана и Гиббса 55
4.1. Газ в поле тяжести E7). 4.2. Газ в поле
центробежных сил E9). 4.3. Распределение Гиббса
F1).
Р а з д е л 5. Флуктуации 64
5.1. Флуктуации числа частиц F5). 5.2. Флуктуации
типа броуновского движения F8). 5.3. Определение
флуктуации по заданному распределению G5). 5.4.
Флуктуации энергии G5). 5.5. Вероятность
флуктуации G7).
Р а з д е л 6. Явления переноса 78
6.1. Теплопроводность (81). 6.2. Вязкость (83).
6.3. Диффузия (87). 6.4. Явления переноса в разре-
женных газах (92). 6.5. Нестационарные процессы
(94).
Р а з д е л 7. Первое начало термодинамики 98
7.1. Работа газа (98). 7.2. Внутренняя энергия, теп-
теплоемкость A00). 7.3. Теплоемкости при разных про-
процессах A05). 7.4. Теплоемкость смеси газов A07).
5. Скорость звука в газе A09). 7.6. Уравнение Бер-
нулли A11).
Р а з д е л 8. Второе начало термодинамики 114
8.1. Определение КПД двигателей A15). 8.2. Опре-
Определение КПД холодильников A18).
Р а з д е л 9. Энтропия. Необратимые процессы 123
9.1. Равенство Клаузиуса A23). 9.2. Изменение энт-
энтропии в обратимых процессах A24). 9.3. Метод
термодинамических функций и соотношения
Максвелла A26). 9.4. Изменение энтропии при не-
необратимых процессах A30). 9.5. Энтропия смеси
идеальных газов A36).
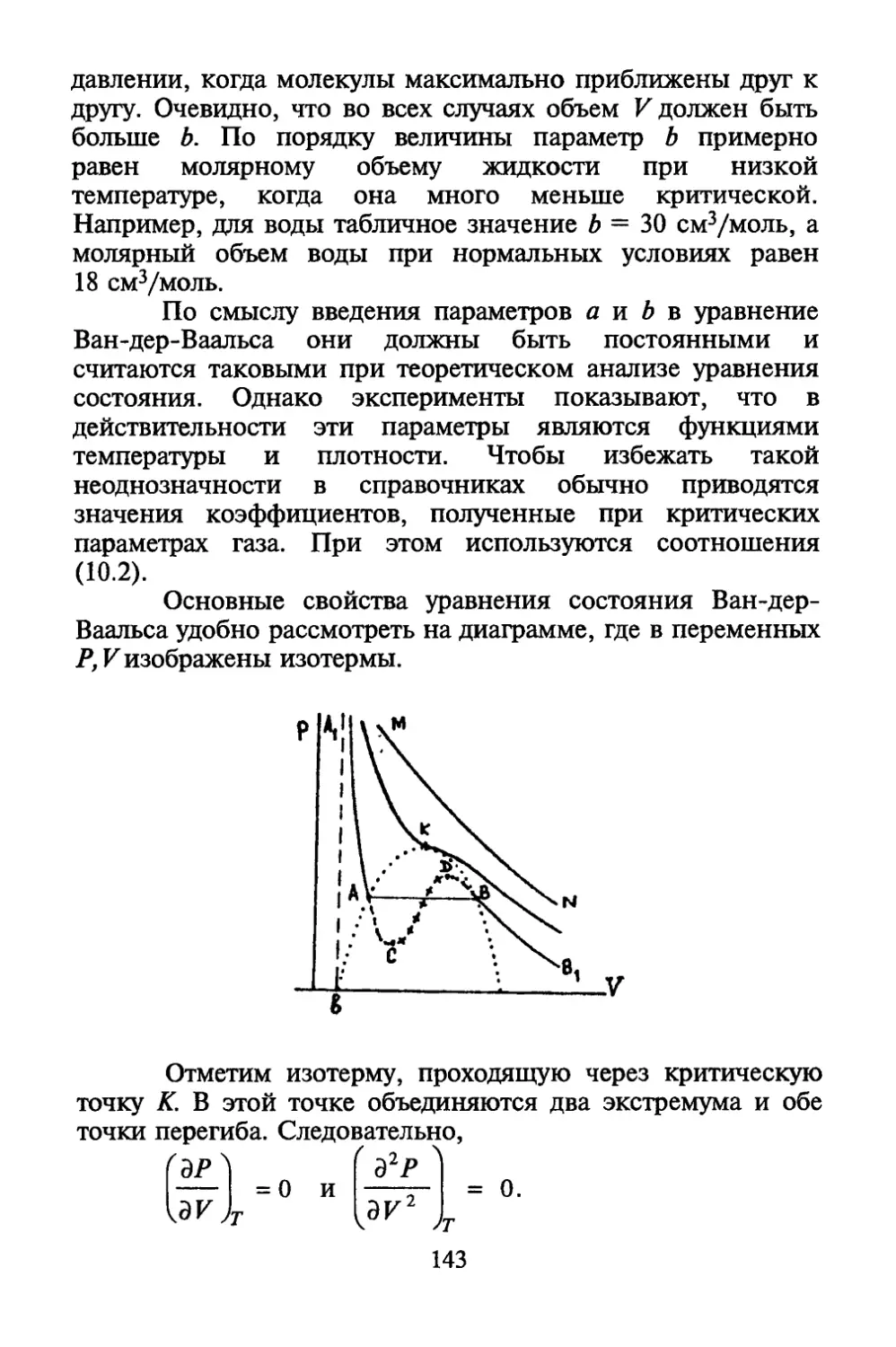
РазделЮ. Реальные газы 141
10.1. Уравнение Ван-дер-Ваальса A41). 10.2. Внут-
Внутренняя энергия и энтропия A45). 10.3. Эффект
Джоуля-Томсона A48).
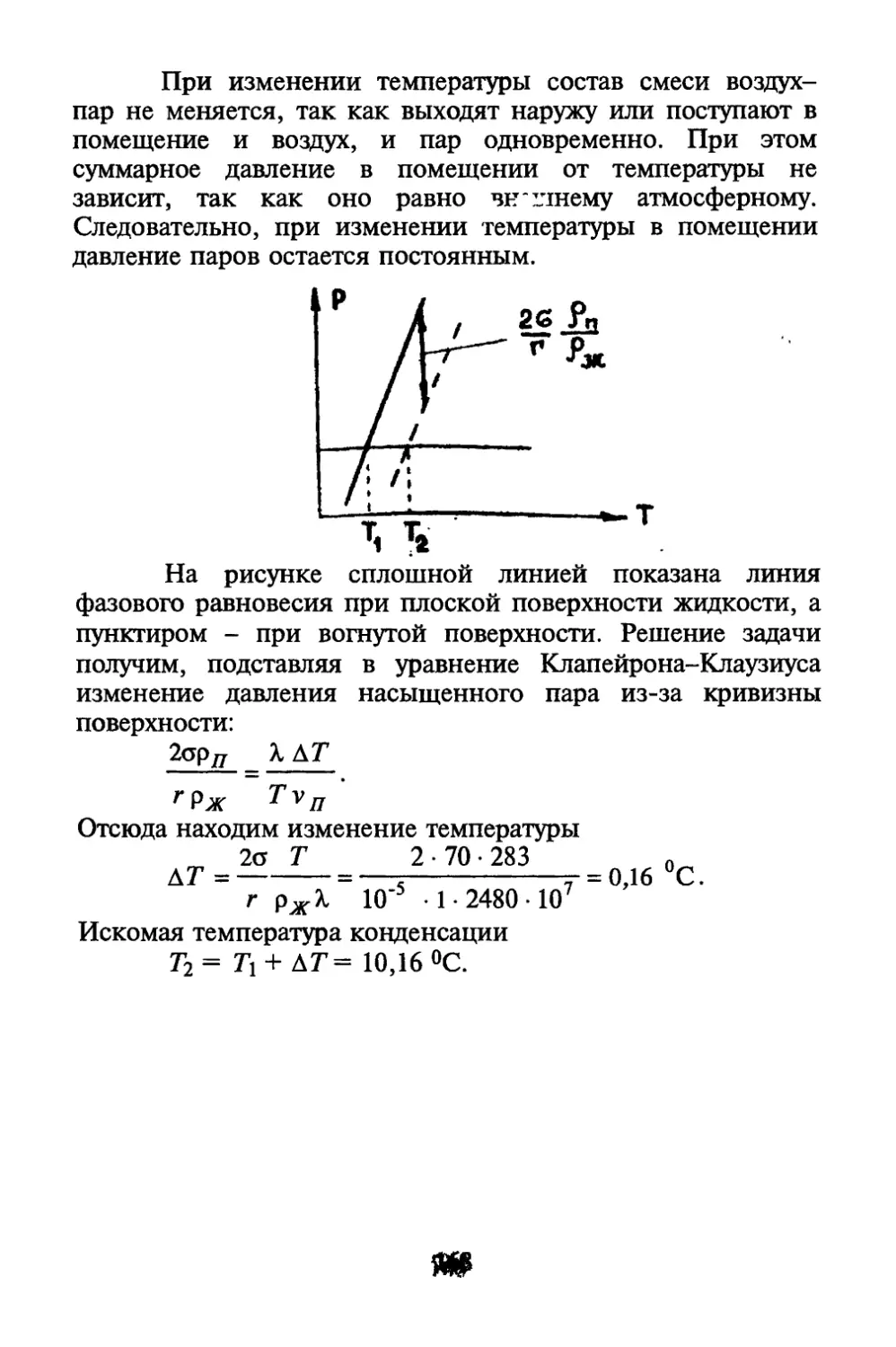
Раздел 11. Фазовые превращения 152
11.1. Уравнение Клапейрона-Клаузиуса A53).
11.2. Приближенное интегрирование уравнения
Клапейрона-Клаузиуса A55).
Р а з д е л 12. Поверхностное натяжение 160
12.1. Давление под кривой поверхностью жидкости
A60). 12.2. Термодинамика поверхностного натяже-
натяжения A63). 12.3. Зависимость давления насыщенно-
насыщенного пара от кривизны поверхности жидкости A66).
ПРЕДИСЛОВИЕ
Предлагаемое учебное пособие написано на основе
семинаров, которые автор проводил на протяжении многих
лет (с 1962 г.) со студентами первого курса Московского
физико-технического института.
Текст издания состоит из двенадцати разделов.
Каждый начинается с небольшого теоретического введения.
Далее следует обсуждение и решение задач, а также анализ
результатов. Представленный материал значительно меньше
объема учебников, он не может их заменить, но при
начальном изучении должен помочь освоить многие
сведения, обычно приводимые в таких книгах, помочь в них
ориентироваться. Объем большинства разделов немного
превышает материал, который можно рассмотреть на
двухчасовом семинаре. Для некоторых больших разделов
(например, 2 и 6) может потребоваться два семинара. По
сложности задачи подобраны ориентировочно для среднего
студента физических специальностей высших учебных
заведений.
Первое издание учебного пособия вышло в 1982 г.,
второе - в 1992 г., оба были предназначены в основном для
преподавателей кафедры общей физики МФТИ. Настоящее
издание частично переработано, а также дополнено в связи
с расширением программы курса по разделам молекулярной
физики.
Условия большей части рассматриваемых задач уже
были опубликованы в ранее вышедших изданиях. Жирным
шрифтом дана нумерация согласно Сборнику задач по
общему курсу физики, часть 1 (термодинамика и
молекулярная физика) под редакцией В.А. Овчинкина (М.:
МФТИ, 1998), а номера в скобках указаны в соответствиии
со Сборником задач по общему курсу физики
(термодинамика и молекулярная физика) под редакцией
Д.В. Сивухина (М.: Наука, 1976). Условия ряда задач
использованы в несколько сокращенном виде. Номера
некоторых задач не указаны, их нет в упомянутых
сборниках. Одни предлагались на экзаменах и в заданиях
МФТИ за последнее время, другие предложены автором.
Автор выражает признательность заведующему
кафедрой общей физики МФТИ профессору А.Д. Гладуну
за интерес к данной работе. Также автор признателен
заведующему кафедрой общей физики МИФИ профессору
А.Б. Хмелинину, доценту этой же кафедры Т.А. Семено-
Семеновой, и профессору А.В. Степанову (ИЯИ РАН), взявшим на
себя труд по рецензированию пособия. Их замечания
способствовали улучшению книги. Автор благодарит
Т.А. Короткову за помощь при наборе текста на компью-
компьютере.
/7.Ф. Короткое
Раздел 1
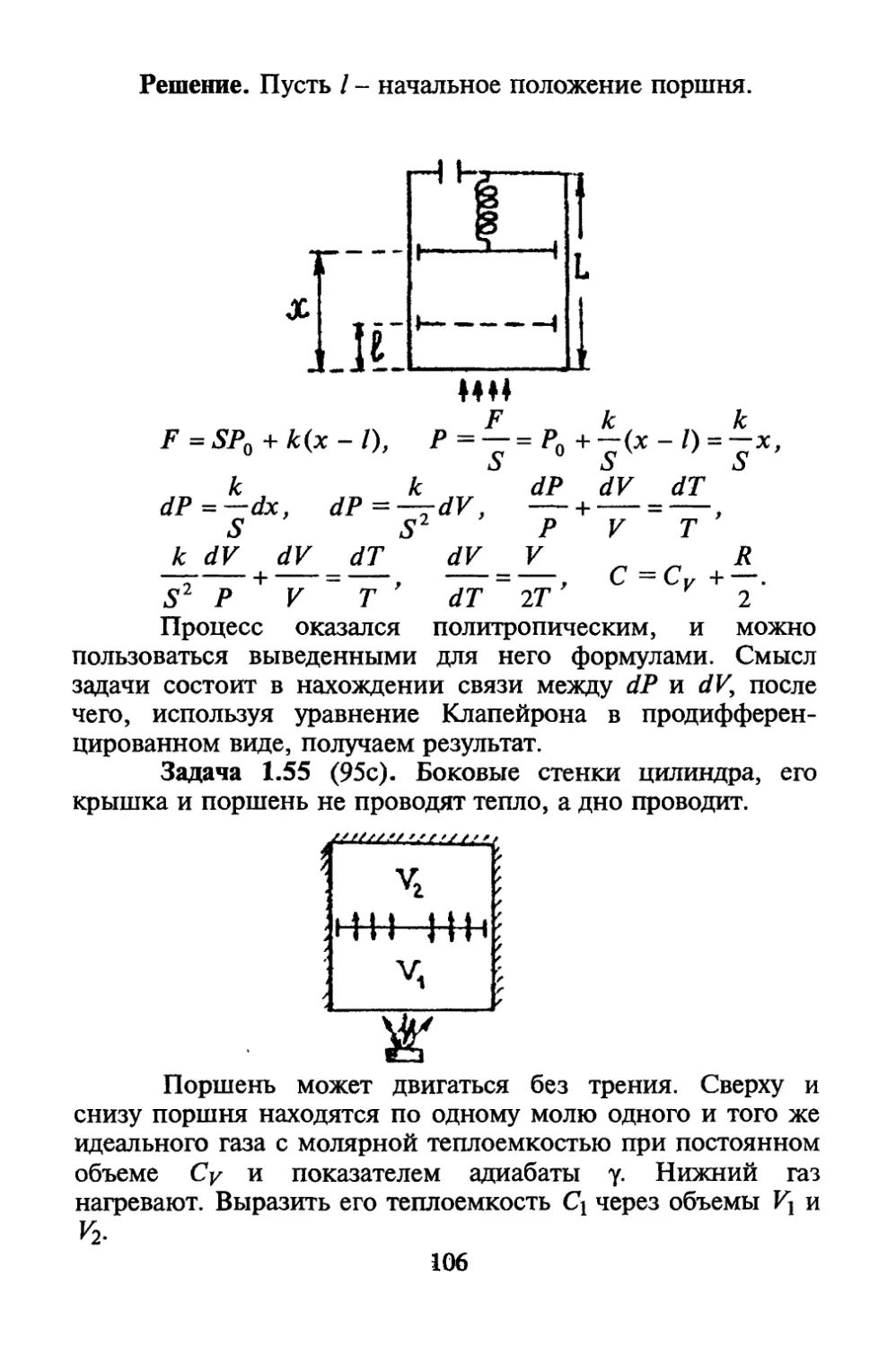
УРАВНЕНИЕ СОСТОЯНИЯ
Для любого вещества между давлением Р,
температурой Т и объемом вещества V существует связь,
которая называется уравнением состояния Р — Р (T,V).
1.1. Идеальный газ
Для идеального газа уравнение состояния имеет вид
PV=vRT, v = — = —. A.1)
NA М<
Это известное уравнение Клапейрона, которое было
получено на основании экспериментальных результатов.
Здесь v - число молей газа, N - количество молекул,
Nл - 6,02 • 1023 1 / моль - число Авогадро, М - масса газа,
ц - молярная масса, R - универсальная газовая посто-
постоянная, равная 8,31-107 эргДмоль-К) = 8,31 Дж/(мольК).
Преобразуем выражение A.1), используя число
частиц в единице объема п = N/V и постоянную Больц-
мана к = R/NA = 1,38-103 Дж/К. Получим
Р=пкТ. A.2)
Это - другой вид уравнения Клапейрона.
Существование уравнения состояния может быть
пояснено с молекулярной точки зрения. Движение молекул
приводит к их соударениям со стенками сосуда, на которые
газ оказывает давление из-за изменения импульса молекул,
т.е. давление получается из-за наличия у молекул импульса.
Температура же зависит от средней кинетической энергии
молекул. Так как для каждой молекулы существует связь
между импульсом и энергией, то при усреднении этих
величин по большому количеству молекул появится связь
между давлением и температурой, то есть уравнение
состояния. При этом, конечно, проявляются и
индивидуальные свойства каждого вещества, такие, как
взаимное притяжение молекул, их способность объеди-
няться, т.е. конденсироваться, превращаться из газа в
жидкость и так далее.
Покажем, как получается уравнение состояния на
примере вывода уравнения Клапейрона, то есть для
идеального газа. Этим названием определяется газ, в
котором взаимодействие между молекулами настолько мало,
что в течение большей части времени движения им можно
пренебречь. Такое пренебрежение допустимо при
достаточной разреженности газа.
Найдем силу F, которую создают молекулы
идеального газа при упругом отражении от небольшой
площадки S, расположенной по нормали к координатной
оси X. За малое время At площадку достигнут все молекулы,
расположенные от нее на расстоянии At Vx, где Vx -
проекция скорости частиц на ось X. В объеме S At Vx
содержится nS At Vx молекул, где п - число частиц в
единице объема. Но только половина попадет на площадку,
так как другая половина будет двигаться в
противоположную сторону из-за равновероятности
направлений. При упругом отражении каждая молекула
передаст площадке импульс 2mVx, а все попавшие на нее
молекулы за время At создадут импульс mnS At V%. Эта
величина согласно второму закону Ньютона равна F At
Следовательно, для давления, которое равно Р — F/S,
получим P-mnV^. Такой результат получен для случая,
когда скорости всех молекул равны. На самом деле,
согласно распределению Максвелла, они разные, поэтому
вместо квадрата скорости следует использовать среднее
значение квадрата скорости всех молекул:
P = mn<Vl >. A.3)
Молекулы движутся не только вдоль X, но и по
направлениям Y и Z В этом случае квадрат модуля
скорости V2 = Vl + Vy + Vl. Так как все направления
равновероятны, то средние квадраты проекций скоростей
равны tyl > = (уу ) = <yl). Следовательно, <К 2) = 3<FX2).
Подставив это выражение в A.3), получим
РЛпа^Х1±ЛпЕк. A.4,
3 2 3 к
Согласно этому уравнению давление идеального газа
пропорционально средней кинетической энергии молекул
т <V2 >
k 2
Сопоставляя A.4) с формулой A.2), получим
соотношение между средней кинетической энергией
молекул и температурой:
m<V2> 3
= -*7\ A.5)
2 2
Более подробное обсуждение полученной формулы
будет дано в разделах 3.1 и 7.2.
1.2. Смеси идеальных газов
Для решения задач о смесях идеальных газов
необходимо использование закона Дальтона: давление смеси
газов равно сумме парциальных давлений каждого газа в
том же объеме. Очевидно, что закон Дальтона справедлив
только для идеального газа, в котором молекулы по-
прежнему не взаимодействуют между собой при
уменьшении расстояния между ними в смесях.
Задача 1.23 D1с). Имеется смесь различных
идеальных газов с массами М\, Мъ Л/з,... и молярными
массами щ, Ц2> Мз>--- соответственно. Показать, что
уравнение состояния такой смеси можно записать в виде
PV =—RT, где М =МХ+М2+М3+... - полная масса
смеси, а постоянная ц играет роль средней молярной массы
смеси. Найти \i.
Решение. Для каждой компоненты смеси имеем
MtRT
равенство Pf = . Суммируя левые и правые части и
\1р
используя закон Дальтона Р =РХ +Р2 +i>3+"-> a также то,
что у всех газов объем и температуры одинаковые, получим
fi/f /? Т7
Р = Е—L , откуда следует M/\i = Z(Af/ /\it) и искомая
\*ч v
формула
Здесь а/ - весовая доля каждой компоненты смеси.
Задача. Найти молярную массу воздуха. Состав
воздуха по массе: С>2 - 23,1%, N2 - 75,5%, Аг - 1,3%, другие
газы -0,1%.
Решение. По формуле A.6) получим
f 0,231 0,755 0,013 т1
II = + + = 29,0.
^ 32,0 28,0 39,9 )
1.3. Барометрическая формула
В качестве примера использования уравнения
Клапейрона приведем вывод барометрической формулы,
которая неоднократно будет использоваться при изучении
курса термодинамики.
Выделим горизонтальный слой воздуха толщиной
dz. Давление выше этого слоя из-за тяжести будет меньше
на величину pgdz, где р = M/V — плотность газа. Откуда
получаем dP = -pgdz . Подставляя выражение плотности из
dP \ig
формулы Клапейрона, получим — = dz . Для
Р RT
интегрирования этого выражения необходимо задать
зависимость температуры воздуха от высоты. Пусть она
будет постоянной, равной Го. Интегрируя, получим
барометрическую формулу
0 V{ RT0J p0 n0 Po
Здесь индексом "О" отмечены параметры при z = 0.
Вычислим высоту атмосферы, на которой давление падает в
V раз. Обозначая ее "Н", получим Н = RTo/(\ig) = 8 км.
10
Отметим, что такая же величина получается для высоты
однородной атмосферы, которая создает то же давление у
поверхности Земли, что и рассмотренная неоднородная.
Атмосфера Земли сохраняет постоянный состав
примерно до высоты 100 км из-за вертикального
перемешивания газов. Если бы перемешивания не было, то
доля легких газов возрастала бы с высотой.
Задача. Найти отношение концентрации газов с
разной молярной массой в зависимости от высоты в изо-
изотермической атмосфере в отсутствии перемешивания.
Решение. Для идеальных газов в изотермической
атмосфере по формуле A.7) получим
Здесь «ю и «20 - концентрации газов на высоте zq.
Задача. Определить на какую высоту поднимется в
изотермической атмосфере герметичный жесткий воз-
воздушный шар из нерастяжимой оболочки, наполненный
гелием. Радиус шара г = 5 м, масса квадратного метра его
оболочки 5 = 0,1 кг/м2, температура воздуха и гелия
/ =0 °С, атмосферное давление у Земли Р = 1 атм, дав-
давление гелия такое же.
Решение. Условие равновесия на максимальной вы-
высоте, где плотность воздуха р, имеет вид
4 з ^ з А г«
— КГ О = — 7СГ Отт^ + 47СГ О.
Отсюда находим
Р = РНе + 38/л
Подставляя найденное значение плотности в
барометрическую формулу, получим
^
= #1п
VI
=
ц цгР J
и
= 13,5км.
Задача. Для изотермической атмосферы получить
зависимость давления воздуха от высоты с учетом
изменения поля тяжести.
Решение. Подставляя в дифференциальное
уравнение равновесия, использованное при выводе A.7),
?oo
зависимость g = — -у, получим после интегрирования
Р = Ро ехр
A.8)
Здесь Rq = 6,4103 км - радиус Земли. При z « Ro
эта формула совпадает с барометрической формулой A.7). В
другом предельном случае, при z-**>, получается конечное
давление воздуха. Следовательно, в реальном поле тяжести
предположение о статическом равновесии приводит к
неверному результату, к бесконечной массе атмосферы.
В действительности на большой высоте равновесие
отсутствует, и Земля непрерывно теряет свою атмосферу.
Восполнение ее идет за счет вулканических газов, а также за
счет выделения кислорода растениями.
1*4. Коэффициент теплового расширения и другие
коэффициенты
Определение уравнения состояния вещества - это
трудная экспериментальная задача. Поэтому часто
ограничиваются отысканием уравнения состояния при
малых изменениях параметров, например, Р и Т. Для этого
пользуются понятиями о коэффициентах, которые опре-
определяются частными производными одних параметров
состояния по другим. Уравнение состояния при этом
превращается в связь между коэффициентами.
Коэффициент объемного расширения позволяет
определить изменение объема тела от нагревания при
постоянном давлении
При постоянной величине а к получим
A.10)
Здесь Vq - начальный объем тела, А Г - приращение тем-
температуры. Индекс "v" при коэффициенте теплового
расширения обозначает, что здесь он относится к
объемному расширению, так как существует еще
коэффициент линейного расширения а^. Можно ввести
также коэффициент расширения площади а,?. Между этими
коэффициентами существует простая связь:
Задача. Шарик стеклянного термометра полностью
наполнен жидкостью. Объем жидкости V, сечение
капилляра S. Найти изменение длины AL столбика
жидкости в капилляре при изменении температуры на AT.
Коэффициент объемного расширения жидкости а,
коэффициент линейного расширения стекла ai . Считать,
что объем капилляра пренебрежимо мал по сравнению с
объемом жидкости.
Решение. При нагревании жидкость будет рас-
расширяться, но при этом будет увеличиваться и объем колбы,
поэтому результат будет зависеть от разницы
коэффициентов объемного расширения жидкости и стекла.
Отметим, что изменение объема колбы не зависит от того,
пустая она или полная.
Пусть объем жидкости, равный AV, войдет в капил-
/ \ &Т
ляр. Тогда получим: AV~ S AL, AL = V [а - За?) .
о
Задача. Найти диаметр D капилляра спиртового и
ртутного термометров при V = 0,50,50,5 = 0,125 см3,
aL =8-10 0С~\ сссп = 108-Ю" °С~Х, если при повышении
температуры на 1 градус длина заполненной части
капилляра увеличивается на 0,1 см (арх= 182-10 °С).
Решение. Используя полученную в предыдущей
задаче формулу, находим для спирта S = 1,05-10-4 см2,
D — J— = 0,011 см. Для ртути диаметр будет больше в
V п
1,4 раза. Диаметр получился очень малым. Чтобы было
13
лучше видно столбик жидкости, его делают не круглым, а
плоским.
Помимо коэффициента теплового расширения
используются еще два других коэффициента: модуль сжатия
К к термический коэффициент давления C:
Ю М1
dVjT P
В формуле, определяющей модуль сжатия, стоит
знак минус, чтобы величина К была положительной, так
как существование веществ с положительной производной
дР) (dV)
или невозможно из-за их неустойчивости по
dV )т \дР )т
отношению к внешнему воздействию.
Отметим, что величина \/К называется коэф-
коэффициентом сжимаемости.
Задача 1.5 C9с). Найти коэффициенты объемного
расширения, модуль сжатия и термический коэффициент
давления для идеального газа.
Решение. Определив соответствующие частные
производные, получим:
То То
Здесь нулевой индекс соответствует начальному
состоянию, при котором вычисляются коэффициенты.
Очевидно, что коэффициенты зависят от того, что принято
за это состояние.
Задачи типа 1.1, 1.2 B8с, 29с). Найти связь между
коэффициентами а, К и р.
Решение. Рассмотрим общий вид уравнения
состояния Р = P(V,T). Запишем дифференциал давления
При dP= О это выражение принимает вид
Ч1й MifK
Входящие сюда частные производные выражаются через
коэффициенты К и р, а отношение дифференциалов dVp и
dTp является в свою очередь частной производной, так как
каждый из дифференциалов берется при постоянном
давлении. Получаем соотношение между производными
дГ]т{дТ)
Отметим, что частную производную можно
рассматривать как отношение дифференциалов в том
случае, если они взяты при одних и тех же условиях.
В полученном выражении сократить дифференциалы
нельзя, так как, например, dPj* dPy.
Используя соответствующие определения коэффи-
коэффициентов, получим
осАУр = Ро. A.13)
Соотношение между коэффициентами оказалось
зависящим от давления, при котором оно определяется.
Обычно это делается при атмосферном давлении.
Формула A.13) часто используется для нахождения
термического коэффициента давления, так как два других
коэффициента находятся из относительно более простых
опытов.
Задача типа 1.3, 1.4 C0с, 31с). По заданным
значениям а = 18-Ю-5 ЧТ1 и \/К = 0,39-10 1/атм
вычислить р при атмосферном давлении и, используя это
значение, определить, на сколько нужно увеличить внешнее
давление, чтобы сохранить постоянным объем ртути при
нагревании ее от 0° до 10 °С.
Решение. Используем формулу A.13)
аК 18 10
0,39 • 10~5
= 46 °С~К
По этой величине находим нужное давление
ДР = Рор AT = 460 атм.
15
Раздел 2
СТАТИСТИЧЕСКИЕ ЗАКОНОМЕРНОСТИ
Все физические величины в термодинамике с
молекулярной точки зрения имеют смысл средних
значений, так как получаются в результате действия
огромного числа молекул. Такими являются и давление, и
температура, и плотность всех веществ. Во многих случаях
реальные вещества можно рассматривать как сплошные
среды, но этого достаточно не всегда. Например, такие
явления, как броуновское движение небольших частиц или
процессы обогащения изотопов урана при прохождении их
в газообразном состоянии через пористые перегородки
могут быть объяснены только с использованием
молекулярных представлений. Эти и многие другие явления
подчиняются статистическим или вероятностным
закономерностям. Отметим некоторые важные положения
теории вероятностей.
2.1. Случайные события
Событие называется случайным, если оно может как
произойти, так и не произойти. Обычно такое имеет место,
когда на результат оказывают влияние множество
различных явлений, учесть которые практически
невозможно. Например, при бросании монеты с быстрым
вращением вокруг диаметра трудно предсказать число
оборотов до падения, а еще труднее рассчитать все
процессы ее остановки при взаимодействии с преградой,
так что заранее не известно, что выпадет - орел или решка
(решетка), каждое из событий является случайным.
Вероятностью события называется отношение числа
благоприятных событий к общему их количеству. Если
возможность осуществления двух событий одинаковая, то
они являются и равновероятными. Естественно, что сумма
вероятностей всех возможных событий равна единице.
и
Например, при бросании монеты возможны всего
два события - выпадение или орла, или решки. Если они
равновероятны, то вероятность каждого равна, очевидно,
1/2. Для этого, конечно, монета должна иметь симмет-
симметричную форму и центр ее массы должен совпадать с
геометрическим центром. Используя свойства симметрии и
однородности, можно во многих случаях еще до опыта
установить так называемую априорную вероятность того или
иного события.
Опытная вероятность устанавливается по большому
числу испытаний N, при условии N » я, где п - число
благоприятных событий. Можно указать предельное
соотношение
P-Um^-jJ-. B.1)
Отметим важное свойство независимых случайных
событий: вероятность одновременного появления нескольких
независимых случайных событий равна произведению их
вероятностей.
Задача. При трехкратном бросании монеты
определить вероятность выпадения орла во всех трех
случаях, а также вероятность выпадения орла хотя бы один
раз.
Решение. Вероятность трехкратного выпадения орла
равна произведению вероятностей, то есть составит
A/2K-1/8.
Для решения второй части задачи используем
вероятность выпадения решки при трех бросаниях, это тоже
равно 1/8. Во всех остальных результатах будет
присутствовать орел. Следовательно, вероятность выпа-
выпадения орла хотя бы в одном случае из трех составит 7/8.
Задача. Из двух пушек одновременно стреляют по
цели. Найти вероятность ее поражения, если вероятность
попадания в цель первой и второй пушками равны 0,6 и 0,8.
Цель считается пораженной, если в нее попал хотя бы один
снаряд.
17
Решение. Сначала найдем вероятность промаха при
обоих выстрелах, которые естественно считать неза-
независимыми. Поэтому вероятность промаха равна произве-
произведению вероятностей 0,4-0,2 = 0,08. Следовательно, вероят-
вероятность поражения цели 0,92.
2.2. Соединения
Перестановками из N элементов называются их
соединения, отличающиеся друг от друга только порядком
входящих в них элементов. Например, перестановки из трех
элементов а, Ъ, с : abc, bca, cab, cba, bac, acb. Число всех
перестановок из N различных элементов равно N!.
Размещениями А# из N элементов по п называются
такие их соединения, которые различаются друг от друга
самими элементами или их порядком. Например,
размещения из 3 элементов а, Ъ, с по 2: ab, ас, be, ba, ca,
cb. Число всех размещений из N по п
Сочетаниями из N элементов по п называются их
соединения, различающиеся друг от друга только самими
элементами. Например, сочетания из трех элементов а, Ь, с
по 2: ab, ас, be. Число всех сочетаний из N различных
элементов по п (обозначается Сдг):
Nf
CnN= • ... B.3)
п ! (N - п) !
Отметим, что С? =C#~W. Кроме того: С% =С% =1
и0! = 1.
Задача. Совершенно случайным образом отобраны
18 человек. Какова вероятность того, что по крайней мере у
двоих из них окажется один и тот же день рождения?
Решение. Сначала найдем вероятность того, что все
дни рождения разные. Число комбинаций разных дней
рождения у 18 человек есть число размещений B.2) из 365
по 18. Именно размещений, а не сочетаний, так как при
перестановке дней получаются новые варианты
комбинации. Например, если у двух людей А и В дни
рождения соответственно 1 января и 1 мая, или же наоборот
- 1 мая и 1 января, то это два варианта, а не один. Получим
18 365 !
А\* = = 365 • 364 - 363 ¦...• 348.
C65-18)!
Полное число возможных дней рождения одного
человека, очевидно, равно 365. У двоих число комбинаций
равно произведению 365-365. У 18 человек полное число
возможных комбинаций дней рождения 36518. Вероятность,
что все дни рождения разные, будет равна отношению числа
таких вариантов к полному количеству комбинаций
А\1< 365-364-363...-348
36518 36518
Теперь найдем вероятность того, что не все дни
рождения разные, а будут и одинаковые:
1 - 0,653 = 0,347.
Задача. В урне два белых и четыре черных шара.
Один человек держит пари с другим, что среди вынутых
трех шаров будет ровно один белый шар. В каком
отношении находятся шансы спорящих?
Решение. Полное число вариантов вынуть три
любых шара из шести с|=20. Число вариантов вынуть
один белый шар из двух С\=2, а вынуть два черных из че-
четырех - с| =6. Всего благоприятных вариантов С\с\ = 12.
Следовательно, вероятность вынуть один белый и два
c\cl з
черных шара Р+=—— =—. Все остальные варианты
св 5
неудачные, их вероятность Р_ = 1 - Р+ = 1 - 3/5 = 2/5.
Искомое отношение вероятностей Р+/Р. = 3/2.
19
2.3. Биномиальное распределение
Получим такое распределение при рассмотрении
физической задачи.
Задача 9.15. Сосуд с N молекулами идеального газа
разделен на две части V\ и V2 . Найти вероятность того, что
в объеме V\ будет содержаться N\, а в объеме V2 будет N2
молекул.
Решение.
1. Число перестановок всех молекул друг с другом
при фиксированных координатах равно N! .
2. В это число входят перестановки N\ молекул
между собой в объеме V\, их число равно N\l.
Соответственно для объема V2 это число равно N2\.
3. Перестановки внутри одного и того же объема не
дают новых распределений. Поэтому число независимых
перестановок, при которых содержится N\ молекул в V\ и
N\
N2 в объеме V2, равно .
NX\N2\
4. Найдем вероятность одного из таких
распределений. Вероятность того, что в объеме V\ находится
одна молекула, есть — . Вероятность, что там
содержится N] молекул, равна ? . Соответ-
ственно для вероятности наличия N2 молекул в объеме V2
f
5. Вероятность одновременного присутствия N\ в V\
\\ ЩъУ2 есть произведение
20
6. Так как такое распределение осуществляется
N\
многими способами, а именно , то искомая
вероятность одновременного нахождения N\ в V\ и N2 в V2
определяется произведением
N\ { Vx ff V2 Г2
P= — *— . B.4)
Здесь N= N1 + N2 .
7. Обозначим вероятность нахождения одной
молекулы в объеме V\ параметром v = —, а в объеме ^
Vx+V2
v2
соответственно параметром q-т:—~- Очевидно, что
р +q = 1. В таких обозначениях формула B.4) будет иметь
вид
^Л, B.5)
NX\N2\
где N\ + N2= Nnp + q = 1.
При несколько других обозначениях, используя я
s JVi и q = 1 - р, получим
р= ,J! ,/"^-^"л- B-6)
n\\N -п)\
И формула B.5), и B.6) называются биномиальным
распределением. Первая имеет симметричный вид как
относительно JVi и N2, так и относительно р и q, но каждая
пара связана указанными ниже формулы B.5)
соотношениями. Если использовать эти соотношения, то
получим распределение B.6), которое является функцией
трех независимых параметров N, п и р. Из него можно
вывести рассматриваемые ниже распределение Пуассона и
распределение Гаусса.
Важными характеристиками случайной величины п
являются ее средняя величина <п> и дисперсия а2, которая
равна среднему значению квадрата отклонения п от
среднего
21
а2 = <(„ _ <n>J>. BJ)
Здесь и дальше угловые скобки обозначают
операцию осреднения.
Задача. Вычислить дисперсию а2 случайной
величины п через ее среднее значение <п> и среднее
значение ее квадрата <п2>.
Решение. Используем осреднение левой и правой
части равенства (я - <п>J = п2 - 2п <п> + <я>2. Получим
<(„ _ <Л>J> = <п2> - 2<л> <я> + <п>2 = <п2> - <п>2.
Следовательно:
а2 = <„2> _ <п>2 щ B.8)
Задача. Вычислить среднее значение <п> и
дисперсию а2 = <(л - <п>J> дискретной случайной вели-
величины п, подчиняющейся биномиальному распределению.
Решение. Сначала отметим, что формула B.6)
получила свое название из-за того, что аналогично
определяются биномиальные коэффициенты в формуле
Ньютона:
? n\(N-n)\
Если аи Ъ в этой формуле заменить на р и q, сумма
которых равна единице, то и сумма в правой части тоже
будет равна единице. Так и должно быть, так как суммарная
вероятность всех событий по формуле B.6) должна быть
равна единице.
Теперь определим среднее значение величины п по
биномиальному распределению. Для этого ее нужно
умножить на вероятность появления по формуле B.6) и
результат просуммировать по всем возможным значениям
»
~ (n-l)\(N-n)V
v^1 (N -1) ! м
Npy\ T~PnQNn = Np (p+q) ~X-Np. B.9)
?> n\{N-n)\P
Для вычисления дисперсии по формуле B.8) сначала
найдем среднее значение вспомогательной величины <(п (п
(отметим, что здесь первые два члена суммы равны нулю,
так как 0 ! = 1, а у следующих в числителе и в знаменателе
можно сократить произведение л (л - 1) и начать суммиро-
суммирование сй = 2, предварительно переместив общие множите-
множители за знак суммы)
= N{N - \)р2{р + q)N~2 = N {N - l)p2.
Вычисленная вспомогательная величина выражается
через средние значения:
<(л (п - 1))> = <л2> - <л>,
так как среднее суммы равно сумме средних величин.
Следовательно <п2> = Np + N(N- l)p2.
Находим а2 по формуле B.8):
а2 = <(„ _ <л>J> = <п2> _ <л>2 =
= Л^ A -Р)= <п> A -Л- B.Ю)
Еще раз отметим, что дисперсия а2 является средним
квадратом отклонения случайной величины от ее среднего
значения и используется как количественная мера
случайного процесса. Эквивалентной мерой служит среднее
квадратичное отклонение а, равное корню квадратному из
дисперсии. Эта величина характеризует разброс случайной
величины около ее среднего значения.
Задача. Человек может двигаться лишь вдоль стены
и только на один шаг: после этого он падает, поднимается,
но забывает, куда двигался раньше, поэтому следующий шаг
делает с равной вероятностью либо влево, либо вправо.
Ш
Найти вероятность того, что сделав N таких движений, он
сместится вправо на Дл шагов.
Решение. Допустим человек сделал влево лл шагов и
Лщ, вправо, следовательно, Пщ> + лл = Ж При этом вправо
было совершено на Ал шагов больше, поэтому
пщ> - пп ~ Аи- Отсюда получим число шагов, которые нуж-
нужно сделать вправо: лпр = (N + Ал)/2. Так как должно полу-
получиться целое число, то обе величины N и An следует зада-
задавать либо четными, либо нечетными. Теперь можно вос-
воспользоваться биномиальным распределением B.6) при
/7 = 1/2 и л = GV + Ал) / 2. Для искомой вероятности
находим
N+An / •
N +Ап), N -AN), \2
Рассмотрим пример. Пусть до двери расстояние
равно An = 3 шагам. Какова вероятность дойти до нее
такому человеку как раз за три шага, при N = 3 ? По
найденной формуле получим довольно малую вероятность Р
= 1/8, что соответствует одновременности трех независимых
событий при вероятности каждого 1/2. Если N = 7, то
вероятность будет более существенной, равной 21/32.
Естественно, что такой способ передвижения оказывается
не очень эффективным.
2.4. Распределение Пуассона
Преобразуем биномиальное распределение B.6) к
виду, удобному для предельного перехода к большим N.
Заменим параметр вероятности р в соответствии с
формулой B.9) р = <n>/N и введем более простое обоз-
обозначение для среднего значения щ = <п> , то есть исполь-
используем р = щ/N. Кроме того, сократим общие члены у N! и
(N - л)!, а также преобразуем показатель степени послед-
последней скобки. Формула B.6) будет иметь вид
24
р =
N{N -l)-(N -и + l) Яр
и! N"
1-
л0
N
1 _ .
JL
N
и!
Перейдем в этом выражении к пределу N -» °° при
фиксированном щ (очевидно, что подобный переход
соответствует также условию р^О), Первая квадратная
скобка при этом будет стремиться к единице, а вторая - к
величине ег*. В результате получим формулу, которая
называется распределением Пуассона:
Рп =
° .-"
B.11)
Можно убедиться, что среднее значение,
вычисленное по этой формуле, совпадает с аналогичной
величиной для биномиального распределения B.9):
=и
0.
B.12)
л=0
Дисперсия распределения Пуассона равна среднему
значению случайной величины
а2 =<(п-п0J >=
B.13)
и находится в соответствии с формулой B.10) при малом р,
которое использовалось в B.11).
Если числа п большие, то вычисление факториала,
входящего в распределение Пуассона, становится
трудоемким, а при л, сопоставимых с числом молекул
воздуха даже в малом объеме и при низких давлениях,
просто невозможно. Однако как раз в таких случаях расчет
может быть сделан по асимптотической формуле Стирлинга:
ь— +.Д и»1. B.14)
<е J V 12л )
Здесь второй член в скобке приведен для того, чтобы
можно было сделать оценку ошибки приближения, в
расчетах он обычно не учитывается. Согласно B.14) уже
при п — 10 погрешность асимптотической формулы Стир-
линга без учета второго члена составляет меньше одного
процента.
Отметим, что в задачах с большим значением п
можно использовать приближенную формулу Стерлинга:
In л ! = л In л - п или п ! = (п/ё)п . B.15)
Однако это выражение менее точное, чем B.14). Но
при вычислении In п ! (не п !) оно приводит к ошибке
меньше одного процента уже при п > 100.
Вернемся к формуле B.11). Для больших п после
использовании формулы Стерлинга B.14) распределение
Пуассона B.11) будет иметь вид
"-"о^ BЛ6)
Рп=
<у/2кп
2.5. Распределение Гаусса
Распределение B.16) имеет максимум вблизи
среднего значения и при больших значениях щ быстро
убывает по обе его стороны. Используя это свойство,
упростим выражение B.16) и получим новое распре-
распределение. Для определения экстремума сначала пролога-
прологарифмируем рассматриваемое выражение, а потом продиф-
продифференцируем и приравняем нулю:
d d Г 1 1 1
— \пРп =——In 2л:-—In п + п In я0 - п In л + п - и0 =
dn dnl 2 2 J
= -— + In na - In n = 0.
2n °
Отсюда следует, что для больших чисел, а именно
при условии In п » —, максимум функции Рп будет при
2п
п = щ, то есть при среднем значении случайной величины.
26
Разложение около максимума начинается с квадратичного
члена. Находим вторую производную при отмеченном
условии больших и, это будет: —— р =-— и получаем
dn n
разложение
In Рп - -— In 271-— In nQ [п - п0) .
2 2 2л0
Отсюда находим:
1
Напомним, что при выводе этой формуле принято,
что среднее значение щ » 1. Существенная величина
вероятности по ней получается только для и, близких к щ.
Если рассматривать такие большие последовательные числа,
то они относительно мало отличаются друг от друга и
также мало отличаются соответствующие вероятности.
В этих условиях вместо дискретного распределения для
отдельных чисел удобно перейти к непрерывному
распределению. Для этого умножим обе части полученной
формулы на dn:
(п-п0J
2n° dn. B.17)
Полученное выражение является частным видом
распределения Гаусса для случая, когда дисперсия равна
среднему значению. Величина Р[п,п0) является
плотностью вероятности, она определяет вероятность
события при значениях п в интервале от п до п + dn и
зависит от одного параметра щ.
Теперь вместо суммирования вероятностей можно
интегрировать соотношение B.17). Например, при значении
по около ста и больше возможна следующая приближенная
замена суммирования интегрированием:
27
л=1ОО ioO
Обратим внимание, что распределение B.17)
нормировано, то есть вероятность всех возможных событий
равна единице. Чтобы убедиться в этом следует
использовать то, что формула симметрична относительно «о
в очень широкой окрестности из-за быстрого убывания
экспоненты при большой величине среднего значения, для
которого оно и выведено. Также вследствие этого быстрого
убывания интегрирование можно производить в
бесконечных пределах: основное значение интеграла
набирается вблизи среднего, а "хвосты" не имеют значения.
Поэтому условие нормировки состоит в выполнении
равенства
которое выполняется, так как приводится к известному
интегралу Пуассона (вычисление имеется в Разделе 3.1):
е~*\
Вернемся еще раз к распределению B.17) и
подчеркнем, что оно является частным видом
распределения Гаусса, так как зависит только от одного
параметра п^, то есть от среднего значения. При этом
дисперсия равна этой величине: с2 = и0.
Найдем более общее двухпараметрическое
распределение Гаусса. Для этого в выражении плотности
вероятности в правой части формулы B.17) в обоих
знаменателях (и перед экспонентой, и в ее показателе)
вместо п0 подставим дисперсию а2, которая наряду с п0
28
будет рассматриваться как второй независимый параметр.
Получится распределение Гаусса, которое, кроме того, еще
называется нормальным распределением:
(*-"оJ
2а2
P[n;no,^jdn= *—е 2<5 dn.
OV27C
B.18)
Как уже отмечалось, корень квадратный из
дисперсии, то есть величина а , называется
среднеквадратичным отклонением. Этот параметр
характеризует эффективный диапазон изменения случайной
величины. При распределении Гаусса вероятность
попадания случайной величины п в интервал п0 ± а равна
0,68, в интервал по±2а - 0,95, а в интервал nQ ± За
соответственно 0,997.
2.6. Энтропия и информация
Для сравнения между собой случайных объектов
(событий, величин, функций) и для использования в теории
информации нужна их количественная характеристика.
Такая величина — энтропия — сначала была введена в
термодинамике Клаузиусом и Больцманом, а потом
применена в информатике Хартли и Шенноном. Эти
разделы науки оказались связаны между собой, но
энтропии, используемые там, различаются между собой
единицами измерения.
Статистическая энтропия Ss служит мерой
неопределенности случайных величин Xt при известной
вероятности их появления Р/
Ss =К^ In (l / P,) при ХЛ = I- B-19)
Здесь К - множитель, зависящий от выбранной
системы единиц измерения энтропии, М — число случайных
величин.
При К = 1/1п2 результат получается в битах, то есть
в двоичных единицах, а найденное выражение определяет
информационную энтропию 5^:
м м
Su = 2>/ log2 A / Л) при 2>< = 1. B.20)
Это формула Шеннона. По сравнению с
приведенной ниже формулой Хартли B.23), в B.20)
использовано среднее значение логарифма вероятности в
соответствии с определением среднего значения некоторой
ым
величины X: < X >=
При К = к, где к = 1,38-103 Дж/К — постоянная
Больцмана, получается статистическое выражение для
термодинамической энтропии S:
м м
S = kYdPi In (l / Р() при 2Л = L B-21)
Вычисленная по этой формуле энтропия получается
в тех же единицах, что и к, то есть в Дж/К. Если известна
ее величина в таких термодинамических единицах, то,
разделив на произведение
0
б ит
30
получим численное значение энтропии в битах. Подробнее
соотношения между разными единицами будут обсуждены
несколько позже, а пока вернемся к анализу определяющей
формулы B.19).
Если одна из величин Р, равна единице, а другие
нулю, то есть информация достоверна и неопределенность
отсутствует, по B.19) получим Ss = О (учтено, что степень
сильнее логарифма). Когда все Р/ одинаковы и равны Р,
неопределенность в информации максимальна и энтропия
принимает наибольшее значение. В этом случае формулы
B.19) — B.21) будут более простыми:
Ss=Kln{l/P). B.22)
Su = log2(l/P). B.23)
Хартли так объясняет смысл последней формулы:
"если в заданном множестве, содержащем N элементов,
выделен какой-то элемент X, о котором заранее известна
лишь его принадлежность к множеству, то чтобы найти X,
необходимо получить количество информации, равное
\og2N бит". Здесь принято, что все элементы одинаковы,
тогда вероятность Р = 1/7V. Таким образом, энтропия — это
информация, которой недостает для полного определения
случайного объекта. Это относится и к выражению B.21).
S = к In (l / P). B.24)
Рассмотрим более подробно формулы B.20) и B.23).
Численная величина информационной энтропии определяет
(с точностью до единицы) среднее число двоичных знаков,
то есть бит, необходимое для различения (или записи)
возможных значений случайной величины. Поэтому
энтропия есть количество добавочной информации,
необходимое для полного определения случайной величины
даже в термодинамических единицах.
it
0 =
1 =
2 =
3 =
0
1
10
11
4 =
5 =
6 ==
7 =
100
101
110
111
Двоичная система широко используется в
вычислительной технике, так как оперирует всего с двумя
возможностями, например, включением или выключением
какого-нибудь элемента в электрической схеме. Любое
число записывается последовательностью нулей и единиц. В
таблице приведено соответствие записей в десятичных
единицах и в двоичной системе.
8 = 1000 12 = 1100 16= 10000
9 = 1001 13 = 1101 17 = 10001
10=1010 14=1110 18=10010
11 = 1011 15=1111 19=10011
Задача. Какое количество бит содержится в
произвольном трехзначном числе?
Решение. Трехзначные числа — это числа от 100 до
999, всего их 900. Они ничем не выделены друг от друга,
поэтому вероятности появления любого из чисел при
случайной выборке одинаковые, равные 1/900. Количество
бит, необходимое для устранения неопределенности, равно
информационной энтропии B.23):
$и = Iog2900 = 9,8 бит.
Число двоичных знаков для записи конкретного
числа может быть только целым, поэтому результат следует
округлить до 10 бит. Отметим, что 210 = 1024, следова-
следовательно, количество найденных знаков действительно
достаточно для описания любого трехзначного числа. В
этом примере было определена информация в битах,
которая необходима для выделения определенного
трехзначного числа из всего многообразия таких чисел. Это
подтверждает, что энтропия есть количество добавочной
информации, необходимое для полного определения
случайной величины.
32
Задача. В русском алфавите используется 33 буквы
и пробел между словами, всего 34 знака. Найти
информационную энтропию, то есть число бит,
приходящихся на один знак.
Решение. Сначала решим задачу при предположении
о равной вероятности появления букв, при этом Р = 1 / 34.
Для расчета используем формулу B.23):
^и = Iog2 34 = 5,09 бит.
Но частоты, то есть вероятности появления букв в
русском тексте, разные, они приведены в таблице.
Вероятности Р, букв в русском языке
пробел 0,175 р 0,040 я 0,018 х 0,009
о
е, ё
а
и
т
н
с
0,090
0,072
0,062
0,062
0,053
0,053
0,045
в
л
к
м
д
п
У
0,038
0,035
0,028
0,026
0,025
0,023
0,021
ы
3
ь, ъ
б
г
ч
й
0,016
0,016
0,014
0,014
0,013
0,012
0,010
ж
ю
ш
ц
щ
э
ф
0,007
0,006
0,006
0,003
0,003
0,003
0,002
Результат получим по формуле Шеннона B.20):
5И = 0,175 log2 A/0,175) + 0,090 log2 A/0,090) +
+ ... +0,002 log2 A/0,002) = 4,35 бит.
Это число заметно меньше, чем 5,09 бит, полученное при
предположении о равной вероятности. Так и должно быть,
так как вычисления проводились яри наличии некоторой
дополнительной информации о частоте появления букв.
Напомним, что информационная энтропия определяет
число бит, необходимое для выделения одной буквы.
Использование дополнительной информации уменьшило
неопределенность задачи и энтропия соответственно
снизилась. Как уже отмечалось, энтропия максимальна при
равной вероятности появления случайных величин.
Если система, в которой происходят случайные
события, получает некоторую информацию /, то
неопределенность уменьшается и энтропия падает. Сумма
этих величин остается постоянной:
?+/= const. B.25)
Новое значение энтропии S можно определить по
B.20) или B.23), а потом вычислить полученную
информацию / по ее уменьшению из B.25).
Рассмотрим задачу об определении победителя на
скачках при игре в тотализатор. Пусть в заезде участвует 16
лошадей. Пока мы ничего не знаем об их особенностях, то
должны считать, что шансы выиграть заезд у всех
одинаковы. Начальную энтропию находим по B.23), а
начальная информация, очевидно, равна нулю:
Sq = Iog2 16 = 4 бита,
Если нам каким-то образом становится известна
дополнительная информация, например, что лошади темной
масти, которых половина в данном заезде, резвее, то
победителя нужно выбирать среди них, то есть среди 8
лошадей. Получим
8 = 3 бита,
34
h = So - Si = 4 - 3 = 1 бит.
Энтропия уменьшилась и стала равна 3-м битам, а
полученная нами информация о том, что выиграют черные,
равна 1-му биту.
Далее мы продолжаем поиски и узнаем, что быстрее
скачут высокие лошади, которых среди темных тоже
половина. Следовательно, нужно выбирать уже среди
четырех претендентов. Учитывая это, найдем
^2 = 1°ё2 4 = 2 бита,
h = So - S2 = 4 - 2 = 2 бита.
Энтропия уменьшилась до 2-х бит, а вся полученная
информация также стала равняться 2-м битам. Если далее
нам удастся узнать еще два подобных признака, то
победитель будет определен, окончательная энтропия равна
нулю, а вся полученная информация будет равна 4-м битам.
Отметим, что начальная энтропия, то есть начальная
неопределенность, тоже составляла 4 бита. В результате
получения 4-х бит информации неопределенность
уменьшилась до нуля.
2.7. Статистическое и термодинамическое определение
энтропии
В термодинамике бесконечно малое изменение
энтропии dS определяется для обратимых процессов
формулой dS = 5Q /Т, где 5Q — бесконечное малое
количество теплоты, Т - абсолютная температура. При
изменении объема идеального газа и одной и той же
температуре, то есть при ТА =Г2, используя первое начало
термодинамики, для разности энтропии в Разделе 9
получено:
S2-Sx= Nk ln(F2 / К,) . B.26)
Здесь N — число молекул, к — постоянная
Больцмана, V\ и Vi — начальный и конечный объем газа.
Соотношение между энтропией системы в
некотором состоянии и вероятностью того же состояния
определяется формулой Больцмана:
S = kln W, B.27)
где W — число возможных вариантов осуществления
данного состояния газа. Величина W называется
статистическим весом.
Если число вариантов равно N и все они
равновероятны, то W= N. Кроме того, вероятность каждого
Р = 1/N, поэтому в данном случае W = 1/Р. При таком
условии формула Больцмана совпадает с информационной
энтропией, выраженной в термодинамических единицах
B.24). Покажем, что подобная связь имеется и в более
сложном случае.
Задача. Выразить энтропию идеального газа через
вероятности, используя формулу Больцмана B.27).
Решение. Сначала найдем статистический вес.
Разместим мысленно N молекул идеального газа по М
объемным ячейкам так, чтобы в каждой было
соответственно по Щ, iV2, ... Nmчастиц. Получим
N\
W = . B.28)
NJ-Ntl. ... -NM\
36
Вывод формулы следует из того, что полное число
вариантов размещения N частиц путем их перестановок
между собой равно N !. Но в это количество не должны
входить перестановки fy молекул между собой внутри
каждого /-го объема. Число таких перестановок в любом
объеме равно Nj !. Они не приводят к новым состояниям
ввиду тождественности рассматриваемых частиц. Поэтому
величину N ! нужно разделить на число таких перестановок
в каждом объеме.
Для упрощения выражения B.28) воспользуемся
приближенной формулой Стирлинга B.15). Получим
B-29)
м
Подставим найденный результат в B.27) и
используем то, что вероятность Pt нахождения N( молекул в
ячейке равна Nj/N.
( #,
S = kln\N]nN -2^Ni In N; \=
= к In \N In N - N2JPl In (NP,) \= B.30)
"^ In
Следовательно, энтропия по формуле Больцмана
B.27), преобразованная к виду B.30), выражается через
вероятности для одной молекулы в ансамбле, т.е. при N = 1,
аналогично тому, как информационная энтропия в
термодинамических единицах B.21).
Задача. Найти увеличение энтропии идеального газа
при его расширении в пустоту из объема V\ до объема
V2 = nVx, где п — целое число, по формуле Больцмана и по
формуле, полученной в термодинамике в Разделе 9.4.
Решение. Считаем, что через некоторое время после
расширения в пустоту все N молекул будут распределены по
объему равномерно и в каждом из п объемов их будет по
N/n, При вычислении статистического веса можно
использовать приближенную формулу B.29), так как для
газа N и N/n - очень большие числа. Получим
w. "' ¦¦„'¦
[{N I n)
N/пЛ"
Используя B.27), найдем
у
. B.31)
Ух
До расширения газа энтропия, в соответствиии с
B.27), равна нулю, так как для единственного объема по
B.28) величина W = 1. Поэтому найденный результат
согласуется с изменением энтропии при вычислении по
формуле B.26), полученной в термодинамике. Отметим, что
при расширении идеального газа в пустоту его температура
в конечном состоянии равна начальной, так как газ не
совершает работы. Более подробно такая задача будет
рассмотрена в Разделе 9.4.
Задача. N молекул идеального газа находятся в
объеме V. Вычислить выигрыш информации А/, если в
результате некоторого процесса молекулы были вытеснены
из малого объема AV« V. Принять N » 1.
Решение. Результат B.31) был получен для целого п,
но формула B.26) верна при любом отношении объемов,
38
что естественно принять и для B.31). Полагая —— = 1 -
и используя разложение логарифма, получим
AV
—¦ B-32)
Энтропия газа уменьшилась, так как уменьшилась
неопределенность в связи с уменьшением объема.
Следовательно, в соответствии с B.25) информация о газе /
увеличилась на такую же величину. В B.32) энтропия
выражена в термодинамических величинах, таких же как и
постоянная Больцмана к. Для получения результата в битах
его нужно разделить на произведение к In 2, как это уже
отмечалось при обсуждении формулы B.21). Следовательно,
выигрыш информации будет
B.33)
Kin 2
Задача. Вычислить затрату энергии для получения 1-
го бита информации в предыдущей задаче, если температура
газа Г=300К.
Решение. При вытеснении молекул из объема AV
была совершена работа АА = р А V, где р — давление газа.
При этом выигрыш информации в соответствии с B.33)
составил А/ бит. Следовательно, расход энергии для
получения 1-го бита информации будет составлять
АА pVln 2 23
= = кТ\п 2 = 1,38 • 10 3 • 300 • In 2 =
А/ N
= 3 • 10~21 Дж/бит.
Такова в данном случае энергетическая стоимость
одного бита информации, она оказалась очень небольшой.
Последние две задачи являются иллюстрацией того, что для
получения информации требуется вполне определенная
затрата энергии. Отметим, что при решении последней
задачи было использовано уравнение состояния идеального
газа A.2).
40
Раздел 3
РАСПРЕДЕЛЕНИЕ МАКСВЕЛЛА
Распределение Максвелла используется для
определения числа молекул, имеющих определенные
значения как компонент, так и абсолютных значений
скоростей. Кроме того, различаются распределения для
одно-, двух- и трехмерных случаев. Основным является
соотношение для одномерного распределения по
компонентам скорости, которое может быть получено из
распределения Гаусса B.17). Это распределение применимо,
когда имеется большое количество независимых случайных
величин. Скорости огромного числа молекул газа
удовлетворяют этому условию. Обозначим Nq - полное
количество молекул, dN - число молекул, имеющих
проекции скорости в интервале vx, vx + dvх.Применяя
B.17), получим
'
NQ
-»*,. C..)
х
Здесь учтено, что среднее значение скорости vx
равно нулю, так как и в положительном, и в отрицательном
направлениях оси л: движется равное число молекул.
Параметр а является среднеквадратичным значением
случайной величины, в данном случае a2 =<v2 >. Для
определения <v2 > используем связь этой величины с
температурой аналогичную A.5). Из A.1) и A.2) получим:
т <vl > I 2 = кТ I 2. Отсюда находим <угх > и
подставляем в C.1) вместо а2:
е C.2)
No \2kT
3.1. Распределение вероятностей для компоненты
скорости
Соотношение C.2) является распределением
Максвелла для компоненты скорости vx (одномерное
распределение). Напомним значение использованных в нем
параметров: т - масса молекулы, к - постоянная
Больцмана, Т- абсолютная температура. При этом скорости
молекул по направлениям у и z могут быть любыми.
Очевидно, что в интервале скоростей от -во до +«>
содержатся все #0 молекул газа, поэтому интеграл от правой
части C.2) по всем возможным скоростям молекул должен
равняться единице. Сделаем такую проверку.
г j. dx. C.3)
л/я
—w OO
Здесь была сделана очевидная замена переменных и
вычисления свелись к определению интеграла, который
называется интегралом Пуассона.
Задача. С помощью полярных координат вычислить
Т х2
интеграл Пуассона: / = J e dx.
Решение. Удобно вычислить произведение двух таких
интегралов
/2 =
Введем полярные координаты:
х2 + у 2 = г2, dxdy = rdrdy.
42
В них переменные разделяются и после вычислений
получим
/2 = J dq>) ре р ф = п, J = л/я.
о о
Используя этот результат, убеждаемся, что
соотношение C.3) равно единице.
Отметим, что квадрат интеграла Пуассона равен
объему между плоскостью ху и поверхностью, образованной
вращением экспоненты вокруг оси z- Этот интеграл часто
применяется при использовании распределения Максвелла.
Кроме него часто встречаются интегралы вида
о
где п - целое число. Эти интегралы при п нечетном берутся
по частям, а при п четном приводятся к интегралу Пуассона
тоже интегрированием по частям. Для справки приведем
значения часто встречающихся интегралов:
Т -^ Т -I J = —
/о = 2 ' l ~ 2 'Jl 4 '
/Зв1,/4 = 3? , 1в C.4)
2 8
Вернемся к рассмотрению распределения Максвелла
для компоненты скорости, которое, как отмечалось, можно
еще называть одномерным распределением. Формулу C.2)
можно также представить в следующем виде:
dN{vx) , ч
Nodvx
Зависимость ?ух) является плотностью
вероятности, так как для получения относительного числа
частиц ее нужно умножить на интервал скоростей dvx.
Часто ее называют функцией распределения
Максвелла (в данном случае для компоненты скорости).
Плотность вероятности <p(vx) является, как это видно по
левой части приведенного выше выражения, производной
от числа молекул по скорости, отнесенной к общему числу
молекул. Ее значение определяет относительное количество
молекул, имеющих скорость vx в единичном интервале
скоростей. Произведение q(vx)dvx равно относительному
числу молекул, имеющих скорости в интервале v*, vx + dvx.
Это произведение имеет более простой физический смысл,
чем плотность распределения (p(vx), хотя именно
зависимость cp(vx) может быть наглядно изображена на
рисунке.
Отметим, что наиболее вероятная скорость,
соответствующая максимуму функции распределения, и
средняя скорости для распределения Максвелла по компоненте
скорости равны нулю. Такой результат получился потому, что
распределение симметрично, поскольку молекулы движутся с
равной вероятностью как в положительном направлении оси х,
так и в противоположную сторону.
Задача. Найти среднюю по абсолютному значению
скорость в одномерном распределении .Максвелла, а также
скорость vx лер, соответствующую точке перегиба кривой
распределения.
44
Решение.
<lvJcl> = Jlvxl
-mvl/BkT) ,
vxe x dv x =
' nm ~Q Люд
В точке перегиба кривой вторая производная равна
нулю:
= 0, отсюда
xnep'\ m •
dvx
Найденные скорости показаны на рисунке,
приведенном выше.
Задача 7.2 C12с). Исходя из распределения
Максвелла найти средний квадрат х-компоненты скорости
молекул газа. Найти отсюда среднюю кинетическую
чергию, приходящуюся на одну степень свободы
юступательного движения молекулы газа.
Решение. Для определения средней величины
квадрата скорости нужно v^ умножить на число
олекул N0<p(vx)dvx, имеющих такую скорость,
..росуммировать по всем возможным скоростям и разделить
на общее число молекул, которое определяется
ютветствующим интегралом. При таком подходе
остоянная А сокращается, и ее не нужно помнить.
г
2kTdvx JxV* dx
2 _ 2kT
* 2 +*>
mvx m T _X2 m
Ae~2kTdvx Je" dx
I
Здесь использована типичная для задач на
распределение Максвелла замена переменных:
mvl I BkT) = x2. Из найденного результата получим
среднее значение кинетической энергии молекулы газа,
приходящуюся на одну степень свободы:
<гх >=<mvl /2>=kT /2.
Отметим, что задачу можно решать несколько иначе:
не записывать в знаменатель интеграл, равный единице, а
использовать вычисленное ранее значение постоянной А.
Получим
< vx >=
3.2. Распределение вероятностей для абсолютной
величины скорости
Рассмотрим теперь распределение Максвелла в
трехмерном случае. Будем считать, что распределения
скоростей молекул по направлениям у и z такие же, как и
для направления х, поскольку все направления равноправны
и ничем не выделены.
Если рассматривать движение по направлению у
части молекул dN(vx), скорости которых по направлению
х лежат в интервале V* ,vx + dvx, то только у некоторой
доли таких молекул скорости по направлению у находятся
в интервале vyy vy + dvy. Эта доля равна
dN(vy) / No = ф у )dvy . По направлению оси z соответст-
соответствующая часть молекул будет составлять величину
dN (у z) I No = cp(v z )dv z. Поскольку вероятность совпа-
совпадения независимых событий равна произведению
вероятностей, то в интервале скоростей dvydvydvz будет
находиться часть молекул, равная произведению
соответствующих вероятностей:
Tp = <P(vjc) Фу) Фz) dvxdvydvz =
=fej2g ^Л^Л«' C-5)
46
Это распределение удовлетворяет условию
нормировки, так как здесь три раза использовано
одномерное распределение, каждое из которых
нормировано (то есть интеграл по всем возможным
скоростям от минус бесконечности до плюс бесконечности
равен единице).
Для определения распределения Максвелла по
абсолютной величине скорости удобно использовать
фазовое пространство скоростей vX9 vy, vz. Вместо элемента
объема такого пространства dvxdvydvz , использованного в
предыдущей формуле, для получения распределения,
зависящего только от абсолютного значения скоростей,
возьмем объем сферического слоя 4%v 2dv, где
v2 =v2 +v2 +v2. Скорости из этого слоя равны по
величине. Для нахождения числа молекул, скорости
которых лежат в интервале v, v + dv, нужно подставить
объем сферического слоя вместо элементарного объема
z. Получим
dN ( т ^2 mv2
= 4п \-^—\ v2e 2kTdv. C.6)
Эту формулу можно также представить в следующем
виде:
mv2
v2e ж . C.7)
iv q \Z7C/C/ J
Здесь F[v) - функция распределения Максвелла для
абсолютной величины скорости в трехмерном случае. Она
удовлетворяет условию нормировки J F(v)dv - 1.
о
Рассмотренный вывод поможет облегчить
запоминание сложной формулы и показывает
происхождение множителя v2.
47
3.3. Средние скорости
Исследуем функцию F(v) - распределение Макс-
Максвелла для абсолютного значения скорости в трехмерном
случае.
Задача. Найти наиболее вероятную скорость vm по
распределению Максвелла для абсолютного значения
скорости молекул газа.
Решение. Такая скорость соответствует максимуму
функции распределения, то есть решение получается из
условия dF/dv = 0. Выполнив дифференцирование,
получим: vm = ^2кТ / m . Эта скорость является наиболее
характерной для распределения, поэтому целесообразно
запомнить ее или вывод.
Задача. Исходя из распределения Максвелла для
абсолютного значения скорости молекул, найти среднюю
скорость <v> и средний квадрат скорости молекул газа <^>.
Решение. Еще раз напомним способ решения
подобных задач. Число молекул, скорости которых
находятся в интервале v, v + dv, равно N$F(v)dv. Умножив
это число на v, получим сумму скоростей молекул,
находящихся в рассматриваемом интервале. То же самое
можно написать и для частиц, имеющих скорости в других
интервалах. Все это нужно сложить, то есть в данном случае
проинтегрировать, и разделить на полное число молекул N$.
В результате находим величину средней скорости
\ \v
—
3e 2kT
v3e 2kT dv = J—. C.8)
Для среднего квадрата скорости будем иметь
\\ ve Л
Отсюда для среднеквадратичной скорости получим
(з.9)
48
Задача. Выразить скорость звука в газе через
наиболее вероятную скорость молекул vm.
Решение. Подробное рассмотрение вопросов,
связанных со скоростью звука, производится дальше в
разделе 7.5. Здесь приведем лишь сведения, необходимые
для решения задачи. Адиабатическая скорость звука в газе
С =
зависит от показателя адиабаты газа у, равного
отношению теплоемкостей при постоянном давлении и при
постоянном объеме, следовательно, эта скорость различна
для газов с разным составом молекул. Согласно закону о
равномерном распределении энергии по степеням свободы
для одноатомных газов величина у = 5/3 = 1,66 и для
скорости звука получим Q = 0,91уш.
Для двухатомных газов при умеренных температурах,
когда еще не возбуждены колебательные степени свободы,
у=7/5 = 1,40 и скорость звука в этом случае С2 = 0,84vm.
Для многоатомных газов у = 4/3 = 1,33 и соответственно
С3 = 0,82vw.
Скорости звука для всех трех типов молекул
оказываются меньше наиболее вероятной скорости и
меньше, следовательно, всех средних скоростей. На рисунке
показано их расположение.
Отметим, что если в распределении Максвелла в
качестве независимой переменной принять отношение v/vm,
то функция распределения уже не будет зависеть ни от
температуры, ни от массы молекул.
3.4. Двумерное распределение Максвелла
Получим распределение Максвелла для абсолютного
значения скорости молекул в двумерном случае, когда она
определяется только скоростями vx и vy : v2=v^+v^.
Сначала напишем распределение Максвелла для компонент
скорости в двумерном случае. Повторяя рассуждения,
проведенные для трехмерного варианта, получим
dN m
Фх)Фу)AухAуу
Вместо фазового объема dvxdvy (можно считать, что
это фазовая площадь) в плоскости vx , vy используем пло-
площадь кольца 2nvdv и подставим это соотношение в
полученное выражение. В результате найдем искомое
распределение:
dN m
No kT
e 2kTvdv. (ЗЛО)
Задача 7.14 C23c). В диоде электроны, эмитируемые
накаленным катодом, попадают в задерживающее поле
анода. Считая, что тепловые скорости эмитированных
электронов распределены по закону Максвелла с
температурой 1150 К, определить долю электронов а ,
преодолевающих задерживающий потенциал U = 0,2 в.
Катодом является тонкая прямолинейная нить, натянутая
по оси цилиндрического анода.
Решение. В данном случае скорость электронов,
направленная вдоль катодной нити, не имеет значения,
определяющей является абсолютное значение скорости в
плоскости, нормальной к нити. Минимальная скорость
электронов, достигших анода, определяется из формулы
mV^ 12 = eU, где е - заряд электрона. Остается
подсчитать относительное число частиц, у которых скорость
больше этой величины. Получим
50
= T
J
кТ
4,81(Г100,2
3.5. Распределение вероятностей для энергии молекул
Вместо распределения вероятностей для скоростей
молекул иногда удобно рассматривать распределение для их
кинетической энергии е. Например, при сравнении
распределения Максвелла с другими распределениями,
которые выводятся для энергии частиц.
Основой для получения искомого распределения
служит соотношение f(z)de = F(v)dv . Оно основано на том,
что число молекул, имеющих скорости в заданном
интервале скоростей, равно числу молекул, имеющих
кинетические энергии в соответствующем интервале
энергии, так как скорость и энергия связаны между собой:
e = mv2/2. Отсюда получим связь между интервалами
скорости и энергии: dz = mvdv . Теперь сделаем подстановку
в распределение для абсолютного значения скорости.
Получим
/() /(JРТ2л? Г». C.11)
/(г)Рл? Г
No dz \%kT )
Задача. Найти наиболее вероятное значение
кинетической энергии молекул газа zm.
Решение. Наиболее вероятное значение
сбответствует максимуму функции распределения, то есть
df(z)/de = 0. Отсюда следует гт = кТ / 2. Отметим, что
скорость молекул газа, соответствующая этой энергии,
конечно не равна наивероятнейшей скорости для
распределения Максвелла по абсолютной величине
скорости, так как распределения для энергии молекул и для
их скоростей разные.
Отметим также, что распределение Максвелла для
энергии молекул не зависит от массы молекул.
Следовательно, в смеси разных газов распределения по
энергии для разных молекул одинаковые, а по скоростям -
разные.
3.6. Перетекание газа через очень малое отверстие
Рассмотрим явление нагревания газа, вытекающего
через очень малое отверстие. Для этого процесса
существенное значение имеет то, что скорости молекул в
сосуде имеют разные величины. Зная распределение
молекул по скоростям, можно вычислить как температуру
вытекающего газа, так и необходимый подвод тепла к газу в
сосуде для поддержания его постоянной температуры.
Для решения такой задачи нужно знать число
молекул, падающих в единицу времени на небольшую
площадку, размеры которой меньше длины свободного
пробега. Это число для единицы площади равно nv/A, где
п - число молекул в единице объема, имеющих скорость v.
Задача 7.24 C28с). В тонкостенном сосуде,
содержащем идеальный газ при температуре Г, имеется
очень малое отверстие, через которое молекулы вылетают в
вакуум. Определить среднее значение энергии вылетевших
молекул.
Решение. Пусть в единице объема сосуда имеется dn
молекул, имеющих скорости в интервале v, v + dv.
В единицу времени через единичную площадку вылетит
dnv/A молекул. Они унесут энергию (dnv/4)(mv2/2). Полная
энергия молекул, вылетевших в единицу времени, учитывая
C.7), равна
Iv mv2
F(v)dv.
о
Число вылетевших молекул будет
n)—F(y)dv.
о4
Средняя энергия вылетевших молекул равна
отношению этих интегралов:
52
Средняя энергия вылетевших молекул равна
отношению этих интегралов:
)v5e~2kTdv ]x5e~x2dx
кг
2 °? ^ Т 3 х2
J
3 х2
Vdv J e~ dx
о °
Полученная величина существенно превышает
среднюю кинетическую энергию молекул в сосуде, равную
ЗкТ/2. Если умножить разницу между ними на число
вылетевших молекул, то можно получить энергию, которую
нужно подводить для поддержания постоянной температуры
остающегося газа. Причина необходимости подвода тепла в
том, что вытекающий газ обогащается быстрыми
молекулами, так как их больше падает на отверстие. Газ в
сосуде при этом охлаждается.
3.7. Пределы применимости распределения Максвелла
Максвелловское распределение скоростей основано
на классической статистике и поэтому оно справедливо,
если квантово-механическими эффектами пренебречь. Это
можно сделать в случае, если расстояния между объектами
L велики по сравнению с их дебройлевской длиной волны
X = h/p, где h = 6,6-10~27 эрге - постоянная Планка,
р = mv - импульс, который можно оценить, например, по
наиболее вероятной скорости молекул v = ^]2кТ / m .
Окончательно получим X = h / л12пгкТ .
Типичные расстояния L между молекулами можно
оценить по их концентрации: L «%JV / N = 1 / !fn , где V-
объем газа, N - число молекул, п - их количество в единице
объема.
Условие применимости классического приближения
можно записать в виде следующих неравенств:
L»X, 1 / л/п » h I 4lmkf. To есть оно применимо,
если газ достаточно разрежен, температура его велика, а
масса молекул не слишком мала.
Рассмотрим гелий при нормальных условиях.
Вычислим для него ЬиХ.
Р 1,013-106 19 ,
п = = г: = 2,7 • 1019 см,
кТ 1,38 • 10~16 • 273
L = 1 / Чп = 33 • 10"8 см,
h 6,6-107
л» —
д/2D/F,02 1023)) ¦ 1,38 • КГ16 • 273
= 0,9310"8см.
Расстояние между молекулами оказалось в 35 раз
больше, чем длина волны де Бройля, поэтому
приблизительно можно считать, что классическое
рассмотрение применимо. Однако для молекул с
меньшими скоростями, например, у которых скорость в сто
раз меньше A0 м/с), чем наиболее вероятная A,06 км/с),
распределение Максвелла уже неприменимо.
Для таких молекул длина волны де Бройля больше
расстояния между ними, и молекулы уже не могут
рассматриваться как независимые частицы, которые
двигаются по определенным классическим траекториям.
Таким образом, квантовые явления ограничивают
применение распределения Максвелла для медленных
частиц.
Распределение ограничено и для очень быстрых
частиц. На этот раз условия накладывает специальная
теория относительности, которую нужно учитывать при
скоростях, близких к скорости света. Дело в том, что
распределение Максвелла допускает существование частиц,
двигающихся быстрее света, но это невозможно.
54
Раздел 4
РАСПРЕДЕЛЕНИЯ БОЛЬЦМАНА И ГИББСА
Распределение Больцмана используется для
определения концентрации частиц в разных участках
пространства при наличии силового поля. Это
распределение можно вывести из барометрической
формулы A.7). Для этого давление в A.7) нужно выразить
через число частиц в единице объема п = N/V. Еще следует
воспользоваться соотношением между постоянными
R=NAk, которое применялось при выводе A.2), а также
формулой (I = yyiNa , где т - масса молекулы. Получим
п = пое кТ .
Отметим, что числитель в показателе экспоненты -
это потенциальная энергия молекулы в поле тяжести.
Подобное распределение числа частиц справедливо и в
более общем случае, когда на молекулы действуют другие,
не гравитационные силы F, но такие, что молекулы в их
поле имеют потенциальную энергию Ер = -JFdr. После
замены будем иметь:
_ ЕР
п = пое кТ . D.1)
Воспользуемся равенством п = dN/dV и подставим
его в D.1). В результате получим распределение Больцмана:
dN=Ae kT dV. D.2)
Здесь dN - число частиц в объеме dV, имеющих
потенциальную энергию Ер. Постоянная А находится по
йолному числу частиц в заданном объеме. Отметим, что
потенциальная энергия, как всегда, определяется с
точностью до постоянного множителя, выбор которого
влияет на величину постоянной А
Если по распределению Максвелла можно найти
число частиц, имеющих некоторую скорость в заданном
интервале скоростей, то распределение Больцмана
определяет число частиц, имеющих известную
потенциальную энергию в заданном интервале координат,
то есть в заданном объеме. При этом потенциальная
энергия является функцией координат.
Задача 8.39 C75с). Вычислить среднюю энергию
<Е> моля одноатомного газа, состоящего иэ молекул,
имеющих два дискретных уровня энергии: ?i и z-i > г\.
Показать, что при очень низких температурах теплоемкость
такого газа равна C/2)Л Для упрощения записи формул
принять ?1=0и82=е.
Решение. По распределению Больцмана
f е,) ( г2 \
и, = А ехр L п2 = А ехр .
1 { кТУ 2 { кТ)
Находим среднюю внутреннюю энергию одной
/ v г.пл +г7п2
молекулы (?, > = -i—i —. При ?i = 0 и г^ = ? получим
пх + п2
?
1 + ехр
кТ
Средняя энергия теплового движения
одной молекулы <?w> = (Ъ/2)кТ. Следовательно, средняя
суммарная энергия одной молекулы равна
1 + ехр
кТ
Для моля получим
здесь Na - число Авогадро. Отметим, что при Т -* 0 первый
член, определяющий внутреннюю энергию, очень быстро
обращается в ноль, так как падает число возбужденных
молекул. Тепловая энергия уменьшается не так сильно, она
представлена последним членом, который в данном случае
является главным. Он определяет теплоемкость, которая
равна С = C/2)Д.
56
Задача 8.38. Пользуясь распределением Больцмана,
найти среднюю потенциальную энергию молекул
идеального газа в поле Щх) = ах2, а > 0.
Решение. По распределению Больцмана D.2) для
среднего значения < U> получим
axV^dx
з—-^г- <4-3>
ах 2
е kTdx
о
При вычислениях были использованы численные
значения интегралов, приведенные в C.4).
4.1. Газ в поле тяжести
Задача 8.5 C45с). Найти среднюю потенциальную
энергию <?#> молекулы газа в изотермической земной
атмосфере, считая поле тяжести однородным. Найти
теплоемкость газа С в этих условиях.
Решение. В данном случае е# = mgz. Потен-
Потенциальная энергия молекул газа в интервале высоты
mgz
z, z + dz равна mgzdN = Amgze kT dz. Потенциальная
«у _ mgz
энергия всех частиц Ajmgze kT dz, количество частиц
о
mgz
А]е кТ dz. Среднее значение энергии получим, взяв
о
отношение этих интегралов
j
хе dx
}e~xdx
О
57
Полная энергия молекул равна сумме потенциальной
и внутренней энергии
Cv Т + NkT = (Ск + Л)Г.
Здесь N - полное число молекул, Na - число Авогадро. Для
1-го моля получим величину теплоемкости
С = CV + R =СР. Теплоемкость газа в постоянном поле
тяжести оказалась равной теплоемкости при постоянном
давлении. Это объясняется тем, что при нагревании газа в
поле тяжести давление в каждом малом объеме,
включающем одни и те же молекулы, остается неизменным,
так как оно определяется весом вышележащего газа и не
меняется при увеличении температуры и подъеме данного
объема.
Задача 8.6 C16с). Теплоизолированный герме-
герметический цилиндрический сосуд высоты Н, наполненный
газом, подвешен в вертикальном положении в однородном
поле тяжести. Температура газа в сосуде везде одинакова и
равна Г. Найти среднюю потенциальную энергию молекулы
газа <гц>.
Решение. В данном случае высота ограничена, но и в
пределах ограниченной высоты справедлива формула
Больцмана. Для полного числа молекул в сосуде N и их
потенциальной энергии ?# получим следующие выражения:
^ кТ ,
N=A)e-mgz/kTdz=A—(l-e
о т8
ТТ
EN =A\mgze-mgz/kTdz =
и >= = кТ , а = . D.4)
U N l~a kT K '
mg { кТ J
mgH
1-е-" ' кТ
Задача 8.7 C47с). Найти теплоемкость идеального
газа в условиях предыдущей задачи, считая rngH « кТ.
Решение. Высота реального сосуда, конечно, мала по
сравнению с высотой однородной атмосферы
58
Яо = кТ I mg = 8 км, следовательно, вполне оправдано
заданное условие малой высоты Н , в соответствии с
которыми в формуле D.4) величина а « 1. Поэтому можно
воспользоваться разложением в ряд выражения D.4):
(-а + ос2/2-а3/б)
2/2 2\ в)
а-а2/2 2\ в
Используя этот результат, находим для одной
молекулы
^ k
dT 12I кТ )
Следовательно, теплоемкость моля газа, учитывая
„ ^ R (mgH
тепловую составляющую, равна С =CV Л
12^ кТ )
4.2. Газ в поле центробежных сил
Задача 8.25. Найти, на сколько возрастает
теплоемкость вращающегося газа по сравнению с
теплоемкостью неподвижного газа. Аргон с молярной
массой \i = 40 заполняет цилиндр радиуса R — 2,5 см и
вращается вокруг оси цилиндра с угловой скоростью
со= 2 • 103 с1 при температуре Т= 300 К.
Решение. Найдем потенциальную энергию одной
молекулы г в поле центробежных сил. Используя de = -Fdr
и jF = rm со2, получим
dr1 2 а2 - г2
2 2
При интегрировании принято, что при г = а
величина г = 0, так как при нулевой температуре Т = 0 все
частицы будут находиться на периферии. Для определения
числа частиц dN в тонком кольцевом слое единичной
длины, объем которого равен dV = 2nrdr, используем
распределение Больцмана:
59
V()
dN =Ae l r 2nrdr,
A 2/ 2 2x - mco2fa2-r2Wr)
</?д, =— mto2(a2 -r2)e v ' 2rdr.
Отсюда для средней энергии одной молекулы
получим
о ,
где использованы обозначения:
i2 40-4- 106 6,25
p = = = 0,0201.
2kT 6 1023 • 2 • 1,38 106 • 300
Разложение при малом р совпадает с разложением
D.5) по а, найденным в предыдущей задаче. Используя его,
получим для одной молекулы:
ШТ
dT 4%{ кТ
Теплоемкость моля вращающегося газа возрастет на
величину
ДС=.
л dT
= —@,020lJ • 8,31 = 2,77 • 10 Дж/(мольК).
60
4.3. Распределение Гиббса
Распределение Гиббса является обобщением
распределений Максвелла и Больцмана. Оба этих
распределения имеют одинаковый экспоненциальный вид, а
в показателях экспонент кинетическая или потенциальная
энергии частицы относятся к тепловой энергии. Поэтому
очевидным обобщением является использование суммы
этих энергий. Кроме того, вместо энергии одной частицы
рассматривается энергия определенного их числа. При этом
термодинамическая система представляется состоящей из
большого количества групп или ансамблей частиц,
содержащих или фиксированное, или заданное среднее
число частиц, обладающих или фиксированной, или
средней заданной энергией. Соответственно существуют три
вида распределения Гиббса. При рассмотрении
фиксированного числа частиц и заданной энергии ансамбля
получается микроканоническое распределение, при
фиксированном числе частиц в ансамбле и средней его
энергии - каноническое распределение Гиббса и при заданных
значениях среднего числа и средней энергии - большое
каноническое распределение.
В данной работе будет рассматриваться только
каноническое распределение Гиббса:
— = Ае kTdxdp. D.6)
vo
Здесь vo - полное число ансамблей, dv - число
ансамблей, сумма кинетической и потенциальной энергии у
которых равна Е(х,р), а обобщенные координаты х,- и
импульсы pi имеют фазовый объем dxdp (например, для N
частиц в ансамбле при использовании декартовых
координат объем будет
dxdp ^dx1dy1dzldpXldpY}dpzl • dxNdyNdzNdpXNdpYNdpZN.
Величина А - постоянная, не зависящая от координат и
импульсов. Отметим, что в распределении Гиббса с
тепловой энергией кТ сравнивается энергия всех частиц
ансамбля, число которых может быть очень велико и велика
их энергия. Поэтому эффективная ширина такого
61
распределения значительно меньше, чем у распределения
для одной частицы.
В случае идеального газа и отсутствия внешних
силовых полей при N = 1, то есть для одной частицы в
ансамбле, распределение Гиббса переходит в
распределение Максвелла C.2).
Используем распределение Гиббса D.6) для
определения среднего значения энергии ансамбля.
Постоянная А определяется интегрированием правой части
D.6) по всем возможным значениям координат и
импульсов. Для среднего значения энергии <Е> получим
г -А
\Ее kTdxdp
<Е>= -^ . D.7)
\е~ kTdxdp
Здесь интегрирование производится по всем
возможным значениям х и р частиц, входящим в ансамбль.
Обозначим знаменатель параметром Zn выразим <Е> через
эту величину, используя преобразование
dZ f - —
p- = -J?e kTdxdp=-<E>Z.
Отсюда находим
Аналогично можно определить среднее значение
квадрата энергии, применяя преобразование
V kTdxdp=<E2>Z.
Следовательно
62
kTdxdP ! a2z
D.9)
Полученные формулы будут использованы при
рассмотрении флуктуации в следующем разделе.
63
Раздел 5 .
ФЛУКТУАЦИИ
Отклонения физических величин от их средних
значений, обусловленные тепловым движением, называют-
называются флуктуациями. Флуктуации термодинамических величин
обычно малы из-за большого количества атомов или
молекул, составляющих рассматриваемую систему.
Для решения задач нужно дать математическое
определение флуктуации и привести ее связь со средними
характеристиками соответствующей термодинамической
функции, которая будет рассматриваться как случайная
величина.
По определению флуктуация А/ термодинамической
величины / равна ее разности со средним значением
А/=/-</>. Естественной характеристикой для случай-
случайной величины, которой является флуктуация, служит
среднее значение ее квадрата <(А/J>, то есть дисперсия,
поскольку среднее значение флуктуации, очевидно, равно
нулю.
Эквивалентной мерой является также средняя
квадратичная флуктуация д/< (А/J > = о, равная средне-
среднеквадратичному отклонению случайной величины. Этой
характеристикой удобно пользоваться при сравнении
флуктуации со средним значением и при расчете
относительной флуктуации. Отметим, что для случайных
величин вычисление дисперсии производилось в B.8) и
B.10). Вычисления для флуктуации аналогичны и являются
лишь повторением проделанных там вычислений.
Задача C82с). Для произвольной флуктуационной
величины / выразить средний квадрат флуктуации <(А/J>
через </2> и </>2.
Решение.
(А/J = 0 " </>J = /2 - 2/</> + </>2,
2 </2> - 2<fXf> + <f>2 = </2> - </>2. E.1).
Эта формула часто используется при решении задач.
64
5.1. Флуктуации числа частиц
Оценка флуктуации числа частиц может быть
сделана на основании биномиального распределения
B.4) - B.6). Это распределение применимо, если события
независимые, в данном случае это означает, что молекулы
двигаются независимо друг от друга, испытывая лишь
редкие столкновения.
Задача 9.4 C85с). В закрытом сосуде в отсутствии
силовых полей находится N молекул идеального газа.
Определить среднее число молекул и его флуктуации в
объеме v, являющегося малой частью объема V.
Решение. Разделим большой объем V на малые
объемы v. Так как все они одинаковые и вероятность
нахождения в них молекул тоже одинаковая, равная v/K, то
число молекул в малом объеме есть случайная величина со
v
средним значением п0 =—N. По условию задачи
v / V «1 и в таком случае средний квадрат флуктуации,
совпадающий с дисперсией, согласно B.10) будет
0 V
Задача 9.5 C87с). В сосуде объема V = 1 литр при
комнатной температуре находится N атомов идеального газа.
Оценить величину N, при которой вероятность для этих
атомов хоть один раз собраться в одну половину сосуда на
протяжении эпохи порядка возраста Вселенной
(Г« 1010 лет) сравнима с единицей.
Решение. Вероятность собраться в одной половине
сосуда Р = (l / 2) . Время т пребывания в этом разде-
разделенном состоянии порядка размера сосуда, который можно
оценить по его объему VF, поделенного на среднюю
скорость молекул. Для наших целей эту величину можно
считать приблизительно равной скорости звука С3.
Следовательно х = lIV / С3. Величина Т/% равна числу
независимых возможностей осуществить различные
состояния, из которых должна реализоваться одна с
65
вероятностью единица. Поэтому РТ / т = 1. Отсюда
получим
Т ТС
N = - = — = 70.
lg 2 Ig2
Здесь было использовано: 1 год = 365-24-3600 = ЗД5107 с,
С3 = 340 м/с, VV = 10 см.
Задача 9.19 C91с). Имеется два сосуда с разными
объемами, в каждом по одному молю молекул N Какое
число п молекул должно перейти из одного сосуда в другой,
чтобы возникшее состояние было бы в а = е раз менее
вероятно, чем исходное.
Решение* Используем формулу B.4) при V\ = V>i для
двух случаев, а именно, когда в сосудах равное число
молекул, и когда в одном на п молекул больше. Получим
{2N)\ (\^N B7V)! (
0 ~ N\N !U J ' a ~" {N - n)\ [N + /i)lU.
По условию задачи Ра = Po/a, следовательно
(N - n)\ (N + и)!
a- . Распишем факториалы и произведем
N\N\
сокращение общих множителей числителя и знаменателя
{N + \){N + 2) ¦ - ¦ (N + л)
а "* GV - л + l)(N -n+2)---N~
1 Y 2) ( п
— 1 + — ••• 1 + —
NX N) К N
Логарифмируем это выражение и каждый логарифм
раскладываем в ряд, ограничиваясь первым членом
.1 2 п \ ( I 2 п-\
In а -\ — + —+...+— + — + —+...+-
N N N) \N N N
2 , . п п2
= —(l + 2+...+я)- — = .
N N N
66
Отсюда получим п = JN In a. При а = е имеем
п = л/Ж = >/б • 1023 = 7,8 • 1011.
Задача 9.13, Два одинаковых сообщающихся сосуда
заполнены газом при нормальных условиях. Каким должен
быть объем К каждого сосуда, чтобы вероятность состояния,
при котором давление в сосудах изменится на 0,1%, была
бы в е100 раз меньше, чем вероятность исходного состояния?
Решение. Эта задача опять на ту же тему с
использованием полученной формулы п = <JN In a . При
переходе из одного сосуда в другой п молекул давление в
сосудах изменится на величину АР = ±—кТ, а начальные
давления связаны с начальным числом частиц в каждом
N
сосуде обычным соотношением Р = —кТ.
АР п fin a
Отсюда получим = — = J . Используя
Р N V N
V /Vo =N /NA, где Ко = 22,4 литра, NA - число
Авогадро, находим = 1—2 . Следовательно
Р у NAV
^VQlna (АР \2 _ 22,4 ¦ 103 ¦ ( In вш) ¦ 106 ^
NA [ Р J 6 • 1023
= 3,7102cm3.
В таком объеме при нормальных условиях содержится
N = NaV/Vq = Ю8 молекул, а линейный размер объема
равен L = W = 1,5-10 см.
Из-за большой величины числа Авогадро
флуктуации термодинамических величин очень малы.
Заметная флуктуация порядка 0,1% может происходить
лишь в малом объеме. Но очень малая флуктуация порядка
10~7 может наблюдаться и в макроскопическом объеме
V - 3,1 см3. (В условии задачи использовано очень малое
отношение вероятностей состояния с флуктуацией и
исходного состояния).
67
5.2. Флуктуации типа броуновского движения
Наблюдаемые в микроскоп очень маленькие
взвешенные в жидкости частицы совершают движение,
направление и скорость которых все время изменяются, это
броуновское движение. Оно объясняется тем, что молекулы
жидкости, находящиеся в тепловом движении, передают
беспорядочным образом свое движение более крупной
частице, которая тоже, следовательно, совершает тепловое
движение. На каждую степень ее свободы, как и у молекул,
приходится энергия (\/2)кТ, поскольку частица имеет
температуру жидкости. Отсюда получим
— <v2 >=-kT, —<v >=-kT.
2 2 2 2
Здесь первая формула относится к одномерному
движению, когда нас интересует только одна компонента
скорости частицы, а во второй v - модуль скорости в трех-
трехмерном пространстве, m - масса частицы. Чем больше мас-
масса, тем меньше ее тепловая скорость. Масса пропорцио-
пропорциональна числу атомов Nm, следовательно, флуктуационная
скорость частицы порядка 1 / ^N m . Даже в очень малых
телах число атомов велико, поэтому их тепловые скорости
малы по сравнению со скоростями молекул. Однако иног-
иногда тепловые движения имеют принципиальное значение.
Задача 9,27. Предел чувствительности пружинных
весов ограничивается тепловым движением механизма.
Найти ту малую массу Am, которая может быть определена
при однократном взвешивании на пружинных весах, если
жесткость пружины равна а, а температура Т.
Решение. Как известно, у гармонического осцил-
осциллятора средняя кинетическая энергия равна средней
потенциальной, отсюда можно определить среднеквад-
среднеквадратичное удлинение пружины, обусловленное бомбарди-
бомбардировкой молекулами окружающей среды:
68
Здесь учтено, что пружина имеет одну степень
свободы. Из-за теплового движения молекул среды пружина
постоянно имеет какое-то удлинение, которое и
ограничивает точность весов. На фоне флуктуационных
отклонений можно различить отклонение, вызванные
весом, которое не больше среднеквадратичного случайного.
Отсюда получим оценку предельной массы:
Am = .
g
Величина предельной массы зависит от жесткости весов.
Для оценки чувствительности можно пользоваться
несколько другой характеристикой. Рассмотрим весы такие,
что некоторая известная масса то вызывает отклонение на
величину ло, следовательно, то g = oocq и а = гщ g /х$ .
Используя это равенство, получим
Am I кТ
m0 \mQgx0
Здесь под корнем находится отношение тепловой энергии
осциллятора к потенциальной энергии в поле тяжести
заданной массы т^ При то = 10 г и ^ = 1 мм, что
примерно соответствует эффективной чувствительности
аналитических весов, получим Ат/т — 0,6- КГ6. Предель-
Предельная масса оказалась очень малой, и смещение чашки весов
при этом тоже очень мало. Но это малое смещение можно
сильно увеличить с помощью светового луча, отраженного
от закрепленного на весах зеркала, так что малость
смещения не накладывает принципиальных ограничений
на возможности взвешивания. Такие ограничения накла-
накладывает тепловое движение.
Задача типа 9.22 C98с). Рассчитать тепловые
флуктуации объема на основании модели, в которой
происходят флуктуации объема газа, находящегося в
цилиндре с поршнем, к которому с внешней стороны
приложено постоянное давление.
69
Решение. Сила, действующая на поршень, равна
разности давлений изнутри Р и снаружи Pq цилиндра,
умноженной на площадь поршня Ф
(Р-Ро)ф=
Ф2х,
где х - смещение от положения равновесия, AV = Фх -
изменение объема. Производная вычисляется при
постоянной энтропии S, если цилиндр и поршень не
проводят тепло.
Уравнение движения поршня
т
х { ЪР\ 2
эк!
является уравнением для гармонического осциллятора, так
как для устойчивости вещества нужно (dP/dV)s < 0.
Средняя потенциальная энергия поршня равна
тепловой энергии одной частицы:
dV
Ф2
кТ
Отсюда
E.2)
Можно рассмотреть ту же задачу для цилиндра и
поршня, сделанных из материала, хорошо проводящего
тепло, и помещенных в среду с постоянной температурой. В
таком случае в итоговой формуле следует брать
производную при постоянной температуре.
70
Задача. Теплоизолированный цилиндр, напол-
наполненный идеальным газом, герметически разделен
теплоизолированным подвижным поршнем на два нерав-
неравных объема V\ и Г2, но с равными давлениями и темпера-
температурами. Определить относительную флуктуацию каждого из
этих объемов, если число частиц в одном из них равно N\, a
В ДРУГОМ Л^.
l
1
i
1*.
Решение. Метод решения такой же, как и задачи
(9.22), но нужно учесть, что в данном случае давление при
смещении поршня изменяется с обеих сторон. Сила,
действующая на поршень, равна
(р1-р2)ф=
Отсюда, следуя решению задачи (9.22), получим
кТ
При наличии второго объема флуктуации меньше,
так как он препятствует движению поршня и податливость
системы уменьшается.
Для идеального газа можно получить соотношение
(dV/dp)s = -V/(yp), используя которое, находим
71
При N\ « N2 решение совпадает с решением задачи
(9.22). При V\ = V2 будем иметь N\ = Л^ и флуктуации
каждого объема станут меньше в V2 , чем в предыдущей
задаче. Второй объем, как отмечалось, уменьшает
податливость системы.
Задача. Вычислить относительную и абсолютную
флуктуацию объема идеального газа при постоянной
температуре и при постоянной энтропии.
Решение. Для идеального газа находим
fdV] __V_ fdV] _V_
\ъР)т~ Р' Up|" уР'
После подстановки в формулу E.2) и использования
соотношения kN = vR получим
((AVJ) =—, -
V 'It \f '
n
is yjsf у
Относительная флуктуация объема идеального газа
оказалась обратно пропорциональной квадратному корню
из числа молекул 1 / -/лГ, а коэффициент пропор-
пропорциональности при условии постоянства температуры равен
единице. При неизменной энтропии он несколько меньше.
Отметим, что из формулы для флуктуации объема
E.2) следует, что абсолютная величина флуктуации при
щ
любом уравнении состояния пропорциональна
Температура и давление не изменяются при одно-
одновременном увеличении и объема, и числа частиц, то есть
когда V пропорционально N. Но, конечно, коэффициент
пропорциональности зависит от уравнения состояния и в
величине абсолютной, и в величине относительной
флуктуации. С физической точки зрения это можно
объяснить тем, что реальное уравнение состояния отражает
взаимодействие молекул между собой. Ясно, что
флуктуация таких молекул будут отличаться от флуктуации
газа, состоящего из невзаимодействующих молекул.
Можно также отметить, что относительная флуктуа-
флуктуация любой термодинамической величины пропорциональна
Задача 9.28 C99с). Найти среднюю квадратичную
относительную флуктуацию объема капельки ртути радиуса
г = 0,01 мм в воздухе при температуре Т = 300 К.
Изотермическая сжимаемость ртути КА = 3,9-10~6 атм.
Решение. Используем определение величины
-1
V
и формулу E.2) для флуктуации объема. Получим
кТК~1
2 , откуда находим искомое значение
Ч
(AVJ > \kTK~l ll,38 • 106 • 300 • 3,9 • 10
-к • 10'9 • 0,981 • 106
3
= 6,26-Ю-9.
Вычислим приближенное значение этой же величины,
исходя из того, что относительная флуктуация любой
термодинамической величины пропорциональна 1 / -JW.
Сначала найдем число молекул в заданной капельке ртути, а
потом определим флуктуацию
73
m 4nr3pNA 4ti • 10~9 • 13,6 • 6 • 1023 14
—NA = ^-^- = » = 1,7.10м,
|i Зц 3-200
= 7,7 10 8.
к
Флуктуации по приближенной зависимости оказа-
оказались больше, чем по точной. Это можно объяснить тем, что
реальные силы сцепления уменьшают величину флуктуации
(напомним, что для идеального газа приближенная формула
совпадает с точной). Однако при начальном изучении
флуктуации возможно ограничиться приближенной
формулой, которая дает правильное выражение с точностью
до одного порядка даже для конденсированного вещества.
Рассмотрим задачу, в которой флуктуации реального
вещества в особых условиях оказываются больше, чем по
простой оценке.
Задача 9,33. В сосуде находится газ Ван-дер-
Ваальса в условиях, когда средний молярный объем равен
критическому, а температура Т превышает критическую
Ткр. Найти изотермическую среднеквадратичную флук-
флуктуацию объема <(AVJ> небольшого элемента этого газа,
имеющего равновесный объем К
Решение. Для определения флуктуации по формуле
E.2) найдем производную, используя уравнение Ван-дер-
Ваальса при V^ = Зв и Гкр = $a/B7eR). Получим
<(ДКJ> AT
V2 9М(Т-Ткр\
Из-за большой сжимаемости вблизи критического
состояния флуктуации сильно возрастают по сравнению с
закономерностью 1 / 4W. Однако это возрастание локали-
локализуется в небольшой окрестности около критической точки.
Например, для воды Гкр = 647 К и при отклонении от этой
(АКJ > 17
величины в один градус получим
отклонении в одну десятую градуса относительная
флуктуация будет равна 54 / 4W.
74
И в таких условиях оценка по формуле 1 /
оказывается неплохой, так как число N даже для малых
наблюдаемых объемов велико (для объема с линейным
размером порядка длины световой волны 10~4 см,
плотностью 1 г/см3, и молекулярной массой несколько
десятков получим N ~ 1010; оценка относительной флук-
флуктуации объема по формуле 1 / 4W равна 10~5, и даже вблизи
критической точки при возрастании флуктуации в
несколько десятков раз они все равно остаются очень
малыми).
5.3. Определение флуктуации по заданному
распределению
Задача. Исходя из Максвелловского распределения
(для модуля скорости в трехмерном случае) найти
флуктуацию модуля скорости одной молекулы.
Решение. По распределению Максвелла определены
средние скорости C.8) и C.9):
ЫкТ 2 ЪкТ
<v >= | , <v >= .
V nm m
Используя формулу E.1), находим
2 2 2 2кТ SkT kT
<(AvJ >=<v2 >-<v >2= = 0,453 .
m nm m
Относительная флуктуация скорости для одной молекулы
оказывается весьма существенной величиной:
(AvJ >
<v >
Эта флуктуация обусловлена столкновениями данной
молекулы с другими и показывает, что скорость отдельной
частицы испытывает значительные изменения, что
естественно при столкновениях равных масс.
5.4. Флуктуации энергии
Для определения флуктуации энергии ансамбля
частиц воспользуемся формулой E.1). Средние значения
75
энергии D.8) и ее квадрата D.9) были найдены с
использованием распределения Гиббса D.6) в Разделе 4.
Применяя эти результаты и используя для удобства
обозначение (J = 1 / кТ, получим
г 2 2 I 32z
< (АЕJ >=< Е2 > - < Е > = г-
v ' z эр2
d(ldZ) Ъ<Е> Ъ<Е> ггг
apU*J эр ГО
д<Е>
Воспользуемся соотношением = vCv, где
v - число молей в ансамбле, Су - молярная теплоемкость
при постоянном объеме. Подставляя в E.3), получим
<(АЕ)
Задача. Найти флуктуацию энергии N молекул
одноатомного идеального газа при температуре Г.
Решение. Среднее значение энергии одной молекулы
идеального одноатомного газа равно C/2)кТ. Для N молекул
эта величина, очевидно, в N раз больше. Следовательно,
средний квадрат флуктуации энергии данного газа согласно
E.3):
<(АЕJ >=C/2)Nk2T2.
Для относительной флуктуации получим
4
< (Д?J > I 2
\3N
В результате решения найдено, что абсолютная ве-
величина среднеквадратичной флуктуации энергии N моле-
молекул пропорциональна корню из их числа, а относительная -
обратно пропорциональна корню из этой величины.
Задача 9.35. Вычислить среднюю относительную
флуктуацию потенциальной энергии внутримолекулярных
колебаний двухатомной молекулы идеального газа, а также
одного моля таких молекул.
Решение. При решении задачи 8.38 в Разделе 4 была
найдена средняя энергия таких колебаний для одной
76
молекулы <Е> = ?7/2. Для N молекул средняя энергия
будет в N раз больше. Используя это и применяя формулу
E.3), получим средний квадрат флуктуации энергии
колебаний N молекул:
<(АЕJ >=k2T2N /2.
Для относительной среднеквадратичной флуктуации
N молекул находим
^—" = JE-5)
J > ГГ
> \N
Очевидно, что решение применимо и для одной
молекулы, т.е. при JV = 1 (поскольку распределение Гиббса
справедливо в этом случае), и для моля молекул при
N = АГд. В этой задаче, как и в предыдущей, получилось,
что относительная флуктуация обратно пропорциональна
корню из числа молекул. Для одной молекулы
относительные флуктуации энергии велики, порядка самой
энергии, а для моля очень малы: д/2 / F • 1023) = 2 • 10~12.
Такой результат - очевидное следствие формулы E.3), в ле-
левой части которой стоит квадрат флуктуации энергии, а в
правой - производная от средней энергии ансамбля. Сред-
Средняя энергия пропорциональна числу частиц в ансамбле.
5.6. Вероятность флуктуации
Распределение вероятностей для различных значе-
значений флуктуации А/ физической величины / определяется
распределением Гаусса B.18), в котором нужно обозначить
п = А/, а= д/< (А/J >, принять щ = <А/> = 0 и исполь-
использовать соответстующие параметры вместо / (например, AN,
А К, АЕ, для которых выше найдены среднеквадратичные
флуктуации, а также АР, А Г, для которых их можно найти).
Задача. Найти отношение вероятности среднеквад-
среднеквадратичной флуктуации к вероятности нулевой ее величины.
Решение. Подставляя в B.18) п =а= \< (А/J > и
п = О, получим искомое отношение 1 / 4е = 0,61. **
77
Раздел 6
ЯВЛЕНИЯ ПЕРЕНОСА
При хаотическом тепловом движении молекулы
переносят вместе с собой массу, импульс и энергию. Если
среднее значение этих величин в единице объема
изменяется в каком-то направлении, то возникает перенос
соответствующей величины и обусловленное им явление:
при переносе массы - диффузия, при переносе импульса -
внутреннее трение, вязкость, перенос энергии приводит к
теплопроводности. Природа этих явлений одинаковая,
поэтому удобно рассмотреть их одновременно и сделать
вывод основных соотношений, при котором выявляются
особенности каждого типа переноса. При этом важными
характеристиками газа являются скорости молекул,
особенности которых уже были рассмотрены в Разделе 3, и
длина свободного пробега.
Длина свободного пробега. Молекулы идеального газа
не все время движутся свободно, а время от времени
сталкиваются друг с другом. Среднее расстояние, на
котором молекулы двигаются без столкновений, называется
длиной свободного пробега и обозначается X.
Сферическая молекула радиуса г может задеть
другую такую же молекулу, если ее центр удален не более,
чем на 2г от траектории центра первой. На расстоянии X это
в среднем случается один раз. Поэтому в объеме цилиндра
пBгJХ может быть центр только одной другой молекулы.
Следовательно пBгJХ = 1, где п ~ среднее число молекул в
единице объема. Отсюда получим
где а - эффективное сечение столкновений. Для сфери-
сферической молекулы а = %BгJ. Эта величина больше соб-
собственного сечения молекулы в четыре раза.
Отметим, что существует более точная формула для
расчета X, учитывающая взаимное движение молекул. Эта
формула содержит в знаменателе дополнительный множи-
78
тель л{2. Но этот множитель вряд ли имеет существенное
значение из-за оценочного характера сделанных выкладок.
Приведем вывод основных формул явлений переноса.
Перенос массы Перенос импульса Перенос энергии
Поток массы Касат. напряжение Поток энергии
J-
АМ_
SAt
=—m<v>x
6
_ A(MVX)
и SAt
= — n < v > x
6
x(«j-«2)= x/w(Kxl-K;c2) =
= —m < v > x
3
dn
xA,— =
dz
= —X,<v >x
= —n < v > m x
3
xX-
dz
= —X.<v > px
dC
x ; С = mn;
dz
J-D%.K.t>
1
~" 3
= — n <v >x
6
2
=—n<v>—kx
3 2
xX,-
dT
dz
= —X< v > p x
3 Ц
dT
dz dz
dV dT
-4—. F.2) *=-*—. F.3)
= — X.<v>p,
3
==—A< V >
3
D - коэффициент r\ - коэффициент % - коэффициент
диффузии вязкости теплопроводности
79
На рисунке пунктиром показана контрольная
площадка, через которую происходит перенос. Кроме того,
отмечены две поверхности 1 (внизу) и 2 (вверху), отстоя-
отстоящие от площадки на длину свободного пробега X.
Приближенно будем считать, что на единичную
1
площадь в единицу времени падает — п < v > молекул, где п
6
- их число в единице объема, <v > - средняя скорость
1
(точное число падающих молекул равно —n<v>, при
4
использовании этого выражения усложняются выкладки,
однако они приводят к тому же результату, что и
полученный ниже) .
Рассмотрим переход молекул через выделенную
площадку в случаях, когда в среде имеются градиенты
концентрации, скорости и температуры и выведем основные
законы диффузии, вязкости и теплопроводности.
Одновременно получим выражения соответствующих
коэффициентов через молекулярные характеристики среды.
Каждый из коэффициентов переноса пропор-
пропорционален средней длине свободного пробега молекул X, а
поскольку эта величина обратно пропорциональна числу
частиц в единице объема, то коэффициенты вязкости и
теплопроводности не зависят от давления газа. Очевидно, до
тех пор, пока длина свободного пробега остается
существенно меньше размеров сосуда.
Отметим также, что коэффициенты тепло-
теплопроводности и вязкости связаны простым соотношением
%/г\ = Су/\х, здесь Су/уь - удельная теплоемкость при
постоянном объеме. Опыт подтверждает наличие подобной
закономерности, но коэффициент пропорциональности
оказывается несколько больше единицы: 1,3-2,5.
Наряду с коэффициентом вязкости и коэффици-
коэффициентом теплопроводности часто рассматриваются коэф-
коэффициенты кинематической вязкости:
v = Л/Р F.4)
и температуропроводности:
а = JC/[p(CvAi)]. F.5)
80
Величины Д v и а имеют одинаковую размерность
(в системе СИ м2/с) и согласно приведенному простому
выводу все три коэффициента равны между собой (по
экспериментальным данным они равны с точностью до
порядка, и приведенный здесь вывод отражает это важное
свойство общности явлений переноса).
6.1. Теплопроводность
Задача 10.14 B64с). Найти распределение
температуры в пространстве между двумя
концентрическими сферами с радиусами R\ и ifc,
заполненном проводящим тепло однородным веществом,
если температуры обеих сфер постоянны и равны Т\ и Т^
Решение. В стационарной задаче полный поток
тепла F.3) через поверхность сферы остается постоянным
4nr2q = Q, так как тепло нигде не накапливается, поскольку
температура остается неизменной. Отсюда получим
-Х^47сг2=<2, Г = -^-- + С. F.6)
а г 4тг х г
Используя граничные условия, находим Qn С:
4nR2
а^Ь.. c = ^^. F.7)
Отметим, что в этой задаче для поддержания
перепада температур требуется подвод тепла, который за
единицу времени равен Q.
В предельном случае, при R\ » R2, имеем условие R\
- Ri = d « R\, используя которое получаем решение для
плоской задачи. При этом поток тепла равен
Т - Т
а
81
Задача. Решить предыдущую задачу, считая, что
коэффициент теплопроводности зависит от температуры по
закону х = Хо^ (этот закон соответствует тому, что
коэффициент теплопроводности газов пропорционален
средней скорости молекул).
Решение. И в этом случае из условия сохранения
полного потока тепла имеем 4nr 2q = Q. Отсюда находим
AT
Для определения постоянных Q и С можно
использовать решение предыдущей задачи, формально
JL "х / о
заменяя величину Г на величину — Т ' . Получим
2
Л R_Ri , C .
Если Т\ > Т2, то коэффициент теплопроводности
уменьшается с расстоянием, и для сохранения постоянства
полного потока тепла градиент температуры должен
меняться с расстоянием более медленно, и, следовательно,
температура будет падать меньше, чем в случае постоянного
коэффициента теплопроводности. Это следует, конечно, и
из решения.
Задача 10.27 B71с). Определить толщину льда,
образующегося в течение заданного времени t на спокойной
поверхности озера. Считать, что температура Т\
окружающего воздуха постоянна и равна температуре
наружной поверхности льда, удельная теплота плавления
льда г, плотность р.
Решение. Будем считать, что теплоемкостью льда
при небольшом морозе можно пренебречь по сравнению с
теплотой плавления. Тогда в образовавшемся слое льда
устанавливается линейный профиль температуры, так как
тепло нигде не накапливается.
82
Количество тепла, переданное воздуху за малое
4*
тг=о°с
время dt, равно теплу, выделенному при замерзании воды в
малом слое dx. Получим
— l
dt =S dxpr,
= t + const.
* 2 X[T2 -
Так как при t = 0 величина х = О, то const = О,
следовательно х = Л / .
V ?г
Для льда % = 2,22-105 эргДсмсК), г = 3,35-109 эрг/г,
р = 0,9 г/см3. При 7\ = 0 °С и Г2 = -10 °С получим
толщину замерзшего слоя за сутки
\l • 2,22 • 105 ^
\ 0,9- 3,35 109
-24-3600 =11,3 см.
За 100 дней толщина льда станет больше в десять раз
и будет около метра, что примерно соответствует толщине
льда, образующегося к концу зимы в средней полосе
страны.
6.2. Вязкость
Задача 10.66 D18с). Определить расход массы газа М
при стационарном изотермическом пуазейлевом течении
его вдоль цилиндрической трубы длиной L и радиуса R, на
концах которой поддерживаются давления Р\ и Pj.
83
Решение. Внутри трубы выделим короткий соосный
цилиндр длиной dx и радиуса г.
Сила, толкающая цилиндр в положительном
направлении оси х, равна разности давлений, умноженной
на площадь основания. Сила сопротивления действует на
боковую поверхность и равна произведению касательного
напряжения F.2) на ее площадь vlnrdx. При стацио-
стационарном движении обе силы равны:
2 dP J dvx
-nr dx = -r|——2%rdx.
dx dr
Интегрируя это соотношение при условии, что
скорость на стенке трубы равна нулю, получим
Vx =
Знак минус показывает, что в направлении скорости
давление падает. Объём жидкости или газа, протекающего
через сечение трубы в единицу времени, равен
>4' dP_
dx
Q =
litrv xdr = ¦
Масса жидкости или газа, протекающая в единицу
времени, то есть расход массы, связан с объемным
расходом соотношением М = pQ. Для несжимаемой жид-
жидкости р = const, отсюда следует, что и объем протекающей в
единицу времени жидкости О& не зависит от X. Получим
84
Для газа можно учесть, что его плотность изменя-
изменяется при изменении давления в соответствии с уравнением
состояния идеального газа A.1). Используя это уравнение,
= const. После интегри-
будем иметь MT=-zr\-^ ^ rt
рования находим решение задачи:
Мг=
8л RT 2L
Если перепад давления небольшой Pi - Р\ « Л т0
получается формула для несжимаемой жидкости.
Отметим, что при изотермическом движении газа
плотность его падает вдоль трубы из-за падения давления, а
так как расход массы остается постоянным, то скорость
возрастает. В конце трубы скорость больше, чем в начале во
столько раз, во сколько уменьшились плотность и давление.
Задача 10.82 D33с). Определить, на какой угол <р
повернется диск, подвешенный на упругой нити, если под
ним на расстоянии h = 1 см вращается такой же диск с
угловой скоростью ш = 50 рад/с. Радиус дисков R = 10 см,
модуль кручения нити / = 100 динсм/рад, вязкость воздуха
считать равной ц = 1,810 динс/см2. Краевыми эффек-
эффектами пренебречь, движение воздуха считать ламинарным.
Решение. Рассмотрим полый цилиндрический слой
воздуха радиуса г и толщиной dr, расположенный на
рисунке вертикально.
Верхняя его часть неподвижна, а нижняя вращается
со скоростью cor. Разобьем слой на горизонтальные кольца
высотой cfe. Каждое кольцо вращается с постоянной
85
скоростью, поэтому напряжения трения, действующие на
верхнее и нижнее основания каждого кольца, одинаковы
т = -цdV I dz = const, отсюда т = ~х\аьг / h и не зависит от
высоты. Вычислим момент сил М9 который создают эти
г2пг - dr - ц&г
напряжения: dM = . Интегрируя, получим
А
2Л
Момент силы упругой нити связан с углом
закручивания нити М = ф/ . Приравнивая выражения для
моментов, найдем
тел со Д4 тс 1,8 -10 - 50 -104
Ф = — = —¦ = 1,41 рад = 81°.
У 2Л/ 2-1.100
Задача 10.83 D34с). Решить предыдущую задачу в
предположении, что диски помещены в сильно
разреженный воздух с давлением Р = 10 мм рт. ст., когда
длина свободного пробега молекул воздуха велика по
сравнению с расстоянием между дисками. Для упрощения
расчета считать, что все молекулы движутся с одинаковыми
по абсолютному значению скоростями, равными средней
скорости молекул воздуха v = 450 м/с.
Решение. На верхнем неподвижном диске выделим
кольцо радиуса г и шириной dr. На площадь кольца в
единицу времени падает 2nrdr(l/4)nv молекул. Каждая
молекула приобретает импульс <огт при соударении с
нижним вращающимся диском и, двигаясь к верхнему без
соударений, передает ему такой же импульс. Сила,
действующая на выделенное кольцо, равна переданному ему
импульсу за единицу времени:
dF — — mnv<Qr2dr.
2
Умножив обе части уравнения на радиус, слева
будем иметь момент силы. После интегрирования получим
полный момент сил:
М =— mwvcoi?4.
8
Отсюда находим угол закручивания ф2 = M/f,
86
Далее используем соотношение между числом частиц
в единице объема, давлением и скоростью молекул (по
условию все скорости равны): Р = mnv 2 / 3. Получим
fc.3«i •*!.,„,„_ ода».
8 v /
Угол закручивания оказался значительно меньше,
чем в предыдущей задаче. Сравнивая соответствующие
формулы, имеем
ЗА
Ф2=-Ф,
При h « X из полученного результата следует, что
Ф2 « ФЬ
Решение последней задачи носит оценочный
характер не только из-за предположения о постоянстве
скоростей теплового движения, но также из-за
фактического использования того, что от нижнего диска к
верхнему молекулы летят, сохраняя расстояние от оси
дисков, то есть вертикально. Это приближение тем лучше,
чем больше радиус R по сравнению с расстоянием между
дисками А.
6.3. Диффузия
Задача 339с. Какова была бы мгновенная скорость
испарения воды с каждого квадратного сантиметра ее
поверхности, если бы над этой поверхностью был вакуум, а
температура воды в этот момент равнялась Т = 300 К?
Табличное значение упругости насыщенного водяного пара
при этой температуре Р = 27 мм рт. ст. Сравнить получен-
полученную величину с величиной скорости испарения при обыч-
обычных условиях (т.е. когда над ее поверхностью находится
воздух при нормальном давлении) и объяснить получив-
получившееся расхождение.
Решение. В условиях равновесия число молекул,
падающих на единичную площадь поверхности за единицу
времени в воду со стороны пара nv/4, равно числу
испарившихся молекул. Следовательно, при разлете в
вакуум с каждой единицы площади поверхности в единицу
87
времени улетело бы такое же их количество. Умножая эту
величину на массу молекулы, получаем поток массы
dM I dt = mnv 14. F.8)
Используя выражение для средней скорости молекул
v = А и уравнение состояния идеального газа Р = пкТ,
27 6 18
= 106 =
dt V 2пкТ 760 ^ 6 • 1023 • 2% • 1,38 • 10~16 ¦ 300
=0,38 г/(см2с). F.9)
Из этого решения следует, что если бы все молекулы
насыщенного пара, находящегося около поверхности
жидкости в равновесии с жидкостью, беспрепятственно
улетели, то слой воды в 0,38 см испарился бы за одну
секунду (при условии постоянной температуры жидкости,
для осуществления которого требуется значительный подвод
тепла, равный теплоте испарения). В действительности
такой слой воды испаряется за несколько часов. Причина
расхождения в том, что не все молекулы покидают слой
насыщенного пара около поверхности беспрепятственно,
этому мешают молекулы воздуха и пара.
Задача 10.108. Вода из чайного блюдца испаряется в
комнате за время порядка суток. Оценить соотношение
между числом вылетающих из жидкости в секунду молекул
N\ и числом возвращающихся в жидкость N2. Оценить
время испарения, пренебрегая токами воздуха в комнате.
Решение. Разница между этими числами
соответствует молекулам, испарившимся в реальных
условиях, а время испарения в вакуум соответствует числу
молекул, вылетевших из жидкости. Поэтому отношение
можно оценить по отношению соответствующих
времен испарения t\lti , где t\ - время, подсчитанное с
88
учетом диффузии по решению предыдущей задачи для слоя
воды глубиной около сантиметра, а ^ - реальное время
испарения:
U 1 5
— = = 10 5.
Nx t2 24 • 3600
Из этой оценки следует, что в реальных условиях
испарение с поверхности жидкости происходит достаточно
медленно, поэтому около нее находится насыщенный пар,
что и следует использовать при решении задач о диффузии
испаряющейся жидкости.
При испарении воды из блюдца в воздухе возникает
движение, так как молекулы воды, смешиваясь с воздухом,
повышают давление смеси, что приводит к возникновению
увлажненных потоков от сосуда. Если этими движениями
пренебречь, то время испарения будет определяться
процессом диффузии молекул воды в воздухе на большие
расстояния. Реальная геометрия движения диффузионных
потоков является трехмерной, требующей численных
расчетов. Однако для оценки времени испарения можно
использовать более простую модель, учитывающую главное
в этом явлении, а именно - радиальное движение паров на
большое расстояние, в пределе - на бесконечность.
Начинается оно от некоторой условной полусферы радиуса
порядка радиуса блюдца, на которой будем считать давление
пара меньше насыщенного в отношении площадей
полусферы и блюдца, которое равно 2. Таким способом
обеспечивается сохранение потока испарившейся массы.
Поток массы при диффузии определяется формулой
F.1). При сферической симметрии используемая в формуле
производная определяется по решению стационарной
задачи диффузии, которое аналогично задачи
теплопроводности F.6 - 6.7). При отсутствии паров воды на
бесконечности для производной на условной сфере, радиус
которой примем равным радиусу блюдца а, получим
(dn I dr)a = -na I а. Здесь па - концентрация на условной
сфере. Поток массы с единицы поверхности блюдца,
89
учитывая равенство всей испарившейся массы и прошедшей
через условную полусферу, будет
(dM) mn I n (dM\ 4\
=D = -\<v > т — = \ =
\dt )д а Ъ a \dt )в За
= 0,38 • — = 0,38 • 2 ¦ ИГ6 г/(см2с).
3 • 6
При испарении в воздух поток пара оказался в
к/а = 2'Ю~6 раз меньше, чем при испарении в вакуум
согласно решению F.9). В приведенном расчете принято,
что радиус блюдца а равен 6 см. Средняя длина свободного
пробега молекул воды в воздухе X взята примерно равной
длине свободного пробега молекул воздуха в соответствии с
рекомендациями в задачах 10.107 и 10.110. Отметим, что
если слой воды глубиной 0,38 см испарился бы в вакуум
согласно F.9) за 1-у секунду (эта численная оценка,
конечно, условная, верная только при постоянной
температуре испаряющейся жидкости, для чего требуется
очень интенсивный тегаюподвод), то в воздухе для этого
понадобится 5-Ю5 с = 6 суток. При глубине воды 1 см
испарение будет продолжаться примерно 15 суток.
Отметим, что при реальном испарении в вакуум
температура верхнего слоя воды будет понижаться, так как
на испарение затрачивается тепло. Только в первые
мгновения температура будет меняться мало, поскольку
скорость подвода тепла за счет теплопроводности сначала
будет большой. Затем скорость уменьшается, что можно
оценить по формуле F.10) (согласно этой формуле скорость
волны теплопроводности уменьшается обратно
пропорционально корню из времени). При понижении
температуры падает скорость молекул пара и соответ-
соответственно уменьшается скорость испарения и в воздух, и в
вакуум, притом в равной мере, если изменение
температуры одинаково. В таком случае отношение между
скоростями испарения остается тем же, то есть
пропорциональным отношению длины свободного пробега
молекул водяного пара к радиусу блюдца. Однако
испарение в воздухе осуществляется очень медленно и
90
поэтому охлаждение воды мало из-за подвода тепла от
окружающей среды. Быстрое испарение воды в вакуум под
колоколом воздушного насоса будет сопровождаться
понижением ее температуры, так как нагревание за счет
теплопроводности - процесс медленный. При уменьшении
температуры еще более быстро падает давление
насыщенного пара, поэтому скорость испарения будет
снижаться. Постепенно часть воды превратится в лед,
который, однако, тоже будет испаряться.
Задача 10.111. Узкий цилиндрический сосуд, диаметр
которого мал по сравнению с его высотой Щ = 20 см,
целиком заполнен водой при температуре 300 К. Сосуд
обдувается сверху поперечным потоком сухого воздуха, так что
давление пара на верхнем конце сосуда можно считать равным
нулю. Учитывая диффузию пара в сосуде, найти время, через
которое испарится вся вода. Плотность насыщенного пара при
указанной температуре р# = 3 10~5 г/см3, а коэффициент
диффузии паров воды в воздухе D = 0,3 см2/с Считать, что
давление пара непосредственно над поверхностью жидкости
равно Pff.
Решение. При медленном испарении диффузи-
диффузионный поток по высоте постоянен, так как через каждое
\
сечение за единицу времени проходит одинаковое число
молекул. Отсюда получим
j = -D (dn/dz) = -D [п„/(Н0 - Щ].
Здесь учтено, что при z — Щ величина п = 0.
91
Поток массы испарившихся молекул равен jm (m —
масса молекулы). Его следует приравнять массе жидкости,
испарившейся в единицу времени с единичной площади
po(dH/dt), Получим уравнение
dH nH m
Ро = -Я— •
Следовательно, dt = —— (#0 -Jt)dH.
Интегрируем, используя условие Н' = Щ при / = 0, и
находим t =— (яо - н) . Вода полностью испарится
2pHD
при Н = 0, поэтому искомое время
ро#о 1 • 202 7
г==Л2_о_ = = 2,22 • 107 с = 257 суток.
2pHD 2-3 10 0,3
С математической точки зрения уравнения диффу-
диффузии и теплопроводности полностью совпадают, в частности,
рассмотренная задача аналогична задаче о промерзании
водоема 10.27 B71с).
6.4. Явления переноса в разреженных газах
Задача 423с. Теплопроводность газа, как известно,
не зависит от давления. Объяснить, зачем из пространства
между двойными стенками сосуда Дьюара выкачивают
воздух, создавая в этом пространстве возможно более
высокий вакуум?
Решение. Теплопроводность не зависит от давления
в газе до тех пор, пока длина свободного пробега молекул в
сосуде меньше расстояния между стенками, а потом она
уменьшается обратно пропорционально давлению.
Следовательно, откачка до невысокого давления беспо-
бесполезна, эффект наступает только при очень малом давлении.
При атмосферном давлении длина свободного пробега
молекул порядка 10~5 см. Поэтому при расстоянии между
стенками примерно 1 см для достижения эффекта умень-
уменьшения теплопередачи сосуд нужно откачать до давления
92
меньше, чем 10 5 атм = 0,0076 мм рт. ст. Если давление
уменьшить до 10~7 атм, то теплопроводность воздуха
уменьшится примерно в 100 раз по сравнению с
теплопроводностью при атмосферном давлении.
Задача. Две половины сосуда разделены тонкой
перегородкой, в которой имеется очень маленькое
отверстие. В обеих половинах находится один и тот же газ,
но левая половина поддерживается при температуре 7\, а
правая — при температуре Г2. Определить равновесное
отношение давлений газа (тепловая эффузия — эффект
Кнудсена).
Решение. Условие равновесия состоит в том, что в
единицу времени слева и справа проходит одинаковое
количество молекул. Отсюда — nl<vl>=— n2<v2>. При
4 4
не одинаковой температуре в обеих половинах сосуда
устанавливается разная концентрация молекул, поэтому
Л Р2
давления тоже разные: -р= = -т==.
т т
Задача 10.62 D31с). Изотермическая эффузия газа
через пористую перегородку (поры которой малы по
сравнению с длиной свободного пробега) используется для
разделения изотопов. Естественная смесь изотопов
помещается в сосуд с пористыми стенками. Газ,
прошедший через поры сосуда, в результате эффузии
откачивается и собирается в специальном резервуаре.
С ним производится второй цикл эффузии, затем третий и
так далее, пока не будет достигнута требуемая степень
разделения изотопов. Сколько циклов эффузии необходимо
произвести, чтобы отношение концентрации частиц легкого
и тяжелого изотопов увеличить в а = 10 раз, если
относительные молекулярные массы их равны соответ-
соответственно цд = 235 и цт = 238 (изотопы урана) ?
Решение. В отличие от предыдущей задачи здесь
процесс неравновесный, молекулы каждого изотопа
переходят в резервуар, где их концентрация меньше. Но
число перешедших молекул разное. Эффект разделения
основан на том, что у изотопа с меньшей массой молекул
93
скорость больше, поэтому через перегородку в единицу
времени проходит больше легких молекул. Число
прошедших молекул пропорционально скорости, поэтому
после первого цикла, то есть в первом резервуаре,
пл\ I пло I Ыт
отношение концентраций будет = I , а после
п { ]
N циклов получим ш = Ло —— . Отсюда
nTN ПТ0 {^Л )
2 lg a 2 lg 10
N= / ч = —т^гл = 363.
Если использовать условие — — «1, то можно
получить приближенный результат N « 4,60 = 360.
6.5. Нестационарные процессы
Время достижения стационарного состояния для
процессов диффузии или теплопроводности можно оценить
по теории размерности, используя, что размерность
коэффициентов диффузии F.1) D = (l/3)A,<v> и
температуропроводности F.5) а = г|/(рОЛ0 равна квад-
квадрату длины, поделенному на время, например, в системе
СИ будет м2/с Пусть в некоторой задаче температура или
концентрация зависят от координаты X и времени t Если в
задаче нет существенных параметров с размерностью длины
или времени, то результат должен зависеть только от
безразмерной величины, составленной из D (или а), X и /,
например, от параметров X2/(Dt) или X2/(at). Одному и
тому же значению такого безразмерного параметра будет
соответствовать одна и та же концентрация С или
температура Т. Фиксируя параметр, например, полагая его
равным единице, получим закон распространения
94
определенной величины С или Т. Отметим, что в задаче о
нагревании полупространства значение параметра единица,
то есть
X2 = at, F.10)
согласно точному решению (его можно найти в справочной
литературе), соответствует движению точки, у которой
температура примерно равна среднему значению между
температурами горячей и холодной сред.
Задача 10.30. Оценить глубину промерзания почвы L
на широте Москвы за бесснежную зиму (t ~ 120 суток).
Теплопроводность грунта принять % « 1 Вт/(м-К), его тегг-
лоемкость с ~ 106 Дж/(м3К).
Решение. Решение находим из формулы F.10),
используя обозначения F.5) и то , что в условии задачи
приведено значение теплоемкости на единицу объема
-М-
120 ¦ 24 • 3600
- = 3,2 м.
10°
Отметим, что в решении предполагается, что
содержание воды в почве очень мало, так как не
учитывается выделение теплоты замерзания (80 кал/г).
Теплоемкость грунта приблизительно равна 0,3 кал/г. Чем
сильнее мороз и чем меньше влажность, тем лучше
использованное приближение. При температуре воздуха
-25 °С и содержании воды в грунте 0,5% (совсем немного)
выделение теплоты при замерзании будет примерно в
десять раз меньше, чем количество тепла, нужное для
охлаждения грунта. Соответственно ошибка из-за пренеб-
пренебрежения теплотой замерзания составит примерно 10%.
Задача 10.51. В дальнем углу комнаты открыли
флакон с духами. Человек чувствует запах духов через одну
минуту. Температура воздуха в комнате Ц = 30 °С. Оценить
время, через которое человек почувствует запах духов в той
же комнате в том же месте, если температура воздуха упадет
до t2 = -30 °С.
95
Решение. Задача также решается на основании
теории размерности: концентрация духов С будет зависеть
только от безразмерного параметра X2/(Dt). Одна и та же
концентрация, предельная для обоняния человека, будет на
том же самом расстоянии при неизменном произведении
Dt, следовательно, Т2Л1 = А/^2- Далее используем, что
коэффициент диффузии пропорционален средней скорости
молекул, то есть корню квадратному из температуры, и
длине свободного пробега. Эта величина обратно пропор-
пропорциональна числу частиц в единице объема, то есть про-
пропорциональна температуре в первой степени, если сделать
естественное предположение, что атмосферное давление в
комнате не изменилось. Отсюда находим D « Г3/2.
Следовательно:
Ч = 11(Тг/Т2)У2 = 60C03/243K/2 = 84 с.
Отметим, что полученный результат является точным, его
можно получить из решения дифференциального уравне-
уравнения для нестационарной диффузии.
Задача 14.32 (из раздела "Механика"). Бочка меда с
вязкостью ци = 100 П (пуаз) и бочка дегтя (% = 10 П)
одинаковы по размерам (R = 10 см) и массе. Бочки
помещаются рядом на горизонтальную поверхность и им
сообщается одинаковая скорость поступательного движе-
движения vq = 1 м/с. Оценить, на какое расстояние одна бочка
будет опережать другую, когда их качение станет равно-
равномерным. Массой тары и трением качения можно пре-
пренебречь, а плотности меда и дегтя считать порядка 1 г/см3.
Решение. Добавим условие, что поверхности бочек и
горизонтальная поверхность сильно шероховатые и из-за
трения между ними оболочка тары быстро тормозится, тогда
как для раскручивания жидкости времени требуется
значительно больше. Это время можно оценить по
соотношению размерностей F.10), используя вместо
коэффициента температуропроводности а коэффициент
кинематической вязкости v = г|/р F.4), так как их размер-
размерности одинаковы. Получим t -R2 /v. Характерный раз-
размер, очевидно, в данном случае равен радиусу бочки. Чем
меньше вязкость, тем больше времени tl-R2/vl
96
раскручивается жидкость' и тем дольше бочка 1 с дегтем, у
которого вязкость меньше, сохранит более высокую
скорость и будет обгонять другую бочку 2, то есть с медом.
Конечные скорости v бочек с разными жидкостями
одинаковы, они определяются из закона сохранения
момента импульса относительно любой точки на гори-
горизонтальной поверхности:
mv«R = mvR + /со, ш = —, v= —.
0 R \ + I/{mR2)
Для сплошного цилиндра момент инерции
/ = mR2 I 2, следовательно, конечные скорости обеих бочек
будут v = 2vo/3.
Так как в течение времени t\ существует разница
скоростей, то путь бочки с дегтем S\ можно оценить по
среднему значению начальной и конечной скорости
Sx =(v0 + v)tx / 2. Вторая бочка с медом приобретет
конечную скорость v раньше, поэтому ее путь будет
состоять из двух частей: за время ti путь равен
(vo+v)f2/2, да еще за оставшееся время tx -t2
существования разницы скоростей бочка с медом пройдет
расстояние [t{ -t2)v. Полный путь второй бочки составит
S2 = (v0 + v)t2 I 2 + (tx - t2)v. Следовательно:
Si-S2=(v0-v)(tx-t2)/2.
При t > t\ расстояние L между бочками изменяться
не будет, оставаясь равным значению при t =f,. Используя
найденные оценки для времен установления скоростей,
получим
v0pR2( I l) 100- МО2 ( 1 1 ,
U1=150 см.
ц2) 6 U0 100
97
Раздел 7
ПЕРВОЕ НАЧАЛО ТЕРМОДИНАМИКИ
Первое начало термодинамики представляет собой
закон сохранения энергщг. количество тепла 5Q,, получен-
полученное системой, равно приращению ее внутренней энергии dE
и совершенной ею работе ЪА:
6Q= dE+ЪА. G.1)
Здесь dE является полным дифференциалом, то есть
ydE = 0, а величины 8Q и ЪА не являются таковыми, поэ-
поэтому для них используется символ 5 (дельта), а не d.
7.1. Работа газа
Работа, совершенная газом при бесконечно малом
изменении объема, равна ЪА — PdV, а при конечном
изменении определяется интегралом А = J P[V,T{V)]dV.
Давление в соответствии с уравнением состояния зависит от
двух параметров К и Г, поэтому для вычисления работы в
общем случае необходимо задать зависимость температуры
от объема. Работа газа, следовательно, зависит от процесса,
который должен быть известен. На плоскости Р, V работа
газа - это площадь под линией Р = P(V). Она может быть
задана либо одной функцией, либо участками нескольких
функций.
Следующая задача показывает, что работа газа
зависит не только от начального и конечного состояния
газа, но и от промежуточных состояний, т.е. от процесса.
Задача. Точки 1 и 2 лежат на одной изотерме
идеального газа. Вычислить работу при переходе из
состояния 1 в состояние 2 по изотерме, а также по изобаре
с изохорой и по изохоре с изобарой.
Решение. Как и при решении всех задач, где
приходится вычислять работу, целесообразно изобразить
98
процессы на плоскости Р, V. При этом видно, что работа тем
больше, чем выше проходит соответствующая кривая.
Для одного моля газа получим:
xA=]l
A. Изотерма: А = J PdV = RT In — ;
Б. Изобара + изохора: А = P\(V2 - V\);
B. Изохора + изобара: А = Pi{Vi - V\).
Очевидно, что при изохорическом процессе работа
не совершается, хотя состояние газа изменяется. Отметим,
что если переменить направлении процесса, т. е. произ-
производить переход из состояния 2 в состояние 1, то газ будет
совершать отрицательную работу, как, например, при
сжатии в цилиндре.
Задача 1.43. Положительную или отрицательную
работу совершает идеальный газ при круговом процессе
1-2-3-1 ? Чему равна эта работа для т граммов азота?
Известно, что — = —
99
Решение. Построим заданный процесс в координатах
Р, V. Замечаем, что линия 1-2 является изобарой, уравнение
V — V
которой в переменных Т, К имеет вид V = — -Т.
т —Т
i2 il
Далее находим Р12 = —Л — -. Работа на изобаре
\i VV
А =
- У\) , на изохоре А =0, на изотерме получим
m \ Л
m V, m \т2 тЛ
А = —RTX In—1-. Полная работа Л = —RTA — - 1 - In— L
Эта работа положительная, что видно по графику в
переменных P,V9 где цикл проходится по часовой стрелке.
Такой же результат можно получить формально из решения,
Т (т 1
так как — - In — > 1 при Т2 /Тг> 1.
тх {тг) 2/ 1
7.2. Внутренняя энергия, теплоемкость
Первое начало термодинамики G.1) содержит
дифференциал внутренней энергии, которая для реального
газа зависит как от температуры, так и от удельного объема
Е= E(T,V). Дифференциал определяется выражением
100
С учетом этого соотношения первое начало
термодинамики G.1) будет иметь вид
= Cy{T,V)dT+\p[T,1
)
dV. G.2)
Здесь Cv =
Отметим, что для решения конкретных задач нужно
знать не только термическое уравнение состояния
Р = P(V ,Т), но и зависимость внутренней энергии от
температуры и объема Е = E(V,T) (калорическое урав-
уравнение состояния), чтобы найти Cy(T,V).
Теплоемкостью тела называется отношение беско-
бесконечно малого количества тепла 5Q, полученного телом, к
изменению dT его температуры:
С=—. G.3)
dT
Теплоемкость единицы массы вещества называется
удельной теплоемкостью и обозначается малой буквой с.
Часто используется теплоемкость одного моля вещества,
которая называется молярной теплоемкостью и
обозначается большой буквой С.
Теплоемкость зависит не только от свойств тела, но
также от процесса, при котором происходит подвод тепла,
так как одновременно может совершаться еще работа.
Используя уравнение G.2), получим
[l G.4,
Из второго начала термодинамики можно показать,
что для идеального газа, т.е. газа, имеющего уравнение
состояния Клапейрона A.1), внутренняя энергия не зависит
от объема, а определяется только температурой, то есть
(dE/dV)m = 0. Следовательно, для идеального газа имеем
й . G.5)
dl Jprocess
101
Однако для использования этого соотношения даже
в случае идеального газа нужно знать зависимость
теплоемкости при постоянном объеме Су от температуры.
В часто встречающихся задачах эта теплоемкость обычно
принимается постоянной, что соответствует пропор-
пропорциональности внутренней энергии газа его температуре.
В таком случае используется простая модель идеального
газа, состоящего из жестких невзаимодействующих
частиц, на каждую степень свободы которых приходится в
среднем, как показывается в статистической физике,
энергия A/2)кТ, где к — постоянная Больцмана, равная
1,3810-23 Дж/К. При / степенях свободы энергия одной
частицы равна (i/2)kT, а внутренняя энергия моля такого
газа и теплоемкость при постоянном объеме СУ равны:
Е = (i/2)kNAT = (i/2)RT, Cv= (i/2)R. G.6)
Для одноатомных газов / = 3, так как у них три посту-
поступательных степени свободы, для двухатомных / = 5, пос-
поскольку добавляются еще две вращательные степени свобо-
свободы. Для более сложных атомов, у которых три вращатель-
вращательные степени свободы, / = 6 (без учета колебательных).
Отметим, что степени свободы некоторого типа,
например, вращательные могут не возбуждаться при низ-
низких температурах, поэтому в таких условиях теплоемкость
двухатомного газа при постоянном объеме равна C/2)J? .
При высоких температурах возбуждаются еще
колебательные степени свободы молекул, на каждую из
которых приходится энергия кТ, поэтому теплоемкость
двухатомного газа может возрасти до G/2O?, например, у
водорода. Однако у других веществ такого значения не
наблюдается, так как молекулы раньше распадаются на две
части, т.е. диссоциируют.
Ниже на рисунке нанесена зависимость тепло-
теплоемкости при постоянном объеме от температуры для
газообразного водорода по данным Дж. Орира.
При более высокой температуре, чем показана на
рисунке, происходит диссоциация, общее число частиц
удваивается, поэтому в таком случае Cv = 2(з / 2)if = 3R.
Ш
I»
i*
I»
т. к
100 1DOO ЮООО
Задача 1.30 (80с). Рассматривая воздух как
идеальный газ, показать, что при нагревании воздуха,
находящегося в комнате, его внутренняя энергия Е не
изменяется, если только внешнее давление остается
постоянным.
Решение. Так как комната не изолирована от
внешней атмосферы, то давление воздуха в ней равно
давлению снаружи, т.е. при нагревании не изменяется, и
часть воздуха выходит на улицу, унося с собой энергию
газа, бывшего ранее в комнате.
Е = CVT = Cv ——.
ц R
Здесь V - объем комнаты, Р - давление в ней. Из
решения следует, что внутренняя энергия газа в комнате не
изменяется при нагревании, т.е. увеличение внутренней
энергии у каждой части массы, еще остающейся в комнате,
в точности компенсируется убыванием энергии за счет
выхода газа из комнаты. Масса газа в комнате при условиях
задачи обратно пропорциональна температуре:
ц PV
m =— .
R Т
Обратимый процесс без подвода тепла называется
адиабатическим. Получим его уравнение для идеального
газа в случае независимости теплоемкости при постоянном
объеме от температуры. Полагая в G.2) 8Q = 0 и
(Э2? / dV)T =0, будем иметь:
103
dT dV
CydT +PdV =0, Cv + R = 0,
TVRICv =const, PV[Cv+R)lCv =const. G.7)
Найдем теплоемкость идеального газа при
постоянном давлении и введем показатель адиабаты у:
СР=С?+р[^-\ =CV+R, уш?*-. G.8)
\О1 )р by
Из G.6) и G.8) для моделей одноатомного,
двухатомного и многоатомного газов получим следующие
значения показателей адиабаты: 5/3, 7/5, 4/3.
Отметим, что воздух представляет собой в основном
смесь двухатомных газов - кислорода и азота, по простой
модели жесткой "гантели" для него должно быть у — 1,400.
Эксперимент дает близкое значение 1,405.
В общем случае теплоемкость газов зависит от
процесса, при котором подводится или отводится тепло, так
как при этом еще может совершаться работа. Она может
быть как положительной, так и отрицательной. Поэтому
при подведении тепла температура газа может и
повышаться, и уменьшаться.
Задача 1.38 (85с). Политропическим процессом
называется процесс, проходящий с постоянной
теплоемкостью С Найти уравнение политропы для
идеального газа, теплоемкость С которого не зависит от
температуры.
Решение. Используя формулы G.5) и A.1) для
одного моля газа, а также условия задачи, получим
RT dT СР - Су dV
V ' Т ~ С-Су V '
TV пЛ = const, PV n = const,
С С С иГ
п= -, С=— ?-. G.9)
С-Су 1-я
При С = 0 получается адиабата Пуассона PVy = const. При
С -* ±оо получается изотерма PV = const.
Из формулы PVn = const следует dP/dV = -nP/V,
откуда получаем, что политропы с п > 0 имеют
104
отрицательную производную, в том числе адиабата и
изотерма.
7.3. Теплоемкости при разных процессах
К этой части раздела относятся задачи, в которых по
заданным условиям можно найти уравнение процесса с тем,
(dV)
чтобы по нему определить производную , а потом
\"-* У process
и теплоемкость.
Задача 1.45 (87с). Нагревается или охлаждается
идеальный газ, если он расширяется по закону PV2 = const?
Какова его молярная теплоемкость?
Решение. Будем рассматривать данную задачу в более
конкретной формулировке: подводится или отводится тепло
при расширении газа? Так как процесс политропический, то
применяем формулу G.9) и находим
С=(СР-2Су)/0- -2) = 2СУ-СР= СУ-Д>0,
т.е. bQjdT > 0. Газ расширяется, поэтому dV > О.
Используем A.1) для замены давления в уравнении
политропы на температуру. При п = 2 и dV > 0 величина
dT < 0, поэтому 6Q < 0, т.е. в данном процессе тепло
отводится от газа. Одновременно его температура падает.
Задача 1.54 (94с). Моль идеального газа нагревается
в цилиндре под поршнем, удерживаемом в положении
равновесия пружиной, подчиняющейся закону Гука. Стенки
цилиндра и поршень адиабатические, а дно проводит тепло.
Начальный объем газа Vq, при котором пружина не
деформирована, подобран так, чтобы P0S2 - kV0, где Ро -
наружное атмосферное давление, S - площадь поршня, к -
коэффициент упругости пружины. Найти теплоемкость для
такого процесса.
105
Решение. Пусть / - начальное положение поршня.
dP=-dx,
к dV dV
к к
+ — (x - /) = —x,
S S
dP dV dT
dP=-TdV, —
РУТ
dT dV _V_ _ R
dT IT 2
Sl P V T
Процесс оказался политропическим, и можно
пользоваться выведенными для него формулами. Смысл
задачи состоит в нахождении связи между dP и dV, после
чего, используя уравнение Клапейрона в продифферен-
продифференцированном виде, получаем результат.
Задача 1.55 (95с). Боковые стенки цилиндра, его
крышка и поршень не проводят тепло, а дно проводит.
пи ни
Поршень может двигаться без трения. Сверху и
снизу поршня находятся по одному молю одного и того же
идеального газа с молярной теплоемкостью при постоянном
объеме Су и показателем адиабаты у. Нижний газ
нагревают. Выразить его теплоемкость С\ через объемы V\ и
106
Решение. Уравнение процесса для газа в верхней
части известно, равенство давлений на поршень сверху и
снизу позволяет найти процесс для газа в нижнем объеме.
R Г, const 9
Р2К2*= const,, Л=Р2, —L = —у->
У \ *2
dT, dVy dV7 dTx Г, ТА
Т V V dV V V
C,=CV+P\ = С v + .
Отметим, что полученный процесс не является
политропическим, так как его теплоемкость зависит от
изменяющихся объемов. При V\ « V2 будем иметь
С\= Ср.
В этом случае давление в нижнем объеме почти не
меняется, поскольку смещение поршня мало влияет на
большой верхний объем. С ростом V\ величина С\ падает и
при V\ » V2 стремится к Су, так как в этом случае почти
не меняется нижний объем.
Задача (96с). Как изменится ответ предыдущей
задачи, если верхнюю крышку сделать теплопроводящеи и
температуру в верхнем объеме поддерживать постоянной?
Решение. В данном случае в верхней части
цилиндра процесс будет изотермическим, поэтому получим
PiVi = const. Дальнейшие выкладки совпадают с решением
предыдущей задачи, поэтому ответ находим из него при
у=1:
п
С, =CV + .
1 1 + к/^
7.4. Теплоемкость смеси газов
Внутренняя энергия смеси идеальных газов равна
сумме внутренних энергий каждого газа в отдельности,
занимающего тот же объем, так как у такого газа
внутренняя энергия не зависит от объема, т.е. от
расстояний между молекулами (очевидно, что у смеси газов
оно меньше).
Пусть е/ - внутренняя энергия на единицу массы
каждого газа, го, - его масса. Для смеси идеальных газов
получим
Me = т\в\ + т2е2 + ще3.
После дифференцирования по температуре найдем
Л%л Wlr, nt-y
су = ТГсм +ТГСК2 + ТГскз- GЛ0>
МММ
Здесь М - суммарная масса смеси: М = тг + т2+ т3,
су - удельная теплоемкость при постоянном объеме смеси,
т,
отношение весовая доля каждой компоненты смеси.
М
Если задана не масса каждого газа mh а число молей
V/, то, используя соотношения
из GЛ0) получим
с ^№у\+УгУгсУг+УъУъсУъ G П)
V^i +V2^i2 +V3II3
Напомним, что здесь рассматриваются удельные
теплоемкости с, т.е. теплоемкости на единицу массы.
Переход к молярной С осуществляется по формуле
С= ц,с.
Для вычисления теплоемкости смеси при постоян-
постоянном давлении можно воспользоваться аналогичными
формулами, заменив всюду су на ср .
В смеси газов имеем Р = Р± + Р^ + Р$. Каждый газ
занимает один и тот же объем V, поэтому
PV=PXV+ P2V+ P3V;
Me + PV= mxex +PXV+ m2e2 + P2V+ m3e3 + P3V.
Величина / = e + PV/M (V - объем массы М)
называется удельной энтальпией, для нее получаем
соотношение, аналогичное использованному для энергии
Mi = nt\i\ + m2i2 + ^3/3»
Производная от энтальпии по температуре есть
теплоемкость при постоянном давлении сР = (di/dT)p .
108
Окончательное выражение для ср смеси подобно формуле
G.11) для су, в которой вместо су нужно использовать ср.
Отметим, что для справедливости полученных
формул необходимо, чтобы состав смеси оставался
постоянным при изменении температуры.
Задача 1.80 C56с), Подсчитать по классической
теории удельную теплоемкость при постоянном давлении
газа ср следующего молярного состава: Не - 20%, Нг - 30%,
СН4 - 50%.
Решение. В задаче задан относительный молярный
состав смеси, т.е. величины v,- = v,- /{v\ + V2 + V3). Решение
следует из формулы G.11), в которой V/ нужно заменить на
V/ и использовать Ср вместо Су , а также применить
формулу Сп=усп
Ср — — ~~-
V! Ц! + V2 Ц2 + V3 [i3
5 1
0,2-R +0,3-R +0,5 4R пл
2 2 71 R
0,2 • 4 + 0,3 • 2 + 0,5 • 16 188
7.5. Скорость звука в газе
Скорость звука - это скорость распространения
малых возмущений таких величин, как давление, плотность
или скорость смещения частиц газа. В условиях, близких к
нормальным, теплообмен между участками газа с
повышенной и пониженной температурой не успевает
происходить, а при звуковых частотах не существенна и
вязкость. Поэтому сжатие и разрежение газа происходит без
изменения энтропии, в адиабатических условиях.
Адиабатическая скорость звука в газе или жидкости при
произвольном уравнении состояния определяется
[ТэрГ
выражением С3 ~ \ — , где производная берется при
V V Эр J«
I > 'О
постоянной энтропии S (Р - давление, р - плотность газа).
109
Отметим, что при очень высокой температуре,
например, в огненном шаре ядерного взрыва, теплообмен
велик, так как осуществляется, в основном, излучением. В
таких условиях распространение звука происходит
изотермически.
Напомним, что в идеальном газе уравнение адиабаты
= const (у = Ср/Су - показатель адиабаты), используя
Й
которое найдем С3 = J— =
V Р
Задача. Вычислить скорость звука в воздухе при
комнатной температуре.
Решение. При 20 °С получим
[
1,4 • 8,3 • 107 • 293
— = 343 м/с.
29
Задача 2.4 C67с). Найти выражение для скорости
звука в смеси V], V2, V3 ... молей различных идеальных газов
при температуре Г.
Решение. При использовании формулы для скорости
звука нужно определить молярную массу смеси и
теплоемкости при постоянном давлении и при постоянном
объеме. Применяя выведенные выше формулы, получим
V\ +V2CK2 +V3CF3 •••
_ \c_p_
Су =
cP =
vlCPl+v2CP2+v3C
+m2 /jn2
VV1
+v3CP3+...
Задача 2.5 C68c). Вычислить скорость звука в
кислороде при температуре Т— 1 кэВ.
Решение. Энергия ионизации внешнего электрона
всех атомов порядка энергии ионизации атома водорода
«10 эВ, а внутреннего электрона при заряде ядра Z будет
примерно «10Z2. Для кислорода при Z — 8 получим
ПО
640 эВ, т.е. при Т = 1 кэВ кислород будет полностью
ионизован. Каждый атом распадется на 8 электронов и
ядро, из одной молекулы кислорода при рассматриваемой
температуре образуется 18 частиц. Считаем, что можно
пренебречь их взаимодействием, и они представляют собой
идеальный одноатомный газ, следовательно, у = 5/3.
Для молекулярного кислорода Р = пкТ или
Р = pRT I |iO2. У полностью ионизованного кислорода
частиц в единице объема будет в 18 раз больше, поэтому
Р = ISnkT или Р = 18рИГ / \iOl, откуда получим
р
= 3,0-107 см/с.
Скорость звука возрастает не только
непосредственно из-за увеличения температуры, но также
из-за возрастания числа частиц и показателя адиабаты.
Определение численной величины скорости связано
с переводом энергетического выражения температуры в
градусы. Значению кТ = 1 эВ соответствует температура
Т «11 600 К, т.е. при условиях задачи температура газа
будет около 107 К.
7.6. Уравнение Бернулли
Это уравнение получается при применении первого
начала термодинамики к стационарному движению газа.
При больших скоростях газа сила тяжести обычно роли не
играет, поэтому ею можно пренебречь. Тогда уравнение
Бернулли имеет вид закона сохранения вдоль линии тока:
v2 /2 + /= const. G.12)
Для идеального газа найдем
v2 /2 + сРТ=срТ0. G.13)
Если вместо температуры ввести скорость звука,
получится соотношение
111
v_ + Jb_ = ±3L G.14)
2 у-1 у-1
Здесь Сзо - скорость звука в точке торможения потока,
где v = 0. Используя температуру торможения 7Ь, найдем
( Y-l v2l
Г0=Л1 + . Величина Го зависит от числа Маха
М — v/Сз , равного отношению скорости потока v к
скорости звука С$ в данной точке :
Г0=Г 1 + ^—!-М21 G.15)
Задача 2.20. Оценить давление у самого "носа"
ракеты, если число Маха М = 5, а давление на высоте
полета ракеты Р = 0,3 атм. Считать процесс сжатия газа
адиабатическим с показателем адиабаты у, а скорость газа
относительно ракеты у ее "носа" равной нулю.
Решение. Отношение температуры торможения к
атмосферной находится по уравнению G.15), а давление -
(т Т^"
по уравнению адиабаты в переменных Р, Т: Ро = Р — г .
При у = 1,4 получим То/Т= 1 + 0,2-25 = 6 и
Pq/P = б3»5 = 529, следовательно, Pq= 159 атм.
Необходимо отметить, что впереди летящего со
сверхзвуковой скоростью тела образуется ударная волна, в
которой энтропия растет с увеличением числа М, поэтому
адиабатическое приближение для определения давления тем
хуже, чем больше М. Точно приближение выполняется
только при М < 1. Однако для определения температуры
такого ограничения нет, так как уравнение Бернулли
справедливо и при переходе линии тока через ударную
волну.
Задача 2.18. Найти скорость v адиабатического
истечения струи идеального газа из сосуда через маленькое
отверстие в вакуум, если известны скорость звука в газе Сзо
и показатель адиабаты у.
112
Решение. При истечении в вакуум газ расширяется
до нулевого давления и, следовательно, до нулевой
температуры. Скорость звука при этом равна нулю.
Используя уравнение G.14), получим
Г
Отметим, что даже при очень большом давлении в
сосуде такая высокая скорость газа может получиться,
только если канал истечения сначала сужается, а потом
расширяется. В самой узкой части скорость будет равна
местной скорости звука. Если же канал только сужается, то
потоком будет достигнута лишь местная скорость звука.
При v = Сз из G.14) находим
Эта скорость меньше скорости звука в газе,
находящегося в сосуде, так как при увеличении скорости,
согласно уравнению Бернулли, температура газа снижается.
113
Раздел 8
ВТОРОЕ НАЧАЛО ТЕРМОДИНАМИКИ
Второе начало термодинамики определяет направ-
направление протекания самопроизвольных процессов, а для
состояния равновесия позволяет получить ряд важнейших
термодинамических соотношений между различными
физическими свойствами вещества. Существует несколько
формулировок второго начала, все они являются постула-
постулатами, т.е. недоказуемыми утверждениями.
Постулат Клаузиуса: тепло не может само по себе
перейти от системы с меньшей температурой к системе с
большей температурой. Эквивалентным является постулат
Кельвина: невозможно непрерывно получать работу, только
охлаждая отдельное тело ниже температуры самой холодной
части окружающей среды. Более краток постулат
Оствальда: невозможно построить вечный двигатель второго
рода (т.е. двигатель, работающий только за счет охлаждения
теплового резервуара).
Несмотря на качественный характер формулировок
второго начала термодинамики, оно приводит к далеко
идущим количественным следствиям. Прежде всего оно
позволяет определить максимальный коэффициент полез-
полезного действия (КПД) тепловой машины. Для получения
других многочисленных количественных соотношений
удобно использовать математическую формулировку второ-
второго начала термодинамики, заключающуюся в двух положе-
положениях:
1. Существует энтропия как функция состояния
системы;
2. При реальных необратимых процессах энтропия
возрастает.
114
8.1. Определение КПД двигателей
Коэффициент полезного действия двигателей равен
отношению совершенной работы к затраченному, т.е.
подведенному теплу. Работа может быть вычислена либо по
площади цикла на плоскости Р, V, либо, пользуясь законом
сохранения энергии, по алгебраической сумме подведен-
подведенного и отведенного тепла на всех участках цикла:
А = \pdV = |б0.
При последнем способе приходится определять
участки цикла, где тепло подводится. Границами участков,
где тепло подводится и отводится, являются точки касания
гладких участков цикла с адиабатой, на которой 5Q = 0.
Задача. На диаграмме Р, V изображен цикл в виде
эллипса, совершаемый с идеальным газом. Показать участки
подвода тепла, а также участки, где температура рабочего
тела возрастает. Цикл обходится по часовой стрелке.
Решение. Проведем изотермы и адиабаты,
касательные к заданному эллипсу. На рисунке показано их
относительное расположение для идеального газа.
Температура возрастает (dT > 0) на участке 4-1-2
(между изотермами). Тепло подводится EQ > 0) на участке
1-2-3 (между адиабатами). Отметим, что на участках 2-3 и 1-
4 теплоемкость отрицательная.
115
Задача 3.7 A66с). На рисунке изображен обратимый
цикл, состоящий из изотермы, изохоры и изобары,
Р
выполняемый молем идеального газа в тепловой машине.
Найти работу и подводимое тепло на каждом участке цикла,
считая, что рабочим веществом является идеальный газ.
Решение. QAb = Cj+T2 - Тг), А^ = (Q- Су) (Т2 - Тг),
<2вв = ~Су(Т2 - ГО, Аъв = 0э Qba = -RTX \n(T2/Tx),
Работа на участке АБ определена как разность
подведенного тепла и приращения внутренней энергии в
соответствии с первым началом термодинамики.
Использовано также то, что на изотерме и изобаре
изменение объема одинаковое. Тепло подводится на участке
изобары, а на изохоре и изотерме оно отводится. Для
коэффициента полезного действия т| получим
Ср{Т2-Тх)
Задача A74с). Найти КПД цикла Клапейрона,
состоящего из двух изотерм и двух изохор, с идеальным
газом в качестве рабочего вещества.
Решение. На изотерме внутренняя энергия
идеального газа не меняется, здесь произведенная работа
равна подведенному теплу. Тепло подводится на изохоре V2,
поскольку здесь возрастает температура, и на изотерме Т\9
так как на этом участке совершается положительная работа.
116
Qn=An «
Qv% = Cv(Ti - T2).
v,
л =
Задача ЗЛ6, Во сколько раз изменится КПД
двигателя внутреннего сгорания, если коэффициент
объемного сжатия а увеличить с 5 до 10 ? Реальный цикл
двигателя заменить идеальным замкнутым циклом,
состоящим из двух изохор и двух адиабат, а рабочее
вещество считать идеальным многоатомным газом.
Решение. На рисунке тепло подводится на левой
изохоре и отводится на правой.
Qn = 0, Q23 = -Су(Т2- 7з); <2з4 =0; Q*i = CV(JX - Т4),
-Тг)
Т -Т
117
Используя уравнение адиабаты TVY ' = const и
определение коэффициента объемного сжатия а = Va/Vw,
получим Ту = З^а7, Г4 = Т3ау~1. Подставляем и находим
= 1 -
= 1 - of
1-10
-1/3
-1/3
= 1,29.
ti2 i-a^-ч 1-5
Здесь было учтено, что для многотомных газов у = 4/3.
Отметим, что при увеличении степени сжатия КПД растет и
в пределе стремится к единице, но довольно медленно.
8.2. Определение КПД холодильников
При работе холодильника затрачивается меха-
механическая работа А, а полезная его деятельность состоит в
отборе тепла \QX\ от более холодного резервуара. Отметим,
что по закону сохранения энергии горячему резервуару
передается тепло I QT\ = I Qx\ + А. Следовательно, КПД
холодильника г|х можно определить как отношение
Чх = \Qx\M = IflJ/dftl - \QX\. Для цикла Карно КПД
холодильника, как и КПД двигателя, зависит только от
температуры холодного Тх и горячего Тт резервуаров тепла
и равен
Заметим, что это выражение не совпадает с обратной
величиной КПД двигателя, так как здесь в числителе стоит
более низкая температура.
118
При работе холодильника тепло \QT\, переданное
горячему резервуару, больше, чем тепло I Qx\, отобранное от
холодного резервуара на величину затраченной работы А.
Это используется в тепловом насосе.
Обратим внимание на то, что КПД холодильника
может быть больше единицы, поэтому вместо КПД иногда
используется термин "эффективность холодильника".
Задача 3.29. В комнате постоянная температура
tx =18 °С поддерживается электронагревателем мощностью
Pw — 500 ватт. Температура воздуха снаружи t2 = -21 °С.
Вместо электронагревателя для поддержания в комнате той
же температуры можно использовать тепловой насос
(тепловую машину, работающую по холодильному циклу).
Какую мощность Pj будет потреблять из электросети
тепловой насос, работающий с максимальной эффек-
эффективностью?
Решение. В данном случае в комнату отдается тепло
Q2, которое состоит из взятого с улицы тепла Q\, и
превращенной в тепло работы двигателя Q2 - Q\ . Тепловой
111
насос работает в обратную сторону по сравнению с
тепловой машиной: он потребляет работу, а отдает тепло.
Его КПД совпадает с КПД машины
Т —Т 39
Рт = Pw — = 500 = 67 Вт (вместо 500 Вт).
Т w Тг 291
Задача 3.37. Какую минимальную работу должен
совершить двигатель идеального холодильника, чтобы
работая в среде, имеющей температуру tc, охладить v молей
воды до to = 0 °С и превратить ее в лед?
119
Решение. В этой задаче "горячая" температура
остается постоянной, а температура Тх падает по мере
остывания воды. Считаем, что идеальный холодильник
Р
работает по циклу Карно. Здесь цикл повторяется много
раз, после каждого обхода на нижней изотерме темпера-
температура уменьшается на малую величину dTx, то есть нижняя
линия цикла является изотермой лишь приближенно.
dA =^
где С - молярная теплоемкость воды.
Найденная работа А\ затрачена на охлаждение.
Работа, затраченная на замерзание воды при температуре
7о, равна Ai = qy{Tc - Tq)/Tq, где q - молярная теплота
плавления льда. Полная совершенная работа
1] + А2 = v
cin^+U--c \(тс-т0)
Холодильник начинает работать, когда температура
воды и среды одинаковы, при этом его КПД стремится к
бесконечности, так как и подвод и отвод тепла осуществ-
осуществляется при одной и той же температуре. По мере охлаж-
охлаждения воды КПД уменьшается.
Отметим, что КПД идеального холодильника,
работающего по циклу Карно, при tx = -13 °С и комнатной
температуре /г = + 20 °С равен 260/33 = 7,9, т.е. гораздо
больше единицы. Также следует обратить внимание на то,
120
что с помощью холодильной машины может быть создана
разность температур некоторых сред, но для этого нужно
затратить работу.
Задача типа 4.1 A92с). Динамическое отопление
Томсона. Топливо сжигается в топке двигателя, который
приводит в действие холодильную машину. Холодильная
машина отнимает тепло от природного резервуара тепла,
например подземного, и отдает ее воде в отопительной
системе.
Одновременно вода в отопительной системе служит
холодильником теплового двигателя. Найти эффективный
КПД такой системы при tD = 210 °С, t0 = 60 °С,
tx = +15 °С.
Решение. На рисунке показан один из частных
случаев расположения циклов холодильной машины и
двигателя. Площади их одинаковые, поскольку работы
равны. Средняя изотерма Tq - это температура отопи-
отопительной системы. Стрелками отмечено тепло, которое
поступает в эту систему сверху из двигателя Q\ и снизу из
холодильника Cfe-
Считаем, что обе машины работают по циклу Карно.
Для двигателя величина Qn - это затраченное тепло,
полученное от сжигания топлива
При этом А = Qd- Q\, следовательно, Qd/Td= Q\/To.
Для холодильника имеем аналогичные соотношения
121
Находим полное тепло Q, поступающее
отопительную систему и эффективный КПД:
f Ш 7 ^Т^ ^1^ ^^^ ^Г^
Q = Q +Q =i0_Q +12. —L*. 'В " »Q =
a a» ^7^ ^^^ ^^^ ^^^ ^7^ ^^^ ^"^
_T0 TD -Tx
td- то-тх'
= ^_ = Zk Td ~Tx ^ 333 195
П Gz> T7/) ^o-^x 483 45 '
При динамическом отоплении с использованием
идеальных машин в данном случае достигается тройной
эффект в использовании топлива. При этом после работы
двигателя 0,69 часть сожженного топлива идет на
нагревание отопительной системы, только 0,31 часть
используется двигателем. Но и это тепло после работы
холодильной машины полностью возвращается в
отопительную систему, да еще дополнительно отбирается от
природного источника тепла двойное количество в
единицах сожженного топлива. Отметим, что при условиях
задачи КПД холодильника равен 640% .
Из последней формулы следует, что Q > Qd при
условии Td > То . Так как это условие всегда выполняется,
то динамическое отопление с использованием идеальных
машин передает в отопительную систему больше тепла, чем
непосредственное нагревание при сжигании топлива.
122
Раздел 9
ЭНТРОПИЯ. НЕОБРАТИМЫЕ
ПРОЦЕССЫ
9.1. Равенство Клаузиуса
Для обратимого кругового процесса имеет место
соотношение
= 0, (9.1)
которое называется равенством Клаузиуса. При подводе
тепла 80 > О, при отводе тепла от рассматриваемой
системы 5Q < 0. Важно отметить, что количество тепла,
полученное системой, зависит от пути интегрирования, то
есть от способа подвода тепла, в частности от того,
совершается или не совершается при этом работа. Поэтому
5Q не является полным дифференциалом. Согласно
равенству Клаузиуса (9.1) полным дифференциалом
является отношение 56 к температуре Т, определяющее
дифференциал функции состояния S, которая называется
энтропией:
dS=5Q/T. (9.2)
Значение интеграла от этой функции JE Q/ 7) в
соответствии с (9.1) не зависит от пути интегрирования, а
только от начального и конечного состояния среды.
Задача 4.10. Термодинамическая система с
произвольным веществом совершает круговой процесс,
состоящий из изотермы 1-2 (температура 7\), изобары
2-3 и адиабаты 3-1. Температура в точке пересечения
изобары и адиабаты равна 7з . Теплоемкость на изобаре Ср
постоянна. Вычислить работу А, совершаемую системой в
этом цикле.
Решение. Особенность задачи в том, что не задано
уравнение состояния и, следовательно, неизвестна
зависимость Р (К), которая нужна для вычисления работы -
интеграла \Р (V)dV. Поэтому работу следует вычислять по
разнице подведенного и отведенного тепла.
На изобаре теплоемкость задана, поэтому отведенное
тепло вычисляем по разнице температур. На изотерме
температура постоянна, следовательно, при использовании
равенства Клаузиуса ее можно вынести за знак интеграла и
получить величину подведенного тепла. По первому началу
термодинамики А = Q\2 + (?23- На изобаре
Для вычисления Qyi применим равенство Клаузиуса
(9.1):
— = 0 ; 5Q = СpdT \ QX1 = *~СрТ\ 1п—,
А =-С
Д + С
Можно проверить, что А > 0, особенно просто это сделать
при 7i - 7з « 7з.
9.2. Изменение энтропии в обратимых процессах
Для обратимых процессов дифференциальным
определением энтропии является равенство (9.2), из
которого следует интегральное определение
^2 =J(8Q/7').
124
В эту формулу не входит уравнение состояния,
поэтому для некоторых простых процессов, происходящих с
постоянной температурой, например, плавление или
испарение, или для процессов с постоянной теплоемкостью,
не трудно найти изменение энтропии даже без знания
уравнения состояния.
Задача 4,60 B19с). Найти изменение энтропии
М =30 т льда при превращении его в пар, если начальная
температура льда / = -40 °С, а температура пара t = 100 °С.
Теплоемкости воды и льда считать постоянными, а все
процессы - происходящими при атмосферном давлении.
Удельная теплоемкость льда сл = 0,5 кал/(г-К), теплота
плавления q = 80 кал/г, теплота испарения воды
X = 539 кал/г.
Решение. Используя определение энтропии (9.2),
получим при нагревании льда dS = cAdT/T. Так как
сл = const, то после интегрирования находим увеличение
энтропии А*У12 = тсл ln(T2 / Tj), где Tj - температура
плавления льда. При плавлении температура не изменяется,
поэтому Ад$2 = тц/Тъ
Нагревание воды также сопровождается увеличением
энтропии AiS23 = тсв In (Г3/Г2). Наконец, при испарении
получим Абз = тХ/Тз. Суммируем изменение энтропии во
всех четырех процессах
AS = ml сл In-1- + — + св In-1- + — =64 кал/К.
\ Т Т Т Т \
Поскольку нагревание происходит при атмосферном
давлении, то использованные в задаче теплоемкости есть
теплоемкости при постоянном давлении.
Задача типа B09с). Найти выражение для изменения
энтропии одного моля идеального газа.
Решение. TdS = CydT + PdV,
dT dV TV
dS = Cv + R , S-Sn =Cvln— + Rln—.
V T V ° V To Vo
Применяя уравнение состояния A.1), заменим Г на Р
125
Р V PV1 I
S - SQ = Cv In— + CP In— = Cv In 7 .
P V \ P Vy \
Задача типа 4.8 B06c). Найти КПД цикла,
изображенного на плоскости Т,S, состоящего из изотермы,
адиабаты и прямой линии. Уравнение состояния рабочего
Т2
тела не известно.
Решение. Сравнивая с циклом Карно, замечаем, что
здесь подведенное тепло то же самое, а совершенная работа
вдвое меньше, поскольку вдвое меньше площадь цикла.
Поэтому Г| = (Тх - Т2) I B7^). Отметим, что КПД циклов,
нанесенных сплошной линией и пунктиром со стрелками,
одинаковые.
В качестве простых задач целесообразно вывести
КПД теплового двигателя и холодильника, используя
энтропию, а также показать геометрический смысл КПД
как отношения площадей на графике Т' - S.
9.3. Метод термодинамических функций и соотношения
Максвелла
Согласно второму началу термодинамики энтропия
является функцией состояния, следовательно, после замены
величины 5Q на TdS первое начало термодинамики для
обратимых процессов превращается в соотношение между
полными дифференциалами:
dS = —dE + — dV. (9.3)
Т Т
В качестве независимых переменных удобно
использовать две из четырех величин: Р, V, Т, S.
Дифференциалы выбранной пары оставляют в правой части
dE=TdS-PdV; Г= — , ^ =4 • (9.4)
Если известна зависимость E(S,V), то из (9.4)
получаем Т и Р путем дифференцирования. Поэтому иногда
внутреннюю энергию Е называют термодинамическим
потенциалом. С помощью замены переменных можно
ввести еще три потенциала, каждый из которых тоже будет
полным дифференциалом.
Энтальпия : / = Е + pV,
V =\— . (9.5)
Свободная энергия : \i/= Е- TS,
( ?wt Л
(9.6)
Термодинамический потенциал: Ф = Е + PV- TS,
, К=(— J . (9.7)
Задание одной функции в виде любого из четырех
потенциалов сразу определяет и термическое, и
калорическое уравнения состояния, следовательно, каждый
потенциал содержит в себе больше информации о свойствах
вещества, чем уравнение состояния (соотношение между
Р, V, Т).
Задача 5.9 B28с). Пользуясь методом
термодинамических функций (соотношениями Максвелла),
найти производную (dE/dV)m.
Решение. Как следует из постановки задачи,
независимыми переменными нужно взять Г и К Из первого
начала термодинамики G.2) и определения энтропии (9.2)
получим
Г'Э?
dV
127
Так как согласно второму началу термодинамики dS
является полным дифференциалом, то множители при dT и
соответствующие частные производные:
\дТ)у ~т{дТ)у ' {dV)T~[
Величины смешанных вторых производных не
зависят от порядка дифференцирования
Применяя это соотношение, находим
d2S d2S
ГЭ7ЭК U
Окончательно получим
«Г»! +Ц?\ *
Используем соотношение (9.8) для идеального газа.
По уравнению состояния A.1) находим производную,
имеющуюся в правой части (9.8), и получаем: (dE/dV)m = О,
т.е. внутренняя энергия идеального газа не зависит от
объема.
Приведенный способ получения формул носит
название метода термодинамических функций, а
полученные формулы называются соотношениями
взаимности или формулами Максвелла.
Задача 5.11 B31с). Используя понятие энтропии и
соотношения Максвелла, получить выражение для разности
теплоемкостей Ср- Су.
Решение. Применим общую формулу для
теплоемкости G.4) и подставим туда соотношение (9.8) для
(dE/dV)m. Получим
'process
Используя изобарический процесс, находим
(9.9)
128
Отметим, что теплоемкости относятся к той же массе
вещества, что и объем К Для идеального газа
(дР) mR (дУЛ mR
— = , = .Отсюда
[дТ)у \iV Ьт)Р iiP
Ср -Cv =—R. (9.10)
В полученном выражении (9.10) теплоемкости
относятся ко всей массе газа.
Задача 5.18. Серебряная проволока диаметра
d = 1 мм адиабатически нагружается при комнатной
температуре Т = 300 К силой F = 10 Н. Полагая, что
теплоемкость с =0,234 Дж/(г-К), плотность р = 10 г/см3, а
линейный коэффициент теплового расширения
ах, = 1,9-10**5 К, определить изменение температуры AT
проволоки.
Решение. Напряженное состояние проволоки
отличается от состояния всестороннего давления,
характерного для жидкости и газа. При использовании
полученных для таких сред формул в данной задаче следует
принять, что давление равно 1/3 напряжения растяжения,
учитывая таким образом отсутствие боковых напряжений
F
АР = -—. Учтем также, что объемный коэффициент
ЗЛ
теплового расширения втрое больше линейного
В задаче задан коэффициент теплового расширения,
а для ответа на поставленный вопрос нужно найти
производную (дТ/дР)$, которую определим методом
термодинамических функций.
Рассмотрим соотношения (9.5). Из последних двух
формул (9.5) следует равенство (дТ/дР)$ = (dV/dS)p . Далее
используем определение теплоемкости при постоянном
(dS)
давлении Ср =7|— . С помощью этой формулы
преобразуем величину (dV/dS)p:
129
,as )p {dTdsjp [dTjp
Подставляя результат в ранее найденное выражение,
получим
I—I = — [—1 . (9.11)
\ог Js \у,р )\о1 Jp
В этом соотношении величины Ср и V относятся к
одному и тому же количеству вещества: либо к одному
молю, либо к единице массы. Будем использовать второе
определение, так как в задаче дана теплоемкость единицы
массы проволоки.
Из (9.11) определим изменение температуры, считая
его малым. Окончательно будем иметь
Т
сРр
300 • 1,9 • 10 -4-Ю6
= -0,031 К.
0,234 • 107 • 10 -л • 0,01
9.4. Изменение энтропии при необратимых процессах
Как уже отмечалось, изменение энтропии, исходя из
ее определения, можно найти только для обратимых
процессов. При вычислении энтропии в необратимых
процессах используется то важное свойство, что она
является функцией состояния. В подобных задачах следует
найти конечное состояние термодинамической системы, т.е.
определить характеризующие ее два параметра. Далее в это
состояние нужно прийти подходящими обратимыми
процессами и на них определить изменение энтропии,
которое будет таким же, как при необратимом процессе.
Задача типа 4.57 B11с). Найти увеличение энтропии
идеального газа массы М, занимающего объем V\b при
расширении его в пустоту в объем Vj .
130
Решение. Уточним условия задачи, а именно
отметим, что стенки сосудов, где происходит перетекание,
являются жесткими, поэтому газ внешней работы не
совершает - нет перемещения приложенных сил давления.
Кроме того отметим, что стенки теплоизолированные,
следовательно, подвода тепла нет.
XX ХХХХХ X X X XXX
X X X У X XX XX X XX
Проинтегрируем первое начало термодинамики G.1)
для всей массы газа по рассматриваемому процессу от
начального состояния 1 и до конечного состояния 2:
J6Q = ]dE + )ЪА , Е2
т = т
1 1 1
Интегралы подведения тепла и работы будут равны
нулю, поэтому в данном процессе сохраняется внутренняя
энергия. Для идеального газа это означает сохранение
температуры. Энтропия его была определена в разделе 9.2.
Конечное состояние газа определено, а так как
энтропия является функцией состояния, то находим
к,+
Решение задачи
получается
простое,
но
промежуточные состояния очень сложны. При расширении
в пустоту после разрыва перегородки происходит быстрое
движение газа до правой стенки и резкое торможение, при
котором возникает ударная волна. Она распространяется
навстречу потоку и останавливает его. В ударной волне из-
за процессов вязкости и теплопроводности в тонком
переходном слое с большими градиентами скорости и
температуры возрастает энтропия. Окончательное
успокоение движения происходит под действием вязких
131
сил, при этом кинетическая энергия переходит в тепловую,
а энтропия возрастает. Необратимость термодинамического
процесса обычно связана с относительно быстрым
неконтролируемым изменением состояния газа, как это
происходит в рассмотренной задаче.
В следующих двух задачах температура и энтропия
возрастают в процессе успокоения колебаний поршня из-за
вязкости реального газа.
Задача А. Вертикальный теплоизолированный сосуд
частично заполнен газом с температурой Т\ и
адиабатической постоянной у. Газ закрыт подвижным
поршнем, уравновешивающим своею тяжестью давление
газа Р\, так что P\S = mg , где m - масса поршня, S - его
площадь, g - ускорение силы тяжести. Поршень медленно
поднимают на высоту, в п раз большую начального
расстояния от дна, а затем отпускают, он падает, сжимая
газ. Найти конечную температуру газа 7з и изменение
энтропии. Для газа выполняется уравнение состояния
Клапейрона A.1).
Решение. Медленный подъем поршня является
адиабатическим процессом, поэтому имеем Т2=Тгп~^у ,
где п =
. При падении используем закон сохранения
ч
JLX)
энергии
Так как Р3 = Ри то — = —
V Т
у1 м
122
При я = 3, у = 1,4 получим Т^/Т\ = 1,32. Отсюда при
T\ = 300 К следует Т$ - 7\ = 96 К. Заметное повышение
температуры происходит из-за неравновесного процесса при
падении поршня: В начале движения вес поршня превышал
силу давления газа, поэтому скорость поршня
увеличивалась, он проходил положение равновесия по
инерции. На рисунке показана примерная зависимость
высоты поршня h от времени t. Возникшие колебания
затухли из-за вязкости реального газа. Кинетическая
энергия поршня перешла во внутреннюю энергию газа,
поэтому температура газа возросла. Если бы вязкость
отсутствовала, то колебания продолжались бы, и энтропия
не возрастала.
Задача Б. Вертикальный теплоизолированный сосуд
частично заполнен газом с температурой Т\ и
адиабатической постоянной у. Газ плотно закрыт
подвижным поршнем, который сначала удерживается от
падения, так как его масса m в п раз больше той, которую
может уравновесить давление газа Р\\ mg = nP\S, где S -
площадь поршня, g - ускорение силы тяжести. Затем
поршень отпускают, он падает и после успокоения
движения и остановки его медленно поднимают на
начальную высоту. Найти конечную температуру газа Т^ и
изменение энтропии. Для газа выполняется уравнение
состояния Клапейрона A.1).
Решение. При падении поршня используется закон
сохранения энергии: vCvG2 - Т\) = nP\(V\ - Vi)\ здесь в
правой части записана в преобразованном виде работа
поршня, равная rng{h\ - h^.
133
Используя уравнения состояния A.1), получим
I ^i) = ^2 / Tv Подставив это соотношение в закон
сохранения энергии, найдем TjJT\ = [1 + п(у - 1)]/у. При
подъеме поршня происходит адиабатическое расширение
газа, поэтому имеем
r- 2 ^п s v/ 1 ) л 1 \п у у У
Из найденного решения при п -> 1 следует 7з ->
как это и должно быть. При п = 3 получим Г3/Г1 = 1,22.
Если 7\ = 300 К, то 7з - 7i = 66 К.
В правой части рисунка показана примерная
зависимость положения поршня от времени. После падения
возникают колебания, при затухании которых из-за
вязкости газа механическая энергия переходит в тепловую,
и по этой причине энтропия возрастает.
Отметим, что при большой вязкости газа колебания
могут не возникнуть, в этом случае вся диссипация энергии
будет происходить в процессе опускания поршня (при
продолжительных колебаниях эта часть мала). Несмотря на
медленность движения, происходит переход механической
энергии в тепловую, и энтропия возрастет на столько же,
как и при быстром падении. Так происходит потому, что
конечные состояния одинаковые, они не зависят от
скорости. Для увеличения энтропии получим
Задача 4.47 B23с). Идеальный одноатомный газ в
количестве v = 10 молей, находящийся при температуре
Т{ = 300 К, расширяется без подвода и отвода тепла в
пустой сосуд через турбину, необратимым образом
134
совершая работу. После установления равновесия газ
приобретает температуру Т2 = 200 К. После этого газ
квазистатически сжимается: сначала изотермически, а
затем адиабатически, возвращаясь в первоначальное
состояние. При этом сжатии затрачивается работа
А = 15 кДж. Найти изменение энтропии газа при
расширении.
Решение. На рисунке изображены: А - сосуд с
газом, Б - сосуд, куда газ перетек, совершив по пути
работу.
После окончания процесса расширения газ с
помощью поршня заталкивается назад, на этот раз
обратимым способом, т.е. медленно. Расширение в вакуум -
это неуправляемый быстрый процесс, такой процесс всегда
является необратимым. Он условно изображен в нижней
части рисунка волнистой линией, там же показаны изотерма
и адиабата.
Найдем изменение энтропии при обратимых
процессах сжатия, когда газ переводится в исходное
состояние. На таких процессах можно проинтегрировать
первое начало термодинамики. Для этого полученное тепло
следует выразить через приращение энтропии и учесть, что
последний интеграл задан в условии задачи. Получим
J TdS = ]dE + JЬА, T2(Si - S2) = Ex - E^ -A.
2 2 2
Как видно, соотношение легко интегрируется:
энтропия меняется на изотерме при постоянной
температуре, поэтому Т выносится за интеграл.
135
При сжатии совершается работа над газом, поэтому
сам газ совершает отрицательную работу. Дальше
учитывается, что внутренняя энергия идеального газа
зависит только от температуры
10.-8,31. C00-200)
= 2 + НЯ 13ДЖ/К.
200 200
В этой задаче прямой процесс - необратимый,
обратный - обратим, поэтому естественно было
воспользоваться обратным процессом для вычисления
энтропии, так как ее изменение одинаково при обоих
процессах, поскольку энтропия - функция состояния.
9.5. Энтропия смеси идеальных газов
Так как молекулы идеального газа не
взаимодействуют ни друг с другом, ни с молекулами другого
газа, то энтропия смеси равна сумме энтропии каждого газа
в отдельности при той же температуре и в том же объеме.
Можно доказать, что смесь разных газов можно
разделить без затраты работы. Пусть у нас имеется смесь
разных молекул, при этом первый газ представлен
удлиненными молекулами, занимающими всегда только
горизонтальное положение, а второй газ состоит из
удлиненных молекул, всегда занимающих только
вертикальное положение. Сосуд двойной: он состоит из
ящика с горизонтальными отверстиями и второго ящика с
вертикальными отверстиями. Первый ящик пропускает
горизонтальные молекулы и задерживает вертикальные,
второй действует наоборот.
Начнем раздвигать ящики. На рисунке видно, что в
левую часть первого ящика попадут только вертикальные
молекулы, так как они свободно проходят через
вертикальные отверстия и поэтому не давят на дно второго
ящика. На его дно действуют только горизонтальные
молекулы, они давят и на левое дно, и на правое, поэтому
суммарная сила равна нулю. Следовательно второй ящик
можно выдвинуть из первого без затраты работы, что и
требовалось доказать.
В рассмотренном примере такая необычная форма
молекул была взята, конечно, только для облегчения
представления о том, что если газы разные, то они должны
чем-то действительно различаться и поэтому, используя эти
различия, их можно разделить.
Задача типа 4.69 B17с). В двух неодинаковых
сосудах находятся разные идеальные газы с известными
параметрами их состояния. Найти изменение энтропии этих
газов после того, как емкости соединили трубкой и газы
перемешались. Сосуды считать жесткими и
теплоизолированными.
Решение. Сразу после соединения сосудов возникает
быстрое движение газов из-за наличия перепада давления, а
также начинается более медленный процесс выравнивания
температуры. Оба явления необратимы. Однако конечное
состояние системы легко найти, так как внутренняя энергия
системы не меняется:
J7* 1 ТТ -— С7
Jb\ т &1 — jbc .
Из этого условия можно найти конечную температуру Тс'
Ш ^2 1
Учтем, что окончательное значение объема каждого
газа равно суммарному начальному объему. Зная по два
параметра состояния как для начального, так и для
конечного состояния системы, определяем изменение
энтропии идеального газа:
137
[ 2 V 2
Важно отметить, что из полученного решения нельзя
получить ответ для случая, когда оба газа одинаковые, так
как в таком варианте не происходит расширения каждой
части до суммарного объема, не происходит взаимного
проникновения молекул, изменяющего состояние системы.
Неправомерность такого перехода особенно видна,
если рассматривать перемешивание газов с одинаковыми
давлениями и температурами, а также одинаковыми
теплоемкостями и молекулярными массами, но все же с
различающимися молекулами. Тогда из решения следует
результат
М
AS = 2—R 1п2 ,
который соответствует тому, что объем каждого газа
удвоился, газы перемешались, поэтому энтропия смеси
возросла. Однако если молекулы газов неразличимы,
тождественны, то должно быть AS = 0, так как при
соединении сосудов состояния газов не меняются и их
энтропия не может возрасти. Имеющее место взаимные
перемещения молекул одного и того же газа ничего не
изменяют, поэтому энтропия должна оставаться
постоянной. Новое состояние может получиться только при
перемешивании чем-то различающихся молекул.
Таким образом, в полученном решении задачи
невозможен предельный переход к одному и тому же газу в
обеих частях сосуда. В невозможности такого предельного
перехода состоит так называемый парадокс Гиббса.
Задача 4.70. В двух сосудах находится по одному
молю разных идеальных газов. Температура в обоих сосудах
одинакова. Давление в первом сосуде Рь а во втором ?ъ
Определить, на сколько изменится энтропия системы, если
138
сосуды соединить. Как изменится результат, если газы
одинаковы?
Решение. Из закона сохранения энергии следует, что
температура после соединения сосудов останется прежней и
в случае разных газов, и в случае одинаковых.
Учитывая это, изменение энтропии для разных
газов найдем по приведенной выше формуле, заменяя
отношение начальных объемов с помощью уравнения
состояния идеального газа на отношение начальных
давлений: V\/V2 = Р2/Рь Отсюда получим
Следовательно, при смешивании разных газов с
одинаковыми начальными давлениями и температурами
AS = 2Rki2.
Для решения задачи в случае одинаковых газов
представим, что они разделены некоторой подвижной
перегородкой, препятствующей перемешиванию, но
позволяющей сжиматься одному газу за счет расширения
другого вплоть до уравнивания давлений. Тогда сумма
начальных объемов газов будет равна сумме конечных
объемов: Vx + V2 = V\k + V2& Отсюда, используя уравнение
состояния идеального газа и то, что температура одна и та
же, находим конечное давление газов: Р^ = 2/{\/Р\ + 1/Р2).
Следовательно, для изменения объемов получим
V2k/V2 = Рт/Рк- Pid/Pi + 1/Рт>/2.
Отметим, что эти изменения в два раза меньше, чем
изменения объемов разных газов, полученные в
рассматриваемой задаче ранее.
Увеличение энтропии в случае одинаковых газов
определим по отношению конечных и начальных объемов:
Ух
139
Увеличение энтропии меньше, чем при смешении
разных газов, на величину 2R 1п2, так как для одинаковых
газов меньше изменения объемов. Отметим частный случай:
при равенстве начальных давлений изменение энтропии по
найденной формуле равно нулю, как это и должно быть.
140
Раздел 10
РЕАЛЬНЫЕ ГАЗЫ
Изучение свойств реальных газов удобно проводить
на модели, отражающей разницу между реальными газами и
идеальными, а также включающей в себя важные свойства
реальных газов, главным из которых является способность
их конденсироваться, превращаться в жидкость. Такой
математической моделью реальных газов является уравнение
состояния Ван-дер-Ваальса.
ДОЛ. Уравнение Ван-дер-Ваальса
Для реальных газов уравнение Клапейрона PV = RT
выполняется приближенно и тем точнее, чем меньше
плотность газа и выше его температура. При большой
плотности и достаточно низкой температуре газы могут
быть переведены в жидкое состояние, что было бы
невозможно, если бы свойства газов точно соответствовали
уравнению Клапейрона. В реальных газах между
молекулами действуют силы, причем на близких
расстояниях это силы отталкивания, а на больших -
притяжения. Одним из простых уравнений, учитывающих
взаимодействие молекул, является уравнение состояния
Ван-дер-Ваальса.
Это уравнение имеет вид (для 1 моля)
A0.1)
Для v молей вместо V нужно использовать V/v, то
есть в уравнение Ван-дер-Ваальса входит молярный объем.
В формуле A0.1) параметры аи b - это коэффициенты Ван-
дер-Ваальса, которые при теоретическом анализе считаются
постоянными.
Величина а/V2 учитывает уменьшение давления
реального газа по сравнению с идеальным из-за взаимного
притяжения молекул. Давление на некоторую площадку
141
пропорционально числу молекул в единице объема около
площадки, а его уменьшение из-за притяжения
окружающими молекулами пропорционально этой же
величине. Поэтому уменьшение давления пропор-
пропорционально квадрату количества молекул в единице объема,
то есть обратно пропорционально квадрату молярного
объема.
Отметим, что этот вывод не зависит от степени п в
зависимости силы притяжения / от расстояния г между
двумя молекулами: / « 1 / гп. Однако для сходимости
интеграла при суммировании по всем притягивающимся
частицам сила должна убывать быстрее, чем 1 / г3, то есть
величина п должна быть больше 3. Это связано с тем, что
число частиц в полусфере толщиной dr увеличивается
пропорционально квадрату расстояния и при п — 3 в
результате интегрирования получается расходящийся на
бесконечности логарифм.
На больших расстояниях притяжение возникает
благодаря взаимодействию между электрическими зарядами,
входящими в состав атомов и молекул (электроны и
протоны). В целом атомы и молекулы нейтральны, но
заряды противоположного знака в присутствии
электрического поля соседних частиц (или даже без поля в
случае полярных молекул) не совмещены в одной точке,
частицы поляризуются и поэтому притягиваются друг к
другу.
По закону Кулона сила взаимодействия между двумя
электрическими зарядами убывает обратно
пропорционально квадрату расстояния между ними. Отсюда
можно вычислить, что сила между двумя "жесткими"
диполями, в которых заряды не смещаются под действием
поля, убывает обратно пропорционально четвертой степени
расстояния. В случае образования диполей из-за
поляризации убывание происходит еще быстрее. Таким
образом, для электрически нейтральных атомов и молекул
условие п > 3 выполняется.
Параметр Ъ определяет минимальный объем,
который может занять моль вещества при боглшом
142
давлении, когда молекулы максимально приближены друг к
другу. Очевидно, что во всех случаях объем К должен быть
больше Ъ. По порядку величины параметр Ь примерно
равен молярному объему жидкости при низкой
температуре, когда она много меньше критической.
Например, для воды табличное значение Ь = 30 см3/мольэ а
молярный объем воды при нормальных условиях равен
18 см3/моль.
По смыслу введения параметров а и Ъ в уравнение
Ван-дер-Ваальса они должны быть постоянными и
считаются таковыми при теоретическом анализе уравнения
состояния. Однако эксперименты показывают, что в
действительности эти параметры являются функциями
температуры и плотности. Чтобы избежать такой
неоднозначности в справочниках обычно приводятся
значения коэффициентов, полученные при критических
параметрах газа. При этом используются соотношения
A0.2).
Основные свойства уравнения состояния Ван-дер-
Ваальса удобно рассмотреть на диаграмме, где в переменных
Р, V изображены изотермы.
Отметим изотерму, проходящую через критическую
точку К. В этой точке объединяются два экстремума и обе
точки перегиба. Следовательно,
эк
= 0 и
Э2Р
= 0.
143
У к =», Тк =—-, Рк =—. A0.2)
Отсюда получим
8а
21 Rb' *K 21b1'
На изотерме А\ - В\ пунктиром отмечены мета-
стабильные состояния: А С - перегретая жидкость, DB -
переохлажденный газ. Такие состояния используются,
соответственно, в пузырьковой камере и в камере Вильсона
для регистрации элементарных частиц.
Показанный крестами участок CD является
неустойчивым, так как здесь | > 0. Такому условию
ЭК )т
не может удовлетворять никакое реальное вещество,
поэтому этот участок уравнения Ван-дер-Ваальса нужно
исправить. Вместо кривой ACDB используется
горизонтальная прямая АВ, проведенная в соответствии с
правилом Максвелла: площади между прямой и изотермой
Ван-дер-Ваальса сверху и снизу равны между собой. Это
следует из того, что при обходе по замкнутому контуру,
составленному из изотерм с одной и той же температурой,
сумма подведенного и отведенного тепла равна нулю
(следствие равенства Клаузиуса), поэтому равна нулю
работа, то есть площадь на плоскости P,V. Отметим, что
знак площади зависит от направления обхода контура.
Область двухфазного состояния отмечена линией,
состоящей из точек. Слева на границе имеется только
жидкость, справа только газ; внутри области массы
жидкости и газа обратно пропорциональны расстоянию по
горизонтали до соответствующей границы.
Задача 6.17. После демонстрации критического
состояния вещества ампула, заполненная эфиром,
охлаждается. Оказалось, что при некоторой температуре Т
жидкость, плотность которой рж = 1,9 ркр, заполняет ровно
половину пробирки. Определить эту температуру Т.
Критическая температура эфира Ткр = 467 К.
Решение. Обозначим объем пробирки V. Масса
жидкости в критическом состоянии равна pKpV, а при
температуре Т масса в пробирке будет состоять из
144
жидкости и газа: ржУ/2 + ргУ/2, где рг - плотность газа. Из
условия сохранения массы получим рг = 2ркр - рж = ОДр^.
Запишем уравнение Ван-дер-Ваальса для двух
крайних состояний перехода от жидкости к газу, при
которых в пробирке содержится или только жидкость, или
только газ (на рисунке это точки Аи В, при переходе от А к
В меняется соотношение между массами жидкости и газа,
но их плотности не меняются, так как вдоль АВ постоянны
температура Г и давление Р):
Г RT ±_ г RT a
уъ l' vb ]'
Приравниваем давления и из полученного уравнения
находим температуру
>(Г-*)
v2v2
Y жг г
Используем соотношения A0.2) и заменим постоянные а
и Ъ на Ткр и VKp:
кр
кр
кр
кр
кр
кр
кр )
= 0,7975
кр
уКР
Здесь было использовано VKp/V2 = 0,1 и Укр/Уж =1,9
согласно ранее найденному отношению плотностей.
Окончательно получим Т= 0,7975467 = 373 К = 100 °С.
10.2. Внутренняя энергия и энтропия
Используя уравнение состояния Ван-дер-Ваальса,
можно получить выражение для внутренней энергии. С
этой целью применим формулу (9.8) из раздела 9:
дЕ } (дР )
— = т\ — - Р. Определяем производную и
dv)T Уът)у
дЕЛ а
dV)T=V2-
подставляем в формулу. Получим
145
Интегрируем это выражение Е = +f{T). Выразим
произвольную функцию через теплоемкость. По
определению — = Cv (T), следовательно:
\дТ )у
E = - — + jcv{T)dT.
Часто принимается, что Су не зависит от
температуры, в этом случае получим
Е= CyT-a/V. A0.3)
Задача 6.26 D75с). Какое количество тепла надо
подвести к одному молю газа Ван-дер-Ваальса, чтобы при
расширении в пустоту от объема V\ до объема Vi его
температура не изменилась?
Решение. Если стенки сосуда теплоизолированы и
являются жесткими, то при расширении в пустоту
сохраняется внутренняя энергия A0.3) независимо от того,
обратимый процесс или нет. Поэтому изменение
температуры газа при расширении в пустоту равно
Ф1
1
У Гг)
Отсюда следует, что газ Ван-дер-Ваальса при
расширении в пустоту охлаждается. Для достижения
первоначальной температуры его следует нагреть (при
постоянном объеме). Получим
1
Температура идеального газа при расширении в
пустоту не изменяется, а температура газа Ван-дер-Ваальса
изменяется, причем всегда уменьшается. Часть тепловой
энергии идет на увеличение потенциальной, которая растет
при увеличении расстояния между молекулами, так как они
притягиваются.
Отметим, что в выражение для внутренней энергии
не вошла постоянная Ь, однако, нужно помнить, что
146
формулой для внутренней энергии можно пользоваться
только при условии V> b.
Задача D79с). Найти выражение для энтропии газа
Ван-дер-Ваальса.
Решение. Используя общее выражение для
изменения энтропии при обратимых процессах
и значение производной
T V -Ъ
Интегрируя это уравнение при постоянной величине
Су от начального состояния 1 до конечного 2, находим
S2 -S\ =Cv\n — + R\n-± . A0.4)
2 l V Тг Vx-b
Это выражение получено для одного моля газа. Для
v молей, число которых остается постоянным при
рассматриваемом процессе, всю правую часть нужно
умножить на число молей v и, кроме того, умножить на v
постоянную Ь. Эта процедура аналогична переходу к v
молям в уравнении состояния Ван-дер-Ваальса A0.1).
Задача. Найти изменение энтропии одного моля газа
Ван-дер-Ваальса при расширении его в пустоту от объема V\
до объема V^ Начальная температура равна 7\.
Решение. Подставляя найденное в задаче изменение
температуры в формулу A0.4), получим
-Ь
AS = Су In
1-
1 1
CVTX
4- Л In-
Vx-b
Интересно отметить, что величина второго члена
здесь больше, чем при расширении до того же объема
идеального газа. Однако первый член, как и в A0.4),
отрицательный, так как температура реального газа падает
при расширении в пустоту, и по этой причине энтропия
147
несколько уменьшается. В целом при расширении в пустоту
энтропия возрастает, но нужно обратить внимание на то,
что при низких температурах расширения в пустоту может
не происходить, так как уравнение Ван-дер-Ваальса
допускает существование не только нулевого давления, но
даже отрицательного.
10.3. Эффект Джоуля-Томсона
Эффект заключается в том, что при медленном
перетекании реального газа через пористую перегородку
(дросселировании) происходит либо повышение, либо
понижение температуры. При таком стационарном процессе
и отсутствии теплопередачи через стенки энтальпия любого
газа не меняется. Вывод о сохранении энтальпии основан
на том, что при стационарном движении изменение
внутренней энергии газа равно работе по его продвижению
через перегородку, т.е. на законе сохранения энергии.
Отсюда следует, что у идеального газа, энтальпия которого
зависит только от температуры, эффект отсутствует, то есть
его температура не меняется.
Задача 6.68 D85с). Показать, что газ,
подчиняющийся уравнению Ван-дер-Ваальса с а = 0, в
опыте Джоуля-Томсона всегда нагревается. Определить
повышение температуры при расширении.
Решение. Условие сохранения энтальпии для такого
газа
DTT/
L = CyT0
V2-b
Отсюда получим — = р
Су
Су
Vx-b\
RV2
h
Это выражение больше единицы при V2 > Vj (газ
расширяется), причем знак изменения температуры не
зависит от величины расширения.
Задача 6.69 D86с). Показать, что газ, подчи-
подчиняющийся уравнению Ван-дер-Ваальса, с Ъ = 0 в опыте
Джоуля-Томсона всегда охлаждается. Определить
понижение температуры при расширении.
Решение. Условие сохранения энтальпии для такого
газа приводит к равенству
откуда получаем
Т - Т -
Знак неравенства соответствует очевидному условию
V] < V2. И в этом случае знак изменения температуры не
зависит от степени расширения газа, она всегда падает.
Отметим, что в рассмотренных задачах проявилось
то свойство уравнения Ван-дер-Ваальса, что постоянные а и
Ъ оказывают противоположное влияние на изменение
температуры газа в опыте Джоуля-Томсона. При
совместном влиянии может быть и повышение, и
понижение температуры.
Задача 6.72 D92с). Расширение газа в процессе
Джоуля-Томсона проводится от начального состояния
(Т, V) до сильно разреженного состояния, в котором газ
может считаться идеальным. Найти кривую инверсии
интегрального эффекта Джоуля-Томсона в переменных
Т, V.
Решение. Считаем, что в конечном состоянии " газ
идеальный, поэтому условие сохранения энтальпии имеет
вид
Подставляя вместо начального давления Pi его
значение по уравнению Ван-дер-Ваальса, получим
149
Rb 2a
Rb 2a
Температура будет повышаться если Тх — >
О, то
есть при условии Тг >
2аУг-Ь
Rb Vx
При меньшей температуре газ в процессе Джоуля-
Томсона будет охлаждаться. Отметим, что при комнатной
температуре дросселирование воздуха приводит к
понижению температуры газа, а водорода к повышению.
Задача. Для газа, подчиняющегося уравнению Ван-
дер-Ваальса, найти в общем случае уравнение кривой
инверсии, т.е. такой кривой в плоскости Т, V, при переходе
через которую эффект Джоуля-Томсона меняет знак.
Решение. В начальном и конечном состоянии
энтальпии газа равны: Е\ + Pi V\ = JE2 + Pj V^ Подставляем
сюда значение давлений по уравнению Ван-дер-Ваальса
A0.1) и используем условие, что в точках инверсии
начальные и конечные температуры газа одинаковы
Т\ = 7^. В результате получим температуру инверсии
7л {У,-Ь){Уг-Ъ)
Т =
Rb
A0.5)
В общем случае температура инверсии газа Ван-дер-
Ваальса зависит не только от начального, но и от
конечного состояния газа, то есть от степени его
расширения. Отметим предельные случаи формулы A0.5).
150
При Vi - V\ « V\ полним температуру инверсии для
дифференциального эффекта:
га{Ух-Ъ)г
Rb Vl
В другом предельном случае, при V2->°°, получается
температура инверсии при сильном расширении газа, когда
в конечном состоянии его можно считать идеальным:
Rb Vi
151
Раздел 11
ФАЗОВЫЕ ПРЕВРАЩЕНИЯ
Фазами вещества называются его однородные части,
различающиеся по физическим свойствам, отделенные друг
от друга границами раздела. Лед и вода, в которой он
плавает, - пример твердой и жидкой фазы. Вода и водяной
пар в чайнике - пример жидкой и газовой фазы.
Понятие фаз является более общим понятием, чем
понятие об агрегатных состояниях, которыми считаются
твердое, жидкое или газообразное вещество. Различные
фазы могут существовать и в пределах одного и того же
агрегатного состояния. Твердое состояние одного и того же
вещества может быть в разных фазах. Известными
примерами являются: графит и алмаз; сера, в которой
образуются ромбические (обычная желтая сера) и
моноклинные кристаллы; белое олово с тетрагональной
структурой, которое при атмосферном давлении и
температуре ниже 14 °С переходит в серое олово (этот
переход известен как "оловянная чума").
Для равновесия между фазами необходимо как
механическое равновесие, так и тепловое, то есть равенство
давлений и температур. Но этого недостаточно, поскольку
масса одной фазы может изменяться за счет другой. Только
при определенном соотношении между давлением и
температурой вдоль кривой фазового равновесия,
определяемой равенством удельных термодинамических
потенциалов, осуществляется постоянное отношение между
числом молекул в одной фазе и числом в другой. Линия
фазового равновесия определяется дифференциальным
уравнением Клапейрона-Клаузиуса.
МЙ2
11 Л. Уравнение Клапейрона-Клаузиуса
Задача 11.4 E45с). Рассмотрев цикл Карно для
системы, состоящей из жидкости и ее насыщенного пара, и
применив к нему теорему Карно, выразить производную
давления насыщенного пара по температуре dP/dT через
удельные объемы пара vn и жидкости уЖу и удельную
теплоту парообразования q.
Решение. На плоскости Р, V рассмотрим бесконечно
малый по давлению цикл Карно, состоящий из двух
протяженных изотерм 1-2 и 3-4 и двух коротких адиабат
2-3 и 4-1.
Площадь цикла равна затраченной работе
КПД цикла Карно равен
dA
dT
Т
и
dP
dT
'12
dT
T
следовательно:
q т ai T{vn -v
Следствие. При произвольном фазовом переходе из
фазы 1 в фазу 2 получим
— —7^=^- (ИЛ)
dT T(v2-Vl)
Это уравнение Клапейрона-Клаузиуса. В нем #1-_>2 -
удельная теплота перехода из первой фазы во вторую
(с учетом знака). Например, при испарении воды
q = 539 кал/г, а при конденсации q = -539 кал/г. При этом
153
в знаменателе с плюсом стоит удельный объем второй фазы.
Наклон кривой фазового равновесия одинаков в обоих
случаях, так как в уравнении A1.1) меняется знак и в
числителе, и в знаменателе.
Задача. Сравнить тангенсы углов наклона кривых
фазового равновесия около тройной точки.
Решение. На рисунке показано взаимное
расположение твердой, жидкой и газообразной фазы около
тройной точки.
Г05
Отметим некоторые характерные особенности линий
фазовых переходов.
Линия сублимации расположена круче, чем линия
испарения жидкости. Это объясняется тем, что теплота
сублимации qrr около тройной точки равна сумме теплот
плавления дтжк испарения джг- Такой результат Следует из
рассмотрения бесконечно малого цикла вокруг тройной
точки. Он совершается при бесконечно малом отличии от
изотермического цикла и согласно равенству Клаузиуса (9.1)
алгебраическая сумма подведенных теплот при постоянной
температуре равна нулю.
Используя уравнение A1.1), получим искомое
отношение тангенсов или производных:
ЯтгУг -уж) Ятг
^L) Яжг^г -vr) Яжг
)
= 1 +
A1.2)
154
В последнем соотношении учтено, что удельный
объем газа много больше, чем удельные объемы и
жидкости, и твердого тела.
У большинства веществ удельный объем жидкости
больше, чем у твердого тела, так как молекулы жидкости
более подвижны и должны располагаться несколько дальше
друг от друга, чем у твердого тела. В таких случаях согласно
уравнению Клапейрона-Клаузиуса кривая плавления имеет
положительный наклон. Однако молекулярная структура
некоторых тел такова, что плотность твердого тела меньше
плотности жидкости, как, например, у воды и льда, у
чугуна, ряда других веществ. В таких случаях кривая
плавления имеет отрицательный наклон.
Линия испарения жидкости имеет малый наклон, так
как удельный объем газа обычно большой по сравнению с
удельным объемом и жидкости, и твердого тела. Эта линия
оканчивается в критической точке, поэтому говорить о
жидкости или газе можно только в условиях фазового
равновесия, когда они присутствуют одновременно и
различаются по плотности.
При низких температурах все вещества находятся в
твердой фазе, за исключением гелия, который при малом
давлении остается жидкостью вплоть до нулевой
температуры.
11.2. Приближенное интегрирование уравнения
Клапейрона-Клаузиуса
Задача E58с). Найти зависимость давления
насыщенного пара от температуры при следующих
предположениях: удельную теплоту парообразования q
считать не зависящей от температуры; удельный объем
жидкости пренебрежимо мал по сравнению с удельным
объемом пара; к пару применимо уравнение состояния
идеального газа. (Эти упрощения допустимы вдали от
критической точки, если интервал изменения температур не
слишком большой) .
155
Решение. Используем уравнение Клапейрона-
Клаузиуса при условии уж « vn и применяем уравнение
dP \iq dT
Клапейрона vn = RT/(\iP). Получим — = -. Интег-
Р R Т
рируя, находим
Р = Ро ехр
(И.З)
где Pq ~ давление насыщенного пара при температуре То.
По этой формуле найдем давление водяного пара
дри О °С, исходя из давления паров воды, кипящей при 100
°С (го = 373 к) и атмосферном давлении Pq = 760 мм рт. ст.
Получим Р = 6,3 мм рт. ст., что несколько превышает
действительное значение, равное 4,6 мм. Отличие связано с
тем, что в действительности при понижении температуры
теплота парообразования растет, поэтому отрицательный
показатель экспоненты на самом деле несколько больше.
Задача 11.41 E46с). Найти изменение температуры
А Г плавления льда при повышении давления на
АР = 1 атм. Удельный объем воды при 0 °С vb = 1 см3Д,
удельный объем льда vjj = 1,091 см3/г, удельная теплота
плавления льда q = 80 кал/г. По найденному значению А Г
рассчитать приближенно температуру тройной точки воды.
Решение. Подставляя указанные значения в
уравнение Клапейрона-Клаузиуса, получим
dP
— = -137 атм/К,
dT '
dT
dP
= 0,0073 К/атм.
Переход лед-вода при 0 °С происходит при
атмосферном давлении, то есть давление и воды, и льда
равно 1 атм. Кривая фазового равновесия лед-вода на
плоскости Р, Т из-за малой разности удельных объемов идет
очень круто, почти вертикально, поэтому температуру
тройной точки приближенно можно оценить, полагая в ней
давление насыщенного пара равным нулю. На графике
видно, что это можно сделать для определения
температуры. Тройная точка обозначена ТТ,
экстраполированная для определения температуры точка
обозначена цифрой ", точка " соответствует кипению
при атмосферном давлении.
iam
По найденному значению производной получаем
приближенно температуру тройной точки, равную
+0,0073 °С. Табличное значение +0,010 °С.
Давление в тройной точке много меньше
атмосферного, приближенно его можно оценить по кривой
фазового равновесия жидкость-пар. Эта кривая вблизи
нулевой (по Цельсию) температуры идет полого, и поэтому
давление в тройной точке приближенно равно давлению
насыщенного пара при 0 °С, которое, как отмечалось в
предыдущей задаче, равно 4,6 мм рт. ст.
Задача 11.56. Тонкая проволока, охватывающая
петлей брусок льда, под действием нагрузки способна
пройти через лед. Полагая, что скорость движения
проволоки v определяется скоростью подвода тепла через
проволоку от области над проволокой, где вода замерзает, к
области под проволокой, где плавится лед, оценить
величину скорости v . Теплопроводностью льда пренебречь.
Температура льда 0 °С, теплота плавления д = 335 Дж/г,
плотность льда р = 0,917 г/см3. Диаметр проволоки
D = 0,1 мм, коэффициент теплопроводности
X = 130 ВтДм-К), давление, создаваемое под проволокой,
принять равным 10 атм.
Решение. Обозначим удельные объемы льда \д и
воды Уд . Под проволокой температура плавления льда из-за
повышенного давления меньше 0 °С на величину
АТ=Р(ул-ув)Т/д.
157
За малое время At количество тепла, прошедшего
поперек проволоки на единицу ее длины, можно оценить по
одномерному приближению закона теплопроводности
Q ~ (Di dT/dz)At« (D)c AT/D)At =%ATAt.
Это тепло проплавит лед толщиной Az, на что нужно
его количество, равное рлЯ& Д& в установившемся режиме
из равенства теплот находим % AT At = рлдО Az. Так как
скорость движения проволоки есть v = Az/At, то получим
- рл)
130 • 273 • 106 • 83
Q 9л Pbd C35 • 103) • 9172 • 1000 • 10
= 0,31 мм/с.
Следует заметить, что оценка по одномерному
приближению лучше подходит для проволоки не круглого, а
квадратного сечения со стороной D. Также отметим, что в
стационарном режиме для плавления льда не требуется
дополнительного подвода тепла, так как при замерзании
воды над проволокой выделяется такое же его количество,
которое необходимо для плавления льда под ней. Поскольку
плотность воды больше, чем льда, то жидкость будет
достаточно свободно обтекать проволоку.
Задача 11.13. Гейзеры могут рассматриваться как
большие подземные резервуары, наполненные грунтовой
водой и прогреваемые подземным теплом (в нижней части
рисунка стрелками условно обозначен подвод воды и
тепла). Выход из них на поверхность Земли осуществляется
через узкий канал, который в "спокойный" период
заполнен водой. Считая, что "активный" период наступает,
когда закипает вода в подземном резервуаре, и что во
время извержения гейзера канал заполнен только паром,
который и выбрасывается наружу, оценить, какую часть
воды теряет резервуар гейзера во время одного
извержения. Глубина канала h — 90 м. Молярная теплота
испарения воды Л = 41 кДж/моль.
Решение. Когда вода в подземном резервуаре
нагреется настолько выше 100 °С, что закипит при давлении
-Ро + PS*1 = Ю а™> то в°Да из выходного канала будет
выброшена, и он заполнится паром, плотность которого
примерно в 103 раз меньше. Поэтому давление в резервуаре
упадет почти до одной атмосферы, и вода будет кипеть до
тех пор, пока ее температура не понизится до 100 °С.
Теплота, идущая на испарение, берется за счет того, что
вода была нагрета выше 100 °С. Отсюда получаем баланс
тепла Am (Л/ц) = тс А Т и, следовательно:
Am I m = |nc AT / Л.
Температуру кипения воды при давлении 10
атмосфер определим по формуле A1.3). Окончательно
получим
т = ^о373
RTQ P 8.31-373
1 In — 1 г- In 10
Л Ро 41 • 103
„ O,Y Am 18- 4,18- 78,6
АТ= 78,6 К, = ¦ =—— = 0,144.
m 41 103
Отметим, что помимо канала, через который
происходит извержение, у подземного резервуара должен
быть еще снабжающий его водой источник, например,
фильтрационные воды. Период работы гейзера
определяется, в основном, временем его наполнения и
прогревания. Время извержения обычно невелико по
сравнению с временем подготовки.
159
Раздел 12
ПОВЕРХНОСТНОЕ НАТЯЖЕНИЕ
Вдоль поверхности жидкости действует сила, лежа-
лежащая в касательной плоскости. Величина ее определяется
коэффициентом поверхностного натяжения а, который по
определению равен силе, действующей на единицу длины
границы поверхности жидкости. Размерность а равна
отношению силы к длине, в системе СИ получим Н/м, а в
системе СГС будет дин/см.
12.1. Давление под кривой поверхностью жидкости
Если граница между жидкостью и газом искривлена,
то из-за поверхностного натяжения по разные ее стороны
существует разность давлений, которая зависит от кривизны
поверхности и определяется формулой Лапласа
Ai>4i+i) A2Л)
где R\ и /?2 - радиусы двух взаимно перпендикулярных
нормальных сечений поверхности раздела. Сумма их
обратных величин, использованная в формуле, не зависит
от выбора положения нормальных сечений.
Отметим, что давление всегда больше там, где
расположен центр касательной окружности (если их две, то
больше там, где находится центр окружности с меньшим
радиусом). При этом давление может быть больше и внутри
жидкости, и вне ее в зависимости от задачи. Например,
капля жидкости в воздухе и воздушный пузырек в воде
сжаты силами поверхностного натяжения, давление внутри
них выше, чем давление в окружающей среде.
Другой пример - подъем жидкости при смачивании
по капилляру и опускание при несмачивании. В обоих
случаях давление воздуха равно атмосферному давлению, но
радиус касательной окружности в первом варианте
расположен в воздухе, поэтому там давление выше, то есть
160
в капилляре при подъеме жидкости силами поверхностного
натяжения создается разрежение, из-за чего она и
поднимается. В случае несмачивания радиус касательной
окружности расположен внизу, в жидкости, там создается
повышенное давление по сравнению с атмосферным и
жидкость опускается.
Задача E06с). Чему равно добавочное давление АР
внутри мыльного пузыря с диаметром d = 0,8 см, если
поверхностное натяжение мыльной воды а = 40 дин/см?
Решение. Учитывая что пленка имеет две
поверхности, по формуле Лапласа A2.1) получим
B 2} 8а 8-40 , -> л «
АР = 2а ¦— + —-= — = = 400 дин/см2 = 0,3 мм рт. ст.
U d) d 0,8
Эту задачу можно решить другим способом,
рассматривая силы, действующие на каждую полусферу
условно разрезанного пузыря: по окружности действуют
силы поверхностного натяжения, равные 2ncd (здесь учтено,
что пленка имеет две поверхности). Они уравновешены
силами давления воздуха, действующими изнутри на
полусферы: (nd2/4)AP. Приравнивая, получим тот же
результат.
Задача 12.22 E26с). Капля воды с массой т = 0,1 г
введена между двумя плоскими и параллельными между
собой стеклянными пластинками, смачиваемыми водой,
причем краевой угол равен нулю. Как велика сила
притяжения между пластинами F, если они находятся друг
от друга на расстоянии d = 10~4 см? Поверхностное
натяжение воды (при 18 °С) а = 73 дин/см.
Решение. Центры соприкасающихся окружностей
двух главных сечений расположены один в жидкости,
другой в воздухе, поэтому в формуле Лапласа знаки
радиусов разные. Давление выше там, где расположен
меньший радиус, то есть в воздухе. Пластинки оказываются
прижатыми друг к другу атмосферным давлением. Находим
те-1- 10"
=17,8 см.
161
2 1 l
¦ - — = 1^46 • 106 дин/см2.
18 J
F= nR2AP = 71-A7,8J1,46Ю6дин = 1490 кг.
Вне площади сжатой капли давление с каждой
стороны пластинок равно атмосферному, то есть
уравновешено. Сила притяжения пластинок получилась
очень большой из-за малости расстояния между ними. При
расстоянии в 100 раз больше, равным 0,01 см (толщина
волоса или листа бумаги), сила будет в 104 раз меньше,
всего 149 грамм.
Задача 12.3 D97с). Капля несжимаемой жидкости
совершает пульсационные колебания, становясь
\
\
последовательно вытянутой, сферической, сплюснутой,
сферической, снова вытянутой и так далее. Как зависит
период этих пульсаций т от плотности р, поверхностного
натяжения а и радиуса капли R ?
Решение. Действительные колебания капли носят
сложный двумерный характер. Рассмотрим простую модель,
позволяющую сделать оценочные расчеты.
162
В тех частях капли, где радиус уменьшился на
величину А/?, давление будет больше на величину
AP=(c/R2) AR,
поэтому на эту часть капли будет действовать избыточная
сила, равная приблизительно APnR2. Эта сила будет
приводить в движение примерно одну четвертую часть
массы капли
Используя такую модель, получим уравнение
колебаний
d2
т —j(AR) + тю(ДЛ) = 0.
Отсюда находим период пульсаций
За
Ввиду приближённого характера модели численный
коэффициент здесь тоже приближённый, но вывод
уравнения отражает механизм возникающих колебаний.
Отметим, что с точностью до множителя период
колебаний капли можно получить из соображений теории
размерности, так как из величин р, а и R, от которых
зависит период - других заданных параметров нет - можно
составить единственную комбинацию с размерностью
времени: х« р1/2 R3/2 c~1/2.
12.2. Термодинамика поверхностного натяжения
Задача 12,5 D99с). Рассмотрев цикл Карно для
пленки жидкости в предположении, что температуры
нагревателя и холодильника бесконечно мало отличаются
друг от друга, и применив к этому циклу теорему Карно,
найти производную поверхностного натяжения а жидкости
по температуре.
Решение. Обозначим площадь пленки Ф и
рассмотрим на плоскости а, Ф бесконечно малый цикл
Карно. Растянем пленку изотермически из состояния 1 в
состояние 2, увеличив ее площадь на малую величину АФ.
При этом к пленке нужно подвести тепло д-АФ, где q -
теплота, необходимая для изотермического образования
единицы площади пленки. Внешняя работа по растяжению
пленки равна а-АФ, следовательно, работа самой пленки
будет (-а АФ ). Отметим, что коэффициент поверхностного
натяжения зависит от температуры и при одной и той же
ее величине постоянен. Затем растянем пленку
адиабатически из состояния 2 в положение 3. Далее по
изотерме 3-4 и адиабате 4-1 вернемся в исходное состояние.
Работа пленки за цикл равна площади цикла в
переменных а, Ф:
da
АА=-Ао ДФ=~ АГ АФ.
dT
Подведенное тепло AQ = #АФ. Коэффициент
АА AT
полезного действия цикла Карно равен величине = 3
АО Т
откуда получаем искомое соотношение:
q = -~Tdc/dT. A2.2)
Так как q > О, то производная поверхностного
натяжения по температуре отрицательна: da/dT < 0, то есть
коэффициент поверхностного натяжения падает с ростом
температуры. Это согласуется с тем, что при критической
температуре он равен нулю.
Отметим, что исследованный цикл аналогичен
рассмотренному ранее бесконечно малому циклу Карно с
насыщенным паром. Аналогом давления Р является
коэффициент поверхностного натяжения с другим знаком
(-а), аналогом объема V - площадь пленки Ф. При
сделанном анализе величина а была взята со знаком
минус, так как работа газа равна PdV, а работа пленки
будет (-о-ДФ).
Задача 12.6 E00с). Найти выражение для внутренней
энергии U пленки.
Решение. По первому началу термодинамики
8Q = dU - ЫФ, При изотермическом процессе
dS
bQ = qdO = -Т dO, Из этого выражения следует
dT
( dS)
dU = а- Г — аФ. Так как а зависит только от Т. но не от
I dT)
Ф, то, интегрируя, получим
( \
Задача 12.9 E03с). В сосуде с адиабатическими
стенками находится мыльный пузырь радиуса г = 5 см.
Общее количество воздуха в сосуде и в пузыре v = 0,1 моля,
его температура. Т = 290 К (предполагается, что она
одинакова внутри и вне пузыря). При этой температуре
поверхностное натяжение а = 70 дин/см,
daJdT = -0,15 динДсм-К). Как изменится температура
воздуха в сосуде, если пузырь лопнет? Теплоемкостью
образовавшихся капелек пренебречь.
Решение. Увеличение температуры воздуха
происходит за счет внутренней энергии пленки
(двусторонней) лопнувшего пузыря
v Cv AT = 2 • 4лт2[о- —Т
V { dT
2f d^)
дг . Г a J. 1«ИG0 + 0.15 ¦ 290) ,
5vR 5 0,1 8,31 • 107
12.3. Зависимость давления насыщенного пара от
кривизны поверхности жидкости
Линия фазового равновесия на плоскости Р, Т может
смещаться в зависимости от кривизны поверхности раздела.
Хотя у поверхности жидкости пар почти всегда является
насыщенным, но его давление зависит не только от
температуры, но и от формы поверхности раздела.
Для вывода искомой зависимости рассмотрим
закрытый сосуд с насыщенным паром, на дне которого
имеется жидкость с плоской поверхностью, в которую
погружена капиллярная вертикальная трубка с внутренним
радиусом г.
Если жидкость смачивает стенки капилляра, то она
поднимется вверх, если не смачивает, то опустится. Чтобы
нельзя было сделать вечный двигатель, основанный на
разнице давлений насыщенного пара над вогнутым
мениском Р., который расположен на высоте h от плоской
поверхности, давление там должно быть меньше давления
пара над плоской поверхностью Ро на ту же величину, на
которую уменьшается давление газа в поле тяжести на
высоте А: Р_ = Ро - Pngh или АЛ = - pjjgh, где рп -
плотность пара. Высота подъема жидкости получается из
равенства давления жидкости в основании капилляра и у
плоской поверхности: -2a/r + p%gh = pjjgh , где рж -
плотность жидкости.
А п 2а р/т 2а рп
АР = И т И- A2.4)
г Рж - Рп г Рж
ИВ
Приближенное выражение справедливо, когда плотность
пара мала по сравнению с плотностью жидкости, то есть
вдали от критической точки.
Над выпуклой поверхностью давление насыщенного
пара больше, чем над плоской, на величину
ж
По этой причине капли воды в воздухе будут
испаряться даже при 100% влажности.
Задача 12.52. Пары воды, находящиеся в
помещении, начинают конденсироваться на гладкой
поверхности при охлаждении ее до 7\ = 10 °С, Начиная с
какой температуры Ti они начнут конденсироваться на
пористом теле с радиусом пор г = 10~5 см? Удельная теплота
парообразования воды X = 2480 кДж/кг, коэффициент
поверхностного натяжения а = 70 дин/см. Угол смачивания
поверхности пор равен нулю .
Решение. В данном случае давление пара у
пористой поверхности определяется его давлением в
комнате, поэтому оно одинаковое и у выпуклых, и у
вогнутых участков поверхности. Но при этом около
вогнутой поверхности пар может быть насыщенным, а
около плоской поверхности и тем более выпуклой - еще
ненасыщенным, так как давление насыщенного пара около
вогнутой поверхности меньше на величину
. Поэтому
при снижении температуры пар начнет конденсироваться
сначала на вогнутых участках поверхности, а для
конденсации на плоской поверхности нужно еще
дополнительно снизить температуру.
При изменении температуры состав смеси воздух-
пар не меняется, так как выходят наружу или поступают в
помещение и воздух, и пар одновременно. При этом
суммарное давление в помещении от температуры не
зависит, так как оно равно внтлнему атмосферному.
Следовательно, при изменении температуры в помещении
давление паров остается постоянным.
На рисунке сплошной линией показана линия
фазового равновесия при плоской поверхности жидкости, а
пунктиром - при вогнутой поверхности. Решение задачи
получим, подставляя в уравнение Клапейрона-Клаузиуса
изменение давления насыщенного пара из-за кривизны
поверхности:
2<уря ХАТ
гРж Tvn '
Отсюда находим изменение температуры
2а Т 2-70-283 0
г ржХ КГ5 -1-2480-107
Искомая температура конденсации
т= 10,16 °С.
ЗАМЕЧЕННЫЕ ОПЕЧАТКИ
стр строка напечатано надо
N~AiV
N- Ал
24 13 сверху
37 8 снизу 5 =
37 7 снизу S - к 1п(ЛГ1пЛГ-... 5
56 12 снизу
60 2 сверху
66 6 сверху с разными с равными
* (ЛПпЛ/Ч..
<е >
<?т>
75 11 снизу
84 1 снизу
85 6 сверху
85 7 сверху
85 6 снизу
104 10 снизу
165 9 сверху
165 10 сверху
2кТ
m
р2-р,«р
полый
ЪкТ
m
pf-p,«p,
(это слово убрать)
Су
dS da
dT dT
dS da
dT dT