Комбинаторные алгоритмы теория и практика - Липатова Е.П., Алексеева В.Б.

Автор: Липатова Е.П. Алексеева В.Б.
Теги: компьютерные технологии математика математический анализ комбинаторика переводная литература теория и практика
Год: 1980
Похожие
Алгоритмы. Руководство по разработке
Лекции по математике Т.10. Перебор и эффективные алгоритмы Краткое и ясное изложение предмета
Программирование в алгоритмах
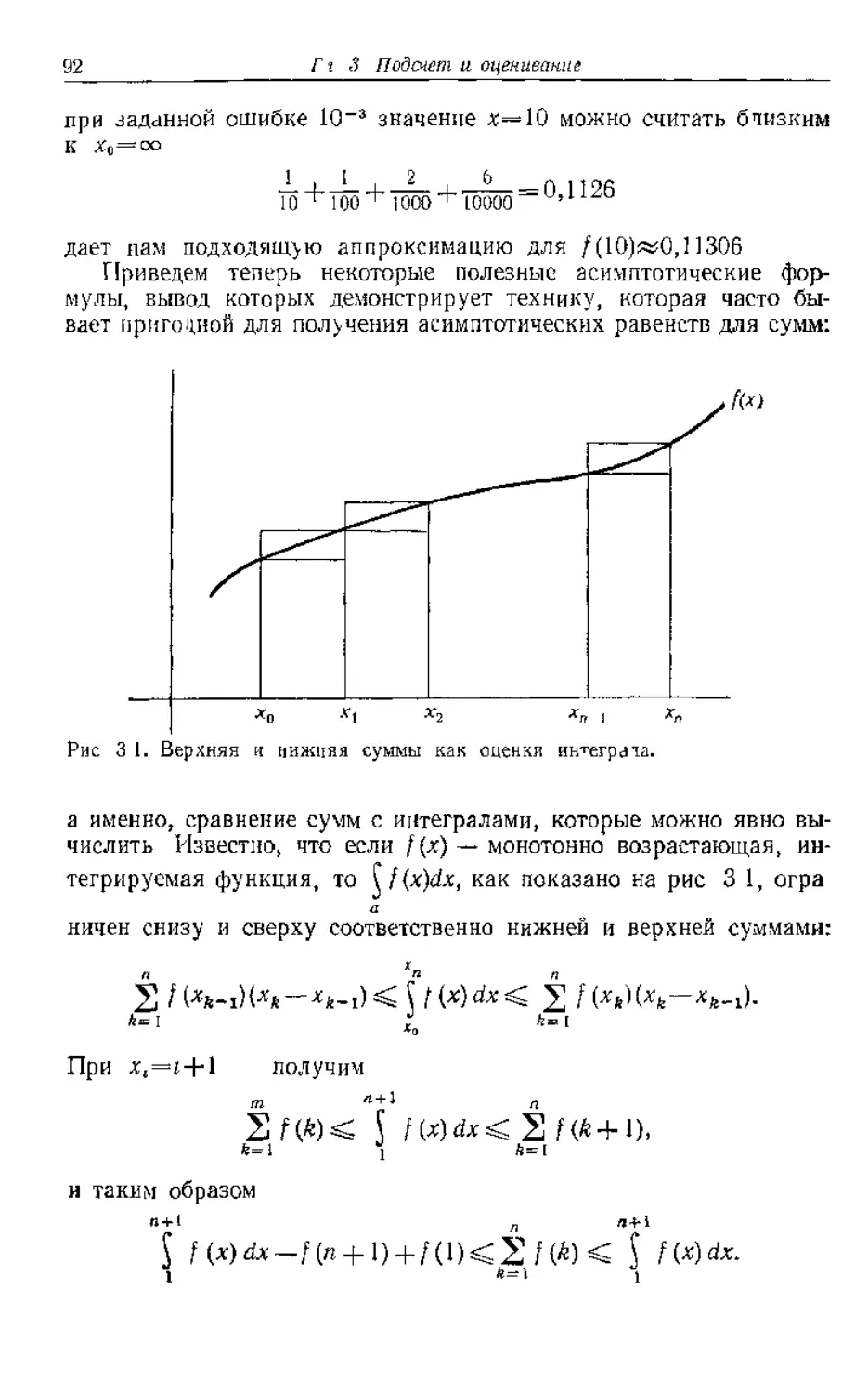
Текст
                    Э. РЕЙНГОЛЬД. Ю. НИВЕРГЕЛЬТ.НДЕО
КОМБИНАТОРНЫЕ
АЛГОРИТМЫ
ТЕОРИЯ И ПРАКТИКА
COMBINATORIAL
ALGORITHMS
THEORY
AND PRACTICE
EDWARD M REINGOLD
Department of Computer Science
University of Illinois at Urbana-Cbampaign
JURC NIEVERGELT
Department of Computer Science
University of Illinois at Urbana Champaign
Swiss Federal Institute of technology, Zurich
NARSINGH DEO
Department of Electrical Engineering and Computer
Science Programme
Indian Institute of Technology, Kanpur
Prentice-Hall, Inc , Englewood Cliffs,
New Jersey 07632
1977
Э. РЕЙНГОЛЬД, Ю. НИВЕРГЕЛЬТ, Н.ДЕО
КОМБИНАТОРНЫЕ
АЛГОРИТМЫ
ТЕОРИЯ
И ПРАКТИКА
Перевод с английского
Е П ЛИПАТОВА
под редакцией
В. Ь. АЛЕКСЕЕВА
ИЗДАТЕЛЬСТВО «МИР» МОСКВА 1980
УДК 681 142 2
(М.: Мир. 1у77). паписаннои совместно с Дж Фарраром, В данной
Редакция литературы по математический наукам
1702070000	, г. х г. ,
© 1977 by Prentice-Hall, Inc.,
20204-028	Englewood Cliffs, New Jersey 07632
041(01)-8O	'	© Перевод на русский язык, «Мир», 1980
ОТ РЕДАКТОРА ПЕРЕВОДА
Задачи алгоритмического характера на дискретных конечных
структурах встречаются в практике постоянно. Однако долгое
время они не привлекали к себе внимания исследователей, так как
в большинстве случаев для их решения находился какой-либо
естественный алгоритм (обычно тина перебора) Поиск более хо-
роших алгоритмов не мог представлять интереса ни для задач
малой размерности, ни для задач большой размерности, поскольку
в первом случае такие алгоритмы ненамного лучше естественного,
а во втором — они так же, как и естественный алгоритм, не при-
водят к решению из-за большого объема вычислений
Повсеместное применение ЭВМ существенно изменило положе-
ние, так как стало возможным решать задачи большей размерности
Оказалось, что для таких задач различные усовершенствования
естественных алгоритмов могут давать существенный выигрыш во
времени работы или требуемой памяти Необходимость практи-
ческого решения широкого круга комбинаторных задач привела
к появлению большого количества усовершенствований естествен-
ных алгоритмов, а во многих случаях и к построению принципи-
ально новых алгоритмов, Это в свою очередь потребовало разра-
ботки теоретических методов сравнения их качества, а также
исследования общих принципов построения хороших комбинатор-
ных алгоритмов.
Этим вопросам и посвящена данная книга В ней методы оценки
эффективности и общие принципы построения алгоритмов иллю-
стрируются на различных комбинаторных задачах, среди которых
наибольшее внимание уделяется очень важным для работы с боль-
шими массивами данных алгоритмам поиска и сортировки, а также
получившим широкое развитие алгоритмам на графах
В последние годы появилось три довольно исчерпывающих
издания на русском языке, систематически освещающих вопросы,
связанные с комбинаторными алгоритмами. Khvt Д Искусство
программирования для ЭВМ, т 1 — 3 — М.: Мир, 1976—1978, Кри-
стофидес Н Теория графов Алгоритмический подход- At. Мир,
1978, Ахо А , Хопкрофт Дж , Ульман Дж Построение и анализ
вычислительных алгоритмов — М • Мир, 1979
Предлагаемую вниманию читателей книгу М Рейнгольда,
Дж Нивергельта и Н. Део отличает удачное сочетание компакт-
ности изложения с весьма подробной разработкой темы, что позво-
ляет легко и быстро ознакомиться с предметом
Определенные трудности при переводе вызвала терминология,
так как в рассматриваемой области она еще не устоялась В боль-
шинстве случаев здесь использована терминология, принятая в
переводах упомянутых выше монографий Д Кнута и А. Ахо, Дж
Хопкрофта и Дж. Ульмана.
В Б Алексеев
ПРЕДИСЛОВИЕ
Комбинаторные алгоритмы предназначаются для выполнения
вычислений на дискретных конечных математических структурах
Это новое направление, и лишь несколько лет тому назад оно стало
превращаться из набора не связанных между собой вычислитель-
ных приемов в систематическую область знаний Становлению
этой новой дисциплины способствовали следующие три фактора
Возрастающая роль вычислении комбинаторного характера в
прикладных задачах по сравнению с другими вычислениями
Явный прогресс разработки и анализа алгоритмов, касающийся
прежде всего математической стороны дела
Переход от изучения частных комбинаторных алгоритмов к
исследованию свойств, присущих классу алгоритмов
Совокупность этих факторов и выделила комбинаторные алго-
ритмы как новую важную дисциплину на грани программирования
и математики Курсы комбинаторных алгоритмов и примыкающие
к ним курсы анализа алгоритмов теперь изучаются в колледжах
и университетах на отделениях программирования, математики,
электротехники и исследования операций
Способы представления комбинаторных алюритмов довольно
разнообразны, и лекции или учебники по этому предмету могут
предназначаться для разных аудиторий Настоящая книга обра-
щена к читателю, которого можно охарактеризовать как обладаю-
щего больше программистской, нежели математической квалифи-
кацией, к читателю, который интересуется комбинаторными алго-
ритмами в силу их практического значения. Таким образом, при
написании книги мы руководствовались в основном следующими
целями.
Выбрать те темы, которые имеют отношение к практическим
вычислениям (и все же отдельные вопросы, представляющие не
столько практическим, сколько математический интерес, были в
книгу включены).
Выделить аспекты алгоритмов, важные с точки зрения их реа-
лизации, и опустить детали, которые может восполнить любой ком-
петентный программист.
Представить математические рассуждения, там где они необ-
ходимы, в интуитивно понятной форме
Уровень подготовки читателя. Подготовка, требующаяся для
понимания материала книги, несколько меняется от главы к главе
Минимум необходимых познаний в программировании соответст-
вует уровню первокурсника-программиста, уже научившегося
писать довольно пространные программы Этой подготовки было бы
достаточно для понимания обсуждаемых атгоритмов, которые
представлены в обозначениях, аналогичных современным языкам
программирования высокого уровня Кроме того весьма желательно
знакомство со структурами данных и обработкой списков в объеме
второго курса факультета программирования Необходимый уро-
вень математического образования соответствует типичной подго
товке студента, прослушавшего ряд математических курсов помимо
математического анализа
Разделы со звездочкой. Два раздела этой книги помечены зна-
ком * Раздел 3.4 помечен потому, что для его чтения требуется
знакомство с нетривиальными математическими понятиями, а
раздел 8 6 — потому, что он сложен по существу Эти разделы
можно рассматривать как необязательные Звездочкой помечены
и соответствующие им упражнения, а также другие упражнения,
требующие серьезной математической подготовки или имеющие
необычно сложное решение.
Общая организация. Зависимость между девятью главами обо-
значена на следующей диаграмме, в которой «сильная» зависимость
показана сплошными стрелками, а «слабая»—пх актирными
В гл 1 дается обзор содержания всей книги В ней также пред-
ставлены отдельные темы и методы, которые вновь появляются в
последующих главах
В гл. 2 и 3 обсуждаются соответственно структуры данных и
методы перечисления Весь материал, содержащийся в этих двух
главах, кроме разд 3 4, служит основой для остальной части книги
Однако, возможно, удобнее было бы раскрывать темы этих глав,
когда они необходимы для изложения материала последующих
глав Здесь использован иной подход с целью попытаться сделать
гл 4—9 по возможности не зависящими друг от друга
Материал гл 4 об исчерпывающем поиске важен для понимания
гл 5, в которой фактически методы гл 4 пересматриваются для
случая простых комбинаторных объектов По некоторым причинам
материал гл 4 является решающим для понимания многих раз-
делов гл 8 об алгоритмах на графах Глава 9 служит продолже-
нием гл. 4 и 8, в ней исследуются некоторые теоретические вопросы,
возникающие в связи с неудачами программистов и математиков в
поиске «эффективных» алгоритмов для решения некоторых из
обсуждаемых задач. В гл. 6 и 7 описываются наиболее распро-
страненные комбинаторные алгоритмы: поиск и сортировка. Эти
главы больше других опираются на материал гл 2 и 3.
Благодарности
В словаре Г У. Фаулера (Н W Fowler, A Dictionary of Modern
English Usage, sec ed , revised and edited by Sir Ernest Gowers,
Oxford University Press, New York and Oxford, 1965) статья «Не-
логичность» начинается так
Нам посчастливилось иметь много таких критически настроенных
читателей, изучивших всю или часть рукописи этой книги, и они
помогли найти различные примеры «нелогичностей» Мы очень
признательны Джеймсу Р Битнеру, Эллану Б Бородину, Джеймсу
Э Филлу, У Д Фрейзеру, Брайену Э Хенше, Уилфреду Дж Хан-
сену, Эллису Горовицу, Алону Йтаи, Дональду Б Джонсону,
Джону Э. Коху, Дер-цзай Ли, Карлу Либергерру, К Л Лю,
Прабхакеру Матети, Иешуа Перлу, Дэвиду Э Плайстеду, Эндрю
Г. Шерману, Роберту Э Тарьяну, Дэниелю С Ватанабе, Ли Дж.
Уайту, Томасу Р Уилкоксу и Герберту С Уилфу Без их неоце-
нимой помоши книга была бы хуже
Мы в особом долгу перед Джеймсом Э филлом за его тщатель-
ную подготовку ответов к упражнениям.
Мы обязаны Университету штата Иллинойс в Урбана — Шам-
пейн, Швейцарской высшей технической школе, Научной лабора-
тории Лос-Аламоса, Вейцмановскому институту науки, Универ-
ситету штата Вашингтон и Индийскому технологическому инсти-
туту в Канпуре за обеспечение благоприятных условий для подго-
товки этой кни1и Их поддержка сильно облегчила нашу задачу.
Наконец, мы хотели бы выразить признательность и благодар-
ность Конни Носбич и Джун Уинглер, нашим секретарям в Уни-
верситете штата Иллинойс, за терпеливую, добросовестную и ква-
лифицированную перепечатку (в том числе иногда неоднократную)
рукописи
Эдвард М Рейнгольд
Юрг Нивергелып
Парсинг Део
Глава 1. Что такое комбинаторные
вычисления?
Предметом теории комбинаторных алгоритмов, часто называ-
емой комбинаторными вычислениями, являются вычисления на
дискретных математических структурах Это новое направление
исследований Лишь в последние несколько лет из наборов искус-
ных приемов и разрозненных алгоритмов сформировалась система
знаний о разработке, реализации и анализе атгоритмов
Может быть полезно провести аналогию с более устоявшейся
дисциплиной- комбинаторные вычисления находятся в таком же
отношении к комбинаторной математике (дискретной, конечной
математике), как численные методы анализа к анализу. Мы явля-
емся свидетелями того, что комбинаторные вычисления развиваются
сегодня так же, как и численные методы анализа в 50 е годы, а
именно
интенсивно изобретаются новые алгоритмы;
происходит быстрый прогресс, главным образом в математи-
ческом плане, в понимании алгоритмов, их разработки и
анализа,
происходит переход от изучения отдельных алгоритмов к
исследованию свойств, присущих классам алгоритмов
Активизации комбинаторных вычислении в последнее время,
несомненно, способствовало растущее практическое значение вы-
числений комбинаторного характера Есть все основания считать,
что в прикладных программах объем вычислений комбинаторного
характера будет расти быстрее, чем объем численных расчетов,
поскольку, за исключением традиционных областей приложения
математики к физическим дисциплинам, дискретные математические
структуры встречаются чаще, чем непрерывные, и доля машинного
времени, затрачиваемою на физические задачи, убывает Следова-
тельно, пользователи и прикладные программисты вероятно, будут
вынуждены решать задачи больше комбинаторного, чем численного
характера
В отличие от некоторых других разделов математики комбина-
торные вычисления не имеют «ядра», т е некоторого количества
«фундаментальных теорем», составляющих суть предмета, из ко-
торых выводится большинство результатов Сначала может пока-
12
заться, что в целом эта область состоит из наборов специальных
методов и хитрых приемов Действительно, остроумные приемы
играют здесь известную роль и, для того чтобы проиллюстрировать
это, в данной главе мы рассмотрим некоторые примеры техники
«игры на двоичности» Однако, после того как было исследовано
много комбинаторных алгоритмов, стали вырисовываться неко-
торые общие принципы Именно эти принципы делают комбина
торные вычисления связной областью знании и позволяют изло
жить ее и систематизированном виде
Цель данной главы состоит в том, чтобы проиллюстрировать
на примерах некоторые из этих главных принципов' кроме того,
она является введением в некоторые темы и методы, которые в
последующих главах будут изучены более глубоко
Глава построена так, что изложение переходит от конкретных
задач к более абстрактным принципам, причем применение не-
которых из этих принципов к анализу алгоритмов требуез раз
витой математической теории Поэтому абстрактные разделы главы
являются более сложными, чем остальные; в этом смысле первая
глава точно отображает ту область науки, введением в которую
она является В разд. 1 1 и 1 2 приводятся примеры творческого
подхода и изобретательности при синтезе эффективно работающих
алгоритмов В разд 1 3 и 1 4 изложены общие принципы синтеза
алгоритмов И наконец, в разд. 1 5 и 1 6 приведены методы анализа
алгоритмов Разработка, анализ и реализация алгоритмов состав-
ляют сущность комбинаторных вычислений
1.1. ПРИМЕР. ПОДСЧЕТ ЧИСЛА ЕДИНИЦ В ДВОИЧНОМ
НАБОРЕ
Двоичные наборы, т е последовательности на нулей и единиц,
являются носителями информации фактически во всех современных
вычислительных устройствах Однако большинство программистов
редко работают с информацией на уровне двоичных наборов Это,
траммист обычно имеет дело с арифметическими операциями и
редко касается вопросов внутреннего представления чисел С дру-
гой стороны, в областях, не так хорошо устоявшихся, как числен-
ные расчеты, некоторые важные операции над данными нельзя
ввести в вычислительное устройство или языки программирования
высокого уровня, Так, в некоторых часто встречающихся в комби-
наторных вычислениях классах операции для эффективного про-
граммирования необходимо знание алгоритмов, которые работают
на уровне двоичных символов Со временем, когда эти операции
будут более широко известны, они, вероятно, будут вводиться в
вычислительные устройства и языки программирования Пока же
такие операции являются необходимым инструментом для каждого,
кто программирует комбинаторные алгоритмы
В качестве примера рассмотрим задачу подсчета числа единиц
в двоичной последовательности B~bnbn 3 babi длины п Такая
операция является естественной, если представить себе, чго набор
В задает подмножество S некоторою множества U с п этементами
так, что единицы указывают на те элементы множества U, которые
принадлежат S Тогда указанная операция определяет число эле-
ментов в S
Сразу на ум приходит следующий алгоритм решения такой
задачи- последовательно просматривать каждый раздел и, если
он равен единице, в счетчике задават ь соответствующее приращение.
Дпя некоторых вычислительных устройств алгоритм 1 1 может
оказаться наиболее разумным, однако, большинство вычислитель-
ных устройств имеет специфические особенности, которые позво-
ляют для этих целей использовать более быстрые алгоритмы. Пред-
положим, что память состоит из ячеек, которые могут хранить дво-
ичные слова длины п и что вычислительное устройство может вы-
полнять логические или булевы операции параллельно над каждым
разрядом слова Предположим, кроме того, что вычислительное
устройство может производить арифметические операции, которые
интерпретируют эти слова как беззнаковые целые неотрицательные
числа, записанные в двоичной системе счисления.
Рассмотрим алгоритм 12. Высказывание «В^-В/\(В—I)» со-
держит интересную операцию, использующую сделанные выше
предположения Д — логическая операция «и», которая опери
рует параллельно с каждыми дв>мя соответствующими разрядами
пары аргументов В и В—1 «—» — арифметическая операция вы-
читания над двоичными целыми числами На примере очень хорошо
видно что операция В/\ (В—1) заменяет у В самую правую единицу
нулем.
В	Н 1001000
В - 1	111000111
В л (В - 1) I 11000000
Цикл в алгоритме 1 2 повторяется до тех пор, пока В не станет
равным нулю, т е не будет состоять из одних нулей В то время,
как цикл в алгоритме 1 1 всегда повторяется п раз, в алгоритме 1 2
цикл повторяется лишь столько раз, сколько единиц в наборе В
Иначе говоря, алгоритм I 2 работает только с единицами в В, не
зная a priori их расположения Этот алгоритм, очевидно, эффек-
тивен, когда он применяется к «разреженным» словам, т. е. наборам
с малым числом единиц Он является «хитрым» в том смысле, что
сложным образом зависит от способа представления чисел (осо-
бенно отрицательных) в вычислительном устройстве, что с точки
зрения первоначальной постановки задачи является совершенно
посторонним
Более интересен алгоритм, изложенный далее. С алгоритмом 1 1
он имеет одно общее важное свойство повторение цикла фикси-
рованное число раз, зависящее от п и не зависящее от В. В ю же
время в отличие от алгоритма I 1, повторяющего свой цикл п раз,
в алгоритме 1 3 (подробного изложения которого мы не даем) цикл
повторяется только Ign") раз1) Для типичного слова длины 32
(или 64) цикл повторяется пять (соответственно шесть) раз, т. е.
алгоритм 1.3 является значительно более быстрым, чем алгоритм
1 1 Алгоритм 1 3 исходит из тех же предположений о возможностях
вычислительного устройства, что и алгоритм 1 2 Дополнительно
требуется, чтобы существовал способ быстро сдвигать слово на 1, 2,
4, 8 разрядов
Этот алгоритм лучше всего объяснить на конкретном примере
в
Ья	Ь7	Ь6	Ь5	Ь4	6,	Ьг	bi
1	1	0	1	0	0	0	1
1 Сначала выделяются разряды с нечетными номерами Ь., &6,
bi и слева от каждого из них приписываются пули Полученный
таким образом набор обозначим Внеч
Затем выделяются четные координаты и сдвигаются вправо на
один разряд на места разрядов Ь7, Ьь, Ьз, bt соответственно К каж
дому из разрядов припишем слева нуль, а полученную таким об-
разом строку обозначим Вчег
(Нули, приписанные разрядам, выделены мелким шрифтом, чтобы
отличить их от нулей, входящих в набор В ) После этого склады-
ваем два числа, двоичными представлениями которых являются
И Вчст Через В' обозначим набор, представляющий собой
двоичную запись результата суммирования
b's ft? Ь'ь b's Ь, Ь'з b'2 Ъ*1
Впеч
В'
0	10	1	0	0	0	1
0	1 0	0	0	0	0	0
1	0 0	1	0	0	0	1
к.
о 0	1 о о 0	1
Виет I О
о 1	0 и о О О
Складываем два числа Вкеч и Вчет Двоичную запись этой
суммы обозначим В”
3 Берем разряды b'it b3, b~,, й'( и приписываем к этой четверке
слева четыре нуля, в результате чего получим набор б''1еч.

о о 0 0 0 1
Точно так же берем разряды Ь~е, Ь\, bt, й5, сдвигаем их вправо на
четыре разряда па места b"t, b"3, b“t, bi соответственно, приписываем
к ним слева четыре нуля и получаем набор В^,„.
I	Ьх by Ь/, b$
Вчет | о и о о О	0	1	1
Наконец, складываем два числа, двоичными представлениями
которых являются Внсч и В"чет. Последовательность В"' = (00000100),
представляющая собой двоичную запись результата суммирования,
одновременно является двоичной записью суммы разрядов слова В
(в данном случае — четыре)
Если п — произвольное и не является степенью двойки, то к
слову В припишем предварительно слева нули так, чтобы суммар-
ная длина стала степенью двойки, ближайшей сверху к п После
такого предварительного замечания легко обобщить алгоритм на
случай слов любой длины
Рекомендуем читателю доказать, что в общем виде предложен-
ный алгоритм корректен В разд 1 4 описан общий принцип син-
теза алгоритмов, из которого прямо следует и алгоритм 1 3, и до-
казательство его корректности Этот принцип является хорошей
иллюстрацией нашего утверждения о том, что комбинаторные
алгоритмы имеют общие идеи и методы, из которых следуют многие
частные случаи
Существуют ли более быстрые алгоритмы для вычисления
числа единиц в слове? Существует ли «оптимальный» алгоритм?
Вопрос оптимальности алгоритмов важен, но он требует конкрети-
зации Для того чтобы показать оптимальность алгоритма, не-
обходимо точно определить класс допустимых алгоритмов и кри-
терий оптимальности В случае алгоритмов подсчета числа единиц
в наборе такая конкретизация была бы сложной и весьма нечеткой,
включающей подробности о способах работы вычислительного уст
ройства. В разд 1 5 мы обсудим проблему оптимальности ачго
ритмов в более упрощенной постановке.
Однако мы можем привести правдоподобные доводы в пользу
того, что предложенный далее алгоритм суммирования числа еди-
ниц (алгоритм 1 4) является самым быстрым из всех возможных,
так как он, используя поисковую таблицу, получает результат в
следующего вида
Какой самый быстрый путь поиска В в этой таблице’5 При тех
же предположениях, что и в предыдущих алгоритмах, можно счи-
тать В адресом ячейки памяти, содержащей сумму единиц в В
Этот факт и дает нам алгоритм, требующий только одного обращения
к памяти
Завершая раздел, отметим большое разнообразие существующих
алгоритмов вычисления числа единиц в наборе, которые основаны
на совершенно разных принципах Алгоритмы 1 1 и 1 4 решают
задачу «в лоб» алгоритм 1 1 просматривает каждый разряд и
поэтому требует много времени, алгоритм 1 4 хранит решение для
каждого набора и поэтому требует большого объема памяти Ал-
горитм 1 3 является изящным компромиссом между ними.
1,2. ПРОБЛЕМА ПРЕДСТАВЛЕНИЯ:
КОДЫ, СОХРАНЯЮЩИЕ РАЗНОСТИ
Следующей чрезвычайно важной проблемой в комбинаторных
вычислениях является задача эффективного представления объек-
тов, подлежащих обработке Эти объекты могут быть такими же
простыми, как двоичные наборы в предыдущем примере, или та-
кими сложными, как сети дорог или органические молекулы Про-
блема возникает по той причине, что обычно имеется много воз-
можных способов представления сложных объектов более простыми
структурами, которые можно заложить в вычислительное устрой
ство или языки программирования, но не все такие представления
в одинаковой степени эффективны с точки зрения времени и памяти
Более того, идеальное представление зависит от вида производи-
мых операций
В данном разделе эта ситуация проиллюстрирована приме-
рами, в которых мы хотим определить весьма специфические опе-
рации над целыми Целые определяются как данные простейшего
типа почти во всех вычислительных устройствах и языках програм-
мирования, и, таким образом, проблема представления, как
правило, не возникает; имеющееся представление (выбираемое кон-
структором вычислительной машины) почти всегда наилучшее.
Однако существуют некоторые заслуживающие внимания исклю-
чения, когда выгодно (или даже необходимо) использовать пред-
ставление целых в вычислительном устройстве иным способом
&ги исключения появляются в следующих случаях-
1)	необходимы целые, большие имеющихся непосредственно
в аппаратном оборудовании,
2)	необходимы только небольшие целые, и требуется сэкономить
память, упаковывая их по несколько в одну ячейку,
3)	действия с целыми производятся не общепринятыми ариф-
метическими операциями,
4)	целые используются для представления других типов объек-
тов, и необходимо иметь возможность легко обращать целое в со-
ответствующий ему объект и образно (этот важный случай преды-
дущего исключения появится в 1л 5).
Обсуждаемая в этом разделе проблема кодов, сохраняющих
разности, касается случаев 2 и 3
В задачах распознавания образов и классификации для решения
вопроса, будут ли два объекта X и У эквивалентными, стандартной
является следующая процедура X и Y представляются векторами
признаков (лг, х2, ..xt) и (yt, у2,	, У/) соответственно, где каж-
дая компонента означает признак объекта, выраженный целым
значением Считается, что X и У эквивалентны тогда и только
тогда, когда
где t — целое, называемое порогом.
В типичных приложениях (таких, как денситометрия в задачах
представлания непрерывных сигналов цифровыми, подсчет числа
букв в английских словах или подсчет числа вершин в графе, ко-
торый является абстрактным представлением написанной от руки
буквы) можно считать, что и компоненты, и порог принимают лишь
небольшие целые значения В этих случаях несколько компонент
EEEEEEEEEEEHEEEE1ZZD
Ячейка. 1
запо, что выделенные зоны могут даже состоять из частей двух
соседних ячеек памяти
На первый взгляд кажется, что для вычисления Six;—yd не-
обходимо последовательно выделять пары соответствующих компо-
нент векторов признаков и затем сдвигать каждую из них на соот-
ветствующее место для вычитания В этом разделе будет показано,
что если целые представить в специальном виде (в виде кодов, со-
храняющих разности), операцию сравнения суммы разностей с
порогом можно значительно ускорить, если выполнять все операции
над потной ячейкой памяти, игнорируя при этом границу между
зонами Ускорение особенно эффективно в вычислительных уст-
ройствах с длинными словами и аппаратно реализованной опера-
цией нахождения числа единиц в стове
Код 3>, сохраняющий разности (DP-код), есть отображение
множества {!, 2, . , jV} в множество {0, 1 }п двоичных
последовательностей длины п со следующими свойствами Для всех
целых I, j, таких, что
1) из |т—следует H(Dlt Dj}-=\t
2) из U—/Г>£ следует H(Dt,
где H(D„ Dj) — расстояние Хемминеа между двумя кодовыми
словами D, и DJt т е число разрядов, в которых они различаются,
a t — порог Интуитивно ясно, что код Я) сохраняет малые раз-
ности, а большие разности смешивает все вместе 3) называют
п-разрядным DP-t-кодом ранга N, или иногда (п, fj-кодом ранга N
Легки проверить, что ес ш компоненты двух векторов призна-
выполпепо, если и только если хсммингово расстояние между пред-
ставлениями X и Y не больше I Это свойство позволяет эффективно
сравнивать векторы признаков, что указывалось выше.
В приведенном ниже примере код имеет ранг N—8, длину п=4
равным единице
щими целыми числами) Заметим, что смежными являются только
те кодовые слова, номера которых отличаются на единицу
В табл 1 1 приведены максимальные ранги, которые можно
получить для п^б Соответствующие оптимальные коды довольно
легко можно построить вручную для nsCo и с помощью ЭВМ для
п=6 Мы не знаем рангов оптимальных кодов для п—7, так как
J
программа построения их для п-~6 не позволяет в реальное время
решить эту же задачу для н=7 Случай п—6 подробно рассмотрен
в разд 4 1 5 Это рассуждение иллюстрирует эмпирическое пра-
вило, которое удивительно часто присутствует в комбинаторных
алгоритмах Учитывая, что многие интересные комбинаторные
задачи содержат параметр, который естественным образом опреде-
параметром является длина слова и), эмпирическое правило гласит.
1.3.	СПОСОБЫ композиции
Дпа предыдущих примера проникнуты духом «игры на двоично-
сти»— остроумной и изобретательной, но весьма специфической
техники, которая хорошо работает па одно» задаче, но нс обобща-
ется и не переносится на другую. С целью предупредить читателя
от заключения, что комбинаторные вычисления представляют собой
лишь набор разрозненных искусных приемов, в этом и следующем
разделах мы обсудим два общих принципа; мы покажем также, как
их можно использовать в таких специальных задачах, как построе-
ние алгоритма для подсчета числа единиц в двоичном наборе и кон-
струирование кодов, сохраняющих разности Излагаемые ниже
принципы композиции решений и декомпозиции задачи обладают
такой общностью, что возможность их применения не ограничи-
вается только комбинаторными вычислениями, оба они полезны при
решении любой математической задачи.
Принцип композиции, который является предметом этого раз
дела, приводит нас к построению сложных объектов путем соеди
нения более простых. Чы проиллюстрируем этот принцип на при
мере конструирования больших DP-кодов Заметим, что для малых
значений рани ,V и порога t (особенно если /=1) DP-коды легко
строятся вручнупо. Чтобы построить коды большого ранга и/или
двух способов композиции, один из которых увеличивает ранг без
изменения порога, а другой, увеличивая порог, лишь незначительно
увеличивает ранг. Оба способа композиции базируются на идее
образования составного кодового слова из слов двух различных
кодов путем приписывания их друг к дрхп
Сложение порогов. Пусть Dlt D 2,	, есть (п, .
,	, Ем есть (т, и) код Тогда последовательность
Ци + .^за ъ	>,

7И И +	1 р в противном случае

Если Nite&M/u, то ран! составного кода приблизительно равен
N+M Например, при композиции оптимальных (3, 1)- и (4, 2)-
кодов, получается (7, 3)-код ража 9
Fx = OOOO
E-, - 0001
E, = OOH
/-4=0111
Es = Illi
£6 = 1110
D,Et = 0000000
P2t( = 0010000
£)гЕг = 0010001
DjE, = 00100H
D,E, = 011001 1
/>,е4 - 011(11 I I
DJ-< - Ollllll
D,F< Hill 10
есть (n+m, f)-Koj ранга
Например, при композиции оптимального (3, 2) кода ранга 4 с
самим собой, мы получим (6, 2)-код ранга 50
рвчг R - IО
D, = Еу = ООО
[)2 - Е2= 001
Dy = £, = 011
D„ = £4 = 111
= 000000
= 000001
= 000011
= 00011J
= Oil 111
= 111111
= HIGH
’ 111001
- 111000
1.4	СПОСОБЫ ДЕКОМПОЗИЦИИ
Принцип декомпозиции приводит нас к решению задачи о сложном
объекте путем разложения его на какое то число меньших, решению
той же самой задачи для каждого из меньших объектов и затем
композиции найденных решений. Дчя того чтобы обеспечить окон-
чание процедуры, достаточно для простых объектов прекратить
процесс декомпозиции и решать задачу непосредственно для них
Именно этот принцип приводит к эффективному и изящному алго-
ритму суммирования единиц в двоичной последовательности длины
п (алгоритм 1 3 из разд 1 1)
Пусть B=bn . b2bi — двоичный набор длины п., и пусть S (В) —
сумма единиц в нем Зададимся некоторым h и разделим В на две
части Вl—bn ..bh+1 и ВГ=ЬЬ . b-J^ S(B), очевидно, удовлетворяет
следующему рекуррентному соотношению
3(В) = 5(В;)+Ж)
Это означает, что 3 (В) можно получить за одну операцию сложе-
такие же рассуждения для Bt и Вг, затем для поднаборов, которые
они порождают, и т д, мы получим процесс вычисления S(B)
при условии, что мы можем подсчитать число единиц в достаточно
коротких наборах Если фразу «достаточно короткий» понимать
как «длины один» и считать S(B)=B для n—1, то станет ясно, как
можно вычислить число единиц в наборе последовательным сумми
рованием Очевидно, этот процесс зависит от способа разбиения
набора В и его поднаборов
Рассмотрим две экстремальные стратегии разбиения В первой
выберем h=n—1, тогда Bi=bn и Br—bn t Ь2Ьг В этом случае
последовательно слева направо просматриваются все разряды
При такой стратегии требуется п— 1 сложений (алгоритм 1 1)
Во втором случае положим	Тогда В(=&Г1	|<i и
Ву=^_л-[. .ЬгЬи Этот способ решения задачи, при котором оди-
наково обрабатываются обе части набора В (Bt и Вг) и В всегда
разбивается примерно пополам, приводит к алгоритму 1.3, по для
того, чтобы это стало очевидным, требуется остроумная идея
Заметим, что в этом алгоритме все еще надо осуществить п—1 ело
вать п—1 сложений (упражнение 5) Следовательно, дтя того чтобы
получить логарифмическую скорость работы алгоритма 1.3, мы
должны сделать так, чтобы несколько операций сложения в корот-
ких наборах производились путем применения единственной one
рации в длинных. Как это сделать, показано па рис 1.3 S(B)
теперь означает не только сумму единиц в наборе, но также (что
более существенно) — набор, который является двоичной записью
числа единиц в слове В, дополненный слева пулями до соответст-
15 Классы аггоритчов
ООО ... ООО । rl ।
+ ООО ... ООО ।	।
=	5(ЯГ)|
1.5.	КЛАССЫ АЛГОРИТМОВ
при таком определении становится возможным говорить, что дан-
ный алгоритм является оптимальным по отношению к некоторому
свойству, если он работает по крайней мере так же хорошо (отно-
сительно этого свойства), как любой другой алгоритм из рассмат-
риваемого класса Знание того, что имеющийся алгоритм является
оптимальным, может предотвратить поиск не существующего 4V4-
шего алгоритма
Как можно строго определить (возможно, бесконечный) класс
алгоритмов? Исследуем этот вопрос на примере задачи о фальшивой
монете Рассматриваемый в этом примере класс алгоритмов порож-
дает более обширный и более важный класс алгоритмов — так
называемые деревья решений
Одна из формулировок задачи о фальшивой монете такова
Имеется п монет, о которых известно, что п—1 из них являются
настоящими и не более, чем одна монета фальшивая (легче или
тяжелее остальных монет). Дополнительно к группе из п сомни-
тельных монет дается еще одна монета, причем заведомо известно,
что она настоящая. Имеются также весы, с помощью которых мы
можем сравнивать общий вес любых т монет в общим весом любых
других т монет и гем самым установить, имеют ли две группы
по т монет одинаковый вес, либо одна из групп легче другой За-
дача состоит в том, чтобы найти фальшивую монету (если она есть)
за наименьшее число взвешиваний, или сравнений Число срав-
нений, необходимых в алгоритме, можно определять различными
способами; наиболее разумными являются рассмотрение среднего
числа сравнений и числа сравнений в худшем случае Этот вопрос
мы обсудим в дальнейшем после определения рассматриваемого
класса алгоритмов
Пусть сомнительные монеты занумерованы числами 1, 2,	, п;
монете, о которой известно, что она настоящая, поставим в со-
ответствие номер 0. Пусть теперь S={0, 1, 2, п}— множество
монет Если Si, S2— иепересекающиеся непустые подмножества
множества S, то через Ss, . S2 обозначим операцию сравнения весов
множеств St и S2 При сравнении возможны три исхода, которые
мы будем обозначать следующим образом Si<S-3, Si=S2 или Si>S2
в зависимости от того, является ли вес St меньшим, равным или
большим веса S2
Рассматриваемые алгоритмы можно представить в форме (тер-
нарного) дерева решений. Дерево на рис. 1 4 для случая четырех
монет иллюстрирует введенные нами понятия и обозначения В тех
случаях, когда это не вызывает путаницы, мы при обозначении
множеств будем опускать скобки Корень дерева на рис 1 4 изоб-
ражен в виде кружка и помечен отношением 1 : 2, это означает,
что алгоритм начинает работу сравнением весов монет с номерами
I и 2 Три исходящие из корня ветви ведут к поддеревьям, опреде-
ляющим продолжение работы алгоритма после каждого из трех
возможных исходов первого сравнения Квадраты, называемые
листьями дерева, означают, что работа алгоритма заканчивается.

работы требует алгоритм в среднем, однако для этого требуется
задать вероятности различных исходов Если мы предположим,
что все девять исходов 1L, IН, 2L, 2Н, 3L, ЗН, 4L, 4Н, G равнове-
роятны, то тогда этот алгоритм требует в среднем 7/3 сравнений
На одну чашку весов мы можем положить больше одной монеты.
Например, можно начать сравнения, положив на одну чашку весов
монеты 1 и 2, а на другую — монеты 3 и 4 (рис 1.5) Если посчаст-
ливится, задачу можно решить за одно сравнение — это может
произойти, когда все монеты настоящие. Однако ясно, что неза-
висимо от того, как дополняется это дерево решений, в худшем
случае задача все равно потребует тех же трех сравнений, поскольку
единственное тернарное решение, вообще говоря, не может иден-
тифицировать один из четырех исходов, которые возможны на вет-
ви, помеченной символом «С», так же как и один из четырех ис-
ходов на ветви, помеченной символом «>» К tomv же независимо
от того, как дополняеюя это дерево решений, оно потребует в сред-
нем по крайней мере 7/3 сравнений (почему’), и в этом смысле оно
не лучше, чем дерево на рис. 1.4.
1 Каждый узел помечен сравнением Sx • S2, где Sx и S2 — не-
пересекающиеся непустые подмножества множества S={0, 1, 2,
,, п} всех монет.
2 Каждый лист либо не помечен (что соответствует невозмож-
ному исходу в предположении существования не более чем одной
фальшивой монеты), либо помечен одним из исходов :L, гН, G,
означающим соответственно, что монета с номером i является лег-
кой или тяжелой или что все монеты настоящие
Четко определив подлежащий дальнейшему рассмотрению класс
алгоритмов, мы можем теперь исследовать свойства, которыми
должно обладать каждое дерево из этого класса; мы можем также
задаться вопросом, как найти алгоритмы, являющиеся в некотором
смысле оптимальными Мы сделаем это в начале для чешрех монет,
а затем перейдем к общему случаю
Поскольку в задаче о четырех монетах требуется различить
девять возможных исходов, любое дерево решений дтя этой задачи
должно иметь по крайней мере девять листьев и, следовательно,
не менее двух ярусов Поэтому дерево на рис 1.6 является опти
мальным и в смысле худшего случая, и в среднем Существуют ли
другие оптимальные деревья? Для ответа на этот вопрос мы должны
рассмотреть множество всех деревьев решений для задачи о че-
тырех монетах Нашу задачу облегчит любое рассуждение, которое
позволит исключить из дальнейшего рассмотрения какую-либо
часть этого множества деревьев решений Прежде всего видно, что
путем любой перестановки множества {1, 2,	, п} сомнительных
монет из одного дерева, приведенного на рис 1.6, можно получить
другие оптимальные деревья; все они будут изоморфны дереву па
рис 1 6 Исходя из этого, мы теперь уточним постановку задачи
и будем интересоваться попарно неизоморфными деревьями.
Зададимся затем вопросом, существует ли оптимальное дерево
среди тех, у которых в корне не используется монета с номером О
При таком ограничении в корне дерева можно сделать только два
различных сравнения, а именно 1:2 и 1, 2.3, 4 Рассмотрим раз-
биение исходов по трем ветвям, выходящим из корня, как показано
на рис 1 5 Для получения такого, как на рис 1.6, полного двухъ-
ярусного тернарного дерева, девять возможных исходов должны
были бы быть разбиты в отношении (3, 3, 3), они же вместо этого
разбиваются соответственно в отношении (2, 5, 2) и (4, 1, 4) Таким
образом, мы заключаем, что задачу для четырех монет нельзя ре-
шить за два сравнения, не используя дополнительную настоящую
монету
Наконец, рассмотрим те деревья решений, которые используют
монету 0 в корне В этом случае видно, что в корне фактически
возможны только два сравнения (0 • 1) и О, 1 : 2, 3 Для первого
сравнения набор исходов будет (1, 7, 1), в связи с чем все алгоритмы,
начинающиеся таким способом, для нас непригодны; набор же
исходов (3, 3, 3) приводит к оптимальному дереву, показанному на
рис 1 6 Аналогичным образом устанавливается, что для оптималь-
ного дерева сравнения в первом от корня ярусе определяются един-
ственным образом. Отсюда мы заключаем, что для задачи о четырех
монетах фактически существует только одно оптимальное дерево
Интересно посмотреть, что происходит, когда используемые
для анализа задачи о четырех монетах идеи переносятся на про-
извольный случай В некоторой степени все идеи обобщаются на
случай любого числа монет, однако некоторые из них нс имеют
практического значения, когда п значительно больше четырех
В принципе оптимальные деревья решений всегда можно найти
путем систематического поиска в множестве деревьев решении,
поскольку для любого заданного п в качестве кандидатов требуется
рассмотреть лишь конечное число деревьев решений В главе 4
мы обсудим технику исчерпывающего поиска в таких конечных
множествах Однако, если даже поиск организован разумно и рас-
сматриваются лишь существенно различные (не изоморфные) де-
ревья, эта процедура не может служить практическим способом
отыскания оптимальных деревьев решений С ростом п число де-
ревьев растет экспоненциально, и поэтому техника исчерпывающего
поиска имеет практическое значение только для малых значений п
Поскольку совершенно очевидно, что число листьев в дереве
решений должно быть по крайней мере таким же, как и число воз-
можных исходов задачи (2л+1 для задачи об п монетах), сразу же
можно получить нижнюю оценку необходимого числа сравнений
(или, что эквивалентно, верхнюю оценку числа монет для данного
числа сравнений)
Теорема 1.1 Если п>-^-(3‘—1), то задачу для и монет нельзя
решить за I сравнений в худшем случае.
В разд 2 3 3 мы воспользуемся той же идеей для доказательства
более сильного утверждения:
Теорема 1.2, Если n>-i-(3f—1), то задачу для п монет невоз-
можно решить за I сравнений в среднем
Заметим, что локальные данные о разбиении исходов по вет-
вям, выходящим из некоторого узла, позволяют делать выводы о
свойствах, присущих всему дереву решений. Мы воспользуемся
этим замечанием для получения трех общих результатов Ими
являются
1	Отрицательный результат относительно алгоритмов, которые
не используют настоящую монету О
2	Изящное утверждение, обратное теореме 1 1, которое уста
навливает, что в случае	—1) для решения задачи об п мо-
нетах достаточно I сравнений, а также явное построение оптималь-
ных деревьев решений для п= ^-(Зг—1)
3	Эвристическое правило, позволяющее эффективно получать
хорошие (но не обязательно оптимальные) деревья решений, когда
указанное выше изящное решение для отыскания оптимальных
деревьев не пригодно
Теорема 1.3. Если n>y(3z—1), то задачу для п монет невоз
можно решить за / сравнений, не использхя монету О
Доказательство Из теоремы 1 1 следует, что достаточно только
показать, что если 2п+1=3(, то не существует I уровнего дерева

решений для задачи об п монетах в эгой ограниченной форме Для
некоторого /,	в корне любого такого дерева мы сравни-
вали бы / монет с номерами, скажем, 1,2,	, / с другим множе-
ством из / монет, пусть, к примеру, они имеют номера /+1, ,2/
(рис 1.7). Заметим, что каждой из ветвей с символом «С» и «>»
соответствует 2/ исходов, а оставшиеся 2л4-1—4/ исходов соот-
ветствуют ветви с символом «=» Для того чтобы можно было скон-
струировать нужное дерево решении с /=log3 (2/i-M) уровнями,
каждой из перечисленных выше ветвей должна соответствовать
треть исходов (почему3) Тогда имело бы место соотношение 2/ =
—2п-Н—4/ или эквивалентное ему соотношение 6/=2/1т1, что
для целых / и п невозможно, гак как 6/ четко, тогда как 2н+1 не-
четно
Стоит отметить утверждение, обратное тому, которое использо-
валось при доказательстве теоремы 1 3 если можно найти дерево,
такое, что в каждом узле множество возможных исходов делится
на три равные части, то это дерево должно быть оптимальным.
Эта идея является ключевой при доказательстве следующей тео-
ремы
Теорема 1.4. Если пСу(3'—1), то задачу для п монет можно
решить за I сравнений.
Доказательство Пусть Кг=(Зг—1). Рассмотрим случаи n=Ki
(случай n<Kt мы оставляем для упражнения 7) Поскольку в по-
следующем числа Ki играют важную роль, полезно отметить два
тождества:
2Kt + 1 = Зг
Заметим, что Xt=l и что для одной монеты п-Kt задачу можно
решить одним сравнением 0 : 1 Мы должны показать, что в общем
случае для К/ монет задачу можно решить за I сравнений, мы сде-
лаем это, указав алгоритм, который при любом заданном зна-
чении I можно использовать для построения необходимого для нас
дерева решений.
В процессе выполнения этого алгоритма мы аккуратно будем
следить за всеми сведениями о множестве монет, причем эта ин-
формация будет всегда принадлежать к одному из трех типов
В ходе работы алгоритма при любом значении I, изменяющемся
от I до 1, алгоритм всегда находится в одном из трех состояний
Состояние 1 мы имеем Л, подозрительных монет (т е. если в
рассматриваемом нами множестве существует фапьшивая
монета, то она находится именно среди этих монет), и нам
для окончания решения разрешается сделать i сравнений
Случай !— I соответствует начальному состоянию задачи
Состояние 2 мы имеем множество из К,+1 монет и другое мно-
жество из Ki монет; в нашем распоряжении имеется i срав-
нений, и мы знаем, что или в множестве из Хг+1 элементов
находится тяжелая монета, или в множестве из элемен-
тов находится легкая монета
Состояние 3 то же, что и состояние 2, но теперь мы знаем, что
или в множестве из /С+1 элементов находится легкая
монета, или в множестве из элементов находится тяжелая
монета.
Для каждого из этих трех состояний алгоритма мы указываем,
какое надлежит сделать следующее сравнение, с помощью функции
переходов /, показанной на рис 1 8, мы утверждаем, что предпи
санное действие будет всегда приводить нас к одному из тех же са-
мых состояний (при этом i убывает на единицу). Когда i примет
значение 1, задача решится единственным сравнением, как быдо
отмечено выше Алгоритм имеет следующую структуру
Рис

Для завершения доказательства остается проверить некоторые
детали Для каждого перехода в диаграмме состояний, приведен-
ной на рис 1 8, вы должны просто проверить согласование мно-
жеств монет в начальном и конечном состояниях Вы должны
также проверить, используя рекуррентное соотношение Кг=
= ЗХг-1+1, что возможные для каждого состояния исходы распа-
даются по трем ветвям, выходящим из этого состояния, на группы
одинаковой мощности
Для большинства комбинаторных задач не существует изящ-
ного и эффективного пути отыскания оптимального решения,
такого, как алгоритм I 5 для задачи о фальшивой монете В этом
отношении литература по комбинаторным алгоритмам зачастую
вводит читателя в заблуждение, поскольку она сосредоточивает
внимание на элегантных решениях, даже если они применяются
только к отдельным задачам Красивые решения часто страдают
большим пороком если задачу слегка изменить, решение стано-
вится неприменимым Такая ситуация возникнет, например, при
доказательстве теоремы 1.3, если в задаче о фальшивой монете
предположить существование по крайней мере двух фальшивых
монет вместо одной Идеи, устойчивые по отношению к небольшим
изменениям формулировки задачи, имеют общий характер, подобно
идее рассмотрения разбиения исходов по ветвям дерева решений,
Проиллюстрируем другое применение этой идеи.
Важный принцип практических вычислений утверждает, что
если точно решить задачу трудно, то следует попытаться найти
эвристический алгоритм, который позволит эффективно находить
приближенные решения В случае деревьев решений для задачи
с данным числом исходов очевидным эвристическим соображением
является следующее попытаться удержать число уровней в дереве
решений как можно меньшим. Этого можно достигнуть, если де-
рево делать как можно более широким Тернарное дерево решений
с данным числом листьев можно сделать широким, если в каждой
вершине исходы разбить на три группы примерно равной мощности
В случае задачи с четырьмя монетами при девяти возможных
исходах нам хотелось бы выбрать в корне такое сравнение, чтобы
на каждой из ветвей, выходящих из корня, оставались возможными
три исхода Однако, как мы видели, этого достичь невозможно,
есчи нам дополнительно не дана настоящая монета В такой ог-
раниченной постановке задачи с четырьмя моментами в корне можно
сделать только два существенно различных сравнения, а именно
1 2 и 1,2 : 3,4 Они разбивают девять исходов на части (2, 5, 2)
и (4, 1, 4) соответственно Какая из них более однородная, т е
ближе к идеальному разбиению (3, 3, З)2 Введем важную меру од-
нородности таких разбиений Мы не имеем возможности привести
здесь полное обоснование выбора этой специфической меры До-
полнительные соображения по этому поводу будут приведены в
гл 6 и 7
Рассмотрим вектор вероятностей (pi, рг, ..., рп); здесь каждое
pi — неотрицательное действительное число, и	® примере
на рис 1.4 разбиение (2, 5, 2) порождает вектор вероятностей
pj=2/9, ps=5/9, р»=2/9; в предположении, что все девять исходов
равновероятны, эти величины представляют собой вероятности
появления каждой из трех ветвей, выходящих из корня. Нам нужна
функция %?(plf рг, .... рп) со следующими свойствами:
1	Она симметрична относительно pi, pt, .... рп, т. е не зависит
от взаимного расположения pi
2	Она достигает своего максимума на векторе с максимальной
однородностью: pt=pi=.. .=рп= —
3	. Она достигает своего минимума, равного нулю, на векторе
с минимальной однородностью- Pi=l, Рг=Рз= ..=рп=0.
4	Она монотонно возрастает от точки минимума до точки мак-
симума: если а изменяется от 0 до—,5^11—(п—1)а, а, ,,,, а],
монотонно возрастает
Такими свойствами обладает хорошо известная в теории инфор-
мации функция — энтропия
Я{рх....
Эта функция удовлетворяет также другим требованиям, жела
тельным с различных точек зрения
Используя эту функцию для измерения степени однородности
двух векторов, соответствующих корням двух деревьев решений в
задаче о четырех монетах, получим
44-4, 4Н4+44+44-+39
Та же самая мера, примененная к идеальному разбиению (3, 3, 3),
дает
Таким образом, согласно этой мере, разбиение (2,5, 2) ближе к одно-
родному, чем (4, 1, 4) Эвристический принцип выбора сравнения,
приводящего к наиболее однородному разбиению множества всех
исходов, корректно устанавливает, что корнем паилучшего дерева
решений для ограниченной задачи о четырех монетах должно быть
сравнение 1 2, Поскольку большинство задач о наилучшем дерева
решении не имеет процедур отыскания оптимальных решений, от
личных от полного перебора, этот простой эвристический принцип
стоит помнить
В этой части мы продемонстрировали полезность точного оп
ределения класса алгоритмов Из простой идеи рассмотрения раз
биения множества исходов по ветвям дерена решений оказалось
возможным получить границы необходимого числа сравнений,
эффективный алгоритм построения оптимального дерева для спе
циального случая и ценный эвристический принцип, который при
меняется к любой задаче о дереве решений
1.6. АНАЛИЗ АЛГОРИТМОВ
В процессе разработки и реализации алгоритма естественным
образом раскрываются некоторые его свойства Например, из
описания алгоритма 1 3 в разд 1 1, очевидно, следует, что дво
ичный набор длины п ои обрабатывает за pign-] итераций. По
мере того как алгоритмы становятся все более и более сложными,
все менее и менее вероятно, что их важные свойства проявятся на
стадиях разработки и реализации Как правило, некоторые важные
аспекты поведения алгоритма, такие, как его корректность, не-
обходимое число операций или объем памяти, определить трудно
Поэтому обычно глубокое понимание нового алгоритма предваряет
очень длинная стадия его анализа
Из-за трудностей анализа алгоритмов им зачастую просто пре
небрегают, вместо этого программа выполняется, чтобы увидеть
что получится (например, измеряется время работы) Такой подход
можно признать удовлетворительным, если есть основание пола
гать, что тестовые задачи достаточно хорошо характеризуют ра
боту алгоритма и в общем случае, если же Это не так, то описанный
выше подход даст мало ценной информации Даже если тест пре
красно характеризует работу алгоритма, он никогда не даст ответ
на придирчивый вопрос, могут ли существовать лучшие алгоритмы
для решения той же самой задачи. Проблему оптимальности алго
ритма можно решить только путем его анализа
В анализе алгоритмов существуют две фундаментальные про
блемы
1. Какими свойствами обладает данный алгоритм5
2 Какие свойства должен иметь любой алгоритм, решающий
данную проблему5
Фундаментальная разница между этими дв>мя вопросами состоит
в подходе к ответу на них В первом случае алгоритм задан и за
37
ключения выводятся путем изучения свойств, присущих ему.
Во втором случае задается проблема и точно определяется струк-
тура алгоритма, заключения выводятся на основе изучения суще-
ства проблемы по отношению к данному классу алгоритмов
Обсуждение задачи о фальшивой монете в разд 1 5 содержит
примеры обоих типов проблем в ситуации, когда решить их можно
сравнительно легко В этой главе мы продолжим изучение кодов»
сохраняющих разности, для того, чтобы привести нетривиальные
примеры анализа отдельного алгоритма и класса всех алгоритмов,
предназначенных для решения данной проблемы
Анализ алгоритма построения кода. Рассмотрим алгоритм, ко-
торый порождает последовательность	£2>г, кодов, сохра-
няющих разности, начиная с произвольного кода и который
строит S>t путем композиции с самим собой согласно проце-
дуре увеличения ранга, изложенной в разд 1.3 Вычислим ранг
кода построенного по такому алгоритму, считая его функцией
длины кодового слова. Пусть R (п) — ранг п разрядного кода
и соответственно R(2n)— ранг кода S>i + 1, полученного компо-
зицией кода S)i с самим собой Тогда из уравнения (1 1) разд 1.3
мы знаем, что
Для того чтобы определить вид функции, удовлетворяющей этому
уравнению и, в частности, скорость роста его решения, упростим
правую часть (не слишком сильно ее изменяя) и изучим видоизме-
ненное функциональное уравнение
г(2«) = Ш^,	(12)
надеясь, что г (я) не слишком сильно отличается от R (п) В упраж-
нении И поставлена задача выяснить, насколько хорошо г (и)
аппроксимирует R(n)
Систематические процедуры решения таких рекуррентных урав-
нений более подробно обсуждаются в гл 3, но в данном случае
достаточно метода проб и ошибок. После некоторого эксперимен-
тирования мы придем к экспоненциальному решению вида
r(n) — c2an,
где с и а— константы, которые надлежит определить Подставляя
это предполагаемое решение в 1 2, получим уравнение
c2ian =!
которое удовлетворяется, если c=t~\ 1, независимо от значения а.
Таким образом, алгоритм, увеличивающий ранг, строит коды с
рангами, которые приближенно имеют вид
Само рекуррентное уравнение не ограничивает выбора а, но
существует другое ограничение, которое должно быть удовлетво-
рено, а именно начальные условия, ранг и длина кода ®0, с кото-
рого начиналась схема композиции. Если в качестве мы выберем
оптимальный четырехразрядный DP-I-код ранга 8, то получим на-
чальное условие
г(4) = 8 = ;
из которого вытекает а= у, и, следовательно
Таким образом, алгоритм, увеличивающий ранг, начинающийся с
этого частного кода строит «-разрядные коды, имеющие около
+ 1 кодовых слов из 2п возможных двоичных наборов длины п
Сформулировать этот результат можно, например, так Только
половину разрядов в коде можно использовать для информации;
другая половина определяется частично задачей (условием, что
код должен сохранять разности) и частично рамками, устанавли-
ваемыми процедурой увеличения ранга
Можно ли сделать лучше? Можно ли найти алгоритмы, которые
строят «-разрядные коды, ранги которых более близки к 2я? К этому
вопросу можно подойти двумя различными путями Один очевид-
ный — постараться улучшить данный алгоритм Более тонкий
подход состоит в том, чтобы сначала посмотреть, можно ли добиться
улучшения Прежде чем обсуждать более тонкий подход, кратко
остановимся на первом
В нашем примере можно получить частичное улучшение, если
начать процедуру увеличения ранга с более эффективного кода
Например, оптимальный 5-разрядный DP-1-код ранга 14 дает г(5)=
= 14=2-260 или а= у lg7«0,56, что уже несколько лучше Однако
уравнение (1 3) с учетом того, что а<1 (ранг кода длины п, оче-
видно, не может превзойти 2"), говорит нам, что в любом коде,
построенном на основе применения алгоритма увеличения ранга,
долю длины кодового слова, равную (1—а), нельзя использовать
для записи информации. Для тою чтобы получить более сущест
венное улучшение, мы должны отказаться от описанной процедуры
увеличения ранга и исследовать другие принципы построения ко-
дов Мотивировкой таких обширных исследований служит резуль-
тат следующего анализа.
39
Верхняя граница ранга (гг,/)-кодов. Требования, предъявляемые
к кодам, сохраняющим разности;
1) если |t—то H(D„ Dj)=]i—/], и
2) если |t—/|>/, то H(Dit
вынуждают кодовые слова Di находиться на определенных мини-
мальных расстояниях друг от друга, а это обстоятельство в свою
очередь не дает возможности использовать все вершины «-мерного
куба в качестве кодовых слов «-разрядного кода Это явление
проиллюстрировано на рис. 1 2 В данном разделе мы выведем
верхнюю оценку ранга «-разрядного DP-1-кода, имея лишь его
определение и ничего более не предполагая. Следовательно, эта
оценка, которая зависит только от самой задачи, должна иметь
место для любого алгоритма построения кода
Верхняя оценка ранга N «-разрядного DP /-кода, которую
мы получим, имеет следующий вид:
£.c2nr,
где с зависит от I и не зависит от п Правая часть этого неравенства
растет значительно быстрее, чем оценка >•(«)= (/-J-l)2°", <з>1,
которая была получена из уравнения (1 3) для кодов, построенных
в соответствии с процедурой увеличения ранга. Расхождение
между этой верхней оценкой и нижней оценкой, которую дает
уравнение (1.3), оставляет большую неопределенность в том, какие
же ранги достижимы, иначе говоря, остается неясным, завышена
ли верхняя оценка или не эффективна процедура увеличения
ранга. Эта неопределенность в исследуемой задаче является ти-
пичной ситуацией. Наша задача слишком специальна, чтобы про-
должать здесь дальнейшее обсуждение Скажем только, что верх-
няя оценка достаточно хорошая и что можно построить коды с
рангами, близкими к верхней оценке Для дальнейшего ознаком-
ления можно рекомендовать литературу, указанную в разд 1 7.
Здесь же мы намеревались только очертить проблемы, которые
необходимо преодолеть при анализе нетривиальных алгоритмов.
Мы изложим только схему вывода неравенства (1.4), оставляя
читателю возможность самому заполнить пробелы в доказательстве.
Доказательство неравенства 1.4. Пусть	Dt, .DN}—
«-разрядный DP-Z-код; отождествим кодовые слова Dc с вершинами
«-мерного куба, как показано на рис. 1.2. Положим
и каждой вершине V «-мерного куба сопоставим вес (V), равный
числу кодовых слов, которые находятся на хемминговом расстоянии
г от вершины V:
WT (И)=(число кодовых слов D,, таких, что H(V,
Сначала покажем, что
1ГГ (V)^zi,
D 0 1 t О
1 0 1 0 t
110 11
и проверим, что
1	Каждая строка имеет точно г единиц, и отсюда общее число
единиц в матрице равно sr,
2	, В каждом столбце матрицы находится по крайней мере г
единиц (проверка этого утверждения предлагается в упражнении
12), и, следовательно, общее число единиц в матрице не превосходит
Сопоставляя эти два утверждения, получаем, что зг^пг, или s^n.
(Как будет показано в разд 3 4,2, простой прием подсчета эле-
ментов матрицы по строкам и столбцам и приравнивания этих
результатов заходит удивительно далеко )
Установив, что 1УГ(К)С«, отметим теперь следующие свой-
ства распределения весов в л-мерном кубе
1	Общий вес в кубе равен N (?), поскольку каждое из У ко-
довых слов дает вклад i в вес каждой из (") вершин, находящихся
на расстоянии г от кодового слова;
2	Общий вес кодовых слов Dt равен 2(W—г) (упражнение 13),
и отсюда общий вес всех вершин, не принадлежащих коду ££>,
3	Поскольку существует 2"—W вершин V, не принадлежащих
и каждая из них имеет вес Ц7Г (К)й^/?, общий вес всех вершин,
не принадлежащих S>, не превосходит (2’—Afjzi.
Объединяя (2) и (3), получаем неравенства
N -2 (Л/ -г) С (2й — /V) и
п2"—2г.
Для фиксированного г и растущего п величина (?) растет при-
мерно как Ьпг, где b зависит от г и не зависит от п. Учитывая это,
можно показать, что
а это соотношение и есть неравенство (1 4)
Читатель, который старательно проработал эту главу, начи-
ная с тривиального алгоритма подсчета числа единиц в наборе»
просматривающего все разряды по очереди, и кончая заполнением
пробелов в выводе верхней оценки (1.4), имеет теперь общее пред-
ставление о полном спектре комбинаторных алгоритмов. В част-
ности, каждая тема, встречающаяся в этой книге, будет некоторым
напоминанием принципов разработки алгоритмов, приведенных
в разд. 1 3 и 14, рассмотрения проблем реализации, приведенных
в разд. 1 1 и 1 2, и математических процедур анализа алгоритмов,
изложенных в разд 1 5 и 1.6.
1.7. КОММЕНТАРИИ И ССЫЛКИ
Хотя комбинаторная математика является старой дисциплиной
(она получила свое наименование в 1666 г от Лейбница и его Dis-
sertatio de Arte Combinatorial, комбинаторные алгоритмы с их
акцептом на разработку, анализ и реализацию практических алго-
ритмов являются продуктом века вычислительных машин Ссылки
на первые работы, касающиеся специальных вопросов этой области,
будут лапы в последующих главах, но список работ, носящих более
общий характер, приводится ниже
Lehmer D Н Combinatorial Problems with Digital Computers,
Proc Fourth Canadian Math Congress, 1957, University of
Toronto Press, 1960, 160—173.
Lehmer D. H Teaching Combinatorial Tricks to a Computer, Chapter
15 in Combinatorial Analysis, R Bellman and M Hall (eds),
Proc. Symp Applied Math , Vol 10, American Math. Society,
Providence, R. I , I960, 179—193
Lehmer D. H. The Machine Tools of Combinatorics, Chapter 1 in
Applied Combinatorial Mathematics; E F Beckenbach (Ed),
Willey, New York, 1964, 5—31
Hall M , Knuth D. E Combinatorial Analysis and Computers, Ame-
rican Math Monthly, 72, Pt II (1965), 21—28
Укажем более современные руководства
Wells М. В Elements of Combinatorial Computing, Pergamon Press,
Oxford, 1971
Even S Algorithmic Combinatorics, Macmillan, New York, 1973
Aho A V , Hopcroft J. E , Ulman J D The Design and Analysis
of Computer Algorithms, Addison-Wesley, Reading, Mass., 1974
[Имеется перевод: Ахо A , Хопкрофт Дж, Ульман Дж Пост-
роение и анализ вычислительных алгоритмов.— М : Мир, 1979 |
Nijenhuis А , Wilf II S. Combinatorial Algorithms, Academic Press,
New York, 1975
Обширные сведения по комбинаторным алгоритмам можно найти
в книге
Knut D Е The Art of Computer Programming, Vol 1, Fundamental
Algorithms (1968), Vol 2, Semmumerical Algorithms (1969),
Vol 3, Sorting and Searching (1973), Vol 4, Combinatorial
Algorithms (to appear), Addison-Wesley, Reading, Mass [Имеет-
ся перевод. Кнут Д. Искусство программирования для ЭВМ,
т 1, 2, 3 —М Мир, 1976, 1977, 1978.]
Логарифмический алгоритм суммирования единиц в двоичном
наборе, приведенный в разд 1 1, был, вероятно, получен неза-
висимо несколькими авторами. Одним из первых его реализовал
Давид Мюллер из Иллинойсского университета, который исполь-
зовал этот алгоритм в программе для машины Illiac I в 1954 i
Описанные в разд 1 2 коды, сохраняющие разности, или не-
значительные их вариации известны под различными названиями
(цепные коды, циклические коды) с тех пор, как в работе
Kautz W Н Unit-Distance Error-Checking Codes, IRE Trans.
Electronic Computers, EC-7 (1958), 179—180
был рассмотрен специальный случай /=1 Эта работа, как и неко-
торые последующие, касается приложений таких кодов к задачам
обнаружения и исправления ошибок, в особенности при представ-
лении непрерывных сигналов цифровыми Обсуждение проблем
применения кодов, сохраняющих разности, к задачам распозна-
вания, а также соо1ветствующая библиография приведены в работе
1 8 Упражнения
Preparata F. P., Nievergelt J. Difference-Preserving Codes, IEEE
Trans. Information Theory, IT-20 (1974), 643—649
Анализ задачи, более общей, чем рассмотренная в разд I 6
задача о фальшивой монете, приводится в работе
Smith С. А В The Counterfeit-Coin Problem, The Mathematical
Gazette, 21 (1947), 31-39
Проблема анализа комбинаторных алгоритмов привлекла за
последнее время много внимания. Приведем две обзорные статьи,
посвященные этой теме
Knuth D. Е. Mathematical Analysis of Algorithms, Information
Processing 7i (Proceedings of the 1971 1FIP Congress), North-
Holland Publishing, Co , Amsterdam, 1972, 19—27.
Frazer W. D Analysis of Combinatory Algorithms — A Sample of
Current Methodology, Spring Joint Computer Conference, AFIPS
Conference Proceedings, Vol. 40 (1972), 483—491.
1.8. УПРАЖНЕНИЯ



этом\олжно выполняться следующее условие: па каждом стержне ни в^какой
для попечения (nH 1) разрядного DP-1-кода ранга
к алгоритму, требующему я—1 сложений.
11 Эта задача касается оценки различия между апnj оксимацией г (п) и фуьк-
(а) Покажите что для любого целого/>1 и любого начального условия /?(!)=
—с^1 функция Rin) монотонно возрастает.
всех л>1 выполняется неравенство R(п)^г(л).
(с) Рассмотрите рекуррентную формулу
Покажите, что при одинаковых начальных условиях R(1)W(1)^1 пя всех
п>\ выполняется неравенство R(n)<r(n)
(d) Найдите компактное выражение для решения г(п) рекуррентного срав
ошибки аппроксимации г (п) функции R (п) Определите скорость роста этой гра
13 Покажите, что для DP-f-кода ранга Л'и для
Глава 2. Представление комбинаторных
объектов
Большинство вычислительных устройств в качестве основных
объектов допускает только двоичные наборы, целые и символы,
поэтому, прежде чем работать с более сложными объектами, их
необходимо представить двоичными наборами, целыми или сим-
волами Например, числа с плавающей запятой кодируются парой
целых — мантиссой и порядком этого числа, но такое кодирование
обычно незаметно для пользователя. В противоположность этому
рассмотренные в данной главе способы кодирования объектов (мно-
жества, последоватетьности и деревья) почти всегда адресованы
пользователю.
Любой заданный класс объектов может иметь несколько возмож-
ных представлений, и выбор наилучшего из них решающим обра-
зом зависит от того, каким образом объект будет использовав,
а также от типа производимых над ним операции Все эти сооб-
ражения побуждают пас рассмотреть не только свойства самих
представлений, но также и некоторые приложения.
2.1.	ЦЕЛЫЕ
Целые являются основными объектами в вычислительной ком-
бинаторике, и хотя их легко можно использовать во всех вычисли-
тельных устройствах, иногда удобно представлять их в форме,
отличном от непосредственно заданной в машине В различных
вычислительных теоретико-числовых исследованиях изучаются са-
ми целые числа, но мы будем использовать их главным образом
при подсчете и индексировании В последнее время установлено,
чю полезны различные представления В этом разделе мы обсудим
важный и общий класс позиционных представлений, оставляя
ipyi-ие более специальные случаи для упражнений 4, 5 и 6.
Мы будем рассматривать только неотрицательные целые О, 1,
2,	, поскольку, вообще говоря, при подсчетах и индексировании
нет необходимости в отрицательных целых Кроме того, к любому
представлению неотрицательных целых легко присоединить оди-
ночный знаковый двоичный разряд.
Позиционные системы для представления целых чисел очень
широко известны, поскольку они встречаются во многих разделах
46
математики, начиная с «новой математики» и кончая углубленным
курсом теории чисел. В системе счисления с основанием г каждое
положительное целое число имеет единственное представление в
виде конечной последовательности
в которой каждое dt — целое, удовлетворяющее условию
и dh=?M). Нуль представляется последовательностью (0). г назы-
вается основанием системы (г>1) Целое, соответствующее после-
довательности (2 1), имеет вид
N — d0 -Ed/?4-dar34-... 4-dsr*,
что принято выражать следующим образом-
На протяжении истории использовались различные значения г
Например, древние вавилоняне использовали г=60, а индейцы
племени майя г—20 Сегодня наиболее широко используется г=
= 10 — десятичная система, которую мы унаследовали от арабов,
и г=2— двоичная система, которая лежит в основе современных
вычислительных устройств В действительности она используется
лишь на самом низком уровне аппаратного оборудования, в слож
ных вычислительных устройствах и базисных языках удобнее
использовать г=8 или г=16
Единственность этого представления можно доказать методом
от противного Числа М=0 и N= 1, очевидно, имеют единственное
представление. Предположим, что представление не единственно,
и пусть V>1 будет наименьшим цепым числом, имеющим два
различных представления
Если то без потери общности предположим, что k>l. Тогда,
поскольку

и поскольку мы заключаем, что
ИА-1 (fA-,	(2 21
что невозможно Таким образом, мы должны иметь k-l. Анало
гично, если мы имели бы снова неравенство (2 2) и отсюда
С необходимостью dk—ek. Следовательно, число
2 I Це we
имеет два различных представления, что противоречит предполо-
жению, что N — наименьшее из таких чисел
Для доказательства того, что каждое положительное целое
имеет представление по основанию г, достаточно задать алгоритм,
конструирующий (с необходимостью единственное) представление
данного числа W Как мы увидим, такую процедур} осуществляет
алгоритм 2 1 Он строит последовательность d„, di, d2, dh путем
повторения деления на г и записи остатков Пусть на первом шаге
при делении N на г остаток будет d« Частное, полученное в резуль-
тате первого шага, делим на г, вновь полученное частное делим
на г и т. д Полученная в результате такого процесса последова-
тельность остатков и будет требуемым представлением Л/ по ос-
нованию г.
Очевидно, что последовательность d0, db , dh, вычисленная
посредством применения алгоритма 2 1, для всех d, удовлетворяет
условию Os^di<r и dft=#0, за исключением случая ЛГ^О Простым
методом индукции можно показать, что ^=^d/,
Важным обобщением систем счисления с основанием г являются
смешанные системы счисления, в которых задается не единственное
основание г, а последовательность оснований ra, rt, г2,	, и по-
следовательность (2 1) соответствует целому
где теперь каждое d, удовлетворяет неравенству 0^/{<гг и d^O,
если М=#0 Тот факт, что каждая такая последовательность соот-
ветствует единственному числу и каждое положительное целое
число имеет единственное представление, следует из простого обоб-
щения результатов для обычных систем счисления, которые яв-
ляются частным случаем смешанных систем при r^—r, i^O
Смешанные системы счисления могут вначале показаться стран-
ными, но в действительности в повседневной жизни они встреча-
48
ются почти так же часто, как и десятичные. Рассмотрим, напри-
мер, нашу систему измерения времени — секунды, минуты, часы,
дни недели и годы Это — в точности смешанная система с го=6О,
В главе 5 мы будем использовать некоторые смешанные системы
для установления соответствия между перестановками и целыми
числами В частности, мы будем использовать систему счисления
с факториалами, в которой последовательность (2 1) соответствует
петому числу
O<d,<t+I и <4=т±0для всех Л^О, заметим, что всегда d9=0 Это —
смешанная система счисления, в которой — Для фиксиро-
ванного значения n>k мы будем использовать также систему
счисления с убывающими факториалами, в которой последователь-
ность (2 I) соответствует целому числу
i и для в этом случае всегда dn-i=0 Это —
смешанная система счисления, в которой rt^=n—i,
Представление целого Л' в смешанной системе счисления (г0,
г,, . ) осуществляется с помощью алгоритма 2.2, который являет-
ся простым обобщением алгоритма 2.1. Вместо того чтобы для
получения dj, в качестве делителя всегда использовать г, в алго-
ритме 2 2 используются
2.2.	ПОСЛЕДОВАТЕЛЬНОСТИ
Бесконечная последовательность
формально определяется как функция /, областью определения
которой является множество положительных целых чисел
Z>1. Во многих случаях индексирование последовательности более
удобно начинать с нуля; тогда областью определения / будет мно-
жество целых неотрицательных чисел. Аналогично определим ко-
нечную последовательность или список
как функцию, областью определения которой является множе-
ство {!, 2,	?г} Примером бесконечной последовательности
явтяются простые числа
i	1234	5	6 7	8 9 10..
Pi	2 3 5 7	11	13	17	19	23 29
перестановка
П (1, 2, 3, 4, 5, 6)= <6, 2, 5, 1, 3, 4)
2.2.1. Последовательное распределение
С вычислительной точки зрения простейшим представлением
конечной последовательности является точный список ее членов,
расположенных по порядку в последовательных ячейках памяти
Так, Si хранится, скажем, начиная с ячейки /t, st хранится, начи
ная с ячейки It—li+d, ss хранится, начиная с ячейки 4-2d
и т. д., где d— число ячеек, требуемых для хранения одного эле
мента последовательности. Это последовательное представление
проиллюстрировано на рис. 2.1
Описанное выше представление последовательности имеет ряд
преимуществ Во-первых, оно легко осуществимо и требует не-
больших расходов в смысле памяти. Кроме того, оно зачастую
еще полезно и потому, что существует простое соотношение м^жлу
i и адресом ячейки, в которой хранится s,-
Это соотношение позволяет организовать прямой доступ к любому
элементу последовательности. Наконец, последовательное пред-
ставление имеет достаточно широкий диапазон и включает в себя в
качестве специального случая представление многомерных мас-
сивов (упражнение 7)
Например, чтобы представить массив размером пХт
(2.4)
будем рассматривать его как последовательность Si, $2, sn,
в которой каждое s, в свою очередь является последовательностью
из т элементов i'-й строки нашей матрицы. Таким образом, число
ячеек, требуемых для записи элемента s, (будем обозначать это
число символом d), равно md, 1де d — число ячеек, требуемых
для записи элемента ац Поскольку последовательность Sj начи-
нается в ячейке
ячейка для atJ б\дет иметь стедующий адрес.
Это представление известно как построчная запись матрицы, по-
столбцовая запись получается, если массив (2 4) рассматривать как
последовательность tL, t2,	, im, в которой каждое tt в свою оче-
редь является последовательностью из п элементов i го столбца
матрицы.
Последовательное распределение, наряду с преимуществами,
имеет некоторые значительные недостатки Например, такое пред-
ставление становится неудобным, если требуется изменить после-
довательность путем включения новых и исключения имеющихся
там элементов Включение между 5, и s! + l нового элемента требует
сдвига	s/ + 2, , sn вправо на одну позицию, аналогично, ис-
ключение в, требует сдвига тех же элементов на одну позицию влево
С точки зрения времени обработки такое передвижение элементов
может оказаться дорогостоящим, и в случае динамических последо-
вательностей лучше использовать технику связанного распреде
ления, обсуждаемую в следующем разделе.
Характеристические векторы. Важной разновидностью после-
довательного распределения является случай, когда такому пред-
ставлению подвергается подпоследовательность некоторой основ-
ной последовательности $3, а2, а» .?). В этом случае можно предста-
вить последовательность более удобно, используя характеристиче-
ский вектор — последовательность из нулей и единиц, где i-й разряд
равен единице, если принадлежит рассматриваемой последова-
тельности, и нулю в противном случае
Например, характеристический вектор начального сегмента
последовательности (2 3) простых чисел имеет вид
характеристический вектор
для простых чисел:
123456789 10
0 1 10 10 10 0 0
Здесь основной последовательностью является последовательность
целых положительных чисел. В ЭВМ с 32-разрядными словами для
запоминания простых чисел, меньших 10е, потребуется 10s'32=
=31250 слов Замечая далее, что для £>1 число 2< не простое,
мы можем сэкономить половину этого поля, выписывая разряды
только для чисел вида 2t (-1,	1, и запоминая, что простое число 2
отсутствует Таким образом, простые числа, меньшие чем 10е,
можно записать только 15625 словами Поскольку число простых
чисел, меньших 10е, равно 78498, последовательное представление,
описанное ранее, потребовало бы поля в пять раз меньшего размера
Характеристические векторы почезны в ряде случаев метода
решета, которые обсуждаются в разд. 4 2 Вообще их полезность
вытекает из их компактности, существования простого фиксиро-
ванного соотношения между i и адресом г-го разряда и возможности
при таком представлении очень легко исключать элементы Дей-
ствительно, все примеры из разд. 4 2 вычисляют нужную подпо-
следовательность (например, простые числа) путем последователь-
ного удаления из основной последовательности (например, целых
положительных чисел) элементов, которые не входят в подпосле-
довательность.
Главное неудобство характеристических векторов состоит в
том, что они не экономичны Исключение составляют «плотные»
подпоследовательности последовательностей st, sg, s4, ... Кроме
того, их трудно использовать, если не существует простого соот-
ношения между i и s. Если такое соотношение сложное, то исполь-
зование характеристических векторов может быть очень не эконо-
разуют подпоследовательность последовательности простых чисел 2, 3,
И 13, 17, 19, 23, 29 ... .
мичпым в смысле времени обработки. Если последовательности не
достаточно плотные, то значительным может оказаться объем
памяти. В случае простых чисел между i и s, имеется простое соот-
ношение. S;=i (или s£=2i —1, если использовать только нечетные
числа) Теорема о простых числах утверждает, что число простых
чисел, меньших п, приблизительно равно п/in п, таким образом,
простые числа относительно плотно распределены в множестве
целых чисел.
2.2.2. Связанное распределение
Неудобство включения и исключения элементов при последо-
вательном распределении происходит из-за того, что порядок сле-
дования элементов задается неявно требованием, чтобы смежные
элементы последовательности находились в смежных ячейках
памяти В результате многие элементы последовательности во
время включения или исключения должны передвигаться Если
это требование опущено, то мы можем выполнить операции вклю-
чения и исключения без того, чтобы передвигать элементы после-
довательности. Конечно, необходимо сохранять информацию о
способе упорядочения последовательности элементов, но можно
сделать это явным образом вместо того, чтобы использовать неко
горое неявное требование. В частности, при связанном распреде-
лении последовательности (связанном списке) каждому постав-
ки в соответствие указатель Р1Г отмечающий ячейку, в которой
записаны s;+i и Р,+1 Существует также указатель Ро, который
указывает начальную ячейку последовательности, т е. ячейку с
символами Si и Рг. Все сказанное выше проиллюстрировано на
Здесь каждый узел 1) состоит из двух полей В поле INFO
размещен сам элемент последовательности, а в поле LINK— ука-
затель на следующий за ним элемент Поскольку дня s„ = INFO(L,)
мента Stu, если ячейка для s, известна Для этого необходимо лишь
изменить значения некоторых указателей Например, чтобы ис-
ключить элемент s2 из последовательности, изображенной на рис 2 3,
необходимо только положить L1NК (/i)=LINК (/2); после такой
операции элемента s2 в посчедователыюсти больше не будет (рис
2.4) Чтобы в последовательность на рис 2 3 включить новый
подпоследовател ьности
на рис 2.5, мы должны фактически использовать операцию get-cell
для того, чтобы найти значение Мы будем полностью игнори-
ровать проблему сбора ненужных ячеек памяти, предполагая лишь,
что их каким-то образом собирают для последующего использо-
вания (такой процесс носит название сбора мусора)
С помощью связанных распределений мы добились большей
гибкости, но потеряли некоторую информацию При последова-
тельном представлении фиксированное соотношение между i и
ячейкой s, позволяет, в частности, иметь быстрый и прямой доступ
к любому элементу последовательности В связанном распреде-
лении такого соотношения не существует, и доступ ко всем эле-
ментам последовательности, кроме первого, не является прямым
и эффективным Например, при последовательном представлении,
если длина последовательности задана, то легко найти средний ее
элемент, это же самое сделать труднее, если последовательность
задается связанным списком. Кроме того, приходится тратить па-
мять на указатели Р,.
В приложениях при выборе последовательного или связанного
представления разумно сначала проанализировать типы операций,
которые будут выполняться над последовательностью Если опе-
рации производятся преимущественно над случайными элементами,
осуществляют поиск специфических элементов (см гл 6) или про-
изводят упорядочение элементов (см гл 7), то обычно лучше по-
следовательное распределение Связанное распределение предпо-
чтительнее, если в значительной степени используются операции
включения и/или исключения элементов, а также сцепления иуили
разбиения последовательностей
Разновидности связанных списков. Тривиальной модификацией
связанного списка, изображенного на рис 2.3, будет стедующее
несколько более гибкое представление последовательности если
Рп указывает на slr как показано па рис 2 6, то мы имеем так назы-
ваемый циклический список. Такая форма списка дает возможность
достигнуть (хотя и не прямо) любой элемент из любого другого
элемента последовательности Включение и исключение элементов

Еще большая гибкость достигается, если использовать дважды
связанный список, когда каждый элемент s( последовательности
вместо одного имеет два связанных с ним указателя Как показано
на рис 2 7, они указывают на элементы s,-5 и s^i. В таком списке
для любого элемента имеется мгновенный прямой доступ к преды-
дущему и последующему элементам, в связи с чем облегчаются
такие операции, как включение нового элемента перед st и исклю-
чение элемента s, без предварительного знания его предшествен-
ника Если есть необходимость, дважды связанный список очевид-
ным образом можно сделать циклическим
2.2,3. Стеки а очереди
В комбинаторных алгоритмах особую важность представляют
две структуры данных, основанные на динамических последова-
тельностях, т е последовательностях, которые изменяются вслед-
ствие включения новых и исключения имеющихся элементов
В обоих случаях операции включения и исключения, которым
подвергается последовательность, имеют ограниченный вид они
производятся только в концах последовательности Стек есть
последовательность, у которой все включения и исключения про-
исходят только в ее правом конце, называемом вершиной стека
(соответственно левый конец последовательности называется ос-
нованием) Таким образом, элементы включаются в стек и исклю-
чаются из него в соответствии с правилом «Первым пришел — по-
следним ушел». Очередь — это последовательность, в которой все
включения производятся на правом конце списка (в конце очереди),
в то время как все исключения производятся на левом конце (в
начале очереди) В противоположность стеку очередь onepnpver
в режиме. «Первым пришел — первым ушел»
Стеки и очереди имеют важное значение в бухгалтерском деле.
Для выполнения какой-либо определенной задачи может потребо-
ваться выполнение ряда подзадач Каждая подзадача может в
свою очередь привести к другим требующим выполнения подзада-
чам. И стеки, и очереди являются механизмом, посредством ко-
торого запоминаются подзадачи, подлежащие выполнению, а также
порядок, в котором они должны быть выполнены В некоторых
случаях порядок таков «Первым пришел — последним ушел»,
тогда удобно использовать стеки Если порядок подчиняется пра-
вилу «Первым пришел — первым ушел», то подходящим инстру-
ментом являются очереди В разд 2 3 2 будут приведены примеры
каждого из этих случаев
Поскольку операции включения в стеки и очереди и исключе-
ния из них широко используются в обсуждаемых в этой книге ал-
юритмах, введем следующие обозначения
D<^x Добавить х к D. Если D—стек, то х помещается
в вершину, если же D — очередь, то х добавляется
в конец
x<^D Присвоить переменной х значение верхнего
элемента D, если D—сгек, или начального эле-
мента D, если D—очередь Этот элемент затем
из D исключается
Введенные нами понятия мы будем использовать, не обращая
внимания на технику построения стеков и очередей.
Последовательная реализация. Для стеков это распределение
весьма удобно Все, что нам нужно, это переменная, скажем t,
чтобы следить за вершиной стека S Предположим, что для 5 от-
ведены ячейки S (1), S (2),	, S (т), тогда пустой стек соответствует
отучаю 1=0, и операции включения и исключения следующие:
m then overflow
then underflow

Здесь underflow (нехватка) означает, что делается попытка уда-
непосредственно перед началом очереди, а переменную г в качестве
указателя ее конца, то очередь будет состоять из элементов Q(/4-l),
Q(f-L2), , , Q (г) Согласно этому определению, пустая очередь
соответствует случаю г— f Мы имеем

г >—(г4-1) mod т
if г — f then overflow
else Q (r) -— x
ifr = f then underflow
else J /-(Z-rDmod,»
I x— Q(fl
Как и в случае стеков, underflow означает, вообще говоря, окон-
чание, a overflow — ошибку Заметим, что оператор overflow по-
является, когда к очереди из т—1 элементов добавляется m-й эле-
мент, это означает, что одна из отведенных т ячеек оставляется
пустой.
Связанное распределение. Связанное распределение стека такое
же легкое, как и последовательное распределение Мы сохраняем
символ t в качестве указателя ячейки, являющейся вершиной стека,
и используем поле LINK элемента стека для указания элемента,
находящегося под данным элементом в стеке Нижний элемент
стека имеет пустой указатель \ в поле LINK, и 1—.\ означает
пустой стек ОДы имеем
/ — get-cell
INFO (/) —х
L INK (!) t
ift^A then underflow
|x<- INFO(0
elSe | LINK(t)
58
В этом случае условие overflow появляется в операции get-cell,
если никакие ячейки недоступны.
Для очередей связанные распределения по существу те же са-
мые, что и для стеков (т. е. LINK (х) указывает на элемент очереди,
идущий после х). Незначительные изменения состоят в том, что мы
используем f вместо I в качестве указателя начала и, кроме тою,
г—в качестве указателя конца. Чтобы к очереди добавить эле-
мент, мы используем
I get-cell
INFO (0*—.
LINK (/)*-
LINK (/)♦—
Как и прежде, условие overflow неявным образом присутствует
в операции get-cell
Пустую очередь удобно задавать условием /=Л, но при этом
мы должны обеспечить определение значения г для пустой очереди
так, чтобы алгоритм включения элементов работал правильно при
включении первого элемента После некоторых размышлений ста-
новится ясным, что мы должны хранить f в поле LINK узла, кото-
рый указан символом г Исключение элемента производится тогда
следующим образом:
2.3.	ДЕРЕВЬЯ
Конечное корневое дерево Т формально определяется как непу-
стое конечное множество упорядоченных узлов, таких, что суще-
ствует один выделенный узел, называемый корнем, дерева, а ос-
тавшиеся узлы разбиты на ni^O поддеревьев 7\, Т г, , Тт. (За
исключением гл. 8, все деревья в этой книге считаются корневыми,
а термин «дерево», вообще говоря, будет означать корневое дерево )
Узлы, не имеющие поддеревьев, называются листьями-, остальные
узлы называются внутренними узлами Введенные нами понятия
проиллюстрированы на рис 2.8
В гл. 1 мы кратко использовали деревья при изучении необхо-
димого числа взвешиваний в задаче о фальшивой монете с п моне-
тами Так рано деревья появились не случайно, ибо понятие дерева
используется в различных важных аспектах в каждой главе книги.

Посредством деревьев изображаются иерархические организации,
поэтому они являются наиболее важными нелинейными струк-
турами данных в комбинаторных алгоритмах
В описании соотношений между узлами дерева мы используем
терминологию, принятую в генеалогических деревьях Так мы
говорим, что в дереве (или поддереве) все узлы являются потом-
ками его корня, и наоборот, корень есть предок всех своих потом-
ков Далее, корень мы будем именовать отцом корней его подде-
ревьев, которые в свою очередь будут сыновьями корня Напри-
мер, на рис, 2 8 узел А является отцом узлов B,Gu1,JhK — сы-
Все рассматриваемые нами деревья будут упорядочены, т е.
для них будет важен относительный порядок поддеревьев каждого
узла Таким образом, деревья
считаются различными
Определим лес как упорядоченное множество деревьев, в связи
с этим мы можем перефразировать определение дерева- дерево
есть непустое множество узлов, такое, что существует один выде-
ленный узел, называемый корнем дерева, а оставшиеся узлы об-
разуют лес с поддеревьями корня
Важной разновидностью корневых деревьев является класс
бинарных деревьев Бинарное дерево Т либо пустое, либо состоит
из выделенного узла, называемого корнем, и двух бинарных под-
деревьев левого Т, и правого Тг Бинарные деревья, вообще го-
воря, не являются подмножеством множества деревьев, они пол-
ностью отличаются по своей структуре, поскольку две следующие
картинки
не изображают одно и то же бинарное дерево Как деревья, однако,
они обе не отличимы от
Различие между деревом и бинарным деревом состоит в том,
что дерево не может быть пустым, и каждый узел дерева может
иметь произвольное число поддеревьев; в то же время бинарное
дерево может быть пустым, каждая из его вершин может иметь 0, 1
или 2 поддерева, и существует различие между левым и правым
поддеревьями
2.3.1.	Представления
Почти все машинные представления деревьев основаны на свя-
занных распределениях (представления в виде последовательных
распределений для некоторых типов бинарных деревьев будут вве-
дены в разд 63 1 и 7.3 1) Каждый узел состоит из поля INFO
и некоторых полей для указателей Например, представление,
которое будет удобным для изложения разд 2 4, для каждого узла
имеет единственное поле для указателя FATHER, указывающего
на отца данного узла При этом приведенное на рис 2 8 дерево
будет выглядеть так, как показано па рис 2 9 Такое представление
полезно, если необходимо, как в разд 2 4, подниматься по дереву
от потомков к предкам 1акая операция встречается довольно
редко, чаще требуется опуститься по дереву от предков к потомкам
Представление дерева (или леса) с использованием указателей,
ведущих от предков к потомкам, довольно сложно, поскольку
узел, имея не более чем одного отца, может в то же время иметь
произвольно много сыновей Другими словами, при таком пред-
ставлении узлы должны различаться по размеру, что является
определенным неудобством. Один из путей обхода этой трудности
состоит в том, чтобы определить соответствие между деревьями и
бинарными деревьями, поскольку бинарные деревья легко пред-
ставить узлами фиксированного размера Каждый узел в этом слу-
чае имеет три поля LEFT (указатель местоположения корня ле-
вого поддерева), INFO (содержимое узла) и RIGHT (указатель

местоположения корня правого поддерева) Все сказанное выше
проиллюстрировано на рис 2 10
Мы можем представлять деревья как бинарные деревья (исполь-
зуя узлы фиксированного размера), представляя каждый узел
леса в виде узла, состоящего из полей LEFT, INFO и RIGHT При
полями LEFT, INFO и RIGHT
этом поле LEFT предназначается для указания самого левого сына
данного узла, а поле RIGHT —для указания следующего брата
данного узла. Например, лес, показанный на рис 2 11(a), пре-
образуется в бинарное дерево, показанное на рис 2 11(b) Таким
образом, мы используем поле LEFT некоторого узла для указателя
на связанный список сыновей этого узла, этот список связывается
с помощью полей RIGHT Такое представление мы будем называть
естественным соответствием между лесами и бинарными деревьями
Другие представления бинарных деревьев и лесов обсуждаются
в упражнениях 17—20
2.3.2,	Прохождения
Во многих приложениях необходимо пройти лес, заходя в
узлы (т е обрабатывая их) некоторым систематическим образом
Посещение каждого узла может быть связано с простой операцией,
такой, как печать содержимого или со сложной, такой, как вычис
ление функции Единственное, что мы будем предполагать,—
это то, что при посещении узла структура леса не меняется Пред-
ставляются полезными следующие четыре основных способа про-
хождения леса а именно в глубину, снизу вверх, в горизонтальном
порядке и для бинарных деревьев в симметричном порядке

При прохождении в глубину, известном так же, как прохож-
дение в прямом порядке, узлы леса проходятся в соответствии со
следующей рекурсивной процедурой1
1	Посетить корень первого дерева
2	. Пройти в глубину поддеревья первого дерева (если они есть)
3	Пройти в глубину оставшиеся деревья, если они есть.
Например, для леса, показанного на рис 2.11(a), узлы будут про-
L, М, N, О, Р, Q, R, S Название «в глубину» отражает тот факт,
что после посещения некоторого узла мы продолжаем прохождение
в глубь дерева всякий раз, когда это возможно Как мы увидим
в гл 4, 5 и 8, такой порядок особенно полезен в процедурах поиска
Для бинарных деревьев эга процедура упрощается и выглядит
следующим образом
1.	Посетить корень
2.	Пройти в глубину левое поддерево
3.	Пройти в глубину правое поддерево
В этом случае пустое дерево проходится без выпотнения каких-
либо действий Заметим, что прохождение леса в глубину в точ-
ности такое же, как и прохождение в глубину бинарного дерева,
являющегося его представлением Именно этот факт и делает ука
заниое выше соответствие «естественным».
Прохождение снизу вверх, известное так же, как обратный
порядок или концевой порядок, осуществляется согласно следую-
щей рекурсивной процедуре
1 Пройти снизу вверх поддеревья первого дерева, если они есть
2 Посетить корень первого дерева
3. Пройти снизу вверх оставшиеся деревья, если они есть
Название «снизу вверх» связано е- тем, что в момент посещения
произвольного узла все его потомки оказываются уже пройден-
ными Такой порядок прохождения полезен, в частности, потому,
что он позволяет вычислять рекурсивно определенные функции
на лесах (см упр. 22 и 23) При этом порядке прохождения узлы
леса, показанного на рис. 2 11(a), проходятся в следующем порядке
процедура прохождения снизу вверх применительно к бинарным
деревьям имеет следующий вид-
1	Пройти снизу вверх левое поддерево
2	Пройти снизу вверх правое поддерево
3	Посетить корень
Симметричный порядок для бинарных деревьев определяется
рекурсивно следующим образом.
1	Пройти в симметричном порядке левое поддерево.
2	Посетить корень.
3	Пройти в симметричном порядке правое поддерево.
Такой способ прохождения известен также как лексикографический
порядок (причины такого названия станут ясны в гл 6) или внутрен-
ний порядок Заметим, что прохождение леса снизу вверх эквива-
лентно прохождению в симметричном порядке соответствующего
этому лесу (при естественном соответствии) бинарного дерева
Сравнивая рекурсивные процедуры прохождения бинарных
деревьев в глубину, снизу вверх и в симметричном порядке, можно
обнаружить их значительное сходство:
прохождение
в глубину
1	посетить корень
2	леное поддерево
3	правое поддерево
симметричный
порядок
1.	левое поддерево
2.	посетить корень
3.	правое поддерево
прохождение снизу
вверх
1.	левое поддерево
2.	правое поддерево
3	посетить корень
следующие операции
посетить корень посетить узел р
левее поддерево if lEFT(p)=/= X then S <= (LEFT (р), I)
правее поддерево if R IGHT (p) A then S <= (RIGHT (/?), 1)
Так, например, прямая конкретизация алгоритма 2.3 для прохож-
дения бинарного дерева в глубину приводит к алгоритму 2 4(a).
Операции
5<=(Р 2)
I ,S <= (р, 3)
"i if LEFT (p) # \ tl en S <= (LEFT (p), 1)
if RIGHT(p)?=A then S<=(RIGHT(p) 1)
while S' # пусто do \ |f RKjHT <р) = Л then S <= R 1GHT (p)
V if LEFT (p)	\ then S <= I FFT (p)
3 № 780
3 <= (корень, ])
I 5<=(р, 2)
1 if LEFT (p)^Athen 3 <5= (LEFT (p), 1)
। S <= (p, 3)
t=2 ' il LEFT (p)	\
I then 3 <= (R IGHT (p), 1)
2.3.3. Длина путей
В некоторых разделах этой книги деревья используются не
только как способ представления структуры данных, но так же,
как средство для анализа поведения определенных алгоритмов
В этой связи возникает потребность в количественных измерениях
различных характеристик деревьев и, в частности, бинарных
деревьев
Наиботее важные количественные характеристики деревьев
связаны с уровнями узлов Уровень р определяется рекурсивно и
считается равным нулю, если р — корень Т, в противном случае
уровень р определяется как 1 4- уровень (FATHER (/?)). Понятие
уровня дает нам возможность просто определить высоту h(T)
дерева Т:
h (T) max уровня (p).
ft (О) - о
— 1 + max h( T')
тересуют среднее расстояние от корня до узла в исходном дереве
и среднее расстояние от корня до внешних узлов в расширенном
бинарном дереве В расширенном бинарном дереве с п внутренними
узлами всегда существует л-Н внешних узлов (упр 25)
Длина внешних путей Е(Т) расширенного бинарного дерева
Ten внутренними узлами есть сумма уровней всех внешних узлов,
длина внутренних путей ЦТ) есть сумма уровней всех внутренних
узлов.
На рис 2 12(b) длина внешних путей равна 21, а длина внутрен-
них путей равна 9 Эти суммы, поделенные соответственно на число
внешних и число внутренних узлов, дают искомое среднее
Среднее расстояние до внешнего узла =	.
Среднее расстояние до внутреннего узла =
заметим,
Чтобы понять рекурсивную часть определения (2.5), ......
что Т\ и Тт содержат вместе п—1 внутренних узлов и что добавле-
ние внутреннего узла над ними в качестве корня увеличивает уро-
вень каждого из них на единицу Аналогично истолковывается
рекурсивная часть определения (2 6) Мы можем установить связь
между Е(Т) и ЦТ), рассмотрев разность D(T)=E(T)—ЦТ) Ис-
пользуя (2.5) и (2 6), получим
£>(□) = О
откуда следует (упр 26), что для расширенного бинарного дерева
Гел внутренними узлами D{T)=2n Таким образом,
£(Г)=ЛП^2л,	(2 7)
откуда следует, что для определения свойств обеих величин нам
достаточно только изучать или Е (Т) или I (Г)
В последующих главах нас будет особенно интересовать диапа-
зон значений функций £(Г) и У (Г) Например, легко видеть
(упр, 27), что среди всех расширенных деревьев с п внутрен-
ними узлами показанное на рис 2 13 дерево имеет максимальное
значение /(Г). В этом случае
/(?) = £
ElD-i'Hn + S)-
В упр. 18 гл. 3 мы рассмотрим среднее значение У (Г), когда все
возможные расширенные бинарные деревья с п внутренними >з-
лами равновероятны Это среднее оказывается равным ириблизи-
Осгавшаяся часть этого раздела посвящена выводу минималь-
ного значения для /(7). Легче, однако, получить минимальное зна-
чение для Е(Т) и затем воспользоваться соотношением (2 7) Спра-
ведлива
Лемма 2.1. 2» расширенного бинарного дерева с п внутренними
узлами и минимальной длиной внешних путей все внешние узлы
находятся на уровнях / и /+1, где I — некоторое целое число
Такое дерево называется полностью сбалансированным бинарным
деревом с п внутренними узлами
Доказательство Пусть Г — расширенное бинарное дерево с ми
нимальной длиной внешних путей, и пусть L и I будут соответст
венно максимумом и минимумом всех уровней, на которых появ-
ляются внешние узлы, L^l Предположим, что L^l—2 Удалим
два внешних узла, которые являются братьями на уровне/., в ре-
зультате чего их oieu, станет внешним узлом Затем эту пару при-
соединим к внешнему узлу на уровне /, который в результате та-
кой операции станет внутренним Описанная процедура пока-
зана на рис 2 14 Такая модификация дерева сохраняет число
внешних и внутренних узлов, но уменьшает длину внешних путей
па L—(/+1), поскольку L>/+2, это число положительное. Это
про1иворечит предположению о минимальности длины внешних
путей дерева Т
Лемма 2.2. Если llt I........ ln+I — уровни п4-1 внешних узлов
в расширенном бинарном дереве с п внутренними узлами, то
2 2-', =1.
Доказательство предла1ается провести читателю в качестве
упражнения 28
Теперь мы готовы вычислить минимальную длину внешних
путей расширенного бинарного дерева с п внутренними и п+1
внешними узлами Используя лемму 2 1, предположим, что на
уровне / будет k, а на уровне /-Ч будет н+1— k внешних узлов.
уровне I) Из леммы 2 2 следует, что
и отсюда
(2 8)
Поскольку k^l, то 22+1>п+1, а поскольку &<«+!, то 2^п+1,
/- Llg^ + DJ-
(2 9)
Объединение (2 8) и (2 9) дает
Л?_ 2L U(n+j)
и, следовательно, минимальная длина внешних путей равна
+ (? + W^-l-*) = (»+ П L'g^+n J +
(2 Ю)
Таким образом, мы доказали следующую теорему
Теорема 2.1. Минимальная длина внешних путей расширенного
бинарного дерева с п внутренними узлами равна
(f!+l)lg(rt+l)^(n + l)(2-()-2^)
где e=lg(«+l)—LIg(«+l)J, о<9<!
Нетрудно получить аналогичную формулу для расширенных
/-арных деревьев с п внутренними узлами В этом случае аналог
соотношения (2 7) будет иметь вид
Е(7')-(/-1)7(7') Ч п
и минимальная длина внешних путей равна
[я(/- 1R 1] 1- +Ф +1 п, I- Llog,[(<- 1)»+ 1]J
Мы можем применить формулу (2.11) к задаче о фальшивой
монете из гл 1, взяв 1 = 3 В этом случае мы находим, что минимум
длины внешних путей расширенного тернарного дерева с п внутрен-
ними узлами (и, следовательно, с 2п + 1 внешними узлами, см.
упр 25) есть
где 0<0<1, 6=log, (2я-|-1)—[_logs(2n+')J Таким образом, ми
нимально возможное среднее расстояние от корня до внешнего
log, (2„+ 1) + 4 (3-20-3>-!)
Поскольку любое решение задачи о фальшивой монете с п моне-
тами соответствует расширенному тернарному дереву (тернарному
ключаем, что никакое решение не может использовать меньше чем
logs(2n + l) взвешиваний в среднем и что это среднее достижимо,
если и только если 0=0, т с если и только если 2« + 1 является
степенью тройки. Это доказывает теорему 1 2
2.4. МНОЖЕСТВА И МУЛЬТИМНОЖЕСТВА
S={s1, з2, sn},

Здесь вес s, различны и /дг — кратность элемента st
мощность S равна
В этом случае
Наиболее общими операциями иа множествах и мультимножествах
являются операции объединения и пересечения Для множеств эти
операции мы будем обозначать U н Г), а для мультимножеств |±| и
соответственно
Последовательное и связанное представление последователь-
ностей (разд. 2 2) можно использовать для множеств и мульти-
множеств очевидным способом. Индуцируя искусственный порядок
элементов множества или используя собственный порядок, если он
существует, мы можем рассматривать множество как последова-
тельность Аналогично как последовательность можно рассматри-
вать и мультимножество, или, для того чтобы сэкономить место,
его можно рассматривать как последовательность пар, каждая из
которых состоит из элемента и его кратности Методы хеширова-
ния из 1л 6 можно использовать для представления множеств,
в которых нет никакого естественного порядка
Как и для последовательностей, наилучший метод представле-
ния множеств или мультимножеств существенно зависит от опе-
раций, которые мы собираемся выполнять над ними Предположим,
например, что мы имеем дело с непересекающимися подмножест-
вами множества S—{sl( sa, , sn) и что над ними необходимо вы-
полнять две следующие операции объединение двух .множеств и
отыскание подмножества, содержащего данное s, Таким образом,
в любой момент времени мы имеем разбиение S на непустые непере
секающиеся подмножества В оставшейся части этого раздела будет
рассмотрено представление множества, которое позволяет весьма
эффективно реализовывать операции объединения и отыскания
С целью идентификации считаем, что каждое из непсресекаю-
щихся подмножеств множества S имеет щия Имя — это просто
один из элементов подмножества или иначе — представитель под-
множества В дальнейшем, когда мы будем ссылаться на имя под-
множества, мы будем под этим подразумевать его представителя
Рассмотрим, например, множество
разбитое на четыре нспересскающихся подмножества
<1,6,®,8,И} (®| (®,4,5) |9@}	(2 12)
В каждом из подмножеств обведенный кружочком элсмещ является
его именем Если нам нужно найти подмножество, в котором со-
держится восьмерка, искомым ответом будет 7, т е имя подмно-
жества, содержащего восьмерку Если нам нужно взять объедине-
ние подмножеств с именами 2 и 10, мы получим разбиение мно-
жества S следующего вида
<1,6,®, 8, 11} (@,4,5} (@}и{9, @}
Именем множества {@}и\9л@| может быть или 2, или 10.
Мы предполагаем, что вначале имеется разбиение множества
S={si, s2,	, s„) на п подмножеств, каждое из которых состоит из
одного элемента'
(©1 (©) ... (©}
(2 13)
и имя каждого из них есть просто этот единственный элемент Это
разбиение преобразуется путем применения операций объединения
вперемешку с операциями отыскания Такая, кажущаяся на пер
вый взгляд надуманной, задача чрезвычайно полезна в определен-
ных комбинаторных алгоритмах, пример ее полезности мы увидим
в «жадном» алгоритме разд. 8 2 1
Для реализации операций объединения и отыскания мы будем
задавать процедуры UNlON{x, у) и FlND{x) соответственно Про-
цедура UNION (х, у) по именам двух различных подмножеств х и у
образует новое подмножество, содержащее все элементы множеств
х и у Процедура FIND (%) выдает имя множества, содержащего х.
Например, если мы хотим множество, содержащее а, объединить
с множеством, содержащим Ь, мы должны выполнить следующую
последоватетьносш операторов
х-—FlND(c)
у* FIND (6)
Предположим, что мы имеем и операций объединения, переме-
шанных с / операциями отыскания, и что мы начинаем с множества
S —{sj, $2, , , sn}, разбиюго на подмножества, состоящие из одного
элемента (см. (2 13)) Мы хотим иметь такую структуру данных для
представления непересекающихся подмножеств множества S, чтобы
последовательность операций можно было производить эффективно
Структура данных, которую мы будем использовать, является
представлением в виде леса с указателями отца, как показано на
рис 2.9 Каждый элемент 5, множества будет узлом леса, а отцом
его будет другой элемент из того же подмножества, что и ©. Если
элемент пе имеет отца (т е является корнем), то он будет именем
своего подмножества В соответствии с этим разбиение 2 12 может
быть представлено так, как показано на рис 2 15
При таком представлении операция FIND(x) состоит в передо
дах ле указателям отцов от х до корня (т е имени) ею подмно
жества Операция UNlON(x, у) состоит в связывании вместе не-
которым образом деревьев, имеющих корни х и у Например, такую
После и операций объединения наибольшее из возможных под
множеств, получающихся в результате разбиения S, будет содер-
жать «+1 эдементов Далее, поскольку каждое объединение умень-
насколько эффективно можно выполнить последовательность из
О 0 0-0
t
начинается внизу цепи из п-М элементов множества, то ясно, что
Время, требуемое на операции отыскания, будет пропорционально
/•(«+!) Очевидно, оно не может быть больше, чем константа, ум-
ноженная на f-(uH-l) Действуя более умно, мы можем сущест-
венно уменьшить эту опенку
Для большей ясности рассмотрим более подробно наихудший
случай Если операция UNION(x, у) удерживает деревья в лесу
«сбалансированными» путем назначения корня большего подмно
жества отцом корня меньшего подмножества, то мы немного прок-
рываем в памяти, поскольку каждый узел леса должен содержать
информацию о мощности находящегося под ним поддерева, но зато
можно доказать следующую лемму
Лемма 2.3. Пусть s? — произвольный элемент множества S.
Обозначим через r(sz) ранг элемента т е высоту поддерева
с корнем Sf, и через d(sf)—число узлов в этом поддереве Если
в операции объединения используется балансировка, rod(s£)^2'ls<'
для каждого sf £ S
Доказательство Доказательство будем проводить индукцией
по и, т е числу выполненных операций объединения Для п=0
лемма, очевидно, справедлива, поскольку каждый элемент $,£5
является корнем дерева, состоящего из единственного узла, и та-
ким образом, мы имеем г (s;) = 0, d(S()=l, предположим, что лемма
верна для u=k и посмотрим, что может получиться на (/г-И)-й
операции объединения UNION(x, у) По предположению индук-
ции перед этой последней операцией объединения мы имеем d(x)^
'^2Г‘Х> и 4/(р)>2л Без нарушения общности можно считать
d{x)~^d(у) Тогда операция UKIONfx, у) вынужтает х стать от-
цом у, и после объединения ранг х будет равным тпах[г(х), г (</)+11
После объединения мы также будем иметь d {x)^2d{y)^2r '^fI
Следовательно, и до последней операции и после нее, имеем d(x)>
Из леммы 2 3 следует, что после и операций объединения для
каждого элемента s$ € S выполняется неравенство
а это в свою очередь означает, что на / операций отыскания будет
требоваться количество времени не более чем константа, умножен
нал на / 1g (« +1) Поскольку fczu, общее время на объединение и
отыскание будет также не больше, чем константа, умноженная
на / lg(u+i) Легко видеть, что полное бинарное дерево с и+1
узлами может быть получено путем объединений, т е существует
пример, в котором время отыскания достигает верхней границы
Мы можем повысить эффективность операций отыскания, ис-
пользуя операцию сжатий пути. После операции F!ND(x) х и все
Например, если мы выполним операцию	па лесе, показан-
кания.
Операция объединения с балансировкой приведена в алгорит-
ме 2 7, а операция отыскания со сжатием пути — в алгоритме 2 8.
В каждом из этих алгоритмов мы предполагаем, что элемент s;
множества представлен узлом леса в ячейке Ц, причем узел состоит
из трех полей: ELT (/;)=$*, FATHER (/,-) —это ячейка узла, соот
ветствующего отиу s,, и SIZE (/<) — это d(st), число элементов в под-
дереве с корнем s(
SIZE (
FATHER (lx)
SIZE (ly) <— S
Для анализа эффективности одновременного использования ба-
лансировки и сжатия пути введем две важные функции Опреде-
лим
и функцию Ь, которая на самом деле обратна функции 1g*;
п	(11	2	3	4	5
ig* п	0 1	2	3	3	4
16 17	65536 65537	2И,>'’
4 5.5	6	.6
п 0 1 2 3 4	5
Ъ(п) 0 1 2 4 16 65536 l'*™
следуем по пути от х до наивысшего предка у соответствующею
объединению, которое выполняется перед FlND(x) в первоначаль-
ной последовательности операций. Таким образом, задача сводится
к случаю, когда выполняется последовательность из п операций
объединения, за которыми следует f частичных операции отыскания.
Пусть F — лес, полученный в результате применения операций
объединения, и пусть для любого элемента st$S величина г(зг)
будет его рангом в F Подчеркнем, что величина r(s,) определена
и фиксирована относительно она не изменяется даже в случае,
когда лес будет изменяться из за выполнения частичных операций
отыскания Заметим, что если перед операцией частичного отыс-
кания х является отцом у и х'=£х — отец у после выполнения этой
операции, то г(г)<у(х') Следовательно, даже после изменения
леса F ранги вдоль любого пути F, проходимого при операции час-
тичного отыскания, всегда будут строго возрастать
Разобьем элементы s g S на lg*(w-|-l) f-1 групп Go, Gs, ...
. •Gtg’iu + i) следующим образом.
Из такого разбиения следует, что Gc есть множество всех элементов
с рангом 0 (т е множество узлов исхода), G,— множество всех
элементов с рангом 1, G2 — множество всех элементов с рангами 2
или 3, G3— множество всех элементов g рангами 4, 5, ... 15,
G, — множество всех элементов с рангами 16, 17...65535	и т д
Мы будем использовать это разбиение элементов s, g S для разбие-
ния связей, ведущих от сыновей к отцам в f операциях частичною
отыскания
Время, требуемое для выполнения / операций отыскания, оче
видно, пропорционально числу связей, ведущих от сыновей к отцам
и встречающихся при выполнении / операций отыскания Разобьем
эти связи на классы
L= (связи, ведущие от сыновей к отцам и являющиеся послед-
ними на пути некоторого частичною отыскания}-,
D = {связи, ведущие от сыновей к отцам, не являющиеся послед-
ними на пути частичного отыскания и такие, что отец и сын
находятся в различных группах Gz};
и тля &=0, 1, ..., Ig* (u+1)
Ек связи, ведущие от сыновей к отцам, не являющиеся послед-
ними на пути частичного отыскания и такие, что отец и сын
Очевидно, что каждый п\ть частичного отыскания содержит
точно одну постеднюю связь и, следовательно,
1А1=/	(2 14)
Поскольку существует не более чем 1g* (и+ 1) + ! групп G;, каждый
путь частичного отыскания содержит не более чем lg*(u->-l) свя
вей идущих от элемента одной группы к элементу другой Таким
образом,
ЮК/ lg*(u^I)
Если мы сможем доказать, что для некоторой константы С
(2.16)
то ie\i самым мы докажем теорему, поскольку
так как мы предположили, что t пропорционально п Из этого ре-
зультата, а также из (2.14) и (2 15) следует, что общее число связей,
имеющихся в / процедурах частичного отыскания и равное 1Л +
-,-\D| -|-S|£fe|, не превосходит константы, умноженной на f lg*(u—1)
Чтобы доказать (2,16), отметим, что для любого элемента х из
б/, каждая связь, проходимая в некоторой процедуре частичного
отыскания (за исключением последней связи в этой процедуре)
и ведущая от х к его отцу в Gh, дает элемен1у х нового отца более
высокого ранга Поскольку в 6^. существует не более 6(^—1)—blk)
различных рангов, то для любого элемента из Gh может быть не
более чем b(k-\-V)—b(k) таких связей, встречающихся в процедурах
частичного отыскания. Таким образом, для каждого из IGJ эле-
ментов 6k и Ek может быть не более b (£—1)—b (k) цепочек Заметим,
что по лемме 2 3 существует не более и/27 элементов ранга г, по-
скольку каждый элемент ранга г есть корень поддерева, содержа
щего по крайней мере 2Г элементов Поэтому
£ V
и, следовательно,
2п'
,2ц
Сравнивая эту теорему с предыдущим результатом, находим,
что если число операций объединения и число операций отыскания,
выполняемых на {sb s2, . ., s^}, пропорционально п, то общее время,
требуемое для этих операций, пропорционально
если не используется ни балансировка, ни сжатие пути,
если используется балансировка и не используется
сжатие,
если используется балансировка и сжатие
2.5. КОММЕНТАРИИ И ССЫЛКИ
.Материал, представленный в разд 2 1, 2.2 и 2 3, является ос-
новой не только для комбинаторных алгоритмов, но и вообще для
программирования Содержание элих разделов не является исследо-
ванием всех представляющих интерес и важных проблем; наша
задача состояла в том, чтобы только установить определенную тер-
МИНОЛО1ИЮ и изложить основные результаты, необходимые для
последующих 1лав Заинтересованному в более подробном изло-
жении читателю рекомендуется обратиться к книге
Knuth D E. The Art of Computer Programming, Voh> 1 and 2,
Addison-Wesley, Reading, Mass., 1968 and 1969 [Имеется пере-
вод Кнут Д Искусство npoiраммирования для ЭВМ, т 1
(1967). т 2 (1977).—М • Мир ]
о списках стеках, очередях и деревьях
Алгоритмы объединения и отыскания и их анализ имеют инте-
ресную историю Проблема вначале возникла в связи с обработкой
предложений EQUIVALENCE в ФОРТРАНе, непосредственное
представление их в виде леса (без балансировки и сжатия пути)
приведено в работе
Galler В А , Ficher М J An Improved Equivalence Algorithm,
Сотт ACM, 7 (1964), 301—303
В статье
Fischer М. J Efficiency of Equivalence Algorithms, in Complexity
of Computer Computations, Miller R. E and Thatcher J W
(Eds), Plenum Piess, New York, 1972,
Hopcroft J E ,
Comput, 2
Ullman J D Set-Merging Algorithms, SIAM J.
(1973), 294—303,
Чтобы понять окончатетьпые результаты, касающиеся про-
блемы объедипеиия/отыскания, необходимо ввести некоторые по-
нятия Пусти функция A (i, ]) определена на парах целых неотри-
цательных чисел I, I следующим образом:
Эта функция растет с огромной скоростью, например,
Л (3, 4)=-23
65536
дв-'ек.
(2.17)
Пусть
65537
двоек .
Более того, Тарьян показал, что существует последовательность
\ао А С. С On the Average Behavior of Set Merging Algorithms
(extended abstract), Proceedings of Seventh Annual ACM Sym-
posium on Theory of Computing (1976), 192—195.
2 6. УПРАЖНЕНИЯ

Докажите, что любое положительное целое число может быть единственным об-
разом представлено как сумма чисел Фибоначчи

что любое целое V из области 0<Л <П?=1ш, имеет единственное представление
(rj, г2, ,гп) в котором Л?=г, (тос1 т;) и Осг, <т, для 1<1<л Постройте алго-
9' Трехдиагональной называется матрица Л= (а(у), в которой аг,— 0, если

0(7 должен быть простой функцией i j и адреса ячейки для ап

чисел вида меньших п, где а и Ь —- взаимно простые числа приближенно
lx. I M'liKnr.v .тлтщттм для кпишюшшпя цикличспдио списка
пулевые. Построите связанное представление для разреженной матрицы в которое
входят только ненулевые элементы Постройте алгоритм дтя копирования такой
14. Пусть х и у — ячейки первых элементов двух связанных списков Какое
procedure MYSTERY (х у)
ii х = Л then MYSTERY <—у
(/ <— get-cell
(NFO (/) <— 1КГО(х)
LINK (/) <— MYSTERY (1 INK (»), y)
MYSTERY I

15 Дек — это линеипыи список, в котором псе включения и исключения
производятся на обоих концах списка. Опишите последовательное и связанное
оритет Включения производятся в конец очереди, а исключения производятся
в любом месте очереди, поскольку исключаемым элемент — это всегда элемент
УЗЕЛ BDEFCGJKlLHAOPfrRQ S М
СТЕПЕНЬ 00 0 030002024002 0 103
порядках
является связью RIGHT) От обычных связей нити отличаются путем присоети
2 6.

(а)	Какой смысл иьеют такие нити в бинарном дереве сопоставленном про-
извольному дереву при естественном соответствии?
(Ь)	Опишите очень простой алгоритм прохождения прошитого дерева в сим
метричном порядке
(с)	Опишите простой алгоритм отыскания последующего узла в прошитом
дереве при прохождении в глубину
21	Какие из порядков прохождения дерева подходят для построения алго-
ритма копирования дерева? Постройте такой алгоритм
22	. Нумерация Штралера узлов бинарного дерева определяется следующим
образом. Пустое дерево имеет номер Штралера 0. Если бинарное дерево Т имеет
поддеревья 7\ и Тг номер Штратера S(T) для него определяется следующим
образом:
o(/	\ S(T)21 в Противном случае
Постройте алгоритм вычислеииг SCT) щя бинарного депева Т, основанный та
23	Арифметические выражения с операциями -ф,	*, / могут очевидным
образом быть представлены расширенными бинарными деревьями, если в каче-
стве операторов взять внутренние узлы, а операндами считать листья. Например
выражение (А+ВУС—Е соответствуют следующему дереву;	’
85

представленного с помощью естественного соответствия бинарным деревом
имеется (t—•])«+! внешних узлов
!>(□)= О
узлами
расширенного бинарного дерева ел внутренними узлами достигается на дереве,
Глава 3. Подсчет и оценивание
Вся область комбинаторных алгоритмов насыщена задачами,
которые требуют подсчета или оценивания числа элементов в ко-
нечном множестве или перечисления без повторений всех этих
элементов в некотором специальном порядке Следовательно, стан-
дартные процедуры подсчета и оценивания являются необходимым
инструментом для каждого, кто имеет дело с комбинаторными алго-
ритмами При подсчете и перечислении наиболее широкое приме-
нение имеет процедура поиска с возвращением (и ее варианты),
поскольку она предъявляет меньше всего требований к исследуе-
мому множеству, более подробно мы обсудим эту процедуру
в разд 4 1 В этой гтаве будут рассмотрены процедуры подсчета,
которые применимы, когда исследуемое множество (или семейство
множеств) имеет хорошую структуру При использовании такой
структуры эти процедуры часто позволяют применять аналитиче-
ские методы в противоположность вычислительному подходу поиска
с возвращением
Существуют два вида задач подсчета В более простом случае
задается конкретное множество и требуется определить точно число
элементов в нем Техника исчерпывающего поиска, описанная
в гл. 4, и теория перечисления Пока, изложенная в разд 3 4, имеют
дело с таким классом задач Более общим, однако, является случаи,
когда имеется семейство множеств, заданное некоторым парамет-
ром, и нас интересует мощность множеств как функция параметра
В этом случае редко требуются точные значения Чаще бывает до-
статочной оценка порядка, и иногда требуется только оценка ско-
рости роста функции Например, если известно, что мощность не-
которого подлежащего рассмотрению множества растет по некото
рому параметру экспоненциально, то этого может оказаться доста
точно для того, чтобы вообще отказаться от предложенного подхода
к изучению пробчемы, не занимаясь различными деталями Изло-
женные в разд 3.1, 3 2 и 3 3 процедуры асимптотических разложе-
ний, рекуррентных соотношений и производящих функции приме-
няются ко второму типу проблем.
Поскольку излагаемые в данной главе методы |ребуют достаточно
основные идеи, а заинтересованному в более глубоком изучении
Гл 3 Подсчет и оценивание
читателю рекомендуем обратиться к специальной литературе (см
разд. 3 5) К счастью, основные идеи этих методов подсчета, как мы
вам со сложной структурой, где могут потребоваться глубокие ма-
тематические знания.
3.1. АСИМПТОТИКИ
Асимптотики—это искусство оценивания и сравнения скорос-
тей роста функций Vlbi юворим, что при х->со функция (Цхг)/х
«ведет себя как t» или «возрастает с такой же скоростью как х»,
и при х-»-0 «ведет себя как Р'х» Мы говорим также, что «log х при
х—»-оо и любом е>0 растет медленнее, чем хе и что при п->-оо 2 log «
растет не быстрее, чем п log п» Такие неточные, но интуитивно яс-
ные утверждения полезны при сравнении функций так же, как от-
ношения <, ^ и = при сравнении чисел В этом разделе будет
показано, как высказанные выше утверждения формулируются
более корректно Определим три основных асимптотических соот-
ношения
Определение. /(x)~g(x) при х—*-x(i, если и только если
В этом случае мы будем говорить, что функция /(х) асимптотически
равна функции g(x), или что ) (х) растет с такой же скоростью,
как и g(x)
Определение. f(*)=o(.g(x)) при х->х0, если и только если
Мы будем говорить, что при х->х0/(х) растет медленнее, чем g(x),
или что /(х) «есть о-малое» от g(x)
Определение, /(г)—O(g(x)) при х—>х0, если и только если су-
ществует константа с, такая, что
В этом случае мы говорим, что f(x) растет не быстрее, чем g(x), или
что при х->х«/(х) «есть о-большое» от g(x).
Мы не будем записывать условие х->-Х|), когда значение х0 оче-
видно, поскольку пас главным образом будут интересовать скорости
роста для больших значений независимой переменной, мы всюду
(если это специально не оговорено) в этой книге предполагаем х0 = оо
Соотношение ?(x)=g(x)-‘-o(/i(x)) означает, что /(х)—g(x)^=
=о(й(х)) Аналогично f(xj=g(x) -О (к (х)) означает, 4rof(x)—g(x)^=
~O(h.(x)) Выражения О( ) и о( ) будут использоваться также
и в неравенствах Например, неравенство
х I о(х)^2х при V-*ce
означает, что дтя любой функции /(х), такой, что /(х)=о(х), при
х->ос имеет место соотношение x+f{х)г^.2х для всех достаточно
больших значений х
гЬ=> H>fj)’1-7T"(7)=I+’(I1
Приведем теперь некоторые полезные асимптотические ра-
венства Внимательно их изучая, читатель может проверить свое
понимание предыдущих определений
Полином асимптотически равен своему старшему члену
2	а^' ^0 (xft)	при ,	(3 1)
	г' -= о (tfr+1)	при -	(3 2)
		при ;	и	(3 3)
Суммы степеней целых чисел удовлетворяют соотношениям
Отсюда, в частное! и, имеем
У I* у При II —г СЮ,
я 1
2	Hft + 1-|-O(nft + 1) при П.—’-'Я
и для любого целого fe^O; (3.5)
2	=	+ при п~^оо и для любого	(3.6)
Заметим, что (3.4) и (3 5) содержат в точности одну и ту же инфор
манию, а (3 6) является несколько более сильным утверждением,
чем (3 4) и (3 5) Соотношение
z2fft —	1 + ул* + О при п —юс для любого k 1 (3.7)
еще более сильное, поскольку оно содержит второй член асимпто-
тического разложения ^2 1>< при п->-<х>
Для того чтобы продемонстрировать принципы, используемые
прн получении асимптотического разложения заданной функции,
на этом примере стоит остановиться более подробно Равенство (3 4)
утверждает, что ^2 £* растет как nft+1/(fe-J-l) Прй п.->оо. Предполо-
жим, что мы хотим получить больше информации о разности между
этими двумя функциями (непосредственно из определения можно
получить лишь, что эта разность есть o(n* + 1), что представлено
равенством (3 5)) Рассмотрим разность
” I
2 1* — I---с «А Ь1 при п -> co
и зададимся вопросом, как быстро она растет Естественно пред-
положить, что порядок ее роста равен п" Индукцией по k можно
показать (упр 2), что
2	— уn^ + Ofn^-1) при л-^оо.
Аналогичные рассуждения можно провести относительно разности
между функциями У i" и	... пт д , получая на каждом
шаге одно слагаемое асимптотического ряда для 2 г*«
Вообще
является асимптотическим рчдом для f (х) ити асимптотическим
разложением /(х) при х-*-Го, обозначаемым
2) для каждого п
Асимптотический ряд не обязательно должен схотшься На-
пример рассмотрим ряд

который является асимптотическим разложением функции

(см. упр. 4) и который не сходится ни для каких значении х Разли-
чие между сходящимися и асимптотическими рядами состоят в том,
что с точки зрения сходимости мы имеем дело с поведением час
тичных сумм sn для фиксированного значения х и /w-оо, в то время
как с точки зрения асимптотики мы имеем дело с поведением час-
тичных сумм sn для каждого фиксированного значения п и х-^хц
Расходящийся асимптотический ряд /(x)~2c/gj(x) при х—*-х0
обычно можно использовать для хорошей аппроксимации f(x)
при условии, что независимая переменная х находится досоточно
близко к х„ и что окончание суммирования выбрано корректно.
Типичной является ситуация, когда для любою фиксированного
значения х члены ряда вначале убывают, а затем неограниченно
растут Бели суммирование продолжить достаточно далеко до того
места, где члены ряда начинают возрастать, значения частичных
сумм становятся все более отличающимися oi значений функции
f(x) Хорошим местом остановки суммирования является или пер
вое значение i, для которого Ctgt(x) меньше, чем допустимая ошибка,
или значение i, для которого c,g,(x) является минимальным, а
именно то I, которое меньше Так для функции
f W = е~‘
1 I 1 I___2 I fl — П 1 1 OR
10^100^1000^ 10000
а именно, сравнение сумм с интегралами, которые можно явно вы-
числить Известно, что если ){х)— монотонно возрастающая, ин-
тегрируемая функция, то ^f(x)dx, как показано на рис 3 1, огра
ничен снизу и сверху соответственно нижней и верхней суммами:

При х,=г+1 получим
и таким образом
п+1	п	л+1
J f (x)dx — /(л + 1) + /(1)<21/(ЧС J f(x)dx.
можно взять /(x)=in х, так что In х dx=x In х—х н
(п4 1) In («+ 1)—п — In («4-1)	2 'п (л-- 1) ln(n-i- 1) — п.
В более слабой форме это можно переписать так
2 In k = (п 4- 1) in (п + 1) — п 4-0 (logп).	(3,8)
Далее, разделив левые и правые части равенства (3 8) на In 2,
Slg* = (n-l)lg(n+D— 42 + 0<1°S'1>	(39>
Заметим, что константа поглощается «о-большим» Аналогичным
образом (упр. 5) находим
£б1пб=^Ц-К|п(п + 1)--!4гг+о('11о£'!) (З-Ю)
и, разделив левую и правую части на In 2, преобразуем (3.10)
к следующему виду
SHog4_fc±^lg(n+l)-4t^ + O(nlo8I1)	(3.11)
Используя в качестве нижних и верхних оценок более точные
аппроксимации f(x)dx, мы можем уточнить соотношение (3 8)
и вывести хорошо известную формулу Стирлинга для факториалов
л1~|/2лп ппе~п при п —* <х>	(3.12)
Наконец, эта техника позволяет определить скорость роста
гармонических чисел
S-
(3 13)
Соотношение (3 13) можно уточнить
(3.14)
где 7«0,577 называется постоянной Эйлера

3 2. РЕКУРРЕНТНЫЕ СООТНОШЕНИЯ
Понятие рекуррентных соотношений проиллющрируем на клас-
сической проблеме, поставленной л изученной около 1200 года
Леонардо из Пизы, известным как Фибоначчи. Удивительная важ-
ность чисел Фибоначчи для анализа комбинаторных алгоритмов
делает этот пример весьма подходящим
Фибоначчи поставил свою проблему в форме рассказа о ско-
рости роста популяции кроликов при следующих предположениях
Все начинается с одной пары кроликов Каждая пара кроликов
становится фертильной через месяц, после чего каждая пара рож-
дает новую пару кроликов каждый месяц Кролики никсида не
умирают и их воспроизводство никогда не прекращается
Пусть Fn — число пар кроликов в популяции по прошествии п
месяцев, и пусть эта популяция состоит из Уп пар приплода и Оп
«старых» пар, т е r„=Nn+On. Таким образом, в очередном ме-
сяце произойдут следующие события
дичится на чисто родившихся в момент
времени п
Nn¥i^On	Каждая старая пара в момент времени п
производит пару приптода в момент вре-
мени (и-]-1)
В последующий месяц эта картина повторяется.
Объединяя эти равенства, мы получим следующее рекуррентное
соотношение:

Выбор начальных условий для последовательности чисел Фибо-
наччи не важен; существенные свойства этой последовательности
определяются рекуррентным соотношением Мы будем предпола-
3.2.1. Линейные рекуррентные соотношения
с постоянными коэффициентами
Последовательность Фибоначчи является частным случаем одно-
родных линейных рекуррентных соотношений с постоянными коэф-
фициентами:
(3.16,
где коэффициенты не зависят от п и хг, х2, .xh считаются задан
ными Существует общий метод решения (т е. отыскания хп как функ-
ции п) линейных рекуррентных соотношений с постоянными коэф-
фициентами. Этот общий метод мы будем сначала использовать для
последовательности Фибоначчи, а затем обсудим общий случай
Ищем решение в виде
с постоянными сиг. Подставляя эго значение в рекуррентное со-
отношение Фибоначчи, получим

Это означает, что Fn=crn является решением, если либо с—0,
либо г=0 (и отсюда Fn =0 для всех и), а также (и это более интерес-
ный случай) если г2—г—1—0 Тогда и константа с произвольна
г = у (1 + |/5) или ,'Ц() —КЮ
Число у(1 + )/5)»1,618 известно как зоютое сечение, поскольку
с древних времен считалось, что треугольник со сторонами 1 и
-у(1 1 J/5) имеет наиболее приятные пропорции
Сумма двух решений однородного линейного рекуррентного
соотношения, очевидно, также является решением, и можно на
самом деле показать, что общее решение последовательности Фи-
боначчи имеет вид
(3 17)
где константы с и с' определяются начальными условиями Поло-
жив Гл=0, Fi=l, мы получим следующую систему линейных урав-
нений
решение которой дает
(3 18)
Для всех начальных условий, при которых последователь-
ности, удовлетворяющие соотношению Фибоначчи, растут при-
мерно как	j . поскольку вклад члена ед 1 ? J очень
мал (и в абсолютном, и в относительном смысле), так как
|4 (1 -/5)| < 1 < 4<1 +J/5).
Таким образом, для начальных условий Fo=O, А\ = ] числа Фибо-
наччи асимптотически растут как
Изложим теперь без доказательства, как только что описанная
процедура применяется к установлению асимптотического поведе-
ния решений общих рекуррентных линейных соотношений с по-
стоянными коэффициентами Мы начнем с однородных соотноше-
ний, а затем обсудим неоднородный случай, когда к правой части
добавляется постоянное слагаемое. Подстановка хп=гп приводит
нас к алгебраическому уравнению
k корней которого даю1 решения вида хп=Г;' для i = ], 2,	, k
Если все эги корни различны, то k решении образуют базис прост-
ранства всех решений: они независимы (т с никакое решение rf
не может быть получено в виде линейной комбинации остальных)
и покрывают все пространство (т е все остальные решения урав-
нения (3 16) обладают том свойством, что каждое из них может
быть представлено в виде линейной комбинации этих решений)
Таким образом, для случая различных корней общее решение ре-
куррентного соотношения (3 16) имеет вид
Если нас интересует только асимптотическое поведение последо-
вательности лт, л'2,	, то достаточно рассмотреть лишь члены
С/г", у которых rt имеет максимальное абсолютное значение среди
тех членов, у которых с,#=0
Начальные условия, при которых некоторые коэффициенты
всех возможных начальных условий), и в том же самом смысле
рекуррентные соотношения, у которых корни имеют равные по
абсолютной величине значения, являются исключительными в мно-
жестве всех рекуррентных соотношений. Поэтому наиболее частым
и заслуживающим внимания является случай, когда один корень
доминирует по абсолютной величине, т е
97
В этой ситуации асимптотическое поведение хп имеет вид
и эта формула часто дает хорошую аппроксимацию даже для не
очень больших значений п. Когда |rj<l, г=2, 3, .... k, абсолют-
ная ошибка этой аппроксимации, т. е величина
стремится к нулю при п-*-оо Если же для некоторого t=2, 3, ..k,
|rj>l, то с ростом п стремится к нулю только относительная ошибка
аппроксимации хп~С1Г%, т е величина (х„—С1Г?)/хга.
Если некоторые из корней rt, rs......rk совпадают, например
/J=r2=ra> то решения	не являются независимыми и не
образуют базиса в пространстве всех решений Можно показать,
что в этом случае общее решение имеет вид
Обобщение этой формулы для соотношений с произвольным числом
кратных корней очевидно
Неоднородное линейное рекуррентное соотношение имеет вид
Хп^арсп^+а^п 2+ . .+аьхп_й+&	(3 19)
Его общее решение представляет собой сумму частного решения
соотношения (3 19) и общего решения соответствующего ему одно-
родного соотношения
которое находится описанным выше способом. Это приводит к ре-
шению с k параметрами, которые используются для того, чтобы
удовлетворить k начальным условиям уравнения (3.19).
Частное решение (3.19) находится следующим образом Если
2 йг#=1, то существует частное решение хп—с, где с определяется
из уравнения
Если = l и 2 то существует частное решение хл=сп,
где с определяется из уравнения
cn^a-Ldri—i)+a2c(/i—2)+ , .+akc(n~k)-\-b,
В общем случае частное решение вида ха=спт для некоторого
m<.k можно найти, подставляя это выражение в соотношение (3 19)
и сравнивая коэффициенты Используя рекуррентные соотношения,
нужно соблюдать некоторую осторожность. В комбинаторных при-
ложениях обычно необходим только анализ свойств решения, а не
вычисление последовательности по заданным рекуррентным соот-
ношениям С этой точки зрения достаточно предыдущего анализа
Если необходимо вычислить последовательность численно в cooi
ветствии с рекуррентным соотношением и если это вычисление не
может быть выполнено в целых числах (или с какой угодно точ-
ностью), численные расчеты следует проводить с осторожностью,
чтобы при вычислениях избежать ловушек (эффект неустойчивости),
которые могут сделать бесполезным любое вычисление, основанное
па методе, кажущемся простым Обсуждение проблемы устойчи
вости, которая возникает при численных вычислениях линейных
рекуррентных соотношений, можно найти в любой книге по чис-
ленным решениям дифференциальных уравнений
3.2.2. Общие рекуррентные соотношения
Рекуррентные соотношения, отличные ог линейных соотноше-
ний с постоянными коэффициентами не имеют общего метода ре-
шения, сравнимого с тем, который был рассмотрен в предыдущем
разделе Общие рекуррентные соотношения решаются (или их ре-
шения аппроксимируются или оцениваются) методом проб и оши-
бок Если метод проб и ошибок основан на общих идеях, изложен-
ных в этом разделе, он по меньшей мере дает хорошую оценку
асимптотического поведения решения большинства рекуррентных
соотношений
Сокращение числа членов в соотношении. Рассмотрим рекуррент-
ное соотношение
3 2. Рекуррентные соотношения
где хп задается как начальное условие. Это линейное рекуррентное
соотношение, но оно не принадлежит к классу, рассмотренному
в предыдущем разделе. Его, однако, можно преобразовать в линей-
ное рекуррентное соотношение с постоянными коэффициентами,
ести заметить, что

xn+I=zxn
Решение последнего уравнения, как сразу можно определить,
имеет вид
Аналогичные наблюдения часто позволяют упростить рекуррент-
ные соотношения, которые включают взвешенные суммы (с постоян-
ными весами) всех предшествующих членов, например, соотношение
приводится к виду
хп+1=(ап+1—а„)Ч-(1+М хп
Таким образом, решение можно выписать в замкнутой форме в виде
суммы произведений, но если коэффициенты ап+1—ап и ] +ЬЛ не
имеют простой структуры, то мы в результате ничего не выиграем
Определение скорости роста решения. При анализе трудоемко-
сти алгоритма типа декомпозиции (см разд. 1 4) иногда встречается
рекхррентное соотношение вида
(3 20)
где х(| — заданное начальное условие Посмотрим сначала, как
возникает это соотношение, а затем изложим способ его решения.
Представим себе класс проблем Рп, п=1, 2, .., размерность,
или сложность которых измеряется целым параметром п Пусть
хп означает среднее количество работы, требуемое для решения
проблемы Рп Например, предположим, что Рп требует построения
бинарного дерева над последовательностью из п элементов е2,
.., еп следующим образом Сначала последовательность просмат*
ривается, скажем слева направо, и некоторый, определенный эле-
мент выбирается в качестве «корня дерева» Количество работы,
требуемой для этого, пропорционально п, что учитывается слагае-
мым ап в уравнении (3.20), При такой интерпретации разумно счи-
)ать й>0 Затем выполняется некоторая работа над элементом ец,
и мы обозначим ее через Ъ.
Элемент ek разбивает последовательность е, е2, ... еп на ле-
вую часть Bi, еа, .. , е^~1 а правую часть е^,	, еп (Одна или обе
они могут быть пустыми ) Таким образом, мы разложили проблему
Рп на две подпроблемы Р^ и Pn-h Для решения Рп должны быть
решены и Pa-i, и Р„-ь, причем на них затрачивается соответственно
количество работы и хп k Отсюда при фиксированном k полу-
чим
Предположим, что в результате просмотра последовательности лю-
бой из элементов еа, ег может быть выбран в качестве корня
с одинаковой вероятностью, или, что эквивалентно, k может
принимать любое значение от 1 до п с вероятностью 1/п Тогда
среднее количество работы хп, требуемое для решения проблемы
Рп, удовлетворяет соотношению
+ •X'n-fe)
которое легко приводится к соотношению (3.20)
Изложим теперь систематическую процедуру проб и ошибок,
с помощью которой можно определить асимптотическое поведение
решения рекуррентного соотношения (3 20) Мы начнем с попытки
найти простейшее возможное решение — константу Подстановка
в (3 20) х„=с приводит к соотношению
с= 2с+ап +Ь,
откуда следует, что хп=с не является решением Однако эта по-
пытка говорит нам намного больше, поскольку из нашего предпо-
ложения а>0 следует, что правая часть соотношения больше, чем
левая. Другими словами, попытка положить хп=с приводит к не-
равенству
4S Ч + ап+Ь.
Таким образом, для равенства левых и правых частей хп должно
быть большим, чем Xi, хг, , хп-г, т е как функция п решение
рекуррентного соотношения должно расти быстрее, чем хп=с.
Поэтому на следующем шаге испытаем линейную функцию
t=c/i Подставив ее в рекуррентное соотношение, получим

В этом соотношении имеется несколько различий между левой и
правой частями, но на данном этапе необходимо сосредоточить
внимание только на главных членах, т е на сп в левой и (с+а) п
в правой частях Несовпадение главных членов свидетельствует
о юм, что линейная функция не может быть решением, более того,
тот факт, что для достаточно больших п правая часть больше, чем
левая, говорит нам, что линейная функция также растет слишком
медленно для того, чтобы быть решением нашего соотношения
В третьей попытке выберем функцию, которая растет быстрее,
чем линейная Положив хп—сп2, получим
спг
При достаточно больших значениях п правая часть будет меньше
левой, а это в свою очередь означает, что квадратичная функция
растет слишком быстро для того, чтобы быть решением
Имея нижнюю и верхнюю границы скорости роста решения, на
следующем шаге выберем функцию, у которой скорость роста ле-
жит между линейной и квадратичной Степень п, скажем xn=nJ/«,
будет опять же приводить к несовпадению главных членов На са-
мом деле для любого е>0 х„=п1+€ растет слишком быстро Это
обстоятельство наводит на мысль положить xn—cn\gn, что при-
водит к соотношению
cnlgn — ‘^	klgk + an+b.
Используя грубый вариант равенства (3,11), получим
У, ft IgA = у л3 lgn + o(na iog n),
(3 21)
и наше предполагаемое равенство примет вид
Таким образом, хп—сп 1g п удовлетворяет первому необходимому
требованию, а именно требованию совпадения главных членов
в обеих частях Мы можем теперь заключить, что для некоторой
неизвестной пока константы с решение имеет следующее асимпто-
102
Гл. 3. Подсчет и оценивание
тическое поведение
хп~сп 1g п.
Выписанное выше равенство не позволяет определить с, поскольку
мы потеряли слишком много информации при переходе от (3 11)
к (3 21), собирая все члены, за исключением главного члена — н® 1g п,
в слагаемое o(zz3 log л)
Использование равенства (3 11) в его полном виде для получе-
ния последующего члена в асимптотическом разложении 2А 1g k
позволяет получить дополнительные условия, с помощью которых
можно определить с:
сп. 1g п = 
и отсюда
сп 1g и = сп 1g п + (а —« + О (log п).
Для совпадения линейных членов в обеих частях мы должны
выбрать с так, чтобы

Теперь мы знаем, что решение рекуррентного соотношения (3 20)
имеет следующий вид
хп=а In 4 п 1g п+о(п log п),
для большинства практических целей этой информации достаточно
Дальнейшие члены асимптотического разложения хп можно по-
лечить путем увеличения числа алгебраических манипуляций, по
большого интереса они не представляют.
Рекуррентное соотношение (3.20) мы исследовали главным об
разом для того, чтобы продемонстрировать метод решения соответ-
ствующего класса соотношений. В гл 6 и 7 мы столкнемся с этим
соотношением в различных контекстах, где его решение буде1 ис-
пользоваться для анализа некоторых процедур поиска и сорти-
ровки
Предложенный нами способ отыскания решения не является
строгим. На самом деле требуется установить много больше, чтобы
завершить доказательство того, что In 4 п 1g п при п~-*-оо
Сравнеаие левых и правых частей, приводившее вас к поиску ре-
шений, которые растут медленнее или быстрее текущего прибли-
103
жения, производилось без упоминания некоторых предположений
Главным образом, мы молчаливо воспользовались тем фактом, что
решение является монотонно возрастающей функцией от п Отсутст-
вие математической строгости можно оправдать тем, что мы пытались
только подобрать решение довольно сложного соотношения. Все
годится для достижения такой цели, и единственным разумным
критерием при отборе средств является успех, т. е. получение пра-
вильного решения Все это — лишь первая половина процесса
решения если мы уверены, что угадали правильное решение, то
остается доказать, что это так Эта вторая половина является пре-
имущественно чисто математической — трудоемкой, но ясной Ис-
следование соотношения (3 20) с этой точки зрения мы продолжим
в упр 11 (см также упр 12)
3.3. ПРОИЗВОДЯЩИЕ ФУНКЦИИ
Как показано в предыдущем разделе, «подсчет» часто означает
вычисление или определение свойств некоторой последователь-
ности чисел Xi, x-i, , где xk соответствует проблеме Р-Р. из некото-
рой последовательности проблем Pt, Рг, .. Структура этих
проблем индуцирует отношение между элементами соответствую-
щей последовательности, и обработка таких последовательностей
является важным аспектом многих задач, связанных с подсчетом.
В этом разделе мы предлагаем полезный инструмент для работы
с последовательностями Идея состоит в том, чтобы каждой числовой
последовательности сопоставить функцию действительного или
комплексного переменного таким образом, чтобы обычные операции
над последовательностями соответствовали простым операциям над
соответствующими функциями. Аналитические методы опериро-
вания с функциями действительного или комплексного перемен-
ного часто оказываются проще и сильнее, чем комбинаторные ме-
тоды непосредственного оперирования с последовательностями;
поэтому такой подход часто приводит к изящным результатам,
в то время как прямое решение повлекло бы за собой громоздкие
вычисления
Имеется много возможных способов отображения последова-
тельностей в функции, но наиболее общим в комбинаторике яв-
ляется сопоставление последовательности ха, хц х2, функции
действительной переменной s X называется производящей функ-
цией последовательности ха, xlt хг, . В табл 3 1 содержатся
примеры, которые читатель может проверить, разлагая произво-
дящую функцию в ряд Тейлора в окрестности з—0 (упр 14)
104
Поскольку последовательность может быть восстановлена по
своей производящей функции, любые сведения о функции дают неко-
торую информацию о последовательности Однако основная цен-
ность производящих функций состоит в том, что многие обычные
операции нал последовательностями соответствий! простым ал-
гебраическим или аналитическим операциям над функциями.
В этом разделе мы рассмотрим наиболее важные из операций Че-
рез Xfe, z/й, zJ(, fe=0, 1, 2,	, мы будем обозначать последователь-
ности, а соответствующие им производящие функции — через
Линейные операции
Если а и b — константы, то последовательность zk~axh+byk
имеет производящую функцию Z (s)*=aX (s)+bY (s).
Сдвиг начала
Последовательнос!ь, определяемая следующим образом
имеет производящую функцию У(з)=Х($)5' Аналогично, последо-
вательность
имеет производящую функцию
В качестве примера использования линейных операций и сдвига
начала рассмотрим оценку для суммы
которая появляется при анализе алгоритмов в разд. 5.2 2. Пусть
и для каждого фиксированного значения t будем рассматривать
х(] как последовательность, задаваемую индексом /, с производя-
щей функцией
Нас интересует последовательность у}, определенная следующим
образом.

105
Таблица 3.1
Некоторые распространенные производящие функции
Последовательность ** fr = U 1 2	фук^и™’
(1) х4=1	—L—
(2) хА=й + 1	1 (1-ь)2
(3) хо=О	‘"(га)
	
(4) хо = 0	In (1 -4-S)
хЛ = у, если k нечетно	
Xh = —, если h > 0 четно	
(5)	г произвольное	(1-НХ
В = ф	es
(7) tft = —, г произвольное	ers
Производящая функция этой последовательности получается путем
применения линейных операций
и»)-	(s)=E(i+s)"--(i+s)”E	.
Последнее выражение легко оценивается как сумма членов геомет-
рической прогрессии, и таким образом мы находим
y(s) ,Jt + s)n +
Как (14-s)*/s, так и (I-i-s)'1-,/s являются простыми сдвигами начала
для функций (l-Hs)" и	соответственно, и мы заключаем,
Частичные суммы
Если yh — У *<> ^=0, 1, 2, . , то
Это следует из правил линейных операций и сдвига начала (упр 15)
Дополнительные частичные суммы
Если существует X(l) = ^£ xh и если уь = xt, fe=0, 1,2,.
Изменение масштаба
Последовательность y^-kx^, 6=0, 1,2,... имеет производящую
функцию У (s)=sX'($). а последовательность	—произ-
водящую функцию
Эти последние два правила в сочетании с правилами линейных
операции и сдвига начала позволяют нам вычислить У (s) из X (s)
для любого преобразования последовательностей
где R(k) — произвольная рациональная функция k
Изменение масштаба также полезно при оценке сумм Рассмот-
рим сумму
которую можно переписать следующим образом.
Обозначив
9-8.
Производящие функции
107
мы получим и» таким образом,
Y (s)=^sZ'(s).
Поскольку Xh^tyb, мы также имеем
X (s)=sy'(s)=sZ'(s)+saZ'(s).
Но из габл. 3.1 мы знаем, что Z (s)=(1 откуда
X(s) — s(n — l)(l+s)»-2 + ss(n — 1)(п—2)(1 у s)"-3.
Очевидно

что означает
*2 (Л— k) (»—£)(„—=	— !)2”-’ — ("—D*
Это и аналогичные суммирования появляются при анализе алго-
ритма в разд 4 1 7.
Свертка
Последовательность	А=0, I, имеет производя-
щую функцию Z(s)=X (s) Y(з).
Это правило, вероятно, является наиболее важным доводом
в пользу применения производящих функций, поскольку свертка
является распространенным явлением в комбинаторных задачах
и непосредственный подсчет приводит к громоздким суммам. В про-
тивоположность этому соответствующая операция над производя-
щими функциями является простой операцией умножения.
Чтобы проиллюстрировать использование производящих функ-
ций, мы обсудим теперь заслуживающую внимания задачу подсчета
числа бинарных деревьев с п узлами. Формула свертки играет
основную роль при решении этой задачи
Напомним (см гл 2), что бинарное дерево Тп с п узлами при
rt—0 пусто Если п>0, то бинарным деревом является тройка
(Т (, г, Tn-t-t), где г — выделенный узел, называемый корнем дере-
ва 1\, Ti — бинарное дерево с I узлами для некоторою/=0, 1,
, п—1, называемое левым поддеревом дерева Тп, и Tn-i-, —
бинарное дерево с п—I—1 узлами, называемое правым поддере-
вом Тп
Каково же число хп различных бинарных деревьев Тп с п уз-
лами5 Из определения следует, что ха—1, очевидно также, что
*1=1, х2—2, х3=5 Из определения Тп выводится следующее ре-
куррентное соотношение
(3 23)
Это рекуррентное соотношение довольно трудно решить методами,
изложенными в разд. 3 2 Можно легко установить, что хп растет
быстрее, чем полином от п, но что экспоненциальная функция есп
растет слишком быстро для того, чтобы быть решением.
Заметим, однако, что правая часть соотношения (3 23) представ-
ляет собой свертку, и в связи с этим рассмотрим производящую
функцию
Используя тот факт, что свертка последовательностей соответствует
умножению производящих функций, мы пишем
Поскольку замена п на А+1 в (3 23) приводит к соотношению
- £
мы можем упростить правую часть и получить уравнение для про
изводящей функции
Учитывая, что г0=1, получим
(3 24)
Разложение бинома К1—4з дает
(1 — 4s)i/3 =
4s)ft
I 4	, 2 \	2 1	,,	2 \	1 ) \	'21,.,.,
- 1 -y4s+ х2- < (4s)1--------2-----jp----L (4s)>+.
Коэффициенты при s*, A^l, этого ряда можно записать в следую-
щем виде'
109
так что
(1-4S)1'’-! -Ё |(2L1)S*	(3'25>
Поскольку результат подстановки (3 25) в (3.24) должен быть ря-
дом по неотрицательным степеням ь, решение (l/2s)(H-prl—4$)
в (3.24) является посторонним Подставляя (3 25) в решение
получим
Отсюда получаем, что число бинарных деревьев е п узлами равно
(3.26)
для п:
Как правило, невозможно найти простое компактное выраже-
ние для нетривиальной комбинаторной последовательности Ком-
пактные выражения элегантны и иногда полезны, но они не всегда
дают ответ в наиболее удобной форме. Например, чтобы определить
скорость роста хп как функции п, перепишем (3.26) следующим
образом
и, используя формулу Стирлинга (3 12), получим
(3 27)
Было бы весьма трудно получить эту формулу методом проб и оши
бок, используя прямо соотношение (3,23).
*3.4. ПОДСЧЕТ КЛАССОВ ЭКВИВАЛЕНТНОСТИ:
ТЕОРЕМА ПОЙА
Первая трудность при подсчете элементов в множестве часто
состоит в том, чтобы четко определив объекты подсчета Рассмот-
рим, например, задачу из разд. 3.3 о числе бинарных деревьев
с п узлами. Если мы не будем отличать «левое» от «правого», то
следующие четыре картинки, которые при данной ранее формули-
ровке изображали различные деревья, теперь будут представлять
одно и то же дерево:
вует графов с п вершинами и е ребрами, обычно подразумевается,
что следующие две картинки:
3.4,1. Пример: раскраска узлов бинарного дерева
Рассмотрим полное бинарное дерево с семью узлами и всевоз-
можные различные варианты раскраски его узлов белым или чер-
ным цветом в предположении, что мы не отличаем «левое» от «пра-
вого» На следующем примере приведены различные представле-
ния одной п той же раскраски дерева:

В противоположность этому каждая из следующих картинок пред-
ставляет собой отличную от других раскраску дерева
XX /Сх Х\ /Сх
Чтобы уяснить, какое же множество объектов подлежит пере-
счету, определим множество S представлений. Каждой картинке
такого типа, как показанные выше, поставим в соответствие функ-
цию из области D семи узлов в область R двух цветов
D - {1,2,3,4,5,6,7},
4	5 6	7
Заметим, что S состоит из 2’= 128 элементов, называемых представ-
лениями Например, приведенные выше представления f3 и /4
соответствуют функциям
/<(l) = f>(3) = fI(5)^f,(7) = o,
А (2) -А (4) =-/3(6) = .
f, (1) - f. (3) = /. (5) ’ f, (6) - О. f. (2) - Л (4) = f. (7) = .
На множестве S всех функции, отображающих D в R, определим
отношение эквивалентности Y и каждый класс эквивалентности
отождествим с одним из подлежащих пересчету объектов (раскра-
сок дерева).
Интуитивно ясно, что ft и /4 должны принадлежать одному клас-
су эквивалентности относительно у Почему это так5 В области D
существует подстановка л, которая переставляет двух сыновей
узла 3, а именно узлы 6 и 7, и две функции /3 и /4 отличаются только
«по модулю л», г е	или, что эквивалентно, функция /4
получается применением сначала подстановки л к О и последую-
щим отображением D на R посредством функции f3. Поскольку мы
не отличаем «левое» от «правого» и л только переставляет левою и
правого сыновей узла 3, две функции такого же типа, как /8 и /4,
должны быть эквивалентны
112
<1)(23)(46)(57)
4	5674	57 б
(1)(2)(3)(4)(5)(67)
проблемы относится к области интуиции и здравого смысла, по-
скольку мы только интуитивно и до некоторой степени неопреде-
ленно сформулировали выражение «левое и правое не должны раз-
личаться».
Группа G подстановок, относительно которых раскраски де-
рева инвариантны, порождается тремя подстановками, показан-
ными на рис 3 2, эти подстановки переставляют поддеревья с уз-
лами 1, 2 и 3 соответственно Компактным способом представления
подстановок является циклическая запись При таком представ-
лении множитель вида е2, ек) называется циклом и озна-
чает, что подстановка отображает et на ₽2, е2 на е3,	, на ек
Всевозможные произведения подстановок пь и Л; образуют
группу G из восьми подстановок, показанных в табл. 3.2. В этой
таблице столбец под названием «цикловой индекс» сопоставляет
каждой подстановке некоторое выражение, которое описывает ее
циклическую структуру. Эти выражения содержат неизвестные
Перестановка	apegcS^e
	(1)(2)(3)(4)(5)(6)(7)	x] (1Х23Х46У57)	x.x?
	(1Д2)(3)(45)(6)(7)	x?x2 (1)(2)(3)(4)(5)(67)	x,x2
it-ХП} ~ ,r3jr2	(1){2)(3)(45)(67)	x,x2
Trjfr2 = TTjITi	(1)(23)(4657)	x,x2x4
art 77 3 — 77 *771	(П(23)(4756)	x,x2x4
77,772773	(1)(23)(47)(56)	x,xl
Xi, хг, , при этом показатель при xk означает число циклов длины k
в подстановке Так, цикловой индекс соответствующий под-
становке л,, означает, что состоит из одного цикла длины ] и
трех циклов длины 2 Цикловой индекс подстановки л нс сохраняет
никакой информации о том, какому циклу л принадлежит тот или
иной элемент множества D
Теперь мы ютову определить центральное понятие, исполь-
зуемое в теореме Пойа Если дана группа подстановок G, то цик-
ловым индексом Рв группы G называется полином относительно
неизвестных хг, хг, , который представляет среднее арифмети-
ческое цикловых индексов, взятых по всем подстановкам л из
группы G В нашем примере
Цикловой индекс группы подстановок—это функция, которая
описывает некоторые свойства группы так же, как производящая
функция описывает свойства последовательности Однако, в то
время как производящая функция описывает соответствующую ей
последовательность однозначно, цикловой индекс не определяет
единственную i руппу подстановок. Различные и не изоморфные
группы подстановок могут иметь один и тот же цикловой индекс.
Однако, как будет видно из теоремы Пойа, цикловой индекс содер-
жит достаточно информации для подсчета классов эквивалентности
отношения у, индуцированного группой G Число классов эквива-
лентности на множестве S функций, отображающих D в R, при
отношении эквивалентности у (индуцированном группой подста-
новок G на множестве D) получается сопоставлением значения
(мощности множества R) каждому неизвестному' х,- в цикловом
индексе Ро группы G. В нашем примере \R 1 = 2, и отсюда получим
Читателю предлагается проверить путем систематического конст-
руирования, что в нашем примере число различных раскрасок де-
рева действительно равно 42
3.4.2. Теорема Пойа и лемма Бернсайда
В этом разделе мы с более формальных позиций рассмотрим спе-
циальный случай теоремы Пойа, проиллюстрированный на примере
из разд 3 4 2, и набросаем его доказательство Это доказательство
включает результат, известный как лемма Бернсайда, который
сам по себе представляет интересную технику подсчета. Хотя тео-
рему Пойа легче использовать механически, лемма Бернсайда более
ясно раскрывает математическую суть, на которой основана идея
подсчета классов эквивалентности.
Если дано конечное множество D, называемое областью опреде-
ления, и конечное множество R, называемое областью значений,
а также группа подстановок G на множестве D, то определим
2 Отношение эквивалентности у на 3, индуцируемое G fyg
для f и g из S, если и только если существует подстановка л в G,
такая, что f=gn
3 Цикловой индекс Р0(Л1, х2, .. , xlDi) группы G (т. е, полином
относительно неизвестных х}, х2, .... XiO,).
• • X|D|
где /Цл) — число циклов длины k в подстановке л
Теорема (Пойа). Число классов эквивалентности относительно
у равно Ро(|7?|, ]А?|,	, |/?|), где |/?| — мощность множества R
множестве S. Определим на S отношение эквивалентности у, инду-
цируемое группой G' fyg, если и только если в G' существует под-
становка л, такая, что f—n(g) Определим I (л) как число элемен-
тов множества S, инвариантных относительно подстановки л (f из
S инвариантен относительно подстановки п, если и только если
Лемма (Бернсайд). Число классов эквивалентности относитель-
но у равно
I о 1
115
Мы выбрали обозначения таким образом, чтобы объекты, ис-
пользуемые в теореме Пойа и лемме Бернсайда, имели одно и то же
наименование Заметим, что группы подстановок б и б' действуют
на различных множествах G действует на D, a G' — на S
В качестве примера используем лемму Бернсайда для подсчета
числа раскрасок дерева в задаче из разд 3 4 1 Вспомним, что
D = {1, 2, 3, 4, 5, 6, 7} — множество вершин, /?={о, •} — мно-
жество красок и S — множество функций Группа подоановок
6	7 4	5
nt, рассматриваемая как подстановка на множестве S раскрасок
дерева, просто отображает одну раскраску на другую, при этом
переставляются цвета вершин 2 и 3, 4 и 6, 5 и 7 Таким образом,
раскраска инвариантна относительно если и только если сов-
116
ных раскрасок дерева равно

теории групп Мы приведем только основные шаги доказательства,
подробности доказательства оставляем в качестве упражнении 23.
(а)	В декартовом произведении G’xS рассмотрим все «инва-
рианты», т. е все пары (л, f), такие, что nf—f, и выразим их число
двумя способами
2 /
где J (f) означает число подстановок, относительно которых инва-
риантна функция Д а /(л), как и прежде, число элементов S, ин-
вариантных относительно подстановки л. Это равенство является
частным случаем общего тождества 2Za^=S2au, которое можно
установить, указывая инварианты путем расстановки меток в мат-
рице на рис. 3.3.
117
(Ь)	Если f и g эквивалентны, то J </)=J (g), т е каждый столбец
внутри класса эквивалентности в матрице на рис 3 3 имеет одно
и то же число инвариантов
(с)	Если / и g эквивалентны, то число подстановок, которые
переводят / в g, равно J (f), т е числу подстановок, которые ос-
тавляют / инвариантным.
(d)	Внутри каждого класса эквивалентности в матрице на рис 3 3
существует точно |G'| инвариантов
(е)	Из п (d) следует немедленно утверждение леммы Бернсайда
2 / (тс) - У, J (?) — | G' (-(чисто классов эквивалентности)
С^юрмулированный в начале эюго раздела специальный слу-
чай теоремы Пойа легко сводится к лемме Бернсайда, поскольку
можно почленно приравнять суммы, выражающие число классов
эквивалентности в этих двух теоремах Если вместо каждого из
неизвестных х, подставить значение |/?|, теорема Пойа примет
следу ющий вид
Число классов
эквивалентности = j-y: V,1 R
а лемма Бернсайда будет выглядеть следующим образом.
Число классов
эквивалентности =-j~q-	/ (л).
Теперь замечаем, что
1) если то G и G’ изоморфны,
2) функция / D-t-R инвариантна относительно подстановки л
(л рассматривается как подстановка, заданная па S), если и только
если / есть константа на каждом цикле подстановки л (л рассмат-
ривается как подстановка на D).
Отсюда следует, что
а это в свою очередь устанавливает эквивалентность двух теорем.
Изложенное выше краткое введение представляет наиболее важ-
ные идеи теории перечисления Пойа Эта теория применима в ос-
новном к проблемам, обладающим большой симметрией, выражен-
ной через богатую группу подстановок. Более общая формулировка
3.5. КОММЕНТАРИИ И ССЫЛКИ
Краткое изложение методов асимптотического разложения функ-
ции можно найти во многих учебниках по прикладной математике.
Более обширное изложение этого материала можно найти в следую-
щих трех книгах
De Bruijn N G , Asymptotic Methods in Analysis, North-Holland
Publishing Co , Amsterdam, 1961 [Имеется перевод Де
Брейн Н. Г Асимптотические методы в анализе — М ИЛ,
1961.]
Dingle R В , Asymptotic Expansions Their Derivation and Inter-
pretation, Academic Press, New York, 1971,
Copson E T , Asymptotic Expansions, Cambridge University Press,
New York, 1971 [Имеется перевод Копсон Э Т Асимптоти-
ческие разложения — М' Мир, 1966]
Кроме комбинаторики, рекуррентные соотношения появляются
естественным образом во многих разделах математики. Любая книга
из таких книг
Hildebrand F. В Finite-Difference Equations and Simulations,
Prentice-Hall, Englewood Cliffs, N Y , 1968
Рекуррентные соотношения играют важную роль также при пост-
роении случайных чисел По этому поводу см гл. 3 книги
Knuth D Е The Art of Computer Programming, Vol 2 (Seminume-
rical Algorithms), Addison-Wesley, Reading, Mass., 1969.
[Имеется перевод Кнут Д. Искусство программирования для
ЭВМ, т 2 Получисленные алгоритмы — М.: Мир, 1977.]
Производящие функции являются также стандартным аппаратом
в теории вероятностей и статистике. С.м , например, гл 11 кнши
119

Feller W An Introduction to Probability Theory and Its Applica-
tions, Vol 1 (3rd edition), Wiley, New York, 1958. [Имеется
перевод Феллер В Введение в теорию вероятностей и ее при-
ложения, т 1, изд 2 — М Мир, 1967 1
Теорема Пойа была опубликована в работе «Комбинаторное оп-
ределение числа групп, графов и химических соединений»'
Polya G. Kombinatorische Anzahlbestimmungen fur Gruppen,
Graphen and chemische Verbindungen, Acta Math., 68 (1937),
145—254
Некоторые аспекты этой теории перечисления были предвосхищены
в работе
Redfield J. Н. The Theory of Group-Reduced Distributions, Am J
Math , 49 (1927), 433—455
Во многих учебниках существуют обзоры по теории перечисле-
ния Пойа. Из них можно рекомендовать1)
De Bruijn N G Polya’s Theory of Counting, Chapter 5 in E F Be-
ckenbach (Ed) Applied Combinatorial Mathematics, Wiley,
New York, 1964. [Имеется перевод Де Брейн Н I Теория
перечисления Пойа, в сб «Прикладная комбинаторная мате-
матика» — М Мир, 1968.1
и гл 5 книги
Liu С. L Introduction to Combinatorial Mathematics, McGraw-
Hill, New York, 1968
3.6. УПРАЖНЕНИЯ
с е'	(£—1)1
-Л-1"
120



и, испотьззя асимптотическое разложение илтс! радов докажите затем что
k In k = ^- In л — -J-0 (n log n)


), когда «


с точным решением Как вы'объясняете различие?
9 Найдите общее решение рекуррентного соотношения
10 Найдите обшее решение рекуррентного соотношения

g(0=4 js^ds+i—L

(b) Покажите что/(/)=2((+2)ln (T—2)—т2 In 3^ (/-г2)+о есть решение
интегрального уравнения

отношением
*	о = О,
*	я = 42-
удовлетворяет неравенству
(d) Докажите, что
*	„ = (1п 4) п In м-1- о (п log л).
+ (х0—Зо |-fr)n-“X0 ) (Указание-, ^из пхп вычтите (п—i и поделите результат

In ni, jg [1g и jg (1g fej
15. Докажите корректность правил композиции для производящих функций,
соответствующих операциям, приведенным в разд 3 I (линейные операции,
16 Пусть случайная величина х принимает значения 0 1,2, .. с вероятно-
производящая функция Пусть у — случайная величина, полученная' путем
сложения п независимых копии случайной величины х и пусть «о. щ_, уг ..
венно Показать что производящая функция Y (s)= равна X (з)" (Оказание
*18. Цель этого примера — определить среднюю длину внутренних путей
(см. разд. 2.3.3) расширенного бинарного дерева (. п внутренними узлами в пред-
положении, что все (пл)/ (п-Н) деревьев равновероятны Пусть хяа — число

путей т. Докажите, что

производящей функции для хпт Используйте эту формулу для вычисления
ии=«!М

(а) Аккуратно определите требуемою группу подстановок.
(с) Решите задачу, используя формулу перечисления Пойа
*21 Конструктор интегральных схем строит чипы с 1G элементами, располо-
к<енныии в виде матрицы размера 4X4'
3.6

Q®(D®
®®®@
® @ @ @
@ @ @ @

180е
Используйте теорему Пойа или лемму Бернсайда Для каждой фигуры точно
23 Заполните пробелы в доказательстве леммы Бернсайда в разд 3.4.2.
Глава 4. Исчерпывающий поиск
Использование ЭВМ для ответа на такие вопросы, как «сколько
существует способов », «перечислите все возможные или
«есть ли способ обычно требует исчерпывающего поиска мно-
жества всех возможных решений Например, не известен метод
отыскания всех простых чисел, меньших 104, который бы не требо-
вал просмотра некоторым образом каждою целого числа .между 1
и 104, или если мы хотим найти все пути прохода через лабиринт,
мы должны исследовать все пути, начинающиеся от входа
В этой главе предлагаются два общих метода организации та-
кого поиска Первый, поиск с возвращением, работает постоянно,
пытаясь расширить частичное решение На каждом шаге поиска,
если расширение текущего частичного решения невозможно, мы
возвращаемся к более короткому частичному решению и пытаемся
снова его продолжить Поиск с возвращением используется в ши-
роком классе задач поиска, включающих грамматический разбор,
игры и составчение расписаний. Второй метод, метод решета, яв-
ляется логическим дополнением к поиску с возвращением, при его
использовании мы пытаемся исключить объекты, не являющиеся
решениями, вместо того, чтобы искать сами решения Методы ре-
шета полезны прежде всего в теоретико-числовых задачах.
Нужно помнить, однако, что поиск с возвращением и метод ре-
шета представляют собой только общие, методы Непосредственное
их применение обычно ведет к алгоритмам, время работы которых
недопустимо велико Современный уровень быстродействия ЭВМ
практически не позволяет производить исчерпывающий поиск
в множестве, состоящем более чем из 10й элементов Поэтому для
того, чтобы эти методы были полезны, к ним нужно относиться как
к схемам, с которыми следует подходить к задаче Схемы должны
быть хорошо приспособлены (часто это требует большей изобрета-
тельности) к конкретной задаче, так чтобы в результате алгоритм
юдился для практического использования
4.1. ПОИСК С ВОЗВРАЩЕНИЕМ
Идею поиска с возвращением (backtrack) легче всего понять
в связи с задачей прохода через лабиринт наша цель — попасть
из некоторого заданного квадрата в другой заданный квадрат путем
125

последовательного перемещения по квадратам. Трудность состоит
в том, что, как показано на рис. 4 1, нас ограничивает существование
преград, запрещающих некоторые перемещения Один из способов
прохода через лабиринт — это двигаться из начального квадрата
в соответ(твии с двумя правилами
1. В каждом квадрате выбирать еще не исследованный путь
2 Если из исследуемого в данный момент квадрата не ведут
неисследованные пути, то нужно вернуться на один квадрат назад
по последнему пройденному пути, по которому вы пришли в данный
квадрат
из тупика В этом и состоит сущность поиска с возвращением: про-
должать расширение исследуемого решения до тех пор, пока это
возможно, и когда решение нельзя расширить, возвращаться по
нему и пытаться сделать другой выбор на самом близком шаге, где
имеется такая возможность.
4.1.1.	Общий алгоритм
В самом общем случае мы полагаем, что решение задачи состоит
из вектора (с1( а2, ..) конечной, но не определенной длины, удов-
летворяющего некоторым ограничениям Каждое af является эле-
ментом конечного линейно упорядоченного множества Аг Таким
образом, при исчерпывающем поиске должны рассматриваться эле-
менты множества АхАх .х<4( для i=0, 1, 2, . . в качестве
возможных решений В качестве исходного частичного решения
126
Гл. 4. Исчерпывающий поиск
обозначим это подмножество через Si В качестве а/ выбираем наи-
меньший элемент множества 5Ъ в результате мы имеем частичное
решение (аД В общем случае различные ограничения, описываю-
щие решения, говорят о том, из какого подмножества S^ множества
еще дальше и выбираем новый элемент йь_2 и т д
Этот процесс удобно описать в терминах процедуры прохожде-
гия дерева в глубину, описанной в разд 2 32 Исследуемое под-
множество множества Л]Х/)2х	х/1, для i=0, 1, 2, представ
ляется как дерево поиска следующим образом Корень дерева (ну
левой уровень) есть пустой вектор Его сыновья суть множество
кандидатов для выбора оь и в общем случае узлы А-го уровня яв
127
все решения, мы хотим получить все такие узлы
Процедура поиска с возвращением для нахождения всех решс
ний формально описывается алгоритмом 4 1 Если нужно найти
только одно решение, то программа заканчивает работу после его
записи, в этом случае останов в конце цикла while означает, что
решений нет Когда процесс останавливается, значение count
есть число исследованных узлов дерева
Для того чтобы увидеть, как этот алгоритм применяется к кон-
кретным задачам, рассмотрим задачу расстановки как можно боль-
шего числа ферзей на шахматной доске размера пХп таким образом,
что ни один ферзь не атакует другого Поскольку ферзь атакует
все поля в своей строке, своем столбце и диагоналях, ясно, что на
шахматной доске можно расставить мактмум п ферзей так, чтобы
ни один из них не атаковал друюго Таким образом, задача сво-
дится к определению возможности расставить п не атакующих друг
друга ферзей и, если есть возможность расстановки, к определе-
нию, сколькими способами это можно сделать
В каждом столбце может находиться в точности один ферзь,
а это означает, что решение можно представить вектором , а»),
в котором а, — номер строки ферзя из столбца с номером i Более
того, в каждой строке может быть в точности один ферзь, и поэтому
если 1=£], то а^й]. Наконец, поскольку ферзи могут атаковать
Друг друга по диагонали, мы должны иметь |а,—а7|=#=|<—/I, если
i^j. Таким образом, для того, чтобы определить, можно ли доба-
128
вить ah к (аь . , Ол-i), мы просто сравниваем с каждым at,

while i < fe and flag do-I then flag'—false
Используя эту процедуру, программу поиска с возвращением
для нахождения всех решений задачи о не атакующих друг друга
ферзях на доске размера пХл ............ _ ------ -----------
образом
можно представить следующим
while k
while sft
do
while sft SZn and
ферзь не может
быть поставлен в
строку $й столбца k
do sfet— sft+l
if k — n then записать
как решение
й + 1
while sk^n and ферзь
не может быть по-
ставлен в строку sft
столбца k
do - s., I 1
[[все решения найдены]]
Заметим, что в процессе приспосабливания общей процедуры
поиска с возвращением к задаче о ферзях мы не вычисляли и не
хранили явно множества Ss В этом случае легче хранить только
наименьшее значение из Sk, т е s*, и следующее значение вычис
лять по мере необходимости. Проверка условия 5^0 соответ
ствует условию s^n, поскольку вычисляемое значение sn+j не
меньше, чем п4-1, то Sn+I всегда пусто
4.1.2.	Усовершенствования
В программе поиска с возвращением для нахождения всех ре
шений задачи о не атакующих Друг друга ферзях на доске размера
лХл мы не пытались исследовать все (п‘) (около 4,4х 10е для /г=8)
129

возможных способов расстановки п ферзей на доске размера пхп
Вместо этого мы заметили, что каждый столбец содержит самое
большее одного ферзя, что дает только пп расстановок (для п = 8
около 1,7х 10!). Более того, как было отмечено, никакие два ферзя
нельзя поставить в одну строку, а поэтому, для того чтобы вектор
(Qi....ап) был решением, он должен быть перестановкой элемен
тов (1, 2,	, п), что дает только п\ (для п = 8 около 4,0х104) воз-
можностей Тот факт, что никакие два ферзя не могут находиться
на одной диагонали, сокращает число возможностей еще больше,
так что для л=8 в лесу остается только 2056 узлов С помощью ряда
наблюдений мы исключили из рассмотрения большое число возмож-
ных расстановок п ферзей на доске размером пХп. Использование
подобного анализа для сокращения процесса поиска называется поис-
ком с ограничениями (или отсечением ветвей в связи с тем, что при
этом удаляются поддеревья из дерева) Например, размещение
ферзя на клетке (1, 2) (первый столбец, вторая строка) дает огра-
ничение: оно запрещает размещение другого ферзя на клетке, ска-
жем, (2, 3)
Процесс ограничений в задаче о ферзях можно продолжить
дальше. Два решения можно считать эквивалентными, если одно
из них переводится в другое с помощью ряда вращений и/или от-
ражений Ясно, что если мы найдем все попарно неэквивалентные
решения, то мы сможем построить все множество решений. Заме-
тим, что ферзь, расположенный в любом углу доски, атакует все
другие угловые поля, поэтому решений, в которых ферзи стоят
более чем в одном угл^, нет Следовательно, любое решение с фер
зем в клетке (1, 1) может быть переведено вращением и/или отраже-
нием в эквивалентное, в котором клетка (1, 1) пуста Таким образом,
мы можем начать с а{=2 и получить, однако, все неэквивалентные
решения. Мы сразу обрываем у дерева большое поддерево.
Другим усовершенствованием является слияние, или склеива-
ние, ветвей. Идея состоит в том, чтобы избежать выполнения дважды
одной и той же работы если два или больше поддеревьев данного
дерева изоморфны, мы хотим исследовать лишь одно из них В за-
даче о ферзях мы можем использовать склеивание, заметив, что
если п/2"|, то найденное решение можно отразить и полу-
чить решение, дтя которого гг/2 . Следовательно, деревья
в лесу, соответствующие, например, случаям <з£=2 и аг—п—1,
изоморфны. В результате, не беспокоясь об исследовании деревьев,
соответствующих случаям dj= Г п/2 +1, aj= п/2 “| — 2, ,а2-п,
мы все же найдем все неэквивалентные решения Кроме того, по-
скольку использование такого склеивания не влияет на ограниче-
ние в клетке (I, 1) (почему5), нам нужно найти решения только для
Г п/2 ] Когда п нечетно и ai~ п/2 “], мы можем ограни
читься случаем а2^. р п/2 ~| —2 в соответствии с тем же самым прин-
ципом (На самом деле, если п нечетно, лучше ограничиться случаем
S Л 780
2^01^ |_ п/2 J Почему?) Экономия, получаемая при этом, не|ри
виальная, в случае размера доски 8x8 лес сводится уже к 801 узлу,
и остающиеся в результате вычисления можно проделать вручную
за несколько часов
В добавление к ограничениям и склеиванию, которые, очевидно,
могут сократить поиск в случае, если ищутся все решения на
полном дереве, существует эвристический метод, который может
оказаться полезным, когда существование решения вызывает сом-
нения или когда вместо всех решений нужно найти только одно
Этот метод, называемый переупорядочениепоиска, можно использовать
несколькими способами Во-первых, если интуиция подсказывает,
что все решения будут иметь некоторый определенный вид, то благо-
разумно строить поиск так, чтобы раньше других исследовать воз-
можные решения именно этого вида Во-вторых, если возможно,
то дерево следует перестроить так, чтобы узлы меньшей степени
(т е имеющие относительно мало сыновей) были бы близки к вер-
шине дерева, например, дерево на рис 4 3(a) предпочтительнее,
чем дерево, показанное на рис 4 3(b) Почему это может оказаться
полезным13 В общем случае, для того чтобы обнаружить, что путь
не может вести к решению, должно быть накоплено несколько огра-
ничений, и обычно это случается на фиксированной глубине де-
рева В результате большее число узлов будет запрещено, если
большая часть ветвлений будет находиться ближе к листьям, чем
к корням Конечно, нужно понимать, что такой вид перестройки
дерева может оказаться бесполезным, если должно быть исследовано
все дерево Более того, даже если не требуется исследовать все
дерево, перестройка может переместить решения не ближе к началу
поиска, а дальше от него
Последнее усовершенствование состоит в использовании метода
декомпозиции, описанного в разд 1.4, т е в разложении задачи
на k подзадач, решении этих подзадач и затем композиции решений
подзадач в решение исходной задачи. В этом случае требования
к объему памяти могут быть очень высокими, поскольку нужно
хранить все решения подзадач, однако, скорость может значи-
тельно возрасти Например, если для решения задачи размера п
требуется время с-2", то использование метода декомпозиции по-
зволит уменьшить время до величины А*с-2"'*+Т, где Т — время,
требуемое для композиции решений подзадач Если число решений
подзадач мало и объединить их нетрудно, то Т будет относительно
малым, и в результате этот метод даст огромную экономию
Важно понимать, что такие попытки усовершенствований нужно
делать не только при анализе задачи перед программированием,
но также и во время работы программы. В задаче о ферзях, напри-
мер, анализ позволяет нам ввести небольшие ограничения уже при
составлении программы, но ограничение, состоящее в том, что
ферзи, стоящие на одной диагонали, бьют друг др} га, можно при-
менять только в процессе появления конфигураций, так как для
этого ограничения известного анализа нет Аналогично, склеива-
ние и перестановку поиска можно применять в некоторых ситуа-
циях во время работы Применение склеивания во время работы
означает возможность распознать одинаковые поддеревья по час-
тичному решению в корне поддерева Использование процедуры
перестройки поиска во время работы означает либо то, что делается
обоснованное предположение о том, что текущее дерево не пред-
ставляет интереса и поэтому его просмотр надо отложить, либо то,
что для частичного решения	aft) остальные компоненты
решения ищутся в некотором динамически определяемом порядке
вместо обычного порядка а^+г, ....
4.1.3.	Оценка сложности выполнения
Типично, что поиск с возвращением приводит к алгоритмам,
экспоненциальным по своим параметрам Это является простым
следствием того, что в предположении, что все решения имеют длину
не более п, исследованию подлежат приблизительно П1А1 узлов
дерева (здесь I4J означает число элементов в 4,) Даже при ши-
роком использовании ограничений и склеивании лучшее, что мы
можем ожидать для I4J—это константа, при этом получаются
деревья примерно с С” узлами для некоторого OI Поскольку
размеры дерева растут так быстро, разумно попытаться определить
возможность осуществления поиска путем оценки числа узлов
в дереве
Аналитическое выражение для оценки удается получить редко,
поскольку трудно предсказать, как взаимодействуют различные
ограничения по мере того, как они появляются при продвиже-
нии в глубь дерева Существует, однако, интересный метод Монте-
Карло оценки размеров дерева Идея состоит в проведении несколь-
ких испытаний, при этом каждое испытание представляет собой
проведение поиска с возвращением со случайно выбранными зна-
132
чениями at Предположим, что мы имеем частичное решение (аи
аг, , а*_1) и что число выборов для обоснованное на том, вво-
дятся ли ограничения или осуществляется склеивание, равно
Xk~ISJ Если хА=#0, то Qk выбирается случайно из S<, и для каж-
дого элемента вероятность быть выбранным равна 1/хь. Если х ),=•(),
то испытание заканчивается. Таким образом, если x^lSJ, toOi S>
выбирается случайно с вероятностью 1/Xi; если xs = IS2l, то при
условии, что а, было выбрано из Si, aa€S2 выбирается случайно
с вероятностью 1/хг и т д Математическое ожидание
в точности равно числу узлов в дереве, отличных от корня, т е
оно равно числу случаев, которые будут исследоваться алгоритмом
поиска с возвращением
Для доказательства этого предположим, что Т — фиксирован-
ное дерево, размеры которого надо оценить На узлах х£ Т опреде-
лим две функции следующим образом
11,	если х—корень Т,
k-p (FATHER (х)), если х не корень Т и
FATHER (х) имеет k
сыновей.
которые проходятся во
время испытания,
в противном случае
Тогда ясно, что
результат испытания — случайная величина

и ее математическое ожидание равно
Е(Х) = £|	2 Р
Но р(х) фиксировано относительно х£Т и поэтому не зависит от
испытания, так что
Е(Х)= 2 />W £('«)
По построению вероятность того, что узел х£Т проходится во
время испытания, равна 1/р(х), т е £(/(х)) = 1//?(х) Таким об-
)33
разом,
£(Х) =	2	1 = число узлов в Т, отличных от корня.
что и требовалось доказать.
Общий алгоритм поиска с возвращением легко преобразуется
применительно к реализации таких испытаний; для этого при
Sfc=0 вместо возвращения мы просто заканчиваем испытание
Алгоритм 4 2 осуществляет N испытаний для аппроксимации числа
узлов в дереве.
Эго вычисление по методу Монте-Карло можно использовать для
оценки эффективности алгоритма поиска с возвращением путем
сравнения его с эталоном, полученным для задачи с меньшей раз-
мерностью Например, при прогоне задачи о ферзях с ограниче-
ниями и склеиванием в соответствии с описанной выше процеду-
рой для отыскания всех решений в случае доски размером 10x10
требуется поиск на дереве с 14 566 узлами В случае 11X11 после
1000 испытаний по методу Монте-Карло опенка числа узлов была
70 806, и поэтому можно ожидать, что вычисления потребуют при-
мерно в 4,9 раза больше времени, чем в случае 10х 10 При прогоне
программы в случае 11x11 оказалось, что фактически дерево
имеет 70 214 узлов и время вычисления в 5,3 раза больше, чем в
случае 10x10.
4.1,4.	Два способа программирования
До сих пор мы представляли алгоритм поиска с возвращением
в виде двух вложенных циклов — внутреннего цикла для расши-
рения решения и внешнего цикла для возвращения. Этот же алгоритм
Можно запрограммировать двумя другими существенно различными
способами' один с использованием языка программированиявысокого
Уровня с рекурсией и другой в использованием языка ассемблера
средствами макрорасширения В последнем случае мы предпола-
гаем, что решениями могут быть только листья дерева.
134
Рекурсивный подход полезен прежде всего для алгоритмов на
графах (см, разд 8.2 2 о поиске в глубину) Общий алгоритм поиска
с возвращением можно представить рекурсивно так, как это еде
дано в алгоритме 4 3 Символ II означает конкатенацию векторов
где ( ) — пустой вектор Заметим, что все возвращения скрыты
в механизме, реализующем рекурсию
BACKTRACK (( ), 1)
procedure BACKTRACK (vector, t)
a£Si do BACKT RACK {lector ]](a), s + 1)
Подход к поиску с возвращением с позиций языка ассемблера
основывается на предположении, что наиболее важным аспектом
программы является ее быстродействие Многие приложения про
цедуры возвращения требуют относительно малой памяти, и поэто
му будет разумным значительно расширить требования к памяти
для того, чтобы существенно уменьшить требуемое время. Одна идея
состоит в применении средств макрорасширения ассемблера для
производства высоко специализированных программ, в которых все
или некоторые циклы не являются вложенными; такой подход устра-
няет определенные логические проверки и уменьшает число команд
для контроля циклов Если все решения имеют длину п, ю это
можно сделать, например, написав макрокоманду (назовем ее
CODE,), тело которой следующее
вычислить St
L[ if Si — 0 then goto Л(_,
at-—элемент в S,
Эта макрокоманда CODEj повторяется для/=1, 2,..., п, порождая
программу вида
CODE,
COD Ег
CODE„
записать (д,,	в качестве решения
goto Ln
Lo Цвсе решения найдены]]
135
Заметим, что такой подход требует, чтобы все решения имели
одну и ту же фиксированную длину Это часто встречающийся слу-
чаи, и преимущество описанного выше подхода очевидно макро-
команду CODE, можно организовать так, что main будут приспособ-
лены для S; Например, в задаче о не атакующих друг друга ферзях
нам нужно было ограничение 2 аг |" /2/2“|, и если п нечетно и
<ji—Г л/2"|. то 1 а2 Г ге/2",—2 Включение этих проверок в
общий алгоритм возвращения, написанный с циклами while, дорого,
так как некоторые проверки нужно осуществлять каждый раз во
внутреннем цикле, даже несмотря на то что они редко что-либо
дают Используя макроподход, команды для проверок можно вклю-
чить в программу только там, где это необходимо Конечно, этот
подход можно использовать и без макросредств, но это неудобно.
Существенно, что для каждого уровня в дереве используются
отдельные программы В задаче о ферзях это позволяет нам, напри-
мер в системе IBM/360, осуществлять почти всю работу в регистрах
вместо (относительно) более медленной памяти Так в случае доски
размером 15х 15 регистры 1—15 можно использовать соответственно
для записи позиций ферзя в столбцах 1—15. Использование этого
метода для случая 15х 15 требует только 25-минутного прогона на
IBM 360/75 (по сравнению с 170 минутами при очевидной програм-
ме), а решение для случая 16х 16 требует 168 минут
Есть другие пути использования макросредств для ускорения
программ поиска с возвращением В задачах о покрытии (таких,
как упражнения 1(h), 1 (k), 1 (1)) можно написать макрокоманду,
которая порождает отдельную часть кода для каждой позиции,
подлежащей покрытию, или для каждой покрывающей фигуры.
Описанный выше макроподход применительно к задаче о ферзях
можно рассматривать так' CODEZ размещает на доске г-го ферзя
Пример использования в поиске с возвращением макрокоманд, не
требующих, чтобы все решения имели одну и ту же длину, описан
в конце следующего раздела
4.1.5.	Пример. Оптимальные коды, сохраняющие
разности
В разд 1 2 мы обсудили коды, сохраняющие разности, и привел»
таблицу максимальных рангов, которые можно получить для раз-
личных длин кодов и порогов. Здесь мы обсудим, как можно вычис-
лить элементы этой таблицы, используя различные методы, рас-
смотренные в предыдущих разделах данной главы В особенности
обратим внимание на ранги оптимальных «-разрядных кодов.
Сохраняющих разности, с порогом 1, эти методы так же хорошо
Применяются и к другим значениям порогов
Для нашей задачи наиболее очевидным методом поиска с воз-
вращением было бы исследование всех 21П возможных подмножеств
136
кодовых слов, аналогичное исследованию всех (J}3) возможных
расстановок п ферзей на доске размера пХл в задаче о ферзях Даже
для п=5 осуществить такой просмотр было бы практически невоз
можно. Вместо этого мы используем некоторые внутренние свойства
симметрии, присущие таким кодам
Назовем два кода изоморфными, если и только если один может
быть получен из другого отрицанием и/или перестановкой столб-
цов Должно быть ясно, что на свойства разностей DP-/ кодов эти
операции не влияют Такое понятие изоморфизма приводит к двум
полезным свойствам симметрии
Свойство симметрии 1. Любой DP /-код с рангом ?+3 изо-
морфен коду, у которого первые Н-3 слов следующие
.00...000
00.. 001
00
t— 2 разрядов
Доказательство. Мы можем считать, что первое кодовое слово
состоит из одних нулей, поскольку ко всем столбцам, в которых
первое кодовое слово имеет единицу, можно применить отрицание
Для I — 1 второе кодовое слово должно состоять из всех нулей и
одной единицы, и мы можем поменять столбцы местами так, чтобы
единица занимала самую правую позицию Далее, мы знаем, что
третье кодовое слово должно иметь две единицы (из сравнения его с
первым и вторым кодовыми словами) и что одна из этих единиц долж-
на занимать самую правую позицию (из сравнения со вторым сло-
вом) Таким образом, мы можем переместить другую единицу в сле-
дующую после самой правой позицию, переставляя столбцы и не
изменяя первые два слова Такое же рассуждение показывает, что
четвертое слово можно привести к виду 00 0111 без изменения
первых слов и поэтому для t — 1 имеет место свойство симметрии
Доказательство продолжается по индукции Предположим, что
свойство симметрии выполняется для t — 1, мы хотим доказать, что
это свойство выполняется для t Поскольку любой DP-i-код есть
описано в свойстве симметрии. Рассмотрим кодовое слово с номером
I + 3 Код является DP-Лкодом, и поэтому мы можем сравнить сло-
во с номером t + 3 с первым и (I + 2) м словами и заключить, что
137
оно должно иметь t + I единиц справа и одну единицу где нибудь
еще. Поэтому одна перестановка превращает его в слово желае-
мой формы без изменения предыдущих слов.
Свойство симметрии 2. Любой DP-Z-код изоморфен коду, в кото-
ром для 1 i < п первая единица в столбце с номером i (считая
справа) встречается раньше первой единицы в столбце с номером
Доказательство Это свойство симметрии очевидно, гак как
мы всегда можем переставить нужные столбцы
Например, коды
ооооооо	0000000
0000001	0000001
0000011	0000011
0000111 И 0000111
1000111	0001Ш
1001111	оонш
1101111	0111111
изоморфны, так как мы можем переставить четыре левых стглбцэ
одного кода, чтобы получить другой код
Применение этих двух свойств симметрии к задачам отыскания
оптимальных DP-1-кодов существенно сокращает дерево поиска
Первое свойство симметрии говорит о том, что мы должны начать
поиск, скажем, с {000000, 000001, 000011, 000111} для п=6 Па
рис. 4.4 продемонстрировано, как используется второе свойство
138
симметрии, пунктирные линии
показывают, какие поддеревья
выбрасываются Эти выбрасыва-
ния появляются прямо у корня,
и поэтому число узлов, удален-
ных из дерева, значительно
Была написана и пропуще-
на программа, использующая
эти два метода сокращения для
случаев п=5 и и=6, в которой
исследовалось 348 я 651 138 уз-
лов соответственно Для п=5
оптимальный найденный код
имел ранг 14, а для п~6 имел
ранг 27 В процессе попыток
(a)
<Ь)
уменьшить размеры поиска так,
чтобы можно было осуществить
решение задачи для п=7, было
исследовано полное дерево для
п=5на наличие других свойств
симметрии Часто встречающая-
ся ситуация в дереве показана
на рис 4 5 После нескольких
проб и ошибок было открыто
свойство симметрии 3
Свойство симметрии 3. Рас-
смотрим дерево поиска для л-раз-
рядного DP-1-кода Предполо-
жим, что узел Р имеет сыно-
вей Sj и S8, таких, что Sj име
ет только одного сына Sn, a S21
является одним из сыновей St,
кроме того, — такое же ко-
довое слово, что и Su. Тогда лю-
бой код в поддереве с корнем
S2i является кодом в поддереве
с корнем Sn.
139
Доказательство Предположим, что для образования DP-1-
кода ниже узла S21 может быть добавлена последовательность
Vi, ^2.	, Vh (см рис 4.5(a)) и предположим, что добавление
V,, Vt, , Vh ниже узла Sn не образует DP 1-кода Кодовые сло-
ва, расположенные выше Sj и 32, одинаковы, таким образом, един-
ственной причиной того, что добавление Va, . , Vh ниже узла
Sn может не образовывать DP-1-код, является то, что одно из V,
слишком близко к S,, т е H(SU < 1. Ясно, что Я(5Ь V,)^=0,
иначе было бы S^V^, и тогда Н(Р, Vi) — I, что противоречит
предположению, что Vs, , Vh можно добавить ниже S21 с
образованием DP-1-кода, V'i = S11=Sai также невозможно Таким
образом, мы должны иметь H(Si, Vj=l и	— За1, но а
этом случае V, также должно быть сыном Si, тем самым противореча
тому, что S, имеет только одного сына Si,
Мы заключаем, что любое расширение кода из узла S21 не длин-
нее, чем некоторое расширение кода из узла Sn Нас интересует
лишь отыскание единственного оптимального кода, что означает, что
в таких случаях мы можем оборвать поддерево с корнем в Sal
Можно ожидать, что свойство симметрии 3 относительно слабое,
но фактически оно уменьшает число узлов в дереве примерно на 60%;
например, при л=5 в дереве осталось только 145 узлов С исполь-
зованием трех свойств симметрии для п=7 было проделано вычисле-
ние по методу Монте-Карло для оценки числа узлов в дереве.
В двух прогонах с 3500 и 10000 испытаниями соответственно число
узлов оценивалось примерно как 2х 1012 Так как программа обра-
батывает узлы со скоростью 6000 узлов в секунду, поиск оптималь-
ного DP 1-кода длины п=7 не осуществим; он потребовал бы более
десяти лет вычислений
В качестве попытки ускорения работы программы были исполь-
зованы макрокоманды для порождения коротких подпрограмм для
каждого из 2" возможных кодовых слов. Например, если W — ко-
довое слово и IV'i, U/3,	— кодовые слова, смежные с W, мак-
рокоманда создаст подпрограмму вида
добавить W в код
if этот код длиннее, чем ранее порож-
денный самый длинный код then
записать его
if ITj можно добавить then call
if можно добавить then call
if 1ГЛ можно добавить then call Wa
удалить W из кода
return
140
4.1.6.	Метод ветвей и границ
Хорошо известный вариант поиска с возвращением, называе-
мый методом ветвей и границ, на самом деле является лишь специ
альным типом поиска с ограничениями Ограничения основывают-
ся на предположении, что каждое решение связано с определенной
стоимостью и что нужно найти оптимальное решение (решение с
наименьшей стоимостью) Для применения метода ветвей и границ
стоимость должна быть четко определена для частичных решений;
кроме того для всех частичных решений (й!, aSl.	и для всех
расширений (а,, а2,..ak) мы должны иметь
cost (Uj, Я2, • • • ’ afc-i) cos^ (at> ai. - • > ak-i ’ as)-
Когда стоимость обладает этим свойством, мы можем отбросить
частичное решение (аъ а2,	at,), если его стоимость больше
или равна стоимости ранее вычисленных решений. Это ограничение
легко включается в общий алгоритм поиска с возвращением, как
видно из алгоритма 4 4В большинстве случаев функция стоимо
сти неотрицательная и даже удовлетворяет более сильному требо-
ванию
где C(oi,) 0 — функция, определенная для всех а>, Это условие,
конечно, слегка упрощает алгоритм 4 4
Задача коммивояжера является типичной задачей оптимизации,
которую можно решить с помощью метода ветвей и границ В этой
задаче коммивояжер должен посетить п городов и возвратиться
141
в исходный пункт, при этом требуется минимизировать общую стои-
мость путешествия Переезжая из города i в город j он терпит убы-
ток Clt Например, если матрица стоимостей равна
2	3	4	5	6	7
1	оо	3	93	13	33	9	57
2	4	со	77	42	21	16	34
3	45	17	оо	36	16	28	25
4	39	90	80	оо	56	7	91
5	28	46	88	33	оо	25	57
6	3	88	18	46	92	со	7
7	44	26	33	27	84	Зр	оо
то стоимость пути 1—2—5—7—3—6—4—1 равна 277, в то время
как стоимость оптимального пути, скажем 1—4—6—7—3—5—2—1,
равна только 1261'
К этой задаче легко применить общий метод ветвей и границ,
получая алгоритм, который возвращается всякий раз, когда стои-
мость текущего частичного решения равняется или превосходит
стоимость лучшего решения, найденного до сих пор Эта проверка
устраняет просмотр некоторых частей дерева, но на самом деле она
достаточно слабая, допускающая глубокое проникновение внутрь
дерева до того, как ветви обрываются Более того, произвольный
фиксированный порядок городов является причиной того, что много
времени теряется на исследование путей, которые начинаются с
маршрута 1—2, если города 1 и 2 отстоят далеко друг от друга. Эчо
является иллюстрацией тому, как техника перестройки дерева
применяется к методу ветвей и границ, почти оптимальные решения
следует находить на раннем этапе поиска
В задаче коммивояжера относительно успешной техникой пере-
стройки дерева является разбиение на каждом шаге всех оставших-
ся решений на две группы те, которые включают выделенную дугу,
и те, которые ее не включают Дута, используемая для разбиения
множества решений, выбирается соответственно эвристике (описы-
ваемой ниже), преследующей цель отсечения максимального коли-
чества ветвей деревьев. Конечно, каждому узлу в дереве, теперь,
очевидно, бинарном, будет сопоставляться нижняя граница стои-
мости всех решений, вырастающих из него
Метод использует тот факт, что если из любой строки или лю-
бого столбца матрицы стоимостей вычитается константа, то оптималь-
ное решение не меняется Стоимость оптимального решения, ко-
142
нечно, меняется, но сам путь не меняется На самом деле стоимость
оптимального решения отличается в точности на количество, вычтен-
ное из строки или столбца Поэтому, если произведено вычитание,
такое, что каждый столбец и строка содержат нуль и все Сц еще не-
отрицательны, то общая вычтенная сумма будет нижней границей
стоимости любого решения Например, приведенная выше матрица
стоимостей может быть преобразована вычитанием 3, 4, 16, 7, 25,
3 и 26 из строк 1—7 соответственно и затем вычитанием 7, 1 и 4
из столбцов 3, 4 и 7 соответственно, в результате чего преобразо-
ванная матрица будет равна
2	3	4	5	6	7
1	со	0	83	9	30	6	50
2	0	оо	66	37	17	12	26
3	29	1	оо	19	0	12	5
4	32	83	66	оо	49	0	80
5	3	21	56	7	оо	0	28
6	0	85	8	42	89	оо	О
7	18	О	О	0	58	13	оо
границей стоимости любого решения 1огда первоначально мы име-
ем корень бинарного дерева и соответствующую нижнюю границу,
Как этот узел распадается на поддеревья3 Предположим, что
мы выбираем дугу 4—6, по которой происходит разбиение дерева
Правое поддерево будет содержать все решения, которые исключают
дугу 4—6, зная, что дуга 4—6 исключена, мы можем изменить мат
рицу стоимостей, положив С4,е = оо. Тогда у получившейся матрицы
из четвертой строки можно вычесть 32, и поэтому правое поддерево
имеет нижнюю границу 96 Н-32 =128 Левое поддерево будет содер
жать все решения, которые включают дугу 4—6, и поэтому четвер-
тая строка и шестой столбец матрицы стоимостей должны быть уда
лены, поскольку теперь мы никогда не можем идти из 4 куда-нибудь
еще и не придем в 6 откуда-либо еще В результате мы будем иметь
матрицу стоимостей на единицу меньшего размера Далее, посколь-
ку все решения в этом поддереве используют дугу 4—6, дуга 6—
4 больше не используется, и нужно положить Сб1 = со Наконец, мы
можем теперь вычесть 3 из четвертой строки результирующей маг-
143
задачи, в то время как правые ребра только добавляют значения оо
и, возможно, несколько новых нулей без изменения размерностей
Не трудно определить, какая дуга дает наибольший рост нижней
границы правого поддерева следует выбрать нуль, который при
замене па бесконечность разрешает вычитать наибольшее число из
его строки и столбца
Применяя метод ветвей и границ к приведенной выше в качест-
ве примера матрице стоимостей, мы замечаем некоторую сложность
Первое включенное ребро есть 4—6, следующее — 3—5 и третье —
2—I (см самый левый путь из корня дерева на рис 4 7) В этом
узле нижняя граница равна 112, а преобразованная матрица стои-
мостей имеет вид
144
2	3	4	7
1	оо	74	0	41
5	14	со	0	21
6	85	8	со	О
7	О	О	0	со
замене на бесконечность позволяет вычесть
Нуль, который при ________ ________________ _________ _______
наибольшее количество из соответствующей строки и столбца, на-
ходится на месте i — 1, /=4. Поэтому мы расщепляем данный узел,
используя ребро 1—4 В левом поддереве мы получаем нижнюю
оценку 126 и преобразованную матрицу стоимостей
5	14	21
б	85	б	О
7	О	0	«
И вообще, если ребро, добавленное к частичному обходу, есть
ребро, идущее из ги в /1( и частичный обход содержит пути —г,—.
—ia и jt — )ц— .. — i0, то нужно предотвратить использование
ребра /0 —б.
Применение этого метода к матрице стоимостей, приведенной
выше, в качестве примера дает бинарное дерево, показанное на
рис 4.7 Заметим, что первое найденное решение оптимально, мы
145
данных можно сделать предположение, что для случайной пУ.п-
матрицы расстояний число исследуемых узлов равно О (1,26я)
а-р-отсечение. Существенно другой разновидностью метода
ветвей и границ является метод, встречающийся при построении
деревьев игр Дерево игры — это дерево, которое появляется в ре
зультате исследования способом поиска с возвращением всевозмож-
ных последовательностей ходов: корень есть начальная конфигура-
ция игры, сыновья корня — это возможные положения после хода
Первого игрока, сыновья этих узлов — это возможные положения
после ответного хода второго игрока и т д Например, на рис 4.8
показаны фрагменты дерева игры в крестики-нолики, где первым

ставится крестик (X), на дереве показаны только неэквивалентные
(с точностью до вращения и/или отражения) сыновья узла
Каждый лист дерева игры представляет собой возможное оконча
ние игры, в случае игры в крестики и нолики окончанием можетбыть
победа крестиков, победа ноликов или ничья Нас интересует оцен-
ка дерева игры с позиции первого игрока, каждый лист помечается
значением вышрыша первого игрока 4-1 в случае победы, —1 в
случае поражени?! и 0 при ничьей Значения других узлов опреде
ляются значениями их сыновей. Для узла Af с сыновьями А\, А», .
. , Nit значение V (Л') имеет вид
| max(V(A\),.. .,У(У*)), если уровень четный,
| min (V (Afj), .. ,V(Nk)), если уровень N нечетный
Это означает, что первый игрок пытается максимизировать
свой выигрыш, в то время как второй игрок пытается минимизиро-
вать свой проигрыш. При таких условиях хорошо известно, что
значение корня дерева, показанного на рис 4 8, равно нулю, что
означает, что при условии минимакса игра всегда кончается ничьей.
Мы могли бы применить просто очевидную технику возвращения
для оценки всех узлов дерева и определить значение в корне Од-
нако существует лучший метод, называемый а, ^-отсечением,
который использует идею метода вегвей и границ для обрывания
поддеревьев дерева игры Заметим, что, как только узел оценен,
становится кое что известно о значении, которое будет присвоено
его отцу В частности, если отец узла принадлежит уровню дерева,
на котором вычисляется максимум, то значение, присвоенное узлу,
есть нижняя граница значения его отца. Такая нижняя граница
уровня, в котором вычисляется максимум, называется а значением.
В симметричной ситуации, когда отец находился на уровне, в кото-
ром вычисляется минимум, получающаяся верхняя оценка его
значения называется ^-значением
В примере на рис 4.9, как только узлу d присваивается значе-
ние 3, сразу же получается Р-значение 3 для узла т, и мы полу-
чаем, что значение в т будет не больше чем 3 Располагая такой
информацией, мы рассуждаем следующим образом Если можно
показать, что значение любого другого потомка узла т будет боль
ше 3, мы можем спокойно игнорировать оставшуюся часть дерева,
расположенную ниже этого потомка Поэтому мы можем тогда
действовать так, как если бы эти ветви и узлы были оборваны
Такая ситуация называется ^-отсечением, и она встречается всегда,
когда обнаруживается, что узел, расположенный на два уровня ниже
узла с p-значением, имеет большее значение, чем это р На уровне,
в котором вычисляется максимум, имеем сходную ситуацию. Возв-
ращаясь снова к примеру и обнаружив, что для узла т значение
равно 3, мы имеем для корня дерева а значение 3, так что, если
влиять па окончательное значение корня Эта процедура назы-
вается а отсечением.
Преимущество такой процедуры над алгоритмом исчерпывающе-
го поиска очевидно, вместо всех нам нужно проверить только часть
узлов дерева Однако мы быстро замечаем, что на количество сэко-
номленной работы сильно влияет порядок узлов дерева, так как
этот порядок определяет время появления а- и 0-отсечений Несмот-
ря на эту очевидную зависимость от порядка поиска, мы можем
сказать кое-что об относительной эффективности а-0-отсечения по
сравнению с прямым алгоритмом поиска с возвращением Рассмот
рим дерево, изображенное на рис. 4 10 Здесь значение А есть ниж
няя граница для значения корня С Предполагая, как раньше, что
оценка узлов происходит слева направо, от Вг к Вп, мы можем
определить d, расстояние до а-отсечения как наименьшее i, 1 п,
такое, что Bt А Мы хотим узнать, как ведет себя величина d
с изменением п, для того чтобы это стало возможным, мы делаем
некоторые предположения о значениях узлов. Мы знаем, что среди
«среднее расстояние до а отсечения»:
D(n, р) = У k Рг (отсечение в k)1)
- 2 k Рг(Й!> А, В2> А, . ...В^^А и
=	— р)
= (1— P)fe2
При п -> оо мы имеем частичные суммы сходящегося ряда, так что
D(n, р) всегда ограничено сверху его пределом
£»(оо, р) = (1 — р) Д kpk~l
Другими словами, на дереве, удовлетворяющем предыдущим пред-
положениям, a-0-отсечение ограничивает ветвление дерева в соот-
ветствии с некоторым значением, не зависящим от фактического
150
его ветвления Предположим, например, что все В, имеют одну и
ту же вероятность быть больше ити меньше А, т е р=1—Р~—
Это предположение можно считать разумным в отсутствие любых
специальных сведений о распределении значений на дереве Тогда в
соответствии с нашим анализом мы можем ожидать, что среднее
расстояние до обрыва не больше чем D(oo, ~)=2, независимо от
того, сколько будет В,
4.1,7. Динамическое программирование
Задача коммивояжера из предыдущего раздела является приме-
ром многошагового процесса решения, т е. процесса, при котором
осуществляется последовательность решений, возможный выбор ко-
торых зависит от текущего состояния системы, т е предыдущих
решений Для задачи коммивояжера решением на каждом шаге яв-
ляется город, который надо посетить следующим В таком процессе
задача состоит в определении оптимальной последовательности ре-
шений, т е. такой последовательности, которая минимизирует
(или, возможно, максимизирует) некоторую целевую функцию В за
даче коммивояжера целевой функцией, которую надо минимизиро-
вать, является стоимость обхода
При решении таких задач с помощью динамического программи-
рования мы основываемся на принципе оптимальности
Оптимальная последовательность решений обладает тем свой
ством, что какими бы ни были начальное состояние и начальное
решение, остальные решения должны быть оптимальной после-
довательностью решений по отношению к состоянию, получаю-
щемуся в результате первого решения
Применение этого принципа к решению комбинаторных задач по
существу означает использование принципа декомпозиции вначале
находятся решения подзадач, затем они используются для отыска-
ния решения больших подзадач и, наконец, для решения самой
задачи
Для задачи коммивояжера определим
стоимость оптимального маршрута из i в 1,
который проходит через каждый из городов
h, Is, • • •, ik в точности один раз в любом
порядке и не проходит ни через какие
другие города.
151
Принцип оптимальности утверждает, что
». ......+ /1. /........................../.-1.
где, как в предыдущем разделе, Ctj — стоимость прямого переезда
из города i в город /. Далее, по определению мы имеем
Т(у, () = С„+С„	(4 2)
Мы заинтересованы в вычислении Т(1, 2, 3, .... п) и нахожде-
нии маршрута такой длины Соотношения (4 1) и (4.2) определяют
рекурсивную процедуру вычисления 7’(1, 2, 3, .., п), последо-
вательность значений jm, получаемых при рекурсивном применении
равенства (4 1), дает оптимальный маршрут Для п=5 последова-
тельность рекурсивных обращений показана в виде дерева на
Обратите внимание на то, что здесь присутствует значительное
дублирование в листьях, для больших значений п встречаются
деревья большей высоты, с дублированием на более высоких уров-
нях дерева. Чем выше в дереве появляются дублирования, тем они
дороже При рекурсивном вычислении дерева в глубину (см.
разд 4.1.4) трудно распознать идентичные поддеревья и преду-
предить дублирующие вычисления. Используя принципы склеива-
ния ветвей и переупорядочивания поиска, мы организуем вычисле-
ния снизу вверх, уровень за уровнем Так как значения Т на одном
уровне зависят от значений Т на ближайшем снизу уровне, мы
можем начинать с листьев (уровень с номером п—2), значения ко-
торых мы знаем из равенства (4 2), и производить обработку по
направлению вверх к корню (уровень с номером 0), уровень за
уровнем Конечно, этот подход требует большей памяти, чем поиск
в глубину Если для каждого отдельного узла дерева мы использу-
ем одно слово памяти, то всего слов памяти потребуется 11
Такое относительно большое требование к памяти типично для та-
кого поуровневого применения динамического программирования
Число сложений, требуемых для вычисления (4.1) и (4 2), равно
1 для каждого листа, 2 для каждого узла, чьи сыновья являются
листьями, 3 для каждого узла, чьи внуки являются листьями, и
т д , т е п — i—1 сложений для каждого узла на уровне с номе-
7(2,3.4 5)
7(345)	7(4:3,5)	7(5:3,4)	7(2;4,5)	7(4,2,5)	7(5,24) Т(2;3,5)	7(3,2 5) 7(5,2,3)	7(2 3 4)	7(3:2,4)	7(4,2 3)
Рис 4 11 Рекурсивное вычисление Т (1 2, 3, 4, 5) Узлы, обведенные в кружок, являются повторениями, т е гакос же вычис-
ление выполняется раньше
153
ром i, а всего сложений будет
2 (число узлов на уровне t) (п—i — 1)
Число сравнений почти то же самое, что и число сложений, а именно
п — i — 2 для каждого узла из уровня с номером t, таким образом,
общее число сравнений равно
Заметим, что при движении снизу вверх уровень за уровнем объем
требуемой работы является функцией только числа городов и не
зависит от элементов матрицы стоимостей в противоположность ме
тодам ветвей и границ, при поиске в глубину, которые существенно
зависят от порядка строк и столбцов, а также от элементов матрицы
К сожалению, применение принципа оптимальности и динами-
ческою программирования к задаче коммивояжера не уменьшает
существенно времени вычисления, оно только реорганизует его
Однако для других задач принцип оптимальности может резко
уменьшить объем поиска, и поэтому динамическое программиро-
вание может существенно сократить время вычисления (см
упр 5, 6 и 7) Пример такого сокращения мы увидим в разд 6 3,2,
в котором время вычисления уменьшается с величины, пропорцио-
нальной 4’7/1’s, если пользоваться очевидным исчерпывающим ал-
горитмом, до О(п3) при подходе с позиций динамического про-
граммирования, улучшение действительно существенное
Наша неудача в попытке отыскать эффективный метод поиска
оптимального решения задачи коммивояжера, которая рассматри
валась в этой главе, будет подробно исследована в гл 9
4.2.	МЕТОДЫ РЕШЕТА
Как можно предположить из самого названия, решето представ-
ляет собой метод комбинаторного программирования, который рас-
сматривает конечное множество и исключает все элементы этого
множества, не представляющие интереса. Этот метод является
логическим дополнением к процессу поиска с возвращением, опи-
санного в предыдущем разделе, который перечисляет все элемен-
ты множества, представляющие интерес.
Методы решета полезны прежде всего в теоретико-числовых
вычислениях Например, одним из наиболее известных методов
154
между0б^^Зб: 7, 11, 13, П, 19, 23, 29, 31	Р
4.2.1. Нерекурсивное модульное решето
Решето Эратосфена мы можем интерпретировать как поиск всех
чисел междс N и №, которые одновременно являются членами
одной из арифметических прогрессий в каждом из следующих мно-
^+1},
{ЗА+1, 3fe + 2},
{5А+1, 5ЙЦ-2, 5fe + 3, 5Л + 4},
{7fe+l, ..,7^ + 6},
{1U + 1...Ш-hlOf,
{ph +1...ph-rp— 1},
где р — наибольшее простое число, меньшее или равное W Тот
факт, что число принадлежит прогрессии вида 26+1, означает,
что оно нечетно, факт, что оно принадлежит одной из прогрессии
3k rl или 36+2, означает, что оно не является кратным 3, и т д
Таким образом, между /V и № простыми являются только те числа,
которые удовлетворяют всем этим условиям
Рассмотрим еще одну средневековую головоломку о женщине и
яйцах По пути на базар, куда женщина несла продавать яйца, ее
случайно сбил с ног всадник, в результате чею все яйца разбились
Всадник предложил оплатить убытки и спросил, сколько у нее было
яиц Женщина сказала, что точного числа она не помнит, но когда
она брала яйца парами, то оставалось одно яйцо Одно яйцо остава-
лось также, когда она брала сразу по 3, 4, 5 и 6 яиц, но когда
она брала сразу по 7 штук, го в остатке ничего не было. Ясно, что
она могла бы иметь (V яиц, если и только если Л' одновременно яв-
ляется членом каждой из арифметических прогрессий
26 + 1, 36 + 1, 4бф I, 56+1, 66+1 и 76
Как moi ла бы женщина определить все возможные значения числа
яиц, меньшие lOOCP Для решения этой задачи можно использовать
решето, выписывая целые числа 1,	, 1000 и затем удаляя все эле-
менты, не принадлежащие различным прогрессиям: сначала все чет-
ные числа, потом числа вида 3k или 36+2 и т д Оставшиеся чиста
и будут возможными решениями
И решето Эратосфена, и решето для средневековой головоломки
являются специальными случаями обобщенного модульного решета
Пусть ти тг, т3,	, mt — множество из t целых чисел (называе-
мых модулями) Для каждого т, рассмотрим nt арифметических
прогрессий
Задача состоит в отыскании всех целых чисел, заключенных в
пределах между А и В, которые для каждого т, одновременно
принадлежат одной из п{ прогрессий В решете Эратосфена мы
имеем /«1=2, т4=3, тя=5,. , т^р (наибольшее простое число,
-1 и ац—j В задаче о женщине и
меньшее или равное TV), zip
Если модули попарно взаимно просты, то мы можем объединить
все прогрессии и получить одно множество из Пи, прогрессий с мо-
дулем Пт, Это осуществляется повторным применением следующей
техники объединения прогрессий mikA-a-i и т26+а2 в одну прогрес
сию т-рпгк-\-а Поскольку по предположению наибольший общий
делитель и равен единице, алгоритм Евклида п гарантирует
156
существование целых чисел и и v, таких, что mlu-\-iniv=\. Выбирая
a—mLua2+m2Vai, мы находим, что x^a(mod т^ц), если и только
если (modmJ и (mod m2) Таким образом, для того чтобы
определить, какие целые числа из отрезка между А и В удовлет-
воряют требованиям одной из п, прогрессий для каждого т(, мы
можем взять каждое целое из этого отрезка, разделить его на П/пв
и посмотреть, является ли остаток одним из П/г, приемлемых остат-
ков Конечно, мощность вновь получившегося множества быстро
растет, так быстро, что, имея только 10 множеств из трех прогрес-
сий каждое, можно получить одно множество из п=31и=59049
прогрессий. Следовательно, пришлось бы вычислять эти 59049 зна-
чений и затем просматривать их для каждого остатка, который будет
получен Это большая работа, и обычно более практично использо-
вать решето
Пользу обобщенного модульного решета можно ощутить, рас-
сматривая задачу проверки первого миллиона чисел Фибоначчи с
целью отыскания потных квадратов Поскольку
мы получаем, что
т е. Fioooeoo имеет более 200000 десятичных знаков. Очевидно, «ло-
бовой» метод порождения первого миллиона чисел Фибоначчи и
проверки каждого из них, не является ли оно полным квадратом, не
осуществим, но методом решета вычисление можно легко провести
за несколько минут
Вычисление начинается с установления в памя1И миллиона раз-
рядов для характеристического вектора г-и разряд представляет
целое число Лг, если этот разряд равен единице, то может бьпь
квадратом, если он равен нулю, то /•, квадратом быть не может
Сначала все разряды будут единицами, и в процессе отсеивания на
каждом шаге некоторые из этих разрядов становятся нулями.
После окончания просеивания, если окажется, что какой-либо из
разрядов равен единице, то соответствующее число Фибоначчи
нужно исследовать на предмет, не является ли оно полным квадра-
том Миллион разрядов памяти, требующихся для характеристичес-
кого вектора,— это много, но не чрезмерно, например, в машине с
32-разрядными словами потребуется только 31250 слов памяти.
Рассмотрим последовательность Фибоначчи по модулю р, где
р — простое число Пусть это будет последовательность Pit Р2,
определяемая следующим образом
Эта последовательность периодическая, причем период начинается
с Л = 1 Для доказательства этого утверждения рассмотрим р2-М
упорядоченных пар целых чисел
(Рг, Рг),(Р4, РЙ), ...,(РР=, Р^+1), (Рр!+1. Рр! + 2)
Поскольку по модулю р существует только р2 различных упорядо-
ченных пар целых чисел, две из этих лар должны совпадать Пусть
(Рг, P,+i) и (Р„ Pt^L) будут самыми левыми совпадающими парами
Если г>1, то мы имеем
что противоречит предположению о том, что (Pr, Pr+i) и (Рг.
Раи) — самые левые совпадающие пары Таким образом, числа
Фибоначчи образуют по модулю р периодическую последователь-
ность, начинающуюся с Pt и такую, что Pi-=Pi+nT для некоторого
По модулю любого числа п существует несколько квадратов
(обычно называемых квадратичными вычетами по модулю п'}
и несколько пеквадратов Например, 0, 1, 2 и 4 являются квадра
тичными вычетами по модулю 7, в то время как 3, 5 и 6 являются
квадратичными невычетами Таким образом, любое из чисел т^З, гу
или 6 (mod 7) не может быть квадратом, потому что оно является
квадратичным невычетом по модулю 7 Поскольку для каждого
простого р числа Фибоначчи по модулю р образуют периодическую
последовательность с периодом Тр, мы производим отсеивание,
используя арифметические прогрессии 7'^4-т для каждого i, та-
кого, что Pi является квадратичным невычетом по модулю р Для
иллюстрации процесса отсеивания рассмотрим случай р=7 Ряд,
Фибоначчи по модулю 7 представляет собой последовательность из
16 элементов
повторяющихся периодически с периодом 7,=16 Поскольку 3, 5
и 6 — квадратичные невычеты, мы знаем теперь, что P4+1<n. Fs-n№,
Ft+un, #9+ien. Ло+ien. Fn+itn и fu+ien не являются квадратами для
n^O, iax что значения в разрядах, соответствующих этим числам,
можно поменять с единицы на нуль
После отсеивания квадратичных невычетов первых 32 простых
чисел мы обнаруживаем, что все значения разрядов, кроме перво
го, второго и двенадцатого, изменены на нули Не изменившие зна-
чений разряды соответствуют трем числам Fi=F2=l и FiS = 144,
поэтому можно заключить, что среди первого миллиона чисел
Фибоначчи только они являются квадратами На самом деле дока-
зано что только они являются квадратами среди чисел Фибоначчи
4.2.2.	Рекурсивное решето
Существует много решет, в которых модули т^, т2, заранее
не заданы; значение т[ будет зависеть от чисел, не удаленных после
просеивания по модулю т4-1 Многие решета строятся рекурсив-
ным образом Фактически, решето Эратосфена обычно так и стро-
ится после выписывания чисел 2, 3,	, N мы вычеркиваем все числа,
кратные 2, кроме самой двойки Затем, поскольку наименьшее
оставшееся число, чьи кратные остались неудаленными, равно
трем, удаляются все числа, кратные трем, кроме самой троики, и
Заметим, что на каждом шаге первое удаленное число является
квадратом числа, с которого начинается просеивание, например,
первым числом, исключаемым двойкой, будет 4, тройкой — 9 и т д
Когда число, относительно которого производится просеивание,
становится больше V Лг, никакие числа уже не могут быть удалены,
и процесс заканчивается
Обычно мы удваиваем размер ячеек решета Эратосфена, осуще
ствляя предпросеивание для двойки; другими словами, мы начинаем
только с нечетных чисел, отсеивая кратные 3, 5, 7, 11 и т д
Пусть X — двоичный набор, тогда рекурсивный вариант решета
Эратосфена (с предпросеиванием для двойки) для нечетных простых
чисел до 2У4-1 показан в алгоритме 4 5.
for A = 3 to	by 2 do
Другое хорошо известное рекурсивное решего порождает счаст-
ливые числа Из списка чисел 1, 2, 3, 4, 5, удаляется каждое
второе число, в результате чего получается список 1, 3, 5, 7, 9
Поскольку тройка является первым числом (исключая единицу)
159

которое не использовано в качестве просеивающего, из оставшихся
чисел мы удаляем каждое третье число, получая в результате спи-
сок I, 3, 7, 9, 13, 15, 19, 21, .Теперь удаляется каждое седьмое
число, в результате чего получается список 1, 3, 7, 9, 13, 15,21,
Числа, которые никогда не удаляются из списка, называются «счаст-
ливыми»
Неслютря на большую схожесть решега Эратосфена и решета для
получения счастливых чисел, последнее реализуется труднее Труд-
ность возникает потому, что числа, отсеиваемые на k-м шаге, по-
зиционно зависят от еще неисключенных элементов, а не от элемен-
тов первоначального множества В предположении, что для пред-
ставления чисел используется двоичная последовательность в решете
для счастливых чисел нужно будет считать, скажем, каждый седь-
мой единичный разряд вместо вообще седьмого разряда Эта задача
существенно облегчается, если использовать бирки Вместо исполь-
зования полного машинного слова для представления возможных
решений, которые мы должны просеять, мы используем часть этого
слова для хранения счетчика числа единиц в остальной части слова.
Например, в ЭВМ со словом, состоящим из четырех байтов, каждый
из которых состоит из восьми разрядов, мы можем использовать
слово так, как это показано на рис 4 13 Правый байт содержит
счетчик числа единичных разрядов в трех левых байтах С ш. поль-
зованием бирок отыскание /-го невычеркнутого элемента (/-го еди-
ничного разряда) легко осуществляется путем суммирования бирок
до тех пор, пока сумма S не станет большей или равной /, соответ-
ствующий элемент будет (S—/+1) м единичным разрядом справа в
левых байтах последнего слова, чья бирка суммировалась
Очевидно, навешивание бирок не приводит к экономии времени,
если из каждого слова исключается один или более разрядов По
этой причине имеет смысл осуществить просеивание для нескольких
шагов без бирок и начинать их использовать, когда подлежащие
отсеиванию элементы становятся достаточно редкими Точное число
шагов, прогоняемых без бирок, зависит от типа решета и размера
слова Например, для решета счастливых чисел с 32-разрядными
словами и 8-разряднои биркои лучше сделать первые три-четыре
шага без бирки.
Навешивание бирок можно расширить до бирок более высокого
порядка, выбирая целое т 2 и подсчитывая сумму бирок в бло-
ках из т слов. Обычно эти бирки должны храниться вне исходного
поля, поскольку их значения могут стать большими. Можно исполь-
зовать бирки еще более высокого порядка, накладывая на множество
нечто вроде структуры дерева, по через некоторое время начинается
процесс уменьшения отдачи, и выигрыш становится незначитель-
ным. Как и бирки первого порядка, бирки высоких порядков стоит
использовать только в тех случаях, когда исключается менее од-
ного разряда на блок
Рекурсивное решето несколько другого характера можно ис-
пользовать для вычисления следующей последовательности U Вна-
чале 2) Если вопрос о вхождении в U решен для всех целых
чисел, меньших п, то U тогда и только тогда, когда п является
суммой единственной пары различных элементов из U Таким обра-
зом </=(1, 2, 3, 4, 6, 8, 11, 13, 16, 18, 26, .) Эту последова-
тельность можно вычислить с помощью двух параллельных просеи-
ваний; целое должно быть просеяно (должно быть суммой, полу-
чаемой не менее чем одним способом) и не должно быть отсеяно (дол-
жно быть суммой, получаемой не более, чем одним способом)
Используем два двоичных вектора. Для i>2
Лг = 1, если и только если t представимо в виде суммы не менее
чем одним способом
У,=1, если и только если i представимо в виде суммы не более
чем одним способом
«Двойное решето» для вычисления элементов U до некоторого
числа N приводится в алгоритме 4 6. Значение счетчика k увеличи-
вается до тех пор, пока оно не достигнет первого целого числа,
большего предыдущего элемента из U, представимого точно одним
способом. Это целое принадлежит U, и поэтому разряды, соответ-
ствующие всем целым k+i для i<_k, должны быть обновлены.
161
4,2.3,	Решето, отбраковывающее изоморфные
объекты
Иногда из данного множества объектов необходимо выделить
максимальное подмножество попарно неизоморфных объектов. Мы
имеем, скажем, объекты
Находим все o-t s ог, г>1, и вычеркиваем их Если оа — первый
невычеркнутый после otобъект, находим все огз£о0, £>ап и вычер-
киваем их. Продолжая в том же духе, мы получаем максимальное
множество неэквивалентных объектов. Таким образом, решето,
отбраковывающее изоморфные объекты, является специальным слу-
чаем рекурсивного решета
Рассмотрим, например, задачу о не атакующих друг друга фер
зях на доске размера пХп Если мы нашли ЛГ решений и хотим
просеять их, чтобы выделить решения, не эквивалентные относи-
тельно вращения и/или отражения, мы можем сделать это при
помощи решета, отбраковывающего изоморфные объекты. В этом
случае, однако, не обязательно производить явное просеивание,
поскольку решения (перестановки) находятся в возрастающем лек-
сикографическом порядке 1). После нахождения очередной переста-
новки мы порождаем все перестановки, эквивалентные ей Если ка-
кая-либо из них с лексикографически меньше, чем данная
перестановка, то она уже найдена раньше, и данную перестановку
мы можем игнорировать Например, в случае 7x7 находятся 16 пе-
рестановок — решений Они находятся в следующем порядке:
4,	1,	3,	6,	2,	7,	5
4,	1,	5,	2,	6,	3,	7
4,	2,	7,	5,	3,	1,	6
6 Л» 7 80
162
Найдя перестановку (2, 4, 1, 7, 5, 3, 6), мы ее записываем; по-
скольку она является первой из найденных, ни одно из эквивалент-
ных решений с at=£l не будет лексикографически меньше, чем
она Продолжая процесс, находим перестановку (2, 4, 6, 1, 3, 5,7)
Вычисляя все эквивалентные решения, мы находим, что меньше
этой перестановки будет только перестановка (1, 3, 5, 7, 2, 4, 6).
Так как для нее а, = 1, записываем (2, 4, 6, 1, 3, 5, 7) Следующей
находится перестановка (2, 5, 1, 4, 7, 3, 6) После вычисления
всех эквивалентных решений мы находим, что ни одно из них не
меньше, чем эта перестановка, поэтому она записывается Следую-
щей находится перестановка (2, 5, 3, 1, 7, 4, 6), и, поскольку
она эквивалентна перестановке (2, 4, 1, 7, 5, 3, 6), она отбрасы
вается Процесс продолжается до тех пор, пока не будут нсследо
ваны все 16 перестановок и не будет найдено шесть неэквивалент-
ных решений
4.3.	ПРИБЛИЖЕНИЯ ИСЧЕРПЫВАЮЩЕГО ПОИСКА
Рассмотренная в разд. 4.1 6 задача коммивояжера является
одной из комбинаторных оптимизационных задач, для которых эф-
фективные алгоритмы не известны Эмпирические данные показы-
вают, что для средней (т е случайной) задачи с л городами, ме-
тод ветвей и границ (см рис 4.7) требует деревьев поиска с числом
узлов, пропорциональным 1 26" Подход с позиций динамического
программирования, изложенный в разд 4 1 7, требует деревьев
поиска примерно с п2п узлами Все известные алгоритмы требуют
поиска в объеме, экспоненциальном относительно числа городов
Для таких трудных с вычислительной точки зрения проблем один
из подходов состоит в том, чтобы ослабить требование, что алго
ритм должен давать оптимальный результат, и требовать лишь, что-
бы результат был разумно близким к оптимальному Ослабление
ограничений на оптимальность часто приводит к более эффективным
алгоритмам, поскольку в этом случае исчерпывающий поиск яв-
ляется только «приближенным» При этом ожидается, что проигрыш
в стоимости найденных (квазиоптиматьных) решений будет умерен-
Обычно легко изобрести эвристические алгоритмы, которые бы-
стро находят решение, в действительности можно обнаружить, что
большинство, но не все решения, задаваемые эвристикой, являют-
ся хорошими Например, в разд 6 2 3 мы обсудим эвристические
алгоритмы для построения бинарных деревьев поиска, качество
среднего построенного дерева достаточно хорошее, но иногда полу-
чается, что строятся очень плохие деревья Обычно невозможно
доказать, что эвристический алюритм всегда находит решение,
близкое к оптимальному
В этом разделе мы исследуем эвристические алгоритмы для за
дачи коммивояжера В случае п городов алгоритмы требуют вре-
меня лишь 0(п9), и можно показать, что они дают маршруты, стои-
мость которых не слишком отличается от стоимости оптимально! о
маршрута, если матрица стоимостей симметрична и удовлетворяет
неравенству треугольника Такие приближенные алгоритмы имеют
большую практическую ценность для задач, в которых время, не-
обходимое для отыскания оптимального результата, растет быстро
при увеличении размера задачи.
Типичным эвристическим методом в задачах оптимизации явля-
ется поиск решений, которые в некотором смысле оптимальны
локально, а не глобально В частности, если мы рассматриваем по-
строение маршрута по п городам как последовательность решений,
мы можем принимать каждое решение в соответствии с правилом ло-
кальной оптимальности Рассмотрим, например, очевидный метод
ближайшего соседа построения маршрута по п городам. В качестве
начальной точки произвольно выбираем одни из городов Среди
всех еще не посещавшихся городов в качестве следующего выбираем
ближайший к только что выбранному (т. е. последнему городу,
добавленному к маршруту), если все города уже посещались, воз-
вращаемся в начальный город В этом случае условием локальной
оптимальности является то, что выбираемый на каждом шаге город
является ближайшим к последнему пройденному Это условие не
обязательно является условием глобальной оптимальности, посколь-
ку небольшое отклонение в начале пути может дать существенную
экономию позже.
Алгоритм ближайшего соседа можно легко реализовать за время,
пропорциональное (упр 9) Если — порожденный этим
алгоритмом маршрут мины ]VR' и Оп—оптимальный маршрут
длины ]О„|, то справедлива
Теорема 4.1. Если С — «хл-матрица стоимостей (*1^2), которая
симметрична (С-^—Сц для любых i и /) и удовлетворяет неравен-
Доказательство. Пусть длины ребер в маршруте Nn> построен-
ном по методу ближайшего соседа, будут 1-^1^ ^1», так что
Лпя доказательства теоремы докажем следующие три
неравенства
о.|> 2/,
|О,|>2 £ 1„
(4 4)
2
(4 5)
Когда п четно, неравенство (4.5) является частным случаем не-
равенства (4 4) Утверждение теоремы легко следует из этих нера
венств если в (4.4)взять fe—1,2,2*, >2Г1ё«1—2 и сложить эти
[“ Ig/il—1 неравенств с неравенствами (4 3) и (4 5), то получим
(rlg»1 + 1) I о„| >2 i /, = 2|«,|,
откуда и следует утверждение теоремы
Неравенство (4 3) является тривиальным следствием из неравен-
ства треугольника, симметричности матрицы стоимостей С и то-
го факта, что п^2 Для доказательства неравенства (4 4) будем
считать, что — город, в котором при построении маршрута
по методу ближайшего соседа было добавлено ребро Пусть при
заданном k,	Ah — множество городов {съ с2, сал}
н Th — маршрут по городам из множества Ак, проходящий по
ним в том же циклическом порядке, что и оптимальный маршрут.
Из неравенства треугольника имеем
Нам нужно показать только, что правая часть неравенства (4 4)
является нижней оценкой IZ’hl Пусть с, и ^—-города в Ак и
Ci—с, — ребро в Th. В соответствии с построением по метолу бли-
жайшего соседа, если с, был добавлен к Nn перед с}, то CCjC ^lt. С
другой стороны, если город с} был добавлен к Nn раньше города с,,
то СС/С(—Поскольку один из городов ci и с} должен быть
добавлен раньше другого, мы имеем
Суммируя это неравенство по всем ребрам в 7\, находим
1Л1=	2	С„,> X min(/„/,)	(46)
Наименьшее ребро ъТк имеет длину по крайней мере Z2h, наименьшее
из следующих ребер имеет длину не меньше и т д Таким об-
разом, наименьшее слагаемое tnin (/*, 1}) в равенстве (4 6) есть !>к>
следующее наименьшее — 1^., и т д Поскольку ребро 1„
^i^2k, встречается в сумме не более двух раз и в 7\ имеется 2k
ребер, сумма в неравенстве (4 6) по крайней мере вдвое больше сум
мы k наименьших ребер.
|Л|> X	т>п(/„/,)>2(/,, + /„_,+ • ,.+/,„) = 2 £ /„
с;-е/ В Гк	l = *+1
и поэтому правая часть неравенства (4 4) будет нижней оценкой
|7\|, что и требовалось доказать
165
Доказательство неравенства (4.5) аналогично, и мы оставляем
его в качестве упражнения 11.
Теорема 4 1 дает только верхнюю оценку величины |АП |/|О„ |
и не говорит о том, насколько плохим на самом деле может быть
это отношение Можно построить симметричную пХп-матрицу рас-
стояний, удовлетворяющую неравенству треугольника, для кото-
рой алгоритм ближайшего соседа порождает маршрут, стоимость
которого более, чем в -ylg п раз больше стоимости оптимальною
маршрута.
Мы можем получить лучшие результаты, используя более искус-
ную локально-оптимальную стратегию Алгоритм включения бли-
жайшего города проводит маршрут по подмножеству из п городов;
на каждом шаге к маршруту добавляется новый город, и процесс
продолжается до тех пор, пока в маршрут не будут включены все
п городов Алгоритм начинается с маршрута, состоящего из одною
произвольно выбранного города Новый город, добавляемый на
каждом шаге, выбирается из городов, еще не вошедших в маршрут,
как город,ближайший к некоторому городу, уже принадлежащему
маршруту, новый город тогда включается в маршрут следующим
после того города из маршрута, который является ближайшим к
Хотя этот алгоритм сложнее, чем алгоритм ближайшего соседа,
его также можно реализовать за время, пропорциональное пг, если
для каждого, еще не вошедшего в маршрут города хранить данные о
ближайшем к нему городе из маршрута Определение города, кото-
рый должен быть добавлен к маршруту, решение о том, где он должен
быть включен и обновление данных о ближайших городах можно
сделать за время, пропорциональное п Поскольку в маршрут
входит п городов, общее число операции пропорционально п1.
В алгоритме включения ближайшего города условие локальной
оптимальности более тонкое, чем в алгоритме ближайшего соседа,
и поэтому можно ожидать, что он порождает маршрут, для которого
гарантируется, что его стоимость ближе к стоимости оптимального
маршрута, чем верхняя оценка из теоремы 4.1 Это действительно
так Как и прежде, пусть Оп — оптимальный маршрут длины |ОП|.
Пусть 1п — маршрут, порождаемый алгоритмом включения бли-
жайшего города и |/„| —длина маршрута 1п Справедлива
Теорема 4.2. Если С — матрица стоимостей размеров пХп,
2, которая симметрична и удовлетворяет неравенству тре-
угольника, то
Доказательство Пусть сь с2,	, сп — города, взятые в том
порядке, в котором они добавлялись в маршрут алгоритмом вклю-
166
Гл 4 Исчерпывающий поиск
чения ближайшего города Мы будем доказывать теорему путем по-
строения взаимно однозначного соответствия между городами <?2. ,
.. , сп и всеми наибольшими ребрами в Оп таким образом, чтобы стои-
мость включения города c,t между городами с, и су, т е величина
—С^1), быта не больше удвоенной стоимости
ребра в Оп, соответствующего Таким образом, на самом деле мы
включения ближайшего города следит не только за текущим марш-
рутом Ci, сг,. , ct,	но и за паукообразной конфигураци-

J 67
мы покажем, что увеличение стоимости маршрута при включении Cj
16S
не больше чем в два раза превосходит стоимость, равную длине
удаленного ребра. Таким образом, будет установлено соответствие
между городами с2, .сп и ребрами Оп — {1тзх} и теорема будет
доказана
Предположим, что город ck должен быть включен в маршрут
алгоритмом включения ближайшего города, причем ск является
ближайшим к городу ст из маршрута, как это изображено на
рис 4 15 Стоимость включения ck между ст и смежным городом,
скажем ch равна С^+С^—СС(С(в Пусть сх— точка маршрута,
к которой присоединяется нога, включающая Сь, и пусть сх— су —
первое ребро этой ноги (не исключено, что	Поскольку
алгоритм выбирает для включения город, ближайший к маршруту,
мы имеем
(4 7)
н по неравенству треугольника
Используя симметрию, мы можем объединить их и получить
Сложение (4 7) и (4 8) дает

что эквивалентно соотношению
2Сс
Следовательно, включение Ck между с; и сп стоит самое большее
2СсЛсу После того как ck включено, ребро vx — cv из конфигурации
удаляется (конфигурация при этом остается паукообразной) и ал-
горитм продолжает работать
Итак, каждый город с^, k=2,..., п, соответствует единственно-
му ребру сх—Су из Оп—{Zmax} таким образом, что стоимость вклю-
чения не превосходит удвоенной длины соответствующего ребра
в О — {/тах}. Поскольку стоимость 1п явтяется суммой стоимостей
включений, мы имеем
откуда следует утверждение теоремы
Таким образом, теперь мы знаем, что алгоритм включения бли-
жайшего города всегда порождает маршруты, стоимость которых
превышает стоимость оптимального маршрута не больше чем в два
раза. Кроме того, можно показать, что существует задача с п горо-
дами (л>6), для которой алгоритм включения ближайшего города
порождает маршрут, длина которого почти в два раза больше
169

длины оптимального маршрута Рассмотрим матрицу стоимостей
С, определяемую следующим образом
Такое задание означает, что Cj7=C7< = I для ;=i +1 (mod п) и CtJ=
=СЛ — есть длина кратчайшего пути из t в /, следующего по ду-
гам типа k—(fe±l)(mod п) Эта конфигурация изображена на
рис 4 16 для /1=8 Города образуют цикл, и каждый город нахо-
Рис 4 16 Задача коммивояжера, для которой алгоритм включения ближайшего
Рис 4 17 Т8, возможный результат работы алгоритма включения ближайшего
дится на расстоянии 1 от его последующего и предыдущего. Расстоя-
ние между двумя несмежными городами есть длина кратчайшего
пути по циклу между этими двумя городами
Пусть для этой задачи с п городами маршрут состоит из ребер
рут Тв Маршрут Тп включает два ребра длины 1 и п—2 ребра длины
2, а общая длина Тп равна 1Тп1=2п—2 Очевидно, оптимальный
маршрут Оп, состоящий из ребер I—и и г—(t'+l),	—1, имеет
длину п, и поэтому
В предположении, что маршрут Т„ может быть получен в резуль
тате применения алгоритма включения ближайшего города, это
отношение является наибольшим, допускаемым теоремой 4 2, по-
скольку
Для доказательства того, что маршрут Тп можно получить в
результате применения алгоритма включения ближайшего города,
заметим, что алгоритм может начинать работу с города 1, затем
добавлять к нему город 2, затем — город Зит д , поскольку
каждый добавленный город находится на расстоянии 1 (наименьшем
возможном) от города, входящего в маршрут Пусть Tk, 3s^k^n,—
маршрут, полученный атгоритмом включения ближайшего города
после включения города k Осталось доказать по индукции, что Tk
может состоять из ребер 1—2, (k—1)—k и i—(i-t-2) для	2
Это, очевидно, верно для k—З поскольку Ts — единственный путь
1—2—3—1 Предполагая, что это верно для 3^/^/?, заметим, что
Tk+1 получается из Tk включением города k Fl между городами
4.4.	КОММЕНТАРИИ И ССЫЛКИ
Lucas Е Recreations Mathematiques, Gauthier-Villar'-., Pans, 1891,
где он использован для решения задачи о выходе из лабиринта
Первое описание общего алгоритма проводится в работе
Walker R J An Enumerative Technique for a Class of Combinatorial
Problems, in Combinatorial Analysis (Proceedings of Symposia
in Applied Mathematics, Vol X), American Mathematical So-
ciety, Providence, R I , 1960,
371
Рекурсивная форма процедуры поиска с возвращением была исполь-
зована Робертом Тарьяном в различных алгоритмах на графах Его
статья
Tarjan R Е Depth-First Search and Linear Graph Algorithms,
SMAf J Comput, 1(1972), 146-160,
подробно обсуждается в разд 8 2 2
Приведенная в разд 4 1.3 техника проведения оценок по методу
Монте-Карло была предложена в статье
Hall М., Knuth D Е Combinatorial Analysis and Computers, Amer.
Math Monthly, 72, Part II (February 1965), 21—28
Она была глубоко проанализирована в работе
Knuth D. Е Estimating the Efficiency of Backtrack Programs,
Math Comp . 29 (1975), 121 — 136
Макрокоманды для построения программ поиска с возвращением
впервые были применены при отыскании покрытий в пентамино (см.
упражнение 1(h)) в работе
Fletcher J G., A Program to Solve the Pentonuno Problem by the
Recursive Use of Macros, Comm. ACM, 8(1965), 621—623.
С тех пор они успешно использовались дтя решения многих комби-
наторных задач, см статью
Bitner J R , Reingold Е М Backtrack Programming Techniques,
Сотт ACM, 18 (1975), 651—656
Раздел 4.1 5, в котором рассматривается пример применения
поиска с возвращением для отыскания оптимальных кодов, сохра-
няющих расстояние, основан на неопубликованной работе
Дж Р Битнера. Вопрос о длине оптимального «-разрядного DP-/-KO-
да остается открытым даже для t= 1 Однако в статье
Евдокимов А А Максимальная длина цикла в единичном «-мер-
ном кубе, Матем заметки, 6 (1969), 309—329,
доказано, что длина оптимальною «-разрядного DP-1 кода равна
с2п, где с—некоторая константа’).
Метод ветвей и границ успешно применялся в оптимизационных
задачах с конца 1950-х годов. Название метода произошло, по-ви-
димому, от расщепления пространства решений на подмножества
(ветвление) и ограничений функции стоимости на подмножествах
пространства решений. Многие разнообразные применения этого
метода описаны в обзоре
ДАН СССР, 228, N«S (1976}, 1273^- 1276 — При и Рред.П ’	Н€*‘
Lawler E. L., Wood D. E Branch-and-Bound Methods. A Survey,
Operations Research, 14 (1966), 699—719,
и в книге
Lawler E L. Combinatorial Optimization Networks and Matroids,
Holt, Rinehart & Winston, New York, 1976
Наиболее искусный подход к задаче коммивояжера (показанный
на рис. 4 7) обязан своим появлением работе
Little J D t, Murty К. G , Sweeney D. W , Karel С. An Algorithm
for the Traveling Salesman Problem, Operations Research, 11
(19b3), 972—989
Этот метод и другие подходы прекрасно обсуждаются в работе
Gomory R Е The Traveling Salesman Problem, in Proceedings of
the IBM Scientific Computing Symposium on Combinatorial
Problems, IBM Data Processing Division, White Plains, N. Y ,
1966
Дополнительный материал о деревьях игр и их опенках можно
найти в книге
Nilsson N J Problem-Solving Methods in Artificial Intelligence,
McGraw-Hill, New York, 1971 (Имеется перевод- Нильсон
H. Дж Искусственный интеллект Методы поиска решений —
Гораздо более глубокий анализ алгоритма ct-P-отсечения и его обоб-
щение дается в статье
Knuth D. Е , Moore R W An Analysis of Alpha-Beta Pruning,
Artificial Intelligence, 6 (1975), 293—326
Динамическое программирование — это детище Ричарда Велл-
мана, который о нем много написал Общее обсуждение этого метода
вместе с большим числом упражнений можно найти в книге
Bellman R. Dynamic Programming, Princeton University Press,
N J., 1957 [Имеется перевод Веллман P Динамическое
программирование — М ИЛ, I960 )
Подробное описание применения его к комбинаторным задачам да-
но в работе
Bellman R Combinatorial Processes and Dynamic Programming,
in Combinatorial Analysis (Proceedings of Symposia in Applied
Mathematics, Vol X), American Mathematical Society, Provi-
dence, R I , 1960.
4.4 Комментарии и ссылки
173
Процедура применения динамического программирования к задаче
коммивояжера появилась независимо в статьях
Bellman R Dynamic Programming Treatment of the Travelling Sales-
man Problem, J ACM, 9 (1962), 61—63 [Имеется перевод.
Веллман P Применение динамического программирования к
задаче о коммивояжере. Киб сборник, вып. 9, старая серия —
М . Мир, 1964, 219—222 ],
Held М Karp R М A Dynamic Programming Approach to Sequen-
cing Problems, J, Soc Induct Appl. Math, 10 (1962) 196—210.
[Имеется перевод. Хелд M , Карп Р М. Применения динами-
ческого программирования к задачам упорядочения Киб сбор-
ник, вып 9, старая серия — №.. Мир, 1964, 202—218 1
Метод решета, безусловно, восходит к Эратосфену из Кирен, ко-
торый жил около 200 года до н э. Обобщенное модульное решето
было представлено в работе
Lehmer D. Н The Sieve Problem for All-Purpose Computers, Math
Tables Aids Comput, 7 (1953), 6—14
Метод, используемый для объединения пар прогрессий со вза-
имно простыми модулями, основан на знаменитой «Китайской
теореме об остатках» Интересное изложение этой и смежных с ней
тем см в гл 10 книги
Ore О. Number Theory and Its History, McGraw-Hill., New York,
1948
Решето для определения точных квадратов среди чисел Фибо-
наччи приведено в статье
Wunderlich М С. On the Existence of Fibonacci Squares, Math
Comp , 17 (1963), 455—457.
Доказательство того, что 1 и 144 являются единственными такими
квадратами, можно найти в статье
Cohn J Н. Е Square Fibonacci Numbers, Fibonacci Quart, 2 (1964),
109—113
Счастливые числа и относящиеся к ним последовательности опи-
саны в статье
Hawkins D Mathematical Sieves, Set Amer., 199, No 6 (December
1958), 105-112
Использование бирок в решетах для вычисления этих последова-
тельностей вместе с некоторыми другими применениями методов ре-
шета обсуждается в обзорной статье
Wunderlich M C Sieving Procedures on a Digital Computer, J ACM,
14 (1967), 10-19
Решето, отбраковывающее изоморфные объекты, обсуждается в ра-
боте
Swift J D Isomorph Rejection in Exhaustive Search Techniques,
in Combinatorial Analysis (Proceedings of Symposia in Applied
Mathematics, Vol X), American iMathematical Society, Provi-
dence, R I , I960
Rosenkrantz D. J , Stearns R E , Lewis P M An Analysis of Se-
veral Heuristics for the Travelling Salesman, S/AAl J Comput,
6 (1977), 563—581,
Christofides N Worst-case Analysis of a New Heuristic for the Tra
veiling Salesman Problem, Technical Report of the Graduate
School of industrial Administration, Carnegie-Mellon Universitx,
Pittsburgh, Pa , 1976,
гих комбинаторных задач можно найти в книге
4 5

175
Graham R L Bounds on the Performance of Scheduling Algorithms,
Chapter 5 of Computer and Job-Shop Scheduling Theory,
E G Coffman, Ji (Ed), Wiley, New York, 1976, 165—227
4.5.	УПРАЖНЕНИЯ
нерассмотренных случаев.
4x11	13 х 1		
	5 х 10	13 х 3	
		7x7	6x9
16x2			
прямоугольниками, имеет размер 27x27 Существует ли еще меньший?
на все клетки доски, кроме центральной Фишка переносится на свободную клетку
176

Найдите последовательность «прыжков», такую, чтобы на доске осталась всего
одна фишка в центральной клетке
(е) Сим иетричная пХ п задача о не бьющих друг друга ферзях Найдите все
решения «X «-задачи о не бьющих друг друга ферзях, инвариантные относительно
поворотов на 90°, 180° и 270°. В такой постановке каждый ферзь, помещенный не
в центре, определяет положение трех других ферзей
(1) Минимальное множество не атакующих друг друга ферзей и доминирующих
друг друга ферзей и все возможные их распределения так, чтобы каждая нсзаня
тая клетка шахматной доски находилась под боем,
точно один раз и возвращается в исходную точку?

Найдите все решения для прямоугольников размера 6X10 и 5X12
(1) Кубики сома Следующие семь элементов можно сложить вместе многими
способами для того, чтобы составить куб размером 3X3X3


' (к) У пенталина Найти наименьшее п, такое, что область размера 12X5/1
eBzo
Найдите все значения л, для которых это возможно
(1) Из тождества
I’-]- 2г4-32+ . 4-24s = 4900 = 70®
можно предположить, что имеется возможность покрыть квадрат размера 70 X 70,
(гл) Дан куб размера лХллл. состоящий из пл ячеек; заполнить ячейки куба
(п) Магические квадраты Магический квадрат порядка п представляет собой
Поскольку

сумма должна быть равна ул(л®+1) Так, например.
1	15	24	8	17
23	7	16	5	14
20	4	13	22	6
12	21	10	19	3
9	18	2	11	25
является магическим квадратом порядка 5 в каждой строке, каждом столбце
вивалентных (относительно вращений н/или отражений) магических квадратов
порядка п


для покрытия плоскости, любой лХп квадрат является пандиагональным маги-
мера пХп, в которой в каждой клетке находится целое число от 1 до п и такая,

ортогональны квадрату из п. (р) и на самом деле ортогональны друг другу. Най
и границ для решения задачи коммивояжера.
рования для решения предлагаемых ниже задач
работ, стоимость назначения i-ro человека на у-ю работу равна Сл-. задача со
В каждой ячейке можно поместить только^однукомпоненгу, и каждая компонента
179


и k операторов, параллельно выполняющих эти работы- время, требуемое для
P=(pi/\, такая, что Pi;——1. если работа I должна быть выполнена перед работой
раторов минимизирующее время всей работы от начала до конца'
странстве, если игра проводится на трех досках размера 3X3? Что можно ска
зать об игре на четырех досках размера 4X4?
где Mt имеет размеры ri_xXr, Используйте подход динамического программа
6 Предположим, что нам даны координаты п вершин выпуклого л-угольиика
(Ь)	Покажите, как применение динамического программирования к исчерпы
вающему поиску позволяет найти триангуляцию наименьшей стоимости за время
180

дение
(с)	Последовательности сумм Модифицируйте решето для последователт
ности U (разд. 4.2.2) так чтобы после того, как решен вопрос о принадлежности
различных элементов последовательности не более чем двумя способами, (3) в
(d)	Псевдоквадраты Пусть р — простое число и Np — наименьшее положи-
тельное целое число, не являющееся полным квадратом и имеющее вид 8*4-1,
меньших или равных р Числа iVp называются псевдоквадратами, поскольку
они в некотором смысле ведут себя как квадраты
наибольшее положительное целое не представимое в виде суммы п х степеней
венство	верно при всех Если существует неотрицательное целое
жается как сумма различных членов последовательности /п,, mt,
(f)	Суммы простых чисел Пусть Pq=(Pi, ...}={2Г 3,	— последова
тельность простых чисел, и пусть Рп — подпоследовательность Ро, рекурсивно
определяемая следующим образом Рп= {pilt£P4-i} Пусть tn—наибольшее
положительное целое число, которое не представимо в виде суммы различных
181

показать,^что Рп удовлетворяет ее условию Используйте следующие результаты.
9.	Опишите реализацию алгоритма ближайшего соседа для задачи комми-
вояжера на п городах за время, пропорциональное п?.
10.	Приведите примеры, для которых алгоритм ближайшего соседа порож
дает оптимальный маршрут. Приведите примеры, для которых оп дает маршруты,
12.	Один из недостатков алгоритма ближайшего соседа состоит в том, что
сделать гак чтооы выполнялось неравенство треугольника, дооавляя к каждому
элементу матрицы max {С//} Означает ли это, что теоремы 4 1 и 4.2 верны для
выполняется’
для включения город, включение которого требует наименьшей стоимости, иначе
говоря, город k (взятый не из текущего маршрута) включается между смежными
городами i и j (из текущего маршрута) так, чтобы выбор I, / и k минимизировал
сумму С/дЧ-Су—С//. Установите результат, аналогичный теореме 4.2, для алго-
ритма <амого дешевого включения. Какое число операций как функция от п не-
обходимо для реализации алгоритма самого дешевого включения в задаче с п
Глава 5. Порождение элементарных
комбинаторных объектов
В комбинаторных алгоритмах часто
исследовать все элементы некоторого
необходимо порождать
.. __________ ____ _______________г____ класса комбинаторных
объектов Наиболее общие методы решения таких задач, основанные
на поиске с возвращением, рассматривались в гл 4, однако во мно-
гих случаях объекты настолько просты, что целесообразнее приме
нять специализированные методы В этом разделе мы обсудим
процедуры порождения некоторых комбинаторных объектов, кото-
рые обычно встречаются на практике В каждом случае существуют
две возможные цели — систематическое порождение всех возмож-
ных конфигураций и порождение равномерно распределенных
случайных конфигураций
Задачи, требующие систематического порождения, часю возни-
кают при вычислении комбинаторных формул Например, часто
необходимо вычислять суммы, имеющие вид
2/(«>.
где суммирование выполняется по всем последовательностям
ху, хг, .., xk, удовлетворяющим некоторым ограничениям
Вычисление такой суммы включает в общем случае порождение
каждой из возможных конфигураций элементов х,- в некотором си-
стематическом порядке Конечно, можно использовать изложенный
в гл 4 общий метод поиска с возвращением, но во многих случаях
конфигурации достаточно хорошо просматриваются и их порож-
дение можно сильно упростить Это верно для комбинаторных
объектов, обсуждающихся в этой паве перестановок, подмножеств,
сочетаний, композиций и разбиений целых чисел
Алгоритм систематического порождения состоит из трех ком
понент выбор начальной конфигурации, трансформация одного
объекта в следующий и условие окончания, говорящее о том, когда
остановиться. Всюду в этой главе общая форма такого алгоритма
будет иметь следующий вид.
выбрать начальную конфигурацию
while not условие окончания do
вывести объект
преобразовать в
следующий объект
Заметим, что в рамках такой схемы выбор начальной конфигу-
рации должен учитывать тот факт, что алгоритм предпринимает
еще одно преобразование после того, как распечатан последний объ
ект. Поскольку это постороннее преобразование не должно приво-
дить к ошибке в программе, некоторые из операций выбора началь-
ной конфигурации могут присваивать значения на вид посторон
ним переменным, например нулевому или (п + 1)-му элементу мас-
сива, в то время как массив обычно имеет эпементы только с номе-
рами от 1 до п Обращение к этой посторонней переменной или из-
менение ее значения часто можно использовать как условие окон-
чания
Процедуру, последовательно производящую объекты путем по-
следовательных обращений, можно прямо записать по данным опе-
рации выбора начальной конфигурации, трансформации и условию
окончания
procedure GENERATE (объект, flag)
.f r. .. I выбрать начальную конфигурацию
it flag then	{a)se
else преобразовать в следующий объект
return
В этой процедуре flag используется как сигнал вновь начать порож-
дение (вызов с flag=true) и как сшнал порождения последнего
объекта (возврат с flag=true)
В алгоритме порождения всех элементов множества нас прежте
всего интересует общее количество времени, требующегося для по
рождения всего множества В частности в некоторых алгоритмах
можно порождать все множество за время, пропорциональное его
мощности Такие алгоритмы, называемые линейными, желательны,
ибо их эффективность — асимптотически наилучшая из возможных
Представляет также интерес количество изменений, которые про-
исходят при переходе к последующим объектам Иногда желательно,
чтобы такого рода изменения были возможно малыми, например, в
разд. 5 1 мы исследуем алгоритм порождения перестановок, в ко-
тором последовательные перестановки различаются лишь тран-
спозицией соседних элементов Такие алгоритмы называются адго
ритмами с минимальным изменением Точное определение мини
мяльного изменения зависит от рассматриваемых комбинаторных
конфигураций
Задачи, требующие случайного порождения элементов в классе
комбинаторных объектов, возникают при оценке сложности по
методу Монте Карло (см. разд 4 1 3) Например, если мы не можем
удовлетворительно проанализировать поведение алгоритма в сред-
нем, дтя суждений об эффективности, возможно, придется испытать
его на большом числе случайно выбранных входных конфигураций.
184
Случайное порождение часто затруднено тем, что мы требуем равно-
вероятности всех возможных конфигураций
Один из способов подхода к систематическому и случайному
порождению состоит в задании определенного соответствия между
целыми числами 0, 1,	, N—1 и N объектами Систематическое
порождение тогда осуществляется перечислением целых чисел от
О до N — 1 и обращением каждого числа в объект, в то время как
случайное порождение осуществляется случайным порождением
целого числа от 0 до /V — 1 и обращением его в объект. Процесс
обращения, однако, может быть дорогостоящим, и обычно лучше
его избегать, если эго возможно
5.1.	ПЕРЕСТАНОВКИ РАЗЛИЧНЫХ ЭЛЕМЕНТОВ
п! перестановок множества {аь а3, . , ап} (различных)элемен-
тов относятся к часто порождаемым комбинаторным объектам Без
ограничения общности мы полагаем, что элементами множества
являются целые числа от 1 до п, т е рассматриваются только пере
становии целых чисел oi 1 дол. Такое упрощение будет возможно
также провести для других комбинаторных объектов, таких, как
подмножества и сочетания
5.1.1.	Лексикографический порядок
Последовательность перестановок на множестве {1, 2...и}
представлена в лексикографическом порядке, если она записана
в порядке возрастания получающихся чисел. Например, лексико-
графическая последовательность перестановок трех элементов имеет
вид 123, 132, 213, 231, 312, 321 В общем случае если ст = (dj, о2, ..,
. ., оп) и т=(тъ т2,	, тп) — перестановки, то мы говорим, что
ст лексикографически меньше т, если и только если для некоторого
мы имеем ст>—т; для всех /<А и о&<л>.
Легко точно определить соответствие между целыми числами
О, 1, 2	, д'—1 и л1 перестановками из множества {I, 2, . ., п},
записанными в лексикографическом порядке индекс перестановки
11= (nlf ла, . . , лп) определяется как
индекс! [(1)]-=0
индексп(П)= (лх—1)(л—1)1+индекс п-1(П'), гдеП'= (л,, л’,,. ,
 > л«-1) — перестановка, полученная из П удалением л,
и уменьшением на единицу всех элементов, больших Л1
Когда рекурсивное определение индекса итерируется для по
рождения ГГ, П"= (ГГ)' ит д , последовательность величин —1,
л,—1, Л1—1, состоит из цифр представления индексап(П) в
системе счисления с факториалами Таким образом, при данном
значении i мы можем вычислить перестановку с номером i в лекси-
185
кографическом списке, обращая i в его факториальное представле-
ние (см разд 2 1)
и, поступая далее рекурсивно, образуем П', перестановку на мно-
жестве {1, , n—1}, индекс которой равен dj! 4 -+dn_2(п—2)!,
и увеличиваем на единицу все элементы, большие чем dn_,; затем
dn_,+l прибавляется в качестве первого элемента перестановки.
Как и выше, перестановка одного элемента с номером 0 есть (1)
Как отмечалось в разд 4 2 3, явное применение алгоритма поиска
с возвращением (разд. 4 1.1) к перестановкам порождает их в лекси-
кографическом порядке Перестановки можно порождать одну за
другой следующим образом Начиная с перестановки (1, 2, . , п),
мы переходим от П— (ль л2, . . , лп) к ее последующей путем про-
смотра П справа налево в поисках самой правой позиции, в которой
ntO/+1. Найдя ее, мы теперь ищем л,, наименьший элемент, рас-
положенный справа от л, и больший его, затем осуществляется тран-
спозиция элементов л7 и л( и отрезок л/+1,	, л„ (элементы которо-
го расположены в порядке убывания) переворачивается Например,
для п=8 и П= (2, 6, 5, 8, 7, 4, 3, I) мы имеем лг=5 ИП|=7 Меняя их
местами и переворачивая л|+1, . , л„, получаем (2,6, 7, 1, 3, 4,
5, 8), перестановку, следующую за П в лексикографическом порядке.
Алгоритм 5 1 реализует эту процедуру.
Алгоритм 5 1, очевидно, начинает работу с распечатки П—
(!, 2,	, п), первой в лексикографическом порядке переста-
новки, и останавливается только, когда 1=0, что происходит, если
которые систематически порождают перестановки
Заметим, что в лексикографически упорядоченной последова-
тельности перестановок существует полная подпоследовательность
k' перестановок из k правых элементов, в которой остальные элемен-
ты не перемещаются Это наблюдение позволяет нам получить ре-
куррентное соотношение для и Ck числа транспозиций «лг«-»лр>
или «л,ч-»лу» и числа сравнений «лг>л/т1» или «nt>n/> соответ
ственно использованных алгоритмом 5.1 для порождения первых АН
из п\ перестановок. В частности, заметим, что для каждого из п
возможных значении ль т е для каждой подпоследовательности
перестановок, соответствующих л — 1 самым правым компонентам,
используется /п_1 транспозиций Трансформация последней пере-
становки одной из этих подпоследовательностей в первую пере-
становку следующей подпоследовательности требует |_(n+l)/2j
перестановок, и всего таких преобразовании будет п—1, Таким
образом, за исключением преобразования, которое осуществляется
при i=0, имеется п!п ,+ (п—1)|_ (п— 1)/2 J транспозиций, а поэтом1»
Пусть
187
тогда
2 _ „/о	,	•.	_ J 0, если п нечетно,
п \ n-i+ п-i)'	если п четно
Решение этого соотношения легко получить
(2L<« - 1>/2 J) 1) '
Поэтому
Добавление |_ (n+2)/2 J транспозиций, осуществляемых при 1=0 в
алгоритме 5 1, дает всего
Транспозиций Поскольку
Е -jjyr® ch 1^ 1 54308,
мы получаем, что алгоритм для порождения п! перестановок ис-
пользует приблизительно 1 54308гг.’ транспозиций Аналогично,
в упражнении 2 мы найдем, что С„« (у е— 1)и1«3 07742 п’
Чуть более эффективный алгоритм лексикографического порож-
дения перестановок рассматривается в упражнении 13 Следует
однако подчеркнуть, что лексикографический порядок не может
порождаться так эффективно, как другие порядки, преобразование
одной перестановки в другую в этом случае — это сложный про
цесс Важность лексикографического порядка определяется его
простотой и естественностью
5.1.2.	Векторы инверсий
Пусть Х=(хь х2,	х„) есть последовательность чисел Пара
(х„ Xj) называется инверсией X, если ;</ и х,>х; Вектор инверсий
последовательности X—это последоватетьность целых чисел
таких, что dj— число элементов xlt таких, что (X/, ху) является ин-
версией Другими словами, d;— это число элементов, больших Ху
и стоящих слева от него в последовательности, так что
188
Например, вектором инверсии перестановки
будет
Простое доказательство по индукции показывает, что вектор
инверсий (dj, ds, . dn) однозначно определяет перестановку
множества {1, 2,	, п) (упр 7), что хорошо видно на следую-
щем примере Предположим, что мы имеем вектор инверсий
Вычисляем соответствующую перестановку, заметив, что, посколь
ку 1, мы должны иметь л5=4 Затем так как d4=0, то л4=5
Аналогично, так как d9=2, то л9=1 Поскольку ds—1, то л4=2,
и поэтому Л!=3 Таким образом, перестановка имеет вид П=(3,
Замечая, что ограничения	/=!, 2, .	, п почти те же,
что предъявляются к цифрам в системе счисления с факториалами,
мы получаем другую нумерацию перестановок множества {1, 2, ...
Пусть
имеет вектор инверсий
Тогда, поскольку di=0,
Эта нумерация дает нам другой путь порождения перестановок,
однако путь этот плохой, потому что построение перестановки по
ее вектору инверсий требует порядка па операций Более того,
порождение следующей перестановки из предыдущей в порядке,
индуцированном векторами инверсий, как и при лексикографическом
порядке, является беспорядочным процессом, однако преимущество
последнего в его естественности. Наш интерес к векторам инверсий
основан на том факте, что вектор инверсий (и особенно сумма его
компонент) несет информацию о количестве «беспорядка» в переста-
новке. Эго оказывается полезным при анализе некоторых алгорит-
мов сортировки из гл 7.
5.1.3.	Вложенные циклы
Одним ид простейших видов перестановок является единственный
цикл, перестановка, в которой некоторые элементы циклически
ных элементов фиксировано Например,
/1	2	3	4	5	6	7Х
\3	4	5	1	2	6	7/
есть циклическая перестановка порядка 5 и степени 3
Такие перестановки интересны потому, что каждая переста-
новка П из {1, 2, п} может быть записана в виде произведения
п=р„р„., . р,р„
где Р,— циклическая перестановка порядка i (очевидно, что Ру—
тождественная перестановка, и ее можно игнорировать) и умноже-
ние производится слева направо Чтобы понять это, рассмотрим,
как бы мы записали перестановку П= (4, 3, 5, 2, I) в виде та-
кого произведения Мы хотим, чтобы

Поскольку Р,, Ря и Р2 все не изменяют 5 и П (3)=5, мы должны иметь
Р6(3)=5 и поэтому Рв=(3, 4, 5, i, 2) Теперь мы имеем
и, поскольку Рд и Рг оставляют 4 инвариантной, П (1)=4 и Ps(l)=3,
мы должны иметь Р4(3)=4, а поэтому Р4=(2, 3, 4, 1, 5) или
то время как Р4(Р,(2))—1, и
должны иметь А’8(1)=3, т е
Аналогично, поскольку П(2)=3, в
Pi оставляет 3 инвариантным, мы
Рз=(3, 1, 2, 4, 5) Таким образом,
/1 2 3	4 5\ = /1	2	1 4 5W1	2 3 4	5\
U 3 5	2 1J " \3	4	5 1 2Л2	3 4 1	5/
Наконец, поскольку П(4)=2, в то время, как Р9 (Р* (Р$ (4))) —!, мы
должны иметь Р2(1)=2 или Ps—(2, 1, 3, 4, 5), что в результате
дает
/1	2	3	4	5\	/1	2	3	4	5\/1	2	3	4	5\
\4	3	5	2	1/	\3	4	5	1	2/\2	3	4	1	5/
/1	2	3	4	5\/1	2	3	4 5\
\3	1	2	4	5/\2	1	3	4 5Л
Мы представляем читателю показать по индукции, что в общем слу-
чае каждая перестановка может быть записана единственным спо-
собом в виде такого произведения.
Таким образом, мы можем выписать все перестановки п элемен-
тов систематическим перебором всех возможностей для Рп, Рп-1,
, Р, Простой способ сделать эго состоит в том, чтобы начать с
перестановки (1.2, .	, п} и последовательно сдвигать по циклу на
один разряд все п элементов Когда сдвиг по циклу на один разряд
первых п элементов возвращает нас к ранее порожденной переста-
новке (т е Р„ становится тождественной перестановкой), мы сдви
гаем по циклу первые п—1 элементов на один разряд Если этот шаг
возвращает нас к ранее порожденной перестановке (т е Рп-\ ста
ловится тождественной перестановкой), мы сдвигаем по циклу пер-
вые п—2 элементов на один разряд После того, как мы получим
новую перестановку, мы \ нсс снова сдвигаем по циклу все п эле-
ментов Детали этой процедуры показаны в алгоритме 5.2
191
Чы можем явно задать индексацию, определяемую этим алго-
ритмом, замечая, что на каждом шаге мы пытаемся увеличить сте-
пень Рп па единицу Если при этом Р„ становится тождественной,
то мы пытаемся увеличить степень Р„ , на 1, и т д Таким образом,
мы просто считаем в системе счисления с убывающими факториа-
лами (см разд 2 1), и поэтому если
и степень Pt равна dh 0^.(1,<i, то
индекс, (П) = dn^ + d„_x
Порядок, определяемый этими «вложенными циклами», нельзя
породить эффективно Преобразование одной перестановки в сле-
дующую может потребовать в худшем случае п2 транспозиций и
эффективно Даже если циклический сдвиг рассматривается как
элементарная операция, преобразование в худшем случае все равно
требует по порядку п операций, что все еще не дает линейного алго-
ритма По-видимому, метод вложенных циклов, хотя и представляет
некоторый исторический н теоретический интерес, имеет малую прак-
тическую ценность
5.1.4.	Транспозиция смежных элементов
Последовательность л! перестановок на множестве {1, 2,
.. , л), в которой соседние перестановки различаются так мало, как
только это возможно,— лучшее, на что можно надеяться с точки
зрения минимизации объема работы, необходимого для порождения
последовательности Для того чтобы такое различие было мини
мально возможным, любая перестановка в нашей последователь-
ности должна отличаться от предшествующей ей транспозицией
двух соседних элементов Такая последовательность перестановок
может быть полезной в некоторых приложениях, например, рассмо-
трим величину
min | (11 (%), a) |,
где х и а — фиксированные векторы из п элементов, (х, а) — ска-
лярное произведение двух векторов и П пробегает множество пере-
становок из п элементов. Последовательные скалярные произведе-
ния вычисляются наиболее эффективно, если к на каждом шаге изме-
няется только с помощью одной транспозиции (почему?) В случаях,
когда количество работы, необходимой для транспозиции двух эле-
ментов, пропорционально расстоянию между ними, нам хотелос >
бы делать транспозиции смежных элементов
192
Такую последовательность перестановок легко построить рекур-
сивно Для п—1 единственная перестановка (1) удовлетворяет на-
шим требованиям. Предположим, что мы имеем последовательность
П1, П2, перестановок на множестве {1, 2, . , п—1}, в которой
последовательные перестановки различаются только транспозицией
смежных элементов Мы будем расширять каждую из этих (п—I)!
перестановок, вставляя элемент п на каждое из п возможных мест
Весь фокус, однако, в том, чтобы расположить эти п перестановок
в порядке, удовлетворяющем требованию минимального изменения.
Немного подумав, мы найдем очевидный способ сделать это п до-
бавляется к Ift последовательно во все позиции справа налево, если I
нечетно, и слева направо, если i четно. Порядок порождаемых та-
ким образом перестановок будет следующим’
-12'
1.21'
[1234
123 1243
123) 1423
(.4123
(4132
132 1432
11342
(1324
[3124
1312 3142
J1Z 3412
(4312
(4321
-321J3421
J2i]3241
|3214
(2314
„„ 12341
23112431
(4231
[4213
•213 2413
2143
(2134
Конечно, практически трудно порождать весь список последо-
вательностей целиком Однако ту же последовательность перестано-
вок можно порождать итеративно, получая каждую перестановку из
предшествующей ей и небольшого количества добавочной информа-
ции Это делается с помощью грех векторов: текущей перестановки
193
П— (nt1 л2,,, , лп), обратной к ней перестановки Р= (рх,р2,.. -,РпУ)
и записи направления d„ в котором сдвигается каждый элемент i
(—1, если он сдвигается влево, т1, если вправо, и 0, если не сдви-
гается). Элемент сдвигается до тех пор, пока не достигнет элемента,
большего, чем он сам, в этом случае сдвиг прекращается. В этот
момент направление сдвига данного элемента изменяется на проти-
воположное и передвигается следующий меньший его элемент, кото-
рый можно сдвинуть. Поскольку хранится перестановка, обратная к
П, то в П легко найти место следующего меньшего элемента Алго-
ритм 5 3 представляет собой реализацию этого метода. Заметим, что
мы присваиваем л0=ял+,=п-|-1, чтобы прекратить передвижение
п, и dj = O, чтобы в тех случаях, когда т становится равным 1 во
внутреннем цикле, остаток внешнего цикла был правильно опре-
делен

Корректность алгоритма 5.3 доказывается простой индукцией
по п, как только мы докажем, что когда записывается перестановка
П=(лъ п2, . ., лп), значения di,	являются в точности
теми же, что и соответствующие значения, которые получаются,
когда во время порождения всех перестановок на множестве {1,2,
, п—1} алгоритм записывает П—п (перестановку П с удалением
п) Это свойство d, можно в свою очередь доказать индукцией по
числу порожденных перестановок на множестве {1, 2,	., п}
Это очевидно верно после записи первой перестановки (1,2, . , п)
Предположим, что это верно, когда записывается k-я переста-
новка П— (яь л2,	, лп) Необходимо рассмотреть два случая
Во первых, если пр то ни одно из не меняет значения.
7 Л» 7B0
194
С другой стороны, если Rpn+dn > п, мы присваиваем d„->-------dn
и продолжаем цикл с т=п—1 Это, однако, означает, что
сделанные изменения будут как раз теми, которые мы долж
пы были бы произвести при записи П—п, и, следовательно,
индукционная гипотеза справедлива и для следующей за П пере-
становки, т е для перестановки, которая должна быть записана
Алгоритм 5 3 — один из наиболее эффективных алгоритмов для
порождения перестановок, хотя и его можно несколько улучшить
Внутренний цикл может быть исключен за счет существенного услож-
нения алгоритма, без увеличения скорости его работы (см упр. II)
Алгоритм линеен, поскольку проверка условия во внутрен-
нем цикле делается всего У il=nl-|-o(n!) раз (упр. 12) Более эф-
фективный алгоритм получается применением метода макрорасши-
рений, описанного в разд 4.1 4, поскольку в п—1 из каждых п
сдвигов сдвигается элемент п (упр 13)
Легко видеть из рекурсивного определения последовательности,
что нумерация перестановок, порождаемых этим алгоритмом, имеет
( п—k, если ипдекс„_1(П—и)
индексп(П) = п индекс__.(П—п)4-< ,	. четный,
'	* п 1V	— 1,если индекс,^ (II—п)
(	нечетный,
где k определяется из соотношений лк=п.
5.1,5.	Случайные перестановка
Любую из обсуждавшихся выше последовательностей можно
использовать для порождения случайных перестановок, так как
существует четкое соответствие между целыми числами и переста-
новками Выбирая случайное целое между 0 и и1—1, мы тем самым
выбираем перестановку Однако в дополнение к задаче выбора,
скажем, случайного целого между 0 и 52’ — 1 существует еще зада-
ча превращения этого числа в перестановку. Это превращение тре-
бует порядка п2 операций.
Эффективный метод порождения случайных перестановок осу-
ществляют последовательности из п—1 транспозиций Начиная с
любой перестановки П=(п1, п2, . . , лп), элемент лп перестав-
ляется с одним из элементов л2, . ., лга, выбираемым
случайно Затем меняется местами с одним из элементов
л3, . .	Лп-2, выбираемым случайно, и т д.
195
Рг (П = 2) = Рг (лй = ой) Рг [(л„ ....	=
= (ot, .. .О*.-!) при условии, ЧТО ЛЙ = ОЙ]
Рг(1Ь-=Ч = 4.
что и требовалось
5.2.	ПОДМНОЖЕСТВА МНОЖЕСТВ
Порождение подмножеств множества {alt as, . ,,ап} экви-
Ясно, что наиболее прямым способом порождения всех двоичных
под
До-
196
{i -—О
«hile tfo
Алгоритм 5 6 линеен, так как проверка условия «аг $5» осуще-
ствляется один раз для каждого двоичного набора, еще раз для
каждого второго набора, еще раз для каждого четвертого набора и
т д, или 2п4-2',_’+ 4-2-М=2',+*—I раз. Однако алгоритм не
является алгоритмом минимального изменения, и порядок, в котором
порождаются подмножества, не имеет каких либо специальных
свойств, которые говорят в его пользу (естественный лексикографи-
ческий порядок получается применением алгоритма возвращения
для порождения подмножеств). В следующем разделе излагается
несколько более эффективный алгоритм минимального изменения
В следующем за ним разделе обсуждается процедура порождения
всех подмножеств мощности к, т. е. сочетаний из п элементов по k.
5.2.1.	Коды Грея
Наименьшим возможным изменением при переходе от одного под-
множества к другому является добавление или удаление одного
элемента множества В терминах двоичных наборов это означает,
что последовательные наборы должны различаться в одном разряде.
Такие последовательности двоичных наборов известны как коды
Грея\ более точно, «-разрядный код Грея есть упорядоченная цик-
лическая последовательность 2" «-разрядных наборов (кодовых
слов}, такая, что последовательные кодовые слова различаются в
одном разряде (ср. эти коды с DP-Z-кодами из гл 1) Коды Грея
можно удобно представить их последовательностью переходов, т е
упорядоченным списком номеров разрядов (пронумерованных спра-
ва налево), которые меняются при переходе от одного кодового сло-
ва к другому Обычно начальным кодовым словом является (00 . 0),
хотя на самом деле это несущественно, поскольку код циклический.
Существует много «-разрядных кодов Грея, но мы будем иметь
дело только с одним специальным классом, который обладает неко-
торыми полезными свойствами Предположим, что
G(n) = |

очевидно есть (п-Н)-разрядный код Грея Всюду в этом разделе
мы будем рассматривать только так называемые двоично-отраженные
коды Грея, получаемые в процессе применения этого рекурсивного
определения, начиная с тривиального 1 разрядного кода Грея
Занумеровав столбцы G(n) справа налево, можно рекурсивно
определить последовательность переходов Тп кода G(n). Если

есть последовательность переходов для «-разрядного кода, то, оче-
видно,
Заметим, ЧТО 7'перевернутое = ^^ и П0ЭТ0Му ПО ИНДУКЦИИ
^перевернутое —дЛЯ всех п faKJ1M обрЭЗОМ, рекурСИВНОЦ
определение упрощается и имеет следующий вид.
Например, для 4-разрядного кода
последовательность переходов имеет вид
I, 2, 1, 3, 1, 2, 1, 4, 1, 2, 1, 3, 1, 2, 1.
Такая же последовательность переходов
рекурсивного определения, а именно
получается из другого
Тя+1= 1, /, + 1, 1, /,+ 1, 1,	.... 1, r.z.-.+ l, 1, (5 1)
где7’п=/1, /2,	, #2"—1 Это дает другое рекурсивное определение
тех же кодов Если
G(n) =
₽сть «-разрядный код, то (n-l 1) разрядный код можно иначе опре-
делить следующим образом
G(n + 1) =|
Пусть Kn—kx,kt, . . , k2,l_l— последовательность, такая, что kt—1
есть разряд, в котором перенос прекращается, когда к до-
бавляется 1 Из рекурсивного определения (п-Ч)-разрядных дво-
ичных чисел очевидно, что
Кп+1= 1, kr +1,1, k,+ 1,1, 63-Н, . , 1,	1,1;
и поскольку Xi=l, мы имеем Кп = 7'п Таким образом, разряд, ко-
торый изменяется при переходе от G, к Gt t в G (п), это разряд, рас-
положенный слева от разряда, в котором прекращается перенос,
когда 1 добавляется к i— (bnbn.l Ь0)г Это наблюдение позволя-
ет предложить способ прямого получения G, из двоичного пред-
ставления I. Если

где
Равенство
= + (mod 2),	(5 2)
(5 2) позволяет нам вычислять номер кодового слова
прямо по Gi Пусть помер i представлен в двоичной системе:
Г=(ЬПЬП 1 • bob
200
Поскольку 0^t<2n, мы имеем Ьп=0. Вместе с равенством (5 2)
это по индукции дает
b,= S gCT(mod2), 0.
Сложение двух разрядов по модулю 2 то же самое, что ис-
ключающее «или» двух разрядов, и поэтому равенство (5 2) позволяет
нам очень быстро превратить i—(bnbn 5	b0j2,	в
Gt с помощью двоичного вычислительного устройства Мы просто
сдвигаем разряды i на одну позицию влево и выполняем операцию
исключающего «или»
исключающее «или»
Операции сдвига и исключающего «или» не эффективны в язы
ках программирования высокого уровня, поэтому мы заинтересо
ваны также в порождении элементов G (л) последовательно, переходя
от одного кодового слова к следующему за ним, без хранения номера
и превращения его каждый раз в соответствующее кодовое слово
Достаточно иметь возможность порождать последовательность Тп
эффективно, и мы можем делать это, используя стек, действующий
следующим образом.
Вначале стек содержит элементы п, п—1,	, 1 (с 1 в вершине)
Алгоритм выталкивает верхний элемент i и помещает его в последо-
вательность; после этого в стек добавляются элементы i—1, t—2,
. . ,1 Именно таким образом алгоритм 5 7 (а) порождает код Грея
gi *~gi
Заметим, что стек в алгоритме 5 7 (а) работает при сильных огра
ничениях; всякий раз, когда ;>1 помещается в стек, мы знаем а
priori, что над ним будут размещены элементы /—1, .	1 Разум
ное использование этих сведений позволяет нам в качестве стека
применять массив (тп, тп.п т0) следующим образом тю ука
зывает верхний элемент стека, и для каждого т;— это элемент,
находящийся в стеке под /, если / находится в стеке Если элемента
201
I в стеке нет, то значение ту не может оказывать влияния на вычис-
ление, и его значение можно восстановить равным /+1, так как мы
знаем, что когда в следующий раз элемент /4-1 будет помещен в
стек, элементом, расположенным над ним, будет /. Более того,
так как элементы i—1, . , 1 будут помещены в стек после удаления
элемента i, нам нужно только присвоить г,, полагая, что для
всех /, l^/<i—2, значение т> было восстановлено, когда / было уда-
лено. Наконец, для z=/= 1 элементы t—1,	,1 помещаются в стек
с помощью операции т0«— I. В результате алгоритм становится таким,
как алгоритм 5,7 (Ь)
i^=l, если же/= 1, то утверждение	немедленно исправляет
неправильное значение, присвоенное т0. Таким образом, оконча1ель-
ным алгоритмом будет алгоритм 5.7 (с)
Заметим, что реализация стека таким способом не уменьшает
числа стековых операций, но она исключает внутренний цикл в
котором 1—1, , 1 заносятся в стек Таким образом, алгоритм
переходит от одного кодового слова к следующему за постоянное
время и без лишних затрат на внутренний цикл.
202
Для доказательства корректности алгоритма 5 7 (с) нам нужно
только показать, что последовательность значений переменной i
есть Т„ Рассмотрим цикл
I вывести i
while т0 < k 4-1 do. 1
начинающийся, когда	где <Xj=i I 1 для Q^j<Zk
и aft^A+1. Цикл в алгоритме 5 7 по существу совпадает с этим цик-
лом, только в нем изменено условие окончания таким образом,
чтобы порождалось последнее кодовое слово Следовательно, все
будет доказано, если мы покажем, что этот цикл порождает последо-
вательность Г/,, останавливаясь с tj—/' —1 для и т0=ай^А-Н.
Эго, очевидно, верно для k—\ Предположим, что это верно для
k=n—1, и рассмотрим, что получится, когда k=n Так как в этом
случае условия для к=п—1 также удовлетворены, то по предполо-
жению индукции мы знаем, что вначале будет порождено Тп_|,
после чего будет т>=/-Н для —1 и т0=ап_1=п Следующая
итерация порождает п и после нее	для 0^/<п—1 и тп_! =
==ал^п+1 Далее, опять по предположению индукции мы знаем,
что порождается Тп-! до того момента, когда будет т«=ап^д+1, при
этом выполняется т;—1 для	—1, и, следовательно, в
целом будет порождена последовательность Tn-i, и, Tn-t=Tn.
5,2.2,	k-подмножества (сочетания)
Обычно требуются не все подмножества множества {а1( а2,
.. .,ап\, а только те, которые, удовлетворяют некоторым ограничени-
ям; наиболее общим ограничением является мощность подмножеств
Особый интерес представляют подмножества фиксированной мощ-
ности k, т е (?) сочетаний из п предметов по k штук. В этом разделе
мы обсудим их порождение в лексикографическом порядке, порожде
ние в порядке минимального изменения, основанное на кодах Грея
из предыдущего раздела, а также процедуру случайного порождения
Лексикографический порядок. Как обычно, мы делаем упроща-
ющее предположение, что основным множеством является множест-
во натуральных чисел {1, 2,	, м}; таким образом, мы хотим по-
рождать все сочетания мощности k из целых чисел {1,2,	., п}
Наиболее естественным является возрастающий лексикографиче
ский порядок, с компонентами в каждом сочетании, расположенны-
ми в порядке возрастания слева направо Так, например, (|)=20
сочетаний из шести предметов по три (т е трехэлементные подмно-
жества множества {1, 2, 3, 4, 5, 6}) записываются в лексикогра-
фическом порядке следующим образом:
234
235
236
245
246
123
124
125
126
134
135
136
145
146
156
256
345
346
356
456
Рекуррентное соотношение для индекса позиции сочетания
(flZi, тг, , mh) в списке k подмножеств множества {1, 2,
. , п}, где 1^/И|<т4<	можно найти, замечая, что
если fc=l, то индекс равен л:г, в то время как при ^2он равен
индексу сочетания (т2—mt, т3—mlt . . , ть—т,) из п—т, эле
ментов по k~ 1 плюс число сочетаний из п элементов no k, которые
начинаются с первой компоненты, меньшей тк Таким образом,
индекс (mt, ms........mk)
= индекс,
индекс,, t (mj) =
Полагая /по=0, мы находим, что
“"Мчс». »™,.............'»»)	= 1 + У У.
1=0	1=1	4
С помощью тождества (3 22)
при T=m]ty—Ш]—1, N—n—и J—k—/—1 последняя формула
приводится к виду

что в. свою очередь можно упростить и получить следующую фор-
Сочетания в лексикографическом порядке можно порождать по-
следовательно простым способом. Начиная с сочетания (1,2,..., А),
204
следующее сочетание находится просмотром текущего сочетания
справа налево с тем, чтобы определить место самого правого эле
мента, который еще не достиг своего максимального значения Этот
элемент увеличивается на единицу, и всем элементам справа от не-
го присваиваются новые наименьшие возможные значения, как по-
казано в алгоритме 5.8.
Общую производительность алгоритма 5.8 можно легко опреде
лить, если мы знаем, сколько раз выполняется сравнение «с>=
=п—k+jn Это сравнение осуществляется один раз для каждого со-
четания 1т е, (?) раз], еще раз для каждого сочетания с ск = п [т е.
(EzJ) раз], еще по разу для каждого сочетания с cs_i=n—1 и
ск—п [т е (Jz|) раз], . и еще по разу для каждого сочетания с
ct=n—ct=n—k+2, , ch=n (т e	раз] Таким
образом, оно осуществляется
раз Зная это, легко видеть, что присваивание	выпол-
няется CV) — (?)—(fe-i) раз Сравнение «/^=0», очевидно, выпол-
няется (£)+1 раз, и, таким образом, поведение алгоритма пол-
ностью определено Поскольку (nkl)—(k) [(«•+ l)/(n—^+1)1 и
(s-i)i=(fe)^/(n—£+1), алгоритм линеен, за исключением тех слу-
чаев, когда k = n—о(п) В этом случае алгоритм можно применять
для порождения сочетаний из п предметов по п—k, эти сочетания
затем можно «дополнить» для получения сочетаний из п предметов
Порядок минимального изменения. Наименьшим изменением,
возможным в последовательных сочетаниях в списке всех сочета-
ний из п элементов по k, является замена одного элемента другим
В терминах двоичных наборов это означает, что мы хотим выписать
все «-разрядные наборы, содержащие точно k единиц, так что после-
довательные наборы различаются ровно в двух разрядах (в одном
нуль заменяется единицей, в другом единица нулем).
205
Пусть G(n)— двоично-отраженный n-разрядный код Грея из
предыдущего раздела, и пусть G (п, k), Q^k^n,— последовательное! ь
кодовых слов ровно с k единицами Эта последовательность G(л, k),
очевидно, обладает требуемым свойством, чтобы все кодовые слова
содержали точно k единичных разрядов Теперь мы должны пока-
зать, что последующие кодовые слова различаются ровно в двух
разрядах
Теорема 5.1. Первым кодовым словом в G(n) ровно ck единицами
будет О"-* 1А, а последним —]0я-А1А—для и 0п, если k=Q й)
Доказательство Доказательство проводится индукцией по п
для всех фиксированных А>1. Теорема, конечно, справедлива
для всех п, если £=0, и для n=k, поскольку в этих случаях только
одно кодовое слово имеет допустимый вид, таким образом, теорема
выполняется для п, равного I Предположим, что теорема верна для
G(n), ri^l. Пусть G(n)R— последовательность кодовых слов (строк)
из G(n), взятых в обратном порядке; тогда G(n+1) формируется ре-
курсивно из G(n) следующим образом:
й<'1 + 1) = (?ой«).
и поэтому первое кодовое слово с единицами в G(n+1) есть
первое такое слово в G(n) с приписанным слева нулем. Иными
словами, это есть 0п+1"*1*. как и требовалось Аналогично, по-
следнее кодовое слово с единицами в G(«+l)— это первое
кодовое слово с k—1 единицами в G(n) с приписанной слева едини-
цей, т е это	как и требовалось
Теорема 5.2. Соседние кодовые слова в G (и, k) различаются ровно
в двух разрядах
Доказательство Доказательство проводится индукцией по п.
Теорема, очевидно, верна для п=1, поскольку /?=0 или k=l
Предположим, что утверждение справедливо для п и всех k, 0^k^.n
Мы должны показать, что оно верно для n -J-1 и любого k, 0<J^n+l
Если 6=0 или k=n+l, оно тривиально справедливо, так как
содержит только одно кодовое слово без единичных разрядов и
только одно кодовое слово с п+1 единицами Для теорема
выполняется по предположению индукции, если соседние кодовые
слова оба либо в 0G(n), либо в lG(n)ff
vvvvvvvvvvvvvvvv
\/
\/
V
V
\/
V
Таким образом, осталось только показать, что последнее кодо-
вое слово с k единичными разрядами в О G (п) отличается ровно в
двух разрядах от первого кодового словасй единицами lG(n)ff. Из
теоремы 5 1 мы знаем, что для 6=1 эти два кодовых слова будут
соответственно 010п-1 и ЮО"-1; для они будут 010п~*1*-1 =
=010я-*11*-г и 1	10п—*01*—а соответственно
Для эффективного последовательного порождения кодовых слов
G(n, k), n^k^O, полезно дать рекурсивное определение, аналогия
ное первому определению кода Грея G(n). Для ri>k>0 мы имеем
Доказательство индукцией по п показывает, что такое определение
действительно задает последовательность, совпадающую с той, ко-
торая получается удалением из G(n) всех кодовых слов с числом
единиц, не равным k
Рекурсивная структура G (n, k) показана в виде бинарного дерева
на рис. 5 1. Простое доказательство по индукции показывает, что
листья дерева (не изображены на рисунке) должны быть либо
10(/л, 0)й, либо 0G(m, т) Задача последовательного порождения
кодовых слов сводится тогда к задаче прохождения листьев показан-
ного на рис 5 1 дерева сверху вниз Это прохождение выполняется
процедурой типа поиска с возвращением, в которой продвижения
вперед и возвращения упрощаются за счет рекурсивной структуры
дерева.
Для перехода от одного кодового слова к другому мы рассмат-
риваем путь из текущего листа в корень дерева и следуем по этому
пути в направлении корня до тех пор, пока узлы являются нижними
сыновьями По достижении узла, который является верхним сыном,
мы идем к его брату (нижнему сыну) и следуем по верхним сыновьям
к листу. Например, на рис 5 1 мы следовали бы по жирной сплош-
ной линии справа налево и затем по жирной пунктирной линии еле
ва направо. Из-за рекурсивной природы дерева узел G(n, k) на
рис 5 1 .можно рассматривать как корень поддерева большего дере-
ва Таким образом, рис 5 1 является примером преобразования про-
извольного кодового слова в следующее
В процессе порождения мы храним путь из корня к текущему
листу в виде текущего кодового слова (gn, gn_t, , gt) Мы также
храним стек узлов g£ G(i—1, t), в которые мы должны возвратить-
ся ’) Поскольку мы легко можем вычислить значение t, нет необ-
ходимости хранить его в стеке, хранится только значение i Заме-
тим, что I является счетчиком числа единичных разрядов среди
Тщательное изучение дерева совместно с теоремой 5 1 показы-
& = 0	1 .. ОЮ’”1!!”2 I	
t > 1	1 1
	а"1 г	[ .. 010‘ 2	1 1	;
	.. ЮО'-2	1
1	6. = 1
! 1
;	. 11О'"'“2О1' 1
I	1 t > о
;	. ою‘ '~2п''
&—I
. 100’ 2
i <-0
.. 010' 2
Эти преобразования влияют на число единичных разрядов, распо-
меняемых преобразованием,— это gt и
gt-i.	если	g, = 0	и	/>1,
g/-it	если	gz = 0	и	^ = 1,
gt,	если	gz=l	и	;>0,
g,.,,	если	gj = 1	и	/=0
В дополнение к предыдущей информации мы должны добавить
в стек узлы из пути между текущим узлом и текущим листом с
тем, чтобы обеспечить последующее возвращение. Так как это за-
висит от узла в вершине стека, значение t может снова измениться.
Если t=0 или t=i—1, то ясно, что в стек никакие новые узлы не
добавляются, поскольку узел, в котором мы находимся, есть
g,G(i—1, i—1) или giG(t— 1, 0)ff — лист в том и другом случае
Для элемента в вершине стека значение t должно быть вычислено
заново, и мы утверждаем, что в этом случае новое значение t всегда
209
равно /+1 Это верно, поскольку мы идем влево от gt, пока не до-
стигнем узла, который является верхним сыном своего отца, но
легко показать, что если 1G (т, t)R— нижний сын, то его отец должен
быть верхним сыном Аналогично, если 0G(m, i')p — нижний сын,
то его отец также будет нижним сыном
С другой стороны, в случае /^0 и t^=i—1 мы должны включить
в стек узлы i—1, i—2, , 1, за исключением того случая, когда
gi-t~ =gi=0, в этом же случае в стек включается только i—1.
Значение t должно быть вычислено заново, и, поскольку среди
gi-irgi г, , gt-ц единицей может быть только gi-1( мы можем при-
своить t*-t—gi i Если при этом t становится равным 0, мы должны
иметь gi-г— . =8\=0
Все детали даны в алгоритме 5 9.
Заметим, что в алгоритме 5 9 стек реализуется таким же способом,
как в алгоритме 5.7(c) ь— указатель вершины стека, и каждый
элемент в стеке немедленно получает повое значение, как только
он исключается из стека Поскольку мы присвоили т,.то од-
но присваивание тг»-t-f-1 служит для введения в стек i—1, . .
210
, ?4-1. Доказательство корректности алгоритма 5.9 для n^k>G
можно провести таким же образом, что и доказательство коррект
ности алгоритма 5 7(c). Алгоритм 5 9 работает неправильно, если
fe=0, поскольку неправильно начинается стек В этом случае тре
буются лишь некоторые незначительные изменения (какие?)
Для порождения кодового слова из предыдущего алгоритм 5.9,
очевидно, требует лишь ограниченное число операций, не зависящее
от п и k Мы сможет определить точное число операций, необходимое
для порождения всех (") кодовых слов из G(n, k), как только мы
будем знать, сколько раз во время порождения G(n, fe) мы имеем
gi = l и /=4=0 в утверждении «if g~l» и сколько раз мы имеем
( —1—1 или I — 0 в утверждении «if l=i—1 or /=0» В других
случаях число необходимых операций распределяется равномерно
по всем возможным вариантам
Пусть a,, k— число раз, когда = 1 и ^0 во время порождения
G(n, k) в предложении «if gt—1», исключая последний проход через
цикл после порождения последнего кодового слова При этом по
следнем проходе мы имеем i=nJ-\ и g/=0, что означает, что пред-
ложение	не будет выполняться Таким образом, ап<к
является точным числом раз выполнения его во время порождения
G(n, А) Пусть — число раз наступления события gj=l и /#=0
во время порождения G(n,k)R (последний проход через цикл после
порождения последнего кодового слова исключается) При переходе
от последнего кодового слова из 0G(n—1, k) к первому кодовому
слову из lG(n—1, k—1)я мы имеем и gn=0 При переходе от
последнего кодового слова из IG(n—1, k—1) к первому кодовому
слову из 0G(n—1, k)R мы имеем t=n, gn~l и £=4=0, если и только
если /г>1 Таким образом, имеются рекуррентные соотношения
Аналогично, пусть с„,к- число раз наступления события t = i—1
или /=0 в предложении «if t = i—1 or 1=0» во время порождения
наступления этого события вовремя порождения G(n,'k)K, исключая
последний проход Как и выше, мы можем вывести рек} ррептные
соотношения
211
в остальных случаях
Такие рекуррентные соотношения можно решить, использ\я
производящие функции Мы покажем, как это сделать для
и оставляем (аналогичное) решение для ап, k в качестве трудного
упражнения для читателя Определим производящие функции
С (л, у) =--
£>(v, у)-
Рекуррентные соотношения для сп h и dn>s дают
С(х, у) = хС(х, у) + хуО(х, +
D(x, y)—xD(x, у) + хуС(х, +
откуда мы получаем
С(л, ») Ц_(1 + й х] [1 _9(1 _х](1 __w),
что в свою очередь можно выразить как
Для п>£>0 коэффициент при xnyk в С(х, у) есть сп ь, и поэтому
Это соотношение можно упростить и получить следующее соотноше-
О,	если п — 1г.
212
Как было замечено ранее, предложение then в утверждении «И t=
— с—1 or t — Q* выполняется	раз во время порождения
G(n, Л)
Случайные A-множества. Для порождения случайного подмно-
жества 5 множества {аь а2, . , ап} с k элементами мы выбираем
один из п элементов случайно (вероятность выбора at равна 1/п)
и затем выбираем случайное (k—1)-подмножество из оставшихся п—1
элементов Вероятность выбора fe-подмножества {а, , als, , а1/г),
появляющегося в результате такой процедуры, есть произведение
следующих вероятностей:
Рг (первый выбранный элемент —
один из k элементов ац, . . , а,*)
Рг (второй выбранный элемент —
один из k—1 оставшихся элементов) ='
Рг (третий выбранный элемент —
один из k—2 оставшихся элементов) = -
Рг (&-й выбранный элемент —
последний оставшийся элемент)^
что дает
Таким образом, все (?) fe-подмножеств равновероятны.
Алгоритм можно реализовать, используя дополнительный мае
сив для хранения номеров еще не выбранных элементов После
того, как выбраны первые /—Isgfe элементов, ps, pJ+t, , р„ бу-
дет записью п—/4-1 элементов, которые еще не выбраны (см алго-
ритм 5 10) Если порядок множества сохранять не обязательно, то
массив р можно исключить, используя алгоритм, аналогичный ал-
горитму для случайных перестановок (алгоритм 5 4), который дает
случайные перестановки на первых k местах множества
5.3.	КОМПОЗИЦИИ И РАЗБИЕНИЯ ЦЕЛЫХ ЧИСЕЛ
Здесь мы рассмотрим задачу порождения разбиении положитель-
ного числа п в последовательность неотрицательных целых чисел
{Pi> Р»г •	> Рк}> так что Pi+p8-t-	В частности, мы рас-
смотрим задачу с различными ограничениями на рг Если порядок
чисел pt важен, то (р,, р2,	, р^) называется композицией п, в
этом случае мы обычно накладываем ограничение pt>0 Случается,
однако, что значение k фиксировано, и тогда разрешается, чтобы
р,=0; эти композиции называюгся композициями п из k частей
Возможны другие ограничения, например, на максимальную или
минимальную мощность pt или на число повторений каждого из
них, но такие композиции менее интересны. Если порядок рс не
важен и pf>0, то {pi, рг, . ., рь) является мультимножеством и
называется разбиением п. В этом случае на р{ также могут быть на-
ложены дополнительные ограничения
Различие между композициями, композициями из k частей и
разбиениями можно легко понять, рассматривая в качестве примера
случай Композициями являются (3), (1,2), (2,1), (1,1,1),
композициями из двух частей являются (0, 3), (1,2), (2,1), (3,0) и раз-
биениями — (3), (1, 2), (1, 1, 1)
5.3.1.	Композиции
Удобное представление композиций получается из рассмотрения
целого числа п как отрезка прямой, состоящего из п отрезков еди-
ничной длины Линия разделена (п—I) точками, и композиция по-
лучается пометкой некоторых из них Элементами композиции явля-
ются просто расстояния между смежными точками На рис 5 2 по-
казана композиция (2, 1, 2, 2, 1) для п=8.
Ясно тогда, что каждая композиция п соответствует способу
выбора подмножества из п—1 точек Каждой точке мы можем со-
поставить двоичную цифру, и, таким образом, композиции п будет
соответствовать (п—1) разрядное число Далее, композиция из k
частей соответствует(п—1 (-разрядному числу ровно с&—1 единица-
ми, и поэтому существует (211) таких композиций
Мы можем рассматривать композиции п из k частей как спосо-
бы выбора k—1 точек на линии, разделенной n-\-k—1 точками на
n+k единичных отрезков В этом случае расстояние между последо-
вательно выбранными точками на единицу больше, чем соответству-
214
ющая компонента композиции При такой интерпретации, например,
рис 5.2 представляет графическое изображение композиции из пяти
частей (1, 0, 1, 1, 0) числа 3 Тотда в общем случае существует
композиций п из k частей.
Ясно, что методы предыдущего раздела можно легко применить
к последовательному и случайному порождению композиций Лек
сикографический порядок рассматривается в упражнении 30.
5.3.2.	Разбиения
Разбиения п отличают! я от композиций п тем. что порядок ком
понент не важен, так что, например, не делается различия между,
скажем, 1 + 1+2, 1+2+1 и 2+1 + 1 В частности обычно удобно
задавать разбиение {р,, рг, , р-к} числа п с компонентами, рас-
положенными в некотором порядке, например р^р^ СРл
Разбиения п с / компонентами можно порождать в возрастаю-
щем лексикографическом порядке, начиная с pi = pi — =pi ! =
= 1, pi=n— /+1 и продолжая процесс следующим образом Для по
лучения следующего разбиения из текущего просматриваем эле-
менты справа налево, останавливаясь на самом правом pt, таком,
и после этого заменяем pi на п—^р, Например, если п=12,1=5 и
разбиение имеет вид (1, I, 3, 3, 4), мы находим, что 4 больше самой
правой единицы на 2, и поэтому следующее разбиение будет
{1 2, 2, 2, 5} Когда ни один из элементов разбиения не отличается
от последнего больше, чем на единицу, мы процедуру заканчиваем.
Доказательство того, что этот процесс, лежащий в основе алгорит-
ма 5 11, работает, мы оставляем для упражнения 31.
«“ 2р/
Попытки анализа этого алгоритма не предпринимаются, потому
что алгоритм можно существенно улучшить, если использова1ь
215
обозначения для мультимножества, введенные в разд 2 4 Разбие-
ние п записывается, как
где имеется mi вхождении рх, т2 вхождений ръ и т д
Это представление исключает необходимость просмотра справа
налево, давая более эффективный алгоритм (упр 32) Однако еще
более эффективно порождать разбиения в «словарном» порядке, в
котором каждое разбиение удовлетворяет условию ?i>p2> >Pi-
Для п=7 разбиения будут порождаться следующим образом,
Идея, использованная в аноритме 5 12, состоит в том, чтобы
начинать сл»1 и переходить от одного разбиения к следующему,
рассматривая самый правый элемент разбиения, mt*pi Если гп tp t
достаточно велико (тг>1), мы можем исключить два pt для того, чтобы
добавить еще одно р,—1 (или включить одно pt+1, если в текущий
момент его нет) Если /Л;=1, то pi-t—m, pt достаточно велико
для того, чтобы добавить pt I-Ll. В любом случае то, что остается,
превращается в соответствующее число единиц и формируется но-
вое разбиение Алгоритм 5.12 использует этот процесс для порожде-
ния разбиений числа п
216
Ясно, что алгоритм 5 12 линеен, так как число операции, не-
обходимых для перехода от одного разбиения к следующему, ог
раничено константой, не зависящей от п и I Доказательство его
корректности мы оставляем в качестве упражнения 33
Случайные разбиения. В этом разделе мы обсудим весьма общин
метод порождения случайных комбинаторных объектов; в частно-
сти, этот метод применяется при порождении случайных разбиений
числа п Как обычно, задача состоит в том, чтобы убедиться, что
все возможные объекты равновероятны.
Предположим, что существует ап объектов «размерности» п и
что ап удовлетворяет рекуррентному соотношению
0B= S “.А.,
Предположим далее, что существует «конструктивное» доказатель-
ство этого тождества; другими словами, предположим, что существу-
ет четкая процедура, при которой ат объектов размерности т рас-
ширяются до атп ат объектов размерности п. Тогда мы можем слу-
чайно выбрать объект, выбирая сначала случайное значение т в
соответствии с распределением
рг(т) = М», Osjmsjn-I,
и затем рекурсивно выбирая случайный объект размерности т
и расширяя его до объекта размерности п таким образом, чтобы все
возможные расширения были равновероятны.
Пусть Р (п) — число разбиений п, где Р (0) — I по определению.
Тождество Эйлера устанавливает, что
пР(п}— 2 а(п — т)Р(т),	(5 3)
где
о (т)—сумма положительных делителем числа т.
Мы можем переписать равенство (5.3) в виде
пР (и) = 2	2 dP(m),
и все, что нам нужно,— это конструктивное доказательство этого
тождества
Пусть П — фиксированное разбиение числа т<.п, и пусть d
делит (п—т) Сопоставим (П, d) d копии разбиения П', построенного
путем присоединения (п—m}fd элементов d к П:
(П, d)
Когда d пробегает делители п—т и П разбиения т, 0^.т^.п—1,
каждое возможное разбиение числа п появляется в списке справа ров-
но п раз, подтверждая равенство (5 3). Для того чтобы убедиться в
этом, рассмотрим XV—{niyipi..mr»pz}— произвольное фик-
сированное разбиение числа п Тогда П' получается присоединением
k элементов pt к разбиению п—kpt, полученному путем удаления k
элементов pt из П' для	и Каждое такое разбиение
повторяется р, раз. Таким образом, П' встречается всего
2} i) = 2тл = "
Детали этой процедуры даны в алгоритме 5.13.
Доказательство того, чтоалгоритмб 13 порождает фиксированное
разбиение П числа п с вероятностью	осуществляется не-
посредственно по индукции Для «=0 пустое разбиение порождается
с вероятностью 1 = ГР(0). Предположим, что алгоритм работает
для всех п'<п. Вероятность появления П тогда равна
Рг(П) =	2 Рг(1Г)Рг(ГГ расширено до II) =
~У, Рг (П' расширено до П)
Но вероятность того, что ГГ расширено до II, равна пулю, за исклю-
чением тех случаев, когда П можно получить из ГГ в результате
присоединения к П' k копий р{ разбиения П числа т, и поэтому
Рг(ГТ расширено до П) = Рг (т—п — kpt) Рг (d-p/)
Таким образом,
что и требовалось доказать
5.4.	КОММЕНТАРИИ И ССЫЛКИ
Алгоритмы порождения всевозможных комбинаторных конфи-
скаций можно найти в разделе алгоритмов Communications of the
АСМ за период с февраля 1960 г. по июнь 1975 г., когда этот раздел
был переведен в ACM Transactions on Mathematical Software Эти
алгоритмы перепечатаны в Collected Algorithms from ACM
Комбинаторные свойства перестановок квалифицированно об-
суждаются в книге
Knuth D. Е The Art of Computer Programming, Vol 3 (Sorting and
Searching), Addison-Wesley, Reading, Mass., 1973 1Ймеется пе-
ревод Кнут Д Искусство программирования для ЭВМ, т 3
(Сортировка и поиск) —М Мир, 1978 1
219
Общий обзор и библиография по порождению перестановок приво-
дятся в
Ord-Smith R. J. Generation of Permutation Sequences, Computer
J , 13 (1970), 152-155 and 14 (1971), 136—139,
Sedgewick R. Permutation Generation Methods, Computing Surveys,
9 (1977), 134—164
Лексикографические алгоритмы для перестановок открывались
независимо много раз Первое упоминание о них восходит к Л Л Фи-
шеру и К К Краузе в 1812 г. Наиболее эффективный алгоритм,
известный в этом случае, описан в упражнении 4, он взят из работы
Ord-Smith R J Algorithm 323 Generation of Permutations in Le-
xicographic Order, Comm ACM, 11 (1968), 117
Сведения об этом алгоритме см также в [Сотт АСМ, 12 (1969),
512], а примечания к нему — в [Сотт, АСМ, 16 (1973), 577—578]
Наблюдение, что вектор инверсий однозначно определяет соответ-
ствующую перестановку, принадлежит Маршаллу Холлу мл См ра-
боту
Tompkins С В Machine Attacks on Problems whose Variables Аге
Permutations,, in Numerical Analysis (Proceedings of Symposia
in Applied Mathematics, Vol 6), American Mathematical Society,
Providence, R I , 1956
В этой статье также в общих чертах описано порождение пере-
становок с помощью вложенных циклов и описан ряд вычислитель-
ных задач, в которых требуется последовательное порождение пере-
становок.
То, что перестановки можно порождать с помощью транспозиций,
впервые было опубликовано в статье
Wells М. В. Generation of Permutations by Transposition, Math.
Comp , 15 (1961), 192—195.
В методе Уэллса, однако, не всегда делаются транспозиции
смежных элементов Метод, изложенный в разд 5 1 4, в котором
всегда осуществляются транспозиции смежных элементов, был поч-
ти одновременно открыт Троттером и Джонсоном и опубликован
в статьях
Trotter Н F Algorithm 115: Perm, Сотт АСМ, 5 (1962), 434—435,
JohnsonS М Generation of Permutations by Adjacent Transpositions
Math Comp , 17 (1963), 282—285
Эта специфическая последовательность перестановок имеет
интересное приложение в музыке, подробности см в статье
Papworth D G Computers and Change-Ringing, Computer J ,
3 (1960), 47-50
Наиболее эффективный из известных сейчас способов порожде-
ния перестановок с минимальным изменением получен с помощью
применения метода макрорасширения, изложенного в разд 4 1 4,
к алгоритму минимальною изменения, приведенному в разд 5 1.4
(см. упражнение 13) См. статьи
Ehrlich G Algorithm 466 Four Combinatorial Algorithms, Comm.
ACM, 16 (1973), 690—691,
Dershowitz N A Simplified Loop-Free Algorithm for Generating
Permutations, SIT, 15 (1975), 158—164
Статья Эрлиха также содержит линейный алгоритм порождения
сочетаний и композиций в порядке минимального изменения Теория
этих и аналогичных алгоритмов для кодов Грея и алгоритмов раз-
биения множеств изложена в статье
Ehrlich G. Loopless Algorithms for Generating Permutations, Com-
binations, and Other Combinatorial Configurations, J ACM, 3
(1973), 500—513
Алгоритм порождения случайных перестановок впервые был опуб-
ликован в статье
Moses L Е , Oakland R V Tables of Random Permutations, Stan-
ford University Press, Stanford, Ca , 1963
On был независимо опубликован в статье
Durstenfeld R Algorithm 235 Random Permutation, Comm ACM, 7
(1964), 420
и в работе
De Balbine G \ote on Random Permutations, Math Comp , 21
(1967), 710-712
И в работе де Бальбина, н в статье
Pike М С. Remark on Algorithm 235, Сотт. АСМ, 8 (1965), 445,
отмечено, что этот метод можно применять для получения алгорит-
ма случайных сочетаний, приведенного в разд. 522
Коды Грея были использованы в девятнадцатом веке в качестве
решения головоломки, известной как «китайское кольцо» Название
эти коды получили по имени Фрэнка Грея, который развил теорию
кодов, предупреждающих ошибки при передаче определенных сиг-
налов. Впервые эти коды были опубликованы в работе
Gray F Pulse Code Communication, U S. Patent 2632058, March 17,
1953.
Дальнейшие подробности истории кодов Грея можно найти в
статье
Heath F. G Origins of the Binary Code, Scientific American, 227,
2 (August 1972), 76—83
См также раздел математических игр в том же номере Scien-
tific American, где Мартин Гарднер обсуждает код Грея.
Существует много кодов Грея Однако наиболее широко изве-
стен двоично отраженный код Грея, обсуждавшийся в разд 5 2 1,
и зачастую именно оп рассматривается как собственно код Грея.
Алгоритм 5 7(c) порождения полного двоично-отраженного кода
Грея взят из работы
Bitner J R , Ehrlich G., Reingold E. M. Efficient Generation of
the Binary Reflected Gray Code and its Applications, Comm.
ACM, 19(1976), 517-521
Аналогичный алгоритм описан в статье
Misra J Remark on Algorithm 246, ACM Trans Math Software, I
(1975), 285.
Алгоритм порождения сочетаний в лексикографическом порядке
впервые появился в статье
Mifsud С J Algorithm 154: Combination in Lexicographic Order,
Comm ACM, 6 (1963), 103,
хотя в этой работе не дается анализа требуемого времени или функ-
ции индекс Приведенный в данной книге анализ принадлежит
Брайану Хенше. Возможность построения алгоритма порождения
сочетаний в порядке минимальною изменения на основе кода Грея
была продемонстрирована в статье
Tang D Т , Liu С N Distance-2 Cycle Chaining of Constant Weight
Codes, IEEE Trans Computers, 22 (1973), 176—180
Их алгоритм, который появился в работе
Liu С. N , Tang D Т. Algorithm 452 Enumerating Combinations
of m Out of n Objects, Comm. ACM, 16 (1973), 485,
необычайно сложен Алгоритм и анализ, данные в разд 5 2 2, взя-
ты из указанной выше статьи Битнера, Эрлиха и Рейнгольда
Композиции и разбиения целых чисел являлись областью ин-
тенсивного математического исследования в течение более 300 лет,
с тех пор как Лейбниц спросил Бернулли, исследовал ли он Р(п),
число разбиений числа п Подробную историю вопроса н сведения
об имеющихся вплоть до 1920 года результатах можно найти в гл 3
книги


Dickson L. Е History of the Theory of Numbers, Vol 11, Diophan-
tine Analysis, Chelsea Publishing Co , New York, 1971
Дополнительные подробности и более поздние результаты можно
найти в большинстве книг по комбинаторике, см., в частности, книгу
Hall М. Combinatorial Theory, Blaisdell, Waltham, Mass., 1967
[Имеется перевод Холл М , Комбинаторика — М.‘ Мир, 1970 1
Здесь стоит упомянуть один результат (см, стр. 39—42 книги Холла)
PW
Первый алгоритм порождения разбиении, приведенный в
разд 5 3.2, очень сгар и открыт К. Ф. Гинденбургом в 1778 г Второй
и гораздо более эффективный способ порождения разбиений принад-
лежит Гидеону Эрлиху
Общий метод порождения случайных комбинаторных объектов
и его применение к разбиениям взяты из статьи
Nijenhuis A., Will Н. S. A Method and Two Algorithms on the
Theory of Partitions, J. Combinatorial Theory (&.), 18 (1975),
219—222
5.5.	УПРАЖНЕНИЯ
и найдите решение этого рекуррентного соотношения [Указание подставьте
Тп—С„\ (Зя+1)/2 ] Используйте величины 1П и Сп для того, чтобы дать полный
затрагивают элементы перестановки Считайте операцию*-» равнозначной трем
операциям <— и рассматривайте каждое сравнение как арифметическую опера-
дельности "перестановок, который следит за факториальным представлением
для транспозиции л/«-»л/. Проанализируйте этот алгоритм и сравните его с ана
лизом в упражнении 2
5 Модифицируйте алгоритм, описанный в упражнении 4 так. чтооы вместо

по числу операций с алгоритмом из упражнения 4.
6 (а) Найдите вектор инверсий для перестановки (4, 3 6, 7, 2, 5, 8, 9 1)
(Ь) Найдите перестановку вектор инверсий которой есть
9 Каковы последние две перестановки на множестве {1 2,	, п} в последо-
вательности с минимальными изменениями, описанной в разд. 5 I 4?
(при подходящей технике обработки списков) с тем, чтобы сделать время, требу
ющееся для преобразования одной перестановки в следующую, постоянным, не
зависящим от п. [Указание: Прочтите разд. 5.2 1] Посте выполнения упражнения
12 определите, дает ли это изменение экономию
раз Объясните, почему сравнение «п=/= 1 > вино шяется п' Н раз Используйте
операций, требуемых для порождения п' перестановок и сравните ответы с ре-
зультатами упражнений 2 и II
относительно малое число элементов делают большинство передвижений. На-
пример в лексикографической последовательности самый правый элемент дви-
гается половину времени, в то время как в последовательности с минимальными
более быстрые алгоритмы, записывая особый код для этих часто встречающихся
выполнения в общем цикле. Эта идея встречалась в разд. 4.1.4 при использовании
Р14 Предположим, что мьРизменяем алгоритм порождения случайных пере
for i = 1 to п do л,<->лпП(1(1кгП
те на I м шаге i й элемент транспонируется с элементом случайно выбранным
из всех п элементов. Остаются ли перестановки равновероятными? {Указание:
п! для л>3 ие является делителем пп ) Полагая, что вначале n, = i,	вы-
числите вероятность тождественной перестановки {Указание: покажите, что
15 Напишите программу для "определения при разных значениях п числа
перестановок 11= (л, л3, .... nJ па множестве {1,2 .., и}, которые обладают
16 Постройте и проанализируйте алгоритм порождения всех перестановок
224

18. Постройте и проанализируйте алгоритм вычисления обратной переста-
новки х) на месте *)
19. (а) Беспорядком на множестве 1, 2, .... п} называется перестановка
П= (л„ л2, ,пп}, у которой для любого I. Сколько существует беспоряд-
ков на множестве (1, 2, .	я}’ [Указание установите рекуррентное соотношение
порядков.на множестве {1, 2, п} [Указание: используйте рекуррентное соот-
{1, 2, .. . nf. такой чтобы все беспорядки были равновероятны. [Указание: ис-
пользуйте технику из разд. 5.3.2 и рекуррентное соотношение из п. (а) ]
ротов и отражений) способов размещения элементов множества {1, 2, п}
по окружности Придумайте и проанализируйте алгоритм порождения венков
(Ь) Придумайте алгоритм для порождения случайного венка, полагая, что
все (п—1)! венков равновероятны и докажите корректность этого алгоритма
единиц, 1<&<л—1 Докажите, что для некоторого ОО
в виде
+ +(?) 
где 0<Пз<а?< ..<а#<тг Как это можно использовать при порождении соче-
Грея, данную в разд 5.2 1	[ '	“
исходов нужно только Igfn!/(п—й)!й!? двоичных разрядов. Как теряются Igfel
порядке возрастания длин в лексикографическом порядке для каждой фиксиро-
’) См сноску на стр 193.— Прим, ред
элементов перестановки См стр 309 — Прим ред.
5 5 Упражнения
225
29 Придумайте и проанализируйте алгоритм минимального изменения ком-
30 Покажите что композиции числа п из k частей можно порождать в воз
(Оказание. определите pt—i>j—d^t j-

индекс 1(рь ръ .. , ps)] =


рождал только такие разбиения п, в которых компоненты удовлетворяют условию
(Ь) Сконструируйте алгоритм, анало1ичный алгоритму (а), для порождения
для некоторого и )<й<л. (Указание, порождайте разбиения в словарном по
ваться^перемещёнием одного элемента из одною подмножества в другое
к разбиениям множества. (Указание: пусть ап — число разбиений множества из п

и (Uj u2,	• ип} с целочисленными компонентами Придумайте и проанализи-
руйте алгоритмы для порождения точек решетки в лексикографическом порядке
8 Я= 780
Глава 6. Быстрый поиск
Задача поиска является фундаментальной в комбинаторных ал
горитмах, так как она формулируется в такой общности, что вклю-
чает в себя множество задач, представляющих практический инте-
рес При самой общей постановке «Исследовать множество Т с тем,
чтобы найти элемент, удовлетворяющий некоторому условию С»,
о задаче поиска едва ли можно сказать что-либо стоящее Удиви-
тельно, однако, что достаточно незначительных ограничений на
структуру множества Т, чтобы задача стала интересной' возникает
множество разнообразных стратегий поиска различной степени эф-
фективности
В гл 4 мы имели дело с таким положением, когда необходимо ис
следовать все множество Т или большую его часть, чтобы наверняка
найти элемент, отвечающий спецификации (если таковой существу-
ет). Для множества из п элементов при таком подходе время поиска
составляет О (п). В этой главе будут сделаны некоторые предполо
жения о структуре множества Т, позволяющие исследовать Т за
время 0(log п) или 0(1) Большинство алгоритмов поиска попадает
в одну из трех категорий, характеризуемых временем поиска 0(п),
О (log п) и 0(1)
6.1.	ПОИСК И ДРУГИЕ ОПЕРАЦИИ НАД ТАБЛИЦАМИ
Любой способ поиска оперирует с элементами, которые будем
называть именами, взятыми из множества имен S, называемого
пространством имен. Это пространство имен может быть конечным
или бесконечным Самыми распространенными пространствами имен
являются множества целых чисел с их числовым порядком (нумера-
цией) и множества последовательностей символов лад некоторым ко-
нечным алфавитом с их лексикографическим (т. е. словарным) по
рядком
Каждый из алгоритмов поиска, обсуждаемых в этой главе, ос
новая на одном из трех следующих предположений о пространст-
Предположение 1. На S определен линейный порядок, называе-
мый естественным порядком и обозначаемый знаком <С. Такой по-
рядок имеет следующие свойства:
1	Любые два элемента х, усравнимы, т е должно выпол-
няться в точности одно из трех условий- х<у, х=у, у<.х
2	Порядок обладает транзитивностью, т е если х<у и у<г,
то х<г для любых элементов х, у, z£S Мы используем обозначе-
ния >, 5s в очевидном смысле. При анализе эффективности ал-
горитма поиска полагаем, что исход «, — или >) сравнения х . у
получается за время, не зависящее от мощности |S| пространства
имен S и от мощности п исследуемой таблицы Т
Предположение 2. Каждое имя в S есть последовательность
символов или цифр над конечным линейно упорядоченным алфави-
том А = {аи а2,	 , ас} Естественным порядком на S является
лексикографический порядок, индуцированный линейным поряд-
ком на А Мы полагаем, что исход «, = или >) сравнения двух
символов (не имен) получается за время, не зависящее от IS1 или п.
Предположение 3. Имеется функция h- S {0, 1,	, m— I},
которая равномерно отображает пространство имен S в множество
{0, 1, . . , m—1}, т е все целые i,	—1, приблизительно с
одинаковой частотой являются образами имен из S при отображении
h Мы полагаем, что функция h может быть вычислена за время, не
зависящее от IS! и п
Предположение 1 очень сильное, поскольку нет теоретического
обоснования того, почему возможно сравнение имен за время, не
зависящее от размерности пространства имен Однако это часто вы-
полняется на практике, когда для имени отводится фиксированное
число ячеек памяти Предположение 2 является самым реалистич-
ным из трех предположений Предположение 3 с его требованием,
чтобы время вычисления h не зависело от ISI, с теоретической точки
зрения выглядит шатко, но с практической — довольно реально.
Как уже было отмечено, поиск производится не в самом прост-
ранстве S имен, а в конечном подмножестве Г—{хь х2, • . хп]
множества S, называемом таблицей На большинстве таблиц, кото-
рые мы рассматриваем, определен линейный порядок, называемый
табличным порядком ему соответствует нижний индекс имени (т. е.
Xi есть первое имя в таблице, х2 — второе и т п ) Табличный по-
рядок часто совпадает с естественным порядком, определенным на
пространстве имен, однако такое совпадение не обязательно
Мощность таблицы Т обычно намного меньше, чем мощность
пространства имен S, даже если S конечно Например, телефонная
книга большого города может содержать 10е записей, или имен,
которые можно рассматривать как имена, взятые из пространства
последовательностей с не более чем 20 символами над алфавитом,
состоящим приблизительно из 30 разных букв При этом предполо-
жении имеем п = |Г|«10в и |S|«103° Обычно на практике простран-
ства имен бывают такими большими, что часто становится безраэ-
228
личным, считать пространство имен конечным или бесконечным
В примере с телефонной книгой мы с тем же успехом могли предпо
лагать, что пространство имен состоит из всех последовательностей
букв произвольной (конечной) длины.
Представление о таблице как об упорядоченном множестве имен,
существенно для многих целей, но иногда бывает необходимо рас
содержать одно имя Например, если процесс включения нового
имени рассматривать более подробно, то обнаружится, что сначала
нужно расширить табчипу добавлением ячейки, для того чтобы за
готовить место для новой записи только потом туда заносится новое
Всюду в этой главе мы будем предполагать, что имена появляют-
ся в таблице не больше одного раза (исключение составляет переход-
ный период, в течение которого заносится новое имя, в таблице до-
пускается два вхождения одного имени) В большинстве случаев
вследствие такого предположения таблица с п именами имеет ровно
п ячеек Однако важный класс ачгоритмов, основанных на вычисле-
нии адреса (разд 6 5), опирается на предположение о том, что таб
лица содержит больше ячеек, чем имен Эти алгоритмы должны че1
ко принимать во внимание наличие пустых ячеек
Существует ряд синонимов для объектов, именуемых здесь таб-
лицей и именем- В обработке данных существуют файлы, элемента
ми которых являются записи, каждая запись есть последователь-
ность полей, одно из которых (участвующее в поиске) называется
ключом. Если сам файл проходится во время поиска, то «файл» и
«ключ» представляют собой то, что мы называем «таблицей» и «име-
нем» соответственно (Эта терминология несколько двусмысленна,
поскольку понятие «ключ» можно отнести либо к самой ячейке, либо
к содержимому ячейки.) Однако при поиске в большом файле часто
не подразумевается просмотр самого файла; вместо этого поиск осу-
ществляется на справочнике или указателе файла. При успешном по-
иске найденная в указателе отдельная запись указывает на соответ-
ствующую запись в файле При таком типе организации файлов на-
шему понятию таблицы соответствует указатель или справочник
В настоящей главе обсуждается много алгоритмов поиска имени
г в таблице Из всех операций, производимых над таблицей, отыска-
ние одного элемента является наиболее общей. Действительно, су-
ществуют таблицы, на которых после их построения никогда не
производится других операций Тут разумно не пожалеть усилий
и построить Эти таблицы так, чтобы минимизировать время поиска
Это положение иллюстрируют оптимальные бинарные деревья по-
иска (разд 6.3 2) и некоторые методы вычисления адреса (разд 6 5)
На большинстве таблиц, однако, производятся операции, отлич
ные от поиска имен Самые важные из них такие, модификация таб
лицы, запись имен в нужном порядке, объединение нескольких таб-
229
ном выполнении некоторых из этих операций, мы уже не в состоянии
так оптимизировать структуру таблицы, чтобы добиться наибыст-
рейшего возможного поиска Компромиссом здесь будет решение,
в котором время поиска удлиняется из соображений более гибкой
организации таблицы, т е такой организации, которая позволяет
выполнять некоторые виды операций с относительном легкостью
Почти все алгоритмы поиска из данной главы — результат этого
компромисса.
Мы рассматриваем только четыре табличные операции поиск,
включение, исключение и распечатка Подробное определение того,
что должны делать эти операции над таблицей 7 = {xt, х3,	, х„},
зависит от структуры данных, использованной для реализации
таблицы
поиск z
вкчючение г
переменной i присвоить такое значение, что
г -ху, в противном случае указать, что zfrT
юшее место
включить г на т-е место
включить имя z сразу после имени
исключить г
До включения 71={х11
*. + 1...Ч}.
После включения Г = {х,.
. . , X,_LZ, X;,	. , хп\
если г g Т, то исключить его
иногда реализуется процедурой по*
последующей процедурой
исключить с i-го места
исключить х, из Т.
До исключения 7' = ^х1, .. , х,_{,
Л-„ х; + 1,	х„\
После исключения Т = -[Хр . .
Таблица, в которой осуществляются включения или исключе-
ния, называется динамической; в противном случае она носит назва-
ние статической
Последней операцией, которую мы будем рассматривать для каж-
дой табличной структуры, является
распечатка выпечатать все имена из Т в их естественном
порядке
Если табличный порядок соответствует естественному, распечат-
ка является простой операцией, если же они не связаны, как в
большинстве методов вычисления адресов, распечатка предполагает
и сортировку
Среди всех операций, которые можно производить над таблица-
ми, четыре, рассматриваемые в этой главе (поиск, включение, исклю-
чение и распечатка), и сортировка (гл 7) — наиболее важные Сор-
тировка обсуждается отдельно, потому что время ее выполнения
значительно превышает времена выполнения четырех других опера-
ций" она требует времени не менее сп log п, тогда как все другие
операции для большинства табличных структур (исключая распе-
чатку элементов в естественном порядке для большинства методов вы-
числения адресов) можно выполнить за время О(п)
6.2.	ПОСЛЕДОВАТЕЛЬНЫЙ ПОИСК
Под последовательным поиском мы подразумеваем исследование
имен в том порядке, в котором они встречаются в таблице При та-
ком поиске в таблице в худшем случае получается просмотр всей
таблицы, даже в среднем последовательный поиск имеет тенденцию
к использованию числа операций, пропорционального п Для боль-
ших таблиц его не следует относить к методам быстрого поиска, по-
скольку последовательный поиск асимптотически гораздо медлен-
нее других алгоритмов, описанных в этой главе Несмотря на его
низкие асимптотические возможности, имеется ряд причин, по ко-
торым этот метод следует обсудить вначале Во-первых, хотя идея
его проста, он позволяет нам ввести важные понятия и методы, при-
менимые к поиску вообще Во-вторых, последовательный поиск яв-
ляется единственным методом поиска, применимым к отдельным
устройствам памяти и к тем таблицам, которые строятся на прост-
ранстве имен без линейного порядка. Наконец, последовательный
поиск является быстрым для достаточно малых таблиц и для боль-
ших таблиц, организованных иерархическим способом более быст-
рый метод используется для исследования окрестности верхушки
иерархии, а последовательный поиск — для подтаблиц на нижнем
уровне иерархии
Для последовательного поиска по таблице T={xj, х2, .. ,
мы предполагаем, что имеется указатель i, значение которого при-
надлежит отрезку	или, возможно, О^г'^п+1 Над этим
указателем разрешается производить только следующие операции
первоначальное присваивание ему значения 1 или п (или, если удоб-
нее, 0 или п+1), увеличение и/или уменьшение его на единицу и
сравнение его с О, I, п или п+1. При таких соглашениях наиболее
231
очевидный алгоритм поиска в таблице Т первого вхождения данного
имени г имеет вид алгоритма 6 1 Здесь, как и во всех других алго-
ритмах поиска, изложенных в настоящей главе, мы полагаем, что
алгоритм останавливается немедленно по отыскании г или установ-
лении, что г в таблице нет
Рассмотрим некоторые аспекты эффективности последователь-
ного поиска, начиная со стандартных методов программирования.
В программе, построенной в виде одного цикла, как алгоритм 6 1,
любое значительное ускорение должно быть следствием улучшения
кода в цикле Для того чтобы увидеть, какие операции выполняются
внутри цикла, необходимо переписать алгоритм 6 i в форме, близ-
кой к языку машины
цикл if г == х, then
if i = n then
[найдено]]
[не найдено])
goto
ЦИКЛ
За каждую итерацию выполняется до четырех команд два срав-
нения, одна операция увеличения и одна передача управления
Для ускорения внутреннего цикла общим приемом является до-
бавление в таблицу специальных строк, которые делают необяза
тельной явную проверку того достиг ли указатель границ таблицы.
Это можно сделать в алгоритме 6 1 Если перед поиском мы добавим
искомое имя z в копие таблицы, то цикл всегда будет завершаться
отысканием вхождения г, таким образом, нам не нужно в цикле каж-
дый раз делать проверку i=n В конце цикла проверка условия с>л,
выполняемая лишь однажды, говорит о том, является ли найден-
ное вхождение z истинным или специальным элементом таблицы Эта
техника демонстрируется в алгоритме 6.2
232
Улучшение алгоритма 6.1 будет наиболее очевидным, если мы
перепишем алгоритм 6 2 в тех же близких к языку машины обозна-
чениях, которые использовались раньше.

if z = x, then goto возможно
возможно
goto цикл
if 1^.п then [[найдено, i указывает на г[]
else [[не найдено]}
При каждой итерации выполняю! ся лишь три действия вместо че-
тырех, как это было в алгоритме 6.1. Таким образом, в большинстве
вычислительных устройств цикл в алгоритме 6.2 будет выполняться
гораздо быстрее, чем в алгоритме 6 1, и поскольку скорость цикла
определяет скорость всей программы, такое же сравнение имеет ме-
сто для двух программ
Печально то, что фокус с добавлением г в конец таблицы перед
поиском удается, только если мы имеем прямой непосредственный
доступ к концу таблицы Это возможно, если таблица хранится в па-
мяти с произвольным доступом, но невозможно в общем случае, ког-
да используется связанное размещение или память с последователь
ным доступом (такая, как лента)
Единственным недостатком алгоритма 6 2 является то, что при
безуспешном поиске (поиске имен, которых нет в таблице) всегда
просматривается вся таблица Если такой поиск возникает часто,
то имена надо хранить в естественном порядке, это позволяет завер
шать поиск, как только при просмотре попалось первое имя, боль-
шее или равное аргументу поиска В этом случае в конец таблицы
следует добавить фиктивное имя оо для того, чтобы гарантировать
выполнение условия завершения (сю — это новое имя, которое по
предположению больше любого имени из пространства имен 5)
Таким образом, получаем алгоритм 6.3.
Для того чтобы проанализировать время последовательного по
иска в таблице, содержащей п имен, за единицу времени примем
время, требующееся для исследования одного элемента таблицы Ис-
следование строки таблицы включает сравнение пары имен, увели-
чение указателя, передачу управления и, возможно, в менее эф-
фективных алгоритмах сравнение пары указателей Таким образом,
для нахождения т-го имени Xt в таблице требуется t единиц времени.
Для вычисления среднего времени поиска мы должны задать ин-
формацию о частоте обращения к отдельным именам Простым и
самым естественным предположением в отсутствие специальной ин-
формации о фактической частоте является предположение о том, что
частота обращения распределена равномерно, т. е. что ко всем име-
нам в таблице обращаются одинаково часто Это означает, что сред-
нее время поиска Sn для успешного поиска равно всего лишь

Для безуспешного поиска среднее время равно приблизительно п/2,
когда имена хранятся в естественном порядке, или равно п, когда
это не так (см упр I) Предположение о равномерной частоте об-
ращения редко оказывается справедливым обычно основное время
поиска уходит на малую долю имен Если таблица является стати-
ческой (или если модификации появляются лишь изредка), можно
собрать статистику о частоте обращения и, используя эмпирически
установленное распределение, реорганизовать таблицу так, чтобы
уменьшить время поиска Если а; обозначает частоту обращения к
имени л?(, т е аг^0 и ^аг=1, то среднее время поиска
минимально, когда имена встречаются в таблице в порядке невоз-
растания частоты обращения, т. е при табличном порядке
. .^а„. (См доказательство в упр 2 и обобщение в упр 3 )
На практике частоты обращения часто далеко не одинаковы, так
что обращение к таблице в порядке невозрастания частот обращения
может существенно уменьшить среднее время поиска Например,
одно из распределений частот, на основании которого проводится
обращение ко многим таблицам на практике, есть закон Зипфа.
— для i = 1, 2.......п,
где нормирующая константа с выбирается так, что
Таким образом,
234
согласно равенству (3.13) В случае, когда имена в таблице упорядо-
чены в соответствии с убыванием частоты обращения,удовлетворяю-
щей закону Зипфа, среднее время успешного поиска равно
s„=L'

что примерно в In л раз быстрее, чем соответствующее среднее
время у(л—1) для таблиц, хранящихся в естественном порядке
допивание имен приводит к существенному изменению среднего вре-
мени успешного поиска.
Заметим, что при уменьшении среднего времени успешного по-
иска мы увеличили время, требующееся при безуспешном поиске, с
у до л, поскольку табличный порядок отличается от естественного
Когда распределение частот a prion неизвестно и эмпирические
наблюдения невозможны или неудобны, все равно следует исполь-
зовать преимущество различных частот обращения для уменьшения
среднего времени успешного поиска В самоорганизующемся файле
при пользовании таблицей так меняется табличный порядок, что
имена, к которым обращаются часто, передвигаются в направлении
начала таблицы Эта тема разрабатывается в упр 5
Мы видели, что реализация и производительность алгоритмов
поиска зависят сп таких свойств таблицы, как хранение имен в ес-
тественном порядке. Для других распространенных табличных
операций эта зависимость даже более резко выражена Например,
выписывание имен в естественном порядке есть последовательный
просмотр с временем О(п), когда табличный порядок совпадает с ес-
тественным. но требует сортировки (процедура с временем О (п log п),
см гл. 7), если это не так С другой стороны, включение и исключе-
ние зависят главным образом от структуры данных, выбранной для
представления таблицы, нежели от порядка имен в таблице
Двумя наиболее важными структурами данных для последова
тельного поиска являются связанные списки, которые можно ис
пользовать только в случае памяти с произвольным доступом, и по
следовательно распределенные списки, которые можно использо
включение и исключение в связанном списке требует только из
менения нескольких указателей, если известно соответствующее
место (см рис 24 и 2.5) Таким образом, если отыскание точного
местоположения отделено от фактического включения или исключе-
ния, последние две операции могут быть выполнены за время, не за-
висящее от размера таблицы.
235
В последовательно распределенной таблице последовательные
имена хранятся в последовательных ячейках (см рис. 2.1) Поэтому
исключение имен образует пропуск, который должен быть запол-
нен, а включение имен требует, чтобы был образован пропуск.
В обоих случаях в таблице должно быть передвинуто или перепи-
сано много имен, и, как показывает алгоритм 6.4, эти операции
требуют времени 0{п)
В этом разделе мы увидели, что даже простой последовательный
поиск требует выбора разумной конструкции. Но, что важнее, мы
поняли, что использование метода, улучшающего алгоритм в одном
отношении, может ухудшить его в других. Например, таблицу обыч-
но нельзя хранить одновременно в естественном порядке и порядке
невозрастания частот обращения Следовательно, создание струк
туры таблицы и соответствующих ей алгоритмов часто должно быть
компромиссом между несколькими желаемыми, но взаимно несов
местимыми свойствами К сожалению, в оставшейся части главы мы
обнаружим, чго эти конструктивные решения становятся более
трудными, когда приходится иметь дело с более сложными структу-
рами данных и алгоритмами поиска
6.3.	ЛОГАРИФМИЧЕСКИЙ ПОИСК В СТАТИЧЕСКИХ
ТАБЛИЦАХ
Мы говорим о логарифмическом времени поиска, как только воз-
никает возможность за время с, не зависящее от п, последовательно
свести задачу поиска в таблице, содержащей п имен, к задаче поиска
в таблице, содержащей не более ап имен, где а<1 — константа
В этом случае время t(n), требующееся для поиска в таблице с п
именами, удовлетворяет рекуррентному соотношению
решение которого имеет 8 ид
где b определяется начальными условиями и коэффициент с при ло»
гарифме есть время, требуемое для уменьшения размера табтицы от
п имен до ап.
Самыми распространенными предположениями, которые дают
возможность уменьшить размер таблицы от п до ап за время, не за
висящее от п, являются предположения о том, что пространство
имен S линейно упорядочено и что сравнение двух имен х,у из S (для
определения х<у, х—у и х>у) есть элементарная операция, тре
бующая постоянного количества времени, не зависящего от п В ре
зультате время, необходимое для большинства логарифмических
алгоритмов поиска естественно измеряется числом сравнений (с тре
мя исходами) пар имен Для некоторых алгоритмов, однако, более
естественны сравнения с большим, но фиксированным числом ис
ходов
В этом разделе мы рассматриваем только статические таблицы,
т е таблицы, в которых включение и исключение либо не ветре
чаются, либо так редки, что когда они появляются, строится новая
таблица Динамические структуры таблиц, допускающие логариф
мическое время поиска, так же как и эффективные алгоритмы вклю
чения и исключения, обсуждаются в разд 6 4 Для статических таб
лин нужно обсудить лишь алгоритмы поиска и построения таблицы
Алгоритмы поиска достаточно просты, но некоторые из алгоритмов
построения таблицы сложны Такая ситуация возникает потому, что
в случае статической таблицы разумно считать частоты обращения
известными, и может быть стоит затратить существенные усилия на
построение оптимальной таблицы — таблицы с минимальным сред-
ним временем поиска (относительно данных частот обращения) 4л
горктмы построения таблиц и их анализ являются наиболее важны-
ми темами этою раздела
6.3.1.	Бинарный поиск
Когда ячейки таблицы последовательно распределены в памяти
с произвольным доступом и имена хранятся в таблице в их естест
венном порядке, возможен бинарный поиск — один из наиболее
широко используемых методов поиска Идея этого метода состоит
в том, чтобы искать имя z в интервале, крайними точками которого
являются два заданных указателя I (для «низа») и h (для «верха»).
Новый указатель т (для «средней точки») устанавливается где-то
около середины интервала, и либо z находится в ячейке, на которую
указывает т, либо сравнение 2 с именем в этой ячейке сводит интер
вал поиска к одному из интервалов [/, т—1] или [т+1, /г] Ьсли ин
тервал становится пустым, поиск завершается безуспешно
Для получения логарифмического времени поиска существенно
устанавливать указатель т за время, не зависящее от длины интер
вала, это требование делает непригодным бинарный поиск на боли
шиистве вспомогательных запоминающих устройств Требование,
чтобы т помещалось точно в середине интервала, несущественно,
хотя выбор средней точки в качестве т обычно дает самый эффектив
237
ный алгоритм В некоторых частных случаях, однако, полезно раз-
бить интервал на подынтервалы длины а(Л—/+1) и (1—a)(h—/+1)
для фиксированного значения а, отличного от Va (см упр. 7) Когда
таблица размещена не последовательно, а хранится в виде списка
древовидной структуры, доля а должна, вероятно, меняться от
интервала к интервалу (см разд 63 2, 642и64 3)
Бинарный поиск по идее прост, но с деталями условия завер-
шения поиска нужно обращаться осторожно Частные случаи
h—1= 1 и h—1=0 требуют пристального внимания в любой програм-
ме бинарного поиска В алгоритме 6 5 эти случаи обрабатываются
тем же кодом, что и в общем случае, и поучительно посмотреть, как
это делается, проследив за выполнением алгоритма для п=2 и
Корректность алгоритма 6 5 следует из утверждения, данного в
комментарии в начале тела цикла Он устанавливает, что если г
находится где-либо в таблице, то оно должно находиться в интер-
вале [I, Л1, иначе говоря, при нашем предположении, что имя появ-
ляется в таблице не больше одного раза, утверждается, что г не
встречается ни в интервале [1, /—1], ни в интервале [й+1, л] Это
утверждение очевидно первый раз, когда мы входим в цикл при 1= 1
и h=n, и непосредственно по индукции проверяется, что оно вы-
полняется при каждом проходе через цикл Когда мы выходим из
цикла, то должно быть f>/t, и поэтому утверждение принимает вид
?${хъ	, х, и г£{хЛ+ь , хп}, откуда следует, что z£{xj,
При анализе алгоритма 6 5 полезно описать последовательность
сравнений «г : хр как расширенное бинарное дерево (см разд
2 3.3) Первое сравнение — это корень дерева, и его левое и пра-
срав
Дере-
 
ветственно
Легко доказать индукцией по h—I, что высота дерева T(l, ft),
определяемая равенством (bl), равна {”lg(ft—/+2)“| Таким об-
разом, высота Т (1, п) дерева, соответствующего бинарному поиску
в таблице с п именами, равна lg (n+1)Поскольку высота дере
ва равна числу сравнений z хс, которые требуется сделать в худ-
шем случае, мы заключаем, что для таблицы с п именами бинарный
поиск требует не больше f lg(n-H)"| сравнений
Чтобы проанализировать среднее число сравнений, требуемых
для бинарного поиска, рассмотрим две величины Sn — среднее
число сравнений г хг при успешном поиске (обиар\живающем, что
г присутствует в таблице) и Vn — среднее число сравнений г . х,
239
в случае безуспешного поиска (обнаруживающего, что г в таблице
Sn =1-1-2- [длина внутренних путей дерева 7(1, п)|
и Pr(z<Xi) = Pr(z>rn)=l/(n+l), имеем
' (длина внешних путей дерева 7(1, л)]
Используя равенство (2 7), получаем отсюда интересное соотноше-
S. =(1+1)(7.-1.	(6 2)
Объединяя равенство (6.2), тот факт, что 7(1, и) — полностью сба-
лансированное бинарное дерево с 2п+1 узлами (почему5), и равен-
ство (2 10) приходим к
(« + 1) + 2—0 — 2-й,
S. ^(1+4)[|г(" + 1) + 2-0-2‘’в]-1.
где 0=lg(n | I)—+
240

6.3.2.	Оптимальные деревья бинарного поиска
соответствует промежутку в таблице Таким образом, дерево на
241
рис 6 1 фактически представляет собой дерево бинарного поиска
над именами х2, .. , х10. Тот факт, что симметричный порядок
узлов является естественным порядком, означает, что для каждого
тественпом порядке и все имена в правом поддереве узла xt следуют
за х( в естественном порядке.
На рис 6 2 показаны четыре различных дерева бинарного поис-
ка на множестве имен {А, В, С, D} Деревья (а) и (Ь) вырожденные,
поскольку они по существу являются линейными списками, которые
должны просматриваться последовательно
Поиск имени г в дереве бинарного поиска осуществляется путем
сравнения г с именем, стоящим в корне Тогда
1	Если корня нет (дерево пусто), го г в таблице отсутствует в
поиск завершается безуспешно
2	Если z совпадает с именем в корне, поиск завершается ус-
пешно
3	Если z предшествует имени в корне, поиск продолжается ниже
в левом поддереве корня
4	. Если г следует за именем в корне, поиск продолжается ниже
в правом поддереве корня
Если бинарное дерево имеет вид дерева из гл 2, то каждый узел
представляет собой тройку (LEFT, NAME, RIGHT), где LEFT и
RIGHT содержат указатели левого и правого сыновей соответствен
но, и NAME содержит имя, хранящееся в узле Указатели могут
иметь значение Л, означающее, что поддерево, на которое они ука-
зывают, пусто Если указатель корня дерева есть Л. то само дерево
пусто Как и следовало ожидать, успешный поиск завершается во
внутреннем узле дерева бинарного поиска и безуспешный поиск
завершается во внешнем узле
Эта процедура нахождения имени z в таблице, организованная
в виде дерева бинарного поиска Т, показана в алгоритме 6.6 Отме-
тим его сходство с алгоритмом 6 5 (бинарный поиск)
NAME (р) р — LEFT (р)
NAME(p) р — RIGHT (р)
Для того чтобы в дереве бинарного поиска выписать все имена
док обхода бинарных деревьев (см. разд 2 3 2)
Пусть |3|, |32,	, (5П обозначаю-i частоты обращения к именам
•Xi, л 2,	. . R, соответственно и аи, ....ап — частоты, с кото-
242
рыми безуспешный поиск заканчивается в каждом из (п4-1) листьев
дерева бинарного поиска Т Тогда среднее время поиска в Т (по
всем поискам, успешным и безуспешным) можно выразить как
2 [1 4-уровень (X/)j4-	2 ai уровень (у/).
Пусть
I Т I -= 2 0/ уровень 4-	2 «т уровень (уг)
есть взвешенная длина пути в Т. Таким образом, среднее время по-
иска в Т есть
и поскольку не зависит от структуры Т, можно сосредоточить
свое внимание на величине 171
Если частоты а{ и интерпретируются как вероятности, они
должны быть неотрицательными и нормированными так, чтобы
2», + 2b-i
Нам в данном случае важна неотрицательность, а не нормирован
ность, поскольку нормирующую константу 2а«+2^> которая вхо-
дит в \Т\ лишь в качестве сомножителя, можно интерпретировать
как часть единицы измерения Ненормированные величины а, ир,
называются весами (весами листьев и весами узлов соответственно)
Продолжая рассматривать деревья на рис. 6 2, предположим, что
имена А, В, С, D имеют частоты обращения (или веса внутренних
узлов) Pj==1, р2^6, р3 =4, р4 —5 соответственно и что безуспешного
поиска не бывает (все веса листьев равны нулю) На рис. б 3 пока-
заны четыре дерева поиска, соответствующих деревьям рис 6.2
с удаленными внешними узлами и именами, замененными их весами;
приведена также получающаяся взвешенная длина пути. Заметим,
что среднее время поиска в первых двух деревьях более чем в два
раза превосходит среднее время поиска в третьем дереве
Мы заинтересованы в отыскании оптимального дерева бинарного
поиска над множеством имен с данными частотами. При данных весах
строить дерево бинарного поиска Т над упорядоченным множеством
имен X], х2,	, хп, такое, что взвешенная длина пути |Т| мини
матьна
Эта задача дает яркий пример эффективности динамического про-
граммирования, изложенного в разд 4.1 7 Так как существует при-
243
мерно 4re/(nj/ лп) бинарных деревьев с п узлами (см, формулу (3 27)
времени, экспоненциально растущего с ростом п. Динамическое
поиска удовлетворяет следующему принципу оптимальности опти-
мальное дерево бинарного поиска Т с весами а0, рх, alt . , 0Л, ап
имеет некоторый вес в корне, левым поддеревом корня является
оптимальное дерево бинарного поиска Тг с весами 0lt аь ,
р,_1, af-i и правым поддеревом корня является оптимальное дерево
бинарного поиска Тг с весами atl рг+ъ , рл, a„. Оптимальное де-
рево бинарного поиска также удовлетворяет другому требованию
динамического программирования, а именно взвешенную длину
пути ITI можно вычислить с помощью «локальной» информации о
двух поддеревьях Тг и Тг, в частности, |Т| можно вычислить по взве-
шенным длинам путей \7\\ и и суммам всех их весов Wi и Wr
соответственно-
1Л= |Т(Ц-|Гг| + Гг-|-^г,
(6.3)
где
+ 2₽, и»'г=2а,+ 2 р,.
,=0 г = с '	1=1 i=i+i 1
Принцип оптимальности гласит, что для того, чтобы выбрать
корень оптимального дерева, нужно вычислить для каждого узла
с весом (3; оптимальную взвешенную длину пути в предположении,
что является корнем Т Это требует знания оптимальных правого
и левого поддеревьев и если вычисление проводится по рекурсив-
ной схеме сверху вниз, то одни и те же оптимальные поддеревья бу-
дут вычисляться повторно (обсуждение этой проблемы см. в разд
4 1 7) Следовательно, алгоритм построения оптимального дерева
им n + i—1 оптимальных деревьев на i последовательных весах уз-
244
ei только одно дерево Когда процесс заканчивается при i — n, мы
имеем искомое оптимальное дерево на п последовательных весах
На рис 6 4 показано, как этот алгоритм строит оптимальное
дерево на четырех именах А, В, С, D с весами узлов 1,6,4, 5 соот-
ветственно и весами листьев, равными нулю Работа, требуемая на
каждом шаге, явно показана на последнем шаге примера, где опти-
мальное дерево на всех четырех именах выбирается путем сравнения
его взвешенной длины пути с такой же длиной для трех других воз
можных кандидатов Поддеревья, обведенные пунктирной линией,
являются оптимальными деревьями, построенными на ранних эта-
пах алгоритма Хотя в этом примере имеется единственное оптималь-
ное дерево, в общем случае единственность не имеет места
На рис 6 5 показано то же самое вычисление, организованное
в виде матрицы Каждый элемент матрицы содержит всю необходи-
мую информацию об оптимальном дереве, построенном на последова-

тельных именах (начиная с имени, указанного в левой части матри-
цы, и кончая именем, указанным в матрице сверху), в виде
1)	корня оптимального дерева,
2)	суммы весов всех узлов дерева,
3)	взвешенной длины пути в дереве.
Например, верхний правый элемент матрицы описывает опти-
мальное дерево над всеми именами (от А до D), оно имеет корнем С,
су'мма весов всех узлов равна 16 и взвешенная длина пути равна 13
Для того чтобы воссоздать полное оптимальное дерево, достаточно
найти информацию о его левом поддереве, т е. оптимальном дереве
па узлах Л и В Для вычисления взвешенной длины пути в каждом
элементе матрицы используется формула (6.3) Например, взвешен-
ная длина пути оптимального дерева TAncD на четырех именах Л,
В, С, D вычисляется через длины путей |ТЛВ| и |ТД| его оптималь-
ных поддеревьев и сумм их весов и WD соответственно1
Н звсоНР + H +	+	+ / +	15
В примере на рис 6 4 спучай нулевых весов листьев взят только
для простоты представления Когда веса листьев аг не равны нулю,
удобно рассматривать верхний треуюльник в (пЧ I) х (п+ 1)-матрице
вместо лХп-матрицы из предыдущего примера. Каждый элемент
матрицы содержит три величины Для	имеем
Rtf —номер корня оптимального дерева на последова-
тельности весов ah р/+1, az+I, , (3/, af,
— сумма весов сс;+0,+1 + . . Ц-Эу-f-tXy,
Р, —взвешенная длина пути оптимального дерева на
последовательности весов а,, Рг + 1, а,+1, . pz, az
(когда i — j, дерево состоит из одного листа и эта
величина равна нулю)
Заметим, что для вычисления элемента этой матрицы с номером
i, ] нам нужны элементы с номерами u=i, и v=j, u^i Поэтому
структура алгоритма 6.7 проста Два внешних цикла просматривают
все элементы над диагональю (п-t-l) Х(л+1)-матрицы Присваиваю-
щее предложение
RtJ->—любое значение k,
минимизирующее сумму Р( A_t +
+ Pi,/^VI.,„+Wk,	
247
Теорема 6.1. Пусть Rt< j-i — корень оптимального дерева над
а,, Р/+1, .	. P/-I, а;-х и Ri+It } — корень оптимального дерева
над ai+i, Р1+2,	, aJr где 1<!—1 Тогда над а„ +
а} существует оптимальное дерево, корень которою Rij удовлетво-
ряет неравенствам
R, Rh/<
Рис 6 7 иллюстрирует утверждение теоремы о том, что сущест-
предложение алгоритма 6 7 так:
248
Ri_f*—любое значение k, Rt <. k /?, + 1 f,
минимизирующее сумму Pt k~i + Pk,+
+ Wt.k_,^WKf,
6.3.3. Почта оптимальные деревья бинарного поиска
горитма 6 7 практически неприменим (за исключением малых таб-
лиц). Более того, поскольку как правило частоты обращения а
усилий на построение оптимального дерева. Однако существует эф-
фективный (с временем и памятью 0 (/г)) эвристический алгоритм для
построения деревьев, среднее время поиска на которых близко
к среднему времени поиска на оптимальном дереве бинарного по-
иска, и такой алгоритм имеет практическую ценность В этом раз-
деле мы обсудим различные примеры эвристических алгоритмов и
предложим способы избежать плохие эвристики
При данной последовательности частот обращения существуют
две правдоподобные эвристики для построения дерева бинарного
поиска Первая эвристика состоит в том, чтобы поддерживать дерево
«сбалансированным», насколько это возможно. Эта эвристика ес-
249
943	94	29	12
Щ“35	|Г| =34	|П-28
2
рифмического, которое мы ждем от деревьев бинарного поиска. Сре-
ди нескольких понятий «сбалансированности» следующие два име-
ют смысл в этом контексте, выбрать корень (как всего дерева, так
и каждого поддерева) так, чтобы у его левого и правого поддеревьев
максимально близкими были либо (а) число узлов, либо (Ь) суммы
весов. Вторая эвристика состоит в том, чтобы помещать наиболее
часто вызываемые имена около корня При последовательном при-
менении эта эвристика приводит к деревьям, у которых веса узлов
монотонно не возрастают вдоль любого пути от корня к листу, та-
кие деревья называются чонотонными (сравните это с определени
ем пирамиды в разд 7 1 3)
Для иллюстрации этих эвристик на рис 6 8 показаны различные
деревья бинарного поиска на шести именах с частотами обращения
лагаем, что частоты безуспешных поисков, т е веса листьев а,
равны нулю (Все обсуждаемые эвристики обобщаются различными
способами на случай произвольных весов листьев ) Заметим, что от-
ношение среднего времени поиска для «худшего» и «лучшего» среди
предположительно «хороших» деревьев рис 6 8(a) равно 35/20=
= 1 75 Легко удостовериться в том, что одно из четырех деревьев,
имеющее сбалансированное число узлов, оптимально, но в общем
случае это не обязательно Пример также показывает, что дерево,
которое имеет максимально сбалансированные суммы весов, не обя-
зательно оптимально. Главный интересующий нас вопрос состоит
в том, насколько близки к оптимальным могут быть деревья, по-
строенные в соответствии с этими различными эвристиками
Один из способов ответить на этот вопрос — провести экспери-
менты на ЭВМ, при которых порождается много последовательно-
стей весов, строить деревья в соответствии с разными алгоритмами
и собирать статистические данные о результатах. В некоторых ис-
следованиях такого рода, опубликованных в печати, утверждается,
что при эвристических алгоритмах, основанных на объединении
принципов сбалансированных деревьев и монотонных деревьев,
среднее время поиска отличается лишь на несколько процентов от
оптимального. Имеет смысл дать интуитивное объяснение этого яв-
ления, поскольку оно возникает во многих комбинаторных задачах
Представим себе пространство всех деревьев, построенных по дан-
ной последовательности весов и рассмотрим взвешенную длину пути
как функцию деревьев этого пространства Очевидно, для большин-
ства последовательностей (но, конечно, не для всех) эта функция
очень ровная в окрестности своего минимума, т е существует мно
го деревьев, взвешенная длина пути которых близка к оптимальной
Следовательно, легко найти хорошее дерево, но трудно найти опти-
мальное, поскольку оптимальное дерево мало отличается oi других
близких деревьев в его окрестности
Другим способом определения эффективности различных эври-
стик являются статистические предположения о распределении по-
следовательности весов и анализ математического ожидания взве-
шенной длины пути деревьев, построенных в соответствии с различ-
ными алгоритмами Здесь «математическое ожидание» означает взве-
шенное среднее по всем возможным последовательностям весов
Приведем результаты сравнения математического ожидания взве-
шенной длины пути четырех типов деревьев в предположении, что
веса п внутренних узлов pi, р2, .. , рп выбираются последователь-
но как независимые выборки из множества неотрицательных дейст-
вительных чисел с данным распределением вероятностей и что веса
листьев равны нулю. Пусть р — средний вес и Оп, Вп и Мп —мате-
матические ожидания взвешенных длин путей оптимального сбалан-
сированного (относительно числа узлов) и монотонного деревьев
бинарного поиска соответственно, построенных по этим последова-
тельностям весов Пусть Rn — математическое ожидание взвешен-
ной длины пути «случайного» дерева бинарного поиска на п узлах,
такого, что все >злы имеют одинаковую вероятность Гл быть кор-
нем, и что если }зел i — корень, то его левым поддеревом является
случайное дерево бинарного поиска на узлах i, , i— 1 и правым
поддеревом — случайное дерево бинарного поиска на узлах z +1,
, п Эти случайные бинарные деревья служат основой оценки
эффективности других алгоритмов, если оказывается, что деревья,
построенные в соответствии с некоторым эвристическим принципом,
несущественно лучше случайных деревьев, то эвристика сомни-
тельна
В качестве примера техники, используемой для получения по-
лезных статистических результатов, рассмотрим математическое
ожидание взвешенной длины пути Rn случайных деревьев на п уз-
лах Если такое дерево Т имеет корень k, l^k^n, то случайное де-
рево Тi на k—1 узлах будет его левым поддеревом и случайное дере-
во Тг на п—k узлах — его правым поддеревом Взвешенная длина
пути удовлетворяет равенству
Если считать, что все значения k от 1 до п равновероятны и матема-
тическое ожидание суммы всех весов в п—1 раз больше среднего веса
Р, то, рассматривая математическое ожидание обеих частей этого ра-
венства, получаем равенство
которое можно преобразовать к виду
к,
Последнее представляет собой частный случай уравнения (3 20),
которое было решено в разд 3.2.2 Дополнительные аспекты таких
преобразований приводятся в упр. 12.
252
Результаты сравнения различных эвристик неожиданны.
£« =^ilgn + O(n),
Д, =pnlg« + O(n),
Л4„ = (2 1п 2)^>п 1g/1 + 0 (и),
Rn = (2 In 2)p/i lgп -J 0(п)
Другими словами, асимптотически для больших п в среднем по клас
су всех весовых последовательностей, выбираемых в ссильек вин
с описанной выше процедурой, сбалансированные деревья так же
хороши, как оптимальные деревья, и монотонные деревья так же
плохи, как случайные деревья Аналогичные результаты имеют
место в общем случае, когда веса листьев ненулевые и выоираются
независимо из множества неотрицательных вещественных чисел с
другим распределением вероятностей
Плохие свойства эвристик, которые помещают большие веса
около корня, можно понять следующим образом. При наших пред-
положениях все узлы имеют одинаковую вероятность получить наи-
больший вес, т е стать корнем монотонного дерева. Таким образом,
процесс выбора корня всего дерева, так же как корней всех подде-
ревьев, для монотонных деревьев такой же, как для случайных де-
ревьев; этот процесс в результате приводит к сбалансированному
дереву со степенью несбалансированности, указываемой множите-
лем 2 In 2л 1.4 Единственной компенсацией несбалансированности,
получающейся в процессе выбора наибольшего из оставшихся весов
в качестве корня каждого поддерева, является то, что один-един
ственпый вес умножается на меньший номер уровня. Однако в боль-
шинстве весовых последовательностей один вес совсем ненамного от-
личается от суммы других весов. В предшествующем анализе пере-
мещение больших весов вверх по дереву оказывает влияние только
на член 0(п), в то время как эффект несбалансированности дерева
определяет множитель 2 In 2 в главном члене Рп 1g «
Для деревьев бинарною поиска, сбалансированных по сумме
весов, существуют более точные результаты Пусть Оп — взвешенная
длина пути оптимального дерева бинарного поиска для нормиро-
ванного распределения частот (£р, +2а<= и ПУСТЬ Wn — взве-
шенная длина пути сбалансированного относительно сумм весов де-
рева бинарного поиска Тогда можно показать, что
где 5^=5? (ав1 р15	р3,	, ап_ъ р„, ап) — энтропия (см разд
1 5) Другими словами, бинарные деревья поиска, сбалансирован-
ные по суммам весов, никогда не далеки от оптимального
Эти результаты означают, что разумная эвристика состоит
в том, чтобы начинать с некоторого сбалансированного дерева
253
и изменять дерево локально, помещая большие веса ближе к корню,
стараясь не слишком сильно нарушить сбалансированность дерева
в этом процессе Хорошим способом производить такие локальные
изменения являются «вращения», обсуждаемые в разд 6 4.2 Эти
результаты также означают, что если файл статический и если все
записи требуют одинакового объема памяти, то последовательно
распределенная таблица обладает весьма подходящими свойствами
она может быть построена сортировкой (О(п log н)-операция); не
требует расхода памяти на указатели, допускает бинарный поиск,
соответствующим полному бинарному дереву, которое почти так же
хорошо, как оптимальное дерево для большинства практических
случаев
6.3.4. Цифровой поиск
Методы поиска, обсуждавшиеся до сих пор, были основаны толь-
ко на предположении о том, что па пространстве имен S определен
линейный порядок и что время, требующееся для сравнения двух
имен, не зависит от мощности пространства S Не обязательно было
рассматривать детали представления имени и того, как определить,
предшествует ли одно имя другому. Однако, хотя имена обычно
представляются таким образом, что они могут сравниваться простым
вычислением над их представлениями, пространство имен неиз-
бежно будет иметь гораздо более сложную структуру, чем просто
абстрактный линейный порядок, и для таких ситуаций можно скон
струировать некоторые методы поиска Методы цифрового поиска
используют ют факт, что имя или его представление можно всегда
интерпретировать как последовательность букв над некоторым ко-
нечным алфавитом (в крайнем случае над двоичным алфавитом
В качестве примера цифрового поиска рассмотрим построение
таблицы следующих последовательностей десятичных цифр — при-
ближений хорошо известных математических констант:
/2 » 1 414,
ТГТ " 1 44’
е«2 718,
л«3 14159,
Эти шесть последовательностей цифр можно представить в виде
дерева (рис 6 9)
Заметим, что последовательность цифр для каждого имени полу-
чается при прохождении некоторого пути от корня дерева к листу,
заметим также, что идентичные префиксы (т. е начальные подпосле-
довательности) различных имен объединяются до тех пор, пока это
254
возможно. Таким образом, поиск имени г с цифрами dx, d2,	, dt
начинается в корне и продолжается сравнением самой левой еще
несравнивавшейся цифры d} с метками всех ветвей, выходящих из
текущего узла Если d, совпадает с меткой некоторой ветви, то мы
следуем по этой ветви до следующего узла Если ни одна метка с d,
Если все цифры
не совпадает, то поиск завершается безуспешно
имени г найдены, то поиск завершается успешно
Пример из рис 6 9 отличается тем, что ни одно из имен в таблице
не является префиксом другого имени Для многих приложений это
нехарактерно, и поэтому мы представляем два метода, с помощью
которых можно конструировать деревья цифрового поиска для имен,
которые являются префиксами других имен в таблице. Первый ме-
тод состоит в юм, чтобы добавить разряд «конец имени» к каждому
узлу дерева, отмечая таким способом конец слова в этом узле На-
пример, если мы хотим, чтобы 314 было именем и 314159 тоже было
именем, то в узлах, содержащих цифры 4 и 9, надо положить этот
разряд равным 1, а во всех других узлах вдоль пути 314159 надо по-
ложить этот разряд равным 0 Второй метод состоит в том, чтобы
слегка модифицировать имена таким образом, чтобы ни одно имя не
могло быть префиксом другою Например, если именами являются
английские слова, к концу каждого слова нужно присоединить про-
бел; при этом методе «А » и «AN » не будут префиксами «AND»
Дерево цифрового поиска можно представить в ЭВМ многими
способами, по для эффективной реализации представление должно
позволять одновременное сравнение символа в имени с пометками
всех ветвей, выходящих из узла Разбиением слова на составляющие
его буквы ничего не достигается, если эти сравнения осуществляются
путем поочередного просмотра всех выходящих из узла ветвей,
такой метод был бы почти наверняка медленнее бинарного поиска,
который сравнивает два имени целиком в одной элементарной опе-
рации. Один способ превращения многократного просмотра ветвей
255
которое использует эту компоненту). Каждая цифра в подлежащем
поиску имени используется как индекс или указатель соответствую-
щей компоненты такого вектора, которая в свою очередь определяет
следующий шаг поиска. Представленное таким способом дерево циф-
рового поиска называется бором *) На рис 6 10 цифровое дерево по-
иска из рис. 6 9 представлено в виде бора Для экономии объема
памяти последовательность узлов вдоль пути, где ветвление не про-
исходит (как в случае пути, помеченного 14159), сжата в один узел,
изображенный в виде эллипса Поэтому, когда такой узел достн-
25S
гается, оставшиеся буквы искомого имени должны сравниваться
с буквами в узле
Поиск по бору можно проиллюстрировать следующим примером
Для поиска по бору из рис. 6.10 имени 2718 мы используем цифру 2
как индекс в векторе, сопоставленном корню Заметим, что нам не
нужно рассматривать другие компоненты этою вектора, и поэтому
время, требующееся для выполнения этой операции, не зависит от
размера алфавита Найденная компонента является указателем ,ipv
того узла, в котором мы используем в качестве индекса цифру 7
Здесь мы находим указатель специального узла, содержащего суф
фикс имени 18 Соединяя префикс 27, который сопоставляется пу ги в
этот узел, и суффикс 18, который хранится явно, мы получаем полное
имя Заметим, что 2718 найиено за два шага, мы исследовали мини-
мальное число цифр, которые могут выделить это имя просмотром
слева направо из всех остальных имен в таблице Если бы мы искали
имя 23, то натолкнулись бы на пустой суффикс в специальном пус-
том узле, расположенном на конце пути, помеченного 23 Этот пустой
узел необходим для обозначения того, что 23 является именем из
таблицы При отыскании 012345 пустой указатель для нулевой ком-
поненты вектора, сопоставленного корню, определяет поиск как
безуспешный и за один шаг дает ответ, что этого имени нет в таб
Этот пример иллюстрирует два характерных свойства боров они
допускают быстрый поиск, особенно в случае безуспешных поисков,
и они имеют тенденцию к излишнему расходу памяти. Неэффектив
ное использование памяти возникает потому, что схема размещения
поля для каждой буквы алфавита в каждом узле лучше приспособ-
лена для представления всего пространства имен, а не содержимого
конкретной таблицы, поэтому бор обычно содержит место для мно-
гих имен, не принадлежащих таблице.
В общем случае излишний объем памяти возникает в узлах вбли-
зи нижней части бора, в то время как узлы около корня имеют тен-
денцию к полноте Попытки использовать скорости боров без боль-
шого расхода памяти обычно приводят к объединению методов по-
иска по борам для отдельных префиксов имен с некоторыми другими
методами поиска для суффиксов Эта идея используется в словарях
с побуквенными высечками они позволяют определить с одного
взгляда, где начинаются и кончаются слова с любой заданной на-
чальной буквой, но требуют некоюрого другого способа отыскания
конкретного имени внутри этой более узкой области
Методы цифрового поиска заменяют сравнение между двумя
именами последовательностью сравнении между символами в их
представлениях Так как на каждый символ представления требует-
ся только по одному такому сравнению, то время поиска пропорцио-
нально (средней) длине имен. При алфавите из с символов средняя
длина п разных имен не может быть .меньше, чем logcn, таким обра-
зом, цифровой поиск дает время поиска, логарифмическое относи-
тельно размера таблицы, так же как и бинарный поиск Коэффици-
ент пропорциональности зависит от многих факторов, но на практи-
ках многопутевое разветвление от одного символа (для алфавита с с
буквами это обычно с-путевое разветвление) в основном не длиннее,
чем двухпутевое разветвление при сравнении двух имен В этом
отношении цифровой поиск аналогичен одновременно сильно вет-
вящимся деревьям из разд 6 4 4 и методам вычисления адреса из
разд 6.5 Цифровой поиск анало! ичен методам вычисления адреса
и в том отношении, что имеет тенденцию к неэффективному исполь-
зованию памяти — как правило, таблица включает поле для многих
несуществующих имен
Цифровой поиск отличается в важном отношении от всех дру-
гих методов, описанных в этой главе для данного множества имен
существует только одно дерево цифрового поиска, таким образом,
нет вопроса о построении оптимального дерева Любой статистиче-
ский анализ среднего времени поиска зависит только от допущений
о содержимом таблицы Для методов, в которых мы рассматриваем
сравнение имен как элементарную операцию, любое множество п
имен ведет себя так же, как и любое другое (в предположении, что
все перестановки этого множества равновероятны, см разд 6 4 1).
В деревьях цифрового поиска различные множества имен приводят
к борам разного вида и, в частности, длины имен оказывают важное
влияние на время поиска и память, необходимую для боров Анализ
и эксперименты только подтверждают естественное заключение о
том, что в таблице с п именами над алфавитом из с символов поиск
требует в среднем приблизительно logcn шагов с с исходами на каж-
дом шаге.
Включение и исключение в бору прямые (упр. 13), и с этой точки
зрения цифровой поиск можно считать подходящим методом для
динамических таблиц Цифровой поиск обсуждался в связи со стати-
ческими таблицами, поскольку у него нет характерного свойства,
излагаемых в разд 6 4 алгоритмов для динамических таблиц, он не
гарантирует логарифмического относительно размера таблицы вре-
мени поиска в худшем случае
6.4. ЛОГАРИФМИЧЕСКИЙ ПОИСК В ДИНАМИЧЕСКИХ
ТАБЛИЦАХ
Здесь мы рассмотрим организацию в виде деревьев для таблиц,
в которых часто встречаются включения и исключения Что проис-
ходит с временем поиска в дереве, которое модифицировалось путем
включения и исключения’ Если включенные и исключенные имена
258
выбраны случайно, то оказывается, что в среднем время поиска мало
изменяется, но в худшем случае поведение плохое — деревья могут
вырождаться в линейные списки, поиск в которых нужно осуществ-
лять последовательно Проблема вырождения дерева в линейный
список, приводящая к времени поиска 0(п) вместо 0 (log п) в прак-
тических применениях выражена более резко, чем это указывается
теоретическим анализом Такой анализ обычно предполагает, что
включения и исключения появляются случайным образом, но на
практике часто это не так
В этом разделе представлены три различных метода, гаранти-
рующие логарифмическое время поиска даже в худшем случае
Каждый метод основан на деревьях, которые в некотором смысле
«сбалансированы», таким образом, асимметричных деревьев, кото
рые приводят к большому времени поиска, удается избежать
Главной проблемой, которую надо решать в любом таком методе,
является проблема восстановления сбалансированности дерева пос-
ле того, как включение и исключение нарушили его. Этот процесс
восстановления сбалансированности должен осуществляться за
время 0 (log я) с тем, чтобы гарантировать логарифмическое время
поиска, включения и исключения
6.4.1. Случайные деревья бинарного поиска
Как ведут себя деревья бинарного поиска без ограничений
в качестве динамических деревьев^ Другими словами, предполо
жим, что дерево бинарного поиска меняется при случайных вклю-
чениях и исключениях, какова будет средняя стоимость поиска на
таком дереве с помощью алгоритма 6 6? Ответ на этот вопрос даст
нам основание для сравнения утонченных методов, обсуждающихся
в разд 6.4 2 и 6 4 3 Однако до рассмотрения вопроса необходимо
точно описать механику включения и исключения
Для включения г мы используем незначительную модификацию
алгоритма 6.6. Если г не было найдено, мы получаем для z новую
ячейку и связываем ее с последним узлом, пройденным во время
безуспешного поиска z Соответствующее предложение нельзя од
нако просто добавить в конце алгоритма 6 6, поскольку при нор-
мальном окончании цикла while указатель р не указывает больше
на последний пройденный узел, а вместо этого имеет значение А
В связи с этим мы должны производить включение до того, как вы-
полняется предложение p*-LEFT(p) или д *-RIGHT (д), мы
можем осуществить это, сделав процедуру включения рекурсивной,
как в алгоритме 68 Процедура INSERTS, Т) выдает в качестве
значения указатель на дерево, в которое добавлено г Таким обра
зом, T-*-INSERT(z, Т) используется для включения z в Т.
259
T INSERT (г, T)
procedure INSERS (г, T)
INSERT-
NAME (p) •— г
LEFT (д) — RIGHT (p)*— Л
•aseJ name (£):’	(г, LEFT (p))
' г > NAME (p): RIGHT (p)^—INSERT (z, RIGHT (p))
Исключение гораздо сложнее включения, и мы изложим здесь
только основную идею Если подлежащее удалению имя z имеет
самое большое одного сына, то при исключении г его сын (если он
вообще есть) объявляется сыном отца г (см рис 6 11 (а)) Если z
имеет двух сыновей, его прямо удалить нельзя Вместо этого мы
находим в таблице либо имя у,, которое непосредственно предшест-
вует г, либо имя уг, которое непосредственно следует за г в естест-
венном порядке Оба имени принадлежат узлам, которые имеют не
больше одного сына (почему?), и, таким образом, г можно исключить
заменой его либо именем yt, либо именем уг, и затем исключением
узла, который содержал yt или у3 соответственно (рис 6 11(b)).
Частичный ответ на вопрос о влиянии включений и исключений
на вид дерева бинарного поиска дается теперь путем анализа слу-
чайных деревьев из разд 6.3.3 Если алгоритмом 6 8 последователь-
но включаются п имен в первоначально пустое дерево, и если все
перестановки входной последовательности равновероятны, то это
«построение повторным включением» порождает деревья, случайные
в том смысле, как об этом было сказано в разд 6.3.3, с (5(=1,
Отсюда среднее время поиска в таких деревьях, измеряемое
числом пройденных узлов, равно (2 In 2)lg п+О(1), т. е приблизи-
тельно в 1.4 раза больше, чем Ign-i-O(l) —среднее время поиска
в полностью сбалансированном дереве с п узлами
В большинстве приложений можно считать допустимым время
поиска, приблизительно на 40% большее, чем в полностью сбаланси
рованных бинарных деревьях, но деревья бинарного поиска без
ограничений на практике не надежны, поскольку вероятно появле-
ние «пристрастных» последовательностей включений имен в некото-
ром приближенном порядке, и получающиеся в результате деревья
будут не случайны Более того, в худшем случае поведение является
линейным относительно величины таблицы, а не логарифмическим
Схемы балансировки, представленные в следующих трех разделах,
гарантируют логарифмическое время поиска без требований каких
бы то ни было допущений о последовательности включений и ис-
ключений.

6.4.2. Бинарные деревья, сбалансированные по высоте
Наиболее очевидный путь для того, чтобы динамическое дерево
не стало асимметричным, поддерживать его как можно более сбалан-
сированным во все моменты времени Таким образом, если при вклю-
чении в дерево нового имени В, как показано слева на рис б 12,
дерево становится не полностью сбалансированное, ю оно перест-
раивается так, как это показано на рисунке К сожалению, такое
преобразование обычно меняет все дерево в примере на рис 6 12
ни одно из отношений отец — сын не остается неизменным Таким
образом, эта операция перестройки в общем случае требует количе-
ства работы, пропорционального п
Методы балансировки, обсуждаемые здесь и в следующем раз-
деле, имеют то свойство, что если после исключения или включения
требуется преобразование дерева, оно может быть выполнено ло-
кальными изменениями вдоль одного пути от корня к листу; как мы
увидим, это требует времени 0 (log п) Для обеспечения такой гиб-
кости деревья должны иметь возможность отклоняться от пол-
ностью сбалансированных бинарных деревьев, но в настолько малой
степени, чтобы среднее время поиска в них было лишь немногим
больше, чем в полностью сбалансированном бинарном дереве.
Как и в гл 2, пусть А (Г) обозначает высоту бинарного дерева Т,
т е длину самого длинного пути от корня к листу Высота дерева
с одним единслвенным узлом равна 0, и по определению мы считаем
высоту любого пустого дерева равной —1
Определение. Бинарное дерево Т сбалансировано по высоте тогда
и только тогда, когда два поддерева корня Tt и Тг удовлетворяют
условиям
1 |А(Т|)-А(7’,М1,
2 Tt и Тг сбалансированы по высоте
Пустое бинарное дерево, не имеющее ни корня, ни поддеревьев,
удовлетворяет этим условиям и, следовательно, является сбаланси-
рованным по высоте Дерево с единственным узлом является сбалан-
сированным по высоте в соответствии с соглашением о высоте пусто-
го дерева На рис. 6.13 показаны некоторые сбалансированные по
высоте деревья и одно бинарное дерево, не являющееся таковым Ог-
раничение высоты предупреждает сбалансированные по высоте би-
нарные деревья от слишком большого уклонения от полностью сба-
лансированного бинарного дерева Действительно, на рис 6 13(a)
показаны три «наиболее асимметричных» сбалансированных по вы-
соте бинарных дерева среди деревьев высоты 1,2 и 3 соответственно.
Несмотря на то что сбалансированные по высоте бинарные де-
ревья могут выглядеть разреженными, время поиска, которое сии
требуют, лишь слегка больше, чем в полностью сбалансированных
бинарных деревьях Экспериментальные данные позволяют предпо
262
дожить, что средняя длина внутренних путей в сбалансированном
по высоте бинарном дереве с п узлами равна и 1g n+O(n), следова-
тельно, среднее время поиска равно 1g л+О(1), что асимптотически
отличается от среднего времени поиска в полностью сбалансирован-
ном бинарном дереве лишь константой
ны, трудно даже просто перечислить сбалансированные по высоте
бинарные деревья с л узлами (см. упр 18), не говоря уже об анализе
их вида Однако если рассматривать наихудшее (наиболее асиммет-
ричное) сбалансированное по высоте бинарное дерево, то можно
проанализировать максимальное время поиска в дереве (высоту)
и среднее время успешного поиска в дереве (длину внутренних путей,
разделенную на число узлов).
Наиболее асимметричное сбалансированное по высоте бинарное
дерево Тh высоты h имеет наиболее асимметричное бинарное дерево
Тh-i высоты h—1 в качестве одного из своих поддеревьев и наиболее
асимметричное бинарное дерево 7\_2 высоты h—2 в качестве дру-
гого, как показано на рис, 6 14. Наиболее асимметричные сбаланси
263
рованные по высоте бинарные деревья, показанные на рис. 6 13(a)
для h=i, 2 и 3, построены по правилу типа Фибоначчи при началь-
ных пустом дереве T-i и дереве Та с одним узлом
Обозначая число узлов в Th через и длину внутренних путей
в Th через ph, получаем рекуррентные соотношения
(6-4)
Ph = Ph~i + Pfl~2 + nh— 1,	р_1 = ро = 0	(6.5)
Первое решается методом из разд 3.2 2 и дает общее решение
Принимая во внимание начальные условия, получаем
(6.6)
Обращая равенство (6 6), находим
(6.7)
~ 1вГ(1+ У 5)/2]
Таким образом, время поиска в худшем случае (т е высота наибо-
лее асимметричного бинарного дерева) в сбалансированных по вы-
соте бинарных деревьях приблизительно на 44% больше, чем сред-
нее время поиска 1g п в полностью сбалансированных бинарных де-
ревьях и примерно такое же, как среднее время поиска в случайно
построенных деревьях бинарного поиска
Приближенный анализ среднего (в большей степени отражаю-
щего истинное положение, чем худший случай) времени успешного
поиска Sh—Ph/n-h в наиболее асимметричном сбалансированном по
высоте бинарном дереве даже более удобен Деление рекуррент-
ного соотношения (6.5) на лает

Опуская член —1/лй и используя выражение (6.6) для замены
rth-i/rth и ti], г/пк их приближениями [(]4-К5)/2Н и [(1 +Кб)/2|_*
соответственно, получаем
(6.8)
Это рекурр женным в +И5)/21-> ного рекур	ентное соотношение снова можно решить методом, изло- разд 32 2 Используя тождество 1(14-К5)/2]-14-[(1 = 1, находим, во первых, что общее решение однород- рентного отношения, соответствующего (6-8), есть 8л^с	с'	ж с при
и, во-вторь или, более	ях, что (6 8) имеет частное решение вида SA=const-ft, точно, S,, = —к	h, - РР Л ® 0.72Л
Отсюда по.	пуяаем решение соотношения (6 8)
S,	,-ЦрЛ + с + о(1)«ррЛ при	(69)
Для ср< метричных средним вр деревьях м	шнения этого среднего времени поиска в наиболее асим сбалансированных по высоте бинарных деревьях со еменем поиска в полностью сбалансированных бинарных !Ы подставляем <6 7) в (6 9} и получаем |g[(|+^)i2]lgn,«1.04„.	(6 10)
Таким образом, среднее время поиска в наиболее асимметричных сба-
лансированных по высоте бинарных деревьях примерно лишь па
4% больше, чем в полностью сбалансированных бинарных деревьях
Этот результат вместе с тем фактом, что сильно асимметричными
будет только малая доля сбалансированных по высоте деревьев,
подтверждает ранее полученные эмпирическим путем данные о том,
что среднее время поиска в сбалансированных по высоте бинарных
деревьях, усредненное по всем таким деревьям, равно 1g п+О(\)
Проведенный анализ устанавпивает, что сбалансированные по
высоте деревья имеют короткое время поиска; теперь нужно пока-
зать, что включения и исключения можно легко производить, сохра-
няя деревья сбалансированными
Два преобразования деревьев, называемые вращением и двойным
вращением, позволяют нам перестроить сбалансированные по вы-
соте деревья, сбалансированность которых была нарушена после
включения или исключения На рис 6 15 приведены эти два типа
преобразований и показано, как они восстанавливают сбалансиро
ванность дерева, нарушенную включением В левых частях
рис 6 15(a) и (Ь) показано поддерево сбалансированною по высоте
бинарного дерева, в которое только что был включен новый узел
NEW Эго включение может послужить причиной нарушения огра-
ничения на высоту во многих узлах, рассмотрим из них самый ниж-
в узлах, расположенных в дереве выше, будут восстановлены авто-

матически ) В случае вращения два узла с именами А и В, явно по-
казаны на рис. 6.15(a) вместе с их кодами состояний \ и — соот-
ветственно, которые указывают, что перед включением правое под-
дерево дерева А имеет большую высоту, чем его левое поддерево, и
высоты двух поддеревьев дерева В равны (код состояния / появ-
который является, конечно, необходимым условием для выполне-
ния поиска алгоритмом 6.6
Остается определить условия, при которых применяются пока-
занные на рис. 6 15 вращение и двойное вращение (и симметричные
варианты) Это лучше делать неформально
Алгоритм включения. После того как алгоритмом 6 8 включено
новое имя, путь из корня в лист проходится в обратном направле-
нии (Из-за того, что бинарное дерево, как правило, не обеспечивает
явные связи FATHER, это возвращение обычно подразумевает, что
спускающийся путь хранится в стеке ) Действие, предпринимаемое
при прохождении каждого узла по восходящему пути, зависит, во-
первых, от условия на высоту в этом узле (/, — или \) и, во-вто-
рых, в случае, когда условие имеет вид / или \, от направления
последнего шага или двух последних шагов вверх по этому пути
Правила эти следующие
1	Если текущий узел имеет условие на высоту —, то оно ме-
няется на условие \, если последний шаг начинается из правого
сына, и на /, если он начинается из левого сына. Мы продолжаем
следовать вверх по пути до тех пор, пока текущим узлом не станет
корень, и в этом случае процедура заканчивается
2	Если текущий узел имеет условие на высоту / или \
и последний шаг начинается из более короткого из двух поддеревьев
текущего узла, то это условие меняется на — и процедура завер-
шается
3	. Если текущий узел имеет условие на высоту / или \ и по-
следний шаг начинается из более высокого из двух поддеревьев те-
кущего узла, то
(а)	если последние два шага осуществлялись в одном направле-
нии (оба из левых сыновей или оба из правых сыновей), то выпол-
няется соответствующее вращение;
(Ь)	если два последних шага делались в противоположных на-
правлениях, то выполняется соответствующее двойное вращение
В обоих случаях процедура заканчивается
Алгоритм исключения. Сначала имя исключается в соответствии
с алгоритмом на рис 6 11 Это служит гарантией того, что узел,
который исключается, имеет не меньше одного пустого поддерева
Если исключаемый узел имеет ровно одно пустое поддерево, то,
согласно ограничению на высоту поддеревьев, другое поддерево со
стоит из одного узла, как показано на рис 6 16. В этом случае влия-
ние на сбалансированность дерева по высоте такое же, как если бы
исключался лист, следовательно, нам надо рассмотреть только этот
последний случай Когда лист исключается, поддерево, состоящее
именно из этого узла, теряет одну единицу высоты (его высота ме-
няется от 0 до —1). Теперь мы проходим путь от этого исключенного
267
случаях преобразование восстанавливает высоту поддерева до той,
которая была до исключения, если это так, то алгоритм заканчи-
вается, поскольку исключение не влияет на условие на высоту всех
1. Если текущий узел имеет условие на высоту —, то укорачи-
вание дерева не влияет на высоту дерева, имеющего корнем теку-
щий узел Алгоритм заканчивает работу.
268
(а) Подходящее вращение восстанавливает ограничение на вы-
корнем текущий узел, укоротилось
(с) Подходящее двойное вращение восстанавливает ограничение
на высоту поддеревьев в текущем узле Продолжается движение
6 4
2G9
В случаях 2, 3(b) и 3(c), если текущий узел — корень, алгоритм
заканчивает работу
бующему не более одного преобразования, этот алгоритм исключе-
ния может требовать \_h)2 J преобразований, где h — высота всего
дерева (см. упр. 19). Однако в большинстве случаев алгоритм исклю-
чения (и также алгоритм включения) не потребует прослеживания
восходящего пути до самого корня, обычно алгоритм завершается
после некоторого числа шагов, которое не зависит от высоты дерева
(см упр 20)
6.4.3. Бинарные деревья, сбалансированные по весу
В предыдущем разделе мы рассматривали деревья, сбалансиро-
Определение. Пусть Тп — бинарное дерево с узлами, в ко-
тором корень имеет правое и левое поддеревья Ti и Тг с 2^0 и
узлами соответственно Тогда балансом Р(7'п) называется величина
и(т,)=(±].
Заметим, что Р(ТП) определяет относительное число узлов в левом
поддереве дерева Тп и всегда удовлетворяет условию 0<р
поскольку 1+г—п—1
270
Определение, Для у бинарное дерево Тп с узлами
называется деревом с балансом весов а или деревом из множества
WB [а], если выполнены два следующих условия:
1) а«Ж)С1-а,
2) два поддерева Tt и Тг корня дерева Тп принадлежат WB fee]
Пустое бинарное дерево То по определению входит в WB loci
Класс WB [al становится все более и более ограниченным по
мере того, как а меняется от 0 до 1/2. Поскольку а=0 не наклады
вает ограничений вообще, WB 10] представляет собой класс всех
бинарных деревьев Случай а=1/2 означает, что левое и правое под-
деревья каждого узла содержат одинаковое число узлов, поэтому
WB [1/2] принадлежат только полностью сбалансированные би-
нарные деревья с n = 2h—1 узлами В примере на рис 6 17 ба
ланс каждого поддерева выписан рядом с корнем каждого подде-
рева, минимум этих балансов — это максимальное а, такое, что
данное дерево принадлежит WB [а]
Замечание 1 Для любого а из интервала 1/з<а<1/г выполняет-
ся WB [a]=WB [1/г]
Доказательство пусть дерево Т не является полностью сбалан-
сированным бинарным деревом, т е пусть оно не принадлежит
WB Р/J; тогда рассмотрим минимальное поддерево Т (дерево наи-
меньшей высоты) дерева Т, не принадлежащее WB Р/J, т е, не
являющееся полностью сбалансированным бинарным деревом Де-
рево Т' должно иметь два полностью сбалансированных поддерева
ТI, Тг с l=2s— 1 и r=2l—I узлами соответственно, где (скажем,
s<i) Тогда имеем баланс [3 (Т1')—1/(1 -}-2'--s)^y, отсюда Т не может
принадлежать WB lai для любого а>у.
Замечание 2. Для любого а, 0<а< у, в WB[a| существуют
деревья, не являющиеся сбалансированными по высоте,
Доказательство Четвертое дерево на рис 6.17 принадлежит
WB [l/8lsWB [al, но не является сбалансированным по высоте,
Замечание 3. Для любого а, 0-Са^у существуют сбалансиро-
ванные по высоте деревья, не принадлежащие WB [al.
Доказательство Рассмотрим дерево Т, левое поддерево кото-
рого является наиболее асимметричным сбалансированным по вы-
соте _деревом высоты й, показанным па рис 6 14, с nh«1.9 1(1-f-
4-|/5)/2]л узлами, и правое поддерево которого — полностью сба-
лансированное бинарное дерево высоты h с 2л+‘—I узлами Дерево Г
сбалансировано по высоте, но р (Г) -> 0 при h -> оо.
271
Мы заключаем, что видом сбалансированных по весу деревьев
можно управлять, непрерывно изменяя параметр а в отрезке 0<1а^
^2- Более того, сбалансированность по весу и сбалансированность
по высоте являются независимыми критериями сбалансированности.
Для того чтобы показать, что сбалансированные по весу деревья
гарантируют логарифмическое время поиска в динамических табли-
цах, мы должны ограничить время поиска в деревьях из WB [al
и показать, как в дереве, вышедшем из WB [а] в результате включе-
ния или исключения, можно восстановить баланс за логарифмиче-
ское время Восстановление баланса будет сделано для 0<а^
<11—J/ 2/2«0.29 с использованием таких же преобразований (вра-
щения и двойного вращения), как в сбалансированных по высоте
деревьях.
Чтобы получить границу для времени поиска рассмотрим наи-
более асимметричное дерево Тп с п узлами в WB [al («наиболее асим-
метричное» означает теперь нечто иное, чем в предыдущем
разделе). Это дерево имеет a(n-j-l)—l«an узлов в одном из его
поддеревьев (скажем, в левом) и (1—a)(n+l)—1«(1—a)n узлов
272
в другом Оба поддерева являются наиболее асимметричными, от-
сюда высота ha(n) этого наиболее асимметричного дерева Тп в
WB [а] удовлетворяет jекуррентному соотношению
ha(n)=- 1	а) (га + 1)— 1] х 1 +/га[(1 — а)л],
с решением
+ 0(1).
Для полностью сбалансированных бинарных деревьев (а=у) эта
формула дает
^1/2 (n)» lg(n + l),
что и нужно Для а=1—К2/2 — наибольшего значения а, для ко
торого работает описываемый ниже алгоритм перестройки,— имеем
Таким образом, самое большое время поиска в наиболее асиммет
ричном дереве из WB [1—J/2/2] лишь в два раза больше времени
поиска в полностью сбалансированных бинарных деревьях Как и в
сбалансированных по высоте деревьях, среднее время поиска в наи-
более асимметричных деревьях из WB [а] гораздо лучше, чем в худ-
шем случае, как показывает следующая теорема
Теорема 6.2. Если Тп входит в WB [al, то длина внутренних
путей I (Тп) удовлетворяет неравенству
ЦТ..У-
где 5? (а)=—а 1g а—(l--a)lg(l— а) — простой частный случай эн-
тропии, введенной в разд 1 5
Доказательство упр 22
Следствием теоремы 6 2 является тот факт, что среднее время ус
пешного поиска / (Тп)/п в наиболее асимметричных деревьях из
WB [а] не больше [l/,?^ (a)]lg(ra-|-l)+0(l), иначе говоря, от време-
ни успешного поиска в полностью сбалансированных деревьях оно
отличается не больше чем сомножителем 1/3£(а) Для а=1 — р 2/2
имеем l/^f(a)«l 15, так чго для деревьев из WB [1—K2/2J время
поиска увеличивается самое большее на 15% по сравнению с пол-
ностью сбалансированными бинарными деревьями
Лишь малая доля деревьев в WB [al является максимально
асимметричными, и намного большую часть составляют деревья,
близкие к полностью сбалансированным бинарным деревьям Таким
образом, среднее время поиска, усредненное по всем деревьям, су-
щественно лучше, чем определяет теорема 6 2, возможно оно даже
равно 1g п-|-О(1) Тем не менее никакого математического исследо-
влияние этих преобразований на баланс поддеревьев, участвующих
274
но, 1/(2—а)С1—а, т. е а*—За+1^0, которое выполняется для
а^(3—j/5)/2«0.38 По замечанию 1 промежуток WB (-^]—
—WB [0 38] пуст, и поэтому а^О 38 в действительности совсем не
является ограничением Для Рл на рис. 6,19 показано, что имеется
малый отрезок ₽2>(1—2а)/(1— а), где ₽д>1—а, т е где для вос-
становления сбалансированности дерева нельзя использовать вра-
щение. Однако для	г^(1—2«)/(1—а) балансы и Рд принадле-
жат отрезку [а, 1—а! и ближе к 1/а, чем было р4 Поэтому наше пер-
вое правило восстановления сбалансированности таково.
Правило вращения. Вращение восстанавливает сбалансирован-
ность поддерева, когда баланс Pi поддерева равен а и баланс рг
его правого поддерева не больше (1—2а)/(1—а). Симметричное пра-
вило устанавливает, что если pj=l—а и баланс рг левого поддерева
не меньше а/(1—а), то вращение восстанавливает сбалансирован
ность дерева.
Когда узел включается или исключается, для дерева с п узлами
балансы изменяются не непрерывно, а дискретно малыми шагами
величины примерно 1/п Хотя предшествующее вычисление произво-
дилось в предположении ₽!=а, ясно, что результат будет аналогии-
275
ным, когда pi близко к а. В частности, когда Pi опускается немного
ниже а (из-за того, что узел был удален из более легкого поддерева
или добавлен к более тяжелому поддереву), правило вращения ос-
тается верным (рассмотрите, как выглядит (Зй — ₽i+(l—Pi)Pa, когда
Р]=сс—е) Единственное ограничение — это го, что правило не
— у 272
должно применяться к очень маленьким поддеревьям (менее чем с
четырьмя узлами), где включение или исключение узла влечет за
собой большое изменение pi Эти малые поддеревья легко обрабаты-
ваются как специальные случаи
Что делать, когда pi=a и (1—2сс)/(1—а)^р2-^1—а3 В этом civ
чае используется двойное вращение, дающее в результате балансы
27b
как показано на рис. 6 18(b) На рис 6.20 показаны рл, ₽в и Рс как
функции независимой переменной р2Рз с ограничением
поскольку, когда применяется двойное вращение,	—а и
(1—2а)/(1—а)^р2<Д—а. Относительно этой независимой перемен-
ной графики для и такие же, как на рис 6 19, но интересую-
щий нас отрезок другой Для того чтобы обеспечить принадлежность
(Зл и рй отрезку fa, 1—al, мы должны иметь два неравенства
что приводит к а^(3—рг5)/2«0 38 и, таким образом, не налагает
нового ограничения, и
что приводит к а<1—К2/2«0 29 и, таким образом, ограничивает
допустимый отрезок изменения а несколько ниже верхней границы
1/з. Используя ограничение а^1—V 2/2, можно непосредственно
подсчитать, что a^Pc^I—а для допустимых отрезков ₽2 и р8
(упр 23). Таким образом, наше второе правило восстановления
сбалансированности таково
Правило двойного вращения. Двойное вращение восстанавли-
вает сбалансированность поддерева, когда баланс корня некото-
рого поддерева равен а^1—J/2/2 и баланс ра его правого поддерева
не меньше (I—2а)/(1—а) Симметричное правило устанавливает, что
если Рх= 1—а и баланс ра левого поддерева не больше а/(1— а), то
двойное вращение восстанавливает сбалансированность дерева
Для реализации сбалансированных по весу деревьев каждый
узел должен содержать информацию, достаточную для вычисления
его баланса. Вместо непосредственного хранения балансов, удобно
хранить целое значение, такое, как мощность поддерева с корнем
в этом узле (т е число узлов, которое оно содержит) или ранг хра-
нящегося в этом узле имени относительно поддерева с корнем в этом
узле (т е единица плюс мощность левого поддерева этого узла), ба
ланс узла можно вычислить по такой информации, хранимой в узле
(как5) Дополнительное преимущество хранения другой величины
состоит в том, что важные операции, такие, как отыскание /г-го
имени в таблице, g-й кванили или числа имен между двумя данными
именами и у2, все можно выполнить за время О (log п) (упр 24),
эти задачи обычно требуют времени, пропорционального п, если
информация о мощности не хранится явно
Теперь легко описать алгоритм включения или исключения дан-
ного имени z Мы ищем г в дереве, начиная от корня и следуя по
пути к листу При прохождении каждого узла информация о мощно-
сти обновляется, и, если поддерево с корнем в этом узле становится
несбалансированным, выполняется подходящее преобразование де-
рева Как только г найдено (в случае исключения) или найдено
его место (в случае включения), применяются манипуляции с ука-
зателями для включения или исключения узла, описанные в
разд 6 4.1. Затем алгоритм заканчивается, так как все обновления
и восстановления сбалансированности были сделаны во время по-
иска г Заметим, что поскольку уравновешенные по весу деревья не
требуют возвращения по пути вверх к корню, нет необходимости
хранить путь в стеке
Что происходит, когда имеется постороннее включение или ис-
ключение, т е. когда алгоритм включения применяется к уже при-
сутствующему имени или когда алгоритм исключения применяется
к имени, которого нет в дереве’’ В таких случаях вся информация о
мощности должна быть исправлена при втором проходе вниз по де-
реву, но преобразования, выполненные при первом проходе, унич-
тожать не следует Они не нужны, но улучшают сбалансирован-
ность дерева
Если мы сделаем некоторые предположения о распределении ба-
лансов в дереве из WB [а], можно будет оценить математическое
ожидание числа преобразований, которые нужно выполнить во
время включения или исключения. Включения и исключения сдви
гают балансы по интервалу [а, 1—се], и, таким образом, каждый
баланс можно рассматривать как случайное блуждание в непрерыв-
ном интервале с отражающими границами Когда на некотором
шаге баланс выходит из интервала, применяется преобразование
и баланс перемещается ближе к ’/2 Если баланс отражается на то
же расстояние, на которое он пытался уйти, то один из результатов
теории вероятностей утверждает, что получающееся распределение
будет равномерным на интервале [а, 1—а) Однако можно увидеть
из рис 6 19 и 6 20, что ситуация даже более благоприятна, в боль-
шинстве случаев баланс, который достиг границы интервала, сильно
отражается по направлению к Но даже при (слабом) предполо-
жении, что распределение балансов в дереве из WB [о-] равномерно
на [а, 1—а], можно показать, что математическое ожидание числа
преобразований, требующихся для включения или исключения
узла, меньше чем 2/(1—2а) и не зависит от п (упр 25) Для
например, требуется в среднем меньше четырех преобразований.
6.4.4. Сбалансированные сильно ветвящиеся деревья
Деревья бинарного поиска естественным образом обобщаются до
т арных деревьев поиска, в которых каждый узел имеет k-ё^т. сыно-
вей и содержит й 1 имен Имена в узле делят множество имен
278

на k подмножеств, каждое подмножество соответствует одному из k
дерева утверждает только, что каждый узел имеет не более т сыно-
вей и содержит не более т—1 имен Ясно, что на m-арных деревьях
можно осуществлять поиск так же, как на бинарных деревьях
Для поддержания сбалансированности /я-ариых деревьев потре-
буем, чтобы все пути из корня к листу были одинаковой длины и что
бы каждый узел (кроме корня) имел от [* ат до т сыновей для не
которой константы 0<а<1 (Мы будем обсуждать только случай
а=1/«. но возможны и другие значения а ) Этот критерий сбаланси-
рованности гарантирует логарифмическое время поиска (почему?),
и, как мы увидим, в этом случае легко поддерживать сбалансиро-
ванность дерева во время включений и исключений
Как и в деревьях бинарного поиска, полезно различать внутрен
ние узлы и листья Внутренний узел содержит имен, записан
пых в естественном порядке, и имеет fe-H сыновей, каждый из кото-
рых может быть либо внутренним узлом, либо листом Лист не со-
держит имен (разве что временно в процессе (включения), и, как
раньше, в листьях — завершаются безуспешные поиски Обычно за
очевидностью мы на рисунках их опускаем
Определение. Сбалансированное сильно ветвящееся дерево поряд-
ка т есть m-арное дереве, в котором
1)	все листья расположены на одном уровне,
2)	корень имеет k сыновей,
3)	другие внутренние узлы имеют k' сыновей, р т/2 “] ^.k'^rn
На рис 6 22 показано сбалансированное 5-арное дерево, кото-
рое получается в результате включения имени Z в дерево из рис. 6 21
при условии сохранения свойств сбалансированного 5-арного дере-
ва Постепенное исследование преобразования дерева из рис 6 21
в дерево, показанное на рис. 6 22, поясняет процесс включения для
сбалансированных /n-арных деревьев
Включение имени Z начинается с поиска Z. Поиск заканчивается
безуспешно, что можно интерпретировать как то, что Z находится
в листе в соответствии с рис. 6.23 (а) В противоположность деревьям
бинарного поиска сбалансированным сильно ветвящимся деревьям
поиска запрещается расти в листьях, вместо этого их вынуждают
расти в корне Поэтому Z продвигается вверх, в узел, занятый име-
нами И, W, X и У Если бы этот узел не был уже полностью занят,
в него просто включилось бы новое имя. В нашем примере, однако,
узел уже содержит т—1 —4 имени и поэтому в нем нет места еще для
одного имени Пять имен, пытающихся разместиться в этом узле,
нужно разбить на две группы и среднее имя X нужно продвинуть
в узел-отец для тою, чтобы оно служило разделителем между двумя
частями, как показано на рис 6.23(b) Если бы узел-отец не был
полностью занят, то процесс включения закончился бы, но в нашем
примере он уже заполнен до отказа и его необходимо расщепить
Среднее имя Р используется как разделитель между Е, К и U, X
и продвигается вверх. Когда расщепляется корень, создается новый
узел, который становится новым корнем, и дерево вырастает на один
уровень Таким образом, мы получаем дерево рис. 6.22.
Для иллюстрации процесса исключения рассмотрим исключение
имени U из дерева рис 6 22 Поскольку U служит разделителем ме-
жду двумя множествами Q, R, S, Т и V, W, его нельзя просто вы-
черкнуть. Вместо этого оно заменяется своим непосредственным
предшественником в дереве, именем Т (которое может служить раз-
В узле с единственным именем W нарушается условие тою, что каж-
b 4 Логариф чическии поиск в динамических таблицах
281
(С)
Рис (> 24 Исключение имени U из дерева на рис. 6.22. (а) Промежуточная стадия
U исключено из дерева из рис. 6.22 Узел с единственным именем
ним брата (с) Недозаполиенный узел й7 и минимально полный узел
282
дай узел, отличный от корня, должен иметь по крайней мере
Г т/2~| сыновей и, следовательно, должен содержать не меньше
Г т/ 2 "J —1 имен
Узлу, который после расщепления оказался недостаточно за-
полненным, может не хватать только одного имени. Поэтому мы пы-
таемся занять имя в одном из смежных с ним братьев На рис 6 24(a)
левый брат W имеет достаточный запас имен, и поэтому мы можем
добавить разделитель V к узлу W и продвинуть 7 вверх в качестве
нового разделителя, как показано на рис 6.24(b)
Если нет смежного брата, который может одолжить имя, то дол-
жен существовать смежный брат, который заполнен минимально,
т е который содержит ровно Г сгГ2”[—I имен (правый брат W на
рис 6 24(a)) Поскольку недозаполненный узел содержит т/2“]—2
имен после исключения, этот узел, его минимально заполненный
брат и их разделитель в узле-отце могут быть объединены в один
узел с т—1 или т—2 именами. Если мы объединим W и Y, Z на
рис 6 24(a) таким образом, то получим дерево, показанное на
рис 6.24(c). Теперь узел, содержащий V, стал недозаполненным,
и этот же процесс повторяется в следующем более высоком уровне
дерева. В худшем случае алгоритм исключения завершается в кор-
не, тогда высота дерева может уменьшиться на один ярус, как в на-
шем примере Когда мы объединяем V с его левым братом Е, К и с
разделителем Р, мы получаем полностью сбалансированное, пол-
ностью заполненное дерево с двумя уровнями (рис 6.24(d)).
6,5.	МЕТОДЫ ВЫЧИСЛЕНИЯ АДРЕСА
Термин «метода вычисления адреса», известный также как пре-
образования ключа в адрес, методы рассеянной памяти и хеширова-
ние или хешированное кодирование, относится к любому методу по-
иска, который начинается с вычисления адреса по имени. Такие ме-
тода используют свойства памяти с произвольным доступом больше,
чем другие методы поиска
В этом разделе предполагается, что мы имеем память, состоящую
из т ячеек Mj,	—1, при этом каждая ячейка может содер-
жать одно имя, и что при данном значении / мы можем обращаться
к М} за постоянное время, не зависящее от т Эти предположения
выполняются в современных ЭВМ для больших т, и поэтому методы,
описанные в данном разделе, часто применяются на практике
Главным достоинством методов вычисления адреса является то,
что соответствующее им математическое ожидание времени поиска
не зависит от размера таблицы, если вся таблица укладывается в
оперативную память Асимптотически и часто также на практике
они являются самыми быстрыми из известных методов поиска, но
имеют три недостатка Во-первых, табличный порядок имен обычно
не связан с их естественным порядком Во-вторых, при таких мето-
283
дах худший случай может оказаться хуже, чем при последователь-
ном поиске Наконец, таблицы, основанные на вычислении адреса,
расширить динамически непросто: это может приводить к потере
памяти, если таблица слишком велика, или к малой производитель-
ности, если таблица слишком мала Тем не менее методы вычисления
адреса в некоторых случаях являются ценными; многие таблицы, на-
пример, не обязательно записывать в естественном порядке, худшим
случаем часто можно пренебречь, если он возникает достаточно
редко, и размеры многих таблиц можно точно оценить a priori
В разд 6 5 1 основные идеи этих методов иллюстрируются про-
стыми примерами В последующих разделах более подробно обсуж-
даются самые популярные методы
6.5.1.	Хеширование и его варианты
Начнем с очень простого примера, в котором пространство имен
необычно мало Рассмотрим пространство имен S = {/1, В, , Z},
память или хешированную таблицу М={Л40,	..., Л124'} из
26 ячеек с пространством адресов А = {О, 1, ... , 25} и преобразова-
ние ключей в адреса или хеш-функцию h S-> А, которая отобра-
жает буквы в адреса так, чтобы сохранить алфавитный естественный
порядок имен в S (т е h(A)=0,	. , h(Z)-—25) Таблица
7'={х1, х2,	, x„}sS хранится в памяти следующим образом,
в ячейках Л1Л( , размещаются имена х/, а в пустых ячейках — спе-
циальный символ, не принадлежащий S (скажем, —), как показано
на рис. 6 25.
284
Четыре табличные операции выполняются простыми и быстрыми
алгоритмами
поиск г
— 2 then ([найдено: Ь(г) указывает на гД
else [не найдено: г нет в таб тине]]
включение г.
исключение г
распечатка
for I <—0 tom—I do if — then вывести
Отметим, что в алгоритме поиска отсутствует явный цикл, эта
черта характерна для идеального случая метода вычисления ад-
реса Важно, чтобы любой цикл, присутствующий в вычислении
хеш-функции h, не зависел от размера таблицы. В этом случае,
как в предыдущем примере, h можно вычислить в большинстве
ЭВМ за фиксированное число поразрядных операции над двоичными
кодами символов В этом простом примере распечатку имен в ес-
тественном порядке можно выполнить путем простого линейною
просмотра памяти, что весьма не характерно для процедур вычис-
ления адреса. Здесь так получитось потому, что объем памяти ока-
зался равным размеру пространства имен, что является очень
необычным случаем; обычно память слишком мала, чтобы вместить
все пространство имен.
Один способ вычисления адреса применяется к статическим
таблицам, когда хеш-функцию можно выбрать после того, как ста-
нет известно содержимое таблицы В этом случае, воспользовав-
шись специальными хитроумными методами, можно найти легко
вычислимую функцию, которая взаимно однозначно отображает
множество хранящихся в таблице имен в пространство адресов
Особенно легко найти такую функцию, когда память содержит
больше ячеек, чем имен Рассмотрим, например, размещение пяти
слов AN, AT, NO, ON и PI в памяти Af0, Mi, , Ме. Предполо-
жим, что каждая буква представлена 5-разрядным кодом А соот-
ветствует 00000, В — 00001, С — 00010 и т д ’’’— '—
пять слов имеют такое представление'
Таким образом,
AN
ON
PI
цепочка btb6bi однозначно определяет
Заметим, что двоичная
каждое из этих пяти слов и что значения этих двоичных цепочек,
рассматриваемых как двоичные целые числа, лежат в пространстве
адресов Л =-{0,1,2,3,4,5,6). Таким образом, хеш функция h(x) —
285
™*(,ЪЛЬ&Ь^)Я отображает множесгво пяти имен впамя1Ь, более того,
при этом сохраняется естественный алфавитный порядок.
Когда содержимое таблицы известно до того, как строится хеш-
функция, само пространство имен не имеет значения В этом при-
мере мы могли предположить, чю пространство имен было просто
данным множеством из пяти стов, чю оно было множеством всех
наборов из двух букв или чю это было множество всех наборов
произвольной дпины
При обычном применении метода вычисления адреса, часто на-
зываемом хешированием, точно определяется большое пространство
имен S вместе с некоторой неопределенной информацией о содер-
жимом таблицы. Мы можем знать, например, что число имен, кото
рые нужно хранить в таблице, не превысит некоторой границы, что
некоторые имена встречаются с большей вероятностью, чем другие,
или что имена, вероятно, встречаются в кластерах, определяемых
общими свойствами На основании такой информации мы выбираем
размер памяти т и строим хеш-функцию, которая отображает S
в пространство адресов А — {0,1, ... /п— 1}. Окончательным кри-
терием нашего выбора т и h является их эффективность на прак-
тике, теоретического анализа в общем случае не достаточно, по-
скотькс такой анализ обычно основан па предположениях о содер-
жимом таблицы, которые слишком примитивны
Рассмотрим, например, пространство имен S всех двоичных
цепочек фиксированной длины 8 и предположим, что известен мак-
симачьный размер таблицы — шесть имен Допустим, что мы вы-
брали память из восьми ячеек Ма, Mt, .., /И, и выбрали простую
хеш-функцию, которая отображает цепочку в три самых правых
разряда, интерпретируемых как двоичное целое Эта функция имеет
два преимущества: ее легко вычислить и она рассеивает прост-
ранство имен равномерно по пространству адресов.
Допустим, таблица состоит —...............
из пяти имен
л( = 00010110
х2 = 00100100
Кг = 00111010
х4 » 10101100
х5 = 11110000
й(к1) = (Л0)2 = 6,
- (1()())2 = 4.
А(х,) = (010), = 2,
/Кл4) - (ЮО). = 4,
= (000) - о.
Л!и, первую свободную
ячейку, следующую за его собственным
286
адресом h(xd~^ Наша память теперь выглядит так, как пока-
зано на рис 6 26. Заметим, что табличный порядок не связан с ес-
тественным порядком имен; поэтому распечатка имен в естественном
порядке требует их сортировки
Когда память больше размера хранимой таблицы, пустые ячейки
должны отличаться от занятых Эго обычно делается либо добавле-
нием лишнего разряда
к каждой ячейке, как предлагается на
рис 6 26, либо, если можно, использованием специального значе-
ния, не принадлежащего пространству имен, для обозначения пу
стой ячейки Мы будем просто предполагать, что у нас есть способ
получения ответа на вопрос «Является ли М, пустой'3» за постоян-
ное время; нам не важно, как это реализуется
Когда возникает коллизия, поиск становится существенно бо-
лее сложным, чем в рассмотренном ранее примере, и обычно вклю
чает цикл, который может выполняться до т раз в худшем случае
При способе разрешения коллизий из приведенного выше примера
(т е использовании первой незанятой ячейки, следующей за собст-
венным адресом) поиск требует последовательного просмотра па
мяти; при этом нужно начинать с собственного адреса г и перехо-
дить от ячейки M4-i к Мо циклически, как показано в алгорит-
ме 6 9 Поиск завершается безуспешно, если встречается пустая
ячейка или когда просмотрена вся память Мы можем избежать
явной проверки последнего случая, если по крайней мере одна
ячейка памяти оставлена пустой, это мы и предполагаем в алго-
ритме 6 9.
287
while Mt не
Во время включения мы должны явно проверять, что память
не полна, т е что существует более одной пустой ячейки. В алго-
ритме 6.10 это осуществляется сравнением числа п уже входящих
в таблицу имен, с размером памяти т. Во всех предыдущих методах
поиска мы просто расширяли таблицу, если нужно, но сделать это
для метода вычисления адреса не просто, поскольку хеш-функция h
явно зависит от размера памяти Расширение памяти требует но
вого хеширования памяти, т е отыскания новой хеш-функции и
перемещения всех ранее размещенных имен в соответствии с новой
хеш-функциеи
Удивительно, что очевидный способ исключения имени из
Л1(, когда М-, помечается как пустая, является неправильным для
большинства схем хеширования! Для того чтобы понять, почему
это так, посмотрим, что происходит с таблицей на рис 6 26, если
мы исключаем х2, помечая Mt как пустую ячейку, Если мы теперь
ищем xt, то последовательный поиск, начинающийся в 4, собствен-
ном адресе имени х4, находит, что пусто, и ошибочно заключает,
что имени xt в таблице нет, х4 находится в Мь, где оно хранилось
из-за того, что оно вступало в коллизию с х2 Пока была занята
ячейка Л14, имя х4 было достижимо, но когда Л14 стала пустой, х,
стало недостижимым для алгоритма 6 9 В идеале исключение х2
должно производить перемещение х4 из Мь в его собственный адрес
М4 Однако, чтобы гарантировать, что пусгая ячейка М5 не делает
недоступным еще какое-нибудь имя, нужно проверить, что ячейка
Ah пуста и что /i(xj)=#4 и Л(х,)#=5 В более тонких схемах разре-
шения коллизий такая перестройка таблицы требует широкого по-
иска и проверки и, как правило, исключение осуществляется иначе.
Если мы будем считать, что каждая запись в столбце на рис 6 26,
помеченном «занято», допускает одно из трех значений «занято»
(j/), «пусто» (пробел) или «исключено» (d), то исключение имени
выполняется пометкой его ячейки как «исключено»
Когда имеются ячейки с пометкой «исключено», алгоритм 6 9
(поиска в хеш-таблице) для правильной его работы нужно модифи-
цировать так, чтобы «исключенные» ячейки игнорировались во
время поиска Алгоритм 6 10 (включение в хеш-таблицу) нужно
модифицировать так, чтобы новое имя вводилось в пустую или
«исключенную» ячейку в зависимости от того, какая из них встре-
тится первой, в любом случае испотьзованная ячейка помечается
как занятая (см упр 30) Заметим, что, хотя исключенная ячейка
ведет себя как пустая относительно включения, она ведет себя как
заполненная ячейка относительно поиска Это влечет за собой то,
что безуспешный поиск, который завершается, когда встречается
первая пустая ячейка, становится очень неэффективным, если по
следователыюсть включений и исключений оставляет все меньше
и меньше ячеек с пометкой «пусто», даже если общее число имен
в таблице остается, грубо говоря, постоянным’ В копие концов
при безуспешном поиске будет просматриваться вся память
Первые два примера этого раздела иллюстрировали методы вы-
числения адреса ограниченной применимости когда пространство
имен меньше доступной памяти или когда содержимое таблицы из-
вестно до выбора хеш-функции Третий пример самый важный, он
иллюстрирует метод, полезный, когда пространство имен велико и
хеш-функция и схема разрешения коллизий должны быть выбраны
до того, как станет известным содержимое таблицы Более подробно
эти задачи обсуждаются в следующих разделах
6.5.2.	Хеш-функции
В идеале хеш-функция h S^-A должна была бы легко вычис-
ляться и отображать пространство имен в пространство адресов
так, чтобы равномерно рассеять имена по памяти. Если второе
требование истолковать так, что каждый адрес i$A является об-
разом примерно одинакового числа имен x£S, то приемлемы про-
стые хеш-функции, например функции, в которых подцепочки имени
интерпретируются как двоичные целые Однако на самом деле мы
заботимся только о том, рассеивается ли содержимое таблицы, а
не все пространство имен по памяти равномерно Таким образом,
хеш-функция должна была бы быть построена так, чтобы равно
мерно рассеять по памяти те подмножества множества S, которые
могут встретиться в качестве содержимого таблицы Эти вероятные
подмножества редко можно охарактеризовать точно, следовательно,
289
построение хеш-функций является искусством, которое не подчи-
няется анализу, использующему математические формулы, и вместо
этого опирается на несколько правил, основанных на здравом
смысле. К счастью, как мы увидим, хеш-функция не является са-
мым важным фактором техники хеширования Любая разумная
хеш функция будет удовлетворительно работать на большинстве
множеств имен, и в то же время для любой хеш-функции существуют
множества имен, на которых она работает плохо. В этом разделе
описывается, как избежать хеш-ф\нкций, которые плохо работают
на некоторых распространенных множествах имен.
Правила, устанавливающие, что некой функции h следует из-
бегать, всегда опираются на экспериментальные данные о том, что
множества имен, которые, вероятно, встретятся, содержат много
имен, которые h отображает в малое множество адресов Подобное
окучивание имен появляется по разным причинам. Если имена
выбраны кем-то, то это могут быть последовательности вида XI,
Х2, ХЗ или ACOST, BCOST, CCQST Если вначале имена имеют
разные длины, то их можно дополнить пробелами в хвосте так,
чтобы все они имели стандартную длину Если имена ограничены
алфавитом, меньшим, чем множество символов алфавита ЭВМ, то
в представлениях имен некоторые комбинации разрядов могут воз-
никать чаще, чем другие. Следует избегать хеш-функций, которые
склонны отображать такие скученные имена в скученные адреса
Хеш-функции без столь ярко выраженных недостатков будут при-
емлемыми, если их легко можно вычислить и если они хорошо ра-
ботают на контрольных данных
Для того чтобы обеспечить быстрое вычисление хеш-адресов,
большинство хеш-функций близки к примитивным операциям,
допустимым для ЭВМ, в связи с чем они лучше описываются на
уровне операций над двоичными наборами в представлениях имен
и адресов Поэтому будем полагать, что имена и адреса представ-
лены двоичными наборами длины /пате и Zaddress соответственно
Часто /,1аше меньше или равно длине машинного слова, и во всех
представляющих интерес случаях /nanie>^ddress’ так как> если
^iMme^^address- каждому имени можно приписать свой адрес (как
в первом примере разд 6 5 1)
Простейшие xeiu-функции выбирают некоторое специальное
подмножество из /dddte,s разрядов из строки с /пате разрядами и
используют их для формирования адреса, как во втором и третьем
примерах из разд 6.5 1 Из нашего более раннего обсуждения оче-
видно, что опасность этого метода состоит в том, что он имеет тен-
денцию порождать чрезмерное количество коллизий, так как все
имена, представления которых оказываются совпадающими по
подмножеству разрядов, выбранному хеш функцией, отображаются
вается с множеством разрядов, общих для некоторого окучивания
10 № 780
имен, эти имена будут отображаться в малое множество адре-
Такие наблюдения приводят к требованию, чтобы каждый из
/add[es5 разрядов адреса зависел от всех /пагае разрядов имен Наи-
более эффективный путь достижения этой зависимости состоит
в том, чтобы производить арифметические операции, результаты
которых зависят от всех разрядов имени, и затем выделять /addres5
разрядов из этого результата Большинство используемых хеш-
функций основано на таком подходе, по при этом следует избегать
некоторых ловушек Например, один из самых первых методов пост-
роения хеш-функций, метод середины квадрата, состоит в гом, что
имя представляется целым числом, затем находится его квадрат,
после чего из середины представления квадрата выделяются /addrcss
разрядов Хотя этот метод часто является удовлетворительным, при
нем возможны свои подводные камни, поскольку возведение в квад-
рат не сохраняет равномерности распределения, если х — равно-
мерно распределенная случайная величина на отрезке 1с, 5], то
Xs не будет равномерно распределенной величиной на отрезке
[а2, 52| Особенно неприятно проявляется такое нарушение рас-
пределении, когда представление оканчивается нулями Его квад-
рат имеет в конце вдвое больше нулей, и эти нули могут распрост-
раняться на среднюю область представления квадрата, тем самым
искажая получающийся в результате адрес Посколькх задачей
хеширования является равномерное распределение имен в памяти,
от метода середины квадрата в общем случае отказываются
Умножение па константу свободно or недостатков, присущих
методу квадрата Если х — равномерно распределенная случайная
величина в отрезке 1а, 5], то величина сх равномерно распределена
в отрезке [со, с&1, и этот отрезок можно отобразить на пространство
адресов {0, 1,	, т—1} многими способами, которые сохраняют
равномерность Это обстоятельство является основой метода муль-
типликативного хеширования Конечно, при построении фактиче-
ской хеш-функции мы должны помнить, что представления имен
нельзя считать равномерно распределенными и что арифметические
действия выполняются в некоторой дискретной конечной системе
счисления, свойства которой (в частности, основание системы счис-
ления и дтину слова) необходимо учитывать, чтобы избежать вы-
рожденных случаев, которые приводят к очень большому числу
коллизий Основная опасность мультипликативного хеширования
относится ко многим возникающим на практике таблицам, которые
содержат подмножества имен с представлениями, образующими ариф-
метические прогрессии Мультипликативные хеш-функции отобра-
жают такие прогрессии имен в арифметические прогрессии адресов,
скажем, с разностью i Если с или т выбраны произвольно, то i
может оказаться делителем т и эти подмножества будут использо-
вать только 1/х. часть объема памяти Следствием этого является
291
порождение стольких коллизий, сколько можно было бы ожидать
при использовании лучшей хеш-функции с меньшей памятью
Метод хеширования, основанный на делении, использует хеш-
функцию типа
Л (х) = (представление х, рассматриваемого как целое) modm,
где т — объем памяти Выбор т является решающим в этом ме-
тоде Например, если т. четно, то h(x) четно тогда и только тогда,
когда представление х будет четным целым; эта неравномерность
может оказаться серьезной Если т — степень основания системы
счисления, применяемой в ЭВМ, то Л(х) будет зависеть только от
самых правых букв х, что является еще одной серьезной потенциаль-
ной опасностью неравномерности Вообще к проблемам может
всего, чтобы tn было простым, простота пг гарантирует еще и то,
что каждая цифра хеш-адреса зависит от всех букв имени.
6.5,3.	Разрешение коллизий
Пока хеш-табтица не слишком полна (скажем, заполнена на
50% объема), коллизии появляются редко, и производительность
схемы хеширования определяется прежде всего временем, требую-
щимся для вычисления хеш-функции Когда память становится
более заполненной, доступ к именам требует все больше и больше
времени из-за коллизий Поэтому когда память используется в боль-
шой степени, схема разрешения коллизий определяет эффективность
схемы хеширования Отсюда выбор схемы разрешения коллизии
обычно важнее выбора хеш-функции
Схема разрешения коллизий каждому имени х присваивает
последовательность адресов ап=Л(х), аь а2,	Алгоритм
включения проверяет ячейки до тех пор, пока не найдет пустую
Для гарантии того, что пустая ячейка встречается, если она су-
ществует, каждый адрес г,	—1, должен появляться в после-
довательности точно один раз По существу, эту последовательность
можно представить двумя способами, которые соответствуют по-
следовательному и связанному распределению списков (см.
разт 2 2)
Открытая адресация. В третьем примере разд 6 5.1 мы исполь-
зовали простейшую форму открытой адресации, называемой ли-
нейным опробованием, которое порождает последовательность адре-
сов аг=(/1(х)+г)тоб т Если память не является почти пустой,
простота полученной таким путем последовательности не компен-
сирует серьезный недостаток, который делает ее обычно неудовлет-
ворительной Этим недостатком является вторичное скучивание.
Первичное скучивание возникает, когда таблица содержит много
ю*
292
имен с одинаковыми хеш-адресами Вторичное скучивание возни-
кает, когда имена с различными хеш-адресами имеют одинаковые
(или почти одинаковые) последовательности адресов сс1( сс2,
Когда возникает первичное екучивание, линейное опробование по-
рождает последовательность занятых следующих одна за другой
ячеек и все имена, попадающие в любые из этих ячеек в результате
хеширования, порождают последовательность адресов, которая
пробегает эти занятые ячейки.
Если h есть хеш функция, основанная на делении, то эффект
вторичного скучивания может возрасти из-за наложения схемы
разрешения коллизий на практике многие таблицы содержат под-
множества имен, которые различаются только в последних буквах
(такие, как Al, А2, АЗ, или PARTA, PARTB PARTG, )
и представления таких имен часто образуют наборы последователь-
ных чисел Эти имена могут отобразиться в последовательные ад-
реса, если с хеш-функцией, основанной на делении, используется
линейное опробование.
Вторичного скучивания и наложения можно избежать, исполь-
зуя линейное опробование с приращением Д(х), которое является
функцией имени х. Это приращение дает последовательность адре-
сов (x)4-r‘A(x))mod т, которая будет опробовать каждую
ячейку, ещти Л (х) и т взаимно просты Поскольку Д(х) по существу
является другой хеш-функцией, этот метод называется двойным хе-
шированием Если мы хотим обеспечить, чтобы последовательности
проб просматривали всю память, двойное хеширование является
наилучшим методом разрешения коллизий для открытой адреса-
Метод пеночек Метод цепочек —это способ построения после-
довательности указателей из собственного адреса Л(х) в ячейку,
где х размещается окончательно С помощью некоторою расхода
памяти (для хранения указателей) такой способ помогает избежать
проблемы вторичного скучивания во время поиска, но не во время
включения. Рис 6 27 иллюстрирует это Предположим, что х и у
образую! котлизию х размещается по своему собственному адресу
а0=/г(х) и у размещается по следующему адресу а, в последователь
пости разрешения коллизий для ап (рис 6.27(a)) Предположим те-
перь, что имя г нельзя записать по его собственному адресу h(z) =
= р0 и что, следуя по его последовательности разрешения коллизии
Pi, рг, , мы перешли через а0 и сч например, Pj —а0 и рг=а.
Для отыскания пустой ячейки во время включения мы, возможно,
должны просмотреть а0 и но как только г размещено в ячейке
р3, привязываем р3 непосредственно к	так что при поиске 2
производится меньше проб, чем при его включении (рис 6 27(b))
В этом раздече мы обсудили методы разрешения коллизий, ко-
торые использмот ячейки только из хеш-таблицы А\ожно помещать
293
образующие коллизии имена в отдельной дополнительной области.
Это эквивалентно комбинации разных методов поиска, хеширо-
вание используется на первом шаге, а другие методы используются
6.5.4.	Влияние коэффициента загрузки
В предположениях, что время доступа к любой ячейке в памяти
постоянно и что хеш-функция отображает пространство имен на
пространство адресов равномерно, а также чго содержимое таблицы
есть беспристрастная выборка из пространства имен, ожидаемая
эффективность метода вычисления адреса не зависит от и, т. е от
числа имен в таблице Вместо этого она зависит в основном от
коэффициента загрузки Х^п/гп, т е степени заполнения памяти
В экстремальном случае X— 1, когда память используется пол-
ностью, очевидно, что быстрого времени доступа достигнуть не-
возможно. Однако важно рассмотреть эффективность метода вы-
числения адресов, когда память почти полна Как показывает сле-
дующее рассуждение и подтверждает опыт, коэффициент загрузки
294
90?4 допускает приемлемую эффективность, таким образом, ис-
пользование методов вычисления адреса не приводит к значитель-
ной потере памяти.
От чего зависит хорошая эффективность методов вычисления
адреса^* Возможно, секрет лежит в выборе разумной хеш-функции,
которая по возможности предотвращает коллизии. Однако в ре-
альных <лучаях хеш-функция выбирается до тою, как содержимое
таблицы становится известным, а это означает, что способа избе-
жать коллизий не существует Даже если хеш-функция отображает
имена на пространство адресов равномерно, доля А-/2 имен в таб-
лице будет образовывать коллизию с ранее введенными именами
(см упр 32) Поскольку А обычно близко к 1, почти половина
имен приводит к коллизиям, следовательно, даже самая лучшая
хеш функция не может предотвратить большого числа коллизий
К счастью, число коллизий имеет слабое влияние на эффективность
методов вычисления адреса; коллизия удлиняет последователь
ность проб топько на одну ячейку Отсюда следует, что выбор
хеш функции не является решающим моментом в разработке мето-
дов вычисления адреса; наиболее важным является то, что проис-
ходит после возникновения коллизии, т е схема разрешения коп
тизии
Дадим приближенный анализ двойного хеширования. Предпо-
ложим, что последовательность а0=/1(г), аь а2. .. адресов, при-
писанная имени г, обладает тем свойством, что каждый адрес аг
с равной вероятностью может быть любым из адресов 0,	, т—1
независимо от других При этом предположении (которое при-
близительно верно для двойного хеширования), если таблица имеет
коэффициент загрузки р и г не принадлежит таблице, вероятность
использования проб при безуспешном поиске равна
Рг (использовано k проб)^Рг(Лф
заполнены,
пусто) =
Таким образом, математическое ожидание t/(p) числа проб, не-
обходимых дтя безуспешного поиска z в хеш-таблице с коэффициен-
том загрузки р равно

Заметим, что число проб, необходимых для отыскания г после
тою, как оно попало в хеш-таблицу, такое же, как число проб
в безуспешном поиске, когда оно включается Рассмотрим теперь
хеш-таблицу, строящуюся по мере того, как в последовательность
включаются имена, с коэффициентом загрузки р., растущим от О
245
до его конечного значения X Разумным допущением является то,
что в интервале (О, Л) и изменяется не дискретно, а непрерывно,
и для математического ожидания числа проб S(X), необходимых
для успешною поиска с коэффициентом загрузки X, мы получаем
Функции J (X) и S(X) стремятся к 1 при Х-х», указывая, таким
образом, корректно, что при поиске в почти пустой таблице доста-
точно одной пробы. Функции U (К) и S(X) неограниченно растут
при Х->1, но это является следствием интерпретации р как непрерыв-
ной величины, что равнозначно предположению о бесконечной па-
мяти Мы имеем
0 95	0 99
U(X}
5(A)
10 0 20 0 1000
Таким образом, если адреса, порожденные .методом разрешения
коллизий, независимы и равномерно распределены на пространстве
адресов, как обычно бывает при двойном хешировании, то среднее
число требуемых проб мало даже для такого большого коэффициен-
та загрузки, как 90%.
6.6.	КОММЕНТАРИИ И ССЫЛКИ
Широкое обсуждение методов поиска, изложенных в этой главе,
дано в книге
Knuth D. Е, The Art of Computer Programming, Vol 3 (Sorting and
Searching), Addison-Wesley, Reading, Mass , 1973 [Имеется
перевод Кнут Д, Искусство программирования для ЭВМ.
Т. 3. Сортировка и поиск.— М . Мир, 1978 I
В этой книге содержится также краткая история развития различ-
ных методов
Идея организации таблицы для последовательного поиска
таким образом, что имена располагаются в невозрастающем по-
рядке частот, была впервые проанализирована в работе
Smith W. Е. Various Optimizers for Single-Stage Production, Laval
Research Logistics Quart , 3 (1956), 59— 66
В этой статье имеется также интересное обобщение (см упр 3)
Использование самоорганизующихся файлов (упр 5), когда
частоты a priori не известны, было впервые предложено в работе
McCabe J On Serial Files with Relocatable Records, Operations Res.,
12 (1965), 609—618.
Подробный анализ различных стратегий см в работах
Rivest R L On Self-Organizing Sequential Search Heuristics, Comm
ACM, 19 (1976), 63--67
Bitner J R Heuristics that Dynamically Alter Data Structures to
Decrease Their Access Time, Ph D thesis, University of Illi
nois, Urbana, 111 , 1976
Первая опубликованная корректная реализация бинарного
поиска для таблиц всех размеров (т е нс только для случая 2fe—1)
имеется в статье
Bottenbruch Н Structure and Use of Algol 60, J ACM, 9 (1962),
161—221,
хотя она, конечно, должна была быть сделана гораздо раньте
Вариант в упр 6 (равномерный бинарный поиск) принадлежит
А К Чандре [Ashok К Chandra (1971)1 Интересное применение
метода бинарного поиска и тонкий анализ его эффективности содер-
жится в статье
Bentley J L , Yao А С С An Almost Optimal Algorithm for Un-
bounded Searching, Info Proc Let , 5 (1976); 82—87
Первое описание бинарных деревьев поиска дано в работе
Wmdley Р F. Trees, Forests and Rearranging, Comp J , 3 (I960),
84 —88 [Имеется перевод Уайндли П Ф Деревья, леса и
переупорядочения Киб сб , вып 1 (новая серия) — М Мир,
1965, 87—98 [
Идея оптимальных деревьев бинарного поиска берет свое начало
в теории кодирования, см
Gilbert Е N., Moore Е F Variable-Length Binary Encodings, Bell
System Tech J , 38 (1959), 933—968 (Имеется перевод. Гил
берт Э Н , Мур Э Ф Двоичные кодовые системы переменной
длины Киб еб, вып 3 (старая серия) — М Мир, 1961,
103-141 ]
В частном случае, когда веса внутренних узлов равны нулю (не
очень пригодном для деревьев бинарного поиска, поскольку это
означает, что поиск только безуспешный, но важном в построении
деревьев за время О (п log п) и с памятью О (л) См. работы
Hu Т С , Tucker А С. Optimal Computer Search Trees and Variable-
Length Alphabetic Codes, SIAM J Appt Math , 21 (1971),
514—532
HuT, C, A Neu Pioof of the T-C Algorithm, SIAM J Appt. Math ,
25 (1973), 83- 94
297
В общем случае алгоритм 6 7 требует О (л2) времени и памяти, он
взят из работы
Knuth D Е Optimal Binary Search Trees, Acta Informatica, 1 (1971),
14-25
Некоторые обобщения алгоритма Кнута приводятся в статье
Itar A Optimal Alphabetic Trees, SIAM J Comput., 5 (1976),
Эвристические алгоритмы построения почти оптимальных де-
ревьев описаны в работах
Bruno J , Coffman L G Nearly Optimal Binary Search Trees, Proc.
Ц-IP Congress 71, North-Holland Publishing Co, Amsterdam,.
1972, 99- 103
Walker W A , Gotlieb С C. A Top Down Algorithm for Construc-
ting Nearly Optimal Lexicographic Trees, in Graph Theory and
Computing, R Read (Ed), Academic Press, New York, 1972,
303—323.
Анализ среднего времени поиска в оптимальных, сбалансированных
(ио узлам) и случайных деревьях (описанный в разд 6 3 3) взят из
статьи
Nievergelt J , WongC К On Binary Search Trees, Proc IFIPCongress
71, North-Holland Publishing Co, Amsterdam, 1972, 91—98.
Эта статья также дает частичный анализ среднего времени поиска
в монотонных деревьях, полный анализ этого случая приведен
в докторской диссертации Дж Битнера (James Bitner) из Иллинойс-
ского университета Анализ среднего времени поиска в деревьях
бинарного поиска, сбалансированных по суммам весов, взят из
работы
Bayer Р J Improved Bounds for Binary Search Trees, Ada Informa-
tica, в печати
Боры впервые были предложены в работе
Tredkin Е. Trie Memory, Сотт АСМ, 3 (1960), 490—500
Sussenguth Е Н Use of Tree Structures for Processing Files, Comm.
ACM, 6 (1963), 272—279
Walker W A Hybrid Trees as a Data Structure, Ph D Thesis,
Department oi Computer Science, University of Toronto, 1975.
Создание такого гибрида методов преследует цель обеспечить быст-
рое сильное ветвление около корня дерева, но при этом избежать
потери памяти, характерной для незаполненных узлов в нижних
уровнях бора
Деревья, сбалансированные по высоте, известные также как
АВЛ-деревья, были введены в работе
Адельсон Вельский Г М , Ландис Е М Один алгоритм организа-
ции информации — ДАН СССР, 146, № 2 (1962), с 263—266
Очевидное обобщение на случай, в котором разность высот двух
поддеревьев каждого узла не больше h, обсуждается в работах
Foster CCA Generalisation of AVL Trees, Comm ACM, 16 (1973),
513—517
Luccio F , Pagii L On the Height of Height-Balanced Trees, IEEE
Trans Comput , 25 (1976), 87-90
Различные эмпирические результаты о сба таксированных по вы-
соте деревьях и их обобщение обсуждаются в статье
Karlton Р. L., Fuller S Н , Scroggs R Е , Kaehler Е В Performance
of Height-Balanced Trees, Comm ACM, 19 (1976), 23—28
Сбалансированные по весу деревья разд 6 4 3 были введены
в работе
Nievergelt J , Remgold Е М Binary Search Trees of Bounded Ba
lance, SMAl J Comput, 2 (1973), 33—43
Разновидность деревьев, сбалансированных по весу, в которой кри-
терий сбалансированности зависит от длины внешних путей, описы-
вается в работе
Baer J L Weight-Balanced Trees, AFIPS Conference Proceedings
44 (1975 National Computer Conference Proceedings), 467—472
Сбалансированные сильно ветвящиеся деревья (разд 6 4 4)
порядка т были впервые описаны в статье
Bayer R , McCreight Е Organization and Maintenance of Large Or-
dered Indexes, Acta Informatica, 1 (1972), 173—189
Частный случай m=3, называемый (3-2)-деревом, был независимо
открыт Дж. Хопкрофтом (John Hopcroft) в 1971 г Этот частный слу-
чай подробно обсуждается в гл 4 книги
Aho А V., Hopcroft J Е , Ullman J D The Design and Analysis of
Computer Algorithms, Addison-Wesley, Reading, Mass , 1974
[Имеется перевод Ахо A , Хопкрофт Дж , Ульман Дж По-
строение и анализ вычислительных алгоритмов — М Мир,
1979.1
6 6
299
Иногда сбалансированные сильно ветвящиеся деревья полезно пред-
ставлять как бинарные деревья, см работу
Bayer R Symmetric Binary В Trees: Data Structure and Mainte-
nance Algorithms, Acta !nformatica, 1 (1972), 290—306
Важным соображением в использовании сильно ветвящихся
деревьев является степень заполненности узлов по объему, очевидно,
большая часть памяти не используется, если многие узлы лишь
минимально заполнены. Можно показать, что в сбалансированных
сильно ветвящихся деревьях порядка т коэффициент использова-
ния памяти асимптотически равен 1п2я?69% для больших т.
Подробности можно найти в статье
Yao А С-С , On Random 3 2 Trees, Ada 1 nformatica, to appear
Методы вычисления адреса (разд 6 5) были впервые предложены
разными авторами в начале 50-х годов, по но этому поводу Ди ра-
Dumey A 1 Indexing tor Rapid Random-Access Memory, Computers
and Automation, 5 (1956), 6—8,
ничего не было опубликовано Основные направления развития
метода изложены в трех наиболее существенных работах
Peterson W W Addressing for Random Access Storage, IBM J.
Res. and Dev. I (1957), 130—146
Buchholz W File Organization and Addressing, IBM Syst J , 2
(1963), 86-111.
Morris R Scatter Storage Techniques, Comm ACM, 11 (1968), 38—
43
Последний обзор по хеш функциям приведен э статье
Knott G D Hashing Functions, Computer J., 18 (1975), 265—278.
Схема коллизий, сочетающая в себе преимущества хеширования и
достоинства последовательного поиска в упорядоченной таблице
(упр 36), описана в статье
Amble О , Knuth D Е Ordered Hash Tables, Computer J , 18 (1974),
135—142
Во многих приложениях процедуры быстрого поиска, связан-
ных с информационным поиском, предмет поиска определен не
полностью Например, нас может интересовать поиск всех пяти-
буквенных английских слов вида ST*R*, где «*»—«все равно,
какой» символ, таким образом, будут найдены такие слова, как
STARE, START, STORM н STERN Применения различных ме-
300

годов вычисления адреса и цифрового поиска к таким частично
определенным задачам поиска описаны в статье
Rivest R L Partial-Match Retrieval Algorithms, SIAM J Comput,
5 (1976), 19—50
6 7. УПРАЖНЕНИЯ
довательпого поиска по таблице с п именами приблизительно равно п/2 Этот
результат опирается на ряд предположений; даже если мы полагаем, что все
от того, каким способом производится поиск
(а)	Заполните таблицу, указав среднее число сравнений, требующихся для
	поиск	
(абличныи порядок сов		
		
(Ь)	Рассмотрим таблицу с именами, расположенными в естественном порядке,
в которой поиск можно осуществлять последовательно в прямом и обратном по
любом месте, где остался указатель таблицы при завершении предыдущего по
иска. Чему равно среднее число сравнений на каждый поиск в предположении
перестановок имен в таблице перестановки с частотами обращения в монотонно
невозрастающем порядке имеют минимальное среднее время поиска
случай безуспешного поиска?
30i

4. (а) Пусть a/—2~l,	1 и ач=2-'1 + 1— частоты обращения к п име-
(Ь) Каково оптимальное дерево оинарного поиска на п именах с этими ча
торая группа имен ищется многократно)
6 Равномерный бинарный поиск. Перепишите алгоритм 6 5 так чтобы вместо
трех указателей и т были бы только два указателя — текущая позиция т
при этом*интервал поиска длины F/, + 1 разбивается на два подынтервала длин
Fk nFk- ^соответственно, приводя к делению на две части с а= ( )^5— ])/2«0 62
Р 9 Построите все различные деревья бинарного поиска на четырех и пяти
поиска требует (я2) обращений к элементам матрицы, показанной на
до О	в '	6 3 3
(a) B„=P«1g«-|-0
от весов не зависит.)
*(b) (2ln2)Pnlg«- O (п).

302	Гл 6 Быстрый поиск
Тогда среднее	п,=»5+2; 2 £W
где £	/,•) - Тп через f(x)	- математическое ожидание величины w,A/t Найдите выражение Jim —— = 2 В, л_ю п 1п п “1’’
	
13 Построите алгоритмы включения и исключения в дереве цифрового по-
Постройте таблицу Т с выбранными случайно п«2( именами, полагая, что имена
лсния каждого именш Средствами машинного моделирования исследуйте среднее
него поисков
16 Докажите следующие утверждения о деревьях бинарною поиска
x,_i — непосредственный предшественник х/ в естественном порядке — не
имеет правого сына.
обязательно пройти узел х(-_,.
(с) При безуспешном поиске имени г между х;_, и х, необходимо просмат
равно большему из чисел 1) число сравнений, требуемых для поиска х, _р и 2)
успешного поиска в случайном дереве бинарного поискав п именами,"и пусть
Un — соответствующее число для случайного безуспешного поиска Докажите
имени, совпадает с числом сравнений, требующихся для его включения,)
* (Ь) Используйте рекуррентное соотношение для изучения асимптотическою
19	Докажите, что алгоритм исключения дтя сбалансированных по высоте
20	Предположим, что существуют фиксированные вероятности р, q, г, где
условие на высоту /, — или \"с вероятностью р, q, г соответственно независимо
предполагать что р=г/ При этих предположениях покажите, что средняя длина
6 7. Упражнения
303
от мощности дерева
21	Допустим, что мы изменяем определение сбалансированного по высоте
поддеревьев каждого узла равнялась 2 (вместо 1). Построите алгоритм восста-
новления сбалансированности так, чтобы гарантировалось логарифмическое время
поиска. Каковы наиболее асимметричные сбалансированные по высоте деревья
в этом случае? Каково время поиска в худшем случае и каково среднее время
22	Используйте индукцию по числу узлов для доказательства неравенства
(Л+П Igf/i+O-Sn
?3	. предположениях^ указанных на рис 6 20 и в сопровождающем тексте,
этом уме
щеннй, требуемых для включения или исключения узла, меньше 2/(1—2а). (Ум-
ных различных значений I и г, и все они равновероясны. Только дтя двух из
может стать причиной того, что дерево выйдет из класса WB [а] Таким образом,
из интервала [а, ]—а| равна 1/[(1—2а)п]).
(а)	Пусть j-e имя в естественном порядке х, находится в узле, не принадле-
(Ь)	Безуспешный поиск имени г между x(_i и х( включает сравнение как с
27. Докажите, что если сбалансированное сильно ветвящееся дерево стро
ится путем включения п имен одного за другим и полученное в результате дерево
(по всем п включениям), равно V — I Используйте этот результат для оценки
среднего числа расщеплений на одно включение.
28 Постройте алгоритм распечатки всех имен, хранящихся в сильно ветвя
щемся дереве в естественном порядке
адресов в статической таблице, такую, что коллизий не возникает Например,
предположим, что пространство имен состоит из букв от А до Z и что буквы коди
жение чисел от 1 до 26. Предположим, что должны записать восемь имен Я। У
304

A. 00001'
E 00101
F 00110
J 01010
K. 01011
Q: 10001
T- 10100
W 10111
000
001
010
on
100
101
ция отображает Л-^000^/-Jobl, jL-010?K^Ol К	T~>1010, V-ShY)
КЛЮчСНО»
31. Придумайте алгоритм исключения для хеш-таблицы и метода разрешения
ными именами (X — коэффициент загрузки).
вательно распределенной в резидентной области таблице с 10 000 имен 80%
просмотров таблицы приходится на поиск 20% имен. Вместо того чтобы выпол-
по алфавиту^ и низкочастотную таблицу, где остальные 8000 имен располагаются
34. Т У Годум (см. упр 33) заметил, что обращение ко многим таблицам
подчиняется закону Зипфа. Годума интересуют утверждения типа «Доля р всех
просмотров таблицы приходится на долю а имен в таблице», и поэтому он хочет
с п записями в которой частоты обращения подчиняются закону Зипфа. доля
Рп(а) всех просмотров приходится на |_аг1 J наиболее часто отыскиваемых имен
(а)	Каковы рл (0) и ₽„ (I)?
(Ь)	Дайте приближенную формулу для Р„ (а)
(с)	Опираясь на результаты п (а) и (t>) начертите примерный i ра ртк для
Р2.ю2в (а) (Указание 22026««е10.)
35 Т У Говум (см. упр 33 и 34j создает общую теорию расщеплении одной
таблицы с п именами на" две таблицы, высокочастотную таблицу, ^содержаш\'ю
iO5

три типа таблиц
следовательно,
(с) хеш-таблицы
частотная и низкочастотная таблицы должны быть одного типа. Для каждого из
трех классов таблиц Годум имеет полный ответ на вопрос. «Для какой области
кочастотную?» Создайте независимо элементарную теорию Т У. Голема.
В более глубокой теории Т. У Годума типы таблиц могут быть различными,
эта теория пока еще разрабатывается
36 Упорядоченные хеш-таблицы В интересном варианте хеш таблиц исполь-
так\то а/= (й(х)+1Д (х)) mod т, 0<Л(х)<т, 1-<Д(х)<т. и 1 (х) и т взаимно
i	d ( Д( )) d

। —» й (х)
. . .. . л . f if М: < х then Л1,>
»h,l,	+ 4W)
таблицы.
(с) Докажите, что множество п имен хг х2 ..., хл можно расположить в упо
рядоченной хеш-таблице одним и только одним способом так, чтобы к ней был
крайней мере одна организация таблицы существует Какой порядок вхождения
имен по принятому алгоритму гарантирует что хеш-таблица является упорядо-
чи» организаций две, и пусть х;- — наибольшее имя, располагающееся в различных
(d) Пусть Sfi — среднее^число проб в общепринятом хешировании для слу-
число в стучайном безуспешном поиске Пусть 5Я и Un — соответствующие числ--


(Указание, рассуждайте, как в упр< 17, и используйте резул£таты п (с)). Таким
образом, §„=-S4 I. е. упорядоченные я обычные хеш-таблицы имеют одинаковое
"(с) Пусть Сп — среднее число проверок условия в цикле while во время вклю-
чения в упорядоченную хеш-таблицу. Покажите, что Cj-|-C2+.. -\-Cn=nS„
одного из ключей увеличивается на единицу.) Объедините это с результатами
п (d) для того, чтобы доказать, чго C„=Un^t
Глава 7. Сортировка
Рассматриваемые здесь задачи можно отнести к наиболее часто
встречающимся классам комбинаторных задач Почти во всех ма-
шинных приложениях множество объектов должно быть перераз-
мещено в соответствии с некоторым заранее определенным поряд-
ком Например, при обработке коммерческих данных часто бывает
необходимо расположить данные по алфавиту или по возрастанию
номеров В числовых расчетах иногда требуется знать наибольший
корень многочлена (см разд 3 2 1)
Как и в гл 6, будем считать заданной таблицу с п именами,
обозначаемыми х1( х2,	, хп. Каждое имя xt принимает значение
из пространства имен, на котором определен линейный порядок
Далее, мы считаем, что никакие два имени не имеют одинаковых
значений; т е. любые х, обладают тем свойством, что если i^j,
то либо либо хг>х, Ограничение хг£х; при упрощает
анализ без потери общности, ибо и при наличии равных имен коррект-
ность идей и алгоритмов не нарушается Наша цель состоит в том,
чтобы выяснить что-нибудь относительно перестановки Л = л 4,...
..лп), для которой хп,<хЯ1< • .<Ай В задаче полной сорти-
ровки требуется полностью определить П, хотя обычно это делается
неявно путем переразмещения имен в порядке возрастания В за
дачах частичной сортировки требуется извлечь либо только час
тичную информацию о 11 (например, П, для нескольких значений г),
либо полностью определить П по некой заданной частичной инфор-
мации о ней (так обстоит дело при слиянии двух упорядоченных
таблиц)
В разд 7.1 обсуждается внутренняя сортировка, т е решается
задача полной сортировки для случая достаточно малой таблицы,
умещающейся непосредственно в адресной памяти. Раздел 7 2 по
священ внешней сортировке, представляющей собой задачу полной
сортировки для случая такой большой таблицы, что доступ к ней
организован по частям, расположенным на внешних запоминающих
устройствах Наконец, задачи частичной сортировки — задачи
выбора i-го наибольшего имени и слияния двух упорядоченных таб-
лиц — обсуждаются в разд 7 3.
7.1. ВНУТРЕННЯЯ СОРТИРОВКА
Существуют по крайней мере пять широких классов алгоритмов
внутренней сортировки
1 Вставка. На i-м этапе (-е имя помещается на надлежащее
место между i—1 уже отсортированными именами.
Обмен
3 Выбор На I м этапе из неотсортированных имен выбирается
Z-е наибольшее (наименьшее) имя и помещается на соответствую-
щее место
309
Эти классы нельзя назвать ни взаимоисключающими, ни ис-
черпывающими одни алгоритмы сортировки можно с полным осно-
ванием отнести более, чем к одному классу (пузырьковую сор-
тировку из разд 7 i 2 можно рассматривать и как выбор, и как
обмен), а другие не укладываются ни в один из классов (упр I)
Тем не менее перечисленные пять классов достаточно удобны для
классификации обсуждаемых алгоритмов сортировки
В настоящем разделе сосредоточим внимание на первых четырех
классах алгоритмов сортировки Хотя алгоритмы, основанные на
слиянии, и приемлемы для внутренней сортировки, более естест-
венно рассматривать их как методы внешней сортировки, и поэтому
отнесем их к разд. 7 2
В описываемых алгоритмах сортировки имена образуют после-
довательность, которую будем обозначать хь х2, . , хп незави-
симо от возможных пересылок данных, таким образом, значением xt
является любое текущее имя в i-й позиции последовательности
Многие алгоритмы сортировки наиболее применимы к массивам,
в этом случае х, обозначает i-й элемент массива Другие алгоритмы
более приспособлены для работы со связанными списками- здесь хг
обозначает i-й элемент списка Следующие обозначения исполь-
зуются для пересылок данных-
значения имен xt и х, меняются местами.
г, *- у значение у присваивается имени хс
у-'—х, значение имени ху присваивается у.
Таким образом, операция Xi+-Xj, которая встречается в различных
что никакие два имени не имеют одинаковых значений. Однако это
условие всегда обязательно восстанавливается
В каждом из рассматриваемых алгоритмов будем считать, что
имена нужно сортировать на месте Другими словами, переразмеще-
ниеимен должно происходить внутри последовательности х2,
, хп, при этом существуют одна или две дополнительные ячейки,
в которых временно размещается значение имени Ограничение
«па месте» основано на предположении, что число имен настолько
велико, что во время сортировки не допускается перенос их в другую
область памяти Если в распоряжении имеется память, достаточная
для такого переноса, то некоторые из обсуждаемых в этой главе
алгоритмов можно значительно ускорить. Эти рассмотрения за-
ставляют нас в алгоритмах распределяющей сортировки и сорти-
ровки слиянием реализовать последовательность х,, х2, . , хп как
связанный список
Нижние оценки. Прежде чем изучать различные алюрнтмы сор
тировки, рассмотрим задачу сортировки с теоретической точки
зрения с тем, чтобы получить некоторое представление об ожидае-
основанные на представлении имен, которое не влечет за собой
сортировки число сравнений является хорошей мерой производи
мой работы, и вследствие этого представляет интерес минимальное
число сравнений, требующееся для сортировки п имен.
Чтобы исключить из этого теоретического рассуждения алго-
ритмы сортировки, основанные больше на представлении имен,
чем на их сравнении, будем рассматривать только те алгоритмы,
которые основаны на абстрактном линейном упорядочении прост-
ранства имен для любой пары имен х,, х}, i^i, либо xt<iXj, либо
х£>хг (Не трудно распространить это рассуждение па случай,
когда разрешены равные имена, см упр 3 ) Любой такой алгоритм
сортировки можно представить в виде расширенного бинарного
дерева решений (разд 1 5 и 2 3 3), в котором каждый внутренний
узел соответствует сравнению имен, и каждый лист (внешний
узел) — исходу алгоритма Это дерево можно рассматривать как
блок схему алгоритма сортировки, в котором все циклы «размо
таны» и показаны только сравнения имен Два сына узла изобра
жают, таким образом, два возможных исхода сравнения Напри-
мер, на рис 7 1 показано бинарное дерево решений для сорти-
ровки трех имен В оставшейся части этого раздела мы будем рас-
сматривать только те алгоритмы сортировки, которые можно
записать в виде таких деревьев решений
В любом таком дереве решений каждая перестановка определяет
единственный путь от корня к листу Поскольку мы рассматриваем
только те алгоритмы, которые правильно работают на всех п1 пере
становках имен, листья, соответствующие разным перестановкам,
должны быть разными. Тогда ясно, что в дереве решений для сор-
тировки п имен должно быть по крайней мере п! листьев
Заметим, что высота дерева решений равна числ^ сравнений,
требующихся алгоритму в наихудшем случае Пусть S(n) обозна-
чает минимальное число сравнений, выполняемых любым алгорит-
мом сортировки в худшем случае, т е
S(n)= nun [max (число сравнении)].
Поскольку бинарное дерево высоты h может иметь не больше 2*
листьев, заключаем, что
и поэтому по формуле Стирлинга (формула (3 12))
Таким образом, любой алгоритм сортировки, основанный на срав-
нении имен, в наихудшем случае потребует не меньше п 1g п срав-
нений
Можно также получить нижнюю оценку величины S(n) — мини-
мального среднего числа сравнений имен, выполняемых алгорит-
мом, который правильно сортирует все п] перестановок при усло-
вии, что все они равновероятны; т. е
S(n) — min
шсло сравнений) j .
Длина внешних путей (см разд 2.3,3) дерева решений равна сумме
всех расстояний от корня до листьев; деление ее на п! дает среднее
число сравнений для соответствующего алгоритма По теореме 2 1
в расширенном бинарном дереве с N листьями минимальная длина
внешних путей равна Mlg М4-0(М), положив Л'=п’, находим
Поэтому любой алгоритм сортировки, основанный на сравнении
имен, потребует в среднем не меньше п 1g п сравнений имен
что эти результаты выводятся только из свойств бинарных деревьев,
и поэтому справедливы для любых алгоритмов сортировки, основан
пых на бинарных деревьях решений произвольного вида
7.1.1.	Вставка
Алгоритм 7 1, представляющий собой простейшую сортировку
Эффективность этого алгоритма как и большинства алгоритмов
сортировки, зависит от числа сравнений имен и числа пересылок
данных, осуществляемых в трех случаях худшем, среднем (в пред-
положении, что все перестановок равновероятны) и лучшем.
Ключом к анализу алгоритма 7 1 является число проверок условия
«Х<Х» в цикле while, поскольку, если это число известно, легко
вывести число пересылок данных «X-*—х>»,	и «х, Нч-Х»
Таким образом, поведение алгоритма 7.1 полностью зависит от
чиста инверсий в сортируемой таблице Сравнение «Х<х,» произ-
водится ^(1+d/) раз, где dj -- число имен, больших х} и стоящих
слева от него ((dt, dit , dr) — вектор инверсий (разд 5 1 2) для
Xi, хг, ..., хГ1), и, следовательно, сравнение «Х<х;» производится
п—14-J£djpa3 Так как O^d^j—1 и величины d, независимы,
то максимальное ц минимальное значения л—равны соот-
ветственно у(н- 1)(л{-2) и л —1 Нетрудно показать, что среднее
значение Jfdj по всем перестановкам равно ^’У'/=ТП —0. 11
1 2 ] 1 '
поэтому среднее значение п- Л-У//? равно —(п—1) (л 1-4) Внут-
ренняя часть цикла while выполняется "^d, раз, так что число пере-
сылок данных будет равно (л—1) |-(л—1)+Х60’ т е yfa—1)(^+4)
в худшем случае, 2п—2 в лучшем случае и —(л—1)(л-;-8) — в сред-
Можно ли усовершенствовать сортировку вставками? Используя
бинарный поиск (разд 6 3 1), мы могли бы делать бинарные вставки
и, следовательно, не больше Г 1g/-] сравнений имен для вставки /-го
имени Таким образом, было бы достаточно всего Г 1g I "1 ig п
сравнений имен (ср с S(n)) К сожалению, после отыскания места,
в которое нужно вставить х!г ограничение «на месте» влечет за собой
то, что сама вставка требует в среднем у/ пересылок имен, и ал-
горитму все равно потребуется порядка пг операций В противо-
положность этому можно было бы использовать связанный список
для сортируемой части таблицы, делая тем самым вставку более
эффективной Конечно, в этом случае для отыскания места, куда
можно вставить xj, бинарный поиск неприменим, и нам пришлось бы
воспользоваться последовательным поиском Для полученной в ре-
зультате алгоритма сортировки потребовалось бы порядка п2 опе-
раций
Если бы можно было объединить легкость поиска в последова-
тельно распределенном списке с легкостью вставки в связанном
списке, мы имели бы возможность получить алгоритм, требующий
О(п 1g л) времени Это можно сделать, инючьзуя схемы сбаланси-
314

7.1.2.	Обменная сортировка
Обменная сортировка некоторым систематическим образом ме-
няет местами пары имен, не отвечающие порядку до тех пор, пока
такие пары существуют Фактически алгоритм 7 1 можно рассмат-
0 0 2 3 1 0 5 2
0 1 2 0 0 4 1 0
0 1 0 0 3 0 0 0
00020000
0 0 1 0 0 0 0 0
00000000
00000000
рива|Ь как обменную сортировку, в которой имя х, меняется мес
тами >о своим соседом слева до тех пор, пока не оказывается на
правильном месте В этом разделе мы обсуждаем два типа обменных
сортировок: хорошо известную, но относительно неэффективную
пузырьковую сортировку и быстрмо сортировку — один из лучших
со всех точек зрения алгоритмов внутренней сортировки
315
В алгоритме 7 2 используется переменная Ь, значение которой в на
чале цикла while равно наибольшему индексу I, такому, что про
имя Х( еще не известно, стоит ли оно на окончательной позиции
На рис. 7 3 показана работа алгоритма на примере таблицы с и —8
именами
Анализ пузырьковой сортировки зависит от трех факторов-
числа проходов (т е числа выполнений тела никла while), числа
сравнений «х/>х,+1» и числа обменов «х^х]+1» Число обменов
равно, как в алгоритме 7 1, числу инверсий 0 в лучшем случае,
-уЩп—1) в худшем случае и — п(п—1) — в среднем Рис 7 3 дает
возможность предположить, что каждый проход пузырьковой сор-
тировки, исключая последний, уменьшает на единицу каждый нену-
левой элемент вектора инверсий и циклически сдвигает вектор на
одну позицию влево, легко доказать, что это верно в общем случае,
и поэтому число проходов равно единице плюс наибольший элемент
вектора инверсий В лучшем случае имеется всего один проход,
в худшем случае — п проходов и в среднем — проходов, где
Ph— вероятность того, что наибольшим элементом вектора инвер-
сии является k—1 Согласно упр 7, имеем JPkPИли/2 г—к
Общее число сравнений имен трудно определить, но
можно показать, что оно равно п— 1 в лучшем случае, уп(п -1)
в худшем случае и ^-(п2—п!пп)+О(п) — в среднем
Пузырьковую сортировку можно несколько улучшить (упр 8),
но при этом она все еще не сможет конкурировать с более эффек-
тивными алгоритмами сортировки Ее единственным преимущест-
вом является простота
Как в простой сортировке вставками (алгоритм 7 1), так и в пу-
зырьковой сортировке (алгоритм 7 2) основным источником неэф-
фективности является тот факт, что обмены дают слишком малый
эффект, так как в каждый момент времени имена сдвигаются только
на одну позицию Как будет показано в упр 9, такие алгоритмы
непременно требуют порядка п2 операций как в среднем, так и
в худшем случаях. Таким образом, обнадеживающим усовершенст-
от друга, что делает сортировку с убывающим шагом (упр 5 и 6)
316
асимптотически достаточно эффективной Другой прием, приводя-
щий к тому, что каждый обмен совершает больше работы, исполь-
зуется в быстрой сортировке
Быстрая сортировка. Идея метода быстрой сортировки состоит
в том, чтобы выбрать одно из имен в таблице и использовать его
для разделения таблицы на две подтаблицы, составленные соот-
ветственно из имен меньших и больших выбранного, которые затем
рекурсивно сортируются с использованием быстрой сортировки
Разделение можно реализовать, одновременно просматривая таб-
лицу слева направо и справа налево, меняя местами имена в не-
правильных частях таблицы Имя, используемое для расщепления
таблицы, затем помещается между двумя подтаблицами, и две под-
таблицы сортируются рекурсивно
В алгоритме 7 3 показаны детали быстрой сортировки (QUICK-
SORT) для сортировки таблицы (xf, х/+1, . , лД, где лу используется
для разбиения таблицы на подтаблицы На рис 7 4 показано, как
алгоритм 7 3 использует два указателя i и / для просмотра таблицы
во время разбиения В начале цикла «while i<p i и j указывают
соответственно на первое и последнее имена, о которых известно,
317
что они находятся не в тех частях файла, в которых требуется.
Когда i и / встречаются, т е когда i^], все имена находятся в со-
ответствующих частях таблицы и х, помещается между двумя час-
QUICKSORT (/, J—1)
QUICKSORT (/-(-I, Z)
Доказательство того, что алгоритм 7 3 производит сортировку
правильно, предлагается в качестве упр 10
Для анатиза общего числа сравнений имен «хгОу» и «х/>ху»
в алгоритме 7 3 заметим, что в конце цикла «while i<]» все имена
Х/+1,	, хг сравнивались один раз с X/, исключая имена xs и xs+i
(где просмотры встречаются), которые сравнивались с xt дважды.
Пусть Сп — среднее число сравнений имен для сортировки таб-
лицы из п разных имен, предполагается, что все п1 перестановок
таблицы равновероятны Очевидно, что Со=С!=О, и в общем слу-
чае имеем
где
ps — (вероятность того, что х, есть s-е наименьшее имя)= —,
поскольку две подтаблицы, порожденные разбиением, случайны,
318
т е поскольку все (s—1)1 перестановок имен в левой подтаблице
равновероятны и все (п—з)! перестановок имен в правой подтаблице
равновероятны (упр 11). Это рекуррентное соотношение можно
упростить
Последнее аналогично соотношению (3 20), и, проведя такой же
анализ, как в разд 3 2.2, получим
Более точный анализ с помощью метода, приведенного в упр. 12
Легко показать по индукции, что в худшем случае чисто срав
пений имен Сп не больше	Этот результат, очевидно, верен
для ns^2, поскольку непосредственная проверка дает С9=0, С\=0,
С,—3 Предположим, что это справедливо для всех t<n, п^З
Имеем
так что по предположению индукции
Максимум достигается при £ = 1 или /?-=п; поэтому
для п.^3 Если быстрая сортировка применяется к уже отсортиро-
ванной таблице (’), то производится (п4-1)+«+ .+3 сравнений
имен, и мы заключаем, что
Поскольку среднее значение Сп равно О (п log л), такое колос-
сальное количество работы на случайных таблицах производится
редко, но сам по себе факт, чго алгоритм сортировки так плохо себя
ведет на уже отсортированной таблице усложняет дело Более тою,
встречающиеся на практике таблицы не являются случайными, а
часто бывают почти упорядоченными, так что указанное экстремаль
319
ное значение становится более вероятным Трудность составляет
выбор элемента, по которому осуществляется разбиение таблицы,
когда таблица чже почти упорядочена, первое имя вряд ли делит
таблицу на равные части Мы можем улучшить быструю сорти-
ровку (для неслучайных таблиц), используя для расщепления таб-
лицы случайно выбранное имя Это изменение легко включит
в алгоритм 7.3 добавить предложение	прямо перед
предложением «г<-/+1»
Быструю сортировку можно еще улучшить, используя для рас-
щепления таблицы медиану малой случайной выборки из k имен.
Если 6=3, можно показать, чго I88nlgn, даже в этом слу-
чае Сп пропорционально пг
Анализ величины 1п — среднего числа обменов	и
«Х/<-»х7»—аналогичен анализу С„, но сложнее Можно показать
(упр. 12), что
+ 3 + П
В худшем случае число /п, очевидно, удовлетворяет неравенству
та} (Л-1 +
и легко показать по индукции, что in^n\gn Применяя быструю
сортировку к таблице, в которой имя, используемое для расшевле
ния таблицы, является па каждом шаге медианой, мы видим, что
1g п Таким образом,
Алгоритм 7 3 изящен, ио непрактичен Проблема состоит в том,
чю рекурсия используется для записи подтаблиц, которые рас-
сматриваются на более поздних этапах, и в худших случаях (когда
таблица уже отсортирована) глубина рекурсии может равняться п.
Следовательно, для стека, реализующего рекурсию, необходима
память, пропорциональная п, для больших п такое требование
становится неприемлемым. Кроме тою, второе рекурсивное обраще-
ние к быстрой сортировке в алгоритме 7 3 может быть легко исклю
чено (как?) По этим причинам мы предлагаем алгоритм 7 4, ите-
рационный вариант быстрой сортировки, в которой стек ведется
явно Элементом стека является пара (/, /), когда пара находится

в стеке, это значит, что нужно сортировать соотве!Ствующие лу, .
, Х{. Алгоритм 7 4 помешает в стеке большую из двух подтаблиц
и немедленно применяет алгоритм к меньшей подтаблице. Это умень-
шает глубину стека в худшем случае примерно до 1g п (упр 13)
Заметим, что подтаблииы длины I игнорируются, и что расщепле-
ние подтаблицы делается с использованием случайно выбранного
имени в этой подтаблице.


while t < I do । "hlle



else । ца длиниее]]

Для быстрой сортировки можно сделать другое значительное
усовершенствование Вместо того, чтобы использовать быструю
сортировку для всех подтаблиц, мы применим ее только к «боль-
шим» подтаблицам, скажем, длины не меньше т и воспользуемся
321
простой сортировкой вставками для «маленьких» лодтаблиц длины
меньше т Поскольку для «маленьких» таблиц среднее число срав-
нений имен в быстрой сортировке больше, чем среднее число срав-
нений имен в простой сортировке вставками, отсюда следуег, что
подходящий выбор т улучшит эффективность быстрой сорти-
ровки (упр 14)
7.1.3.	Выбор
В сортировке посредством выбора основная идея состоит в том,
чтобы идти по шагам (=1, 2, ..п, находя <-е наибольшее (наимень-
шее) имя и помещая его на его место на (-ом шаге Простейшая форма
сортировки выбором представлена алгоритмом 7 5- (-е наибольшее
имя находится очевидным способом просмотром оставшихся п—г+1
имен Число сравнений имен на г-м шаге равно п—(, что приводит
к общему числу сравнении имен (п—1) + (п—2)+ +1=уп(л—1)
независимо от входа, поэтому ясно, что это не очень хороший спо-
соб сортировки
Несмотря на неэффективность алгоритма 7 5, идея выбора мо-
жет привести и к эффективному алгоритму сортировки Весь воп-
рос в том, чтобы найти более эффективный метод определения (-го
наибольшего имени, чего можно добиться, испопьзуя механизм
турнира с выбыванием Суть его такова, сравниваются ч ха,
х3 хл, х,,	, хп, затем сравниваются «победители» (т е.
большие имена) этих сравнений и т д, эта процедура для п=16
показана на рис 7 5 Заметим, что для определения наибольшего
имени этот процесс требует п—1 сравнений имен (упр 16); но опре-
делив наибольшее имя, мы обладае.м большим объемом информации
о втором по величине (в порядке убывания) имени оно должно
быть одним из тех, которые «потерпели поражение» от наибольшего
имени Таким образом, второе по величине имя теперь можно оп-
ределить, заменяя наибольшее имя на —со и вновь осуществляя
сравнение вдоль пут и от наибольшего имени к корню На рис 7 6
эта процедура показана для дерева из рис 7 5
Поскольку дерево имеет высоту Г 1g п “| (почему?), второе по
величине имя можно найти за [" 1g п —1 сравнений вместо п—2,
используемых в алгоритме простого выбора Этот процесс, очевидно,
можно продолжить Найдя второе по величине имя, заменяем его

322
разумным методом сортировки при условии, что пересыпки имен
происходят эффективным образом (вспомним, что бинарные вставки,
с которыми мы имели дело в разд 7 11, используют только п 1g п
сравнении имен, но Сп2 обменов)
Идея турнира с выбыванием прослеживаекя при сортировке
весьма отчетливо, если имена образуют пирамиду Пирамида — это
полностью сбалансированное бинарное дерево высоты h, в котором

324
все листья находятся на расстоянии Л или Л—1 от корня (разд. 2.3.4)
и все потомки узла меньше его самого, кроме того, в нем все листья
уровня h максимально смещены влево На рис 7 7 показано мно-
жество имен, организованных в виде пирамиды. Чтобы получить
удобное линейное представление дерева, пирамиду можно хранить
по уровням в одномерном массиве сыновья имени из i й позиции
есть имена в позициях 2i и 2i+1. Таким образом, пирамида, пред-
ставленная на рис 7 7, принимает вид
94 93 75 91 85 44 51 18 48 58 10 34
Заметим, что в пирамиде наибольшее имя должно находиться
в корне и, таким образом, всегда в первой позиции массива, пред-
ставляющего пирамиду. Обмен местами первого имени с n-м поме-
щает наибольшее имя в его правильную позицию, но нарушает
свойство пирамидальности в первых п—1 именах Если мы можем
сначала построить пирамиду, а затем восстанавливать ее эффек-
тивно, то все в порядке, так как тогда можно производить сорти-
ровку следующим образом:
Это общее описание пирамидальной сортировки.
Как преобразовать в пирамиду данное бинарное дерево, все
листья которого максимально сдвинуты влево и оба поддерева кото-
рого являются пирамидами'5 Сравниваем корень с большим из
сыновей Если корень больше, дерево уже является пирамидой;
но если корень меньше, мы меняем его местами с большим сыном
и применяем рекурсивно алгоритм восстановления к поддереву,
корень которого заменялся (рис 7 8) Таким образом, процедура
RESTORE (/, k) восстановления пирамиды из последовательности
Xj, Xy+i, , xh в предположении, что все поддеревья суть пирамиды,
такова-
procedure RESTORE (/, k)
RESTORE (m k)
Переписывая это итеративным способом и дополняя деталями, мы
получаем алгоритм 7 6 Заметим, что х} является листом тотда и
только тогда, когда	<УПР
325
Для построения пирамиды вначале заметим, что свойство пира-
мидалыюсти уже выполняется (тривиально) для каждого листа
(х,, г= L J+1, • , п) и что обращение к RESTORE(1, п) для
i=L4'2J’ L-y21 J—1’	’ 1 преобразует таблицу в пирамиду па
for » =	20 ' by—• do RESTORE (;, n)
lor . = » to 2 by —I do (	(|
Поведение пирамидальной сортировки в среднем не известно,
и поэтому мы рассмотрим только худший случай Нам нужно знать
объем работы, выполняемой во время обращения к RESTORE (f, I)
В частности, если Л. — высота поддерева (изолированный узел имеет
высоту 0) с корнем в xf, то в процессе восстановления производится
не больше 2/г сравнений имен и не больше h обменов, таким образом,
нам необходимо определить h. Заметим, что левый сын Xf есть xtj,
левый сын которого есть х4/ и т д Поддерево имеет высоту Л, где
h — наибольшее целое число, такое, что самый левый потомок
XjAz существует, т е такое, что 2/!f^l, откуда следует, что
h= |_ 1g-— J , эта формула легко доказывается по индукции (упр 19)
Поэтому в фазе построения совершается не больше
обменов и, следовательно, О(п) сравнений имен. Аналогично, в фазе
выбора происходит не больше
обменов и поэтому всего лишь 2n 1g п+О (а) сравнений имен. Таким
образом, для пирамидальной сортировки любой таблицы требуется
O(nlogn) операций, в противоположность быстрой сортировке,
в которой при некоторых таблицах совершается Сп2 операций. Не-
смотря на это, эмпирические данные показывают, что в среднем
быстрая сортировка более эффективна, чем пирамидальная (упр 20)
7.1.4.	Распределяющая сортировка
Обсуждаемый здесь алгоритм сортировки отличается от рассмат-
ривавшихся до сих пор тем, что он основан не на сравнениях между
именами, а на представлении имен, в этом отношении он напоми-
нает цифровую обменную сортировку, описанную в упр. 15. Мы по-
лагаем, что каждое из имен xj, х2, . , хп имеет вид
и их нужно отсортировать в возрастающем лексикографическом по-
рядке, т е.
тогда и только тогда, когда для некоторого t^p имеем х;1/=х;,( для
поэтому имена можно рассматривать как целые, представленные
но основанию г, так что каждое имя имеет р r-ичных цифр Чтобы
327
не было имен разной длины, более короткие имена дополняются
нулями
Цифровая распределяющая сортировка основана на наблюдении,
что если имена уже отсортированы по младшим разрядам /, /—1, .
I, то их можно полностью отсортировать, сортируя только по
старшим разрядам р, р—1, . , Z+1 при условии, что сортировка
осуществляема таким образом, чтобы не нарушить относительный
порядок имен с одинаковыми цифрами в старших разрядах (допол-
нительно об этом типе сортировок сказано в упр 25) Эта идея ле-
жит в основе механических сортировальных устройств для перфо-
карт, для сортировки карт в полях, скажем, от 76-й до 80-й колонки,
они сортируются в возрастающем порядке по 80-й колонке, потом
по 79-й колонке, затем по 78-й, затем по 77-й и, наконец, по 76-й
колонке Каждая сортировка по колонке состоит из чтения колонки
каждой карты и физического перемещения карты на верх стопки,
которая отвечает цифре, пробитой в этой колонке карты Как только
все карты помещены в соответствующие стопки, стопки объеди-
няются вместе в порядке возрастания, затем процесс повторяется
для следующей колонки слева Эта процедура проиллюстрирована
на примере трехзначных десятичных чисел (рис 7 9)
Заметим, что как к стопкам, так и к самой таблице обращаются
по правилу «первым включается — первым исключается», и поэтому
лучшим способом их представления являются очереди В частности,
предположим, что с каждым ключом ассоциируется поле связи
LINK,; тогда эти поля связи можно использовать для сцепления
всех имен в таблице вместе во входную очередь Q При помощи полей
связи можно также сцеплять имена в очереди Qo, Qt, . , Qr-Jt
используемые для представления стопок После того как имена рас-
пределены по стопкам, очереди, представляющие эти стопки, свя-
зываются вместе для получения вновь таблицы Q Алгоритм 7.8
представляет эту процедуру в общих чертах, подробности, связан-
ные с применением методов, изложенных в разд 2 2 3 для построе-
ния очередей, отнесены в упр. 23 В результате применения алго-
ритма очередь Q будет содержать имена в порядке возрастания;
т е имена бу’дут связаны в порядке возрастания полями связи,
начиная с головы очереди Q

U; U '-О '<LJ1 '~bfJ '-kJ i'IJ ’'iJ \1д1
I------310 181 522 534 (94 334 095 595 646 376,207 917 198.809 209 799. 139
^уууууууууц
Рис 7.9. Цифровая pacnpeie.'iHiouwM сортировка Пунктирные стрелки показывают как столки имен объединяются в таблицу
329
Анализ алгоритма 7 8 должен отличаться от анализа других
алгоритмов сортировки, поскольку мы не можем подсчитывать
число сравнений имен и перестановок Вместо этого мы будем
подсчитывать общее число операций очереди Всегда имеется р
проходов ио таблице, и каждый проход требует исключения из
Q каждого имени и включения его в одну из очередей Qt Отсюда
всего в очередях имеется 2пр операций включения/исключения
Каждый проход требует также г—1 сцеплений для получения Q
из Qo, , Qr-i, и поэтому имеется всего (г—1)р операций сцепле-
ния очередей Из разд. 22 3 следует, что операция включения/
исключения или операция сцепления может быть выполнена за
постоянное время Поэтому алгоритм 7 8 для сортировки имен
Хг, хп, где х, имеет вид (х, р, х,_ p.lt , O^xt<l<r, тре-
бует времени О(пр+гр)
7.2.	ВНЕШНЯЯ СОРТИРОВКА
В методах сортировки, обсуждавшихся в предыдущем разделе,
мы полагали, что таблица умещается в быстродействующей внут-
ренней памяти Хотя для большинства реальных задач обработки
данных это предположение слишком сильно, оно, как правило, вы-
полняется для комбинаторных алгоритмов, в которых сортировка
обычно используется только для некоторою сокращения времени
работы алгоритмов, когда оно недопустимо велико даже для задач
«умеренных» размеров Например, часто бывает необходимо сор-
тировать отдельные предметы во время исчерпывающего поиска
(гл 4), но поскольку такой поиск обычно требует экспоненциаль-
ною времени, маловероятно, что подлежащая сортировке таблица
будет настолько большой, чтобы потребовалось использование
внешних запоминающих устройств Однако задача сортировки
таблицы, которая слишком велика для основной памяти, служит
хорошей иллюстрацией работы с данными большого объема, и
поэтому в этом разделе мы обсудим важные идеи внешней сорти-
ровки Более того, будем рассматривать только сортировку таблицы
путем использования вспомогательной памяти с последовательным
доступом, такой, как магнитная лента
Будем считать, чго имеется <+1 лент, на одной из которых за-
писана таблица имен xlt х2,х3, . , и t рабочих лент, при этом лента
с записанными на ней именами служит для ввода данных Будем
также считать, что внутренняя память вместе с другими данными,
программами и т п может содержать одновременно только т имен
Предполагается, разумеется, что количество имен входной таблицы
значительно превышает т
Общей стратегией в такой внешней сортировке является
использование внутренней памяти для сортировки имен из ленты
по частям так, чтобы производить исходные отрезки (известные
также как цепочки) имен в возрастающем порядке По мере порож-
дения эти отрезки распределяются по t рабочим лентам, и затем
производится их слияние по I отрезков обратно на исходную (/+1)-ю
ленту так, что она будет содержать меньшее число более длинных
отрезков. Затем отрезки снова распределяются по остальным t
лентам и чнова производится их слияние по t штук обратно на
(/ —1)-ю ленту Процесс продолжается до тех пор, пока не получится
один отрезок, т е пока таблица не будет полностью отсортирована.
Имеются, саким образом, две отдельные проблемы как порождать
исходные отрезки и как осуществлять слияние
Самый очевидный метод для получения исходных отрезков
состоит в том, что можно просто считывать т имел, рассортировы-
вать их во внутренней памяти и записывать их на ленту в виде
отрезка, продолжая такой процесс до тех пор, пока небудуг исчер-
паны все имена. Все полученные таким образом исходные отрезки
содержат т имен (исключая, возможно, последний отрезок). По-
скольку число исходных отрезков в конце концов определяет время
слияния, мы хотели бы найти некоторый метод образования более
длинных исходных отрезков и, следовательно, меньшего их коли-
чества. Эго можно сделать, используя для сортировки идею тур
нира (пирамидальную сортировку) из разд 7 1 3 При этом под
холе т имен, которые умещаются в памяти, хранятся в виде такой
пирамиды, что сыновья узла больше узла (вместо того, чтобы быть
меньше нею). Этот метод отвечает определению «победителя» при
сравнении имел в сортировках типа турнира как меньшего из двух
имен, и это позволяет нам следить за наименьшим именем
Порождение исходных отрезков продолжается следующим об
разом Из входной ленты считываются первые т имен и затем из
них формируется пирамида, как описано выше Наименьшее имя
выводится как первое в первом отрезке и заменяется в пирамиде
следующим именем из входной ленты в соответствии с алгоритмом
7 6 (RESTORE), модифицированным так, чтобы для восстановления
пирамиды следить за наименьшим, а не за наибольшим именем
Процесс, известный как выбор с замещением, продолжается таким
образом, что к текущему отрезку всегда добавляется наименьшее
в пирамиде имя, большее или равное имени, которое последним
добавлено к отрезку; при этом добавленное имя заменяется на сле-
дующее из входной ленты и восстанавливается пирамида Когда
в пирамиде нет имен, больших, чем последнее имя в текущем от-
резке, отрезок обрывается и начинается новый отрезок Этот про-
цесс продолжается до тех пор, пока все имена не сформируются
в отрезки
Разумный путь реализации этой процедуры состоит в том, чтобы
рассматривать каждое имя х как пару (г, х), 1де г есть номер от-
резка, в котором находится х Иначе говоря, считается, что пирамида
состоит из пар (л, xj, (гг, х2),	, (fm, хт), сравнения между па
331
рами осуществляются лексикографически. Когда считывается имя,
меньшее последнего имени в текущем отрезке, оно должно быть
в следующем отрезке, и благодаря наличию номера отрезка это
имя будет ниже всех имен пирамиды, которые входят в текущий
отрезок Подробности алгоритма выбора с замещением отнесены
в упр 28 и 29
Порождает ли этот выбор с замещением длинные отрезки? Ясно,
что он делает это по крайней мере не хуже, чем очевидный метод,
так как все отрезки (кроме, возможно, последнего) содержат не
меньше т имен На самом деле можно показать, что средняя дайна
отрезков, порождаемых выбором с замещением, равна 2m (упр 30),
что вполне можно считать улучшением по сравнению с очевидным
методом, в котором средняя длина отрезков равна т Конечно,
в лучшем случае все закапчивается только одним исходным отрез-
ком, т. е. отсортированной таблицей.
После того как порождены исходные отрезки, возникает задача
повторного распределения их по рабочим лентам и слияния их
вместе до тех пор, пока в конце концов мы не получим окончатель-
ную отсортированную таблицу. Простейший метод здесь состоит
в том, чтобы распределить отрезки по лентам 1,2,...,/ равномерно
и произвести их слияние на ленту /-М Получаемые в результате
отрезки снова равномерно распределить по лентам 1, 2,	, t и
снова произвести слияние, образуя более длинные отрезки на
ленте /-М Процесс продолжается до тех пор, пока на ленте /-(-1
не останется только один отрезок (отсортированная таблица) От-
метим, что на простое переписывание отрезков сленты/+1 на другие
ленты тратится совсем немного времени. Каждый «проход» сокра-
щает число отрезков в t раз. Следовательно, если имеется г исход-
ных отрезков, то потребуется riogtr~| проходов, где каждый про-
ход состоит из фазы переписывания, за которой следует фаза слия-
ния Таким образом, имеется 21" log/"1^(2 1g 0Г1ёг~1 проходов
по именам, половина которых никак не уменьшает числа отрезков
Для /+1 лент (т. е. слияния отрезков по/) иг исходных отрезков
число проходов по данным примерно таково.
2 0001g г
1 262 1g/-
1 000 1g г
0.8611g/-
0 774 1g г
07121g/-
0.667 lg г
0.631 lg г
О 471 1g/
10
20
Если немного подумать, то фазу переписывания можно исклю-
чить. Предположим, что 57 исходных отрезков распределены по
332
лентам 1, 2, 3 и4,как показано на рис 7 10. На этом рисунке
означает п отрезков порядка i, и отрезок порядка i есть результат
слияния i исходных отрезков Отрезки сливаются так, как показы-
вают стрелки на рисунке Идея этого многофазного слияния состоит
в том, чтобы организовать исходные отрезки так, что после каждого
слияния, кроме последнего, имеется ровно одна пустая лента —
эта лента будет принимающей при следующем слиянии Далее, мы
хотим, чтобы в последнем слиянии участвовало бы только по одному
отрезку с каждой из t непустых лент. Распределение исходных от
резков < такими свойствами называется совершенным распределе
Предположим, что имеется не 4, a Z+1 лент Идею многофазного
слияния обобщить легко, так что вычислим совершенное распреде
ление для общего случая Проделаем это в обратном направлении
Пусть cikj — число отрезков на /-й ленте, когда остается осущест
вить k фаз слияния Более того, мы будем считать, что при слиянии
число отрезков	,
на ленте /.100... 0	0 0
когда больше проходов со слиянием не остается, т. е в самом конце.
Если, когда остается k слияний, имеем распределение
число отрезков
на ленте /: aftil ak ч ... f
то следующее слияние оставляет распреде 1епие
число отрезков
Легко показать, что для имеем	и переключение
логических номеров лент, при котором числа отрезков расположены
в убывающем порядке, дает
число отрезков
на ленте /: йА1 t ак> ,—аь<
Поэтому
Следовательно, совершенные распределения для Z+1 лент таковы:
334
Гл. 7 Сортировка
1 042 lg г
0.764 lg г
O.6221gr
0.536 lg г
0 479 Igr
0 438 lg г
0 4071g г
О 383 lg г
0 275 Igr
7.3.	ЧАСТИЧНАЯ СОРТИРОВКА
ность алгоритма Это верно для обсуждаемых здесь алгоритмов
выбора и слияния
335
7.3.1. Выбор
Как при данных именах хъ xs, . , хп можно найти 6-е из наи-
больших в порядке убывания^ Задача, очевидно, симметрична
отыскание (п—6+1) го наибольшего (6 го наименьшего) имени
можно осуществить, используя алгоритм отыскания 6-го наиболь
шего, но меняя местами действия, предпринимаемые при резуль
татах < и > сравнений имен Таким образом, отыскание наиболь-
шего имени (6=1) эквивалентно отысканию наименьшего имени
(Jt—n); отыскание второго наибольшего имени (6=2) эквивалентно
считать, что	|" -±-п ~] Особый интерес представляет задача
отыскания квантилей k= |“ ап ~[, 0<а< 1, и, в частности, медианы
Конечно, все перечисленные варианты задачи выбора можно
решить, используя любой из методов полной сортировки имен,
изложенных в разд 7.1, и затем тривиально обращаясь к 6-му
наибольшему. Как мы видели, такой подход потребует порядка
п log п сравнений имен независимо от значения k Но при этом мы
получаем гораздо больше информации, чем требуется, так что еле
дует поискать лучшие пути Итак, сначала изучим применение
различных алюритмов сортировки к задаче выбора п затем опишем
алгоритм, который требует только О(п) сравнений имен независимо
При использовании алгоритма сортировки для выбора наиболее
подходящим будет один из алгоритмов, основанных на выборе,
т. е либо простая сортировка выбором (алгоритм 7 5), либо пира
мидальная сортировка (алгоритм 7 7) В каждом случае мы можем
остановиться после того, как выполнены первые k шагов Для
простой сортировки выбором это означает использование
сравнений имен, а для пирамидальной — использование п (-6 1g п
сравнений имен В обоих случаях мы получаем больше информа-
ции, чем нужно, потому что мы полностью определяем порядок k
наибольших имен Это не страшно, если k — константа, не завися
тая от и, так как обрабатывается очень малое количество допол
нительнон информации, но когда k - |“ ап “|, (Ха^у, мы сорти-
руем таблицу длины ап и, таким образом, имеем дело с большим
объемом лишней информации
Хотя с первого взгляда этого не видно, идея быстрой сортировки
дает разумный метод выбора 6-го наибольшего имени из имен
хь , хп Таблица разбивается на две подтаблицы выше Xi
336
Предположим, что обнаружено, что Xi попадает в позицию / (т. е.
что это /-е наибольшее имя) Если k=], то процедура заканчивается,
если k<Z/, мы ищем k е наибольшее имя среди *i, , х7_,, и если
k>j, мы ищем (k—наибольшее имя среди Xj+i, .., хп Алго-
ритмы 7.3 и 7 4 (быстрая сортировка) легко модифицировать, чтобы
они использовали эту технику для отыскания А-го наибольшего
имени Задачи перестройки этих алгоритмов мы предлагаем в ка-
честве упражнений.
Наскочько эффективен этот алгоритм? Если C,r> k—число
сравнений имен, требующееся в среднем, то
и можно тривиально показать по индукции, что Сп k = O(n) К.сожа-
лению, число сравнений имен в худшем случае Сп ь иропорцио
нально и2, и поэтому, хотя этот алгоритм и хорош’в среднем, он
может быть чрезвычайно неэффективным.
Неэффективность возникает из-за того, что имя, используемое
для разбиения таблицы, может оказаться слишком близким к од
ному из двух краев таблицы вместо того, чтобы быть ближе к сере-
дине, как нам хотелось бы (для расщепления таблицы почти по
полам) Таким образом, для улучшения этого алгоритма нужно
открыть способ эффективно находить некоторое имя, которое за
ведомо близко к середине таблицы Следующий индуктивный ме-
тод показывает, как это сделать. Предположим, что мы имеем
алгоритм выбора, который находит k е наибольшее из п имен за
28л сравнений. Эю, конечно, зерно для п<50, поскольку 28п>
^-уп(п—1) сравнений имен достаточно для полной сортировки
имен при использовании пузырьковой сортировки при п^50.
Предположим, что 28/ сравнений имен достаточно для «и Сначала
делим таблицу с п именами на п/7 “| «п/7 подтаблиц по 7 имен
в каждой, добавляя, если нужно, несколько фиктивных имен типа
—оо для дополнения последней подтаблины (т е когда п не яв-
ляется кратным 7) Затем полностью отсортируем каждую из п/7
подтаблцц. Если использовль пузырьковую сортировку, то сор
тировка таблицы с 7 именами требует не больше у7(7—i)—21
сравнения имен, поэтому в целом сортировка всех этих таблиц тре
бует не больше 21 (п/7) = 3п сравнений имен Затем рекурсивно
применяется алгоритм выбора к п/7 медианам п/7 отсортированных
таблиц для отыскания медианы медиан за 28 (п/7) — 4п сравнений
имен Информация об именах в этот момент показана на
рис 7 И
имеется около уН имен Поэтому есть гарантия, что медиана медиан
«близка» к середине таблицы, и мы можем использовать этот факт
для расщепления таблицы, когда применяем идею быстрой сорти-
ровки к выбору
Сколько всего нужно сравнений имен? Чы использовали Зп
сравнении для сортировки подтаблиц, 4п сравнений для отыскания
медианы, п сравнений для расщепления таблицы и не больше
28 (у») сравнений для рекурсивного применения алгоритма (по
скольку может существовать до уп имен в подтаблице, к которой
рекурсивно применяется алгоритм) Таким образом, производили
не больше 28м сравнений имен; и поскольку ясно, что общее коли-
чество работы пропорционально числу сравнений имен, мы имеем
алгоритм выбора с временем работы О(п) Конечно, этот алгоритм
не так эффективен, как пирамидальная сортировка, если не верно,
что 28п<‘2п log п, т е п>2и—16 384 Но мы были слишком ire-
чески это число можно уменьшить еще дальше до па^5 431п,
так что алюритм становится пригодным и для малых значений л.
338
7.3.2. Слияние
Вторым направлением исследования частичной сортировки яв-
ляется задача слияния двух отсортированных таблиц
и	в одну отсортированную таблицу z^z2^ .
^zn+m Существует очевидный способ это сделать-таблицы, под
лежащие слиянию, просматривать параллельно, выбирая на каждом
шаге меньшее из двух имен и помещая его в окончательную таблицу
Этот процесс немного упрощается добавлением имен сторожей
лп+1=//т+1 = оо, как в алгоритме 7 10 В этом алгоритме i и / ука-
зывают соответственно на последние имена в двух входных табли-
цах, которые еще не быти помещены в окончательную таблицу
xn + i'f~ Ут + 1*~
|
Уг
При пхт этот метод стияния достаточно хорош; фактически
для п—т можно показать, что в худшем случае для слияния всегда
необходимо не меньше п ]-т—1 — 2п—1 сравнений имен (упр 42)
Однако при т=1 мы можем слить таблицы гораздо эффективнее,
используя бинарный поиск (алгоритм 6 5) для отыскания места,
куда нужно вставить в связи с этим наша цель теперь состоит
в том, чтобы найти метод слияния, который объединяет лучшее,
что есть в бинарном поиске и алгоритме 7.10
На рис. 7 12 показана основная идея процедуры бинарного
слияния, которая ведет себя как бинарный поиск при т— 1, но как
прямое слияние при пхт Эта процедура является также хорошим
компромиссом для других значений т Пусть п^т, идея состоит в
ут вкладывается в самую правую подтаблицу (используется бинар-
ный поиск), ут и те из подтаблицы, о которых стало известно, что
’ ^-21-^22 |-^23-*-24^25 l-t26-t27x28
I
У1 •  • У5 Уб
они больше ут, можно теперь поместить в выходную таблицу, и
алгоритм продолжается рекурсивно Вспомним, однако, что би-
нарный поиск работает наиболее эффективно для таблиц размера
2*—1 (почему?), и поэтому будет лучше, если в последней подтаб-
лице большей таблицы окажется не около n/tn, a	имен.
Так, для случая, показанного на рис 7 12, мы имеем 2'-1»2S/8-'—I —
=3 и сравниваем с х„5, как показано на рис. 7 13 Если х25>т/в,
то х25, х2в, х27, х2д можно поместить в выходную таблицу, и мы про-
должаем слияние X), х2,	, z24 с ух, у2, . , уй. Если x2i<yb, то
используем бинарный поиск для отыскания места г/„ среди х2вх>7х28
за два сравнения имен и помещаем и xt>y6 в выходную таблицу
Продолжаем процесс, сливая х}х2 лЛ с у^. .у-,, где k — наи-
большее целое, такое, что т/в>«л Общее описание этой процедуры
приведено в алгоритме 7 11 Предложения then и else, относящиеся
к «if т^п», одинаковы во всем, кроме того, что роли г и у (и отсюда
п и т) меняются местами
Сколько делается сравнений^ Пусть Сп!л — число
имен, производимых в худшем случае алгоритмом 7 11
нии *1,	, хп и f/t, , ут Нетрудно показать, что
сравнении
при слия-
(упр 43) Ботее того, из упр 44 имеем
(7 2)
ст «~ст L«2j + "l> 2m
Повторное применение равенства (7 2) и объединение его с равенст-
вом (7.1) дает
с. „-m+jjj-l+r™. т-йп,
При т—п имеем
340
Гл 7 Сортировка
вто время как при т — 1 получаем
т е алгоритм 7 11 работает как прямое слияние на одном краю
и как бинарный поиск на другом
Далее, так как имеется (т£п) возможных исходов алгоритма
слияния (почему*), то по аналогии с анализом величины S (п)
в вводной части разд 7 I мы должны иметь не меньше 1g ("Й") 1
сравнений имен в худшем случае Но, согласно упр 45,
и поэтому бинарное слияние достаточно эффективно для промежу-
точных значений т так же, — •• — —Л............
как и для крайних

Поместить x„ + s_at,
| лицу

Используя t сравнений
имен, вставить ут в
Ли+2 -г'’	•' хп 6инаР
ным поиском Пусть k —
Ут> +	ай + 2’	•» х:;



Поместить	..
... ут в выходямо таб
имен, вставить хп в
Ут+ъ-th • • Ут бнпар
ным поиском. Пусть k —
что хп > уь Поместить
11 n = 0 then Поместить yt, , , дт в выходную таблицу
Алгоритм 7.11. Схема бинарного слияния.
341
7.4.	КОММЕНТАРИИ И ССЫЛКИ
Почти все, что может потребоваться дополнительно узнать о за-
дачах сортировки, обсуждавшихся в этой главе, можно найти
в книге
Knuth D Е The Art of Computer Programming, Vol. 3 (Sorting
and Searching), Addison-Wesley, Reading, Mass., 1973
[Имеется перевод Кнуг Д Искусство программирования для
ЭВМ Т 3 (Сортировка и поиск) — М Мир, 1978 }
Материал, изложенный там, представляет собой энциклопедиче-
ский подход к проблеме в целом Обширную библиографию всех
статей, изученных Кнутом при написании раздела о сортировке,
можно найти в журнале Computing Reviews, 13 (1972), 283—289.
Раздел 5 5 книги Кнута содержит отличное сравнение методов сор-
тировки и краткую историю предмета сортировки
Одна из первых попыток машинной сортировки была предпри-
нята Джоном (рон Нейманом, который запрограммировал внутрен-
нюю сортировку слиянием (упр 27) на машине EDVAC Подроб-
ности, относящиеся к этой работе, см в статье
Knuth D Е. Von Neumann’s First Computer Programni, Computing
Surveys, 2 (1970), 247—260
Пузырьковую сортировку впервые проанализировал Говард
Б Демут в 1956 г в докторской диссертации о сортировке (Стэн-
фордский университет), хотя метод был известен и раньше Пузырь
новая сортировка была, например, частично проанализирована
в более ранней обзорной статье
Friend Е Н Sorting on Electronic Computer Systems, J ACM, 3
(1956), 134—168
В этой статье изложен также метод турнира с выбыванием (пред-
шественник пирамидальной сортировки) и другие новые способы
сортировки
Быстрая сортировка была впервые описана в работе
Ноаге CAR Quicksort, Comp J , 5 (1962), 10—15,
а соответствующие ей алгоритмы 63 и 64—в Communi: tions о/ the
АСМ Модификация с использованием медианы выборки имен для
расщепления таблицы имеется в статье Хоара, но анализ ее эффек-
тивности (с примером из трех имен) сделан в работе
Van Emden М Н Increasing the Efficiency of Quicksort, Comm
ACM, 13 (1970), 563—567.
Быстрая сортировка основана на относительно простой идее,
но существует много ее возможных модификаций и усовершенство-
342
ваний Все они со знанием дела обсуждаются и анализируются
в работе
Sedgewick R Quicksort, Report Number STAN-CS-75-492, Depart-
ment of Computer Science, Stanford University, Stanford, Ca ,
May 1975
Этот отчет является превосходным примером методологии анализа
комбинаторного алгоритма. Наше изложение быстрой сортировки
основано на отчете Седгевика
Поведение быстрой сортировки при наличии равных имен час-
тично анализируется Седгевиком, но более полно изучается в статье
Burge W Н Ал Analysis of Binary Search Trees Formed from Se-
quences of Nondistinct Keys, J ACM, 23 (1976), 451—454.
Пирамидальная сортировка была описана в работе
Williams J W.J Algorithm 232 (Heapsort), Сотт ACM, 7 (1964),
347—348
Эффективным подход к фазе построения был предложен в работе
Floyd R W Algorithm 245 (Treesort), Сотт ACM, 7 (1964), 701
Стоит кратко описать кое-что из того, что известно относительно
наименьшего возможною числа сравнений имен S(n), необходимых
в худшем случае для сортировки п имен «Теоретико-информацион-
ный» разбор, сделанный в вводной части разд. 7 1, в сущности оз-
начает, что если все п' перестановок могут появляться с одинаковой
вероятностью, то мы можем использовать энтропию, введеннмо
в разд 1.5 для получения неравенства
Таким образом, для определения порядка имен, как в худшем слу-
чае, так и в среднем, требуется не меньше 1g п! бинарных решений
(т е сравнений имен) Следующая таблица суммирует все извест-
ные результаты относительно S(n), пС13
19
10 11 12 13
22 26 29 33
22 26 30 ?
Заметим, что для rcsjl I можно отсортировать п имен за Г 1g п! “|
их сравнений Л\етод, который это делает, известный как сортировка
вставками и слиянием, был представлен в статье
343
Ford L., Jr , Johnson S. A Tournament Problem, Amer. Math.
Monthly, 66 (1959), 387—389
и впервые был проанализирован Адяном (Hadian А.) в его доктор-
ской диссертации (Миннесотский университет) в 1969 г Тог факт,
что 5(12) =30, а не Г 1g 12’“| =29, приводится в работе
Wells М. Applications от a Language for Computing in Combinatorics,
Information Processing, 65 (Proceedings of the 1965 1FIP Congress)
Spartan Books, Washington, D C , 1966, 497—498
Этот результат полечен вычислением «в лоб», которое заняло 60
часов на ЭВтМ /Maniac II
Выбор с замещением (для образования исходных отрезков во внеш-
ней сортировке) был впервые предложен Севардом (Seward Н Н )
в диссертации на соискание степени магистра (Массачусетский
технологический институт) в 1954 г. Первый анализ этой про-
цедуры принадлежит Меру (Moore Е F) [см U S. Patent 2983904
(1961)], где Мур показал, что математическое ожидание длины от-
резка равно 2т. Подробности его очаровательного доказательства
вместе с полным анализом математического ожидания длины от-
резков (упр 30) можно найти в монографии Кнута в томе, посвя-
щенном сортировке, о котором говорилось выше
Общее многофазное слияние было предложено в работе
Gilstad R L Polyphase Merge Sorting—Ап Advanced Technique,
Proc AFIPS Eastern Joint Computer Conf , 18 (1960), 143—148
Каскадное слияние (хпр 33) обязано своим появлением работе
Betz В К , Carter W С New Merge Sorting Techniques, ACM Na-
tional Conference, 14 (1959), paper 14
Хоар в своей статье о быстрой сортировке предложил исполь-
зовать каскадное слияние для определения k-ra (в порядке убы-
вания) наибольшего имени среди п имен. Первый полный аиачиз
этою метода дан в статье
Knuth D. Е Mathematical Analysis of Algorithms, Information
Processing, 71 (Proceedings of the 1971 1FIP Congress), North-
Holland Publishing Co , Amsterdam, 1972, 19—27
Подробности его реализации и сравнение с подходом быстрой сор-
тировки содержатся в работе
Floyd R W , Rivest R L. Algorithm 489 (Select), Comm ACM, 18
(1975), 173
Приведенный в разд 7 3.1 алгоритм выбора, использующий
О{п) операций в худшем случае, появился в статье
344

Blum At , Floyd R W , Pratt V , Rnest R L., Tarjan R. E Time
Bounds for Selection, J Comput Sys Sei., 7 (1973), 448—461,
усовершенствование этою алгоритма использовано в работе
Schonhage А . Paterson VI S , Pippenger N Finding the Median,
J Comput Sys Sa , 13 (1976), 184—199
для доказательства того, что среднее из п имен можно наити за
3n+0((n log п)’/«) сравнений имен; это усовершенствование можно
модифицировать для нахождения &-го наибольшего имени за то же
число сравнении
Алгоритм бинарного слияния из разд. 7 3.2 взят из статьи
Hwang I- К , Lin S A Simple Algorithm for Merging Two Disjoint
Linearly Ordered Sets, SMAl </. Comput., 1 (1972), 31—39
7.5.	УПРАЖНЕНИЯ
1 Реализуйте и проанализируйте следующую сортирояку перечислением
соип^,	дли сортировки таблицы. Работает ли алгоритм если имена мо-
2 Продолжите рассуждение приведенное во введении к разд. 7 1, с тем,
чтобы показать, что даже если разрешены равные имена, для сортировки п имев
нений имен для такого алгоритма сортировки равно -|-пН-0(1)
4 Добавьте проверку «!>0» в цикл while алгоритма 7 1 простой сортировки
1, гдеЯ„=21/1А
о Перепишите алгоритм 7 1 так чтобы он в таблице xj, х2 .... хя сортировал
чнсеЛ|б(>д^_|> ' >fir=l, последовательно 6гсортировка, <\_i сортировка
*6 (s') Покажите, что для любых положительных целых end, если таблица
то наибольшее целое, не представимое в виде ul'-rvm, и у>0 равно (I—1) (т— 1)—1
7 5

руюшая часть сортировки с уменьшающимся шагом имеет время прогона О
^Jtl\ 1) П ,	й ,, б	- у, _	*

Каково среднее значение



имен, больших х1г
346
Гл 7 Сортировка


и, таким образом, что
13 Проанализируйте глубину стека в худшем случае для алгоритма 7 4.
[Ответ L. lg (n+1)/3 _J н>2.)
)1ч. Модифицируйте алгоритм / ‘t (нерекурсивная оыстрая соотировка) так.
сортировку вставками из упр. 4, либо добавьте имя-сторож х0——™ (в последнем
него числа сравнений и среднего числа перестановок, определите оптимальное
15 Придумайте и реализуйте алгоритм сортировки аналогичный быстрой
сортировке, в котором расщепление осуществляется на основании самого стар
(а) числа перестановок,
(с) максимальной глубины стека.
Проанализируйте средние случаи для (а), (Ь) и (с), считая, что имена, кото-
16. Покажите, что побои метод определения наибольшею имени в таблице
(Ъ) Используя н. (а), докажите, что первый никл for алгоритма 7 7 пирами
таблицу Xj, х2,	., ха.
19. Докажите, что в пирамиде с п именами поддеревос корнем в X; имеет вы-
7 5

«нелистьев»	)
21 (а) Постройте и проанализируйте алгоритмы добавления имени к пира-
tb) Постройте и проанализируйте алгоритм исключения данного имени х(
22. Исследуйте идею тернарной пирамиды и алгоритм сортировки, основан
устойчивы?
“26 Предположим, что в данной матрице А= (atj) каждая строка сортируется
в возрастающем порядке и затем каждый столбец сортируется в возрастающем
порядке. Останутся ли строки в возрастающем порядке? Обоснуйте ваш ответ
27	Идею слияния можно использовать не только для внешней, но и для „нут-
реннсй сортировки Примените идею из разд 7.2 для получения алгоритма внут-
ваш алгоритм.
28.	Модифицируйте алгоритм 7.6 (восстановление пирамиды) так чтобы имена,
если Ci=z2 и <х2, и тг|К, чтобы'наименьшее имя (а не наибольшее) хранилось

31.	Реализуйте многофазное слияние, описанное в разд. 7.2 Следите за фиг

7 5 Упражнения
349
обходимые для образования совершенною распределения, надо распределять как
33 каскадное слияние лучше всего объяснть на примере. Предположим,
что мы имеем 190 исходных отрезков и 6 лент; мы производим слияние так. как
показано на рис 7 14. Изучите и реализуйте это слияние Можно показать, что
при /+1 лентах (т. е. слиянии по t лентам) и г исходных отрезках число проходов

3	1 042 1g г
4	0.704 ig г
5	0.598 1g г
б	0.5511g г
7	0.5281g/-
8	0.5161g/-
9	0 5091g г
10	0 5051g г
20	0 5001g г
Почему для Н 1=3 число проходов такое же как гри многофазном слиянии?
имеется только две ленты?найдитс метод ленточной сортировки {Указание- сном
бинируйте идеи пузырьковой сортировки и выбора с замещением)
•(b) Проанализируйте математическое ожидание нужного числа сравнении
это сделать за время 0 (я)?
наибольшего имени. Обобщить этот результат.
k го наибольшего из п имен необходимо n—k\ Г lg (fe—i) ~i сравнений имен. (Ука
зание: используйте рассуждение, аналогичное приведенному в конце разд 7 1
рассуждению, которое показывает, что S(n)>lgn!)
41.	Преобразуйте алгоритм 7 10 (прямое слияние) так, чтобы имена хл + 1=
=t/n+1 = oo не были бы нужны, и таким образом постройте алгоритм который
использует не больше п-\-т— 1 сравнений имен для слияния Х|<х2< <хп и
42.	Докажите что 2л—1 сравнений имен необходимо и достаточно для слияния
зует n-j-m— 1 сравнении имен, когда


для 2т<& {Указание: докажите индукцией по т что С,„ п<
заметив что Ст n=tTax(C(i	^ra-t п i Н-1), где t—


Глава 8. Алгоритмы на графах
Множество самых разнообразных задач естественно формули-
руется в терминах точек и связей между ними, г е в терминах
графов Так, например, могут быть сформулированы задачи со
ставления расписаний в исследовании операций, анализа сетей в
электротехнике, установления структуры молекул в органической
химии, сегментации программ в программировании, анализа цепей
Маркова в теории вероятностей В задачах, возникающих в реаль-
ной жизни, оказывается, что соответствующие графы часто так
велики, что их анализ неосуществим без ЭВМ Таким образом,
решение прикладных задач с использованием теории графов воз
можно в той мере, в какой возможна обработка больших графов
на ЭВМ, и поэтому эффективные алгоритмы решения задач теории
графов имеют большое практическое значение В этой главе мы
излагаем несколько эффективных алгоритмов на графах и исполь-
зуем их для демонстрации некоторой общей техники решения задач
на графах с помощью ЭВМ
Конечный граф G=(V, Е) состоит из конечного множества
вершин V={vlt v2,	•} и конечного множества ребер Е= {е,, е2,	}
Каждому ребру соответствует пара вершин если ребро {v, w)
соответствует ребру е, то юворят, что е инцидентно вершинам v
и w Граф G изображается следующим образом: каждая вершина
представляется точкой и каждое ребро представляется отрезком
линии, соединяющим его концевые вершины Граф называется
ориентированным, если пара вершин (с, ш), соответствующая
каждому ребру, упорядочена В таком случае говорят, что ребро е
ориентировано из вершины v в вершину ш, а направление обозна-
чается стрелкой на ребре Мы будем называть ориентированные
графы орграфами В неориентированном графе концевые вершины
каждого ребра не упорядочены, и ребра не имеют направления
Неориентированный и ориентированный графы изображены соот
встственно на рис 81 и 82 Ребро называется петгеи, если оно
начинается и кончается в одной и гой же вершине. Говорят, что
два ребра параллельны, если они имеют одну и ту же пару концевых
вершин (и если они имеют одинаковую ориентацию в случае ори
ентированного графа) Граф называется простым, если он не имеет
ни петель, ни параллельных ребер. Если не указывается против
стыми
будем считать, чю рассматриваемые графы являются про-
обозначения соответственно числа вершин
G=(V, Е)
символы 1VI и \Е\ для
и числа ребер в графе

8.1. ПРЕДСТАВЛЕНИЯ
Наиболее известный способ представления графа па бумаге со-
стоит в геометрическом изображении точек и линий В ЭВМ граф
должен быть представлен дискретным способом, причем возможно
Много различных представлений. Простота использования, так же
353

как и эффективность алгоритма на графе, зависит от подходящего
выбора представления графа В этом разделе обсуждаются раз-
личные структуры данных для представления графов.
Заметим, что в матрице смежностей петля может быть представ-
лена соответствующим единичным диагональным элементом. Крат-
ные ребра можно представить, позволив элементу матрицы быть
больше 1, но это не принято, так как обычно удобно представлять
каждый элемент матрицы одним двоичным разрядом.
Для задания матрицы смежностей требуется двоичных
разрядов Если они помещаются в машинные слова длиной в I
двоичных разрядов, то каждая строка матрицы требует [“ |К|//“|
слов Если каждая строка начинается с нового слова, то для записи
матрицы смежностей требуется | VI • f I V\/l ~| слов У неориенти-
рованного графа матрица смежностей симметрична, и для ее пред-
ставления достаточно хранить только верхний треугольник В ре-
зультате экономится почти 50% памяти, ио время вычислений может
при этом немного увеличиться, потому что каждое обращение
к ац должно быть заменено следующим' «if i>/ then ац else ац»
Нетрудно видеть, что в большинстве алгоритмов на графах
каждое ребро данного графа 6 необходимо рассматривать по край-
ней мере один раз. иначе то единственное ребро G, которым мы
пренебрежем при исследовании, может изменить природу G По
этому в случае представления графа его матрицей смежностей для
большинства адюритмов требуется время вычисления, по крайней
t2 X" 780
354
мере пропорциональное |V|2 (исключения из этого утверждения см.
в упр. t).
Матрица весов. Граф, в котором ребру (t, /) сопоставлено число
wt!, называется взвешенным графом, а число w,j называется весом
ребра (|, /) В сетях связи или транспортных сетях эти веса пред-
ставляют некоторые физические величины, такие, как стоимость,
расстояние, эффективности, емкость или надежность соответст-
вующего ребра Простой взвешенный граф может быть представлен
своей матрицей весов (V=[ay^], где wtj есть вес ребра, соединяю-
щего вершины i и / Веса несуществующих ребер обычно полагают
равными оо или 0 в зависимости от приложений (см., например,
раздел гл 4, в котором рассматривается задача коммивояжера)
Когда вес несуществующего ребра равен 0, матрица весов является
простым обобщением матрицы смежностей
Список ребер. Если граф является разреженным (|Е\ =о (IVIs).
то возможно, что более эффективно представлять ребра графа
парами вершин Это представление можно реализовать двумя мае
сивами g=(gi, gi, , giEi) и Л=(/гь ht, ... Н\е\) Каждый
элемент в массиве есть метка вершины, а г-е ребро графа выходит
из вершины gl и входит в вершину hi. Например, орграф, изобра-
женный на рис 8.3, будет представляться следующим образом:
Ясно, что при этом легко представимы петли и кратные ребра.
Так как для обозначения каждой из п вершин требуется по
крайней мере [“Ign"] разрядов памяти, для представления 1рафа
списком ребер потребуется по крайней мере 2|Е| [“ lg| VI ”| разрядов
памяти Если для обозначения одной вершины используется слово
длины I разрядов (в предположении 1Vl^2'), то это представление
требует 2[Е|/ разрядов памяти
Поскольку число двоичных разрядов для хранения графа в
виде его матрицы смежностей пропорционально IVI2, решение
вопроса о том, является ли список ребер более экономичным (асимп-
тотически), зависит от того, как растет |Е| при изменении IVI
Если |E|~c|VI2, то для большого IVI список ребер является менее
экономичным. Если |£|=o(|Vl2), то список ребер для больших
| VI может быть более экономичным Поэтому выбор представления
часто зависит от того, являются ли рассматриваемые нами графы
разреженными, такими, что |£| =р(|VI2), или плотными, такими,
что |£|~с| VI3 Однако для графов, используемых в практических
целях, решающую роль может играть длина слова I.
Структуры смежности. В ориентированном графе вершина у
называется последователем другой вершины х, если существует
Если для хранения метки вершины используется одно машин-
ное слово, то структура смежности ориентированного графа требует
|V| + |E| слов Если граф неориентированный, нужно ]VI+2]£|
слов, так как каждое ребро встречается дважды.
Структуры смежности могут быть удобно реализованы масси-
вом из |V| линейно связанных списков, где каждый список содер-
жит последователей некоторой вершины Поле данных содержит
метку одного из последователей, и поле указателей указывает следу-
ющего последователя (разд 2 2 2) Хранение списков смежности
в виде связанного списка желательно для алгоритмов, в которых
в графе добавляются или удаляются вершины
В дополнение к этим известным представлениям графов сущест-
вуют другие, менее употребляемые Одно из них обсуждается в
упр 2
Во многих задачах на графах выбор представления является
решающим для эффективности алгоритма С другой стороны, пере-
ход от одного представления к другому относительно прост и может
быть выполнен за О(|И|2) операций (упр. 3) Поэтому если решение
задачи на графе обязательно требует числа операции, по крайней
мере пропорционального |У|2, то время ее решения не зависит от
вида, а котором представлен граф, так как представление его может
быть изменено за O(|V|2) операций,
12»
8.2. СВЯЗНОСТЬ И РАССТОЯНИЕ
Говорят, что вершины х и у в графе смежны, если существует
ребро, соединяющее их Говорят, что два ребра смежны, если они
имеют общую вершину Простой путь, или, для краткости, просто
путь, записываемый иногда как (оь v2,	о&),— эго последова-
тельность смежных ребер (оь о2), (vt, v3),	. (oft 2, oft..i), (Oh-i,
yk), в которой все вершины о,, о2, ••, vh различны, исключая,
возможно, случай o^Ofc В орграфе этот путь называется ориенти-
рованным из У1 в Os, в неориентированном графе он называется
путем между и vn. Число ребер в пути (в данном случае k—1)
называется длиной пути На рис 8 1 последовательность (о* о4),
(о4, v,), (о1, и,) = ФЛ, 0.1, О], о2) есть путь длины 3 между ов и о,. В орг-
5, 7, 1) есть путь длины 4 из вершины 3 в 1 Расстояние от вершины
а до вершины b определяется как длина кратчайшего пути (т е.
пути наименьшей длины) из а в b Цикг— это путь, в котором
первая и последняя вершины совпадают На рис 8 1 (о3, у3> Vt, vly
уя) есть цикл длины 4, на рис 8 3 (3, 4, 5, 3) — цикл длины 3 Граф,
который не содержит циклов, называется ациклическим
Подграф графа 6= (V, Е) есть граф, вершины и ребра которого
лежат в G Подграф графа G, индуцированный подмножеством S
множества V вершин [рафа G,— это подграф, который получается
в результате удаления всех вершин из V — S и всех ребер, инци-
дентных им.
Неориентированный граф G связен, если существует хотя бы
одни путь в G между каждой парой вершин о, и v_, Ориентированный
। раф G связен, если неориентированный граф, получающийся из G
пхтем удаления ориентации ребер, является связным Говорят,
что ориентированный граф сильно связен, если для каждой пары
вершин vt и и} существует по крайней мере один ориентированный
путь из vt в v, и по крайней мере один из о; в о,. Граф, состоящий
из единственной изолированной вершины, является (тривиально)
связным Максимальный т) связный- подграф графа G называется
связной компонентой или просто компонентой G Несвязный  раф
состоит нз двух или более компонент Максимальный сильно связ-
ный подграф называется сильно связной компонентой
Большинство основных вопросов о графе касается связности,
путей и расстояний Нас может интересовать вопрос, является ли
граф связным; если он связен, ю может оказаться нужным найти
кратчайшее расстояние между выделенной парой вершин или оп-
ределить кратчайший путь между ними. Если граф несвязен, то
может потребоваться найти все его компоненты В этом раздете
строятся алгоритмы для решения этих и дру|их подобных во-
просов
8.2.1. Остовные деревья
Связный неориентированный ациклический граф называется
деревом, множество деревьев называется лесом Мы уже встреча-
лись в предыдущих главах с корневыми деревьями и лесами, обра-
зованными корневыми деревьями, но (некорневые) деревья и леса,
обсуждаемые в этой главе, являются графами весьма специального
типа и играют важную роль во многих приложениях
В связном неориентированном графе G существует по крайней
мере один путь между каждой парой вершин, отсутствие циклов
в д означает, что существует самое большое один такой путь между
любой парой вершин в G Поэтому, если G — дерево, то между каж-
дой парой вершин в G существует в точности один путь Рассуж-
дение легко обратимо, и поэтому неориентированный граф G будет
деревом тогда и только тогда, когда между каждой парой вершин
в G существует в точности один путь Так как наименьшее число
ребер, которыми можно соединить п вершин, равно.»—1 (почему?)
и дерево с п вершинами содержит в точности п—1 ребер (упр 4),
то деревья можно считать минимально связными графами. Уда-
ление из дерева любого ребра превращает его в несвязный граф,
разрушая единственный путь между по крайней мере одной парой
вершин
Особый интерес представляют остовные деревья графа G, т е.
деревья, являющиеся подграфами графа G и содержащие все его
вершины Если граф G несвязен, то множество, состоящее из ос-
товных деревьев каждой компоненты, называется остовным лесом
графа Для построения остовного дерева (леса) данного неориен-
тированного графа G, мы последовательно просматриваем ребра G,
оставляя те, которые не образуют циклов с уже выбранными
Во взвешенном графе д=(Е, Е) часто интересно определить
остовное дерево (лес) с минимальным общим весом ребер, т е
дерево (лес), у которого сумма весов всех его ребер минимальна
Такое дерево называется минимумом остовных деревьев 1) Минимум
остовных деревьев можно найти, применяя описанную выше про-
цедуру исследования ребер в порядке возрастания их весов Дру-
358
гимн словами, на каждом шаге мы выбираем новое ребро с наи-
меньшим весом (наименьшее ребро), не образующее циклов с уже
выбранными ребрами, этот процесс продолжаем до тех пор, пока
не будет выбрано IVI—1 ребер, образующих остовное дерево Т
Этот процесс известен как жадный алгоритм
Легко видеть, что жадный алгоритм конечен Минимальность
результирующего дерева Т не так очевидна, но это можно доказать
следующим образом Предположим, что Т не является минимумом
остовных деревьев. Пусть жадный алгоритм прибавляет к Т ребра
б2, . , еп так, что эти ребра идут в порядке невозрастания весов
Пусть Тта есть минимум остовных деревьев, который включает
ребра elt е2, .e,_i для наибольшего возможного i Ясно, что
г>1, н так как Т не является минимумом остовных деревьев, то
i^n Добавление et к Tmln приводит к тому, что образуется цикл,
который должен включать ребро х^=е},	Поскольку х и elt
е2.	., Ct-i принадлежат Тт\а, в котором нет циклов, и поскольку
жадный алгоритм добавляет ребро наименьшей стоимости, которое
не образует циклов, мы знаем, что вес х по крайней мере равен весу
е/ (иначе бы к elf е2,	, вместо в; было бы добавлено х). Если
вес х больше, чем вес в,, то Tn,;,,= (7'min—{x,})(/(6f} будет остовным
деревом с меньшим общим весом, чем — противоречие По-
этому веса х и е, должны быть равны, в связи с чем 7"^in будет
минимумом остовных деревьев, что противоречит предположению,
что i наибольшее из возможных Поэтому Т должно быть минимумом
остовных деревьев.
Жадный алгоритм может быть выполнен в два этапа Сначала
ребра сортируются по весу и затем строится остовное дерево путем
выбора наименьших из имеющихся в распоряжении ребер Время,
требуемое для сортировки |Е| ребер, равно 0(|£|loglГ|) (гл 7)
Используя эффективные алгоритмы на множествах из разд, 2 4
для отыскания и объединения частично построенных деревьев
с добавлением на каждом шаге ребра, дерево можно «вырастить»
за о(t£[loglBI) операций Поэтому выбор алгоритма сортировки
будет существенным образом определять эффективность алгоритма
в целом
Существует другой метод получения минимума остовных де-
ревьев, который ле требует ни сортировки ребер, пи проверки на
цикличность на каждом шаге,— так называемый алгоритм ближай-
шего соседа Мы начинаем с некоторой произвольной вершины а
в заданном графе Пусть {а, Ь) — ребро с наименьшим весом, пн
цлдентное а, ребро (я, Ь) включается в дерево Затем среди всех
ребер, инцидентных либо а, либо &, выбираем ребро с наименьшим
весом и включаем его в частично построенное дерево В резуль-
тате этого в дерево добавляется новая вершина, скажем с По
вторяя процесс, ищем наименьшее ребро, соединяющее а, Ь или с
С некоторой другой вершиной графа Процесс продолжаете; до
359
тех пор, пока все вершины из G не будут включены в дерево, т е
пока дерево не станет остовным Доказательство того, что эта
процедура приводит к минимуму деревьев, аналогично доказа-
тельству для жадного алгоритма и предлагается в качестве упр 5
Наихудшим для этого алгоритма будет случай, когда G—полный
граф (т е когда каждая пара вершин в графе соединена ребром),
в этом случае для того, чтобы найти ближайшего соседа, на каждом
шаге нужно сделать максимальное число сравнений. Чтобы выбрать
первое ребро, мы сравниваем веса всех 171- 1 ребер, инцидентных
вершине а, и выбираем наименьшее, этот шаг требует 17|—2 срав-
нений Для выбора второго ребра мы ищем наименьшее среди
возможных 2(| 71—2) ребер (инцидентных а или Ь) и делаем для
этого 2(171—2)—1 сравнений Таким образом, ясно, что для выбора
г-го ребра требуется t(|7|—i)—1 сравнений, и поэтому в сумме
потребуется
сравнений для построения минимума остовных деревьев.
Однако можно поступить умнее и уменьшить число сравнений
примерно до [VIs Пусть алгоритм для каждой вершины и, которая
еще не принадлежит дереву, хранит указатель вершины дерева,
ближайшей к v. Эта информация позволяет нам найти х-ю добав-
ляемую вершину всего лишь за 171—i сравнений при i^2 Первая
вершина дерева выбирается произвольно и поэтому вообще не
требует сравнений К тому же после добавления к дереву t-й вер-
шины информацию о ближайших вершинах можно скорректировать
за 171—i операций, сравнивая для каждой вершины v (из 171—i
вершин), не принадлежащей дереву, расстояния от нее до только
что добавленной вершины и до той вершины, которая перед этим
была в дереве ближайшей к ней (Ср. этот процесс с алгоритмом
ближайшего соседа для задачи коммивояжера из разд 4 3 ) От-
сюда для (>2 добавление к дереву i-й вершины требует 2 (17|—i)
сравнений, а общее число сравнений равно
Запись текущей ближайшей вершины в дереве для каждой из
вершин, еще не попавших в него, можно осуществить при помощи
двух массивов dist(v) для расстояний (весов) и near(v) для назва-
ний вершин. В алгоритме 8 1 эта техника используется для по-
строения минимума остовных деревьев T={VT, Ет) с общим весом
WT в предположении, что граф G=(V, Е) задан матрицей весов
= и что веса несуществующих ребер равны оо На i-м шаге
360
цикла while множество V—Vr имеет 17|—i элементов, и поэтому
первый шаг цикла требует |и|—i—1 сравнений. Следующие три
шага в цикле требуют лишь фиксированного числа операций, и
последний шаг — цикл for — требует IVI—i—1 сравнений adist(x)>
Поэтому общее число операций равно 0(1 И|г)
Заметим, что если граф G несвязен, алгоритм порождает мини-
мум остовных лесов, т е множество минимумов остовных деревь
ев по одному для каждой связной компоненты G Эти остовные
деревья связаны вместе ребрами с бесконечными весами Поэтому
в данном случае в конце алгоритма W7?- =оо
Другой подход к нахождению минимума остовных деревьев см.
в vnp 6 Упражнение 7 показывает, как такой подход приводит
к алгоритму, требующему 0 (IЕIloglogl VI) операций.
Построение всех остовных деревьев. Иногда нас интересуют
все остовные деревья графа
Эта задача возникает, например, при анализе электрических схем,
когда схема представлена в виде графа Так как с увеличением
числа вершин число остовных деревьев растет экспоненциально
(полный граф с п вершинами имеет пп~2 остовных деревьев; см.
упр. 10), то эта задача становится невыполнимой даже для графов
дение производилось эффективно
Наиболее удачный алгоритм порождения всех остовных деревь-
ев графа аналогичен показанному на рис 4.17 методу ветвей и
границ для решения задачи коммивояжера Множество всех ос
товных деревьев графа G делится на два класса класс, содержащий
выделенное ребро (u, v), и класс, его не содержащий Остовные
деревья, которые содержат (ы, р), состоят из ребра (и, v) и остов-
ного дерева графа Gl!tfl, получающегося из G склеиванием вершин
из G ребра (и, о)
параллельные ребра. Эти ребра сохраняются, как показано на
требует О (I VI+1 £1 + |£|/) операций, где I— число остовных
деревьев графа G (упр 16).
8.2.2. Поиск в глубину
Один из
исследования
прохождения
наиболее
ес гествеиных
способов
систематического
всех вершин и ребер графа исходит из процедуры
графа методом поиска с возвращением, подобным
362
тированном графе G=(V, Е) поиск в глубину осуществляется сле-
Структура снежности Лроидынм фа<р 2
Рис
применяем процесс рекурсивно к w Если все ребра, инцидентные
вершине V, уже просмотрены, мы идем назад по ребру (и, v), по
которому пришли в и, и продолжаем исследование ребер, инци-
дентных и Процесс заканчивается, когда мы пытаемся вернуться
назад из вершины, с которой начиналось исследование Как мы
увидим в этом и следующих разделах только что предложенная
техника чрезвычайно полезна при определении различных свойств
как ориентированных, так и неориентированных графов
На рис 8 5 показано, как поиск в глубину исследует иеориен
тированный граф G, представленный структурой смежности Мы
начинаем с произвольно выбранной вершины а и идем по первому
встретившемуся нам ребру (а, Ь) Так как вершину b мы никогда
раньше нс посещали, остаемся в b и проходим по первому непрой-
денномх ребру, инцидентному Ь, а именно (Ь, с) Теперь в вершине с
первым непройденным ребром оказывается ребро (с, а) Проходим
(с, а) и обнаруживаем, что вершина а уже посещалась ранее По
этому возвращаемся вс и каким-либо образом помечаем ребро (с, а)
(на рис 8 5 — пунктирной линией), чтобы отличить его от ребер
типа (Ь, с), которые ведут в новые вершины Вернувшись в вер-
шину с, мы ищем другое пепройденное ребро и идем по первому
встретившемуся из них, скажем (с, d). Так как d — новая вершина,
снова остаемся в d и ищем непройденное ребро, в данном случае
(d, b) Поскольку вершина b посещалась ранее, помечаем ребро
(d, b) пунктирной линией и возвращаемся в d Из за того, что не
пройденных ребер, инцидентных d, не осталось, мы возвращаемся
в с В с обнаруживаем непройденное ребро (с, е) и проходим его.
Поскольку е — новая вершина, остаемся вен ищем непройденное
ей инцидентное ребро, которое оказывается ребром (е, а) Так
как а — уже пройденная вершина, помечаем ребро (е, а) пунктир-
ной линией Теперь вершина е полностью просмотрена, и мы воз-
вращаемся вс В с нет ребер, оставшихся непройденными, поэтому
двигаемся назад в b и, наконец, в а Все ребра, инцидентные а,
пройдены, что означает конец процедуры.
Как показано на рис 8 5, поиск в глубину превращает исход-
ный неориентированный граф G в орграф G, индуцируя на каждом
ребре направление (направление прохождения) Чиста около
ребер графа G на рис 8 б указывают порядок, з котором проходи-
лись ребра Ребра графа G, приводящие во время прохождения в
новые вершины (на рис 8 5 они изображены сплошными пиниями),
образуют ориентированное остовное дерево (леев случае несвязного
графа), т е дерево Т, являющееся остовом графа G, в котором
имеется выделенная вершина г, называемая корнем и такая, что
имеется ориентированный путь из г в любую вершину Т, но не
существует ориентированного пути из любой вершины Т в корень г.
Если в ориентированном остовном дереве имеется путь из вершины
х в вершину у, то говорим, что х — предок у, а у — потомок х.
Если этот путь не пуст (т е х=£у}, мы говорим, что х — собствен-
ный предок у, в у — собственный потомок х
Ориентированное остовное дерево, которое получается в резуль-
тате поиска в глубину на простом связном неориентированном
графе, будем называть DFS-деревом Ребра графа G, не принад-
лежащие DE'S-дереву, называются обратными ребрами, так как
они ведуг назад в пройденные ранее вершины На рис 8 5 обратные
ребра обозначены пунктирными линиями Заметим, что обратное
ребро должно идти от потомка к предку (почему?).
Для реализации процедуры поиска в глубину нам необходимо
отличать уже пройденные вершины от еще яепройденных Этого
можно достигнуть путем постепенной нумерации вершин числами
от 1 до |lz[ по мере того, как мы в них попадаем Сначала положим
num(v)=0 для всех Vв знактого, что пи одна вершина нс прой-
дена, и когда попадем в вершину о в первый раз, придадим num (у)
ненулевое значение Способ поиска в глубину представлен алго-
ритмом 8 2 Рекурсивная процедура DFS(v, и) осуществляет поиск
в глубину на графе G={V, Е), содержащем с, и строит для графа
ориентированное остовное дерево (V, Т), и является отцом и в де-
реве Граф задан структурой смежности, и Adj (и) означает множе-
ство вершин, смежных с v Элементы множества Т — это ребра
дерева, а элементы множества В — обратные ребра Если граф G
несвязен, то (V, Т) б>дет тесом
364
Заметим, что если num(w)=0, то (v, w) — ребро дерева, тогда как
если num (ш)=Н=0, то условием того, что (у, го) будет обратным реб-
ром, являются соотношения пит (w)<.num (с) и w^=u Если пит (©)<
<num(v), это значит, что вершина w была пройдена раньше вер
шины v Поэтому (т>, w) является обратным ребром, если оно не
является ребром дерева Т, пройденным от отца v к и, т е при
условии, что а#=и.
Поскольку для каждой вершины, которая проходится впервые,
мы обращаемся к DFS ровно один раз, всего обращений к DFS
требуется IVI При каждом обращении количество производимых
действии пропорционально числу ребер, инцидентных рассматри-
ваемой вершине Поэтому время поиска в глубину на неориенти-
рованном графе равно 0(|У|—1£|)
Связные компоненты. Простейшим случаем применения тсхни
ки поиска в глубину на неориентированном графе является способ
отыскания связных компонент неориентированного графа G— (V, Е)
Алгоритм 8.3 присваивает общий номер compnum(v) каждой вер-
шине а1, принадлежащей компоненте, в которую попадает вершина и
COMP (0
-0 then СОЛ1Р(и)
365
Легко видеть, что этот алгоритм так же, как алгоритм 8 2,
требует 0(1У|+Ш1) операций.
сортировкой вершин графа G. Например, вершины орграфа на
рис 8 6 (а) топологически отсортированы, а на рис. 8 6 (Ь) нет
Топологическая сортировка может рассматриваться как процесс
отыскания линейного порядка, в который может быть вложен
данный частичный порядок Нетрудно показать, что топологиче-
ская сортировка вершин орграфа возможна тогда и только тогда,
когда он является ациклическим (упр 17) Топологическая сорти-
ровка полезна при анализе схем действия, где большой и сложный
план представляется как орграф, вершины которого соответствуют
целям плана, а ребра — действиям Топологическая сортировка
дает порядок, в котором могут быть достигнуты цели
Топологическая сортировка начинается с отыскания вершины
графа G—(V, Е), из которой не выходят ребра (такая вершина
существует, если G не имеет циклов), и присвоения этой вершине
наибольшего номера, а именно IVI. Эта вершина удаляется из
графа G вместе с входящими в нее ребрами Поскольку оставшийся
орграф также ациклический, мы можем повторить процесс н при
своить следующий наибольший номер IVI—1 вершине, из которой
не выходят ребра, и т д Для того чтобы алгоритму потребовалось
О (I VI +1Д1) операций, нужно избежать поиска в модифицирован
ном орграфе вершины, из которой не выходят ребра Это будет
сделано, если мы произведем единственный поиск в глубину на
данном ациклическом орграфе G Дополнительно к обычному мас-
сиву num нам потребуется еще один массив label объема IVI для
ЗС6

записи меток топологически отсортированных вершин Это озна-
чает, что если в графе G имеется ребро (и, и), то label (u)<label(v)
Полный поиск и процедура присвоения меток TOPSORT приво
дятся в алгоритме 8.4
Время работы алгоритма 8 4 равно О (I У| +1£|), так как каждое
ребро проходится один раз и для каждой вершины один раз вызы-
вается TOPSORT
8.2.3.	Двусвязность
Такая вершина называется точкой сочленения или разделяющей
вершиной. Граф, содержащий точку сочленения, называется раз-
делимым. Например, вершины b, f и i на рис 8 7(a) являются
точками сочленения, при этом других точек сочленения нет Граф
без точек сочленения называется двусвязным или неразделимым.
Максимальный двусвязный подграф графа называется двусвязной
компонентой или блоком Отыскание точек сочленения и двусвяз-
ных компонент данного графа важно при изучении надежности
коммуникационных и транспортных сетей Это важно также и при
определении других свойств графа G, таких, например, как пла-
нарность, так как часто полезно разложить G на его двусвязные
компоненты и изучать каждую из них в отдельности (разд. 8 6)
Вершина о неориентированного связного графа является точ-
кой сочленения тогда и только тогда, когда существуют две другие
вершины х и у, такие, что любой путь между х и у проходит через
вершину v; в этом и только в этом случае удаление v из графа G
разрывает все пути между х и у (т е делает G несвязным) Эю
соображение позволяет нам использовать поиск в глубину для
нахождения точек сочленения н двусвязных компонент графа за
О(|V|+|£|) операций.
367

procedure TOPSORT (у)
if пит(и’) = 0 then TOPSORT (w)
Основную идею можно понять при изучении примера на рис. 8 8,
который схематически изображает связный граф, состоящий из
двусвязных компонент Gt,	и точек сочленения Vj, IC/-SC5
Если мы начинаем поиск в глубину, скажем, из вершины s в Ga,
то можем перейти из Ge, скажем, в С4, проходя через вершину va.
Но по свойствам поиска в глубину, все ребра в G4 должны быть
пройдены до того, как мы вернемся в о2, поэтому С4 состоит в точ-
ности из ребер, которые проходятся между заходами в вершину
Для других двусвязных компонент дело обстоит несколько слож-
нее так, например, если мы уходим из С4, идем вО8и оттуда — в G2
через с'3> то окажемся в 62, пройдя ребра из G9, G3 и 62. К счастью,
однако, если хранить ребра в стеке, то во время прохождения назад
в G3 через вершину os все ребра графа Gs будут на верху стека
После их vдaлeния на верху стека будут ребра из G3, и мы снова
будем проходить Gs Таким образом, если можно распознавать
точки сочленения, то применяя поиск в глубину и храня ребра в
стеке в той очередности, в какой они проходятся, можно также
определить двусвязные компоненты, ребра, находящиеся на верху
стека в момент обратного прохода через точку сочленения образуют
двусвязную компоненту
Для определения точки сочленения для каждой вершины v
графа в процессе поиска в глубину требуется вычислять новую
функцию lowpttv) Определим lowpitp) как наименьшее значение
niimfx), тде х— вершина графа, в которую можно попасть из v,
проходя последовательность из нуля или более ребер дерева, за
368
полезна благодаря следующей теореме
Теорема 8.1. Пусть (j=(V, Е) — связный граф с DFS-деревом Т
и .множеством обратных ребер В Вершина a£V будет точкой сочле-
нения тогда и только тогда, когда существуют вершины о,
такие, что (а. о) £ Т. w=£a и го не является потомком и в! и lowot (v)^
^num (а).

Доказанная нами теорема дает способ распознавания точки
вершину V, такую, что.(а, v) £ Т и lowpt (y'f^num (а), то а будет либо
Таким образом, алюритм 8 5 определяет двусвязные компоненты
(процедура BICON) графа G— (V, £) Поскольку он осуществляет
8.2.4.	Сильная связность
ния сильно связных компонент, но полученная структура будет
более сложной, чем множество ребер дерева и множество обратных
ребер. Эта сложность возникает потому, что ребра в орграфе уже
ориентированы, и мы не можем свободно проходить их в выбранном
нами направлении, как мы делали при поиске в глубин} на неори-
ентированных графах
Посмотрим, что будет, если мы должны проходить ребра орграфа
G по их направлениям во время поиска в глубину на G Как и
прежде, каждой вершине х присваиваем порядковый номер пит(х),
когда попадаем в нее впервые. Эти номера присваиваются вершинам
навсегда и обозначают порядок, в котором посещались вершины
Когда нам встречается ребро (и, ни), которое еще не проходилось,
вершина w может быть или не быть ранее пройденной Если w
прежде не посещалась, то (у, w) маркируется как ребро дерева,
так же как и в случае неориентированного графа. Если и> уже
пройдена, то она может быть или не быть предком v в противопо-
ложность случаю неориентированного графа, в котором вершина
w всегда была предком и. Если w — предок вершины и, то, оче-
видно, пит (а>)<пит (о) и (о, w) будет обратным ребром.
Если w не является предком v и num(wj>num(v), то вершина w
должна быть потомком v; в этом случае ребро (с, w) называется
ребром, направленным вперед', ребро (v, w) представляет собой
дополнительный путь из v в w. Если num(w)<.num(y) и w не яв-
ляется ни предком, ни потомком с, то ребро (v, w) называется по-
перечным ребром.
На рис. 8 10 показан поиск в глубину на орграфе и получаю-
щееся в результате разбиение ребер на четыре подмножества
Предполагается, что орграф представлен структурой смежности,
показанной на рисунке и поиск в прямом порядке начинается ит
произвольно выбранной вершины а Номера вершин пройденного
орграфа представляют собой значения пит, т. е порядок, в котором
проходились вершины. Жирные пинии означают ребра дерева,
тонкими линиями обозначены обратные ребра, перечеркнутыми —
поперечные ребра и пунктирными линиями — ребра, направленные
вперед
Очевидно, дерево (или лес), порожденное поиском в глубину,
несдинственно и классификация ребер зависит от произвольного
порядка, в котором вершины и ребра исходного орграфа задаются
в структуре смежности, а также от выбора начальной вершины. Тем
не менее разбиение ребер, которое следует из поиска в гаубицу на
орграфе, можно использовать для определения его сильно связных
компонент Заметим, что направленные вперед ребра можно и>-
норировать, так как они нс влияют на сильную связность Далее
заметим, что исходящие из v обратные ребра и поперечные ребра
могут идти только в такие вершины х, для которых num (v)>num (х)
Пусть v и w принадлежат одной и той же сильно связной ком-
поненте графа G, и без ограничения общности предположим, что
for x £ V do if num (x)= 0 then BICON (x, 0)
procedure В ICON (v u)
num (v) *— 1
I(l, v) — ребро дерева!
В ICON (®, о)
for u. £ Adj (v) do if num(w)=0 then
верха стека включая (о, да) Исключить зги

lowpt (0-L- min (lowpl (v), пит (из))
Алгоритм 8.5. Определение дв^связных компонент графа G— (V, Е).
372
(a)
(b)
Рис 8 10. (а) Орграф 6 и его структура смежности, (b) Орграф 0, пройденный при
замы жирной линией), 3 обратных ребер (показаны тонкой линией),
вперед (пунктирные линии).
nuin(v)<Hufn(w) По определению в G существует путь р из и в ш
Путь р не должен содержать поперечных ребер, идущих из одного
дерева DFS-леса в другое, так как num{v)<.num(w) и поперечные
ребра идут только в вершины с меньшими номерами, т е ситуация
373
невозможна Так как имеется поддерево, которое с его попереч-
ными и обратными ребрами включает путь р, то будем считать г
корнем минимального такого поддерева В силу минимальности
поддерева, если р не проходит через корень г мы должны иметь
что невозможно Итак, путь р проходит через корень г, откуда
следует, что г находится в той же самой сильно связной компо-
ненте, что v и а Таким образом, если 5 — сильно связная компо-
нента графа G, то вершины S определяют дерево, которое является
подграфом остовного леса Обратное утверждение не верно не
каждое поддерево соответствует сильно связной компоненте
Определение корней поддеревьев, соответствующих сильно
связным компонентам, позволит определить сами сильно связные
компоненты так же, как определение точек сочленения позволило
нам найти двусвязные компоненты Для отыскания этих корней
определим lowllnklv) как наименьший номер среди номеров вершин
в той сильно связной компоненте., в которой находится вершина v,
эти вершины можно достичь по пути из нуля или большего числа
ребер, за которыми следует не больше одного обратного или одного
поперечного ребра Значения lowlink дают информацию, которая
нужна нам для отыскания корней сильно связных компонент,
вершина v будет таким корнем тогда и только тогда, когда lowlink(v)—
=uum(v) (упр 21) К счастью, эти значения lowlink легко можно
вычислить в процессе поиска в глубину. Процедура STRONG для
определения сильно связных компонент орграфа G—(V, Е') пред-
ставлена алгоритмом 8.6
В случае когда для определения наличия в стеке вершины w
используется двоичный булев массив (вершина w находится в стеке
тогда и только тогда, когда она принадлежит той же сильно связной
компоненте, что и предок у), алгоритм 8.6 представляет собой уточ-
нение поиска в глубину, в ходе реализации которого требуются
некоторые дополнительные операции при прохождении каждото
ребра 1 рафа. Каждая вершина включается в стек и исключается из
него в точности один раз Поэтому алгоритм 8 6 требует времени,
равного 0(|К|4-|Е|)
Для доказательства корректности алгоритма 8 6 требуется
лишь показать, что значения lowlink вычисляются корректно; до-
казательство можно провести по индукции (упр. 22).
374
8.2.5.	Транзитивное замыкание
вершины граф, то решается так легкс	задан граф G=(V, Е), нас может интересовать, какие связаны между собой. Если G — неориентированный задача сводится к определению его связных компонент и применением алгоритма 8.3 Если G — орграф, то задача । не решается В этом разлете мы обсудим один метод ре-
шения и его обобщение, другие подходы рассматриваются в упр
23, 24, 25.
Предположим, что орграф G—(V, Е) представлен матрицей
смежностей A = [ai7| размера ||/| X |V|, где <1^=1, если имеется ребро
чить матрицу связности /l*=a’z|, определяемую условиями
вида a'j = \, если в графе G имеется путь из i в /, и й'7-=0, если
такого пути нет. Если множество Е ребер трафа 6 рассматривать
как бинарное отношение па множестве V вершин графа G, то А*
будет матрицей смежностей для графа G*-=(V, Е*), в котором Е*—
транзитивное замыкание бинарного отношения Е. На рис 8 II
показан орграф и его транзитивное замыкание G”.

Мы можем вычислить матрицу А* по матрице А, определяя
последовательность матриц Л10) = 1а^И’	, 4ukl,=
— [й’-}к|,1 следующим образом
Мы утверждаем, чю А •=Д(|1'1’, Дтя того чтобы понять, почему
это так, заметим, что по индукции легко доказать, что а--’ = 1 тогда
и только тогда, когда существует путь из t £ V в / $ V с промежу-
точными вершинами, выбираемыми только из множества {1, 2, .
=o)/'1’V (й!7_1’А^/_1>) равно единице тогда и только тогда, когда
либо 1>=_1 (существует путь из t в /, использующий вершины
только из {1, 2,	,1—1}), либо одновременно aji-1'и равны
единице (имеются пути из i в / и из I в /, использующие вершины
только из множества {1, 2,	,/—!}) Итак, утверждение спра-
ведливо для I
Хотя соотношение 8 1 полезно для понимания способа вычис-
ления 4*, оно неудобно для фактического выполнения вычислений,
так как хотелось бы преобразовать А в А* на месте, т е мы хо-
тели бы преобразовать А в 4*. используя лишь фиксированный
объем дополнительной памяти. Это можно сделать, рассматривая
соотношение (8 1) в другой форме
Заметим, что если задана матрица А'‘~11, то ее можно преоб-
разовать в Д‘п следующим образом. Если а$-1)=0, то просто
имеем а)/’ ^ац-1> > и если ,=Ь имеем
Обозначив но строку матрицы А через at *, получим
(8 2)
Далее, для i=£l значение аг‘~1> используется только при вычис-
лении а^\, поэтому его шачения могут меняться, не влияя на
вычисления a‘k‘‘, для k^=i Элемент а““1’ используется для вычне-
В алгоритме 8 7 используется соотношение (8.2) для преобра-
зования А в А* Здесь, очевидно, потребуется O(|VIS) операций,
однако мы замечаем, что в самом внутреннем цикле основной
являеюя операция «или» двух строк матрицы А В большинстве
вычислительных устройств это можно сделать за одну операцию,
если строка матрицы А целиком помещается в машинное слово
Значительная экономия получается, даже если строка требует не-
скольких слов

8.2.6.	Кратчайшие пути
В этом разделе мы рассмотрим алгоритмы, отвечающие на во-
прос о расстоянии между узлами в простом орграфе с неотрицатель-
ными весами К таким орграфам сводятся мноте типы графов,
так, если данный орграф не является простым, его можно сделать
таковым, отбрасывая все петли и заменяя каждое множество па-
раллельных ребер кратчайшим ребром (ребром с наименьшим
весом) из этого множества Если граф неориентирован, то можно
просто рассматривать граф, который получается из данного заменой
каждого неориентированного ребра (t, /) парой ориентированных
ребер (i, j) и (j, i) с весом, равным весу исходного неориентирован-
ного ребра Если граф невзвешен, можно считать, что все ребра
имеют один и гот же вес Позднее .мы будем рассматривать и отри-
цательные веса
Нас интересуют следующие вопросы,
1	Какова длина кратчайшего пути между двумя выделенными
вершинами? Что это за путь’
2	Каковы длины кратчайших путей между выделенной вершиной
и всеми остальными вершинами графа? Каковы эти пути^
3	Каковы длины путей между всеми парами вершин^ Что это за
пути^
Будем предполагать, что ответить на эти вопросы надо для
простого взвешенного орграфа, в котором выполнение условия
не требуется, а выполнение неравенства треугольника
необязательно Несуществующие ребра будем счи-
тать ребрами с бесконечным весом Сумма весов ребер в пути будет
называться весом или длиной этого пути,
Первая задача, отыскание длины кратчайшего пути между двумя
вершинами s (начало) и f (конец) и отыскание самого пути, может
быть решена методом, похожим на алгоритм 8 1, т е методом
ближайшего соседа для отыскания минимума остовных деревьев
графа Мы начинаем из вершины s и просматриваем граф в ширину
(упр 28) в противоположность поиску в глубину, используемому
в разд. 8 2 2, 8.2.3 и 8 2 4, помечая вершины значениями их рас-
стояний от s Процесс заканчивается, когда вершина / помечена
значением ее расстояния от s.
До окончательной пометки вершине присваивается временная
метка присвоенное вершине число будет расстоянием от начала s,
когда множество рассмотренных путей не состоит из всех возмож-
ных путей Алгоритм прекращает работу только тогда, когда метка,
присвоенная вершине Д далее не меняется Таким образом, в каж-
иметь окончательные метки, а остальная часть нет.
Вначале вершине s присваивается окончательная метка 0 (ну-
левое расстояние до самой себя), а каждой из остальных |1/|—1
вершин присваивается временная метка со На каждом шаге одной
вершине с временной меткой присваивается окончательная и поиск
продолжается дальше Таким образом, на каждом шаге метки
меняются следующим образом
1	Каждой вершине /, не имеющей окончательной метки, присваи-
вается новая временная метка — наименьшая из ее временной
метки и чисел а^-гокончательная метка i, где I— вершина,
которой присвоена окончательная метка на предыдущем шаге
2	Находится наименьшая из всех временных меток, которая и
становится окончательной меткой своей вершины В случае
равенства выбирается любая из них
Процесс продолжается до тех пор, пока вершине f не присваи-
вается окончательная метка
Первой помеченной окончательной вершиной будет $, которая
находится на нулевом расстоянии от себя. Следующей, получившей
окончательную метку, будет вершина, ближайшая к s. Третьей
вершиной, получившей окончательную метку, будет вторая по
близости к s и т д Легко видеть, что окончательная метка каждой
вершины — это кратчайшее расстояние от этой вершины до начала
s, это утверждение легко доказать по индукции (упр 29)
Для иллюстрации найдем расстояние от вершины b до вершины
g в орграфе на рис 8 12 Мы используем массив dist для хранения
меток вершин в процессе решения Окончательные метки обведены
квадратиками, а жирными квадратиками выделены самые первые
приписывания окончательных меток Процесс присвоения меток
Сам путь можно вычислить в процессе работы алгоритма, ис-
пользуя указатели pre (v) когда метка вершины v становится окон-
чательной, pre(v) указывает на вершину с окончательной меткой,
ближайшую к вершине а, т. е pre(v) — вершина, предшествующая
вершине у в кратчайшем пути Отсюда вершины, входящие в крат-
чайший путь, имеют следующий вид
s, , pre {pre (pre (/))), pre (pre (f)), pre(f), f
Алгоритм 8 8 находит кратчайший путь (и его длину) от s к /
в графе G= (V, Е), представленном в виде матрицы весов И'/=
Булев массив final (и) используется для определения того, какие
метки являются окончательными [final (и)=true] и какие — времен-
ными [//no((y)=talse] Значением last является вершина, последняя
из тех, которые уже получили окончательную метку. В конце
алгоритма 8 8 label (f) есть длина кратчайшего нуги между верши-
нами s и /, если /абе/(/)=оо, то такого пути не существует и не-
которые из значений pre (и) не будут определены. В упр 30 обсуж-

7 I 01 2	“	00
6	j 0 ]	| 2 |	«.	7	~
0	H	0	'	7	"
[~6~|	|~~O~|	fT]	10	7
0 0 0-»0-
И	Ш	И	io	И	14
Ш	Ш	DO	0	□	'4
Ш	И	0	0	□	14
0 0 0HB 14












дается модификация алюрнтма 8 8 для порождения всех кратчай-
Алгоритм 8.8 обращается к тел} цикла while не более чем [Ю —1
раз, и число операций, требующихся при каждом таком обращении,
очевидно, равно O(|lz|) Поэтому алгоритму требуется О(ДТ)
операций.
Если мы хотим найти длины кратчайших путей от s до всех
остальных вершин, то просто заменим цикл while на
while V not final (х) do.
При этом все равно алгоритму требуется только OfIV'P) операции.
В упр 31 обсуждается модификация, необходимая для порождения
самих путей

Отрицательные веса. До сих пор мы считали, что веса положи-
тельны Если некоторые из весов отрицательны, алгоритм 8 8
работать не будет, так как после присвоения вершине окончатель-
ной метки мы не можем ее изменять Алгоритм можно модифици-
ровать для орграфов с отрицательными весами при условии поло-
жительности суммы весов каждого цикла в орграфе Задача плохо
определена, если в цикле с отрицательным весом имеется вершина
на пути, направленном из s в /, гак как тогда кратчайшего пути из
s в f нет
Для модификации потребуется, чтобы на каждом шаг е каждая
вершина с окончательной меткой потучала бы также новую вре-
менную метку, если эта временная метка оказывается меньше,
чем окончательная Такая модификация увеличивает время вычис-
лений с OdVl2) до 0(|V|2Vl); в связи с этим отметим, что суще-
ствует более эффективный метод нахождения кратчайших путей
при наличии отрицательных весов Рассмотренный ниже алюритм
ограничивается временем, равным О(|И3|)
Кратчайшие пути между всеми парами вершин. Для иахожде
ния кратчайших путей между всеми |V|(|V|—1) упорядоченными
парами вершин в данном орграфе (или |V'|(|V'|—1)/2 неупорядочен-
ными парами в случае неориентированного графа) мы можем мо-
дифицировать алгоритм 8 8, который предназначен для нахож-
дения всех кратчайших путей, начинающихся в одной вершине,
и применить его к каждой вершине орграфа, т. е |к| раз Такой
подход, очевидно, дал бы алгоритм, требующий O(||/|d) операций
для графов с неотрицательными весами, но в случае наличия от-
рицательных весов после модификации потребуется О(|У|32'1'*)
операций. Вместо этого мы изложим более общий метод, в котором
нужно О (|V| ) операций даже дня i рафов с отрицательными весами.
Пусть №=|а>,7| —матрица весов графа G-=(V, Е), и мы хотим
вычислить матрицу W* =[^71, в которой — длина кратчай-
8.2.5 определим последовательность матриц = стедующим
образом:
(8 3)
полагая, что вес несуществующего ребра равен оо, х+оо = оо и
min(x, оо)=х для всех х Значение есть длина кратчайшею
пути из i£V в / £ с промежуточными вершинами, принадлежа-
щими только множеству {1,2,	, l}giV. Алгоритм 8 9, основанный
на равенствах (8.3), очень напоминает алгоритм 8 7 вычисления
транзитивного замыкания графа G, отличие состоит в том, что
расширен самый внутренний цикл, неявным образом присутству-
ющий в алгоритме 8 7 вследствие того, что для обозначения полной
строки матрицы А используется а,, Алгоритму 8 9, очевидно,
потребуется О(|1/р) операций
Заметим, что на алгоритм О1рицательность весов не влияет, но
в целом задача становится бессмысленной, если имеется цикл от-
рицательной длины. Интересно отметить, что алгоритм 8 9 является
наиболее эффективным из всех методов вычисления единственного
кратчайшего пути в плотном орграфе с отрицательными весами.
Алгоритм 8.9 не порождает явно |1 |([|/|—1) кратчайших путей,
382
он только задает их длины. Сами пути можно построить из матрицы
путей Р = (ре;], в которой pi} — вторая вершина на кратчайшем
пути из i 6 V в / V. Кратчайший путь из t в / представляет собой
последовательносгь ребер (о,, ys), (у2, оэ), ..., {^_1, fa), fj=t, va=f,
в которой vt=pt_l<f для
Матрицу Р легко вычислить в алгоритме 8 9. Положим сначала
Если на шаге с номером I имеем шг{+шг/<и',-7, то полагаем pij-*~pu
Легко доказагь, что в конце работы алгоритма Рм—О, в том и только
том случае, когда &'ц=,х>, т. е. тогда и только тогда, когда пути
из । в / не существует.
8.3. ЦИКЛЫ
В этом разделе изучим алгоритмы решения задач, имеющих
отношение к структуре циклов графа Простейшей задачей, ко-
нечно, является определение того, содержит ли ориентированный
или неориентированный граф циклы. Поиск в глубину достаточен
для ответа на этот вопрос как для ориентированных, так и для
неориентированных ]рафов граф или орграф имеет цикл тогда
и только тогда, когда DFS-дерево содержит обратное ребро Чуть
более трудной является задача определения минимального множе-
ства циклов неориентированного графа, из которого могут быть
построены все циклы графа (так называемое фундаментальное мно-
жество циклов) Еще труднее определить все циклы орграфа.
8.3.1. Фундаментальные множества циклов
Рассмотрим остовное дерево (V, Т) связного неориентированного
графа G=(V, Е) Любое ребро, не принадлежащее Т, т. е любое
ребро из £—Т, порождает в точности один цикл при добавлении
его к Т Такой цикл является элементом фундаментального множе-
ства циклов графа G относительно дерева Т Поскольку каждое
остовное дерево графа G включает ]У|—I ребер, в фундаментальном
множестве циклов относительно любого остовного дерева графа G
имеется |£|— |Р’Ц 1 циклов
Полезность фундаментального множества циклов вытекает из
того факта, что это множество потностью определяет циклическую
структуру графа- каждый цикл в графе может быть представлен
комбинацией циклов из фундаментального множества. Пусть F-
={Sb S2,	, <S|£|_|V4 i } — фундаментальное множество циклов,
где каждый цикл S, является подмножеством ребер G, т. е S^E
Тогда любой цикл графа G можно записать в виде ((8'(1ф5,а)ф )ф
, где символ @ обозначает операцию симметрической
разности, Д<^б = {х|л. £ A U В, х(£<4Пб} Например, на рис 8 14
показаны граф и фундаментальное множество циклов, получаю-
щихся из выделенного жирной линией остовного дерева графа,
здесь цикл (a, b, е, h, g, f, с, а) есть	в то время как цикл
384
(с, d, f, с) представляется в виде	Заметим, что не каждая
такая сумма является циклом, например, Si®S5 состоит из двух
не связанных между собой циклов
Поиск в гтубипу является естественным подходом, использу-
емым при порождении фундаментальною множества циклов, он
строит остовное дерево (DFS-дерево), и каждое обратное ребро
порождает цикл относительно этого дерева. Когда алгоритм дости-
гает обратного ребра (п, да), цикл состоит из ребер дерева, идущих
от да к v, и обратного ребра (v, да) Для того чтобы следить за ребрами
дерева, мы применяем поиск в глубину со стеком, в котором хра-
нятся все вершины из пути, идущего от корня к вершине, которая
проходится в данный момент Когда попадаем на обратное ребро,
сформированный цикл будет состоять из этого ребра и ребер, сое-
диняющих вершины из верха стека Алгоритм 8 10 строит фунда-
ментальное множество циклов {S(, S2,	, S|£|_ivi+i} графа
G--(V, Е), используя этот метод (процедура FNDCYC).
С первого взгляда может показаться, что алгоритм 8 10 должен
быть линейным по числу ребер |Е|, но это не так. Верно, что в цикле
for каждое ребро (и, да) просматривается лишь дважды, но одно
и то же ребро входит во многие циклы S;, и поэтому на самом деле
просматривается много раз Число операций алгоритма 8 10 равно
в действительности 0(|И| + [Е|-Н), где I — сумма длин всех по-
рожденных циклов
Величина I зависит от графа так же, как и от порядка вершин
в списках смежности. Так как каждый цикл имеет длину не больше
чем ]ГЬI, то ясно, что (И-1)(|£|- 1Г| + 1)<|(IИ-1)41И-
—2) В полном графе с |К| вершинами и |Е| =у[И ([VI—1) ребрами,
упорядоченными в структуре смежности так, что первое ребро,
выходящее из вершины i, идет в вершину i+l, 1C<<|V|, поиск в
глубину порождает yGH—1) (|К|—2) циклов следующих длин
один цикл длины [V |—I, два — длины |V|—2, три — длины |У|—3,
- , |К|—2 циклов дзины два Сумма длин этих циклов равна
Атгоригму 8 10 требуется, таким образом, O(|V|3) операций
8.3.2. Порождения всех циклов
В таких приложениях, как изучение выполнения вычислитель-
ных программ или размыкание обратных связей в системах конт-
роля, необходимо перечислять все циклы графа. Такой подход,

num (i) «- i
else if num (и)
num (s) и then
S7 — цикл


siackt=w.
Заметим,
чго blacky
Алгоритм 8.10. Фундаментальные циклы графа.
386
как просмотр подмножеств множества фундаментальных циклов,
неэффективен, поскольку многие подмножества будут приводить
к вырожденным циклам; более того, в этом случае не будет аналога
для орграфов. Мы рассмотрим только задачу порождения циклов
орграфа, любой алгоритм порождения всех циклов орграфа можно
также использовать для неориентированных графов, преобразуя
их в орграфы путем замены каждого ребра парой ребер с противо-
положными направлениями. (Что происходит в этом случае с цик-
лами графа?)
Так же, как и число остовных деревьев, число циклов ор]рафа
может быть экспоненциальным относительно числа вершин Дей-
ствительно, полный орграф с п вершинами и п (п—1) ребрами со-
держит (?)(/—1)’ циклов длины I, а значит, всего
циклов Таким образом, едва ли можно ожидать, что алгоритм
будет полиномиальным относительно объема введенной инфор-
мации Мы можем, однако, попытаться построить алгоритм, кото-
рый порождает циклы за время О ((|V’|4-|E|) (е-Н)), где «—число
циклов в орграфе Такой алгоритм будет близок к оптимальному,
так как время, требующееся только для распечатки циклов, должно
равняться £'(, где £— средняя длина цикла, о которой можно
В орграфе циклы можно порождать в процессе поиска в глубину,
в котором ребра добавляются к пути до тех пор, пока не получится
цикл Если поиск е возвращением осуществляется не очень проду-
манно, то в процессе порождения будем исследовать юраздо больше
путей, чем это необходимо, и эффективность алгоритма снизится
Для того чтобы быть уверенным в том, что каждый цикл порож-
дается только однажды и что дополнительной работы проделывается
очень мало, необходимо аккуратно сократить поиск
Для того чтобы гарантировать, что каждый порожденный цикл
будет новым и не будет получаться просто в результате перестановки
ребер в полученном ранее цикле, мы полагаем, что вершины пред-
ставлены цепыми числами от 1 до jV|, и считаем, что каждый цикл
имеет корень в его наименьшей вершине Начинаем поиск в вер
шине s и строим (ориентированный) путь (s, Oj, vt, , vh), ,акои,
следующая вершина равна s После порождения цикла (s,
Vi. Vz> • - s) исследуем следующее ребро, выходящее из vk.
Если все ребра, выходящие из вершины уже исследованы,
возвращаемся к предыдущей вершине и пробуем исходящие из
нее пути и т. д Этот процесс продолжается до тех пор, пока мы
не увидим, что пытаемся вернуться за начальную вершину s, тогда
387
все никлы, содержащие вершину s, построены Процедура повто-
ряется для s—1, 2,	, |V|
Чтобы предупредить прохождения циклов, начинающихся в
вершине vt во время поиска циклов с корнем в вершине s, необхо-
димо указать, что все вершины рассматриваемого пути (кроме s)
будем помечать как недоступную путем присвоения значения false
переменной avail (v), как только и присоединяется к рассматрива-
емому пути Вершина v будет оставаться недоступной по крайней
мере до тех пор, пока мы не возвратимся за вершину v к предыдущей
вершине рассматриваемого пути. Если рассматриваемый путь,
идущий в вершину v, не приводит к циклу с корнем в вершине $,
то v будет оставаться недоступной некоторое время даже после тою,
как мы возвратимся за нее. Это позволяет избежать поиска циклов
в тех частях графа, в которых такой поиск раньше был безуспешным
В процессе поиска вершины рассматриваемого пути хранятся
в стеке, называемом path, вершина v добавляется на верх стека
перед тем, как продолжить поиск (с помощью рекурсивного обра-
щения к процедуре), и удаляется с верха стека при возвращении
(при возвращении из рекурсивного обращения к процедуре) Эта
вершина помечается как недоступная при включении ее в стек и,
если она приводит к циклу, имеющему корень в вершине s, стано-
вится вновь доступной после того, как она исключается из стека.
Если вершина не привела к циклу с корнем в s, то она временно
остается недоступной Для записи предшественников всех недо-
ступных вершин, которые не принадлежат рассматриваемому пхти,
будем хранить множества В (zz>) дзя каждой вершины w g V
S (&.')= {о £ VI (v, w)£E и v недоступна и пе находится на рас-
сматриваемом пути}.
Иными словами, B(w) — множество недоступных предшественников
вершины w
Обратимся к ситуации, когда рассматриваемый путь есть (s,
Vi, v2,	, Vh) и следующее ребро, которое надо пройти, есть (и^,
Оы-i) Возможны три случая
1	Если 0s + 1 = S, то МЫ построим НОВЫЙ ЦИКЛ ($, Cl, Vi, , Vh, S)
Выводим этот цикл и присваиваем/7ag*-true, указывая тот факт,
что цикл (с корнем $), проходящий через vh, найден
2	Если ys+i#=s и доступна, то добавляем к рассматрива-
емому пути посредством рекурсивного обращения к процедуре
порождения цикла
3	. Если вершина Vh+i недоступна, то пропускаем ее и ищем другое
ребро, начинающееся в вершине vk Если неисследованных
ребер, начинающихся в вершине vb, нет, vk удаляется из пути,
и мы возвращаемся назад в vh-i Возвращаясь в вершину oh_lt
388
делаем снова доступной, если она привела к циклу (т. е flag
имеет значение true). Иначе опа остается недоступной, и для
вершин ш, которые являются последователями Uk, вершина
добавляется в множество В(и>)
Этот процесс описан как рекурсивная процедура CYCLE в
алгоритме 8 1) (а)
Для того чтобы вершину и сделать вновь доступной, мы должны
изменить значение avail (и) на true Однако, если вершина и стано-
вится снова доступной, то же самое происходит со всеми ее недо-
ступными предшественниками, не принадлежащими рассматрива-
емому пути (почему?). Таким образом, все э тементы множества В(и)
должны быть сделаны доступными (предшественники вершины и,
не находящиеся в В (и), уже доступны по определению В (и)) и В (и)
следует положить равным а.
Когда эти вершины становятся вновь доступными, становятся также
доступными их недоступные предшественники, не принадлежащие
рассматриваемому пути, и т, д. Этот процесс расширения множе-
ства вершин, становящихся доступными, дается в алгоритме 8 11 (Ь)
рекурсивной процедурой UNMARK.
procedure UNMARK (и)
□of atail (w) then UNMARK (w)
Для завершения описания алюритма заметим, что любой цикл
в орграфе целиком лежит внутри сильно связной компоненты
Поскольку граф на такие компоненты можно разложить, используя
алгоритм 8 6, то в каждый момент времени мы будем применять
процедуру CYCLE к одной сильно связной компоненте
Adj
CYCL1 (s, /)
UNMARK-
После обращения к процедуре CYCLE (s, f) будут порождены все
циклы, содержащие .s, и вершину s можно удалить из графа Это,
конечно, изменит сильно связные компоненты графа В предпо
ложении, что граф G=(lz, £), V —{1, 2,	, IVI}, представлен
структурой смежности Adj0, управляющая программа для CYCLE
дается в алгоритме 8 11 (с).
Доказательство корректности алгоритмов 8 11 (а), (Ь) и (с)
оставляем в качестве упр 36 Из этого упражнения можно заклю-
чить, что между последовательными порождениями циклов про-
ходит не более 0(1 УЦ-|£|) времени (упр. 37), и поэтому в целом
процедура требует 0((|УЦ-|£|)(«+1) операций, где с — число
порожденных циклов
8.4. КЛИКИ
А^аксимальный полный подграф графа G называется кликой
графа G, другими словами, клика графа G есть подмножество его
вершин, такое, что между каждой парой вершин этого подмноже-
ства существует ребро, и, кроме того, это подмножество не принад-
лежит никакому большему подмножеству с тем же свойством
Например, на рис. 8 15 показан граф и его клики. Клики графа

следует аккхратио. Каждая клика должна порождаться в точности
один раз так, чтобы не тратилось время на повторную работу
Простая техника, использованная в разд 8 3 2, рассматривающая
произвольный никл, как помеченный в вершине с наименьшим
номером, для клик слишком неэффективна Для порождения всех
клик требуется дрхгая техника, и, как мы увидим, предназначенный
для этих целей алгоритм является наиболее сложным из всех, об-
суждавшихся в данной главе.
Вначале рассмотрим естественный поиск клик с возвращением,
т е поиск, в котором не делается никаких попыток упростить
дерево поиска Каждый узел в дереве поиска соответствует полному
подграфу графа, и каждое ребро соответствует вершине графа
Сын данного узла С получается добавлением к С вершины х£с,
которая смежна с каждой вершиной из С Ребро, идущее от С к
сыну Си {•*}, соответствует вершине х На рис 8 17 показаны не-
который граф G и дерево поиска Т, которое проходится в процессе
естественного поиска с возвращением. Заметим, что каждая клика
порождается много раз каждое из подмножеств {1, 2, 3} и {3, 5, 6}
порождается шесть раз, а подмножество {2, 4} порождается дважды;
Гл 8 Алгоритмы на графах
14	<5>	<61
'1	i >	10	14	<5>	(6}
Л А /Ж I А А
Рис 8 17 Граф G и результат поиска с возвращением без ограничении клик G
Теорема 8.2. Пусть S — узел в дереве поиска Т (т е S есть
подмножество вершин графа G, которое индуцирует полный под
граф графа 6), и пусть первый сын узла S в дереве Т, который
надо исследовать, является множеством Su {*} (т е вершина х
™АфЙЬ’ еС™ поддерев° с корнем в 5и^} i>Ke йсследовалось и
смежна с каждой вершиной из S) Предположим, что все поддеревья
узла SU {*} в дереве Т уже исследованы и порождены все клики,
включающие Su{x} Тогда необходимо исследовать только те из
сыновей Su{y}, для которых o^Adj(x) (рис. 8 18).
8 4 KviKti
Отметим, что теорем}' 8 2 нельзя повторно применять к дереву,
когда исследуются сыновья узла S, т е после применения теоремы
для обрывания поддерева с корнем в S и {у,} (рис 8 18) при условии
ut£Adj(x) мы не можем оборвать поддерево с корнем в SU {^},
когда fh £ Adj (Vj) для некоторой вершины y,$Adj(x) (упр 38)
Другими словами, теорема 8 2 применяется только к первому ис-
следуемому сыну S и неприменима к оставшимся ею сыновьям,
К счастью, имеет место следующий простой результат.
Теорема 8.3 Пусть S — узел в дереве поиска Т, и пусть SczS—
собственный предок S в Т Если все поддеревья узла S U {*} уже
исследованы, так что порождены все клики, включающие S U {/},
то все неисследованные поддеревья с корнями S (J {х} можно про-
игнорировать
Таким образом, для того, чтобы воспользоваться теоремой 8 2,
процедура CLIQUE выбирает произвольную вершину уда-
ляет / из V и исследует поддерево S U {/}, обращаясь к процедуре
EXPLORE Согласно теореме 8 2, нам нужно исследовать лишь
поддеревья xcjV, когда x^Adj (/) Поддеревья S исследуют-
ся тогда с помощью EXPLORE.
Второй параметр D процедуры CLIQUE представляет собой
множество, состоящее из всех вершин, смежных со всеми верши
нами из 5, но таких, которые по теореме 8 3 не нужно добавляю
394
и поддерево 8 и {х} исследовалось для некоторого
Как и прежде, множества 8 — это предки S в дереве поиска,
и поэтому множества SU {<} суть братья, дяди, «ирадяди», «прапра-
дяди» и т д. множества 5 в дереве поиска
Так как SsV всегда является полным подграфом графа G,
и есть множество всех вершин, смежных с каждой вершиной
в S, то 8 будет кликой тогда и только тогда, когда N иD^0 Из
теоремы 8 3 следует, что если N= 0 и D=£0, то все клики, вклю-
чающие S, уже порождались Если Л #=0, то мог}т оставаться клики,
включающие S, которые еще не порождались Поэтому CLIQUE
и D-J=0 и исследует (или обрывает) поддеревья Su{x}, x£N при
М¥=0
Алгоритм 8 12 можно улучшить с помощью более аккуратно
го выбора вершины /—корня первого исследуемого поддерева
Очевидно, что в соответствии с теоремой 8 2 полезно выбрать f
так, чтобы N П Adj (/) было бы как можно больше, такой выбор
позволит обрывать большинство деревьев. Фактически нам даже не
нужно выбирать Можно взять V (J0 так, чтобы N р Adj (f)
было возможно наибольшим; если то первым исследуем под
дерево 8 U {]} Если f^D, то, согласно теореме 8.3, не нужно ис-
следовать 8 U {/}; мы просто начинаем исследовать остальные
поддеревья Итак, в алгоритме 8 12 заменяем
[[исследовать первое поддерево]
EXPLORE (/)

•вершина в которая максимизирует | М f) Adj(f)|
I [[исследовать первое поддерево]
explorer
Эта модификация дает наиболее эффективный на практике из
известных алгоритмов порождения всех клик графа. Не известно,
каково время его работы, но, как показывает граф Муна — Мозера
(рис 8 16), оно не выражается полиномом относительно [VI или |£|.
Кроме того (что важнее), время работы пемодифицировапного
алгоритма 8.12 не может быть выражено полиномом относительно
числа клик Рассмотрим граф на рис 8.19. Этот граф имеет 2" клик,
CLIQUE (V. 0)
procedure CLIQUE (Л, D)

LXPiORE (f)

, , . „,,,	. , ,f4	, | v •— вершина в Л Л (I — Adj (/))
whde Л fW- Adj (/))	0 do .1 EXpLOlR£ (y)

"U {“}
Алгоритм 8.12. Порождение клик графа
каждая из них состоит из kn вершин, и дерево поиска содержит
по крайней мере (А+1)" узлов дня алгоритма 8 12 (но не для его
модификации Почему?) Выбирая /! = lg&, получим граф с 2AlgA
вершинами, k кликами и fe*s* узлами в дереве поиска
Корректность алгоритма 8 12 и его модификации может быть
доказана одновременным использованием математической индук-
ции по N и теорем 8 2 и 8 3 (упр 39)
8.5. ИЗОМОРФИЗМ
Два графа 0л=(1/л, Ел) и GS=(VB, £в) называются изоморф-
ными (это обозначается СЛ^СВ), если существует взаимно одно-
значное соответствие f V^Ve, такое, что (v, ш)£Ел тогда и
только тогда, когда (/(о), f(w))£Ea, т е существует соответствие
между вершинами 1 рафа G4 и вершинами графа GB, сохраняющее
отношение смежности Например, на рис 8 20 показаны два изо-
морфных орграфа' вершины a, b, с, d, е, f в орграфе G2 соответствуют
вершинам 2,3, Ь, 1,4, 5в указанном порядке в орграфе Gj Вообще
говоря, между Ц и FB может быть более чем одно соответствие,
и на рис. 8 20 1рафы имеют на самом деле второй изоморфизм-
а, Ъ, с, d, е, f соответствуют в указанном порядке вершинам 2, 3,
6, 1, 5, 4 Изоморфные графы отличаются только метками вершин,
в связи с чем задача определения изоморфизма возникает в ряде
практических ситуаций, таких, как информационный поиск и оп-
ределение химических соединений
Заметим, что, как и е случае порождения всех циклов графа
(разд. 8 3.2), можно о!раличиться орграфами Любой неориенти-
397
рованный граф превращается в орграф заменой каждого ребра двумя
противоположно направленными ребрами Два полученные таким
образом орграфа, очевидно, изоморфны тогда и только тогда, когда
изоморфны исходные графы.
Самый прямой метод проверки изоморфизма графов состоят в
поиске с возвращением с целью исследования п1 возможных соот-
ветствий между вершинами двух «-вершинных орграфов При
н>13 этот естественный способ становится неудовлетворительным
из-за величины «I. Однако при подходящем укорачивании дерева
поиска такой метод дает основу для построения приемлемого алго-
ритма установления изоморфизма графов
Определим полустепень захода {полустепень исхода) вершины
в орграфе как число ребер, входящих в вершину (выходящих из
вершины) Очевидно, вершина yt в <?i не может изоморфным образом
соответствовать вершине v2 в если не верно, что одновременно
полустепень захода (о1) = пол\степени захода (у2) и полустепень
исхода (у1)=полустепени исхода (и3) Так, на рис 8 20 изоморфизм
ограничивается соответствиями между следующими подмноже-
ствами вершин.

Так что в действительности необходимо проверить только 31=6
соответствий вместо 61=720, а это дает значительную экономию.
398
Именно этот подход мы используем при построении алгоритма
установления изоморфизма орграфов
Предположим, что нам даны два орграфа GX=(EX1 Тх} и Gy —
= (Vy, Су) и требуется выяснить, изоморфны ли они .Мы пола
не могут быть изоморфными Пусть один из орграфов, скажем Gx,
выбран в качестве эталона. Пусть Gx(£) — подграф графа Gx,
индуцируемый вершинами {1,2,	k), Q^k^n. Ясно, что Gx(0) —
пустой подграф н Gx(l)—подграф, состоящий из единственной
вершины 1 и не содержащий ребер
При определении того, изоморфны ли графы Сх и Су, исполь-
зуем технику поиска с возвращением Очевидно, Gx(0) изоморфен
пустому подграфу Gv Предположим, что на некотором шаге най-
ден подграф Gy, состоящий из вершин SsVy, который изоморфен
Gx(k) Попытаемся продолжить изоморфизм на GA(£+1), выбирая
вершину —S, соответствующую k-\-\^Vx Есяи такая вер-
шина v найдена, то зафиксируем соответствие /?1 и попытаемся
продолжить изоморфизм на Gx(k |-2) Если такой вершины и не
существует, то возвращаемся в Gx(k—1) и пытаемся выбрать дру
гую вершину, соответствующую k £ Vx Этот процесс продолжается
до тех пор, пока не будет найден изоморфизм между Gx(n)=Gx
и Су, в противном случае возвращаемся к Gv(0), заключив, что
Этот процесс представлен в алгоритме 8 13 Использованная
там процедура MATCH выдает значение true если k можно сопо-
ставить v, и false в противном случае В остальной части настоящего
раздела описывается предварительная работа, необходимая для
простой реализации процедуры MATCH.
/ Ik V
I ISOMORPH(S и {о})
399
где t= I" logio(n+l) 1 Пусть Xdeg(i) и Ydeg(t) обозначают эти
составные числа для i х вершин в Gx и Gy соответственно Заметим,
что Xdeg(i) = Ydeg(]) тогда и только тогда, когда вершина i в Gx и
вершина / в Gv имеют одинаковые полустепени захода н исхода. За-
метим также, что мультимножества (Xdeg(i)\ l^ngCn} и {Ydeg(i)\
Для того чтобы дерево поиска стало возможно более узким
вверху (разд 4,1,2), сделаем так, чтобы возможно меньшее число
вершин в Gy соответствовало Gx(l) С этой целью перенумеруем
вершины Gx, проделав на нем поиск в глубину, начиная из вершины
V’x. для которой имеется наименьшее количество вершин Vx,
таких, что Xdeg(x)=Xdeg (v). С этого момента будем рассматривать
только такое перенумерованное представление Gx, отбросив исход-
ные метки вершин. «Перемеченные» вершины имеют полезное до-
полнительное свойство, состоящее в том, что вершина, для которой
в данный момент ищется соответствующая, обычно смежна с вер-
шинами, для которых соответствующие найдены раньше, этот
факт ограничивает возможное число соответствий, сокращая тем
По мере того как в процессе поиска в глубину встречаются
ребра, мы будем организовывать их в массив, обозначающий номер
вершины, из которой каждое данное ребро выходит, и номер вер-
шины, куда ребро заходит. В дополнение к ребрам, с самого начала
входившим в Gv, в этот массив будут также включены «фиктивные»
ребра, идущие к корням деревьев DFS леса из фиктивной вершины
О Затем производится сортировка ребер так, что все ребра, при-
надлежащие подграфу G\(k), располагаются перед ребрами, инци-
дентными вершине i>k
Рассмотрим приведенный на рис 8 21 пример, где показаны
два орграфа Gx и G}, а также их структуры смежности Полусте-
пени захода, исхода и составные степени равны
21
22
12
22
12
22
21
22
12345678
1	2	2	2	2	2	1	2
2	2	1	2	1	2	2	2
12	22	21	22	21	22	12	22
400
две — с Xd£g=21 и четыре — с Xdeg=‘2‘2, начинаем поиск в гпу-
чнсло соответствий между Gx{i) и подграфами графа Gy Пусть
401
|£х1+/, где/ — число деревьев в DFb-лесу Здесь г-е встретившееся
ребро выходит из вершины [гот, и идет в вершину 1о„
Для примера на рис 8 22 имеем
10
Эти ребра сортируются в неубывающем порядке в соответствии с
grapht, где grapht=max(fromi, to,) есть наименьшее k, такое, что
ребро (fromi, tot) принадлежит Gx(k) Для описанных выше ребер
переупорядоченным массивом будет
12
13
14
15
16
1 2
Теперь мы гоювы описать процедур) MATCH, которая в алго-
ритме 8 13 определяет, может ли вершина v£Vv соответствовать
вершине	Поскольку найден изоморфный образ Gx(k— 1)
в Gy, мы знаем, что для всех г, /<£ пара (i, /) является ребром
графа Gx(k—1) тогда и только тогда, когда (/,, fj) есть ребро в Gy.
Вершина и в GY может соответствовать вершине k в Gx при ус-
ловии, что (I, /г) является ребром Gx(k), тогца и только тогда, когда
(/,, и) является ребром Gy, и, аналогично, (k, i) является ребром
402
Gx(k) тогда и только тогда, когда (v, f,) является ребром в Gy
Это легко проверяется, так как у нас есть массивы from, to graph
и f. Подробности процедуры MATCH мы оставляем в качестве
упр 43 Алгоритм 8 13 в худшем случае требует 0 (к!) операций,
т е обрывание деревьев может оказаться бесполезным и все (или
почти все) п! возможных соответствий могут потребовать проверки
*8.6. ПЛАНАРНОСТЬ
Граф называют планарным, если существует такое изображение
на плоскости его вершин и ребер, что (а) каждая вершина v ичобра
жается отдельной точкой v' на плоскости и (Ь) каждое ребро (о, аг?)
изображается простой кривой, имеющей концевые точки (v', ш'),
причем (с) эти кривые пересекаются только в общих концевых точ-
ках Задача определения того, можно ли изобразить граф на пло
скости без пересечений ребер, имеет большой практический инте
чатных плат необходимо выяснить, можно ли окончательную схему
вложить в плоскость)
Определение планарности графа отличается от других задач,
обсуждаемых в этой главе, поскольку при изображении точек
и линий на плоскости приходится больше иметь дело с непрерыв
ными, а не дискретными величинами Взаимосвязь между диск-
ретными и непрерывными аспектами планарности заинтересовала
математиков и привела к различным характеристикам планарных
графов (упр 45) С точки зрения математики эти характеристики
изящны, но эффективных алгоритмов определения планарности
они не дают Наиболее успешный подход к определению планарно-
сти состоит просто в том, что граф разбивается на подграфы и затем
делается попытка разместить его на плоскости, добавляя подграфы
один за другим и сохраняя при размещении планарность
Вначале сделаем несколько простых, но полезных наблюдений
Поскольку орграф планарен тогда и только тогда, когда планарен
соответствующий неориентированный граф, полученный игнори-
рованием направления ребер, го достаточно рассматривать только
неориентированные графы Поскольку неориентированный i раф
планарен тогда и только тогда, когда все его связные компоненты
планарны, достаточно рассматривать лишь связные неориентиро-
ванные графы Более того, легко видеть, что неориентированный
граф планарен тогда и юлько тогда, когда все его двусвязные
компоненты планарны Поэтому, если неориентированный граф
является разделимым, мы можем разложить его на двусвязные
компоненты и рассматривать их отдельно Наконец, поскольку
параллельные ребра и петли всегда можно добавить к графу или
удалить из него без нарушения свойства планарности, достаточно
рассматривать только простые графы Поэтому при определении

планарности будем предполагать, что граф неориентированный,
простой и двусвязный.
Нетрудно нарисовать на плоскости полный граф с четырьмя
вершинами без пересечений ребер, следовательно, неплоский граф
должен иметь по крайней мере пять вершин. Аналогично можно
показать, что неплоский граф имеет по крайней мере девять ребер
(упр 45) В общем случае можно использовать теорему Эйлера,
связывающую число граней, вершин и ребер планарного графа
(число I раней) [-(число вершин) — (число ребер) —2,
компоненты удовлетворяю! условиям |У|>5 и 9^|£7КЗ[К|— 6
Алюритм планарности должен затем рассматривать только эти
двусвязные графы, имеющие О(!И|) ребер Алгоритм определения
планарности в этом случае достаточно сложен, и оставшаяся часть
данного раздела посвящена постепенному его построению
графе G наити цикл С, разместить С на плоскости в виде простой
замкнутой кривой, разложить оставшуюся часть G — С на непере-
нам удалось разместить так весь граф G, то он планарен, в про-
тивном случае он непланарен Трудность этого способа заключается
в том, что при размещении п\тей можно выбирать либо внутрен
ность, либо внешность С, и мы должны обеспечить, чтобы непра-
вильный выбор области размещения на ранней стадии не устранял
вести нас к неверному заключению, что планарный граф нсплаиарсн.
Гл 8 Алгоритмы на графах
Например, на рис 8.23 (а) предположим, что начальным циклом
внутри указанного цикла, как показано на рисунке Теперь обна-
руживается, что последнее ребро (a, d) нельзя добавить ни вовнутрь,
ни вовне цикла Было бы неправильно заключить, что граф G не
является планарным, так как другое размещение на рис. 8 23 (Ь)
показывает, что граф G планарен. Таким образом, необходимо
иметь возможность порождать пути систематически, выбирать
подходящие области для их размещения и в случае необходимости
переставлять уже размещенные пути с тем, чтобы можно было
добавить новые пути
Порождение путей. Для порождения путей в некотором требу-
емом порядке переупорядочим вершины и списки смежности
Точный смысл этого переупорядочения прояснится позже
Сначала на данном простом двусвязном графе осуществляем
поиск в глубину, превращая граф G в орграф G, состоящий из IVI—1
ребер дерева и |Е|—IVJ + 1 обратных ребер, как говорилось в разд
8 2 2 С этого момента будем игнорировать исходные метки вершин
и обозначать вершины их значениями пит Такой просмотр в глу-
бину и переобозначение вершин важны из-за простой структуры
в G Пусть, так же как в разд 8 2 3, lowpt (v) — наименьшая зану-
мерованная вершина, достижимая из вершины v или любого ее
потомка (в DFS-дереве) с помощью не более одного обратного ребра
В случае когда с помощью одного обратного ребра невозможно
достичь вершины, лежащей ниже и, сама о является lowpt (и) Ана-
логично, пусть nexlopt (v)— следующая самая низкая вершина, за
исключением lowpt (и), расположенная под о, которая может быть
достигнута таким же образом Если такой вершины нет, nexlopt (о)
приравнивается v Точнее, если Sv — множество всех вершин, ле-
жащих на любом пути из вершины v, состоящем из 0 или более
ребер дерева и заканчивающемся не более чем одним обратным
ребром, ю
lowpt (a) = min(Sp)
nexlopt (v) — тшп ({г} и (Sv — {lowpt (v)}))
На рис 8 24 изображен граф G, преобразованный в орграф G
с перенумерованными вершинами Тот же орграф G показан на
рис. 8 25, где старые метки вершин опущены и значения пит ис-
пользованы в качестве имен вершин. Значения lowpt и nexlopt
показаны в виде упорядоченных пар (lowpt (v), nexlopt (v)), распо-
ложенных рядом с каждой вершиной v Заметим, что в силу дву-
связности G теорема 8 1 гарантирует, что v^nexlopt (v)>lowpt (v),

пути в G порождались в некоторой желаемой поспедовательности.
численную функцию Ф
12w, если (у, и>) — обратное ядро,
2 lowpt (w), если (у, w) — ребро дерева
и ne'clopt (ш)	1>,
2lowpt(w) + \, если (ц, ш) — ребро дерева
и nexlopt{w) < с.


После этого для каждой вершины и сортируем все ребра (v, w)
в порядке неубывания значений функции Ф и используем этот
порядок в списках смежности J) Новые списки смежности для G
будут называться Padj (о) — правильно упорядоченными списками
смежности Па рис. 8.26 приведены значения функции Ф для ребер
графа, изображенного на рис 8 25, а на рис. 8 27 приведены списки
Padj(p) Заметим, что в переупорядоченных списках смежности
обратное ребро, идущее к более низкой вершине, всегда предшест-
вует обратному ребру, идущему к более высокой вершине, ipv6o
говоря, ребра (v, w) дерева появляются в порядке неубывания их
возможностей приводить в расположенную ниже v иопттчч; пл
одному обратному ребру.
вершину по
Рис 8 25 (foxpZ (a) nexlnpl (□))
рис 8 23 (b)
Ребра (pj wj	4[(f. *»
(1,2)	2
(2,3)	2
(3,4)	3
(4,5)	3
Ребра	(5,6)	3
дерева	(6,7)	5
(6.8)	3
(8.9)	3
(9, 10)	9
1(10 11)	9
(9,1)	2
(7.2)	
(6,3)	6
Обратные SI'*).	6
ребра (11,4)	3
(8 5)	10
(И 5)	10
(10,8)	16
(11.9)	18
1^ебер орграф G из рис


86
107
= (6 3)
Рис 8 27 Орграф G, его правильно упорядоченные списки смежности Раф (у)
Получив правильно упорядоченные списки смежности, пред-
ставляющие орграф <3, применим теперь просмотр в глубину для
разложения G на один цикл С и некоторое число непересекающихся
по ребрам путей pi. Начиная из вершины 1, мы продолжаем путь
по ребрам дерева до тех пор, пока не встретится вершина г, такая,
что первое ребро в списке Padj (z) есть обратное ребро (которое,
как мы увидим, идет в вершину 1) Это обратное ребро вместе со
сформированным до сих пор путем (от 1 до г) составляет первый
408
дующему ребру, исходящему из г Каждый раз, когда мы проходим
ребро дерева, мы продолжаем построение пути, когда мы проходим
обратное ребро, оно становится последним ребром текущего пути.
Таким образом, каждый путь состоит из последовательности ребер
дерева (их число ^0), за которыми следует одно обратное ребро.
Новый путь начинается из начальной вершины последнего обрат-
ного ребра, если в этой вершине неисследованных ребер больше
нет, возвращаемся к предыдущей вершине на последнем пути Про-
цесс продолжается до тех пор, пока в графе G не исчерпаются не-
пройденные ребра Алгоритм 8 14 осуществляет это разложение
орграфа на пути и цикл На рис. 8.27 показано, как этот алгоритм
раскладывает орграф, изображенный на рис. 8.25 (представленный
правильно упорядоченными списками смежности, приведенными
г 4— о
Pt 0
PATH (1)
procedure PATH (с)

В процедуре PATH каждый путь закапчивается обратным реб-
ром. Из всех обратных ребер, доступных в конкретной вершине,
алгоритм 8.14 всегда выбирает неиспользованное ребро, ведущее к
наименьшей вершине. Это следует из того факта, что каждый список
Padj (о) идет в порядке неубывания функции Ф, и значение ф [(о, и.)1
на обратном ребре (п, а») равно 2ш Этот факт объясняе> также,
почему на рис 8 26 путь (11 5) порождается перед путем (11, 9)
Следующие свойства порождаемых путей опредетяются специ-
альным упорядочением списков Padj (с)
начальной вершины зг в конечную вершину f, Если при прохожде-
нии первого ребра в пути pt рассмотреть все обратные ребра, кото-
рые еще не использованы ни в каком пути, то будет наименьшей
вершиной, достижимой из s, по пути, состоящему из ребер дерева и
любого одного из этих обратных ребер Более того, если v — внут-
ренняя вершина пути pi (т е если v(-pt, v^s,, то fi— наи-
меньшая вершина в DFS-дереве, достижимая из v или любого из ее
потомков по цепочке, состоящей из ребер дерева и любого обратного
ребра в G
Доказательство Это свойство следует из того факта, что когда в
р( проходится первое ребро, все ребра, идущие из вершины v и ее
потомков, еще не пройдены, а также из переупорядочения ребер в
соответствии со значениями функции Ф
Свойство 2. Пусть pt и pj, />г^1,— два порожденных пути с
начальными и конечными вершинами s,, Sj и flt f, соответственно.
Если Sj — предок (не обязательно собственный) вершины s7, то
Доказательство. Это свойство верно потому, что когда порож-
дается путь pt, обратное ребро, завершающее путь р/г не использу-
ется, а также потому, что по свойству 1 путь р, использует обратное
ребро, идущее дальше всего вниз в G
Свойство 3. Пусть pt и р;,	два порожденных пути,
имеющих одну и ту же пару начальных и конечных вершин s и f
Пусть Xi—вторая вершина в пути pi, a Xj — вторая вершина в
пути р) (первая вершина каждого из этих п\тей—-это общая началь-
ная вершина s) Если ребро (s, х,) не является обратным ребром
(т. е если x^f) и nexlopl(xt)<s, то (s, Xj) не будет обратным реб-
ром и nexlopt(xj)<s
Доказательство. По свойству 1 имеем f—lowpt(xt}. Так как
(s, xt) — ребро дерева (Х|=/=/) и nexlopt (xt)<s, значение функцииФ
410
на нем по определению будет
Поскольку р, порождается после pt, в правильно упорядоченном
списке смежности Padj(s) вершина х, должна появиться позже, чем
хг Отсюда следует
Таким образом, (s, xj не может быть обратным ребром и Xj-^f.
Таким же образом nexlopt (xy)<s, иначе мы имели бы
— противоречие
Польза этих свойств станет ясна позже Заметим, что именно
свойство 3 требует вычисления значений nexlopt. Эти значения поз-
воляют нам оборвать связь между двумя ребрами дерева (и, и) и
(и, w), начинающимися в общей вершине и, когда значения lowpt
для v и w совпадают
Сегменты. Когда ребра цикла С=р0 удаляются из G, ребра
оставшегося орграфа G—С распадаются на один или более связных
кусков. Каждый из этих связных кусков состоит из одного или ботее
сегментов, определяемых следующим образом Сегмент (графа G
относительно цикла С) есть либо (а) одно обратное ребро (uit w),
не принадлежащее С, по такое, что вершины у,, wQC, либо (Ь) под-
граф, состоящий из ребра дерева (vt, w), vt g C, w£C, и ориентиро-
ванного поддерева, имеющего корнем w, вместе со всеми обратными
ребрами из этого поддерева Вершина vt в С, из которой начинается
сегмент, называется базовой вершиной сегмента На рис 8 28 пока-
заны начальный цикл С и четыре сегмента орграфа, приведенного
Каждый сегмент — это связный подграф в G—С, но не каждая
связная компонента G—С является сегментом, так как два или
более сегментов могут иметь общую базовую вершину, как, напри-
мер, сегменты Si и S4 па рис 8 28. Процедура PATH порождает
сегменты в порядке убывания их базовых вершин, и все пути одного
сегмента порождаются раньше, чем пути следующего сегмента
Ясно, что все пути, принадлежащие сегменту, должны размещаться
вместе — либо все внутри С, либо все вне С Это является причиной
объединения путей в сегменты
Позже мы увидим, что размещая сегмент, можно применять ал-
горитм рекурсивно и порождать сегменты внутри сегмента (относи-
тельно другого цикла) Таким образом, понятие сегмента является
решающим для понимания алгоритма планарности
(а)	(Ь)

♦12
Вложение. Цикл С, состоящий из ребер (1, ц2), (vs, о3),
, (fft-i, tpj, (ffe, 1), укладывается на плоскости в виде простой зам-
кнутой кривой, и затем укладываются сегменты Цикл С делит пло-
скость на внешнюю и внутреннюю области Говорят, что сегмент с
первым ребром (иг, ш) укладывается внутри С, если при обходе по
часовой стрелке вокруг точки v, на плоскости, порядок встречаю-
щихся ребер будет следующий (v,_L, U,), (Vi, W), (vt, Ц1+1) Говорят,
что сегмент укладывается вне С, если порядок ребер имеет вид:
(Vi-,, yf), (ot, vi + !), (у,, л)1) (рис 8 29). Обратное ребро (х, v}),
принадлежащее сегменту, размещенному внутри С, называется
входящим в С в вершине V, изнутри Ясно, что порядок ребер при
обходе вокруг вершины у; по часовой стрелке будет следующим:
{Vj-i, v3), (х, и}), (v}, P) + i). Аналогично для ребра возвращения
(х, Vj), входящего в Св точке v} снаружи, этот порядок будет еле-
После укладки С мы пытаемся разместить сегменты орграфа G—С
по одному в том порядке, в котором они порождаются процедурой
PATH Для размещения сегмента S мы берем первый путь р в S,
порожденный процедурой РАТИ, и выбираем сторону С, скажем
внутреннюю, на которой будет размещен путь р Исследуя ранее
размещенные пути, мы можем определить, размещается ли р внутри
С Если р так уложить можно, мы размещаем его, в противном
случае все те ранее размещенные внутри С сегменты, которые ме-
шают размещению р, переносятся во внешнюю область С Перенос
этих сегментов наружу может заставить некоторые другие сегменты
переместиться из внешней области внутрь и т д Если р все-таки
нельзя разместить внутри С даже после этих перемещений сегмен-
тов, то граф G неплапарен Если р можно разместить внутри С,
мы размещаем ею и затем пытаемся уложить оставшуюся часть
сегмента S, применяя рекурсивно алгоритм размещения Если это
удается, то мы делаем то же самое со следующим сегментом
проверяемый критерий для определения того, можно ли на данном
этапе разместить первый путь сегмента на определенной стороне
цикла С Такой критерий дает
Теорема 8.4. Пусть р — первый путь в текущем сегменте S,
идущий из V, (базовой вершины S) в v, (другую вершину в С) Если
все сегменты, порожденные раньше S, уже размещены, то р можно
разместить внутри С при условии, что среди ранее размещенных об-
ратных ребер нет ребра (г, п(), входящего в С изнутри между вер-
шинами v, и v„ т е ни для одного обратного ребра (х, vt), разме-
413
щенною внутри, не выполняется условие Vj<.Vi<vi. Более того,
если такое обратное ребро существует, то сегмент 3 не может быть
размещен внутри С.
Доказательство Поскольку сегменты порождаются в порядке
убывания их базовых вершин, ни одно из размещенных до этого
момента времени ребер не может выходить из вершин, меньших,
чем v, в С Поэтому если ни одно обратное ребро не входит в С из-
нутри между у, и V], то ничто не мешает нам уложить р внутри С,
поместив его достаточно близко к С
Пусть существует уложенное обратное ребро с возвраще-
оно должно принадлежать порожденному ранее сегменту, скажем
S', который размещен внутри С Пусты», — базовая вершина этого
сегмента (S' может быть единственным обратным ребром с воз
вращением (х, Vt), в этом случае vq—x.) ПоскотькуЗ' порожден
раньше, чем 3, имеем vq^v, Если vQ>vlt ясно, что последова-
тельность ребер в S', идущая из vq в vt, будет мешать размеще-
Другая возможность — это vq=v,, т, е. сегменты 3' и 3 имеют
общую базовую вершину. В этом случае будем рассматривать
первый порожденный в сегменте 3' путь, скажем р‘. Путь р' идет из
uq в vr (и о4, vr принадлежат С) Из свойства 2 путей следует, что
vr^v}. Поэтому вершина vT отличается от vt, и в сегменте S' имеются
по крайней мере два пути, один из которых входит в С в вершине
vlt а другой — в вершине иг Поэтому первый путь р' в S' не может
состоять только из обратного ребра
Далее, если t»r<o> (рис 8 30 (Ь)), то ясно, что путь р не может
быть размещен внутри С В результате остается только одна воз-
можность, а именно пути р и р' имеют общие концевые вершины,
т е. vt=vq и Vj=vT К этому случаю имеет отношение свойство 3.
Пусть w и w' — вторые вершины путей р и р' соответственно
Поскольку первое ребро в р' не является обратным ребром, получа-
ем w'=£vr. Более того, имеется по крайней мере два обратных ребра,
идущих из S' и входящих в С ниже у,(=О(), а именно в точках vT
и V/, так что nexlopt (w'}<Zvq. Поэтому в силу свойства 3 (т е.
путь р состоит не из одного обратного ребра) и Vj<nexlopt
Другими словами, в сегменте S имеются по крайней мере два обрат-
ных ребра (ведущих из вершины w или из ее потомков), одно из
которых идет в вершину vj, а другое — в вершину nexlopKw), кото-
рая лежит выше но ниже vt. Последовательность ребер сегмен-
та S, идущих из вершины о, в вершину nexlopt (w) вместе с путем р,
блокирует размещение сегмента 3 внутри С (рис. 8 30 (с)).
Следствием этой теоремы является тот факт, что для проверки
планарности достаточно имен начальной и конечной вершин путей,
i \ , v / / / / / 1	/ \ \ г \ \ \ к— \ X	/ /у ! \ \ v”' । 	1 (Ь) ц, = и, , и, < v, -* и, vr 	= 1
поскольку возможность уктадки пути определяется его концевыми
вершинами
Рекурсия. До этого момента мы рассматривали размещение толь-
ко первого пути р в сегменте 3. Следует также определить, можно ли
на плоскости уложить оставшуюся часть сегмента, т е 3—р. Для
того чтобы это сделать, заметим, что подграф S—р можно добавить
к планарному размещению (которое теперь состоит из никла С, всех
сегментов, порожденных до 5, и пути р) тогда и только тогда, когда
подграф G~SljC планарен (упр 50) Таким образом, сталкиваемся
теперь с задачей определения планарности подграфа G Мы можем
это определить, применяя к G рекурсивно критерии разместимости.
В этой рекурсии путь р вместе с ребрами дерева пути из/ (конечная
вершина р) в s (начальная вершина р) будет служить начальным
циклом С в G Удаление цикла С из G может далее разбить остав-
шийся орграф G—С на сегменты (сегменты G относительно С),
которые в свою очередь обрабатываются рекурсивно Этот процесс
продолжается до тех пор, пока все пути в сегменте S не разместятся
на плоскости или окажется, что некий путь (первый путь сегмента
некоторого сегмента некоторого сегмента ) не может быть уложен
В качестве простого примера рассмотрим сегмент приведен-
ный на рис 8 28 Его первый путь р = (9, 10, 11, 4), причем s—9
и /=4 Строим граф G=S3 (J С, который состоит из 14 ребер, и ис-
следуем G на планарность Начальным циклом G будет С=(4, 5, 6,
8, 9, 10, 11, 4) Оставшийся орграф G—С состоит из семи ребер,
причем четыре являются частью С Каждое из оставшихся трех ре-
бер (11,5), (11,9), (10, 8) является обратным ребром и само по
себе составляет сегмент (в G относительно С) Следующий уровень
рекурсии не требуется
Структуры данных. При размещении сегмента, начинающегося
в вершине vt в С, необходимо знать, какие вершины в С, располо-
женные под vt (меньшие, чем vt) имеют обратные ребра, входящие
либо извне, либо изнутри. При наличии этой информации можно
использовать теорему 8.4 для того, чтобы решить, можно ли раз-
местить данный сегмент Организуем два стека 1ST и OST для хра-
пения вершин с обратными ребрами, входящими изнутри и извне
соответственно Мы увидим, что эти два стека имеют следующее свой-
ство вершины в них располагаются в порядке их возрастания (наи-
большая вершина на верху стека).
Когда в сегменте 3 порождается первый путь, идущий из вер-
шины s в вершинч / (обе они из С) вершина / должна быть добавле-
на на верх стека 1ST1), поскольку новый сегмент мы всегда пытаемся
416
добавить внутрь Аналогично, во время рекурсивного применения
алгоритма должны быть добавлены в стеки конечные вершины дру-
гих путей в сегменте S Заметим, что конечную вершину / текущего
пути можно добавлять в стек тогда и только тогда, когда / больше,
чем конечная вершина самого раннего из построенных путей, ска-
жем р, который проходит через начальную вершину текущего пути.
Иначе, если / совладает с конечной вершиной пути р, то / уже была
добавлена в стек и учтена. Вершина f, разумеется, не может быть
меньше, чем конечная вершина пути р.
Когда во время порождения (и размещения) сегментов мы воз-
вращаемся вниз по ребру дерева	то знаем, что все сегменты,
начинающиеся в вершине vt (или выше), порождены и успешно
размещены Поскольку сегменты порождаются в порядке \бывания
их базовых вершин (в С), ни один из еше непорожденных сегментов
не может начинаться в вершине, большей ог_,, поэтому по теореме
8 4 ни одно обратное ребро, входящее в вершину t'!_i или выше,
не может мешать размещению следующего сегмента В связи с этим
можно вытолкнуть из стеков 1ST и OST все вхождения вершины
при прохождении ребра (o,-i, fj).
Когда югменты перемещаются изнутри вовне и обратно, должны
передвигаться соответствующие элементы в стеках 1ST и OST.
Этот шаг может повлечь за собой сдвиг элементов вперед и назад
много раз, и было бы более эффективно сдвигать элементы группами,
а не по отдельности. Для этой цели определим связку как максима-
льное множество элементов в 1ST и OST, соответствующих обрат-
ным ребрам такое, что размещение одного обратного ребра опреде-
ляет размещение всех других
Из определения ясно, что связки меняются при изменении со-
держимого стеков Однако связки всегда определяют разбиение па
классы элементов в обоих стеках. Более того, из порядка, в котором
исследуются пути, и из тою факта, что элементы в стеке для новою
сегмента всегда добавляются на верх стека, следует, что все эле-
менты в каждом стеке, принадлежащие определенной связке, смеж-
Рассмотрим размещение внутри цикла С нового сегмента S,
первый путь которого идет из s в / Когда все элементы, соответ-
ствующие обратным ребрам в S, добавлены в 1ST, формируется
новая связка В, содержащая эти элементы для S, а также элементы,
соответствующие обратным ребрам, которые мешают S, т. е. все
вершины Vi, удовлетворяющие условию f<jut<Zs Другими словами,
для формирования новой связки В каждая связка, содержащая
любой элемент V;, должна быть объединена с новыми элементами.
Во всех других связках вершины v должны удовлетворять условию
v<f. Таким образом, вершина г из 1ST или из OST должна удов-
летворять двум условиям.



Рис 8 31 Содержимое стеков 1ST, OST и BST для рис. 8.27 на различных эта-
пах. (а) После размещения четырех путей в первом сегменте Si (b)
щенпя 'сегмента S2= (р5}=--- ((8,5)} (d) После размещения обоих пттей
з сегменте S3 и рекурсивного возвращения (е) Посте размещения
сегмента Sj= (ра}= {(6,3)}.
J4 \ 7о0
418
1) если f<Z.z<Z.s, то г принадлежит связке В;
2) если 2>s или ?</, то г не принадлежит связке В
В общем случае некоторые этемешы последней связки В будут в
/ST, а остальные — в OST, но в обоих стеках они будут наверху
Введение связок полезно, так как укладка любого обратного ребра,
принадлежащего связке В, полностью определяет укладку всех
обратных ребер из В и укладка обратного ребра из одной связки не
влияет на укладку обратных ребер, не принадлежащих этой связке
Информацию, относящуюся к связкам, удобно хранить в третьем
стеке, называемом BST Каждый элемент в BST представляет собой
упорядоченную пару (х, у), где с — самый нижний элемент в 1ST,
принадлежащий данной связке, а у — самый нижний элемент в
OST, принадлежащий той же связке. Равенство х=0 означает, что
данная связка не имеет элементов в 1ST, и z/=0 означает, что связка
не имеет элементов в OST На рис 8 31 показано содержимое трех
стеков 1ST, OST и BST в разное время при применении процедуры
размещения к разложенному орграфу, приведенному на рис 8 28
Как мы вскоре увидим, элементы (х, у) в BST являются на самом
деле скорее не элементами, а указателями на элементы в 1ST и
О ST
Полный алгоритм определения планарности. Теперь мы гото-
вы дать подробное описание алгоритма определения планарности во
всей его полноте Используя описанную ранее процедуру поиска
путей, будем порождать пути по очереди и попытаемся разместшь
очередной путь прежде, чем начаю порождать следующий Сразу
после того, как первый путь Р из первого сегмента S, идущий из
вершины s в вершину / (обе они из цикла С), размещен внутри С
в соответствии с описанной выше процедурой, на верху стека 1ST
будет элемент f Теперь попытаемся рекурсивно уложить оставшу-
юся часть сегмента S. Для того чтобы отличить в стеке элементы,
добавляемые во втором уровне рекурсии, поместим маркер «конец
сгека» на верх стека OST В 1ST элемент / на верху стека сам по
себе служи"! маркером «конец стека», поскольку ни одно обратное
ребро, выходящее из S, не ведет в вершину, меньшую /
Предположим, чго на сегменте S рекурсия успешно завершена,
и мы только что вернулись к верхнему уровню рекурсии В общем
случае размещение S будет добавлять элементы в стеки 1ST и OST
(выше / и маркера «конец стека» соответственно) Если имеется
новая связка, содержащая обратные ребра, входящие с обеих сю-
остаток цикла С мы не можем добавить к планарному размещению
не планарен и граф G Обратно, если каждая новая связка имеет
обратные ребра, входящие в цикл С изнутри или извне, но ле с
имущество такого представления состоит в том, что, когда мы пере-
водим связку элементов из одного стека в другой, перемещать сами
элементы на самом деле не нужно, нужно только изменить указа-
тели начала и конца связки Поскольку возможно много перемеще-
ний связок вперед и назад, такое представление важно. Заметим,
что элементы массива stack, будучи помещенными в массив, больше
не изменяются, меняются только элементы массива next При такой
реализации стек связок BST содержит пары указателей (х, у),
указывающих на массив stack
420
Шаг С. Этот шаг повторяется до тех пор, пока 1ST и OST не
пусты и их верхние элементы мешают размещению текущего пути р,
который заканчивается обратным ребром (v, w) Если верхние эле-
менты в 1ST и OST одновременно больше, чем w, то путь р не мо-
жет быть уложен, и G не планарен Если, однако, больше w только
верхний элемент в OST, т е если stack (next (—!))>&' то путь мож-
но разместить внутри без всяких проблем. Если больше w только
верхний элемент в 1ST, т е. еспи slack (пгл7(0))>ш, то перемещаем
Если р— не начальный цикл, то имеем path($<p, и поэтому либо
f(path(s)) уже добавлена в стек 1ST, либо ее добавлять совсем не
нужно. Поэтому конечная вершина f(p)=w текущего пути должна
добавляйся к 1ST, только если (ро/й(s)) Поскольку avail—
Заключение. Легко видеть, что в части алгоритма 8.15, в которой
происходит поиск путей, требуется 0 (| V|4- |Е |) операций. Для части
алгоритма, посвященной размещению, требуется информация, со-
стоящая из конечных точек |£|— [К] порождаемых путей (т е.
путей, отличных от цикла р0) Размещающая часть атгоригма со-
стоит исключительно из последовательности манипуляций над сте-
ками, и включение'исключение элемента требует постоянного вре-
мени. Общее число элементов в 1ST, OST и BST будет 0(|У|-г-|£j);
поэтому в полном алгоритме будет только 0(|У[+|£|) операций.
Более тою, поскольку |£|^3|V|—6 (в противном случае граф дол-
жен быть непланарным), алгоритму требуется 0([Р|) операций.
Аналогично, объем необходимой памяти будет
Мы показали только, как исследовать граф на планарность,
а не как фактически разместить его на плоскости, если он планарен
Само размещение графа на плоскости можно осуществить, проделав
некоторую дополнительную работу (упр 51)

423

[исключить вершины из BSTj
(x,y)<^=BST
if stack (x) S’ у then x «— 0
if stack (y) S- v then у -— 0
( [вытолкнуть элемент из
hl ?( 1)^0 d f fe( /(!))-- d ’ °S7,fl
I	<— next (next( —1))
while next (0) ?± 0 and stack (ne cl (0)) v do J [КЫТО'1КН>'ГЬ элемент из ISTj
I next ((I) *— next (next (Q))

in •— 0
then if stack (y) > f (path) (^) then
else in
while stack (х) > / (path (w)) or
(stack (у) > f (path (w))
and stack (next (- 1)) OJ do

next (in) next (—1)
next (—1) •*— next (y)

исключенными связками [теми, которые оораызвапись в резулыате укладки


Гл 8 Алгоритмы на графах
if л 5= 0 and j'₽ 0 then if slack (next (in)) > w then if stack (next (out))>(w)
дующии (у)

temp «— next (x)

next (avail)«— next (0)
next (C) -<— avail
if in = O then in <— avail
Алгоритм 8.16(d). Добавление w к /ST
if in 0 or cut r 0 or
<t then BST <= (in, out)
Алгоритм 8 16 (e)
Корректировка BST.
if i s then do

8 7 КОММЕНТАРИИ И ССЫЛКИ
Неовой опубликованном работой по теории графов является
статья Эйлера 1736 г , посвяшенная решению задачи о кенигсберг-
ских мостах, однако самостоятельной ветвью математики теория
графов не была до 1930-х г История развития теории графов и
описание многочисленных ее приложений приводятся в книге
Deo N. Graph Theory with Applications to Engineering and Computer
Science, Prentice-Hall, Englewood Cliffs, N J , 1974
Имеются три к 1ассические книги по теории графов
Berge С The Theory of Graphs and Its Applications, Wiles, New York,
1962 [Имеется перевод: Берж К Теория графов и ее применс
ние — М.. ИЛ, 1962)
Harary Ь Graph lheory, Addison Wesley, Reading, Mass., 1969
[Имеется перевод Харрарн Ф Теория графов —М Мир,
1973 ]
Огс О Theory of Graphs (Cambridge Colloquium Publications,
Vol 38), American Mathematical Society, Providence, R I ,
1962 [Имеется перевод: Ope О Теория графов — М.: Нахьа,
1968 1
Очень элементарное изложение можно найти в книге
Ore О, Graphs and Their Uses, Random House and the L W Singer
Company, New York, 1963 [Имеется перевод: Ope О Графы и
их применение — М Мир, 1965)
Хотя большая часть результатов в теории графов была полу-
чена в тридцатые и сороковые годы, попытки отыскания практиче-
ских алгоритмов обработки больших графов начались только в пя-
тидесятые годы. Эти работы развивались как часть исследования
операций и были прямым следствием растущей популярности и
достуипоши вычислительных машин Среди первых рассмотренных
иробчем были построение минимума остовных деревьев, определе-
ние кратчайшего пути, задача коммивояжера, задача о назначениях
и задача о потоках в сетях
Жадный алгоритм построения минимума остовных деревьев
обязан своим появлением работе
Kruskal J. В. On the Shortest Spanning Subtree of a Graph and the
Traveling Salesman Problem, Proc Amer Math Soc , 7 (1965),
48—50
Алгоритм ближайшего соседа для построения минимума остов-
пых деревьев (алгоритм 8 1) впервые был опубликован в статье
Prim R, С, Shortest Connection Networks and Some Generalizations,
Bell Syst Tech J., 36 (1957), 1389—1401	[ Имеется пере
вод Прим Р. К Кратчайшие связывающие сети и некоторые
обобщения, Киб сборник, вып. 2 (старая серия), 1961, 95—107 I
и независимо в статье
Dijkstra Е Two Problems in Connexion with Graphs, Num. Math.,
I, (1959), 269—271
Алгоритм Краскала требует О(|£|log|£|) операций, а алюритм
Дейкстры — Прима требует 0 (i/|2) операций. Вскоре были найдены
алгоритмы, требующие О (]£ floglogl/|) операций. Первый такой
алгоритм был приведен в работе
Yao А. С. С Ап О (|£|loglog|Kj) Algorithm for Finding Minimum
Spanning Trees, info. Proc Let, 4 (1975), 21—23
(ynp 7), иной метод обсуждается в работе
Cheriton D , Tarjan R. E. Finding Minimum Spanning Trees, SIAM
J Comput , 5 (1976), 724—742
Основная идея порождения всех остовных деревьев была опи-
сана в работе
Minty G J A Simple Algorithm for Listing All the Trees of a Graph,
IEEE Trans Circuit Theory, 12 (1965), 120
Сравнительно неэффективная рекурсивная программа, основанная
на той же самой идее, была опубликована в статье
McIlroy М. D Algorithm 354 Generator of Spanning Trees, Comm
ACM, 12 (1969), 511
Более эффективные алгоритмы опубликованы в статьях
Read R С , Tarjan R Е Bounds on Backtrack Algorithms for
Listing Cycles, Paths, and Spanning Trees, Networks, 5 (1975),
237—252
(cm ynp 16) 11
Gabou H. N Two Algorithms for Generating Weighted Spanning
Trees in Order, 5/444 J. Comput, 6 (1977), 139—150.
Алгоритмы Габова порождают все остовные деревья в порядке воз-
растания стоимости.
Техника просмотра в глубину (поиск с возвращением) исполь-
зовалась в алгоритмах на графах долгое время, однако степень,
с которой эта процедура позволяет раскрыть свойства графа, была
обнаружена недавно Первой работой в этом направлении является
статья
Tarjan R Е Depth-First Search and Linear Graph Algorithms, SIAM
J Comput, 1 (1972) 146—160
В этой работе представлена основная процедура поиска в глу-
бину (алгоритм 8 2) и алгоритмы отыскания двусвязных компонент
(алгоритм 8 5) и сильно связных компонент (алгоритм 8 6).
Некоторые из этих алгоритмов появились также в работе
Hopcroft J Е., Tarjan R Е Algonhm 447. Efficient Algorithms
for Graph Manipulation, Comm. ACM, 16 (1973), 372—378.
427
Дополнительные приложения процедуры поиска в глубину, вклю
чающие алгоритмы 8.4 топологической сортировки на ациклическом
орграфе, описаны в статье
Tarjan R. Е Finding Dominators m Directed Graphs, SIAM J Com-
put., 3 (1974), 62—89
Еще другие приложения обсуждаются в работе
Tarjan R. Е Testing Flow Graph Reducibihty, J. Comput Sys Sa ,
9 (1974), 335—365.
^-связный граф — это граф, в котором любые k вершин можно
удалить без нарушения связности Трехсвязность (6 = 3) можно
определить за 0(|71+1£|) операций с помощью поиска в глубину
Hopcroft J, Е , Tarjan R Е. Dividing a Graph into Triconnected
Components, S/AM J. Comput., 2 (1973), 135—158
Для	|7| лучший из известных алгоритмов требует O(k\К|3)
операций; его можно найти в работе
Even S. An Algorithm for Determining Whether the Connectivity of a
Graph is at Least k, SIAM J. Comput , 4 (1975) 33—396
Идея алгоритма транзитивного замыкания (алгоритм 8 7) впер-
вые была высказана в работе
KleeneS С Representation of Events ш Nerve Nets and Finite Auto-
mata, in Automata Studies, С E. Schannon and J McCarthy
(Eds.), Princeton University Press, Princeton, N. J , 1956 [Имеет
ся перевод Клини Ф. К Представление событий в нервных сетях
и конечных автоматах, Сб статей «Автоматы» под ред Шеннона
и Маккарти—М, ИЛ, 1956, 15—67]
в качестве метода доказательства теоремы о конечных автоматах.
Сам алгоритм был независимо получен позже и появился в статье
Warshall S A Theorem on Boolean Matrices, J. ACM, 9 (1962),
11 — 12.
Когда матрица смежности размещается так, что самый вну!ренний
цикл можно реализовать одной или двумя машинными инструк-
циями, этот алгоритм является в общем случае наиболее эффектив
ным из всех известных Эмпирические данные, подтверждающие это
высказывание, см в работе
Syslo AL AL, Dzikiewicz J Computational Experience with Some
Transitive Closure Algorithms, Computing, 15 (1975), 33—39
Модифицированную версию алгоритма, приспособленную для очень
больших разреженных орграфов, особенно при страничной органи-
зации памяти, можно найти в статье
428
Warren H S A Modification of Marshall’s Algorithms for the Transi-
tive Closure of Binarv Relations, Comm ACM, 18 (1975), 218—
220
дальнейшие ссылки даны в статье
Munro J 1 Efficient Determination of the Transitive Closure of a
Directed Graph, Info Proc Let , 1 (1971), 56—58.
O'Neil P E , O’Neil E J A Fast Expected Time Algorithm for
Boolean Matrix Multiplication and Transitive Closure, Informa-
tion and Control, 22 (1973), 132—138
статье
Moore E F The Shortest Parth Through a Maze, pp 285—292 m
Proceedings of the International Symposium on the Theory of
Switching, Part II, Harvard Universitv Press, Cambridge, Mass,,
1959
Johnson DBA Note on Dijkstra’s Shortest Path Algorithm, J. ACM
20 (1973), 385—388,
вершин в графе взят из работы
Floyd R W. Algorithm 97 Shortest Path, Comm ACM, 5 (1962),
345

Этот алгоритм является также наиболее эффективным из всех из-
вестных алгоритмов отыскания одного кратчайшего пути в графе с
отрицательными весами ребер Другой алгоритм отыскания всех
кратчайших путей в графе, такой же эффективный, как алгоритм
8 9, описан в статье
Tabouner Y. All Shortest Distances in a Graph: Ап Improvement
to Dantzig’s Inductive Algorithm, Discrete Math, 4 (1973), 83—87
Обзоры проблем и результатов о кратчайших путях приведены
в работах
Johnson D В Algorithms for Shortest Paths, Technical Report
73—169, Department of Computer Science, Cornell University,
Ithaca, N Y , 1973,
Yen J Y. Shortest Path Network Problems (Mathematical Systems
in Economics, Heft 18), Verlag Anton Hain, Meisenheim am
Gian, 1975
Обширную библиографию работ по кратчайшим путям, минимумам
остовных деревьев и смежным задачам можно найти в работе
Pierce A. R. Bibliography on Algorithms for Shortest Path, Shortest
Spanning Tree, and Related Circuit Routing Problems (1956—
1974), Networks, 5 (1975), 129-149
Алгоритм 8 10 отыскания фундаментального множества цик-
лов обязан своим появлением работе
Paton К An Algorithm for Finding a Fundamental Set of Cycles of a
Graph, Comm. ACM, 12 (1969), 514—518
Вариант Этого алгоритма, несколько отличный от предложенного
в разд 8 3, можно найти в работе
Gibbs N. W. Algorithm 491* Basic Cycle Generation, Comm. ACM,
18 (1975), 275—276,
Приведенный в разд 8 3 2 алгоритм порождения всех циклов
орграфа заимствован из работы
Johnson D В Finding AU the Elementary Circuits of a Directed
Graph, SIAM J Comput, 4 (1975), 77—84
Ьыто предложено много других алгоритмов порождения всех ник-
лое орграфа Обзор этих алгоритмов и их относительных достоинств
можно найти в статье
Mateti Р , Deo N On Algorithms for Enumerating All circuits of
a Graph, SIAM J Comput, 5 (1976), 90-99.
430
Поправки к этой статье были опубликованы в работе
Mulligan G. D , Corneil D G Correction to Bierstone's Algorithm for
Generating Cliques, J ACM, 19 (1972), 244—247
/(») =
n -^= 0 (mod 3),
n 1 (mod 3),
n — 2 (mod 3),
(конструкция на рис. 8 J6 дана для «аО (mod 3), каковы соотвст-
Moon J W , Moser L On Cliques in Graphs, Jsrael J Math , 3
(1965), 23-28
Pauli M. C Unger S H. Minimizing the Number of States in Incomp-
letely Specified Sequenciai Switching Functions, JRE Trans
Elect Comput, 8 (1959), 356—367
числа ктик (упр
40), икая реализация приведена в работе
8.7 Комментарии и ссылки
431
Tsukiyama S , Ide М., Ariyoshi Н , Ozaki Н. A New Algorithm for
Generating AU the Maximal Independent Sets, SIAM J. Comput,
6 (1977), 505—517
Unger S. H., GIT — A Heuristic Program for Testing Pairs of Di-
rected Line Graphs for Isomorphism, Comm ACM, 7 (1964),
26—34.
Совершенно другой подход
Bertziss А. Т. A Backtrack
к задаче можно найти в статье
Graphs, J ACM, 20. (1973), 365—377
Procedure for Isomorphism of Directed
Все известные алгоритмы изоморфизма орграфов требуют в
худшем случае экспоненциальною относительно числа вершин ко-
личества операций Однако в некоторых специальных случаях
реализация осуществляется намного лучше Если графы планарны,
изоморфизм можно установить за О (IVI logl 71) операций, по этому
поводу см.
Hopcroft J. Е , Tarjan R Е А V log V Algorithm for Izomorphism
of Triconnected Planar Graphs, J. Comput. Syst. Sa., 7 (1973),
323—331.
Доказано даже, что планарные графы на изоморфизм можно прове-
рить за 0(1 VI) операций Подробности см. в работе
Hopcroft J. Е., Wong J К Linear Time Algorithm for Isomorphism
on Planar Graphs, Proc. Sixth Annual ACM Symposium on Theory
of Computing (1974), 172-184.
более ранняя характеризация планарных графов принадлежит
который они в конечном счете улучшили до 0(1/1) в работе
Hopcroft J Е , Tarjan R. Е. Efficient Planarity Testing, J ACM,
21 (1974), 549-568
Изложенный в разд 8 6 алгоритм планарности взят из этой статьи
В ней также описывается, как построить планарное представление,
если данный граф планарен (см. упр. 51). Некоторые исправления
к этой работе приведены в статье
Deo N. Note on Hopcroft and Tarjan Planarity Algorithm, J. ACM,
23 (1976), 74-75.
Техника теории 1рафов стала важной в решении больших разре-
женных систем линейных уравнений методом исключения Гаусса
Приложение теории графов в этой области дало много новых
интересных алгоритмов на графах, см.
Tarjan R Е Graph Theory and Gaussian Elimination, in Sparse
Matrix Computations, by J R Bunch and D J Rose (eds),
Academic Press, New York, 1976
Эпилог. В этой 1лаве было представлено несколько задач, свя
занпых с графами, и алгоритмы их решения, поэтому будет полезно
расклассифицировать эти задачи в соответствии с числом операций,
которого они требуют в худшем случае
1	Задачи, для которых имеются алгоритмы, требующие числа
операций, пропорционального
2	Задачи, для которых известные алгоритмы требуют/(|7|, |Е|)
операций для некоторой нелинейной но не более чем полиноми-
альной функции f
3	Задачи, о которых нельзя сказать, что они обязательно эк
споненциальны по сложности, но для которых неизвестны алгорит-
мы, требующие меньше, чем экспоненциальное число операций.
4	Задачи, которые обязательно требуют числа операций, эк-
споненциального относительно размерности входа, потому что они
включают порождение экспоненциального числа подграфов
Первый класс задач включает отыскание остовного дерева, связ-
ных, двусвязных или сильно связных компонент, топологическую
сортировку и определение планарности Поскольку большинство
нетривиальных алгоритмов требует просмотра всех вершин и ребер
графа, то мы не можем ожидать что сложность алгоритмов будет
меньше, чем 0 (|/I + [£!), за исключением некоторых специальных
случаев Одно из таких исключений см в упражнении 1, в работе
Rivest R , Vuillemin J A Generalization and Proof of the Aanderaa-
Rosenberg Conjecture, in Theoretical Computer Sci , to appear
обсуждаются свойства, которыми должно обладало любое такое
исключение
8.8. Упражнения
433
Разделение задач на первые три класса зависит ог степени ма-
стерства До 1971 г задача проверки планарности была во втором
классе, но открытие нового алгоритма передвинуло ее в первый
класс Аналогично, возможно, но маловероятно, что в третьем
классе будут открыты полиномиальные алгоритмы, однако не по-
хоже, что это в действительности произойдем В настоящий момент
второй класс включает в себя задачи отыскания минимума остов-
пых деревьев, кратчайших путей или фундаментального множества
циклов
Четвертый класс задач включая в себя порождение всех остов
ных деревьев графа, всех циклов графа или всех клик графа. Не
существует возможности открытия нового алгоритма, который позво-
лял бы переместить задачи из этого класса в один из первых двух
классов, поскольку эти задачи обязательно экспоненциальны
относительно размерности входа (хотя относительно размерности
выхода, возможно, и линейны).
Третий класс задач, включающий задачу коммивояжера, опре-
деление изоморфизма, нахождение максимальной клики и многие
другие, представляет собой загадку Хотя ни одна из задач этого
класса не кажется безусловно экспоненциальной с точки зрения
требования ко времени, известных полиномиальных алгоритмов для
них нег Далее, о многих задачах из этого класса известно, что они
имеют следующее свойство полиномиальный алгоритм дтя любой
одной из них дат бы полиномиальный алгоритм для всех задач из
класса Третий ктасс задач является предметом гл 9
8.8. УПРАЖНЕНИЯ
l.^ Cmoxo.ii пристогО|орграфа	\' называется вершина с | V — 1 33^°‘
двоичная матрица А~[а.;] размера |Й| X |£|, где тогда и только тогда,
когда вершина с номером i инцидентна ребру с номером г. в противном случае
Можно ли идею такого представления распространить на орграфа? Каковы Пре-
S. Постройте алгоритмы для преобразования друг в друга Всех пар ел еду ющнх
представлении графа:
Сколькс/операций необходимо для каждого из обращений?
4. Докажите что если неориентированный граф G~ (И, £) состоит из k связ-
ных компонент, то	—h Докажите что если ]/:|>|VJ— k, то Q содержит
а Докажите, чю метод ближайше! о соседа в том виде, в каком он был испить
434
Гл 8. А егоритмы на графах
алгоритмов из разд 2.4.)
O(l£|loglog| VI) операций. (Указание; для каждой вершины о инцидентные ей ребра
разбиваются на f- lg| V| ”| подмножеств Sj (ц), S2 (о).^rigiVn^’ таких- что
для 1</ вес любого ребра в S/(o) больше или равен веса любого ребра в Sj(p).
Это можно сделать за O(|£|log 1og|V|) операций, многократно используя алго-
ритм, показанный на рис. 7.11. Сколько ребер теперь необходимо исследовать на
каждом шаге алгоритма, приведенного в упр. 6?)
Я. Определим 1 дерево неориентированного графа как осговпое дерево с одним
добавленным внешним ребром (это ребро является причиной образования цикла).
9 Предположим, что нам дана матрица стоимостен С размера пХщ которая
треугольника. Мы "можем считать С матрицей весов взвешенного неориеитиро-
(Ь) Каким образом можно использовать минимум остовных деревьев для
задаче'о коммивояжере получить за O(ns) операций маршрут, стоимость кото-
совсршенное паросочетание в графе с 2ft вершинами есть множество k, не пе-
ресекающихся по вершинам ребер Используйте факт, что минимум стоимости
совершенного паросочетания во взвешенном графе G— (V, £) может быть по-
лучен за время О (I VIя) ]
помеченными числами 1, 2, . п. (Указание: рассмотрите следующую процедуру
и само ребро Повторяем этот процесс, удаляя вершины t»g, с2, .гл1_2до тех
пор пока граф не примет вид
., были смежны во время их удаления. Покажите, что каждая из п"-2 после
доватечыюстей (w,, с3 ш„_2) Кш/Сга. соответствует единственному де
13 По аналогии с lowpH'S) определим luglipt(v) как наибольший номер вер-

модифицировать алгоритм 8 2 для вычисления значений lughpt.
num{v). Пусть nd (у) — число потомков вершины v (включая саму о). Докажите?
<num(w)<num(y)-rnd(y) Докажите, что nd(t>)—1+V Jnd(tc'). Покажите
жите, что ребро (v, w) графа G будет мостом тогда и только топа когда (v, w)
является ребром дерева и lvwpt(wy^num(w).)
1 рафа G Используя этот результат, улучшите ваш алгоритм из упр. 11 так/чтобы
он требовал только О(|VI-Hi'1-HilZ) операций где г — число остовных деревьев
графа G Как будет веста себя ваш алгоритм на графе упр 1!?
19 В ациклическом орграфе G= две вершины и и w назовем несвязан
биение V па котором ребра Е индуцируют частичную упорядоченность)
нент неориентированного графа (Указание используйте индукцию по числу
связной компоненты, то что вытекало бы из соотношения
сильно связной компоненты. Рассмотрите первое ребро на .тюбом пути цз v в а.
for ) to | V | do
for i — 1 to [ V | do
for ! -= 1 to | V1 do al} <— au v (aa л ay)
436
Гл 8 Алгоритмы на графах
Обоснуйте в^ш °™®7 алгоритм корректен то при каких условиях он лучше,

ипьвть ж е ля	4 разумным образом1*
25 Пусть
Л1( = (йц + й22> (i’ll + ^22),
— (й11 +й12) ^22,

Mi — (а1а—даз) (д21-|~ Ь22)
Покажите,^ как это тождество приводит ^алгоритму умножения д^ух пХп-мат-
*27. "транзитивное сокращение орграфа G~ {V, Е) есть граф GT— (V, ЬТ].
шим числом ребер, обладающего этим свойством. Как задача отыскания транзи-
проходим вес ребра, инцидентные г; пусть эти ребра будут "(г, aj, (г. аг), ..(г, а&)
Затем исследуем ребра инцидентные alt a2, .	а*. Пусть эти ребра будут
до тжаем до тех пор пока не будут исследованы все ребра дерева (Если G — ие-
зание: используйте очередь.) Используйте этот тип прохождения графа для оп-
29 Докажите, что значение окончательной метки вершины в алгоритме 8 8

зуйте индукцию по числу^вершин с окончательными метками.)
31."Расширьте идею из упр 30 так. чтобы находить все кратчайшие пути из $
32. Приведите пример орграфа, в котором некоторые из ребер имеют отри-
цательные веса, но в котором не существует цикла с суммарным отрицательным
результат	фа G (V Z) .	(	[	)
ритм в.в^можно модифицировать и использовать только два двоичных разряда па
*35. Постройте, проанализируйте и докажите корректность эффективного
что задано фундаментальное множество циклов
для любой вершины x^=s существует обращение к процедуре UNMARK(v),
которая присваивает avail (x)-*-true тогда и только тогда, когда
дает каждый никл в точности один раз.
37. Докажите, что в алгоритме 8 Идисло операции выполняемых в проме-
ЗЭ.Рдокажите что модифицированный алгоритм в lz порождает каждую
дую клику в подграфе, индуцированном Л'из/в точности один раз.)
вершин {1 2,... i}. Рассмотрим следующим' индуктивный метод отыскания
(1)	Если Q=Adj (i) то С [J {i}£
(ii)	Если CgtAdj (г), то С£^/.
(iii)	Если Cfi£Adj(i), то FCDAdj (i)J(J {;} является полным подграфом С, и


8 8


*50. Предположим, что в алгоритме проверки на планарность цикл С, все
проходит по ребру в точности один раз. Докажите, что смзный граф G— (У, Ё)
когда существует нечетное число инцидентных ей ребер) Постройте алгоритм
для отыскания эйлерова^ пути с О(|У|+|£0 операциями.
от корпя к у должен проходить через х Каждая вершина является домипатором
вершины г можно линейно упорядочить (от корня до г включительно) в соответ-
ствии с порядком их вхождения в кратчайший путь oi корня до г. Соотношения
«а доминирует 6» можно, таким образом, представить деревом, называемым до-
минаторным деревом графа G. Придумайте алгоритм построения доминаторного
дерева корневого ациклического орграфа G в предположении, что корень G из
55. Вершинная база орграфа G— (У, £) — это минимальное подмножество
B=V, такое, что в каждую вершину V существует путь длины пуль или больше
из некоторой вершины, принадлежащей В Покажите, что
захода, нс может принадлежать никакой вершинной базе;
(Ь)	ациклический орграф содержит единственную вершинную базу
(с)	каждая вершинная база орграфа содержит одно и то же число вершин
рациями^	к 1	। н 1	4 G л	б
большего чем /VI числа реоер. Построите алгоритм для отыскания максимума на
(Ь) О — любой граф
57 В неориентированном графе G= (V, £) разрез относитетьно пары вершин
х у _ это минимальное подмножество Ss£, такое, что по крайней мере одно
ребро любого пути между' х и у принадлежит S (Таким образом, удаление S из G
делает вершины х и у несвязными, и никакое собственное подмножество S этим
свойством не обладает.) Придумайте алгоритм для отыскания разреза относительно
V 58. Пусть G — неотрицательно взвешенный связный орграф н котором вес
ребра представляет его пропускную способность (т. е количество чего-либо, про
его ребер Если имеется в точности одна вершина х не имеющая исходящих из
нес ребер, и в точности одна вершина у, не имеющая ребер заходящих в нес, то
G называется транспортной сетью. Потоком в такой сети называется функция,
сопоставляющая каждому ребру (i, /) неотрицательное число Л/так 4rofij<Wij
для каждого ребра (i, j) и	Для каждой вершины	(если ребра,

потока.	7	i
(а) Теорема о максимальном потоке и минимальном разрезе. Покажите, что
59. Пусто G= (V Д) - неориентированный связный граф. Предюложим,
такое, что каждын цикл орграфа G содержит но" крайней мере одну вершину из S
т е. вершинного множества вершин оорагных связей с наименьшим возможным
61 По аналогии с определением наименьшего вершинного множества обраг
реберное '‘множество обратных с/язей Постройте алгоритм для отыскания такого
если все вершины G можно раскрасить, используя k различных цветов так, чтобы
*(с) каждый планарный граф '> раскрашиваемый
юший минимально возможное число красок и такой, что никакие две смежные
Глава 9. Эквивалентность некоторых
комбинаторных задач
В этой главе мы близко познакомимся с третьим классом задач,
описанным в конце гл. 8: задачи, которые не кажутся по существу
трудными, но для которых известны только алгоритмы с экспонен-
циальным временем. В результате нашего исследования мы увидим,
какие драматические последствия будет иметь открытие алгоритма
с полиномиальным временем для задачи коммивояжера Таким обра-
зом, не удивительно, что «хитрые» трюки из гл 4 не дают алгоритмов
с полиномиальным временем.
В восьми первых главах этой книги мы игнорировали точное
определение того, что такое алгоритм и что такое оценка времени,
полагая, что читатель по опыту знает, что это такое, даже без фор-
матных определений. Но для доказательства результатов о послед-
ствиях существования алгоритмов с полиномиальным временем
для различных комбинаторных задач требуется более точное поня-
тие «алгоритма с полиномиальным временем».
Любой алгоритм в этой книге можно рассматривать как «черный
ящик», который по входной последовательности производит выход-
ную последовательность Эта ситуация изображена на рис 9 1.
В частности, мы будем требовать, чтобы входная и выходная после4
довательности были последовательностями из нулей и единиц, кото-
рые кодируют входы задачи и выходы алгоритма в виде двоичных
чисел Тогда алгоритм можно рассматривать как последователь-
ность элементарных двоичных операций, таких, как или, и, не,
печать и т д , работающих с памятью из двоичных символов,
которая может бьпь произвольно большой
Эти предположения относительно алгоритма сильно противо-
речат представлению алгоритма на языке высокого уровня, которое
использовалось раньше Однако эти предположения эквивалентны
ным к экспоненциальным временем остается неизменным: поскольку
все паши л ипы данных содержат конечное число двоичных символов,
перевод алгоритмов с языка высокого уровня на уровень двоичных
символов увеличивает число операций только полиномиально,
переходе от операций высокого уровня к двоичным операциям
Таким образом, полиномиальный или экспоненциальный характер
времени работы алгоритма инвариантен, поскольку Р (Т (/)) огра-
ничивается сверху некоторым полиномом относительно /, если и
только если Т (I) ограничивается некоторым полиномом относитель-
но I Далее, такое же рассуждение показывает, что если входные и
выходные последовательности кодируются «разумным» ]) способом,
полиномиальный или экспоненциальный характер длины выходной
последовательности как функции длины входной последовательности
также инвариантен
Для того чтобы сделать ясной эту инвариантность относительно
полиномиального изменения, рассмотрим задачу коммивояжера с п
городами Здесь входом является гаХга матрица расстояний и выхо
дом—перестановка множества {1, 2,. , п}. Если k— наиболь-
шее расстояние между городами (предполагается, что все они целые
числа), то вход можно закодировать с помощью rfig k двоичных сим-
волов, и выход можно закодировать примерно nigra двоичными
символами Подход с позиции динамического программирования,
изложенного в разд 4 7 1, использует 0(па2") арифметических и
логических операций над элементами матрицы расстояний и, та-
ким образом, только O(ra22f'log k) операций над двоичными разря-
дами Ясно, что замена кодирования, скажем, на десятичное,
не повлияет на полиномиальный или экспоненциальный характер
используемых функций, но опа может увеличить или уменьшить их
полиномиально
Мы будем говорить, что данный алгоритм является алгоритмом
с полиномиальным временем, если время его работы, т е число
элементарных двоичных операций, которые он выполняет, на вход-
ной строке длины I ограничено сверху некоторым полиномом Р{1)
9 1 Кюссы <J>

Обозначим класс всех задач, которые можно решить такими алго
ритмами, через У. Все обсуждавшиеся в этой книге задачи с алго-
ритмами, для которых показано, что время их работы ограничено
полиномом относительно числа входов, очевидно, входят в У, и все
задачи с алгоритмами, для которых доказано, что время их работы,
иличисло выходов, с необходимостью экспоненциально относительно
числа входов, не входят в У.
Чтобы понять, какие следствия будут вытекать из того, что У
содержит задачу коммивояжера или одну из многих других зага-
дочных задач, необходимо ввести класс с№У задач, которые можно
решить за полиномиальное время с помощью недетерминированного
алгоритма. Неформально мы определяем состояние алгоритма как
комбинацию адреса выполняемой в текущий момент команды и зна-
чений всех переменных Все алгоритмы, рассматривавшиеся до сих
пор, были детерминированными, иначе говоря, во всех них для
любого данного состояния существует не больше одного вполне
определенного «следующего» состояния Другими словами, де-
терминированный алгоритм в каждый момент времени может делать
только что-то одно В недетерминированном алгоритме для любого
данного состояния может быть больше одного допустимого следую-
щего состояния; другими словами, недетерминированный алгоритм
в каждый момент времени может делать больше одной вещи.
Недетерминированные алгоритмы не являются в каком-либо смысле
вероятностными или случайными алгоритмами; они являются
алгоритмами, которые могут находиться одновременно во многих
состояниях.
Недетерминированность легче всего понять, рассматривая ал-
горитм, который производит вычисления до тех пор, пока не до-
ходит до места, в котором должен быть сделан выбор из нескольких
альтернатив Детерминированный алгоритм исследовал бы одну
альтернативу и потом возвращался бы для исследования других
альтернатив Недетерминированный алгоритм может исследовать
все возможности одновременно, «копируя», в сущности, самого себя
для каждой альтернативы Все копии работают независимо, не сооб-
щаясь друг с другом каким-либо образом. Эти копии, конечно, ме-
тут создавать дальнейшие копии и т д Если копия обнаруживает,
что она сделала пеправичьный (или безрезультатный) выбор, она
прекращает выполняться Если копия находит решение, она объ
являет о своем успехе, и все копии прекращают работать
444
Мы будем представлять недетерминированный алгоритм, ис-
пользуя три основных оператора: выбор, неудача и успех. Выбор
S — это многозначная функция, значениями которой являются
элементы конечного множества S Неудача заставляет копию алго-
ритма прекращать работу, успех заставляет все экземпляры ал-
горитма перестать работать и отмечает успешное завершение вы-
числения.
Очевидно, никакое физическое устройство не способно на неогра-
ниченное недетерминированное поведение; недетерминированные
алгоритмы—это абстракция, которая позволяет нам игнорировать
некоторые проблемы программирования поиска с возвращением
Например, алгоритм 9 1 является недетерминированной версией
алгоритма 4 1 (общий алгоритм поиска с возвращением). Сравнивая
алгоритм 9.1 с алгоритмом 4 1, мы видим сильное различие алго-
ритм 9.1 не содержит возвращения, если достигается тупик, потому
что функция выбор заставляет исследовать все пути
Определим как класс всех задач, которые мо/кпо решить не-
детерминированными алгоритмами, работающими в течение поли-
номиального времени, г е недетерминированными алгоритмами,
в которых всегда есть путь успешного вычисления за время, полино-
миальное относительно длины входной строки; очевидно
Поскольку путей вычисления может быть экспоненциально много
вероятно, что алгоритмы, допустимые в этом случае, намного силь-
нее, чем детерминированные алгоритмы, допустимые для задач из
У. Например, задача входит в ^3', если она может быть решена
недетерминированным алюритмом поиска с возвращением (алго-
ритм 9 1), в котором
1)	для всех k операции «вычислить 5й» и проверки «Верно ли, что
Sb^0>» и «Является ли («I, «2,	, «ь) решением?» можно
сделать за полиномиальное относительно длины входной строки
время,
2)	длина каждого пути вычисления ограничена полиномом отно-
сительно длины входной строки.
cost >— О
9.2.	^-ТРУДНЫЕ И оТ^-ПОЛНЫЕ ЗАДАЧИ
труднее.
Последствия существования детерминированного полиномиаль-
ного алгоритма для сО’-трудиой или с/Г^-полной задачи драмати-
ческие: это означало бы, что классы У и olfj' совпадают, так что
возвращением, в котором каждый из путей вычисления можно
исследовать за полиномиальное время, может быть решена детер-
минированным алгоритмом, который работает в течение полиноми-
ального времени. Это было бы чересчур удивительным, и поэтому
является сильным аргументом против существования детермини-
рованных полиномиальных алгоритмов для любой «АГ^-трудной или
Л^-полной задачи
В этом разделе мы исследуем различные комбинаторные задачи,
включая задачу коммивояжера, и докажем, что они являются ^ХЗ'-
трудными или сЛ^^-полными Для доказательства того, что задача
является Л’5>-трудной, мы должны доказать, что если для задачи
имеется детерминированный полиномиальный алгоритм, можно
частный случай задачи Pt можно преобразовать за полиномиальное
стного случая задачи Рг.
полноты
Определение. Задача является ^З’-труднои, если каждая за-
дача из Л1^ преобразуется в нее, и задача является ^З-полной,
если она одновременно является -трудной и входит в ЗЗЗ1
Поэтому для доказательства того, что задача является ^З*-
трудной, необходимо доказать, что некоторая Л^-трудиая задача
преобразуется в нее Трудность состоит в том, чтобы изначально
установить, что некоторая частная задача является Л^-трудной;
затем можно использовать эту задачу для доказательства Л55-
трудности других задач
9.2.1.	Выполнимость
Нашей отправной точкой будет задача о выполнимости из ма
тематической логики Пусть Х2, Х3,	— булевы переменные,
и пусть Х2, Х8, Хя, обозначают отрицания этих переменных
447
Соо1вегственно, так что истинно, если и тотько если X, ложно
Символы Хь Хъ Х2, Хг, . называются литералами Как обычно,
пусть V и д обозначаю! булевы операции «или» и «и» соответст-
венно Дизъюнкт — это множество литералов, объединенных one
рацией «или», например X2vX5vX,VXlu является дизъюнктом
Булево выражение в конъюнктивной нормальной форме — это мно-
жество дизъюнктов, объединенных операцией «и», например,
является булевым выражением в конъюнктивной нормальной форме.
Легко видеть, что любое булево выражение можно представить
в конъюнктивной нормальной форме, используя правила Де Моргана
и тождество
Булево выражение называется выполнимым, если существует
некоторое присваивание переменным значений истинно и ложно,
такое, что выражение имеет значение истинно. Так выражение
является выполнимым, потому что его значением является истинно,
если Xi—Х3=Х4=ложно и Х2=истинно. С другой стороны, выра-
не является выполнимым, потому что любое присваивание перемен-
ным значений истинно и ложно дает значение выражения ложно
Задача о выполнимости состоит в определении, является ли выпол-
нимым булево выражение, представленное в конъюнктивной нор-
мальной форме Имеется следующий основной результат
Теорема 9.1. Задача о выполнимости является оХ^-полной
Доказательство эгой теоремы выходит за рамки нашей кнши,
но мы можем выделить его главные этапы Легко показать, что про-
верка выполнимости входит в алгоритм 9 3 представляет
собой недетерминированный полиномиальный алгоритм, определяю-
щий, является ли булево выражение £(ХЬ Х2, . , Хп) выполни-
мым Доказательство того, что детерминированный полиномиальный
алгоритм для проверки выполнимости влечет за собой существова-
ние детерминированного полиномиального алгоритма для каждой
задачи из е№.!Р, не сложно, но оно требует очень подробного описа-
448
входной последовательности можно выполнить за полиномиальное
время Опираясь на этот результат, можно показать, что существует
последовательность таких булевых выражений, соответствующая
разрядам выходной последовательности для любого алгоритма из
dV’J’ и любой входной последовательности.
Следствие 3 выпо щимость является сЛ^-полпой
Доказательство Из алгоритма 9.3 немедленно следует, что 3-
вынолнимость принадлежит сО"1 Мы должны показать, что выпол-
нимость преобразуется в 3-выполнимость, т е что имея булево
выражение Е{Х^ Х2,	, Хп), представленное в конъюнктивной
нормальной форме, можно за полиномиальное время построить
ной форме, в которой каждый дизъюнкт имеет самое большое три
титерала, так что Е является выполнимым, если и только если Е
выполнимо Такое Ё можно построить из Е следующим образом
Заменяем в Е каждое предложение a, V^V \/аю где ai — Дите
ралы и /г^4, выражением
(a, j a, v Z) л (а, V... V’> VZ),
9 2 <№£? трудные и ^ср-полные задачи
449
где Z — новая переменная, этот процесс повторяем до тех пор,
пока ни один дизъюнкт не будет иметь больше трех литералов.
Полученное в результате выражение Е является выполнимым, если
и только если исходное выражение Е является выполнимым
(упр 7(a)), и, кроме того, Ё можно построить за время, полиномиаль-
ное относительно длины Е (чир 7(b))
Естественно спросить теперь, можно ли ограничить задачу
выполнимости еще больше, скажем только до двух литералов в
дизъюнкте, и так, чтобы вопрос о ее принадлежности 5* остался
открытым Ответ на этот вопрос отрицательный.
Теорема 9.2. 2-выполнимость принадлежит З1
Доказательство упр 8
Задачи и их дополнения. Прежде чем рассматривать различные
другие .^-полные задачи, обсудим некоторое аномальное свойство
недетерминированных алгоритмов. Рассмотрим задачи разрешения,
ответами в которых являются просто еда» или «нет» (например, «Яв-
ляется ли это булево выражение выполнимым?»), и определим допол-
нение такой задачи Р как задачу Р, в которой ответы обратны
(например, «Является ли это булево выражение невыполнимым?»).
Если существует детерминированный полиномиальный алгоритм для
Р, то простым отрицанием выхода мы получаем детерминированный
полиномиальный алгоритм для дополнения Р, таким образом,
PG3*, если и только если Р£3*. Для <№3* такой результат не из-
вестен Другими словами, не известно, что существование недетер-
минированного полиномиального алгоритма для задачи Р гаранти-
рует существование такого алгоритма для Р.
Тот факт, что задача разрешения и ее дополнение могут быть
неодинаковой сложности, противоречит нашему интуитивному пред-
ставлению Трудность здесь проистекает из необычной природы
недетерминированного вычисления, ответ «да» должен соответство-
вать оператору успех, мы не можем просто взять дополнение к выходу
недетерминированного алгоритма, поменяв местами успех и неудача,
поскольку окончательный успех требует только одного успешного
пути вычислений, в то время как окончательная неудача требует,
чтобы все пути вычисления вели к неудаче Таким образом, оказы-
вается, что недетерминированное вычисление более приспособлено
для задачи существования типа «существует ли элемент х, такой, что
некоторое свойство для него выполняется?», чем для дополнительных
к ним задач несуществования типа «выполняется ли некоторое свой-
ство для всех х?»
Существуют примеры задач разрешения Р£<№3\ о которых не
известно, что они входят в 3>, для которых Р^^З* (см. упр. 3),
15 № 760
но они являются исключениями. Для большинства задач разреше-
ния из для которых неизвестно, что они входят в 53, не известно,
входят ли в (№5^ их дополнения Алгоритм 9.3, например, ясно
показывает, что задача о выполнимости входит в но не из-
вестно, входит ли в задача о невыполнимости (определяемая
следующим образом, при всех ли присваиваниях значений истин-
ности булево выражение имеет значение ложно) На самом деле легко
доказать, что для любой о№^-полной задачи Р дополнение Р входит
в в том и только в том случае, если класс замкнут относи-
тельно дополнения, т. е. если и только если дополнение каждой за-
дачи из <№5* также входит в <^5*
Невыясненная асимметрия между большинством задач разре-
шения и их дополнениями объясняет, почему о задачах оптимизации,
обсуждающихся в разд 9.2 2 и 9 2 3, доказано только, что они яв-
ляются сЯ^-трудными, и не доказано, что они являются еАГ^-пол-
ными. Например, задача «Существует ли маршрут коммивояжера
стоимости не больше входит в согласно алгоритму 9 2; но
не известно, входит ли в J^S3 задача-дополнение «Верно ли, что все
маршруты имеют стоимость больше №». Определение оптимального
маршрута требует ответа на оба вопроса, и поэтому теорема 9 6 из
разд 9.2 3 устанавливает только, что задача определения оптималь-
ного маршрута коммивояжера является -трудной.
9.2.2.	Некоторые ^Р-полные задача
Теперь мы готовы исследовать в свете понятия сЛ^-полноты
некоторые комбинаторные задачи, аналогичные рассмотренным в
гл. 8 (т е основанные на графах)
Вспомним (гл. 8), что полный подграф неориентированного
графа G=(V, £)—это граф G' — (V, Е'}, для которого V'^V,
Е'^Е, и между каждой парой вершин из Е' существует ребро в V'.
Теорема 9,3. Задача определения того, содержит ли неориенти-
рованный граф G—(V, Е) полный подграф с k вершинами, является
аО^-полной.
Доказательство Опишем сначала простои недетерминированный
полиномиальный алгоритм для определения того, содержит ли G
полный подграф с k вершинами. Алюритм недетерминированно
выбирает подмножество из k вершин и проверяет за время О (А2),
является ли оно полным Этим доказано, что задача входит в класс
^З3. Теперь мы должны доказать, что задача является сМ’5>-труд
ной, мы сделаем это, показав, что в нее преобразуется задача выпел
нимости.
Предположим, что дано булево выражение С1ДСгЛ /\Ck,
представленное в конъюнктивной нормальной форме, где каждое
9 2 ^-трудные и $'<3’-полные задачи
Ct является дизъюнктом. Преобразуем вопрос о его выполнимости в
вопрос существования полного подграфа с k вершинами в графе,
который можно построить из данного выражения за время, полино-
миальное относительно его длины Рассмотрим неориентированный
граф G=(V, Е), определяемый следующим образом:
И = {а, г)|а—литерал в дизъюнкте CJ,
F =-{((сс, 0, (0,	иа#ф}.
Интуитивно ясно, что для каждого вхождения литерала в выраже-
ние граф G имеет вершину и ребра соединяют такие пары литералов
из различных дизъюнктов, которым можно одновременно придать
значение истинно. Полный подграф с k (число дизъюнктов) верши-
нами в G соответствует k литералам из разных дизъюнктов, которым
одновременно можно придать значение истинно так, что литералы,
дизъюнкты и отсюда само выражение имеют значение истинно Та-
ким образом, выражение является выполнимым, если G содержит
полный подграф с k вершинами. Обратно, если выражение является
выполнимым, то существует распределение значений истинно и лож-
но по переменным, такое, что выражение истинно Иначе говоря,
каждый из fe дизъюнктов содержит литерал, значение которого есть
истинно, и вершины, соответствующие этим буквам, образуют пол-
ный подграф с k вершинами Таким образом, граф G= (V, Ё) содер-
жит полный подграф с k вершинами, если и только если выражение
является выполнимым Очевидно, G можно построить по выражению
за полиномиальное время.
Клика (см. разд 8 4) — максимальный полный подграф гра-
фа Полный подграф С графа G является максимумом клик графа G,
если другой полный подграф G не содержит больше вершин, чем С.
Следствие. Определение максимума клик неориентированного
графа G=(V, Е) является <А№’-трудной задачей.
Множество R^V является вершинным покрытием графа G, если
каждое ребро G инцидентно некоторой вершине в R Задача, кото-
рая вполне аналогична задаче определения, существует ли в не-
ориентированном графе полный подграф с k вершинами, состоит в
определении, имеет ли неориентированный граф G=(V, Е) вершин-
ное покрытие мощности / Например, множество вершин {2, 4, 5, 6,
7} является вершинным покрытием для графа из рис 9 3(a) Каждое
вершинное покрытие G соответствует полному подграфу в дополне-
нии G'—(V, Е'} ''рафа G, образованном из вершин G и множества
всех ребер, не входящих в G (почему5) На рис 9 3(b) показано до-
полнение графа из рис 9 3(a); полным подграфом, соответствующим
А
вершинному покрытию {2, 4, 5, 6, 7}, является граф, порожденный
множеством вершин {], 3}
Двойственность полных подграфов графа и вершинных покры-
тий его дополнения позволяет тривиально доказать следующие ре-
зультаты
Теорема 9.4. Определение того, имеет ли неориентированный граф
G=(V, Е) вершинное покрытие мощности I, является «V’^-полной
задачей
Следствие. Определение максимума вершинных покрытий, не-
ориентированного графа G=(V, Е) является J^-трудной задачей.
его нет.

Теорема 9.5. Задача определения того, имеет ли орграф гамиль-
тонов цикл, является сЬГ^-полной
Доказательство. Как и в других доказательствах, сила не-
детерминированных алгоритмов дает возможность тривиально по-
казать, что задача входит в Для доказательства того, что она
о^-полна, мы покажем, что в нее преобразуется задача определе-
ния существования вершинного покрытия мощности I. Иначе гово-
ря, покажем, как, имея любой неориентированный граф G=(V, Е),
построить орграф G=(P, Ё) за полиномиальное время так, чтоб
имеет вершинное покрытие мощности I, если и только если G имеет
гамильтонов цикл, д определяется следующим образом Множество
вершин таково-
е, 6)|о	е££, такие, что е инцидентно о, <5 — 0 или 1} и
где 01, аг, ... , at — новые символы То есть множество вершин G
состоит из I вершин а9, ... , ai вместе с парой вершин для каж-
дого ребра и инцидентной вершины графа G Эти пары вершин в G
показаны на рис. 9.5 в клетках. Ребра G лучше описывать не фор-
мально Каждому ребру е 6 Е графа G, соединяющему вершины и и о,
соответствует подграф с четырьмя вершинами и шестью ребрами из
G, как показано в выделенной части на рис. 9 5 Далее, для каждой
вершины графа G подграфы, соответствующие ребрам, инцидент-
ным V, соединяются ребрами, как показано на рис 9 5 Порядок
ребер в этом «реберном списке» произвольный, но фиксированный.
Реберные списки для вершин и и v показаны на рис 9 5В дополне-
ние ко всем этим ребрам имеется ребро, идущее из каждого а,
^1, в первый элемент каждого реберного списка, и ребро, идущее
в каждое а„	из последнего элемента каждого реберного
списка.
Предположим, что G имеет вершинное покрытие (оь и2, .. , vj
Мы должны показать, что G имеет гамильтонов цикл. Пусть
ei. 1» ei, ’• , ei, — ребра G, инцидентные v,,	в том поряд-
ке, в котором они появляются в «спиках» в G Рассмотрим цикл
а,, (“1. е.,1. °). («I.	<)> (»!, «I.., °). (“1, Ч,„ !>>---
•	(»1,	0), (»,.	1),
«.,1. 0).	1, 1), (»„	0),	I), ...
  (t>..	0), (»>,	I).
“l,	«1,1. °), (”«.	<) (°., «I,.. °).
1). «V



9 2, ^ср-трудные и ^^’•полкые задачи
455
Этот цикл проходит через все вершины в V, кроме вершин из ребер-
ных списков, соответствующих вершинам в V, отличным от vt,
Однако, поскольку {oi, с2, .,. , ог) является вершинным по-
крытием G, каждая вершина V—{fi, vs.........yj, которой инци-
дентно хотя бы одно ребро, смежна какой-нибудь из вершин vf, т. е.
в Е имеется ребро е=(о,, w) Рассмотрим вершины (ш, е, 0) и (w, е, 1)
в И в реберном списке для w Мы можем расширить цикл с тем, что-
бы включить в него эти вершины, заменяя ребро из вершины (о„ е, 0)
в вершину (и,, е, 1) в цикле путем
(о,, е, 0), {w, е, 0), е, 1), (у,, е, 1).
Это можно сделать для каждой вершины из V, которая не входит
в цикл. В результате получается цикл в G, который содержит все
вершины из V, т. е гамильтонов цикл
Обратно, предположим, что G имеет гамильтонов цикл Посколь-
ку цикл содержит каждую вершину в V, он должен содержать все
а„	и поскольку в Ё нет ребер между любой парой вершин
at, гамильтонов цикл можно разбить на I нетривиальных непересе-
кающихся путей, каждый из которых начинается в некотором й}
и кончается в некотором не имея внутри других аг Исследование
конфигурации из жирных линий на рис 9 5 показывает, что любой
гамильтонов цикл, входящий в такую конфигурацию в вершине
(и, е, 0) должен выходить из вершины {и, е, I), он не может выходить
где-либо и затем возвращаться в (u, а, 1) позже (почему?) Следова-
тельно, каждому из I путей между вершинами at можем сопоставить
вершину V, такую, что каждая вершина в У на данном пути, не
имеющая вид (v, е, 6), имеет вид (ш, е, 6), где w смежна с v в G по
ребру е$Е Эти I вершин в V образуют вершинное покрытие G.
Следствие. Определение того, имеет ли неориентированный граф
гамильтонов цикл, является оО’-полной задачей
Доказательство Как обычно, ясно, что задача входит в
Чтобы показать, что она Л^-полна, мы докажем, что в нее преоб-
разуется задача определения наличия гамильтонова цикла в ор-
графе Для данного орграфа G=(V, £) построим неориентирован-
ный граф Ё), заменяя каждую вершину v g V трехвершинной
4£6
конфигурацией, показанной на рис 9 6 Другими словами,
6)| v € V, 6 = 0, 1 или 2}
£={((«, 2), (у, 0))](и,	{((у, 0), (у,	U
U {(а, 1), (у, 2))| И)
Очевидно, G имеет гамильтонов цикл, если он имеется в G, но G так-
же имеет гамильтонов цикл, если он имеется в G, поскольку любой
такой цикл в G должен входить в конфигурацию, соответствующую
способа включить в цикл (о, 1), среднюю вершину конфигурации
9.2.3.	Еще раз о задаче коммивояжера
Теорема 9.6. Определение оптимального маршрута в симметрич-
ной задаче коммивояжера с п городами (т. е. симметричной матри-
цей стоимости) является Ж^-трудной задачей
Доказательство. Симметричную задачу коммивояжера можно
рассматривать как задачу отыскания гамильтонова цикла мини-
мальной стоимости во взвешенном неориентированном графе. Имея
это в виду, легко доказать, что задача определения существования
гамильтонова цикла в неориентированном графе преобразуется в
задачу коммивояжера
Имея неориентированный граф G=(V, Е), |VI=n, строим сим-
метричную задачу коммивояжера с п городами следующим образом
Пусть V = {i»i, оа, ,. , vn}. Стоимость проезда между городами i и /
9 2 Jff? трудные и полные задачи
457
определяется следующим образом
£'у I 2 в противном случае
Ясно, что стоимость оптимального маршрута равна п, если G со-
держит гамильтонов цикл, если G не содержит гамильтонов цикл,
стоимость оптимального маршрута должна быть не меньше п-Н
(п—1 ребер стоимости 1 и одно ребро стоимости 2)
Следствие. Определение оптимального маршрута в общем слу-
чае (т. е не обязательно симметричном) задачи коммивояжера с п
городами является ЖЗ^-трудной задачей
Следствие. При данной границе b задача определения, сущест-
вует ли маршрут стоимости не больше b в симметричной задаче ком-
мивояжера, является о^^-полной
Доказательство Как следует из нашего обсуждения в разд 9 1,
задача входит в Она является о/<У-трудной, согласно рассуж-
дению, аналогичному рассуждению, которое использовалось при
доказательстве теоремы 9 6
На самом деле дело обстоит еще хуже, чем это кажется из теоре-
мы 9 6 и ее следствий. В разд. 4 3 мы привели алгоритм включения
ближайшего города, который работает полиномиальное время и вы-
числяет маршрут, стоимость которого с гарантией не больше, чем
удвоенная стоимость оптимального маршрута Это доказательство
существенно опиралось на симметрию матрицы стоимости и допуще-
ние о том, что стоимости удовлетворяют неравенству треугольника
Можно было надеяться на аналогичный «приближенный» алгоритм
в общем случае, т е когда неравенство треугольника не выполнено;
однако, к сожалению, даже эта задача является о№^-трудной Если
мы определим г-субоптимальный маршрут как маршрут, стоимость
которого не больше, чем в 14-е раз больше стоимости оптимального
маршрута, то справедлива
Теорема 9.7. Для любого е>0 задача отыскания е-субоптималь-
ного маршрута для симметричной задачи коммивояжера с п города-
ми является о^-трудной
Доказательство. Доказательство анало!ично доказательству тео-
ремы 9 6 По данному неориентированному графу G-=(V', Е), V=
= {&!, .. , vn} строим симметричную задачу коммивояжера, опреде-
'lj | Гпе“|+2 в противном случае.
458
Ясно, что стоимость оптимального маршрута равна п, если и только
если G содержит гамильтонов цикл, если G не содержит гамильто-
нов цикл, стоимость оптимального маршрута должна быть по край-
ней мере «+|“п8*| + 1 Поскольку
" + , , ,
маршрут, стоимость которого больше п, является 8-субоптималь
ным, если и только если он оптимален, т е. если и только если 6
не имеет гамильтоновых циклов
Следствие. Для любого е>0 отыскание 8-субоптимального марш-
рута для общей задачи коммивояжера с п городами является
<№^-трудной задачей.
9.3.	КОММЕНТАРИИ И ССЫЛКИ
В этой главе мы исследовали множество комбинаторных задач,
которые эквивалентны в том смысле, что либо все они могут быть ре-
шены детерминированным полиномиальным алгоритмом, либо ни
одна из них не может быть решена таким способом (упр 19) Класс
этих эквивалентных задач широк и включает задачи из разных об-
ластей прикладной и «чистой» математики и исследования операций
В конце раздела мы рассмотрим несколько интересных ^МУ^-полных
и сО*-трудных задач, не вошедших в текст или упражнения этой
главы.
Недетерминированное вычисление восходит к раннему периоду
развития математической логики и теории вычислимости: все мо-
дели вычисления, основанные па так называемых системах перепи-
сывания, неявно являются недетерминированными Первым явным
использованием недетерминированности является способ вычисле-
ния, предложенный М Рабином и Д Скоттом летом 1957 г Их ре-
зультаты впервые были опубликованы в статье
Rabm М О , Scott D Finite Automata and Their Decision Problems,
IBM J Res. Develop., 3 (1959), 114—125 [Имеется перевод
Рабин M О , Скотт Л Конечные автоматы и задачи их разре-
шения Киб сборник, вып 4 (старая серия) — М Мир, 1962,
Эта статья была перепечатана в книге
Moore Е F Sequential Machines Selected Papers, Addison-Wesley,
Reading, Mass , 1964
Идея использования недетерминированных алгоритмов как сред-
ства выражения поиска с возвращением взята из работы
459
Floyd R. W Nondeterministic Algorithms, J ACM, 14 (1967),
636—644.
Результаты, доказывающие, что одну задачу можно преобразо-
вать в другую, являются общими в математической логике и тео-
рии вычислимости, но такие результаты сильно отличаются по духу
от тех, которые представлены здесь Результаты такого же типа, как
приведенные в этой главе, имеются в математическом программиро-
вании, например, в работе
Dantzig G В On the Significance of Solving Linear Programming
Problems with Some Integer Variables, Econometrica, 28 (1960),
30—44
доказано, что множество комбинаторных задач можно преобра-
зовать в задачи линейного программирования. Аналогично, в
работе
Dantzig G В., Blattner W. О., Rao М R All Shortest Routes from а
Fixed Origin in a Graph, Theory of Graphs, International Sympo-
sium, Rome, July 1966 Proceedings published by Gordon and
Breach, New York, 1967, and by Dunold, Paris, 1967 , 85—90
доказано, что задача коммивояжера преобразуется в задачу опреде-
ления кратчайшего (без циклов) пути из одной вершины взвешенно-
го орграфа во все вершины орграфа, когда веса могут быть положи-
тельными, нулевыми, отрицательными или равными оо (упр 17).
Ключевым результатом этой главы является теорема 9 1 о том,
что задача выполнимости является Л^-полной Этот результат
взят из статьи
Cook S. A The Complexity of Theorem-Proving Procedures, Proc.
Third ACM Symposium on Theory of Computing (1971), 151—158.
[Имеется перевод- Кук С. А Сложность процедур вывода тео-
рем- Киб сборник, вып 12 (новая серия) — М ' Мир, 1975,
Основополагающая статья Кука содержит следствие теоремы 9 1 о
том, что 3-выполнимость является о^^-полной, и замечание, что 2-
выполнимость принадлежит 5s (теорема 9 2), основанное на резуль-
татах работы
Da\is М , Putnam Н. A Computing Procedure for Quantification
Theory, J ACM, 7 (1960), 201—215
Теорема 9.3 неявно содержится в доказательстве Кука утвержде-
ния о том, что задача изоморфизма подграфов является $“3* пол-
Богатство класса Я'Р полных задач было показано в работе
Karp R M Reducibility Among Combinatorial Problems, Complexity
of Computer Computations, R F Miller and J W Thatcher
(Eds.), Plenum Press, New York, 1972, 85—104 [Имеется пере
сборник, вып 12 (новая серия) — М.: Мир, 1975 16—38 1
Эта важная статья содержит теоремы 9 4 9.5 и 9 6 и множество дру-
гих подобных результатов Важное усиление теоремы 9 6 дано в ра-
боте
Garey М R., Graham R L , Johnson D S Some оО1-Complete
Geometric Problems, Proc Eighth ACM Symposium on Theory
of Computing (1976), 10—22,
где доказано, что задача коммивояжера явтяется сА^-полной,
даже если ес органичить множеством точек с евклидовым расстоя
нием Теорема 9 7 была доказана в 1974 г одновременно и незави-
симо друг от друга Полом и Сани и Гонзалесом в работах
Pohl 1 Practical Complexity and the Design of Algorithms, Informa-
tic, 17 (1975), 205-211,
Sahni S , Gonzalez T Р-Complete Approximation Problems, J ACM,
23 (1976), 555—565
Прежде чем обращаться к литературе, читателю следует ознако-
миться с различными терминами, которые являются синонимами
зывает «сводимым» го, что мы называем «преобразуемым», и Кук
называет «полиномиально сводимым» пли «^-сводимым» нечто бо-
лее общее, чем «преобразуемое». Для обозначения аУ^-полноты
Карп использовал термин «полиномиально полный» или просто
«полный» Термины «преобразуемый» и «аЛГЗ'-полный» стали стан-
дартными благодаря появлению статей
Knuth DEA Terminological Proposal, SIGACT News, 6, I (Janu-
ary 1974), 12—18
Knuth D E Postscript about hard Problems, SIGACT News, 6,
2 (April 1974), 15—16
Для будущих исследовании имеется еще много открытых вопро-
сов В дополнение к вопросу о том, верно ли, что У>=<#'53, имеются
нерешенные вопросы, относящиеся к отдельным комбинаторным
задачам Например, о задаче коммивояжера известно, что она яв-
ляется -трудной, но не известно, является ли она -полной,
т. е. входит ли она в О задаче определения изоморфизма двух
графов известно, что она принадлежит cY^5, но не известно, являет-
ся ли она еМ’^-нолной.
461
Оставшаяся часть этого раздела посвящена описанию несколь-
ких <ЛГ5*-трудных и (АГ^-полных задач с целью показать их разно-
образие
Дискретная задача о многопродуктовом потоке формулируется
следующим образом. Имеется граф и множество k непересекающихся
пар вершин исток — сток (5г, (,).	требуется определить,
существует ли множество k не пересекающихся по вершинам путей
pt,	где pt — путь от st до tt. Доказательство того, что в
случае неориентированного графа эта задача является ЦУ’^-иолной,
принадлежит Д Кнуту и появилось в статье
Karp R. М On the Computational Complexity of Combinatorial
Problems, Networks, 5 (1975), 45—68
(Эта обзорная статья является великолепным введением в предмет
аУ’^'-полных задач ) Результат Кнута усилен в статье
Even S., Itai A., Shamir A On the Complexity of Timetable and
Multicommodity Flow Problems, SIAM J Comptil , 5 (1976),
691—703,
в которой доказано, что для А=2 задача сЛГ^-полна и для ориенти-
рованных, и для неориентированных графов
В статье Илена, Итан и Шемирэ также устанавливается с^^-лол-
нота задачи составления расписания Предположим, что нам дано
множество часов в педеле, набор п учителей, каждый из которых
имеет возможность преподавать в течение некоторого подмножества
часов, множество т классов, каждому из которых в расписании от
водится только несколько часов в неделю, и пХт матрица неотри-
цательных целых чисел, в которой U, /)-й элемент означает число ча-
сов, в течение которых i-й учитель должен преподавать в /-м классе
Мы хотим определить, возможно ли назначить время уроков и
распределить учителей так, чтобы каждый класс собирался в тре
буемые часы, каждый учитель мог быть в своих классах, был бы
только один учитель на класс и ни один учитель не был бы н тзначен
одновременно в два класса.
Граф является k-раскрашиваемыя, ести все его вершины можно
раскрасить в k разных цветов, так чтобы никакие две смежные вер-
шины не имели одного и того же цвета Из упр. 62 гл. 8 мы знаем,
что каждый планарный граф является 5-раскрашивасмым. Также
легко доказать, что задача проверки 2-раскрашиваемости пркнадле
жит 5» (упр 64 гл 8) и, конечно, задача проверки 4-раскрашивае-
мости всех планарных графов, завися! от знаменитой теоремы о че-
тырех красках В статье
StOvkmever L Planar 3-Colorability js Polinoniial Complete, SIGACT
News, 5, 3 (July 1973), 19 -25
462
доказано, чю определение того, является ли планарный граф 3-рас-
крашиваемым, является <ЛГ^-полной задачей. Этот результат уси-
лен в работе
Garey М R , Johnson D S , Stockmeyer L. Some Simplified
Complete Problems. Theoretical Comput Set., 1 (1976), 237—267
для задачи определения 3 раскрашиваемости в планарных графах,
каждая из вершин которых имеет не больше четырех инцидентных
ребер
Пусть дана разреженная матрица (см упражнение 11 гл 2)
А и вектор Ь, и мы хотим решить систему линейных уравнений
по методу Гаусса, используя преимущество разреженности матри-
цы А, т. е возможность не хранить или не производить арифметиче-
ские операции над некоторыми или всеми нулями В то же время мы
можем искать х, применяя метод исключения Гаусса к эквивалент-
ной переставленной системе
(PAQ) (Qrx) = Pb,
где Р и Q — перестановочные матрицы (т. е матрицы из 0 и 1, со-
держащие ровно одну I в каждой строке и столбце) Задача опреде
ления Р и Q так, чтобы минимизировать время или память, требуе-
мые для применения метода исключения Гаусса для переставлен-
ной системы, является сАГ^-полной Две различных версии этой за-
дачи см. в работах
Rose D J , Tarjan R Е Algorithmic Aspects of Vertex Elimination
in Directed Graph, SIAM J Appl. Math., 34 (1978), 176—197
Papadimitriou С H. The JV’S’-Completeness of the Bandwidth Mini
mization Problem, Computing, 16 (1976), 263—270
Если имеется таблица имен, которую нужно организовать в виде
бора (см разд 6 3 4), то не обязательно, чтобы корень проверял
первую букву, сыновья корня проверяли вторую букву и т д На
самом деле мы можем получить меньший бор (т е бор с меньшим
числом внутренних узлов), рассматривая буквы в разных порядках
Задача определения бора с минимально возможным числом впу
тренних узлов, является Л'ЬТ’-полной. Аналогично, если все листья
бора равновероятны, определение бора с минимальным средним вре
менем поиска является а№У5-полной задачей Детали этого и соот
ветствующие результаты можно найти в работе
Comer D , Sethi R The Complexity of Trie Index Construction,
J. ACM, 24 (1977), 428-440.
9.4 Упражнения
463
Для данного конечного множества разреженных комплексных
полиномов от одной переменной с целыми коэффициентами, пред-
ставленных в виде последовательности упорядоченных пар (коэф-
фициент, степень) для каждого ненулевого коэффициента, задача
определения наименьшего общего кратного этого множества поли-
номов является а^^-трудной Определение числа различных комп-
лексных корней произведения таких полиномов является также
off?-трудной задачей. Эти и другие аналогичные результаты пред-
ставлены в работах
Plaisted D A Sparse Complex Polynomials and Polynomial Reduci-
bility J. Comput. Sys Set, 14 (1977), 210—221
Plaisted D A Some Polynomial and Integer Divisibility Problems
are cA^-Hard, Proc Seventeenth Annual Symposium on Founda-
tions of Computer Science (1976), 264—267.
9.4.	УПРАЖНЕНИЯ
входят ли в задачи, которые они решают Есть ли среди сформулированных
в предыдущих главах задач задачи, не входящие в
ритмы для решения упражнений 1(b), 1(f) l(k) l(m), 3(a), 3(b), 3(c), 3(d) и 3(e)
4. Докажите, что если	то все задачи из01У’5> являются (ДС5’-иолиыми
(а)	((Х^Х^л ((ХЛХ^У (Х,ЛХ7)»УХ3
(b)	(Xiл Х3 лХ8)у (Х,лХ3л (Х3уХз))у (X,лХ8)

464

двух литералов, т е в виде (а, уаг)Л (а:1 VttjA...Л («s-i Va*) гдеа(-, ]</<£ —
для целочисленной матрицы С и целочисленного вектора d. Докажите, что эта
0, в остальных случаях
и вектора
d, — 1 — (число отрицаний переменных в t м дизъюнкт) )
рованный граф подграф, изоморфный второму неориентированному графу^ явля
ется -полной (Указание используйте теорему 9 3)
непересекающихся множеств '(Указание; используйте теорему 9.3)
есть множество R—V. такое что каждый цикл G содержит вершину из R. Дока-
ставляет собой кратчайший путь с ровно одним циклом из вершины в нее саму?)
9 4 Упражнения
работает следующим образом. При данной лХл-матрице С расстояний между
городами в задаче коммивояжера с п городами, в которой каждый элемент мат-
границей стоимости любого маршрута, и таким образом, стоимость оптимального
(см. разд. 6.3.1) на отрезке [0, яа2*]. достаточно только lg(na2ft)=fe-[-2]gn приме-
является р^.^-трудной, а не оу,^-полной, например задача отыскания оптималь-
коммивояжера может быть решена детерминированным полиномиальным алго-
20* Сноска на стр 442 утверждает, что было бы неразумно разрешить коди-
бы было разрешено кодирование числом разрядов, пропорциональным л?
ПРЕДМЕТНЫЙ
УКАЗАТЕЛЬ
б™58—360? 425
165—170ИЯ	™жаишего города
отыскания (см. также Алгоритм
объединения отыскания) 74
слияния множеств (ем также
двоичном наборе 12—17, 24—25,
42
Алюритмы па графах 352—440
вершинная база 433
связей 440
двквязные ком оненты 366
жадный алгоритм 74, 358 425
изоморфизм	396—402 431—432,
459—460
клика (максимальная) 433, 437, 451
клики (все) 389—396, 430, 433, 437
кратчайшие пути 377—382, 452
428—429 333 , 451
максимальное независимое множе
остовное дерево (минимальное)
357—360 425, 433—434
остовные деревья (все) 357—360,
425 433—434
планарность 402—424 433.
поток в сет?439—440 461
раскраска 440, 461—462
438
426
реберное множество обратных свя-
зей 440
С 373. 426. 436 К
366?427 *432 С Р Р
транзитивное замыкание 374—376,
427—428, 436
транзитивное сокращение 436
циклы (все) 384—389, 429, 433, 437
U"ctbo) 382—384* 429, 437 ”
сетей 351? 360
Асимптотики 38—94
Асимптотические ряды 90—91
Бернсайда лемма 114, 116—117
Боры ^255—256, 297, 462
Брат (в дереве) 59
Венок перестановок 224
Вершина (графа) 351
последователь 354
предшественник 355
соседи 355
Вершинное покрытие 452
Ветви и 1раницы 140—150 171 360
Взвешенная длина пути 242, 249—252
Включение
в последовательно размещенные
списки 49—51
Предметный	указатель	467
парные деревья поиска 261—266 в таблицу хеширования 287, 291— в упорядоченные хеш-таблицы 305 Вложенные циклы (в перестановке) 189—191 Внутренние узлы (дерева) 58 Возвращение 87, 124—153, 168—170, 171, 183, 185, 196 361, 386, 391 ветви и границы 140—150, 171, 360 ^150—153, 172, Р24§, ' 437^442 использование макрорасширений 133-134, 139, 171 недетерминированный алгоритм 453, 454, 458 общий алгоритм 125—128 выполмеаия применение к DP 1 кодам 135— 140 171 Вращение х64—х65. 274—276 двойное 264—265, 276—277, 303 Выполнимость 446—450 Высота (дерева) 66	связные компоненты 356 Г 369—374, 426, Деревья 26—28. 58—72, 357 бинарного поиска 162, 240—254 бинарные 54, 107—109 длина внешних путей 66—72, 298, 311 239 ^121—Ь2,Р24о”Х	66—721 длина минимальная 70—72 естественное соответствие между бинарными деревьями и лесами 62, 64 игры 126—149 монотонные 249—253, 297 остовные 357—361, 425—426, 433 пирамида 250, 322—324 нарные 70, 239 представления 60—62 прошитые 84—85 прохождения 62—66, 126 пустые бинарные 59 раскраска узлов НО—116
Гамильтонов цикл 452—456 Грамматическим раэбор 124 Граф 351 ациклический 356 гомеоморфный 438 двусвязный 366—369 изоморфный 396—398 Муна — Мозера 390—391, 430 несвязный 356	расширенные бинарные 68 расширенные Аарные 86 решений 26—28, 311 сбалансированные 248—283, 261— 277, 297—298 Сб277НС^8В 303Ые П° ВеСаМ Сб269ВС298ад303Ые П° ВЫСОТе * сильно ветвящиеся 278—282, 298, 303 случайны^, бинарные 3-2-деревья 298 Д 153, 437, 442Р	’ р п н е 1 Дважды связанный список 55 Двойное хеширование 292, 293—295 Е 294	Р Д *	Ц > парными деревьями и чесами) 62 64
468

Задачи
К°162^°7^,е₽354, 425 ’445, 45о’
456—458, 459
о потоке 439—440, 461
о ферзях 127—131, 135, 136, 161—
162, 176
составления расписании 124, 175,
Закон Зипфа 233, 234 304
Зототое сечение 95, 156	263—264
Имена 226
Инверсия (в перестановке) 187
выбор инверсий 187—188 219,223,
315
списков 49—51
бинарных деревьев поиска 269
бинарных деревьев поиска 281 —
282
тоды вычисления адреса) 2«л
Коды Грея 43, 196—202, 220—221,
224—225
двоично-отраженные 197—198, 221
порождение 191—202, 205—212
197—198
Коды оптимальные 20—21, 23, 135—
140, 171
сохраняющие разности 17—25,37—
41, 44 196
сложение порогов 22—23
увеличение ранга 23, 37—38
коллизия 285—286
Комбинаторные вычисления 22
221 —222*,И 225ЛЬ1Х ЧИС&П> 213—2141
Конъюнктивная нормальная форма 447
Коэффициент загрузки 293—295
КР425?428-429ТИ433,	3&2'
из одной вершины с другую 377—
378
Mtgg^Di:e“ арЭМ веР
Исходные отрезки 32У—330. 343
Китайское кольцо 220
Классы алгоритмов 25—36, 309—310
°430,Д433 437 *
Ключ 228
перестановок 181, 184—187 219,
222-223
разбиений 214—218, 225
сочетаний 202—204, 221
Л *84	'


469

Магические квадраты 177
в возвращении 133—135 139 171
в порождении перестановок 194,
220, 223
Максимум кпик 433. 438, 451
Максимальный и максимум 356
Маркова цепи 351
Массива размещение 49—50 83
щение) з
перемножение 179, 428
436
Начальная ячейка последовательности
Недетерминированные алгоритмы 453—
445, 458
для поиска с возвращением 458
Неоднородные рекуррентные соотно-
шения 97—98
слияния 338—340"
сортировки 309—313
Новое хеширование 287
Нумерация Штралера 69
282—299

^131—1W 139^ 171 183Щ	*
решета 153—162, 173—174
ду Р
отбраковк^ _рфш
решето 154—155 158—
159
174, 180
цепочек 292—293
М433М>М	Д Р
Минимальный и мииимем 35b
Множество 72
Мост (в графе) 436
вания 290
150
ности 20—23, 135—140 171
двоичном 46 19а
с убывающими факториалами 48,
с факториалами 48 1 84 188
уравновешенной тернарной 82
Открытая адресация 291


графах) 439
470

Перестановки 110—118, 182, 184—195,
218—219
венки5224
187. 222—223
191—194 220, 223
ч'амн 189—194' 219
случайные 194—195 220, 223, 224
Петля (в графе) 351
Пирамида 250, 322—324
Пандиагоаальные магические квадраты
178
Пентамиио 176
Подграфы 356
изоморфизм 459
индуцированные 356
максимальные полные ( клики)
полные 450
Поиск 125—170, 226—295
быстрый 226—296
в глубину 134, 761, 366, 426
вычисление
общий бинарный 296, 301, 236—240
последовательный 230—235
са^Рг™1изуюшиеся а лы
Поле 228
INFO 52
LINK 52
NAME 241
Захода вершины 397
исхода вершины 397
«о-малое» 88—89
Поперечное ребро 370
254,
сочетания 202—212
для перестановок 191—193 220,223
для сочетаний 204—205, 221
переходов 196
Поток в сети 425. 439—440. 461
тов 44—86
графы 352—356
леса 60—62
вычетами 83
двоичная система 46
система по основанию г 46—47
уравновешенная тернарная систе-
ма 82
Предшественник (вершины) 355
Приближение Стирлинга 93, 120 311
Принцип оптимальности 150
Производящие функции 86, 103—109,
118, 211
линейные операции 104
свертка 107—109
Простой путь (в графе) 356
в глубину^62—66, 84 126
Предметный указатель
471
Псевдоквадраты 180
простой 356
Разбиения (целых чисел) 213—218, 221,
225
лексикографический порядок
случайные 216—218, 222
Разделяющая вершина (=точка
Размещение памяти
*254 С еА
последовательное распределение
Разрез 439
Разреженные полиномы 463
Раскраска 110—114 440, 461—462
Расстояние Лемминга 19
Ребро (графа) 351
Ребро, направленное вперед 370
Рекуррентные соотношения 86, 94—
103, 107—108, 118
неоднородные 97—98
Ряд Тейлора 103
Сбалансирование 74—77, 249—253,
261—277, 297—298
Сбор мусора 54
Сводимая задача 460
Связанный список 52—55, 84
ния/отыскания) 76
дерева 64
234
Слияние 129 " 15*1 308 338—340
бинарное 338—340, 344, 350
прямое 338—339. 349
венок* перестановок 224
деревья 250—251, 258—261, 297
перестановки 194—195, 220, 222—
224
разбиения (целых чисел) 216—218
сочетания 209 , 220
фазном слиянии)' 332
быстрая 316—321, 344—350
внешняя 329—334
внутренняя 308—329
вставками 312—314, 344
выбором 321—326
линейный алгоритм выбора 335
наименьшая занумерованная вер*
шина 404
нижние оценки 309—312
обменная ^314—321
ровна Шелла) 344
слиянием 330—334 , 338—340
топологическая 365—366, 427
цифровая обменная 346
Сосед (вершины) 355
Способы** декомпозиции 23—25, 150
с возвращением 130—131
Способы композиции 21—23
Стек 55 —58
Сток 433
Сын (в дереве) 59
472

статическая 229. 235—236
гряфов 424—425
решетки 225
Транзитивное замыкание 374—377, 427,
436
Транзитивное сокращение 436
Транзитивный орграф 436
Трехсвязность 427
числения адреса) 73. 282—288
Хроматическое число 440
в графе 358
вложенные в перестановках 189
384—38(L 42SL 433. 43?В Р
фундаментальное множество 382—
Числа Спрэга 180
Эилера постоянная 93, 217, 424, 438
Эйлеров путь 439
Указатель 228
FATHER 60
RIGHT 61
Упаковка множества 464
Упорядочение дерева (—техника пере
Упорядоченные прохождения дерева
Упорядоченные таблицы хеширования
299 305
Успех 444
. а-отсечепие 147
a-fi-отсеченне 145—150 172, 179
В деревья (см Сильно ветвящиеся
деревья)
DFS-дерево 363—364
DP-Z-код (см. также Коды сохрани
ющие разности) 49
Файл 228
Фибоначчи (=Леонардо из Пизы) 94
деревья (= наиболее асимметрия
ные деревья, сбалансированные
по высоте) 262—263
квадраты 156 157, 173
поиск 300—301
числа 94—96, 156, 157, 173
(в графе) 382—386
Функции хеширования 288—291, 299
методы деления 2S1
H(D( Оу)=Хеммингово расстояние
стями £>( и Df, т е число разрядов,
(Р1,	, Рп) — энтропия
= — У’р, Jgpz (для г; Se 2) 35
(а) — частный случай энтропии^
- _а lga-(l—a) lg(l— а) 272
Н„ — nt гармоническое число—
= ^21/1=1пл+0'1) 93
1LUAC 1 42
4-выполнимость 448
/(-подмножества (сочетания) 202—212,
220
Характеристический вектор (последо-
порядок^минимально о
Предметный	указатель	473
lg*( (повторный логарифм по основа НИЮ 2) 77 lavlittk <у) 373 lotupt tv) 367—368 Maniac II 343 441 вершинное покрытие^ 452 раскрашиваемость 461—462 Р зей 464	цело* е е программирование о^^-трудные задачи 464—465 вАГ^-трудный 445 nexlopt (v) 404 num (v) 363 overflow 56 5> 441 Padj (v) 406 ran ci (k I) (94 U (= последовательность У лама) 160 WB (a) 270
ОГЛАВЛЕНИЕ
Предисловие
Глава 1 Что такое комбинаторные вычисления?
I I Приксу, Подсчет числа единиц в двоичном наборе . .
25
Глава 2 Представление комбинаторных объектов . .





.4.2.1. Линейные рекуррентные соотношения i иоионинымн
3.4. Подсчет классов эквивалентности: теорема Пойа

Глава 4. Исчерпывающий поиск . .
4 1.3 Оценка сложности выполнения .
Оглавление
475
4.1.4	Два способа программирования
4.1.5.	Пример Оптимальные коды, сохраняющие разности
4.1.6.	Метод ветвей и границ	...............
4.1.7.	Динамическое программирование...........
4.2.1. Нерекурсивное модульное решето............
4.2.3 Решето, отбраковывающее изоморфные объекты .
Приближения исчерпывающего поиска................
Комментарии и ссылки ............................
133
135
140
150
153
154
158
161
162
175
5.1 Перестановки различных элементов.................
5.1.1 Лексикографический порядок.................
5 1 3 Вложенные циклы	...............
5.1.4. Транспозиция смежных элементов............
5.1.5 Случайные перестановки ....................
5 2 Подмножества множеств	...............
5 2 1. Коды Грея ... .	....................
5 2 2 fe-подмножества (сочетания) ...............
5 3 Композиции и разбиения целых чисел ..............
5.3.2 Разбиения..................................
182
184
184
187
189
191
194
195
196
202
213
213
214
218
222
Глава 6 Быстрый поиск ......................................
6 1 Поиск и другие операции над таблицами .	...
6 3 I Р бинарный поиск	.	. . .
6 3.2. Оптимальные деревья бинарного поиска . .
6.3.3. Почти оптимальные деревья бинарного поиска
6 4 Логарифмический поиска динамических таблицах
6.4.2 Бинарные деревья сбалансированные пи высоте
6.4.4 Сбалансированные сильно ветвящиеся деревья.
6.5	Методы вычисления адреса	..............
6.5.1.	Хеширование н его варианты ...........
6.5.2.	Хеш-функции........	..............
6.5.3.	Разрешение коллизий ..................
6.5.4.	Влияние коэффициента загрузки.........
6.6	Комментарии и ссылки ... .	..............
226
226
230
235
236
240
248
253
257
258
261
269
277
282
283
288
291
293
295
300
Глава 7. Сортировка...........................
7.1	. Внутренняя сортировка.........
7.1.1.	Вставка	............
7.1.3.	Выбор
7.1.4.	Распределяющая сортировка
7.2	Внешняя сортировка . .
307
ЗОН
312
314
326
329
334
476
Оглавление
7.3.1 Выбор
341
344
8.2. Связность и расстояние................
8.2.2 Поиск в глубину..................
8.2.3 Двусвязность.....................
8 2.5 Транзитивное замыкание...........
8.2.6. Кратчайшие пути ... ....
8 3 Циклы .	...
8.0. Изоморфизм............................
8 7 Комментарии и ссылки...............  .
8 8 Упражнения . ..........................
351
352
356
361
369
374
377
382
382
384
402
424
433
Глава 9. Эквивалентность некоторых комбинаторных задач
9 1 Классы 5s и  		..........
9 2 (ДР^-трудпые и <^5* полные задачи............
9 2.2 Некоторые	задачи...........
9 2 3 Еще раз о задаче коммивояжера . . . ,
9.3. Комментарии и ссылки .	................. . .
9.4. Упражнения .	. .	.................
441
441
445
446
450
456
458
463
466