ИЗДАТЕЛЬСТВО
* к

С. М. Окулов
ПРОГРАММИРОВАНИЕ
В АЛГОРИТМАХ
4-е издание
*-
Москва
БИНОМ. Лаборатория знаний

УДК 519.85(023)
ББК 22.18
0-52
Серия основана в 2008 г.
Окулов С. М.
0-52 Программирование в алгоритмах / С. М. Окулов. —
4-е изд. — М. : БИНОМ. Лаборатория знаний, 2017. —
383 с. : ил. — (Развитие интеллекта школьников).
ISBN 978-5-9963-0848-4
Искусство программирования представлено в виде
учебного курса, раскрывающего секреты наиболее популярных
алгоритмов. Освещены такие вопросы, как комбинаторные
алгоритмы, перебор, алгоритмы на графах, алгоритмы
вычислительной геометрии. Приводятся избранные олимпиадыые
задачи по программированию с указаниями к решению.
Практические рекомендации по тестированию программ являются
необходимым дополнением курса.
Для школьников, студентов и специалистов, серьезно
изучающих программирование, а также для преподавателей
учебных заведений.
УДК 519.85(023)
ББК 22.18
Учебное издание
Серия: «Развитие интеллекта школьников»
Окулов Станислав Михайлович
ПРОГРАММИРОВАНИЕ В АЛГОРИТМАХ
Редактор О. А. Полежаева
Художественный редактор Н. А. Нова к
Технический редактор Е. В. Денюкова
Компьютерная верстка: Л. В. Катуркина
Подписано в печать 07.02.13. Формат 60x90/16.
Усл.печ. л.24.
Издательство «БИНОМ. Лаборатория знаний»
125167, Москва, проезд Аэропорта, д. 3
Телефон: (499) 157-5272
© БИНОМ. Лаборатория знаний,
ISBN 978-5-9963-0848-4 2013

Содержание
Предисловие 6
1. Арифметика многоразрядных целых чисел 8
1.1. Основные арифметические операции 8
1.2. Задачи 22
2. Комбинаторные алгоритмы 27
2.1. Классические задачи комбинаторики 27
2.2. Генерация комбинаторных объектов 34
2.2.1. Перестановки 34
2.2.2. Размещения 44
2.2.3. Сочетания 50
2.2.4. Разбиение числа на слагаемые 58
2.2.5. Последовательности из нулей и единиц длины N
без двух единиц подряд 64
2.2.6. Подмножества 67
2.2.7. Скобочные последовательности 71
2.3. Задачи 76
3. Перебор и методы его сокращения 87
3.1. Перебор с возвратом (общая схема) 87
3.2. Примеры задач для разбора
общей схемы перебора 89
3.3. Динамическое программирование 106
3.4. Примеры задач для разбора идеи метода
динамического программирования 108
3.5. Метод ветвей и границ 116
3.6. Метод «решета» 121
3.7. Задачи 126
4. Алгоритмы на графах 158
4.1. Представление графа в памяти компьютера 158
4.2. Поиск в графе 159
4.2.1. Поиск в глубину 159
4.2.2. Поиск в ширину 161
4.3. Деревья 162

Содержание
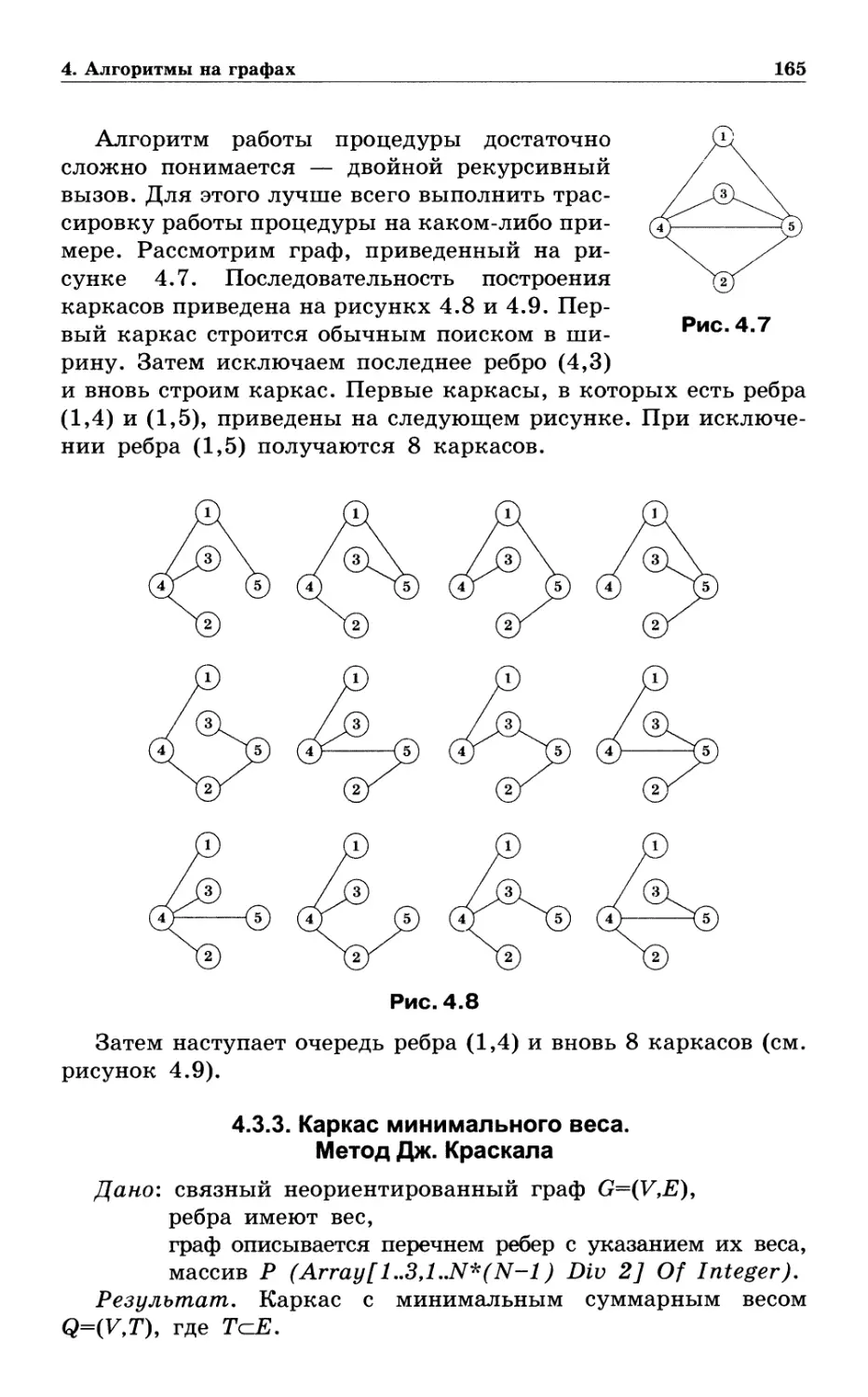
4.3.1. Основные понятия. Стягивающие деревья 162
4.3.2. Порождение всех каркасов графа 163
4.3.3. Каркас минимального веса. Метод Дж. Краскала . . 165
4.3.4. Каркас минимального веса. Метод Р. Прима 168
4.4. Связность 170
4.4.1. Достижимость 170
4.4.2. Определение связности 172
4.4.3. Двусвязность 173
4.5. Циклы 176
4.5.1. Эйлеровы циклы 176
4.5.2. Гамильтоновы циклы -177
4.5.3. Фундаментальное множество циклов 179
4.6. Кратчайшие пути 180
4.6.1. Постановка задачи. Вывод пути 180
4.6.2. Алгоритм Дейкстры 182
4.6.3. Пути в бесконтурном графе 183
4.6.4. Кратчайшие пути между всеми парами вершин.
Алгоритм Флойда 186
4.7. Независимые и доминирующие множества 188
4.7.1. Независимые множества 188
4.7.2. Метод генерации всех максимальных независимых
множеств графа 189
4.7.3. Доминирующие множества 194
4.7.4. Задача о наименьшем покрытии 195
4.7.5. Метод решения задачи о наименьшем разбиении . . 196
4.8. Раскраски 202
4.8.1. Правильные раскраски 202
4.8.2. Поиск минимальной раскраски вершин графа .... 203
4.8.3. Использование задачи о наименьшем покрытии
при раскраске вершин графа 207
4.9. Потоки в сетях, паросочетания 208
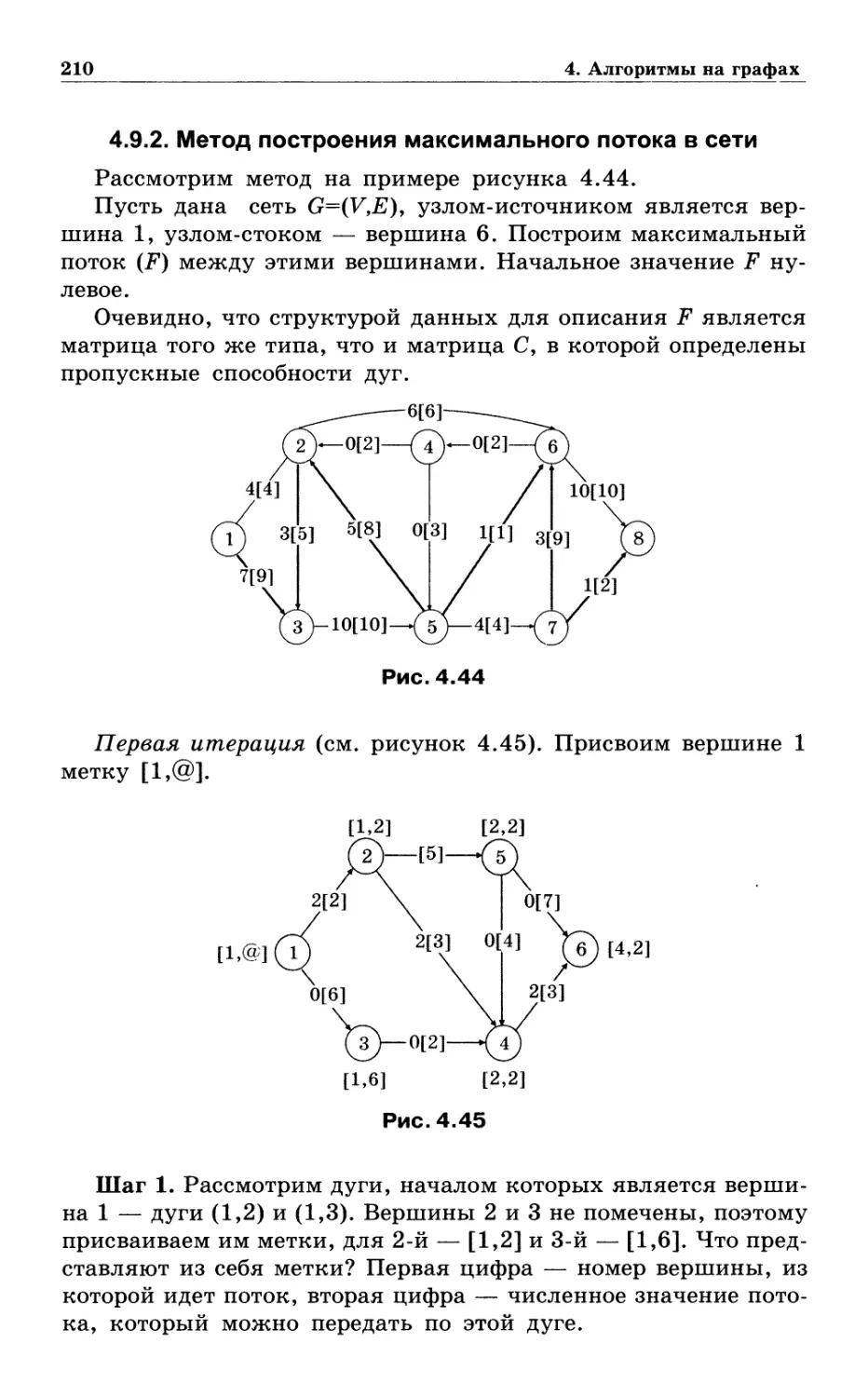
4.9.1. Постановка задачи 208
4.9.2. Метод построения максимального потока в сети ... 210
4.9.3. Наибольшее паросочетание в двудольном графе ... 215
4.10. Методы приближенного решения задачи
коммивояжера 219
4.10.1. Метод локальной оптимизации 219
4.10.2. Алгоритм Эйлера 222
4.10.3. Алгоритм Кристофидеса 225
4.11. Задачи 227

Содержание 5
5. Алгоритмы вычислительной геометрии 249
5.1. Базовые процедуры 249
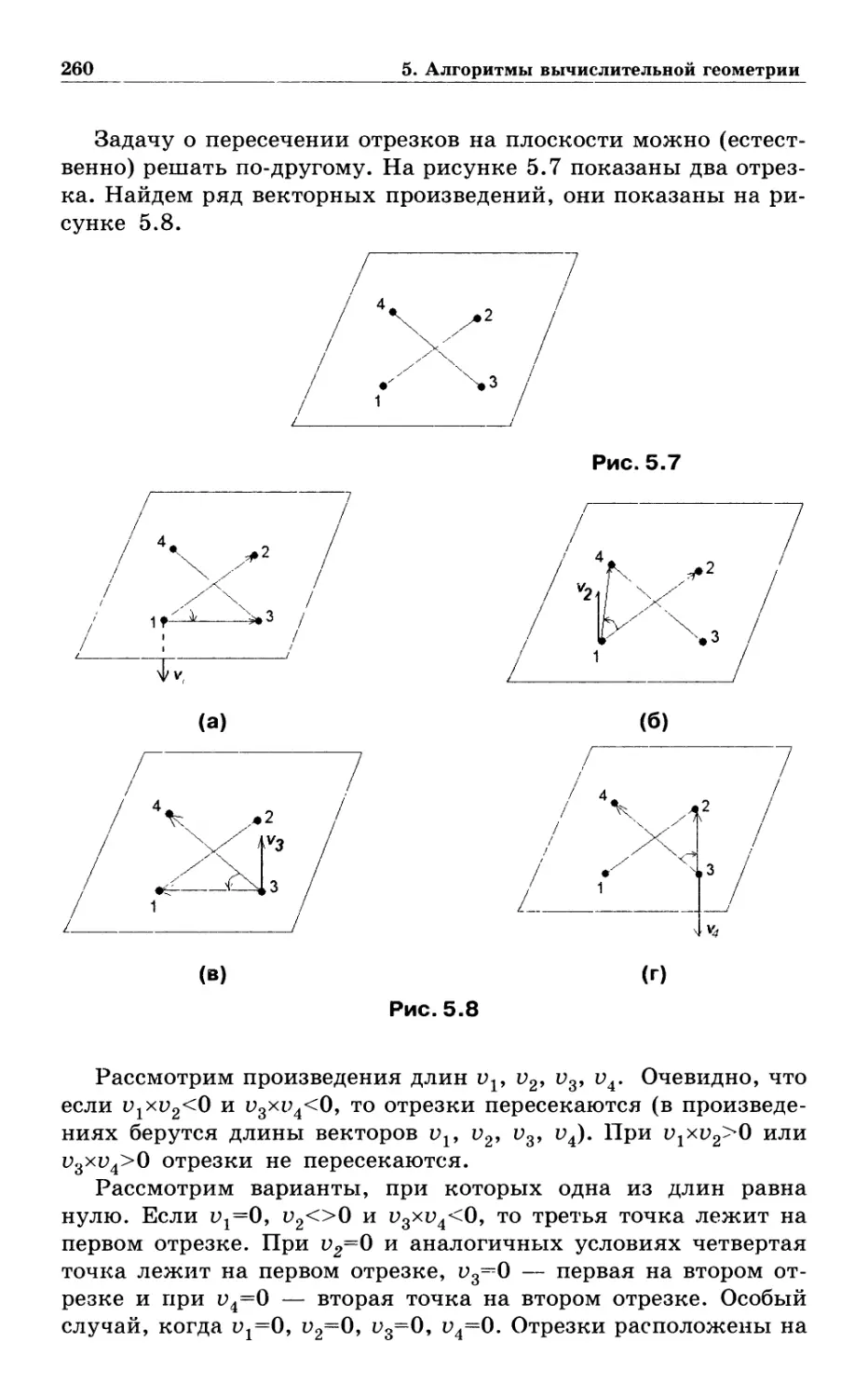
5.2. Прямая линия и отрезок прямой 255
5.3. Треугольник 262
5.4. Многоугольник 266
5.5. Выпуклая оболочка 272
5.6. Задачи о прямоугольниках 284
5.7. Задачи 293
6. Избранные олимпиадные задачи
по программированию 300
7. Заметки о тестировании программ 358
7.1. О программировании 359
7.2. Практические рекомендации 360
7.3. Тестирование программы решения задачи
(на примере) 370
Библиографический указатель 382

Единственной женщине посвящаю.
Предисловие
Курс «Программирование в алгоритмах» является
естественным продолжением курса «Основы программирования». Его
содержание достаточно традиционно: структурное
программирование, технологии «сверху — вниз» и «снизу — вверх». Освоению
обязательной программы курса автор придает огромное
значение. Она обязана стать естественной схемой решения
задач, если хотите — культурой мышления или познания.
Только после этого, по нашему глубокому убеждению,
разумно переходить на объектно-ориентированное программирование,
работу в визуальных средах, на машинно-ориентированное
программирование и т. д. Практика подтвердила жизненность
данной схемы изучения информатики. Ученики
физико-математического лицея г. Кирова многие годы представляют регион на
различных соревнованиях по информатике, включая
Международные олимпиады. Возвращение их без дипломов или
медалей — редкое исключение. Переходя в разряд студентов,
выпускники лицея без особых хлопот изучают дисциплины по
информатике в любом высшем учебном заведении России, а
также успешно выступают в командных чемпионатах мира среди
студентов по программированию.
Для кого предназначен учебник! Во-первых, для учителей и
учащихся школ с углубленным изучением информатики.
Во-вторых, для студентов высших учебных заведений,
изучающих программирование и стремящихся достичь
профессионального уровня. Особенно он будет полезен тем, кто готовится
принять участие в олимпиадах по программированию, включая
широко известный чемпионат мира по программированию,
проводимый под эгидой международной организации ACM
(Association for Computing Machinery).
О благодарностях, ибо не так часто вслух предоставляется
возможность сказать коллегам о том, что ты их безмерно
уважаешь. Во-первых, это касается моих учеников и учителей
одновременно. Без сотрудничества с ними вряд ли автор смог
написать что-то подобное. Первая попытка написания книг
такого рода была предпринята в 1993 году с Антоном
Валерьевичем Лапуновым. То было совместное вхождение в данную
проблематику. Для Антона более легкое, для автора достаточно

7
трудное. Затем последовало сотрудничество с Виталием
Игоревичем Беровым. Наверное, благодаря ему автор нашел ту схему
изложения алгоритмов на графах, которую он затем применял
в работе даже с восьмиклассниками. Сотрудничество с
Виктором Александровичем Матюхиным в пору его ученичества
было не таким явным, но после того, как он стал студентом
МГУ и в настоящее время, оно, на мой взгляд, очень
плодотворно. Влияние Виктора на развитие олимпиадной
информатики в г. Кирове просто огромно. С братьями Пестовыми,
Андреем и Олегом, написаны книги. Более трудолюбивых и
отзывчивых учеников автору не приходилось встречать.
Сотрудничество с такими ребятами не было бы возможным без
высочайшего профессионализма Владислава Владимировича
Юферева и Галины Константиновны Корякиной, директора и
завуча физико-математического лицея г. Кирова. Особые слова
признательности хотелось бы выразить Владимиру
Михайловичу Кирюхину, руководителю сборной команды школьников
России по информатике. В 1994 году он привлек автора к
работе в жюри российской олимпиады школьников. За эти годы
автор воочию увидел весь тот тяжелейший труд, который стоит
за победами российских школьников на Международных
олимпиадах. Иосиф Владимирович Романовский сделал ряд ценных
замечаний по газетной версии главы 5, за что автор благодарит
его и желает дальнейших творческих успехов в деле обучения
петербургских студентов. Многие годы главный редактор
газеты «Информатика» Сергей Львович Островский поддерживал
автора в его работе, и признательность за это остается
неизменной.
Об ошибках. Учебники такого плана не могут не содержать
ошибок. Для многих алгоритмов можно, естественно, найти
другие схемы реализации. Автор с признательностью примет
все замечания. Присылайте их, пожалуйста, по адресу
okulo v@ vspu. kir о ν. ru

1. Арифметика многоразрядных
целых чисел
Известно, что арифметические действия, выполняемые
компьютером в ограниченном числе разрядов, не всегда
позволяют получить точный результат. Более того, мы ограничены
размером (величиной) чисел, с которыми можем работать. А
если нам необходимо выполнить арифметические действия лад
очень большими числами, например
30!= 265252859812191058636308480000000?
В таких случаях мы сами должны позаботиться о
представлении чисел и о точном выполнении арифметических операций
над ними.
1.1. Основные арифметические операции
Числа, для представления которых в стандартных
компьютерных типах данных не хватает количества двоичных
разрядов, называются иногда «длинными». В этом случае
программисту приходится самостоятельно создавать подпрограммы
выполнения арифметических операций. Рассмотрим один из
возможных способов их реализации.
Представим в виде:
30!=2х(104)8+6525х(104)7+2859х(104)6+8121х(104)5+9105(104)4+
+8636х(104)3+3084х(104)2+8000х(104)1+0000х(104)0.
Это представление наталкивает на мысль о массиве.
Номер
элемента
в массивеА
1 Значение
0
9
1
0
2
8000^
3
_3084_
4
8636^
5
J9105
6
8121
7
2859^
8
6525
9
2
Возникают вопросы. Что за 9 в А[0], почему число хранится
«задом наперед»? Ответы очевидны, но подождем с ними.
Будет ясно из текста.
Примечание
Мы работаем с положительными числами!
Первая задача. Ввести число из файла.
Но прежде описание данных.

1. Арифметика многоразрядных целых чисел
9
Const MaxDig=1000;{^Максимальное количество цифр -
четырехзначных.*}
Osn=10000;{^Основание нашей системы счисления, в
элементах массива храним четырехзначные числа.*}
Type TLong=Array[0..MaxDig] Of Integer;{^Вычислите
максимальное количество десятичных цифр в нашем числе.*}
Прежде чем рассмотреть процедуру ввода, приведем
пример. Пусть в файле записано число 23851674 и основанием
(Osn) является 1000 (храним по три цифры в элементе массива
А). Изменение значений элементов массива А в процессе ввода
отражено в таблице 1.1. В основу положен посимвольный ввод,
для этого используется переменная ch.
Таблица 1.1
А[0]
3
0
1
1
1
2
2
2
3
3_
А[Ц
674
0
2
23
238
385
851
516
167
674
А[2]
851
0
0
0
0
2
23
238
385
851
А[3]
23
0
0
0
0
0
0
0
2
23
ch
-
2
3
8
5
1
6
7
4
1
Примечание
Конечное состояние
Начальное
состояние
1-й шаг
2-й шаг
3-й шаг
4-й шаг
5-й шаг
6-й шаг ι
7-й шаг
Итак, в А[0] храним количество задействованных
(ненулевых) элементов массива А — это уже очевидно. И при
обработке каждой очередной цифры входного числа старшая цифра
элемента массива с номером i становится младшей цифрой
числа в элементе i+Ι, а вводимая цифра будет младшей цифрой
числа из А[1].
Примечание (методическое)
Можно ограничиться этим объяснением и разработку процедуры
вынести на самостоятельное задание. Можно продолжить
объяснение. Например, выписать фрагмент текста процедуры переноса
старшей цифры из A[i] в младшую цифру Α[ΐ+1], τ. е. сдвиг уже
введенной части на одну позицию вправо:

10
1. Арифметика многоразрядных целых чисел
For i:=А[0] DownTo 1 Do
Begin
A[i + 1] :=A[i + l] + (Longlnt (A[i])*10) Div Osn;
A[i] := (Longlnt (A[i] ) *10) Mod Osn;
End;
Пусть мы вводим число 23851674 и первые 6 цифр уже
разместили «задом наперед» в массиве А. В символьную
переменную ch считали очередную цифру многоразрядного числа — это
«7». По нашему алгоритму она должна быть размещена как
младшая цифра в А[1]. Выписанный фрагмент программы
освобождает место для этой цифры. В таблице 1.2 отражены
результаты работы этого фрагмента.
Таблица 1.2
i
2
2
1
ащ
516
516
160
А[2]
238
380
385
А[3]
0
2
2
ch
7
После этого остается только добавить текущую цифру кА[1]
и изменить значение А[0].
В конечном итоге процедура должна иметь следующий вид:
Procedure ReadLong(Var A:TLong);
Var ch:Char;i:Integer;
Begin
FillChar(A,SizeOf(A),0);
Repeat
Read(ch);
Until ch In ['0' . .' 9' ]
{^Пропуск не цифр в начале файла.*}
While ch In [Ό' . .' 9' ] Do
Begin
For i : =A [ 0 ] DownTo 1 Do
Begin{^"Протаскивание"
старшей цифры в числе из A[i] в младшую
цифру числа из A[i + 1] . *}
A[i + 1] :=A[i + l] + (Longlnt (A [i])*10) Div Osn;
A[i] : = (Longlnt (A[i] ) *10) Mod Osn;
End;

1. Арифметика многоразрядных целых чисел
11
A[l]:=A[1]+Ord(ch)-Ord('0');
{^Добавляем младшую цифру к числу из А[1] . *}
If A[A[0]+1]>0 Then Inc(A[0]);
{^Изменяем длину, число задействованных
элементов массива А.*}
Read(ch);
End;
End;
Вторая задача. Вывод многоразрядного числа в файл или
на экран.
Казалось бы, нет проблем — выводи число за числом.
Однако в силу выбранного нами представления числа необходимо
всегда помнить, что в каждом элементе массива хранится не
последовательность цифр числа, а значение числа, записанного
этими цифрами. Пусть в элементах массива хранятся
четырехзначные числа. И есть число, например, 128400583274. При
выводе нам необходимо вывести не 58, а 0058, иначе будет
потеря цифр. Итак, нули также необходимо выводить. Процедура
вывода имеет вид:
Procedure WriteLong(Const A:TLong);
Var Is,s:String;
i : Integers-
Begin
Str(Osn Div 10,1s);
Write(A[A[0]]);{*Выводим старшие цифры числа.*}
For i:=А[0]-1 DownTo 1 Do
Begin
Str(A[i],s);
While Length(s)<Length (Is) Do s:='0'+s;
{*Дополняем незначащими нулями.*}
Write(s);
End;
WriteLn;
End;
Третья задача. Сложение двух положительных чисел.
Предварительная работа по описанию способа хранения,
вводу и выводу многоразрядных чисел выполнена. У нас есть
все необходимые «кирпичики», например, для написания
программы сложения двух положительных чисел. Исходные числа
и результат храним в файлах. Назовем процедуру сложения
SumLongTwo. Тогда программа ввода двух чисел и вывода
результата их сложения будет иметь следующий вид:

12
1. Арифметика многоразрядных целых чисел
Var A,B,C:TLong;
Begin
Assign(Input,'Input.txt'); Reset (Input);
ReadLong(A);ReadLong(B);
Close (Input);
SumLongTwo(А,В,С);
Assign(Output,'Output.txt'); Rewrite(Output);
WriteLong(C);
Close(Output);
End.
Трудно ли объяснить процедуру сложения? Используя
простой пример — нет.
Пусть А=870613029451, Б=3475912100517461.
Результат — С=3476782713546912. Алгоритм имитирует
привычное сложение столбиком, начиная с младших разрядов.
И именно для простоты реализации арифметических операций
над многоразрядными числами используется машинное
представление «задом наперед». Ниже приведен текст процедуры
сложения двух чисел.
Procedure SumLongTwo(Const А,В:TLong;Var C:TLong);
Var i,k:Integer;
Begin
FillChar (CSizeOf (C) , 0) ;
If A[0]>B[0] Then k:=A[0] Else k:=B[0];
For i :=1 To k Do
Begin
C[i+1]:=(C[i]+A[i]+B[i])Div Osn;
C[i]:=(C[i]+A[i]+B[i]) Mod Osn;
{*Есть ли в этих операторах ошибка?*}
End;
If C[k+1]=0 Then C[0] :=k Else C[0] :=k+l;
End;
Таблица 1.3
1
2
3
ЛИ
9451
1302
8706
0
7461
51
9121
3475
6912
6912
6912
6912
C[2]
1
1354
1354
1354
0
0
7827
7827
cm
о
о
1
3476

1. Арифметика многоразрядных целых чисел
13
Четвертая задача. Реализация операций сравнения чисел:
А=В, А<В, А>В, А<В, А>В.
Функция А=В имеет вид.
Function Eq(Const A,B:TLong):Boolean;
Var i:Integer;
Begin
Eq:=False;
If A[0]=B[0] Then
Begin
i:=l;
While (i<=A[0]) And (A[i]=B[i]) Do Inc(i);
Eq:=(i=A[0]+l);
Ends-
End;
Реализация функции А>В также прозрачна.
Function More(А,В:TLong):Boolean;
Var i : Integers-
Begin
If A[0]<B[0]
Then More:=False
Else
If A[0]>B[0]
Then More:=True
Else
Begin
i:=A[0];
While (i>0) And (A[i]=B[i]) Do Dec(i);
If i=0
Then More:=False
Else
If A[i]>B[i]
Then More:=True
Else More:=False;
End;
End;
Остальные функции реализуются через функции Eq и More.
Function Less(A,B:TLong):Boolean;{A<B}
Begin
Less:=Not(More(A,B) Or Eq(A,B));
End;

14
1. Арифметика многоразрядных целых чисел
Function More_Eq(A,B:TLong):Boolean;
Begin
More_Eq:=More(A,B) Or Eq(A,B);
End;
И наконец, последняя функция А<В.
Function Less_Eq(A,B:TLong):Boolean;
Begin
Less_Eq:=Not(More(A,B));
End;
Для самостоятельного решения может быть предложена
следующая более сложная задача. Требуется разработать
функцию, которая выдает 0, если А больше Б, 1, если А меньше В и
2 при равенстве чисел. Но сравнение должно быть выполнено с
учетом сдвига. О чем идет речь? Поясним на примере.
Пусть А равно 56784, а Б — 634. При сдвиге на 2 позиции
влево числа Б функция должна сказать, что Б больше А, без
сдвига — что А больше Б. Или А равно 567000, а Б — 567 и
сдвиг равен 3, то функция должна «сказать», что числа равны.
Решение может иметь следующий вид.
Function More(Const А, В: TLong; sdvig: Integer):
Byte;
Var i : Integers-
Begin
If A[0]>(B[0]+sdvig)
Then More:=0
Else
If A[0]<(B[0]+sdvig)
Then More:=l
Else
Begin
i:=A[0];
While (i>sdvig) And (A[i]=B[i-sdvig]) DoDec(i);
If i=sdvig
Then
Begin
More:=0;{^Совпадение чисел с учетом
сдвига.*}
For i:=l To sdvig Do
If A[i]>0 Then Exit;
More:=2;{*Числа равны, "хвост" числа А
равен нулю.*}

1. Арифметика многоразрядных целых чисел
15
End
Else More:=Byte(A[i]<B[i-sdvig]);
End;
End;
Пятая задача. Умножение многоразрядного числа на
короткое.
Под коротким числом понимается целое число, не
превосходящее основание системы счисления.
Процедура очень похожа на процедуру сложения двух
чисел.
Procedure Mul(Const A: TLong;Const К: Longlnt;
Var C: TLong) ;
Var i : Integer;
{^Результат - значение переменной С.*}
Begin
FillChar(C, SizeOf(C), 0);
If K=0
Then Inc (C[0]) {^Умножение на ноль.*}
Else
Begin
For i:=l To A[0] Do
Begin
C[i+1]:=(Longlnt(A[i])*K+C[i]) Div Osn;
C[i] : = (Longlnt (A [i])*K +C[i]) Mod Osn;
End;
If C[A[0]+1]>0
Then C[0] :=A[0]+1
Else C[0]:=A[0];
{^Определяем длину результата.*}
End;
End;
В качестве самостоятельной работы можно предложить
разработку процедуры умножения двух чисел. Возможный
вариант процедуры приведен ниже.
Procedure MulLong(Const А, В: TLong; Var С: TLong);
{^Умножение "длинного" на "длинное".*}
Var i, j : Word;
dv: Longlnt;
Begin
FillChar(C, SizeOf(C), 0);
For i:=l To A[0] Do

16
1. Арифметика многоразрядных целых чисел
For j :=1 To B[0] Do
Begin
dv:=LongInt (A[i])*B[j ] + C[i + j-l];
Inc(C[i+j], dv DivOsn);
C[i + j-l] :=dv Mod Osn;
End;
C[0]:=A[0]+B[0];
While (C[0]>1) And (C[C[0] ]=0) Do Dec(C[0] ) ;
End;
Шестая задача. Вычитание двух многоразрядных чисел с
учетом сдвига.
Если суть сдвига пока не понятна, то оставьте ее в покое, на
самом деле вычитание с учетом сдвига потребуется при
реализации операции деления. Выясните алгоритм работы
процедуры при нулевом сдвиге.
Введем ограничение: число, из которого вычитают, больше
числа, которое вычитается.
Работать с длинными отрицательными числами мы не
умеем. Процедура была бы похожа на процедуры сложения и
умножения, если бы не одно «но» — не перенос единицы в
старший разряд, а «заимствование единицы из старшего разряда».
Например, в обычной системе счисления мы вычитаем 9 из
11 — идет заимствование 1 из разряда десятков, а если из
10000 той же 9 — процесс заимствования несколько сложнее.
Procedure Sub(Var A: TLong;Const B: TLong;
sp: Integer);
Var i, j : Integer; { *Из А вычитаем В с учетом
сдвига sp, результат вычитания в А.*}
Begin
For i:=l To B[0] Do
Begin
Dec(A[i+sp], B[i]);
{^Реализация сложного заимствования*} {*)
j:=i; {*)
While (A[j+sp]<0) And (j<=A[0]) Do
Begin {*)
Inc(A[j+sp], Osn);Dec(A[j+sp+l]);Inc(j); {*}
End; {*}
End;
i:=A[0];
While (i>l) And (A[i]=0) Do Dec(i);

1. Арифметика многоразрядных целых чисел
17
А[0]:=i; (^Корректировка длины результата
операции*)
End;
Если строки, отмеченные {*}, заменить на нижеприведенные
операторы:
{^Реализация простого заимствования*}
If A[i+sp]<0 Then
Begin
Inc(A[i+sp], Osn);
Dec(A[i+sp+l]);
End;
то, по понятным причинам, алгоритм не будет работать при
всех исходных данных. Можно сознательно сделать ошибку и
предложить найти ее — принцип «обучение через ошибку».
Рекомендуется выполнить трассировку работы данной
процедуры, например, для следующих исходных данных.
А=100000001000000000000,
Б=2000073859998.
Седьмая задача. Деление двух многоразрядных чисел, т. е.
нахождение целой части частного и остатка.
Написать исходный (без уточнений) алгоритм не составляет
труда:
Procedure LongDivLong(Const А, В: Tlong;
Var Res, Ost: TLong);
Begin
FillChar(Res, SizeOf(Res), 0); Res[0]:=l;
FillChar(Ost, SizeOf(Ost), 0); Ost[0]:=l;
Case More(A, B, 0) Of
0: MakeDel (A, B, Res, Ost); {*A больше В, пока
не знаем, как выполнять операцию, -
λλвыносим" в процедуру.*}
1: Ost:=A; {*A меньше В.*}
2: Res[l]:=l; {Нравно В.М
End;
End;
А дальше? Дальше начинаются проблемы. Делить
столбиком нас научили в школе. Например:

18
1. Арифметика многоразрядных целых чисел
1000143123567
73859998
_261543143
221579994
_399631495
369299990
_303315056
295439992
_78750647
73859998
7385999^
13541(Целая часть частного)
4890649 (Остаток)
Что мы делали? На каждом этапе в уме подбирали цифру (1,
3, 5 и т. д.), такую, что произведение этой цифры на делитель
дает число меньшее, но наиболее близкое к числу. Какому? Это
трудно сказать словами, но из примера ясно. Зачем нам это
делать в уме? Пусть делает компьютер. Однако упростим пример,
оставим его для тестирования окончательной логики, тем более
что и числа длинные. Пусть число А будет меньше BxlO, тогда
в результате (целая часть деления) будет одна цифра.
Например, А равно 564, а Б — 63 и простая десятичная система
счисления. Попробуем подобрать цифру результата, но не методом
прямого перебора, а методом деления отрезков пополам. Пусть
Down — нижняя граница интервала изменения подбираемой
цифры, Up — верхняя граница интервала, Ost равен делимому.
Таблица 1.4
Down
0
1 5
I
! 7
1
! 8
1 8
Up
10
10
10
10
ι 9
C=B*{(Down+Up) D/V2)
315
441
504
567
504
Osi-564 |
C<Ost
C«Dst ι
C<Ost
OOst I
C<Ost
Итак, результат — целая часть частного равна (Down+Up)div 2,
остаток от деления — разность между значениями Ost и С.
Нижнюю границу Down изменяем, если результат (С) меньше
остатка, верхнюю Up, если больше. В таблице 1.4 приведены
результаты вычислений.
Усложним пример. Пусть А равно 27856, а Б — 354.
Основанием системы счисления является не 10, а 10000. В таблице
1.5 приведено поэтапное решение этой задачи.

1. Арифметика многоразрядных целых чисел
19
Таблица 1.5
1 Down
0
0
0
0
0
0
0
78
78
1 78
| 78
78
78
78
Up
10000
5000
2500
1250
625
312
156
156
117
97
87
82
80
79
С
1770000
885000
442500
221250
110448
55224
27612
41418
34338
30798
29028
28320
27966
27612
Osi-27856
OOst
OOst
OOst
OOst
OOst
OOst
C<Ost
OOst
OOst
OOst
OOst
OOst
OOst
C<Ost
Целая часть частного равна 78, остаток от деления — 27856
минус 27612, т. е. 244.
Пора приводить процедуру. Используемые «кирпичики»:
функция сравнения чисел (More) с учетом сдвига и умножения
многоразрядного числа на короткое (Mul) описаны выше.
Function FindBin(Var Ost: TLong;Const В: Tlong;
sp: Integer) : Longlnt;
Var Down, Up: Word;
C: TLong;
Begin
Down:=0;Up:=Osn;{^Основание системы счисления.*}
While Up-l>Down Do
Begin {*У преподавателя есть возможность сделать
сознательную ошибку. Изменить условие цикла на
Up>Down. Результат - зацикливание программы.*}
Mul (В, (Up+Down) Div 2, С);
Case More(Ost, C, sp) Of
0: Down:= (Down+Up) Div 2;
1: Up:= (Up + Down) Div 2;
2: Begin Up:=(Up+Down) Div 2; Down:=Up; End;

20
1. Арифметика многоразрядных целых чисел
End;
End;
Mul (В, (Up+Down) Div 2, С);
If More(Ost,C,0)=0
Then Sub(Ost, C, sp)
{*Находим остаток от деления.*}
Else
Begin Sub(С,Ost,sp); 0st:=C; End;
FindBin:=(Up+Down) Div 2;{*Целая часть частного.*}
End;
Осталось разобраться со сдвигом — значением переменной
sp в нашем изложении.
Вернемся к обычной системе счисления и попытаемся
разделить числа, например, 635 на 15. Что мы делаем? Вначале
делим 63 на 15 и формируем, подбираем в уме, первую цифру
результата. Подбирать с помощью компьютера мы
научились. Подобрали — это цифра 4, и это старшая цифра
результата. Изменим остаток. Если вначале он был 635, то сейчас
стал 35. Вычитать с учетом сдвига мы умеем. Опять
подбираем цифру. Вторую цифру результата. Это цифра 2 и
остаток 5. Итак, результат (целая часть) 42, остаток от деления 5.
А что изменится, если основанием будет не 10, а 10000?
Алгоритм совпадает, только в уме считать несколько труднее, но
ведь у нас же есть молоток под названием компьютер —
пусть он вбивает гвозди.
Procedure MakeDel(Const А, В: Tlong;
Var Res, OstrTLong);
Var sp: Integers-
Begin
Ost:=A;{^Первоначальное значение остатка.*}
sp:=A[0]-B[0];
If More (A, B, sp)=l Then Dec (sp);
{* B*0sn>A, в результате одна цифра.*}
Res [0] :=sp+l;
While sp>=0 Do
Begin
{*Находим очередную цифру результата.*}
Res[sp+1]:=FindBin(Ost, B, sp) ;
Dec(sp);
End;
End;

1. Арифметика многоразрядных целых чисел
21
Примечание
В результате работы по данной теме каждый учащийся обязан
иметь собственный модуль для работы с многоразрядными
числами, который должен содержать следующий (примерный) перечень
функций и процедур (описательная часть). Курсивом выделены
процедуры и функции, не рассмотренные в данной главе.
Function Eq(Const А, В: TLong): Boolean;
{^Сравнение чисел А=В*}
Function Less(Const А, В: TLong): Boolean;
{^Сравнение чисел А<В*}
Function More(Const А, В: TLong): Boolean;
{^Сравнение чисел А>В*}
Function Less_Eq(Const А, В: TLong):Boolean;
{^Сравнение чисел А<В*}
Function Могe_Eq(Const А, В: TLong): Boolean;
{^Сравнение чисел А>В*}
Function LongTurnShort(Const A: TLong;
Var К: Longlnt): Boolean;
{^Преобразование многоразрядного числа в число
типа Longlnt.*}
Function LongModShort(Const A: TLong;
Const K: Word) : Word;
{^Остаток от деления многоразрядного числа на
короткое типа Word.*}
Function HowDigits(Const A: TLong): Longlnt;
{^Подсчет числа десятичных цифр в многоразрядном
числе.*}
Procedure Mul(Const A: TLong; К: Word;
Var В: TLong) ;
{^Умножение многоразрядного числа на короткое типа
Word.*}
Procedure MulLong(Const А, В: TLong; Var C: TLong);
{^Умножение двух многоразрядных чисел*}
Procedure SumLongTwo(Const A, B: TLong;
Var С: TLong) ;
{^Сложение двух многоразрядных чисел*}
Procedure Sub(Var A: TLong;Const B: Tlong;
Const sp:Integer);
{^Вычитание многоразрядных чисел*}

22
1. Арифметика многоразрядных целых чисел
Procedure ShortTurnLong(К: Longlnt; Var A: TLong);
{^Преобразование числа типа Longlnt в многоразрядное
число.*}
Procedure LongDivShort(Const A: TLong;
Const К: Word; Var В: TLong);
{^Целочисленное деление многоразрядного числа на
короткое типа Word.*)
Procedure LongDivLong(Const A, B: TLong;
Var C, ost: TLong);
{*Деление двух многоразрядных чисел*}
Procedure SdvigLong(Var A: TLong; Const p: Word);
{*Сдвиг влево на р длинных цифр.*}
1.2. Задачи
1. Для представления многоразрядных чисел использовался
одномерный массив. Каждая цифра числа (или группа цифр)
хранилась в отдельном элементе массива. Рассмотрим
представление многоразрядных чисел в виде двусвязного списка.
Каждая цифра числа — элемент списка. На рисунке 1.1
представлено число 25974.
N
'
head
4
Mil
s
*
ν
' 7
Ν.
s
ч
9
•ч
ζ'
V
5
tail
Ν
?
4
\
t
2
Nil
Рис. 1.1
Число хранится «задом наперед». Такое представление
удобно при выполнении арифметических операций, а для вывода у
нас есть адрес предшествующего элемента. Элемент списка
можно описать следующим образом:
Const Basis=10;{^Основание системы счисления.*}
Typept=^elem;
elem=Record
data:Integer;
next,pred:pt
End;
Var head, tail :pt;

1. Арифметика многоразрядных целых чисел
23
Разработать программы выполнения основных
арифметических операций при таком способе хранения многоразрядных
чисел.
2. Написать программу вычисления N1, при Л7>100.
3. Написать программу вычисления 3^, при N>100.
4. Написать программу извлечения квадратного корня из
многоразрядного числа.
Указание. Пусть требуется найти целую часть результата.
Возможна следующая схема решения задачи [9].
Шаг 1. Многоразрядное число разбивается на несколько пар
(граней) чисел. Если число содержит четное количество
разрядов, тогда первая грань содержит две цифры, если нечетное, то
одну. Так, число 236488 разбивается на три грани, каждая из
которых содержит две цифры: 23 64 88, а для числа 15385
первая грань состоит из одной цифры 1.
Число граней определяет количество разрядов ответа. В
качестве примера возьмем число 574564 и разобьем его на грани:
57 45 64. Таким образом, ответом является трехразрядное
число (обозначим через г/).
Шаг 2. Рассматривается первая грань 57 и подбирается
число χ такое, чтобы х2 было как можно ближе к 57, но не
превосходило его. Таким образом, х=7, так как 7х7=49<57, а
8х8=64>57. Первая цифра ответа у равна 7.
Шаг 3. Находится разность между первой гранью 57 и
х2=49: 57-49=8. Эта разность приписывается к следующей
грани, получается число 845.
Шаг 4. Подбирается следующая цифра. Находится новое
значение х, такое, чтобы (2хг/х10+х)хх не превосходило 845 и
было наиболее близким к 845. Это число 5, так как
(14χ10+5)χ5=725<845, а (14х10+6)х6=876>845. Итак, вторая
цифра ответа 5 и г/=75.
Шаг 5. Повторятся шаг 3. Находим разность: 845-725=120,
ее «подклеим» к следующей грани — 12064.
Шаг 6. Выполняются действия шага 4.
(2хг/х10+х)хх<=12064. Значение χ равно 8, так как
(150х10+8)х8=12064. Итак, г/=758.
Пояснений требует шаг 4, а именно, не понятно, почему
используется такая формула для подбора очередной цифры
ответа.
Пусть 10хг/+х =4ζ. Возведем в квадрат число 10хг/+х.
Получим 100хг/2+10хг/хх+10хг/хх+х2=<г.

24
1. Арифметика многоразрядных целых чисел
Значение у подобрано на шаге 2, оно дает вклад ЮОхг/2 в
число ζ. Подбор цифры χ обязан дать максимальный вклад в
число г-ЮОхг/2.
Примечание
Если корень не извлекается в результате повторения шагов 3, 4, то
после последней цифры заданного числа ставят запятую и
образуют дальнейшие грани, каждая из которых имеет вид 00. В этом
случае процесс извлечения корня прекращается при достижении
требуемой точности.
5. Определить, встречаются ли в записи некоторого
многоразрядного числа две подряд идущие цифры, например 9?
6. Определить наибольший общий делитель двух
многоразрядных чисел.
7. Определить наименьшее общее кратное двух
многоразрядных чисел.
8. Определить, являются ли два многоразрядных числа
взаимно простыми.
9. Определить количество делителей многоразрядного числа.
10. Написать программу проверки того, что число
2i9936x(2i9937_;[) является совершенным, т. е. равным сумме
своих делителей, кроме самого себя.
11. Написать программу перевода многоразрядного числа в
системы счисления с основаниями 2, 8, 16.
12. Написать программу разложения многоразрядного числа
на простые множители.
13. Известно, что целочисленное деление (умножение) на 2
равносильно сдвигу числа на один разряд вправо (влево). Два
обычных числа а и Ъ можно сложить с помощью следующего
алгоритма:
• если а и Ъ четные числа, тоа+Ь=—+ — х2;
V2 2)
. . (а-1 Ь-1 А 0
• если а и о нечетные числа, то а + о = + + 1 χ 2;
{2 2 )
• если а — четное, а Ъ — нечетное, то α + Ь = — + χ 2 + 1;
U 2 )
• если а — нечетное, ab — четное, то а + Ъ = I + — χ 2 + 1.
1 2 2)

1. Арифметика многоразрядных целых чисел
25
Заметим, что при нечетном значении а для целочисленного
а -1 а
деления = —.
2 2
Приведенный алгоритм выполнения операции сложения
реализуется с помощью следующей рекурсивной функции:
Function Sum(χ,у:Integer):Integer;
Begin
If x=0
Then Sum:=y
Else
If y=0
Then Sum:=x
Else
If (x Mod 2 =0) And (y Mod 2 =0)
Then Sum:=Sum(x Div 2, у Div 2) *2
Else
If (x Mod 2 =1) And (y Mod 2 =1)
Then Sum:=Sum(x Div 2, у Div 2 +1)*2
Else Sum:=Sum(x Div 2, у Div 2) *2 + l;
End;
Написать аналогичную процедуру сложения (не обязательно
рекурсивную) двух многоразрядных целых чисел а и Ъ.
Деление и умножение на 2 заменить соответствующими операциями
сдвига на один разряд.
14. Два числа а и Ъ можно перемножить, используя только
сдвиги на один разряд и операцию сложения.
Например, Ь=125, а=37.
Выпишем следующий столбик чисел:
125x37
250x18+125
500x9+125
1000x4+500+125
2000x2+500+125
4000x1+500+125.
И результат: 125x37=125+500+4000=4625 (в каких случаях
изменяемое число Ъ входит в сумму?). Он основан на
следующих тождествах:
• если а четное число, то α χ Ь = — χ 6 χ 2;
• если а нечетное число, то α χ Ъ - \ χ Ь \ χ 2 + Ъ.

26
1. Арифметика многоразрядных целых чисел
Этот алгоритм реализуется с помощью следующей
рекурсивной функции:
Function RecMul(χ,у:Integer):Integer;
(^Естественно предполагается, что результат не
выходит за пределы Integer.*}
Begin
If x=0
Then RecMul:=0
Else
If χ Mod 2 = 0
Then RecMul:=RecMul(x Div 2,y)*2
Else RecMul:=RecMul(x Div 2,y)*2+y;
End;
Написать аналогичную процедуру умножения (не
обязательно рекурсивную) двух многоразрядных целых чисел а и Ъ.
Деление и умножение на 2 заменить соответствующими
операциями сдвига на один разряд.
15. Написать программу сложения двух знаковых
многоразрядных чисел [2].
Указание. Необходимо заменить ί-разрядное отрицательное
число numb на его дополнение до числа 10*, то есть на число
10^ -\numb |.
Алгоритм получения дополнительного кода отрицательного
числа известен [2, 23]. Находят обратный код десятичного числа
путем замены каждой цифры i на 9-i. Прибавление единицы к
обратному коду дает дополнительный код. После замены
отрицательных слагаемых на их дополнительный код работает
алгоритм сложения многоразрядных чисел, рассмотренный в 1.1.

2. Комбинаторные алгоритмы
Одна из главных целей изучения темы, помимо
традиционных, заключается в том, чтобы учащиеся осознали суть
«отношения порядка» на некотором множестве объектов.
На множестве объектов типа Word, Integer, Char, Boolean
отношение порядка воспринимается как нечто очевидное.
Объяснить, что на типе Real его нет, гораздо сложнее. Однако
осознание того факта, что компьютер что-то может делать с каким-то
множеством объектов только в том случае (по крайней мере,
перебрать их все), если на этом множестве введено какое-то
отношение порядка, требует длительной работы. А выработка
автоматических навыков «вычленения» отношения порядка на
множестве данных конкретной задачи — работа многих дней.
2.1. Классические задачи комбинаторики
При решении практических задач часто приходится
выбирать из некоторого конечного множества объектов
подмножество элементов, обладающих теми или иными свойствами,
размещать элементы множеств в определенном порядке и т. д. Эти
задачи принято называть комбинаторными задачами.
Многие из комбинаторных задач решаются с помощью двух
основных правил — суммы и произведения. Если удается
разбить множество объектов на классы и каждый объект входит в
один и только один класс, то общее число объектов равно
сумме числа объектов во всех классах (правило сложения).
Правило умножения чуть сложнее. Даны два произвольных
конечных множества объектов А и Б. Количество объектов в А равно
N, в В — М. Составляются упорядоченные пары аЪ, где asA (a
принадлежит А) и ЬеВ. Количество таких пар (объектов) равно
ΝχΜ. Правило обобщается и на большее количество множеств
объектов.
Перестановки (ΡΝ — число перестановок).
Классической задачей комбинаторики является задача о
числе перестановок — сколькими способами можно
переставить N различных предметов, расположенных на N различных
местах.

28
2. Комбинаторные алгоритмы
Объяснение примеров
1. Сколькими способами можно переставить три монеты 1, 2, 5
рублей, расположенных соответственно на трех местах с
номерами 1, 2, 3? Ответ: 6.
2. Сколькими способами можно пересадить четырех гостей А,
Б, В, Г, сидящих соответственно на четырех местах 1, 2, 3,
4? Ответ: 24.
3. Сколькими способами можно переставить буквы в слове
«эскиз»! Ответ: 120.
4. Сколькими способами можно расположить на шахматной
доске 8 ладей так, чтобы они не могли бить друг друга?-От-
вет: 40320.
N различных предметов, расположенных на N различных
местах, можно переставить
N\ (Af-факториал) = 1χ2χ3χ...χΝ способами (PN=Nl).
Отвлекаясь от природы объектов, можно считать их для
простоты натуральными числами от 1 до N. При этой
трактовке понятие перестановки можно дать следующим образом.
Перестановкой из N элементов называется упорядоченный набор
из N различных чисел от 1 до N. Места также нумеруются от 1
до N. Тогда перестановку можно записать таблицей с двумя
строками, из которых каждая содержит все числа от 1 до N.
(12 3 4 5 6^
Например, F =\
[3 5 1 6 4 2у
Перестановку
1
2 3 4
2 3 4
N
N
называют тождественной.
По перестановке F однозначно определяется перестановка
F'1, такая, что FF'1=E.
, Γΐ 2 3 4 5 6^
Так, для нашего примера F
2 3 4
3 6 15 2
Под суперпозицией перестановок F и G понимают
перестановку FG, определяемую следующим образом: FG(i)=F(G(i)).
Так, если F совпадает с приведенной выше перестановкой, а
G =
12 3 4 5 6
6 3 5 13 2
, то FG
^1 2 3 4 5 6^
2 14 3 15

2. Комбинаторные алгоритмы
29
Каждую перестановку можно представить графически в
виде ориентированного графа с множеством вершин от 1 до N.
(1 2 3 4 5 6^
Для перестановки F =
(351642;
ориентированный граф изображен на рисунке 2.1
соответствующий
(бЬ^-Θ
Рис. 2.1
Графическая иллюстрация облегчает введение понятия
цикла перестановки. Видим, что перестановка F представима
двумя циклами: F=[l, 3], [2, 5, 4, 6].
Пару f. и /·, (где i<j) называют инверсией перестановки F,
если f>fj. Число инверсий (К) определяет знак перестановки
(-1)^. Для нашего примера число инверсий равно 6, а знак
перестановки положительный. Произвольную перестановку,
являющуюся циклом длины 2, обычно называют транспозицией.
Размещения ( А%).
Задача формулируется следующим образом: сколькими
способами можно выбрать и разместить по Μ различным местам
Μ из N различных предметов?
Объяснение примеров
1. Сколькими способами можно выбрать и разместить на двух
местах 1, 2 две из трех монет 1, 2, 5 рублей? Ответ: 6.
2. Сколькими способами можно выбрать и разместить на двух
местах 1, 2 двух из четырех гостей А, Б, В, Г? Ответ: 12.
3. Сколько трехбуквенных словосочетаний можно составить
из букв слова эскиз? Ответ: 60.
4. В чемпионате по футболу принимают участие 17 команд и
разыгрываются золотые, серебряные и бронзовые медали.
Сколькими способами они могут быть распределены? Ответ:
4080.
5. Партия состоит из 25 человек. Требуется выбрать
председателя партии, его заместителя, секретаря и казначея.
Сколькими способами можно это сделать, если каждый член
партии может занимать лишь один пост. Ответ: 303600.

30
2. Комбинаторные алгоритмы
Число размещений вычисляется по формуле
A™ =Nx(N -l)x(N -2)χ...χ(ΛΓ -Μ +1),
или Ам = - —
N (N-M)\
Сочетания (выборки) (С™ \
Другой классической задачей комбинаторики является
задача о числе выборок: сколькими способами можно выбрать Μ из
N различных предметов?
Объяснение примеров
1. Сколькими способами можно выбрать две из трех монет 1,2,
5 рублей? Ответ: 3.
2. Сколькими способами можно выбрать двух из четырех
гостей А, Б, В, Г? Ответ: 6.
3. Сколькими способами можно выбрать три из пяти букв
слова эскиз! Ответ: 10.
4. В чемпионате по футболу России принимают участие 17
команд и разыгрываются золотые, серебряные и бронзовые
медали. Нас не интересует порядок, в котором располагаются
команды-победительницы, ибо все они выходят на
Европейские турниры. Сколько различных способов представления
нашего государства на Европейских турнирах? Ответ: 680.
5. Партия состоит из 25 человек. Требуется выбрать
председателя партии и его заместителя, ибо они представляют
партию в президиуме межпартийных форумов. Сколькими
способами можно это сделать, если каждый член партии может
занимать лишь один пост? Ответ: 300.
6. Сколькими способами можно поставить на шахматной доске
8 ладей (условие о том, что ладьи не могут бить друг друга,
снимается)? Ответ: 4328284968.
7. Сколько различных прямоугольников можно вырезать из
клеток доски размером ΝχΜ (стороны прямоугольников
проходят по границам клеток)?
Пояснение. Горизонтальные стороны могут занимать любое
из М+1 положений. Число способов их выбора — С2м+1,
аналогично для вертикальных сторон. Ответ: С2М + 1 χ C2N+l.
Сочетание можно определить и как подмножество из Μ
различных натуральных чисел, принадлежащих множеству чисел
из интервала от 1 до N. Число сочетаний вычисляется по
формуле

2. Комбинаторные алгоритмы
31
С! =' "!
' N
Μ\χ(Ν -Μ)!
Полезные формулы:
С» =С; =1 (Ю>1)
С^ =C%~M (правило симметрии)
С™ =С™:1 +С^_Х (ЛГ>1, 0<М<ЛГ) (правило Паскаля)
Ν
Σ^ιΝ =2Ν . Эта формула является следствием известного
/=0 соотношения под названием бином Ньютона:
/г=0
При х=у=1 бином Ньютона дает приведенную формулу.
Размещения с повторениями (А^).
Даны предметы, относящиеся к N различным типам. Из них
составляются всевозможные расстановки длины k. При этом в
расстановки могут входить и предметы одного типа. Две
расстановки считаются различными, если они отличаются или
типом входящих в них предметов, или порядком этих предметов.
Объяснение примеров
1. Найти общее количество шестизначных чисел.
Ответ: 9x10x10x10x10x10=900000.
2. Найти число буквосочетаний длины 4, составленных из 33
букв русского алфавита, и таких, что любые две соседние
буквы этих буквосочетаний различны.
Ответ: 33x32x32x32=1081344.
3. Ячейка памяти компьютера состоит из 16 бит (/?). В каждом
бите, как известно, можно записать 1 или 0 (Ν). Сколько
различных комбинаций 1 и 0 может быть записано в
ячейке? Ответ: 216=65536.
Общая формула для подсчета числа размещений с
повторениями
AkN =Nk.
Перестановки с повторениями.
Выше рассмотрены перестановки из различных предметов.
В том случае, когда некоторые переставляемые предметы
одинаковы, часть перестановок совпадает друг с другом.
Перестановок становится меньше. Задача формулируется следующим

32
2. Комбинаторные алгоритмы
образом. Имеются предметы k различных типов. Сколько
перестановок можно сделать из Νλ предметов первого типа, Ν2 —
второго, ..., Nk — k-vo типа (Ν\+Ν2+...+Νk=N)?
Объяснение примеров
1. Сколько различных буквосочетаний можно получить из
букв слова папа? Ответ: 6 (папа, паап, ппаа, апап, аапп,
аппа).
2. Сколько различных буквосочетаний можно получить из
букв слова капкан? Ответ: 180.
3. Сколькими способами можно расположить в ряд 2
одинаковых яблока и 3 одинаковые груши? Ответ: 10.
4. Сколько различных сообщений можно закодировать, меняя
порядок 6 флажков: 2 красных, 3 синих и 1 зеленый? Ответ:
60.
5. Для выполнения работы необходимо в некотором порядке
выполнить дважды каждое из трех действий (а, Ь, с).
Например: ааЪЪсс, саЪЪас. Сколько существует различных
способов выполнения работы? Ответ: 90.
Общая формула для подсчета перестановок с повторениями
имеет вид:
N\
Ρ(Ν„ Ν2, ..., Ν.) = — ,
где Ν=Ν\+Ν2+...+Νk — общее число элементов.
Эта формула следует из
P(NV N2, ..., Nk) = CNl *CN2_Ni x---xCNk_Ni_ Nk .
Сочетания с повторениями.
Имеются предметы N различных типов. Сколько существует
расстановок длины k, если не различать порядок предметов в
расстановке (различные расстановки должны отличаться хотя
бы одним предметом)?
Схема рассуждений. Пусть N=4 и k=l'. Закодируем
расстановку с помощью последовательности из нулей и единиц.
Запишем столько единиц, сколько предметов первого типа, затем
нуль, а затем столько единиц, сколько предметов второго типа,
и т. д. (нуль, единицы, соответствующие предметам третьего
типа, нуль и единицы для предметов четвертого типа).
Суммарное количество единиц в последовательности равно 7,
количество нулей — N-1 или 3, т. е. длина равна 10. Количество
таких последовательностей определяется количеством способов
записи 3 нулей на 10 мест, или Cf0=120.

2. Комбинаторные алгоритмы
33
Общая формула для подсчета числа сочетаний с
повторениями имеет вид
гл k s-λΝ -\ ζ-лк
Объяснение примеров
1. Четверо ребят собрали в лесу 30 белых грибов. Сколькими
способами они могут разделить их между собой? Ответ:
2. Сколькими способами можно выбрать 3 рыбины из трех
одинаковых щук и трех одинаковых окуней? Ответ: 4 (N=2,
k=3).
3. Сколькими способами можно выбрать 13 из 52 игральных
карт, различая их только по масти? Ответ: 560 (N=4, /г=13).
4. Сколько всего существует результатов опыта,
заключающегося в подбрасывании 2 одинаковых игральных костей (если
кости различные, то 36)? Ответ: 21 (Af=6, k=2).
5. Сколько существует целочисленных решений уравнения
х1+х2+х3+х4=7? Ответ: 120 (N=49 k=7, пример решения —
1101101101).
Разбиения.
Требуется подсчитать число разбиений конечного множества
предметов S, где |S|=iV (количество предметов), на k различных
подмножеств S=S1uS2u...uSk, попарно не пересекающихся,
|в4|=/г4, i=l, 2, ..., k и n1+n2+...+nk=N.
Схема рассуждений. Sx можно сформировать С^1
способами, S2 -С%2_м способами, ... Sk -C^"_N _ _N способами.
Таким образом, число разбиений равно
или
Ν,Ι χΝ21 χ...χ Nkl
Объяснение примеров
1. Сколькими способами можно разбить три монеты 1, 2, 5
рублей на три группы по одной монете? Ответ: 6.
2. Сколькими способами можно разбить четырех гостей А, Б,
В, Г на две группы? Ответ: 6.

34
2. Комбинаторные алгоритмы
Сколькими способами можно разбить пять букв слова эскиз
на три группы так, чтобы в первой группе была одна буква, а
5!
во второй и третьей по 2? Ответ: = 30.
1! х2! х2!
Сколькими способами можно расселить 8 студентов по трем
комнатам: одноместной, трехместной и четырехместной?
8!
Ответ:
1! хЗ! х4!
280.
5. Сколькими способами можно раскрасить в красный,
зеленый и синий цвет по 2 из 6 различных предметов? Ответ:
6! =90.
2! х2! х2!
Число Стирлинга второго рода S(N,k) определяется как
число разбиений Af-элементного множества на k подмножеств.
Так, S(4,2)=7: {[1, 1, 3], [4]}, {[1, 2, 4], [3]}, {[1, 3, 4], [2]}, {[1,
2], [3, 4]}, {[1, 3], [2, 4]}, {[1, 4], [2, 3]} и {[1], [2, 3, 4]}.
Считается, что S(0,0)=1.
Если k>N, то S(N,k)=0.
При k=N S(N,N)=1.
В общем случае справедлива формула
S(iV,^)=S(iV-l,bl)+^(iV-l^) для 0<k<N.
2.2 Генерация комбинаторных объектов
2.2.1. Перестановки
Первая задача. Вычислить число перестановок для
заданного значения N.
Известно, что число перестановок равно факториалу числа
Ν (ΛΠ=1χ2χ3χ...χΛ0. В таблице 2.1 приведены значения N1 для
N от 1 до 30.
Таблица 2.1
N
1
2
3
I 4
5
I б
Ν\ ]
1
2
6
24
120
720 j

2. Комбинаторные алгоритмы
35
1 7
8
9
10
11
12
I 13
I
I
; зо
5040(Последнее число типа Integer) |
40320
362880
3628800
39916800
479001600(Последнее число типа Longlnt)
6227020800
265252859812191058636308480000000
Рекурсивное определение: Nl=Nx(N-l)l
Функция вычисления ΝΙ имеет ограниченную область
применения.
Function Fac(k:Longlnt):Longlnt;
Var r,i: Longlnt;
Begin
r:=l;
For i:=l To k Do r:=r*i;
Fac:=r;
End;
Функция Fac работоспособна при Ν, меньшем или равном
12. Для больших значений N требуется использовать
«длинную» арифметику: умножение «длинного» числа на короткое;
вывод «длинного» числа (глава 1).
Вторая и третья задачи. Перечислить или сгенерировать
все перестановки для заданного значения Ν, что требует
введения отношения порядка на множестве перестановок. Только в
этом случае задача имеет смысл.
Предполагаем, что перестановка хранится в массиве Ρ
длины N. Лексикографический порядок на множестве всех
перестановок определяется следующим образом:
ρΐ<ρ2 тогда и только тогда, когда существует такое £>1, что
Px[t]<P2[t] и P1[i]=P2[i] для всех i<t.
При решении данной задачи решается и задача получения
следующей в лексикографическом порядке перестановки.
Антилексикографический порядок на множестве всех
перестановок определяется следующим образом:
pi<p2 тогда и только тогда, когда существует такое t<N, что
Ρχ[ί]>Ρ2[ί] и p![i]=P2[i] для всех i>t.

36
2. Комбинаторные алгоритмы
Пример. N=3. В таблице 2.2 приведены все
лексикографические и антилексикографические порядки на множестве всех
перестановок для N=3.
Таблица 2.2
1 Лексикографический (А)
123
132
213
231
312
321
Антилексикографический (В) |
123
213
132
312
231
321
Пример. N=4. В таблице 2.3 столбцы, обозначенные буквой
А, означают генерацию перестановок в лексикографическом
порядке, буквой В — антилексикографическом.
Таблица 2.3
А
1234
1243
1324
1342
1423
| 1432
В
1234
2134
1324
3124
2314
3214
А
2134
2143
2314
2341
2413
2431
В
1243
2143
1423
4123
2413
4213
А
3124
3142
3214
3241
3412
3421
В
1342
3142
1432
4132
3412
4312
А
4123
4132
4213
4231
4312
4321
~~в~1
2341
3241
2431
4231
3421
4321 |
Пример. Перестановка 11, 8, 5, 1, 7, 4, 10, 9, 6, 3, 2. Какая
следующая перестановка идет в лексикографическом порядке?
Рис. 2.2

2. Комбинаторные алгоритмы
37
Находим «скачок» — 4 меньше 10. Затем «в хвосте»
перестановки находим первый элемент с конца перестановки,
больший значения 4, на рисунке 2.2 это значение 6. Меняем
местами элементы 4 и 6 и «хвост» перестановки ухудшаем
максимально, т. е. расставляем элементы в порядке
возрастания. Процедура получения следующей в лексикографическом
порядке перестановки имеет вид:
Procedure GetNext;
Var i,j:Integer;
Begin {*Для перестановки Ν, Ν-1,...,1 процедура
не работает, проверить.*}
i:=N;
While (i>l) And (P [i] <P [i-1 ] ) DoDec(i);
(*Находим "скачок".*}
j:=N;
While P[j]<P[i-l] Do Dec(j); {*Находим первый
элемент, больший значения Ρ[i-1].*}
Swap(PLi-l],P[j]);
For j:=0 To (N-i + 1) Div 2 - 1 Do
Swap (P [i+j ], Ρ [N-j ]) ; { *Переставляем элементы "хвоста"
перестановки в порядке возрастания.*}
End;
Procedure Swap(Var a,b:Integer);
Var t:Integer;
Begin
t:=a;a:=b;b:=t;
End;
Фрагмент общей схемы генерации:
Init;{^Инициализация: в массиве Ρ - первая
перестановка, в массиве Last - последняя.*}
Print;{*Вывод перестановки.*}
While Not(Eq(P,Last)) Do
Begin{*Функция Eq
определяет равенство текущей перестановки
и последней; если не равны,
то генерируется следующая*}
GetNext;
Print;
End;

38
2. Комбинаторные алгоритмы
Изменим задачу. Необходимо перечислить все перестановки
чисел от 1 до N так, чтобы каждая следующая перестановка
получалась из предыдущей с помощью транспозиции двух
соседних элементов.
Например: 321->231->213->123->132->312.
Возьмем перестановку ρν ρ2, ..., ρΝ и сопоставим с ней
следующую последовательность целых неотрицательных чисел
yvy2> — > У ν- Для любого i от 1 до N найдем номер позиции s, в
которой стоит значение / в перестановке, т. е. такое s, что ps=i,
и подсчитаем количество чисел, меньших i среди pv p2, ..., ps_v
это количество и будет значением уг
Пример:
Таблица 2.4
i
t,
1_А_
1
11
0
2 ' 3
8
1
5
1
4
1
1
5
7
0
6
4
3
7
10
2
8
9
0
9
6
5
10
3
5
11~Ί
2 J
0 ]
Очевидно, что 0<yt<i. Всего таких последовательностей NI,
т. е. множества перестановок и последовательностей чисел
совпадают по мощности. Построение последовательности чисел из
перестановки очевидно, как и то, что разным перестановкам
соответствуют разные последовательности чисел. Таблица 2.4
называется таблицей инверсий. Пару (pifPj), такую, что i<j и
р>Р:, называют инверсией перестановки. Каждая инверсия как
бы нарушает порядок в перестановке, единственная
перестановка, не имеющая инверсий, — это (1, 2, 3, ..., Ν). Μ. Холл
установил, что таблица инверсий единственным образом
определяет соответствующую перестановку — обратное построение.
Пример. Последовательность 0111. Четверка записана на
втором месте, ибо только одна цифра в перестановке «стоит»
левее ее; имеем *4**. Тройка с учетом занятого места
находится на третьем месте — *43*. Двойке с учетом занятых мест
принадлежит четвертое место, т. е. получаем перестановку
1432.
Еще примеры. Дана последовательность чисел 0023.
Четверка стоит на четвертом месте (3+1), тройка находится на
третьем месте (2+1) — **34, двойка (0+1) — на первом месте —
получаем 2134. Еще одна последовательность — 0112.
Четверка на третьем месте (2+1), тройка на втором (1+1), двойка на
втором (1+1), но с учетом занятых мест на четвертом получаем
перестановку 1342. Идею осознали?

2. Комбинаторные алгоритмы
39
В таблице 2.5 приведены последовательности чисел и
соответствующие перестановки для N=4.
Таблица 2.5
i 0000
0001
! 0002
Г 0003
0013
0012
4321
3421
3241
3214
2314
2341
0011
0010
0020
0021
0022
0023
2431
4231
4213
2413
2143
2134
0123
0122
0121
0120
0110
0111
1234
1243
1423
4123
4132
1432
0112
0113
0103
0102
0101
0100
1342 Π
1324
3124
3142
3412
4312^
Зрительный образ предлагаемой схемы генерации. Пусть
есть доска в форме лестницы (см. рис. 2.3). Высота i вертикали
равна i. В первоначальном состоянии шашки стоят на первой
горизонтали. Стрелки указывают направление движения
шашек (вверх). За один ход можно передвинуть одну шашку в
направлении стрелки. Если шашку передвинуть нельзя, то
осуществляется переход к следующей слева шашке. После того
как найдена шашка, которую можно передвинуть помимо
передвижения шашки, осуществляется смена направления
движения всех шашек справа от найденной. Ниже на рисунке 2.3
приведена смена состояний шашек на доске при N=4, начиная
с последовательности чисел 0023. Под последовательностями
чисел записаны соответствующие им перестановки.
* Ψ I I
1111 1^1 ι ι мн ич ψ
^Α ^ ^ ^
0023
2134
0123
1234
0122
1243
0121
1423
Рис. 2.3
Оказывается, что изменение на единицу одного из элементов
последовательности соответствует транспозиции двух соседних
элементов перестановки. Увеличение y[i] на единицу
соответствует транспозиции числа i с правым соседом, уменьшение — с
левым соседом. Итак, помимо генерации последовательностей
необходимо уметь находить число i в перестановке и менять его
местами с одним из «соседей», но это уже чисто техническая
задача.

40
2. Комбинаторные алгоритмы
Опишем используемые данные.
Const Nmax=12;
Var P:Array[1. .Nmax] Of 0. .Nmax;
{^Хранение перестановки.*}
Υ:Array[1..Nmax] Of O..Nmax-l;
{^Хранение последовательности чисел.*}
D:Array[1..Nmax] Of -1..1;
{^Направление движения "шашек".*)
Процедура формирования начальной перестановки и
начальных значений в массивах Υ и D.
Procedure First;
Var i:Integer;
Begin
For i :=1 To N Do
Begin
P[i]:=N-i+l; Υ[i]:=0;D[i]:=1;
End;
End;
Поиск номера «шашки», которую можно передвинуть,
При D[i\=\ и Y[/]=/-l или D[i]=-1 и Y[i]=0 шашку с
номером / нельзя передвинуть.
Function Ok:Integer;{*Если значение функции равно
1, то нет ни одной шашки, которую можно
передвинуть.*}
Var i : Integers-
Begin
i:=N;
While (i>l) And (((D[i]=l) And (Y[i]=i-1)) Or
((D[i]=-1) And (Y[i]=0))) Do Dec(i);
Ok:=i;
End;
Основной алгоритм генерации перестановок имеет вид:
Begin
First;
pp:=True;
While pp Do
Begin
Solve(pp);
If pp Then Print;
End;
End;

2. Комбинаторные алгоритмы
41
Уточним процедуру генерации следующей перестановки.
Procedure Solve(Var q:Boolean);
Var i,j,dj:Integer;
Begin
i:=Ok; q:=(i>l);{*Находим номер шашки, которую
можно передвинуть.*}
If i>l Then
Begin
Υ[i]:=Y[i]+D[i];{^Передвигаем шашку - изменяем
последовательность чисел.*}
For j :=i + l To N Do D [ j ] :=-D [ j ] ; { ^Изменяем
направление движения шашек, находящихся
справа от передвинутой.*}
j:=Who_i(i);{*Находим позицию в перестановке,
в которой записано число i . *}
dj:=j+D[i];{^Определяем соседний элемент
перестановки для выполнения транспозиции.*}
Swap(Ρ[j], P[dj]);{^Транспозиция.*}
End;
End;
Остался последний фрагмент алгоритма, требующий
уточнения, — поиск в перестановке позиции, в которой находится
элемент i. Он достаточно прост.
Function Who_i(i:Integer):Integer;
Var j:Integer;
Begin
j:=N;
While (j>0) And (P[j]oi) DoDec(j);
Who_i:=j;
End;
Четвертая задача. По номеру определить перестановку
относительно порядка, который введен на множестве перестановок.
Остановимся на лексикографическом порядке. Рассмотрим
идею решения на примере.
Пусть N равно 8 и дан номер L, равный 37021. Найдем
соответствующую перестановку. Пусть на первом месте записана
единица. Таких перестановок 7!, или 5040 (1*******). При 2 тоже
5040 (2*******). Итак, 37021 Div 5040=7. Следовательно, первая
цифра в перестановке 8. Новое значение L (37021 Mod
5040=1741) 1741. Продолжим рассуждения и оформим их в виде
таблицы 2.6.

42
2. Комбинаторные алгоритмы
Таблица 2.6
1 /
1
2
I 3
4
! 5
6
7
8
/. П
37021
1741
301
61
13
1
1
0
ρ
^старая
********
8*******
83******
834*****
8345****
83456***
834561**
8345617*
Ρ
7Ι-5040
6!=720
5!=120
4!=24
3!=6
2!=4
1!=1
0!=1
LDivP
7
2
2
2
2
0
1
LModP
1741
301
61 ^
13
1
1
0
Ρ Ι
гновая
8*******
83******
834*****
8345****
83456***
834561**
8345617*
83456172
Обратим внимание на третью строку, в которой на третье
место записывается цифра 4. То, что записываются не цифры 1
и 2, очевидно: их требуется пропустить. Цифра три «занята»,
поэтому записываем 4. Точно так же в строках 4, 5 и 7.
О программной реализации. Пусть ЛК12, таким образом,
значение L не превосходит максимального значения типа
Longlnt. Определим следующие константы.
Const Nsmall=12;
ResSm:Array[0..Nsmall] Of Longlnt
-(1,1,2,6,24,120,72 0,504 0,4 032 0,362 880,3 6288 00,39916
800,479001600); {^Значения Ν! для N от 0 до 12.*}
И процедура.
Procedure GetPByNum(L:Longlnt);
Var Ws:Set Of Byte;
i,j,sc:Integer;
Begin
Ws:=[];{^Множество для фиксации цифр,
задействованных в перестановке.*}
For i :=1 To N Do
Begin
Sc:=L Div ResSm[N-i];L:=L Mod ResSm[N-i];
While (scoO) Or (j In Ws) Do
Begin
If Not (j In Ws) Then Dec(sc) ;
Inc (j);
End;
Ws:=Ws+[j];{*Нашли очередную цифру.*}

2. Комбинаторные алгоритмы
43
P[i]:=j;
End;
End;
Для более глубокого понимания сути приведем часть
трассировки работы процедуры для ранее рассмотренного примера.
Результаты трассировки приведены в таблице 2.7.
Таблица 2.7
| /
1
2
L 3
!
! 4
I
Sc
7
6
5
4
3
2
" ■
1
^~ 0
2
1
0
2
1
1
0
2
1
1
1
0
L
37021
1741
301
61
13
•^ J ^_
J
1
2
3
4
5
6
7
8
1
2
3
1
2
3
4
1
2
3
4
5
Ws
[]
[8]
[3,8]
[3,4,8]
[3,4,5,8]
ρ Ί
••••••••
о********
83******
834******
Γ " " 1
I J
I
8345**** !
Пятая задача. По перестановке получить ее номер, не
выполняя генерацию множества перестановок.
Начнем с примера. Пусть N равно 8 и дана перестановка
53871462.
Схема:
7!* <количество цифр в перестановке на 1-м месте, идущих
до цифры 5, с учетом занятых цифр — ответ 4>
6!* < количество цифр в перестановке на 2-м месте, идущих
до цифры 3, с учетом занятых цифр — ответ 2>

44
2. Комбинаторные алгоритмы
5!х < количество цифр в перестановке на 3-м месте, идущих
до цифры 8, с учетом занятых цифр — ответ 5>
4!х < количество цифр в перестановке на 4-м месте, идущих
до цифры 7, с учетом занятых цифр — ответ 4>
3!х < количество цифр в перестановке на 5-м месте, идущих
до цифры 1, с учетом занятых цифр — ответ 0>
2!х < количество цифр в перестановке на 6-м месте, идущих
до цифры 4, с учетом занятых цифр — ответ 1>
1!х < количество цифр в перестановке на 7-м месте, идущих
до цифры 6, с учетом занятых цифр — ответ 1>
Итак,
7!χ4+6!χ2+5!χ5+4!χ4+3!χ0+2!χ1+1!χ1=4χ5040+2χ720+5χ120+4χ
x24+0x6+lx2+lxl=22305.
Function GetNumByP:Longlnt;
Var ws:Set Of Byte;
i,j,sq:Integer;sc:Longlnt;
Begin
ws:=[];{^Множество цифр перестановки.*}
sc:=l; {*Номер перестановки.*}
For i :=1 To N Do
Begin
j : =1; sq:=0;{^Определяем количество цифр.*}
While j<P[i] Do
Begin
If Not(j In ws) Then Inc(sq);
Inc (j ) ;

Endows : =ws+[P[i]];{*Цифра P[i] задействована.*}
sc:=sc+ResSm[N-i]*sq;{^Умножаем число
перестановок на значение текущей цифры.*}
End;
GetNumByP:=sc;
End;
2.2.2. Размещения
Первая задача. Подсчитать количество размещений для
небольших значений N и Μ можно с помощью следующих
простых функций.
Function Plac (n,m:Longlnt) :Longlnt;
Var i,ζ:Longlnt;
Begin
z:=l;

2. Комбинаторные алгоритмы
45
For i :
Plac: =
End;
= 0 То m-1 Do z:=z* (n-i) ;
:z;
Рекурсивный вариант реализации.
Function Plac(η,m:Longlnt):LongInt;
Begin
If m=0
Then Plac:=l
Else Plac:=(n-m+1)*Plac (n,m-l);
End;
Функции дают правильный результат при N<12. Для
больших значений N необходимо использовать «длинную»
арифметику.
Вторая задача. Сгенерировать все размещения для
заданных значений N и Μ в лексикографическом порядке.
Пример. N=4, М=3. В таблице 2.8 приведены размещения в
лексикографическом порядке.
Таблица 2.8
Г 123
124
132
134
142
143
213
214
231
234
241
243
312
314
321
324
341
342
412
413
421
423
431
432 |
Текст решения имеет вид:
Program GPlac;
Const n=4; m=3;{^Значения пит взяты в качестве
примера.*}
Var A:Array[1..m] Of Integer;{^Массив для
хранения элементов размещения.*
S: Set Of Byte;{*Для хранения использованных
в размещении цифр.*}
Procedure Solve(t:Integer);{^Параметр t
определяет номер позиции в размещении
Var i:Byte;
Begin
For i:=l To η Do{*Перебираем цифры и находим
1-ю неиспользованную.*}
If Not (i In S) Then
Begin
}

46
2. Комбинаторные алгоритмы
S:=S+[i];{^Запоминаем ее в множестве занятых
цифр.*}
А[t]:=i;{^Записываем ее в размещение.*}
If t<m Then Solve(t+1) Else Print;{*Если
размещение не получено, то идем
к следующей позиции, иначе
выводим очередное размещение.*}
S :=S- [i];{^Возвращаем цифру в число
неиспользованных.*}
End;
End;
Фрагмент основной программы.
Begin
S: = []; Solve (1);
End.
Для генерации размещений можно воспользоваться
процедурой генерации перестановок из предыдущего пункта.
Требуется только уметь «вырезать» из очередной перестановки
первые Μ позиций и исключать при этом повторяющиеся
последовательности.
Третья задача. По заданному размещению найти
следующее за ним в лексикографическом порядке.
Свободными элементами размещения назовем те элементы
из множества от 1 до Ν, которых нет в текущем размещении
(последовательности из Μ элементов).
Пример. N=5, М=3 и размещение 13 4. Свободными
элементами являются 2 и 5. Первый вариант решения
заключается в том, чтобы дописать в размещение свободные элементы в
убывающем порядке (13 4 5 2), сгенерировать следующую
перестановку (1 3 5 2 4) и отсечь первые Μ элементов (1 3 5).
Получаем следующее размещение. Реализация этой же идеи, но
без обращения к генерации следующей перестановки
приводится ниже по тексту.
Ее суть:
• Начинаем просмотр размещения с последнего элемента Μ
и идем, если необходимо, до первого.
• Находим первый свободный элемент, который больше,
чем элемент в рассматриваемой позиции размещения.
• Если такой элемент найден, то заменяем им текущий, а в
«хвост» размещения записываем свободные элементы в
порядке возрастания и заканчиваем работу.

2. Комбинаторные алгоритмы
47
• Если такого элемента не найдено, то переходим к
следующей позиции.
Const n=4; m=3;
Var A:Array[1..т] Of Byte;
Procedure GetNext;
Var i,j,k,q:Integer;
Free:Array[1..n] Of Boolean;{^Массив для
хранения признаков занятости элементов
в размещении.*}
Function FreeNext(t:Byte):Byte;{^Функция поиска
первого не занятого элемента.*}
Begin
While (t<=n) And Not (Free [t] ) Do Inc(t);
{ *Находим первый свободный элемент.*}
If t>n
Then FreeNext:=0{*Если такого элемента
нет, то значение функции равно нулю.*}
Else FreeNext:=t;{*Номер первого свободного
элемента.*}
End;
Begin
For i:=l To η Do Free[i]:=True;{*Массив
свободных элементов.*}
For i :=1 To m Do Free [A[i] ] :=False; {*По
размещению исключаем занятые элементы.*}
i :=m;{*Начинаем с конца размещения.
Предполагаем, что анализируемое
размещение не является последним.*}
While (i>0) And (FreeNext(A[i])=0) Do
Begin
{*Пока не нашли позицию в размещении,
элемент в которой допускается изменить,
выполняем действия из цикла. При нашем
предположении такая позиция обязательно
существует.*}
Free[A[i]]:=True;{*Освобождаем элемент,
записанный в позиции i . * }
Dec(i);{*Переходим к следующей позиции.*}
End;
Free[A[i]]:=True;{*Переводим текущий элемент
в найденной позиции в свободные.*}
q:=FreeNext(А[i]+1) ;{*Находим свободный
элемент, больший текущего.*}

48 2. Комбинаторные алгоритмы
Free[q]:=False;{^Считаем его занятым.*}
A[i]:=q;{^Записываем его в размещение.*}
к:=1;{^Формируем "хвост" размещения.*}
For j :=i + l To m Do
Begin{*Co следующей позиции
до конца размещения.*}
While (k<=n) And Not(Free[k]) Бо{*Пока не
найдем первый свободный элемент.*}
If k>=n Then k:=l Else Inc(k);
A[j] :=k;j ^Записываем найденный элемент
в размещение.*}
Free[k]:=False;{^Считаем его занятым.*}
End;
End;
Четвертая задача. При заданных значениях N и Μ по
номеру размещения L определить соответствующее размещение
(упорядочены в лексикографическом порядке).
Рассмотрим размещения из 5 по 3 элемента, их 60. В
таблице 2.9 часть размещений, вместе с их номерами, приводится в
лексикографическом порядке. Первому размещению
соответствует номер 0.
Таблица 2.9
\ °
1 1
2
I з
! 4
| 5
123
124
125
132
134
135
6
7
8
9
10
LJlJ
142
143
145
152
153
154
12
13
14
15
16
17
213
214
215
231
234
235
ι 1
18
19
20
21
22
23
241
243
245
251
253
254
24
25
26
27
28
29
312
314
315
321
324
325
30
31
32
33
34
341~Ί
342
345
351
352
Значение А2А (в общем случае А^~_1) равно 12. Количество
размещений с фиксированным значением в первой позиции
равно 12, а это уже путь к решению.
Пусть нам задан номер 32 и массив свободных элементов 1 2
3 4 5 (номера элементов массива считаются с 0). Вычисляя 32
Div 12, получаем 2, следовательно, в первой позиции записана
цифра, стоящая на 2-м месте в массиве свободных элементов, а
это цифра 3. Оставшееся количество номеров 32 Mod 12 =8,
массив свободных элементов 12 4 5. Продолжим процесс
вычисления — 8 Div 3=2 (Ад1 =3), следующая цифра 4. Оставшееся
количество номеров 8 Mod 3 =2, массив свободных номеров 1 2
5. Продолжим — 2 Div 1 =2, что соответствует цифре 5.

2. Комбинаторные алгоритмы
49
Const n=5;m=3;
Var A:Array[l..m] Of Integer;
L:Longlnt;{*Номер размещения.*}
Procedure GetPByNum(L:Longlnt);{*B процедуре
использована функция Plac - вычисления
количества размещений.*}
Var i,j,q,t:Longlnt;
Free:Array[1..n] Of Byte;{^Массив свободных
элементов размещения.*}
Begin
For i:=l To η Do Free [i] : =i; { ^Начальное
формирование.*}
For i :=1 To m Do
Begin{*i - номер позиции
в размещении.*}
t:=Р1ас(n-i,m-i);{*Количество размещений,
приходящихся на один фиксированный
элемент в позиции i . *}
q:=L Div t;{^Вычисляем номер свободного
элемента размещения.*}
А[i]:=Free[q+1];{^Формируем элемент
размещения.*}
For j:=q+l To n-i Do Free[j]:=Free[j+1];
{^Сжатие, найденный элемент
размещения исключаем из свободных.*}
L:=L Mod t;{*Изменяем значение номера
размещения (переход к меньшей
размерности).*}
End;
End;
Пятая задача. По размещению определить его номер
(размещения упорядочены в лексикографическом порядке).
Поясним идею решения на примере. Дано размещение 345.
Количество свободных элементов, меньших 3, равно 2
(12x2=24). Количество свободных номеров, меньших 4, также
2 — 24+3x2=30. И наконец, меньших пяти, также 2.
Ответ: 12x2+3x2+1x2=32.
Function GetNumByP:Longlnt;{*Используется
процедура Plac вычисления количества
размещений.*}
Var L,i,jrnum:Longlnt;
ws:Set Of Byte;{^Множество элементов
размещения.*}

50
2. Комбинаторные алгоритмы
Begin
ws : = [ ] ;
L:=0;
For i :=1 To m Do
Begin{*i - номер позиции
размещения.*}
num:=0;{*Счетчик числа незанятых элементов.*}
For j :=1 To A[i]-1 Do
If Not(j In ws) Then Inc (num) ; {*Если элемента
j нет в ws, то увеличиваем значение
счетчика числа незанятых элементов,
которые встречаются до значения A[i]. *}
ws:=ws+[А[i]];{^Элемент А[i] задействован
в размещении.*}
L:=L+num*Plac(n-i,m-i);{^Значение счетчика
умножаем на количество размещений,
приходящихся на одно значение
в позиции с номером i . * }
End;
GetNumByP:=L;
End;
2.2.3. Сочетания
Между /г-элементными подмножествами N-элементного
множества и возрастающими последовательностями длины k с
элементами из множества целых чисел от 1 до N (сочетаниями)
существует взаимно однозначное соответствие. Так, например,
подмножеству [2, 6, 1, 3] соответствует последовательность
чисел 1, 2, 3, 6. Таким образом, решая задачи подсчета и
генерации всех сочетаний, мы решаем аналогичные задачи для k-эле-
ментных подмножеств. Лексикографический порядок на
множестве последовательностей определяется так же, как и
для перестановок.
Пример. В таблице 2.10 приведен лексикографический
порядок для С g.
Таблица 2.10
1234 j
! 1235
|
| 1236 I
1245 [
1246
1256
1345
1346
1356
1456
2345
2346
2356 Π
2456
3456

2. Комбинаторные алгоритмы
51
Первая задача. Подсчитать количество сочетаний для
данных значений N и k.
Использование формулы С* = явно не продук-
N k\ x(N-k)l
тивно. Факториал представляет собой быстровозрастающую
функцию, поэтому при вычислении числителя и знаменателя
дроби может возникнуть переполнение, хотя результат —
число сочетаний — не превышает, например, значения Maxlnt.
Воспользуемся для подсчета числа сочетаний формулой
С* =С*;11 +С*.Х, где АГ>1, 0<k<N.
Получаем знаменитый треугольник Паскаля (см.
таблицу 2.11). Просматривается явная схема вычислений. Очевидно,
что если в задаче не требуется постоянно использовать значения
CkN для различных значений N и /г, а требуется только
подсчитать одно значение С^ , то хранить двумерный массив в памяти
компьютера нет необходимости.
Таблица 2.11
Г44^ к
\ N ^\
0
1
2
3
4
5
6
| 7
8
L 9
0
1
0
1
2
3
4
5
6
7
8
9
2
0
0
1
3
6
10
15
21
28
36
3
0
0
0
1
4
10
20
35
56
84
4
0
0
0
0
1
5
15
35
70
126
5
0
0
0
0
0
1
6
21
56
126
6
0
0
0
0
0
1
7
28
84
7
0
0
0
0
0
0
1
8
36
8
0
0
0
0
0
0
0
1
9 I
0
0
0
0
о
0
0 I
I ^ ι 1 ι
Приведем процедуры вычисления CkN для того и другого
случая. Подсчет всех значений ChN .
Const MaxN=100;
Var SmallSc:Array[0..MaxN,0..MaxN] Of Longlnt;
{^Нулевой столбец и нулевая строка необходимы,
это позволяет обойтись без анализа на выход
за пределы массива.*}
Procedure Fi11SmallSc;
Var i,j:Integer;

52
2. Комбинаторные алгоритмы
Begin
FillChar(SmallSc,SizeOf(SmallSc), 0) ;
For i:=0 To N Do SmallSc [i, 0] :=1;
For i :=1 To N Do
For j :=1 To к Do
If SmallSc[i-l,j]*1.0+SmallSc[i-l,j-1]>
MaxLonglnt
Then SmallSc[i,j]:^MaxLonglnt
Else
SmallSc[i,j]:=SmallSc[i-l,j]+SmallSc
[i-l,j-l]; {^Умножение на 1 . 0 переводит
целое число в вещественное, поэтому
переполнения при сложении не происходит.
Стандартный прием, обязательный при "игре"
на границах диапазона целых чисел.*}
End;
Второй вариант реализации процедуры.
Type SmallSc=Array[0..MaxN] Of Longlnt;
Function Res(к:Integer):Longlnt;
Var A,B:SmallSc;
i,j:Integer;
Begin
FillChar(A,SizeOf(A) , 0) ;
FillChar(B,SizeOf(B) ,0) ;
A[0]:=1;A[1]:=1;
For i :=1 To N Do
Begin
B[0]:=1;B[1]:=1;
For j:=1 To к Do В[j]:=A[j]+A[j-1];{*Если
число больше максимального значения типа
Longlnt,то необходимо работать с "длинной"
арифметикой. Данная операция должна быть
изменена - вызов процедуры сложения двух
"длинных" чисел.*}
А:=В;
End;
Res:=A[k];
End;
Вторая задача. Сгенерировать все сочетания в
лексикографическом порядке.
Рассмотрим пример для N=7 и k=6. Число сочетаний равно
21 (см. таблицу 2.12).

2. Комбинаторные алгоритмы
53
Таблица 2.12
0
! 1
| 2
3
I 4
5
6
12345
12346
12347
12356
12357
12367
12456
7
8
9
10
11
12
13
12457
12467
12567
13456
13457
13467
13567
14
15
16
17
18
19
20
14567 Ί
23456
23457
23467
23567
24567
34567
Начальное сочетание равно 1, 2, ..., k, последнее — N-k+1,
N-k+2, ..., N. Переход от текущего сочетания к другому
осуществляется по следующему алгоритму. Просматриваем
сочетание справа налево и находим первый элемент, который можно
увеличить. Увеличиваем этот элемент на единицу, а часть
сочетания (от этого элемента до конца) формируем из чисел
натурального ряда, следующих за ним.
Procedure GetNext;{^Предполагается, что текущее
сочетание (хранится в массиве С) не является
последним.*}
Var i,j:Integer;
Begin
i:=k;
While (C[i]+k-i+l>N) DoDec(i); {*Находим
элемент, который можно увеличить.*}
Inc (С[i]);{^Увеличиваем на единицу.*}
For j :=i + l То k Do С [ j ] :=C [ j-1] +1; {^Изменяем
стоящие справа элементы.*}
End;
Третья задача. По номеру L определить соответствующее
сочетание.
Для решения этой задачи необходимо иметь (вычислить)
массив SmallSc, т. е. использовать первую схему вычисления
числа сочетаний (первая задача) для данных значений N и k.
Порядок на множестве сочетаний лексикографический. В
таблице 2.12 номера с 0 по 14 имеют сочетания, в которых на
первом месте записана единица. Число таких сочетаний — С*
(«израсходован» один элемент из N и один элемент из k).
Сравниваем число L со значением С*. Если значение L больше С*,
то на первом месте в сочетании записана не единица, а большее
число. Вычтем из L значение С% и продолжим сравнение.

54
2. Комбинаторные алгоритмы
Procedure GetWhByNum(L:LongInt);
Var i,j,sc,Is:Integer;
Begin
sc:=n;
Is:=0;{*Цифра сочетания.*}
For i:=l To к Do
Begin{*i - номер элемента в сочетании;
k-i - число элементов в сочетании.*}
j:=l; {*sc-j - число элементов (η) , из которых
формируется сочетание.*}
While L-SmallSc[sc-j,k-i]>=0 Do
Begin{*Для данной позиции в сочетании и числа
элементов в сочетании находим тот элемент
массива SmallSc, который превышает
текущее значение L.*}
Dec(L,SmallSc[sc-j , k-i] ) ;
Inc (j);{^Невыполнение условия цикла While
говорит о том, что мы нашли строку
таблицы SmallSc, т.е. то количество
элементов, из которых формируется
очередное сочетание, или тот интервал
номеров сочетаний (относительно
предыдущей цифры), в котором находится
текущее значение номера L.*}
End;
С[i]:=ls+j;{^Предыдущая цифра плюс приращение.*}
Inc(Is,j);{*Изменяем значение текущей цифры
сочетания.*}
Dec(sc, j);{*Изменяем количество элементов,
из которых формируется остаток
сочетания.*}
End;
End;
В таблицах 2.13, 2.14 и 2.15 приведены результаты ручной
трассировки процедур GetWhByNum для различных N, /г и L.
Таблица 2.13
N=7, ft=5, L=17.
ι
j 1
Γ2
j
1
2
1
L
17
2
2
sc
7
7
5
Is
0
0
2
SmallSc[sc-j,k-i]
15
5
5
^ $сновое ι '^новое j
!
2****
23***
5 I 2 !
4
I 3 !

2. Комбинаторные алгоритмы
55
Г3
4
L5
1
1
2
1
2
2
0
0
ι 4 ! з
3
3
1
4
4
6
3
2
1
1
234**
234**
2346*
23467
3
1
0
4
6
7 |
Таблица 2.14
N=1, *=5, L=0.
ι—:—'
i /
1
2
3
4
5
/_
0
0
0
0
0
sc
7
6
5
4
3
Is
0
1
2
3
4
SmaltSc[sc-j,k-i]
15
10
6
3
1
С
1****
12***
123**
1234*
12345
SCHOBoe
6
5
4
3
2
^новое
1
2
3
4
5 J
Таблица 2.15
N=7, fe=5, L=20.
| /
1
I 2
I 3
! 4
| 5
J
1
2
3
1
1
1
1
L
20
5
0
0
0
0
0
sc
7
7
7
4
3
2
1
Is
0
0
0
3
4
5
6
SmallSc[sc-j,k-i]
15
5
С
•••••
•••••
3****
34***
345**
3456*
34567
SCHOBoe
-
-
4
3
2
1
0
'SHosoe
-
-
3
4
5
6
7 |
Для полного понимания алгоритма выполните ручную
трассировку при N=9, /г=5, L=78. Ответ — 23479. Однако
достаточно, пора и честь знать.
Четвертая задача. По сочетанию получить его номер.
Как и в предыдущей задаче, необходимо иметь массив
SmallSc. Эта задача проще предыдущей. Требуется аккуратно
просмотреть часть массива SmallSc. Эта часть массива
определяется сочетанием, для которого ищется номер. Например, на
первом месте в сочетании стоит цифра 3 (N=79 k=4). Ищется
сумма С^ +С|! +Cj? — количество сочетаний, в которых на
первом месте записана цифра 1, цифра 2 и цифра 3. Аналогично
для следующих цифр сочетания. Предполагаем, что С[0] равно
О — технический прием, позволяющий избежать лишних
проверок условий.

56
2. Комбинаторные алгоритмы
Function GetNumByWhiLonglnt;
Var scrLonglnt;
i,j:Integer;
Begin
sc:=1;
For i :=1 To к Do
For j:=C[i-l]+l To C[i]-1 Do Inc(sc,SmallSc[N-j,k-i]) ;
GetNumByWh:=sc;
End;
В таблицах 2.16 и 2.17 приведены результаты ручной
трассировки функции GetNumByWh для различных N, k и L.
Таблица 2.16
N=9, ft=5, С=023479.
1 /
1
j 2
3
4
[_5
/
1
от 3 до 2, цикл по у не работает
от 4 до 3, цикл по/ не работает
5
6
8
sccrapoe
1
71
71
71
75
78
SmallSc[N-j,k-i]
70
-
-
4
3
1
SCHOBoe
71
!
-
75
78
79 |
Таблица 2.17
N=1, ft=5, C=023467.
/
! 1
2
3
i 4
I 5
У
1
от 3 до 2, цикл по у не работает
от 4 до 3, цикл по/ не работает
5
sccrapoe
1
16
16
16
от 7 до 6, цикл по/не работает J^ 18
SmallSc[N-j,k-i]
15
-
-
2
-
5сновое !
16
-
-
18 !
- J
Обратите внимание на то, что нумерация сочетаний в
задачах 3 и 4 различна. В задаче 3 сочетания нумеруются с 0, а в
задаче 4 — с 1.
Пятая задача. Выберем для представления сочетания
другой вид — последовательность из 0 и 1. Последовательность
храним в массиве С из N элементов со значениями 0 или 1, при
этом С[/]=1 говорит о том, что элемент (Ν-i+l) есть в сочетании
(подмножестве).

2. Комбинаторные алгоритмы
57
Пусть Af=7, k=5. В таблице 2.18 представлены
последовательности в той очередности, в которой они генерируются, и
соответствующие им сочетания.
Таблица 2.18
0
1
| 2
I з
4
5
[ 6
0011111
0101111
0110111
0111011
0111101
0111110
1001111
12345
12346
12356
12456
13456
23456
12347
7
8
9
10
11
12
13
1010111
1011011
1011101
1011110
1100111
1101011
L 1101101
12357
12457
13457
23457
12367
12467
13467
14
15
16
17
18
19
20
1101110
1110011
1110101
1110110
1111001
1111010
1111100
23467 |
12567
13567 ι
23567
14567
24567
34567
Принцип генерации последовательностей.
Начинаем с конца последовательности. Находим пару С[/]=0
и C[i+l]=l. Если такой пары нет, то получена последняя
последовательность. Если есть, то заменяем на месте i нуль на
единицу и корректируем последовательность справа от i.
Последовательность должна быть минимальна с точки зрения введенного
порядка, поэтому вначале записываются 0, а затем 1, при этом
количество 1 в последовательности должно быть сохранено.
Опишем основные фрагменты реализации этого алгоритма.
Const MaxN=...;
Type MyArray=Array[1..MaxN] Of 0..1;
Var Curr, Last:MyArray;{*Текущая и последняя
последовательности.*}
i,j ,Num,N,k:Integer;
Begin
For i :=1 To N Do
Begin Curr[i]:=0;Last[i]:=0;End;
For i :=1 To k Do
Begin Curr[N-i+l]:=l;Last[i]:=1; End;
{^Формируем начальную
и последнюю последовательности.*}
While Not Eq (Curr, Last) Do
Begin
i:=n-l;
While (i>0) And Not ( (Curr [i] =0) And
(Curr[i+l]=l)) Do Dec(i);
{*Находим пару 0-1, она есть, так как
последовательность не последняя.*}

58 2. Комбинаторные алгоритмы
Num:=0;
For j:=i + l To η Do Inc (Num,Curr[j]);
{^Подсчитываем количество единиц.*}
Curr[i]:=1;
For j:=i+l To n-Num+1 Do Curr[j]:=0;{^Записываем
нули.*}
For j:=n-Num+2 To η Do Curr[j]:=1;{^Записываем
единицы.*}
End;
End;
2.2.4. Разбиение числа на слагаемые
Дано натуральное число N. Его можно записать в виде
суммы натуральных слагаемых:
N=a1+a2+...+ak, где k, av ..., ak больше нуля.
Будем считать суммы эквивалентными, если они
отличаются только порядком слагаемых. Класс эквивалентных сумм
приведенного вида однозначно представляется
последовательностями bv ..., bk, упорядоченными по невозрастанию. Каждую
такую последовательность bv ..., bk назовем разбиением числа
N на. k слагаемых.
Как обычно, решаем четыре задачи: подсчет количества
различных разбиений числа; генерация разбиений относительно
определенного отношения порядка, введенного на множестве
разбиений; получение разбиения по его номеру и задача,
обратная третьей.
Первая задача. Приведем пример для N=8 (см. таблицу
2.19), а затем рассуждения, позволяющие написать
программный код.
Таблица 2.19
1
2
3
4
5
6
7
L8
11111111
2111111
221111
22211
2222
311111
32111
3221
9
10
11
12
13
14
15
16
3311
332
41111
4211
422
431
44
5111
17
18
19
20
21
22
521 ]
53
611
62
71
8

2. Комбинаторные алгоритмы
59
Число разбиений числа N на k слагаемых обозначим через
P(N,k), общее число разбиений — P(N). Очевидно, что значение
P(N) равно сумме P(N,k) по значению k. Считаем, что
Р(0)=Р(1)=1. Известен следующий факт.
Теорема. Число разбиений числа N на k слагаемых равно
числу разбиений числа N с наибольшим слагаемым, равным к.
Теорема доказывается простыми рассуждениями на основе
диаграмм Феррерса. Пример такой диаграммы приведен на
рисунке 2.4.
• · ·
15=6+4+3+1+1 15=5+3+3+2+1+1
Рис. 2.4
Главное, что следует из этого факта, — реальный путь
подсчета числа разбиений. Число разбиений P(i,j) равно сумме
P(i-j,k) по значению к, где k изменяется от 0 до у. Другими
словами, j «выбрасывается» из i и подсчитывается число способов
разбиения числа i-j на k слагаемых. Проверьте этот алгоритм с
помощью таблицы 2.20.
Таблица 2.20
1
2
3
4
I 5
6
I 7
L8
0
0
0
0
0
0
0
0
0
2
0
1
1
2
2
3
3
4
3
0
0
1
1
2
3
4
5
4
0
0
0
1
1
2
3
5
5
0
0
0
0
1
1
2
3
6
0
0
0
0
0
1
1
2
7
0
0
0
0
0
0
1
1
3
0
0
0
0
0
0
0
1
1
2 |
3
5
7
11
15
l_?2j
Например, Р(8,3)=Р(5,0)+Р(5)1)+Р(5,2)+Р(5,3).
Определим данные.

60
2. Комбинаторные алгоритмы
Const MaxN=100;
Var Ν:Longlnt;
SmallSciArray[0..MaxN,0..MaxN] Of Longlnt;
Procedure FillSmallSc;
Var i,j, k:Integer;
Begin
FillChar(SmallSc,SizeOf(SmallSc) , 0) ;
SmallSc[0,0]:=l;
For i :=1 To N Do
For j :=1 To i Do
For k:=0 To j Do
Inc(SmallSc[i,j], SmallSc[i-j,k]);
SmallSc[0,0]:=0;
End;
Таблица значений сформирована, она нам потребуется для
решения других задач. Для подсчета же числа разбиений
осталось написать простую процедуру.
Procedure Calc;
Var i:Integer;
Res:Longlnt;
Begin
Res:=SmallSc[N,1];
For i: =2 To N Do Res : =Res + SmallSc [N, i ] ;
WriteLn(Res);
End;
Вторая задача. Генерация разбиений.
Во-первых, необходима структура данных для хранения
разбиения. По традиции используем массив:
Var Now:Array[0..MaxN] Of Integer;
В Now[0] будем хранить длину разбиения, т. е. число
задействованных элементов массива Now.
Возьмем из таблицы 2.19 одно из разбиений числа 8,
например «41111», следующее «4211». В каком случае можно
увеличить Now[2]7 Видим, что Now[l] должно быть больше
Now[2], т. е. в текущем разбиении находится «скачок» —
Now[i-l]>Now[i]9 Now[i] увеличивается на единицу, а все
следующие элементы разбиения берутся минимально
возможными. Всегда ли возможна данная схема изменения разбиения?
Например, разбиение «44», следующее — «5111». Таким
образом, или «скачок», или i равно 1. Кроме того, изменяемый эле-

2. Комбинаторные алгоритмы
61
мект не может быть последним, ибо увеличение без
уменьшения невозможно.
Procedure GetNext;
Var i,j,sc:Integer;
Begin
i:=Now[0]-1;{*Предпоследний элемент разбиения.*}
sc:=Now[i + 1]-1;Now[i + 1]:=0;{*B sc накапливаем
сумму, это число представляется затем
минимально возможными элементами.*}
While (i>l) And (Now [i ] =Now [i-1 ] ) Do
Begin
sc:=sc+Now[i];Now[i]:=0;Dec(i);
{*Находим "скачок".*}
End;
Inc(Now[i]);{^Увеличиваем найденный элемент
на единицу.*}
Now[0]:=i+sc;{^Изменяем длину разбиения.*}
For j :=1 To sc Do Now [ j+i] :=1; { ^Записываем
минимально возможные элементы,
τ . е. единицы.*}
End;
А будет ли работать данный алгоритм для последнего
разбиения (в нашем примере для «8»)? Оказывается, что нет.
Проверьте.
Считаем, что в Now хранится первое разбиение, а в массиве
Last — последнее. Они формируются, например, в процедуре
типа Init. Схема генерации:
While Not(Eq(Now,Last)) Do
Begin{*Фунция Eq дает
"истину", если текущее распределение
совпадает с последним, и "ложь"
в противном случае, можно сделать проще -
While Now[0]<>l Do ....*}
GetNext;
Print;{*Вывод разбиения.*}
End;
Третья задача. По номеру разбиения (L) получить само
разбиение Now.

62 2. Комбинаторные алгоритмы
Нумерация разбиений осуществляется относительно
введенного отношения порядка. Пусть L равно 0. Сделаем «набросок»
алгоритма.
sc:=N;i:=1;{*sc - число, которое представлено
разбиением, i - номер позиции в разбиении.*}
While sc<>0 Do
Begin{*Пока число не исчерпано.*}
j:=1;{*Число, которое должно записываться
на место i в разбиении.*}
??????{^Значение j определяется по значению
L, пока не знаем как.*}
Now[i]:=j;sc:=sc-j;Inc(i);{*Формируем текущую
позицию разбиения и готовимся к переходу для
формирование новой.*}
End;
Как это ни странно, но если вместо знаков «??????» оставить
пустое место («заглушку»), то при L, равном 0, данный
набросок будет работать — на выходе мы получим начальное
разбиение, состоящее из единиц.
Пусть L равно 1. Обратимся к таблице 2.20. Проверяем
SmallSc[8,l]. Если L больше или равно этому значению, то мы
уменьшим значение L на SmallSc[8,l], увеличим значение j на
единицу и, в конечном итоге, получим разбиение 2111111.
Итак, что нам необходимо сделать? Да просто просмотреть
строку массива SmallSc с номером sc и определить последний
элемент строки, его номер в у, который меньше текущего значения
L. Мы последовательно отсекаем разбиения числа sc,
начинающиеся с чисел у. Ниже приведен полный текст процедуры.
Procedure GetWhByNum(L:Longlnt);
Var i,j,sc:Integer;
Begin
sc:=N;i:=1;
While sc<>0 Do
Begin
j:=l;
While L>=SmallSc[sc,j] Do
Begin
Dec(L,SmallSc[sc,j]);Inc (j);
End;
Now[i]:=j;sc:=sc-j;Inc(i);

2. Комбинаторные алгоритмы
63
End;
Now[0]
End;
= i-l; {^Корректируем длину разбиения.
Четвертая задача. По разбиению (Now) получить его
номер.
Принцип прост. Брать текущее число из разбиения, начиная
с первого, и смотреть на его «вклад» в количество номеров.
Например, разбиение «22211». Определяем, сколько номеров
приходится на первую 2, затем на вторую и т. д.
Function GetNumByWh:Longlnt;
Var i, jk,p:Integer;
sc:Longlnt;
Begin
sc:=1;{^Формируем номер разбиения.*}
jk:=N;{*Номер строки в массиве SmallSc.*}
For i:=l To Now[0] Do
Begin{^Просматриваем
разбиение.*}
For p:=0 To Now[i]-1 Do sc:=sc+SmallSc[ jk,p];
{^Значение числа из разбиения определяет
число столбцов в массиве SmallSc.*}
jk:=jk-Now[i];{^Изменяем номер строки.*}
End;
GetNumByWh:=sc;
End;
В таблице 2.21 приведена ручная трассировка функции
GetNumByWh для N=8, Now=22211.
Таблица 2.21
sccrapoe
1
2
3
4
I 4
^старое
8
6
4
2
1
/
1
2
3
4
5
Ρ
0
1
0
1
0
1
0
0
5Сновое
1
2
3
4
4
4
^новое
6
4 J
2
1 l
0 J
Итак, номер определен, он равен 4.

64
2. Комбинаторные алгоритмы
2.2.5. Последовательности из нулей и единиц длины N
без двух единиц подряд
Первая задача. Подсчет числа последовательностей из
нулей и единиц длины N без двух единиц подряд.
В таблице 2.22 приведен пример для N=4. Таких
последовательностей 8.
Таблица 2.22
Г оооо
0001
0010 ~~[ 0101
0100 __j 1000
1001
1010
Как подсчитать количество таких последовательностей
(обозначим через P(N))7
Пусть есть последовательность длины N. На первом месте в
последовательностях записан ноль. Число этих
последовательностей P(N-l).
Рассмотрим случай, когда на первом месте записана
единица. Тогда на втором месте обязательно должен быть записан 0.
Число таких последовательностей P(N-2). Итак, получили
формулу:
P(N)=P(N-1 ;+Р(ЛГ-2),
а это не что иное, как формула вычисления чисел Фибоначчи.
Таким образом, число последовательностей длины N, в
которых нет двух идущих подряд 1, равно iV-му числу Фибоначчи.
Ограничимся диапазоном чисел типа Longlnt (N<44).
Для вычисления количества последовательностей при
больших значениях N требуется использовать «длинную»
арифметику, в частности процедуры сложения и вывода длинных чисел.
А при наших ограничениях можно ввести результаты в массив
констант.
Const NSmall=44;
ResSm: Array[0..NSmall] Of LongInt= (1, 2, 3, 5, 8,
13, 21, 34, 55, 89, 144, 233, 377, 610, 987,
1597, 2584, 4181, 6765, 10946, 17711, 28657,
46368, 75025, 121393, 196418, 317811, 514229,
832040, 1346269, 2178309, 3524578, 5702887,
9227465, 14930352, 24157817, 39088169,
63245986, 102334155, 165580141, 267914296,
433494437, 701408733, 1134903170, 1836311903);
Процедура вычисления количества последовательностей:
Function GetSmall(N: Integer): Longlnt;
Begin

2. Комбинаторные алгоритмы
65
If N>NSmall Then GetSmall:=MaxLongInt
Else GetSmall:=ResSm[N];
End;
Вторая задача. Генерация последовательностей.
Рассмотрим пример, приведенный в таблице 2.23, для N=6
(номер последовательности, последовательность).
Таблица 2.23
Го
1
2
3
4
5
|_6
000000
000001
000010
000100
000101
001000
001001
7
8
9
10
11
12
13
001010
010000
010001
010010
010100
010101
100000
14
15
16
17
18
19
20
100001
100010
100100
100101
101000
101001
101010
Принцип перехода к следующей последовательности.
Начинаем с конца последовательности,
подпоследовательности типа ..0010... переходят в тип ...0100... и типа ..001010... в
тип 010000....
Формализация этого принципа приведена в следующей
процедуре. Для хранения последовательности используется массив
Now.
Procedure GetNext;
Var i: Integer;
Begin
i:=N;
While (Now[i]=l) Or ((i>l) And (Now [i-1 ] =1) ) Do
Begin
Now[i]:=0;Dec(i);
End;
Now[i]:=1;
End;
Третья задача. По номеру получить последовательность.
Зададим себе простой вопрос. Если значение L больше, чем
число последовательностей длины ЛГ-1, то что находится на
первом месте (слева) в последовательности — 0 или 1? Ответ
очевиден: 1. Вычтем из значения L число последовательностей длины
N-1 и продолжим сравнение с новым значением L. В этом суть
решения, которая реализована в процедуре GetWhByNum.

66
2. Комбинаторные алгоритмы
В таблице 2.24 приведена ручная трассировка процедуры
GetWhByNum для ЛГ=6, L=15.
Таблица 2.24
L
15
2
2
2
2
0
/
1
2
3
4
5
6
Ρ
13
8
5
3
2
1
/Vow(******)
·« •••••
10****
100***
1000**
10001*
100010
Procedure GetWhByNum(L: Longlnt);
Var i: Integer;
Begin
For i :=1 To N Do
If L>=GetSmall(N-i) Then
Begin
Now[i]:=1;
L:=L-GetSmall(N-i) ;
End
Else Now[i]:=0;
End;
Четвертая задача. По последовательности получить ее
номер в соответствии с введенным отношением порядка.
Если в последовательности на месте i находится 1, то в
номере есть вклад от числа всех последовательностей длины N-i.
Итак, следует просмотреть последовательность и по значению 1
подсчитать сумму количества последовательностей
соответствующих длин.
Function GetNumByWh: Longlnt;
Var i: Integer;
sc: Longlnt;
Begin
sc:=1;
For i:=l To N Do If Now[i]=l Then
Inc (sc, GetSmall (N-i)) ;
GetNumByWh:=sc;
End;

2. Комбинаторные алгоритмы
67
2.2.6. Подмножества
Проблема. Научиться работать с подмножествами
^-элементного множества натуральных чисел от 1 до N такими, что
каждое следующее подмножество отличалось бы от
предыдущего только на один элемент.
Решаем традиционные четыре задачи:
подсчет количества подмножеств;
генерация подмножеств;
определение подмножества по номеру;
определение номера по подмножеству.
Первая задача. Подсчет количества подмножеств.
Количество подмножеств множества из N элементов равно
2χΝ. Эта задача проста, если значение N не очень большое.
Однако уже при N=15 количество подмножеств 32768, поэтому
тип данных Integer требуется использовать осторожно.
Пусть N меньше или равно 100. При таких значениях N
необходимо использовать элементы «длинной» арифметики, а
именно: умножение «длинного» числа на короткое (пятая
задача 1-й главы, процедура Mul) и вывод «длинного» числа
(вторая задача 1-й главы, процедура SayTLong).
Процедура вычисления количества подмножеств множества
из N элементов.
Есть небольшой «нюанс». Возводить двойку в степень N —
утомительное занятие, сократим его по возможности.
Procedure Calc;
Var i: Integer;
Tmp: TLong;
Begin
i:=N;{^Информация для размышления. Основанием
системы счисления в нашей задаче является
10000, а два в степени 13 равно 8192.*}
Res [ 1] : =1; Res [ 0] :=1;{*Два в степени 0 равно 1.*}
While i>0 Do
Begin
If i>13 Then
Begin
Mul(Res, 1 shl 13, Tmp); i:=i-13;
End
{^Напомним, что команда shl - сдвиг влево,итак
1 сдвигается на 13 разрядов влево, т.е. мы
умножаем на 213.А почему нельзя умножать на 214?*}
Else

68
2. Комбинаторные алгоритмы
Begin
Mul(Res, 1 shl i, Tmp) ; i:=0;
End;
Res:=Tmp;
End;
End;
Вторая задача. Генерация подмножеств.
Подмножества Л^-элементного множества натуральных
чисел от 1 до N будем представлять двоичными
последовательностями длины N — Now[l], Now[2], ..., Now[N] (массив Now).
Элемент Now[i], равный единице, говорит о том, что N—i+1
принадлежит подмножеству.
Таблица 2.25
Число
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
L 15
Двоичное
представление числа
(В)
0000
0001
0010
0011
0100
0101
0110
0111
1000
1001
1010
1011
1100
1101
1110
1111
Двоичная
последовательность
(Now)
0000
0001
0011
0010
0110
0111
0101
0100
1100
1101
1111
1110
1010
1011
1001
1000
Подмножество
[]
[1]
[1.2]
[2]
[2,3]
[1,2,3]
[1.3]
[3]
[3,4]
[1,3,4]
[1,2,3,4]
[2,3,4]
[2,4]
[1,2,4]
[1,4]
_W J
Во втором столбце таблицы 2.25 записаны двоичные
представления чисел от 0 до 24-1. Каждое из чисел мы подвергли
преобразованию (кодирование по Грею), заменив каждую
двоичную цифру, кроме первой, на ее сумму с предыдущей
цифрой по модулю 2, таким образом, получив элементы массива
Now. Т. е., Now[l]:=B[l] и Now[i]:=B[i]@B[i-l] для всех i от 2
до N.

2. Комбинаторные алгоритмы 69
В четвертом столбце таблицы 2.25 записаны подмножества,
построенные по единичным элементам массива Now. Обратите
внимание на то, что каждое следующее отличается от
предыдущего только на один элемент.
Запишем формирование массива Now в виде процедуры.
Procedure TransferB;
Var i : Integer;
Begin
FillChar(Now, SizeOf(Now), 0) ;
Now[1]:=B[1];
For i:=2 To N Do Now[i] :=B[i] Xor B[i-1] ;
End;
Обратное преобразование:
B[l]:=Now[l], B[i]:=Now[i]0B[i-l] для i от 2 до N.
Procedure TransferToB;
Var i, j : Integers-
Begin
FillChar(B, SizeOf(B), 0) ;
В[1]:=Now[1];
For i:=2 To N Do B[i] :=Now[i] Xor B[i-1] ;
End;
Воспринимая данное преобразование как факт, осмысление
которого лежит за пределами данного материала, генерацию
подмножеств можно осуществлять с использованием массива Б.
В качестве материала для самостоятельного осмысления
предлагается следующая изящная процедура генерации
очередного разбиения.
Procedure GetNext;
Var i : Integers-
Begin
i:=N+l;
Repeat
Dec (i);
В [ i ] : =B [ i ] Xor 1 ;
Until B[i]=l;
Now[i] :=Now[i] Xor 1 ;
End;{*Будет ли работать данная процедура для
последовательности 1111 (N=4)?*}
Можно решать задачу по-другому. Вспомним зрительный
образ «лесенки» со стрелками, который мы использовали при

70
2. Комбинаторные алгоритмы
генерации перестановок, таких, что каждая следующая
отличалась от предыдущей только одной транспозицией соседних
элементов. В данной задаче следует использовать не лесенку, а
прямоугольное поле 2χΝ. Шашки в начальный момент
находятся в первой строке (она соответствует нулевым значениям в
двоичной последовательности) и двигаются в направлении
стрелок. Определяется первая справа шашка, которую можно
сдвинуть в направлении стрелки. Сдвигаем ее, а у шашек,
находящихся справа от нее, меняем направление движения.
Последовательности 0000 при N=4 соответствует следующая
«картинка» — рисунок 2.5.
Г "
1 f
i ι
t
t
t
1 ]
0 _J
Рис. 2.5
А последовательности 0100 соответствует рисунок 2.6.
|_t
t
4-
1
I
ι 1
1
Ι ο ι
Рис. 2.6
Следующее состояние поля будет иметь вид
(последовательность 1100), приведенный на рисунке 2.7.
ΐ
4-
t
t
1 |
0 J
Рис. 2.7
Процесс генерации окончится при состоянии
(последовательность 1000), изображенном на рисунке 2.8.
Τ
ι
i
1 J
ι 1 о |
Рис. 2.8

2. Комбинаторные алгоритмы
71
Третья задача. Определение подмножества по номеру.
Получение последовательности В по номеру разбиения на
подмножества L соответствует записи числа L в двоичной
системе счисления с использованием массива В. Двоичный разряд
числа L — это значение соответствующего элемента массива В.
Procedure GetWhByNum (L: Longlnt);
Var i: Integer;
Begin
For i :=1 To N Do
Begin
B[N-i+l]:=L And 1;{^Выделяем младший разряд
числа L.*}
L: =L shr 1; { ^Уменьшаем L в два раза (деление
на 2).*}
End;
End;
Четвертая задача. Определение номера по подмножеству.
Алгоритм получения номера разбиения на подмножества по
последовательности В соответствует в нашем случае переводу
числа из двоичной системы счисления в десятичную.
Function GetNumByWh: Longlnt;
Var sc: Longlnt;
i: Integers-
Begin
s с : = 0 ;
For i:=l To N Do sc:=sc*2 + B[i];
GetNumByWh:=sc+l;
End;
2.2.7. Скобочные последовательности
Последовательность из 2χΝ скобок правильная, если для
любого значения i (1 < i < 2χΝ), число открывающих скобок,
например «(», больше или равно числу закрывающих скобок «)»
и общее число открывающих скобок в последовательности
равно числу закрывающих.
Пример. Последовательность (())()() — правильная (N=4),
последовательность (()))(() — не является правильной.
Мы по-прежнему решаем наши четыре задачи. Однако
изменим порядок их рассмотрения. Начнем с генерации
последовательностей.

72
2. Комбинаторные алгоритмы
Пусть N равно 4. В нечетных столбцах таблицы 2.26
приведены номера последовательностей, а в соседних —
соответствующие последовательности.
Таблица 2.26
г°~
1
2
з
4
5
I 6
()()()()
()()(())
()(())()
()(()())
()((()))
(())()()
(ОКО)
7
8
9
10
11
12
13
(00)0 ]
(000)
(()(()))
((()))()
(((»())
(«к»)
(((О))) I
Что же мы делаем? Какое отношение порядка введено на
множестве последовательностей? Сколько существует таких
последовательностей для заданного значения ΝΊ Вопросов
много, ответов пока нет.
Пусть наша последовательность хранится в переменной
строкового типа Now. Мы просматриваем строку справа налево
до первой комбинации скобок типа «)(». Она обязательно
должна встретиться, ибо, считаем, что текущая
последовательность не является последней. Заменяем эту комбинацию скобок
на «()». Подсчитываем с начала строки (последовательности),
на сколько число открывающих скобок больше числа
закрывающих, дописываем это количество закрывающих скобок, и
если строка не длины 2χΝ, то дополняем ее комбинациями
скобок «о».
Procedure GetNext;
Var i, j, sc: Integer;
Begin
i:=N*2;
While (i>l) And (Now[i-l] + Now [i ]<>')(' )
Do Dec (i) ; { *Поиск комбинации λλ) (".*}
Now[i-l] :=' ('; Now[i] :=')';{*3амена.*}
Now:=Copy(Now,1,i);
sc:=0;{*Подсчет разности числа открывающих и
числа закрывающих скобок.*}
For j :=1 To i Do
If Now[j]=' ('
Then Inc (sc)
Else Dec(sc);
While sc<>0 Do
Begin

2. Комбинаторные алгоритмы
73
{^Дополнение подпоследовательности
закрывающими скобками.*}
Now:=Now+')';Dec (sc);
End;
While Length(Now)<2*N Do Now:=Now+'()';
{^Дополняем строку, максимально "ухудшая"
ее, т.е. из остатка строки делаем ее
начальное значение.*}
End;
Даны две последовательности Рх и Р2, например ()()(()) и
()(()())· Какая из них имеет больший номер? Просматриваем
последовательности слева направо, сравнивая соответствующие
символы. Найдем первое значение i, при котором P1[i]<>P2U]-
Если окажется, что Pi[i]=')', a P2U]=:'С > то Рх имеет меньший
номер, чем Р2. Можно записать сей факт и в математических
обозначениях, но суть не изменится, поэтому воздержимся.
Перейдем к первой задаче. Введем понятие частично
правильной скобочной последовательности. Последовательность
частично правильная, если для любой позиции в
последовательности число открывающих скобок больше или равно числу
закрывающих, естественно, что количество тех и других
считается от начала последовательности. Так, последовательность
«(((((» является частично правильной, а последовательность
«(()))((» — нет, для позиции 5 число закрывающих больше
числа открывающих скобок.
Оформим наши дальнейшие рассуждения в виде таблицы
2.7. Номер строки указывает на число скобок в
последовательности, номер столбца — на разность между числом
открывающих и закрывающих скобок, имя таблицы ScSmall, элемент
таблицы ScSmall[i,j] равен количеству частично правильных
последовательностей из ί скобок, причем разность между
числом открывающих и закрывающих равна у. Это ключевой
момент для понимания: «разность — номер столбца». На диагонали
таблицы 2.7 записаны 1, число последовательностей, состоящих
из одних открывающих скобок, а они попадают под
определение частично правильной последовательности. Элементы
таблицы 2.7 ScSmall[iJ] равны 0, если i и j числа разной четности.
Примеры.
ScSma/Z[3,l]=2: ((), ()(.
ScSmall[4,2]=3: (((), (()(, ()((.
ScSmall[4,0]=2: ()(), (()).
ScSmall[5,l]=5: ()()(, (())(, ((()), (()(), ()(().

74 2. Комбинаторные алгоритмы
И «крохотный факт»:
ScSmall[59l]=ScSmall[4,0]+ScSmall[4,2l
Дописываем в конец последовательностей из ScSmall[4,0]
открывающую скобку, а в конец ScSmall[4,2] —
закрывающую. А это уже реальный путь подсчета числа
последовательностей. Ответом задачи будет ScSmall[2xN,0].
Таблица 2.27
!
0
1
2
3
4
5
6
7
L JL.
-1
0
0
0
0
0
0
0
0
^J__
~F^
1
0
1
0
1
0
1
0
2
2 · 0
I
0 5
5 ' 0
0
14
14
_1_
2
3
0 I 0
0
1
0
3
0
9
0
0
1
0
4
0
0 14
28 _J 0
4
0
0
0
0
1
0
5
0
20
5
0
0
0
0
0
1
0
6
0
6
0
0
0
0
0
0
1
0
7
0
0
0
0
0
0
0
1
: 7 г*-
ι 1
8 |
о
о |
0 J
0 1
0
0
0 J
0
LjJ
Ограничимся при вычислениях диапазоном типа Longlnt.
Const SmallN=37;
Var ScSmall: Array [-1.. SmallN + 1, -L.SmallN + 1]
Of Longlnt;
Процедура формирования таблицы вряд ли нуждается в
пояснениях.
Procedure Fi11SmallSc;
Var i, j: Integer;
Begin
FillChar(ScSmall, SizeOf(ScSmall), 0) ;
ScSmall[0, 0]:=1;
For i:=l To SmallN-1 Do
For j :=0 To SmallN Do
ScSmall[i,j]:-ScSmall[i-1,j-1]+
ScSmall[i-1,j+1];
End;
Дополним ее функцией определения количества частично
правильных последовательностей из массива SCSmall.
Function GetSmallSc (N, Up: Longlnt) : Longlnt;
Begin
If (N<0) Or (Up<0)

2. Комбинаторные алгоритмы
75
Then GetSmallSc:=0
Else
If (N>SmallN) Or (Up>SmallN)
Then GetSmallSc :=MaxLongInt
Else GetSmallSc:=ScSmall [N, Up];
End;
Вычисление последовательности по номеру и обратное
преобразование можно вынести на самостоятельную часть работы.
Ниже приведены соответствующие процедура и функция. В
переменной Up, как и выше, формируется текущая разность
между числом открывающих и закрывающих скобок.
Procedure GetWhByNum (L: Longlnt);
Var i, Up: Integer;
P: Longlnt;
Begin
Now:-''; Up:=0;
For i:=l To N*2 Do
Begin
P:=GetSmallSc(N*2-i, Up-1);
If (L>=P) Then
Begin
Now:=Now+'('; Inc(Up); L:=L-P;
End
Else
Begin
Dec (Up); Now:=Now+')';
End;
End;
End;
Function GetNumByWh: Longlnt;
Var sc: Longlnt;
i, Up: Integer;
Begin
sc:=l; Up:=0;
For i:=l To N^2 Do
If Now[i] =' (' Then
Begin
sc:=sc+GetSmallSc(N*2-ifUp-1) ;Inc (Up) ;
End

76
2. Комбинаторные алгоритмы
Else Dec(Up);
GetNumByWh:=sc;
End;
2.3. Задачи
1. Разработать программу генерации всех
последовательностей длины k из чисел 1, 2, ... N. Первой последовательностью
является 1, 1, ...,1, последней — Ν, Ν, ..., N.
2. Разработать программу генерации всех
последовательностей длины k, у которых i-й элемент не превосходит значения
i. Первой последовательностью является 1, 1, ...,1,
последней — 1, 2, ..., k.
3. Перечислить все разбиения натурального числа N на
натуральные слагаемые (разбиения, отличающиеся лишь
порядком слагаемых, считаются за одно) в следующих порядках
например, при N=4:
4, 3+1, 2+2, 2+1+1, 1+1+1+1;
4, 2+2, 1+3, 1+1+2, 1+1+1+1;
1+1+1+1, 1+1+2, 1+3, 2+2, 4.
4. Разработать программу генерации всех последовательностей
длины 2χΝ9 составленных из N единиц и N минус единиц, у
которых сумма любого начального отрезка неотрицательна, т. е.
количество минус единиц в нем не превосходит количества единиц.
5. Определить, что делает следующая процедура. Первое
обращение — R(N,1).
Procedure R(t,k:Integer);
Var i:Integer;
Begin
If t=l Then
Begin
A[k]:=1;<вывод к элементов массива А>;
End
Else
Begin
A[k] :=t;<BbiBOfl k элементов массива А>;
For i:=l To t-1 Do
Begin A[k]:=t-i;R(i,k+1);End;
End;
End;

2. Комбинаторные алгоритмы
77
6. На множестве перестановок задается
антилексикографический порядок. Решить задачи 2-5 из п. 2.2.1.
7. Решить задачи 1-5 из п. 2.2.1 для перестановок с
повторениями.
8. Решить задачи 1-5 из п. 2.2.2 для размещений с
повторениями.
9. Решить задачи 1-5 из п. 2.2.3 для сочетаний с
повторениями.
10. Путем трассировки приведенной программы [18]
определите ее назначение и алгоритм работы.
Const n=4 ;
Var A:Array[1..η] Of Integer;
i : Integers-
Function Place (i, m: Integer) : Integers-
Begin
If (m Mod 2 = 0) And (m>2)
Then
If i<m-l
Then Place:=i
Else Place:=m-2
Else Place:=m-l;
Ends-
Procedure Perm(m:Integer);
Var i,t: Integers-
Begin
If m=l Then
Begin
For i:=l To η Do Write (A [i] :3) ; WriteLn;
End
Else
For i :=1 To m Do
Begin
Perm (m-1) ;
If i<m Then
Begin
t:=A[Place(i,m) ]; A[Place(i,m) ] :=A[m] ;A[m] :=t;
Ends-
End;
Ends-
Begin
For i :=1 To η Do A[i] :=i;

78
2. Комбинаторные алгоритмы
Perm(n);
End.
11. Путем трассировки приведенной программы [18]
определите ее назначение и алгоритм работы.
Const n=4;
Var A:Array [1 . .η] Of Integer;
i, j ,ρ, 1: Integers-
Begin
For ι :=1 To η Do А И 1 :=0;
i:=0;
Repeat
For 1:=1 To η Do Write (A [1] :3) ;
WriteLn;
i:=i+l;p:=l;j:=i;
While j Mod 2=0 Do
Begin
j:=j Div 2;p:=p+l;
End;
If p<=n Then A[p] :=1-A[p] ;
Until p>n;
End.
12. Путем трассировки приведенной программы [18]
определите ее назначение и алгоритм работы.
Const n=5;
к=3;
Var A:Array [1 . .η] Of Integer;
i, j,ρ:Integer;
Begin
For i:=l To к Do A[i]:=i;
p:=k;
While p>=l Do
Begin
For i:=l To к Do Write (A[i] :3) ;
WriteLn;
If A[k]=n Then p:=p-l Else p:=k;
If p>=l Then
For i:=k DownTo ρ Do A[i] : =A [p]+i-p+l ;
End;
End.

2. Комбинаторные алгоритмы
79
13. «Взрывоопасностъ». На одном из секретных заводов
осуществляется обработка радиоактивных материалов, в
результате которой образуются радиоактивные отходы двух типов: А
(особо опасные) и Б (неопасные). Все отходы упаковываются в
специальные прямоугольные контейнеры одинаковых
размеров, после чего эти контейнеры укладываются в стопку один
над другим для сохранения. Стопка является взрывоопасной,
если в ней соседствуют два ящика с отходами типа А.
Требуется написать программу, которая подсчитывает
количество возможных вариантов формирования невзрывоопасной
стопки из заданного общего числа контейнеров N (1 < N < 100).
Входные данные. Во входном файле input.txt содержится
единственное число N.
Выходные данные. В выходной файл output.txt необходимо
вывести искомое число вариантов.
Пример входных и выходных данных
представлен на рисунке 2.9.
Указание. Обозначим опасный контейнер 1,
а неопасный — 0. Моделью стопки является
последовательность из 0 и 1. Взрывоопасная
стопка есть последовательность из 0 и 1, в
которой соседствуют хотя бы две 1 подряд.
Задача сводится к подсчету числа
последовательностей длины N без двух соседних 1. Приведем
пример. При N=4 таких последовательностей
8, они представлены в таблице 2.28.
Таблица 2.28
Гоооо
1 0001
0010 0101
0100
1000
1001
1010 J
Как подсчитать количество таких последовательностей
(обозначим через P(N))?
Пусть есть последовательность длины N. На первом месте в
последовательности записан 0. Число таких
последовательностей P(N-1).
Рассмотрим случай, когда на первом месте записана 1. Тогда
на втором месте обязательно должен быть записан 0. Число
таких последовательностей P(N-2).
Итак, получили формулу: Ρ(Ν)=Ρ(Ν-1)+Ρ(Ν-2), а это не что
иное, как формула вычисления чисел Фибоначчи. Таким
образом, число последовательностей длины N, в которых нет двух
Пример.
input.txt
4
output.txt
8

80
2. Комбинаторные алгоритмы
идущих подряд 1, равно N-му числу Фибоначчи. Тип данных
Longlnt достаточен только для вычислений при N<44. Для
вычисления количества последовательностей при больших
значениях N требуется использовать «длинную» арифметику, а
именно процедуры сложения и вывода «длинных» чисел.
Если задачу чуть-чуть изменить — вычислять количество
взрывоопасных стопок, то потребуется процедура вычитания
«длинных» чисел. Из 2N необходимо вычесть число
невзрывоопасных стопок.
14*. Натуральные числа от 1 до N (1 < N < 13) поступают на
обработку в определенной последовательности. Например, 3, 4,
6, 2, 5, 1. Числа размещаются в таблице следующим образом:
последовательно просматриваются числа из первой строки и
сравниваются с поступившим числом k. Если число k больше
всех чисел строки, то оно размещается в конце строки. Если же
найдено (первое) число £, такое, что t>k, то число k
записывается на это место, а число t «выдавливается» из
строки и размещается во второй строке по
этому же принципу, затем в третьей (если
потребуется) и τ .д., пока для числа (k или
«выдавливаемого») не будет найдено место. Для
приведенной последовательности вид
размещения представлен на рисунке 2.10.
Требуется по конечному результату
восстановить все возможные входные
последовательности чисел, обработка которых по данному
алгоритму приводит к этому размещению.
Так, для примера из формулировки задачи,
ответом являются 16 последовательностей,
приведенных на рисунке 2.11.
Указание. Простейший способ решения
заключается в генерации всех перестановок и
проверке — удовлетворяет ли очередная
перестановка «правилам игры». Однако если
ввести ограничение на время решения, то этот
способ не выдерживает элементарной
критики. Обратим внимание на следующие
моменты. На обработку поступила
последовательность (N=6) 1, 2, 3, 4, 5, 6. Ее размещение '
имеет вид: 12 3 4 5 6. Обратный порядок по- Рис. 2.11
Рис. 2.10
32 1465
32 1645
342 165
324 165
326145
362 145
342615
3462 15
324615
3264 15
3624 15
34265 1
3462 5 1
32465 1
'32645 1
I 36245 1
Задача с международной олимпиады школьников 2001 г. (формулировка
сокращена).

2. Комбинаторные алгоритмы
81
1 4
2 6
3 5
ю :
Рис
7
8
9
11
12 !
!
i
.2.12
ступления дает размещение по одному элементу
в строке: в первой — 1, во второй — 2 и т. д.
Зададим себе вопрос: а возможны ли размещения,
при которых элементы в столбцах (не в строках!)
идут не в порядке возрастания, как, например,
приведенное на рисунке 2.12. Оказывается,
нет.** Мы всегда получаем размещения,
элементы в столбцах и строках которых записаны в порядке
возрастания. Если так, то первое решение получается простым
выписыванием элементов по столбцам в обратном порядке. Для
примера из формулировки задачи это будет 3 2 16 4 5.
Второй вариант решения может заключаться в том, что из
полученной (первой) последовательности путем перестановки
соседних элементов мы получаем какую-то
последовательность. Проверяем ее на «пригодность» и если она
удовлетворяет «условиям игры», то запоминаем ее в очереди. Итак,
выполняем все перестановки соседних элементов в исходной
последовательности, а затем переходим к очередному
необработанному элементу очереди, если он есть.
Недостаток алгоритма очевиден. Мы можем получать одну и
ту же последовательность несколькими способами. Поэтому
приходится их хранить и перед записью в очередь проверять,
нет ли дублирования. А это уже потеря времени и, естественно,
данное решение (приведем его «костяк») является только
очередным приближением, хотя и работающим, к окончательному
варианту.
Const NMax=13;
Type MyArray=Array[1 . .NMax] Of Word;
Var A:MyArray;
Function Check (Const PiMyArray) -.Boolean;
{*Функция проверки - удовлетворяет ли очередная
последовательность условиям задачи?*}
Begin
End;
Procedure Solve;
Type pnt=AIlem;
В этом заключается неточность в формулировки задачи на международной
олимпиаде. Если проверять по несуществующим размещениям, то часть
решений, включая опубликованные в газете «Информатика», будут
генерировать неизвестные входные последовательности.

82
2. Комбинаторные алгоритмы
Ilem=Record{^Описываем элемент очереди.
Очередь размещаем "в куче". Обычный список.
Записываем в конец - указатель ykw,
считываем первый элемент - указатель ykr.*}
Next:pnt;
Data:MyArray
End;
Var R,Q:MyArray;
ykr,ykw, p:pnt;
i:Word;
headrpnt;
Function NotQue:Boolean;{^Функция проверки -
есть ли данная последовательность в очереди?*}
Begin
End;
Begin
New(ykw);ykwA.Data:=A;ykwA.Next:=Nil;head:=ykw;
{^Записываем первый элемент в очередь.*}
ykr:=head;
While ykrOnil Do
Begin {*Пока очередь не пуста.*}
R:=ykrA.Data;{*Берем элемент из очереди.*}
For i:=l To N-l Do
Begin
{*Генерируем все возможные последовательности
путем перестановок соседних элементов.*}
Q:=R;
Swap(Q[i]fQ[i + l]) ;
If Check (Q) And NotQue Then
Begin
{*Если последовательность удовлетворяет
условиям задачи и ее нет в очереди, то
записываем в очередь.*}
New(p);pA.Data:=Q;pA.Next:=Nil;
ykwA.Next:=p;
ykw:=p;
Print(Q) ; {*Процедура вывода элементов
одномерного массива в файл не приводится.*}
End;
End;
ykr:=ykrA.next;{*Переходим к следующему
элементу очереди.*}
End;

2. Комбинаторные алгоритмы
83
End;
Begin
{^Основная программа. Ввод данных. Формирование
первой последовательности массив А) . * }
Solve;
End.
15. На клетчатой полоске бумаги высотой в одну клеточку и
длиной N клеток некоторые клетки раскрашены в зеленый и
белый цвета. По этой полоске строится ее код, которым является
последовательность чисел — количества подряд идущих зеленых
клеток слева направо. Например, для полоски на рисунке 2.13
;г- ■:~г: : : Г 1..:-... -.г.".ι с
Рис. 2.13
кодом будет последовательность 2 3 2 8 1. При этом количество
белых клеток, которыми разделяются группы зеленых клеток,
нигде не учитывается (главное, что две группы разделяются, по
крайней мере, одной белой клеткой). Одному и тому же коду
могут соответствовать несколько полосок. Например,
указанному коду соответствует полоса, изображенная на рисунке 2.14:
- " ;i τι ι rm "
Рис. 2.14
Задача состоит в том, чтобы найти
количество полосок длины N, соответствующих
заданному коду.
Входные данные. В единственной строке
входного файла input.txt записано число N —
длина полоски (1 < N < 200), затем число К —
количество чисел в коде (0 < К < (iV+l)/2) и
далее К чисел, определяющих код.
Выходные данные. В выходной файл output.txt
записывается количество полосок длины iV,
соответствующих заданному коду.
Указание. Добавляем к каждому числу кода
по единице (соответствует пробелу), получаем
:J
Примеры
input.txt
40
output.txt
1_
input.txt
5 2 12
output.txt
3
input.txt
J 4 2 2 2 __
i
i output.txt
!_o__
Рис. 2.15

84
2. Комбинаторные алгоритмы
значение s. Остается решить задачу о подсчете числа
размещений N-s пробелов по известному количеству мест —
количеству чисел в коде плюс единица. Естественно, что ограничения
требуют применения многоразрядной арифметики.
На рисунке 2.15 приведены возможные значения входных
данных (файл input.txt) и соответствубщие значения выходных
данных (output.txt).
16. Между числами av...,aN нужно вставить знаки
арифметических операций +, -, * так, чтобы результат вычисления
полученного арифметического выражения был равен
заданному целому числу Б.
Входные данные. Во входном файле
input.txt записано сначала требуемое число
В (-2х109 < В < 2х109), затем число N —
количество чисел в арифметическом
выражении (1 < N < 12), а затем целые числа
av...,aN (0 < α. < 20)
Выходные данные. В выходной файл
output.txt вывести искомое
арифметическое выражение или число 0, если его
построить не удается. Если решений
несколько, вывести любое из них.
Указание. Количество мест для
расстановки знаков — N-1. Требуется
сгенерировать все строки этой длины, состоящие из
символов +, -, *, их З^"1. Для каждой Рис. 2.16
строки вычислить арифметическое
выражение и, в зависимости от результата,
продолжить процесс генерации или закончить
работу.
На рисунке 2.16 приведены возможные значения входных
данных (файл input) и соответствующие значения выходных
данных (файл output).
Представляет определенный интерес алгоритм вычисления
выражения. Приведем его.
В строке В (глобальная переменная относительно
приведенных функций) записана очередная последовательность из
символов +,-,*, а в массиве А — последовательность чисел.
Function GetRes: Comp;
Var tm: Comp;
ρ:Integer;
Примеры
input.txt
1053
6
5 6 7 10 15 8
output.txt
5+6+7*10*15-8
input.txt
12
2
1 2
output.txt
0

2. Комбинаторные алгоритмы
85
Begin
р:=1;
tm:=GetMul(p);
While (p<N) And (B[p] In ['+' , '-']) Do
Begin
Inc (p);
Case B[p-1] Of
'+': tm:=tm+GetMul(p);
'-': tm:=tm-GetMul(p) ;
End;
End;
GetRes:=tm;
End;
И функция, вычисляющая произведение очередных
сомножителей.
Function GetMul(Var p: Integer): Comp;
Var tm: Comp;
Begin
tm:=A[p];
While (p<N) And (B[p]='*') Do
Begin
tm:=tm*A[p+l];
Inc (p);
End;
GetMul:=tm;
End;
Обратной задачей является поиск количества «счастливых
билетов» (например, троллейбусных, т. е. шестизначных).
Общая формулировка задачи. Последовательность из 2χΝ цифр,
каждая цифра от 0 до 9, называется счастливым билетом,
если сумма первых N цифр равна сумме последних N цифр.
Операции даны, требуется найти числа.
Пусть нам необходимо подсчитать количество счастливых
чисел в диапазоне [А,В], где А, В — заданные натуральные
числа, имеющие в десятичной записи не более 20 цифр. Пусть
N=3, А=1, Б=999999. Ответ задачи — 55251.
Следующая функция является наброском решения. Она
правильная, но работает достаточно медленно.
Function Rec(k,Sum:Longlnt):Comp;{^Параметрами
рекурсии являются к - номер позиции в числе и
Sum - сумма цифр в числе до позиции к.*}

86
2. Комбинаторные алгоритмы
Var i:Integer;
Ans rLonglnt;
Begin
If k=2*N+l
Then
If Sum=0 Then Rec:=l Else Rec:=0
Else
Begin
Ans:=0;
For i:=0 To 9 Do
If k<=N
Then Ans:=Ans+Rec(k+1,Sum+i)
Else
If i<=Sum Then Ans:=Ans+Rec(k+1,Sum-i);
Rec:=Ans;
End;
End;
Работа алгоритма ускоряется за счет следующего приема.
Схема рекурсивного подсчета замедляется из-за многократного
подсчета одного и того же значения, например Rec(3,8) при
N=2. Следует ввести структуру данных для хранения
подсчитанных значений сумм типа
Μ: Array [1. .20,0. .90] Of Comp .
Пусть начальное значение элементов массива равно -1.
После того, как вычислено какое-то значение, оно запоминается в
массиве и используется при дальнейшей работе. Проведите
соответствующее изменение алгоритма.
17. На плоскости заданы N точек с целочисленными
координатами. Требуется выделить те точки этого множества,
которые образуют выпуклую оболочку (вырожденные случаи — все
точки на одной прямой и т. д. не рассматриваются).
Указание. Специальные методы построения выпуклой
оболочки будут рассмотрены в главе 5. В данном случае можно
воспользоваться следующим фактом. Точка (х, у) принадлежит
выпуклой оболочке, если она не лежит внутри любого
треугольника, образованного остальными точками исходного
множества. Всего треугольников, которые можно построить из N
точек, — C3N , общая временная сложность задачи 0(N4).

3. Перебор
и методы его сокращения
Обучение программированию, алгоритмизации —
сверхсложное дело*. Знание конструкций языка программирования,
способов описания алгоритмов не решает проблемы. Требуется
проделать огромную работу для того, чтобы сформировать
стиль мышления, присущий специалисту по информатике.
Этот стиль характеризуется, на наш взгляд, двумя
основополагающими моментами: язык информатики (он не зависит от
конкретного языка программирования) должен стать
естественным языком выражения своих мыслей (рассуждений);
методология решения задач, присущая информатике, должна
быть освоена не на фактографическом уровне. Тема «перебор и
методы его сокращения» является одной из ключевых в этой
системе обучения. Весь процесс обучения построен через
решение задач, естественно, с использованием компьютера.
3.1. Перебор с возвратом (общая схема)
Даны N уопрядоченных множеств Uv U2, ..., UN (N —
известно), и требуется построить вектор Α=(αν α2, ..., αΝ)> где
агеи19 a2GU29 ..., aNGUNy удовлетворяющий заданному
множеству условий и ограничений.
В алгоритме перебора вектор А строится покомпонентно
слева направо. Предположим, что уже найдены значения первых
k-Ι компонент, Α=(αν α2, ..., akv ?, ..., ?), тогда заданное
множество условий ограничивает выбор следующей компоненты ak
некоторым множеством SkczUk. Если *S^<>[ ] (не пустое), мы
вправе выбрать в качестве ak наименьший элемент Sk и перейти
к выбору k+Ι компоненты и так далее. Однако если условия
таковы, что Sk оказалось пустым, то мы возвращаемся к выбору
k-Ι компоненты, отбрасываем ah_x и выбираем в качестве
нового ak_x тот элемент Sk_v который непосредственно следует за
только что отброшенным. Может оказаться, что для нового ак_х
условия задачи допускают непустое Sk, и тогда мы пытаемся
Может быть, это явилось одной из причин, по которой, после появления
мощных персональных компьютеров, образовательная информатика с таким
энтузиазмом «бросилась» в изучение так называемых информационных
технологий.

88
3. Перебор и методы его сокращения
снова выбрать элемент ak. Если невозможно выбрать ak_v мы
возвращаемся еще на шаг назад и выбираем новый элемент ak_2
и так далее.
/К начало
yfC д выборы для aj
f I \ \ / \ Выборы ДЛЯ 8ί2
/\ Л\ Жч ПРИ Данном ai
• 1 # 1 Ъ / I \^N* выборы для а3
А · L д ПРИ Данных ai> а2
/ I выборы дляи а4
• · при данных ах, а2, а3
Рис. 3.1
Графическое изображение — дерево поиска (см. рисунок
3.1). Корень дерева (0 уровень) есть пустой вектор. Его сыновья
суть множество кандидатов для выбора av и, в общем случае,
узлы k-το уровня являются кандидатами на выбор ak при
условии, что αν α2, ..., ak_x выбраны так, как указывают предки
этих узлов. Вопрос о том, имеет ли задача решение, равносилен
вопросу, являются ли какие-нибудь узлы дерева решениями.
Разыскивая все решения, мы хотим получить все такие узлы.
Рекурсивная схема реализации алгоритма.
Procedure Backtrack(<вектор,i>);
Begin
If <вектор является решением>
Then оаписать его>
Else
Begin
<вычислить SL>;
For <aeS1>Do Backtrack (<вектор| I a>, i + 1) ;
{*| I - добавление к вектору компоненты.*)
End;
End;
Оценим временную сложность алгоритма. Данная схема
реализации перебора приводит к экспоненциальным алгоритмам.
Действительно, пусть все решения имеют длину N, тогда иссле-

3. Перебор и методы его сокращения
89
довать требуется порядка | иг\ х| U2\ x...x| UN\ узлов дерева. Если
значение Ui ограничено некоторой константой С, то получаем
порядка CN узлов.
3.2. Примеры задач для разбора
общей схемы перебора
1. «Задача о расстановке ферзей».
Для разбора общей схемы одной из лучших задач является
задача о расстановке ферзей. На шахматной доске ΝχΝ
требуется расставить N ферзей таким образом, чтобы ни один ферзь
не атаковал другого.
Отметим следующее.
Все возможные способы расстановки ферзей — С^2 (для
N=8 около 4,4х109).
Каждый столбец содержит самое большее одного ферзя, что
дает только NN расстановок (для N=8 1,7х107).
Никакие два ферзя нельзя поставить в одну строку, а
поэтому, для того чтобы вектор (αν α2, ..., αΝ) был решением, он
должен быть перестановкой элементов (1, 2, ..., Ν), что дает
только ЛП (для N=8 4,0x104) возможностей.
Никакие два ферзя не могут находиться на одной
диагонали, это сокращает число возможностей еще больше (для N=8 в
дереве остается 2056 узлов).
Итак, с помощью ряда наблюдений мы исключили из
рассмотрения большое число возможных расстановок N ферзей на
доске размером ΝχΝ. Использование подобного анализа для
сокращения процесса перебора называется поиском с
ограничениями или отсечением ветвей в связи с тем, что при этом
удаляются поддеревья из дерева.
Второе. Другим усовершенствованием является слияние,
или склеивание, ветвей. Идея состоит в том, чтобы избежать
выполнения дважды одной и той же работы: если два или
больше поддеревьев данного дерева изоморфны, мы хотим
исследовать только одно из них. В задаче о ферзях мы можем исполь-
зовать склеивание, заметив, что если ал>\ — I, то наиденное
1 2
решение можно отразить и получить решение, для которого
αχ<Γ—1. Следовательно, деревья, соответствующие, например,
Li
случаям ах=2 и α1=Λ^-1, изоморфны.
Рисунок 3.2 иллюстрирует сказанное и поясняет ввод
используемых структур данных.

90
3. Перебор и методы его сокращения
12 3 4
1
#
#
#
#
#
@
#
2
#
@
#
@
@
#
[1.1]
12 3 4
[2,3]
1
#
#
#
#
#
3
@
#
@
#
&
#
2
@
#
12 3 4
#
#
3
&
1
#
#
#
#
#
@
4
#
2
#
@
I
-> 6
12345678
/
/
/
/
/
/
/
/
15
16
i 12 3 4 5 6 78
и
3
4
5
6
7
\
\
\
S
\
\
\
\
N
\
\
\
\
\
\
\
76
Рис. 3.2
Структуры данных.
Up:Array[2..16] Of Boolean;{^Признак занятости
диагоналей первого типа.*}
Down:Array[-7..7] Of Boolean;{*Признак занятости
диагоналей второго типа.*}
Vr:Array[1..8] Of Boolean;{*Признак занятости
вертикали.*}
X:Array[1..8] Of Integer;{*Номер вертикали,
на которой стоит ферзь на каждой горизонтали.*}
Далее идет объяснение «кирпичиков», из которых
«складывается» решение (технология «снизу вверх»).
Procedure Hod(i,j:Integer); {^Сделать ход.*}
Begin
X[i]:=j;Vr[j]:=False;Up[i+j]:=False;
Down[i-j]:=False;
End;
Procedure 0_hod(i, j:Integer);{^Отменить ход.*}

3. Перебор и методы его сокращения
91
Begin
Vr[j]:=True;Up[i+j]:=True;Down[i-j]:=True;
End;
Function D_hod(i,j:Integer):Boolean;
{^Проверка допустимости хода в позицию (i,j) . *}
Begin
D_hod:=Vr[j] And Up[i+j] And Down[i-j];
End;
Основная процедура поиска одного варианта расстановки
ферзей имеет вид:
Procedure Solve(i:Integer;Var q.-Boolean);
Var j:Integer;
Begin
j:=0;
Repeat
Inc(j);q:=False;{*Цикл по вертикали.*}
If D_hod(i,j) Then
Begin
Hod(i,j);
If i<8
Then
Begin
Solve(i + 1,q);
If Not q
Then O_hod(i,j);
End
Else q:=True;{*Решение найдено.*}
End;
Until q Or (j=8) ;
End;
Изменим формулировку задачи. Пусть требуется найти все
способы расстановки ферзей на шахматной доске ΝχΝ. Для
доски 8x8 ответ 92.
Возможный вариант реализации приведен ниже по тексту.
Procedure Solve(i:Integer);
Var j:Integer;
Begin
If i<=N
Then
Begin
For j :=1 To N Do

92
3. Перебор и методы его сокращения
If D_hod(i, j) Then
Begin
Hod(i,j);
Solve(i+1);
O_hod(i,j);
End;
End
Else
Begin
Inc(S);{*Счетчик числа решений, глобальная
переменная.* }
Print;{*Вывод решения.*}
End;
End;
Продолжим изучение задачи. Нас интересуют только
несимметричные решения. Для доски 8x8 ответ 12. Это задание
требует предварительных разъяснений. Из каждого решения
задачи о ферзях можно получить ряд других при помощи
вращений доски на 90°, 180° и 270° и зеркальных отражений
относительно линий, разделяющих доску пополам (система
координат фиксирована). Доказано, что в общем случае для
любой допустимой расстановки N ферзей возможны три
ситуации:
• при одном отражении доски возникает новая расстановка
ферзей, а при поворотах и других отражениях новых
решений не получается;
• поворот на 90° и его отражение дают еще две расстановки
ферзей;
• три поворота и четыре отражения дают новые
расстановки.
Для отсечения симметричных решений на всем множестве
решений требуется определить некоторое отношение порядка.
Представим решение в виде вектора длиной N, координатами
которого являются числа от 1 до N. Для ферзя, стоящего в i-й
строке, координатой его столбца является i-я координата
вектора. Для того, чтобы не учитывать симметричные решения,
будем определять минимальный вектор среди всех векторов,
получаемых в результате симметрии. Процедуры Siml, Sim2,
Sim3 выполняют зеркальные отображения вектора решения
относительно горизонтальной, вертикальной и одной из
диагональных осей. Известно (из геометрии), что композиция этих
симметрии дает все определенные выше симметрии шахматной
доски, причем не принципиально, в какой последовательности

3. Перебор и методы его сокращения
93
выполняются эти процедуры для каждой конкретной
композиции. Проверка «на минимальность» решения производится
функцией Стр, которая возвращает значение True в том
случае, когда одно из симметричных решений строго меньше
текущего решения.
Возможный вариант реализации (отсечение на выводе
решений) приведен ниже по тексту.
Type TArray=Array [ 1. .Ν] Of Integer;
Procedure Siml(Var XiTArray);
Var i:Integer;
Begin
For i:=l To N Do X[i] :=N-X[i]+1;
End;
Procedure Sim2(Var X:TArray);
Var i,r: Integers-
Begin
For i:=l To N Div 2 Do
Begin
r:=X[i]; X[i]:=X[N-i+l];X[N-i+l]:=r;
Ends-
End;
Procedure Sim3(Var X:TArray);
Var YrTArray;
i : Integers-
Begin
For i:=lToNDoY[X[i]]:=i;
X:=Y;
Ends-
Function Cmp(X,YrTArray):Boolean;
Var i:Integer;
Begin
i:=l;
While (i<=N) And (Y[i]=X[i]) Do Inc(i);
If i>N
Then Cmp:=False
Else
If Y[i]<X[i] Then Cmp:=True Else Cmp:=False;
Ends-
Procedure Solve(i:Integer);
Var j:Integer;f:Boolean;
YrTArray;

94
3. Перебор и методы его сокращения
Begin
If i<=N
Then
Begin
For j :=1 To N Do
If D_hod(i,j) Then
Begin
Hod(i,j);
Solve(i+1);
O_hod(i,j);
End;
End
Else
Begin
f:=True;
For j :=0 To 7 Do
Begin
Y:=X;
If j And 1 =0 Then Siml (Y) ;
If j And 2 =0 Then Sim2 (Y) ;
If j And 4 =0 Then Sim3 (Y) ;
If Cmp(Y,X) Then f:=False;
End;
If f Then
Begin
Inc(S);{*Счетчик числа решений, глобальная
переменная.* }
Print;{*Вывод решения.*}
End;
End;
End;
Примечание
Программу решения задачи о шахматных ферзях можно написать
по-разному. Ниже по тексту приведено одно из возможных
решений*. Решение очень компактное, по-своему изящное, но не будем
комментировать его. Попробуйте разобраться с ним и ответить на
вопрос: в чем заключается отличие в стилях при написании
программ в этом примере и в целом в данном учебнике.
Текст программы из учебника по информатике для студентов
педагогических вузов.

3. Перебор и методы его сокращения
95
Program Ferz;
Uses Crt;
Const N=8;
Var B:Array [1. .N] Of Integers-
Procedure Rf(i:Integer);
Var j , k,p, t: Integers-
Begin
For j :=1 To N Do
Begin
B[i]:=j;k:=l;p:=0;
While (k<l) And (p=0) Do
Begin
If (B[k]=B[i]) Or (Abs(k-i)=Abs(B[k]-B[i]))
Then p:=l;
Inc(k);
End;
If p=0 Then
If i<N
Then Rf(i+1)
Else
Begin
For t:=l To N Do Write (B[t] :3) ;
WriteLn;
Ends-
End;
Ends-
Begin
ClrScr;
Rf (1);
End.
2. «Задача о шахматном коне».
Существуют способы обойти шахматным конем доску,
побывав на каждом поле по одному разу. Составить программу
подсчета числа способов обхода.
Разбор задачи начинается с оценки числа 64! — таково
общее число способов разметки доски 8x8. Каждую разметку
следует оценивать на предмет того, является ли она способом
обхода конем доски (решение в «лоб»). Затем оцениваем порядок
сокращения перебора исходя из условия — алгоритм выбора
очередного хода коня. Будем считать, что поля для хода
выбираются по часовой стрелке. Объяснение иллюстрируется
следующими рисунком 3.3.

96
3. Перебор и методы его сокращения
8 1
1
4
7
10
6
9
3
2
5
8
1
4
9
6
10
7
3
2
5
8
8
11
6
3
1
4
9
12
10
7
2
5
Рис. 3.3
Структуры данных.
Const N= ; М= ;
DxrArray[1..8] Of Integer^(-2,-1,1,2,2,1,-1-2) ;
Dy:Array[l. .8] Of Integer^(1,2,2,1,-1,-2,-2,-1) ;
Var AiArray[-1..N+2,-1 . .M+2] Of Integer;
t:Integer;
Основной фрагмент реализации — процедура Solve.
Procedure Solve(χ,у,q:Integer);
Var ζ, i,j:Integer;
Begin
A[x,y]:=q;
If q=N*M
Then Inc (t)
Else
For ζ :=1 To 8 Do
Begin
i:=x+Dx[z];j:=y+Dy[z] ;
If A[i,j]=0 Then Solve(ifj,q+l)
End;
A[x,y] :=0;
End;
Часть текста из основной программы имеет вид:
For i :=-l To N+2 Do
For j:=-1 То M+2 Do A[i,j]:=-1;{^Записываем
ХЛбарьерные" элементы, тем самым исключая лишние
операторы If, утяжеляющие текст программы.*}
For i :=1 To N Do
For j :=1 То Μ Do A[i, j] :=0;
t:=0;
1
4
6
3
5
2

3. Перебор и методы его сокращения 97
For i :=1 To N Do
For j : =1 То Μ Do Solve (i, j , 1) ;
WriteLn('число способов обхода конем доски ',
Ν,'*',Μ,' - ',t);
Если попытаться составить таблицу из числа способов
обхода конем шахматной доски для значений N и М, то окажется,
что быстродействия вашего компьютера не хватит для решения
этой задачи (а вы им так гордились!).
Изменим решение задачи о шахматном коне так, чтобы
находился только один вариант обхода конем доски. Применим
обход доски, основанный на правиле Варнедорфа выбора
очередного хода (предложено более 150 лет тому назад). Суть
последнего в том, что при обходе шахматной доски коня следует
ставить на поле, из которого он может сделать минимальное
количество перемещений на еще не занятые поля, если таких
полей несколько, можно выбирать любое из них. В этом случае
в первую очередь занимаются угловые поля и количество
«возвратов» в алгоритме значительно уменьшается. Найдите, для
каких значений N и Μ ваш компьютер будет справляться с
этой задачей?
Вариант процедуры Solve для этого случая.
Procedure Solve(x,у,q: Integer);
Var W: Array[1..8] Of Integer;
xn, yn,i,j,m,min: Integer;
Begin
A[x,y]:=q;
If (q<N*M) Then
Begin
For i :=1 To 8 Do
Begin{^Формирование массива W.*}
W[i] :=0;xn:=x+Dx[i];yn:=y+Dy[i] ;
If (A[xn,yn]=0)
Then
Begin
For j :=1 To 8 Do
If (A[xn+Dx[j],yn+Dy[j]]=0)
Then Inc(W[i]);
End
Else W[i] :=-l;
End;
i:=l;
While (i<=8) Do

98
3. Перебор и методы его сокращения
Begin
min:=Maxint;
т:=1;{*Ищем клетку, из которой можно сделать
наименьшее число перемещений.*}
For j : =2 То 8 Do
If W[ j ] <min Then
Begin m:=j;min:=W[j];End;
If (W[m]>=0) And (W[m]<Maxint) Then
Begin
Solve(x+Dx[m],y+Dy[m],1+1);
W[m]:=Maxint;{*Отмечаем использованную
в переборе клетку.*}
End;
Inc(i);
End;
End
Else
Begin
<вывод решения>;
halt;{^Исключение этого оператора, нарушающего
структурный стиль процедуры, одна из
требуемых модификаций программы.*}
End;
А[х,у]:=0;
End;
3. «Задача о лабиринте».
Классическая задача для изучения темы. Как и предыдущие
задачи, ее не обходят вниманием в любой книге по
информатике. Формулировка проста. Дано клеточное поле, часть клеток
занята препятствиями. Необходимо попасть из некоторой
заданной клетки в другую заданную клетку путем
последовательного перемещения по клеткам. Изложение задачи опирается на
рисунок произвольного лабиринта и «прорисовку» действий по
схеме простого перебора.
Классический перебор выполняется по правилам,
предложенным в 1891 году Э. Люка в «Математических
развлечениях»:
• в каждой клетке выбирается еще не исследованный путь;
• если из исследуемой в данный момент клетки нет путей,
то возвращаемся на один шаг назад (в предыдущую
клетку) и пытаемся выбрать другой путь.

3. Перебор и методы его сокращения
99
Э. Люка в 1891 году сформулировал общую схему решения
задач методом перебора вариантов.
Решение первой задачи.
Program Labirint;
Const Nmax=...;
Dx:Array[l..4] Of Integer=(1,0,-1,0);
Dy:Array[l..4] Of Integer=(0,1,0,-1);
Type MyArray=Array[0..Nmax+1,0..Nmax+1]
Of Integer;
Var AiMyArray;
xn,yn,xk,yk,N:Integer;
Procedure Init;
Begin
{*Ввод лабиринта, координат начальной и конечной
клеток. Границы поля отмечаются как
препятствия.*};
End;
Procedure Print;
Begin
{*Вывод матрицы А - метками выделен путь выхода
из лабиринта.*};
End;
Procedure Solve(χ,у,k:Integer);
{*k - номер шага,
χ, у - координаты клетки.*}
Var i : Integers-
Begin
А[х,у] :=k;
If (x=xk) And (y=yk)
Then Print
Else
For i :=1 To 4 Do
If A[x+Dx[i],y+Dy[i]]=0
Then Solve(x+Dx[i],y+Dy[i],k+1);
A[x,y] :=0;
End;
Begin
Init;
Solve(xn,yn,1);
End.

100
3. Перебор и методы его сокращения
С помощью данной схемы находятся все возможные
варианты выхода из лабиринта. Их очередность (массивы констант
Dx, Dy) определяется правилом просмотра соседних клеток.
Если требуется найти один выход из лабиринта, то требуется,
естественно, изменить решение.
Проделайте работу, сохранив при этом структурный вид
программного кода.
Второй способ решения задачи о лабиринте (поиск
кратчайшего по количеству перемещений пути) называют «методом
волны ».
Изложим суть метода. Начальную клетку помечают,
например, меткой со значением 1, а затем значение метки
увеличивается на единицу на каждом шаге (см. рисунок 3.4). Очередное
значение метки записывается в свободные клетки, соседние с
клетками, имеющими предыдущую метку. В любой момент
времени множество клеток, не занятых
препятствиями, разбивается на три
класса: помеченные и изученные; помеченные
и неизученные и непомеченные. Для
хранения клеток второго класса лучше всего
использовать структуру данных
«очередь» (мы предполагаем, что она изучена
ранее, например, по книге автора
«Основы программирования»). Процесс
заканчивается при достижении клетки выхода из лабиринта (есть
путь) или при невозможности записать очередное значение
метки (тупик). На рисунке 3.4 иллюстрируется этот процесс.
Темные клетки означают препятствия. Начальная клетка
находится вверху слева, конечная — внизу справа. Кроме того, из
рассмотрения примеров должно следовать понимание того
факта, что выход из лабиринта имеет кратчайшую длину.
Program Labirint;
Const NMax=...;
MMax=...;
DxrArray[1..4] Of Integer^(-1,0,1,0);
Dy:Array[1..4] Of Integer=(0,1,0,-1);
Type MyArray=Array[0..NMax+1,0..MMax+1] Of Integer;
Var A:MyArray;{*Глобальные переменные.*}
Ν,Μ:Integer;
χη,yn,xk,yk:Integer;
Function Solve:Boolean;
Type Och=Array[1..NMax*MMax,1..2] Of Integer;

3. Перебор и методы его сокращения 101
Var t,i,j,ykr,ykw:Integer;
0:0ch;{*0чередь.*}
Υ:Boolean;
Begin
A[xn,yn]:=l; ykr:=0{^Указатель чтения из
очереди.*};
ykw:=l; {^Указатель записи в очередь.*}
Υ:=False;{^Начальное присвоение.*}
О[ykw,1]:=хп;О[ykw,2]:=уп;{^Заносим координаты
начальной клетки в очередь.*}
While (ykr<ykw) And Not (Y) Do
Begin
{*Пока очередь не пуста и не найдено решение.*}
Iпс(ykr);i:=0[ykr,1];j:=0[ykr,2];{*Πο
указателю чтения берем элемент из
очереди.*}
If (i=xk) And (j=yk)
Then Y:=True
{*Если это клетка выхода из лабиринта, то
решение найдено.*}
Else
For t:=l To 4 Do
If A[i + Dx[t] ,j+Dy[t] ]=0 Then
Begin
{*B этой клетке мы еще не были.*}
A[i+Dx[t], j+Dy[t]]:=A[i,j]+l;
{^Присваиваем значение метки.*}
Inc(ykw);0[ykw,1]:=i+Dx[t];
0[ykw,2]:=j+Dy[t];{^Записываем
координаты клетки в очередь.*}
End;
End;
Solve:=Y;{^Результат работы функции Solve.*}
End;
Основная программа имеет вид:
Begin
Init;{*BBOfl лабиринта, координат начальной
и конечной клеток. Текст процедуры
не приводится.*}
Assign(Output,'Output.txt');Rewrite(Output);
{*Выводим результат (массив А) в файл.*}
If Solve

102
3. Перебор и методы его сокращения
Then Print{*Текст процедуры Print в силу
ее очевидности не приводится.*}
Else WriteLn('Нет пути');
Close(Output);
End.
Модифицируйте предыдущее решение так, чтобы находился
не один путь, а, например, t путей, если они существуют.
4. «Задача о рюкзаке (перебор вариантов)».
В рюкзак загружаются предметы N различных типов
(количество предметов каждого типа не ограничено). Максимальный
вес рюкзака W. Каждый предмет типа i имеет вес и>{ и
стоимость у. (/=1,2, ..., Ν). Требуется определить максимальную
стоимость груза, вес которого равен W.
Обозначим количество предметов типа i через ki9 тогда
требуется максимизировать
v1xk1+v2xk2+...+vNxkN
при ограничениях
wlxkl+w2xk2+...+wNxkN=W,
где k{ — целые (0 < /г. < [W/w.]), квадратные скобки означают
целую часть числа.
Рассмотрим простой переборный вариант решения задачи,
работоспособный только для небольших значений N
(определить, для каких?). Итак, данные:
Const MaxN=...;
Var Ν,W:Integer;
{^Количество предметов, максимальный вес.*}
Weight,Price:Array[l..MaxN] Of Integer;
{*Bec, стоимость предметов.*}
Best,Now:Array[1..MaxN] Of Integer;
{*Наилучшее, текущее решения.*}
MaxPrice:Longlnt;{^Наибольшая стоимость.*}
Решение, его основная часть — процедура перебора:
Procedure Solve(k,w:Integer;st:Longlnt);
{*k - порядковый номер группы предметов, w - вес,
который следует набрать из оставшихся
предметов, st - стоимость текущего решения.*}
Var i:Integer;
Begin
If (k>N) And (st>MaxPrice)

3. Перебор и методы его сокращения
103
Then
Begin {*Найдено решение.*}
Best:=Now;MaxPrice:=st;
End
Else If k<=N Then
For i:=0 To W Div Weight [k] Do
Begin
Now[k]:=i;
Solve(k+l,W-i*Weight[k],st+i*Price[k]);
End;
End;
Инициализация переменных, вывод решения и
вызывающая часть (Solve(19W,0)) очевидны.
5. «Задача о коммивояжере».
Классическая формулировка задачи известна уже более 200
лет: имеются N городов, расстояния между которыми заданы;
коммивояжеру необходимо выйти из какого-то города,
посетить остальные N-1 городов точно по одному разу и вернуться
в исходный город. При этом маршрут коммивояжера должен
быть минимальной длины (стоимости).
Задача коммивояжера принадлежит классу ЛГР-полных т. е.
неизвестны полиномиальные алгоритмы ее решения. В задаче с
N городами необходимо рассмотреть (iV-Ι)! маршрутов, чтобы
выбрать маршрут минимальной длины. Итак, при больших
значениях N невозможно за разумное время получить
результат.
Оказывается, что и при простом переборе не обязательно
просматривать все варианты. Это реализуется в данной
классической схеме реализации.
Структуры данных.
Const Мах=...;
Var A:Array[1..Мах,1..Max] Of Integer;
{*Матрица расстояний между городами.*}
В:Array[1..Мах,1..Max] Of Byte;{^Вспомогательный
массив, элементы каждой строки матрицы
сортируются в порядке возрастания, но сами
элементы не переставляются, а изменяются
в матрице В номера столбцов матрицы А.*}
Пример. На рисунке 3.5 приведены матрицы А и Б (после
сортировки элементов каждой строки матрицы А).

104
3. Перебор и методы его сокращения
А В
г г
| @ ! 27
1 7
20
21
I 12
|_23
@
П^
16
13 | @
16 ι 25
46
5
27
5
16
1
35
@
48
9
"~3(Г 26 !
30 ι 25
5 0
18
@
5
18 ί
5
_@j
РН 6~
|_4_[_1_
| 6 j 5
2 1 5
! 6 ! 1^
lZI
3
ΓΎ~
3
2
6
3
5
5
6
1
1
2
4
3 Ί
5
4
3
4
1
1
2
3
4
5
_d
Рис. 3.5
Примечание
Символом @ обозначено бесконечное расстояние.
Way,BestWay:Array[1..Max] Of Byte;{^Хранится
текущее решение и лучшее решение.*}
Nnew:Array[1..Max] Of Boolean;{^Значение
элемента массива False говорит о том,
что в соответствующем городе коммивояжер
уже побывал.*}
BestCost:Integer;{^Стоимость лучшего решения.*}
Идея решения. Пусть мы находимся в городе с номером υ.
Наши действия.
Шаг 1. Если расстояние (стоимость), пройденное
коммивояжером до города с номером υ, не меньше стоимости найденного
ранее наилучшего решения (BestCost), то следует выйти из
данной ветви дерева перебора.
Шаг 2. Если рассматривается последний город маршрута
(осталось только вернуться в первый город), то следует
сравнить стоимость найденного нового решения со стоимостью
лучшего из ранее найденных решений. Если результат сравнения
положительный, то значения BestCost и BestWay следует
изменить и выйти из этой ветви дерева перебора.
Шаг 3. Пометить город с номером υ как рассмотренный,
записать этот номер по значению Count в массив Way.
Шаг 4. Рассмотреть пути коммивояжера из города υ в ранее
не рассмотренные города. Если такие города есть, то перейти
на эту же логику с измененными значениями υ, Count, Cost,
иначе на следующий шаг.
Шаг 5. Пометить город υ как нерассмотренный и выйти из
данной ветви дерева перебора.
Прежде чем перейти к обсуждению алгоритма,
целесообразно разобрать этот перебор на примере. На рисунке 3.6 приведен
пример и порядок просмотра городов. В кружках указаны но-

3. Перебор и методы его сокращения
105
мера городов, рядом с кружками — суммарная стоимость
проезда до этого города из первого.
Третье отсечение
Θ ©
Первое отсечение
1J Вторая оценка (JZJ Первая оценка
Рис. 3.6
Итак, запись алгоритма.
Procedure Solve(v,Count:Byte;Cost:Integer);
{*v - номер текущего города; Count - счетчик числа
пройденных городов; Cost - стоимость текущего
решения.*}
Var i:Integer;
Begin
If Cost>BestCost Then Exit;{^Стоимость текущего
решения превышает стоимость лучшего из
ранее полученных.*}
If Count=N Then
Begin
Cost:=Cost+A[v,1];Way[N]:=v;{^Последний город
пути. Добавляем к решению стоимость
перемещения в первый город и сравниваем
его с лучшим из ранее полученных.*}
If Cost<BestCost Then
Begin BestCost:=Cost; BestWay:=Way;End;
Exit;{*0ператор нарушает структурный стиль
программирования - "любой фрагмент логики
должен иметь одну точку входа и одну точку
выхода. Следует убрать его" . *}
End;

106
3. Перебор и методы его сокращения
Nnew[v]:=False;Way[Count]:=v;{*Город с номером ν
пройден, записываем его номер в путь
коммивояжера.*}
For i :=1 To N Do
If Nnew[B[v,i]] Then
Solve(B[v,i], Count+l,Cost+A[v,B[v,i]]);
{*Поиск города, в который коммивояжер
может пойти из города с номером v.*}
Nnew[v]:=True; {^Возвращаем город с номером ν
в число непройденных.*}
End;
Первый вызов — Solve(l,l,0). Разработка по данному
«шаблону» работоспособной программы — техническая работа. Если
вы решитесь на это, то есть смысл проверить ее
работоспособность на примере матрицы А, приведенной на рисунке 3.7.
Решение имеет вид 189256107431, его стоимость 158.
@
32
19
33
22
41
18
15
16
I 31
32
@
51
58
27
42
35
18
17
34
19
51
@
23
35
49
26
34
35
41
33
58
23
@
33
37
23
46
46
32
22
27
35
33
@
19
10
23
23
9
41
42
49
37
19
@
24
42
42
10
18
35
26
23
10
24
@
25
25
14
15
18
34
46
23
42
25
@
1
32
16
17
35
46
23
42
25
1
@
32
31
34
41
32
9
10
14
32
32
@
Рис. 3.7
Задание. Оцените время работы программы. Если у вас
мощный компьютер, то создайте матрицу А[1..50,1..50] и
попытайтесь найти наилучшее решение с помощью разобранного
метода. Заметим, что набор 2500 чисел — утомительное
занятие и разумная лень — «двигатель прогресса».
3.3. Динамическое программирование
Идея метода. Это важнейший раздел изучаемой темы,
поэтому вполне применим принцип: чем больше разнообразных
задач, тем лучше. Разбор основной идеи метода и ее
обсуждение можно сделать на классической задаче о Черепашке.

3. Перебор и методы его сокращения
107
Черепашке необходимо попасть из пункта А в пункт Б. На
каждом углу она может поворачивать только на север или
только на восток. Время движения по каждой улице указано на
рисунке 3.8. Требуется найти минимальное время, за которое
Черепашка может попасть из пункта А в пункт Б.
3*
А1
2Ж 3
8 В
6А
6 7
Рис. 3.8
20
15
X
16
18
13
17
А*
21
11
16
19
4 6
Рис. 3.9
Υ
10
12
Путь, показанный на рисунке 3.8 линиями со стрелкой,
требует 21 единицу времени. Отметим, что каждый путь состоит
из 6 шагов: трех на север и трех на восток. Количество
возможных путей Черепашки 20 (Cg).
Мы можем перебрать все пути и выбрать самый быстрый.
Это метод полного перебора (ответ — 21). Для вычисления
каждого времени требуется пять операций сложения, а для
нахождения ответа — 100 операций сложения и 19 операций
сравнения. Задача решается вручную. Однако при N, равном 8, у
Черепашки уже 12870 путей. Подсчет времени для каждого
пути требует 15 операций сложения, а в целом — 193050
сложений и 12869 сравнений, то есть порядка 200000 операций.
Компьютер при быстродействии 1000000 операций в секунду
найдет решение за 0.2 секунды, а человек?
Предположим, что N равно 30, тогда количество различных
путей 60!х(30!х30!). Это очень большое число, его порядок 1017.
Количество операций, необходимых для поиска решения,
равно 60х1017. Компьютер с быстродействием 1000000 операций в
секунду выполнит за год порядка 3.2х1013 операций
(подсчитайте). А сейчас нетрудно прикинуть количество лет,
требуемых для решения задачи.
Вернемся к исходной задаче. Начнем строить путь
Черепашки от пункта Б. Каждому углу присвоим вес, равный
минимальному времени движения Черепашки от этого угла до пункта
Б. Как его находить? От углов Χ, Υ решение очевидно. Для
угла Ζ время движения Черепашки в пункт Б через угол X
равно 15 единицам, а через угол Υ — 11 единицам. Берем минима-

108
3. Перебор и методы его сокращения
льное значение, т. е. вес угла будет равен 11. Продолжим
вычисления. Их результаты приведены на рисунке 3.9. Путь,
отмеченный стрелками, является ответом задачи. Оценим
количество вычислений. Для каждого угла необходимо
выполнить не более двух операций сложения и одной операции
сравнения, т. е. три операции. При N, равном 300, количество
операций — 3x301x301, это меньше 1000000, и компьютеру
потребуется меньше одной секунды. Итак, много лет при N=30 и
1 секунда при N=300.
Идея второго способа решения задачи основана на методе
динамического программирования. Заслуга его открытия
принадлежит американскому математику Ричарду Беллману.
Выделим особенность задачи, которая позволяет решить ее
описанным способом. Мы начинаем с угла В (см. рисунок 3.9), и
для каждого угла найденное число является решением задачи
меньшей размерности. Поясним эту мысль. Если бы мы
решали задачу поиска пути Черепашки из пункта Τ в пункт Б, то
найденное число 17 — решение задачи. Для каждого угла
найденное значение времени не изменяется и может быть
использовано на следующих этапах.
3.4. Примеры задач для разбора идеи метода
динамического программирования
1. «Треугольник».
На рисунке 3.10 изображен треугольник из чисел.
Напишите программу, которая вычисляет наибольшую сумму чисел,
расположенных на пути, начинающемся в верхней точке
треугольника и заканчивающемся на основании треугольника.
7
! 3 8 |
I 8 10 I
2 7 4 4 I
|_4 5 2 6 5J
Рис. 3.10
• Каждый шаг на пути может осуществляться вниз по
диагонали влево или вниз по диагонали вправо.
• Число строк в треугольнике больше 1 и меньше 100.
• Треугольник составлен из целых чисел от 0 до 99.

3. Перебор и методы его сокращения
109
7
3
8
2
0
8
1
7
0
0
0
4
0
0
0
4
0
0
0
0
0
0
0
0
0
7
10
18
20
24
15
16
25
30
15
20
27
19
26
24
Рис. 3.11 Рис. 3.12
Рассмотрим идею решения на примере, приведенном в
тексте задачи. Входные данные запишем в матрицу D. Значения
элементов матрицы D приведены на рисунке 3.11
Будем вычислять матрицу R:array[l..MaxN,0..MaxN]
следующим образом, предварительно обнулив ее элементы:
R[l,l]:=D[1,1];
For i: =2 To N Do
For j :=1 To i Do
R[i, j]=max(D[i,j]+R[i-l,j] , D [i, j ] +R [ i-1, j-1 ] ) ;
где max — функция вычисления максимального из двух
чисел.
Осталось найти наибольшее значение в последней строке
матрицы R, оно равно 30 (см. рисунок 3.12).
2. «Степень числа».
Даны два натуральных числа N и k. Требуется определить
выражение, которое вычисляет kN. Разрешается использовать
операции умножения и возведения в степень, круглые скобки
и переменную с именем k. Умножение считается одной
операцией, возведению в степень q соответствует q-Ι операция.
Найти минимальное количество операций, необходимое для
возведения в степень N. Желательно сделать это для как можно
больших значений N.
Так, при N=5 требуются три операции — (kxk)2xk.
Определим массив Ор, его элемент Op[i] предназначен для
хранения минимального количества операций при возведении
в степень i (Op[l]=0). Для вычисления выражения, дающего
N-ю степень числа k, арифметические операции применяют в
некоторой последовательности, согласно приоритетам и
расставленным скобкам. Рассмотрим последнюю примененную
операцию.
Если это было умножение, тогда сомножителями являются
натуральные степени числа /г, которые в сумме дают N. Сте-

110
3. Перебор и методы его сокращения
пень каждого из сомножителей меньше N, и ранее вычислено,
за какое минимальное число операций ее можно получить.
Итак:
opnl:=Min{no всем ρ:1<ρ<Ν, Op[ρ]+0ρ[η-ρ]+1}.
Если последней операцией являлось возведение в степень, то
opn2:=Min;{ для всех ρ (^1) - делителей Ν,
Op[N div ρ]+ρ-1} .
Результат — Op[N]=Min(opnl,орп2). Фрагмент реализации:
Const MaxN=1000;
Var N, k: Integer;
Op: Array [1 . .MaxN] Of Integer;
Procedure Solve;
Var i, j : Integers-
Begin
For i: =2 To N Do
Begin
0p[i]:=0p[i-l]+l;
For j :=2 To i-1 Do
Begin
0p[i]:=Min(0p[i], 0p[j]+0p[i-j]+l);
If i Mod j=0 Then
0p[i]:=Min(0p[i], Op[i Div j]+j-l);
End;
End;
End;
3. «Алгоритм Нудельмана—Вунша» (из молекулярной
биологии).
Молекулы ДНК содержат генетическую информацию.
Моделью ДНК можно считать длинное слово из четырех букв (А, Г,
Ц, Т). Даны два слова (длины Μ и Ν), состоящие из букв А, Г,
Ц, Т. Найти подпоследовательность наибольшей длины,
входящую в то и другое слово.
Пусть есть слова ГЦАТАГГТЦ и АГЦААТГГТ. Схема
решения иллюстрируется рисунком 3.13. На рисунке закрашены
клетки, находящиеся на пересечении строки и столбца с
одинаковыми буквами.
Принцип заполнения таблицы W следующий: элемент W[i,j]
равен наибольшему из чисел W[i-l,j], W[iJ-l], а если клетка
<i,j> закрашена, то и W[i-l,j-l]+l.

3. Перебор и методы его сокращения
111
ί
|ц
τ
г
г
А
Τ
А
ц
Г
1
1
1
1
1
1
1
0
0
А
2
2
2
2
1
1
1
1
Г
Г
3
2
2
2
2
2
2
2'
1
ц
3
3
3
3
3
3
ι
3*
/
2
1
А
4
4
4
4
-4-
3
5
5
4
4
5
5
5
6
6
71
7
б*Ге|
5^5
U-r<
4J
гЗ^З
2
1
А
2
1
Τ
4
3
2
1
Г
4
4
3
2
1
Г
5
4
4
3
2
1
Τ
Рис. 3.13
Формирование первой строки и первого столбца
выполняется до заполнения таблицы и осуществляется так: единицей
отмечается первое совпадение, затем эта единица автоматически
заносится во все оставшиеся клетки.
Например, W[3,l] — первое совпадение в столбце, затем эта
единица идет по первому столбцу. Подпоследовательность
формируется при обратном просмотре заполненной таблицы от
клетки, помеченной максимальным значением. Путь — это
клетки с метками, отличающимися на единицу, буквы
выписываются из закрашенных клеток. Последовательность этих
букв — ответ задачи. Для нашего примера две
подпоследовательности: ГЦААГГТ и ГЦАТГГТ.
Фрагмент основного алгоритма.
For i:=l To Length (SI) Do
For j:=l To Length (S2) Do
Begin
A[i,j]:=Max(A[i-l,j],A[i,j-l]);
If Sl[i]=S2[j] Then
A[i,j] :=Max(A[i,j], A[i-1,j-1]+1);
End;
WriteLn ('Ответ: ',A[Length(SI),Length(S2)]);
4. «Разбиение выпуклого N-угольника».
Дан выпуклый Af-угольник, заданный координатами своих
вершин в порядке обхода. Он разрезается N-2 диагоналями на

112
3. Перебор и методы его сокращения
треугольники. Стоимость разрезания определяется суммой
длин всех использованных диагоналей. Найти разрез
минимальной стоимости.
Идея решения разбирается с использованием рисунка 3.14.
■^-/^
\ / А[к,1] многоугольник
Рис. 3.14
Обозначим через S[k,l] стоимость разрезания
многоугольника A[k,l] диагоналями на треугольники. При l=k+\ или k+2
S[k,l]=0, следовательно, l>k+2. Вершина с номером i, i
изменяется от /г+1 до 1—1, определяет какое-то разрезание
многоугольника A[k,l]. Стоимость разрезания определим как:
S[k,l]=min{dAUHa диагонали <к,г>+длина диагонали
<U>+S[&,i]+S[U]}. При этом следует учитывать, что при i=k+l
диагональ <k,i> является стороной многоугольника и ее длина
считается равной нулю. Аналогично при i=l-l.
5. «Задача о камнях».
Из камней весом pv p2,...., pN набрать вес W или, если это
невозможно, максимально близкий к W снизу вес.
Рассмотрим идею решения на следующих данных:
N равно 5, рг=5, ρ2=4* Рз=9> Р4=И» Рь=13, W=19.
Сформируем матрицу A (A:Array[l..N,0..W] Of Integer), в
которой номер строки соответствует номеру камня, а номер
столбца — набираемому весу. В нулевой столбец запишем
нули, в первую строку (по столбцам) до веса первого камня
нули, а затем вес первого камня (пытаемся набрать
требуемый вес одним камнем). Во второй строке фиксируем
результат набора веса с помощью двух камней и т. д. После
заполнения А имеет вид, показанный на рисунке 3.15. Вес 19
набрать нельзя, ближайший снизу вес 18.

3. Перебор и методы его сокращения
113
1
гг
2
3
4
|_5
и
0
0
0
0
0
1
0
0
0
0
0
2
0
0
0
0
0
3
0
0
0
0
0
4
0
0
0
0
0
ь
5
5
5
5
5
6
5
5
5
5
5
/
5
7
7
7
7
В
5
7
7
7
7
9
5
7
9
9
9
10
5
7
9
9
9
11
5
7
9
11
11
12
5
12
12
12
12
13
5
12
12
12
12
14
5
12
14
14
14
15
5
12
14
14
14
16
5
12
16
16
[l6j
17
5
12
16
16
16
18
5
12
16
18
18
19
5
12
16
18 \
18\
Рис. 3.15
Для заполнения текущей строки достаточно знать только
предыдущую строку (результат решения задачи меньшей на
единицу размерности), а в элементе массива A[i,j] записывается
решение задачи о камнях при N=i и W=j.
Программный код решения компактен и не требует
пояснений.
Procedure Solve;
Var i, j :Integer;
Begin
For i: =2 To N Do
For j :=1 To W Do
Begin
If j-P[i]>=0
Then
A[i,j]:= Max(A[i-l,j],
A[i-l,j-P[i]]+P[i])
Else A[i,j] :=A[i-l,j] ;
End;
End;
Для ответа на вопрос, «из каких камней набирается вес»,
решение необходимо дополнить простой рекурсивной
процедурой. В таблице на рисунке 3.15 курсивом выделена часть
элементов, задействованных при работе процедуры, а жирным
шрифтом те значения i и у, при которых осуществляется вывод
веса камня Ρ[ΐ].
Procedure Way(i,j:Integer);
Begin
If (i=l) And (A[i,j]=0)
Then Exit
Else
If i = l

114
3. Перебор и методы его сокращения
Then
Begin
Way(i,j-P[i]);
Write(P[i], ' ');
End
Else
If A[i,j]OA[i-l,j]
Then
Begin Way(i,j-P[i]);Write(P[i],' ') ;End
Else Way(i-1,j);
End;
6. «Задача о рюкзаке (к весу камней добавляется и их
стоимость)».
Напомним формулировку задачи. В рюкзак загружаются
предметы N различных типов (количество предметов каждого
типа не ограничено). Вес рюкзака должен быть меньше или
равен W. Каждый предмет типа i имеет вес wt и стоимость и.
(ί=1,2, ..., Ν). Требуется определить максимальную стоимость
груза, вес которого не превышает W.
Рассмотрим случай, когда вес рюкзака в точности равен W.
Обозначим количество предметов типа i через /г., тогда
требуется максимизировать и1х/г1+и2х/г2+...+иА^х/^ при ограничениях
wlxkl+w2xk2+...+wNxkN=W,
где hi — целые (0 < kt < [W/wJ), квадратные скобки означают
целую часть числа.
Формализуем задачу следующим образом. Шаг i ставится в
соответствие типу предмета i=l,2,...,iV. Состояние yi на шаге ί
выражает суммарный вес предметов, решение о загрузке
которых принято на шагах Ο,Ι,.,.,ί. При этом yn=W, i/.=0,l,...,W
при i=l,2,...,Af-l. Варианты решения к{ на шаге i описываются
количеством предметов типа i, 0 < kt < [W/wJ.
Уточним идею на конкретных данных. Пусть W=6, и дано
четыре предмета (см. таблицу 3.1).
Таблица 3.1
i
1
2
! з
4
Wj
2
3
1
4
Vi Ί
50 Ι
90
30
140

3. Перебор и методы его сокращения
115
Схема работы для данного примера приведена на рисунке
3.16. В кружочках выделены только достижимые состояния
(суммарные веса для каждого шага в соответствии с
приведенной выше формализацией) на каждом шаге. В круглых скобках
указаны стоимости соответствующих выборов, в квадратных
скобках — максимальная стоимость данного заполнения
рюкзака. «Жирными» линиями выделен способ наилучшей
загрузки рюкзака.
Рис. 3.16
Текст решения.
Const MaxN=...;
МахК=
Type Thing=Record
W,V: Word
End;
Var A: Array[1..MaxN,0..MaxK] Of Word;
P: Array[1..MaxN] Of Thing;
01d,NewA:Array[0..MaxK] Of Longlnt;
N,W:Integer;
Procedure Solve;
Var k,i,j:Integer;
Begin
FillChar(Old,SizeOf(Old),0);
For k:=l To N Do

116
3. Перебор и методы его сокращения
Begin{*Цикл по шагам.*}
FillChar(NewA,SizeOf(NewA),0);
For i:=0 To W Do {*Цикл по состояниям шага.*}
For j:=0 To i Div P[k] .W Do {*Цикл по вариантам
решения - количеству предметов каждого
вида.*}
If j*P[k].V+01d[i-j*P[k].W]>=NewA[i] Then
Begin
NewA[i]:=j*P[k].V+Old[i-j*P[k].W];
A[k,i]:=j;{*3десь j количество предметов?*}
End;
01d:=NewA;
End;
End;
Вывод наилучшего решения.
Procedure OutWay(k,1:Integer);
Begin
If k=0 Then Exit
Else
Begin
OutWay(k-1,1-A[k,1]*P[k].W);{*A здесь
вес.*}
Write(A[k,1],' ' ) ;
End;
End;
Первый вызов — OutWay(N,W). Эту схему реализации
принято называть «прямой прогонкой». Ее можно изменить. Пусть
пункт два формализации задачи звучит следующим образом.
Состояние г/, на шаге i выражает суммарный вес предметов,
решение о загрузке которых принято на шагах i, i+1, ..., N при
этом yx=W, г/.=0,1,...,Ж при i=2,3, ...,N. В этой формулировке
схему реализации называют «обратной прогонкой».
Иллюстрация к этой схеме приведена на рисунке 3.17.
3.5. Метод ветвей и границ*
Идея метода ветвей и границ обычно излагается по работе
Дж. Литтла. Не отступим и мы от этой традиции. Суть идеи
проста. Все перебираемые варианты следует разбить на классы
Литтл Дж., Мурти К., Суини Д., Кэрел Е. Я. Алгоритм решения задачи
коммивояжера. //Экономика и математические методы. 1965. №1. С. 13-22.

3. Перебор и методы его сокращения
117
Рис. 3.17
(блоки), сделать оценку снизу (при минимизации) для всех
решений из одного класса, и если она больше ранее полученной,
то отбросить все варианты из этого класса. Весь вопрос в том,
как разделять на классы.
Пусть решается задача о коммивояжере. Дана матрица
расстояний — полный граф (см. рисунок 3.18).
1
2
3
4
5
6
1
-
9
13
5
16
6
2
7
-
3
3
4
2
8
11
5
6
13
9
4
10
5
9
-
10
8
5
17
8
11
3
-
4
6
5
6
14
6
8
-
Рис. 3.18
Если мы будем вычитать одно и то же число из всех
элементов строки или столбца, то суммарная стоимость пути
коммивояжера не изменится. При вычитании константы из
элементов строки стоимость любого пути уменьшится на эту
константу, ибо числа в строке соответствуют выезду из
города, а выезд из этого города обязательно присутствует в пути.
Точно так же и вычитание из элементов столбца — въезд в
город. Вычитаемая константа входит в оценку пути, но не
рассматривается дальше, после изменения матрицы. Найдем
минимум в каждой строке и вычтем его. Получается матрица,

118
3. Перебор и методы его сокращения
которая приведена на рисунке 3.19. Сумма вычитаемых
констант равна 24.
1
2
3
4
5
6
1
-
5
11
2
8
2
2
4
-
0
5
3
1
3
0
0
-
3
5
5
4
7
1
7
-
2
4
5
14
4
9
0
-
0
6
2
2
12
3
0
-
Рис. 3.19
Аналогичную операцию выполним со столбцами: из
элементов первого вычитаем 2, а из элементов четвертого — 1.
Итоговая сумма — 27. Все пути коммивояжера уменьшились на это
значение.
1
2
3
4
5
6
1
-
3
9
0
6
0
2
4
-
0
5
3
1
3
0
0
-
3
5
5
4
6
0
6
-
1
3
5
14
4
9
0
-
0
6
2
2
12
3
0
-
Рис. 3.20
Если получается выбор по одному нулю в каждом столбце и
строке (они выделены курсивом в матрице на рисунке 3.20), то
тем самым мы получаем путь коммивояжера со стоимостью 27.
Это путь (1-^3->2—»4—»5—»6—»1) с минимальной стоимостью,
любой другой путь имеет большую стоимость. Значение 27 —
это оценка снизу всех маршрутов коммивояжера. В данном
случае она достигается на конкретном маршруте. Очевидно,
что мы просто очень удачно подобрали пример. Не обязательно
после приведения существование пути по ребрам с нулевой
стоимостью. Продолжим рассмотрение. Пусть дана другая
матрица расстояний, она приведена на рисунке 3.21.

3. Перебор и методы его сокращения
119
1
2
3
4
5
6
1
-
2
3
7
6
5
2
1
-
4
6
5
4
3
2
3
-
5
4
3
4
3
4
5
-
3
2
5
4
5
6
7
-
1
6
5
6
7
8
2
-
Рис. 3.21
После приведения по строкам и столбцам (сумма констант
приведения равна 14) получаем новую матрицу, которая
представлена на рисунке 3.22.
1
2
3
4
5
6
1
-
0°
0
4
4
4
2
О1
-
1
3
3
3
3
0°
0
-
1
1
1
4
1
1
1
-
0
0°
5
3
3
3
1
-
0
6
4
4
4
0
0°
-
Рис. 3.22
Рис. 3.23
Выделенные курсивом нули дают путь,
но это не путь коммивояжера. Его вид
показан на рисунке 3.23. Наши дальнейшие
действия (шаг ветвления). Рассмотрим
нули в приведенной матрице (см. рисунок
3.22), именно нуль в позиции (1, 2). Он,
естественно, означает, что стоимость переезда из первого во
второй город равна нулю. Однако если исключить (запретить)
переезд из первого во второй город, то въезжать во второй
город все равно придется. Цены въезда указаны во втором
столбце — въезжать из третьего города дешевле всего. Так как
выезжать из первого города нам когда-либо придется, то дешевле
всего выехать в третий город — нулевая стоимость. Вычисляем
сумму этих минимумов, она равна 1+0=1. Суть этой единицы в
том, что если не ехать из первого города во второй, то
придется заплатить не менее 1. Эта оценка нуля указана в матрице
верхним индексом. Сделаем оценки всех нулей и выберем
элемент с максимальной оценкой. Если таких нулей несколько,

120
3. Перебор и методы его сокращения
то выбираем любой. Итак, в чем суть ветвления. Все маршруты
коммивояжера разбиваются на два класса, содержащих ребро
(1,2) и не содержащих ребро (1,2). Для последнего класса
оценка снизу увеличивается на единицу, т. е. равна 15. Для
маршрутов из первого класса продолжаем работать с матрицей.
Исключаем (вычеркиваем) первую строку и второй столбец. Кроме
того, в уменьшенной матрице на место (2,1) следует поставить
прочерк, означающий невозможность соответствующего
переезда. После этих манипуляций матрица примет следующий
вид, приведенный на рисунке 3.24.
2
3
4
5
6
1
-
О5
4
4
4
3
О2
-
1
1
1
4
1
1
-
0°
0°
5
3
3
1
-
о1
6
4
4
О1
0°
-
Рис. 3.24
Продолжим наши действия по оценке маршрутов из первого
класса (см. рисунки 3.25, 3.26, 3.27). Сокращенную матрицу, к
сожалению, приводить нельзя — минимальные элементы во
всех строках и столбцах равны нулю. Таким образом, оценка
снизу для класса маршрутов, содержащих (1,2), остается
равной 14. С сокращенной матрицей выполним аналогичные
действия — оценим нули, выберем нуль, соответствующий
переезду из третьего города в первый. Суть действий в разбивке этого
класса маршрутов на подклассы по той же самой схеме — с
(3,1) и без (3,1). Для второго подкласса оценка снизу 14+5=19.
С первым подклассом аналогичные действия — исключаем
столбец и строку, на место (2,3) в таблице пишем запрет на
перемещение. Матрица допускает операцию приведения.
Вычитаем единицу из элементов первой строки и первого столбца.
2
4
5
6
3
-
0°
0°
0°
4
О2
-
0°
0°
5
2
1
-
О1
6
3
0°
0°
-
2
4
5
6
3
-
1
1
1
4
5
1 3
- I 1
0
0
-
0
6
4
0
-
1
4
5
6
3
-
0°
5
1
-
о° | о0
6
О1
0°
-
Рис.3.25
Рис. 3.26
Рис. 3.27

3. Перебор и методы его сокращения
121
Нижняя оценка маршрутов этого
подкласса возрастает на два,
итого 14+2=16. Следующий шаг
приводит к матрице еще
меньшего размера. Весь процесс работы
по рассматриваемой схеме
представлен на рисунке 3.28.
Вершины этого дерева представляют
классы решений. Черта над
цифрами означает, что
соответствующий класс не содержит какой-то
конкретный переезд из города в
город. Числа у вершин дерева Рис· 3.28
означают оценки снизу для
маршрутов из данного класса. Итак, получена первая оценка — 16
для маршрута 1—»2—»4—»6—»5—»3—»1. Все подклассы решений, у
которых оценка снизу больше или равна 16, исключаются из
рассмотрения — очевидный факт после изложения схемы
решения. Остался только подкласс без переезда из первого города
во второй, его оценка равна 15. Однако после первого же
ветвления получаются подклассы с оценками 16 и 17. Обработку
можно заканчивать. Найден наилучший маршрут
коммивояжера, стоимость проезда по этому маршруту равна 16.
Программная реализация метода ветвей и границ —
хорошая проверка техники программирования (структурного стиля
самого процесса написания программы). Что лучше? Или
работать с матрицами различной размерности, или вводить
дополнительные структуры для хранения исключенных номеров
строк и столбцов? Вопросы можно продолжить. Ответ даст
эксперимент с различными версиями программ реализации
алгоритма.
В п. 3.2.2 рассмотрена одна схема решения задачи
коммивояжера, в данном пункте — другая. В чем их отличие для
различных значений размерности задачи N? По некоторым
оценкам, с помощью метода ветвей и границ можно решать задачи с
ЛК100.
3.6. Метод «решета»
Идея метода. Решето представляет собой метод
комбинаторного программирования, который рассматривает конечное
множество и исключает все элементы этого множества, не
представляющие интереса. Он является логическим дополнением к
процессу поиска с возвратом (backtrack), в котором мы пытаем-

122
3. Перебор и методы его сокращения
ся постепенно перечислить все возможные варианты решения.
В решете идут от обратного — от всего множества решений
задачи.
Решето Эратосфена. Эратосфен — греческий математик,
275-194 гг. до наглей эры. Классическая задача поиска
простых чисел в интервале [2..N] — инструмент для обсуждения
метода. Объяснение строится на основе рисунка 3.29 и
фрагмента алгоритма.
Исходная последовательность:
2 3 4 I 5 | 6 7 8 9 10 11 I 12 13 14 I 15 I 16 17 18 19 20 21 22 23 24 25 I 26 27 28 29 30 31 32
| 2 | 3 ! 4
11J12 13 14 15 !6Jl7 181 19J20 21 f22 23 24125 26 27 28 29 30 31 35
Выделенные элементы последовательности отбрасываются, в
результате получаем:
»
3
5
со
7
9 10
11
13
15
17
19
21
23
25
27
29
31
2
3
5
6
7 J9^ 10 | 11
13 15 17
19 21
23
25 27 29
31
Выделенные элементы последовательности отбрасываем, в
результате получаем:
Τ
10
11 I 13
17 | 19 23
25 29
31
Рис. 3.29
Const N= . . .; {*Верхняя граница интервала чисел.
Type Number=Set Of 2..Ν;{решето, Ν<256}
Var S:Numbe r;
Procedure Search(Var S:Number);
Var i,j:2..N;
Begin
S:=[2..N];
For i : =2 To N Div 2 Do
If i In S Then
Begin
j:=i+i;
While j<=N Do
Begin S:=S-[j];j:=j+i; End;
End;
End;

3. Перебор и методы его сокращения
123
Логическим развитием задачи является ее решение при N
больших 256. В этом случае необходимо ввести массив с
множественным типом данных элементов.
«Быки и коровы»*.
Компьютер и ребенок играют в следующую игру. Ребенок
загадывает последовательность из четырех (не обязательно
различных) цветов, выбранных из шести заданных. Для удобства
будем обозначать цвета цифрами от 1 до 6. Компьютер должен
отгадать последовательность, используя информацию, которую
он получает из ответов ребенка.
Компьютер отображает на экране последовательность, а
ребенок должен ответить (используя для ввода ответа
клавиатуру) на два вопроса:
• сколько правильных цветов на неправильных местах;
• сколько правильных цветов на правильных местах.
Пример. Предположим, что ребенок загадал
последовательность 4655. На рисунке 3.30 приведена последовательность
шагов по отгадыванию числа.
Компьтер
1234
5156
6165
5625
5653
4655
Ответ ребенка
1 0
2 1
2 1
1 2
1 2
0 4
Рис. 3.30
Один из возможных способов отгадать последовательность
такой:
написать программу, которая всегда отгадывает
последовательность не более чем за шесть вопросов, в худшем случае — за
десять.
Правильный выбор структур данных — это уже половина
решения. Итак, структуры данных и процедура их
инициализации.
Const Pmax=6*6*6*6;
Type Post=String [4];
Var A-.Array [1. .Pmax] Of Post;
B:Array[1..Pmax] Of Boolean;
Модификация задачи Антона Александровича Суханова.

124
3. Перебор и методы его сокращения
cnt:Integer;{*Счетчик числа ходов.*}
ok:Boolean;{^Признак - решение найдено.*}
Procedure Init;
Var i,j,k,1:Integer;
Begin
For i:=l To 6 Do
For j :=1 To 6 Do
For k:=l To 6 Do
For 1 :=1 To б Do
A[(i-1)*216+(j-l)*36+(k-1)*6+l]:=
Chr (i+Ord('0' ) )+Chr (j+Ord('0' ) ) +
+Chr (k+Ord('0' ) ) +Chr (1+OrdC 0' )) ;
For i:=l To Pmax Do B[i] :=True;
cnt:=0;ok:=False;
End;
Поясним на примере идею решета. Пусть длина
последовательности равна двум, а количество цветов — четырем.
Ребенок загадал 32, а компьютер спросил 24. Ответ ребенка 1 О,
фиксируем его в переменных kr (1) и bk(0).
Таблица 3.1
А
11
12
13
14
Ρ 21
22
23
24
31
| 32
33
34
41
42
I ^
44
В
True
True
True
True
True
True
True
True
True
True
True
True
True
True
True
True
В (после анализа Ьк)
False
False
False
False
False
False
False
В (после анализа кг)
False
False
False
False
False
Результат
False
True ]
False
False
False
False
False \
False
False
True I
False
False
True j
False
True I
False

3. Перебор и методы его сокращения
125
Итак, было 16 возможных вариантов, после первого
осталось четыре (см. таблицу 3.1) — работа решета. Функция,
реализующая анализ элемента массива А по значениям
переменных kr и bk, имеет вид:
Function Pr (a, b: Post; kr,bk: Integer) .-Boolean;
Var i,χ:Integer;
Begin
{^Проверка по "быкам".*}
x:=0;
For i:=l To 4 Do
If a[i]=b[i] Then Inc(x);
If xobk Then
Begin Pr:=False;Exit;End;
{^Проверка по "коровам".*}
x:=0;
For i:=l To 4 Do
If (a[i]ob[i]) And (Pos (b [i] , a) <>0)
Then Inc(x);
If xokr Then
Begin Pr:=False;Exit;End;
Pr:=True;
End;
Логика — «сделать отсечение» по значению хода А.
Procedure Hod(h:Post);
Var i, kr,bk: Integers-
Begin
Inc(cnt);Write(cnt:2,' . ' ,h, '-' ) ;
ReadLn(kr,bk);
If bk=4 Then
Begin ok:=True;<вывод результатам-End
Else
For i:=l To Pmax Do
If B[i] And Not Pr (A[i] , h,kr,bk)
Then В[i]:=False;
End;
Основная программа.
Begin
ClrScr;
Ι η ί t;

126
3. Перебор и методы его сокращения
Hod ('1223');
While Not ok Do
Begin
Г выбор очередного хода из А |
Hod(h) ;
End;
End.
Дальнейшая работа с задачей требует ответа на следующие
вопросы:
• Зависит ли значение cnt от выбора первого хода?
Установите экспериментальным путем.
• Как алгоритм выбора очередного хода влияет на результат
игры? Исследуйте. Например, выберите тот элемент А
(соответствующий элемент В должен быть равен True), в
котором количество несовпадающих цифр максимально.
Примечание
Рассмотренные задачи носят учебный характер. Обычно идеи
метода решета используются в совокупности с другими методами.
3.7. Задачи
1. Задача о парламенте*.
На острове Новой Демократии каждый из жителей
организовал партию, которую сам и возглавил. Любой из жителей острова
может состоять не только в своей партии, но и в других партиях.
К всеобщему удивлению, даже в самой малочисленной партии
оказалось не менее двух человек. К сожалению, финансовые
трудности не позволили создать парламент, куда вошли бы, как
предполагалось по Конституции острова, президенты всех
партий. Посовещавшись, островитяне решили, что будет достаточно,
если в парламенте будет хотя бы один член каждой партии.
Помогите островитянам организовать такой, как можно
более малочисленный парламент, в котором будут представлены
все партии.
Исходные данные: каждая партия и ее президент имеют один
и тот же порядковый номер от 1 до Ν (4<Ν < 150). Вам даны
списки всех N партий острова Новой Демократии. Выведите
предлагаемый вами парламент в виде списка номеров ее членов.
Например, для четырех партий результат приведен в таблице 3.2.
Межгосударственная олимпиада по информатике 1992 года, автор задачи
Ю. Корженевич.

3. Перебор и методы его сокращения
127
Таблица 3.2
Список членов парламента 2 состоит из одного жителя с
номером 2.
Указание. Задача относится к классу NP-полных задач. Ее
решение — полный перебор всех вариантов. Начиная с
подмножеств мощности 1, требуется генерировать все возможные
подмножества множества жителей (до подмножеств мощности N
Div 2) и заканчивать процесс в том случае, когда будет найдено
решение для подмножеств определенной мощности.
Покажем, что ряд эвристик позволяет сократить перебор
для некоторых наборов исходных данных.
Представим информацию о партиях и их членах с помощью
следующего зрительного образа — таблицы (см. таблицу 3.3).
Номером строки является номер партии, номером столбца —
номер жителя.
Таблица 3.3
Номер
партии
1
2
3
[ 4
Номер жителя |
1
1
0
1
0
2
1
1
1
1
3
1
1
1
0
4
1
0
1
0 J
Тогда задачу можно переформулировать следующим образом.
Найти минимальное число столбцов, таких, что множество
единиц из них «покрывает» множество всех строк. Очевидно, что
для нашего примера это один столбец — второй.
Рассмотрим еще один пример (см. рисунок 3.31). Из
первоначальной таблицы можно исключить третий столбец,
соответствующий третьему жителю, — множество партий, в которых
он состоит, содержится в множестве партий, в которых состоит
второй житель. После сокращения таблицы могут появиться
строки с одной единицей (партия представлена одним
жителем). Таких жителей необходимо включать в парламент.
Включаем второго жителя. После этого останется представить в
парламенте только четвертую партию. Итак:

128
3. Перебор и методы его сокращения
жители
π
a /l 1 1 0 \ /lll\
Ρ 0101 J 0 10
τ 0 1 1 0 Ί Oil
и \ 1 0 0 1 / \100/
и
Рис. 3.31
• во-первых, требуется проверять, есть ли житель,
представляющий все множество не представленных в
парламенте партий;
• во-вторых, исключать часть жителей из рассмотрения,
если есть жители, представляющие большее количество
партий, и это множество партий содержит партии
исключаемого жителя;
• в-третьих, если в результате предыдущей операции
появляются партии, представленные одним жителем, то этих
жителей обязательно требуется включать в парламент.
Вывод: перебор следует выполнять не по всем жителям и не
для всех партий. Второе и третье действия необходимо
выполнить до момента начала перебора вариантов (предварительная
обработка) и только затем выполнять схему перебора. Первое
действие должно выполняться как на стадии предварительной
обработки, так и в процессе перебора.
Общая схема перебора реализуется как обычно. Приведем
часть описания данных для того, чтобы она была понятна.
Const Nmax=150;
Type Nint=0..Nmax+l;
Sset=Set Of 0..Nmax;
Var A:Array[Nint] Of <информация по каждому жителю>;
Ν:Integer;{*Число жителей на острове*.}
Один из вариантов решения.
Procedure Solve(k:Nint;Res,Rt:Sset); {*k- номер
элемента массива A; Res - множество партий,
которые представлены в текущем решении; Rt -
множество партий, которые следует "покрыть"
решением; min - минимальное количество членов
в парламенте; mn - число членов парламента
в текущем решении; Rbest - минимальный парламент;
Rwork - текущий парламент; первый вызов -
Solved, Π, [1. -Ν]) .*}
Var i:Nint;

3. Перебор и методы его сокращения 129
Begin
1 блок общих отсечений |
If Rt=[]
Then
Begin
If nm<min
Then
Begin min:=mn; Rbest:=^Rwork End;
End
Else
Begin
i:=k;
While i<=N Do
Begin
Г блок отсечений по i |
Include(i);{*Включить жителя, информация
по которому записана на месте i в
массиве А, в решение.*}
Solve(i+1,Res+A[i].part,Rt-A[i].part);
Exclude(i);{^Исключить из решения.*}
Inc (i);
End;
End;
End;
В качестве примера действий в блоке общих отсечений
можно взять следующий алгоритм. Подсчитать для каждого
значения ί (1 <i<t) множество партий, представляемых жителями,
номера которых записаны в элементах массива с г по ί (массив
C:Array[l..N] Of Sset). Тогда, если Res — текущее решение, а
Rt — множество партий, требующих представления, то при
Res+C[i\ < Rt решение не может быть получено и эту ветку
перебора следует «отсечь».
Пример отсечений по i — если при включении элемента с
номером i в решение значение величины Rt не изменяется, то
это включение жителя, информация по которому записана на
месте i в массиве А, бессмысленно.
2. Какое наименьшее число ферзей можно расставить на
доске так, чтобы они держали под боем все ее свободные поля?
Модификация задачи. Найти расстановку ферзей, которая
одновременно решает задачу для досок 9x9, 10x10 и 11x11.

130
3. Перебор и методы его сокращения
Указание. Задачу можно решать как обычным перебором,
так и, представив доску как граф, путем поиска минимального
доминирующего множества вершин.
3. Расставить на доске ΝχΝ(Ν < 12) N ферзей так, чтобы
наибольшее число ее полей оказалось вне боя ферзей.
4. Расставить на доске как можно больше ферзей так, чтобы
при снятии любого из них появлялось ровно одно неатакован-
ное поле.
5. Задача о коне Аттилы («Трава не растет там, где ступил
мой конь!»).
На шахматной доске стоят белый конь и черный король.
Некоторые поля доски считаются «горящими». Конь должен
дойти до неприятельского короля, повергнуть его и вернуться на
исходное место. При этом ему запрещено становиться как на
горящие поля, так и на поля, которые уже пройдены.
6. Магараджа — это фигура, которая объединяет в себе ходы
коня и ферзя. Для доски 10x10 найти способ расстановки 10
мирных (не бьющих друг друга) магараджей.
7. Пронумеровать позиции в матрице (таблице) размером
5x5 следующим образом. Если номер i (1 < i < 25) соответствует
позиции с координатами (х,г/), вычисляемыми по одному из
следующих правил:
(z,w)=(x±39 у);
(z,w)=(x, у±3);
(z,w)=(x±2, y±2).
Требуется:
• написать программу, которая последовательно нумерует
позиции матрицы 5x5 при заданных координатах
позиции, в которой поставлен номер 1 (результаты должны
быть представлены в виде заполненной матрицы);
• вычислить число всех возможных расстановок номеров
для всех начальных позиций, расположенных в правом
верхнем треугольнике матрицы, включая ее главную
диагональ.*
Третья международная олимпиада по информатике, 1991 год.

3. Перебор и методы его сокращения
131
8. Замок*.
На рисунке 3.32 изображен план замка.
12 3 4 5 6 7
w<-
Рис. 3.32
N
->Е
Написать программу, которая определяет:
• количество комнат в замке;
• площадь наибольшей комнаты;
• какую стену в замке следует удалить, чтобы получить
комнату наибольшей площади.
Замок условно разделен на ΜχΝ клеток (М < 50, N > 50).
Каждая такая клетка может иметь от 0 до 4 стен.
План замка содержится во входном
файле в виде последовательности
чисел, по одному числу,
характеризующему каждую клетку. В начале файла
расположено число клеток в направлении с
севера на юг и число клеток в
направлении с запада на восток. В последующих
строках каждая клетка описывается
числом ρ (0 <р < 15). Это число
является суммой следующих чисел: 1 (если
клетка имеет западную стену), 2
(северную), 4 (восточную), 8 (южную). Внутренняя стена
считается принадлежащей обеим клеткам. Например, южная стена в
клетке (1,1) также является северной стеной в клетке (2,1).
Пример входного файла представлен на рисунке 3.33.
Замок содержит по крайней мере две комнаты.
В выходном файле должны быть три строки. В первой
строке содержится число комнат, во второй — площадь
наибольшей комнаты (измеряется количеством клеток). Третья строка
содержит три числа, определяющих удаляемую стену: номер
Пример.
4
7
11 6 11 6 3 10 6
7 9 6 13 5 15 5
1 10 12 7 13 7 5
13 11 10 8 10 12
13
Рис. 3.33
Шестая международная олимпиада по информатике, 1994 год.

132
3. Перебор и методы его сокращения
строки, номер столбца клетки, содержащей удаляемую стену, и
положение этой стены в клетке (N — север, W — запад, S —
юг, Ε — восток).
9. Автозаправка.
Вдоль кольцевой дороги расположено Μ городов, в каждом
из которых есть автозаправочная станция. Известна стоимость
Z[i] заправки в городе с номером i и стоимость C[i] проезда по
дороге, соединяющей i-й и (/+1)-й города, С[М] — стоимость
проезда между первым и М-м городами. Для жителей каждого
города определить город, в который им необходимо съездить,
чтобы заправиться самым дешевым образом, и направление —
«по часовой стрелке» или «против часовой стрелки», города
пронумерованы по часовой стрелке.
Указание. Переборный вариант решения задачи сводится к
проверке всех 2хМ вариантов для жителей каждого города,
итого — 2хМхМ проверок.
Введем два дополнительных массива
On, Ag: Array [1..M] Of Record
wh, pr:Integer
End; .
On[i] означает, где следует заправляться (wh) и стоимость
заправки (рг) жителям /-го города, если движение разрешено
только по часовой стрелке. В этом случае жители города i
имеют две альтернативы: либо заправляться у себя в городе, либо
ехать по часовой стрелке. Во втором случае жителям города i
надо заправляться там же, где и жителям города i+Ι, или в
первом, если i=M. Итак, On[i]=min{Z[i],C[i]+On[i+l].pr}.
Откуда известно значение Оп[/+1].рг? Необходимо найти город j с
минимальной стоимостью заправки — On[j]:=(j,Z[j]). После
этого можно последовательно вычислять значения On[j-l],
On[j-2], ..., Οτι[/'+1].
Аналогичные действия необходимо выполнить при
формировании массива Ag[i], после этого для жителей каждого города i
следует выбрать лучший из On[i].pr nAg[i]pr вариант заправки.
10. В массиве A (Aran/[1.JV,1..M] Of Byte), заполненном 0 и
1, найти квадратный блок максимального размера, состоящий
из одних 0.
Указание. Пусть N=5, М=6 и массив А заполнен следующим
образом (см. таблицу 3.4). Определим массив В (Array[l..N,l..M]
Of Byte) следующим образом. Элементы первой строки и
первого столбца инвертируются относительно соответствующих

3. Перебор и методы его сокращения
133
(B[i,j]=l-A[ifj]) элементов массива А. И далее, при i=2..N и
j=2..M B[i,j]=0, если A[i,j]=\, и B[i,j]=Min(B[i-l,j],B[i,j-l],
B[i-lJ-l])-\1, если А[i,j]=0. Для нашего примера В
представлен в таблице 3.5. Ответ задачи — 3.
Таблица 3.4
0
1
0
1
1
о I о
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0 I 1
о _ t 1
1
0
1
0
1
Таблица 3.5
1
0
1
0
0
1
2
2
2
2
1
0
1
2
3
1
1
1
0
0
0
1
0
1
0
Как изменится решение, если потребовать нахождение
прямоугольного блока максимального размера? Решает ли
следующий фрагмент программного кода задачу?
Procedure Solve;
Var i, j, k, nx: Integer;
Begin
sqa:=0;{*Результат.*}
For i :=1 To N Do
For j :=1 To Μ Do
If A[i, j]=0
Then Β [ί, j]:=B[i, j-l]+l
Else
B[i, j]:=0;{*B массиве А исходные данные,
в В - результаты подсчета.*}
For i :=1 To N Do
For j :=1 То Μ Do
Begin
nx:=B[i, j] ;
For k:=i DownTo 1 Do
Begin
nx:=Min(nx, B[k, j]);

134
3. Перебор и методы его сокращения
If nx*(i-k+1)>sqa Then sqa:=nx*(i-k+1);
End;
End;
End;
11. Задача о паркете*.
Комнату размером ΝχΜ единиц требуется покрыть
одинаковыми плитками паркета размером 2x1 единиц без пропусков и
наложений (М < 20, Ν <8, Μ, Ν — целые). Пол можно покрыть
паркетом различными способами. Например, для М=2, N=3
все возможные способы укладки приведены на рисунке 3.34.
Рис. 3.34
Требуется определить количество всех возможных способов
укладки паркета для конкретных значений Μ < 20, Ν <8.
Результат задачи — таблица, содержащая 20 строк и 8 столбцов.
Элементом таблицы является число, являющееся решением
задачи для соответствующих N и М. На месте ненайденных
результатов должен стоять символ «*».
Указание. Пусть i — длина комнаты (1 < i < 8), j — ширина
комнаты (1 <j < 20). «Разрежем» комнату на части. Разрез
проводится по вертикали. Плитки, встречающиеся на пути
разреза, обходим справа, т. е. при движении сверху вниз на каждом
шаге либо обходим справа выступающую клетку, либо нет.
При других укладках паркета могут получиться другие
сечения. Все варианты сечений легко
пронумеровываются, ибо это не что иное,
как двоичное число: обход справа
плитки соответствует 1, отсутствие
обхода — 0. На рисунке 3.35 сечение
выделено «жирной» линией, ему
соответствует двоичное число 00100011 (35).
Количество различных сечений 2'
(пронумеруем их от 0 до 2'-1), где i —
длина комнаты.
Задача Сергея Геннадьевича Волченкова с VI Всероссийской олимпиады
школьников по информатике 1994 год.

3. Перебор и методы его сокращения
135
Не будем пока учитывать то, что некоторые из сечений не
могут быть получены. Обозначим парой (k,j) комнату с
фиксированной длиной iy правый край которой не ровный, а
представляет собой сечение с номером h. B[k,j] — количество
вариантов укладки паркета в такой комнате. Задача в такой
постановке сводится к нахождению B[0,j] — количества
укладок паркета в комнате размером (i,j) с ровным правым краем.
Считаем, что В[0,0]=1 при любом i, ибо комната нулевой
ширины, нулевого сечения и любой длины укладывается
паркетом, при этом не используется ни одной плитки. Кроме этого
считаем B[k,0]=0 для всех сечений с номерами /г<>0, так как
ненулевые сечения при нулевой ширине нельзя реализовать.
Попытаемся найти B[k,j] для фиксированного i.
Предположим, что нам известны значения B[l,j-1] для всех сечений с
номерами I (О < I < 2'-1). Сечение I считаем совместимым с
сечением k9 если путем добавления целого числа плиток паркета из
первого можно получить второе. Тогда B[kJ]=^B[lJ-l]f
суммирование ведется по всем сечениям Z, совместимым с сечением к.
Налицо динамическая схема решения задачи. Схема ее
реализации имеет вид:
Var B:Array[0. .255,0. .20] Of Comp;
A:Array[1. .8,1 . .20] Of Comp;
{*Результирующая таблица.*}
Procedure Solve;
Var i, j , k, 1,max:Integer;
Begin
For i : = 1 To 8 Do
Begin {*Цикл по значению длины комнаты.*}
max:=2Shli-l;{^Вычисляем 2 в степени i минус 1. *}
FillChar(В,SizeOf(В),0);
В[0,0]:=1;
For j :=1 To 2 0 Do
Begin {*Цикл по значению ширины комнаты.*}
For k:=0 To max Do { *Сечение с номером к.*}
For 1:=0 To max Оо{*Сечение с номером 1.*}
If Can(kf1/i) Then B[k,j]:=B[k,j]+B[1, j-1] ;
{^Совместимость сечений "зарыта"
в функции Сап(k,l,i).*}
А [ i,j] :=В[0,j];
End;
End;
End;

136
3. Перебор и методы его сокращения
При решении вопроса о совместимости сечений следует
различать понятия совместимость сечений в целом и
совместимость в отдельном разряде. При анализе последнего входными
данными являются значения разрядов сечений и информация о
предыстории процесса (до текущего разряда) — целое или
нецелое количество плиток уложено. Выходными данными —
признак — целое, нецелое количество плиток, требуемых для
перевода сечения I в сечение &, или решение о том, что анализ
продолжать не следует — сечения несовместимы. Оставим эту
часть работы и доведение схемы решения до работающего
варианта на самостоятельное выполнение.
Еще несколько замечаний.
Во-первых, если произведение N на Μ нечетно (размеры
комнаты), то количество укладок паркетом такой комнаты равно 0.
Во-вторых, при М=\ и четном N ответ равен 1.
В-третьих, результирующая таблица симметрична
относительно главной диагонали.
В-четвертых, для комнат размером 2xt достаточно просто
выводится следующая рекуррентная формула: Α[2,ί]=Α[2,ί-1]+Α[2,ί-2]
(ряд Фибоначчи).
Эти замечания реализуются на этапе предварительной
обработки и приводят к незначительной модификации алгоритма
процедуры Solve. Еще одно замечание касается точности
результата. Для больших значений N и Μ необходимо организовать
вычисления с использованием «длинной» арифметики (/=8,
/=20), ибо результат равен 3547073578562247994.
12. «Канадские авиалинии»*.
Вы победили в соревновании, организованном канадскими
авиалиниями. Приз — бесплатное путешествие по Канаде.
Путешествие начинается с самого западного города, в который летают
самолеты, проходит с запада на восток, пока не достигнет самого
восточного города, в который летают самолеты. Затем
путешествие продолжается обратно с востока на запад, пока не достигнет
начального города. Ни один из городов нельзя посещать более
одного раза за исключением начального города, который надо
посетить ровно дважды (в начале и в конце путешествия). Вам также
нельзя пользоваться авиалиниями других компаний или другими
способами передвижения. Задача состоит в следующем: дан
список городов и список прямых рейсов между парами городов;
найти маршрут, включающий максимальное количество городов и
удовлетворяющий вышеназванным условиям.
Задача с Пятой Международной олимпиады школьников по информатике
1993 года.

3. Перебор и методы его сокращения
137
Указание. Пусть нам необходимо попасть из самого
западного города в самый восточный, посетив при этом максимальное
количество городов. Связи между городами будем записывать с
помощью массива West:
West[i,j] =
True, есть авиалиния между городами
с номерами i и j ;
False, авиалинии нет.
Пусть мы каким-то образом решили задачу для всех
городов, которые находятся западнее города с номером ί, τ. е. для
городов с номерами Ι.,(ί-Ι). Что значит решили? У нас есть
маршруты для каждого из этих городов, и нам известно, через
сколько городов они проходят. Обозначим через Q. множество
городов, находящихся западнее i и связанных с городом i
авиалиниями (см. рисунок 3.36). Для этих городов задача решена,
т. е. известны значения d[j] (yeQ.) — количество городов в
наилучшем маршруте, заканчивающемся в городе с номером у.
Итак:
d[i]:=0;
For jeQx Do If d[j]+l>d[i] Then d [i] :=d[j]+1;
Остается открытым вопрос, а где же маршрут? Ибо значение
d дает только количество городов, через которые он проходит.
А для этого необходимо запомнить не только значение d[i], но
и номер города у, дающего это значение. Возможно
использование следующей структуры данных:
A:Array[1..max] Of Record
d, l:Byte;
End; .
В данной схеме мы видим не что иное, как метод
динамического программирования в действии. Как обобщить этот
набросок решения для первоначальной формулировки задачи? Для
удобства перенумеруем города в обратном порядке — с востока
на запад. Изменим массив А:

138
3. Перебор и методы его сокращения
Array[I..max,I..max] Of Record
d,1:byte;
End;
Под элементом A[i,j].d (путь из города i в город у) понимается
максимальное число городов в маршруте, состоящем из двух
частей: от i до 1 (на восток) и от 1 до j (на запад). По условию
задачи нам необходимо найти наилучший по числу городов
путь из Ν-το города в iV-й. Считаем, что A[l,l].d=l и
AliJ]=A[J>ii Через Qt обозначим множество городов, из которых
можно попасть в город i. Верны следующие соотношения:
A[i, j ] .d=max (A[k, j ] . d+1) , при keQi, k<>j , если jol;
A[i, i] . d=max (A[k, i] .d) , при i>l и keQi.
13. Реп1ить предыдущую задачу методом полного перебора
вариантов.
Указание. Определим структуры данных, а именно:
New:Array[l..max] Of Boolean;
way, way_r:Array[1..2*max] Of Byte;
Первый массив необходим для хранения признака —
посещался или нет город (New[i]=True — города с номером i нет в
маршруте). Во втором и третьем массивах запоминаются по
принципу стека текущий и наилучший маршруты
соответственно. Для работы со стеками необходимы указатели —
переменные yk и ykrnax. Алгоритм перебора поясняется рисунком
3.37. Ищем путь из города с номером i.
West
pp=true
for j:=i+l to η do
Рис. 3.37
Фрагмент основной части программы.
Begin
FillChar(New,SizeOf(New),True);
yk:=1;Way[yk]:=1;pp:=True;yk_max:=0;
pp=false
for j:=l to i-1 do

3. Перебор и методы его сокращения
139
Solve (1) ;
End.
И процедура поиска решения.
Procedure Solve(i:Byte);
Var j , pn,pv:Byte;
Begin
If i=N Then pp:=False; (^Меняем направление.*}
If (i = l) And Not pp Then
Begin {*Вернулись в первый город.*}
If yk>yk_max Then
Begin {*Запоминаем решение.*}
yk_max:=yk; way_r:=way;
End;
pp:=True;{^Продолжаем перебор.*}
End;
{*По направлению определяем номера просматриваемых
городов.*}
If pp Then
Begin pn:=i+l; pv:=n; End
Else
Begin pn:=l; pv:=i-l; End;
For j : =pn To pv Do
If West[i,j] And New[j] Then
Begin {*B город с номером j летают самолеты
из города i, и город j еще не посещался.*}
Inc(yk);Way[yk]:=j;New[j]:=False; {*Включаем
город j в маршрут . * }
Solve (j) ;
New[j]:=True;Way[yk]:=0;Dec(yk); {^Исключаем
город j из маршрута.*}
If j=N Then pp:=True; {*Если исключается
самый восточный город (Ν) , то меняем
направление движения.*}
End;
End;
14. Ресторан.
В ресторане собираются N посетителей. Посетитель с
номером i подходит во время Г. и имеет благосостояние Рг Входная
дверь ресторана имеет К состояний открытости. Состояние
открытости двери может изменяться на одну единицу за одну

140
3. Перебор и методы его сокращения
единицу времени, т. е. она или открывается на единицу, или
закрывается, или остается в том же состоянии. В начальный
момент времени дверь закрыта (состояние 0). Посетитель с
номером i входит в ресторан только в том случае, если дверь
открыта специально для него, то есть когда состояние
открытости двери совпадает с его степенью полноты Sr Если в момент
прихода посетителя состояние двери не совпадает с его
степенью полноты, то посетитель уходит и больше не возвращается.
Ресторан работает в течение времени Т.
Цель состоит в том, чтобы, правильно открывая и закрывая
дверь, добиться того, чтобы за время работы ресторана в нем
собрались посетители с максимальным суммарным
благосостоянием.
Входные данные.
В первой строке находятся значения N, К и Г, разделенные
пробелами (1 < N < 100, 1 < К < 100, 0 < Τ < 30000).
Во второй строке находятся времена прихода посетителей
Τν Т2, ...,ΤΝ, разделенные пробелами (0 < Т. < Г, для всех
i=l,2,...,N).
В третьей строке находятся величины благосостояния
посетителей Ρν Р2,... Рдг, разделенные пробелами (0 < Pt < 300, для
всех /=1,2,...,Ν).
В четвертой строке находятся значения степени полноты
посетителей Sv S2, ... SN, разделенные пробелами (1 < S. < К,
для всех ί=1,2,...,Λ0. Все исходные данные — целые числа.
Выходные данные. Выводится одно число, являющееся
максимальным значением суммарного благосостояния
посетителей. В случае, если нельзя добиться прихода в ресторан ни
одного посетителя, выходной файл должен содержать значение 0.
Классическая задача на метод динамического
программирования. Состояния открытости двери можно представить
«треугольной решеткой», изображенной на рисунке 3.38. Каждая
Рис. 3.38

3. Перебор и методы его сокращения
141
вершина определяет степень открытости q в момент времени t.
Некоторым вершинам решетки приписаны веса, равные
величине благосостояния посетителя, приходящего в момент
времени t и имеющего степень полноты, равную Sr Что осталось
сделать? Найти путь по решетке, проходящий через вершины,
сумма весов которых имеет максимальное значение. Следует
отметить, что нет необходимости хранить оценки всех вершин.
Нам нужно подсчитать оценки для момента времени t. Это
возможно, если известны их значения для момента времени t—1.
15. Имеется клеточное поле размером ΝχΜ. Из каждой
клетки можно перемещаться в одну из соседних, если она есть
(вверх, вправо, вниз, влево). Коммивояжер стартует из
какой-то клетки. Может ли он обойти все клетки и вернуться в
исходную клетку?
16. Даны два массива Α[1..Ν] и Β[1..Ν]. Матрица расстояний
между городами формируется по правилу: C[i,/]=A[i]+£[y] или
C[i,j]=Min(A[i],B\j]) при ioj. Решить задачу коммивояжера для
этих случаев.
17. Черепашка находится в городе, все кварталы которого
имеют прямоугольную форму, и ей необходимо попасть с
крайнего северо-западного перекрестка на крайний юго-восточный.
Пример.
Φ © ®-
<5
(9) @_^_@ @
Рис. 3.39
ю
На некоторых улицах проводится ремонт, и по ним
запрещено движение (например, на рисунке 3.39 между
перекрестками 3 и 7, 5 и 6, 10 и 11), длина, а значит и стоимость проезда
по остальным улицам задается. Кроме того, для каждого
перекрестка определена стоимость поворота. Так, если Черепашка
пришла на 7-й перекресток и поворачивает к 11-му, то она
платит штраф, а если идет в направлении 8-го, то платить ей не
приходится. Найти для Черепашки маршрут минимальной
стоимости.

142
3. Перебор и методы его сокращения
Исходные данные:
• N — количество перекрестков, определяется через два
числа I, m и N=lxm (1<Z, т<11);
• длина улиц (стоимость проезда) и стоимость поворота на
перекрестках — целые числа.
Указание. Определим для каждого перекрестка два числа:
стоимость перемещения на юг и стоимость перемещения на
восток. Начнем их вычисление с крайнего юго-восточного
перекрестка (см. рисунок 3.40). Алгоритм вычислений имеет вид:
A[i,j]/восток+ Min(A[i,j+1]/восток,A[i,j + 1] /
юг+А[i,j +1]/поворот)
A[i,j]/юг+Min(A[i+1,j]/юг,A[i+1,j]/восток+А[i + 1,
j]/поворот).
При этом i изменяется от Ы до 1, ау от т-1 до 1.
Иллюстрация к этому алгоритму приведена на рисунке 3.40 (max —
обозначено отсутствие движения в данном направлении). Итак,
стоимость минимального маршрута равна 40. Дальнейшее
решение во многом зависит от удачности выбора структур
данных. Если определить:
Const Nmax=ll;
Type Cross=Record
Right, Down, Turn : Integer
End;
Var A:Array[1..Nmax,1..Nmax] Of Cross;
то программная реализация будет достаточно компактна.
9 10
ίο
ДЗ
J4
15
40 //
I
30 >/
/2&
max/
/11
35 /"
lb/
/21
max у/
/ 6
10S/
/nmx
2 /
/max
0 /
Рис. 3.40
18. Задано прямоугольное клеточное поле ΝχΜ (2<=Ν>Μ<8)
и число k. Построить k различных непрерывных разрезов этого
поля на два клеточных поля равной площади. Разрез должен
проходить по границам клеток. Пример разреза приведен на
рисунке 3.41.

3. Перебор и методы его сокращения
143
Указание. Задача логически разбивается на | 1 I I 1 ΤΊ
следующие части: N ~Н
• построение разреза между двумя точками Ι ΓΊ I I XJ
на границе клеточного поля; Рис. 3.41
• подсчет площадей;
• вывод результата.
Наиболее интересной является первая часть. Перенумеруем
точки на границе поля по часовой стрелке. После этой
операции появляется возможность перебирать по две точки и
строить между этими точками разрез. Организация перебора
очевидна. Номер первой точки (i) изменяется от 1 до L, где L —
количество точек на границе, номер второй от значения i+1 до
L. Для построения разреза используется классический
волновой алгоритм (задача о лабиринте). Дальнейшее решение
зависит от выбора структур данных. Целесообразно хранить
координаты точек линии разреза. В этом случае площадь — это
сумма площадей прямоугольников.
19. Имеется механизм, состоящий из N расположенных в
одной плоскости и свободно надетых на зафиксированные оси
пронумерованных шестеренок, зубья которых соприкасаются
друг с другом. Информация о механизме ограничивается тем,
что для каждой шестеренки перечислены все те, с которыми
она находится в непосредственном зацеплении. Напишите
программу, определяющую, есть ли такая шестеренка,
поворачивая которую мы приведем в движение весь механизм.
20. Дано N конвертов с размерами А.хБ. и N прямоугольных
открыток с размерами C.xD^ i=l, ..., N. Возможно ли разложить
открытки по конвертам и если да, то привести все варианты
раскладки.
21. «Американские кубики».
Даны четыре кубика — на рисунке 3.42 изображены их
развертки. Требуется сложить из них башню 1x1x4 так, чтобы на
каждой боковой грани встречались все четыре цифры.
Определить форматы входных и выходных данных. Написать
программу поиска всех вариантов (если они есть) раскладки
кубиков, удовлетворяющих условию задачи.
ГП Γ7Ί ГТ] [Τ]
[Т~| |4~| р~[ ГП
I 4 I 3 I3 I I 1 I 3 1 I I 1 2 2 I |4 | 3 \2 |
1 2 3 3
Рис. 3.42

144
3. Перебор и методы его сокращения
22. Клетки доски 8x8 раскрашены в два цвета: белый и
черный. Необходимо пройти из левого нижнего угла в правый
верхний так, чтобы цвета клеток перемежались. За один ход
разрешается перемещаться на одну клетку по вертикали или
горизонтали.
Программа должна (если путь существует):
• находить хотя бы один путь;
• находить путь минимальной длины.
Указание. Для решения задачи применим метод «волны» с
учетом условия задачи — чередования клеток разного цвета.
23. Дана матрица iVxiV (iV<=10), состоящая из целых чисел.
За одну операцию разрешается изменить знаки всех чисел
произвольно выбранной строки или столбца на противоположные.
Требуется сделать суммы чисел во всех строках и столбцах
неотрицательными .
Программа должна ввести матрицу и вывести в качестве
результата последовательность операций. Количество операций
должно быть минимальным.
Указание. Задача решается перебором вариантов. У нас есть
2xiV элементов, N строк и N столбцов. Необходимо
генерировать /г-элементные подмножества из множества 2xiV элементов,
k изменяется от 1 до 2xiV, и проверять матрицу после
изменения знаков в строках и столбцах, принадлежащих очередному
подмножеству.
24. Круг разбили на 8 секторов*. Какие-то два соседних
сектора пусты, а в остальных расположены буквы, Р, О, С, С, И, Я
в некотором порядке, по одной в секторе (см. рисунок 3.43).
За один ход разрешается взять любые
две подряд идущие буквы и перенести их
в пустые сектора, сохранив порядок. При
этом сектора, которые занимали
перенесенные буквы до хода, становятся
пустыми. Номером хода назовем номер первого
из секторов в порядке обхода по часовой
стрелке (ЧС), содержимое которого
переносится.
Состояние круга назовем правильным,
если начиная с сектора 1 по ЧС можно
прочесть слово «РОССИЯ». При этом мес-
Рис.3.43
Задача предложена для одной из кировских олимпиад по информатике
Антоном Валерьевичем Лапуновым.

3. Перебор и методы его сокращения
145
тоположение пустых секторов может быть произвольным.
Состояние круга можно закодировать строкой из 8 символов,
получающихся при чтении круга по ЧС, начиная с сектора 1,
если пустому сектору поставить в соответствие символ
подчеркивания '_'. Эту строку из 8 символов будем называть кодом
круга.
По заданному коду найти кратчайшую последовательность
ходов, переводящую круг в правильное состояние. Если
решений несколько, то необходимо выдать только один вариант.
Указание. Задача решается перебором вариантов. Из
каждого состояния круга генерируются все состояния, в которые
можно попасть из него. Запоминаем состояния в структуре
данных типа очередь. Повторяющиеся состояния в очередь не
записываются. Процесс перебора заканчивается при достижении
состояния, эквивалентного состоянию «РОССИЯ».
25. Заданы две символьные строки А и Б, не содержащие
пробелов. Требуется вычислить, сколькими способами можно
получить строку В из строки А, вычеркивая некоторые
символы. Например, если строки А и В имеют соответственно вид Са-
маринаИрина и Сара, то искомое число равно 7, для строк
аааввввссс и авс это число равно 36.
Таблица 3.6
0
а
b
с
0
1
0
0
0
а
1
1
0
0
а
1
2
0
0
а
1
3
0
0
b
1
3
3
0
b
1
3
6
0
b
1
3
9
0
b
1
3
12
0
с
1
3
12
12
с
1
3
12
24
с |
1
з I
12П
36_J
Написать программу, находящую требуемое число способов.
Указание. Рассмотрим идею решения на примере,
приведенном в таблице 3.6. Для клеток, у которых символы на
горизонтали и вертикали не совпадают, значение
переписывается из соседней по горизонтали клетки. Например, символ 'а' и
первый символ *Ь' по горизонтали. Способов получения
строки 'а' из строки 'aaab9 столько же, сколько из строки 'ааа\
Для случая совпадения символов, например *Ь' по вертикали
и второе *Ь' по горизонтали, количество способов — это сумма
способов для строк *аЬ' и 'aaab' (без последнего символа во
второй строке), а также — 'а' и 'aaab9 (последние символы
строк совпадают).

146
3. Перебор и методы его сокращения
26. В вашем распоряжении имеется по четыре экземпляра
каждого из чисел: 2, 3, 4, 6, 7, 8, 9, 10. Требуется написать
программу такого размещения их в таблице 6x6 (см. таблицу
3.7), чтобы в клетках, обозначенных одинаковыми значками,
находились равные числа и суммы чисел на каждой
горизонтали, вертикали и обеих диагоналях совпадали.
Таблица 3.7
ГТН
| ""
! #
+
L 11
@
@
1
$
11
| $
1
#
+
11
#
+
@
@
1
Л
~гП
'<
#
$
_JLJ
Примечание
Обратите внимание на то, что число 11 уже записано в таблице 4
раза.
Указание. Метод решения задачи традиционный — перебор
вариантов, но организовать его следует достаточно грамотно.
Первоначально необходимо выбрать числа для помеченных
клеток, а затем дополнять до значения суммы элементов,
которая вычисляется очень просто — сложить все числа и
разделить на шесть (она равна 40).
27. Возьмем клетчатую доску ΜχΝ (1<Μ,Ν<4). Воткнем в
каждую клеточку штырек. В нашем распоряжении есть К
(0<К<20) абсолютно одинаковых колечек, каждое из которых
можно нанизывать на штырек, причем на один штырек
разрешается надеть несколько колечек. Подсчитать, сколькими
способами можно распределить все эти колечки по штырькам. Два
распределения считаются разными, если на каком-то из
штырьков находится разное количество колечек, и одинаковыми в
противном случае.
Входные данные: Μ, Ν, К.
Для входных данных: 2, 2, 2, результат: 10.
Указание. Заметим, что клеточная доска дана для
«устрашения». С таким же успехом задачу можно решать на линейке
из ΜχΝ клеток. Допустим, что найдено решение для L клеток,
то есть определено число способов для всех значений колечек
от 1 до К. При L+1 клетке решение получается очевидным
способом — в клетке L+1 размещаем ρ колечек, а в клетках от 1
до L — оставшиеся. Традиционная схема, называемая
динамическим программированием.

3. Перебор и методы его сокращения
147
28. Для известной игры «Heroes of Might and Magic III»
генератор случайных карт создает острова, на которых
изначально будут расположены герои. Но при случайной генерации
карты острова получаются различными по величине. Назовем
коэффициентом несправедливости отношение площади
наибольшего острова к площади наименьшего. Необходимо
подсчитать этот коэффициент. Карта представляет собой
прямоугольник ΝχΜ, в каждой клетке которого записан 0 (вода) или 1
(земля). Островом считается множество клеток, содержащих 1,
таких, что от любой до любой из них можно пройти по клеткам
этого множества, переходя только через их стороны.
Входные данные (см. рисунок 3.44). В
первой строке входного файла содержатся
числа N и Μ (размеры карты, 1<Ν, Μ<1000).
В следующих Μ строках записано по N
чисел (разделенных пробелами), каждое из
которых либо 0, либо 1.
Выходные данные. В выходной файл
вывести коэффициент несправедливости с 5
знаками после запятой. Если на карте нет ни
одного острова, вывести 0.
Указание. Упростим задачу. Пусть
размеры поля не превышают по каждому
измерению значения 100. Проблем с оперативной
памятью в этом случае нет, и решение
хорошо известно — алгоритм волны (выход из лабиринта). Суть:
«цепляем» первую ненулевую клетку поля и пытаемся
распространять «волну» по всем ненулевым соседним клеткам
(обходом в ширину), гася при этом единичные значения в клетках
поля и подсчитывая количество таких клеток.
Изменение размерности, а именно 1<ЛГ,М<1000, приводит к
совершенно другому решению. Сложность задачи возрастает на
порядок. Описание карты следует считывать по строкам, ибо нет
возможности хранить ее полностью в памяти (количество
клеток умножим на 4 — по два байта на координату — это
приводит к значению 4х106, явная нехватка памяти). Что изменится в
решении? Пусть данные обработаны из N строк, считываем
данные по (ЛЧ-1)-й строке. Каждый остров, сформированный по
данным из первых N строк и активный к этому этапу обработки,
имеет уникальный идентификатор. Заметим, что если при
добавлении строки размер острова не увеличился, то из этого
следует, что остров не вышел на (N+1) строку (если это единствен-
Пример.
f.in \
7 6
110 0 0 0 0 |
0 10 10 0 0 |
lioiioo !
10 0 0 10 0 |
0 0 0 1110 |
1110 0 10 i
f.out I
2.33333 !

148
3. Перебор и методы его сокращения
ный выход острова на данную строку), его площадь следует
проверить на значения минимума, максимума и исключить из
дальнейшего рассмотрения.
Как происходит обработка очередной строки?
Просматриваем ее слева направо. Если встречаем единичный элемент
(остров), то возможны следующие ситуации:
• слева и сверху в предыдущей строке не было единичных
элементов — создаем описание нового острова;
• слева или сверху есть единичный элемент (остров) —
описание острова существует, присоединяем элемент к острову;
• слева и сверху есть единичные элементы, текущий
элемент «склеивает» ранее созданные острова, объединяем
их (пример приведен на рисунке 3.45 — обработка
«темной» клетки приводит к склеиванию ранее созданных
связных областей).
После этих действий необходимо проверить, все ли острова
подтвердили свою активность. Если есть острова, не
подтвердившие свою активность, то следует проверить их площади на
минимум и максимум, откорректировать последние и
исключить их из дальнейшей обработки.
29. «Полигон»*.
Существует игра для одного игрока, которая начинается с
задания Полигона с N вершинами. Пример графического
представления Полигона при N=4 показан на рисунке 3.46. Для
каждой вершины Полигона задается значение — целое число, а
для каждого ребра — метка операции + (сложение) либо *
(умножение). Ребра Полигона пронумерованы от 1 до N.
Первым ходом в игре удаляется одно из ребер.
Каждый последующий ход состоит из следующих шагов:
• выбирается ребро Ε и две вершины Vx и F2, которые
соединены ребром Е;
3
4
5
6
6
7
8
9
Ри
с.З
.45
10 11
У
@—^
1 +
* 3
®-^г~®
Рис. 3.46
Задача с Международной олимпиады школьников по информатике
1999 года.

3. Перебор и методы его сокращения
149
• ребро Ε и вершины Vx и V2 заменяются новой вершиной со
значением, равным результату выполнения операции,
определенной меткой ребра Е, над значениями вершин V1nV2.
Игра заканчивается, когда больше нет ни одного ребра.
Результат игры — это число, равное значению оставшейся
вершины.
Пример игры (см. рисунок 3.47). Рассмотрим полигон,
приведенный в условии задачи. Игрок начал игру с удаления
ребра 3. После этого игрок выбирает ребро 1, затем — ребро 4 и,
наконец, ребро 2. Результатом игры будет число 0.
ι +
(йЬгЧ?)
4 *
©
®-J-0 ®-Ч£>
2
+
@-L-©
Рис. 3.47
Требуется написать программу, которая по заданному
Полигону вычисляет максимальное значение оставшейся вершины и
выводит список всех ребер, удаление которых на первом ходе
игры позволяет получить это значение.
Входные данные. Файл pol.in (см. рисунок 3.48) описывает
Полигон с N вершинами. Файл содержит две строки. В первой
строке записано число N. Вторая строка содержит метки ребер
с номерами 1, ..., Ν, между которыми записаны через один
пробел значения вершин (первое из них соответствует вершине,
смежной ребрам 1 и 2, следующее — смежной ребрам 2 и 3 и
так далее, последнее — смежной ребрам N и 1). Метка ребра —
это буква £, соответствующая операции +, или буква х,
соответствующая операции *.
Выходные данные. В первой строке выходного
файла pol.out (см. рисунок 3.48) программа
должна записать максимальное значение оставшейся
вершины, которое может быть достигнуто для
заданного Полигона. Во второй строке должен быть
записан список всех ребер, удаление которых на
первом ходе позволяет получить это значение.
Номера ребер должны быть записаны в
возрастающем порядке и отделяться друг от друга
пробелом.
Пример.
pol.in
4
t-7t4x2x5
pol.out
33
1_2_
Рис. 3.48

150
3. Перебор и методы его сокращения
Ограничения. 3<N<50. Для любой последовательности ходов
значения вершин находятся в пределах [-32768, 32767].
Указание. После удаления первого ребра остается
выражение, в котором необходимо так расставить скобки, чтобы его
значение было максимальным. Например, пусть удалено
первое ребро в примере из формулировки задачи. Остается
выражение -7+4x2x5. Способы расстановки скобок: (-7)+(4х2х5),
(-7+4)χ(2χ5), (-7+4χ2)χ5.
Введем следующий массив
Max:Array [1 . .MaxN,1. .MaxN] Of Longlnt,
где константа MaxN равна 50 (по условию задачи). Элемент
Max[i,j] определяет максимальное значение выражения длины у,
начиная с вершины i (ключевой момент). Например, Мах[1,3] —
для выражения -7+4x2. Очевидно, что Max[i,l] равно
значениям вершин для всех i. Явно просматривается традиционная
динамическая схема. Единственная сложность — отрицательные
числа. При умножении отрицательных чисел может быть
получен максимум. В силу этого необходимо считать и
минимальные значения для каждого выражения. Просчитаем наш
пример «вручную». Рассмотрим только массив Мах. Результаты
ручного просчета приведены в таблице 3.8. Выбор
максимального значения из последнего столбца таблицы дает ответ
задачи — максимум выражения и номера ребер.
Таблица 3.8
-7+4=-3
4 | 4*2=8
2*5=10
4 I 5 | 5+(-7)=-2
-7+(4*2)=1
(-7+4)*2=-6
4*(2*5)=40
(4*2)*5=40
(-7)+(4*2*5)=33
(-7+4)*(2*5)=-30
(-7+4*2)*(5)=5
(4)*(2*5+(-7))=12
(4*2)*(5+(-7))=-16
(4*2*5)+(-7)=33
2*(5+(-7))=-4
(2*5)+(-7)=3
(5)+((-7)+4)=2
(5+(-7))+4=2
(2)*(5+(-7)+4)=4
(2*5)+((-7)+4)=7
(2*5+(-7))+4=7
(5)+((-7)+4*2)=6
(5+(-7))+(4*2)=6
(5+(-7)+4)*2=4

3. Перебор и методы его сокращения
151
30. «Почтовые отделения»*.
Вдоль прямой дороги расположены деревни. Дорога
представляется целочисленной осью, а расположение каждой
деревни задается одним целым числом — координатой на этой оси.
Никакие две деревни не имеют одинаковых координат.
Расстояние между двумя деревнями вычисляется как модуль
разности из координат.
В некоторых, не обязательно во всех, деревнях будут
построены почтовые отделения. Деревня и расположенное в ней
почтовое отделение имеют одинаковые координаты. Почтовые
отделения необходимо расположить в деревнях таким образом,
чтобы общая сумма расстояний от каждой деревни до
ближайшего к ней почтового отделения была минимальной.
Напишите программу, которая по заданным координатам
деревень и количеству почтовых отделений находит такое
расположение почтовых отделений по деревням, при котором
общая сумма расстояний от каждой деревни до ее ближайшего
почтового отделения будет минимальной.
Входные данные. В первой строке
файла post.in (см. рисунок 3.49)
содержатся два целых числа: первое число —
количество деревень V, 1 < V < 300,
второе число — количество почтовых
отделений Р, 1 < Ρ < 30, Ρ < V. Вторая строка
содержит V целых чисел в
возрастающем порядке, являющихся
координатами деревень. Для каждой
координаты X выполняется 1 < X < 10000.
Выходные данные. Первая строка файла post.out (см. рисунок
3.49) содержит одно целое число S — общую сумму расстояний
от каждой деревни до ее ближайшего почтового отделения.
Вторая строка содержит Ρ целых чисел в возрастающем порядке.
Эти числа являются искомыми координатами почтовых
отделений. Если для заданного расположения деревень есть несколько
решений, то программа должна найти одно из них.
Указание. При размещении одного почтового отделения
эта задача известна как задача Лео Мозера (1952 год). Ответ
V Div 2+1 (V — нечетное число) и любая из двух средних
деревень (V — четное). Решение задачи с одним почтовым отделе-
Задача с Международной олимпиады школьников по информатике
2000 года.
Пример.
post.in
10 5
1 2 36 7 9 11 22 44 50
post.out
9
2 7 22 44
Рис.
50
3.49

152
3. Перебор и методы его сокращения
нием на взвешенном графе основано на использовании
алгоритма Флойда и поиска вершины с минимальной суммой
расстояний до других вершин. При увеличении количества
почтовых отделений эти идеи «не проходят». Переборные
схемы также не работают при данных ограничениях. Остается
поиск динамической схемы. Рассмотрим пример, приведенный в
формулировке задачи. Размещаем одно почтовое отделение в
деревне с номером i. Оценим расстояние до деревень,
находящихся левее ее. Результаты оценки приведены в таблице 3.9.
Таблица 3.9
I 1
2
|__0_1Л__
3
3
4^ 5
12
16
6
26
7
8
38 115
9
291
Г ю I
345 J
Что это дает? Пока ничего. Попытаемся решить задачу для
двух почтовых отделений. Рассмотрим деревни с номерами от 1
до i. Одно почтовое отделение размещается в деревне с номером
i. Найдем место второго почтового отделения, дающего
минимальную сумму расстояний. Пример (i равно 5). Крестиками на
рисунке 3.50 обозначены деревни с почтовыми отделениями.
Справа на рисунке приведены суммы расстояний до ближайших
почтовых отделений. Из четырех вариантов выбираем второй,
дающий минимальную оценку — 3. Просчитаем для всех
значений i. Массив оценок имеет вид, приведенный в таблице 3.10.
1
1
1
·-
-·—·
2 3
V ш
1-к
• А.
2 3
—«—·
т—
6
6
-4т
А
А
Рис. 3.50
Таблица 3.10
\ 1
2
оо | 0
3
1
4
2
5
3
6
7
7 [ 12
8
L^_j
9
I ю II
I 37 j 43 |l
Символом оо обозначен бессмысленный случай — два
почтовых отделения в одной деревне.
Продолжим рассмотрение — три почтовых отделения. На
рисунке 3.51 приведен случай при i=l (в 7 деревнях
размещаются 3 почтовых отделения). Первый справа отрезок
характеризует вариант, при котором два почтовых отделения расположе-
1 2 3
-к

3. Перебор и методы его сокращения
153
1 2 3
•—·—·
6 7
·—♦—
1 2 3
•—·—·
1 2 3
9 1J * * *
~~"* * 1 2 3
•—·—·
1 2 Ъ
1 2 3
—*-·
6 7
·—♦—
-М-
-^2-
6 7
·—·—
6 7
·—·—
-«7
-4-«5
-4-4^5
-i-Ую
-Ui 11
Рис.3.51
ны в деревнях с 1-й по 6-ю. Он подсчитан (равен 7, третье
отделение в седьмой деревне, итоговая оценка не изменяется и
равна 7), мы почти «нащупали» динамическую схему. Второй
отрезок — два почтовых отделения в деревнях с 1-й по 5-ю. Из
предыдущего рассмотрения стоимость этого случая равна 3,
расстояние от 6 деревни до ближайшего почтового отделения 2,
итого 5. Окончательные оценки при 3, 4 и 5 отделениях
приведены в таблице 3.11.
Таблица 3.11
| 1
00
00
00
2
00
00
ОС
3
0
00
00
4
1
0
ОС
5
2
1
0
6
3
2 Ί
1
7
5
3
2
8
9
5
3
9
21
9
5
1
10
27
15
9 J
Осталось сделать последний шаг. Оценка расстояний в
нашей схеме проводилась до деревень, расположенных слева. К
этим оценкам следует прибавить сумму расстояний до
деревень, находящихся справа. Окончательные оценки приведены
в таблице 3.12.
Таблица 3.12
1
ОС
2
00
3
00
4
00
5
6
7
101 | 92 J 85
8
53
9
I 11
ιο~Ί
9_J
Итак, общая сумма расстояний от каждой деревни до ее
ближайшего почтового отделения равна 9. Это минимум в
окончательном массиве оценок. Как зафиксировать в этой схеме
деревни с почтовыми отделениями? Как обычно в алгоритмах
типа Флойда, при улучшении оценки, запоминать
соответствующую ситуацию.

154
3. Перебор и методы его сокращения
Пример.
palin.in
5
Ab3bd
palin.out
2
31. Палиндром* — это симметричная строка, т. е. она
одинаково читается как слева направо, так и справа налево. Вы
должны написать программу, которая по заданной строке
определяет минимальное количество символов, которые необходимо
вставить в строку для образования палиндрома.
Например, вставкой двух символов строка «Ab3bd» может
быть преобразована в палиндром («dAb3bAd» или «AdbSbdA»),
а вставкой менее двух символов палиндром в этом примере
получить нельзя.
Входные данные. Файл palin.in (см. рисунок
3.52) состоит из двух строк. Первая строка
содержит одно целое число — длину N входной строки,
3 < N < 5000. Вторая — строку длины N, которая
состоит из прописных (заглавных) букв от Ά' до
*Z\ строчных букв от 'а' до 'ζ' и цифр от Ό' до '9'.
Прописные и строчные буквы считаются различ-
ными· Рис. 3.52
Выходные данные. Файл palin.out (см. рисунок 3.52) состоит
из одной строки. Эта строка содержит одно целое число,
которое является искомым минимальным числом символов.
Указание. Рассмотрим идею решения задачи. Формируем
матрицу R[i,j] (i,j=l..N), где R[i,j] — минимальное количество
букв, которые необходимо вставить в строку S(i,j) с i-го
символа по у-й символ строки S для того, чтобы получить из нее
палиндром. Искомый результат — R[1,N].
Как формируется матрица R1 Во-первых, заполняется только
одна часть матрицы, выше или ниже главной диагонали,
включая ее. Во-вторых, если S[i]=S[y], то R[i,j]=R[i+l,j-l]. В-третьих,
если S[i]<>S[fl, то Wj]=Min(H[i+l,j]9H[i,j-l])+l.
Потренируемся на примерах.
S='Ab3bd'. Матрица R имеет вид, приведенный в таблице
3.13.
Таблица 3.13
Г о
-
-
1 -
1 -
1
0
-
-
__-
2
1
0
-
-
1
0
1
0
-
2 ]
1
2
1
0
Задача с Международной олимпиады школьников по информатике
2000 года.

3. Перебор и методы его сокращения
155
S='abcdba3'. Матрица R имеет вид, приведенный в таблице
3.14.
Таблица 3.14
; о
-
-
! -
1 -
!_:
1
0
-
-
-
-
-
2
1
0
I
-
-
-
г^'1
2
1
0
-
■
L -
I
1
2
1
0
-
1
2
3
2
1
0
г~2-1
3 !
4 1
з 1
2 Ί
1
L?J
Естественно, что хранить в памяти компьютера всю матрицу
не следует. Достаточно одномерных массивов.
32. Двое играют в следующую игру: они разложили
однокопеечные монетки в стопки (в разных стопках может быть
различное количество монет), а стопки расположили в ряд слева
направо на столе перед собой. Затем игроки по очереди делают
ходы. На каждом ходе участник берет слева несколько стопок
(не меньше одной), но не больше, чем перед этим взял его
противник (первый игрок своим первым ходом берет не более К
стопок). Игра заканчивается, когда стопок не осталось.
Требуется вычислить, какое максимальное число монет может
заполучить первый игрок, если второй тоже старается ходить так,
чтобы получить как можно больше.
Входные данные. Во входном файле input.txt
(см. рисунок 3.53) записано число стопок N
(1 < N < 180). Затем N чисел, задающих
количество монет в стопках слева направо
(количество монет в стопке — не менее 1 и не более
20000), и в конце число К, ограничивающее
количество стопок, которые допускается
брать на первом ходе (1 < К < 80).
Выходные данные. В выходной файл
output.txt (см. рисунок 3.53) выводится
одно число — максимальное количество
монет, которое заведомо может заполучить
первый игрок, как бы ни играл второй.
Указание. Суть решения отражена в
следующей процедуре и выводе результата
А[1,К], где А — Array[\..MaxN+\, Ο,.ΜαχΚ]
Of Longlnt.
Рис. 3.53
Примеры.
input.txt
3 4 9 18
output.txt
14
input.txt
4 12 2 7
output.txt
5
input.txt
5 34817 2
output.txt

156
3. Перебор и методы его сокращения
Выполните трассировку процедуры и разработайте
программу решения задачи.
Procedure Solve;
Var i, j: Integer;
sum: Longlnt;
Begin
sum:=0;
For i : =N DownTo 1 Do
Begin
sum:=sum + Pr[i];
For j :=1 To К Do
Begin
A[i, j] :=A[i, j-1];
If i+j<N+2 Then
A[i, j]:=Max(A[i, j], sum-A[i + j, j]);
{*Обычная функция определения
максимального из двух чисел.*}
End;
End;
End;
33. Задача о магических квадратах.
В квадратной таблице ΝχΝ записать числа 1, 2, 3, ..., ΝχΝ
так, чтобы суммы по всем столбцам, строкам и главным
диагоналям были одинаковы. Примеры магических квадратов
приведены на рисунке 3.54.
1 ®~~
' 3
| 4
1
5
9
6 ]
7
2
Г2 "
I 9
4
7
5
3
1 |
8~|
т
12
13
L 8
2
14
7
11
15
3
10
6
16 I
5 I
4
9 |
Рис. 3.54
Указание. Задача имеет решение лишь для Л7>3. Сумма всех
чисел квадрата равна №х(№+1)/2. Таким образом, искомая
сумма равна Afx(Af2+l)/2. Чудовищный алгоритм решения: вы-

3. Перебор и методы его сокращения
157
тягиваем квадрат в линейку, генерируем все перестановки
чисел 1, 2, 3, ..., ΝχΝ и проверяем каждую перестановку на
предмет ее пригодности требованиям магичности квадрата. Не
используется даже факт знания значения суммы чисел. Из 9!
перестановок при N=3 только 8 перестановок удовлетворяют
условиям задачи, а из 161=20922789888000 - 7040
перестановок. Проверьте свой компьютер на выживаемость при N=4. Во
время его счета оцените вручную временные затраты
алгоритма (допускается прибавить к производительности вашего
компьютера несколько миллионов операций в секунду). После
этого (при условии, что глава вами проработана достаточно
тщательно) с помощью ряда эвристик, сокращающих перебор,
вы быстро напишете новый вариант алгоритма и получите все
решения при N=4. О дальнейшем продвижении в сторону
увеличения значения N позвольте умолчать.

4. Алгоритмы на графах
Данная глава посвящена алгоритмам на графах, точнее
прикладным аспектам этой темы. Если при изложении материала
избежать многочисленных дефиниций и доказательств (к чему
стремился автор), то он, в силу своей наглядности и простоты,
становится доступным и школьнику. Работа по этой
проблематике значительно обогащает алгоритмическую культуру
учащихся, совершенствует технику написания программ, так как
алгоритмы являются неиссякаемым источником задач любого
уровня сложности.
4.1. Представление графа в памяти компьютера
Определим граф как конечное множество вершин V и набор
Ε неупорядоченных и упорядоченных пар вершин и обозначим
G=(V,E).
Количество элементов в множествах V τι Ε будем обозначать
буквами N и М.
Неупорядоченная пара вершин называется ребром, а
упорядоченная пара — дугой.
Граф, содержащий только ребра, называется
неориентированным; граф, содержащий только дуги, — ориентированным,
или орграфом.
Вершины, соединенные ребром, называются смежными.
Ребра, имеющие общую вершину, также называются
смежными. Ребро и любая из его двух вершин называются
инцидентными. Говорят, что ребро (и, υ) соединяет вершины и и υ.
Каждый граф можно представить на плоскости множеством
точек, соответствующих вершинам, которые соединены
линиями, соответствующими ребрам. В трехмерном пространстве
любой граф можно представить таким образом, что линии (ребра)
не будут пересекаться.
Способы описания. Выбор соответствующей структуры
данных для представления графа имеет принципиальное значение
при разработке эффективных алгоритмов. При решении задач
используются следующие четыре основных способа описания
графа:
• матрица инциденций;

4. Алгоритмы на графах
159
• матрица смежности;
• списки связи;
• перечни ребер.
Мы будем использовать только два: матрицу смежности и
перечень ребер.
Матрица смежности — это двумерный массив размерности
NxN.
J 1, вершина с номером i смежна с вершиной с номером j
[О, вершина с номером i не смежна с вершиной с номером j
Для хранения перечня ребер необходим двумерный массив
R размерности Мх2. Строка массива описывает ребро.
A[iJ]
4.2. Поиск в графе
4.2.1. Поиск в глубину
Идея метода. Поиск начинается с некоторой
фиксированной вершины υ. Рассматривается вершина ζ/, смежная с υ. Она
выбирается. Процесс повторяется с вершиной и. Если на
очередном шаге мы работаем с вершиной q и нет вершин,
смежных сдине рассмотренных ранее (новых), то возвращаемся из
вершины q к вершине, которая была до нее. В том случае,
когда это вершина υ, процесс просмотра закончен.
Очевидно, что для фиксации признака, просмотрена
вершина графа или нет, требуется структура данных типа:
Nnew : Array[l..N] Of Boolean.
Пример. Пусть граф описан матрицей смежности А. Поиск
начинается с первой вершины. На рисунке 4.1 приведен
исходный граф, а на рисунке 4.2 у вершин в скобках указана та
очередность, в которой вершины графа просматривались в
процессе поиска в глубину.
Рис. 4.1

160
4. Алгоритмы на графах
Алгоритм поиска.
Procedure Pg(v:Integer);
{^Массивы Nnew и А глобальные.*}
Var j:Integer;
Begin
Nnew[v]:=False; Write(v:3);
For j :=1 To N Do
If (A[v,j]<>0) AndNnew[j]
Then Pg (j);
End;
Фрагмент основной программы.
FillChar (Nnew,SizeOf(Nnew),True);
For i :=1 To N Do
If Nnew [i] ThenPg(i);
В силу важности данного алгоритма рассмотрим его
нерекурсивную реализацию. Глобальные структуры данных
прежние: А — матрица смежностей; Nnew — массив признаков.
Номера просмотренных вершин графа запоминаются в стеке St,
указатель стека — переменная yk.
Procedure Pgn(ν:Integer);
Var St:Array.[l-.Ν] Of Integer;
yk, t, j:Integer;
pp:Boolean;
Begin
FillChar(St,SizeOf (St),0); yk:=0;
Inc(yk);St[yk]:=v;Nnew[v]:=False;
While yk<>0 Do
Begin {*Пока стек не пуст.*}
t:=St[yk];{*Выбор "самой верхней" вершины
из стека.*}
j:=l;pp:=False;
Repeat
If (A[t,j] <>0) AndNnew[j]
Then pp:=True
Else Inc (j);
Until pp Or (j>=N); {"^Найдена новая вершина
или все вершины, связанные с данной
вершиной, просмотрены.*}

4. Алгоритмы на графах
161
If рр Then
Begin
Inc (yk);
St[yk]:=j;
Nnew[j]:=False;{^Добавляем номер вершины
в стек.*}
End
Else Dec(yk); {^"Убираем" номер вершины
из стека.*}
End;
End;
4.2.2. Поиск в ширину
Идея метода. Суть (в сжатой формулировке) заключается в
том, чтобы рассмотреть все вершины, связанные с текущей.
Принцип выбора следующей вершины — выбирается та,
которая была раньше рассмотрена. Для реализации данного
принципа необходима структура данных очередь.
Пример. Исходный граф на рисунке 4.3. На рисунке 4.4
рядом с вершинами в скобках указана очередность просмотра
вершин графа.
Рис. 4.3 Рис. 4.4
Приведем процедуру реализации данного метода обхода
вершин графа.
Алгоритм просмотра вершин.
Procedure Pw(v:Integer);
Var Og:Array[1..N] Of 0..N;{*Очередь . *}
ykl, yk2:Integer;{^Указатели очереди,
ykl - запись; yk2 - чтение.*}
j:Integer;
Begin

162
4. Алгоритмы на графах
FillChar(Og,SizeOf(Og),0);
ykl:=0;yk2:=0;{^Начальная инициализация.*}
Inc(ykl);Og[ykl]:=v;Nnew[v]:=False;
{*B очередь - вершину v.*}
While yk2<ykl Do
Begin {*Пока очередь не пуста.*}
Inc(yk2);v:=Og[yk2]/Write(v:3);
{*"Берем" элемент из очереди.*}
For j:=l To N Do {^Просмотр всех вершин,
связанных с вершиной v.*}
If (A[v,j]<>0) AndNnew[j] Then
Begin
{*Если вершина ранее не просмотрена, то
заносим ее номер в очередь.*}
Inc (ykl);Og[ykl] :=j;Nnew[j] :=False;
End;
End;
End;
4.3. Деревья
4.3.1. Основные понятия. Стягивающие деревья
Деревом называют произвольный связный
неориентированный граф без циклов. Его можно определить и по-другому:
связный граф, содержащий N вершин и N-1 ребер. Для
произвольного связного неориентированного графа G=(V,E) каждое
дерево (V,T), где ТеЕ, называют стягивающим деревом
(каркасом, остовом). Ребра такого дерева называют ветвями, а
остальные ребра графа — хордами.
Примечание
Понятие цикла будет дано позже. В данной теме ограничимся его
интуитивным пониманием.
Число различных каркасов полного связного
неориентированного помеченного графа с N вершинами равно NN~2.
Пример. На рисунке 4.5 приведены граф и его каркасы.

4. Алгоритмы на графах
163
Поиск единственного стягивающего дерева (каркаса). Методы
просмотра вершин графа поиском в глубину и в ширину
позволяют построить одиночный каркас. В вышеописанные программы
необходимо вставить запись данных по ребрам, связывающих
текущую вершину с ранее не просмотренными в некую структуру
данных, например, массив Tree (Array [1. .2,1. .Ν] Of Integer).
Пример. На рисунке 4.6 приведены граф и его каркасы,
построенные методами поиска в глубину и в ширину. В круглых
скобках указана очередность просмотра вершин графа при
соответствующем поиске.
Рис.4.6
4.3.2. Порождение всех каркасов графа
Дано. Связный неориентированный граф G=(V,E).
Найти. Все каркасы графа.
Каркасы не запоминаются. Их необходимо перечислить.
Для порождения очередного каркаса ранее построенные не
привлекаются, используется только последний.
Множество всех каркасов графа G делится на два класса:
содержащие выделенное ребро (υ,и) и не содержащие. Каркасы
последовательно строятся в графах G(u,u) и G-(v,u)- Каждый из
графов G(u,u) и G-(u,u) меньше, чем G. Последовательное
применение этого шага уменьшает графы до тех пор, пока не будет
построен очередной каркас, либо графы станут несвязными и
не имеющими каркасов.
Для реализации идеи построения каркасов графа G
используются следующие структуры данных:
• очередь — Turn (Array[1..Ν] Of Integer) с нижним
(Down) и верхним (Up) указателями;
• массив признаков Nnew;
• список ребер, образующих каркас, — Tree;
• число ребер в строящемся каркасе — numb.
Начальное значение переменных:

164
4. Алгоритмы на графах
FillChar(Nnew,SizeOf(Nnew),True);
FillChar (Tree,SizeOf(Tree),0);
Nnew[1]:=False;
Turn[l]:=l; Down:=1;Up:=2; { *B очередь заносим
первую вершину.*}
numb:=0;
Procedure Solve(ν,q:Integer);{*v - номер вершины,
из которой выходит ребро, q - номер вершины,
начиная с которой следует искать очередное
ребро каркаса .*}
Var j:Integer;
Begin
If Down>=Up Then Exit;
j :=q;
While (j<=N) And (numb<N-l) Do
Begin
{*Просмотр ребер, выходящих из вершины с номером v.*}
If (A[v,j]<>0) AndNnew[j] Then
Begin
{*Есть ребро, и вершины с номером j еще нет
в каркасе. Включаем ребро в каркас.*}
Nnew[j]:=False;
Inc(numb);Tree[1,numb]:=v;Tree[2,numb]:=j;
Turn[Up]:=j;Inc(Up);{*Включаем вершину
с номером j в очередь.*}
Solve(v,j+1); {^Продолжаем построение
каркаса.*}
Dec (Up);Nnew[j] :=True;Dec(numb);
{^Исключаем ребро из каркаса.*}
End;
Inc (j);
End;
If numb=N-l Then
Begin <вывод каркаса>; Exit End;
{*Bce ребра, выходящие из вершины с номером ν,
просмотрены. Переходим к следующей вершине
из очереди и так до тех пор, пока не будет
построен каркас.*}
If j=N+l Then
Begin
Inc(Down);
Solve(Turn[Down],1);
Dec(Down);
End;
End;

4. Алгоритмы на графах
165
Алгоритм работы процедуры достаточно (D
сложно понимается — двойной рекурсивный / \
вызов. Для этого лучше всего выполнить трас- /^^®^\
сировку работы процедуры на каком-либо при- @— —®
мере. Рассмотрим граф, приведенный на ри- ^ч\ //
сунке 4.7. Последовательность построения \£)
каркасов приведена на рисункх 4.8 и 4.9.
Первый каркас строится обычным поиском в ши- Рис. 4.7
рину. Затем исключаем последнее ребро (4,3)
и вновь строим каркас. Первые каркасы, в которых есть ребра
(1,4) и (1,5), приведены на следующем рисунке. При
исключении ребра (1,5) получаются 8 каркасов.
Рис. 4.8
Затем наступает очередь ребра (1,4) и вновь 8 каркасов (см.
рисунок 4.9).
4.3.3. Каркас минимального веса.
Метод Дж. Краскала
Дано: связный неориентированный граф G=(V,E),
ребра имеют вес,
граф описывается перечнем ребер с указанием их веса,
массив Ρ (Array[1..3,l..N*(N-l) Div 2] Of Integer).
Результат. Каркас с минимальным суммарным весом
Q=(V,T), где TczE.

166
4. Алгоритмы на графах
Рис. 4.9
Пример. Граф и процесс построения каркаса по методу Кра-
скала.
Шаг 1. Начать с графа Q, содержащего N вершин и не
имеющего ребер.
Шаг 2. Упорядочить ребра графа G в порядке неубывания их
весов.
Шаг 3. Начав с первого ребра в этом перечне, добавлять
ребра в граф Q, соблюдая условие: добавление не должно
приводить к появлению цикла в Q.
Шаг 4. Повторять шаг 3 до тех пор, пока число ребер в Q не
станет равным N-1. Получившееся дерево является каркасом
минимального веса.
Рис. 4.10
Какие структуры данных требуются для реализации шага
3? Стандартным в программировании методом является
введение массива меток вершин графа (Mark:Array[l..N] Of
Integer). Начальные значения элементов массива равны номерам
соответствующих вершин (Mark[i]=i для i от 1 до N). Ребро
выбирается в каркас в том случае, если вершины, соединяемые

4. Алгоритмы на графах
167
им, имеют разные значения меток. В этом случае циклы не
образуются. Для примера, приведенного на рисунке 4.10, процесс
изменения Mark показан в таблице 4.1.
Таблица 4.1
| Номер итерации
Начальное значение
I 1
2
I 3
I 4
Ребро
-
<1,4>
<4,5>
<2,3>
<2,5>
Значения элементов Mark |
[1,2,3,4,5]
[1,2,3,1,5]
[1,2,3,1,1]
[1,2,2,1,1]
_[_VU , 1,11 J
И алгоритм этого фрагмента.
Procedure Chang_Mark(l,m:Integer);
{^Массив Mark глобальный.*}
Var i,t:Integer;
Begin
If m<l Then Begin t :=1; 1: =m;m:=t End;
For i:=l ToNDo
If Mark[i]=m Then Mark[i]:=1;
End;
Фрагмент основной части программы.
Program Tree;
Const N=. . ;
Var P:Array[l. .3,1- -Ν* (Ν-1) Div 2] Of Integers-
Mark -.Array [ 1 . .N] Of Integer;
k, i,t:Integer;
M:Integer;{^Количество ребер графа.*}
Begin
<ввод описания графа - массив Р>;
<сортировка массива Ρ по значениям весов ребер>;
For i:=l To N Do Mark[i] : =i;
k:=0;t:=M;
While k<N-l Do
Begin
i:=l;
While (i<=t) And (Mark[P[1,i]]=Mark[P[2,i]])
And (P[l,i]<>0) Do Inc(i);
Inc(k) ;
Оапоминание ребра каркаса>;
Change_Mark(Mark[P[l,i]],Mark[P[2,i]]);
End;
End;

168
4. Алгоритмы на графах
4.3.4. Каркас минимального веса.
Метод Р. Прима
Дано: связный неориентированный граф G=(V,E),
ребра имеют вес,
граф описывается матрицей смежности
A (Array[L.NJ..N] Of Integer),
элемент матрицы, не равный нулю, определяет вес
ребра.
Результат. Каркас с минимальным суммарным весом
Q=(V,T), где ГсЯ.
Отличие от метода Краскала заключается в том, что на
каждом шаге строится дерево, а не ациклический граф, т. е.
добавляется ребро с минимальным весом, одна вершина которого
принадлежит каркасу, а другая нет. Такой принцип
«добавления» исключает возможность появления циклов. Для
реализации метода необходимы две величины множественного типа
SM и SP (Set Of 1..N). Первоначально значением SM являются
все вершины графа, a SP пусто. Если ребро (i,j) включается в
Г, то один из номеров вершин i и j исключается из SM и
добавляется в SP (кроме первого шага, на котором оба номера
переносятся в SP).
Пример. На рисунке 4.11 приведен граф, для которого
последовательно строится каркас. Процесс построения
(изменение SM и SP) показан на рисунках 4.12 и 4.13.
Рис. 4.11
Алгоритм построения каркаса.
Procedure Tree; {*А - глобальная структура данных.*}
Var SM,SP:Set Of 1..Ν;
min,i,j,l,k,t:Integer;

4. Алгоритмы на графах
169
SM=[7] SP=[1..6] SM=[] SP=[1..7]
(з) @ (ь) (г\ (л) (5)
(?) ® >® ® ®
Рис. 4.12
SM=[1,2,5..7] SP=[3,4]
® Θ
SM=[5..7] SP=[1..4]
© Θ
SM=[1,5..7] SP=[2..4]
Φ Θ
SM=[5,7] SP=[1..4,6]
Cs) 0
® ® Θ—®
Рис. 4.13
Begin
min:=maxint; SM:=[1..N];SP:=[];{^Включаем первое
ребро в каркас . * }
For i:=l To N-l Do
For j:=i+l To N Do
If (A[i,j ]<min) And (A[i,j]<>0) Then
Begin min:=A[i,j];1:=i;t:=j; End;
SP: = [1,t];SM:=SM-[1,t]; <выводим или
запоминаем ребро <l,t>>;
{^Основной цикл.*}
While SM<>[] Do
Begin
min:=maxint;1:=0;t:=0;
For i :=1 To N Do
If Not (i In SP) Then
For j :=1 To N Do
If (j In SP) And (A[i,j]<min) And (A[i,j]<>0)
Then Begin min:=A[j , k]; 1:=i;t:=j;End;
SP:=SP+[1];SM:=SM-[1] ;
{выводим или запоминаем ребро <l,t>};
End;
End;

170
4. Алгоритмы на графах
4.4. Связность
4.4.1. Достижимость
Путем (или ориентированным маршрутом)
ориентированного графа называется последовательность дуг, в которой
конечная вершина всякой дуги, отличной от последней, является
начальной вершиной следующей. Простой путь — это путь, в
котором каждая дуга используется не более одного раза.
Элементарный путь — это путь, в котором каждая вершина
используется не более одного раза. Если существует путь из
вершины графа υ в вершину г/, то говорят, что и достижима из υ.
Матрицу достижимостей R определим следующим образом:
1, если вершина с номером и достижима из ν
[U, при недостижимости
Множество Щи) — это множество таких
вершин графа G, каждая из которых может
быть достигнута из вершины υ. Обозначим
через Γ(υ) множество таких вершин графа G,
которые достижимы из у с использованием
путей длины 1. Γ2(υ) — это Γ(Γ(υ))9 τ. е. с
использованием путей длины 2 и так далее. В
Рис 4 14
этом случае: " "
Щи)={и}иГ(и)иГ2(и)и...иЩи).
При этом ρ — некоторое конечное значение, возможно,
достаточно большое.
Пример (см. рисунок 4.14).
Д(1)={1М2,5}и{1,6}и{2,5,4}и{1,6,7}={1,2,4,5,6,7}.
Выполняя эти действия для каждой вершины графа, мы
получаем матрицу достижимостей R.
Procedure Reach; {^Формирование матрицы R,
глобальной переменной. Исходные данные -
матрица смежности А, глобальная
переменная.*}
Var S,T:Set Of 1. .Ν;
i,j,1:Integer;
Begin
FillChar(R,Size0f(R),0);
For i :=1 To N Do
Begin
{^Достижимость из вершины с номером i . * }

4. Алгоритмы на графах
171
T:=[i];
Repeat
S:=T;
For 1:=1 To N Do
If 1 In S Тпеп{*По строкам матрицы А,
принадлежащим множеству S.*}
For j :=1 To N Do
If A[1,j]=1 Then Τ:=T+[ j ] ;
Until Б=Т;{*Если Т не изменилось, то найдены все
вершины графа, достижимые из вершины
с номером i . *}
For j :=1 To N Do
If j In Τ Then R [ i, j ] : =1 ;
End;
End;
Q[v,u] =
Матрицу контрдостижимостей Q определим следующим
образом:
1> если из и можно достигнуть ν
[О, при недостижимости
Множеством Q(v) графа G является множество таких
вершин, что из любой его вершины можно достигнуть вершины υ.
Из определения следует, что столбец υ матрицы Q совпадает со
строкой υ матрицы R, т. е. Q=Rt, где R* — матрица,
транспонированная к матрице достижимостей R.
Для примера на рисунке 4.15 приведены матрицы A, R и Q.
А =
0100100 >\
1000000
0101000
0000001
1000010
0001000
0000010
R =
1101111 >
1101111
1111111
000101 1
1101111
000101 1
000Ю11 ;
Q =
1110100
1110100
0010000
1111111
1110100
1111111
1111111
Рис. 4.15
Дополнения.
1. Граф называется транзитивным, если из существования
дуг (ν,и) и (u,t) следует существование дуги (v,t). Транзитивным
замыканием графа G=(V,E) является граф G2=(V,EuE')9 где
Еч — минимально возможное множество дуг, необходимых для
того, чтобы граф Gz был транзитивным.
Задание. Разработать программу для нахождения
транзитивного замыкания произвольного графа G.

172
4. Алгоритмы на графах
2. Щи) — множество вершин, достижимых из v, a Q(u) —
множество вершин, из которых можно достигнуть и.
Определить, что представляет из себя множество R(v)c\Q(u).
Задание. Разработать программу нахождения этого типа
множеств.
4.4.2. Определение связности
Определения.
Неориентированный граф G связен, если существует хотя бы
один путь в G между каждой парой вершин i и /'.
Ориентированный граф G связен, если неориентированный
граф, получающийся из G путем удаления ориентации ребер,
является связным.
Ориентированный граф сильно связен, если для каждой
пары вершин i и у существует по крайней мере один
ориентированный путь из i в у и по крайней мере один из у в i.
Максимальный связный подграф графа G называется
связной компонентой графа G. Максимальный сильно связный
подграф называется сильно связной компонентой.
Рассмотрим алгоритм нахождения сильно связных
компонент графа.
Идея достаточна проста. Для примера на рисунке 4.14
значение Я(1Н1}и{2,5}и{6М4М7Н1,2,4,5,6,7}, a Q(l)={l}u{2,5}u{3}.
Пересечение этих множеств дает множество С(1)={1,2,5}
вершин графа G, образующих сильную компоненту, которой
принадлежит вершина графа с номером 1. Продолжим рассмотрение:
Д(ЗН1,2,3,4,5,6,7}, Q(3)={3} и С(3)={3}; Л(4)={4}и{7}и{6}={4,6,7}
и Q(4)={4}u{6}u{7}={4,6,7} и С(4)={4,6,7}. Итак, мы нашли
сильные компоненты графа G.
Граф G*=(V*,E*) определим так: каждая его вершина
представляет множество вершин некоторой сильной компоненты
графа G, дуга (/*, у*) существует в G* тогда и только тогда,
когда в G существует дуга (i,y), такая, что i принадлежит
компоненте, соответствующей вершине i*9 ay — компоненте,
соответствующей вершине у*. Граф G* называется конденсацией графа G.
Некоторые факты по изложенному материалу.
1. G* не содержит циклов.
2. В ориентированном графе каждая вершина i может
принадлежать только одной сильной компоненте.
3. В графе есть множество вершин Р, из которых достижима
любая вершина графа и которое является минимальным в том
смысле, что не существует подмножества в Р, обладающего та-

4. Алгоритмы на графах
173
ким свойством достижимости. Это множество вершин
называется базой графа.
4. В Ρ нет двух вершин, которые принадлежат одной и той
же сильной компоненте графа G. Любые две базы графа G
имеют одно и то же число вершин.
Задание. Разработать программу нахождения базы графа.
Схема решения. База Р* конденсации G* графа G состоит из
таких вершин графа G*, в которые не заходят ребра.
Следовательно, базы графа G можно строить так: из каждой сильной
компоненты графа G, соответствующей вершине базы Р*
конденсации G*, надо взять по одной вершине — это и будет базой
графа G.
4.4.3. Двусвязность
Иногда недостаточно знать, что граф связен. Может
возникнуть вопрос, насколько «сильно связен» связный граф.
Например, в графе может существовать вершина, удаление которой
вместе с инцидентными ей ребрами разъединяет оставшиеся
вершины. Такая вершина называется точкой сочленения, или
разделяющей вершиной. Граф, содержащий точку сочленения,
называется разделимым. Граф без точек сочленения
называется двусвязным, или неразделимым. Максимальный двусвяз-
ный подграф графа называется двусвязной компонентой, или
блоком.
Пример. На рисунке 4.16 показаны разделимый граф и его
двусвязные компоненты. Точки сочленения вершины с
номерами 4, 5 и 7.
© ® ® ®
Рис. 4.16
Точку сочленения можно определить иначе. Вершина t
является точкой сочленения, если существуют вершины или,
отличные от £, такие, что каждый путь из и в υ (предполагаем,
что существует по крайней мере один) проходит через вершину
с номером t.

174
4. Алгоритмы на графах
Наша задача — найти точки
сочленения и двусвязные компоненты графа.
Основная идея. Есть двусвязные
компоненты Gl9 G2, G3, G4 и G5 и точки
сочленения 1, 2, 3 (см. рисунок 4.17).
Осуществляем поиск в глубину из вершины
£, принадлежащей Gr Мы можем перей- G4
ти из Gx в G2, проходя через вершину 1. g
Но по свойству поиска в глубину все
ребра G2 должны быть пройдены до того,
как мы вернемся в 1. Поэтому G2 состо- Рис. 4.17
ит в точности из ребер, которые
проходятся между заходами в вершину 1. Для других чуть сложнее.
Из Gx попадаем в G3, затем в G4 и G5. Предысторию процесса
прохождения ребер будем хранить в стеке. Тогда при
возвращении в G4 из G5 через вершину 3 все ребра G5 будут на верху
стека. После их удаления, т. е. вывода двусвязной компоненты из
стека, на верху стека будут ребра G4, и в момент прохождения
вершины 2 мы можем их опять вывести. Таким образом, если
распознать точки сочленения, то, применяя поиск в глубину и
храня ребра в стеке в той очередности, в какой они проходятся,
можно определить двусвязные компоненты. Ребра,
находящиеся на верху стека в момент обратного прохода через точку
сочленения, образуют двусвязную компоненту.
Итак, проблема с точками
сочленения. Рассмотрим граф на рисунке 4.18.
В процессе просмотра в глубину все
ребра разбиваются на те, которые
составляют дерево (каркас), и множество
обратных ребер. Обратные ребра выделены на
рисунке более жирными линиями.
Что нам это дает? Пусть очередность
просмотра вершин в процессе поиска в
глубину фиксируется метками в массиве Рис. 4.18
Num. Для нашего примера Num —
(1,2,3,4,5,6,7,9,8). Если мы рассматриваем обратное ребро
(υ,и), и ι; не предок г/, то информацию о том, что Num[v]
больше Num [и] у можно использовать для пометки вершин υ τι и
как вершин, принадлежащих одной компоненте двусвязности.
Массив Num использовать для этих целей нельзя, поэтому
введем другой массив Lowpg и постараемся пометить вершины
графа, принадлежащие одной компоненте двусвязности, одним
значением метки в этом массиве. Первоначальное значение

4. Алгоритмы на графах
175
метки совпадает со значением соответствующего элемента
массива Num. При нахождении обратного ребра (υ,и) естественной
выглядит операция: Lowpg[v]:=Min(Lowpg[v],Num[u]) —
изменения значения метки вершины и, так как вершины υ и и из
одной компоненты двусвязности. К этому алгоритму
необходимо добавить смену значения метки у вершины υ ребра (υ,и) на
выходе из просмотра в глубину в том случае, если значение
метки вершины и меньше, чем метка вершины υ (Lowpg[u]:=
Min(Lowpg[v],Lowpg[u])). Для нашего примера массив меток
Lowpg имеет вид: (1,1,1,2,4,4,4,9,8). Осталось определить
момент вывода компоненты двусвязности. Мы рассматриваем
ребро (υ,и), и оказывается, что значение Lowpg[u] больше или
равно значению Num[v]. Это говорит о том, что при просмотре в
глубину между вершинами υ к и не было обратных ребер.
Вершина υ — точка сочленения, и необходимо вывести очередную
компоненту двусвязности, начинающуюся с вершины и.
Итак, алгоритм.
Procedure Dvy(v,p:Integer);{*Вершина р - предок
вершины v. Массивы A, Num, Lowpg и переменная
nm - глобальные.*}
Var u .'Integer ;
Begin
Inc(nm);Num[ν]:=nm;Lowpg[v]:=Num[v];
For u:=l To N Do
If A[v,u]<>0 Then
If Num[u]=0
Then
Begin
<сохранить ребро (v,u) в стеке>;
Dvy(u,ν);
Lowpg[ν]:=Min(Lowpg[ν],Lowpg[u]); {*Функция,
определяющая минимальное из двух чисел.*}
If Lowpg[u]>=Num[v] Then <вывод компоненты>;
End
Else
If (uop) And (Num[v] >Num[u] ) Then
Begin
{ *u не совпадает с предком вершины v.*}
<сохранить ребро (ν,и) в стеке>;
Lowpg[v]:=Min(Lowpg[v],Num[и]);
End;
End;

176
4. Алгоритмы на графах
Фрагмент основной программы:
FillChar(Num,SizeOf(Num),0);
FillChar(Lowpg,SizeOf(Lowpg),0);
nm:=0;
For v:=l To N Do
If Num[v]=0 Then Dvy(v,0) ;
Мостом графа G называется каждое ребро, удаление
которого приводит к увеличению числа связных компонент графа.
Задание. Разработать программу нахождения всех мостов
графа. Покажите, что мосты графа должны быть в каждом
каркасе графа G. Каким образом знание мостов графа может
изменить (ускорить) алгоритм нахождения всех его каркасов?
4.5. Циклы
4.5.1. Эйлеровы циклы
Эйлеров цикл — это такой цикл, который проходит ровно
один раз по каждому ребру.
Теорема. Связный неориентированный граф G содержит
эйлеров цикл тогда и только тогда, когда число вершин
нечетной степени равно нулю.
Не все графы имеют эйлеровы циклы, но если эйлеров цикл
существует, то это означает, что, следуя вдоль этого цикла,
можно нарисовать граф на бумаге, не отрывая от нее карандаша.
Дан граф G, удовлетворяющий условию теоремы. Требуется
найти эйлеров цикл. Используется просмотр графа методом
поиска в глубину, при этом ребра удаляются. Порядок просмотра
(номера вершин) запоминается. При обнаружении вершины, из
которой не выходят ребра, мы их удалили, ее номер
записывается в стек, и просмотр продолжается от предыдущей
вершины. Обнаружение вершин с нулевым числом ребер говорит о
том, что найден цикл. Его можно удалить, четность вершин
(количество выходящих ребер) при этом не изменится. Процесс
продолжается до тех пор, пока есть ребра. В стеке после этого
будут записаны номера вершин графа в порядке,
соответствующем эйлерову циклу.
Procedure Search(v:Integer);{*Глобальные
переменные: А - матрица смежности, Cv - стек;
ук - указатель стека.*}

4. Алгоритмы на графах
177
Var j:Integer;
Begin
For j :=1 To N Do
If A[v, j ]<>0 Then
Begin
A[v,j]:=0;A[j,v]:=0;
Search(j)
End;
Inc(yk);Cv[yk]:=v;
End;
На рисунке 4.19 приведен пример графа и содержимое стека
Си после работы процедуры Search.
(2}——©-.
Cv: 13567254321
Рис. 4.19
4.5.2. Гамильтоновы циклы
Граф называется гамильтоновым, если в нем
имеется цикл, содержащий каждую вершину
этого графа. Сам цикл также называется гамиль-
тоновым. Не все связные графы гамильтоновы.
На рисунке 4.20 дан пример графа, не
имеющего гамильтонова цикла.
Дан связный неориентированный граф G. Требуется найти
все гамильтоновы циклы графа, если они есть.
Метод решения — перебор с возвратом {backtracking).
Начинаем поиск решения, например, с первой вершины графа.
Предположим, что уже найдены первые k компонент решения.
Рассматриваем ребра, выходящие из последней вершины. Если
есть такие, что идут в ранее не просмотренные вершины, то
включаем эту вершину в решение и помечаем ее как
просмотренную. Получена (&+1) компонента решения. Если такой
вершины нет, то возвращаемся к предыдущей вершине и
пытаемся найти ребро из нее, выходящее в другую вершину. Решение
получено при просмотре всех вершин графа и возможности
достичь из последней первой вершины. Решение (цикл)
выводится, и продолжается процесс нахождения следующих циклов.
<Ξ>

178
4. Алгоритмы на графах
На рисунке 4.21 приведен пример графа и часть дерева пере
бора вариантов, показывающего механизм работы данного ме
тода.
Рис. 4.21
Procedure Gm(k:Integer); {* k - номер итерации.
Глобальные переменные: А - матрица смежности; St -
массив для хранения порядка просмотра вершин
графа; Nnew - массив признаков: вершина
просмотрена или нет.*}
Var j,v:Integer;
Begin
v:=St[k-l]; {*Номер последней вершины.*}
For j :=1 To N Do
If (A[v,j]<>0) Then {*Есть ребро между
вершинами с номерами ν и j . * }
If (k=N+l) And (j = l)
Then <вывод цикла>
Else
If Nnew[j] Then
Begin {*Вершина не просмотрена.*}
St[k]:=j;
Nnew[j]:=False;
Gm(k+1);
Nnew[j]:=True;
End;
End;
Фрагмент основной программы.
St[1]:=l;Nnew[l]:=False; Gm(2);

4. Алгоритмы на графах
179
4.5.3. Фундаментальное множество циклов
Каркас (V,T) связного неориентированного графа G=(V,E)
содержит N—1 ребро, где N — количество вершин G. Каждое
ребро, не принадлежащее Г, т. е. любое ребро из Е-Т, порождает в
точности один цикл при добавлении его к Т. Такой цикл
является элементом фундаментального множества циклов графа G
относительно каркаса Т. Поскольку каркас состоит из N-1
ребра, в фундаментальном множестве циклов графа G
относительно любого каркаса имеется M-N+1 циклов, где Μ —
количество ребер в G.
Пример графа, его каркаса и множества фундаментальных
циклов приведен на рисунке 4.22.
Рис. 4.22
Поиск в глубину является естественным подходом,
используемым для нахождения фундаментальных циклов. Строится
каркас, а каждое обратное ребро порождает цикл относительно
этого каркаса. Для вывода циклов необходимо хранить
порядок обхода графа при поиске в глубину (номера вершин) —
массив St9 а для определения обратных ребер вершины следует
«метить» (массив Gnum) в той очередности, в которой они
просматриваются. Если для ребра (v,j) оказывается, что значение
метки вершины с номером j меньше, чем значение метки
вершины с номером υ, то ребро обратное и найден цикл.
Начальная инициализация переменных.
пит:=0;ук:=0;
For j : =1 То N Do Gnum [ j ] : =0;

180
4. Алгоритмы на графах
Основной алгоритм.
Procedure Circl(v:integer);{^Глобальные
переменные: А - матрица смежности графа; St -
массив для хранения номеров вершин графа в том
порядке, в котором они используются при построении
каркаса; ук - указатель записи в массив St; Gnum -
для каждой вершины в соответствующем элементе
массива фиксируется номер шага (num), на котором
она просматривается при поиске в глубину.*}
Var j : Integers-
Begin
Inc(yk);St[yk]:=v;
Inc(num);Gnum[v]:=num;
For j :=1 To N Do
If A[v,j]<>0 Then
If Gnum[j]=0
Then Circl[j] {*Вершина j не просмотрена.*}
Else
If (j<>St[yk-l]) And (Gnum[j]<Gnum[v])
Then <вывод цикла из St>{*j не предыдущая
вершина при просмотре, и она была
просмотрена ранее.*};
Dec(yk);
End;
Название «фундаментальный» связано с тем, что каждый
цикл графа может быть получен из циклов этого множества. Для
произвольных множеств А и Б определим операцию
симметрической разности АФВ=(АиВ)\(АглВ). Известно, что произвольный
цикл графа G можно однозначно представить как
симметрическую разность некоторого числа фундаментальных циклов.
Однако не при всех операциях симметрической разности получаются
циклы (вырожденный случай).
Задание. Разработать программу нахождения всех циклов
графа.
4.6. Кратчайшие пути
4.6.1. Постановка задачи. Вывод пути
Дано:
ориентированный граф G=(V,E),
веса дуг — A[ifj] (i,/=l JV, где N — количество вершин графа),
начальная и конечная вершины — s, tsV.

4. Алгоритмы на графах
181
Веса дуг записаны в матрице смежности А, если вершины i
и j не связаны дугой, то A[i,j]=co. Путь между s и t оценивается
ZA[i,/].
г , j € пути
Результат: путь с минимальной оценкой.
Пример. Кратчайший путь из 1 в 4
проходит через 3-ю и 2-ю вершины и
имеет оценку 6 (см. рисунок 4.23).
Особый случай — контуры с
отрицательной оценкой.
Пример.
При s=l и t=6, обходя контур Рис. 4.23
3—>4—>2—>3 (см. рисунок 4.24)
достаточное число раз, можно сделать так, что
оценка пути между вершинами 1 и 5
будет меньше любого целого числа.
Оценку пути назовем его весом или
длиной. Будем рассматривать только графы
без контуров отрицательного веса.
Нам необходимо найти кратчайший Рис. 4.24
путь, т. е. путь с минимальным весом,
между двумя вершинами графа. Эта задача разбивается на две
подзадачи: сам путь и значение минимального веса.
Обозначим минимальные веса через D[s,t]. Неизвестны
алгоритмы, определяющие только D[s,t], все они определяют
оценки от вершины s до всех остальных вершин графа. Определим
D как Array[l..N] Of Integer. Предположим, что мы определили
значения элементов массива D — решили вторую подзадачу.
Определим сам кратчайший путь. Для s и t существует такая
вершина υ, что D[t]=D[v]+A[v,t]. Запомним υ (например, в
стеке). Повторим процесс поиска вершины г/, такой, что
D[v]=D[u]+A[u,v], и так до тех пор, пока не дойдем до вершины
с номером s. Последовательность t, υ, и, ..., s дает кратчайший
путь.
Procedure Way(s,t:Integer);{*D, A - глобальные
структуры данных. St - локальная структура
данных для хранения номеров вершин.*}
Var v,u:Integer;
Procedure Print; {^Выводит содержимое St.*}
Begin
End;

182
4. Алгоритмы на графах
Begin
<почистить St>;
<занести вершину с номером t в St>;
v:=t;
While v<>s Do
Begin
и:=<номер вершины, для которой D[v]=D[u]+A[u,v]>;
<занести вершину с номером ν в St>;
ν: =u;
End;
End;
Итак, путь при известном D находить мы умеем. Осталось
научиться определять значения кратчайших путей, т. е.
элементы массива D. Идея всех известных алгоритмов
заключается в следующем. По данной матрице весов А вычисляются
первоначальные верхние оценки. А затем пытаются их улучшить
до тех пор, пока это возможно. Поиск улучшения, например
для D[v], заключается в нахождении вершин г/, таких, что
D[u]+A[u,v]<D[v]. Если такая вершина и есть, то значение
D[v] можно заменить на D[u]+A[u,v].
4.6.2. Алгоритм Дейкстры
Дано:
ориентированный граф G=(V,E),
s — вершина-источник; матрица смежности A (Array\l..N,\.JST\
Of Integer);
для любых ζ/, иеТ^вес дуги неотрицательный (A[u,v] >0).
Результат: массив кратчайших расстояний D.
В данном алгоритме формируется множество вершин Г, для
которых еще не вычислена оценка расстояние и, во-вторых (это
главное), минимальное значение в D по множеству вершин,
принадлежащих Г, считается окончательной оценкой для вершины,
на которой достигается этот минимум. С точки зрения здравого
смысла этот факт достаточно очевиден. Другой «заход» в эту
вершину возможен по пути, содержащему большее количество дуг, а
так как веса неотрицательны, то и оценка пути будет больше.
Пример. Граф и его матрица смежности.
В таблице 4.2 приведена последовательность шагов
(итераций) работы алгоритма. На первом шаге минимальное значение
D достигается на второй вершине. Она исключается из
множества Т9 и улучшение оценки до оставшихся вершин (3,4,5,6)
ищется не по всем вершинам, а только от второй.

4. Алгоритмы на графах
183
3
00
1
00
ОС
7
2
X
ОС
1
00
ОС
4
ОС
ОС
00
ОС
4
1
00
00
1
00
5
3
V ос оо ос
Рис. 4.25
Таблица 4.2
№ итерации
1
2
3
4
I 5 ,
D[1]
0
0
0
0
о
D[2]
3
3
3
3
3
D[3]
7
5
5
5
5
0[4]
00
00
6
6
6
D[5]
00
00
00
9
7
D[6]
00
4
4
4
4
τ Ι
[2,3,4,5,6]
[3,4,5,6]
[3,4,5]
[4,5]
[5]
Procedure Dist;{*A, D, s, N - глобальные величины.*}
Var ir и: Integer;
T:Set Of 1..N;
Begin
For i : =1 To N Do D [ i ] : =A [ s, i ] ;
D[s]:=0;
T:=[l..N]-[s];
While T<>[ ] Do
Begin
и:=<то значение 1, при котором достигается
min(D[l])>;
T:=T-[u];
For i :=1 To N Do
If i In Τ Then D[i]:=min(D[i],D[u]+A[u,i]);
End;
End;
Время работы алгоритма teO(N2).
4.6.3. Пути в бесконтурном графе
Дано:
ориентированный граф G=(V,E) без контуров,
веса дуг произвольны.
Результат: массив кратчайших расстояний (длин) D от
фиксированной вершины s до всех остальных.

184
4. Алгоритмы на графах
Утверждение — в произвольном бесконтурном графе
вершины можно перенумеровать так, что для каждой дуги (i,j)
номер вершины i будет меньше номера вершины у.
Пример.
Введем следующие структуры данных:
• массив Numln, Numln[i] определяет число дуг, входящих
в вершину с номером i;
• массив Num, Num[i] определяет новый номер вершины i;
• массив St, для хранения номеров вершин, в которые
заходит нулевое количество дуг. Работа с массивом
осуществляется по принципу стека;
• переменная пт, текущий номер вершины.
Идея алгоритма. Вершина г, имеющая нулевое значение
Numln (а такая вершина на начальном этапе обязательно есть в
силу отсутствия контуров в графе), заносится в St, ей
присваивается текущее значение пт (запоминается в Num), и
изменяются значения элементов Numln для всех вершин, связанных с
i. Процесс продолжается до тех пор, пока St не пуст.
Рис. 4.26
На рисунке 4.26 приведен пример графа, а в таблице 4.3
представлены результаты трассировки работы алгоритма для
этого примера.
Таблица 4.3
№ итерации
1 начальная
1
2
3
4
5
L 6
Numln
[2,2,2,1,0,1]
[2,2,1,0,0,1]
[1,2,0,0,0,1]
[0,2,0,0,0,0]
[0,1,0,0,0,0]
[0,0,0,0,0,0]
[0,0,0,0,0,0]
Num
[0,0,0,0,0,0]
[0,0,0,0,1,0]
[0,0,0,2,1,0]
[0,0,3,2,1,0]
[0,0,3,2,1,4]
[5,0,3,2,1,4]
[5,6,3,2,1,4]
St
[5]
[4]
[3]
[6,1]
[1]
[2]
[]
Nm^\
0
1
2
3
4 |
5
6 |

4. Алгоритмы на графах
185
Procedure Change_Num;{*A, Num — глобальные
структуры данных.*}
Var Numln,St:Array [1 . .Ν] Of Integer;
i, j,u,nm,yk:Integer;
Begin
FillChar(Numln,SizeOf(Numln) , 0) ;
For i :=1 To N Do
For j :=1 To N Do
If A[i,j]<>0 Then Inc(Numln[j]);
nm:=0;yk:=0;
For i:=l ToNDo
If Numln [i]=0 Then
Begin Inc (yk) ; Stack [yk] :=i; End;
While yk<>0 Do
Begin
u:=Stack[yk];Dec[yk];Inc(nm);Num[u]:=nm;
For i :=1 To N Do
If A[u,i]<>0 Then
Begin
Dec(Numln[i]);
If Numln[i]=0 Then
Begin Inc(yk); Stack[yk]:=i; End;
Ends-
End;
End;
Итак, пусть для графа G выполнено условие утверждения
(вершины перенумерованы) и нам необходимо найти
кратчайшие пути (их длины) от первой вершины до всех остальных.
Пусть мы находим оценку для вершины с номером i.
Достаточно просмотреть вершины, из которых идут дуги в вершину с
номером i. Они имеют меньшие номера, и оценки для них уже
известны. Остается выбрать меньшую из них.
Procedure Dist;{*D, A - глобальные величины.*}
Var i,j: Integers-
Begin
D[l]:=0;
For i:=2 To N Do D[i]:=Мах1п1-<максимальное
значение в матрице смежности
А>;{^Определите, с какой целью вычитается
из Maxlnt максимальный элемент матрицы А.*}
For i:=2 To N Do
For j :=1 To i-1 Do

186
4. Алгоритмы на графах
If А[ j, i]<>oo
Then D[i]:=Min(D[i],D[j]+A[j, i]);
End;
Процедура написана в предположении о том, что / и у —
новые номера вершин и A[i,j] соответствует этим номерам. Однако
это не так. Новые номера по результатам работы предыдущей
процедуры хранятся в массиве Num. Требуется «стыковка»
новых номеров и матрицы А. Как это сделать наилучшим образом?
Время работы алгоритма teO(N2).
4.6.4. Кратчайшие пути между всеми парами вершин.
Алгоритм Флойда
Дано:
ориентированный граф G=(V,E) с матрицей весов
A(Array[l..N,l~N] Of Integer).
Результат: матрица D кратчайших расстояний между
всеми парами вершин графа и кратчайшие пути.
Идея алгоритма. Обозначим через Dm[i,j] оценку кратчайшего
пути из i в у с промежуточными вершинами из множества [1..га].
Тогда имеем:
D°[i,j]:=A[i,j] и
D(m+1)[i,y]= Mm{Dm[i,y],Dm[i,m+l] +Dm[m+l,y]}.
Второе равенство требует пояснения. Пусть мы находим
кратчайший путь из i в у с промежуточными вершинами из
множества [1..(га+1)]. Если этот путь не содержит вершину (га+1), то
D(m+1Xi,j]=Dm[i,j]. Если же он содержит эту вершину, то его
можно разделить на две части: от i до (га+1) и от (га+1) до у.
Время работы алгоритма teO(Ns).
Procedure Dist; {*A, D - глобальные структуры
данных.*}
Var m,ΐ,j:Integer;
Begin
For i:=l To N Do
For j : =1 To N Do D [ i, j ] : =A [ i, j ] ;
For i:=lToNDoD[i,i]:=0;
For m:=l To N Do
For i :=1 To N Do
For j : =1 To N Do D [ i, j ] : =Min { D [ i , j ] ,
D[i,m]+D[m,j]};
End;

4. Алгоритмы на графах
187
Пример. На рисунке 4.27 представлены граф и значения
матриц типа D при работе процедуры.
Рис. 4.27
Верхний индекс у D (см. рисунок 4.28) указывает номер
итерации (значение т в процедуре Dist).
D°=
0 12 1
2 0 7ос
65 0 2
,1 оо 4 0.
D1 =
(О 1 2 Ϊ
2043
6 5 0 2
V1 2 3 0.
D2=D1
D3=D2
D4=
Γθ 1 2 1
2043
340 2
12 3 0
Рис. 4.28
Расстояния между парами вершин дает D. Для вывода
самих кратчайших путей введем матрицу Μ того же типа, что и
D. Элемент M[i,j] определяет предпоследнюю вершину
кратчайшего пути из ί в у.
Процедура Dist претерпит небольшие изменения. В том
случае, когда D[i,j] больше D[i,m]+D[mj], изменяется не только
D[i,j], но и M[i,j]. M[i,j] присваивается значение M[m,j]. Для
нашего примера изменения Μ показаны на рисунке 4.29.
м°=
1111
2 2 2 2
33 33
V4 4 4 4,
М1 =
1 1 1 Я
2 2 11
3 3 33
V4 1 1 А)
М2=М1 М3=М2' М*=
Ί 1 1 Ϊ
2 2 11
4 133
4 114^
Рис. 4.29
Например, необходимо вывести кратчайший путь из 3-й
вершины во 2-ю. Элемент М[3,2] равен 1, поэтому смотрим на
элемент М[3,1]. Он равен четырем. Сравниваем М[3,4] с 3-й.
Есть совпадение, мы получили кратчайший путь: 3—>4—»1—» 2.
Procedure All_Way(i,j:Integer);{*Вывод пути между
вершинами i и j . * }

188
4. Алгоритмы на графах
Begin
If M[i, j]=i Then
If i=j Then Write (i) Else Write (i, ' - f, j )
Else
Begin
All_Way(i,M[i,j]); All_Way (M [ i,j],j) ;
End;
End;
4.7. Независимые и доминирующие множества
Задача поиска подмножеств множества вершин V графа G,
удовлетворяющих определенным условиям, свойствам,
возникает достаточно часто.
4.7.1. Независимые множества
Дан неориентированный граф G=(V,E). Независимое
множество вершин есть множество вершин графа G, такое, что любые
две вершины в нем не смежны, т. е. никакая пара вершин не
соединена ребром. Следовательно, любое подмножество S,
содержащееся в V, и такое, что пересечение S с множеством
вершин смежных с S пусто, является независимым множеством
вершин.
Пример.
Множества вершин (1, 2), (3, 4, 5), (4, 7),
(5, 6) независимые (см. рисунок 4.30).
Независимое множество называется
максимальным, когда нет другого независимого
множества, в которое оно бы входило. Если
Q является семейством всех независимых
множеств графа G, то число
a[G]=max\s\ Рис. 4.30
называется числом независимости графа G, а множество S*, на
котором этот максимум достигается, называется наибольшим
независимым множеством. Для примера на рисунке 4.30
a[G]=3, а S* есть (3, 4, 5).
Понятие, противоположное максимальному независимому
множеству, есть максимальный полный подграф (клика). В
максимальном независимом множестве нет смежных вершин, в
клике все вершины попарно смежны. Максимальное независи-

4. Алгоритмы на графах
189
мое множество графа G соответствует клике графа G\ где G —
дополнение графа G.
Для примера на рисунке 4.30 дополнение G приведено на
рисунке 4.31(a), клика графа (^'(рисунок 4.31(6)) соответствует
максимальному независимому множеству графа G. Число
независимости графа G равно 4, максимальное независимое множество
(2, 5, 7, 8), ему соответствует клика графа G (рисунок 4.31(e)).
Рис. 4.31
4.7.2. Метод генерации всех максимальных независимых
множеств графа
Задача решается перебором вариантов. «Изюминкой»
алгоритма является отсутствие необходимости запоминать
генерируемые множества с целью проверки их на максимальность путем
сравнения с ранее сформированными множествами. Идея
заключается в последовательном расширении текущего
независимого множества (k — номер шага или номер итерации в
процессе построения). Очевидно, что если мы не можем расширить
текущее решение, то найдено максимальное независимое
множество. Выведем его и продолжим процесс поиска.
Будем хранить текущее решение в массиве Ss (Array[l..N] Of
Integer), его первые k элементов определяют текущее решение.
Алгоритм вывода решения очевиден (процедура Print).
В процессе решения нам придется многократно
рассматривать вершины графа, смежные с данной. При описании графа
матрицей смежности — это просмотр соответствующей строки,
при описании списками связи — просмотр списка. Упростим
нахождение смежных вершин за счет использования нового
способа описания графа. Используем множественный тип
данных. Введем тип данных:
Type Sset=Set Of 1..N

190
4. Алгоритмы на графах
и переменную
Var A:Array[l. .N] Of Sset.
Итак, чтобы определить вершины графа, смежные с
вершиной i, необходимо просто вызвать соответствующий элемент
массива А.
Пример. Основная сложность алгоритма в выборе очередной
вершины графа. Введем переменную Gg для хранения номеров
вершин — кандидатов на расширение текущего решения.
Значение переменной формируется на каждом шаге k (см. рисунок
4.32). Что является исходной информацией для формирования
Gg? Очевидно, что некоторое множество вершин, свое для
каждого шага (итерации) алгоритма. Логически правомерно
разбить это множество вершин на не использованные ранее
(Qp) и использованные ранее (Qm). Изменение значений Qp и
Qm происходит при возврате на выбор k-vo элемента
максимального независимого множества. Мы выбирали на k шаге,
например, вершину с номером /, и естественно исключение ее из
Qp и Qm при поиске следующего максимального независимого
множества. Кроме того, при переходе к шагу с номером (k+1)
из текущих множеств Qp и Qm для следующего шага
необходимо исключить вершины, смежные с вершиной i, выбранной на
данном шаге (из определения независимого множества), и,
разумеется, саму вершину i.
&ί yd)—Θ
Рис. 4.32
Итак, общий алгоритм.
Procedure Find(k:Integer; Qp,Qm:Sset);
Var Gg:Sset;
i:Byte;
Begin
If (Qp=[ ]) And (Qm=[ ]) Then
Begin Print(k); Exit; End;
формирование множества кандидатов Gg для
расширения текущего решения (к элементов
в массиве Ss) по значениям Qp и Qm - "черный
ящик А" . >;
А[1]=[2,3]
А[2Н1,4]
А[3]=[1,4]
A[4]=[2,3,o]
АГ5]=[4]

4. Алгоритмы на графах
191
i:=l;
While i<=N Do
Begin
If i In Gg Then
Begin
Ss[k]:=i;
Find(k+l,Qp-A[i]-[i],Qm-A[i]-[i]);
<изменение Qp, Qm для этого уровня
(значения к) и, соответственно, изменение
множества кандидатов Gg - "черный ящик Б".>;
End;
Inc (i);
End;
End;
Продолжим уточнение алгоритма. Нам потребуется простая
функция подсчета количества элементов в переменных типа
Sset.
Function Number(A:Sset):Byte;
Var i, cnt:Byte;
Begin
cnt:=0;
For i :=1 To N Do
If i In A Then Inc (cnt) ;
Number:=cnt;
End;
Используем метод трассировки для того, чтобы найти
дальнейший алгоритм уточнения решения. Будем делать разрывы
таблицы для внесения пояснений в работу черных ящиков (см.
таблицу 4.4).
Таблица 4.4
к
1
2
Ор
[1.-5]
[4,5]
Qm
[]
[]
Gg
[1-5]
[4,5]
Ss
(1)
(1.4)
Примечания
Выбираем первую вершину
Вершины 2,3 исключаются из списка
кандидатов, остаются вершины с
номерами 4,5 |
Первое уточнение «черного ящика А».
If Qm<>[] Then <корректировка Gg с учетом ранее
использованных вершин>
Else Gg:=Qp;

192
4. Алгоритмы на графах
Его суть в том, что если выбирать из ранее использованных
вершин нечего, то множество кандидатов совпадает со
значением Qp, и далее по алгоритму мы «тупо» выбираем первую
вершину из Qp. Переходим к следующему вызову процедуры Find
(см. таблицу 4.5).
Таблица 4.5
3
2
[]
[5]
[]
[4]
[]
[5]
(1,4)
(1,5)
Вывод первого максимального
независимого множества и выход в
предыдущую копию Find
Исключаем вершину 4 из Qp и ι
включаем ее в Qm \
I
Продолжает работу цикл While процедуры Find с
параметром k, равным 2. Выбираем следующую вершину — это
вершина 5. И вызываем процедуры Find с другими значениями
параметров (см. таблицу 4.6).
Таблица 4.6
3
2
[]
[]
[]
[4,5]
[]
[]
(1,5)
Вывод второго максимального
независимого множества
Цикл While закончен, выход в
предыдущую копию процедуры
Rnd(/<=1)
Уточнение «черного ящика Б».
Первое: необходимо исключить вершину i из Qp и включить
ее в Qm.
Второе: следует откорректировать множество Gg. Выбор на
этом шаге вершин, не смежных с /, приведет к генерации
повторяющихся максимальных независимых множеств, поэтому
следует выбирать вершины из пересечения множеств Qp и A[i].
Итак, «черный ящик Б».
Qp:=Qp-[i];Qm:=Qm+[i];
Gg:=Qp*A[i];
Следующий шаг — выход в предыдущую версию Find, при
этом значение k=l (см. таблицу 4.7).

4. Алгоритмы на графах
193
Таблица 4.7
П~"
1
I 2
[2.-5] [1]
[ 1. .5] | ! Однако после работы «черного ящика
; | Б» имеем следующие значения
| переменных |
[2..5J [1] | [2..3] Ι (2) ! |
[3,5] ! [] Ι [3,5]
! 3 j [5] ' []
| 4 [] , И
' ' !
1 3
ί 2
ι
ί 1 _^
Γ 2
[] ί [5]
[5]
[3..5]
[5]
[3]
[1,2]
[2]
Г [5]
[]
[]
[]
[2,3]
(2,3)
(2,3,5)
(3)
1
Вывод третьего максимального
независимого множества !
!
Согласно логике «черного ящика Б»
множество кандидатов Gg становится
пустым
Итак, мы первый раз попадаем в
процедуру Find, и множество Gm при
этом не пусто
Должен работать алгоритм «черного ящика А» при
непустом значении Gm.
Замечание 1. Если существует вершина у, принадлежащая
Qm, такая, что пересечение А[у] и Qp пусто, то дальнейшее
построение максимального независимого множества
бессмысленно — вершины из А[у] не попадут в него (в нашем примере как
раз этот случай).
Замечание 2. Если нет вершин из Qm, удовлетворяющих
первому замечанию, то какую вершину из Qp следует
выбирать? Ответ: вершину iG(QpnA[j]) для некоторого значения
jsQm, причем мощность пересечения множеств A[j] и Qp
минимальна. Данный выбор позволяет сократить перебор.
Итак, окончательный алгоритм «черного ящика А».
Begin
delt:=N+l;
For j :=1 To N Do
If j In Qm Then
If Number(A[j]*Qp)<delt Then
Begin
i:=j; delt:=Number(A[j]*Qp);
End;
Gg:=Qp*A[i];
End

194
4. Алгоритмы на графах
Закончим трассировку примера.
Таблица 4.8
Г 2 [5]
|_L L I5L _
[2]
[1,2,32
Γΐτη ι
_JLJ I
Выход в основную программу I
Независимые максимальные множества графа найдены.
4.7.3. Доминирующие множества
Для графа G=(V,E) доминирующее множество вершин есть
множество вершин SaV, такое, что для каждой вершины у, не
входящей в S, существует ребро, идущее из некоторой
вершины множества S в вершину у. Доминирующее множество
называется минимальным, если нет другого доминирующего
множества, содержащегося в нем.
Пример.
Доминирующие множества (1, 2, 3),
(4, 5, 6, 7, 8, 9), (1, 2, 3, 8, 9), (1, 2, 3,
7) и т. д. Множества (1, 2, 3), (4, 5, 6, 7,
8, 9) являются минимальными. Если (?
Q — семейство всех минимальных
доминирующих множеств графа, то число
$[G]=min | S |
SzQ Рис. 4.33
называется числом доминирования графа, а множество S*, на
котором этот минимум достигается, называется наименьшим
доминирующим множеством. Для примера на рисунке 4.33 β [G]=3.
Задача. Пусть город можно изобразить как квадрат,
разделенный на 16 районов (см. рисунок 4.34). Считается, что
опорный пункт милиции, расположенный в каком-либо районе,
может контролировать не только этот район, но и граничащие с
ним районы. Требуется найти наименьшее количество пунктов
милиции и места их размещения, такие, чтобы
контролировался весь город.
Представим каждый район вершиной графа и ребрами
соединим только те вершины, которые соответствуют соседним
районам. Нам необходимо найти число доминирования графа и
хотя бы одно наименьшее доминирующее множество. Для
данной задачи β [<2]=4, и одно из наименьших множеств есть (3, 5,
12, 14). Эти вершины выделены на рисунке 4.34 (б).

4. Алгоритмы на графах
195
1
5
9
13
2
6
10
14
3
7
11
15
4
8
12
16
(а) (б)
Рис. 4.34
4.7.4. Задача о наименьшем покрытии
Рассмотрим граф. На рисунке 4.35 показана его матрица
смежности А и транспонированная матрица смежности с
единичными диагональными элементами А*. Задача определения
доминирующего множества графа G эквивалентна задаче
нахождения такого наименьшего множества столбцов в матрице
А*, что каждая строка матрицы содержит единицу хотя бы в
одном из выбранных столбцов. Задачу о поиске наименьшего
множества столбцов, «покрывающего» все строки матрицы,
называют задачей о наименьшем покрытии.
В общем случае матрица не обязательно является
квадратной, кроме того, вершинам графа (столбцам) может быть
приписан вес, в этом случае необходимо найти покрытие с
наименьшей общей стоимостью. Если введено дополнительное
ограничение, суть которого в том, чтобы любая пара столбцов
не имела общих единиц в одних и тех же строках, то задачу
называют задачей о наименьшем разбиении.
^01000000^
0 0 10 10 0 0
0 0 0 1 10 0 0
0 0 0 0 10 0 0
0 110 0 10 0
10 0 0 0 0 10
10 0 0 0 0 0 1
U 10 0 0 0 0 0;
Рис. 4.35
А* =
(Ί 0 0 0 0 1 1 1
110 0 10 0 1
0 110 10 0 0
0 0 110 0 0 0
0 11110 0 0
0 0 0 0 110 0
0 0 0 0 0 110
[θ 0 0 0 0 0 1 1
Предварительные замечания.
1. Если некоторая строка матрицы А* имеет единицу в
единственном столбце, т. е. больше нет столбцов, содержащих еди-

196
4. Алгоритмы на графах
ницу в этой строке, то данный столбец следует включать в
любое решение.
2. Рассмотрим множество столбцов матрицы А*, имеющих
единицы в конкретной строке.
Для нашего примера:
Е7Н1, 6, 7, 8),
U2=(l, 2, 5, 8),
Е/8=(2, 3, 5),
U4=(3, 4),
!У5=(2, 3, 4, 5),
£/6=(5, 6),
£/7=(6, 7),
*У8=(7,8).
Видим, что U4aU5. Из этого следует, что 5-ю строку можно
не рассматривать, поскольку любое множество столбцов,
покрывающее 4-ю строку, должно покрывать и 5-ю. Четвертая
строка доминирует над пятой.
4.7.5. Метод решения задачи о наименьшем разбиении
Попытаемся осознать метод решения задачи, рассматривая,
как обычно, пример.
У нас есть ориентированный граф, его матрица смежности и
транспонированная матрица смежности с единичными
диагональными элементами (см. рисунок 4.36). Исследуем структуру
матрицы А*. Нас интересует, какие столбцы содержат единицу
в первой строке, какие столбцы содержат единицу во второй
строке и не содержат в первой и так далее. С этой целью можно
было бы переставлять столбцы в матрице А*, но оставим ее «в
покое». Будем использовать дополнительную матрицу Б/, ее
тип:
Type Pr = Array [l..MaxN, l..MaxN+l] Of Integer;
Var Bl:Pr;
Ί 0 1 1 0 1 0]
110 0 10 1
1 1 10 0 0 0
0 0 1 10 0 0
0 0 0 1 10 0
0 10 0 110
1 1 0 0 1 1 lj
A =
0
0
1
1
0
1
0
1
0
0
0
1
0
1
1
1
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
1
0
0
0
0
1
0
0
1
0
0
1
1
0
0
1
1
0
A* = \
Рис. 4.36

4. Алгоритмы на графах
197
где MaxN — максимальная размерность задачи. Почему плюс
единица (технический прием — «барьер»), будет ясно из
последующего изложения (процедура Press).
При инициализации матрица В1 должна иметь вид: в первой
строке — [12 3.. N 0], а все остальные элементы равны нулю.
Наше исходное предположение заключается в том, что все
столбцы матрицы А* имеют единицы в первой строке.
Проверим его. Будем просматривать элементы очередной строки (/)
матрицы В1. Если Bl[i,j]<>09 то со значением Bl[iJ], как
номером столбца матрицы А*, проверим соответствующий элемент
А*. При его неравенстве нулю элемент В1 остается на своем
месте, иначе он переписывается в следующую строку матрицы Б/,
а элементы текущей строки В1 сдвигаются вправо, сжимаются
(Press). Итак, для N-1 строки матрицы В1.
Для нашего примера матрица В1 после этого преобразования
будет иметь вид:
BI-
1 3 4 6 0 ... 0 ^
2 5 7 0 0 ... 0
0 0 0 0 0 ... 0
V0 0 0 0 0
0 )
В задаче заданы стоимости вершин графа или стоимости
столбцов матрицы А*, и необходимо найти разбиение
наименьшей стоимости. Пусть стоимости описываются в массиве Price
(Array[ 1 ..MaxN] Of Integer) и для примера на рисунке 4.36
имеют значения [15 134 38 9 10]. Осталась чисто техническая
деталь — отсортировать элементы каждой строки матрицы В1
по возрастанию стоимости соответствующих столбцов матрицы
А*. Результирующая матрица В1 имеет вид:
В1 =
4 3 6 1 0 ... 0
5 7 2 0 0 ... 0
0 0 0 0 0 ... 0
V0 0 0 0 0
0 /
а алгоритм формирования описан в процедуре Blocs.
Procedure Blocs;{^Выделение блоков, В1 -
глобальная переменная.*}
Procedure Sort;
Begin

198
4. Алгоритмы на графах
End;
Procedure Press(i, j:Integer);{*Сдвигаем элементы
строки с номером i, начиная с позиции
(столбца) j, на одну позицию вправо.*}
Var k:Integer;
Begin
k:=j;
While Bl[i,kj<>0 Do
Begin{*Поэтому размерность
матрицы с плюс единицей. В последнем
столбце строки всегда записан 0 . *}
Bl[i,k]:=Bl[i,k+l];
Inc(k);
End;
End;
Var i,j,cnt:Integer;
Begin
FillChar(Bl,SizeOf(Bl), 0) ;
For i :=1 To N Do Bl [1, i] :=i; { ^Предполагается, что
в первом блоке все столбцы.*}
For i :=1 To N-l Do
Begin
j:=1;cnt:=0;
While Bl[i,j]<>0 Do
Begin
If A*[i,Bl[i,j]]=0 Then
Begin{*Столбец не в этом блоке.*}
Inc(cnt) ;
Bl[i + 1,cnt]:=B1[i,j];{^Переписать в следующую
строку.*}
Press (i,j) ;
Dec(j) ;
End;
Inc (j);
End;
End;
Sort;
End;
Изменим чуть-чуть А* (A*[2,7]=0, A*[4,7]=l). Какой вид
будет иметь матрица Bl?

4. Алгоритмы на графах
199
После этой предварительной работы мы имеем вполне
«приличную» организацию данных для решения задачи путем
перебора вариантов. Матрица В1 разбита на блоки, и необходимо
выбрать по одному элементу (если соответствующие строки еще
не покрыты) из каждого блока. Процесс выбора следует
продолжать до тех пор, пока не будут включены в «покрытие» все
строки или окажется, что некоторую строку нельзя включить.
Продолжим рассмотрение метода. Если при поиске
независимых множеств мы шли «сверху вниз», последовательно
уточняя логику, то сейчас попробуем идти «снизу вверх»,
складывая окончательное решение из сделанных «кирпичиков».
Как обычно, следует начать со структур данных. Во-первых,
мы ищем лучшее решение, т. е. то множество столбцов,
которое удовлетворяет условиям задачи (не пересечение и
«покрытие» всего множества строк), и суммарная стоимость этого
множества минимальна. Значит, необходима структура данных
для хранения этого множества и значения наилучшей
стоимости и, соответственно, структуры данных для хранения
текущего (очередного) решения и его стоимости. Во-вторых, в
решении строка может быть или не быть. Следовательно, нам
требуется как-то фиксировать эту информацию. Итак, данные.
Type Model=Array[1..MaxN] Of Boolean;
Var Sbetter-.Model; Pbetter : Integer; { *Лучшее
решение.*}
S:Model; P:Integer;{^Текущее решение.*}
R:Model;{*R[i]=True - признак того, что
строка i "покрыта" текущим решением.*}
Алгоритм включения (исключения) столбца с номером k в
решение (из решения) имеет вид:
Procedure Include(k:Integer); {^Включить столбец
в решение.*}
Var j:Integer;
Begin
Ρ:=P+Price[k];{*Текущая цена решения.*}
S[k]:=True;{^Столбец с номером к в решение.*}
For j :=1 To N Do
If A*[j,k]=l Then R[j] :=True; {*Строки,
"покрытые" столбцом к.*}
End;
Procedure Exclude(k:Integer);{^Исключить столбец
из решения.* }
Var j:Integer;

200
4. Алгоритмы на графах
Begin
p:=p-Price[к];
S[k]:=False;
For j :=1 To N Do
If (A*[j,k]=l) AndR[j] Then R[j]:=False;
End;
Проверка, сформировано ли решение, заключается в том,
чтобы просмотреть массив R и определить, все ли его элементы
равны истине.
Function Result:Boolean;
Var j:Integer;
Begin
While (j<=N) And R[j] Dolnc(j);
Result:=j=N+l;
End;
Кроме перечисленных действий, нам необходимо уметь
определять — «можно ли столбец с номером k включать в решение».
Для этого следует просмотреть столбец с номером k матрицы А*
и проверить, нет ли совпадений единичных элементов со
значением True соответствующих элементов массива R.
Function Cross(k:Integer):Boolean; {^Пересечение
столбца с частичным решением, сформированным
ранее.*}
Var j:Integer;
Begin
While (j<=N) AndNot(R[j] And (A* [j,k]=l) ) Do Inc(j);
Result:=j=N+l;
End;
Заключительная процедура поиска Find имеет в качестве
параметров номер блока (строки матрицы В1) — переменная
bloc и номер позиции в строке. Первый вызов — Find(l,l).
Procedure Find(bloc,jnd:Integer);
Begin
If Result Then
Begin
If P<Pbetter Then
Begin
Pbetter:=P;

4. Алгоритмы на графах
201
Sbetter:=S;
End;
End
Else
If Bl[bloc,jnd]=0
Then Exit
Else
If Cross(Bl[bloc,jnd])
Then
Begin
Include(Bl[bloc,jnd]);
Find(bloc+l,l);
Exclude(Bl[bloc,jnd]);
End
Else
If R[bloc] Then Find(bloc+1,1)
Else Find(bloc,jnd+1);
End;
Будет ли правильно работать процедура Find при
измененной матрице А* (изменение приведено выше по тексту)?
Исправьте неточность.
Нам осталось привести основную программу, но после
выполненной работы она не вызывает затруднений.
Program R_min;
Const MaxN=...;
Type ...
Var ...
Procedure Init; {*Ввод и инициализация данных.*}
Begin
End;
Procedure Print;{*Вывод результата.*}
Begin
End;
{^Процедуры и функции, рассмотренные ранее по тексту.*}
Begin {^Основная логика.*}
Init;
Blocs;
Find(1,1);
Print;
End.

202
4. Алгоритмы на графах
4.8. Раскраски
4.8.1. Правильные раскраски
Пусть G=(V,E) — неориентированный граф.
Произвольная функция f:V->{ 1,2,...,&}, где k принадлежит
множеству натуральных чисел, называется вершинной &-рас-
краской графа G.
Раскраска называется правильной, если f(u)^f(v), для
любых смежных вершин и и v.
Граф, для которого существует правильная fc-раскраска,
называется ^-раскрашиваемым. Минимальное число &, при
котором граф G является й-раскрашиваемым, называется
хроматическим числом графа и обозначается χ((3).
Пример. x(G)=S. Меньшим количеством цветов граф
правильно раскрасить нельзя из-за наличия треугольников. Рядом с
«кружками» — вершинами графа — указаны номера цветов
(см. рисунок 4.37).
Рис. 4.37
Метод получения правильной раскраски достаточно прост —
закрашиваем очередную вершину в минимально возможный
цвет.
Введем следующие структуры данных.
Const Nmax=100; {^Максимальное количество вершин
графа.*}
Type V=0..Nmax;
Ss=Set Of V;
MyArray=Array[1..Nmax] Of V;
Var Gr:MyArray;{*Gr - каждой вершине графа
определяется номер цвета.*}
Для примера, приведенного на рисунке 4.37, массив Gr
имеет вид: Gr[l]=Gr[3]=Gr[5]=l; Gr[2]=Gr[4]=Gr[7]=2; Gr[6]=3.

4. Алгоритмы на графах
203
Фрагмент основного алгоритма.
формирование описания графа>;
For i:=l To N Do Gr[i] : = [Color (i,0)];
<вывод решения>;
Поиск цвета раскраски для одной вершины можно
реализовать с помощью следующей функции:
Function Color(i,t:V):Integer;{*i - номер
окрашиваемой вершины, t - номер цвета,
с которого следует искать раскраску данной
вершины, А - матрица смежности, Gr -
результирующий массив.*}
Var Ws:Ss;
j:Byte/
Begin
Ws:=[ ];
For j :=1 To i-1 Do
If A[j,i]=l Then Ws:=Ws+[Gr[j]];
{^Формируем множество цветов, в которые
окрашены смежные вершины с меньшими
номерами.*}
j:=t;
Repeat {*Поиск минимального номера цвета,
в который можно окрасить данную вершину.*}
Inc (j);
Until Not(j In Ws) ;
Color:=j;
End;
Пример. Для графа на рисунке 4.38
получаем правильную раскраску:
Gr[l]=l, Gr[2]=Gr[4]=2, Gr[3]=3, Gr[5]=4.
Однако минимальной раскраской является:
Gr[l]=l, Gr[2]=Gr[5]=2 и Gr[3]=Gr[4]=3,
и хроматическое число графа равно трем.
Рис. 4.38
4.8.2. Поиск минимальной раскраски вершин графа
Метод основан на простой идее [16], и в некоторых случаях
он дает точный результат.

204
4. Алгоритмы на графах
Пусть получена правильная раскраска графа, q —
количество цветов в этой раскраске. Если существует раскраска,
использующая только q-Ι цветов, то все вершины, окрашенные в
цвет q, должны быть окрашены в цвет g, меньший q.
Согласно алгоритму формирования правильной раскраски
вершина была окрашена в цвет q, потому что не могла быть
окрашена в цвет с меньшим номером. Следовательно,
необходимо попробовать изменить цвет у вершин, смежных с
рассматриваемой. Но как это сделать?
Найдем вершину с минимальным номером, окрашенную в
цвет q, и просмотрим вершины, смежные с найденной.
Попытаемся окрашивать смежные вершины не в минимально
возможный цвет. Для этого находим очередную смежную вершину и
стараемся окрасить ее в другой цвет. Если это получается, то
перекрашиваем вершины с большими номерами по методу
правильной раскраски. При неудаче, когда изменить цвет не
удалось или правильная раскраска не уменьшила количества
цветов, переходим к следующей вершине. И так, пока не будут
просмотрены все смежные вершины.
Опишем алгоритм, используя функцию Color предыдущего
параграфа.
Var MaxC,MinNum,i:V;
Procedure MaxMin(Var c,t:V);
Begin
End;
Procedure Change(t:V);
Begin
End;
Begin
<ввод данных, инициализация переменных>;
For i:=l To N Do Gr[i] :=Color (i,0);{^Первая
правильная раскраска.*}
MaxC:=0;MinNum:=0;
Repeat
<найти вершину с минимальным номером(MinNum) ,
имеющую максимальный цвет раскраски(МахС) -
процедура MaxMin(MaxC,MinNum)>;
<изменить цвет раскраски в соответствии
с описанной идеей - процедура
Change(MinNum)>;

4. Алгоритмы на графах
205
Until MaxC=Gr [MinNum] ; { *До тех пор, пока метод
улучшает раскраску.*}
<вывод минимальной (или почти минимальной!)
раскраски>;
End.
Если работа процедуры MaxMin достаточно очевидна, то
Change требует дальнейшего уточнения.
Procedure Change (t:V) ;
Var r,q:V;
Ws:Ss;
Function MaxCon (1: V;Rs : Ss) :\/;{*Находим смежную
с 1 вершину с наибольшим номером и
не принадлежащую множеству Rs . * }
Var i,w:V;
Begin
i:=l-l; w:=0;
While (i>=l) And (i In Rs) And (w=0) Do
Begin
If A[l,i]=l Then w:=i;
Dec(i);
End
MaxCon:=w;
End;
Begin
Ws : = [ ] ;
q:=MaxCon(t,Ws);
While q<>0 Do
Begin
r:=Color(q,Gr[q]);
If r<MaxC Then <изменить цвет у вершин
с номерами, большими t, по методу
правильной раскраски>
Else Ws:=Ws+[q];
q:=MaxCon(tfWs);
End;
End;
Осталось заметить, что при изменении цвета у вершин с
номерами, большими значения £, по методу правильной
раскраски следует запоминать в рабочих переменных значения Gr и
МахС, так как при неудаче (раскраску не улучшим) их
необходимо восстанавливать, и на этом закончить уточнение логики.

206
4. Алгоритмы на графах
При любом упорядочении вершин допустимые цвета j для
вершины с номером i удовлетворяют условию j < i. Это
очевидно, так как вершине i предшествует i-Ι вершина, и,
следовательно, никакой цвет j > i не использовался.
Итак, для вершины 1 допустимый цвет 1, для 2 — цвет 1 и 2
и так далее.
С точки зрения скорости вычислений вершины следует
помечать (присваивать номера) так, чтобы первые q вершин
образовывали наибольшую клику графа G. Это приведет к тому, что
каждая из этих вершин имеет один допустимый цвет и процесс
возврата в алгоритме можно будет заканчивать при
достижении вершины из этого множества.
В алгоритме рассматриваются только вершины, смежные с
вершиной, окрашенной в максимальный цвет. Однако следует
работать и с вершинами, являющимися смежными для
смежных.
На рисунке 4.39 приведены примеры графов и их раскраски.
Рис. 4.39
Первая цифра в круглых скобках обозначает значение цвета
при правильной раскраске, вторая — при минимальной.
ля графов на рисунках 4.39(a) и 4.39(b) алгоритм дает пра -
вильный результат. Для графа на рисунке 4.39(6) при
изменении цвета вершины с номером 6 необходимо просматривать
вершины, смежные к смежным с шестой вершиной.
Рассмотренный алгоритм требует очередной модификации.
Самый интересный случай на рисунке 4.40. Мы не можем
получить минимальную раскраску с помощью рассмотренного

4. Алгоритмы на графах
207
алгоритма (даже если будем
рассматривать все вершины, смежные к
смежным), хотя она, конечно, существует и
совпадает с предыдущей. Итак,
результат работы алгоритма зависит от
нумерации вершин графа, а таких
способов — способов нумерации N!.
4.8.3. Использование задачи о наименьшем покрытии
при раскраске вершин графа
При любой правильной раскраске графа G множество вершин,
окрашиваемых в один и тот же цвет, является независимым
множеством. Поэтому раскраску можно понимать как разбиение
вершин графа на независимые множества. Если рассматривать
только максимальные независимые множества, то раскраска — это не
что иное, как покрытие вершин графа G множествами этого типа.
В том случае, когда вершина принадлежит не одному
максимальному независимому множеству, допустимы различные раскраски
с одним и тем же количеством цветов. Эту вершину можно
окрашивать в цвета тех множеств, которым она принадлежит.
Исходным положением метода является получение всех
максимальных независимых множеств и хранение их в
некоторой матрице Μ(Νχλ¥), где W — количество максимальных
независимых множеств. Элемент матрицы M[i,j] равен
единице, если вершина с номером i принадлежит множеству с
номером у, и нулю в противном случае. Если затем каждому столбцу
поставить в соответствие единичную стоимость, то задача
раскраски не что иное, как поиск минимального количества
столбцов в матрице М, покрывающих все ее строки. Каждый
столбец соответствует определенному цвету.
Пример. На рисунке 4.41 представлено пять максимальных
независимых множеств и два варианта решения задачи о
покрытии (строки А и Б). В обоих случаях вершина 4 может быть
окрашена как во второй, так и в третий цвета.
1
2
3
4
5
А
В
1
1
1
0
0
0
*
2
1
0
0
0
1
*
3
0
0
1
1
0
*
*
4
0
1
0
1
0
*
5
0
0
0
1
1
*
Рис.4.41
Рис. 4.40

208
4. Алгоритмы на графах
4.9. Потоки в сетях, паросочетания
4.9.1. Постановка задачи
Одной из задач теории графов является задача определения
максимального потока, протекающего от некоторой вершины s
графа (источника) к некоторой вершине t (стоку). При этом
каждой дуге (граф ориентированный) (/,/) приписана некоторая
пропускная способность C(i,j), определяющая максимальное
значение потока, который может протекать по данной дуге.
Содержательных интерпретаций задачи достаточно много,
и, безусловно, они усилят и сделают более понятными
сложные занятия по этой проблематике.
Метод решения задачи о максимальном потоке от s к t был
предложен Фордом и Фалкерсоном, и их «техника меток»
составляет основу других алгоритмов решения многочисленных
задач, являющихся обобщениями или расширениями
указанной задачи.
Одним из фундаментальных фактов теории потоков в сетях
является классическая теорема о максимальном потоке и
минимальном разрезе. Разрезом называют множество дуг,
удаление которых из сети приводит к «разрыву» всех путей,
ведущих из s в t. Пропускная способность разреза — это суммарная
пропускная способность дуг, его составляющих. Разрез с
минимальной пропускной способностью называют минимальным
разрезом.
Теорема (Форд и Фалкерсон). Величина каждого потока из s
в t не превосходит пропускной способности минимального
разреза, разделяющего s и t, причем существует поток,
достигающий этого значения.
Теорема устанавливает эквивалентность задач нахождения
максимального потока и минимального разреза, однако не
определяет метода их поиска.
Пример. На рисунке 4.42 показана
сеть, источник — вершина 1, сток —
вершина 6, в скобках у дуг указаны их
пропускные способности. Минималь- (7
ный разрез — дуги (1, 2) и (3, 4),
следовательно, согласно теореме
максимальный поток равен 4. Разрез определен
путем простого перебора. Алгоритм его Рис. 4.42
«лобового» поиска очевиден.
Осуществляем перебор по дугам путем генерации
2) [5]
[2]
6]
[7]
[3] [4] Г£
3 ) [2] -0

4. Алгоритмы на графах
209
всех возможных подмножеств дуг. Для каждого подмножества
дуг проверяем, является ли оно разрезом. Если является, то
вычисляем его пропускную способность и сравниваем ее с
минимальным значением. При положительном результате сравнения
запоминаем разрез и изменяем значение минимума.
Удачный выбор данных позволяет сделать программный код
компактным, но очевидно, что даже при наличии различных
отсечений в переборе метод применим только для небольших
сетей. Однако, как найти максимальный поток, т. е. его
распределение по дугам, по-прежнему открытый вопрос.
«Техника меток» Форда и Фалкерсона заключается в
последовательном (итерационном) построении максимального
потока путем поиска на каждом шаге увеличивающейся цепи, то
есть пути (последовательности дуг), поток по которой можно
увеличить. При этом узлы (вершины графа) специальным
образом помечаются. Отсюда и возник термин «метка».
Пример из работы [9]. На рисунке 4.43 рядом с
пропускными способностями дуг указаны потоки, построенные на этих
дугах. На рисунке поток через сеть равен 10 и найдена
увеличивающаяся цепочка, выделенная двойными линиями.
Обратите внимание на ориентацию дуг, входящих в цепочку. По
данной цепочке можно пропустить поток, равный 1, пропускная
способность дуги (5, 6). Изменяем суммарный поток, его
значение становится равным 11. Поток увеличен, необходимо
продолжить поиск увеличивающихся цепочек; если окажется, что
построить их нельзя, то результирующий поток максимален.
Заметим, что для данного примера это значение потока
окончательное. Обратите внимание на то, как изменен поток на дугах
сети в зависимости от их ориентации.
^— б[6]-
^ °L°J —^_^
(5Γ0[2]^7)^0[2]-Λ
Λ 4[5] 6f8] 0[3] 0[1] 4^9] ±8
6[9]
0[2]
Рис. 4.43

210
4. Алгоритмы на графах
4.9.2. Метод построения максимального потока в сети
Рассмотрим метод на примере рисунка 4.44.
Пусть дана сеть G=(V,E), узлом-источником является
вершина 1, узлом-стоком — вершина 6. Построим максимальный
поток (F) между этими вершинами. Начальное значение F
нулевое.
Очевидно, что структурой данных для описания F является
матрица того же типа, что и матрица С, в которой определены
пропускные способности дуг.
-б[б]-
2 Ь-0[2]—ЛУ-0[2]—( 6 ;
Рис. 4.44
Первая итерация (см. рисунок 4.45). Присвоим вершине 1
метку [1,@].
[ΐ>@](ι
2[3] 0[4] КГ) [42]
2[3]
Шаг 1. Рассмотрим дуги, началом которых является
вершина 1 — дуги (1,2) и (1,3). Вершины 2 и 3 не помечены, поэтому
присваиваем им метки, для 2-й — [1,2] и 3-й — [1,6]. Что
представляют из себя метки? Первая цифра — номер вершины, из
которой идет поток, вторая цифра — численное значение
потока, который можно передать по этой дуге.

4. Алгоритмы на графах
211
Шаг 2. Выберем помеченную, но непросмотренную вершину.
Первой в соответствующей структуре данных записана
вершина 2. Рассмотрим дуги, для которых она является началом —
дуги (2,4) и (2,5). Вершины 4 и 5 не помечены. Присвоим им
метки — [2,2] и [2,2]. Итак, на втором шаге вершина 2
просмотрена, вершины 3, 4, 5 помечены, но не просмотрены,
остальные вершины не помечены.
Шаг 3. Выбираем вершину 3. Рассмотрим дугу (3,4).
Вершина 4 помечена. Переходим к следующей вершине — четвертой,
соответствующая дуга — (4,6). Вершина 6 не помечена.
Присваиваем ей метку [4,2]. Мы достигли вершины-стока, тем
самым найдя путь (последовательность дуг), поток по которым
можно увеличить. Информация об этом пути содержит метки
вершин.
В данном случае путь или увеличивающаяся цепочка
1->2->4->6. Максимально возможный поток, который можно
передать по дугам этого пути, определяется второй цифрой
метки вершины стока, то есть 2. Поток в сети стал равным 2.
Вторая итерация (см. рисунок 4.46).
[l,@](l
1[6]
(з)—1[2]—^4j
[1,6] [3,2]
Рис. 4.46
Шаг 1. Присвоим вершине 1 метку [1,@]. Рассмотрим дуги,
началом которых является помеченная вершина 1. Это дуги
(1,2) и (1,3). Вершина 2 не может быть помечена, так как
пропускная способность дуги (1,2) исчерпана. Вершине 3
присваиваем метку [1,6].
Шаг 2. Выберем помеченную, но не просмотренную
вершину. Это вершина 3. Повторяем действия. В результате вершина
4 получает метку [3,2].
Шаг 3. Выбираем вершину 4, только она помечена и не
просмотрена. Вершине 6 присваиваем метку [4,1].

212
4. Алгоритмы на графах
Почему только одна единица потока? На предыдущей
итерации израсходованы две единицы пропускной способности
данной дуги, осталась только одна. Вершина-сток достигнута.
Найдена увеличивающая поток цепочка, это 1->3->4->6, по
которой можно «протащить» единичный поток. Результирующий
поток в сети равен 3.
Третья итерация (см. рисунок 4.47). Вершине 1
присваиваем метку [1,@].
[1,@]( 1
2[б]
1[3] 0[4] Г^[5Д]
λ
3[3]
[1,5] [3,1]
Рис. 4.47
Шаг 1. Результат — метка [1,5] у вершины 3.
Шаг 2. Метка [3,1] у вершины 4.
Шаг 3. Пропускная способность дуги (4,6) израсходована
полностью.
Однако есть обратная дуга (2,4), по которой передается
потоку не равный нулю (обратите внимание на текст,
выделенный курсивом — «изюминка» метода). Попробуем
перераспределить поток. Нам необходимо передать из вершины 4 поток,
равный единице (зафиксирован в метке вершины). Задержим
единицу потока в вершине 2, то есть вернем единицу потока из
вершины 4 в вершину 2. Эту особенность зафиксируем в метке
вершины 2 — [-4,1]. Тогда единицу потока из вершины 4 мы
передадим по сети вместо той, которая задержана в вершине 2,
а единицу потока из вершины 2 попытаемся «протолкнуть» по
сети, используя другие дуги. Итак, вершина 4 просмотрена,
вершина 2 помечена, вершины 5 и 6 не помечены.
Шаг 4 и 5 очевидны. Передаем единицу потока из вершины
2 в вершину 6 через вершину 5. Вершина-сток достигнута,
найдена цепочка 1->3->4->2—»5->6, по которой можно передать
поток, равный единице. При этом по прямым дугам поток
увеличивается на единицу, по обратным — уменьшается.
Суммарный поток в сети — 4 единицы.

4. Алгоритмы на графах
213
Четвертая итерация. Вершине 1 присваиваем метку [1,@].
2)—Ц5]—л о
[1>@](1
Рис. 4.48
1[7]
1[3] 0[4] ,6-
3[3]
Шаг 1. Помечаем вершину 3 — [1,4].
Шаг 2. Рассматриваем помеченную, но не просмотренную
вершину 3. Одна дуга — (3,4). Вершину 4 пометить не
можем — пропускная способность дуги исчерпана. Помеченных
вершин больше нет, и вершина-сток не достигнута.
Увеличивающую поток цепочку построить не можем. Найден
максимальный поток в сети. Можно заканчивать работу.
Итак, в чем суть «техники меток» Форда и Фалкерсона?
1. На каждой итерации вершины сети могут находиться в
одном из трех состояний: вершине присвоена метка, и она
просмотрена; вершине присвоена метка, и она не просмотрена, то
есть не все смежные с ней вершины обработаны; вершина не
имеет метки.
2. На каждой итерации мы выбираем помеченную, но не
просмотренную вершину υ и пытаемся найти вершину и,
смежную с υ, которую можно пометить. Помеченные вершины,
достижимые из вершины-источника, образуют множество
вершин сети G. Если среди этих вершин окажется вершина-сток,
то это означает успешный результат поиска цепочки,
увеличивающей поток, при неизменности этого множества работа
заканчивается — поток изменить нельзя.
Входные данные.
Сеть, описываемая G=(V,E) матрицей пропускных
способностей C[1.JV,1.JV], где N — количество вершин.
Вершина-источник s и вершина-сток t.
Выходные данные.
Поток, описываемый матрицей F[1..N,1..N].
Рабочие переменные.
Структура данных для хранения меток — P[1.JV,1..2].

214
4. Алгоритмы на графах
Элемент Р[/,1] — номер вершины, из которой можно
передать поток, равный Р[/,2], в вершину с номером /.
Логическая переменная Lg, значение True — есть цепочка,
увеличивающая поток, False — нет.
Основной алгоритм.
Begin
<ввод данных и инициализация переменных(Lg:=True)>;
While Lg Do
Begin
FillChar(P,SizeOf(Ρ),0);
<процедура расстановки меток(Mark), если
вершину t не смогли пометить, то Lg:=False;
результат работы - значение Ρ (метки вершин) >;
If Lg Then <процедура Stream(t) - изменение
потока по дугам найденной цепочки от
вершины-стока t до вершины-источника s; входные
данные - массив Р, результат - измененный массив
F>;
End;
<вывод потока F>;
End.{конец обработки}
Уточним алгоритм расстановки меток (не лучший вариант).
Procedure Mark;
Var M: Set Of 1. .Ν;
i, 1: integers-
Begin
M:=[1..N]; {*Непросмотренные вершины.*}
Ρ[s,1] :=s;Ρ[s,2] :=maxint;{^Присвоим метку
вершине-источнику.*}
l:=s;
While (P[t,l]=0) And Lg Do
Begin
For i:=l To N Do {*Поиск непомеченной вершины.*}
If (P[i,l]=0) And ((C[l,i]<>0) Or (C[i,l]<>0))
Then
If F[l,i]<C[l,i] Then
Begin{*Дуга прямая ? *}
P[i,l]:=1;
If P[l,2]<C[l,i]-F[l,i]
Then P[i,2]:=P[l,2]
Else P[i,2]:=C[l,i]-F[l,i];
End

4. Алгоритмы на графах
215
Else
If F[i,l]>0 Then
Вед1п{*Дуга обратная?*}
P[i,l]:=-l;
If P[l,2]<F[i,l]
Then P[i,2]:=P[1,2]
Else P[i,2] :=F[i,lb-
End;
M:=M-[1];{*Вершина с номером 1 просмотрена.*}
1:=1;{*Находим помеченную и непросмотренную
вершину.*}
Repeat
Inc(l)
Until (1>N) Or ((P[1,1]00) And (1 In M) ) ;
If 1>N Then Lg:=False;
End;
End;
Алгоритм изменения потока F имеет вид:
Procedure Stream(q:Integer);
Begin {^Определяем тип дуги - прямая или обратная,
знак минус у номера вершины - признак обратной
дуги.*}
If P[q,l]>0
Then F[P[q,l],q]:=F[P[q,l],q]+P[t,2]
Else F[q,abs(P[q,l])]:=F[q,abs(P[q,1])]-P[t,2];
If Abs(P[q,ll)<>s Then
Begin
{*Если не вершина-источник, то переход к
предыдущей вершине цепочки.*}
q:=Abs(P[q,ll) ;
Stream(q);
End;
End;
Итак, рассмотрение метода построения максимального
потока в сети завершено.
4.9.3. Наибольшее паросочетание в двудольном графе
Паросочетанием в неориентированном графе G=(V,E)
называется произвольное множество ребер М<^Е, такое, что никакие
два ребра из Μ не инцидентны одной вершине.

216
4. Алгоритмы на графах
Вершины в (3, не принадлежащие ни одному ребру паросоче-
тания, называют свободными.
Граф G называют двудольным, если его множество вершин
можно разбить на непересекающиеся множества — V=XuY,
ΧηΥ=0, причем каждое ребро ееЕ имеет вид е=(х,у), где хеХ,
г/еУ. Двудольный граф будем обозначать G=(X,Y,E).
Задача нахождения наибольшего паросочетания в
двудольном графе сводится к построению максимального потока в
некоторой сети. Рассмотрим схему сведения. На рисунке 4.49
показан исходный двудольный граф G.
Рис. 4.49
Построим сеть S(G) с источником s и стоком t следующим
образом:
• источник s соединим дугами с вершинами из множества
X;
• вершины из множества У соединим дугами со стоком t;
• направление на ребрах исходного графа будет от вершин
из X к вершинам из У;
• пропускная способность всех дуг C[i,y]=l.
Найдем максимальный поток из s в t для построенной сети.
Он существует [18]. Насыщенные дуги потока (они выделены
«жирными» линиями на рисунке) соответствуют ребрам
наибольшего паросочетания исходного графа. Найденное наибольшее
паросочетание не единственное. Проверьте, это ли паросочета-
ние получается при помощи алгоритма нахождения
максимального потока. Найдите другие паросочетания.
Рассмотрим другой метод построения наибольшего
паросочетания в двудольном графе. Введем понятие чередующейся
цепи из X в Υ относительно данного паросочетания М.
Произвольное множество дуг PczE вида:
Р={(х0,уг), (yvxx), (xvy2)> ·.·» (yk'xi)> (хк'Ук+1Я>
где k>0,
все вершины различны,

4. Алгоритмы на графах
217
х0 — свободная вершина в X,
yk+1 — свободная вершина в У,
каждая вторая дуга принадлежит М, то есть
PnM^iy^J, (y2,x2), ..., (yk,xk)}.
Теорема [18]. Паросочетание Μ в двудольном графе G
наибольшее тогда и только тогда, когда в G не существует
чередующейся цепи относительно М.
Теорема подсказывает реальный путь нахождения
наибольшего паросочетания. Пусть найдено некоторое паросочетание в
графе G, на рисунке 4.50 оно выделено «жирными» линиями.
Ищем чередующуюся цепь — ее дуги выделены линиями со
стрелками. Она состоит из «тонких» дуг и «жирных», причем
начинается и заканчивается в свободных вершинах. Длина
цепи нечетна. Делаем «тонкие» дуги «жирными» и наоборот.
Паросочетание увеличено на единицу.
Рис.4.50
Общий алгоритм.
Begin
<ввод и инициализация данных>;
<найти первое паросочетание>;
While <есть чередующаяся цепочка> Do <изменить
паросочетание>;
<вывод результата>;
End.
Очередь за определением данных и последовательным
уточнением алгоритма.
Граф описывается матрицей A[N,M], где iV — количество
вершин в множестве X, а М — в У.

218
4. Алгоритмы на графах
Паросочетание будем хранить в двух одномерных массивах
XN и YM. Для примера на рисунке 4.50 X/V=[0,l,2,4] и
УМ=[2,3,0,4,0].
Уточнение фрагмента «найти первое паросочетание» не
требует разъяснений. Можно начать и с одного ребра в первом па-
росочетании, но в этом случае количество итераций в основном
алгоритме возрастает.
For i :=1 To N Do
Begin {^Назначение переменных i,
j , рр очевидно.*}
j:=1; pp:=True;
While (j<=M) And pp Do
Begin
If (A[i,j]=l) And (YM[j]=0) Then
Begin
XN[i]:=j;YM[j]:=i;
pp:=False;
End/
Inc (j);
End;
End;
Как лучше хранить чередующуюся цепочку, учитывая
требование изменения паросочетания и продумывая алгоритм ее
построения? Естественно, массив, пусть это будет Chain:
Array[l..NMmax] of NMmax.. NMmax,
где NMmax — максимальное число вершин в графе, и его
значение для рассмотренного примера равно [1, -4, 4, -2, 3, -3], т. е.
вершины из множества YM хранятся со знаком минус (вспомните
метод построения максимального потока).
Итак, поиск чередующейся цепочки.
Function FindChain:Boolean;
Var p,ук,г:Word;
Begin
<инициализация данных, в частности ук:=1;>;
<нахождение свободной вершины в XN>;
If <вершина не найдена>
Then FindChain:=False
Else
Begin
ρ:=<номер первой свободной вершины>;
Chain[yk]:=р;

4. Алгоритмы на графах
219
Repeat
г:=<очередная вершина из Chain>;
For <для всех вершин, связанных с r> Do
If <вершина из XN>
Then
Begin
If <ребро "тонкое") Then <включить
ребро в цепочку>
End
Else
Begin
If <ребро "толстое") Then
<включить ребро в цепочку>
End;
Until <просмотрены все вершины из Chain> or
<текущая вершина принадлежит YM,
и она свободна>;
FindChar:=<текущая вершина принадлежит YM,
и она свободна>;
End;
End;
Процесс дальнейшего уточнения алгоритма вынесем в
самостоятельную часть работы.
4.10. Методы приближенного решения задачи
коммивояжера
4.10.1. Метод локальной оптимизации
Попытаемся отказаться от перебора вариантов при решении
задачи о поиске гамильтоновых циклов или, если граф
«нагруженный», о поиске путей коммивояжера. При больших
размерностях задачи (значение N) переборные схемы не работают —
остаются только приближенные методы решения. Суть
приближенных методов заключается в быстром поиске первого
решения (первой оценки), а затем в попытках его улучшения. В
методе локальной оптимизации в этих попытках просматриваются
только соседние вершины графа (города) найденного пути.
Шаг 1. Получить приближенное решение (первую оценку).
Шаг 2. Пока происходит улучшение решения, выполнять
следующий шаг, иначе перейти на шаг 4.

220
4. Алгоритмы на графах
Шаг 3. Для всех пар номеров городов i,j, удовлетворяющих
неравенству (l<i<j<N), проверить: diX i^di^dj^χ>άίΛ ^djiJrdi j+l
для смежных городов, т. е.
для несмежных городов.
Примечание
На рисунке 4.51 даны графические иллюстрации первого и второго
неравенств. «Жирными» линиями обозначены участки старых
маршрутов, «тонкими» — новых.
Рис. 4.51
Если одно из неравенств выполняется, то найдено лучшее
решение. Следует откорректировать ранее найденное решение
и вернуться на шаг 2.
Шаг 4. Закончить работу алгоритма.
Для реализации алгоритма достаточно матрицы расстояний
А и массива для хранения пути коммивояжера Way.
Вид общей алгоритма:
Begin
1пд.1:;{*Ввод из файла матрицы расстояний,
инициализация глобальных переменных.*}
OneWay;{*Поиск первого варианта пути
коммивояжера.*}
Local;{^Локальная оптимизация.*}
0и1:;{*Вывод результата.*}
End.
Продолжим уточнение алгоритма.
Работа процедур Init, OneWay, Out достаточно очевидна.
Естественным приемом является вынесение ее в самостоятельную
часть работы школьников на занятии.

4. Алгоритмы на графах
221
Нам необходимо уточнить процедуру Local. Работаем не с
частностями, а на содержательном уровне. Предположим, что
мы имеем функции Bestl и Best2, их параметры — индексы
элементов массива Way, определяющих номера городов в пути
коммивояжера, а выход естественный — истина или ложь, в
зависимости от того, выполняются неравенства или нет.
Рассуждаем дальше. Если неравенство выполняется, то нам
необходимо изменить путь (соответствующие элементы массива
Way). Пока не будем заниматься деталями. Пусть эту работу
выполняет процедура Swap, ее параметры — индексы элементов
массива Way). Эта процедура, вероятно, должна сообщать о том,
что она «что-то изменила», ибо нам необходимо продолжать
работу до тех пор, пока что-то меняется, происходят улучшения.
Итак, алгоритм процедуры Local.
Procedure Local;
Var i,j: Integers-
Change :Boolean;
<здесь функции Bestl и Best2, а также процедура
Swap>;
Begin
Repeat
Change:=False;
For i:=l To N-l Do
For j:=i+l To N Do
If i = j+l Then
Begin
If Bestl (i,j) Then Swap (i,j) ;
End
Else
If (i = l) And (j=N)
Then
Begin
If Bestl (i,j ) Then Swap (i,j) ;
End { *0б этой проверке лучше первоначально
умолчать, чтобы было о чем спросить,
"если совсем будет плохо" - все понимают
и нет вопросов.*}
Else
If Best2(i,j) Then Swap (i,j);
Until Not(Change);{*Из логики неясно - кто
изменяет значение переменной Change на True.
Определите, учитывая, что функции Bestl,
Best2 и процедура Swap локальные по
отношению к процедуре Local.* }
End;

222
4. Алгоритмы на графах
4.10.2. Алгоритм Эйлера
Этот алгоритм и следующий работоспособны в том случае,
если выполняется неравенство треугольника. Его суть в том,
что для любой тройки городов /, у, k (между которыми есть
связь) выполняется неравенство di-Jrd-b>dih.
Рассмотрим идею алгоритма.
Шаг 1. Строится каркас минимального веса (алгоритмы
Прима или Краскала).
Примечание. Это не есть первое приближение, как в
предыдущем алгоритме.
Шаг 2. Путем дублирования каждого ребра каркас
преобразуется в эйлеров граф.
Шаг 3. Находим в построенном графе эйлеров цикл.
Шаг 4. Эйлеров цикл преобразуем в гамильтонов цикл (или
маршрут коммивояжера). Метод преобразования:
последовательность вершин эйлерова цикла сокращается так, чтобы
каждая вершина графа в получившемся цикле встречалась ровно
один раз.
Шаг 5. Закончить работу алгоритма. Получено
приближенное решение задачи коммивояжера.
Покажем, что стоимость приближенного решение CostAp не
превосходит удвоенной стоимости оптимального решения Cost Bet.
Пусть стоимость каркаса — CostFr. Тогда CostFr<CostBet,
так как при удалении из оптимального пути коммивояжера
ребра получаем каркас с весом не большим, чем CostAp. Из
правила построения эйлерова графа получаем, что вес построенного
эйлерова цикла 2xCostFr. Неравенство треугольника
обеспечивает результат: следующую оценку шага 4 — CostAp<2xCostFr, a
значит, CostAp<2xCostBet.
Пример.
Рассмотрим пример на рисунке 4.52.
1-8-9-2-9-8-1-7-5-10-6-10-5-7-1-3-4-3-1
Рис. 4.52

4. Алгоритмы на графах
223
Для исходных данных, приведенных в таблице 4.9,
«жирным» шрифтом выделен каркас минимального веса. В таблице
выделены те ребра графа, которые включаются в каркас с
помощью алгоритма Прима.
Таблица 4.9
1
2
I 3
4
5
6
I 7
Γδ
9
10
1
@
32
19
33
22
41
18
15
16
31
2
32
@
51
58
27
42
35
18
17
34
3
19
51
@
23
35
49
26
34
35
41
4
33
58
23
@
33
37
23
46
46
32
5
22
27
35
33
@
19
10
23
23
9
6
41
42
49
37
19
@
24
42
42
10
7
18
35
26
23
10
24
@
25
25
14
8
15
18
34
46
23
42
25
@
1
32
9
16
17
35
46
23
42
25
1
@
32
10 ]
31
34
41
32
9
10
14
32
32
@
Последовательность включения ребер в каркас: (8,9), (8,1),
(9,2), (1,7), (7,5), (5,10), (10,6), (1,3) и (3,4).
«Тонкие» линии добавляются на шаге 2. Получаем эйлеров
граф. Затем эйлеров цикл (его стоимость 244) преобразуется в
путь коммивояжера (шаг 4). Согласно неравенству
треугольника мы получаем:
d2^dW>d2V ά2$+ά*Λ>ά2,ύ d2,X+dl,l>d2,V
Суммируя левые и правые части неравенств, получаем:
d2,9+ii9,8+ii8,l+dl,7>ii2,7·
Аналогичные преобразования осуществляются и для других
фрагментов сокращения эйлерова цикла. Для рассмотренного
примера Cost Ар равна 202.
Оцените, насколько стоимость этого маршрута больше
стоимости оптимального?
Структуры данных. Помимо названных ранее массивов
А — матрица расстояний и массива Way — хранение искомого
пути, требуется «что-то» для хранения описания каркаса.
Пусть это будет массив В:
Array[1..Nmax,l..Nmax] Of Boolean.
Элемент B[i,j], равный True, говорит о том, что ребро (i,j)
графа принадлежит каркасу.

224
4. Алгоритмы на графах
Общий алгоритм.
Begin
1пл_1:;{*Ввод описания - матрица расстояний;
инициализация данных.*}
Solve;{*Решение задачи.*}
0и1:;{*Вывод результата.*}
End.
Процедуры Init и Out очевидны (должны создаваться «на
автомате»). Уточняем процедуру Solve. Первый «набросок».
Procedure Solve;
Var ?{*Пока не знаем.*}
<процедуры и функции>;
Begin
InitSolve;{^Инициализация переменных процедуры
Solve.*}
FindTree;{^Построение каркаса.*}
EilerWay;{*Поиск эйлерова цикла.*}
KommWay;{*Поиск пути коммивояжера.*}
End;
Прежде чем продолжать уточнение, необходимо определить
структуры данных этой части алгоритма и взаимодействие его
составных частей. Во-первых, при построении каркаса
необходимо иметь список ребер, отсортированный в порядке
возрастания их весов (алгоритмы Краскала и Прима). Следовательно,
на входе процедуры FindTree должна быть матрица расстояний
А, на выходе — В, рабочие структуры — массив для хранения
списка ребер. Внутренние процедуры: формирование списка
ребер и сортировки.
Продолжим рассмотрение. Эйлеров цикл необходимо где-то
хранить. Пусть это будет массив St (Array[l..N*(N-l) Div 2]
Of Byte). Количество ненулевых элементов в St — значение
переменной Count. Эти величины описываются в разделе
переменных процедуры Solve, их инициализация — в процедуре
InitSolve. Процедуру поиска эйлерова цикла сделаем
рекурсивной, поэтому первый вызов изменится — EilerWay(l).
Выбор начальной вершины при поиске эйлерова цикла не имеет
значения.
Итак, классический алгоритм поиска эйлерова цикла
приводится с целью показа работы процедуры KommWay, ибо
последняя не есть поиск гамильтонова цикла в обычной
трактовке.

4. Алгоритмы на графах
225
Procedure EilerWay(v:Byte);
Var j : Integers-
Begin
For j :=1 To N Do
If В [v, j ] Then
Begin
В[v,j]:=False; В[j,v]:=False;EilerWay(j);
End;
Inc (Count) ;St[Count] :=v;{*Заносим номер вершины
в эйлеров цикл.*}
End;
Procedure KommWay;
Var s:Set Of L.Nmax;
i, j : Integers-
Begin
i:=0;s: = [];
For j:=l To Count Do{^Исключаем повторяющиеся
номера вершин из эйлерова цикла.*}
If Not (St [j] In s) Then
Begin
Inc(i) ;
Way[i]:=St[j];
s:=s+[St[j]] ;
Ends-
End;
4.10.3. Алгоритм Кристофидеса
Отличается от предыдущего алгоритма построением
маршрута из каркаса минимального веса. Неравенство треугольника
выполняется.
Шаг 1. Строится каркас минимального веса (алгоритм
Прима или Краскала).
Шаг 2. На множестве вершин каркаса (обозначим их через
V), имеющих нечетное число ребер каркаса, находится паросо-
четание минимального веса. Таких вершин в любом каркасе
четное число. Метод поиска паросочетания — чередующиеся
цепочки.
Шаг 3. Каркас преобразуется в эйлеров граф путем
присоединения ребер, соответствующих найденному паросочетанию.
Шаг 4. В построенном графе находится эйлеров маршрут.
Шаг 5. Эйлеров маршрут преобразуется в маршрут
коммивояжера.

226
4. Алгоритмы на графах
Итак, данный метод отличается от предыдущего только
шагами 2 и 3. Все этапы реализуются за полиномиальное время.
Известно [16], что для этого метода оценка приближенного
метода имеет вид CostAp<l.SxCostBest и эта оценка является
лучшей для приближенных полиномиальных алгоритмов решения
задачи о коммивояжере с неравенством треугольника.
Маршрут Эйлера:
1-7-5-10-6-4-3-1-8-9-2-1
Рис. 4.53
На данных из предыдущего параграфа на рисунке 4.53
показан пример каркаса («жирными» линиями) и паросочетание
минимального веса («тонкими» линиями), построенное на
вершинах каркаса с нечетными степенями (вершинах 1, 2, 4, 6).
Подграф имеет матрицу расстояний, приведенную в таблице
4.10.
Таблица 4.10
\ 1
00
32
33
41
2
32
00
58
42
4
33
58
00
37
6
41
42
37
00
Путь коммивояжера имеет стоимость Cost Ар, равную 191.
В алгоритм Solve (см. предыдущий алгоритм) добавляется
процедура построения паросочетания минимального веса (Р).
Назовем ее Pair. Ее входными данными является матрица В
(описывает каркас), выходными — новая матрица С (элементы
логического типа), соответствующая графу, получаемому
добавлением к каркасу ребер Р.

4. Алгоритмы на графах
227
Procedure Pair;
Var ?{*Пока не знаем.*};
<процедуры и функции, вложенные в Pair>;
Begin
InitPair;{^Инициализация переменных процедуры,
формирование массива с номерами вершин,
имеющих нечетную степень.* }
First;{*Поиск первого паросочетания.*}
Find;{*Поиск Р.*}
Ad;{^Добавление ребер, образующих Р, к каркасу -
матрица С.*}
End;
4.11. Задачи
1. Дан ориентированный граф с N вершинами (iV<50).
Вершины и дуги окрашены в цвета с номерами от 1 до Μ (Μ<6).
Указаны две вершины, в которых находятся фишки игрока и
конечная вершина. Правило перемещения фишек: игрок
может передвигать фишку по дуге, если ее цвет совпадает с
цветом вершины, в которой находится другая фишка; ходы можно
делать только в направлении дуг графа; поочередность ходов
необязательна. Игра заканчивается, если одна из фишек
достигает конечной вершины.
Написать программу поиска кратчайшего пути до конечной
вершины, если он существует.
2. Некоторые школы связаны компьютерной сетью. Между
школами заключены соглашения: каждая школа имеет список
школ-получателей, которым она рассылает программное
обеспечение всякий раз, получив новое бесплатное программное
обеспечение (извне сети или из другой школы). При этом, если
школа В есть в списке получателей школы А, то школа А
может не быть в списке получателей школы Б.
Написать программу, определяющую минимальное
количество школ, которым надо передать по экземпляру нового
программного обеспечения, чтобы распространить его по всем
школам сети в соответствии с соглашениями.
Кроме того, надо обеспечить возможность рассылки нового
программного обеспечения из любой школы по всем остальным
школам. Для этого можно расширять списки получателей
некоторых школ, добавляя в них новые школы. Требуется найти
минимальное суммарное количество расширений списков, при
которых программное обеспечение из любой школы достигло
бы всех остальных школ. Одно расширение означает добавле-

228
4. Алгоритмы на графах
ние одной новой школы-получателя в список получателей
одной из школ.
3. Задан неориентированный граф. При прохождении по
некоторым ребрам отдельные (определенные заранее) ребра могут
исчезать или появляться.
Написать программу поиска кратчайшего пути из вершины
с номером q в вершину с номером w.
4. Заданы два числа N и Μ (20<M<iV<150), где N —
количество точек на плоскости. Написать программу построения
дерева из Μ точек так, чтобы оно было оптимальным.
Дерево называется оптимальным, если сумма всех его ребер
минимальна. Все ребра — это расстояния между вершинами,
заданными координатами точек на плоскости.
5. Даны два числа N и М. Написать программу построения
графа из N вершин и Μ ребер. Каждой вершине ставится в
соответствие число ребер, входящих в нее. Граф должен быть
таким, чтобы сумма квадратов этих чисел была минимальна.
6. Задан ориентированный граф с N вершинами, каждому
ребру которого приписан неотрицательный вес. Написать
программу поиска простого цикла, для которого среднее
геометрическое весов его ребер было бы минимально.
Примечание
Цикл называется простым, если через каждую вершину он
проходит не более одного раза, петли в графе отсутствуют.
7. Компьютерная сеть* состоит из связанных между собой
двусторонними каналами связи N компьютеров (N не
превосходит 50, а количество каналов N+5), номера которых от 1 до N.
Эта сеть предназначена для распространения сообщения от
центрального компьютера всем остальным. Компьютер,
получивший сообщение, владеет им и может распространять его
дальше по сети. Запрещается передавать сообщения одному и тому
Рис. 4.54
Задача предложена Антоном Александровичем Сухановым для
Всероссийской олимпиады школьников в 1993 году.

4. Алгоритмы на графах
229
же компьютеру дважды. Время передачи сообщения по каналу
связи занимает одну секунду, при этом передающий и
принимающий компьютеры заняты на все время передачи данного
сообщения. На рисунке 4.54 приведен возможный вариант такой сети.
В начальный момент времени центральный компьютер
может передать сообщение одному из непосредственно связанных
с ним компьютеров, т. е. соседу. После окончания передачи
этим сообщением будут владеть оба компьютера. Каждый из
них может передать сообщение одному из своих соседей и так
далее, пока все компьютеры не будут владеть сообщением. Для
сети, показанной на рисунке, возможный порядок
распространения сообщения от центрального компьютера с номером 6
имеет вид:
Секунда 1: 6->4
Секунда 2: 4->3
6->7
Секунда 3: 3->1
4->5
Секунда 4: 3->2
Написать программу определения и вывода порядка
передачи сообщения за минимальное время.
8. Внутрь квадрата с координатами левого нижнего угла
(0,0) и координатами верхнего правого угла (100, 100)
поместили Af (l<Af<30) квадратиков. Написать программу поиска
кратчайшего пути из точки (0,0) в точку (100,100), который бы не
пересекал ни одного из этих квадратиков. Ограничения:
• длина стороны каждого квадратика равна 5;
• стороны квадратиков параллельны осям координат;
• координаты всех углов квадратиков — целочисленные;
• квадратики не имеют общих точек.
Указание. Строится граф из начальной, конечной точек и
вершин квадратиков (ребра не должны пересекать квадраты).
Затем ищется кратчайший путь, например, с помощью
алгоритма Дейкстры.
9. Задан неориентированный граф с N вершинами,
пронумерованными целыми числами от 1 до N. Написать программу,
которая последовательно решает следующие задачи:
• выясняет количество компонент связности графа;
• находит и выдает все такие ребра, что удаление любого из
них ведет к увеличению числа компонент связности;
• определяет, можно ли ориентировать все ребра графа
таким образом, чтобы получившийся граф оказался сильно
связным;

230
4. Алгоритмы на графах
• ориентирует максимальное количество ребер, чтобы
получившийся граф оказался сильно связным;
• определяет минимальное количество ребер, которые
следует добавить в граф, чтобы ответ на третий пункт был
утвердительным.
10. Задан ориентированный граф с N (l<iV<33) вершинами,
пронумерованными целыми числами от 1 до N. Напишите
программу, которая подсчитывает количество различных путей
между всеми парами вершин графа.
11. Ребенок нарисовал кружки и некоторые из них соединил
отрезками. Кружки он пометил целыми числами от 1 до iV
(l<iV<30), а на каждом отрезке поставил стрелочку. Затем он
приписал каждому кружочку вес в виде некоторого целого
числа и определил начальный и конечный кружочки. Из первого
он должен выйти, а во второй попасть.
Ребенок решил для себя следующее:
• набрать максимально возможное суммарное количество
очков;
• по каждому отрезку пройти ровно один раз;
• если в кружок он попадает при движении по направлению
стрелки, то к суммарному количеству очков вес этого
кружка прибавляется;
• если в кружок он попадает при движении против
направления стрелки, то из суммарного количества очков вес
этого кружка вычитается.
Написать программу, которая бы помогла ребенку
построить путь, удовлетворяющий всем этим требованиям.
12. Имеется поисковая система, состоящая из броневика и
нескольких разведчиков. Эта система была направлена для
поисков сейфа с секретной документацией противника. В
лабиринте (см. рисунок 4.55) один из посланных разведчиков
обнаружил цель поисков — сейф. Сам разведчик вывезти сейф не в
состоянии, но броневик, с которого были посланы разведчики,
может это сделать. Разведчик составил план своего пути в виде
списка команд U (вверх), D (вниз), L (влево), R (вправо). Путь
разведчика не обязательно является кратчайшим, но он точно
безопасен (в лабиринте есть мины). Броневик поедет по пути,
проходящему по пути разведчика (причем из квадрата А в
соседний квадрат В он может ехать только в том случае, если
разведчик тоже проходил из А в Б, а проход разведчика из Б в А
не обеспечивает безопасности) так, чтобы истратить как можно
меньше топлива. Написать программу, определяющую,
сколько топлива нужно броневику, чтобы доехать до сейфа.

4. Алгоритмы на графах
231
1 Li—I—к-
ϊ гтт
Нн j ι1[
Π ^TrlF^·
хгЙП
Η И н
I—i—i—i---4-—-jpi
—! τ ! !—г
_ U L4
I : Π
kl : j !
"":"■ Γ ": !~~
1 m\ [
1
-1-
ι -1 j
№1fn J
■ ] |Lh!
1 : ! : 1 j
1—h
рн ι i mil
Ρ ! t Fftttt+н
путь разведчика
_ путь броневика
Рис. 4.55
Входные данные.
В первой строке входного файла записаны целые числа Μ и
Τ (Μ — сколько топлива нужно на движение на 1, Τ —
сколько топлива нужно на поворот на 90°). 1<М, Т<100.
Во второй строке записано целое число N (0<iV<100).
В третьей — строка из N символов, задающая движение
разведчика, каждый символ которой — это один из четырех
символов С/, D, L, R.
Выходные данные.
Выведите в выходной файл минимальное количество
топлива, необходимое броневику для того, чтобы доехать до сейфа.
Примеры.
input.txt
2 1
51
DRURRRRRDDRDRRRDDLLLLLLLURULUUUUUUUULLL-
DRRRRDRRDDLU
output.txt
44
input.txt
10 1
9
RULDRUDUL
output.txt
32

232
4. Алгоритмы на графах
Указание. Упростим задачу. Пусть
нет стоимостей поворота. Так как путь
описывается строкой не более чем из
100 символов, то по нему можно
построить ориентированный граф, в
котором будет максимум 100 вершин.
Стоимость дуг известна, и она
постоянна в этом случае. Осталось с помощью
известного алгоритма Дейкстры (поиск
пути с минимальным весом) найти
решение. Что изменяется при введении
стоимости поворота? Рассмотрим пример, приведенный на
рисунке 4.56. Из точки А дошли до точки В, затем вернулись в
точку А и другим путем снова пришли в точку В. Таким
образом, из точки А в точку В можно попасть двумя способами.
Верхний путь содержит 7 перемещений и 4 поворота,
нижний — 9 перемещений и 3 поворота. Пусть стоимость
перемещения равна 2, а стоимость поворота — 3. Тогда верхний путь
имеет общую стоимость 26, а нижний — 27. Казалось бы, что
следует выбирать верхний путь. Однако, если оценить
стоимости перемещений до точки С, то окажется, что верхний путь
имеет стоимость 30, а нижний — 28. Из этого следует, что для
каждой вершины необходимо хранить не одну минимальную
стоимость ее достижения, а четыре стоимости — по каждому
направлению, строить соответствующий граф и применять
алгоритм Дейкстры. В этом заключается «изюминка» задачи.
13. «Химическая тревога». Произошло радиоактивное
заражение местности. Составлена карта зараженности. Она
представляет собой прямоугольную таблицу ΝχΜ, в клетках которой
записана зараженность соответствующего участка. Написать
программу поиска пути из левой верхней клетки таблицы в
правую нижнюю клетку с минимальной суммарной дозой радиации.
Входные данные. В первой строке входного файла input.txt
записаны числа N и М, а в следующих N строках — по Μ
чисел — карта зараженности местности. Числа в строке
разделяются одним или несколькими пробелами. l<iV<30, 1<M<30,
зараженность участка — целое число от 0 до 100.
Выходные данные. В файл output.txt записывается одно
число — суммарная доза радиации.
На рисунке 4.57 приведен пример заполнения входных и
выходных данных.
Указание. В явном виде динамическую схему применить
нельзя, ибо даны не два направления движения, как в классиче-
i<jr
1
I
ТТ'
!
1 ! :1
Ί
|
ί
В
Q

4. Алгоритмы на графах
233
Пример.
input.txt
3 5
2 100
1 100
1 0
О 100 100 |
0 0 0 !
3 100 2
| output.txt
1э
Рис. 4.57
ских задачах о Черепашке, а четыре.
Однако если клетки таблицы рассматривать
как вершины графа с ребрами,
означающими возможность перехода из одной
клетки в другую, то задача сводится к
поиску пути в графе между заданными
вершинами с минимальной стоимостью. Так
как стоимости положительные, то
применим алгоритм Дейкстры. Данная схема в
чистом виде неприменима. Например,
при описании графа с использованием
матрицы смежности потребуется
использовать двумерный массив 900x900 байт. Оперативной памяти
явно не хватит. Следует идти другим путем. Достаточно
ограничиться массивом оценок достижения каждой клетки
таблицы (Мп). На каждом шаге обработки находим элемент Мп с
минимальной оценкой. Согласно алгоритму Дейкстры эта
оценка окончательна. Вычисляем стоимости достижения клеток,
соседних с найденной, помечаем клетку как обработанную
(знак минус у значения оценки стоимости достижения данной
клетки), и находим следующий элемент из Мп. Для примера
на рисунке 4.56 окончательный вид массива Мп представлен в
таблице 4.11. Ответ задачи — значение Abs(Mn[N,M]).
Таблица 4.11
1
| 1
! 2
! з
1
-2
-3
2
-102
-103
-4
3
-7
-7
-7
4
-107
-7
-107
5 j
I
-7 !
-9J
14. Дана доска 8x8. На ней размещены один король и N
коней (0<iV<63). Фигуры перемещаются по шахматным
правилам. В процессе перемещений в одной клетке разрешается
размещать несколько фигур. Цель перемещений — собрать все
фигуры в одной клетке, причем за минимальное общее
количество перемещений. Дополнительное условие — если король и
конь находятся в одной клетке, то их можно переместить
вместе по правилу хода коня, причем это перемещение засчитыва-
ется за один ход.
Входные данные. Файл input.txt содержит одну строку
символов без пробелов, описывающую начальное расположение
фигур на доске. Строка содержит последовательность клеток

234
4. Алгоритмы на графах
Пример.
input.txt
D4A3A8H1H8
ι
! output.txt
ы
Рис. 4.58
доски, первая из которых — клетка короля,
остальные — клетки коней. Каждая клетка
описывается парой буква-цифра.
Выходные данные. Файл output.txt должен
содержать одно число — минимальное
количество перемещений, за которое все фигуры
можно собрать в одной клетке доски.
На рисунке 4.58 приведен пример
заполнения входных и выходных данных.
Указание. Представим доску в виде графа
(см. рисунок 4.59). Клетки (вершины)
соединены ребром, если из одной в другую можно
попасть ходом коня (матрица смежности
графа). Расстояние между двумя вершинами —
это количество ходов, которые требуется
сделать коню, чтобы попасть из одной клетки в
другую. С помощью стандартного алгоритма
находим кратчайшие пути между всеми
парами вершин (алгоритм Флойда).
Предположим, что пока решается задача только для
коней. Для ответа на вопрос задачи
необходимо найти клетку, до которой расстояние от
всех клеток с конями минимально. При
известных кратчайших расстояниях это поиск
минимального значения по массиву.
Количество ходов для короля из клетки (/, у) в (ρ, ζ)
равно Max(Abs(i-p), Abs(j-z)).
Рассмотрим случай, когда конь может «подвозить» короля.
Пусть клетка (i,j) — место встречи фигур и sc — оценка
количества ходов коней до этой клетки. Необходимо найти коня и
клетку доски, в которой он подхватит короля, причем вклад в
общую оценку ходов при этом должен быть минимальным.
15. Задан ориентированный граф с N вершинами,
пронумерованными целыми числами от 1 до N. Написать программу,
которая подсчитывает количество различных путей между всеми
парами вершин графа.
Входные данные. Входной файл input.txt содержит
количество вершин графа N (1<N<33) и список дуг графа, заданных
номерами начальной и конечной вершин.
Выходные данные. Вывести в выходной файл output.txt
матрицу ΝχΝ, элемент (i,y) которой равен числу различных путей,
ведущих из вершины / в вершину у или -1, если существует
бесконечно много таких путей.
Рис. 4.59

4. Алгоритмы на графах
235
Пример
На рисунке 4.60 приведен пример заполнения входных и
выходных данных.
| input.txt \
Ί 2 !
2 4 |
'3 4
14 1
15 3 |
!ϋ J
Рис. 4.60
Указание. В алгоритмах на графах есть очень изящный
метод определения кратчайших путей между всеми парами
вершин — алгоритм Флойда. Используем его идею для решения
нашей задачи. Пусть в матрице F[1..N,1»N] в текущий момент
времени хранится количество путей длины г между всеми
парами вершин, и нам необходимо найти количество путей длины
Н-1. Что делать? При F\i,k]<>0 между вершинами i и k есть
какое-то количество путей длины г и если при этом A[k,j]<>0, то
между вершинами / и j есть пути длины Н-1. Просчитывая для
всех значений £, мы получаем количество путей между всеми
парами вершин длины Н-1. Второе соображение касается
циклов в графе, ибо они определяют значение бесконечности (число
путей) задачи. Очевидно, что если выявлен цикл, то до всех
вершин этого цикла существует бесконечно много путей.
Выявленный цикл — это ненулевой элемент на главной диагонали
матрицы F при какой-либо из N итераций. Почему N? Да очень
просто, N — это длина максимального цикла в графе.
16. Дано прямоугольное клетчатое поле ΜχΝ клеток.
Каждая клетка поля покрашена в один из шести цветов, причем
верхняя левая и нижняя правая имеют различный цвет. В
результате поле разбивается на некоторое количество
одноцветных областей: две клетки одного цвета, имеющие общую
сторону, принадлежат одной области.
Правила игры. За первым игроком закреплена область,
включающая левую верхнюю клетку, за вторым — правую
нижнюю. Игроки ходят по очереди. Делая ход, игрок
перекрашивает свою область по своему выбору:
• в любой из шести цветов;
• в любой из шести цветов, за исключением цвета своей
области и цвета области противника.
, output.txt
-1-10-10
i-1 -10-10
1-1 -10-10
1-1-10-10
-1-11-10

236
4. Алгоритмы на графах
! Пример
! input.txt
I;
ι output.txt |
3 I
L4 j
Рис.4.61
В результате хода к области игрока присоединяются все
прилегающие к ней области выбранного цвета, если такие
имеются. Если после очередного хода окажется, что области
игроков соприкасаются, то игра заканчивается.
Написать программу, которая определяет минимально
возможное число ходов, по прошествии которых игра может
завершиться.
Входные данные. Цвета пронумерованы
цифрами от 1 до 6. Первая строка входного файла
input.txt содержит Μ и N — размеры поля (1<М,
Ν<60). Далее следует описание раскраски поля —
Μ строк по N цифр (от 1 до 6) в каждой без
пробелов. Первая цифра файла соответствует цвету
левой верхней клетки игрового поля. Количество
одноцветных областей не превосходит 50.
Выходные данные. В выходной файл output.txt
необходимо вывести искомое количество ходов
для каждого из пунктов.
На рисунке 4.60 приведен пример заполнения
входных и выходных данных.
Указание. Сведем задачу к некоторой графовой
модели. Рассмотрим идею решения на примере,
приведенном в формулировке задачи. Преобразуем
исходную матрицу (Т) (см. рисунок 4.61) в
матрицу областей (Ob) (см. рисунок 4.62), определим
цвет каждой области (массив С) и подсчитаем их
количество (k). Для примера Ob будет выглядеть
следующим образом. Массив С — (1, 2, 1, 1, 4, 3, 3, 2), k равно
8. А затем по этой матрице построим матрицу смежности графа
(G), определяющего связи между областями (см. рисунок 4.63).
После этих замечаний решение первого
пункта задачи сводится к поиску
кратчайшего пути, точнее количества ребер в пути,
между вершинами 1 и 8 (см. рисунок 4.64).
Для этого можно использовать алгоритм
Дейкстры или обход графа в ширину.
Ответ задачи — значение уровня вершины 8
(при обходе в ширину) минус единица.
Чем отличается решение по второму
пункту задачи? Нельзя окрашивать область в
цвета своей области и области противника. Это приводит к
тому, что мы можем остаться в той же вершине графа
областей. Опишем состояние игры кортежем (х,у,play,color), где χ —
Рис. 4.62
0
1
0
0
0
0
0
0
1
0
1
1
1
0
0
0
0
1
0
0
0
1
0
0
0
1
0
0
1
0
1
0
Рис,
0
1
0
1
0
1
1
0
0
0
1
0
1
0
0
1
0
0
0
1
1
0
0
1
.4.63
0
0
0
0
0
1
1
0

4. Алгоритмы на графах
237
Рис. 4.64
номер области первого игрока, у — номер области второго
игрока, play — номер игрока и color — номер цвета, в который
игрок окрашивает область. Как выполнить такой просмотр
состояний игры? Да опять же традиционным обходом в ширину в
пространстве состояний. Завершением обхода будет или
просмотр всей очереди, или достижение одного из конечных
состояний. Принцип обхода в ширину дает минимальное возможное
число ходов, по прошествии которых игра завершается.
17. Корпоративная сеть состоит из N компьютеров,
некоторые из них соединены прямыми двусторонними каналами
связи. В целях повышения секретности при проектировании сети
количество каналов связи было сокращено до минимума с тем
условием, чтобы любые два компьютера имели возможность
обмена информацией либо непосредственно, либо через другие
компьютеры сети.
Хакер хочет прослушивать все передаваемые в сети
сообщения. Для этого он разработал вирус, который, будучи
установленным на какой-либо из компьютеров, передает ему всю
информацию, проходящую через этот компьютер. Оказалось, что
материальные затраты, необходимые для установки вируса на
конкретный компьютер, различны.
Требуется определить набор компьютеров, которые хакер
должен заразить вирусом, чтобы минимизировать общие
материальные затраты.
Входные данные. Первая строка входного файла input.txt
содержит N — количество компьютеров в сети (l<iV<500). В i-й
из последующих N строк содержатся номера компьютеров, с
которыми непосредственно связан компьютер с номером /.
Далее следует N целых чисел из диапазона [1,1000] —
материальные затраты, связанные с установкой вируса на каждый из
компьютеров.
Выходные данные. В выходной файл output.txt требуется
вывести минимально возможные суммарные затраты и список но-

238
4. Алгоритмы на графах
I Пример
1 input.txt
ι 5
15
4
4
2 3 5
4 1
1 5 5 2 10
output.txt
3
1 4
Рис. 4.65
меров компьютеров, которые необходимо
инфицировать, упорядоченный по возрастанию.
На рисунке 4.66 приведен пример заполнения
входных и выходных данных.
Указание. В условии задачи в «сверхзавуали-
рованной» форме сказано о том, что связи
компьютеров описываются некоторой древовидной
структурой, ибо в противном случае «сокращение
до минимума» каналов связи невозможно. Итак,
мы имеем какое-то дерево (связное),
описывающее связи между компьютерами. Это ограничение
дает возможность решать задачу и для 500
компьютеров. При связях компьютеров, описываемых
произвольным связным графом, вероятно, ничего
другого, кроме перебора с некоторыми
эвристиками, не остается делать. А это уже достаточно безнадежно
Идея решения. Рассматриваем
вершины дерева по принципу обхода в
ширину. Мы находимся в вершине с
номером k (см. рисунок 4.66), и нам
требуется оценить (с учетом
требования задачи — все связи между
компьютерами должны быть под контролем):
• B[k] — стоимость заражения
компьютеров из поддерева, при
условии, что и компьютер с
номером k заражается;
• W[k] — то же самое, только компьютер с номером k не
заражается.
Так как используется обход в ширину, то оценки В и W для
всех компьютеров с номерами kv k2, ..., kY уже получены. В
первом случае — при оценке B[k] — компьютеры kv k2,..., hi мы
можем как заражать, так и не заражать, т. е. необходимо найти
ВЩ+тт{В\к^Щк$+тт^
Во втором случае — не заражаем компьютер k — компьютеры
kv k2, ..., &· необходимо заражать, в противном будет нарушено
условие задачи, т. е. W[k]=B[k1]+B[k2\+...+B[ki]. Ответом на
первый пункт задачи будет значение min(B[j],W\j]), где j —
номер вершины, с которой начинается обход в ширину.
18. Дан ориентированный граф. Вершинам приписаны веса.
Требуется найти путь между начальной и конечной вершинами
(они заданы) с максимально возможным суммарным весом.
Путь должен удовлетворять следующим условиям:
Рис. 4.66

4. Алгоритмы на графах
239
• по каждой дуге разрешается пройти один раз;
• если в вершину попадаем по входящей дуге, то к
суммарному весу вес этой вершины прибавляется;
• если в вершину попадаем по выходящей дуге, то из
суммарного веса вес этой вершины вычитается.
Входные данные. Входной файл input.txt содержит данные в
следующей последовательности:
• N хг х2 ... xN — количество вершин графа и их веса
(l<iV<30, 1<х.<30000);
• bt e — номера начальной и конечной вершин;
• Μ — количество дуг;
• ix Ji — номера вершин, соединяемых
первой дугой;
• *2 h — номера вершин, соединяемых
второй дугой;
*м
1м
номера вершин, соединяемых ду-
Пример
input.txt \
5 1 3 5 100:
23
1 4
5
1
2
5
2
4
output.txt
-72
12 5 3 2
Рис. 4.67
гой с номером М.
Выходные данные. В выходной файл
output.txt требуется вывести максимальный вес
пути и путь, на котором он достигается. В
случае, если решение не существует, выходной
файл должен содержать единственную строку
«по solution».
На рисунке 4.67 приведен пример
заполнения входных и выходных данных, а на рисунке
4.68 — граф, соответствующий входным
данным.
Указание. Задача на поиск
эйлерова пути в графе между заданными
вершинами. Так как требуется найти не
просто путь, а путь с наилучшей
оценкой, то перебор вариантов, — это,
наверное, единственный способ решения
задачи. Эйлеров путь между
вершинами бие существует (теорема Эйлера) в
связном графе в том и только том
случае, если вершины Ъ и е имеют
нечетные степени, а все остальные — четные степени.
Следовательно, на стадии предварительной обработки требуется выяснить
существует ли в принципе путь между заданными вершинами.
Для сокращения перебора разумно ввести дополнительную
структуру данных, в которой для каждой вершины определе-
Рис.4.68

240
4. Алгоритмы на графах
на последовательность просмотра остальных вершин графа.
Для нашего примера она может иметь вид, приведенный на
рисунке 4.69.
гг^
! 5
! 2
! 2
!___3___
^~"о
3
5
0
0
1
0
0
0
0
4
0 J
0
L_0__
г"о"1
о !
о !
0 ~Ί
_Αϋ
Рис. 4.69
Так, из вершины 2 очередность просмотра вершин — 5, 3, 1,
4. Вероятность того, что при этом на первых шагах перебора
получается оценка, близкая к оптимальной, возрастает, если
не рассматривать специально подобранные тесты. Кроме того,
следует ввести оперативную проверку связности
непросмотренной части графа. Пусть мы идем по ветке перебора 1-4-6, как
показано на рисунке 4.71. В процессе поиска решения —
эйлерова пути — пройденные ребра
«выбрасываются». Перечеркнутые ребра
удалены, они пройдены, и мы
находимся в 6-й вершине. Может
оказаться, во-первых, что появятся
изолированные вершины и, во-вторых, что
нарушится связность оставшейся части
графа. Например, так, как это
показано на рисунке 4.70. Необходимо
попасть из 1-й вершины в 7-ю. Очевидно,
что вершины 2, 3, 4 уже никак не
попадут в путь, поэтому дальнейший
поиск пути в этом варианте решения не
имеет смысла. Поиск эвристик,
сокращающих перебор, можно продолжить.
19. «Стены»* . В некоторой стране
стены построены таким образом, что
каждая стена соединяет ровно два
города, и стены не пересекают друг
друга. Таким образом, страна разделена на
отдельные области. Чтобы добраться
Рис. 4.70
Рис. 4.71
Задача с Международной олимпиады школьников по информатике
2000 года.

4. Алгоритмы на графах
241
из одной области в другую, необходимо либо пройти через
город, либо пересечь стену. Два любых города An В могут
соединяться не более чем одной стеной (один конец стены в городе А,
а другой — в городе В). Более того, всегда существует путь из
города А в город В, проходящий вдоль каких-либо стен и через
города.
Существует клуб, члены которого живут в городах. В
каждом городе может жить либо один член клуба, либо вообще ни
одного. Иногда у членов клуба возникает желание встретиться
внутри одной из областей, но не в городе. Чтобы попасть в
нужную область, каждый член клуба должен пересечь какое-то
количество стен, возможно равное нулю. Члены клуба
путешествуют на велосипедах. Они не хотят въезжать ни в один город
из-за интенсивного движения на городских улицах. Они также
хотят пересечь минимально возможное количество стен, так
как пересекать стену с велосипедом довольно трудно. Исходя
из этого, нужно найти такую оптимальную область, чтобы
суммарное количество стен, которые требуется пересечь членам
клуба, называемое суммой пересечений, было минимальным из
всех возможных.
Города пронумерованы целыми числами от 1 до N , где N —
количество городов. На рисунке 4.71 пронумерованные
вершины обозначают города, а линии, соединяющие вершины,
обозначают стены.
Предположим, что членами клуба
являются три человека, которые
живут в городах с номерами 3, 6 и 9.
Тогда оптимальная область и
соответствующие маршруты движения членов
клуба показаны на рисунке 4.72.
Сумма пересечений равняется 2, так как
членам клуба следует пересечь две
стены: человеку из города 9 требуется
пересечь стену между городами 2 и 4,
человеку из города 6 требуется пересечь стену между городами 4
и 7, а человек из города 3 не пересекает стен вообще.
Требуется написать программу, которая по заданной
информации о городах, областях и местах проживания членов клуба
находит оптимальную область и минимальную сумму
пересечений.
Входные данные. Файл имеет имя walls.in. Первая строка
содержит одно целое число: количество областей М, 2<М<200.
Вторая строка содержит одно целое число: количество городов
N, 3<iV<250. Третья строка содержит одно целое число: количе-

242
4. Алгоритмы на графах
ство членов клуба L, 1<L<30, L<N. Четвертая
строка содержит L различных целых чисел в
возрастающем порядке: номера городов, где
живут члены клуба.
Оставшаяся часть файла содержит 2М строк,
по паре строк для каждой из Μ областей.
Первые две строки из них описывают первую
область, вторые две строки — вторую область, и
т. д. В каждой паре первая строка содержит
количество городов I на границе области; вторая
строка содержит номера этих I городов в
порядке обхода границы области по часовой стрелке.
Единственным исключением является
последняя область — это находящаяся снаружи
(внешняя) область, окружающая все города и другие
области, и для нее порядок следования городов
на границе задается против часовой стрелки.
Порядок описания областей во входном файле
задает целые номера этим областям. Область,
описанная первой во входном файле, имеет
номер 1, описанная второй — номер 2, и т. д.
Обратите внимание, что входной файл содержит
описание всех областей, образованных городами и
стенами, включая находящуюся снаружи
(внешнюю) область.
Выходные данные. Файл имеет имя walls.out.
Первая строка этого файла содержит одно целое
число: минимальную сумму пересечений. Вторая
строка содержит одно целое число: номер
оптимальной области. Если существует несколько
различных решений, вам необходимо выдать лишь одно из них.
На рисунке 4.73 приведен пример заполнения входных и
выходных данных, а на рисунке 4.74 — граф,
соответствующий входным данным.
Пример
walls.in
10
10
3
3 6 9
3
1 2 3
3
1 3 7
4
2 4 7 3
3
4 6 7
3
4 8 6
3
6 8 7
3
4 5 8
4
7 8 10 9
3
5 10 8
7
7 9 10 5 4
2 1
walls.out
2
lL j
Рис. 4.73
Рис. 4.74

4. Алгоритмы на графах
243
Указание. В формулировке задачи содержится подсказка
решения. Описание исходного графа, а это явная задача на
графовые алгоритмы, дано, например, не в виде матрицы
смежности, а заданием областей. Требуется построить граф,
вершинами которого являются области, а ребрами — стены между
областями. Естественно, что должна быть вершина и для
внешней области. После формирования графа областей находим
кратчайшие расстояния между всеми парами вершин
(алгоритм Флойда). Для каждого члена клуба и каждой области
определяем минимальное расстояние, за которое он добирается
до этой области. Осталось просуммировать эти расстояния по
всем членам клуба и выбрать минимум.
20. Два графа Ga=(Va,Ea) и Gb=(Vh,Eb) называются
изоморфными, если существует взаимно однозначное соответствие
f-'Va->Vb, такое, что сохраняется отношение смежности между
вершинами графа, т. е. (v,w)eEa тогда и только тогда, когда
(f(v),f(w))eEb. Даны два графа. Определить, изоморфны ли они.
На рисунке 4.75 приведены примеры изоморфных графов.
Рис. 4.75
Рекомендации. Прямой метод решения, заключающийся в
генерации всех возможных перестановок N!, где N —
мощность множеств Va и Vb, и проверке сохранения отношения
смежности для каждого случая работоспособен для небольших
значений Ν (Ν<12). Несколько сократить перебор позволяет
введение массивов для хранения степеней вершин (число
ребер, инцидентных вершине) и установка соответствия только
между вершинами, имеющими одну степень. Для графов,
приведенных на рисунке 4.75 и имеющих одно значение степени,
это сокращение не работает.
21. Максимально полный подграф графа G называется
кликой. В клике между каждой парой вершин существует ребро.
Число клик в графе может расти экспоненциально
относительно числа вершин. Так, в графах MN Муна-Мозера с 3xiV вер-

244
4. Алгоритмы на графах
Рис. 4.76
шинами вершины разбиты на триады (1, 2, 3), (4, 5, 6), ...
(3xiV-2, 3xiV-l, SxN). Ребер между вершинами любой триады
нет. Однако вершины триады связаны ребрами со всеми
вершинами, не принадлежащими данной триаде. На рисунке 4.75
приведен граф Муна-Мозера при N=2 (первый на рисунке), на
рисунке 4.76 — при iV=3.
Графы Муна — Мозера имеют 3^ клик, каждая из которых
содержит N вершин. Перечислить для небольших значений N
клики в графах Муна-Мозера.
Примечание
В общем случае задача о поиске клик в графе G решается
достаточно сложно. Однако понятие клики противоположно понятию
максимально независимого множества. Строим дополнение графа G\
Находим в G' максимально независимые множества (это мы умеем
делать) — они соответствуют кликам исходного графа.
22. Рассмотрим четыре множества £^=[2, 3], S2=[l, 2, 4],
S3=[3, 4], S4=[l, 3, 4]. Требуется выбрать такие различные
четыре числа хх, х2, х3> xv что xiG^p i==l> 2> 3, 4. Этими числами
могут быть хх=2, х2=4, xs=3, x4=l, они представляют данную
систему множеств. Несложно привести пример множеств, для
которых данное представление невозможно. Ф. Холлом
доказана теорема о существовании системы различных
представителей. Система M(S)={SV S2, ..., SN} имеет систему различных
представителей тогда и только тогда, когда для любой
подсистемы {Sz 9Sl ,...,Sl }(^M(S) выполняется неравенство
1К
> k, т. е. количество элементов в объединении любых k
J~l
подмножеств должно быть не менее k.

4. Алгоритмы на графах
245
Пусть S= [1, 2, ..., Ν]. Определить, имеет ли M(S)={SV S2,
..., SN} систему различных представителей.
Указание. По M(S) требуется построить двудольный граф.
Система различных представителей существует тогда и только
тогда, когда в двудольном графе есть максимальное паросоче-
тание из N ребер.
23. Дан массив ΝχΜ, в клетках которого произвольным
образом поставлены числа от 1 до ΝχΜ. Горизонтальным ходом
называется такая перестановка любого числа элементов
массива, при которой каждый элемент остается в той строке, в
которой он был. Вертикальным ходом называется такая
перестановка любого числа элементов массива, при которой каждый
элемент остается в том столбце, в котором он был.
Разрешаются только горизонтальные и вертикальные ходы''.
Разработать программу, которая за возможно меньшее
количество ходов расставляет элементы массива по порядку, т. е.
в первой строке — от 1 до М, во второй строке — от М+1 до
2М, и т. д.
Указание. Рассмотрим метод поиска системы различных
представителей для нашей задачи на примере представленном
на рисунке 4.77.
1 6
: 1
ί 9
Li?.
8
11
2
_
~~8
11
14
3
10
5
2
Пб""1
5
12
4
По]
13
2 :
s, j
s_2_[_
s3 I
S4±
6
5
2
=Lj
Рис. 4.77
Обозначим элементы каждой строки нашей таблицы как Sv
S2, S3, S4. Считаем, что есть множества S- (l<Z<iV),
составленные из элементов, которые необходимо разбить на N классов Кь
по принадлежности к строке результирующей таблицы. Эти
множества удовлетворяют теореме Холла, то есть любые q
множеств содержат элементы не менее чем q классов.
Начинаем работу.
Первая итерация (первый столбец правой таблицы). Из Sx
выбираем 6^К2, из S2 — lei£\, из Ss — 9εΚ3, так как 2
выбрать нельзя, класс Кг занят, из S4 — 16, так как 3, 4 и 7
выбирать не имеем права по той же причине.
По мнению автора, это — одна из лучших олимпиадных задач Сергея
Геннадьевича Волченкова.

246
4. Алгоритмы на графах
Вторая итерация. По этому же
алгоритму из Sj — 8, S2 — 11, Ss — 2.
Выбрать из S4 нечего — все классы
заняты. Строим чередующуюся цепочку
(построение паросочетания в
двудольном графе), она начинается в S4 и
состоит из ребер (S4,3), (3,S3), (S3,14).
Эти ребра на рисунке 4.78, помечены
одинарными стрелками. Меняем
представителя у Ss на 14 из К4, и для S4
появляется представитель — 3 из ϋΓ1
(третий столбец правой таблицы).
Третья итерация. Выбираем для
Sx — 10, для S2 — 5, для Ss — 2.
Проблемы выбора для S4. Строим
чередующуюся цепочку: (S4,4), (2,S3), (S3,12),
(10,Sx), (Sx,15), она выделена на
рисунке двойными стрелками и меняем представителей (пятый
столбец правой таблицы).
Четвертая итерация. Выбор представителей однозначен.
Второй вертикальный и третий горизонтальный ходы
очевидны. При вертикальном — каждый элемент столбца
перемещаем в свою строку, а это можно сделать — у нас по одному
представителю; при горизонтальном — каждый элемент строки
перемещается в свой столбец.
24. Дан взвешенный (ребрам приписаны веса) граф G=(V,E),
естественно связный.
Обозначим через D(v,u) минимальное расстояние между
вершинами v,u^V.
Величина D(G) = Max(D(v,u)) называется диаметром графа.
Величина R(v) - Adax(D(v,u)) максимальным удалением в
графе от вершины υ.
Величину R(G) -- Min(R(v)) называют радиусом графа.
Любая вершина teV, такая, что R(t)=R(G), называется
центром графа.
Написать программу поиска диаметра, радиуса и центров
графа.
Указание. Первый шаг решения заключается в
формировании матрицы минимальных расстояний между всеми парами
вершин графа. Дальнейшее очевидно.

4. Алгоритмы на графах
247
25. Плоским графом называется граф, вершины которого
являются точками плоскости, а ребра — плоскими
непрерывными линиями без самопересечений, соединяющими
соответствующие вершины и не имеющими общих точек, естественно,
кроме инцидентных им обеим вершинам. Граф, допускающий
изображение в виде плоского, называют планарным. Известна
теорема Понтрягина-Куратовского: «Граф планарен тогда и
только тогда, когда он не содержит в качестве частей графы Къ и
К33 (может быть с добавочными вершинами степени 2)».
Графы Къ и К3 з приведены на рисунке 4.79.
Kj.3
Рис. 4.79
Планарных графов достаточно мало при
больших значениях N (количества
вершин), и выделение в G подграфов типа Къ и
К3 з — достаточно сложная задача.
Определить, какие подграфы содержатся в так
называемом графе Петерсона, приведенном
на рисунке 4.80.
26. Гранью (S) называют часть
плоскости, окруженную простым циклом (циклом
без самопересечений) и не содержащую
внутри себя других элементов графа. Формула Л. Эйлера
(1758 г.) связывает число граней, число вершин и ребер пла-
нарного графа G=(V,E), где | v\ =N, \E \ =М: £+АГ=М+2. Если
граф G без петель и кратных ребер (а в нашем рассмотрении
участвуют именно такие графы), то каждая грань ограничена
по крайней мере тремя ребрами графа. Из этого факта
получается оценка снизу удвоенного числа ребер графа 3xS<2xM.
Отсюда следует оценка количества ребер планарного G графа —
Μ<3χΝ-6 (при Ν>3). Проверить то, что графы Къ и Ks 3 не
являются планарными.
27. Согласно теореме Д. Кенига (1936 г.) для двудольности
графа необходимо и достаточно, чтобы он не содержал циклов
нечетной длины. Определить, является ли граф двудольным.

248
4. Алгоритмы на графах
Указание. При поиске в ширину вершины графа
помечаются метками 0, 1, 2 и т. д. Первой вершине, с которой
начинается просмотр, приписывается значение 0, вершинам, связанным
с ней, — метка 1 и т. д. Разобьем граф после просмотра на две
части: X включает вершины с четными метками, У — с
нечетными. Если оба подграфа пусты — исходный граф является
двудольным.
28. Задача Штейнера на графах. В связном взвешенном
графе G с выделенным подмножеством вершин U (C/czV) требуется
найти связный подграф Т, удовлетворяющий двум условиям:
• множество вершин подграфа Τ содержит заданное
подмножество U;
• граф Τ имеет минимальный вес среди всех подграфов,
удовлетворяющих первому условию.
Указание. Очевидно, что искомый подграф является
деревом, оно называется деревом Штейнера. Задача сводится к
нахождению дерева минимального веса в подграфах графа G,
множество вершин которых содержит U. Эффективных
алгоритмов решения задачи неизвестно, поэтому ничего другого не
остается, как перебрать варианты при небольших значениях N.
29. Задача о пяти ферзях. На шахматной доске 8x8
расставить наименьшее число ферзей так, чтобы каждая клетка
доски была под боем.
Указание. Построить граф для данной доски с учетом
правил перемещения ферзя. Всякой искомой расстановке
соответствует наименьшее доминирующее множество в графе.
30. Подмножество вершин графа, являющееся как
независимым, так и доминирующим, называется ядром. Найти ядра
графа.
Указание. Независимое множество является максимальным
(не обязательно наибольшим) тогда и только тогда, когда оно
является доминирующим. Таким образом, ядра графа — это
независимые максимальные множества вершин.

5. Алгоритмы
вычислительной геометрии
В этой главе рассматриваются алгоритмы, связанные с
геометрией. Они служат хорошим «подспорьем» в изучении
данного раздела математики. Но это не главное. Главное в том, что
вычислительная геометрия (определение Ф. Препарата, В. Шей-
моса [24]) является, во-первых, одним из разделов информатики
и, во-вторых, источником большого количества научных и
прикладных задач. Эта обширная область знаний, естественно, не
рассматривается полностью, а только ее отдельные аспекты,
доступные школьникам. Дело в том, что задач по информатике,
связанных с вычислительной геометрией, достаточно много, а
соответствующих публикаций достаточно мало. В какой-то
степени материал этой главы восполняет данный пробел. Кроме
того, специфика задач по вычислительной геометрии такова,
что их реализация позволяет формировать у школьников
структурный стиль написания программ.
5.1. Базовые процедуры
Прежде чем перейти к основным алгоритмам, рассмотрим
типы данных и базовые процедуры работы с ними.
Точка на плоскости описывается парой вещественных
чисел.
При использовании вещественного типа операции сравнения
лучше оформить специальными функциями. Причина
известна, на вещественных типах данных в системе
программирования Паскаль нет отношения порядка, поэтому записи вида а=Ь,
где а и Ь вещественные числа, лучше не использовать.
Приведем пример, объясняющий это положение.
Пусть для хранения вещественного типа используются два
десятичных разряда для порядка и шесть разрядов для
хранения мантиссы. Есть два числа:
α=0,34567χ104 и Ь=0,98765х10 4.
При сложении и вычитании осуществляется: выравнивание
порядков, сложение (вычитание) мантисс и нормализация
результата. После выравнивания порядков число Ь=0,0000000098765x104.
После сложения мантисс имеем: 0,3456700098765х104.

250 5. Алгоритмы вычислительной геометрии
Так как для хранения мантиссы у нас шесть десятичных
разрядов (в реальном компьютере тоже есть ограничение,
например, для типа Real в Турбо Паскале — 11-12 цифр), то
результат округляется и он равен 0,345670*104.
Итак, а+Ь=а при Ь>0!!! Компьютерная арифметика не
совпадает с обычной арифметикой.
На протяжении всей главы используются описанные ниже
типы данных, функции и процедуры.
Type Real=Extended;
TPoint=Record
χ, у: Real
End;
Const_Eps: Real=le-3;{^Точность вычисления.*}
ZeroPnt: TPoint = (X:0; У:0);{*Точка
с координатами 0,0.*}
Реализация операций сравнений: =, <, >, <, >.
Function RealEq(Const a, b: Real): Boolean;
{*Строго равно.*}
Begin
RealEq:-Abs(a-b)<=_Eps;
End;
Остальные функции RealMore (строго больше), RealLess
(строго меньше), RealMoreEq (больше или равно), RealLessEq
(меньше или равно) пишутся по аналогии.
Для определения максимального из двух вещественных
чисел приведенные выше функции уже можно использовать.
Function RealMax(Const a, b: Real): Real;
(^Максимальное из двух вещественных чисел.*}
Begin
If RealMore (a, b) Then RealMax:=a Else RealMax:=b;
End;
Аналогично пишется функция RealMin (поиск
минимального числа) и функция EqPoint совпадения двух точек на
плоскости.
Function EqPoint(Const А, В: TPoint):Boolean;
{^Совпадают ли точки ?*}
Begin
EqPoint:=RealEq(A.x, В.χ) And RealEq(А.у, В.у);
End;

5. Алгоритмы вычислительной геометрии
251
Функция вычисления расстояния между двумя точками на
плоскости (см. рисунок 5.1) имеет вид.
Function Dist(Const А, В: TPoint): Real;
{^Расстояние между двумя точками
на плоскости.*}
Begin
Dist:=Sqrt(Sqr(Α.χ-Β.χ) + Sqrt(A.y-B.у));
{^Вспомним теорему Пифагора - "квадрат
гипотенузы прямоугольного треугольника равен
сумме квадратов катетов".*}
End;
Каждую точку плоскости можно считать вектором, начало
которого находится в точке (0,0). Обозначим координаты точки
(вектора) υ через (их,иу), w=(wx,wy), q=(qx>Qy)·
Для векторов определены следующие операции:
• сумма: q=v+w, qx=vx+wx, qy=uy+wy;
• разность: q=v-w, qx=vx-wx, qy=vy~wy>
• скалярное произведение: v*w=vxwx+v w ;
• векторное произведение: vxw=(vxw -υ wx)k.
Скалярным произведением вектора υ на вектор w
называется число, определяемое равенством
νχιν= I у Ι χ I м; | xcos(cp),
где символом | | обозначается длина вектора, а φ — угол между
векторами.
Скалярное произведение обращается в нуль в том и только
том случае, когда по крайней мере один из векторов является
нулевым или когда векторы ν и w ортогональны.
Для скалярного произведения справедливы следующие
равенства:
(v+z)xw=v*w+vxz
(λ ν)χιν =υχ(λ w)=X(vxw).

252
5. Алгоритмы вычислительной геометрии
Если векторы заданы своими координатами в ортонормиро-
ванном базисе £,/, т. е. v=(vx,v ) w=(wx,w ), то формула для
скалярного произведения с учетом перечисленных свойств
записывается
vxw=vxwjixi)+uywx(jxi)+uxwy(ixj)+uy^^
=VxWx(ixi)+VyWy(M)=VxWx+VyWy.
Для скалярного произведения векторов (ν,α) и (ι#,β),
изображенных на рисунке 5.2, справедливо соотношение
vxw=vxwx+v w =v cos(a) w cos(P) +v sin(a) w sin{fi)=v w cos(ct-P).
При общей начальной точке у двух векторов скалярное
произведение больше нуля, если угол между векторами острый, и
меньше нуля, если угол тупой.
V*W
> X
Рис. 5.2
Рис. 5.3
Векторным произведением vxw называется вектор (см. рисунок
5.3), такой, что:
• длина вектора νχιυ равна
Ι υ\ χ I w\ xsin(ip);
• вектор νχιν перпендикулярен векторам ι; и до, т. е.
перпендикулярен плоскости этих векторов;
• вектор νχιν направлен так, что из конца этого вектора
кратчайший поворот от ν к w виден происходящим против
часовой стрелки.
Длина векторного произведения
численно равна площади параллелограмма,
построенного на перемножаемых векторах
υ hw как на сторонах (см. рисунок 5.4).
Пусть векторы ν и w заданы своими
координатами в базисе i, /, k
(wx,wy,wz).
Векторное произведение
(Vx'VyVz) И
Рис. 5.4

5. Алгоритмы вычислительной геометрии
253
νχιν = (vxi+vj+v2k, wJL+wJ+wJk) ζ=ζνχινχ ixi + νχιν ixj + νχιυ2 ixk
+ vywx jxi + υ w jxj + vyw2 jxk 4- vzwx kxi +v2wy kxj +v2w2 kxk.
Векторные произведения координатных ортов равны:
ixi =0, jxj =0, kxk =0, ixj =k, jxi=~k, jxk=i, kxj =-£, kxi =j и ixk =-/.
Формула имеет вид:
νχιν =(vyw2-v2wy)i 4- (v2wx-vxw2)j 4- (vxwy-vywx)k.
Ее можно записать в другом, более компактном виде (через
определитель):
их и? =
J
и>.
k
Vz
Раскрывая определитель, мы получаем ту же самую
формулу. Учитывая наш случай, а именно то, что координаты v2 и ιν2
векторов равны нулю, получаем vxw=(vxwy-vywx)k. После
несложных преобразований получаем
0X10 =(vxcos(a)xwxsin(fi)-vxsin(a)xwxcos(ft) )k=(vxwxsin(fi-a) )k.
Векторное произведение ненулевых векторов равно нулю
тогда и только тогда, когда векторы параллельны.
Пример. Найти площадь треугольника
ОАВ (см. рисунок 5.5).
Очевидно, что его площадь равна
половине площади параллелограмма ОАСВ, а
площадь последнего равна модулю
векторного произведения векторов О А и ОВ. На-
Y
ходим, SOACB=AxxBy-AyxBx, отсюда
ю
-> X
А^ χ В,
-А хВ
у *
JOAB
Рис. 5.5
Отметим, что значение SOBA имеет другой знак
(ориентированная площадь).
Тип данных для описания векторов имеет вид:
Type TVecCart=TPoint; (*Record x, у: Real End*)
Рассмотрим процедуры работы с векторами в декартовой
системе координат.
Procedure AddVecCart(Const a, b: TVecCart;

254
5. Алгоритмы вычислительной геометрии
Var c:TVecCart);
{*Сумма двух векторов в декартовой системе координат.*}
Begin
с.х:=а.х+Ь.х;с.у:=а.у+b.у;
End;
Аналогично пишутся и процедуры вычисления разности двух
векторов SubVecCart, умножения вектора на число MulKVecCart,
а также функции нахождения скалярного произведения
SkMulCart и векторного произведения VectMulCart векторов в
декартовой системе координат. Например:
Function SkMulCart (Const a, b: TVecCart): Real;
{* Скалярное произведение.*}
Begin
SkalarMulCart:=a.x*b.x+a.y*b.y;
End;
Вектор ν можно задать в полярной системе координат через
его длину (модуль) υ и угол α относительно оси X. Координаты
полярной системы координат (υ, α) и прямоугольной
декартовой (νχ,υ ) связаны соотношениями:
vx=vxcos(a), v =vxsin(a),
v=Sqrt(vx2+vy2), tan(a)=vy/vx.
Тип данных для описания вектора в полярной системе
координат имеет вид
Type TVecPol=Record
rst, angle: Real
End;
Операции перевода из одной системы координат в другую
реализуются с помощью следующих процедур и функций.
Функция определения угла используется при переводе в полярную
систему координат.
Function GetAngle(Const χ, у: Real): Real;
{ ^Возвращает угол от 0 до 2*Pi в радианах.*}
Var rs, с: Real;
Begin
rs:=Sqrt(Sqr (x) + Sqr(y)) ;{^Вычисляется
расстояние от точки (0,0) до (χ, у) . Можно
воспользоваться функцией Dist.*}

5. Алгоритмы вычислительной геометрии
255
If RealEq(rs, 0)
Then GetAngle:=0
Else
Begin
с:=x/rs;
If RealEq(c, 0)
Then c:=Pi/2
Else
c:=ArcTan(Sqrt(Abs(1-Sqr(c))) /c) ;
If RealLess(c, 0) Then c:=Pi+c;
If RealLess(y, 0) Then c:=2*Pi-c;
GetAngle:=c;
End;
End/
Procedure CartToPol(Const a: TVecCart;
Var b:TVecPol);{*Перевод из декартовой системы
координат в полярную.*}
Begin
b.rst:=Sqrt(Sqr (a.x) + Sqr(a.y));
b.angle:=GetAngle(a.x, a.y);
End;
Procedure PolToCart (Const a: TVecPol;
Var b: TVecCart) ;
{^Перевод из полярной системы координат
в декартовую.*}
Begin
b.x:=a.rst*cos(a.angle);
b.y:=a.rst*sin(a.angle);
End;
5.2. Прямая линия и отрезок прямой
Прямая линия на плоскости (см. рисунок 5.6), проходящая
через две точки (νχ9υ ) и (wx,wy), определяется следующим
линейным уравнением от двух переменных:
(WX-VX)X(y-Vy) = (Wy-Vy)X(X-VX)-
После преобразований получаем:
~(wy-vy)xx +(wx-vx)xy + (wy-vy)xvx - (wx-vx)xvy=0
или, после соответствующих обозначений:
Ахх+Бхг/+С=0,
где A=v.y-w.y, B=w.x-v.x, C=-(v.xx(v.y-w.y)+v.yx(w.x-v.x)).

256
5. Алгоритмы вычислительной геометрии
Параметры прямой линии описываются с помощью
следующего типа данных:
Type TLine=Record
А, В, С: Real
End;
Procedure Point2ToLine(Const ν, w: TPoint;
Var LrTLine);
{^Определение уравнения прямой
по координатам двух точек.*}
Begin
L.A
L.B
L.C
End;
= ν . у - w. у ;
= w.χ -ν. χ;
=-(v.x*L.A + v.y*L.B);
Если прямые заданы с помощью уравнений
Агхх+В {ху+С г=0 и А2хх+В2ху+С2=0, то точка их пересечения,
в случае ее существования, определяется по формулам
(А1хБ2-А2хБ1<>0):
х=(С1хВ2-С2хВ1)/(А1хВ2-А2хВ1),
y^A^C^A^C^/iA^B^A^B^
обычным решением системы двух уравнений с двумя
неизвестными.
Функция CrossLine определяет существование точки
пересечения (с учетом тех погрешностей, которые определяются
введенной точностью вычислений), а в процедуре Line2ToPoint
вычисляются координаты точки пересечения.
Function CrossLine(Const LI, L2 : TLine) : Boolean;
{^Определяет существование точки пересечения
двух прямых. Значение функции равно True,
если точка есть, и False, если прямые
параллельны.*}

5. Алгоритмы вычислительной геометрии
257
Var st: Real;
Begin
st:=LI.A*L2.B-L2.A*L1.B;
CrossLine:=Not RealEq(st,0);
End;
Procedure Line2ToPoint(Const LI, L2 : Tline;
Var Ρ:TPoint);{^Определение координат точки
пересечения двух линий.*}
Var st: Real;
Begin
st:=Ll.A*L2.B-L2.A*L1.B;
P.X:=(L1.C*L2.B-L2.C*L1.B)/st;
P.Y:=(L1.A*L2.C-L2.A*L1.C)/st;
End;
Координаты точек отрезка можно задать двумя
параметрическими уравнениями от одной независимой переменной t:
X==Vx']r(Wx~Vx)Xt^
y=yx+(wy-vy)xt.
При 0<£<1 точка (х,у) лежит на отрезке, а при t<0 или £>1 —
вне отрезка на прямой линии, продолжающей отрезок.
Для проверки принадлежности точки Ρ отрезку необходимо
выполнение равенства в уравнении (wx-vx)x(y-v )=-(w -υ )χ(χ-υχ)
и принадлежность координаты, например, χ точки Ρ интервалу,
определяемому координатами χ концов отрезков.
Function AtSegm(Const А, В, Ρ: TPoint): Boolean;
{^Проверка принадлежности точки Ρ отрезку АВ.*}
Begin
If EqPoint(А, В)
Then AtSegm:=EqPoint(A, P)
{*Точки А и В совпадают, результат
определяется совпадением точек А и Р.*}
Else
AtSegm:=RealEq((B.x-A.x)*(Р.у-А.у), (В.у-А.у)*
(Р.х-А.х)) And ( (RealMoreEq (Р.χ, Α.χ) And
RealMoreEq(Β.χ,Ρ.χ))
Or (RealMoreEq(P.χ, Β.χ)
And RealMoreEq(Α.χ, Ρ.χ)));
End;
Задание. Измените функцию для случая, когда отрезок
описывается параметрическими уравнениями.

258
5. Алгоритмы вычислительной геометрии
Процедура, с помощью которой определяются координаты
точки пересечения двух отрезков, пишется на основе ранее
приведенных процедур построения прямой по двум точкам и
нахождения точки пересечения прямых (не утверждается то,
что точка пересечения принадлежит отрезкам).
Procedure FindPointCross(Const fL, fR, sL, sR:
TPoint; Var rs : TPoint);{*Если точки пересечения
не существует, то значение rs равно (0,0) . *}
Var LI, L2: TLine;
Begin
Point2ToLine (fL, fR, LI);
Point2ToLine (sL, sR, L2);
If CrossLine(Ll,L2)
Then Line2ToPoint (LI, L2, rs)
Else rs:=ZeroPnt;
End;
Примечание
Процедуру следует доработать в том случае, если точка
пересечения прямых совпадает с точкой (0,0).
Пусть два отрезка находятся на одной прямой. Требуется
определить их взаимное расположение.
Function SegmLineCross(Const fL, fR, sL, sR:
Tpoint): Byte; {^Отрезки находятся на одной
прямой, проверка их взаимного расположения.
Результат равен 0, если отрезки пересекаются
в одной точке, 1 — не имеют пересечения и 2 —
есть пересечение более чем в одной точке.*}
Var Minf, Maxf,Mins,Maxs: Real;
Begin
Minf:=RealMin(Dist(fL,ZeroPnt),Dist(fR,ZeroPnt));
Maxf:=RealMax(Dist(fL,ZeroPnt),Dist(fR,ZeroPnt));
Mins:=RealMin(Dist(sL,ZeroPnt),Dist(sR,ZeroPnt));
Maxs:=RealMax(Dist(sL,ZeroPnt),Dist(sR,ZeroPnt));
If RealEq(Minf,Maxs) Or RealEq(Maxf,Mins)
Then SegmLineCross:=0
Else
If RealMore(Mins,Maxf) Or RealMore(Minf,Maxs)
Then SegmLineCross:=1
Else SegmLineCross:=2;
End;

5. Алгоритмы вычислительной геометрии
259
Даны два отрезка на плоскости, заданные координатами
своих концов. Определить их взаимное расположение (до
написания функции попробуйте прорисовать все возможные случаи).
Function SegmCross(Const fL, fR, sL, sR: Tpoint):
Byte; {* Результат равен 0, если отрезки пересекаются
в одной точке и лежат на одной прямой, 1 - не имеют
пересечения и лежат на одной прямой, 2 - отрезки лежат
на одной прямой и есть пересечение более чем в одной
точке, 3 - отрезки лежат на параллельных прямых, 4 -
отрезки не лежат на одной прямой и не имеют точки
пересечения, 5 - отрезки не лежат на одной прямой и
пересекаются на концах отрезков, б - отрезки не лежат на
одной прямой, точка пересечения принадлежит одному из
отрезков и является концом другого отрезка, 7 -
отрезки не лежат на одной прямой и пересекаются в одной
точке, не совпадающей ни с одним концом отрезков.*}
Var rs:TPoint;
Ll,L2:TLine;
Begin
Point2ToLine (fL, fR, LI);
Point2ToLine (sL, sR, L2);
If CrossLine (LI,L2)
Then
Begin
Line2ToPoint(LI, L2, rs)
If EqPoint (rs, fL) Or EqPoint(rs,fR) Or
EqPoint(rs,sL) Or EqPoint (rs,sR)
Then SegmCross: =5
Else
If AtSegm(fL,fR,rs) And AtSegm(sL,sR,rs)
Then SegmCross:= 7
Else
If AtSegm(fL,fR,rs) Or AtSegm(sL,sR,rs)
Then SegmCross:=6
Else SegmCross:=4;
End
Else
If EqPoint(L1.A*L2.B,L2.A*L1.B) And Not
(EqPoint (LLC, L2.C) )
Then SegmCross:=3
Else SegmCross:= SegmLineCross( fL, fR,
sL, sR);
End;

260
5. Алгоритмы вычислительной геометрии
Задачу о пересечении отрезков на плоскости можно
(естественно) решать по-другому. На рисунке 5.7 показаны два
отрезка. Найдем ряд векторных произведений, они показаны на
рисунке 5.8.
/ 7
Ч /'<
ι
ι ·
Чз
Рис. 5.7
1f-
4*3 /
/
ψ ν
Cl·
Чз /
(а)
/
I
I 4
(б)
/
ν
чз
7
(в)
Рис. 5.8
(г)
Рассмотрим произведения длин υν v2, vs, v4. Очевидно, что
если υ1χυ2<0 и vs*v4<0, то отрезки пересекаются (в
произведениях берутся длины векторов υν v2, vs, v4). При ι;χχι;2>0 или
υ<όχυ4>0 отрезки не пересекаются.
Рассмотрим варианты, при которых одна из длин равна
нулю. Если 1^=0, ν2<>0 и vsxv4<0, то третья точка лежит на
первом отрезке. При v2=0 и аналогичных условиях четвертая
точка лежит на первом отрезке, vs=~0 — первая на втором
отрезке и при υ4=0 — вторая точка на втором отрезке. Особый
случай, когда и1=0, v2=0, t>3=0, v4=0. Отрезки расположены на

5. Алгоритмы вычислительной геометрии
261
одной прямой, необходимы дополнительные проверки для
выяснения того, перекрываются они или нет. Все ли особые
случаи рассмотрены?
Задание. Определите значения векторных произведений при
совпадении каких-либо двух точек, например 2-й и 3-й.
Задание. Разработайте процедуру определения взаимного
расположения двух отрезков на плоскости с использованием
рассмотренных векторных произведений.
Еще один вариант решения задачи о пересечении отрезков
возможен при использовании параметрической формы записи
уравнения прямой. Отрезки заданы координатами своих
концов:
(*0'#о) ~ (*ι>#ι) и (х2,у2) - (х3,у3).
Уравнения имеют вид:
x=x0+t1x(xl-x0), 3/=3/о+*1хО/1"#о)»
где txs[09l]9 и x=x2+t2x(xs-x2), y=y2+t2x(ys-y2), где f2e[0,l].
В точке пересечения, при ее существовании выполняются
равенства:
(1 1 ν Ι Ω/ Хп\ТпХуХо Xq)
Уо+*1х(У1~Уо) = У2+*2х(Уг~У2)-
Есть система двух уравнений с двумя неизвестными ΐΎ и t2.
Если существует единственное решение и tv t2<=(0,l), то
отрезки пересекаются. Если одно из значений tx и t2 равно 0 или 1, а
второе принадлежит [0,1], то отрезки пересекаются в одной из
вершин, в остальных случаях отрезки не пересекаются.
Задание. Разработайте процедуру, определяющую
пересекаются ли отрезки. На основании выше изложенного материала.
Нормальным вектором η к прямой L
(Ахх+Вху+С=0) называют всякий
ненулевой вектор, перпендикулярный
этой прямой (см. рисунок 5.9).
Известно, что координаты вектора
определяются значениями А и Б в уравнении
линии L - п=(А,В). Для того, чтобы Рис. 5.9
найти уравнение прямой на плоскости
L (см. рисунок 5.10, проходящей через
заданную точку М0 перпендикулярно заданному направлению
п=(А,В), необходимо раскрыть скалярное произведение
(г-г0, л)=0. Оно равно Ах(х-х0) +£х(г/-г/0)=0.
\

262
5. Алгоритмы вычислительной геометрии
Рис. 5.10
Procedure PerLine(Const n: TLine; Const P: Tpoint;
Var L: TLine) ;
(*Линия, перпендикулярная η,
проходящая через точку Р.*}
Begin
L.A:=n.B;
L.B:=-n.A;
L.C:=-L.A*P.X-L.B*P.Y
End;
Расстояние от точки Р(х0,г/0) до прямой L вычисляется по
\L.Axx0 +L.Bxy0 + L.CI
формуле: p(P,L) = — -
JL.A2 +L.B2
Function DistPointToLine(Const Ρ: TPoint;
Const L:TLine): Real;{^Расстояние от точки до
прямой.*}
Begin
DistPointToLine:=Abs((L.A*P.x+L.B*P.y+L.C))
/Sqrt(Sqr(L.A)+Sqr(L.B));
End;
5.3. Треугольник
Даны три отрезка α, b, с. Для существования треугольника с
такими длинами сторон требуется одновременное выполнение
условий (а+Ь>с), (b+c>a) и (а+с>Ъ).
Function IsTrian(Const а, b, с: Real): Boolean;
{^Проверка существования треугольника
со сторонами а, Ъ, с.*}
Begin
IsTrian:=RealMore(a+b, c) And RealMore(a+c, b)
And RealMore(b+c, a);
End;

5. Алгоритмы вычислительной геометрии
263
Рис. 5.11
Площадь треугольника (см. рисунок 5.11).
Если известны длины сторон треугольника, то
для вычисления площади треугольника
обычно используется формула Герона
S^P х (Ρ -ο) χ (р -Ъ) χ (р -с)
где р=(а+Ь+с)/2.
Function Sq(a,b,с:Real):Real;
Var ρ:Real;
Begin
p:= (a+b+c)/2;
Sq:=Sqrt(p*(p-a)*(p-b)*(p-c));
End;
Возможно использование и других формул:
S =
α χ h axb χ sin c α χ sin Β χ sin С
h χ sin A
2 2 2 χ sin A 2 χ sin Б χ sin С
где большими буквами А, Б, С обозначены углы против
соответствующих сторон.
Гораздо интереснее второй способ вычисления площади
треугольника — через векторное произведение. Длина вектора дает
удвоенную площадь треугольника, построенного на этих
векторах.
Пусть даны три точки ρ^(χνν^)9 р2=(х2,у2), р3=(Хз»Уг) на
плоскости, определяющие вершины треугольника. Совместим
начало координат с первой точкой.
Векторное произведение равно
4*^3
J
-χ, у2 -у>
■х> Уз ~У>
Вычисление длины вектора равносильно раскрытию
определителя
х9
Ух
Уг
Уз
1
1
1
=х1Чу2-УзУУ1х(х2~хз)+(х2хУз~хгхУ2) (Рас"
крываем по первой строке).
Function SquareTrian(Const pi, p2, p3: TPoint) :
Real; {^Вычисление ориентированной площади
треугольника.*}
Begin
SquareTrian:=(pi.χ*(ρ2.У~рЗ.у)-pi.у(р2.х-рЗ.χ)
+ (р2.х*р3.у-р3.х*р2.у))/2;
End;

264
5. Алгоритмы вычислительной геометрии
2
-1
1
2
1
-1
2
-1
-2
2
-2
-1
1
1
1
1
1
1
Пример. Вычислим удвоенную
площадь треугольника, изображенного на
рисунке 5.12.
Значение определителя
равно 9.
Значение определителя
первом случае угол считался против часовой стрелки, во
втором — по часовой стрелке.
Υ
(-ML-
. \
^
-ν
/ -χ
(1,-2)
Рис. 5.12
равно -
■9. Отличие: в
Пример. Рисунок 5.13.
4-11
Определитель
а определитель
О
-2
4
3
-2
О
3
(-2,3)
равен 10,
2
3
равен 15.
Рис. 5.13
Вывод: при обходе против часовой стрелки получаем
положительные величины, а при обходе по часовой стрелке —
отрицательные значения.
Замечательные линии и точки в треугольнике.
1. Высоту треугольника, опущенную на
сторону а, обозначим через ha (см. рисунок
5.14). Через три стороны она выражается
формулой
йя =
2 ~ ^Рх(р-а)х(Р~Ь)х{р-с)
где р=(а+Ь+с)/2.
Рис. 5.14
Function GetHeight(Const a, b, с: Real):
Real; {^Вычисление длины высоты, проведенной
из вершины, противоположной стороне треугольника
с длиной а. * }
Var ρ: Real;
Begin
p: = (a+b+c)/2;

5. Алгоритмы вычислительной геометрии
265
GetHeight:=2*Sqrt(ρ*(р-а)*(p-b)*(р-с))/а;
End;
2. Медианы треугольника пересекаются в
одной точке (всегда внутри треугольника),
являющейся центром тяжести треугольника. Эта
точка делит каждую медиану в отношении 2:1,
считая от вершины. Медиану на сторону а (см.
рисунок 5.15) обозначим через та. Через три
стороны треугольника она выражается
формулой
Рис. 5.15
тл
л/2хЬ2 +2хс2 -а2
Function GetMed(Const a, b, с:
Real) : Real; {^Вычисление длины
медианы, проведенной из вершины,
противоположной стороне треугольника с длиной а.*}
Begin
GetMed:=Sqrt(2*(b*b+c*c)-a*a)/2;
End;
3. Три биссектрисы треугольника
пересекаются в одной точке (всегда внутри
треугольника), являющейся центром вписанного
круга (см. рисунок 5.16). Его радиус
вычисляется по формуле
Рис. 5.16
(р-а)х(р-Ь)х(р-с)
Биссектрису к стороне а обозначим через βα, ее длина
выражается формулой
βα
2 x.yb хс χ рх(р -а)
Ъ -f с
, где ρ — полупериметр.
Function GetRadlns(Const a, b, с: Real): Real;
{^Вычисление радиуса окружности, вписанной
в треугольник с длинами сторон а, Ъ, с.*}
Var p: Real;
Begin
p:=(a+b+c)/2;
GetRadlns:=Sqrt((p-a)*(ρ-b)* (p-c)/p);
End;

266
5. Алгоритмы вычислительной геометрии
Function GetBis (Const а, b, с: Real) : Real;
{^Вычисление длины биссектрисы, проведенной
из вершины, противоположной стороне треугольника
с длиной а.*}
Var p: Real;
Begin
p:=(a+b+c)/2;
GetBis:=2*Sqrt(b*c*p*(p-a))/(b + c);
End;
4. Три перпендикуляра к сторонам
треугольника, проведенные через их
середины, пересекаются в одной точке,
служащей центром описанного круга (см.
рисунок 5.17). В тупоугольном
треугольнике эта точка лежит вне треугольника, в
остроугольном — внутри, в
прямоугольном — на середине гипотенузы. Его
радиус вычисляется по формуле
ахЪ хс
К = —- —
4^px(p-a)x(p-b)x(p-c)
В равнобедренном треугольнике высота, медиана и
биссектриса, опущенные на основание, а также перпендикуляр,
проведенный через середину основания, совпадают друг с другом; в
равностороннем то же имеет место для всех трех сторон. В
остальных случаях ни одна из упомянутых линий не совпадает с
другой. Центр тяжести, центр вписанного круга и центр
описанного круга совпадают друг с другом только в
равностороннем треугольнике.
Function GetRadExt(Const а, b, с: Real): Real;
{^Вычисление радиуса окружности, описанной около
треугольника с длинами сторон а, Ь, с.*}
Var p: Real;
Begin
p:= (a+b+c)/2;
GetRadExt:=a*b*c/(4*Sqrt(p*(p-a)*(p-b)*(p-c)));
End;
5.4. Многоугольник
Многоугольник назовем простым, если никакая пара
непоследовательных его ребер не имеет общих точек. Требуется
определить, является ли заданный многоугольник простым.

5. Алгоритмы вычислительной геометрии 267
Для решения этой задачи у нас разработан аппарат, ибо суть
решения в определении взаимного расположения сторон
многоугольника. Если нет ни одного пересечения сторон, включая
случай их частичного наложения, то многоугольник простой.
Запрещенные ситуации пересечения сторон многоугольника
показаны на рисунке 5.18 (цифрами обозначены концы
отрезков, соответственно первого и второго).
2
ι ^ \
2 2 V1
Рис. 5.18
Function IsPoligonSimple
(Const A:Array Of TPoint;Const N:Word):Boolean;
{^Проверка простоты многоугольника. Значение функции
равно False, если многоугольник не является простым, и
True, если он простой. Точки в массиве А заданы в
порядке обхода по часовой или против часовой стрелки.
Предполагаем, что если отрезки лежат на одной прямой и
пересекаются в одной точке, то это один отрезок.*}
Var i, j : Integer;
pp:Boolean;
Begin
pp:=True;
i:=l;
While (i<=N-l) And pp Do
Begin
j:=i+l;
While (j<=N) And pp Do
Begin
Case SegmCross (A[i] ,A[i+l] ,A[j] ,A[ (j + 1) Mod N] )
0£{*Функция проверки взаимного
расположения двух отрезков описана ранее.*}
0,2,6,7: pp:=False;
End;
Inc (j ) ;
End;

268
5. Алгоритмы вычислительной геометрии
Inc(i);
End;
IsPoligonSimple:=рр;
End;
Задача. Дана точка ρ и простой Af-угольник Q. Определить,
принадлежит ли точка ρ внутренней области простого
^-угольника Q, включая его стороны.
Проведем через точку ρ прямую L, параллельную оси X.
Если L не пересекает Q, то ρ не принадлежит Q, она внешняя
по отношению к Q. Найдем количество пересечений (w) луча,
выходящего из точки ρ влево или вправо. Точка ρ лежит
внутри Q тогда и только тогда, когда w нечетно. Это общий
(идеальный) случай. В этой, как и в любой геометрической задаче,
есть частные случаи.
На рисунке 5.19 для первой точки все хорошо, она внешняя,
количество пересечений четно (считаем вправо). Для второй и
третьей точек ситуация чуть хуже — на прямой L лежит одна
из сторон многоугольника; прямая L проходит через вершину
многоугольника.
Рис. 5.19
Вырожденные случаи. Лучше повернуть чуть-чуть прямую
L против часовой стрелки, что устранит вырожденность и
позволит считать по схеме, приведенной ниже.
Function IncludPoint(Const A: Array Of TPoint;
Const N: Word; Const P: TPoint): Boolean;
{^Проверка принадлежности точки многоугольнику
(включая стороны).*}
Var i, nxt, sc: Integer;
If, rg: TPoint;
nx: Real;
Begin
sc:=0; IncludPoint:=True;
For i:=0 To N-l Do

5. Алгоритмы вычислительной геометрии
269
Begin {*Для каждой стороны
многоугольника находим координату χ точки
пересечения с горизонтальным лучом.*}
nxt:= (i + 1) Mod N;
If AtSegm(A[i], A[nxt], Ρ) Then Exit;{^Проверка
принадлежности точки Р отрезку
(A[i],A[nxt]).*}
lf:=A[i]; rg:=A[i];
If RealLess(A[i].y, A[nxt].y)
Then rg:=A[nxt]
Else If:=A[nxt];
If RealLess(If.y, A[i].y) And RealLessEq
(A[i].y, rg.y) Then
Begin
Nx: = ( (rg.x-lf.x)*P.y+lf.x*rg.y-lf.y*rg.x)/
(rg.y-lf.y); (^Вычисление координаты х
точки пересечения стороны многоугольника
с прямой, параллельной оси X. Для решения
задачи достаточно в уравнение
(wx-vx) * (y-vy) = (wy-vy) * (x-vx) подставить
координаты соответствующих точек, раскрыть
скобки и сократить подобные члены.*}
If RealMore(nx, P.x) Then Inc(sc);
End;
End;
IncludPoint:=Odd(sc);
End;
Задача. Вычислить площадь простого плоского
многоугольника.
Метод. Соединяем начало координат отрезками с
вершинами многоугольника. Последовательно вычисляем
ориентированные площади треугольников. В результате получим площадь
нашего многоугольника.
Рассмотрим задачу на примере. Удвоенная площадь
прямоугольного треугольника вычисляется по формуле axb (a,b —
стороны треугольника, образующие прямой угол), а
трапеции — (a+b)xh, где a, b — длины оснований, h — высота. Пусть
наш многоугольник является четырехугольником Ро/^р^з' гДе
p^ix^yj). Вычислим площадь треугольников, показанных на
рисунке 5.20:
51=х1хг/1-х0хг/0-(г/1+г/0)х(х1-х0)=х0хг/1-х1хг/0
S2=x2xy2-x1xy1-(y2+y1)x(x2-x1)=x1xy2-x2xy1

270
5. Алгоритмы вычислительной геометрии
^3==Х3ХУЗ~-Х2ХУ2-(УЗЛ'У2)Х(Х3-Х2)=:Х2ХУЗ-Х3ХУ2
^4=хохУо-хзхУз~(Уо+Уз)х(хо-хз)^хзхУо~хохУз
Мы могли бы это же самое сделать с помощью векторных
произведений, рассмотренных выше (эта формула уже
получена ранее), но пусть будет так — другой способ.
ί
S2
\
(б)
У
Л
S4
(с)
Рис. 5.20
После суммирования и группировки получаем:
Убедитесь в правильности наших
рассуждений на следующем примере,
изображенном на рисунке 5.21. Площадь
многоугольника (S) равна 3,5. По нашим
формулам
2xS=lx(l-2)+4x(4-l)+lx(3-l)+lx(3-4)+
+2χ(2-3)+2χ(2-3)+1χ(1-2)=7.
(1Д>
(4Д)
Рис. 5.21
После этих рассуждений и примеров можно написать
функцию вычисления площади простого многоугольника.
Function Square(Const A: Array Of TPoint;
Const N:Word): Real;{^Ориентированная площадь
многоугольника из N точек.*}
Var i: Word;

5. Алгоритмы вычислительной геометрии
271
sc: Real;
Begin
If N<3
Then Square:=0
Else
Begin
Sc:=A[0].x*(A[1].y-A[N-l].y)+A[N-1].x*
(A[0] .y-A[N-2] .y) ;
For i:=l To N-2 Do
sc:=sc+A[i].x*(A[i+1].y-A[i-l].y);
Square:=sc/2;
End;
End;
Задача. Дан многоугольник. Определить, является ли он
выпуклым.
Многоугольник выпуклый, если все диагонали лежат
внутри него. Сумма внутренних углов в выпуклом многоугольнике
равна 180°x(iV-2), где N — число сторон многоугольника.
Решить задачу определения выпуклости можно и
по-другому. Все треугольники, образованные тройками соседних
вершин в порядке их обхода, имеют одну ориентацию. При этом
следует учесть тот факт, что нахождение тройки вершин на
одной прямой не нарушает факта выпуклости. Первые два
многоугольника на рисунке 5.22 выпуклые, третий, независимо от
направления обхода, не является выпуклым.
oo<i
Рис. 5.22
Function IsPoligonConvex(Const A: Array Of TPoint;
Const N: Word) : Boolean;
{^Проверка выпуклости многоугольника, значение
функции равно True, если многоугольник выпуклый.*}
Var bn, nw: Byte;
i: Integer;rp: Real;
Begin
IsPoligonConvex:=False;
If N>3 Then
Begin

272
5. Алгоритмы вычислительной геометрии
Ьп:=1;
For i:=0 To N-l Do
Begin
rp:=SquareTrian(A[(i+N-1) Mod N] , A[i], A[(i + 1)
Mod N]); {^Ориентированная площадь
треугольника, построенного по трем
соседним вершинам многоугольника.*}
If RealEq(rp, 0)
Then nw:=l{*To4KH находятся на одной прямой.*}
Else
If RealLess(rp, 0) Then nw:=0 Else nw:=2;
If (bn=l) Then bn:=nw
Else
If (nw<>l) And (nwobn) Then Exit; {*Вершины
многоугольника лежат не на одной прямой,
ориентация треугольников не совпадает -
многоугольник не выпуклый.*}
End;
End;
IsPoligonConvex:=True;
End;
5.5. Выпуклая оболочка*
На плоскости задано множество S, содержащее N точек.
Требуется построить их выпуклую оболочку.
Идея алгоритма Грэхема. Тройки последовательных точек
проверяются в порядке обхода против часовой стрелки на
предмет того, образуют ли они угол, больший или равный π. Если
угол q1q2(l3 больше или равен π, то считают, что qxq24^ образуют
«правый поворот», иначе они образуют «левый поворот».
Алгоритм (см. рисунок 5.23):
• найти внутреннюю точку t;
• используя t как начало координат, отсортировать точки
множества S по неубыванию в соответствии с полярным
углом и расстоянием от t;
• выполнить обход точек, исключая точки типа q2
образующие «правый поворот».
Этот алгоритм можно упростить. Можно находить не
внутреннюю точку, а самую левую и верхнюю. Она заведомо при-
Идеи всех алгоритмов этого параграфа взяты из прекрасной книги Ф.
Препарата и Μ Шеймоса [24].

5. Алгоритмы вычислительной геометрии
273
надлежит выпуклой оболочке. При этом значения углов
вычисляются относительно этой точки.
Известно, что сортировка N элементов может быть
выполнена за время 0(NxlogN) (методы Хоара, слияния, пирамидальной
сортировки). Это самая трудоемкая по времени часть алгоритма.
Обход может быть выполнен за время, пропорциональное N.
Значит, выпуклую оболочку можно построить за время,
пропорциональное NxlogN.
Опишем структуры данных.
Var A:Array[1..MaxN] Of TPoint;{*Координаты точек.*}
Ν: Integer;{^Количество точек.*}
Μ: Integer;{^Количество точек в выпуклой
оболочке.*}
Is: Array[1..MaxN] Of Integer;{*Номера точек.
В процедуре типа Init необходимо
выполнить следующее присваивание:
For i:=l To N Do ls[i] :=i.*}
bb: Array[1..MaxN] Of Boolean;{^Признак
принадлежности точки выпуклой
оболочке, начальное присвоение -
FillChar(bb, SizeOf(bb), True), все
точки принадлежат выпуклой оболочке.*}
Rd: Array[1. .MaxN] Of Real;{*Оценки углов.* }
Фрагмент вывода результата решения задачи имеет вид:
WriteLn(Μ);
For i:-l To N Do
If bb[i] Then Write (Is [i] , ' ');

274
5. Алгоритмы вычислительной геометрии
Сейчас мы знаем, к чему стремиться, поэтому перейдем к
основной процедуре.
Procedure Solve;
Var aa: TPoint;
i, j, r: Integer;
Begin
j:= 1;{^Предполагаем, что самой левой верхней
точкой множества по значению координаты X
является первая точка.*}
For i: =2 То N Do {*Поиск точки, заведомо
принадлежащей выпуклой оболочке.*}
If RealMore(A[j].х, A[i].x)
Or (RealEq(A[i].χ, A[j].x)
And RealMore(A[i].y, A[jJ.y))
Then j:=i;
aa:=A[l];A[l]:=A[j];A[j]:=aa;
r:=ls[1];Is[1]:=ls[j];Is[j]:=r;{*Меняем точки,
на первом месте в массиве записана точка,
принадлежащая выпуклой оболочке.*}
{^Вычисляем значения синусов углов, углы принадлежат
первой и четвертой четвертям, если брать их с
противоположным знаком и затем отсортировать в
порядке неубывания, то выпуклая оболочка будет
построена обходом против часовой стрелки.*}
For i:=2 ToNDo
Begin
aa.x:=A[i].x-A[l].x;aa.у:=A[i].y-A[1]. y;
Rd[i]:=-aa.y/Sqrt(Sqr(aa.x) + Sqr(aa.y));
End;
Sort (2, N);{*Обычная сортировка, например по
Ч.Э.Р.Хоару. Следует только не забывать,
что при перестановке ключей - Rd[i]
необходимо переставлять и соответствующие
элементы в массивах Is и А (процедура не
приводится).*}
{^Осталось выполнить обход множества точек.*}
If N>3 Then Rounds;{*Обход.*}
End;
И наконец, последняя из рассматриваемых процедур.
Procedure Rounds;
Var If, md, rg: TPoint;
lfi, mdi, rgi: Integer;

5. Алгоритмы вычислительной геометрии
275
г: Real;
Function Predd(ldi: Integer): Integers-
Begin
Dec(ldi);
While Not (bbfldi] ) Do ldi := (ldi+N-2) Mod N + 1;
Predd:=ldi;
End;
Begin
M:=N;{^Количество точек в выпуклой оболочке.*}
lf:=A[2]; md:=A[3]; rg:=A[4];
lfi:=2; mdi:=3; rgi:=4;
While rgi<>2 Do
Begin
r:=-SquareTrian(If, md, rg) ; {^Ориентированная
площадь треугольника.*}
If Not(RealMore(r, 0))
Then
Begin
{^Исключаем точку с номером mdi из
выпуклой оболочки.*}
bb[mdi]:=False;mdi:=lfi;md:=lf;
Ifi:=Predd(Ifi);{^Определяем номер
предыдущей точки.*}
If:=A[lfi];
Dec(Μ);
End
Else
Begin {^Переходим к следующей точке.*}
lfi:=mdi; mdi:=rgi; rgi:=rgi Mod N + 1;
lf:=md; md:=rg; rg:=A[rgi];
Ends-
End;
End;
Рассмотрим другой способ построения выпуклой оболочки —
алгоритм Джарвиса. Он основан на следующем утверждении.
Отрезок L, определяемый двумя точками, является ребром
выпуклой оболочки тогда и только тогда, когда все другие точки
множества S лежат на L или с одной стороны от него. Из этого
утверждения «вытекает» следующий алгоритм. N точек
определяют С^ , т. е. порядка 0(N2) отрезков. Для каждого из этих
отрезков за линейное время можно определить положение
остальных N-2 точек относительно него. Таким образом, за время,

276
5. Алгоритмы вычислительной геометрии
пропорциональное 0(iV3), можно найти
все пары точек, определяющих ребра
выпуклой оболочки. Затем эти точки
следует расположить в порядке
последовательных вершин оболочки. Джар-
вис заметил, что данную идею можно
улучшить, если учесть следующий
факт. Если установлено, что отрезок
qxq2 является ребром оболочки, то
должно существовать другое ребро с
концом в точке q2, принадлежащее выпуклой оболочке. Уточнение
этого факта приводит к алгоритму с временем работы,
пропорциональным 0(N2). Рисунок 5.24 служит иллюстрацией данной
идеи.
Структуры данных:
Const MaxN=100;
Var A: Array[1..MaxN] Of TPoint;{*Массив
с координатами точек плоскости.*}
Ν: Integer;{^Количество точек.*}
rs: Array[1..MaxN] Of Integer;{*Номера точек,
принадлежащих выпуклой оболочке,
в процедуре типа Init (инициализации
и ввода исходных данных) необходим
оператор FillChar(rs,SizeOf (rs),0) . * }
Μ: Integer;{^Количество точек в выпуклой
оболочке.*}
Найдем номер самой левой нижней точки. Она принадлежит
выпуклой оболочке. Задача эквивалентна поиску номера
минимального элемента в массиве.
Function GetLeft: Integer;
Var i, If: Integers-
Begin
If—1;
For i:=2 To N Do
If RealLess (A[i] .x, A[lf].x) Or
(RealEq(A[i] .x, A[lf].x) And
RealLess(A[lf] .y, A[i].y))
Then If:=i;
GetLeft:=lf;
End;

5. Алгоритмы вычислительной геометрии
277
Основная процедура.
Procedure Solve;
Var nx: Integer-
Is: TPoint;
Begin
M:=0;{^Количество точек в выпуклой оболочке.*}
nx:=GetLeft;{*Находим самую левую и нижнюю
точку.*}
While (M=0) Or (nx<>rs[l]) Do
Вед1п{*Пока не вернулись к первой точке.*}
Inc(M); rs[M]:^пх;{^Очередная точка выпуклой
оболочки.*}
If M>1 Then Is : =А [rs [M-l ] ] { ^Предыдущая точка
выпуклой оболочки.*}
Else
Begin ls:=A[rs [1]]; Is.у:=ls.y-1; End;
{*Если рассматриваемая точка является
первой точкой выпуклой оболочки, то
искусственно уменьшаем на единицу
ординату у первой точки и считаем ее
предыдущей точкой оболочки.*}
nx:=GetNext (Is, A[rs[M]]) ; {*Поиск
следующей точки выпуклой оболочки,
параметрами функции являются координаты
двух предыдущих точек оболочки.*}
End;
End;
Перенесли, как обычно, всю «тяжесть» алго- ^АГП
ритма на следующую часть — функцию GetNext
(метод последовательного уточнения,
технология «сверху — вниз» в действии). Рассмотрим, 4^*gn
как осуществляется поиск точки выпуклой обо- ^^
л очки, изображенной на рисунке 5.25. Требует- ^
ся найти точку множества, такую, что угол,
образованный лучами (A[i],gn) и (gntpr), имеет Рис. 5.25
минимальное значение. Если таких точек
несколько, то выбирается точка, находящаяся на максимальном
расстоянии от точки gn. Таким образом, мы опять возвращаемся к
задаче поиска минимального элемента в массиве.
Function GetNext(Const pr, gn: TPoint) : Integer;
Var i, fn: Integer;
mx, rsx, nw: Real;

278
5. Алгоритмы вычислительной геометрии
Begin
mx:=-10;{^Использование явных констант в «теле»
программного кода - дурной тон, но простит
нас читатель за эту маленькую слабость.*}
For i :=1 To N Do
Begin
nw:=GetAngle (pr, gn, A[i]);{*Найдем угол.* }
If RealLess(mx, nw)
Then
Begin
fη:=i;mx:=nw; rsx:=Dist(gn, A[i]);
End
Else
If RealEq(nw, mx) Then
Begin
nw:=Dist(gn, A[i]);
If RealLess (rsx, nw) Then
Begin
fn:=i; rsx:=nw;
End;
End;
End;
GetNext:=fn;
End;
Осталось уточнить функцию вычисления угла по трем
точкам. Она отличается от ранее рассмотренной функции, поэтому
необходимо сказать несколько слов.
Пусть Lx и L2 — две прямые, заданные уравнениями
А2хх+Б2хг/+С2=0, А2хА2+В2хВ2>0 п
соответственно (см. рисунок 5.26). Угол п^
α между прямыми Lx и L2 равен углу \_1
между нормальными векторами ;
ηχ={ΑνΒ^ и п2={А2,В2} этих прямых. ^""%
Отсюда следует, что
Рис. 5.26
cos α =
(п19п2)
\П 1 Х \П 2 |
Ах χ А2 + Вх χ В2
д/а* +В2 х^А22 + В22
Function GetAngle(Const А, В, С: TPoint): Real;
Begin
If RealEq(Dist (С,В) , 0)

5. Алгоритмы вычислительной геометрии
279
Then GetAngle:=-ll
Else GetAngle:=((B.x-A.x)*(C.x-B.x)+(B.y-A.y)*
(C.y-B.y))/(Dist(A,B)*Dist(C,B));
End;
Метод «разделяй и властвуй» при построении выпуклой
оболочки, основан, как обычно для этого типа алгоритмов, на
принципе сбалансированности, суть которого в том, что
вычислительная задача разбивается на подзадачи примерно одинаковой
размерности. Они решаются, и затем результаты объединяются.
Метод эффективен, если время, требуемое на объединение
результатов, незначительно.
Суть данного алгоритма построения выпуклой оболочки.
Множество S разделяется на два подмножества Sx и S2
примерно равной мощности. Для каждого из подмножеств строится
выпуклая оболочка. Если время объединения оболочек
пропорционально количеству вершин в них — O(N), то временная
зависимость имеет вид: T(iV)<2T(A72)+O(A0.
Итак, разбиваем множество S из N точек на два
подмножества, каждое из которых будет содержать одну из двух
ломаных, соединение которых даст многоугольник выпуклой
оболочки (см. рисунок 5.27). Найдем точки war, имеющие,
соответственно, наименьшую и наибольшую абсциссы.
Проведем через них прямую L, тем самым получим разбиение
множества точек S на два подмножества Sx (выше или на прямой
L) и S2 (ниже прямой L). Определим точку h, для которой
треугольник <whr> имеет наибольшую площадь среди всех
треугольников {<wpr>:p^S1}. Если точек имеется более одной, то
выбирается та из них, для которой угол <hwr> наибольший.
Точка h гарантированно принадлежит выпуклой оболочке.
Действительно, если через точку h провести прямую,
параллельную L, то выше этой прямой не окажется ни одной точки
Рис. 5.27

280
5. Алгоритмы вычислительной геометрии
множества S. Через точки w и h проведем прямую Lv через
точки h и г — прямую L2. Для каждой точки множества S;
определяется ее положение относительно этих прямых. Ни
одна из точек не находится одновременно слева как от Lp так и
от L2, кроме того, все точки, расположенные справа от обеих
прямых, являются внутренними точками треугольника <wrh>
и поэтому могут быть удалены из дальнейшей обработки.
Процесс продолжается до тех пор, пока слева от строящихся
прямых типа Lx и L2 есть точки.
Перейдем к описанию более детального решения.
Const MaxN=100;
Type TSpsk = Array[0..MaxN] Of Integer;
Var A: Array[1..MaxN] Of TPoint;
N: Integer;
rs: TSpsk;{*Храним номера точек, составляющих
выпуклую оболочку, в rs[0] фиксируется
количество точек.*}
Вывод результата очевиден уже в данный момент:
WriteLn(rs[0]);
For i:=l To rs [0] Do Write(rs [i], ' ');
Опишем ряд вспомогательных функций и процедур, прежде
чем разобрать алгоритм (технология «снизу — вверх»).
Нам потребуется определять взаимное расположение точки
и линии на плоскости — функция Get Sign. Значение функции
равно 0, если точка находится на линии, плюс единице при
нахождении в левой полуплоскости и минус единице — в правой.
Function GetSign(Const L: TLine; Const A: TPoint):
Integer;
Var rs : Real;
Begin
rs:=A.x*L.A + A.y*L.B + L.C;
If RealEq(rs, 0)
Then GetSign:=0
Else
If RealMore (rs, 0)
Then GetSign:=1
Else GetSign:=-l;
End
Площадь треугольника по координатам трех вершин
определяется точно так же, как и ориентированная площадь — функ-

δ. Алгоритмы вычислительной геометрии
281
ция SquareTrian (рассмотрена ранее), только берется ее
абсолютное значение.
Function Square(Const А, В, С: TPoint): Real;
Begin
Square:=Abs((Α.χ*(B.y-C.y) + Β.χ*(С.у-А.у) + С.х*
(А.у-В.у))12);
End;
Договоримся, что мы работаем с номерами точек.
Координаты точек хранятся в массиве А. Пусть имеется некоторое
множество точек, их номера в массиве /V. Через две заданные
точки (Z/, rg) проводится прямая линия (L). Требуется в массив rs
записать номера тех точек из исходного множества, которые
находятся в другой полуплоскости относительно линии L, чем
заданная точка (пп). Считаем, что точки, по которым строится
линия, должны быть в результирующем множестве. Решение
этой задачи обеспечивает следующая процедура.
Procedure SelectPoints (If, rg: Integer;
Const nn: TPoint;
Const fr: TSpsk;
Var rs: TSpsk);
Var i, lzn, nw: Integer;
L: TLine;
Begin
rs[0]:=2; rs[l]:=lf; rs[2]:=rg;
Point2ToLine(A[If] , A[rg], L);{^Построение линии
по двум точкам, процедура описана ранее . * }
lzn:=GetSign(L, nn);{^Определяем знак
полуплоскости, в которой находится точка
с номером пп.*}
For i:-3 To fr[0] Do
Begin
nw:=GetSign (L, A[fr[i]]);
If nw*lzn=-l Then
Begin Inc(rs[0]);rs[rs[0]]:=fr[i]; End;
End;
End;
Пусть есть множество точек. Их номера хранятся в массиве
(ow). Требуется найти номер той точки, которая наиболее уда-

282
5. Алгоритмы вычислительной геометрии
лена от двух точек с номерами из первых двух элементов
массива. Эта задача решается с помощью следующей функции.
Напомним, что в нулевом элементе массива хранится количество
точек множества.
Function MDist(Const ow: TSpsk): Integer;
Var max, nw: Real;
i, rs: Integers-
Begin
max:=Square(A[ow[l]], A[ow[2]], A[ow[3]]);
r s : = 3 ;
For i:=4 To ow[0] Do
Begin
nw:=Square(A[ow[l]], A[ow[2]], A[ow[i]]);
If RealMore (nw, max) Or (RealEq(nw, max) And
RealMore(A[ow[rs]].x, A[ow[i]].x))
Then
Begin max:=nw;rs:=i;End;
End;
MDist:=ow[rs];
End;
Еще одна очевидная процедура. В исходном множестве
точек находим номера самых крайних левой и правой, а также
формируем первоначальный массив номеров точек. При этом
на первое и второе места записываем номера найденных
точек — они заведомо принадлежат выпуклой оболочке.
Procedure FindMinMax(Var If, rg: Integer;
Var All:TSpsk);
Var i, sc: Integer;
Begin
lf:=l; rg:=1;{*Находим номера точек
с минимальным (If) и с максимальным (rg)
значениями координаты х, при равных
значениях χ выбираются точки с меньшим
значением координаты у.*}
For i :=1 To N Do
Begin
If RealMore (A[i] .x, A[rg].x) Or
(RealEq(A[i].x, A[rg].x)
And RealMore(A[rg].y, A[i].y))
Then rg:=i;
If RealMore(A[lf].x, A[i].x) Or
(RealEq(A[i].x, A[lf].x)

5. Алгоритмы вычислительной геометрии
283
And RealMore(A[lf].у, A[i].y))
Then If:=i;
End;
A11[0]:=N;A11[1]:=lf; All[2]:=rg; sc:=2;
For i:=l To N Do
If (iolf) And (iorg) Then
Begin Inc(sc); All[sc]:=i; End;
End;
А сейчас одна из ключевых процедур алгоритма. Для
множества точек, описываемых их номерами из массива ow,
формируется множество точек из их выпуклой оболочки.
Procedure GetSpisok(Const ow: TSpsk; Var rs: TSpsk);
Var i, nw: Integer;
If, rg, rssc: TSpsk;
Begin
rs:=ow;
If ow[0]>2 Then
Begin
nw:=MDist(ow);{*Находим максимально удаленную
точку от точек ow [ 1 ] и ow[2] .*)
SelectPoints(ow[1], nw, A[ow[2]], ow, If) ;
{^Определяем множество точек, находящихся
в другой полуплоскости, чем точка с номером
ow[2], относительно прямой, проходящей
через точки с номерами ow [ 1 ] и nw.*}
SelectPoints (nw, ow[2], A[ow[l]], ow, rg) ;
{^Определяем множество точек, находящихся
в другой полуплоскости, чем точка
с номером ow[1], относительно прямой,
проходящей через точки с номерами nw
и ow[2].*}
GetSpisok(If, rs);{^Рекурсивно продолжаем
строить выпуклую оболочку для выделенного
множества точек. Если мощность выделенного
множества точек равна 2, то процесс
заканчивается.*}
GetSpisok(rg, rssc);
For i :-=2 To rssc [0] Do rs [rs [0] + i-l ] :=rssc [i] ;
{^Объединяем два множества точек.*}
Inc(rs [0], rssc[0]-l) ;
End;
End;

284
5. Алгоритмы вычислительной геометрии
Основная процедура после проделанной работы достаточно
«прозрачна».
Procedure Solve;
Var If, rg, i: Integer;
fr, frl: TSpsk;
nw: TPoint;
Begin
FindMinMax(If, rg, rs) ;{*Находим крайние по
значению координаты χ точки исходного
множества.*}
nw:=А[1f];nw.у:=nw.у-10;
SelectPoints (If, rg, nw, rs, fr);{*B fr
формируется список номеров точек, лежащих
по одну сторону от прямой, проходящей через
точки If и rg . * }
nw.у:=nw.y+2 0;
SelectPoints (rg, If, nw, rs, frl);{*B frl - no
другую сторону.*}
GetSpisok(fг, rs);{^Строим выпуклую оболочку для
множества точек с номерами из fr.*}
GetSpisok(frl, fr);{*CTpoHM выпуклую оболочку
для множества точек с номерами из frl.*}
For i:=2 To fr[0]-l Do rs[rs [0]+i-l] :=fr [i];
{*Объединяем выпуклые оболочки.*}
lnc(rs[0], fr[0]-2);
End;
5.6. Задачи о прямоугольниках
1. Дано Ν (0<iV<5000) прямоугольников со сторонами,
параллельными координатным осям. Каждый прямоугольник
может быть частично или полностью перекрыт другими
прямоугольниками. Вершины всех прямоугольников имеют
целочисленные координаты в пределах [-10000, 10000] и
каждый прямоугольник имеет положительную площадь.
Периметром называется общая длина внутренних и внешних границ
фигур, полученных путем наложения прямоугольников. Найти
значение периметра.
На рисунке 5.28(a) показана фигура из 7 прямоугольников.
Соответствующие границы полученной фигуры показаны на
следующем рисунке 5.28(6).

5. Алгоритмы вычислительной геометрии
285
(а) (6)
Рис. 5.28
Пример входного файла:
7 (количество прямоугольников)
-15 0 5 10 (границы прямоугольника — нижняя левая и
верхняя правая)
-5 8 20 25
15 -4 24 14
0 -6 16 4
2 15 10 22
30 10 36 20
34 0 40 16
Ответ: 228.
Рассмотрим более простую задачу. На прямую «набросали»
какое-то количество отрезков. Последние могут пересекаться,
находиться один внутри другого и т. д. Требуется определить
количество связных областей, образованных этими отрезками.
На рисунке 5.29 даны три отрезка (2, 5), (4, 6) и (8,10).
Количество связных областей две. Как их найти?
1 2 12 3 3
# ·—·—· · ·—
2 4 5 6 8 10
Рис. 5.29
Используем стандартный прием. Записываем в один массив
координаты отрезков, в другой признаки начала (1) и конца
отрезков (-1). Сортируем элементы первого массива по
неубыванию, одновременно переставляя соответствующие элементы
второго массива. После этого осталось считать сумму значений
признаков. Если ее текущее значение равно нулю, то выделена
очередная связная область.

286
5. Алгоритмы вычислительной геометрии
Вернемся к исходной задаче. Очевидно, что можно считать
периметр отдельно, по частям. Например, первоначально его
составляющую по оси У, а затем по оси X.
Рассмотрим идею решения на примере рисунок 5.30. Даны
четыре прямоугольника. Считаем составляющую периметра по
оси У. Ось разбивается координатами прямоугольников на
следующие участки: (0,1), (1,2), (2,3), (3,4) и (4,6). Рассматриваем
каждый участок, т. е. определяем прямоугольники (точнее их
координаты по X с признаками начала и конца интервала),
которые могут дать «вклад» в периметр. Для первого участка —
один прямоугольник, для второго — три, для третьего — два,
для четвертого — три и для пятого — один. Выписав для
каждого участка координаты X с соответствующими признаками,
выполняем сортировку и находим количество связных
областей. Так, на рисунке 5.30 для первого сечения (отмечено
цифрой 1) количество связных областей равно 1, а для второго
сечения — 2. После этого достаточно длину этого участка умножить
на количество связных областей и удвоить результат.
Получаем составляющую периметра по оси У на этом участке.
1:(1,1)-(6,4)
γ 2:(5,0)-(8,2)
I 3:(7,1)-(9,4)
6 + 4:(4,3)-(10,6)
1 б 10
Рис. 5.30
^Х
После этих замечаний можно приступить к разбору
решения. Как обычно, начинаем со структур данных.
Const MaxN=5001;
Type MasPn=Array[1..MaxN*2] Of Integer;
MasSw=Array[1..MaxN*2, 1..2] Of Integer;
{ *Для записи координат и соответствующих
признаков начала и конца отрезков.*}
Var N, i: Integer;
Ax, Ay: MasPn;{*Для хранения координат
прямоугольников.*}

5. Алгоритмы вычислительной геометрии
287
Основная программа.
Begin
Assign (Input, '...' ) ; Reset (Input) ;Read (N) ;
For i :=1 To N Do
Begin
Read(Ax[i*2-l], Ay[i*2-1]);
Read(Ax[i*2], Ay[i*2]);
End;
Close(Input);
Assign (Output, '...' ) ; Rewrite (Output) ;
WriteLn(GetPerim(Ax, Ay) + GetPerim(Ay, Ax));
Close(Output);
End.
Вспомогательную процедуру сортировки по любому методу с
временной оценкой O(NxlogN) описывать не будем.
Procedure Sort(Var nn: MasSw; If, rg: Integer);
Begin
End;
Функция GetPerim.
Function GetPerim(Const Ax, Ay: MasPn): Longlnt;
Var i: Integer;
sc: Longlnt;
D: MasSw;
Begin
sc:=0;{^Значение периметра по одному из
направлений.*}
FillChar(D, SizeOf(D), 0) ;
For i:=l To 2*N Do D[i, 1] :=Ax[i] ; (^Массив
координат по этому направлению.*}
Sort(D, 1, 2*N);{*Сортировка.*}
For i:=l To N*2-l Do
If D[i, l]OD[i + l, 1] Тпеп{*Если координаты не
равны, то вычисляем количество связных
областей на этом сечении - функция GetPr,
умножаем на длину участка и на 2 . * }
sc:=sc+GetPr(Ax, Ay, D[i, 1]) * (D[i+1, 1] -
D[i, 1]) * 2;
GetPerim:=sc;
End;

288
5. Алгоритмы вычислительной геометрии
Следующий шаг уточнения. Вычисляем количество связных
областей на сечении, определяемом значением переменной х.
Function GetPr(Const Ax, Ay: MasPn; x: Integer) :
Integer;
Var i, b, d, sc: Integer;
nn: AMasSw;{*Число прямоугольников многовато
(до 5000), задействуем «кучу».*}
Begin
New (nn) ;
GetRect (Ax, Ay, χ, nnA, sc) ; { ^Определяем
прямоугольники, имеющие отношение к
рассматриваемому сечению, их количество -
значение переменной sc, а координаты в
массиве ппА.*}
If scoO Then Sort(nnA, 1, sc) ; { ^Выполняем
сортировку с одновременной перестановкой
признаков начала и конца отрезков.*}
Ь:=0;{*Для хранения суммы значений признаков.*}
If sc>0 Then d:=l Else d:=0;
For i:=l To sc-1 Do
Begin
b:=b+nnA[i, 2] ;
If (b=0) And (nnA[i+l, l]OnnA[i, 1])
Then Inc(d);{*Если текущее значение b равно нулю
и координаты не совпадают, то увеличиваем
счетчик числа связных областей.*}
End;
GetPr:=d;
Dispose(nn) ;
End;
Последний шаг уточнения алгоритма — определение
характеристик сечения.
Procedure GetRect(Ax, Ay: MasPn; χ: Integer;
Var nn: MasSw;Var sc: Integer);
Var i : Integer;
Begin
sc:=0;
For i:=l To N Do
If (Ax[i*2-l]<=x) And (x<Ax[i*2]) Then
Begin
{*Если прямоугольник имеет отношение
к сечению, то запоминаем координаты
по соответствующему направлению (они
в массиве Ау) и признаки начала
и конца отрезка.*}

5. Алгоритмы вычислительной геометрии
289
Inc (sc);
nn[sc, 1]:=Ay[i*2-l];nn[sc+l, 1]:=Ay[i*2];
nn[sc, 2]:=l;nn[sc+1, 2]:=-l;
Inc (sc);
End;
End;
2. На плоскости задано Ν (1<Ν<300) прямоугольников со
сторонами, параллельными координатным осям (пример на
рисунке 5.31(a)). Координаты вершин прямоугольника (х,у) —
вещественные числа с точностью до двух знаков после запятой.
Написать программу поиска площади фигуры (см. рисунок
5.31(6), получающейся в результате объединения
прямоугольников.
Продлим все вертикальные линии до пересечения с осью X.
Эти линии определяют на оси X множество интервалов, внутри
каждого из которых длина сечения по оси У будет постоянной
(рисунок 5.31(b)). Поэтому для нахождения площади
достаточно отсортировать точки на оси X, рассмотреть все сечения и
добавить к площади <длину интервала> * <длину сечения>. Для
поиска длины сечения используем метод из предыдущей
задачи. Началу каждого отрезка присвоим значение признака,
равное 1, а его концу — -1 и отсортируем точки по значению
координаты У. Считаем сумму значения признаков. Если она не
равна нулю, то соответствующий интервал «плюсуем» к длине
сечения.
а) 6) в)
Рис. 5.31
Из структур данных приведем только те, которые требует
уровень детализации объяснения.
Const MaxN=300;
Туре TPoint=Record
Χ, Υ:Real
End;
Var PrM: Array[1..2,1..MaxN] Of TPoint;

290
5. Алгоритмы вычислительной геометрии
N: Longlnt;
Res: Real;
Ox, Oy: Array[1..MaxN*2] Of Real;
В процедуре инициализации и ввода данных координаты
вершин прямоугольника записываются в массиве РгМ, причем
в РгМ[1] (это массив) — координаты первой вершины, а в
РгМ[2] — второй. Вершина прямоугольника с меньшими
значениями (Χ,Υ) записывается в РгМ[1]. Кроме того, значения X
запоминаются в массиве Ох.
На рисунке 5.32 приведен пример записи входных данных и
ответ, соответствующий этим входным данным.
| Пример.
4 (количество прямоугольников)
0 0 10.1 5.2 (координаты нижнего левого и правого верхнего углов)
|-3 3 5.36 7
| 1 6 9 15
|8 3 20 8
ι Ответ.
|195.188
Рис. 5.32
Основная процедура вычисления площади объединения
прямоугольников выглядит следующим образом.
Procedure Solve;
Var i: Longlnt;
m: Real;
Begin
Sort(Ox, 1, N*2);{^Сортируем по неубыванию
значения координаты X прямоугольников.
Процедура, в силу ее очевидности, не
приводится.*}
т:=0;Res:=0;{*т - длина сечения, Res - значение
площади объединения прямоугольников.*}
For i:=l To N*2 Do
Begin
If iol Then Res:=Res + Abs ( (Ox[i] -Ox[i-l] ) *m) ;
{^Прибавляем площадь очередного сечения.*}

5. Алгоритмы вычислительной геометрии
291
If (i=l) Or Not(Eq(Ox[i], Ox[i-l])) Then Calc
(Ox[i], m) ; {^Определяем новое значение длины
сечения.*}
End;
End;
Уточнению подлежит процедура Calc.
Procedure Calc(Const x: Real; Var rs: Real);
Var i, M: Longlnt;{*M - количество интервалов
на данном сечении.*}
Begin
<Инициализация переменных процедуры, в частности
М:=0>
For i:=l To N Do{^Формируем массив ординат для
данной координаты х.*}
<Если есть пересечение прямоугольника с прямой,
параллельной оси Υ и проходящей через точку х, то
занести координаты Υ прямоугольника в рабочий массив,
не забыв при этом сформировать признаки начала и
конца отрезка. Количество пересечений - значение
переменной М.>;
If M=0 Then rs:=0
Else
Begin
<Сортируем границы интервалов по оси Y,
переставляя одновременно соответствующие элементы
массива признаков>;
<Вычисляем новую длину сечения - значение
переменной rs>;
{*Так, для примера на рисунке 5.33 длина сечения
равна 10.*}
End;
End;
12 12 3 4 4 3
··· ·· · · · ·
12 6 8 101112 13
Рис. 5.33
Дальнейшее уточнение алгоритма вынесем на
самостоятельную работу.
3. Найти площадь пересечения N прямоугольников со
сторонами, параллельными осям координат.
Входные данные. Число N (количество прямоугольников
2<iV<1000) и N четверок действительных чисел XiV YiV Xi2,

292
5. Алгоритмы вычислительной геометрии
У-2, задающих координаты левого нижнего и правого верхнего
углов прямоугольника.
Выходные данные. Площадь пересечения (общей части) всех
данных прямоугольников, либо выдать, что они не пересекаются.
На рисунке 5.34 приведен пример входных
данных и соответствующий ему ответ.
Задача предельно проста. Приведем ее с
целью «закрыть» тему «Прямоугольники на
плоскости со сторонами, параллельными осям
координат, их периметр и площади». Оказывается,
что можно независимо найти область
пересечения интервалов на прямой отдельно по осям X и
У. Эти интервалы определяют прямоугольник,
являющийся пересечением заданных
прямоугольников.
Const MaxN=1000;
Eps=le-7;
Type Segm=Record
L, R: Real
End;
SegmArray=Array[1..MaxN] Of Segm;
Var N: Integer;
OnX, OnY: SegmArray;
ObX, ObY: Segm;
Procedure I nit;
Begin
<ввод данных>
End;
Г,
Пример.
3
О 0 10 10
5 5 15 15
-1.5 0 7 8
Ответ: 6
Рис. 5.34
=A.L Else New.L:=B.L;
=A.R Else New.R:=B.R;
Function Cross(А,В:Segm;Var New:Segm):Boolean;
{^Устанавливаем факт пересечения двух
отрезков А и В.*}
Begin
If (B.L-A.L)<Eps Then New.L:
If (A.R-B.R)<Eps Then New.R:
Cross:=(New.L-New.R)<Eps;
End;
Function SolSegm(Const On: SegmArray;
Var Ob: Segm): Boolean;{^Определяем область
пересечения интервалов на прямой, если
она есть.*}

5. Алгоритмы вычислительной геометрии
293
Var i: Integer;
Begin
Ob:-On[1];
i:=2;
While (i<=N) And Cross (On [ i] , Ob, Ob) Do Inc(i);
SolSegm:=i>N;
End;
Begin
Init;{^Стандартный ввод данных.~ }
Write('Ответ > ' ) ;
If SolSegm(OnX, ObX) And SolSegm(OnY, ObY)
Then WriteLn('Площадь ',
Abs ( (ObX.L-ObX.R)*(ObY.L-ObY.R) ) :0:6)
Else WriteLn(^Пересечения нет.*);
End.
5.7. Задачи
1. Дана прямоугольная призма, основанием которой
является выпуклый iV-угольник (l<iV<50). Необходимо разделить ее
на К частей (1<К<Ъ0) равного объема. Разрешается проводить
прямые вертикальные разрезы от одной границы призмы до
другой. Различные разрезы могут иметь общие точки лишь в
своих концевых вершинах.
Написать программу построения требуемых К—1 разрезов.
Указание. В основании призмы
лежит выпуклый многоугольник, в этом
вся суть решения, его определенная
простота. Задача решается на уровне
многоугольника, лежащего в
основании. Через его вершину всегда можно
провести отрезок прямой и «отсечь»
площадь, меньшую площади исходного м
многоугольника, причем оба
получившихся многоугольника будут выпуклы- Рис. 5.35
ми. Отсюда следует, что многоугольник
можно «разрезать» на куски площади £МНОгоугольника/<число ча_
стей>, проведя все разрезы через одну вершину. Число прямых
равно числу частей минус 1.
Пусть мы нашли площадь треугольника A1ANAN_1> она
меньше площади отрезаемого куска. Добавляем к ней площадь
треугольника A1AN_1AN_2. Если по-прежнему площадь куска не
превышена, то продолжаем процесс. В общем, мы рано или

294
5. Алгоритмы вычислительной геометрии
поздно придем к случаю, когда потребуется отсечь от какого-то
треугольника треугольник площадью S' (площадь второго
получаемого треугольника (S") также известна), причем одна
точка разреза — вершина, а вторая «плавает» по
противоположной стороне. Нам необходимо вычислить координаты точки Μ
(см. рисунок 5.35). Высоты треугольников равны, поэтому
S' AM
S" ~ MB'
После этого следует изменить выпуклый многоугольник
(«выкинуть» из него те точки, которые мы включили в
отрезанный кусок). Легче это сделать, если начать процесс
отрезания с ΑχΑΝ, затем А^м__19 а не АгА2, А^АЪ и т. д. В этом случае
не придется сдвигать элементы массива А.
2. Дан простой многоугольник со сторонами,
параллельными осям координат. Три последовательно соединенных
вершины многоугольника не лежат на одной прямой. Требуется
определить, существует ли такая точка внутри многоугольника, из
которой видимы все внутренние точки многоугольника.
Число вершин многоугольника N (iV<100) и их координаты
заданы в порядке обхода по часовой стрелке. Все
координаты — целые. Ответом является сообщение Yes или No.
Воспользуемся следующим
алгоритмом: все вертикальные отрезки
поделим на две группы — восходящие и
нисходящие (см. рисунок 5.36).
Аналогично и для горизонтальных
отрезков (идущих вправо и влево). Среди
первых выберем отрезок с
максимальной абсциссой (max), среди второй
группы — с минимальной абсциссой
(min). Назовем условие выполнимым, Рис. 5.36
если max<min. Искомая точка
существует в том случае, если это условие выполняется как по оси
X, так и по оси У. Объяснение этому факту достаточно простое.
Искомая точка находится в заштрихованной полуплоскости
для каждого рассматриваемого отрезка. Если условие не
выполняется, то полуплоскости не пересекаются. Приведите
возможный текст решения.
3. Отражение агрессии. Для своевременного отражения
возможной воздушной агрессии на город необходимо
обнаруживать средства воздушного нападения противника в момент
подлета к границе «опасной зоны» — на расстояние R от центра

5. Алгоритмы вычислительной геометрии
295
города, который мы примем за начало координат. Имеются N
комплексов ПВО, расположенных в точках с координатами (xv
уг), (х2, г/2), ..., (xN, yN). Для каждого комплекса i (l<i<N)
известен радиус его действия Rr
Напишите программу, которая:
• определяет, надежно ли защищен город от нападения,
т. е. верно ли, что обнаружение происходит при подлете к
границе «опасной зоны» с любого направления;
• в случае отрицательного ответа на первый пункт
определяет диапазоны «опасных» направлений, т. е. таких
направлений, с которых при подлете обнаружение не
происходит. Направление задается углом (от 0° до 360°), на
который нужно повернуть луч Ох против часовой
стрелки, чтобы он совпал с этим направлением. Например,
направление на точку (R,0) соответствует числу 0, а на
точку (0,R) — числу 90.
В первой строке входного файла содержится натуральное
число N (l<iV<50) и вещественное число R. В последующих
строках записано N троек вещественных чисел (xit г/·, #·),
каждая из которых задает координаты и радиус действия одного из
комплексов ПВО. Числа разделяются пробелами и/или
символами перевода строки. Все вещественные числа по модулю не
превосходят 1000.
Первая строка выходного файла должна содержать ответ
Yes /No. В случае отрицательного ответа вторая строка должна
содержать количество диапазонов «опасных» направлений (К),
а каждая из последующих К строк — начало и конец
очередного из диапазонов. Диапазоны должны быть перечислены в
порядке обхода против часовой стрелки.
Указание. Рассмотрим рисунок 5.37.
Лучше вначале проверить, не защищает ли
какая-нибудь одна ПВО весь город. Если да,
то ответ очевиден, иначе определим все
точки пересечений зон ПВО и зоны города.
Точки типа 2 и 3 исключаем, а точки типа 1,2,
4, 5 сортируем по значению полярного угла.
Все эти точки являются защищенными, а
значит, те интервалы, которые они (точки)
разделяют, не объединяются. После этого
остается проверить интервалы на
принадлежность какой-нибудь зоне ПВО.

296
5. Алгоритмы вычислительной геометрии
4. На плоскости заданы треугольник и отрезок. Определить
их взаимное расположение.
5. На плоскости заданы два треугольника (координатами
своих вершин).
Определить взаимное расположение треугольников и найти
замкнутую ломаную линию, ограничивающую область, общую
для обоих треугольников (если она есть).
6. На плоскости заданы два треугольника. Используя
перемещения и повороты, определить, можно ли один из
треугольников вложить в другой.
7. Даны два прямоугольника со сторонами, параллельными
осям координат. Определить их взаимное расположение. Для
случая, когда прямоугольники пересекаются, вычислить:
• замкнутую ломаную, ограничивающую область,
объединяющую оба прямоугольника;
• замкнутую ломаную, ограничивающую область, общую
для обоих прямоугольников;
• площадь области, общей для обоих прямоугольников.
Снять ограничение о параллельности сторон
прямоугольников осям координат. Исследовать задачу.
8. На плоскости координатами своих вершин заданы два
прямоугольника. Путем их перемещений и поворотов
установить, можно ли один из прямоугольников вложить в другой.
9. На плоскости задано N точек. Найти две наиболее
удаленные друг от друга точки (диаметр множества).
Утверждение. Диаметр множества равен диаметру его
выпуклой оболочки.
10. На плоскости задано N точек. Требуется разбить их на k
групп Sv S2, ..., Sk таким образом, чтобы максимальный из
диаметров групп был минимален.
11. На плоскости заданы N точек. Найти две из них,
расстояние между которыми наименьшее.
12. На плоскости заданы N точек. Найти ближайшего
«соседа» для каждой точки.
13. Из заданного множества точек на плоскости выбрать две
точки так, чтобы количество точек, лежащих по сторонам от
прямой, проходящей через эти две точки, различалось
наименьшим образом.
14. Определить радиус и центр окружности, на которой
лежит наибольшее число точек заданного на плоскости
множества точек.

5. Алгоритмы вычислительной геометрии
297
15. На плоскости задано множество N произвольным
образом пересекающихся отрезков прямых линий. Перечислить
множество всех треугольников, образованных указанными
отрезками.
16. На плоскости заданы N точек. Найти минимальное
количество прямых, на которых можно разместить все точки.
17. Евклидово минимальное остовное дерево (каркас). На
плоскости заданы N точек. Построить дерево, вершинами
которого являются все заданные точки, и суммарная длина всех
ребер минимальна.
18. Триангуляция. На плоскости заданы N точек. Соединить
их непересекающимися отрезками таким образом, чтобы
каждая область внутри выпуклой оболочки этого множества точек
являлась треугольником.
19. Минимальное евклидово паросочетание. На плоскости
задано 2χΝ точек. Объединить их в пары, соединив отрезками
так, чтобы сумма длин отрезков была минимальна.
Примечание
Известен алгоритм со сложностью 0(JV3).
20. Наименьшая охватывающая окружность. На плоскости
заданы N точек. Найти наименьшую окружность (по значению
радиуса), охватывающую все заданные точки.
Примечание
Эта задача известна под названием «минимаксная задача о
размещении центра обслуживания». Требуется найти точку ^о=(хО'#о)
(центр окружности), для которой наибольшее из расстояний до
точек заданного множества минимально. Точка t0 определяется
критерием Мт{Мах{(хгх0)2+(УгУ0)2}}-
21. Наибольшая «пустая»
окружность. На плоскости заданы N точек.
Найти наибольшую окружность (см.
рисунок 5.38), не содержащую внутри
ни одной точки этого множества. Центр
окружности должен находиться внутри
выпуклой оболочки множества точек.
Примечание
Известно, что как задачу о наименьшей
охватывающей окружности, так и задачу о наибольшей «пустой»
окружности можно решить за время, пропорциональное
O(NxLogN).

298
5. Алгоритмы вычислительной геометрии
22. Даны два выпуклых многоугольника Q1 и Q2 с iV и Μ
вершинами соответственно. Построить их пересечение.
Указание. Пересечением выпуклых многоугольников с Ν η
Μ вершинами является выпуклый многоугольник, имеющий
не более Ν+Μ вершин.
23. Даны два выпуклых многоугольника Qx и Q2 с N и Μ
вершинами. Найти выпуклую оболочку их объединения.
Указание. Метод обработки (см. рисунок 5.39). Находим
некоторую внутреннюю точку t многоугольника Qx (центр масс
трех любых вершин Qx). Определяем, является ли точка t
внутренней точкой многоугольника Q2 (за время, пропорциональное
O(N)). Если точка t является внутренней точкой Q2, то вершины
как Qv так и Q2 упорядочены в соответствии со значением
полярного угла относительно точки t. За время, пропорциональное
O(N), получаем упорядоченный список вершин как Qv так и Q2
путем слияния списков вершин этих многоугольников. К
полученному списку точек применяем метод обхода Грэхема. Если
точка t не является внутренней точкой Q2, то многоугольник Q2
лежит в клине с углом, меньшим или равным π. Этот клин
определяем двумя вершинами и и υ многоугольника Q2, которые
находим за один обход вершин многоугольника Q2. Вершины и и υ
разбивают границу Q2 на две цепочки вершин, монотонные
относительно изменения полярного угла с началом в точке t. При
движении по одной цепочке угол увеличивается, при движении
по другой — уменьшается. Одну из этих цепочек удаляем (ее
точки являются внутренними относительно строящейся
оболочки). Другая цепочка и граница Qx являются упорядоченными
списками. Соединяем их в один список вершин, упорядоченный
по полярному углу относительно точки t, и выполняем обход.
Рис. 5.39
24. Определить принадлежность точки ρ выпуклому
N-угольнику Q. (см. рисунок 5.40)
Указание. Методом двоичного поиска находим «клин».
Точка ρ лежит между лучами, определяемыми qt и q^v тогда и то-

5. Алгоритмы вычислительной геометрии
299
Рис. 5.40
лько тогда, когда угол (ptqi+1) положительный, а угол (ptqj
отрицательный. Сравниваем ρ с единственным ребром. Точка ρ
внутренняя тогда и только тогда, когда угол (qtqi+1p)
отрицательный.
25. Разработать функции:
• построения окружности по трем точкам;
• нахождения пересечения прямой и окружности;
• нахождения точек пересечения двух окружностей.
26. Построить выпуклую оболочку для множества точек на
плоскости без использования операций с вещественным типом
данных.
Указание [2]. Строим выпуклую оболочку в порядке обхода
против часовой стрелки. Находим самую правую нижнюю
точку (х0,г/0). Она принадлежит выпуклой оболочке. Следующей
является точка (х1,у1), для которой угол между осью X и
вектором (х0,г/0) ~ (χι>#ι) минимален. Если таких точек несколько, то
выбирается точка, расстояние до которой максимально.
Суть идеи заключается в том, чтобы угол не вычислять, а
вычислять знак выражения (xi+l-x^*{y-yj) - (г/.+1-г/-)*(х-лг.),
где (χ,,*/,) — очередная точка, вошедшая в выпуклую оболочку,
(л:.+1,г/.+1) — следующая точка выпуклой оболочки, а (х,у) —
координаты любой точки, не вошедшей в выпуклую оболочку.
Выражение отрицательно, и это является «ключом» решения
задачи.
27. На плоскости заданы N точек. Построить замкнутую
ломаную без самопересечений и самокасаний, координатами
которой должны стать все заданные точки.
Указание. Построить часть выпуклой оболочки между
самой левой и самой правой (по координате X) точками.
Оставшиеся точки отсортировать по координате X и затем
последовательно соединить отрезками.

6. Избранные олимпиадные
задачи по программированию
1. Дано целое неотрицательное число N (iV<32767). При запи
си N в двоичной системе счисления получается последователь
ность из 1 и 0. Например, при iV=19 получаем 19]0 =
1 24+0 23+0 22+1 241 2°, т. е. в двоичной системе I 10011
число запишется как 100112. При циклическом
сдвиге вправо получаются другие числа. Найти максима- , oil 10
льное среди этих чисел. Так, для числа 19 список ! 00111
последовательностей показан на рисунке 6.1, а резу- ' 10011
льтатом является число 1 24+1 23+1 22+0 2х+0 2° = L
28. Рис. 6.1
Указание. Находим старший значащий разряд в
двоичном представлении числа N, ибо бессмысленно,
например, в числе 000000001010 выполнять лишние сдвиги,
соответствующие первым нулям. После того, как значение числа
сдвигов найдено, последовательно изменяем значение N и находим
его максимум. Задача становится более интересной, если снять
ограничение по N (iV>32767). Как минимум не избежать
длинной арифметики и моделирования выполнения операций
сдвига на один двоичный разряд.
Procedure Solve;
Var i, j: Integer;
Begin
Res:-N; i:=0;
While ( (N shr i)>l) Do Inc (i) ;{ ^Определяем место
первой единицы справа в двоичном
представлении числа N.*}
j:=i;{*Число сдвигов*}
While j<>0 Do
Begin
N:=(N shr 1) + (N And 1) shl i; { *Сдвигаем вправо
на один разряд и приписываем старшую
единицу.*}
If N>Res Then Res:=N;
Dec (j) ;
End;
End;

6. Избранные олимпиадные задачи по программированию
301
2. «Кратеры на Луне». Время от времени пролетающие
вблизи нашего спутника Луны астероиды захватываются ее
гравитационным полем и, будучи ничем не задерживаемы,
врезаются с огромной скоростью в лунную поверхность, оставляя в
память о себе порядочных размеров кратеры приблизительно
круглой формы.
Требуется найти максимально длинную цепочку вложенных
друг в друга кратеров.
Формат входных данных. Первая строка входного файла
(см. рисунок 6.2) содержит целое число N — количество
кратеров, отмеченных на карте (l<iV<500). Следующие N строк
содержат описания кратеров с номерами от 1 до N. Описание
каждого кратера занимает отдельную строку и состоит из трех
целых чисел, принадлежащих диапазону [-32768, 32767] и
разделенных пробелами. Первые два числа представляют собой
декартовы координаты его центра, а третье — радиус. Все
кратеры различны.
Формат выходных данных. Первая [пример. ~ΐ
строка выходного файла (см. рисунок 6.2) d.in \d.out
должна содержать длину искомой цепочки \ л я
кратеров, вторая — номера кратеров из ' о 0 30 3 4 1!
-15 15 20 ' '
15 10 5 ! !
этой цепочки, начиная с меньшего кратера
и кончая самым большим. Номера
кратеров должны быть разделены пробелами. | 1Q 1Q 1Q \ \
Если существует несколько длиннейших
цепочек, нужно вывести любую из них.
Указание. Ответить на вопрос о принадлежности одного
кратера другому достаточно просто. Пусть координаты центров
кратеров и их радиусы хранятся в массивах. Для решения
задачи будем использовать данные:
Const MaxN=50 0;
Var Ax, Ay, Ar: Array [ 1. .MaxN] Of Longlnt;)
В каком случае кратер с номером i вложен в кратер с
номером у? Если точки с координатами
Αχ[ϊ\+Ατ\ΐ\, Ay[i],
Ax[i]-Arli], Ay[i],
Ax[i], Ay[i]+Ar{r\9
Ax[i), АуЩ-АгЩ
принадлежат кратеру с номером у, то и весь кратер с номером i
находится в кратере с номером у. Точка находится внутри
окружности (кратера) в том случае, если расстояние между
точкой и центром окружности меньше радиуса.

302
6. Избранные олимпиадные задачи по программированию
Рассмотрим еще пример, изображенный на
рисунке 6.3. Пусть в массивах Sc и Ls(Array[l.JST\
Of Integer;) каким-то образом оказались
следующие данные: Sc — (3, 0, 1, 0, 1, 2) и
Ls — (6, 0, 2, 0, 4, 5).
Найти максимальный элемент тх в массиве
Sc и его номер k несложно. Если вывести
значение найденного максимума WriteLn(mx+\) и вызвать
процедуру SayRes(k) (в нашем случае будет SayRes(l))
Procedure SayRes(k: Integer);
Begin
If Ls[k]<>0 Then SayRes(Ls[k] ) ;
Write(k, ' ')/
End;
то получим:
4
4 5 6 1,
что и является ответом задачи. Итак, осталось понять, как
формировать значения элементов массивов Sc и Ls.
3. На клеточном поле задано N точек (в узлах
клеточного поля).
Требуется найти точку, до которой суммарное
расстояние от заданного множества точек
минимально. Расстояние считается при прохождении по
границам клеток.
Формат входных данных (см. рисунок 6.4).
Первая строка входного файла содержит число
N — количество точек (l<iV<500). Каждая из последующих N
строк содержит координаты точки — два целых числа из
диапазона [-32767, 32767], разделенных пробелом.
Формат выходных данных (см. рисунок 6.4). Ваша
программа должна вывести в выходной файл координаты точки —
два целых числа, записанных через пробел.
Указание. Зачем нам плоскость? Почему задачу нельзя
решить отдельно для каждого измерения?
Результат решения на плоскости — это результат решения
на двух прямых, т. е. нашли точку на X, нашли точку на Y, тем
самым получили координаты точки на плоскости. Решаем
задачу на прямой линии. Пусть не N точек, а две. Очевидно, что
точку следует размещать в том месте, где находится одна из точек.
А если три точки? Например, (1,5, 1000). В этом случае ответом
является 5.
Пример.
4
0 0
0 0
1 1
2 2
01

6. Избранные олимпиадные задачи по программированию
303
4
1
2
3
обратная
Рис. 6.5
4. «Печать буклета». При печати до- лицевая
кумента обычно первая страница
печатается первой, вторая — второй,
третья — третьей и так далее до конца. Но
иногда, при создании буклета, порядок
печати должен быть другим. При печати
буклета на одном листе печатаются
четыре страницы: две — на лицевой
стороне, и две — на обратной. Когда вы
сложите все листы по порядку и согнете их пополам, страницы
будут идти в правильном порядке, как у обычной книги.
Например, четырехстраничный буклет (см. рисунок 6.5) должен быть
напечатан на одном листе бумаги: лицевая сторона должна
содержать сначала страницу 4, потом — 1, обратная — 2 и 3.
Если в буклете число страниц не кратно четырем, то в конце
можно добавить несколько пустых страниц, но так, чтобы
количество листов бумаги при этом было минимально
возможным.
Ваша задача — написать программу, которая считывает из
входного файла количество страниц в буклете и генерирует
порядок его печати.
Входные данные. Входной файл (a.in, см.
рисунок 6.6) содержит количество страниц в буклете —
натуральное число, не превышающее 500.
Выходные данные. В выходной файл (a.out, см.
рисунок 6.6) необходимо выдать порядок печати
данного буклета — последовательность команд,
каждая из которых располагается на отдельной
строке и состоит из четырех чисел. Числа
разделяются пробелом и обозначают следующее:
• номер листа, на котором происходит печать;
• сторону: 1 — если печать происходит на
лицевой стороне, и 2 — если на обратной
стороне.
Два оставшихся числа — номера страниц
буклета, которые должны быть напечатаны. Пустая
страница задается числом 0. Если целая сторона
должна быть оставлена пустой, команду для ее
печати выводить не обязательно.
Указание. Необходимо дополнить число страниц
до значения, кратного четырем, а затем аккуратно
выводить информацию по лицевым и обратным
сторонам листа буклета. На лицевых сторонах листов
Пример.
a.in
1
a.out
110 1
a.in
4
a.out
114 1
12 2 3
a.in
14
a.out
110 1
12 2 0
2 1 14 3
2 2 4 13
3 1 12 5
3 2 6 11
4 1 10 7
4 2 8 9
Рис. 6.6

304
6. Избранные олимниадные задачи по программированию
буклета правая страница должна быть нечетной, а на
обратных — четной.
Фрагмент решения.
Var n:Integer;
Function Out (q: Integer) : Integers-
Begin
If q<=n Then Out:=q Else Out:=0;
End;
Procedure Solve;
Var i, nn : Integers-
Begin
If n=l Then WriteLn ( ' 1 1 0 1 ' ) ;
Else
Begin
nn:=n;
nn:=nn+(4-nn mod 4);{^Увеличиваем количество
страниц до значения, кратного 4.*}
For i:=l To nn Div 2 Do
Begin
If i Mod 2 = 1
Then WriteLn ( (i-tl) Div 2,' 1 ■ ,
Out(nn+l-i), ' ', Out (i) )
{^Выводим лицевые стороны.*}
Else WriteLn (i Div 2, ' 2 ',0ut(i),' ',0ut (nn-H-i)) ;
{*Выводим обратные стороны.*}
Ends-
End;
End;
5. В стране Гексландии каждое графство
имеет форму правильного шестиугольника,
а сама страна имеет форму большого
шестиугольника, каждая сторона которого состоит
из N маленьких шестиугольников (на
рисунке 6.7 iV=5). Графства объединяются в
конфедерации. Каждая конфедерация раз в год
выбирает себе покровителя — одного из 200
жрецов. Этот ритуал называется Великими
перевыборами жрецов и выглядит так: конфедерации
одновременно подают заявления (одно от конфедерации) в Совет
жрецов о том, кого они хотели бы видеть своим покровителем (если
заявление не подано, то считают, что конфедерация хочет
оставить себе того же покровителя). После этого все заявки удов-

6. Избранные олимпиадные задачи но программированию
305
летворяются. Если несколько конфедераций выбирают одного
и того же жреца, то они навсегда объединяются в одну. Таким
образом, каждый жрец всегда является покровителем не более
чем одной конфедерации.
Требуется написать программу, позволяющую Совету
жрецов выяснить состав каждой конфедерации после Великих
перевыборов.
В Совете все графства занумерованы (начиная с 1) с
центрального графства по спирали (см. рисунок). Все жрецы
занумерованы числами от 1 до 200 (некоторые из них сейчас могут не
быть ничьими покровителями).
Входные данные. Во входном файле (b.in, \
см. рисунорк 6.8) записано число N —
размер страны (1<N<128) — и далее для
каждого графства записан номер
жреца-покровителя конфедерации, в которую оно входит
(графства считаются по порядку их номеров).
Затем указаны заявления от конфедераций в
виде пар чисел: первое число — номер
очередного жреца-покровителя, второе — номер
желаемого жреца-покровителя. Все числа во
входном файле разделяются пробелами и
(или) символами перевода строки.
Выходные данные. В выходной файл (b.out, см. рисунок 6.8)
вывести для каждого графства одно число — номер его
жреца-покровителя после Великих перевыборов. Сначала — для
первого графства, затем — для второго и т. д.
Указание. Задача на принцип косвенной адресации.
Использовать два массива (начальный и конечный) для хранения номеров
жрецов для графств нельзя — оперативной памяти явно не
хватит. Обозначим через f(N) количество графств в стране со
стороной из N шестиугольников. Тогда /(1)=1. Заметим, что при
увеличении размера страны добавляется «внешний пояс» графств,
их количество — 6x(iV-l). Итак, /(A0=/(iV-l)+6x(iV-l), или
l+3x(N-l)xiV. При N, равном 128, получаем 48769 графств.
Vara: Array [ 1.. 200 ] Of Word;
b : Array[1..50000] Of Byte;
i,n,k,t : Word;
f : Text;
Begin
Assign(f, 'b.in');Reset(f);
Read(f,n);
n:=l + 3* (n-1)*n;
Пример.
b.in
2
115 3
5 1
1 3
b.out
3 3 13
Рис.
1 5
3 1
6.8
1
3

306
6. Избранные олимпиадные задачи по программированию
For i - 1 То 200 Do a[i]-i;
For i : = 1 To η Do Read (f, b [ i ] ) /
While Not SeekEof (f) Do
Begin
Read(f,k,t)/a[k]:=t;
End;
Close (f);
Assign (f, 'b.out');
Rewrite (f)/
For i := 1 To η Write(f,a [b [i]]) /
{^Косвенная адресация.*}
Close(f);
End.
А что, если N больше 128, например, равно 1000?
Количество графств приближается к 3 миллионам. Есть ли выход?
Оказывается, есть. Массив для хранения номеров жрецов для
графств вообще не требуется.
6. «Игра в слова». Надеемся, что вам
знакома следующая игра. Выбирается слово, и из
его букв составляются другие осмысленные
слова, при этом каждая из букв исходного
слова может быть использована не более такого
количества раз, которое она встречается в
исходном слове.
Напишите программу, помогающую играть
в эту игру.
Входные данные. В первой строке входного
файла (c.in, см. рисунок 6.9) записано
выбранное для игры слово. В последующих строках
задан «словарь» — множество слов, которые
мы считаем осмысленными. Их количество не
превышает 10000. Слово — это
последовательность не более чем 255 маленьких латинских
букв. Каждое слово записано в отдельной
строке. Заканчивается словарь словом "ZZZZZZ"
(состоящим из заглавных букв), которое мы не
будем считать осмысленным. Слова в словаре,
как это ни странно, не обязательно
располагаются в алфавитном порядке.
Выходные данные. В выходной файл (c.out,
см. рисунок 6.9) необходимо выдать список
слов, которые можно получить из исходного
I Пример.
soundblaster
sound
ι sound
! blaster
i soundblaster
i master
last
task
sos
test
bonus
done
ZZZZZZ
c.out
sound
\ sound
i blaster
j soundblaster
j last
; sos
;bonus
ι done
!zzzzzz
Рис. 6.9

6. Избранные олимпиадные задачи по программированию
307
слова. Слова должны быть выданы в том же порядке, в
котором они встречаются в словаре. Каждое слово должно быть
записано в отдельной строке. Список слов должен заканчиваться
все тем же неосмысленным словом «ZZZZZZ».
Указание. Требуется проверить: можно ли из букв одного
слова получить другое слово. «Запутанные» решения основаны
на анализе соответствия букв исходных слов. При простом
решении следует сформировать маски — количество букв (а, Ь,
с,.., г) в каждом из слов. Если такие маски есть, то задача
сводится к проверке вхождения маски слова из словаря в маску
первого слова.
7. «Делители». Даны два положительных целых числа А и
В. Определить возможность их разложения на N
положительных делителей αν α2, ..., aN, bv b2, ..., bN таких, что произведения
этих делителей совпадают. Т. е. требуется выполнение
следующих условий: αχχα2χ...χαΝ=Α, b1xb2x...xbN=B и alxb1=a2xb2=
=...=aNxbN, где αρ α2, ..., αΝ — делители числа A, a bv b2, ...,
bN — делители числа Б. Число 1 в этой задаче считается
делителем.
Входные данные. В единственной строке
входного файла (d.in, см. рисунок 6.10) через
пробел записаны числа А, В и N. Произведение
чисел А и Б не превышает значения
2147483647, а значение N — 31.
Выходные данные. В первую строку
выходного файла (d.out, см. рисунок 6.10) через
пробел записываются числа а19 а2, ..., αΝ, а во
вторую — Ьг, Ь2, ..., bN (достаточно вывести одно
из решений). Если решение отсутствует, то в
выходной файл записывается сообщение «по».
Указание. Произведение делителей чисел А и Б совпадает и
равно, обозначим его как h. Нахождение h сводится к
вычислению
h:=Round(Exp(ln((A*1.0)*B)/N)).
Пусть мы нашли число j такое, что h и А делятся нацело на
у, а В нацело делится на h Div у. В этом случае А следует
разделить на у, а В — на h Div у. После этого процесс поиска
делителей следует продолжить. Если мы найдем iV таких чисел у, то
задача решена.
Пример. Если А равно 320, В — 2278125 HJV — 6, то после
вычислений получим /г, равное 30, а в результирующих
массивах будет записано соответственно (2, 2, 2, 2, 2, 10) и (15, 15,
15, 15, 15, 3).
Пример.
d.in
4^16 2_
d.out
2 2
4 4

308
6. Избранные олимииадные задачи по программированию
I Пример.
Ί
200 100 200 200I
2 19 I
8. «Мотоциклисты». Среди мотоциклистов г. Кирова
популярно следующее соревнование: на одной из улиц города
выбирается прямой участок, на котором установлено несколько
(1<Ν<100) светофоров, имеющих только красный и зеленый
цвета. Мотоциклист проезжает выбранный участок на
постоянной скорости, причем нарушать правила дорожного движения,
т. е. проезжать перекресток на красный свет, категорически
запрещается, кроме случаев, когда мотоциклист пересекает
перекресток в момент переключения светофоров. Мотоциклист,
изменивший скорость движения, либо проехавший на красный
свет, либо выбравший скорость, меньшую 5 м/с,
дисквалифицируется. Побеждает мотоциклист, проехавший трассу за
минимальное время.
Требуется найти оптимальную скорость движения по трассе.
Входные данные. В первой строке
входного файла (m.in, см. рисунок 6.11)
записано N — число светофоров. В следующей
строке ΛΗ-1 чисел: первое — расстояние от
точки старта до первого светофора,
второе — расстояние между первым и вторым
светофорами, ... последнее число —
расстояние от последнего светофора до точки
финиша (расстояния — числа из интервала от 1
до 100000). В третьей строке записаны N
чисел — времена работы в красном и
зеленом режимах (оно одинаково) для каждого
светофора (числа из интервала от 1 до 300).
Выходные данные. В выходной файл (m.out, см. рисунок
6.11) записывается одно число (с точностью до четырех
знаков) — искомая скорость или сообщение «по», если решения
нет.
Указание. На рисунке 6.12 по горизонтальной оси
откладываем расстояния, а по вертикальной — время. Времена работы
каждого светофора в красном режиме выделены на
соответствующих расстояниях «черным отрезком». Каждой скорости
движения мотоциклиста соответствует
наклонная прямая. Для решения задачи
необходимо провести прямую из начала
координат с наименьшим угловым
коэффициентом, проходящую через
«светлые» участки рисунка 6.12. Обратим
внимание на то, что «лучшая» прямая касается
хотя бы одного отрезка в верхней точке. Рис. 6.12
m.out
\ 55.5556
Рис. 6.11
I /
х\

6. Избранные олимпиадные задачи по программированию
309
Действительно, если она не касается ни одного отрезка в
верхней точке, то ее можно сдвинуть («повернуть») вниз, уменьшая
при этом угол, т. е. увеличивая скорость, до соприкосновения с
первой возможной точкой. Из вышесказанного следует
решение: необходимо проверить все возможные «верхние» точки
«темных отрезков» на предмет их принадлежности искомым
прямым и выбрать наилучшую.
9. «Троллейбусы». Троллейбусы одного маршрута проходят
через остановку каждые k (1<£<500) минут. Известны времена
прихода Ν (1<Ν< 100000) жителей г. Кирова на остановку (N, k —
целые числа). Если человек приходит на остановку в момент
прихода троллейбуса, то он успевает войти в этот троллейбус.
Необходимо написать программу определения времени
прибытия первого троллейбуса на остановку (это число от 0 до k-1),
такого, чтобы:
• суммарное время ожидания троллейбуса для всех
граждан было минимально;
• максимальное из времен ожидания троллейбуса было
минимально.
Входные данные. В первой строке входного
файла (t.in, см. рисунок 6.13) записано число k, во
второй — N, а затем N строк со временем прихода
жителей на остановку (числа от 0 до 100000).
Выходные данные. В выходном файле (t.out, см.
рисунок 6.13) записываются два числа, каждое в
своей строке, являющиеся ответами на первый и
второй вопросы задачи соответственно. Если
вариантов решения задачи несколько, то выдать один
из них. При решении только одного пункта задачи
строка, соответствующая другому пункту,
остается пустой.
Указание. Достаточно подсчитать время
прихода жителей по модулю k. После этого в каждый
момент времени от 0 до k-Ι имеем количество
пришедших жителей (см. рисунок 6.14). Для ре-
| Пример.
! t.in
;юо
15
ίο
210
99
551
99
t.out
10
Рис. 6.13
0 12 3 .... k-1
Рис. 6.14

310
6. Избранные олимпиадные задачи по программированию
шения задачи достаточно проверить время прихода первого
троллейбуса от 0 до Ы и выбрать из них наилучшее для
первого и для второго пунктов.
Так, например, алгоритм решения первого пункта задачи
выглядит следующим образом.
Procedure SolvePA;
Var i, j: Longlnt;
sc, Min: Longlnt;
Begin
Min:=MaxLongInt;
For i:=0 To k-1 Do
Begin{*Время прихода первого троллейбуса.*}
sc:=0;{*Находим сумму времени ожидания
троллейбусов для всех жителей.*}
For j :=0 То k-1 Do sc:-sc + ( (k - j + i) Mod k) * A[j] ;
If sc<Min Then
Begin ResA:=i;Min:=sc;End;
{^Сравниваем.*}
End;
End;
10. «Посылки». Весь воскресный день родители решили
посвятить отправке посылок голодному в г. Москве
сыну-студенту. Для этого родители привозят посылки на вокзал и
отправляют их на любом идущем в г. Москву поезде. А сын в
г. Москве приезжает к приходу этого поезда на вокзал,
получает посылку и отвозит ее в общежитие. При этом родители не
могут сразу принести на вокзал более одной посылки (так как
очень тяжело!). Студент также не может носить по несколько
посылок сразу (он голодный!). Время, необходимое родителям,
чтобы добраться от дома до вокзала, равно Τ (оно равно
времени переезда от вокзала до дома). В г. Москве, как известно,
поезда приходят на разные вокзалы. Для каждого вокзала
известно время, необходимое студенту на дорогу от общежития до
этого вокзала (оно равно времени на дорогу от этого вокзала до
общежития). Дано расписание движения поездов из г. Кирова в
г. Москву. Договоримся, что поезда в пути не обгоняют друг
друга (т. е. поезд, который раньше другого отправляется из
г. Кирова, прибывает в г. Москву тактке раньше).
Написать программу определения максимального
количества посылок, которые родители смогут послать за воскресный
день голодному студенту (он все их должен встретить и отвезти
в общежитие).

6. Избранные олимпиадные задачи по программированию
311
I Пример.
\p.in
!70
|2
!40
!50
4
60 1200 2
200 1120 1
1200 1440 2
\p.out
Рис. 6.15
Входные данные. Во входном файле (p.in, см.
рисунок 6.15) заданы в следующем порядке
целые числа:
• Τ — время на дорогу родителей от дома до
вокзала в г. Кирове;
• Μ — количество вокзалов в г. Москве
(0<М<20);
• Μ строк, в каждой из которых записано
одно число — время переезда от
соответствующего вокзала до общежития;
• N — количество поездов (0<iV<1000);
• N строк, каждая из которых содержит 3
числа: время отправления поезда из г.
Кирова, время в пути, номер вокзала в г.
Москве, на который прибывает данный поезд.
Црим^чание
Список поездов дан в отсортированном по времени отправления
порядке. Время в задаче — абстрактное число из интервала от 0 до
5000. В одну единицу времени отправляется не более одного
поезда. Все данные — целые числа.
Выходные данные. В выходном файле (p.out, см. рисунок 6.15)
необходимо вывести одно число — максимальное количество
посылок, которые родители смогут отправить за воскресенье.
Указание. Предположим, что родители
отправили посылку с первым поездом.
Принимаем решение по второму поезду.
Возможны два варианта. Если они успевают
съездить за второй посылкой, то они ее
отправляют с поездом, и количество
отправленных посылок к этому моменту времени
будет равно двум, а если нет, то первую посылку они могут
отправить не с первым, а со вторым поездом. Продолжим
последовательно этот процесс. Пусть для всех поездов с номерами i
от 1 до k-Ι найдено максимальное количество посылок,
которые успеют отправить родители к моменту отправления поезда
i. Решаем задачу для поезда с номером k (рисунок 6.16),
предполагая, что с ним также отправляется посылка. Для
нахождения этого числа (посылок) достаточно рассмотреть все
предыдущие поезда, с которыми можно было отправить предпоследнюю
посылку и успеть отправить посылку на поезде с номером k.
Естественно, что из этих чисел выбирается максимальное.
Схема динамического программирования в действии.
Рис. 6.16

312 6. Избранные олимпиадные задачи по программированию
Рассмотрим основную процедуру — она проста, если не
вдаваться в детали, что и не требуется делать на данном этапе
решения.
Procedure Solve/
Var i, j: Integer;
Begin
ResΡ:=0; {* Результат.*}
For i:=1 To N Do
Begin {^Решаем задачу для поезда
с номером i . *}
Res[i]:=1;{*Мы всегда можем отправить первую
посылку с этим поездом, "проспав" все
предыдущие.*}
For j:=l To i-1 Do{^Согласуем отправку посылки
с поездом i с отправками посылок на
предыдущих поездах.*}
If IfPossib(j,i) Then Res[i]:=Max(Res[j]+l,Res[i]);
{*Если между поездами с номерами i и j
родители успевают съездить домой, студент
- в общежитие, то сравниваем Res[j]+1 и
Res[i] .*}
ResP:=Max(Res[i] , ResP);{*Может быть результат,
полученный для поезда с номером i, Res[i]
являться ответом задачи, например, в том
случае, когда все следующие поезда
отправляются через каждую секунду.*}
End
End;
Итак, все технические сложности задачи сконцентрированы
в функции IfPossib проверки совместимости отправки посылок
поездами с номерами ί и у.
11. «Закраска прямой». Интервал прямой с
целочисленными координатами [а,Ь) содержит левую границу — точку а, и
не содержит правую границу — точку Ь. Итак, интервал от 0 до
1.000.000.000 выкрасили в белый цвет. Затем было выполнено
N (l<=iV<=100) операций перекрашивания. При каждой
операции цвета в интервале, границы которого задаются,
меняются на противоположный (белый на черный, черный на белый).
Написать программу поиска самого длинного интервала
белого цвета после заданной последовательности операций
перекрашивания.

6. Избранные олимпиадные задачи по программированию
313
ί Пример.
14
j 20 50
! 10 35
| 40 90
I100 1000000000
z.out
L15
Рис. 6.17
Входные данные. Входной файл (z.in, см.
рисунок 6.17) содержит в первой строке
число N и затем N строк с границами
интервалов (числа в диапазоне Longlnt).
Выходные данные. В выходной файл
(z.out, см. рисунок 6.17) выводится одно
число — длина самого большого белого
интервала.
Указание. Решение с отслеживанием
всех перекрашиваний достаточно
трудоемко. Порисуем чуть-чуть. На рисунке
изображен один интервал. Вверху указан номер
границы, внизу — цвет интервала.
Значения границ не изображены. Границы с номерами 0 и 3
соответствуют предельным значениям.
Пусть есть два интервала. Различные варианты размещения
интервалов показаны на рисунке 6.18. Кружками большего
размера отмечены границы второго интервала. Можно продолжить
рисование: много отрезков, интервалы, начинающиеся в одной
точке и т. д., но эти рисунки будут только подтверждать идею.
Если отсортировать все границы в порядке возрастания, то белые
участки после всех перекрашиваний начинаются с четных
номеров границ.
0
•—
0
1
—ft
6
1
2
—♦—
ч
3
2
6
4
-*—
3
5
—·
0 1
6
1 3 i 5
ч 6 ч 6
Рис. 6.18
12. «Отрезки». На прямой линии расположено N (l<iV<500)
отрезков. Из них нужно выбрать наибольшее количество
попарно не пересекающихся. Отрезки пересекаются, если они
имеют хотя бы одну общую точку.
Входные данные. В первой строке файла (o.in* см. рисунок
6.19) записано число N — количество отрезков. В каждой из
последующих N строк заданы координаты отрезка.

314
6. Избранные олимпиадные задачи по программированию
Выходные данные. В выходной файл (o.out, см. j Пример, ί
рисунок 6.19) записываются координаты концов ! |
отрезков (целые числа из диапазона Integer). Каж- I * ι
дый отрезок в отдельной строке. ί 3 !
Указание. Попытки решения задачи перебор- ^ \
ными методами не имеют успеха. Сгенерировать 4 6
все возможные подмножества множества из 500 | j
элементов при любых эвристических приемах со- j °'out I
кращения перебора не реально, поэтому следовало 11 3
сразу искать другое решение. Задача относится к |_^_.?_ j
классу задач, решаемых с помощью «жадных» ал-
п Рис. 6.19
горитмов. Суть: сортируем отрезки по значениям
правых концов, а затем последовательно идем по
отсортированным отрезкам и берем в качестве следующего
отрезка такой первый отрезок, у которого правая граница больше
левой границы текущего отрезка.
Основной фрагмент реализации имеет вид:
Const NMax=500;
Var A:Array[0. .NMax,1. .2] Of Longlnt;
Procedure Solve;
Var i:Integer;
t:Longlnt;
Begin
t:=-MaxLongInt;
For i:=1 To N Do
If A[i,l]>t Then
Begin
Writeln(A[i, 1] , ' \A[i,2]); t:=A[i,2];
End;{*Если левая граница больше значения t, то
включаем отрезок в решение и присваиваем
переменной t значение правой границы
отрезка.*}
End;
Обоснуйте правильность его работы.
13. «Поезда». Имеется ветка метро, станции которой
пронумерованы по порядку числами 1 (центр), 2, ..., N (2<iV<30). Из
центра (станция с номером 1) и самой дальней станции (номер
N) одновременно отправляются два поезда.
Требуется выяснить, где и когда произойдет встреча, если
движение поездов удовлетворяет следующим условиям:
• на каждой из станций, кроме первой и последней, поезда
стоят Μ часов;

6. Избранные олимпиадные задачи по программированию 315
• поезда разгоняются и тормозят мгновенно;
• во время движения поезда имеют одну и ту же скорость V;
• в случае, если поезда встречаются на станции, выдать
самое раннее время встречи.
Входные данные. В первой строке файла (p.in,
см. рисунок 6.20) задано число V — скорость
поезда (в км/час). Во второй строке задано число М. В
третьей строке задано число N — количество
станций. В четвертой строке задан набор чисел d2,..., ] 0.5 ι
dn> где число di является расстоянием от станции с I ^ |
номером (/-1) до станции с номером i (в километ- j 1
pax). Все числа, кроме N, вещественные. ^p.out |
Выходные данные. В выходной файл (p.out, см. 12.5 I
рисунок 6.20) требуется записать время встречи (в | 2.0 |
часах, с одной цифрой после точки) и расстояние
от места встречи до центра (с одной цифрой после Рис. 6.20
точки).
Указание. Задача не требует знаний специальных
алгоритмов. Можно решать путем моделирования движений того и
другого поездов. Однако есть более простой способ. Общее
время в пути (t) подсчитать несложно — сумма времен
остановок на станциях и время перемещений между станциями
(скорость — постоянная величина). Время встречи поездов равно
t/2, если оно не совпадает с моментом остановки. При встрече
на какой-то станции требуется сделать небольшое уточнение.
Кстати, задача значительно усложняется, если скорость
поездов непостоянна (разгон, торможение, остальное время —
постоянная скорость). В этом случае необходимо уметь очень
аккуратно решать квадратные уравнения. Вернемся к нашей
задаче. Рассмотрим, как обычно, пример: V=1.0, M=5.0, iV=3 и
расстояния 10.0 и 7.0. Общее время в пути 22 единицы.
Половина этого значения 11. Но к этому моменту времени второй
поезд стоит на станции уже 4 единицы времени, а первый — 1
единицу. Значит, время встречи 11-1 или 10 единиц времени.
14. Имеется N (10<iV<100) ламп, пронумерованных от 1 до
N. Каждая лампа может иметь два состояния — включена,
выключена. Четыре кнопки позволяют управлять лампами
следующим образом:
• кнопка 1 — при нажатии все лампы изменяют свое
состояние на противоположное;
• кнопка 2 — при нажатии изменяется состояние всех
ламп, имеющих нечетные номера;
Пример.
p.in
1

316
6. Избранные олимпиадные задачи по программированию
10
1
-1 I
7; -i
Output.Txt
0000000000
0110110110
0101010101
• кнопка 3 — при нажатии изменяется состояние ламп,
имеющих четные номера;
• кнопка 4 — при нажатии изменяется состояние всех
ламп, имеющих номера 3&+1(£>0), т. е. 1, 4, 7, ...
Первоначально все лампы включены. Имеется счетчик С
(1<С<10000), который учитывает суммарное число нажатий
всех кнопок.
Требуется по значению числа С и конечному состоянию
некоторых ламп определить все возможные, конечные,
различные конфигурации N ламп.
Входные данные. Файл Input.txt (см. рису- п~ ι
а о1ч 'Пример. |
нок 6.21) содержит четыре строки: | I
• количество ламп Ν; \Input.Txt \
• значение счетчика С;
• номера тех ламп, которые в конечной
конфигурации включены;
• номера тех ламп, которые в конечной
конфигурации выключены.
Номера ламп в третьей и четвертой строках
записываются через пробел, списки номеров
ламп заканчиваются числом -1.
Выходные данные. В файл Output.txt (см.
рисунок 6.21) записываются все возможные Рис. 6.21
конечные конфигурации (без повторений),
каждая — в отдельной строке. Конфигурация — это строка
длины N (первый символ — состояние первой лампы, N-й —
состояние N-й лампы), где 0 означает, что лампа выключена,
а 1 — включена.
Примечание
Количество ламп, о которых известно, что в конечной
конфигурации они включены, меньше или равно 2. Гарантируется, что
существует хотя бы одна конечная конфигурация для каждого входного
файла.
Указание. Заметим, что перебирать все 4е вариантов, при
С=10000 — бесполезное занятие, попытаемся упростить
задачу. Во-первых, последовательное действие любых двух кнопок,
например, 1-2, эквивалентно их действию в противоположном
порядке, т. е. 2-1 (коммутативность). Во-вторых,
последовательное применение какой-либо кнопки два раза подряд не
изменяет состояние лампочек. Поэтому любое значение С, большее
4, уменьшается на 2. Итак, нечетные С, большие 4, заменяются
на С, равное 3, а четные С, большие 5, на С, равное 4. Остается
перебрать различные варианты конечных конфигураций при

6. Избранные олимпиадные задачи по программированию
317
С<4, их всего 15 (1; 2; 3; 4; 1,2; 1,3; 1,4; 2,3; 2,4; 3,4; 1,2,3;
1,2,4; 1,3,4; 2,3,4; 1,2,3,4), что, безусловно, не 4е. Необходимо
только не забыть о том, что, например, при С, равном 3,
следует проверять и конфигурации, получаемые при С, равном 1.
15. «Звездная ночь». Посмотрите на ночное небо, где
светящиеся звезды объединены в созвездия (кластеры) различных
форм. Созвездие — это непустая группа рядом расположенных
звезд, имеющих соседями звезды либо по горизонтали, либо по
вертикали, либо по диагонали. Созвездие не может быть
частью другого созвездия.
Рис. 6.22
Созвездия на небе могут быть одинаковыми. Два созвездия
являются одинаковыми, если они имеют одну и ту же форму
независимо от их ориентации. В общем случае число
возможных ориентации для созвездия равно восьми, как показано на
рисунке 6.22.
Ночное небо представляется картой неба, которая, в свою
очередь, является двумерной матрицей, состоящей из нулей и
единиц. Элемент этой матрицы содержит цифру 1, если это
звезда, и цифру 0 — в противном случае.
Для заданной карты неба отметить все созвездия, используя
при этом маленькие буквы. Одинаковые созвездия должны
быть отмечены одной и той же буквой; различные созвездия
должны быть отмечены различными маленькими буквами.

318
6. Избранные олимпиадные задачи по программированию
Для того чтобы отметить созвездие, необходимо заменить
каждую единицу в созвездии соответствующей маленькой
буквой.
Входные данные. Входной файл с именем starry.in содержит
в первых двух строках ширину W и высоту Η матрицы,
соответствующей карте неба. Далее в этом файле следует Η строк, в
каждой из которых содержится W символов.
Выходные данные. Файл starry.out содержит ту же самую
матрицу карты неба, что и файл starry.in, только созвездия в
ней отмечены так, как описано в условии задачи.
Ограничения:
О < ^(ширина карты неба) < 100,
0 < //(высота карты неба) < 100,
0 < Число созвездий < 500,
0 < Число различных созвездий < 26(а..г),
1 < Число звезд в каждом созвездии < 160.
Пример
starry.in
23
15
Таблица 6.1
^
!°
ί 0
1 о
0
|о
1
0
0
I о
0
о
I о
[о
0
1
1
0
0
0
0
0
0
0
0
0
0
0
0
τ
1
0
0
0
0
0
1
0
0
0
0
1
0
0
0
0
0
0
0
0
0
0 1
1 0
0
0
0
0
1
1
0
0
0
1
0
1
1
0
0
0
0
1
0
0
1
0
0
1
0
0
0
0
0
1
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
1
1
1
0
0
1
0
1
1
0
0
0
0
0
0
0
0
0
1
1
1
1
о| 1
I
1 | 1
0
1
1
1
1
1
0
0
0
1
1
1
1
0
1
0
1
0
0
0
1
0
0
0
0
0
0
0
0
0
0
1
0
1
0
1
0
1
1
1
1
1
0
0
0
0
1
0
0
0
1
0
1
0
0
0
1
0
0
0
0
1
1
1
1
1
0
1
0
1
0
1
0
1
1
0
0
0
0
0
0
0
1
0
0
0
1
0
0
0
г
0
0
0
0
0
0
1
1
1
1
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
1 Ϊ0
I
1 ! 1
0
0
0
0
0
0
1
0
0
1
1
1
0
0
0
0
1
1
0
0
0
0
0
lJL
0
1
1
0
0
0
0
0
1
0
0
0
0
0
1
0
1
1
0
0
0
0
0
1
0
0
0
0
1
0
0
0
1
0
0
0
0
0
1
1
0
0
0
0
0
о I
1
1
0
о I
о !
0
0
1
0
0
0
0
ι !
L°J

6. Избранные олимпиадные задачи по программированию
319
starry.out
Таблица 6.2
,0
1 ч
о
a
U а
i 0J0
]о о
о
ί 0
Ιο
! о
1°
! о
Ιο
1 о
0
0
0
0
0
0
0
0
0
0
0 1 0
a j a
0
0
0
0
0
b
0
0
0
0
g
0
0
0
0
0
0
0
0
0
0
g
0
0
0
a
a
о
0
0
e
0
f
f
0
0
0
0
b
0
0
a
0
0
e
0
0
0
0
0
b
0
0
0
L^
(Γ
0
0
0
e
0
0
0
0
0
0
0
0
0
0
oi
0
0
0
e
e
e
0
0
d
0
d
d
0
d
0
0
0
0
0
0
0
0
0
d
d
d
d
d
d
0
с
с
с
с
с
0
0
0
d
d
d
d
0
d
0
с
0
0
0
с
0
0
0
0
0
0
0
0
0
0
c
0
b
0
с
0
с
с
с
с
с
0
0
0
0
с
0
0
0
с
0
с
0
0
0
с
0
0
0
0
с
с
с
с
с
0
с
0
b
0
с
0
f
f
0
0
0
0
0
0
0
с
0
0
0
с
0
0
0
ьп
0
0
0
0
0
0
с
с
с
с
с
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0_
0
0
0
0
d
d
0
0
о
0
0
0
а
0
0
е
е
е
0
0
d
0
0
о
0
а
а
0
0
0
0
0
е
0
d
d
0
0
0
0
0
а
0
0
0
0
0
е
Т1
d
d
0
0
0
0
0
а
0
0
0
0
е
L^
0
0
d
0
0
0
0
0
а
а
0
0
0
0
0
°]
d
d ι
0
0
0
о I
οΊ
a
0
0
0
0
b
0
В таблице 6.2 представлен один из возможных вариантов
выходного файла для представленного выше входного файла,
содержащего карту неба в таблице 6.1.
Указание. Пусть карта описывается массивом А:
А:Array[0..MaxN+1,0..MaxN+1] Of Byte;
где MaxN=100, максимальный размер карты. Вместо 1,
описывающей звезду созвездия, элементу А в процессе обработки
будем присваивать код (ASCII) соответствующей буквы.
Попробуем «набросать» общий алгоритм.
For i :=1 To N Do
For j :=1 To M Do
If A[i,j]=l Then
Begin
<Обход созвездия, начиная с клетки (i,j), по
принципу обхода в ширину. Результат в переменной Work_Star
(описание созвездия) и в переменной d (фиксируется
отклонение влево от координаты j)>/
<Получение всех симметричных созвездий. Проверка
совпадения найденного созвездия с ранее полученными.
Результат - код ASCII созвездия. Если совпадения не
было, то полученное созвездие запоминается>;
<Пометка полученного созвездия кодом ASCII>/
End;

320
6. Избранные олимпиадные задачи по программированию
Подумаем об используемой оперативной памяти.
Максимальный размер карты — 100x100. Одно созвездие может
использовать всю карту, т. е. при описании созвездия необходимо
«закладывать» максимальный размер 10000. С другой стороны,
созвездий может быть 26, итого требуется 260000 байт. Цифра
большая. Необходимо сокращать, использовать побитовое
хранение описаний созвездий. Делим на 8 и получаем 32500 байт,
что уже допустимо.
Определим структуры данных и сделаем первое уточнение
алгоритма решения.
Const MaxN=100;{^Максимальный размер карты.*}
МхСп^2 6;{*Количество различных созвездий.*}
StArt-97;{*ASCII код буквы а.*}
Dx: Array[1..8] Of Integer-( 0, 0, 1, 1,
1,-1,-1,-1);{*Приращения, используемые
при обходе в ширину.*}
Су: Array[1..8] Of Integer-( 1,-1, 1,
0,-1, 1, 0,-1);
Type MasSt-Array[0..MaxN+1, 0..(MaxN+8) Div 8] Of
Byte;{*KapTa отдельного созвездия,
используется побитовое хранение.*}
Star=Record
A: MasSt;
Ν, Μ: Integer-
End;
(^Описание созвездия.*}
Var A: Array[0..MaxN+1, О..МахМ+l} Of Byte;
{*Описание карты.*}
Ν, Μ: Integer;{*Размер карты.*}
Rs: Array [1. .MxCh] Of Star;{*Массив для
хранения различных созвездий.*}
Sc: Integer;{*Число различных созвездий.*}
При таком определении структур данных основная
процедура Solve имеет вид.
Procedure Solve;
Var i, j, d: Integer;
WorkJStar:
Starrer Byte;
Begin
For i:=l To N Do
For j : =1 To Μ Do
If A[i, j]=l Then

6. Избранные олимпиадные задачи по программированию
321
Begin
d:=GetSt(i,j,Work_Star);{*Обход в ширину,
d - отклонение влево от начала точки
обхода. Стандартный обход в ширину
должен быть модифицирован так, чтобы
подсчитывался размер созвездия -
прямоугольник наименьшего размера,
в который помещается созвездие. Кроме
того, требуется выполнять битовую
кодировку созвездия.*}
c:=Check(Work_Star);{*Проверка на совпадение
с ранее полученными созвездиями.*}
SetUp(i, j-d,с,Work_Star);{*Пометка созвездия
буквой алфавита.*}
End;
End;
Дальнейшее уточнение алгоритма предоставим читателю.
Самая трудоемкая ее часть — проверка созвездий на совпадение.
16. «Самый длинный префикс». Структура некоторых
биологических объектов представляется последовательностью их
составляющих. Эти составляющие обозначаются заглавными
буквами. Биологи интересуются разложением длинной
последовательности в более короткие последовательности. Эти
короткие последовательности называются примитивами. Говорят, что
последовательность S может быть образована из данного
множества примитивов Р, если существует η примитивов рг,...,рп в
Р, таких, что их конкатенация (сцепление) ρν...>ρη равняется
S. При конкатенации примитивы р19...,рп записываются
последовательно без разделительных пробелов. Некоторые
примитивы могут встречаться в конкатенации более одного раза, и не
обязательно все примитивы должны быть использованы.
Например, последовательность АВАВАСАВЛАВ может быть
образована из множества примитивов {А, АВ, BAt CA, ВВС}.
Первые К символов строки S будем называть префиксом
строки S длины К.
Требуется написать программу, которая для заданного
множества примитивов Ρ и последовательности Τ определяет
длину максимального префикса последовательности Т, который
может быть образован из множества примитивов Р.
Входные данные (см. рисунок 6.23) расположены в двух
файлах. Файл input.txt описывает множество примитивов Р, а
файл data.txt содержит последовательность Т, требующую
проверки. Первая строка input.txt содержит η — количество при-

322
6. Избранные олимпиадные задачи по программированию
митивов в множестве Ρ (1<я<100). Каждый
примитив задан в двух последовательных строках.
Первая из них содержит длину L примитива
(1<L<20), а вторая — строку из заглавных букв
(от Ά' до Z') длины L. Все η примитивов
различны. Каждая строка файла data.txt содержит одну
заглавную букву в первой позиции. Файл data.txt
заканчивается строкой с символом V (точка) в
первой позиции. Длина последовательности не
меньше 1 и не больше 500 000.
Выходные данные (см. рисунок 6.23). В первую
строку файла output.txt требуется записать длину
максимального префикса последовательности Г,
который может быть образован из множества Р.
Указание. Введем переменную с именем
МахРг типа Longlnt для хранения значения
длины максимального префикса. Ответим на вопрос:
как задействовать примитив в сравнениях? Если
сравнение начинается с первой позиции
последовательности символов, то понятно — примитивы
начинаются с этой же буквы. А если нет?
Мы в какой-то позиции последовательности с
номером t. Новое подмножество примитивов для
сравнения выбирается только в том случае, если МахРг
равно t-l\ ! ! Это означает, что закончено сравнение
по какому-то примитиву, он полностью входит в
конкатенацию, и есть полное право подключать к
процессу новое подмножество примитивов. Если t-1
не равно МахРг, то процесс сравнения символов
последовательности продолжается только с
символами ранее выделенных примитивов. В том случае,
когда множество выделенных примитивов пусто, обработка
закончена. То, что мы нашли, — значение МахРг — ответ задачи.
А в какие моменты времени изменяется значение МахРг?
Как только заканчивается сравнение хотя бы с одним
примитивом, изменяем значение МахРг.
Для хранения «активных» примитивов следует ввести
структуру данных Ρ — массив из Μ строк и ΜαχΝ плюс один столбец
(Array[l..M,0..MaxN] of Integer). Почему Μ? Нет необходимости
хранить предысторию процесса сравнения на большую глубину,
ибо максимальная длина примитива М. В элементе же нулевого
столбца Ρ фиксируем количество записей в соответствующую
строку. С этой структурой данных следует предусмотреть
следующие операции: вставка элемента (открытие нового примитива,
| Пример.
input.txt
!5
1
1А
!2
;АВ
(ВВС
,2
СА
2
ВА
data.txt
ΙΑ
!В
\й
|С
А
!в
1а
|А
|В
с
в
output.txt
11
Рис. 6.23

6. Избранные олимпиадные задачи по программированию
323
перевод его в состояние «активный»); исключение элемента
(сравнение очередного символа активного примитива и строки
дало отрицательный результат); сжатие данных (если
действительно для хранения активных примитивов выбран массив).
17. Дан текст, набранный символами одинаковой ширины
(включая пробелы). Длина строки при печати этим шрифтом
на листе бумаги равна S. Назовем пустой последовательность
пробелов между соседними словами в строке, а также от начала
строки до первого слова в ней и от последнего слова в строке до
конца строки.
Требуется преобразовать текст так, чтобы сумма кубов
пустот по всем строкам была минимальна.
Для достижения этой цели разрешается заменять
произвольную пробельную последовательность (непустую
последовательность подряд идущих пробелов и/или символов перевода
строки) любой другой последовательностью.
Входные данные. Первая строка входного файла содержит
целое число S (1<S<80). В последующих строках записан текст,
содержащий не более 500 слов. Длина каждого слова не
превосходит S.
Выходные данные. В первую строку выходного файла
записывается минимально возможная сумма кубов пустот по всем
строкам. В последующих строках выводится преобразованный
текст.
1 input.txt
10
aaa-bbb—bbbb
аааа
110
aa-bb—bb
аа
10
aaaa-bbbb—bbbb
аааа
13
aaaaa-aaaa-aaa-aa-a
13
aaaaaa-aaaaa-aaaa-aaa-aa-a
13
aaaaaaa-aaaaaa-aaaaa-aaaa-
aaa-aa-a
I
output, txt I
15
-aaa—bbb-bbb
b-aaaa-ccc-ccc
c-
8
-aa-bb-bb-aa-c
c-cc- ι
6
aaaa-bbbb-bbb
b-aaaa-cccc-cc
cc-
35
-aaaaa—aaaa—
aaa—aa—a—
5 I
aaaaaa-aaaaa-
aaaa-aaa-aa-a
59
—aaaaaaa—a
aaaaa-aaaaa—a i
^aa^aaa-aa-a- |
Рис. 6.24

324
6. Избранные олимпиадные задачи по программированию
Для осознания сути задачи на рисунке 6.24 приведены
примеры входных и соответствующих выходных файлов (в
таблице символом «-» обозначен пробел — удобнее считать).
Указание. Решение основано на факте — сумма кубов
минимальна в том случае, когда количество пробелов между
словами совпадает, и если этого достичь нельзя, то эти значения
(количество пробелов) наиболее близки друг другу. Пусть мы
размещаем в строке q слов, количество символов в словах
равно w. Длина строки известна — S позиций. Обязательное
количество пробелов на каждом месте (d), а их (#+1), подсчитываем,
находя целую часть частного от деления количества пробелов
(S-w) на количество мест q+Ι. Оставшееся число пробелов
(m:=(S-w) Mod (#+1)) необходимо распределить по одному к
пробелам на т местах.
18. «Парковка»*. Парковка около Великой Стены состоит из
длинного ряда парковочных мест, полностью заполненного
машинами. Один из краев считается левым, а другой — правым.
Каждая из машин имеет свой тип. Типы перенумерованы
натуральными числами, и несколько машин могут иметь один и тот
же тип. Рабочие решили упорядочить машины в парковочном
ряду так, чтобы их типы возрастали слева направо.
Упорядочение состоит из нескольких этапов. В начале каждого этапа
рабочие одновременно выводят машины с их мест и затем ставят
машины на свободные места, образовавшиеся в результате
выезда машин на данном этапе, т. е. меняют их местами. Каждый
рабочий перемещает только одну машину за этап, и некоторые
рабочие могут не участвовать в перемещении машин на этапе.
Эффективность процесса упорядочивания машин определяется
количеством этапов.
Предположим, что на парковке находится N машин и W
рабочих.
Требуется написать программу, которая находит такое
упорядочивание, при котором количество этапов не превосходит
значения N/(W-1), округленного в большую сторону, т. е.
[N/(W-1)\ Известно, что минимальное число этапов не
превосходит [N/(W-1)\
Рассмотрим следующий пример. На парковке находятся 10
машин типов 1, 2, 3, 4 и четверо рабочих. Начальное положение
машин слева направо, заданное их типами — 2334421131.
Задача с Международной олимпиады школьников 2000 года.

6. Избранные олимпиадные задачи по программированию
325
Минимальное количество этапов — 3, и они могут быть
выполнены так, что расположение машин по типам после
каждого из этапов следующее:
• 2114423331 — после первого этапа,
• 2112433341 — после второго этапа,
• 1112233344 — после третьего этапа.
Входной файл имеет имя саглп (см. ри-
10 4 4
233442 113 1
car.out
3
427387283
3 4 9 9 6 6 4
3 1 5 5 10 10 1
сунок 6.25). Первая строка входного файла j Пример,
состоит их трех чисел. Первое — количест- | Car.in
во машин N, 2<iV<20000. Второе —
количество типов машин М, 2<М<50, причем тип
машины является натуральным числом от
1 до М. На парковке есть хотя бы одна
машина каждого типа. Третье — количество
рабочих W, 2<W<M. Вторая строка
содержит N целых чисел, где i-e число является
типом i-й машины в парковочном ряду,
считая слева направо. Рис.6.25
Выходной файл имеет имя car.out (см.
рисунок 6.25) Первая строка выходного файла содержит число
R — количество этапов. Далее следует R строк, где Z+1 строка
выходного файла описывает i-й этап. Формат строки,
описывающей этап, следующий. Первое число — количество машин С,
перемещаемых на данном этапе. Далее следует С пар чисел,
определяющих перемещения машин на данном этапе. Первое
число пары — позиция, с которой машина перемещается,
второе число пары — позиция, на которую машина перемещается.
Позиция машины является целым числом от 1 до N и отсчиты-
вается с левого конца ряда.
В случае, если существует несколько оптимальных
решений, выдайте только одно из них.
Оценка решения. Предположим, что количество этапов,
выданных вашей программой, — Д, a [N/(W-1)\ = Q. Если
какой-то из R этапов выдан некорректно или после выполнения
всех этапов типы машин не выстраиваются в возрастающем
порядке, вы набираете 0 очков за тест. В противном случае ваши
очки будут начислены в соответствии со следующими
правилами:
• R<Q 100% очков
• #=Q+1 50% очков
• R=Q+2 20% очков
• R>=Q+3 0% очков

326
6. Избранные олимпиадные задачи по программированию
Указание. Прагматика и еще раз прагматика торжествует в
решении данной задачи. Поиск минимального количества
этапов в задаче не требуется. Необходимо осуществить
перестановку машин на стоянке за Q этапов — это дает 100%-ный балл.
Если за один этап на свои места ставится W-1 машина, то этот
результат достигается. Так как на стоянке работают W
рабочих, W-1 машина всегда ставится на свои места на одном
этапе, с помощью простого эвристического алгоритма.
• Взять машину, стоящую не на своем месте, и переставить
ее на место в том промежутке, где она должна стоять,
занятое машиной, также стоящей не на своем месте;
• продолжить этот процесс (с последней машиной) до тех
пор, пока не окажутся задействованными в перестановке
все рабочие или не получится цикл. При этом машина,
вытесненная последней, ставится на первоначальное место, с
которого начинался процесс перестановки. Последняя
машина не обязательно попадает в свой промежуток. В
случае цикла и оставшегося количества рабочих более одного,
алгоритм повторяет свою работу с этими рабочими над
машинами, стоящими, естественно, не на своих местах.
Для примера из формулировки задачи этот алгоритм дает
этапы работы, приведенные в таблице 6.3.
Таблица 6.3
этапа
1
L 2
I з
1__—„
Место i
1
2
2
1
1
2
3
3
3
3
3
3
3
L 1 Tj_
4
4
2_
2
2 ~
5
4
4__~
_2
2
6
2
3
3
3
[7 ! 8
Ϊ ! Г4
г- Гт 1 -i
1
3__
1
_3
9
3
4
4
4
10 |
1
1
4
4 |
Ответ (файл car.out):
4 9 9 6 6 1
5 10 10 1 2 2
7 2 3 8 8 3
Решение состоит не из минимального числа этапов, но оно
отвечает требованию задачи.
19. «Медианная энергия»*. В новом космическом
эксперименте участвуют N объектов, пронумерованных от 1 до N. Изве-
Задача с Международной олимпиады школьников 2000 года.

6. Избранные олимпиадные задачи по программированию
327
стно, что N — нечетно. Каждый объект имеет уникальную, но
неизвестную энергию У, выражающуюся натуральным числом,
l<Y<iV. Назовем объектом с медианной энергией такой объект
X, для которого количество объектов с энергией, меньшей, чем
у X, равно количеству объектов с энергией, большей, чем у X.
Требуется написать программу, которая определяет объект с
медианной энергией. К сожалению, сравнивать энергии можно
только с помощью устройства, способного для трех различных
заданных объектов определить, какой из них имеет медианную
энергию.
Библиотека. Вам предоставляется библиотека device с
тремя операциями:
• GetN', вызывается только один раз в начале программы;
не имеет аргументов; возвращает значение N;
• Med3, вызывается с тремя различными номерами
объектов в качестве аргументов; возвращает номер объекта,
имеющего медианную (среднюю) энергию;
• Answer, вызывается только один раз в конце программы;
единственный аргумент — номер объекта X, имеющего
медианную энергию. Эта функция корректно завершает
выполнение вашей программы.
Библиотека device генерирует два текстовых файла
median.out и median.log. Первая строка файла median.out
содержит одно целое число: номер объекта, переданного
библиотеке при вызове Answer. Вторая строка содержит одно целое
число: количество вызовов Med3, которое было сделано вашей
программой. Диалог между вашей программой и библиотекой
записывается в файл median.log.
Инструкция для программирующих на языке Pascal:
включите строку uses device; в текст вашей программы.
Экспериментирование. Вы можете поэкспериментировать с
библиотекой, создав текстовый файл device.in. Файл обязан
содержать две строки. Первая строка — одно целое число:
количество объектов N. Вторая строка — целые числа от 1 до iV в
некотором порядке: i-e число является энергией объекта с
номером i.
Пример
device.in
5
2 5 4 3 1
Файл device.in, указанный выше, описывает 5 объектов с их
энергиями. Эту информацию можно представить в виде
таблицы 6.4.

328
6. Избранные олимпиадные задачи по программированию
Таблица 6.4
Номер объекта
j| Энергия
1
^__,
2
L_5_J
3
L_A_
4_
■ 3 -
5 !
1 1
—J ι
1.
2.
3.
4.
5.
4.
4.
Ниже приведена корректная последовательность с пятью
обращениями к библиотеке:
GetN возвращает 5.
Med3(l,2,S) возвращает 3.
Med3(3,4,l) возвращает
Med3(4,2,5) возвращает
Answer(4)
Ограничения:
• количество объектов N нечетно, и 5<iV<1499;
• для объекта с номером / выполняется l<i<N;
• для энергии объекта У выполняется l<Y<iV, и все энергии
различны;
• библиотека для Pascal содержится в файле: device.tpu
• объявление функций и процедуры на Pascal:
Function GetN:Integer;
Function Med3(xtytz:Integer):Integer;
Procedure Answer(m:Integer);
• в ходе исполнения программы разрешается использовать
не более 7777 вызовов функции Med3;
• ваша программа не должна читать или писать какие-либо
файлы.
Указание. Пусть есть массив с энергиями объектов (см.
таблицу 6.5).
Таблица 6.5
1 Номер
Энергия
1
8
2
1
3
3
4
7
5
5
6
4
"ТТЛ
13
ю
9
_2J
10
11
11
12 [ 13 j
12 9 | 6 |
Все, что мы можем сделать с помощью операции Med3, это
разбить массив на три части, выбрав случайным образом два
несовпадающих номера (а и Ъ) элементов. Не деление пополам,
как в бинарном поиске, а деление на три части — «тринарный»
поиск. Пусть а=5 и Ь=12. Просматриваем все номера объектов,
помеченные признаком True. В начальный момент времени для
всех объектов этот признак равен True. Если операция
Med3(a,b,i) дает в качестве результата:
• значение а, то помечаем объект с номером / как элемент,
принадлежащий левой части (признак Left);

6. Избранные олимпиадные задачи по программированию
329
• значение i, то помечаем объект с номером i как элемент,
принадлежащий средней части (признак Middle);
• значение Ь, то помечаем объект с номером i как элемент,
принадлежащий правой части (признак Right).
В таблице 6.6 буквами L, M, R обозначены признаки _Left,
Midlle, Right. Буквой N обозначен признак _None, элемент
не рассматривается на данном шаге анализа.
Таблица 6.6
ι ■ '
ι Номер ι 1
Признак Μ
2
L
3
L
4
Μ
5
Ν
6
L
7
R
8
R
~^
L
^
R
11
R
12
N
^
Μ \
Итак, разбили, а что дальше? Напрашивается единственно
разумный ход — выбрать одну из трех частей и продолжить
поиск (другого не дано).
Вся сложность задачи — в выборе параметров поиска и в
аккуратном переходе от одного этапа поиска к другому. Какую
часть выбрать для следующего этапа поиска? Мы имеем в
левой части результата поиска 4 элемента, в правой — 4 и в
средней (без учета а и Ь) — 3. Первоначально осуществлялся поиск
элемента с медианной энергией 7 в массиве из 13 элементов.
После этого этапа необходимо искать элемент со вторым
значением энергии среди элементов, помеченных признаком _Мid-
die. Часть параметров поиска определена: количество и
признак элементов, среди которых ищется искомый; номер
значения энергии объекта. Еще один параметр — одно из
предыдущих значений а или Ъ — требует пояснений (это самый
сложный момент). Поясним рисунком 6.26.
ас be be ас
*μ
ΦΙ an bn \
\ φ Φ Χ
Если Med3(an,bn,ac)<>bn To ...
Рис. 6.26
Оказалось, что поиск следует продолжать в левой (по
отношению к а) части. Генерируем новые значения а Ь (обозначены
как an, bn). Если после этого средний элемент (Med3(an,bn,ac))

330
6. Избранные олимпиадные задачи по программированию
находится не на месте Ьп, то структура последующего поиска
нарушается. Необходимо поменять значения у an и Ъп. Так,
если после первого этапа поиска мы выяснили, что его следует
продолжать в левой части, то и следующее деление на три
части должно осуществляться с учетом этого результата.
Примечания.
1. Прервите чтение и проделайте ручной просчет поиска по данным
из условия задачи без смены значений. Результат уже на этом
простом примере окажется отрицательным.
2. Сделайте еще два рисунка и выясните особенности
использования функции Med3 при продолжении поиска в средней и правой
частях.
Позволим себе привести полный текст решения этой
красивой задачи*.
Program Median;
Uses device;
Const MaxN = 1500;
Type TDir = (_None, _Middle, _Left, _Right);
Var n: Integer;
Mas : Array [L.MaxN] Of TDir;
Lt, Rt : Integer; (^Количество элементов
в подмножествах *)
Procedure MakeMiddle(Dir: TDir);{^Помечаем
элементы, среди которых осуществляется поиск.*}
Var i: Integer;
Begin
For i := 1 To N Do
If Mas [i] = Dir Then Mas [i] := _Middle
Else Mas[i]:= _None;
End;
Procedure Swap(Var a,b: Integer);
Var c: Integer;
Begin с := a; a := b; b := c; End;
Procedure GetNext(Var a,b: Integer; len: Integer);
{^Генерируем номера а и b.*}
Var i,t,ca,cb: Integers-
Begin
t := 0;
Это одна из версий программы решения задачи. Разработана Дмитрием
Сергеевичем Шулятниковым.

[збранные олимпиадные задачи по программированию
331
са := Random(len)+1;
cb := Random(len)+1;
While ca=cb Do cb := Random(len)+1;
For i := 1 To N Do (^Сложность в том, что номера
оставшихся элементов для поиска идут
не подряд.*}
If Mas[i] = _Middle Then
Begin
inc (t)/
If ca = t Then a := I;
If cb = t Then b := i;
End;
End;
Procedure Doit(Dir: TDir; res, len, lb: Integer);
(^Основная процедура, параметры поиска
описаны ранее.* }
Var а, b, i, t: Integer;
Begin
MakeMiddle(Dir); (^Выделяем элементы, среди
которых осуществляется поиск.*}
If len - 1 Then
Begin
a := 1;
While Mas[a] <> _Middle Do inc (a);
Answer(a);
End
Else
Begin
GetNext(a,b,len);
If (Dir=_Right)
Then
Begin
If Med3 (lb,a,b) о а
Then Swap(a,b)
End
Else
If Med3(a,b,lb) <> b
Then Swap(a,b);
{^Корректируем значения а и b с учетом
предыдущего поиска. Пояснение приведено
на рисунке в тексте.х}
If len - 2 Then

332
6. Избранные олимпиадные задачи по программированию
Begin
If res = 1 Then Answer (a) Else Answer (b)
End
Else
Begin
It := 0; rt := 0;
Mas[a] := _None; Mas[b] := _None;
For i : = 1 To η Do
If Mas[i] = _Middle Then
Begin
t := Med3(a,b,i) ;
If t = b
Then
Begin inc(rt); Mas[i] := _Right End
{*Пишем в правую часть.*}
Else
If t = a Then
Begin inc (It) ; Mas [ i] : = _Lef t End;
End/
If Res = lt + 1
Then Answer (a)
Else {^Искомый
элемент попал на границу интервала,
поиск завершен.*}
If Res = len-rt
Then Answer(b)
Else
If res < lt+1 Then Doit (_Left, res, It, a)
(*Поиск с новыми параметрами.*}
Else
If res < len-rt
Then Doit(_Middle, res-lt-1,
len-lt-rt-2,b)
Else Doit(_Right,res-len+Rt,Rt,b);
End;
End;
End;
Procedure Solve;
Begin
η := GetN; Randomize;
FillChar(Mas, SizeOf(Mas), _Middle);
Doit(_Middle,n shr 1+1, n, 1);{*Первый вызов, η
shr 1+1 - среднее значение энергии, 1-

6. Избранные олимпиадные задачи по программированию
333
условно считаем, что ранее был первый
номер (обеспечивает правильный поиск).*}
End;
Begin Solve End.
20. В компьютерной графике* для обработки черно-белых
изображений используется их преобразование в строку из
десятичных чисел. Изображение или его часть (квадрат меньшего
размера) последовательно делится на 4 равных квадрата. Если
все точки в квадрате одного цвета (черного или белого), то
процесс деления этой части изображения заканчивается.
Квадраты, содержащие как черные, так и белые точки, опять делятся
на 4 равных квадрата. Процесс продолжается до тех пор, пока
каждый из квадратов не будет содержать точки только одного
цвета.
Например, если использовать 0 для белого и 1 для черного,
то изображение на рисунке 6.27(a) будет записано матрицей из
нулей и единиц, как представлено на рисунке 6.27(6).
0
0
0
о о о о
0
0
0
0
о о о о
0
0
0
0
0
0
1
1
1
0
0
0
0
1
1
1
1
0
0
1
1
1
1
1
1
0
0
0
0
0
1
1
1
1
0
0
0
0
1
1
1
1
0
0
13
14
7 8
11 12 15 16 1Э
17 18
(а)
(б)
Рис. 6.27
(в)
Матрица будет разделена на квадраты, как показано на
рисунке 6.27(b), где квадраты, выделенные серым, те, которые
содержат только черные точки.
Преобразование выполняется следующим образом. Корень
дерева представляет все изображение. Каждая вершина дерева
описывает некий квадрат. Она может иметь 4 исходящих ребра
к другим вершинам, представляющим квадраты, на которые
делится исходный квадрат. Вершины без исходящих ребер со-
Одна из самых красивых задач, с которой пришлось работать автору.

334
6. Избранные олимпиадные задачи по программированию
ответствуют квадратам, состоящим из точек одного цвета.
Например, приведенному выше изображению на рисунке 6.27(b) с
разбивкой на квадраты соответствует дерево, изображенное на
рисунке 6.28. Серые вершины обозначают квадраты,
содержащие 2 цвета, а белые и черные — квадраты, состоящие из
точек одного цвета (такого же, как цвет квадрата).
7 8 9 10
Рис. 6.28
4&
15 16 17 18
В дереве вершины пронумерованы в соответствии с
нумерацией квадратов на рисунке 6.27(b). Квадраты обходятся
слева-направо и сверху-вниз, начиная с верхнего левого угла
(верхний левый (В-Л), верхний правый (В-П), нижний левый
(Н-Л), нижний правый (Н-П)). Каждая черная вершина
дерева кодируется следующим образом: поднимаемся от вершины
по ребрам к корню, записывая при этом подряд цифры от 1 до
4 в соответствии с тем, где находится текущий квадрат по
отношению к вышестоящему (верхний левый — 1, верхний
правый — 2 , нижний левый — 3, нижний правый — 4 ).
Получившееся число записано по основанию 5, запишем его по
основанию 10.
Например, вершина с номером 4 имеет путь Н-Л, В-П.
Получается число 325 (по основанию 5) или 1710 (по основанию 10).
Вершина с номером 12 имеет путь Н-Л, Н-П, или 435 и 2310
соответственно. Вершина с номером 15 имеет путь В-Л, Н-Л,
Н-П, или 1345=4410. После этого дерево кодируется строкой
чисел: 9 14 17 22 23 44 63 69 88 94 113.
Требуется написать программу перевода изображения в
строку чисел и обратного преобразования — строки чисел в
изображение.
Входные данные. Файл содержит описание одного или
нескольких изображений. Все изображения — это квадратные
рисунки, сторона квадрата которых имеет значение длины,
являющееся степенью двойки. Входной файл начинается с целого числа

6. Избранные олимпиадные задачи по программированию
335
п, где \п\ — длина стороны квадрата (\п\ < 64). Если число η
больше 0, то затем следует \п\ строк по \п\ знаков в строке,
заполненных 0 и 1. При этом 1 соответствует черному цвету. Если η
меньше 0, то затем следует описание изображения в виде строки
из десятичных чисел, оканчивающейся -1. Полностью черному
квадрату соответствует кодировка из одного 0. Белый квадрат
имеет пустую кодировку (ничего не вводится). Признаком конца
входного файла является значение п, равное 0.
Выходные данные. Для каждого изображения из входного
файла выводится его номер. В том случае, когда изображение
задается с помощью 0 и 1, в выходной файл записывается его
представление в виде строки из десятичных чисел. Числа в
строке сортируются в порядке возрастания. Для изображений,
содержащих больше 12 черных областей, после каждых 12
чисел вывод начинается с новой строки. Количество черных
областей выводится после строки из десятичных чисел. В том
случае, когда изображение задается строкой из десятичных чисел,
в выходной файл записывается его представление в виде
квадрата, в котором символ V соответствует 0, а символ '*' — 1.
Пример входного и выходного файлов приведен в таблице 6.7.
Таблица 6.7
1 Входной файл
8
00000000
00000000
00001 111
00001111 |
0001 1111 I
Г 001 1 1 1 1 1 Г
00111100
00111000
-8
ι 9141722234463698894113-1
12
|00
! оо i
ι ι
ί -4 ;
!ο-ι |
! I
ι
! ι
| |
Выходной файл
Изображение 1
914 17 22 2344 63 69 88 94113 |
Общее число черных областей 11
Изображение 2
• • • • I
• • • • ι
• • • • •
•••**•
• • • •
• • •
Изображение 3
Общее число черных областей 0
Изображение 4
• • • • |
• • * * |
• * * *
i

336
6. Избранные олимпиадные задачи по программированию
Указание. Очередной раз используем технологию «сверху
вниз» в наших рассуждениях.
Основная программа не требует пояснений.
Begin
Readln(N);{*Вводим размерность изображения.*}
While NOO Do
Begin
If N>0 Then SolveA Else SolveB; {*Первая
процедура преобразует изображение в виде матрицы
в строку десятичных чисел, вторая процедура
выполняет обратное преобразование.*}
End;
End.
Дальнейшее уточнение требует осознания того, каким
образом в нашей задаче описывается очередной квадрат. Итак, это
координаты левого верхнего угла квадрата, длина его стороны
и тот путь по изображению, который предшествовал
попаданию в этот квадрат.
Формирование пути по изображению следует из
формулировки задачи — строка из цифр от 1 до 4.
Назовем функцию обработки квадрата RecA, ее заголовок —
Function RecA(i,j,d:Integer;Var Way:String):Boolean;
Значение функции True говорит о том, что квадрат черный.
Другим очевидным соображением является введение
массива для хранения результата — десятичных чисел,
описывающих изображение. Пусть это будет массив
Ср:Array[1..MaxCn] Of Longlnt;
где MaxCn — константа, равная 64x64, а счетчиком числа
записей в Ср является значение переменной Cut.
Мы совсем забыли сказать о том, что исходное изображение
записано в массиве
A:Array[1..MaxN,l..MaxN] Of Boolean;
где MaxN — константа, равная 64. Значение элемента массива
A[ij], равное True, соответствует черной клетке с
координатами (/,/), а при False — белой. Итак, SolveA.

6. Избранные олимпиадные задачи по программированию
337
Procedure SolveA;
Var i:Integer;
Begin
ReadA;{*Вводим описание изображения из входного
файла, формируем А.*}
Cnt:=0;
If RecA(l,Ι,Ν,'') Then
Begin Cnt:=l; Cp[Cnt] :=0; End/
{*Если все изображение состоит из
одного черного цвета, то записываем в
первый элемент массива Ср ноль
и заканчиваем обработку этого теста, во
всех остальных случаях массив Ср
сформирован рекурсивной функцией RecA.*}
Sort; {^Сортируем массив Ср.*}
PrintA;{*Выводим результат в выходной файл
OutPut.*}
End;
Функция RecA имеет вид.
Function RecA(i,j,d:Integer;Way:String):Boolean;
Var k:Integer; с:Boolean;
Begin
If d=l
Then c:=A[i,j] {*Дошли до квадрата
единичной длины, значение функции
определяется цветом квадрата.*}
Else
Begin
k : = d Div 2 ;
c:=RecA(i, j,k, Ί'+Way) And RecA(i,j+k, k, '24-Way)
And RecA(i + k, j,d, '3'+Way)
And RecA(i+k,j+k,d,' 4'+Way);
{^Значение функции на данном уровне
рекурсии определяется значениями функции
на квадратах меньшего размера.*}
If с Then Dec(Cnt,4);{*Если все составляющие
квадраты черные, то и данный квадрат
черный.*}
End;
If с Then Begin
Inc(Cnt);{*Квадрат черный, преобразуем путь
(строка, описывающая число в пятеричной
системе счисления) в десятичное число и
записываем результат.*}

338
6. Избранные олимпиадные задачи по программированию
Ср[Cnt]:=<преобразовать строку символов,
описывающую число в пятеричной системе счисления, в
число в десятичной системе счисления>/
End;
RecA:=c;
End;
На этой ветке алгоритма осталось уточнить функцию
преобразования пути по квадрату в десятичное число.
Процедуры Sort и PrintA (мы вызываем их из процедуры
SolveA) «прозрачны» для человека, прочитавшего книгу до
этого места. Описание алгоритма получения матрицы,
описывающей изображение, из строки десятичных чисел чуть сложнее.
Вся суть в аналогичной процедуре RecB. Квадрат описывается
координатами верхнего левого угла и длиной стороны,
безусловно, что они являются параметрами процедуры. Кроме того,
у нас есть путь, представленный пятеричным числом. Вопрос.
Как из очередной цифры этого числа сделать переадресацию по
квадрату, т. е. перейти к одному из четырех квадратов
меньшего размера? Ответив на него, можно
программировать как процедуру RecB, так и
весь алгоритм SolveB. Поясним ситуацию
рисунком 6.29. Пусть координаты левого
верхнего угла квадрата задаются
значениями переменных i и у, а длина стороны
нового квадрата — значение г. Цифры в
кружках — это значения переменной k,
получаемой из очередной цифры
пятеричного числа с помощью операции
k:=Way Mod 5-1; Рис. 6.29
Итак, в зависимости от значения
переменной k с помощью операций
i + r*(kDiv2) и j+r*(kMod2)
мы переходим к левым верхним углам любого из четырех
квадратов меньшего размера. Для убедительности
проиллюстрируем этот фрагмент рассуждений примером из таблицы 6.8.
Таблица 6.8
i Номер вызова процедуры RecB
:ί 1
L 2
!| з
/
1
1
col
i
1
5
L^_
d
8
4
2
Way
325или1710
3
^ 0
* Ί
1
2
-
г
4 !
2 !
"
Θ
i+rj
ij+r
CO
i+rj+r
(0

6. Избранные олимпиадные задачи по программированию
339
Дальнейшую работу по уточнению алгоритма оставим
заинтересованному читателю.
21. На числовой прямой отметили несколько отрезков,
каждый из которых обозначили одной из букв латинского
алфавита (различные отрезки — различными буквами). Используя эти
значения как операнды, а также операции объединения (+),
пересечения (*), разности (-) множеств и круглые скобки, было
составлено теоретико-множественное выражение.
Множество точек, являющееся результатом вычисления
составленного выражения, разбивается на некоторое количество
связных частей, каждая из которых является либо отдельной
точкой, либо промежутком, т. е. отрезком, интервалом или
полуинтервалом. Если потребовать, чтобы число частей в
разбиении было минимальным (никакие две части нельзя объединить
в большую), то такое представление окажется единственным.
Написать программу, представляющую результирующее
множество точек в указанном виде.
Входные данные. В первой строке входного файла (input.txt,
см. рисунок 6.30) содержится натуральное число N —
количество отрезков на прямой. В каждой из следующих N строк
находится описание одного из отрезков: буква, приписанная
этому отрезку, и координаты его левого и правого концов. Все
координаты — целые числа из диапазона [0, 109], строчные и
прописные буквы считаются различными. В следующей строке
содержится выражение длиной не более 250 символов.
Выражение не содержит пробелов и лишних скобок.
Выходные данные. В выходной файл (output.txt, см. рисунок
6.30) записывается разбиение результирующего множества на
связные части. Порядок вывода частей должен соответствовать
порядку их следования на числовой прямой, ι ;
если передвигаться по ней слева направо. ; РимеР· |
Точка представляется указанием ее целочис- \ input.txt \
ленной координаты в фигурных скобках, 13 :
числовые промежутки представляются со- А 0 30
гласно стандартным правилам: квадратная I а 10 15 ■
скобка означает, что соответствующая конце- ι b 15 20 ;
вая точка принадлежит промежутку; круг- |L_"3*—)LI<L_lj
лая — не принадлежит. Целочисленные ко- output.txt \
ординаты левого и правого концов го· 10)
промежутка должны быть разделены точкой |{15} !
с запятой, каждую из частей разбиения еле- (20;30] |
дует записать в отдельную строку выходного ! —
файла. Рис. 6.30

340 6. Избранные олимпиадные задачи по программированию
Указание. Заданные отрезки определяют множество точек на
прямой, назовем их граничными. Так, для примера на рисунке
6.29 это [0, 10, 15, 15, 20, 30] (после сортировки).
В результате выполнения теоретико-множественного
выражения интервал между двумя соседними граничными точками,
например (0, 10), или принадлежит, или не принадлежит
результирующему множеству (не может часть интервала (0, 10)
принадлежать результату, а другая нет). Для проверки
принадлежности интервала достаточно проверить, а принадлежит ли
его средняя точка результату. Множество граничных точек
преобразуется и имеет вид: [0, 5, 10, 12.5, 15, 15, 15, 17.5, 20,
25, 30]. Количество точек для N интервалов — iVx4-l.
Что дальше? Берем каждую точку и проверяем, анализируя
выражение. Операция объединения (А-КВ) заменяется на (A Or
Б), (А-В) — на {A And Not В) и (А*Б) — на (A And В). Запись
выражения в форме Бэкуса-Наура имеет вид:
<выражение>=<слагаемое>{<операция><слагаемое>}
<операция>=+|-|*
<слагаемое>=(<выражение>)|<идентификатор>
<идентификатор>=а|Ь|с..г|А|В|С..г
Определим «узловые» моменты решения задачи.
Из структуры данных (они даны не все) приведем
следующие.
Const MaxN=52;{^Максимальное количество интервалов,
2 6 символов алфавита.*}
Var OnX:Array[1..MaxN*2] Of Longlnt;{^Начальное
множество граничных точек.*}
N:Integer;{^Количество интервалов.*}
Numb:Integer;{^Рабочая переменная, определяет
номер символа в выражении при его анализе.*}
Мы должны просматривать все множество граничных точек,
их iVx4-l, а в массиве ОпХ только часть из них, средние точки
интервалов не присутствуют. Не будем дописывать их в ОпХ, а
попытаемся просто вычислять по номеру с помощью
следующей функции.
Function Get(k:Integer):Real;
Begin
If к Mod 2 = 0
Then Get:=(0nX[k Div 2]*1.0+OnX [k Div 2+1])/2

6. Избранные олимпиадные задачи по программированию
341
Else Get:=OnX[k Div 2 + 1];
End;
Результат вызова функции Get на множестве граничных
точек из нашего примера представлен во 2-м столбце таблицы
6.9.
Таблица 6.9
! *
1
2
I 3
4
5
6
I 7
8
9
10
L υ.,
Get(k)
0
(0*1.0+10)/2=5
10
(10*1.0+15)/2=12.5
15
(15*1.0+15)/2=15
15
(15*1.0+20)/2=17.5
20
(20*1.0+30)/2=25
30
Atln(Get(k)) \
True
True ι
False ,
False
True
True
True
False
False
True |
True J
Функция Atln дает истину или ложь в зависимости от того,
принадлежит или нет точка прямой результирующему
множеству. Ее вид:
Function Atln(x:Real):Boolean;
Begin
Numb:=0;{*Номер обрабатываемого символа
в выражении.*}
Atln:=Expr(x);{^Перенесем очередной раз тяжесть
на следующую функцию (не будем пока ее
рассматривать) - вычисления выражения, это
позволит нам до конца выяснить отношения с
процедурой WriteRes.*}
End;
Итак, основной алгоритм обработки заключен в процедуре
WriteRes.
Procedure WriteRes;
Var a,b:Integer;
i:Integer;
Begin
i:=l;

342
6. Избранные олимпиадные задачи по программированию
While (i<=N*4-l) And (Not Atln (Get (i) ) ) Do
Inc(i); { *Пропускр.ем граничные точки до тех пор,
пока не дойдем до точки, принадлежащей
результирующему множеству.*}
While i<=N*4-l Do
Begin
a:=i;{*Левая граница интервала из результирующего
множества.*}
While (i<=N*4-l) And Atln(Get(i)) Do Inc(i);
{^Пропускаем точки, принадлежащие
результирующему множеству.*}
b:=i;{*Правая граница интервала.*}
SayRes(a,b)/{*Выводим интервал. Процедура
не приводится.*}
Inc (i) ;
While (i<=NM-l) And (Not Atln (Get (i) ) ) Do
Tnc(i); {*Снова пропускаем граничные точки до
тех пор, пока не дойдем до точки, принадлежащей
результирующему множеству.*}
End;
End;
Закончим рассмотрение. Осталось уточнить процедуру
SayRes — вывода найденного интервала и вычисления
выражения Ехрг при конкретном значении х, а также основной
алгоритм и ввод данных.
22. Дана последовательность, состоящая из нулей и единиц.
Требуется найти N (0<iV<20) битовых подпоследовательностей
длиной от А до Б (0<А<В<12) включительно, которые
встречаются в исходной последовательности наиболее часто.
Входные данные. Файл input.txt (см. рисунок 6.31) содержит
данные в следующем формате. В первой строке — число А, во
второй — Б, в третьей — число N, в четвертой —
последовательность символов 0 и 1, заканчивающуюся символом 2.
Примечание
Размер входного файла не превышает 2-х мегабайт.
Выходные данные. В файл output.txt (см. рисунок 6.31)
записываются не более N строк, каждая из которых содержит
одну из N наибольших частот вхождения и соответствующие ей
подпоследовательности. Строки располагаются в порядке
убывания частот вхождения и имеют следующий вид:
частота подпоследовательности подпоследовательность ...
подпоследовательность,

6. Избранные олимпиадные задачи по программированию
343
где частота — это количество вхождений указанных далее
подпоследовательностей. Подпоследовательности в каждой строке
должны располагаться в порядке убывания длины. При равной
длине — в порядке убывания их числового значения. Если в
последовательности встречается менее N различных частот,
выходной файл будет содержать меньше N строк.
I Пример. j
ι input.txt
\1
110
1010100100100010001111011000010100110011110000100100111100100000002
output.txt I
|23 00 I
|15 10 01 I
12 100 I
11 001 000 11 I
10 010 |
|8 0100
|7 1001 0010 |
|6 0000 111 |
5 1000 110 011 I
4 1100 ООН 0001
Рис. 6.31
Указание. Входной файл очень большой. Следует провести
обработку за один его просмотр.
Количество различных подпоследовательностей не так
велико, как кажется. Их 8191 (21+22+23+...+212-213-1=8191) и это
путь к реальному решению задачи. Введем массив D для
хранения частоты встречаемости каждой подпоследовательности.
Обрабатывая разряд за разрядом исходной последовательности,
будем добавлять по единице к соответствующему элементу D.
Ниже в таблице 6.10 приводятся результаты обработки первых
10 разрядов из примера, приведенного в условии задачи
(единственное отличие — А считается равным 1). В первом столбце
указана длина подпоследовательности, во втором — номер
элемента массива D, в третьем — соответствующая
подпоследовательность, далее номер обрабатываемого разряда и в последнем
столбце — результат обработки.

344
6. Избранные олимпиадные задачи по программированию
Таблица 6.10
L
1
L 2
3
|
I
:4
—
|
I
:
i
I
|
I 5
Λ/~]
Ι 1
2
0 0 | 1 |
1 ί 1 ί i 1
2
00
3 ' 01
4
~5 Ι
6
7
8
9
10
11
12
13
10
11
000
001
010
011
100
101
110
111
14 | 0000
15 0001
16 ! 0010
17 0011
18
19
20
21
22
0100
0101
0110
0111
1000
3
2
4
! 2
ι
Ι 1 ! 2
ι
1
ι
1 !
ι
1
!
! !
ι
ι
!
23 | 1001 Ι
24
25
26
27
1010
1011
1100
1101
28 ! 1110
29 1111
30 00000
!
12 4094 0...0
I
1
1
!
5
6
3 4
1
2
2
1
!
'
ι
i
1
1
7
8
9
5 ί 6
3 .
3
1
3
3
ι
1
2
ίο | ...
:
4
4
Γ~Τ
2
!
ι
|
i
!
24- -
Ι ' ι
ι
1 ;
2
2
Γ^Ί
39 |
26
23 i
15
15
11 !
11 !
11 I
10 |
5
12
3
5
6 I
6
4
7
4
8 I
2 I
2 !
5
7 [
2 I
1 '
4
I 1 !
'з !
h 1
I
|
I
. ■
После того, как сформирован массив D, остается найти
первые N максимальных значений и вывести затем
соответствующие подпоследовательности. Остановимся на ключевых
моментах обработки.

6. Избранные олимпиадные задачи по программированию
345
Разумно в массиве констант определить индексы для D,
которые определяют первые последовательности заданной длины,
что мы и сделаем.
Const Rt:Array[0. .13] Of Integer= (0, 0, 2, 6, 14,
30, 62, 126, 254, 510, 1022, 2046, 4094,
8190);{*Rt[i] определяет, с какого
номера начинаются последовательности
длины i . *}
МахВ=12;
MaxN=21;
Var D: Array[0..8190] Of Longlnt;
Α, Β, Ν: Integer;
При обработке очередного символа требуется вычислять
последовательности, а лучше их номера, образуемые
предыдущими символами и текущим символом из входной строки. Как это
сделать?
Пусть в массиве Sold хранятся номера последних
обработанных подпоследовательностей, например (0, 1, 1, 5, 5).
Обработана следующая часть исходной последовательности — 0101, и
мы обрабатываем символ Ό' (Значение В равно 4, поэтому 5
элементов в массиве Sold). Что это значит (вспомните о массиве
Rt)? В Sold хранятся текущие смещения, получаемые из
последних символов входной строки, относительно первых
констант заданной длины в массиве D. Так, первая единица
означает, что последней была обработана последовательность Ί',
находящаяся на первом месте в своей группе
последовательностей. Вторая единица — первая последовательность длины 2,
т. е. '01' (начинаем отсчет в каждой группе с нулевого
индекса). Первая пятерка — обрабатывалась последовательность
длины 3 с пятого места, т. е. '101'. Последняя пятерка —
обрабатывалась последовательность длины 4 с пятого места, т. е.
Ό101'.
Еще раз повторим. Подпоследовательности:
• длины 1 имеет 1-й номер, начиная с 0 (0+1=1 и
соответствует последовательности Ί' в массиве D);
• длины 2 — 1-й номер (2+1=3 и соответсвует
последовательности '01' в массиве D);
• длины 3 — номер 5 (6+5=11 и соответствует
последовательности '101' из таблицы);
• длины 4 — 5-й номер (14+5=19 и соответсвует
последовательности '0101' из таблицы).

346
6. Избранные олимпиадные задачи по программированию
Переходим к вычислению новых номеров при обработке
очередного символа Ό' из входной строки:
• длины 1 - 0x2+0, 0-й номер;
• длины 2 - 7x2+0, подпоследовательность '10' имеет 2-й
номер;
• длины 3 - 7x2+0, подпоследовательность '010' имеет 2-й
номер;
• длины 4 - 5*2+0, подпоследовательность '1010' имеет
10-й номер
и массив Sold имеет вид: (0, 0, 2, 2, 10). Обрабатываем
следующий символ Ό'.
• длины 1 - 0x2+0, 0-й номер;
• длины 2 - 0x2+0, 0-й номер;
• длины 3 - 2x2+0, 4-й номер;
• длины 4 - 2x2+0, 4-й номер.
Результат Sold — (0, 0, 0, 4, 4). Подпоследовательности Ό' и
'00' находятся на нулевых местах. Подпоследовательности
'100' и '0100' на четвертых местах в своих группах. Проверьте.
Откуда берем цифры выше по тексту, выделенные курсивом?
В таблице 6.11 приведено изменение значения элементов
массива Sold при обработке первых 10 разрядов
последовательности, приведенной в условии задачи.
Таблица 6.11
1 № символа
! 1
I 2
3
4
5
| "" ~6 "
7
8
I 9 "
L_ ю
Символ
0 _|
7 1__ ~\
0
1
0
о"
1
0
1 о ~"
1
Sold
|_0, 0,-1,-1,-1 |
0,1,1,-1,-1 !
0,0,2,2,-1 I
0,1,1,5,5 j
0,0,2,2,10
0,0,0,4,4 1
0,1,1,1,9
0,0,2,2,2
0,0,0,4,4 |
0,1,1,1,9 |
Procedure Solve;
Var: nch: Char;
Sold,Nw:Array[0..MaxB] Of Integer;
i:Integer;
Begin
FillChar(Nw, SizeOf(Nw), 0) ;
For i:=l To MaxB Do Sold[i] :=-l;
Sold[0]:=0;

6. Избранные олимпиадные задачи по программированию
347
Read(nch);
While ncho'2 ' Do
Begin{*Пока не прочитали последний символ.*}
For i :=1 To В Do
Begin
If Sold[i-l]<>-l
Then
Begin
Nw[i]:=Sold[i-l] *2 +
Ord(nch)-Ord('0') ;
If (i>=A) Then Inc(D[Rt[i] +Nw[i]]);
{^Прибавляем единицу к соответствующему
элементу массива D.*}
End
Else Nw[i]:=-l;
End;
Sold:=Nw;{^Запоминаем вычисленную
последовательность номеров.*}
Read(nch);{*Читаем следующий символ.* }
End;
End;
Приведем еще одну вспомогательную процедуру. Мы
работаем с номерами последовательностей, а на заключительном
этапе требуется сама последовательность. Этот перевод
осуществляется с помощью следующей простой процедуры.
Procedure SayW(num: Integer);{*По номеру
подпоследовательности вычисляем ее вид.*}
Var i, j: Integer;
s: String;
Begin
i:=MaxB;
While (i>0) And (Rt[i]>num) Do Dec(i);
{^Определение длины.*}
num:=num - Rt[i]; s:='';
For j :=0 To i-1 Do
Begin
s:=Chr(num Mod 2 + Ord ( ' 0' ) ) + s;
num: = num Div 2;
End;
Write (' ' , s) ;
End;

348
6. Избранные олимпиадные задачи по программированию
23. Даны «цепочки» из нулей и единиц одинаковой
(большой) длины. Над ними можно выполнять поразрядно операции
NOT, AND и OR.
Таким образом: OR(a,b)=NOT(AND(NOT(a),NOT(b))).
Написать программу, которая вводит натуральное число N
(iV<1995), четыре цепочки а, Ь, с, и d длины N и определяет:
• можно ли последовательным применением
перечисленных операций получить d из а, Ъ и с;
• при удовлетворительном ответе строит нужную
последовательность операций (достаточно одной
последовательности).
Пример 1. Для iV=6, α=011000, b=111010, c=010001 и
d=100010 вывод программы может быть следующим:
• на первый вопрос — «Да»;
• на второй вопрос — AND(NOT(a),OR(bta)).
Пример 2. Для iV=6, α=0110000, b=l 11010, с=010001 и
d=000010, ответ на первый вопрос отрицательный.
Указание. Если рассматривать разрядные «срезы» цепочек
а, Ъ и с, то различных всего восемь. Это наводит на мысль о
том, что алгоритм обработки должен быть независим от длины
цепочек, естественно, после их какой-то первоначальной
обработки.
Поясним это утверждение на примерах.
Пусть:
а=11111111 01010101 10101010
Ь=10 10 10 10 00110011 00001111
с=010 10 10 1 00001111 11110000
2 «среза» 8 «срезов» 4 «среза»
сЮ 10 1010 1 10100101 11011010
Из этого факта следует, что цепочки при предварительной
обработке необходимо «сжать». Это первое. Кроме того,
очевидно, что если одному значению разрядных срезов (срезы по
порядку различные) цепочек а, Ъ и с соответствуют различные
значения в соответствующих разрядах цепочки d, то на первый
вопрос задачи имеется отрицательный ответ — «из одних и тех
же данных невозможно получить два различных результата».
Так, для третьего примера ответ —«Нет», первому и третьему
разрядным срезам соответствуют различные значения в
соответствующих разрядах цепочки d. Итак, предположим, что мы
умеем сводить наши длинные цепочки (а, Ь, с и d) к цепочкам с
длиной не более восьми разрядных срезов и решать первую
часть задачи. Что из этого следует? Количество различных це-

6. Избранные олимпиадные задачи по программированию
349
почек длины не более 8 — 256. Это первое. И второе, какие бы
операции над цепочками а, Ъ и с мы ни выполняли, наш
результат — это одна из 256 цепочек. Значит, необходимо
организовать перебор вариантов не по различным
последовательностям операций (NOT, AND и OR), а по результатам этих
операций. А это уже только техника перебора и не более.
Приведем часть структур данных, которые, на наш взгляд,
соответствуют решаемой задаче.
Const Мах=25б;
Ch=Array[l. .3] Of Char= ('а', Ъ','с') ;
Type Action=Record
operation: 0..3;{*0 - нет операции; 1 -
NOT; 2 - OR; 3 - AND.*}
opl,op2:Word;{*Номера операндов - индексы
элементов в массиве типа А.*}
result:Byte{*Результат данной операции.*}
End;
Var A: Array[0..Max] Of Action;
cnt,oldcnt:Word;{*Счетчики числа записанных
элементов в массив А.*}
ok:Boolean;
Первые четыре элемента массива А описывают исходные
данные задачи после операции сжатия — значения полей operation,
opl, ор2 равно нулю, A[0].result=d, A[l].result==at A[2].result=b
и A[3].result=c.
В качестве примера приведем одну из процедур — вывода
результата. Входным параметром является номер (индекс)
элемента массива А — первая операция, которая имеет результат,
равный d.
Procedure Out(p:Word);
Begin
With A [p] Do
Case operation Of
0: Write(Ch[p]);
1: Begin Write(' NOT ');Out(opl);End;
2: Begin Write('(')/Out(opl);Write (' OR ');
Out(op2);Write(')');End;
3: Begin Write С О;Out(opl);Write С AND ');
Out(op2);Write(')');End;
End;
End;

350
6. Избранные олимпиадные задачи по программированию
И основной алгоритм.
Begin
<сжать исходные данные>;{^Результат - первые 4
элемента массива А и логическая переменная, в которой
фиксируется признак отсутствия решения.*}
If <нет решения>
Then <вывод сообщения>
Else
Begin
cnt:=3;ok:=False;
Repeat
oldcnt:=cnt;
<Перебор>;
Until (oldcnt=cnt) Or ok;
End;
End;
24. Заданы две строки An В длины N (l<iV<100), состоящие
из символов 0 и 1 (двоичные слова)*. Допускается следующее
преобразование строк. Любую подстроку А или Б, содержащую
четное число единиц, можно перевернуть, т. е. записать в
обратном порядке. Например, в строке 11010100 можно
перевернуть подстроку, составленную из символов с 3-й по 6-ю
позиции. Получится строка 11101000.
Две строки считаются эквивалентными, если одну из них
можно получить из другой с помощью описанных преобразований.
Написать программу, которая:
• определяет эквивалентность заданных
строк А и В;
• если строки эквивалентны, предлагает один
из возможных способов преобразования
строки А в строку В.
Входные данные расположены в файле с
именем input.txt (см. рисунок 6.32). В первой строке
файла содержится число N. Следующие две
строки содержат слова А и В соответственно. Слова
записаны без ведущих и «хвостовых» пробелов.
Выходные данные. Результат работы
программы выводится в файл с именем output.txt (см.
рисунок 6.32). Если заданные слова не эквивалент- Рис. 6.32
Задачу предложил для одной из областных олимпиад по информатике
Виталий Игоревич Беров.
Пример.
input.txt |
9 |
100011100
ooioiiooi!
!
output.txt Ι
yes j
6 9
3 8 I

6. Избранные олимпиадные задачи по программированию
351
ны, то выходной файл должен содержать только сообщение по.
Если слова эквивалентны, то в первую строку выходного файла
нужно вывести сообщение yes, в последующие —
последовательность преобразований слова А в слово В. Каждое
преобразование записывается в отдельной строке в виде пары чисел i, у
(разделенных пробелом), означающей, что переворачивается
подстрока, составленная из символов с номерами /, Н-1, ..., у.
Указание. Основная идея решения задачи формулируется
следующим образом. На множестве всех слов W следует
выделить подмножество S (SczW), такое, что для любого слова t^W
можно указать эквивалентное ему слово reS.
Алфавит и слова у нас заданы, преобразования тоже.
Осталось определить множество S, свести каждое слово к
представителю из множества S, и если представители совпадают, то
слова эквивалентны.
Из каких слов состоит S? Слов вида 11... 100...0100...О,
причем как первая группа единиц, так и первая группа нулей, а
также следующая единица (слово из одних 0) могут
отсутствовать. Заметим, что вывод преобразований, в случае
эквивалентности слов, чисто техническая деталь. Она требует
дополнительной структуры данных (массива) для запоминания значений
i и у при каждом перевертывании.
Другая схема решения (автор приводит рассуждения одного
из восьмиклассников, решавших данную задачу). Как обычно,
ребенок вначале рисует, рисует примеры слов и
преобразований над ними. Попытаемся воспроизвести его рисунки. В
таблице 6.12 столбцы с заголовком «?» — это уже выводы из
рисунков.
Таблица 6.12
П№
1
2
П3
4
! 5
! 6
ί 7
! в
! 9
i 10
I 11
слово
1111000010
11111001
0000001000
10010001100
11000100100
11100100000
0100101101
1001001101
1100100101
1110010001
1111000100
число 1
5
6
1
4
4
L___ 4 __
5
5
5
5
5
?
4
0
6
5
5
5
3
3
3
3
3
? Ί
ι Ί
2
3
2 I
2
2 1
2_J
2 Π
2 J
2
2_j

352
6. Избранные олимпиадные задачи по программированию
Его вывод заключается в том, что количество нулей после
четного числа единиц (4-й столбец) и после нечетного числа
единиц (5-й столбец) в слове постоянно — не изменяются в
процессе преобразования слов (строки таблицы с номерами 4-6 и
7-11). После этого он пишет небольшой фрагмент подсчета этих
чисел (сразу после их ввода)
cnt:=0;
chl:=0;ch2:=0;
For i:=l To Length (S) Do
If S[i]=,01 Then
If cnt Mod 2 = 0 Then Inc(chl) Else Inc(ch2)
Else Inc (cnt);
и выписывает результат — слово после его приведения.
Нулевая позиция в слове считается при этом четной, например
числа 1, 5 (5 нулей после четного числа единиц — нулевого), 4
(4 нуля после нечетного числа единиц) однозначно определяют
слово 0000010000.
Обоснуем результат рассуждений. Инвариантом
преобразования является знакочередующаяся сумма вида:
H-iyxa^,
где i — номер единицы, а at — номер позиции / единицы.
Схема доказательства. Обозначим через s номер позиции в
подстроке, соответствующий центру переворачиваемой
подстроки. Пусть χ — номер позиции до «переворота», у — номер
этой позиции после операции «переворота». Очевидно, что
(x-H/)/2=s, т. е. y=2s-x, или ai-^2s-ai.
Количество элементов в сумме четно, знаки чередуются и
Z(-iyxa.=Z(-l)/x(2s-a/).
Поэтому после ввода слов следует подсчитать количество 1 в
каждом из них и суммы указанного типа. Если они совпадают,
то слова А и В эквивалентны.
Например, для строки 0101 сумма равна
(-l)xx2 +(-1)2χ4=2,
после переворачивания — 1010, сумма —
(-1)1х1+(-1)2хЗ=2.
Они совпадают, строки эквивалентны. Для примера (110100
и 110001) эти суммы равны -3 и -5, строки неэквивалентны.

6. Избранные олимпиадные задачи по программированию
353
9
101010011
Дополним задачу при ограничении l<iV<60. Необходимо
найти количество слов, эквивалентных заданному слову А.
Входные данные расположены в файле с име- . ,
нем input.txt (см. рисунок 6.33). В первой строке ! Пример. j
файла содержится число N. Следующая строка ι input.txt
содержит слово А, записанное без ведущих и
« хвосг овых » пробелов.
Выходной файл с именем output.txt (см. рису-
с ооч ; output.txt
нок о.33) должен содержать искомое количество
слов. I 30 j
Задача на умение использовать динамические
схемы подсчета, плюс — «длинная»
арифметика.
Рассмотрим первую часть задачи. Мы подсчитали
количество 0 после четного числа 1 в слове и после нечетного. Из
вышеизложенного ясно, что перемещение 0 из той или другой групп
по соответствующим позициям (после четного числа единиц
или после нечетного) приводит к эквивалентным словам.
Приведем пример для пояснений. Пусть есть слово
101010010. Количество нулей после всех четных единиц в
сумме равно 2, после нечетных — 3. Количество позиций, на
которые можно переставлять нули из первой группы, равно 3, из
второй — 2.
Выделим их — lOlOlOOlO.
Переставляем «крупные» нули:
101100100, 101001001, 001011001, OlOlOlOOl, OlOllOOlO
(подчеркнута та подстрока, которая переворачивается, но в
данном случае это уже не принципиально).
Переставляем «мелкие» нули:
lOlOlOOlO. llOlOOOlO, ΙΟΟίΟΐΟΐΟ, lOOOlOllO.
Найдем для каждого случая количество эквивалентных
слов, эти значения необходимо перемножить, результат —
ответ задачи. Для нашего примера первое значение 6, второе —
4. Ответ — 24.
Возвращаясь к предыдущим рассуждениям, подсчитаем
инварианты, например, для двух последних строк:
(-1)1χ1+(-1)2χ4+(-1)3χ6+(-1)4χ8=-1+4-6+8=5
и (-lJ^l+i-l^xo+i-^xT+i-l^xS^-l+o-T+e^.
Совпадают, строки эквивалентны.
Приведем текст процедуры, назовем ее Find, параметрами
которой являются числа k и I — число позиций и число нулей,
результат — число эквивалентных слов типа Longlnt.

354
6. Избранные олимпиадные задачи по программированию
Пусть найдено решение для t позиций, т. е. определено
число способов размещения для всех количеств нулей от 1 до I.
При (ί-Μ)-ή позиции решение получается очевидным
способом — в позиции с номером £+1 размещаем определенное
количество нулей, в позициях с номерами от 1 до t — оставшиеся
(они уже подсчитаны). Один из возможных вариантов
реализации этой схемы приведен ниже, разумеется, это не
единственный способ.
Function Find (k,1:Integer) :LongInt;
Var Q:Array[1..2,0..MaxN] Of Longlnt;
i,j:Integer;
Begin
Fill Char(Q,SizeOf (Q),0);
For j : =0 To 1 Do Q [ 1,j] :=1;
For i :=1 To k-1 Do
Begin
Q[2,0]:=1;
For j:=l To 1 Do Q[2,j] :=Q [1, j ]+Q [2, j-1] ;
Q[l]:=Q[2];
End;
Find:=Q[l,l] ;
End;
25. Алгоритм Евклида для нахождения наибольшего общего
делителя двух целых чисел хорошо известен и изучается в
курсе основ информатики. Рассмотрим задачу повышенной
сложности, идея решения которой основана на алгоритме Евклида.
Даны натуральные числа ρ и q. Разработать программу
определения последовательности натуральных чисел наибольшей
длины N, такой, что значение суммы любых ρ идущих подряд
элементов этой последовательности было бы положительно, а
любых q — отрицательно*.
Разумно предположить, что последовательность имеет
некоторую регулярную структуру, т. е. она не случайна. И эту
регулярность следует найти.
Можно считать, что значение N>max(ptq). Случай, когда
q=lp или p^tq (одно из чисел делится нацело на другое)
отсекается моментально. Действительно, пусть q=lp и построена
последовательность а19 α2, ..., αΝ.
Автор благодарит Александра Николаевича Семенова за помощь в разборе
данной задачи.

6. Избранные олимпиадные задачи по программированию
355
Из равенства
q ρ 2р 1*р
Σα.· =Σα. + Σα<+···+ Σα.· >0
ί=1 / =1 г-p + l t=(Z-l)*p+l
следует противоречие.
Сделаем два предположения: q>p (иначе просто меняем
знаки у элементов последовательности); ρ и q взаимно просты, т. е.
НОД(р,д)=1. Затем результат обобщим.
Действия учащегося, ум которого не обременен техникой
доказательств, выглядят достаточно просто — он пытается
прорисовать последовательности. Попытаемся воспроизвести эти
действия с помощью следующей таблицы 6.13 для
произвольных значений ρ и q (на последний столбец таблицы пока не
обращаем внимания).
Таблица 6.13
Г~№
Г1
I 2
3
4
5
6
I 7
8
Q
6
11
7
12
8
13
9
14
Ρ
5
5
5
5
5
5
5
5
Схема Евклида
6"=1*5++Г
1Г=2*5++Г
7~=Г5++2~
5+=2*2~+1+
12"=2*5++2"
5"""=2*2~+1 +
8~=1*5++3~
5+=1*3~+2+
3~=1*2++Г
13~=2*5++3~
5+=ГЗ~+2+
3~=1*2++Г
9~=1*5++4~
5+=1*4~+1+
14"=2*5++4"
5+=Г4"+1 +
Последовательность
+_!___?
+ +_| ?
+-+-++-|+-+?
+-+-++-+-++-|+-+?
_+—+_+_|_+_?
-+—+-+—+-+-|-+-?
+++-++++-|+++?
+++-++++-++++-|+++?
L
9
14
10
15
11
16
12
17
9 |
-2,9 |
-3,13
-7,5
-10,7
-5,8
-7, 11
-11,3
-15,4
Первая строка — #=6, р=6. Схема Евклида дает условный
символ «-» (назовем его базовым). Конструируем из него
последовательность. Сумма пяти элементов должна быть
положительна. Добавляем другой символ — « + ». Сумма шести
элементов — отрицательна, поэтому добавляем «-». В таблице 6.13
эта часть отделена от остальной символом « | ».
Что происходит дальше? Три базовых элемента (повторяют
начало) не меняют структуры исследуемого нами объекта. В
позицию, отмеченную «?», мы не можем записать ни «-», ни
« + ». Запись «-» на эту позицию делает последнюю сумму из
пяти элементов отрицательной. Запись « + » — сумму из шести
последних элементов положительной.

356
6. Избранные олимпиадные задачи по программированию
Чем отличается вторая строка таблицы 6.13?
Последовательность « l·» повторяется два раза (множитель 2 в схеме
Евклида).
Третья строка таблицы более интересна. Из базового
элемента мы конструируем последовательность из двух элементов
(сумма их отрицательна). Из нее мы получаем
последовательность длины пять и только затем длины семь, добавляя ранее
полученную последовательность длины два.
Из этих же экспериментов определяется и максимальная
длина L - L=(p+q-2) при Н0Д(р,д)=1.
Действия математика (на наш взгляд) несколько
отличаются от тех, что приведены. Он, быть может, тоже рисует
последовательности, но в конечном итоге его результат выглядит
иначе. Следует предположение о том, что L>p+q-2. Затем
выполняются рассуждения по индукции, получается
противоречие, и следствием является доказанный факт о том, что
L<p+q-2.
Итак, пусть мы получили последовательность (регулярную!)
из « + » и «-». Требуется определить, какие натуральные числа
соответствуют им (последний столбец таблицы). Должна быть
зависимость от значений ρ, q и соотношения количеств «+» и
«-» на различных периодах последовательности.
Обозначим через ivt число « + » на периоде tp тогда
отношение числа «-» к числу « + » выражается (t-w^/w^ Вернемся к
таблице 6.13 и попытаемся определить, как связаны эти
отношения на соседних периодах.
После некоторых усилий устанавливается следующий факт:
(t-wj/w^it^-w^/w^
при четном значении i и «>» при нечетном /.
Доказательство истинности этого факта математик проводит
методом индукции. Что из него следует? Пусть tx=q, t2=p и i=l.
Мы имеем неравенство
(q-w1)/w1>(p-w2)/w2 (i — нечетно).
Средневзвешенное чисел в правой и левой частях неравенства
принадлежит интервалу, определяемому этими числами, т. е.
(q-wx)/wx>(q+p-wl-w2)/(wx+w2)>(p-w2)/w2.
Заменим « + » на число x=p+q-wx-w2 и «-» на число
y=-(wl-\-w2). Из последнего неравенства получаем, что сумма
любых ρ чисел, идущих подряд, равна
w2xx+(p-w2)xy>0,

6. Избранные олимпиадные задачи по программированию
357
а сумма любых q чисел — равна
w;1xx+(g-w;1)xi/<0.
После этого можно поставить точку в рассуждениях и
перейти к написанию программы.
А случай НОД(р,#)=^>1? Для значений p/d и q/d мы можем
построить наш объект. Добавим между каждыми элементами
построенной последовательности, а также справа и слева по
(d-Ι) нулей. Условия положительности и отрицательности
сумм выполняются, а длина равна
(p/d+q/d-2)*d+d-lf или p+q-d-1.

7. Заметки о тестировании
программ
При написании этой главы на память приходит один пример
из собственной практики автора. После окончания
университета автору пришлось разрабатывать программы (а это было
начало 80-х годов прошедшего столетия) для
специализированных вычислительных комплексов. В силу определенной
живости натуры автор быстро стал ведущим разработчиком и
отвечал за весь цикл разработки программ и их внедрение,
будучи заместителем генерального конструктора по этим
вопросам. Одну программную ошибку в комплексе, прошедшем все
испытания и принятом заказчиком, автору пришлось искать не
менее полугода.
Среди решаемых задач комплекса было построение связных
областей (от любой точки области до любой точки можно
попасть по точкам связной области) в четырехмерном
пространстве параметров. Эти области изменялись во времени, одни точки
области исчезали, другие добавлялись, области могли
объединяться и наоборот. Вот такую динамичную картинку
требовалось обрабатывать в реальном масштабе времени, причем поток
входной информации (подлежащий обработке) был весьма
значительным.
Периферийных устройств не было. Программы хранились в
ПЗУ, и каждое изменение требовало его
перепрограммирования. Для того, чтобы что-то просмотреть, необходимо было
остановить соответствующий процессор и с помощью
тумблеров набрать адрес регистра или ячейки, содержимое которых
после этого отображалось с помощью диодов. Ошибка
проявлялась нестабильно, только на определенных входных потоках,
причем в одних случаях происходило зацикливание (не
обязательно в одном месте), в других — бессмысленное
«размножение» связных областей. Ошибка проявлялась достаточно редко,
и это, а также то, что знание комплекса разработчиками было
доскональное, позволило, видимо, пройти все испытания.
По характеру мигания светодиодов определялось место
работы программы, устройства. Некоторые сбои устранялись
простым ударом кулака по определенному месту соответствующей
стойки и т. д. Ошибка оказалась достаточно простой.

7. Заметки о тестировании программ
359
В том случае, когда связные области в процессе изменений
превращались в одиночные (или почти одиночные) точки и
располагались в пространстве параметров примерно так, как
черные клетки на шахматной доске, нехватало места в
оперативной памяти для хранения их описания. Контроля на выход за
пределы соответствующих структур данных не было (примерно
так же, как выход индекса за пределы массива). Никто не
предполагал такой ситуации, по всем предварительным
расчетам ее не могло быть, однако... было получено огромное
удовлетворение от проделанной работы.
Появление книги Э. Йодана [12] и др. было воспринято
автором как должное, ибо нечто подобное он уже делал на
практике, когда, например, в режиме «сухого плавания» (комплекса
под рукой не было) искал описанную выше ошибку.
Приверженность технологии нисходящего проектирования
программ осталась неизменной все эти годы. Дальнейшее
развитие программирования, как науки, так и отрасли
производства, только подтвердило правильность революционных идей,
высказанных в свое время профессором Э. Дейкстрой.
7.1. О программировании
Программирование — теоретическая и практическая
деятельность по обеспечению программного управления обработкой
данных, включающая создание программ, а также выбор
структуры и кодирования данных — классическое определение.
Попробуем определить несколько иначе, более конструктивно,
рассматривая то, чем занимается программист.
Есть задача или проблема. В первую очередь программист
должен определить возможность ее решения, выбирая
соответствующий метод. Затем разработать проект программы,
состоящий из алгоритма на каком-либо из языков программирования,
доказать правильность работы программы и предусмотреть
возможность ее изменения, внесения изменений на этапе
сопровождения. Таким образом, в укрупненном виде мы видим три
этапа:
• до программирования,
• программирование,
• после программирования.
Есть еще и четвертый этап. После того, как все казалось бы
сделано, ответить на вопрос — «а что если все не так?».
Только часть работы связана с выбором структур данных и
кодированием — использованием языков программирования.
Программирование есть, если так можно выразиться, инженер-

360 7. Заметки о тестировании программ
ная работа по конструированию некой целостной системы
обработки данных. Отличие программы, например, от некоторой
механической системы, в том, что число взаимодействующих
частей в программе настолько велико, что не поддается
никакому разумному объяснению и проверить работу этой
программной системы, перебирать все возможные способы
взаимодействия ее частей немыслимо даже на сверхбыстродействующих
компьютерах в разумные сроки.
Итак, выделим это положение: программа (назовем так по
традиции) — сверхсложная система. Где же выход при
создании таких сверхсложных систем, при достижении их
работоспособности? Видимо, только в технологиях, обеспечивающих на
выходе качественный и надежный продукт, важнейшим
элементом которых является умение тестировать программные
решения.
7.2. Практические рекомендации
Общие положения.
Практические рекомендации по написанию программ
основаны на технологии нисходящего проектирования.
О строгом математическом доказательстве правильности
работы обычно не может быть и речи при достаточно сложной
программе. Успешная трансляция не есть признак работающей
программы, а правильность работы на некотором наборе тестов
еще не означает, что программа всегда будет работать
правильно, — следует помнить, что различных комбинаций входных
данных бывает, как правило, бесконечно (или «практически»
бесконечно) много. Основная идея — не пытаться
программировать сразу. Пошаговая детализация автоматически
заставляет формировать понятную структуру программы. При этом
требуется отслеживать правильность детализации, создавая набор
контрольных точек и просчитывая значения данных в них.
Контрольные точки обычно проходятся при любых начальных
данных (как точка сочленения в графе).
Выбор представления данных — один из фундаментальных
аспектов разработки программы. Н. Вирт так определял
критерии этого действия:
• естественность, структуры данных обязаны «вытекать»
из специфики задачи;
• привычность, структуры данных выбираются так, чтобы
программирование приближалось к утверждению «как
говорю, так и пишу программу, ничего лишнего»;

7. Заметки о тестировании программ
361
• оптимальность, структуры данных выбираются так,
чтобы была возможность построения эффективного
алгоритма.
Например, решая задачу о построении каркаса
минимального веса в графе, естественно выбрать список ребер, а не
матрицу инциденций или матрицу смежности.
Примеры плохого программирования.
Приведем ряд примеров, которые не соответствуют
технологии структурного написания программ.
1. Следует придерживаться правила о том, что любой
фрагмент программного кода (алгоритма) должен иметь одну точку
входа и одну точку выхода (пусть даже в ущерб эффективности
использования памяти). Ниже приводится пример того, как
небольшой фрагмент имеет две точки выхода.
While <условие 1> Do
Begin
If <условие 2> Then Exit;
End;
Использование конструкции бесконечного цикла только
усугубляет ситуацию.
While True Do
Begin
If <условие 2> Then Exit;
End/
2. Искусственные приемы, как, например,
продемонстрированный ниже случай «насильного» выхода из циклической
конструкции типа For, приводят, при внесении изменений в
программу, к многочисленным и трудно устранимым
ошибкам.
For i :=1 To N Do
Begin
If <условие> Then i:=N+l;
End/

362
7. Заметки о тестировании программ
3. Увлечение параметрами при работе с процедурами и
функциями является «болезнью роста» при освоении технологии
нисходящего проектирования программ.
Type BArray=Array [1. .Ν] Of Byte;
Procedure Swap(Var В:BArray;i,k:Byte)/
Var χ:Byte;
Begin
x:=B[i];B[i]:=B[k];B[k]:=x;
End;
и вызов Swap(B,i,k) вместо следующего простого текста
процедуры:
Procedure Swap(Var у, ζ :Byte);
Var x:Byte;
Begin
x:=y;y:=z;ζ:=χ;
End;
и вызова Swap(B[i],B[k]).
4. Один профессиональный программист сказал автору в
частной беседе о том, что для него критерием подготовленности
выпускников высшего учебного заведения к работе является
понимание (глубокое) рекурсии и знание динамических
структур данных.
Procedure Generate;{*t - глобальная переменная*}
Begin
t:=t+l;
Generate;
t:=t-l;
End;
Логичнее выглядел бы следующий фрагмент (вопрос об
экономии места в стеке адресов возврата не ставится, оно есть и
точка).
Procedure Rec(t:Byte);
Begin
Rec (t + 1) ;
End;

7. Заметки о тестировании программ
363
5. Очень трудно убедить школьников в том, что если
переменная используется только в процедуре, то она и должна
определяться в этой процедуре, пусть и с дублированием
программного кода. Только через большое количество занятий,
после многочисленных ошибок приходит понимание факта.
Типичный пример такого написания программ приводится ниже.
Program
Var i,j:Integer;
Procedure A;
Begin
{Работа с переменными i, j};
End;
Procedure B;
Begin
{Работа с переменными i, j};
End;
{**}
Begin
{Работа с переменными i, j}
End.
Временная сложность(1).
Обычно на время решения задачи накладываются
определенные ограничения. Размерность задачи опишем величиной
N. Временная сложность алгоритма является линейной при
t~0(N), полиномиальной при t~0(№), где q равно обычно 2
или 3, и экспоненциальной при t~0(qN). Эффективными
являются алгоритмы первых двух типов.
Обычно подсказка о том, какой существует алгоритм
решения, содержится в формулировке задачи (имеется в виду олим-
пиадный вариант). Если дано N, большее 50, то следует искать
быстрый алгоритм, в противном случае сосредоточиться на
эвристиках, сокращающих традиционный перебор с возвратом.
Ответим на вопрос: как оценить время работы программы в
среде Турбо Паскаль?
Обычно используют тот факт, что к ячейке с абсолютным
адресом $40:$6С (назовем ее Timer) один раз в 1/18.2 секунды
аппаратно прибавляется единица (или один раз в каждые 55
миллисекунд).
Допустим, что программа должна работать 5 секунд
(зафиксировали время в ячейке с именем TimeTest). В начале работы
программы значение из $40:$6С запомнили в некоторой пере-

364
7. Заметки о тестировании программ
менной, например TimeOld. После этой подготовительной
работы в расчетной части программы осталось проверять условие
Timer-TimeOld > 18.2xTimeTest.
Если оно выполняется, то время решения задачи истекло.
Так как обычно перед завершением задачи требуется записать
в выходной файл результат (хотя бы промежуточный,
например наилучшее из найденных решений в переборной задаче), а
для этого требуется время, то условие пишут с учетом этого
факта
Timer-TimeOld > 18.2x(TimeTest-0.5).
Ниже приведен текст фрагмента, в котором считается
количество прибавления единицы к ячейке в зависимости от
времени, выделенного на работу программы.
Program TimeCheck;
Uses Crt;
Const N=5;
Var TimerrLonglnt Absolute $40:$6C;
TimeOld,TimeTest,L,i:Longlnt;
pp:Boolean;
Begin
ClrScr;
For i :=1 To N Do
Begin
TimeOld:=Timer;{Запоминаем значение таймера.}
pp:=True;
TimeTest:=i;{*Время решения задачи.*}
L:=0;
While pp Do
Begin {*Пока не истекло время,
отведенное на решение задачи.*}
Inc(L);{^Прибавляем единицу к счетчику.*}
If Timer-Time01d>18.2*(TimeTest{-0.5}) Then
Begin
pp:=False;
WriteLn(L);
End;
End;
End;
End.

7. Заметки о тестировании программ
365
Приемы контроля правильности работы программы.
Сформулируем ряд приемов, позволяющих избежать
простых ошибок в разрабатываемых программах.
1. Обычно формат входных данных задачи строго определен.
Если в формулировке требуется контролировать корректность
ввода данных, то следует выделить эту часть алгоритма в
отдельную процедуру(ы). Однако в последние годы от требования
проверки входных данных отказались (видимо, из-за
простоты) — они считаются корректными. Несмотря на это, после
ввода данных их следует сразу вывести и проверить, что
позволит избежать ошибок этого типа (на них обычно не обращают
внимания и только после значительных усилий возникает
вопрос — «а правильно ли в программе вводятся данные»).
2. Иногда полезно отслеживать (не в пошаговом режиме)
трассу работы определенной части программы. Так, при входе
в процедуру можно выводить ее имя и значения входных
параметров или выводить промежуточные данные в определенных
точках программы. К этому же приему относится и введение
дополнительных счетчиков, контролирующих прохождение
различных ветвей алгоритма.
3. Синтаксические ошибки устраняются обычно
моментально. Для поиска, если так можно выразиться, логических
ошибок первого типа в среде Турбо Паскаль рекомендуется вести
отладку с включенными директивами. Начало программы
после нажатия Ctrl+O+O выглядит следующим образом:
{$A+9B-j)+^^^-9G-j+,L+,N-9o-jp-,Q-M-,s+,T-y+9x+}
{$М 16384,0,655360}.
Изменение, например, R- на R+ позволяет контролировать
выход индексов за пределы массива.
Логические ошибки следующего уровня сложности связаны
обычно с тем, что задача была понята неверно, т. е. решена не
та задача, которая была поставлена. В этом случае лучше всего
«прогнать» решение на примере, просчитанном «вручную»
(обычно такой пример приводится в формулировке задачи).
Неверным может оказаться замысел алгоритма. Правильные
решения получаются не для всех исходных данных. Это,
вероятно, самый сложный тип ошибок и его рассмотрению посвящен
следующий параграф данной главы.
О тестировании программ.
Тест является совокупностью исходных данных для
проверки работоспособности программы. Одного теста обычно
недостаточно для проверки каждой ветви программы, и говорят о

366
7. Заметки о тестировании программ
системе тестов. Кроме того, с помощью тестов проверяются
количественные ограничения на исходные данные и временные
ограничения. Исходя из этого, разумно формировать систему
тестов, например, следующим образом:
первый тест должен быть максимально простым;
следующие тесты должны проверять вырожденные случаи
(например, при поиске решений квадратного уравнения
проверяются вырожденные случаи);
обязательно следует проверять граничные случаи (результат
описан как тип Integer, а значение превосходит 32767);
предельные тесты проверяют решение при наибольших
значениях входных параметров задачи, и, разумеется, требуется
постоянный контроль над временем выполнения программы
(при превышении ограничений по времени выбран не
эффективный алгоритм решения).
Автоматизация проверки.
Обычно в задаче имена входного и выходного файлов
определены. Постоянное изменение имени не очень рационально.
Рассмотрим, как выходить из данной ситуации.
Во-первых, создается директория для работы с программой,
и она является текущей в системе программирования Турбо
Паскаль. Программа ищет входной файл в текущей
директории и записывает в нее выходной файл.
Пусть есть следующая «варварская» программа — из файла
считываются два числа, их сумма записывается в выходной
файл. Кроме того, в программу вставлены не очень понятные
операторы. Однако они написаны, и с ними проводится отладка.
Program add;
Var a,b : Integer;
Begin
Assign(input,'input.txt'); Reset(input);
ReadLn(a,b);
Close(input);
While a=10 Do;
If a = 20 Then b := Round (a/0) ;
Assign(output,' output.txt'); Rewrite(output);
WriteLn(a+b);
Close(output);
End.
Создаем систему тестов (см. таблицу 7.1). В текущей
директории записываем файлы с каждым тестом (имена i.tst, где i —

7. Заметки о тестировании программ 367
номер теста) и результирующие файлы (имена i.ans, где i —
номер теста).
Таблица 7.1
j Имя входного
файла
I l.tst
2.tst
[ 3.tst
4.tst
[ 5.tst
Тест
25
4545
35
1010
20 0
Имя выходного
файла
l.ans
2.ans
3.ans
4.ans
S.ans
Результат
7 I
91 I
ft
8 i
20 ;
20 !
Переименование входных файлов в файл с именем input.txt
и пятикратный запуск программы при очевидных результатах
утомительно и не очень удобно. Требуется минимальная
автоматизация процесса тестирования программ.
Ниже приведен текст программы. Следует набрать и
сохранить его в файле Checker.dpr (текущей директории), а затем
откомпилировать, используя среду Delphi. После этого запустите
программу Checker.exe. Ее входными параметрами (они
задаются в командной строке) являются:
имя исполняемого файла (рассмотренный выше пример
следует откомпилировать в текущей директории, например, с
именем ту.ехе);
количество тестов;
ограничение по времени (в секундах).
Вид командной строки —
Checker.exe ту.ехе 5 2 (5 тестов, 2 секунды на тест).
Результат очевиден. Итак, имея программу Checker, мы
значительно упрощаем процесс отладки решений.
Program* Checker;
{$app.type console} -(^Консольное приложение.*}
uses Windows,SysUtils,Classes;
var SInf : StartUpInfo;{* Установки для
функции CreateProcess . * }
PInf : Process_Information;{^Информация
о созданном процессе.*}
TickCount : Longint;{* Количество миллисекунд.*)
Программа разработана студентом 4-го курса факультета информатики
Вятского государственного педагогического университета Московкиным
Алексеем Александровичем.

368
7. Заметки о тестировании программ
YourAnswer: TStringList;{*Ответ тестируемой
программы.*}
RightAnswer: TStringList;{^Правильный ответ.*}
FileName: String;{*Имя тестируемой
программы.*}
FeedBack: String;{^Результат тестирования.*}
TestCount: Integer;{^Количество тестов.*}
TimeLimit: Integer;{^Ограничение
по времени.*}
IsTimeLimit: Boolean;{*Индикатор окончания
лимита времени.*}
ExitCode: Cardinal;{*Код завершения
тестируемой программы.*}
i: Integer;
begin
FileName:= ParamStr(1);{*Первый параметр - имя
файла.*}
TestCoun:= StrToInt(ParamStr(2));{*Второй -
количество тестов.*}
TimeLimit:= StrToInt(ParamStr(3));{*Третий -
ограничение по времени.*}
for i:=l to TestCount do
begin
RenameFile(IntToStr(i) +' . tst','input.txt');
{^Переименовать входной тест в input.txt.*}
FillChar(SInf,SizeOf(SInf), 0);
SInf.cb:= SizeOf(PInf);{*Заполнить
структуру.*}
SInf.dwFlags:= STARTF_USESHOWWINDOW;
StartUpInfo
SInf.wShowWindow:= sw_Hide;{*Сделать окно
процесса невидимым.*}
CreateProcess(PChar(FileName),nil,nil,nil,
false,{*3апуск тестируемой программы.*}
CREATE_NEW_CONSOLE or NORMAL_PRIORITY_CLASS,
nil,
nil,SInf,PInf);
TickCount := GetTickCount;{*Запомнить время.*}
IsTimeLimit := true;
While ((TickCount+TimeLimit*1000) >-
GetTickCount)and IsTimeLimit do

7. Заметки о тестировании программ
369
if WaitForSingleObject(PInf.hProcess, 0) <>
WAIT_TIMEOUT ЪЬеп{*Ждать, пока программа
закончит работу или истечет тайм-аут.*}
IsTimeLimit := false;
if IsTimeLimit then
begin {*Если истек тайм-аут,
закончить работу программы.*}
TerminateProcess(PInf.hProcess, 0) ;
FeedBack := 'Time limit exceeded!';
{^Превышение лимита времени.*}
end
else
begin
GetExitCodeProcess(PInf.hProcess,ExitCode);
(^Получить код завершения программы.*}
if ExitCodeoO
then FeedBack := 'Run-time error!'
{*Если код завершения не равен нулю, то
ошибка времени выполнения.*}
else
begin
YourAnswer := TStringList.Create;
RightAnswer := TStringList.Create;
YourAnswer.LoadFromFile('output.txt' );
{*3агрузить файл с ответами тестируемой
программы.*}
RightAnswer.LoadFromFile(IntToStr(i)+ '.ans');
{*3агрузить файл с правильными
ответами.*}
if YourAnswer . TextORightAnswer . Text
then
Feedback := 'Wrong answer ...' {*Если
они не совпадают, то тест не пройден,*}
else
FeedBack := 'Ok.';{*иначе все в порядке.*}
YourAnswer.Free;
RightAnswer.Free;
end;
end;
RenameFile('input.txtf,IntToStr(i)+' .tst');
(^Переименовать входной тест.*}
Writeln ('Test '+IntToStr(i)+' : '+FeedBack);
{*Выдать результат теста.*}
end;

370 7. Заметки о тестировании программ
DeleteFile(' output.txt');{*Удалить ненужный
файл.*}
writeln('Completed ...');{*Выдать сообщение об
окончании.*}
Readln;
end.
7.3. Тестирование программы
решения задачи (на примере)
Рассмотрим следующую задачу.
Даны два квадратных клеточных поля (см. рисунок 7.1).
Размер клетки 1x1. Клетки поля закрашены в белый или
черный цвет. Совпадающая часть квадратов — это множество
клеток, имеющих одинаковый цвет. Она разбивается на какое-то
количество связных областей. Найти площадь наибольшей
связной области совпадающей части квадратов.
Пример
Наибольшая связная
область
(окрашен а в
черный цвет) имеет
площадь 4
Рис. 7.1
Описание квадратов хранится в текстовых
файлах (см. рисунок 7.2). Символ «1» во
входных файлах соответствует черной клетке, символ
«0» — белой. В выходном файле должно быть
одно целое число, равное площади наибольшей
связной области общей части.
Ограничения. Размер поля N в интервале от 2
до 1000. Время работы — не более 5 секунд.
Анализ и решение задачи. В идейном плане
задача очень простая. Ее суть сводится к следующему:
If <Клетка[i, j ] 1-го квадрата>=Клетке [i, j ]
2 квадрата
Then <Клетке[i, j ] результатам = 1
Else <KneTKa[i,j] результатам = О,
+ =
1-й квадрат 2-йквадрат Результат
| Пример.
\Photol.txt |
!4
! оюо
j 1000
liio I
j hoi |
• Photo2.txt
Ϊ4
от !
i 1011
jooio
ιοοοι
Ι Result.txt I
Рис. 7.2

7. Заметки о тестировании программ
371
а затем найти связную область с наибольшей площадью.
Проработав этот учебник до данной страницы, программное
решение представленное ниже, пишется за считанные минуты.
Структуры данных.
Const
Size = 100;{*Размер квадрата.*}
Dx: Array[1..4] Of Integer = (0, -1, 0, 1);
{^Вспомогательные массивы Dx, Dy
используются в волновом алгоритме обхода
связной области.*}
Dy: Array[1..4] Of Integer = (-1, 0, 1, 0);
Type
PhotoMatch = Array [L.Size, L.Size] Of Byte;
{*Для хранения результирующего квадрата.*}
Helper = Array [1..Size*Size] Of Integer;
{^Вспомогательный тип для хранения очереди
при обходе в ширину.*}
Var
PhotoM : PhotoMatch;{*Результирующий квадрат.*}
Ох,Оу: Helpers-
Result, TempRes,N: Integer;
Напомним алгоритм волнового алгоритма (п. 3.2).
Function Get(Const k,p : Byte): Integer;{*Обход
совпавшей части квадратов.*}
Var i, dn, nx, ny, up : Integer;
Begin
Ox[l] := k; Oy [ 1 ] : = p; dn : = 1 ; up : = 1 ;
(^Заносим координаты первой клетки
в очередь.* }
PhotoM [k,ρ]:=0;
Repeat
For i:=l To 4 Do
Begin
nx := Ox [dn] + dx [i]; ny := Oy [dn] + dy [i];
If (nx>0) And (ny>0) And (nx<=N) And (ny<=N)
And (PhotoM[nx,ny]=1)
Then
Begin{*Заносим в очередь.*}
PhotoM [nx, ny] := 0; Inc(up); Ox [up]:= nx;
Oy [up]:= ny;
End;
End;

372
7. Заметки о тестировании программ
Inc(dn);{*Переходим к очередному элементу
очереди.*}
Until с1п>ир;{*Пока очередь не пуста.*}
Get := up;{*Количество элементов в очереди равно
площади общей части.*}
End;
Процедура ввода данных.
Procedure Init;
Var photol, photo2: Text;
charl, char2 : Char;
x, у : Integer;
Begin
Assign (photol, 'photol.txt'); Reset(photol);
{*Входные файлы.*}
Assign (photo2, 'photo2.txt'); Reset(photo2);
ReadLn(photol,N);ReadLn(photo2,N);
For у : = 1 To N Do
Begin
For χ := 1 To N Do
Begin
Read(photol, charl); Read(photo2, char2);
PhotoM [x,y]:=Ord(charl=char2);{*Если
"закраска" совпадает, то ...*}
End;
ReadLn(photol); ReadLn (photo2);
End;
End;
Главная процедура.
Procedure Solve;
Var i, j,t :Integer;
Begin
Result:=0;
For i : = 1 To N Do
For j : = 1 To N Do
If (PhotoM[i,j]=l) Then
Begin
t:=Get(i,j);
If t>Result Then Result:=t;{*Площадь
наибольшей связной области.*}
End;
End;

7. Заметки о тестировании программ
373
Вывод результата.
Procedure WriteAnswer;
Var f: Text;
Begin
Assign (f , 'result.txt'); Rewrite(f);
Write (f, Result); Close(f);
End;
Основная программа.
Begin
Init;
Solve;
WriteAnswer;
End.
Итак, часть тестов, вне всякого сомнения, проходит, и есть
база для проведения экспериментов. Изменение значения
константы Size до требований задачи (даже до значения 200)
приводит к сообщению Error 22: Structure too large. He хватает
оперативной памяти. Напомним, что в среде Турбо Паскаль
для задачи выделяется порядка 64 Кбайт*.
Размерность задачи такова, что результирующее клеточное
поле хранить в оперативной памяти можно только с
использованием динамических структур, битовых записей, или еще
каким-нибудь оригинальным способом. А требуется ли хранить?
Возможна построчная обработка поля.
Пусть обработана строка. При обработке следующей строки
возможны ситуации (см. рисунок 7.3):
область 1 продолжается в следующей строке;
область 2 закончилась; области 3 и 4 «сливаются» в одну;
область 5 только начинается.
Рис. 7.3
В настоящее время происходит отказ от среды Турбо Паскаль на
Международных олимпиадах по программированию. В новых средах таких жестких
ограничений по оперативной памяти, как правило, нет. Автор считает, что
ограничения — один из «двигателей» развития. Вспомним 1-й и 2-й этапы
развития технологий программирования. Ограничения по ресурсам ЭВМ
являлись мощнейшим рычагом создания эффективных алгоритмов и их
исследования.

374
7. Заметки о тестировании программ
Единственная небольшая сложность — правильно
отслеживать изменение значений площади при слиянии областей.
Основные процедуры этого варианта программы приводятся
ниже по тексту.
Const Size = 1000;{*Размер поля.*}
Туре
Answer = Array [O..Size] Of Longlnt;{*Массив
ответов (ячейки с площадями).*}
PhotoLine = Array [O..Size] Of Integer;{*Для
обработки строки поля.*}
Var
OldLine, NewLine : PhotoLine;{*01dLine -
предыдущая, NewLine - новая строки.*}
wrlnd : Integer;{*Рабочая ячейка, для поиска
свободного номера связной области.*}
Result : Integer;{^Результат.*}
TempRes : Answer;
filel, file2 : Text;
' Procedure Init;
! Begin
I FillChar( OldLine, SizeOf(OldLine), 0);
j FillChar( TempRes, SizeOf(TempRes) , 0);
I wrlnd := 1;
i Result:=0;
I End;
Procedure Change(Dellnd, Newlnd: Integer);
{^Заменяем номера устаревших связных областей
на новое значение.*}
Var i : Integers-
Begin
For i := 1 To Size Do
Begin{^Выполняется при
слиянии двух связных областей.*}
If NewLine[iJ=DelInd Then NewLine[i]:= Newlnd;
If OldLine[i]=DelInd Then OldLine[i]:= Newlnd;
End;
End;
Procedure CompareLines;{^Сравнения предыдущей и
новой строк. Находим, какие связные области
сливаются или дают "потомство".*}

7. Заметки о тестировании программ
375
Var i :Integer;
charl, char2 :Char;
Begin
FillChar( NewLine, SizeOf(NewLine), 0);
For i := 1 To Size Do
Begin
Read(filel, charl); Read(file2, char2);
If charl = char2 Then
Begin {^Правило одинаковой
"закрашенности" . * }
If (NewLine[i-l] = 0) Or (i = 1)
Then
Begin
(*Новая связная область.*}
While TempRes[wrlnd]<>0 Do
If wrInd<Size
Then Inc( wrlnd )
Else wrlnd:= 1;
NewLine [i] := wrlnd
End
Else NewLine[i] := NewLine[i-1];{*Простое
дополнение к связной области.*}
If (OldLine[i]<>0) And (NewLine [i] oOldLine [i] )
Then
Begin {^Слияние или наследование.*}
TempRes[ 01dLine[i] ] := TempRes
[ 01dLine[i] ] + TempRes[ NewLine[i] ];
{^Сложение значений площадей.*}
If TempRes[ NewLine[i]]<>0
Then
Begin
{^Слияние.*}
TempRes[ NewLine [i] ] := 0;
{^Уничтожение устаревшего описания
связной области.*}
Change(NewLine[i], 01dLine[i]);
End
Else NewLine [i] := OldLine [i];
{^Наследование.*}
End;
Inc ( TempRes[ NewLine [i] ] );
End
Else NewLine [i] := 0;

376
7. Заметки о тестировании программ
End;
ReadLn(filel); ReadLn(file2);
End;
Procedure Solve;
Var i, j : Integer;
Begin
Assign(filel, 'photoA.txt'); Reset(filel);
Assign(file2, 'photoB.txt'); Reset(file2);
For i := 1 To Size Do
Begin
CompareLines;{^Сравниваем строки.*}
For j := 1 To Size Do
If (TempRes[j]<>0) And (TempRes[j] > Result)
Then Result :=TempRes[j];
OldLine := NewLine;{*Новую строку считаем
старой.*}
End;
Close(filel);Close(file2);
End;
Продолжим тестирование решения. Вопросы с оперативной
памятью решены. Остались временные ограничения — 5
секунд на работу программы с одним тестом. С этой целью
необходимо разработать достаточно полную систему тестов. Один
тест максимального размера еще не говорит о том, что
выполняются требования задачи. Один из файлов (для простоты)
можно заполнить единицами (первая вспомогательная
программа). А затем? Напрашивается создание файлов
максимального размера по принципам, приведенным на рисунке 7.4, и,
конечно, файла со случайными значениями, а это еще четыре
вспомогательные программы (не ручным же способом
заполнять файлы).
Рис. 7.4
Этим, вероятно, не исчерпываются все возможности, но
ограничимся приведенными тестами — их достаточно для на-

7. Заметки о тестировании программ
377
шего изложения. Затем необходимо организовать учет времени
решения задачи одним из способов, описанным выше (лучше,
естественно, вторым). Что выясняется? Оказывается, только на
одном из тестов временное ограничение не выполняется, а
именно на тесте со структурой — «зубья» (см. рисунок 7.5).
И5ЯОТ5И
Рис.7.5
Почему именно на этом тесте? Вернемся к решению. Ответ
просматривается — частота слияния связных областей на тесте
значительно возрастает, что вызывает работу процедуры Change,
т. е. лишний цикл (подсчитайте — сколько раз выполняется
процедура Change для области 1000x1000, заполненной по
принципу «зубьев»).
Можно ли без принципиальных изменений на идейном
уровне и в программной реализации добиться выполнения
требований задачи? Оказывается, да! Используем идею косвенной
адресации. Исключим, точнее изменим, процедуру Change из
решения. В процедуре просматривался весь массив с целью
поиска существующих «родственников». Изменим смысловую
нагрузку элемента массива. Она будет содержать:
• или данные о площади;
• или ссылку (информацию) на ту ячейку, в которой
записано значение площади при слиянии связных областей;
• или ссылку на ссылку при многократном слиянии
связных областей.
Как их отличить друг от друга? Стандартный прием —
отрицательное значение является признаком косвенной адресации.
Исключение многократного просмотра длинных цепочек (при
слиянии большого количества связных областей)
осуществляется одноразовым прохождением по цепочке, после которого во
всех ячейках указывается адрес конечной ячейки со значением
площади. Еще один момент рассматриваемой идеи требует
упоминания. В предыдущем варианте признаком свободного
номера связной области являлось нулевое значение элемента в
массиве TempRes. В данном варианте этот массив используется для
косвенной адресации к ячейкам со значением площади, поэто-

378
7. Заметки о тестировании программ
му требуется введение дополнительного массива с элементами
логического типа для этой цели, назовем его Used.
Type UsedAn = Array [L.Size] Of Boolean; {*Тип для
хранения информации об использованных номерах
связных областей.*}
Var Used:UsedAn;
При этом предположении поиск свободного номера связной
области выглядит следующим образом.
Procedure NextWrlnd/{*Массив Used необходим,
значение Usedfi], равное E'alse, говорит о том,
что значение i - свободный номер связной
области.*}
Begin
While Used[wrlnd] Do
If wrInd<Size Then Inc ( wrlnd ) Else wrlnd := 1;
TempRes [ wrlnd ] := 0;
End;
Ключевая функция поиска номера ячейки, указывающей на
значение площади. При выходе из рекурсии изменяем
значения ссылок.
Function FindLast( ind : Integer ) :Integer;{*Ищет
итоговый номер, указывающий на значение
площади.*}
Begin
If TempRes [ ind ] > 0
Then FindLast := ind
Else
Begin
TempRes [ ind ] := -FindLast ( Abs ( TempRes
[ind] ) ) ;
FindLast := Abs ( TempRes [ ind ] );
End;
End;
Процедура сравнения соседних строк претерпит
незначительные изменения. Приведем ее для сравнения с предыдущей.
Procedure CompareLines;
Var i : Integer;
charl, char2 : Char;
Begin

7. Заметки о тестировании программ
379
FillChar( NewLine, SizeOf(NewLine), 0);
For i :- 1 To Size Do
Begin
Read(filel, charl); Read(file2, char2);
If charA = charB Then
Begin
If (NewLine[i-l] = 0) Or (i = 1)
Then
Begin
NextWrlnd;{*Новый вариант поиска
свободного номера связной области.*}
newLine[i] := wrlnd;
End
Else NewLine [ i] := NewLine[i-1] ;
If (OldLine[i]<>0) And
(NewLine [ i ] OOldLine [ i ] )
Then
If TempRes [ 01dLine[i] ] > 0
Then
Begin
{^Простое слияние.*}
TempRes[OldLine[i]]:=
TempRes[OldLine[i] ] +
TempRes[NewLine[i]]; {^Суммируем
площади.*}
TempRes[ NewLine [i] ]:= - OldLine [i];
{^Преобразуем ячейку со значением
площади в ячейку ссылочного типа.*}
NewLine[i] := OldLine [i]
End
Else NewLine [i] := FindLast ( OldLine
[i] ); {*При слиянии со связной
областью, которая при данном
значении i помечена ячейкой
ссылочного типа, находим ячейку со
значением площади этой связной
области. *}
Inc ( TempRes[ NewLine[i] ] );
Used [NewLine [i] ] := True ;
End;
End;
ReadLn(filel);ReadLn(file2);
End;

380
7. Заметки о тестировании программ
И наконец, новый вариант процедуры Solve.
Procedure Solve;
Var i:Integer;
Begin
InitTemp;
Assign(fileA, 'photoA.txt'); Reset(fileA);
Assign(fileB, 'photoB.txt'); Reset (fileB) ;
For i := 1 To Size Do
Begin
CompareLines;
FillChar ( used , SizeOf(used), False);
{*Считаем все номера свободными.*}
For j := 1 To Size Do
Begin
If TempRes [ NewLine [j] ] < 0 Then
NewLine [j] := FindLast ( NewLine [j] );(*Этим
действием мы сокращаем количество
переадресаций по ссылочным ячейкам при
поиске ячейки с площадью, значительно
ускоряя тем самым обработку следующей
строки при слиянии связных областей.*}
If (TempRes [ NewLine [j] ] > 0) And Not Used
[NewLine [j]] Then
Begin
If TempRes [ NewLine [j] ] > Res Then
Res := TempRes [ NewLine [j] ];
Used [ NewLine [j] ] := True;
End;
End;
OldLine := NewLine;
End;
Close(fileA);Close(fileB);
End;
Для иллюстрации алгоритма, а именно изменения значений
в массивах NewLine и TempRes (см. таблицу 7.2), рассмотрим
простой пример, первые две строки которого изображены на
рисунке 7.6.
Рис. 7.6

7. Заметки о тестировании программ 381
Таблица 7.2
i
1
2
3
4
5
9
10
NewLine
1 020304050
6000000000
1000000000
1 100000000
1120000000
1 1 22000000
1 122330000
1 1 22334450
1 122334455
5555555555
TempRes
1111 100000
11111-1 0000
21111-1 0000
31111-1 0000
341 1 1 -10000
-241 1 1 -10000
-251 1 1-10000
-261 1 1 -10000
-2-381 1 -1 0000
-2-3-4-514-1 0000
-2-3-4-515-10000
-5-5-5-515-10000
Примечание
После обработки 1-й
строки сформировано
пять связных областей,
площадь каждой из них
равна 1
Обрабатываем 2-ю строку.
В 1 -м столбце таблицы
указывается номер клетки
строки
Указывается
последовательное
изменение значений в
массивах при работе
логики
Простое добавление к
связной области
«Склейка» связных
областей. Площадь
записана во второй
ячейке. Первая переходит
в разряд ссылочных
Простое добавление к
связной области
«Склейка» с 3-й связной
областью из предыдущей
строки. Приводится
окончательный вид
массива TempRes
«Склейка» с 5-й связной
областью из предыдущей
строки
Работа процедуры
CompareLines окончена
Готовим данные для
следующего вызова
CompareLines. Цепочка
ссылок сокращена до
одной - на ячейку с
площадью
Этот вариант программы «разбирается» с тестом типа «зубьев»
размером 1000x1000 за 3 секунды. Можно ли продолжить
совершенствование программы решения задачи? Безусловно, ибо нет
предела совершенству. Мы не использовали динамические
структуры данных. А может быть, есть вариант не построчного
сравнения клеточных полей. Да даже написание программ,
генерирующих входные файлы различных типов, интереснейшая задача.

Библиографический указатель
1. Алексеев А. В. Олимпиады школьников по информатике.
Задачи и решения. — Красноярск: Красноярское книжное
издательство, 1995.
2. Андреева Е. В., Фалина И. Н. Информатика: Системы
счисления и компьютерная арифметика. — М.: Лаборатория
Базовых Знаний, 1999.
3. Бабушкина И. Α., Бушмелева Η. Α., Окулов С. М.,
Черных С. Ю. Конспекты занятий по информатике (практикум по
Паскалю). — Киров: Изд-во ВятГПУ, 1997.
4. Бадин Н. М., Волченков С. Г., Дашниц Н. Л.,
Корнилов П. А. Ярославские олимпиады по информатике. —
Ярославль: Изд-во ЯрГУ, 1995.
5. Беров В. И., Лапунов А. В., Матюхин В. Α.,
Пономарев А. А. Особенности национальных задач по информатике. —
Киров: Триада-С, 2000.
6. Брудно А. П., Каплан Л. И. Московские олимпиады по
программированию. — М.: Наука, 1990.
7. Виленкин Н. Я. Комбинаторика. — М.: Наука, 1969.
8. Вирт Н. Алгоритм+структуры данных=Программы. —
М.: Наука, 1989.
9. Гусев В. Α., Мордкович А. Г. Математика: Справочные
материалы. — М.: Просвещение, 1990.
10. Дагене В. Α., Григас Г. К., Аугутис К. Ф. 100 задач по
программированию. — М.: Просвещение, 1993.
11. Емеличев В. Α., Мельников О. И., Сарванов В. И.,
Тышкевич Р. И. Лекции по теории графов. — М.: Наука, 1990.
12. Йодан Э. Структурное проектирование и
конструирование программ. — М.: Мир, 1979.
13. Касаткин В. Н. Информация. Алгоритмы. ЭВМ. — М.:
Просвещение, 1991.
14. Касьянов В. Н., Сабельфельд В. К. Сборник заданий по
практикуму на ЭВМ. — М.: Наука, 1986.
15. Кирюхин В. М., Лапунов А. В., Окулов С. М. Задачи по
информатике. Международные олимпиады 1989-1996. — М.:
«ABF», 1996.

Библиографический указатель
383
16. Кристофидес Н. Теория графов. Алгоритмический
подход. — М.: Мир, 1978.
17. Лапунов А. В., Окулов С. М. Задачи международных
олимпиад по информатике. — Киров, Изд-во ВятГПУ, 1993.
18. Липский В. Комбинаторика для программистов. — М.:
Мир, 1988.
19. Окулов С. М., Пестов А. А. 100 задач по
информатике. — Киров, Изд-во ВятГПУ, 2000.
20. Окулов С. М., Пестов Α. Α., Пестов О. А. Информатика в
задачах. — Киров, Изд-во ВятГПУ, 1998.
21. Окулов С. М. Конспекты занятий по информатике
(алгоритмы на графах): Учебное пособие. — Киров, Изд-во ВятГПУ,
1996.
22. Окулов С. М. Задачи кировских олимпиад по
информатике. — Киров, Изд-во ВятГПУ, 1993.
23. Окулов С. М. Основы программирования. — М.:
Лаборатория Базовых Знаний, 2001.
24. Препарата Ф., Шеймос М. Вычислительная геометрия:
введение. — М.: Мир, 1989.
25. Савельев Л. Я. Комбинаторика и вероятность. —
Новосибирск: Наука, 1975.
26. Усов Б. Б. Комбинаторные задачи// Информатика. 2000.
№ 39.

Для заметок

РАЗВИТ Е ИНТЕЛЛЕКТ ШКОЛЬНИКОВ
Очередная книга из серии «Развитие интеллекта школьников» снова
вводит вас в мир программирования.
Внимательно изучайте эту книгу - и вам откроются секреты
популярных алгоритмов!
Вы познакомитесь с комбинаторными алгоритмами, перебором,
алгоритмами на графах, алгоритмами вычислительной геометрии, а также
получите навыки решения олимпиадных задач
Станислав Михайлович ОКУЛОВ
Декан факультета информатики Вятского государственного
гуманитарного университета, кандидат технических наук, доктор
педагогических наук, профессор, почетный работник высшего
профессионального образования РФ. Автор 9 изобретений по элементам
ассоциативных вычислительных структур и автор (соавтор) 15 книг
по информатике для школьников и студентов.
Книги автора, вышедшие в серии «Развитие интеллекта
школьников»:
«Основы программирования»
«Ханойские башни»
«Абстрактные типы данных»
«Алгоритмы обработки строк»
«Динамическое программирование»
Область интересов: развитие интеллектуальных способностей
школьника при активном изучении информатики, методика
преподавания информатики в школе и вузе
С Ί 993 по 2003 год деятельность в вузе совмещал с работой
учителя информатики. За это время его ученики отмечены 33
дипломами (1-й и 2-й степени) на российских олимпиадах школьников
по информатике; трое из них представляли Россию на
международных олимпиадах
ISBN 978-5-9963-0848-4